Общий курс физики. Том 1. Механика - Хайкин С.Э.

Автор: Хайкин С.Э.

Теги: физика

Год: 1947

Похожие

Физика 10 класс. Учебник для общеобразовательных учебных заведений

Общий курс физики Т.1. Механика

История и методология механики

Общий курс физики. Том I. Механика.

Текст

ОБЩИЙ КУРС ФИЗИКИ
той i
с. а. х л и в и д
МЕХАНИКА
ИЗДАНИЕ ВТОРОЕ
ДОПОЛНЕННОЕ И ПЕРЕРАБОТАННОЕ
Допущено Министерством высшего
образования СССР в качестве
учебника для университетов.
огиз
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 19 4 7 ЛЕНИНГРАД

Редактор Г. И. Колъченко. Техн. редактор Н. А. Тумаркина.
Подписано к печати lOZVil 1947 г, 36 печ. л. 44,2 авт. л. 44,95 уч.-изд. л. 61 000 тип. зи.
в печ. л. АШ76. Тираж 25 000 экз. Цена 16 р. Переплет 1 р. Заказ J4 6825.
1-я Образцовая типография треста «Полиграфкнига» Огиза при Совете Министров СССР.
Москва, Валовая, 28,

ОГЛАВЛЕНИЕ
Стр.
Предисловие ко второму изданию 7
Из предисловия к первому изданию 8
Глава I. Введение 11
§ 1. Реальный объект и идеализированная схема A1). —§2. Из-
Измерение физических величин A5). — § 3. Системы единиц A8).—
§ +. Размерность физических величин B0). —§ 5. Физические
законы и размерности величин B2). — § 6. Правило размер-
размерностей B4).
Г л а в а II. Кинематика . • 23
§ 7. Простраиственно-времеииые системы отсчёта B8).—§8. Пе-
Перемещение точки C1). —§9. Скорость C2). —§10. Ускоре-
Ускорение C4). —§ It. Тангенциальное и нормальное ускорения C6). —
§12. Перемещения твёрдого тела C9). —§ 13. Вращательное
движение D2). — § 14. Связь между векторами линейной и уг-
угловой скоростей D6).
Глава III. Движущиеся системы координат 49
§ 15. Отсчёт времени в движущихся системах координат D9).—
§ 16. Движущиеся системы координат E1).—§ 17. Вращающие-
Вращающиеся системы координат E5) § 18. Некоторые случаи движения
твёрдого тела F3).
Глава IV. Законы Ньютона 71
§ 19. Выбор системы отсчёта G1). — § 20. Материальная точка
G2).— §21. Силы в механике Ньютона G3). —§ 22. Измере-
Измерение сил G6). — § 23. Связь между силой и ускорением G8).—
§ 24. Масса. Второй закон Ньютона (80). — § 25. Количество
движения (83). — § 26. Третий закон Ньютона (84). — § 27. За-
Законы Ньютона и определение массы (86). — § 28. Уравнения
движения (89).—§29. Инерциальные системы координат (90).—
§.30. Опыт, Фу ко. (94).
Глава V. Силы и деформации 96
§ 31. Возникновение деформаций (96). — § 32. Деформации при
вращательном движении (98). — § 33. Деформации при «сложных»
движениях A01). — §34. Силы и деформации A04).
Г лав а VI. Движения под действием силы тяжести 106
§ 35. Земное притяжение A06).—§ 36. Взвешивание тел A08). —
§ 37. Определение массы взвешиванием A11). —§38. Деформа-
Деформации тяжёлого тела (ИЗ).

4 ОГЛАВЛЕНИЕ
Глава VII. Равновесие материальной точки 115
§ 39. Состояния равновесия и их устойчивость A15). — § 40. Аб-
Абсолютно жёсткие связи A16). — §41. Равновесие при наличии
абсолютно жёстких связей A17).
Глава VIII. Силы трения 119
§ 42. Силы трения A19). — §43. Измерение сил трения A21).—
§44. Сухое и жидкое трение A22). — § 45. Зависимость силы
жидкого трения от скорости A23). — 6} 46. Падение тел в со-
сопротивляющейся среде A24).—§ 47. Парашютный прыжок
A25). — § 48. Падение при малых скоростях A26). — § 49. Трение
покоя A27). — § 50. Трение скольжения A30). — § 51. Роль
сухого трелия A31). —§ 52. Явление застоя A32). —§ 53. Су-
Сухое трение и устойчивость состояний равновесия A35).
Глава IX. Закон сохранения количества движения 137
§54. Закон сохранения количества движения A37). — § 55. При-
Применения закона сохранения количества движения A38).—
§ 56. Абсолютно неупругий удар A41).
Глава X. Закон сохранения момента количества движения. . . 143
§ 57. Момент силы и момент количества движения A43). —
§ 58. Уравнение моментов A46). — § 59. Математический маят-
маятник A49). — § 69. Закон сохранения момента количества дви-
движения для системы точек A51).—§61. Изменение направле-
направления момента количества движения A55).
Глава XI. Работа и энергия 163
§62. Работа силы A63). —§ 63. Работа сил трения A66).—
§ 64. Потенциальная энергия A67). — § 65. Потенциальная
энергия и состояния равновесия A70). — §66. Закон сохране-
сохранения энергии A71). — §67. Колебания при возникновении силы
A74). —;§, 68. Закон сохранения энергии и закон сохранения
момента количества движения A76). — §69. Закон сохранения
энергии и силы трения A78).—§ 70. Мощность A79). — §71. Пе-
Передача работы A81). — § 72. Абсолютно упругий удар A83).—
§ 73. Законы сохранения в движущихся системах коорди-
координат A87).
Глава XII. НеинерЦиальные системы координат 190
§74. Силы инерции A90). —§ 75. Системы координат, движу-
движущиеся прямолинейно A93). — § 76. Вращающаяся система ко-
координат A96). — § 77. Кориолисова сила инерции B00).—
§ 78. Движение иа поверхности Земли B04). — § 79. Неинер-
циальпые системы координат и законы сохранения B08). —
§ 80. Эквивалентность сил инерции и сил тяготения B11).
Глава XIII. Механика твёрдого тела , 213
§ 81. Твёрдое тело как система материальных точек B13). —
§82. Движение Центра тяжести твёрдого тела B14). —§83. Дви-
Движение тела, закреплённого на оси. Момент инерции B17). —
§84. Пренебрежение моментом инерции тел B21).—§85. Фи-
Физический маятник B22).—§86. Измерение силы тяжести B25).—
§ 87. Уравнения движения твёрдого тела. Равновесие твёр-
твёрдого тела'B26). — §88. Рычажные весы B29). — §89. Плоское дви-
движение твёрдого тела B31). — §90. Закон сохранения момента
количества движения для системы тел B35). — § 91. Качение
тел. Тренне качения B38). — § 92. Самодвижущиеся экипажи

ОГЛАВЛЕНИЕ 5
B41). — § 93. Свободные оси B45). — § 94. Движение тела,
закреплённого водной точке B49). — § 95. Гироскопы B54).
§ 98. Применения гироскопов B61).
Глава XIV. Всемирное тяготение 265
§ 97. Закон всемирного тяготения B65). — § 98. Гравитационная
постоянная B68). —§ 99. Приливы B72).
Глава XV. Механика упругих тел .....,..,,.,.,.., 274
§ 100. Сплошные тела B74). — § 101. Типы деформаций B75).—
§ 102. Упругие тела B79). — § 103. Упругие напряжения B82).—
§ 104. Напряжения в точке B85).—§ 105. Изотропные и ани-
анизотропные тела B89). — § 106. Энергия упругой деформации
B90). — § 107. Упругое равновесие. Устойчивость упругого рав-
равновесия B93). — § 108. Распространение "импульса в упругом
теле B96). — § 109. Течение энергии в упругом теле C00).
Глава XVI, Гидростатика и аэростатика 304
§ 110. Общие свойства жидкостей и газов C04). — § 111. Давле-
Давление в жидкости и газе C07). — §112. Сжимаемость жидкостей
и газов C09). — § 113. Распределение давлений в покоящихся
жидкости и газе C12). — § 114. Подъёмная сила. Плавание тел
C14). — § 115. Изменения давления с высотой. Барометрическая
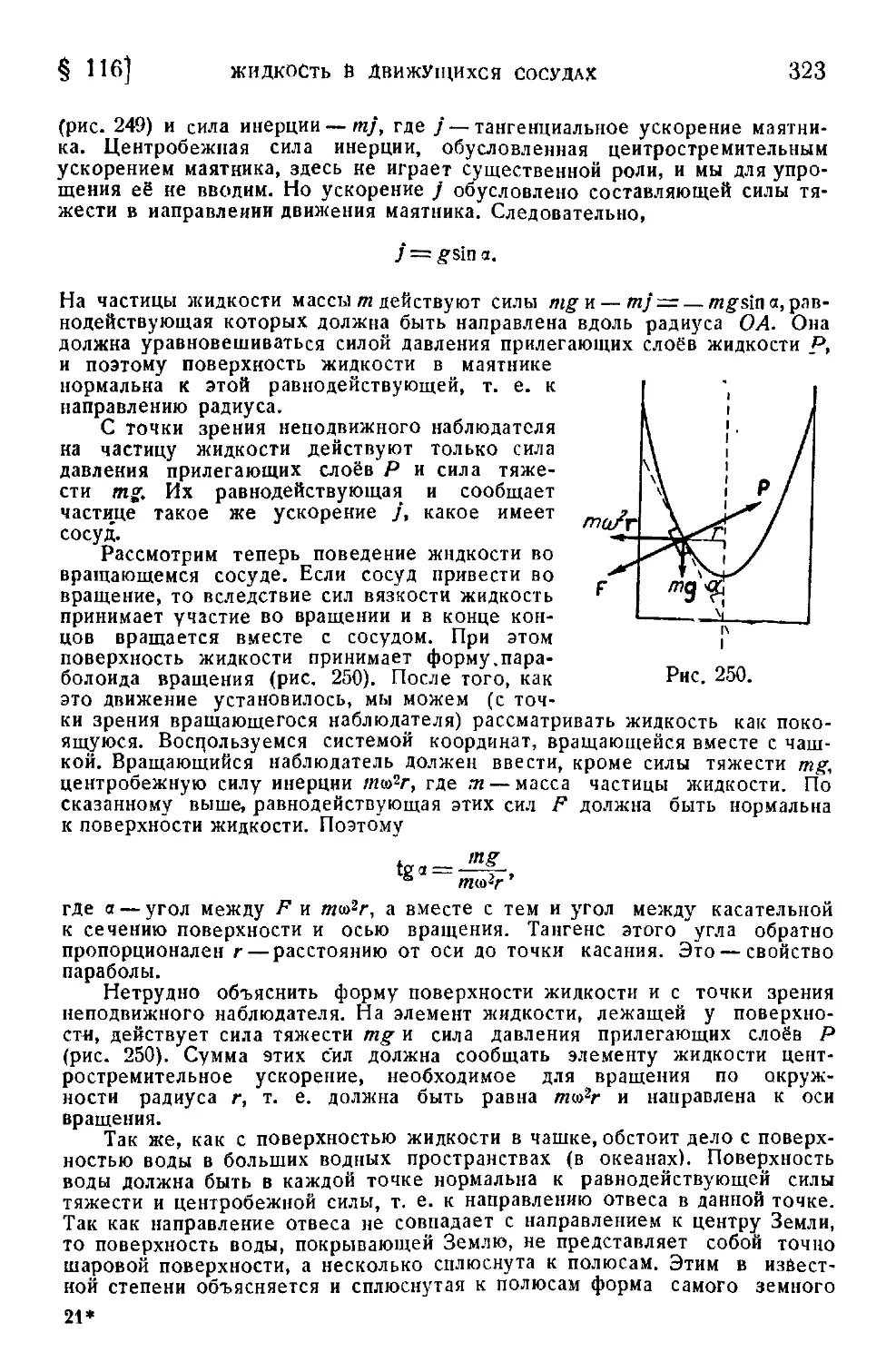
формула C19). — § 116. Жидкость в движущихся сосудах C22).—
§ 117. Поверхностные явления C25).
Глава XVII. Гидродинамика и аэродинамика 328
§118. Стационарный ток жидкости C28). — § 119. Давление
в текущей жидкости. Закон Бернулли C31). — § 120. Примене-
Применение законов сохранения к движению жидкостей C37). —
§ 121. Реактивное движение C39).—§ 122. Роль вязкости
C41). — §123. Движение тел в жидкости или газе C47).—
§ 124. Обтекание тел идеальной жидкостью C52).—§ 125. Обте-
Обтекание тел вязкой жидкостью C56). — § 126. Сопротивление
давления и сопротивление трения C61). — §127. Подъёмная
сила C64). —§ 128. Крыло самолёта C71). — § 129. Эффект
Магнуса. Циркуляция C72). — § 130. Полёт самолёта C79). —
§ 131. Устойчивость полёта и управление самолётом C82).—
§ 132. Распространение импульса в жидкости и газе C87).
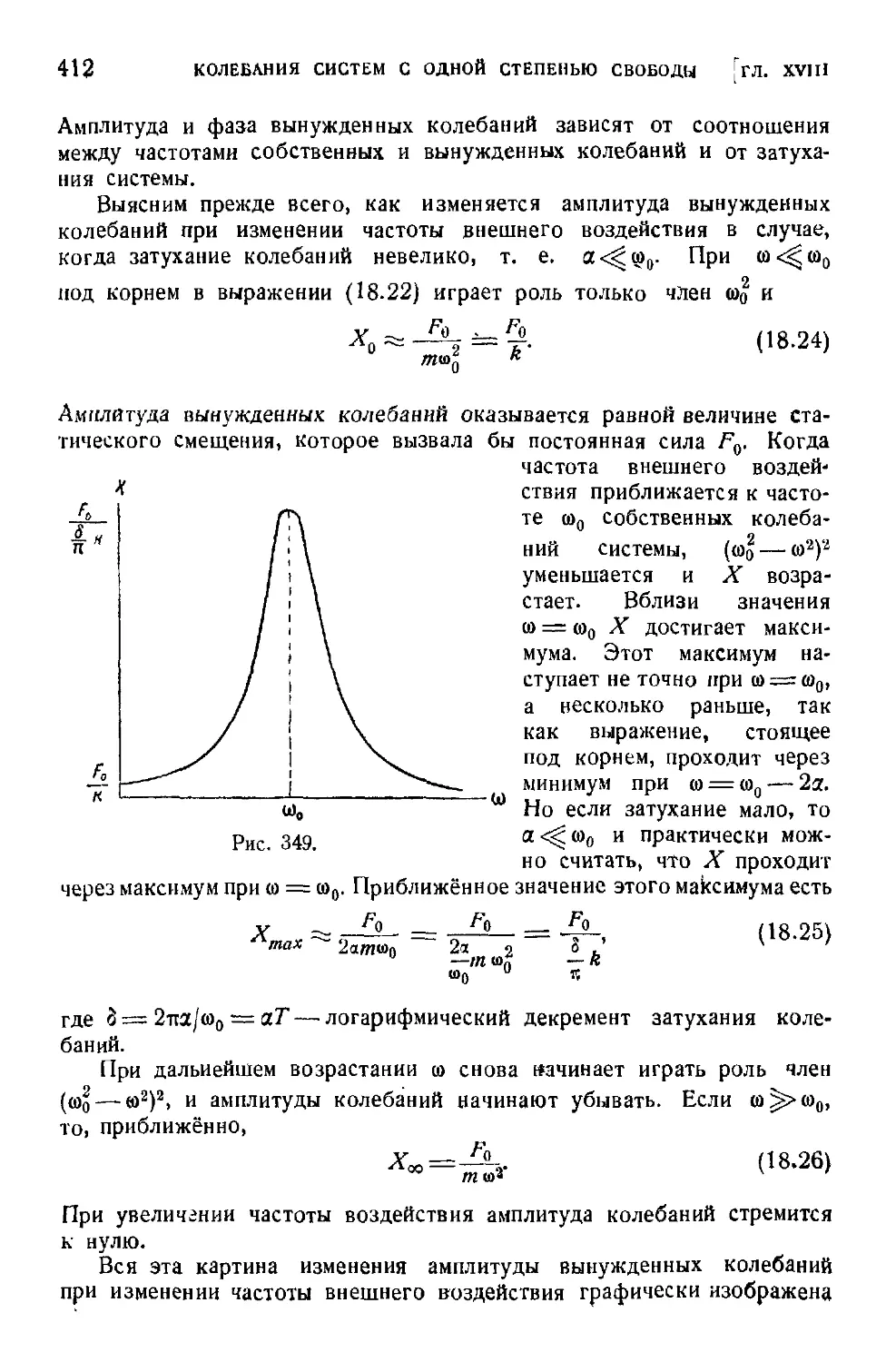
Глава XVIII. Колебания систем с одной степенью свободы . . 394
§ 133. Колебательные движения C94). — § 134. Гармонические
колебания C95). — § 135. Собственные колебания D00).—
§ 136. Собственные колебания при большом трении D06). —
§ 137. Автоколебания D08). — § 138. Вынужденные колебания
D10). — § 139. Резонанс D17). — § 140. Негармоническое внеш-
внешнее воздействие D20).
Глава XIX. Колебания систем со многими степенями свободы . 425
§ 141. Колебания систем с двумя степенями свободы D25).—
§ 142. Колебания связанных систем D28). — § 143. Колебания
в сплошных телах D35). — § 144. Нормальные частоты сплош-
сплошной системы D42). — § 145. Частоты колебаний струны D46). —
§ 146. Поляризация поперечных колебаний D48). § 147. Па-
Параметрическое возбуждение колебаний D49).
Глава XX. Волны 451
§ 148. Бегущие волны D51).—§ 149. Стоячие волны D57).—
§ 150- Колебания сплошных систем как стоячие волны D63), —

6 ОГЛАВЛЕНИЕ
§ 151. Волны в сплошной среде D67).—§152. Волны на поверх-
поверхности жидкости D69). — § 153. Интерференция волн D72). —
§ 154. Принцип Гюйгенса D75). — § 155. Диффракция волн D78).
Глава XXI.,Акустика 482
§ 156. Звуковые волны D82). — § 157. Распространение звука
в атмосфере D88). — § 158. Бинауральный эффект. Эффект Доп-
плера D91). — § 159. Звуковые волны в трубах D94).—
§160. Акустический "резонатбры D97). — § 161. Источники
звука E00). — § 162. Ультразвуки E06).
Глава XXII. Механика специальной теории относительности. . 509
§ 163. Роль скорости света в механике E09). — § 164. Сокра-
Сокращение размеров тел при движении E18).—§ 165. Замедление
хода движущихся часов E24).— §166. Принцип относительности
E30). — § 167. Кинематика теории относительности E40).—
§ 168. Масса и сила в механике теории относительности E50). —
§ 169. Закон движения механики теории относительности E58).
Литература 567
Предметный указатель 568

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Второе издание учебника в некоторых местах существенно пере-
переработано и значительно дополнено, вследствие чего объём его заметно
увеличился. В связи с этим я считаю необходимым подчеркнуть, что
вовсе не следует весь материал, помещённый в учебнике, рассматри-
рассматривать как обязательный для курса физики физико-математических фа-
факультетов. Всё то, что, по моему мнению, нельзя рассматривать как
обязательный материал, напечатано мелким шрифтом*) и может быть
опущено при работе над книгой (во всяком случае при первом чте-
чтении). При этом я стремился к тому, чтобы эти пропуски не
нарушали последовательности изложения н не затрудняли чтения
книги.
Многие параграфы**) могут быть пропущены целиком, так как они
посвящены вопросам, которые не входят в программу курса физики
для физико-математических факультетов, или освещают эти вопросы
гораздо более подробно, чем предусмотрено программой.
За шесть лет, прошедших со времени выхода первого издания
учебника, и особенно в последнее1 время, в связи с подготовкой
второго издания, я получил большое число отзывов об учебнике
и отдельных замечаний как от товарищей, с которыми я вме-
вместе работал, так н от преподавателей других высших учебных заве-
заведений. Многие из этих рецензий и замечаний очень помогли мне
при переработке книги, и я выражаю их авторам свою искреннюю
признательность. Пользуюсь случаем ещё раз горячо поблагодарить
академика С. И. Вавилова, академика М. А. Леонтовича, академика
Г. С. Ландсберга, члена-корреспондента Академии наук УССР
Д. И. Блохинцева и профессора С. М. Рытова, которые просма-
*) За исключением главы, посвященной теории относительности,
, конечно, тоже нельзя рассматривать как обязательный материал.
**) А именно §§: 33, 40, 41, 47, 48, 52, 53, 61, 71, 73, 79, 80, 84, 91, 92, 96,
108, 109, 116, 117, 128-131, 137, 146, 147, 155, 157, 159, 162^169.

S ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
тривали рукопись второго издания учебника и дали мне ряд ценных
советов, и кандидата физико-математических наук М. А. Исаковича,
внимательно прочитавшего всю рукопись и сделавшего много важных
замечаний, которые очень помогли мне при окончательной обработке
книги.
При подготозке второго издания учебника я уже не мог обра-
обращаться за советами к моему покойному учителю академику Л. И.
Мандельштаму, скончавшемуся в 1944 г. Я с новой остротой по-
почувствовал, как велика эта утрата.
С' Хайкан
Октябрь 1946 г.
Москва
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Эта книга представляет собой изложение первой части общего
курса физики, читанного автором в течение ряда лет для студентов
физического, а в некоторые годы и механико-математического фа-
факультетов Московского государственного университета.
Курс физики, предназначенный для студентов-физиков, занимает
особое положение. Прежде всего он должен дать достаточно пол-
полное и глубокое представление в целом о предмете, который являет-
является будущей специальностью студента. Далее он должен дать уча-
учащемуся обширные фактические знация, необходимые для дальнейшего
изучения курса теоретической физики и специальных курсов. На-
Наконец, он должен научить студента применять свои знания к конкрет-
конкретным вопросам — научить его объяснять наблюдаемые явления. Этими
требованиями и определяются, с одной стороны, характер изложения,
а с другой, — объём излагаемого материала.
Характер изложения в настоящем курсе во многом отличается
от общепринятых методов изложения раздела механики в общем
курсе физики. Я стремился возможно полнее разъяснить физическое
содержание тех понятий, которыми пользуется механика, и возможно
отчётливее нарисовать ту физическую картину, которая кроется за
обычно применяемыми в механике схемами рассуждений. Выполнение
этой задачи потребовало гораздо больше места, чем то, которое
отводится обычно в курсах физики для изложения основ механики.
Но особенно третья из указанных выше задач привела к значитель-

ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗД\НИЮ 9
ному увеличению объёма курса. Для того чтобы научить применять
общие положения и законы к конкретным явлениям, необходимо
рводить в курс большое число примеров, поясняющих общие за-
законы и иллюстрирующих их применение; эти примеры в настоящей
книге занимают много места.
В курсе общей физики, читаемом в аудитории, важную роль иг-
играют демонстрации. Они не только служат в качестве иллюстрации
тех или иных уже формулированных законов, но во многих случаях
воспроизводят опытные факты, на основании которых затем форму-
формулируются физические законы. Поэтому демонстрации в курсе физики
играют не только вспомогательную роль, но имеют и самостоятель-
самостоятельное значение.
В книге, конечно, нет возможности сохранить за демонстрациями
то место и значение, которые принадлежат нм в курсе, читаемом
в аудитории. Сохранены лишь наиболее поучительные демонстрации,
органически связанные с курсом. Значительная часть этих демонстра-
демонстраций является оригинальной и описывается впервые. Они осущест-
осуществлены в физическом кабинете МГУ М. В. Колбановым и С. И. Уса-
гиным.
Конечно, ни одно описание опыта, даже самое подробное, не
даст читателю того, что даёт опыт, произведённый в аудитории. Од-
Однако, ясное представление об идее опыта даёт очень много для по-
понимания явлений. В книге было бы нецелесообразно описывать опыты
во всех деталях. Для уяснения содержания опыта описывается лишь
упрощённая схема его осуществления. Но при таком упрощении на
читателя возлагается задача возможно конкретнее представить себе
описываемый опыт (или восстановить в памяти опыт, уже виденный
в аудитории). Для облегчения этой задачи иллюстрации ко многим
опытам даны в виде рисунков, а не чертежей. Эти рисунки выпол-
выполнены М. П. Плещеевой.
В книге почти не затрагиваются вопросы, касающиеся техники
физических измерений и конструкции измерительных приборов. Это
сделано сознательно. Я полагаю, что методам физических измере-
измерений и физического эксперимента нельзя научиться по книге—•
это задача учебных лабораторий. Точно так же по книге нельзя
научиться самостоятельно решать конкретные расчётные задачи—•
Для этого нужно много задач решать самому. Поэтому в настоящей
книге почти отсутствуют расчётные примеры.

10 ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Настоящий курс рассчитан на студентов первого курса физиче-
физического факультета. Поэтому он требует знаний по физике в объёме
курса физики средней школы и знакомства с элементами высшей
математики (понятие производной, операции дифференцирования и ин-
интегрирования, понятие о декартовой системе координат).
Как при чтении курса, так и при работе над этой книгой я все-
всегда широко пользовался советами академика Л. И. Мандельштама,
за что ещё раз выражаю Л. И. свою глубокую признательность.
Я весьма благодарен также моим рецензентам — члену-корреспонденту
Академии наук СССР М. А. Леонтовичу и члену-корреспонденту
Академии наук СССР С. А. Христиановичу, которые прочли рукопись
книги и сделали много ценных замечаний. Этими замечаниями я, ко-
конечно, воспользовался. Я очень благодарен также редактору изда-
издательства Г. Н. Кольченко, который оказал мне большую помощь при
окончательной обработке рукописи.
С. Хайкин
Август 1940 г.
Москва

ГЛАВА I
ВВЕДЕНИЕ
§ 1. Реальный объект и идеализированная схема
Наблюдая то или иное физическое явление, мы обнаруживаем,
что одни свойства реальных объектов существенно сказываются на
ходе явлений или их конечном результате, другие играют второсте-
второстепенную роль и практически на ход явления не влияют. Так, если мы
изучаем распределение сил, с которыми действует тяжёлая балка на
две опоры, на которых она лежит, то мы обнаружим на опыте, что
распределение это существенно зависит от расположения опор и не
зависит от прогиба балки, если она достаточно жестка и прогиб мал.
Это значит, что при достаточной жёсткости балки её упругость не
влияет на распределение сил давления на обе опоры. Поэтому при
расчёте этих сил мы можем реальную балку, обладающую конечной
упругостью и способную деформироваться, заменить воображаемой
абсолютно жёсткой, недеформируемой балкой. Так мы приходим
к представлению об абсолютно твёрдых, недеформируемых телах —
представлению, которое широко применяется в механике.
Точно так же, наблюдая вертикальные колебания груза, подвешен-
подвешенного на пружине, мы обнаружим, что период их существенно зависит
от массы груза, но не зависит от его размеров и формы. Поэтому
при изучении этих колебаний груза на пружине мы можем реальный
груз, обладающий определённой массой, размерами и формой, заме-
заменить материальной точкой, т. е. воображаемым материальным телом,
имеющим ту же массу, что и груз, но не обладающим протяжён-
протяжённостью. Это представление о материальной точке тоже широко приме-
применяется в механике.
Замена реального тела конечных размеров материальной точкой
той же массы существенно упрощает теоретическое рассмотрение
задачи и вместе с тем позволяет ответить на интересующий нас во-
вопрос, так как при этой замене правильно учитывается то свойство
реального объекта, от которого зависит период колебаний груза—.
его масса.
Такая замена необходима при построении всякой физической
теории. Приступая к теоретическому анализу всякого физического

'2 ВВЕДЕНИЕ [ГЛ. I
явления, мы должны выделить то главное, от чего существенно за-
зависит изучаемое явление, и отбросить второстепенные обстоятельства,
которые в этом явлении не играют роли. Без такого упрощения
задачи теоретическое исследование физических явлений было бы вообще
невозможно: самые простые явления приводили бы нас к чрезвычайно
сложным, не разрешимым теоретическим задачам. Чтобы сделать воз-
возможным теоретический анализ явления, мы вынуждены заменять реаль-
реальные физические системы некоторыми упрощёнными идеализированными
схемами, лишь приближённо отражающими свойства реального объекта.
Конечно, эти идеализированные схемы мы не можем выбирать произ-
произвольно. Они должны правильно передавать те свойства реального
объекта, которые играют существенную роль в изучаемых явлениях,
хотя при этом могут и не передавать тех свойств реального объекта,
которые не сказываются на характере этих явлений. Именно поэтому
мы можем пользоваться в теории такими представлениями, которые
не отражают полностью всех свойств реальных объектов. Так, мы
пользуемся представлениями о материальной точке, т. е. о теле,
обладающем массой, но не обладающем протяжённостью; об абсолютно
твёрдом теле, т. е. теле, которое ни при каких условиях не меняет
своей формы; представлением о точечных электрических зарядах, т. е.
о зарядах, сосредоточенных в одной точке, и т. д. Вводя в соответ-
соответствующих случаях эти представления, мы будем каждый раз остана-
останавливаться на их происхождении. Но уже сейчас уместно подчеркнуть,
что в природе не существует ни материальных точек, ни абсолютно
твёрдых тел, ни точечных электрических зарядов, ни множества дру-
других образов, которыми мы пользуемся при теоретическом рассмотре-
рассмотрении физических проблем. Всё это — абстракции, которыми мы поль-
пользуемся для того, чтобы сделать возможным теоретическое рассмотрение
проблемы.
Поэтому, при построении теории прежде всего требуется решить,
какой идеализированной схемой можно заменить рассматриваемую
реальную физическую систему; например, в каких случаях можно дан-
данное реальное тело рассматривать как материальную точку, считать
его абсолютно твёрдым и т. д. Зависит это не только от свойств
реального объекта, но и от характера процессов, которые мы изучаем,
а также от содержания тех вопросов, на которые должна ответить
теория. Пусть, например, металлический диск небольших размеров
подвешен горизонтально на проволоке, прикреплённой к центру диска.
Когда нас интересует вопрос о периоде колебаний диска, как обычного
маятника (вокруг горизонтальной оси), мы можем рассматривать этот
диск как материальную точку. Если нас интересует вопрос о периоде
колебаний этого диска вокруг вертикальной оси, т. е. крутильных
колебаний, то мы должны этот диск рассматривать как твёрдое тело.
И, наконец, если нас интересует вопрос о периоде тех звуковых
колебаний, которые будет совершать диск, когда мы его ударим,
то мы должны рассматривать его как упругое тело. Один и тот же

§ 1] РЕАЛЬНЫЙ ОБЪЕКТ И ИДЕАЛИЗИРОВАННАЯ СХЕМА 13
объект рассматривается то как материальная точка, то как абсолютно
твёрдое тело, то как упругое тело именно потому, что в разных
случаях определяющую роль играют разные свойства этого реального
объекта. Период колебаний диска как маятника не зависит от разме-
размеров диска и упругих свойств материала, из которого он сделан.
Поэтому для определения этого периода мы можем пользоваться
представлением о материальной точке, которое не отражает размеров
и упругих свойств реального объекта. Период крутильных колебаний
диска зависит от его размеров, но не зависит от упругих свойств
(если диск достаточно жёсткий). Поэтому мы можем пользоваться
представлением об абсолютно твёрдом теле; это представление может
правильно отражать существенные для нас свойства реального
объекта — массу и размеры диска, но не отражает его упругих свойств.
Наконец, период звуковых колебаний зависит не только от размеров
диска, но и от упругих свойств материала. Следовательно, в данном
случае мы должны пользоваться представлением об упругом теле,
правильно отражающем свойства реального объекта не только в от-
отношении его массы и размероз, но и в отношении его упругих
свойств. Но и это представление вовсе не передаёт всех без исклю-
исключения свойстз реального диска. Всякий металл обладает внутренним
трением; рассматривая тело как абсолютно упругое, мы не учитываем
этого свойства реального объекта. Однако, поскольку внутреннее
трение (пока оно мало) не влияет на период звуковых колебаний
диска, мы можем, и не учитывая внутреннего трения, правильно
ответить на интересующий нас вопрос.
Теперь ясно, какой смысл имеют те абстракции, которыми мы
пользуемся во всякой теории. Когда мы говорим об абсолютно твёр-
твёрдом теле, это возсе не значит, что то реальное тело, которое
участвует в изучаемых явлениях, действительно абсолютна твёрдое —
таких тел в природе нет. Это означает лишь, что в изучаемом на-
нами явлении упругие свойства тела вообще не играют роли. Точно
так же, когда мы говорим об абсолютно упругом теле, то это оз-
означает лишь, что внутреннее трение не играет роли в изучаемом явле-
явлении, и т. д.
Как мы видим, применяемые нами абстракции никогда не передают
всех свойств реального объекта. Но даже в отношении тех свойств,
которые они не передают, эти абстракции всё же отражают объек-
объективную реальность: именно они отражают тот факт, что эти свойства
не играют роли в изучаемом явлении. Если бы это было не так, то
с помощью этих абстракций мы не могли бы правильно описать яв-
явления, протекающие в реальном объекте.
Из сказанного следует также, что всякая теория, поскольку она
пользуется идеализированными схемами, может охватить лишь ограни-
ограниченный круг явлений, протекающих в реальной системе, может отве-
ответить лишь на ограниченный круг вопросов. Если, например, жёсткая
балка лежит не на двух, а на трёх опорах, то распределение давлений

14
ВВЕДЕНИЕ [ГЛ.
между опорами существенно зависит от упругих свойств балки.
Чтобы стало ясно, почему в этом случае упругость балки играет
существенную роль, представим себе, что средняя опора находится
несколько ниже других и балка в ненагруженном состоянии этой
средней опоры вовсе не касается (рис. 1). Нагрузим теперь балку
некоторым грузом. Если балка очень жёсткая, то она почти ие про-
прогнётся и попрежнему ие будет касаться средней опоры—давление
на среднюю опору будет равно нулю. Если же балка не очень же'ст-
.- кая, то она изогнётся сильнее и ляжет на
-д -.—а . /г-* среднюю опору — давление на эту опору уже
\ не будет равно нулю. Распределение давле-
Рис- 1. ний теперь существенно зависит от упругих
свойств балки. Поэтому, предположив, что
балка абсолютно твёрдая, мы вообще не могли бы определить, как
распределяется давление между тремя опорами; для определения этих
трёх давлений Ри Pv P3 (рис. 2) мы имели бы только два ура-
уравнения. Одно из этих уравнений — это условие равенства сил:
Р] + Р^ -Ь Pi = Р> а другое — условие равенства моментов
сил, взятых относительно какой-либо оси (например, оси, проходящей
через точку Л,): Pi(AlAi)-\-P3{A1A3) = P(A1B). Для определения
трёх неизвестных сил Pv Р2 и Ps мы полу- р
чим лишь два уравнения — этого, конечно, Р i2 °
недостаточно. к I
Такие случаи в механике называются М & \2
статически-неопределёнными. Конечно, в су- **Г »^
ществе этого явления ничего неопределён- I
ного нет — в каждом реальном случае да- '
вление некоторым образом распределяется Рис. 2.
между опорами. Но для того, чтобы устано-
установить, как именно распределяются давления, нужно правильно учесть
те свойства балки, от которых это распределение существенно
зависит. Отказываясь от учёта упругости балки, мы лишаемся воз-
возможности ответить на вопрос о распределении давления между тремя
опорами.
Итак, при построении всякой теории выбор идеализированной схемы
существенно зависит от того, какой круг явлений мы хотим охва-
охватить, на какие вопросы хотим получить ответ. От идеализированной
схемы требуется, чтобы она точно передавала те свойства реального
объекта, от которых существенно зависят интересующие нас явления.
Между тем, приступая к изучению явлений, мы ещё не знаем досто-
достоверно, какие именно свойства реального объекта определяют харак-
характер изучаемого явления. Сама теория могла бы нам дать надёжный
ответ на этот вопрос лишь в том случае, если бы мы могли рассмотреть
проблему с учётом всех тех свойств, роль которых нам нужно выяснить.
Например, для того, чтобы теоретически выяснить, какую роль играют;
масса и размеры, упругость и внутреннее трение материала и т. д.

g 2] ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН 15
в указанных выше различных случаях колебания диска, мы должны
были бы развить теорию, учитывающую все эти свойства реального
диска. Если же мы каких-либо из этих свойств в нашей теории не
учтём, то никаких указаний о роли неучтённых свойств мы из теории
уже не получим.
Никакая теория не может содержать в себе обоснования той
исходной идеализации, на которой эта теория построена. Только
опыт может оправдать применение той или иной идеализации. Часто
опыт предшествует теории и даёт указания о роли тех или иных свойств
системы в интересующем нас явлении, а следовательно, и о том, ка-
какие из этих свойств необходимо учесть. Иногда такой непосредствен-
непосредственный опыт оказывается ненужным, так как накопленные нами ранее
сведения, относящиеся не к изучаемому, а к сходным с ним другим
физическим явлениям, позволяют нам более или менее уверенно су-
судить о том, какие свойства реальной физической системы нужно
учесть, чтобы построить теорию протекающего в ней явления. Тем
не менее во всех случаях, после того как теория уже построена, её
результаты необходимо сопоставить с опытом. Только совпадение
результатов теории с данными опыта даёт нам уверенность в том,
что при переходе от реальной физической системы к идеализирован-
идеализированной схеме мы правильно отразили все те черты реальной системы,
которые определяют характер интересующих нас явлений. Как бы
логичны и последовательны ни были физические теории, в основе их
всегда лежит некоторое упрощение реальной обстановки, та или иная
идеализация свойств реальных объектов. И в самой теории не могут
содержаться доказательства законности этих упрощений и идеализа-
идеализации. Только согласие теории с опытом служит этим доказательством.
Поэтому в физике, как и во всех опытных науках, при сопоставлении
всякой теории с опытом решающее слово принадлежит опыту.
§ 2. Измерение физических величин
Всякое измерение представляет собой какую-то определённую
операцию, в результате которой мы получаем значение данной фи-
физической величины. Так, длину какого-либо предмета мы определяем,
прикладывая к этому предмету линейку — эталон длины. Число,
указывающее, сколько раз эталон укладывается вдоль измеряемого
тела, и выражает длину предмета. Точно так же для определения
веса тела мы уравновешиваем это тело на равноплечем рычаге при
помощи эталонов веса (гирь). Число единиц (эталонов) веса, которое
необходимо для того, чтобы уравновесить тело на равноплечем ры-
рычаге, и выражает вес тела.
Для того чтобы в результате измерений можно было получить
числа, мы должны, во-первых, выбрать эталон данной физической
величины (т. е. образец, для которого эта величина принята за
единицу); во-вторых, установить ту операцию, при помощи которой

\б ВВЕДЕНИЕ Г™. I
происходит сравнение данной величины с эталоном, и, наконец,
установить способ сложения эталонов. Например, в указанной выше
операции, служащей для измерения веса тела, содержатся определе-
определение способа сравнения весов тел и способ сложения эталонов: веса
тел равны, если тела уравновешиваются на равноплечем рычаге; вес
нескольких эталонов, положенных на одну чашку весов, равен ариф-
арифметической сумме весов отдельных эталонов.
Точно так же, если в качестве эталона силы мы выбираем
известным образом растянутую пружину, то мы должны опреде-
определить, чему мы будем считать равной силу, которая действует на
тело, если к нему прикреплены две пружины-эталона под известным
углом друг к другу. (Эта сила равна не арифметической, а гео-
геометрической сумме сил, действующих со стороны каждого из эта-
эталонов).
Операции сравнения величии и сложения эталонов, как сказано,
должны быть нами установлены. Однако, выбор этих операций от-
отнюдь не произволен, так как результаты операции должны удовле-
удовлетворять вполне определённым требованиям — повторяемости, однознач-
однозначности и т. д. Например, если бы мы условились считать, что сила,
действующая на тело со стороны двух пружин, равна арифметиче-
арифметической, а не геометрической сумме сил, действующих со стороны каждой
из пружин, то результаты измерений сил оказались бы неоднознач-
неоднозначными: в зависимости от угла между направлениями пружин мы полу-
получили бы разные значения измеряемой силы. Только геометриче-
геометрическое сложение сил, действующих со стороны пружин-эта тонов,
обеспечивает однозначность результатов измерений. Так же об-
обстоит дело и с установлением способов измерения всех физических
величин.
Чтобы удовлетворять требованиям повторяемости, однозначности
и т. д., способы измерения должны отражать свойства измеряв'
мых физических величин. Геометрическое сложение сил, действую-
действующих со стороны пружин, отражает векторный характер силы, ариф-
арифметическое сложение весов эталонов отражает свойство аддитивности
масс и т. д. Выбор того нли иного способа измерения физической
величины подсказывается опытом,и пригодность установаенного спо-
способа измерения испытывается на опыте — результаты измерений
должны удовлетворять указанным выше требованиям.
Таким образом, способы измерения физических величин не выби-
выбираются произвольно, а вырабатываются на основании опыта. Но всё
же эти способы требуют определения. Поэтому, вводя какую-либо
новую физическую величину, мы должны прежде всего установить
способ её измерения.
Указанные выше требования накладывают известные ограничения
и на выбор эталонов. Конечно, самая величина эталона может быть
выбрана совершенно произвольно, но эталон должен обладать вполне
определёнными физическими свойствами. Например, эталон длины —

§ 2] ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН 17
линейка — должен быть сделан из достаточно жёсткого материала.
Если бы в качестве эталона длины мы выбрали не металлическую,
а резиновую линейку, то повторяемость результатоз, конечно, не
была бы обеспечена.
Числа, которые мы получаем в результате измерений, обладают
одной важной особенностью, обусловленной тем, что всякое измере-
измерение мы производим с известной степенью точности; ни одно измере-
измерение неволможно произвести «абсолютно точно». В сущности
при измерении мы никогда не получаем какого-либо определенного
значения физической величины, а лишь пределы, между которыми эта
величина заключена. При усовершенствовании измерительной техники
пределы, между которыми заключена измеряемая величина, могут
суживаться, но только до известной степени. Во всяком измерении
существует некоторый предел точности измерений, которого нельзя
перейти ни ира каком усовершенствовании метода измерений. Так,
пользуясь для измерения длины оптическими приборами, мы не
можел! получить результатов с точностью, много большей, чем длина
световой волны. Такая граница точности существует во всяком
измерении.
То обстоятельство, что всякая физическая величина всегда задаётся
только с известной степенью точности, имеет не только принципиаль-
принципиальное, но и практическое значение, когда мы оперируем с этими вели-
величинами. Точность наших расчётов никогда не должна превышать той
точности, с которой измерены величины, участвующие в расчёте.
Излишняя точность в расчётах не только бесполезна (между тем, чем
больше точность, тем сложнее расчёты), но и вредна, так как она
создаёт неправильное представление о точности результатов. Пусть,
например, при определении плотности жидкости мы измерили объём
и массу некоторого количества жидкости, причём объём измерен
с точностью до одного процента, а масса — с большей точностью, на-
например, до 0,1°/0. Объём жидкости оказался равным 12,5 см%, а её
масса 15,40 г. Для определения плотности нужно разделить массу на
объём, что даст 15,4: 12,5 = 1,232. Однако, не имеет смысла указы-
указывать, что найденная плотность оказалась равной 1,232. Ведь точность,
с которой определена плотность жидкости, во всяком случае не выше,
чем точность измерения объёма, т. е. не выше одного процэнта.
Поэтому четвёртый знак в числе, выражающем плотность, ничего не
даёт. Он не только бесполезен, но н вреден, так как даёт основание
предполагать, что плотность определена с точностью до одной деся-
десятой процента, между тем как в действительности она определена
с точностью до одного процента. Вт почему точность расчётов ни-
никогда не должна быть выше, тем точность измерения тех величин,
которые входят в наши расч^Ш.
То, что физические велрчиньт всегда могут быть заданы толь-
только с известной степенью точности, играет существенную роль ещё
в целом ряде случаев. Так, например, о физических величинах
2 С. Э. Хайкин

18 ВВЕДЕНИЕ [гЛ. t
не имеет смысла говорить, что они несоизмеримы (т. е. не име-
имеют общей меры), ибо, поскольку самые измерения физических
величин производятся всегда с известной степенью точности, с этой
гтепенью точности для двух физических величин. может быть найдена
и общая мера,
§ 3. Системы единиц
Для измерения всякой физической величины нужно установить
способ сравнения этих физических величин и выбрать эталон данной
физической величины. Поэтому, в сущности, мы должны были бы
иметь множество эталонов для всех разнообразнейших физических
величин. Для того чтобы избавиться от необходимости вводить новый
эталон для всякой новой физической величины, поступают следующим
образом. Выбрав несколько эталоноз для основных физических вели-
величин (например, длины, времени, массы), принимают их за основные
единицы. Единицы всех остальных физических величин устанавливают
при помощи эгих основных единиц, пользуясь для этого какими-либо
физическими законами, связывающими между собой нозые физические
величины с теми, для которых эталоны существуют. Так, например,
в качестве эталона силы можно было бы пользоваться сжатой (или
растянутой) на определённую величину пружиной. Но необходимость
о этом эталоне силы отпадает, если мы воспользуемся вторым законом
Ньютона, устанавливающим связь между массой, ускорением и силой.
Так как согласно этому закону сила пропорциональна произведению
массы на ускорение, то за единицу силы мы можем принять такую
силу, которая определённой массе т сообщает определённое ускоре-
ускорение а. Если хранящиеся у нас эталоны позволяют измерять массы
и ускорения, то мы всегда сможем воспроизвести эталон силы, подо-
подобрав силу (например, сжатие пружины) так, чтобы она массе т со-
сообщала ускорение а.
При переходе от основных единиц (т. е. тех, для которых хра-
хранятся специальные эталоны) к проаззодным можно было бы устана-
устанавливать эти новые единицы совершенно произвольно и, например, за
единицу силы принять такую силу, которая определённой массе со-
сообщает некоторое определённое ускорение. Однако, вся система
единиц получается гораздо более стройной и все физические соотно-
соотношения принимают более простой и удобный вид, если при установле-
установлении нозых единиц определять их таким образом, чтобы в выражение
нозой величины через оснозные не входили никакие числовые коэф-
коэффициенты. Тогда за единицу силы мы должны будем принять такую
силу, которая массе, равной единице, сообщает ускорение, равное
единице; за единицу количества электричества мы должны принять
такое количество электричестза, которое с равным ему количеством
электричества на расстоянии, разном единице, взаимодействует с силой,
равной единице, и т. д. Построенные по этому принципу системы
единиц носят название абсолютных.

'§ 3} СИСТЕМЫ ЕДИНИЦ 19
Существует несколько абсолютных систем единиц, отличающихся
выбором тех величин, которые приняты за основные и для которых
установлены специальные эталоны. В физике наиболее употребитель-
употребительна система единиц, в основу которой положены единицы длины (L),
массы (М) и времени (Т). Все остальные единицы выводятся из этих
трёх основных*). Это — так называемая система LMT.
В качестве эталонов в этой системе служат: эталон длины — ли-
линейка, длина которой принята за 1 м; эталон массы — гиря, масса
которой принята за 1 кг, и эталон промежутка времени — средние
солнечные сутки **).
Выбрав те физические величины, эталоны которых в данной си-
системе приняты за основные (в системе LMT это — эталоны длины,
массы и времени), следует установить ещг и самую величину этих
основных эталонов. Например, за единицу длины может быть принят
и метр, т. е. длина того эталона, который хранится в Париже, и
сантиметр, т. е. одна сотая длины эталона. Точно так же, за еди-
единицу массы можно принять и килограмм, т. е. массу эталона, и грамм,
т. е. одну тысячную массы эталона.
Наконец, за единицу времени могут быть приняты либо средние
солнечные сутки, либо некоторая часть их. Для того, чтобы разделить
эталон времени — средние солнечные сутки—на равные части, при-
пригоден всякий периодический процесс, т. е. процесс, повторяющийся
через равные промежутки времени. Обычно для этого пользуются
периодическим движением маятника часов. Сосчитав число колебаний,
которые совершает маятник часов в течение средних солнечных суток,
мы можем воспользоваться в качестве единицы времени продолжитель-
продолжительностью одного колебания маятника, составляющей известную долю
средних солнечных суток. За единицу времени в физике принята 1 се-
секунда, составляющая g ^ долю средних солнечных суток. Таким
образом, часы представляют собой физический прибор, аналогичный
линейке с нанесёнными на ней делениями, расстояние йежду которыми
составляет известную долю эталона длины. Как и всякий физический
измерительный прибор, часы должны удовлетворять известным тре-
требованиям, и, прежде всего, движение маятника должно быть точно
повторяющимся процессом.
В зависимости от выбора единиц длины, массы и времени полу-
получаются . различные системы единиц, например сантиметр — грамм —
секунда (CGS) или метр — килограмм — секунда (MKS). Но, поскольку
основными единицами и в том, и в другом случае служат единицы
*) Впрочем, кроме единицы температуры, которую оказалось удобнее
определять независимо от этих трёх основных единиц.
•*) Эталоны длины и массы хранятся в Парижской палате мер и весов,
а тщательно сделанные с них копии — в других странах. Копии эталонов,
Находящиеся в СССР, хранятся во Всесоюзном институте метрологии
я стандартизации.
2'

20 введение Ггл. i
длины, массы и времени, мы имеем дело с системами единиц, отли-
отличающимися только «масштабами»—величиной основных единиц, а не
их характером. В дальнейшем, когда мы будем говорить об «измене-
«изменении масштабов» единиц, мы будем иметь в виду именно этот случай —
замену в той же системе единиц одних основных единиц другими —
большими или меньшими.
Существуют и другие абсолютные системы единиц, в которых в
основу положены другие основные величины. В механике пользуются,
например, системой единиц, в которой основными единицами служат
единицы длины, силы и времени. Эталоны длины и времени в этой
системе единиц выбираются так же, как в системе LMT, а эталоном
силы служит та сила, с которой гиря-эталон притягивается к земле
на широте 45°. Это — так называемая система LFT.
В физике наиболее распространённой является абсолютная система
единиц LMT, в частности, система CGS. В механике мы будем поль-
пользоваться только системой CGS.
В следующих параграфах мы рассмотрим общие вопросы, связан-
связанные с переходом от одной системы единиц к другой и с изменением
масштабов основных единиц. При этом мы будем для определённости
иметь в виду систему LMT, но все те общие соображения, которые
будут высказаны, в одинаковой мере относятся и ко всем другим аб-
абсолютным системам единиц.
§ 4. Размерность физических величин
В том случае, когда мы пользуемся какой-либо одной абсолютной
системой единиц, часто бывает удобно изменять масштабы единиц,
например, измерять длину в одних случаях в сантиметрах, в других —
в метрах и т. д. Поэтому прежде всего необходимо выяснить, как
изменяются результаты измерения тех или иных физических величин
при таком изменении масштаба. Пока речь идёт о результатах изме-
измерения тех величин, которые лежат в основе данной системы единиц,
дело обстоит просто. Если, например, мы увеличиваем масштаб длины
в 100 раз — переходим от сантиметров к метрам,—то числа, полу-
получающиеся в результате измерения всех длин, уменьшаются в 100 раз.
Но когда мы производим измерения каких-либо других, не основных
величин, например, силы, работы и т. д., то влияние изменения мас-
масштабов на числа, получающиеся в результате измерения этих вели-
величин, не столь очевидно. Между тем часто это бывает важно знать.
Числа, получающиеся в результате этих измерений, вообще го-
говоря, изменяются при изменении масштабов основных единиц, так как
в абсолютной системе единиц при изменении основных единиц изменя-
изменяются и все производные единицы. Действительно, если, например, мы
увеличим в л раз единицу длины, то во столько же раз увеличится
и единица силы; если мы увеличим в л раз единицу времени, то еди-
единица силы уменьшится в л2 раз. Вместе с изменением единиц, служа-

§ 4] РАЗМЕРНОСТЬ ФИЗИЧЕСКИХ ВЕЛИЧИН 21
щих для измерения, изменятся, конечно, и числа, получающиеся в ре-
результате измерения тех или иных физических величин. Очевидно, что
при данном изменении масштабов результаты всех измерений одних и
тех же физических величин изменятся одинаково. Например, если мы
будем измерять самые различные скорости, принимая за единицу
длины метр, а затем перейдём к другой единице длины — километру,
то все числа, выражающие измеренные нами различные скорости,
уменьшатся в 1000 раз. Другими словами, для всякой физической
величины существует вполне определённая связь между изменениями
масштабов основных единиц и изменениями чисел, получающихся
в результате измерения этой физической величины. Размерность фи-
физической величины и выражает эту связь.
Размерность физической величины указывает, как изменяется
число, выражающее результат измерения данной физической ве-
величины, при изменении масштабов применяемых единиц.
Если, например, результат измерения какой-либо физической ве-
величины в системе LMT при изменении единицы длины изменяется
так же, как изменяется результат измерения самой длины (т. е. при
увеличении единицы длины в п раз результат измерения уменьшается
в п раз), но не изменяется при изменении других основных единиц
(массы и времени), то данная физическая величина имеет размерность
длины. Если при увеличении единицы длины в а раз результаты из-
измерения данной физической величины уменьшаются в пр (и не зави-
зависят от выбора других единиц), то, следовательно, данная физическая
величина имеет размерность длины в степени р. Подобным же обра-
образом определяется размерность какой-либо физической величины, если
результаты её измерения зависят от выбора масштабов других осноз-
ных единиц.
Для указания размерности физических величин пользуются симво»
лическими обозначениями, например Ц}Ж~''Т~Г. Это означает, что в
системе LMT число, выражающее результат измерения данной физиче-
физической величины, уменьшится в пР раз, если единицу длины увеличить
в п раз, увеличится в пЯ раз, если единицу массы увеличить в и раз,
и, наконец, увеличится в /гграз, если единицу времени увеличить в и раз.
Размерность физической величины указывает вместе с тем, как в
данной абсолютной системе единиц изменяются единицы, служащие
для измерения этой физической величины, при изменении масштабов
основных единиц. Если, например, сила в системе LMT имеет раз-
размерность LMT~a, то это значит, что при увеличении единиц длины
в и раз единица силы также увеличивается в п раз; при увеличении
единиц массы в п раз единица силы также увеличивается в и раз и,
наконец, при увеличении единиц времени в п раз единица силы умень-
уменьшается в п2 раз.
Размерность всякой физической величины определяется, с одной
стороны, установленным способом измерения данной физической ве-
величины, а с .другой, — выбором системы единиц. Ндпример, если мы

22 ВВЕДЕНИЕ ["гл. I
измеряем скорость отношением пройденного пути к тому промежутку
времени, за который этот путь пройден, то в системе LMT скорость
будет иметь размерность LT, Но мы могли бы измерять скорость
и по-иному, например, сразнивая её с той скоростью, которую будет
иметь свободно падающее тело, и определяя измеряемую скорость по
тому времени, в течение которого падающее тело достигло бы изме-
измеряемой скорости. Тогда за единицу скорости мы должны были бы
принять такую скорость, которую свободно падающее тело достигло
бы за единицу времени. Ясно, что в этом случае единица скорости
изменялась бы так же, как единица времени, и размерность скорости
в системе LMT была бы Т.
Вместе с тем, как уже сказано, размерность физической величины
зависит и от выбора системы единиц. Так, например, плотность, ко-
которую мы определяем как отношение массы тела к его объёму, в
системе LMT имеет, очевидно, размерность L~8M. Если же пользоваться
системой единиц, в основу которой положены единицы длины, силы
и времени, т. е. системой LFT, то размерность массы, а вместе с тем
и плотности, будет зависеть от выбора способа измерения масс.
Измеряя массу по отношению силы к сообщаемому этой силой уско-
ускорению, мы получим для массы размерность силы, делённой на уско-
ускорение, т. е. размерность L~'FT2, а для плотности L~4FT2.
§ 5. Физические законы и размерности величин
Всякий количественный физический закон содержит в себе неко-
некоторое утверждение относительно связей между теми или иными фи-
физическими величинами. Например, во втором законе Ньютона содер-
содержится утверждение, что ускорение тела пропорционально действующей
на это тело силе; в законе Кулона содержится утверждение, что сила
взаимодействия между двумя точечными зарядами обратно пропорци-
пропорциональна квадрату расстояния между ними, и т. д. Для того, чтобы
проверить на опыте эти утверждения, мы должны независимыми спо-
способами одновременно измерить все те величины, к которым относится
наше утверждение. Пока мы не располагаем способами независимого
измерения всех тех величин, которых касается наше утверждение, мы
не можем его проверить. Так, положение, содержащееся во втором
законе Ньютона, что ускорение пропорционально действующей силе,
только тогда можно рассматривать как утверждение, поддающееся
проверке на опыте, если мы располагаем независимыми способами
измерения ускорений и сил. Если же мы не располагаем независимым
способом измерения силы, а определяем силы по тем ускорениям,
которые они сообщают телу, то положение, что ускорение пропор-
пропорционально силе, уже не является утверждением, 'поддающимся опыт-
опытной проверке, а представляет собой определение силы, которое, как
и всякое определение, в непосредственной опытной проверке не
нуждается. Если мы определяем силу по ускорению, заранее считая

§ 5] ФИЗИЧЕСКИЕ ЗАКОНЫ И РАЗМЕРНОСТИ ВЕЛИЧИИ 23
её пропорциональной ускорению, то нет смысла подвергать опытной
проверке положение, что ускорения пропорциональны силам.
При формулировке всяких физических законов нужно ясно отда-
отдавать себе отчёт, в какой мере те или иные положения представляют
собой утверждения, нуждающиеся в проверке на опыте, и в какой
мере они являются лишь определениями новых физических величин.
Различать утверждения и определения необходимо потому, что утвер-
утверждения и определения стоят в совершенно различной связи с опытом.
Утверждения можно и нужно проверять на опыте. Именно постольку,
поскольку эти утверждения поддаются опытной проверке и под'
тверждаются на опыте, они представляют собой физические
законы. Проверка состоит в том, что результаты нескольких неза-
независимых измерений различных физических величин удовлетворяют
соотношению, выражаемому законом. Определения же не поддаются
опытной проверке такого рода. Правда, поскольку в определении
всякой физической величины содержится способ её измерения, этот
способ должен, как указывалось, удовлетворять определённым требо-
требованиям. С этой точки зрения определения подлежат испытанию на
опыте. Однако, это испытание сводится к тому, что результаты
повторных измерений одной и той же физической величины дол-
должны удовлетворять определённым требованиям; в частности, при
неизменных условиях измерения должны давать один и тот же ре-
результат.
Таким образом, испытание на опыте, которому подлежит опреде-
определение, по своему существу отличается от проверки на опыте, которой
должно быть подвергнуто утверждение.
Если бы в физических законах речь шла всегда только о пропор-
пропорциональности между физическими величинами или известными функ-
функциями физических величин, утверждения о том, что между данными
величинами существует пропорциональность, оставались бы правиль-
правильными для любых масштабов единиц (конечно, при условии, что мы
во всей серии измерений, служащих для проверки данного утвер-
утверждения, применяем всё время одни и те же единицы). Действительно,
замена во всех измерениях одних единиц другими изменит результаты
всех измерений в одинаковое число раз, и если между какими-либо
величинами существует пропорциональность в одной серии измерений,
то она сохранится и во всякой другой серии измерений, произведённой
при помощи других единиц.
Таким образом, пока речь идёт только о пропорциональности
между какими-либо величинами, все ограничения при выборе единиц за-
заключаются только в том, что каждую величину мы должны измерять
всё врзмя в одних и тех же единицах. Выбор же самих единиц, слу-
служащих для измерения той или другой величины, остаётся произ-
произвольным.
Иначе обстоит дело, когда мы хотим придать физическому закону
такой вид, чтобы в.нём содержалось утверждение не ,о пропорцио-

24 ВВЕДЕНИЕ [ГЛ. I
нальности, а о равенстве между какими-либо комбинациями физиче-
физических величин. Ясно, что от пропорциональности между какими-либо
величинами всегда можно перейти к равенству между ними, введя
соответствующий коэффициент пропорциональности. Этот коэффициент
пропорциональности мы могли бы определить нз опыта, измерив одни раз
все физические величины, входящие в данный закон. Дальше мы могли бы
утверждать, что результаты измерения нескольких различных физических
величин должны удовлетворять определённому равенству. Например,
второй закон Ньютона можно рассматривать как утверждение, что
произведение массы на ускорение равно действующей силе. Мы ут-
утверждаем, что, измерив какими-либо независимыми способами массу
тела, его ускорение и действующую силу и перемножив числа, по-
полученные в результате первых двух измерений, мы получим число,
равное результату третьего измерения. Но в таком виде это утвер-
утверждение справедливо только при определённом выборе единиц измере-
измерений: например, если мы будем измерять массу в граммах, ускорение
— в CMjcerc2 и силу — в динах. Если же мы бу-дем измерять ма*су в ки-
килограммах, а ускорение и силу — попрежнему в см\секъ и динах, то
равенство между произведением массы на ускорэние и силой, конечно,
нарушится. Следовательно, в этом случае на выбор едлниц измере-
измерений накладываются какие-то более жёсткие требования, чем в том
случае, когда речь идёт только о пропорциональности между физи-
физическими величинами.
§ 6. Правило размерностей
Эти жёсткие требования, казалось бы, заключаются в том, что,
формулируя какой-либо физический закон в виде равенства, мы
должны тут же фиксировать и единицы, в которых следует измерять
все входящие в этот закон вгличины. Однако, эти требования можно
значительно смягчить, если все равенства, выражающие наши физи-
физические законы, будут удовлетворять следующему условию: размер-
размерности обеих частей равенства должны быть одинаковы. В таком
случае требование сводится только к тому, чтобы для измерения всех
величин, входящих в данное равенство, пользоваться одной и той
же абсолютной системой единиц. Масштаб же основных единиц
можно выбирать совершенно произвольно — равенство при этом не
нарушается. Так, во втором законе Ньютона можно, пользуясь систе-
системой LMT, измерять массу в граммах, ускорение — в CMJceic^ и силу — в
г-см\сек2, т. е. в динах. Но можно также пользоваться системой
единиц — километр, килограмм массы, секунда; тогда ускорение
следует измерять в км\секг, а силу — в кг-км'^сек2. Как в том, так и в
другом случае произведение массы на ускорение будет равно дейст-
действующей силе. Обусловлено это именно тем, что во втором законе
Ньютона размерности обеих частей равенства одинаковы: размерность
силы равна произведению размерностей массы и ускорения. Поэтому

§ 6] ПРАВИЛО РАЗМЕРНОСТЕЙ 25
при переходе к новым масштабам результаты измерений отдельных
величин будут изменяться так, что равенство не нарушится.
Это справедливо, конечно, всегда. Соотношения, которые мы
устанавливаем между физическими величинами, не будут зависеть от
выбора масштабов единиц, если знак равенства соединяет выражения,
имеющие одинаковую размерность. Возсе нельзя сказать, что соотно-
соотношения, в которых знак равенства соединяет выражения различной
размерности, не имеют смысла — они лишь не имеют общности. На-
Например, можно утверждать, что давление в воде, выраженное в kzjcm'K
равно одной десятой от глубины погружения в метрах, и записать это
следующим образом:
Эта формула не только имеет вполне определённый смысл, но ею
пользоваться удобнее, чем всякой другой, несмотря на то, что раз-
размерности правой и левой частей в ней различны., Но она не имеет
общности — она верна лишь в jex случаях, когда мы измеряем давление
в кг, см2, а глубину в метрах. Если мы перейдём, например, к изме-
измерению глубины в сантиметрах, то формула окажется неверной.
Каким же образом достигается в физических формулах равенство
размерностей правой и левой частей, обеспечивающее этим форму-
формулам общность, т. е. независимость от .масштабов?
Здесь следует различать два случая. Первый состоит в том, что
в формулу, выражающую данный физический закон, входит какая-
либо физическая величина, для которой единицы измерения устана-
устанавливаются на основании этого1 самого закона. Примером этого может
служить закон Кулона:
Единица количества электричества устанавливается на основании са-
самого закона Кулона: мы принимаем за единицу такое количество
электричества, которое с равным ему количеством электричества,
находящимся на расстоянии, равном единице, взаимодействует с силой,
равной единице. В этом случае одинакоаая размерность правой и
левой частей соблюдается, так сказать, «автоматически».
Действительно, требуя, чтобы закон Кулона был справедлив
при любых масштабах единиц, мы тем самым определяем связь между
единицами количества электричества и единицами силы и длины. Если
мы увеличим единицу силы в т раз, то единица количества электри-
электричества увеличится в \^т раз; если же, не изменяя единицы силы,
мы увеличим единицу длины в п раз, то единица количества электри-
электричества увеличится также в п раз. Размерность количества электриче-
электричества в системе LMT оказывается равной M'^L8'1!*, а размерность
выражения efajr2 оказывается равной размерности силы.
Таким же образом во дсех законах, которыми мы пользуемся для
Установления единиц измерения какой-либо из физических величин.

26 ВВЕДЕНИЕ
ГЛ. I
входящих в этот закон, одинаковая размерность правой и левой ча-
частей равенства всегда будет обеспечена.
Во втором случае в формулу, выражающую данный закон, входят
только такие физические величины, для которых единицы измерения
установлены были ранее либо непосргдственно (в виде эталонов),
либо при помощи каких-либо других законов. При этом, вообще
говоря, может случиться, что наш закон устанавливает пропорциональ-
пропорциональность между комбинациями физических величин, размерности которых
различны. Тогда после перехода от пропорциональности к равенству,
чтобы это равенство не нарушалось, коэффициент пропорциональности
должен изменяться при изменении масштабоз.
Например, в случае закона всемирного тяготения утверждение
состоит в том, что сила взаимного притяжения двух тел прямо про-
пропорциональна произведению масс этих тел и обратно пропорциональна
квадрату расстояния между ними:
Но размерность правой части есть M2L~a, а размерность левой MLT~2;
следовательно, величина числового коэффициента, который нужно
ввести, чтобы от пропорциональности перейти к равенству, будет
зависеть от выбора масштабов.
Мы могли бы написать закон всемирного тяготения в общем виде
следующим образом:
F=Y^, A.1)
где у — некоторый числовой коэффициент. При этом численное зна-
значение Y изменяется при изменении масштабов; следовательно, Y пред-
представляет собой величину, имеющую определённую размерность. И так
как мы каждый раз при переходе к новым масштабам подбираем у
так, чтобы равенство A.1) оставалось справедливым, то тем самым
мы так определяем размерность у> чтобы размерности правой и левой
частей равенства A.1) оказались одинаковыми. Для этого коэффици-
коэффициент у должен иметь размерность UM^T-2 (этот размерный коэффи-
коэффициент у носит название гравитационной постоянной). Но, вводя в за-
закон всемирного тяготения этот коэффициент, размерность которого
определяется из самого же закона всемирного тяготения, мы свели
наш второй случай к первому. А в первом случае, как мы видели,
одинаковая размерность правой и левой частей обеспечивается «авто-
«автоматически:».
Может, конечно, случиться, что.в новом физическом законе, свя-
связывающем между собой величины, единицы измерения и размерность
которых были установлены заранее, размерности правой и левой ча-
частей «сами собой» оказываются одинаковыми. Тогда, хотя при пере-
переходе от выражения пропорциональности к равенству и может оказать-
оказаться необходимым ввести некоторый числовой коэффициент, вели-.

§ 6] ПРАВИЛО РАЗМЕРНОСТЕЙ 27
чипа этого числового коэффициента не будет зависеть от выбора
масштабов единиц, т. е. этот числовой коэффициент окажется без-
безразмерным.
Мы видим, таким образом, что равенствам, выражающим физиче-
физические законы, всегда можно придать такой вид, чтобы эти равен-
равенства не нарушались при изменении масштабов единиц (для этого раз-
размерности правой и левой частей равенства должны быть одинаковы).
Именно в таком общем, не зависящем от выбора масштабов, виде и
принято выражать все физические законы и вообще все соотношения
между физическими величинами.

ГЛАВА II
КИНЕМАТИКА
§ 7, Пространственно-временные системы отсчёта
Движением тела называется изменение его положения со временем.
Для описания движения тел нужно прежде всего установить способ
определения положения, которое занимает тело, и способ отсчёта
момента времени, соответствующего тому или иному положению тела.
Положение тела может быть определено только по отношению к
каким-либо другим телам. Поэтому и о движении данного тела, т. е.
изменении его положения, можно говорить только постольку, поскольку
выбраны другие тела, которые служат для определения положения
данного тела. Эти тела, которые служат для определения положения
движущихся тел, называют системами отсчёта.
Для описания движений на земле в качестве такой системы от-
отсчёта обычно выбирают землю илл (что то же самое) какие-либо
тела, неподвижные относительно земли, например, стены аудитории,
в которой производятся опыты. Но в некоторых случаях оказывается
более удобным выбирать другие системы отсчёта потому, что по от-
отношению к разным системам отсчёта одни и те же тела совершают
различные движения. Надлежащим выбором системы отсчёта можно
упростить описание рассматриваемого движения.
С точки зрения кинематики никакого принципиального различия
между разными системами отсчёта нет и все они совершенно равно-
равноправны. Только в динамике, при изучении законов движения, мы обна-
обнаружим принципиальное различие между некоторыми системами отсчёта
и сможем поэтому привести соображения в пользу выбора одной,
вполне определённой системы отсчёта или, вернее, одного класса си-
систем отсчёта.
После того, как выбрано тело или тела, которые должны служить
системой отсчёта, можно связать с ними какую-либо систему коорди-
координат, например, прямоугольную (декартову), и определять положение
каждой точки движущегося тела тремя координатами в выбранной
системе координат. Этим последним способом чаще всего и поль-
пользуются.
Как уже было указано, для описания движения тел нужно не только
выбрать систему отсчёта, но и установить, каким образом мы будем

§ 7] ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ СИСТЕМЫ ОТСЧЁТА 29
определять моменты времени, в которые та или иная точка движущегося
тела занимает известное положение.
Время обычно отсчитывается по часам и, следовательно, задача
сводится, к определению положения стрелок часов в то мгновение,
когда выбранная точка движущегося тела занимает определённое
положение. Другими словами, должна быть установлена -одновремен-
-одновременность двух событий — прохождение какой-то точки тела через опре-
определённое положение и прохождение стрелки через определённое де-
деление циферблата часов. Если и движущееся тело, и часы находятся
в одном месте, то мы можем непосредственным наблюдением конста-
констатировать однозременность двух событий *). Если же часы и движу-
движущееся тело находятся в разных местах, то речь идёт об установле-
установлении одновременности двух событий, из которых одно происходит «здесь»
(стрелка часов проходит через определённое деление), а другое —
«там» (движущееся тело проходит через определённое положение).
А это нечто совсем иное. Нужен какой-то сигнал, который дал бы
нам знать, что «там» это событие произошло. В качестве этого сиг-
сигнала мы условимся пользоваться световыми сигналами или радиосиг-
радиосигналами. В тот момент, когда «там» произошло событие (точка тела
проходит через определённое положение), посылается световой сигнал
(или радиосигнал). Получив этот сигнал, мы отмечаем положение
стрелки часов. Однако, не этот момент мы будем считать моментом,
когда «там» произошло событие. Если в момент получения сигнала
часы показывают время t, то моментом, когда «там» произошло событие,
мы будем считать время
V = t — Tlt B.1)
*
где г, — промежуток времени, в течение которого световой сигнал
проходит путь «оттуда»—«сюда». Для определения момента, когда
«там» произошло событие, мы должны знать этот промежуток времени
Xj н отсчитать его от показаний часов. Однако, мы не в состоянии
непосредственно измерить промежуток времени, за который свето-
световой сигнал проходит путь «оттуда»—«сюда», так как для этого
нужно знать момент, когда сигнал вышел «оттуда». Это было бы воз-
возможно только в том случае, если бы в нашем распоряжении был
какой-то другой сигнал, который дал бы нам знать, когда именно
световой сигнал вышел «оттуда», для чего этот другой сигнал дол-
должен был бы распространяться с гораздо большей скоростью, чем
световой (только тогда временем его распространения, по сравнению
с временем распространения светового сигнала, можно было бы пре-
пренебречь).
*) Предполагается, что мы в состоянии сделать это достаточно точно,
но это не существенно. Для того, чтобы исключить' субъективные ошибки
наблюдателя, мы могли бы применить какие-либо объективные методы,
устанавливающие одновременность двух событий, например, моментальную
фотографию.

30 КИНЕМАТИКА [ГЛ. tl
Однако, мы не располагаем никакимл сигналами, распространя-
распространяющимися быстрее, чем световые. Скорость света есть наибольшая ско-
скорость распространения сигналов, которая нам известна. Поэтому мы
не можем непосредственно измерить промежуток времени tj.
Но мы можем измерить промежуток времени, в течение которого
световой сигнал проходит путь туда и обратно. Для этого мы можем,
например, «отсюда» послать световой сигнал на зеркало, находящееся
«там», и отметить моменты, когда сигнал отправлен и когда он воз-
возвратился. Оба эти события (отправление и приход сигнала) происхо-
происходят «здесь», и мы прямо отсчитываем моменты отправления и прихода
¦сигнала*). При этом мы получим какой-то промежуток времени ?.
Он, очевидно, равен сумме двух промежутков времени: т2 — времени
прохождения сигнала туда и Tj — времени прохождения сигнала обратно,
т. е. T' = Ti~f-V
Далее предполагают, что т1 = т2, а следовательно, что Т]=т'/2,
и таким образом определяют промежуток времени т2, который нужно
отсчитать от показаний часов «здесь», чтобы определить момент,
когда «там» произошло событие.
Предположение, что тх = т2, означает, что мы считаем скорость
светового сигнала с в обоих направлениях одинаковой. Это предпо-
предположение не может быть проверено непосредственно на опыте, так
как мы не можем непосредственно измерять промежутки времени Tj
и т2, а всегда лишь их сумму т'. Но, сделав указанное предположе-
предположение, мы можем найти скорость света с, если измерим промежуток т'
и расстояние х «отсюда» — «туда». Тогда
2х
с=-г.
Такие измерения скорости света производились неоднократно раз-
различными методами, причём оказалось, что величина с (в пустоте) всегда
одна и та же и равна 299 796 KMJcerc. Поэтому нет необходимости
каждый раз измерять промежуток г и из него определять т,=т'/2,
для того чтобы определить момент, когда «там» произошло событие.
Если расстояние «отсюда»—«туда» есть х и если в момент полу-
получения сигнала о событии часы «здесь» показывают время t, то момен-
моментом, когда «там» произошло событие, мы будем считать момент
где с — постоянная скорость света. Соотношение B.2) и есть опре-
определение того, что мы называем моментом, когда «там» произошло
событие, или определение одновременности двух событий, происшед-
происшедших в разных местах.
*) Конечно, практически это делается не при помощи часов, а гораздо
ЛР TAMFfUUU U#TAtt!IUU
более тонкими методами.

§ 8] ПЕРЕМЕЩЕНИЕ'ТОЧКИ 31
§ 8. Перемещение точки
Для того чтобы полностью определить движение какого-либо реаль-
реального тела, нужно знать движение каждой его точки. Поэтому прежде
всего необходимо установить способы описания движений точки, т. е.
установить основные положения кинематики точки.
Выбрав систему отсчёта, мы можем определять положение точки
в пространстве при помощи трёх координат, например, в прямоуголь-
прямоугольной (декартовой) системе координат. Если точка движется, то это
значит, что положение её относительно системы отсчёта меняется со
временен, и каждому новому моменту времени соответствуют, вообще
гозоря, другие значения всех трёх координат. Координаты движу-
движущейся точки являются функциями времени. Для описания движения
точки мы должны были бы определить вид этих функций. Однако,
обычно нельзя непосредственно определить вид функций, выражаю-
выражающих зависимость координат от времени, не определив предварительно
ускорения и скорости точки. Кроме того, часто этого и не требуется,
а достаточно знать только скорость и ускорение точки.
Если при движении точка переместилась из Л в В (рис. 3), то
перемещением точки называют отрезок, имеющий длину АВ и на-
направление от Л к В, Если затем точка пере-
переместилась из В в С, то это второе переме-
перемещение выражается отрезком ВС. Результирую-
Результирующее перемещение точки выражается отрезком
АС и представляет собой замыкающую двух
составляющих перемещений или, что то же, диа- fi*
гональ параллелограмма, построенного на со-
составляющих перемещениях. Следовательно, от- Рис. 3.
резки, выражающие перемещения, складываются
геометрически (по правилу параллелограмма). Такие величины, кото-
которые, подобно перемещениям, характеризуются не только значением
величины, но и определённым направлением в пространстве, называются
векторными величинами или векторами. Перемещение точки есть
вектор. Суммой двух векторов называется вектор, построенный на
составляющих векторах по правилу параллелограмма, как это имело
место для результирующего перемещения. Векторные величины мы
будем обозначать либо двумя буквами (соответствующими началу и
концу отрезка) со стрелками наверху, либо одной жирной буквой.
Мы будем, например, писать (рис. 3):
АС=АВ-\-ВС или
Всякое перемещение мы можем рассматривать как сумму несколь-
Ких составляющих перемещений и изображать в виде суммы каких-
либо составляющих перемещений бесчисленным числом способов. Но,
если мы заранее укажем направления тех составляющих перемещений,
в виде суммы которых мы- хотим изобразить данное перемещение, то

32
КИНЕМАТИКА
Ггл. н
задача станет однозначной. Например, если мы изобразим перемеще-
перемещение ОС в виде суммы трёх перемещений, направленных по трём осям
декартовой системы координат (рис. 4), то эти составляющие переме-
перемещения будут равны, соответственно, О А, АВ и ВС или О А', ОВ', ОС
(рис. 5). Эти векторы представляют
собой составляющие (компоненты)
вектора ОС по трём осям координат.
Если направления, в которых мы
берём составляющие данного векто-
вектора, раз навсегда фиксированы, то и
направления составляющих векторов
также остаются неизменными. При
О
-SB
Рис. 4.
изменении вектора ОС изменяются
только абсолютные величины ком-
компонент ОА', Ъв1, и ОС'. Поэтому
с векторами ОА', ОВ' и ОС мы мо-
можем обращаться, как со скалярными величинами (так как они полно-
полностью определены, если известна их величина). Таким образом вся-
всякий вектор мы сможем задавать тремя скалярными величинами — тре-
тремя компонентами по осям координат.
Если вектор а образует с осями
координат х, у, z углы а, В, у> то
его компоненты по этим осям соот-
соответственно равны
, = acos В,
я =а cos а,
А
аг = а cos у»
B.3)
где a = V<ix~\~ay~\~al есть абсо-
абсолютная величина (длина) вектора а.
§ 9. Скорость
Рис. 5.
Вектор перемещения, вообще
говоря, не совпадает с участком
траектории, которую описала движущаяся точка при данном переме-
перемещении (так как траектория может быть криволинейной). Но если
взять достаточно малое перемещение, то с требуемой степенью точ-
точности можно заменить малый участок траектории её хордой и считать,
что вектор перемещения совпадает с соответствующим участком траек-
траектории. Обозначим это достаточно малое перемещение через As. Ком-
Компоненты этого вектора по трём осям х, у, z мы будем обозначать,
соответственно, через Дл:, Ду> Дг. Абсолютная величина вектора Is

§ 9] скорость 33
выражается через его компоненты так:
Если вектор As образует с осями координат углы а, [3, у, то Ах —
= As cos a, \y = is cos р, Az = Ascosy.
Пусть малое перемещение As произошло за время А'. Отношение
As/At есть величина, вообще говоря, не постоянная, зависящая от
выбранной нами величины промежутка времени Д?. Если мы будем
брать промежуток Д/ всё меньше и меньше, то в общем случае (если
движение точки ие является равномерным) отношение Дв/Д^ будет
изменяться. Уменьшая всё дальше и дальше промежуток времени М,
мы обнаружим в конце концов, что отношение Д$/Д^ перестаёт заметно
меняться при дальнейшем дроблении промежутка. Иначе говоря, при
неограниченном уменьшении промежутка времени № отношение &SJM
будет стремиться к некоторому определённому значению, к некото-
некоторому пределу. Предел, к которому стремится отношение Дв/Д* при
беспредельном уменьшении Д^, т. е.
называется линейной скоростью точки*). Следовательно, скорость
точки v есть отрезок, по величине равный пределу отношения вели-
величины перемещения As к соответствующему промежутку времени Д?
при бесконечном уменьшении Д? и по направлению совпадающий
с вектором As.
Легко видеть, что скорость v также представляет собой вектор,
так как она получена из вектора As умножением его на скалярную
величину 1/Д/. Вектор скорости, как и всякий вектор, можно задавать
тремя компонентами по осям координат. Компоненты вектора скоро-
сти v=hm дт по осям координат соответственно равны:
osa' *>=[йовН' 'HlSo&W B-4)
где а, р, у— углы вектора v с осями координат. С другой стороны,
компоненты вектора As по осям координат соответственно равны
Дл: = As cos a, Ay = Д$ cos j}, Аг = д$ cos у,
13№ а, р, у — те же углы, так как направления As и v совпадают.
Следо вате льно,
•) Когда речь идёт только о линейной скорости и другие скорости не
рассматриваются, термин «линейная» обычно опускают.
3 С. Я VdHvuu
С. Э. Хайкин

34 КИНЕМАТИКА [l.1. II
т, е. компоненты вектора скорости выражаются производными по вр>
мени от соответствующих координат точки.
Таким образом, если известен вид функций, выражающих зависи-
зависимости координат от времени, то компоненты скорости мы получим,
дифференцируя зги функции повремени. Наоборот, если нам известно,
как компоненты скорости точки зависят от времени, то при помощи
обратной операции — интегрирования — мы можем найти вид функций,
выражающих зависимость координат от времени. При этом, однако,
в результате интегрирования мы получим функции, содержащие по
одной произвольной постоянной (постоянной интегрирования). Чтобы
определить эти произвольные постоянные и иметь возможность нахо-
находить значения координат в любой момент времени, необходимо знать
значения координат для какого-либо определённого момента времени.
Поясним сказанное на простейшем примере. Пусть, например, из-
известно, что компонента скорости по координате х постоянна и равна
v0. Другими словами, —- = v0 или dx = vodf. Интегрируя, получим.
jc = ] v0 dt — vot -f- C, B.6)
где С—постоянная интегрирования. Если нам известно, что в момент
t = tl x=^xA, то, подставляя в уравнение B.6) эти значения, найдем
л-, = Vq*! -J-С, откуда С=лг,—votx и, следовательно,
x = xiJrvo{t — t1).
§10. Ускорение
При движении точки скорость её, вообще говоря, может изме-
измениться как по направлению, так и по величине. Пусть, например, иек-
торы v, и v3 изображают скорость точки, соответ-
Ау ственно, в моменты времени tl и t2 (рис. 6). Из-
Изменение скорости есть v2 — v,, т. е. вектор Ду.
Этот вектор Ду, выражающий изменение скорости
движения за промежуток времени M = t^ — tv бу-
будет, вообще говоря, изменяться со временем, даже
рис 6 если продолжительность промежутка времени №
остаётся неизменной.
Взяв отношение Ду/Д^, мы получим некоторый новый вектор, вели-
величина и направление которого, вообще говоря, будут различны для
различных промежутков времени. Вектор Ду/Д? будет изменяться, если
мы, выбрав какой-либо промежуток времени Д?, будем затем его умень-
уменьшать. Однако, если мы веб дальше и дальше будем уменьшать проме-
промежуток времени Д', то в конце концов мы перестанем обнаруживать
изменения вектора Ду/Д^. Другими словами, при неограниченном умень-
уменьшении промежутка времени Д' отношение Ду/Д^ стремится к некоторому
определённому пределу, называемому ус/горением точки.

10] УСКОРЕНИЕ 35
Итак, ускорение точки
^- B.7)
г
есть вектор, длина которого равна пределу отношения Ду/Д', а на-
направление совпадает с направлением вектора Ду, изображающего
изменение скорости за малый промежуток времени Д?.
Очевидно, Ду может не совпадать по направлению с ,v, и, следо-
следовательно, направление вектора ускорения, вообще говоря, не совпадает
с направлением вектора скорости.
Если компоненты вектора Ду суть Avx, Ди \vz, то, рассуждая
так же, как и при определении компонент вектора скорости, нетрудно
убедиться, что компоненты вектора ускорения выразятся так
.. Д»~ dvr . ,. &vv dvv . ,. Д». dv, ,,->„.
Принимая во внимание B.5), получим:
/ _ <**? j _ *У_ i — d2L B Q\
J*—dt3 ' h dP ' Jz—dt ' x '
т. е. компоненты вектора ускорения выражаются вторыми производ-
производными по времени от соответствующих координат точки.
Если нам известен вид функций, выражающих зависимость коор-
координат от времени, то двукратным дифференцированием их мы найдём
компоненты вектора ускорения, а вместе с тем его величину и направ-
направление. Наоборот, если известен вид функций, выражающих зависи-
зависимость компонент ускорения от времени, то обратной операцией —
интегрированием — мы найдём функции, выражающие зависимость коор-
координат от времени. Однако, при двукратном интегрировании в функции,
выражающие зависимость координат от времени, войдут по две произ-
произвольные постоянные (постоянные интегрирования), для определения
которых необходимо знать либо значения координат в какие-нибудь
Два определённых момента времени, либо значения координат и ком-
компонент скорости в какой-нибудь определённый момент времени. По
известным значениям компонент скорости в какой-либо момент вре-
времени мы сможем определить постоянную интегрирования, появившуюся
после первого интегрирования, а по значениям координат в некоторый
момент времени — вторую постоянную, появившуюся в результате вто-
второго интегрирования. Пусть, например, тело движется 6 направлении
ови а; с постоянным ускорением
Интегрируя это уравнение, получим:
3*

36 КИНЕМАТИКА [l'-Т. И
Интегрируя уравнение второй раз, получим:
^ B.12)
Если, например, известно, что при t — 0 vx — v0, а лг=О, то, под-
подставив t = 0 и lvx=='°4 B уравнение B.11), мы определим первую
постоянную интегрирования: С, = и0. Подставив / = 0 и ;е = О в урав-
уравнение B.12), найдём вторую постоянную: С2=0. Тогда
Это — известная формула пути, проходимого при равномерно-уско-
равномерно-ускоренном движении с ускорением а и начальной скоростью va.
Таким образом, если нам иззестны компоненты ускорений, как
функции времени, то для того, чтобы определить координаты точки
в любой момент' времени, необходимо, помимо выполнения чисто мате-
математической операции—двукратного интегрирования, знать ещё зна-
значения координат точки и компонент её скорости в какой-либо опре-
определённый момент времени. Обычно в задачах механики бывают известны
координаты и скорость точки в один и тот же момент времени, ко-
который является начальным моментом рассматриваемого движения, —
начальные условия. Для полного описания движения точки достаточно,
следовательно, определить ускорения, которые испытывает точка в каж-
каждый момент времени, и знать начальные условия.
§ 11. Тангенциальное и нормальное ускорения
Часто бывает важно знать компоненты вектора ускорений в на-
направлении скорости движения и в перпендикулярном направлении. Рас-
Рассматривать эти компоненты ускорения отдельно
полезно потому, что их роль в изменении ха-
характера движения различна.
При выяснении роли различных составляю-
составляющих вектора ускорений мы ограничимся для
простоты только случаем движения точки на
плоскости. Разложим вектор ускорения на две
взаимно перпендикулярные составляющие — тан-
тангенциальную ],, совпадающую по направлению с
вектором скорости, и нормальную }п, перпенди-
перпендикулярную к нему (рис. 7). За малый промежуток
рис j времени № тангенциальная составляющая уско-
ускорения даст малое изменение скорости на вели-
величину Avt — JtM в направлении вектора v, т. е. в направлении самой
скорости. Поэтому
Л=?. BЛЗ>
где v — величина скорости, взятая как скаляр.

ТАНГЕНЦИАЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ
37
Нормальная составляющая ускорения даст за это время малое
изменение скорости Avn = jni^, направленное перпендикулярно к самому
вектору скорости (рис. 8). Легко видеть, что изменение Av, вектора,
направленное по самому вектору v, изменит только величину v, но
не изменит его направления. С другой стороны, изменение Дуя, направ-
V
W
Рис. 8.
Рис. 9.
ленное перпендикулярно к v, если оно мало, изменяет только направ-
направление вектора v, а не его величину. Действительно, после изменения
на Avn вектор v превратится в вектору' (рис. 9). Но o'2 = i/2-j-Ai/2,
и так как lvn достаточно мало, то с точностью до величины второго
порядка малости v' = v.
Таким образом, тангенциальная составляющая ускорения изменяет
только величину скорости, а нормальная составляющая — только её
направление. Так как вектор скорости совпадает по направлению
с касательной к траектории, то нормальная составляющая ускорения
всегда должна быть направлена в ту сторону, куда поворачивается
касательная, т. е. внутрь траектории движения; поэтому и полное
ускорение всегда направлено внутрь траекто-
траектории. Если полное ускорение будет направ-
направлено вперёд от нормали — в направлении
движения (рис. 7), то тангенциальная соста-
составляющая ускорения совпадает с направле-
направлением скорости, т. е. абсолютная величина
скорости увеличивается. Наоборот, если пол-
полное ускорение направлено назад от нормали
(рис. 10), то тангенциальное ускорение на-
направлено против скорости, и абсолютная
величина скорости уменьшается.
Найдём величину нормального ускоре-
ускорения в наиболее простом случае равномер-
равномерного движения по окружности. Пусть точка Рис' Ю.
за некоторое время М переместилась из А
в В (рис. 11). Скорости точки в Л и В изобразятся равными по
величине векторами vt и v2. Перенеся вектор vt в точку В, получим
вектор Av, изображающий изменение скорости за время Д'. Но тре-
треугольники BCD и ОАВ подобны, как равнобедренные с одинаковыми
углами при вершинах. Поэтому CDlBC=AB\OA, или
Дг; = -.4В. B.14)

38
КИНЕМАТИКА
[гл. п
При беспредельном уменьшении Д? угол между v} и v2 стремится
к нулю, а угол между v2 и Ду — к прямому: значит, вектор Ду при-
приближается к направлению нормали к траектории, т. е. к направлению
радиуса. Следовательно,
Um&=/.. B-ЬЗ)
Но, с другой стороны, при М—»-0 длина хорды АВ приближается
h длине дуги Д$, которая представляет собой путь, пройденный точ-
точкой за время \t. Поэтому при малых
мы можем вместо B.14) написать.
— As. Деля обе части на Д? и
переходя к пределу, получим:
О
in-
г
B.16)
Рис. И.
Это ускорение направлено к центру
окружности, почему его и называют
центростремительным.
Такую же величину имеет нор-
нормальное ускорение и в случае нерав-
неравномерного движения по окружности.
В этом случае вектор v2 будет но ве-
величине отличаться от v,. Однако, это
изменение величины вектора v связано
с наличием тангенциального ускорения /,. Нормальное же ускорение
саязано только с изменением направления вектора v и поярежнему
шражается формулой B.16).
Итак, в случае неравномерного движения по окружности
in— 7'
B.17)
Jt~~
df
Следовательно, зная скорость движения точки как функцию времени
и радиус траектории, мы можем найти нормальную и тангенциальную
компоненты ускорения. Так как эти компоненты взаимно перпенди-
перпендикулярны, то полное ускорение равно
B.18)
Когда величина скорости постоянна, то полное ускорение направлено
к центру окружности и постоянно по величине. Если точка движется
прямолинейно, то г = оо и существует только тангенциальное уско-
ускорение (г. е. /й —0).

§ 12] ПЕРЕМЕЩЕНИЯ ТВЁРДОГО ТЕЛА 39
Соотношения, полученные нами для частного случая движения по
окружности, справедливы для всякого плоского движения. Всякий
достаточно малый участок криволинейной траектории мы можем заме-
заменить дугой окружности. Эта окружность называется кругом кривизны
для данной точки кривой.
Рассматривая отдельные элементы плоской криволинейной траек-
траектории как элементы окружностей, мы получим для них те же резуль-
результаты, что и для движения по окружности*). Только вместо радиуса
окружности г мы должны подставить радиус круга кривизны, или,
короче, радиус кривизны кривой р; следовательно, для всякого
плоского криволинейного движения
Ы
Но, в отличие от движения по окружности, р меняется от точки к
точке. Если тангенциальное ускорение отсутствует, то полное уско-
ускорение направлено по нормали, и движение происходит со скоростью,
постоянной по величине, но переменной по направлению—это кри-
криволинейное равномерное движение. Если движение происходит но
окружности, то для равномерного движения необходимо, чтобы пол-
полное ускорение было всегда направлено по нормали к окружности,
т. е. по рациусу. При этом ускорение всегда направлено в одну
и ту же точку — к центру. Если же при движении но любой другой
криволинейной траектории ускорение всегда направлено в одну и ту
же точку, то оно уже не может везде оставаться нормальным к тра-
траектории (так как только для окружности нормаль всё время направ-
направлена в одну и ту же точку). В некоторых частях траектории непре-
непременно будет существовать тангенциальная составляющая ускорения,
и скорость не может оставаться постоянной но величине. Отсюда,
например, видно, что движение планет по эллиптическим орбитам
должно происходить с переменной по величине скоростью, так как
ускорение планет всегда направлено к солнцу.
§ 12. Перемещения твёрдого тела
Чтобы описать движение какого-либо реального тела, вообще
говоря, необходимо знать движение каждой его точки. Однако, очень
*) Когда речь шла об определении скорости движения, мы могли эле-
элемент криволинейной траектории заменить элементом прямой. При опреде-
определении ускорений мы уже не можем этого сделать, так как наличие ускоре-
ускорения обусловливает искривление траектории. Поэтому необходимо учесть
кривизну траектории. Эту кривизну траектории и определяет круг кривизны,
элементом которого мы заменяем элемент траектории.

40 КИНЕМАТИКА [ГЛ. II
часто мы можем определить движение любой точки тела, если будем
знать движение ограниченного числа отдельных его точек. Это имеет
место в случае, когда взаимное расположение отдельных точек тела
при движении практически не изменяется, т. е. тело при движении
почти не деформируется. Если деформации тела при движении малы
и не играют принципиальной роли в рассматриваемом вопросе, то
ими вообще можно пренебречь и рассматривать тело как абсолютно
твёрдое. Тогда для определения положения тела достаточно задать
положения любых трёх точек этого тела, не лежащих на одной пря-
прямой, иначе говоря, задать положение произвольного треугольника,
жёстко связанного с телом.
Для определения положения одной точки в пространстве нужно
знать три её координаты. Определение положения трёх произвольных
точек в пространстве требует задания девяти величин — трВх троек
координат. Однако, если эти точки образуют жёсткий треугольник,
то расстояние между каждой парой точек выражается определён-
определённым образом через координаты точек. Девять координат вершин тре-
треугольника не независимы, а связаны между собой тремя ура-
уравнениями. Поэтому, чтобы определить положение абсолютно
твёрдого тела в пространстве, нужно задать шесть независимых
величин.
Количество независимых величин, которые должны быть заданы
для определения положения тела или системы тел, называется числом
степеней свободы системы. Следовательно, свободное абсолютно
твёрдоэ тело обладает шестью степенями свободы.
Если абсолютно твёрдое тело не вполне свободно, то оно обла-
обладает меньшим числом степеней свободы. Так, если абсолютно твёр-
твёрдое тело закреплено неподвижно в одной точке, вокруг которой
оно может вращаться, то из шести независимых координат три фн-
ксирозаны, и для определения положения тела должны быть заданы
только три координаты. Следовательно, абсолютно твёрдое тело,
жёстко закреплённое в одной точке, обладает тремя степенями сво-
свободы.
Если абсолютно твёрдое тело закреплено на неподвижной оси,
вокруг которой оно может вращаться, то это означает, что фиксиро-
иано положение двух вершин треугольника. Из шести независимых
координат заранее фиксированы пять (координат двух вершин тре-
треугольника, т. е. двух точек, расстояние между которыми также
фиксировано), и для определения положения тела должна быть задана
только одна координата. Следовательно, абсолютно твёрдое тело,
закреплённое на оси, вокруг которой оно может вращаться, обла-
обладает одной степенью свободы.
При изучении движения твёрдого тела мы в большинстве случаез
будем рассматривать только плоские движения, при которых все
точки тела перемещаются в параллельных плоскостях. В этом слу-
случае жёсткий треугольник ABC, которым мы определяли положение

§ 12) ПЕРЕМЕЩЕНИЯ ТВЕРДОГО ТЕЛЭ 41
тела, можно выбрать так, чтобы он всё время лежал в одной из
таких параллельных плоскостей (рис. 12 и 13). При этом для опре-
определения положения треугольника достаточно задать только положение
одной из его сторон, например, стороны АВ. Задать положение
отрезка АВ мы можем при помощи двух пар координат его концов
на плоскости. Но так как расстояние между концами неизменно, эти
две пары координат связаны одним уравнением. Поэтому положение
отрезка на плоскости определяется
заданием трёх независимых вели-
величин — твёрдое тело, совершающее
плоское движение, обладает тремя
степенями свободы.
О числе степеней свободы мож-
можно говорить не только в примене-
применении к твёрдым телам, но и в при-
применении к отдельным точкам. Из
самого определения ясно, что от- Рис. 12. Рис. 13.
дельная свободная точка обладает
тремя степенями свободы. Точка, которая может двигаться только по
какой-либо фиксированной поверхности, обладает двумя степенями
свободы; точка, которая может двигаться только по какой-либо
фиксированной линии, обладает одной степенью свободы.
Если движущееся тело заметно изменяет свою форму при движе-
движении, то положение трёх точек тела уже не определяет положения всех
остальных его точек. Всякое реальное тело обладает определённым
ограниченным числом степеней свободы (не превышающим шести)
лишь постольку, поскольку мы рассматриваем его как недеформи-
руемое.
При движении твёрдого тела различные точки совершают, вообще
говоря, различные перемещения. В частном случае, когда все точки
тела совершают одинаковые перемещения, движение его называется
поступательным. В этом случае любая прямая, проведённая в теле,
движется, оставаясь параллельной самой себе. Другой важный частный
случай движения — это случай, когда какие-либо две точки тела всё
время остаются неподвижными. Такое движение называется враща-
вращательным. Прямая, соединяющая эти две неподвижные точки (и также
остающаяся неподвижной), называется осью вращения. При посту-
поступательном движении все точки тела движутся одинаково, и, определив
движение какой-либо одной точки тела, мы вместе с тем определим
движение любой его точки. Поэтому при описании поступательного
движения тела не возникает никаких новых вопросов по сравнению
с теми, которые возникали при описании движения точки. При вра-
вращательном движении различные точки тела движутся, вообще говоря,
по-разному. Однако, и вращательное движение легко описать таким
образом, чтобы это описание сразу определило движение всех точек
вращающегося тела.

42
КИНЕМАТИКА
[ГЛ, 11
X
i
§ 13. Вращательное движение
При вращении абсолютно твёрдого тела вокруг неподвижной оси
все точки тела описывают окружности, лежащие в плоскостях, пер-
перпендикулярных к оси вра-
вращения XX (рис. 14). Цент-
Центры этих окружностей ле-
лежат на оси вращения. Ра-
Радиусы Гг и г3 этих окруж-
окружностей за одно и то же
время поворачиваются на
один и тот же угол а. Этот
угол называется угловым
перемещением тела.
Угловой скоростью (о
называется предел, к кото-
которому стремится отношение
углового перемещения
Рис. 14.
к промежутку времени Д/, за который это перемещение произошло,
при бесконечном убывании Д?, т. е.
л, Ая da.
<о = lira T7 =-jr .
B.20)
Для иллюстрации представления об угловой скорости можно восполь-
воспользоваться методом стробоскопического освещения*). Если чёрный диск
с белой чертой по радиусу привести в быстрое вращение (например, наса-
насадив его на ось мотора), го при обычном освещении нельзя будет разглядеть
черты, диск будет казаться серым. Если же освещать диск стробоскопиче-
стробоскопически, то глаз будет отмечать отдельные положения белой черты, соответ-
соответствующие моментам, > когда стробоскоп даёт вспышку света. Поэтому на
диске мы увидим несколько белых линий, составляющих равные углы между
собой (рис. 15). Это соответствует постоянной угловой скорости. Эти линии
могут перемещаться в ту или другую сторону в зависимости от соотношеиия
между числом оборотов диска и числом вспышек стробоскопа в секунду,
но углы между всеми линиями будут равны **). Если же резко затормозить
диск, то во время остановки диска можно заметить, что углы между лини-
линиями постепенно уменьшаются (рис. 16). Угловая скорость при торможении
уменьшается.
*) Стробоскопическим называется освещение отдельными кратковре-
кратковременными вспышками, следующими через равные промежутки времени. Это
достигается, например, с помощью диска с отверстием, вращающегося перед
источником освещения.
**) Если число вспышек стробоскопа в точности кратио числу оборотов
диска, то линии на диске остановятся, причём число этих линий будет равно
отношению числа вспышек стробоскопа к числу оборотов диска (за каждый
оборот диска стробоскоп даст и вспышек, которые застанут белую черту
в и различных положениях, отличающихся на угол 2Щп).

13]
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
43
Точка тела, лежащая на расстоянии г от осн вращения, при пово-
повороте на малый угол Да опишет малую дугу Д$ = гДа (рис. 17). Раз-
Разделив обе части равенства на элемент времени Д/, за который
Рис. 15.
Рис. 16.
Ри^.. 17.
произошло это перемещение,
перехода к пределу:
мы получим Д$/Д^=
или после
B.21)
угловая
где v — линейная скорость рассматриваемой точки, a w -
скорость вращения.
Таким образом, зная угловую скорость и расстояние точки от
оси вращения, мы сможем найти скорость любой точки вращающе-
вращающегося тела. Скорости всех точек тела перпендикулярны к радиусам,
проведённым из оси вращения, и пропорцнональны расстоянию от
оси вращения. Концы векторов скорости для точек, лежащих на од-
одном радиусе, лежат на одной прямой, образующей с радиу-
радиусом угол а, причём tga пропорциона-
пропорционален угловой скорости со (рис. 18). Угло-
Угловым ускорением называется предел отно-
отношения изменения угловой скорости Дш за
промежуток времени Д^ к этому проме-
промежутку времени при бесконечном умень-
уменьшении последнего, т. е. угловое ускоре- I 0\
нне
и, на основании B.20),
B.22)
B.23)
Рис. 18.
Зная угловую скорость и угловое ускорение, нетрудно иаЙти
ускорение любой точки вращающегося тела. Как мы видели (§ 11)',
при плоском криволинейном движении точка имеет нормальное уско'-

44
КИНЕМАТИКА
[гл. il
рение jn, направленное к центру и по абсолютной величине равное
v^Jr. Подставляя значение v из соотношения B.21), получим:
Л=
B.24)
dv
Тангенциальное ускорение точки jt = jr; дифференцируя выраже-
выражеj|
ние B.21), найдём (так как г постоянно) —j| = r-jj? = nj. Следова-
Следоваdt~
тельно,
Полное ускорение точки есть
B.25)
B.26)
Зная угловую скорость и угловое ускорение вращающегося тела,
а- также расстояние от точки до оси вращения, мы можем найти
величину и направление ускорения
для любой точки тела.
Так как отношение тангенциаль-
тангенциального ускорения к нормальному
/У/'п = Г(/(о3 одинаково для всех то-
точек тела, то вектор полного уско-
ускорения для всех точек тела образует
с радиусом, проведённым к этой
точке, одни и тот же угол J5, при-
причём tgj$ = 7j/<o2 (рис. 19). Вели-
Величина полного ускорения пропор-
пропорциональна расстоянию до оси вра-
вращения. Поэтому для всех точек,
лежащих на одном радиусе, концы
векторов ускорения лежат на одной
прямой. При 7) = 0 (вращение с по-
постоянной угловой скоростью) [$=0, и полное ускорение для всех
точек направлено по радиусу к оси вращения (центростремительное
ускорение).
Введённые таким образом угловая скорость и угловое ускорение
ничего не говорят о том, как ориентирована ось вращения в про-
пространстве. Можно ввести такое определение угловой скорости, кото-
которое будет указывать не только величину угловой скорости, но и
ориентировку вращения в пространстве, если изображать угловую
скорость отрезком прямой, которая совпадает с осью вращения,
а длина отрезка в некотором условном масштабе выражает величину
угловой скорости. Однако, чтобы полностью определить направление
вращения, требуется задать не только ось вращения, но и указать,
в какую сторону происходит вращение. Для этого условились при-
Рис. 19.

13]
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
45
писывать отрезку, изображающему угловую скорость, определённое
направление, которое с направлением вращения связано правилом
буравчика. Угловой скорости приписывают то направление, в котором
будет двигаться (ввинчиваться или вывинчиваться) буравчик, если его
вращать в направлении изображаемого вращения (рис. 20 иллюстри-
иллюстрирует это правило).
Итак, угловую скорость задают при помощи отрезка определённой
длины, имеющего определённое направление, т. е. так, как задают
векторные величины.
Однако, этого мало, чтобы иметь право утверждать, что угловая
скорость есть вектор — нужно убедиться, что заданная таким образом
угловая скорость действительно об-
обладает всеми свойствами векторных
величин. Нетрудно показать, что
в этом смысле угловая скорость
совершенно аналогична линейной
скорости и, как и последняя, пред-
представляет собой вектор. Установлен-
Установленный выше способ задания угловой
скорости соответствует тому, что
и малые угловые перемещения мы
изображаем отрезками, направлен-
направленными по правилу буравчика вдоль
осей, вокруг которых происходят
эти перемещения, причём длина
отрезка в определённом масштабе
выражает величину углового пере-
перемещения.- Так (рис. 21), угловое
перемещение Да, соответствующее перемещению точки из А в В,
изображается отрезком ОВ\ угловое перемещение Др, соответствующее
' -• перемещению точки из В
i в С, изображается отрез-
• С ком ОС и т. д. Каждому
Лд перемещению точки по дуге
соответствует отрезок, на-
А правленный вдоль оси вра-
вращения, т. е. перпендику-
перпендикулярно к плоскости дуги, и
длины этих отрезков пропорциональны длинам дуг. Но так как уг-
угловые перемещения малы, то длины дуг гДа, гЩ и т. д. малы по
сравнению с радиусом вращения г, и эти дуги можно заменить
Я»рдами. Иначе говоря, пока угловые перемещения малы, соответ-
соответствующие им перемещения точки можно считать прямолинейными.
Каждому такому линейному перемещению соответствуем отрезок,
выражающий угловое перемещение, который пропорционален линей-
линейному перемещению и повёрнут относительно него на 90°.
Рис. 20.

46 КИНЕМАТИКА [1Л. II
Таким образом, переход от самих перемещений точки к отрезкам,
выражающим малые угловые перемещения, связан только с измене-
изменением масштаба и поворотом, одинаковым для всех отрезков. Отсюда
видно, что отрезки, изображающие малые угловые перемещения, во
всём подобны линейным перемещениям, и следовательно, так же как
линейные перемещения, представляют собой векторные величины.
Однако, если малое угловое перемещение Да изображается вектором,
направленным вдоль оси вращения, то и угловая скорость
« = Ига^, B.27)
д -+о-"
получающаяся умножением Да на скалярную величину 1 А', изобра-
изображается вектором, направленным вдоль оси вращения.
Наше доказательство векторного характера угловой скорости
основано на том, что малые угловые перемещения аналогичны линей-
линейным перемещениям, и переход к угловой скорости от малых угловых
перемещений аналогичен переходу к линейной скорости от малых
линейных перемещений. Следует подчеркнуть, что только малые
угловые перемещения аналогичны линейным перемещениям. Что ка-
касается конечных угловых перемещений, то к ним наше рассуждение
неприменимо. Если бы конечные угловые перемещения изображались
при помощи отрезков, то эти отрезки не были бы подобны линейным
перемещениям и не являлись бы векторными величинами.
Поскольку угловая скорость есть вектор, то и изменение угло-
угловой скорости есть вектор. Следовательно, угловое ускорение
TQ=lira-^ B.28)
есть вектор, совпадающий по направлению с вектором Дю, т. е.
вектором изменения угловой скорости за достаточно малый промежу-
промежуток времени. Если направление оси вращения остаётся неизменным,
то вектор 7) лежит на этой же оси. Он совпадает по направлению
с со, если угловая скорость возрастает по величине, и направлен
в противоположную сторону, если ю уменьшается.
Угловую скорость и угловое ускорение можно, как и все век-
векторы, разлагать на компоненты по определённым направлениям,
в частности, задавать тремя компонентами по трём осям координат.
§ 14. Связь между векторами линейной и угловой скоростей
связь между векторами угловой и соответствующей
линейной скорости. Связь между абсолютными величинами угловой
скорости ю«и линейной v нами была найдена: v — шг. Будем считать
радиус г также вектором, направленным от оси вращения. Определим
теперь связь яежду направлениями векторов v, ю иг. Расположение

^ СВЯЗЬ МЕЖДУ ЛИНЬЙНОЙ И УГЛОВОЙ СКОРОСТЬЮ 47
этих векторов указано на рис. 22. Как видно, вектор v перпендику-
перпендикулярен и к вектору со, и к вектору г. Направление v можно опре-
определить, пользуясь правилом буравчика. Если мы расположим бурав-
буравчик так, чтобы его рукоятка сначала совпадала с вектором ш (рис. 22),
а затем поаериём его кратчайшим путём так, чтобы рукоятка сов-
совпала с г, то движение самого буравчика совпадёт с направлением v*).
gT0 _ частный случай операции векторного перемножения двух век-
topoB. _^ _^
Векторным произведением двух вектороз АВ и АС называете я
вектор, перпендикулярный к векторам АВ и АС, направленный по
\
Рис. 22.
правилу буравчика и равный по величине произведению величин век-
векторов А~В и АС на синус угла между ними. Легко видеть (рис. 23),
что произведение -АВ-АС' sin а равно удвоен-
удвоенной площади треугольника ABC или площади
параллелограмма ABCD. Следовательно, век-
векторное произведение двух векторов АВ и ВС
есть вектор, перпендикулярный к плоскости па-
-—> Рис. 2о.
раллелограмма, образованного векторами АВ
и ВСт и равный по величине площади этого параллелограмма. На-
Направление вектора определяется правилом буравчика.
Обозначается векторное произведение следующим образом:
[АВ-Ъ~С] или АВХВС-
Очевидно, векторное произведение меняет направление, т. е. ме-
меняет знак, при изменении порядка сомножителей, так как при этом
меняется направление вращения буравчика. Следовательно,
{АВ-АС] = —[АС-АВ].
Как видно из Определения операции векторного умножения, век-
вектор линейной скорости v представляет собой векторное произведение
*) Мы могли бы совместить рукоятку буравчика с вектором г, вращая
буравчик в обратном направлении. Поэтому правило становится определен-
определенным только тогда, когда берётся кратчайшее направление, при котором угол
поворота до совмещения с г будет наименьшим.

48 кинематика [гл. и
векторов и иг. 6 нашем частном случае векторы ш и г перпенди-
перпендикулярны; поэтому синус угла между ними равен 1 и вектор v по
величине равен просто произведению векторов ш и г. Следовательно,
v = [o>.r]. B.29)
Поскольку мы рассматриваем радиус г как вектор, выражения
B.24) и B.25) для нормального и тангенциального ускорений при
вращении вокруг неподвижной оси можно записать в векторной форме.
Нормальное ускорение
|„ = —ю»г; B.30)
знак минус взят потому, что это ускорение направлено к оси вра-
вращения, а направление радиуса-вектора г мы уже выбрали — от оси
вращения. Тангенциальное ускорение j/ направлено по касательной
в ту же сторону, что и линейная скорость, если угловая скорость
возрастает по величине, т. е. если вектор углового ускорения 1}
совпадает по направлению с вектором to. Поэтому
h=[ri-r]. B.31)
Если угловая скорость убывает по величине, то 7) направлена в сто-
сторону, противоположную ш, и j^ направлено в сторону, противопо-
противоположную линейной скорости.
Напомним, что все полученные нами выражения относятся к слу-
случаю вращения вокруг неподвижной оси.

ГЛАВА III
ДВИЖУЩИЕСЯ СИСТЕМЫ КООРДИНАТ
§ 15. Отсчёт времени в движущихся системах координат
При описании движений часто бывает необходимо переходить от
одной системы отсчета к другой, известным образом движущейся
относительно первой. Задача заключается в юм, чтобы, зная движе-
движение точки в первой системе координат, найти её движение во вто-
второй системе координат.
В этой задаче в новой форме возникает вопрос о способе отсчёта
времени. Установленный выше способ отсчета времени относился
к одной системе координат, в которой описывались все движения.
Сейчас мы рассматриваем две различные системы координат, и возни-
возникает вопрос об отсчёте времени в системах координат, движущихся
друг относительно друга.
Мы могли бы сохранить наш прежний способ отсчёта времени
(при помощи световых сигналов) — по часам, связанным с первой
системой координат. Но это означало бы, что мы пользуемся в двух
системах координат различными способами отсчёта времени. Действи-
Действительно, если бы мы пользовались только одними часами, связанными
с первой системой координат, то это означало бы, что в первой
системе координат мы отсчитываем время по неподвижным часам, а
во второй — по движущимся.
Чтобы применять а обеих системах координат один и тот же
установленный нами способ отсчёта времени, мы должны в каждой
системе координат установить свои часы, т. е. пользоваться в двух
системах координат различными часами, причём одни часы движутся
относительно других.
Для определения момента времени, когда «там» произошло собы-
событие, мы должны, попрежнему, от показаний часов отсчитать время
распространения сигнала «оттуда»—«сюда»—до часов, по кото-
которым производится отсчёт. Но за время распространения сигнала
часы успеют несколько переместиться друг относительно друга, и
пути, проходимые сигналом в двух системах координат, окажутся
разными. Вследствие этого и поправки, которые мы должны будем
вводить к показаниям часов в двух системах координат, будут раз-
различны.
4 с. э. хайкин

50 ДВИЖУЩИЕСЯ СИСТЕМЫ КООРДИНАТ [гл. III
Как же связаны между собой результаты определения в двух раз-
различных системах координат момента времени, когда произошло какое-
либо событие? Ясно, что этот вопрос возчик только потому, что
сигналы, которыми мы пользуемся, распросграняются с конечной
скоростью, и за время распространения сигналов расстояния, кото-
которые входят в рассмотрение, успевают изменяться. Если ''бы мы
воспользовались сигналами, которые распространяются мгновенно,
т. е. с бесконечно большой скоростью, то вопрос отпал бы. Однако,
такими сигналами мы не располагаем, и это —принципиальное обстоя-
обстоятельство, с которым в физике необходимо считаться. Но если за
время распространения сигнала те расстояния, которые входят в рас-
рассмотрение, не успевают заметно измениться, т. е. если скорости,
с которыми нам приходится иметь дело, малы по сравнению со ско-
скоростью распространения сигналов (скоростью света), то вэирос так-
также отпадает. При этих условиях результаты определения в двух
разных системах координат момента времени, когда произошло то
или иное событие, практически будут совпадать.
В макроскопической механике, т. е. в механике тел, состоящих из
множ:ства элементарных частиц, эти условия обычно соблюдаются.
Во всяком случае, на Земле нам не приходится встречаться с макро-
макроскопическими движениями, скорости которых превышают десятки
километров в секунду, в то время как скорость света составляет
около 300 000 клецек*). Даже в небесной механике, где приходится
иметь дело со скоростями в сотни километров в секунду, в боль-
большинстве случаев результаты определения момента времени, когда
произошло какое-либэ событие, практически совпадают в различных
системах координат.
Поэтому, пока скорости, с которыми нам приходится иметь дело,
малы по сравнению со скоростью света, можно считать, что данное
событие происходит во etex системах координат одновременно. На
этом предположении построена вся «классическая механика», кото-
которая вследствие этого оказывается справедливой лишь приближённо,
но тем более точно, чем меньшз (по сравнению со скоростью света)
те скорости, с которыми нам приходится иметь дело. Это первое
приближение оказывается достаточно точным для всех без исключе-
исключения задач о движении макроскопических тел на Земле и для подав-
подавляющего большинства задач небесной механики. Поэтому классиче-
классическая механика, несмотря на свой принципиально приближённый
характер, имеет огромное практическое значение, так как обеспечи-
обеспечивает вполне достаточную точность во всех указанных случаях.
Несмотря на это, вопрос о том, как связаны между собой ре-
результаты определения в разных системах координат момента времени,
когда произошло данное событие, имеет большое принципиальное
*) Элементарные частицы — атомы, электроны и т. д. — могут двигаться
СО скоростями, не малыми но сравнению со скоростью света.

§ 16] движущиеся системы координат 51
значение. Рассмотрение этого вопроса привело А. Эйнштейна к за-
заключению о необходимости дополнить и уточнить целый ряд самых
основных положений не только механики, но и физики вообще. Все
эти дополнения, внесённые А. Эйнштейном в основные положения
классической физики, получили название теории относительности. Ме-
Механика теории относительности включает в себя классическую меха-
механику как приближение, справедливое до тех пор, пока скорости дзи-
жений малы по сравнению со скоростью света.
Механика теории относительности (как и вся теория относитель-
относительности)- имеет всё же не только принципиальное, но и практическое
значение. Так, при рассмотрении быстрых движений элементарных
частиц приходится применять механику теории относительности, чтобы
получить результаты, согласующиеся с опытом. Но механика элемен-
элементарных частиц составляет предмет специального раздела физики. По-
Поэтому мы ограничимся изложением классической механики*).
§ 16. Движущиеся системы координат
Как указывалось, в механике часто возникает следующая задача:
движение точки определено по отношению к системе отсчета, кото-
которая, в свою очередь, известным образом движется относительно ка-
какой-то другой системы отсчёта; требуется найти движение точки по
отношению к этой второй системе отсчёта. Например, известно дви-
движение находящихся в вагоне тел относительно eat она, который,
в свою очередь, движется по отношению к Земле. Требуется найти
движение этих тел относительно Земли.
При рассмотрении подобных задач первую систему координат
(в нашем примере — связанную с вагоном) принято называть «движу-
«движущейся», а вторую (в нашем примере — связанную с Згмлёй)— «не-
«неподвижной». В соответствии с этим движение относительно «движу-
«движущейся') системы координат принято называть «относительным», а
движение по отношению к «иеподзижной» системе координат — «абсо-
«абсолютным». Наконец, движение «движущейся» системы координат отно-
относительно «неподвижной» назызают переносным.
Некоторые из этих терминов совершенно условны. Прежде всего,
не имеет смысла говорить о системе координат, что она «непо-
«неподвижна вообще», пока не указана какая-либо другая система отсчёта,
по отношению к которой поколтея эта «неподвижная». С другой
стороны, не имеет смысла разделять движения на «абсолютные» и
«относительные», поскольку вообще можно говорить только о дви-
движении по отношению к какой-либо системе отсчёта. Однако, эти
термины широко применяются, так как сокращают изложение. По-
аггому мы будем ими пользоваться, но, чтобы не забывать об их услов-
условности, будем ставить их в кавычки.
*) Механика теорил относигельиогти будет кратко изложена в коаце
книги.

ДВИЖУЩИЕСЯ СИСТЕМЫ КООРДИНАТ
ГЛ. Ш
В этих терминах сформулированная в начале этого параграфа
задача вьплядит так: заданы «относительное» и переносное дви-
движения; требуется найти «абсолютное» движение. Точнее гоаоря, нам
заданы координаты какой-либо точки в движущейся системе коор-
координат и координаты точек движущейся- системы координат относи-
относительно «неподвижной», как функции времени. Требуется найти коор-
координаты рассматриваемой точки в «неподвижной» системе координат,
как функции времени. Зная все координаты, как функции временя,
мы всегда сможем (путём однократного и двукратного дифференци-
дифференцирования) найти, соответственно, скорости и ускорения рассматриваемой
точки в «относительном» и «абсолютном» движении.
В таком общем виде эту задачу приходится решать сравнительно
редко. Обычно можно ограничиться более частной задачей: зная ско-
скорости и ускорения «относительного» и переносного движения, найти
скорости и ускорения «абсолютного» движения.
Поэтому в общем виде мы рассмотрим задачу1, только для про-
простого случая, когда движущаяся система координат движется пря-
прямолинейно относительно «неподвижной». Для случаев же более
сложного переносного движения мы ограничимся указанной выше
более частной задачей.
Рассмотрим сначала простейший случай, когда система коорди-
координат х', у, z' движется относительно «неподвижной» х, у, г не только
прямолинейно, но и равномерно со скоростью v0. Иллюстрацией
к этому случаю может служить движение тела относительно вагона
в прямолинейно и равномерно движущемся поезде. Движение тела от-
относительно вагона за-
дано, требуется опре-
определить это движение
относительно Земли.
Так как система коор-
координат х\ у', z' дви-
движется прямолинейно,
то скорости всех её
? j- х' точек относительно
«неподвижной» систе-
системы координат х, у, z
одинаковы и равны v0.
Следовательно, v0 есть
общая для всех точек системы координат х', у1, z' скорость
переносного движения. Для упрощения выберем системы координат
так, чтобы они совпадали в момент / = 0 и ось х была направлена
по скорости 1»0 (рис. 24). Тогда координаты у и у', z и z' рассма-
рассматриваемой точки в любой момент времени соответственно равны
в обеих системах координат, ,т. е. у = у\ z = z', координаты же х'
и х будут связаны соотношением х = х'-\-х0, где хй — координата
точки Q' в первой системе координат в рассматриваемый момент вре-

§ 16] ДВИЖУЩИЕСЯ СИСТЕМЫ КООРДИНАТ 53
мени. Но гак как xa = vQt, то
х — х' -\- vuK
Соотношения
x = x'-\-v,f, у=У, г = г} C.1)
носят название галилеевых преобразований координат. Они отра-
отражают переход от одной системы координат к другой в случае, когда
одна из систем координат движется относительно другой прямоли-
прямолинейно и равномерно вдоль оси х.
Из соотношений C.1), дифференцируя их дважды по времени, сразу
можно получить связь между компонентами скоростей и ускорений
в обеих системах координат. Так как v0 от времени не зависит, то
т, е. компоненты ускорения, а значит, и всё ускорение движущейся
точки в обеих системах координат, одни и те же. Компоненты же
скорости v точки во второй системе координат равны сумме соот-
соответствующих компонент скорости vr и скорости v0. Следовательно,
v = v' + v0, C.2)
J=J'. C.3)
т. е. «абсолютная» скорость v всякой движущейся точки равна гео-
геометрической сумме «относительной» скорости v' и переносной
скорости v0; «абсолютное» же ускорение j равно «относительному»
ускорению j'.
Перейдём теперь к случаю, когда система координат х', у', z'
движется по отношению к х, у, z прямолинейно, но с ускорением.
В этом случае, попрежнему, в любой момент времени спразедлизы со-
соотношения:
х = х'-\-х0^ у = У, г — *. C.4)
Попрежнему скорость и ускорение всех точек движущейся системы
координат по отношению к неподвижной будут одни и те же, причём
dxn . d2Xn
скорость переносного движения vQ = ——-, а его ускорениеу0 = -~-.
Поэтому, дифференцируя соотношения C.4) дважды но времени, мы
получим:
vx = v'x + vo> vy = v'y' V* = K>
Jji—Jx~T~J0 ->y — Jy >z Js'
В этом случае не только скорости, но и ускорения в обеих си-
системах координат различны, причём
v = v'-r-v0, C.5)
J=i'+Jo. C.6)
т. е. «абсолютная» скорость равна геометрической сумме «относ'к-

54 движущиеся системы координат [гл. in
тельной» и переносной скоростей, и «абсолютное» ускорение равно
геометрической сумме «относительного» и переносного ускорений.
Этот результат, полученный нами для прямолинейного переносного
Движения, справедлив также при всяком поступательном переносном
движении. Это обусловлено тем, что при поступательном перенос-
переносном движении, так же как при прямолинейном, все точки движущейся
системы координат имеют по отношению к неподвижной одни и те
же скорости и ускорения. Поэтому к «отиосительной» скорости рас-
рассматриваемой точки, независимо от её положения в движущейся си-
системе координат, прибавляется одна и та же скорость переносного
движения, и к «относительному» ускорению точки прибавляется одно
и то же ускорение — именно ускорение переносного движения.
В случае непоступательного переносного движения скорости раз-
различных точек движущейся системы координат относительно «непо-
«неподвижной» различны. Но при этом, попрежнему, абсолютное перемеще-
перемещение рассматриваемой точки представляет собой геометрическую
сумму её «относительного» перемещения и переносного перемещения
той точки движущейся системы координат, в которой в данный мо-
момент находится рассматриваемая точка. Поэтому «абсолютная» ско-
скорость рассматриваемой точки попрежнему представляет собой геомет-
геометрическую сумму «относительной» скорости этой точки и переносной
скорости той точки движущейся системы координат, в которой в дан-
данный момент находится рассматриваемая точка тела. Следовательно,
всегда «абсолютная» скорость рассматриваемой точки представляет
собой геометрическую сумму «относительной» и переносной ско-
скоростей.
С «абсолютным» ускорением дело обстоит иначе. Только в рас-
рассмотренном выше частном случае поступательного переносного дви-
движения «абсолютное» ускорение пргдетавляет собой геометрическую
сумму «относительного» и переносного ускорений. В случае же не-
непоступательного переносного движения, когда скорости движения раз-
различных точек движущейся системы координат относительно «непо-
«неподвижной» различны, к «относительной» скорости рассматриваемой точки
тела прибавляется скорость переносного движения, которая зависит
от положения точки в движущейся системе координат. Так как по-
положение рассматриваемой точки тела в движущейся системе коор-
дираг изменяется вследствие «относительного» движения, то «абсо-
«абсолютная» скорость изменяется вследствие трёх причин:
1) изменения «относительной» скорости рассматриваемой точки
тела;
2) изменения переносной скорости той точки движущейся системы
координат, в которой в данный момент находится рассматриваемая
точка;
3) изменения переносной скорости вследствие перехода рассмат-
ризаемой точки из одной точки движущейся системы координат
в другую.

ВРАЩАЮЩИЕСЯ СИСТЕМЫ КООРДИНАТ
55
Каждое из этих изменений скорости связано с наличием соотзет-
ствующего ускорения, а именно:
1) «относительного» ускорения, зависящего только от характера
«относительного» движения;
2) переносного ускорения, зазисящего только от характера пере-
переносного движения;
3) некоторого дополнительного ускорения, зависящего от харак-
характера как «относительного», так и переносного движения. Это допол-
дополнительное ускорение, впервые рассмотренное Кориолисом, назызают
кориолисовым ускорением.
«Абсолютное» ускорение рассматриваемой точки тела представляет
собой сумму этих трёх ускорений. Таким образом, в то время как
«абсолютная» скорость при любом характере переносного движения
представляет собой сумму «относительной» и переносной скоростей,
«абсолютное» ускорение представляет собой сумму не только «отно-
«относительного» и переносного, но и кориолисова ускорений. Только
в частных случаях кориолисово ускорение обращается в пуль, на-
например, в рассмотренном выше случае поступательного переносного
движения.
§ 17. Вращающиеся системы координат
В общем случае нахождение «абсолютного» ускорения представ-
представляет собой сложную задачу. Поэтому мы ограничимся только част-
частным случаем, когда движущаяся система координат вращается отно-
относительно «неподвижной», вокруг неизменной оси
с постоянной угловой скоростью. Примером
этого случая могут служить движения тел от-
относительно Земли, которая, в свою очередь,
совершает относительно Солнца суточное вра-
вращение вокруг своей оси с постоянной угло-
угловой скоростью. (Годовое движение Земли от- ^- '
носительно Солнца происходит с гораздо мень-
меньшей угловой скоростью, и поэтому в большин-
большинстве случаев его можно не принимать во вни-
внимание.)
Расположим обе системы координат — вра-
вращающуюся х', у, г' и «неподвижную» х, у,
z — так, чтобы оси z и г' совпадали с на-
направлением оси, вокруг которой происходит
вращение с постоянной угловой скоростью со (рис. 25). Переходя
от координат рассматриваемой точки х', у', г' во вращающейся си-
системе коорцинат к координатам этой же точки х, у, z в «непо-
«неподвижной» системе координат и выразив их как функции времени, мы
смогли бы дифференцированием найти «абсолютную» скорость и
«абсолютное» ускорение, подобно тому как это было сделано в прг-
z,z'
Ci)
Рии 25.

56
ДВИЖУЩИЕСЯ СИСТРМЫ КООРДИНАТ
[гл. ш
дыдущем параграфе. Однако, мы не будем проделывать этих выкла-
выкладок, а воспользуемся более наглядными кинематическими соображе-
соображениями.
Начнём со специального случая, когда рассматриваемая точка М
покоится во вращающейся системе координат, т. е. «относительная»
скорость v' = 0. Тогда относительно «неподвижной» системы коор-
координат эта точка вращается вокруг оси z с постоянной угловой ско-
скоростью со и описывает при этом окружность радиуса г (рис. 26).
При этом, как мы знаем, точка обладает скоростью
[<»• г]
и центростремительным ускорением
Так как это — скорость и ускорение движения относительно «не-
«неподвижной» системы координат, то это и есть искомые «абсолютные»
скорость и ускорение. Следователь-
но, в случае, когда «относитель-
«относительная» скорость равна нулю, «абсо-
Рис. 26.
лютная» скорость равна переносной, и «абсолютное» ускорение равно
переносному. Первое совершенно очевидно, второе становится понятным,
если принять во внимание, что «относительное» ускорение равно нулю,
а кориолисово ускорение, обусловленное движением точки во вращаю-
вращающейся системе координат, в нашем случае также равно нулю (так
как точка не движется во вращающейся системе координат).
Рассмотрим теперь более сложные случаи, когда «относительная»
скорость не равна нулю. Начнём со случая, когда рассматриваемая
точка движется вдоль прямой, проходящей через ось вращения и пер-
перпендикулярной к ней. Иллюстрировать этот случай можно следующей
моделью (рис. 27). Прямая штапга АВ вращается вокруг перпенди-
перпендикулярной к ней оси 00' с угловой скоростью w. Тело М движется
по штанге со скоростью v' относительно штанги. Требуется найти
скорость и ускорение этого тела относительно «неподвижной» системы
координат.

§ Щ
ВРАЩАЮЩИЕСЯ СИСТЕМЫ КООРДИНАТ
Рис. 28.
Прежде всего заметим, что в «неподвижной» системе координат
рассматриваемое движение уже не будет прямолинейным. В этом легко
убедиться, если представить себе, что тело М, двигаясь, прочерчи-
прочерчивает след на столе, над которым вращается штанга. Ясно, что вслед-
вследствие вращения штанги этот след, т. е. траектория тела в «непо-
«неподвижной» системе координат, будет
представлять собой некоторую
кривую (рнс. 28). Следовательно,
наряду с тангенциальным ускоре-
ускорением в «неподвижной» системе
координат должно существовать и
нормальное ускорение /я, направ-
направленное внутрь траектории тела. Со-
Составляющая этого ускорения в
направлении, нормальном к штан-
штанге, как мы увидим, и есть корио-
лисово ускорение.
Для вычисления этого ускоре-
ускорения положим, что относительная
скорость v', т. е. скорость тела относительно штанги, по величине
остаётся постоянной. (Это ограничение не принципиально и, как бу-
будет показано, не изменяет результатов.) При этом, однако, «абсолют-
«абсолютная» скорость тела v изменяется как по величине, так и по направ-
направлению. Так как тело движется вдоль
штанги, а сама штанга вращается,
то «абсолютная» скорость тела на-
направлена как-то под углом к штан-
штанге. Разложим эту скорость на две
составляющие: vr, направленную
вдоль штанги, и \и, направленную
перпендикулярнокштанге (рис.29).
Составляющая vr обусловлена движением относительно штанги и
равна относительной скорости vr; составляющая \п обусловлена вра-
вращением штанги и равна переносной скорости той точки, где нахо-
находится тело М, т. е. vn=cor. (Как всегда, «абсолютная» скорость
равна сумме «относительной» и переносной ) Если бы тело М оста-
оставалось неподвижным на штанге, то составляющая vn изменялась бы
только по направлению, и это изменение, обусловленное переносным
ускорением (как в первом примере этого параграфа), как раз раз-
разно coV и направлено к центру. Следовательно, переносное ускорение
изменяет направление составляющей vn.
Однако, этим не исчерпываются изменения составляющих Vn и vr.
Вследствие вращения штанги изменяется направление составляющей vr,
а вследствие движения тела по штанге и изменения г — абсолютная
величина составляющей vn. Так как v,. направлена вдоль штанги, то
изменение её направления есть изменение скорости, нормальное
О
м
Рис. 29.

58 ДВИЖУЩИЕСЯ СИСТЕМЫ КООРДИНАТ [ГЛ.III
к штанге. С другой стороны, так как v направлена перпендикулярно
к штанге, то изменение её величины есть также изменение скорости,
нормальное к штанге. Таким образом, при равномерном движении
тела по равномерно же вращающейся штанге в «неподвижной» си-
системе координат будет существовать не только переносное ускоре-
ускорение jc — — war, направленное к центру и вызывающее изменение на-
направления скорости vn, но и нормальное к штанге ускорение ]k,
вызывающее изменение направления скорости vr и величины ско-
скорости vn.
Чтобы определить величину этого ускорения, нужно иайти указан-
указанные изменения скоростей за малый промежуток времени hi. Для этого
сравним значения vr и vn для двух положений точки, М и М', раз-
разделённых промежутком времени
№ (рис. 30). Так как нас инте-
интересует изменение только вели-
величины vn, а не его направления,
то мы должны сравнивать толь-
только абсолютные величины \п в
двух положениях. Поэтому
вектор vn мы должны перено-
переносить из положения /И в положе-
положение М', не сохраняя его направления, а наоборот, совмещая его
с вектором \'п — новым вектором скорости vra. В результате мы по-
лучим отрезок \vn, выражающий изменение величины вектора vn.
Наоборот, для вектора vr мы должны найти изменение его направ-
направления; поэтому vr мы должны переносить, сохраняя его направление.
В результате мы получим отрезок Avr, выражающий изменение на-
направления скорости vr. Сумма отрезков Avn и Avr представляет собой
полное изменение «абсолютной» скорости тела в направлении, нормаль-
нормальном к штанге за элемент времени Ы.
Нетрудно подсчитать величину этого ускорения. Если за время \t
штанга повернулась иа угол Да = шД?, то
Дг>г = г»гАа = ?7,<1Ш; C.7)
с другой стороны, за время Д? тело прошло по штанге путь hr = vr At
и при этом скорость vn = <ar возросла по величине на
\vn = Дг ш = vr со М. C.8)
Оба эти изменения скорости равны по величине н направлены в одну
и ту же сторону. Поэтому полное изменение скорости в направле-
направлении, нормальном к штанге, есть Дг»г -\- Дип = 2vr w Д? и ускорение,
направленное нормально к штанге,
h = Шп ~r-±^-n = 2uvr. C.9)

§ 17]
ВРАЩАЮЩИЕСЯ СИСТЕМЫ КООРДИНАТ
59
Это ускорение, зависящее как от «относительной» скорости v' = vr,
так и от переносной (скорости вращения ш) и представляет собой
кориолисово ускорение для нашего случая. Направление этого ускоре-
ускорения зависит как от напразления v', так и от направления вращения.
Совершенно очевидно, что при изменении направления вращения
направление \k изменится на обратное. Легко убедиться и в том, что
при изменении направления
v' направление \k также из-
изменяется на обратное. Дей-
Действительно, при движении
точки М от центра к пери-
периферии скорость \п возра-
возрастала по величине, а на-
направление vr менялось в сто-
сторону перемещения штанги. Рис 31.
При движении же точки М от
периферии к центру (рис. 31) скорость vn уменьшается по величине,
а направление vr изменяется в сторону, противоположную переме-
О)
Ш <*>
I
(О О)
Рис. 32.
щению штанги. Следовательно, в этом случае Avra и Avr, а значит,
и \k направлены в сторону, противоположную перемещению штанги.
Как легко видеть, во всех случаях, если рассматривать ш как
вектор» то направление \k будет определяться (см. рис. 32) по

60
движущиеся системы координат
[гл. lit
10)
правилу буразчика, считая от ш к v\ Так как в нашем случае векторы ш
и v' взаимно перпендикулярны, то jfe можно определить как удвоен-
удвоенное векторное произведение векторов ю и v':
j, = 2[o).v']. C.10)
Это выражение остаётся справедливым и в том случае, когда
вращающаяся штанга образует не прямой, а произвольный угол [S
с осью вращения (рис. 33), т. е. описывает не плоскость, а конус.
Действительно, разложим vr на две
составляющие — ttrsinp, лежащую в
плоскости, нормальной к оси враще-
вращения, н t>rcosp, направленную вдоль
оси вращения. Изменять направление
при вращении штанги будет только
первая составляющая 7Jrsm[$. С дру-
другой стороны, расстояние тела от оси
вращения будет возрастать только
за счёт этой же составляющей ско-
скорости г>г sin 3- Всё будет происхо-
происходить так же, как и в рассмотренном
выше плоском случае, если бы тело двигалось по штанге со ско-
скоростью г»,, sin [5. Следовательно, \k по абсолютной величине равно
2<uVr sin (ш, vr), а направление его попрежнему определяется правилом
буравчика, т. е. и в этом случае )k выражается формулой C.10).
Полное ускорение тела в «неподвижной» системе координат, т. е.
«абсолютное» ускорение, равно геометрической сумме )е и )k.
Если бы тело двигалось вдоль штанги не равномерно, а с ускоре-
ускорением ]' («относительное» ускорение), то все наши выводы относи-
относительно ускорения \k остались бы в силе, так как мы рассматривали
только малые элементы времени Д/1, за которые скорость v' можно
считать постоянной. Однако, вследствие наличия «относительного»
ускорения j' «абсолютное» ускорение будет равно геометрической сумме
не двух (как было в случае постоянной «относительной» скорости),
а трёх ускорений:
Рис. 33.
где j' — «относительное» ускорение, зависящее от характера относи-
относительного движения; \с = — ю2г—переносное ускорение, зависящее
от угловой скорости переносного движения и положения рассматри-
рассматриваемой точки в движущейся системе координат; jft = 2 [ш¦ «>г] — кори-
олисово ускорение, зависящее как от «относительной» скорости, так
и от угловой скорости переносного движения.
Мы пришли для нашего конкретного случая к тому же выводу,
который в общем виде был сформулирован в конце предыдущего
параграфа. Однако, полученные нами количественные результаты
относятся только к одному случаю относительного движения, когда

§ 17J
вращающиеся системы координат
61
Рис. 34.
относительная скорость всё время лежит в плоскости, проходящей
через ось вращения (рис. 34). Чтобы убедиться, что это выражение
справедливо при любом направлении относительной скорости, нужно
ещё показать, что оно справедливо при от-
относительной скорости, направленной нор-
нормально к плоскости, в которой лежат рас-
рассматриваемая точка и ось вращения. Для
этого рассмотрим случай, когда относитель-
относительное движение представляет собой вращение
вокруг той же оси, вокруг которой проис-
происходит вращение движущейся системы ко-
координат.
Пусть рассматриваемая точка вращается
вокруг оси z с угловой скоростью со' относительно движущейся системы
координат, которая в свою очередь вращается вокруг той же оси с
угловой скоростью о) относительно «неподвижной» системы координат
(рис, 35). Для определённости положим, что
оба вращения происходят в одну и ту же
сторону. «Относительная» скорость v' = w'r
и направлена нормально к радиусу г (т. е.
нормально к плоскости, проходящей через
ось вращения, — этот именно случай нас ин-
интересует). Угловая скорость вращения точки
в «неподвижной» системе координат пред-
представляет собой сумму углоаых скоростей
to и со' (так как обе направлены в одну
сторону) и «абсолютная» скорость точки
г> = (ш-|-юг)г направлена так же, как и относительная скорость v'.
Так как «абсолютная» скорость по величине постоянна и движение
происходит по окружности, то «абсолютное» ускорение направлено к
центру, причем
у =
J/1 = <огг
co'V + 2в)ш'г,
но ш'2г есть «относительное» ускорение (так как «относительное»
движение есть вращение с постоянной угловой скоростью т'), а
(oV — переносное ускорение (так как система координат вращается
с угловой скоростью (о). Следовательно, «абсолютное» ускорение,
кроме «относительного» и переносного, содержит ещё дополнитель-
дополнительное ускорение 2аш'г. Поскольку a>'r=v', то это дополнительное
ускорение равно 2«w', т. е. по величине совпадает с найденным нами
выше выражением для кориолисова ускорения. Сопоставляя направ-
направления векторов со и v' (рис. 35), мы убедимся, что направление этого
дополнительного ускорения определяется правилом буравчика, в на-
направлении от «о к v'. Таким образом, это дополнительное ускоре-
ускорение jft=2[<o-v'] и есть кориолисово ускорение, выражающееся так
же> как и в рассмотренном выше случае.

ДВИЖУЩИЕСЯ СИСТЕМЫ КООРДИНАТ
[гл. ш
uf
Как и прежде, «абсолютное» ускорение равно сумме «относитель-
«относительного», переносного и кориолисова ускорений. Однако, роль ко-
риолисова ускорения в обоих рассмотренных случаях несколько раз-
различна. В то время как в перзом случае кориолисово ускорение
изменяло и величину, и направление «абсолютной» скорости, во вто-
втором случае корнолисово ускорение изменяет только направление
«абсолютной» скорости, действуя в этом случае «совместно» с «отно-
«относительным» и переносным ускорениями. В этом случае кориолисово
ускорение появляется потому, что «относительная» и переносная
скорости направлены в одну сторону и складываются арифметически —
так же, как «относительное» и пере-
переносное ускорения. Между тем при уве-
увеличении скорости центростремительное
ускорение должно возрастать пропор-
пропорционально квадрату скорости. А это
и значит, что помимо «относительного»
и переносного ускорений, каждое из
которых пропорционально квадрату со-
соответствующей угловой скорости, долж-
должно появиться ещё дополнительное уско-
U> рение, пропорциональное удвоенному
рис- зб. произведению этих угловых скоростей.
Если скорости ш и (о' направлены в
противоположные стороны, то сумма «относительного» и перенос-
переносного ускорений оказывается больше, чем «абсолютное» ускорение,
и кориолисово ускорение
должно быть направлено в
противоположную сторону,
т. е. от центра. В этом легко
убедиться из рассмотрения
(рис. 36).
Мы рассмотрели два слу-
случая относительного движе-. /
ния — когда скорость лежит V
в плоскости, проходящей Чч^
через ось вращения, и когда
она нормальна к этой пло-
плоскости. В общем случае Рис. 37.
произвольно направленную
относительную скорость v' мы можем разложить на две составля-
составляющие— одну, лежащую в плоскости, проходящей через ось
вращения v'', и другую, нормальную к этой плоскости,—v'" (рис. 37).
Для каждой из этих составляющих справедливы результаты, получен-
полученные нами выше; следовательно, они справедливы и для v' в целом. По-
Поэтому, когда точка движется произвольным образом со скоростью v'
относительно системы координат, вращающейся с постоянной угловой

§ 18] НЕКОТОРЫЕ СЛУЧАИ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 63
скоростью о), абсолютное ускорение точки
|=j'—m»r-f 2[mv'], C.11)
где j' — «относительное» ускорение, — ш2г — переносное ускорение, и
2[(ov'] — кориолисово ускорение.
Переносное ускорение всегда направлено к оси вращения. Корио-
Кориолисово ускорение направлено нормально к векторам to и v'; поэтому
оно всегда лежит в плоскости, перпендикулярной оси вращения; его
ориентировка в этой плоскости зависит от направления вектора v'.
§ 18. Некоторые случаи движения твёрдого тела
В предыдущей глазе мы рассмотрели простейшие случаи дзиже-
нии твёрдого тела, поступательное, когда все точки тела движутся
одинаково, и вращательное, когда все точки тела описывают окруж-
окружности вокруг одной и той же неподвижной осн. Пользуясь взедён-
ными в настоящей глазе движущимися системами координат, можно
рассматривать и более сложные случаи дзижения твЗрдого тела. При
этом поступают следующим образом.
Помимо «неподвижной» системы коор-
координат, в которой рассматривается дзи-
жение твёрдого тела, вводится неко-
некоторая вспомогательная система коорди-
координат. Эта вспомогательная система коор-
координат выбирается так, чтобы движение
тела по отношению к ней оказалось
болге простым, чем по отношению к
«неподвижной» системе координат. Дви-
Движение тела относительно «неподвижной»
системы координат рассматривается как
результат его движения относительно
движущейся (вспомогательной) системы Рис. 38.
координат («относительного» движения)
и дзижения этой системы координат относительно неподвижной (пере-
(переносного движения). Пользуясь этим приёмом, мы рассмотрим прежде
всего случай плоского дзижения твёрдого тела.
В случае плоского движения, как мы видели (§ 12), достаточно
задать дзижение на плоскости отрезка прямой, жестко связанного
с телом. Если мы определим перемещение этого отрезка, то мы вместе
с тем определим и перемещение всех точек тела. Но перемещение
отрезка АВ на плоскости в любое положение А2В2 можно рассмат-
рассматривать как результат двух перемещений (рис. 38): поступательного,
при котором отрезок перемещается параллельно самому себе в поло-
положение -4M,, и поворота отрезка вокруг точки О на угол а до совпадения
с положением А2В2. Вместе с поступательным перемещением отрезка
АВ такое же поступательное перемещение созерщают и все точки

64 Движущиеся системы координат [гл nt
тела. Вместе с поворотом отрезка поворот на тот же угол и вокруг
той же оси совершают и все точки тела. Следовательно, всякое
плоское перемещение тела можно рассматривать как результат двух
перемещений — поступательного и вращательного.
Конечно, разделение это неоднозначно. Если мы изменим величину
поступательного перемещения, то изменится при этом и положение
оси, вокруг которой нужно повернуть отрезок -4,6,, чтобы он со-
совместился с отрезком Л2В2. Но при этом, как легко убедиться, не из-
изменится угол, на который нужно повернуть отрезок Л,й, до совме-
совмещения с Л3В2. Всякое плоское перемещение твёрдого тела можно
различными способами представить как сумму поступательного и вра-
вращательного перемещений, причём ось, вокруг которой происходит
поворот, в разных случаях будет разной, а угол поворота будет во
всех случаях один и тот же.
Элементарное перемещение тела можно представить себе как
результат двух перемещений: поступательного is, при котором все
точки тела перемещаются на одну и ту же величину As, и поворота
Да, при котором все точки тела поворачиваются на один и тот же
угол Да относительно одной и той же оси.
В соответствии с этим мы можем ввести вспомогательную систему
координат, которая, двигаясь поступательно, совершает такое же
элементарное перемещение As, как и все точки тела. Тогда по отно-
отношению к этой системе координат перемещение тела будет представ-
представлять собой элементарное вращение Да. Следовательно, вспомогательная
система координат будет двигаться поступательно со скоростью
v0 = lim ~ ,
а тело относительно этой системы координат будет вращаться
с угловой скоростью
„ Да
@= lim -гт.
Таким образом, переносная скорость будет одинакова для всех точек
тела (так как система координат движется поступательно) и равна v0.
«Относительная» скорость точек тела будет равна
где г — расстояние до оси вращения. Полная («абсолютная») скорость
всякой точки тела
Таким образом, плоское движение твёрдого тела мы можем пред-
представить как результат вращения тела относительно системы координат,
которая сама движется поступательно. Соответственно скорость каж-

18]
НЕКОТОРЫЕ СЛУЧАИ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
дой точки твёрдого тела мы можем рассматривать как сумму двух ско-
скоростей— поступательной и обусловленной вращением тела вокруг
некоторой оси. Для определения скорости всех точек тела достаточно
знать скорость поступательного движения v0, угловую скорость вра-
вращения (о и положение оси вращения.
Разделение скорости точек тела на поступательную и обусловлен-
обусловленную вращением так же неоднозначно, как и разделение перемещений.
Всегда можно изменить скорость поступательного движения, тогда
соответствующим образом изменится и положение оси вращения, но
угловая скорость остаётся неизменной. Всё это прямо следует из кар-
картины сложения перемещений. Однако, для пояснения можно привести,
более наглядные соображения.
Пусть, например, движение тела в какой-то момент времени мы
представили в виде поступательного движения со скоростью v0 и вра-
вращения вокруг оси О с угловой скоростью ш. Обусловленная этим
вращением линейная скорость точек тела есть г>' = <яг, где г—рас-
г—расстояние данной точки от оси О
(рис. 39). Концы векторов скоростей
точек А, В, С, ..., М лежат на пря-
прямой, образующей с направлением
AM угол а, пропорциональный
угловой скорости ш. Увеличим те-
теперь поступательную скорость на
Дг»0, а от обуслевленной вращением
скорости каждой точки отнимем эту
же величину Дг>0. При этом, очевидно,
результирующая скорость всех точек
остаётся неизменной. Но после умень-
уменьшения на одну и ту же величину
Дг>0 всех скоростей, обусловленных
вращением (рис. 40), концы векто-
векторов, изображающих эти скорости,
снова расположатся на прямой, об-
образующей тот же угол с направле-
направлением AM (эта прямая переместится
параллельно самой себе). Следовательно, новые скорости, обусловленные
вращением, соответствуют вращению с прежней угловой скоростью,
но вокруг новой оси, проходящей через точку О'. Это — точка, в ко-
которой v*= — Д?>0.
Мы можем произвольно выбирать поступательную скорость тела;
при этом будет изменяться положение оси вращения. Но угловая
скорость вращения будет во всех случаях одна и та же. В частно-
частности, мы можем положить поступательную скорость равной нулю.
Тогда скорость всякой точки тела выразится как линейная скорость,
обусловленная только вращением вокруг некоторой оси с прежней
угловой скоростью со, т. е. v' = <о г, где г — расстояние от точки тела
5 С. 3. Хайкин
Рис. 40.

66
движущиеся системы координат
[гл. ш
до этой оси. Эта ось проходит через точку, скорость которой в дан-
данный момент равна нулю.
Мы всегда можем изобразить скорость всех точек тела в данный
момент только как результат вращения вокруг этой осн. В следую-
следующий момент мы также сможем это сделать, но положение оси враще-
вращения, вообще говоря, будет уже другим. Ось, выбранная таким обра-
образом, что скорости всех точек тела можно изобразить только как
результат вращения вокруг.этой оси, будет изменять свой положение
относительно тела. Поэтому она называется мгновенной осью.
Картину сложения поступательной скорости и скорости, обусловленной
вращением, а также представление о мгновенной оси можно поиснить с по-
помощью следующей установки. На ось патефонного моторчика *) насажен
белый круг с чёрными точками. Моторчик с кругом укреплён на тележке,
Которая может перемещаться по рельсам (рис. 41). При одновременной
Рис. 41.
вращении моторчика и движении тележки каждая точка круга движется со
скоростью, которая равна сумме поступательной скорости тележки и линей-
линейной скорости, обусловленной вращением диска вокруг оси моторчика. Эта
последняя равна v' = <or. Пусть, например, круг вращается по часовой
стрелке; линейные скорости о' некоторых его точек, обусловленные этим
вращением, изображены на
рис. 42а. К скорости о' в- ка-
каждой точке прибавляется одна
н та же скорость поступатель-
поступательного движения тележки р0.
Вследствие этого получится
распределение результирую-
результирующих скоростей и, указанное
на рис. 42Ь. В точке, где р'=»
— — °о> результирующая ско-
•> рость ва=0. Через эту точ-
точку О' и проходит мгновенная
Рис. 42. ось вращения; она лежит на
расстоянии г = Ро/й> от оси
моторчика. Положение мгновенной оси хорошо видно на круге, так как
чёрная точка на круге, через которую проходит мгновенная ось, не
размывается. Другие же точки размываются и оставляют след в виде
окружностей с центром на мгновенной оси (рис. 43а). Мгновенная ось
перемещается вместе с тележкой, так как точка, где v = 0, всегда лежит
на вертикали, проходящей через центр круга. В результате сложения посту-
*) Ось моторчика делает примерно 1,25 оборота в секунду.

§ 18] НЕКОТОРЫЕ СЛУЧАИ ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА 67
пательного движения со скоростью v0 и вращения вокруг оси О с угло-
угловой скоростью и получается вращение с той же угловой скоростью <о во-
вокруг мгновенной оси О', которая сама движется прямолинейно со скоростью
vu. При изменении знака va мгновенная ось располагается по другую сторону
от точки О и опять на том же расстоянии (рис. 43, Ь). При увеличении ско-
скорости поступательного движения мгновенная ось удаляется от точки О и
может уйти за пределы круга. Тогда ни одна точка на круге не будет
иметь скорости, равной нулю. Все точки круга будут описывать окружно-
окружности с центром, лежащим вне круга, а сам центр будет попрежнему пере-
перемещаться со скоростью г/0.
Если колесо катится без скольжения по какой-либо поверхности, то
соотношение между линейной скоростью центра колеса и угловой скоростью
вращения оказывается фиксированным (иначе
происходило бы скольжение). Именно линей-
линейная скорость центра колеса р0 =«>/?, где
<о — угловая скорость вращения колеса, а
R—его 'радиус. С другой стороны, ско-
скорость, обусловленная' вращением, есть v' = и>г.
Поэтому точка, где v1 ~vu, лежит под осью
на расстоянии R от оси, и мгновенная ось О
совпадает с образующей, соприкасающейся р ' ,3
с поверхностью. Качение колеса без сколь-
скольжения можно рассматривать как вращение
вокруг мгновенной оси, проходящей через точку, в которой колесо опи-
опирается на поверхность.
Пользуясь таким же приёмом, можно рассмотреть другой важный част-
частный случай — движение твёрдого тела, имеющего одну неподвижную
точку. В этом случае, очевидно, ни «относительное», ни переносног
движение не может быть поступательным, так как скорость одной
точки тела всегда остаётся равной нулю. Движение тела, имеющего
одну неподвижную точку, можно рассматривать как вращение тела
относительно оси, как-то связанной с вспомогательной системой
координат, которая, в свою очередь, вращается относительно «непо-
«неподвижной». При этом линейная скорость каждой точки тела, как и
всегда, равна геометрической сумме линейных скоростей «относи-
«относительного» движения данной точки тела и переносного движения той
точки движущейся системы координат, в которой в данный момент
находится рассматриваемая точка тела. Это общее положение спра-
справедливо при любом характере переносного движения и не требует
в нашем случае специального доказательства. Однако, более удобно
рассматривать не линейные скорости отдельных точек, а угловые ско-
скорости вращений и определять результирующее движение при помощи
этих угловых скоростей.
Мы рассмотрим эту задачу не для общего случая движения тела,
имеющего одну неподвижную точку, а для частного случая, когда
движение тела можно рассматривать как вращение вокруг некоторой
неподвижной относительно тела оси («относительное» движение),
которая, в свою очередь, вращается вокруг другой оси, жёстко свя-
связанной с «неподвижной» системой координат (переносное движение).
Как мы увидим, в этом случае результирующее («абсолютное») дви-
5*

68
ДВИЖУЩИЕСЯ СИСТЕМЫ КООРДИНАТ
[гл. m
жение тела представляет собой вращение с угловой скоростью, равной
геометрической сумме угловых скоростей «относительного» и пере-
переносного движений.
Чтобы убедиться в этом, воспользуемся тем, что уже было сказано
выше (§ 13) о связи между малыми угловыми перемещениями и соот-
соответствующими им линейными перемещениями. Пусть (рис. 44) вектор О В'
Рис. 44.
изображает элементарное угловое перемещейие Да, обусловлен-
обусловленное вращением тела вокруг оси хх', т. е. «относительным» движе-
движением, а вектор ОС — элементарное угловое перемещение Др, обу-
обусловленное вращением оси хх' относительно другой «неподвижной»
оси уу, т. е. переносным движением. Какая-то точка А движущегося
тела вследствие поворота Да вокруг оси хх' переместится по дуге
АВ, а вследствие поворота оси хх' относительно оси уу' на угол Др
переместится но дуге АС. Результирующее угловое перемещение
Рис. 45.
изобразится углом Ду, а результирующее линейное перемещение — ду-
гой AD. Так как углы Да и Др малы, то сферический параллелограмм
ABDC можно считать плоским. Очевидно, этот параллелограмм подобен
параллелограмму O'B'D'O, так как стороны этого последнего полу-
получаются из сторон параллелограмма ABDC одинаковым изменением

§ 18] НЕКОТОРЫЕ СЛУЧАИ ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА 69
масштаба и поворотом иа угол тс/2. Поэтому и диагональ OD' полу-
получается из диагонали AD таким же преобразованием масштаба
и направления. Следовательно, вектор OD' выражает результирующее
угловое перемещение Ду. Разделив все векторы на элемент времени Д^,
за который происходят рассматриваемые элементарны© перемещения,
мы получим (рис. 45) из ABDC параллелограмм, построенный на
линейных скоростях v'-— «относительного» движения и v0 — пере-
переносного движения точки А; из OB'D'C мы получим параллелограмм,
построенный иа соответствующих угловых скоростях обоих вращений —
а>' и со0? И так же, как вектор OD' изображает результирующее угло-
угловое перемещение, вектор а>' изображает результирующую угловую
О'
Рис. 46.
скорость, которой соответствует результирующая линейная скорость v
точки А.
Таким образом «абсолютную» линейную скорость всякой точки
тела можно рассматривать как результат вращения тела с угловой
скоростью (о, которая представляет собой геометрическую сумму
«относительной» угловой скорости <*>' и переносной угловой скоро-
скорости <о0. Иначе говоря, угловые скорости «относительного» и пере-
переносного движений складываются геометрически.
Для демонстрации геометрического сложения угловых скоростей может
служить следующая установка.
Шар с- нанесёнными на него отчётливыми точками (белыми на чёр-
чёрном фоне, или наоборот) может вращаться на оси, подшипник которой
устанавливается наклонно на втулке центробежной машины (рис. 46, а),
таким образом, шар может вращаться вокруг своей оси ОА с уг-
угловой скоростью тА («относительное» движение), В свою очередь, ось шара

70
ДВИЖУЩИЕСЯ СИСТЕМЫ КООРДИНАТ
гл. Щ,
О А может вращаться вокруг осн центробежной машины' О1 В с угловой ско~
ростью шв (переносное движение). Раскрутив шар (рис. 46, Ь), а затем приведя
в движение центробежную машину, мы получим одновременно
оба вращения (рис. 46, с). Результирующая угловая скорость ш
должна быть равна геометрической сумме слагаемых скоро-
скоростей, <од и шв (рис. 47). О положении вектора результирующей
угловой скорости можно судить по тому, что точки, лежащие
вблизи этого вектора, имеют малые линейные скорости и по-
поэтому должны быть хорошо видиы. Все остальные точки из-за
больших линейных скоростей размоются и в отдельности не
будут видны—они прочерчивают линии, близкие к окружно-
окружности. Вектор результирующей угловой скорости перпендику-
перпендикулярен к плоскостям, вблизи которых лежат эти волнистые
линии. При вращении хорошо видно, что между осями ОА
и ОВ лежит вектор результирующей угловой скорости.
Рис. 47

ГЛАВА IV
ЗАКОНЫ НЬЮТОНА
§ 19. Выбор системы отсчета
Когда мы говорим «тело движется>, то имеем в виду изменение
положения данного тела относительно каких-либо других тел. С этими
«другими телами» мы связываем ту или иную систему координат и от-
относительно неё отсчитываем положение движущегося тела.
По отношению к равным системам координат одно и то же тело
может двигаться совершенно по-разному. Чтобы подметить общие
черты, свойственные в одинаковой мере всем наблюдаемым движениям,
следует выбрать одну определённую систему координат и пользоваться
ею при описании всех изучаемых нами разнообразных движений.
В качестве такой системы координат естественнее всего, казалось
бы, выбрать систему координат, жёстко связанную с Землёй. Такая
система отсчёта была бы достаточно удобной для описания движений,
происходящих на Земле. Но уже для описания движения внеземных
тел (планет) такая система отсчёта была бы гораздо менее удобной.
Однако, система отсчёта, связанная с Землёй, обладает гораздо более
принципиальным недостатком (в чём ои заключается, будет ясно из
дальнейшего). Поэтому мы выберем сразу другую, свободную от этого
недостатка систему отсчёта, связанную с Солнцем и звёздами. Пред-
Представим себе, например, крест, образованный тремя взаимно перпенди-
перпендикулярными осями координат, и поместим центр этого креста (начало
координат) в центр Солнца; три оси направим на какие-либо три
звезды, выбранные таким образом, чтобы направления иа них из центра
Солнца были взаимно перпендикулярны. К этой системе координат
мы и будем относить изучаемые движения. В дальнейшем эту систему
координат мы будем называть «неподвижной».
Этим мы вовсе не имеем в виду сказать, что она неподвижна. По-
Поскольку выбранная нами система отсчёта единственная, которой мы
будем пользоваться, в утверждение, что она неподвижна, нельзя было
бы вложить никакого содержания. Мы будем пользоваться термином
«неподвижная» по отношению к этой системе координат только для
краткости, а чтобы это не повлекло за собой недоразумений, так же,
как и прежде, будем брать этот термин в кавычки.

72 ЗАКОНЫ НЬЮТОНА [ГЛ. IV
Система координат, жёстко связанная с Землёй, будет двигаться
относительно «неподвижной», так как Земля совершает суточное
и годовое движение относительно Солица и звёзд. Однако, угловая
скорость этою движения невелика, и ускорение Земли относительно
«неподвижкой» системы координат практически сказывается лишь
в некоторых специальных случаях. Поэтому, хотя принципиально мы
в дальнейшем должны всё время иметь в виду «неподвижную» систему
координат, но практически сможем в большинстве случаев пользо-
пользоваться в качестве системы „ отсчёта Землёй, в частности, отно-
относить все движения к стенам аудитории, в которой производятся
опыты. Те случаи, когда этого делать нельзя, будут специально
оговорены.
§ 20. Материальная точка
Изучение динамики мы начнём с изучения законов движения так
разываемой материальной точки.
Во многих задачах о движении тел размеры и форма тела не
играют роли, а существенную роль играет лишь масса тела. Поэтому
мы можем реальное тело заменить точкой. Но при этом мы должны
считать, что та точка, которой мы заменили наше реальное тело,
обладает массой этого тела. Так мы приходим к представлению о теле,
не имеющем протяжённости, но обладающем конечной массой, т. е.
к материальной точке.
Круг вопросов, при решении которых движущиеся тела можно
рассматривать как материальные точки, и составляет предмет того
раздела механики, который носит название механики материальной
точки.
Однако, даже в тех случаях, когда размеры и форма тел не ска-
сказываются на характере изучаемых движений, всё же, как мы убедимся,
существенную роль играют взаимодействия отдельных частей тела
между собой.
Чтобы выяснить картину движения тела во всех деталях, необ-
необходимо принимать во внимание эти взаимодействия. А для этого
нужно рассматривать 1ела как протяжённые (какими и являются
все реальные тела в действительности), ибо говорить о взаимодей-
взаимодействии между отдельными частями материальной точки, конечно, не
имеет смысла. Поэтому в механике точки мы, в сущности, всё же
будем рассматривать протяжённые тела, но изучать только такие
движения, характер которых не зависит от размеров и формы тел.
Практически это сведётся к тому, что мы ограничимся только такими
случаями, когда движение тела можно рассматривать как поступатель-
поступательное. Поэтому мы сможем не различать скоростей и ускорений раз-
различных точек протяжённого тела и говорить о скорости и ускорении
тела вообще.

§21] СИЛУ В МЕХАНИКЕ ИЬЮТОНД 7'<$
§ 21. Силы в механике Ньютона
Если мы будем изучать разнообразные движения, но относить
их всегда к «неподвижной» системе координат, то мы у всех дви-
движений обнаружим одну общую черту: всякое ускорение тела всег-
всегда вызывается действием на данное тела каких-либо других
тел.
Для иллюстрации может служить следующий опыт. На гладком,
горизонтальном стекле помещён стальной шар. Шар этот остаётся
в покое, пока иа него не действуют другие тела. Конечно, мы не мо-
можем осуществить опыта, при котором на данное тело не действовали
бы никакие другие тела, так как на все тела, находящиеся на земле
или вблизи неё, действует земля. В нашем опыте действие земли на
шар компенсируется действием стекла на шар. Для того чтобы при
движении шара стекло не влияло на шар каким-либо иным образом
(кроме компенсации действия земли), стекло должно быть по возмож-
возможности гладким.
Если.шар толкнуть, т. е. сообщить ему начальную скорость, то
он покатится по стеклу прямолинейно и почти с постоянной ско-
скоростью. Следовательно, в отсутствии других тел, кроме земли и стекла,
шар либо покоится, либо движется прямолинейно и равномерно. Земля
и стекло вм«сте не сообщают шару никаких ускорений. Но если
к шару прикрепить предварительно растянутую пружину, то он начнёт
двигаться, т. е. приобретёт ускорение.
Ускорение шару могут сообщать и другие тела, например, по-
постоянный магнит, находящийся на некотором расстоянии от шара.
Приближая и удаляя магнит, мы убедимся, что именно он является
причиной ускорения шара. Располагая магнит с разных сторон и сооб-
сообщая шару различные начальные скорости, мы будем наблюдать раз-
различные движения шара, но ускорение шара во всех случаях будет
направлено к- магниту.
Если шар прикрепить к концу нерастянутой пружины, то под
действием магнита шар начнёт двигаться, а пружина — растягиваться.
При каком-то определённом растяжении пружины дальнейшее движе-
движение шара прекратится (рис. 48). Это значит, что растянутая пру-
пружина и магнит, действуя на шар одновременно, не сообщают ему
ускорений.
Вообще, если на данное тело действует несколько других тел, то
может случиться, что они вместе не сообщают ему ускорения. Но
если тело испытывает ускорение, то мы всегда обнаружим другое
тело или другие тела, которые это ускорение вызывают.
Таким образом, опыт показывает, что всякое ускорение данного
тела есть результат действия других тел. Это утверждение яв-
является одним из основных положений механики Ньютона..
Продолжая изучение различных движений, мы обнаружим ещё
одну общую для всех движений черту: если тело А сообщает какое-

8АК0НЫ НЬЮТОНА
[гл.
либо ускорение телу В, то и тело В, в свою очередь, всегда сооб-
сообщает некоторое ускорение телу А. Для демонстрации этого положе-
положения можно несколько видоизменить опыт с шаром и магнитом,
описанный выше. Если магнит на стекле поместить на катках так,
Ряс. 48.
чтобы он мог легко двигаться, то, приближая к магниту стальной
шар, мы убедимся, что шар сообщает магниту ускорение.
Если шар и магнит иа катках прикрепить к пружинам (рис. 49),
то, сообщая ускорение друг другу, они оба придут в движение. Пру-
Пружины будут растягиваться, и при, определённой величине растяжения
^
Рис. 49.
дальнейшее движение шара и магнита прекратится. Как и в предыду-
предыдущем случае, это означает, что, действуя одновременно, растяну-
растянутая пружина и магнит не сообщают ускорения шару, а растякутая
пружина и шар ие сообщают ускорения магниту.
Этот опыт показывает, что шар действует на магнит во всех от«
ношениях так же, как магнит на шар.

§ 21] СИЛЫ В МЕХАНИКЕ НЬЮТОНА 75
Поэтому основное положение ньютоновой механики мы можем сей-
сейчас сформулировать следующим образом: ускорения всегда являются
результатом взаимодействия тел.
Эти действия тел друг на друга, в результате которых взаимодей-
взаимодействующие тела могут сообщать друг другу ускорения, мы называем
силами. Таков смысл понятия силы в механике Ньютона. В дальней-
дальнейшем мы встретимся ещё с другими применениями термина «сила».
Уже в механике, не говоря о других разделах физики, нам придётся
в дальнейшем расширить понятие силы. Но пока под силами мы бу-
будем понимать только действие одних тел на другие. Поэтому мы
всегда сможем указать как тело, на которое сила действует, так
и тело, со стороны которого сила действует. Например, при враще-
вращении груза на верёвке мы будем говорить о силе, действующей на груз
со стороны вербвки и направленной к центру, о силе, действующей
со стороны груза на верёвку и направленной от центра, и т. д. Для
этих сил часто применяют специальные названия «центростремитель-
«центростремительная сила» и «центробежная сила». Конечно, этими названиями можно
пользоваться для того, чтобы дать дополнительные указания о на-
направлении силы. Но для того, чтобы исчерпывающим образом опре-
определить, о какой силе идёт речь, всегда нужно указывать, на какое
тело и со стороны какого тела она действует.
В механике мы встретимся с тремя типами сил: 1) Силы взаимного
притяжения между телами, действующие на расстоянии. Это — так
называемые силы всемирного тяготения или гравитационные силы,
существование которых открыл Ньютон. Примером этих снл может
служить притяжение тел землёй, 2) Силы, возникающие при непо-
непосредственном соприкосновении тел и обусловленные деформацией со-
соприкасающихся тел. Это — так называемые упругие силы. Примерами
сил этого типа могут служить силы, действующие на тело со стороны
сжатой или растянутой пружины. К этой же категории относится
и сила, с которой верёвка действует на привязанный к её концу
груз, илн сила, с которой действует стол на лежащий на нём груз,
и т. д. Правда, деформации этих тел, например, растяжение верёвки
или прогиб стола, часто бывают незаметны. Но упругие силы, о ко-
которых у нас идёт речь, всегда обусловлены деформациями, происшед-
происшедшими при соприкосновении тел. Абсолютно жёстких (недеформиру-
емых) тел в природе нет. Все физические тела в этом смысле
подобны пружинам — они могут деформироваться и в деформирован-
деформированном состоянии могут действовать с известной силой на другие тела,
с которыми они непосредственно соприкасаются. 3) Наконец, третий
тип сил — это также силы, возникающие при непосредственном со-
соприкосновении тел, но обусловленные не общей деформацией сопри-
соприкасающихся тел, а явлениями, происходящими непосредственно около
поверхности соприкосновения. Примером сил этого типа могут слу-
служить силы трения, возникающие при скольжении одного тела по
другому.

7 6 законы ньютона [гл. iv
Когда силы, с которыми человек действует на какие-либо тела,
относятся ко второй из рассмотренных нами категорий сил, то они
обусловливаются деформацией соответствующих мышц. С этими- де-
деформациями и связаны определённые физиологические ощущения, ко-
которые испытывает человек, когда он сообщает ускорение телу.
Тремя рассмотренными типами сил отнюдь ие исчерпываются все
силы, которые могут возникать между телами. Так, наэлектризован-
наэлектризованные или намагниченные тела, или два провода, по которым текут
электрические токи, действуют друг на друга с определёнными си-
силами и могут сообщать друг другу ускорения. Однако, рассмотрение
этих других типов сил относится к другим разделам физики. Пока
мы ограничиваемся собственно механикой, мы будем встречаться
только с указанными тремя типами сил: гравитационными, упругими
и силами треиия. Вопрос о том, почему возникают те или иные силы,
например, упругие, выходит за рамки механики и рассматривается
в других разделах физики. Для механики важно лишь знать, когда
(при каких условиях) эти силы возникают и какова их величина в том
или другом случае.
Пользуясь представлением о силах, мы можем основные утвержде-
утверждения механики Ньютона сформулировать в следующих трёх положениях:
1. Всякое ускорение тела вызывается какой-либо силой.
2. Всякая сила обусловлена действием на данное тело каких-
либо других тел.
3. Все силы носят характер взаимодействий.
Этими тремя положениями исчерпываются с качественной стороны
законы Ньютона. Чтобы перейти к количественному изучению этих
законов, необходимо располагать методами измерения сил и ускоре-
ускорений. Метод измерения ускорений нам уже известен. Установив метод
измерения сил, мы сможем на опыте изучать количественные соотно-
соотношения между силами и ускорениями.
§ 22. Измерение сил
Для установления способа измерения сил мы должны выбрать,
во-первых, эталон силы, а, во-вторых, способ сравнения других сил
с этим эталоном. Возьмём какую-то вполне определённую пружину,
растянутую (или сжатую) до известной величины. Эталоном силы мы
будем считать ту силу Fo, с которой эта пружина при фиксирован-
фиксированном растяжении действует на прикреплённое к любому из её концов
тело, и считать, что направлена эта сила вдоль оси пружины. Способ
сравнения других сил с эталоном мы установим следующий: будем
считать измеряемую силу равной по величине и противоположной
rfo таправлениЕО эталону силы, если при одновременном действии на
тело силы-эталона Fo и измеряемой силы F^ (рис. 50) .тело остаётся
в покое,

§ 22]
измерение сил
-77
Приведенным способом мы сможем установить, равна ли измеря-
измеряемая сила F^ эталону силы Fo, ио не сможем измерить любую силу.
Для этой последней цели воспользуемся тем, что установленный нами
способ сравнения сил позволяет воспроизводить силу-эталон в любом
количестве экземпляров. Достаточно взять любую пружину и подо-
подобрать ей растяжение так, чтобы при одновременном действии этой
пружины Кх и пружины-эталона К* в противоположных направлениях*)
тело т оставалось в покое (рис. 51). Зафиксировав подобранное
К
/С
Рис. 50.
Рис 51.
таким образом растяжение пружины Kv мы сможем дальше пользо-
пользоваться ею также в качестве эталона силы. Располагая несколькими
эталонами силы, мы установим способ измерения снл, величина ко-
которых не равна эталону силы. Прикрепим к телу т, на которое дей-
действует измеряемая сила F^, две пружины-
эталона и расположим их иод такими
углами (рис. 52), чтобы тело т не испы-
испытывало ускорения. Тогда мы будем счи-
считать, что измеряемая сила равна взятой
с обратным знаком геометрической сум-
сумме сил, действующих со стороны эта-
эталонов, т. е. что
Fх ~ (^oi ~Г Рог)"
Так мы сможем измерять силы, только
меньшие, чем 2F0. Но, располагая пружины Рис. 52.
параллельно, мы сможем воспроизвести
эталоны в 2F0, а затем 4F0 и т. д., а далее с их помощью измерить
силы любой величины (а не только меньшие, чем 2F0). Конечно, прак-
практически нет никакой надобности производить каждый раз -вакие из-
измерения. Мы можем взять любую подходящую пружину и измерить
по нашему способу силу, действующую со стороны этой пружины
при различных растяжениях. Такими калиброванными пружинами —
динамометрами — и пользуются на практике для измерения сил.
Располагая способом измерения сил, мы сможем установить, при
каких условиях возникают силы, от чего зависит их величина в тех
или иных случаях, и установить количественную связь между силами
н ускорениями.
*) При этом растяжение пружин-эталонов должно Всё время оставаться
неизменным —таким, какое мы зафиксировали, выбирая эталон силы.

78 законы ньютона [гл. iv
Прежде всего мы сможем убедиться, что все силы, независимо от
их природы, всегда складываются геометрически, т. е. ведут себя,
как векторы*). Пусть, например, мы имеем тело т, на которое дей-
действуют силы притяжения Fj и F2 со стороны двух других тел (рис. 53).
Каждую из этих сил, если бы она действовала отдельно, мы могли
бы измерить по нашему способу; мы нашли бы эти силы F, и F2.
Если же на тело т действуют одновременно оба другие тела, то,
чтобы тело т не испытывало ускорений, к нему,
как показывает опыт, нужно приложить силу
F= — (Fj-^F^)- ^a этом основании мы можем
всегда заменять несколько сил их равнодействую-
равнодействующей (геометрической суммой) и всякую силу раз-
разлагать на составляющие, геометрическая сумма
которых равна данной силе.
рис 53 Далее, измеряя силы трёх типов, встречающиеся
н механике, — гравитационные, упругие и силы
1 рения — мы сможем убедиться в том, что силы первых двух типов
зависят только от взаимного расположения тел, т. е. от их кон-
конфигурации. В случае гравитационных сил величина силы зависит от
формы и размеров тел и расстояний между ними. В случае же
упругих сил величина сил зависит от деформации тел, т. е. в конеч-
конечном счёте также от конфигурации отдельных частей тела. Наконец,
силы третьего типа — силы, трения — кроме конфигурации зависят и
от относительной скорости взаимодействующих тел.
Если мы исключим из рассмотрения силы трения, то можно счи-
считать, что силы в механике зависят только от конфигурации тел. Это
позволит нам в дальнейшем особенно отчётливо представить себе
содержание основных законов движения.
§ 23. Связь между силой и ускорением
Поскольку мы умеем независимо измерять ускорения и силы, мы
можем на опыте установить связь между ними. Для этого может слу-
служить, например, следующий опыт (рис. 54). К тележке, которая мо-
может (с.малым трением) двигаться по рельсам, прикреплена калибро-
калиброванная пружина со шкалой (динамометр). К другому концу пружины
прикреплена нитка с грузом М, переброшенная через блок. По вели-
величине растяжения пружины мы сможем определить силу, действующую
на тележку со стороны пружины**). Измеряя, с другой стороны, уе«
*) Силы, действующие со стороны двух одинаковых пружин-эталонов,
по определению складываются геометрически (так как в установленном спо-
способе сравнения сил мы берём геометрическую сумму сил, действующих со
стороны пружин-эталонов). Но для всех других сил, например, для несколь-
нескольких неодинаковых пружин или для сил всемирного тяготения, это утвер-
утверждение нуждается в опытной проверке.
**) Сила эта при движении тележки с ускорением не равна, а меньше ве-
веса груза М. Вопрос этот будет специально рассмотрен позднее.

§ 23]
СВЯЗЬ МЕЖДУ ХИЛОЙ И УСКОРЕНИЕ!!
79
корение тележки, мы обнаружим прежде всего, что независимо от скоро-
скорости, которой обладает тележка, ускорение её под действием данной силы
будет всегда одно и то же. Ускорение тележки однозначно опре-
определяется действующей на неё силой. Далее, прикрепляя к нити раз-
различные грузы и создавая тем самым различные растяжения пружины
(динамометра), мы обнаружим, что ускорение тележки пропорцио-
пропорционально действующей на неё силе.
Рис. 54.
Результаты, полученные нами в опытах с тележкой, оказываются
справедливыми и во всех других случаях. Всякий раз, когда мы бу-
будем измерять, с одной стороны, силы, действующие на данное тело,
и, с другой стороны, соответствующие ускорения, мы обнаружим,
что ускорение j однозначно определяется действующей силой
и пропорционально действующей силе F.
Далее, при помощи соответствующих опытов мы сможем устано-
установить, что направление ускорения совпадает с направлением силы, вы-
вызывающей данное ускорение. Для этого могут служить, например,
описанные нами опыты со стальным шаром на стекле. Наконец, про-
производя опыты, с телом, на которое одновременно действует несколько
сил (со стороны нескольких тел), мы обнаружим, что ускорение
тела пропорционально равнодействующей всех сил и совпадает
с ней по направлению.
Следовательно, если | есть вектор ускорения, a SF — геометри-
геометрическая сумма всех действующих на тело сил, то
Это справедливо для любого тела, однако, только до тех пор, пока
достигнутые телом скорости много меньше скорости срета. Опыты
с движением тел, скорости которых сравнимы со скоростью света,
показали, что при столь больших скоростях ускорение тел уже не
растёт пропорционально действующей силе. Однако, как уже указы-
указывалось, скорости, при которых это обстоятельство практически ста-
становится заметным, не могут быть достигнуты в опытах с макроскопи-
макроскопическими телами.
Для того чтобы тело, обладающее конечным ускорением, приобрело
некоторую конечную скорость, действие силы должно продолжаться

80 ЗАКОНЫ НЬЮТОНА [ГЛ. IV
конечное время. Другими словами, под действием сил тело приобре-
приобретает или изменяет скорость не сразу, а постепенно. Это именно об-
обстоятельство и имеют в виду, когда говорят, что тела обладают
инерцией. Свойство инерции непосредственно вытекает из того фак-
факта, что силами определяются ускорения (именно, ускорения, а не ско-
скорости) тел.
Один из наиболее наглядных опытов, служащих для демонстрации инер-
инерции тел, заключается в следующем: два больших одинаковых груза подвеши-
подвешиваются на одинаковых нитях, один под другим (рис. 55). Нить подбирается
так, чтобы она выдерживала натяжение, равное весу одного
груза, и обрывалась при натяжении, равному весу обоих грузов.
Тогда, если плавно опустить сначала верхний груз, поддерживая
нижний, а затем плавно же опустить нижний груз, то верхняя
нит!) обрывается. Если же опустить нижний груз не плавно, а
сразу, выдернув нз-под него подставку, то оборвётся-не верх-
верхняя, а нижняя нить.
Чтобы смысл описанного опыта был совершенно ясен, не-
необходимо принять во внимание, во-первых, что нить действует
с известной силой на груз, только когда она растянута, и, во-вто-
во-вторых, что обрывается нить тогда, когда её удлинение превосхо-
превосходит некоторый определённый предел. Учтя оба эти обстоятель-
р .,. ства, легко объяснить описанный опыт.
Когда нижний груз падает с некоторой высоты, обрывается
не верхняя, а нижняя нить потому, что верхний груз не может
«сразу» (за очень малый промежуток времени) приобрести заметную ско-
скорость, а нижний не может «сразу» потерять свою Скорость, т. е. потому,
что грузы обладают инерцией.
Ясно, что чем менее растяжима нить, тем меньше должна быть скорость
нижнего груза (т. е. практически высота его падения) для того, чтобы ниж-
нижняя нить оборвалась. Если бы нить была совсем иерастяжима, то совсем ма-
малой начальной скорости груза было бы достаточно, чтобы оборвать нить.
Действительно, груз не может мгновенно остановиться, когда нить вытянется
до нормальной длины, так как для этого потребовались бы бесконечно боль-
большие силы.
Свойство инерции представляет собой качественную сторону того поло-
положения, которое было сформулировано выше: ускорения тел однозначно оп-
определяются действующими на них силами и при этом оказываются пропор-
пропорциональными действующим силам. Это положение заключает в себе и все
те особенности поведения тел, которые называют инерцией. Инерцию тел
иногда описывают как свойство тел «сопротивляться» изменению скорости.
Однако, слово «сопротивляться» вряд ли здесь уместно. Это слово было бы
уместно, если бы, несмотря на действие сил, тело всё же сохраняло свою
скорость постоянной. Между тем, как только на тело начнёт действовать
сила, скорость тела тотчас же начинает изменяться. Таким образом, термин
«сопротивляться» не даёт правильного представления о действительном по-
положении вещей.
§ 24. Масса. Второй закон Ньютона
Мы установили, что данному телу одна и та же сила сообщает
всегда одно и то же ускорение. С другой стороны, опыт показывает,
что различным телам одна и та же сила сообщает, вообще го-
говоря, различные ускорения. Убедиться в этом можно при помощи
описанных уже опытов с тележкой (prfc. 54). Если мы будем на тележ-1

§ 24} МАССА. ВТОРОЙ ЗАКОН НЬЮТОНА 81
ку класть различные грузы, то при одном и том же растяжении
пружины ускорение тележки будет различно. Чем больше груз,
положенный на тележку, тем меньшее ускорение получает тележка
под действием данной силы.
Следовательно, величина ускорения, которое приобретает тело
под действием данной силы, зависит не только от величины действу-
действующей силы, но и от свойств самого тела. Для каждого данного
тела ускорение пропорционально силе, но коэффициент пропорцио-
пропорциональности для различных тел оказывается различным. Этот коэф-
коэффициент пропорциональности т и определяет величину массы или,
точнее, инертной массы*) данного тела, характеризующей степень
инертности тела. Введя понятие об инертной массе тела, мы можем
связь между силой и ускорением выразить следующим образом:
mJ = SF, D.1)
причём масса т есть для данного тела величина постоянная, пока
достигнутые телом скорости не очень велики. Если же достигнутая
телом скорость становится сравнимой со скоростью света, то, как
уже было указано, прямой пропорциональности между силой и ус-
ускорением не существует: чем больше достигнутая телом скорость,
тем меньше -ускорение, сообщаемое телу данной силой. Мы можем
толковать это так, что соотношение D.1) остаётся всё же справед-
справедливым при любых скоростях, но зато с увеличением скорости масса
тела возрастает; масса тела зависит от той скорости, которой уже
обладает тело. Однако, пока скорости тел малы по сравнению со
скоростью света, эта зависимость массы От скорости не играет роли.
Поэтому в задачах механики, с которыми мы будем иметь дело
в дальнейшем, мы всегда сможем считать массу тела постоянной,
если тело не разрушается, от него не отделяются какие-либо ча-
части и т. д.
Итак, произведение массы на ускорение равно сумме действу-
действующих сил — это одна из возможных формулировок второго закона
Ньютона**).
Для данного тела, измеряя силы, мы всегда можем опреде-
определить ускорение тела или, наоборот, измеряя ускорение тел г,
*) Массу тела, определяющую связь между силой и ускорением, т. е.
определяющую динамические или инерционные свойства тел, называют инерт-
инертной массой в отличие от гравитационной массы, которая определяет вза-
взаимное тяготение тел. Понятие гравитационной массы будет введено позднее.
Пока для краткости мы будем говорить не «инертная масса», а просто
«масса».
**) Формулировка второго закона движения, данная самим Ньютоном,
будет приведена ниже. Ньютон сформулировал законы движения в своей
знаменитой книге сМатематические начала натуральной философии», вышед-
вышедшей впервые в 1б86 г. Эта книга переведена на русский язык академиком
А. Н. Крыловым.
6 с э. хайкин

82 законы ньютона [гл. tv
мы можем определить сумму действующих на него сил, ес-
если хотя бы один раз для этого тела мы произвели одновремен-
одновременно измерение и действующей силы, и сообщаемого ускорения.
В этом и можно видеть физическое содержание второго закона
Ньютона.
При этом толковании второго закона Ньютона для установления
способа измерения массы тела используется тот же второй закон
Ньютона. Величина массы определяется одновременным измерением
силы и ускорения. Следовательно, второй закон Ньютона в этом
случае, с одной стороны, содержит утверждение, что ускорение про-
пропорционально силе, которое может быть проверено на опыте, а, с дру-
другой,— представчяет собой определение массы тела как отношения
силы, действующей на тело, к сообщаемому этой силой ускорению*).
Опытной проверке второй закон Ньютона доступен лишь в той мере,
в какой он представляет собой утверждение. Если бы мы установили
независимый от второго закона Ньютона способ измерения массы, то
второй закон приобрёл бы целиком характер утверждения, поддаю-
поддающегося опытной проверке. Такой способ будет указан нами в даль-
дальнейшем.
Так как уравнение D.1) — векторное, то оно эквивалентно трём
уравнениям для трёх компонент векторов ускорения и силы, взятых
по трём осям координат. Если мы обозначим эти компоненты соот-
соответственно индексами х, у, z, то эти три уравнения будут иметь вид:
Мы пользовались всё время совершенно произвольно выбранной
единицей силы — принимали за единицу силы ту силу, с которой дей-
действует какая-то произвольно выбранная пружина при каком-то произ-
произвольно фиксированном растяжении. Но закон Ньютона устанавливает
связь между единицей силы и единицей массы. При нашем способе
измерения масс массой, равной единице, будет обладать такое тело,
которому сила, равная единице, сообщает ускорение, также равное
единице. Поэтому, если единица силы выбранг, то единица массы бу-
будет тем самым определена. Однако, в физике поступили наоборот:
произвольно выбрали единицу массы и тем самым определили еди-
единицу силы. Такой путь предпочли потому, что хранить и воспроиз-
воспроизводить эталон массы гораздо удобнее, чем эталон силы. В системе
CGS за единицу силы принята такая сила, которая массе в 1 г сооб-
сообщает ускорение в 1 cMJcerc2. Эта единица силы названа диной. Рас-
Располагая эталоном массы, т. е. массой в 1 г, и измеряя ускорения,
сообщаемые этой массе какой-либо пружиной, мы сможем прокалиб-
прокалибровать эту пружину в динах.
*) Практически, как известно, для измерения масс пользуются другим
методом, о котором у нас будет итти речь ниже.

§ 25] КОЛИЧЕСТВО ДВИЖЕНИЯ 83
§ 25. Количество движения
В формулировке Ньютона во второй закон движения входит не
ускорение, а изменение количества движения. Количество движения mv
есть вектор, равный по величине произведению массы тела на его
скорость и по щщавлению совпадающий с направлением скорости.
Если масса тела или рассматриваемой части тела остаётся постоян-
постоянной, то изменения количества движения тела могут происходить
только вследствие изменения его скорости.
Если за бесконечно малый промежуток времени dt скорость тела
массы т изменилась на dv, то изменение количества движения тела
за это же время будет d(m\)=-md\. Но ускорение тела ]=z— и
изменение количества движения связано с ускорением тела соотно-
соотношением
Выражая во втором законе Ньютона произведение массы на ус-
ускорение через изменение количества движения, получим:
d{mv) — ^Fdt. D.3)
Это и есть выражение второго закона движения в том виде, как его
формулировал Ньютон: «Изменение "^""НРГТМ дщщШШ ЩЦЩЩЦ!0"
нально приложенной движущей силе и происходит по -направлению
той прямой, по которой эта сила действует».
Очевидно, что пока масса тела постоянна, эта формулировка
второго закона движения эквивалентна той, которая была приведена
выше. Если же при движении масса тела изменяется, то обе приве-
приведённые формулировки не эквипалентны, так как изменение количе-
количества движения может происходить и за счёт изменения массы. Но
мы этих случаев рассматривать не будем.
Выражение второго закона Ньютона D.3) можно переписать так:
D.4)
т.. е. производная вектора количества движения по времена равна
геометрической сумме действующих сил.
Это уравнение также связывает векторные величины и поэтому
оно эквивалентно трём уравнениям для компонент векторов количе-
количества движения и силы. Обозначая эти компоненты индексами х, у, г,
мы можем эти три уравнения записать следующим образом:
d ^ d тгч «f . . iri
6*

84 ЗАКОНЫ НЬЮТОНА [ГЛ IV
§ 26. Третий закон Ньютона
Мы рассматривали до сих пор только одну сторону вопроса—¦
связь между силами, действующими на данное тело со стороны дру-
других тел, и его ускорением. Но, как уже указывалось, силы, дейст-
действующие со стороны одних тел на другие, всегда носят характер
взаимодействий. Если тело А сообщает ускорение телу В, то и тело В
сообщает ускорение телу А. Поэтому возникает вопрос, как связаны
между собой эти ускорения, сообщаемые телами друг другу, или как
связаны между собой силы, с которыми тела действуют друг на
друга.
Если взаимодействуюише тела не обладают ускорением, то непо-
непосредственным измерением сил мы обнаружим, что силы, возникающие
при взаимодействии тел, равны
по величине и противоположны
| \ f& по направлению.
Для этого можно воспользоваться
р ее снова описанным выше опытом со
' стальным шаром и магнитом на стекле.
Если поместить магнит на катки и
прикрепить как шар, так и магнит при помощи одинаковых пружии, то, как
покажет опыт, магнит и шар только тогда остаются в покое (не имеют уско-
ускорений), когда обе пружины растянуты одинаково (рис. 56). Так как шар
и магнит при этом не имеют ускорений, то мы должны заключить, что
сила F1f с которой шар действует на магнит, равна силе F2, с которой дей-
действует на магнит прикрепленная к нему пружина; с другой стороны, сила F,,
с которой магнит действует на шар, равна силе F4, с которой иа шар дей-
действует прикрепленная к нему пружина. А так как обе пружины растянуты
одинаково, то F2 = — Ft, и, следовательно,
В тех же случаях, когда взаимодей- I r-A L^mvJ г-Д I
ствующие тела сообщают друг другу уско- 60 &) ^1R>—(So
рения, мы можем при помощи второго за- ^^
кона Ньютона по этим ускорениям опре-
определить силы, с которыми тела действуют рис, 57.
друг на друга.
Определить силы, возникающие при
взаимодействии тел, нам позволит, например, следующая серия опытов,
представляющая собой видоизменение описанного выше опыта с тележкой.
Возьмем сначала одну тележку и, прикрепив к ней динамометр и груз
(рис. 54), одновременно измерим действ) ющую силу и сообщаемое ею ге-
лежке ускорение; тем самым мы определим массу тележки т\. Повторим
затем этот опыт с друюй тележкой и определим массу второй тележки
/и2. Поставим теперь на рельсы обе тележки и заставим их каким
yi одно способом взаимодействовать между собой. Можно, например,
соединить тележки пружиной (рис. 57) или установить на одной из
тележек маленький электромотор, на вал которого накручивается
нитка, привязанная другим концом ко второй тележке (рис. 58).
Независимо от способа взаимодействия мы обнаружим, что всегда тележки
сообщают друг другу противоположные по направлению ускорения \х и ]а
причем величины ускорений, которыми обладают обе тележки в любой (но
один и тот же) момент времени, обратно пропорциональны массам тележек,
1 еУ/' т\

§ 26 J ТРЕТИЙ ЗАКОН НЬЮТОНА 85
Опыт показывает, что для любых двух тел, при любом характере
их взаимодействия ускорения, сообщаемые телами друг другу, обрати©
пропорциональны массам тел и направлены в противоположные сто-
стороны, т. е.
Отсюда на основании "второго закона Ньютона мы должны заключить,
что силы, с которыми действуют какие-либо два тела друг на
друга, всегда равны по величине и направлены в противополож-
противоположные стороны. Это положение и составляет содержание третьего за-
закона Ньютона.
Рис. 58.
Сам Ныоток формулировал третий закон следующим образом:
«Действию всегда есть равное и противоположное противодействие,
иначе — взаимодействия двух тел друг на друга между собою равны
и направлены в противоположные стороны».
Не следует, однако, думать, что «противодействие» чем-либо
принципиально отличается от «действия». Сила «противодействующая»
по своей природе и происхождению ничем не отличается от силы
«действующей». Если «действующая» сила обусловлена всемирным
тяготением, то и «противодействующая» сила обусловлена той же
причиной. Если «действующая» сила обусловлена деформацией какого-
либо из соприкасающихся тел, то, как будет показано ниже (§ 31),
«противодействующая» сила обусловлена деформацией другого из
соприкасающихся тел. Поэтому при рассмотрении вопроса о проис-
происхождении сил никогда не следует выделять «противодействующие»
силы и какую-то специальную категорию сил.
В принятой нами схеме изложения третий закон Ньютона не со-
содержит никаких определений и представляет собой утверждение, под-
поддающееся опытной проверке. Непосредственным измерением сил или
на основании второго закона Ньютона (измерив массы тел и испыты-
испытываемые телами ускорения) мы можем путем независимых измерений
проверить на опыте правильность третьего закона Ньютона. Однако,
после того как второй закон Ньютона сформулирован, третий закон
уже не представляет собой целиком самостоятельного утверждения.

86 ЗАКОНЫ НЬЮТОНА [ГЛ. IV
Новым в третьем законе Ньютона я-зляется лишь утверждение, что
при взаимодействии двух тел сообщаемые ими друг другу ускорения
всегда обратно пропорциональны массам этих тел *).
Остальное вытекает уже из второго закона, так как ес^ли ускоре-
ускорения обратно пропорциональны массам, то, согласно второму закону
Ньютона, силы должны быть равны по величине.
Второй и третий законы Ньютрна представляют собой основные
законы движения. Все остальные законы движения, как мы увидим,
могут быть выведены из этих двух основных законов.
Что же касается первого закона Ньютона, то он вообще не пред-
представляет собой самостоятельного закона, так как не содержит ника-
никаких новых утверждений. Первый закон Ньютона целиком содержится
во втором законе, частным случаем которого он является. В самом
деле, если действующая на тело сила равна нулю, то по второму
закону Ньютона и ускорение тела равно нулю, т. е. тело может либо
находиться в состоянии покоя, либо двигаться прямолинейно и рав-
равномерно. А ведь этим и исчерпывается содержание перзого закона
Ньютона.
В частном случае двух сий, действующих на одно и то же тело,
первый закон Ньютона вообще не содержит никакого утверждения,
так как если ускорение равно нулю, то по определению (содержа-
(содержащемуся в нашем способе измерения сил) обе силы разны и противо-
противоположны. Однако, поскольку он относится не только к случаю двух
сил, а к любому числу сил, он содержит утверждение, что ускорение
равно нулю, если сумма всех действующих сил равна нулю (однако,
это утверждение не новое, так как оно уже заключено во втором
законе Ньютона).
§ 27. Законы Ньютона и определение массы
В том изложении основных законов движения, которое было при-
приведено выше, способ измерения массы был заимствован из второго
закона Ньютона. Вследствие этого второй закон Ныогона уже нельзя
было рассматривать целиком как утверждение, поддающееся опытной
проверке. Можно, однако, поступить иначе, а именно, — заимствовать
способ измерения массы из третьего закона Ньютона. Тогда характер
утверждений, содержащихся во втором и третьем законах Ньютона,
соответствующим образом изменится. Этот новый способ измерения
массы тела может быть установлен следующим образом. Независимо
от второго закона Ньютона мы можем установить на опыте (напри-
(например, при помощи описанных уже опытов с двумя тележками), что два
*) Второй закон Ньютона утверждает, что ускорение, сообщаемое данной
силой, обратно пропорционально массе тела; но он не утверждает, что при
любом взаимодействии двух тел их ускорения обратно пропорциональны
массам.

§ 27] ЗАКОНЫ НЬЮТОНА И ОПРЕДЕЛЕНИЕ МАССЫ 87
взаимодействующих тела сообщают друг другу ускорения, отноше-
отношение которых всегда остаётся постоянным. Абсолютную величину
этого постоянного отношения мы и примем за обратное отноше-
отношение масс взаимодействующих тел. Тогда, выбрав массу тх какого-либо
определённого тела за эталон, мы можем заставить этот эталон массы
любым способом взаимодействовать с тем телом, массу которого /я2
мы должны определить. Измерив в какой-либо момент ускорения эта-
эталона /i и измеряемого тела J2, мы найдём массу измеряемого тела:
Характер и условия взаимодействия не играют при этом никакой роли;
самые измерения ускорений мы можем произвести в любой момент
времени. Как уже было указано, отношение ускорений всегда будет
одно и то же.
Теперь мы располагаем независимыми методами измерения всех
трёх величин, входящих во второй закон Ньютона. Измеряя незави-
независимо массу, силу и ускорение, мы -убедились бы, что всегда произ-
произведение массы на ускорение равно действующей силе. Конечно, для
этого мы должны были бы пользоваться надлежащим образом выбран-
выбранными единицами массы, ускорения и силы, например, в системе CGS
единицами: грамм, cMJceK2 и дина. (Если бы мы выбрали единицы как-
либо случайно, то в закон Ньютона вошёл бы некоторый постоянный
числовой коэффициент, одинаковый для всех опытов и всех тел.)
С этой точки зрения второй закон Ньютона весь целиком приоб-
приобретает характер утверждения, которое может быть полностью про-
проверено на опыте. Но, позаимствовав способ измерения массы из
третьего закона Ньютона, мы изменили характер утверждений, соцер-
жащихся в этом законе. Положение «ускорения тел обратно пропор-
пропорциональны их массам» уже не может быть проверено на опыте, так
как мы не располагаем способом измерения масс, независимым от
третьего закона Ньютона. В третьем законе Ньютона остаётся лишь
следующее утверждение: отношение ускорений двух взаимодействую-
взаимодействующих тел всегда остаётся постоянным, независимо от характера и ус-
условий взаимодействия, Это утверждение можно проверить на опыте,
так как мы располагаем способом измерения ускорении. В остальной
своей части третий закон Ньютона представляет собой либо опреде-
определение (определение массы), либо следствие из второго закона Ньютона.
Итак, в зависимости от того, как мы выберем способ измерения
массы, характер утверждений, содержащихся во втором и третьем за-
законах Ньютона, оказывается различным. Но и в том, и в другом слу-
случае в законах Ньютона помимо некоторых утверждений должно со-
содержаться и определение массы. Не прибегая к законам Ньютона,
этого определения дать невозможно.
Попытки определить инертную массу незазисимо от динамики,
например, как количество вещества (как это делал Ньютон), не дадут

88 законы ньютона [гл. iv
ничего нового, так как у нас нет независимого способа определения
«количества вещества» и для установления этого способа потребуется
привлечь на помощь динамику. Инертная масса есть понятие дина-
динамики» и определить её можно только на основании законов динамики.
Оба указанные способа измерения массы, конечно, одинаково за-
законны. Однако, второй способ обладает тем преимуществом, что,
применяя его, мы, как было показано, превращаем второй закон
Ньютона в утверждение, целиком поддающееся опытной проверке.
Поскольку из второго закона Ньютона вытекают уравнения движения,
он с этой точки зрения является основным законом механики. Есте-
Естественно выбрать такой способ измерения масс, который именно этому
основному закону придаёт характер экспериментального закона. По-
Поэтому мы остановимся на втором способе измерения масс — по отно-
отношению ускорений, сообщаемых телами друг другу, и именно этот
способ будем рассматривать как определение массы.
Если мы отказываемся от определения массы как «количества веще-
вещества» и определяем её из динамики, то вовсе ие очевидно, что общая масса
двух тел равна сумме масс обоих тел. В действительности масса обладает
этим свойством аддитивности, и это можно показать на основании законов
механики. Возьмём для наглядности две свинченные гири с массами mi и /п2.
Пусть на одну из них действует сила Fi и на другую F2 (рис. 59). Кроме
того, через соединяющий их стержень массы пц и /я2 могут действовать
друг на друга с какими-то силами Ф! и Ф% причём
согласно третьему закону Ньютона Ф1 = — Ф2. Уско-
?-•" рения масс ]j и j3 определяются на основании второго
закона Ньютона:
Рис. 59.
Но так как гири свинчены между собой, то оии
движутся вместе, т. е. ji = j2. Складывая оба уравнения вместе и учиты-
учитывая, что <!>! = —Ф2( мы получим:
Но Fj-J-Fj есть сумма сил, действующих на оба тела вместе, a j — их
общее ускорение. Значит, тело, составленное из двух тел с массами /nj и
pi2 ведёт себя так же, как одно тело, обладающее массой т1-!Гт2. Если
оба закона Ньютона верны для любых тел, то общая масса двух тел равна
сумме их масс. Масса тел обладает свойством аддитивности.
Хотя все реальные тела обладают конечной массой, однако в целом
ряде случаев оказывается возможным пренебречь массой некоторых движу-
движущихся тел. Это пренебрежение возможно тогда, когда ускорение рассмат-
рассматриваемого движения практически не зависит от массы того или иного тела.
Например, если к телу большой массы М привязана лёгкая нить массы т,
а к другому концу нити приложена сила F, то ускорение тела и нити зави-
еит практически только от массы М. Действительно, по второму закону
Ньютона
{М-\-т)\ — ?
и если М^>т, то мы можем-, ие делая заметной ошибки, отбросить массу т;
Этим приёмом часто пользуются в механике. Но при атом обычно идут
дальше, и не только пренебрегают массой некоторых тел, но упрощают
и самую картину взаимодействия между телами. Эти упрощения ^очень* по-

§ 28] УРАВНЕНИЯ ДВИЖЕНИЯ 89
лезиы, но нужно себе ясно представлять, почему они возможны и с чем
связаны.
Этот прийм мы рассмотрим на следующем конкретном примере. Две
массы тг и т% связаны лё! кой иитью массы т0 (рис. 60). На массу т1
действует сила F и поэтому обе массы и иить движутся с общим ускоре-
ускорением J = Fj(mi-\-mi-\-tn<)). При этом обе массы действуют на нить с силами
F] и F2. В свою очередь, нить действует на
обе массы с силами F3 и F4. Для каждого из Т}.....* г . тг
тел (двух масс и нити) мы можем написать «•¦
1 i,
Рис 60
где/ — ускорение, одинаковое для всех тел.
Но если масса та очень мала, то это значит,
что и /*1 — F2 очень мало, так как ускорение / определяется, главным
образом, массами т{ и щ и даже при /и0—>-0 остаётся конечным.
Поэтому, пренебрегая массой нити, мы вместе с тем должны считать, что
F,=^Fa, несмотря на то» что нить движется с ускорением, а не покоится.
Мы пришли к этому заключению на основании второго закона Ньютона.
С другой стороны, на основании третьего закона Ньютона мы можем
утверждать, что Р^ = Р3 н F^^Ft, и так как при т0—>-0 Fl = Fij то
Fs = Fit т. е. силы, с которыми действует нить на оба тела, равны (и про-
противоположны). Но мы можем тогда выбросить все промежуточные рассу-
рассуждения с нитью и просто сказать, что тела т^ и т% действуют друг на друга
через нить с равными и противоположными силами.
1 Таким приёмом часто пользуются в механике. Пренебрегают массой
нитей, рычагов, пружин и т. д. и прямо говорят о взаимодействии тел,
которые в действительности действуют не друг на друга, а на концы нити,
пружины, рычага и т. д.
§ 28. Уравнения движения
Исключим пока из рассмотрения силы трения и будем рассмат-
рассматривать только силы всемирного тяготения и упругие силы. Эти оба
типа сил зависят только от конфигурации взаимодействующих тел,
т. е. от координат тел или их отдельных частей. В таком случае
силы всегда могут быть выражены в виде некоторых функций от
^координат *). (Отыскание вида этих функций, т. е, определение зави-
зависимости сил от координат, составляет задачу соответствующих раз-
разделов физики — учения о тяготении и учения об упругих свойствах
уел.) Следовательно, если отсутствуют силы трения, то, применяя
второй закон Ньюгона, мы всегда выразим ускорения, т. е. вторые
производные от координат по времени, через известные функции
самих координат и придём к дифференциальным уравнениям второго
порядка, в которых независимой переменной является время, а функ-
функцией — координаты." Полученные дифференциальные уравнения движе-
движения вместе с начальными условиями определяют вид этих функций,
т. е. зависимость координат от времени. В некоторых случаях
*) Принципиально это "всегда возможно сделать в механике. Случаи,
когда это практически трудно или неудобно делать — тогда присутствуют
так- называемые «абсодютно жёсткие» связи, будут рассмотрены позднее.

90 законы ньютона [гл. IV
дифференциальные уравнения движения легко можно проинтегрировать,
т. е. зависимость координат от времени можно выразить в виде
каких-либо известных функций. Иногда это интегрирование оказы-
оказывается весьма трудным, но это трудность чисто математическая.
Мы можем теперь по-и,юму формулировать основное положение
механики Ньютона: для системы тел в .любой момент времени
вторые производные по времени от координат тел однозначно
определяются координатами этих тел. Это означает, что для
определения ускорений в системе тел в любой момент времени нужно
знать только конфигурацию всех тел системы в этот момент времени.
Образно выражаясь, для определения ускорений системы тел в какой-
либо момент времени нужно иметь только моментальную фотографию
системы, соответствующую этому моменту, и совершенно не нужно
знать, движутся ли тела или покоятся. Если мы имеем две одинако-
одинаковые системы тел, которые движутся совершенно по-разному, но если
«моментальные фотографии» этих систем окажутся для каких-либо
двух моментов идентичными, то в эти моменты обе системы будут
обладать одинаковыми ускорениями.
Однако, дальнейший характер движения тела после момента, к
которому относится «моментальная фотография», определяется не
только тем ускорением, которым обладает тело в данный момент,
но и той скоростью, которой оно к этому моменту достигло.
Скорость же при данной конфигурации может быть различной (она
зазисит от предшествующего движения). Но если конфигурация
(а значит, и ускорение) и скорость в данный момент времени из-
известны, мы сможем найти конфигурацию и скорость в следующий
момент времени и, продолжая далее это рассмотрение, найти конфи-
конфигурацию и скорость в любой момент времени, т. е. определить всё
последующее движение. Конфигурация и скорость в данный момент
времени—это начальные условия. Если известны дифференциальные
уравнения движения и заданы начальные условия, всё дальнейшее
движение системы определено *).
§ 29. Инерциальные системы координат
Мы условились пользоваться всё время «неподвижной» системой
координат. Однако, практически часто удобнее пользоваться другими
системами координат, например, системой координат, связанной с
Землёй, которой фактически мы уже пользовались. Между тем самое
содержание установленных нами основных положений механики таково,
что они не могут быть справедливы в любых системах координат.
Действительно, будем рассматривать какое-либо движение одновре-
*) Напомним, что это утверждение, как и вся механика, которую мы
шуса .излагаем, справедливо только д|я выбранной нами «нбпОдвфкной»
системы координат.

§ 29] ИИРРЦИАЛЫШЕ СИСТЕМЫ КООРДИНАТ 91
менно в дзух системах координат: нашей прежней «неподвижной»
и другой, которая движется относительно «неподвижной» с некото-
некоторым ускорением. Тогда ускорение одного и того же тела в этих
двух системах координат будет различно. Между тем силы, опреде-
определяемые конфигурацией тел, останутся прежними, гак как расстояния
между телами или между отдельными частями тел зависят только от
разностей координат, т. е. не изменяются при переходе к новой
системе координат. Если ускорение, наблюдаемое в одной системе
координат, мы можем объяснить действием каких-либо других тел,
то мы не сможем сделать этого в другой системе координат, так
как ускорения оказались другими, а конфигурация тел, а следова-
следовательно, и силы остались прежними*).
«Неподвижная» система координат и система координат, связан-
связанная с Землёй, обладают ускорением одна относительно другой. Это
ускорение обусловлено суточным вращением Земли относительно
Солнца и звёзд, а также годовым движением Земли. Поэтому уста-
установленные нами основные положения механики Ньютона не могут
относиться и к «неподвижной» системе координат, и к системе коор-
координат, связанной с Землёй. Они верны либо в той, либо в другой
системе координат. Но опыты, которые мы до сих пор производили,
были столь грубы, что не давали возможности установить, в какой
из двух систем координат верно утверждение, что ускорения одно-
однозначно определяются конфигурацией. Более того, наши опыты были
столь грубы, что они не позволили заметить разницы межцу двумя
системами координат (между тем эта разница заведомо должна суще-
существовать). Поэтому при дальнейшем уточнении опытов может ока-
оказаться, что наше утверждение несправедливо ни для той, ни для
другой из этих систем координат. Специальные точные опыты должны
указать ту систему координат, в которой справедливо утверждение,
что все ускорения обусловлены действием каких-либо тел и одно-
однозначно определяются конфигурацией этих тел.
Первым опытом, который дал ответ на этот вопрос, был класси-
классический опыт Фуко с маятником. Опыт этот заключался в наблюдении
за движением плоскости качаний маятника по отношению к Земле.
Плоскость качаний маятника Фуко на разных широтах движется по-
разному. Проще всего это движение выглядело бы на полюсе. На
основании тех опытов, которые производились на разных широтах,
легко установить, как двигалась бы плоскость качаний на полюсе.
Чтобы выяснить самую идею опыта, мы рассмотрим -спераа вообра-
*) То же самое мы могли бы сказать, если бы принимали во внимание
силы треичя. Тогда мы должны были бы утверждать, что ускорения взаи-
взаимодействующих тел определяются их конфигурацией и относительными ско-
скоростями взаимодействующих тел (так как силы трения зависят от относи-
относительной скорости тел). Но относительные скорости тел так.же не изменяются
при переходе к другой системе координат.

92
ЗАКОНЫ НЬЮТОНА
[гл. IV
жаемый опыт на полюсе, а затем опишем результаты реального опыта
в топ виде, как он был произведён впервые Фуко.
Представим себе, что длинный маятник, подвешенный на вращаю-
вращающемся подвесе (так, что точка подвеса может вращаться вокруг вер-
вертикали, не закручивая нити), помещён на северном полюсе. Сообщим
маятнику толчком начальную скорость в каком-либо определённом
горизонтальном направлении. Маятник начнёт совершать колебания
в той вертикальной плоскости, в которой лежит сообщённая маят-
маятнику начальная скорость. Наблюдая за плоскостью качаний маятника,
мы обнаружили бы, что плоскость качаний маятника всё время пово-
поворачивается относительно Земли (в направлении по часовой стрелке,
если смотреть сверху) с углозой скоростью в 2тт радиан/сутки.
Вместе с тем она сохраняет неизменным своё положение относительно
Солнца и звёзд. Какой вывод
мы можем сделать из этого
наблюдения?
На маятник действуют две
силы — сила притяжения Земли
mg, направленная к центру
Земли, и 'сила натяжения
нити f (рис. 61). Начальная
скорость определяет ту пло-
плоскость, в которой маятник
начал совершать колебания.
Рис- 61. В этой же вертикальной пло-
плоскости лежат и обе силы,
действующие на маятник. Эти силы не могут отклонить ско-
скорость маятника v от той плоскости, в которой она лежала
в начальный момент. Поэтому, если маятнику сообщают ускорения
только нить и Земля, то плоскость качаний маятника должна оста-
оставаться неизменной. Но именно так обстоит дело, если мы будем
отсчитывать положение плоскости качаний относительно Солнца и
звёзд, т. е. пользоваться «неподвижной» системой координат. Если
же мы будем отмечать положение плоскости качаний относительно
Земли, т. е. пользоваться системой координат, связанной с Землёй,
то окажется, что плоскость качаний не остаётся неизменной, а пово-
поворачивается. Между тем никаких тел, которые могли бы сообщать уско-
ускорения, не лежащие в плоскости качаний, мы указать не можем. Сле-
Следовательно, если мы будем относить ускорения маятника к
Солнцу и звёздам, т. е. пользоваться «неподвижной-» системой
координат, то мы сможем объяснить все ускорения действием
каких-то определённых тел. Если же мы будем пользоваться
системой координат, связанной с Землёй, то помимо ускорений,
обусловленных действием определённых тел, мы встретимся
и с такими ускорениями, причиной которых не являются какие-
либо определённые тела. Это' и есть <зтвет на поставленный вопрос.

§ 29] ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ К.ООРДИНАТ §3
Такие системы координат, в которых все ускорения обусловлены
действием каких-либо тел, носят название инерциальных систем
координат *\. Опыт Фуко позволяет, следовательно, утверждать, что
выбранная нами «неподвижная» система координат является инер-
циальной; система же координат, связанная с Землёй, не является
инерциальной.
Правда, первое из этих утверждений не имеет столь категориче-
категорического характера, как второе. Возможно, что более тонкие и более
точные опыты покажут, что и в выбранной нами «неподвижной»
системе координат существуют такие ускорения, которые ие могут
быть объяснены действием каких-либо определённых тел. Но тогда
Эти же опыты покажут, как нужно выбрать систему координат, чтобы
она была инерциальной. Усовершенствование и уточнение опытов
может внести уточнение и в определение инерциальной системы
координат. Но всегда, при любой точности наших опытов, мы смо-
сможем указать систему координат, которая с этой степенью точности
является инерциальной. Пока же не только опыт Фуко, но и все
аналогичные опыты дают результаты, которые позволяют считать
систему координат, связанную с Солнцем и звёздами, инерциальной.
Поэтому мы и условились с самого начала пользоваться «неподвиж-
«неподвижной» системой координат, связанной с Солнцем и звёздами. Как мы
теперь виДим, именно в этой системе координат справедливы все те
основные положения механики, которые мы формулировали выше.
Легко видеть, что всякая система координат, которая по отно-
отношению к данной инерциальной системе координат движется прямоли-
прямолинейно и равномерно, также является инерциальной. Действительно,
в этом случае ускорения тела в обеих системах координат будут
одни и те же. И если в одной системе координат эти ускорения
можно объяснить действием других тел, их конфигурацией, то и в
другой системе координат их можно объяснить таким же образом.
Следовательно, все системы координат, которые движутся прямоли-
прямолинейно и равномерно по отношению к «неподвижной», также явля-
являются инерциальными. В них во всех справедливы те положения и
законы механики, которые были формулированы выше.
Во всех инерциальных системах координат движение данной
системы тел описывается одними и теми же уравнениями. Поэтому,
если в двух системах координат, движущихся друг относительно
друга прямолинейно и равномерно, мы будем наблюдать две одина-
одинаковые системы тел, поставленные а одинаковые начальные условия,
*) Происхождение этого названия связано с тем, что только в таких
системах координат справедлив первый закон Ньютона, т. е. утверждение,
Что тело, не подвергающееся действию других тел, движется прямолинейно
н?равномерно. Такое движение и называется движением по инерции, и пер-
первый закон Ньютона часто называют «законом инерции». Отсюда произошло
и название «инерциальные системы координат», так как только в них спра-
справедлив «закон инерции».

94 ЙАКОНЫ НЬЮТОНА [гл. IV
то все дальнейшие движения этих тел будут одинаковы. Другими
словами, если в различных инерциалъных системах координат мы
будем производить одни и те же механические опыты, то эти
опыты во всех случаях дадут один и тот же результат. Это
положение, высказанное впервые Галилеем, носит название прин-
принципа относительности Галилея.
Из этого принципа следует, что механическими опытами нельзя
обнаружить прямолинейное и равномерное движение системы отсчёта
относительно Солнца и звёзд. Но ускоренное движение системы
отсчёта относительно Солнца и звёзд может сказаться на результа-
результатах механических опытов, как это имеет место, например, в опыте
Фуко.
Часто встречаются такие движения, на которых практически не
сказывается то обстоятельство, что система координат, связанная
с Землёй, не является инерциальной. Таковы именно были все те
опыты, которые мы описывали в предыдущих параграфах. Поэтому
мы и могли при рассмотрении этих опытов пользоваться системой
координат, связанной с Землёй, и в этой системе координат приме-
применять законы, которые, строго говоря, справедливы только в «непо-
«неподвижной» системе координат. В пределах этих опытов система коор-
координат, связанная с Землёй, практически была инерциальной.
§ 30. Опыт Фуко
Реальный опыт впервые был произведён Фуко в Париже в 1850 г.
Хотя принципиальное содержание опыта, изложенное в предыдущем пара-
параграфе, при атом не изменяется, тем не менее характер движений маятника
будет иным. На полюсе плоскость качаний маятника сохраняла бы неиз-
менным своё положение относительно звёзд
(т< е- вращалась бы относительно Земли в на-
направлении, противоположном вращению Земли
относительно звёзд, и с той же угловой ско-
скоростью 2тс радиан/сутки). Во всех других точках
земного шара этого уже не будет и, как легко
видеть, не может быть. Ведь, во всяком случае,
плоскость качаний маятника всегда проходит
через вертикаль данного места, а вертикаль
всякой точки Земли (кроме полюсов) при вра-
вращении Земли изменяет своё положение отио-
Рис. 62. сительно звёзд. Поэтому плоскость качаний
маятника уже не будет сохранять неизменным
своё положение относительно звёзд; относительно Землн она также
будет двигаться по-иному.
Характер движения плоскости качания маятника в этом случае можно
установить при помощи следующих соображений. Будем рассматривать
движение маятника относительно «неподвижной» системы координат. Раз-
Разложим угловую скорость вращения Земли ю на две составляющие: верти-
вертикальную e*i и" горизонтальную щ (рис. 62). Так как силы, действующие на
маятник со стороны Земли и нити^ попрежнему лежат в вертикальной пло-
плоскости, то они не могут вызвать вращения плоскости качаний маятника
вокруг вертикальной оси. В отношении вертикальной составляющей враще.

§30]
опыт фуко 95
ния Земли всё будет обстоять так же, как на полюсе. Но поскольку эти
силы всё время удерживают маятник в плоскости, проходящей через верти-
вертикаль данного места, оии тем самым заставляют плоскость качаний вместе
с вертикалью вращаться вокруг горизонтальной оси. Таким образом, силы,
действующие на маятник, не увлекают плоскости качаний маятника вслед
за Землёй во вращении щ и полностью увлекают плоскость качаний
вслед за Землёй во вращении ео2. Относительно звёзд плоскость качаний
маятника будет вращаться с угловой скоростью w2. Земля же будет «ухо-
«уходить» из-под плоскости качаний маятника с угловой скоростью Wj (так как
в этой части вращения Земли плоскость качаний маятника не участвует).
Следовательно, по отношению к Земле плоскость качаний маятника будет
вращаться в направлении, противоположном вращению Земли относительно
звёзд (т. е. по часовой стрелке, если смотреть сверху), с угловой скоро-
скоростью о»! = ш sin if, где if — широта данного места. Поэтому угловая скорость
вращения плоскости качаний маятника будет меньше, чем на полюсе. Для
Москвы, например, sin <р = 0,83 и плоскость качаний маятника совершила
бы полный оборот приблизительно в 29 час.

ГЛАВА V
СИЛЫ И ДЕФОРМАЦИИ
§ 31. Возникновение деформаций
Задачу, которая стоит перед нами, когда мы хотим рассмотреть
какое-либо движение, мы можем формулировать следующим образом.
Нам заданы конфигурация, т. е. взаимное расположение и деформа-
деформации тел системы, и их скорости в какой-либо момент времени (на-
(начальные условия). Для того, чтобы определить дальнейшие движения
в системе, мы должны прежде всего найти ускорения, которые будут
иметь отдельные тела или части тел системы в начальный момент.
Эти ускорения мы найдём, определив из начальной конфигурации
силы, действующие в системе (предполагается, что мы знаем, как
именно силы зависят от конфигурации). Зная скорости и ускорения
в начальный момент, мы сможем определить, как будет происходить
движение в следующий момент времени и как при этом изменится
конфигурация тел —,их взаимное расположение и деформации. От-
Отсюда мы найдём, как изменятся силы, действующие в системе, и
какие ускорения будет иметь система в следующий момент времени.
Продолжая это рассмотрение дальше, мы сможем шаг за шагом про-
проследить движения в системе. Таким образом, начальное состояние
системы определяет всё её последующее движение.
Применим теперь эту схему рассуждений
. к отдельным конкретным задачам. В каче-
F А ; 8 if стве простейшего примера рассмотрим та-
-—-/№fwj__| I—I кую задачу: тело массы т сначала нахо-
находится в покое и в недеформированном
Рис. 63. состоянии. Затем на одну из точек тела
начала действовать некоторая постоянная
сила F, например, к этой точке тела прикреплена пружина, которую
мы внезапно растянули до некоторой определённой величины и затем
следим за тем, чтобы растяжение пружины всё время оставалось
неизменным. Для упрощения мы будем рассматривать тело удли-
удлинённой формы и будем считать, что сила F действует на всё сечение
тела (рис. 63).
На основании второго закона Ньютона мы можем утверждать,
что всё тело как целое будет двигаться с постоянным ускорением

§ 311 ВОЗНИКНОВЕНИЕ ДЕФОРМАЦИЙ 97
jz=^F{m. Но, чтобы проследить картину возникновения движения,
необходимо применить схему рассмотрения, изложенную выше.
В начальный момент тело не деформировано. Следовательно,
нет никаких сил, которые действовали бы со стороны тела на пру-
пружину или со стороны одних частей тела на другие. Но когда пру-
пружина оказалась растянутой, на левый конец тела, к которому пру-
пружина прикреплена, начнёт действовать сила, которая сообщит этому
чонцу тела некоторое ускорение, и он начнёт двигаться. Остальные
части тела сначала будут оставаться в покое, так как на них не
действуют ещё никакие силы. Но если левый конец тела начал дви-
двигаться, а правый остаётся в покое, то тело будет растягиваться.
Вследствие деформации тела в нём возникнут внутренние силы, дей-
действующие между отдельными частями тела.
Разделим мысленно тело плоскостью X на две части: А и ВС;
вследствие растяжения на часть ВС со стороны части А будет дей-
действовать сила, направленная влево. Под действием этой силы часть ВС
также начнёт двигаться влево. Но вначале, пока деформации и силы
е\цё малы, ускорение части ВС также будет мало, и она будет
отставать от части А. Деформация будет возрастать, вследствие чего
будет увеличиваться сила, действующая на часть ВС, а вместе с тем
будет возрастать и её ускорение. Вместе с тем часть ВС будет дей-
действовать на часть А с силой, направленной вправо, и поэтому уско-
ускорение части А будет постепенно уменьшаться. В конце концов дол-
должен наступить момент, когда ускорение обеих частей тела А и ВС
и вообще всех точек тела окажется одинаковым. Тогда дальнейшая
деформация тела должна прекратиться*).
Следовательно, с того момента, когда всё тело будет двигаться
с одинакозым ускорением j=Fjm, оно будет находиться в некото-
некотором неизменном деформированном состоянии.
Ясно, что деформации различных частей тела будут различны. Разделим
мысленно тело плоскостями X н У на части А, В и С (рис. 63). Легко
видеть, что деформация тела у плоскости X должна быть больше, чем у
плоскости Y. Чем дальше от точки приложения силы, тем меньше деформа-
деформация тела.
Обычно мы имеем дело с телами очень жёсткими; поэтому возникаю-
возникающие в них деформации очень малы и обнаружить их трудно. Но если взять
тело нежёсткое, то легко даже на-глаз обнаружить деформации, возни-
возникающие в том случае, когда тело испытывает ускорение. Для этой цели
можег служить следующая демонстрация.
На резиновую ленту надет ряд одинаковых свинцовых грузиков на рав-
«ом расстоянии E—10 см) друг от друга (рис. 64, а). Если ленту с грузами
положить иа гладкое горизонтальное стекло и затем резко дёрнуть за один
*) Строго говоря, дальнейшая деформация тела прекратится ие тогда,
когда ускорения всех точек тела окажутся равными, а когда окажутся
равными скорости всех точек тела. Но в этот момент ускорения их будут
уже снова различны: в теле возникнут упругие колебания. Но с точки зре;
нйя нашей задачи — это побочное явление, и поэтому мы н,е будем его при-
принимать во внимание.
7 С. э. ХаПкин

98 силы и деформации [гл. v
её конец, то все участки ленты растянутся по-разному (рис. 64, Ь). Эти
растяжения повторяют в увеличенном виде всю картину деформаций в рас-
рассмотренном выше примере.
Так как ускоряемое тело при движении оказывается деформиро-
деформированным, то оно действует на прикреплённую к нему пружину с не-
некоторой силой. Ускоряемое тело действует на ускоряющее именно
потому, что оно деформировано. Если бы оно не испытывало уско-
рения, но было так же де-
деформировано, как в нашем
случае, то оно действовало
w бы на пружину точно с той
же силой. Деформацией
тела объясняется проис-
происхождение той силы, ко-
которая согласно третьему
закону Ньютона должна
действовать со стороны
тела на ускоряющую его
пружину.
Если пользоваться терминологией Ньютона, то силу, действующую
со стороны пружины на тело, следует назвать «действием», а силу,
действующую со стороны тела на пружину, — «противодействием».
Но по своей природе «противодействие» ничем не отличается от
«действия»; «действие» обусловлено тем, что деформирована пру-
пружина, а «противодействие» тем, что деформировано тело.
§ 32. Деформации при вращательном движений
Рассмотрим теперь также подробно случай движения тела по
окружности с постоянной угловой скоростью. Пусть, например, тело
массы т, прикреплённое на пружине к не-
неподвижной точке О, вращается с постоян-
ной угловой скоростью (о (рис. 65). Вра- „
щение с постоянной угловой скоростью есть f -"
движение с ускорением, направленным к
центру. Это центростремительное ускорение Рис. 65.
телу сообщает растянутая пружина, которая
действует на тело с определённой силой. Как мы уже знаем (§ 13), при рав-
равномерном движении по окружности тело испытывает ускорение jn = wV,
т. е. пружина должна на него действовать с силой F = raaJr.
Чтобы составить полную картину возникновения рассматриваемого
движения, необходимо выяснить, почему пружина оказалась растяну-
растянутой. Для этого рассмотрим какой-либо конкретный случай возникно-
возникновения вращательного движения.
В нашем, примере мы могли бы получить равномерное вращение сле-
следующим образом. Пусть вначале тело покоится, а пружина не растянута.

§ 32] ДЕФОРМАЦИИ ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ 99
Сообщим ему некоторую начальную скорость v в направлении, пер-
перпендикулярном к ОА (рис. 66). Вначале, пока на тело не действуют
никакие силы, оно должно двигаться прямолинейно и равномерно
в направлении начальной скорости v. При этом расстояние О А будет
увеличиваться, а пружина растягиваться. Возникает сила, действую-
действующая со стороны пружины на тело в направлении О, тело приобретёт
ускорение в этом направлении и перестанет
двигаться прямолинейно*). Сначала, пока
растяжение пружины мало, ускорение, сооб- _
щае.мое телу, также будет мало, и траекто- О—'1"
рия движения будет лишь слегка искривлена.
Удлинение пружины будет продолжаться и рис> gg.
сообщаемое ею ускорение будет возрастать.
Траектория будет становиться всё более и более искривлённой.
Растяжение пружины прекратится, когда она будет сообщать телу
ускорение, необходимое для того, чтобы траектория превратилась в
окружность. Для этого пружина должна действовать иа тело
с силой
После этого и установится равномерное вращение тела с угловой
скоростью (о = г»|/-, где г—радиус вращения**).
Эту картину установления вращения можно продемонстрировать при
помощи следующего опыта (рис. 67). На гладкое горизонтальное стекло
помещён тяжёлый шарик, прикреплённый к
I мягкой пружине. Другой конец пружины за-
закреплён неподвижно. Если шарик сильно уда-
ударить, т. е. сообщить ему начальную скорость
в направлении, перпендикулярном к оси пру-
пружины, то можно наблюдать описанную выше
картину. Вначале траектория шарика будет
заметно отличаться от окружности и лишь в
дальнейшем, когда пружина достаточно рас-
растянется, траектория превратится в окружность.
Ясно, что при установлении вращения
будет деформироваться не только пру-
67- жина, но и само тело. Это будет про-
происходить примерно так, как и в пре-
предыдущем примере. Так как пружина прикреплена только к од-
одной стороне тела, то она только прилегающей к ней части тела
*) Строго говоря, вначале скорость будет изменяться не только по напра-
направлению, но и по величине, так как сила, действующая со стороны пружины, не
будет точно перпендикулярна к скорости v. Но если пружина достаточно
жесткая и растяжение её мало, то этим можно пренебречь и принимать
во внимание только изменение направления скорости.
**) Мы опять пренебрегаем побочными явлениями в виде упругих коле-
колебаний, которые могут возникнуть и в этом случае.
7*

100 силы и деформация [гл. V
будет сообщать ускорение к центру. Поэтому вначале только
ближайшие к пружине части тела начнут двигаться криволинейно,
а наружные будут двигаться прямолинейно. Расстояние между от-
отдельными частями тела будет возрастать — тело будет растяги-
растягиваться. Возникнут упругие силы, действующие между отдельными
частями тела, и эти силы начнут сообщать ускорение внешним частям
тела. Изменение деформации тела прекратится только тогда, когда
возникшие внутри тела упругие силы окажутся достаточными для
того, чтобы всем частям тела сообщить ускорения, необходимые для
движения по окружностям. Таким образом, к моменту установления
равномерного вращения не только пружина, но и само тело окажется
деформированным (растянутым).
'Величину растяжения в разных частях тела мы сможем примерно
оценить, если опять для упрощения будем рассматривать удлинённое
тело малого сечения (рис. 68) и
считать, что сила со стороны пру-
-J жины приложена ко всему сечению.
Если размеры тела малы по срав-
рио g§ нению с радиусом вращения, то ха-
характер деформации будет примерно
такой же, как и в случае прямолинейного движения с ускоре-
ускорением j=m'r.
Вращающееся тело оказывается деформированным и поэтому дей-
действует на пружину в направлении от центра. Как и в предыдущем
примере, наличием деформации ускоряемого тела объясняется
происхождение силы, которая должна действовать со стороны
тела на пружину, т. е. силы ^противодействия», которая должна
существовать по третьему закону Ньютона. Если бы тело не
вращалось, но было деформировано так же, как и при вращении,
оно действовало бы на пружину точно с той же силой.
Эту силу, которая действует со стороны вращающегося тела на
пружину, называют «центробежной», так как она направлена от
центра. Но, применяя этот термин, всегда следует помнить о про-
происхождении этой силы. Она возникает потому, что вращающееся
тело оказывается деформированным, и по своей природе ничем не
отличается от центростремительной силы, с которой растянутая пру-
пружина действует на вращающееся тело.
Применяя это рассмотрение, мы легко объясним, почему в некоторых
случаях происходит разрушение быстро вращающихся тел, например, раз-
разрыв маховиков. Внутренние части маховика (спицы) должны сообщать
внешним частям ускорения, необходимые для движения по окружности. Для
этого они должны развивать достаточные силы. Если даже при наибольших
допустимых деформациях внутренние части маховика всё ещё не развивают
сил, необходимых для движения внешних частей по окружности, то эти
внешние части будут двигаться по раскручивающимся спиралям, деформа-
деформации внутренних частей будут нарастать, превзойдут наибольший допусти-
допустимый предел и маховик разлетится на части.

§ 33] ДЕФОРМАЦИЙ ПРИ «СЛОЖНЫХ» ДВИЖЕНИЯХ 101
Можно сказать, что причиной разрыва маховика является отсутствие
сил, достаточных для того, чтобы сообщить внешним частям маховика нуж-
нужные ускорения. Силы необходимы для того, чтобы маховик вращался как
целое, не разрываясь, и маховик разрывается, когда этих сил нет или они
недостаточно велики.
§ 33. Деформации при «сложных» движениях
Во многих случаях изучаемое движение удобно рассматривать как дви-
движение относительно системы координат, которая, в свою очередь, движется
относительно другой «неподвижной». При таком рассмотрении обычно го-
говорят, что результирующее «абсолютное» движение представляет собой
«сложное» движение.
Мы рассмотрим с той же точки зрения, как и в предыдущих двух па-
параграфах, вопрос о силах и происхождении деформации для одного типа
«сложных» движений, именно когда переносное движение представляет
собой вращение с постоянной угловой скоростью. Этот случай особенно
интересен потому, что к нему сводится задача о движениях земных тел,
когда приходится учитывать суточное движение Земли.
Как уже неоднократно указывалось, законы движения в том виде, как
они сформулированы выше, справедливы только в инерциальных системах
координат. Поэтому мы ие можем пока решать задачи о движении тел
во вращающейся системе координат. Но если «относительное» движение
тела нам задано, то, зиая переносное движение, мы найдём и «абсолют-
«абсолютное» движение тела относительно «неподвижной»,
т. е. инерциальной, системы координат, в которой
справедливы законы Ньютона в том виде, как они
сформулированы выше. В этой инерциальной си-
системе координат мы и будем рассматривать вопросы
о действующих силах и возникающих деформа-
деформациях *). При этом мы должны будем определить
ускорения, которые испытывает тело относительно
этой ииерциальной системы координат, т. е. найти
«абсолютное» ускорение движущегося тела. Эта
задача была детально рассмотрена в § 17.
Воспользуемся снова моделью, которой пользо-
пользовались при этом рассмотрении—телом, движущимся вдоль вращающейся штан-
штанги. Ограничимся ради простоты случаем, когда вдоль штанги тело движется
с постоянной скоростью. Обеспечить это можно, прикрепив к телу соответству-
соответствующим образом подобранную пружину (рис. 69), обладающую коэффициентом
упругости & = дао>3 (т. е. пружину нужно подобрать под заданную угловую
скорость вращения штанги — <л). Если пружина не растянута, когда тело т
лежит на оси вращения, то в любой точке между О и В на тело т со сто-
стороны пружины будет действовать направленная к центру сила Ar = /n<eV,
где г — расстояние до оси. Это значит, что в любом положении тела т
пружина сообщает ему как раз такое центростремительное ускорение,
какое испытывало бы это тело, вращаясь с угловой скоростью <о по окруж-
окружности радиуса г, и тело т может при любом г оставаться неподвижным
на вращающейся штанге. Если же мы сообщим телу какую-то начальную
скорость р' вдоль штанги, то оно будет двигаться с этой скоростью до
конца штанги (мы предполагаем, что трение отсутствует).
*) В дальнейшем, когда мы установим, какой вид имеют законы дви-
движения в тех или иных неинерциальных системах координат, мы сможем
поступать иначе — прямо решать задачи о движении тел во вращающейся
координат.

102 силы и дкформации [гл. v
Каково же «абсолютное» ускорение тела, движущегося с постоянной
скоростью о' вдоль штанги, которая вращается с постоянной угловой ско-
скоростью л»? Так как в нашем случае относительное ускорение равно нулю, то
«абсолютное» ускорение есть геометрическая сумма переносного ускорения
направленного к центру, и кориолисова ускорения
J* = 2[«.v'J,
направленного нормально к штанге в сторону ей вращения, так как тело
движется от центра. Задача состоит в том, чтобы объяснить происхожде-
происхождение этих ускорений.
Как легко видеть, переносное ускорение как раз равно тому уско-
ускорению, которое сообщает телу растянутая пружина, так как сила, с кото-
которой она действует, равна т<я*г и направлена к центру. Таким образом, ту
компоненту «абсолютного» ускорения, которая направлена вдоль штанги,
тело получает под действием пружины.
Перейдём теперь к вопросу о происхождении корнолисова ускорения,
направленного нормально к штанге. Так как пружина действует вдоль
штанги, то она не может сообщать этого ускорения. Следовательно, един-
единственное тело, которое может сообщать это ускорение, это сама штанга,
которая может давить на тело в'бок. Но для этого штанга должна быть
соответствующим образом изогнута. Именно, для
того, чтобы сила, действующая на тело со стороны
штанги, была направлена в сторону перемещения
штанги — вперёд, сама штанга должна быть вы-
выгнута назад. Необходимо, следовательно, объяснить,
почему штанга оказывается изогнутой.
Чтобы сделать более наглядным происхожде-
происхождение деформаций штанги, представим себе несколько
иную модель, в которой очень гибкая штаига за-
закреплена только на оси вращения. Но тогда сила, с которой она мо-
может давить на тело т, будет очень мала и не сможет заметно изменить
скорость тела. Между тем, находясь вблизи центра, тело обладает малой
скоростью \п< нормальной к штанге, так как расстояние до оси вращения
мало. Если, удаляясь от центра, тело сохраняет ту малую скорость vn, ко-
которую оно имело вблизи центра, то оно отстанет от движения штанги и
изогнёт ей назад (рис. 70). Механизм возникновения деформации прин-
принципиально такой же, как и в примерах предыдущих параграфов. Разница
заключается лишь в том, что после того, как тело дойдёт до конца штанги
и остановнтся, деформация штангн исчезнет. Если штанга достаточно жестка,
то её деформации, возникающие при движении, заметить не удастся. Однако,
вти деформации возникают во всякой штанге, причём величина этих дефор-
деформаций в каждый момент такова, что обусловленная ею сила давления на
груз как раз равна 2tn[<o-v'], т. е. сообщает грузу нужное кориолисово
ускорение. Если бы эта сила была меньше, то груз в направлении, нор-
нормальном к штанге, двигался бы с недостаточным ускорением и штанга
изогнулась бы сильнее. Вместе с тем возросла бы до нужной величины
сила, действующая со стороны штанги на тело т.
Конечно, при движении тела т. по вращающейся штанге деформиро-
деформированной оказывается ие только штанга, но и само тело. При этом передняя
часть тела оказывается сжатой, а задняя растянутой. (Возникновение этих
деформаций после всего сказанного читатель без труда объяснит сам.)
Вследствие этого не только штанга давит на тело, ио и тело давит на штангу
с такой же по величине силой, но направленной в противоположную
сторону, т. е. навстречу движению штанги, если груз движется от

§33]
ДЕФОРмацин при «сложных» движениях
103
Рнс. 71.
Го» Ш
центра К периферии. Эта сила, следовательно, равна — 2т [<av'J или
2m[v'o>].
Кориолисово ускорение, как мы видели, изменяет направление на об-
обратное при изменении направления относительной скорости v'. Значит,
когда тело движется по штанге от периферии к центру, то ускорение,
а следовательно, и давление штанги на тело направлены навстречу движе-
движению штанги. А для «того штанга должна быть изогнута вперёд (рис. 71).
Такая деформация штанги возникает потому, что, двигаясь к центру,
т. е. переходя в области, где vs меньше, тело опе-
опережает штангу и изгибает ев ¦ направлении её дви-
движения.
В рассмотренной нами модели деформации жесткой
штанги малы, я наблюдать их непосредственно невоз-
невозможно. Однако, описанную выше картину можно на-
наблюдать на специальном демонстрационном приборе,
в котором роль штанги играет резиновая трубка, а
роль движущегося по штанге тела — текущая по
трубке вода (рис. 72). Патрубки, на которые надета
трубка, соединены с двумя концентрическими трубами, служащими валом
прибора. При помощи фланца, не препятствующего вращению вала, эти
трубы соединяются с неподвижными трубками, через которые ток воды
подводится к прибору. Таким образом можно пропускать ток воды через
резиновую трубку при вращении прибора.
Чтобы иметь возможность наблюдать форму трубки при быстром вра-
вращении, применяется стробоскопическое освещение. Удобнее всего осущест-
осуществить его следующим образом: источник света
помещается позади прибора, а на валу укреп-
укрепляется дЪкк в радиальной щелью. Впереди
прибора устанавливается зеркало. Свет от
источника, проходя через щель и отражаясь
от зеркала, освещает трубку отдельными ко-
короткими вспышками при одном и том же по-
положении трубки. Трубка благодаря этому ка-
кажется неподвижной и форма ей хорошо вид-
видна. Если привести прибор во вращение, не про-
пропуская воды по трубке, то последняя остаётся
прямой. При пропускании воды трубка изги-
изгибается тем сильнее, чем быстрее вращение и
ток воды. При изменении направления враще-
вращения или направления течения воды трубка
изгибается в другую сторону. Так как трубка изогнута, то значит,
вода давит на трубку, а трубка, в свою очередь, давнт на воду и со-
сообщает частицам воды нужное кориолисово ускорение.
Поскольку в этом и аналогичных случаях силы, действующие на дви-
движущееся тело, сообщают ему кориолисово ускорение, эти силы иногда на-
называют кориолисовыми силами, так же как и те силы обратного направле-
направления, с которыми действует движущееся тело на направляющую (трубку,
штангу и т. п.). Однако, как мы видели, эти силы ничем не отличаются
от «обычных» упругих сил, с которыми мы имели дело раньше. Движуще-
Движущееся тело давит на вращающуюся штангу и штанга давит на тело потому,
что они деформированы. Но для таких «обычных» упругих сил, с которыми-
действуют друг на друга деформированные тела, пет никакой необходимости
вводить специальные названия. Мы поэтому не будем называть этн силы
кориолисовыми, а сохраним этот термин для нового типа сил, которые бу-
будут введены в дальнейшем н для которых, действительно, потребуется
специальное название.
?
Рис. 72.

Ю4 силы и д формации [гл. V
§ 34. Силы и деформации
Рассмотренные примеры достаточно поясняют физическую картину
в тех случаях, когда взаимодействия обусловлены непосредственным
соприкосновением тел *).
Конечно, вся картина иногда может быть сложнее, чем в рассмот-
рассмотренных примерах, но общий характер явлений остаётся тем же. При
соприкосновении тел сначала приобретают ускорения только непо-
непосредственно соприкасающиеся их части. Отдельные части одного и
того же тела движутся вначале по-разному, и тело начинает дефор-
деформироваться. Поэтому нсякое тело, испытывающее ускорение в резуль-
результате непосредственного соприкосновения с другими телами, всегда
оказывается деформированным. Этими деформациями ускоряемых тел
и объясняется происхождение сил, с которыми ускоряемые тела дей-
действуют на ускоряющие, т. е. сил «противодействия», которые должны
существовать по третьему закону Ньютона.
Деформации ускоряемых тел часто называют динамическими де-
деформациями, чтобы подчеркнуть их отличие от статических дефор-
деформаций неподвижных тел. Конечно, происхождение статических и ди-
динамических деформаций по существу одно и то же. Как те, так и
другие являются результатом того, что разяые части тел в течение
некоторого времени двигались по-разному. Но если взаимодействуют
более чем дза тела, то может случиться, что силы, возникшие в ре-
результате деформаций, в конце концов уравновесятся и ускорения тел
прекратятся; вместе с тем прекратятся дальнейшие изменения дефор-
деформации. Эти неизменные деформации, которыми тела обладают в от-
отсутствие ускорений, и называются статическими деформациями*'").
Обычно, чтобы объяснить происхождение статических деформаций,
ограничиваются только тем, что указывают силы, которыми «дан-
«данная деформация выззана». Однако, это объяснение неполное. Силы
являются причиной движений, а деформации—-результатом дви-
движений. Поэтому, не рассматривая движений, нельзя дать полной
картины возникновения деформаций. Чтобы объяснить происхождение
статических деформаций, строго говоря, нужно так же, как и для
объяснения динамически* деформаций, на основании законов движе-
движения объяснить, почему отдельные части деформированного тела в те-
течение некоторого 'времени двигались по-разному. Правда, в случае
статических деформаций связь между силами и движениями, с одной
стороны, и между движениями и деформациями,—с другой, столь
очевидна, что можно обойтись без детального рассмотрения и прямо
связывать силы с деформациями. Но в случае динамических деформа-
*) Мы пока всё ещё оставляем в стороне силы трения.
**) Дальнейшие изменения деформаций прекратятся сразу, только если
до этого они протекали очень медленно. В противном случае в системе воз-
возникнут колебания, и статические деформации установятся только после
того, как эти колебания затухнут.

§ 34] СИЛЫ И ДЕФОРМАЦИИ 105
ций эта связь далеко не столь очевидна, и для обьясненкя их проис-
происхождения необходимо (как это было сделано в наших примерах)
рассмотреть движения, в результате которых данная деформация воз-
возникла.
Силы, действующие со сторвны ускоряемого тела на ускоряющее,
иногда называют «силами инерции». Однако, термин этот очень не-
неудачен прежде всего потому, что самое разделение тел на ускоряю-
ускоряющие и ускоряемые весьма условно и часто вообще не имеет смысла.
Далее, этот термин даёт основания думать, что между силами, дей-
действующими со стороны ускоряющие тел и со стороны ускоряемых,
есть какое-то принципиальное различие. Между тем, как мы видели,
силы эти по существу друг от друга ничем не отличаются, и их
происхождение и природа совершенно одни и те же. Эгот термин
неудачен, наконец, ещЭ и потому, что им обозначают обычно еще'
и силы сонсем другого происхождения, которые действительно сле-
следует выделять. С атим нозым типом сил мы встретимся позднее и их
мы н будем называть силами инерции. Что же касается сил, с кото-
которыми ускоряемые тела действуют на ускоряющие, то силами инерции
их назызать не следует.

ГЛАВА VI
ДВИЖЕНИЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
§ 35. Земное притяжение
Приведённые выше примеры и высказанные затем общие сообра-
соображения откосились к случаям, когда действуют упругие силы, обу-
обусловленные непосредственным соприкосновением тел.
Рассмотрим теперь случай, когда действуют силы всемирного
тяготения, ие обусловленные непосредственным соприкосновением.
Для этого, не рассматривая законов всемирного тяготения, поясним
лишь некоторые факты, касающиеся движения под действием земного
притяжения.
Как известно, все тела в данной точке под действием земного
притяжения испытывают одинаковые ускорения. Различное ускорение
некоторых тел пр,и падении, например, куска металла и куска бумаги,
объясняется только тем, что помимо Земли на эти тела при движе-
движении действует ещё и окружающая среда (воздух). Если же падение
происходит в беввоздушном пространстве, то все тела падают с оди-
одинаковым ускорением. Этот факт можно продемонстрировать при по-
помощи известного опыта с падением различных тел в стеклянной
трубе, из которой удалён воздух; бумажка и металлический шарик
в этой трубе падают с одинаковыми скоростями.
В данной точке эемного шара все свободно падающие тела об-
обладают одним и тем же ускорением. В различных же точках уско-
ускорение свободно падающего тела оказывается различным. Прежде
всего ускорение зависит от высоты тела над землёй — оно обратно
пропорционально квадрату расстояния от тела до центра земного
шара, т. е. убывает с высотой в отношении
Я* __ Я*
(/?+Л)а~Я3+2Л/?-|-#1'
где R — раднус земли и h — высота над уровнем моря. Так как
обычно h<*tR, то членом Аа можно пренебречь по сравнению с R}
и приближённо записать это соотношение в виде \j (l 4" 2-^ J. Сле-
Следовательно, при подъёме на 3 км от уровня моря ускорение сво-

§ 35] ЗЕМНОЕ ПРИТЯЖЕНИВ 107
бодного падения убывает лишь на 0,001 своей величины. Поэтому
при изменении высоты тела даже на сотни метроз ускорение свобод-
свободного падения практически можно считать постоянным.
Если мы будем измерять ускорение падающих тел в различных
точках у поверхности земного шара (на различных широтах) и будем
при этом пользоваться выбранной нами «неподвижной» системой ко-
координат, то ускорение падающих тел будет везде Одно и то же.
Впрочем в действительности это не совсем верно. Земля, как известно,
по форме несколько отличается от шара: она имеет слегка сплюс-
сплюснутую в направлении полюсов форму, так что расстояние от поверх-
поверхности Земли до центра её меньше у полюсов, чем на экваторе. По-
втому притяжение тел Землёй на уровне моря уменьшается от по-
полюсов к экватору приблизительно на 0,002 своей величины. Однако,
это различие не играет принципиальной роли в рассматриваемом нами
вопросе, и мы будем этим обстоятельством пренебрегать, т. е. будем
считать, что во всех точках на поверхности земного шара Земля
сообщает всем телам одинаковое ускорение относительно «непо-
«неподвижной» системы координат.
Ускорение же свободно падающего тела относительно Земли
(а не относительно «неподвижной» системы координат) на различных
широтах будет различно, так как точки на поверхности Земли вслед-
вследствие суточного движения Земли имеют различное ускорение по от-
отношению к «неподвижной» системе координат.
Ускорение g, отсчитываемое относительно «неподвижной» системы
координат, у полюсов равно 983 см\сек?, а у экватора 981 см\секг.
Поскольку мы пренебрегаем этим различием, мы примем g= 982 cMJcerc2
(что примерно соответствует широте в 45°) и будем считать его
одинаковым на всех широтах.
Если ускорение силы тяжести для всех тел, независимо от их
массы, оказывается одинаковым, то сама сила, с которой тело при-
притягивается к Земле, должна быть пропорциональна массе тела. Дей-
Действительно, если тело массы mi обладает ускорением g, то, как
следует из второго закона Ньютона, на него действует сила /7=тм1§-.
Точно так же на тело массы т2 действует сила Ръ = tn2g. Но так
как ускорение силы тяжести g для всех тел одно и то же, то
Силы, с которыми тела притягиваются к Земле, пропорциональны
инертным массам тел (/га, и т2 — массы, входящие во второй закон
Ньютона, т. е. как раз инертные массы тел).
Поскольку силы, с которыми тела притягиваются к Земле, про-
пропорциональны инертным массам тел, мы можем сравнивать инертные
массы тел, сравнивая силы, с которыми тела притягиваются к Земле.
Для измерения этих сил можно применять взвешивание тел.

108 движения иод действием силы ТЯ1К-СП1 [гл. vi
§ 36. Взвешивание тел
Взвешивание тел можно производить при помощи рычажных или
пружинных весов. В первом случае непосредственно сравниваются два
тела, масса одного из которых принята за эталон. Массы тел счи-
считают разными, когда система весов оказывается в равновесии. При-
Применяются и такие конструкции весов, где равновесие наступает не
при равенстве масс, а при каком-то определённом отношении между
ними (например, десятичные весы). Но принципиально это ничего не
меняет. Во всех этих случаях непосредственно сравниваются массы
двух тел.
В пружинных весах дело обстоит иначе. Массы двух тел сравни-
сравниваются не непосредственно, а косвенным образом. Взяв какую-либо
пружину, нагружают её конец известными массами и отмечают рас-
растяжение пружины, вызванное той ичи иной известной массой. На-
Нагружая затем весы неизвестной массой и отсчитывая вызванное ею
растяжение пружины, определяют величину этой массы.
Как в пружинных, так и в рычажных весах для взвешивания не-
необходимо констатировать, что система находится в равновесии, т. е.
не обладает ускорением и скоростью. Но для этого необходимо
пользоваться какой-то системой координат, относительно которой мы
смогли бы констатировать отсутствие ускорений.
Практически в качестве такой системы координат
мы всегда пользуемся Землёй: взвешивая тела, мы
устанавливаем, что чашки весов покоятся отно-
относительно стен лаборатории.
Между тем мы условились считать равными
такие дзе силы, которые, одновременно действуя
на тело, не сообщают ему ускорения относитель-
относительно «неподвижной» системы координат.
Таким образом, принципиально мы должны
Рис. 73. были бы при взвешивании констатировать отсут-
отсутствие ускорений относительно «неподвижной»
системы координат, а практически констатируем отсутствие
ускорений относительно Земли.
На результатах взвешивания с помощью пружинных весов эта
«подмена» может сказаться. Чтобы выяснить этот вопрос, рассмот-
рассмотрим, какую роль играет то обстоятельство, что сами пружинные
весы вместе с висящим на них телом обладают ускорением по от-
отношению к «неподвижной» системе координат.
Представим себе, что мы производим взвешивание на пружинных
весах, которые находятся в лифте (рис. 73), опускающемся вниз
с некоторым постоянным ускорением а. (если это ускорение а ве-
велико — порядка g, то несущественно, брать ли ускорение а относи-
относительно Земли или относительно «неподвижной» системы координат).
Каково будет растяжение пружины весоа, если мы повесим на них

§36]
ВЗВЕШИВАНИЕ ТЕЛ
109
массу /и? После того, как установится «равновесие», т. е. пру-
пружина перестанет растягиваться, масса т будет двигаться вместе
с точкой подвеса весов, т. е. также с ускорением а. (В дейст-
действительности это вовсе не равновесие, так как масса обладает уско-
ускорением.)
Под действием силы тяжести mg и натяжения пружины / тело
обладает ускорением а. Поэтому на основании второго закона Ньютона
мы можем написать:
или
ma — mg—f
f=m{g—a).
В опускающемся с ускорением а лифте натяжение-пружины оказы-
оказывается равным не mg, каким оно было бы в покоящемся лифте, а
меньшим на величину та. В частности, если лифт
падает с ускорением g, то натяжение пружины исче-
исчезает. Так оно и должно быть: если лифт, а вместе
с ним и груз падают с ускорением g, то это значит,
чго на груз не действуют никакие силы, кроме
притяжения Земли.
Иллюстрацией этого последнего случая являются
опыты Любимова. На лёгкой рамке, которая может почти
без трения скользить вдоль вертикальных направляющих
проволок, укреплены на одинаковых пружинах два или
три груза разной массы. Когда рамка покоится, грузы
эти по-разному растягивают пружины (рис. 74). Но если
ошустить рамку так, чтобы она свободно падала, то рас-
растяжение пружин исчезает и все три груза располага-
располагаются иа одинаковой высоте, соответствующей длине не-
нерастянутых пружин.
Легко объяснить, почему при освобождении рамки в
самом начале свободного падения деформация пружин
исчезает. В первый момент на рамку, кроме силы тяже-
тяжести, действует направленное вниз натяжение пружии, на
которых висят гири, и поэтому рамка падает с уско-
ускорением, большим g. Сами же гири вначале падают с
ускорением, меньшим g, так как на иих (кроме силы тя-
тяжести) действует сила натяжения пружин, направленная
вверх. Поэтому рамка догоняет гири"и растяжение пру-
пружин уменьшается. Так будет продолжаться до тех пор,
пока ие прекратится действие всех пружин, т. е. пока
все пружины не сократятся до нормальной длины. После
этого рамка вместе с грузами будет падать с одинаковым
ускорением, равным ускорению свободного падения ").
Рис. 74.
Ясно, что в случае, если лифт движется с ускорением вверк,
натяжение пружины будет больше, чем mg, на величину та.
*) Мы опять пренебрегаем теми колебаниями грузов, которые возник-
возникнут в первый момент после освобождения рамки.

110 ДВИЖЕНИЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ [гл. VI
Если мы взвешиваем тело на пружинных весах, которые движутся
ускоренно, то натяжение пружины не равно силе земного притяже-
притяжения mg, а меньше или больше в зависимости от того, куда направ-
направлено ускорение весов — к Земле или от Земли. Конечно, притяжение
Земли во всех случаях остаётся одинаковым, так как оно зави-
зависит только от конфигурации тел и не зависит от того, движется
ли тело или нет. Но притяжение Земли не равно натяжению пру-
пружины, так как тело вовсе ие покоится относительно снеподвиж-
ной» системы координат, а движется по отношению к ней с уско-
ускорением и.
Точно так же, как с взвешиванием в лифте, обстоит дело с взве-
взвешиванием в разных точках земного шара. Так как Земля вращается*)
относительно «неподвижной» системы координат, то все точки Земли,
а вместе с тем и подвешенные в этих точках весы обладают уско-
ускорением по отношению к «неподвижной» системе координат. Это уско-
ускорение направлено к центру той окружности, которую описывает
данная точка Земли (рис. 75), и равно ю2г
(w — угловая скорость Земли, г—радиус па-
параллельного круга), т. е. для различных широт
различно. Оно достигает максимума на экваторе
и падает до нуля на полюсах.
Взвешивгя тело на пружинных весах в раз-
различных точках земного шара, мы как бы по-
повторяем опыты со взвешиванием в ускоренно
движущемся лифте, причём различным широтам
земного шара соответствуют различные ускоре-
Рис. 75. Ния лифта. Только на полюсе натяжение пружины
будет равно силе, с которой взвешиваемое тело
притягивается Землёй (так как на полюсе взвешиваемое тело не имеет
ускорения по отношению к «неподвижной» системе координат). Во
всех других точках земного шара тело, покоящееся на пружинных
весах, обладает направленным к земной оси ускорением относительно
«неподвижной» системы координат и, так же как в опускающемся
с ускорением лифте, натяжение пружины будет меньше, чем при-
притяжение Земли. На экваторе натяжение пружины будет меньше,
чем на полюсе на величину na = mv>*R, где ш — угловая скорость
вращения Земли, равная примерно 7,3>10~5 радиан/сгл:, и R — ра-
радиус Земли, равный примерно 6,3-108 см. Наибольшая разница (ме-
(между полюсом и экватором) будет составлять, следовательно, около
О.З»/,,.
Весом тела называют ту силу, с которой тело действует на
покоящийся относительно Земли подвес (или подставку), к ко-
*) В рассматриваемой нами задаче мы учитываем только суточное
движение Земли (вращение вокруг своей оси). Роль годового Движения
Земли (обращения вокруг Солнца) будет выяснена позднее (§ 78).

§ 37] ОПРЕДЕЛЕНИЕ МАССЫ ВЗВЕШИВАНИЕМ 111
торому оно прикреплено (а не силу притяжения тела Землёй). Сле-
Следовательно, вес тела зависит от широты, на которой производится
взвешивание.
§ 37. Определение массы взвешиванием
Теперь легко выяснить, при каких условиях можно сравнивать
массы тел с помощью взвешивания. Как рычажные, так и пружинные
весы отмечают вес тела, т. е. силу, с которой тело давит на под-
подставку или тянет за подвес весов. Эта сила, как мы видели, равна
m(g— а), где а — вертикальная составляющая ускорения*) самих
весов относительно «неподвижной» системы координат; g есть вели-
величина постоянная, а а зависит от широты места. В рычажных весах
обе массы — эталон и измеряемая — всегда находятся в одной точке
земного шара (длиной плеч весов можно, конечно, пренебречь). По-
втому, когда оба тела покоятся на рычажных весах, а для обеих
масс одно и то же. И если веса' тел равны, то
"МиГ— а)=т^— а)
и, следовательно, т2 = mv
С пружинными весами может случиться, что мы их прокалибро-
прокалибровали в одном месте, где вертикальное ускорение самих весов, обу-
обусловленное суточным движением Земли, равно а1( а взвешиваем тело
в другом месте (иа другой широте), где вертикальное ускорение
весов другое, аг. Масса-эталон т1 при калибровке весов вызовет
растяжение пружины, соответствующее силе F1 = m1{g — а,). Взве-
Взвешиваемая же масса щ вызовет растяжение F2=m2(g— а2). Если
растяжение весов в обоих случаях окажется одинаковым, т. е. F1 = F2,
то ml^=mi, если ах=^а2.
Таким образом, с помощью пружинных весов мы можем сравни-
сравнивать массы тел только при том условии, что весы калибруются и
применяются на одной и той же широте. (Строго говоря, следовало
бы калибровать и применять весы даже в одной и той же точке
земного шара, так как и величина g немного меняется от точки
к точке вследствие отступлений от шарообразной формы и неодно-
неоднородности Земли.)
Силы притяжения тел Землёй всегда пропорциональны массам
тел. Однако, веса тел будут также пропорциональны их массам
лишь в том случае, „когда при измерениях ускорения обоих сравни-
сравниваемых тел будут одинаковы относительно «неподвижной» системы
координат.
*) Полное ускорение данной точки Земли направлено по радиусу па-
параллельного круга. Для рассматриваемого вопроса существенна только вер-
вертикальная составляющая этого ускорения, т. е. проекция его на вертикаль
данного места. Роль горизонтальной составляющей будет выяснена позд-
позднее (§ 78).

112
ДВИЖЕНИЯ ПОД ДЬЙСТВИЬЧ СИЛЫ ТЯИЙСТИ
[гл. vt
В пружинных весах это условие (равенство ускорений) может не
соблюдаться, если мы помещаем весы в разных точках земного шара.
В рычажных весах это условие обычно соблюдается само собой. Но
ее ш условие равенства ускорений будет нарушено в рычажных весах,
тс и в этом случае равновесие весов не позволяет утверждать, что
массы тел равны. Это имеет место, если одно из взвешиваемых тел
движется с ускорением. Если, например, на платформе рычажных
(дясягнчных) весов уравновешен человек, который затем приседает
на корточки, то во
время движения чело-
человека равновесие будет
нарушено, хотя масса
его тела, конечно, не
изменилась.
Очень убедительной
демонстрацией этого слу-
случая может служить взве-
взвешивание на рыча*.ных
весах так называемого
диска Максвелла — мас-
массивного диска, подвешен-
подвешенного на двух нитях, об-
обмотанных вокруг оси
диска (рис. 76). Законы
движения диска Макс-
Максвелла мы рассмотрим в
главе о движении твёр-
дого тела- Но в обп*ем
движение диска Макс-
велла таково, что диск
опускается вниз и под-
поднимается вверх с направ-
направленным вниз постоянным
ускорением, составляю-
составляющим некоторую долю
ускорения силы тяжести
(как если бы он скаты-
скатывался с не очень крутой
горы и затем вкатывался
на другую, такую же
гору). Опыт со взвеши-
взвешиванием диска Максвелла
на рычажных весах по-
показывает, что если урав-
Рис. 76.
новесигь покоящийся
диск па весах, то щш движении диска равновесие нарушается. Для восстанов-
восстановления равновесия нужно снять часть груза с другой чашки весов. Диен
оказывается «легче» как при движении вниз, так и при движении вверх. (Это
и понятно, так как ускорение диска в обоих случаях направлено вниз.) Равно-
Равновесие на рычажных, как и на пружинных, весах дает право считать массы
равными только при условии, что обе сравниваемые массы имеют одинако-
одинаковое ускорение по отношению к «неподвижной» системе координат, а в
описанном опыте это условие не соблюдено.

§ 38]
дефэрмщии тяжёлого тела
ИЗ
§ 38. Деформации тяжёлого тела
При движении тел под действием силы тяжести, так же как и в случае
непосредственного соприкосновения, принципиальную роль играет то обсто
ятельство, что все реальные тела в большей пли меньшей степени способны
деформироваться и что в результате этих деформаций возникают силы
Однако, вследствие различия в характере сил, возникающих при непосред-
непосредственном соприкосновении, и сил всемирного тяготения деформации движу-
движущихся тел в обоих случаях оказываются различными.
Все тела при свободном падении испытывают одно и то же ускорение;
поэтому, если мы разделим тело на части, то все эти части также будут
падать с одинаковым ускорением — с таким же, с каким они падали бы,
если бы были соединены между собой. Следовательно, отдельные
части свободно падающего тела не сообщают друг др}гу никаких уско-
ускорений.
Каждая часть тела приобретает ускорение под действием силы земного
притяжения, действующей непосредственно на эту часть тела, и величипа
этой силы пропорциональна массе соответствующей части тела. Такие силы,
действующие на каждый элемент тела н пропорциональные массе этого
элемента, носят название массовых сил.
Различие в хаоактере действия массовых сил и сил, возникающих при
непосредственном соприкосновении, и приводит к существенному различию
в картине деформаций. Чтобы выяснить эти различия, рассмотрим след>ю
щии конкретный пример. Тело массы т, опять удлинен-
удлиненной формы и постоянного сечения, подвешено на нити
за один из концов. Тело покоится потому, что на него
действуют две равные по величине силы — сила тяжести
mg и сила натяжения нити /. Нить действует на тело
потому, что она растянута. Происхождение этого растя-
растяжения легко объяснить таким же образом, как мы это де-
делали в предыдущей главе.
Легко видеть, что в нашем случае должна быть
растянута не только нить, но и само тело. Действителььо,
нить действует только на верхний конец тела (для упро-
упрощения будем считать, что она действует на всё верхнее
сечение). Но земное притяжение действует на все части
тела. Поэтому сила земного притяжения, действующая на
нижнюю часть тела, должна быть уравновешена силой,
действующей на эту часть тела со стороны верхней.
А для этого тело должно быть деформировано (растянуто).
Растяжение должно быть наибольшим у верхнего конца
тела и постепенно уменьшаться до нуля к нижнему концу
1ела. Этой деформацией обусловлена та сила, с которой
подвешенное тело действует на нить.
Если висящее тело начинает свободно падать, то
сначала верхние слои его имеют большее ускорение,
чем нижние (так как помимо сил тяжести иа верхние
слои действуют ещё упругие силы, направленные вниз,
а на нижние слои действуют упругие силы, направленные вверх). Деформа-
Деформации исчезают, и свободно падающее тело оказывается недеформиро-
ванным.
Для иллюстрации всей этой картины может служить мягкая пружина,
свитая из толстой проволоки. Такая пружина, поднятая за один конец, ока-
оказывается растянутой вверху сильнее всего; книзу растяжение пружины бу-
будет постепенно уменьшаться (рис. 77, а). Картина деформации пружины
в утрированном виде повторяет картину деформации всякого тяжёлого
тела, подвешенного за верхний конец. Если верхний конец пружины отпус
8 С. Э. Хайкин
Рис. 77.

114 ДВИЖЬКИЯ ПОД Д..ЙСТВИ..М С.ЛЫ ТЯЖЕСТИ [гл. VI
тить, то пружина сжимается, растяжения её исчезают и дальше она падает
в недеформированном состоянии (рис. 77, Ь).
Таким образом, тело, испытывающее ускорение только под действием
силы тяжести, оказывается недеформированным, между тем как тело, испы-
испытывающее ускорение благодаря непосредственному прикосновению других
тел, всегда оказывается деформированным. Это различие обусловлено тем,
что сила тяжести является массовой силой н сама сообщает одинаковые
ускорения всем частям тела.
Рассмотренная картина позволяет объяснить физическую природу того
неприятного ощущения, которое испытывает человек при падении. При нор-
нормальных условиях в ре^льтате действия силы тяжести отдельные органы
человеческого тела оказываются деформированными н определённым обра-
образом давят друг на друга. Это состояние для человека является нормаль-
нормальным. Когда начинается свободное падение, то деформации исчезают н от-
отдельные органы перестают давить друг на друга. Это исчезновение при-
привычных деформации и давлений и лежит а осцове «ощущения падения».

ГЛАЙЛ VII
РАВНОВЕСИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 39. Состояния равновесия и их устойчивость
В механике нас часто интересует вопрос о том, в каких поло-
положениях тело (или система тел) может находиться длительное время.
Для этого прежде всего скорость тела должна быть равна нулю, так
как иначе оно из данного положения уйдёт. Но, кроме того, и уско-
ускорение тела должно быть равно нулю, так как в противном случае
тело приобретает скорость и также уйдёт из данного положения.
Таким образом, чтобы тело могло длительно находиться в неизмен-
неизменном положении, его скорость и ускорение в этом положении должны
одновременно обратиться в нуль. Для того же, чтобы ускорение тела
в данном положении обратилось в нуль, сумма сил, действующи* на
тело в этом положении, должна быть равна нулю, т. е. это должно
быть положение равновесия. Если в положении равновесия к тому
же и скорость тела равна нулю, то говорят, что тело находится
в состоянии равновесия.
Однако, если тело оказалось в состоянии равновесия, то этого ещё
недостаточно для того, чтобы в реальных условиях оно оставалось
в этом состоянии как угодно долго. Дело в том, что в реальных усло-
условиях на всякое тело действуют случайные толчки, «возмущения». Эти
малые случайные толчки принципиально неустранимы; они всегда
будут сообщать телу малые отклонения от положения равновесия или
малые начальные скорости. Чтобы знать, что произойдёт дальше,
нужно исследовать, как ведёт себя тело не в состоянии равновесия,
а вблизи него.
При отклонении от положения равновесия силы изменяются и сумма
сил уже не будет равна нулю. Если эта сумма сил такова, что она
не вызывает дальнейшего увеличения начальных отклонений или на-
начальных скоростей тела, то тело не будет дальше уходить от состояния
равновесия. Малые толчки никогда не уведут тело далеко от состоя-
состояния равновесия. Такое состояние равновесия называется устойчивым.
Если же сила, возникшая при отклонении от положения равнове-
равновесия, такова, что она увеличивает начальные отклонения или начальные
скорости, то, как бы ни были малы начальные отклонения или ско-
8*

116
РАВНОВЕСИЕ МАТйРИАЛЬНОЙ ТОЧКИ
[гл. vii
рости, они дальше будут возрастать под действием возникших сил.
Тело будет уходить от состояния равновесия и в конце концов уйдёт да-
далеко от него. Такое состояние равиовесия называется неустойчивым.
В реальных условиях тело может длительное время находиться
только в состояниях устойчивого равновесия. Поэтому решение вопро-
• са об устойчивости состояний равновесия так же
важно, как и отыскание самих состояний равиовесия.
Устойчивость состояний равновесия, как мы
видели, зависит, от того, какие силы возникают
при отклонении от положения равновесия. Для
устойчивости необходимо, чтобы возникшие силы
возвращали тело к положению равновесия. На-
Например, на шарик, лежащий в чашке (рис. 78),
действуют сила тяжести mg и сила давления чашки F. Если
дно чашки и шарик достаточно гладкие, то сила, действующая
на шарик, нормальна к поверхности чашки (силы треиия отсутствуют).
В положении равновесия (внизу чашки) эти силы равны по величине
и противоположны по направлению. Если шарик не-
немного отклонится от положения равновесия, то рав-
равнодействующая F, сил F и mg уже не равна нулю
и будет возвращать шарик в положение равновесия.
Следовательно, состояние равновесия устойчиво.
Если же шарик лежит на вершине гладкого ку-
купола (рис. 79), то это положение также представляет
собой положение равновесия. Но при отклонении
шарика от вершины равнодействующая Fj силы тя-
тяжести и давления купола будет удалять шарик от положения равно-
равновесия. Состояние равновесия оказывается неустойчивым. И, действи-
действительно, как бы точно мы ни укладывали гладкий шарик на вершину
купола, он на ней не останется и скатится вниз.
Случай, когда шарик находится на горизонтальной плоскости,
представляет собой промежуточный случай между двумя рассмотрен-
рассмотренными. При смещении шарика равнодействующая всех сил всегда ос-
остаётся равной нулю. Такой случай, когда при смещении от положе-
положения равновесия силы вообще не возникают, принято называть без-
безразличным равновесием.
С точки зрения нашего определения безразличное равновесие так-
также является устойчивым, так как при нём не возникает сил, которые
увеличивали бы начальные отклонения тела.
§ 40. Абсолютно жёсткие связи
При решении ряда вопросов в механике применяется одно, хотя и со-
совершенно формальное, но очень важное представление, которое удобно
выяснить на рассмотренных выше примерах.
Если бы чашка и шарик были совершенно гладкие, то сила, действу-
действующая со стороны чашки, всегда была бы нормальна к поверхности чашку
Рис. 79.

§ 41] РАВНОВЕСИЕ ПРИ НАЛИЧИИ АБСОЛЮТНО ЖЁСТКИХ СВЯЗЕЙ 117
(отсутствовало бы трение). Поэтому она ие играет никакой роли при пере-
перемещениях шарика вдоль чашки. И если мы рассматриваем только переме-
перемещения шарика вдоль поверхности чашки, то мы можем вовсе не рассмат-
рассматривать сил давления чашки н принимать во внимание только составляющую
силы тяжести в направлении вдоль поверхности чашки. Она как раз будет
равна равнодействующей силе Fi. Составляющая же силы тяжести в направ-
направлении, нормальном к поверхности чашки, уравновесится силой давления
чашки. При этом чашка и шарик должны быть известным образом дефор-
деформированы. Но если шарик н чашка достаточно жёсткие, то этими дефор-
деформациями можно пренебречь. Пренебрегая деформациями чашки, мы припи-
приписываем ей такие свойства: уже при исчезающе малых деформациях чашки
могут возникнуть силы, необходимые для того, чтобы уравновесить силу
тяжести и прекратить дальнейшую деформацию чашки. Мы считаем чашку
недеформированной и всё же нормальную составляющую силы тяжести
уравновешенной давлением чашки.
Так как только составляющая силы тяжести вдоль поверхности чашки
может вызвать перемещения вдоль этой поверхности, то направление этой
составляющей решает вопрос об устойчивости состояний равновесия.
Этим приёмом часто пользуются в механике, и мы также будем нм
пользоваться. Если движение тел происходит вдоль каких-либо жёстких
н гладких направляющих или ограничено какими-либо жёсткими рычагами,
мало растяжимыми нитями и т. д., то мы часто можем не принимать во
внимание деформаций этих связей. Мы приписываем этим связям такие
свойства, как чашке: уже при исчезающе малых деформациях связей в них
возникают такие силы, которые прекращают дальнейшее увеличение дефор-
деформаций. Связи всегда деформируются41, так как только при" этом они могут
действовать на тело с некоторыми силами. Но если связи очень жёсткие,
то мы можем не принимать во внимание их малых деформаций и рассмат-
рассматривать эти связи как абсолютно жёсткие.
Рассматривая связи как абсолютно жёсткие, мы должны считать, что
возможны только такие перемещения, при которых не происходит дефор-
деформации связей. Сил, действующих со стороны связей, мы не мо^ем опреде-
определить из конфигурации (потому что мы не учитываем деформации связей).
Но это оказывается и ненужным, так как эти силы исключаются из задачи
о равновесии. После того, как задача о равновесии решена, мы сможем,
если это нужно, вычислить силы, действующие со стороны связей.
Представление об абсолютно жёстких связях хотя и не передаёт точно
свойств реальных связей, но часто оказывается применимым. Если связи
очень жёстки, то степень их жёсткости перестаёт играть роль в целом
ряде вопросов. Поэтому о жёсткости очень жёстких связей мы часто можем
сделать предположение, что она бесконечно велика.
Конечно, представление об абсолютно жёстких связях не всегда может
дать правильный ответ на вопросы, нас интересующие. Например, если
купол, на котором лежит шарик, может заметно деформироваться, то ша-
шарик на прогнувшемся куполе может оказаться в состоянии устойчивого
равновесия. Как и всегда, только опыт может решить вопрос о том, при-
пригодна ли.данная идеализация (представление об абсолютно жёстких связях)
для решения интересующей нас конкретной задачи.
§ 41. Равновесие при наличии абсолютно жёстких связей
Воспользуемся представлением об абсолютно жёстких связях для реше-
решения следующей задачи.
Гладкий шарик массы М может быть помещён на внутреннюю (рнс.80)
или внешнюю сторону (рис. 81) гладкой .цилиндрической поверхности.
К шарику прикреплена нить, перекинутая через блок. К концу нити под-

118 равновесие материальной точки [гл. vii
вешен груз т. Требуется определить условия равновесия шарика н иссле-
исследовать их устойчивость для того и другого случая.
Если цилиндрическая поверхность достаточно жёсткая, то мы можем
считать её недеформируемой. Далее, так как шарик н поверхность гладкие,
то силы, действующие на шарик
со стороны поверхности, нормаль-
нормальны к этой поверхности.
Если М > т, то шарик всегда
должен касаться поверхности.
Поэтому возможны перемещения
шарика только вдоль поверхности
цилиндра. Для решения вопроса
достаточно принять во внимание
только силы, действующие в
У/^\ направлении этого возможного
f/Wg /' fWq перемещения, т. е. вдоль поверх-
/ иости. В этом направлении дей-
ствуют составляющая силы тяже-
РиС- °"- ™с- 8*• сти Mg и составляющая натяже-
натяжения нити f. Для равновесия эти
силы должны быть равны. Так как f=mg, то условие равновесия в
обоих случаях напишется в виде:
Mgsin я = mgcos ?.
Это условие совершенно аналогично условию равновесия на наклонной
плоскости, образующей угол а с горизонтом. Шарик окажется в равновесии
в такой точке поверхности, где касательная к ней образует с горизонтом
угол а, а нить образует с горизонтом угол a-f-P, причём sin а/cos fi = т[М.
Зная положение равновесия, мы легко могли бы найти и силу давления по-
поверхности на шарик. Эта сила определится из условия, что сумма проекций
сил Afg и f на нормаль к поверхности должна уравновешиваться реакцией
поверхности.
Для упрощения дальнейшего выберем такое положение блока, чтобы
положению равновесия соответствовал угол [! = 0. В этом случае условие
равновесия примет вид:
Это условие аналогично условию равиовесня на наклонной плоскости, когда
иить параллельна наклонной плоскости.
Исследуем теперь вопрос об устойчивости обоих состояний равновесия.
Для этого мы должны найтн силы, которые возникнут при малых смеще-
смещениях шарика относительно положения равновесия. Пока смещения малы,
можно считать, что направление нити всё время совпадает с касательной
к поверхности, т. е. р=гО. Тогда в первом случае (рис. 80) при смещении
шарика влево угол а уменьшится и, значит, Мg sin я < mg, т. е. равнодей-
равнодействующая будет направлена вправо — будет возвращать шарик к положению
равновесия. При смещении вправо угол а увеличится и Mg sin a > mg, т. е.
возникшая сила будет также возвращать шарик к положению равновесия. Сле-
Следовательно, на внутренней стороне цилиндра равновесие шарика устойчиво.
Наоборот, на внешней стороне цилиндра (рис. 81) при смещении шари-
шарика влево угол а увеличится, т. е. Mgsina > mg, н равнодействующая этих
сил будет ещё дальше отклонять шарик от положения равновесия. При сме-
смещении шарика вправо угол я уменьшится и Mg sin a <^ mg. Опять возникшая
сила будет удалять шарик от положения равновесия. На внешней стороне
цилиндра равновесие шарика неустойчиво.

ГЛАВА VIII
СИЛЫ ТРЕНИЯ
§ 42. Силы трения
Силы трения по своему характеру существенно отличаются от
упругих сил и сил всемирного тяготения. Отличие состоит в том,
что силы трения в той или иной мере зависят не только от конфи-
конфигурации тел, но и от их скоростей. Впрочем это различие не идёт
так глубоко, как можно было бы думать. Вероятно, в конечном счёте
силы трения всё-таки зависят только от конфигурации тел, ио эта
зависимость не выступает так явно, как в случае сил всемирного тяго-
тяготения и упругих сил. Однако, вопрос о происхождении сил трения
выходит за рамки механики. В механике мы огра-
ограничимся только изучением свойств сил трения,
как механических сил,и той роли, которую они
играют при движении.
Силы, действующие между соприкасающи-
соприкасающимися твёрдыми телами, могут быть, вообще
говоря, направлены не по нормали к поверхно-
поверхности раздела соприкасающихся тел. Например, Рис. 82.
изогнутая стальная пружина (рис. 82) может
действовать на брусок, к которому она прикасается, с силой F,
направленной под каким-то углом к поверхности соприкосновения.
При этом величина и направление действующей силы . зависят не
только от внутренних упругих свойств пружины и бруска, но и от
состояния их поверхностей.
Разложим силу, действующую на брусок со стороны пружины,
на две составляющие — нормальную Fn и тангенциальную F^ (рис. 82).
Каждую из составляющих мы можем измерить обычным способом
(с помощью динамометров).
Изменяя состояние соприкасающихся поверхностей, например,
степень их шероховатости и т. п., мы обнаружим, что нормальная
составляющая Fn не зависит от свойств поверхностей, а лишь от
величины деформации тела и пружины. Это уже известный нам тип
сил — упругие силы. Между тем тангенциальная составляющая F,
существенно зависит от свойств поверхностей и при изменении их
изменяется в широких пределах.
Ь.

120 силы трения [гл. via
В случае, если соприкасающиеся твёрдые тела движутся друг
относительно друга (например, одно тело скользит по другому),
также возникают такие тангенциальные силы. Эти тангенциальные
силы, возникающие между соприкасающимися телами, и называ-
называются силами трения.
Тангенциальные силы возникают при известных условиях не толь-
только между поверхностями твердых тел, но и между соприкасающи-
соприкасающимися поверхностями твердого тела и- жидкости или твёрдого тела и
газа. В этом случае тангенциальные силы возникают только при
движении жидкости (или газа) относительно
твёрдого тела. Покоящаяся жидкость или
газ может действовать на твёрдое тело только
с силой, нормальной к поверхности сопри-
соприкосновения. Между тем в случае твёрдых
тел тангенциальные силы могут возникать
и между неподвижными телами.
Обнаружить тангенциальные силы, возникаю-
возникающие между движущимся газом и твёрдым телом,
рис gg можно при помощи следующего опыта (рис. 83).
На ось мотора насажен гладкий диск. Парал-
Параллельно ему укреплена пластинка, которая может
легко вращаться вокруг оси. Эта пластинка удерживается в опреде-
определённом положении при помощи мягкой спиральной пружниы. К пла-
пластинке причреплен указатель, конец которого движется вдоль шкалы.
Если мотор привести во вращение, то пластинка поворачивается на неко-
некоторый угол в направлении вращения мотора н остаётся в этом положении.
Очевидно, что это может быть вызвано только тангенциальными силами,
действующими на пластинку со стороны воздуха (так как диск с пластин-
пластинкой непосредственно не соприкасается). Воздух, приведённый в движение
диском, действует на пластинку с силами, направлен шми вдоль поверхно-
поверхности соприкосновения воздуха н пластинки. В жидкости этот опыт дал бы
ещё более заметный эффект.
Эти тангенциальные силы, действующие со стороны движу-
движущейся жидкости или газа на твёрдые тела, также называют
силами трения. В эгом случае силы трения зависят как от состоя-
состояния поверхности твёрдого тела, соприкасающейся с жидкостью, так
и от свойств самой жидкости.
При относительном движении твёрдого тела и соприкасающейся
с ним жидкости или газа могут возникать и другие силы, кроме
тангенциальных. Например, если плоская пластинка движется в жидко-
жидкости нормально к своей поверхности, то изменяются нормальные
силы, действующие на поверхность пластинки. Обусловленные дви-
движением изменения нормального давления таковы, что давление на
переднюю сторону пластинки больше, чем на заднюю, и поэтому
равнодействующая нормальных давлений направлена навстречу дви-
движению.
Эта сила, возникающая при движении тела в результате измене-
изменения нормальных давлений, носит название сопротивления среды.

§ 43] ИЗМЕРЕНИЕ СИЛ ТРЕНИЯ 121
Силы сопротивления среды могут быть гораздо больше, чем силы
трения, например в случае тонкой пластинки при продольном движе-
движении пластинки возникающие силы обычно гораздо меньше, чем при
её движении в направлении нормали. Поэтому при движении тела
в жидкости или газе сопротивление среды часто играет ббльшу.о
роль, чем силы трения. Происхождение этих двух типов сил, их
зависимость от свойств тел (формы, состояния поверхностей и т. д.)
совершенно различны *). Но как силы трения, так и силы сопротив-
сопротивления среды зависят от скорости движения и качественно одинаково
влияют на характер движения. "Поэтому с точки зрения механики
эти силы целесообразно объединить и рассматривать их вместе.
В этой главе под силами трения мы будем понимать и собствен-
собственно силы трения, и сопротивление среды, не разделяя их.
§ 43. Измерение сил трения
Для измерения сил трения мы будем пользоваться тем же мето-
методом, каким мы пользовались для измерения всех другие сил: силы
равны и противоположны, если, действуя одновременно на огно и то
же тело, они не сообщают ему ускорений. Поэтому, чтобы найти
силу трения, действующую на какое-либо тело, достаточно измерить
ту силу, которую необходимо приложить к телу, чтобы оно двигалось
без ускорения, т. е. с постоянной скоростью. Этим способом обычно
и пользуются для определения силы трения.
Например, для того, чтобы определить силу трения (и сопротивления
среды), действующую со стороны жидкости на движущееся в ней тело,
прикрепляют динамометр одним концом к испытуемому телу, а дру[ им —
к движущейся с постоянной скоростью тележке. Измеряя показания дина-
динамометра при различных скоростях тележки, тем самым определяют и силу
треиия при разных скоростях. Для таких измерений строятся специальные
гидроканалы.
Для измерения сил трения и сопротивления среды в случае движения
в воздухе пользуются тем обстоятельством, что силы трения и сопротивле-
сопротивления среды должны быть одинаковы в обоих случаях, когда тело движется
с постоянной скоростью в среде или когда тело покоится, а среда движется
с той же скоростью в обратном направлении.
Поэтому, если мы закрепим тело при помощи динамометров и будем
обдувать его потоком воздуха, имеющим известную скоэость v, то показа-
показания динамометров дадут нам величину и направление сил, действующих на
тело со стороны движущегося воздуха, а вместе с тем и те силы, которые
действовали бы на тело, если бы оло двигалось с той же скоростью v в
покоящемся воздухе.
Для получения быстрого и однородного (т. е. имеющего одинаковую
скорос.ь по всему сечению) потока воздуха применяют аэродииамичесю е
трубы, в которых движение воздуха создаётся при помощи мощных венти-
вентиляторов.
*) Происхождение этих сил и их свойства будут выяснены в механика
жидкостей и газов (гл. XVII).

122 силы трения [гл.
VIII
Для измерения сил трения, действующих между твёрдыми телами, одно
из соприкасающихся тел укрепляется при помощи динамометров, которые
и измеряют тангенциальные силы, действующие на это тело со стороны
другого. Это второе тело может покоиться или двигаться (скользить) отно-
относительно первого, и таким образом измеряют силы трения, соответствую-
соответствующие различным скоростям движения соприкасающихся тел. Такие приборы
называются трибометрами.
Измеряя силы трения, возникающие при различных движениях,
мы сразу обнаружим, что эти силы зависят от скорости движения
одного из соприкасающихся тел относительно другого. Эту скорость
мы для краткости будем называть относительной скоростью (хотя,
как мы уже неоднократно указывали, всякая скорость по существу
своему относительна).
Повседневный опыт показывает, что сила треиия всегда направ-
направлена навстречу относительной скорости. Чтобы поддерживать движе-
движение тела с постоянной скоростью, всегда нужно прикладывать силу
в направлении относительной скорости движущегося тела. Следоза-
тельно, сила трения зависит от относительной скорости уже по од-
одному тому, что при изменении направления относительной скорости
изменяется и направление силы трения. Но и величина силы трения
всегда в ббльшей или меньшей степени зависит от величины отно-
относительной скорости.
§ 44. Сухое и жидкое треиие
Характер зависимости от скорости для сил треиия между двумя
твёрдыми телами и сил трения между твёрдым телом и жидкостью
{или газом) оказывается совершенно различным. Наиболее существен-
существенным в этом различии является совершенно разное поведение тех
и других сил при малых скоростях*. Именно, в случае соприкосно-
соприкосновения твёрдых тел, как бы ни была мала скорость их относитель-
относительного движения, силы трения всегда имеют конечную величину и со-
сохраняют конечную величину, когда относительная скорость движения
надает до нуля. В случае же соприкосновения твёрдого тела с жид-
жидкостью или газом все силы трения (в том числе и сопротивление среды)
с уменьшением скорости также уменьшаются и исчезают, когда ско-
скорость тела относительно среды падает до нуля.
Это существенное различие между силами трения в обоих случаях
можно продемонстрировать при помощи следующего опыта. Если деревян-
деревянный брусок лежит в сосуде с водой, то, как бы малы ни были силы, дей-
действующие на брусок, они заставят его медленно двигаться (плыть). Чтобы
привести брусок в движение, достаточно слегка подуть на него. Значит,
малая сила, действующая при этом на брусок, всё же больше, чем сила
трения, действующая со стороны воды. Но если этот же брусок лежит на
столе, то, слегка подув на него, мы уж не приведём его в двяжение. Даже
более значительные силы не всегда приведут брусок в движение. Следова-
Следовательно, сила трения уравновешивает действующую Tia брусок силу, т. е.
сила трения имеет конечную величину и тогда, когда брусок покоится от-
относительно сюла.

§ 45] ЗАВИСИМОСТЬ СИЛЫ ЖИДКОГО ТРЕНИЯ ОТ СКОРОСТИ 123
По этой же причине человек, упираясь шестом в дио, может двигать
баржу весом в сотни тонн (конечно, очень медленно), но никогда не смо-
сможет сдвинуть с места поезд того же веса.
Различия в характере зависимости сил трения от скорости приво-
приводят к тому, что оба тина сил трения совершенно по-разному влияют
иа характер движений. Поэтому при изучении влияния сил трения на
движение тел необходимо различать эти два типа сил. Принято на^
зывать сухим трением силы трения, которые не обращаются в нуль,
когда относительная скорость равна.нулю, жидким трением—силы
трения, которые обращаются в нуль вместе со скоростью.
Мы рассмотрим сначала влияние жидкого 1рения на движение
тел.
§ 45. Зависимость силы жидкого трения от скорости
Силы жидкого трения возникают при движении твёрдого тела
в жидкости или газе, причём эти силы зависят от относительной
скорости тела и среды и растут со ско-
скоростью сначала медленно, а затем быстро.
Зависимость силы трения / от относитель-
относительной скорости v выглядит примерно так, как
показано на рис. 84. При малых относитель-
относительных скоростях <о зависимость силы трения от
скорости можно выразить линейным законом:
/ = — kxvx (8.1)
где fcj — коэффициент трения (знак минус
) казывает, что сила направлена навстре- Уж. 84.
ч/ относительной скорости). При больших
относительных скоростях силу трения можно выразить в виде:
1 — ±.Ь&\ (8.2)
причём должен быть взят знак, противоположный знаку v (так как
сила трения направлена навстречу скорости). Значения коэффициен-
коэффициентов fe, и k2 зависят от свойств среды, формы тел и состояния их
поверхности.
В частности, коэффициент kx растёт с увеличением вязкости сре-
среды. Поэтому, например, коэффициент k1 для движения в воде гораз-
гораздо больше, чем для движения в воздухе, а в .глицерине больше, чем
в воде. Коэффициент k2 для тел, не имеющих резких изгибов
и острых выступов («обтекаемая форма» тел), гораздо меньше, чем
для тел, имеющих выступы, резкие изгибы и т. д. Кроме того, зна-
значение обоих коэффициентов зависит от размеров тел. Чем меньше
поперечные размеры тел, тем меньше и коэффициенты k{ и k2.
Теоретический расчёт коэффициентов /г, и kt возможен только
для тел простейшей формы. Поэтому величины коэффициентов kx и ?2

124 силы трения [гл. vuj
обычно определяют опытным путём, измеряя силу, действующую на
тело со стороны среды, при различных скоростях движения. Напри-
Например, когда речь идет о движении тел в воздухе, коэффициенты
fej и k2 определяют путём «продувки» тела в аэродинамической трубе.
Необходимо, однако, иметь в виду, что не только самые вели-
величины коэффициентов /г, и /г3, но и те области скоростей, в которых
можно считать силы трения линейно или квадратично зависящими от
скорости, также зазисят от размеров и формы тел и свойств среды.
Таким образом, нельзя придавать сколько-нибудь общего значения при-
приведённым формулам зависимости сил трения от скорости. Но всё же
расчёты, производимые при помощи этих формул, дают известное
представление о характере движения тел в сопротивляющейся среде.
§ 46. Падение тел в сопротивляющейся среде
Приведёнными выше формулами мы воспользуемся, в частности, для
того, чтобы произвести некоторые расчёты, касающиеся падения тел в воз-
воздухе и вообще в сопротивляющейся среде.
Уравнение движения для тела, падающего под действием силы тяжести
в сопротивляющейся среде, можно написать следующим образом:
^ = Р~ЦР), (8.3)
где f(v) — сопротивление среды, направленное навстречу движению тела,
т. е. вверх, а Р—сила притяжения Земли (нли, точнее, разность между
силой притяжения и «выталкивающей» силой окружающей среды — воздуха
или воды). В большинстве случаев эту силу Р можно считать постоянной.
Если падение началось без начальной скорости, то в начале f(v) = 0.
Поэтому в начальный момент тело имеет такое же ускорение, как и в от-
отсутствие сопротивления среды. Но при возрастании скорости возрастает
и /(»); при этом сумма сил, действующих на тело, Р—/(с) уменьшается
и вместе с тем уменьшается и ускорение. Когда скорость достигнет такого
значения »о, при котором f(v9) = P, то ускорение обратится в нуль и даль-
дальше тело будет падать с постоянной, «установившейся» скоростью *).
Величина установившейся скорости зависит, с одной стороны, от веса
тела, а, с другой, — от того, как изменяется'сила f (v) со скоростью. Чем
меньше Aj или k^ в формулах, выражающих зависимость сопротивления
среды от скорости, тем больше должно быть vq, чтобы f(t>o) достигло зна-
значения Р. Но ki и k2 уменьшаются с уменьшением размеров тел. Поэтому,
чем больше вес тела при данных его размерах, т. е. чем плотнее тело,
тем больше установившаяся скорость (и тем больший должен быть пройден
путь, для того чтобы эта скорость была достигнута).
Установившуюся скорость е0 можно найти из условия f(vu) = P, если
нам известно, как именно зависит сила f(v) от скорости. Для тел доста-
достаточно плотных при падении в воздухе установившаяся скорость во всяком
случае настолько велика, что можно применять формулу (8.2). Тогда
*) При падении тел с большой высоты нужно принимать во внимание
изменение плотности воздуха с высотой. Поэтому при приближении к Зем-
Земле сопротивление воздуха возрастает и скорость падения не толькд пере-
перестаёт возрастать, но даже начинает уменьшаться. Для упрощения мы, од-
однако, не будем принимать во внимание этого обстоятельства.

§ 47] парашютный прыжок 125
u\i. Установившаяся скорость падения в воздухе для тел одинако-
одинаковых размеров и формы (для которых k2 одно н то же) растёт пропорцио-
пропорционально квадратному корню из веса тел*).
При одной и той же форме тел кг растёт примерно пропорционально
квадрату линейных размеров тел, а в некоторых случаях даже медленнее
(но во всяком случае не быстрее). Вес же тел, если они сделаны из одина-
одинакового материала, растёт пропорционально объёму (т. е. кубу линейных
размеров), следовательно, во всяком случае быстрее, чем k3. Поэтому тела
одинаковой формы и сделанные из одинаковых материалов, брошенные с
большой высоты, достигают Земли с тем большей установившейся скоростью,
чем больше вес тела.
Например, сброшенные с высоты более 5000 — 6000 м авиационные
бомбы достигают Земли уже с установившейся скоростью. При этом устано-
установившаяся скорость возрастает с увеличением веса бомб. Для малых бомб уста-
установившаяся скорость составляет 150—200 м/сек, а для больших достигает
300 м/сек. По той же причине тела малых размеров даже при большой плотности
имеют сравнительно незначительную установившуюся скорость. Падающая
с большой высоты шрапнель или мелкие осколки снарядов достигают Земли
со скоростями, не превышающими 100 м/сек.
§ 47. Парашютный прыжок
Для человеческого тела (вследствие относительно больших его размеров
и мало благоприятной формы) коэффициент ?г сравнительно велик — в системе
CGS он равен примерно 2 г/см (коэффициент kiy конечно, зависит от поло-
положения тела и его ориентировки по отношению к скорости; приведённое зна-
значение даёт лишь порядок величины).
Принимая вес человека Р = 70 уг =а7• 107 дн, мы получим для скорости
установившегося движения значение v0 = У'l-107/2 =s6-10?см\сек = 60м/сек.
С какой бы высоты ни падал человек, если высота падения достаточно ве-
велика — примерно более 700 м,— то он достигнет Земли всегда с одной и той
же скоростью, около 60 м/сек.
Для парашюта (вследствие его больших поперечных размеров и спе-
специальной формы) ki примерно в 100 раз больше, чем для человеческого
тела, т. е. *3 = 200 г\см.
При прыжке с парашютом установившаяся скорость равна поэтому
5—6 м/сек и соответствует той скорости, которая была бы достигнута при
прыжке без парашюта с высоты около 2 м.
Если парашютист прыгает с раскрытым парашютом (прыжок с трениро-
тренировочной парашютной вышки), то его скорость монотонно возрастает, пока не
достигнет значения установившейся скорости (примерно 6 м/сек). Если па-
парашют при прыжке раскрывается не сразу, скорость парашютиста сначала
быстро растёт и, если затяжка составляет более 700 м, парашютист дости-
достигает установившейся скорости падения без парашюта (примерно 60 м\сек).
После раскрытия парашюта сразу возникают очень большие силы, дейст-
действующие на парашют со стороны воздуха. Поэтому скорость падения быстро
уменьшается до установившейся скорости падения с парашютом F м/сек).
Большие ускорения при раскрытии парашюта представляют собой наи-
наиболее серьёзное физическое испытание для организма парашютиста nptf
затяжном прыжке. Само же падение с установившейся хотя и большой
*) В некоторых специальных случаях установившаяся скорость ока-
оказывается столь большой (например, для тяжёлых авиационных бомб, сбро-
сброшенных с большой высоты), что достигает и даже превосходит скорость
звука C30 м/сек). Тогда формула / = tafl перестаёт быть верной.

126
СИЛЫ ТРЕНИЯ
ГЛ. VIII
скоростью не связано ни с какими физическими изменениями в организме,
так как, поскольку движение происходит равномерно, все органы находят-
находятся в таком же состоянии, как и у покоящегося человека.
С физической точки зрения человек, падающий с по-
постоянной скоростью в 60 м\сек% находится в таком жо
состоянии, как и покоящийся человек, которого обдувает
ветер скоростью в 60 м\сек.
Воспроизвести картину прыжка с раскрытым пара-
парашютом можно при помощи описанной нами падающей
рамки, если к рамке приделать большой парашют из тка-
ткани (рис. 85). В начале падения натяжение пружин, на кото-
которых висят гири, исчезнет, как в опыте без парашюта (ско-
(скорости малы и сопротивление воздуха незначительно). Но
после 3—4 м падения скорость, а вместе с тем и сопро-
сопротивление воздуха заметно возрастают. Ускорение умень-
уменьшается, и пружины снова начинают растягиваться. Если
парашют достаточно большой, то падение от потолка до
пола аудитории F—7 м) оказывается достаточным для
того, чтобы скорость почти достигла установившейся; пру-
пружины к концу падения растягиваются почти до того поло-
положения, которое они занимали при покоящейся рамке.
В примерах с падением авиационной бомбы и пара-
парашютным прыжком мы предполагали, что падающее тело не
имеет начальной скорости. В действительности дело обыч-
обычно обстоит не так. Сброшенная с самолёта бомба или
выпрыгнувший парашютист имеет начальную скорость,
равную скорости самолёта.
Для рассмотрения задачи в этом более общем случае
следует разложить начальную скорость падающего тела
на вертикальную и горизонтальную составляющие. Для
вертикального движения тела мы получим прежнюю задачу
падения под действием силы тяжести, но с некоторой на-
начальной скоростью, равной вертикальной составляющей
начальной скорости тела. Для горизонтального движения
мы получим другую задачу: движение в сопротивляющейся
среде с начальной скоростью, ио без действия внешней
силы. Горизонтальная составляющая скорости тела будет всё время
уменьшаться, стремясь к нулю (установившаяся скорость равна нулю).
§ 48. Падение при малых скоростях
В тех случаях, когда скорость установившегося движения невелика
и движение начинается без начальной скорости (или с очень малыми на-
начальными скоростями), во всё время движения можно считать, что f(v) =
= — fcjtt, и уравнение движения имеет вид:
dv n .
mjf = P-bP, (8.4)
где Р—разность между весом тела и «выталкивающей силой», действующей
со стороны окружающей среды. Установившаяся скорость тогда будет
Р
Рис 8*5
Влияние размеров и формы тела на скорость установившегося движения
в общих чертах такое же, как и в предыдущем случае. Чем больше размеры
тела, тем меньше установившаяся скорость падения тела при данном его
весе. Опять-таки, поскольку /fej растёт во всяком случае не быстрее, чем
пропорционально квадрату линейных размеров тела, а вес растёт пропорци-

§ 49}
ТРЕНИЯ ПОКОЯ
12?
онально объёму, т. е. кубу линейных размеров, то с увеличением линейных
размеров тел установившаяся скорость их падения растёт. Поэтому, напри-
например, крупные капли тумана опускаются быстрее мелких, а крупные частицы
песка оседают в воде быстрее, чем мелкие.
Медленное движение с установившейся скоростью и влияние размеров
тел можно наблюдать, опуская в сосуд с глицерином небольшие фарфоровые
шарики. Шарики опускаются примерно с постоянной скоростью и крупные
шарики опускаются быстрее мелких.
Для тел шарообразной формы при медленном движении коэффициент kt
оказывается пропорциональным радиусу шара, т. е. растёт, как линейные раз-
размеры тел. Вес же шара растёт пропорционально кубу радиуса и уже не-
небольшое увеличение размеров шарика заметно сказывается на увеличении
скорости установившегося движения.
Для тел шарообразной формы при медленном движении коэффициент kx
был вычислен теоретически Стоксом. Оказалось, что
где а — радиус капли, а р — постоянная, характеризую-
характеризующая вязкость среды, Так называемый коэффициент вяз-
вязкости.
С помощью формулы Стокса по скорости установив-
установившегося движения тела можно определить радиус тела,
если известна вязкость среды. Этим часто пользуются
для определения размеров мелких шарообразных частиц —
капель, зёрен эмульсии и т. д. Наоборот, при известных
размерах шариков формула Стокса позволяет определить
коэффициент вязкости среды. Влияние вязкости среды на
величину установившейся скорости можно продемонстри-
продемонстрировать, бросая фарфоровые шарики я сосуд с водой и
глицерином. В воде шарики падают гораздо быстрее, чем
в глицерине (рис. 86).
Все наши расчёты относились к установившемуся
движению. Поэтому мы ничего не могли сказать о том,
1
о
я
1
1
И
о
С
i
Ыо
Рис. 86.
за какое время тело достш авт установившейся скорости и какой путь оно
при этом проходит. На все эти вопросы можно получить ответ, только
проинтегрировав уравнение движения. Рассмотрение этой задачи показы-
показывает, что чем больше установившаяся скорость, тем больше времени тре-
требуется, чтобы она установилась.
§ 49. Трения покоя
Силы сухого трения возникают, например, между несмазанным»
соприкасающимися поверхностями твёрдых тел. На величину этих
сил и характер их зависимости от скорости существенно влияют со-
состояние поверхностей, их обработка, наличие загрязнений и т. д.
Вместе с тем величина этих сил зависит от величины нормального
давления между поверхностями. Сила трения между соприкасающимися-
твёрдыми телами обладает характерной чертой сухого трения — она
не обращается в нуль вместе со скоростью. Сила трения, которая
может существовать между соприкасающимися, но не движущимися
телами, носит название трения покоя.
Для демонстрации особенностей силы трения покоя может служить сле-
следующий опыт (рис. 87). На столе лежит тело М, к которому прикреплена
перекинутая через блок нить с чашкой на конце. Пока на чашке нет

128 силы трения [гл. vi и
груза (весом чашки пренебрегаем), тело, конечно, покоится и сила трения
равна нулю. Положим теперь на чашку небольшой груз Р; тело всё же
остаётся в покое. Следовательно, кроме натяжения ннти на тело действует
ещё сила трения, равная по величине натяжению нити и направленная в
противоположную сторону. При увеличении груза на чашке тело будет
оставаться в покое, пока груз этот не достигнет определённой величины
(после чего возникает скольжение). Пока не возникло скольжение,сила тре-
ния всё время остаётся равной натяжению
нити и изменяется при изменении этого иа-
тяжения. То же самое происходило бы
при изменении направления нити.
Величина и направление силы тре-
трения покоя определяются величиной
р „ и направлением той внешней силы,
которая должна была бы вызвать
скольжение. Сила трения покоя всегда равна по величине и про-
противоположна по направлению этой внешней силе.
Сила трения покоя может иметь любую величину и любое напра-
направление в плоскости соприкосновения, но по величине не может пре-
превосходить некоторого определённого значения, которое называют
максимальной силой трения покоя. До тех пор, notfa внешняя
сила не превосходит максимальной силы трения покоя, скольже-
скольжение не возникает. Сила трения покоя «автоматически» принимает
такое значение, чтобы скольжение не возникло.
Законы сухого трения были сформулированы Кулоном. Величина
максимальной силы трения покоя fwax зависит от величины силы нор-
нормального давления между поверхностями. _ Если в нашем опыте
(рис. 87) увеличивать силу нормального давления, то примерно про-
пропорционально этой силе будет возрастать и величина того груза, ко-
который нужно положить на чашку, чтобы возникло скольжение. Сле-
Следовательно,
где N— сила нормального давления.
Как показывает опыт, величина /тах зависит от состояния сопри-
соприкасающихся поверхностей, но не зависит ет их размеров. Если тело
в нашем опыте (рис. 87) имеет форму прямоугольного параллелепи-
параллелепипеда с одинаково обработанными поверхностями и мы положим era
на другую грань, имеющую другие размеры, то fnax не изменится.
При одинаковых условиях по всей поверхности соприкосновения силу
трения, приходящуюся на единицу площади, можно рассчитать, раз-
разделив всю силу трения на площадь поверхности соприкосновения.
Максимальная сила трения покоя, отнесённая к единице площади со-
соприкосновения S, /1тах выразится в виде:
f f max •• _
J\n,ax 5 ^ S '
и так как NjS = P есть нормальное давление, то
f\max ~~ V-P'

¦§49]
ТРЕНИЯ ПОКОЯ
129
Это — так называемый закон трения Кулона. Величина ц носит на-
название коэффициента трения покоя.
Закон Кулона соблюдается лишь приблизительно и притом лучше
для больших давлений, чем для малых. Его можно применять также
и тогда, когда давление в разЕШх точках соприкосновения различно.
Но тогда для подсчёта результирующей силы трения f,,aX нужно
разбить всю поверхность соприкос-
соприкосновения на отдельные малые эле-
элементы, на которых давление можно
считать одинаковым, и просуммиро-
просуммировать все силы трения, действующие
на отдельные элементы поверхности
(т. е. взять интеграл силы f\max по
поверхности соприкосновения).
Для определения jj. можно поль-
зоватьсч методом предельного угла.
Если два тела, для которых нужно
измерить ц, положить одно на другое и затем наклонять их (рис.
88), то при определённом угле наклона оц верхнее тело начнёт сколь-
скользить по нижнему. Этот угол наклона и называется, предельным углом.
Зная угол наклона а, легко подсчитать величину нормальной и тан-
тангенциальной составляющих, действующих со стороны нижнего тела
на верхнее:
Fn = mg cos a, />= mg sin а,
где т — масса верхнего тела.
Если предельный угол есть а.х, то для этого угла FtjS=fli^lx
(S—площадь соприкосновения), и так как FJS=^P, то
Рис.
Для иллюстрации ниже приводится таблица значений коэффициен-
коэффициентов трения покоя для некоторых материалов при различном состеянии
соприкасающихся поверхностей.
Коэффициент трения покоя ц
Пара тел
Сталь по сталн — поверхности смазаны маслэм .
Металл по дереву, сухие
Металл по дереву, смазанные маслом
Дерево по дереву, сухие
Кожа по металлу, сухие
Кожа по металлу, смоченные водой
Сталь по льду . .
0,15
0,12
0,5
0,1
0,65
0,6
0,2—0,1
0,6
0,027
9 С. Э. Хаакщ

130
СИЛЫ ТРЕНИЯ
[гл. viir
-ь-
§ 50. Треиие скольжения
Когда внешняя сила достигает величины fmaX, возникает сколь-
скольжение. При этом сила трения продолжает существовать — она назы-
называется в этом случае трением скольжения. Силы трения скольжения
зависят от материала тел и состояния поверхностей, но, кроме того,
они зависят и от скорости скольжения (относительной скорости тел).
Самый характер зависимости силы трения скольжения от скорости
для различных тел и различной обработки поверхностей весьма раз-
различен, но для разнородных мате-
материалов (если поверхности не под-
подвергались какой-либо специальной
обработке и очистке) сила трения
скольжения обычно вначале падает
с увеличением скорости, а затем
снова начинает возрастать.
Характер зависимости силы
трения от скорости скольжения
изображён на рис. 89. Эта харак-
характеристика силы трения передаёт
также и особенности силы треиия
покоя. При относительной скорости, равной нулю, сила трения (тре-
(трение покоя), как мы знаем, может иметь любое значение, не пре-
превосходящее /тах. Этому соответствует вертикальный участок харак-
характеристики, совпадающий с осью ординат.
Таким образом, сила трения как функция скорости скольжения
f(v) неоднозначна при значении v = 0. При v=0 она не имеет
производной, и поэтому её не всегда можно дифференцировать. Эти
обстоятельства необходимо учиты-
учитывать, когда /(^) входит в уравнения
движения.
Изменение нормального давления
между соприкасающимися телами
влияет на величину силы трения
скольжения качественно так же, как
и на величину трения покоя. Чем
больше нормальное давление, тем
больше сила трения скольжения
при той же скорости скольжения.
В некоторых специальных случаях (для однородных твёрдых мате-
материалов или при специальной обработке соприкасающихся поверхно-
поверхностей) сила трения скольжения оказывается очень мало зависящей от
скорости и примерно равной максимальной силе трения покоя; харак-
характеристика силы трения в этих случаях имеет вид, приведённый на
рис. 90. Сила трения скольжения остаётся всё время примерно равной
силе трения покоя, и к ней также может быть применён закон Кулоиа.
Г
-V
и
-f
Рис. 90.

§ 51] РОЛЬ СУХОГО ТРЕНИЯ 131
Входящий в него коэффициент трения ц будет относиться не только
к максимальной силе трения покоя, но н к силе трения скольжения.
Вообще же, поскольку сила трения скольжения не остаётся постоян-
постоянной при данном давлении (так как она меняется при изменении ско-
скорости скольжения), смысл коэффициента jj. для трения скольжения
становится определённым, только если речь идёт о какой-нибудь оп-
определённой скорости скольжения.
§ 51. Роль сухого трения
Трудно указать не только какую-либо машину или механизм, но
и вообще движение тзёрдых тел на земле (за исключением полета и
плавания), где сухое трение не играло бы принципиальной роли. При
этом сухое трение не всегда играет вредную роль, препятствующую
движению. Очень многие движения без сухого трения, со всеми его
особенностями, были бы незозможны. Примеров таких движений можно
привести множество. Достаточно указать, что человек не мог бы хо-
ходить, если бы отсутствовали силы трения. Именно силы трения-, воз-
возникающие при ходьбе между подошвами и землёй (обычно силы тре-
трения покоя), двигают тело человека. Там, где силы сухого трения
являются причиной движения, обычно играют роль силы трения покоя,
несмотря на то, что тела, между которыми возникают эти силы, дви-
движутся. В этом смысле особенно типичны случаи вращения и качения,
причиной которых являются силы сухого трения.
Примером вращения, вызызаемого силами сухого трения, является
движение ремённого приводного механизма. Ведущий шкив вращается
вместе с двигателем, на вал которого он насажен. Сам ремень и ве-
ведомый шкив приводятся в движение силами трения, действующими
между шкивами и надетым на иих ремнём. При этом нормально ремень
и шкивы движутся так, что линейные скорости на окружности шкива'
и внутренней поверхности ремня одинакозы. Поэтому не происходит
тангенциальных смещений соприкасающихся точек ремня и шкива
друг относительно друга — скольжение отсутствует*), и между со-
соприкасающимися поверхностями действует трение покоя. Величина этой
силы определяется величиной других сил **), действующих на шкив
со стороны нагрузки — вращаемого механизма. Если силы, действую-
действующие на шкив со стороны нагрузки, оказываются очень большими, то
максимальной силы трения покоя между ремнём и шкивом оказывается
недостаточно дли поддержания нужной скорости вращения шкива, и
возникает скольжение. Так как сила трения скольжения обычно меньше
*) Строго говоря, скольжение отсутствует ие на всей поверхности со-
соприкосновения. В некоторых местах происходит проскальзывание ремня, но
мы для упрощения картины не будем принимать это во внимание.
**) Здесь правильнее было бы говорить не о силах, а о моментах сил.
Но для простоты мы говорим о силах, так как ничего принципиально нового
переход к моментам сил в наше рассмотрение не внесёт,

132 СИЛЫ ТРЕНИЯ [ГЛ. VIИ
силы трения покоя, то после возникновения скольжения скорость
ведомого шкива ещё больше падает и часто он вообще останавли-
останавливается. Для нормальной работы приводного ремня необходимо, чтобы
скольжение вообще не возникало.
При качении колёс самодвижущихся экипажей (поезда, автомобиля)
дело обстоит совершенно таким же образом. В нормальных условиях
качение колёс происходит без скольжения, и поэтому силы, действую-
действующие со стороны земЯи на колёса, — это силы трения покоя. И именно
на использовании особенностей сил трения покоя основано действие
ведущих колёс экипажа и принципы торможения. Эти вопросы будут
изложены в главе о движении твёрдого тела, где они могут быть
рассмотрены полнее.
§ 52. Явление застоя
Наличие трения покоя приводит к тому, что во всех случаях, где дей-
действующие силы должны вызвать скольжение соприкасающихся поверх-
поверхностей, нужны конечные силы для того, чтобы вызвать движение. Это
обстоятельство играет важную роль в ряде случаев, например, в различных
измерительных приборах. Большинство наших измерительных приборов, не
только механических, но и электрических, основано на измерении смещений
стрелки или другого указателя под действием тех или иных сил. Измеряя
смещения указателя, мы определяем силы, вызвавшие это смещение, н по
ним судим об измеряемой величине (давлении, ускорении, силе тока и т. д.).
Но движение указателя в обычных технических приборах почти всегда свя-
связано с возникновением скольжения. Ось стрелки прибора обычно укреп-
укрепляется в подшипниках, и вращение стрелки связано со скольжением оси
в подшипнике. Движение стрелки может начаться только после того,
как действующая на стрелку сила (которую мы и хотим измерить) достиг-
достигнет некоторого конечного значения, превосходящего максимальную силу
трения покоя в подшипниках *).
Это явление «застоя» ставит предел увеличению чувствительности при-
приборов, в которых стрелка укреплена на подшипниках (и вообще приборов,
в которых движение указателя связано с возникновением скольжения). Явле-
Явление застоя сказывается не только на чувствительности прибора, но и иа точ-
точности его показаний. Если бы треиие покоя отсутствовало, то стрелка всякий
раз устанавливалась бы в таком положении, где внешняя (измеряемая) сила и
упругая сила, возвращающая стрелку к положению равновесия, были бы равны.
Но из-за наличия трения покоя стрелка может остановиться не точно в этом
положении, а лишь вблизи него. Не только в начале, но и в любой точке
шкалы существует область застоя. Прибор даёт показания с некоторой ошиб-
ошибкой, которая может быть тем больше, чем больше область застоя.
Для демонстрации явления застоя может служить следующая модель
(рис. 91). На горизонтальной планке лежит груз, к которому с двух сторон
прикреплены пружины. Трение груза о подставку вызывает явление застоя.
Если отвести груз от положения равновесия и предоставить его самому себе,
то он начнёт двигаться к положению равновесия, но остановится, вообще
говоря, не точно в положении равновесия, а в какой-то точке в области
застоя (в какой именно, зависит от начального отклонения груза, т. е. от
скорости, с которой он вошёл в область застоя).
*) При вращении стрелки также играют роль не силы, а моменты сил.
Введение моментов сил и здесь ничего принципиально нового в наши рас-
рассуждения не внесёт.

§ 52]
ЯВЛЕНИЕ ЗАСТОЯ
133
Явление застоя, характерное для приборов, в которых движение указа-
указателя связано со скольжением, отсутствует в приборах, в которых не возни-
возникает скольжения, например, приборах на подвесе. В подвесных приборах
подвижная система укрепляется на тонкой и длинной (и потому очень легко
закручивающейся) нити. Так как силы сухого трения в этом случае отсут-
отсутствуют,, то подвижная система начинает перемещаться под действием сколь
Рис. 91.
угодно малой силы и в конце концов останавливается в таком положении,
в котором измеряемая сила точно равна упругой силе, действующей на
подвижную систему. Поэтому в подвесных приборах увеличение точности
отсчёта положения подвижной системы (при помощи зеркального отсчёта
или микроскопа) позволяет нтти очень г
далеко в смысле увеличения чувст- Т '
вителыюсти и точности прибора. *v<
F-
Q
D
Рис. 92.
Рис. 93.
Конечно, и в подвесных приборах действуют силы трения и сопротив-
сопротивление среды (или электромагнитные силы, подобные силам трения), но это
всегда силы, относящиеся к типу жидкого трения. Они влияют не на поло-
положение равновесия, а лишь на скорость движения подвижной системы. Как
мы видели, если сила жидкого трения достигает величины внешней силы, то
движение происходнт с установившейся скоростью, тем меньшей, чем меньше
величина внешней силы. Поэтому обычно, чем чувствительнее прибор (т. е.
чем меньше действующие на него силы), тем медленнее он устанавливается!
Эта связь между чувствительностью и скоростью установления приборов,'
обнаруженная нами на одном частном случае, янляется весьма общей и ха-
характерной чертой всех измерительных приборов. Различными методами мы
можем увеличивать чувствительность приборов, но это всегда связано
с увеличением времени установления прибора в новом положении.
Несмотря на наличие сухого трения, явление застоя иногда может от-
отсутствовать. Поясним это па конкретном примере (рис. 92). На широкой
ленте, движущейся с большой постоянной скоростью vn, неподвижно лежнг
Груз. Для этого, конечно, к грузу должна быть приложена сила F, уравно-
уравновешивающая силу трения скольж.ения. Затем под действием силы Ft

134
СИЛЫ ТРЕНИЯ
[гл
VI!!
возникло движение с малой скоростью V[ в направлении, перпендикулярном
к vn (рис. 93). Какова будет составляющая силы треиия, действующая на
i руз со стороны ленты в этом направлении?
Сила трения всегда направлена навстречу скорости относительного дви-
движения. Когда возникает движение в направлении vt, то скорость скольжения
будет paeia геометрической сумме v0-f Vi, т. е. изобразится вектором v2.
Значит, сила трения F'2 будет направлена навстречу v2, а по величине
равна F' (если величину силы трения можно считать постоянной). Тогда со-
составляющая силы трения в направлении, перпендикулярном к Vq, F^ —
=: Z7' sm a. Ho vjun = tg a, и если v± -^ »0, то угол a мал и sina=s:tg<i. Сле-
Следовательно, F1. = — F'. Таким образом, составляющая силы трения в направ-
лении, перпендикулярном к v0, оказывается пропорциональной vl — скорости
движения в этом направлении. И если vx стремится к нулю, то и составляю-
составляющая силы трения стремится к нулю. Для движений, перпендикулярных к v0,
сила трения приобретает характерные черты жидкого трения. Сила Fi, дей-
действующая в этом направлении, может быть как угодно мала, и она всё же
Рис. 94.
вызовет движение в этом направлении, т. е. застой отсутствует. Это явле-
явление используется для устранения застоя в некоторых измерительных при
борах (гирокомпас Брауна).
Для демонстрации явления «превращения сухого трения в жидкое» может
служить так называемый зажим Проии, который применяется для измерения
сил трения и для некоторых других целей. Устройство зажима Прони изо-
изображено на рис. 94. Если сильно сжать колодки, то трение покоя очень
велико и пока вал неподвижен, для движения зажима вдоль вала нужны
очень большие силы. Но если привести вал в быстрое вращение, то возни-
возникает скольжение вала относительно зажима со скоростью v0. Тогда зажим
легко скользит вдоль вала, т. е. в направлении, перпендикулярном к v0.
Это явление имеет практическое значение. Им объясняется, например,
тот факт, что приводные ремни соскальзывают при остановке или резкЪм
уменьшении скорости ведомого шкива (когда на токарном станке заел резец).
При нормальной работе станка скольжение ремня отсутствует. При резком
изменении скорости ведомого шкива возникает скольжение ремня. Тогда
достаточно самых малых сил в направлении, перпендикулярном скольжению,
чтобы ремень начал двигаться вдоль оси шкива и соскочил с него. Обычно
этн малые силы существуют всегда вследствие не вполне параллельной уста-
установки ведущего и ведомого шкивов.

§ 53] СУХОЕ ТРЕНИЙ И УСТОЙЧИВОСТЬ СОСТОЯНИЙ РАВНОВЕСИЯ 135
Этим же обстоятельством объясняется и тот факт, что при резком тор-
можеиии автомобиля его часто заносит. Нормально колеса автомобиля ка-
Tfljcfl по земле без скольжения *). Но при резком торможении скорость
вращения колес быстро уменьшается и возникает скольжение. Скорость
скольжения направлена вдоль движения автомобиля. Поэтому в перпендику-
перпендикулярном направлении достаточно самых малых сил для того, чтобы автомо-
автомобиль начал скользить.
Важную роль играет это явление при вращательном бурении. Только бла-
благодаря быстрому вращению всей колонны, несущей бур, трение этой колонны
о стенки скважины а направлении вдоль скважины невелико. Если вращение
прекращается, то трение вдоль скважшсы резко возрастает и для преодоле-
преодоления этого трения, например, при подъеме бурового инструмента, требуются
большие силы. Поэтому поднимать из глубоких скважин вращающийся-бу-
вращающийся-буровой инструмент гораздо легче, чем остановленный.
§ 53. Сухое трение и устойчивость состояний равновесия
Рассмотренные выше явления можно объяснить, предполагая, что сила
трения по величине не зависит от скорости скольжения, но направлена
навстречу скольжению. В действительности, как уже было указано, сила тре-
трения скольжения часто вначале падает при увеличении скорости скольжения.
Наличие падающего участка в характеристике трения может быть причиной
также очень своеобразного явления.
Мы рассмотрим это явление на том же конкретном примере (рис. 92).
На ленте, движущейся с постоянной скоростью v0, лежит груз, удерживае-
удерживаемый на ней пружиной. Состояние равновесия груза определяется условием
/гх ~\-f @$) = 0, где kx — упругая сила пружины, возникающая прн смеще-
смещении х, a f (v0) — сила трения скольжения при скорости va. Только в этом
одном положении силу трения, действующую на покоящийся груз, можно
уравновесить натяжением пружины. Допустим, что мы нужным образом на-
натянули пружину и положили груз на ленту. Это состояние будет состоянием
равновесия. Но сможет ли груз оставаться в этом состоянии долго? Как мы
сейчас увидим, — не всегда. Допустим, что мы поместили груз совершенно
точно в положение, соответствующее состоянию равновесия (практически
абсолютно точно сделать этого, конечно, нельзя). Но все же в дальнейшем
всегда неизбежны малые толчки, которые будут выводить груз из состояния
равновесия, например, сообщать ему небольшие начальные скорости.
Дальнейшее поведение груза зависит от того, как будет изменяться
сила треиия скольжения при изменении скорости скольжения. Положим, что
скорость скольжения v0 такова, что она соответствует падающему участку
характеристики трения, т. е. »0<mnin (рис. 95). Допустим, например, что
груз в результате толчка получил скорость в направлении движения ленты.
Тогда относительная скорость груза и ленты (скорость скольжения) умень-
уменьшится, так как она будет равна разности скоростей движения груза и ленты.
А от этого сила трения возрастёт. Следовательно, сила треиия окажется
больше упругой силы (так как раньше, при скорости скольжения с0, они
были равны). Равнодействующая будет направлена в сторону начальной
скорости груза и будет ускорять груз; скорость, которую груз получил от
толчка, в дальнейшем будет увеличиваться. Толчок в направлении движения
ленты навсегда выведет груз из состояния равновесия. Нетрудно убедиться,
что то же самое произойдет при толчке в направлении против движения
ленты. Состояние равновесия оказывается неустойчивым. Эта неустойчи-
неустойчивость обусловлена тем, что скорость скольжения соответствующая состоя-
*) Во всяком случае, между некоторой частью шины и землёй скольже-
скольжение отсутствует.

136
СИЛЫ ТРЕНИЯ
[гл. viil
нию равновесия, лежит на падающем участке характеристики треиия. Поль-
зуясь'аналогичными рассуждениями, легко убедиться, что когда скорость
скольжения v0 лежит на поднимающемся участке характеристики трения,
т. е. больше i»min (рис. 95), то состояние равновесия
Г будет устойчивое.
Если состояние равновесия груза неустойчиво,
то груз не сможет находиться в нём сколько-нибудь
долго. Но так как нигде других состояний равно-
равновесия нет, то груз нигде не может оставаться в по»
кое. С другой стороны, движения груза ограничены
j пружиной, и он ие может уходить как угодно да-
далеко. Почти очевидно, что груз должен всё время
совершать колебания около положения равновесия.
Так оно в действительности и происходит.
Все эти явления можно также продемонстриро-
продемонстрировать на зажиме Прони. Если скорость вращения вала велика (»0>Pmin),
то зажим остаётся в покое, в отклонённом положении. При этом ynpyi ая
сила пружин, удерживающих зажим, как раз уравновешивает силу трения.
Если же скорость вращения вала мала (vu < tfmin), то зажим не остается
в покое в отклонённом положении, а совершает колебания около этого
положения.
Рис. 95.

ГЛАВА IX
ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
§ 54. Закон сохранения количества движения
Закон сохранения количества.движения является прямым следст-
следствием законов движения. Для изолированной материальной точки этот
закон является очевидным следствием второго закона Ньютона. Если
на точку не действуют никакие силы, то скорость её, а, значит, и
количество движения остаются постоянными. В случае же больше чем
одной точки закон сохранения количества движения является не столь
очевидным следствием законов движения и оказывается спразедливым
лишь при известных условиях.
Рассмотрим систему из нескольких материальных точек, которые
взаимодействуют между собой, но не подвергаются действию извне
никаких других тел. Система, которая включает в себя все взаимо-
взаимодействующие тела (так, что ни на одно из тел системы не действуют
другие тела, кроме включённых в систему), называется замкнутой
системой. Силы, действующие между телами, образующими замкнутую
систему,* называют внутренними силами (для этой системы тел).
Итак, рассмотрим замкнутую систему, состоящую из материальных
точек с массами тх, тъ тв, ... Пусть скорости этих точек — Vj, v2,
v3 а внутренние силы, действующие между ними, — F12, Fl3,...,
F2I, F2J, ... , F31, F32, ... (F12 — сила, действующая на точку / со
стороны точки 2, и т. д.). Напишем уравнения второго закона Нью-
Ньютона для каждой из этих точек:
¦-г. \ГП. V,)= Г «o-f- Г ,о-4- . . • 1
fit '11' 1ь| 1о 1 '
Складывая все эти уравнения, мы получим слева производную по вре-
времени от общего количества движения, а справа — сумму всех» сия,
действующих в системе. Но так как система замкнута, то сумма
всех сил в ней равна нулю. Действительно, в этой сумме встретятся

138 ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ [гл. IX
попарно силы F12 и F21, F23 и F32 и т. д , причём всякой силе Fik бу-
будет соответствовать сила Fw. Но по третьему закону Ньютона
Поэтому полная сумма сил в замкнутой системе всегда равна нулю.
Следовательно, во всякой замкнутой системе
ivl = 0 и ]^/и^ = const. (9.1)
— полное количество движения замкнутой системы есть величина
постоянная.
Если система не является замкнутой, т. е. на точку системы дей-
действуют внешние силы со стороны каких-либо других тел, не входя-
входящих в систему, то общее количество движения системы уже не будет
оставаться постоянным. Действительно, пусть эти внешние силы будут
Ф1( Ф2,... Тогда:
Если мы сложим уравнения движения для всех точек, то сумма всех
внутренних сил ?lk попрежнему будет равна нулю. Следовательно,
Производная от общего количества движения системы точек равно,
геометрической сумме всех внешних сил-, действующих на систему.
Внешние (и только внешние) силы изменяют общее количество дви-
движения системы.
§ 55. Применения закона сохранения количества движения
При применении закона сохранения количества движения к движе-
движениям иа Земле необходимо принимать во внимание, что на все тела
действует притяжение Земли. Поэтому ни одна система тел на Земле не
является замкнутой, если в эту систему не включена Земля. Конечно,
мы могли бы в эту систему включить Землю и получили бы замкну-
замкнутую Систему. Однако, тогда пришлось бы учитывать изменения коли-
количества движения Земли. Мы могли бы, например, рассматривать зам-
замкнутую систему, состоящую из падающего на Землю камня и Земли.
Количество движения, которое приобретает при этом Земля, равно
количеству движения, которое приобретает камень. Но, вследствие
того, что масса Земли гораздо больше массы камня, изменение ско-
скорости Земли будет исчезающе мало. Поэтому, если мы вклю-

§ 55] ПРИМЕНЕНИЯ ЗАКОНА СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ 139
чаем Землю в замкнутую систему, всякие расчёты с применением за-
закона сохранения количества движения лишаются практического значе-
значения, а демонстрации теряют свою наглядность. Но, не включая Земли
в нашу систему тел, мы никогда замкнутой системы не получим.
Однако, так как уравнение (9.2) есть уравнение векторное, то
оно эквивалентно трём уравнениям для сумм компонент количеств
движения по трём осям координат:
<9-3>
где 2^*> 2^%' 2(^«'г СУТЬ суммы компонент всех внешних сил по
каждой из трёх осей. Следовательно, если внешние силы Ф,, действу-
действующие на незамкнутую систему, такозы, что сумма компонент всех
этих сил в каком-либо определённом направлении, например, в направле-
направлении оси х, равна нулю, то для этого направления
= const.
(9.4)
Составляющая общего количества, движения системы в направле-
направлении, в котором не действуют внешние силы, есть величина по-
Рис 96.
стоянная. Незамкнутая система в этом направлении будет вести себя
как замкнутая. В приведённых ниже примерах система тел не является
замкнутой, но в горизонтальном направлении ведёт себя как замкнутая.

140
ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
[гл. IX
Из закона сохранения количества движения следует, что внутрен-
внутренние силы, действующие в системе, не могут изменить общего коли-
количества движения системы, а позволяют лишь отдельным телам системы
обмениваться количествами движения.
Рис. 97.
Обшеизвестную демонстрацию с отдачей при выстреле из «пушки» можно
изменить так, чтобы было особенно ясно, что при выстреле пушка и сиа-
ряд только обмениваются количеством движения. Если пушка скатывается
с наклонной плоскости (рис. 96) и при выстреле имеет уже соответствую-
соответствующую скорость, то после выстрела она останавливается. При выстреле пушка
передала снаряду все то количество движения, которым она обладала.
Рис. 98,
Для демонстрации закона сохранения количества движения в случае
трёх тел может служить следующий опыт. На тележку, движущуюся с ма-
малым трением по рельсам, поставлен ящик с песком. По двум пблосам угло-
углового железа, укрепленным наклонно навстречу друг другу, в тележку могут
скатываться стальные шары. Если в тележку падает один шар (рис. 97), то
она начинает двигаться в направлении, э котором двигался шар. Если в те-

§ 56]
АБСОЛЮТНО НЕУПРУГИЙ УДАР
141
лежку падают одновременно два шара равной массы, опущенные с одина-
одинаковой высоты, то тележка остаётся на месте (рис. 98).
Закон сохранения количества движения устанавливает, что количество
движения в замкнутой системе в любой момент времени равно количеству
движения, которым система обладала в начальный момент. Однако, знание
общего количества движения системы ещё не дает исчерпывающих указаний
о скоростях тел, входящих в систему, даже в простейшем случае двух тел.
Если в начальный момент система имела количество движения р0, то в лю-
любой момент времени /и^-}-"^^ —Ро- Из этого одного уравнения мы не
можем найти двух неизвестных vt и v2. Одного закона сохранения количе-
количества движения, вообще говоря, недостаточно для определения скоростей тел
системы.
§ 56. Абсолютно неупругий удар
В случае абсолютно неулругого удара двух тел из закона сохранения
количества движения можно все же определить скорости движения тел.
Абсолютно неупругим называют такой удар, после которого скорости
обоих соударяющихся тел оказываются одинаковыми. Для этого, очевидно,
соударяющиеся тела должны обладать определёнными свойствами.
Это возможно,^например, если силы определяются не деформациями,
а зависят от скорости изменения деформаций. В природе часто встречаются
такие тела, в которых значительные силы возникают только при быстрых
изменениях деформаций, медленные же изменения деформаций не связаны
с возникновением заметных сил. Такими свойствами обладает, например,
мягкая глина и некоторые другие пластические тела. Поэтому медленно их
можно деформировать, прикладывая очень малые силы. Для быстрых же
изменений деформаций нужны очень значительные силы: удар молотка очень
мало расплющивает глиняный шар, в то время как рукой его легко можно
расплющить, если это делать медленно. Если тело обладает такими свой-
свойствами, то после того, как прекратится
изменение деформации, исчезнут и силы.
Поэтому тела, обладающие такими свой-
свойствами, не восстанавливают своей формы.
При соударении таких тел (например,
глиняных шаров) произойдёт следующее.
В момент столкновения возникнут быстрые
деформации — шары будут быстро сжи-
сжиматься; поэтому возникнут значительные
силы, которые будут в разные стороны
изменять скорости обоих шаров. Так будет
продолжаться до тех пор, пока скорости
шаров не окажутся равными. В этот мо-
меит деформации шаров перестанут изме-
изменяться, а, значит, исчезнут и силы (так как
они существуют только до тех пор, пока
деформации изменяются). Поэтому перестанут изменяться и скорости шаров,
и оба шара будут продолжать двигаться с одинаковой скоростью. Это и
есть случай абсолютно неупругого удара.
Реальные пластические тела не обладают такими идеально неупругими
свойствами. Однако, если скорости соударяющихся пластических тел не
очень велики, то удар практически оказывается абсолютно неупругим.
Продемонстрировать этот случай абсолютно неупругого удара можно
при помощи шаров из пластилина (глины), подвешенных на нитках (рис. 99).
После удара оба шара будут двигаться вместе с одинаковой скоростью.
Если удар оказывается абсолютно неупругич, то определить требуется
только одну общую скорость обоих тел' после удара. Закон сохранения
Рис. 99.

142
ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
[гл.
IX
количества движения и знание начальных условий достаточны для опре-
определения этой скорости.
Напишем в общем виде закон сохранения количества движения для
случая центрального абсолютно неупругого удара, т. е. для случая, когда
скорости шаров лежат на линии, соединяющей их центры (рис. 100). Если
массы тел ту и /п2, их скорости до
удара Vj и v2, а их общая скорость
после удара v, то
(9.5)
Скорость после удара будет на-
направлена по той прямой, по которой
направлены обе скорости до удара. Поэтому уравнение (9.5) можно рассма-
рассматривать как скалярное. Скорость после удара будет
„ mMi -f mivi
Если шары движутся навстречу друг другу, то они вместе будут продол-
продолжать двигаться в ту же сторону, в которую двигался шар, обладавший
большим количеством движения. Если, в частности, количества движения
обоих шаров равны по величине, то оба шара остановятся. Если оба шара
движутся в одну сторону, то они после удара будут двигаться в ту же сто-
сторону со скоростью большей, чем скорость первого шара, и меньшей, чем
скорость второго (догнавшего первый). В частном случае, если массы ша-
шаров равны,
В случае нецентрального удара (рис. 101) можно разложить обе скоро-
скорости на составляющие vn в направлении линии, соединяющей центры шаров,
и составляющие V(—в перпендикулярном направлении (.рис. 101Ь). Для
составляющих vn\ и v„2 всё будет об-
обстоять так же, как и при центральном и,
ударе. Они в конце концов окажутся
равными, и для них мы можем напи-
написать то же соотношение, что и при
центральном ударе. Для составляю-
составляющих же vtl и vt% дело будет обстоять а
иначе. Их могут изменять толь^ тан-
тангенциальные силы, т. е. силы трения.
Но силы трения вызовут вращение
шаров, » вся картина очень осложнится. Во всяком случае, нельзя утвер-
утверждать, что составляющие скоростей в направлении, перпендикулярном" к ли-
линии центров после удара, окажутся равными. Поэтому закон сохранения
количества движения позволит нам определить только составляющую резуль-
результирующей скорости в направлении линии центров. Для составляющих ско-
скоростей после удара в направлении, перпендикулярном к линии центров',
закон сохранения количества движения, конечно, тоже справедлив, но эти
составляющие после удара могут быть различными. Двух же скоростей на
основании одного закона сохранения количества движения определить нельзя.
Рис. 101.

ГЛАВА X
ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
§ 57. Момент силы и момент количества движения
Для замкнутых систем оказывается справедливым и другой закон
сохранения, именно закон сохранения моментов количества движения.
Однако, особый интерес закона сохранения моментов количества дви-
движения заключается в том, что в ряде случаев он оказывается спра-
чеСТВЗ,
Для того чтобы формулировать закон сохранения моментов коли-
количества движения, необходимо ввести два новых физических понятия —
момента силы и момента количества движения.
Для упрощения мы введём эти понятия и сфор- ?*
мулируем закон сохранения моментов количества ,У "%^
движения сначала для случая, когда силы и ско-
скорости лежат в плоскостях, перпендикулярных к
оси моментоз.
Моментом силы относительно какой-либо оси
называется, как известно, произведение силы F на
плечо d, т. е. на перпендикуляр, опущенный из ^ис- Ю2.
оси О на направление силы (рис. 102). Следовательно, по величине
момент силы равен удвоенной площади треугольника ОАВ, т. е.
площади параллелограмма, построенного на векторах г и F,
где г — радиус-вектор, проведённый из точки О (след оси) к точке
приложения силы. Моменту силы приписывают определённое направле-
направление, а именно то^ в котором будет двигаться вдоль оси буравчик,
если его рукоятка вращается по направлению силы (рис. 103). Итак,
момент силы F относительно оси, проходящей через точку О, есть
вектор М, перпендикулярный к плоскости вектора F и радиуса-век-
радиуса-вектора г, равный по величине площади параллелограмма, образованного
векторами т и F, и направленный по правилу буравчика, т. е.
M = [r-F]. A0.1)
Нам придётся в дальнейшем находить результирующий момент
нескольких сил, действующих на данное тело. Покажем, что момент

144
ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ [гЛ. X
Рис. 103.
суммы сил Fj и F2 относительно какой-либо оси равен сумме момен-
моментов этих сил относительно той же оси *).
Найдём, например, момент суммы сил F, и F2, лежащих в пло-
плоскости чертежа, относительно оси, проходящей через точку О (рис. 104)
перпендикулярно к плоскости чертежа.
Перенесём для этого сиЛы Fx и F2 в
точку их пересечения А. Как следует из
самого определения, моменты сил ие из-
изменяются, если точка приложения силы
переносится вдоль направления силы.
Поэтому моменты сил F, и F2 направлены
перпендикулярно к чертежу и выража-
выражаются площадями параллелограммов, по-
построенных, соответственно на векторах F^
и FjH радиусе-векторе г. Момент же суммы сил F, и F'2, т. е. их
равнодействующей F, также перпендикулярен к чертежу и выражается
площадью параллелограмма, по-
построенного на векторе F и радиусе-
векторе г. Легко видеть, что эта
площадь ADEO равна сумме площа-
площадей AKLO и АВСО, построенных
соответственно на векторах F 'х и
Fj. Это видно из того, что парал-
параллелограмм АВСО равен параллело-
параллелограмму KDEL, а треугольник ADK
равен треугольнику OEL. Следова-
Следовательно, вектор, выражающий момент
суммы сил F, и Fa, равен сумме векто-
векторов, выражающих моменты сил Fl и F2.
Совершенно аналогично моменту силы определяется и момент
количества движения. Ограничимся опять случаем, когда ось момен-
моментов выбрана таким образом, что вектор количества движения лежит
в плоскости, перпендикулярной к оси. Моментом количества дви-
движения относительно некоторой оси (рис. 105) называют вектор,
направленный вдоль этой оси по правилу буравчика и равный по ве-
величине произведению количества движения mv на длину перпендику-
перпендикуляра, опущенного на этот вектор из заданной оси. Следовательно,
момент количества движения N есть векторное произведение
радиуса-вектора г на вектор количества движения mv:
N=[r • mv].
(Ю.2)
*) Это прямо вытекает из свойств векторного произведения и не требует
специального доказательства. Однако, для читателей, незнакомых с вектор-
векторной алгеброй, приводимый вывод может быть полезен.

§ 57]
МОМЕНТ СИЛЫ И МОМ2НТ КОЛИЧЕСТВА ДВИЖЕНИЯ
145
Ось мо-
ментоб
N
Чтобы найти момент количества движения тела относительно ка-
какой-либо неподвижной оси, нужно было бы учесть все количества
движения, которыми обладают отдельные части тела, находящиеся
на разных расстояниях от оси. Но если
размеры тела малы по сравнению с рас-
расстоянием до выбранной оси, то радиусы-
векторы, проведённые к различным точкам
тела, практически будут совпадать, и мы
можем рассматривать тело как материаль-
материальную точку. Так как мы изучаем сейчас
механику точки, то мы ограничимся только
этими случаями.
Случаи, когда размеры тела сравнимы
с расстоянием до оси моментов, мы рас-
рассмотрим в главе о движении твёрдого
тела.
О
УПМ
Рис. 105.
Поясним представление о моменте силы и моменте количества движения
некоторыми конкретными примерами. Отметим прежде всего, что момент
количества движения, которым обладает тело, движущееся прямолинейно
и равномерно (рнс. 106), есть величина постоянная. Действительно, хотя
радиус-вектор г всё время изменяется, но момент количества движения
остаётся постоянным, так как остаётся неизменной длина перпендикуляра d,
опущенного из точки О на направление вектора тм.
Очевидно, в замкнутой системе точек, в которой общее количество
движения постоянно, общий момент количества движения относительно лю-
любой оси также будет оставаться постоянным. Закон сохранения моментов
• количества движения справедлив для любой замкнутой
fa системы.
Но, как уже было сказано, интерес представляют
как раз те случаи, когда количество движения изменяется,
а момент количества движения относительно какой-либо
оси остаётся постоянным. Простейшим примером этого
случая является движение точки, по окружности с по-
постоянной скоростью. Так как направление скорости при
этом всё время изменяется, то вектор количества дви-
движения также изменяется (по направлению, но не по ве-
величине). Если за ось моментов мы выберем ось, прохо-
проходящую через центр вращения, то момечт количества
движения относительно этой оси будет оставаться постоянным. Вектор
момента количества движения будет направлен всё время по осн и по
величине равен произведению постоянных величин mv и г (угол между
mv и г всё время остаётся прямым). Конечно, если бы за ось моментов
мы выбрали ось, не проходящую через центр окружности, то момент
количества движения относительно этой осн не оставался бы постоянным,
так как в векторном произведении [r-mv] изменялась бы величина г и угол
между г и mv.
Точка, движущаяся по окружности, не является замкнутой системой,
так как на неё всё время должна действовать какая-либо внешняя сила,
сообщающая ей центростремительное ускорение (например, натяжение
нити, которой точка привязана к центру). Эта сила н изменяет количество
движения системы, но не изменяет момента количества движения точки
относительно оси, проходящей через центр вращения.
10 с. Э. Хайкин
Рис. 103.

t46 ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ [гЛ. X
§ 58. Уравнение моментов
Установим связь между моментом внешних сил и моментом коли-
количества движения точки (в соответствии с предыдущим ограничимся
случаем плоского движения). Если на материальную точку массы т
действует сила F (это может быть равнодействующая многих сил),
то уравнение движения имеет вид:
Выберем какую-либо неподвижную ось, перпендикулярную к пло-
плоскости движения точки. Пусть след этой оси есть точка О (риС. 107),
и проведём от точки О радиус-вектор г. При
движении точки этот радиус-вектор изменяется,
т. е. г есть функция времени. Умножим векторно
обе части уравнения движения на г:
[r.|mv]=[rF]. A0.3)
Рис. 107. Правая часть этого уравнения есть момент сил,
взятый относительно выбранной нами оси. Левая
же часть, как мы увидим, есть производная по времени от момента
количества движения тела относительно выбранной оси. Так как про-
производная векторного произведения выражается аналогично производной
произведения скалярных величин, то
1[г • mv] = [^ ¦ mv] + [г- jt (mv)] . A0.4)
Но rfr есть элементарное изменение радиуса-вектора (рис. 108), т. е.
элементарное перемещение тЪчки за время
dt, и значит, ^ = v- Таким образом, пер-
первый член в правой части A0.4) есть век-
векторное произведение двух колинеарных век* ^/'^-'Т'йг
торов (v и mv), которое, как известно,
равно нулю. Следовательно,
Рис. 108.
Поэтому уравнение A0.3) можно записать следующим образом:
или
f = M, A0.5)
где М = [rF] — момент сил, а N = [г • mv] — момент количества-
движения, взятые относительно любой (но одной и той же) непо-
двидсной оси.

§ 58]
УРАВНЕНИЕ МОМЕНТОВ 147
Производная от момента количества движения точки относи-
относительно какой-либо оси равна моменту действующих сил относи-
относительно этой оси.
В частности, если М = 0, то
N = const. A0 6)
Силы не изменяют момента количества движения относительно
какой-либо оси, если сумма моментов сил относительно этой оси
равна нулю.
В нашем примере с равномерным движением по окружности сила натя-
натяжения нити ие изменяет момента количества движения тела относительно
оси, проходящей через центр вращения, именно потому, что момент силы
относительно этой оси равен нулю (сила проходит через ось). Если бы мы
выбрали ось, не проходящую через центр
вращения, то момент силы не был бы равен
нулю и поэтому изменялся бы момент коли-
количества движения системы относительно этой
осн.
Примером движения, к которому может
быть применён закон сохранения моментов,
служит движение планет по своим орбитам
(рис. 109). Так как сила, действующая со сто-
стороны Солнца на планету, всегда направлена
к центру Солнца S, то момент количества ™с- '09.
движения планеты относительно оси, про-
проходящей через центр Солнца, всегда остаётся постоянным. Отсюда
видно, что скорость планеты в перигелии Р должна быть больше скорости
движения в афелии А в отношении гг/гъ так как моменты количества дви-
движения mvin и и»,/2 должны быть равны (угол между г и v в обоих слу-
случаях прямой). Для промежуточных положений нужно принять во внимание,
что угол между гии изменяется. Однако, как легко видеть, г sin а для'
любой точки больше, чем /•], и поэтому скорость
в любой точке меньше, чем в перигелии.
Уравнение моментов A0.5) указывает, как из-
изменяется момент количества движения материальной
- с w точки под действием сил..Так как dN = M<#, то
момент сил, совпадающий по направлению с момен-
Рис. ПО. том количества движения, увеличивает момент ко-
количества движения (rfN совпадает по направле-
направлению с N). Если же момент сил направлен на-
навстречу моменту количества движения, то этот последний уменьшается
(dN противоположно N).
Применим эти соображения к конкретному примеру (рис. 110): к круг-
круглой палочке на нерастяжимой нити привязан шарик (сил тяжести не будем
принимать во внимание). Сообщим шарику начальную скорость v0 в на-
направлении, перпендикулярном к нити. Шарик начнёт вращаться вокруг па-
палочки, причём нить будет накручиваться на палочку и шарик будет дви-
двигаться по закручивающейся спирали. Относительно оси О, совпадающей
с осью палочки, момент силы не равен нулю (так как нить не проходит
через ось палочки), и, следовательно, момент количества движения относи-
относительно этой оси не будет оставаться постоянным. Легко видеть, что он бу-
будет уменьшаться. В рассматриваемом случае скорость шарика всегда дол-
должна быть нормальна к направлению ннти. Поэтому нить может изменять
только направление, а не абсолютную величину скорости шарика (как и
10*

148 ЗАКОН СОХРАНЕНИЯ MOMt-HTA КОЛИЧЕСТВА ДВИЖЕНИЯ [гЛ. X
в случае вращения по окружности). С другой стороны, радиус-вектор г
будет всё время уменьшаться по величине (вследствие закручивания нити),
а угол между раднусом-вектором и скоростью шарика будет всё время
оставаться близким к прямому. Поэтому момент количества движения [r-mv]
при движении будет убывать. Это уменьшение момента количества движе-
движения шарика обусловлено тем, что на шарнк действует момент силы натя-
натяжения инти F, направленный навстречу начальному моменту количества
движения шарика. Действительно, в нашем примере начальный момент ко-
количества движения относительно оси О, [r-wvo], направлен на наблюдателя,
а момент силы натяжения нити относительно этой оси направлен за чертёж.
Следовательно, dN также направлено за чертёж, т. е. навстречу N. По-
Поэтому начальный момент количества движения будет при движении умень-
уменьшаться.
Уравнение моментов справедливо для любой произвольно вы-
выбранной неподвижной оси. Но оно приобретает особенно простой
вид для случая вращения по окружности, если в качестве оси мо-
моментов выбрать ось, проходящую через центр окружности. Тогда
радиус-вектор остаётся постоянным по величина, и направление его
всегда перпендикулярно к направлению вектора количества дзиже-
ния. В этом случае абсолютная величина вектора момента количества
движения N= m^v. Так как, с другой стороны, для вращения
по окружности г> = «у, где ш — угловая скорость вращения, то
N=mr2o) A0.7)
и
rf.V „ du>
ш=тг ж-
Уравнение моментов A0.5) принимает вид
тг*? = М. A0.8)
Это уравнение записано нами в скалярной форме. Однако, для
рассмотренного частного случая легко восстановить его векторный
характер, рассматривая угловую скорость и угловое ускорение как
векторы. Так как ось вращения постоянна, то вектор угловой ско-
скорости изменяется только по величине и, следовательно, вектор угло-
углового ускорения направлен по оси вращения. Вектор момента силы
также направлен по оси вращения; эти векторы совпадают по на-
направлению, и мы можем написать уравнение моментов в следующем
виде:
/f = M, A0.9)
где /=w/ для нашего частного случая представляет собой неко-
некоторую скалярную величину. В таком виде это уравнение совершенно
аналогично уравнению Ньютона для линейных ускорений, но вместо
сил в него входит момент сил, а вместо массы — величина / = /иг8.
Эта величина носит название момента инерции материальной точки

§ 59] МАТЕМАТИЧЕСКИЙ МАЯТНИК 149
массы* т относительно данной оси. При помощи момента инерции
удобно выражать и момент количества движения тела. Как видно из
A0.7), при движении по окружности момент количества движения от-
относительно оси вращения есть
N = /@. A0.10)
Это выражение справедливо и для случая, когда движение про-
происходит не по окружности и для любых неподвижных осей, но мы
пока его получили и будем им пользоваться только для движения по
окружности и для оси, проходящей через центр вращения. Опять
для нашего частного случая мы можем просто переписать это соот-
соотношение в векторной форме. Вектор момента количества движения
в случае неподвижной оси вращения совпадает с направлением оси
вращения, т. е. с направлением вектора угловой скорости. Поэтому
В таком виде это выражение аналогично выражению для количества
движения, только вместо линейной скорости в него входит угловая
скорость, а вместо массы — момент инерции.
§ 59. Математический маятник
Применим уравнение моментов к задаче о движении так называе-
называемого «математического маятника», т. е. тела, подвешенного на
столь длинной нити, что размерами тела по сравнению с длиной
нити можно пренебречь. За ось моментов выберем горизонтальную
ось, проходящую через точку подвеса, перпендикулярно к пло-
плоскости качаний маятника. Момент силы натяжения нити относительно
этой оси всегда равен нулю. Момент же силы тяжести выразится
так:
М =
где / — длина нити, a — угол отклонения от вертикали. Момент
инерции маятника относительно оси, проходящей через точку под-
подвеса, I = ml2 и уравнение моментов A0.9) даёт:
rf» m^ls'n а
Знак минус взят потому, что момент силы тяжести сообщает маят-
маятнику ускорение в направлении, обратном отклонению. Так как
dv> d4
ш=ш>то
~~ 5Р = 7"
Это — дифференциальное уравнение, определяющее угол отклонения а,
как функцию времени. Для общего случая определение вида функ-

150 закон сохранения момента количества движения [гл. х
ции a(t) из полученного дифференциального уравнения представляет
большие трудности. Но если ограничиться малыми углами а, то за-
задача весьма упрощается. При малых углах можно заменить sin a
через а, и тогда уравнение движения маятника принимает вид:
сРя. в
Это уравнение показывает, что а должна быть такой функцией
времени, чтобы вторая производная от этой функции в любой момент
была равна самой функции, умноженной на величину — gjl. Такими
свойствами, как известно, обладают гармонические функции сииус и
косинус. Следовательно, при колебаниях маятника а должна меняться
со временем по гармоническому закону, например, по закону я =
= a0cosp(, где а0 — амплитуда колебаний, а р = 2пп, причём я
есть частота колебаний, т. е. число колебаний, совершаемых маят-
маятником в 1 сек. Очевидно, р есть число колебаний за 2тт секунд;
р называют угловой частотой колебаний.
Однако, не всякая гармоническая функция будет удовлетворять
полученному нами дифференциальному уравнению, т. е. обращать
его в тождество. Подставив a —a0cosp/ в уравнение A0,11), полу-
получим:
p2a0 cos pt = ¦— a0 cos pt.
Для того чтобы уравнение удовлетворялось, должно быть р2 —#//
или
«=/!¦
Это и есть угловая частота колебаний маятника. Следовательно,
a = a0 cos l/ y t.
Маятник совершит полное колебание за время Т, в течение ко-
которого повторяется значение функции синус или косинус. Это время
определяется из условия Ту gil = 2n; отсюда время полного коле-
колебания маятника — период маятника —
Это — известная формула маятника.
При подстановке решения а = а0соз/^ в дифференциальное
ураменне A0.11) а0 сократилась, т. е. амплитуда колебаний ай не

§ 60] ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ 151
определяется из уравнения движения. При выбранном нами законе
колебаний a = a0cosp/a0 представляет собой то значение, которое
принимает а при / = 0, т. е. начальное отклонение маятника. Ам-
Амплитуда колебаний маятника а0 определяется начальными условиями,
в частности, в нашем случае величиной начального отклонения. Если
бы мы приняли, что колебания маятника происходят по закону <z =
= otosinp/, то это значило бы, что в момент t=.Q я = 0, т. е. что
начало отсчёта времени совпадает с одним из моментов, когда маят-
маятник проходит через среднее положение. Замена косинуса синусом
соответствует только изменению начала отсчёта времени на Т\4.
Амплитуда колебаний маятника и в том и в другом случае опреде-
определяется начальными условиями.
Наше рассмотрение показывает, что период колебаний маятника
зависит от его длины (и ускорения силы тяжести), но не зависит от
амплитуд. При любых амплитудах период колебаний будет один
и тот же. Это свойство называется изохронностью колебаний ма-
маятника.
Однако, всё наше рассмотрение справедливо только при малых
отклонениях (когда sin а можно заменить через я). В частности, и
свойство изохронности имеет место только при этих предположениях.
При больших отклонениях это уже не будет справедливо: момент
силы тяжести будет расти медленнее, чем угол а (так как момент
пропорционален sin а), и маятник будет медленнее возвращаться
к положению равновесия, т. е. период колебаний будет возрастать,
и тем заметнее, чем больше отклонения. При больших отклонениях
маятник уже не обладает свойством изохронности, так как период
колебаний зависит от амплитуды.
Рассматривая колебания маятника, мы не учитывали того, что на
маятник будут действовать силы трения и сопротивления среды. Эти
силы приведут к тому, что колебания маятника будут постепенно
затухать, т. е. уже не будут подчиняться закону a = a0cospt, где
а0 — постоянная величина. Величина <z0 будет с течением времени
уменьшаться. Но если силы трения невелики, то это уменьшение
величины <z0 будет происходить очень медленно, а период маятника
будет оставаться практически неизменным. Поэтому колебания маят-
маятника являются одним из наиболее удобных методов отсчёта постоян-
постоянных промежутков времени.
§ 60. Закон сохранения момента количества движения
для системы точек
От уравнения моментов для одной точки легко перейти к урав-
уравнению моментов для системы точек. Пусть у нас есть ряд матери-
материальных точек с массами mv тг, тг,.. . (рис. 111). На эти точки дей-
действуют внутренние силы со стороны других точек системы F,2, Fu ,. .. ,
F?1, Fj8,... и т. д. Кроме того, на все точки могут действовать

152
ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
[гл. х
внешние силы со стороны других тел, не входящих в систему. Обо-
Обозначим эти силы через Ф,, Ф2,. . . Уравнения движения для каждой
из точек системы будут иметь вид:
mtv1
Ограничимся опять случаем, когда все
силы и все скорости лежат в одной и той
же плоскости (или в параллельных плоско-
плоскостях), и возьмём ось моментов, перпендику-
перпендикулярную этой плоскости. (Точка О на рис. 111
есть след этой оси.)
Проведя радиусы-векторы rv r2, г3,... ко
всем точкам системы, мы получим (как и прежде):
A0.12)
Ш У3 ¦ «vaj = [г, • F2I] + [г, • F23] +.. . + [г, • ФJ,
Сложив все эти уравнения, получим слева
где N — общий момент количества движения всех точек системы,
а справа—сумму моментов всех сил (внутренних и внешних),
действующих в системе. Но сумма моментов всех внутренних сил
должна быть равна нулю, так как внутренние силы всегда попарно равны
и противоположны по направлению, и моменты этих сил относительно
одной и той же оси также всегда попарно равны и противоположны
по направлению. Поэтому после сложения всех уравнений A0.12)
мы получим справа только сумму моментов внешних сил. Уравнение
моментов принимает вид:
dN— м
где М — момент только внешних сил.
Производная общего момента количества движения системы
относительно какой-либо оси равна моменту всех действующих
на систему внешних сил относительно этой же оси.
В частности, если для какой-либо оси М = 0, то
N = const.

60]
ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ 153
— общий момент количества движения системы относительно
этой оси остаётся постоянным.
Внутренние силы не могут изменить общего момента количества
движения системы, а могут лишь вызвать обмен моментами коли-
количества движения между различными точками системы. В незамкнутой
системе общий момент количества движения системы может изме-
изменяться в результате действия моментов внешних сил. Но если можно
выбрать такие оси, относительно которых момент всех внешних сил
равен нулю, то общий момент количества движения системы отно-
относительно этих осей будет оставаться постоянным.
Иллюстрацией закона сохранения момента количества движения мо-
может служить следующий простой опыт. На металлический стержень наса-
насажены две одинаковые массы т, которые могут свободно скользить вдоль
стержня. Стержень укреплён в подпятнике, в котором он может вращаться
с малым трением. Массы связана нитью так, что очи находятся примерно
на половине длины стержня по обе стороны от оси. Если раскрутить стер-
стержень и затем пережечь нить, то массы соскользнут на края стержня; уг-
угловая скорость стержня при этом уменьшится так, что момент количества
движения останется неизменным. Если пренебречь массой стержня, то пол-
полный момент количества движения двух масс т относительно оси вращения
Он должен оставаться постоянным (так как момент внешних сил относи-
относительно оси вращения равен нулю). Поэтому, если вначале угловая скорость
была tflj и расстояние масс до оси Г\, а в конце, соответственно, а>ч и г%, то
Следует отметить, что и линейная скорость при этом также уменьша-
уменьшается.-Действительно, ь» = <1)ги если o>i/«>2 = r\\r\ , то о1/о3 = га/г1,т.е. линей-
линейная скорость после перемещения грузов уменьшилась в отношении, обрат-
обратном отношению радиусов. Уменьшение линейной скорости масс вызывается
силами, с которыми на массы действует стержень.
Как мы видели (§ 33), при движении тела вдоль вращающегося стержня
могут возникать силы давления со стороны стержня на тело, обусловлен-
обусловленные деформацией стержня. Однако, мы рассматривали там случай, когда
угловая скорость стержня остаётся постоянной. Теперь же при движении
масс вдоль стержня его угловая скорость быстро уменьшается. Поэтому
вся картина возникновения деформаций и сил оказывается гораздо более
сложной, и мы не будем её рассматривать. Но из того, что линейная ско-
скорость масс уменьшилась, мы должны заключить, что во время движения
масс по стержню он был изогнут вперёд, так что силы, действующие со сто-
стороны стержня на массы, были направлены навстречу их движению, обу-
обусловленному вращением стержня.
Ещё более убедительной получается эта демонстрация, если её произ-
произвести в обратном порядке — заставить грузы приближаться к оси. Для
этого их можно соединить достаточно тугой пружиной, а затем при помощи
нити, идущей от грузов к концам стержня, растянуть грузы к краям стержня.
Если прн вращении стержня пережечь нитку, то пружина стянет грузы
к оси. Прн этом угловая скорость вращения стержня резко возрастает.
(Момент инерции уменьшается, а момент количества движения не изме-
изменяется.) В этом случае линейные скорости грузов увеличиваются, так как
угловая скорость растёт быстрее, чем уменьшается расстояние до оси.
Аналогичные опыты можно произвести на так называемой скамье
Жуковского. Скамья Жуковского укреплена так, что она может свободно

154
ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ. X
вращаться вокруг вертикальной оси. Человек с гирями в руках, находя-
находящийся на скамье (рис. 112), представляет собой систему, для которой момент
количества движения относительно вертикальной осн должен оставаться
постоянным. Поэтому, если скамью с человеком, который держит грузы
в вытянутых руках, привести во вращение, то угловая скорость заметно
увеличивается, когда чело-
человек прижимает руки с гру-
грузами к груди. Происходит
это потому, что момент
инерции системы умень-
уменьшается, а момент количе-
количества движения должен
оставаться неизменным.
Уравнение моментов
определяет, как именно
изменяется момент коли-
количества движения системы,
рис_ из. если момент сил не ра-
равен нулю. Но связь между
изменениями момента количества движения и изменениями ско-
скоростей различных точек системы в общем случае сложна. По-
Поэтому мы пока ограничимся опять только простейшим случаем,
когда все точки системы движутся с одинаковой угловой скоростью ш
по концентрическим кругам. (Круги эти могут лежать не в одной
плоскости, а в параллельных плоскостях.) Взяв за ось моментов
прямую, проходящую через центр вращения (и перпендикулярную
к плоскости движения), мы можем выразить момент количества дви-
движения всей системы следующим образом:
n= 2 w/=2 »v>=B mtrl)»=B'/) »•
Сумма моментов инерции всех точек системы, взятых относи-
относительно какой-либо оси, есть общий момент инерции системы отно-
относительно этой же оси. Обозначая этот общий момент инерции
через /, мы можем написать уравнение моментов для системы точек
в таком же виде, как получили его раньше для одной точки:
где м—сумма моментов всех внешних сил относительно оси вра-
вращения.
Такой простой вид уравнение моментов принимает только в рас-
рассматриваемом случае вращения всех точек системы вокруг одной
и той же неподвижной оси с общей угловой скоростью. Мы пока
только этим случаем и ограничимся. Некоторые более сложные слу-
случаи будут рассмотрены в динамике твёрдого тела.
Иллюстрацией к этому простейшему случаю может служить так назы-
называемый крест Обербека (рис. 113). Два крестообразно скреплённых стержня
могут свободно вращаться вокруг горизонтальной оси. По стержням могут

§ 61] ИЗМЕНЕНИЕ НАПРАВЛЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ 155
Рис. ИЗ.
передвигаться четыре груза большой массы (моментом инерции креста по
сравнению с суммой моментов инерции грузов можно пренебречь). К оси,
на которой вращается крест, прикреплено несколько шкивов разного радиуса.
К концу одной из интей, намотанных
на шкивы, прикрепляется груз, и
сила натяжения нити создаёт мо-
момент, сообщающий кресту некоторое
угловое ускорение. (Момент силы
тяжести равен нулю, если грузы
расположены симметрично.) Изменяя
величину груза и радиус шкива,
можно изменять величину момента
внешней силы. С другой стороны,
переставляя грузы, можно изменять
момент инерции системы. При этом
угловое ускорение креста возрастает
при увеличении момента внешней
силы и уменьшается при увеличении
момента инерции системы.
Мы рассматривали пока только
такие случаи, когда все силы
лежат в плоскости, перпендику-
перпендикулярной к оси моментов. Если
это условие не соблюдено, то
всё рассмотрение усложняется.
Начнём с рассмотрения наиболее
простого из этих случаев, когда
движение происходит вокруг неподвижной (закреплённой) оси и эта ось
выбрана за ось моментов. Если сила F не лежит в плоскости, перпендику-
перпендикулярной к этой оси (рис. 114), то её можно разложить на две состав-
составляющие: F,, лежащую в этой пло-
плоскости, и FB, перпендикулярную к этой
плоскости. Для составляющей F, спра-
справедливо всё то, что было сказано выше
для сил, лежащих в плоскости, перпенди-
перпендикулярной к оси. Составляющая Fn, на-
направленная вдоль оси, не может изме-
изменить момента количества движения от-
относительно этой оси и вызовет только
дополнительное давление на опоры оси.
Поэтому в случае закреплённых осей
вращения мы можем всегда брать только составляющие внешних
сил, лежащие в плоскостях, перпендикулярных к оси вращения,
и свести этот случай к уже рассмотренному.
§ 61. Изменение направления момента количества движения
Когда ось вращения закреплена, внешние силы, как бы они нн были
направлены, могут изменять только величину момента количества движения,
но не могут изменять ei о направления. Но если ось вращения может изме-
изменять своё направление в пространстве, то внешние силы, вообще говоря,
Рис. 114.

156
ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
[гл. х
изменяют не только величину, но и направление момента количества дви-
движения.
Этот более сложный случай мы не будем рассматривать в общем виде,
а ограничимся только одним конкретным примером, на котором можно
будет выяснить, как происходят изменения направления момента количе-
количества движения.
Воспользуемся для этого следующей моделью (рис. 115). Тело массы т
закреплено неподвижно на жёсткой, невесомой штанге длиной г, которая
вращается вокруг перпен-
дикулярной к ней оси 00'
с угловой скоростью (о. Пло-
Плоскость (перпендикулярную
к 00'), в которой движется
штанга, мы для краткости
будем называть «плоско-
стью штанги». Подшинники
оси вращения укреплены
так, что эта ось может
свободно поворачиваться
вокруг двух горизонтальных
осей *) XX' и YY>.
Положим, что штанга
вращается вокруг оси 00',
и на эту ось через подшип-
подшипники действуют внешние
силы F и F' , создающие
внешний момент М, кото-
который начнёт поворачивать плоскости штанги вокруг оси XX' по часовой
стрелке (рис. 115). Пока плоскость штанги неподвижна, тело т может испы-
испытывать ускорения, лежащие только в плоскости штанги. Но если плоскость
шташи начнёт поворачиваться вокруг оси XX', то должно возникнуть
ускорение тела от, перпендикулярное к плоскости штанги.
Что такое ускорение, помимо дру! их ускорений, должно гозникнуть,
видно из сопоставления направления линейных скоростей тела v1 в двух
близких точках, лежащих по обе стороны оси XX' (рис. 116). Так как
в этих местах линейные скорости, обусловленные вращением вокруг оси XX',
очень малы, то можно считать, что абсолютная скорость тела определяется
только вращением вокруг оси 00', и- поэтому линейные скорости в каждой
точке лежат в плоскостях штанги. За время пока тело перешло из точки /
в точку 2, эта плоскость немного повернулась и соответственно измени-
изменилась скорость v' от v( до v%. Изменение скорости равно dv', и, значит,
существует ускорение, направленное нормально к плоскости штанги, вверх
со стороны X и вниз со стороны X'. Наоборот, на концах диаметра, пер-
перпендикулярного к XX', такое ускорение отсутствует, так как поворот пло-
плоскости штанги около оси XX' не вызывает изменения направления линей-
линейной скорости v' в этих местах.
Таким образом, вследствие вращения плоскости штанги вокруг оси XX'
возникает зависящее от положения штанги переменное ускорение, напра-
направленное нормально к плоскости штанги. Это ускорение тела вызывается
давлением со стороны штанги, которая для» этого должна быть соответ-
соответствующим образом изогнута вниз на передней стороне круга и вверх — на
задней. (Возникновение этих деформаций штанги нетрудно объяснить, поль-
*) Этого можно достичь, применив, например, так называемый карданов
подвес. На рисунке, чтобы его не загромождать, способ крепления под-
подшипников не показан.

§ 61] ИЗМЕНЕНИЕ НАПРАВЛЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ 157
зуясь теми же соображениями, которые мы применяли при рассмотре гаи
аналогичного вопроса в § 33.)
Чтобы определить величину и направление этих сил давления при раз-
разных положениях штанги, нужно найти сообщаемое ею ускорение в напра-
направлении, нормальном к плоскости штанги*). Для этого будем рассматривать
вращение тела т в системе координат, жёстко связанной с осью 00' и
плоскостью штанги, как «относительное», а вращение этой системы коор-
динаЧ1 вокруг оси XX' как переносное.«Относительное» движение представляет
собой вращение вокруг оси 00' с угловой скоростью ю, а переносное
вращение —вокруг оси XX' с некоторой угловой скоростью, которую мы
обозначим через Я (рис. 117). «Абсолютное» ускорение будет равно сумме
«относительного», переносного, лежащих в плоскости штанги, и корио-
лисова, направленного перпендикулярно к векторам «относительной» ско-
скорости v' и угловой скорости Я. Все эти три ускорения телу т может сооб-
сообщать только штанга, так как только она на тело действует. Так как первые
два лежат в плоскости штанги, то, для того чтобы сообщать их телу,
штанга должна быть соответствующим образом деформирована — растянута
и изогнута в своей плоскости. Наконец, для того чтобы сообщать телу кориоли-
сово ускорение, штанга должна быть изогнута в направлении, перпендику-
перпендикулярном к плоскости штанги. Это— как раз та деформация, в необходимости
которой мы убедились выше.
Кориолисово ускорение
*) Хотя штанга слегка изогнута, но можно в прежнем смысле говорить
о «плоскости штанги».

158
ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
[гл.
в нуль, так как в этом месте
При перемещении штанги меняет величину вследствие изменения угла
между У и v'. На диаметре, перпендикулярном к XX', \ь обращается
и у' колинеариы (рис. J17). Пройдя через
нуль, \k меняет знак и начинает снова
возрастать по величине. На диаметре
XX' значение \к проходит через макси-
максимум, так как здесь v7 перпендикуляр-
перпендикулярно к Я.
Таким же образом изменяется и
сила давления штаиги на тело
Сила R, с которой, в свою очередь,
давит тело*) на штангу, равна по ве-
величине силе F и направлена в противо-
противоположную сторону, т. е.
R = 2m,[\'Q]. A0.13)
Величина и направление этой силы для
различных точек (положений штанги)
указаны на рис. 118.
Рассматривая направления давления
тела на штангу, мы обнаружим сле-
следующее. При переходе тела через ось
XX1 сила R не меняет направления,
поэтому её момент относительно этой
оси меняет направление. Вследствие
этого среднее значение момента
силы R относительно оси XX' за один
оборот штанги равно нулю и при быстром вращении тела этот момент
ие играет существенной роли. Наоборот, при переходе тела через ось УУ
сила R меняет направление, и поэтому её момент относительно этой оси
направлен всё время по оси УУ, так что он должен поворачивать плоскость
штанги вокруг оси УУ против часовой
стрелки, если смотреть со стороны У
(рис. 118).
Этот пульсирующий по величине, но
постоянный по направлению (и поэтому не
равный нулю в среднем за оборот) момент
относительно оси УУ будет постепенно
поворачивать плоскость штанги так, что
нижний конец О' оси 00' будет уходить
назад к концу X' оси XX'. Но вниз, по
оси 00', направлен вектор угловой скоро-
скорости ю, а значит, и вектор момента количе-
количества движения N (рис. 115). С другой сто--
роны, за чертёж по оси XX' направлен МО'
мент внешних сил М. Таким образом, как
только внешний момент М вызовет враще-
вращение плоскости штанги вокруг оси XX'
(вдоль которой направлен этот момент), тотчас же возникает давление тела на
штангу. Момент этой силы давления R относительно оси УУ1 вызовет вра-
вращение плоскости штанги вокруг оси YV в таком направлении, что момент
*) Тело давит на штангу потому, что оно также оказывается дефор-
деформированным; здесь опять всё происходит так же, как в примерах, разо-
разобранных нами в гл. V.

§ 61] ИЗМЕНЕНИЕ НАПРАВЛЕНИЙ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ 159
Рис. 119.
количества движения тела N будет поворачиваться в направлении
внешнего момента М.
При этом, как мы видели, момент силы R оказывается не постоянным
по величине, а пульсирующим. Вследствие этого и обусловленное им вра-
вращение плоскости штанги вокруг оси УУ' будет неравномерным. Однако,
при большой скорости ш вращения тела вокруг оси 00' эти пульсации
происходят очень быстро (с частотой вращения тела). Поэтому, как будет
показано ниже, вращение вокруг оси XX' происходит почти так же, как
если бы момент силы R имел постоянную величину, равную среднему
значению пульсирующего момента за один
оборот штанги. На этом основании мы
будем считать, что сила R создаёт неко-
некоторый постоянный во времени (а не пуль-
пульсирующий с частотой вращения тела т)
момент. (После того, как задача будет
рассмотрена до конца, выяснится, почему
это можно было сделать и какая ошибка
при этом допущена.)
Итак, вращение вокруг оси XX', обу-
обусловленное внешним моментом М, вызовет
появление силы R, дающей некоторый
момент М' относительно оси УУ. Этот мо-
момент вызовет вращение плоскости штанги
вокруг оси УУ с угловой скоростью У
(рис. 119), причём момент количества движе-
ния N будет приближаться к направлению внешнего момента М. Но, как
только возникнет вращение плоскости штанги вокруг оси УУ', появится сила
давления R' со стороны тела на штангу, подобно тому, как появилась сила
давления R при повороте вокруг оси XX'. Так как угловая скорость У
повёрнута относительно Q на 90° по часовой стрелке, то и вся картина
для силы R' повернётся относительно картины для силы R на 90° в ту же
сторону. Момент этой силы R' относительно
оси XX' также будет изменяться по ве-
величине, но направлен он будет всё время
в одну сторону— к концу X оси XX'. Так
же, как и для момента силы R, этот пуль-
пульсирующий момент можно заменить средним
значением за один оборот тела. Этот сред-
средний момент М", как видно из рисунка, бу-
будет направлен навстречу внешнему мо-
моменту М. Поэтому, когда вращение вокруг
оси У У достигнет такой скорости ^', при
которой средний момент М' силы R'станет
равным внешнему моменту М, вращение
вокруг оси XX' прекратится *). Вместе
с тем исчезнет и момент сил R, вызвав-
вызвавший вращение плоскости штанги вокруг
оси УУ'. Но само это вращение будет
продолжаться с достигнутой скоростью Q',
так как никаких моментов относительно оси УУ, которые могли бы
остановить движение или вообще изменить его углочую скорость, уже нет.
Итак, внешний момент М сначала вызывает вращение плоскости
штанги вокруг оси XX' с возрастающей угловой скоростью 8 (рис. 120).
х'
Рис. 120.
*) В этой картине установления мы опускаем ряд деталей, которые для
нас сейчас несущественны. Более подробно вся эта картина будет рассмо-
рассмотрена в § 94.

160
ЗАКОН СОХРАНЕНИЙ МОМЕНТА КОЛИЧЬ.СТВА ДВИЖЕНИЙ
[гл.
Вследствие этого появляется момент М', вызывающий вращение плоскости
итанги вокруг оси УУ с возрастающей угловой скоростью Й'. При эюм по-
появляется момент М", направленный навстречу внешнему моменту М.
После того как угловая скорость й' возрастёт настолько, что М" достигнет
значения М, вращение вокруг оси XX' прекратится *), а вращение во-
вокруг оси УУ' будет продолжаться с достигнутой скоростью й\
Конечный результат действия внешнего момента М состоит в^ том, что
момент количества движения N начинает вращаться с постоянной угловой
скоростью Я' в направлении внешнего момента М. Роль внешнего моиента
состоит в том, что он уравновешивает мо-
момент М", с которым при этом движении вра-
вращающееся тело действует на ось.
Если действие внешнего момента М пре-
прекращается, то существующий при вращении
тела вокруг оси УУ момент М" оказывается
неуравновешенным. Он вызывает вращение
плоскости штанги вокруг оси XX' в напра-
направлении, противоположном тому, в котором
она вращалась сначала, когда появился
внешний момент М. Это вращение вызовет
появление момента М', так же противополож-
противоположного тому, который существовал вначале
н вызвал вращение вокруг оси УУ. Под
действием этого момента скорость Я' будет
уменьшаться, и вращение вокруг оси УУ
быстро прекратится. Внешний момент М не-
необходим для поддержания вращения вокруг оси УУ. Когда внешний
момент исчезнет, это движение почти сразу прекращается.
Как сказано, угловая скорость 4У должна быть такой, чтобы обусло-
обусловленный ею момент М" был равен по величине внешнему моменту М. Из
этого условия определяется и то значение угловой скорости й', которое
устанавливается под действием внешнего момента М.
Для определения й' найдём в соответствии со сказанным выше среднее
значение момента М" за один оборот штанги. Аналогично A0.13), сила R'
определяется выражением:
Рис. 121.
Переходя от векторной записи к скалярной и выражая линейную ско-
скорость v' через угловую скорость вращения тела «о, получим (рис. 121):
= 2т<яг Й' sin a,
A0.14)
где а —угол между векторами v' и Я'. При этом справа от оси XX1
сила R' направлена на наблюдателя, а слева от оси XX'—от наблюдателя.
Момент её в обоих случаях направлен к концу X оси XX' и равен:
*) Как уже сказано, здесь опущены некоторые детали. В действитель-
действительности, когда М" достигнет значения М, вращение Q ещё не прекратится.
Поэтому скорость Й' будет продолжать растн и М" станет больше М. Уг-
Угловая скорость Q не только упадёт до нуля, но и изменит направление;
появится момент М', обратного направления, и скорость й' уменьшится.
Словом, будут происходить колебания угловых скоростей Я около значения,
равного нулю, и Q' около значения, соответствующего условию — М" = М.

§ 61] ИЗМЕНЕНИЕ НАПРАВЛЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ 161
так как плечо силы есть г sin а. Среднее значение sin2 а за период есть 1/2, и
поэтому среднее значение момента М" есть
М" = mr*u> Q'. A0.15)
Но /пг2 = /—момент инерции тела относительно оси вращения, a lu> = N —
момент количества движения относительно этой оси; поэтому
Так как установившаяся скорость должна быть такова, чтобы М"=М, то
С такой угловой скоростью будет поворачиваться вектор N в направ-
направлении внешнего момента М. За время М он повернётся на угол Да = Й'Д*
и изменится на величину ДД/ = Л/Да = N Й* Ы (рис. 122). Подставляя отсюда
значение О' в A0.14), найдём:
fif=M. A0.17)
Так как вектор Ш перпендикулярен к вектору N, то он совпадает по на-
направлению с вектором М. Поэтому мы можем рассматривать уравнение
A0.15) как векторное и, переходя к пределу, получим:
^=М. A0.18)
Это — уже известное нам уравнение моментов, полученное нами раньше
(§ 58) для случая, когда М и N совпадают по направлению. Сейчас на
частном примере мы получили это же уравнение для случая, когда М пер-
перпендикулярно к N. Следовательно, это уравнение
справедливо и в общем случае, когда М и N обра-
образуют какой угодно угол. Действительно, разлагая М на
две составляющие: Mi — в направлении N и М2— в
направлении, перпендикулярном к N, мы получим
оба рассмотренных случая, когда справедливо, как
мы убедились, уравнение A0.18). При этом составляю- „ .„9
щая Mi изменяет величину вектора N, а составляю-
составляющая Щ — его направление.
Итак, если постоянный момент внешней силы М остаётся всё время
перпендикулярным к моменту количества движения N, то этот последний
будет вращаться, «стремясь догнать» вектор М, причем угловая скорость
этого вращения определяется выражением A0.16). Если же вектор М непо-
неподвижен в пространстве, то вектор N в этом вращении не только «стремится
догнать», но догоняет вектор М. Угол между М н N уменьшается, и угло-
угловая скорость вращения вектора N уже не остаётся постоянной, а умень-
уменьшается (так как уменьшается составляющая вектора М в направлении,
перпендикулярном к N).
Теперь мы можем обосновать ту замену пульсирующего момента Сред-
Средним значением, которая была сделана выше. Как уже указывалось, это
законно только при большой скорости вращения тела вокруг своей оси,
т. е. при большом N. В самом деле, с увеличением ЛГУ уменьшается,
а, значит, наибольшие значения, которых достигает пульсирующий момент М",
пропорциональные произведению /V9', остаются неизменными, но частота
пульсации увеличивается (увеличивается <о). Но чем чаще пульсации мо-
момента, тем меньше изменение скоростей, которые этими пульсациями вызы-
И С. Э. Хайкин

162 ЗАКОН СОХРАНЕНИЯ КОЛИЧЬСТВЭ ДВИЖЕНИЯ [ГЛ. X
ваются. Скорость вращения не успевает измениться за полупериод пульса-
пульсации, в течение которого момент сил изменяется от наибольшего значения
до нуля или обратно. Иначе говоря, тело само усредняет пульсации, если
они достаточно быстрые. Поэтому и можно при быстром вращении заменять
пульсирующий момент его средним значением. Поэтому же можно вообще
не учитывать тех моментов, среднее значение которых за период равно
нулю, например, момента силы R относительно оси XX'.
Уравнение моментов A0.18) всё же оказывается при этом не вполне
точным, а приближённым. Действительно, под действием постоянного внеш-
внешнего момента момент количества движения должен изменяться с постоянной
скоростью; между тем пульсации скорости хотя и малы, но всё же они
имеют место. Дело в том, что вполне точным уравнение моментов является
не для момента количества движения тела вокруг оси вращения, а дли
суммы всех трёх моментов количества движения, которыми обладает тело
при вращении вокруг трёх взаимно перпендикулярных осей. Следовательно,
в нашем случае N в точном уравнении A0.16) есть геометрическая сумма
момента N, которым обладает тело вследствие вращения вокруг осн 00',
я момента N', которым оно обладает вследствие вращения вокруг оси YY',
причём N'=/'Q', где /'—момент инерции тела относительно осн УУ. Так
как расстояние от тела т до оси УУ при вращении его вокруг 00' меняется,
то момент N' меняется по величине, даже когда й' остаётся постоянным,
а именно N' пульсирует с частотой to. Но если геометрическая сумма мо-
моментов N н N' должна изменяться с постоянной скоростью, а момент N'
пульсирует с частотой и, то и момент N должен пульсировать с частотой ю.
Однако, если даже наибольшее значение пульсирующею момента N' мало
по сравнению с N, то пульсации момента N очень малы и ими можно пре-
пренебречь. Это условие соблюдается, если угловая скорость ь> вращения
вокруг осн 00' очень велика, как мы н предположили при замене пульси-
пульсирующего момента силы его средним значением. Следовательно, уравнение
A0.18) можно применить непосредственно к моменту количества движения
относительно оси вращения лишь при условии, что скорость этого враще-
вращения достаточно велика.
На рассмотренном частном примере обнаруживается общая черта, свой-
свойственная всем быстро вращающимся телам. Под действием внешних момен-
моментов ось быстро вращающегося тела поворачивается ие в той плоскости,
в какой она поворачивалась бы, если бы не было быстрого вращения, а в
плоскости, ей перпендикулярной. При этом движение оси под действием
постоянного момента происходит не с ускорением, а с постоянной угловой
скоростью и продолжается только пока действует внешний момент. Когда
прекращается действие внешнего момента, практически сразу прекращается
и движение оси. Эти особенности движения оси быстро вращающегося тела
нашли себе важные практические применения в так называемых гироско-
гироскопических приборах, которые б)дут рассмотрены ниже.

ГЛАВА XI
РАБОТА И ЭНЕРГИЯ
§ 62. Работа силы
Если точка приложения силы F совершает элементарное переме-
перемещение 4s, то при этом сила F совершает элементарную работу
1lA=FUscos(F, As)=FsAs, A1.1)
где р^ — проекция силы на направление перемещения. Произведение
абсолютных величин двух векторов на косинус угла между ними
носит название скалярного произведения этих векторов и обозначается
(F-As), следовательно, работа силы равна скалярному произведе-
произведению векторов силы и перемещения:
A,4 = (F-As). (П.2)
Если угол между F и As острый, то cob(F, As)^>0 и совершённая
работа положительна. Если угол между F и As тупой, то
cos(F, As)<^0 и работа, совершённая силой, отрицательна. В таком
случае иногда говорят, что не сила совершила отрицательную работу
а совершена работа против данной силы.
В том случае, когда перемещение происходит в направлении,
перпендикулярном к действию силы, cos (F, As) = 0 и сила не совер-
совершает работы.
Для того чтобы подсчитать работу, совершенную силой на каком-
либо конечном пути, на котором величина силы изменяется, нужно
весь путь разбить на ряд отдельных, достаточно малых элементарных
перемещений, на каждом из которых силу можно считать постоянной,
а затем взять алгебраическую сумму работ, совершённых силой иа
каждом таком элементарном перемещении.
Если весь путь разбит на отдельные малые участки длины As, то
работа на всём пути
^F, As).
Для каждого из участков должны быть взяты значения (силы F и угла
(F> Sit), соответствующие этому участку. Этому подсчёту соответ-
соответствует математическая операция интегрирования вадль пути переме-
11*

164 РАБОТА И ЭНЕРГИЯ [гл. XI
щення. Работа силы F при перемещении s может быть выражена
в виде интеграла:
А = J (F ds) = J Fsds, A1.3)
т. е. на каждом бесконечно малом участке пути ds должно быть
взято произведение Fs (проекции силы на направление пути) на ве-
величину участка ds и эти произведения должны быть просуммированы
по всему пути s.
За единицу работы, как н всегда при построении абсолютных
систем единиц, должна быть принята такая работа, которую сила,
равная единице, совершает при перемещении, равном единице (при-
(причём направление перемещения совпадает с направлением силы). В си-
системе CGS (сантиметр-грамм-секунда) единицей силы служит дина (дн),
а единицей работы — дн.см. Эта единица носит название эрга. Приме-
Применяется и более крупная единица работы — джоуль; 1 дж=107 эрг.
В систете MKS (метр-кнлограмм-секунда) единицей силы служит
килограмм-сила.' Поэтому в качестве единицы работы должна быть
принята работа, совершённая силой в 1 кг при перемещении на 1 м,
т. е. килограммометр. Так как 1 кг = 9,8-106 дн, то 1 кг-м=^
= 9,8-10' <Эк = 9,8 дж.
Найдём выражение работы для некоторых простейших случаев.
Если на всём пути проекция силы на направление пути остаётся
постоянной, то Fs — Fcos(F, <\s) для всех элементов суммы будет одно
и то же. Поэтому Ps может быть вынесено из-под знака суммы:
Сумма же элементов пути равна всей длине пути. Когда проекция силы
на направление перемещения на всём пути постоянна, работа силы равна
произведению проекции силы на длину пути.
Примером может служить движение тела по наклонной плоскости.
Работа, совершённая силой тяжести mg на пути s по наклонной плоскости'
есть '
A —
Работа зависит не от длины пути по наклонной плоскости, а от высоты ft,
иа которую опустилось тело.
Если величина силы F остаётся постоянной, но величина её проекции
на направление пути изменяется (потому что изменяется направление
пути), то нз-под знака суммы можно вынести не Fs, a F:
A —^Fbs cos(F, As) = .F2 As cos (F, As).
Под знаком суммы стоит проекция элементарного перемещения на посто-
постоянное направление силы. Но сумма проекций всех элементов пути на
постоянное направление равна проекции всего пути на это направление.
Следовательно, работа силы в этом случае будет:
где Sp—длина проекции всего пути на постоянное направление силы F.

§ 62] РАБОТА СИЛЫ 165
Примером может служить работа силы тяжести при движении тела по
какому-либо криволинейному пути*). Так как длина проекции пути на
йаправление силы тяжести, т. е. на вертикальное направление, есть просто
изменение высоты тела ft, то и в этом случае работа силы тяжестя зави-
зависит не от длины пути, а от изменения высоты
тела: А — tngh, где h — изменение высоты тела.
Во всех случаях работа, совершённая силой
тяжести при перемещении тела, не зависит от
пути, по -которому происходило перемещение,
и определяется только высотой, на которую
опустилось тело, т. е. начальным и конечным _ лр>~ w
положением тела. Подобным же свойством об д*?. ]'
ладают и упругие силы. "" " в" *¦
В этом мы можем убедиться на таком при-
примере. К какому-либо телу прикреплена растя- Рнс. 123.
нутая пружина. Другой конец пружины закреплён
неподвижно в точке О (рис. 123). Подсчитаем работу, которую совершает
сила, действующая со стороны пружины, при перемещении тела из точки С
в точку В по различным путям. Начнём с пути CDB. Положим для опреде-
определённости, что сила, с которой действует пружина, подчиняется закону
Гука; тогда сила пружины P=kr, где г — удлинение пружины. На пути CD
при элементарном перемещении — Дг сила пружины совершит работу
ДЛ = — Frbr = — kr Дг
[так как cos(F, Дг)= 1]. Чтобы вычислить работу на всём пути ACD, нужно
взять сумму элементарных работ по всему пути, т. е. вычислить опреде-
определённый интеграл, взятый в пределах от ги соответствующего точке С,
до г2, соответствующего точке D:
При перемещении по пути DB сила пружины не совершит никакой работы,
так как путь DB есть дуга окружности и cos (F, Дв) = 0. Следовательно,
полная работа силы пружины на пути
CDB есть
Ясно, что при перемещении по пути
„а,- yj.-i.j-.L.^. СЕВ сила пружины совершит ту же
в ? работу.
р 124 На пути СВ будет изменяться не
• только величина силы, но и угол
(F, As) между направлением силы и
направлением перемещения (рнс. 124). Работа силы Р на пути СВ будет:
Асв = 2 Иг Д* cos a.
Сравним теперь работу силы по путям СВ и CD. Пути СВ и CD мы
можем разбить на одинаковое число элементов (рис. 124). Тогда проекция
каждого элемента Д* по направлению силы есть Ar1 = Ascosa. Поэтому на
*) Однако, при этом изменение высоты тела должно быть достаточно
мало, чтобы силу тяжести можно было считать постоянной.

166 РАБОТА И ЭНЕРГИЯ [гл. Xt
соответствующих элементах путей CD и СВ совершается одинаковая эле-
элементарная работа, и так как число элементов одно и то же, то вся работа
на пути СВ равна работе на пути CD. Полная работа силы пружины во
всех трёх случаях будет одна и та же.
Работа силы пружины не зависит от пути и определяется только на-
начальным и конечным положением конца пружины. Этим свойством обла-
обладают не только сила пружины, но и вообще всякие упругие силы, т. е.
силы, возникающие при деформациях тел и однозначно определяемые
этими деформациями.
Работа сил тяготения и упругих сил не зависит от пути
и определяется только начальным и конечным положением точки
приложения силы. Но в таком' случае работа зтнх сил по любому
замкнутому пути всегда должна быть равна
нулю. Действительно, пусть точка приложения
силы переместилась нз В в С по пути BDC, а
затем по тому же са.\гаму пути обратно из С в
В (рис. 125). На обратном пути сила в каждой
точке будет' равна силе, действовавшей в этой
точке на пути туда. Но направление перемеще-
Рис. 125. ния на обратном пути будет противоположно
направлению перемещения на пути туда. По-
Поэтому работа на обратном пути ACDB по величине будет равна
работе на прямом пути ABDC и противоположна ей по знаку, т. е.
^bdc~^~ ^cdb^1®' Пусть теперь обратное перемещение происходит
по другому пути СЕВ. Работа силы не зависит от пути, и, следова-
следовательно, ACDB^= ACFB, откуда АСЕВ^=—Ardc и на вс§м пути
ЛВОСБа = 0. Путь этот мы выбрали совершенно произвольно. Сле-
Следовательно, работа упругих сил и сил тяготения по любому
замкнутому пути всегда равна нулю.
§ 63. Работа сил трения
Иначе обстоит дело в случае сил, зависящих от скоростей, — на-
например, сил трения. Легко видеть, что при наличии сил трения
работа по замкнутому пути, в частности, работа по одному и
тому же пути, пройденному туда и обратно, может быть не
равна нулю. Действительно, сила трения всегда направлена на-
навстречу скорости относительного движения. Поэтому, если, например,
тело движется в сопротивляющейся среде, то и на прямом пути, и
на обратном сила трения будет совершать отрицательную работу
и сумма этих работ по замкнутому пути не будет равна нулю.
Не следует, однако, думать, что сила трения всегда совершает отрица-
отрицательную работу. При известных условиях работа эта может быть положи-
положительна, и работа сил трения на замкнутом пути может оказаться положи-
положительной илн равной нулю. Дело в том, что сила трения направлена всегда
навстречу относительной скорости движения тел; поэтому она может ока-
оказаться направленной в сторону движения данного тела, если другое тело,
со стороны которого эта сила действует, движется в ту же сторону с боль-

§ 64] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 167
шей скоростью. Примером этого могут служить случаи, рассмотренные
нами в главе о тренни (§ 52). Если тело лежит на подставке, движущейся
со скоростью »0, и движется в том же направлении с меньшей скоростью »,
то относительная скорость тела направлена навстречу v, а сила трения Р
направлена в сторону движения тела, на которое она действует. Поэтому
сила трения совершает положительную работу. При движении тела в обрат-
обратном направлении сила трения направлена попрежнему в сторону щ (так
как v < vо н направление относительной скорости не изменилось) и сила
трения совершает отрицательную работу. Если при этом сила трения по
величине не зависит от величины относительной скорости, то работа силы
при перемещении тела в одном 'И в другом направлении будет одинакова
по величине и противоположна по знаку, т. е. работа по замкнутому пути
будет равна нулю. Более того, если сила трения уменьшается со скоростью
(т. е. 1>о лежит на падающем участке характеристики трения), то на пути,
совпадающем с направлением с0, относительная -скорость будет меньше, а
сила трения больше, чем на обратном пути. Поэтому и положительная ра-
работа силы трения на пути, совпадающем с направлением »0, будет больше,
чем отрицательная работа на обратном пути, и работа силы трения по
замкнутому пути будет положительна.
Положительную работу может совершать н сила трения покоя. Напри-
Например, в случае приводного ремня сила трения покоя всё время совершает
положительную работу, так как точка приложения силы трения (точки на
окружности шкива) всё время перемещается в направлении действия силы.
Работа силы трения по замкнутому пути может быть не равна
нулю потому, что эта работа зависит не только от начального и ко-
конечного положений точек приложения силы, но н от пути н скорости
перемещения.
§ 64. Потенциальная энергия
В системе тел, в которой действуют только силы, зависящие от
конфигурации, всякая работа этих сил связана с изменением конфи-
конфигурации (так как если система вернулась к прежней конфигурации,
то работа сил должна быть равна нулю). И если силы, действующие
в системе, совершают положительную работу, то конфигурация при
этом всегда изменяется так, что в конце концов способность системы
совершать работу оказывается исчерпанной. Например, если сила рас-
растянутой пружины совершает положительную работу, то прн этом
тфужина сокращается. В конце концов пружина сократится до нор-
нормальной длины и не сможет более совершать работу. Растянутая
пружина обладает определенным ограниченным запасом работы, кото-
которую она может совершить. Величина этого запаса работы опреде-
определяется начальным растяжением пружины, т. е. её начальной конфи-
конфигурацией.
Всякая система тел, в которой действуют силы тяжести и упру-
упругие силы, обладает определённым ограниченным запасом работы, ко-
которую эти силы могут совершить. Этот запас работы, обусловленный
конфигурацией тел системы, представляет собой потенциальную
внергию системы.
Например, потенциальная энергия растянутой пружины есть вся
та работа, которую может совершить сила пружины при сокращении

168 РАБОТА И ЭНЕРГИЯ [ГЛ. XI
пружины до нормальной длины. Как мы видели (§ 62) при сокраще-
сокращении растянутой пружины (если она подчиняется закону Гука) сила
пружины может совершить работу Л=- (х2— jc|), где хг и х2—
начальное и конечное растяжения пружины. Если растянутая пружина
сокращается до нормальной длины, то jc2 = O, и потенциальная энер-
энергия пружины, растянутой на величину хх:
U=^L. A1.4)
Эта энергия связана с наличием упругих деформаций в материале
пружины. В этих случаях потенциальную энергию называют энергией
упругой деформации.
Так же выразится и потенциальная энергия сжатой пружины,
если JCj — её сжатие (опять, если пружина подчиняется закону Гука).
Если тело опускается вниз, то сила тяжести при этом может со-
совершить некоторую определённую работу, величина которой зависит
от начальной высоты тела. Тяжёлое тело, поднятое на некоторую
высоту, обладает потенциальной энергией, равной той работе, кото-
которую совершит сила тяжести, когда тело опустится до «наинизшего»
уровня. Однако, «наинизшая» конфигурация для сил тяжести не мо-
может быть так естественно определена, как для пружины. Для пру-
пружины и вообще для упругих сил «наинизшей» конфигурацией будет
та, при которой деформации отсутствуют. Для тяжёлого тела нан-
низшим положением может быть в зависимости от условий опыта
уровень пола, уровень земли и т. д. Уровень, относительно которого
отсчитывается потенциальная энергия тела, поднятого на некоторую
высоту, может быть выбран совершенно условно. Но эта условность
никогда не скажется, так как нас интересует всегда не величина
потенциальной энергии, а её изменения (нужно лишь всегда отсчи-
отсчитывать потенциальную энергию относительно одного и того же уровня).
Если тело опускается с высоты ftj до высоты А2> т0 сила тяжес-
тяжести mg (когда её можно считать постоянной) совершает работу
A==mg{ht — А2), т. е. потенциальная энергия тела массы т равна
U=mgh, A1.5)
где h — начальная высота тела над уровнем, от которого отсчиты-
отсчитывается потенциальная энергия тела.
Всякий раз, когда силы, действующие в системе, совершают поло-
положительную работу, происходят такие изменения конфигурации, при
которых потенциальная энергия системы, уменьшается. Наоборот,
если силы, действующие в системе, совершают отрицательную работу,
то конфигурация изменяется так, что потенциальная энергия возрас-
возрастает. Чтобы силы, действующие в системе, совершали отрицательную
работу, точки приложения этих сил должны перемещаться в направ-
направлении, противоположном действию сил. Этого можно достигнуть, на-

§ 64] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 169
пример, прикладывая к телам системы внешние силы. Тогда эти
внеш-ше силы совершают гюложительную работу и увеличивают по-
потенциальную энергию системы.
Так, сила, растягивающая пружину, совершает работу и увеличивает
потенциальную энергию системы. Прн этом, если мы растягиваем пружину
медленно, работа внешней силы как раз равна увеличению потенциальной
энергии пружины. Действительно, для медленного растяжения достаточно
приложить к пружине (с закреплённым неподвижно другим концом) силу F
и постепенно увеличивать эту силу, чтобы она всё время лишь немного пре-
превышала силу, действующую со стороны пружины. Если затем пружина бу-
будет сжиматься, то она совершит такую же работу, какую совершила внеш-
внешняя сила прн растяжении пружины. Следовательно, при медленном растя-
растяжении пружины работа, совершённая внешней силой, как раз равна
увеличению потенциальной энергии пружины. При быстром растяжении
это уже не будет иметь места, так как, для того чтобы конец пружины
двигался с значительным ускорением, нужно, чтобы F было заметно больше
силы, действующей со стороны пружины, и тогда работа внешней силы
будет больше, чем увеличение потенциальной энергии пружины. Только
при медленных движениях работа внешних сил как раз равна увеличению
потенциальной энергии системы.
Рассмотрим ещё одни конкретный пример, из которого можно б|дет
вывести некоторое общее заключение. Две пружины соединены своими кон-
концами. Второй конец одной из пружин закреплён, а на второй конец другой
пружины действует сила F, изменяющаяся так, что происходив медленное
растяжение пружин. Положим, что обе пружины подчиняются закону Гука,
причём коэффициенты упругости их k\ н ?2 различны. В каждый момент и,
в частности, в конечном состоянии силы, действующие со стороны пружин
друг на друга, равны. Поэтому klxl = kixi, где хх и ^—соответственные
растяжения пружин. Отсюда xllx2 = k2/ki. Потенциальные энергии растяну-
растянутых пружин, соответственно, будут
<*=-г и "•=-?¦• т-е- t/^
Заменяя отношение X\jx2 через krfki, получим:
Ь -Ь.
и3 ~ ъ •
Распределение энергии в пружинах обратно отношению коэффициентов
упругостей пружины. Если одна пружина гораздо жёстче другой, то прак-
практически вся работа идёт на увеличение энергии упругой деформации более
мягкой пружины.
Очень жёсткие (мало деформируемые) тела подобны пружине с очень
большим *. Полагая, что *->-со, мы всё же получим в таких пружинах
конечные силы (так как соответственно уменьшаются деформации и f = kx
остаётся конечным). Но потенциальная энергия таких пружин стремится
к нулю, так как kx»/2 = p\2k -*¦ 0 при ?-»-оэи / конечном. Поэтому, вводя
представление об абсолютно жёстких телах илн связях, мы можем считать
энергию их упругой деформации прн всяких (конечных) силах равной нулю.
Если в системе, кроме сил тяжести и упругих сил, действуют и
силы трения, то они также могут совершать работу — положительную
или отрицательную. Однако, та работа, которую могут совершить
эти i-члы, не определяется, как мы видели, конфигурацией тел. На-

170 РАБОТА И ЭНЕРГИЯ [ГЛ. XI
пример, если тело падает в сопротивляющейся среде, то силы трения,
действующие на тело, совершают отрицательную работу (так как
сила направлена навстречу перемещению). Однако, эта работа не
увеличивает потенциальной энергии падающего тела. Попрежнему
потенциальная энергия определяется положением тела (его высотой).
Когда в системе действуют силы трения, потенциальная энергия си-
системы попрежнему определяется только силами, зависящими лишь от
конфигурации тел.
§ 65. Потенциальная энергия и состояния равновесия
Чтобы состояние равновесия было устойчиво, как уже было ука-
указано, необходимо, чтобы при отклонении от положения равнозесия.
возникали силы, возвращающие систему снова к положению равнове-
равновесия. (Это условие должно соблюдаться для любого направления,
в котором может произойти отклонение системы.) При этом возник-
возникшие силы совершают положительную работу. Если в системе дейст-
действует только силы тяготения и упругие силы, то совершаемая ими
положительная работа соответствует уменьшению потенциальной энер-
энергии системы. При приближении системы к положению устойчивого
равновесия потенциальная энергия должна уменьшаться, с какой бы
стороны ни приближа-
приближалась система к поло-
положению равновесия. А
это возможно только
в том случае, когда
положение равновесия
соответствует миниму-
Рис. 126. му потенциальной энер-
энергии.
Состояние равновесия устойчиво в том и только в том слу-
случае, если ему соответствует минимум потенциальной энергии.
В промежуточном случае безразличного равновесия при смещении
от положения равновесия вообще не возникает никаких сил, т. е.
потенциальная энергия вообще не изменяется при отклонении системы
от положения равновесия.
Для иллюстрации этой связи между характером состояний равновесия
и потенциальной энергией системы воспользуемся примером равновесия
шарика на цилиндрической поверхности, рассмотренным нами в § 41. При
этом кы опять будем пользоваться представлением об абсолютно жёстких
недеформируемых связях. Считая поверхность и нить недеформируемымн,
мы можем не принимать во внимание энергии уиругой деформации. При
этих предположениях потенциальная энергия системы обусловлена толъ-ко
силой тяжести, действующей на оба груза, и равна
U ^ M g й[ -(- tng h%,
гае hi и ft8 —высоты обоих грузов (рис. 126). Нам нужно выяснять, как
изменяется потенциальная энергия при изменении положения грузов.

§ 66] ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ 171
Попрежнему ограничимся случаем, когда нить параллельна касательной
к поверхности в точке, соответствующей положению рапновесия, и будем
считать, что направление нитн не изменяется при малых перемещениях
шарика (блок далеко). Условие равновесия для этого случая мы получим
(§ 41) в виде:
Если бы шарик М перемещался по наклонной плоскости С углом наклона а,
и соответственно перемещался груз т, то потенциальная энергия системы
оставалась бы постоянной.
В случае, когда шарик лежит на внутренней поверхности цилиндра, он
при тех же самых перемещениях груза т поднимается на большую высоту,
а опускается на меньшую высоту, чем в случае, когда он двигался бы по
наклонной плоскости с углом наклона а. Поэтому при обоих перемзщеииях
0.
Потенциальная энергия в обе стороны от положения равновесия возрастает.
Положение равновесия соответствует минимуму потенциальной энергии —
оно устойчиво.
Когда шарик лежит на внешней поверхности цилиндра, он при тех же
перемещениях груза т поднимается на меньшую высоту, а опускается на
большую высоту, чем в случае, когда он двигался бы по наклонной пло-
плоскости с углом наклона а. Поэтому при обоих перемещениях
Д?/= Mgbhy -f- mgbh2 < 0.
Потенциальная энергия в обе стороны от положения равновесия убывает.
Положение равновесия соответствует максимуму потенциальной энергии —
оно неустойчиво. Эти результаты совпадают с теми, к которым мы пришли
в § 41, рассматривая непосредственно силы, возникающие при. отклонении
шарика от положения равновесия.
Наши выводы относительно связи между характером изменений
потенциальной энергии и устойчивостью состояния равновесия спра-
справедливы только для систем, в которых отсутствуют силы трения.
Силы трения, в частности, наличие падающего участка на характери-
характеристике трения, могут сделать неустойчивыми и такие состояния равно-
равновесия, которым соответствует минимум потенциальной энергии. Про-
Происхождение неустойчивости в этом случае было нами выяснено в § 53.
§ 66. Закон сохранения энергии
Способность тел совершать работу определяется не только их
конфигурацией, но и скоростями, которыми эти тела обладают. Весь
запас работы, которую может совершить
тело вследствие того, что оно обладает
определенной скоростью, представляет
собой кинетическую энергию тела.
Подсчитаем кинетическую энергию для Рис. 127.
следующего конкретного примера: к концу
нерастянутой пружины (рис. 127) прикреплено тело массы т. Сообщим
этому телу начальную скорость vr При движении тела пружина
будет растягиваться и скорость тела будет убывать. Уравнение дви-

172 РАБОТА И ЭНЕРГИЯ [ГЛ. XI
жения тела будет иметь вид.
da ,. х
т — = f ух),
где f(x) — сила, действующая на тело со стороны пружины. Умно-
Умножим обе части этого уравнения на элементарное перемещение dx.
Принимая во внимание, что — =v, мы получим:
mvdv—f{x)dx. 01-6)
Так как сила, с которой действует тело на пружину, есть—/(•*). то
на пути dx эта сила созершит работу
dA = —f{x)dx = — mvdv. 0 1-7)
Чтобы подсчитать нею работу, совершённую телом до полной оста-
остановки, нужно взять сумму элементарных работ, совершённых при
изменении скорости от v0 до 0, т. е. проинтегрировать выражение
A1.7) в пределах от va до 0. Производя интегрирование и подставив
пределы, получим:
о
. Г j 1 иг»2
А — — \mv dv= —
о mv\
Такова работа, которую созершит тело до полной остановки. Значит,
тело массы т, движущееся со скоростью v, обладает кинетической
энергией
Г = 5?. A1.8)
При изменении скорости тела на dv кинетическая энергия тела изме-
изменяется на dT = mvdv, причём, как следует из уравнения (П.7),
dT = f{x)dx, т. е. изменение кинетической энергии тела равно эле-
элементарной работе внешней силы, действующей на тело.
В общем случае, если действующая на тело сила по направле-
направлению не совпадает со скоростью, то обе части уравнения движения
m-TT = t следует скалярно умножить на ds: m(v-dv) = (i-ds). Сила f
совершает работу (f-ds) и изменяет кинетическую энергию тела на
dT = (v • dv) = v dvt, где dvt — проекция вектора dv на направле-
направление V.
Изменение кинетической энергии происходит только при наличии
тангенциального ускорения. Если сила сообщает телу только нор-
нормальное ускорение, то при этом она не совершает никакой работы;
вместе с тем не изменяется и абсолютная величина скорости и ки-
кинетическая энергия тела остаётся неизменной.
Рассмотрим теперь, как изменяется потенциальная и кинетическая
энергии какой-либо замкнутой системы, в которой отсутствуют силы

§ 66] ЗАКОН СОХРАНЕНИЯ ЭНЬРГНИ 173
трения, т. е, действуют только упругие силы и силы тяготения. Для
материальных точек системы, обладающих массами mv /и3)... , та,
мы можем написать:
dt
Пусть все точки за какой-то элемент времени dt довершают пере-
перемещения dxv flfxS)..., dxn. Умножим каждое из уравнений ска-
лярно на соответствующее перемещение. Мы получим (так как
¦7r = v, и т. д.):
m, (v^Vl) — (F18 + F18 + ... ) dxl = О,
щ (v2flfv2) — (F81 + Fs3 + ... ) dx2 = 0,
>K (v/vn) - (Fnl + Fn2 + ...) dxa = 0.
Сложив все этн уравнения, мы получим:
2 /», (v^V/) - 2 (F/i -Ь рй + • • •) ^х,-=о-
2 'И/ (v/rfv^) = dT есть бесконечно малое изменение кинетической
энергии всей системы, а — 2 (Fn + F;2 + • ¦)d\l = dU— взятая
с обратным знаком бесконечно малая работа всех сил, действующих
в системе, т. е. бесконечно малое изменение потенциальной энергии
системы. Следовательно, для всей системы в целом
dT + dU = 0, A1.9)
откуда полная энергия системы
W= U-\- T= const. A1.I0)
Значение этой постоянной определяется значением кинетической энер-
энергии То и потенциальной энергии Ua системы в какой-то (один и тот
же) момент времени:
Полная энергия замкнутой системы, в которой
шалши#пругие силы и силы всемирного тяготения, есть вели-
величина постоянная. Это и есть закон сохранения энергии в меха-
механике. Он, как мы убедились, непосредственно вытекает из закона
движения.

174 РАБОТА И ЭНЕРГИЯ [ГЛ. XI
Однако, не для всех сил, действующих в системе, оказывается
возможным или удобным учитывать нх работу в виде изменения по-
потенциальной энергии системы. Прежде всего работа сил трения не
может быть учтена в виде изменений потенциальной энергии. Но и
силы, не зависящие от скоростей, иногда бывает удобно рассматри-
рассматривать как внешние и не учитывать их работы в виде изменений потен-
потенциальной энергии системы. Тогда закон сохранения энергии должен
быть формулирован иным образом. Обозначим силы, работа которых
учитывается в виде изменений потенциальной энергии, попрежнему
через Fik, а внешние силы, т. е. силы, работа которых не учиты-
учитывается в виде изменений потенциальной энергии, через Фа. Уравне-
Уравнения движения материальных точек системы после скалярного умно-
умножения их на «соответствующие бесконечно малые перемещения dxi
будут иметь вид:
т, (VjflfVj) — fFu-f- Fl3-f... )dxl^ (Ф^х,),
Щ (v3^v2) — (F21 + F23 4- . .. ) dx2 = (
Сложив эти уравнения, мы получим слева попрежнему сумму бес-
бесконечно малых изменений ' потенциальной н кинетической энергии си-
системы, а справа — сумму бесконечно малых работ всех внешних сил.
При конечных изменениях конфигурации изменение полной энергии
системы будет равно всей работе А, совершённой внешними силами ф^.
При переходе системы из состояния / в какое-либо другое состоя-
состояние 2 мы получим:
2
) = Allt A1.11)
т. е. изменение полной энергии системы при переходе из одного
состояния в другое равно работе, совершенной при этом внеш-
внешними силами. Это и есть более общая формулировка закона сохра-
сохранения энергии в механике.
§ 67. Колебания при возникновении силы
Воспользуемся законом сохранения энергии для рассмотрения следую-
следующей конкретной задачи. На тело массы т, прикрепленное к пружине (под-
(подчиняющейся закону Гука), в какой-то момент начинает действовать посто-
постоянная сила Fo. Силы трения отсутствуют. Смещение тела х будем отсчиты-
отсчитывать от положения, при котором пружина не растянута (рнс. 128).
При перемещении тела от начального положения х0 до положения х1
изменение полной энергии системы должно быть равно работе силы t\:
mv\ kx\ \ (mv\ kxl

§ 67]
КОЛЕБАНИЯ ПРИ ВОЗНИКНОВЕНИИ СИЛЫ
где t>i и Vq — скорости тела в точках х± и х$. Пусть в начальный момент
тело покоится (р0 = 0) и пружина не растянута (хй = 0), т. е. энергия си-
системы в начальный момент равна нулю. Посмотрим прежде всего, каковы
будут потенциальная и кинетическая энергии в тот момент, когда сила пру-
пружины достигнет величины Fq, т. е. когда отклонение достигнет значения
Так как в начальный момент То-\- ?/0=0, то полная энергия си-
системы равна работе, совершённой
внешней силой, т. е. Tl~\-U1="
и так как F<> = kx1, то _
" -X ' X
Но U\ = kx
Тх = Arf/2.
следовательно,
X, JCg
Рис. 128.
При движении тела работа внеш-
внешней силы /=Ъ идёт на увеличение отча-
отчасти потенциальной, а отчасти кинетической энергии системы. Как раз в момент,
когда натяжение пружины достигнет величины Fq, потенциальная и кинети-
кинетическая- энергии системы окажутся равными, т. е. как раз к этому моменту
половина работы внешней силы пойдет иа увеличение потенциальной энер-
энергии, а половина — на увеличение кинетической. Но если mv\\2= kx2x\2, то в
этот момент тело обладает скоростью »i=.*"iУ kfm. Оно будет продолжать
двигаться дальше с убывающей скоростью, причем за
счёт работы внешней силы и кинетической энергии
тела будет увеличиваться потенциальная энергия пру-
пружины до тех пор, пока тело не остановится. К этому
моменту вся работа внешней силы полностью пойдёт
на увеличение потенциальной энергии пружины. Отсю-
Отсюда мы можем определить то наибольшее отклонение,
которого достигнет тело. При этом отклонении
Ьу\*У — F* v т a v О А* \Ь
КЛп\^ 1 Q Лч) I . С Лч —- *?i Q/K.
Если бы внешняя сила возрастала очень медленно
до величины Fo (а не возникла сразу, как в нашем
примере), то статическое отклонение тела было бы
равно xi = Folk. Наибольшее отклонение, которого до-
достигает тело при мгновенном возникновении внешней
силы, оказывается вдвое больше статического откло-
отклонения. Дальше тело начнёт двигаться обратно с воз-
возрастающей скоростью; в положении Ху его скорость
снова достигнет значения »j = X\ \k\tn. При дальней-
дальнейшем движении скорость и вместе с тем кинетическая
энергия упадут до нуля. Пусть это будет положение х%. Прн этом
снова вся работа силы на пути от 0 до дг2 и затем обратно от х2 до хв,
т. е. работа FqXb, должна быть равна потенциальной энергии пружины
Адг|/2. Следовательно, Р(,х$ = кх\12. Решение 2F0 = kx% невозможно, так
как при растяжении, меньшем лг2, везде 2Fq > kx. Следовательно, je3 —(L
После этого все движения будут повторяться, т. е. тело будет совершать
колебания около положения xi = Fulk в обе стороны на величину х-у. При
этом скорость тела будет изменяться в пределах от нуля (в крайних точ^
ках) до Vy = хх Vk\m в средней точке (при x = Xi).
Рассмотренную нами картину можно иллюстрировать при помощи сле-
следующего опыта. Рели груз на пружине (рис. 129) подтянуть ниткой так,
чтобы пружина вначале не была растянута, а затем нитку пережечь, то
Рис. 129.

176 РАБОТА Н ЭНЕРГИЯ [гл. XL
груз будет совершать колебания около положения, соответствующего ста-
статическому растяжению пружины. Размахи колебаний будут как раз равны
величине статического растяжения. Пережигание ннтн соответствует «мгно-
«мгновенному включению» силы тяжести, которая раньше была уравновешена
натяжением нити.
Всякое мгновенное возникновение илн вообще изменение внешней силы
при наличии упругих сил неизбежно вызывает колебания около того стати-
статического отклонения, которое соответствует медленному изменению силы до
того же постоянного значения. С такими колебаниями, возникающими при
быстрых изменениях силы, нам уже приходилось встречаться при рассмот-
рассмотрении вопроса о происхождении деформаций, но там мы этнмн колебаниями
для упрощения пренебрегали. Конечно, на практике мы обычно имеем дело
не с мгновенно возникающими, а лишь с постепенно изменяющимися си-
силами Но если они изменяются быстро, то все же колебания возникают
При всяких быстрых изменениях силы всегда некоторая часть работы силы
превращается в энергию упругих колебаний, подобных тем, которые мы
сейчас рассматривали. Эти колебания в конце концов затухают вследствие
наличия сил трения в системе.
§ 68. Закон сохранения энергии и закон сохранения момента
количества движения
Кинетическая энергия движущегося тела (рассматриваемого как
материальная точка) равна mv2j2. Если движение тела представляет
собой вращение вокруг достаточно удалённой *) неподвижной осн,
то кинетическую энергию удобно выражать через угловую скорость
вращения. Так как v = wr, то
т
2 2 2 '
где / — момент инерции тела относительно оси вращения. Это же
выражение справедливо и для системы тел, вращающихся с общей
угловой скоростью вокруг одной и той же, удалённой от всех тел оси.
Если в отсутствии моментов внешних сил момент инерции си-
системы изменяется, то происходит и соответствующее изменение
угловой скорости, так как момент количества движения остаётся
постоянным; но, если /ю остаётся неизменным, то /ю2 уже не может
оставаться неизменным; когда при неизменном моменте количества
движения момент инерции увеличивается, то кинетическая энергия
уменьшается, и наоборот. Эти изменения кинетической энергии
обусловлены работой тех сил, которые вызывают изменения момента
инерции вращающейся системы.
Выяснить это обстоятельство проще всего иа конкретном примере вра-
вращения шарика на нити. Представим себе, что нить пропущена в отвер-
отверстие О, служащее центром вращения (рнс. 130), и момент инерции шарика
отногнтельно оси, проходящей через точку О, можно изменять, изменяя
длину ннти. При закреплённом конце нити сообщим шарику некоторую на-
начальную скорость »q, т. е. некоторый момент количества движения
Nq = /Wo»o = f^l^o (Mo — начальная угловая скорость, а г$ — начальная
длина ннти). Будем изменять момент инерции вращающегося шарика, мед-
*) Чтобы можно было рассматривать тело как материальную точку.

§ 68]
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
177
_*
Рис. 130.
ленно втягивая или отпуская ннть. При этом момент количества движения
относительно оси вращения не будет изменяться, так как сила натяжения
нити проходит через ось моментов. Так как /и = const., то при увеличении
радиуса вращения (возрастании /) кинетическая энергия
шарика /ь>-/2 будет уменьшаться. Для того, чтобы удер-
удерживать коиец нити, мы должны к ней приложить внеш-
внешнюю силу F=nt(i>ir. Если шарик удаляется от оси, то
¦точка приложения силы F перемещается в направлении,
противоположном направлению силы. Сила F совершает
отрицательную работу. Эта отрицательная работа внеш-
внешней силы н уменьшает кинетическую энергию шарика
(за счёт кинетической энергии шарика совершается работа
«против силы F»).
Наоборот, если нить втягивать, то кинетическая энер-
энергия Шарика ^улет увеличиваться (так как/уменьшается).
Но при этом внешняя сила F совершает положительную
работу, так как точка приложения силы F перемещается
в направлении силы. Эта работа идёт на увеличение ки-
кинетической энергии шарика.
Изменение кинетической энергии шарика связано с
изменением его линейной скорости v (так как в конечном счёте кинетическая,
энергия шарик* есть тиЦ1). Причиной изменения линейной скорости шарика
является сила, действующая со стороны нити. При изменении радиуса
вращения (длины нити) шарик движется по некоторой спирали, и поэтому
направление нити не перпендикулярно к скорости ша-
шарика. Появляется тангенциальная составляющая уско-
ускорения, изменяющая абсолютную величину скорости.
При раскручивающейся спирали нормаль к спирали
оказывается впереди радиуса-вектора (рис. 131). Со-
Составляющая натяжения нити Ft, а значит, и танген-
тангенциальное ускорение будут направлены в сторону,
противоположную скорости, и будут уменьшать ско-
скорость. При скручивающейся спирали, наоборот, нор-
нормаль к спирали оказывается позади радиуса-вектора,
тангенциальное ускорение направлено в сторону ско-
скорости и будет её увеличивать.
Во всех случаях, когда внешние силы изменяют момент инерции вра-
вращающейся системы, они совершают работу и изменяют кинетическую энергию
системы. Если же момент инерции вращающейся системы изменяется не под
действием внешних сил, а вследствие изменения связей в системе, напри-
например, в результате пережигания иитей в опытах, описанных в § 60, то кар-
картина получается иная. В этих случаях внешние силы отсутствуют и, следо-
следовательно, они не могут быть причиной изменения кинетической энергии
системы. Но в этих случаях перемещения отдельных тел системы происхо-
происходят быстро и неизбежно связаны с возникновением упругих деформаций,
а значит, и колебаний, аналогичных тем, которые рассмотрены в преды-
предыдущем параграфе. Часть энергии системы превращается в энергию этих
1 колебаний. Эта энергия вследствие затухания колебаний рассеивается
в виде тепла. Поэтому энергия системы в конечном счёте уменьшается.
Во втором из этих опытов, описанных в § 60, копа грузы движутся
к центру под действием пружины, кинетическая энергия системы в конце
оказывается больше, чем вначале. Это объясняется тем, что силы, дейст-
действующие со стороны пружины, совершают положительную работу и увели-
увеличивают кинетическую энергию системы. Однако, и в этом случае возникают
колебания, при которых рассеивается часть энергии, и поэтому кинетиче-
кинетическая энергия системы в конце оказывается меньше, чем сумма начальной
кинетической энергии сиетемы н потенциальной энергии растянутой пружины.
12 С. э. Хайкин
Рис. 131.

178 РАБОТА И ЭНЕРГИЯ [гЛ. XI
§ 69. Закон сохранения энергии и силы трения
Если в системе действуют силы, зависящие от скоростей, напри-
например, силы трения, то работа этих сил не учитывается изменениями
потенциальной энергии системы. Поэтому работу сил трения нужно
учитывать отдельно так, как мы учитывали работу внешних сил
в § 66. Если в замкнутой системе действуют силы трения, то так же,
как и в случае действия внешних сил,
где А12 — работа сил трения, действующих в системе. Силы трения
направлены навстречу перемещениям тел и работа, совершаемая ими,
оказывается отрицательной, т. е. А12<^0 и полная энергия замкну-
замкнутой системы при движении убывает.
Примеры такого уменьшения механической энергии системы в резуль-
результате действия сил трения мы наблюдаем на каждом шагу. Всякий раз,
когда отсутствуют внешние силы, работа которых могла бы пополнить
убыль энергии, вызванную силами трения, движения в системе затухают.
Прн макроскопических движениях, с которыми мы имеем дело и механике,
всегда в той илн иной мере присутствуют силы трения, и поэтому энергня
замкнутой системы уменьшается при движении.
В замкнутой системе, в которой действуют силы трения,
полная механическая энергия системы при движении убывает*).
Следовательно, в этих случаях закон сохранения энергии в узко ме-
механическом смысле несправедлив. Однако, при таком «исчезновении»
механической энергии всегда возникает эквивалентное количество
энергии другого вида. В частности, если уменьшение механической
энергии обусловлено действием сил трения, то при этом всегда вы-
выделяется определённое количество тепла, эквивалентное «исчезнув-
«исчезнувшему» количеству механической энергии.
Не только силы трения, но и другие механические силы, зави-
зависящие от скоростей, могут вызывать уменьшение механической энергии
системы. К этому типу относятся, например, силы, действующие
на электрический проводник, движущийся в магнитном поле. Поэтому
для поддержания вращения динамомашины внешние силы должны со-
совершать положительную работу, равную отрицательной работе снл,
зависящих от скоростей. Механическая энергня динамомашнны остаётся
постоянной, хотя внешние силы совершают работу. За счёт механи-
механической работы в динамомашине выделяется электрическая (и отчасти
тепловая) энергня, эквивалентная затраченной механической работе.
Все эти превращения энергии можно продемонстрировать при помощи
небольшой динамомашины, приводимой в движение опускающимся грузом
*) Напомним, что это справедливо только для замкнутой системы.
В незамкнутой сисгеме не только работа внешних сил может быть больше,
чем отрицательная работа снл трения, и увеличивать энергию системы,
но и сами силы трения могут совершать положительную работу, увели-
увеличивающую энергию системы. Пример этого был приведён в § 53.

§ 70]
мощность
179
(рис. 132). Если цепь динамомашины не замкнута, то силы взаимодействия
между якорем дииамомашииы и её статором отсутствуют. При этом груз
опускается с заметным ускорением и достигает нижней точки с большой
скоростью. Почти вся потенциальная энер1ия груза превратилась в кине-
кинетическую энергию самого груза и вращения якоря. Если же замкнуть цепь
динамомашины на лампочку накаливания или маленький электрический
мотор, то груз будет опускаться вниз гораздо медленнее. Уже не вся по-
потенциальная энергия груза будет превращаться в кинетическую энергию.
Силы, действующие между якорем и статором, зависят от скорости враще-
вращения и направлены навстречу вра-.
щению. Отрицательная работа этих
сил приведёт к тому, что полная
механическая энергия системы будет
уменьшаться. Но при этом динамо-
машина будет отдавать эквивалент-
эквивалентное количество электрической энер-
энергии, которая может быть снова
превращена в механическую (в мо-
моторе), в тепловую (в электрической
лампочке накаливания) нли в какой-
либо другой вид энергии.
Всякий раз, когда будет «ис-
«исчезать» энергия одного вида, бу-
будет появляться эквивалентное ко-
количество энергии других видов.
Энергия никогда не исчезает и
не появляется вновь; она лишь
превращается из одного вида в
другой. В этом заключается закон
сохранения анергии в его об- Рис. 132.
щем физическом смысле.
Закон сохранения энергии в механическом смысле представляет
собой лишь следствие, и притом не всегда справедливое (если силы
зависят от скоростей), из законов движения. Всеобщее же значение
закона сохранения энергии выступает именно там, где он не является
следствием из законов движения. Там, где закон сохранения энергии
в узко механическом смысле оказывается несправедливым, мы всегда
сможем указать другие виды энергии, в которые превратилась «ис-
«исчезнувшая» механическая энергия.
§ 70. Мощность
Все механизмы — двигатели, машины, станки и т. д. — служат
в конечном счёте для выполнения той или иной механической работы.
При этом одни механизмы совершают работу за счёт механической же
энергии. Например, водяные турбины совершают работу за счёт ки-
кинетической энергии движущейся воды. В других случаях машины
совершают механическую работу за счёт электрической энергии —
таковы, например, электрические моторы.
12*

180 РАБОТА И ЭНЕРГИЯ [гЛ. XI
Для характеристики всякого механизма важно знать, как быстро
он совершает работу. Мощность механизма, есть отношение ра-
работы., которая совершена механизмом, к тому промежутку вре-
времени, за который эта работа совершена. Если это отношение не
остаётся постоянным, то для определения мощности нужно брать
столь малые промежутки времени, чтобы дальнейшее нх дробление
не изменяло отношения работы к промежутку времени. Следователь-
Следовательно, если за промежуток времени At сове'ршена работа ДЛ, то мощ-
мощность механизма есть
w= hm м =~ (П.13)
Единицей мощности в абсолютной систе'ме единиц должна служить
такая мощность, при которой за единицу времени совершается ра-
работа, равная единице. Поэтому единицей мощности в системе GQS
служит эрг в секунду. Если же за единицу работы принять джоуль,
то единица мощности есть джоуль в секунду. Эта единица носит
название ватта:
1 вт = 10т эрг\сек.
В системе MKS' единицей мощности служит килограммометр
в секунду. Применяется и другая единица — лошадиная сила:
1 л.с. — 7Ь кгм\сек.
Элементарная работа, созершённая за промежуток времени dt,
есть
dA = (Fds),
Где ds есть бесконечно малое перемещение точки приложения силы
за элемент времени dt. Поэтому мощность
Где v — скорость точки приложения силы. Этим соотношением обычно
н'пользуются для измерения мощности механизмов.
Например, при измерении мощности двигателей зажимом Прони, кото-
который был описан выше (рис. 94), шкив, установленный на валу двигателя,
помещают в зажим и устанавливают давление зажима так, чтобы двш а-
тель мог вращаться. При помощи динамометра, прикреплённого к зажиму,
измеряют момент сил трения скольжения, с которыми шкив действует на
зажим. Этот момент можно заменить моментом некоторой силы F, прило-
приложенной к окружности шкива. Зиая число оборотов шкива п и его радиус
R, находят мощность w, развиваемую двигателем. Так как да = Fv, где v —
Линейная скорость точек окружности шкива, то
Однако, при этом двигатель всю свою мощность расходует на работу
против сил трения в зажиме. Поэтому для измерения мощности, отдаваемой
двигателем в обычных условиях работы на полезную нагрузку, используется
другой принцип.

§ 71] ПЕРЕДАЧА РАБОТЫ 181
Для того, чтобы механизм совершал работу, движущиеся части меха-
механизма должны действовать друг на друга с определёнными силами, т. е.
должны быть определённым образом деформированы: приводной ремень
должен быть растянут, вал двигателя должен быть скручен и т. д.
Из деформации движущихся частей можно определить те силы, с ко-
которыми действуют друг на друга эти части. Зиая скорости движения, мы
найдём мощности, передаваемые тем или иным механизмом. Для измерения
сил, действующих межДу движущимися частями механизмов, в каком-
либо месте вставляют упругий, легко деформирующийся элемент, по де-
деформации которого и определяют развиваемые им силы (например,
между валом двигателя и валом механизма, приводимого во вращение,
вставляют упругую муфту, которая может скручиваться). Зная число
оборотов вала, определяют мощность, передаваемую муфтой шкиву.
В некоторых случаях деформации движущихся частей бывают так значи-
значительны, что их можно измерять непосредственно. Например, длинные валы
при работе закручиваются настолько, что их скручивание легко измерить.
Этим пользуются для измерения мощности,отдаваемой судовым двигателем
гребиому винту.
Так как мощность механизма определяется произведением силы, кото-
которую развивает движущаяся часть механизма (вал, шкив, шестерня и т. д.),
на скорость, с которой эта часть движется, то для увеличения мощности
нужно лчбо увеличивать эти силы, либо увеличивать скорости движения.
Но увеличение сил всегда связано с увеличением размеров движущихся
частей. Например, чтобы вал при наибольших допустимых деформациях
развивал большие силы, нужно взять больший диаметр вала. Поэтому npif
данной скорости увеличение мощности механизма всегда связано с увели-
увеличением его размеров. Можно, однако, не увеличивая размеров механизмов,
повысить его мощность, увеличивая скорость движущихся частей. При
одних и тех же размерах быстроходный механизм всегда мощнее тихоход-
тихоходного; при одинаковых мощностях быстроходный механизм компактнее
тихоходного.
§ 71. Передача работы
Деформации движущихся частей механизма, совершающего работу,
играют принципиальную роль во всём процессе передачи работы.
Рассмотрим этот процесс на конкретном примере работы приводного
ремня (рис. 133). Пусть левый шкив служит ведущим, а правый ведомым;
следовательно, работа передаётся от левого
шкива к правому. Ремень, верхняя часть Г, f
которого растянута, действует на ведомый
шкив с силой F, направленной в сторону вра-
вращения шкива и поэтому совершающей поло-
положительную работу *). На ведущий шкив
ремеиь действует с силой f-\, направленной
навстречу движению шкива, и, значит, сила Рис. 133,
F1 совершает отрицательную работу (поло-
(положительную работу совершает сила, действующая со стороны ведущего
шкива на ремень).
Растянутая часть ремня обладает определённой энергией упругой де-
деформации. Эта энергия распределена во всей деформированной части
ремня. Если бы растянутый ремень покоился, то и энергия упругой де-
деформации оставалась бы иа месте, в растянутой части ремня. Так как ре-
ремень движется, то растянутыми оказываются всё новые и новые участки
*) Для упрощения мы опять говорим о силах: переход к моментам
сил не внесёт ничего принципиально нового, а лишь усложнит рассу»
Ждения.

182 РАБОТА И ЭНЕРГИЯ [гЛ.
XI
ремня, вступающие в верхнюю область между шкивами. При эгом, оче-
очевидно, энергия упругой деформации, которой облатает растянутый ремень,
не остается неподвижной в одних и .тех же местач ремня, а переходит из
одних его участков в другие, так что она оказывается локализованной
в части ромня, находящейся в данный момент между шкивами. Следова-
Следовательно, энергия движется по ремню в направлении, противоположном дви-
движению самого ремня, но с той же скоростью. Этот случай представляет
собой одни из простейших примеров течения энергии в движущемся упруго
деформированном теле. Вообще, когда упруго деформированное тело или
отдельные его участки движутся, с этим связано и перемещение энергии
упругой деформации, т. е. течение энергии.
Картину течения энергии в упругом теле мы рассмотрим детально
в § 109. Но уже сейчас мы должны принять во внимание течение упругой
энергии в ррмне, если хотим проследить процесс передачи работы от ве-
ведущего шкива к ведомому.
Ведущий шкив совершает положительную работу, которая идёт иа соз-
создание энергии упругой деформации ремня. Эта энергия течёт по ремню
к ведомому шкиву и там за счёт неё снова совершается механическая ра-
работа по вращению ведомого шкива. При стационарном режиме (постоянных
оборотах и постоянной нагрузке) у ведущею шкива в ремень втекает
столько же энер[ии, сколько её вытекает у ведомого шкива, и поэтому
анергия упругой деформации ремня всё время остаётся постоянной. В ста-
стационарных случаях мы не можем непосредственно обнаружить движения
энергии по ремню. Мы можем установить, что эиерг ия движется только
потону, что количество энергии в данном объёме изменяется и, значит,
энергия втекает или вытекает из этого объёма.
Поэтому при стационарном движении (когда деформации ре пня остаются
постоянными) мы ие будем иметь непосредственных указаний о движении
энергии от ведущего шкива к ведомому. Однако, в случае нестационар-
нестационарного движения легко было бы обнаружить, как энергия упругой деформа-
деформации движется от ремня к ведомому шкиву.
Если бы, например, конец ремня, находящийся у ведущего шкива,
внезапно остановился, то ремень мог бы совершить ещё некоторую работу.
Действительно, он действовал бы на ведомый шкив с некоторой силой
до тех пор, пока его деформация ие исчезла, и совершал бы положитель-
положительную работу *). Энергия упругой деформации ремня продолжала бы течь
по ремню к шкиву. В этом случае мы обнаружили бы, что энергия, нахо-
находившаяся в одном месте, переместилась в другое место, т. е. наблюдали бы
движение энергии в пространстве. Это даёт нам основание говорить о дви-
движении энергии и в стационарном случае.
Совершенно такую же картину движения энергии мы наблюдали бы
и во всех других передаточных механизмах и вообще во всех случаях,
когда работа передаётся из одних точек простраЕгства в другие. При этом,
однако, направление движения энергии не связано однозначно с направле-
направлением движения деформированных тел —оно зависит также от характера
деформации. В растянутом ремне, как мы видели, энергия движется в на-
направлении, противоположном движению ремия. В толкающем (сжатом) ры-
рычаге энергия течёт в том же направлении, в котором движется рычаг.
При изменении деформации (замена растяжения сжатием) направление те-
течения энергии меняется иа обратное. Во вращающемся скрученном валу
работа передаётся от одного конца вала, иа котором находится двигатель,
к другому концу, на котором находится нагрузка, т. е. энергия движется
в направлении оси вала. Между тем все точки вала движутся в плоскостях,
перпендикулярных к оси.
*). Мы ие говорим о три работе, которую мог бы совершить ремень
вследствие того, что он обладает кинетической энергией.

72]
АБСОЛЮТНО УПРУГИЙ УДАР 183
После всего сказанного совершенно ясно, что упругие деформации тел,
передающих работу, играют существенную роль. Если бы мы считали эти
тела недеформируемыми, то мы ие могли бы проследить всей картины
движения энергии. Для иедеформируемых тел нельзя было бы говорить
об энергии упругой деформации, а значит, и о движении энергии. Если бы,
например, мы считали ремень абсолютно иерастяжимым, то мы должны
были бы считать, что у ведущего конца шкива работа исчезает, а у ведо-
ведомого вновь появляется. Представление об абсолютно твёрдых иедеформи-
иедеформируемых телах так же непригодно для построения физической картины пе-
передачи работы (движения энергии), как оно непригодно для построения
физической картины «передачи» силы. Говоря, что «сила передаётся» или
«работа передаётся», мы в случае абсолютно недеформируемых тел никаких
физических представлений с этими словами связать не можем.
§ 72. Абсолютно упругий удар
Один лишь закон сохранения энергии обычно ие может дать полного
ответа иа вопрос о характере происходящих движений. Как и закон сохра-
сохранения количества движения, он даёт только одно уравнение и поэтому для
случая более чем одного тела ие позволяет определить скоростей гел.
Только в случае одного тела скорость этого тела в любой момент может
быть определена по начальным условиям на основании закона сохранения
энергии.
Для случая двух тел можно найти скорости обоих тел, применяя два
закона сохранения: сохранения количества движения и сохранения энергии
(конечно, если он соблюдается для данной системы тел). Эти два закона
дают два независимых уравнения, которые и позволяют определить две не-
неизвестные скорости в любой момент по начальным скоростям. Классиче-
Классическим примером применения законов сохранения является задача о так назы-
называемом абсолютно упругом ударе.
Абсолютно упругим удъром называют такое кратковременное взаимо-
взаимодействие тел, после которого в обоих взаимодействующих телах не
остаётся никаких деформаций. Поэтому вся та кинетическая энергия,
которой обладали тела до удара, после удара снова превращается в ки-
кинетическую энергию.
Для того, чтобы удар был абсолютно упругий, тела должны были бы
обладать вполне определёнными свойств-ами. Прежде всего все силы, воз-
возникающие в телах, должны зависеть только от деформаций. Если бы в те-
телах возникали силы, зависящие от скоростей деформаций, то деформации
не исчезали бы полиостью после прекращения взаимодействия тел. При
этом часть работы сил, действующих между телами, превращалась бы
в тепло и кинетическая энергия после удара была бы меньше, чем до
удара. Таким образом, для того, чтобы удар был абсолютно упругим,
должны отсутствовать силы, зависящие от скоростей. Реальные тела ие
обладают такими идеально упругими свойствами, но всё же в некоторых
реальных телах силы, зависящие от скоростей, могут быть очень малы.
Таковы, например, хорошие сорта стали, слоновая кость и т. д.
Соударение таких тел будет происходить следующим образом. Kai:
и при абсолютно неупругом ударе, будут возникать деформации соударяю-
соударяющихся тел и в результате этого возникать силы, изменяющие скорости тел.
Так будет продолжаться до тех пор, пока скорости обоих тел не окажутся
равными. До этого момента всё происходит так же, как и при абсолютно
неупругом ударе. Но с этого момента всё будет происходить иначе. При
абсолютно неупругом ударе в момент, когда скорости станут равны, силы
исчезают и скорости тел в дальнейшем остаются равными. В случае же
упругого удара в этот момент силы не исчезнут и скорости будут продол-
продолжать изменяться в том же направлении, что и раньше. Поэтому шары

184 РАБОТА И ЭНЕРГИЯ [гл. XI
будут «отодвигаться» друг от друга и деформации будут уменьшаться,
пока вовсе не исчезнут. К этому моменту упругие силы, возникающие
в шарах, совершат такую же положительную работу, какая была затрачена
на деформацию. Вся кинетическая энергия, которой обладали тела до удара,
снова превратится в кинетическую. Правда, при этом часть кинетической
энергии может быть связана с движением деформированных частей обоих
тел, т. е. с упругими колебаниями самих-тел, а не с движением тела как
целого. Но если соударяющиеся тела достаточно упруги и скорости до удара
невелики, то эта энергия бывает очень незначительна и кинетическая
энергия движения тел, как целого, после удара практически оказывается
равной кинетической энергии до удара.
Если удар можно считать абсолютно упругим, то для соударяющихся
тел можно написать два уравнения, выражающих закон сохранения,коли-
сохранения,количества движения и закон сохранения энергии:
2\2, A1.15)
Y~' AUb)
где vt и v2 —скорости шаров до удара, а V, и v2 — скорости их после
удара.
Рассмотрим сначала случай центрального улара. Уравнение A1.15)
в этом случае можно рассматривать как скалярное (все скорости до удара
do papa
до удара
т,
*после увара
после удара ...
Рис. 134. Рис. 135.
и после удара направлеЕШ по линии центров) и переписать уравнения
A1.15) и A1.16) в таком виде:
») OT( ) (П17)
mi(v'?-vl)=:m.i(vl-v'l), A1.18)
Разделив второе уравнение на первое, получим:
Умножая это уравнение один раз на от2, а другой раз на /»i и вычитая
его из уравнения A1,17), получим выражения для обеих скоростей после
удара:
' (ffll — ГП2) Р] -(- 2«2г/2 ' (ffl2 — «l) V2 + 2ffill'l /11 IQ4
»i= 7^+^Г2 ' P2=- т^щ ' AU9)
В общем виде эти выражения несколько сложны. Мы рассмотрим
только два частных случая, охватываемых этими соотношениями:

72] АБСОЛЮТНО УПРУГИЙ УДАР
1) Один шар до удара покоится: о2 —0. Тогда
485
После удара второй шар движется в ту же сторону, куда двигался первый
до удара. Скорость t>2 и поведение первого шара зависят от соотношения
масс.
a) Если /«!>/«2, то первый шар продолжает двигаться в том же на-
направлении, как и до удара, но с меньшей скоростью. Скорость второго
шара после удара больше, чем скорость первого
до удара (рис. 134).
b) Если ту < mi< T0 направление движения
первого шара при ударе изменяется — шар от-
отскакивает обратно. Второй шар движется в ту
сторону, в которую двигался первый до удара,
ио с меньшей скоростью (рис. 135).
2) Массы шаров одинаковы: /Я| = /я3 = т.
Тогда
( 2mv.2 i 1т vy _
Pl ~~ ~2m~ Vv V2~~~2m *'
т. е. шары равной массы при ударе обмениваЕотся
скоростями.
Все эти случаи можно продемонстрировать
при помощи стальных или костяных шаров, ка-
катящихся по гладкбму горизонтальному стеклу.
Конечно, наше рассмотрение, строго говоря,
не относится к случаю качения шаров по пло-
плоскости. Но если стекло достаточно гладкое, то
центры шаров движутся примерно так, как это следует из нашего рас-
рассмотрения.
В случае нецентрального удара можно разложить скорости шаров на
составляющие (рис. 136): »1я и о2л в направлении линии центров и vu и
v2t-— в перпендикулярном направлении и написать два уравнения, выра-
выражающих закон сохранения количества движения (штрихами попрежнему
отмечены скорости после удара):
Рис. 136.
+ т1Р2п> (И-20)
mvvyt -f m2°2/ = mYv\t + т-Р%- О 1.21)
Так как v2 = v\ -f- v2n, то закон сохранения энергии мы можем написать
в виде:
.2
[v'l +¦ »12„)
2
2
A1.22)
Для четырёх неизвестных компонент скорости vu, vw v2t, v2n мы получи-
получили только три уравнения. Однако, поскольку мы сделали предположение,
что энергия при ударе сохраняется, мы должны считать, что силы трения
отсутствуют (шары абсолютно гладкие). Но тогда шары при ударе и? мо-
могут изменить тангенциальных составляющих своих скоростей (так как для
этого нужны тангенциальные силы). Поэтому вместо уравнения A1.21) мы
можем прямо написать:

186 РАБОТА И ЭНЕРГИЯ [гЛ. XI
Соответствующие члены в уравнении A1.22) сократятся, и для нор.
мальных составляющих мы получим два уравнения:
+ тчР1п = т\Ры -f m2v'2n,
2 "•" 2 ~~ 2 ' 2
Эти уравнения совершенно аналогичны тем, которые мы получили для
полных скоростей в случае центрального удара. Таким образом, при не-
нецентральном абсолютно упругом ударе гладких шаров нормальные со-
составляющие скоростей ведут себя так же, как при центральном ударе;
тангенциальные же составляющие не изменяются.
В частности, в случае нецентрального удара шаров равной массы они
обмениваются нормальными составляющими скоростей, а тангенциальные
составляющие остаются неизменными.
Случай нецентрального удара также можно продемонстрировать при
помощи стальных или костяных шаров, катящихся по стеклу.
Остановимся ещё на одном случае нецентрального удара. Положим,
что масса одного из шаров гораздо больше массы другого шара (щ^> Ш\).
До удара этот шар покоится (i/2 = 0). Из соотношений A1.19), пренебрегая
«j по сравнению с /я2;мы получим для нормальной составляющей первого шара:
Тангенциальная составляющая скорости после удара не изменится. Полная
скорость шара после удара изменит лишь своё направление. Это справед-
справедливо и для случая абсолютно упругого удара о гладкую стенку. При этом
«угол падения» а будет равен «углу отражения» fi (рис. 137).
Отметим одно обстоятельство, очень характерное для законов сохране-
сохранения. Так как мы получили выражения для скоростей после удара, разделив
уравнение A1.18) на A1.17), то при этом мы, оче-
видно, потеряли одно решение, при котором обе
части уравнения A1.17) обращаются в нуль, а
именно решение:
р ,.,-j которое также удовлетворяет законам сохранения.
Но это решение соответствует тому, что скорости
шаров вообще ие изменились при ударе: шары как
бы прошли Один сквозь другой, не изменяя своих скоростей. Мы знаем,
конечно, что это невозможно, ио знаем это на основании совсем других
соображений, а не законов сохранения. С точки же зрения законов сохра-
сохранения такое решение вполне возможно. Это — не случайное обстоятельство,
а очень характерная и принципиальней черта законов •сохранения. Законы
сохранения никогда не дают и ие могут дать однозначного ответа на вопрос
о том, что произойдёт. Но если мы, исходя из каких-либо других соображе-
соображений, можем указать, чтб именно должно произойти, то законы сохранения
дают ответ иа вопрос, как это должно произойти. С точки зрения закона
сохранения энергии свободное тело может остаться «висеть» в воздухе, так
как при этом энергия его остаётся неизменной. Но если мы знаем, что те-
тело будет падать, то закон сохранения энергии позволяет установить, как
будет меняться скорость тела с высотой. Понятно, почему законы сохра-
сохранения не могут дать однозначного ответа на вопрос о том, что произойдёт.
Ведь законы сохранения во всяком случае будут соблюдены, если вообще
ничего не произойдёт. Даже тогда, когда законы сохранения дают ответ на
вопрос, они дают его в виде альтернативы: либо ничего ие произойдёт, либо
произойдёт то-то и то-то.

§ 73] ЗАКОНЫ СОХРАНЕНИЯ В ДВИЖУЩИХСЯ СИСТЕМАХ КООРДИНАТ 187
§ 73. Законы сохранения в движущихся системах координат
Как было показано, ^применяемые нами законы движения справедливы
не только в «неподвижной» системе координат, по и в любой инерциальиой
системе координат. Поэтому не требуется доказывать, что законы сохране-
сохранения, которые являются прямым следствием законов движения, также должны
быть справедливы в любой инерциальной системе координат. Однако, это
положение полезно разъяснить и иллюстрировать на отдельных конкретных
примерах *).
С законом сохранения количества движения дело обстоит просто. Если
скорости материальных точек, образующих замкнутую систему в неподвиж-
неподвижной системе координат, равны vb v3, v3, ..., то в движущейся системе коор-
дниат они будут равны \'1=z\l — \g, \'2= v2 — v0, ..., где v0 —скорость
второй системы координат относительно первой «неподвижной». Соответ-
Соответственно полное количество движения всех тел в «неподвижной» системе
координат будет равно:
а в движущейся системе координат;
' ^ -f wav2 4" • • • — («i + mi + • • •) vo •
Второе отличается от первого иа постоянную величину (nti -\-mi~\- ...) vn.
Одна и та же система обладает разным количеством движения в разных
системах координат. Но если количество движения в «неподвижной» системе
координат остаётся постоянным, то оно остаётся постоянным и в системе
координат, движущейся прямолинейно и равномерно относительно неподвиж-
неподвижной. Закон сохранения количества движения справедлив для замкнутой
системы в любой инерциальной системе координат.
Закон сохранения энергии также справедлив для любой ииерциальиой
системы координат; однако, это не столь очевидно, как для закона сохране-
сохранения количества движения. Прежде всего ясно, что потенциальная энергия
данной системы точек во всех инерциальных системах координат будет одна
и та же. Действительно, потенциальная энергия данной системы зависит
только от их конфигурации, т. е. от разностей координат. Но это взаимное
расположение не зависит от выбора системы координат. Поэтому потенциаль-
потенциальная энергия данной системы материальных точек во всех инерциальных
системах координат будет одна и та же.
Кинетическая же энергия в различных системах координат будет раз-
различна. Если в «неподвижной» системе координат скорости точек v1; Vj, . ..,
то кинетическая энергия каждого тела будет соответственно равна
т _ Щ0* т _ Щ°*
В движущейся системе координат скорости точек будут v'1 = v1 — Vo,
V2 = V2~ vo> • • •> a кинетическая энергия каждой из них;
11 — —g — —2 mi ^VlV°' '
тг (v2v0) 4-
4VO
*) Как обстоит дело с законами сохранения в неинерциальных системах
координат, мы рассмотрим в § 79.

188 РАБОТА И ЭНЕРГИЯ [ГЛ. X*
Следовательно,
Тх- r1=«1(v1ve)
—Тъ=Щ (v2v0)
Если скорости v1( \ь ... изменяются, то ие только самая величина кинети-
кинетической энергии, но и изменения кинетической энергии каждой точки в раз-
различных системах, координат будут различны.
Общая кинетическая энергия всей системы в движущейся системе ко-
координат 7"'= 7^+ Т^Н будет отличаться от общей кинетической энер-
энергии в неподвижной системе координат Т= Ту -\- Тъ-\- .. . на величину
(/я, 4- т» 4- ...) vl
r-r = («iv1 + «,v, + ...)ve 2 * <1L23)
Полная энергия W данной системы материальных точек в движущейся
систрме координат будет отличаться от полной энергии W в «неподвижной»
системе координат на ту же величину. Второй член правой части выраже-
выражения A1.23) всегда остаётся постоянным, так как Vo постоянно. Первый же
член, вообще говоря, может изменяться при изменении скоростей. Но
в замкнутой системе сумма т^у^ -j- w2v2 -f-. .. должна оставаться постоян-
постоянной, так как она представляет собой полное количество движения всех
материальных точек системы. Поэтому, если для данной системы достается
постоянным, то W—W, а, значит, и W\ остаётся постоянным. Если закон
сохранения энергии справедлив для данной системы материальных точек в
«неподвижной» системе координат, то он будет справедлив для неё и в любой
инерциальной системе координат. Кинетическая, а, следовательно, и полная
энергия системы в различных системах координат, будет различна, но в лю-
любой инерциальной системе координат сумма кинетической и потенциальной
энергии замкнутой системы будет оставаться постоянной.
Если на систему действуют внешние силы (т. е. система не является
замкнутой), то её полная энергия ни в одной из систем координат не оста*
нется постоянной. Но при этом и разность W— W уже ие остаётся постоян-
постоянной, так как общее количество движения системы (которое входит в эту
разность) для незамкнутой системы изменяется. Следовательно, не только
полная энергия системы, № и изменения этой энергии для различных систем
координат оказываются различными. Но всё же изменение полной энергии
системы, в каждой из систем координат равно работе внешних сил. Не-
Необходимо лишь принять во внимание, что перемещения материальных точек,
а, следовательно, и работа внешних сил в разных системах координат, так-
также оказываются различными.
Поясним эго на следующем простом примере. Пусть на тело массы т
начинает действовать постоянная внешняя сила F. Будем рассматривать зто
движение в двух системах координат, из которых вторая движется относи-
относительно первой в направлении, ПРОТИВОПОЛОЖНОМ F, С ПОСТОЯННОЙ СКОрОСТЬЮ V(j.
Ускорение тела в обеих системах координат будет одно и то же: a^F\m.
Если в начальный момент скорость тела равна нулю в первой системе ко-
координат, то в момент времени t она будет равна
т
В движущейся системе координат в этот момент Скбрость будет

§ 73] ЗАКОНЫ СОХРАНЕНИЯ В ДВИЖУЩИХСЯ СИСТЕМАХ КООРДИНАТ 189
Соответственно, кинетическая энергия в двух системах координат вы-
выразится так:
Так как кинетическая энергия тела в начальный момент в первой системе
была равна нулю, а во второй Го = /иУд/2, то изменения кинетической энер-
энергии в обеих системах координат за время t будут:
АГ &T' Ft+
2/д - и ' Ъп
С другой стороны, пути, пройденные телом в обеих системах координат,
выразятся так:
aV Ft* , . at* . . Ft*
8 *' V+ ^+
а работы силы F на этих путях будут, соответственно, равны:
Р2/2
Следовательно, Д7"=/5, ДГ' = /5'. Изменения кинетической энергии и работа
силы F в обеих системах координат различны, но и в той и в другой си-
системе координат работа внешней силы равна изменению энергии системы.

ГЛАВА XII
НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ
§ 74. Силы инерции
Как было показано (§ 30), основные положения механики Ньютона,
а, значит, и все вытекающие из них следствия, могут быть справед-
справедливы только для систем координат, движущихся друг относительно
друга прямолинейно и равномерно. Далее опыты (в частности, опыт
Фуко) показали, чго основные положения механики Ньютона справед-
справедливы в нашей «неподвижной» системе координат. Значит, «неподвиж-
«неподвижная» система координат вместе со всеми системами координат, не
обладающими по отношению к ней ускорением, образует класс инер-
циальных систем координат, в которых справедливы основные положе-
положения механики Ньютона.
- Однако, практически часто удобно пользоваться системами коор-
координат, которые имеют ускорение по отношению к Солнцу и звёздам.
В таких неинерциальных системах координат механика Ньютона уже
не справедлива. Классическим примером этого случая является си-
система координат, связанная с Землёй. Для того, чтобы определить
ускорение тел по отношению к Земле, нельзя пользоваться основ-
основными положениями механики Ньютона в том виде, как они были
сформулированы выше. Между тем часто нас интересуют движения
тел именно по отношению к Земле. Поэтому возникает вопрос: нельзя
ли изменить и дополнить механику Ньютона так, чтобы её можно
было применять и к системе координат, связанной с Землей? Вообще,
что и как нужно изменить в механике' Ньютона, чтобы её можно
было применять в данной неинерциальной системе координат?
Рассмотрим с этой точки зрения основные положения механики
Ньютона:
1. Ускорения тел вызываются силами.
2. Силы обусловлены действием тел друг на друга и однозначно
определяются конфигурацией тел или их относительными скоростями.
При переходе к системе координат, обладающей ускорением но
отношению к Солнцу и звёздам, ускорения движущихся тел изменя-
изменяются, а конфигурация и относительные скорости тел, а, значит, и
силы, остаются прежними. Поэтому оба основных положения вместе

§ 741 силы инт-рции 191
не могут быть сохранены при переходе к неинерциальным системам
координат. От одного из этих положений нужно отказаться. В меха-
механике отказались от второго из положений механики Ньютона, чтобы
сохранить в силе первое. Следовательно, в механике неинерциальных
систем координат попрежнему ускорения вызываются силами, но силы
необязательно обусловлены действием тел друг на друга. В неинер-
неинерциальных системах координат появляются силы, возникновение
которых уже нельзя объяснить действием каких-либо отдельных
тел. Их появление обусловлено тем, что система координат обла-
обладает ускорением по отношению к Солнцу и звёздам. Эти силы
мы будем называть силами инерции*).
Введение сил инерции позволяет сохранить для неинерциальных
систем координат первое положение механики Ньютона. Вместе с тем
сохраняют свой прежний вид и уравнения движения, вытекающие из
этого положения. Попрежнему в уравнениях движения слева будут
стоять произведения масс тел на их ускорения (но уже относительно
данной неинерциальной системы координат), а справа — силы. Но среди
этих сил, кроме «обычных» сил, обусловленных действием других
тел на данное, будут встречаться и силы инерции.
В то время, как в инерциальных системах координат уравнение
движения имеет вид:
wj = 2F- 02.1)
где 2^ — сумма сил, действующих на данное тело со стороны других
тел, в неинерциальных системах координат уравнение движения того
же тела имеет вид:
2 2 02.2)
где 2F —те же самые силы, действующие на данное тело со сто-
стороны других, a 2F/—сумма сил инерции, действующих на данное
тело вследствие того, что неинерциальная система координат обла-
обладает ускорением по отношению к «неподвижной».
Однако, уравнения движения только тогда имеют смысл, когда
входящие в него силы мы умеем определить. Для «обычных» сил мы
всегда сможем (по крайней мере принципиально) сделать это, зная
конфигурацию тел и их относительные скорости. То же самое мы
должны суметь сделать и для сил инерции. Конечно, силы инерции
должны зависеть не только от координат и скоростей тел, но и от
ускорения нашей системы координат (по отиошеню к «неподвижной»),
так как их появление именно этим ускорением и обусловлено. Но
если нам задано движение системы координат, то мы должны суметь
*) Мы говорим «мы будем называть» потому, что нередко в механике
силами инерции называют силы, действующие со стороны ускоряемых тел
на ускоряющие. Как уже было сказано, мы не будем применять этот тер-
термин в таком смысле и будем называть силами инерции только силы, появ-
появляющиеся в неинерциальиых системах координат и обусловленные тем, что
система координат обладает ускорением по отношению к Солнцу и звёздам.

192 НЕИНгРЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ [гл XII
определить силы инерции, т. е. выразить их через координа-
координаты и скорости тел, и скорость и ускорение самой системы коор-
координат.
Указание о том, как определить силы инерции, действующие в той
или иной неинерциальной системе координат, мы найдем, сопоставляя
уравнения движения одного и того же тела в двух системах коор-
координат — инерциальной A2.1) и неинерциальной A2.2). Вычитая
первое уравнение из второго и принимая во внимание, что ^F — это
одни и те же силы, не зависящие от выбора систеуы координат
и поэтому одинаковые в обоих случаях, Получим:
где j' — ускорение в данной неинерциальной, a j — ускорение в
инерциальной системе координат.
Очевидно, j'—j—это то дополнительное ускорение, которое
добавляется к ускорению в инерциальной системе координат вслед-
вследствие того, что неинерциальная система координат движется по
отношению к инерциальной. Это дополнительное ускорение не вы-
вызывается действием каких-либо других тел, так как действие тел
остаётся таким же, как в инерциальной системе координат, и* со-
сообщает рассматриваемому телу то же ускорение j, что и в инер-
инерциальной системе координат. Возникновение этого дополнительно! о
ускорения j' — j и должны объяснить силы инерции. А для этого
сумма сил инерции должна быть равна произведению этого допол-
дополнительного ускорения на массу того тела, на которое эти силы дей-
действуют.
Следовательно, чтобы ' определить силы инерции, действующие
в том или ином случае, мы должны найти разность ускорений в не-
неинерциальной и инерциальной системах координат. Эта задача была
нами подробно рассмотрена в гл. III. Там мы определяли, как свя-
связаны между собой «относительное» и «абсолютное» ускорения при
различных движениях системы координат — различных переносных
движениях. В нашем случае — ускорение в «неинерциальной» системе
координат—это «относительное», а ускорение в инерциальной си-
системе координат—«абсолютное». Разность между первым и вто-
вторым— это как раз те дополнительные ускорения, которые нужно
прибавить к ускорению в инерциальной системе координат, чтобы
получить ускорение в неинерциальной системе координат. Таким об-
образом, общий способ определения сил инерции, действующих в том
или ином случае, нами найден: сумма сил инерции, действующих
на данное тело, равна произведению массы тела на дополни-
дополнительное ускорение, которое нужно добавить к «абсолютному»
ускорению, чтобы получить «относительное».
Зная, как выражаются силы инерции в том или ином случае дви-
движения неинерциальной системы координат (переносного движения),
мы могли бы сразу рассматривать движения в этой системе коорди-

§ 75] СИСТЕМЫ КООРДИНАТ, ДВИЖУЩИЕСЯ ПРЯМОЛИНЕЙНО 193
нат, не интересуясь уже картиной этих движений в инерциальной
системе координат. Однако, для того, чтобы освоиться с этим но»
еым приёмом, мы рассмотрим примеры движений как в инерциаль-
инерциальной, так и в иеинерциальной системах координат при различных
переносных движениях и сопоставим между собой результаты того
и другого рассмотрения.
При сопоставлении движения в инерциальной и неинерциальной
системах координат мы для краткости будем пользоваться термина-
терминами, общепринятыми для этих случаев, — будем говорить о «непо-
«неподвижном и движущемся наблюдателях». Не следует, однако, думать»
что какую-либо роль при этом играют субъективные ощущения
«наблюдателей». Вместо наблюдателей мы могли бы с двумя систе-
системами координат связать какие-либо регистрирующие приборы (фото-
(фотоаппараты, приборы для записи ускорений и скоростей и т. д.), кото-
которые объективно регистрировали бы движение тела относительно той.
и другой систем координат. Эту объективную регистрацию движений
мы и будем иметь в виду, когда будем говорить о результатах на-
наблюдений «неподвижного и движущегося наблюдателей».
§ 75. Системы координат, движущиеся прямолинейно
Сопоставим прежде все^о движения тела в двух системах коор-
координат, из которых одна движется по отношению к другой с ускоре-
ускорением, но прямолинейно. Иллюстрацией этому могут служить различ-
различные опыты на тележке, движущейся по рельсам с ускорением.
«Поместим» одного наблюдателя в аудитории, а другого на тележке.
Конечно, и наблюдатель, находящийся в аудитории, не будет, строго
говоря, «неподвижным», так как но отношению к Солнцу и звёздам
он движется с ускорением (вместе с Землёй). Но в рассматриваемых
нами опытах это никак не скажется — система координат, связанная
с Землёй, с точки зрения этих опытов будет практически инерциаль-
ная. Поэтому наблюдателя, находящегося в аудитории, мы будем
называть неподвижным.
Произведём следующий опыт. Положим на тележку гладкое стек-
стекло и на него шарик. Если мы толкнём тележку, то шарик начнёт
перемещаться относительно тележки в направлении, противополож-
противоположном движению тележки. Для неподвижного же наблюдателя шарик
попрежнему остаётся в покое (конечно, пока шарик свободно лежит на
стекле и не соприкасается с краем тележки). Так оно и должно
быть с точки зрения законов Ньютона, ибо на шарик не действуют
никакие силы (давление стекла уравновешивает силу тяжести, а си-
силы трения практически отсутствуют). Но для движущегося с тележ-
тележкой наблюдателя шарик приобретает ускорение, когда мы толкаем
тележку. Между тем никаких новых тел, которые могли бы вызвать
ускорение шарика, не появилось (рука ведь действует на тележку,
а не на шарик). И если движущийся наблюдатель объясняет все
13 С. Э. Хайкин

194 HI ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ КО0РДИН\Т [гл. XII
наблюдаемые им ускорения действием сил, то он должен предполо-
предположить, что на шарик начала действовать некоторая сила, не обуслов-
обусловленная действием каких-либо других тел. Это и есть сила инерции,
которая появляется потому, что система координат, с которой связан
наблюдатель, приобретает ускорение по отношению к инерциальной.
Шарик по отношению к тележке приобретает ускорение, противо-
противоположное тому, которым обладает тележка по отношению к ауди-
аудитории. Следовательно, появившаяся сила инерции направлена на-
навстречу тому ускорению, которым обладает движущаяся система
координат.
Легко подсчитать и величину этой силы инерции. Для неподвиж-
неподвижного наблюдателя шарик покоится; следовательно, для движущегося
•он обладает ускорением-/„, где /0— ускорение тележки. Но, для
того чтобы шарик обладал ускорением—/0, на него должна дейст-
яозагь сила инерции Р=— /п/0, где т — масса шарика.
Рис. 138.
Но—/0 — это то ускорение, которое как раз нужно добавить к «аб-
«абсолютному», чтобы получить «относительное» ускорение в случае
поступательного переносного движения. Сила инерции, как видим,
равна этому дополнительному ускорению, умноженному на массу те-
тела, на которое она действует.
К этому же выводу нас приведёт и другой опыт. Поместим на
тележку маятник (рис. 138). Пока тележка покоится, маятник рас-
расположен отвесно. Если же сообщить тележке ускорение при помощи
груза, перекинутого через блок, то маятник отклонится от огвеса
в сторону, противоположную движению тележки, и останется в та-
таком отклонённом положении на всё время, пока тележка движется
с постоянным ускорением *).
*) Маятник вначале будет качаться около отклонённого положения.
Чтобы колебания маятника не возникли, нужно сделать так, чтобы ускоре-
ускорение тележки возникло не сразу, а постепенно.

§ 75] СИСТЕМЫ КООРДИНАТ, ДВИЖУЩИЕСЯ ПРЯМОЛИНЕЙНО 195
Неподвижный наблюдатель объяснит движение маятника следую-
следующим образом: на маятник действует только сила тяжести и натяже-
натяжение подвеса. Вначале, пока маятник, расположен отвесно, натяжение
подвеса не может сообщить ему ускорения в горизонтальном направ-
направлении. Поэтому тележка вместе с точкой
подвеса уходит от покоящегося маятника. .
Но тогда направление подвеса перестаёт I ,
быть вертикальным (рис. 139) и составляю- щк
щая этого натяжения /since сообщает маят- ^gl
нику горизонтальное ускорение. Отклонение
отвеса будет увеличиваться, пока составляю- ' /-s /~\~~| ' *"J<7
щая / since не достигнет значения mj\ (j0—
ускорение тележки и т — масса маятника). Рис. 139.
Тогда маятник будет двигаться с тем же
ускорением jn, что и тележка, и отклонение отзеса перестаёт
изменяться. Сумма действующих на маятник сил должна быть равна
'"Jai т- е>
Для движущегося наблюдателя маятник вначале имеет ускорение
в направлении, противоположном движению тележки, а затем, когда
отклонение перестаёт изменяться, ускорение маятника исчезает. При
этом сумма сил, действующих на маятник со стороны Земли и под-
подвеса, равна т\й (эти силы для обоих наблюдателей одинаковы). Так
как ускорение маятника движущийся наблюдатель обнаруживает
только вначале, то он должен предположить, что на маятник начала
действовать сила — т}а, сначала вызвавшая отклонение маятника, а за-
затем уравновесивщая силы nig и f, действующие на маятник. Это
и есть сила инерции, появление которой обусловлено ускорением
тележки относительно неподвижной системы координат.
Когда система координат движется с ускорением, но пря-
прямолинейно по отношению к инерциальной, в ней действуют си-
силы инерции
F/ = — ink,
где j0 — ускорение системы координат, а т — масса тела, на кото-
которое эта сила инерции действует. Зная, как выражается сила инер-
инерции, мы можем уже сразу, не рассматривая предварительно движе-
движения в инерциальной системе координат, определить характер
движений в системе координат, движущейся с ускорением, но пря-
прямолинейно.
В качестве примера рассмотрим опыты с лёгким маятником, подвешен-
подвешенным на падающей рамке. Если масса рамки велика по сравнению с массой
маятника, то можно считать, что его движение никак не сказывается на
движении рамки, и она падает с ускорением свободного падения g. Рас-
Рассматривая движение маятника с точки зрения «неподвижного» наблюдателя,
было бы трудно в общем виде ответить на вопрос о движении маятника
при паленин рамки. С точки же зрения наблюдателя, находящегося на
13s

196
НЕИНЕРЦЙАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ
[гл. XI t
рамке, ответ на этот вопрос можно дать сразу. Так как рамка падает сво-
свободно, т. е. с ускорением g, то движущийся наблюдатель должен кроме
сил, действующих на маятник со стороны Земли и штанги, ввести ещё
направленную вверх силу инерции — т%, где
т — масса маятника. Поэтому для наблюдате-
—з--ц ля, находящегося на рамке, сила инерции как
раз уравновешивает силу тяжести *). По от-
отношению к рамке маятник движется так,
ф ; | 6-! как будто сила тяжести на него ие действует,
а действует только штат а. Но если тело жёстко
скреплено с осью, вокруг которой оно может
вращаться, и никакие другие силы на него не
действуют, то оно будет вращаться с той по-
постоянной скоростью, которую имело в начальный
момент. После начала падения чаятиик будет
продолжать вращаться вокруг точки подвеса с
той скоростью, которую он имел в момент, когда
началось падение. В частности, если маятник
в момент начала падения находился в положе-
положении наибольшего отклонения, а скорость его
была равна нулю, то он будет продолжать оста-
II I ваться в отклонённом положении (неподвижном
I T по отношению к рамке) во всё время падения
I (рис. 140). Если в момент начала падения иаят-
Рис. 140. Рис. 141. ник проходил через низшее положение и имел
наибольшую скорость, то во время падения он
будет продолжать вращаться с этой наибольшей скоростью (рис. 141).
§ 76. Вращающаяся система координат
Перейдём теперь к случаю вращения системы координат с постоян-
постоянной угловой скоростью. Опять путём сопоставления движений одного
и того же тела в инерциальной системе координат и в системе
координат, вращающейся относительно инерциальной, мы должны
будем найти выражения для сил
инерции, появляющихся в этом
случае.
Произведём для этого опыт
с отвесами на вращающейся
горизонтальной подставке (рис.
142). При вращении подставки
отвесы отклоняются от верти-
вертикали наружу (от оси вращения).
В случае постоянной угловой
Рис. 142.
скорости вращения подставки каждый отвес отклоняется иа оп-
определённый угол и дальше отклонение отвесов прекращается.
Величина этого отклонения тем больше, чем больше расстояние от
отвеса до оси вращения. Отвес, находящийся на оси вращения, не
отклоняется вовсе.
*) Так можно, с точки зрения движущегося наблюдателя, объяснить
И опыт Любимова, который был описан в § 36.

§ 76] ВРАЩАЮЩАЯСЯ СИСТЕМА КООРДИНАТ 197
Выясним, как нозникают отклонения отвесов. Когда подставка на-
начинает вращаться, отвес висит вертикально, и действующие на него
силы — притяжение Земли и натяжение нити — ие могут ему сооб-
сообщить никаких ускорений в горизонтальной плоскости. Поэтому под-
подставка вместе с точкой подвеса начинает уходить от покоящегося
груза. Нить натягивается сильнее и отклоняется от вертикали. Появ-
Появляется составляющая натяжения нити в горизонтальной плоскости.
Она сообщает ускорение грузу, и он начинает принимать участие
в движении подставки. Вместе с тем увеличение натяжения нити вы-
вызывает появление и вертикальной составляющей ускорения — груз
начинает подниматься. Изменения угла отклонения отвеса прекратятся
тогда, когда груз приобретёт ту же скорость, что и лежащая под
ним точка подставки, т. е. будет полностью участвовать во вращении
подставки. При этом шарик будет описывать окружность и угловая
скорость вращения будет равна о). Для этого на него должна дей-
действовать центростремительная сила ти>2г, т. е. такой должна быть
составляющая натяжения нити в горизонтальном направлении. С дру-
другой стороны, вертикальная составляющая натяжения нити должна
уравновешивать вес шарика. Следовательно, f sin а = тюгг и fcosa=:
= mg, откуда tgct — wV/g.
Рассмотрим теперь это же движение с точки зрения наблюдателя,
находящегося на подставке. Отклонение отвеса от вертикали вращаю-
вращающийся наблюдатель объясняет появлением сил инерции. Детальное
объяснение того, как возникает отклонение грузов для вращающе-
вращающегося наблюдателя, оказывается довольно сложным (из дальнейшего
будет ясно, почему). Но при установившемся отклонении отвесов
легко найти силы инерции, действующие на грузы. Со стороны Зем-
Земли и нити на каждый из грузов действуют силы, сумма которых
равна т<йгг и направлена к центру вращения (так же, как для не-
неподвижного наблюдателя). Однако, для вращающегося наблюдателя
отвесы покоятся, и поэтому сумма всех сил, действующих на .груз,
должна быть равна нулю. Поэтому вращающийся наблюдатель должен
предположить, что на каждый из отвесов действует сила инерции,
направленная от центра и равная /им2г. Это — так называемая
центробежная сила инерции *).
Когда для вращающегося наблюдателя тело покоится, этот
наблюдатель должен ввести центробежную силу инерции, направ-
направленную от оси вращения и равную пш2г, где т — масса тела, на
которое эта сила действует, ш — угловая скорость вращения наблю-
наблюдателя (относительно «неподвижной» системы координат), г—радиус-
*) Таким же образом наблюдатель, движущийся вместе с шариком,
объясняет и простейший случай вращения шарика на нитке. На шарнк
действуют сила притяжения иити (центростремительиая сила)—тш2г и центро-
центробежная сила инерции /nmV. Вторая уравновешивает первую, и поэтому
шарик ие имеет ускорения (для наблюдателя, вращающегося вместе с ша-
шариком, шарик покоится).

198
НЕИНЬРЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ
[гл
XII
вектор. Но — о>2г есть переносное ускорение той точки вращаю-
вращающейся системы координат, в которой находится тело. В этом случае,
так как тело покоится во вращающейся системе координат, «относи-
«относительное» ускорение равно нулю, а «абсолютное» равно переносно-
переносному. Поэтому дополнительное ускорение, которое нужно прибавить
к «абсолютному», чтобы получить «относительное», равно ы2т —
переносному ускорению, взятому с обратным знаком. Сила инерции
равна этому дополнительному ускорению, умноженному на массу
тела.
Сделав этот вывод, мы можем теперь уже сразу рассматривать
движение тела с точки зрения вращающегося наблюдателя. Это
весьма упростит решение некоторых вопросов
Рис, 143.
Рис. 144.
та>гт
Рассмотрим в качестве примера опыт с лёгким пробковым шариком,
помещенным во вращающуюся шарообразную чашку (рис. 143). При не-
небольшой угловой скорости вращения чашки шарик лежит на дне. Однако,
если угловая скорость чашки достаточно велика, то шарик уже не остается
лежать на дне, а, поднявшись по стенке чашки, вращается вместе с чаш-
чашкой, оставаясь на некоторой определённой высоте,
тем большей, чем больше угловая скорость враще-
вращения чашки (рис. 144).
Такое поведение шарика с точки зрения наблю-
наблюдателя, вращающегося вместе с чашкой,объясняет-
чашкой,объясняется весьма просто Так как шарик легкий и вместе
с тем шероховатый, то силы трения достаточно ве-
велики, для того чтобы увлечь шарик за чашкой.
Поэтому мы можем считать, что, двигаясь вдоль
стенки чашки, шарик нигде не отстает от враще-
вращения чашки, т. е. все движения шарика происходят
по одному и тому же меридиаЕ1у чашки. В дей-
действительности это не совсем так, ио это обстоятельство не помешает
иам объяснить поведение шарика Поэтому мы можем представить себе,
что шарик одет (в виде бусииы) па вращающуюся проволочную дугу, по
которой он может свободно передвигаться (рис. 145). Для неподвижною
дар
Рис. 145.

§ 76]
ВРАЩАЮЩАЯСЯ СИСТЕМА КООРДИНАТ 199
наблюдателя на шарик действуют сила тяжести mg и давление со стороны
проволоки N. С точки зрения вращающеюся наблюдателя на покоящийся
шарик действует, кроме того, центробежная сила инерции misfit, 1де <о —
у[ловая скорость вращения наблюдателя (чашки). Состояния равновесия
шарика определяются из условия, что сумма моментов силы тяжести и си-
силы инерции относительно центра дуги О равна нулю *). Из рисунка видно,
что момент силы тяжести М± = —mgR sin а, где R — радиус дуги (знак мн-
иус взят потому, что момент действует в направлении, противоположном
отклонению). Сила инерции есть /»(oV= mu>2./?sin се, и её момент относитель-
относительно точки О равен М^ = tmo^R- sin a cos а (знак -f- взят потому, что момент дей-
действует в направлении отклонения). Поэтому результирующий момент есть
М = m^R? sin а ( cos а $-). A2.4)
Из условия равновесия М — 0 получаем два значения угла, при которых
возможно равновесие-sin * = 0 и cos a =ь §/«>-#. Первое условие может быть
осуществлено при любом <о, второе — только при условии ?/ш2/?< 1 Ц^ли
со2 >§¦//?. Таким образом, при малых угловых скоростях существует только
одно положение равновесия шарика — в нижней точке (а = 0). При больших
угловых скоростях появляется и другое положение равновесия, определяе-
определяемое из второго условия. Угол, соответствующий этому положению равнове-
равновесия, тем больше, чем больше ш.
Для того чтобы определить поведение шарика, нужно не только найти
состояния равновесия, но и решить вопрос об их устойчивости. Если мо-
момент сил, возникающих при отклонении от положения равновесия, возвра-
возвращает шарик к положению равновесия, то состояние равновесия устойчиво;
в противном случае состояние равновесия неустойчиво. Таким образом,
для устойчивости состояния равновесия необходимо, чтобы результирующий
момент обеих сил был по знаку противоположен отклонению от положения
равновесия Из выражения A2.4) вилно.'что вблизи положения равновесия
а = 0 знак момента противоположен знаку отклонения при cos a < gl^fiR-
Так как мы рассматриваем малые отклонения от положения а = 0, то
cosa~l и наше условие принимает вид: ?/а>Ч?>1. Это и есть условие
устойчивости нижнего положения равновесия Но вместе с тем, как мы виде-
видели, это — и условие существования только одного (нижнего) положения
равновесия. Поэтому, пока существует только одно нижнее положение рав-
равновесия, оно всегда устойчиво—шарик может в нем находиться как
уюдно долго. При ббльшпх оборотах чашки, когда ?-/ш2/? < 1, появляет-
появляется другое положение равновесия (cos а = gj^R), а нижнее становится
неустойчивым.
Таким же образом, как эта было сделано выше, можно убедиться
в том, что верхнее положение равновесия, если оно существует, всегда
устойчиво.
Рассмотренный пример является хорошей иллюстрацией преимуществ
применения движущихся систем координат. В «неподвижной» системе ко-
координат мы должны были бы рассматривать сложные движения и решать
грудный вопрос об устойчивости этих движений Применив вращающуюся
систему координат, мы свели задачу к гораздо более простой — отысканию
состояний равновесия и определению их устойчивости.
*) Если бы мы взяли моменты сил относительно какой-либо другой
точки, то нам пришлось бы учесть н моменты той силы N, с которой про-
проволока давит иа шарик. Но так как эта сила нормальна к проволоке (тре-
(трения пет), то её момент относительно точки О равен нулю.

200 НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ [гл. ХЦ
§77. Кориолисова сила инерции
На тело, которое покоится во вращающейся системе координат,
действует центробежная сила инерции. Отсутствие ускорения у покоя-
покоящегося тела вращающийся наблюдатель сможет объяснить, лишь
учтя эту силу инерции. Если же тело движется относительно вра-
вращающейся системы координат, то действующая в этой системе коор-
координат сила инерции носнт более сложный характер. Одной только
центробежной силой инерции вращающийся наблюдатель не сможет
объяснить наблюдаемых им ускорений.
Чтобы выяснить характер силы инерции, возникающей в этом
случае, мы должны, как и прежде, найти то дополнительное ускоре-
ускорение, которое нужно добавить к ускорению в «неподвижной» системе
координат, чтобы получить ускорение во вращающейся системе коор-
координат. Проще всего выглядит эта задача, если тело не обладает
ус^рением в «неподвижной» системе координат, т. е. покоится или
движется прямолинейно и равномерно. Тогда ускорение во вращаю-
вращающейся системе координат как раз равно интересующему нас допол-
дополнительному ускорению. Действительно, на тело не действуют никакие
силы со стороны других тел, и всё ускорение во вращающейся си-
системе координат есть ускорение, обусловленное силами инерции.
В случае, когда «абсолютное» ускорение j —0, «относительное»
ускорение во вращающейся системе координат
J' = -b-J*. A2.5)
где je = — со2г— переносное, а ]А = 2[а>'У']^-кориолисово ускоре-
ускорение Следовательно, интересующее нас дополнительное ускорение
есть
w2r-]-2fv'.(i>]
(вместо изменения знака во втором члене мы изменили порядок со-
сомножителей), а сила инерции
F, = m(<o2r-f 2 fv'<¦>]). A2.6)
Таким образом, сила инерции в нашем случае состоит из двух
частей — первой, зависящей только от угловой скорости вращения, и
второй, зависящей также и от «относительной» скорости. Можно
сказать, что на тело, движущееся во вращающейся системе коорди-
координат, действуют сразу две силы инерции. Первая,
Fc = mo>2r, A2.7)
представляет собой уже известную нам центробежную силу инерции,
действующую также и на покоящееся тело во вращающейся системе
координат. Вторая,
Fft = 2»i[v'<e], A2.8)
представляет собой добавочную силу инерции, появляющуюся

§ 77] кориолисова сила инерции 201
тогда, когда тело движется во вращающейся системе координат;
когда скорость этого движения v' обращается в нуль,— эта сила ис-
исчезает. Эта сила инерции связана, как мы видели, с существованием
кориолисова ускорения, и поэтому её обычно называют кориолисовой
силой инерции. Для этой силы инерции мы и сохраняли название, от
применения которого мы отказались в § 33. Нужно, однако, помнить,
что кориолисова сила инерции вызывает не то ускорение 2[w-v'],
которое называют кориолисовым, а обратное ему дополнительное
ускорение 2fv'«o>], которое появляется при переходе от «неподвиж-
иой> к вращающейся системе координат.
Мы полагали для упрощения, что в «неподвижной» системе коор-
координат тело движется прямолинейно и равномерно. Если же в «непо-
«неподвижной» системе координат тело движется с ускорением, то значит,
на него действуют какие-то силы со стороны других тел. Во
вращающейся системе координат эти силы действуют попрежнему и
имеют то же значение, но
к ннм добавляются две силы ft
инерции — центробежная и
кориолисова. Сумма всех
этих сил и должна быть равна
произведению массы тела на -—•-,
его ускорение во вращаю- р ..g
щейся системе координат. ис>
Для пояснения рассмот-
рассмотрим, как и в предыдущих параграфах, какое-либо движение с
точки зрения как неподвижного, так и движущегося наблюдателя.
В качестве такого примера воспользуемся опять моделью, на ко-
которой мы изучали деформации (§ 69). Напомним, как происходит
движение тела по вращающейся штанге с точки зрения неподвиж-
неподвижного наблюдателя (рис. 146). На тело действуют две силы fc со
стороны пружины н fft со стороны изогнутой штанги. С другой
стороны, если тело относительно штанги движется равномерно, зна-
значит, его относительное ускорение j' = 0 и абсолютное ускорение
l = lt-\-lk, где \с — переносное ускорение, направленное к центру,
и \k — кориолисово ускорение, направленное нормально к штанге
в сторону её движения (если тело движется от оси). Центростре-
Центростремительное ускорение \с телу сообщает сила fc, действующая
со стороны пружины, а корнолисово ускорение — сила fft, действую-
действующая со стороны изогнутой штанги.
Посмотрим теперь, как объяснит всю картину наблюдатель,
вращающийся вместе со штангой. Так как тело движется относительио
штанги с постоянной скоростью, то для вращающегося наблюдателя
рно движется прямолинейно и равномерно (для него штанга непо-
неподвижна). Между тем на тело действуют силы fc со стороны пружины
и fft — со стороны штанги (эти силы, действующие со стороны одних
тел на другие, одинаковы во всех системах координат). Чтобы о,бьч<;*

202 неин^рниальные системы координм1 [гл. хп
нить, почему, несмотря на действие этих сил, тело всё же движется
прямолинейно и равномерно, движущийся наблюдатель вводит силы
инерции (рис. 147) — центробежную ?с, направленную от центра и
уравновешивающую натяжение пружины, и i'k—направленную в сто-
сторону, противоположную кориолисову ускорению, и уравновешивающую
давление штанги.
С точки зрения вращающегося наблюдателя можно сказать, что
кориолисова сила «прижимает тело к штанге и изгибает штангу».
При этом, однако, нужно
иметь в виду, что давление
тела на штангу — это во-
вовсе не кориолисова сила
0 | —g, инерции. Это давление —
«обычная» сила, действу-
f* ющая со стороны одного
Рис J47 тела на дРУгое и обу-
обусловленная тем, что дви:
жущееся по штанге тело оказывается деформированным. Но воз-
возникновение этой деформации вращающийся наблюдатель объясняет
действием на тело кориолисовой силы. Здесь дело обстоит совершен-
совершенно так же, как, например, в случае тяжёлого тела, лежащего на
подставке. На подставку действует не притяжение Земли, а дефор-
деформированное тело. Но тело оказалось деформированным потому, что
на него действует сила тяжести.
В разобранном примере направления центробежной и кориолисо-
кориолисовой сил инерции не совпадают. Но в случае, когда тело во вращаю-
вращающейся системе координат само „
вращается вокруг той же оси, * ^ш ~ f T f( l fк'
что и система координат, ко- °^0 ш 'V *-
риолисово ускорение, как мы °
видели (§ 18), направлено так- Рис. 148.
же к оси вращения или от неё,
в зависимости от направления вращения. В этом случае и кориоли-
кориолисова сила инерции либо совпадает по направлению с центробежной,
либо направлена ей навстречу. Приведём и для этого случая рас-
рассмотрение с точки зрения неподвижного и вращающегося наблюдателя
Пусть тело массы т, прикреплённое на нити, вращается вокруг
точки О с угловой скоростью (о относительно «неподвижной» системы
координат. Другая система координат вращается вокруг той же
точки О с угловой скоростью ш0 относительно «неподвижной»
(рнс. 148). Для определенности положим, что ш и ш0 направлены в
одну сторону и ш]>AH. Для неподвижного наблюдателя на тело
массы т действует натяжение нити /= яш2г, которое и сообщает
телу центростремительное ускорение, необходимое для вращения с
угловой скоростью (о.

КОг"ИОЛИСОБА СИЛА ИНЕРЦИИ
203
Для вращающегося наблюдателя угловая скорость тела есть
(й — ш0, а линейная скорость v' = (ш— шо)г. Следовательно, для него
сумма сил, действующих на тело, должна быть равна/' = тя((о — «>0)V
и направлена к центру. Эта сумма составляется из направленной к
центру силы натяжения нити f=moi2r, направленной от центра цен-
центробежной силы /е = — т<й?г и также направленной от центра корио-
лисовой силы Д —— 2ш?'ш0 — — 2/и(а — ао)гшо. Сопоставляя зна-
значения /, /с и Д, можно убедиться, что действительно
В случае, 1фгда соо^>ш, но направлено в ту же сторону, линей-
линейная скорость v' меняет знак. Вместе с тем меняет знак и кориоли-
сова сила — она будет в этом случае направлена к центру (рис. 149).
f :
Рис. 149.
ft
Рис. 150.
В частности, когда тело покоится в неподвижной системе координат
(@ = 0), кориолисоза сила Д=2/лсо2г направлена к центру и по ве-
величине вдвое больше центробежной. Если система координат вращает-
вращается в сторону, противоположную вращению
тела, то кориолисова сила также направлена
к центру (рис. 150).
Мы рассматривали до сих пор случаи, когда
скорость тела во вращающейся системе коорди-
координат v' лежит в плоскости, перпендикулярной к
угловой скорости вращения системы координат.
Но так же, как и для кориолисова ускорения,
полученное нами выражение для кориолисовой
силы справедливо и тогда, когда это условие
не соблюдается. Например, если точка движется
прямолинейно в «неподвижной» системе коорди-
координат, то в системе координат, вращающейся
вокруг оси, параллельной направлению движения
точки, её движение будет происходить по вин-
винтовой линии (рис. 151). Поэтому скорость во
вращающейся системе координат V' не будет
•параллельна оси вращения и кориолисова сила
будет существовать.
На плоскости, перпендикулярной к оси вращения и вращающейся вме»
сте с наблюдателем с угловой скоростью ю0, проекция движущейся точки
будет вращаться с угловой скоростью сой. Кориолисова сила при
этом как мы уже знаем, будет равна 2mwfy и направлена к осн вращения.
Рис. 151.

204 неинёрциальные системы коо?линлт [гл. хп
Кориолисова сила инерции всегда направлена нормально к скорости v'
во вращающейся системе координат. Поэтому она изменяет только направ-
направление и не может изменять величины скорости v'. Центробежная сила инер-
инерции, вообще говоря, может быть как угодно направлена относительно v' и
Может изменять как величину, так и направление этой скорости.
§ 78. Движение на поверхности Земли
Применение вращающейся системы координат особенно удобно
при рассмотрении движений на поверхности Земли. Система коорди-
координат, связанная с Землёй, участвует в суточном и годовом движениях
Земли и поэтому не является инерциальной. Чтобы законы Ньютона
были справедливы для земного наблюдателя, нужно к силам, действую-
действующим со стороны других тел, прибавить силы инерции*. При этом, так
как Земля относительно «неподвижной» системы координат вращается
вокруг своей оси и вокруг Солнца, нужно было бы ввести силы инер-
инерции, обусловленные ускорениями и суточного, и годового движений.
Однако, силы инерции, обусловленные вторым ускорением, обычно
не приходится учитывать и вот почему. Так как размеры Земли малы
по сравнению с расстоянием до Солнца, то всем телам на Земле
Солнце сообщает примерно одинаковое ускорение — такое же, какое
оно сообщает самой Земле. Другими словами, Солнце действует на
всякое тело массы т на Земле с силой, примерно равной /raj, где
\—центростремительное ускорение Земли в её годовом движении.
Но, с другой стороны, в системе координат, связанной с Землёй,
иа всякое тело массы m действует обусловленная этим ускорением
центробежная сила инерции—-/я], направленная от Солнца. Эта сила
инерции как раз уравновешивает снлу притяжения Солнца, и вместо того,
чтобы учитывать их обе, можно просто не вводить ни той, ни другой.
Как сказано, это справедливо лишь постольку, поскольку можно
пренебречь разницей в расстояниях от Солнца до центра Земли и до»
рассматриваемой точки на её поверхности. Но так как в действитель-
действительности эти расстояния различны, то сила притяжения Солнца не точна
равна центробежной силе инерции, обусловленной вращением Земли
вокруг Солнца, а может быть и больше, и меньше её. Это вы-
вызывает на Земле приливные явления, которые дальше будут специально
рассмотрены. Если же пренебречь приливными явлениями, то можно
считать, что сила притяжения Солнца как раз уравновешивается цен-
центробежной силой инерции, которая обусловлена ускорением Земли,
направленным к Солнцу. Поэтому, например, сила притяжения Солнца
не сказывается на результатах взвешивания тел на пружинных весах.
Показания весов днём, когда притяжение Солнца направлено против
притяжения Земли, и ночью, когда они направлены в одну сторону,
всё же оказываются одинаковыми*).
*) С точки зрения «неподвижного» (в 'еземного) наблюдателя одинаковый
вес тел днём и ночью объясняется тем, что Солнце не только притягивает
взвешиваемое тело с силой mj, ной сообщает Земле ускорение/, направлен^-

§ 78] ДВИЖЕНИЕ НА ПОВЕРХНОСТИ ЗЕМЛИ 205
Всё сказанное относится не только к Солнцу, но и ко всем вообще
небесным телам, в частности, к Луне. Поэтому при помощи пружин-
пружинных весов и вообще динамометров на Земле нельзя обнаружить при-
притяжения других небесных тел, кроме Земли, хотя само по себе при-
притяжение это (например, в случае Солнца) вовсе не мало и легко
могло бы быть обнаружено,
если бы оно действовало только
на взвешиваемое тело, но не
на Землю. Приливные же силы,
обусловленные разницей в рас-
расстояниях до центра Земли и до
взвешиваемого тела, как будет
показано ниже, гораздо меньше
самих сил притяжения.
Что касается кориолисовой
силы, обусловленной враще-
вращением Земли вокруг Солнца, то
вследствие малой угловой ско- Рис. 152.
рости этого вращения ею во-
вообще можно пренебрегать *). Таким образом, кроме силы зем-
земного притяжения достаточно ввести только силы инерции, обус-
обусловленные суточным движением Земли, именно, центробежную силу
fc =/жо^г, где г — радиус-вектор, проведённый от земной оси, и ко-
риолисову силу fft= 2mfv'<o0], где v'—скорость движения тела от-
относительно Земли (рис. 152); fc направлена по радиусу вращения от
оси, fft всегда лежит в плоскости параллельного круга данной точки
Земли, но может быть направлена различно, в зависимости от напра-
направления v'.
Если тело покоится на Земле, то на него действует только цен-
центробежная сила инерции. Эуой силой земной наблюдатель объясняет
уменьшение веса тел (уменьшение натяжения подвеса) с приближе-
приближением к экватору н отклонение отвеса от вертикали по направлению
к экватору. Вертикальная составляющая центробежной силы те, умень-
уменьшающая натяжение подвеса на широте <р, равна (рис. 152)
fc cos <p = nunfr cos if = /tto>2 /? cos2 <p.
Она увеличивается с приближением к экватору, и поэтому вес
иое в ту же сторону^ Происходит то же самое, что и при взвешивании тел в
ускоренно движущемся лифте (§ 36). Днём «лифт» (Земля) имеет ускоре-
ускорение вверх, а ночью вниз. В обоих случаях изменения в показаниях весов
вносимые этим ускорением, как раз компенсируют притяжение Солнца.
*) Отношение кориолисовой силы к центробежной равно 2p'ti>o/(«>(j/0 =
— 2i>4vq, где Vq — линейная скорость движения Земли по орбите; ио вез
скорости v', с которыми мы имеем дело на Земле, гораздо меньше линей-
линейной скорости Земли, которая составляет около 30 км/сек.

206
НГИНЕРЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ
[гл. xil
(натяжение подвеса) уменьшается. Горизонтальная составляющая цен-
центробежной силы fe, отклоняющая отвес к экватору, равна
/с sin ср = tm^r sin <р = mui^R cos tp sin у = -к- mta^R sin 2:p.
Она достигает максимума при <р=45° и на экваторе снова падает до
нуля.
При движении тел относительно Земли для земного наблюдателя
появляется также кориолисова сила, которой объясняется ряд харак-
характерных явлений. Прежде всего корнолисовой силой с точки зрения
земного наблюдателя объясняется вращение плоскости качаний маят-
маятника Фуко. Если снова, как мы это делали (§ 30), рассмотреть вооб-
воображаемый опыт на полюсе, то скорость маятника (при большой длине
подвеса) можно считать всё время перпендикулярной к земной оси,
т. е. v' и ш0 взаимно перпендикулярны и кориолисова сила равна
fk=2mv'<n0.
Она лежит в горизонтальной плоскости, перпендикулярна к vr и на-
направлена по правилу буравчика, т. е. вправо, считая по направле-
Рис. 163.
Рис. 154.
нию движения маятника (рис. 153). Под действием этой силы ско-
скорость v' всё время отклоняется вправо и маятник вычерчивает розетку,
изображённую (в утрированном виде) на рис. 153. Плоскость качаний
маятника вращается относительно Земли в направлении часовой стрелки
и делает один оборот в сутки. Если же опыт делается не на полюсе,
а на широте <f (рис. 154), то горизонтальную составляющую корио-
лисовой силы ft=2m[v'«B0] получим, взяв проекцию вектора <о0 на
направление вертикали данного места. Эта проекция равна a)osintp,
и горизонтальная составляющая кориолисовой силы
fh = 2г»'ш0 sin <р.
На полюсе, где действующая на маятник кориолисова сила вся лежит
в горизонтальной плоскости и равна /ft = 2ядо'ш0, плоскость качаний
вращается с угловой скоростью 2тг —; на широте tp, где горизон-

§ 78]
ДВИЖЕНИЕ НА ПОВЕРХНОСТИ ЗЕМЛИ
207
Рис. 155.
тальная составляющая кориолисовой силы меньше в отношении sin ^: 1,
вращение будет происходить со скоростью 2тс sin tp — . На экваторе
(рис. 154) кориолисова сила, перпендикулярная к <о0, напразлена по
вертикали и поэтому не может вызвать поворота плоскости качаний.
Для того чтобы выяснить одну деталь в характере движения маятника
Фуко, вернёмся снова к опыту иа полюсе. Мы предполагали, что колебания
маятника вызваны начальным толчком. В этом случае в крайних точках
скорость маятника для «неподвижного» наблюдателя будет равна нулю.
Поэтому для земного наблюдателя скорость маятника
в этих точках направлена по касательной к окруж-
окружности, охватывающей розетку, а кориолисова сила на-
направлена к полюсу — розетка в этих точках касается
окружности (рис. 153). Однако, в реальном опыте
маятнику сообщается не начальная скорость, а началь
ное отклонение (маятник оттягивают нитью, а затем
нить пережигают). Поэтому вначале, и всякий раз в
крайней точке, скорость маятника для земного наблю-
наблюдателя (а не для «неподвижного», как в первом случае)
равна нулю. Следовательно, и кориолисова сила в этих
точках равна нулю. В конце движения туда и в начале
движения обратно направления скорости маятника
совпадают. Розетка не касается окружности, а имеет
на окружности точки заострения (рис. 155).
Кориолисовой силой объясняется ещё ряд особенностей движений, про-
происходящих на Земле. Например, на движущийся по рельсам поезд должна
действовать кориолисова сила. Горизонтальная составляющая кориолисовой
силы в северном полушарии прижимает реборды колёс к внутренней сто-
стороне правого (по движению поезда) рельса. Поэтому на двухпутных ли-
линиях правый рельс стирается изнутри. (При однопутном движении в обе
стороны проходит примерно одинаковое число поездов и оба рельса стира-
стираются одинаково.)
С точки зрения внеземного наблюдателя кориолисовой силы не суще-
существует. Поезд, двигаясь, например, по меридиану с севера на юг, дол-
должен принимать участие во враще-
вращении Земли, и его линейная ско-
скорость, обусловленная вращением
Земли, при этом должна возрастать.
С точки зрения неподвижного на-
наблюдателя правый рельс стирается
потому, что рельсы, участвуя в дви-
движении Земли, «уходят* из-под по--
езда влево и правый рельс прижи-
прижимается к реборде колеса.
Кориолнсовой силой с точки
зрения земного наблюдателя объяс-
объясняется и различный характер бере-
берегов рек. У рек в северном полуша-
полушарии правый берег обычно бывает
более крутой и подмытый, чем левый
(закон Вера). Кориолисова сила прижимает воду к правому берегу и она
подмывает берег. Точно так же объясняются искривления направлений
постоянных ветров, дующих с севера на юг и с юга на север (пассатные
ветры).
Кориолисовой силой обусловлено также и отклонение падающих тел к
востоку (рис. 156). В случае, изображённом на рисунке, иа падающее тело
Рис. 156.

208 неинерциаЛьные системы координат ("гл. Ш
действует кориолисова сила, направленная вперёд, т. е. к востоку. Оиа и
вызывает отклонение падающего тела от вертикали. С точки зрения вне-
внеземного наблюдателя (для которого кориолисовой силы не существует) от-
отклонение объясняется тем, что покоящееся относительно Земли тело имеет
горизонтальную скорость, обусловленную вращением Земли и направленную
к востоку. Эта скорость больше, чем скорость точки, находящейся на той
же вертикали на поверхности Земли (так как у последней радиус вращения
меньше). При свободном падении тело сохраняет горизонтальную скорость,
которую оно имело в момент начала падения, и поэтому опережает ту точку
Земли, над которой оно находилось в начале падения.
§ 79. Неинерциальные системы координат и законы сохранения
Введение сил инерции позволило сохранить неизменным второй закон
Ньютона и вытекающие из него уравнения движения. Но зато появились
силы, к которым третий закон Ньютона не применим. Силы инерции нельзя
рассматривать как силы взаимодействия, так как происхождение их не свя-
связано с отдельными взаимодействующими телами.
Это не значит, конечно, что возникновение сил инерции вообще никак
не связано с действием каких-либо материальных тел. Наоборот, естественно
предположить, что возникновение сил инерции в системах координат, обла-
обладающих ускорением по отношению к Солнцу и звёздам, связано именно с
действием массы всех звёзд. Особые свойства системы координат, связанной
с Солнцем и звёздами, её ннерциальиость, тем ft обусловлены, что эта
система координат неподвижна по отношению ко всей совокупности звёзд,
т. е. тел, обладающих огромной^ общей массой. Совместное действие всех
этих масс, повидимому, и является причиной того, что всякое тело, изоли-
изолированное от непосредственного воздействия других отдельиых тел, движется
прямолинейно и равномерно по отношению к Солнцу и звёздам.
Однако, эти соображения можно высказать только предположительно,
так как нельзя поставить опыта, который показал бы, какую роль играет
масса всех звёзд. Мы не можем «убрать» звёзд и посмотреть, что было бы,
если бы они отсутствовали. Мы, конечно, не можем «убрать» и Солнца, ио
мы можем делать опыты при разных положениях Солнца (днём н ночью),
на разных расстояниях от Солнца и, таким образом, мы можем выяснить,
как влияет Солнце на те или иные движения. Со всей массой звёзд мы ие
можем делать таких опытов, так как по отношению ко всей совокупности
звёзд наше положение практически не меняется.
Поскольку нельзя сделать опыта, который ответил бы на вопрос о том,
какую роль играет вся масса звёзд в возникновении сил инерции, в рамках
классической физнкн этот вопрос остаётся открытым*). Когда мы говорим,
что возникновение сил инерции нельзя объяснить действием каких-либо
определённых тел, то это значит лишь, что нельзя указать таких отдельиых
тел, действием которых обусловлено возникновение сил инерции. Этим силы
инерции н отличаются от «обычных» сил (возникновение которых всегда
можно объяснить действием отдельных тел).
Из этого различия вытекает принципиально важное следствие. В иеинер-
циальных системах координат не существует замкнутых систем тел.
Силы инерции для всякой ограниченной системы тел являются внешними.
Отсюда ясно, как обстоит дело с законами сохранения в иеинерциальных
системах координат. Второй закон Ньютона в них справедлив, и поэтому
справедливы и все вытекающие из него следствия. Но все следствия, кото-
которые вытекают из применения второго закона Ньютона к замкнутым систе-
*) В общей теории относительности самая постановка этого вопроса
приобретает иной смысл. В общих чертах эта ниая постановка вопроса в
теории относительности будет выяснена в следующем параграфе.

§ 79] неинерциальнь!е йисгемЫ коорДинАт и ЗА^Оны сохранения 209
мам тел, ие справедливы в неинерциалышх системах координат. Из второго
закона Ньютона вытекает, что производная общего количества движения
системы тел равна сумме внешних сил, действующих на систему. Это
остаётся справедливым и в неинерциалышх системах координат, ио в число
внешних сил должны быть включены и силы инерции, действующие на все
тела системы. Далее, из второго закона Ньютона вытекает, что изменение
полной энергии системы тел (в отсутствие сил трения) равно работе внешних
сил, действующих на тела системы. Это также остаётся справедливым для
неинерциальных систем координат, но должна быть учтена работа всех сил
инерции. Наконец, то же самое можно сказать и о моменте количества
движения системы тел: производная от момента количества движения си-
системы тел равна сумме моментов внешних сил, в том числе и моментов
всех сил инерции.
Поясним всё сказанное на классическом примере с камнем, падающим
на Землю. Сумм? количества движения камня и Земли для «неподвижного»
{внеземного) наблюдателя остаётся постоянной, так как камень и Земля
представляют собой замкнутую систему тел. Обозначим массы камня и
Земли через т и М. Тогда между ускорениями и скоростями камня и Земли
для внеземного наблюдателя будут существовать соотношения:
Jm m ' *м '« '
где/т hj'm, vm и vM — ускорения и скорости камня и Земли, соответственно,
по отношению к «неподвижной» системе координат. Для наблюдателя, свя-
связанного с Землёй, ускорение камня будет jm-\-J1м, ускорение Земли — нуль и,
соответственно, скорости будут vm-\-vM и нуль. Следовательно, общее
количество движения системы камень—Земля для земного наблюдателя,
равно т(vm-f-vM) или {M-^-m)vM (так как vJvM = Mjm). С другой сто-
стороны, так как Земля обладает ускорением—]м по отношению к «неподвиж-
«неподвижной» системе координат, то для земного наблюдателя существуют силы
инерции, направленные навстречу—jм. На камень действует сила инерции
mjм и на Землю—сила инерции MJm- Сумма этих сил равна (М-j-m)j^, a
? (М + т) vM = (М + m)jM<
т. е. производная от полного количества движения для земного наблюдателя
равна сумме всех внешних сил, действующих на тела системы. В рассмат-
рассматриваемом случае внешними силами являются только силы инерции, действу-
действующие на камень и Землю.
Тот же результат получится и для наблюдателя, связанного с камнем.
Для него ускорение камня равно нулю, а ускорение Земли jm-\-JM и ско-
скорость Земли vm-\-VM. Количество движения системы камень—Земля для
наблюдателя, связанного с камнем, равно М (vm-\-vM) или (М-\-т)ат (так
как vmlvM = Mjm). С другой стороны, наблюдатель, падающий с камнем,
должен ввести силы инерции. Та*к как его ускорение (относительно «непо-
«неподвижной» системы координат) есть—_/т, то он должен ввести силы инерции:
т]т, действующую на камень, и Mjm, действующую на Землю. Сумма этих
сил
т. е. опять производная количества движения системы камень—Земля, равна
сумме действующих сил инерции. Всё огромное количество движения система
приобретает благодаря действию сил инерции.
Теперь посмотрим, как с точки зрения наблюдателя, падающего с кам-
камнем, обстоит дело с энергией системы камень—Земля. Потенциальная энер-
14 С. Э. Хайкин

210 НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ [гл. XII
гия системы камень—Земля будет одинакова для всех наблюдателей, так
как она зависит только от конфигурации тел. Поэтому её изменения мы мо-
можем для упрощения подсчитать с точки зрения неподвижного наблюдателя.
На основании закона сохранения энергии, который справедлив для замкну-
замкнутой системы камень—Земля (для «неподвижного» наблюдателя система
камень—Земля замкнута), можно утверждать, что уменьшение потенциаль-
потенциальной энергии равно увеличению кинетической, т. е. уменьшение потенциаль-
потенциальной энергии
mvm
Это изменение потенциальной энергии одинаково для всех наблюдателей.
Полная кинетическая энергия системы для наблюдателя, падающего с кам-
ием, будет равна кинетической энергии Земли, движущейся со скоростью
vm-\-vM, т. е.
Т — — M(vm + »д|)* = -g- + MvmvM-\—2~ .
Появление только малой части этой огромной энергии наблюдатель,
связанный с камнем, объяснит убылью потенциальной энергии на величину
Ш. Для наблюдателя, связанного с камнем, появится огромный избыток
кинетической энергии над убылью потенциальной. Он будет равен
MvL mvL
или4так как vmjvM = M\m и
С другой стороны, на Землю действует сила инерции Mjm (так как ускоре-
ускорение наблюдателя относительно «неподвижной» системы координат равно —/т).
Вместе с тем для наблюдателя, связанного с камнем, Земля пройдёт путь
s—{oM-\-vm)t\2. Работа силы инерции Mjm на этом пути
как раз будет равна Т—Ш—избытку кинетической энергии системы над
потенциальной. Весь огромный избыток энергии системы, оцениваемой
наблюдателем, связанным с камнем, объясняется работой сил инерции, дей-
действующих на систему камень—Земля.
Полученные нами результаты совершенно понятны. Поскольку для не-
инерциальных систем координат силы инерции играют такую же роль, как
и «обычные» силы, они так же могут изменять количество движения и, со-
совершая работу, изменять энергию системы.
Точно так же в вопросе о происхождении деформаций силы инерции для
движущегося наблюдателя играют такую же роль, как и «обычные» силы.
Чтобы объяснить происхождение деформаций, как уже указывалось, необ-
необходимо установить, как двигались различные части деформирующегося тела
и как эти движения привели к возникновению наблюдаемой деформации.
При рассмотрении движений различных частей тела движущийся наблюда-
наблюдатель должен вводить силы инерции, которые, так же как и обычные силы,
вызывают ускорение тех тел или частей тел, на которые они действуют.

§ 80] ЭКВИВАЛЕНТНОСТЬ СИЛ ИНЕРЦИИ И СИЛ ТЯГОТЕНИЯ 211
Если речь идёт и статических {с точки зрения движущегося наблюдателя)
деформациях, то, для того чтобы «объяснить» зти деформации силами, дви-
движущийся наблюдатель должен учитывать и силы инерции. Например, в слу-
случае тела, ускоряемого пружиной (рис. 63), для наблюдателя, движущегося
вместе с телом, деформации тела являются статическими. Чтобы объяснить
происхождение этих деформаций, движущийся наблюдатель должен учесть,
что на все элементы тела действуют силы инерции. Он объяснит проис-
происхождение деформации совершенно аналогично тому, как «неподвижный»
наблюдатель объясняет происхождение деформаций неподвижного тела,
находящегося под действием силы тяжести (§ 38).
§ 80. Эквивалентность сил инерции и сил тяготения
При переходе от одной системы координат к другой «обычные» силы,
зависящие от конфигурации тел (или от их относительных скоростей),
остаются неизменными.
Если мы переходим от одной иперциальной системы координат к дру-
другой, движущейся по отношению к первой прямолинейно и равномерно, то
ускорение тела во второй системе координат будет такое же, как и в пер-
первой. Уравнения движения в обеих системах координат будут одни и те же.
При одинаковой конфигурации и одинаковых начальных условиях все тела
в обеих системах координат будут двигаться одинаково. Поэтому никакими
механическими опытами, производимыми в двух инерциальных системах коор-
координат, нельзя обнаружить движения одной ил них относительно другой
[эго уже известный читателю принцип относительности Галилея*)].
При переходе от инерциальной системы координат к другой, движу-
движущейся с ускорением, появятся силы инерции: в уравнениях движения справа
будут стоять другие силы. Поэтому и движения будут другими. Одни и те
же опыты, производимые в этих двух системах координат, дадут различные
результаты. Например, если в ускоренно движущемся вагоне мы будем
делать опыты с падением тела, то мы обнаружим его отклонение от вер-
вертикали. На Земле же все.тела падают по вэртикали **).
Приведённый пример можно иллюстрировать следующим опытом.
Электромагнит, укреплённый на штативе, удерживает маленький стальной
шарик. Внизу помещена стальная или стеклянная плита. Если выключить
ток в электромагните и затем быстро включить его снова, то шарик, уда-
ударившись о плиту и подпрыгнув, снова прилипает к электромагниту. Поме-
Поместив всю эту установку на движущуюся тележку, можно воспроизвести
«опыт в движущемся вагоне». Если тележка движется равномерно, то шарик
после удара снова прилипает к электромагниту. При движении тележки
с достаточным ускорением шарик к магниту не прилипает, так как, подско-
подскочив, он оказывается заметно впереди или позади магнига (в зависимости
от направления ускорения).
Таким образом, опыты в равномерно и ускоренно движущемся вагоне
дают разные результаты. Какое можно вывести заключение, сопоставляя
только результаты этих опытов? Не зная, что происходит с вагоном
(представим себе, что мы находимся внутри вагона и окна его закрыты
шторами), мы не сможем однозначно истолковать эти опыты. Мы можем
предположить, что вагон приобрёл ускорение, но с таким же основанием
*) Этот принцип, который был распространен Эйнштейном на все вообще
физические явления (а не только на механические), получил название
«специального принципа относительности» (см. гл. XXII).
**) Мы говорим о грубых опытах, при которых не играет роли отклоне-
отклонение падающих тел к востоку. В рамках этих грубых опытов Земля является
практически инерциальной системой.
14 s

212 неинёрцИаЛьныё системы координат [гл. xiI
мы можем допустить, что вагон наклонился. В этом последнем случае тело
тоже будет отклоняться от перпендикуляра, опущенного к полу вагона.
Правда, если мы будем точно измерять ускорение шарика, то мы обнару-
обнаружим, что не только направление, но и величина ускорения стала другой.
Мы должны будем предположить, что не только направление, но и величина
силы тяжести изменились. Но, во всяком случае, мы сможем объяснить
результаты опыта либо появлением силы инерции, либо изменением силы
тяготения. Силы инерции мы всегда можем заменить эквивалентными изме-
изменениями сил тяготения. Эта эквивалентность сил инерции и сил тяготе-
тяготения обусловлена тем, что п те, и другие пропорциональны массам тел,
на которые они действуют *). Сила инерции, так же как и сила тяжести,
сообщает всем телам, помещаемым в данную точку пространства, оди-
одинаковые ускорения. Поэтому все тела, с которыми мы будем делать опыты
в ускоренно движущемся вагоне, будут падать одинаково. Это и даёт нам
основание высказать предположение, что изменилась сила тяжести. Этой
особенностью — действием, эквивалентным изменению силы тяжести, обла-
обладают только силы инерции и не обладают никакие другие силы. Мы не
могли бы заменить силы инерции, например, какими-либо воображаемыми
пружинами, поскольку определённая пружина будет сообщать телам разной
массы различные ускорения.
Эквивалентность сил инерции и сил тяготения лишает нас возможности
различать, что произошло — появились ли новые силы инерции или измени-
изменились силы тяготения. Различные результаты опытов при переходе от одной
системы координат к другой, движущейся с ускорением относительно пер-
первой, мы можем объяснить и тем и другим. При переходе к новой системе
координат мы можем считать либо, что появились силы инерции, либо, что
изменились силы тяготения. Первая из этих точек зрения принята в клас-
классической физике, вторая — в теории относительности.
Таким образом, с точки зрения теории относительности сил инерции не
существует. Но зато силы тяготения при одной и той же конфигурации тел
в различных ^системах координат, движущихся друг относительно друга,
вообще говоря, оказываются различными. Следует, однако, отметить, что
последовательное проведение этой точки зрения в теории относительности
встречается с принципиальными трудностями.
*) Мы пока не различаем инертной и тяжёлой масс теп н прямо поль-
пользуемся тем фактом, что силы тяготения пропорциональны инертным массам
тел. Значение этого факта для рассматриваемого нами вопроса станет яснее
после того, как будет введено понятие тяжёлой массы (!л. XV).

ГЛАВА XIII
МЕХАНИКА ТВЁРДОГО ТЕЛА
§ 81. Твёрдое тело как система материальных точек
В вопросах, которые мы рассматривали выше, размеры и форма
движущихся тел не играли сущестаенной роли, и мы могли ответить
на интересующие нас вопросы, принимая тело за материальную
точку. Однако, в целом ряде случаев это оказывается невозможным,
так как именно размеры и форма тел определяют характер интере-
интересующего нас движения. При этом часто играют роль только размеры
и форма тел и их масса, но не играют роли их упругие свойства.
Тогда тело можно рассматривать как абсолютно твёрдое. Вопросы,
на которые можно ответить, рассматривая тело как абсолютно
твёрдое, и составляют предмет механики твёрдого тела.
В задачах механики твёрдого тела существенную роль играют
размеры и форма тел. Но мы всегда можем мысленно разделить
тело на отдельные столь малые части, что размеры и форма каждой
такой части не будут играть роли в её движении. Насколько малы
должны быть эти части, зависит от условий задачи. Обычно дело
сводится к тому, что размеры каждой отдельной части тела должны
быть малы по сравнению с теми или иными расстояниями, играющими
роль в данной задаче. Например, при рассмотрении вращения тела
вокруг оси размеры отдельных, частей тела должны быть малы по срав-
сравнению с расстоянием до оси. Если размеры всего тела сравнимы с
расстоянием до оси, мы всегда сможем разбить тело на столь малые
части, чтобы размеры каждой такой части были малы по сравнению
с расстоянием до оси. Мы это сможем сделать даже тогда, когда ось
проходит через тело. Представим себе, что мы высверлили в теле
вдоль оси очень тонкий канал. Это, конечно, не может изменить
характера движения тела. А тогда всякая часть тела будет находиться
уже на некотором расстоянии от оси, и мы всегда сможем раз-
разбить .её на части, размеры которых малы по сравнению с расстоянием
до оси. Каждую такую малую часть тела мы сможем рассматривать
как материальную точку. Мы сведём таким образом задачу о движе-
движении твёрдого тела к задаче о движении большого числа отдельных
материальных точек, т. е. к задаче, которую мы рассматривали.
Так как мы считаем тело недеформируемым, то в системе матери-

214 МЕХАНИКА ТВЁРДОГО ТЕЛА [гл. XIII
альных точек, которыми мы заменим твёрдое тело, все расстояния
между отдельными материальными точками мы будем считать неиз-
неизменными. Этим наша новая система точек будет отличаться от ранее
рассматривавшейся, в которой расстояния между отдельными точками
системы могли изменяться.
Отдельные смежные части, на которые мы разбиваем твёрдое тело,
могут действовать друг на друга с известными силами, так же как
отдельные точки в системе материальных точек. Но, рассматривая тело
как абсолютно твёрдое, мы предполагаем, что уже при исчезающе
малых деформациях тела эти силы достигают таких значений, при
которых дальнейшие деформации тела прекращаются. Мы приписываем
С'члам, действующим между отдельными частями твёрдого-тела, такие
же свойства, как и силам, действующим со стороны абсолютно жёст-
жёстких связей. При этом, как и в случае абсолютно жёстких связей, мы
лишаемся возможности определить эти силы из конфигурации (по
деформациям тела). Но это не вызовет никаких затруднений, потому
что эти внутренние силы, действующие между отдельными частями
твёрдого тела, не играют роли в движении всего тела, как целого.
Действительно, как мы видели, в силу третьего закона Ньютона сумма
всех внутренних сил, действующих в системе материальных точек,
разна нулю. Поэтому при рассмотрении движения твёрдого тела внут-
внутренние силы выпадают. Чтобы найти движение твёрдого тела, не
нужно знать внутренних сил, действующих в этом теле. Потом,
когда движение тела будет определено, мы сможем (как и в случае
абсолютно жёстких связей) найти и внутренние силы, действующие»
между отдельными частями тела при данном движении.
¦Как и прежде, мы можем вводить силы, не определяемые из кон-
конфигурации (поскольку мы пренебрегаем деформадиями тел, мы не мо-
можем вычислить внутренних сил из конфигурации) только потому, что
эти силы сразу исключаются. В противном случае введение этих сил
лишило бы нас возможности решить задачу, так как до того, как за-
задача решена, мы не можем этих сил определить.
При разбиении твёрдого тела конечных размеров на отдельные
элементы мы всегда могли бы взять достаточно малые, но конечные
части. Однако, при решении задачи нам требуется находить сумму
большого числа таких малых частей. Нахождение этой суммы упро-
упрощается, если мы заменим её суммой бесконечно большого числа беско-
бесконечно малых частей и воспользуемся методами интегрального исчис-
исчисления. Каждый из этих бесконечно малых элементов можно рассмат-
рассматривать как материальную точку бесконечно малой массы (так как
плотность тела конечна, а объём элемента тела бесконечно мал).
§ 82. Движение центра тяжести твёрдого тела
Уравнения движения твёрдого тела должны дать указания о дви-
движении всех точек тела. Применяя законы Ньютона к отдельным эле-
элементам тела, мы прежде всего установим законы движения одной

§ 82] ДВИЖЕНИЕ ЦЕНТРА ТЯЖЕСТИ ТВЁРДОГО ТЕЛА 215
фиксированной точки твёрдого тела — именно, законы движения его
центра тяжести.
Разбив твёрдое тело на отдельные малые элементы, мы сможем каж-
каждый из эгих элементов рассматривать как материальную точку и приме-
применить к каждому из элементов второй закон Ньютона. Обозначив массу
элемента номера / через kmt и его скорость через v^, мы можем для
каждого из элементов написать второй закон Ньютона в виде:
где Ф[—внутренние силы, действующие на данный элемент тела со
стороны других его элементов, a F^—внешние силы, действующие
на этот элемент.
Складывая уравнения для всех элементов тела, мы получим (так
как 2Ф;=0 по тРетьему закону Ньютона):
| . A3.1)
Так же, как и для всякой системы материальных точек, производ-
производная от общего количества движения тела равна сумме всех внешних
сил, действующих на тело. Но в случае твёрдого тела это уравнение,
как мы увидим, гораздо больше говорит о движении тела, чем оно го-
говорило о движении системы материальных точек. Обусловлено ьто
тем, что в твёрдом теле расстояние между отдельными точками (от-
(отдельными элементами тела) всегда остаётся неизменным, в то время
как в системе материальных точек оно может изменяться.
Чтобы извлечь из уравнения A3.1) более детальные указания
о характере движения твёрдого тела, посмотрим, как связано общее
количество движения твёрдого тела с движением его центра масс
(центра тяжести).
Центр масс твёрдого тела определяется следующим образом. Обо-
Обозначим координаты элемента массы Д/и,- через xt, _y,, zr Составим вы--
ражения Длга^, hm^^ t^mizl и просуммируем эти выражения по всем
элементам масс тела, т. е. найдём 2 Д'^Л. 2 ^ЩУр 2 ^mizr Раз-
Разделим, наконец, каждую из этих сумм на 2^"^., т. е. на общую массу
тела. Полученные величины
- 2* '
представляют собой координаты центра масс тела. Нетрудно убедиться,
что определённая таким образом точка тела созпадает с точкой при-
приложения равнодействующей сил тяжести, действующих на все элементы
тела, т. е. центр масс совпадает с центром тяжести тела.

21S
МЕХАНИКА ТВЁРДОГО ТЕЛА
[гл. хпг
Действительно, если две параллельные силы РА и Рв приложены в точ-
точках Л ни то равнодействующая этих сил приложена в точке С, лежащей
на прямой'/Ш, причём AC'jCB — FB\FА. Если силы РА и Рв суть силы тя-
тяжести, то они пропорциональны массам элементов тела ЬтА и &mg. Поэтому
ACICB = \mBj\mA, т. е. центр тяжести двух точек делит прямую, соеди-
соединяющую эти точки, в отношении, обратном отношению их масс. Следователь-
Следовательно, если мы обозначим координаты элементов тела \тх и &тг через лгь _уь
z{ и х2, _у2, г2 (рис. 157), то координаты х, у, г центра тяжести этих двух
элементов тела будут удовлетворять соотношениям:
х2 — х
х — Xi
Д/и2
у—
г — zx
Из этих соотношений получаем
х —
z =
A3.4)
т. е, значения координат х, у, г совпадают с выражениями A3.2), опреде-
определяющими координаты 4eHTpt масс.
Прибавляя к этим элементам масс третий, четвёртый и т. д., мы убе-
убедимся, что центр масс, координаты которого определяются соотношением
A3.2), совпадает с центром тяжести тела.
Понятие центра масс является более общим, чем центра тяжести,
так как оно не ограничено одним определённым типом сил, действую-
действующих на элементы тела. Между тем поня-
понятие центра тяжести связано с предста-
представлением об определенном типе сил (сил
тяжести). Центр масс является точкой
приложения не только равнодействующей
сил тяжести, но и равнодействующей вся-
всяких массовых сил, действующих на тело,
при условии, что силы, действующие на
все элементы •вела, параллельны друг
другу. Центр тяжести совпадает с цент-
центром масс только постольку, поскольку
силы тяжести, действующие на все эле-
элементы тела, можно считать параллельны-
параллельными. А это верно только до тех пор, пока размеры тела не очень
велики. Центр масс называют так же и центром инерции. Мы будем
дальше "пользоваться и прежним привычным термином «центр тяжести».
Дифференцируя по времени выражения A3.2), мы получим:
Ж
A3.5)

§ 83] ДВИЖЕНИЕ ТЕЛА, ЗАКРЕПЛЁННОГО НА ОСИ 217
Справа в этих выражениях стоят компоненты по тргм осям общего
количества движения системы, а слева — масса тела, умноженная #а соот-
dx dy dz - „
ветствующие компоненты скорости центра масс -jr, v, .f • Следо-
Следовательно,
i»v
где v — вектор скорости центра масс, а т — масса всего тела. Твёр-
Твёрдое тело обладает таким количеством движения, каким Обладала
бы материальная точка массы, равной массе тела, и движущаяся
так, как движется центр масс тела. Иначе говоря, пока речь
идёт о количестве движения твёрдого тела, мы всегда можем заме-
заменить твёрдое тело материальной точкой, помещённой в центр масс
данного тела.
Подставляя полученное выражение для количества движения в урав-
уравнение A3.1), получим:
d '
или, так как масса твёрдого тела постоянна,
- 03.7)
Это уравнение совершенно аналогично уравнению движения матери-
материальной точки.
Центр масс твердого тела движется так же, как двигалась
бы материальная точка той же массы под действием тех внеш-
внешних сил, которые действуют на данное тело.
Уравнение A3.7) определяет движение центра масс твёрдого тела,
т. е. вполне определённой, фиксированной точки этого тела. Это урав-
уравнение применимо и к системе материальных точек и определяет дви-
движения центра масс системы. Однако, для системы материальных точек
центр масс не есть какая-либо фиксированная точка этой системы.
Поскольку расстояние между точками системы может изменяться, центр
масс меняет своё положение в системе. Зная, как движется центр
масс, мы ещё ничего не могли бы сказать о том, как движется какая-
либо определённая точка системы. Но веб же закон движения центра
масс в применении к системе материальных точек даёт определённые
указания о характере движения системы. Так, например, "из закона
движения центра масс следует, что в годовом движении вокруг Солнца
по эллипсу движется именно центр масс Земли и Луны, а не центр
Земли.
§ 83. Движение тела, закреплённого на оси. Момент инерции
Рассмотрим движение твёрдого тела, закреплённого на неподвиж-
неподвижной оси, вокруг которой оно может свободно вращаться. Точка О —¦
след этой оси (рис. 158). К одной из точек тела А приложена внеш-
внешняя сила F. Кроме внешней силы F на тело действуют и силы со сто-

218
МЕХАНИКА ТВЁРДОГО ТЕЛА
[гл. хит
роны связей (реакции связей) — в нашем случае давление подшипников,
в которых закреплена ось тела. Но это давление нормально к оси, если
силы трения отсутствуют. Поэтому, если мы выберем ось вращения за
ось моментов, то момент сил реакции относи-
относительно этой оси будет равен нулю. Момент от-
относительно оси вращения даёт только внешняя
сила F. Разбив тело на отдельные малые эле-
элементы, мы можем рассматривать его как си-
систему материальных точек. Как и для системы
материальных точек, в нашем случае справед-
справедливо уравнение A0.5):
Рис. 158.
?=«.
A3.8)
¦ момент внешней
где N — момент количества движения тела, а М
силы F относительно оси вращения.
В рассматриваемом случае вращения вокруг неподвижной оси мо-
момент количества движения тела легко выразить через угловую скорость
вращения. Элемент массы Д/ях (рис.. 158) обладает моментом коли-
количества движения
Полный момент количества движения тела N=2AN(-, причём сумма
должна быть взята по всем элементам, на которые разбито тело. Так
как тело твёрдое, то расстояние от каждого элемента тела до оси
вращения всё время остаётся неизменным и линейная скорость всякого
элемента перпендикулярна к радиусу-вектору, проведённому к этому
элементу. Поэтому vl = iorl и
Так как моменты всех элементов направлены по оси вращения, и ю
для всех элементов одно и то же, то полный момент количества дви-
движения тела
где / = 2]А»2г.г?—момент инерции всего тела относительно непо-
неподвижной оси. Так как все rt в нашем случае постоянны, то
dJV ^^ ,i о\ ^w / ^w
dt *<— * i dt dt
И уравнение моментов A3.8) принимает вид:
,dco
I
dt
¦ М.
A3.9)

§ 83] ДВИЖЕНИЕ ТЕЛА, ЗАКРЕПЛЁННОГО НА ОСИ 219
Кинетическую энергию вращающегося тела также удобно выразить
при помощи момента инерции:
где vt—линейная скорость элемента массы Lmr
Выражения для момента количества движения и кинетической энер-
энергии аналогичны тем, которые мы получили для системы материальных
точек, расстояние которых от оси вращения остаётся неизменным. Од-
Однако, вычисление момента инерции в рассматриваемом случае представ-
представляет собой более сложную задачу, так как вместо отдельных точек
мы рассматриваем сплошное тело. Поэтому для вычисления / нужно
взять сумму большого числа малых элементов 2^/п/г?- Эту сумму
можно вычислить путём интегрирования. Заменив малые конечные
элементы тела бесконечно малыми, мы получим;
где интегрирование должно быть распространено на все элементы
тела. Таким образом, вычисление момента инерции тела сводится
к объёмным интегралам. Мы ограничимся только
простейшими случаями вычисления момента
инерции.
Положим, что наше тело представляет собой
сплошной однородный цилиндр или диск тол-
толщины h (рис. 159). Найдем момент инерции
диска относительно его геометрической оси.
Разобъём диск на отдельные бесконечно малые
элементы при помощи концентрических цилинд- Рис. 159.
ров, отстоящих друг от друга на расстоянии dr.
Мы получим ряд колец с внутренним радиусом г и внешним r-\-dr. Момент
инерции каждого такого кольца мы можем вычислить, пренебрегая dr по
сравнению с г, т. е. считая, что расстояние от всех точек одного кольца
до оси равно г. Поэтому для каждого отдельного кольца момент инер-
инерции равен d/—'?lAmr2 = r2'2jkm, где ^\т есть масса всего кольца.
Сечение кольца есть hdr и его длина 2тгг; поэтому объём кольца
есть 2nhrdr, и если материал диска однороден, то масса всего кольца
2^"i= p-2-nhrdr, где р — плотность материала кольца. Следовательно,
момент инерции кольца равен dl =2nhprsdrx а всего диска
R
1= \dl = 2nh? \r4r, A3.11)
о
где R — радиус диска. Произведя интегрирование и подставив пределы,
получим

220
МЕХАНИКА ТВЕРДОГО ТЕЛА
ГЛ. XIII
Но nhR2 есть объём диска. Поэтому масса диска равна m —
и момент инерции диска массы т и радиуса R выразится так:
1
A3.12)
г'
Ч
л.
Моменты инерции других тел могут быть найдены принципиально тем же
путём. Однако, практически расчёт получается достаточно простым
только для тел вращения, особенно для тел цилиндрической формы.
Например, для полого цилиндра момент инерции относительно геометри-
геометрической оси вычисляется так же, как для сплошного диска, с той разницей,
что в выражении A3.11) в качестве нижнего предела интегрирования нужно
взять не нуль, а внутренний радиус полого цилиндра Ц1ш При одной и той
же it'acce и одном и том же внешнем радиусе момент инерции полого ци-
линдрг всегда больше, чем момент инерции сплошного цилиндра. Поэтому,
если на оба цилиндра действует один
и тот же момент сил, то сплошной
цилиндр будет иметь большее угловое
ускорение, чем полый.
Для тел неправильной формы или
неоднородных (с пустотами) вычисление
моментов инерции усложняется. Этих
расчётов мы приводить не будем. Для
. качественного сравнения моментов инер-
инерции двух тел одинаковой массы, но рас-
распределённой по-разному, часто можно
пользоваться следующими соображения-
соображениями. Если одинаковые элементы массы в
одном теле расположены дальше, чем
в другом, то момент инерции первого
тела будет больше, чем второго. Эти
соображения можно, например, применить к моментам инерции однород-
однородного прямоугольного параллелепипеда. Из трёх моментов инерции относи-
относительно трёх осей, проходящих через середины противоположных граней
параллелепипеда, наибольшим будет момент инерции относительно самой
короткой из осей. Это сразу станет ясно, если принять во внимание, что
для самой короткой из осей те же самые элементы массы будут распо-
расположены на большем расстоянии, чем для самой длинной.
Если нам известен момент инерции тела относительно оси, проходящей
через его центр тяжести, то легко найти момент инерции тела относительно
любой параллельной ей оси.
Рассмотрим сначала тело, состоящее из двух элементов масс Д/их и &т2
(рис. 160). Центр тяжести тела лежит в точке О на расстояниях г^ и г2 от
обеих масс, причём г,/г2 = Д/и2/Д/Я!. Момент инерции тела относительно оси,
проходящей через точку О перпендикулярно к чертежу, есть
Момент инерцин этих же двух масс относительно оси, проходящей через
точку О' перпендикулярно к чертежу, есть
Из чертежа (рис. 160) видно, что
Рис. 160.

§84]
Следовательно,
ПРЕНЕБРЕЖЕНИЕ МОМЕНТОМ ИНЕРЦИИ ТЕЛ 221
\-f \tnirl + (dmi + ^2)di-f 2оГ(Л/я11/' rf — h\ — Д/м3 Кг22- й|).
Но так как треугольники ОЛ1б1 и ОАгВг подобны, a r\jrt = \m2j\mu то
AOTlKri— h\=^y r\— h\. Поэтому
П = /„-{-(Нищ+ ±тг)(Р,
где d — расстояние между осями.
В действительности тело состоит из множества элементов Дди/. Но так
как точка О есть центр тяжести, то мы всегда сможем так попарно ском-
скомбинировать элементы \trif и Д/яй, чтобы их общий центр тяжести лежал
в точке О. Поэтому для каждой пары соответствующих элементов масс мо-
момент инерции относительно оси О' будет отличаться от момента инерции
относительно оси О на величину (Ат^^т^Ф. А момент инерции всего
тела массы т относительно оси О' будет отличаться от момента инерции
относительно оси О на величину тсР. Таким образом, момент инерции тела
относительно любой оси
A3.13)
где /0 — момент инерции относительно параллельной ей оси, проходящей через
центр тяжести, d — расстояние между осями и т — масса тела-. Эго—так
называемая теорема Штейнера.
§ 84. Пренебрежение моментом инерции тел
Во многих механизмах движение частей механизма связано с вращением
различных вспомогательных колёс, блоков и т. д., массы которых часто не
влияют существенно на ускорения в механизме. В таких,
случаях можно пренебречь моментом инерции этих вспо-
вспомогательных колёс. Выясним, когда это можно делать на
конкретном примере машины Атвуда, которая применяется
для демонстрации законов ускоренного движения. Ма-
шнна Атвуда (рис. 161) представляет собой блок, через
который перекинута нить с висящими на ней двумя гру-
грузами равной массы т. Грузы могут двигаться вдоль вер-
вертикальной шкалы с делениями. Если на один из грузов по-
положить небольшой добавочный грузик Дте, то грузы начи- , . -
нают двигаться с ускорением. На шкале укреплено кольцо, т\Ц} УПГЩ$
которое на ходу снимает добавочный грузик Д/л., После
этого грузы продолжают двигаться равномерно с достиг-
достигнутой к этому моменту скоростью. Измеряя эти скорости,
можно установить связь между массой перегрузки р .„.
Д/л и достигнутой скоростью. ¦
Рассмотрим движение (рузов в машине Атвуда, не пренебрегая момен-
моментом инерции блока.
На каждый из грузов кроме притяжения Земли действует натяжение
нитей /i и /2 (рис. 161). Ускорения грузов у и—j (грузы движутся в про-
противоположные стороны) выразятся так:
А. —mj — tng—/2- A3. '4)
Вычитая второе из первого, мы получим:
/,-Л. A3.15)
На блок действуют те же натяжения дпух нитей /j и /,, соэдшщие
моменты, направленные в противоположные стороны. Если радиус блока /о(

222 Механика твёрдого теЛа [гл. xnt
а его мо лент ингрцчи /, то уравнениг моментов для блока будет иметь вид:
_ .. . du>
Если нить не скользит по блоку, то j = ro—-, и уравнгние моментов можно
переписать в виде:
j-J=h~h- A3.16)
Исключая из уравнений A3.15) и A3.16) величину /j — /3, мы оконча*
тельно получим следующее выражение для у:
~\mg. A3.17)
Момент инерции, вообще говоря, влияет на ускорение грузов. Но даже
в самом неблагоприятном случае, когда почти вся масса блока яг0 распре-
распределена по ободу, всё-таки /</Wq/-03. Поэтому, если mo<^.m, то //го2<^2/я, и
в уравнении A3.17) величину //л02 можно отбросить. Если момент инерции
блока стремится к нулю, то / стремится не к бесконечности, а к конечному
значению
Поэтому произведение Ij/ro4- в уравнении A3.16) стремится к нулю. Следо-
Следовательно, должна стремиться к нулю и правая часть этого уравнения. Пред-
Предположение, что / — 0, приводит к равенству /j=/3. Так как всякий блок
обладает некоторым моментом инерции, то натяжение нити с двух сторон
блока всегда будет различным (при наличии ускорения). Но, пренебрегая
моментом инерции блока, мы можем прямо считать, что грузы «через нить»
действуют друг на друга с равными по величине, но противоположно на-
направленными силами.
Приведённый конкретный пример в достаточной мере разъясняет, когда
можно пренебрегать моментом инерции вспомогательных частей механизма
и что из этого вытекает. Это пренебрежение вполне аналогично случаю
пренебрежения массой тел, рассмотренному в § 28.
§ 85. Физический маятник
Рассмотрим теперь один важный случай движения твёрдого тела
вокруг закреплённой оси, когда момент внешних сил обусловлен дей-
действием силы тяжести. На каждый элемент тела дей-
действует сила тяжести king, создающая определённый
момент относительно оси. Сумма моментов этих сил
равна моменту разнодействующей сил тяжести, кото-
которая приложена к центру тяжести тела. Поэтому, если
центр тяжести тела лежит в точке С (рис. 162), то
момент силы тяжести относительно оси О равен
М = mgd sin or,
где d — расстояние от оси вращения О до центра тя-
Рис 162 жести С, а а-—угол между прямой ОС и вертикалью.
Если тело закреплено на оси, не проходящей через
центр тяжести, то на него всегда действует момент силы тяжести.
Так закреплённое тело и называется физическим маятником [в отличие

§85]
ФИЗИЧЕСКИЙ МАЯТНИК
223
от математического маятника (§ 59), для которого размерами тела можно
пренебречь по сравнению с расстоянием до оси вращения]. Так как
da>
—
d^z ,
z=~, то уравнение моментов будет иметь вид:
или
md
A3.18)
A3.19)
\
Сравнивая это уравнение с аналогичным уравнением для математи-
математического маятника A0.10), мы видим, что эти уравнения отличаются
только постоянным множителем. Там, где
для математического маятника стоит мно-
множитель 1/Л для физического маятника
входит множитель tndjl. Поэтому физиче-
физический маитник будет вести себя так же,
как и математический, длина которого
la = Jjmd. Выведенный из состояния рав-
равновесия, физический маятник будет совер-
совершать колебания с таким же периодом, как
и математический маятник длиной /0; /0 на-
зызается приведённой длиной данного фи-
физического маятника.
Если к оси физического маятника под-
подвесить грузик на нити длиной, равной
приведённой длине данного физического
маятника (рис. 163), то отклонённые на
одинаковый угол физический маятник и
грузик колеблются вместе, так что грузик
всё время находится в одной и той же
точке физического маятника. Эта точка
(лежащая на расстоянии приведённой дли-
длины от оси вращения) называется центром качаний данного физи-
физического маятника.
Приведённая длина /0 всегда больше d, т. е. центр качаний всегда ле-
лежит ниже центра тяжести. Действительно, по теореме Штейнера, момент
инерции относительно оси маятника /=/0-[-яи22, где /п — момент инерции
относительно оси, проходящей через центр тяжести. Поэтому приведённая
длина будет
L = .— ~d-\—*г, A3.20)
" md ' md
т. е. больше d.
Если амплитуды колебаний малы, та период математического
маятника равен
Т = 2
Рис. 163.

224 МЕХАНИКА ТВЁРДОГО ТЕЛА [гл. ХН1
Подставив вместо / значение приведённой длины /0, мы получим период
малых колебаний физического маятника
7 = 2тт 1/ —'—,. A3.21)
У grnd l '
Физический маятник так же, как математический, обладает свойст-
свойством изохронности, пока отклонения малы. Период колебаний физи-
физического маятника тем больше, чем больше его момент инерции и чем
меньше расстояние от оси до центра тяжести.
Эти зависимости можно продемонстрировать на описанном выше (§ 60)
кресте Обербека. Если поставить грузы несимметрично, то центр тя-
тяжести креста не будет совпадать с осью вращения. Крест, отклонённый от
положения равновесия, будет совершать колебания. Период этих колебаний
будет тем больше, чем дальше расположены грузы (так как при этом ра-
растёт /) и чем ближе к симметричному расположение грузов (так как при этом
уменьшается d).
Так как период маятника зависит от g, то маятником можно поль-
пользоваться для определения величины g. Впервые Ньютон воспользо-
воспользовался маятником для измерения ускорения силы тяжести. Наблюдая
качания маятников, сделанных из различных материалов, он со всей
доступной тогда точностью установил, что ускорение силы тяжести
в данной точке Земли для всех тел одно и то же.
При точных измерениях, конечно, уже ни один реальный маятник
нельзя рассматривать как математический. Поэтому при точных измере-
измерениях силы тяжести для периоДа физического маятника
пришлось бы пользоваться формулой A3.21). Но расчёт
момента инерции маятника также не может быть произ-
произведён с большой точностью. Для устранения этих труд-
трудностей можно воспользоваться особым свойством центра
качаний, которое заключается в следующем. Если мы
перенесём точку подвеса физического маятника в центр
качаний, то прежняя точка подвеса окажется новым
центром качаний. Точка подвеса и центр качаний
обратимы. Поэтому период колебаний физического маят-
маятника остаётся прежним (так как прежней осталась приве-
приведённая длина).
Это свойство центра качаний также можно продемои-
р .g. стрнровать с помощью модели, изображённой на рис. 163.
Если укрепить маятник в центре качаний, т. е. в точке,
против которой находился раньше грузик, то при ко-
колебаниях грузик (при той же длине нити) будет попрежнему двигаться вместе
с маятником, находясь всё время против той точки, которая прежде слу-
служила точкой подвеса. Прежняя точка подвеса сейчас является центром
качаний.
Обратимость точки подвеса и центра качаний можно доказать сле-
следующим образом (рис. 164). Расстояние СО' от центра тяжести до новой
оси" d'--/0 — d, где 10=:ОО' — прежняя приведённая длина, a d = OC — рас-
расстояние от центра тяжести до прежней оси. Поэтому новая приведённая
длина будет равна:
/'
~~ т (/0 — d) »

§ 86]
ИЗМЕРЕНИЕ СИЛЫ ТЯЖЕСТИ
225
где /' — момент инерции маятника относительно оси С. По теореме
Штейнера
где /0—момент относительно оси С. Из двух предыдущих соотношеплЙ
получаем:
^ d). A3.22)
Но, с другой стороны, как видно из формулы A3.20), /0 — d=z Iol(md).
Подставляя это выражение для /0 — d в формулу A3.22), получим:
f /
md'
Q"
Сопоставляя с формулой A3.20), получаем;
Воспользовавшись обратимостью точки подвеса и центра качаний, можно
опытным nyfe'M иайти положение центра качаний. Это — точка, в которой
нужно укрепить маятник, чтобы обер 1утый он колебался с тем
же периодом, что и прежде. Для этого у «оборотного» маятника
(рйс. 165) кроме неподвижного упора с ножами О' делается
перецвижной упор О". Передвигая этот упор, находят такое его
положение, при котором оборотный маятник колеблется с тем
же периодом. Тогда расстояние между ножами и даёт при-
ведённую длину маятника. Зная приведённую длину и период
колебаний, можно найти g. Измерение приведённой длины (изме-
рение расстояния) можно произвести с гораздо большей точ-
точностью, чем определение момента инерции. Поэтому при точ-
точных измерениях g всегда пользуются оборотным маятником.
Оборотный маятник предложен Картером в 1822 г.
§ 86. Измерение силы тяжести
Ускорение свободного падения относительно Земли в разных Рис. 165.
точках земного шара различно. Как уже было указано, эти из-
изменения отчасти обусловлены не изменением силы притяжения Земли, а
различным ускорением разных точек Земли по отношению к «неподвижной»
системе координат. Однако, влияние этого фактора легко учесть, т. е. по
существу пересчитать ускорения свободного падения к «неподвижной» системе
координат. Пересчитанные таким образом ускорения определяются уже только
силой притяжения, которая в разных точках Земли также различна."Изменения
силы тяжести от точки к точке обусловлены, с одной стороны, отклонением
формы Земли от шарообразной, а с другой, — различными местными неодно-
родностями в строении Земли (так называемые аномалии силы тяжести).
Точное измерение силы тяжести в различных точках Земли, с одной стороны,
даёт-указания о форме Земли, а с другой, — позволяет обнаруживать раз-
различные местные неоднородности в строении Земли. Поэтому точное изме-
измерение силы тяжести в различных местах Земли имеет большое принципиаль-
принципиальное и-практическое значение.
Основным прибором для измерения силы тяжести является оборотный
маятник. Определив на опыте центр качаний и измерив расстояние между
центром качаний и точкой подвеса, мы найдем приведённую длину /0,
входящую в форлулу периода физического маятника:
•p Q 1 / ^jj_
A3.23)
15 С. Э. Хайкин

226 МЕХАНИКА ТВЁРДОГО ТЕЛА [гЛ. XIII
Измерив при помощи хронометра период колебаний маятника, можно
по этой формуле иайти значение g, откуда путём пересчёта к «неподвижной»
системе координат определяется абсолютная величина силы тяжести в месте
установки маятника. Такие измерения'силы тяжести называют абсолютными.
Однако, даже при весьма точных измерениях приведённой длины и пе-
периода маятника для получения точных окончательных результатов необхо-
необходимо учесть влияние ещё целого ряда факторов, которых не учитывает
формула A3.23). Прежде всего, эта формула получена в результате замены
sin а на а. Поэтому оиа по существу является приближённой. Для уменьше-
уменьшения ошибки измерения производятся при очень малых амплитудах колеба-
колебаний маятника, и при этом вводится поправка, которая для малых амплитуд
может быть рассчитана с большой точностью. Далее приходится учитывать
поправки на температуру, так как с изменением температуры изменяются
все размеры маятника (вследствие теплового расширения). Ошибки вносят
также и силы трения, действующие на маятник со стороны подвеса и окру-
окружающего воздуха—они также несколько изменяют период колебаний. Для
устранения этих ошибок по возможности уменьшают трение в подвесе (под-
(подвешивают маятник иа агатовой призме) и вводят поправку на давление,
учитывающую изменение влияния воздуха. Учёт всех этих поправок позволяет
достичь огромной точности в измерении силы тяжести. В наиболее точных
измерениях ошибка не превышает 2-10~8 от измеряемой величины.
Большая точность при абсолютных измерениях силы тяжести, как видно
из всего сказанного, требует весьма сложных и кропотливых измерений. По-
Поэтому производство большого числа абсолютных измерений весьма затруд-
затруднительно. Для получения большого числа данных применяется метод отно-
относительных измерений силы тяжести. Этот метод основан на измерении
периода, с которым один и тот же маятник колеблется в различных
точках земного шара. Из сопоставления периодов определяется отношение g
в разных точках земного шара. В ряде случаев (для изучения аномалий
силы тяжести) этих относительных измерений вообще достаточно. Для опре-
определения же абсолютной величины силы тяжести достаточно знать абсолютное
значение силы тяжести в какой-либо одной из тех точек, где произведено
относительное измерение силы тяжести.
При относительных измерениях весьма упрощается учёт всех ошибок.
Влияние температуры, давления и т. д. на данный маятник везде будет одно
и то же. Поэтому для исключения ошибок достаточно определить на опыте
влияние всех этих факторов. Зная, как влияют все факторы, можно привести
результаты всех измерений к одним и тем же условиям. Большинство изме-
измерений силы тяжести в различных точках земного шара произведено именно
с помощью относительного метода.
Местные аномалии силы тяжести являются признаками присутствия горных
пород большой плотности, например, железных руд. Поэтому измерение
силы тяжести является одним из методов обнаружения полезных ископаемых.
С помощью этого метода гравиметрической разведки был обнаружен и изу-
изучен целый ряд крупных рудных месторождений.
§ 87. Уравнения движения твёрдого тела. Равновесие твёрдого тела
Рассмотрим теперь, как ставится задача о движении твёрдого тела
в общем виде.
Твёрдое тело в общем случае имеет шесть степеней свободы, и
движение его определяется шестью уравнениями. Три из этих урав-
уравнений" мы получим из закона движения центра тяжести твёрдого тела:

§ 87] уравнЕния движения твёрдого тела 227
где х, у, z — координаты центра тяжести тела, а
суммы компонент внешних сил по осям X, Y, Z.
Три других уравнения мы получим, составив уравнения моментов
относительно осей х, у, z (эти уравнения справедливы для любых
неподзижн&х осей):
* — \ ЛА У — \ АЛ . z —* \ М f 1 Я 9П\
Hi яал л tit ^^ s at *¦¦* й
Здесь Nx, Ny, Nz — моменты количества движения системы относи-
относительно осей X, Y, Z, а 2А?Х, ?jMy, zJMz —суммы моментов внеш-
внешних сил относительно этих осей. Однако, в общем случае связь
между моментами количества движения и скоростями отдельных точек
тела оказывается сложной, и определение скоростей точек тела пред-
представляет собой трудную задачу. Мы не будем рассматривать эту за-
задачу в общем виде и ограничимся в дальнейшем толькэ отдельными
частными случаями. В общем виде мы воспользуемся уравнениями
A3.24) и A3.25) только для определения услозий равновесия твёр-
твёрдого тела. Но прежде приведём некоторые соображения, прямо вы-
вытекающие из вида этих уравнений.
Если мы будем переносить силы вдоль их направления, т. е. за-
заменим силы Fn F2, F3 и т. д. силами F>1, p\, F и т. д. (рис. 166),
то не изменятся ни компоненты сил Fx, Fy, Fz, ни компоненты мо-
моментоз сил Мх, My, Mz (так как «плечи» сил останутся прежними);
следовательно, не изменится и движение тела. Поэтому точки
приложения сил, действующих на тзёрдое
тело, можно переносить вдоль направле-
направления сил — приём, которым постоянно поль-
пользуются. Это можно делать именно потому,
что уравнения A3.24) и A3.25), опреде-
определяющие движение тела, при этом не из-
изменяются.
Далее, как видно из этих уразнений,
силы, действующие на отдельные части тзйр-
дого тела, можно заменять одной результи-
результирующей силой, такой, чтобы она била
равна геометрической сумме всех дей-
действующих сил, а её момент (относительно любой оси) был равен
сумме моментов этих сил. Это можно делать потому, что уравнения
движения, а значит, и характер движений, останутся прежними. Но
из равенства моментоз определяется только прямая, вдоль которой
результирующая сила должна быть направлена, а не точка приложе-
приложения этой силы. В частности, когда силы тяжести, действующие на
отдельные элементы тела, мы заменяем их равнодействующей, то из
условия равенства сил и моментоз следует, что разнодейств"ующая
должна быть направлена по вертикали, проходящей через центр масс
тела. Но при изменении положения тела величина н направление сил
15*

228
МЕХАНИКА ТВЕРДОГО ТЕЛА
[гл. хш
тяжести, действующих на отдельные элементы тела, не изменяются.
Чтобы не изменялась и точка приложения равнодействующей сил тя-
тяжести, следует считать, что она приложена к центру масс тела. Таким
образом, точка приложения равнодействующей сил тяжести опреде-
определяется не из условий равенства сил и моментов при определённом
положении тела, а из сопоставления сил и моментов, действующих
при различных положениях тела.
Отметим, кстати, еще раз, что перенос сил вдоль их направления
и замена сил, действующих на отдельные элементы тела, их резуль-
результирующей допустимы лишь в том случае, если нас не интересует
вопрос о деформациях тела, и мы можем рассматривать его как абсолютно
твёрдое. Так, например, мы не могли бы дать правильного ответа на
вопросы о деформации тел, если бы в примере, рассмотренном в § 31,
переносили точку приложения силы, или в примере § 38 считали бы
силу тяжести приложенной к центру тяжести тела.
Из уравнений A3.24) и A3.25) сразу вытекают условия равнове-
равновесия твёрдого тела. Для равновесия необходимо, чтобы
Fx = Fy = Ft = 0, Мх = Му = Мг = 0. A3.26)
Оси X, Y, Z мы можем выбрать созершенно произвольно, но так,
чтобы они не лежали в одной плоскости (иначе одно из трах уразнений
A3.26) будет предста-
представлять собой следствие
двух других). Оси удоб-
удобно выбирать так, чтобы
наибольшее число мо-
моментов сил обратилось
в нуль (чтобы внешние
силы проходили через
выбранные оси).
Рассмотрим, напри-
например, условия равновесия
на горизонтальной пло-
плоскости треножника, на-
нагружённого массой т
(рис. 167). На тренож-
треножник действуют сила тя-
тяжести mg и силы давления со стороны пола Ft, F2, Fs. Выберем оси
так, как указано на рисунке. Так как все силы вертикальны, то вместо первых
трёх уравнений A3.26) мы получим только одно:
A3.27)
в,
/&.
д
/У
*
Ч\ X
с
Рис. 167.
Вместе с тем и уравнение моментов относительно оси г тождественно
обратится в нуль.
Пусть точка О есть проекция центра тяжести треножника с грузом на
плоскость опоры. Ргссматривая расположение ножек А, В, С и точки О на
этой плоскости (рис. 167), мы сможем составить два уравнения моментов
относительно осей хну, лежащих в этой плоскости:
0. A3.28)

§ 88]
РЫЧАЖНЫЕ BF.CbI
229
Эти три уравнения и определяют условия равновесия. Для того, чтобы
они удовлетворялись, проекция точки О должна лежать между осями
х и у, иначе моменты сил mg и Рг или F8 будут одного знака. Из этих же
уравнений определяются и наибольшие значения d\ и d2, при которых урав-
уравнения A3.28) могут удовлетворяться (так как в силу A3.27) ни одна Р не
может быть больше mg). Как легко видеть, эти наибольшие значения rfj
и fl?2 как раз таковы, что проекция точки О не должна выступать за линии,
соединяющие ножки стола. Из уравнений A3.27) и A3.28) мы можем опре-
определить и все три силы Plt Fv Fs, т. е. давления на ножки стола.
Заметим кстати, что если бы мы рассматривали стол на четырёх нож-
ножках, то мы получили бы тоже только три уравнения. Мы нашли бы условия
равновесия, но не смогли бы определить четырёх сил давления Ръ Fs, Fs, Ft.
Этот случай аналогичен примеру с жёсткой балкой на трёх опорах, приве-
приведённому во введении. Распределение давлений на ножки стола существенно
зависит от упругих свойств стола и его деформаций. Поэтому определить
эти давления, рассматривая стол как твёрдое тело, невозможно.
К твёрдому телу применимы и все те выводы относительно связи между
потенциальной энергией и характером состояний равновесия, которые были
получены для материальной точки (§ 65).
Чтобы состояние равновесия тела было устойчивым, потенциальная
энергия тела в этом положении должна иметь минимум. Поэтому тело, на-
находящееся под действием силы тяжести, будет находиться в устойчивом
равновесии только при условии, что центр тяжести тела занимает наинизшее
положение по сравнению со всеми возможными ближайшими положениями.
§ 88. Рычажные весы
Применим условия равновесия твёрдого тела для рассмотрения вопроса
о чувствительности рычажных весов. Схема устройства рычажных весов
изображена на рис. 168.
Коромысло весов АВ под-
В'
Р+Р
if
\
I
В
пёрто в средней точке О,
вокруг которой оно мо- t С \ 0 _---"*"
жет свободно вращаться. '
К концам коромысла под-
подвешены чашки, на кото-
которые накладываются взве-
взвешиваемые грузы (точ-
(точки подвеса А, В находят-
находятся на одной прямой с с V
точкой О). Коромысло,
следовательно, находится
под действием двух сил
веса, действующих со
стороны чашек с груза-
грузами. К середине коромы-
коромысла прикреплена стрел-
стрелка ON, которая указы-
указывает положение коро-
коромысла на шкале S. Если „,,. „,, ..„.....,.,.,„¦ .„, , щ^,^.
веса чашек с грузами I . н
равны, то коромысло \Q t j
остановится в среднем '" *
положении и стрелка Рис. 108.
будет находиться против
нуля шкалы. Если на одну из чашек весов —например, левую — по-
положить некоторый добавочный груз, то коромысло уйдёт из горизон-
горизонтального положения и после колебаний установится в новом положе-
\
N

230 МЬХАНИКА ТВЁРДОГО ТЕЛА [гл. ХШ
нии равновесия А'В'. При этом конец стрелки весов отклонится иа некото-
некоторое расстояние h по шкале. При малых отклонениях величина h пропор-
пропорциональна весу добавочного груза.
Чувствительностью весов называется коэффициент пропорциональности
между весом добавочного груза и величиной вызванного им отклонения
конца стрелки на шкале. Чем больше чувствительность весов, тем меньше
добавочный груз, присутствие которого мы сможем обнаружить, т. е. тем
точнее может быть произведено взвешивание.
Для определения чувствительности рассмотрим условия равновесия
весов в отклоненном от горизонтального положении. Пусть это отклонение
обусловлено тем, что, помимо лежащих на двух чашках равных грузов, вес
каждого из которых вместе с чашкой равен Р, на одну из чашек положен
добавочный груз веса р. Обозначим через / половину длины коромысла,
т. е. О А и ОВ, через Р§— вес коромысла со стрелкой. Для того, чтобы весы
находились в состоянии устойчивого равновесия, центр тяжести их должен
лежать ниже точки опоры. Обозначим через d расстояние от центра тя-
тяжести коромысла и стрелки (точки Е) до точки О. За ось моментов выбе-
выберем ось, проходящую через точку О. Условие равновесия есть условие ра-
равенства моментов сил относительно этой оси:
—P-OD — PrOF= 0.
Так как OC = OD, то уравнение моментов принимает вид:
р-ОС—Р0 OF.
Если коромысло отклонено на угол у, то
p и OF=
Подставляя эти выражения в уравнение моментов, получим:
pi cos f = Ро d sin <р, или ig^ = ?-.
Отклонение конца стрелки по шкале равно h = rtgip, где г— длина
стрелки. Следовательно,
rl
н
Коэффициент пропорциональности между р и Н, т. е. чувствительность
весов,
Следовательно, чувствительность весов прямо пропорциональна длине
коромысла и длине стрелки и обратно пропорциональна весу коромысла
и расстоянию от его центра тяжести до точки подвеса. Чувствительность
весов не зависит от величины взвешиваемых грузов и веса чашек. Это
свойство весов обусловлено тем, что точки прикрепления чашек лежат на
одной прямой с точкой подвеса О и направление сил Р всегда остаётся
вертикальным. Если бы эти условия не были соблюдены, то чувствитель-
чувствительность весов зависела бы от величины веса чашек и грузов. Поэтому весы
всегда конструируют так, чтобы точки подвеса чашек лежали на одной
прямой с точкой О и чашки могли свободно поворачиваться вокруг точек
подвеса.

§ 89] ПЛОСКОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА 231
Из формулы A3.29) легко усмотреть, каковы пути повышения чувстви-
чувствительности весов. Прежде всего для повышения чувствительности следует
увеличивать длину коромысла и длину стрелки. Предел, однако, ставится
тем, что очень длинное коромысло и очень длинная стрелка будут сами
изгибаться, если не делать их достаточно массивными. Увеличение же их
массивности, т. е. их веса Ро, уменьшает чувствительность весов. Последняя
возможность увеличения чувствительности весов это уменьшение d—рас-
d—расстояния между центром тяжести и точкой подвеса. Для регулировки
чувствительности весов в некоторых пределах обычно этим пользуются.
На коромысле весов над или под точкой О помещается грузик, положение
которого можно изменять при помощи винта. Поднимая грузик, мы при-
приближаем центр тяжести весов к точке О и тем самым увеличиваем
чувствительность весов. Однако, и в этом направлении нельзя итти слишком
далеко, поскольку весы представляют собой физический маятник и умень-
уменьшение d увеличивает период колебаний этого маятника. Чем меньше rf,
тем дольше нужно ждать, пока весы установятся в новом положении
равновесия. Здесь мы^снова сталкиваемся с той принципиальной трудностью,
которая возникает всегда при увеличении чувствительности приборов: чем
чувствительнее прибор, тем больше требуется времени для отсчёта его
показаний.
Тем не менее при конструировании чувствительных весов в этом
направлении идут довольно далеко. Чувствительные весы делают с очень
большим периодом колебаний и, не дожидаясь, пока весы установятся
в положении равновесия, наблюдают наибольшие отклонения весов при
колебаниях. Из этих наблюдений определяют положение равновесия, около
которого весы колеблются.
Чувствительность весов зависит ещё от одного обстоятельства, кото-
которого мы пока не учитывали, именно от сил сухого трения в точке подзеса.
Силы сухого трения вызовут появление «застоя» у весов, так же как во
всяком измерительном приборе. Поэтому только в грубых рычажных весах
коромысло одевается иа ось, вокруг которой оно может вращаться. В точ-
точных же весах коромысло опирается на острую грань призмы, сделанной из
возможно более твёрдых материалов (специальных сортов стали, агата
и т. п.). При достаточно острой и твёрдой грани призмы явление застоя
практически может быть устранено.
Все указанные меры повышения чувствительности весов тем легче
осуществимы, чем меньше нагрузка, на которую рассчитаны весы. При
больших нагрузках коромысло весов приходится делать более массивным
(или более коротким), чтобы оно не гнулось. Точно так же при больших
нагрузках поверхность соприкосновения призмы и коромысла нельзя делать
очень малой, так как удельные давления в поверхности соприкосно-
соприкосновения были бы очень велики и вызвали бы разрушение материала.
Поэтому, чем больше нагрузка, на которую рассчитаны весы, тем меньше
абсолютная чувствительность к, которой можно достигнуть, т. е. тем меньше
абсолютная точность взвешивания. Например, в наиболее чувствительных
весах, предназначенных для взвешивания грузов до 1 г, удалось достичь
абсолютной точности в 10~8 г. В наиболее точных весах, предназначенных
для взвешивания грузов до 1 кг, абсолютная точность составляет лишь 10—5 г,
§ 89. Плоское движение твёрдого тела
Рассмотрим простейший случай движения тела, не имеющего
закреплённых точек, именно случай плоского движения. -Примером
этого типа движений может служить качение цилиндра по плоскости.
Другим примером может служить движение уже упоминавшегося
(§ 37) маятника Максвелла.

232 м:х\чик\ тзёрдэго тела [гл. хш
Движение центра тяжести твёрдого тела определяется уравне-
ннсм A3.17):
SZ <13-30>
где v — скорость центра тяжести и ^jF -— сумма всех внешних сил,
действующих на тело.
Для того, чтобы полностью определить движение тела, нужно,
кроме того, написать уравнение моментов относительно какой-либо
произвольно выбранной оси (так как уравнение моментов справед-
справедливо для любой неподвижной оси). Однако, положение движущегося
тела относительно неподвижной оси будет всё время изменяться
и связь между моментом количества движения и угловой скоростью
будет сложной. Зная, как изменяется момент количества движения,
цш ещё очень мало можем сказать о том, как изменяются скорости
различных точек тела.
Задача существенно упростится, если мы выберем ось моментов,
жёстко связанную с телом. Но это значит, что мы составляем
уравнение мойентов в движущейся системе координат, которая при
ускоренном движении тела окажется неинерциальной. В этой системе
координат будут действовать силы инерции, и при составлении
уравнения моментов должны быть учтены моменты сил инерции, что
опять усложнит задачу.
Однако, для случая плоского движения твёрдого тела можно
сразу указать такую ось, связанную е телом, относительно которой
моменты сил инерции оказываются равными нулю и поэтому уравне-
уравнение моментов имеет такой же вид, как и для осей неподвижных
в пространстве. Именно этим свойством будет обладать ось, движу-
движущаяся поступательно (т. е. перпендикулярная к плоскостям, в
которых движутся точки тела) и проходящая через центр тяже-
тяжести тела.
В самом деле, положим, что плоское движение тела происходит так,
что все точки тела движутся в плоскостях, параллельных координат-
координатной плоскости ху. Свяжем с телом подвижную систему координат
так, что её оси х\ у' остаются всё время параллельными осям х,
у, а ось г' жёстко связана с телом и проходит чергз его центр
тяжести. Вследствие того, что движение плоское, ось г' будет всё
врем» оставаться параллельной оси г, и подвижная система коор-
координат х\ у', г' по отношению к неподвижной х, у, z будет дви-
двигаться поступательно. Но в таком случае, как уже указывалось
(§ 16), «абсолютное» ускорение j получается из «относительного»
добавлением только переносного ускорения у'о, одинакового для
всех точек тела. Поэтому и дополнительное ускорение—у0, появляю-
появляющееся при переходе от «неподвижной» системы координат х, у, g
к выбранной на.ми движущейся х\ у', г', будет одинаково для всех
точек тела. Следова i ельно, в этой системе координат силы инерции,

§ 89]
плоскоз двилсенй: твердого
233
действующие на отдельные элементы тела массы Amlt будут равны
-\m.Ju и параллельны друг другу. Равнодействующая этих сил, так
же как и сил тяжести, будет приложена к центру тяжести тела,
и момент её относительно оси, проходящей через центр тяжести,
будет равен нулю. Вследствие этого относительно оси г', выбранной
так, как указано выше, уравнение моментов будет иметь такой же
вид, как и для неподвижной оси, — в него будут входить только
моменты внешних сил.
Поэтому при рассмотрении плоского движения за ось моментов
мы будем всегда выбирать ось, проходящую через центр тяжести
тела и перпендикулярную к плоскости, в которой происходит
движение тела. Например, в случае плоского движения цилиндра
этой осью будет служить его геометрическая ось. Поскольку эта ось
неподвижна относительно тела, мы сразу можем написать выражение
момента количества движения относительно этой оси:
где / — момент инерции тела относительно этой же оси. Уравнение
моментов -jT = M принимает вид:
A3.31)
где /И —момент внешних сил относительно той же оси. Уравнение
A3.30) определяет скорость поступательного движения тела, а уравне-
уравнение A3.3Л) — угловую скорость вращательного движения (пйсле того
как ось выбрана, разделение движения иа поступательное и враща-
вращательное становится однозначным).
Применим полученные уравнения к движению маятника
Максвелла (рис. 169). На диск массы т действуют сила тя-
тяжести т* и натяжение нити /. Поэтому ускорение J центра
тяжести диска определится уравнением
mj~mg—f. A3.32)
Ось моментов, как условлено, выберем так, чтобы она
проходила через центр тяжести диска (т. е. совпадала с
его геометрической осью О). Момент силы тяжести отпо-
си-тельно этой оси равен нулю, а момент силы натяжения
нити M = fr, и уравнение моментов имеет вид:
•%=*¦
A3.33)
(/@
Из кинематических соображений легко найти связь между у и — . Так
как центр тяжести опускается как раз настолько, насколько раскручивается
нить, то его перемещение s и угол поворота диска а связаны соотношением
s=ar. Дифференцируя это соотношение дважды по времени, получим

234 МЕХАНИКА ТВЁРДОГО ТЕЛА |"ГЛ. XIII
/ — /¦—, и уравнение A3.33) можно переписать в виде:
¦jJ = fr. A3.34)
Из уравнений A3.32) и A3-34) найдём j и /:
Ускорение диска тем меньше, а натяжение нити тем больше, чем больше
момент инерции диска.
Дойдя до нижнего положения, когда нить полностью раскрутилась, диск
снова начнёт подниматься вверх с той начальной скоростью, которой он
достиг в нижней точке. Ускорение его будет прежнее и попрежнему
направлено вниз.
Движение всякой точки диска мы можем представить как поступатель-
поступательное движение со скоростью о, равной скорости центра тяжести, и вращение
вокруг геометрической оси * угловой скоростью ю.
Полную скорость любой точки получим, прибавив к скорости tf = v>r,
обусловленной вращением, скорость поступательного движения о. В точке А,
где нить отделяется от оси, эта полная скорость равна нулю. Через эту
точку проходит мгновенная ось движения диска.
Мгновенную ось можно было бы принять за ось моментов. Тогда момент
натяжения нити был бы равен нулю (сила натяжения нити проходит через
мгновенную ось), и угловое ускорение было бы обусловлено моментом силы
тяжести относительно этой осн. Это представление очень наглядно, но при
составлении уравнения моментов возникли бы затруднения. С одной сто-
стороны, нужно было бы принять во внимание момент сил инерции (который
относительно оси, не проходящей через центр тяжести, не равен нулю).
С другой стороны, нужно было бы вычислять момент количества движения
относительно оси, которая не остаётся неподвижной в теле (мгновенная
ось перемещается относительно диска).
Как уже указывалось, эти затруднения не возникают, если за ось
моментов выбирается ось, проходящая через центр тяжести тела и жёстко
связанная с телом.
Подсчитаем кинетическую энергию тела, совершающего плоское
движение. Если рассматривать движение тела как вращение вокруг
мгновенной оси, то элемент массы Ат{ имеет в данный момент
линейную скорость г^ = «>/7, где /у— расстояние от этого элемента
до мгновенной оси. Кинетическая энергия отдельного элемента тела
будет
а кинетическая энергия всего тела
где /j — момент инерции тела относительно мгновенной оси. Но по
теореме Штейнера /t = / -)- тг%, где /•„ — расстояние от мгдовенной

§ 90] ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ 235
оси до центра тяжести и / — момент инерции тела относительно оси,
проходящей через центр тяжести. Поэтому
_ 1 О о | /(О2
Введя в это выражение линейную скорость центра тяжести v = u>r0,
получим:
7 —-jT ' 1Г ' (\о.6()
Полная кинетическая энергия твёрдого тела равна сумме
кинетической энергии поступательного движения и кинетической
энергии вращения вокруг оси, проходящей через центр тяжести,
§ 90. Закон сохранения момента количества движения
для системы тел
К системе, состоящей из твёрдых тел, так же как к системе
материальных точек, могут быть применены законы сохранения коли-
количества движения и момента количества движения. При суммировании
уравнений движения и уравнений моментов внутренние силы, дей-
действующие между отдельными твёрдыми телами, исключаются (в силу
третьего закона Ньютона). Поэтому? если на систему твёрдых тел
не действуют внешние силы, то её общее количество движения
остаётся постоянным. Точно так же, если сумма моментов всех внеш-
внешних сил равна нулю, го общий момент количества движения, системы
твёрдых тел остаётся постоянным. Применение закона сохранения
количества движения к системе твёрдых тел даёт, по существу, то же
самое, что и в случае системы материальных точек,—¦закон движения
центра тяжести системы тел.
Закон сохранения моментов количества движения в применении
к системе твёрдых тел даёт нечто новое по сравнению с системой
материальных точек. Твёрдое тело может вращаться вокруг осей,
проходящих через тело или вблизи него, и с этим вращением связаны
определённые моменты количества движения, которых мы не могли
бы учесть, рассматривая тела как материальные точки. Поэтому в це-
целом ряде случаев закон сохранения моментов количества движения
даёт ответ на вопрос только "в том случае, когда мы рассматриваем
систему твёрдых тел, а не систему материальных точек.
Для пояснения сказанного может служить следующая демонстрация.
Если на «снаряд» пушки, которой мы уже ранее пользовались, сбоку наса-
насадить массивный груз — например, кусок свинца (рис. 170), то при выстреле
пушка откатывается не прямо назад, а вбок, в ту сторону, с которой
находился добавочный груз до выстрела. Если бы пушка была свободна
(не действовали бы силы трения), то, откатываясь, она вращалась бы во-
вокруг своей оси. Между тем центр «снаряда» после выстрела движется прямо-
прямолинейно (так как после выстрела на него никакие силы не действуют). Если

236
МЕХАНИКА ТВЁРДОГО ТЕЛА
[гл
XIII
бы мы рассматривали снаряд как материальную точку и, следовательно,
считали бы, что, двигаясь прямолинейно, он не обладает моментом крли-
честаа движения, то закон сохранения моментов количества движения был
бы нарушен. В действительности же снаряд при движении вращается во-
вокруг вертикальной оси^ проходящей через его центр тяжести, т. е. обладает
определённым моментом количества движения относительно этой оси. Так
как никакие моменты внешних сил относительно вертикальной оси на
систему пушка—снаряд не действуют (если пренебречь силами трения"»,
то пушка после выстрела долж ia обладать таким же, как снаряд, по
величине, но противоположным по знаку моментом количества движения
относительно вертикальной оои, т. е., откатываясь, должна вращаться.
Рис. 170.
Применим теперь закон сохранения моментов количества движения
к вопросу о вращении двигателя. Силы, действующие в двигателе — давле-
давление пара (в паровой машине), давление разов, образовавшихся при взрыве
(в моторе внутреннего сгорания), илн, наконец, электромагнитные силы (в
электромоторе), — это всегда внутренние силы, которые не могут создавать
моментов количества движения всей системы в целом. Между тем все эти
двигатели вращаются, т. е. обладают определённым моментом количества
движения бтносительно оси двигателя.
Как объяснить это с точки зрения закона сохранения момента коли-
количества движения? Дело в том, что эти двигатели никогда не являются
замкнутыми системами. Станина двигателя всегда укреплена на каком-то
фундаменте, и давление со стороны этого фундамента и создаёт внешний
момент относительно оси двигателя. Для этого, конечно, давление фунда-
фундамента должно быть с одной стороны^ больше, чем с другой. В этом можно
убедиться, если поставить электрический мотор на пружинную подставку.
При включении мотора подставка перекосится: пружины е одной стороны
сожму,тея, а с другой растянутся. Разное давление пружин с двух сторон
и создаёт относительно оси мотора момент внешних ^сил, необходимый для
того, чтобы возник момент количества движения всей системы в целом.

§ 90]
ЗАКОН СОХРАНЕНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
237
Если бы на статор мотора ие действовали внешние силы со стороны
подставки, то внутренние силы, действующиг между статором и ротором,
сообщали бы статору и ротору вращение в разные стороны — общий мо-
момент количества движения системы оставался бы равным нулю. Это можно
продемонстрировать при помощи небольшого, специально приспособленного
электромотора. Приспособление состоит в том, что статор мотора устанавли-
устанавливается иа подшипниках, в которых он может свободно вращаться вокруг
той же оси, что и ротор (рис. 171). Ток к статору подводится чер^з спе-
Рис. 171.
цчальные кольца со щетками (так, как обычно ток подводится к ротору).
В гаком виде мотор представляет собой замкнутую систему момент внеш-
внешних сил относительно оси мотора равен нулю. И, действительно, при
включении тока статор и ротор начинают вращаться в разные стороны (на
рисунке слева) с одинаковой скоростью (если их моменты инерции одина-
одинаковы). Если задержать рукой статор, то вращается только ротор. Если же
задержать рукой ротор, то вращаекя один статор в противоположном
направлении. Величина и направление общею момента количества движе-
движения зависят от величины и направления тех внешних сил, которые прило-
приложены к мотору. Внутренние силы во всех случаях остаются одни и те же.
Рис. 172.
Рис. 173.
Рис. 174.
В приведённых примерах применения закона сохранения момента коли-
количества движения для системы твёрдых тел рассматривались моменты коли-
количества движения относительно параллельных осей, и поэтому цело своди-
сводилось к алгебраическому сложению моментов количества движения. Для

238 МЕХАНИКА ТВЁРДОГО ТЕЛ\ [>Л. XIII
иллюстрации векторного характера закона сохранения моментов количества
движения могут служить опыты с вращающимся массивным колесом па
скамье Жуковского.
Человек с колесом в руках, находящийся на скамье Жуковского, пред-
представляет собой систему, на которую не действуют никакие моменты сил
относительно вертикальной оси. Поэтому общий момент количества движе-
движения системы относительно вертикальной оси должен оставаться постоянным.
И, действительно, если находящийся на скамье человек раскручивает ко-
колесо, то он сам со скамьёй начинает вращаться в обратную сторону во всех
случаях, когда ось колеса не лежит в горизонтальной плоскости. Если же
ось колеса горизонтальна, то, раскручивая его, человек остаётся в покое
(рис. 172). Можно видоизменить опыт, передав в руки человека на скамье
уже раскрученное колесо в определённом положении, т. е. сообщив системе
определённый момент количества движения N (рис. 173). Тогда при всяком
изменении положения колеса, связанном с изменением величины проекции
вектора N на вертикальную ось, человек со скамьёй начинает вращаться
так, что сумма момента количества движения человека со скамьёй и про-
проекции момента количества движения колеса на вертикальную ось остаются
постоянными. Например, если опустить ось колеса книзу, то скамья начинает
вращаться в сторону, противоположную вращению колеса (рис. 174).
На этом примере особенно ясна ценность применения законов сохра-
сохранения. Мы можем определить, как будет двигаться человек со скамьёй на
основании закона сохранения моментов количества движения, не вникая в
то, какие силы вызывают это движение.
В дальнейшем, когда мы применим к этим движениям законы динамики,
выяснится и происхождение сил, вызывающих вращение человека со
скамьёй.
§ 91. Качение тел. Трение качения
К задаче о плоском движении твёрдого тела сводятся и все про-
простейшие случаи качения тел. Однако, в этих случаях существенную
роль играют силы трения со всеми их спе-
специфическими особенностями. Поэтому мы
рассмотрим несколько примеров качения тел.
Рассмотрим сначала скатывание цилиндра
с наклонной плоскости (рис. 175). На ци-
цилиндр действуют две силы — сила тяжести
рис J75 mg и сила трения F. Нормальная составляю-
составляющая силы тяжести уравновешивается реак-
реакцией наклонной плоскости, и для движения цилиндра играет роль
только составляющая силы тяжести вдоль плоскости mg sin а. Уравне-
Уравнение движения центра тяжести цилиндра напишется в виде:
m/=mgs\na — F. A3.38)
Уравнение моментов относительно геометрической оси цилиндра имеет
вид:
Id-^ = Fr A3.39)
(так как момент силы тяжести относительно этой оси равен нулю).
Если сила трения имеет достаточную величину, то цилиндр будет

§ 91]
КАЧЕНИЕ ТЕЛ. ТРЕНИЕ КАЧЕНИЯ
239
скатываться без скольжения. Тогда точки на окружности цилиндра
должны проходить ту же длину пути, что и центр цилиндра, т. е.
dm , . dv>
j и -j— должны быть связаны соотношением j — r-rr, и уравнение мо-
моментов A3.39) можно записать так:
Из уравнений A3.38) и A3.39) находим:
1gsina F m
J =
gsina, F=
gsina.
A3.40)
A3.41)
Ускорение цилиндра тем меньше, чем больше его момент инерции.
С другой стороны, и сила трения зависит от момента инерции (уве-
(увеличивается ,с увеличением момента инерции).
При качении без скольжения играет роль сила трения покоя. Она
может иметь любое значение, не превышающее, однако, некоторого
максимального значения fmax. При скатывании цилиндра устанавливается
как раз такая сила трения покоя, чтобы не возникло скольжение.
Если же для этого потребовалась бы сила, большая максимальной
силы трения покоя, т. е. если бы оказалось, что
(например, при очень крутом наклоне плоскости), то возникло бы
скольжение. В этом случае полученные нами уравнения уже непри-
неприменимы.
В качестве другого примера рассмотрим поведение «непослушной»
катушки (рис. 176). Если катушку, лежащую на плоскости, плавно
Рис. 176.
Рис. 177.
тянуть за конец нитки, образующей достаточно большой угол с- пло-
плоскостью, то катушка будет откатываться назад. Чтобы притянуть катушку
к себе, нужно держать нитку почти параллельно плоскости (рис. 177).
Чтобы объяснить, почему в разных случаях центр тяжести катушки
движется по-разному, нужно принять во внимание силу трения, действую-
действующую на катушку со стороны плоскости. Обозначив эту силу"*через Р, а иа-
тяжение нити через / (рис. 176 и 177), мы можем написать уравнение дви-
движения центра тяжести катушки:
mj =

240 МЕХАНИКА ТВЁРДОГО ТЕЛА
и уравнение моментов относительно оси вращения:
[рЛ. XIII
(мы сразу предполагаем, что скольжение отсутствует и, следовательно,
/?-тт ^/')- Исключая из этих уравнений /, мы получим соотношение ме-
между / и F:
mR ~ cos а ) ' \ mR
Отсюда видно, что при л/cos а < R, т. е. при достаточно (талом а,
и центр тяжести движется в сторону силы /. При большом a rjcos a > R и
/ cos a < F.
Поэтому центр тяжести катушки движется в сторону, противоположную
той, куда мы тянем клтушку. граничное значение л определяется из условия
г = R cos а0.
Как видно из рис. 176, этому соответствует такое направление нитки, при
котором её продолжение проходит через мгновенную ось.
При качении тел шрает роль ещё один тип сил трения, именно так
называемое трение качения. О том, что эти силы существуют, говорит
следующий факт. Если цилиндр катится по
горизонтальной плоскости без скольжения (рис.
178), то скорость цилиндра постепенно убывает,
и причём это не связано с возникновением сколь-
скольжения. Скорость центра тяжести цилиндра
. уменьшается потому, что на нею цействует
внешняя сила, направленная против движения,—
сила трения F. Но момент этой силы мог бы
только увеличивать угловую скорость вращения
цилиндра, так как он направлен в ту же сторону, что и вращение.
Следовательно, если бы при качении существовала только тангенци-
тангенциальная сила трения, то она не могла бы одновременно уменьшать обе ско-
скорости цилиндра — поступательную и вращательную так,' чтобы не возникло
скольжения *). Так как в действительности при замедлении движения ци-
цилиндра скольжение не возникает, значит, существует ещё какой-то момент
силы, который направлен навстречу моменту тангенциальной силы трения
и, превосходя его по величине, замедляет вращение цилиндра как раз так,
чтобы не возникло скольжения. Эти и есть момент силы трения качения.
Величину этого момента можно найти, измерив отрицательное ускорение
цилиндра при качении. Уравнения движения цилиндра суть:
mJ = F, I^=M-FR, A3.42)
Рис. 178.
*) Без скольжения цилиндр мог бы двигаться только равномерно (ко-
(конечно, при условии, что F—0 и что в начале движения скольжение отсут-
отсутствует, т. е. ; = /? — ).

§ 92] САМОДВИЖУЩИЕСЯ ЭКИПАЖИ 241
где Р—тангенциальная сила тремя, а М — момент силы трения качения.
Так как движение происходит без скольжения, то j = R ~тт и уравнения
принимают вид:
mj = F, ±-j = M-FR. A3.43)
К
Исключая из этих уравнений F, мы получим:
Зная т, /? и / и измерив /, мы найдём М.
Исключая из уравнений A3.43) j, найдем:
Так как величина F ограничена значением наибольшей силы трения по-
покоя jтах, то при больших значениях момента силы трения качения М си-
силы F может оказаться недостаточно для того, чтобы обеспечить необходи-
необходимое замедление движения центра тяжести. Скорость качения цилиндра
будет убывать быстрее, чем скорость движения центра тяжести. Наряду
с качением цилиндра будет происходить скольжение, направленное вперёд.
Обратный случай невозможен, так как F может иметь любое значе-
значение от 0 до fmax- Как бы ни было мало М, всегда установится такое зна-
значение F, при котором скольжения не происходит.
Момент сил трения качения можно объяснить существованием таких
сил, действующих со стороны плоскости на цилиндр, равнодействующая
которых направлена вертикально, но не проходит через ось цилиндра. На
покоящийся цилиндр в вертикальной направлении действует нормальное
давление плоскости, но его равнодействующая проходит через ось цилиндра.
Добавочная вертикальная сила, возникающая прн качении и не проходящая
через ось цилиндра, и представляет собой результирующую сил трения ка-
качения. Происхождение сил трения качения ещё не вполне выяснено. Впро-
Впрочем вопрос о происхождении сил трения качения, как и вопрос о происхо-
происхождении других сил трения, выходит за рамки механики.
§ 92. Самодвижущиеся экипажи
Законы движения твёрдого тела позволяют рассмотреть задачу о дви-
движении колёсных самодвижущихся экипажей (автомобиль, паровоз). Так как
все силы, возникающие в двигателе, — это силы внутренние, то в конечном
счбте они не могут быть причиной изменения количества движения системы,
т. е. изменения скорости движения экипажа. Точно так же моменты этих
внутренних сил не могут изменять момента количества движения системы,
которое определяется моментом количества движения колёс, поскольку сам
экипаж не вращается. Поэтому при рассмотрении движения экипажей сле-
следует ответить иа два вопроса: как изменяется количество движения эки-
экипажа и как изменяется его момент количества движения.
Ответ на первый вопрос должен дать закон движения центра тяжести,
а на второй — уравнение моментов. Хотя оба эти вопроса, как будет видно
из дальнейшего, тесно связаны между собой, но рассматривать их удобнее
16 С. Э. Хайкин

МЕХАНИКА ТВЁРДОГО ТЕЛА [гл. XIII
порознь. Рассмотрим сначала вопрос об изменении количества движения
экипажа.
Единственные внешние силы, действующие на экипаж в горизонтальном
направлении, это силы трения, которые и являются причиной изменения
скорости экипажа (сопротивлением воздуха мы пренебрегаем). Рассмотрим
детально, как это происходит. Для конкретности будем рассматривать элек-
электрический самодвижущийся экипаж, схематическая модель которого приве-
приведена на рис. 179. Электромотор, помещённый
на раме, соединён приводом с одной парой
колёс. Сначала мы рассмотрим только силы
трения F, действующие на ведущие колёса.
(Силы трения, действующие на другие ко-
колёса, мы рассмотрим позже.)
При включении мотора возникают силы,
которые должны вызвать вращение ведущих
Q колбе. Но если бы колёса начали вращать-
Рис. 17У. СЯ| а экипаж оставался неподвижным, то
должно было бы возникнуть скольжение веду-
ведущих колёс по рельсам. Поэтому возникает сила трения покоя между колё-
колёсами и рельсами. Эта сила всегда направлена в сторону, противоположную
той, в которую должно было ^5ы возникнуть скольжение. При вращении
мотора скольжение колёс по рельсам в нашем случае должно было бы про-
происходить вправо, и тогда сила трения будет направлена влево. Эта внешняя
сила F и будет сообщать экипажу ускорение f — Flm (m—масса экипажа).
Вместе с тем сила трения будет создавать вращающий момент относительно
оси колёс, противоположный вращающему моменту М, действующему со
стороны мотора. Угловое ускорение колёс определится разностью этих
моментов сил, т. е. 1—гг = М — Fr, где /—момент инерции колёс, г — их
радиус. Чтобы не возникло скольжение колёс, необходимо, чтобы соблюда-
соблюдаем
лось соотношение г-тт =/• Поэтому при отсутствии скольжения движение
экипажа будет определяться уравнениями:
откуда
Так как обычно масса колёс очень мала по стравнению с массой всего
экипажа, то /<^mr3 и приближённо
/=¦= — . A3.46)
Величина момента М может изменяться в широких пределах регули-
регулировкой силы тока в электромоторе или давления пара в цилиндре паро-
Еоза. Между тем сила трения покоя F не может превосходить определённей
величины fmax- Поэтому, если окажется, что /та* < М/г, то второе из урав-
уравнений A3.45) уже не может быть справедливо. При этом окажется, что
г -уг >J> т. е. возникает скольжение. Колёса будут буксовать.
Совершенно так же происходит и торможение экипажа. Пусть экипаж
уже движется с постоянной скоростью, без скольжения. Если пренебречь
силами трения качения и трения в осях, то при движении с постоянной
скоростью без скольжения сила трения вообще отсутствует. Сила трения

§92]
САМОДВИЖУЩИЕСЯ ЭкИПАЖЙ $43
покоя возникает только тогда, когда без неё должно было бы возникнуть
скольжение. При нажатии тормозной колодки Т (рис. 180) возникнет сила
трения скольжения Fx, действующая на колёса и направленная в сторону,
противоположную скольжению колёс под колодкой. Эта сила должна за-
замедлить вращение колёс. Если бы скорость экипажа при этом не изменя-
изменялась, то должно было бы возникнуть скольжение колёс по рельсам, на-
направленное вперёд. Вследствие этого со стороны
рельсов на колёса начинает действовать сила
трения покоя F, направленная назад (рис. 180),
Эта внешняя сила и уменьшает скорость эки-
экипажа. И в этом случае, до тех пор пока не воз-
никло скольжение колёс по плоскости, справед- " f "~
ливо уравнение A3.42), но в нём М — это момент
сил трения, действующих со стороны тормозных Рис. 180.
колодок. Если колодки прижать так сильно, что
M]r~>fmaxi T0 возникает скольжение. При этом со стороны рельсов на
колёса тоже действует сила трения, замедляющая движение экипажа, но
это уже сила трения скольжения (а не трения покоя). Так как трение
скольжения обычно меньше максимального трения покоя, то торможение
происходит медленнее, чем под действием максимальной силы трения покоя.
Наивыгоднейшие условия торможения получаются тогда, когда Mjr лишь
немного не достигает fmax. Искусство торможения состоит в том, чтобы
нажать тормозные колодки как раз до предела, при котором ещё только-
только не возникает скольжение колёс.
Рассмотрим теперь, как в результате действия внутренних сил, возни-
возникающих в моторе, изменяется общий момент количества движения системы.
Под действием этих внутренних сил ротор мотора и колёса экипажа начи-
начинают вращаться в одну сторону, а статор мотора вместе с корпусом эки-
экипажа должен был бы начать вращаться в другую сторону (на рис. 179 —
по часовой стрелке), подобно тому, как это происходило со статором мо-
мотора в опытах, описанных в § 90. Однако, вследствие наличия второй пары
колёс экипажа, это вращение не возникает, но зато давление рельсов на
задние (на рис. 166 — правые) колёса увеличивается, а на передние умень-
уменьшается *). Вследствие увеличения давления рельсов на задние колёса и
уменьшения давления на передние и возникает внешний момент, который
и обусловливает изменение момента количества движения всей системы.
Конечно, и При выключенном моторе существует давление со стороны
рельсов на колёса, а следовательно, и момент внешних сил относительно
любой горизонтальной оси, параллельной оси колёс. Но этот момент, как
следует из условий равновесия, равен по величине и противоположен по
направлению моменту силы тяжести относительно той же оси. Таким обра-
образом, результирующий момент внешних сил относительно какой-либо оси,
параллельной оси колёс, равный нулю до включения двигателя, после его
включения становится отличным от нуля. Этот момент внешних снл и обу-
обусловливает возникновение момента количества движения всей системы
в целом. Что касается задних (на рис. 179 — правых) колёс, то поскольку
они не соединены приводом с двигателем, они вообще не вращались бы,
если бы на них не действовали какие-либо силы трения. Поэтому в вопросе
о трогании с места этн колёса не играют принципиальной роли.
Наоборот, в случае торможения на задние (на рис. 180 — правые) ко-
колёса их роль становится существенной, но зато не играют роли ведущие
колёса (мы полагаем, что перед началом торможения мотор был выключен^
*) Это изменение давлений можно заметлть при трогании с места авто-
автомобиля. При резком включении сцеплеаия передои автомобиля немного
подбрасывает кверху.
16*

244 МЕХАНИКА ТВЁРДОГО ТЕЛА. [ГЛ. XIII
Возникает вопрос, как внутренние силы, действующие между колёсами и
тормозной колодкой, могут уменьшить момент количества движения этих
колёс, т. е., в конечном счёте, момент количества движения всей системы
в целом. Как и в случае трогания с места, при торможении возникают
моменты внешних сил, обусловленные изменением давления со стороны
рельсов. Легко видеть, что при торможении увеличивается давление на пе-
передние (на рис. 180 — левые) колёса.
Действительно, если бы передних колёс не было, то под действием сил
трения со стороны задних колёс на тормозную колодку передний (на
рис. 180—левый) конец экипажа стал бы опускаться вниз. Аналогично
тому, как это происходит при трогании с места, изменение внешних дав-
давлений на колёса приводит к появлению результирующего момента внешних
сил относительно какой-либо горизонтальной оси, параллельной оси колёс.
Этот внешний момент и обусловливает уменьшение момента количества
движения всей системы в целом.
В нашем рассмотрении существенную роль играет наличие двух пар
колёс, так как только поэтому возникают внешние моменты, обусловленные
изменениями нормального давления. Нормальное давление не может соз-
создать момента относительно оси той пары колёс, к которой оно приложено.
Экипаж на одном колесе при включении двигателя должен был бы начать
вращаться в сторону, противоположную вращению колеса (как статор мо-
мотора в опыте, опиоанном в § 90). Однако, принципиально возможны и одно-
одноколёсные самодвижущиеся экипажи. Например, на велосипеде можно ездить
на одном колесе, по тогда центр тяжести экипажа должен находиться не
над осью колеса, а впереди неё. (Для того, чтобы ездить на одном колесе,
нужно наклониться вперёд.) Момент силы тяжести относительно оси колеса
является внешним моментом; он и обусловливает возникновение момента
количества движения в системе (без чего не могло возникнуть вращение
колеса).
Выясним теперь, какую роль играют силы трения, действующие на
другие колёса экипажа (например, на колёса вагонов, прицепленных к па-
паровозу). Пусть на вторую пару колёс действуют силы трения со стороны
оси, на которой они вращаются. Если бы действовала только эта сила тре-
трения, то при движении экипажа колёса не стали бы вращаться, возникло бы
скольжение колёс по рельсам вперёд. Поэтому со стороны рельсов на ко-
колёса начинает действовать сила трения покоя F2, препятствующая возник-
возникновению скольжения (рис. 179). Так как сила F3 всегда принимает такое
значение, что скольжения не возникает, то эта сила будет тем больше,
чем больше трение в оси. (Если пренебречь моментом инерции колёс, то
момент силы F2 должен быть всё время равен моменту сил трения в оси.)
Но сила Ft направлена назад и уменьшает ускорение экипажа. Ускорение
экипажа в этом случае определяется уравнением mj = F1 — F%.
Таким образом внутренние силы — трение в осях колёс — влияют иа
ускорение всего экипажа в целом. Так как F не может быть больше, чем
fmax> т0 чем больше F3, тем меньше ускорение экипажа j. Если окажется,
что F%>fmax> T0 экипаж вообще не может сдвинуться с места. Поэтому
паровоз часто не может сдвинуть с места большого состава и «буксует» —
сумма сил Fit действующих на колёса всех вагонов, оказывается больше,
чем сила Flt действующая на ведущие колёса паровоза.
Нетрудно дополнить всю картину, введя силы трения качения. При ка-
качении колёс по рельсам эти силы создают момент, который так же, как и
момент сил трения в осях, должен быть уравновешен моментом силы тре-
трения F-j. Чем больше момент силы трения качения, тем больше будет сила
трения F3, действующая на колёса со стороны рельсов. Таким образом, для
движения экипажа благоприятны следующие условия: возможно большая
величина fmax между ведущими колёсами и землёй и возможно меньшая
величина сил трення в осях и сил трения качения.

§ 93] свободные оси 245
В заключение рассмотрим ещё один вопрос, касающийся самодвижу-
самодвижущихся колёсных экипажей, именно, почему поворачивается автомобиль, если
повернуть его передние колёса? Для того, чтобы направление движения
автомобиля изменилось, на него должна действовать внешняя сила F
(рис. 181). Происхождение этой силы легко объяснить, приняв во внимание,
что сила трения покоя противоположна тому
направлению, в котором должно было бы у*
возникнуть скольжение. Допустим, что авто-
автомобиль продолжает двигаться прямолинейно. ___
\
у
> Uj>
' <7
При этом колёса его будут продолжать вра-
вращаться. Движение колёс будет представлять
собой качение в направлении X и скольже-
скольжение в направлении У*). В результате этих
двух движений колёса и перемещаются в на-
направлении Z. Рис. 181.
Скольжение, которое должно было бы
возникнуть, было бы направлено по Y, следовательно, возникает сила тре-
трения F, направленная навстречу. Эта внешняя сила и изменяет направление
движения автомобиля. На скользком месте, где силы трения малы, авто-
автомобиль не только буксует, но и не слушается руля.
§ 93. Свободные оси
В рассмотренных выше примерах вращения тела вокруг закре-
закреплённой оси или плоского движения ось вращения сохраняла неизмен-
неизменным своё направление в пространстве. Это обеспечивалось опреде-
определёнными внешними условиями. При вращении тела вокруг неподвижной
оси эта ось удерживается в неизменном положении подшипниками.
При скатывании цилиндра направление перемещения оси задавалось
наклонной плоскостью. Однако, после того, как цилиндр скатился
с наклонной плоскости, он продолжал бы вращаться вокруг той же
оси, и хотя ось вместе с центром тяжести двигалась бы уже не
прямолинейно, а по параболе, но она сохраняла бы неизменным
своё направление в пространстве. Такие оси вращения, которые сами
(без действия внешних сил) могут сохранять неизменным своё направ-
направление в пространстве, называются свободными осями тела. Возмож-
Возможность существования таких свободных осей и условия, которыми они
определяются, мы выясним на простейшем примере.
Введём предварительно понятие о моменте сил относительно
точки (а не относительно оси). Моментом силы относительно
точки О называется момент силы относительно оси, проходящей
через эту точку и перпендикулярной к плоскости, в которой
лежат сила и точка. В этом понятии в сущности нет ничего нового
по сравнению с понятием момента силы относительно оси. Но вместо
того, чтобы говорить о моменте относительно оси, перпендикулярной
к плоскости, и т. д., короче говорить о моменте относительно точки.
*) Это можно продемонстрировать при помощи колеса или валика, на-
насаженного на ось. Если двигать валик по столу под углом к оси, то он
будет вращаться вокруг оси и скользить в направлении, перпендикулярном
к оси.

246
МЕХАНИКА ТВЕРДОГО ТСЛА
[ГЛ. ХЩ
В качестве примера, поясняющего возможность существования
свободных осей, рассмотрим два тела массы т1 и //г3, прикреплённых
на стержнях, массой которых можно пренебречь, к оси, проходящей
через точку О (рис. 182). При вращении тел вокруг этой оси с уг-
угловой скоростью о) со стороны этих тел на стержни (и через стержни
на ось) действуют силы /1 = m10Jr1 и /3 = m2<oV2. Сумма этих сил
- уразновешивается давлением под-
% г-} г' гг q ¦*, шипников, удерживающих ось в не-
fnt 0 jriz изменном положении. Но если
mj'x^^intfz-i T0/i—/2- СуммаД
и /2 равна нулю, если вращение
происходит вокруг оси, проходя-
проходящей через точку, определяемую условием mIr1 = m2r2, т. е. через центр
тяжести обоих тел. Однако, этого недостаточно: ось вращения, кро-
кроме того, должна быть перпендикулярна к прямой, соединяющей эти
тела. Если бы это условие не было соблюдено (рис. 183), то хотя
сумма сил Д и /2 и был» бы равна нулю, момент этих сил отно-
Рис. 182.
сительно центра тяжести не был бы равен нулт>. Чтобы удержать
неизменным вращение вокруг оси 00', потребовались бы подшипники.
Со стороны подшипников на ось действовали бы силы Рх и Р2, мо-
ме-нт которых уравновесил бы моменты сил fl и /2. Только прямая,
проходящая через центр тяжести тел и перпендикулярная к линии,
их соединяющей, может сохранять сзоё направление неизменным
без давления со стороны подшипников, т. е. является свободной
осью.
Перейдём теперь к более сложному случаю (рис. 184). Рассмо-
Рассмотрим шесть различных масс mv тг, та, /и4, ть, тв, укреплённых на
концах трёх стержней, скредлённых в одной точке перпендикулярно
друг к другу (массой стержней попрежнему можно пренебречь). Рас-

§ 93] свободные оси 247
стояния всех масс от центра креста подобраны так, что соблюдены
условия /и1г1 = /»2г2, msrs — /я4г4, т&гъ = тйг6, т. е. центр тяжести
тел совпадает с центром креста О.
В этом случае при вращении вокруг любого из стержней по-
попарно сумма сил Д и /2, /3 и /4, /5 и /6, с которыми вращающиеся
массы действуют на стержень, и сумма моментов этих сил относи-
относительно точки О будут равны нулю. Действительно, две массы будут
лежать на оси вращения и вообще не будут играть роли; четыре
другие массы будут попарно лежать на прямых, перпендикулярных
к оси вращения, и, значит, для них, как и в первом примере, сумма
сил / и сумма моментов этих сил относительно точки О будут равны
нулю. Следовательно, для нашей модели все три направления кре-
креста будут свободными осями. Вместе с тем ясно, что, вообще го-
говоря, ни одно другое напразление не будет являться свободной
осью для нашей модели. Для любой оси, не совпадающей с од-
одним из трёх направлений креста, моменты сил / не будут равны
нулю.
Так же обстоит дело и со всяким телом произвольной формы.
В нём всегда существуют такие три взаимно перпендикулярные оси,
проходящие через центр тяжести тела, которые могут служить сво-
свободными осями вращения. Эти оси называются главными осями
инерции.
Для тел правильной фор^ы эти оси инерции легко могут быть
найдены. Например, для прямоугольного параллелепипеда они могут
быть указаны просто по аналогии с нашей моделью из шести тел.
Главными осями инерции параллелепипеда являютси оси, проведён-
проведённые через центры его противоположных граней.
F-сли тело приведено во вращение вокруг одной из главных осей
и момент внешних сил относительно центра тяжести тела отсутст-
отсутствует, то направление оси вращения должно было бы оставаться не-
неизменным в пространстве. Однако, практически мы никогда не можем
привести тело во вращение совершенно точно вокруг одной из глав-
главных осей. А если бы нам это и удалось сделать, то всякие неизбеж-
неизбежные случайные толчки немного нарушили бы это движение. Поэтому
в реальных условиях можно наблюдать длительное вращение вокруг
свободной оси только в том случае, когда небольшие отклонения
от этого вращения в дальнейшем не нарастают. Для этого силы,
действующие на ось со стороны вращающихся частей тела, при не-
небольшом нарушении движения должны снова возвращать тело к вра-
вращению вокруг главной оси, т. е. вращение вокруг главной оси дол-
должно быть устойчивым.
Оказывается, не все три главные оси инерции удовлетворяют
этому требованию. Можно доказать (мы не будем приводить этого
доказательства), что в отсутствии внешних сил устойчивыми яв-
являются только главные оси, соответствующие наибольшему и на-
наименьшему моментам инерции тела. Вращение вокруг сси, соот-

248 МЕХАНИКА ТВЁРДОГО ТЕЛА [гл. ХШ
ветствующей среднему моменту инерции, оказывается неустой-
неустойчивым.
Свободные оси прямоугольного параллелепипеда и их устойчивость
можно продемонстрировать, подбрасывая картонную прямоугольную ко-
коробку так, чтобы она прн этом вращалась вокруг одной из своих главных
осей. Если коробку заставить вращаться вокруг самой короткой или самой
длинной оси, то она во время падения сохраняет неизменной свою ось вра-
вращения. Если же, подбрасывая коробку, сообщить ей вращение вокруг
средней оси, то направление оси не будет оставаться неизменным — падая,
коробка будет качаться.
В телах вращения одной из трёх главных осей инерции всегда является
геометрическая ось тела (это ясно нз соображений симметрии). Другими
главными осями могут быть любые две взаимно перпендикулярные прямые,
лежащие в плоскости, проходящей через центр тяжести тела и перпенди-
перпендикулярной к геометрической осн.
Практически редкЪ приходится иметь дело с совершенно свободным
вращением вокруг одной из главных осей. Обычно на вращающееся тело
действуют силы трения, и для поддержания вращения нужно прикла-
прикладывать момент внешних сил. В этом случае уже неприменимо утверж-
утверждение относительно устойчивости вращения вокруг главных осей, ко-
которое приведено выше. ОбычнЪ в этих случаях устойчивой осью оказы-
оказывается только одна главная ось, соответствующая наибольшему моменту
инерции.
Это можно продемонстрировать, вращая тела различной формы на
центробежной машине. Если к оси центробежной машины подвесить на нити
за конец палочку так, что направление нити совпадает с осью палочки
(соответствующей наименьшему моменту инерции), то при вращении па-
палочка постепенно раскачивается, затем, поднимется и начинает вращаться
в горизонтальном положении, т. е. вокруг оси, соответствующей наиболь-
наибольшему моменту инерции. Это вращение устойчиво. Нить только уравнове-
уравновешивает силу тяжести и сообщает телу некоторый небольшой вращающий
момент, необходимый для компенсации сил трения (сопротивления воз-
воздуха).
Свойства свободных осей имеют очень большое практическое значение.
Во всех машинах с быстро вращающимися ч?"тями возникали бы огром-
огромные силы, действующие со стороны вращающихся частей на ось, если эту
ось выбрать произвольно. Эти силы должны были бы уравновешиваться
соответствующим давлением подшипников. Особенно опасно то, что на-
направление этих сил связано с расположением масс вращающегося тела, и
поэтому силы «вращаются» вместе с телом. Эти большие переменные на-
нагрузки на подшипники действуют разрушительно на всю машину, и их надо
всячески избегать. Путь для этого ясен — нужно сделать так, чтобы ось
вращения, заданная подшипниками, была по возможности близка к сьо-
бодной оси тела. Тогда силы, действующие на ось, со стороны различных
частей вращающегося тела будут почти уравновешивать друг друга. Для
этого быстро вращающимся частям придают форму, возможно более близ-
близкую к телам вращения, и ось вращения возможно точнее совмещают
с геометрической осью тела. Однако, сделать это. абсолютно точно, ко-
конечно, невозможно. Между тем «неуравновешенные» (в смысле сил, дейст-
действующих на ось при вращении) массы, даже если они очень малы, при
больших оборотах действуют на ось с огромными силами (силы пропор-
пропорциональны квадрату угловой скорости).
Так как даже при самом тщательном изготовлении машин нельзя пол-
полностью уравновесить силы, действующие на ось, то в современных быстро-
быстроходных машинах (например, паровых турбинах, делающих до 30 000 обо-
оборотов в минуту) применяют гибкие, или самоцентрирующиеся, валы. Если

§ 94]
ДВИЖЕНИЕ ТЕЛА, ЗАКРЕПЛЁННОГО В ОЦНОЙ ТОЧКЕ
249
вал не очень жёсткий и вместе с тем его ось близка к свободной оси, то
при достаточно большой скорости вращения вал нужным образом из-
изгибается, так что устанавливается вращение
как раз вокруг свободной оси тела.
Действие гибкого вала можно продемон-
продемонстрировать следующим образом. На тонкую
ось, сделанную из стального прутка, наса-
насажен слегка эксцентрично металлический ци-
цилиндр (рис. 185). Ось закрепляется в подшип-
подшипниках так, чтобы она М01ла вращаться
(нужно принять меры к тому, чтобы ось не
вырвало нз подшипников). При медлен-
медленном вращении такой вал сильно «бьёт»
(рисг 185). При увеличении числа оборо-
оборотов, если, успокоив рукой колебания вала,
приблизить вращение к свободной оси,
колебания прекрашаются и вал перестаёт
бить. Вращение тогда происходит совершен-
совершенно спокойно;* можно заметить, что вал при этом изогнут (рис. 185, с).
§ 94. Движение тела, закреплённого в одной точке
Рассмотрим теперь случай движения твёрдого тела, закреплённого
в однрй точке. В этом случае тело не может совершать поступа-
поступательного движения, так как скорость одной его точки всегда равна
нулю, и движение можно представить как вращение вокруг мгновенной
оси, которая изменяет своё положение и в теле, и в пространстве,
но всё время проходит через неподвижную точку тела. Мы могли бы
выбрать три неподвижные оси, проходящие через эту точку, и на-
написать уравнения моментов A3.25) относительно этих трёх осей.
Однако, положение этих осей в теле будет изменяться, и связь между
моментами количества движения относительно трёх осей и скоростями
точек тела будет сложной. С другой стороны, если мы выберем оси,
жёстко связанные с телом, то связь между моментами количества
движения относительно этих осей и скоростями точек тела будет
достаточно простой, но определение характера движения этих осей
окажется сложной задачей. Поэтому мы не будем рассматривать
в общем виде задачи о движении тела, имеющего одну закреплён-
закреплённую точку, а ограничимся только одним специальным, но важным
случаем, когда тело вращения уже быстро вращается вокруг своей
геометрической оси, и требуется определить, как будет двигаться
Ovb тела под действием внешних моментов.
При рассмотрении этой задачи в качестве осей, жёстко связан-
связанных с телом, выбирают три главные оси инерции. Обозначим моменты
инерции тела относительно этих осей, соответственно, через Iv /2,
73. Взяв проекции мгновенной угловой скорости о) на эти оси, <ov <o2,
<о3, составляют выражения /jO),, /2<o2, /Зш3. Эти выражения можно
рассматривать как компоненты некоторого вектора N.
Вектор N, компоненты которого по трём главным осям инерции
соответственно равны
Л^ = /1ш1, М? = /2ш2, Л4 = /аш3, A3.47)

250
МЕХАНИКА ТВЁРДОГО ТЕЛА
[гл. хш
называют главным моментом количества движения твёрдого тела.
Аналогично моменты внешних сил относительно соответствующих
осей можно рассматривать как компоненты некоторого вектора М.
Зная момент внешних сил М, можно определить, как изменяется
вектор N со временем. Но даже зная, как изменяются величина и
направление N, мы в общем случае еще ничего не могли бы ска-
сказать о том, как движется тело — как изменяются величина мгновен-
мгновенной угловой скорости и направление мгновенной оси в пространстве.
Дело в том, что направление N не совпадает с направлением мгно-
мгновенной оси. Действительно, вектор полной угловой скорости со, на-
направленный по мгновенной оси, имеет по осям, жёстко связанным
с телом (главным осям инерции), компоненты <nv <о2, <о3. А вектор N
по тем же осям имеет компоненты N1 = /1<uv iV2 = /2@2, Л/д = /3(й3>
где /,, /2, /3— моменты инерции относительно трёх главных осей,
вообще говоря, различны по величине. Следовательно,
щ
ш.
Рис. 186.
т. е. N и со не колинеарны. Однако, в интересующем на,с спе-
специальном случае можно установить приблизительно связь между на-
празлением N и со и их расположением относительно движущегося
тела. Действительно, если те-
телу задано очень быстрое вра-
вращение вокруг одной из глав-
_ i ных осей инерции (скажем,
,1--" 1 оси 1), и если оно и вра-
вращается, но не быстро, относи-
относительно других осей, <i)j гораз-
гораздо больше, чем <о2 и оK,
значит, вектор со всё время лежит очень близко к оси / (рис. 186).
Вместе с тем и умножение <ov <o3 и ш3 на разные, но одного
порядка величины Iv /2, /3 мало изменит дело: Nx будет гораздо
больше Л/2 и NB. Следовательно, N и © хотя и не совпадают, но
лежат близко друг к другу и вместе с тем близко к главной
оси /. Можно доказать, что в рассматриваемом случае для главного
момента количества движения N и момента М справедливо уравне-
уравнение моментов в обычном виде:
^- = М. A3.48)
Зная, как изменяется направление N, мы сможем приблизительно
сказать, как изменяется направление со, а вместе с тем и как движется
ось 1, относительно которой задано быстрое вращение.
Мы приведём элементарный вывод уравнения моментов AS.48). Он
хотя и громоздок, но зато наглядно объясняет особенности поведения
быстро врагцающихся тел.

§ 94]
ДВИЖЕНИЕ ТЕЛА, ЗАКРЕПЛЁННОГО В ОДНОЙ ТОЧКЕ
251
Рис. 187.
Будем рассматривать массивный диск, вращающийся с большой угловой
скоростью <о вокруг своей геометрической оси (рис. 187). Эта ось закре-.
плена так, что она может поворачиваться в любом направлении, но центр
диска при этом остаётся неподвижным (для этого может служить например,
карданов подвес). Если внешние силы
будут создавать момент относительно
оси вращения диска, то будет изме-
изменяться только величина момента коли-
количества движения, направление же его
будет оставаться неизменным. Веб
будет происходить так же, как в слу-
случае тела, имеющего закреплённую ось.
Существенно новые движения будут
происходить в том случае, когда
момент внешних сил не совпадает по
направлению с имеющимся уже у тела
моментом количества движения. В этом
случае внешний момент будет изменять
не только величину, но и направление
момента количества движения. Наша
задача состоит в том, чтобы выяснить, как происходят эти изменения.
Расположим оси координат так, как указано на рисунке, и посмотрим,
что произойдёт, если на диск начали действовать внешние силы, создающие
момент М относительно оси XX'. Под действием этого момента диск дол-
должен начать поворачиваться вокруг этой оси так же, как если бы он не
вращался вокруг своей оси. Но так будет происходить только в самом
начале, пока диск не приобретёт некоторой конечной угловой скорости
в своём вращении вокруг оси XX'. А тогда скажется то обстоятельство,
¦что вследствие вращения диска вокруг своей оси все частицы его имеют
линейные скорости, лежащие в плоскости диска. При повороте диска во-
вокруг оси XX' должно происходить изменение этих линейных скоростей,
а для этого на каждый элемент массы диска должны действовать соответ-
соответствующие силы со стороны других частей диска. В свою очередь, каждый
элемент массы диска будет действовать на весь диск с силами противопо-
противоположного направления. Характер этих сил мы уже установили на модели,
рассмотренной в § 61. Веб, что было там установлено для тела, вращаю-
вращающегося на штанге, остаётся справедливым для каждого отдельного элемента
массы диска.
Чтобы от отдельных элементов массы перейти к сплошному диску, мы
можем себе представить, что диск состоит из большого числа отдельных
масс &т[, каждая из которых отдельной жёсткой н не имеющей массы
штангой скреплена с осью диска. Тогда к каждому отдельному элементу &mt
мы можем применить результаты § 61.
Масса Ьт( действует на «свою штангу», т. е. на диск, с силой
Rl~2\mi[v'Q'],
где v' — линейная скорость элемента массы &mt, обусловленная вращением
диска вокруг своей оси, a Q' — угловая скорость вращения вокруг оси XX'.
Эта сила через «штангу» действует на ось диска и создаёт момент, кото-
который должен поворачивать ось диска вокруг оси YY'. Как было показано,
момент этот при вращении элемента Дот, меняется по величине, но сохра-
сохраняет неизменным своё направление. Отсюда ясно, что все элементы
диска А/Я; действуют на «штангн» с силами, создающими момент одного
и того же направления. Чтобы подсчитать значение этого результирую-
результирующего момента сил, следовало бы просуммировать мгновенные значения мо-
моментов, создаваемых всеми элементами Д/fy. Но совершенно ясно, что
-вследствие осевой симметрии диска результирующий момент будет равец

252 МЕХАНИКА ТВЁРДОГО ТЕЛА [гл. XIII
сумме средних значений моментов от всех элементов диска, взятых за один
полный оборот диска.
Среднее значение момента силы R' относительно оси YY' для отдель-
отдельного элемента массы мы уже нашли в § 61. Аналогично A0.15) для эле-
элемента массы Д
Результирующий момент, действующий на ось диска со стороны всех его
элементов, равен сумме этих средних значений по всем элементам kmf
где It=2j\mirf—момент инерции диска, а N — его момент количества
движения относительно геометрической оси. Сила {?, действующая со сто-
стороны каждого отдельного элемента Дай/, будет создавать момент также и
относительно оси XX', но, как было показано в § 61, этот момент изме-
изменяется не только по величине, но и по направлению, и его среднее значе-
значение за оборот равно нулю. Поэтому сплошной диск при вращении вокруг
оси XX' вообще не будет создавать момента относительно этой оси.
Итак, если под влиянием внешнего момента М возникнет вращение
диска вокруг оси XX' с угловой '•'скоростью й', то со стороны вращающихся
масс диска на его ось начнёт действовать только момент М' относительно
оси YY', равный МЗ' и направленный по правилу буравчика от N к Й'.
Следовательно,
M' = [N-Q']. A3.49)
Такие моменты, возникающие со стороны вращающихся масс при из-
изменении направления оси вращения, называют гироскопическими мо-
моментами.
Так как ось диска свободна, то под действием момента М' она начнёт
поворачиваться вокруг оси YY' так, что вектор N будет приближаться
к вектору внешнего момента М (рис. 188), т. е. возникнет вращение оси
диска вокруг оси YY' с какой-то угловой
скоростью й. При этом совершенно так же, как
и при вращении вокруг оси XX', возникнет ги-
гироскопический момент
/ но направленный по оси XX'. Этот момент на-
/ правлен навстречу внешнему моменту М. Пока
/ вызванное внешним моментом М вращение й' бу-
/ дет ускоряться, будет возрастать гироскопиче-
гироскопический момент М', а значит, будет возрастать и
скорость вращения Й. Вследствие этого будет
Рис. 188. возрастать и гироскопический момент М". Когда
он достигнет значения М, то сумма моментов
относительно оси XX' обратится в нуль и ускорение вращения й' пре-
прекратится. Но постоянной скорости вращения й' соответствует постоянный
гироскопический момент М', который будет продолжать ускорять враще-
вращение й. Поэтому будет продолжать расти гироскопический момент М", за-
замедляющий вращение й', так что возникшее сначала вращение й', в конце
концов не только прекратится, но и изменит направление. Вместе с тем из-
изменит знак гироскопический момент М', и вращение й начнёт замедляться;
от этого уменьшится момент М" и т. д. Следовательно, сразу после того,
как приложен внешний момент, возникнут движения вокруг обеих осей и ко-
колебания угловых скоростей. Эти колебания будут происходить около состоя»

§ 84]
ДВИЖЕНИЕ ТЕЛА, ЗАКРЕПЛЁННОГО В ОДНОЙ ТОЧКЕ 253
ния, при котором моменты, действующие на ось диска, будут равны нулю. Для
этого гироскопический момент М" должен быть равен по величине внеш-
внешнему моменту М, а гироскопический момент М' должен быть равен нулю.
Это соответствует вращению только вокруг оси YY' с такой угловой ско-
скоростью, при которой М" = М или
M = NQ.
Возникшие в начале колебания в конце концов-затухнут вследствие
трения в подшипниках и сопротивления воздуха. После этого останется
только вращение вокруг оси YY' с угловой скоростью
М
9 = -?. A3.50)
Так как при этом никаких моментов сил относительно оси YY' нет, то воз-
возникшее вращение будет происходить с постоянной угловой скоростью.
В этом смысле оно сходно с движением по инерции. Однако, для этого
«движения по инерции» необходим внешний момент М относительно оси XX',
уравновешивающий гироскопический момент М". Если внешний момент
исчезнет, то под действием гироскопического момента М" возникнет вра-
вращение 2' в направлении, обратном тому, которое возникало при появ-
появлении момента М. Это вызовет появление гироскопического момента М'
также обратного направления, который быстро затормозит вращение Q.
После нескольких колебаний ось диска остановится. Следовательно, если
пренебречь колебаниями в момент возникновения и исчезновения внешнего
момента, то можно считать, что ось диска движется с постоянной угловой
скоростью, пока действует постоянный внешний момент, и сразу останавли-
останавливается, когда внешний момент исчезает. В этом смысле можно сказать,
что движение оси диска не обладает инерцией.
Легко сообразить, как изменится картина, если при вращении от-
относительно осей XX' и YY' действуют силы трения или сопротивления
среды. Внешний момент М непосредственно преодолевает моменты сил
трения относительно оси XX'. Преодолеть же моменты сил трения от-
относительно оси YY' может только гироскопический момент М'. А для этого
должно существовать вращение 2'. Поэтому при наличии больших сил тре-
трения вращение Q' не прекратится вскоре после появления внешнего момен-
момента М, а будет продолжаться наряду с вращением Q.
Полученный нами вывод относительно направления и скорости враще-
вращения оси диска можно сформулировать в виде одного векторного уравнения,
аналогично тому, как это было сделано в § 61. За время М вектор N по-
М
ворачивается на угол Да —ЙЛ?= — \t и изменяется на величину /Ш=ЛГ-Ь.
Следовательно, вектор ДЫ = М-М н направлен по М. Поэтому, переходя
к бесконечно малым изменениям, мы можем написать:
^ = М. A3,51)
Как было показано в § 61, уравнение A3.51), полученное для случая, когда
М перпендикулярен к N, остаётся справедливым и тогда, когда они распо-
расположены под любым углом.
Уравнение A3.51) по виешнему виду совпадает с уравнением для глав-
главного момента количества движения A3.48), которое мы привели без дока-
доказательства. Поэтому можно «читать, что наш вывод представляет собой
это доказательство уравнения A3.48) для рассмотренного частного случая.
Однако, нужно иметь в виду, что это доказательство является приближён-
приближённым и вот почему. Уравнение A3.48) относится к главному моменту коли-

254
МЕХАНИКА ТВЁРДОГО ТЕЛА
[ГЛ. XIII
чества движения. Мы же рассматривали момент количества движения,
связанный с вращением тела вокруг геометрической оси и направленный
по этой оси. Если возникает вращение ещё вокруг какой-либо другой оси,
то появляются и соответствующие компоненты момента количества дви-
движения, так что главный момент количества движения уже не направлен
по геометрической оси. Но, как видно нз A3.51), если момент количества
движения, обусловленный вращением тела вокруг геометрической оси, ве-
велик, то угловая скорость вращения вокруг других осей будет мала. Вместе
с тем будут малы и другие компоненты момента количества движения, и
главный момент количества движения будет очень мало отклоняться от
геометрической оси.
Всё же нужно помнить, что по отношению к моменту N, связанному
с быстрым вращением вокруг геометрической оси тела, уравнение A3.51)
является приближённым, и что внешний момент точно определяет не дви-
движение геометрической оси тела, а изменение главного момента количества
движения.
§ 95. Гироскопы
Гироскопом в общем смысле называется всякое тело вращения,
быстро вращающееся вокруг своей оси. Колесо, которым мы поль-
пользовались в опытах на
скамье Жуковского, пред-
представляет собой гироскоп.
Пользуясь выводами
предыдущего параграфа,
рассмотрим сначала сво-
свободный уравновешенный
гироскоп, т. е. гироскоп,
у которого ось вращения
может принимать любое
направление в простран-
пространстве, а центр тяжести
закреплён. Такой гиро-
гироскоп может быть осуще-
осуществлён, например, прн
помощи карданова под-
подвеса, допускающего по-
поворот колеса гироскопа
вокруг трёх взаимно пер-
перпендикулярных осей. Для
демонстрационных целей
иногда пользуются гиро-
гироскопами другой конструк-
конструкции, изображённой на рис. 189. Колесо гироскопа насажено
на ось, которая может поворачиваться как вокруг горизонтальной, так
и вокруг вертикальной оси, т. е. может принимать любое направление
в пространстве. (Отклонения оси по вертикали в этой конструкции
ограничены не очень большими углами.) Для того, чтобы центр тяжести
гироскопа совпадал с точкой пересечения трёх осей вращения, на
Рис. 189.

§' 95] Гироскопы 255
другой конец оси надевается контргруз. Колесо гироскопа приводится
в быстрое вращение при помощи маленького электромотора. Схема-
Схематически свободный уравновешенный гироскоп изображён на рис. 190
и следующих.
Так как момент сил тяжести относительно точки О равен нулю,
то ось вращающегося гироскопа в отсутствие каких-либо других
внешних сил остаётся не-
неподвижной. Гироскоп обла- М JL~
дает постоянным моментом I ff
количества движения N, |_| q
направленным вдоль непо-
движной оси вращения гиро- рис 190
скопа. Если на гироскоп
начинают действовать внеш-
внешние силы, то его ось начинает двигаться — появляется враще-
вращение и вокруг других осей. Тогда вектор N уже не совпадает с осью
гироскопа, но, по сказанному выше, всегда остаётся близким к ней.
Поэтому, зная, как изменяется вектор N, мы сможем сказать, как
приблизительно движется ось гироскопа.
Из уравнения A3.48) видно, что вектор N изменяется только
тогда, когда действует момент М. Следовательно, ось гироскопа
может заметно перемещаться только до тех пор, пока действуе- мо-
момент М, изменяющий направление N. Изменения N за короткие
промежутки времени Д? определяются тем же уравнением
При кратковременном действии внешних сил (удар) Д^ мало, по*
этому и AN мало — N почти не изменяется. Следовательно, очень
мало должно изменяться и направление оси гироскопа. Действительно,
после резкого удара ось гироскопа не уходит далеко, а дрожит,
оставаясь почти на месте. N после удара перестаёт изменяться. Но
ось гироскопа не должна совпадать с направлением N, а должна
быть лишь близка к нему. Она может совершать малые движения
около направления N. Такие движения оси гироскопа около направ-
направления N носят название нутаций. Дрожание оси гироскопа после
удара и представляет собой один из видов нутаций. В быстро вра-
вращающемся гироскопе нутации очень малы и ими вполне можно пре-
пренебречь. Тогда изменения направления N определяют движение оси
гироскопа. В дальнейшем мы будем считать, что направление N со-
совпадает с осью гироскопа.
При длительном воздействии внешних сил вектор N будет изме-
изменять своё направление в пространстве. Вместе с ним будет изменять
своё направление и ось гироскопа. Направление AN совпадает с на-
направлением М, т. е. не с направлением силы, а с направлением
момента силы относительно оси О. Если сбоку давить на гироскоп
с некоторой силой F (рис. 190), то ось его будот двигаться в на-

256
МЕХАНИКА ТВЁРДОГО ТЕЛЛ
[гл. хш
правлении момента силы М, т. е. будет подниматься вверх. Если
сила F давит на гироскоп вверх (рис. 191), то ось его будет пово-
поворачиваться в горизонтальной плоскости по часовой стрелке (глядя
сверху). Когда на гироскоп постоянно действует сила, создающая
момент М, то направление N будет изменяться за элемент вре-
времени At на величину AN = MA^. Соответственно будет двигаться
Рис. 192.
и ось гироскопа. Такие движения оси гироскопа под действием
внешних моментов называются прецессией. В частном случае, когда
момент М всё время направлен нормально к оси гироскопа, век-
вектор N будет вращаться, оставаясь всё время в плоскости, проходя-
проходящей через М и ось гироскопа. В этой же плоскости будет вращаться
и ось гироскопа. Это один из случаев прецессии.
Прецессию этого типа можно продемонстрировать, подвесив на ось
гироскопа небольшой груз (рис. 192). Вес груза Р будет создавать момент М,
веб время лежащий в горизонтальной плоскости; в этой же плоскости вра-
вращается ось гироскопа.
Если подталкивать прецессирующий гироскоп в направлении прецессии,
то, каь видно из сопоставления рис. 190 и 192, тот конец оси, на котором
висит груз, будет подниматься. Наоборот, если давить на гироскоп против
направления прецессии, то конец осн с грузом будет
. • опускаться. Внешние силы, препятствующие прецес-
[&JT' сии> приводят к тому, что груз опускается. При прецес-
\5с*^ сии на вертикальную ось действуют силы трения в под-
I шипнике, препятствующие прецессии; поэтому ось пре-
цесснрующсго гироскопа не остаётся в горизонталь-
нон плоскости — конец оси, на котором виснт груз, по-
постепенно опускается.
Это может служить иллюстрацией к общим сооб-
соображениям о роли сил трения, приведённым в предыду-
предыдущем параграфе. Вследствие трения вращение, возни-
возникающее вначале под действием внешнего момента,
не прекращается. Поэтому груз всё время продолжает
опускаться.
Этот же тип прецессии можно продемонстрировать
следующим образом. Гироскоп подвешивается одним
концом к нити (рис. 193). Если расположить ось гиро-
гироскопа горизонтально, то она не опускается, а вращается
в горизонтальной плоскости. В этом случае прецессия вызвана моментом
силы тяжести, действующей на весь гироскоп. И здесь закручивание
нити и сопротивление воздуха препятствуют прецессии и приводят к тому,
что ось гироскопа постепенно опускается.
Если бы силы трения отсутствовали, то ось гироскопа в обоих приве-
приведённых примерах двигалась, оставаясь всё время в горизонтальной плоско-
Рис. 193.

§95]
ГИРОСКОПЫ
257
Рис. 194.
сти. Это обусловлено тем, что ось гироскопа вначале была горизонтальна,
т. е. перпендикулярна к направлению внешней силы.
В общем случае, когда вначале ось гироскопа образует какой-то про-
произвольный угол с постоянным направлением силы, создающей внешний
момент, гироскоп, прецессируя, описывает конус около этого постоянною
направления силы. Так, например, когда ось неурав-
неуравновешенного гироскопа в начальный момент накло-
наклонена к горизонту, возникает прецессия, при которой
ось гироскопа описывает конус вокруг вертикали,
т. е. вокруг направления силы тяжести (рис. 194).
Другой случай прецессии, при которой ось гиро-
гироскопа описывает конус вокруг постоянного направ-
направления внешней силы, можно продемонстрировать,
привязав к концу оси длинную мягкую резинку
(достаточно длинная резинка действует на ось гиро-
гироскопа" с силой, направление которой практически
можно считать постоянным). Если резинку натя-
натянуть так, чтобы она составляла небольшой угол с
осью гироскопа, ю эта ось будет описывать конус
вокруг направления резинки. Направление прецессии
определяется, как н прежде, направлениями М и N. Движение, которое в
этом случае совершает ось гироскопа, изображено пунктиром на рис. ]89.
Движение оси гироскопа по конусу обусловлено тем, что она движется
не в направлении силы, а в направлении момента силы, т. е. всегда пер-
перпендикулярна к направлению силы. Поэтому при по-
постоянном направлении силы ось гироскопа описывает ко-
конус вокруг этою направления. Только в частном слу-
случае, когда вначале ось перпендикулярна к направлению
силы, конус превращается в плоскость.
В рассмотренном выше примере неуравновешиваемого
гироскопа, прецессирующего под действием момента силы
тяжести, центр тяжести гироскопа смещён относительно
точки закрепления (чем и обусловлено наличие момента
силы тяжести), но лежит на оси гироскопа. В этих случаях,
представляющих интерес с точки зрения практических
применений, гироскоп называют гироскопическим маят-
маятником.
Найдём угловую скорость прецессии гироскопического
маятника. Пусть О — точка закрепления гироскопа и
С—его центр тяжести (рис. 195). Момент силы тяжести
M=Pl sin f,
где Р_ вес гироскопа, а / — расстояние ОС. Этот мо-
момент вызывает движение конца вектора момента количества движения N
по окружности радиуса JVsin у. За элемент времени &t вектор N изменяется
на величину
AN = !Л It.
Это есть путь, пройденный концом вектора N по окружности, и поэтому
где Да— угол, на который за время Д/ переместилась проекция вектора N
иа горизонтальную плоскость. Следовательно,
С, э. хайкин

258 механика твёрдого тела [гл. хш
и угловая скорость прецессии
Д*
Nsiny '
Подставив значение М, получим:
S = ^'. A3.52)
Легко видеть, что выражение A3.52) для угловой скорости прецессии
В горизонтальной плоскости представляет собой частный случай общего
вы~ажения A3.50).
Период обращения оси гироскопа, или «период гироскопического маят-
маятника»,
т=2?=2*% <13-53>
зависит от параметров гироскопа, но не зависит от угла <р, который обра-
образует ось гироскопа с вертикалью. В этом смысле гироскопический маятник
можно сравнивать с физическим маятником. Так же, как физический маят-
маятник совершает малые колебание около вертикали с периодом T=^2nVlo]g,
где /о — его приведёчная длина, i нроскопический маятник прецессирует
вокруг направления вертикали с периодом, определяемым формулой A3.53),
т. е. аналогичен физическому маятнику с приведённой длиной
A3.54)
Если скорость вращения гироскопа велика, то его «приведённая длина»
может во много раз превышать приведённую длину того физического маят-
маятника, котооый представлял бы собой этот гироскоп, если бы он не вращался.
Соответственно и скорость движения оси вращающегося гироскопа может
быть гораздо меньше, чем скорость движения этого же гироскопа, если он
остановлен. Так например, даже в сравнительно неблагоприятном с этой
точки зрения случае, изображённом иа рис. 194, период прецессии гиро-
гироскопа составляет десятки секунд и «приведённая длина» — десятки метров.
Этот же гироскоп, не вращающийся и подвешенный в точке прикрепления
нити, представлял бы собой физический маятник с приведённой длиной
в несколько сантиметров и периодом в доли секунды.
Благодаря быстрому вращению гироскопа изменение положения его
оси под действием заданных внешних сил происходит не только в другом
направлении, но и гооаздо медленнее, чем в случае, если бы гироскоп не
вращрлся. Иначе говоря, для того, чтобы вызвать столь же быстрые изменения
положения оси, нужно в случае вращающегося гироскопа приложить гораздо
большие силы, чем в случае, когда он не вращается. Вместе с тем пре-
прецессия гироскопа происходит только пока действует внешний момент
н ппекоащается сразу же, кэк только этот момент исчезает. Как уже ука-
указывалось, движение оси гироскопа в этом смысле не обладает инерцией,
тгк как скорость движения оси определяется действующими силами (инер-
(инерция же есть проявление того, что ускорение определяется силами). Поэтому,
если внешние силы действуют на гироскоп непродолжительное время, то
ось его не успеет намного изменить своё положение и после прекращения
действия сил остановится в новом положении, близком к исходному. Именно
все эти особенности поведения оси гироскопа н имеют в виду, когда гово-
говорят, что ось гироскопа «обладает устойчивостью», что она «стремится
сохранить своё положение в простоанстве» и т. д.
Обыкновенный волчок представляет собой также гироскопический маят-
маятник, однако отличающийся тем, что точка опоры у него всегда лежит ниже

§ 95]
Гироскопы
259
центра тяжести. Для физического маятника в случае, когда точка опоры
лежит ниже центра тяжести, положение равновесия оказывается неустойчи-
неустойчивым. Для гироскопического маятника при достаточной скорости вращения
гироскопа это положение становится устойчивым, и поэтому волчок, пока
он вращается достаточно быстро, не падает, а прецессиоует вокруг верти-
вертикали. Более того, наклонно пущенный волчок
выпрямляется, таь что угол между его
осью и вертикалью уменьшается. Объяс-
Объясняется это действием сил трения между
ножкой волчка и плоскостью опоры.
Так как точка "опоры волчка лежит ни-
ниже его центра тяжести (рис. 196), то момент
силы тяжести М направлен так, что направ-
направление прецессии совпадает с направлением
вращения самого волчка *). Поэтому, когда
ось волчка наклонена, сг'лы трения, дей-
действующие на ножку волчка со стороны пло-
плоскости, направлены так, что они ускоряют
прецессию**). А это, как мы зиаем, приведёт
к тому, что центр тяжести волчка поднимет-
поднимется. Однако силы трения, ускоряя прецес-
прецессию, замедляют вращение самого волчка.
Когда вращение замедляется до некоторого
критического значения, волчок теряет устой-
устойчивость и падает.
В случае уравновешенного — «астатического»—гироскопа момент силы
тяжести равен нулю и ось гироскопа остаётся неподвижной до тех пор,
пока на гироскоп не действуют какие-либо внешние силы. Если эти
внешние силы создают момент относительно точки закрепления гиро-
гироскопа, то ось гироскопа начинает цвигаться в направлении момента внеш-
внешних сил.
Чтобы вызвать быстрое движение оси гироскопа, внешние силы должнн
создавать большой внешний момент. В свою очередь, поворачивающийси
гироскоп создаёт большой гироскопический момент, направленный навстречу
внешнему моменту. Внешний момент обычно передаётся на ось гироскопа
в виде давления на подшипники, в которых она закреплена. В свою оче-
очередь, возникающий гироскопический момент приводит к тому, что сама ось
давит на подшипники с силами, равными внешним по величине и противо-
противоположными по направлению.
В частности, если подшипники оси гироскопа жёстко связаны с каким-
либо телом, то гироскопические моменты действуют на это тело при всяком
движении этого тела, сопровождающемся изменением направления оси
гироскопа. Эти силы часто играют заметную роль.
Рис. 196.
*) Если точка опоры лежит выше центра тяжести, то гироскопический
маятник, как это видно, например, из рис. 195, прецессирует в направлении,
противоположном собственому вращению гироскопа.
**) Дело в том, что ось волчка практически опирается на плоскость не
одной точкой. Конец наклонённой оси волчка можно рассматривать как
тупой конус, касающийся плоскости по своей образующей. Если этот конус
вращается вокруг своей оси, то вследсавие наличия сил трения он начнёт
катиться по плоскости, поворачиваясь вокруг своей вершины. При этом
качение будет происходить в ту же сторону, что и вращение конуса вокруг
своей оси. Отсюда видно, что силы трения действуют в том же направл&
иии, в котором происходит прецессия волчка, т. е. ускоряют эту пре-
прецессию.
17*

560
МЕХАНИКА ТВЕРДОГО ТЕЛА
[гл. хн|
Рис. 197.
Например, вращающиеся части машины парохода представляют со-
собой гироскоп, обладающий большим моментом количества движения. Ось
этого «гироскопа» расположена вдоль судна. При килевой качке кораб-
корабля (когда нос корабля поднимается и опускается) изменяется направле-
направление момента количества движения машины. Вследствие этого возникают
силы давления со стороны вала на подшипники; они лежат в горизон-
горизонтальной плоскости и поворачивают корабль вокруг вертикальной оси.
Это «рыскание по курсу» заметно у малых судов с мощными машинами
(буксиры).
Силами, действующими со стороны гироскопа, объясняются движения,
возникающие при повороте оси велосипедного колеса на скамье Жуковского
(§ 90). Когда, например, человек, находящийся на скамье, желает поднять
ось колеса вверх (рис. 197), то он должен надавливать на него вбок с си-
силами Pi и /*2. Вместе с тем возникает и давление со стороны оси на руку,
направленное в противоположную сторону. Это давление и создаёт момент,
вызывающий вращение человека со скамьёй вокруг
вертикальной оси. Определив для различных случаев
направление этих сил, можно убедиться, что всегда
возникает вращение в таком направлении, что.бы
общий момент количества движения системы оста-
оставался постоянным.
Все описанные свойства гироскопа объясня-
объясняются тем, что движение оси гироскопа подчиняет-
подчиняется уравнению A3.48). Движение осн гироскопа
определяется ре направлением силы, а направ-
направлением момента внешних сил. Но этот момент определяется силами, спе-
специально приложенными извне к гироскопу, только тогда, когда гиро-
гироскоп вполне свободен, т. е. когда конструкция прибора допускает любое
положевие его оси. Если же гироскоп не вполне свободен, то нужно
принимать во внимание и моменты тех сил, которые могут действовать
на ось гироскопа со стороны подшипников, в которых он закреплён.
Эти моменты сил могут совершенно изменить поведение гироскопа под
действием внешних снл. Например, если в демонстрационном гироскопе,
которым мы пользовались, закрепить вертикальную ось н сделать возмож-
возможным вращение оси гироскопа только в горизонтальной плоскости, то он
становится совершенно «послушным» Под действием силы F, приложен-
приложенной к гироскопу в горизонтальной
плоскости, ось его не поднимается
кверху, как а случае свободного
гироскопа, а поворачивается в на-
направлении действия силы. Это изме-
изменение в поведении гироскопа объяс-
объясняется тем, что наряду с моментом
силы F иа ось действует момент сил
и со стороны подставки, ,в которой
он закреплён. Возникновение этого
момента легко объяснить. Вначале,
пока на гироскоп не действует
сила F, на него не действуют мо-
моменты и со стороны подставки.
Гироскоп «не знает», что он закре-
закреплён. Поэтому сначала он ведёт себя
как вполне свободный гироскоп:
Рис. 198.
под действием силы F, создающей момент М, направленный вверх, конец
оси гироскопа начинает подниматься (рис. 198). Вертикальная ось, с кото-
которой жёстко связана ось гироскопа, немного изгибается, и воз .икает момент
упругих сил, действующих на ось гироскопа. Под действием этого момента Mj

§ 96J ПРИМЕНЕНИЯ ГИРОСКОПОВ 261
ось гироскопа будет перемещаться в горизонтальной плоскости, как раз
в том направлении, в котором действует сила F. Поэтому гироскоп и ока-
оказывается «послушным». Он ведёт себя так, как будто быстрое вращение
вокруг его геометрической оси отсутствует.
§ 96. Применения гироскопов
Установленные выше свойства гироскопов нашлн себе разнообразные
практические применения. Одним из наиболее важных н широких приме-
применений гироскопов является нарезное оружие. Винтовые нарезы в стволе
орудия сообщают вылетающему снаряду быстрое вращение вокруг оси
и превращают его в гироскоп с большим собственным моментом количе-
количества движения. После вылета из ствола центр тяжести снаряда движется
по параболе и касательная к траектории постепенно опускается вниз
(рис. 199). Действующее на снаряд сопротивление воздуха создаёт момент,
который должен был бы опро-
опрокинуть снаряд. Поэтому, если
бы снаряд не вращался вокруг
своей оси, то направление
этой оси могло бы меняться
самым произвольным образом. ,
В случае же быстрого» враще- • -/
ния вокруг оси снаряд превра- \у
щается в гироскоп и внешний v'
момент М вызывает лишь пре- ./
цессию оси снаряда вокруг на- ~t'
правления касательной к тра- /'/
ектории. Направление прецес- уу
сии. при этом совпадает с на-
направлением собственного вра-
вращения снаряда. В этом отно-
отношении снаряд подобен волчку,
и так же, как в случае волчка,
чтобы прецессия "была устой- Рис. 199.
чива, собственный момент
количества движения снаряда должен превосходить некоторую критиче-
критическую величину. Для этого винтовые нарезы в стволе орудия должны
быть достаточно крутыми (не менее одного оборота нарезов на участке ствола
длиной в несколько десятков калибров).
Так прост) обстоит дело, однако, только в случае очень настильных
траекторий, когда касательная к траектории мало изменяет своё направле-
направление в пространстве. В случае навесных траекторий задача осложняется,
так как ось снаряда должна быть близка к направлению касательной
и вместе с ней изменять своё направление в пространстве. Это возможно
только в случае, если момент количества движения снаряда вокруг оси не
очень велик. Таким образом, для того, чтобы ось снаряда во всех слу-
случаях оставалась близкой к направлению касательной к траектории, собствен-
собственный момент количества движения снаряда должен лежать между некото-
некоторыми определёнными, довольно узкими пределами.
. Лоугим важным применением гироскопов являются различные гиро-
скогичгкие навигационные приборы — гирогоризонт, гирокомпас и т. д.
Создание искусственного горизонта является одной из важнейших задач,
как морской, так и аэронавигации. Для астрономических измерений геогра-
географической широты нужно знать положение горизонтальной плоскости или
вертикали в данной точке. Если линия горизонта не видна, то для опреде-
определения вертикали можно пользоваться отвесом. Однако,-на экипаже, движу-
движущемся с ускорением, отвес не будет направлен по вертикали. Поэтому на

262.
МЬХАНИКЛ ТВЁРДОГО ТЕЛА
ГгЛ. XII!
корабле или самолете обычный отвес для определения вертикали, конечно,
непригоден вследствие неизбежных ускорений при наборе скорости, пово-
поворотах и качке. В этих случаях задачу можно решить при помощи специ-
специального гироскопического маятника, так называемого гирогоризонта.
Для выяснения принципа действия гирогоризонта мы рассмотрим пове-
поведение гироскопического маятника в экипаже, обладающем ускорением. Пока
Экипаж не обладает ускорением, гироскопический маятник, ось которого
расположена вертикально, сохраняет неизменным своё положение. Если
возникло ускорение экипажа, то в системе координат, связанной с экипа-
экипажем, появляются силы инерции. Их действие можно учесть как некоторое
эквивалентное изменение направления силы тяжести. Направление оси
гироскопического маятника уже не будет
совпадать с направлением силы тяжести, и
гироскоп начнёт прецессировать. Но «приве-
«приведённую длину» гироскопического маятника
можно сделать очень большой (порядка согни
километров!), так что период прецессии бу-
дет составлять десятки минут. Если ускоре-
ние длится короткое время, то ось гироскопа
вследствие медленности движения не успеет
уйти далеко от направления вертикали, ко-
которое она занимала прежде. Поэтому кратко-
кратковременные ускорения во'обще заметно не от-
отклоняют оси гирогоризонта от вертикали.
Большого ускорения одного направления
экипажи обычно не могут иметь длительное
время. Наиболее неблагоприятный и этом
отношении случай —это набор скорости, ко-
который может длиться значительное время
и вызвать хотя и не очень большие, но всё
же заметные отклонения оси гироскопа. При
поворотах ускорения длятся короткое время,
а при качке они меняют направление, и от-
отклонения оси гироскопа под влиянием этих
ускорений очень невелики. Таким образом,
Гироскопический маятник с большим перио-
периодом прецессии может служить искусствен-
искусственным горизонтом. Такие гирогоризонты сей-
сейчас широко применяются на морских судах для астрономических на-
наблюдений, на самолетах при слепом полёте и для различных специаль-
специальных цеЛей.
Другое важное применение гироскопов — поддержание заданного на-
направления движения экипажа — например, торпеды или самолета («авто-
(«автопилот»). Для этой цели применяются уравновешенные («астатические»)
гироскопы на кардановом подвесе. В этом случае нет никаких внешних
моментов, которые могли бы изменить направление оси гироскопа, и она
сохраняет своё направление в пространстве независимо от движе шя эки-
экипажа. Конечно, осуществить такой вполне свободный гироскоп практически
невозможно вследствие неизбежного трения в подшипниках карданова под-
подвеса. Однако, если собственный момент количества движения гироскопа
велик, а силы трения малы, то моменты этих сил, возникающие при пово-
поворотах экипажа, мало изменяют направление оси гироскопа в пространстве.
Поэтому при отклонении направления"* экипажа от направления, зада того
осью гироскопа, связанная с экипажем рама, на которой укреплён гироскоп,
поворачивается относительно оси гироскопа. Возникающие при этом откло-
не <ия при помощи тех или иных приспособлений вызывают отклонения
рЗ'лей. возвращающие экипаж к заданному направлению.
Рис. 200.

§ 96]
ПРИМЕНЕНИЯ ГИРОСКОПОВ
263
В случае движения в плоскости, например, торпеды Уайтхеда, достаточно
одного гироскопа с осью, ориентированной по направлению движения.
В случае движения в пространстве на самолёте нужны два' гироскопа —
один с вертикальной осью, задающий горизонтальную плоскость, в которой
должен оставаться самолёт, и другой с горизонтальной осью, ориентиоо-
ванной вдоль оси самолёта, задающий курс самолёта. Оба гироскопа дают
соответствующую «команду» рулям и другим элементам управления, под-
поддерживающим горизонтальный полёт самолёта по заданному курсу. Такими
«автопилотами», освобождающими лётчика от необходимости всё время
управлять самолётом, оборудованы почти все современные самолёты, пред-
предназначенные для длительных полётов.
Наконец, последнее важное применение гироскопа в навигации,
это — гироскопический компас. В гирокомпасах испольчуются свойства не
Рис. 201.
Рис. 202.
вполне свободного гироскопа, ось которого может двигаться только в одной
фиксированной плоскости, которую мы для краткости будем называть пло-
плоскостью оси (рис. 200).
Пусть подставка, на которой закреплён такой не вполне свободный
гироскоп, вращается р постоянной угловой скоростью*» вокруг оси, обя-
обязующей некоторый угол с плоскостью оси
гироскопа. Так как гироскоп не вполне
свободен, то со стороны вращающейся
подставки на него может действовать не-
некоторый внешний момент. Чтобы опреде-
определить направление этого момента, разло-
разложим угловую скорость вращения под-
подставки ю на составляющие — в плоскости
оси а>/ и перпендикулярную к ней <ол
Это второе вращение никак не влияет на
гироскоп, так как относительно этой оси
он в подставке не закреплён. По отноше-
отношению к вращению <а( гироскоп несвободен,
и со стороны подставки на гироскоп
действует внешний момент М/, направлен-
направленный по a>f. Под влиянием этого момента
ось гироскопа будет поворачиваться в
своей плоскости, пока не совпадёт с М.
Это свойство не вполне свободного гироскопа можно продемонстриро-
продемонстрировать следующим образом. На подставке, которая может быть приведена во
вращение вокруг вертикальной о:и, установлен уравновешенный не вполне
Рис. 2U3.

264 МЬХАНИКА ТВЕРДОГО ТЕЛА [ГЛ. «II
свободный гироскоп, ось которого может вращаться в какой-либо наклон-
наклонной плоскости (рис. 201). Пока подставка неподвижна, ось гироскопа может
занимать любое положение в этой плоскости. Если привести подставку во
вращение, то после нескольких качаний ось гироскопа устанавливается
в направлении проекции угловой скорости вращения подставки на плоскость
вращения оси гироскопа и притом так, что момент количества движения
гироскопа по направлению совпадает с направлением* проекции угловой
скорости (рис. 202). Поэтому, если изменить направление вращения под-
подставки, то ось гироскопа поворачивается на 180е.
Аналогично будет вести себя не вполне свободный гироскоп под влия-
влиянием вращения Земли. Если ось его может вращаться только в горизон-
горизонтальной плоскости данного места, то под влиянием угловой скорости
вращения Земли ю она установится в направлении а>/ проекции <о на гори-
горизонтальную плоскость, т. е. в направлении меридиана данного места, причём
вектор момента количества движения будет иметь направление на север
(рис. 203). Таким образом, не вполне свободный гироскоп в комбинации
с устройством, удерживающим его в горизонтальной плоскости (например,
с гирогоризонтом), может служить компасом.
Гироскопические компасы обладают по сравнению с магнитными рядом
преимуществ. На их показания не влияют находящиеся поблизости массы
железа и магнитные бури; они менее чувствительны к вибрациям и качке
к г. д. Поэтому гирокомпасы сейчас играют основную роль в навигации.

ГЛАВА XIV
ВСЕМИРНОЕ ТЯГОТЕНИЕ
§ 97. Закон всемирного тяготения
Закон всемирного тяготения, как и все физические законы, пред-
представляет собой обобщение опытных фактов. Факты, из которых Нью-
Ньютон вывел закон всемирного тяготения, были установлены Кеплером.
Это так называемые «законы Кеплера», которым подчиняются все
планеты солнечной системы. Факты эти следующие:
1. Все планеты движутся по эллипсам, в одном из фокусов кото-
которых находится Солнце.
2. Радиус-вектор планеты описывает в равные времена равные
площади.
3. Квадраты времён обращения планет относятся, как кубы боль-
больших полуосей.
Из этих фактов могут быть сделаны вполне определенные заклю-
заключения об ускорениях., сообщаемых планетам Солнцем. Чтобы упро-
упростить вывод этих заключений, мы заменим эллиптические орбиты
круговыми. Из первых двух законов Кеплера следует, что сила, дей-
действующая на все планеты, направлена н одну и ту же точку, к центру
Солнца. Третий закон Кеплера для круговых орбит гласит:
7? Я»
12
где Тл и 7^— времена обращения, а /?, и R2 — радиусы орбит.
При движении по круговой орбите планета должна испытывать
центростремительное ускорение j=<a2R. Поэтому отношение ускоре-
ускорений для двух различных планет равно
Так как в>1('о>2= ^V^i» то
h u'iR*

266 ВСЕМИРНОЕ ТЯГОТЕНИЕ ГгЛ. XIV
Подставляя отношение квадратов времён обращения A4.1), полу-
получаем:
h — _5
Так как третий закон Кеплера справедлив для всех планет в их
движении нокруг Солнца, то, значит, для любой планеты ускорение
равно
/=%> A4.2)
где С—константа, одинаковая для всех планет, a R — расстояние
от планеты до Солнца.
Солнце сообщает всем планетам ускорение, направленное к
центру Солнца и обратно пропорциональное квадрату расстояния
от Солнца. Это и есть тот вывод, который может быть сделан из
законон Кеплера. Этот вывод; полученный нами для круговых орбит,
справедлив также и для эллиптических орбит.
Если мы применим выражение A4.2) к движению Луны вокруг
Земли, то постоянная С будет иметь другое значение. Отсюда сле-
следует, что эта постоянная С зависит от свойств ускоряющего тела.
Наконец, из сопоставления ускорений, сообщаемых Землёй Луне
и различным телам, находящимся у поверхности Земли, следует,
что Земля сообщает Луне ускорение в 3600 раз меньшее, чем
всем телам, находящимся у поверхности Земли. Так как расстояние
от центра Земли до центра Луны в 60 раз больше радиуса Земли,
то и для ускорений, сообщаемых Землёй любым телам (в том~ числе
и Луне), спранедливо соотношение
У = §1, A4.3)
где Сг одинаково для всех тел, ускоряемых Землёй.
Таковы факты, которыми располагал Ньютон. Из этих фактов он
вывел заключение, что ускорения, сообщаемые небесными телами
друг другу, и ускорения, сообщаемые различным телам Землёй, обу-
обусловлены силами, имеющими одну и ту же природу. Это — силы все-
всеобщего тяготения или гравитационные силы, действующие между
всеми телами, будь то Солнце и планета, или Земля и «ньютоново
яблоко». На основании этих же фактов Ньютон установил те законы,
которыми определяются силы взаимного тяготения. Прежде всего,
силы взаимного тяготения должны быть обратно пропорциональны
квадрату расстояния между центрами тел (для тел шарообразных).
Далее, силы эти должны зависеть от свойств ускоряющих тел (так
как постоянная С для различных ускоряющих тел различна). Наконец,
так как различным телам данное тело сообщает одно и то же уско-

§ 97] вакон всемирного тяготения 267
рение, то силы эти должны зависеть также и от свойств ускоряемых
тел. (Если бы силы не зависели от свойств ускоряемых тел, то
ускорения были бы не одинаковы, а обратно пропорциональны инерт-
инертным массам тел.)
На основании этих соображений Ньютон и высказал предположе-
предположение, что сила нзаимного тяготения
» A4.4)
где г — расстояние между телами, а /и, и >л2 — постоянные, характе-
характеризующие гравитационные свойства каждого из тел. Постоянные т1
и /л2 называются гравитационной (или тяжёлой) массой тела.
Закон всемирного тяготения A4.4) не является целиком утвержде-
утверждением, поддающимся опытной проверке, так как мы не располагаем
способом независимого измерения тяжёлых Nsacc тел. В законе все-
всемирного тяготения содержится только утверждение, что силы тяготе-
тяготения обратно пропорциональны квадрату расстояния между телами
(это утверждение может быть проверено на опыте—законы Кеплера
являются его подтверждением). Кроме того, в нём содержится опре-
определение тяжёлой массы тела. Это определение таково: если мы изме-
измерим силу, с которой какое-либо тело А притягивается к телу В,
а затем вместо тела В поместим другое тело С и измерим силу
притяжения между А и С, то отношение сил притяжения и будет
определять отношение тяжёлых масс тел В к С. Но это мы и делаем
при взвешивании; следовательно, взвешиванием мы определяем тяжё-
тяжёлые массы тел.
Совсем другим способом (по отношению взаимных ускорений или
по отношению между силой и ускорением) мы определяем инертные
массы тел. И заранее вовсе нельзя утверждать, что отношение тяжё-
тяжёлых масс тел должно быть равно отношению их инертных масс.
Однако уже самые грубые наблюдения подтверждают это. Так как
все тела падают к Земле с одинаковым ускорением, то силы, с кото-
которыми они притягиваются Землёй, пропорциональны их инертным мас-
массам. С другой стороны, по определению, отношение этих сил равно
отношению их тяжёлых масс. Следовательно, отношение тяжёлых
масс тел пропорционально отношению их инертных масс. Чтобы про-
проверить это со всей возможной точностью, Ньютон произвёл специ-
специальные опыты с маятниками, сделанными из различных материалов,
и убедился, что все маятники одинаковых размеров и формы колеблются
с одинаковым периодом. Совпадение периодов маятников свидетель-
свидетельствует о том, что g для всех тел одно и то же. Эти опыты повто-
повторялись неоднократно "всё с большей и большей точностью и всегда
давали тот же результат. Таким образом, со всей доступной сейчас
высокой точностью установлен тот факт, что тяжёлые массы тел
пропорциональны их инертным массам,

268 всемирное тяготение [гл. xiv
С точки зрения классической физики этот факт представляется порази-
поразительным, «случайным совпадением», так как инертные и гравитационные
свойства тел в классической физике никак не связаны между собой. В клас-
классической физике законы динамики никак не связаны с существованием сил
тяготения. С точки зрения классической физики законы динамики могли бы
существовать и сохранить свой смысл и вид, даже если бы не существовало
вообще сил тяготения. С точки же зрения теории относительности самое
происхождение законов Ньютона тесно связано с существованием сил тяго-
тяготения. Поэтому пропорциональность инертной и тяжёлой масс с точки зре-
зрения общей теории относительности не является «случайным совпадением»,
а отражает ту глубокую связь, которая существует между законами дина-
динамики и явлением всемирного тяготения.
§ 98. Гравитационная достоянная
Если тяжёлая и инертная массы тела пропорциональны друг другу»
то мы можем считать их равными. Другими словами, тот же плати-
платиновый куб, который мы приняли за единицу инертной массы, мы
можем считать и единицей тяжёлой массы. В физике так и посту-
поступили. Тогда в законе всемирного тяготения A4.4) у нас уже заранее
выбраны единицы для измерения всех величин, входящих в этот
закон. Если мы сохраним этот закон в том виде, как он написан
(т. е. н виде пропорциональности), то он останется справедливым
при любом выборе единиц измерения. Но, если мы хотим заменить
пропорциональность равенством, то мы должны ввести некоторый
коэффициент пропорциональности:
Однако размерности / и тхтг\гг при выбранных нами единицах изме-
измерения тяжёлой массы оказываются различными. Это значит, что при
изменении масштабов единиц должно изменяться и численное зна-
значение коэффициента у, чтобы соотношение A4.5) оставалось спра-
справедливым, т. е. у имеет определённую размерность. Чтобы равенство
A4.5) не зависело от выбора масштабов, размерности правой и леной
частей должны быть одинаковы, и поэтому размерность у в системе
LM.T будет
Размерный коэффициент у называется гравитационной постоян-
постоянной. Гравитационной постоянной у можно придать определённый
наглядный смысл. Если мы положим /и, = 1, т2=1 и г=\, то
/ = у, т. е. у равно той силе, с которой притягиваются два тела
с массами, равными единице, и находящиеся иа расстоянии, равном
единице.
Теперь понятно, почему мы прежде вообще могли не различать
инертной и тяжёлой масс. Массы эти оказались пропорциональными,

§ 98]
ГРАВИТАЦИОННАЯ ПОСТОЯННАЯ 269
а единицы мы выбрали так, чтобы они оказались к тому же и рав-
равными. Поэтому мы и можем говорить о массе тела, не уточняя, идёт
ли речь об инертной или о тяжёлой массе.
Мы могли поступить иначе: выбрать единицу тяжёлой массы так, что-
чтобы не только закон всемирного тяготения был справедлив при любом вы-
выборе масштабов единиц, но и чтобы ^ оставалась постоянной и не завися-
зависящей от выбора масштабов единиц. Тогда f была бы величиной безразмерной,
ио зато размерность тяжёлой массы оказалась бы другой, не такой, как
размерность инертной массы. Именно, размерность тяжёлой массы в систе-
системе LMT была бы:
'/. •/•
[me] — L М Т-1.
Это значит, что хотя тяжёлая масса данного тела и остаётся пропор-
пропорциональной инертной массе, но эти массы уже не равны, независимо от
выбора масштабов единиц (так как размерности этих масс различны).
Для инертной массы мы имеем эталон — определённое тело, масса кото-
которого принята за единицу. Единицу тяжёлой массы следовало бы считать
производной единицей, для которой мы не должны иметь эталонов, а долж-
должны его воспроизводить при помощи закона всемирного тяготения и основ-
основных эталонов (инертной масеы, длины н времени). Если бы мы хотели
последовательно строить абсолютную систему единиц LMT, то эталон инерт-
инертной массы нельзи было бы в то же время рассматривать как эталон тяжё-
тяжёлой массы *).
Тем, что мы одно и то же тело выбираем за эталон и инертной, и тя-
тяжёлой масс, т. е. заранее считаем их равными при всяком выборе масшта-
масштабов, мы предопределяем изменения коэффициента г при изменении масшта-
масштабов, т. е. определяем размерность этого коэффициента.
Для определения значения коэффициента у мы должны один раз
одновременно измерить все величины, входящие н закон всемирного
тяготения, т. е. измерить силу взаимного тяготения двух тел, массы
которых нам заранее известны. Поэтому мы не можем определить у
из сил притяжения планет к Солнцу (так как массы планет нам
неизвестны).
Значение у можно было бы определить из силы притяжения тел
к Земле, если бы масса Земли была измерена независимо (путём
сравнения с какой-либо известной массой). На этом и были основаны
первые измерения у.
Ньютон предложил идею определения массы Земли путём сравнения её
с массой горы. Эту последнюю можьо приближённо определить по разме-
размерам горы, если плотность горных пород известна. Идея^ заключается в из-
измерении отклонения, которое испытывает отвес под действием притяжения
Земли. Если отвес укреплён у подошвы горы (рис. 204), то кроме силы
притяжения Земли F на него действует сила притяжения со стороны го-
горы f, вызывающая отклонение отвеса. Угол отклонения отвеса f опреде-
определяется соотношением tg<p=//.rT. Этот угол <р можно измерить путём астро-
*) Можно было бы поступить ещё иначе: выбрать хранящийся в Пари-
Париже платиновый куб за эталон тяжёлой массы. Тогда нельзя было бы этот
же куб рассматривать как эталон инертной массы. Единица инертной массы
оказалась бы производной единицей, которую нужно воспроизводить по
«талону тяжёлой массы, длины и времени.

270
ВСЕМИРНОЕ ТЯГОТЕНИЕ
Ггл. xiv
номических определений вертикали данного места. По отношению сил / и
F можно найти отношение масс горы и Земли. Так как масса горы
известна, то измерение позволяет определить массу Земли.
Такие измерения были произведены Маскелином A755 г.) и Джемсом
и Кларком A856 г.). Последние измерения дали для массы Земли значение
М = 5,75-1027г, т. е. уже достаточно близкое к тому, которое было уста-
установлено более точными дальнейшими измерениями. Зная массу Земли, по
силе притяжения Землёй тела известной массы
можно из закона всемирного тяготения найти
гравитационную постоянную.
Некоторое видоизменение этого метода пред-
ставлют собой измерения, впервые произведён-
произведённые Карлини A824 г.). Измеряя период колебаний
одного и того же маятника на вершине горы и на
ровном месте, можно определить относительное
увеличение силы тяжести, обусловленное при-
притяжением горы, а затем отношение сил притяже-
притяжения Земли и гооы. Если масса последней извест-
известна, то может быть найдена и масса Земли.
Несколько иной принцип сравнения массы
Земли с известной массой был использован Эйри
A866 г.). Измеряя период колебаний одного н
того же маятника на поверхности Земли и в глубокой шахте, можно найти от-
отношение сил притяжения в этих двух точках. Эти силы имеют разную вели-
величину потому, что верхний слой Земли по-разному действует в точках, на-
находящихся на поверхности Земли и в глубине шахты. Поэтому из сопостав-
сопоставления результатов измерений в этих двух точках можно найти отношение
массы верхнего слоя к массе всей Земли. С другой стороны, зная среднюю
плотность верхнего слоя Земли, можно рассчитать его массу. Поскольку
известна масса верхнего слоя и её отношение к массе всей Земли, можно
определить массу Земли. Измерения Эйри дали величину, примерно на 2О°/о
большую, чем действительное значение.
В дальнейшем этот метод был уточнён и
дал для массы Земли значение, очень близ-
близкое к истинному.
Рис. 204.
Вторую группу составляют методы
определения у по силам взаимодействия
между двумя телами, массы которых
могут быть непосредственно измерены.
Главная трудность в осуществлении
этих методов состоит в том, что при г - -
не очень больших массах, которыми ,' , \
можно пользоваться в этих методах, \ /
силы притяжения оказываются очень *"ж
малыми, Кавендиш впервые построил IJhc- 20j.
прибор, на котором эти малые силы
могут быть измерены A798 г.). Схема прибора изображена на
рис. 205. Коромысло с двумя одинаковыми массами т, подвешен-
подвешенное на очень тонкой и длинной нити, находится в положении
равновесия (рис. 205, а). Если ;<. массам т приблизить сбоку другие
массы М {рис. 205, Ь), то силы взаимного тяготения закручивают
коромысло с нитью на определённый угол. Приближение масс М к

§ 98]
ГРАВИТАЦИОННАЯ ПОСТОЯННАЯ
271
массам т с другой стороны вызывает закручивание коромысла в дру-
другом направлении. В смещённом положении равновесия момент сил
притяжения, действующих на массы т, т со стороны масс М, М,
равен моменту упругих сил, действующих со стороны подвеса. Зная
упругость подвеса, можно определить силы, действующие на массы т
в новом положении равновесия. Так как массы т и М и расстояние
между ними известны, то из значения найденной силы можно опре-
определить величину у-
Выполнение этих измерений требует больших предосторожностей,
так как измеряемые силы очень малы.
Измерения, произведённые Кавендишем, дали значение у =
= 6,66-10~8сл3-г~|-сек~2. Прибор Кавендиша в дальнейшем был
усовершенствован Бойсом A893 г.).
Его измерения дали значение
К этой же группе относится и метод
Жоли. Измерение силы притяжения
между двумя массами производится при
помощи чувствительных рычажных весов
(рис. 206). На весах уравновешивается
шар известной массы от, а затем к нему
подносится другой шар большой массы
М. Сила притяжения, действующая со
стороны этого большого шара, нару-
нарушает равновесие весов. По величине гру-
груза, который нужно положить на другую чашку весов, чтобы восстановить
равновесие, "определяется сила притяжения между шарами. Чтобы
шар М не действовал иа грузы, находящиеся на второй чашке ве-
весов, шар т подвешивается к коромыслу весов на очень длинной нити.
К5ниг и Рихард усовершенствовали метод Жоли и получили для у
значение, которое сейчас считается наиболее точным:
Y = 6,685. КГ8-си3-г-ш<Г2.
После того как у определена, можно найти и массу Земли. Так
как ускорение на поверхности Земли g=yMjR2, где М—масса
Земли, R — её радиус, то, подставляя известные значения g"=
= 982 см\секги R = 6,4-108 см, мы найдём М. Масса Земли, найденная
из непосредственных измерений у, оказывается равной
Рис. 206.
г.
По ускорению, сообщаемому Земле Солнцем, можно таким же
образом определить и массу Солнца. Наконец, по ускорению, сооб-
сообщаемому Земле Луной, можно определить и массу Луны.

272 ВСЕМИРНОЕ ТЯГОТЕНИЙ [ГЛ. XIV
§ 99. Приливы
На явлениях, происходящих на Зепле, обычно не сказывается то обсто-
обстоятельство, что силы всемирного тяготения зависят от расстояния. Только
в специальных опытах большой точности (подобных опыту Кавендиша) это
обстоятельство становится заметным. Есть, однако, очень важное явление
на Земле, в котором изменение сил всемирного тяготения с расстоянием
играет принципиальную роль. Это — явление приливов.
Схематически явление приливов заключается в том, что на поверхности
океана с двух противоположных сторон земного шара образуются «горбы».
Положение этих горбов определяется, главным образом, положением Луны,
однако горбы не лежат точно пол Луний и с противоположной стороны
Земли. Но смещение горбов вызывается некоторыми не играющими прин-
принципиальной роли обстоятельствами. Поэтому при выяснении природы явле-
явления приливов мы ке будем учитывать этих обстоятельств и будем считать,
что горбы лежат как раз под Луиой и с противоположной стороны Земли
(рис. 207). При вращении Земли гор-
горбы сохраняют своё положение от-
Луно . 'f \\ носительио Луны — Земля вращается
OJ, [ I J > JA ' «под ними». Поэтому два раза в
•, \ I' сутки происходит повышение и по-
понижение уровня воды в океане. Это
н вызывает приливы и отливы у бе-
регов океана.
Ряс. l\il. для объяснения явления прили-
приливов, как уже сказано, необходимо
принять во внимание изменение снл всемирного тяготения с расстоянием.
Притяжение Луны сообщает определённое ускорение Земле и всем телам,
находящимся на поверхности Немли. Но так как расстояние от Луны до
разных точек на поверхности Земли различно, то сила притяжения, а вме-
вместе с тем н ускорение также оказываются различными. Всей Земле в це-
целом (кал твёрдому телу) Луна сообщает ускорение /, примерно такое,
какое она сообщала бы телу, помещённому в центре земного шара. Массам
воды, находящимся со стороны Луны, т. е. ближе, Луна сообщает ускоре-
ускорение /j, большее, а массам, находящимся с противоположной стороны Земли,
ускорение it, меньшее, чем всему темному шару в целом. С тЧ>чки зрения
внеземного («неподвижного») наблюдателя при «падении» Земли на Луну *)
массы воды, находящиеся со стороны Луны, опережают Землю, а массы,
находящиеся с другой стороны, отстают от Земли в её падении. Поэтому
и образуются два горба.
~^ Нетрудно объяснить это явление и с точки зрения земного наблюда-
наблюдателя. Чтобы не повторять потом снова соображения «неподвижного» на-
наблюдателя, мы здесь уже сразу приведём некоторые количественные соот-
соотношения, которые нам понадобятся дальше.
Луна сообщает всему земному шару ускорение / = тмо//-2,где щ—мас-
щ—масса Луны, /•(, — расстояние между центрами Земли и Луны. Поэтому земной
наблюдатель должен ввести силу инерции /, = — mj = — 1тщ1г\, где т —
масса, на которую эта сила действует. С другой стороны, на массу воды т
Луна действует с силой / = ¦\mrnl)jr^, где г—расстояние от центра Лупы до
данной массы воды. Для тел, находящихся на стороне, обращенной к Луне,
эта сила будет Д = к/и/ио/''i, а на противоположной стороне/3 =~\тт^г2,
причем /-1 < л0 < гг. Поэтому /i > // > /V Силу /( земной наблюдатель
*) Конечно, это «падение» не связано с приближением к Луне, так как
Земля и Луна вращаются вокруг общего центра тяжести.

§ 99]
Приливы
273
должен прибавить к силам притяжения Земли и Луны. Со стороны Луны fx
направлена против земного притяжения, a ft — в сторону земного притя-
притяжения, и так как /i>//, они вместе уменьшают силу земного притяжения.
С противоположной стороны /2 направлена в сторону земного притяжения,
а // — против него, и поскольку /2 < /г, они также уменьшают силу зем-
земного притяжения. Под Луной и с противоположной стороны все тела,
и вода в том числе, «легче», чем в других местах земного шара. Поэтому
и образуются горбы на поверхности океана.
Возникновение приливной волны можно продемонстрировать в аудито*
рии. Как мы видели, явление приливов обусловлено тем, что «сосуд» (зеы-
ной шар) и вода, в нём находящаяся, имеют разные ускорении. При этом
и должна возникать приливная волна.
'ЩТППЯР—3
Рис. 208.
Рис. 209.
Если плоскую банку с подкрашенной водой подвесить в виде маятника
(рис. 208), то при колебаниях вода в сосуде будет двигаться вместе с со-
сосудом А). Поверхность воды остаётся плоской и неподвижной по отношению
к сосуду. Никаких приливных явлений на поверхности воды в этом случае
не наблюдается, так как ускорения сосуда и воды обусловлены только при-
притяжением Земли и поэтому оказываются в каждом положении одинаковыми.
Если же к сосуду прикрепить Две мягкие пружины (рис. 209), то эти
пружины будут немного изменять ускорение сосуда. Ускорение же воды
попрежнему будет определяться притяжением Земли. Вследствие различия в
ускорениях сосуда и воды они движутся, по-разному, уровень воды не ос-
остаётся плоским! По поверхности воды в сосуде пробегает приливная волна.
Янление приливов на Земле должна вызывать не только Луна, но и
Солнце. Величина приливов определяется разностью ускорений в центре
землн н на её поверхности, обусловленных данным небесным телом. По-
Поэтому, хотя для Земли сила притяжения Солнца больше, чем сила притя-
притяжения Луны, но так как Луна находится от Земли на расстоянии гораздо
меньшем, чем Солнце, то разность ускорений, сообщаемых Луной, оказы-
оказывается больше, чем разность ускорений, сообщаемых Солнцем. Прилги
на Земле, вызванные Солнцем, малы по сравнению с приливами, вызывае-
вызываемыми Луной.
*) Когда маятнику сообщено начальное отклонение, уровень воды в
сосуде горизонтален, а не параллелен дну сосуда, как при колебаниях.
Поэтому сначала вода колеблется в сосуде, но скоро успокаивается и дви-
движется вместе с сосудом.
18 с. Э. Хайкин

ГЛАВА XV
МЕХАНИКА УПРУГИХ ТЕЛ
§ 100. Сплошные тела
Все реальные тела способны деформироваться, и поэтому раз-
различные части тела могут двигаться по-разному. Для того чтобы
изучить движение деформируемого тела, строго говоря, нужно рас-
рассмотреть движение всех отдельных элементов тела, которые могут
двигаться друг относительно друга. Такими элементами являются
атомы, из которых построено всякое тело. (Атомы реального тела
никогда не бывают абсолютно жёстко связаны между собой, поэтому
тело и способно деформироваться.)
Однако, в механике сплошных тел задача ставится по-иному.
Если интересующее нас движение таково, что большое число смеж-
смежных атомов движется одинаково, то мы можем описывать движение
этого элемента тела, забывая о том, что он состоит из отдельных
атомов. Таким образом, мы приходим к представлению о сплошных
телах. Мы разбиваем реальное тело на отдельные малые элементы,
и силы, действующие между смежными элементами, рассматриваем
как внешние силы, действующие со стороны одного элемента на
другой. К этим элементам тела мы применяем обычные законы ме-
механики. Мы имеем право это делать только потому, что в каждый
отдельный элемент входит очень много атомов. Действительно, зако-
законы механики являются обобщением опытных фактоз, которые были
установлены на основании опытов с макроскопическими телами (со-
(состоящими из многих атомов). И мы не имеем никакого права утвер-
утверждать, что эти же законы справедливы и для каждого отдельного
атома. Законы днижения отдельных атомов могут быть установлены
только на основании опытов с отдельными атомами. Эти опыты по-
показали, что к отдельным атомам, вообще говоря, неприменимы те
законы механики, которыми мы всё время пользуемся. Но если в вы-
выделенный элемент входит ещё очень много атомов, то мы вправе
применять к этому элементу обычные законы механики.
Конечно, отдельные атомы выделенного элемента никогда не
движутся одинаково, так как они все совершают хаотическое тепло-
тепловое движение. Но если атомов в элементе много, то именно вслед-

§ 101] типы деформаций 275
ствие хаотичности теплового движения общее количество этого дви-
движения всегда равно нулю. Поэтому мы и можем не учитывать этого
теплового движения, если выделенный элемент объёма содержит до-
достаточно много атомов.
С обеих точек зрения наше рассмотрение законно только до тех
пор, пока в выделенный элемент входит большое число атомов. Для
этого размеры элементов, ьа которые мы разбиваем тело, должны
быть велики по сравнению со средними расстояниями между, атомами.
Но, с другой стороны, размеры элементов должны быть столь малы,
чтобы все атомы элемента при рассматриваемом движении днигались
практически одинаково. Только в том случае, когда мы сможем рдз-
бить тело на отдельные> элементы так, чтобы были соблюдены оба
эти условия, рассмотрение реальных тел, как сплошных, оказывается
возможным.
§ 101. Типы деформаций
Рассматривая тело, как сплошное, мы должны научиться находить
те «внешние» силы, с которыми отдельные элементы тела действуют
друг на друга. В абсолютно упругих телах эти силы однозначно
определяются состоянием взаимодействующих элементов тела — их
деформациями. Поэтому мы должны прежде всего устанозить способ
описания деформаций сплошного тела.
Рис. 210. Рнс. 211. Рис. 212.
При всём разнообразии деформаций тел оказывается возможным
любую деформацию тела свести к двум основным типам деформаций,
которые поэтому называются элементарными деформациями. Этими
элементарными деформациями являются растяжение (и сжатие)
и сдвиг. Для того чтобы ясно представить себе эти основные де-
деформации и их связь с другими типами деформаций, удобно пользо-
пользоваться моделью, изображённой на рис. 210. Ряд одинаковых пластин
(кусков фанеры) соединён между собой по четырём углам одинако-
одинаковыми пружинками. Нижняя пластина прикреплена к столу.
Растяжение тела мы получим, оттягивая верхнюю пластину вверх
(рис. 211), сжатие,—нажимая на неё вниз (рис. 212). Изменение
расстояний между пластинами происходит таким образом, что рас-
18*

276 МЕХАНИКА УПРУГИХ ТЕЛ fr.1. XV
стояния между соседними пластинами во всех точках остаются оди-
одинаковыми. Такая деформация называется однородным растяжением
или сжатием-
Деформацию сдвига мы получим, сдвигая верхнюю пластину па-
параллельно самой себа (рис. 213). При этом расстояния между пла-
пластинами останутся неизменными, но точки соседних пластин, лежащие
на одной вертикали, сдвинутся друг относительно друга в одном
направлении и на одну и ту же величину. Такая деформация назы-
называется однородным сдвигом.
Рис. 213. Рис. 214. Рис. 213.
На этой же модели мо>. но показать и некоторые другие типы
деформаций. Так, изгиб мы получлч, наклонив верхнюю пластину
(рис. 214). При этом расстояния между соседними пластинами в раз-
разных местах изменятся по-разному. С одней стороны, они увеличатся,
с другой — уменьшатся. Таким образом, деформация изгиба сводится
к растяжениям и сжатиям, различным в различных частях, тела, —
неоднородному растяжению и сжатию. Кручение мы получим, повер-
повернув верхнюю пластину вокруг вертикальной оси (рис. 215). При
этом расстояние между пластинами останется неизменным, но точки
пластин, лежавшие на одной вертикали, сдвинутся друг относительно
друга. Этот сдвиг в разных местах будет различен. Например,
в центре сдвига совсем не будет, у переднего ребра он будет на-
направлен вправо, у заднего — влево. Таким образом, деформация
кручения сводится к деформациям сдвига, различным в различных
частях тела, т. е. к неоднородному сдвигу. Другие, более сложные
типы деформаций могут быть сведены к одновременно существующим
двум деформациям неоднородного растяжения и сжатия и неодно-
неоднородного сдвига. Поэтому, введя величины, характеризующие дефор-
деформации растяжения и сдвига, можно потом с помощью этих же вели-
величин характеризовать и все другие типы деформаций.
Деформацию растяжения можно охарактеризовать величиной отно-
относительного удлинения. Если /—длина тела до растяжения, а /,—
после растяжения, то абсолютное удлинение тела при растяжении
есть A/ = /j—/. Относительное удлинение
z=% A5.1)

§ 101] ТИПЫ ДЕФОРМАЦИЙ 277
характеризует величину растяжения или сжатия, причём s соответ-
соответственно положительно или отрицательно. Очевидно, что при одно-
однородном растяжении или сжатии величина ? во всех точках тела одна
и та же.
Деформация сдвига определяется величиной относительного сдви-
сдвига. Если мы отметим какие-либо точки тела, лежащие на одной
прямой, например, на левой грани (рис. 216), то при деформации
абсолютный сдвиг АА', ВВ', СС' и т. д.. для различных точек будет
различным. Но отношение этого сдзига к
расстоянию до точки О будет одно и то же.
Эта величина у и называется относи-
относительным сдвигом. Одно из направлений ,,.,.
сдвига выбирается за положительное, а дру-
другое— за отрицательное. Если деформации малы, то tga= a и y=a.
Относительный сдвиг есть измеренный в радианах угол сдвига. При
деформации однородного сдвига величина у во всех точках тела одна
и та же.
В рассмотренных двух простейших случаях деформация опреде-
определяется одной величиной г или у. Более сложные деформации уже
нельзя определить заданием одной величины. Однако, пока дефор-
деформации достаточно малы, можно всякую деформацию рассматривать
как результат некоторых растяжений и сдвигов. Если мы выберем в
теле какие-либо три взаимно перпендикулярных направления, то
всякую деформацию мы сможем представить как результат трёх рао
тяжений по этим трём взаимно перпендикулярным направлениям
и трёх сдвигов в плоскостях, перпендикулярных к этим направлениям.
Если значения этих трёх растяжений и трёх сдвигов будут заданы,
то мы сможем найти по ним вызванное деформацией изменение рас-
расстояний между любыми двумя точками тела и изменение угла между
любыми двумя направлениями в теле. Таким образом, любая малая
деформация вполне определяется заданием шести указанных величин
(трёх растяжений и трёх сдвиюв).
В общем случае шесть величин, определяющих любую деформа-
деформацию в разных точках тела, различны. Поэтому, чтобы определить
деформацию тела, нужно указать, как изменяются эти шесть вели-
величин от точки к точке, т. е. нужно задать их как функции координат
точек тела.
При рассмотрении деформаций растяжения и сжатия мы пока
оставили в стороне одно сопутствующее этим деформациям явление.
Всякое растяжение тела всегда сопровождается соответствующим
сокращением его поперечного сечения и, наоборот, сжатие—соот-
сжатие—соответствующим увеличением поперечного сечения. На нашей модели
этого явления продемонстрировать, конечно, нельзя. Для демонстра-

278 механика упругих тел [гл. xv
ции поперечного сокращения тел при растяжении может служить
следующий простой опыт. На расположенную вертикально резиновую
трубку плотно одето металлическое кольцо, которое благодаря тре-
трению держится на трубке. Если трубку растянуть, то её диаметр
уменьшается и кольцо соскальзывает вниз.
Характеристикой этого изменения поперечных размеров при рас-
растяжении и сжатии является относительное поперечное расширение
или сжатие
d,-d id A53)
где d—поперечный размер тела до деформации, a rf, — после де-
деформации. При растяжении тел поперечные размеры его уменьшаются
и s <^0; при сжатии е„^>0. Таким образом, s и гд всегда различ-
различны по знаку.
Отношение т =— elsg называют коэффициентом поперечно-
поперечного сжатия или коэффициентом Пуассона. Коэффициент Пуассо-
Пуассона не зависит от размеров тел и для всех тел, сделанных из дан-
данного материала, имеет одно и то же значение. Поэтому коэффи-
коэффициент Пуассона является константой, характеризующей свойства ве-
вещества.
Деформации растяжения и сжатия, вообще говоря, связаны с
изменением объёма тел. Куб с рёбрами в единицу длины после
растяжения на малую величину s будет иметь длину l-(-s и сече-
сечение A -\-г J = 1 -\-2е (ед мало). Объем куба V, до деформации
равный 1, после деформации окажется равным
Изменение объёма
) = s(l— 2v), A5.5)
Где v = — е 'е=1'яг, т. е. величина, обратная коэффициенту Пуас-
Пуассона. У всех реальных тел при растяжении объём увеличивается,
при сжатии-—уменьшается. Это свойство реальных тел можно фор-
формулировать в более общем виде. Если мы н отдельных местах при-
приложим к поверхности тела силы, направленные только наружу, то
объём тела всегда увеличивается. Наоборот, если все силы, дей-
действующие на поверхность тела, направлены только внутрь, то объём
тела всегда уменьшается.
В силу этого свойства реальных тел для них всегда AV и г
должны быть одного знака, а для этого должно быть y<^1li»n»
т~^>2. В предельном случае, если бы тело вообще не изменяло
своего объёма при растяжении и сжатии, должно было бы быть
> = 1/а и т = 2.

§ 102] упругие тела 279
§ 102. Упругие тела
Дальнейшая наша задача состоит в том, чтобы установить, какие
силы возникают в теле при тех или иных деформациях. Очевидно,
что самая постановка этой задачи предполагает, что силы однозначно
связаны с деформациями. Однако реальные тела не обладают этим
свойством в полной мере.
При рассмотрении абсолютно неупругого удара (§ 56) мы даже
предполагали, что возникающие в телах силы определяются не де-
деформациями, а, главным образом, скоростью изменения деформаций.
Но для многих реальных тел при известных условиях силы можно
считать зависящими только от деформаций. Таким образом, мы при-
приходим к представлению об абсолютно упругом теле, в котором силы
однозначно связаны с деформациями. Каждой данной деформации со-
соответствует вполне определённое распределение сил, возникающих
в теле. И, наоборот, каждому данному распределению сил в теле
соответствует вполне определённая деформация. Поэтому есть толь-
только одно состояние тела, в котором отсутствуют силы, действующие
со стороны данного тела на другие или между отдельными частями
тела. Это состояние тела и называется недеформированным.
Мы будем считать, что покоящееся упругое тело, не подвергаю-
подвергающееся действию внешних сил, находится в таком недеформирован-
ном состоянии. Правда, в реальных твёрдых телах, даже в том
случае, когда они не подвергаются действию внешних сил, могут
существовать внутренние силы, действующие между отдельными
элементами тела. Эти внутренние силы или внутренние натяжения
возникают потому, что при образовании твердого тела, например, при
затвердевании расплава, некоторые элементы тела оказываются де-
деформированными. Отжиг металлических отливок или стеклянных
изделий и имеет целью устранение этих внутренних натяжений. Мы
в дальнейшем будем считать, что эти внутрен-ние натяжения отсут-
отсутствуют и что в недеформированном теле никакие силы между от-
отдельными его элементами не действуют.
Если в упругом теле по той или иной причине возникли дефор-
деформации, то в свободном покоящемся теле эти деформации в конце
концов исчезнут и тело вернётся к недеформированному состоянию.
Абсолютно упругое тело должно восстанавливать свою форму. Спо-
Способность тела в конце концов восстанавливать свою форму, ка-
какие бы деформации в нём ни происходили до этого, и Можно
считать определением абсолктно упругого тела.
Конечно, реальные тела вовсе не обладают этой способностью
в полной мере. Только пока деформации тела не превосходят извест-
известных пределов, оно восстанавливает свою форму и то, конечно,
лишь с известной степенью точности. Этот предел, до которого
реальные тела ведут себя приблизительно как абсолютно упругие,
называется пределом упругости данного реального тела. Различные

280 мьханика упругих тьл [гл. XV
тела обладают различным пределом упругости, но для всех тел су-
существует предел, после которого тело уже в заметной степени
сохраняет изменения формы. Такие деформации носят название оста-
остаточных или пластических деформаций. Ряд методов обработки
материалов (ковка, прокатка и т. д.) по существу состоит в создании
таких остаточных деформаций.
Рассматривать тела как абсолютно упругие имеет смысл только
при том условии, что деформации тел заведомо не достигают преде-
предела упругости. Правда, и до того, как достигнут предел упругости,
уже наблюдаются малые остаточные деформации. Но эти остаточные
деформации играют роль только в том случае, когда происходят
быстро повторяющиеся деформации тела. Поэтому при малых и мед-
медленных деформациях многие реальные тела можно рассматривать
как абсолютно упругие. Во-
Г ' | ^^ N^ прос о том, как малы и мед-
медленны должны быть деформа-
деформации, чтобы данное реальное
тело можно было рассма-
рассматривать как абсолютно упру-
упругое, должен быть решён
путём изучения поведения
тела при различных вели-
величинах деформаций.
Рис 217 ¦^ля этой цели пРиме*
няются специальные маши-
машины, в которых образцы
испытуемого материала подвергаются различным деформациям. При
этом обычно изучается связь величин деформаций с силами, ко-
которые приложены к испытуемому образцу, или, что то же
самое (пока деформации происходят медленно), с силами, возникаю-
возникающими в самом образце. Так как для большинства применяемых на
практике материалов даже большие силы вызывают сравнительно
малые деформации, то машины, применяемые для испытания материа-
материалов, должны, с одной стороны, развивать большие силы, а с дру-
другой,— позволять измерять малые деформации. Поэтому конструкции
этих машин сложны, и мы не будем их здесь описывать. Принцип
же их действия ясен из самой цели, для которой они служат. Ре-
Результаты испытания материалов даются обычно в виде графиков,
изображающих связь между деформациями образца и силами, в нём
возникающими.
Примеры таких графиков, полученных при испытании на растяже-
растяжение чугуна (а) и стали (Ь), приведены на рис. 217. Как видно из
этих графиков, при малых деформациях силы F растут пропорцио-
пропорционально деформации г, т. е.
F = k$. A5.6)

§ 102] УПРУГИЕ ТЕЛА 281
Пропорциональность между силой и деформацией впервые отметил
Роберт Гук. Поэтому наличие пропорционааьности между силой иде-
формацией называют законом Гука. Эта область называется также
«областью пропорциональности». Далее силы растут медленнее, чем
деформации. В этой области и лежит предел упругости тела. Точ-
Точного определения предела упругости дать вообще невозможно, так
как малые остаточные деформации наблюдаются всегда.
Пределом упругости считаются такие деформации, после которых
остаточные деформации достигают некоторой определённой, условно
выбранной доли (например, 0,001°/0) от той наибольшей деформации,
которой подвергался образец. Этот предел упругости лежит обычно
близко'за пределом пропорциональности. Дальше начинается область
текучести материала — наибольшие деформации, которым подвергся
материал, почти целиком сохраняются как остаточные деформации,
но целость материала при этом ещё не нарушается. При ещё боль-
больших деформациях возникающие в материале силы уже не только не
растут, но даже уменьшаются с увеличением деформаций. Это и пре-
предопределяет разрушение материала. Уже без дальнейшего увеличе-
увеличения внешней силы деформации материала продолжают увеличиваться
и достигают предела, при котором наступает разрушение.
Область упругих деформаций в большинстве применяемых на практике
материалов очень незначительна (например, для стали пределу упругости
соответствует значение е порядка 0,01). Поэтому наибольшие деформации,
которые может выдержать данный материал без разрушения, определяют-
определяются, главным образом, величиной области текучести. Материалы, для кото-
которых эта область мала, способны выдерживать без разрушения только
малые деформации — эти материалы хрупки. Материалы же, у которых
область текучести велика, способны без разрушения выдерживать большие
деформации. Такие материалы называются вязкими. Например, чугун
и сталь (как видно из рис. 217) имеют примерно одинаковую область упру-
упругих деформаций и примерно одинаково ведут себя в этой области —они
в одинаковой мере упруги. Но область текучести у чугуна гораздо меньше,
чем у стали, поэтому он гораздо более хрупок.
В дальнейшем мы не только будем рассматривать тела как аб-
абсолютно упругие, но будем предполагать, что все деформации не
выходят за пределы области пропорциональности, т. е. что для них
справедлив закон Гука — сила пропорциональна деформации. Такая
область принципиально должна существовать для всякого материала,
у которого силы однозначно определяются деформациями. Это скорее
математическое утверждение, чем физический закон: сила как функ-
функция деформации может быть разложена в ряд Тэйлора, и поэтому
для малых изменений аргумента всегда можно ограничиться первым
членом ряда. Утвер кдение, заключающееся в законе Гука, состоит
в том, что существует достаточно широкая область, в которой силы
пропорциональны деформациям, и что вне этой широкой области
сразу начинаются резкие отклонения от пропорциональности. Однако
о том, как велика эта область, закон Гука ничего ие говорит. Этот
вопрос должен быть решён опытом для каждого конкретного случая.

282 МЕХАНИКА УПРУГИХ ТЬЛ [ГЛ. XV
§ 103. Упругие напряжения
Рассмотрим связь между деформациями и силами в простейшем
случае однородного растяжения (рис. 218). К концу однородного
стержня с сечением S приложена постепенно возрастающая сила F.
Другой конец стержня закреплён. Под действием силы F конец
стержня начнёт двигаться — стержень будет растягиваться. Когда
прекратится возрастание силы F, установится
статическая деформация, которой будут соответ-
соответствовать определённые силы, действующие со сто-
стороны одной части стержня на другую.
Разделим мысленно стержень на две части се-
сечением S н определим силы, с которыми эти
7 части стержня действуют друг на друга. Так как
V обе частн стержня находятся в равновесии, то
I сумма сил, действующих на каждую из них, долж-
* на быть равна нулю. Поэтому на нижнюю часть
Рис ^18 стержня со стороны верхней действует сила — /7.
Такая ж? сила по третьему закону Ньютона
действует со стороны нижней части на верхнюю.
Так как стержень однороден и деформация его также однородна,
то сила Р равномерно распределена по всему сечению стержня.
Отношение силы к сечению, на котором она действует, назы-
называется напряжением в данном сечении. Напряжение в сечении 5
равно
-f
В общем случае, если деформации а различных местах сечения
различны, то для определения напряжения нужно брать столь малые
элементы сечения, чтобы на этом элементе силу можно было счи-
считать распределённой равномерно, т. е.
a = llm ?=%. A5.7)
В рассматриваемом примере направление силы нормально к вы-
выбранной нами площадке и возникающее в этом случае напряжение
jia площадке 5 является нормальным напряжением. Очевидно, что
в рассматриваемом случае напряжение а одинаково для всех площа-
площадок, параллельных сечению 5.
Опыт показывает, что для стержней разного сечения и длины,
но сделанных из одного и того же материала, деформация стержня s
при данной силе F*) обратно пропорциональна сечению стержня. S>
*) Что касается связи между деформацией е и силой Р, то мы заранее
ограничились случаями, когда между ними существует прямая пропорци-
пропорциональность.

§ 103]
УПРУГИЕ НАПРЯЖЕНИЯ
283
т. е.
Ев =
A5.8)
где Е— коэффициент пропорциональности, зависящий от свойств
материала стержня, но уже не зависящий от его размеров. Этот
коэффициент называется модулем упругости или модулем Юнга
данного материала. И так как a — FjS, то
— Ег.
A5.9)
Это соотношение и даёт связь между деформацией и напряжением
в рассматриваемом случае. Модуль Юнга считается положительным,
так что знак напряжения совпадает со знаком деформации. Еслл
модуль Юнга для данного материала известен [а его легко найти
на основании соотношения A5.8) из
опытов с растяжением стержня], то мы
можем по заданным деформациям растя-
растяжения найти напряжения, и наоборот.
Рассмотрим теперь напряжения,
возникающие при сдвиге. Для того
чтобы получить деформацию сдвига,
нужно закрепить одну из граней парал-
параллелепипеда, а к противоположной грани
приложить силу F, лежащую в плоско-
плоскости этой грани (рис. 219). Мысленно
разделим тело на две части сечением S. Для того чтобы верхняя часть
тела находилась в равновесии, на неё со стороны нижней части тела
должна действовать сила F. И в этом случае сила равномерно рас-
распределена по всему сечению S. Напряжение т в сечении S раяно
отношению силы к площади сечения, т. е. при однородном сдвиге
у''
*
I —
1
1
1
;
/
и
Рис. 219.
или в общем случае
A5.10)
В рассматриваемом случае сила лежит в плоскости площадки, на
которую она действует. Возникающее в этом случае напряжение на
площадке S является тангенциальным напряжением. Очевидно,
что в рассматриваемом случае напряжение т одинаково для всех пло-
площадок, параллельных сечению S (параллельных плоскости сдвига).
Опыт показывает, что для параллелепипедов разных размеров, но
сделанных из одного и того же материала, при одной и той же

284 МЕХАНИКА УПРУГИХ ТЕЛ [ГЛ. XV
силе F*) относительный сдвиг у обратно пропорционален сечению S
(сечению плоскости сдвига), т. е.
A5.11)
1
где G также зависит только от свойств материала образца, но не
зависит от его размеров и формы. Этот коэффициент называется
модулем сдвига данного материала. И так как x = F|5, то
t = Gy. A5.12)
Модуль сдвига также считается положительным, так что напряжение
совпадает со знаком сдвига. Определив Из опыта G [с помощью
соотношения A5.11)], можно по заданным деформациям сдвига найти
напряжения, и наоборот. Обе введённые нами упругие константы Е
и G имеют размерность напряжения (так как е и у—безразмерные
величины), т. е. в системе CGS измеряются в дн\см*. Значения этик
констант для некоторых распространённых материалов приведены
в таблице. В этой же таблице приведены и напряжения ашах. со-
соответствующие пределу упругости материала.
Материал
G
Чугуи
Литая сталь
Сталь хромо-никелевая
Алюминий
Медь
Свинец
Латунь
Дуб
12- 10й
21.10й
7-10"
12,5-10»
1,7-ЮИ
9-10"
1 • 10"
8,5-10"
8-10"
8-10"
2,7-10"
4,7-10"
0,6-10"
3,5-10"
12-Ю3
20—40-108
120—140-108
5-Ю8
12-10s
МО»
20-108
2-Ю»
Как уже указывалось выше, злкон Гука справедлив для всех
упругих тел, но только пока деформации не превосходят извест-
известного предела. Обычно при рассмотрении задач механики упругих
тел предполагают, что деформации не превосходят этого предела
пропорциональности. Это упрощает все расчёты и позволяет приме-
применять одно очень важное положение, так называемый принцип су-
суперпозиции, который заключается в следующем. Представим себе,
что мы подвергли тело какой-либо деформации, например, растяже-
растяжению, а затем друюй деформации, например, сдвигу. Модули Е и О,
характеризующие упругие свойства тела, являются константами, не
зависящими от того, деформировано уже тело или нет. Поэтому при
сдвиге в теле возникнут такие же дополнительные напряжения T=Gy,
как и в том случае, если бы тело не было предварительно растя-
*)См. предыдущую сноску.

§ 104] напряжения в точке 285
нуто. Общее напряжение в теле будет представлять собой сумму
тех напряжений, которые возникли бы, если бы тело было подверг-
подвергнуто только растяжению или только сдвигу. Это и есть принцип су-
суперпозиции (наложения) в применении к нашему конкретному случаю.
Он справедлив потому, что упругие свойства тела не зависят от де-
деформации (соблюдается закон Гука). Поэтому всякая новая деформа-
деформация вызывает такие же добавочные напряжения, как если бы все
прежние деформации отсутствовали. В резулыате мы получим на-
напряжение, равное сумме всех тех напряжений, которые возникли бы,
если бы каждая из деформаций существовала отдельно.
Как было указано (§ 101), любую малую деформацию в теле
можно представить в виде суммы элементарных деформаций растя-
растяжения и сдвига. Следовательно (это следует из принципа суперпо-
суперпозиции), напряжения, возникающие при любой деформации, мы можем
представить в виде суммы напряжений, возникающих при элемен-
элементарных деформациях растяжения и сдвига.
§ 104. Напряжения в точке
В механике сплошных тел приходится определять «внешние»
силы, действующие на рассматриваемый элемент тела со стороны со-
соседних. Эти силы действуют через площадки, служащие границами
данного элемента, и мы должны будем по упругим напряжениям
определять величину и направление тек сил, которые действуют на
ту или иную площадку.
В простейшем случае однородного растяжения или сжатия, зная
одно только нормальное напряжение в плоскости S, мы фазу смо-
сможем определить силу, действующую на ту или иную площадку AS,
параллельную плоскости S. Эта сила Д/=аДЛ; направление её нор-
нормально к площадке, поскольку на данной площадке существует
только нормальное напряжение.
Но уже в случае однородного сдвига одна величина тангенциаль-
тангенциального напряжения не определяет полностью снлы, действующей на
площадку AS, лежащую в плоскости сдвига S. Величина этой силы
Д/ = тД5, но о направлении этой силы мы можем сказать только то,
что она лежит в плоскости 5 (так как напряжение тангенциальное).
Мы определим напразление этой тангенциальной силы, задав две
величины—две компоненты тангенциального напряжения — по двум
взаимно перпендикулярным направлениям, лежащим в плоскости пло-
площадки Д5. Умножая каждое из напряжений на величину площадки,
мы получим две компоненты тангенциальной силы, действующей на
площадку AS, и тем самым определим величину и направление силы Д/.
В общем случае произвольной деформации сила, действующая на
площадку, может быть ориентирована как угодно. Чтобы опре-
определить её величину и направление, нужно знать три компоненты этой
силы по Трём заданным направлениям. Для нахождения этих трёх

286
МЬХАНИКА УПРУГИХ ТЕЛ
[ГЛ.
компонент нужно задать три величины — три компоненты напряжения
иа данной площадке: нормальную и две тангенциальные. Умножая их
на величину площадки, мы и найдём три компоненты вектора силы,
действующей на данную площадку, — нормаль-
нормальную и две тангенциальные.
Таким образом, для того чтобы определить
силу, действующую на данную определённую
площадку, нужно зиать три напряжения для
данной площадки. Но площадки, служащие
границами рассматриваемого элемента сплош-
сплошного тела, могут быть расположены как угодно.
Чтобы найти «внешние» силы, действующие на
данный элемент, нам придётся находить силы,
действующие на любую площадку, находящуюся
в данной точке тела, но произвольно ориенти-
ориентированную. Ясно, однако* что напряжение для
данной площадки зависит от выбора площадки,
к которой мы это напряжение относим.
Например, в случае растяжения стержня
напряжение, отнесённое к площадке, лежащей
в плоскости S' (рис. 220), будет отлично от напряжения для
площадки, лежащей в плоскости сечения 5. Действительно, сила,
действующая со стороны одной части стержня на другую через
сечение S, попрежнему равна Р, а площадь
сечения S1 больше, чем сечения 5. Поэтому
напряжение для площадки, лежащей в сече-
сечении S', меньше, чем для площадки в сечении
5. Вместе с тем для сечения S' сила уже
не нормальна к площадке, для которой мы
определяем напряжение. Мы должны поэтому
задать напряжение двумя составляющими —
нормальной <jj и тангенциальной т,. По этим
двум составляющим напряжения мы найдём
нормальную Fn и тангенциальную Ft состав-
составляющие силы, действующей через площадку
S'. Точно так же и в случае сдвига напря-
напряжение для площадки в сечении 5 (рис. 221)
меньше, чем для площадки, лежащей в сечении
5. Вместе с тем сила уже не лежит в плоскости площадки, для кото-
которой мы определяем напряжение. Мы должны поэтому задать этэ
напряжение двумя составляющими а2 и х2. По ним мы сможем найти
компоненты Fn и Ft силы, действующей через площадку S'.
В приведённых примерах однородной деформации напряжение для
всех отдельных элементов данного сечения S (или S') одинаково.
Поэтому мы могли говорить о дапряжении для всей площадки конеч-
конечных размеров (S1 или 5). Однако при неоднородной деформации
Рис. 221.

§ 104] НАПРЯЖЕНИЯ В ТОЧКЕ 287
напряжение для отдельных малых элементов площадки, вообще говоря,
различно. В таком случае, как уже указывалось, для определения
напряжения нужно брать бесконечно малые площадки dS. Положение
такой бесконечно малой площадки можно определять одной точкой,
принадлежащей этой площадке, и ориентировкой площадки. Для ка-
каждой точки тела существует бесчисленное множество таких бесконечно
малых площадок, различным образом ориентированных. Поскольку
напряжение для этих различных площадок зависит от их ориен-
ориентировки, то напряжение, отнесённое к определённой площадке, ещё
не характеризует тех сил, которые действуют на любую площадку
в данной точке. Только в том случае, когда могут быть определены
напряжения для всевозможных малых площадок, лежащих в данной
точке тела, напряжённое состояние в этой точке будет полностью
определено.
В рассмотренном выше простейшем случае равномерного растяже-
растяжения, зная одну величину з, мы сразу могли бы найти напряжение
для любой площадки, ориентированной известным образом. Заданием
одного нормального напряжения для одной площадки мы вполне
характеризуем напряжение в любой точке тела. В общем же случае
неоднородных деформаций должны быть заданы напряжения для трёх
взаимно перпендикулярных площадок. Тогда по этим напряжениям
может быть найдено напряжение для любой площадки. Но напряже-
напряжения для каждой данной площадки, как
уже было указано, в свою очередь
должны быть заданы тремя величинами
(одним нормальным и двумя танген-
тангенциальными напряжениями). Следова-
Следовательно, для определения напряжений
на трёх взаимно перпендикулярных
площадках должны быть заданы девять
величин—три нормальных напряжения 0
и шесть тангенциальных. Однако не
все эти напряжение независимы; при
статических деформациях три тан- Рис. 222.
генциальные напряжения из шести
должны быть попарно равны. Поэтому для характеристики
напряжения в данной точке требуется задание не девяти, а только
шести величин.
Чтобы пояснить сказанчое, мы рассмотрим простейший случай неодно-
неоднородной деформации, именно плоскую деформацию, при которой все напряже-
напряжения для всех площадок лежат в параллельных плоскостях и соогветствующие
напряжения одинаковы для всех этих параллельных плоскостей. Пусть
плоскость чертежа (рис. 222) будет одной из та*их плоскостей. Тогда мы
должны задать напряжения только для двух взаимно перпендикулярных
площадок Si и S2, перпендикулярных вместе с тем к плоскости чертежа;
О А и ОВ — следы этих площадок на плоскости чертежа. По напряжениям
на этих площадках мы можем найти напряжение на любой площадке S,

J
288 МЕХАНИКА УПРУГИХ ТРЛ [ГЛ XV
образующей угол ? с площадкой О А {АВ — след площадки S). Обозначим
нормальные н тангенциальные составляющие напряжений на всех трех
площадках соответственно через ау, хх, ах, ху, а, т (эти обозначения ука-
указаны на чертеже). Напряжения оуг хх, ах, ху мы считаем заданными; тре-
требуется найти напряжения о и т.
При статической деформации всякий элемент деформированного тела
должен находиться в равновесии. Рассмотрим условия равновесия трёх-
трёхгранной призмы, образованной площадками Si, 52 и S. Для равновесия
необходимо, чтобы сумма всех сил, дей-
действующих на грани, и сумма моментов этих
сил относительно любой оси, нерпендику-
„, j,n лярной к плоскости чертежа, были равны
"г4^ / ^* нулю. Компоненты сил, действующих на
эти грани, мы получим, умножив соответ-
соответствующие напряжения иа площади граней.
Обозначим эти силы через /,, Л, и /
(рис. 223).
X Напишем сначала уравнение моментов,
О У\ А выбрав в качестве оси прямую, проходя-
^г 1 щую через середину грани 5 (точка
ff "f/д С—след этой прямой). Так как напряже-
р ,w ния по всей площадке одни и те же (мы
Рис. <.~г>. всегда можем выбрать столь малые пло-
площадки), то равнодействующие сил, дей-
действующих на все грани, приложены к центрам граней. Поэтому момент
силы / относительно оси С будет равен нулю. Моменты сил f\ и /2 будут
определяться только их тангенциальными составляющими fu и f2t (нормаль-
(нормальные составляющие fln и /2я проходят через точку С). Поэтому уравнение
моментов будет иметь вид-
ОВ ОА_
tit ~2 /2'~2" ~~
Но f1(r=xxSi, a f2t~tySi- Поэтому
т s OS_t SaOA_Q
х l 2 У 2 2
Так как Sy\OA = St\OB, то
Тангенциальные напряжения на взаимно перпендикулярных гранях должны
быть равны. Это и есть одно из тех соотношений, которые существуют
между компонентами напряжений на взаимно перпендикулярных гранях
и уменьшают число независимых величин, необходимых для определения
напряжения в данной точке.
Для дальнейшего упрощения положим теперь, что тд:г=ту = 0, т. е. что
на гранях Sj и 52 существуют только нормальные напряжения (это пред-
предположение упростит выкладки, но не лишит смысла нашу задачу). По двум
заданным напряжениям ах и ау мы должны теперь определить компоненты
напряжения о и т (рис. 222). Эти компоненты определятся из первого
условия равновесия-
Но /i^zdyS!, /8 —a^Sa, fn = aS, ft — xS. Проектируя/, и f2 на направле-
направления о и t и приравнивая нулю суммы всех компонент сил по каждому из
направлений, получим:
eS = a^Si COS <p 4- 4^S4 sin ?, tS = aySi sin sp — oxSt COS f.

§ 105] ИЗОТРОПНЫЕ И АНИЗОТРОПНЫЕ ТЕЛА 289
Принимая во внимание, что Sj = S cos sp и S2 = S sin sp, окончательно получим:
о = оу cos2 ip + ** sin8», A5.13)
х = (ау — ох) sin f cos sp. A5.14)
По напряжениям на гранях Sx и S2 мы нашли напряжения на грани S.
§ 105. Изотропные и анизотропные тела
Когда мы говорили об упругих свойствах материала, мы полагали, что
свойства эти одинаковы по всем направлениям и упругие константы мате-
материала для всех направлений одни и те же. Многие материалы, применяемые
на практике, действительно обладают такими свойствами, однако далеко не
все. В частности, отдельные кристаллы обычно обладают различными упру-
упругими свойствами в разных направлениях. Например, куб, вырезанный из
кристалла, под действием одной и той же силы, приложенной к различным
его граням, вообще говоря, испытывает различные деформации.
Тела, которые обладают одинаковыми механическими (и вообще физи-
физическими) свойствами во всех направлениях, называются изотропными.
Тела, свойства которых в различных направлениях различны, называются
анизотропными. Выше, когда мы рассматривали связь между деформациями
и напряжениями, мы говорили только о материале, из которого сделан
деформируемый образец, ио не оговаривали направления, в котором этот
образец вырезай. Это значит, что мы имели в виду изотропные тела.
Упругие свойства анизотропного тела можно охарактеризовать некото-
некоторыми упругими константами так же, как упругие свойства изотропного
тела можно характеризовать двумя константами — модулем Юнга и моду-
модулем сдвига. Однако для анизотропного тела этих констант существует не
две, а больше — 21 в самом общем случае. Число констант уменьшается,
если анизотропное тело обладает некоторой симметрией (в некоторых
направлениях свойства тел одинаковы).
Для изотропных тел, кроме двух основных констант (модуля Юига
и модуля сдвига), мы ввели выше ещё одну упругую константу — коэффи-
коэффициент Пуассона. Но эти три константы, Е, и и т, в изотропных телах не
независимы, а связаны между собой соотношением*):
0 = E . A5.15)
0i)
Упругие свойства твёрдого тела вполне определяются двумя из трёх
констант Е, G, т = \\ч. Так как т > 2, то для всех тел G должно быть
немногим меньще, чем ?/2. Впрочем для технических материалов, под-
подвергшихся специальной обработке (например, прокатке), это соотноше-
соотношение между G и Е не соблюдается. Это обьясняется тем, что подвергшиеся
специальной обработке материалы уже нельзя рассматривать как вполне
изотропные тела.
Для изотропных тел можно ввести ещё одну константу, характеризую-
характеризующую упругие свойства вещества (конечно, уже не независимую,-а связан-
связанную с константами Е, G и /я). При одностороннем сжатии куба, как было
*) Это соотношение можно получить, рассматривая деформацию куба,
подвергнутого растяжению в одном направлении. При этом происходит
поворот диагональных плоскостей куба, т. е. сцвиг. Таким образом, растяже-
растяжение, сокращение поперечных размеров и сдвиг оказываются связанными
между собой.
19 С. э. Хайкин

290 МЕХАНИКА УПРУГИХ ТЕЛ [ГЛ. XV
показано [формула A5.5)], объём куба изменяется на AV=(l —2v)s.
Поэтому при одинаковом сжатии по всем трём парам граней (всесторон-
(всестороннее сжатие) объём куба уменьшится на
= 3 A - 2у) t = 111=М 0 _ Ка.
Величина /С= 3A—2v)/E называется коэффициентом сжимаемости ве-
вещества. Часто вводится величина Ki=^IK-
* = 8(г!з)! A5Л6)
она называется объёмным модулем сжатия. Если бы тело было абсолютно
несжимаемо, то для него v=1/2, и коэффициент сжимаемости /С=0
№=00).
Объяснение всех механических свойств тел, как изотропных, так
и анизотропных следует искать в природе и характере тех сил, которые
действуют между отдельными атомами и молекулами твердого тела. Это,
Конечно, —задача атомной и молекулярной физики, а ие механики, и мы
её не будем касаться (впрочем и атомная физика ещб далеко ие справилась
с этой задачей). Мы ограничимся только самыми общими соображениями
о соотношении между изотропными и анизотропными телами.
Всякий отдельный крнсталл (монокристалл) построен нз атомов, рас-
расположенных в определённом порядке. Расположение атомов и расстояние
между ними в различных направлениях, вообще говоря, различны. Поэтому
отдельный кристалл может обладать различными свойствами в различных
направлениях. И, действительно, все монокристаллы в той или иной мере
обладают анизотропией. Но если тело построено из множества мелких
кристаллов (поликристаллические тела), то, несмотря на анизотропию
отдельных кристаллов, всё тело в целом может быть изотропным, когда
отдельные кристаллики расположены беспорядочно, без всякой системы.
Тогда свойства отдельных кристалликов усредняются по всем направлениям
и в среднем оказываются одинаковыми. Поэтому поликристаллические те-
тела, к которым принадлежат почти все применяемые в технике материалы,
часто бывают изотропны. Однако при специальной обработке (волочении
н т. п.) может произойти упорядочение в расположении отдельных кри-
кристаллов тела. Свойства отдельных кристалликов уже не усредняются,
и поликристаллическое тело может оказаться анизотропным. И, действи-
действительно, поликристаллические материалы, подвергшиеся специальной обра-
обработке, нередко обладают анизотропией.
§ 106. Энергия упругой деформации
При деформации тел внешняя сила, вызывающая деформацию,
совершает работу. С другой стороны, деформированное тело при
исчезновении деформации само совершает работу. Если тело абсо-
абсолютно упруго, то оно может совершить такую же работу, которая
была затрачена на деформацию тела. В абсолютно упругих телах
вся работа, затраченная на деформацию тела, идёт на уве-
увеличение потенциальной энергии упругой деформации. В реальных
телах это не имеет места: возникающие в них силы всегда зависят
не только от величин деформаций, но и от скорости изменения
деформаций. Эти последние силы подобны силам трения (их обычно

§ 106] ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ 291
и называют свнутренним трением»), и работа против этих сил идёт
иа нагревание тела, а не на увеличение потенциальной энергии
упругой деформации. С этим связано и наличие остаточных дефор-
деформаций во всяком реальном теле. Поскольку реальное тело не вос-
восстанавливает полностью своей формы, оно не отдаёт полностью и всей
той работы, которая была затрачена на деформацию. Однако для
многих реальных тел при малых и медленных деформациях остаточ-
остаточные деформации очень малы. Поэтому можно считать, что вся работа,
затраченная на медленную деформацию, увеличивает потенциальную
энергию упругой деформации. В таком случае энергию упругой
деформации деформированного тела можно подсчитать следующим
образом. Положим, что тело подвергается медленному растяжению.
Выделим в деформируемом теле элемент объёма в виде куба с гра-
гранями /. На грань элемента перпендикулярно к направлению растяже-
растяжения действует со стороны соседнего элемента сила
(мы, как всегда, предполагаем, что закон Гука справедлив). При
перемещении этого элемента на расстояние Да; будет совершена
работа
bA f\EPb A5.17)
С этим перемещением связано увеличение растяжения на величину
Де = Дл?//, откуда Дл: = /Дз. Подставляя в выражение A5.17) это
значение Дл:, получим:
Переходя от малых перемещений к "бесконечно малым и интегрируя
бесконечно малые элементы работы на всём пути от 0 до деформа-
деформации s, мы получим:
Эта работа и выражает ту энергию упругой деформации U, кото-
которой обладает выделенный элемент тела, деформированный до рас-
растяжения г. Так как /8 есть объём рассматриваемого элемента *), то
плотность энергии равна
Пользуясь соотношением <з^Ег, можно формулу A5.18) привести
к другому виду:
w ~2~ '2==2Ё' A5.19,
*) Изменением объёма, происходящим при деформации, можно прене-
пренебречь, так как оно мало при малых деформациях.
19*

292 МЕХАНИКА УПРУГИХ ТЕЛ ГгЛ. XV
При заданной деформации плотность энергии прямо пропорциональна Е,
при заданном напряжении обратно пропорциональна Е. Поэтому,
если силы (а, значит, и напряжения) заданы, то чем жёстче тело,
тем меньше энергия его упругой деформации. Здесь всё обстоит так
же, как и с жёсткими пружинами (§ 64).
Энергию упругой деформации всего деформированного тела мы
получим, просуммировав энергию всех элементов объёма тела. Если
деформация однородна, то полная энергия будет
где К —объём тела. При неоднородной деформации нужно разбить
тело на отдельные малые элементы объёма Д1/, в которых деформа-
деформацию можно считать однородной, и просуммировать выражения
'/2 Esz W по всему телу. Эта сумма может быть найдена как взятый
по всему объёму тела интеграл:
Таким же образом можно вычислить и энергию упругой дефор-
деформации при сдвиге. На грань куба с рёбрами /, лежащую в плоскости
сдвига, действует сила
При сдвиге Ду происходит перемещение верхней грани на величину
Дл: = /Ду. При этом совершается работа
LA — Gy/3 Ду.
Переходя к бесконечно малым изменениям, находим, что при сдвиге
от 0 до у совершается работа
г
о
Плотность энергии в деформированном элементе (объём элемента /3):
Полученные выражения справедливы, только пока применим закон
Гука. Но и когда закон Гука не соблюдается, работа, затрачиваемая
на малую деформацию элемента объёма, выражается соотношениями:
ДЛ,—/Длг = /3аДвг (для растяжения)
и
ААу =/Да; = 1Н Ду (для сдвига).
Полная работа соответсхвенно равна
; 1
\

§ 107] упругое равновесие 293
Поэтому, если мы изобразим связь между а и е или т и у в виде
кривой, то полная работа деформации выражается площадью, ограни-
ограниченной этой кривой и осью абсцисс (осью s или осью у).
Наличие остаточных деформаций при переменных деформациях
сказывается в том, что при обратном ходе тем же самым деформа-
деформациям соответствуют меньшие напряжения. Поэтому кривая з=/(е)
[или t=/(y)j при обратном ходе деформации проходит ниже, чем
при прямом (рис. 224). Напряжение в теле
исчезает до того, как исчезла деформация,—
при <5 = 0 в теле существует остаточная
деформация е0. Если продолжать деформиро-
деформировать тело в, другом направлении, то оста-
остаточная деформация исчезнет только тогда,
когда в теле будет уже существовать неко-
некоторое напряжение — <50. Это явление носнт
название упругого гистерезиса.
При периодически повторяющихся де-
деформациях изменения е и а изображаются
замкнутой кривой ABCDEF (рис. 224), рис. 224.
которая называется петлей гистерезиса.
При деформации тела от Е до А будет совершена работа, ббльшая,
чем та, которую отдаст тело при обратном ходе от А до В. Раз-
Разность этих работ, идущая на нагревание тела, выразится площадью
верхней части петли гистерезиса. Точно так же при деформации
BCDE работа, идущая на нагревание тела, выразится нижней частью
петли гистерезиса. При периодически меняющейся деформации за
каждый цикл выделяется тепло, пропорциональное площади петли
гистерезиса.. Чем больше петля гистерезиса, тем сильнее нагревается
тело при периодических деформациях. При быстро повторяющихся
деформациях за единицу времени в теле выделяется -заметное коли-
количество тепла. Вследствие этого все тела, подвергающиеся быстрым
периодическим деформациям, всегда в большей или меньшей степени
нагреваются. Для уменьшения этого нагревания особо ответственные
детали машин, подвергающиеся быстрым периодическим деформациям
(например, пружины клапанов в моторах), делаются из специальных
сортов стали, в которых площадь петли гистерезиса очень мала.
§ 107. Упругое равновесие.
Устойчивость упругого равновесия
Зная упругие свойства тела, мы всегда сможем определить
деформации, которые возникают в теле при действии заданных внеш-
внешних сил, т. е. найти форму, которую принимает тело. Это — задача
о равновесии упругого тела. Мы определяем деформации тела, при
которых силы, возникшие в теле, уравновесят внешние Силы. Простей-

294
МЕХАНИКА УПРУГИХ ТЕЛ
[ГЛ. XV
шие задачи этого типа мы и решали, когда рассматривали однород-
однородные деформации растяжения и сдвига. В случае более сложных
деформаций (кручения, изгиба и т. д.) задача ставится таким же
образом. Упругие свойства тела позволяют определить, как силы,
действующие со стороны тела, связаны с деформациями. Из условия,
что эти силы должны уравновесить внешние силы, приложенные
к телу, мы можем (по крайней мере принципиально) найти и те
деформации, при которых наступит равновесие.
Однако, для того чтобы тело могло длительно находиться в со-
состоянии равновесия, необходимо, чтобы это состояние равновесия
было устойчивым. Это значит, что при не-
р больших отклонениях от состояния равновесия
упругие силы должны изменяться таким об-
образом, чтобы они снова возвращали тело
к состоянию равновесия. Если это условие
не будет соблюдено, то состояние равно-
равновесия будет неустойчиво. Малые отклонения
от состояния равновесия всегда неизбежны,
и поэтому в реальных условиях тело не
может находиться в состоянии неустойчивого
равновесия. Вопрос об устойчивости упругого
равновесия впервые исследовал Эйлер. Так
как исследование этого вопроса представляет
собой сложную задачу, мы ограничимся только
качественными соображениями и поясним эти
соображения на конкретном примере.
Рассмотрим равновесие упругого стержня,
закреплённого в шарнирах и находящегося
под действием силы F, направленной вдоль
стержня (рис. 225). Если верхний шарнир
может перемещаться в направлении силы
F, то под действием этой силы стержень сожмётся. Равновесие
наступит тогда, когда деформация сжатия достигнет значения
Рис. 225.
г ~~ Е ~~ SE'
где S—сечение стержня. Чтобы определить, является ли
это состояние равновесия устойчивым, нужно исследовать, какие
силы возникнут, если стержень цемного отклонится от положения
равновесия, например, слегка выгнется. При этом возникнут упругие
силы, стремящиеся вернуть стержень в положение равновесия. Од-
Одна/со, с другой стороны, сила Р стремится изогнуть его ещё больше.
Дальнейшее поведение стержня определится тем, каков будет ре-
результат одновременного действия двух этих сил. Если сила F не пре-
превосходит известного предела, то стержень вернётся к положению
равновесия. Если сила F превооходит этот предел, то стержень

§ Ю7]
УПРУГОЕ РАВНОВЕСИЕ
295
будет выгибаться ещё сильнее. Равновесие стержня окажется не-
неустойчивым.
При дальнейшем изгибании стержня упругие силы будут увели-
увеличиваться, и при определённом изгибе стержня снова наступит со-
состояние равновесия, уже устойчивое. Этому новому состоянию равно-
равновесия соответствует синусоидальная форма стержня.
Таким образом, для данного стержня существует некоторое
наибольшее «критическое» значение силы F, после которого стер-
стержень неизбежно изогнётся. Так как силы, возникающие при изгибе
стержня, тем больше, чем меньше его длина и чем больше сечение,
то и критическое значение силы F будет при этом расти. "На-
"Наоборот, чем больше длина стержня и чем меньше его сечение,
тем меньше и критическое значение силы F.
Рис. 227.
Поведение стержня при продольной *Нагрузке можно продемон-
продемонстрировать при помощи следующей установки (рис. 226). Тонкий стальной
пруток устанавливается иа штативе так, чтобы «го верхний конец свободно
проходил через отверстие в верхней лапке штатива. Если на пруток одеть
сверху достаточно большой груз, то пруток изгибается и принимает форму
синусоиды. Короткий пруток при том же грузе не изгибается; чтобы он
изогнулся, требуется гораздо большая нагрузка. Если середину стержня
также пропустить через лапку, которая препятствовала бы изгибу (рис. 227),
то критическое значение F увеличивается (это эквивалентно уменьшению
длины стержня). Но если увеличить F выше критического значения, со-
соответствующего этой меньшей длине стержня, пруток снова изгибается
в виде синусоиды. Но на длине стержня укладывается уже не половина
синусоиды, а целая синусоида.
Возникновение неустойчивости при продольной нагрузке стержней
имеет большое практическое значение. Например, при увеличении высоты
колони, нагруженных сверху, необходимо увеличивать и сечение колонн,
хотя -бы нагрузка и оставалась прежней.

296
МЕХАНИКА УПРУГИХ ТЕЛ
[гл.. xv
Неустойчивость продольно сжатых стержней может возникнуть ещё
задолго до того, как напряжение в стержне достигнет предела упругости.
Стержень легко выдерживал бы ту же самую нагрузку, если бы она вызывала
не сжатие, а растяжение стержня. Поэтому, например, толкающие рычаг»
в машинах приходится делать ббльшего сечения, чем тянущие. Это отно-
относится и к другим конструкциям, в которых возникают деформации сжатия.
Сосуды, которые должны выдерживать давление снаружи (при этом в ма-
материале возникает сжатие), должны иметь более прочную конструкцию,
чем сосуды, которые то же давление должны выдерживать изнутри (в ма-
материале возникают растяжения). С этим приходится считаться, например,
при постройке подводных лодок.
§ 108. Распространение импульса в упругом теле
Все рассмотренные - нами вопросы относились к статике упругого
тела. Рассмотрим теперь одну из основных задач динамики упруго-
упругого тела.
Представим себе длинный упругий стержень (рис. 228), по торцу
которого мы ударяем молотком. Этот удар вызовет движение частиц
прилежащего к торцу слоя стерж-
стержня. Движение частиц первого
слоя вызовет деформацию сле-
следующего слоя стержня. В этом
слое возникнут упругие силы, под
J
1
I
Рис. 228.
действием которых частицы пер-
первого слоя потеряют свою' скорость.
Но при этом будут приобретать
скорость частицы второго слоя. Так как частицы второго слбя будут
двигаться, а первого слоя оста1овятся, то деформация во втором
слое исчезнет, но зато будет возникать деформация следующего
слоя. Так, движения частиц и деформации будут передаваться от слоя
к слою. По стержню будет распространяться импульс деформаций
и скоростей.
Картину распространения импульса в стержне можно продемонстри-
продемонстрировать на специальной модели (рис. 229), состоящей из большого числа
одинаковых шариков, подвешенных на длинных нитях и связанных между
собой одинаковыми пружинками. Если ударить крайннй шарик, то хорошо
видно, как от шарика к шарику передаётся скорость и от пружинки к пру-
пружинке передаётся деформация (рис. 230). Конечно, в сплошном стержне
картниа будет иной. В нашей модели пружинки обладают только упру-
упругостью и практически не обладают массой. Шарики же обладают массой,
но практически не деформируются. В сплошном стержне эти свойства
равномерно распределены по телу. Если мы разобьем стержень на отдель-
отдельные малые элементы — тонкие слои, то 'массе рассматриваемого слоя
стержня в нашей модели будет соответствовать шарик, а силам взаимо-
взаимодействия между слоями будут соответствовать пружинки.
Скорость распространения импульса зависит от упругих свойств
стержня. Если бы стержень был абсолютно жёсткий, то он мог бы
двигаться только весь как целое. Импульс мгновенно достиг бы

§ 108]'
РАСПРОСТРАНЕНИЕ ИМПУЛЬСА В УПРУГОМ ТЕЛЕ
297
другого конца стержня. Скорость распространения была бы беско-
бесконечно большая. Это ещё один пример того, как представление об
абсолютно жёстких телах приводит к физически неприемлемым ре-
результатам. С точки зрения
теории относительности ни-
никакой импульс (сигнал) не
может распространяться со
скоростью, большей скорости
света.
Для определения скоро-
скорости распространения ' им-
импульса рассмотрим, что про-
происходит в каком-либо сече-
сечении стержня в то время,
когда через это сечение
проходит импульс. Пусть
импульсу сжатия соответ-
соответствует деформация г и ско-
скорость распространения этой
деформации с. Сжатие стерж-
стержня сопряжено с увеличением
плотности стержня на вели-
величину Др = 5р, где р — плот-
плотность недеформчрованного
стержня. Распространение импульса можно представлять себе как движе-
движение «уплотнения» Др, распространяющегося с той же скоростью с, что
и импульс деформации. За время Д? через сечение стержня пло-
площадью S пройдёт «участок уплотнения» \х = сМ. Масса этого
участка уплотнения
Дот = 5 Дл; Др = Ssp • с hi,
двигаясь со скоростью с, несёт
с собой количество движения
Риг. 229.
Рис. 230.
Но изменение количества дви-
движения справа от рассматриваемого сечения должно быть равно им-
импульсу упругой силы, действующей со стороны левой части сечения
на правую. Этот импульс равен
Приравнивая изменение количества движения импульсу силы, по-
получим
откуда
A5.21)

298 МЕХАНИКА УПРУГИХ ТЕЛ [ГЛ. XV
Скорость распространения импульса зависит от упругих свойств и
плотности стержня.
Эту зависимость легко продемонстрировать на описанной выше мо-
модели стержня (рнс. 229). Увеличению плотности стержня соответствует уве-
увеличение массы шариков в модели. Если надеть на часть шариков доба-
добавочные свинцовые массы, то скорость распространения импульса по этой
части модели заметно уменьшается. Если на двух частях модели установить
лруживкн разной жёсткости, то скорость распространения импульса будет
больше в той части модели, где пружинки жёстче.
В металлах модуль упругости очень велик (порядка 1011—
10t2 дн\смг), а плотность порядка 10 г\см%. Поэтому скорость рас-
распространения импульса оказывается порядка 105 см\сек. Уследить
за распространением так быстро движущегося импульса (не говоря
о том, что и сами деформации очень малы и поэтому не видны)
было бы невозможно. Поэтому нам и приходится для демонстрации
картины распространения импульса пользоваться моделью (рис. 229),
в которой скорость распространения импульса сравнительно мала.
Скорость распространения импульса сжатия зависит только от
свойства тела, но не зависит от величины сжатия. В нашем рассмо-
рассмотрении всё время фигурируют скорость импульса и скорость уплот-
уплотнения, а не скорость отдельных элементов тела. Мы подсчитывали
количество движения, которое связано с движущимся уплотнением,
а не с движением отдельных частиц тела. Характер и скорость дви-
движения отдельных частиц тела зависят от характера импульса, вели-
величины сжатия в отдельных его частях и т. д. Всего этого не нужно
знать, чтобы найти скорость распространения импульса. Существенно,
однако, что отдельные части стержня движутся в том же на-
направлении, в котором распространяется импульс. Поэтому рас-
рассматриваемый импульс называется продольным.
Совершенно таким же образом в стержне будет распространяться
и импульс растяжения. Такой импульс возник бы, если бы на конец
стержня подействовала кратковременная сила /•", направленная от
стержня. Распространение импульса будет происходить так же,
как и в случае сжатия. К этому случаю применимы все те расчёты,
которые были проведены для импульса сжатия, с той разницей, что
нужно рассматривать не уплотнение, а «разрежение». При этом от-
отдельные части стержня движутся в направлении, противоположном
распространению импульса. Но это также продольный импульс, по-
поскольку движение частиц стержня происходит вдоль направления
распространения импульса.
В твёрдом теле могут«распространяться импульсы и другого типа.
Если ударить по концу стержня в направлении, перпендикулярном
стержню, то этот удар вызовет движение крайнего слоя стержня.
Вследствие этого движения возникнет деформация сдвига. Упругие
силы, которые при этом возникнут, вызовут движение соседнего слоя.
Вместе с тем скорости первого слоя будут уменьшаться. От слоя
К слою будет распространяться импульс скоростей и деформаций

§ 108] РАСПРОСТРАНЕНИЕ ИМПУЛЬСА В УПРУГОМ ТЕЛЕ 299
сдвига. На модели такой импульс можно получить, толкнув крайний
шарик вбок (рис. 231). В импульсе сдвига направление движения
отдельных частиц стержня перпендикулярно к направлению рас-
распространения импульса. Такой импульс называется поперечным.
В поперечном импульсе уже не происходит уплотнений. Поэтому
представления, которыми мы пользовались для расчёта скорости про-
продольного импульса, здесь уже неприменимы. Как показывают расчёты,
скорость поперечного импульса в
упругом теле, как и скорость про-
продольного импульса, зависит от
плотности и упругих свойств тела.
Однако вместо упругих сил,
возникающих при сжатии, в слу- "^ттть
чае импульса сдвига играют роль
упругие силы, возникающие при Рис. 231.
сдвиге. Поэтому скорость -попе-
-поперечного импульса зависит не от модуля Юнга Е, а от модуля сдвига G.
Рассмотрим теперь, что произойдёт, когда импульс (для опреде-
определённости будем рассматривать импульс сжатия) достигнет конца
стержня. Частицы последнего слоя стержня получат от предыдущего
некоторую скорость. Если бы дальше находился следующий слой,
СЖвЯШе то скоРость частиц передалась бы этому
, следующему слою. Но последний слой справа
{ свободен. Поэтому его частицы будут про-
продолжать двигаться дальше (рис. 232). Движе-
растяжение ние крайнего слоя стержня прекратится
р „2 только тогда, когда на него начнут действо-
действовать силы, направленные в противоположную
сторону (на рис. 232 — влево). А для
этого на конце стержня должно возникнуть растяжение. Под
действием упругих сил, обусловленных этим растяжением, частицы
последнего слоя потеряют свою скорость, но зато возникнет ско-
скорость у частиц соседнего слева слоя, направленная в ту же сторону.
Эти растяжения и скорости будут передаваться от слоя к слою,
ио уже в обратном направлении. Таким образом, импульс, дошедший
до конца стержня, отразится и пойдёт обратно. При этом, однако,
характер деформации в импульсе изменится. Деформация сжатия
превратится в деформацию растяжения. Скорости же частиц в от»
ражённом импульсе попрежнему будут направлены вправо, т. е.
в ту же сторону, что и в пришедшем импульсе (так как в импульсе
растяжения частицы движутся в направлении, противоположном на-
направлению распространения импульса).
В случае импульса растяжения на конце стержня произойдёт
следующее (рис. 233). Последний слои приобретает скорости, на-
направленные влево. Если бы дальше находился следующий слой, то
эти скорости передались бы его частицам. Но так как справа по-

300 МЕХАНИКА УПРУГИХ ТЕЛ Г ГЛ. XV
следний слой свободен, то его частицы потеряют скорость только
после того, как возникнет сжатие соседнего слева слоя. Растяже-
Растяжение превратите» в сжатие, и в таком виде импульс будет распро-
распространяться в обратном направлении. Скорости же частиц в отражён-,
ном импульсе будут попрежнему направлены влево.
Совершенно так же будет обстоять дело и в случае импульса
сдвига. Если к концу стержня пришёл импульс сдвига, то частицы
свободного конца стержня не потеряют скоростей до тех пор, пока
не возникнет сдвиг обратного направления. При этом последний
Оастяжвние слой пеРедаст час™чам следующего слоя
" - п скорости, направленные так же, как были
направлены скорости в пришедшем сдвиге.
Во всех случаях при отражении импульса
от свободной границы упругого тела изме-
р „до няется знак деформации и остаётся прежним
знак (направление) скоростей частиц. При
отражении от неподвижно закреплённой границы упругого тела проис-
происходит обратное. Так, в случае импульса сжатия, если правый край
стержня неподвижно закреплён, сжатие последнего слоя ие может
исчезнуть и в виде сжатия же вернётся снова к соседнему слева
слою. Но при этом скорости частиц окажутся .направленными влево
(а не вправо, как в пришедшем импульсе). В отражённом импульсе
сжатие останется сжатием, а скорости частиц изменят знак на обрат-
обратный. Подобными рассуждениями можно показать, что так будет об-
обстоять дело со всяким импульсом при отражении от закреплённой
границы упругого тела: знак деформации будет оставаться прежним,
а знак скоростей частиц будет изменяться.
§ 109. Течение энергии в упругом теле
Как мы убедились, при отражении импульса изменяют знак либо
деформации, либо скорости, но не меняют знака н те и другие од-
одновременно. Только поэтому импульс и отражается, т. е. движется
в обратном направлении. Что так именно и должно происходить,
вытекает из картины распространения энергии в упругом теле. Им-
лульс несёт с собой определённую потенцнальную энергию упругой
деформации и кинетическую энергию движения частиц. Распростра-
Распространение импульса в теле связано поэтому с движением энергии, т. е.
с течением энергии в упругом деформированном теле. Выше мы уже
сталкивались с простейшим случаем течения энергии в упругом де-
деформированном теле (§71) — в приводном ремне или передаточном
валу привозного механизма. Однако там мы имели дело с однород-
однородной и не меняющейся со временем деформацией. В интересующем
-нас сейчас случае упругого импульса течение, энергии связано с дви-
движением неоднородной деформации, т. е. с деформацией, изменяю-
изменяющейся кдк.во времени, так и от точки к точке. Эта общая задача

$ 109] ТЕЧЕНИЕ ЭНЕРГИИ В УПРУГОМ ТЕЛЕ 801
о течении энергии в упругом теле была изучена русским учёным
Умовым, В этом общем случае вся картина оказывается гораздо бо-
более сложной, чем для однородной и не меняющейся со временем,
деформации.
Однако некоторые основные выводы, которые легко могут быть
сделаны для простейшего случая, оказываются справедливыми и для
распространения импульса. Чтобы сделать эти выводы, рассмотрим
подробно следующий конкретный пример.
Тело М приводится в движение силой F, действующей на конец
упругого стержня (рис. 234). Поллжим для определённости, что
стержень, толкает тело. При движении на тело М со стороны пло-
плоскости действует постоянная сила трения F', равная—F, так что
движение происходит с
постоянной скоростью v
и деформация (сжатие)
стержня не изменяется.
Движение деформиро- р 4
ванного стержня как це-
целого уже само по себе
связано с движением энергии в пространстве, так как вместе
со стержнем движется и та энергия упругой деформации, которой
он обладает. Такой тип переноса, когда энергия (или количество
движения и т. п.) переносится вместе с частицами тела, которые
этой энергией обладают, называется конвективным переносом, или
конвекцией. Поток конвекции энергии, т. е. количество энергии,
протекающей через единицу нормального сечения за единицу времени,
равен, очевидно, плотности упругой энергии в стержне, умноженной
иа скорость его движения. Так как плотность упругой энергии
где а — напряжение в стержне, а ? — его относительное сжатие, то
ноток конвекции энергии
\=%v. A5.21)
Но помимо конвекции происходит течение энергии по стержню.
В самом деле, иа одном конце стержня работа, совершаемая силой F,
идёт на увеличение энергии деформации (сжатия) стержня. На другом
конце за счёт энергии упругой деформации стержня совершается
такая же работа против силы трения. Столько же энергии, сколько
втекает в стержень с одного конца, вытекает с другого. Через ка-
каждое сечение стержня за некоторый промежуток времени протекает
количество энергии, равное работе, совершённой силой F за тот же
промежуток времени. Эта работа за элемент времени Д? выразится
так:

302 МЕХАНИКА УПРУГИХ ТЕЛ [1Л. XV
где а — напряжение в стержне, a S—его сечеиие. Следовательно,
за единицу времени через единицу поперечного сечения стержня
протекает поток энергии
2 = то. A5.22)
Таким образом, поток энергии упругой деформации пропорцио-
пропорционален произведению напряжения в деформированном теле и скорости
движения тела. Направление этого потока в рассматриваемом случае
совпадает с направлением скорости тела v. Если бы стержень тянул
тело, то скорость движения частиц стержня была направлена в об-
обратную сторону (на рис. 234 — влево), а энергия попрежнему
текла бы от начала стержня к его концу (на рис. 234 — вправо).
Но при этом стержень был бы растянут, т. е. изменился бы и знак
деформации.
Таким образом, при растяжении стержня поток энергии направ-
направлен навстречу скорости тела. Чтобы выражение A5.22) определяло
направление потока энергии, нужно принять во внимание, что на-
напряжению а следует приписывать (так же, как деформации е) знак -J-
при растяжении и знак — при сжатии. Если при этом рассматривать
поток энергии 2 и скорость v как векторы, а <з — как скаляр, то
2 = —.jv. A5.23)
Из сопоставления выражений для конвекции A5.21) и течения
A5.23) энергии видно, что конвекция энергии по сравнению с те-
течением энергии в стержне исчезающе мала, так как е в жёстком
стержне очень мало. Во всех аналогичных случаях, когда упругие
тела мало деформируются, основную роль играет течение энергии
в упругом теле, а не конвекция энергии вместе с телом. Заметим
кстати, что из выражения для конвекции энергии видно, что на-
направление конвекции энергии в отличие от направления течения
энергии зависит только от направления движения тела (знака v) и
не зависит от знака а (так как а и е всегда одного знака). Что это
должно быть так, ясно из самой сущности явления конвекции.
Выражение для потока энергии A5.23), полученное нами для
случая однородной и неизменной во времени деформации, остается
справедливым и для деформации, распространяющейся в теле. Если
в каком-либо сечении упругого тела существует нормальное напря-
напряжение з и лежащие в этом сечеиии частицы тела имеют скорость v,
направленную нормально к сечению, то через единицу площади се-
чеиия течёт поток энергии 2, определяемый выражением A5.23).
Именно этот случай течения энергии имеет место при распростра-
распространении продольного импульса в упругом теле.
При деформациях сдвига направление течения энергии не со-
совпадало с направлением движения частиц. В этом мы уже убедились
на примере вала, передающего работу. Вращающийся вал при пере-
передаче работы должен быть скручен. В каждом сечении вала суще-
существуют тангенциальные напряжения и скорости отдельных элементов

§ Ю9] ТЕЧЕНИЕ ЭНЕРГИИ В УПРУГОМ ТЕЛЕ 303
вала лежат в плоскости сечения.1 Энергия же течёт вдоль вала, т. е.
в направлении, перпендикулярном к направлениям напряжений и
скоростей. Но и в этом случае поток энергии изменяет своё направ-
направление на обратное при изменении направления сдвига или направ-
направления скорости частиц и остаётся неизменным, если одновременно
изменяются и направление сдвига, и направление скорости частиц.
В этом легко убедиться, проследив за тем, что происходит при
изменении направления вращения двигателя или при перестановке
местами двигателя и нагрузки (без изменения направления вращения).
Так же обстоит дело и при распространении деформации сдвига
в упругом теле. Если в каком-либо сечении тела существуют тан-
тангенциальные напряжения и лежащие в этом сечении частицы тела
движутся в направлении этих напряжений, то существует поток
энергии в направлении, 'нормальном к этому сечению. Этот случай
имеет место при распространении поперечного импульса в упругом теле.
Так как энергия упругой деформации связана с самим импульсом,
то направление течения энергии, очевидно, всегда совпадает с на-
направлением распространения импульса. Поэтому при отражении импуль-
импульса должно изменяться на противоположное и направление течения энер-
энергии. Но поток энергии меняет направление на противоположное либо
при изменении знака скорости ча?тиц упругого тела, либо при измене-
изменении знака деформации. Поэтому для изменения направления рас-
распространения импульса должен изменяться знак либо деформа-,
ции, либо скорости частиц. Если бы они не изменяли знака или
изменяли его обе одновременно, то энергия, а вместе с тем и им-
импульс не изменяли бы направления распространения.
Картину отражения импульса от свободного и закреплённого конца
стержня также можно продемонстрировать на модели стержня <рис. 229).
Если последний шарик модели свободен, то сжатие при отражении пре-
превращается в растяжение и, наоборот. Если же последний шарик закреплен,
растяжение отражается в виде растяжения, а сжатие — в виде сжатия.
Отражение импульса происходит не только от границы упругого тела,
но и от границы между двумя упругими телами, если упругие Свойства
или плотность этих тел различны. В этом случае, однако, происходит
только частичное отражение импульса, а частично импульс проходит во
второе тело.
Отражение импульса от границ тела приводит к возникновению
колебаний. Отразившись от второго конца стержня, импульс снова
возвращается к первому концу, затем снова отражается и т. д. Кар-
Картина повторяется через определёиные промежутки времени — в стержне
возникают колебания. В результате импульса такие колебания всегда
возникают в теле ограниченных размеров, обладающем массой и уп-
упругостью. Всякое резкое нарушение равновесия, вообще резкое изме-
изменение состояния упругих тел, представляет собой импульс и сопро-
сопровождается колебаниями. Именно поэтому колебания так часто возникают
в механических системах.

ГЛАВА XVI
ГИДРОСТАТИКА И АЭРОСТАТИКА
§ ПО. Общие свойства жидкостей и газов
Всякий объём жидкости или газа способен как угодно изменять
свою форму под действием сколь угодно малых сил *). Это общее
свойство жидкостей и газов являемся вместе с тем и их общим от-
отличием от твёрдых тел. Но для изменения самого объёма жид-
жидкости или газа, так же как и в случае твёрдых тел, необходимы ко-
конечные внешние силы. Это значит, что при изменении объёма
жидкости или газа в нём возникают силы, в конце концов уравно- "
вешивающие действие внешних сил.
Правда, под действием малых сил изменение формы жидкости или
газа может происходить очень медленно; но оно всегда будет проис-
происходить до тех пор, пока действуют внешние силы. Любое движение
твёрдого тела в жидкости или газе может служить этому подтвер-
подтверждением. Движение тела в жидкости или газе связано с изменением
взаимного расположения отдельных частей жидкости или raja. Ме-
Между тем это движение возникает под действием каких угодно
малых сил.
Жидкости и газы ведут себя как упругие тела только- в от-
отношении изменения объёма. Из двух элементарных деформаций —
сжатия (растяжения) и сдвига — только первая связана с изменением
объёма. Поэтому только в отношении деформаций сжатия и растяже-
растяжения жидкости и газы ведут себя, как упругие тела. Однако и в от-
отношении этой деформации есть существенное различие в поведении
жидкостей и газов, с одной стороны, и твёрдых тел, — с другой.
Твёрдое тело можно растянуть илн сжать в каком-либо
одном направлении. Его можно также сжать во всех направ-
направлениях, т. е. подвергнуть всестороннему сжатию или растяжению.
В жидкостях же и газах практически приходится иметь дело толь-
только со всесторонним сжатием. Правда, в специальных условиях
жидкость может быть подвергнута растяжению; при этой деформа-
*) За исключением случаев, когда размеры объёма в каком-либо на-
направлении очень малы, т. е. жидкость образует плёнку. Эти случаи будут
рассмотрены особо (§ 117).

§ 110} ОБЩИЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ 305
ции в ней также возникают силы, подобные упругим силам
в твёрдом теле. Но в задачах механики эти специальные условия
обычно не возникают, и поэтому практически приходится иметь дело
только с всесторонним сжатием в жидкости. Что же касается газов,
то в них принципиально имеют место только деформации сжатия.
Какой бы объём ни занимала данная масса газа, газ всегда оказы-
оказывается сжатым, так как в отсутствие внешних сил объём газа будет
увеличиваться беспредельно. Между тем жидкость ч отсутствие внеш-
внешних сил занимает определённый объём.
Однако, мы сейчас не рассматриваем различия между жидкостя-
жидкостями и газами (это будет сделано позже), а лишь отмечаем их общие
черты, отличающие их от твёрдых тел. Общая черта жидкостей и
газов состоит в том, что только в отношении деформации всесто-
всестороннего сжатия они ведут себя, как упругие тела. При сжатии жид-
жидкости или газа в них, как и в твёрдом теле, возникают упругие
силы, определяемые величиной деформации, т. е. степенью сжатия
жидкости или газа. Если бы мы все деформации жидкости относили
к нормальному её состоянию, то мы всегда встречались бы с дефор-
деформациями одного знака (сжатием). Как сказано, для газа такое нор-
нормальное, несжатое состояние вообще не • имеет смысла вводить.
Рассматривая же определённую степень сжатия газа как нормальное
состояние, мы встретимся и с увеличением, и с уменьшением степе-
степени его сжатия, т. е. с деформациями различных знаков. То'чно так же
и для жидкости часто удобно определённую степень сжатия рассма-
рассматривать как «нормальное» состояние и вводить деформации различных
знаков. Формально всё будет обстоять так же, как с упругими те-
телами,-— можно говорить о сжатии и о «растяжении» жидкости или
газа, хотя фактически речь будет итти лишь о разной степени
сжатия.
Изменениям формы, не связанным с изменением объёма, соответ-
соответствует элементарная деформация сдвига. При быстрых деформациях
сдвига а жидкости и газе могут возникать заметные силы; однако,
эти силы зависят не от величины деформации, а от скорости изме-
изменения деформации. И если скорость деформаций стремится к нулю,,
Хр и силы стремятся к нулю. Поэтому эти силы следует рассматри-
аать не как упругие силы, а как силы трения. Эти силы внутрен-
внутреннего трения называют силами вязкости. С силами вязкости прихо-
приходится считаться только при рассмотрении достаточно быстрых
движений, когда сдвиги в жидкости или газе изменяются с доста-
достаточно большой скоростью. Какая скорость окажется «достаточно.-
большой» в этом смысле, зависит от свойств жидкости или газа
и конкретных условий задачи. Но во всяком случае, для всех кон-
конкретных условий можно указать ст^ль медленные движения, при ко-
которых с силами, возникающими в жидкости и газе при сдвигах,
можно не считаться. Разумеется, с этими силами можно не счи->
таться при рассмотрении задач о равновесии жидкостей и газов.
20 С. Э. Хайкин

Зоб Гидростатика и аэростатика [гл. xvt
Общая черта жидкостей и газов — наличие лишь одного типа
упругой деформации всестороннего сжатия — позволяет целый ряд
вопросов механики жидкостей и газов рассматривать с общей точки зре-
зрения. Но между жидкостями и газами есть и ряд существенных различий,
которые приводят к различной постановке некоторых вопросов меха-
механики в отношении жидкостей и газов. Например, существенное раз-
различие жидкостей и газов состоит в том, что упругие свойства газов
в гораздо большей степени, чем жидкостей, зависят от температуры.
Однако, мы будем полагать, что свойства тел нам заданы и всё вре-
время остаются неизменными, в частности, что все рассматриваемые
явления протекают при неизменной температуре. Там, где необходимо
учесть изменения температуры газа, будут делаться специальные
оговорки.
Жидкость и .газ, так же как и твёрдые тела, мы будем разби-
разбивать на отдельные малые элементы. Эти элементы должны быть
столь' малы, чтобы можно было считать все отдельные их атомы
движущимися одинаково. Здесь опять речь идёт о регулярном, а не
о хаотическом движении атомов. Того обстоятельства, что отдельные
атомы вследствие хаотического движения выходят за пределы дан-
данного элемента, и их место занимают другие, в макроскопической ме-
механике жидкостей и газов можно не учитывать.
К отдельным малым элементам (которые должны, однако, содер-
содержать ещё много атомов) мы будем применять общие законы механи-
механики. Всякий объём жидкости или газа мы будем рассматривать как
систему таких элементов. Но эти отдельные элементы могут изме-
изменять взаимное расположение. Поэтому к данному объёму жидкости
или газа мы не можем, вообще говоря, применять представлений
механики твёрдого тела, так как в твёрдом теле взаимное располо-
расположение отдельных элементов мы считали неизменным. Для объёма
жидкости или газа в общем случае справедливы только положения
механики системы точек, не связанных жёстко между собой. Но в
том случае, когда речь идёт о покоящейся жидкости или газе или
о таких движениях, при которых взаимное расположение отдельных
элементов рассматриваемого объёма ие изменяется, мы можем итти
дальше и применять к этому объёму положения динамики твёрдого
тела. В частности, в таких случаях можно говорить о центре тяже-
тяжести объёма, как о некоторой фиксированной точке, о моменте сил,
действующих на объём, перемещать точки приложения сил вдоль
направления сил, применять условия равновесия твёрдого тела и т. д.
Этог приём получил название принципа отвердения. Мы представ-
представляем себе рассматриваемый объём отвердевшим и применяем к нему
законы механики твёрдого тела. Ясно, что этот приём допустим
только в том случае, если мы заранее уверены, что отдельные эле-
элементы объёма не изменяют своего взаимного расположения. В частно-
частности, принцип отвердения всегда можно применять к покоящимся жид-
жидкостям и газам.

§ 111]
ДАВЛЕНИЕ В ЖИДКОСТИ И ГАЗЕ
307-
§ 111. Давление в жидкости и газе
Степень сжатия жидкости или газа определяет величину тех сил,
с которыми отдельные части жидкости или газа действуют друг на
друга или иа соприкасающиеся с ними тела. Силы, с которыми
действуют друг на друга отдельные части жидкости или газа, в из-
известном смысле подобны тем упругим силам, с которыми действуют
друг на друга отдельные части деформированного твёрдого тела.
Если мы разделим какой-либо объём жидкости или газа на две части,
то со стороны одной части на другую будут действовать силы, за-
зависящие от степени сжатия жидкости или газа. Как и в упругих
телах, дли того чтобы находить силы, действующие на ту или иную
площадку, вводят напряжения, т. е. относят силы к той площади,
через которую они действуют. Однако, в жидкости и газе при сдви-
сдвиге не возникает сил и все силы обусловлены только деформациями
сжатия. Поэтому сила, действующая со стороны одного элемента
на другой, всегда нормальна к площадке, на которую эта сила
действует. Для всякой площадки в жидкости существует толь-
только нормальное напряжение
p = lim ?g, A6.1)
где AF — сила, a AS—площадка, через которую эта сила действует.
Это нормальное напряжение называют давлением в жидкости
или газе*) (его принято обозна-
обозначать буквой р, а не з,-как в твёр-
твёрдых телах).
В жидкости или газе до:та-
точно задать величину давления
для какой-либо одной площадки в
данной точке, чтобы определить
давление для люб^й площадки в
этой точке. Действительно, рас-
рассмотрим, как мы это делали для
твёрдого тела, условия равновесия
выделенной в жидкости малой
прямоугольной трёхгранной призмы
(рис. 235) с гранями 5,, Sit S3 и
So. Размеры призмы выберем столь
малыми, чтобы давление жидкости
(или газа) можно было считать Рис. 235.
одинаковым на двух параллель-
параллельных площадках So. Тогда силы, действующие на эти площадки,
*) В движущейся жидкости (или газе), как сказано, могут .существо-
.существовать силы, обусловленные сдвигом слоев друг относительно друга. Но эти
силы зависят от скоростей, и их не следует рассматривать как упругие
напряжения.
20*

308 ГИДРОСТАТИКА И АЭРОСТАТИКА [гл. XVt
уравновесятся, и их можно не принимать во внимание. Пусть нам
задано давление р, на грань S,. Нужно найти давление р2 и р3
на грани Sz н 53, Силы, действующие на все три грани (рис. 236),
соответственно равны
Для равновесия необходимо, чтобы
Эти силы образуют замкнутый тре-
Рис. 236. угольник, который подобен тре-
треугольнику сечения призмы (так как
f,, f2 и f3 перпендикулярны к соответствующим граням призмы).
Следовательно,
где /,, /2, /3 — длины сторон треугольника сечения. Так как площади
граней пропорциональны сторонам сечения lv /2, /в, то
откуда на основании A6.2)
Давления иа все три грани равны по величине (но на каждой грани
направлены перпендикулярно к этой грани). Этот вывод справедлив
и для случая, когда на жидкость или газ действуют ещё какие-либо
массовые силы, например, сила тяжести. Так как массовые силы
убывают, как объём призмы, а силы давления — как площадь призмы
(т. е. медленнее), то мы всегда можем выбрать столь малую призму,
чтобы массовыми силами можно было пренебречь.
Наш вывод справедлив и для движущейся жидкости. Двигаясь
вместе с призмой, мы должны были бы ввести силы инерции, кото-
которые являются массовыми и поэтому для малой призмы не играют
роли. При движении призмы могли бы появиться силы вязкости, но
давления (упругие силы) попрежнему должны удовлетворять получен-
полученному соотношению.
Величина давления в данной точке жидкости или газа одина-
одинакова для всех направлений площадки, к которой давление от-
отнесено.
Для измерения давления в жидкости или газе мы должны изме-
измерить силу, с которой действует на какую-либо площадку жидкость
или газ, прилегающие к этой площадке с одной стороны. Простей-
Простейшим образом эта задача осуществляется в мембранных манометрах
и барометрах-анероидах. В жидкость или газ помещается герметиче-

§ 112] СЖИМАЕМОСТЬ ЖИДКОСТЕЙ И ГАЗОВ 309
ски закрытая коробка *), одна из стенок которой может заметно де-
деформироваться под действием измеряемых сил. По величине этой
деформации, отсчитываемой при помощи стрелки и шкалы, опреде-
определяется давление в жидкости или газе. В этих приборах принципиально
важно, чтобы коробка была герметически закрыта и жидкость или
газ давили на упругую стенку только с одной стороны (иначе давле-
давление с двух старой уравновешивалось бы и не вызывало бы деформа-
деформации стенки).
Помещая манометр в жидкость или газ, мы как-то изменяем со-
состояние жидкости или газа. Поэтому нельзя заранее утверждать, что
сила, действующая на стенку коробки, будет такая же, какая действо-
действовала на жидкость, место которой заняла коробка. Однако, если жидкость
или газ находится в равновесии и манометр этого равновесия не на-
нарушил, то, следовательно, сила, с которой прилегающая жидкость
действует на коробку, равна той силе, с которой она действовала
прежде на соседний объём жидкости.
Давление в жидкости в системе CGS измеряется в дн]см%. В си-
системе LFT давление измеряется в граммах или килограммах силы
на квадратный сантиметр. Единица кг смг называется технической
атмосферой.
§ 112. Сжимаемость жидкостей и газов
Давление в данной точке жидкости или газа зависит от степени
сжатия в этой точке. Так же, как и в твердых телах, связь между
давлением (напряжением) и сжатием (деформацией) определяется упру-
упругими свойствами тела. Упругие свойства жидкостей и газов пол-
полностью характеризуются объемной упругостью, т. е. соотношением
между изменениями объёма данной массы жидкости или газа и из-
изменениями давления в них. Здесь выступает второе различие между
жидкостями и газами — их совершенно разная объёмная упругость.
Объёмная упругость жидкостей может быть охарактеризована с
количественной стороны отношением возникшего напряжения к вели-
величине относительного изменения объема, которым это напряжение
вызвано. Пусть объем жидкости при некотором нормальном давлении
равен V, и при изменении давления на Ар он изменился на ДУ.
Следовательно, относительная деформация есть kV\V, а соответству-
соответствующее напряжение Др. Коэффициент -сжимаемости равен
р V
или модуль сжатия
Ьр V Ьр ч '
*) Впервые такой прибор был построен Види, Поэтому все подобны^
Конструкции носят название коробок Види,

310 ГИДРОСТАТИКА И АЭРОСТАТИКА [гл. XVI
Знак минус взят затем, чтобы А" было положительно (&V и Др всегда
противоположны по знаку).
Коэффициент сжимаемости жидкостей очень мал и измерение его тре-
требует специальных предосторожностей. При значительном увеличении дав-
давления в жидкости сосуд, в котором находится жидкость, изменяет свой
объём («раздувается» от давления), и определить малое изменение объёма
жидкости очень трудно. Оно полиостью может маскироваться увеличением
объёма сосуда. Чтобы объём сосуда заметно не изме-
изменялся, Эрстел A822 г.) впервые применил приём, который
затем получил широкое распространение. Сосуд с испы-
испытуемой жидкостью подвергают внешнему давлению, тако-
такому же, как давление жидкости. Схема прибора, кото-
который позволяет это осуществить (так называемого пьезо-
пьезометра), изображена на рис. 237. Внешний сосуд В содер-
содержит дчугой сосуд А, в который пометена испытуемая
жидкость. Капилляр, которым оканчивается сосуд А, по-
погружен в ртуть. Во внешнем сосуде В создается .высокое
давление (для этого обычно ярибор наполняют волой и
присоединяют к гидравлическому прессу). При сжатии
объём жидкости в сосуде А уменьшается и ртуть по ка-
капилляру поднимается. По изменению высоты столба ртути
определяется изменение объёма жидкости. В дальней-
дальнейшем этот принцип был усовершенствован Реньо, кото-
который получил первые надёжные данные о сжимаемости
жидкостей.
Рис. 237. Измерения сжимаемости жидкостей показали,
что изменение давления в широких пределах пропор-
пропорционально относительному изменению объёма. Коэффициент сжимаемо-
сжимаемости К в широких пределах оказывается постоянным.
При очень больших давлениях коэффициент сжимаемости пааает
(сжимаемость жидкостей уменьшается). Коэффициент сжимаемости К
зависит от температуры жидкости. Значения К при небольших давле-
давлениях и температуре 0э для некоторых жидкостей приведгны в таблице.
Сжимаемость жидкостей в см^\кг
Вода 5- Ю-5 Алкоголь 8-Ю-5
Эфнр 1Ы0-в Льняное масло . . .5,2-Ю-5
Ртуть 3,8-10-6 Глицерин 2,2-10~5
Для газов, как известно, связь между объёмом и давлением дан-
данной массы газа даётся законом Бойля-Мариотта (температуру мы
условились считать постоянной):
Q
/)К— COnSt., ИЛИ Р = Т7 •
Изменения давления, вообще говоря, не пропорциональны изменению
объема. Но дли достаточно малых изменений объёма пропорциональ-
пропорциональность между изменениями объёма и давления, конечно, должна суще-
существовать. Действительно, взяв малые изменения объёма ДУ и давле;-

§ 112] СЖИМАЕМОСТЬ ЖИДКОСТЕЙ И ГАЗОВ 8П
ния Др, мы можем на основании закона Бойля*Мариотта написать:
(p-\-kp)(V-\- &V)=pV или, пренебрегая малым произведением
ДДК
Если выражение, стоящее слева, мы так же, как и для жидкостей,
назовём коэффициентом сжимаемости, то коэффициент сжимаемости
газов будет
Сжимаемость газов тем меньше, чем больше давление.
Бели для газов мы ограничимся такими же малыми изменениями
объёма (а не давления), с которыми обычно имеют дело в жидкостях,
то сжимаемость газов можно считать постоянной и сравнивать её с
сжимаемостью жидкостей при том же давлении. При давлении
p = l kzjcm2 для всех газов К=\ смг\кг. Так как для воды при
р = \ kzjcm2 АГ= 5-10—5 смъ\кг, то сжимаемость газов при атмосфер-
атмосферном давлении в 20 000 раз больше, чем сжимаемость воды.
Большое количественное различие в сжимаемости жидкостей и газов
приводит к существенным различиям в их поведении. Очень эффектно это
различие выступает в следующем опыте. Если в эбонитовую банку, нали-
налитую водой, выстрелить (из мелкокалиберной винтовки) так, чтобы пуля
попала выше уровня воды, то байка остаётся целой (пуля лишь пробивает
небольшое отверстие). Если же пуля пробивает банку на несколько санти-
сантиметров под уровнем воды, то банка разлетается вдребезги. Объясняется
это очень малой сжимаемостью волы. Когда пуля «вгоняется» в воду, она
должна либо сжать воду на величину своего объёма, либо вытеснить её
наверх. Не только в первом, но н во втором случаях в воде должны возник-
возникнуть огромные силы (так как пуля вгоняется быстро и вода должна вытес-
няться с большим ускорением). Эти силы и разрывают банку.
Аналогичные явления происходят и при разрыве глубинных бомб,
применяемых против погрузившихся подводных лодок. При разрыве бомбы
иа глубине вследствие малой сжимаемости в воде возникают очень боль-
большие силы, которые раздавливают лодку.
Малая сжимаемость жидкостей позволяет во многих случаях вооб--
ще пренебрегать изменениями объёма жидкости, т. е. рассматривать
абсолютно несжимаемые жидкости. Это значит, что мы приписываем
жидкости следующие свойства: уже при очень малых изменениях
объёма жидкости под действием внешних сил возникают столь боль-
большие упругие силы, что дальнейшее уменьшение объёма жидкости
прекращается. В дальнейшем мы в большинстве случаев будем рас-
рассматривать жидкость как несжимаемую (обратное мы всегда будем
оговаривать).

312
ГИДРОСТАТИКА И АЭРОСТАТИКА
[ГЛ. XVI
§ 113. Распределение давлений в покоящихся
жидкости и газе
При исследовании давления в различных точках покоящихся жид-
жидкости и газа мы можем применять условия равновесия твёрдого тела
к любому конечному объёму, выделенному из жидкости или газа. Но
в этом случае уже нельзя пренебречь массовыми силами, т. е. силой
тяжести, как мы это делали, рас-
рассматривая очень малый объём.
Рассмотрим прежде всего усло-
условия равновесия для элемента объ-
объёма в виде расположенного го-
горизонтально параллелепипеда с
очень малой площадью сечения.
(Всё сказанное ниже относится в
одинаковой мере к жидкостям и
газам, но для краткости мы бу-
будем говорить только о жидкости.)
Силы, действующие на торцы
параллелепипеда, должны быть
равны, так как в горизонтальном
направлении никакие другие силы
не действуют. Так как основания
Рис. 238. параллелепипеда имеют одинако-
одинаковую площадь и силы равны, то
давления также должны быть равны. Во всех точках жидкости,
лежащих в одной горизонтальной плоскости (на одном уровне),
давление одно и то же. Для вертикально расположенной прямой
призмы фис. 238) силы давления на боковые стенки уравновесятся,
и условия равновесия примут вид:
Где f1 и /2 — соответственно силы давления на верхнее и нижнее
основания параллелепипеда, а Р—вес жидкости в рассматриваемом
объёме.
Разделив все три члена равенства на площадь основания парал-
параллелепипеда S, мы получим:
Pi-}- Pi=P2>
где рх и р2 суть давления на уровнях: 1—верхнего и 2— нижнего
оснований, а Р1 — вес столба жидкости, площадь которого равна
единице, а высота — разности уровней / и 2.
Разность давлений между двумя уровнями равнг весу вер-
вертикального столба жидкости между этими уровнями с площадью
сечения, равной единице..Поэтому покоящийся вертикальный столб
жидкости может служить для измерения разности давлений между
нижним и верхним концами столба.

§ \\S\ РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЙ В ЖИДКОСТИ И ГАЗЕ 313
Этот принцип измерения давлений используется в жидкостных
манометрах и барометрах. В жидкостном манометре высота столба
измеряет разность давлений между нижним и верхним открытым
концом столба, т. е. избыток давления у основания трубки над
атмосферным давлением. В жидкостном барометре второй конец трубки
закрыт и из него удалён воздух (давление практически равно нулю).
Поэтому высота столба в барометре измеряет всё давление у основа-
основания трубки. Вместо веса столба давление обычно указывается прямо
в высотах столба определённой, жидкости—миллиметрах ртутного
или водяного столба.
Вес данного объёма жидкости зависит от ее плотности, с одной
стороны, и от высоты и географической широты места, — с другой.
Поэтому при точных измерениях давления приходится приводить
показания к определённой температуре—обычно к 0J и к весу на
уровне моря на широте 45Э. При этих услозиях вес столба ртути
в 1 см2 сечения и 1 мм высоты составляет 1,36 грамм-силы. Сле-
Следовательно, давление в 1 мм Hg равно 1,36 г\смг. При точных
измерениях давлений приходится учитывать также явление капилляр-
капиллярности (см. ниже), вследствие которого высота столба ртути всегда
меньше' той, которая соответствует давлению на открытый конец
барометра. Накрнец, дазление в закрытом конце барометра также
не равно нулю, а определяется давлением, которое создают пары
ртути при данной температуре. Однако, это давление очень мало,
и им вполне можно пренебрегать.
Рассмотрим теперь распределение плотностей в покоящейся жид-
жидкости. Для этого сравним две одинаковые прямые вертикальные
призмы, расположенные на одной и той же высоте в разных местах
жидкости. Так как давление во всех тйчках жидкости, лежащих на
одной высоте, одно и то же, то разность давлений на нижнее и верх-
верхнее основания для обеих призм должна быть одинакова, а значит,
веса призм должны быть равны. Поскольку это справедливо для двух
призм любой (но одинаковой) высоты, то, следовательно, плотность
жидкости (или газа) во всех точках, лежащих на одной и той же
высоте, должна быть одинакова. Этот вывод справедлив и для не-
нескольких различных жидкостей, расположенных одна над другой,
и для жидкости и расположенного над ней газа. Если этот ряд
жидкостей или жидкость и газ находятся в равновесии, то, рас-
рассматривая условия равновесия для призмы, части которой располо-
расположены по обе стороны от границы раздела, мы придём к тем же самым
выводам. Следовательно, граница раздела двух жидкостей разной
плотности или жидкости и газа должна быть горизонтальной.
Призму, для которой рассматриваются условия равновесия, мы
можем продолжить вверх до верхней границы жидкости или газа
(для газа имеет смысл говорить о верхней границе только тогда,
когда ОН заключён в замкнутый сосуд). Тогда
/»=/>» +Л. A6.5)

ЗН ГИДРОСТАТИКА И АЭРОСТАТИКА. [гл. XVI
где р0 — давление на верхней границе жидкости или газа (внешнее
давление), а Рх — попрежнему вес единичного столба. Если жидкость
имеет где-либо свободную поверхность, то давление в данной гори-
горизонтальной плоскости определяется весом единичного столба жид-
жидкости— высотой от этой горизонтальной плоскости до свободной
поверхности. При этом р0 есть давление на свободную поверхность
(в случае открытых сосудов — атмосферное давление).
Если внешнее давление р0 столь велико, что даже для самого
высокого столба (от верхней до нижней границы жидкости, или газа)
ро^>Рр то этим последним можно пренебречь и считать, что p=.pQ.
Можно считать, что давление жидкости или газа во всех точках
сосуда практически одинаково. Например, в баллоне со сжатым га-
газом при давлениях в десятки атмосфер можно с большой точностью
считать, что давление сжатого газа во всех точках баллона одно
и то же. Точно так же практически можно считать одинаковым
давление жидкости во всех точках цилиндра гидравлического пресса,
где жидкость сжата до давления в сотни атмосфер.
Из полученных нами результатов относительно распределения
давления в жидкости и газе вытекает ряд следствий, хорошо извест-
известных из элементарного курса физики, — закон сообщающихся сосудов,
распределение давления на стенки и дно сосуда и т. д.
§ 114. Подъёмная сила. Плавание тел
Распределением давлений по высоте объясняется и возникновение
подъёмной силы, действующей со стороны жидкости или газа на
погруженное в них тело. Давление жидквсти на каждый элемент
поверхности погруженного тела нормально к этому элементу (рис. 239),
но при этом чем ниже расположен элемент поверхности, тем больше
давление. Вследствие этого результирующая всех сил, действующих
на отдельные элементы поверхности тела, всегда направлена вверх.
Э.по и есть подъёмная или «.выталкивающая* сила.
• Для определения величины и направления подъёмной силы восполь-
воспользуемся принципом отвердения. Представим себе, что мы удалили
погруженное в жидкость тело и снова заполнили объем, который
оно занимало, жидкостью. При этом жидкость будет находиться
в равновесии и, следовательно, можно будет применить принцип
отвердения: считать отвердевшей ту часть жидкости, которая занимает
место погруженного тела. На эту часть жидкости действует сила
тяжести, равная весу жидкости и приложенная к её центру тяжести.
Так как «отвердевшая» часть жидкости находится в равновесии, то,
значит, результирующая сил давления, действующих со стороны
окружающей жидкости, равйа весу отвердевшей части, направлена
вертикально вверх и проходит через центр тяжести «отвердевшего»
Объёма.

§ П4]
ПОДЪЁМНАЯ СИЛА. ПЛАВАНИЕ ТЕЛ
315
Рис. 2ЛЭ.
Что касается точки приложения подъёмной силы, то для её
определения можно применить те же соображения, которые были
приведены при определении точки приложения равнодействующей
сил тяжести (§ 87). Если мы сравним два различных положения
одного и того же. выделенного
объёма (рис. 240), то в обоих по-
положениях подъёмная сила F долж-
должна быть направлена по верти-
вертикали АВ, проходящей через центр
тяжести выделенного объёма. Как
и в случае равнодействующей сил
тяжести, для того чтобы точка
приложения подъёмной силы не
перемещалась относительно выде-
выделенного объёма, эту силу сле-
следует считать приложенной к цен-
центру тяжести объёма. Иначе говоря,
поскольку центр тяжести — это
единственная точка, через кото-
которую проходит подъёмная сила
при любом положении выделен-
выделенного объёма, следует считать, что
подъемная сила приложена именно к центру тяжести выделенного объёма.
Если мы снова заменим «отвердевший» объём погруженным телом,
то сила давления на него со стороны окружающей жидкости должна
оставаться прежней. Значит, на погруженное в жидкость или газ тело
действует подъёмная сила, равная весу
жидкости (или газа) в об ьёме, занимаемом
телом, направленная по вертикали и при-
приложенная к центру тяжести вытесненного
объёма.
При подсчёте веса жидкости или газа
в объёме, занимаемом телом, нужно, ко-
конечно, считать, что плотность, жидкости
или газа во всех точках внутри объёма
такая же, как плотность окружающей
жидкости или газа на том же уровне.
В большинстве случаев плотность жидко-
жидкости или газа между наивысшей и наи-
наинизшей точками тела меняется очень мало и тогда её можно считать
постоянной.
Чтобы тело, целиком погруженное в жидкость или газ, находилось
в равновесии, подъёмная сила и сила тяжести должны быть равны
и лежать на одной прямой, т. е. центр тяжести тела и центр тяжести
вытесненного объёма должны лежать на одной вертикаЛи. Это
положение равновесия будет устойчиво, если лри отклонении от
А
F
0
i
'в
А
р /
/fs
/ 1 /
f I
' le
Рис. 240.

316 ГИДРОСТАТИКА И АЭРОСТАТИКА |ГЛ. XVI
него возникают моменты сил, которые снова возвращают тело в по-
положение равновесия. При отклонении тела от положения равновесия
сила тяжести, приложенная к центру тяжести тела, и подъёмная
сила, приложенная к центру тяжести вытесненного объёма, создают
вращающий момент. Если центр тяжести тела Q лежит ниже центра
тяжести вытесненного объёма С (рис. 241), то вращающий момент
возвращает тело к положению равновесия. В противном случае
(рис. 242) возникший вращающий момент ещё дальше отклоняет
тело от положения равновесия.
=z3r Поэтому, для того, чтобы равно-
— весие было устойчиво, центр тя-
тяжести тела должен лежать ниже
центра тяжести вытесненного объ-
объёма. Это условие должно быть
соблюдено, например, в подводной
лодке, для того, чтобы в погру-
рис 241 Рис 242 женном состоянии она не опроки-
опрокидывалась.
Для демонстрации условий
устойчивости погруженного в жидкость тела можно воспользоваться
куском парафина, утяжелённого металлическим грузом ровно на-
настолько, чтобы тело плавало в воде, целиком в неё погрузившись, или
.погружалось очень медленно (для этого нужно весьма тщательно
подобрать груз). Кусок парафина, опущенный в воду грузиком вверх,
перевёртывается в воде (центр тяжести тела немного смещён от центра
тела в сторону грузика).
' Если подъёмная сила, действующая на тело? целиком погруженное
в жидкость, больше, чем вес тела, то тело всплывёт на поверхность;
подъёмная сила (вес вытесненной жидкости) убывает до тех пор, пока
не окажется равной весу тела. Условия равновесия попрежнему сво-
сводятся к тому, что центр тяжести тела и центр тяжести вытесненного
объёма должны лежать на одной вертикали. Однако, условия устой-
устойчивости равновесия будут уже иными. Равновесие может быть устой-
устойчивым и тогда, когда центр тяжести тела О лежит выше центра
тяжести вытесненного объёма С. Иначе устойчивое плавание одно-
однородных тел на поверхности жидкости вообще было бы невозможно,
так как их центр тяжести всегда лежит выше центра тяжести
вытесненного объёма. Это различие обусловлено тем, что для тел,
плавающих на поверхности, изменение положения тела всегда связано
с изменением взаимного расположения центра тяжести тела и центра
тяжести вытесненного объёма.
Рассмотрим условия устойчивости для плавающего на поверхности
жидкости прямоугольного параллелепипеда. Из условий равновесия
следуе** что целиком погруженная грань параллелепипеда должна
быть горизонтальна. При отклонении параллелепипеда от положения
равновесия центр -тяжести вытесненного объёма перемещается в ту

§ 114]
ПОДЪЕМНАЯ СИЛА. ПЛАВАНИЕ ТЕЛ
317
же сторону, куда наклонился параллелепипед. Возникает момент силы
тяжести и подъёмной силы. Если полностью погруженная грань парал-
параллелепипеда больше, чем частично погруженная (рис. 243), то возник-
возникший момент будет возвращать тело к положению равновесия —
равновесие будет устойчиво. В противном случае (рнс. 244) равнове-
Рис. 243.
сие будет неустойчиво. Условие устойчивости равновесия, как легко
зидеть, сводится к тому, чтобы точка М пересечения направления
подъёмной силы с прямой АВ лежала выше центра тяжести тела О.'
Точка М — пересечение направления подъёмной силы с плоскостью
симметрии тела — носит название метацентра. Условие устойчивости
сводится, следовательно, к тому, чтобы центр тяжести тела лежал
ниже метацентра.
Условия устойчивого плавания тел можно продемонстрировать при
помощи деревянного бруска прямоугольной формы, плавающего на воде.
Брусок, опущенный в воду в любом положении, всегда принимает такое
положение, при котором целиком погруженной в воду оказывается его
наибольшая грань. Если утяжелить бру-
брусок металлическим грузом В так, чтобы
центр тяжести О лежал достаточно низ-
низко, то брусок будет плавать в верти-
вертикальном положении (рис. 245). Для того,
Чтобы корабль устойчиво держался на
воде (обладал «остойчивостью»), мета-
метацентр М должен лежать выше центра
тяжести корабля О (рнс. 246). Для тел
произвольной формы положение мета-
метацентра изменяется при изменении
положения тела. Поэтому прн неко-
некотором достаточно большом наклоне метацентр сможет оказаться ниже
центра тяжести тела и тело опрокинется. Кораблям придается такая форма,
чтобы положение метацентра практически не изменялось даже прн значи-
значительном крене корабля. И если центр тяжести корабля лежит ниже мета-
метацентра, то корабль может выдерживать очень больщрй крен» не опро*
кидываясь.
Подъёмная сила исчезает, если на нижнее основание тела не действует
давление со стороны окружающей жидкости (основание тела лежит на дне).
Поэтому, если обычную пробку плотно придавить к дну чашки, наполнен-
наполненной ртутью, то пробка не всплывает. Она остается прижатдй к дну сосуда
•О
В
Рнс. 245.
Рис. 246.

318 ГИДРОСТАТИКА И АЭРОСТАТИКА [Гл. XVI
своим весом и силой давления ртути на верхнее основание. Нечто подоб-
подобное происходит с подводными лодками, опустившимися на гладкое глиии*
стое дно. Лодку «присасывает» к дну и она не может подняться.
Несколько особый случай представляет собой возникновение подь-
ёмной силы аэростатов. Она обусловлена тем, что при одинаковом
изменении высоты давление в более плотном газе (так же, как и и
более плотной жидкости) изменяется иа большую величину, чем
в менее плотном. Поэтому, например, в сообщающихся сосудах с жид-
жидкостями разной плотности уровень более тяжёлой жидкости стоит
ниже, чем более лёгкой.
Для газов такие «сообщающиеся сосуды» получаются в том слу-
случае, когда сосуд, наполненный каким-либо газом, сообщается с атмо-
атмосферой. Например, стеклянная труба длиной в 1 — l'/s м, затянутая
с одной стороны очень тонкой резиновой плёнкой и открытая с дру-
другой, вместе с окружающей атмосферой образует «сообщающиеся
сосуды». Если наполнить трубу водородом или светильным газом
(более лёгким, чем воздух) и поднять трубу закрытым концом
вверх, то плёнка заметно выпучивается. Наоборот, если опустить
этот конец вниз, то плёнка вдавливается внутрь. В обоих случаях
у открытого конца трубы давления воздуха и светильного газа одина-
одинаковы (как на границе двух жидкостей в сообщающихся сосудах).
Поэтому в первом случае давление у верхнего конца трубы умень-
уменьшается внутри трубы на вес столба светильного газа, а снаружи — на
вес столба воздуха. Так как светильный газ легче, то убыль давле-
давления внутри меньше, чем снаружи, — давление внутри больше, поэтому
плёнка выпучивается наружу. Во втором случае давление вверху
одинаково. Прибыль давления при переходе от верхнего конца к ниж-
нижнему в светильном газе меньше, чем в воздухе, и давление изнутри
меньше — плёнка вдавливается. Если наполнить трубу углекислотой
(газом, более тяжёлым, чем воздух), то картина
получается обратная.
Эта демонстрация поясняет возникнозение подъ-
подъемной силы в аэростата*. Оболочка аэростата не
представляет собой замкнутого объёма, а имеет в
нижней части отросток, сообщающийся с внешней
атмосферой (рис. 247). Оболочка должна сообщаться
с атмосферой потому, что в противном случае на
Рис 247. большой высоте, где внешнее давление мало, вну-
внутреннее давление газа разорвало бы оболочку. Дав-
Давление лёгкого газа, наполняющего оболочку, у отверстия равио давлению
внешнего воздуха. С увеличением высоты А над отверстием давление
внутри падает медленнее, чем снаружи (столб газа весит меньше,
чем столб воздуха). Поэтому в каждой точке давление на оболочку
изнутри больше, чем снаружи, и разность давлений на оболочку
направлена везде наружу (нормально к оболочке). Чем выше над
отверстием, тем больше эта разность давлений. Примерное распре-

§ 115] ИЗМЕНЕНИЙ ДАВЛЕНИЯ С ВЫСОТОЙ 319
деление этих разностей давлений указано на рис. 247 стрелками.
Равнодействующая этих разностей давления и представляет собой
направленную вверх подъёмную силу.
В закрытых оболочках, например, оболочках жёстких дирижаблей,
подъёмная сила обусловлена разностью давлений на различные части обо-
оболочки (верхнюю и нижнюю). В оболочках же с отверстием подъёмная
сила обусловлена разностью давлений с двух сторон на одни и те же
части оболочки. Это различие обусловливает известную разницу в поведе-
поведении оболочек. Если бы мягкая оболочка, наполненная небольшим коли-
количеством газа, была закрыта снизу, то её нижняя часть была бы вдавлена
внутрь. Между тем открытая снизу оболочка никогда не может быть вдав-
вдавлена внутрь. Если в открытой оболочке газа мало, то её нижняя часть
наполнена воздухом, давления снаружи и изнутри одинаковы и оболочка
свободно висит складками, но никогда не бывает вдавлена внутрь. Такую
именно форму имеют у Земли оболочки стратостатов.
§ 115. Изменения давления с высотой.
Барометрическая формула
Как в жидкости, так и в газе изменения давления с высотой
определяются весом расположенного между двумя данными уровнями
столба жидкости или газа, имеющего сечение, равное единице. Но
вес одного и того же столба с изменением высоты изменяется, так
как на разных уровнях жидкость или газ сжаты по-разному и поэтому
плотность жидкости или газа на разных высотах различна. Однако,
вследствие малой сжимаемости жидкостей изменения плотности жид-
жидкости с высотой происходят гораздо медленнее, чем плотности газа.
Плотность жидкости можно считать постоянной, пока давления не
очень велики, т. е. пока рассматриваются не слишком большие глу-
глубины. В таком случае, если высота столба А, то его объём также h
(сечение равно единице) и вес столба равен
где р — постоянная плотность жидкости. Поэтому в жидкости измене-
изменение давления с высотой выражается линейным законом
где рй — давление на уровне Л=0. Вследствие того, что жидкость
всё же немного сжимается, давление при возрастании глубины растёт
несколько быстрее, чем по линейному закону. Однако, отклонение
от линейного закона для жидкостей становится заметным только при
очень больших изменениях глубины.
Изменения плотности газа с высотой вследствие большой сжима-
сжимаемости становятся заметными уже при не очень больших разностях
высот. Плотность можно считать постоянной только для малых изме-
изменений высоты ДЛ. Если эти изменения считать положительными вверх,

320 ГИДРОСТАТИКА И АЭРОСТАТИКА, [ГЛ. ХУГ
то изменение давл'ения на участке ДА будет отрицательно (давление
уменьшается):
A6.7)
Связь между давлением и плотностью даётся законом Бойля-
Мариотта (температуру газа мы считаем постоянной). Так как плот-
плотности обратны обьёмам, то по закону Бойля-Мариотта
? __.?о
Р Ро'
где р и р — давление и плотность на высота А, а р0 и р0 — давле-
давление и плотность на высоте А = 0. Подставляя отсюда выражение
для р в соотношение. A6.7), получим:
\р=— p&gbh.
Ро
Для того чтобы найти изменение давления на конечной высоте А,
нужно взять сумму таких элементарных изменений давления на отдель-
отдельных элементах ДА. Для подсчёта заменим малые элементы ДА и Др
бесконечно малыми:
Р Ро
и возьмём интеграл от этого выражения в пределах от 0 до А:
PoJ
о
Интегрируя и подставляя пределы, пол>чим:
1„ 2. = _??«*.
Ро Ро
Переходя от логарифмических функций к показательным, окончательно
получим:
Эта формула, выражающая изменение давления газа с высотой, на-
называется барометрической формулой. Давление в атмосфере с вы-
высотой уменьшается по показательному закону (рис.# 248). При изме-
изменении высоты по арифметической прогрессии давление убывает по
геометрической прогрессии. (На каждые 5,5 км высоты давление
убывает примерно в 2 раза.) Чем больше высота, тем меньшие, изме-
изменения давления соответствуют одному и тому же изменению выерты.

§ 1151
ИЗМЕНЕНИЯ ДАВЛЕНИЯ С ВЫСОТОЙ
321
Барометрическая формула выведена в предположении, что температура
по всей высоте одна и та же. В действительности температура атмосферы
изменяется с высотой, и в эту формулу должны быть введены соответ-
соответствующие поправки. При введении этих поправок (если, кроме того, известно
давление у Земли ро) формула поз-
позволяет по величине атмосферного
давления определить высоту над
Землёй. На этом принципе и по-
построены авиационные альтиметры,
т. е. барометры-анероиды, в которых
на шкалу вместо давлений прямо
нанесены высоты. Однако, для того
чтобы по, показаниям барометра
можно было точно определить вы-
высоту, нужно знать величину да-
давления у Земли и температуру
воздуха.
Уменьшение плотности атмос-
атмосферы с высотой влечёт за собой
уменьшение подъёмной силы аэро-
аэростатов. Когда подъёмная сила,
уменьшаясь, становится равной весу
аэростата, дальнейший подъём аэро-
аэростата прекращается, аэростат дости-
достигает «потолка». Стратостаты, пред-
предназначенные для подъёма на боль-
большие высоты, должны обладать до-
достаточной подъёмной силой на
большой высоте. При неизменном
объёме их подъёмная сила у Земли
была бы чрезмерно велика (скорость
>3
12
IJ
10
9
8
7
6
5
4
3
2
1
О
\
\
\
\
\
\
\
\
\
\
100 200 300 ЫЮ500 600 700 800мл Нд
Рис. 248.
подъёма была бы недопустимо боль-
большой). Для плавного подъёма необ-
необходимо, чтобы подъёмная сила (вес
вытесненного воздуха) лишь немного
превышала вес аэростата с газом.
Поэтому стратостаты наполняются небольшим количеством лёгкого газа
(водорода или гелия), занимающим у Земли только несколько процентов
от всего объёма оболочки; остальную часть оболочки занимает воздух.
При подъёме водород расширяется и занимает всё ббльшую и большую
часть оболочки. Происходит, с одной стороны, увеличение объёма оболочки,
а с другой, — уменьшение общего веса (воздух выходит наружу). На неко-
некоторой высоте водород полностью заполняет оболочку, давления внутри
везде оказываются больше, чем снаружи, и оболочка принимает правиль-
правильную форму (выполнение). При дальнейшем подъёме водород продолжает
уходить из оболочки. Вес стратостата с газом уменьшается, и это ком-
компенсирует уменьшение подъёмной силы с высотой ещё на некотором
участке (от"высоты выполнения до потолка). С этой точки зрения воз-
воздух и водород, выходящие из оболочки, играют роль сбрасываемого бал-
балласта (воздух до высоты выполнения и водород от высоты выполнения
до потолка). Этот выбрасываемый «газовый балласт» компенсирует умень-
уменьшение подъёмной силы, обусловленное уменьшением плотности воздуха
с высотой.
Однако, использование лёгкого газа в качестве «балласта» приводит
к трудностям при спуске стратостата. Дело в том, что так же, как для
плавного подъёма, подъёмная сила должна лишь совсем немного превышать
вес стратостата, для плавного спуска подъёмная сила должна быть лишь
21 с. Э. Хдчкин

322 гидростатика и аэростатика [i.n. xvi
немного меньше веса стратостата. Практически можно считать, чю как
при подъёме, так и при спуске подъёмная сила должна быть равна весу
стратостата. Между тем, если стратостат поднялся до потолка и, значит,
использовал часть лёгкого газа в качестве «балласта», то при спуске газ
будет занимать меньший объём, чем он занимал на той же высоте при
подъёме. Подъёмная сила окажется заметно меньше, чем вес стратостата,
и для того чтобы обеспечить плавный спуск, необходимо соответственно
уменьшить вес стратостата, выбрасывая балласт. Таким образом, плавный
спуск стратостата, поднявшегося до потолка, невозможен без запаса бал-
балласта. Этот необходимый запас балласта понижает потолок стратостата?
Потолок практически определяется не тем, что стратостат не может под-
подняться выше, а тем, что, поднявшись ещё выше, он не мог бы потом плавно
спуститься.
Мы не учитывали изменений температуры воздуха с высотой и газа
в оболочке (вследствие нагревания Солнцем и теплообмена с окружающим
воздухом). Эти изменения, которые в действительности всегда происходят,
существенно изменяют всю картину и очень усложняют задачу плавного
подъёма и спуска стратостата.
§ 116. Жидкость в движущихся сосудах
Часто встречаются случаи, когда жидкость движется вместе с сосудом
так, что по отношению к сосуду она покоится. Если сосуд движется без
ускорений, то никаких новых вопросов не возникает, так как для этого
случая полностью остаётся в силе всё то, что было сказано выше о покоя-
покоящейся жидкости. Однако, когда сосуд движется с ускорением, также может
оказаться, что жидкость относительно сосуда покоится. Примером может
служить «жидкий маятник», которым мы пользовались для демонстрации
явления приливов (§ 98). Когда маятник колеблется свободно, жидкость
покоится относительно сосуда. В этом случае жидкость ведёт себя не так,
как в покоящемся сосуде. Это видно хотя бы из того, что в колеблющем-
колеблющемся «жидком маятнике» поверхность жидкости не остаётся горизонтальной.
Поведение жидкости в движущемся сосуде удобно рас-
сматривать с точки зрения наблюдателя, движущегося
fr вместе с сосудом.
i\ Прежде всего рассмотрим вопрос о форме поверхно-
<а\ сти жидкости, движущейся вместе с сосудом. Выделим
| ' \ на границе жидкости тонкий элемент объёма, приле-
прилегающий к поверхности жидкости. Со стороны соседних
слоев жидкости на него могут действовать силы давле-
давления, нормальные к границам элемента. Если элемент
взять достаточно тонким, то силы, действующие на бо-
боковые грани, будут исчезающе малы и результирующая
сила Р (рис 249) нормальна к поверхности элемента.
Чтобы выделенный элемент жидкости находился в по-
покое, сумма всех других сил, действующих на него,
должна быть также нормальна к поверхности элемен-
Рис. 249. та- Следовательно, поверхность жидкости всегда уста-
устанавливается таким образом, чтобы сумма всех сил,
действующих на частицы жидкости, кроме сил давле-
давления, была нормальна к поверхности. Поэтому в частном случае, когда
на жидкость действует только сила тяжести, поверхность жидкости гори-
горизонтальна.
Пользуясь этим положением, мы легко сможем объяснить поведение
жидкости в качающемся сосуде. С точки зрения наблюдателя, движущегося
вместе с сосудом, на элемент жидкости действуют сила тяжести mg

§ 116]
жидкость В Движущихся сосудах
323
(рис. 249) и сила инерции — mj, где / — тангенциальное ускорение маятни-
маятника. Центробежная сила инерции, обусловленная центростремительным
ускорением маятника, здесь не играет существенной роли, и мы для упро-
упрощения её не вводим. Но ускорение j обусловлено составляющей силы тя-
тяжести в направлении движения маятника. Следовательно,
то/г
Рис. 250.
На частицы жидкости массы т действуют силы mg и— mj'— — mgsin<x,pan-
нодействующая которых должна быть направлена вдоль радиуса ОА. Она
должна уравновешиваться силой давления прилегающих слоев жидкости р,
и поэтому поверхность жидкости в маятнике
нормальна к этой равнодействующей, т. е. к
направлению радиуса.
С точки зрения неподвижного наблюдателя
на частицу жидкости действуют только сила
давления прилегающих слоев Р и сила тяже-
тяжести mg. Их равнодействующая> и сообщает
частице такое же ускорение /, какое имеет
сосуд.
Рассмотрим теперь поведение жидкости во
вращающемся сосуде. Если сосуд привести во
вращение, то вследствие сил вязкости жидкость
принимает участие во вращении и в конце кон-
концов вращается вместе с сосудом. При этом
поверхность жидкости принимает форму.пара-
форму.параболоида вращения (рис. 250). После того, как
это движение установилось, мы можем (с точ-
точки зрения вращающегося наблюдателя) рассматривать жидкость как поко-
покоящуюся. Воспользуемся системой координат, вращающейся вместе с чаш-
чашкой. Вращающийся наблюдатель должен ввести, кроме силы тяжести mg,
центробежную силу инерции mafir, где т — масса частицы жидкости. По
сказанному выше, равнодействующая этих сил Р должна быть нормальна
к поверхности жидкости. Поэтому
tg а = —f-,
где а— угол между F и mufir, а вместе с тем и угол между касательной
к сечению поверхности и осью вращения. Тангенс этого угла обратно
пропорционален г — расстоянию от оси до точки касания. Это — свойство
параболы.
Нетрудно объяснить форму поверхности жидкости и с точки зрения
неподвижного наблюдателя. На элемент жидкости, лежащей у поверхно-
поверхности, действует сила тяжести mg и сила давления прилегающих слоев Р
(рис. 250). Сумма этих сил должна сообщать элементу жидкости цент-
центростремительное ускорение, необходимое для вращения по окруж-
окружности радиуса г, т. е. должна быть равна mufir и направлена к оси
вращения.
Так же, как с поверхностью жидкости в чашке, обстоит дело с поверх-
поверхностью воды в больших водных пространствах (в океанах). Поверхность
воды должна быть в каждой точке нормальна к равнодействующей силы
тяжести и центробежной силы, т. е. к направлению отвеса в данной точке.
Так как направление отвеса не совпадает с направлением к центру Земли,
то поверхность воды, покрывающей Землю, не представляет собой точно
шаровой поверхности, а несколько сплюснута к полюсам. Этим в извест-
известной степени объясняется и сплюснутая к полюсам форма самого земного
21*

324
ГИДРОСТАТИКА Н AapOCTAtHKA
[_ГЛ. XVI
шара. Когда Земля была ещё жидкой, её поверхость приняла такую фор-
форму, какую сейчас имеет поверхность воды в океанах*).
Если с точки зрения движущегося наблюдателя жидкость покоится, то
вопрос о распределении давлений в жидкости решается так же, как для по-
покоящейся жидкости. Необходимо лишь принять во внимание, что на покоящую-
покоящуюся в сосуде жидкость действует не только сила тяжести, но и силы инер-
инерции, обусловленные ускорением сосуда. Например, сразу ясно, что в жид-
жидкости, свободно падающей вместе с сосуном, давление во всех точках бу-
будет одно и то же. Сила тяжести будет уравновешена силой инерции,
и изменения давления с высотой, обусловленные силой тяжести, исчезнут.
Исчезнет также давление жидкости на стенки и дно сосуда и подъёмная сила.
Точно так же для жидкости, вращающейся вместе с сосудом, кроме
силы тяжести, нужно ввести ещё центробежную силу инерции. Эта послед-
последняя в описанном выше опыте с вращающимся сосудом лежит в горизон-
горизонтальной плоскости, поэтому она изменяет распре-
распределение давлений только по горизонтали. По вер-
вертикали изменения давления с высотой должны быть
такими же, как в покоящейся жидкости (условия
равновесия для вертикальной призмы остаются
прежними). Отсюда сразу видно, что на данном
уровне давление в горизонтальной плоскости растёт
от оси к стенкам чашки (так как растёт высота
столба до свободной поверхности). На каждый
элемент жидкости с внешней стороны действует
п rj-vi^ большая сита, чем с внутренней: Рх> Р* (рис. 251).
•*{?*¦ i Равнодействующая этих сил и сообщает эле-
"¦" * менту жидкости необходимое центростремитель-
центростремительное ускорение (с точки зрения неподвижного
наблюдателя). Эта разность давлений в горизонталь-
горизонтальной плоскости является причиной возникновения
своеобразной «подъёмной силы», направленной от
периферии к оси вращения (так же, как разность
давлений по вертикали является причиной возникновения обычной подъём-
подъёмной силы).
Если во вращающуюся жидкость погружено тело меньшей плотности,
чем жидкость, то эта «подъёмная сила» приводит к тому, что тело движет-
движется к оси вращения. Для объяснения представим себе, что мы удалили
тело и заполнили его место жидкостью. Вследствие разности давлений на
элемент жидкости будет действовать как раз та-
такая сила тч>гг, которая необходима для движения
элемента жидкости по окружности. Вернём те-
теперь тело в жидкость. Если плотность тела мень-
меньше, чем плотность жидкости (масса меньше массы
объёма жидкости), то оно получит центростре-
центростремительное ускорение, большее, чем жидкость, и,
значит, будет приближаться к оси. Наоборот, тело
более плотное, чем жидкость, получит меньшее
ускорение, чем то, которое нужно для вращения,
и будет удаляться от оси. Это обстоятельство и
исполыуется в центрифугах, сепараторах и т. д. В центрифуге более тяжё-
тяжёлые частицы (муть) движутся наружу. В молочном сепараторе более
лёгкие частицы (жир) перемещаются к оси вращения.
Рис. 251.
Рис. 252.
*) Таким же образом можно было бы более детально, чем это было
сделано раньше, объяснить и явление приливов. Задача опять сводится
к определению формы, которую примет жидкость в движущемся сосуде,
роль которого играют водные бассейны земного шара.

§ П7]
Поверхностные явления 325
Принцип действия центрифуги и сепаратора можно продемонстрировать
с помощью следующего устройства. В изогнутую стеклянную трубку, на-
наполненную водой, помещают два щарика с плотностью большей и мень-
меньшей, чем плотность воды (рис. 252). Тяжёлый шарик лежит внизу, а лёгкий
плавает наверху. При быстром вращении трубки лёгкий шарик переме-
перемещается к оси вращения («всплывает наверх»), а более тяжёлый удаляется
от неё («опускается на дно»).
§ 117. Поверхностные явления
Мы предполагали, что силы, действующие между отдельными соприка-
соприкасающимися частями жидкости, — это только силы давления, направленные
нормально к плоскости соприкосновения. Однако, в реальной жидкости
существуют и силы другого типа, которые вызывают ряд явлений, нося-
носящих общее название поверхностных явлений. Мы не будем изучать этих
явлений — это задача молекулярной физики; тем не менее и в механике
жидкостей с этими явлениями иногда приходится считаться. Мы выясним,
при каких условиях эти явления возникают, для того чтобы знать, когда
с ними необходимо считаться.
О существовании каких-то других сил, кроме сил нормального давле-
давления, говорит самый факт существования капель жидкости. Капля ртути на
стекле не расплывается, но принимает сплюснутую
форму (рис. 253). Выделим на поверхности капли
плоский элемент объёма. На него действуют сила
тяжести mg и сила нормального давления Р. Эти
две силы не могут обеспечить равновесия элемента
объёма. Поскольку, од «ко, он находится в равно-
равновесии, то, следовательно, существует ещё какая-jo
третья Сила F, причём
Эта сила F направлена внутрь капли. Роль этой Рис. 253.
силы тем более заметна, чем меньше размеры
капли. Это видно из того, что чем меньше
размер капли, тем менее она сплюснута. Следовательно, в малой капле
сила F имеет большее значение по сравнению с силой mg, чем в большой
капле.
Сила F, направленная внутрь капли, представляет собой результирую-
результирующую тех сил притяжения, которые существуют между отдельными молеку-
молекулами жидкости. Направление и величина равнодействующей этих сил зави-
зависят от расположения молекул вокруг данного элемента объёма жидкости
Если рассматриваемый элемент объёма лежит внутри жидкости, то силы
притяжения, действующие на молекулы объёма со стороны окружающих
молекул, всегда должны в сумме дать нуль (вследствие симметричного
расположения молекул). Если же рассматриваемый элемент объёма лежит
на границе жидкости или прилегает к какому-либо другому телу, то сим-
симметрия в распределении молекулярных сил нарушается и равнодействую-
равнодействующая этих сил оказывается не равной нулю. Тогда-то и возникают новые
явления, с которыми в механике жидкостей иногда приходится считаться.
Прежде всего эти силы сказываются на форме поверхности вблизи
стенок сосуда. Силы притяжения между молекулами жидкости и молеку-
молекулами жидкости и стенки сосуда могут быть различны. Если последние боль-
больше первых, то их равнодействующая F для элемента объёма, близкого к
стенке (рис. 254, а), будет отклонена от нормали в сторону стенки сосу-
сосуда. Поэтому и равЕюдействующая этой силы F и силы тяжести mg бу-
будут отклонены к стеме сосуда. Поверхность жидкости должна быть нор-
нормальна к этой равнодействующей, так как она уравновешивается силой

326
ГИДРОСТАТИКА И АЭРОСТАТИКА
[гл. xvi
нормального давления Р прилегающего слоя жидкости; следовательно, по-
поверхность жидкости должна повышаться к стенке. Поверхность жидкости
у стенки имеет вогнутую форму — жидкость «смачивает» стенку.
Наоборот, если силы молекулярного притяжения между молекулами
жидкости больше, чем между молекулами жидкости и стенки, то равно-
равнодействующая этих сил F будет отклонена в сторону, противоположную
стенке (рис. 254, *). Поверхность жидкости у стенки будет иметь выпуклую
форму — жидкость не смачивает стенки.
Силы молекулярного притяжения не только приводят к искривлению
поверхности, но и придают поверхности жидкости особые свойства. На
молекулы жидкости, лежащие на поверхности, действуют силы молекуляр-
молекулярного притяжения, направленные внутрь жидкости. Поверхность жидкости
?\
Рис. 254.
подобна мягкой плёнке, которая удерживается бесчисленным множеством
упругих нитей, направленных внутрь жидкости.
Поверхностная плёнка жидкости действует с некоторой силой на тела,
с которыми она соприкасается и на которые она «натянута». Эти силы
называют силами поверхностного натяжения. Сила поверхностного на-
натяжения зависит не от площади плёнки, а от длины границы плёнки.
Сила поверхностного натяжения пропорциональна этой длине.
Если поверхность жидкости искривлена, то силы поверхностного натя-
натяжения могут сказаться на поведении всего объёма жидкости (а не только
её поверхностной плёнки). Например, в случае смачивающей жидкости
в тонкой трубке силы поверхностного натяжения вследствие искривления
поверхности дают значительную вертикальную составляющую; поверхност-
поверхностное натяжение как бы втягивает жидкость в трубку. Поэтому в капил-
капиллярных трубках смачивающие жидкости поднимаются выше того уровня,
который они занимают в широких трубках. Вес столба жидкости отчасти
уравновешивается составляющей поверхностного натяжения. Наоборот,
иесмачивающие жидкости (ртуть) в тонких трубках стоят на более низком
уровне, чем в широких. Силы, обусловленные поверхностным натяжением,
растут пропорционально периметру трубки (длине окружности плёнки), а
вес столба жидкости растёт пропорционально сечению трубки, т. е. быст-
быстрее* Поэтому в толстых трубках поверхностное
натяжение не изменяет заметно высоты стол-
столба жидкости. Для измерения давлений следует
брать трубки достаточно большого диаметра.
Точно так же около тел, плавающих иа по-
поверхности несмачивающей жидкости, эта поверх-
поверхность имеет выпуклую форму (рис. 255). Силы
ния дают вертикальную составляющую.
—ч:
Рис. 255.
поверхностного
которая прибавляется к
натяже-
подъём-
иой силе жидкости. " Поэтому иголка, смазанная жиром (чтобы она
не смачивалась водой), плавает по поверхности воды. Но и в это»
случае при увеличении размеров тел силы поверхностного натяжения
растут пропорционально периметру тела, а подъёмная сила — пропорцио-
пропорционально площади. Для тел больших размеров составляющая силы поверх.^

§ 117] ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ 327
ностного натяжения исчезающе мала по сравнению с подъёмной силой.
Если положить на воду большой алюминиевый диск, то он также будет
держаться на воде и даже удерживать некоторый груз. Однако, вес диска
и груза уравновешивается не силами поверхностного натяжения, а давле-
давлением (снизу) воды на слегка погруженный диск. При расчёте подъёмной
силы можно вовсе не принимать во внимание силы поверхностного натя-
натяжения. Их роль сводится только к тому, что они удерживают воду и соз-
создают «борт» по краям диска. Конечно, при увеличении нагрузки диск будет
погружаться больше, «борт» вокруг него разрушится и диск потонет.
В газах силы молекулярного притяжения исчезающе малы и с поверхно-
поверхностными явлениями можно вообще не считаться. Отсутствие поверхностного
натяжения является в сущности одним из основных признаков, по которым
отличают газообразное состояние от жидкого.

ГЛАВА XVII
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
§ 118. Стационарный ток жидкости
При описании движения жидкости и газа можно было бы сле-
следить за движением каждой отдельной частицы жидкости, изучать ее
траекторию, скорость и ускорение. Представление о траектории от-
отдельных частиц жидкости мы могли бы получить, отмечая каким-либо
образом эти отдельные частицы, например, бросая на поверхность
текущей жидкости крупинки какого-либо лёгкого нерастворяющегося
порошка Вместе с тем мы подучили бы представление о скорости
каждой отдельной частицы жидкости.
J? Однако, можно иначе описать дви-
движение жидкости. Вместо того чтобы
следить за каждой индивидуальной
частицей, можно изучать скорости
и ускорения, которые в тот или иной
момент имеет всякая частица, про-
проходящая через определённую точку
потока. В этом случае говорят о
скоростях и ускорениях потока {в от-
отличие от скоростей частиц) Если мы
будем знать распределение скоростей
и ускорений в потоке и зависимость этого распределения от вре-
времени, то движение жидкости будет полностью определено
Распределение скоростей в потоке можно охарактеризовать при
помощи так называемых линий тока. На рис. 256 распределение ско-
скоростей частиц в потоке в данный момент изображено маленькими
стрелками. Проведём линии, которые во всех точках касателыш
к этим стрелкам Такие линии, к которым скорость в каждой точке
является касательной, называются линиями тока.
Распределение скоростей в потоке может изменяться со временем.
Вместе с тем изменится и вид линий тока. Линии тока при этом не
совпадают с траект^иями отдельных частиц Действительна, касатель-
касательными к линии тока являются скорости различных частиц, находя-
находящихся в данный момент, например, в точках А и В (рис. 256). Ка-

§ 118)
СТАЦИОНА°ЧЫЙ ТОК ЖИДКОСТИ
329
сательными же к траектории частицы являются скорости одной и той
же частицы, когда она находится в А и в В, т. е. в различные мо-
моменты времени. И если распределение скоростей в потоке меняется
со временем, то за время, пока данная частица дойдет от А до В,
скорость её в точке В может оказаться другой.
Часто распределение скоростей в потоке не изменяется со време-
временем, хотя скорости отдельных частиц со временем изменяются. Вся-
Всякая частица, пришедшая в какую-либо точку потока, имеет в этой
точке такую же скорость, какую имели в этой точке и все предше-
Хакой
Рис 257.
поток называется стаиио-
наршм.
В апационарном по-
потоке линии тока совпа-
совпадают с траекториями
отдельных частиц, так
как скорость в данной
точке не изменяется за
время движения частицы
Вместе с аем траектории
частиц и линии тока в
стационарном потоке не
изменяются со временем.
Наглядное представле-
представление о линиях тока в ста-
стационарном потоке можно
получить, выпуская в теку-
щую жидкость тонкие
струйки густой краски.
Для этого служит плоский сосуд, снабжённый трубочками с тонкими оъ
верстиями; трубочки погружены в поток жидкости, краска из сосуда под
небольшим давлением медленно вытекает из отверстий (рис. 257). Эти
струйки краски, двигаясь вместе с частицами жидкости, дают представле-
представление о траектории частиц, а значит (в случае ста-
стационарного потока), и о линиях тока С помощью
этой установки можно получить картину распре-
распределения линии тока в различных случаях ста-
ционзрного течения На рис. 258 для примера схе-
схематически изображены линии тока для потока,
обтекающего пластинку.
Если течение стационарно, то поверхность,
образованная линиями тока, представляет собой
как бы непроницаемую трубку. Ни одна из частиц
жидкости, находящихся внутри такой трубки, при
движении не выйдет за ее пределы (так как скорости частиц около по-
поверхности всегда касательны к поверхности) Вся жидкость или газ, про-
прошедшие через одно сечение такой трубки, должны пройти и через
любое другое её сечение. Если сечение трубки выбрать достаточно
Рис. 258

330 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [ГЛ. XVII
малым, то скорость жидкости во всех точках одного и того же се-
сечения можно считать одинаковой. Такие достаточно тонкие трубки
носят название токовых трубок.
Масса жидкости или газа, прошедшая за время \t через какое-
либо нормальное сечение токовой трубки площадью S, выразится
так:
где v — скорость частиц в этом сечении, а р — плотность, которую
имеет жидкость или газ у этого сечения. При стационарном течении
за одни и те же промежутки времени через два различных сечения
S, и S2 одной и той же трубки тока должны проходить одинаковые
массы жидкости или газа. В противном случае изменялось бы коли-
количество жидкости в отрезке трубки, ограниченном сечениями, и тече-
течение не было бы стационарным. Поэтому
где vx и w2 — скорости жидкости или газа, a pj и р3 — их плотности
у сечений S1 и Sv
При стационарном течении не только жидкостей, но даже газов
изменениями плотности обычно можно пренебречь и даже газы рас-
рассматривать как несжимаемые жидкости. Рассматривая жидкости и га-
газы как несжимаемые, мы поступаем так же, как поступали, вводя
представление об абсолютно твёрдом теле. Мы вовсе не пренебре-
пренебрегаем изменениями' сил, т. е. давлений, которые обусловлены именно
изменением степени сжатия. Но мы предполагаем, что уже при ма-
малых изменениях степени сжатия возникают силы, достаточные для
того, чтобы дальнейшее изменение объёма прекратилось. Для жидко-
жидкостей это верно в большинстве случаев. К течению газов это пред-
представление применимо, пока скорости течения и искусственно созда-
создаваемые разности давлений невелики. Например, как будет показано
ниже, при течении газа под давлением, близким к атмосферному,
и при скоростях порядка десятков MeTpjB в секунду разность давле-
давлений в различных местах потока может изменяться только на сотые
доли атмосферного давления. Сами по себа эти разности давлений
весьма существенны для всей картины в потоке, и ими нельзя пре-
пренебрегать. Но относительно атмосферного давления, под которым
находится газ, эти изменения давлений малы, и поэтому связанными
с ними изменениями плотности газа вполне можно пренебречь. По-
Поэтому во всех случаях, когда мы будем рассматривать стационарное
движение жидкостей и газов, мы будем пренебрегать сжимаемостью
не только жидкостей, но и газов. Для краткости мы дальшз будем
говорить только о жидкостях, хотя всё сказанное будет применимо
к газам, пока можно пренебречь их сжимаемостью.

§ 119] ДАВЛЕНИЕ В ТЕКУЩЕЙ ЖИДКОСТИ. ЗАКОН БЕРНУЛЛИ 331
Если плотность жидкости не изменяется, то для двух сечений
токовой трубки вместо A7.1) мы можем написать:
^1 —-3 (\7 2\
Там, где сечение трубки уменьшается, скорость потока возрастает.
Поэтому расположение линий тока позволяет судить о распределении
скоростей в потоке. Например, в случае, изображённом на рис. 256,
скорость в сечении CD больше, чем в сечении EF.
Мы рассматривали достаточно тонкие трубки тока для того, чтобы
иметь право во всём сечении трубки считать скорость потока одинако-
одинаковой. Но если скорости во всех точках каждого сечения потока мало
отличаются друг от друга, то можно говорить о скорости в сечении
потока и вместо тонких трубок тока рассматривать весь поток как
одну трубку тока. Написанные выше соотношения относятся тогда ко
всему потоку в целом.
§ 119. Давление в текущей жидкости. Закон Бернулли
При изучении движения жидкости прежде всего необходимо уста-
установить, как будет измеряться давление в текущей жидкости (мы знаем
пока только, как измеряется дав-
давление в покоящейся жидкости).
Давление — это отнесённая к еди-
единице площади сила, с которой
один элемент жидкости действует
на другой. Чтобы измерить давле-
давление в движущейся жидкости, нуж- Рис. 259.
но вместо одной из частиц жидко-
жидкости Поместить манометр и заставить этот манометр двигаться так, как
двигалась бы частица в потоке. Тогда мы сможем утверждать, что
измеряем силы и давления, с которыми действовали бы друг на друга
две частицы, движущиеся в потоке.
При рассмотрении связи между скоростью и давлением в потоке
жидкости мы будем полагать, что силы вязкости отсутствуют, т. е.
будем рассматривать идеальную (невязкую жидкость). В дальнейшем
мы выясним (правда, только качественно), как влияют силы вязкости
на результаты нашего рассмотрения.
Выделим в стационарном потоке участок трубки тока, ограничен-
ограниченный сечениями 1 а 2 (рис. 259). Обозначим для этих сечений через
Sl и S2 площади, vx и v2 — скорости, />, и р2 — давления жидкости
и, наконец, через hx и /г2 — высоты, на которых находятся сечения.
К элементу жидкости, заключённому между сечениями, мы могли бы
применить второй закон Ньютона. Но поскольку силы трения отсут-
отсутствуют, вместо законов Ньютона можно сразу применить закон со-
сохранения энергии. Изменение энергии рассматриваемого элемента

332 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [ГЛ. XVII
жидкости должно быть равно работе внешних сил. Внешними силами для
рассматриваемого элемента являются сила тяжести и силы давления,
действующие на объём через сечения / и 2. Силы давления, действую-
действующие на боковые стенки трубки, н ^мальны к стенкам и работы не
совершают, так как движения жидкости в направлении, нормальном
к поверхности трубки, не происходит.
За малое время Д? рассматриваемый элемент жидкости переместится
по трубке. Его границы займут положения /' и 2'. Левая граница
переместится на v^t, а правая на v^M. Энергия элемента жидкости
при этом изменится, но так как поток стационарный, то энергия
заштрихованной части элемента останется неизменной, Всё изменение
энергии элемента жидкости будет таким же, как если бы левый слой,
заключённый между / и /', занял бы место правого слоя, заключён-
заключённого между 2 и 2'. При Д', а значит н v\t достаточно малом можно
эти слои считать цилиндрическими. Их объёмы
должны быть равны (так как жидкость несжимаема и поток стацио-
стационарный). Поэтому
Объём AQj обладает массой Д/Kj =*= p\Qv Его потенциальная энер-
энергия:
и кинетическая энергия:
ДГ,= j
Аналогично выразятся потенциальная и .кинетическая энергии
объёма ДС?2:
Д?/3 = р^2Д'ghv ДГ2 = -| 4
Изменение полной энергии всего рассматриваемого обьёма есть
\W= (ДГ3 — Д7\) + (Д?/2 - Af/j) =
-? (s2v\— syj м.
Внешние силы (силы давления), действующие на рассматриваемый
объём через сечение /, направлены в сторону перемещения жидкости
и совершают положительную работу. Наоборот, внешние силы, дейст-
действующие через сечение 2, направлены против перемещения жидкости
и совершают отрицательную работу. Поэтому вся работа внешних
сил pxSx и ргЭг при перемещениях vx\t и v2M будет равна
ДЛ =

§ H9j ДАВЛЕНИЕ В ТЕКУЩЕЙ ЖИДКОСТИ. ЗАКОН БЕРНУЛЛИ 333
По закону Охранения энергии Д№=ДД. Подставляя их выражения
и сокращая на 5,г>,Д^ или S^o^t (так как S1vl = Szvi), получим:
—*i)+ j(vl~ ®?)=Pi — Рг
или
Так как сечения выбраны произвольно, то для всех сечений данной
трубки тока
Это уравнение было выведено Даниилом Бернулли A738 г.). Урав-
Уравнение Бернулли Даёт закон изменения давления р с изменением вы-
высоты h и скорости потока v.
Если скорости потока vt и г>2 у двух сечений трубки равны, то
или
т. е. разность давлений равна весу столба жидкости между уровнями
сечений. В том случае, когда скорость в сечениях трубки одинакова,
разность давлений оказывается такой же, как в покоящейся жидкости.
Если скорость в разных сечениях трубки различна, то распределе-
распределение давлений изменяется по сравнению с тем, которое существовало
бы в покоящейся жидкости:
- *а)+\ К - *?)•
Давление уменьшается там. где скорость потока возрастает.
В частном случае горизонтального потока hx — А2 = 0и
р,—Р1=|И—«D- <17'4)
В этом случае изменения давления в потоке обусловлены только
изменением скорости. Там, где линии тока сгущаются и скорости воз-
возрастают, давление уменьшается. Необходимость этого станет очевид-
очевидной, если рассмотреть движение отдельных элементов жидкости с точки
зрения второго закона Ньютона. Всякий элемент жидкости, двигаясь
по токовой трубке уменьшающегося сечения, должен увеличивать свою
скорость. А для этого на элемент должна действовать сила в направ-
направлении его движения; следовательно, давление на передней границе
элемента должно быть меньше, чем на задней.
Эти изменения давления обусловлены изменениями степени сжатия
текущей жидкости при изменении сечения потока. Как и в случае

334
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл.
XVII
твёрдого тела, для объяснения происхождения сил, возникающих в теле,
необходимо принять во внимание деформации тела. Изменения давле-
давления, вытекающие из закона Бернулли, связаны с тем, что данный
элемент жидкости, «втискиваясь» в более узкое сечеиие трубки тока,
вовсе не уменьшает, а увеличивает свой объём.
Рассматривая жидкость как несжимаемую, мы считали эти объёмы
равными. В действительности же, переходя в более узкое сечение,
данная масса жидкости увеличивает свой объём, степень сжатия её
уменьшается, и поэтому давление в жидкости падает.
Закон Бериулли относится к отдельным трубкам тока. Но если в потоке
можно выбрать такие сечения, в которых скорости по всему сечению оди-
одинаковы, то весь поток можно рассматривать как одну трубку тока и приме-
применять ко всему потоку
закон Бернулли. На-
Например, в трубке с
переменным сечением
(рис. 260) к сечениям
/, 2, 3 можно приме-
применять закон Бернулли.
Если в этих сечениях
установить маноме-
Рис. 260. Рис. 261. трические трубки, то,
как показывает опыт,
уровень воды в трубках устанавливается в соответствии с законом
Бернулли *). В узком сечении, где скорость потока больше, уровень
воды в манометрической трубке ниже, т. е. давление меньше.
Можно видоизменить этот опыт так, как указано на рис. 261. В правом
открытом конце трубы давление равно атмосферному. Поэтому в узкой части
трубы (где скорость больше, чем у отверстия) давление ниже атмосфер-
атмосферного. Вследствие этого
ртуть по манометриче-
манометрической трубке поднимается
вверх. Это явление ис-
используется в водоструй-
водоструйных и пароструйных на-
насосах (инжекторах). —•
Если поместить ие- —
подвижный манометр
внутрь потока жидко-
жидкости, то он будет также
измерять давление в
жидкости, но при этом характер потока вследствие присутствия непод-
неподвижного мандметра изменится. В частности, если манометрическая
трубка поставлена отверстием к потоку (рис. 262), то скорость жидко-
жидкости перед отверстием будет равна нулю. Линии тока возле маномет-
манометра будут иметь вид, изображённый на рис. 263. Применяя к этому
Рис. 262.
Рис. 263.
*) Количественного соответствия с законом Бернулли в этом опыте не
получается. Явление осложняется действием сил вязкости, роль которых
выяснится позднее.

§ 119] ДАВЛ1 I1HL В Ti КУЩСЙ ЖИДКОСТИ. ЗАКОН ВЕРНУЛЛИ 335
случаю закон Бернулли A7.4) и подставляя v2=0, получим:
Неподвижный манометр, обращенный отверстием к потоку, изме-
измерит большее давление, чем манометр, движущийся вместе с потоком.
Избыток давления равен pt>^2. Происхождение этого избыточного
давления совершенно очевидно. Частицы жидкости, останавливаясь
перед манометром, сжимаются, и вследствие этого давление повы-
повышается. Создаётся «динамический напор» *).
Теперь мы можем дать себе отчёт в том, в каких случаях можно пре-
пренебрегать сжимаемостью газов. Наибольшее увеличение давления,
которое может получиться приостановке потока, равно рг;г/2, где г; —
максимальные скорости, встречающиеся в потоке. Это избыточное
давление обусловлено тем, что в местах остановки (или замедления)
потока газ оказывается сжатым сильнее, чем в невозмущённом потоке.
Очевидно, дополнительное сжатие газа будет тем менее заметно, чем
меньше pw2/2 по сравнению с давлением р в невозмущённом потоке.
Следовательно, дополнительное сжатие газа не играет существенной
роли, пока pf2/2<^p или w<^l,4 Vpjp- Как мы увидим ниже (§ 132),
скорость звука в газе с =^ 1,2 V^P/p» и, следовательно, сжимаемостью
газов можно пренебрегать, пока наибольшие скорости в потоке малы
по сравнению со скоростью звука в этом газе.
Неподвижная манометрическая трубка, помещённая отверстием
к потоку, носит название трубки Пито. Так как трубка Пито изме-
измеряет давление
/>2=/>, + У". A7.5)
то, зная давление р1 в движущемся (неостановленном) потоке, по
показаниям трубки Пито можно определить скорость потока.
*) Величину р№/2 иногда называют «динамическим давлением». Вместе
с тем «настоящее» давление р называют «статическим давлением», а сумму
/? —{- рс2/2 — «полным давлением». Термины эти вряд ли можно признать
удачными. В жидкости при данных условиях есть только одно давление, ко-
которое мы обозначали через р. Если жидкость остановить, то это «настоящее»
давление возрастёт на рг»2/2. Следовательно, «динамическое давление» —
это то увеличение давления, которое произойдёт, если жидкость остановить.
«Динамическое давление» — это, так сказать, «будущий избыток давления»,
которого нет в потоке, но который появится при остановке жидкости. Точно
так же и «полное давлении» — это «будущее давление», которому будет равно
«настоящее давление» в остановленном потоке.
Все эти ел жные рассуждения становятся излишни, если не пользо-
пользоваться терминами «статическое», «динамическое» и «полное» давление.
Если же с этими терминами придётся встретиться то нужно лишь помнить,
что «статическое давление» — это и есть единственное «настоящее» давле-
давление в жидкости.

336
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[ГЛ. XVII
к коленам<г~у
нанометра ^-*
Для измерения давления в движущемся потоке необязательно применять
манометр, движущийся вместе с потоком. Если небольшую трубку с отвер-
отверстием в боковой части поместить вдоль потока (рис. 264), то везде, кроме кон-
конца трубки расположение токовых линий остаётся почти таким же, как и в
отсутствии трубки. Поэтому у небольших отверстий в боковых частях трубки
давление будет таким же, как в неостановленном потоке.
Такая трубка называется зондом. Манометр, соединённый
с зондом, показывает давление Pi в неостановленном
потоке.
При помощи какого-либо манометра, измеряющего раз-
разность давлений в трубке Пито и зонде, можно измерить
разность давлений рг и рх и по формуле A7.5) опре-
определить скорость потока. Этим способом очень широко
пользуются для измерения скорости потока. Труб-
• ку Пито и зонд обычно комбинируют в виде двух кон-
Рис. 264. центрических трубок (ряс. 265). Внутренняя трубка
имеет отверстие на конце, наружная — ряд отверстий в
средней части. Обе трубки присоединяются к концам манометра, измеряю-
измеряющего разность давлений. Показания манометра прямо позволяют опреде-
определить скорость потока. Этот же прибор позволяет определить скорость
движения относительно воздуха. Таким указателем
скорости пользуются на самолётах.
Закон Бернулли, строго говоря, применим только
к отдельным токовым трубкам. Для разных токовых
трубок значение постоянной в уравнении Бернулли
A7.3), вообще говоря, будет различным. Но в некото-
некоторых частных случаях закон Бернулли можно применять
ко всему потоку в целом.
Один такой случай был указан выше — именно,
когда скорости во всех сечениях потока одни и те же.
Можно также применять закон Бернулли ко всему
потоку в случае, когда все трубки тока выходят из
области, в которой скорости очень малы (или, наобо-
наоборот, все трубки тока приходят в эту область). Тогда в этой области можно
пренебречь членами с V- в уравнении A7.3), а так как pgh-\-p для покоя-
покоящейся жидкости во всей области
имеет одно и то же значение, то и
постоянная в уравнении Бернулли
для всех токовых трубок будет одна
и та же. Поэтому уравнение Бернул-
Бернулли можно применить ко всему по-
потоку в целом.
Эти соображения можно приме-
применить для объяснения следующего
явления. Если через насадку, изобра-
изображённую на рис. 266, пропускать
струю таза (из баллона со сжатым
газом), то нижняя подвижная пластинка начинает стучать о верхнюю.
Скорость газа у края насадки уже мала. По сказанному выше, уравнение
Бернулли можно применить ко всему потоку в целом. Но токовые
линии расходятся от центра насадки к краям. С другой стороны,
давление у края насадки рапно атмосферному и везде ближе к центру (где
линии тока гуще) оно меньше атмосферного. Внешнее (атмосферное) да-
давление прижимает нижнюю пластину к верхней, и течение газа прекращается.
Но тогда статическое давление газа в баллоне снова отодвигает пластину
и пластина прыгает взад и вперёд.
Рнс. 265.
Рис. 266.

§ 120] применение законов сохранения 337
§ 120. Применение законов сохранения к движению жидкостей
Помимо закона сохранения энергии, на основании которого мы
вывели уравнение Бернулли, к движению жидкостей могут быть при-
применены и законы сохранения количества движения и момента количе*
ства движения.
Внешние силы, действующие на данный элемент жидкости, опреде-
определяют изменение количества движения элемента жидкости, а ма-
мент внешних сил определяет изменение момента количества движения
элемента жидкости. Можно также рассматривать как систему тел неко-
некоторые части жидкости вместе с твёрдыми телами. При помощи этих
соображений очень просто решается
ряд вопросов о движении жидкости,
например, о реакции текущей жидко-
жидкости на стенки сосуда.
Когда струя жидкости вытекает """
с некоторой скорость» из отверстия
в сосуде (рис. 267), она уносит с С\
собой некоторое количество дви- V-
жения. Если внешние силы отсут- Рис. 267.
ствуют, то общее количество дви-
движения системы сосуд — жидкость должно быть равно нулю. .Свободный
от внешних сил сосуд должен двигаться в направлении, обратном дви-
движению жидкости в струе. И, действительно, если сосуд поставить на
тележку, то при истечении жидкости сосуд с тележкой движется в об-
обратную сторону. Причиной движения сосуда являются силы, которые
действуют со стороны жидкости на стенку сосуда. Пока жидкость по-
покоится, силы давления, действующие на противоположные участки
горизонтальных стенок сосуда, уравновешиваются. При истечении
жидкости в соответствии с законом Бернулли происходит изменение
давлений, и давление на заднюю стенку оказывается ббльшим,
чем на переднюю.
При помощи закона Бернулли легко подсчитать скорость истечения
жидкости яз отверстия. Если сосуд широкий, а отверстие мало, то скорости
жидкости в сосуде малы. Поэтому, как уже было указано, можно применить
закон Бернулли ко всему потоку в целом и рассматривать его как одну токо-
токовую трубку. В верхнем сечении этой «трубки» — у поверхности жидкости —
давление р0 равно атмосферному, а скорость » = 0. В нижнем сечении
«трубки» — в отверстии—давление также равно атмосферному. Если ско-
скорость в отверстии обозначить через v, то по уравнению Бернулли для этих
двух сечений получим:
^ + Pa~?gh-+pa или v—
где h — высота уровня воды в сосуде. Истечение происходит с той же ско-
скоростью, какую имело бы всякое тело при падении с высоты А. Вытекаю-
Вытекающая струя жидкости образует параболу. По форме этой Параболы легко
определить скорость истечения.
22 с. э. хайкин

338
ГИДРОДИНАМИКА И АЭРОДИНАМИКА.
|ГЛ. XVI!
Если площадь отверстия равна S, то масса вытекающей за единицу вре-
времени жидкости будет
т = pSv = pS V2gh-
(Это соотношение правильно только приблизительно, так как сечение струи
всегда немного меньше площади отверстия.) Уносимое жидкостью за еди-
единицу времени количество движения есть
mv = pS-2gh.
Следовательно, и результирующая сила, действующая в направлении струи
со стороны стенок сосуда на жидкость, должна быть равна 2pghS. По треть-
третьему закону Ньютона результирующая сила бокового давления воды на
стенки должна быть равна этой же величине.
Если закрыть отверстие пробкой, то сила давления на пробку будет pghS,
а результирующая сил давления на стенки будет равна нулю. В отсутствие же
пробки появляется результирующее давление не pghS, a 2pghS. Эта раз-
разница объясняется перераспределением давлений в жидкости в соответствии
с законом Бернулли. Вблизи отверстия линии тока сгущаются, и, следова-
следовательно, давление уменьшается. Появление при открытом отверстии резуль-
результирующей сил бокового давления 2pghS
обусловлено, с одной стороны, тем, что
исчезает сила давления pghS на площади
отверстия, а с другой,— тем, что умень-
уменьшается давление на стенки сосуда вблизи
отверстия.
Закон сохранения количества движе-
движения поясняет принцип действия гребных
колеси винтов. Гребные колёса*парохода
~* вызывают движение воды назад, т. е. по-
появление всё новых и новых количеств дви-
движения воды. По закону сохранения коли-
количества движения противоположное коли-
количеств*-движения приобретает пароход. Ту
же роль выполняют и гребные винты паро-
создают не только поступательное движение
Рис. 268.
хода или самолёта. Винты у
воды или воздуха назад, но и вращение отдельных частей объёма воздуха
или воды. Однако это последнее не играет принципиальной роли в действии
винта и является даже вредным, так как на создание этого вращения бес-
бесполезно расходуется часть энергии. Полезная работа винта заключается
в том, что он отбрасывает некоторое количество жидкости или газа назад
и тем самым создаёт силу тяги, направленную вперёд.
При течении жидкости по изогнутой трубе (рис. 268) количество
движения некоторого элемента жидкости хотя и может оставаться
постоянным по величине, если сечение трубы постоянно, но изменяется
по направлению. За единицу времени через сечение 5 втекает масса
жидкости т — pSVy Она приносит с собой количество движения
Через выходное сечение 5 уходит та же масса жидкости, которая
уносит с собой количество движения

§ 121]
РЕАКТИВНОЕ ДВИЖЕНИЙ
339
Количество движения внутри трубы при стационарном течении
остаётся неизменным. Следовательно, изменение количества движения
жидкости за единицу времени (так как скорости по величине равны,
т. е. vl — vi~v)
AN = N3 — N ! = pSv (v2 — Vi).
Оно должно быть равно сумме всех сил, действующих на жидкость
со стороны стенок трубы. Равнодействующая сил давления струи на
стенки (реакция струи R) должна быть равна по величине и противо-
противоположна по направлению сумме сил, действующих со стороны стенок.
Следовательно, реакция вытекающей жидкости направлена в сторону,
противоположную изгибу трубы.
Реакция текущей струи на стенки изогнутой трубки используется в водя-
водяных и паровых турбинах. Струя жидкости, протекая по искривлённым кана-
каналам колеса турбины (рис. 269), создает силы реакции, момент которых
и вызывает вращения колеса турбн- ,
ны. В других конструкциях жидкость
или пар вытекает из неподвижных тру-
трубок, расположенных против лопаток
Рис. 269.
Рис. 270.
колеса турбины (рис. 270). Проходя мимо лопаток, жидкость или пар изме-
изменяет своё количество движения и вместе с тем действует с известной си-
силой на лопатки колеса, приводя его во вращение. Момент сил будет наи-
наибольший в том случае, когда обтекающая лопатки колеса жидкость будет
сильнее всего изменять своё количество движения. Однако, с другой стороны,
удар жидкости о лопатки колеса невыгоден, так как он связан с потерями
энергии. Поэтому лопаткам колёс придают такую форму и расположение,
чтобы жидкость без удара притекала бы к лопаткам и, уходя от лопаток,
почти полностью теряла свою скорость. При этом получается наилучшее
использование энергии текущей струи.
§ 121. Реактивное движение
Реакция вытекающей струи используется в качестве движущей силы при
реактивном движении, например, в ракетных снарядах. Схематически устрой-
устройство ракетного снаряда приведено иа рис. 271. В камере ракетного сна-
снаряда происходят взрывы специальной взрывчатой смеси. Образующиеся
при этих взрывах газы с большой скоростью (обусловленной большим да-
давлением в камере) вылетают через специальное сопло. Вследствие большого
сжатия газа в камере давление на противоположную соплу стенку камеры
может быть очень значительно. Величина этой силы регулируется количе-
количеством подаваемой взрывчатой смеси.
22*

340
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvit
Рис. 271.
Принципиальное отличие ракетного снаряда от других самодвижу-
самодвижущихся устройств (автомобиля, парохода, самолёта) состоит в том, что для
ускорения ракетного снаряда не требуется взаимодействия с другими телами
(землёй, водой, воздухом). Ракетный снаряд получает ускорение за счёт
сил взаимодействия не с какими-либо посторонними телами, а с газами, обра-
образующимися в самом снаряде. При этом снаряд приобретает такое же коли-
количество движения, какое уносит с собой струя газа, покинувшего снаряд.
Если бы снаряд и струя газа при движении не встречали сопротивления, то
по закону сохранения количества движения их общий центр тяжести оста-
оставался бы неподвижным.
Для того чтобы ракетный снаряд двигался с ускорением (а при
наличии сопротивления и для того, чтобы он двигался с постоянной ско-
скоростью), он должен выбрасывать некоторые количества газа, т. е. масса его
должна уменьшаться. Чтобы снаряд мог приобрести большую скорость,
масса запаса взрывчатых
веществ в нём должна со-
^ ставлять заметную часть
массы снаряда.
Указанная выше прин-
принципиальная особенность ра-
ракетного движения позво-
позволяет осуществить движение
в очень разреженной атмосфере или безвоздушном пространстве («меж-
(«межпланетные путешествия»). В разреженной атмосфере ракетный снаряд
испытывает очень малое сопротивление движению, благодаря чему увели-
увеличиваются достигаемая снарядом скорость и проходимые им расстояния.
Именно это обстоятельство было использовано в ракетных снарядах, посы-
посылавшихся на расстояния в несколько сот километров. Снаряд взлетает
с Земли почти отвесно и скоро достигает высоких, разреженных слоев
атмосферы, где сопротивление движению
мало. Ббльшую часть пути снаряд летит
в этих высоких слоях атмосферы и по-
поэтому дальность его полёта очень велика.
При использовании ракетных снарядов
взамен обычных артиллерийских снарядов
существенную роль играет ещё одна осо-
особенность реактивного движения. Артилле-
Артиллерийское орудие при выстреле испытывает
большие силы со стороны образовавшихся
при взрыве газов (отдача при выстреле),
что заставляет делать орудия очень проч-
прочными, а потому тяжёлыми. При запуске ракетного снаряда образовавшиеся
газы вылетают прямо в атмосферу, и поэтому подобий отдачи на орудие
ие получается. Приспособления для запуска ракетных снарядов получаются
очень легкими — они должны задать только начальное направление снаряду,
т. е. по существу выдерживать только вес снаряда, а не отдачу при
выстреле.
За время Великой Отечественной войны ракетные снаряды получили
широкое распространение во всех армиях.
Наряду с ракетным принципом применяется и другой принцип реактив-
реактивного движения, используемый в так называемых воздушно-реактивных дви-
двигателях. Воздушно-реактивный двигатель в простейшем виде представляет
собой камеру с двумя отверстиями, причём обычно диаметр переднего
отверстия меньше (рис. 272). При движении камеры в неё через переднее
отверстие поступает воздух из окружающей атмосферы, а через форсунки
забрызгивается жидкое топливо, которое, сгорая, нагревает этот воздух.
Нагретый воздух вылетает назад с ббльшей скоростью, чем поступает еле-
IF
- топлива
~—топлива
Рис. 272.

§ 122] роль вязкости 341
реди, так как ири нагревании объём его увеличивается. Так как масса воз-
воздуха остаётся примерно прежней (даже несколько увеличивается за счёт
массы сгоревшего топлива), а скорость возрастает, струя уносит с собой
некоторое избыточное количество движения. При этом стенки камеры ис-
испытывают реакцию— ситу давления, направленную вперёд. Возникает эта
сила, как и всегда, вследствие того, что давление у передней и задней сте-
стенок камеры неодинаково. В простейшем случае, когда задняя стенка камеры
совсем отсутствует (как на нашем рисунке), существует давление только на
переднюю стенку камеры, направленное вперёд.
В таком виде (без специального нагиетателя) двигатель будет развивать
силу тяги лишь тогда, когда он уже движется и воздух поступает через
переднее отверстие вследствие динамического напора. При этом чем больше
скорость движения, тем больше воздуха поступает в камеру и тем больше
будет избыточное количество движения, уносимое струей, так как будет
больше масса газа, выбрасываемого назад. (Для этого нужно, конечно, ожи-
ожигать больше топлива, чтобы в камере развивалась та же температура и по-
получался тот же прирост скорости.) Поэтому сила тяги растёт с увеличением
скорости движения. Эта характерная черта воздушно-реактивных двигателей
составляет их преимущество по сравнению с воздушным винтом, у ко-
которого, начиная с некоторого значения, сила тяги падает при увеличении
скорости (причины этого будут указаны ниже (см. § 130)).
Чтобы воздушно-реактивный двигатель мог работать и развивал силу
тяги, пока ещё не началось движение (пока нет динамического напора), он
снабжается специальными приспособлениями (например, компрессором, на-
нагнетающим воздух в камеру).
Существенное отличие воздушно-реактивного двигателя от ракетного со-
состоит в том, что в его струе используется воздух из атмосферы, а не масса
самого взрывчатого вещества, как в ракетном двигателе (масса сжигаемого
топлива в воздушно-реактивном двигателе составляет незначительную часть
всей массы струи). Поэтому масса запаса топлива для воздушно-реактив-
воздушно-реактивного двигателя может быть гораздо меньше, чем для ракетного снаряда,
и составлять небольшую долю массы всего снаряда или самолёта. Это пре-
преимущество воздушно-реактивных двигателей делает их более пригодными для
имользования в самолётах, чем ракетные двигатели. Однако для работы
воздушно-реактивного двигателя нужна достаточно плотная атмосфера, т. е.
его применение ограничено не очень большими высотами. Ракетный двига-
двигатель свободен от этого ограничения.
§ 122. Роль вязкости
При движении жидкости возникают силы внутреннего трения, иначе
назынаемые силами вязкости, которыми мы раньше пренебрегали.
Действие этих сил сказывается, например, в .. .. *.
падении давления вдоль трубы постоянного ~ рг--Ц- И
сечения, по которой течёт жидкость. Если в Щ} []}~ Д? - —
разных местах горизонтальной трубы поста- -—=-^—- -—-———
вить манометрические трубки (рис. 273), то .И—^^ ——-—-
высота уровня в этих трубках, одинаковая,
пока жидкость покоится, понижается от труб- Рис. 273.
ки к трубке, когда жидкость течёт по трубе.
Давление в разных сечениях трубы различно, но скорость потока
во всех сечениях трубы одна и та же. Между тем, если бы
в жидкости действовали „только силы давления, то под действием раз-
разности давлений столб жидкости между двумя сечениями 1 и 2 должец

342 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [гл. XVII
был бы испытывать ускорение. В действительности этого не наблю-
наблюдается. Следовательно, на движущийся столб жидкости действуют со
стороны трубы силы, направленные навстречу движению жидкости
и уравновешивающие разность давлений. Такие тангенциальные силы
существуют не только между внешним слоем жидкости и трубой,
но и между отдельными слоями жидкости, скользящими друг относи-
относительно друга.
Наличие тангенциальных сил внутри жидкости принодит к тому,
что слой жидкости, непосредственно прилегающий к трубе, действует
на соседний, внутренний, слой и т. д. Таким образом, тангенциальные
силы, действующие со стороны стенок трубы, влияют на скорость всего
потока жидкости. Прилегающий к трубе слой жидкости практически
вовсе не движется («прилипает» к стенкам). Внутренние же слои
жидкости движутся со скоростью, постепенно
_JT —<~° ^ возрастающей по мере удаления от стенок
' Г" jf*7 трубы.
. ?3 Для того чтобы выяснить, как распреде-
I j-' ляются скорости между слоями и какие при
I к этом возникают силы, рассмотрим более
~Г простую задачу. Представим себе плоский
Рис. 274. СЛой жидкости, заключённый между двумя
пластинками (рис. 274). Верхняя пластинка
движется с постоянной скоростью v0, а нижняя покоится. При этом на
каждую пластинку со стороны жидкости действует сила F, которую мож-
можно измерить. Для данной жидкости сила F оказывается прямо пропорцио-
пропорциональной скорости верхней пластинки и паощади пластинки и обратно про-
пропорциональной расстоянию между пластинками. Кроме того, эта сила
зависит от свойств жидкости, именно от её вязкости. Наприм!^,
для глицерина эта сила при прочих равных условиях больше, чем для
воды. Поэтому силу F можно выразить следующим образом:
F=^, A7.6)
где 5—площадь пластинки, d—расстояние между пластинками, а ц —
коэффициент пропорциональности, различный для различных жидко-
жидкостей. Этот коэффициент называется коэффициентом вязкости данной
жидкости. Коэффициент этот может быть определён, если измерена
сила F*).
Как следует из соотношения A7.6), коэффициент вязкости в си-
системе LMT имеет размерность ML~1T~1. В системе CGS он измеряется.
в •. Эта единица названа «пуазом» в честь Пуазейля (см. ниже),
см • сак
*) Практически коэффициент вязкости измеряют другими способами.
С одним из этих способов мы познакомимся ниже. Для измерения коэффи-
коэффициента вязкости может быть также применен закон Стокса (§ 48),

§ 122]
РОЛЬ ВЯЗКОСТИ
Вязкость жидкостей и газов
343
Вещество
Коэффициент вязкости (в пуазах)
Т— 15°
= 302°
Жидкости
Глицерин
Вода ........
Ртуть
Эфир . .'
Углекислота (жидкая)
Аргон
Гелий
Кислород
Воздух
Азот
Углекислый газ . . .
Водяной пар
Водород
46
1,8-10-2
1,7-10-2
0,29-10-2
15
1,Ы0-2
1,6-10-2
0,26-10-2
0,08-10-2
0,29-10-г
1,2-10-2
0,9-10-2
Газы
210-10-е
189-Ю-6
187-Ю-6
171-10-6
166-Ю-6'
139-10-6
90-10-6
86-10-6
221-10-6
197-10-е
195-10-6
181-10-6
171-10-6
146-Ю-6
97-10-6
89-Ю-ч
220- Ю-8
186-Ю-6
131-10-6
105-10-6
299-10-6
268-10-6
139-10-6
В таблице приведены значения коэффициентов вязкости для неко-
некоторых жидкостей и газов. В таблице указаны также определённые
температуры, так как вязкость жидкостей и газов зависит от темпе-
температуры (н жидкостях с повышением температуры вязкость падает, в га-
газах, наоборот, увеличивается).
Рассмотрим теперь распределение скоростей в слое жидкости для
случая, изображённого иа рис. 274. Верхний слой прилипает к верх-
верхней пластинке и движется со скоростью v0. Нижний слой прилипает
к нижней пластинке, и его скорость равна нулю. В промежуточных
слоях скорэсть непрерывно изменяется, т. е. представляет собой не-
некоторую функцию от z. Производная этой функции по z "называется
градиентом скорости. В рассматриваемом случае все промежуточные
слои находятся в одинаковых условиях, поэтому скорость от слоя
к слою изменяется на одинаковую величину и градиент скорости есть
величина постоянная:
dz~d' V'-'l
где d — расстояние между пластинками *). С другой стороны, все слои
*) Так как скорость может, вообще говоря, зависеть^ от времени, то
в общем случае следует писать частную производную. Для стационарных
случаев можно писать полную производную.

344 ГИД ОДИНАМИКА И АЭРОДИНАМИКА [гЛ. XVII
движутся с некоторой, хотя и различной, но постоянной во времени
скоростью. Следовательно, сумма тангенциальных сил, действующих
на любой слой жидкости, должна быть равна нулю. Поэтому на
любую горизонтальную площадку S, лежащую на границе данного слоя,
со стороны другого слоя должна действовать та же сила, что и на
пластинки, к которым прилегает жидкость, т. е. сила
Заменяя vQjd его значением из A7.7), получаем:
Сила, действующая на единицу площади (аналогично тангенциальному
напряжению), будет равна
x = ,i?. A7.8)
В нашем случае градиент скорости постоянен, поэтому и т в лю-
горизонтальной плоскости одно и то же. Но соотношение A7.8)
справедливо и в общем случае, когда градиент скорости
от точки к точке меняется. Тангенциальные силы, воз-
возникающие между двумя движущимися слоями жидкости,
зависят только от того, как меняется скорость вблизи
границы этих слоев. Тангенциальные силы пропорцио-
пропорциональны градиенту скорости, т. е. производной
от скорости по координате в направлении, перпен-
перпендикулярном к плоскости соприкосновения слоев.
Величина -г- представляет собой, в сущности, скорость сдвига
соседних слоев жидкости. Действительно, рассмотрим точки 1 и 2,
лежащие на прямой, перпендикулярной к скорости на расстоянии Дг
(рк. 275). За время Д^ точки эти сдвинутся, соответственно, на Ахх
и Длг2. Сдвиг будет равен (§ 101)
Деля обе части на Д^, получим:
Дат, Дх„
или, так как -^-1 = fI и "дт —^2> переходя к пределу, получим:
Щ — д* и х —

§ 122,1 роль вязкости 345
Обусловленные вязкостью тангенциальные силы, возникающие
в движущейся жидкости, пропорциональны не величине сдвига, а ско-
скорости изменения сдвига.
Вернёмся теперь снова к стационарному течению вязкой жидкости по
трубе. Мысленно выделим расположенный вдоль оси трубы цилиндр длиной/
и радиуса г. Скорость жидкости в разных точках сечения трубы различна.
Она зависит от расстояния до стенок, и градиент скорости есть —.С внеш-
внешней стороны на единицу поверхности цилиндра действует сила вязкости
dv
T=ji—, а на всю поверхность рассматриваемого цилиндра — сила ¦
Так как двнжеиие происходит с постоянной скоростью, то сила Р должна
уравновешивать разность сил давления рх и р2 на торцах цилиндра. Следо-
Следовательно,
откуда
* = -
Интегрируя, получаем:
4ц/
Но у стенок трубы v = 0 (жидкость прилипает). Отсюда для С имеем зна-
значение:
где У?—радиус трубы. Окончательно
Скорости по сечению трубы растут по квадратичному закону от нуля
у стенок до максимальной скорости и~(пг—р9)Ф/4у.[ у оси трубы. Чтобы
подсчитать ко шчество жидкости, протекающей через в;ё сечение трубы,
нужно разбить сечение на тонкие кольца радиуса г и ширины dr. Через
площадь такого кольца dS = 2wrfr в единицу времени протекает объём
жидкости dQ = 2zrdr-v, а через всё сечение трубы протекает обьем
жидчости
R R
интегрируя, получим:

346 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [гл. XVII
Эта формула была получена Пуазейлем. Соотношения, в ней содержа-
содержащиеся, позволяют очень просто по скорости истечения жидкости измерять
её вязкость. Определение вязкости при помощи формулы Пуазейля является
одним из наиболее распространённых методов измерения вязкости.
Как следует из формулы Пуазейля, при заданном давлении общее коли-
количество вытекающей жидкости чрезвычайно резко уменьшается с уменьше-
уменьшением радиуса трубы. Наоборот, при заданном количестве вытекающей
жидкости падение давления иа единицу длины трубы (pi—p^jl очень
резко возрастает с уменьшением радиуса трубы. Это можно продемонстри-
продемонстрировать, соединив последовательно два отрезка труб разного диаметра,
снабжённых манометрическими трубками. На одинаковых участках труб
падение давления в тонкой трубе гораздо больше, чем в толстой.
Силы вязкости нарушают распределение давлений, вытекающее из
закона Бернулли. Этот закон был получен в предположении, что силы вяз-
вязкости отсутствуют. Между тем все реальные жидкости и газы обладают
вязкостью. Поэтому важно знать, в какой мере закон Бернулли всё же
применим к реальным жидкостям и газам.
Представление об этом могут дать следующие, хотя и не строгие, но
наглядные соображения. Закон Бернулли будет приблизительно справедлив
в том случае, когда потери энергии на трение малы по сравнению с общей
энергией текущей жидкости. Введём среднюю скорость течения- жидкости
по трубе сср = Q/ic/?3. Тогда, по A7.9),
[Pi —р2) я/? = 8r.\tlvcp.
Но it/?2 (p\ — р2) есть разность сил давления. Она должна быть равна силе F,
действующей на столб жидкости длиной / со стороны стенок трубы, т. е.
/7=8ic|i/»(:p. При перемещении этого столба жидкости на расстояние / сила
трения о стенки трубы совершит работу A = Fl, т. е.
Рассмотрим теперь объём жидкости, заключённый в отрезке трубы, длина
которого / равна радиусу трубы /?. Кинетическая энергия единицы объёма
есть рР2ср/2 и всего объёма
Закон Бернулли будет хорошо соблюдаться, если 7"^> А, или если
(числовой коэффициент можно отбросить, так как речь идёт о сильном
неравенстве). Следовательно, чем больше вязкость жидкости, тем больше
должно быть / (т. е. в нашем случае радиус трубы) или скорость, чтобы
закон Бернулли был справедлив.
Соотношение A7.10), полученное нами для одного частного случая тече-
течения по трубе (и притом довольно искусственным способом), имеет весьма
общее и важное значение. Работа сил вязкости зависит от размеров поверх-
поверхности рассматриваемого элемента жидкости и пропорциональна j»p/2, а энер-
энергия элемента жидкости зависит от его объёма и пропорциональна рг>2/3,
где / — линейные размеры элемента жидкости. Поэтому отношение энергии
элемента жидкости к работе сил вязкости, т. е. безразмерная величина
R=&, A7.11)

§ 123] ДВИЖЕНИЕ ТЕЛ В ЖИДКОСТИ ИЛИ ГАЗЕ 347
характеризует относительную роль сил вязкости. Эта величина называет-
называется числом Рейнольдса. Чем меньше число Рейнольдса, тем большую роль
играют силы вязкости в движении жидкости. Основ ше черты движения
жидкости в очень сильной степени зависят от того, насколько значительную
роль играют силы трения. Поэтому число Рейнольдса сразу даёт важные
указания о характере движения жидкости или газа. Например, если размеры
тел, с которыми соприкасается жидкость или газ, очень малы, то" даже при
малой вязкости R будет мало и силы трения будут играть преобладающую
роль. Наоборот, если скорости н размеры тел велики, то даже значитель-
значительная вязкость мало будет влиять на характер движения. Влияние вязкости
будет сказываться только у поверхностей соприкосновения твёрдого тела
и жидкости.
Чисяо Рейнольдса играет очень большую роль при изучении движения
жидкостей на моделях. Для того чтобы геометрически подобная модель
какого-либо гидротехнического сооружения, судна и т. д. обеспечивала
подобие в смысле динамики движения, необходимо, чтобы соотношение
между энергией потока и потерями на трение в модели было таким же,
как в реальном объекте. Между тем при изменении размеров тел соотноше-
соотношение это неизбежно изменяется (так как поверхности н объёмы изменяются
по-разному). Но если, вместе с изменением размеров модели, соответствую-
соответствующим образом изменять и скорость потока так, чтобы число Рейнольдса
оставалось неизменным, то будет обеспечено динамическое подобие самого
объекта и его модели. Однако очень малые модели потребовали бы очень
больших скоростей. Поэтому и модели обычно приходится применять значи-
значительных размеров.
Помимо скорости v и характерного для данной задачи размера /, число
Рейнольдса зависит от отношения вязкости жидкости (или газа) ц к её
плотности р. Существенную роль играет именно отношение этих величин,
так как кинетическая энергия элемента жидкости пропорциональна плот-
плотности р, а работа сил вязкости пропорциональна коэффициенту вязкости ц.
Поэтому относительное влияние сил вязкости определяется величиной
* = ц/р, которую называют кинематической вязкостью жидкости или газа.
Кинематическая вязкость v лучше, чем коэффициент вязкости ц, характе-
характеризует роль вязкости при прочих равных условиях. Так, хотя коэффициент
вязкости |i для воды примерно в сто раз больше, чем для воздуха (при
7"=0°), ио кинематическая вязкость воды почти в 10 раз меньше, чем
воздуха. При прочих равных условиях вязкость будет сильнее влиять иа
характер течения воздуха, чем воды.
§ 123. Движение тел в жидкости или газе
Одной из важнейших задач аэро- и гидродинамики является иссле-
исследование движения твёрдых тел в жидкости или газе, в частности,
изучение тех сил, с которыми эта среда действует на движущееся
тело. Практическое значение этой задачи совершенно очевидно —
она возникает во всех случаях движения тел в воздухе и в воде.
Особенно большое значение приобрела эта проблема в связи
с развитием авиации и увеличением скорости движения морских су-
судов различного типа. Во всех этих случаях решающую роль играют
силы, с которыми среда действует на движущееся тело. Задача опре-
определения этих сил является весьма сложной. Поэтому особое значение
приобретает экспериментальное исследование сил, с которыми среда
действует на движущееся в ней тело. При этом пользуются сообра-
соображением, о котором мы уже упоминали (§ 43), а именно, что среда

348 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [ ГЛ. XVII
действует на движущееся в ней тело с такими же силами, с какими
действовал бы на неподвижное тело поток, набегающий на это тело,
если скорости тела в первом случае и потока во втором равны по
величине и противоположны, по направлению. Поэтому для определе-
определения сил, возникающих при движении в воздухе, тело закрепляется
при помощи динамометров в аэродинамической трубе, в которой
создаётся равномерный поток воздуха. По показаниям динамометров
можно сухить о силах, действующих на тело в различных направле-
направлениях, изучать зависимость этих сил от формы и состояния njeepx-
ностн тел, их расположения в потоке и, наконец, от скорости потока
Чтобы исследовать эти зависимости вплоть до самых больших
скоростей, интересующих сейчас авиацию, строятся трубы, в которых
скорость потока может быть доведена до сотни и -более метров
в секунду. С другой стороны, чтобы изучать силы, действующие,
например, на отдельные части самолёта или даже целые самолеты,
сечение трубы должно быть очень большим. Поэтому современные
аэродинамические трубы представляют собой грандиозные сооружения.
Казалось бы, что применение моделей уменьшенного размера
позволит обойтись без грандиозных и дорогостоящих аэродинами-
аэродинамических труб. Однако значительюе уменьшение размеров моделеЧ
неосуществимо, ибо, как было указано в предыдущем параграфе,
аэродинамическое подобие двух различных движений достигается только
при условии, что число Рейнольдса в обоих случаях имеет одно и
то же значение. Поэтому при уменьшении размеров модели (размер
модели в рассматриваемом случае и является характерным размером /)
нужно соответственно увеличивать скорость потока. Однако, когда
скорость потока приближается к 330 М\сек (скорости звука в воз-
воздухе), существенную роль начинает играть сжимаемость воздуха,
изменяющая характер течения и нарушающая подобие. Поэтому при
больших скоростях, интересующих современную авиацию, приходится
применять модели либо в натуральную величину, либо лишь немного
уменьшенных размеров.
При больших скоростях единственный путь к уменьшению моде-
моделей без нарушения подобия (т. е. с сохранением прежнего значения
числа Рейнольдса)—это увеличение плотности среды. Поэтому при-
применение сильно сжатого воздуха*) или тяжелых газов в аэродинами-
аэродинамических трубах позволяет использовать малые модели. Несмотря на
трудность постройки герметических аэродинамических труб, этот метод
всё же получил практическое применение.
Для демонстрации характера сил. действующих на тела в потоке
воздуха, можно применять малые модели аэродинамических труб.
Одна из таких демонстрационных аэродинамических труб изображена
*) Коэффициент вязкости возауха р очень маю зависит от плотности
последнего (за исключением области больших разрежений) и при повыше-
повышении плотности в десятки раз остаётся практически неизменным.

§ 1231
движений тьл в жидкости или f аз°
на рис. 276. С помощью этой трубы можно качественно установить
характер сил, действующих на различные тела как в направлении
потока воздуха (рис 276а), так и в направлении, перпендикулярном
потоку (рис. 276Ь).
Для обозначения компонент сил, действующих на тело, в технической
аэродинамике принято пользоваться прямоугольной системой коор-
Рис. 276а.
Рис. 276Ь.
динат, у которой ось х направлена по скорости потока (рис. 277).
Опыт пбказывает, что величина и направление силы,с которой поток
действует на обтекаемое тело, зависит от формы тел, их ориентировки
в потоке и скорости потока. Тела, имеющие плоскость симметрии
и расположенные так, что эта плоскость параллельна координатной
пло кости xz (рис. 277), испытывают со стороны потока силу R,
направление которой (как и следовало ожидать иа соображений

350
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvil
симметрии) совпадает с направлением потока. Эта сила R^ носит
название «.лобового сопротивления» *).
Лобовое сопротивление, для данного тела быстро растёт с уве-
увеличением скорости потока, а для различных тел зависит от их
У
Рис. 277.
О
размеров и формы. Лобовое сопротивление растёт с увеличением
поперечных размеров тел. Для тел, имеющих одинаковые поперечные
размеры,— например, диска, шара и сигарообразного тела (рис. 278),—
лобовое сопротивление ока-
J) зывается наибольшим для
диска и наименьшим для
сигары. Причины этого будут
выяснены ниже.
В случае, если тело не-
несимметрично или его пло-
плоскость симметрии располо-
расположена наклонно по отноше-
отношению к потоку (рис. 279),,
результирующая сила R, дей-
действующая на тело со сто-
стороны потока, не совпадает
. с направлением потока. Тог-
Тогда эту силу можно разло-
разложить на две составляющие:
R^, направленную вдоль по-
потока, и Rj, — перпендикулярно к потоку. Составляющая R^. — это уже
рассмотренное выше лобовое сопротивление. Составляющая R^ назы-
называется подъёмной силой. Название это, конечно, совершенно условно.
Составляющая R вовсе ие обязательно должна быть направлена
Рис. 278.
*) Применяя термин «сопротивление», имеют в сущности в виду обрат-
обратный случай, когда тело движется в покоящейся жидкости. Тогда тело дей-
действительно испытывает сопротивление Rx со стороны жидкости. Но это
название сохраняют и для случая текущего потока и покоящегося тела,
хотя здесь, пожалуй, правильнее было бы говорить о лобовом давлении.

§ 123]
ДВИЖЕНИЕ ТЕЛ В ЖИДКОСТИ ИЛИ ГАЗЕ
351
вверх. Если тело наклонено в другую сторону, то подъёмная сила
R направлена вниз (рис. 280).
Подъёмная сила, так же как и лобовое сопротивление, зависит
от скорости потока, формы и размеров тела и его расположения
относительно потока. Например, плоская пластинка, расположенная
Рис. 279.
вдоль потока или перпендикулярно к нему, будет испытывать только
лобовое сопротивление (конечно, различное в обоих случаях). На эту
же пластинку, поставленную наклонно, будут действовать и лобовое
сопротивление, и подъёмная сила. Подъёмная сила, так же как и ло-
лобовое сопротивление, растёт с увеличением поперечных размеров тела
и скорости потока. При этом подъ-
подъёмная сила и лобовое сопротивле-
сопротивление примерно одинаково зависят от
скорости потока (пропорциональны
квадрату скорости потока), и отно-
отношение их при изменении скорости
потока практически остаётся неиз-
неизменным (иначе говоря, при изменении
скорости потока направление резуль-
результирующей силы R не изменяется).
Однако отношение подъёмной
силы к лобовому сопротивлению
существенно зависит от ориентиров-
ориентировки тела в потоке. Величина подъ-
подъёмной силы и лобового сопротивления при изменении ориентировки
тела изменяется, вообще говоря, по-разному. Например, в том же
простейшем случае плоской пластинки, поставленной вдоль потока,
лобовое сопротивление отлично от нуля, подъёмная же сила равна
нулю. При увеличении угла атаки, т. е. угла а, под которым
Рис. 280.

352 ГИДГОДИНАМИКА И АЭРОДИНАМИКА [ ГЛ. XVll
пластинка наклонена к потоку (рис. 281), лобовое сопротивление моно-
монотонно растёт и достигает максимума при a = 90J. Подъёмная сила
при увеличении а сначала растёт, а затем падает и при а = 90° снова
обращается в нуль. Иначе говоря, результирующая сила R, действую-
действующая на пластинку, при изменении угла атаки изменяет своё направле-
направление, отклоняясь от направления набегающего потока на угол, во
всяком случае, меньший тс|2.
Для тела произвольной формы результирующая сила R, действую-
действующая на тело со стороны потока, может иметь составляющие по всем
трём осям — лобовое сопротивление Ях, подъёмную силу R^, и боко-
боковую силу Rz.
Для упрощения задачи обычно ограничиваются такими случаями,
когда боковая сила не играет существенной роли и ею можно пре-
пренебречь. Так, если мы имеем тело, изображённое на рис. 277,
и вообще тела, удлинённые в напра-
направлении оси z и имеющие во всех
сечениях, перпендикулярных к г,
одинаковый профиль, то резуль-
результирующая сила R лежит в плоско-
плоскости, перпендикулярной к z, т. е.
боковая сила не возникает (это сле-
следует из соображений симметрии).
JL При этом, конечно, у поверхностей,
р „8] ограничивающих тело в направле-
направлении оси z, обтекание тела будет
происходить не так, как в средней
его части. Однако при большой длине тела это возмущающее влия-
влияние его концов не играет существенной роли. Можно считать, чго
течение везде такое, как если бы в направлении оси z размеры тела
были бесконечно велики. Тогда во всех сечениях, перпендикулярных
к z, картина течения будет одна и та же, и при исследовании обте-
обтекания тела можно ограничиться рассмотрением одного из сечений,
перпендикулярных к z.
При исследовании подъёмной силы и лобового сопротивления
обычно пользуются указанными выше упрощающими предположениями
и рассматривают только двумерную задачу, т. е. картину обтекания
тел в одной плоскости,—так называемое плоское течение.
§ 124. Обтекание тел идеальной жидкостью
Характер обтекания тел потоком существенно зависит от формы
обтекаемых тел. Рассмотрим сначала простейший случай обтекания
круглого цилиндра, ось которого перпендикулярна к плоскости ху
(рис. 282), предполагая, что силы вязкости отсутствуют.
Картина обтекания передней части цилиндра совершенно ясна.
Линии тока обходят цилиндр с двух сторон; у точки А скорость

§ 124]
ОБТЕКАНИЕ ТЕЛ ИДЕАЛЬНОЙ ЖИДКОСТЬЮ
353
жидкости равна нулю, а у точек В и С линии тока сгущаются,
и скорость жидкости больше, чем скорость набегающего потока. Так
как силы вязкости отсутствуют, то справедливо уравнение Бернулли,
откуда следует, что у точки А, где скорость близка к нулю, давле-
давление рА больше, чем давление р в набегающем потоке. Наоборот,
в точках В и С, где скорость жидкости больше, чем в набегающем
потоке, давление рв (или рс)
меньше р. На основании теоремы
Бернулли можно оценить эти из-
изменения давления в точках А и
В. У точки А, где скорость близ-
близка к нулю, давление примерно
на величину рт>2/2 выше р. Чтобы
оценить, насколько падает дав пе-
пение у точек В и С, нужно при-
приблизительно знать скорость жидко-
жидкости у этих точек. Грубо её мож-
можно оценить следующим образом. рис 2Я9
Сгущение токовых линий в сечении
ВС уже мало в точках В' и С,
т. е. на расстояниях от точек В и С, примерно равных радиусу цилиндра.
Можно считать, что площадь сечения В'С ввиду присутствия цилиндра
как бы уменьшилась примерно в два раза, и, следовательно, скорость
жидкости возросла примерно вдвое. (Конечно, в разных местах сечения
В'С скорость жидкости различна, но при грубой оценке с этим
можно не считаться.) Но если скорость у точки В к С равна 2v,
то, по теореме Бернулли,
чткуда
Этот грубый подсчёт показывает, что уменьшение давления в точ-
точках В и С может в несколько раз превосходить увеличение давления
в точке А.
Если картина расположения линий тока впереди и позади цилиндра
одинакова, то скорость у точки D снова падает ю нуля, а давле-
давление ри повышается до значения р. Это повышение давления создают
частицы жидкости, приходящие из областей В и С н обладающие в этих
областях повышенной скоростью. Так как силы трения отсутствуют,
то частицы жидкости, находящиеся в областях В и С, обладают та-
такой кинетической энергией, которой как раз достаточно, чтобы они
могли создать в области D повышенное давление: Pi,'=Px (Подобно
тому, как в отсутствие сил трения, тело, упавшее с какой-то высоты,
обладает как раз такой кинетической энергией, которая необходима,
чтобы снова подняться на ту же высоту.)
23 С. Э. ХаЯкин

354
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvii
Приведённые соображения показывают, что в случае идеальной
жидкости могло бы происходить «полное обтекание» тела, т. е. такое
течение, при котором картина токовых линий впереди и позади цилиндра,
с одной стороны, и сверху и Лизу, с другой, была бы совершенно
одинакова. Вместе с тем распределение давлений в жидкости было
бы совершенно симметрично. Одна-
Однако это давление в различных точках
различно, а следовательно, и силы,
с которыми жидкость давит на
стенки цилиндра в разных местах,
различны. Изменения давлений, кото-
которые имеют место при обтекании
тела потоком, и представляют собой
те дополнительные силы, с кото-
которыми действует поток на обтекаемое
тело. Часто эти дополнительные
силы называют аэродинамическими.
Однако, как мы видим, эти силы
представляют собой «обычные» си-
силы давления жидкости на стенки
тела. Всё дело лишь в том, что
давления в текущей жидкости отли-
отличаются от давлений в покоящейся
жидкости. Эти дополнительные силы,
действующие на стенки цилиндра
в рассматриваемом случае идеальной
жидкости, изображены стрелками
на рис. 283. Там, где давление жидкости больше, чем в набегающем
потоке, эти дополнительные силы направлены к стенкам цилиндра,
где она меньше, — от сте- . »
нок. Вследствие симме-
симметрии этих сил относитель-
относительно двух взаимно перпен-
перпендикулярных плоскостей
AD и ВС равнодействую-
равнодействующая их равна нулю. Рав-
Равномерный поток идеаль-
идеальной жидкости не дейст-
действует на обтекаемый им
цилиндр.
Таким образом, наше рассмотрение вообще не объясняет проис-
происхождения тех сил (подъёмной силы и лобэвого сопротивления), с кото-
которыми действует поток на обтекаемое тело. Чтобы выяснить причины
этого, сопоставим обтекание цилиндра и полуцилиндра (рис. 284).
Очевидно, для участка ABD полуцилиндра распределение скоростей
и давлений будет такое же, как и для соответствующего участка
Рис. 283.
Рнс. 284.

§ 124}
ОБТЕКАНИЕ ТЕЛ ИДЕАЛЬНОЙ ЖИДКОСТЬЮ
355
Рис. 285.
цилиндра. Вдоль же плоской стенки ACD полуцилиндра скорость,
а следовательно, и давление будут такие же, как в набегающем
потоке. Распределение дополнительных сил давления на полуци-
полуцилиндр приведено на рис. 285.
Равнодействующая сил давления
в направлении скорости потока
попрежнему равна нулю, в напра-
направлении же, перпендикулярном к
скорости потока, — отлична от
нуля, т. е. на полуцилиндр дей-
действует дюдъёмная сила, лобо-
лобовое же сопротивление отсутствует.
Отсюда видно, что отсутствие
подъёмной силы в случае цилин-
цилиндра обусловлено специальной сим-
симметричной формой тела. Что же касается лобового сопротивления, то
оно оказалось равным нулю в обоих рассмотренных случаях, и это
не связано с какой-лиЬо специальной формой обтекаемого тела. Ло-
Лобовое сопротивление оказывается
равным нулю во всех случаях пол-
полного обтекания тела.
Действительно, в случае пол-
полного обтекания тела расположе-
расположение токовых линий определяется
лишь формой тела и не изме-
изменяется, если направление потока
меняется на обратное. Например,
в случае полуцилиндра, плоская
стенка которого перпендикулярна
к потоку (рис. 286), изображён-
изображённое на рисунке распределение
. токовых линий получится при пол-
Рис. 286. ном обтекании тела как справа
налево, так и слева направо-
Связано это с тем, что в невязкой жидкости соблюдается
закон Бернулли. Если соотношение Бернулли соблюдается для какой-
либо токовой трубки при движении жидкости в одном направлении,
то оно будет соблюдаться и при движении жидкости в противополож-
противоположном направлении. Следовательно, в невязкой жидкости расположение
токовых линий не должно изменяться, если направление течения жидко-
жидкости изменяется на противоположное. Однако в этом случае и резуль-
результирующая сила давления на вполне обтекаемое тело не должна изме-,
няться при изменении направления потока на противоположное. Но
тогда лобовое сопротивление для полностью обтекаемого тела должно
быть равно нулю, так как иначе для одного из направлений потока оно
оказалось бы направленным против скорости набегающего потока. Tof
23»

356 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [гл. XVlt
что при полном обтекании тела подъёмная сила может быть не равна
нулю, лобовое же сопротивление всегда оказывается равным нулю,
можно связать со следующими соображениями. В случае наличия
подъёмной силы на жидкость со стороны обтекаемого тела действует
сила, направленная перпендикулярно к скорости потока. Она изменяет
направление количества движения жидкости, не изменяя его вели-
величины. В случае же наличия лобового сопротивления на жидкость со
стороны обтекаемого тела действует сила, направленная против потока.
Она должна уменьшать количество движения жидкости. Иными сло-
словами, при наличии подъёмной силы поток позади обтекаемого тела
должен отличаться от набегающего только направлением скорости;
при наличии же лобового сопротивления поток позади обтекаемого
тела должен иметь величину скорости меньшую, чем в набегающем
потоке. При полном обтекании обтекаемое тело может изменить лишь
направление скорости потока позади себя, но не его величину; по-
поэтому может существовать подъёмная сила, но не может • возникать
лобового сопротивления.
Как уже было указано, в отсутствие сил, зависящих от скоростей,
обтекание всегда должно быть полным. Только при наличии сил,
зависящих от скоростей, т. е. сил вязкости, возможно неполное
обтекание тела и, следовательно, возникновение лобового сопро-
сопротивления. Поэтому, чтобы объяснить возникновение лобового сопро-
сопротивления, необходимо учитывать, что все реальные жидкости и газы
обладают вязкостью и что в потоке реальной жидкости или газа
полное обтекание никогда не имеет места.
Что же касается подъёмной силы, то она может существовать
и в отсутствие сил вязкости. Поэтому для объяснения происхожде-
происхождения подъёмной силы и её подсчёта можно рассматривать идеальную
(невязкую) жидкость. Так и поступают обычно в гидродинамике, ибо
пренебрежение вязкостью очень упрощает теоретическое рассмотре-
рассмотрение. При расчёте лобового сопротивления учитывают вязкость
жидкости, а при расчёте подъёмной силы считают жидкость идеальной.
Однако при рассмотрении качественной физической картины естест-
естественно рассматривать оба вопроса вместе. Так как для объяснения
лобового сопротивления необходимо учитывать вязкость жидкости, то
мы рассмотрим картину обтекания тел вязкой жидкостью, которая
даст нам качественное объяснение происхождения как лобового
сопротивления, так и подъёмной силы.
§ 125. Обтекание тел вязкой жидкостью
Как уже указывалось в § 122, наличие вязкости приводит к тому,
что слой жидкости, непосредственно прилегающий к твёрдой стенке,
не скользит вдоль стенки, а «прилипает» к ней. Следующие за ним
слои жидкости скользят друг относительно друга, так что по мере
удаления от стенки скорость постепенно повышается. При этом ввиду

§ 125] ОБТЕКАНИЕ ТЕЛ ВЯЗКОЙ ЖИДКОСТЬЮ 357
наличия скольжения, т. е. градиента скорости в направлении, нормаль-
нормальном к стенке, между слоями действуют силы вязкости, направленные
навстречу скольжению. Следовательно, на всякий слой жидкости со
стороны соседнего слоя, лежащего ближе к стенке, действует тан-
тангенциальная сила, направленная против потока, а со стороны
слоя, лежащего дальше от стенки, — сила, направленная в сторону
потока. На самую стенку со стороны жидкости действует тан-
тангенциальная сила, направленная в сторону потока. Таким обра-
образом, наличие вязкости непосредственно приводит к возникнове-
возникновению сил, действующих со стороны потока на обтекаемое тело.
Эти тангенциальные силы и представляют собой собственно силы
трения.
Однако силами трения отнюдь не исчерпывается то влияние, кото-
которое оказывает вязкость на характер сил, действующих со стороны
потока на обтекаемое тело. Вязкость жидкости существенно изменяет
характер обтекания тела потоком, а вместе с тем и распределение
давлений жидкости на поверхность обтекаемого тепа, так что равно-
равнодействующая сил давлений оказывается не равной нулю. При боль-
больших скоростях потока эта результирующая сил давления может ока-
оказаться гораздо больше собственно сил трения и' играть преобладаю-
преобладающую роль.
Чтобы выяснить влияние вязкости иа характер обтекания, нужно
учесть действие именно тех тангенциальных сил, которые возникают
в прилегающем к стенке слое жидкости. Когда быстрый поток жидко-
жидкости с малой вязкостью обтекает тело, скорость жидкости, равная
нулю на поверхности тела, очень быстро возрастает по мере удале-
удаления от поверхности, так что уже на небольшом расстоянии от
поверхности скорость жидкости оказывается почти такой, как в на-
набегающем потоке. Другими словами, большие градиенты скорости
в направлении, перпендикулярном к стенке, существуют только
в тонком слое жидкости, близком к стенке; та!генциальные силы
в этом слое значительны (так как они пропорциональны произведению
коэффициента вязкости на градиент скорости) и играют существенную
роль. Вне этого слоя, где градиенты скорости уже очень малы,
силы вязкости не играют заметной роли, и ими вполне можно прене-
пренебречь. Этот прилегающий к поверхности тонкий слой жидкости,
в котором действуют значительные силы вязкости, получил название
пограничного слоя.
Силы вязкости не сказываются заметно на характере течения вне
пограничного слоя," так что ко всему потоку, кроме пограничного
слоя, можно применять законы течения идеальной жидкости, в част-
частности, уравнение Бернулли. В пограничном же слое силы вязко-
вязкости существенно изменяют характер течения — они делают невоз-
невозможным полное обтекание и приводят к отрыву потока от стенок
обтекаемого тела. Позади тела возникает вихреобразное движение
жидкости.

358
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvii
Это весьма важное явление отрыва потока мы рассмотрим на том
же примере обтекания цилиндра (рис. 287). В области Л, где поток
разветвляется, скорость его падает дЪ нуля, а давление рА возра-
возрастает иа pf2/2 по сравнению с давлением в набегающем потоке.
В обе стороны от точки А давление в потоке уменьшается, а
скорости возрастают по тем же причинам, что и в случае идеаль-
идеальной жидкости. В некоторых точках А' и А" давление уменьшается
Рис. 287.
до значения р в набегающем потоке и, продолжая далее умень-
уменьшаться, в областях В и С оказывается меньше, чем в набегаю-
набегающем потоке.
В общем распределение давлений на передней части цилиндра 'мало
отличается oi того, какое получилось бы в случае идеальной жидко-
жидкости. Существенное же отличие состоит в том, что силы вязкости
тормозят движение жидкости в пограничном слое, вследствие чего
частицы жидкости приходят из области А в области В и С с гораздо
меньшими скоростями, чем те, которыми они обладали бы в случае
идеальной жидкости. Так как при дальнейшем движении в погранич-
пограничном слое из областей В и С в направлении D' и D" частицы
жидкости попрежнему тормозятся силами вязкости, то в области D'D''
они могут создать давление, лишь немногим превосходящее рв или
рс. Когда давление в области DD' возрастёт до некоторого значе-
значения pD, большего рв, но меньшего р, струя жидкости, движущаяся
в пограничном слое, не сможет более проникать в область D'D''.
Где-то около точек D' и D' будет происходить отрыв потока от

§ 125]
ОБТЕКАНИЕ ТЕЛ ВЯЗКОЙ ЖИДКОСТЬЮ
359
стенок цилиндра. Область D'D' позади цилиндра будет заполнена
вихреобразно движущейся жидкостью, в которой установится давле-
давление pD, большее чем рв и рс, но меньшее, чем давление р в набега-
набегающем потоке.
На рис. 288 приведено полученное экспериментально распределе-
распределение давлений вокруг обтекаемого цилиндра. Попрежнему стрелками
изображены разности между давлением в данной точке и давлением р
в набегающем потоке. Стрелки, направ-
направленные к поверхности цилиндра, соот-
соответствуют давлению большему, чем в
набегающем потоке, а направленные от
поверхности —меньшему. Качественно
эта картина совпадает с той, которая
вытекает из приведённых выше рассу-
рассуждений.
Стрелки на рис. 288 изображают
также и те дополнительные силы даь-
ления со стороны жидкости на обте-
обтекаемое тело, которые возникают при
обтекании. Результирующая этих сил
не равна нулю вследствие того, что
силы впереди и позади тела не ком-
компенсируют друг друга. Вязкость жидко-
жидкости делает невозможным полное об-
обтекание цилиндра и приводит к тому,
что равнодействующая сил давлений
ма обтекаемое тело оказывается не равной нулю и направлена
в строну течения жидкости. Эта сила называется сопротивлением
давления.
Лобовое сопротивление, которое испытывает цилиндр со стороны
обтекающей его вязкой жидкости, представляет собой сумму сопро-
сопротивления трения и сопротивления давления.
Рассмотрим на том же примере обтекания
цилиндра одно важное явление, сопутствующее
отрыву потока от поверхности тел. В погра-
пограничном слое, как указывалось, скорость частиц
жидкости постепенно возрастает по мере уда-
удаления от стенки. Всякий объём жидкости в
пограничном слое обладает моментом количе-
количества движения относительно оси, проходя-
проходящей через центр объёма О, перпендикуляр-
перпендикулярной к плоскости течения (рис. 289). В таком случае говорят, что
течение обладает завихренностью. Наглядное представление о завих-
завихренности можно получить, предположив, что рассматриваемый элемент
текущей жидкости внезапно затвердел и при этом все его частицы
сохранили свои скорости. В случае отсутствия завихренности он
Рис. 288.
i -°
1
--,
_ 1
Рис. 289

360
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvii
щие завихрением, не могут существовать
и распадаются на отдельные вихри.
Рис. 290.
продолжал бы двигаться поступательно; при наличии завихренности
этот элемент донжен был бы начать вращаться в направлении, ука-
указанном на рис. 289 стрелкой. Наряду с движением центра" тяжести
затвердевшего элемента жидкости возникло бы вращение его вокруг
оси, перпендикулярной к плоскости чертежа и проходящей через
центр тяжести элемента.
Поток жидкости, отрывающийся от поверхности обтекаемого
тела, оказывается завихренным. Но тонкие слои жидкости, обладаю-
долго — они неустойчивы
Поэтому отрыв потока
от поверхности тела связан с обра-
образованием позади тела вихрей, которые уно-
уносятся потоком и прстспенно затухают.
Возникновение вихрей и их движение мож-
можно наблюдать, применяя один из указан-
указанных выше способов — посыпая поверхность
жидкости мелкими, нетонущими и иера-
створяющимися частицами или выпуская
в жидкость тонкие струйки краски. На
рис. 290 приведена картина образования
вихрей позади обтекаемого цилиндра, по-
полученная первым из указанных способов.
Картина образования вихрей во многих случаях носит совершенно
регулярный характер. Вихри возникают, по очереди, в каждом из двух по-
потоков, отрывающихся от поверхности тела, и движутся все с одинаковой
скоростью. (Эта скорость меньше, чем скорость потока; это и понятно:
в вихрях собираются как раз
те частицы жидкости, которые
тормозились при обтекании
тела.^ Возникает система вих-
вихрей, изображённая на рнс.291.
Она называется вихревой до-
дорожкой Кармана, по имени
учёного, теоретически изучив-
изучившего этот случай. Эта вихревая
дорожка носит столь правиль-'
ный характер, что она позво-
позволяет рассчитать лобовое со-
сопротивление, испытываемое
телом. Если подсчитать коли-
количество движения, которое
уносит поток жидкости вместе
с движущейся в нём вихревой
дорожкой, то оно оказывается
меньше, чем то количество
движения, которое приносит с собой набегающий на тело поток (так как вихри
движутся с меньшей, чем поток, скоростью). .Обтекаемое тело уменьшает
количество движения потока вследствие того, что оно действует на жидкость
с некоторой силой, направленной навстречу потоку. Зная потерянное коли-
количество движения, можно определить эту силу, а значит, и равную ей по
величине, но противоположно направленную силу лобового сопротивления.
Рис. 291.

§ 126]
СОПРОТИВЛЕНИЕ ДАВЛЕНИЯ И ТРЕНИЯ
361
Возникновение завихрений играет существенную роль не только при
обтеканий тел, но и при течении жидкости по трубам, При малых скоро-
скоростях жидкость течёт по трубе спокойио. Подкрашенная струя жидкости
представляет собой линию, параллельную оси трубы (рис. 292, а). Скорости
по сечению трубы распределяются так, как было найдено выше (§ 120).
Жидкость течёт как бы отдельными слоями, скользящими друг относительно
друга. Такое течение называется ламинарным (слоистым). Прн увеличении
скорости течения жидкости у стенок трубы возникают завихрения, которые
нарушают ламинарное течение жидкости. Эти завихрения вызывают беспо-
беспорядочные движения жидкости, скорости которых имеют составляющие
в направлении, перпендикулярном к оси трубы. Подкрашенная струя раз-
разрывается, н краска перемешивается в трубе (рис. 292, Ь). Такое течение
называется'турбулентным. При турбулентном течении падение давления
в тоубе резко возрастает — оно оказывается пропорциональным уже ие
скорости течения (закон Пуазейля), а квадрату скорости. Изменяется
и распределение скоростей по сечению трубы. Скорости гораздо быстрее
растут у края трубы и мало изменяются в средней части. Градиент скоро-
скорости у стенок трубы оказывается очень большим.
Возникновение турбулентности также определяется значением числа
Рейнольдса /? = pc^/jx, где / — диаметр трубы. Для определённых условий
втекания жидкости в трубу
турбулентность возникает при
определённых значениях числа
Рейнольдса. Например, для
трубы с острыми краями,
вставленной в гладкую стенку,
турбулентность возникает при
#:=1400. Падение давления в
трубе в случае турбулентного
течения, так же как и в случае
ламинарного, очень сильно
зависит от сечения трубы.
Большое падение давления
в трубах малого сечения (тон-
(тонких щелях) используется для
регулирования при "помощи крана количества вытекающей воды. Чтобы
вода вытекала с малой скоростью, давление по эту сторону крана
должно быть мало. При изменении размеров отверстия в кране ско-
скорость течения воды изменяется так, что падение давления в кране попреж-
нему оетаётся почти равным давлению в водопроводной сети. Пока кран
открыт не очень широко, почти всё давление водопроводной сети теряется
внутри крана. Если же широко отвернуть кран и затем заткнуть пальцем
его отверстие, то давление под пальцем будет равно давлению водопровод-
водопроводной сети (так как падения давления в кране не происходит). Поэтому вода
из-под неплотно прижатого пальца вылетает с большой скоростью.
§ 126. Сопротивление давления и сопротивление трения
Лобовое сопротивление, как уже указывалось, п; етставляет собой
сумму сопротивления трения и сопротивления давления. Соотношение
между этими компонентами лобового сопротивления в различных
случаях различно. В случае цилиндра, например, преобладающую
роль играет сопротивление давления. В случае же гладкой пластинки,
расположенной вдоль потока, лобовое сопротивление обусловлено
почти исключительно тангенциальными силами, действующими на
b
Рис. 292.

362
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvii
пластинку со стороны жидкости, т. е. представляет собой почти це-
целиком сопротивление трения. Наоборот, лобовое сопротивление пла-
пластинки, расположенной перпендикулярно к потоку, обусловлено поч-
почти исключительно избытком давления на переднюю сторону
пластинки по сравнению с давлением на её заднюю сторону, т. е.
представляет собой почти целиком сопротивление давления.
Как сопротивление давления, так и сопротивление трения зависят
от характера обтекания, т. е. в конечном счете от формы тел. Однако
форма тел гораздо сильнее влияет на сопротивление давления, чем
на сопротивление трения*). Поэтому соответствующим выбором формы
обтекаемых тел можно значительно уменьшить сопротивление давле-
давления и снизить его до величины сопротивления трения и даже ниже.
Как этого достичь, ясно из рассмотренной в предыдущем параграфе
картины возникновения сопротивления давления. Вследствие отрыва
потока от поверхности тела, позади тела образуется область понижен-
пониженного давления. Чем больше эта область, тем больше сопротивление
давления.
Рис. 293.
Для уменьшения сопротивления давления следует придать телу
обтекаемую форму, при которой расстояние между точками отрыва
обоих потоков, обтекающих тело сверху и снизу, становится очень
малым. Так, например, в случае длинной пластины, сечение которой
изображено на рис. 293, оба потока полностью обтекают тело, и от-
отрыв их происходит у заднего конца пластины, т. е. почти в одной
и той же точке. Поэтому область пониженного давления позади тела
практически отсутствует и сопротивление давления очень мало. Лобо-
Лобовое сопротивление в этом случае обусловлено почти одним только
сопротивлением трения. Если эту пластину разрезать по пунктирной
линии, то лобовое сопротивление е? передней части отдельно
было бы в 5—6 раз больше, чем всей неразрезанной пластины.
Причина этого ясна, у острых рёбер разреза происходит отрыв
потока, и позади плоской стенки образуется область пониженных
давлений.
Мы говорили всё время о телах, имеющих б.ольшие размеры
в направлении оси z. Однако эти же соображения остаются спра-
*) Поэтому сопротивление давления называют также сопротивлением
формы».

§ 126] СОПРОТИВЛЕНИЕ ДАВЛЕНИЯ И ТРЕНИЯ 363
ведливыми и в случае тел вращения, ось которых расположена
вдоль оси х. В частности, для об ьяснения различного лобового
сопротивления тел, изображённых на рис. 278, могут быть приме-
применены те же соображения. На рис. 294 приведена картина
обтекания тела сигарообразной формы. В отличие от случая обтека-
обтекания цилиндра (рис. 290) позади тела отсутствует завихренная область
пониженного давления.
Уменьшение лобового сопротивления тел во многих случаях имеет
большое практическое значение. Так, для самолёта, дирижабля или
торпеды *) лобовое сопротивление воздуха или воды является един-
единственной силой, тормозящей движение. Поэтому фюзеляжу само-
самолёта**), корпусу дирижабля и торпеды придают хорошо обтекаемую
форму. В быстроходных наземных
экипажах — автомобилях и скорост-
скоростных поездах—лобочое сопротивле-
сопротивление, обусловленное воздухом, хотя
и не является единственным сопро-
сопротивлением, но всё же играет замет-
заметную роль. Для уменьшения лобово-
лобового сопротивления этим экипажам
также придаётся обтекаемая форма. —»„.
Сопротивление давления при не- *sS|? ":
изменном характере обтекания тел """"
растёт пропорционально квадрату ри
скорости потока. Зависимость эту
можно объяснить следующим образом. Если, например, у обтекаемого
тела есть острые кромки, то отрыв потока будет всегда происходить
у этих кромок и, следовательно, характер обтекания не будет суще-
существенно изменяться при изменении скорости потока. Но в, таком
случае сопротивление давления зависит только от величии из-
избытка давления перед обтекаемым телом и недостатка давления по-
позади него.
Эги избыток и недостаток давлений обусловлены остановкой
потока перед обтекаемым телом и «отсасывающим действием» потока
позади тела. Но при неизменном характере течения изменения давле-
давления в потоке по уравнению Бернулли***) пропорциональны pv2, где
v — скорость потола, а р — его плотность, и поэтому сопротивление
давления оказывается пропорциональным pv2.
*) Торпеда (самодвижущаяся мина) движется под водой, и поэтому
к ней применимы выводы, касающиеся тел, обтекаемых однородным пото-
потоком. В случае Движения надводных судов картина осложняется явлениями
на поверхности воды.
* ) Вопрос о лобовом сопротивлении крыльев самолета будет специ-
специально рассмотрен ниже.
***) Как уже указывалось, вне пограничного слоя, где силы вязкости
уже не играют существенной роли, к потоку, обтекающему тело, можно
применять уравнение Бернулли.

364 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [ГЛ. XVII
Сопротивление трения более сложным образом зависит от скоро-
скорости потока, но тоже растёт с увеличением скорости потока.
Сопротивление трения при не очень больших скоростях не зависит
практически от степени шероховатости поверхности. Это легко понять,
вспомнив, что первый слой жидкости, прилегающий к стенке тела,
«прилипает» к ней, и существенную роль играет лишь трение внутри
жидкости. Однако при больших скоростях обтекания, когда погра-
пограничный слой очень тонок, шероховатость стенок может сказываться.
Если размеры неровностей сравнимы с толщиной пограничного слоя,
то они могут вызвать нарушение течения в пограничном слое и уве-
увеличить сопротивление трения. Поэтому, например, скоростным само-
самолётам не только придают хорошо обтекаемую форму, но и полируют
или покрывают гладкой краской все обтекаемые поверхности.
Полное лобовое сопротивление в тех случаях, когда преобладающую
роль играет сопротивление давления, также растёт приблизительно
пропорционально pv2. Вместе с тем для тел одинаковой формы оно
пропорционально площади, характеризующей поперечные размеры тел,
например, площади наибольшего поперечного сечения в случае сига-
сигарообразного тела. Поэтому величину лобового сопротивления можно
выразить так:
A7.12)
где 3—- площадь, характеризующая поперечные размеры тела, а без-
безразмерная величина Сх— коэффициент лобового сопротивления. Вели-
Величина Сх зависит от формы тела и его ориентировки по отношению
к потоку. Теоретический подсчёт Сх очень затруднителен и обычно
его приходится определять экспериментально — путём «продувки» тела
ипи его модели в аэродинамической трубе.
К случаю медленного течения в очень вязкой жидкости все изло-
изложенные в последних параграфах представления не применимы, так как
силы вязкости играют существенную роль не только вблизи тела, но
и на значительном расстоянии от него. В этом случае уже нельзя
выделить тонкий пограничный слой, а весь остальной поток рассма-
рассматривать без учёта сил вязкости. Вследствие этого и вся картина
обтекания тела медленным потоком вязкой жидкости, и механизм воз-
возникновения лобового сопротивления будут совершенно иными. Силы
вязкости тормозят движение не только ближайших, но и далёких
слоев жидкости. Сопротивление при этом оказывается пропорциональ-
пропорциональным первой степени скорости. Частным случаем этого типа зависимости
является уже известный нам закон Стокса (§ 48).
§ 127. Подъёмная сила
Направление результирующей силы, действующей со стороны
потока на тело, зависит от формы тела и его ориентировки в потоке.
Если направление этой результирующей силы не совпадает с напра-
направлением потока, существуют составляющие силы как в направлении:

§ 127]
ПОДЪЕМНАЯ СИЛА
365
потока — лобовое сопротивление, так и в направлении, перпендику-
перпендикулярном к потоку, — подъёмная сила. Соотношение между подъёмной
силой и лобовым сопротивлением зависит от формы тела и его ори-
ориентировки по отношению к- потоку. Так, в случае тонкой пластинки,
поставленной под углом к потоку (рис. 295), равнодействующая сил
давления и сил трения R направлена под некоторым углом к пластинке.
Её составляющие Rt и Rv
7\ R
Рис. 295.
представляют собой, со-
соответственно, лобовое со-
сопротивление и подъёмную
силу.
Подъёмная сила обу-
обусловливается распределе-
распределением сил давления по по-
поверхности обтекаемого
тела. Поэтому для объ-'
яснения происхождения
подъёмной силы нужно
рассмотреть, как рас-
распределяются давления
на отдельные элементы
поверхности обтекаемого
тела.
Картину распределения давлений мы рассмотрим на конкретном при-
примере утолщённой пластинки, профиль которой изображён на рис. 293.
Профили такого типа представляют практический интерес, так как
они применяются для крыльев самолёта (преимущества таких профи-
профилей выяснятся из дальнейшего).
Ориентировка крыла по отношению к потоку характеризуется, как
и в случае пластины, углом атаки а, который отсчитывается от неко-
некоторого условного направления,
связанного с профилем. В рас-
рассматриваемом профиле за эго
условное направление принята
прямая, совпадающая с прямоли-
рис 296 нейной частью нижней границы
профиля.
Рассмотрим распределение давлений на крыло при небольшом угле
атаки—порядка S°. На рис. 297 изображено полученное эксперимен-
экспериментально распределение давлений в потоке для интересующего нас слу-
случая. Так же как и для цилиндра, стрелки, направленные к поверхно-
поверхности крыла, изображают избыток давления по сравнению с давлением
в набегающем потоке, а направленные от крыла — недостаток давле-
давления. Чтобы обьяснить возникающее распределение давлений, мы
воспользуемся тем, что нам уже известно о распределении давлений
при обтекании цилиндра. Прежде всег» в передней части крыла,

366
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvii
имеющей форму, близкую к круглому цилиндру, условия обтекания
и распределение давлений будут такие же, как на передней части
цилиндра. В некоторой точке А поток разветвляется и начинает обте-
обтекать крыло (рис. 298). В месте разветвления потока скорость падает
до нуля и, следовательно, давление повышается на ры,2 по сравне-
сравнению с давлением в набегающем потоке. Далее, в обе стороны от
этой точки, как и в слу-
случае цилиндра, давление
начинает падать. Однако
дальнейшая картина бу-
будет, конечно, отличаться
от картины для цилиндра
вследствие различия фор-
формы тел. Тем не менее, на
основании картины для
Рнс. 297. цилиндра (рис. 288) мож-
можно вывести некоторые
качественные заключения о распределении давлений на крыло. Прежде
всего над крылом условия обтекания будут почти такие же, как на
соответствующей части цилиндра, и давление определяется теми же
условиями, что' и на участке цилиндра выше точки А. При малых
углах атаки обтекающий поток над крылом отрывается только почти
у самой задней кромки — в точке D'. Поэтому распределение давле-
Рис. 298.
ний над крылом будет такое же, как и на участке цилиндра, на
котором ещё не происходит отрыва потока, т. е. на участке AD'.
Следовательно, распределение давлений над • крылом мы получим,
перенеся участок AD' поверхности цилиндра на всю верхнюю поверх-
поверхность крыла. Давление в потоке над всей верхней поверхностью
крыла, начиная от некоторой точки А', близкой к А, будет меньше,
чем в набегающем потоке.
Под крылом картина будет иной, так как во всей этой области
поток набегает на крыло и вызывает некоторое повышение давления.
Поэтому давление в этой области будет выше давления в невозму-
невозмущённом потоке. В начале от точки А вниз давление будет падать
так же, как и в случае обтекания цилиндра, но дальше это уменьше-

§ 127]
ПОДЪЁМНАЯ СИЛА
367
Рис. 299.
ние давления прекратится, и во всей области под крылом давление
будет выше, чем в набегающем потоке.
Таким образом' можно объяснить, конечно, только качественно
я весьма нестрого картину распределения сил давления на крыло,
изображённую на рис. 297. Лег-
Легко видеть,__ что равнодействующая
этих сил R (рис. 299) отлична
от нуля, направлена вверх и лишь
•немного отклонена назад от перпен-
перпендикуляра к потоку. На крыло со
стороны потока действуют подъём-
подъёмная сила Ry и лобовое сопротивле-
сопротивление Rx, причём подъёмная сила по
величине значительно превосходит
лобовое сопротивление. Первая
представляет собой сумму проекций
на ось у сил, действующих на от-
отдельные элементы крыла; второе — сумму проекций тех же сил на ось
х. Как видно из картины распределения давлений (рис. 297), подъём-
подъёмная сила обусловлена в боль-
большей мере пониженным давле-
давлением над крылом, чем повышен-
повышенным давлением под крылом.
Лобовое сопротивление обу-
обусловлено, главным образом,
избыточным давлением впереди
крыла и, отчасти, наличием
составляющих вдоль оси х сил,
действующих на нижнюю и
верхнюю поверхности крыла.
При изменении угла атаки
картина, естественно, изменяется.
При увеличении угла атаки не-
несколько возоасгает давлеггке под
крылом, однако незначительно,
так как даже при очень больших
углах атаки это избыточное дав-
давление не может достигнуть вели-
величины JW-/2. (Этой величины избы-
избыточное давление достигает толь-
только в случае пластинки, перпен-
перпендикулярной к потоку.) Но с уве-
увеличением угла атаки резко пони-
понижается давление над крылом, и
поэтому подъёмная сила сначала
быстоо растёт с увеличением
угла атаки. Однако, когда угол атаки достигает некоторой определённой
величины (для рассматриваемого профиля о<оло 15°), картина обтекания
резко меняется. Условия обтеЪания передней верхней части крыла при
больших углах атаки станозятся сходными с условиями обтекания задней
Рис. 300.

368 ГИДРОДИНАМИКА И \Э?ОДЙНАМИКА [гЛ. XVII
стороны цилиндра и, так же как в случае цилиндра, обтекающий
поток отрывается от крыла уже ие у самой задней кромки; позади
крыла образуется завихренное пространство. С увеличением угла атаки
точка отрыва потока быстро приближается от задней кромки крыла к
передней.
На рис. 300 приведены фотографии потока, обтекающего крыло, при
малом и большом углах атаки. В завихренном пространстве позади крыла
давление хотя и ниже, чем в набегающем потоке, но выше, чем в случае
полного обтекания крыла. Действительно, в области, где поток не отры-
отрывается от крыла, распределение давлений соответствует области AD' при
обтекании цилиндра. После точки отрыва потока от крыла распределение
давлений будет примерно подобно распределению в области uD позади
цилиндра. Но в этой области давление выше (падение давления меньше), чем
в области BD'. Поэтому приближение точки отрыва потока к передней
кромке крыла уменьшает подъёмную силу. Несмотря иа то, что с увеличе-
увеличением угла атаки давление под крылом продолжает расти, подъёмная сила
не только перестаёт увеличиваться, но начинает падать, так как точка
отрыва потока начинает быстро приближаться к передней кромке крыла.
Угол атаки, при котором подъёмная сила начинает падать, называется
критическим углом атаки.
При угле атаки, равном нулю, для рассматриваемого профиля ещё будет
существовать некоторая подъёмная сила, так как давление под крылом
будет такое же, как в набегающем потоке, а над крылом давление будет
понижено. Подъёмная сила обратится в нуль только при некотором неболь-
небольшом отрицательном угле атаки. Дальнейшее увеличение отрицательного
угла атаки вызовет появление «отрицательной подъёмной силы*, направлен-
направленной вниз.
Для поведения тел в потоке существенную роль играет не только
величина результирующей сил давления, но и её «точка приложения», точ-
точнее, направление, вдоль которого она действует. Определяется это направле-
направление из условия, что геометрическая сумма моментов сил давления на все
элементы поверхности тела должна быть равна моменту результирующей
силы (относительно любой оси). Как уже указывалось (§§87 и 114), из этого
условия определяется направление прямой, на которой лежит результирую-
результирующая сила, но не точка приложения её. Однако, так же как и в указанных
случаях (при определении точки приложения силы тяжести и гидростатиче-
гидростатической подъёмной силы), из рассмотрения различных положений тела можно
извлечь указания о выборе точки приложения результирующей силы. При
изменении положения тела относительно потока прямая, вдоль которой
направлена результирующая сила, вообще говоря, изменяет своё положение
в теле. Однако в отличие от случаев силы тяжести и гидростатической
подъёмной силы вообще нельзя утверждать, что эти прямые пересекаются,
а поэтому нельзя указать какую-то определённую точку приложения
результирующей силы. Но если результирующая сила при всех рассматри-
рассматриваемых положениях тела остаётся лежать в какой-то одной плоскости, то
любые два её направления должны пересекаться. С другой стороны, при
непрерывном изменении положения тела относительно потока направление
результирующей силы также непрерывно изменяется. Поэтому пересечение
двух направлений, соответствующих двум близким положениям тела, можно
рассматривать как точку приложения результирующей силы для всех
промежуточных положений тела. Так, если (рис. 301) Ai, Аг> /43, /44 —
направления результирующей силы, соответствующие четырём различным
положениям тела /, 2, 3, 4, то точки С\, С2, С3 можно рассматривать как
точки приложения силы в положениям, лежащих соответственномежду положе-
положениями / и 2,2 и 3,3 и 4 Переходя к бесконечно близким положениям тела /, 2,
3, 4 и т. л., мы получим непрерывный ряд Т'очек приложения результирую-
результирующей силы, соответствующих этим положениям.

§ 127]
Подъёмная Силл
369
Таким образом, даже в том случае, когда все направления результирую-
результирующей силы при разных положениях тела не пересекаются в одной точке," но
лежат в одной плоскости, всё же
можно считать, что результирующая
сила приложена к определенной
точке тела, но эта точка переме-
перемешается в теле при изменении его
положения относительно потока. Та-
Такой способ определения точки при-
приложения силы несколько условен, но
вполне законен, если мы рассматри-
рассматриваем только такие изменения поло-
положения тела, при которых результи-
результирующая сила всё время остается в Рис. 301.
одной плоскости. В дальнейшем, во
всех случаях, когда мы будем
применять представление о точке приложения результирующей, напри-
например, подъёмной силы, речь будет идти только о вполне отделенных
" Ь
Рис. 30J.
изменениях положения тела., при которых указанное условие будет соблю-
соблюдено. Поэтому представление о точке приложения результирующей будет
законно и вместе с тем оно упростит рассмотрение целого ряда вопросоз.
24. с. Э. Хайкин

370 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [ГЛ. XVU
На основании рассмотренной выше картины распределения давлений не-
нетрудно определить, где находится точка приложения подъёмной силы. Так как
в образовании подъёмной силы наиболее существенную роль играет понижен-
пониженное давление над крылом в передней его части, то точка приложения подъём-
подъёмной силы_должна находиться не в середине профиля крыла, а ближе к перед-
переднему краю. И действительно, как показывают измерения, при малых углах
атаки точка приложения подъёмной силы в обычных профилях лежит
примерно на V» расстояния между передней и задней кромкой крыла.
При увеличении угла атаки разрежение над передней частью крыла ра-
растёт, так что его роль в образовании подъёмной силы становится ещё боль-
большей. Вследствие этого в обычных профилях точка приложения подъёмной
силы с увеличением угла атаки приближается к передней кромке крыла.
Это обстоятельство играет весьма существенную роль в вопросе об
устойчивости самолёта. Для пояснения может служить опыт с тонкой пла-
стннкой в потоке воздуха. Распределение давлений вокруг тонкой пластинку
Рис. 303.
обтекаемой потоком, конечно, отличается от рассмотренной нами картины.
Однако для пластинки также наибольшую роль в образовании подъёмной
силы играет пониженное давление над её передней частью, и поэтому
точка приложения подъёмной силы лежит ближе к переднему её краю.
Этим и объясняется поведение в потоке воздуха тонкого диска, который
может вращаться вокруг оси, лежащей в плоскости диска (рис. 302). Если
диск повернуть вдоль потока (рис. 302а), то он не остаётся, в таком поло-
положении, а поворачивается и устанавливается примерно перпендикулярно к
потоку (рис. 302Ь). Причины этого таковы. Когда диск расположен точно
вдоль потока, то на него действует только сопротивление трения — танген-
тангенциальная сила, не дающая момента относительно оси вращения диска. Но
как только диск вследствие случайных толчков поверится хотя бы на не-
небольшой угол к потоку, возникнет подъёмная сила, приложенная не к центру
диска, а несколько впереди него (рис. 303а). Эта сила будет поворачи-
поворачивать диск дальше. Следовательно, положение диска вдоль потока есть по-
положение неустойчивого равновесия. Другое положение равновесия полу-
получается для диска, когда он перпендикулярен к потоку, так как в этом
случае равнодействующая сил давления приложена к центру диска и не
даёт момента относительно его оси. (Но при этом положении равнодей-
равнодействующая сил давления — это уже не подъёмная сила, а лобовое сопротив-
сопротивление.) При отклонении диска от этого положения (рис. ЗОЗЬ) точка при-
приложения равнодействующей сил давления переместится немного вперёд.
Возникнет момент, который будет возвращать диск в положение, перпен-
перпендикулярное к потоку. Следовательно, это положение соответствует устой-
устойчивому равновесию.
Примерно так же обстоит дело с крылом. Положение вдоль потока для
отдельно взятого крыла оказывается неустойчивым. Поэтому в конструк-
конструкцию самолёта приходится вводить специальные элементы, которые устраняют
эту неустойчивость (см. § 130).

§ 128J
КРЫЛО САМОЛЕТА.
371
§ 128. Крыло сзмэлёга
В предыдущем параграфе мы рассматривали обтекание крьпа беско-
бесконечной длины. Для реального крыла самолёта, имеющего конечную дтину,
картина осложняется явлениями, происходящими на торцах крыла. Нетрудно
составить представление о том, как сказываются эти явления на величине
подъёмной силы и лобового сопротивления крыла. Если возникла подъёмная
сила, то под крылом установилось более высокое давление, чем над крылом.
Поэтому у торца крыла возникает движение воздуха снизу вверх, как ука-
указано стрелками на рис. 304. Это движение воздуха у торцов крыла изменяет
распределение скоростей, а следовательно, и распределение давлений в
потоке, обтекающем крыло.
Рис. 304.
Рис. 305.
Оценить в общих чертах, каковы будут эт изменения, можп :> м!
помощи следующих соображений. Воздух, обтекающий торец крыла, i ii-м
под крылом и над крылом вертикальную составляющую скорости, напра-
направленную вниз. Вследствие существования этой дополнительной верти-
вертикальной скорости w (рис. 305) крыло конечного размаха в потоке со
скоростью V находится в таких же условиях, в каких находилось бы беско-
бесконечное крыло в потоке, скорость которого v' несколько наклонена вниз.
Это значит, что результирующая сила давления на крыло конечного раз-
размаха R отклонена несколько назад от того направления, которое имела
бы равнодействующая R' для крыла бесконечной длины. Поэтому соста-
составляющая R* силы R по действительному направлению набегающего потока
увеличивается и лобовое сопротивление возрастает. Следовательно, у крыла
конечного размаха лобовое сопротивление больше, чем у участка беско-
бесконечного крыла той же длины.
Перетекание воздуха снизу вверх у торцов крыла происходит тем
более интенсивно, чем больше разность давлений под крылом и над ним,
т. е. чем больше угол атаки. Вследствие этого при увеличении угла атаки
лобовое сопротивление для крыла конечного размаха растёт гораздо быстрее,
чем для крыла бесконечной длины. Ясно, что эти явления сказываются тем
меньше, чем больше длина крыла по отношению к его ширине, т. е. чем
больше относительный размах крыла. С точки зрения уменьшения лобового
сопротивления выгодно применять крылья с большим относительным раз-
размахом.
В предыдущем рассмотрении мы не касались вопроса о зависимости
подъёмной силы крыла и его лобового сопротивления от скорости набегаю-
набегающего потока. Установить характер этой зависимости можно на основании
следующих соображений. И та, и другая сила обусловлены явлениями, свя-
связанными с законом Бернулли, и поэтому оказываются пропорциональными
24*

372
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл.
ро2, где р — плотность жидкости или газа, a v — скорость потока. Так как,
помимо того, величина подъёмной силы и величина лобового сопротивления
(при данном профиле крыла и его относительном размахе) пропорциональны
площади крыла 5, то их можно выразить следующим образом:
A7.13)
A7.14)
где Сх и Су — как легко убедиться из сопоставления размерностей — без-
безразмерные коэффициенты; Сх называется коэффициентом лобового сопро-
сопротивления, а Су — коэффициентом подъёмной силы.
Очевидно, что всё сказанное выше о зависимости подъёмной силы
и лобового сопротивления от угла атаки и относительного размаха крыла
можно перенести, соответственно, на
коэффициенты Сх и Су.
Коэффициент подъёмной силы Су
с увеличением угла атаки растёт сна-
сначала быстро, а затем медленнее и после
критического угла атаки начинает па-
падать. Коэффициент лобового сопротив-
сопротивления Сх растёт сначала медленно, а
затем быстрее
На рис. 306 приведены графики за-
зависимости Сх и Су от угла атаки для
одного из типов крыльев, применяемых
в авиации. Так как Сх по абсолют-
абсолютной величине много меньше, чем Су,
то для того, чтобы обе кривые удобна
было нанести в одном масштабе, на
графике отложена величина 5 Сх. От
крыла самолёта требуется большая.
Рис. 306. подъёмная сила при малом лобовом
сопротивлении. Крыло тем лучше бу-
будет удовлетворять этому требованию,
чем больше величина k~Cy]Cx, которая поэтому называется качеством,
крыла. Как качество крыла влияет на свойства самолёта, будет выяснено
в § 130.
§ 129. Эффект Магнуса. Циркуляция
Качественные соображения относительно распределения давлеаий,
которыми мы пользовались в предыдущих параграфах, весьма на-
наглядны, но, конечно, не пригодны для расчёта величин подъемной
силы и лобового сопротивления. Для этого нужна" математическая
теория, которая позволила бы количественно описать рассмотренную
выше качественную картину. Создание такой тедрии настолько затруд-
затруднено необходимостью учитывать склы вязкости, что трудностей этих
до сих пор не удалось преодолеть.
Между тем, как уже указывалось (§ 124), подъёмная сила может
существовать и в случае обтекания тела идеальной (невязкой) жидко-
жидкостью. Более того, оказалось, что, не учитывая сил вязкости, можно
не только объяснить происхождение подъёмной силы, но и правильно
оценить её величину. Б_ ли разработаны теоретические методы, позво-

§ 129]
ЭФФЕКТ МАГНУСА. ЦИРКУЛЯЦИЯ
373
ляющие рассчитывать величину подъёмной силы, т. е. решать одну
из наиболее важных задач прикладной аэродинамики. В развитии
этих методов основные заслуги принадлежат русским учёным
Н. Е. Жуковскому и С. А. Чаплыгину, которые разработкой этих
методов, а также и другими своими исследованиями очень много
способствовали прогрессу авиации.
Чтобы выяснить, почему при расчёте подъёмной силы можно не учи-
учитывать сил вязкости и какую роль эти силы всё же играют в возникнове-
возникновении подъёмной силы, мы рассмотрим обтекание вращающегося цилиндра
Рис. 307.
(рис. 307). Этот случай не только удобен для выяснения интересую-
интересующих нас вопросов, но имеет и самостоятельный интерес.
Вращение цилиндра изменит картину обтекания вследствие того,
что силы вязкости в пограничном слое будут действовать по-иному.
Если линейная скорость точек поверхности цилиндра больше, чем
скорость набегающего потока, то силы, действующие со стороны
стенки цилиндра на жидкость в пограничном слое, будут вверху
н внизу цилиндра направлены в противоположные стороны. Там, где
обе указанные скорости направлены в одну сторону (на нашем ри-
рисунке— сверху), силы вязкости не только не тормозят движения
жидкости в пограничном слое (как было при невращающемся цилинд-
цилиндре), но, наоборот, будут способствовать этому движению. С другой
стороны, там, где обе скорости направлены навстречу (на нашем ри-
рисунке— внизу), жидкость в пограничном слое будет тормозиться силь-
сильнее, чем в случае невращающегося цилиндра. Наряду с этим впереди
цилиндра частицы жидкости, находящиеся в пограничном слое, под
действием сил вязкости приобретут скорость, направленную вверх.
Вследствие этого точка А, в которой скорость жидкости равна нулю,
и точки ?)' и D", где обтекающий поток отрывается от поверхности
цилиндра, сместятся относительно тех положений, которые они зани-
занимали в случае невращающегося цилиндра. Точка А, для которой ско-
скорость обращается в нуль, сместится в направлении, противоположном

374
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvi i
Рис. 308.
вращению цилиндра — в область, где скорость, сообщаемая жидкости
стенками цилиндра, направлена навстречу движению обтекающей жидко-
жидкости. Точки D' и D" обе сместятся в направлении вращения цилиндра,
так как поток, обтекающий цилиндр в направлении его вращения, будет
отрываться дальше, а обтекающий протиз его вращения — ближе,'чем
в случае невращающегося цилиндра.
В результате получится картина
обтекания, изображённая на рис.
307. На рис. 308 приведена со-
соответствующая этой картине мо-
моментальная фотография потока, по-
полученная на опыте для рассматри-
рассматриваемого случая.
Чтобы установить распределение
давлений в потоке для этого случая,
необходимо учесть не только сме-
смещение точек, где пото# останавли-
останавливается и отрывается от цилиндра,
но и изменение скоростей потока в областях В и С. В области В
линии тока гуще и, следовательно, скорости больше; наоборот, в
области С линии тока реже и скорость
меньше, чем в случае невращающегося
цилиндра. Поэтому и падение давления
в В будет больше, а в С меньше, чем
в случае невращающегося цилиндра.
Перенеся распределение давлений
с участков ABD н ACD невращаю-
невращающегося цилиндра и учитывая указан-
указанные изменения величины падения да-
давления, получим для вращающегося ци-
цилиндра распределение давлений, при-
примерно изображённое на рис. 309 Легко
видеть, что результирующая этих сил
давления имеет вертикальную составля-
составляющую. Вращающийся цилиндр испыты-
испытывает ие только лобовое сопротивление,
но и подъёмную силу. При этом, как
указывалось выше (§ 124), поток по-
позади цилиндра должен быть откло-
отклонён вниз. На рис. 308 это хороша
видно.
Возникновение подъёмной силы при вращении цилиндра назы-
называется эффектом Магнуса. Это явление можно наблюдать при па-
падении бумажного цилиндра, скатившегося с наклонной доски (рис. 310).
Tax ка'с, скатившись с доски, цилиндр продолжает вращаться, то
при его падении, т. е. обтекании п л оком воздуха, возникает подъ-
Рис. 309.

§ 129]
ЭФФЕКТ МАГНУСА. ЦИРКУЛЯЦИЯ
375
ёмная сила, направленная горизонтально и отклоняющая цилиндр
назад.
Эффект Магнуса применяется для использования силы ветра при дви-
движении судов. На судне устанавливаются вертикально высокие цилинд-
цилиндры, которые приводятся в быстрое вращение. Возникает подъёмная си-
сила, направленная горизонтально, перпен-
перпендикулярно к ветру (роторный . корабль).
В последнее время делаются попытки
заменить крылья самолёта вращающими-
вращающимися горизонтальными .цилиндрами. При
движении самолета возникает подъёмная
сила, достаточная для того, чтобы под-
поддерживать самолёт.
Эффектом Магнуса объясняется, на-
например, непрямолинейный полёт тенисно-
го мяча после «резаного» удара, при
котором ракета сообщает мячу не толь-
только поступательное, но и вращательное
движение.
При рассмотрении картины обтекания вращающегося цилиндра
особенно легко проследить происхождение подъёмной силы н лобового
сопротивления и роль сил вязкости в их возникновении. Подъёмная
сила обусловлена тем, что скорость жидкости над цилиндром
оказывается больше, чем под ним, и поэтому, в соответствии с зако-
законом Бернулли, давление под цилиндром выше, чем над ним. Лобовое
Рис- 310#
Рис. 311.
сопротивление обусловлено, главным образом, неполным обтеканием
цилиндра—-наличием позади него области с пониженным давлением.
Все определяется характером обтекания тела, которое существенно
зависит от наличия сил вязкости, играющих принципиальную роль
в возникновении той или иной картины обтекания. Но представим

376
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvii
себе, что после того, как установилась картина обтекания, изобра-
изображённая на рис. 307, силы вязкости исчезли. При этом обтекание ци-
цилиндра должно стать полным: точки D' и D", в которых отрывается
поток от стенок цилиндра, сольются с точкой D. Никаких других
существенных изменений в характере потока исчезновение сил вяз-
вязкости не должно вызвать. Таким образом, если бы силы вязкости
исчезли, картина обтекания тела приняла бы вид, изображённый на
рис. 311.
Действительно, как показывает строгое математическое рассмотре-
рассмотрение, невязкая жидкость может обтекать цилиндр так, как показано
на рис. 311. При этом лобовое сопротивление исчезнет (так как оно
Вызывается непэлным обтеканием), подъёмная же сила останется не-
неизменной, так как не изменится распределение скоростей над и под
цилиндром.
Если нас интересует только подъёмная сила, то обе картины,
изображённые на рис. 307 и 311, можно считать эквивалентными.
Как ММ видели, силы вязкости играют принципиальную роль только
ion возникновении этой картины. Следовательно, силы вязкости нужно
•чать, чтобы объяснить возникновение подъёмной силы, но их
v4HTbmaTb, когда обтекание уже установилось, подъёмная
-чует и требуется лишь найти её величину.
^«ние скоростей, установившееся в потоке, было
жидкость как идеальную и применяя тео-
теорему uvj- у -« найти подъёмную силу. Таким образом,
при определении подъёмной силы возникают две задачи: во-первых,
найти распределение скоростей, которое установится при обтекании,
и, во-вторых, по этому распределению скоростей найти подъёмную
силу. При решении первой задачи, вообще говоря, нужно было бы
учитывать силы вязкости, но в отдельных случаях при помощи кос-
косвенных соображений можно найти распределение скоростей в потоке,
не решая задачи для вязкой жидкости. При решении второй задачи
вообще можно рассматривать жидкость как идеальную. При этом
можно пользоваться представлениями, очень упрощающими реше-
решение второй, а в некоторых случаях и первой задачи. Вместе с
тем эти представления очень намядны, и мц их здесь вкратце иа-

§ 129]
ЭФФЕКТ МАГНУСА. ЦИРКУЛЯЦИЯ
377
Сравнивая две картины обтекания цилиндра идеальной жидко-
жидкостью— ту, при которой нет подъёмной силы (рис. 312), и ту, при
которой она существует (рис. 313), нетрудно обнаружить следующее.
Вторая картина получается из первой, если на течение, соответствую-
соответствующее первой картине, наложить течение жидкости вокруг цилиндра
в направлении часовой стрелки (рис. 314).
Такое течение жидкости вокруг обтекаемого тела называется
циркуляционным течением или циркуляцией. Наличие циркуляции
обусловливает разность скоростей над цилиндром и под ним, т. е.
существование подъемной силы. Зная скорость циркуляционного те-
течения, можно найти величину подъёмной силы. Связь между скоростью
циркуляции и величиной подъёмной силы установлена Н. Е. Жуковским.
Положение точек А и D (рис. 311) зависит от соотношения
между скоростью набегающего потока v и скоростью циркуляции w
(чем больше те» — тем ниже лежат эти точки). Поэтому, зная положе-
положение точек А и D (его часто можно определить из некоторых допол-
дополнительных соображений), можно найти скорость циркуляции, а затем
определить и величину подъёмной силы.
В рассмотренном выше случае вращение цилиндра привело к воз-
возникновению циркуляции и появлению подъёмной силы. В других слу-
случаях циркуляция может возникать вследствие других причин, напри-
например, в случае крыла, из-за несимметрии профиля крыла и его
наклонного положения к потоку. Однако и в этих случаях, так же
как и при вращении цилиндра, само возникновение циркуляции обу-
обусловлено действием сил вязкости. Если бы силы вязкости отсутство-
отсутствовали, циркуляция вообще не могла бы возникнуть ни в одном из
этих случаев.- Но если циркуляция уже существует и величина её из-
известна, то существует и подъёмная сила и величину её можно
найти.
Применим представление о.потоке с циркуляцией к случаю обтекания
крыла. При почти полном обтекании крыла (т. е. при малых углах атаки)
Рис. 315.
Рис. 316.
Рис. 317.
ноток отрывается вблизи задней кромки крыла. Поэтому циркуляцию, воз-
возникающую при обтекании крыла, можно приближённо определить из усло-
условия, что точка отрыва потока находится как раз у задней кромки крыла.
Если бы циркуляция отсутствовала, то в идеальной жидкости должна была
получиться картина обтекания, изображённая на рис. 315. В самом деле,
так как циркуляции и .подъёмной силы нет, то направление потока позади
крыла должно быть такое же, как впереди, т. е. точка отрыва потоков,
обтекающих крыло с двух сторон, должна была бы находиться над крылом.
В действительности же отрыв потока происходит у задней кромки. Сл

378 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [гл. XVII
вательно, должна существовать циркуляция, направленная по часовой стрелке
(рис. 316), которая, налагаясь на течение, изображённое на рис. 315, пе-
переносит точку отрыва потока к задней кромке крыла (рис. 317).
Вместе с тем циркуляция увеличивает скорость потока иад крылом и
уменьшает её под крылом. В соответствии с законом Бернулли давление
под крылом возрастает, а над крылом уменьшается, и возникает подъём-
подъёмная сила.
При помощи таких соображений можно определить не только направле-
направление, но и величину циркуляции, а значит, найти и величину подъёмной силы.
Как уже подчёркивалось, эти соображения позволяют утверждать, что цир-
циркуляция должна существовать, и в
некоторых случаях найти её ско-
скорость. Однако без учёта сил вязко-
вязкости нельзя объяснить, почему цирку-
циркуляция возникла, так как её возникно-
возникновение обусловлено действием сил
вязкости.
Возникновение циркуляции во-
вокруг крыла тесио связано с возник-
возникновением вихрей позади крыла. Вна-
Вначале, пока крыло находится в покое,
циркуляция отсутствует, и общий
момент количества движения системы
крыло — окружающая среда равен
нулю. Поэтому и в дальнейшем об-
общий момент количества движения
этой замкнутой системы должен оста-
Рис. 318. ваться равным нулю. Когда поток воз-
воздуха начинает обтекать крыло, в
начальный момент, пока циркуляция
ещё не возникла, картина обтекания должна быть близка к той, которая
изображена на рис.315. Частицы воздуха, обтекающие крыло снизу, поднима-
поднимаются мимо задней его кромки вверх. При этом под действием сил вязкости дви-
движение частиц воздуха становится завихренным — они приобретают вращение
против часовой стрелки. У кромки постепенно образуется вихрь с вращением
против часовой стрелки (рис. 318). Затем этот вихрь отрывается от крыла
и уносится потоком. Но вихрь обладает некоторым моментом количества
движения, соответствующим вращению против часовой стрелки. В силу
закона сохранения моментов количества движения вокруг крыла должна
возникнуть циркуляция, направленная в сторону, противоположную вращению
вихря (по часовой стрелке). Возникшая уже циркуляция могла бы суще-
существовать дальше, как угодно долго, если бы не силы вязкости. Тогда пре-
прекратилось бы и образование вихрей на конце крыла. (Изменившееся вслед-
вследствие наложения циркуляции распределение скоростей таково, что вихрь на
конце крыла не возникает.) Однако, вследствие наличия сил вязкости цирку-
циркуляция вокруг крыла постепенно затухает, и снова появляются условия,
необходимые для возникновения вихря. Позади крыла снова появляется
вихрь и вместе с тем увеличивается циркуляция вокруг крыла.
При постоянной скорости движения самолёта процесс образования вих-
вихрей происходит почти вполне регулярно. От заднего края крыла периоди-
периодически отрываются вихри, которые уносятся потоком воздуха. Эти вихри,
периодически ударяющиеся о хвост самолёта, могут быть причиной опас-
опасных вибраций. Особенно сильны эти вибрации, когда период ударов вихрей
совпадает с периодом собственных колебаний хвоста самолёта или какой-
либо его части. В практике самолётостроения известны случаи, когда вслед-
вследствие резонанса между ударами вихрей и колебаниями хвоста самолёт
разваливался в воздухе,

§ 130] ПОЛЁТ САМОЛЁТА 379
§ 130. Полёт самолёта
Одной из важнейших задач практической аэродинамики является рас-
рассмотрение сил, которые обеспечивают возможность полёта самолёта, сохра-
сохранения его устойчивости в полёте и управления самолётом. Мы рассмотрим
здесь вкратце эти вопросы, используя те результаты, которые были получены
в предыдущих параграфах.
Чтобы самолёт мог летать, его крылья должны развивать подъёмную
силу. Подъёмная сила возникает только тогда, когда крыло обтекается по-
потоком воздуха. Необходимую скорость движения относительно воздуха са-
самолёту сообщает воздушный винт (пропеллер), приводимый в действие мо-
мотором. Вннт самолёта вращается со •скоростью свыше полутора тысяч
оборотов в йинуту и отбрасывает
назад сильный поток воздуха. При
этом возникает «сила тяги», дей-
действующая иа винт со стороны возду-
воздуха и направленная вдоль оси винта.
Происхождение этой силы станет
сразу ясным, если мы сравним винт
с крылом. Элемент винта — поясок,
вырезанный из винта сечениями А и
В (рис. 319), аналогичен участку кры- Рис. 319.
ла, движущегося под некоторым поло-
положительным углом атаки со скоростью w. Эта скорость лежала бы в пло-
плоскости вращения винта, если бы не возникало потока воздуха в направле-
направлении оси винта (в создании этого потока воздуха и заключается роль винта).
Вследствие же движения воздуха результирующая скорость элемента винта
относительно воздуха и отклоняется виерёд. Но мы пока для упрощения
будем пренебрегать этим обстоятельством. В таком случае действующая на
выделенный элемент винта со стороны окружающего воздуха сила R даёт
«подъёмную силу» Т, направленную вдоль оси
винта, и «лобовое сопротивление» Q, направлен-
направленное против направления движения винта. Сумма
«подъёмных сил» Т, действующих на отдельные
-элементы винта, и представляет собой силу тяга
винта. Моменты сил Q, действующих иа отдель-
отдельные элементы винта, дают результирующий мо-
момент, приложенный к оси винта и направленный
навстречу его вращению. Для поддержания рав-
Рис 320 номерного вращения винта приложенный к его
" оси вращающий момент мотора должен быть
равен этому результирующему моменту сил Q.
Мощность мотора будет использована наиболее эффективно, если при
заданном значении момента сил Q винт развивает возможно большую силу
тяги Т. Это достигается надлежащим выбором профиля винта и «угла атаки»
элементов винта, т. е. шага винта. Теоретически эга задача впервые была
успешно решена Н. Е. Жуковским, который предложил систему воздушного
винта, получившую широкое распространение в авиации (винт НЕЖ).
При рассмотрении работы винта в реальных условиях, как уже указы-
указывалось, необходимо учитывать, что винт не только вращается, но и дви-
движется (вместе с самолётом) поступательно. Поэтому всякий элемент винта,
кроме скорости w, обусловленной вращением, обладает ещё скоростью v,
обусловленной поступательным движением (рис. 320). Результирующая ско-
скорость и каждого элемента винта оказывается вследствие этого в большей
или меньшей степени отклонённой вперёд, и поэтому угол атаки элемента
винта уменьшается. Вместе с тем уменьшается и подъёмная сила эле-
элемента винта, и следовательно, результирующая сила R всё больше и больше

380
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvil
отклоняется назад от направления а. Её составляющая в направлении v
уменьшается — сила тяги элемента винта падает. При некотором значении ско-
скорости v направление R отклонится настолько (рис. 321), что окажется пер-
перпендикулярным к v — сила тяги элемента винта упадёт до нуля. При даль-
дальнейшем увеличении V, когда угол атакн примет некоторое отрицательное
значение, подъёмная сила обратится в нуль и сила R будет направлена
по Ц- Её составляющая на направление v будет направлена против V, т. е.
э .емент винта будет давать отрицательную силу тяги (рис. 322).
Рис. 321.
Рис. 322.
Так как для разных элементов винта скорости w различны (вследствие раз-
разного расстояния до оси) и могут быть различны углы атакн, то зависи-
зависимость силы тяги элемента от скорости
v будет различной, но при больших
значениях v сила тяги каждого эле-
элемента винта должна уменьшиться. Тяга
винта уменьшается по мере увеличе-
увеличения скорости самолёта либо монотонно,
либо начиная с некоторого значения
скорости. Легко видеть, что влияние
скорости v будет тем менее заметно,
чем больше w, а значит, чем выше
обороты винта. Йо при приближении
w к значениям скорости звука обте-
обтекание профиля винта ухудшается,
возрастает лобовое сопротивление и
уменьшается эффективность работы
виита. Следовательно, при скоростях
полёта, близких к скорости звука, винт не может развивать большой силы тяги.
При полёте с работающим мотором на самолёт действуют четыре силы:
сила веса, тяга винта, подъёмная сила и лобовое сопротивление. Чтобы
Рис. 323.
средняя сырость
Рис. 324.
Мйлаа страта
самолёт летел с постоянной скоростью, эта система четырёх сил должна
находиться в равновесии. При этом самолёт может лететь горизонтально,
набирать высоту или планировать. Взаимное расположение четырёх сил во
всех этих случаях будет различно, но для того, чтобы скорость самолёта
оставалась постоянной, сумма всех четырёх сил Д1лжна быть равна нулю.
При горизонтальном полёте (рис 323) подъёмная сила Ry должна быть
равна силе веса Q, а тяга винта F — лобовому сопротивлению Rx. Величина
подъёмной силы и лобового сопротивления зависит от угла атаки крыльев
самолёта. Угол атаки крыльев лётчик может изменять, поднимая или опу-
опуская нос самолёта при помощи руля высоты (см. ниже), н горизонтальный полёт

§ 130]
ПОЛЁТ САМОЛЁТА
381
возможен при различных углах атаки. На рис. 324 изображены три положе-
положения самолёта при горизонтальном полёте с разными углами атаки. С уве-
увеличением угла атаки коэффициент подъёмной силы растёт (по<а угол атаки
не достигнет критического значения), и чем больше угол атаки, тем меньше
скорость, при которой подъёмная сила достигает силы веса. Каждому углу
атаки соответствует определённая скорость, тем меньшая, чем больше
угол атаки. Критическому углу атаки соответствует минимальная скорость
горизонтального полёта *). Если при полёте с этой минимальной скоростью
ещё увеличить угол атаки (т. е. сделать его больше критического), то подъ-
подъёмная сила уменьшится и самолёт начнёт «проваливаться» *"*).
При горизонтальном полёте с постоянной скоростью должны соблю-
соблюдаться равенства Rx=zT, Ry=zG; поэтому, пользуясь выражениями A7.13)
и A7.14) для ~RX и Ну (§ 128), можно написать:
A7.15)
A7.16)
откуда
A7.17)
Потребная силатягиГзависит от отношения k—Cv[Cx, которое называется
«качеством самолёта» (аналогично «качеству крыла», § 127;. Минимальная
тяга потребуется при горизон-
горизонтальном полёте с таким углом
атаки, для которого отноше-
отношение Су)Сх имеет наибольшее
значение. Этот наивыгоднейший
угол атаки для современных са-
самолётов лежит в пределах при-
примерно 3—8°. При этом отно-
отношение Су(Сх достигает 10, т. е.
потребная тяга винта при этих
углах должна быть примерно
в 10 раз меньше веса самолё-
самолёта. Отсюда видно, что даже при
горизонтальном полёте потреб-
потребная тяга винта, а значит, и по-
потребная мощность мотора .ра-
.растут с увеличением нагрузки само-
самолёта. «Это связано с тем, что при большей нагрузке самолёт должен
лететь с большей скоростью (при наивыгоднейшем угле атаки, ко-
который остаётся прежним), чтобы развивать прежнюю подъёмную силу, и по-
поэтому тяга винта должна преодолевать большее лобовое сопротивление.
При наборе высоты с постоянной скоростью система сил, действующих
на самолёт, попрежнему должна находиться в равновесии, но расположение
этих сил изменяется (рис. 325). Подъёмная сила Ry уравновешивает только
Рис. 325.
*) При критическом угле атаки полёт становится уже неустойчивым,
и практически наименьшая скорость Соответствует углу атаки, немного
меньшему критического.
**) Если угол атаки увеличивается (нос самолёта поднимается), то по-
появляется вертикальная составляющая силы тяги. Однако так как вся сила
тяги меньше веса самолёта и4 угол между её направлением и верти-
вертикалью близок к я/2, то вертикальная составляющая силы тяги при горизон-
горизонтальном полёте (когда подъёмная сила направлена вертикально) очень мала
и не играет существенной роли.

382 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [гЛ, XVII
составляющую Gy силы веса. Другую её составляющую Gx, так же как
и лобовое сопротивление, должна уравновесить сила Т, т. е. тяга винта
должна быть больше, чем при горизонтальном полёте. Правда, при этом /?-
должно быть меньше G, а значит, скорость может быть меньше, чем при
горизонтальном полёте; соответственно уменьшится и лобовое сопротивле-
сопротивление. Но так как всё лобовое сопротивление во много раз меньше веса,
то величина, иа которую оно уменьшится, будет гораздо меньше, чем та
часть силы веса, на которую должна увеличиться тяга винта. Поэтому при
увеличении крутизны подъёма потребная мощность растёт. Для того чтобы
самолёт мог набирать высоту, мотор должен обладать запасом мощности
по сравнению с той, которая нужна для горизонтального полёта при наивы-
наивыгоднейшем угле атаки. Чем больше этот резерв мощности, тем быстрее
самолёт сможет Иабирать высоту — тем больше его скороподъёмность.
При снижении с постоянной скоростью мы имеем обратную картину:
составляющая силы, веса действует в направлении тяги винта, и потребная
мощность мотора уменьшается. При достаточном угле снижения составляю-
составляющая силы веса полностью компенсирует лобовое сопротивление, т. е. за-
заменяет тягу винта. Самолёт может планировать — снижаться с выключенным
мотором. Как и минимальная тяга винта при горизонтальном полёте, мини-
минимальный угол планирования получается при наивыгоднейшем угле атаки.
Для взлёта самолёт должен разбежаться по земле и набрать скорость,
при которой подъёмная сила может стать больше силы веса. Чтобы ускорить
наступление этого момента, самолёту перед взлётом придают такое полОже-
ние, при котором угол атаки близок к критическому: отрыв от земли про-
происходит при скорости, лишь немного превышающей минимальную. Поэтому
обычно после отрыва от земли самолёт некоторое время летит почти го-
горизонтально и набирает скорость, прежде чем перейти к набору высоты.
При посадке самолёт приближается к земле пологим спуском и на не-
небольшой высоте лётчик переводит его снова на горизонтальный полёт.
Постепенно увеличивая угол атаки, лётчик уменьшает скорость полёта до
минимальной и переводит самолёт в такое положение, какое он должен
занимать при пробеге по земле. От дальнейшего уменьшения скорости са-
самолёт начинает «проваливаться», прикасается колёсами к земле и, пробе-
пробежав некоторое расстояние по земле, останавливается.
Чем больше скорости, при которых происходит отрыв и соприкоснове-
соприкосновение с землёй, тем труднее со всех точек зрения операции взлёта и посадки.
При этом существенна, конечно, величина скорости относительно земли,
между тем- подъёмная сила определяется скоростью относительно воздуха.
Поэтому взлёт и посадку выгоднее производить против ветра.
§ 131. Устойчивость полёта и управление самолётом
При прямолинейном полёте с постоянной скоростью самолёт должен
двигаться поступательно, т. е. не только сумма действующих на самолёт
сил, но и сумма моментов этих сил относительно любой оси должна быть
равна нулю. Однако и этого мало. Случайные причины (порывы ветра,
разрыв снаряда и т. д.) могут немного отклонить самолёт от положения,
соответствующего совершаемому прямолинейному движению. Нужно, чтобы
после этого самолёт (без участия лётчика) возвращался к исходному дви-
движению. Для этого должны возникать силы и моменты сил, которые умень-
уменьшали бы возникшие отклонения. Только при этом условии движение будет
устойчивым.
При рассмотрении условий равновесия моментов сил удобно выбрать
оси, проходящие через центр тяжести самолёта. Чтобы обеспечить равно-
равновесие моментов, при проектировании самолёта, стремятся прежде всего к
тому, чтобы «омент каждой из действующих сил относительно центра тя-

§ 131]
УСТОЙЧИВОСТЬ ПОЛЁТА И УПРАВЛЕНИЕ САМОЛЁТОМ
383
жести в отдельности по возможности был близок к нулю (для силы веса
это получается само собой). Далее, ось винта располагают так, чтобы она
проходила через центр тяжести и чтобы момент силы тяги относительно
центра тяжести был равен нулю. Наконец, при выборе положения крыльев
стремятся к тому, чтобы равнодействующая аэродинамических сил (подъ-
(подъёмной силы н лобового сопротивления) проходила через центр тяжести
самолёта. Конечно, совершенно точно этого сделать нельзя, но, как будет
видно из дальнейшего, это и не требуется. Во всяком случае, ясно, ка-
какое значение имеет положение центра тяжести самолёта, или центровка
самолёта.
элерон
руль
маправ!
Ъ -стабилизатор
рупь высоты
Рис. 326.
злерон
Рис. 327.
Рнс. 328.
При расположении грузов в самолёте необходимо по возможности мало
изменять положение центра тяжести самолёта. Эта задача особенно усло-
усложняется в случае, когда количество и расположение грузов изменяются в
полёте (расходуется горючее, сбрасываются бомбы), так как при этом центр
тяжести самолёта не должен ¦сколько-нибудь
значительно перемещаться.
Для выяснения вопроса об устойчивости само-
самолёта мы рассмотрим моменты сил, возникающие
при повороте самолёта около 'каждой из трёх
его осей, проходящих через центр тяжести С —
продольной, поперечной и путевой (рис. 326).
Так как при повороте самолёта относительно
вертикальной оси (рис. 327) направление полёта
сразу не успевает измениться, возникает да-
давление набегающего потока на киль — верти-
вертикальное, оперение хвоста самолёта. Это да-
давление, представляющее собой «подъёмную силу» вертикально располо-
расположенного крыла, создаёт момент относительно вертикальней оси, воз-
возвращающий самолёт к исходному положению. Таким образом, вертикальное
оперение обеспечивает устойчивость самолёта относительно вертикальной
оси, или устойчивость пути (способность, сохранять направление полёта).
При повороте самолёта относительно поперечной оси (рис. 328) изме-
изменяется угол атаки и перемещается центр приложения подъёмной силы Ry—
вперёд при увеличении угла атаки (для большинства профилей). Это пере-
перемещение центра приложения подъёмной силы привело бы к ещё большему
задиранию иоса самолёта. Но при этом хвост самолёта опускается и на
стабилизатор — горизонтальное оперение хвоста самолёта — начинает дей-
. ствовать подъёмная сила R', направленная вверх. Она создаёт момент отно-
относительно поперечной оси, возвращающий самолёт в горизонтальное положе-
положение. Наоборот, если нос самолёта опускается, то стабилизатор, поднимаясь,
Становится под отрицательным углом атаки к набегающему потоку, ц на

384
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[гл. xvil
него действует «подъёмная сила», направленная вниз. Момент этой силы
поднимает нос самолёта, т. е. возвращает его'к исходному положению. Таким
образом, хотя крыло само по себе неустойчиво относительно поперечной
оси, стабилизатор придаёт самолёту устойчивость относительно этой оси и
обеспечивает сохранение горизонтального (или близкого к горизонтальному)-
положения продольной оси самолёта. Легко видеть, что положение суще-
существенно не изменится, если точка приложения подъёмной силы будет лежать
впереди центра тяжести. При этом нос самолёта будет несколько поднят,
стабилизатор будет уже с самого начала находиться под положительным
углом атаки и давать подъёмную силу, так что сумм,а моментов подъёмной
силы крыльев и стабилизатора относительно поперечной оси будет равна
нулю. Поворот самолёта относи-
относительно поперечной оси нарушит
равенство этих моментов, и воз-
возникший момент будет, как пока-
показано выше, возвращать самолёт к
исходному положению.
Наконец, устойчивость само-
самолёта относительно продольной
оси обычно обеспечивается спе-
специальным расположением крыль-
крыльев, при котором концы крыльев
подняты выше середины (рис. 329). При горизонтальном положении
самолёта подъёмная сипа каждого из крыльев наклонена несколько внутрь,
но их результирующая направлена вертикально и уравновешивает подъём-
подъёмную силу. Если самолёт накренился (рис. 330), то результирующая подъём-
подъёмная сила R также изменит направление, и её горизонтальная составляющая
R' сообщит самолёту горизонтальную скорость в сторону крена (скольже-
(скольжение на крыло). Возникшее при этом движении течение воздуха со скоростью
v' от одного крыла к другому-(в исправлении, противоположном скольже-
скольжению) создаст дополнительную
«подъёмную силу», направлен-
направленную вниз (так как угол атаки
крыльев по отношению к пото- —•
ку v' отрицателен). Эта «подъ- ——*
ёмная сила» Rt будет больше —-
для поднявшегося крыла, чем ¦—»»г
R2 для опустившегося (так как •—»•
отрицательный угол атаки пер-
вого больше). Момент этих сил » г ' .ч
Рнс. 329.
Рис. 330.
)
будет возвращать самолёт в
исходное положение. Если бы
крылья были расположены в
одной плоскости, то их угол
атаки по отношению к возникшему потоку воздуха был бы одинаков. Од-
Однако и в этом случае при скольжении вследств!е перемещения центра
давлений возникал бы момент сил, возвращающий самолёт к исходному по-
положению. Таким образом, и при горизоитальном расположении крыльев мож-
можно было бы обеспечить устойчивость самолёта, ио V-образное располо-
расположение крыльев усиливает его устойчивость относительно продольной оси.
Мы рассматривали прямолинейное движение самолёта. При криволиней-
криволинейном движении вся картина усложняется, н мы ограничимся только вопросом
о способах изменения направления полёта. Для этой цели служат руль на-
направления, изменяющий направление полёта в горизонтальной плоскости, и
руль высоты, изменяющий его направление в вертикальной плоскости.
Рули представляют собой небольшие плоскости, при нейтральном положе-
положении* являющиеся как бы продолжением плоскостей хвостового оперения.

§ 131]
УСТОЙЧИВОСТЬ ПОЛЁТА И УПРАВЛЕНИЕ САМОЛЁТОМ
385
Рис. 331.
вертикальную составляю-
полёт с набором высоты.
Руль направления представляет собой продолжение киля, а руль высоты —
продолжение стабилизатора (рис. 326). При помощи рукояток управления
и передач лётчик может поворачивать рули соответственно относительно
вертикальной и горизонтальной оси. Обычно руль высоты поворачивается
ручным рычагом, а руль направления — педалями. Поворот рулей приводит
к изменению формы поверхности киля или стабилизатора, которые пред-
представляют собой, как мы видели, в сущности вертикальное и горизонтальное
крыло. Вызванное поворотом руля изменение
формы этого крыла приводит к появлению
«подъёмной силы» (или к изменению уже дей-
действующей подъёмной силы) в направлении,
противоположном повороту руля *). Момент
этой возникшей силы вызывает поворот са-
самолёта вокруг соответствующей оси.
Поворот руля высоты (рис. 331) приводит
к повороту самолёта вокруг поперечной оси,
т. е. изменению угла атаки, вследствие чего
увеличивается подъёмная сила, траектория
полита искривляется и самолёт приобретает
щую скорости и переходит в прямолинейный _ . _д_. ...
Поворот руля направления приводит к тому, что самолёт, продолжая
лететь прямо, начинает поворачиваться вокруг своей путевой оси (рис.332).
При этом скорость потока воздуха относи-
относительно крыла, поворачивающегося вперёд
(на рисунке — правого), увеличивается, а
поворачивающегося назад (на рисунке —
левого) уменьшается. Вследствие этого
подъёмная сила, действующая на правое
крыло, возрастает, а на левое уменьшает-
уменьшается. Возникает момент подъёмной силы
относительно продольной оси, вызывающий
крен самолёта — правое крыло поднимает-
поднимается, а левое опускается. Результирующая
подъёмная сила наклоняется влево и дае'т
составляющую в горизонтальном напра-
направлении. Эта составляющая подъёмной силы
и сообщает самолёту ускорение влево —
самолёт начинает описывать траекторию,
искривлённую влево. Помимо этого фюзеляж самолёта также играет некото-
некоторую роль. Он представляет собой как бы вертикальное крыло. Подъёмная
сила, действующая на это крыло, направлена влево и способствует искри-
искривлению траектории.
Таким образом, сила, действующая на руль направления, не вызывает
непосредственно искривления траектории, да и не могла бы вызвать этого
искривления, так как она направлена наружу, а не внутрь описываемой
траектории. Искривление траектории вызывается, главным образом, креном
самолёта. Поворот в горизонтальном направлении можно вызывать или этому
повороту помогать, непосредственно изменяя крен самолёта. Для этого
служат специальные элементы управления — элероны (рис. 333), которые
Рис. 332.
*) Очень упрощая картину, можно было бы сказать, что на руль, откло-
отклонённый от нейтрального положения, начинает действовать подъёмная сила.
Однако, нельзя говорить о подъёмной силе, действующей на отдельный
участок крыла, расположенный у его задней кромки. Поворот рулей изме-
изменяет всю картину обтекания и приводит к возникновению или изменению
подъёмной силы киля или стабилизатора.
25 с. Э. хайккн

386 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [ГЛ. XV!l
представляют собой небольшие плоскости, прикреплённые к задней кромке
крыльев самолёта на некоторой части их длины. В нейтральном положении
элероны являются как бы тодолжеяием крыльев. При помощи рукояток
или штурвала лётчик может поворачивать элероны относительно горизон-
горизонтальной оси—поднимать или опускать их концы (на рис. 333 изображена
часть коыла с опущенным элероном). При повороте штурвала элероны по-
поворачиваются в противоположные стороны, увеличивая подъёмную силу для
одного крыла (у которого элерон опускается) и уменьшая её для
другого крыла (у которого элерон поднимается). Так как элероны обычно
расположены у краёв крыльев, то они изменяют подъёмную силу тех частей
крыла, которые как раз дают большой момент относительно продольной
оси. Поэтому хотя изменения подъёмной силы, вызываемые элеронами, не
велики, но момент сил, обусловленных действием элеронов, получается
значительным, и самолёт кренится — поднимается то крыло, у которого
Рис. 333.
элерон Опущен вниз. При крене появляется горизонтальная составляющая
подъёмной силы, вызывающая искривление траектории самолёта. Руль на-
направления и элероны, поворачивая самолёт вокруг различных осей, при-
приводят в конечном счёте к одному и тому же результату—искривлению
траектории в горизонтальной плоскости.
В общем, как мы видим, силы, возникающие непосредственно при пово-
повороте рулей и элеронов, не велики, и не влияют непосредственно иа траек-
траекторию полёта самолёта. Но моменты этих сил достаточны для того, чтобы
поворачивать самолёт вокруг осей, в результате чего возникают силы, дей-
действующие на весь самолёт в целом и вызывающие искривление его траек-
траектории.
Рассмотренные нами вопросы касались почти исключительно движения
самолёта с постоянной по величине скоростью и сводились к рассмотрению
условий равновесия между силами, действующими на самолёт (за исключе-
исключением случая поворота в горизонтальной плоскости, когда на самолёт дей-
действует неуравновешенная составляющая подъёмной силы). Большей частью
полёт самолёта происходит именно в таких условиях. Однако, для специ-
специальных типов самолётов (истребитель, пикирующий бомбардировщик) боль-
большое значение имеют случаи движения с большими ускорениями, например,
пикирование к выход из пике и т. д. В этих случаях равновесие сил уже не
имеет места, а наоборот, именно отсутствие равновесия обусловливает
большие ускорения самолёта.
Одним из наиболее актуальных вопросов практической аэродинамики
является увеличение скорости самолёта. При этом возникает ряд серьёзных
трудностей.
Прежде всего, как уже указывалось, скорости, с которыми самолёт
отрывается или касается земли, не должны быть велики. Но эти скорости
близки к минимальной скорости полёта самолёта. Поэтому минимальная
скорость полёта не должна быть очень велика. С другой стороны, макси-
максимальную скорость полёта в большинстве случаев желательно сделать боль-
большой, т. е. диапазон скоростей самолёта должен быть достаточно широк

§ 132] РАСПРОСТРАНЕН!!! ИМПУЛЬСА В ЖИДКОСТИ И ГАЗЕ 387
Именно расширение диапазона скоростей представляет собой одну из наи-
наиболее важных и трудных задач конструирования самолёта.
Так как при больших скоростях подъёмная сила на единицу площади
крыла велика, то при больших скоростях требуется меньшая площадь
крыльев. При этом уменьшается их лобовое сопротивление и, следовательно,
легко увеличить скорости. Однако, при этом увеличивается и минимальная
скорость полёта. Для снижения минимальной скорости приходится прини-
принимать специальные меры — устраивать передвижные щитки или закрылки,
увеличивающие коэффициент подъёмной силы (и вместе с тем и коэффици-
коэффициент л^ового сопротивления). В полёте эти закрылки убираются (прижи-
(прижимаются к крыльям); при посадке они выдвигаются и уменьшают посадочную
скорость. Применение этих методов позволяет несколько расширить диапа-
диапазон скоростей самолёта. Однако, недопустимость повышения минимальной
скорости является всё же одной из серьёзных трудностей при конструировании
скоростных самолётов.
Возможности увеличения скорости самолёта открываются при полёте в
верхних, менее плотных слоях атмосферы. Как видно из соотношений
A7.3) и A7.4), как подъёмная сила, так и лобовое сопротивление уменьша-
уменьшаются при уменьшении плотности воздуха р. Уменьшение лобового сопро-
сопротивления позволяет при данной мощности мотора увеличить его скорость,
и это увеличение скорости как .раз компенсирует падение подъёмной силы,
обусловленное уменьшением р*). Вообще же говоря, скорость, которой
может достигать самолёт, определяется мощностью, которую может развивать
его мотор. Применение воздушно-реактивных двигателей (§ 121) позволило
пойти дальше в увеличении скорости самолётов, прежде всего потому, что
они гораздо мощнее бензиновых моторов при тех же габаритах и весах и
обладают запасом мощности (позволяют сильно форсировать режим дви-
двигателя). Эти преимущества позволили строить реактивные самолёты,
скорость которых превышает наибольшие скорости, достижимые для само-
самолётов с мотором и винтом, и приближается к скорости звука. При таких
скоростях обычная аэродинамика, рассматривающая воздух как несжимае-
несжимаемую жидкость, по причинам, указанным в § 119, оказывается несостоятель-
несостоятельной. Вопросы движения газов при скоростях, близких к звуковым и сверх-
сверхзвуковым, в которых принципиальную роль играет сжимаемость газов, рас-
рассматриваются в газовой динамике.
§ 132. Распространение импульса в жидкости и газе
Во всех рассмотренных ранее случаях движения жидкостей и газов
изменение объёма играло второстепенную роль, и поэтому можно
было рассматривать жидкости и газы как несжимаемые. Сейчас мы
рассмотрим явление, в котором сжимаемость играет принципиальную
роль, именно распространение кратковременного импульса в жидкости
и газе. Как и в аналогичных явлениях в твёрдом теле, сжимаемостью
определяется скорость распространения импульса.
Рассмотрим, прежде всего, как может возникнуть кратковременный
импульс в жидкости и газе. Представим себе большую пластину,
помещённую в жидкость или газ (рис. 334). Сообщив пластине
быстрое нормальное перемещение, мы вызовем в прилегающем слое
*) Для того, чтобы мотор самолёта мог развивать полную мощность на
большой высоте, т. е. в разрежённой атмосфере, применяются специальные
меры: воздух, необходимый для образования горючей смеси, сжимается и
-подаётся в мотор компрессором (нагнетателем).
25*

388
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[ГЛ. XVII
жидкости или газа сжатие и вследствие этого повышение давле-
давления. Это давление вызовет движение следующего слоя газа и т. д.
Сжатие и движение частиц будут передаваться от слоя к слою.
В жидкости или газе будет распространяться импульс сжатий и ско-
скоростей. Этот импульс продольный, так как направление распростра-
распространения импульса совпадает с направлением движения частиц. Очевидно,
что с другой стороны пластины будет распространяться аналогичный
продольный импульс, но не сжатия, а разрежения.
Распространение импульса обусловлено наличием упругих сил,
возникающих в жидкости или газе. Но жидкости и газы обла-
обладают упругостью только в отношении изменения объёма и не обла-
обладают упругостью в отношении сдвига. Поэтому,
в отличие от твёрдых тел, в жидкостях и газах
могут распространяться только импульсы сжа-
сжатия и разрежения, т. е. продольные импульсы.
Импульс всегда будет распространяться либо
в направлении, в котором начали двигаться
частицы жидкости или газа в месте возникно-
возникновения импульса (импульс сжатия), либо в про-
противоположном направлении (импульс разре-
разрежения).
Если сообщить пластине быстрое переме-
перемещение не в нормальном направлении, а под
j i углом к нормали, то частицы всё же получат
скорости, направленные по нормали. Действи-
Рис. 334. тельно, между жидкостью или газом и пластиной
действуют только силы нормального давле-
ления; и как бы ни двигалась пластина, она может сообщить части-
частицам только нормальные скорости. Правда, при быстром движении
между пластиной и жидкостью или газом возникают и тангенциальные
силы вязкости, но если они малы, то скорости частиц практически
нормальны к пластине, в жидкости или газе возникнет только продоль-
продольный импульс, нормальный к пластине. Движение жидкости вдоль пла-
пластины, обусловленное силами вязкости, заметно только вблизи неб.
Скорость распространения продольного импульса в жидкости или
газе можно рассчитать совершенно так же, как и скорость продоль-
продольного импульса в твёрдом теле. Пусть импульс сжатия соответствует
увеличению плотности на Др и увеличению давления на Д/>. Через
площадку S, перпендикулярную к направлению распространения им-
импульса, за время Д^ проходит «часть импульса» с It, где с — скорость
распространения импульса. Прохождение этого участка импульса свя-
связано с увеличением массы справа от площади 5 на величину Д/я =
= Др S'cM. При этом через площадку передаётся количество движения
i
i
Вместе с тем слева, на площадку S действует сила F=Skp, Изме-

§ 132] РАСПРОСТРАНЕНИЕ ИМПУЛЬСА В ЖИДКОСТИ И ГАЗЕ 389
нение количества движения должно быть равно F М. Следовательно,
или с2 = ^. A7.18)
Скорость импульса определяется только тем, как изменяется плотность
среды при изменении давления. Скорость импульса не зависит от его
формы и амплитуды. Поэтому всякие быстропеременные давления
в жидкости или газе, и, в частности, звуки распространяются в среде
в большинстве случаев с той же скоростью, с какой распространяются
отдельные импульсы.
Например, для воды при изменении давления на 1 am, т. е. при-
примерно на Ю6 дЩсм?, вода сжимается на 5-10~5 своего объёма, и плот-
плотность возрастает на 5• 10~5 ztCMs. Подставляя эти значения
др=Ю6 дн\см1 и Др=5-10~5 г\смг в формулу A7.18), получим:
са = 2-1010 см'\сек* и с = 1 400 м[сек.
Это и есть скорость распространения импульса (скорость звука)
в воде.
Строго говоря, при этих расчётах следовало бы принять во вни-
внимание, что упругие свойства среды зависят от температуры. Это обсто-
обстоятельство играет роль даже тогда, когда температура среды в сред-
среднем остаётся неизменной. Дело в том, что при быстром сжатии среды
выделяется тепло, которое не успевает распространиться в со-
соседние объёмы. Правда, для воды это обстоятельство не играет за-
заметной роли,' но для газов его необходимо учитывать. Так как при
повышении температуры сжимаемость газа уменьшается, то это обсто-
обстоятельство приводит к увеличению скорости распространения импульса
по сравнению с той, которая имела бы место при неизменной темпе-
температуре. Сжатие газа без отвода тепла носит название адиабатического
сжатия. При адиабатическом сжатии вместо закона Бойля-Мариотта,
который справедлив при неизменной температуре (изотермическое
сжатие), связь между объёмом и давлением даётся соотношением
р\п = const., A7.19)
где у = cp!cv имеет несколько различное значение для различных га-
газов. Для воздуха Y=l,4. Так как плотности обратны объёмам, то
Р __ Ро
откуда dp = '{(Pui?o)?'l~id?1 Если изменения плотности малы, то
рт—х/р^—1== 1 и
^Г=ЧР±, A7.20)
следовательно, скорость распространения импульса
<=lAg. A7.21)

390 ГИДРОДИНАМИКА И АЭРОДИНАМИКА [гл. XVII
где р0 и р0 — давление и плотность газа при средней температуре.
Для воздуха, например, при 0° p0jp0 = 8-\08 см2/сек2 и у=1,4.
Скорость импульса с = 334 м\сек; это и есть скорость звука в воз-
воздухе. Так как отношение />о/ро меняется с температурой (повышается
с увеличением температуры), то скорость импульса в газе растёт с
повышением температуры. При неизменной температуре отношение
ро/ро для данного газа есть величина постоянная (закон Бойля-Мари-
отта) и, следовательно, скорость импульса не зависит от давления
газа.
Скорость звука в воздухе (скорость распространения импульса)
была впервые измерена следующим образом. Из одного пункта од-
одновременно посылались, звуковой и световой сигналы (удар колокола
и вспышка света). В другом пункте измерялось время, на которое
запаздывает приход звукового сигнала относительно светового. По
этому времени и расстоянию между пунктами определялась скорость
звука (так как скорость света в миллион раз больше скорости звука,
то временем распространения светового сигнала вполне можно пре-
пренебречь). Уже эти первые измерения дали величину, близкую к той,
которая следует из полученной формулы*).
В наших расчётах мы неоднократно пользовались тем, что изме-
изменения плотности и давления малы. Поэтому наши результаты спра-
справедливы только для не слишком сильных импульсов. Очень сильные
импульсы сжатия (например, взрывы) распространяются вначале со
скоростью большей, чем это следует из наших расчётов. Наоборот,
очень сильные разрежения распространяются медленнее.
Импульс, возникающий при быстром перемещении бесконечно
большой пластины, представляет собой простейший тип импульса, так
называемый плоский импульс. Во все точки, лежащие в плоскости,
параллельной пластине, импульс приходит в один и тот же момент.
Вообще во всех точках любой плоскости, параллельной пластине,
в каждый момент времени среда находится в одном и том же состоя-
состоянии. Энергия, движущаяся вместе с импульсом, занимает всё время
одинаковый объём, и плотность энергии в импульсе, следовательно,
не меняется — импульс распространяется, не ослабевая. Однако, это
было бы справедливо только для бесконечно больших пластин. При
конечных размерах пластины вследствие явлений, о которых мы будем
говорить в гл. XX, импульс размывается и захватывает всё более
и более широкие области. При этом энергия импульса рассеивается,
распределяется на всё большие и большие объёмы, и плотность энер-
энергии в импульсе уменьшается. Импульс постепенно ослабевает при
распространении. Некоторое ослабление импульса вызывают также
*) Интересно отметить, что в то время, когда производились первые
опыты по измерению скорости звука, пользовались неправильной формулой,
полученной Ньютоном без учёта адиабатического характера процесса и не
содержавшей поэтому под корнем множителя у. Когда обнаружилось рас-
расхождение с опытом, причина этого была выяснена, и формула исправлена.

§ 132] РАСПРОСТРАНЕНИЙ ИМПУЛЬСА В ЖИДКОСТИ И ГАЗЕ 391
силы вязкости, которые возникают в жидкости и газе и на преодо-
преодоление которых расходуется часть энергии импульса.
Другим простым типом импульса является шаровой импульс. Такой
импульс возникает, если шар, помещённый в жидкости или газе,
сразу резко изменит свой объём.
Если среда однородна, то скорость распространения импульса во
все стороны одна и та же, и он в один и тот же момент будет при-
приходить в точки, лежащие на поверхности одного и того же шара.
При распространении такого шарового импульса энергия будет
занимать всё больший и больший объём. Поэтому плотность энергии
импульса будет убывать. Шаровой импульс будет быстро ослабевать
с расстоянием.
Примерно такой характер имеет взрывная волна, образующаяся
в воздухе при взрыве снаряда или бомбы.
Так же, как и большая пластина, всякое движущееся тело создаёт
импульсы в окружающей жидкости или газе. Однако, эти импульсы
будут иметь заметную величину лишь при достаточно быстром движе-
движении тела. Чтобы выяснить, какую роль при этом играет скорость,
положим, что движущаяся в среде пластина имеет малые размеры.
При медленном движении такой пластины давления по-обе стороны
от неё будут выравниваться, так как газ сможет перетекать мимо
краёв пластины из области сжатия в область разрежения. Поэтому
при медленном движении пластина небольших размеров не будет
создавать импульсов в среде. Однако, если пластина движется доста-
достаточно быстро, то давления не будут успевать выравниваться, и в
среде будет возникать импульс такой же интенсивности, как и в слу-
случае движения бесконечной пластины.
Нетрудно сообразить, при каких скоростях движения тела давле-
давления не будут успевать выравниваться. Давления выравниваются и вооб-
вообще передаются со скоростью распространения импульса (распростране-
(распространение импульса как раз и представляет собой передачу давлений).
Поэтому, если даже тело малых размеров движется в среде со ско-
скоростью распространения импульса или большей, оно должно создавать
сильный импульс в окружающей среде. Например, полёт пули или
снаряда со скоростью, превышающей 340 м\сек, сопровождается
• возникновением импульса.
Так как скорость распространения импульса меньше, чем скорость
источника, его порождающего, то характер возникающего импульса
и картина его распространения оказываются весьма своеобразными.
Пуля и снаряд создают впереди себя сжатие, которое распространяется
во все стороны в виде шарового импульса. Но этот импульс не мо-
может обогнать пулю, так как движется с меньшей скоростью. Следова-
Следовательно, перед пулей импульса не будет. Он будет появляться только
позади неё.
Чтобы выяснить характер импульса, представим, себе, что пуля
движется не непрерывно, а равными скачками, причем каждый из атих

392
ГИДРОДИНАМИКА И АЭРОДИНАМИКА
[ГЛ. XVII
Рис. 335.
скачков вызывает возникновение шарового импульса. На рис. 335
цифрами отмечены последовательные положения пули через равные
промежутки времени. Пользуясь указанным представлением, мы должны
рассматривать эти точки как источники шаровых импульсов, возникаю-
возникающих в момент появления пули в данной точке. Так как эти моменты
отделены друг от друга промежутками времени, то импульсы от отдель-
отдельных точек успевают распространиться на разные расстояния. Располо-
Расположение таких отдельных импуль-
импульсов для момента времени, ког-
когда пуля находится в точке 8,
отмечено на рисунке соответ-
соответствующими кругами. Если от-
отдельные скачки будут стано-
становиться всё мельче и мельче,
круги эти будут расположены
всё гуще и гуще. При этом все
шаровые импульсы образуют
сплошную коническую поверх-
поверхность, которая и представляет
собой поверхность создаваемого пулей импульса. Эта поверхность
движется вместе с пулей и с её скоростью. Таким образом, хотя
отдельные импульсы распространяются с меньшей скоростью, но
поверхность импульсов движется с такой же скоростью, с какой
движется пуля. Вместе с пу-
пулей или снарядом в воздухе
распространяется эта «ударная
волна», имеющая форму конуса.
При этом раствор "конуса тем
меньше, чем больше скорость
пули по сравнению со ско-
скоростью распространения им-
импульса в среде.
Ударную волну, создавае-
создаваемую пулей, можно сделать ви-
видимой при помощи специальных
оптических приёмов, исполь-
использующих увеличение коэффи-
коэффициента преломления воздуха при
сжатии. При помощи кратко-
кратковременного освещения электрической искрой были получены моменталь-
моментальные фотографии летящей пули и сопровождающей её ударной волны.
На рис. 336 приведена одна из таких фотографий.
Картина позади пули отчасти напоминает рассмотренные нами выше
случаи неполного обтекания потоком: пуля оставляет позади себя
завихренное пространство. Однако, основную роль при движении
(. большими скоростями играет картина не позади тела, а впереди
Рис. 336.

§ 132]
РАСПРОСТРАНЕНИЕ ИМПУЛЬСА В ЖИДКОСТИ И ГАЗЕ 393
него. На создание ударной волны расходуется часть энергии дви-
движущегося тела, которая уносится импульсом. Это — новый вид сопро-
сопротивления среды, которое возникает при быстром движении тел. При
скоростях, превышающих скорость распространения импульса, этот
вид сопротивления имеет решающее значение. При этом играют роль
не обтекаемость тел, а явления впереди движущегося тела. Величина
сопротивления зависит от формы не задней (как в случае обтекания),
а передней части тела. Для ослабления возникающего импульса (умень-
(уменьшения сопротивления) выгоден острый нос. Поэтому пулям и снаря-
снарядам обычно придают форму, заострённую спереди. Во всяком случае,
им не придают обтекаемой формы, так как скорость пули выше
скорости распространения импульса в воздухе и обтекаемость не
играет заметной роли. Наоборот, малые авиационные бомбы или мины,
выбрасываемые из миномётов, обычно имеют скорость меньшую, чем
скорость импульса. В этом случае сопротивление существенно зависит
от того, как происходит обтекание бомбы воздухом, и для уменьше-
уменьшения сопротивления малым авиационным бомбам и минам придают
хорошо обтекаемую форму.

ГЛАВА XVIII
КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 133. Колебательные движения
Мы уже сталкивались с одним типом колебательных движений,
именно с колебаниями, возникающими при резком изменении состоя-
состояния системы. Колебания этого типа совершает груз на пружине, на
который внезапно подействовала внешняя сила, упругий стержень,
в котором в каком-то месте возник упругий импульс. Часто встречаются
колебания и иного происхождения. Общий признак всех колеба-
колебательных движений состоит в том, что они представляют собой
движения, многократно повторяющиеся или приблизительно по-
повторяющиеся через определённые промежутки времени.
Самый характер движений определяет и те вопросы, которые нас
главным образом интересуют при изучении колебаний. При изучении
«обычных» неповторяющихся движений нас в большинстве случаев
интересует положение, скорость и ускорение движущихся тел в тот
или иной момент времени. При изучении колебательных движений
нас, главным образом, интересует не состояние системы в данный
момент времени, а признаки, характеризующие повторяемость движе-
движений: закон, по которому повторяется движение; время, через которое
система снова приходит к тому же самому состоянию; наибольшие
отклонения, которых достигает движущееся тело, и т. д. По всем
этим признакам мы могли бы затем определить состояние системы
в любой момент времени, но это обычно не представляет интереса.
Для решения конкретных вопросов, с которыми приходится сталки-
сталкиваться при изучении колебательных движений, обычно необходимо
знать лишь самые признаки, характеризующие повторяемость движе-
движений. В этом и заключается специфическая черта задачи, которую мы
ставим себе при изучении колебательных явлений.
Изучение колебательных движений мы начнём с наиболее простых
задач, когда колеблющееся тело можно рассматривать как материаль-
материальную точку или твёрдое тело, а затем перейдём к случаям, когда
принципиальную роль играют деформации самого колеблющегося
тела, т. е. к колебаниям в упругих телах. Ясно, что колебательные
движения твёрдого тела представляют собой предельный случай коле-
колебаний упругих тел, к которому мы должны притти, пренебрегая

§ 134] ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ 395
деформациями упругих тел. Этот предельный случай более прост,
поэтому мы с него и начнём (так же, как это было сделано в меха-
механике). Но после того, как будет рассмотрена общая картина коле-
колебаний упругих тел, выяснится и то место, которое занимает в ней
предельный случай колебаний твёрдого тела.
§ 134. Гармонические колебания
При рассмотрении математического маятника (§ 59) мы убедились,
что при малых отклонениях движение маятника, подчиняющееся
уравнению
происходит по гармоническому закону. Гармоничность колебаний
маятника обусловлена тем, что ускорение маятника пропорционально
смещению и направлено в противоположную сторону. При больших
отклонениях ускорение уже не пропорционально смещению (ускорение
пропорционально sin а), и следовательно, колебания
уже не будут гармоническими.
Точно так же и колебания груза на пружине,
рассмотренные в § 67, будут гармоническими до тех
пор, пока пружина следует закону Гука. В случае
груза, висящего на пружине (рис. 337), движение
груза описывается уравнением:
m g = -** + />, A8.1)
Рис. 337.
где kx—упругая сила пружины, а Р—сила тя-
тяжести. Чтобы привести это уравнение к такому же виду, какой имеет
уравнение малых колебаний маятника, введём новую координату
хх — х — Pjk. Тогда уравнение A8.1) примет вид:
TS? =-='••
И в этом случае ускорение пропорционально смещению и направлено
в противоположную сторону. Следовательно, xt также будет изменяться
по гармоническому закону — груз будет совершать гармонические
колебания около' положения xt=0 или xo = Pjk. По аналогии
с маятником, мы можем определить и период колебаний груза. Вместо
отношения gjl, которое входило в уравнение маятника, в уравнение
колебаний груза входит отношение k'm. Поэтому период колебаний
груза ^

396 КОЛЬБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. XVill
Чем больше масса груза и чем мягче пружина, тем больше период
колебаний груза.
Гармонические «крутильные» или «торсионные» колебания совер-
совершает тело, подвешенное на упругой нити. Уравнение движения тела
имеет вид:
где / — момент инерции тела, а М — момент упругой силы, действую-
действующей со стороны нити. Как и при всяких, не слишком больших
деформациях, этот момент пропорционален деформации, т. е. /И =
=— kz, где к зависит от размеров и упругих свойств материала
нити. В таком случае уравнение движения
аналогично, уравнению движения маятника (при малых отклонениях)
и груза на пружине. Если тело закрутить на некоторый угол, то оно
будет совершать вокруг вертикальной оси гармонические колебания
с периодом
Г=2тг |/ -^ . A8.4)
Период колебаний зависит в этом случае не от массы тела, а от
момента инерции относительно оси, вокруг которой происходят
колебания. Зная упругость нити и измерив период крутильных коле-
колебаний, легко определить момент инерции тела /. Этим часто поль-
пользуются для определения моментов инерции тел. Если же момент
инерции подвижной системы известен, то, измеряя период торсионных
колебаний, можно найти коэффициент упругости k, характеризующий
упругие свойства подвеса. Таким приёмом пользуются, например, для
определения упругих свойств подвеса в приборе Кавендиша (§ 97).
Крутильные колебания совершает подвижная система во многих
типах измерительных приборов. Чем чувствительнее прибор, тем мень-
меньше дочжно быть k (чтобы малые силы заметно отклоняли подвижную
систему) и тем больше период колебаний прибора.
Вообще тело, находящееся в состоянии устойчивого равновесия,
при небольшом отклонении от этого состояния будет совершать
гармонические колебания, если^на тело действует только сила, зави-
зависящая от положения тела и возвращающая его к положению равно-
равновесия. При наличии только такой-«восстанавливающей» силы, которая
при достаточно малых отклонениях всегда пропорциональна смещению,
малые колебания около положения равновесия всегда будут гармони-
гармоническими.
В реальных системах помимо такой восстанавливающей силы
всегда действуют и силы другого типа, -* прежде всего, силы трения.

§ 134]
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
397
Если они достигают значительной величины, то их влияние может
существенно изменить характер колебаний. Но если эти силы малы,
то для тела, обладающего одной степенью свободы, малые колебания
около положения устойчивого равновесия всегда будут близки
к гармоническим. Этим определяется то особое место, которое зани-
занимают гармонические колебания среди всех разнообразных типов
колебательных движений.
При гармонических колебаниях смещение колеблющейся точки
происходит по гармоническому закону:
или x — Xcos(at-\-§). A8.5)
Ясно, что оба эти закона аналогичны, так как соответствующим вы-
выбором величин <р или ф можно перейти от одного закона к другому.
Величина X (наибольшее значение
отклонения) называется амплитудой
колебаний; величина со называется уг-
угловой частотой колебаний. Через про-
промежутки времени 7" = 2тс/й> функция sin
или cos проходит через одни и те же
значения, т. е. движение повторяется.
Этот промежуток времени Т есть период
колебаний. Поэтому
со =т~ 2nf>
A8.6)
где /—частота колебаний, т. е. число
колебаний в единицу времени. Частота
колебаний имеет размерность Т~1. В си-
системе CGS единицей частоты служит
\\сек. Эта единица получила сейчас Рис. 338.
специальное название «герц» (в честь
физика Генриха Герца). Например, частота 50 герц— это частота
в 50 периодов в секунду. Аргумент гармонической функции, т. е.
@^_|-(р или ю?-|-ф называется фазой колебаний. Значения аргумента
при t=zO, т. е. <р или ф, называются начальной фазой колебания.
Для краткости величины (риф часто называют не начальной фа-
фазой, а просто фазой колебаний. Зависимость смещения от времени
при гармоническом колебании изображается, очевидно, синусоидой.
Эту зависимость может «вычертить» само колеблющееся тело. Напри-
Например, колеблющийся маятник с песочницей вычерчивает синусоиду на равно-
равномерно движущейся под ним доске (рис. 338). Такой метод регистрации
колебаний называется «временной развёрткой». При быстрых колебаниях
для временной развёртки применяются специальные приёмы; для демонстра-
демонстрационных целей обычно применяется многогранное вращающееся зеркало
(см. рис. 343). Пучок света, отражённый от зеркальца, прикреплённого
к колеблющемуся телу, попадает на вращающееся зеркало и от него отра-
отражается на экран. Зеркальце на колеблющемся теле устанавливается так,
чтобы при колебаниях пучок света отклонялся на экране вверх и вниз. При

398
колебания Систем с одной степенью свободы ггл. xvni
Рис. 339.
колебаниях пучок света прочерчивает на экране вертикальную светлую
полоску. Вследствие вращения зеркала пучок света, кроме того, бежит по
экрану в горизонтальном направлении. В результате получается временная
развертка (для гармонических колебаний — синусоида).
Если какие-либо два колебания происходят по гармоническому
закону
х1 = Хг sin (»,* -f тЧ)> Х2 = Х2 Sin (Uj* 4" <Рг)|
то разность фаз этих колебаний
есть величина, вообще говоря, переменная (зависящая от времени).
НО еСЛИ (Oj := 0J, ТО
т. е. разность фаз двух колеба-
колебаний одинаковой частоты есть ве-
величина постоянная. Этот «сдвиг
фаз» равен разности начальных
фаз обоих колебаний.
Представление о гармонических
колебаниях и о сдвиге фаз между
ними может дать следующая мо-
модель. На горизонтальном круге, вра-
вращающемся с постоянной скоростью,
укреплены на ножках два шарика, положение которых на круге может
изменяться (рис. 339). Если проэцировать шарики на экран, то тень шарика
на экране будет совершать гармоническое движение. Действительно, коорди-
координата проекции шарика на
экране (рис. 340, а) лг =
=Ц cos а=/? cos tot, где о—
угловая скорость вращения
круга R определяет ампли-
амплитуду колебаний тени на эк-
экране, а о — частоту этих
колебаний. Когда шарики
стоят на одном радиусе
(рис. 340, Ь), но на разных рис 340.
расстояниях от оси, их тени
совершают колебания, сов-
совпадающие по фазе, но разной амплитуды. Когда шарики расположены на
двух радиусах, образующих угол ? (рис. 340, с), то их тени совершают
колебания, сдвинутые по фазе на угол <р.
Если смещение колеблющейся точки изменяется по гармоническому
закону
x = Xsiti(ti>t-{-y),
то скорость и ускорение точки
dx
v — — = аХ cos (at -\- <р),
A8.7)
A8.8)

§ 134]
ГАРМОНИЧЬСКШ. КОЛИ5ЛНИЯ
399
также изменяются по гармоническому закону. При этом амплитуда
скорости V—onX, а амплитуда ускорения А = а>2Х. По фазе скорость
сдвинута на тг/2, а ускорение — на тс относительно смещения. На
рис. 341 графически изображены
изменения смещения, скорости
и ускорения при гармоническом
колебании.
Колебания, совершаемые те-
телом, часто бывает удобно рассма-
рассматривать как результат наложения
нескольких гармонических коле-
колебаний, одновременно совершаемых
телом. Таким образом, возникает
вопрос о сложении гармонических
колебаний. Например, сумма двух гармонических колебаний с одина-
одинаковыми частотами, но разными фазами и амплитудами, представляет
собой также гармоническое колебание с той же частотой, но новой
фазой и амплитудой. Действительно, как известно из тригонометрии,
a sin (at + <?,) + & sin
= X sin (Ы -\- ф),
где
= а2 -\- Ь2 -f- 2ab cos (ipt — <f>5)
asm
a cos <fi -J- b cos <f2 '
причём X и б соответственно амплитуда и фаза результирующего
колебания.
с
¦га
Рис. 342.
Сумма двух колебаний с различными частотами и одинаковыми
амплитудами
a sin o)]^ -\- a sin tn2t*=^ 2a sin Ml T—- t sin -1-^" 21
представляет собой уже не гармоническое колебание. Если о>, и со2
близки по величине, то результирующее колебание можно рассма-

400
КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. XVIII
тривать как колебание с некоторой «средней частотой» (со, Ц-оJ)'2,
амплитуда которого медленно (по сравнению с «средней частотой»)
меняется в пределах от 2а до нуля по закону sinMl ~ "** t. Она досги-
гает максимума, равного 2а, когда фазы складываемых колебаний
совпадают, и падает до нуля, когда они противоположны (рис. 342).
Такие колебания носят название биений. Время т=2тт(|((й1 — о>2)
называется периодом биений, a mt — ю2—угловой частотой биений.
Если складываемые колебания имеют не только различную частоту, но
и различные амплитуды я и 6, то амплитуды результирующих колебаний
уже нигде не спадают до нуля. Они изменяются от а-\-Ь там, где фазы
складываемых колебаний приблизительно совпадают, до а — b там, где
фазы их противоположны. Чем больше отличаются амплитуды вид, тем
меньше «глубина» биений.
Рис. 343.
Картину сложения двух гармонических колебаний можио продемонстри-
продемонстрировать при помощи двух камертонов с электромагнитным возбуждением
(рис. 343). Ножки камертонов совершают колебания, очень близкие к гар-
гармоническим. Луч света последовательно отражается от двух зеркальных
поверхностей на торцах камертонов, а затем от вращающегося зеркала.
Отклонение зайчика на экране пропорционально сумме отклонений ножек
обоих камертонов. Если камертоны колеблются с одинаковой частотой, то
зайчик на экране вычерчивает синусоиду. Если камертоны колеблются
с немного различными частотами, то зайчик на экране вычерчивает кривую
биений. При изменении разности частот камертонов изменяется частота
биений, при изменении амплитуд одрого из колебаний изменяется глубина
биений.
§ 135. Собственные колебания
Колебания, которые совершает система около положения равнове-
равновесия после того, как она каким-либо образом была выведена из со-
состояния устойчивого равновесия, носят название собственных, или
свободных колебаний. Рассмотренные нами колебания маятника или
груза на пружине являются примером собственных колебаний. Соб-
Собственные колебания возникают в результате достаточно резкого

§ 1351 Собственны!: колебаний 401
начального толчка, в результате всякого быстрого изменения силы,
действующей на тело. Чтобы возникли собственные колебания, нужны
столь быстрые изменения силы, при которых величина силы успеет
заметно измениться за время периода колебаний. Только такие, быст-
быстрые по сравнению с периодом колебаний, изменения силы являются
толчком для данной колебательной системы и могут вызвать собствен-
собственные колебания в системе.
Если не учитывать сил трения, то можно Считать, что в системе
с одной степенью свободы малые собственные колебания происходят
по гармоническому закону:
х = X cos {%t -f- <p)»
где х—-координата, характеризующая положение колеблющегося тела
(например, смещение груза, угол отклонения маятника и т. д.). Ча-
Частота собственных колебаний ш0 определяется свойствами самой си-
системы: % = \^kjm, где k — коэффициент упругости (или вообще
коэффициент пропорциональности между восстанавливающей силой
и смещением), а т — масса колеблющегося тела (или его момент
инерции для колебаний вокруг оси). Амплитуда и фаза собственных
колебаний определяются начальными условиями, т. е. смещением
и скоростью колеблющегося тела в момент ^=0. Если при t—Q
смещение лг = лг0, а скорость v = vQ, то, подставляя в выражения
х = X cos (<o0t-\-<е) и -~ = v = ~- (o0X sin
значения ? = 0, л: = лг0, v = v0, мы найдём:
v0 — — WOA' sin <
откуда
В частности, если колеблющемуся телу сообщено только началь-
начальное смещение хй, a v0 = 0, то
Х=хо> <а = 0 и х = ха cos <o0t.
Наоборот, если телу сообщена начальная скорость v0, а л:0 = 0, то
> = — ¦?¦ и * = -9
2 <о0
Начальное смещение и начальная скорость определяют тот началь-
начальный запас потенциальной и кинетической энергии, который сообщён
колеблющемуся телу. Если силы трения отсутствуют, то этот началь-
начальный запас энергии будет оставаться неизменным при колебаниях.
Процесс колебаний будет сопровождаться переходом энергии из по-
потенциальной в кинетическую и обратно. При этом «колебания энер-
26 С. Э. Хайкин

402 КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. XVIII
гии», т. е. переход энергии из потенциальной в кинетическую и об-
обратно, будут происходить с вдвое большей частотой, чем сами
колебания. Дважды за период энергия будет полностью превращаться
в потенциальную (в двух крайних положениях) и дважды за период
в кинетическую (при прохождении через среднее положение). В со-
соответствии с этим выражения потенциальной энергии
U = ~ =| X* cos* (cV + <f) = ^ [1 + cos 2 (со0/ + <р)]
и кинетической энергии
Содержат удвоенную частоту. Изменения потенциальной и кинетиче-
кинетической энергий при гармонических колебаниях графически изображены
VH на рис. 344. Так как амплиту-
амплитуды смещения и скорости связа-
связаны соотношением V=wuX, a
щ=Ук\т, то kX2=mVi, и
полная энергия колеблющегося
тела равна
W=H±U=k-?. = '^. A8.9)
При гармонических колебаниях
Рис- 344- полная энергия колебаний про-
пропорциональна квадрату амплиту-
амплитуды Смещений (или амплитуды скоростей).
Если на колеблющееся тело действует сила трения, то энергия
системы, а вместе с тем и наибольшие смещения и скорости не ос-
остаются постоянными, а убывают (энергия расходуется на преодоление
сил трения и превращается в тепло). Происходит постепенное зату-
затухание колебаний. Такие затухающие колебания уже не являются гар-
гармоническими (гармонические колебания — это колебания с неизменной
амплитудой). К этим негармоническим колебаниям, строго говоря, уже
не применим термин «амплитуда»—он имеет определённый смысл
только для гармонических колебаний. Однако, термин «амплитуда»
применяют и к негармоническим колебаниям, понимая под амплитудами
наибольшие значения, которых достигает соответствующая величина
(смещение, скорость или ускорение) в течение одного периода коле-
колебаний. Затухающие колебания — это колебания, амплитуда которых
убывает со временем. Чем больше сила трения, тем быстрее затухают
колебания. Закон убывания амплитуд колебаний зависит от характера
еил трения, действующих на тело. График затухающего колебания
для одного определённого типа сил трения приведён на рис. 345.

§ 135]
СОБСТВЕННЫЕ КОЛЕБАНИЯ
403
К затухающим колебаниям, строго говоря, не применим и термин
«период», так как эти колебания вообще не являются периодическим
процессом. Периодическим процессом называется такой процесс, при
котором через одинаковые промежутки времени повторяется одно
и то же состояние системы. Этот промежуток времени и назы-
называется периодом процесса. Но в случае затухающих колебаний состо-
состояние колеблющегося тела вообще не повторяется точно, если, напри-
например (рис. 345), отклонения тела в моменты t1 и t% одинаковы (равны
нулю), то скорости в эти моменты
неодинаковы,, так как амплитуды
скорости убывают и f2<Ct'i- Од-
Однако, если трение мало и колеба-
колебания слабо затухают, то значения
скоростей приблизительно повто-
повторяются.
Таким образом, при малом
трении затухающие колебания
представляют собой процесс при-
приблизительно периодический. По-
Поэтому можно говорить о «перио- Рис. 345.
де» затухающих колебаний, хотя
понятие периода для затухающих колебаний несколько условно. «Перио-
«Периодом» затухающих колебаний принято называть время 7\, за которое
система дважды проходит через среднее положение в одном и том же
направлении, или (что то же самое) время, за которое отклонения
в одну и ту же сторону дважды достигают максимального значения
(рис. 345). Силы трения немного замедляют движение системы. По-
Поэтому «период» затухающих колебаний всегда несколько больше, чем
период тех собственных колебаний, которые совершала бы система,
если бы трение отсутствовало. Но если трение мало, то оно очень
мало влияет на «период» затухающих колебаний. При малом трении
практически можно считать, что «период* затухающих колебаний Г
равен периоду колебаний То в отсутствии трения, и угловая частота
затухающих колебаний ю = 2тт/Г совпадает с угловой частотой ш0
в отсутствии трения.
Закон убывания амплитуды колебаний зависит от характера сил трения,
действующих на колеблющееся, тело. Наиболее простым и вместе с тем
наиболее распространённым является случай, когда сила трения пропорцио-
пропорциональна скорости
f= — bv. A8.10)
В этом случае уравнение движения тела имеет вид:
d%x , , dx
или
dx
26*

404 КОЛЕБАНИЯ CHCTFM С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ.
Так как изменение энергии колеблющегося тела должно быть равно
работе сил трения, то при элементарном перемещении их энергия тела из-
изменится на величину
Изменение (убыль) энергии за период колебаний равно
•г
[
Если трение мало, то оно мало изменяет характер колебаний, н мы не
сделаем большой ошибки, если будем считать, что в течение периода ско-
скорость изменяется по закону » = Vcoso>0<- Тогда
Г Ъ С bV*T
= — Ь ] V2cos2 <Vdt = — -j J УЦ1 -f cos 2<o0t) dt = — -tj- . A8.11)
0 о
Если рассматривать период между двумя амплитудными значениями ско-
скорости Vj, и V8, то энергия системы в начале периода будет Wi=^mV\l2 и
в конце W2 = mVlj2. Убыль энергии равна Д 1Г=^ (Vi — Кг) и, по A8.11),
откуда
т
Так как мы рассматриваем случай, когда трение мало, т. е. ЪТ\т <^ 1, то
или
Изменение амплитуды колебаний на величину AV = V1— V2 происходит за
промежуток времени bt=zT. Выражение A8.12) можно записать следующим
образом:
Т = -214(- <18-13>
Рассматривая амплитуду V как непрерывную функцию времени, a AV и й*
как бесконечно малые элементы*), н проинтегрировав выражение A8.3),
V
V
*) Конечно, это имеет смысл только при условии, что колебания слабо
затухают и AV за период мало по сравнению с V.

§ 135] СОБСТВЕННЫЕ КОЛЕБАНИЯ 405
получи»:
, V Ъ
или
- — t
У=Уое 2п , A8.14)
т. е. амплитуды колебаний убывают по показательному закону.
В случае линейного закона трения A8.10), если трение достаточно
мало, затухающие колебания происходят по закону
V=Voe 2m since*. A8.15)
По аналогичному закону происходит и изменение смещения коле-
колеблющегося тела *):
х—Хе 2т cos at. A8.16)
Величина a = b\2m называется показателем затухания; со— угло-
угловая частота затухающих колебаний. Если трение мало (т. е. аг<^ю02),
то изменением «периода» затухающих колебаний вполне можно пре-
пренебречь и считать, что
to sb соо = Vk]m.
Значения двух последовательных амплитуд колебаний Ху и Хг мы
получим, подставив в выражение A8.16) значения ? = 0 и t=T,
Отношение
Q = e" A8.17)
есть величина постоянная — амплитуды колебаний представляют со-
собой геометрическую прогрессию. Натуральный логарифм этого посто-
постоянного отношения
» = 1п^=а7" A8.18)
называется логарифмическим декрементом затухания колебаний.
Показатель затухания а характеризует затухание колебаний за
единицу времени, а логарифмический декремент Ь — затухание
колебаний за период.
Переходя обратно от логарифмической функции к показательной,
разлагая эту функцию в ряд по степеням малой величины Ь и огра-
ограничиваясь первым членом этого ряда из A8.18), получим:
*) Колебания мало отличаются от гармонических и поэтому для них
приблизительно справедливы соотношения между смещением и Скоростью,
которые былн получены для гармонических колебаний.

406
КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [гЛ. XVII
откуда
Таким образом, если затухание мало, то логарифмический декремент
затухания представляет собой просто относительное уменьшение ам-
амплитуды колебаний за один период.
Так как колебания затухают по показательному закону, то теоре-
теоретически они прекращаются только при *=оо. Но практически можно
считать, что колебания прекратились, если амплитуда их упала до
малой доли начальной величины. Обычно принято считать (конечно,
совершенно условно), что колебания затухли, если их амплитуда упала
до 0,01 от начальной величины. Тогда время затухания колебаний т
определяется соотношением
*.-<« = 0,01 или ат = 4,6,
откуда
т ^= 4,6 — =-,-.
1 о
Если, например, 8 = 0,1, то можно считать, что колебания практи-
практически затухают по прошествии 40—50 периодов.
§ 136. Собственные колебания при большом трении
Если трение мало, то оно вызывает затухание колебаний, ио не
изменяет заметно скорости движения тела (периода колебаний). Если же
Рис. 345.
Рис. 347.
трение велико, то оно заметно замедляет движение колеблющегося
тела, но при этом и затухание колебания увеличивается. Процесс всё
больше и больше отличается от периодического, и термин «период»
всё менее и менее применим к этому процессу. В случае сильно за-
затухающих колебаний уже совершенно условно «периодом» колебаний
называют время Т между двумя последовательными прохождениями
тела через нулевое положение или между двумя соседними максиму-
максимумами (рис. 346). Этот «период» растёт с увеличением коэффициента

§ 136] СОБСТВЕННЫЕ КОЛЕБАНИЯ ПРИ БОЛЬШОМ ТРЕНИИ 407
трения. Попрежнему логарифмический декремент равен Ь=ЬТ\2т,
где Г—«период» колебаний. Если коэффициент трения b очень ве-
велик, то колеблющееся тело вообще никогда не проходит дважды
через нулевое положение, а приближается к нему второй раз только
асимптотически (рис. 347). При этом 7"= со, а вместе с тем и 8= со.
Движение тела теряет последние черты колебательного движения.
Такие системы,'в которых вследствие большого трения движение
окончательно теряет колебательный характер, называются апериоди-
апериодическими в отличие от систем колебательных. Переход от колебатель-
колебательного движения к апериодическому происходит в области, где коэф-
коэффициент трения приближается к значению b = 2 V km- При дальнейшем
увеличении Ь возвращение системы к положению равновесия проис-
происходит всё медленнее и медленнее.
Влияние треыия на затухание колебаний и переход от колебательной
системы к апериодической можно продемонстрировать при помощи груза
на пружине, помещая его в среду с различной вязкостью. В воздухе сопро-
сопротивление мало, н поэтому колебания происходят с очень малым затуханием
(декремент порядка 0,01). В воде сопротивление гораздо больше, и затуха-
затухание заметно увеличивается (декремент порядка единицы). Наконец, в масле
отклонённый груз вообще не переходит за положение равновесия — про-
происходит апериодическое движение (? = оо). Измеряя затухание колебаний
тела, погруженного в жидкость, можно определить коэффициент трения Ь
для силы трения, действующей на тело со стороны жидкости. Этот коэф-
коэффициент Ь связан известным образом с коэффициентом вязкости жидкости.
Таким образом, измеряя затухание колебаний тела, погружённого в жид-
жидкость, можно определить коэффициент вязкости жидкости. Этим приёмом
часто пользуются на практике. В жидкость погружают диск или цилиндр,
совершающий торсионные колебания, и по затуханию этих колебаний
определяют коэффициент вязкости жидкости.
В.измерительных приборах при всяком резком изменении измеряемой
силы всегда возникали бы собственные колебания около нового положения
равновесия. Если трение в приборе мало, то колебания эти затухали бы
очень медленно. Приходилось бы долго ждать, пока прибор установится
в новом положении и можно будет произвести отсчёт. Поэтому в измери-
измерительных приборах обычно искусственно увеличивают затухание колебаний
при помощи специальных демпферов — механических или электромагнитных.
Простейшим является воздушный демпфер — лёгкий поршенёк, соединён-
соединённый с подвижной системой прибора и движущийся в трубочке (без трения
о стенки, чтобы не было «застоя»). Сопротивление воздуха при движении
поршенька делает прибор апериодическим. Сопротивление это не должно
быть очень большим, так как тогда оно очень'замедлит движение системы
к новому положению равновесия. Наивыгоднейшим является такое сопро-
сопротивление, при котором подвижная система без колебаний, но наиболее бы-
быстро приближается к новому положению равновесия. Этому условию соот-
соответствует значение b=z2Ykm. Такое значение сопротивления называется
критическим.
Затухание колебаний по показательному закону происходит только в
том случае, когда сила трения пропорциональна скорости. При других ти-
типах сил трення и закон затухания получается иным. Например, в случае
постоянного трения, не зависящего от скорости («сухое трение»), работа
силы трения, т. е. потеря энергии за полупериод колебаний

408 КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [гл. XV1U
где / — постоянная сила трения, a (A"i -f Х2) — пройденный путь, равный
сумме двух следующих друг за другом наибольших отклонений в противопо-
противоположные стороны. В положениях наибольшего отклонения кинетическая
энергия равна нулю, и поэтому полная энергия системы соответственно
равна kXl/2 и kX^2, Убыль энергии тг{Х\ ~Х\) должна быть равна Д№,
Следовательно,
или
Такое же соотношение получится и для двух следующих отклонений Хг
н Х%. Следовательно, убыль амплитуды за период есть
4/
Амплитуды колебаний убывают по арифметической прогрессии с раз-
разностью 4//А. Колебания продолжаются только до тех пор, пока наибольшее
отклонение превосходит fjk, т. е. выходит за пределы области застоя. Ког-
Когда наибольшее отклонение уже не выходит из области застоя, колебания
прекращаются. Колебания затухают не асимптотически, а за конечное чис-
число периодов.
Картину затухания колебаний при наличии постоянного трения можно
продемонстрировать на модели, которой мы пользовались для демонстрации
застоя (рис. 78). Отклонённый от положения равновесия груз совершает
несколько колебаний и останавливается где-либо в области застоя.
Во многих колебательных приборах наряду с трением, пропорциональным
скорости, присутствует и сухое трение (например, в измерительных приборах
на подшипниках). Пока колебания велики, преобладают потери, обуслов-
обусловленные трением, пропорциональным скорости (так как они пропорцио-
пропорциональны квадрату амплитуд), и затухание происходит примерно по показа-
показательному закону. Когда амплитуды уменьшаются, начинают преобладать
потери, обусловленные постоянным трением, и дальнейшее затухание про-
происходит примерно по закону арифметической прогрессии.
§ 137. Автоколебания
Собственные колебания представляют собой колебания около положе-
положения устойчивого равновесия. Амплитуда этих колебаний определяется ве-
величиной начального отклонения и начальной» скорости, т. е. величиной той
энергии, которая сообщена телу начальным толчком. Вследствие наличия
трения эти колебания затухают; собственные колебания в системе никогда
не могут быть незатухающими (стационарными). Для поддержания собст-
собственных колебаний система должна обладать каким-либо источником энер-
энергии, из которого-она могла бы пополнять убыль энергии, обусловленную
затуханием. Чтобы колебания были стационарными, система за период ко-
колебаний должна отбирать от источника как раз столько энергии, сколько
расходуется в ней за это же время. Для этого система должна сама
управлять поступлением энергии из источника. Такие системы называ-
называются автоколебательными, а незатухающие колебания, которые они со-
совершают, — автоколебаниями.

§ 137J АВТОКОЛЕБАНИЯ 409
Типичным примером механической автоколебательной системы является
часовой механизм. Колебания маятника или балансира часов поддержива-
поддерживаются за счёт той энергии, которой обладает поднятая гиря или заведённая
пружина часов. Проходя через определённое положение, маятник приводит
в действие храповой механизм. При этом маятник получает толчок, попол-
пополняющий потери энергии за период. Маятник сам открывает и закрывает
доступ энергии из заводного механизма. При нормальном ходе часов энер-
энергия, которую получает маятник, как раз равна потере энергии на трение
за время между двумя толчками (обычно за полупериод). Поэтому колебания
и оказываются стационарными. Если начальное отклонение маятника боль-
больше нормального, то потери на трение оказываются больше, чем поступле-
поступление энергии из заводного механизма. Колебания затухают до тех пор, пока
потери не окажутся равными поступлению энергии. Автоматически уста-
устанавливается как раз такая амплитуда колебаний, при которой потери на
трение компенсируются поступлением энергии из источника. Следователь-
Следовательно, амплитуда колебаний определяется не величиной начального толчка,
а соотношением между потерями и поступлением энергии, т. е. свойствами
самой колебательной системы. Это — характерная черта автоколебаний,
отличающая их от собственных колебаний (амплитуда которых определяет-
определяется начальными условиями).
Хотя амплитуда колебаний маятника часов и не зависит от начальных
условий, но для того, чтобы часы пошли, маятнику нужно сообщить на-
начальный толчок. Это, однако, не является обязательным для всякой авто-
автоколебательной системы. Во многих автоколебательных системах колебания
могут возникнуть без всякого начального толчка. Примером этого может
служить зажим Прони, в котором при малых оборотах вала колебания воз-
возникают без начального толчка. Как мы видели (§ 53), это обусловлено тем,
что на падающем участке характеристики трения состояние равновесия
оказывается неустойчивым. Достаточно самых малых отклонений системы
от состояния равновесия, чтобы колебания в ней начали нарастать, — про-
происходит самовозбуждение колебаний. Когда амплитуды колебаний зажима
возрастут, изменения скорости выйдут за пределы падающего участка ха-
характеристики, и потери на трение увеличатся. Дальнейшее нарастание
колебаний прекратится — автоматически установятся колебания такой ам-
амплитуды, при которой увеличение энергии за часть периода компенсирует
потери энергии за другую часть периода. Зажим будет совершать авто-
автоколебания.
В технике широко применяются электромеханические автоколебатель-
автоколебательные системы, в которых колебания совершает механическая система, а по-
поступление энергии регулируется специальным электрическим устройством.
Таков, например, электрический звонок. К подобным же автоколебательным
системам относятся и камертоны с электромагнитным возбуждением, о ко-
которых упоминалось в § 125.
Если в автоколебательной системе потерн энергии на трение малы по
сравнению с общей энергией колебаний, то и энергия, необходимая для
компенсации потерь, также мала. Колебания происходят почти так, как
если бы трение вовсе отсутствовало. В этом случае автоколебания будут
близки к гармоническим. Вместе с тем и период автоколебаний близок
к периоду тех собственных колебаний, которые совершала бы система,
если бы потери энергии не компенсировались. Если же потери на
трение велики, а значит, велика и энергия, поступающая от источника,
то автоколебания могут по форме заметно отличаться от гармони-
гармонических и их период может заметно Отличаться от периода собственных
колебаний. Поэтому, например, в хороших часах, в которых потери на
тренне малы, маятник совершает колебания, по форме почти не отличаю-
отличающиеся от гармонических, и с частотой, почти точно совпадающей с частотой
собственных колебаний маятника (этим н обеспечивается точность хода

410 КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. XVIII
часов). В простых ходиках, в которых потери на трение велики, колеба-
колебания маятника даже на-глаз отличаются от гармонических, и период этих
колебаний уже заметно отличен от периода свободных колебаний маят-
маятника.
§ 138. Вынужденные колебания
Если на какое-либо тело действует колеблющаяся по величине
внешняя сила, то это тело будет совершать колебания, характер ко-
которых в той или иной мере повторяет характер
изменений внешней силы. Такие колебания называ-
называются вынужденными.
Вынужденные колебания совершает, например,
якорь электромагнита, питаемого от цепи перемен-
переменного тока (сила тока, а вместе с тем и сила притя-
притяжения магнита, периодически изменяются). Частота
этих колебаний определяется не свойствами самой
системы (как в случае собственных колебаний или
o автоколебаний), а частотой внешнего воздействия. Мы
р -^ рассмотрим сначала простейший случай, когда внеш-
внешняя сила изменяется по гармоническому закону.
Моделью для нашей задачи может служить груз
иа пружине, на который действует внешняя сила F (рис 348),
изменяющаяся по закону
F=F0 sin Ы,
и сила трения /, пропорциональная скорости груза, т. е.
Положим, что в момент, когда начала действовать внешняя сила,
смещение груза и его скорость равны нулю. Под действием внешней
силы груз будет постепенно раскачиваться. Внешняя сила будет со-
совершать работу, которая зависит от величины смещений груза и при
прочих равных условиях растёт пропорционально амплитудам колеба-
колебаний груза. С другой стороны, потери энергии в системе растут про-
пропорционально квадрату амплитуд колебаний. Поэтому вначале работа
внешней силы будет превышать потери энергии, энергия системы бу-
будет возрастать—амплитуды колебаний будут увеличиваться. Так как
потери энергии возрастают быстрее, чем работа внешней силы, то
в конце концов наступит момент, когда работа внешней силы будет
как раз покрывать потери энергии в системе. Дальнейшее нарастание
колебаний в системе прекратится — установятся колебания с некото-
некоторой постоянной амплитудой. Если внешняя сила изменяется по гар-
гармоническому закону, то установившиеся колебания также будут гар-
гармоническими и частота их будет совпадать с частотой внешней силы.
Установлению вынужденных колебаний всегда предшествует по-
постепенное раскачивание системы. Для того чтобы наблюдать уста-
установившиеся колебания, всегда необходимо подождать некоторое

§ 138] вынуждьнные колебания 411
время после включения внешней силы, пока закончится процесс
установления. Как велико должно быть это время, будет видно из
последующего рассмотрения.
Мы изучим сейчас картину установившихся колебаний (в дальней-
дальнейшем мы ещё вернёмся к процессу установления). Для рассматриваемой
нами модели уравнение движения напишется в виде:
Интересующие нас вынужденные колебания происходят по гармони-
гармоническому закону с частотой, равной частоте внешней силы, т. е. по
закону
A8.20)
Чтобы определить амплитуду X и сдвиг фаз <р этих вынужденных
колебаний, подставим выражение A8.20) в уравнение A8.19). Если
A8.20) есть решение уравнения A8.19), мы должны получить тожде-
тождество. Подстановка эта даёт:
—/n(o2^sin((oz!-}-(pL-^M^cos (u>t-\-y)-{-kXsin(u>i-}- tp) =zFosinat.
Разложив синус и косинус суммы at-{-у на синусы и косинусы
от Ы и (р и собрав вместе члены, содержащие синусы и косинусы
от ш, получим:
[( — mco2 -\- k) Xcos (p — btoXsln <p — Fo] sin mi -j-
~\~[{ —inw? -\-ft) Xsin у-\-ЬшХcos ip]
Для того чтобы это выражение представляло собой тождество, необ-
необходимо, чтобы коэффициенты при синусе и косинусе были порознь
равны нулю. Мы получаем, таким образом, два уравнения для опре-
определения X и (р:
[(— mco2 -f- k) cos (p — 6ю sin <p] X=F0, \
[( — mco2-f Л) sin sp-f *(ocostp] ^=0. / A8.21)
Чтобы найти Х, возведём оба уравнения в квадрат и сложим:
ИЛИ
где &l=k\m — угловая частота собственных колебаний груза, аа =
— Ь2т—показатель затухания этих собственных колебаний; <р оп-
определится из второго уравнения A8.21):

412
КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ["гл. XVIH
Амплитуда и фаза вынужденных колебаний зависят от соотношения
между частотами собственных и вынужденных колебаний и от затуха-
затухания системы.
Выясним прежде всего, как изменяется амплитуда вынужденных
колебаний при изменении частоты внешнего воздействия в случае,
когда затухание колебаний невелико, т. е. а-с^со,,. При ^
под корнем в выражении A8.22) играет роль только член (во и
та"
k'
A8.24)
Амшгйгуда вынужденных колебаний оказывается равной величине ста-
статического смещения, которое вызвала бы постоянная сила Fo. Когда
частота внешнего воздей-
воздействия приближается к часто-
частоте со,
ний
о0
собственных колеба-
колебасо2J
системы,
уменьшается и
стает. Вблизи
со2J
X возра-
возразначения
со = <оо X достигает макси-
максимума. Этот максимум на-
наступает не точно при со — ю0,
а несколько раньше, так
как выражение, стоящее
под корнем, проходит через
минимум при со = ю0 — 2а.
Но если затухание мало, то
а <$; <оо и практически мож-
можно считать, что X проходит
через максимум при ю = со0. Приближённое значение этого максимума есть
2а 2
—тщ
где 3 = 2та/<оо = аТ — логарифмический декремент затухания коле-
колебаний.
При дальнейшем возрастании со снова »ачинает играть роль член
(юо—-w2J, и амплитуды колебаний начинают убывать. Если ш^>ю0,
то, приближённо,
A8.26)
При увеличении частоты воздействия амплитуда колебаний стремится
к нулю.
Вся эта картина изменения амплитуды вынужденных колебаний
при изменении частоты внешнего воздействия графически изображена

§ 138]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
413
на рис. 349. Как видно из выражений A8.24) и A8.25), отношение
между максимальной амплитудой вынужденных колебаний ХтаХ и ста-
статическим отклонением Хо зависит только от затухания системы:
Лтах Я ,«о о7\
—р— = -5-. A8.2/)
Если $ мало по сравнению с единицей, то наибольшая амплитуда
вынужденных колебаний во много раз превышает статическое от-
отклонение Хо. Это резкое возрастание амплитуд вынужденных колеба-
колебаний в области., где ш близко к <о0, называется явлением резонанса.
Кривые, подобные изображённой на рис. 349, называются амплитуд-
амплитудными резонансными кривыми.
С помощью соотношения A8.23) можно таким же образом про-
проследить изменение сдвига фаз (р при изменении частоты внешнего
воздействия. При ш<^со0
, 2а<о
tgtpsa g,
т. е. ср близко к нулю. Фаза вынужденных колебаний примерно со-
совпадает с фазой внешней силы. При <о —> о>о
— °о и <р = — -|
— фаза вынужденных колебаний на п/2 отстаёт от фазы внешней
силы. Наконец, при ю^>ю0
т. е. <р близко к — тт. Фаза вынужденных колебаний почти противо-
противоположна фазе внешнего воздействия. Эти изменения (р при измене-
изменении со графически изображены на
рис. 350. Такие кривые называют-
называются фазовыми резонансными кри- q
выми. Если затухание мало, то
в области резонанса происходят
резкие изменения фазы: в не-
небольшой области изменения ча- ^%
стот сдвиг фаз меняется почти на J
180°.
Явление резонанса представляет
собой одни из наиболее удобных
способов измерения частоты колеба- ""*
ний. Располагая набором резонато-
резонаторов (колебательных систем с малым ™с- *0.
затуханием), частота которыхзаранее
известна, можно определить частоту внешней силы. Частота эта совпадает
с собственной частотой того из резонаторов, который наиболее сильно
колеблется под действием внешней силы. Этот принцип используется, на-

414
КОЛКБА.НИЯ СИСТЕМ С ОДНОЙ СТЕПЬВЫО СВОБОДЫ [гл. XVIIt
пример, в язычковом частотомере, который представляет собой набор уп-
упругих пластинок с массами на концах. Каждая пластинка является колеба-
колебательной системой, собственная частота которой определяется величиной
массы и упругостью пластинки. Частоты собственных колебаний этих пла-
пластинок заранее известны. При колебаниях язычка eFo торцевая часть видна
в виде размытой полоски. Амплитуду вынужденных колебаний язычков
легко оценить по величине этого размытия. Измеряемая частота совпадает
с частотой наиболее сильно колеблющегося язычка. Язычковые частотоме-
частотомеры широко применяются для измерения частоты переменного тока. Для
этого измеряемый переменный ток пропускается в обмотку электромагнита,
возбуждающего колебания язычков.
Принцип язычкового частотомера можно использовать для демонстрации
полученных нами зависимостей амплитуды и фазы вынужденных колебаний
от соотношения между частотами собственных и вынужденных колебаний.
Если взять два язычка, один из которых имеет собственную частоту, точно
Рис. 351.
Рис. 352.
равную 100 пер/сек, а другой имеет частоту, отличающуюся на десятые
доли периода, то при возбуждении электромагнита переменным током
в 50 пер/сек *) будут возбуждаться оба язычка (рис. 351). Однако, ампли-
амплитуды их колебаний будут различны. Сильнее будет колебаться тот из
язычков, частота которого точно совпадает с частотой внешней силы. Если
рассматривать язычки в стробоскопическом освещении, при котором часто-
частота вспышек почти совпадает с частотой внешнего воздействия, то ячычки
будут казачьей движущимися очень медленно. Цоэтому легко можно про-
проследить за сдвигом фаз колебаний обоих язычков (рис. 352). Часть периода
язычки движутся навстречу друг другу. Это и значит, что они колеблются
в разных фазах.
От результатов, полученных нами для амплитуды и фазы смеще-
смещения при вынужденных колебаниях, легко перейти к амплитудам и
*) Язычок притягивается к электромагниту при обоих направлениях
переменного тока. Поэтому частота вйешией силы вдвое больше частоты
переменного тока, т. е. равна 100 пер/сек.

§ 138]
вынужденные Колебания
415
фазам скорости и ускорения. Так как вынужденные колебания явля-
являются колебаниями гармоническими, то амплитуда скорости равна
—F° — F* A8.28)
Если
ту
то при
V
т-
* max
Го
2/яа
=
А
тч>
Ь'
t
т. е. при со—»-0 Vo—>-0.
При со ^= ш0 V достигает максимума
Наконец, при
т. е. при ю--»-оо Vqq—> 0.
Эта зависимость амплитуд скоростей от <о изображена на рис. 353.
Таким же образом можно проследить зависимость от со и амплитуд
ускорений (рис. 354).
Наиболее характерные отличия этих зависимостей от зависимости
для амплитуд смещений состоят в том, что амплитуда скоростей па-
падает до нуля как при со —> 0, так
и при (о —>¦ оо, а амплитуда уско-
ускорений падает до нуля при со —>- О
и стремится к конечному значению
-9 при со —>• оо.
т г
Сдвиг фаз между скоростью
и внешней силой и ускорением
и внешней силой мы получим сразу,
приняв во внимание, что ско-
скорость на тт/2, а ускорение на тт
опережают смещение. Поэтому
сдвиг фаз между скоростью и
внешней силой равен ф = (р-{-п/2, Рис. 353.
а между ускорением и внешней
силой ft = (p-|~Tt. При резонансе tp = — тт/2 и ф = 0 скорость
совпадает по фазе с внешней силой. При ю^>ю0, ср-=—-тг и S^O
ускорение совпадает по фазе с внешней силой.
Полученные результаты можно пояснить наглядными физическими
соображениями. Когда частота внешнего воздействия со мала по срав-
сравнению с частотой собственных колебаний системы, в левой части

416
КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ГгЛ, XVIlt
уравнения A8.19) заметную роль играет только член kx и, следо-
следовательно,
kx ч: Fo sin tot.
Внешняя сила идёт, главным образом, на преодоление упругой
силы. Амплитуда смещения Xo—Fojk и смещение совпадают по фазе
с внешней силой. Наоборот,
А когда частота ш очень велика,
играет роль только член т -пт и
т —т- =4r Fa sin tot.
Внешняя сила идёт, главным
образом, на то, чтобы сооб-
сообщать телу ускорение. Ампли-
Амплитуда ускорений AOQ = F0(m, и
ускорение совпадает по фазе
с внешней силой (а смещение
противоположно по фазе).
В области резонанса члены
Рис. 354.
т j-f и kx, хотя, и велики каж-
каждый порознь, но примерно равны по величине и противоположны по
знаку. Действительно, колебания происходят по закону лг =
причём со = <о0. Поэтому
т. -jTj- = — тю2Х sin g>/,
a ^Ar =
Но так как ?//га =
а со = «>0, то
сРх , л„
l№~ ^ эти члена
в уравнении A8.19) компенсируют друг друга и
b -тт =? Fo sin (ot.
Это значит, что в области резонанса пружина сама помимо внешней
силы сообщает массе m необходимое ускорение. Роль внешней силы
сводится только к преодолению силы трения. Амплитуда скорости
VmaX = Fojb, и если трение мало, то Vmav велико. Скорость совпа-
совпадает по фазе с внешней силой. При этом внешняя сила совершает
наибольшую работу, так как направление движения груза всё время
совпадает по знаку с направлением внешней силы. Наоборот, при <о,
заметно отличном от соо, направление движения груза в течение неко-
некоторой части периода совпадает с направлением внешней силы, а в
течение другой части периода противоположно ей. Внешняя сила
совершает почти одинаковую положительную и отрицательную рабо-
работу, и работа за весь период невелика. Таким образом с точки зре-

§ 139]
РЕЗОНАНС
417
Малое затухание
Среднее затухание
Большое затухание
ния энергетической явление резонанса связано с тем, что при со-
совпадении частот со и №0 наступают наиболее благоприятные условия
для поступления в систему энергии от источника внешней силы.
Явление резонанса можно рассматривать как случай, когда под
действием гармонической внешней силы система совершает «почти
собственные» колебания. Роль внешней силы сводится, главным об-
образом, к компенсации действующих в системе сил трения.
§ 139. Резонанс
Амплитуды вынужденных колебаний зависят не только от соот-
соотношения между частотами со и <о0, но и от величины сил трения
в системе. Как видно из выражения A8.22), чем больше затухание а,
тем меньше при прочих равных условиях амплитуда вынужденных ко-
колебаний. Но вдали от резонанса
силы трения вообще не играют
заметной роли; поэтому и измене-
изменение величины сил трения мало из-
изменяет амплитуду вынужденных ко-
колебаний. В области резонанса, где
именно силы трения играют основ-
основную роль, изменение их сущест-
существенно сказывается на изменении
амплитуды вынужденных колебаний.
В частности, при резонансе, как вид-
видно из выражения A8.25), ампли-
амплитуды вынужденных колебаний изме-
изменяются обратно пропорционально 8.
Поэтому с увеличением сил трения вся кризая резонанса опускается
вниз, но максимум этой* кривой опускается гораздо быст-
быстрее, чем области, далёкие от резонанса (рис. 355). Вся кри-
кривая резонанса при увеличении сил трения притупляется. Менее
резкими становятся и изменения сдвига фаз в области резонанса.
С увеличением затухания системы всё явление резонанса становится
всё менее и менее заметным и при больших затуханиях (§ порядка 1
и больше) вообще исчезает. Резонансными свойствами, т. е. спо-
способностью особенно сильно отзываться на колебания одной опреде-
определённой частоты, обладают только системы с малым затуханием.
Поэтому в тех случаях, когда мы хотим использовать явление резо-
резонанса, например, для измерения частоты колебаний, необходимо при-
применять резонаторы с возможно малым затуханием. Иначе явление
резонанса не будет отчётливо выражено, и измерения не будут точ-
точными. Наоборот, в тех случаях, когда явление резонанса играет
вредную роль и его необходимо устранить, следует по возможности
увеличивать затухание колебательной системы. Явление резонанса
часто вызывает очень большие и поэтому опасные вибрации в раз-
27 с. э. хайкин
Рис. 355.

418 КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. XVIII
личных сооружениях и машинах; одним из способов борьбы с этими
опасными вибрациями является увеличение затухания системы.
Установление вынужденных колебаний в резонаторе длится
тем больше времени, чем меньше затухание резонатора. Убе-
Убедиться в этом можно из рассмотрения картины установления колеба-
колебаний при резонансе.
При возникновении внешней силы, как мы знаем, всегда возбуж-
возбуждаются собственные колебания. С другой стороны, при действии
внешней силы в системе должны существовать вынужденные колеба-
колебания. Если справедлив принцип суперпозиции, то мы можем рассма-
рассматривать картину установления как_ наложение двух процессов: собст-
собственных колебаний, вызванных включением внешней силы, и вынуж-
вынужденных колебаний, создаваемых постоянно действующей гармонической
внешней силой. При резонансе частоты этих двух колебаний совпа-
совпадают, и следовательно, смещение колеблющейся системы есть
A8.29)
где Хо — начальная амплитуда собственных колебаний, X — амплитуда
вынужденных (установившихся) колебаний, а ф и (р — их фазы.
X и <р определяются соотношениями, полученными в предыдущем
параграфе, а Хо и ф — начальными условиями.
Из соотношения A8.29) без детального рассмотрения сразу мож-
можно указать на одну важную черту картины установления. Так как
собственные колебания затухают, то, в конце концов, в системе оста-
останутся одни вынужденные колебания. Но чем меньше затухание систе-
системы, тем дольше нужно ждать, пока затухнут собственные колебания,
тем дольше длится процесс установления. Другими словами, чем резче
выражены резонансные свойства системы, тем дольше время
установления резонанса. Это общая и весьма принципиальная черта
всех резонаторов.
Если в момент включения внешней силы л; = 0 и ~г, =0, то из со-
соотношения A8.29), подставляя t = Q, мы получим *):
O. A8.30)
С другой стброны, если а<^шо, то, дифференцируя соотношение A8.29) и
пренебрегая величиной аХц по сравнению с величиной wqXq, мы получим
приближённое выражение для скорости колеблющейся системы:
^щХе-^соа(ч>^ + ^)+Хсоа(^ + ) A8.31)
A8.32)
Подставляя в это выражение t = Q и о = 0, получим:
*) Мы всегда можем выбрать значение начальной фазы <[>0 так, чтобы
моменту включения соответствовало значение f = 0.

§ 139] РЕЗОНАНС
Из соотношения A8.30) и A8.32) следует, что
X
'"А
11
111
11
419
Амплитуда собственных колебаний равна амплитуде вынужденных ко-
колебаний, а их фаза противоположна фазе вынужденных. Поэтому резуль-
результирующее смещение, определяемое выражением A8.29), можно запи-
записать так :
х = X A—е~а') sin (шд(-|- ^). A8.33)
Результат сложения собственных и вынужденных колебаний представляет
собой колебания с амплитудой, нарастающей до значения X по закону
1 —е—at (рис. 356). Если мы за время установления примем время, в тече-
течение которого амплитуда вынужденных колебаний достигает, например, 0,99 А"
(собственные колебания затухают до 0,01 А"), то для «времени установле-
установления» вынужденных колебаний мы получим то
же значение, которое получили выше для
продолжительности, собственных колебаний
(§ 126). Время установления будет т=е 4,6 Г/8.
В хорошем резонаторе с Ь порядка 0,01
должно пройти несколько сот периодов, пока
колебания успеют установиться.
С одной стороны, явление резонанса рез-
резко выражено только в случае малого затуха-
затухания резонатора; с другой, чем меньше за-
затухание резонатора, тем дольше нужно ждать,
чтобы резонанс установился. Поэтому явле-
явления резонанса отчётливо наблюдаются только
а том случае, когда за время устанэвления
резонатора внешнее воздействие ие успевает
прекратиться или вообще измениться. Явление
резонанса позволяет обнаруживать очень
слабые колебательные воздействия, т. е. даёт очень чувствительный способ
обнаружения и измерения колебаний. Но для этого измеряемое воздействие
должно длиться достаточно долго. И в этом случае увеличение чувстви-
чувствительности измерительного прибора (которым служит резонатор) связано с
увеличением длительности наблюдения, а значит, накладывает ограничения
на скорость изменения измеряемых величин.
Если внешняя частота <о несколько отличается от частоты резонато-
резонатора <»0, то картина установления усложняется: собственные и вынужденные
колебания дают биения. Однако, попрежнему начальная амплитуда собст-
собственных колебаний равна амплитуде вынужденных. Вследствие затухания
собственных колебаний глубина биений уменьшается, и биения постепенно
исчезают. Чем меньше разность о> — со0) тем больше период биений. При
со — со0 очень малом собственные колебания успевают затухнуть ещё в те-
течение первого полупериода биений. Картина установления постепенно пе-
переходит в ту, которую мы получили для случая совпадения со и ч>0.
Явление резонанса в таком виде, как оно описано выше, наблю-
наблюдается только в том случае, когда сам резонатор в отсутствие внеш-
внешней силы способен совершать колебания, близкие к гармоническим.
Именно поэтому он отзывается сильнее всего на гармоническое
внешнее воздействие, частота которого совпадает с собственной ча-
частотой резонатора. Как уже было указано, собственные колебания
резонатора будут близки к гармоническим, если пружина подчиняется
закону Гука, т. е. если коэффициент упругости пружины н» зависит
27*
Pi с. 356.

420 колебания систем с одной стьпенью свободы [гл. xviii
от её растяжения. Такие резонаторы называют гармоническими или
линейными *). Гармонический резонатор особенно сильно отзывается
на гармоническое внешнее воздействие, т. е. на такие колебания,
которые близки к собственным колебаниям резонатора.
§ НО. Негармоническое внешнее воздействие
Мы рассматривали до сих пор случай, когда внешняя сила изме-
изменяется по гармоническому закону. Однако, на практике очень часто
приходится иметь дело с негармоническими колебательными воздей-
воздействиями, например, периодическими резкими толчками. Чтобы отве-
ответить на вопрос, как ведёт себя гармонический резонатор при таких
негармонических воздействиях,
можно воспользоваться тем, что
мы уже знаем о воздействии гар-
гармонической внешней силы.
Для гармонического резона-
\ тора справедлив принцип супер-
суперпозиции. Поэтому негармониче-
негармоническое внешнее воздействие мы мо-
можем рассматривать как сумму гар-
гармонических воздействий, каждое
из которых влияет на резонатор
Рис. 357. таК] как если бы все другие
отсутствовали. Но как влияет
отдельное гармоническое воздействие, мы уже знаем. Если мы
сумеем представить негармоническое воздействие в виде суммы гар-
гармонических, то мы сразу получим ответ на интересующий нас вопрос.
Пока мы пользуемся гармоническими резонаторами, вся задача сво-
сводится к тому, чтобы представить данное переменное воздействие
в виде суммы гармонических воздействий. Существуют математические
методы разложения любой функции в ряд синусов и косинусов. Мы
не будем, однако, рассматривать этой математической задачи, а вос-
воспользуемся сразу её результатами, пояснив их на некоторых конкрет-
конкретных примерах.
Прежде всего рассмотрим некоторые примеры негармонического,
но периодического воздействия. Например, негармоническую функ-
функцию f(t) периода Г, изображённую на рис. 557 жирной линией, как
видно из этого же рисунка, можно изобразить в виде суммы двух
синусов с периодами Т и Г 2, т. е. с угловыми частотами ю1 — 2iti T
и ш2 = 2(о,. Синус с частотой @j называется «основным тоном» раз-
разложения данной функции f(i), а синус с частотой 2<о: — вторым
«гармоническим обертоном» этого разложения. Таким образом, раз-
*) Происхождение термина «линейный резонатор» связано с тем, что
резонатор, в котором упругая сила подчиняется закону Гука, описывается
линейным дифференциапьным уравнением.

§ 140]
НЕГАРМОНИЧЕСКОЕ ВНЕШНЕЕ ВОЗДЕЙСТВИЕ
421
ложение функции /(') в гармонический ряд содержит основной тон
и второй обертон.
На рис. 358 жирной линией изображена периодическая функция
с частотой ci)j —2п|7", которая кроме основного тона с частотой шх
содержит ещё второй и третий обертоны с частотами 2o)j и Зо^,
Вообще всякую периодическую, но негармоническую функцию
с частотой со можно разложить в «спектр», т. е. представить в виде
ряда гармонических функций с частотами <av 2(Oj, Ът1 и т. д., крат-
кратными основной частоте. Чем сильнее отличается от гармонической
разлагаемая функция, тем богаче её (пектр, тем больше обертонов
содержится в разложении и тем больше амплитуды этих обертонов.
В общем случае спектр периодической функции содержит бесконе i-
ный ряд гармонических обертонов, амплитуды которых вообще гово-
говоря, убывают (но не-всегда монотонно) с увеличением номера обертона.
Чем богег «плавной» является разлагаемая функцля, тем быстрее
убывают амплитуды обертонов. Хотя
разложение периодической функции
в гармонический ряд даёт в общем
случае бесконечный спектр, но
вследствие того, что обертоны
спектра обычно быстро убывают,-
практически приходится принимать
во внимание наличие только некото-
некоторого конечного (и небольшого) чис-
числа обертонов.
Разложив периодическое воз-
воздействие в гармони шский ряд, мы
сразу сможем ответить на вопрос
о том, как будет вести себя гар-
ионический резонатор, находящий-
находящийся под этим воздействием. Каждая
из гармонических составляющих будет вызывать такой эффект, как
если бы другие составляющее отсутствовали (принцип суперпозиции).
Но мы уже знаем, что гармонический резонатор особенно сильно
отзывается на такое гармоническое воздействие, на которое он «на-
«настроен», т. е. частота которого близка к собственной частоте резо-
резонатора. Из всех гармонических составляющих внешнего воздействия
только эта составляющая вызовет сильные колебания резонатора.
Все остальные гармонические составляющие не вызовут заметных
колебаний резонатора, так как их частоты значительно отличаются
от собственной 'частоты резонатора. Резонатор будет совершать вы-
вынужденные колебания, примерно такие же, как если бы во всём внеш-
внешнем воздействии содержалась только та гармоническая составляющая,
частота которой близка к его собственной частоте. Эти вынужденные
колебания будут почти гармоническими, хотя само влешнее воздей-
воздействие существенно отличается от гармонического.
Рис. 358.

422
КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ {гл. XVH!
Рис. 359.
Если, например, обычный маятник подталкивать малыми толчками один
раз за период его колебаний, то он раскачается и будет совершать вынуж-
вынужденные гармонические колебания, хотя внешняя сила (толчки) вовсе не
является гармонической. Но внешняя сила имеет период, совпадающий
с собственным периодом маятника. Из всего негармонического внешнего
воздействия маятник отзывается только на основной гармонический тон и
совершает почти такие же колебания, как если бы во внешнем воздействии
присутствовал только основной тон.
Если мы будем маятнику сообщать такие толчки один раз за два пе-
периода, то он также будет совершать почти гармонические колебания
с собственной частотой, но с меньшей
амплитудой. В этом случае частота
внешнего воздействия вдвое меньше
частоты маятника, а частота второго
гармонического обертона внешнего
воздействия совпадает с собственной
частотой маятника. Маятник отзывает-
отзывается только на второй обертон внеш-
внешнего воздействия. Так как амплитуда
второго обертона меньше, чем ос-
основного тона, вынужденные колебания
маятника в этом случае слабее, чем
в первом, когда толчки сообщаются
раз в период. Если затухание маятника
мало, то мы могли бы поддерживать
в нём почти гармонические вынужден-
вынужденные колебания, подталкивая маятник один раз за пять или даже за десять
периодов. В этом случае маятник выделял бы из внешнего воздействия
соответственно пятый или десятый гармонический обертон. Точно так же
и всякий гармонический резонатор из всего спектра внешнего воздействия
выбирает тот обертон, на который он настроен.
Если во внешнем воздействии не содержится гармонического обертона,
частота которого была бы близка к собственной частоте резонатора, то
резонатор вообще мало отзывается на внешнее воздействие — резонанса
не наблюдается. Для резонанса необ-
необходимо, чтобы внешнее воздействие
содержало гармоническую составляю-
составляющую с частотой, близкой к собст-
собственной частоте резонатора. Напри-
Например, внешнее воздействие с периодом Т
и частотой (о = 2it/7", изображённое жир-
жирной линией на рис. 359, не содержит
гармонической составляющей с часто-
частотой «в (основной тон отсутствует).
В нём содержатся только составляющие 2ш и За ^изображены тонкими ли-
линиями). Если резонатор настроить на частоту внешнего воздействия ш,
резонанса наблюдаться не будет. Только при настройке резонатора на ча-
частоту 2о> или Зо> будет наблюдаться резонанс.
В случае непериодического внешнего воздействия задача ставится
так же, как и в случае негармонического, но периодического воздействия.
Резонатор отзывается только на гармонические составляющие внешнего
воздействия, на которые он настроен. Но в разложении непериодической
"функции в гармонический ряд содержатся уже не только кратные частоты.
Рассмотрим, например, воздействие с частотой «e=2it/7\ амплитуда ко-
которого изменяется по закону (рис. 360)
Рис. 360.

§ НО]
НЕГАРМОНИЧЕСКОЕ ВНЕШНЕЕ ВОЗДЕЙСТВИЕ
423
Такие колебания называются модулированными. Q называется угловой
частотой модуляции, а т = 2я/й — периодом модуляции. Так как период ко-
колебании Т и период модуляции -с могут быть не кратными друг другу, то
модулированные колебания являются, вообще говоря, непериодическими
колебаниями. Их можно записать следующим образом:
л: = ЛГ0 A — sin Qt) sin at = Xo sin mt — Xo sin Qt sin ief.
Это колебание можно представить в виде суммы трёх гармонических ко-
колебании
х = Хо sin at + Щ cos («4-2) t - ^ cos (и—Q) t
с частотами о>, ю — й, в>-f 2. не кратными друг другу. Спектр такого мо-
модулированного колебания ¦ содержит три гармонических колебания, ампли-
амплитуды н частоты которых можно условно изобразить так, как это сделано
на рис. 361. При воздействии- такого колебания на гармонический оезона-
тор резонанс будет наблюдаться при совпадении частоты
резонатора с каждой из трёх частот.
Это можно продемонстрировать следующим образом.
Если питать язычковый частотомер (рис. 362, а) перемен-
переменным током без прерывателя, то в нём сильно колеблется
только один язычок, частота которого равна 100 пер/сек.,
т. е. совпадает с частотой внешнего воздействия, вдвое
большей, чем частота переменного тока *) (рис. 362, Ь).
Если же в цепь переменного тока включить прерыватель,
который разрывает цепь, например, 6 раз в секунду,
то заметно колеблются и два доугих язычка, с частотами в 94 и
106 периодов в секунду (рис. 362, с). Прерыватель «модулирует»
силу .переменного тока, изменяя её от максимума до нуля и снова до ма-
максимума 6 раз в секунду. Поэтому в разложении внешнего воздействия
(силы, действующей на язычки) в гармонический ряд появляются соста-
44 46 48 SO Ы 54 *>6
i11i
llllllHIIIlllllHIHIIII
40 48 50 5? 54
¦¦lIMIIIIIIIIIIHIIIIlM
Рис. 361.
Рис. 362.
вляющие с угловыми частотами «o-f-Q и о> —S. На них и отзываются два
язычка, расположенных симметрично по обе стороны от язычка с угловой
частотой и. Так как сама модуляция (изменение амплитуды тока) проис-
происходит не по гармоническому закону, то в «спектре модуляции» также со-
содержатся обертоны 29, 38- и т. д. Поэтому в модулированном колебании
*) На шкале частотомера указываются частоты переменного тока,
вдвое меньшие, чем собственные частоты соответствующих язычков.

424 КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ CTilHHbX) СВОБОДЫ [ГЛ. XVHI
содержатся гармонические составляющие с частотами о>-)-22, в> — 29
и т. д. На них отзываются соответствующие язычки частотомера (но ампли-
амплитуды этих составляющих меньше, чем ю -f-2 и со — Q).
В общем случае непериодическое воздействие содержит беско-
бесконечное число гармонических составляющих, которые не находятся
в простых кратных отношениях. В спектре непериодической функции
могут встречаться частоты, как угодно близкие друг к другу. В то
время, как спектр периодической функции всегда является дискрет-
дискретным — «линейчатым», спектр непериодической функции может быть
непрерывным, «сплошным». Не одна частота спектра, а целая полоса
частот может оказаться близкой к собственной частоте резонатора
и вызывать заметные его колебания.
Резонанс будет наблюдаться всякий раз, когда частота собствен-
собственных колебаний резонатора лежит в области, в которой амплитуды
спектра внешнего воздействия имеют достаточно большую величину.
Гармонический резонатор при всяком внешнем воздействии отзывается
только на некоторую узкую полосу спектра воздействия, на которую
он настроен. Зная все составляющие спектра воздействия, мы сразу
сможем оценить, какой эффект оно вызовет. Так как обычно мы
имеем дело с гармоническими резонаторами, то для оценки эффекта
достаточно знать, каков спектр того или иного воздействия. Это и
придаёт математическому приёму разложения функции в гармонический
ряд особый физический интерес.

ГЛАВА XIX
КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
§ 141. Колебания систем с двумя степенями свободы
Мы рассматривали до сих пор такие колебательные системы, по-
положение которых определяется только одной координатой. Для опи-
описания колебательного движения нужно
было определить закон, по которому
изменяется эта единственная коорди-
координата колеблющегося тела. Если колеб-
колеблющееся тело обладает более чем
одной степенью свободы, то при ко-
колебаниях могут изменяться все коорди-
координаты тела. В частности, если колеблю-
колеблющееся тело рассматривать как материаль-
материальную точку, то при колебаниях могут
изменяться все три координаты этой
точки. Примером может служить масса
т, растянутая на шести пружинках
(рис. 363). Колебания могут происхо-
происходить так, что будут изменяться все три
координаты точки т.
Мы ограничимся только простей-
простейшим случаем, когда колебания про-
происходят в одной плоскости, т. е. изменяются только две коор-
координаты точки т. Моделью для этого случая может служить масса,
растянутая на четырёх пружинках (рис. 364). Из того, что мы знаем
о колебаниях систем с одной степенью свободы, мы сможем вывести
ряд заключений о характере колебаний нашей модели.
Начнём с простейшего случая, когда все четыре пружинки оди-
одинаковы. Если мы сместим массу т в направлении х на величину Хо,
то она будет совершать гармонические колебания с определённой
частотой со по закону
х = XQ cos at.
При смещении в направлении у она будет совершать гармонические
колебания с той же частотой по закону
у = YQ cos at.
Рис. 363.

426 КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [гл. XIX
При смещении в каком-либо произвольном направлении (рис. 365)
масса т будет совершать колебания, которые можно рассматривать
как суперпозицию двух колебаний в направлениях х и у, происхо-
происходящих с одинаковыми частотами
и одинаковыми фазами, т. е. по
закону
х = Хо cos at и у = Yo cos at.
Так как при этом х\у=^Хй[Уй-=.
= const., то колеблющаяся точка бу-
будет всё время находиться на одной
и той же прямой, в направлении
которой она была отклонена в
начальный момент. Колеблющаяся
точка будет совершать прямоли-
прямолинейное движение, как и в случае,
когда она была отклонена только
в направлении х или только в на-
направлении у.
Сместим теперь массу иа вели-
величину Хо в направлении х и сообщим
ей толчком начальную скорость Vo
в направлении у (рис. 366). При
этом возникнут колебания, которые
мы можем рассматривать так же,
как суперпозицию двух колебаний в направлениях х и у, происхо-
происходящих с одинаковой частотой, но с различными начальными фазами
(так как начальные условия для обоих колебаний различны). Ко-
Колебания эти будут происходить по закону.
х = Хо cosai, y~Yos'ma>t,
где Y0=Voj® (так как при амплитуде ско-
скорости Vo амплитуда смещений Ко= Voja и
при t = О смещение по оси у равно нулю).
Иначе
-?• = cos at, ~ = sin at.
ло У О
Возведя оба эти выражения в квадрат и сло-
сложив их, получим:
—2-\-^=1- О9-1)
Рис. 364.
Рис. 365.
Это — уравнение эллипса. Колеблющаяся точка будет совершать дви-
движение по эллипсу с полуосями Хо и Уо. Разность фаз между коле-
колебаниями в направлениях х и у приводит к тому, что точка не со-
совершает прямолинейного движения, а описывает эллипс.

КОЛЕБА.НИЯ СИСТЕМ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
427
Рис. 366.
В частности, если подобрать начальную скорость Vo так, чтобы
Yo= V0j<o — X0, то уравнение A9.1) превращается в уравнение
окружности. Колеблющаяся точка будет двигаться по кругу. Оси эллипса
в нашем примере совпадают с осями хну. Это обусловлено опре-
определённым выбором начальных условий. Если мы изменим начальные
условия, то изменится и расположение осей эллипса. Например, если
мы, отклонив массу т в направлении х, со-
сообщим ей начальную скорость Vo, направ-
направленную под углом к оси х, то оси эллипса
будут наклонены -под определённым углом
к осям х и у (рис. 364). Отношение полу-
полуосей эллипса и угол наклона зависят от
амплитуд и фаз колебаний в направлениях
х и у.
Перейдём теперь к случаю, когда обе
пары пружии в нашей модели различны. Тогда
колебания по направлениям х и у будут про-
происходить с различными частотами », и ш2.
В общем случае, если отклонение задано
сразу и в направлении х, и в направле-
направлении у, возникнет колебание, которое можно рассматривать как су-
суперпозицию двух колебаний с разными частотами cOj и ю2. Картина
будет весьма сложная. Но если пружины мало отличаются друг
от друга, то частоты ю, и со2 близки друг к другу. В течение одно-
одного периода картина почти не будет отличаться от той, которую
дают одинаковые частоты, т. е. точка будет описывать эллипс.
Однако, так как частоты всё же различны, то разность фаз ме-
между обоими колебаниями постепенно будет изменяться и вместе
с тем будет деформироваться и эллипс, проходя через все положения,
соответствующие различным сдвигам фаз.
Когда частоты
получается очень
из колебаний в целое число раз больше частоты другого. Пусть, например,
период 7\, колебаний в направлении у вдвое больше, чем
у период Тх колебаний в направлении х.
По прошествии одного периода колебаний Ту точка
должна верлуться в исходное положение (так как за
это же время прошло два периода Тх и, следовательно,
^ig —j-jc отклонение в направлении у также должно повториться).
s^ ^"ч Поэтому траектория движения точки за период зам-
Ч *s кнётся (рис. 367). Но за время Тх точка дважды успеет
пройти через крайние положения Ло и —Хо и один
раз через крайние положения Уо и — Уо- Следовательно,
траектория будет два раза касаться прямых х~Х0
и х=: — Xq и один раз касаться прямых у = Ко и
Самый вид траектории зависит от фаз обоих колебаний, но число точек
касания определяется только отношением частот. Эти траектории носят
.название фигур Лиссажу.
ы о^ и и>, заметно отличаются одна от другой, картина
сложной, по она снова упрощается, если частота одного
б П
Рис. 357.

428
КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ |_ГЛ. XIX
При простых кратных отношениях между обеими частотами фигуры
Лиссажу представляют собой замкнутые кривые, вписанные в прямоуголь-
нлк со сторонами, равными удвоенным амплитудам складываемых колеба-
колебаний. По числу касаний траектории сразу
можно определить отношение частот коле-
колебаний. На рис. 368 и 369 приведены приме-
примеры траекторий, которые получаются при не-
некотором определённом соотношении фаз для
частот, относящихся как 1:3 (рис. 368) и как
3:4 (рис. 359). Если между обеими частотами
нет простого кратного отношения, то траек-
траектории движения являются незамкнутыми и
Рис. 358.
Рис. 369.
вместо фигур Лиссажу получаются области, сплошь заполненные траекто-
траекторией движущейся точки.
Кинематической иллюстрацией рассматриваемых случаев может служить
картина, которую даёт на экране пучок света, последовательно отражаю-
Рис. 370.
щяйся от двух камертонов, колеблющихся с различными частотами. Если
камертоны установить так, чтобы они колебались во взаимно перпендику-
перпендикулярных направлениях (рис. 370), то пятно на экране будет описывать фи-
фигуры Лиссажу.
§ 142. Колебания связанных систем
На практике часто приходится встречаться с колебательными
системами, которые состоят из нескольких тел, так или иначе свя-
связанных между собой. Простей-
Простейшим примером таких систем ^ % /f (
могут служить две маш! тл l^nWr-'mrTmr^^rmW-l
и щ, растянутые на тр§?- пру- J т, тг I
жинках (рис. 371)., Вообще
говоря, мы имеем здесь дело рис 371.
с колебательной системой,
обладающей несколькими степенями свободы. Но такие системы
удобно рассматривать как несколько связанных между собой колеба-
колебательных систем, каждая из которых обладает одной степенью свободы.
Смысл этого рассмотрения заключается в том, что свойства колеба-
колебательных систем с одной степенью свободы нам уже известны. Остаётся

§ 142] КОЛЕБАНИЯ СВЯЗАННЫХ СИСТЕМ 429
лишь установить, как изменяются свойства этих систем от того, что
они связаны между собой.
Разделение связанной системы на отдельные системы с одной
степенью свободы может быть произведено различными способами
(всякое разделение на части, вообще говоря, неоднозначно). Например,
модель, изображённую на рис. 371, мы можем разделить на две си-
системы, закрепив пружинку К2 посредине. Мы можем, конечно, закре-
закрепить не середину пружины /С2, а любую её точку. При этом мы
будем получать различные колебательные системы с одной степенью
свободы, обладающие различными свойствами. Если мы выберем раз
навсегда определённый способ разделения связанной системы на части,
мы сможем, зная свойства этих отдельных частей, вывести опреде-
определённые заключения о свойствах всей системы в целом.
Этот способ состоит в следующем: пусть система состоит из п
материальных точек, каждая из которых обладает одной степенью
Рис. 372.
свободы. Закрепив все точки системы кроме первой, мы получим
первую систему с одной степенью свободы; затем, закрепив все точ-
точки, кроме второй, мы получим вторую систему с одной степенью
свободы, и т. д. Перебрав все точки нашей сложной системы, мы
получим я систем, каждая из которых обладает одной степенью сво-
свободы. Полученные таким образом системы с одной степенью свободы
называют парциальными системами. Изучив свойства этих парциаль-
парциальных систем, мы затем сможем вывести определённые заключения
о свойствах нашей сложной системы, рассматривая её как п парциаль-
парциальных систем, связанных между собой.
Этот общий приём и результаты, которые с его помощью могут
быть получены, мы выясним на модели, приведённой на рис. 371.
Рассмотрим случай, когда обе массы щ и тъ и все три пружины Kv
Kv Кг одинаковы. Закрепим массу яг2 и отклоним массу /щ в на-
направлении, перпендикулярном к пружинам (рис. 372). Эта масса будет
совершать гармонические колебания (затуханием мы пренебрегаем).
Это и будет первая парциальная система. Собственная частота
первой парциальнб'й системы — первая парциальная частота — опре-
определяется величиной массы тг и упругостью пружин /С, и К2. Далее,
если мы закрепим массу т1 и отклоним массу т2 (рис. 373), послед-
последняя будет совершать такие же колебания с той же частотой — это
вторая парциальная система. Йогда обе массы освобождены, то их
можно рассматривать как две парциальные системы с одинаковыми
частотами, связанные между собой. Связь между обеими системами

430' КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ ГЛ. XIX
обусловлена тем, что движение каждой из масс изменяет натяжение
пружины К2, поэтому и сила, с которой пружина К2 действует на
одну из масс, зависит от положения другой массы. Такая связь на-
называется упругой или силовой. Возможны и другие типы связи, когда
сила, действующая со стороны одной массы на другую, зависит не
от положения первой массы, а от её скорости (например, Связь через
„ д. . силы трения) или от её уско-
К Jck&ftOnrfiL i Рения- Этот последний слу-
LYYr)nrrp-*-r^^1 1<ПгЛ чай называется инерциальной
гПНШ щ I связью. Мы в дальнейшем огра-
Рис. 373. ничимся только случаями, по-
подобными только что рассмо-
рассмотренному, когда связь между
системами является силовой. Однако, все общие выводы, которые
будут сделаны для этого частного случая, справедливы и для случая
инерциальной связи.
Выясним прежде всего, какой характер имеют собственные коле-
колебания в связанных системах. Чтобы возбудить собственные колебания
в системе, изображённой на рис. 371, нужно дать какие-то начальные
отклонения обеим массам те, и т2. Эти начальные отклонения могут
быть различны. Рассмотрим сначала два специальных случая, когда
обеим массам сообщены одинаковые отклонения в одну и ту же сто-
Рис. 374. Рис. 375.
рону (рис. 374) и в разные стороны (рис. 375). В первом случае
средняя пружина К2 вообще не будет сообщать обеим массам ника-
никакого ускорения, и на обе массы будут действовать только одинаково
растянутые пружины Кх и Кв. Поэтому ускорения обеих масс будут
одинаковы и последние будут всё время двигаться одинаково. Обе
массы будут совершать колебания в одной и той же фазе и с оди-
одинаковой частотой. Однако, как легко видеть, эта частота будет меньше
одинаковой парциальной частоты обеих систем. Действительно, в том
случае, когда одна из масс закреплена, не только пружина К± или К&,
но и пружина К2 сообщает ускорение колеблющейся массе; между
тем при колебаниях обеих масс в одной фазе пружина /С2 вообще
не играет роли. При колебаниях обеих масс в одной фазе восста-
восстанавливающая сила меньше, чем для каждой из парциальных систем
(при той же величине отклонения), а значит, частота этих колебаний
ниже парциальной частоты.
Если обеим массам сообщены одинаковые начальные отклонения
в разные стороны (рис. 375), то на каждую из масс будут действо-

§ 142] КОЛЕБА.НИЯ СВЯЗАННЫХ СИСТЕМ 431
вать не только одинаково растянутые пружины Кг и А'з, но и растя-
растянутая пружина К2. Силы, действующие на каждую массу, будут не
такие, как в первом случае, но для обеих масс они опять будут оди-
одинаковы. Поэтому и ускорения будут одинаковы; массы будут дви-
двигаться так, что не только вначале, но и в любой момент их откло-
отклонения будут равны по величине и противоположны по знаку. Обе
массы будут совершать гармонические коле-
колебания одной и той же частоты, но противо- Т'
положные по фазе. Легко видеть, что в этом -' |\
случае частота колебаний будет выше общей ,'' \
парциальной частоты обеих связанных систем. ' ' "V—7^~ &
Действительно, при колебаниях в противопо- ^т,
ложной фазе натяжение пружины К2 в каж- ,--~*""Т ~" Т"~~~-~ ;.
дый момент будет больше, чем в случае,
когда одна из масс закреплена. Поэтому ,'''1\
восстанавливающая сила больше, и следова- * \ , f
тельно, частота колебаний выше. \| „-•
Таким образом, при специальном вы юре *''
начальных отклонении Мы можем заставить Рис. 376.
обе массы совершать одинаковые гармониче-
гармонические колебания с одной из двух различных частот. Одна из этих частот
лежит ниже общей парциальной частоты связанных систем, а другая
выше. Эти частоты носят название нормальных частот или частот
связи; гармонические колебания, соответ-
,+! ствующие этим частотам, называются
у' ~**-^т. нормальными колебаниями.
^ :^~й 3 Соответствующим выбором начальных
т>_ т2 условий можно возбудить в обеих свя-
^-"•""I Р"~~-^ fj занных системах либо то, либо другое
_ нормальное колебание. В общем же слу-
^'К чае при произвольном выборе начальных
¦^ "<1 г^" С условий в каждой из связанных систем
v*;"'' возникают сразу оба нормальных коле-
г бания, т. е. два гармонических колебания
Рис. 377. с различными частотами. Действительно,
любые начальные отклонения мы можем
рассматривать как суперпозицию двух начальных отклонений — одного,
при котором обе массы отклонены одинаково в одну сторону, и дру-
другого, при котором обе массы одинаково отклонены в противополож-
противоположные стороны. Например, на рис. 376, а приведено произвольное на-
начальное отклонение масс тх и т2, которое можно представить
в виде суммы двух начальных отклонений: одного, одинакового для
обеих масс (рис. 376, Ь), и другого, противоположного для обеих
масс (рис. 376, с). Поэтому при произвольном начальном отклонении
возникнут сразу оба нормальных колебания, соответствующих обоим
типам начальных условий. Так как оба нормальных колебания имеют

432 КОЛЕБА.НИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [гЛ. XIX
разные частоты, то в результате их одновременного существования
в системе возникнут биения.
В частном случае, когда только одной из масс сообщено началь-
начальное отклонение (рис. 377, а), его можно представить в виде суммы
начальных отклонений двух типов — одинакового (рис. 377, Ь) и про-
противоположного (рис. 377, с), причём величина обоих этих отклоне-
отклонений одна и та же. Значит, в этом случае будут возбуждены два
нормальных колебания одинаковых амплитуд.
Как мы уже знаем, в результате сложения двух гармонических
колебаний с одинаковыми амплитудами и разными частотами полу-
получаются биения, в которых амплитуда колебаний изменяется периоди-
периодически от некоторого максимума до нуля. Амплитуда колебаний от-
отклонённой массы будет постепенно уменьшаться, пока эта масса совсем
не остановится. В это же время будет возрастать амплитуда коле-
колебаний второй массы (которая вначале не была отклонена). После
того, как первая масса остановится, снова начнётся постепенное
нарастание амплитуд колебаний этой массы и уменьшение амплитуд
колебаний второй массы. Дальше вся эта картина будет повто-
повторяться.
Всю эту картину возбуждения одного из нормальных колебаний или
обоих нормапьных колебаний одновременно можно продемонстрировать на
двух одинаковых маятниках, связанных мягкой пружинкой. Если отклонить
оба маятника на одинаковый угол в одну сторону, то они будут совершать
гармонические колебания в одной фазе, н амплитуды колебаний обоих
маятников будут оставаться одинаковыми. Такая же картина получится,
если отклонить оба маятника на одинаковый угол в противоположные сто-
стороны, но если отклонить только один из маятников, то амплитуда его ко-
колебаний будет постепенно уменьшаться, а другого — постепенно нарастать.
Так будет продолжаться до тех пор, пока первый маятник совсем не оста-
остановится; колебания второго маятника к этому моменту достигнут той
амплитуды, которую имел вначале первый маятник. После этого весь про-
процесс будет продолжаться в обратном направлении. Колебания маятников
будут ногить характер биений.
С точки зрения энергии здесь дело обстоит следующим образом. В на-
начальный момент энергией обладает только первый маятнлк. Действуя через
пружину, он начинает раскачивать второй маятник. При этом хотя ампли-
амплитуды колебаний первого маятника и убывают, но он всё время опережает
второй маятник и продолжает его раскачивать (совершает работу) даже
тогда, когда амплитуда колебаний второго маятника" становится больше,
чем первого. Поэтому энергия постепенно переходит от первого маятника
ко второму. Это раскачивание прекратится только тогда, когда первый
маятник остановится, т. е. вся энергия полностью перейдёт ко второму
маятнику. После этого второй маятник начнёт раскачивать первый — энер-
энергия начнёт снова возвращаться к первому и т. д. Благодар"я наличию связи
между маятниками происходит «перекачка» энергии от одного маятника
к другому и обратно.
Частота биений и скорость перекачки энергии зависят от того, насколько
отличаются друг от друга частоты нормальных колебаний. Чем больше их
разность, тем больше частота биений и тем быстрее происходит перекачка
энергии. Чтобы выяснять, _рт чего зависит разность частот нормальных
колебаний, вернёмся к нашей первой модели (рис. 37!). Будем изменять
упругость пружины Л> делая последнюю всё более и более мягкой. При

§ 142] КОЛБА.НИЯ СВЯЗАННЫХ СИСТЕМ 433
этом, чтобы обе массы Ш\ и т2 находились в равновесии в неотклонённом
положении, пружина Д'г должна быть всё более и более растянута. При
очень мягкой пружине К2 расстояние между массами »zj и т2 будет очень
велико (рис. 378), и при их отклонениях растяжение пружины Кг будет
изменяться очень незначительно. Влияние пружины Къ будет становиться
всё менее и менее заметным, связь между системами становится всё более
и более слабой.
Но, как мы видели, различие в нормальных частотах и их отличие от
общей парциальной частоты связанных систем обусловлены именно различ-
различным влиянием пружины Кч, в различных случаях. Чем меньше влияние
пружины Ki, тем меньше будет заметно это различие, тем ближе к парциаль-
парциальной частоте обеих систем будут
обе нормальные частоты н тем „,
меньше будет разница между ни- J "г "г
ми. Чем слабее связь между |ЛЛЛГР*ОГЛГ)ЛЛЛГГ'"''
двумя системами, тем медленнее ' "у
будут биения, возникающие в свя-
связанных системах. Рис. 378.
Принципиально, даже при
очень слабой связи между систе-
системами всё же нормальные частоты будут различны, и в связанных системах
должны наблюдаться биения. Однако, при очень слабой связи эти биения и
перекачка энергии будут происходить очень медленно. Так как вследствие
наличия трения колебания в связанных системах всегда постепенно затухают,
то при очень слабой связи они успеют совсем затухнуть до того, как замет-
заметная доля энергии успеет перейти от одной системы к другой — биения не
будут наблюдаться.
Мы рассмотрели только простейший случай, когда обе связанные ся-
стемы имеют одну и ту же парциальную частоту. В общем случае, когда
связанные системы имеют различные
парциальные частоты (например, в случае
двух связанных маятников разной длины),
явления гораздо сложнее, но основные
полученные нами выводы остаются спра-
справедливыми. Попрежнему, вследствие нали-
наличия связи система обладает двумя нормаль-
нормальными частотами, отличными от парциаль-
ы ных частот обеих связанных систем. Одна
ш» шп из нормальных частот лежит ниже меньшей
из парциальных частот, а другая — выше
Рис. 379. большей из парциальных частот. Чем сла-
слабее связь между системами, тем ближе
лежат нормальные частоты к обеим парциальным частотам.
При действии внешней силы на связанные системы также наблюдаются
явления резонанса. Как и в системе с одной степенью свободы, резонанс
наступает всякий раз, когда гармоническая внешняя сила совпадает по
частоте с одним из тех гармонических колебаний, которые способна со-
совершать сама система. А так как две связанные системы могут совершать
колебания с каждой из нормальных частот, то и резонанс наступает в том
случае, когда частота гармонического внешнего воздействия совпадает
с одной из двух нормальных частот coL и о>2'системы. При медленном измет
нении частоты внешней силы резонанс наблюдается дважды при совпаде-
совпадении с каждой из нормальных частот связанной системы. Резонансная кривая
имеет двугорбый характер (рис.ч379). Таким образом, если мы свяжем два
одинаковых резонатора, то они будут отзываться не на ту парциальную
ча;тоту, которой обладает каждый из них в отдельности, а на две другие
частоты, одна из которых лежит выше, а другая —ниже собственной
28 С. Э. Хайкин

434
КОЛЕБА.НИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [>Л. XIX
частоты резонатора. Это «расщепление» частоты связанных резонаторов
тем более заметно, чем сильнее связь между ними.
Только в одном специальном случае возникают особые явления при
совпадении частоты внешнего воздействия с парциальной частотой одной
из связанных систем (а не с одной из нормальных частот). Это происходит
в том случае, если обе связанные системы обладают различными парциаль-
парциальными частотами o>i и о>2 и внешняя сила с частотой ч>х действует только
на систему с парциальной частотой «в2. Тогда в той системе, на которую
действует внешняя сила, колебания будут очень слабыми. Наоборот, во
второй системе, на которую внешняя сила непосредственно не действует,
но парциальная частота которой
совпадает с частотой внешней
силы, возникнут очень сильные
колебания.
Продемонстрировать этот слу4
чай можно при помощи следую-
следующей установки (рис. 380, а). На
плоской пружине К\ укреплена
масса т, подобранная таким об-
образом, что парциальная частота
этого резонатора заметно отли-
отличается от частоты городского
переменного тока. Однако, не-
несмотря на несовпадение частот,
под действием сильного электро-
электромагнита, питаемого переменным
током, язычок всё же совершает
заметные вынужденные колеба-
колебания. Но если на этом язычке укре-
укрепить другой язычок А, парциаль-
парциальная частота которого точно равна
удвоенной *) частоте переменного
тоха, то этот второй язычок бу-
будет очень сильно раскачиваться,
а амплитуды колебаний первого
язычка заметно упадут (рис.380,Ь).
Если этот второй резонатор («ус-
(«успокоитель») задержать рукой так,
чтобы он не мог колебаться, то
снова первый язычок начинает
сильно колебаться (рис. 380, с).
Причина «успокоения» первого язычка состоит в tojj, что.второй язычок,
совершающий сильные вынужденные колебания, действует на первый с си-
силой, которая по амплитуде почти равна, а по фазе почти противоположна
внешней силе. Второй язычок почти полностью компенсирует действие
внешней силы на первый. Вместе с тем, так как первый язычок почти не-
неподвижен, то резонанс для второго язычка наступает именно на его пар-
парциальной частоте, а не на одной из частот связи.
Это явление широко используется в технике в различного рода успокои-
успокоителях для устранения вредных вибраций машин, уменьшения качки корабля
и т. Д. Для уменьшения качки корабля внутри корпуса корабля помещаются
большие цистерны, наполиеные водой и соединённые трубами (так называемые
цистерны Фрама). При качке корабля происходят колебания уровня воды в
цистернах, и эта колебательная система играет роль успокоителя.
*) Как уже указывалось, частота силы
вдвое больше частоты переменного тока.
притяжения (внешней силы)

§ 143]
КС№Ь\НИЯ В СПЛОШНЫХ ТЕЛА*
435
§ 143. Колебания в сплошных телах
Мы переходим к рассмотрению таких колебаний, при которых
не вей тело колеблется как целое, а отдельные части тел совершают
различные колебания. В этом случае существенную роль играют
деформации колеблющихся тел и упругие силы, возникающие при
этих деформациях.
Примером таких колебаний могут служить колебания, совершае-
совершаемые упругим стержнем или натянутой струний._ Так как различные
части стержня или струны колеблются по-разному, то колебания тел
сопровождаются их деформациями. Эти деформации и являются при-
причиной возникновения тех сил,
которые вызывают ускорения К,
отдельных частей колеблю-
колеблющегося тела.
Из всех разнообразных
типов колебаний в сплош-
сплошных телах мы остановимся,
главным образом, на двух
простейших—продольных ко-
колебаниях стержня и колеба-
колебаниях натянутой струны.
Из рассмотренной нами
картины колебаний в связан-
связанных системах можно полу-
получить некоторые указания о
характере колебаний в
сплошных телах. Для этого
представим себе, что в модели, изображённой на рис. 371, число
отдельных масс и число пружин становятся всё больше и боль-
больше. В случае трёх масс мы получим три связанные системы,
которые обладают тремя различными нормальными частотами.
Каждое из нормальных колебаний в отдельности можно воз-
возбудить, задав соответствующие начальные отклонения всех трёх масс.
На рис. 381 изображены эти три типа начальных отклонений, со-
соответствующие трём различным нормальным колебаниям связанной
системы.
В первом случае (рис. 381, а) начальные отклонения всех трёх масс
подобраны так, что результирующие силы, действующие на них со стороны
пружин, пропорциональны смещениям этих масс. Нетрудно было бы найти
величину отклонений, при которых соблюдается это требование. Но и без
этого расчёга ясно, что отклонение массы т> должно меньше чем вдвое
превышать отклонения масс ntj и т3. Действительно, пружины К\ и К2 тя-
тянут массу nix в разные стороны,vа пружины Кг и Кз тянут массу т3 в од-
одну и ту же сторону. Если бы отклонение массы т3 было вдвое больше, чем
масс mi и /я3, то результирующая сила, действующая на массы rtix и т3,
была бы равна нулю. Если начальные отклонения будут подобраны так, что
силы будут пропорциональны начальным смещениям, то и ускорения, идо-
28*
Рис. 381.

436 КОЛЕБА.НИЯ СИСТЕМ СО МНОГИМИ СТЫ1ЕНЯМИ СВОБОДЫ [гЛ. XIX
стигнутые скорости всё время будут пропорциональны смещениям. Все три
массы будут двигаться, сохраняя своё взаимное расположение, и будут со-
совершать одно гармоническое колебание с одной и той же частотой. Это
будет первое нормальное колебание системы.
Прн начальных смещениях, изображённых на рис. 381, Ь, возникнет
второе нормальное колебание (масса т3 при этом колебании всё время
остаётся в покое). Наконец, если начальные отклонения, изображённые на
рис. 381, с, подобрать так, чтобы результирующие силы были пропорцио-
пропорциональны смещениям, то и в этом случае все три массы будут совершать
одно и то же гармонлческое колебание. Это будет третье нормальное ко-
колебание системы.
Такими же рассуждениями, как и для двух масс, можно убедиться,
что первому типу начальных смещений соответствует нормальное ко-
колебание наименьшей частоты, а третьему — наибольшей. Для четырёх
масс мы получим четыре нормальных колебания, соответствующих
четырём типам начальных смещений, и т. д. При беспредельном уве-
увеличении числа масс будет беспредельно возрастать и число нормаль-
нормальных колебаний связанной системы. Увеличивая беспредельно число
масс, " мы в конце концов подойдём как угодно близко к сплошной
системе. Большое число малых масс, связанных между собой пружи-
пружинами, должно обладать такими ж,е свойствами, как и сплошное тело,
в котором возбуждаются колебания аналогичного типа.
Всё, что мы можем сказать относительно колебаний большого
числа связанных систем, в равной мере относится и к колебаниям
стержня или струны. Стержень и струна обладают множеством нор-
нормальных частот. Так же как частоты нормальных колебаний системы,
состоящей из отдельных масс, зависят от числа и величин этих масс
и упругости пружин, нормальные частоты сплошной системы зависят
от размеров, плотности и упругих свойств сплошной системы. В стер-
стержне эти упругие свойства определяются упругостью самого материала.
При поперечных колебаниях струны зависимость возникающей силы
от величины отклонения определяется натяжением струны. Поэтому
для данного стержня нормальные частоты имеют определённые фи-
фиксированные значения. Нормальные частоты поперечных колебаний
данной струны зависят не только от её размеров и плотности мате-
материала, но и от величины натяжения.
Так же, как в системе, состоящей из отдельных масс, выбором
соответствующих начальных условий в стержне или струне можно
возбудить то или иное из свойственных им нормальных колебаний.
В общем случае в стержне и струне сразу возбуждаются в той или
иной степени все нормальные колебания, которыми обладает эта систе-
система. Всякое колебание стержня или струны, возникающее в результате
начального толчка, представляет собой суперпозицию тех или иных
нормальных колебаний. В системе, состоящей из отдельных масс,
возникновение тех или иных нормальных колебаний определяется ха-
характером начальных отклонений всех масс. Точно так же в струне
возникают различные нормальные колебания в зависимости от харак-
характера начального отклонения струны. Оттягивая струну в различных

§ 143] КОЛЕБАНИЯ В СПЛОШНЫХ ТЕЛАХ 437
точках, мы будем возбуждать в ней, вообще говоря, различные нор-
нормальные колебания. Поэтому и характер звука, издаваемого струной,
будет, вообще говоря, различным.
В системе, состоящей из трёх тел, второе из нормальных колеба-
колебаний таково (рис. 381, Ь), что при этом колебании масса щ все время
остаётся в покое. Точно так же и в сплошной системе каждому из
нормальных колебаний соответствуют определённые точки, которые
при этом колебании остаются в покое. Эти точки называются узло-
узловыми точками данного нормального колебания. Расположение узло-
узловых точек для различных типов нормальных колебаний также можно
выяснить на основании аналогии с системой, состоящей из отдельных
точек. В системе, состоящей из трёх точек, при первом нормальном
колебании с наиболее низкой частотой (рис. 381, а) остаются в по-
покое только крайние точки, в которых закреплены пружины, — эти
точки и являются узловыми точками соответствующего нормального
колебания струны. При втором нормальном колебании, соответствую-
соответствующем более высокой частоте (рис. 381, Ь), кроме крайних точек в по-
покое будет оставаться и масса т2. В струне при соответствующем
нормальном колебании не только две крайние точки, но и средняя
точка будут являться узловыми точками. Наконец, при третьем нор-
нормальном ьолебанни, соответствующем наиболее высокой частоте
(рис. 381, с), не только две крайние точки, но и две точки, лежа-
лежащие между массами тг и ms и т2 и т3, будут оставаться в покое.
В струне этому нормальному колебанию будут соответствовать четыре
узловые точки (две по краям и две в средней части струны), распо-
расположенные так, что они делят струну на три равные части. Вообще,
чем выше частота нормального колебания, тем больше узловых точек
соответствует этому нормальному колебанию. При переходе к каждому
следующему нормальному колебанию число узловых точек струны
увеличивается на единицу, причём эти узловые точки располагаются
так, что они всё время делят струну на равные части.
Первое нормальное колебание, соответствующее наиболее низкой
частоте и двум узловым точкам (на концах струны), называется основ-
основным тоном собственных колебаний струны. Все остальные нормаль-
нормальные колебания, соответствующие более высоким частотам, носят на-
название обертонов струны.
В зависимости от характера начальных отклонений в системе воз-
возбуждаются те или иные обертоны колебаний. Так, например, чтобы
в системе, состоящей из трёх масс, возбудить то нормальное коле-
колебание, при котором средняя масса /и2 остаётся в покое, нужно дать
начальное отклонение массам тх и тг Мы не возбудим этого нор-
нормального колебания, если оттянем только массу тг. Точно так же,
оттянув струну в какой-либо точке, мы не возбудим в ней тех нор-
нормальных колебаний, для которых эта точка является узловой.
Картину возникновения разтичных нормальных колебаний при разных
начальных отклонениях можно продемонстрировать на слабо натянутой ре-

438
КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [гл. XIX
Рис. 382.
зиновой трубке. Такая «струна» обладает сравнительно малой упругостью,
поэтому амплитуды её колебаний могут быть сделаны очень большими н
хорошо видны (особенно в теневой проекции). Если оттянуть струну в сред-
средней точке (рис. 382), то мы сильнее всего возбудим в ней нормальное ко-
колебание наименьшей частоты (основной тон), для которого узловыми явия-
ют i тольчо крайние точки. Если оттянуть две половины струны симмет-
симметрично в противоположные
стороны, то мы возбудим в
ней сильнее всего то нормаль-
нормальное колебание, для которого
средняя точка является узло-
узловой. При этом колебания стру-
струны будут происходить с боль-
большей частотой.
Конечно, колебания струны
вследствие сопротивления воз-
воздуха и внутреннего трения в
резине постепенно затухают.
При этом видно, что не тольчо
уменьшается амплитуда коле-
колебаний струны, но изменяется
и форма колебаний. Это объ-
объясняется тем, что, оттягивая
струну в одной точке, мы воз-
возбуждаем в ней не одно нормаль-
нормальное колебание, а ряд нормаль-
нормальных колебаний (все, для которых эта точка не является узловой). Но частэты
этих колебаний различны и затухают онн с разной скоростью — тем быстрее,
чем больше частота колебаний. Поэтому и изменяется форма колебаний. Под
конец в струне останется
только одно нормальное
колебание, соответствую-
соответствующее наиболее низкой час-
частоте, и колеблющаяся стру-
струна принимает форму сину-
синусоиды (рис. 382). Отдель-
Отдельные точки струны колеб-
колеблются с одной и той же
частотой, но с разными
амплитудами, причём эти
амплитуды распределяются
по закону синуса.
Амплитуды каждого
из нормальных колеба-
колебаний струны распределя-
распределяются вдоль струны по
закону синуса. Узловые
точки — это точки, в ко-
которых этот синус обращается в нуль. Для основного тона на
всей длине струны укладывается только один полупериод синуса
(одна «полуволна»). Для обертонов распределение амплитуд таково,
что на длине струны укладываются две, три и т. д., вообще целое
число полуволн.
Рис. 383.

§ 143]
КОЛЕБАНИЯ В СПЛОШНЫХ ТЕЛАХ
439
Всё сказанное о колебаниях струн при известных условиях спра-
справедливо и для продольных колебаний упругого стержня. Если оба
конца стержня закреплены, то они находятся в таких же условиях,
как и концы струны. По-
Поэтому к такому закреп-
закреплённому стержню отно-
относится всё, что было ска-
сказано относительно стру-
струны. Если концы стержня
не закреплены или закреп-
закреплён только один его ко-
конец, то картина получает-
получается уже не такой, как для
струны. Мы её рассмот-
рассмотрим позднее с несколько
иной точки зрения.
Синусоидальное рас-
распределение амплитуд нор-
нормальных колебаний яв-
является весьма распростра-
распространённым, но всё же не
общим законом распреде-
распределения амплитуд в сплош-
сплошных системах. Чтобы рас-
распределение амптитуд нор-
нормальных колебаний было
Рис. 384.
синусоидально, прежде
всего необходимо, чтобы сплошная система была однородна, т. е. её
плотность и упругость во всех точках были одни и те же. Если, напри-
например, мы нарушим однородность резиновой струны,
насадив на неё три свинцовых грузика, то при ко-
колебаниях струна до самого конца будет сохранять
форму ломаной линии (рис. 383 и 384) и не примет
синусоидальной формы. Вследствие неоднородности
распределение амплитуд нормального колебания пере-
перестанет быть синусоидальным.
Распределение амплитуд нормального колебания мо-
может оказаться несинусоидальным и в однородных сплош-
сплошных системах, если упругие силы, действующие между
отдельными элементами сплошной системы, непропорцио-
непропорциональны величине относительного смещения соседних эле*-
ментов, а зависят от деформаций каким-либо более сложным образом. На-
Например, при поперечных колебаниях упругого стержня возникают деформации
изгиба. Упругие силы зависят от величины изгиба, который через элементар-
элементарные деформации сжатия и растяжения выражается некоторым сложным обра-
образом. Поэтому распределение амплитуд колебаний изгиба упругого стержня
оказывается несинусоидальным (рис. 385, а). Но и в этом случае каждому нор-
нормальному колебанию соответствует определённое расположение узловых
Рис. 385.

440
КОЛЕБА.НИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ |>Л. XIX
•*¦> а
точек. Изогнул упругую пластинку так, как указано на рис. 385, Ь, мы воз-
возбудим в ней нормальное колебание, для которого узловыми точками явля-
являются точки А и В.
Колебания камертона (рис. 386) представляют собой также колебания из-
изгиба упругого стержня, но при этом, в отличие от только что рассмотрен-
рассмотренного случая, сам стержень изогнут, и оба конца его свободны. При ударе в ка-
камертоне возбуждается колебание в основном тоне, и распре-
распределение амплитуд колебаний вдоль каждой ножки камер-
камертона получается примерно таким же, как вдоль стержня на
рис. 385, а. При этом обе ножки камертона движутся в ка-
каждый момент в противоположные стороны (одновременные
положения ножек указаны на рис. 386 одинаковыми буквами),
так что вследствие симметрии ножек общее количество дви-
движения камертона остаётся всё время равным нулю. Это зна-
значит, что при колебаниях на него никакие внешние силы не
должны действовать, поэтому закреплять камертон не нужно.
Между тем для того, чтобы прямой стержень совершал ко-
колебания изгиба, такие как на рис. 385, а, его конец должен
быть жёстко закреплён. В самом деле, при колебаниях коли-
количество движения стержня всё время быстро меняется, я с»
стороны стержня на тиски, в которых он закреплён, действуют
переменные силы, достигающие значительной величины.
Именно для того, чтобы можно было не заботиться о за-
закреплении камертона, а просто держать в руках, ему при-
придают U-образную форму*).
В общих чертах такая же картина, как в струне, будет наблюдаться и
при колебаниях упругих пластинок или плёнок. Если упругую плёнку, напри-
например тонкий лист металла, натянуть на рамку, то такая мембрана будет
обладать также. бесконечным числом нормальных колебаний. Частоты
этих колебаний зависят от размеров и массы мембраны и её натяжения. Но
О
Рис. 386.
Рис. 387.
Рис. 388.
каждому нормальному колебанию соответствуют уже не отдельные узловые
точки, а целые узловые линии, которые при данном колебании остаются в
покое. Такие же узловые линии существуют и при колебаниях упругой
*) В действительности условия закрепления стебля камертона, на кото-
котором укреплены его ножки, играют известную роль. Это связано с тем, что
ввиду конечной толщины ножек камертона в средней точке, где прикре-
прикрепляется стебель, узел колебаний не образуется. Поэтому в стебле так же
возбуждаются упругие колебания, которые передаются дальше подставке,
на которой стебель установлен, или руке, в которой он зажат. Это вносит
некоторое добавочное затухание в колебания камертона.

§ 143]
КОЛГБШИЯ В СПЛОШНЫХ Т?Л«1Х
441
Рис. 339,
пластинки. Обнаружить узловые лииии колеблющейся пластинки можно сле-
следующим образом. Если на металлическую пластинку насыпать слой мелкого
песка и затем возбуждать в ней колебания, проводя по краю пластинки
смычком, то песок будет ссьшаться с колеблющихся частей пластинки и
скопляться в узловых линиях. Полученные таким образом картины рас-
распределения узловых линий, так называемые фигуры Хладни, для не-
некоторых типов колебаний пластинок изображены на рис. 387, 388 и 389.
Рассмотренные нами типы колебаний пред-
представляют собой различные случаи собственных
колебаний сплошных систем. Вследствие наличия
трения эти колебания всегда будут затухающи-
затухающими. В сплошных системах, _так же как и в си-
системе с одной степенью свободы, можно соз-
создать условия, при которых те или иные из нор-
нормальных колебаний системы поддерживаются
за счёт постороннего источника энергии. Из
этого источника колеблющаяся система пополняет
потери энергии. В этом случае мы получим авто-
автоколебания в сплошной системе. Типичным при-
примером таких автоколебаний .является возбуждение
струны смычком. Потери энергии пополняются
за счёт работы силы трения, действующей между
смычком и струной. В рояле и в щипковых музы-
музыкальных инструментах (балалайка, гитара) про-
происходят затухающие собственные колебания струны. В смычковых инстру-
инструментах (скрипка, виолончель) происходят автоколебания, т. е. незатухаю-
незатухающие колебания. Этим, главным образом, и объясняется различие в характере*
ззуков, издаваемых щипковыми и смычковыми инструментами.
Если на сплошную колебательную систему действует переменная
внешняя сила, то она вызывает вынужденные колебания в системе.
Прн атом наблюдаются явления резонанса. Так же, как и в системе
с одной степенью свободы, в сплошных системах в момент возникно-
возникновения внешней силы возбуждаются собственные колебания, которые
постепенно затухают. Для установления явления резонанса необходнмо
известное время — тем большее, чем меньше затухание собственных
колебаний в системе.
Пользуясь аналогией между сплошной системой и системой, со-
состоящей из многих отдельных масс, можно вывести определённые
заключения и о характере явления резонанса в сплошных системах.
Резонанс в сплошных системах будет наблюдаться всякий раз, когда
частота гармонического внешнего воздействия будет совпадать с ча-
частотой одного из нормальных колебаний сплошной системы. Тогда
возникнут сильные вынужденные колебания сплошной системы, харак-
характер которых будет примерно такой же, как и у нормального коле-
колебания, совпадающего с частотой внешнего воздействия. Узловые
точки, соответствующие этому нормальному колебанию, будут оставать-
оставаться в покое при вынужденных колебаниях. Поэтому, если внешняя сила
будет приложена к узловой точке данного нормального колебания,
то она ие будет совершать работы (точка приложения силы не переме-
перемещается) и не будет увеличивать' энергии колебаний сплошной систе-
системы. Колебания не будут нарастать, и явление резонанса не наступит,

442
КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ CTtПЕНЯМИ СВОБОДЫ [гЛ. XIX
Чтобы в сплошной системе наблюдалось явление резонанса, не-
необходимо не только, чтобы частота гармонической внешней силы
совпадала с одной из нормальных частот системы, но чтобы эта
внешняя сила была приложена не в узловой точке данного нормаль-
нормального колебания.
Продемонстрировать явление резонанса в сплошных системах и роль
точки приложения силы можно на железной струне, на которую действует
электромагнит, питаемый переменным
током. Если подобрать натяжение стру-
струны так, чтобы одно из её нормальных
колебаний совпадало с удвоенной ча-
частотой переменного тока, то в струнз
возникнут очень сильные вынужден-
вынужденные колебания. Однако, если переме-
переместить электромагнит в узловую точку
возбуждаемого нормального колебания,
то колебания струны прекратятся.
Другой демонстрацией явления ре-
резонанса в сплошных системах может
служить следующий опыт. На общем
основании (лёгком столике) укреплены
мотор с эксцентрично насаженной не-
небольшой массой н длинная стальная
пластинка, зажатая в тиски (рис. 390).
При вращении мотора неуравновешен-
неуравновешенная масса вызывает колебания стола,
которые действуют на пластинку. Из-
Изменяя число оборотов мотора, можно
достигнуть того, что частота колеба-
колебаний будет совпадать с основным
тоном колебаний пластинки — будет
наблюдаться резонанс. Увеличивая число оборотов мотора, можно достичь
того, что частота внешней силы окажется равной частоте одного из обер-
обертонов колебаний пластинки. При этом снова будет наблюдаться резонанс.
Распределение амплитуд вынужденных колебаний будет совпадать с распре-
распределением, соответствующим тому нормальному колебанию, для которого
HSfeer место резонанс. Кроме зажатого нижнего конца на пластинке появится
ещё одна или несколько узловых точек.
§ 144. Нормальные частоты сплошной -системы
Для того чтобы определить нормальные частоты сплошной
системы, мы могли бы продолжить ту аналогию, которой пользо-
пользовались в предыдущем параграфе: рассчитать нормальные частоты
системы, состоящей из большого числа отдельных малых масс, свя-
связанных между собой. Однако, этот расчёт сложен, и поэтому мы пой-
пойдём по другому пути, который не только упростит расчёты, но и
подготовит переход к вопросам, которые будут рассматриваться
в следующей главе. Мы определим частоты тех собственных колеба-
колебаний, которые возникают в сплошной системе под действием началь-
начальных толчков определённого типа.
Этн колебания возникают вследствие того, что импульс распро-
распространяется в теле с конечной скоростью и затем, отразившись от
Рис. 390.

§ 144] НОРМАЛЬНЫЙ ЧАСТОТЫ СПЛОШНОЙ СИСТЕМЫ 443
границы сплошного тела, возвращается обратно, после чего процесс
повторяется снова. В простейшем случае время, необходимое для того,
чтобы импульс дошёл до границы тела и вернулся снова, и пред-
представляет собой период тех колебаний, которые будут возбуждены
начальным толчком. Этот период определяется скоростью распростра-
распространения импульса и размерами сплошного тела. i
Например, если упругий стержень, концы г 1 а
которого свободны, ударить по одному из
торцов (рис. 391, а), то по стержню побе- . ,^
жит импульс сжатия. Условно обозначим »-i
сжатия стрелками, направленными вверх, „ „.
а растяжения стрелками, направленными
вниз. Направление распространения им-
импульса будем обозначать горизонтальными стрелками. Через вре-
время x = ljc, где / — длина стержня, а с — скорость распростра-
распространения импульса, импульс достигнет другою конца стержня. Там
он отразится в виде импульса растяжения; и через такое же время х
снова вернётся к пер ому концу (рис. 391, Ь). Здесь снова произой-
произойдёт отражение, растяжение снова превра-
'— тится в сжатие, и дальше процесс будет
L—— ^1 а повторяться. Следовательно, возникнут коле-
"*"'¦'', бания с периодом, равным времени распро-
I ^П Ь стРанения импульса туда и обратно, т. е. с
— I периодом 7\=2//с. Так как с = |/Е;р,где
1 Е—модуль Юнга, а р—плотность мате-
риала стержня, то Т1 = 21у р/Е. Зная
/, р и Е, мы найдём Tv
Мы можем возбудить в стержне собственные колебания и с дру-
другим периодом. Представим себе, что в момент, когда первый импульс
достиг правого конца стержня (рис. 392, а), мы снова ударим по
левому концу. Возникший при этом второй импульс сжатия будет
двигаться вправо, в то время как отражённый импульс растяжения
будет двигаться влево. Оба они будут двигаться с одинаковой ско-
скоростью и встретятся в центре стержня. В стержне соблюдается закон
Гука, т. е. справедлив принцип суперпозиции; поэтому каждый из
импульсов будет двигаться так, как будто другого нет, и импульсы
пройдут «один сквозь другой», не повлияв друг на друга. Через
время х = 1 с первый импульс достигнет левого конца (рис. 392, Ь) и
отразится в виде сжатия, а второй достигнет правого конца и отра-
отразится в виде растяжения.
Дальше вся картина будет повторяться. Таким образом, после
двух ударов весь процесс будет повторяться через промежуток вре-
времени, за который импульс пробегает по стержню только в одном
направлении, т. е. период возникших колебаний 7 = /|с вдвое
меньше, чем при одном ударе.

444 колебания систем со многими степенями свободы [гл. xix
Колебания с ещё меньшим периодом мы можем возбудить при помощи
трёх последовательных ударов. Ударим стержень второй раз в тот момент,
когда импульс от перового удара прошёл 2/з длины стержня, т, е. через
промежуток времени *т = 2//3с после первого удара (рис. 393, а). За сле-
следующий такой же промежуток времени т второй импульс дойдёт до точки М,
лежащей на расстоянии 2//3 or левого конца; первый импульс успеет
отразиться и в виде растяжения вернуться в эту точку. В этот момент
ударим стержень в третий раз (рис. 393, Ь). В стержне будут распростра-
распространяться три импульса. Через время т/2 = //Зг первый импульс встретится
с третьим в точке N, лежащей на расстоянии 1\Ъ от левого, а второй до-
достигнет правого конца стержня. Ещё через время т/3 первый импульс дой-
дойдёт до левого конца и отразится в виде сжатия," второй, отразившись от
правого конца в виде растяжения, достигнет точки М, а третий достигнет
этой точки на пути туда (рис. 393, с). Расположение всех трёх импульсов
будет таким же, как в момент третьего удара. Следовательно, в этом слу-
случае вся картина будет повторяться через промежутки времени т = 2//3е,
т. е. возникнут колебания с периодом 7д = 2//3г втрое меньшим, чем в слу-
случае одного удара. Точно так же четырьмя уда-
ударами, повторяющимися через промежутки вре-
а мени Г,/4, мы возбудим колебание с периодом
T = lj2c.
1
t5-
1
1 N
M I
f-
M ' 1
M 1
. Соответствующим числом ритмических
ударов мы можем возбудить колебание с лю-
любым периодом, в целое число раз меньшим
с основного периода Tv
—U ' Правда, каждое из* возбуждаемых таким
образом собственных колебаний ие будет
Рис. 393. представлять собой одно нормальное ко-
колебание стержня, так как при нормальном
колебании амплитуды колебаний должны распределяться по стержню
непрерывно по закону синуса. Но всякое собственное колебание пред-
представляет собой наложение тех или иных нормальных колебаний. Ясно,
что собственное колебание с определённым периодом Г может содер-
содержать в себе только нормальные колебания с периодами Т, Т\2, Г/3
и т. д., так как только сумма таких колебаний может дать колебание с
периодом Т. (В противном случае картина не повторялась бы через
время Г.) И если мы можем возбудить в стержне собственное коле-
колебание с любым периодом Tjn, то, следовательно, все нормальные
колебания стержня должны иметь периоды Tjn, где п — любое це-
целое число.
Если от периодов перейти к угловым частотам, то йI=2тт/Т1 =
= тгс//, или число колебаний в секунду ^ = ^2/, а
где я—любое целое число. Это и есть частоты нормальных ко-
колебаний стержня. При л = 1 мы получим основной тон, а при
/2=2, 3, . . . — обертоны колебаний стержня. Эти обертоны являются
кратными основному тону; они поэтому называются гармоническими
обертонами.

§ 144] НОРМАЛЬНЫЕ ЧАСТОТЫ СПЛОШНОЙ СИСТЕМЫ 445
Частоты нормальных колебаний зависят ие только от скорости
распространения импульса и размеров тела, но и от условий отраже-
отражения импульса от границы тела. Если, например, второй конец стержня
закреплён (рис. 394, а), то импульс сжатия от конца стержня отра-
отразится также в виде сжатия (рис. 394, Ь), но, вернувшись снова к
первому, свободному концу, он отразится от него в виде растяже-
растяжения (рис. 394, с), и следовательно, через
время т = 2/|с картина не повторится. Но *~" ___»
ещё через время т/2 = /'с -импульс растяже- * -|а
ния отразится от закреплённого конца опять •*-*»
в виде растяжения (рис. 394, d), вернётся к ' 1
свободному концу и здесь отразится в ь
виде сжатия (рис. 394, е). После этого 4zz 1c
картина будет повторяться; период воз- * t ,
никших колебаний Тг будет равен вре- '—¦ --~р
мени, за которое импульс дважды проходит t~" Lg
по стержню туда и обратно, т. е. ' ¦ Iе
„ 4/ 2я кс
Гг=— и w1 = y = 2F' Рис.394.
Период основного тона вдвое больше, а частота вдвое меньше, чем
в случае стержня той же длины, у кеторого оба конца свободны.
В стержне, один конец которого закреплён, мы можем ритмиче-
ритмическими ударами возбудить собственные колебания с периодом мень-
меньшим, чем 7"i. Однако, мы не сможем в этом случае двумя ударами возбу-
. дить колебания с периодом Г/2. Действительно,
(-V « если через время \х=.Т-у\1 после первого удара
М |а мы снова ударим по левому концу стержня, то
iy этот удар просто уничтожит растяжение, при-
~р в jj шедшее в этот момент к левому концу, и ко-
°- 1 лебания не возникнут.
(i- -*-\г Но тремя ударами, следующими через про-
М | с межутки времени т=7уЗ, мы сможем возбудить
17 /F" ч колебание с периодом 7"8=ri/3 (рис. 395). Дей-
— :!=тт- 1^ ствительно, к моменту второго удара первый
— Ч 1 импульс успеет отразиться и в виде сжатия
'2* достигнет точки М; находящейся на расстоянии
р 3q. //3 от правого конца (рис. 395, Ь). К моменту
третьего удара первый импульс, отразившись or
правого, а затем левого конца и превратившись
в растяжение, снова окажется в точке М (рис. 395, с). Второй импульс, отразив-
отразившись в виде сжатия от правого конца, также окажется в той же точке. Ещё
через промежуток времени Г^З первый импульс после ещё одного отражения
от правого конца снова достигнет левого конца и превратится в сжатие
(рис. 395, d). В зтот момент вся картина будет такой же, как и в момент
третьего удара. Дальше через промежутки времени 7"i/3 картина будет
повторяться, т. е. возникнут колебания с периодом Гз=Г!/3.
С помощью нескольких ритмических ударов, следующих через
нечётные доли основного периода колебаний, мы сможем возбудить
только колебания с периодами Г/Bя-|-1), где я —целое число. Сле-
I

446
колебаний Систем Со Многими степенями Свободы [гл. xtx
довательно, и нормальные колебания будут иметь частош, только
в нечётное число раз большие, чем частота основного тона. Таким
образом, для стержня, закреплённого одним концом, угловые частоты
нормальных колебаний определяются формулой
Bя~М)кс
2/ '
A9.3)
где п — любое целое число.
Рис. 396.
§ 145. Частоты колебаний струны
Совершенно таким же образом определяются нормальные частоты
поперечных колебаний натянутой струны. Так как оба конца струны закре-
закреплены, то условия отражения поперечного им-
импульса от обоих концов будут одинаковы. Так
же, как для стержня с обоими закреплёнными
(или обоими свободными) концами,основной тон
струны будет иметь угловую частоту и>у=тсе\1,
_? где / — длина струны, ас — скорость расиростра-
ненйя поперечного импульса вдоль струны. Обер-
Обертоны струны будут иметь угловые частоты
<оя = rfitcjl, где п — любое целое число.
Для одного специального типа поперечного
импульса легко найти скорость распространения
импульса по струне. Представим'себе, что натянутая струна продёрнута
через трубку, согнутую в виде кольца (рис. 396), и протягивается
сквозь эту трубку со скоростью с. Определим давление струны на
стенки трубки. Обозначим натяжение струны, т. е. силу, с кото-
которой любой элемент струны действует на соседний, через Т, радиус коль-
кольца через г, а массу единицы длины струны (линейную плотность
струны) через р. Каждый элемент струны,
находящийся внутри трубки, движется по
окружности радиуса г с линейной скоро-
скоростью с. Значит, на элемент струны длины
Дя должны действовать силы, сообщающие
этому элементу центростремительное ускоре-
ускорение сЦг, т. е. должны действовать внешние
силы, сумма которых есть
Рис. 397.
Внешние силы — это, с одной стороны, силы натяжения соседних элементов
струны Д, а с другой, — давление стенок трубки /2. Поэтому давление
стенок /2 = / — Д. Сялы натяжения, действующие со стороны соседних
элементов струны, как видно из рис. 397, дают равнодействующую Д,
направлению к центру, причём
Но так как 2 sin а
то
TAs
Если мы подберём с так, чтобы / = /], то всё необходимое центростре-
центростремительное ускорение элемент струны Дя будет получать за счёт натяжений,

'§ 145] частоты колЕВчний струны 447
действующих со стороны соседних элементов, и давление
струны на стенки трубки будет отсутствовать. Следовательно, при" / = /i
или c^—TIp труба перестанет играть #роль, н мы можем её «распилить»
вдоль н удалить. «Барашек»_будет оставаться иа месте, если струна дви-
движется со скоростью с = УгТ/р. Это значит, что свободный барашек бежит
по струне со скоростью c = \rTjf. При этом радиус барашка не играет
роли. Более того, и специальная форма барашка, которую мы выбрали,
не играет роли — она только упрощает расчёты. Всякий" барашек любой
формы будет двигаться по струне со скоростью с = УтЦ. Но этн бараш-
барашки и представляют собой поперечные импульсы, распространяющиеся
по струне.
Следовательно, скорость распространения поперечного импульса по
струне равна
с = у — • A9.4)
Сма зависит от натяжения струны и её «линейной плотности», т. е. массы
единицы длины струны.
Подставив A9.4) в A9.3), выразим нормальные частоты струны через
её натяжение и плотность. Для обертона струны номера я имеем:
В рассмотренном случае обертоны струны (а также продольных коле-
колебаний стержня) оказывались гармоническими. Это обусловлено упомянутым
в § 143 обстоятельством — пропорциональностью между смещениями и воз-
возникающими силами — и однородностью сплошной системы: плотность и
упругие свойства системы во всех точках одни и те же. Поэтому и ско-
скорость распространения импульса вдоль всей струны одна н та же. Импульс
отражается только от второго конца струны.
Если свойства тела неодинаковы по всей длине, то картина будет со-
совсем иная. Пусть, например, плотность струны или стержня в какой-то
точке Л резко изменяется. Скорость распространения импульса в обеих
частях струны будет различна, и импульс, вызванный первым ударом, ча-
частично отразится в точке А, а частично пройдёт во вторую часть струны
и отразится от её конца. На обратном пути также произойдёт частичное
отражение, и к началу струны вернётся уже не такой импульс, который
возник при ударе. Помимо этого, в струне будут распространяться и частично
отражённые импульсы, которые будут возвращаться к концам струны не
в те моменты, когда к ним возвращается прошедший импульс (так как эти
импульсы проходят разные пути). Собственные колебания не будут перио-
периодическими. А это и значит, что нормальные колебания, из которых состоит
всякое собственное колебание, не будут кратными основному тону. (Сумма
колебаний с кратными частотами всегда дала бы периодический процесс.)
Нарушение однородности сплошной системы делает негармоническими обер-
обертоны системы.
Легко видеть, что гармоничность обертонов системы тесно связана
С равномерным распределением узловых точек вдоль системы. Действительно,
например, для второго обертона (второго нормального колебания) однород-
однородной струны, кроме двух узловых^ точек на концах струны, появляется ещё
узловая точка в середине струны4. Эту узловую точку можно закрепить; мы
этим не нарушим второго нормального колебания струны, которое при этом
превращается в первое нормальное колебание (основной тон) для каждой
из двух половин струны. Но основной тон для половины струны должен

448
КОЛЕБАНИЯ СИСТЕМ CO МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. Xlfc
быть ровно вдвое выше основного тона для всей струны. Поэтому второй
обертон для всей струны дспжен быть ровно вдвое выше её основного тона,
т. е. должен быть гармоническим. Гармоничность обертонов как раз свя-
связана с тем, что узловые точьи делят однородную колеблющуюся систему
на равные части.
§ 146. Поляризация поперечных колебаний
Если, прикрепив струну и ножке камертона с электромагнитным воз-
возбуждением (рис. 398, а), возбуждать в струне колебания, то каждая точка
колеблющейся струны движемся в плоскости, перпендикулярной к струне.
Но в этой плоскости ху каждая точка струны может совершать криволи-
Рнс. 398.
нейное движение. Так же, как и в случае одной материальной точки, ко-
колеблющейся в плоскости ху, каждая точка струны может двигаться так,
что одновременно будут изменяться её координаты х и _у. Движение ка-
каждой точки струны можно рассматривать как результат сложения двух ко-
колебаний, происходящих во взаимно перпендикулярных направлениях, и при-
применять результаты, полученные нами в § 141. Так как для струны все направле-
направления в плоскости ху равноправны, то частота колебаний струны по обоим на-
направлениям будет одна и та же. Поэтому каждая точка струны будет опи-
описывать в плоскости ху некоторый эллипс, отношение бсей которого и их
ориентировка зависят от сдвига фаз между колебаниями по осям х и у.
Поскольку при этом сдвиг фаз между колебаниями в направлениях х и у во
всех точках струны один и тот же к не изменяется со временем, то вся
струна в целом при колебаниях описывает фигуру, по форме напоминающую
веретено (рис. 398, о). Сечения зтой фигуры представляют собой эллипсы.
Такие колебания носят название поляризованных по эллипсу. В круглой
струне очень часто возбуждаются такие зллиптически-поляризованные ко-
колебания. Только приняв специальные меры, можно достичь того, чтобы каж-
каждая точка струны при колебаниях двигалась по одной прямой в плоскости ху.
Например, если струну пропустить сквозь тонкую щель (рис. 398, с),
то при возбуждении в струне колебаний все точки струны будут двигаться
по прямым, "параллельным щели. Движение всех точек струны будет проис-
происходить в одной плоскости, проходящей через струну и щель. Такие колеба-
колебания называются плоско-поляризованными, а плоскость, в которой происхо-
происходят колебания, называется плоскостью поляризации.
Если упругие свойства колеблющегося тела в двух направлениях х и у
неодинаковы, то -и частоты колебаний в этих двух направлениях будут раз-
различны и сдвш физ между обоими колебаниями всё время будет изменяться.

§ 147]
ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ
449
Эллипсы, описываемые точками колеблющегося тела, будут всё время де«
формироваться, превращаться в прямую, снова вытягиваться в эллипс и т. д.
Сдвиг фаз между колебаниями в направлениях х и у не остаётся постоян-
постоянным, а всё время меняется; колебания являются неполяризованными.
Такие неполярцзованные колебания можно продемонстрировать при
помощи упругих стержней прямоугольного сечения. Если сечение стержня
немного отличается от квадратного, то упругие свойства стержня в двух
направлениях немного различны и конец стержня описывает всё время де-
деформирующийся эллипс.
Если сечение стержня подобрано так, что частоты колебаний в обоих
направлениях находятся приблизительно в простом целочисленном отноше-
отношении, то конец колеблющегося стержня вычерчивает соответствующую
этому соотношению фигуру Лиссажу. Однако, вследствие не вполне точного
целочисленного отношения между частотами фигура эта всё время дефор'
мируется.
Ясно, что весь вопрос о поляризации колебаний имеет смысл только
в случае поперечных колебаний. Для продольных колебаний, при которых
направление колебаний всегда совпадает с направлением распространения
импульса, явление поляризации колебаний вообще отсутствует.
§ 147. Параметрическое возбуждение колебаний
Мы рассматривали выше случай возбуждения вынужденных колебаний,
при которых внешнее воздействие непосредственно вызывает движение ко-
колеблющегося тела или отдельных его точек. Однако, колебания могут воз*
никать и в том случае,
когда внешнее воздей-
воздействие не вызывает непо-
непосредственно движения
системы, а лишь перио-
дически изменяет свой»
ства колебательной си-
системы. Когда внешнее
воздействие сводится к
изменению свойств сн*
стемы, то это значит,
что оно изменяет Перио-
Периодически какой-либо из
параметров, характери*
зующих свойства систе-
системы. Такие воздействия
называются параметрит
ческими. Например, па-
раметрическое воздей-
воздействие на струну мояшо
осуществить, прикрепив конец струны к ножке камертона, которая
колеблется вдоль струны (рис. 399). При этом, несмотря на то, что
ножка камертона не будет сообщать никаких поперечных движений точкам
струны, а будет лишь периодически изменять её натяжение, при известных
условиях в Струне всё же возникнут сильные поперечные колебания («опыт
Мельде»). В этих случаях говорят о параметрическом возбуждении ко-
колебаний.
Для того, чтобы выяснить сущность явления параметрического возбу-
возбуждения колебаний, вернёмся к простейшему случаю колебаний маятника.
Одним из параметров маятника, характеризующим свойства маятника как
колебательной системы, является длина маятника. Параметрическое воз-
воздействие на маятник мы можем осуществить, периодически изменяя его
29 С. Э. Хайкин

450 КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [гл. XIX
длину, т. е. втягивая и выпуская нить, на которой висит маятник. Предста-
Представим себе, что маятник уже совершает малые колебания, и мы втягиваем
нить всякий раз, когда маятник проходит через среднее положение, и на
столько же выпускаем нить всякий раз, когда маятник проходит через
крайние положения.
Втягивая нить, мы совершаем положительную работу, т. е. увеличиваем
энергию колебаний маятника. Наоборот, отпуская нить, мы совершаем от-
отрицательную работу, т. е. отбираем энергию у маятника. Однако, энергия,
которую мы сообщаем маятнику, притягивая его в среднем положении,
и отбираем, отпуская маятник в крайних положениях, будет различна. Дей-
Действительно, при колебаниях маятника натяжение нити в среднем положении
будет больше, чем в крайних. Поэтому положительная работа, совершаемая
при втягивании нити в среднем положении, больше отрицательной работы,
совершаемой при выпускании нити в крайних положениях. Энергия, сообща-
сообщаемая маятнику, больше энергии, получаемой от него обратно. И если этот
избыток энергии, сообщаемый маятнику за каждый период колебаний,
бочьше, чем потери энергии в самом маятнике, то колебания маятника
должны нарастать- Мы можем, следовательно, раскачивать маятник при по-
помощи параметрического воздействия, если это воздействие происходит
с надлежащей частотой и в надлежащей фазе. В частности, частота воздей-
воздействия в рассматриваемом случае должна быть вдвое больше частоты соб-
собственных колебаний маятника (так как полупериоду колебаний маятника
соответствует полный период изменений его длины).
Классическим примером такого параметрического возбуждения колеба-
колебаний является раскачивание на качелях. Приседая в крайних положениях
и выпрямляясь в среднем положении, человек, находящийся на качелях,
изменяет момент инерции качелей (т. е. изменяет параметр системы) с ча-
частотой, вдвое большей, чем собственная частота системы. Выпрямляясь
в среднем положении, качающийся человек совершает положительную ра-
работу; приседая в крайних положениях, он совершает меньшую отрицатель-
отрицательную работу, и поэтому энергия колебаний с каждым периодом возрастает.
Для параметрического возбуждения колебаний принципиально необхо-
необходимо, чтобы система уже совершала малые колебания. Однако, вследствие
неизбежных случайных толчков во всякой системе существуют малые соб-
собственные колебания. И если параметрическое воздействие происходит с над-
надлежащей частотой, то эти малые колебания начинают нарастать (необходи-
(необходимое для этого соотношение фаз устанавливается само собой). Так как
явления параметрического возбуждения наблюдаются только при известных
соотношениях между частотой внешнего воздействия и частотой собствен-
собственных колебаний системы, то в этом отношении оно сходно с явлением резо-
резонанса. Поэтому его часто называют параметрическим резонансом.
Параметрическое возбуждение колебаний происходит и в упомянутом
выше случае периодического изменения натяжения струны, прикреплённой
к ножке камертона (рис. 399). Если частота колебаний камертона вдвое
больше частоты основного тона колебаний струны, то в струне возбу-
возбуждается колебание, которому соответствуют два узла на концах струны
(рис. 399, а). Если уменьшать натяжение струны, то частота колебаний ка-
камертона оказывается вдвое больше второго обертона, затем третьего и т. д.
В струне возбуждаются колебания соответственно с узловой точкой по се-
середине струны (рис. 399, Ь), с двумя узловыми точками (рис. 399, с) и г. д.

ГЛАВА XX
ВОЛНЫ
§ 148. Бегущие волны
Мы рассматривали выше движения, которые возникают в сплош-
сплошной системе под действием одного или нескольких кратковременных
импульсов. Теперь мы рассмотрим случай, когда какой-либо точке
сплошного тела сообщён не отдельный нмпульс, а периодическое дви-
движение. Как и отдельный импульс, это движение будет распростра-
распространяться в теле с некоторой конечной
скоростью. Это значит, что и все
другие точки тела постепенно нач-
начнут совершать периодическое дви-
движение с той же частотой. При этом ^^^ш"^^^^^^^^^^^^^^^т
вследствие потерь энергии в теле рис 400
амплитуды колебаний отдельных
точек тела будут постепенно убы-
убывать по мере удаления от точки, которая приводится в колебательное
движение. Эту картину распространения колебаний вдоль сплошного
тела можно продемонстрировать на мягкой и длинной пружине, ле-
лежащей на стекле. Если один конец пружины привести в колебатель-
колебательное движение, то хорошо видно, как это движение распространяется
вдоль пружины, постепенно затухая (рис. 400). Такие движения носят
название волновых движений, или волн.
В достаточно длинной пружине волны успевают затухнуть, не дойдя
до другого её конца, который остаётся в покое. Поэтому, если мы
возьмём достаточно длинное тело, то длина его перестаёт играть роль;
мы можем рассматривать, например, «бесконечно длинный» стержень
или «бесконечно длинную» струну, ограниченные только с одной сто-
стороны. При этом, однако, если мы ограничимся небольшим участком
этого «бесконечно длинного» стержня, то можно пренебречь тем за-
затуханием колебаний, которое происходит на этом участке (если оно
невелико). Таким образом, мы приходим к представлению о «беско-
«бесконечно длинном» стержне, не обладающем затуханием.
С этого идеализированного случая мы и начнём наше рассмотре-
рассмотрение. Пусть конец стержня совершает гармоническое движение по
закону
29*

452 волны [гл. XX
в направлении длины стержня. Это движение, так же как и отдель-
отдельный продольный импульс, будет передаваться по стержню от слоя
к слою. По стержню побежит продольная упругая волна. Точка
стержня, находящаяся на расстоянии х от начала, будет совершать
такое же движение; однако, в этом движении она будет отставать на
время, потребное для распространения волн на расстояние х. Это
время равно х\с, где с — скорость распространения волн вдоль стержня.
Точка, находящаяся на расстоянии к, будет иметь в момент t такое
же смещение, какое начальная точка имела на время х\с раньше, т. е.
в момент t — х\с. Таким образом, точка, находящаяся на расстоянии х
от начала стержня, будет двигаться по закону:
B0.1)
или, так как m = 2ujT(T—период колебаний),
B0.2)
Это выражение представляет собой уравнение волны, распростра-
распространяющейся со скоростью с в направлении возрастающего х. Разные
точки имеют в один и гот же момент времени tt вообще говоря,
различные смещения. Но если мы возьмём на стержне ряд точек,
находящихся на расстоянии сТ друг от друга, то аргументы синуса
в выражении смещения для этих точек будут отличаться на 2тг и по-
поэтому сами смещения будут одинаковы. Любой ряд точек, находя-
находящихся на расстоянии сТ друг от друга, будет в каждый момент иметь
одно и то же смещение. Это расстояние
\=сТ B0.3)
называется длиной волны. Как видно из самого выражения для'Х, длина
волны равна тому пути, который проходит волна за один период
колебаний.
Амплитуда колебаний всех точек стержня в нашем случае одна
и та же, но фаза колебаний различных точек различна. Для двух
точек, находящихся на расстоянии х1 друг от друга, фазы колебаний
сдвинуты на 2iu:1/L На расстоянии одной длины волны фаза коле-
колебаний изменяется на величину 2тг.
Если мы будем наблюдать всё время какую-либо фиксированную
точку стержня, то мы обнаружим, что она совершает гармонические
колебания. Если же мы будем двигаться вдоль стержня со скоростью с,
то мы вообще не обнаружим никаких колебаний. Все сечения стер-
стержня, против которых мы будем находиться в каждый момент, будут
в этот момент иметь одно и то же смещение.
Такое гармоническое движение отдельных сечений стержня, рас-
распространяющееся вдоль стержня с некоторой определённой скоростью,
называется бегущей волной.

§ 148]
БЕГУЩИЕ ВОЛНЫ
453
Рассмотрим теперь, как распределяются в бегущей по стержню
волне скорости и деформации. Прежде всего, если смещение какой-
либо точки стержня изменяется по закону
B0.4)
B0.5)
то скорость этой точки будет
^j* = «*„ COS 2* (?-¦?).
Скорость от точки к точке меняется по тому же закону, что
и смещение, но смещение и скорости сдвинуты друг относительно
друга по фазе на тт/2. Скорость данной точки стержня достигает ма-
максимума, когда смещение этой точки падает до нуля. Представим себе,
ТТТТТТТТТ'
трттгпттг
I | I | II ИМ
ш
г Г г' / г
—"направление бегущей волны
Рис. 401.
что мы сделали моментальную фотографию распределения смещений
и скоростей волны в стержне. Если мы отметим сечения / и /', ко-
которые имеют в данный момент наибольшее смещение (рис. 401, а),
то в этот же момент наибольшую скорость имеют сечения 2 и 2',
находящиеся на расстоянии Х/4 от мест наибольшего смещения. Мож-
Можно сказать, что волна скоростей сдвинута относительно волны смеще-
смещений по времени на Г/4, а в пространстве на Х/4.
Чтобы выяснить характер распределения деформаций в бегущей
волне, нужно принять во внимание следующее. Величина де-
деформации сжатия стержня, вызванной колебаниями, зависит не от
абсолютных величин смещения соседних сечений стержня, а от того,
как быстро изменяется смещение от сечения к сечению. Там, где
смещение наибольшее (в сечениях /, /), стержень вообще не дефор-
деформирован. Наоборот, в сечениях 2, где смещение проходит через нуль,
деформация оказывается наибольшей. Максимумы деформаций в бе-
бегущей волне совпадают с минимумами смещений, т. е. с максимумами
скоростей.

454 волны [гл. хх
Чтобы пояснить эту картину, представим себе, что мы нанесли на
боковой поверхности стержня линии на равном расстоянии друг от
друга. Деформации стержня вызовут изменения расстояний между этими
линиями. На рис. 401, b таким способом излбражено мгновенное рас-
распределение деформаций стержня, соответствующее тому же моменту
времени, для которого на рис. 401, а приведено распределение смеще-
смещений (конечно, смещения и деформации на этих рисунках преувеличены).
Для того чтобы найти распределение деформаций в бегущей
волне, выделим слой стержня толщиной Длг. Пусть продольные смеще-
смещения границ этого слоя соответственно равны $х и ?2; это значит, что
толщина слоя изменилась на Д^ = ?2 — ?р Относительное изменение
толщины слоя, т. е. растяжение, равно е = Д5 \х, или для бесконечно
тонких слоев е — ~.
Если смещение от точки к точке изменяется по закону B0.4), то
деформация в точке х в момент t будет:
Волна деформаций (растяжений) сдвинута относительно волны сме-
смещений также на Х/4, но в другую сторону-, чем волна скоростей.
Следовательно, волна скоростей и волна деформаций сдвинуты на VI.
Другими словами, волна деформаций противоположна по фазе волне
скоростей. Слои стержня, которые в данный момент имеют
положительную скорость (т. е. движутся в направлении-|-х), в этот
же момент имеют отрицательную деформацию, т. е. оказываются
сжатыми. В тот момент, когда изменяется знак скорости слоя, из-
изменяется и знак деформации; она становится положительной. Слои,
движущиеся в направлении—х, оказываются растянутыми.
При распространении бегущей волны распространяются волна ско-
скоростей, несущая с собой кинетическую энергию, и волна деформаций,
несущая с собой потенциальную энергию. Происходит геренос энергии
так же, как при распространении отдельного импульса. Течение энергии
в определённом направлении происходит так же, как и в случае одного
импульса. Деформированные элементы стержня движутся и при этом
передают свою потенциальную и кинетическую энергию следующим
элементам стержня. Энергия течёт по стержню с той же скоростью,
с какой распространяется волна. Но, как мы видели при движении
сжатого упругого тела, энергия течёт в направлении движения тела;
наоборот, при движении растянутого тела энергия течёт в направле-
направлении, противоположном движению тела. Поэтому хотя направление дви-
движения слоев стержня дважды изменяется за период, но направление
течения энергии остаётся неизменным. Энергия всё время течёт в на-
направлении -\-х, т. е. в направлении распространения бегущей волны.
При распространении бегущей волны энергия постепенно рассеи-
рассеивается вследствие внутреннего трения в теле. Но если трение неве-

§ 148] БЕГУЩИЕ ВОЛНЫ 455
лико, то рассеянием энергии на расстоянии немногих длин волн мож-
можно пренебречь и на этом расстоянии рассматривать процесс как
незатухающую бегущую волну. Вместе с тем, если на длине стержня
укладывается очень большое число волн, то бегущая волна успеет
полностью затухнуть, и другой конец стержня или струны не будет
играть роли. Таким образом, результаты, полученные нами для беско-
бесконечно длинного стержня, не обладающего затуханием, применимы
к тем случаям, когда затухание бегущих волн на расстоянии одной
длины волны очень мало,- но на всей длине стержня укладывается
очень большое число волн. Если же при малом затухании на всей
длине стержня укладывается небольшое число длин волн, то бегущая
волна достигает другого конца стержня, почти не затухая. Второй конец
стержня в этом случае играет существенную роль и изменяет всю
картину. Возникают новые явления, которые мы рассмотрим в следую-
следующем параграфе.
г' i
направление бегущей волны
Рис. 402.
Всё сказанное относительно бегущие волн в стержне можно
перенести на случай распространения бегущих волн в струне. Пред-
Представим себе очень длинную натянутую струну, ближний конец кото-
которой мы приводим в гармоническое колебание по закону
в направлении, перпендикулярном к струне. Смещения начальной
точки струны будут передаваться следующим точкам, от них к сле-
следующим и т. д. Вдоль струны побегут поперечные волны смещений,
скоростей и деформаций, причём скорость распространения этих волн
будет такая же, как для одиночного импульса.
Картину распространения бегущей волны по струне можно на-
наглядно представить себе следующим образом. Вообразим трубку,
изогнутую в виде синусоиды с амплитудой Хй и расстоянием между
максимумами \ = сТ, где с — скорость распространения импульса
вдоль струны, а Т—период тех колебаний, которые совершает конец
струны. Продёрнем струну в эту трубку и затем будем двигать трубку
вдоль по струне со скоростью с. Движение тех точек струны, кото-
которые находятся внутри трубки, будет точно таким, как и при 'распро-
'распространении по струне бегущей волны.
С помощью этой модели легко представить себе мгновенное рас-
распределение смещений и скоростей в бегущей волне. Оно изображено
на рис. 402. Так же как и для стержня, волна скоростей сдвинута

456 волны [гл. хх
относительно волны смещений на ХD. Выражения B0.4) и B0.5),
так же как и для стержня, описывают бегущие вдоль стержня, волну
смещений и волну скоростей.
Эти волны для струны имеют такой же характер, как и для
стержня разница лишь в направлении смещений и скоростей. Волна
же деформаций имеет в струне иной характер, чем в стержне.
В струне при малых амплитудах колебаний величину натяжения
можно считать постоянной, и никаких изменений в деформации мате-
материала струны при колебаниях не происходит. Всё дело в изменении .
4 направления, в котором силы натя-
натяжения действуют на данный элемент
струны со стороны соседних. Соста-
Составляющая этих натяжений в напра-
направлении, перпендикулярном к струне,
играет роль восстанавливающей
силы для отдельного элемента стру-
струны. При распространении волн
Рис. 403. в струне возникновение сил обу-
обусловлено изменением направления
отдельных элементов струны, и эти изменения направлений играют
такую же роль, какую играют деформации материала в случае
волн в стержне. Поэтому волна деформации для струны характери-
характеризуется углом, который образует тог или иной элемент струны с направ-
направлением покоящейся струны. А этот угол, как видно из рис. 403,
определяется значением ^- для рассматриваемого элемента струны,
и выражение B0.8) так же, как и в случае стержня, изображает
бегущие вдоль струны волны деформаций.
О расположении в струне волны деформаций по отношению к волне
смещений и волне скоростей можно повюрить всё то, что было
сказано для стержня. Действительно, деформация (угол с направлен
нием х) равна нулю в точках наибольшего смещения / и /', т. е.
волна деформаций сдвинута на Х/4 по отношению к волне смещений.
Таким образом, кинематическая картина для бегущих волн смещения,
скорости и деформации в случае стержня и струны совершенно одна
и та же. Но с точки зрения течения энергии картина в струне ока-
оказывается более сложной, и мы не будем её рассматривать. Всё,
что сказано было выше, а также будет сказано дальше относитель-
относительно течения энергии, относится к продольным волнам в стержне
и к аналогичным случаям (например, волнам в воздухе), но не
к струне.
Мы предполагали, что скорость распространения бегущей волны
совпадает со скоростью распространения отдельного импульса. Осно>
ванием для этого предположения служило то обстоятельство, что
в рассматриваемых простейших случаях продольных колебаний стержня
и колебаний струны скорость распространения импульса не зависит..

§ 149] стоячие волны 457
от формы и характера импульса и для импульсов любого типа оказы-
оказывается одной и той же. Поэтому мы могли считать, что скорость
распространения, бегущей волны, которая представляет собой одну из
разновидностей импульса, совпадает со скоростью импульса. Однако,
это справедливо не всегда. В некоторых случаях скорость распростра-
распространения бегущей волны не совпадает со скоростью импульса. Поэтому,
вообще говоря, следует различать скорость распространения импульса
и скорость распространения волны. Эту последнюю называют фазовой
скоростью, так как с этой скоростью движется фаза распространяю-
распространяющегося колебания.
Фазовая скорость не только может отличаться от скорости импульса,
но может быть различной для колебаний различной частоты. Эти оба
обстоятельства тесно связаны между собой Скорость распространения
импульса оказывается отличной от фазовой скорости именно потому,
что 'сама фазовая скорость зависит от частоты колебаний. Зависимость
фазовой скорости от частоты колебаний называется дисперсией. При
наличии дисперсии скорость отдельного импульса не совпадает с фа-
фазовой скоростью (различной для различных частот). Но в рассматри-
рассматриваемых нами простейших случаях дисперсия отсутствует, и поэтому
фазовая скорость совпадает со скоростью импульса. В дальнейшем
мы встретимся со случаем, юлда имеет место дисперсия волн.
§ 149. Стоячие волны
Когда бегущая волна достигает другого конца стержня или струны,
то на этом конце происходит отражение волны, так же как и в слу-
случае отдельного импульса. Отраженная волна распространяется в обрат-
обратном направлении, и движение каждого сечения стержня или точки
струны можно рассматривать как результат сложения двух волн —
падающей и отражённой. Если при распространении и отражении
волны не происходит их затухания, то обе волны — падающая и отра-
отражённая—будут иметь одинаковую амплитуду. Но фазы обеих волн
в какой-либо точке х будут, вообще говоря, различны. Сдвиг фаз
обусловлен, с одной стороны, тем, что отражённая волна проходит
путь от точки х до конца стержня и обратно; с другой стороны, тем,
что при отражении волн от границы тела, вообще говоря, может
происходить изменение фазы волны. В рассматриваемом случае отра-
отражения от закреплённого конца стержня волна смещений отражается
с поворотом фазы на тг (так же, как импульс смещений отражается от
закреплённого конца стержня с изменением знака смещения). Падающая
волна проходит от начала стержня до точки х путь х, и выражение
для падающей волны имеет вид.
6, = ЛГ0 sin »(/-?)
где ю—2п/7" угдо&ая.^частота волны» Qгражёниая волна лроходит

458 волны [гл. хх
от начала стержня до конца и обратно до точки х путь 21—л:,
и выражение для отражённой волны имеет вид:
B0.7)
(знак минус учитывает изменение фазы при отражении). Результирую-
Результирующее смещение каждого сечения стержня:
или
\ = 2Х0 sin со '-=-^ cos со (t 1-\ B0.8)
Каждое сечение стержня колеблется по гармоническому закону.
Разные сечения колеблются в одной и той же фазе, но с различной
амплитудой:
X=2Xosinu>1-^. B0.9)
Амплитуда колебаний изменяется от точки к точке по закону синуса.
В точках, для которых аргумент синуса обращается в нуль, ампли-
амплитуда колебаний падает до нуля. Эти точки всё время остаются в по-
покое. Это — уже знакомые нам узловые точки. Прежде всего такой
узловой точкой является закреплённый другой конец стержня (х = 1).
Следующие узловые точки лежат на расстоянии хх друг от друга.
Это расстояние определяется из условия @Xj/c = n или
кс сТ X
Х1~ п — ~2— 2"'
т. е. узловые точки отстоят на расстоянии полуволны друг от друга.
В середине между узловыми точками лежат точки, в которых ампли-
амплитуда X достигает максимума, — эти точки называются, пучностями
смещений. Между двумя узлами фаза смещений всех сечений стержня
одна и та же: при переходе через узел фаза смещений сразу ме-
меняется на тт. Амплитуда смещений между двумя узлами изменяется
от нуля до максимума и снова до нуля. Колебания с таким распре-
распределением амплитуд и фаз называется стоячей волной.
Чтобы изобразить распределение амплитуд смещений вдоль стержня,
будем откладывать амплитуды смещения, соответствующие каждому
сечению стержня, в перпендикулярном к стержню направлении (хотя
сами смещения происходят в рассматриваемом случае вдоль стержня).
Построенная таким способом графическая картина распределения
амплитуд смещений вдоль стержня для одного из возможных случаев
изображена на рис. 404, а. Синусоида на этом рисунке изображает
распределение амплитуд смещений вдоль стержня. Точки / и /',
р которых синусоида проходит через нуль, соответствуют узлам сме-

§ 149]
СТОЯЧИЕ ВОЛНЫ
459
щений, точки 2 и 2', в которых она проходит через максимум —
пучностям смещений. На закреплённом конце стержня, как мы убе-
убедились, должен получиться узел смещений.
Что касается первого конца стержня, то его движение задано, —
ему, по нашему предположению, сообщается периодическое движение.
Следовательно, в стержне установится стоячая волна с такой ампли-
амплитудой в пучности, что амплитуда этой стоячей волны на первом конце
стержня как раз равна амплитуде колебаний, заданных этому концу
Рис. 404.
стержня. Отсюда следует, что чем ближе лежит узел образовавшейся
стоячей волны к первому концу стержня, тем больше амплитуда стоя-
стоячей волны в пучности при заданной амплитуде смещений первого
конца стержня. Иначе говоря, для того, чтобы амплитуда стоячей
волны в пучности была велика, нужно, чтобы около первого конца
стержня лежал узел смещений. Так как на втором закреплённом конце
стержня обязательно должен получиться узел смещений, то условие
получения стоячей волны с большой амплитудой сводится к тому, что
на обоих концах стержня должны получиться узлы смещений. Для этого
по длине стержня должно укладываться целое число полуволн.
Если это условие соблюдено точно, то, как следует из наших
рассуждений, амплитуда стоячей волны в пучности должна возрасти
до бесконечности, так как только волна с бесконечно большой ам-
амплитудой в пучности может дать конечную амплитуду на бесконечно
малом расстоянии от узла. Однако, к такому результату мы пришли
только потому, что не учитывали затухания при распространении
волн в стержне. Как мы увидим ниже, затухание приводит к тому,
что и в точке, где образуется узел стоячей волны, амплитуда сме-
смещений всё же не падает до нуля. Поэтому, если задать смещения
с конечной амплитудой концу стержня, на котором должен устано-
установиться узел волны смещений, то амплитуда в пучности волны будет
хотя и большой, но всё же конечной; она будет тем больше, чем
меньше затухание волн в стержне.

460 волны [гл. хх
Чтобы амплитуда стоячих волн была наибольшей, нужно подо-
подобрать такие условия, при которых по длине стержня укладывается
целое число полуволн. Для данного стержня это сводится к выбору
частоты тех колебаний, которые задаются концу стержня. Эта ча-
частота должна быть такой, чтобы соответствующая ей длина волны
в стержне удовлетворяла указанному условию. Следовательно, стоя-
стоячие волны с большой амплитудой можно возбудить в стержне только
при определённых частотах внешнего воздействия. Связь этого об-
обстоятельства с явлением резонанса будет выяснена в следующем па-
параграфе.
Картины распространения бегущих и стоячих волн совершенно
различны. Однако, если мы в обоих случаях буд;м наблюдать дви-
движение только какого-либо одного сечения стержня, то мы не отли-
отличим стоячей волны от бегущей. В обоих случаях отдельное сечение
стержня колеблется по гармоническому закону (кроме узловых точек
в случае стоячей волны). Различие между бегущей и стоячей вол-
волнами мы обнаружим, только если в каждом случае сравним движе-
движение двух разных сечений стержня. В случае бегущей волны разные
сечения стержня колеблются с одинаковой амплитудой, но в раз-
различных фазах. В случае же стоячей волны разные сечения стержня
колеблются в одинаковой фазе, но с различными амплитудами.
Бегущая волна скоростей отражается от закреплённого конца
стержня также с поворотом фазы на 7т (аналогично тому, как при
отражении отдельного импульса от закреплённого конца стержня
скорость изменяет знак). Соотношения между фазами падающей и от-
отражённой волн скоростей получается такое же, как и для волны сме-
смещений. Поэтому узлы скоростей в стоячей волне образуются в тех
же точках, что и узлы смещений. Это и понятно: в узле смещений
сечение стержня всё время остаётся в покое — следовательно, и ско-
скорость в этом сечении всё время равна нулю. Ясно также, что пуч-
пучности скоростей лежат в тех же точках, что и пучности смещений.
Что касается бегущей волны деформаций, то при отражении от
закреплённого конца стержня она не изменяет фазы (также, как не
изменяется знак деформации для отдельного импульса). Соотношение
между фазами падающей и отражённой волн для деформаций будет
не таким, как для смещений и скоростей, вследствие чего узлы де-
деформаций получатся не в тех местах, где узлы смещений. Можно
было бы, складывая падающую и отражённую волны деформаций, как
это было сделано для волны смещений, найти места узлов и пуч-
пучностей. Но, и не производя этих расчётов, можно сразу сказать,
что на закреплённом конце стержня должна получиться пучность де-
деформации, так как в этом месте падающая и отражённая волны де-
деформаций совпадают по фазе.
Таким образом, пучности деформаций совпадают с узлами ско-
ростов., иг .очевидно,, узлы деформаций — с пучностями скоростей.
На рис. 404, b изображено распределение.амплитуд деформадий для.

§ 149] СТОЯЧИЕ ВОЛНЫ 461
того же случая, для которого на рис. 404, а изображено распреде-
распределение амплитуд смещений и амплитуд скоростей. Что касается сдви-
сдвигов во времени между мгновенными значениями смещения, скорости
и деформации (т. е. сдвигов фаз между колебаниями этих величин),
то они останутся такими же, как и в бегущей волне. Скорость бу-
будет во времени сдвинута относительно смещения на Г/4, а деформа-
деформация будет изменяться во времени в той же фазе, в какой изменяется
смещение, т. е. будет сдвинута во времени на TJ4: относительно
скорости.
Так как энергия течёт только в том случае, когда происходит
движение деформированного тела, то ни через узлы смещений, где
сечения стержня неподвижны, ни через узлы деформаций, где сече-
сечения стержня никогда не деформированы, не происходит течения
энергии. Энергия, которой обладает участок стержня длиной в ),/4,
заключённый между узлом смещений и узлом деформаций, остаётся
навсегда в этом участке. Происходит лишь переход заключённой
в этом участке энергии из кинетической в потенциальную и об-
обратно (скорость и деформация сдвинуты по фазе на тс/2). Пол-
Полный переход энергии из кинетической в потенциальную и обратно
происходит дважды за период. В стоячей волне, в отличие от бе-
бегущей волны, не происходит течения энергии. Этого впрочем и
следовало ожидать: мы получили стоячую волну как результат
сложения двух бегущих волн, распространяющихся в противополож-
противоположные стороны. Обе бегущие волны несут с собой одинаковую энер-
энергию в противоположных направлениях. Поэтому результирующая
стоячая волна не связана с переносом энергии.
Из этих соображений сразу видно, как скажется на рассмотренной нами
картине возникновения стоячих волн затухание бегущей волны при распро-
распространении. Вследствие затухания амплитуда отражённой волны всегда будет
меньше, чем волны падающей. Поэтому отражённая волна будет нести
с собой меньше энергии, чем падающая, и в результирующей волне должно
наблюдаться течение энергии в том направлении, в котором распростра-
распространяется падающая волна. А это значит, что результирующая волка не пред-
представляет собой стоячей волны в чистом виде. Она содержит в себе и бе-
бегущую, и стоячую волны.
Действительно, пусть падающая волна имеет в какой-то точке ампли-
амплитуду Х\, а отражённая — меньшую амплитуду Х2. Мы можем разбить падаю-
падающую волну на две волны с амплитудами Л2 и Хг — Х2- Первая волна вместе
с отражённой, имеющей ту же амплитуду Х%, даст чистую стоячую волну,
не связанну» с течением энергии. Второй волне амплитуды Х\ — Л2 не соот-
соответствует никакая отражённая волна, и поэтому она представляет собой
чистую бегущую волну, несущую с собой известную энергию. Эта энергия
рассеивается в остальной части стержня. Таким образом, вследствие нали-
наличия затухания мы никогда не получаем в стержне и вообще во всякой
сплошной системе чистых стоячих воли. Наряду со стоячими волнами всегда
наблюдаются и бегущие волны. Точки, которым соответствуют узлы сме-
смещений стоячей волны, не будут оставаться в покое, а будут совершать
колебания с амплитудой бегущей волны Х1 —Х2. Но чем меньше затухание
волны по всей длине системы, тем меньше амплитуда этой бегущей волны.
При достаточно малом затухании для решения ряда вопросов можно счи-
считать, что в системе возникают только чистые стоячие волны.

462 волны
Ггл#
¦Совершенно так же, как и образование стоячих волн в стержне,
происходит образование поперечных стоячих волн в струне. Если
одному из концов натянутой струны сообщать колебательное движе-
движение в поперечном направлении, например, прикрепив его к ножке
камертона (рис. 398), то по струне будет распространяться попереч-
поперечная бегущая волна. От другого закреплённого конца струны она
будет отражаться так же, как отражается продольная волна от конца
стержня, — фаза волны смещения при отражении будет изменяться на тт.
Поэтому картина распределения узлов и пучностей по струне будет
совершенно такая, как и рассмотренная картина для стержня с за-
закреплёнными концами. Всё сказанное выше справедливо и для струны,
за исключением представлений о течении и распределении энергии;
эту картину, как указывалось, со стержня на струну распространять
нельзя.
Для стержня, в отличие от натянутой струны, может встретиться
и другой случай, когда второй конец его не закреплён. Условия
отражения падающей волны будут иными — соответственно изменится
распределение узлов и пучностей стоячих волн. При отражении от
свободного конца волна смещений и волна скоростей отражаются
без изменения фазы, а волна деформаций изменяет фазу на тт. (Так
же, как в случае отражения отдельного импульса от свободного
ко'нца, не изменяется знак смещения и скорости и изменяется знак
деформации.) Если в падающей волне смещение меняется по закону
то в отражённой без изменения фазы оно описывается уравнением
S2 = Jf0sta«(/-HLzi
и результирующее смещение будет
или
S = 2X0cosw^^-sin<o (t — -?¦). B0.10)
Амплитуда распределяется по закону косинуса (а не синуса, как в
случае закреплённого конца) и при х = 1, т. е. на сзободном конце,
достигает максимума. Таким образом, на свободном конце стержня
стоячие волны образуют пучность смещений и скоростей и узел дефор-
деформаций (волна деформации отражается с изменением фазы на п). В ос-
остальном распределение узлов и пучностей получается такое же, как
в случае закреплённого конца, — узлы и пучности чередуются и лежат
на расстояниях Х/4 друг от друга.
Условие получения стоячлх волн наибольшей амплитуды можно
получить из тех же соображений, что и в случае стержня с закре-

§ 150]
КОЛЕБАНИЯ СПЛОШНЫХ СИСТЕМ, КАК СТОЯЧИЕ ВОЛНЫ
463
пленным вторым концом, У первого конца стержня, движение которого
задано, должен лежать узел смещений образующейся стоячей волны.
Но на свободном конце стержня образуется пучность смещений. Оба
эти условия будут соблюдены, если на длине стержня уложится
нечётное число четвертей волн.
Распределение амплитуд смещений в одном из случаев, возможных
для стержня со свободным концом, изображено на рис. 405, а (по-
прежнему 1—V — узлы, 2— 2'— пучности); распределение амплитуд
деформаций для этого же случая приведено на рис. 405, b B— 2' —
узлы, / — V — пучности).
?
Отражение бегущих упругих волн происходит не только от вполне
свободного или жёстко закреплённого конца тела, но и от всякой гра-
границы, у которой изменяются свойства сплошного тела — его упру-
упругость или плотность. При этом происходит частичное отражение
падающей волны, которое является причиной возникновения стоячих
волн. Таким образом, при наличии достаточно резких нарушений
однородности системы распространение бегущей волны в системе
неизбежно связано с возникновением стоячих волн.
§ 150. Колебания сплошных систем, как стоячие волны
Рассмотренная в предыдущем параграфе картина возбуждения
стоячих волн соответствует, в сущности, вынужденным колебаниям
сплошной системы. Под влиянием периодического внешнего воздей-
воздействия все точки системы совершают вынужденные колебания с раз-
различными амплитудами, и распределение этих амплитуд даёт картину,
соответствующую стоячим волнам. С такой же точки зрения образо-
образования стоячих волн могут быть рассмотрены и собственные колеба-
колебания стержня, струны и вообще ^сплошных систем, а также и явления
резонанса в, сплошных системах.
Собственным колебаниям стержня с закреплёнными обоими кон-
концами соответствует такое распределение стоячих волн, при котором

464
волны
Г гл. хх
оба конца стержня находятся в покое (так как "первый конец стержня
уже не приводится в движение). Поэтому собственным колебаниям
стержня соответствуют такие стоячие волны, для которых на обоих
концах стержня образуются узлы смещений. Так как узлы стоячей
волны отстоят друг от друга на расстоянии Х/2, то на длине стержня
должно укладываться целое число полуволн (рис. 406). Следовательно,
между длиной стоячей волны X, соответствующей тому или иному
собственному колебанию, и дли-
длиной стержня / должно существо-
существовать соотношение:
где п — любое целое число. Так
как Х = 2ттс/ю, то это соотноше-
соотношение можно записать в виде:
Рис. 406. шл —Т">
что совпадает с выражением A9.2)
для угловых частот собственных колебаний стержня, полученным в
предыдущей главе. Нормальные частоты стержня определяются, сле-
следовательно, из краевых условий,
на концах стержня должны ле-
лежать узлы соответствующих стоя-
стоячих волн.
При продольных колебаниях
стержня возможны другие крае-
краевые УСЛОВИЯ — ОДИН ИЗ КОНЦОВ *г.„. --^"fctf *»
стержня может быть свободен.
В этом случае собственным коле-
колебаниям стержня должны соответ-
соответствовать такие стоячие волны, для
которых на неподвижно закреплён- р .._
ном конце стержня образуется
узел смещений, а на свободном —
пучность смещений. Для этого на длине стержня должно укладываться
нечётное число четвертей волн (рис. 407), т. е. между длиной стоячей
волны X, соответствующей тому или иному собственному колебанию,
и длиной стержня должно существовать соотношение:
B/1+1) ?=/,
где я = 0, 1, 2, 3, ..., или, так как Х = 2т:с/ш, to
B/2+1) да;
(о = ¦—-— .
я 21

§ 130] КОЛЕБАНИЯ СПЛОШНЫХ СИСТЕМ, кАК СТОЯЧИЕ ВОЛНЫ 465
что совпадает с выражением A9.3) для угловых частот колебаний
стержня с одним закреплённым и другим свободным концами.
Таким образом, нормальные частоты колебаний системы — это те
частоты, которым соответствуют стоячие волны, удовлетворяющие
краевым условиям. Поэтому условие резонанса в сплошных системах —
совпадение частоты внешнего воздействия с одной из нормальных
частот сплошной системы — сводится к тому, что возникающие в ре-
результате внешнего воздействия стоячие волны должны удовлетворять
краевым условиям. При этом амплитуды возникших стоячих волн бу-
будут наибольшие. В частности, если стержень закреплён с двух кон-
концов, то для наступления резонанса на его длине должно укладываться
целое число полуволн. Если один конец стержня закреплён, а друго'й
свободен, то на его длине должно укладываться нечётное число чет-
четвертей волн.
Условия резонанса в струне аналогичны условиям для стержня с за-
закреплёнными концами. Резонанс в струне будет наблюдаться всякий раз,
когда на длине струны укладывается целое число полуволн. Так, в случае,
изображённом на рис. 398, на струне укладываются две полуволны— частота
колебаний ножки камертона совпадает со вторым обертоном (вторым нор-
нормальным колебатаем) струны. Однако, частоты нормальных колебаний струны
зависят от её натяженчя. Поэтом , уменьшая натяжение струны, мы можем
добиться того, что уже не второй, а третий, четвёотый и т. д. её обертон
будет совпадать с частотой колебаний камертона. При этом всякий раз бу-
будут наблюдаться стоячие волны большой амплитуды, и на длине струны будет
укладываться, соответственно, три, четыре и т. д. полуволн. В рассматри-
рассматриваемом случае внешнее воздействие оказывается приложенным к узлу стоя-
стоячей волны, возбуждаемой в системе. Между тем, как было указано (§ 135),
резонанс не наблюдается, если внешняя сила приложена к узлу возбуждае-
возбуждаемых колебаний. Но дело в той, что в рассматриваемом случае мы имеем
не заданную внешнюю г~ил\>, а заданное движение одной из точек струны.
В этом случае наивыгоднейшие условия для резонанса получаются именно
тогда, когда задано движение в узле возбуждаемого колебания. Действи-
Действительно, амплитуды колебаний в стоячей волне во всех точках должны быть
большими, чем в узле. Поэтому, если мы зададим колебательное движение
какой-либо точке вблизи узла, то амплитуда колебаний в пучности должна
быть гораздо больше, чем амплитуды заданного движения, т. е. будет на-
наблюдаться резонанс. Наоборот, если мы зададим движение с определённой
амплитудой точке, лежащей в пучности возбуждаемого колебания, то ам-
амплитуда колебаний всех др\гих точек будет меньше, и резонанс наблюдаться
не будет. Тачим образом, при возбуждении колебаний внешней силой выгод-
выгоднее всего прикладывать внешнюю силу в пучности возбуждаемого колебания,
а при возбуждении колебаний заданным движением одной из точек тела
выгоднее всего задавать движение в узле возбуждаемого колебания.
Это различие легко объяснить с энергетической точки зрения. При -воз-
-возбуждении колебаний внешней силой, как уже было указано, внешняя сила
совершает наибольшую работу, если смещения точки, к которой она при-
приложена, оказываются наибольшими (так как величина силы задана). Если
же задана не сила, а смещение, то наибольшая работа будет совершаться
тогда, когда к точке, которой задано двяжение, приложены наибольшие
силы. Но наибольшие силы нужно прилагать к той точке струны, в которой
упругие силы, возникающие в самой струне, оказываются наибольшими.
А это'будут точки, в которых лежат пучности деформаций, т. е. узлы сме-
дений. Поэтому наибольшая работа будет совершиться внешними силами
30 С. Э. хайкин

466 волны ^гл. хх
в том случае, когда задано движение в узле смещений возбуждаемого
колебания.
Как мы убедились, под действием внешней силы в случае резонанса
в системе возбуждаются стоячие волны, по характеру распределения ампли-
амплитуд близкие к тому из нормальных колебаний системы, частота которого
совпадает с частотой внешнего воздействия. В других случаях возбуждения
интенсивных колебаний в сплошной системе дело обстоит аналогичным
образом. Так, в случае параметрического возбуждения колебаний (§ 147)
интенсивные колебания возникают, когда частота колебаний ножки камер-
камертона вдвое больше одного из нэрмальных колебаний струны, и распределе-
распределение амплитуд колебаний будет такое же, как для соответствующего нормаль-
нормального колебания струны, — на струне укладывается «половина синусоиды»,
«целая синусоида», «полторы синусоиды» и т. д.
Так же обстоит дело и в случае возбуждения автоколебаний в сплошной
системе. Грубо говс?ря, можно считать, что механизм, обусловливающий
возникновение автоколебаний в системе, компенсируя потери энергии в си-
системе, поддерживает нормальные колебания этой системы. Например, в смыч-
смычковых музыкальных инструментах (скрипка и др.) характеристика силы
тренчя между смычком и струной такова, что часть работы, совершаемой
этой силой, идёт на попотнение потерь энергии, происходящих при колеба-
нчях струны. При автоколебаниях в большинстве случаев возбуждается ко-
колебание, частота которого близка к основному тону системы; однако, в не-
некоторых специальных случаях возможно возникновение автоколебаний,
близких к одному из обертонов системы (например, «флажолеты» на скрипке).
Если затухание собственных колебаний в системе мало, то механизм, под-
поддерживающий автоколебания, подводит к системе за период энергию, состав-
составляющую лишь малую долю всей "энергии, которой обладает колеблющаяся
система. Поэтому он очень мало изменяет характер поддерживаемых коле-
колебаний; автоколебания как по частоте, так и по распределению амплитуд
оказываются близкими к нормальным колебаниям системы. Например, при
игре на скрипке обычно основной тон колебаний таков, что для него вдоль
свободной части струны — от пальца, прижимающего её к грифу, до под-
подставки—укладывается половина длины волны. Частота колебаний скрипичной
струны, возбуждаемой смы чком, совпадает с частотой собственных колебаний,
которые получаются, если эту струну оттянуть, а затем отпустить (пиччикато).
С точки зрения возникновения стоячих волн можно рассматривать и ко-
колебания твёрдых тел, с которых мы начали изучение колебаний. В одно-
однородной сплошной системе возникают стоячие волны, амплитуды которых
вдоль системы распределяются по гармоническому закону. Однакс), нарушение
однородности системы, как мы уже знаем, приводит к нарушению этого за-
закона распределения амплитуд котебаиий вдоль системы. Всякая колебатель-
колебательная система представляет собой сплошную систему, в большей или меньшей
мере неоднородную. Поэтому колебания всякой системы можно рассматри-
рассматривать как стоячие волны, распределение амплитуд которых в той или иной
мере отличается от синусоидального вследствие неоднородности системы.
Например, груз на пружине мы можем рассматривать как сплошную систему,
у которой одна часть (пружина) обладает малой плотностью и малым коэф-
коэффициентом упругости, а другая часть (сам груз) обладает очень большой
плотностью и большим коэффициентом упругости. При колебаниях груза
получается негармоническое распределение амплитуд смещений отдельных
точек системы. Амплитуды смещений точек пружины растут примерно по
линейному закону, а амплитуды смещений всех точек ' руза оказываются
примерно одинаковыми. В системе возникает стоячая волна, однако распре-
распределение амплитуд в этой стоячей волне существенно отличается от синусои-
синусоидального вследствие сильной неоднородности системы.
Неоднородность системы приводит, как мы видели, и к нарушению гар-
гармоничности в распределении нормальных частот системы. Например, в случае

§ 151] волны в сплошной среде
груза на пружине второму обертону этой системы соответствует частота
не вдвое ббльшая, чем частота основного, тона, а в сотни раз большая.
Поэтому, если мы ограничимся областью не очень высоких частот, то можно
считать, что груз на пружине обладает только одной собственной частотой.
Все остальные нормальные частоты системы лежат за пределами интересу-
интересующей нас области частот. И мы можем рассматривать только основной тон
колебаний груза на пружине. А для этого колебания мы можем считать
груз недеформируемым, а пружину не обладающей массой, как мы это де-
делали в гл. XVIII.
Таким образом, колебания отдельных недеформируемых. тел можно рас-
рассматривать как предельный случай колебаний в сплошных системах, обла-
обладающих резкой неоднородности).
§ 151. Волны в сплошной срзде
Мы рассмотрели выше картину распространения бегущих волн
в стержне и струне. В системах такого типа распространение волн
могло происходить только по одному определённому направлению.
Вообще же в упругой сплошной среде, например, в упругом теле
больших размероэ, в воде или в воздухе, волны могут распро-
распространяться по всем направлениям. При этом картина распространения
волн принципиально остаётся прежней, однако возникает ряд новых
вопросов, на которых мы сейчас и остановимся.
Прежде всего при распространении волны во всех направлениях
волна, вообще говоря, захватывает всё большие и большие части
пространства. Поэтому энергия, которую несёт с собой волна, зани-
занимает всё большие и большие объёмы, и при распространении волны
плотность энергии убывает. А это связано с соответствующим умень-
уменьшением амплитуды распространяющейся волны. Таким образом, даже
в отсутствие потерь в среде происходит уменьшение амплитуды волны
при распространении. Только в специальном случае распространения
так называемой плоской волны в среде амплитуда волны остаётся
постоянной.
Такую плоскую волну в среде мы получим, если поместим в упру-
упругую среду большую пластину, колеблющуюся в направлении нормали
к пластине. Все точки среды, прилегающие к пластине, будут совер-
совершать колебания с одинаковыми амплитудой и фазой. Эти колебания
будут распространяться в виде волн в направлении, нормальном
к пластине. Все точки среды, лежащие на любой плоскости, парал-
параллельной пластине, будут совершать колебания в одной и той же фазе.
Эти плоскости, параллельные пластине, будут представлять собой
поверхности равной фазы или волновые поверхности. Энергия волны,
заключённая между двумя поверхностями равной фазы, будет распро-
распространяться вместе с волной, занимая всё время один и тот же объём.
Поэтому плотность энергии в плоской волне будет оставаться неиз-
неизменной, а следовательно, будет оставаться неизменной и амплитуда
волны. Уравнение плоской волны будет иметь вид:
$ = А"о sin (о ^ — jj.
80»

468 волны [гл. хх
где х — расстояние точки от пластины (источника волн), а с — ско-
скорость распространения волн. Плоскую волну, строго говоря, нельзя
осуществить в неограниченной сплошной среде. Только при известных
условиях можно получить в сплошной среде картину, близкую к рас-
распространению плоской волны, т. е. волны, амплитуда которой не из-
изменяется с расстоянием. Во всех других случаях амплитуда изменяется
с расстоянием.
Для того чтобы выяснить, как изменяется амплитуда волны при
распространении, можно воспользоваться связью между амплитудой
волны и плотностью энергии. Эта связь легко может быть установ-
установлена. Так как плотность энергии упругой деформации пропорциональна
квадрату деформации, а плотность кинетической энергии пропорцио-
пропорциональна квадрату скороети, то плотность энергии, которую несёт
с собой волна, пропорциональна квадрату амплитуды волны (ампли-
(амплитуды смещен-ий и амплитуды скоростей волны пропорциональны друг
другу). Поэтому, зная, как изменяется плотность энергии волны, мы
сразу сможем сказать, как изменяется её амплитуда.
Рассмотрим волну, распространяющуюся из одной точки по всем
направлениям в однородном пространстве, т. е. с одинаковой скоростью.
Фаза волны в точке, находящейся на некотором расстоянии от источ-
источника, будет связана с фазой волны у источника так же, как и в слу-
случае волны, распространяющейся по одному направлению. Если у ис-
источника волны колебания среды происходят по закону
? = X s
sin
то в точке, находящейся на расстоянии г от источника, колебания
будут происходить по закону
Во всех точках, находящихся на одинаковых расстояниях от источ-
источника, фаза волны в каждый момент будет одна и та же. 'Всякая
шаровая поверхность, цецтр которой совпадает с источником волны,
будет поверхностью равной фазы. Плоскость, касательная к поверх-
поверхности равной фазы, называется фронтом волны в данной точке.
Выберем какие-либо две близкие поверхности равной фазы, отстоя-
отстоящие на определённом расстоянии друг от друга, и будем следить за
Энергией волны, заключённой между этими поверхностями. Эта энер-
энергия будет двигаться вместе с волной и, следовательно, будет всё
время занимать объём шарового слоя неизменной толщины, заключён-
заключённого между поверхностями равной фазы. Этот объём яри распро-
распространении волны растёт, как г%, и значит, плотность энергии волны
убывает, как 1/г2. А так как энергия пропорциональна квадрату
амплитуды волны, то амплитуда волны будет убывать, как 1/л Следова-.
тельно, если амплитуда волны на расстоянии от источника, равном
единице, есть Хг, то на расстоянии г от источника она будет равна

§ 152] ВОЛНЫ НА ПОВЕРХНОСТИ ЖИДКОСТИ 469
Л\ г, т. е. колебания на расстоянии г будут происходить по закону
B0.11)
Это — уравнение шаровой волны. Шаровую волну в среде возбуждал
бы, например, пульсирующий шар, помещённый в упругой среде. Всем
прилегающим частицам среды этот пульсирующий шар будет сооб-
сообщать колебательное движение, которое и будет распространяться
в среде в виде шаровой волны.
На практике редко приходится иметь дело с такими источниками волк,
как пульсирующий шар. Однако, и тела, колеблющиеся более сложным
образом, создают в окружающей среде волны, которые на достаточно боль-
большом расстоянии от источника часто можно считать шаровыми. В этих
случаях колеблющееся тело можно рассматривать как точечный источник.
Например, звучащий колокол можно считать источником таких шаровых
волн, возникающих в среде (в воде или воздухе), в которую он погружён.
Если волны от источника распространяются во все стороны только
в тонком слое, ограниченном двумя параллельными плоскостями, то в этом
слое картина распространения фазы волны будет такой же, как и в случае
шаровой волны. Поверхностями равной фазы будут служить цилиндры ма-
малой высоты, центр которых совпадает с источником. Вдали от источника
можно считать, что энергия волны, заключённая между двумя поверхностями
равной фазы (двумя коаксиальными цилиндрами), будет двигаться вместе
с этими поверхностями. Объём, заключённый между ними, будет расти
как г; следовательно, плотность энергии будет убывать как 1/г, а ампли-
амплитуда волны будет убывать как \\У г. Уравнение волны вдали от источника
б/дет иметь вид:
У г
— -V B0.12)
с I
где Х\ амплитуда волны на расстоянии от источника, равном единице. Такая
воша носит название круговой волны.
Если очень большое число источников волн, расположенных на одной
прямой близко один от другого, создаёт волны одинаковой фазы и ампли-
амплитуды, то во всех плоскостях, перпендикулярных к этой прямой, будут
распростра1яться круговые волны также одинаковой амплитуды и фазы.
Поверхностями равной фазы будут служить бесконечные коаксиальные
цилилдры, на осях которых лежат источники волны. Такая волна называется
цилиндрической. Уравнение цилиндрической волны имеет такой же вид,
ка< и уравнение круговой волны B0.12), и справедливо для любой пло-
плоскости, перпендикулярной к прямой, на которой лежат источники волн.
§ 152. Волны на поверхности жидкости
Всё сказанное относительно различных типов волн относится
в одинаковой мере как к продольным, так и к поперечным волнам
в сплошной среде. Нужно лишь иметь в виду, что поперечные волны
могут возникать только в упругих твёрдых телах. В жидкостях и га-
газах могут возникать только продольные упругие волны. Есть, однако,
один случай, когда и в жидкости могут возникать поперечные вол-
волны (впрочем они не являются, строго говоря, чисто поперечными

470 волны [гл. хх
волнами). Это волны на поверхности жидкости или на границе двух
жидкостей. Волны на поверхности жидкости являются прекрасной
моделью для наблюдения картины распространения волн.
Возникновение волн на поверхности жидкости обусловлено не
упругими силами в жидкости, а силой тяжести. (Именно поэтому
и могут возникать поперечные волны.) Если в какой-либо точке
поверхность жидкости будет нарушена (например, в воду упадёт
капля), то по поверхности жидкости будут распространяться круговые
импульсы. При этом отдельные частицы жидкости будут двигаться
не только в вертикальном направлении (они будут описывать при-
примерно круговые траектории), и распространяющийся импульс не является,
строго говоря, поперечным. Но если отвлечься от движения отдель-
отдельных частиц жидкости и рассматривать только движение поверхности
жидкости, то мы получим картину распространения поперечного
импульса. При распространении этого импульса сила тяжести играет
такую же роль, какую играют упругие силы, возникающие при сдвиге,
для распространения поперечного импульса в упругом твёрдом теле.
Если импульсы в какой-либо точке повторяются периодически, то
на поверхности жидкости распространяются круговые волны. Все
точки, находящиеся на одной и той же окружности* колеблются
в одинаковой фазе. Расстояние между двумя окружностями, в кото-
которых фаза колебаний отличается на 2к (например, между двумя гор-
горбами), представляет собой длину волны. Как и прежде, \ = сТ, где
с — скорость распространения волны, а Т—период, с которым по-
повторяются импульсы.
Эту картину возникновения круговых волн можно продемонстрирован,
в ванне, наполненной водой (для демонстраций дно ванны обычно делают
из стекла и проецируют картину на экран). Если на поверхности жидкости
поместить вертикально колеблющийся шарик, то от шарика по поверхности
жидкости будут распространяться круговые волны (рис. 408). Амплитуда
этих волн будет постепенно убывать с расстоянием (как это и должно быть
для круговой волны).
На поверхности жидкости можно получить и плоские волны, если
в качестве источника волн вместо шарика взять колеблющуюся палочку
(рис. 409). В этом случае точки, находящиеся на одной и той же прямой,
цараллельной источнику, колеблются в одной и той же фазе; горбы волн'
располагаются параллельно палочке. Амплитуда колебаний почти не убы-
убывает с расстоянием, как это и должно быть для плоской волны. (Небольшое
уменьшение амплитуды обусловлено затуханием волн.)
Скорость распространения волн на поверхности жидкости, как и в слу-
случае упругих волн, зависит от величины сил, возникающих при отклонении
от положения равновесия. Но- сила тяжести, которая в рассматриваемом
случае играет роль восстанавливающей силы, зависит от смещений частиц
не так, как упругие силы, возникающие в случае упругих волн. Поэтому
оказывается, что скорость распространения воли по поверхности жидкости
зависит от длины волны (от частоты колебаний источника волн), т. е.
наблюдается дисперсия волн. Скорость распространения увеличивается
с увеличением длины волны.
Однако, это справедливо только в случае, когда слой жидкости,, на
поверхности которого возникают волны, достаточно глубок — не м-енее

§ 152]
ВОЛНЫ НА ПОВЕРХНОСТИ ЖИДКОСТИ
471
нескольких длин волн. Для тонких слоев жидкости скорость распростране-
распространения волн зависит уже только от глубины слоя (она уменьшается с умень-
уменьшением глубины слоя) и не зависит от длины волны, т. е. дисперсия отсут-
отсутствует. Поэтому наблюдать дисперсию волн на поверхности можно только
в достаточно глубоких сосудах. Явление дисперсии можно наблюдать при
возникновении короткого цуга волн на поверхности жидкости (например,
при падении камня в воду). В таком цуге содержатся волны разной длины,
и хорошо видно, как более'длинные волны опережают короткие, остающи-
остающиеся позади.
Из этого обстоятельства вытекает важное следствие. В случае диспер-
дисперсии короткий цуг волн или отдельный импульс не сохраняет своей формы
Рлс. 408.
Рис. 409.
при распространении. Дисперсия приводит к тому, что короткий цуг волн,
или импульс, расплывается. Поэтому самое понятие скорости импульса
становится не вполне определённым. Его заменяют понятием групповой
скорости, которая представляет собой, грубо говоря, скорость движения
«центра тяжести» цуга волн.
Так же, как быстро движущееся тело (пуля) возбуждает ударную волну
в окружающем газе (§ 132), тело, быстро Движущееся по поверхности жид-
жидкости, возбуждает волны на поверхности жидкости. «Быстро» и в том, и в
другом случае означает, что скорость тела должна быть больше скорости
распространения импульса в среде. Поскольку волны по поверхности жид-
жидкости распространяются с сравнительно небольшой скоростью (порядка
нескольких метров в секунду), то при достаточно быстром движении судно
поднимает такую «носовую» волну на поверхности воды. Аналогично удар-
ударной волне в воздухе, волна эта, расходящаяся от носа судна, имеет форму
клина, тем более острого, чем быстрее движется судно. На создание этих
волн тратится часть работы Сил, движущих судно, т. е. возникает добавоч-
добавочное сопротивление. Для уменьшения этого сопротивления судам придают
специаль iyio форму и очертания (острый нос). Эта же цель достигается
в глиссерах тем, что судно не разрезает поверхность воды, а почти сколь-
скользит по ней.
В случае очень коротких волн, когда радиус кривизны поверхности
достаточно мал, кроме силы тяжести начинают играть заметную роль и си-
чы поверхностного натяжения. Они становятся преобладающими для волн
достаточно малой длины, например, в случае воды для волн короче 1 см.
В этом случае роль восстанавливающей силы практически играют только

472
волны
ГГЛ. XX
•силы поверхностного натяжения. Поэтому короткие волны на поверхности
жидкости называют капиллярными волнами. Скорость распространения
капиллярных волн существенно зависит от свойств жидкости (плотности
и величины поверхностного натяжения). Она зависит также и от длины
волны, т. е. дчя капиллярных волн имеет место дисперсия. Однако, харак-
характер этой зависимости иной, чем в случае волн, обусловленных силой тя-
тяжести: скорость распространения капиллярных волн увеличивается с умень-
уменьшением длины волны.
§ 153. Интерференция волн
В результате сложения двух бегущих волн одинаковой частоты,
распространяющихся в противоположные стороны, возникают, как мы
видели, стоячие волны. В сплошной среде при сложении волн, рас-
распространяющихся в различных направлениях, также возникают стоячие
волны. Однако, в сплошной среде вся картина может быть гораздо
более сложной, так как складываться могут волны, распространяющиеся
не только в двух противополож-
противоположных направлениях, но и под углом
друг к другу. Явления, возникаю-
возникающее при сложении волн, носят
общее название интерференции.
Рассмотренная' нами картина
возникновения стоячих волн в
стержне или струне представляет
собой простейший случай интерфе-
интерференции. К этому же простейшему
случаю приводит и сложение двух
плоских волн, распространяющих-
распространяющихся в сплошной среде в проти-
противоположных направлениях. Если,
например, плоская волна падает
нормально на отражающую стен-
стенку, то в результате сложения
получается система стоячих волн,
узлы и пучности которых лежат
на плоскостях, параллельных отражающей стенке. Расстояние между
двумя плоскостями узлов или двумя плоскостями пучностей попреж-
нему равно половине длины волны. На отражающей стенке обра-
образуется пучность или узел в зависимости от условий отражения.
Картину образования стоячих волн можно продемонстрировать при
помощи волн на поверхности воды. Пользуясь палочкой в качестве вибра-
вибратора, можно получить плоские волны (рис. 40Э). Поместив на пути распро-
распространения волн плоскую стенку (свинцовый экран), можно получить стоячие
волны во всём пространстве между вибратором и экраном. В остальной
части пространства будут распространяться бегущие волны.
Несколько иная интерференционная картина получается в тех слу-
случаях, когда две плоские волны распространяются не в противоположные
стороны, а под углом друг к другу. Например, при частичном отражении
Рис. 410.

§ 153]
ИНТЕРФЕРЕНЦИЯ ВОЛН
47S
плоской волны от экрана, поставленного под углом к направлению волны
(рис. 410), перед экраном получаются стоячие волны, с пучностями, рас-
расположенными на пересечениях фронтов падающей и отражённой волн.
Рассмотрим теперь картину интерференции двух круговых волн,
распространяющихся от двух различных источников. Пусть два
источника О1 и О2 (рис. 411) создают круговые волны одинаковой
частоты и одинаковой фазы. Вследствие того, что обе волны про-
проходят от источников, вообще говоря, различные расстояния, они
будут приходить в
одну и ту же точку
с разными фазами,
причём сдвиг фаз будет
равен 2vtdj\, где d =
= йг — й?2— «разность
хода», т. е. разность
расстояний от данной
точки до обоих источ-
источников. В точки, нахо-
находящиеся на одинако-
одинаковом расстоянии от
обоих источников, обе
волны будут прихо-
приходить в одинаковой
фазе и поэтому будут Риг, 411,
складываться и усили-
усиливать друг друга. Амплитуда результирующей волны во всех этих
точках будет наибольшая. То же самое будет получаться во всех
точках, в которых фаза обеих волн будет отличаться на 2тт, 4тг
и 1. д. Следовательно, во всякой точке, расстояние от которой до
обоих источников будет отличаться на X, 2Х, 3/. и т. д., амплитуда
результирующей волны будет наибольшая. Геометрическим местом
точек, расстояние от которых до обоих источников есть величина
постоянная, являются гиперболы, фокусы которых совпадают с ис-
источниками. Точки, в которых амплитуда результирующей волны
достигает максимума, будут лежать на таких гиперболах.
С другой стороны, в точках, к которым обе волны придут со
сдвигом фаз в нечётное число тт, т. е. в противоположных фазах,
обе волны будут ослаблять друг друга и амплитуда результирующей
волны будет минимальной. Это будет иметь место в точках, для
которых расстояние от обоих источников отличается на Х/2, Щ2,
5>,B и т. д. Следовательно, точки, в которых амплитуда результирую-
результирующей волны падает до минимума, также будут лежать на гиперболах,
расположенных между гиперболами максимумов. В результате полу-
получится интерференционная картина, содержащая ряд максимумов и мини-
минимумов, чередующихся между собой (рис. 412). Если в точки, в кото-
которых фазы обеих $олн противоположны, обе волны приходят примерно

47i
волна
[гл. хх
с одинаковой амплитудой, то результирующая амплитуда практически
будет равна нулю. Но амплитуда круговой волны убывает с расстоя-
расстоянием; поэтому в случае равных амплитуд волн у источников мини-
минимумы амплитуд будут спадать до нуля только при том условии, что
разность расстояний до источников мала по сравнению со всем рас-
расстоянием. Во всех областях, где это условие не соблюдается,
минимумы уже не будут спадать до нуля. Вместе с тем и максимумы
будут тем. менее заметны, чем больше отличаются по амплитуде
обе волны, пришедшие в данную точку. Поэтому отчётливая интер-
интерференционная картина будет наблюдаться только вблизи прямой,
проходящей посередине между источ-
источниками. При удалении от этой
прямой интерференционная картина
будет становиться всё менее и
менее резкой. Отчётливо будут вид-
видны только средний максимум и не-
несколько соседних с ним максимумов
и минимумов.
Рассмотренная нами картина
будет наблюдаться, если оба источ-
источника создают волны одинаковой
частоты и с постоянным сдвигом
фаз у источников. Для упрощения
мы считали этот сдвиг фаз рав-
равным нулю, но это несуществен-
несущественно; важно лишь, чтобы он был
постоянным. Только при этом
условии каждой точке пространства
будет соответствовать вполне определённый и постоянный сдвиг фаз
между обеими пришедшими волнами. Если сдвиг фаз между источ-
источниками не будет оставаться постоянным, то с изменением сдвига фаз
будет изменяться и вся картина. Сдвиг фаз между волнами в каждой
точке будет проходить через все значения от 0 до 2тг. Положения
максимумов и минимумов будут смещаться в пространстве, и неизмен-
неизменного распределения амплитуд волн в пространстве мы уже не получим.
В частности, если частоты волн заметно отличаются друг от друга,
то сдвиг фаз будет изменяться быстро, и вся картина размоется.
Даже кратковременной интерференционной картины наблюдать не
удастся.
Таким образом, от двух источников можно наблюдать неподвиж-
неподвижную интерференционную картину только при условии, что не только
частоты обоих источников, но и сдвиг фаз между ними длительно
остаётся постоянным. Источники, удовлетворяющие этим условиям,
называются когерентными. Обеспечить когерентность двух источ-
источников можно различными способами. Наиболее простым способом
являетс-я получение двух волн от одного и того же источника и по-
Рис. 412.

§ 154] принцип гюйгепса 475
тому когерентных. (Все рассмотренные ранее случаи интерференции
падающих и отражённых волн относились к этому же случаю —
когерентность обеспечивалась тем, что падающая и отражённая вол-
волны происходят из одного источника.) Однако, существуют и другие
методы получения двух когерентных источников упругих волн. На-
Например, для получения двух когерентных источников волн на поверх-
поверхности воды можно применить два малых шарика, насаженных на один
и тот же якорь электромагнита. Так именно получена интерферен-
интерференционная картина, изображённая на рис. 412.
Получаемая картина зависит от расстояния между источниками
Ох и О2. Чем меньше это расстояние, тем дальше от средней линии
лежит точка а, в которой разность хода d достигает по-
половины длины волны (рис. 413). Это значит, что при
сближении источников гипербола, соответствующая первому
минимуму, а вместе с тем и все гиперболы, по которым
располагаются максимумы и минимумы, будут всё более и
более искривляться. Расстояние между максимумами и
минимумами будет увеличиваться. Когда расстояние между
источниками уменьшится -до 1/2, то только в точках, ге-
жащих на прямой, соединяющей источники, разность хода „ ..„
будет составлять Х/2. На этой прямой и будет лежать
первый (и единственный в этом случае) минимум. Об-
Область, которая прилегает к среднему максимуму и заключена
между двумя первыми минимумами, расширится и займёт всё
поле. При дальнейшем уменьшении расстояния между источниками
уже нигде в пространстве не будет точек, для которых разность
хода составляет \/2. Исчезнет и первый минимум, и постепенно кар-
картина будет приближаться к той, которую даёт один точечный источник,
§ 134. Принцип Гюйгенса
Рассмотрим теперь картину, которую даёт длинный ряд точечных
источников, расположенных на одной прямой достаточно близко друг
к другу-. Каждый из источников даёт круговые волны, и все эти
волны интерферируют между собой. В результате получится картина,
характер которой можно установить при помощи следующих сооб-
соображений.
В образовании интерференционной картины в каждой точке
существенную роль играют только источники, лежащие на таких рас-
расстояниях до рассматриваемой точки, которые не очень сильно отли-
отличаются друг от друга. Поэтому пока мы будем рассматривать точки,
лежащие на линии, параллельной источникам, и не слишком близкие
к крайним источникам, то для них результат интерференции должен
быть один и тот же (так как они одинаково расположены по отноше-
отношению к источникам, участвующим в образовании интерференционной
картины). Следовательно, амплитуда и фаза волны во всех точках,

476
волны
[гл. хх
расположенных на прямой, параллельной источникам, должны быть
одни и те же. Поэтому в результате интерференции мы получим
в средней части такую же картину, как и в случае плоской волны.
Только вблизи источников появятся интерференционные максимумы
и минимумы. Интерференция от ряда близких источников изображена
на рис. 414. Вдали от вибраторов полученная картина будет примерно
такой же, какую даёт плоский вибратор (рис. 409).
Вообще мы можем заменить любой источник волн системой коге-
когерентных точечных источников, которые в результате интерференции
дадут ту же картину, что и данный
источник. Эта возможность замены
любого реального источника си-
системой точечных источников, интер-
интерферирующих между собой, подска-
подсказывает идею важного принципа,
применяемого при рассмотрении
вопросов распространения волн.
Всякую волну мы можем в любом
месте «остановить» и заменить её
системой воображаемых точечных
источников. Дальнейшее распро-
распространение волны можно рассматри-
рассматривать как результат интерференции
волн, сознаваемых этими элементар-
элементарными точечными источниками. При
этом амплитуда и фаза волн, соз-
создаваемых всеми точечными источниками, определяются амплитудой
и фазой приходящей волны в той точке, в которой расположен дан-
данный источник. Этот принцип, так называе-
называемый принцип Гюйгенса-Френеля, чрезвы-
чрезвычайно удобен для рассмотрения вопросов
распространения волн.
Применяя принцип Гюйгенса-Френеля,
нужно учитывать интерференцию волн, соз-
создаваемых всеми элементарными источниками.
Эта сложная задача весьма упрощается в тех случаях, когда падающая
волна ничем не ограничена, т. е. когда не приходится рассматривать
«краёв» падающей волны. В таком случае можно пользоваться теми
же рассуждениями, которыми мы пользовались при нахождении интер-
интерференционной картины от ряда близко расположенных точечных
источников. Амплитуда волны в точках а и b (рис. 415), расположен-
расположенных одинаково по отношению ко всем элементарным источникам,
будет одинакова, и никаких интерференционных максимумов и мини-
минимумов наблюдаться не будет. Фазы же результирующей волны в точ-
точках а и b сдвинуты по отношению к фазам ближайших к ним эле-
элементарных источников А и В на одинаковую величину. Это видно
Рис. 414.
Рис. 415.

§ 154] принцип гюйгенса 477
из того, что точки а и Ь расположены совершенно одинаково относи-
относительно ближайших к ним элементарных источников А и В.
Отсюда вытекает способ нахождения поверхности равной фазы
результирующей волны. Нужно найти точки, в которых ближайшие
к ним элементарные источники создают элементарные волны одина-
одинаковой фазы. Эта поверхность и будет поверхностью результирующей
волны. Такое построение для случая круговой волны приведено на
рис. 416. Av Л?, ...—элементарные точечные источники на поверх-
поверхности приходящей волны. Эти источники, колеблющиеся в одинаковой
фазе (так как фаза приходящей волны во всех точках Л,, Аг, ...
одна и та же), создают элементарные круговые волны, которые изо-
изображены на рисунке дугами. При одинаковом
расстоянии Axav A2av ... фаза всех этих эле-
элементарных волн в точках аг, а2, ... в каждый
момент будет одна и та же. Поэтому и фаза
результирующей волны в точках а,, а2, ...
будет одна и та же. Следовательно, поверх-
поверхность, касающаяся всех поверхностей эле-
элементарных волн в точках а,, а2, ..., и представляет собой поверх-
поверхность результирующей волны.
Мы получили совершенно очевидный результат, что круговая волна
и дальше распространяется в виде круговой. Но этот пример поясняет
применение принципа Гюйгенса-Френеля для случаев, когда не при-
приходится принимать во внимание «краёв» волны. Как видно, в этом
случае способ цостроения результирующей волны сводится к следую-
следующему: расположив элементарные источники на поверхности прихо-
приходящей волны, нужно построить элементарные волны, соответствующие
одной и той же фазе. Огибающая этих элементарных волн одина-
одинаковой фазы и будет представлять собой поверхность результирующей
волны. В таком именно виде этот принцип и был впервые форму-
формулирован Гюйгенсом. Позднее Френель указал на необходимость при-
принимать во внимание интерференцию элементарных волн. Но если
падающие волны ничем не ограничены, то картина интерференции не
даёт ничего нового по сравнению с принципом Гюйгенса в его пер-
первой формулировке. Только «края» волны дают новые явления, не
охватываемые принципом Гюйгенса. На этих явлениях мы коротко
остановимся ниже.
Применим принцип Гюйгенса к задаче о преломлении волн. Положим,
что плоская волна падает под некоторым углом на границу двух сред,
в которых скорость распространения волн ^ и с2 различна (рис. 417). Для
определённости положим, что c± > с2. По принципу Гюйгенса заменим вол-
н^, приходящую на границу раздела из первой среды, элементарными
точечными источниками, амплитуда которых во всех точках одинакова,
а фаза определяется фазой приходящей волны в этой точке. Но падающая
волна, для которой поверхности равной фазы параллельны плоскости АВ,
приходит в разной фазе в различные точки на границе раздела. Поэтому
и элементарные источники на поверхности раздела должны иметь различ-
различную фазу — они должны быть сдвинуты по фазе друг относительно друга

478
волны
[гл.
XX
в'
так же, как сдвинута фаза приходящей волны в разных точках. Элементар-
Элементарные волны, создаваемые во второй среде этими источниками, будут иметь
одинаковую фазу на различном расстоянии от источников. Если мы изо-
изобразим элементарные волны, соответствующие одной и той же фазе, то
радиусы их будут различны. Но поверхность результирующей волны во
второй среде есть огибающая всех эле-
элементарных волн, соответствующих одной
и той же фазе, т. е. плоскость А'В'.
Так как скорость распространения
волн в обеих средах' различна, то rf''4=d
и А'В' не будет параллельна АВ, прои-
произойдёт преломление волны. Отношение
d к d' равно отношению скоростей рас-
распространения волн в двух средах: d!\d =
~czl"i- Отсюда может быть получен закон
преломления волн. Он аналогичен закону преломления света.
Картину преломления волн можно показать на поверхностных волнах,
воспользовавшись тем, что скорость распространения этих волн в мелких
Рис. 417.
**4t 4, „ь. him .яг. miM i Л ^&
Рис. 418.
Рис. 419.
сосудах зависит от глубины сосуда и уменьшается с уменьшением глубины.
Если на дно ванны, в которой вибратор возбуждает плоские волны, поло-
положить толстое стекло, уменьшив тем глубину слоя воды, то у границы
стекла будет происходить преломление воли (рис. 418). Придав стеклу
форму линзы, можно наблюдать действие на волны «собирательной линзы»
(рис. 419). Поскольку законы преломления волн здесь такие же, как и в
оптике, и результаты получаются аналогичными.
§ 155. Диффракция волн
Если распространяющаяся волна встречает на пути какие-либо
препятствия или неоднородности конечных размеров, то возникают
новые явления, которые носят общее название диффракции. С точки
зрения принципа Гюйгенса-Френеля явления диффракции представляют
собой результат влияния «краёв» вдлн, которых мы до сих пор не

§ 155]
ДНФФ?АКЦИЯ ВОЛН
479
принимали во внимание. При конечных размерах препятствий и неод-
нородностей вместо бесконечных волновых поверхностей приходится
рассматривать «куски» волновых поверхностей; применение принципа
Гюйгенса-Френеля к этому случаю легко позволяет в общих чертах
объяснить диффракционкые явления.
Рассмотрим, например, картину распространения плоской волны,
на пути которой находится плоский экран с отверстием небольшого
размера (рис. 420). По принципу Гюйгенса-Френеля мы должны вол-
волну, пришедшую к отверстию, заменить элементарными точечными
источниками, колеблющимися в одинаковой фазе. Если отверстие мало
по сравнению с длиной волны, то все эти источники находятся на
расстоянии, малом по сравнению с длиной волны. Они, как и в слу-
случае двух близких точечных источников, не дадут интерференционной
картины, а дадут примерно такой -же результат, как один точечный
источник, помещённый в отверстии, За отверстием образуется круго-
Рис. 420.
Рис. 421.
вая волна (рис. 420). При увеличении размеров щели картина бу-
будет приближаться к той, которую дают много источников, располо-
расположенных близко друг от друга на одной прямой. Щель, размеры кото-
которой велики по сравнению с длиной волны, пропускает плоскую волну,
почти не изменяя её характера. Только по краям вырезанного участка
плоской волны будет наблюдаться искривление фронта волны (рис. 421).
Таким же образом можно рассмотреть и обратную картину — прохожде-
прохождение волны мимо экрана конечных размеров. В этом случае элементарные
источники нужно поместить на всей поверхности плоской волны, кроме
точек, закрытых экраном. По обе стороны от экрана пройдут «куски» пло-
плоских волн. На «краях» этих волк, так же как и в случае широкой щели,
будут наблюдаться искривления фронта волны. Поэтому волны будут отчасти
проникать в область, закрытую экраном. Пока размеры экрана веляки,

480 волны [гл. хх
волны всё же не проникнут в среднюю часть области, закрытой экраном.
При уменьшении размеров экрана проникающие за него волны захватывают
всё большую и большую часть области, закрытой экраном. Когда размеры
экрана становятся малыми по сравнению с длиной волны, волны захваты-
захватывают всю область, закрытую экраном, как будто экран вообще отсутствует.
Экран, малый по сравнению с длиной волны, вообще не является для этих
волн экраном. Поэтому, например, мол, который должен служить экраном
для морских волн, приходится делать больших размеров. При малых разме-
размерах мола морские волны свободно проникали бы в ограждённое молом про-
пространство.
При рассмотрении вопросов распространения волн очень удобным
и наглядным является представление о луче. Лучом называют линию,
касательная к которой в каждой точке совпадает с направлением
распространения волны в этой точке. Так, в случае распространения
плоской волны в однородной среде лучами являются прямые, нормальные
к фронту волны. При преломлении волн на границе двух сред направле-
направление лучей измеряется. В неоднородной среде, свойства которой
в разных местах различны, фронт волны может постепенно повора-
поворачиваться по мере распространения, и тогда лучи будут представлять
собой некоторые кривые. Только для плоской волны в однородной
среде направление лучей в разных участках волны будет одно и то
же; в других случаях оно для разных участков волны, вообще го-
говоря, различно.
Вырезая мысленно из поверхности волны отдельные куски и рас-
рассматривая луч, соответствующий данному «куску волны» (т. е. на-
направление, в котором этот «кусок волны» распространяется), мы мо-
можем получить представление о распространении волн. Однако, только
такие «куски волн», которые можно считать «кусками плоских волн»,
распространяются как целое в одном направлении. Например, отдель-
отдельные части «куска шаровой волны» распространяются в различных
направлениях, и до тех пор, пока размеры «куска шаровой волны»
сравнимы с е'8 радиусом кривизны, распространение этого куска шаро-
шаровой волны нельзя описать одним лучом. Следовательно, только в слу-
случае таких «кусков волн», которые мы вправе рассматривать как пло-
плоские (т. е. таких площадок, для которых амплитуда и фаза волны
во всех точках одни и те же) можно распространение «куска волны»
задать одним лучом.
Казалось бы, что, выбирая «куски волн» достаточно малыми, мы
всегда сможем достичь этого. Однако, в действительности это не
так. В самом деле, если размеры «куска волны» сравнимы с длиной
волны, то даже если бы его можно было считать куском плоской
волны, он не будет распространяться весь в одном направлении.
В этом мы убедились, рассматривая прохождение плоской волны через
узкую щель (рис. 421). Щель вырезает «кусок плоской волны», но
если её ширина сравнима с длиной волны, то после щели этот «ку-
«кусок плоской волны» распространяется во все стороны, а вовсе не
в одном направлении (рис. 420). Поэтому представление о лучах при-

§ 155] днффракция волн 481
менимо только в тех случаях, когда всякий кусок волны, размеры
которого велики но сравнению с длиной волны, можно считать «ку-
«куском плоской волны». Если на волновой поверхности есть такие места,
в которых амплитуда или фаза волны на расстоянии порядка длины
волны сколько-нибудь заметно изменяется, представление о лучах ока-
оказывается неприменимым. Так именно обстояло дело в рассмотренных
выше явлениях диффракцин. Например, вблизи края экрана, где ампли-
амплитуда волны резко изменяется, картину распространения волны нельзя
описать при помощи лучей.
В однородной среде лучи представляют собой прямые, и следовательно,
если представление о лучах применимо, мы должны получить картину
прямолинейного распространения волн, образования геометрической
тени и т. д. В рассмотренных же явлениях этой картины не получа-
получалось именно потому, что создавались условия, при которых на отдельных
участках волновой поверхности амплитуда волны заметно изменяется
на расстоянии длины волны и представление о луче оказывается не-
неприменимым. Отклонения от прямолинейного распространения волн,
обусловленные этими причинами, и называются явлением диффракции.
Диффракционные явления свойственны всяким волновым процессам;
в частности, они наблюдаются и при распространении световых волн.
Однако, так как длина световых волн очень мала (порядка 10~4 см),
то препятствия даже малых, в обычном смысле, размеров всё ещё велики
по сравнению с длиной световой волны. Поэтому-то в оптике так
широко можно применять представление о луче и пользоваться законами
геометрической оптики.
31 С. Э Ха,1кин

ГЛАВА XXI
АКУСТИКА
§ 156. Звуковые волны
Особое по своей важности место среди всех типов упругих волн
занимают звуковые волны. Человеческое ухо воспринимает в виде зву-
звуковых ощущений колебания, лежащие в пределах примерно от 20 до
20 000 колебаний в секунду. Эти колебания обычно достигают уха
в виде упругих волн, распространяющихся в воздухе. Поэтому под
звуковыми волнами обычно понимают упругие волны в воздухе,-частоты
которых лежат в указанных выше пределах.
Звуковая волна представляет собой последовательные сжатия и раз-
разрежения воздуха, распространяющиеся со скоростью, зависящей от
свойств среды (воздуха). В звуковой волне, как и в случае отдельного
импульса, сжатия и разрежения происходят столь быстро, что обмен
теплом не успевает происходить и процесс протекает адиабатически
(см. § 132). Поэтому для скорости распространения звуковых волн
получается такое же выражение, как а для скорости отдельного им-
импульса A7.15):
•Р- B1.1)
Наиболее удобный метод определения скорости звуковых волн
основан на измерении длины стоячих звуковых волн (см. ниже, § 159).
Эти измерения дали результаты, согласные с формулой B1.1), и по-
показали, что скорость звуковых волн разной длины в воздухе одна
и та же, т. е. что' для звуковых волн в воздухе дисперсия отсутствует.
Вместе с тем эти измерения подтвердили, что фазовая скорость зву-
звуковых волн совпадает со скоростью распространения отдельного про-
продольного импульса. (Оба эти результата, как уже указывалось в § 148,
тесно связаны между собой.) Скорость звука в воздухе при темпера-
температуре 0° равна (как и скорость импульса) 334 м сек. Таким образом, часто-
частотам от 20 до 20 000 гц, составляющим пределы звукового диапазона,
соответствуют звуковые волны в воздухе длиной примерно от 15 м до
15 мм. Пределы эти широки, так что во всех тех случаях, когда
существенную роль играет длина звуковой волны, длинные и короткие
звуковые волны могут вести себя по-разному.

§ 156] звуковые волны 483
Звуковая волка, как и всякая упругая волна, представляет собой
волны смещений, скоростей и деформаций, связанные между собой
и распространяющиеся вместе в среде. В гармонической звуковой волне
в каждой точке смещения, скорости и деформации (сжатия) меняются
по синусоидальному закону. Вместе с тем в каждой точке происходят
изменения давления, обусловленные изменением степени сжатия газа.
Изменения давления, вызванные звуковой волной, накладываются на
то среднее давление, которое существует в газе (в случае свободной
атмосферы — атмосферное давление). Эти изменения давления назы-
называют избыточным звуковым давлением или просто звуковым давлением.
Единицей звукового давления служит бар—давление в 1 дн^м2. Бар
составляет, следовательно, около 10~6 атмосферного давления*).
Нетрудно установить связь между звуковыми давлениями и скоро-
скоростями частиц в звуковой волне. Ограничимся для простоты случаем
плоской волны (впрочем, основные наши выводы будут справедливы
и для других типов волн). Пусть плоская волна возбуждается беско-
бесконечной пластинкой, колеблющейся в направлении х по закону
Волна распространяется также в направлении х; смещение частиц, ле-
лежащих в каждой плоскости, нормальной к этому направлению, про-
происходит по закону ?~Xosinu>(t — xjc). Тогда, как было показало
в § 148, относительное изменение толщины слоя, лежащего между
двумя бесконечно близкими плоскостями, есть
Этому изменению расстояния соответствует такое же относительное
изменение объёма слоя, заключённого между двумя плоскостями. Если
относительное сжатие газа, т. е. относительное уменьшение объёма —
dVfVu обозначить через 7), то:
4 ?
С другой стороны, скорость частицы
Сопоставляя два последних выражения, получим связь между
сжатием и скоростью частиц в звуковой волне
а = сц. B1.5)
*) В метеорологии название «бар» применяется для обозначения вели-
величины нормального атмосферного давления, и давление атмосферы изме-
измеряется в миллибарах. Не следует смешивать «бар», применяемый в акустике,
с «баром» метеорологии.
31*

484 АКУСТИКА [ГЛ. XXI
Относительное сжатие ц = — Lv\v есть вместе с тем относительное
увеличение плотности газа в объёме, т. е.
Применяя уже известное соотношение A7.14) между изменением
плотности и изменением давления при адиабатическом процессе, получим:
Ар = Ш B1-6)
Подставляя отсюда 7j в выражение B1.5), получим соотношение между
скоростью частиц и звуковым давлением:
Д/> = I?-а = р са B1.7)
(т к как c = V'yp/p)-
Громким звукам соответствуют звуковые давления в сотни бар.
Следовательно, даже громким звукам в атмосфере соответствуют очень
малые относительные изменения давлений (dpjp менее 0,001). Соот-
Соответственно (так как Y близко к единице) и скорости частиц в звуко-
звуковой волне очень малы по сравнению со скоростью звука, даже для
громких звуков- они менее 10 см\сек.
Как видно из B1.6), ур0 представляет собой коэффициент пропор-
пропорциональности между избыточным цавлением и вызванным им уменьше-
уменьшением объёма, т. е. это уже встречавшийся нам (§ 112) модуль сжи-
сжимаемости, однако не для медленного сжатия при постоянной температуре
(изотермический процесс), а для быстрого сжатия без обмена теплом
(адиабатический процесс). Так как для звуковых волн существенную
роль играет именно адиабатическая сжимаемость, то величину х = YP
принято в акустике называть модулем сжимаемости или коэффици-
коэффициентом объёмной, упругости среды. Применяя это обозначение, можно
упростить запись соотношений B1.1), B1.6) и B1.7):
с= уГ±, B1.8)
B1.9)
?
Ьр=?-и. B1.10)
Звуковая волна несёт с собой потенциальную энергию — энергию
упругой деформации газа и кинетическую энергию движущихся
частиц газа. Подсчитаем потенциальную энергию, заключённую в эле-
элементе объёма, ограниченном двумя стенками площади S, находящи-
находящимися на расстоянии Ал:. Если относительное сжатие в слое есть rj, то
по B1.9) сила, действующая на стенку площади S, есть SAp==Sx7j.
При изменении относительного сжатия на й?7] стенка перемещается на
Длг«Л|, и при этом совершается работа

§ 156] звуковые волны 485
Чтобы подсчитать работу, затраченную на изменение относительного
сжатия от 0 до 7j, нужно проинтегрировать dA в этих пределах.
Этот интеграл
U=Slx7.\ridri = S\x^r
0
и выражает энергию упругой деформации в объёме Six. Следова-
Следовательно, плотность энергии упругой деформации
«*=т- B1Л1>
С другой стороны, кинетическая энергия этого же объёма Six есть
и плотность кинетической энергии
™т=^Щ- B1.12)
Но в каждой точке волны соблюдается соотношение B1.5) между и
и 7j. Подставляя в него значение с из B1.8) и сопоставляя с B1.11)
и B1.12), убеждаемся, что wa = wT, т. е. плотность потенциальной
и кинетической энергии в каждой точке звуковой волны одна и та же.
Звуковая волна несёт с собой одинаковые потенциальную и кине-
кинетическую энергии, так что как та, так и другая энергия составляет
половину полной энергии волны. Энергия, которую несёт с собой зву-
звуковая волна, распространяется вместе с волной и течёт всё времл
в том направлении, в котором распространяется волна. Это следует
из того, что, как видно из выражений B1.3) и B1.4), сжатие и ско-
скорость частиц в волне совпадают по фазе. Когда какой-либо элемент
объёма сжат, то он вместе с тем движется в сторону положительных
значений х, т. е. в направлении распространения волны. В этом же
направлении течёт и энергия. В тот момент, когда знак деформации
меняется, сжатие превращается в разрежение—изменяется и направ-
направление скорости, а энергия продолжает течь в прежнем направлении.
Энергия эта в разных сечениях волны различна", так как различны
сжатия и скорости. Для характеристики действия звуковых волн во
многих случаям удобно пользоваться средней энергией, которую не-
несёт с собой звуковая волна. Для определения средней энергии нужно
подсчитать энергию, содержащуюся в слое, заключённом между стен-
стенками, отстоящими на расстоянии длины волны 1 друг от друга. Раз-
Разделив всю эту энергию на объём слоя, получим среднюю плотность
энергии, которую несёт с собой звуковая волна. Так как И'г = и'„(
то плотность всей энергии звуковой волны

486 акустика [гл. xxi
г) в звуковой волне меняется от точки к точке по закону
где rj0 — амплитуда относительного сжатия. В слое сечения S и юл-
щипы л содержится энергия
W=[ xr,25 dx = 6 y.rf 0 ] cos2 (о ^ — —) й?лг =
2 * + *¦ 9
Средняя плотность энергии в звуковой волне
wCp=-2-. B1.13)
Так как соотношение BL9) справедливо для всяких мгновен-
мгновенных значений Д/j и ц, то оно справедливо и для амплитудных значе-
значений и, следовательно,
(АрK
даср=~аГ» B1.14)
где Др0 — амплитуда звукового давления.
Поток звуковой энергии, который падает за единицу времени на
единицу пллдади, нормальной к направлению распространения волны,
характеризует интенсивность звуковой волны. За единицу времени
на эту площадь упадёт вся энергия, заключённая в столбе с основа-
основанием, равным единице, и высотой, равной с. Следовательно, интенсив-
интенсивность звука
или (так как с2 —-л/р)
, 1 (V)
/ = -2 ре"- B1-15)
Интенсивность звука измеряется в эрг^см^сек. Громкому звуку,
для которого, например, Дро=2ООбйр, соответствует интенсивность
около 5-Ю2 эрг\см?сек. Для наиболее слабых звуков, которые ещё
способно воспринимать ухо человека, Д/?о = 1 -10~4 бар и интенсив-
интенсивность звука составляет около 10~10 эрг\см?сек. Если считать, что
площадь уха составляет 10 см2, то к нему подводится при этом мощ-
мощность в. 10~9 эрг\сек, т. е. 10~1в ватт.
Определение интенсивности звука или амшштуды звуковой волны
может быть произведено по величине тех механических сил, с кото-

звуковые волны 487
рыми звуковая волна действует на то или иное тело. Однако, даже
громкие звуки соответствуют сравнительно небольшим силам. Так
как это давление быстро изменяется, то для непосредственного его
измерения нужен был бы прибор, который успевает следить за из-
изменением силы. Между тем, как неоднократно указывалось, быстрые
механические приборы никогда не могут быть сделаны чувствитель-
чувствительными. Поэтому непосредственное измерение переменного давления
звуковой волны весьма затруднительно, и для измерения амплитуды
звуковой волны пользуются косвенными методами.
Среди механических приборов, служащих для этой цели, наиболее
важным является так называемый диск Рэлея — лёгкий диск неболь-
небольших размеров, подвешенный вертикально на тонкой нити. На такой
диск, помещённый под углом на пути звуковой
волны (рис. 422), так же как и в случае по-
постоянного потока (§ 127), действуют аэроди- *
намические силы, стремящиеся повернуть его ""
перпендикулярно к скорости потока, т. е. в слу- *
чае звуковой волны, перпендикулярно к на- — ».
правлению скорости движения частиц в волне
(перпендикулярно к направлению распростра- Рис- 422>
нения волны). Хотя скорости частиц быстро
меняют не только величину, но и знак, момент аэродинамических
сил, действующих на диск, направлен всё время в одну и ту же сто-
сторону и поэтому в среднем за период он отличен от нуля. Этот мо-
момент пропорционален квадрату амплитуды скорости частиц в
звуковой волне. Определяя величину вращающего момента по
углу поворота диска, можно судить об амплитуде скорости частиц
и, следовательно, о звуковом давлении и интенсивности звуковой
волны.
Если длина измеряемой звуковой волны велика по сравнению с
размерами диска, то можно считать, что диск находится в однород-
однородном потоке, и тогда удаётся подсчитать теоретически момент сил,
действующих на дьск. При этом измерения момента дают прямо аб-
абсолютную величину амплитуды скорости частиц в звуковой волне,
т. е. диск Рэлея позволяет производить абсолютные измерения ам-
амплитуд в звуковой волне. Однако, диск Рэлея сравнительно мало
чувствителен — он даёт заметные отклонения лишь при звуковом да-
давлении в волне по крайней мере в несколько бар (звуки средней
громкости). Кроме того, он обладает и другими недостатками. Вслед-
Вследствие этого большое значение в акустике приобрети косвенные ме-
методы измерения амплитуд волны — при помощи более чувствительных
индикаторов, например, накалённой проволочки, охлаждаемой движе-
движением воздуха в звуковой волне и т. д. Для того чтобы эти приборы
давали абсолютную величину амплитуды давления или скорости в*
звуковой волне, они должны быть предварительно прокалиброваны
(сравнением с диском-Рэлея).

488 акустика [гл. xxt
Диск Рэлея и накалённая проволочка хотя и позволяют обнаруживать
звуковые волны и измерять их амплитуду, однако не воспроизводят тех ко-
колебаний давления и скорости, которые происходят в звуковой волне, т. е.
не являются приёмниками звуковых колебаний. В качестве приемников
звуковых колебаний обычно применяют различного типа микрофоны, поз-
позволяющие превратить звуковые колебания в соответствующие колебания
электрического напряжения или силы тока (для последующего усиления
передачи по проводам к телефону и т. д.). Наиболее распространённым
типом микрофона является угольный, в котором электрическое сопротивле-
сопротивление угольного порошка изменяется под действием давления звуковой волны.
Эти изменения сопротивления следуют за колебаниями давления в звуковой
волне и вызывают соответствующие изменения силы тока в цепи микро-
микрофона. Существуют также и другие типы микрофонов; все они так или
иначе отзываются на колебания давления или скорости в звуковой волне
и превращают эти колебания в электрические.
Чрезвычайно чувствительным приёмником звуковых колебаний является
человеческое ухо. Как уже указывалось выше, нормальное человеческое
ухо начинает воспринимать звуки при давлении звуковой волны . порядка
10~4 бар. Этой наибольшей чувствительностью ухо человека обладает при
частотах около 3500 гц. К звукам большей и меньшей частоты ухо ока-
оказывается менее чувствительным. В сторону низких частот чувствитель-
чувствительность человеческого уха быстро уменьшается, и самый низкий тон, соот-
соответствующий частоте в 20 гц, ухо начинает различать только когда
давление звуковой волны достигает примерно 1 бара, в сторону высоких
частот чувствительность уха медленно падает вплоть до частот порядка
15 000—20 000 гц. В этой области лежит предел, выше которого человече-
человеческое ухо вообще перестаёт воспринимать звуки (для разных людей этот
предел несколько различен). Очень большие звуковые давления вызывают
в ухе человека болезненные ощущения. Для очень низких частот (по-
(порядка 50 гц) эти болезненные ощущения наступают при звуковых давле-
давлениях в несколько сот бар. На частотах порядка 3500 гц болезненные ощу-
ощущения возникают только при давлениях попядка 1000 бар. Таким образом,
ухо человека может приспособляться к изменениям амплитуды звуковых
волн в 107 раз, при этом количество энергии, попадающей в ухо, изменяется
в Ю14 раз.
§ 157. Распространение звука в атмосфере
Мы до сих пор считали, что звуковые волны распространяются в покоя-
покоящейся однородной среде, не обладающей вязкостью. Однако, в действи-
действительности эти условия никогда не соблюдаются. Прежде всего воздух об-
обладает вязкостью, что приводит к поглощению звука — часть энергии
превращается в тепло. Так как силы вязкости пропорциональны произве-
произведению коэффициента вязкости на градиент скорости, то потери энергии
оказываются пропорциональными произведению коэффициента вязкости на
квадрат градиента скорости частиц в звуковой волне *). Но при неизмен-
неизменной длине волны градиент скорости частиц пропорционален амплитуде ско-
скорости. Поэтому потери энергии оказываются пропорциональными квадрату
ампл гтуды скорости частиц, т. е. пропорциональными энергии, которую не-
несёт с собой звуковая волна. Вследствие это о при распространении звуко-
звуковой волны на каждой единице длины пути рассеивается одна и та же доля
всей энергии, которую несёт с собой звуковая волна. Поэтому амплитуда
*) Аналогично тому, как в случае движения тела при наличии трения
потери ¦энергии оказываются пропорциональными произведению коэффици-
коэффициента трения на квадрат скорости (§ 135).

§ 157] РАСПРОСТРАНЕНИЕ ЗВУКА В АТМОСФЕРЕ 489
плоской звуковой волны по мере распространения убывает по показатель-
показательному закону *)
где а — показатель затухания волны. Волна затухает по мере распростра-
распространения.
На расстоянии, равном единице, амплитуда волны убывает в е<* раз.
При этом энергия волны, пропорциональная квадрату амплитуды, убывает
в е21 раз. Поэтому уменьшение интенсивности звука, обусловленное по-
поглощением звуковой энергии, характеризуется показателем 2а.
Так как относительное влияние сил вязкости определяется кинемати-
кинематической вязкостью v —ц/р, где ц — коэффициент вязкости и р—плотность
среды (см. § 122), то показатель затухания а оказывается пропорциональ-
пропорциональным v (при прочих равных условиях). Этим, например, объясняется, что
в воде звуковые волны распространяются лучше (с меньшим затуханием),
чем в воздухе, даже при наиболее благоприятных условиях — во вполне
спокойной атмосфере. Нерегулярные движения воздуха, которые всегда
происходят в свободной атмосфере (турбулентность атмосферы), вызывают
значительное увеличение затухания волн.
Как указывалось, потери' энергии, а значит, и показатель затухания а,
пропорциональны квадрату градиента скорости. Но при данной амплитуде
волны градиент скорости обратно пропорционален длине волны, так как
те же изменения скорости частиц в волне соответствуют тем меньшим
расстояниям, чем короче волна. Поэтому показатель затухания а оказы-
оказывается обратно пропорциональным квадрату длины волны или прямо про-
пропорциональным квадрату частоты звука. Звуки высокого тона поглощаются
в атмосфере гораздо сильнее, чем низкие тона. Если в атмосфере возни-
возникает звук, содержащий как низкие, так и высокие тона, то гораздо дальше
распространяются низкие тона этого звука; высокие тона затухают на
гораздо меньшем расстоянии. Этим, например, объясняется, что когда са-
самолёт близко, в создаваемом им шуме можно расслышать высокие тона
(свист); когда же самолёт находится далеко, то слышен только шум низ-
низкого тона (гудение).
В случае плоской звуковой волны уменьшение амплитуды волны при
распространении обусловлено только поглощением энергии. В шаровой
волне помимо поглощения энергии уменьшение амплитуды волны при рас-
распространении происходит вследствие того, что энергия волны распреде-
распределяется на всё больший и больший объём — рассеивается в пространстве.
Практически в большинстве случаев звуки распространяются не в виде пло-
плоской, а в виде шаровой (вообще «расходящейся») волны, и поэтому умень-
уменьшение амплитуд обусловливается как поглощением, так и рассеянием
энергии. При распространении длинных звуковых волн, для которых по-
поглощение в атмосфере мало, преобладающую роль играет рассеяние энер-
энергии. Для коротких звуковых волн становится заметным поглощение энер-
энергии, и в случае наиболее коротких звукоаых волн оно играет преобла-
преобладающую роль.
На характер распространения звука в свободной атмосфере существенно
влияет неоднородность атмосферы — различия в температуре воздуха, на-
направлении и скорости ветра и т. д. Температура воздуха, как уже указы-
указывалось, влияет на скорость звука — с понижением температуры скорость
звука уменьшается. С высотой температура воздуха понижается (вплоть
*) Здесь опять полная аналогия с законом убывания амплитуды коле-
колебаний в случае, когда на колеблющееся тело действует сила трения, про-
пропорциональная скорости (§ 1Э5).

490
АКУСТИКА
[гл. xxi
Рис. 423,
300 км
до высот в 7—8 км), и поэтому скорость звука в верхних слоях меньше,
чем в нижних. Вследствие этого звуковые волны, исходящие от источника,
находящегося у земли, постепенно преломляются по мере проникновения
в более высокие слои атмосферы — звуковые лучи искривляются, подыма-
подымаясь от земли кЕерху (рис' 423). Это вызывает ослабление слышимости и
образование «звуковой тени» у поверхности земли. Изменение направления
и скорости ветра с высотой также вызывает искривление звуковых лучей.
При наличии ветра скорость звука в
воздухе складывается со скоростью
самих воздушных масс, и если эта по-
последняя изменяется с высотой по ве-
величине и направлению, то и направ-
направление распространения звука может
измениться. Оба эти обстоятельства —
изменение температуры и скорости
ветра с высотой — иногда приводят
к тому, что звуковые лучи сначала
поднимаются в верхние слои атмосферы и затем снова опускаются к земле —¦
звук, неслышный в областях, более близких к источнику («зоны молчания»),
становится снова слышным в более далёких областях («зоны аномальной
слышимости»).
Чрезвычайно характерный пример существования зон аномальной слы-
слышимости даёт схема расположения пунктов, в которых были слышны гром-
громкие взрывы, происходившие в
Москве 9 мая 1920 г. (рис. 424).
На этой схеме заштрихованы зо-
зоны, в которых были слышны
взрывы. Между внутренней зоной
нормальнэй слышимости и внеш-
внешней зоной аномальной слыши-
слышимости лежит зона молчания. Зона
аномальной слышимости начи-
начинается на расстоянии около 150 км
от места взрыва. При распростра-
распространении звука на столь большие
расстояния звуковые волны долж-
должны предварительно достигать
очень высоких слоев атмосферы
B0—30 км). Поэтому изучение
этой картины даёт некоторые
указания о строении и свойствах
высоких слоев атмосферы.
Помимо регулярных измене-
изменений температуры воздуха и ско-
скорости ветра с высотой в свобод-
свободной атмосфере часто встреча-
встречаются нерегулярные неоднород-
неоднородности— резкие изменения температуры или скорости в отдельных
местах. Эти неоднородности, влияя на ход звуковых лучей, могут привести
К резким нерегулярным изменениям слышимости от точки к точке и во
времени. Наконец, при распространении звука в атмосфере существенную
роль могут играть отражения звуковых волн от различных препятствий —.
тор (эхо), от поверхности земли или воды (при наклонном распространении
звуковой волны) и т. д.
Все эти обстоятельства очень усложняют картину распространения
звука в свободной атмосфере. С ними приходится считаться в тех случаях,
Kol-да возникает задача определения положения источника звука, находя-
Рис. 424.

§ 158] бинауральный эффект, эффект допплерл 491
щегося па значительном расстоянии. Эта задача является одной из основ-
основных задач артиллерийской звукометрической разведки, занимающейся
определением положения стреляющих орудий по наблюдению за звуком
выстрела. Несколько звукометрических станций, расположенных в разных
точках, фиксирует момент прихода звука одного и того же выстрела. По
промежуткам времени между этими моментами определяются разности рас-
расстояний от орудия до соответствующей пары звукометрических станций.
Зная эти разности для двух пар станций и положение этих станций, можно
определить положение стреляющего орудия. Однако, при этом предпо-
предполагается, что звук приходит от орудия к звукометрической станции по
кратчайшему пути. Поэтому все указанные выше причины, вызывающие
искривление звуковых лучей в атмосфере, очень затрудняют работу артил-
артиллерийской звукометрической разведки.
§ 158. Бинауральный эффект. Эффект Допплера
Способность ориентироваться по звуку, т. е. определять направ-
направление, в котором находится источник звука, обусловлена, главным
образом, одновременным воздействием звуковой волны на оба уха*).
Разность фаз, с которой проходящая волна воздействует на оба уха,
и является тем физическим фактором, которым различаются волны, при-
приходящие по различным направлениям. Лишь в том случае, когда источник
звука находится прямо впереди или позади человека, звуковая волна
достигает обоих ушей в одной и той же фазе. При всяком другом
положении источника волна будет достигать обоих ушей с разной
фазой. Это и Дсбт возможность определять положение источника
звука. Интересно отметить, что высота расположения источника звука
над землёй не имеет значения для сдвига фаз между волнами, дей-
действующими на оба уха (при нормальном, вертикальном, положении
человека). И действительно, человек в гораздо меньшей степени об-
обладает способностью определять угол возвышения источника над го-
горизонтом, чем положение той вертикальной плоскости, в которой
лежит источник. Влияние сдвига фаз волны, действующей на оба уха,
называется бинауральным эффектом.
Точность определения направления по разности фаз волн, дости-
достигающих двух приёмников, будет тем выше, чем больше расстояние
между обоими приёмниками (чем больше «база»). Этот метод повы-
повышения точности определения направления на источник звука приме-
применяется в современных звукоулавливателях, предназначенных для
определения положения самолётов по издаваемому ими звуку. Звуко-
Звукоулавливатель (рис. 425) состоит из двух пар рупоров, разнесён-
разнесённых на значительное расстояние (метр и .больше) друг от друга.
*) Вследствие диффракции звуковые волны огибают препятствия, раз-
размеры которых не очень велики по сравнению с длиной звуковой 'волны,
в частности, голову человека. В том случае, когда источник звука нахо-
находится по одну сторону от человека, звуковые волны благодаря диффракцин
достигают всё же и другого уха.

492
АКУСТИКА
[гл. xxl
Рупоры расположены попарно в двух взаимно перпендикулярных
плоскостях. Наблюдатель, слушающий шум самолёта через рупоры
одной пары, перемещает ось звукоулавливателя в соответствующей
плоскости до тех пор, пока звуки, достигающие обоих его ушей,
не совпадут по фазе. Когда это положение достигнуто для обоих
наблюдателей, ось звукоулавливателя указывает направление норма-
нормали к фронту приходящей звуковой волны. Однако, это направле-
направление, вообще говоря, не совпадает с истинным в данное мгновение
направлением на самолёт, если он имеет скорость в направлении, нор-
нормальном к линии самолёт — звуко-
звукоулавливатель. Фроит волны, достиг-
достигшей в данный момент звукоулавли-
звукоулавливателя, определяет направление, в
котором самолёт находился несколь-
несколько раньше этого момента. Чтобы
определить истинное направление
на самолёт, нужно ввести поправки
на его скорость. Это обстоятель-
обстоятельство (а также влияние ветра и раз-
различных неоднородностей, о которых
шла речь выше, на распростра-
распространение звука в атмосфере) умень-
' шает точность определения направ-
направления на самолёт, хотя само по себе
определение направления фронта
приходящей волны можно произво-
производить с большой точностью.
Движение источника звука пря-
прямо на приёмник или от него не
сказывается на направлении фронта
волны, но приводит к измене-
изменению частоты принимаемого звука.
Это связано с тем, что скорость
распространения звуковой волны в среде не зависит от скорости
движения источника. Поэтому, если источник звука движется от
приёмника со скоростью и, то за единицу времени мимо приёмника
пройдут не все максимумы и минимумы волны, излучённые за это
время источником, а только часть их. Приёмник отметит меньшее
¦число колебаний, чем создаёт источник. Пусть источник в начале се-
секунды находился на расстоянии с см от приёмника, причём с см\сек —
скорость звука в среде. Тогда через секунду он будет находиться
на расстоянии с -\- и. На этом расстоянии уложатся все / макси-
максимумов, которые за одну секунду созданы излучателем (/ — ча-
частота колебаний излучателя). Но за одну секунду до приёмника дой-
дойдут не все эти максимумы, а только часть их, расположенная на
расстоянии с. Следовательно, приемник отметит меньшую частоту /',
Рис. 425.

§ 158] БИНАУРАЛЬНЫЙ ЭФФЕКТ. ЭФФЕКТ ДОЙПЛЕРЛ 493
причём /'{/ — с[(с-\-и), откуда
/ —1 „ •
Если источник приближается к приёмнику, то
1
/'=/-
и
с
При движении приёмника прямо от источника или к нему также
происходит изменение частоты, но в количественном отношении ре-
результат будет иной. Если приёмник движется к источнику со ско-
скоростью и, то за одну секунду он пройдёт не мимо /, а мимо боль-
большего числа максимумов /', причём f'if=(u-\-c)ic, откуда
Если приёмник удаляется от источника, то он отметит меньшую ча-
частоту
/'=/('-!)•
Это изменение частоты при движении источника или приёмника
называется эффектом Допплера. Этим эффектом объясняется, на-
например, изменение высоты тона паровозного гудка при быстром
движении паровоза или наблюдателя (в другом поезде). Считая в
обоих случаях и положительным, когда расстояние увеличивается,
мы можем написать:
Если и\с <^ 1, то
/'^/(l-f-) и f^f,
и в первом приближении эффект Допплера в обоих случаях (движе-
(движения источника и движения приёмника) оказывается одинаковым. Од-
Однако, если не ограничиваться первым приближением, то эффект Доп-
Допплера в случаях движения источника к приёмнику и приемника к
источнику оказывается различным *).
¦*) В современной технике нередко скорость источника или приёмника
отнюдь не мала о сравнению со скоростью звука (например, скорость
самолётов прибтижается к скорости звука), и тогда эффект Допплера в обоих
случаях даже приблизительно нельзя считать одинаковым.

494 \кУсти!а [гл. xxi
Это, конечно, ни в какой мере не противоречит галилееву
принципу относительности. Дело в том, что в рассматриваемых случаях
кроме источника и приёмника играет роль и среда, в которой рас-
распространяется звук. Движение источника к приемнику и приёмника
к источнику даёт разные результаты именно потому, что в первом
случае источник движется в среде, а приёмник покоится относительно
среды, во втором случае источник покоится относительно среды,
а приёмник движется в ней. Это, конечно, — разные опыты, и поэтому
естественно, что они дают разные результаты.
В том случае, когда источник или приёмник движется не по пря-
прямой, их соединяющей, эффект Допплера определяется не полной
скоростью движения, а её составляющей в направлении этой прямой.
§ 159. Звуковые волны в трубах
Стенки, ограничивающие объём воздуха, существенно влияют на
характер звуковых колебаний в этом объёме. Мы рассмотрим неко-
некоторые наиболее важные случаи звуковых колебаний в объёмах.
Начнём с распространения звуковой волны в трубе, диаметр
которой меньше длины волны, но всё же не слишком тонкой и об-
обладающей гладкими стенками. При этих условиях стенки не вносят
заметного затухания; их роль сводится лишь к тому, чтобы обеспе-
обеспечить распространение колебаний в одном направлении — вдоль трубы.
Если в один из концов трубы вставлен поршень, совершающий гар-
гармонические колебания, то по столбу воздуха, заключённому внутри
трубы, распространяется звуковая волна, которая по своему характеру
совершенно аналогична плоской волне в свободном воздухе. Труба
делает возможным существование «куска плоской волны», размеры
которого меньше длины волны. (В отсутствие стенок так^й «кусок
плоской волны» не мог бы распространяться прямолинейно из-за диф-
фракции.) Если второй конец трубы закрыт твёрдой стенкой, то
звуковая волна будет отражаться от этой стенки, причём фаза волны
деформаций останется прежней, а фаза волны скоростей изменится
на л ( скорость изменяет знак на обратный). Всё будет происходить
так же, как и в случае стержня с закреплённым концом. В трубе
установятся стоячие звуковое волны, причём на закрытом конце трубы
образуются пучность деформаций и узел скоростей.
На открытом конце трубы также будет происходить отражение
звуковой волны, но с изменением фазы деформации на тт — сжатие
будет превращаться в разрежение, и наоборот. Действительно, когда
сжатие в падающей волне подходит к отверстию трубы, частицы
воздуха имеют скорость, направленную в ту сторону, в кото-
которую распространяется волна, т. е. из трубы наружу. Но сна-
снаружи эти частицы уже не вызовут такого сжатия, какое существовало
в падающей волне. Так как снаружи трубы давление воздуха можег
выравниваться во всех направлениях, то сжатие будет гораздо меньше,

§ 159] ЗВУКОВЫЕ ВОЛНЫ В ТРУБАХ 495
чём в волне, распространяющейся внутри трубы. Поэтому частицы
воздуха, вышедшие из трубы, к тому моменту, когда их остановит
давление лежащего впереди слоя воздуха, сместятся дальше, чем сме-
смещаются частицы внутри трубы, и на конце трубы возникнет разреже-
разрежение. Точно так же, когда разрежение подходит к концу трубы, в трубу
устремляются частицы воздуха из слоя, имеющего сечение большее,
чем сечение трубы. Эти частицы, приобретя скорость за счёт разности
давлений, не только скомпенсируют разрежение в конце трубы, но
и создадут в нём сжатие. Таким образом, в обоих случаях фаза
деформаций изменяется на тг. Так как скорости частиц при этом
не меняют знака, то энергия начнёт течь в обратном направлении,
а это и значит, что у открытого конца трубы будет происходить
отражение падающей волны.
Этот механизм отражения звуковых волн от открытого конца
трубы аналогичен отражению от свободного конца стержня (§ 149).
Но в случае стержня происходит полное отражение падающей волны,
в случае же трубы звуковая волна отчасти выходит наружу; открытый
конец трубы является источником шаровых волн в окружающем воз-
воздухе. Легко видеть, что отражение звуковой волны у открытого
конца трубы будет тем менее заметно, чем больше диаметр трубы.
В самом деле, причиной отражения является выравнивание давлений
в воздухе, прилегающем к открытому концу трубы. Но так как
выравнивание давлений происходит со скоростью звука, то в вырав-
выравнивании давлений будут участвовать только области, отстоящие
от краёв трубы на расстоянии, малом по сравнению с длиной волны.
(Выравнивание давлений играет заметную роль лишь в том случае,
когда оно может происходить за промежуток времени, малый по
сравнению с периодом звуковых колебаний.) Поэтому, если диаметр
трубы мал по сравнению с длиной волны, то слои, участвующие
в выравнивании давлений, имеют размеры, сравнимые с диаметром
трубы, и выравнивание давлений играет заметную роль. Если же
диаметр трубы превосходит длину волны, то выравнивание давлений
перестаёт играть роль — отражение от открытого конца трубы стано-
становится всё менее и менее заметным. Но пока диаметр трубы мал по
сравнению с длиной волны, от открытого конца трубы происходит
почти полное отражение звуковых волн и в трубе устанавливаются
стоячие волны. При этом на открытом конце трубы образуются узел
деформаций и пучность скоростей.
Вследствие отражения звуковых волн у концов трубы столб воз-
воздуха, заключённый в трубе конечной длины, так же как и стержень
конечной длины, представляет собой колебательную систему, облада-
обладающую определёнными нормальными колебаниями — основным тоном
и гармоническими обертонами. Частоты этих колебаний и распреде-
распределение их амплитуд вдоль трубы, а также и возникновение резонанса при
вынужденных колебаниях, определяются совершенно теми же условиями,
что и в случае стержня, причём закрытый конец трубы аналогичен

496 АКУСТИКА Ггл_ XXI
закреплённому концу стержня, а открытый конец трубы ~ свободному
(§§ 143 и 149).
Звуковые колебания в трубах, диаметр которых мал по сравнению
с длиной волны, всегда приводят к образованию стоячих волн в трубе.
Для наблюдения картины распределения амплитуд стоячих воли
в трубах можно пользоваться свойствами газового пламени. Слабое
газовое пламя, зажжённое у узкого отверстия в стенке трубы, уве-
увеличивается в местах, где образуются пучности стоячей волны. Пропу-
Пропуская через трубу с большим числом малых отверстий светильный газ
и возбуждая в ней стоячие волны при помощи звучащего репродуктора
(рис. 426), можно наблюдать распределение амплитуд вдоль трубы.
Аналогично случаю со струной, одному концу которой задано дви-
движение, в трубе, у одного конца которой помещён репродуктор,
iJ.i-iLi-fcfcU-.-yJJL.iU'J 8
J.i-iLi-fcfcU-.-yJJL.iU'J 8 ' Щ
2500 пер/сек
/1 Д
4
3500 nep/cek
^ 4
4500 nep/cek
4 "¦
Рис. 426.
а другой конец закрыт, резонанс будет наблюдаться всякий раз,
когда вдоль трубы укладывается нечётное число четвертей волн.
Изменяя частоту тока, питающего репродуктор, можно получить сто-
стоячие волны разной длины (рис. 426).
Измерение длины стоячей волны в трубах представляют собой
один из наиболее удобных способов измерения фазовой скорости
звуковых волн в воздухе или других газах. Расстояние между двумя
пучностями равно половине длины волны \. Зная период возбуждаемых
колебаний Т, из соотношения 1 = сТ находят скорость звука. При
точных измерениях необходимо, конечно, применять более точные
методы определения положения пучностей, а также учитывать влияние
стенок трубы на скорость распространения звуковых волн.
В столбе воздуха, заключённом в трубе, можно возбуждать не только
вынужденные колебания, но также и автоколебания. Колебания, возбужда-

§ 160] акустические резонаторы 497
емые_ в органных трубах и в других духовых инструментах, представляют
собой именно автоколебания. Постоянный ток воздуха, продуваемый через
клапан трубы, возбуждает в трубе автоколебания, которые по частоте
и характеру распределения амплитуд обычно близки к собственным коле-
колебаниям столба воздуха, заключённого в трубе. В трубе, закрытой с обеих
сторон, возникают колебания основного тона, и вдоль трубы укладывается
одна полуволна. В трубе, открытой с одной стороны, возникают колебания
основного тона, для которых вдоль трубы укладывается четверть волны.
При одинаковой длине в органной трубе с закрытым концом возникают
колебания вдвое большей частоты, чем в трубе с открытым концом (тон
вдвое выше).
На органной трубе можно продемонстрировать зависимость частоты
колебаний от скорости звука в газе, заполняющем трубу. Если вместо
воздуха наполнить трубу светильным газом, то частота колебаний в трубе
повышается, так как скорость звука в светильном газе (менее плотном,
чем воздух) выше, чем в воздухе. Это особенно отчётливо можно демон-
демонстрировать на двух трубах одинаковой длины. Пока обе трубы наполнены
воздухом, они дают колебания одинаковой частоты (звучат в унисон). После
того, как одна из труб наполнена светильным газом, трубы дают колебания
несколько различной частоты; при сложении их возникают биения — пери-
периодические изменения силы звука, которые отчётливо слышны.
В случае, когда диаметр трубы очень мал, силы вязкости играют
существенную роль. Вследствие этого при распространении в трубе волна
быстро затухает — акустическая энергия превращается в тепло- тонкие
трубы поглощают подводимую к ним акустическую энергию. Этим объяс-
объясняется сильное поглощение звука пористыми материалами. Поры действуют,
как тонкие трубы, — они поглощают падающую на них акустическую энергию;
поэтому стенки, изготовленные из пористого материала, поглощают значи-
значительную часть падающей на них звуковой энергии.
§ 160. Акустические резонаторы
Одной из задач прикладной акустики является выделение гармо-
гармонических составляющих из сложных (негармонических) звуковых
колебаний. Такая задача возникает при конструировании ряда акусти-
акустических приборов, например, приёмников звука, когда хотят сделать
их более чувствительными к колебаниям одной частоты по сравнению
с другими (выделение «полезного сигнала» из всей м'ассы звуков)
и т. д. Специальный интерес представляет гармонический анализ
звуков, т. е. определение амплитуд гармонических составляющих,
содержащихся в том или ином звуке. Ухо человека снабжено множе-
множеством резонаторов (так называемые кортиевы органы), которые
и позволяют человеку различать высоту звука, т. е. частоту основного
тона звуковых колебаний и его тембр («окраску»), т. е. содержание
обертонов в этом звуке.
Роль акустического резонатора может играть всякий объём воздуха,
ограниченный стенками и обладающий поэтому собственными часто-
частотами колебаний, например, кусок трубы конечной длины. Однако,
такой кусок трубы обладает множеством нормальных колебаний
и поэтому будет резонировать (отзываться) на множество гармониче-
гармонических колебаний. Удобнее, конечно, применять такие резонаторы,
которые отзываются на одну определённую частоту внешнего гармо-
32 С. Э Хайкин

498 АКУСТИКА 1 ГЛ. XXl
нического воздействия. Такими свойствами обладают, например, со-
сосуды шаровой формы с горлом (рис. 427) — так называемые резонаторы
Гельмгольца.
Резонаторы Гельмгольца стоят в таком же отношении к трубам,
кж механическая колебательная система с одной степенью свободы
(груз на пружине) — к однородной сплошной системе (стержню). Как
уже указывалось (§ 150), груз на пружине можно рассматривать как
предельный случай неоднородной сплошной системы. Точно так же
и резонатор Гельмгольца можно рассматривать как предельный случай
трубы переменного сечения.Обертоны такой сплошной
системы вследствие её неоднородности не гармо-
гармоничны и лежат далеко от основного тона. Основной
же тон резонатора, как и в случае груза на пружине,
можно определить, рассматривая его как систему,
в которой масса и упругость сосредоточены в разных
местах.
Так как диаметр горла резонатора мал, то при ко-
Рнс. 427. лебаниях скорость воздуха в нём гораздо больше,
чем в сосуде; поэтому роль колеблющейся массы
играет, главным образом, масса воздуха в горле. С другой
стороны, так как объём воздуха в горле гораздо меньше, чем в
сосуде, то абсолютными изменениями объёма воздуха в горле при
колебаниях можно пренебречь и считать, что весь этот объём колеб-
колеблется как целое, изменяется же только объём воздуха в сосуде и воз-
воздух играет роль пружины. Иначе говоря, воздух в горле можно
заменить поршнем массы m = pSl, где 5 — сечение, а / — длина
горла. Объём V резонатора можно заменить некоторой пружиной,
упругость которой определим следующим образом. Из соотношения
B1.9) (где У. = ЧР), связывающего сжатие 7] с изменением давления,
получаем:
где Ьх — смещение споршня» в горле. Сила, действующая на
«поршень»,
пропорциональна смещению поршня, т. е. объём воздуха в сосуде
действует как пружина с коэффициентом упругости
Угловая частота колебаний массы т, удерживаемой пружиной, с ко-
коэффициентом упругости k, как известно, есть @= т/ Щт. Подстав-

§160]
АКУСТПЧКСКИЕ РЕЗОНАТОРЫ
499
ляя в это выражение найденные значения k и т, получим:
У vi?
или, так как VtPt? - с>
VI?
1Г
VI
B1.15)
Изменяя размеры сосуда и горла, можно получить резонаторы с соб-
собственными частотами, охватывающими весь диапазон звуковых частот.
Из выражения B1.15) частоты собственных колебаний резонатора
для соответствующей длины волны получаем:
B1.16)
Для резонатора, у которого диаметр горла равен длине горла, а длина
горла в несколько раз меньше диаметра сосуда (эти соотношения
между размерами близки к тем, которые применяются на практике),
длина звуковой волны, соответствую-
соответствующей данному резонатору, оказывается в
10—15 раз больше диаметра сосуда, т. е.
размеры резонатора значительно меньше,
чем длина волны.
11111111
ЧпгттаИт 2000 МО сек]
* г—
Рис. 429.
Резонатор Гельмгопьца выделяет из всех действующих на него
гармонических колебаний то колебание, частота которого совпадает
с собственной частотой резонатора. Индикатор (нагретая проволочка,
чувствительное газовое пламя и т. д.), помещённый в горле резона-
резонатора или в специальном отростке, расположенном против горла,
позволяет судить об амплитуде колебаний резонатора. Располагая
большим набором резонаторов, частоты которых лежат достаточно
близко друг к другу, можно определить амплитуды различных гармо-
гармонических составляющих того или иного звука, т. е. произвести
гармонический анализ звуков.
Чистые музыкальные тона представляют собой колебания, близкие
к периодическим, и они дают, следовательно, большую амплитуду
основного тона и некоторое число гармонических составляющих,
амплитуды которых обычно убывают по мере увеличения номера
32*

500 акустика [гл. xxi
гармоники. Распределение амплитуд этих гармонических составляющих
для звуков, создаваемых различными музыкальными инструментами,
различно. Эти различия, как указывалось, и определяют, главным
образом, различный тембр звуков. Содержание гармоник определяется
не только свойствами колебательной системы, являющейся источником
звука, но и способом возбуждения колебаний. Поэтому тоны, полу-
получающиеся при возбуждении струны смычком и «щипком», имеют
разный тембр.
Гласные звуки человеческой речи также представляют собой
колебания, близкие к периодическим и поэтому содержащие, помимо
основного тона, гармонические обертоны. Однако, распределение
этих обертонов гораздо сложнее, чем в чистых музыкальных тонах.
На рис. 428 приведена запись формы колебаний для гласной «а»,
произнесённой низким мужским голосом, а на рис.429 — амплитуды
гармонических составляющих («частотный спектр») этого же звука.
Согласные звуки человеческой речи представляют собой колебания,
уже весьма далёкие от периодических; поэтому их спектр весьма
сложен и содержит негармонические обертоны.
§ 161. Источники звука
Источником звука является всякое тело, колеблющееся с частотой,
лежащей в пределах звукового диапазона, и возбуждающее в окру-
окружающей упругой среде (обычно в воздухе) звуковые волны. Этот
процесс возбуждения волн в окружающей среде носит название излу-
излучения волн. Различные тела в разной степени обладают способностью
излучать звуковые волны. Например, колеблющийся камертон сам
по себе излучает очень слабо. Это объясняется малыми размерами
ножек камертона и характером их колебаний. Как и в случае отдель-
отдельного импульса (§ 132), колеблющаяся ножка камертона вызывает
сжатие воздуха с одной стороны и в то же время разрежение — с
другой, ^следствие того, что выравнивание давления в воздухе про-
происходит очень быстро (со скоростью звука) эти сжатия и разрежения
в сильной степени компенсируют друг друга. Вместо того, что1ы воз-
возбуждать упругую волну в окружающем воздухе, колеблющаяся ножка
камертона лишь «перекачивает» прилегающие к ней слои воздуха
с одной стороны на другую. Звуковые волны возбуждаются только
постольку, поскольку это перекачивание происходит неполностью.
Помимо этой причины, камертон плохо излучает звук ещё и потому,
что ножки его при колебаниях всегда движутся в противоположные
стороны, т. е. колеблются в противофазе. Поэтому и волны, излучаемые
обеими ножками, противоположны по фазе и не усиливают, а осла-
ослабляют друг друга. Камертон излучает лишь постольку, поскольку
излучения каждой из его ножек не вполне компенсируют друг друга.
Если преградить путь звуковым волнам, излучаемым одной из ножек
камертона, одев на эту ножку картонную трубку (рис. 430), то звук

§611
ИСТОЧНИКИ ЗВУКА
501
о
Рис. 430.
усиливается, так как волны, создаваемые одной из его ножек, уже
не ослабляются противоположными по фазе волнами от другой ножки.
Вредная роль непосредственного выравнивания давлений между
сжатиями и разрежениями, возникающими около колеблющегося тела,
сказывается во всех случаях излучения звука. Оно не происходило бы,
если бы за время, малое по сравнению с периодом колебаний, импульс
сжатия, выравнивающий давление, не успевал обежать вокруг колеб-
колеблющегося тела. Но за период Г импульс пробегает путь fT^=l, т. е.
как раз путь, равный длине звуковой волны, возбуж-
возбуждаемой телом. Поэтому колеблющееся тело будет хо-
хорошо излучать только в том случае, когда размеры
его, по крайней мере, сравнимы с длиной излучаемой
волны.
Однако, соблюсти это требование было бы труд-
трудно — излучатели оказывались бы чересчур громоздкими,
и для увеличения излучения применяют иные методы.
Камертон, например, устанавливается на резонаторный
ящик. Вследствие механической связи через стебель
камертон возбуждает колебания столба воздуха в ящике,
а этот последний излучает колебания в окружающий
воздух. При этом, так как ящик с одной стороны за-
закрыт и размерь! его значительны, устраняется эффект
выравнивания давлений, и излучение оказывается гораз-
гораздо более сильным. Нечто подобное происходит и в струнных музы-
музыкальных инструментах, где корпус инструмента играет роль резона-
торного ящика.
В некоторых источниках звука применяются другие методы борьбы
с выравниванием давлений. Например, в обычных громкоговорителях мем-
мембрана имеет размеры, которые сравнимы с длиной волны только для доста-
достаточно высоких звуковых частот (порядка тысячи колебаний в секунду),
для низких же частот (порядка 100 кол/сек) размеры мембраны малы по
сравнению с длиной волны и вследствие выравнивания давлений громко-
громкоговоритель очень слабо излучал бы низкие тона. Для ^устранения этого
мембрана помещается в вырезе большой отражательной доски, которая
препятствует выравниванию давлений и для низких частот.
Возбуждение волн колеблющимся телом связано с излучением
энергии в окружающую среду. В источниках звука эти потери энергии
на излучение могут быть очень значительны (чем лучше излучатель,
тем больше эти потери). Они обусловливают сильное затухание соб-
собственных колебаний излучателя. Влияние этих потерь легко обнару-
обнаружить на камертоне. Камертон без резонансного ящика звучит гораздо
слабее, чем с ящиком, но зато затухание звука при наличии ящика
происходит гораздо быстрее.
В простейшем случае, когда источником звука является колеб-
колеблющаяся пластина, размеры которой велики по сравнению с длиной
возбуждаемой волны, не трудно подсчитать мощность, затрачиваемую
пластиной на создание звуковых волн. При больших размерах

502 акустика [гл. xxi
пластины можно считать, что она создаёт плоскую волну и звуковое
давление dp у всей поверхности пластины одно и то же (диффракция
не играет существенной роли). Если смещение пластины происходит
по закону
S = Хо sin 2 тт j,,
то ? есть вместе с тем смещение частиц в возбуждаемой волне
при л; = 0, т. е. непосредственно около пластины. Поэтому соотно-
соотношение между давлением в звуковой волне и скоростью пластины
будет такое же, как и между давлением и скоростью в самой звуковой
волне B1.7):
Ар = рси. B1.17)
На пластину площади ^ действует со стороны звуковой волны
сила
За время dt пластина пройдёт путь & = udt и совершит работу
Следовательно, мощность, затрачиваемая пластиной на создание зву-
звуковых волн,
P=^ = Slpu, B1.18)
где Ар — давление, создаваемое в звуковой волне, аи — скорость
пластины.
Пользуясь соотношением B1.7) между Др и и, можно выразить
мощность следующим образом:
P=Spcu* = S(^~ . B1.19)
Принимая во внимание, что Ар и и меняются по гармоническому за-
закону и их средние значения за период соответственно равны ДРд/2
и Ид/2 (где Др0 и иа — амплитуды давления и скорости), получим сред-
среднюю мощность, отдаваемую пластиной за период колебаний:
Наши выводы справедливы только для пластины, размеры которой
велики по сравнению с длиной возбуждаемой еад волны. При этом
условии мы могли пренебречь явлениями диффракции непосредственно
у пластины и считать, что возле неё возникает плоская волна. Однако,
так как пластина имеет конечные размеры, то возбуждаемая ею волна
представляет собой не бесконечную плоскую волну, а лишь «кусок
плоской волны». Поэтому вследствие диффракции на краях «куска

§ 1611 источники звука 503
волны» волны будут постепенно расходиться, и это расхождение, по
мере удаления от пластины, будет всё более и более заметно. Энер-
Энергия, излучаемая пластиной, будет постепенно рассеиваться в простран-
пространстве, амплитуда волны по мере удаления от источника будет падать
и тем сильнее, чем быстрее расходится волна. Роль диффракции опре-
определяется отношением поперечных размеров «куска волны» к длине
волны; влияние её будет тем более заметным, чем меньше это отно-
отношение. Всякая пластина даёт вдали, грубо говоря, конус расходящихся
звуковых волн.
При данной длине волны телесный угол этого конуса обратно
пропорционален площади пластины и, наоборот, при данных размерах
пластины этот угол прямо пропорционален квадрату длины волны.
Очевидно, чем меньше угол конуса, т. е. чем уже пучок звуковых
волн, создаваемых пластиной, тем медленнее падает амплитуда зву-
звуковой волны на направлении нормали к пластине. Поэтому во многих
случаях (например, чтобы об-
обслужить звуком длинную, но
узкую площадь) выгодно при-
применять источники звука, даю-
дающие узкий пучок волн, т. е.
направленные источники звука.
Дла этого потребовались бы
пластины, например, мембраны
громкоговорителей, размеры ко-
которых больше длины звуковой
волны. Однако, даже для сред- рис 431
них звуковых частот (волны
длиной 20—30 см) это условие выполнить невозможно. Мем-
Мембраны сами по себе практически не могут дать направленного
излучения звуковых волн. Более того, так как мембраны практически
приемлемых размеров оказываются много меньше длины волн для длин-
длинных звуковых волн, то на низких частотах явление диффракции играет
заметную роль уже в непосредственной близости к мембране. Даже
вблизи мембраны создаваемые ею волны существенно отличаются от
плоских. Поэтому, приведённый выше расчёт излучаемой пластиной
мощности в этом случае неприменим.
Излучаемая мощность падает по мере приближения длины волны к по-
поперечным размерам пластины *). Когда радиус мембраны мал по сравнению
с длиной волны, излучаемая мощность оказывается пропорциональной квад-
квадрату отношения радиуса мембраны к длине волны, т. е. очень быстро падает
по мере увеличения длины волны. Таким образом, мембраны практически
приемлемых размеров не могут дать сколько-нибудь резкой направленности
*) Это уменьшение излучаемой мощности обусловлено явлениями диф-
диффракции впереди пластй"ны, а не эффектом выравнивания давлений, который
может быть устранён применением упомянутых выше отражательны*
экранов.

504
АКУСТИКА
[гл. xxi
I
для средних длин волн звукового диапазона и вообще плохо излучают
длинные звуковые волны.
Чтобы повысить излучение мембраны и придать ему направленность,
применяются рупоры, т. е. трубы, сечение которых постепенно увеличи-
увеличивается (рис. 431). Рупор устраняет явление диффракции на краях «куска
плоской волны», создаваемой мембраной, так что звуковая волна подходит
к устью рупора всё ещё в виде «куска плоской волны», но гораздо боль-
больших, чем у мембраны, поперечных размеров. Если поперечные размеры
устья рупора порядка длины волны, то отражение волн у устья, как и у от-
отверстия широкой трубы (см. § 159), будет мало. Звуковые волны будут
выходить из устья рупора, и вся картина будет примерно такая, как если
бы устье рупора было закрыто колеблющейся пластиной. Рупор как бы
заменяет истинную мембрану малых размеров мембраной больших размеров
(равных поперечным размерам устья рупора). Вследствие этого увеличи-
увеличивается излучение длинных звуковых воли и обеспечивается большая или
меньшая направленность излучения. Ко-
Конечно, при этом направленность излуче-
излучения получается резкой только для волн,
длина которых меньше поперечного раз-
размера устья рупора.
Применение рупора позволяет также
повысить мощность, отдаваемую мембра-
мембраной (увеличить «акустическую отдачу» мем-
мембраны). Средняя мощность, излучаемая
Рис 43*> мембраной при данных ее размерах и ам-
амплитуде колебаний, может быть увеличена
за счет увеличения давления в звуковой
волне, создаваемой мембраной (так как отдача мощности обусловлена работой
мембраны против силы давления, действующей на неё со стороны звуковой
волны). Если поместить мембрану в камеру с отверстием, размеры которого
меньше размеров мембраны, то переменное давление, создаваемое в камере
колеблющейся мембраной, будет выше, чем в отсутствие камеры, и мощ-
мощность, излучаемая мембраной через отверстие в камере, будет выше.
Однако, это достигается за счёт уменьшения поперечных размеров «куска
плоской волны» с вытекающими отсюда вредными последствиями — ухуд-
ухудшением направленности. Но применение рупора с узким горлом позволяет
устранить эти последствия. Поэтому в громкоговорителях обычно приме-
применяют предрупорные камеры и горло рупора делают меньших размеров, чем
мембрана, (рис. 432).
Интенсивность звука, создаваемого тем или иным источником, зависит
не только от свойств источника, но и от свойств помещения, в котором ис-
источник находится. Если стены помещения сильно отражают падающие на них
звуковые волны, то в помещениях могут происходить такие же явления, как
и в трубах, но вся картина гораздо более сложна вследствие того, что рас-
распространение падающих и отраженных волн может происходить по всем
трём направлениям, а не по одному, как это происходило в трубах. При этом
должна была бы возникнуть сложная система стоячих волн. Однако, так
как обычно стены помещения не представляют собой правильных плоско-
плоскостей—-имеют выступы, карнизы и т. Д., в помещениях находятся различ-
различные предметы, также отражающие звук, и кроме того, могут происходить
многократные отражения, то узлы и пучности стоячих волн, образующиеся
при отдельных отражениях, оказываются сдвинутыми друг относительно
друга. Изменения амплитуд от точки к точке, характерные для стоячих
волн, усредняются, и фактически отчётливых стоячих волн в помещениях
обычно не наблюдается. Отражения дают звуковые колебания, интенсив-
интенсивность которых во всех точках помещения примерно одинакова. Поэтоиу
в помещениях с отражающими стенами наряду с звуком, идущим прямо от

§ 161] источники звука 505
источника, в каждую точку со всех сторон приходят отражённые звуки.
Эти последние носят название диффузного (рассеянного) звука. Влияние
помещения на характер звучания в нём («акустика помещения») опреде-
определяется именно существованием этого диффузного звука.
Так как диффузный звук имеет примерно одинаковую интенсивность
во всех точках помещения, а прямой звук убывает по мере удаления от
источника, то диффузный звук вблизи источника играет меньшую роль, чем
вдали от него. Вследствие этого уменьшение громкости звука по мере уда-
удаления от источника происходит медленнее, чем на открытом воздухе (или в по-
помещении, стены которого полностью поглощают падающие на него звуки).
Чтобы обеспечить одну и ту же интенсивность звука, в закрытом помеще-
помещении требуется меньшая мощность источника звука, чем на открытом воздухе,
и притом тем меньшая, чем сильнее отражается звук от стен помещения.
С этой точки зрения казалось бы выгод-
выгодным делать стены помещений возможно 5
лучше отражающими звуки.
Однако, если стены почти полностью
отражают звуки, то в образовании диф-
диффузного отражения заметную роль играют
многократные отражения от стен (так как
при сильно отражающих стенах интенсив-
интенсивность звука после второго или третьего
отражения ещё почти такая же, как после
первого отражения). Но после каждого из
этих многократных отражений звук При-
Приходит в данную точку позже предшеству-
предшествующего, и чем больше отражений происхо-
происходит при образовании диффузного звука,
тем больше времени требуется для того, чтобы он достиг полной ин-
интенсивности. С другой стороны, после того, как источник звука замолчал,
диффузный звук исчезнет не сразу, так как в течение некоторого времени
будут приходить звуки от стен, испытавшие многократное отражение. Диф-
Диффузный звук, а значит, и полное звучание в помещении устанавливается
и прекращается не сразу, а постепенно. Это явление носит название ревер-
реверберации звука. Время, потребное на то, чтобы звучание в помещении прак-
практически исчезло, называют временем реверберации.
На рис. 433 приведён график установления и прекращения звучания
в закрытом помещении (Т—время реверберации). Закон установления и
прекращения звука в помещении совершенно аналогичен закону установле-
установления и прекращения вынужденных колебаний во всякой колебательной си-
системе*). Это понятно ведь рассмотренная картина представляет собой,
в сущности, установление или прекращение вынужденных колебаний в ко-
колебательной системе, которую представляет собой объём воздуха, ограни-
ограниченный отражающими звук стенами.
Из сказанного выше ясно, что чем сильнее отражение звука от стен
помещения, тем больше время реверберации. Поэтому, хотя сильное отра-
отражение от стен выгодно с точки зрения повышения громкости звука (или
уменьшения мощности источника), но оно обусловливает большое время
реверберации. Помещение оказывается слишком гулким, отчётливость речи
уменьшается, качество звучания музыки ухудшается. С другой стороны,
при очень слабом отражении от стен время реверберации мало и качество
звучания приближается к тому, которое получается на открытом воздухе.
Но при этом требуется большая мощность источников звука или при той
*) Так как звук затухает по показательному закону, то время ревербе-
реверберации определяется условно, поскольку полностью звук затухает лишь
при t =со.

506 акустика [гл. xxi
же мощности уменьшается обеспечиваемая ими площадь. С точки зрения
качества звучания музыки очень слабое отражение от стен также нецеле-
нецелесообразно — музыка звучит глухо. Чтобы обеспечить наилучшую «акустику
помещения», подбирают для него время реверберации, наиболее благоприят-
юе с точки зрения той цели, для которой служит помещение. Уменьшение
времени реверберации достигается применением звукопоглощающих мате-
материалов, покрывающих ббльшую или меньшую часть пола, потолка и стен
(портьеры, ковры, щиты из пористых материалов и т. д.).
§ 162. Ультразвуки
Как мы видели, вдали от излучателя невозможно получить узкий, не-
расходящийся пучок волн, поперечные размеры которого сравнимые длиной
волны. Между темг как с точки зрения использования звуковой энергии
(передачи звуковых сигналов на большие расстояния), так и для решения
ряда специальных задач, важно получать возможно более узкие пучки зву-
звуковых волн. Осуществить это можно, только применяя достаточно корот-
короткие акустические волны, лежащие за верхней границей слышимости уха
человека. Такие ультразвуковые волны, или ультразвуки, не только позво-
позволяют решить указанную важную задачу прикладной акустики, но и пред-
представляют интерес и с других точек зрения. Всё сказанное выше об акусти-
акустических волнах и акустических приборах остаётся в общем справедливым
и для ультразвуков, но малые длины волн и, соответственно, высокие частоты
колебаний придают особые черты всей этой области явлений.
Прежде всего излучатели звуковых волн, применяемые в области аку-
акустических частот, оказываются мало пригодными для излучения ультразвука.
Основное затруднение заключается в том, что ускорения мембраны, излу-
излучающей ультразвуки, должны быть очень велики, так как амплитуда уско-
ускорений пропорциональна квадрату частоты (при заданной амплитуде смеще-
смещений). Для того чтобы мембрана, имеющая не слишком малую массу,
совершала вынужденные" колебания высокой частоты и достаточной ампли-
амплитуды, потребовались бы огромные силы. Помимо этого возникает ряд дру-
других трудностей, с которыми не удалось бы справиться, сохранив в ультра-
ультраакустических излучателях принцип обычного громкоговорителя.
Все эти трудности отпадают при использовании так называемых пьезо-
пьезоэлектрических излучателей.
Некоторые кристаллы (кварц, турмалин, сегнетова соль и др.) дают
пьезоэлектрический эффект: под действием упругой деформации на поверх-
поверхности кристалла появляются электрические заряды (прлмой пьезозффект);
и наоборот, под действием электрического поля они испытывают упругие
деформации — сжимаются или растягиваются—в зависимости от направле-
направления поля (обратный пьезоэффект). Поэтому, если пластинку, вырезанную
из пьезоэлектрического кристалла, поместить между обкладками конденса-
конденсатора, к которому подводится переменное электрическое напряжение, то
в пластинке будут возникать переменные упругие деформации, т. е. будут
происходить вынужденные механические колебания. Но сама пластинка, как и
всякое упругое тело, обладает собственными частотами колебаний, завися-
зависящими от размеров пластинки и свойств материала. Если подобрать частоту
внешней силы (переменного электрического поля) так, чтобы она совпала
с одной из собственных частот упругих колебаний пластинки, то наступит
резонанс— амплитуда вынужденных колебаний достигнет больших значений.
Упругие свойства пьезоэлектрических кристаллов таковы, что из них
можно делать пластинки, обладающие очень высокими собственными часто-
частотами колебаний — вплоть до десятков мегагерц. Например, в кварцевой пла-
пластинке могут возникать продольные упругие волны в направлении её толщины.
Так как поверхности пластинки свободны, на них должны получаться

§ 162]
УЛЬТРАЗВУКИ
507
пучности скоростей и узлы деформаций и на толщине пластинки должно
укладываться целое число полуволн. Поэтому частота основного тона этих
колебаний определится из условия, чго на толщине пластины уложится одна
полуволна (рис. 434). Следовательно, длина упругой волны в кварце \k = 2d,
а так как ^=e^//, где ск — скорость распространения упругих волн в кварце, то
Скорость распространения упругих волн в кварце по разным направлениям,
несколько различна (ввиду анизотропии—различных упругих свойств в раз-
разных направлениях), но близ-
близка к 5500 \ П
например,
й
\L~7~.Z
деформации
м\сек. Поэтому,
для пластинки
толщиной в 5 мм частота
собственных упругих коле-
колебаний составит около
550 000 гг?. Вырезая пластин-
пластинки разной толщины, можно
получить различные частоты собственных
происходить упругие колебания других типов
другим направлениям;
d
у
А
скорости
кварцевая
пластинка
|||
Ш
Рис. 434.
колебаний. В пластинке могут
(продольные колебания по
колебания изгиба и т. д.), но в ультраакустике обычно
пользуются только рассмотренным выше типом колебаний —продольными
колебаниями по толщине пластинки.
Если поместить пластинку между обкладками конденсатора, питаемого
переменным напряжением (рис. 435), то в ней можно возбудить вынужден-
вынужденные упругие колебания этого типа. При совпадении частоты внешней силы
с собственной частотой пластинки на-
наступит резонанс и амплитуда вынужден-
вынужденных колебаний достигнет максимума (она
может достигать величины 10-* см).
Прикладывая достаточно большие элек-
электрические напряжения, легко было бы
получить и большие амплитуды, но при
этом деформации в пластинке превос-
превосходят допустимые пределы и она мо-
может разрушиться.
Колеблющаяся таким образом пла-
пластина, так же как и мембрана гром-
громкоговорителя, возбуждает ультразву-
ультразвуковые волны в окружающей среде*) —
воздухе, воде. Так как скорость звука в среде — не только в воздухе, но и
в воде— в несколько раз меньше, чем в кварце, то длина возбуждаемой
в среде волны будет соответственно короче, чем в кварце, т. е. в несколько
раз меньше, чем 2d. Поэтому, если длина и ширина пластинки хотя бы
в несколько раз больше, чем её толщина, то поперечные размеры пластинки
значительно превышают длину волны, возбуждаемой ею в среде. Таким
образом легко реализуется случай пластины, размеры которой велики по
сравнению с длиной возбуждаемой волны. К пьезоэлектрическим излучате-
излучателям этого типа применимо всё то, что было сказано выше о пластине, раз-
размеры которой велики по сравнению с длиной волны. Излучаемый пластин-
пластинкой пучок ультразвуковых волн будет очень мало расхотиться, причём
поперечные размеры этого пучка вблизи пластины будут порядка сантимет-
сантиметров, а по мере удаления они будут медленно увеличиваться.
Рис. 435.
*) Чтобы обкладка конденсатора не мешала излучению, одну из обкладок
заменяют тонким слоем металла, нанесённым на поверхность самой пластины.

508
ЛКУСТИКЛ
[гл. xxi
Рис. 436.
Уменьшение амплитуды волны с расстоянием, обусловленное рассеянием
энергии, будет происходить очень медленно. Но зато поглощение ультра-
ультразвуков, обусловленное вязкостью среды, будет велико, так как оно пропор-
пропорционально квадрату частоты колебаний (§ 158). Поэтому в случае ультразву-
ультразвуков преобладающую роль играет обычно не рассеяние энергии в пространстве,
а поглощение её средой. С этой точки зрения вода является более благо-
благоприятной для распространения ультразвуков средой, чем воздух, так как
вследствие меньшей кинематической
вязкости вода меньше поглощает зву-
звуковые волиы, чем воздух. Поэтому
основное практическое применение
ультразвуки нашли в гидроакустике.
Применению ультразвуков в воде
благоприятствует ещё одно обстоятель-
обстоятельство. Как мы видели (§ 161), средняя
мощность, излучаемая колеблющейся
пластинкой, при данной амплитуде её
' скорости пропорциональна рс. А для
воды рс в несколько тысяч раз боль-
больше, чем для воздуха, так что ультра-
ультраакустический излучатель, при прочих
равных условиях, излучает в воде го-
гораздо лучше, чем в воздухе. Пьезо-
кварцевые излучатели в воде могут
излучать очень значительную мощ-
мощность. Так, кварцевая пластинка, колеб-
колеблющаяся с амплитудой смещения
10-* см и угловой частотой и> =:3- 10s,
имеет амплитуду скорости ао = ЗО см\секЛгм. как для воды г=а 1500 м\сек =
= 1,5-105 см\сек, то пластина в 1 см2 излучает при этом мощность 7 вот.
В воздухе при тех же условиях пластина излучала бы около 2 милливатт.
В качестве приёмников ультразвуков применяются пьезоэлектрические
пластинки такой же толщины, как и пластинка излучателя, волны которого
должны быть обнаружены. Под действием колебаний давления в волне
приёмная пластинка совершает вынужденные колебания. Одинаковая тол-
толщина пластинок обеспечивает резонанс в приёмной пластинке. Упругие коле-
колебания пластины вызывают появления переменных зарядов на пластинке
(прямой пьезоэффект) и переменного напряжения на конденсаторе, между
обкладками которого она помещена. Это переменное напряжение усиливается
затем при помощи лампового усилителя и обнаруживается при помощи того
или иного индикатора.
Ультразвуки впервые были практически применены в эхолоте для изме-
измерения глубины моря. В дне судна помещаются ультразвуковой излучатель,
посылающий короткие сигналы, длящиеся около 0,001 сек, и приёмник
ультразвуков (рис. 436). Отражаясь от дна моря, ультразвуки через некото-
некоторое время достигают приёмника. По промежутку времени, прошедшему
между отправлением сигнала и его возвращением, зная скорость распростра-
распространения ультразвука, определяют расстояние до дна моря.
В дальнейшем этот же метод был применён для обнаружения препят-
препятствий на пути судна (например, айсбергов), обнаружения подводных лодок
и т. д. Ультразвуки применяются также для подводной сигнализации, связи
между подводными лодками и т. д. Ультраакустические приборы занимают
большое место в оборудовании современных подводных лодок, а также
надводных кораблей.

ГЛАВА XXII
МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
§ 163. Роль скорости света в механике
Законы классической механики, в частности, законы Ньютона,
представляют собой обобщение опытных фактов. Эти законы уста-
устанавливались и проверялись на основании наблюдений медленных (по
сравнению со скоростью света) движений. Поэтому мы не имеем
оснований утверждать, что эти же законы окажутся справедливыми
и для быстрых движений. Только специальные опыты, относящиеся
к быстрым движениям, могут дать ответ на этот вопрос. Такие опыты,
произведённые с быстрыми электронами, показали, что для очень быст-
быстрых движений законы классической механики несправедливы — они
должны быть соответствующим образом видоизменены и дополнены.
Вместе с тем оказалось, что изменения, сделаные в механике, не
стоят особняком, а тесно связаны с изменениями, которые одновре-
одновременно пришлось внести в другие разделы физики — электродинамику,
оптику и т. д. Все эти изменения, которые коснулись не только мно-
многих фундаментальных законов физики, но и определений ряда основных
физических понятий, составляют содержание теории относительности.
В то время, когда основы теории относительности были сформу-
сформулированы А. Эйнштейном A905 г.), многие из её следствий ещё не
находили себе подтверждения на опыте. Но за истекшие сорок лет
многочисленные наблюдения и эксперименты блестяще подтвердили
целый ряд важных выводов теории относительности и тем самым пре-
превратили её в общепризнанную теорию, составляющую одну из основ
всей современной физики. Краткому и элементарному изложению тех
новых идей и изменений, которые теория относительности внесла
в механику, посвящена настоящая глава книги.
Однако нужно иметь в виду, что последующее изложение не может
дать полного и отчётливого представления не только об истории раз-
развития идей теории относительности, но и о той огромной роли, кото-
которую эти идеи сыграли в развитии всей физики. Создать такое пра-
правильное и отчётливое представление настоящий очерк не в состоянии
прежде всего потому, что он охватывает лишь вопросы механики те-
теории относительности, между тем идеи теории относительности воз-
возникли и развивались главным образом в связи с проблемами электро-
электродинамики и оптики. Кроме того, в последующем изложении, чтобы

510 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXII
его упростить, сознательно нарушена историческая перспектива. Дело
в том, что только благодаря теории относительности стала ясной по-
постановка некоторых вопросов и содержание, а иногда и бессодержа-
бессодержательность, некоторых утверждений классической физики. Только с
точки зрения теории относительности оказывается возможным отчёт-
отчётливо изложить те разногласия, которые возникли между классической
физикой и теорией относительности, и указать те опыты, которые
должны решить, какая из этих теорий верна. Классическая же физика
была не в состоянии этого сделать. Именно поэтому в настоящем
очерке все вопросы излагаются не так, как они возникали в своё время
в классической физике, а так, как они были освещены позднее в те-
теории относительности. Вследствие этого в последующем изложении
классическая физика и теория относительности выступают как две
равноправные, одинаково ясные и последовательные теории, выбор
между которыми должен быть сделан лишь на основании опыта. Между
тем в действительности дело обстояло не так, ибо не только ответы
на вопросы, но и сама постановка некоторых вопросов в классической
физике оказались неправильными. Тем самым в последующем изло-
изложении нарушается историческая перспектива, но зато устраняются те
трудности, с которыми безуспешно пыталась справиться классическая
физика и которые благодаря правильной и более глубокой постановке
вопросов разрешила теория относительности.
Прежде всего в теории относительности была впервые отчётливо
выяснена та особая роль, которую в физике вообще и в механике,
в частности, играет скорость света. Как уже указывалось (§ 7),
поскольку в механике возникает необходимость отсчитывать момент
времени, когда где-то произошло определённое событие, мы должны
пользоваться теми или иными сигналами, которые дали бы нам знать,
когда «там» это событие произошло. Если бы мы располагали сиг-
сигналами, которые распространяются мгновенно, то мы могли бы отсчи-
отсчитывать момент, когда «там» произошло событие, непосредственно по
часам, находящимся «здесь». Однако, такими сигналами мы не рас-
располагаем. Наиболее быстрые сигналы, которые мы можем использо-
использовать для указанной цели, это световые сигналы, которые распростра-
распространяются хотя и с большой (с точки зрения наших обычных масштабов),
но всё же конечной скоростью. Поэтому в показания часов мы должны
вносить поправку на время распространения светового сигнала «от-
«оттуда»— «сюда»; эта поправка, очевидно, зависит от скорости света.
Таким образом, скорость света играет существенную роль, если для
отсчёта времени в разных местах мы пользуемся одними и теми же
часами*). Скорость света наряду с линейкой и часами входит
*) Если бы для отсчёта времени в разных местах мы пользовались
различными часами, из которых одни находятся в том месте, где произошло
событие, а другие «здесь», то световые сигналы понадобились бы для того,
чтобы сверять между собой часы, и скорость света играла бы столь же
существенную роль. К этому вопросу мы ещё вернёмся.

§ 163] РОЛЬ СКОРОСТИ СВЕТА В МЕХАНИКЕ 511
в набор тех «инструментов», при помощи которых мы производим
измерения промежутков времени и расстояний. Поэтому, наряду с воп-
вопросами о постоянстве длины линеек и хода часов, возникает вопрос о
постоянстве скорости света.
Однако, именно постоянство скорости света нельзя непосред-
непосредственно и полностью проверить на опыте. Как уже указывалось (§ 7),
непосредственное определение скорости света возможно только в ре-
результате измерения промежутка времени, в течение которого свето-
световой сигнал распространяется туда и обратно. Поэтому все непосред-
непосредственные определения скорости света основаны на предположении,
что световые сигналы в обе стороны распространяются с одинаковой
скоростью. Правда, существуют астрономические методы определения
скорости света, в которых измеряется только время распространения
светового сигнала «оттуда сюда». Таков метод Рёмера, в котором
используется видимое нарушение периодичности затмений спутников
Юпитера. Рёмер обнаружил, что время между двумя последующими
затмениями каждого из спутников Юлитера, по мере увеличения рас-
расстояния между Юпитером и Землёй, постепенно возрастает, а затем,
после того как это расстояние начинает уменьшаться, время это
снова постепенно сокращается. Из-за конечной скорости распростра-
распространения света момент, когда затмение наблюдается на Земле, запазды-
запаздывает, если за время между двумя затмениями расстояние между Землёй
и Юпитером возросло, и наоборот, этот момент наступает раньше,
если расстояние уменьшилось. Однако, для того чтобы из этих нарушений
периодичности определить скорость света, нужно считать, что движе-
движение спутников Юпитера строго периодично, т. е. что их движения
подчиняются законам Ньютона. Между тем вопрос о постоянстве
скорости света должен быть решён до того, как сформулированы
законы движения, ибо для формулировки и проверки законов движе-
движения мы уже должны пользоваться световыми сигналами для отсчёта
времени и должны сделать предположения об их свойствах. Чтобы
пояснить, почему метод Рёмера неудовлетворителен с точки зрения
интересующего нас вопроса о пригодности световых сигналов для
отсчёта времени *), можно привести следующую аналогию. Если мы
уже сформулировали первый закон Ньютона, то мы могли бы «про-
«проверять» постоянство длины линейки, измеряя, проходит ли материаль-
материальная точка, движущаяся по инерции, путь от одного конца линейки
до другого за одно и то же время. Однако, ещё до того, как сфор-
сформулированы законы механики, должны быть установлены способы
измерения расстояний, т. е. должна быть выбрана линейка и должны
быть сделаны предположения о её свойствах.
*) Принципиально так же обстоит дело и с другим астрономическим
методом опоеделения скорости света — по аберрации звёзд (метод Брад-
лея). Он основан на использовании определённых физических представле-
представлений, развивать которые можно только после того, как установлены способы
отсчёта расстояний и времени.

512 механика специальной теории относительности [гл. ххи
Принципиально со скоростью света, как «измерительным инстру-
инструментом», дело обстоит совершенно так же, как с линейкой и часами.
Для того чтобы результаты измерения длин удовлетворяли известным
требованиям повторяемости, однозначности и т. д., линейка, которой
мы пользуемся для этой цели, должна обладать определёнными физи-
физическими свойствами (быть достаточно жёсткой). Но пока для измере-
измерения длин мы пользуемся только линейкой, например, метром, храня-
хранящимся в Палате мер и весов, мы лишены возможности проверить на
опыте, не изменяет ли эта линейка своей длины — длина её, по
определению, постоянна*).
Аналогично для того, чтобы результаты измерения промежутков
времени при помощи часов удовлетворяли известным требованиям,
эти часы должны обладать определёнными физическими свойствами
(движение их должно быть точно повторяющимся). Но пока для
измерения промежутков времени применяются только часы, мы не
можем проверить на опыте, равны ли между собой промежутки вре-
времени, за которые стрелка часов делает полный оборот, — эти проме-
промежутки времени по определению одинаковы. Точно так же и световые
сигналы, при помощи которых мы устанавливаем время, когда «там»
произошло событие, т. е. определяем одновременность двух событий,
происходящих в разных местах, должны обладать определёнными
физическими свойствами, чтобы результаты измерения времени удо-
удовлетворяли требованиям однозначности, повторяемости и т. д. Но
мы не можем, например, проверить на опыте, что скорость света
туда и обратно всегда одинакова—она по определению одна и та
же. Словом, если бы для измерения каждой физической величины мы
располагали только одним методом, мы не могли бы проверить на
опыте свойства того инструмента, при помощи которого эти измере-
измерения производятся. Основное свойство каждого «инструмента» (постоян-
(постоянство длины линейки, хода часов и скорости света) пришлось бы
постулировать.
Однако, в действительности дело обстоит не так. Для отсчёта
времени «там» мы должны пользоваться световыми сигналами. В на-
набор основных «инструментов» для измерения расстояний и проме-
промежутков времени помимо линейки и часов должны входить и световые
сигналы. Но при помощи этих трёх «инструментов» измерения и про-
промежутков времени и расстояний можно производить двумя различ-
*) Конечно, применяя разные линейки и сравнивая их между собой,
мы можем обнаружить, что одни из них изменяют длину по сравнению
с другими, но какую-то линейку (самую жёсткую) мы дожны принять за
эталон и её длина по определению является постоянной. В настоящее время
в качестве эталона длины часто используют длину определённой световой
волны, но это значит лишь, что длина этой световой волны по определению
считается постоянной. Пока мы пользуемся одним и тем же методом изме-
измерения расстояний — сравнением с эталоном длины, Мы должны выбрать
этот эталон и не можем проверить на опыте, остаётся ли его длина посто-
постоянной.

§ 163] РОЛЬ СКОРОСТИ СВЕТА В МЕХАНИКЕ 513
ными методами. Поэтому оказывается возможным, сопоставляя резуль-
результаты измерений двумя различными методами, проверять на опыте
свойства самих инструментов. В самом деле, помимо обычного метода
измерения расстояний с помощью линейки, расстояния можно изме-
измерять при помощи световых сигналов и часов следующим образом.
Для того чтобы измерить расстояние между точками А и В, поме-
поместим в точку А источник коротких световых импульсов, а в точку В
зеркало и с помощью часов будем измерять промежуток времени т,
за который сигнал проходит от А до В и обратно. Тогда расстояние
АВ мы будем считать равным ст/2, где с — скорость света*). Сопо-
Сопоставляя результаты измерения расстояний обоими методами, мы смо-
сможем на опыте проверить свойства одного из трёх основных «инстру-
«инструментов». Например, при помощи световых сигналов и часов мы
можем проверить, остаётся ли постоянной длина линейки в разных
случаях.
Точно так же и измерение промежутков времени, помимо обычного
метода (с помощью часов), принципиально возможно производить, поль-
пользуясь линейкой и световыми сигналами. Для этого на двух штрихах
линейки, находящихся ¦ на расстоянии d, мы поместим два зеркала,
одно параллельно другому. Коротккй световой импульс, посланный
от одного из зеркал, будет «бегать» между зеркалами. Тогда проме-
промежуток времени между двумя последовательными отражениями сигнала
от одного из зеркал мы должны считать равным 2d\c, и для того,
чтобы измерить какой-либо промежуток времени, будем «считать»,
сколько раз за это время сигнал отразился от одного из зеркал.
Такое устройство для измерения промежутков времени можно назвать
«световыми часами». Сопоставляя результаты измерений обычными
и световыми часами, мы сможем также проверить на опыте свойства
одного из основных «инструментов», например, выяснить, остаётся
ли неизменным ход обычных часов при различных условиях или зави-
зависит ли скорость света от направления его распространения. Таким
образом, постулируя свойства одних основных «инструментов», мы
получим возможность проверять на опыте свойства других.
Для такой проверки не всегда необходимо сразу привлекать все
три инструмента. Например, можно проверять свойства световых
сигналов, пользуясь только линейками, или наоборот, проверять
линейки, пользуясь только световыми сигналами (и не привлекая на
помощь часы). Расположив пля некоторым углом друг к другу две
*) Конечно, здесь обсуждаются только принципиально возможные,
а не практически пригодные методы. Если бы такие методы осуществить,
то в большинстве случаев они не могли бы дать той точности, которая
достигается при измерении расстояний с помощью линеек. Впрочем, метод
измерения расстояний с помощью коротких электромагнитных импульсов
приобрёл сейчас большое практическое значение: он применяется во всех
радиолокационных установках для определения расстояния до обнаружен-
обнаруженного объекта (например, самолёта).
33 с. Э. Хайкин

514 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXII
одинаковые линейки с зеркалами на концах и посылая световые
сигналы из вершины угла вдоль обеих линеек, можно устано-
установить, одновременно ли возвращаются в вершину угла оба сигна-
сигнала, отразившиеся от концов линеек. Постулируя постоянство дли-
длины линеек, мы таким способом проверяем, одинакова ли скорость
света в разных направлениях. Наоборот, постулируя постоянство
скорости света, мы проверяем, не изменяется ли длина линеек, если
мы по-разному ориентируем их в пространстве. Существенно, од-
однако, что и в этом случае одним из применяемых «инструментов»
непременно должны быть световые сигналы (часы и линейки сверять
между собой невозможно). И только потому, что световые сигналы
входят в набор основных «инструментов», такая проверка одних «ин-
«инструментов» при помощи других становится возможной.
Эта возможность и была использована для решения кардинального
вопроса о влиянии движения основных «инструментов» на их свойства,
а значит, и на результаты производимых с их помощью измерений.
Производя опыты с движущимися телами, сплошь и рядом приходится
те или иные из основных «инструментов»—линейки, часы или источ-
источники света — связывать с движущимися телами, и поэтому необходимо
знать, изменяются ли при этом, и как именно, свойства самих «инстру-
«инструментов». При решении этого вопроса в классической физике постули-
постулировались свойства одного из основных инструментов — именно, пред-
предполагалось, что линейки не изменяют своей длины при движении.
Опираясь на указанный постулат, классическая физика пыталась
выясннтп на опыте физические свойства третьего основного «инстру-
«инструмента» — определить, как влияет движение источника света на ско-
скорость световых сигналов. Результаты этого опыта заставляют сделать
вывод, что скорость света зависит от скорости источника. Вместе
с тем в классической физике, независимо от этого опыта, постули-
постулировались и свойства часов; предполагалось, что часы не изменяют
своего хода при движении. Так обстоит дело со свойствами основных
измерительных «инструментов» в классической физике*).
Теория относительности, наоборот, отказывается от двух основных
постулатов классической физики (постоянство линеек и часов) и при-
принимает третий возможный постулат — постоянство скорости света. При
*) Постулат о постоянстве хода часов, принятый в классической физике,
всё же не позволяет исключить скорость света из набора основных изме-
измерительных «инструментов». Дело в том, что постулат о постоянстве хода
часов относится к случаю их равномерного движения. Между тем при
переносе часов из одного места в другое они, по крайней мере, в течение
некоторого времени испытывают ускорение. Поэтому после установки часов
в новом месте их необходимо сверить с часами, находящимися «здесь»,
при помощи световых сигналов. При этом было бы необходимо считаться
с тем, что скорость света в классической физике зависит от скорости
источника. Только потому, что классическая физика имела дело со скоростями,
очень малыми по сравнению со скоростью света, можно было не учитывать
зависимости скорости света от скорости источника.

§ 163] РОЛЬ СКОРОСТИ СВЕТА В МЕХАНИКЕ 515
этом о свойствах линеек и часов никаких предположений заранее
не делается; их свойства—влияние движения на длину линеек и ход
часов — должны быть установлены на опыте. И тот же самый опыт,
который при предположении о постоянстве линеек заставляет сделать
вывод, что скорость света зависит от скорости источника, при пред-
предположении о постоянстве скорости света приводит к выводу, что
длина линеек зависит от скорости их движения. Этот опыт, на кото-
который мы ссылаемся, был впервые осуществлён Майкельсоном в 1881 г.;
идею и содержание его мы рассмотрим в следующем параграфе. Сейчас
нам достаточно уяснить себе смысл этого опыта и выводы, которые из
него должны быть сделаны. Смысл опыта сводится к проверке свойств
основных измерительных «инструментов» с помощью других. Вывод
же сводится к альтернативе: либо линейки не изменяют своей длины
при движении, а скорость света изменяется при движении источника,
либо скорость света не зависит от движения источника, а линейки
изменяют свою длину при движении.
Разрешить эту альтернативу, опираясь только на опыт Майкельсона,
невозможно; для того чтобы решить, какое из двух исходных положе-
положений правильно, нужно обратиться к другим опытным фактам. Оказывает-
Оказывается, что мы не можем привести никаких фактов, которые подтверждали
бы, что длина линейки и ход часов не изменяются при движении,
и значит, предположение об изменении длины линейки и хода часов
не противоречит опыту. Правда, изменения эти таковы, что обнаружить
их непосредственным сравнением между собой линеек или часов не-
невозможно. Поэтому нам и кажется необычным такое предположение,
ибо наш непосредственный повседневный опыт, как будто, говорит
иное. Но после того, как мы выясним, как именно изменяются длина
линейки и ход часов при движении, станет очевидным, что наш
непосредственный опыт по этому вопросу вообще ничего не говорит.
С другой стороны, ряд фактов, которые будут приведены ниже,
говорит о том, что скорость света не зависит от скорости источника.
Тем самым альтернатива разрешается в пользу второго положения,
т. е. в пользу теории относительности, которая исходит именно из
постулата о постоянстве скорости света.
Прежде чем приводить факты, заставившие принять этот постулат,
уточним его содержание. Постулат о постоянстве скорости света вклю-
включает в себя прежде всего предположения о том, что при распростране-
распространении светового сигнала «туда» и «обратно» скорость его одна и та же.
Далее постулат о постоянстве скорости света содержит ещё и следую-
следующее утверждение. Если мы при помощи линейки и часов, неподвижных
по отношению друг к другу, будем измерять скорость световых сиг-
сигналов в пустоте, то во всех случаях мы получим один и тот же ре-
результат, независимо от того, движется ли источник света по отношению
к линейке и часам, а также независимо от того, движутся ли линейка,
часы и источник света вместе по отношению к звёздам. Иначе говоря,
постулат о постоянстве скорости света содержит утверждения, что
33*

516 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXII
скорость света не зависит ни от скорости источника, ни от скорости
движения всех приборов вместе.
Мы называем эти положения утверждениями потому, что они могут
быть сопоставлены с опытом и находят себе подтверждение на опыте,
точнее, в астрономических наблюдениях. Первое из утверждений, — что
скорость света не зависит от скорости источника — подтверждается
наблюдениями за двойными звёздами. Линейную скорость двойных
звёзд, обусловленную их вращением вокруг общего центра тяжести,
в тех случаях, когда она направ-
Ф > лена от Земли или к Земле, можно
f ^\ определить по смещению спект-
( \ —. ральных линий, содержащихся в по-
l I \^) Земля сылаемом звездой свете (эффект
\. J Допплера). И если скорость посы-
"*^ • лаемого звездой света зависела
s бы от скорости самой звезды, то
рис 437 эт0 Должно было бы вызвать ви-
видимое нарушение периодичности в
движении двойных звёзд. Действительно (рис. 437), если бы свет от звезды,
находящейся в точке А и приближающейся к Земле, распространялся с
большей скоростью, чем свет от звезды, находящейся в точке В и удаля-
удаляющейся от Земли, то при том огромном расстоянии, которое свет прохо-
проходит, эта разница в скоростях вызвала бы значительную разницу во вре-
временах распространения сигнала. Поэтому свет от точки А проходил бы
за время, много меньшее, чем свет от точки В. Для земного наблюдателя
движение звезды по одной по- „, ,.
_, яг, >¦ Скорость движения солнечной
ЛОВИне Орбиты, ОТ А К В, Про- cuantfiuотносительна звезд
должалось бы дольше, чем . Д
движение по другой половине • О ,° •
орбиты, от В к А. Однако, Сш""# я
такое нарушение периодичности Рис 438
никогда не наблюдалось, и
следовательно, скорость света от скорости источника не зависит.
Второе утверждение, — что скорость света не зависит от скорости
движения всех приборов относительно звёзд, также находит себе
подтверждение в астрономических наблюдениях. Дело в том, что ряд
фактов (в частности, смещение спектральных линий в спектрах звёзд)
указывает на то, что вся солнечная система, как целое, движется по
отношению к звёздам. Поэтому Юпитер со своими спутниками, нахо-
находящийся в какой-то момент в положении А (рис. 438), через шесть
лет окажется в положении В (Юпитер совершает полное обращение во-
вокруг Солнца за 12 лет). Скорость движения солнечной системы, как це-
целого, в положении А направлена навстречу скорости света, идущего
от Юпитера к Земле, а во втором положении В — в ту же сторону.
Если бы общее движение «приборов» (Юпитера и его спутников и
астрономических инструментов на Земле) относительно звёзд сказы-

§ 163 РОЛЬ СКОРОСТИ CBtTA В МЕХАНИКЕ 517
валось бы на скорости света, то должны были бы также наблюдаться
нарушения периодичности спутников Юпитера, но связанные не с го-
годовым движением Земли (как обнаруженные Рёмером), а с годовым
движением Юпитера, т. е. с двенадцатилетним периодом. Однако,
такие нарушения периодичности никогда не были обнаружены и, сле-
следовательно, нужно признать, что скорость света не зависит от дви-
движения всех «приборов» относительно Солнца и звёзд.
Таковы факты, на основании которых в теории относительности
в качестве основного постулата принят постулат о постоянстве скорости
света. В постулат о постоянстве скорости света, как мы видим, входят
высказывания, стоящие в различной связи с опытом — предположение
об одинаковой скорости света при распространении «туда» и «обратно»,
которое не может быть проверено на опыте, и заимствованное из наблю-
наблюдений утверждение о независимости скорости света от скорости
источника и двух других приборов (линейки и часов), движущихся
вместе. Но, поскольку эти различные высказывания касаются одного и
того же вопроса о физических свойствах скорости света, как одного
из трах основных «инструментов», они объединены в единый постулат.
Расхождение между классической физикой и теорией относительно-
относительности, касающееся числа и содержания основных постулатов, является
весьма принципиальным *). Однако, практическое значение этого расхож-
расхождения для всего дальнейшего построения физической теории зависит от
того, какие результаты даёт проверка на опыте' свойств линеек и часов,
после того как постулировано постоянство скорости света. Если бы
при этой проверке на опыте оказалось, что длина линейки и ход часов
не изменяются при их движении, т. е. подтвердились бы те свойства
линеек и часов, которые постулируются в классической физике, то
указанное принципиальное различие между классической физикой и
теорией относительности не имело бы никакого практического значения.
Всё ограничилось бы тем, что постоянство длины линеек и хода часов
можно было бы рассматривать, как опытные факты, а не как постулаты.
Но, как сказано, опыт показывает, что длина линейки и ход часов
изменяются при их движении. Следовательно, основные постулаты клас-
классической физики в теории относительности не фигурируют ни как
исходные постулаты, ни как опытные факты. Наоборот, теория отно-
относительности исходит из полученных опытом данных о том, что длина
линейки и ход часов вполне определённым образом зависят от ско-
скорости их движения. Вследствие этого не только в своих исходных
пунктах, но и во всех выводах, теория относительности существенно
*) Напомним ещё раз сказанное в начале главы: весь вопрос о содер-
содержании основных постулатов классической физики и сущности расхождений
между классической физикой и теорией относительности рассматривается
нами в том освещении, какое он получил в теории относительности.
Только Эйнштейн указал на постулативный характер предположений, о по-
постоянстве длины линеек и хода часов, предположений, которьге в классичес-
классической физике рассматривались не как возможные постулаты, а как заимстоо
ванные из опыта факты.

518 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гл. XXII
отличается от классической физики. Однако, при этом теория отно-
относительности отнюдь не противоречит классической физике и не
отвергает её, но существенно её уточняет. Пока скорости движений
линеек и часов малы по сравнению со скоростью света, эти движения
очень мало изменяют длину линейки и ход часов. Поэтому для мед-
медленных (по сравнению со скоростью света) движений, с которыми мы
обычно имеем дело в макроскопической механике, с достаточной для
практики точностью можно считать длину линейки и ход часов не
изменяющимися при движении. Вместе с тем и вся классическая ме-
механика, которая покоится на этих предположениях, оказывается при-
применимой с вполне достаточной для практики степенью точности.
§ 164. Сокращение размеров тел при движении
С той точки зрения, с какой мы излагаем весь вопрос, цель опыта
Майкельсона состояла, как указывалось, в проверке основных изме-
измерительных «инструментов», а именно, в выяснении влияния движения
«инструментов» на их свойства*).
Идею опыта Майкельсона можно пояснить следующим образом.
Представим себе, что в центре большой сферы, выбеленной изнутри
(т. е. не поглощающей света), находятся наблюдатель и источник
световых сигналов, распространяющихся по всем направлениям. Оче-
Очевидно, что если все направления равноправны, то световые сигналы
одновременно достигнут поверхности сферы и одновременно вернутся
обратно. В какой-то момент времени наблюдатель увидит, что вся
сфера сразу осветилась. Однако, если вся сфера вместе с источником
и наблюдателем движется в каком-то направлении, то равноправие
всех направлений в пространстве может быть нарушено. Нельзя за-
заранее утверждать, что вся сфера осветится одновременно. Возможно,
наблюдатель увидит, что сначала освещаются одни частя сферы, а
затем — другие. Опыт Майкельсона и должен был дать ответ на вопрос,
нарушает ли общее движение сферы, источника света и наблюдателя
равноправие всех направлений в пространстве. Ответ на этот вопрос
был отрицателен. Как и в случае неподвижной сферы, наблюдатель
увидел бы, что вся сфера освещается сразу.
Такова идея опыта. Сам же опыт в действительности был осуще-
осуществлён иначе.
Основная трудность в осуществлении опыта состоит в том, что
влияние движения при малых скоростях не может быть заметно, и
для того чтобы его можно было обнаружить, скорость движения
должна быть не очень мала по сравнению со скоростью света. Наибольшая
скорость макроскопических тел, осуществимая в условиях опыта, со-
*) Конечно, когда первый опыт Майкельсона был задуман и осуществлён
(т. е. до возникновения теории относительности), его цель и содержание
формулировались иначе. Однако, следуя принятому методу изложения, мы
чтих формулировок здесь не приводим,

§ 164] СОКРАЩЕНИЕ РАЗМЕ?ОВ ТЕЛ ПРИ ДВИЖЕНИИ 519
вершенно недостаточна для того, чтобы можно было обнаружить
ожидаемый эффект. Поэтому возникла идея использовать для этой
цели скорость движения Земли по её орбите, которая составляет
около 30 км\сек и значительно превышает все скорости макроско-
макроскопических тел на Земле. Конечно, используя эту скорость, мы не можем
останавливать приборы и снова приводить их в движение. Зато, пово-
поворачивая всю установку в горизонтальной плоскости", мы изменяем
расположение приборов относительно этой скорости. Например, если
установка расположена так, что световыз сигналы распространяются
вдоль направления скорости движения Земли по её орбите, то, по-
повернув установку на 90°, мы достигнем того, ч,то направление
распространения световых сигналов окажется перпендикулярным к на-
направлению скорости движения Земли по её орбите.
В опыте Майкельсона, как ясно из сказанного выше, сущность
опыта заключалась в выяснении вопроса, влияет ли поворот установки
на времена распространения двух световых сигна-
сигналов, из которых один распространяется в направ- ^
лении движения установки, а другой — в перпенди-
кулярном направлении. Пользуясь явлением интер-
интерференции световых волн, можно с очень большой
точностью сравнивать между собой промежутки
времени, за которые свет проходит туда и обратно ^ „л
по различным путям. В последних установках |
для осуществления опыта Майкельсоиа при срав- V »-
нении этим способом двух промежутков времени рис 439
была достигнута точность в 10~18 сек. Однако, в кур-
курсе механики было бы нецелесообразно рассматривать те оптические явле-
явления, которые происходят в установке Майкельсона и позволяют достичь
такой точности *). Поэтому мы заменим реальный опыт Майкельсона
некоторым воображаемым опытом, который принципиально эквивалентен
реальному опыту и должен дать те же результаты.
Представим себе (рис. 439), что на жёсткой плите установлен
источник света S, посылающий во всех направлениях очень короткие
световые сигналы. На двух взаимно перпендикулярных направлениях
установлены зеркала Л и В, отражающие световые сигналы обратно
в точку S. В этой точке, помимо источника света, находится устройство,
позволяющее точно констатировать, одновременно ли возвращаются
в точку 5 световые сигналы, отражённые от зеркал А и В.
Пусть сначала установка ориентирована так, что её скорость v
относительно звёзд, направлена по SA. Зеркала устанавливаются так,
чтобы сигналы, отражённые от зеркал А и В, возвращались в точку S
одновременно. После этого установка поворачивается на 90°, так
что скорость v оказывается направленной по SB. При этом оказы-
*) Описание опыта Майкельсона см. Г. С, Ландсберг, Оптика,
Гостехиздат, 1940 г., § 124.

520 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гл. XXII
вается, что сигналы, отражённые от Л и В, попрежнему возвращаются
в точку S одновременно. Иначе говоря, равенство времён распростра-
распространения сигналов, идущих к зеркалам А и В, при изменении направления
скорости установки v не нарушается.
I vzi. Между тем пути, проходимые световыми
' ', \Г ч/~^"< сигналами, оказываются различными для
*._* ?. „ I сигналов, распространяющихся вдоль ско-
>-vrc. L 1л' рости v и перпендикулярно к ней, так
как за время распространения сигнала
точка S и оба зеркала успевают переме-
переместиться относительно звёзд *).
Нетрудно установить, как связано время распространения сигна-
сигналов с расстоянием от точки S до зеркал. Обозначим расстояния,
на которых были установлены зеркала в начале опыта, соответствен-
соответственно, SA через /' и SB — через /. (Напомним, что эти расстояния
были подобраны так, чтобы оба сигнала одновременно возвра-
возвращались в точку S.)
Найдём сначала время распространения продольного сигнала, рас-
распространяющего вдоль скорости v (т. е. отражающегося от зеркала А
в первой части опыта). Если Z\ — время распространения сигнала от S
до А, то за это время зеркало А' удалится на расстояние vt\ и зай-
займёт положение А', а точка S—положение S' (рис. 440). Световой
сигнал должен будет нагонять зеркало, и если скорость света есть с',
то пройденный им путь с'т1 = /'-|-'г'т1> откуда
;
Если время распространения сигнала обратно, от А' до 5", есть Т2 (за
это время точка 5 пройдёт навстречу сигналу расстояние vz2 и займёт
положение 5"), то пройденный сигналом путь
C'l2 = /' — VT2 ,
откуда
Складывая B2.1) и B2Г.2), получим время т', за которое сигнал про-
проходит путь от S до А и обратно:
B2.3)
*) Мы рассматриваем весь опыт в «неподвижной» системе координат,
связанной со звёздами. Поэтому речь везде будет идти о перемещении при-
приборов и о скорости движения приборов относительно звёзд.

§ 164] СОКРАЩЕНИЕ РАЗМЕРОВ ТЕЛ ПРИ ДВИЖЕНИИ 521
Найдём теперь время распространения поперечного сигнала.
Если тх — время распространения сигнала до зеркала В, то за время тг
точка 5 переместится на от, и займёт положение 5' (рис. 441).
Аналогично, если т2 — время распространения поперечного сигнала
обратно от В до S, то за это время точка S' переместится ещё на
расстояние г>т2 и займёт положение S". За всё время распространения
поперечного сигнала туда и обратно T=T1-f-t2 точка 5 переместится
на расстояние vz.
Если с есть скорость распространения поперечного сигнала, то
весь пройденный сигналом путь
«=»/<ч-(?)>-
откуда
"'=-. B2.4)
Это—время, за которое сигнал проходит путь от S до В и обратно.
Так как в начале опыта / и /' были подобраны так, что т' = т, го
правые части выражений B2.3) и B2.4) должны быть равны:
9/' 9/
11 =-=. B2.5)
При повороте установки на 90° продольный и поперечный сигналы
меняются местами; при этом в равенстве B2.5) меняются местами
/ и /', с и с'. Так как в равенство B2.5) си
с' входят по-разному, то при этой замене равен-
равенство должно было бы нарушиться, если бы
с и с', / и /' оставались неизменными. Между
тем опыт Майкельсона показывает, что равен-
равенство т и т', а значит, и B2.5) не нарушается. / |* *\
Таким образом, из опыта Майкельсона следует, ' ^_ _ ч, „
что при повороте установки изменяются s'
либо расстояния до зеркал, либо скорости
распространения сигнала, причём эти измене-
изменения должны быть такими, чтобы равенство B2.5) рис 441
не нарушалось. Это и есть та альтернатива,
о которой шла речь в предыдущем параграфе. Постулируя постоян-
постоянство одной из этих величин, мы определим из равенства B2.5), как
влияет скорость движения установки на другую из этих величин.
В классической физике, как уже указывалось, постулируется, что
длина линеек и вообще твёрдых тел остаётся постоянной. Принимая
этот постулат, мы должны считать, что / = /', так как если / и /' не
изменяются при повороте установки, то вследствие полной «взаимо-

522 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ |>Л. XXII
заменяемости» обоих положений они должны быть равны. При 1 = 1'
равенство B2.5) даёт:
— % . B2.6)
т. е. с'^>с — скорость продольного светового сигнала больше ско-
скорости поперечного. Таков вывод, к которому приводит классическую
физику опыт Майкельсона.
Теория относительности вместо постулата о постоянстве длины ли-
линеек постулирует постоянство скорости света. На основании этого
постулата мы должны положить с = с', и равенстзо B2,5) даёт:
Так как при повороте / и I' меняются местами, а равенство B2.7)
не нарушается, то величины / и /' при повороте изменяют свои значе-
значения. Именно, продольное расстояние /' при повороте, превращаясь
в поперечное, увеличивается в отношении 1:1/1 ^, а поперечное
/, превращаясь в продольное, уменьшается в отношении 1/1 —^ : 1.
Вместе с тем из формулы B2.7) видно, что при г> = 0 должно быть
1 = 1'.
Итак, на основании опыта Майкельсона теория относительности
приходит к следующему выводу: если при помощи световых сигналов
мы сравниваем размеры двух тел, и пока эти тела неподвижны, размеры
их в каком-либо направлении оказываются одинаковыми, то при дви-
движении одного из этих тел в направлении измеренного размера со ско-
скоростью v рассматриваемый размер движущегося тела по сравнению с
размером тела, оставшегося неподвижным, сокращается в отношгнии
1/ 1—^:1. Размеры тела в поперечном направлении остаются при
этом неизменными.
Более подробное рассмотрение показывает, что во всех остальных
направлениях, кроме поперечного, тоже происходит соответствующее
сокращение размеров, так что твёрдое тело, имеющее в'неподвижном
состоянии форму шара некоторого радиуса га, при движении со скоростью
v превращается в эллипсоид вращения с полуосями г0 1/ 1 — ^ , г0,
г0, причём первая полуось лежит в направлении скорости v. Сокра-
Сокращение продольных размеров тел тем больше, чем больше скорость их
движения, и при v = с продольные размеры тел должны были бы
сокращаться до нуля. Однако, как следует из динамики теории отно-
относительности (ниже это будет показано), скорости тел никогда не
могут достичь скорости света.

§ 164] СОКРАЩЕНИЕ РАЗМЕРОВ ТЕЛ ПРИ ДВИЖЕНИИ 523
Напомним, что мы рассматривали опыт Майкельсона в «неподвиж-
«неподвижной» системе координат, и вывод, к которому мы пришли, пока ка-
касается только движения относительно звёзд: если мы сравниваем рас-
расстояния при помощи световых сигналов, то всякое твердое тело, дви-
движущееся относительно звёзд со скоростью v, сокращается в направлении
движения до размера /01/ 1 —^, где за lQ принят размер этого тела,
когда оно покоится относительно звёзд. Очевидно, что этот вывод,
касающийся всех твёрдых тел, относится также и к линейкам, приме-
применяемым для измерения расстояний. Поэтому, если две линейки, пока
они неподвижны относительно звёзд, имеют одинаковую длину, и мы
примем длину этих линеек за /0, а затем одна из них начинает дви-
двигаться вдоль своего направления со скоростью v, то длина этих ли-
линеек оказывается различной; неподвижная линейка будет иметь длину
/0, а движущаяся—длину
¦='./'-?¦
Именно потому, что все твёрдые тела, в том числе и линейки, дви-
движущиеся с одной и той же скоростью, независимо от их свойств
(упругости, плотности и т. д.) сокращаются одинаково, это сокраще-
сокращение продольных размеров не может быть обнаружено непосредствен-
непосредственным измерением. В самом деле, измеряя длину тела при помощи
линейки, мы должны приложить линейку к телу. В таком случае тело
и линейка движутся с одной и той же скоростью и сокращаются оди-
одинаково; поэтому результаты измерения останутся неизменными. Про-
Производя измерение длины движущихся тел так же, как мы производим
это измерение в случае неподвижных тел, т. е. с помощью линейки,
неподвижной относительно тела, мы не обнаружим происходящего при
движении тел сокращения их продольных размеров.
Правда, принципиально возможно производить измерения длины
движущегося тела при помощи неподвижной линейки. Но при этом
тело будет двигаться относительно линейки, и это будет уже не тот
способ, которым мы пользуемся при измерении длины неподвижного
тела, так как в этом последнем случае тело неподвижно относительно
линейки. Поэтому метод измерения длины в случае, когда тело дви-
движется относительно линейки, нуждается в специальном определении,
которое будет дано ниже.
К выводу о сокращении продольных размеров всех тел при дви-
движении приводит отрицательный результат опыта Майкельсона — отсут-
отсутствие эффекта при повороте установки. Если бы размеры тел не изме-
изменялись при движении, то при повороте установки равенство т = т'
должно было бы нарушиться. Поэтому важно знать, достаточно ли •
точно сравниваются эти времена t hi' и можно ли было обнаружить
разницу между т и т\ если бы она в действительности существовала.

524 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ГгЛ. XXII
В самом деле, если бы оказалось, что разница во временах т и т\
которую вообще можно ожидать, меньше, чем достигнутая в установке
точность сравнения, то, конечно, на основании отрицательного резуль-
результата опыта Майкельсона мы никак не могли бы сделать заключения
о сокращении продольных размеров тел. Легко видеть, что если бы
продольные размеры тел не сокращались, то при повороте прибора
должно было бы увеличиться в отношении 1: 1/ 1—^ время т и
уменьшиться в отношении т/ 1 —\i\ время т', причём отношение т:т'
уже было бы равно не единице, а 1: (\ —^Л. Для опыта Майкельсона
v = 30 км/сек и if2/c2 = l -Ю"8, т. е. необходимо было бы обнаружить
разность времён прихода сигналов в т-10~8 сек. Само время распро-
распространения сигнала в наиболее совершенных установках, на которых про-
производился опыт Майкельсона, составляло около 5-Ю"8 сек (длина пути
луча около 15 м), и разность времён прихода, которая должна была бы
получиться (если бы продольные размеры тел не сокращались) соста-
составила бы 5-10~1в сек. Между тем, при сравнении времён распростра-
распространения сигналов в последней установке, как уже указывалось, была
обеспечена точность в 10~18 сек, т. е. во много раз более высокая,
чем та, которая необходима для обнаружения эффекта, если бы он
существовал. Поэтому отрицательный результат опыта Майкельсона
даёт совершенно надёжные основания для вывода о сокращении про-
продольных размеров тел при движении.
Установив на опыте, как влияет движение линейки на её длину,
мы в случае, когда придётся пользоваться движущейся линейкой,
должны будем учитывать происходящее при этом сокращение длины
линейки.
§ 165. Замедление хода движущихся часов
В опыте Майкельсона часы не участвуют, и поэтому о свойствах
часов этот опыт непосредственно ничего не говорит. Но, как уже указы-
указывалось, принципиально возможно измерять промежутки времени двумя
методами при помощи обыкновенных и световых часов и, постулируя
свойства одних, выяснить на опыте свойства других. Однако, такие
измерения не могли быть произведены с требуемой степенью точности,
и свойства часов невозможно было проверить на опыте так непосред-
непосредственно, как свойства линеек проверяются в опыте Майкельсона. Резуль-
Результаты таких принципиально осуществимых, но ещё не осуществлённых
опытов, пришлось предсказывать из косвенных соображений, опираясь
на какие-либо известные факты. Именно на этот путь стала теория
относительности *).
*) Сейчас установлены факты, касающиеся продолжительности жизни
элементарных частиц — мезонов; эти факты можно рассматривать как пря-

§ 165] ЗАМЕДЛЕНИЕ ХОДА ДВИЖУЩИХСЯ ЧАСОВ 525
Следует отметить, что в классической физике задача сравнения
обыкновенных часов со световыми вообще не ставилась. Поскольку
постоянство хода обыкновенных часов постулируется, а световые часы'
для измерений не применяются, вопрос об их свойствах не возникает.
В теории относительности дело обстоит иначе: о свойствах обыкно-
обыкновенных часов не делается никаких предположений, и эти свойства
должны быть установлены, если не непосредственным опытом, то при
помощи каких-либо косвенных соображений. Эти соображения осно-
основываются на тех положениях, которые содержатся в постулате о по-
постоянстве скорости света. В этом постулате, как указывалось, помимо
предположения об одинаковой скорости света в двух направлениях
(которым, как легко видеть, мы уже пользовались при подсчёте вре-
времён распространения- сигналов в опыте Майкельсона), содержатся ещё
два утверждения, основанные на астрономических наблюдениях. Первое
из них — о независимости скорости света от скорости источника — также
было использовано при толковании опыта Майкельсона. Именно на
основании этого утверждения мы положили с = с' и пришли к выводу
о сокращении продольных размеров тел. Второе же утверждение —
о независимости скорости света от общего движения всех прибо-
приборов относительно звёзд—пока ещё никак не было использовано.
Из него как раз и можно извлечь указания о том, какой результат
должно было бы дать непосредственное сравнение обыкновенных и
световых часов.
В самом деле, утверждение, что, измеряя скорость света при по-
помощи линеек и часов, мы всегда получим одинаковый результат, не-
независимо от общего движения всех приборов (линейки, часов и источ-
источника света), как раз и означает, что обыкновенные и световые часы,
двигаясь вместе, должны итти с одинаковой скоростью. Действительно,
если бы обыкновенные и световые часы, идущие одинаково, когда они
неподвижны, при движении разошлись бы, то это значило бы, что
скорость света, измеренная при помощи линейки и часов, в обоих слу-
случаях различна. Таким образом, на основании постулата о постоянстве
скорости света результат опыта по сравнению обычных и световых
часов может быть предсказан: обыкновенные и световые часы, движу-
движущиеся вместе, должны давать одинаковые показания. Что же касается
влияния движения световых часов на их ход, то на основании опять-
таки постулата о постоянстве скорости света и уже известных нам
свойств линеек, оно тоже может быть предсказано.
мое подтверждение изложенных ниже выводов о влиянии движения йа ход
часов, выводов, к которым теория относительности пришла на основании
косвенных соображений. Подтверждением этих выводов можно считать так-
также поперечный эффект Допплера, обнаруженный на каналовых лучах. Ока-
Оказалось, что скорость движения атома влияет на частоту излучаемого им
света совершенно так же, как скорвсть движения часов влияет на их ход.
Иначе говоря, если бы мы проверяли движущиеся часы по частоте колебаний
движущихся вместе с ними атомов, то мы обнаружили бы как раз такое за-
замедление хода часов, которое было предсказано теорией относительности.

52G МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гл. XXll
Вернёмся для этого к установке, при помощи которой был осуще-
осуществлён опыт Майкельсона. Как мы видели, путь светового сигнала при
движении установки относительно звёзд больше, чем у покоящейся уста-
установки. Если расстояние от точки S до зеркал у покоящейся установ-
установки обозначить через /0, то при движении установки для поперечного сиг-
сигнала это расстояние останется неизменным, т. е. /=/0 и путь светового
1 5- .
С
Для продольного сигнала расстояние /' сокращается в отношении
1/1—%:\, т. е. /' = /„1/1—%. Подставляя это значение /'
У Ci " г С1
в формулу B2.3), найдём, что путь продольного сигнала также ока-
зывается равным 2l0j l/ 1 — -j-. Как и следовало ожидать, пути, про-
проходимые продольным и поперечным сигналом, оказываются одинако-
одинаковыми (в противном случае при одинаковой скорости света сигналы не
могли бы одновременно возвращаться в точку S), но большими, чем
в покоящейся установке, в отношении 1: l/l—^-.
Так как скорость света при движении установки не изменяется, то
промежуток времени, в течение которого сигнал, отправленный из точки S
к одному из зеркал А и В (безразлично какому), возвратится в точку 5,
при измерении с помощью движущихся световых часов увеличится в от-
отношении 1: у 1—qj- по сравнению с неподвижными световыми ча-
часами. Иначе говоря, при движении световых часов ход их замедляется
в отношении 1/ 1 -: 1. Но, по сказанному выше, обыкновенные часы
должны итти так же, как световые. Следовательно, при движении обык-
обыкновенных часов ход их также замедляется в отношении у 1 — — :1.
Отсюда вытекает следующее: пусть у нас есть двое одинаковых
часов, т. е. таких часов, которые, будучи неподвижными относительно
звёзд, идут одинаково. Положим, что одни из часов остаются непо-
неподвижными, а другие движутся со скоростью v. В момент, когда движу-
движущиеся часы поравнялись с неподвижными, мы синхронизуем первые со
вторыми, т. е. установим стрелки движущихся часов в то же поло-
положение, в котором в этот момент находятся стрелки неподвижных ча-
часов*). Вследствие того, что движущиеся часы идут медленнее непо-
1—^:^> когда неподвижные часы будут
*) Такая синхронизация необходима, так как часы могли разойтись при
предшествующем движении. Мы также ничего не знаем о том, как ведут
себя часы в момент начала движения, когда они испытывают ускорение.
Ведь все наши выводы касаются только влияния равномерного движения.

§ 165] ЗАМЕДЛЕНИЕ ХОД\ ДВИЖУЩИХСЯ ЧАСОВ 527
показывать время т с момента синхронизации, движущиеся часы будут
показывать время
t' = t у 1—fj". B2.8)
Это соотношение и устанавливает связь между показаниями непод-
неподвижных и движущихся часов, если время т отсчитывается с момента,
когда они находились в одной точке и показывали одно и то же время.
За время т движущиеся часы отстанут от неподвижных на
т-т'=т^1-|/ 1-jrJ, B2.9)
т. е. по мере движения будут отставать всё больше и больше. По-
Поэтому, если мы будем пользоваться движущимися часами, то чтобы свя-
связать их показания с показаниями неподвижных часов, нужно знать не
только, с какой скоростью движутся часы, но и сколько времени прошло
с момента синхронизации. В этом отношении с измерением времени
дело обстоит сложнее, чем с измерением длин, так как для того,
чтобы связать длину движущегося тела с длиной покоящегося, нужно
знать только скорость движения; время, в течение которого происходит
движение, не играет роли.
При установленном нами способе синхронизации нетрудно в соот-
соотношение между показаниями движущихся и неподвижных часов ввести
то расстояние, на которое успели удалиться часы с момента синхро-
синхронизации. Положим, что неподвижные часы находятся в начале коор-
координат, а скорость движущихся направлена по оси х. Тогда в момент т
они будут находиться в точке x-=vz. Преобразуя формулу B2.8)
и подставляя в неё x = in, получим:
V
хи
S B2.10)
Это соотношение связывает показания движущихся часов, находя-
находящихся в точке х, с показаниями неподвижных часов, находящихся
в начале координат, при условии, что в момент т = 0 движущиеся
часы тоже находились в начале координат и были'установлены на то
же показание, что и неподвижные. Очевидно, что это же соотноше-
соотношение справедливо и для часов, движущихся в противоположном напра-
направлении— в сторону отрицательных значений х. При этом, однако, нужно
считать скорость v отрицательной, произведение vx тогда попрежнему
будет положительным, и движущиеся часы, синхронизованные с непо-
неподвижными в момент прохождения мимо начала координат, попрежнему
будут отставать. Теперь мы вправе применять движущиеся часы, так
как, отсчитывая по ним время т', мы можем с помощью соотношения

528 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гл. XXII
B2.10) найти т, т. е. перейти к показаниям неподвижных часов, ко-
которыми мы условились пользоваться.
Пока мы ввели только одни неподвижные и одни движущиеся часы.
Принципиально этого достаточно, так как, пользуясь световыми сигна-
сигналами, мы могли бы как по неподвижным, так и по движущимся часам
отсчитывать время, когда «там» произошло событие. Не отказываясь
от этого метода, мы введём, однако, и другой метод, который практи-
практически часто применяется, а главное поможет нам отчётливее представить
себе результаты отсчёта времени «там» по движущимся часам. Расста-
Расставим множество часов в разных точках пространства и будем отсчиты-
отсчитывать время события в каждой точке по часам, находящимся в этой
точке. Для того чтобы так отсчитывать время в любой точке, мы
должны именно заранее расставить часы во все точки пространства,
так как переносить часы с места на место в процессе измерений мы
не имеем права. В самом деле, всякое движение часов вызывает замед-
замедление их хода, и поэтому после переноса часы будут показывать не то,
что они показывали бы, если бы их не переносили*). Поэтому мы
должны не только расставить часы по местам, но после того, как они
расставлены, синхронизовать их, т. е. установить так, чтобы они по-
показали одно и то же время. Способ синхронизации часов, находящихся
в разных местах, вытекает непосредственно из определения одновре-
одновременности двух событий, происходящих в разных местах, ибо синхронно
идущими мы ведь и называем такие часы, стрелки которых одновре-
одновременно проходят через одно и то же положение. В соответствии
с определением одновременности, принятым в физике (см. § 000),
двое часов А и В идут синхронно, если световой сигнал, отправлен-
отправленный от часов А в момент, когда они показывают время т, достигает
часов В в момент, когда эти последние показывают время
где с — скорость света, а х — расстояние между часами А и В,
измеренное обычным способом, т. е. при помощи линейки.
Пользуясь световыми сигналами, можно, таким образом, синхрони-
синхронизовать все часы, расставленные в разных местах, по каким-либо одним
часам; при этом нужно измерить расстояние от этих последних часов
до всех остальных. Можно, однако, обойтись без этого измерения,
определяя расстояние также при помощи световых сигналов, которые,
достигнув часов В, отражаются от находящегося здесь зеркала и
снова возвращаются в А. Если в момент отправления сигнала часы А
показывают время т, а в момент возвращения T-f-Дт, то в момент,
когда этот световой сигнал достигает часов В, они должны быть
*) Здесь также де/.о осложняется ещё тем, что мы не знаем, как дей-
действуют на часы ускорения, неизбежные в начале и в конце переноса.

§ 165] ЗАМЕДЛЕНИЕ ХОДА ДВИЖУЩИХСЯ ЧАСОВ 529
установлены на время
т' = т + у. B2.12)
Таким образом, мы можем синхронизовать любую пару часов, не
зная заранее расстояния между ними и не зная даже скорости света
(используя лишь предположение, что она одинакова в обе стороны).
В этом смысле второй способ синхронизации обладает преимуществом
перед первым. Но принципиально они эквивалентны, ибо, в соответст-
соответствии с постулатом о постоянстве скорости света, величина х\с в вы-
выражении B2.11), где расстояние между часами х измерено при по-
помощи линейки, всегда будет равна величине Дт/2 в выражении B2.12),
где Дт — время распространения сигнала от одних часов до других
и обратно.
Пользуясь световыми сигналами, мы можем синхронизовать тем
или другим из указанных способов не только любую пару часов, не-
неподвижных относительно звёзд, но и любую пару часов, движущихся
вместе с одинаковой скоростью относи-
относительно ззёзд. Но в этом последнем слу- V, Л__
чае, если мы пользуемся способом син-
хронизации, соответствующим выражению
B2.11), то измерение х следует произво-
производить при помощи линейки, движущейся
вместе с часами.
После того, как установлен способ
синхронизации нескольких движущихся *
вместе часов, может возникнуть вопрос о
связи между показаниями любых из этих
движущихся часов и часов неподвижных.
Представим себе двое часов В и С, движущихся вместе с одинаковой
скоростью v мимо неподвижных часов А в направлении оси д:(рис. 442).
В момент, когда часы В поравняются с часами А, сверим их между собой.
Для простоты положим, что в этот момент и те и другие установлены
на 00 час. 00 мин. Одновременно с установкой на нуль часов А и В
отправим из А световой сигнал для синхронизации часов С. По уста-
установленному способу синхронизации часов в момент прихода сигнала
часы С должны быть установлены на время т'—- х'\с, где х'—расстоя-
х'—расстояние между часами В я С, измеренное при помощи линейки, движу-
движущейся вместе .с ними. Связь между показаниями часов А и В нам
уже известна — она даётся соотношением B2.10), которое получено
именно для применённого нами способа синхронизации часов А и В
(в момент, когда они поравнялись). При этом может возникнуть вопрос:
справедливо ли это соотношение для часов А и С? Для ответа на
этот вопрос мы должны в соотношении B2.10.) подставить вместо х
то расстояние от часов А, на котором находятся часы С в момент
прихода синхронизующего сигнала, а вместо т—показания часов А
в этот момент.
34 С. Э. Хайкин

530 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XX»!
Произведя эти подстановки, мы убедились бы, что соотношение
B2.10) даёт как раз то значение т', на которое должны быть уста-
установлены часы С в момент прихода синхронизующего сигнала для
Того, чтобы они были синхронны с часами В. Иначе говоря, можно
доказать, что если мы имеем ряд часов, движущихся вместе с одина-
одинаковой скоростью v вдоль оси х и синхронизованных между собой при
помощи световых сигналов, то показания любых из этих часов, когда
они находятся в точке с координатой х, связаны с показаниями непо-
неподвижных часов, находящихся в начале координат, соотношением B2.10),
причём время х отсчитывается от момента, когда была произведена
синхронизация одних из движущихся часов по неподвижным и был
послан синхронизующий сигнал для синхронизации всех движущихся
часов между собой *).
Из всего сказанного следует, что, сравнивая между собой несколько
часов, движущихся с одинаковой скоростью, мы никогда не сможем
обнаружить влияния этого движения на ход часов. Не только ско-
скорость хода всех часов будет одна и та же (изменится одинаково),
но и синхронизация часов не нарушится. Так же, как нельзя обнару-
обнаружить сокращения длины линеек, сравнивая между собой только дви-
движущиеся вместе линейки, нельзя обнаружить изменения хода часов,
сравнивая между собой только движущиеся вместе часы.
§ 166. Принцип относительности
Если принять постулат о постоянстве скорости света, то опыт
Майкельсона, как мы убедились, показывает, что длина движущейся
линейки меньше, чем такой же неподвижной, и ход движущихся ча-
часов медленнее, чем таких же неподвижных. При этом, хотя в опы-
опыте Майкельсона идёт речь о линейках, движущихся или непо-
неподвижных относительно звезд, всё же он оставляет открытым следую-
следующий весьма существенный вопрос: обусловлен ли эффект сокраще-
сокращения длины линейки и замедления хода часов их движением
относительно звёзд или же он является следствием их движе-
движения относительно неподвижных линейки и часов? Иначе говоря,
играет ли принципиальную роль то, что в опыте Майкельсона фигу-
фигурирует скорость относительно звёзд, и получили ли бы мы тот же
результат, если бы могли осуществить опыт Майкельсона с прибо-
приборами, движущимися, например, относительно Земли, а не относительно
звёзд? Поскольку этот второй опыт не осуществлён, прямого ответа
на поставленный вопрос нет, и приходится снова прибегать к косвен-
косвенным соображениям для того, чтобы этот ответ дать. Нужно рассмо-
*) Нетрудно убедиться, что вывод справедлив и для часов С, располо-
расположенных сначала где-либо со стороны отрицательных значений х. Именно по-
поэтому синхронизовать с неподвижными можно любые из движущихся часов.
Существенно лишь, в какой момент проведена эта синхронизация, так как
с него начинается отсчёт времени.

§ 166] ПГИНЦИП ОТНОСИТЕЛЬНОСТИ
531
треть оба возможных ответа, выяснить, как согласуются они с дру-
другими известными нам фактами, и на этом основании выбрать один из
ответов.
Рассмотрим первый возможный ответ: эффект сокращения линеек
и замедления хода часов обусловлен их движением относительно
звёзд. Так как это движение равномерное, то система координат,
связанная со звёздами, оказывается принципиально выделенной из
всего класса инерциальных систем координат. В системе координат,
связанной со звёздами, неподвижная линейка была бы длиннее, и не-
неподвижные часы шли бы быстрее, чем линейки и часы, связанные со
всякой другой инерциальной системой координат. Сравнивая между
собой всевозможные линейки и часы, движущиеся друг относительно
друга, мы могли бы в таком случае по этому признаку из всех инер-
инерциальных систем координат выделить ту, которая связана со звёздами.
Иначе говоря, должны были бы существовать какие-либо опыты, ко-
которые в системе координат, связанной со звёздами, давали бы не
тот же результат, что и в других инерциальных системах координат.
Словом, принципиально было бы возможно на опыте обнаружить
прямолинейное и равномерное движение приборов относительно звёзд.
В опыте Майкельсона это движение не обнаруживается лишь потому,
что происходит соответствующее сокращение продольных размеров
твёрдых тел, но это лишь «случайное» обстоятельство. В каких-либо
других опытах прямолинейное и равномерное движение приборов от-
относительно звёзд может быть обнаружено. Принцип относительности
Галилея неверен — он соблюдается лишь приблизительно; при равномер-
равномерном прямолинейном, но достаточно быстром движении приборов от-
относительно звёзд, когда станет заметным сокращение линеек и за-
замедление хода часов, явления могут протекать не так, как в случае
приборов, покоящихся относительно звёзд. Таковы выводы, к которым
приводит предположение, что эффект сокращения линеек и замедле-
замедления хода часов обусловлен движением относительно звёзд.
На этой именно точке зрения стоял Г. А. Лорентц, который ещб
ранее Эйнштейна установил, что опыт Майкельсона указывает на со-
сокращение длины линеек и замедление хода часов.
Эта точка зрения, хотя и содержит совершенно новые для клас-
классической физики представления о сокращении длины линеек и за-
замедлении хода часов, по существу всё же сохраняет характерное
для классической физики представление об особом положении системы
координат, связанной со звёздами. Это особое положение системы
координат, связанной со звёздами, отражалось на всей картине элек-
электромагнитных явлений в классической физике. С точки зрения клас-
классической физики все электромагнитные явления (в том числе и све-
световые) протекают в электромагнитном эфире, заполняющем пространство
и неподвижном относительно звёзд. Особое положение системы ко-
координат, связанной со звёздами, с точки зрения классической элек-
электродинамики обусловлено именно тем, что в этой системе координат
34*

532 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXII
эфир неподвижен. Но тогда приборы, движущиеся относительно звёзд,
движутся и относительно эфира, и можно попытаться обнаружить это
движение.
Опыт Майкельсона раньше рассматривали именно как одну из по-
попыток обнаружить это движение («эфирный ветер»). Но «эфирный
ветер» не был обнаружен не только в опыте Майкельсона, но
и в ряде других электрических опытов, которые были предприняты
с той же целью. Более того, эти опыты приводили к явному проти-
противоречию — для объяснения их нужно было бы предположить, что
эфир покоится по отношению к двум разным комплектам приборов,
которые движутся друг относительно друга. Таким образом, сама по-
постановка вопроса о движении эфира или о движении относительно
эфира приводит к противоречиям.
Но, если нельзя говорить о движущемся или покоящемся эфире,
то с точки зрения электродинамики нет никаких оснований выделять
систему координат, связанную со звёздами.
Поскольку не удаётся не только обнаружить на опыте прямоли-
прямолинейное и равномерное движение относительно звёзд, но и вообще
выделить по каким-либо признакам систему координат, связанную со
звёздами, нужно признать, что эта система координат с точки зрения
электродинамики, так же как и с точки зрения механики, ничем не
отличается от всех других инерциальных систем координат.
Следовательно, принцип относительности Галилея не только верен,
но должен быть распространён на все физические явления (а не на
одни лишь механические, для которых он был сформулирован Гали-
Галилеем). Иначе говоря, во всех системах координат, движущихся прямо-
прямолинейно и равномерно друг относительно друга, любые физические
явления должны протекать одинаково и любые физические опыты
должны давать одинаковый результат.
Это положение получило впоследствии название специального
принципа относительности, так как оно относится к специальному
случаю прямолинейного и равномерного движения. (Более общий
принцип, охватывающий случаи ускоренного движения систем ко-
координат, был назван «общим принципом относительности».) По-
Поэтому все физические законы должны иметь такой вид, чтобы они
удовлетворяли специальному принципу относительности. В частности,
все законы должны выглядеть одинаково как для системы координат,
связанной со звёздами, так и для любой системы координат, движу-
движущейся относительно звёзд прямолинейно и равномерно. Все эти си-
системы координат равноправны, и движение без ускорения относительно
звёзд не может играть никакой специальной роли. Если в каких-либо
явлениях играет роль скорость прямолинейного и равномерного дви-
движения, то это может быть только скорость одних приборов отно-
относительно других, а никак не скорость их движения относительно звёзд.
Такова точка зрения, которая была сформулирована А. Эйнштейном
и принята в теории относительности.

§ *66] ПРИНЦИП ОТНОСИТЕЛЬНОСТИ 533
Очевидно, принцип относительности даёт однозначный ответ на
вопрос, поставленный в начале этого параграфа. Эффект сокращения
длины линеек и замедления хода часов может быть обусловлен только
их движением относительно тех «неподвижных» линеек и часов, с ко-
которыми мы сравниваем движущиеся линейки и часы. И в формулах,
выражающих сокращения длины линейки и замедление хода часов,
скорость v есть скорость движения одной линейки по отношению
к другой, или одних часов по отношению к другим, а не скорость
их движения по отношению
к звёздам. При этом, по- ^7\а' .» &С^
скольку все системы коор- ^ч^ - -*+^
динат равноправны, мы мо-
жем любую из двух движу- ' /^7\а t й
щихся друг относительно \Л/
( )
щихся друг относительно \Л
друга линеек (или часов) Г
Т
считать неподвижными. Тог- р ..,
да вторая линейка, которая
движется относительно выб-
выбранной нами за неподвижную, будет короче, и вторые часы, которые дви-
движутся относительно выбранных нами за неподвижные, будут идти медлен-
медленнее. Наоборот, если мы вторую линейку и вторые часы примем за непо-
неподвижные, то первая линейка окажется короче второй и первые часы бу-
будут идти медленнее вторых. Чтобы
пояснить эти выводы, рассмотрим
следующий конкретный случай.
Возьмём две одинаковые ли-
линейки, которые, будучи измерены
при помощи неподвижного мас-
масштаба, имеют одинаковую длину
хй, и две пары часов, которые,
Рис. 444. «с. 445. будучи неподвижны друг отно-
относительно друга, имеют одина-
одинаковый ход. Укрепим на концах каждой из линеек по паре
часов и заставим одну из линеек L' с часами А' и В' дви-
двигаться относительно другой линейки L с часами А и В с относи-
относительной скоростью v (рис. 443). В момент, когда часы В' поравня-
поравняются с часами А, синхронизуем часы В' с часами А. Для упрощения
положим, что в этот момент и те и другие часы показывают 00 час,
00 мин., а точку, в которой они находятся, примем за начало коор-
координат. В момент, когда мы синхронизуем часы В' с часами А, по-
пошлём из точки, где они находятся, световой сигнал для синхрониза-
синхронизации часов В с часами А и часов А' с часами В'. Это — те же самые
методы синхронизации, которые мы применяли в предыдущем пара-
параграфе, и поэтому для связи между показаниями различных часов
справедливо полученное там соотношение B2.10). Пользуясь этим со-
соотношением и учитывая происходящее при движении линеек сокра-

534 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXII
щение их длин, мы найдём показания различных часов в моменты,
когда часы А' совпадают с часами А (рис. 444) и когда часы В'
совпадут с часами В (рис. 445). Для определённости будем сначала
считать неподвижной линейку L с часами А и В. Так как линейка U
движется, то длина её сокращена до х0 |/ 1— -'-, и значит, путь,
который должны пройти часы А', чтобы поравняться с часами А:
S= хоу\ — v~. Так как движение происходит со скоростью v,
то оно будет продолжаться время Sjv, и в момент, когда часы А'
поравняются с часами А, эти последние будут показывать время
~7> B2.13)
Показания движущихся часов А1 в момент, когда они поравня-
поравняются с часами А, т. е. находятся в точке jc = O, мы найдём из со-
соотношения B2.10), подставив в него х = 0 ит из B2.13):
т = тл __ _?о
~э v ' B2.14)
Как видно, на показаниях часов А' никак не сказывается движение
линейки и часов. Они показывают то же время, что и в случае, если
бы линейка не изменяла своей длины, а часы не изменяли своего хода.
Поскольку мы считаем неподвижной линейку L, этот результат объ-
объясняется тем, что сокращение длины линейки L' и замедление хода
часов А' как раз компенсируют друг друга. Если бы мы выбрали
в качестве неподвижной линейку L', то это означало бы, что часы А
должны пройти путь х0, равный длине покоящейся линейки L', а часы А',
как покоящиеся, не изменяют своего хода, поэтому они и должны
показывать время xg[v. Итак, мы нашли показания часов А и А'
в момент, когда они поравнялись.
Найдём теперь показания часов В и В' в момент, когда они по-
поравняются. Опять будем сначала считать неподвижной линейку L.
Часы В' должны пройти всю длину х0 покоящейся линейки, чтобы
поравняться с часами В, и в этот момент часы В покажут время
*в= ? ¦ B2-15)
Это же время покажут и часы А, находящиеся в начале координат
(так как часы Л и В неподвижны и синхронизованы). Следовательно,
показания часов В' в момент, когда они поравняются с часами В,
мы можем определить из соотношения B2.10), где под х следует по-
понимать показания часов А или В, т. е. хв, а под х — расстояние

§ 166] принцип относительности 535
точки В от начала координат, т. е, х0. После подстановки и простых
преобразований получим:
Если снова считать неподвижной линейку V, этот результат также
очевиден. В этом случае для совпадения В с В' точка В должна
пройти всю длину движущейся линейки L, т. е, хол/ 1 — ~ , Итак,
мы нашли также показания часов В и В' в момент, когда они порав-
поравнялись. Посмотрим теперь, какие выводы можно сделать из сопоста-
сопоставления всех этих показаний.
Прежде всего мы можем сравнить ход движущихся часов с хо-
ходом часов неподвижных. Для этого мы должны сравнить показания
проверяемых часов сначала с показаниями одних, а затем других
часов, мимо которых эти проверяемые часы проходят (само собой
разумеется, что часы, с которыми сверяются, должны быть синхронизо-
синхронизованы друг с другом). Сверим сначала движущиеся часы В' с систе-
системой неподвижных часов А, В. При первом сопоставлении, когда часы В'
находились против часов А, их показания, по условию, совпадали.
Второе сопоставление может быть произведено в момент, когда
часы В' поравнялись с часами В. Как видно из сопоставления выра-
выражений B2.15) и B2.16), в этот момент часы В' показывают время
-?. B2.17)
Как и следовало ожидать, движущиеся часы идут медленнее системы
неподвижных часов А, В в отношении л/ 1 — %-'Л и отстают от не-
подвижных на соответствующую величину.
Будем теперь считать неподвижной систему часов А'В'. Тогда
с ними можно сверить движущиеся часы А, показания которых сна-
сначала сопоставляются с часами В', и, по условию, эти показания со-
совпадают, а затем с часами В в момент, когда они поравнялись друг
с другом. Как видно из выражений B2.13) и B2.14), в этот момент
часы А показывают время
Тл=т*/Йт. B2Л8)
т. е. и в этом случае движущиеся часы А идут медленнее системы
неподвижных часов А', Ь' также в отношении 1/ 1 : 1 и отстают
от них. Таким образом, как бы мы ни выбирали систему неподвижных

536 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXII
часов, мы обнаруживаем, что часы, движущиеся относительно этих
неподвижных, идут медленнее их.
Вообще, если у нас есть две системы синхронизованных часов,
движущихся одна относительно другой, одна А, В, С,... и другая
L, M, N,... и если мы выберем систему часов А, В, С,... за не-
неподвижную, то часы L, М, N,.. . будут идти медленнее, чем А, В, С,...
и отставать от них. Наоборот, если мы выберем за неподвижную си-
систему часов L, M, N,..., то часы А, В, С,... будут идти медленнее,
чем L, М, М,... и будут отставать от них. Так как обе системы часов
совершенно равноправны, то любую из них мы можем выбрать за
неподвижную и по ней производить отсчет времени. Но результаты
отсчёта времени по часам А, В, С,... или L, M, N,... будут различны.
Так же, как нельзя указать избранной абсолютной системы координат,
нельзя указать избранной абсолютной системы часов для отсчйта вре-
времени. Отсчет времени так же относителен, как, например, отсчёт ско-
скорости,— он зависит от того, по какой системе часов мы будем отсчи-
отсчитывать время, так же, как отсчёт скорости зависит от того, какую си-
систему координат мы выберем за неподвижную. Более того, не только
показания часов А, В, С,... и L, М, Л',... в момент, когда произошла
какое-либо событие, будут различны, но и промежутки времени, про-
протекшие между какими-либо двумя событиями, отсчитанные по этим
двум системам часов, будут различны. Это видно непосредственно из
соотношения B2.10), которое как раз связывает результаты отсчёта
промежутка времени между двумя событиями по часам А, В, С,...
и по часам L, М, Л/,... Из этого соотношения видно, что не только
промежутки времени т и т' различны, но когда т = 0, то, вообще
говоря, т'т^О. Если промежуток времени между двумя событиями т = 0,
то это значит, что оба события происходят одновременно, если
же х' =? 0, то, значит, те же соэытия происходят разновременно.
События одновременные при отсчете времени по одной системе часов
оказываются неодновременны ли при отсчёте времени по другой си-
системе часов. Как видно из соотношения B2.10), только в случае * —0
события, одновременные в одной системе часов, оказываются одно-
одновременными и в другой. Но это — случай тривиальный; он соответ-
соответствует тому, что оба события происходят в одном месте. Если
же два события происходят в разных местах, то они могут быть
одновременными только при отсчете времени по какой-либо одной
системе часов. При отсчёте времени по всякой другой системе часов,
движущейся по отношению к первой, эти же события оказываются
неодновременными. Понятие одновременности так же относительно,
как и понятие покоя: оно имеет смысл, только если указана система
часов, по которой производится отсчёт времени, — так же как поня-
понятие покоя имеет смысл, только когда указана система координат,
относительно которой тело покоится.
Таким образом, принцип относительности придаёт всему вопросу
об отсчёте времени совсем нозый смысл. С точки зрения Лорентца

§ 166] принцип относительности 537
эффект замедления хода часов являлся совершенно побочным и не
принципиальным. По часам, неподвижным относительно звёзд, с точки
зрения Лорентца можно отсчитывать абсолютное время. Понятие одно-
одновременности сохраняет абсолютный смысл: события, одновременные
по часам, неподвижным относительно звёзд, можно считать «абсолютно»
одновременными, так же как и время, отсчитываемое по этим часам.
Словом, с точки зрения Лорентца, всё дело сводится к тому, что
часы, движущиеся ртносительно звезд, начинают «врать». Пользуясь
этими часами, нужно вводить соответствующую поправку и приводить
их показания к «абсолютному» времени, отсчитываемому по часам,
неподвижным относительно звёзд. Само же «абсолютное» время
сохраняет свой прежний смысл, который в него вкладывала класси-
классическая физика еще со времён Ньютона.
Однако, как показал А. Эйнштейн, весь вопрос гораздо глубже.
Дело не в том, что какие-то одни часы начинают «врать». Самый
способ отсчёта времени, которым пользуются в физике, — по часам,
синхронизованным между собой световыми сигналами, — таков, что
результат отсчёта времени всегда относителен — он зависит от вы-
выбора системы часов. А так как все системы часов равноправны,
у нас нет никаких оснований выделять ту или иную из них, и по-
поэтому отсчёту времени нельзя придать абсолютного характера. Сле-
Следовательно, и понятие одновременности является относительным.
В том виде, как оно применялось в классической физике, как аб-
абсолютное понятие, оно не имело определённого содержания; вернее —
в различных случаях в него вкладывалось различное содержание.
Именно поэтому классическая физика пришла к принципиальным про-
противоречиям, разрешить которые удалось только теории относитель-
относительности, после того как было уточнено понятие одновременности.
Пересмотр всего вопроса об отсчёте времени и, в частности, об
одновременности событий является одной из наиболее глубоких ре-
реформ, которые внесла в физику теория относительности.
Перейдем теперь к сопоставлению длины линеек. Напомним, что
по условию обе линейки, когда они покоятся, имеют одинаковую
длину х0. Не требуется никакого детального определения того, что
это означает. Если покоящиеся линейки имеют одинаковую длину,
то, уложив их так, чтобы концы А и А' совпадали, мы обнаружим,
что концы В и В' тоже совпадают. При этом, так как линейки не-
неподвижны, то после такого укладывания концы Л и Л' и концы В и В'
всегда будут совпадать. Вопрос о времени не возникает; две непо-
неподвижные линейки можно сравнивать непосредственно, не применяя ни-
никаких других инструментов.
Иначе обстоит дело с движущимися линейками. Положим, что
в какой-то момент концы А и А' двух линеек совпадают. Очевидно,
линейки следует считать равными, если в этот же момент совпа-
совпадают другие их концы В и В'. Следовательно, нужно отметить вре-
время каждого из двух событий, происходящих в разных местах,—

538 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [ГЛ. XXII
совпадение концов А и А' и концов В и 5'. Если эти события
произошпи одновременно, то линейки имеют одинаковую длину. Если
же эти события произошли в разное время, то в зависимости от того,
какое из них произошло раньше, а какое позже, мы сможем устано-
установить, какая из линеек длиннее. Иначе говоря, при непосредственном
сравнении длины двух линеек, из которых одна движется относительно
другой, необходимо пользоваться часами для отсчёта моментов вре-
времени, когда совпадают концы линеек.
Часы должны быть расставлены по концам линеек, чтобы по ним
можно было отсчитывать момент, когда «здесь» произошло это со-
событие*). Ясно, что рассмотренный нами выше случай — две линейки
с часами по концам — как раз даёт возможность сравнить между со-
собой длину линеек. Для этого нужно сопоставить между собой
показания часов А и А', В и В' в моменты, когда концы линеек
поравнялись друг с другом. При этом каждый раз мы должны поль-
пользоваться неподвижными часами, т. е. часами, связанными с той ли-
линейкой, которую мы считаем неподвижной. В первом случае, когда
линейка L неподвижна, а Ц движется мимо неё, мы должны отсчи-
отсчитывать показания но часам А и В. Как видно из выражений B2.13)
и B2.15),
Тл=^в}А-?. B2.19)
Так как тл< те, то концы А и А' линеек поравнялись раньше, чем
концы В и В'. В момент, когда поравнялись концы А и А', конец В'
еще не достиг конца В, а это и значит, что линейка U короче L.
Во втором случае, когда линейка U неподвижна, a L движется мимо
нее, нужно отсчитывать показания по часам А' и В'. Как видно из
выражений B2.14) и B2.16),
Ъ = ТД. |Л-?. B2.20)
Так как та, <Гтл„ то концы линеек В и В1 поравнялись раньше,
чем концы А и Л'. В момент, когда поравнялись концы В и В',
конец А ещё не достиг конца А', а это и значит, что лииейка L
короче линейки U. Так как соотношения B2.19) и B2.20) между
хА и те, с одной стороны, и те, и 1А„ с другой,— одинаковы, то очевидно,
что и сокращения длины движущейся линейки в обоих случаях оди-
одинаковы. Как и должно быть, в обоих случаях движущаяся линейка
короче неподвижной в отношении л/ 1 — 5L ; 1,
*) Вместо часов, расставленных по концам линеек, мы могли бы поль-
пользоваться световыми сигналами, дающими знать о том, когда «там» произо-
произошло событие. Но поскольку мы пользуемся часами, синхронизованными
при помощи световых сигналов, результаты рассмотрения в обоих случаях
должны быть одинаковы. Рассмотрение же в случае расставленных заранее
часов более наглядно.

§ 166] ПРИНЦИП ОТНОСИТЕЛЬНОСТИ 539
Как мы видим, при сравнении длины двух линеек, движущихся
одна относительно другой, всё дело в том, что совпадение концов
А и А' и В и В' происходит не одновременно при отсчёте времени
как по часам А и В, так и по часам А' и В'. При этом по часам
А и В раньше совпадают концы А и А' и позже концы В и В'.
Наоборот, по часам А' и В' раньше совпадают концы В и В' и позже —
концы А и А'. Поэтому-то результат сравнения длины линеек зави-
зависит от того, какими часами мы пользуемся для отсчета времени, т. е.
какую линейку и часы мы считаем неподвижными. Результат сравне-
сравнения длин движущихся линеек самым тесным образом связан с отно-
относительностью отсчёта времени и понятия одновременности двух со-
событий.
Итак, какую бы из линеек мы ни выбрали за неподвижную, вто-
вторая линейка, движущаяся мимо неподвижной, оказывается короче.
Длина линеек так же относительна, как и ход часов, — она зависит
от того, какую из линеек мы будем считать неподвижной, а какую
движущейся. При этом, в полном соответствии с принципом относи-
относительности, все системы координат, движущиеся прямолинейно и рав-
равномерно друг относительно друга, действительно оказываются совер-
совершенно равноправными в отношении поведения линеек и часов. Для
каждой из систем координат получаются одни и те же соотношения
между длинами линеек и ходом часов, покоящихся в этой системе
координат и движущихся относительно неё.
В заключение рассмотрим приведённый нами выше конкретный
пример с точки зрения тех общих соображений, которые были из-
изложены в § 163. Две линейки с часами на концах представляют со-
собой модель опыта, при помощи которого, казалось бы, можно непо-
непосредственно сравнивать длины неподвижной и движущейся линеек
и ход неподвижных и движущихся часов без участия световых сиг-
сигналов. Прежде всего следует отметить, что этот воображаемый опыт
никогда не был произведен и не может быть произведён с требуемой
степенью точности при современных экспериментальных средствах.
Мы можем предсказать, что дал бы этот опыт, только основываясь
на результатах фактически произведённого опыта Майкельсона. Од-
Однако, с принципиальной точки зрения существенно не это, а другое.
Дело в том, что часы, установленные на концах линеек, должны
быть синхронизованы между собой, так как в противном случае весь
опыт не имеет смысла. А для синхронизации часов, находящихся
в разных местах, у нас нет никаких, других средств, кроме световых
сигналов. Поэтому, если бы мы, пользуясь световыми сигналами для
синхронизации часов, не высказывали заранее никаких постулатов
о свойствах световых сигналов, то наш воображаемый опыт, так же
как опыт Майкельсона, можно было бы толковать либо как проверку
свойств линеек и часов при помощи световых сигналов, либо как
проверку свойств световых сигналов при помощи линеек и часов. Так,
сопоставление показаний одних часов, положим В', с показаниями

540 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXII
двух часов А а В можно рассматривать либо как проверку часов В',
если мы заранее считаем, что часы А а В синхронизованы (поскольчу
они сверены при помощи световых сигналов), либо как проверку син-
синхронности часов Аи В, если мы заранее предполагаем, что часы В' не
изменяют своего хода при движении. Но это второе толкование и озна-
означало бы, что мы проверяем свойства световых сигналов — их пригод-
пригодность для синхронизации часов. Точно так же сопоставление показаний
часов А и"/1' и В и В' в моменты, когда они поравнялись, можно
было бы рассматривать либо как сравнение длины двух линеек, если
заранее считать, что часы А и В и А' и В' попарно синхронизо-
синхронизованы, либо опять как проверку синхронности часов, если мы заранее
предполагаем, что линейки не изменяют своей длины при движении.
Это второе толкование опять означало бы, что мы проверяем свой-
свойства световых сигналов при помощи линеек и'часов.
Как видим, дело обстоит именно так, как было изложено в § 163.
Комплект основных измерительных «инструментов», необходимых для
измерения расстояний и промежутков времени—линейки, часы и све-
световые сигналы — даёт возможность производить несколько независи-
независимых измерений, результаты которых должны быть известным образом
связаны между собой. Поэтому, производя эти измерения, мы полу-
получаем возможность проверить на опыте свойства одних измеритель-
измерительных «инструментов» при помощи других.
§ 167. Кинематику теории относительности
Для различных наблюдателей, движущихся друг относительно
друга, физические явления могут протекать по-разному. Однако, фи-
физические законы, управляющие этими явлениями, не могут зависеть
от движения наблюдателя. Это общее положение для частного слу-
случая прямолинейного и равномерного движения выражается в специ-
специальном принципе относительности, согласно которому любой физи-
физический закон, справедливый в какой-либо одной инерциальной системе
координат, должен быть справедлив и во всякой другой инерциаль-
инерциальной системе координат. Иначе говоря, все физические законы должны
иметь форму, инвариантную по отношению к преобразованиям, соот-
соответствующим переходу от одной системы координат к другой, дви-
движущейся по отношению к первой прямолинейно и равномерно. По-
Поэтому вопрос о переходе от одной системы координат к другой,
движущейся прямолинейно и равномерно, с точки зрения теории от-
относительности представляет принципиальный интерес. Преобразова-
Преобразования, соответствующие этому переходу, представляют собой как бы
«пробный камень», на котором должен испытываться всякий физи-
физический закон, — этот закон должен быть инвариантен по отношению
к таким преобразованиям.
Однако, такие требования к физическому закону мы вправе предъ-
предъявлять только в том случае, если при описании физичгских явлений

§ 167]
КИНЕМАТИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
541
нами нигде не была нарушена равноправность различных систем
координат. Это значит, что во всех системах координат мы должны
пользоваться одними и теми же методами измерения физических ве-
величин. Поэтому если в одной системе координат мы пользуемся
для измерения длины линейкой, неподвижной по отношению к этой
системе координат, то в другой системе координат мы должны поль-
пользоваться линейкой, неподвижной по отношению к этой второй системе
координат. То же самое относится к часам и ко всем вообще приме-
применяемым измерительным приборам. При переходе же от одной системы
координат к другой необходимо будет принимать во внимание уже
известные нам свойства линеек и часов —
сокращение длин движущихся линеек и
замедление хода движущихся часов по
сравнению с принятыми за неподвижные.
Принимая во внимание эти сооб-
соображения, нам необходимо пересмотреть
заново вопрос о том, как преобразуют-
преобразуются различные кинематические величины
при переходе от одной системы коор-
координат к другой, движущейся относитель-
относительно первой прямолинейно и равномерно.
Рассмотрим так, как мы это уже делали (гл. III, § 16), две системы
координат: первую х, у, z, или систему К, и вторую х', у', г', или
систему К', движущуюся относительно первой в направлении оси х с
постоянной скоростью v (рис. 446). Для упрощения положим, что в
начальный момент начала координат О и О' и направления осей
совпадают. В началах координат О и О' поместим двое часов — одни
неподвижные и другие движущиеся, и в момент, когда они поравня-
поравняются, т. е. как раз в начальный момент, сверим их между собой.
Кроме того, в каждой системе координат мы можем установить ещё
сколько угодно часов и в начальный момент синхронизовать их при
помощи световых сигналов (одним из двух упоминавшихся выше
способов).
Как мы видели (§ 166), если система движущихся часов таким
образом синхронизована и сверена с неподвижными, находящимися
в начале координат, то показания любых движущихся часов V свя-
связаны с показаниями неподвижных часов t соотношением:
Рис. 445.
V*
B2.21)
где х — координата этих движущихся часов в системе К- Но так
как все часы системы К были синхронизованы между собой, то од-
одновременно с часами, находящимися в начале координат, все осталь-
остальные часы системы К показывают время t. (Нужно помнить, что здесь

542 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [ГЛ. XXII
идёт речь об одновременности в системе К.) Следовательно, в ка-
какой-то момент времени, в который все часы системы К показывают
одно и то же время t, все часы системы К показывают различное
время Р, определяемое соотношением B2.21). Времени t в системе К
соответствует своё местное время f в каждой точке системы К'.
Мы условились в каждой точке отсчитывать время по неподвижным
часам, находящимся «здесь» , и поэтому соотношение B2.21) и пред-
представляет собой формулу преобразования времени при переходе от
системы К к системе К' для точки, имеющей координату х в си-
системе К-
Так как системы координат К и К! совершенно равноправны, то
те же самые рассуждения мы можем повторить и для преобразова-
преобразования времени от системы К' к системе К, с той лишь разницей, что
система К движется относительно К' в обратном направлении, т. е.
со скоростью — v. Следовательно, если в какой-то момент времени,
когда все часы системы К' одновременно показывают время V (здесь
речь идёт уже об одновременности в системе К'), то все часы си-
системы К показывают различное время
<=- г——.• B2.22)
Это соотношение представляет собой формулу преобразования вре-
времени при переходе от системы А" к системе К для точки, имеющей
координату х' в системе 1С.
В классической физике вместо этой формулы применяется соот-
соотношение
t = f, B2.23)
вытекающее из постулата о неизменности хода часов во всех систе-
системах координат. Нетрудно проследить, при каких условиях формулы
преобразования теории относительности могут быть приближённо за-
заменены соотношением B2.23), применяемым в классической физике.
Для этого необходимы условия;
%<1 и %<*- B2-24)
Первое соотношение означает, чтр скорость v должна быть доста-
достаточно мала по сравнению со скоростью света. Второе соотношение
содержит ещё и другое требование, а именно, чтобы xjc было мало
по сравнению с t, т. е. чтобы времена распространения световых
сигналов на расстояния, фигурирующие в наших задачах, были малы
по сравнению с интересующими нас временами. Оба эти условия
хорошо соблюдаются во всех задачах макроскопической земной ме-
механики и большинстве задач небесной механики.

§ 16?] КИНЕМАТИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 543
Перейдём теперь к вопросу о преобразовании координат. Рассмот-
Рассмотрим точку, имеющую в момент t в системе К координату х, т. е.
лежащую на расстоянии х от точки О, причём это расстояние изме-
измерено при помощи линейки, неподвижной в системе К. Точка О' в
этот момент лежит от точки О на расстоянии vt, измеренном также
при помощи линейки, неподвижной в системе К. Следовательно, рас-
рассматриваемая точка отстоит от точки О' в этот момент на расстоянии
х — vt, измеренном опять-таки при помощи линейки, неподвижной в си-
системе К. Но координату точки в системе К' нужно измерять при помощи
линейки, неподвижной в системе 1С, т. е. движущейся в системе К.
Эта движущаяся линейка будет в отношении l/ I — ^-: 1 короче не-
неподвижной. Поэтому в результате измерения расстояния от рассма-
рассматриваемой точки до точки О' при помощи движущейся линейки мы
получим число, в 1/1/1 — ^5 раз большее, чем при измерении при
помощи неподвижной.
Таким образом, координата рассматриваемой точки в системе К'
есть
х~=; B2.25)
что касается координат у' и z', то они, очевидно, остаются рав-
равными у и z, так как лииейка, движущаяся в направлении х', не ис-
испытывает сокращения в направлениях у' и г', т. е. не изменяет
своей длины при измерении расстояний вдоль осей у' и г'.
Окончательно мы ¦ получаем следующие формулы преобразования,
так называемые преобразования Лорентца-Эйнштейна:
t-~
*L., У'=У, *'=*, *'= ,-fL-, B2.26)
/
отражающие переход от системы координат Кк системе К', движущейся
по отношению к К с постоянной скоростью v в направлении оси лг-ов.
При соблюдении условий B2.24) эти формулы могут быть заме-
заменены галилеевыми преобразованиями C.1), отражающими тот же
переход от системы К к системе К в классической физике. Как раньше
указывалось, условия B2.24) хорошо соблюдаются в большинстве задач
макроскопической механики. Именно поэтому классическая механика
даёт достаточную точность при рассмотрении почти всех макроско-
макроскопических движений.
Если бы нам понадобилось перейти, наоборот, ©т системы К1 к
системе К, то так же, как это было сделано для преобразования
времени B2.22), легко сделать это для координаты х. Заменяя в

544 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гл. XXII
формулах B2.26) х на х', у на у', z на z', t на ? и v на — о,
получаем преобразования Лорентца-Эйнштейна для перехода от систе-
системы К' к системе К:
х=уЩ у=у *=л '=ут^- B2-27)
Зная, как преобразуются координаты при переходе от системы К к
системе К1 или обратно, нетрудно установить, как преобразуются
скорости при этих переходах. Для этого нужно найти соотношения
между бесконечно малыми приращениями координат и времени в двух
системах К и К1. Так, например, для того чтобы от «относитель-
«относительной» *) скорости и' в системе К1 перейти к «абсолютной» скорости
и в системе К, нужно продифференцировать выражения B2.27):
^^ B2.28)
Пусть какая-либо точка обладает в системе К1 «относительной»
скоростью и' с компонентами
и'1—^ и— $2- и'—**1 A9 1Я\
"х—dti > "у— dtn uz — ^Г> \ЛЛЪ)
а в системе К «абсолютной» скоростью и с компонентами:
«*=& *,=% :=S- B2.зо)
В эти соотношения мы должны подставить выражения B2.28) для
dx, dy, dz и dt. Принимая во внимание, что — = a^., мы можем вы-
выражения для dx и dt записать так:
nxv
dx= a*JlL= dt1 и dt = —¦ ci dt1; B2.31)
V a V l &
подставляя ¦ их в соотношения B2.30), получим:
I --/^
*) Термины «относительная», «абсолютная» и переносная скорость
применяются здесь в том же условном смысле, в каком они были введены
в § 16 и применялись во всей книге.

§ 167] КИНЕМАТИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 545
Это формулы преобразования компонент скорости при переходе
от системы К1 к системе К. Зная величины компонент скорости и'
в системе К', мы по этим формулам найдём компоненты скорости и
в системе К. Для перехода от системы К к системе К в этих формулах
следует вместо компонент и поставить компоненты и', и наоборот,
a v заменить на — v.
Аналогичным образом можно получить формулы преобразования
ускорений при переходе от системы К' к системе К или обратно.
Пусть какая-либо точка обладает в системе К ускорением '}' с ком-
компонеаи
понентами
dnx ,, du'v ,, dnz
J J
~d
F'
а в системе К— ускорением j с компонентами
_dux . __ duy . _dn1
J* dt' Jy dt ' Jz~ at'
Дифференцируя выражения B2.32), мы найдём связь между бес-
бесконечно малыми приращен 1ями компонент скорости в системе К, du ,
du , duz и в системе К', dux, duy и duz. Разделив полученные выра-
выражения на dt и воспользовавшись выражением B2.31), связывающим
dt и d ', мы выразим компоненты ускорения в системе К через ком-
компоненты ускорения в системе К'.
Однако в таком общем виде эти выражения несколько' громоздки,
потому что в общем случае все три компоненты скорости их, иу, иг
изменяются со временем, так как ускорение может быть направлено
произвольным образом. Формулы существенно упрощаются, когда
в начальный момент скорость и' направлена по оси х, а ускорение j
по направлению либо совпадает со скоростью и' (тангенциальное
ускорение), либо перпендикулярно к нему (нормальное ускорение).
Для задач динамики, которые нам предстоит рассмотреть, этих двух
случаев будет достаточно, и мы ими ограничимся.
В первом случае — тангенциального ускорения, — так как вначале
скорость и' направлена по оси х', она всё время остаётся направлен-
направленной по оси х\ т. е. их=и', иу = 0, иг = 0. Принимая это во вни-
внимание и дифференцируя выражение B2.32), получим:
Деля обе части равенства на dt и принимая во внимание связь
между dt и dt', найдём связь между тангенциальными ускорениями в
35 С. Э. Хайкин

54б МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. ХШ
системах К и К':
]t= - с-—- ft, B2.33)
где
. _ du ( — d^_
Следует подчеркнуть, что это соотношение справедливо лишь в рас-
рассматриваемом случае, когда скорость и ускорение не только совпадают
по направлению, но и направлены по оси х', т. е. совпадают по на-
направлению с переносной скоростью.
Перейдём теперь к другому случаю, когда ускорение нормально
к оси х', например, направлено по оси у'. В этом случае dux — 0
и du'z = 0, и при дифференцировании B2.32) их нужно считать посто-
постоянной:
daу=- ~du'y.
Деля обе части равенства на dt и принимая во внимание, что мы рас-
рассматриваем момент, когда скорость и' направлена по оси х' и, следова-
du ЯИ„ /
тельно, и направлена по оси х, и что ~^ = Jn и —f=jni найдём связь
между нормальными ускорениями в системах К и К1'.
{22M)
Опять следует иметь в виду, что это соотношение справедливо лишь
для того момента, когда не только ускорение нормально к скорости,
но и скорость и' направлена по оси х', т. е. совпадает по направле-
направлению с переносной скоростью.
Полученные нами выражения для тангенциального и нормального
ускорений понадобятся нам в дальнейшем. А пока вернёмся к фор-
формулам преобразования скоростей. Численная величина скорости в лю-
любой прямоугольной системе координат выражается через компоненты
этой скорости известной формулой:

§ 1671 кинематика теории относительности 547
Подставляя из формул B2.32) значения компонент скорости их, иу, иг,
найдём;
Это — формула сложения скоростей теории относительности, выражаю*
щая величину «абсолютной» скорости и, если компоненты «относи-
«относительной» скорости равны и'х, иу, иг и переносная скорость v на-
направлена по оси х. В классической механике этот случай сложения
скоростей выражается формулой:
которая представляет собой запись правила параллелограмма скоростей
для рассматриваемого случая.
В простейшем случае, когда скорость и' направлена по оси х\
т, е. их = и, иу — 0, и'г = 0, формула сложения скоростей теории
относительности принимает вид:
l±I B2.37)
u'v
r. e. «абсолютная» скорость не равна алгебраической сумме «отно-
«относительной» и переносной, как это имеет место в классической механике,
а меньше их суммы, если обе скорости направлены в одну сторону,
и больше их разности, если они направлены в противоположные
стороны.
Из сопоставления выражений B2.36)"и B2.37) видно, что правило
параллелограмма скоростей классической механики является прибли-
приближённым — оно применимо лишь в случае, если соблюдаются условия:
Как легко видеть, эти ограничения эквивалентны ограничениям B2.24),
при которых вообще применима классическая механика. В обоих
случаях дело сводится к тому, что все скорости, с которыми прихо-
приходится иметь дело, малы по сравнению со скоростью света.
Формула сложения скоростей теории относительности обладает
характерной особенностью, отражающей ту особую роль, которую
играет величина скорости света. Особенность эта состоит в том, что
если одна из складываемых скоростей — относительная «' или пере-
переносная v — равна скорости света с, то и результирующая скорость а
оказывается равной с. В самом деле, пусть относительная скорость
35 s

54& МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ГгЛ
и'~с. После простых преобразований формулы B2.35) и принимая
во внимание, что и*-\-иу2 -\-и/ = с2, получим:
-Zi 7^—^'
Результат этот верен при любом направлении скорости и', но он
особенно нагляден в двух частных случаях, когда скорость и' направ-
направлена по оси х и перпендикулярна к ней. В первом случае, как видно
из относящейся к этому случаю формулы B2.37), при и' = с, так-
также и и = с, независимо от значения v. Переносное движение вообще
ничего не изменяет, если относительная скорость уже равна с, В случае,
когда и' перпендикулярно к х, например, их=*0, иу — и' и и'г — 0, для
компонент скорости и из B2.32) получаются выражения:
иеслии^=с, то ttj,— у с2 — v2, т. е. компонента результирующей
скорости по оси у сокращается как раз настолько, что численная
величина скорости и = у u%-\-Uy оказывается равной с. Перенос-
Переносное движение не изменяет величины «абсолютной» скорости, если
«относительная» скорость уже равна с, а лишь поворачивает её в на-
направлении V.
Точно так же, если переносная скорость v=c, то формула
B2.35) даёт
= с>
т. е. независимо от величины и направления «относительной» скорости и'
«абсолютная» скорость равна с, если переносная скоростьv-= с. Иначе
говоря, если система К1 движется относительно системы К со скоростью
света, то, как бы ии двигались отдельные точки в системе К', они все
движутся со скоростью с относительно системы К', и их взаимное рас-
расположение в системе К не изменяется. В системе К при этих условиях
нельзя наблюдать никаких движений, происходящих в системе К'.
В частности, движущиеся стрелки часов, находящихся в системе К!t

§ 167] КИНЕМАТИКА ТЕОРИИ OfНОСИТЕЛЬНОСТИ 349
в системе К будут неподвижны. Часы, идущие нормально в системе К
и движущиеся вместе с нею относительно системы К со скоростью
света, для системы К будут остановившимися.
Этот результат вполне согласуется с уже известным нам обстоя-
обстоятельством — замедлением хода движущихся часов. В самом деле, как
следует из формулы замедления хода часов при движении B2.8),
для системы координат, по отношению к которой часы движутся со
скоростью света, стрелки часов должны стоять на месте, т. е. их
положение относительно циферблата не должно изменяться. Конечно,
приведённые соображения нельзя рассматривать как подтверждение
правильности формулы, выражающей зависимость хода часов от их
движения. Эта зависимость установлена опытом (правда, не прямым,
а косвенным), и в основу кинематики теории относительности
положены именно эти, установленные на опыте, свойства часов. Но
если бы из кинематики теории относительности вытекало, что стрелки
часов, движущихся со скоростью света относительно системы К,
в этой системе изменяют своё расположение относительно циферблата,
то это означало бы внутреннее противоречие между исходными по-
положениями и конечным результатом. Дело в том, что, поскольку
формулы кинематики уже получены, мы можем, ничего не говоря
о физических свойствах часов, рассмотреть кинематическую задачу:
зная, как движутся стрелки относительно циферблата в системе К1, найти,
как они движутся в системе К. Как видим, в результате такого рас-
рассмотрения никакого противоречия не возникает.
Можно было бы убедиться, что в тех случаях, когда «относи-
«относительная» и переносная скорости каждая меньше скорости света,
«абсолютная» скорость не достигает скорости света, даже если
сумма «относительной» и переносной больше скорости света. Для
частных случаев, рассмотренных выше, когда и' параллельно или
перпендикулярно к оси х, это сразу видно из соответствующих формул.
В общем случае это также нетрудно было бы доказать, но вывод
несколько громоздок, и мы поэтому его не приводим.
Таким образом, если в исходной системе координат мы не встре-
встречаемся со скоростями, ббльшими скорости света, то ни в какой
другой системе координат, которая движется по отношению к первой
со скоростью, не превосходящей скорости света, мы также не встре-
встречаемся со скоростями, ббльшими, чем скорость света. Как будет
видно из динамики теории относительности, ии одному телу не может
быть сообщена скорость, ббльшая скорости света, и следовательно,
скорость света в механике теории относительности играет роль пре-
предельной скорости. Поэтому тот факт, что формулы теории относитель-
относительности теряют смысл при скоростях, ббльших скорости света, отнюдь не
является ограничением области применимости теории относительности..
Дело не в. том, что теория относительности не верна при скоростях,
ббльших скорости света, а в том, что невозможно сообщить телу
скорость, большую, чем скорость света.

550 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ГгЛ. XXII
§ 168. Масса и сила в механике теории относительности
Основное качественное содержание классической динамики со-
сохраняется и в динамике теории относительности. Как и в механике
Ньютона, в механике теории относительности ускорения тел (в ииер-
циальных системах координат) вызываются силами, а силы предста-
представляют собой действия тел друг на друга. И задача динамики поиреж-
нему заключается в определении ускорений, которые тела сообщают
друг другу. Однако количественные законы механики Ньютона
ие могут быть непосредственно перенесены в динамику теории отно-
относительности. Они должны быть пересмотрены и уточнены. Но эти
уточнённые законы должны быть таковы, чтоэы для медленных дви-
движений они совпадали с законами классической механики. Поэтому
основная задача динамики теории относительности заключается в
отыскании закона, который связывал бы между собой силы и сооб-
сообщаемые ими ускорения и для медленных движений совпадал бы со
вторым законом Ньютона.
Для формулировки и проверки этого закона необходимо предва-
предварительно (как это пришлось делать и в классической механике) уста-
установить способы измерения массы тела и силы, действующей на тело.
При этом, поскольку речь идёт не об отыскании совсем новых зако-
законов, а об уточнении и дополнении законов классической механики,
Следует стремиться не устанавливать новые методы измерения массы
и силы, а сохранить те методы, которые применяются в классической
механике, лишь дополнив и уточнив их, если это окажется необхо-
необходимым. Эти дополнения и уточнения подсказываются теми требова-
требованиями, которые в теории относительности предъявляются ко всяким
измерениям.
Прежде всего установленныз методы измерений не должны нару-
нарушать равноправия различных инерциальньк систем координат, т. е.
в каждой системе координат измерение должно производиться оди-
одинаковым способом. Далее, если это требование соблюдено, то со-
сопоставление результатов различных измерений не должно противо-
противоречить принципу относительности. Иначе говоря, принцип относитель-
относительности требует, чтобы результаты одинаковых измерений, произведён-
произведённых в одинаковых условиях в двух разных системах координат, дви-
движущихся одгш относительно другой прямолинейно и равномерно, со-
совпадали между собой.
Поясним сказанное на уже знакомом нам примере измерения
Длины движущихся линеек (§ 166). Принцип относительности вовсе
не требует, чтобы одинаковые линейки L и ?', измеренные в одной
системе координат, например К, имели одинаковую длину. Но он
требует, чтобы линейка V, измеренная в системе К, имела ту же
длину, какую имеет линейка L, измеренная в системе К'. В самом
деле, принцип относительности требует, чтобы одинаковые измерения
давали в системах К и К' Одинаковый результат. Но одинакорые

§ 168j МАССА И СИЛА В МЕХАНИКЕ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 551
измерения в обоих случаях — это измерения движущихся линеек,
т. е. именно линейки V в системе К и линейки L в системе К.
Измерение же линеек L и L' в системе К— это измерение первый
раз неподвижной, а второй раз движущейся линейки, т. е. два раз-
различных измерения.
Такие же требования мы предъявим к методам измерения масс
и сил. Начнем с измерения масс. В классической механике мы onpw-
деляли отношение масс двух
тел по обратному отношению
ускорений, сообщаемых те- ш"
лами друг другу (§ 27); „ , .,, .„ ; п
этот же метод мы сохраним •* *Jh—0—!1+ S—-Q ?
и в динамике теории отно- / ! 2
сительности. Однако, как | ,.
мы сейчас увидим, он тре- р 447
бует уточнения. Дело в
том, что в классической ме-
механике отношение ускорений, сообщаемых телами друг другу, можно
было считать постоянным и не зависящим не только от рода взаимо-
взаимодействующих сил, но и от скоростей, которыми обладают взаимо-
взаимодействующие тела.. Но, как вытекает из кинематики теории относи-
относительности, т. е. из более точного рассмотрения, отношение ускорений,
сообщаемых телами друг другу, должно зависеть (и притом вполне
определённым образом) oi
j* скоростей взаимодействую-
j- 1 ;,' I', ^ цг' х" Щих тел- Мы убедимся в
tJ7 *~ * С? *~ этом на простейшем примере
' ! * двух одинаковых тел, сооб-
<у' щающих друг другу только
р 448 тангенциачыюе или только
нормальное ускорение.
Рассмотрим два одинаковых шара / и 2, движущихся с некото-
некоторой скоростью один относительно другого (рис. 447). Выберем си-
систему координат 1С с осями х' и у', связанную с первым шаром.
Второй шар в этой системе координат движется с некоторой ско-
скоростью и'т Пусть эти два шара как-то взаимодействуют между
собой (через пружину, вследствие того, что они заряжены, или
ещё каким-либо способом) и сообщают друг другу относительно
выбранной системы коор'динат ускорения /[ и f2, по направлению
совпадающие со скоростью а'2_ Найдём теперь ускорения /j' и j'%
этих же шаров в системе координат К' с осями х" и у', связанной
со вторым шаром (рис. 448), т. е. движущейся относительно системы К'
со скоростью v' — u'2. Так как ускорения попрежиему остаются тан-
тангенциальными, т. е. направлены вдоль переносной скорости системы1
координат /С'» т& .мы можем применить формулу преобразования

552 механика специальной теории относительности [гл. ххп
тангенциальных ускорений B2.33), выведенную именно для этог»
случая. В системе К' и[ = 0 (первый шар покоится), а сама система А?
движется относительно К" со скоростью z» = —и'2. Поэтому на ос-
основании формулы B2.33) получим:
/ и'2 \ 3'2
-3/2
Уже из этих формул ви^но, что два одинаковых шара, из кото-
которых один движется, а другой покоится, сообщают друг другу раз-
различные ускорения. Действительно, если бы, например, в системе К1
оба шара сообщали друг другу одинаковое ускорение, т. е. если бы
было /( — /у т.°> как следует из полученных формул, должно быть
f^=^zf'r Между тем оба случая в системах К1 к К" совершенно рав-
равноправны, так как шары одинаковы и в обоих случаях рассматри-
рассматриваются ускорения покоящегося и движущегося шаров. Поэтому
если бы оказалось, что j'x=f2, a j"x=^j'v то принцип относительности
был бы нарушен. Следовательно, j[^j'T Более того, исходя из прин-
принципа относительности, можно найти связь между ускорениями j[
и /2. В самом деле, в системе К' j[ есть ускорение неподвижного,
a j'2—ускорение движущегося тела. В системе К' j есть ускорение
неподвижного, а;','—ускорение движущегося шара. Поскольку в
остальном оба опыта совершенно равноправны, на основании принци-
принципа относительности мы можем утверждать, что должно быть:
;•;=;; B2.40)
На основании этих равенств и принимая во внимание, что по абсо-
абсолютной величине скорость первого шара и"^ в системе К" равна
скорости второго и'г в системе А", из соотношений B2.38) и B2.39)
получаем:
/ / г»'2 \ 3/2
Н)
' <22-43>
Из этих выражений следует, что отношение ускорения движуще-
движущегося шара к ускорению неподвижного шара в обеих системах коор-
двдат одинаково (как и должно быть согласно принципу относитель-

§ 168] Масса и сила в механике теории относительности
553
ности) и равно A — ^-) , т. е. меньше единицы. Хотя шары оди-
одинаковы, движущийся шар сообщает неподвижному большее ускорение,
чем неподвижный движущемуся. Отношение тангенциальных ускоре-
ускорений, сообщаемых шарами друг
другу, не остаётся постоянным, \у' \у
а зависит от скоростей, которы-
которыми шары обладают.
Аналогично найдём отноше-
отношение нормальных ускорений, ко-
которые сообщают друг другу два
одинаковых шара. В системе К'
(рис. 449) первый шар имеет ско-
скорость и\ = 0 и ускорение j[,
второй — скорость и'2 -ф 0 и уско-
ускорение /2. Скорость и'2 направле-
направлена по оси х', а оба ускорения
Л' и Л—"по оси У
i,'
оси у , т.
к скорости и
I/
Рис. 449.
JT
У
Рис. 450.
нормально
В системе К" (рис. 450; первый шар имеет скорость «*= и' и
ускорение /*, второй — скорость и — 0 и ускорение j\. Пользуясь
формулой B2.34) для преобразования нормальных ускорений и при-
принимая во внимание, что w^= —и'2, найдём:
B2.44)
fr B2.45)
Как и в предыдущем случае, на основании принципа относительности
мы можем утверждать, что должно быть
1. = /п И /„= Л .
с'-
|2\-1
Принимая во внимание эти равенства, окончательно получим:
А'
B2.46)
B2.47)
Как и в случае тангенциальных ускорений, движущийся шар сооб-
сообщает неподвижному большее ускорение, чем неподвижный движущемуся.
Попрежнему отношение ускорений, сообщаемых шарами друг другу,
зависит от скоростей, которыми эти шары обладают, но количественно

554 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ.ХХП
эта зависимость несколько иная, чем в случае тангенциальных уско*
рений.
Если бы, так же как и в классической механике, мы определяли
отношение масс двух тел просто как величину, обратную отношению
ускорений, то оказалось бы, что отношение масс двух одинаковых
тел не только зависит от их скоростей, но что эта зависимость раз-
различна для тангенцаальных и нормальных ускорений. Следовательно,
пользуясь этим способом измеренля масс, мы должны были бы раз-
различать продольную и поперечную массы движущегося тела. Так именно
поступал Эйнштейн в своих первых работах по теории относитель-
относительности. Однако тогда масса перестает быть скалярной величиной,
какой 'бна была в классической механике, почему этот метод изме-
измерения масс и был признан нецелесообразным и от него в дальнейшем
отказались. При этом, однако, нет необходимости отказываться от
самого метода измерения, масс, принятого в классической механике.
Достаточно лишь несколько дополнить его, чтобы масса тела попреж-
нему оказалась скалярной величиной. Оказывается, что если за отно-
отношение масс двух тел мы примем не просто величину, обратную отно-
отношению их ускорений, а эту величину, умноженную на некий «попра-
«поправочный множитель», то соответствующим выбором этого множителя
можно достичь того, что масса тела окажется скалярной величиной.
Так, если мы для сравнения масс двух тел будем пользоваться отно-
отношением сообщаемых ими друг другу тангенциальных ускорений, то
нужно ввести «поправочный множитель» 1 ~, чтобы масса тела
оказалась скалярной величиной.
Конечно, в этом выборе способа измерения массы есть некоторая
условность. Но всякий способ измерений является в известной сте-
степени условным — он должен, быть нами установлен. Однако не сле-
следует думать, что выбор способа измерения той или иной физической
величины произволен. Этот выбор, в конечном счёте, отражается на
формулировке физических законов, в кэторые входит данная физиче-
физическая величина. Поэтому выбор метода измерения масс предопределяет
ту форму, какую будут иметь законы движения в механике теории
относительности. Для того, чтобы этим законам придать форму, наи-
наиболее близкую к законам классической механики, надлежит ввести
указанный «поправочный множитель», т. е. установить следующий
способ измерения массы тел. Чтобы измерить массу т какого-либо
движущегося тела, нужно заставить его так взаимодействовать с по-
покоящимся телом, масса которого /га0 принята за эталон, чтобы дви-
движущееся тело испытывало только тангенциальное ускорение. Измерив
скорость и ускорение движущегося тела, а и У, и ускорение тела-
эталона Уо (в начальный момент, пока оно ещё не успело приобрести
заметной скорости), мы найдём отношение масс двух тел;
1tL—h(\_t\ B2.48}
Щ j \ с"-) ?

§ 168] МАССА И СИЛА В МЕХАНИКЕ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 555
Это и есть определение массы движущегося тела, принятое в ме-
механике теории относительности. Ясно, что оно совтадает с опреде-
определением массы, принятым в классической механике, если и достаточно
мало, так что величиной и2/с2 можно пренебречь по сравнению с еди-
единицей. Действительно, в этом случае «поправочный множитель» об-
обращается в единицу и отношение масс есть просто обратное отно-
отношение ускорений.
Заметим, что оговорки в приведённом выше определении массы —
необходимость производить измерения только в начальный момент и
только при тангенциальном ускорении — не являются принципиаль-
принципиальными. Так как формулы преобразования скоростей и ускорений в
общем случае известны, можно было бы сформулировать способ из-
измерения масс по сообщаемым ими друг другу ускорениям и в общем
случае. Однако в этом нет необходимости, поскольку при устано-
установлении метода измерения той или иной физической величины мы мо-
можем вводить любые специальные требования, лишь бы они были прин-
принципиально осуществимы. Как легко видеть, все те оговорки, которые
были сделаны при формулировке метода измерения масс, этому тре-
требованию удовлетворяют.
Применяя этот способ измерения массы тела к рассмотренному
выше случаю взаимодействия двух одинаковых шаров, когда движу-
движущийся шар испытывает только тангенциальное ускорение, мы найдём
отношение масс движущегося и покоящегося шаров. Подставляя в
формулу B2.48) найденное нами отношение B2.42), где j'2—j и
т = т2 (движущийся шар), a j\=j§ и ml=mQ (покоящийся шар),
получаем:
т ]=^=. B2.49)
Следовательно, в случае двух одинаковых шаров масса движущегося
шара больше массы покоящегося в отношении 1: у 1—^-.
Итак, выбранный способ измерения масс приводит к следующей
зависимости массы от скорости. Если какое-либо тело, когда оно
покоится, обладает «покоящейся массой» w0, то при движении со ско-
скоростью и оно обладает массой
HL B2.50)
Мы получили этот результат при рассмотрении тангенциальных уско*
рений. Однако, как будет видно из дальнейшего, наш выбор метода
измерения масс позволяет сохранить скалярный характер массы. По-
Поэтому формула B2.50) выражает зависимость массы от скорости во
всех случаях, при.любом направлении ускорения, испытываемого телом.

556 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXII
Поскольку масса тела зависит от скорости, то в разных си-
системах координат одно и то же тело обладает различной массой.
На основании соотношения B2.50), пользуясь формулой преобра-
преобразования скоростей, мы могли бы получить формулу преобразования
массы тела при переходе от одной системы координат к другой в
общем виде. Однако в таком общем виде эта формула нам не по-
понадобится, так как мы ограничимся только такими частными случаями,
когда в одной системе координат тело покоится. Тогда в системе
координат, движущейся со скоростью v относительно первой, оно
будет обладать скоростью — v. И если в первой системе координат
оно обладает массой т0, то во второй системе координат его масса
У 1~ж
B2.51)
Это и есть формула преобразования масс, когда в первой системе
коордигат тело покоится.
Перейдём к вопросу об измерении сил в механике теории отно-
относительности. Как и в классической механике, мы будем измерять силы
при помощи калиброванных пружин
^- (динамометров). Как способ калибровки
"" пружин, так и способ измерения сил
... остаётся таким же, как и в классической
механике (§ 22). Однако в теории
относительности возникает новый во-
вопрос— как ведут себя пружины при движении. Иначе говоря, за-
зависит ли сила, с которой действует пружина на прикреплённое к ней
тело,, от скорости движения тела и пружины. Этот вопрос
совершенно аналогичен вопросу о влиянии движения на
длину линеек и ход часов. И так же, как в отношении
линеек и часов, для ответа иа этот вопрос мы должны
проверить свойства пружин при помощи какого-либо дру-
другого способа измерения сил. Но в механике мы не рас-
располагаем другим способом измерения сил, кроме пружин.
Для этой проверки приходится обращаться к электриче-
электрическим явлениям.
Электродинамика теории относительности приводит к
вполне определённым заключениям относительно влияния р „„
движения на силу взаимодействия между двумя электри-
электрическими зарядами. Именно, оказывается, что если два
заряда движутся в направлении линии, их соединяющей (рис.
451), то сила взаимодействия между зарядами остаётся той же,
что и в случае, когда заряды покоятся. Если же заряды дви-
движутся в направлении, перпендикулярном к линии, их сем
единяющей (рис. 452), то сила взаимодействия, измеренная в дви«
жущейся системе координат,, относительно, которой заряды покоятся^

§ 168J масса и сила в механике теории относительности 557
оказывается в отношении 1: у \ — ^- ббльшей, чем в «неподвиж-
«неподвижной» системе координат, относительно которой заряды движутся со
скоростью v. Иначе говоря, пусть два электрических заряда, движу-
движущихся со скоростью v в системе К, действуют друг на друга
с силой F. Тогда в системе координат К, движущейся относительно
системы К со скоростью v (в системе К' заряды покоятся), сила
взаимодействия между этими зарядами равна F, причём
F' = F, B2.52)
если эта сила направлена вдоль скорости v, и
4==, B2.53)
если сила направлена перпендикулярно к скорости v.
Полученные соотношения для сил взаимодействия между электри-
электрическими зарядами позволяют установить, как влияет движение пру-
пружины на ту силу, с которой она действует на прикреплённое к ней
тело. Для этого прикрепим к зарядам, движущимся со скоростью v
в системе К, испытуемую пружину. Если она будет действовать на
заряжённые тела с такой же силой, с какой заряды будут взаимодей-
взаимодействовать между собой, то заряды и пружина будут находиться в равно-
равновесии. На основании принципа относительности мы можем утверждать,
что равновесие будет иметь место и в системе К', которая движется
относительно К со скоростью v. Следовательно, силы, с которыми
действуют пружины, изменяются при движении так же, как и силы взаимо-
взаимодействия электрических зарядов. Поэтому, если пружина, движущаяся
со скоростью v в системе К, действует на прикрепленное к ней тело
с силой F, то в системе К', в которой пружина покоится (К1 дви-
движется относительно К со скоростью v), эта пружина действует
с силой F', причём
F' = F, B2.52)
если скорость v направлена вдоль оси пружины, и
тяг
если скорость v перпендикулярна к оси пружины.
Итак, для измерения сил, действующих на то или иное тело, мы
попрежнему будем пользоваться калиброванными пружинами, прикре-
прикреплёнными к этому телу. Подобрав растяжение пружины так, чтобы
тело не испытывало ускорения, мы будем отсчитывать силу, действу-
действующую на тело, по показаниям на шкале калиброванной пружины.
Но при этом пружина должна быть прикреплена к телу, т. е. дви-

558 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ' ГЛ. XXlr
гагься вместе с ним. По показаниям такай покоящейся по отноше-
отношению к телу пружины мы измеряем силу, действующую на тело. Если
же нам нужно будет сравнивать силы, действующие на движущиеся
друг относительно друга тела, то необходимо будет принимать во
внимание влияние движения пружины на силу, с которой она дейст-
действует. Здесь дело обстоит так же, как и с измерением длин. Длину
каждого тела мы измеряем при помощи линейки, приложенной к телу,
т. е. покоящейся по отношению к нему. Когда же нам нужно сравни-
сравнивать длины двух тел, из которых одно движется относительно дру-
другого, то ми должны учитывать влияние движения линейки на её
длину — сокращение длины линейки.
Полученные соотношения для преобразования сил справедливы,
очевидно, не только для пружин, ио и для всех вообще сил, так как
к любым силам применимы те же рассуждения. Следовательно, соот-
соотношения B2.52) и B2.53) представляют собой формулы преобразова-
преобразования всяких сил при переходе от одной системы координат к другой,
движущейся со скоростью v. Соотношение B2.52) относится к слу-
случаю, когда сила лежит в направлении скорости v, a B2.53) — к слу-
случаю, когда сила перпендикулярна к этому направлению. В общем слу-
случае, когда сила направлена под углом к скорости v, формулы преоб-
преобразования более сложны. Мы их приводить не будем, так как в даль-
дальнейшем они нам не понадобятся. Установив способы измерения массы
и силы и формулы преобразования масс и сил при переходе от одной
системы координат к другой, мы можем перейти к основной задаче
динамики — установлению связи между массой, ускорением и силой,
т. е. к формулировке закона движения.
§ 169. Закон движения механики теории относительности
Приступая к формулировке закона движения механики теории от-
относительности, мы должны руководствоваться следующими двумя со-
соображениями. Во-первых, как и все физические законы, он должен удо-
удовлетворять принципу относительности, т. е. должен сохранять свой
вид (быть инвариантным) при переходе от одной системы координат к
другой, движущейся прямолинейно и равномерно. Во-вторых, для мед-
медленных движений он должен совпадать со вторым законом Ньютона.
Эти соображения дают указания о том, какой вид должен иметь закон
движения в механике теории относительности. Прежде чем проверять
ту или иную форму закона движения на опыте, следует проверить,
удовлетворяет ли он двум указанным требованиям, так как если закон
этим требованиям ие удовлетворяет, то можно заранее сказать, что
он ие верен, и проверка его непосредственным опытом становится
ненужной.
Исходя из этих соображений, посмотрим, удовлетворяет ли второй
закон" Ньютона принципу относительности. В связи с этим возникает
следующий вопрос. В классической механике второй закон Ньютона

§ 1691 закон движения механики теории относительности 559
может быть записан двумя способами:
т~ = ? B2.54)
или
^(яи) = Р. '22.55)
Поскольку в классической механике масса не зависит от скорости,
обе эти записи, очевидно, эквивааентны. В механике же теории отно-
относительности, так как масса зависит от скорости, эти две записи вы-
выражают различные законы движения.
Нетрудно убедиться, что первая форма B2.54) не удовлетворяет
принципу относительности. Пусть на тело массы т действует пружина
с силой F (рис. 453); для упро-
упрощения рассмотрим случай перехода _/*тоорргч ^ ^^ и- х
от системы А", в которой B2.54) U U U 0 » w х \У *
выражает закон движения, к си- р ,„
стеме А"', в которой движущееся
тело в данный момент покоится
(т. е. система Л движется относительно системы К со скоростью г» — и).
Так как сила F лежит на одной прямой со скоростью тела и, то в системе К
тело обладает только тангенциальным ускорением. Воспользуемся из-
известными нам формулами преобразования масс, ускорений и сил. Обо-
Обозначим через т! массу рассматриваемого тела в системе К!. Так как
это есть покоящаяся масса тела, то в системе К, в которой тело
обладает скоростью и, его масса
т — — B2.56)
Далее иа основании формулы преобразования тангенциального уско-
ускорения B2.33), так как v= и, а «' = 0 (в системе К тело покоится),
получим:
— ^У'2. B2.57)
Наконец, так как ось пружины лежит на одной прямой со скоростью
и, а значит, и со скоростью v, то, как было показано [формула B2.52)],
F=F'. B2.58)
Подстановка полученных выражений в B2.54) показывает, что в такой
форме закон движения не сохраняет своего вида при переходе к си-
системе К, так как связь между величинами т',f и F' получается не
такая, как между величинами т, j и F. Поскольку хотя бы в одном
случае форма B2.54) оказывается неинвариаитной при переходе от

560 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гЛ. XXl't
одной системы координат к другой, движущейся прямолинейно и рав«
номерно, эта форма не может выражать закона движения.
Обратимся теперь ко второй форме закона движения B2.55). Так
каь т есть скалярная функция скорости, то выражение B2.55) можно
записать в таком виде
d\x I dm da „
тж + иш-шг=?' <22-59>
Проверим инвариантность этой формы для того же простейшего слу-
случая, для которого мы проверяли первую форму. В этом случае и из-
изменяется только по величине (есть только тангенциальное ускорение),
и уравнение B2.59) можно рассматривать как скалярное и записать
в таком виде.
Дифференцируя выражение B2.56) (т' в .нашем случае покоящаяся
масса), находим:
н т Т
B2'61)
Подставляя в B2.60) полученное выражение, а также выражения
B2.56), B2.57) и B2.58) для т, ^- и F (которые остаются справед-
справедливыми, поскольку рассматривается тот же случай), получим:
или после очевидных преобразований и сокращений:
, du' с-,
m4i' = F-
Так как в рассматриваемом случае т' постоянно, то полученное вы-
выражение можно записать так:
Таким образом, в рассмотренном простейшем случае выражение B2.55)
оказывается инвариантным по отношению к переходу от системы К
к системе К'.
Нетрудно убедиться, что оно остаётся инвариантным и в другом
простейшем случае, когда тело испытывает только нормальное уско-

§ 169] ЗАКОН ДВИЖЕНИЯ МЕХАНИКИ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 561
рение. Пусть в системе К тело массы т под действием создаваемой
пружиной силы F испытывает ускорение /, нормальное к скорости
тела а (рис. 454). Так как в этом случае скорость тела по абсо-
абсолютной величине остаётся постоянной, то и массу тела можно считать
постоянной и записать уравнение движения B2.55)
в виде:
mj=F. B2.62)
В системе К', которая движется вместе с телом
т, т. е. относительно системы К движется со ско-
скоростью v=a, тело обладает скоростью я' = 0.
Применяя формулу преобразования нормальных
ускорений B2.34), получим связь между ускоре-
ускорениями тела т в системах К и К':
}—[ 1 ——
B2.63)
Рис. 454.
Далее, так как пружина в системе К движется
перпендикулярно к своей оси, то в системе К', в которой пружина
покоится, как было показано в предыдущем параграфе, она будет
действовать с большей силой
Наконец, так как в системе К' тело покоится, применяя формулу
преобразования масс B2.56), относящуюся к этому случаю
т=
т'
B2.65)
где /и' есть покоящаяся масса тела, и подставляя в B2.62) значения
/, F, т из B2.63), B2.64) и B2.65), получим:
m'f = F'. B2.66)
Таким образом, форма B2.55) закона движения инвариантна и в этом
случае.
Конечно, в рассматриваемом случае, так как скорость тела по
абсолютной величине постоянна, масса тела не изменяется со време-
временем, и формы B2.54) и B2.55) эквивалентны. Поэтому случаи нор-
нормального ускорения не дают указаний о том, какую из двух форм
закона движения следует выбрать. На этот вопрос дал ответ рассмо-
рассмотренный выше случай тангенциального ускорения. Но, после того как
форма закона движения выбрана, необходимо проверить, инвариантна
ли она и в случае нормальных ускорений, чтобы убедиться, что масса
тела является скалярной величиной. Поскольку при этой проверке
3d с. Э. Хайкин

562 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гл. XXII
мы пользовались тем же выражением для зависимости массы от ско-
скорости, что и для тангенциальных ускорений, и проверка дала поло-
положительный результат, мы видим, что введение скалярной массы, изме-
измеряемой установленным выше способом, позволяет сохранить в меха-
механике теории относительности форму закона движения, весьма близкую
к форме второго закона Ньютона. Не только в рассмотренных част-
частных случаях, но и в самом общем случае можно было бы убедиться,
что при переходе к системе К', движущейся с любой постоянной
скоростью v относительно системы К (а не со скоростью v = u, как
в рассмотренном простейшем случае), выражение B2.55) остаётся
инвариантным. Поэтому можно ожидать, что именно оно выражает
закон движения. Но, для того чтобы решить вопрос, действительно
ли это есть закон движения, его нужно подвергнуть проверке на
опыте.
Коль скоро установлены независимые способы измерения всех вхо-
входящих в закон движения
^(яю)= F B2.67)
величин, именно массы, ускорения и силы, закон этот представляет
собой утверждение, которое целиком можно проверить на опыте.
Правда, современная техника ещё не позволяет осуществить столь
быстрые движения макроскопических тел, при которых этот закон
движения давал бы результаты, заметно отличающиеся or результатов,
получаемых при помощи второго закона Ньютона. Поэтому непосред-
непосредственная проверка закона движения теории относительности на опыте
с макроскопическими телами до сих пор не была осуществлена. Од-
Однако, в опытах с элементарными частицами (электронами, протонами
и т. д.) найдены вполне надёжные подтверждения закона движения
механики теории относительности.
Так, опыты с быстро движущимися электронами показали, что дан-
данная сила сообщает электрону тем меньшее ускорение, чем больше
скорость, которой электрон в этот момент облагает; причём при дан-
данной скорости электрона нормальное ускорение оказывается ббльшим,
чем тангенциальное. Все эти результаты, как легко видеть, прямо
вытекают из закона движения механики теории относительности, тогда
как по закону движения классической мечаннхи ничего подобного не
должно было бы иметь места.
Многие факты, касающиеся элементарных частиц, не только ка-
качественно, но и количественно хорошо согласуются с законом дви-
движения механики теории относительности и являются весьма убеди-
убедительным его подтверждением. Тем не менее, после появления теории
относительности подтверждающие её факты приходилось специальна
разыскивать и они «давались в руки» с трудом. Сейчас эти факты
нередко сами попадаются на пути и даже становятся «поперёк доро-
дороги». Наиболее ярким примером этого ми.кет служить проблема полу»

§ 169] ЗАКОН ДВИЖЕНИЯ МЕХАНИКИ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 563
чения больших скоростей электронов в так называемом циклотроне.
Принцип циклотрона, устройство которого здесь описывать было бы
нецелесообразно, состоит в применении постоянного магнитного
поля, для того чтобы заставить электроны двигаться по круго-
круговым орбитам с периодом обращения, равным периоду колебаний
быстропёременного электрического поля, которое в определённых
местах орбиты сообщает электронам некоторую добавочную ско-
скорость. Большие скорости- электронов могут быть достигнуты, если
такие электрические толчки повторяются большое число раз и в
нужные моменты времени. Для этого изменения электрического поля
должны быть синхронны с обращением электронов по орбитам. Од-
Однако, период обращения частицы в постоянном магнитном поле по
круговым орбитам зависит от её массы. При возрастании скорости
электрона его масса увеличивается, и период обращения изменяется,
вследствие чего нарушается синхронизм с изменениями электрическо-
электрического поля. Таким образом, зависимость массы от скорости ограничи-
ограничивает возможность ускорения электронов в циклотроне. Препятствие
оказалось столь серьёзным, что для получения пучков быстрых элек-
электронов пришлось разрабатывать другие ускорители, основанные на
иных принципах. Это — если не одно из самых убедительных, то во
всяком случае одно из самых ощутительных доказательств зависи-
зависимости массы от скорости, а вместе с тем механики теории относи-
тельности.
Закон движения механики теории относительности B2.67) внешне
имеет такой же вид, как и второй закон Ньютона в классической
механике. Интересно отметить, что именно в таком виде, а не в ви-
виде B2.54), он был сформулирован самим Ньютоном. Однако, способ
измерения одной из величин, входящих в этот закон, именно массы,
принятый в механике теории относительности, отличается от способа
измерения массы в классической механике. Поэтому по существу за-
закон движения механики теории относительности представляет собой
новый закон, принципиально отличный от второго закона Ньютона.
В заключение рассмотрим вопрос о кинетической энергии тела
в механике теории относительности. Как и в классической механике,
кинетическая энергия определяется той работой, которую совершает
внешняя сила, чтобы сообщить скорость телу. Элементарную работу
силы dA при перемещении dt
dA = Fdr
можно иначе записать следующим образом:
Эга элементарная работа равна dE—увеличению кинетической
энергии тела. Подставляя вместо величины Fdt равную ей по закону
движения B2.67) величину d(mv), получаем выражение дли прираще-
36*

564 МЕХАНИКЛ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [ГЛ. XXII
ния кинетической энергии тела:
dE = {d(mu)} u = mudu-\-u2dm.
Пользуясь выражением B2.50) для массы движущегося тела и для
dm, находим:
т — du
§и du
' B2'68)
Интегрируя это выражение в пределах от 0 до и, найдём кинетиче-
кинетическую энергию тела, имеющего массу покоя гп0 и скорость я:
и
Г тои da _ woct 2 I92M\
? Г /П()С ' B209)
C2
Внешне это выражение совершенно не похоже на выражение для
кинетической энергии в классической механике. Однако, нетрудно
убедиться, что для малых скоростей они совпадают (как и следова-
следовало ожидать). В самом деле, если иг\съ мало по сравнению с едини-
единицей, то приближённо можно написать:
Подставив это выражение в B2.69), получим: Е = гп0а3/2, т. е. выра-
выражение для кинетической энергии в классической механике.
Сопоставление зависимости массы и кинетической энергии тела
от скорости приводит к заключению, которому можно придать весь-
весьма общий характер, выходящий далеко за рамки механики.
Именно, из сопоставления выражений B2.68) и B2.61) видно,
что
dE=c4m, B2.70)
т. е. с увеличением скорости тела масса его растёт пропорционально
росту кинетической энергии. При изменении кинетической энергии
тела на величину dE в том же направлении изменяется и инертная
масса тела на величину dm = dE\c^. Следовательно, изменения кине-
кинетической энергии и инертной массы тела однозначно связаны между
собой. Аналогично для полной кинетической энергии тела соотноше-
соотношение B2.69) даёт:
Е = е2(т — т0). B2.71)
Иначе говоря, масса движущегося тела больше массы покоящегося
на величину
тЕ=%, B2.72)

§ 169] ЗАКОН ДВИЖЕНИЯ МЕХАНИКИ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 565
где Е — кинетическая энергия тела. Увеличение массы движущегося
тела по сравнению с массой покоящегося можно толковать так, что
сама энергия Е обладает массой —$ и эта масса прибавляется к
массе покоящегося тела. Поэтому инертная масса тела зависит от
того, какой кинетической энергией (т. е. какой скоростью) это тело
обладает.
В такой форме это толкование прямо вытекает из механики тео-
теории относительности. Однако, Эйнштейн пошёл дальше и предполо-
предположил, что это справедливо не только для кинетической, но и вообще
для всей энергии, которой обладает тело. Если вся энергия тела
изменяется на величину ДЕ, то масса тела изменяется в том же на-
направлении на величину ДЕ/с2. При всяких изменениях энергии тела
происходят соответствующие изменения его массы.
Вследствие того, что с2 очень велико, эти изменения массы мо-
могут быть обнаружены только при очень больших изменениях энергии
тел. Эйнштейн сам указал явления, на которых можно пытаться прове-
проверить соотношение между массой и энергией. Это — ядерные превра-
превращения, при которых происходят очень значительные изменения энер-
энергии частиц. Эти явления действительно дали блестящие доказательства
справедливости соотношения Эйнштейна B2.72) между энергией
и массой.
Наиболее наглядным подтверждением соотношения Эйнштейна
является так называемый дефект массы в ядрах, состоящих более
чем из одной элементарной частицы. Оказалось, что масса такого
ядра меньше, чем сумма масс частиц (протонов и нейтронов), его
составляющих. Причина состоит в том, что при образовании ядра
силы, удерживающие протоны и нейтроны в ядре («ядерные силы*),
совершают положительную работу, и поэтому общая энергия всех
частиц, образующих ядро, меньше, чем в том случае, когда они этого
ядра ещё не составляли. Соответственно этому их общая масса в
ядре меньше, чем сумма масс, которыми каждый из них обладал до
образования ядра.
Соотношение Эйнштейна между массой и энергией является од-
одним из наиболее фундаментальных соотношений современной физики.
Исходя из этого соотношения и применяя принцип относителности, мож-
можно получить все те "результаты, к которым пришла теория относитель-
относительности изложенным выше путём. Таким образом соотношение между мас-
массой и энергией можно считать основным соотношением теории относитель-
относительности. Помимо огромного принципиального значения оно имеет и важное
практическое значение, прежде всего для всей ядерной физики. По-
Поскольку масса тела определяется содержанием энергии в иём, то при
всех ядерных превращениях, при которых происходят заметные из-
изменения общей массы, выделяются огромные количества энергии.
Можно сказать, что вся ядерная физика является блестящим под-
подтверждением соотношения Эйнштейна межту массой и энергией, а зна-

566 МЕХАНИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ [гл. XXII
чит, и всей теории относительности. С другой стороны, ядерная
физика своими успехами и, в частности, блестящими успехами в прак-
практическом использовании ядерной энергии в не малой степени обязана
теории относительности.
Несмотря на то, что мы ограничились изложением только меха-
механики специальной теории относительности, но уже на этом конкрет-
конкретном материале основная, руководящая идея всей теории относитель-
относительности выступает достаточно чётко. Физические законы не могут
зависеть от выбора системы отсчёта, т. е. от движения наблюда-
наблюдателя. Поэтому они должны быть «безотносительны», иначе говоря,
не должны изменяться при переходе от одной системы координат
к другой. Как мы убедились, действительно физические законы мож-
можно сформулировать так, чтобы было выполнено это требование
обеспечена их инвариантность. Однако, при этом физические поня-
понятия, которые служат для формулировки этих законов, и, прежде
всего, основные понятия интервала длины и промежутка времени,
оказываются относительными. Но относительность физических поня-
понятий отнюдь не противоречит требованию, чтобы физические законы
были «безотносительны». Руководящая идея теории относительности
состоит в том, что можно и нужно ввести в физику целый ряд
относительных понятий, для того чтобы обеспечить ч.безотносител*-
ность*, инвариантность физических законов.

ЛИТЕРАТУРА
По всему курсу
Р. В. Поль, Введение в механику и акустику, ГТТИ, 1933.
Г. А. Л о р е н т ц, Курс физики, изд-во «Матезис», Одесса, 1910.
По отдельным разделам курса
И. В. Арнольд, Теоретическая арифметика, Учпедгиз, 1939.
П. В. Ьриджмен, Анализ размерностей, ГТТИ, 1934.
Н. Е. Жуковский, Теоретическая механика, Оборонгиз, 1939.
A. А. Эйхенвальд, Теоретическая физика, ч. II, Общая механика.
ГИЗ, 1930.
Г. .Галилей, Сочинения, т. I, ГТТИ, 1934.
Р. М а й е р, Закон сохранения и превращения энергии, ГТТИ, 1933.
Г. Гельмгольц, О сохранении силы, ГТТИ, 1934.
С. Э. Хайкии, Что такое силы инерции, ГТТИ, 1940.
B. Л. Кирпичёв, Беседы о механике, ГТТИ, 1933.
Перри, Вращающийся волчок, ОНТИ, 1936.
Архимед, Стевин, Галилей, Паскаль, Начала гидростатики,
ГТТИ, 1933.
Т. Пешль, П. Эвальд, Л. Прандтль, Физика упругих и жидких
тел, ГТТИ, 1935.
К. Ш ю т т, Физика полёта, Гостехиздат, 1942.
Г. Баркгаузен, Введение в учение о колебаниях, Энергоиздат, 1934.
Флеминг, Волны в воде, воздухе и эфире, изд-во Академии Наук СССР,
1937.
C. Н. Ржевкин, Слух и речь, ОНТИ, 1936.
С. И. Вавилов, Экспериментальные основания теории относительности,
ГИЗ, 1928.
М. Бори, Теория относительности Эйнштейна и её физические основы.
ОНТИ, 1938.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютно жёсткие связи 116, 117;
равновесие при наличии их 117 и д.
— неупругий удар 141
— твёрдое тело 13, 40
— упругий удар 183
— упругое тело 279
Абсолютные системы единиц 18: CGS
19, 20, LFT 20, LMT 19, МК? 19
Автоколебания 408 и д.: в сплошных
системах 466, зажима Прони 409,
звуковые в трубах 4S6
Автопилот 262
Адиабатическое сжатие газа 389
Альтиметр 321
Амплитуда 137, 150: вынужденных ко-
колебаний 412, звуковой волны 486
Анизотропные тела 289 и д.
Апериодические системы 407
Атаки угол 351, 365: критический 368
Атвуда машина 221
Атмосфера техническая 309
Атмосферное давление 313
Аэродинамическая труба 347
— силы 354
— подобие 347
Аэростаты 318
Бар 483
Барометрическая формула 319 и д.
Барометры жидкостные 313
Бегущие волны 451 и д., 454 и д.: в
стержне 453, в струне 455
Безразличное равновесие 116
Бернулли закон 330, 332
Биения 400
Бинауральный эффект 491 и д.
Бойля-Мариотта закон 320
Боковая сила 352
Ватт 180
Векторное произведение 47
Векторы 31
Вес тела НО
Весы рычажные 229: чувствительность
их 230, 231
Взвешивание тел 108 и д.
Взрывная волна 391
Види коробка 309
Винт воздушный 379
Вихревая дорожка Кармана 360
Вихрь 360
(Внутреннее трение 291
Внутренние силы 137, 214, 215
Воздушно-реактивный двигатель 339
Волна взрывная 391: ударная 392
Волновые поверхности 467
Волны 451 и д.: бегущие 451 и д., в
сплошной среде 467 и д., деформа-
деформаций 454
— звуковые 482 и д.: в трубах 494
и д., стоячие 496
— капиллярные 472, круговые 469,
на поверхности жидкости 469 и д.,
плоские 467, поперечные 455, 470,
продольные 453, скоростей 453,
цилиндрические 469, шаровые 46Э
Волны уравнение 152.
Восстанавливающая сила 396, 397
Вращательное движение 41, 42
Вращающиеся системы координат 55
и д., 196 и д.
Вращение тела вокруг неподвижной
оси 217 и д.
Вращения ось 41
Временная развёртка 397
Время в движущихся системах коор-
координат 49 и д., 524 и д.
Всемирное тяготение 26, 265 и д.
Всестороннее сжатие 304
Второй закон Ньютона 22, 24, 558
Вынужденные колебания 410 и д.
Выталкивающая сила 314
Вязкая жидкость 356 и д.
Вязкости коэффициент 127, 341
— силы 305
Вязкость 281, 340, 342: кинематиче-
кинематическая 346
Газы 304 и д.
Галилеевы преобразования координат
53, 530 и д.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
569
Галилея принцип относительности 94,
211, 532
Гармонические колебания 395: кру-
крутильные 396
— резонаторы 420
Гармонический анализ звуков 497
Гельмгольца резонаторы 498, 499
Герц 397
Гидродинамика 327 и д.
Гидростатика 304 и д.
Гирогоризонт 262
Гирокомпас 263
Гироскопические навигационные при-
приборы 261 и д.
Гироскопический маятник 257
— момент 252
Гироскопы 254 и д., 261 и д.
Гистерезиса петля 293
Гистерезис упругий 293
Главный момент количества движения
твёрдого тела 250
Гравитационная: масса 267, постоян-
постоянная 26, 268 и д.
Гравитационные силы 75
Градиент скорости 342
Гребные колёса и винты 337
Групповая скорость волн 471
Гука закон 281
Гюйгенса принцип 475 и д.
Давление: атмосферное 314, в газе
307, в жидкости 307, в покоящихся
жидкости и газе 312 и д., в текущей
жидкости 330 и д., динамическое
334, звуковое 483, 484, изменение
с высотой 319 и д., полное 334, ста-
статическое 334
Движение: «абсолютное» 51, волновое
451 и д., вращательное 41, 42, на
поверхности Земли 204и д., «относи-
«относительное» 51, переносное 51, плоское
40, 63, под действием силы тяжести
106 и д., поступательное 41, твёрдо-
твёрдого тела 63 и д., тел в жидкости или
газе 346 и д.
Дефект массы 565
Деформации: возникновение 104, дина-
динамические 96 и д., 104 и д.,
остаточные (пластические) 280, 293,
при вращательном движении 98
и д., при сложных движениях 101
и д., статические 104, тяжёлого тела
112 и д.
Джоуль 164
Динамические деформации 104
Динамический напор 334
Динамическое давление 334
Диск: Максвелла 112, Рэлея 487
Дисперсия волн 457, 471
Диффракция волн 478 и д.
Диффузный звук 505
Длина волны 452
Допплера эффект 493
Единица: времени 19, длины 19, мас-
массы 19
Единицы физических величин 18 и д^
Жидкое трение 122, 123: зависимость
от скорости 123
Жидкости 304 и д.
Жидкость в движущихся сосудах 322
и д.
Жуковского скамья 153, 238
Завихренность течения 359
Зажим Прони 134
Закон всемирного тяготения 26, 265-
и д.
Закон движения в механике теории
относительности 558 и д.
Законы Ньютона 71 и д., 86 и д.
Замедление хода движущихся, часов
524 и д.
Замкнутая система 137
Застоя явление 132
Затухание колебаний 402: при наличии
постоянного трения 408
Затухания: логарифмический декре-
декремент 405, показатель 405
Звуковая тень 490
— энергия 484 ид.: поглощение 488
и д., рассеяние 488 и д.
Звуковое давление 483, 484
Звуковые волны 482 и д.: в трубах
494 и д., источники 500 и д.
Звукоулавитель 492
Звук 482 и д.: поглощение 488, рас-
распространение в атмосфере 488 и д.
Земное притяжение 106
Зонд 335
Зоны: аномальной слышимости 490,
молчания 490
Идеализированная схема 11 и д.
Изгиб 276
Излучение звуковых волн 500
Измерение физических величин 15
и д.
Изотропные тела 289 и д.
Изохронность колебаний маятника 151
Инертная масса 81, 267
Инерциальная связь 430
Инерциальные системы координат 90--
И д„ 550

570
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Инерции: момент 143, 217 и д., силы
105, 190 и д., центр 216
Инерция 80
Источники звука 500 и д.
Интенсивность звуковой волны 486
Интерференция волн 472 и д.
Импульс: в упругом теле 296 и д.,
отражение 303, плоский 390, попе-
поперечный 299, продольный 298, распро-
распространение в жидкости и газе 387 и
д., растяжения 293, сдвига 299, сжа-
сжатия 297, 298, 299, шаровой 391
Кавендиша опыт 270
¦Камертон 500
Капиллярные волны 472
Кармана вихревая дорожка 360
Качение тел 238 и д.
Качество: крыла 372, самолёта 381
Кеплера законы 255
¦Киюграммочстр 180
Кинематика 27 и д.: теории относи-
относительности 540 и д., точки 31
Кинематическая вязкость 346
Кинетическая энергия 171 и д.: в дви-
движущихся системах координат 187,
в механике теории относительности
563 и д., вращающегося тела 219,
связь с массой 564
Когерентность воли 474
Колебания: в сплошных телах 435 и
д., вынужденные 410 и д., гармони-
гармонические 395, камертона 440, крутиль-
крутильные 396, малые собственные 401, мо-
модулированные 423, нормальные 431,
4&5, поперечные 439 и д., при воз-
возникновении силы 174, связанных си-
систем 428 и д.
— систем: с двумя степенями свобо-
свободы 425 и д., с одной степенью сво-
свободы 394 и д., со многими степенями
свободы 425 и д.
— собственные 400 и д.: при боль-
большом трении 406 и д.
— сплошных систем, как стоячие вол-
волны 463 и д., стержня 436, 439 и д.,
струны 436 и д., твёрдых тел 466,
упругой пластинки 440
'Количество движения 83: твёрдого те-
тела 217
"Конвекция энергии в упругом теле 301
Кориолисова сила инерции 200 и д.,
206 и д.
Кориолисово ускорение 55 и д., 61,
Г02
Кориолисовы силы 103 и д.
Критический угол атаки 381
Критическое сопротивление 407
Круговые волны 469
Крутильчые колебания 396 и д.
Кручение 276
Крыло самолёта 365, 371
Кулона закон трения 128, 129
Ламинарное течение 361
Линейная скорость 33, 45 и д.
Линейные резонаторы 420
Линии тока 327
Лиссажу фигуры 427
Лобовое сопротивление 350, 359' коэф-
коэффициент 364
Логарифмический декремент затуха-
затухания 405
Лорентца-Эйнгатейна преобразования:
координат 543, скоростей 544, уско-
ускорений 545
Лошадиная сила 180
Луч 480
Любимова опыты 109
Магнуса эффект 372 и д.
Майкельсона опыт 515 и д., 518 и д.
Максвелла: диск 112, маятник 233
Малые собственные колебания 401 и д.
Масса 80 и д.: в механике теории от-
относительности 550 и д., гравитаци-
гравитационная 267, движущегося тела 554,
555, зависимость от скорости 555 и
д., измерение её в механике тео-
теории относительности554 ид., инерт-
инертная 81, 267, определение 86 и д., оп-
определение взвешиванием 411 и д.
Массовые силы 113
Математический маятник 149
Материальная точка 11, 72
Маятник: гироскопический 257, Макс-
Максвелла 233, математический 149, обо-
оборотный 225, физический 222 и д.,
Фуко 206 и д.
Мгновенная ось вращения 66
Метацентр 317
Микрофоны 488
Модулированные колебания 423
Модуль: сдвига 284, 289, сжимаемости
484, упругости 283, Юига 283, 289
Момент гироскопический 252
— инерции 143, 217: диска 219, поло-
полого цилиндра 220, пренебрежение им
221, тел неправильной формы 220
— количества движения 144; главный
250, изменение его направления 155 н
д., полный 218
— силы: относительно оси 143, отно-
относительно точки 245

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
571
Мощность 179 ид.
Музыкальные тоны 499
Наложение гармонических колебаний
399
Напряжение: в данном сечении 282,
в точке 285 и д., нормальное 282,
тангенциальное 283
Негармоническое внешнее воздейст-
воздействие 420 и д.
Неииерциальные системы координат
190: и законы сохранения 208 и д.
Неупругий удар 141
Неустойчивое равновесие 116
Нормальное ускорение 36
Нормальные колебания 431
— частоты 431, 435: сплошной си-
системы 442 и д.
Нутации 255
Ньютона законы 71 и Д.: второй 22,
24, 80 и д., 86 и д., первый 86,
третий 84, 98
Обербека крест 154
Обертоны 420, 437, 444
Оборотный маятник 225
Обтекаемая форма тел 362
Обтекание тел вязкой жидкостью 356
и д., идеальной жидкостью 352 и д.,
полное 354
Объёмной упругости коэффициент 484
Объёмный модуль сжатия 290
Одновременность двух событий 536
и д.
Однородное растяжение (сжатие) 276
Однородный сдвиг 276
Основной тон 437
Остаточные деформации 280, 293
Остойчивость 317
Ось вращения 41
Отвердения принцип 306
Относительная скорость 122
Относительное движение 51
— поперечное расширение (сжатие)
278
— удлинение 276
Относительности: принцип 530 и д.,
теории 509 и д.
Относительный сдвиг 277
Падение тел: в сопротивляющейся сре-
среде 124, при малых скоростях 126
Параметрический резонанс 450
Параметрическое возбуждение коле-
колебаний 449 и д.
Парашютный прыжок 125
Парциальные системы 429
Первый закон Ньютона 86
Перемещение твёрдого тела 39 и д.,
угловое 42
— точки 31
Переносное движение 51
Период гироскопического маятника
258
Периодический процесс 403
Период: биений 400, колебаний 150.
396, 397
Петля гистерезиса 293
Пито трубка 334
Плавание тел 314 и д.
Пластические деформации 280
Плоский импульс 390
Плоское движение 40, 63, 231 и д.
Поверхности равной фазы 467
Поверхностное натяжение 326
Поверхностные явления 325 и д.
Поворот самолёта: относительно вер-
вертикальной оси 383, относительно
поперечной оси 383, относительно
продольной оси 384
Поглощение звуковой энергии 488 и д.
Пограничный слой 357
Подобие аэродинамическое 347
Подъёмная сила 314, 350, 364 и д.,
аэростата 321
Подъёмно! силы коэффициент 372
Показатель затухания 405
Полёт самолёта 379 и д.: горизонталь-
горизонтальный 380, при взлёте 382, при набо-
наборе высоты с постоянной скоростью
381, при посадке 382, при снижении
с постоянной скоростью 382, устой-
устойчивость 382 и д.
Поляризация поперечных колебаний
448: плоская 448, эллиптическая 448
Поперечная ось самолёта 383
Поперечного сжатия козффициент 278
Постоянство скорости света 511, 514
и д.
Поступательное движение 41
Потенциальная энергия 167, 170
Поток стационарный 328
— энергии упругой деформации 302
Правило размерностей 24 и д.
Предел упругости 279
Предельный угол 129
Преломление волн 477
Преобразования координат Галилея
53
— Лорентца-Эйиштейна: координат
543, скорости 544, ускорения 545
Прецессия 256
Приведённая длина физического маят-
маятника 223
Приливы 272

572
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Принцип отвердения 306
— относительности 530 и д., Галилея
94, 211, специальный 532
— суперпозиции 284
Продольная ось самолёта 383
Продольные колебания стержня 464
Прони зажим 134
Пропеллер 379
Пространственно-временные системы
отсчёта 28 и д.
Пуаз 341
Пуазейля формула 344, 345
Пуассона коэффициент 278, 289
Путевая ось самолёта 383
Пьезоэлектрические излучатели звука
506
Пьезоэффект 506
Работа 163 и д.: передача 181, сил тре-
трения 166, сил тяготения 166, упругих
сил 166
Равновесие и потенциальная энергия
170
— материальной точки 115 и д.: без-
безразличное 116, неустойчивое 116,
устойчивое 115
— плавающего тела 315, 316, при на-
наличии абсолютно жёстких связей 117
и д., твёрдого тела 226 и д., упру-
упругого стержня 294
Радиус кривизны 39
Размерности физических величин 20
и д., 22 и д.: и физические законы
22 и д., 24 и д.
Ракетный снаряд 338 и д.
Растяжение 275: всестороннее 304
Рассеяние звуковой энергии 488 и д.
Реактивное движение 338
Реверберация звука 505
Резонанс 413, 417 и д.: в сплошных
системах 441, 442, 465 и силы тре-
трения 417
Резонансные кривые: амплитудные
413, фазовые 413
Резонанс параметрический 450
Резонаторы акустические 497: Гельм-
гольца 498
— гармонические (линейные) 420
Рейнольдса число 361
Рупоры 504
Рычажные весы 229: чувствительность
их 230, 231 "
Рэлея диск 487
Самодвижущиеся экипажи 241 и д.
Свободные колебания 400 и д,
— оси 245 и д.
Связанные системы 428 и д.
Связь: инерциальная 430, упругая (си-
(силовая) 430
Сдвиг 275: относительный 277, фаз 398
Сдвига модуль 284
Сжатие 275: всестороннее 304, одно-
однородное 276
Сжимаемости коэффициент 290, 309
Сжимаемость жидкостей и газов 309
и д.
Сила: боковая 352, в механике теории
относительности 550 и д., восстана-
восстанавливающая 396,397, измерение в ме-
механике теории относительности 556
и д.
— инерции: кориолисова 200 и д.,
, центробежная 197
— подъёмная 314 и д.. 318, 350, 364
и Д., связь с ускорением 78, тяги
379, тяжести 106 и д., 225 и д., цен-
центробежная Ш0
Силовая (упругая) связь 430
Силы 73 и д.: аэродинамические 354,
внутренние 137, 214, 215, всемирно-
всемирного тяготения 75, вязкости 305, гра-
гравитационные 75 и деформации 95 и
д., 104 и д., измерение 76, инерции
105, 190 и д., 197, 200 и д., 208, 211,
массовые 113, поверхностного натя-
натяжения 326
— трения 75, 119 и д.: измерение 121
и д., работа их 166
— упругие 75
Системы единиц физических величин
18 и д.: абсолютные 18
— координат: вращающиеся 55 и д.,
196, движущиеся 49 и д., 51 и д.,
движущиеся прямолинейно 193,
ииерциальные 90 и д., 186, 550, не-
инерциальные 190
— отсчёта 26, 71
Скольжения трение 130; зависимость
от скорости 130
Скорость 32 и д.
— волн: групповая 471, на поверх-
поверхности жидкости 471, фазовая 471
— звука 390, 482, истечения жидко-
жидкости из отверстия 336, линейная 46
и д., относительная 122, распро-
распространения импульса 296, самолёта
386
— света 30: её роль в механике 509,
постоянство 511, 514 и д.
— угловая 42, 46, установившаяся
124
Сложение: гармонических колебаний
399, векторюв 31

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
573
Смачиваемость 325
Собственные колебания 400 и д.: ма-
малые 401, при большом трении 406
и д., стержня 463
Сообщающиеся сосуды 318
Сопротивление: давления 359,361, кри-
критическое 407, лобовое 350, 359, сре-
среды 120, трения 359, 361
Свхраиение количества движения 137
и д.: применения 138 и д.
— момента количества движения 143
ид., 176 и д.: для системы тел 235,
для системы точек 151 и д.
— энергии 171 и д., 176 и д.: в инер-
циальных системах координат 187
и силы трения 17-8
Сохранения законы 186: в движущихся
системах координат 187, в инерци-
альных системах координат 187, 208
и д., применение к движению жид-
жидкостей 336 и д.
Спектр модуляции 423
Специальная теория относительности
509 и д.
Специальный принцип относительно-
относительности 532 и д.
Сплошные тела 274
Статические деформации 104
— давления 334
Стационарное течение вязкой жидко-
жидкости 340, 344 и д.
Степени свободы системы 40
Стокса формула 127
Стоячие волны 457 и д., 463 и д.: зву-
звуковые в трубах 496, в стержне 457
и д., в струне 462 и д.
Стробоскопическое освещение 42
Суперпозиции принцип 284
Сухое трение 122, 123, 128, 131 и
устойчивость равновесия 135
Тангенциальное: напряжение 283,
ускорение 36 и д.
Твёрдое тело 13, 213 и д.: плоское
движение 231 и д., равновесие 226
и д., уравнения движения 226 и д.
Текучесть материала 281
Техническая атмосфера 309
Течение: ламинарное 361, стационар-
стационарное 340, 344 н д., турбулентное 361,
циркуляционное 377
— энергии в упругом теле 300 и д.
Токовые трубки 329
Торможение экипажа 242
Точка материальная 11, 72
Точность измерения физической вели-
величины 17
Трение: влияние на затухание колеба-
колебаний 407, внутреннее 291, качения
238 и д., жидкое 122, 123, покоя 127,
скольжения 130, сухое 122, 123, 128.
131, сухое и устойчивость равнове-
равновесия 135
Трения покоя коэффициент 129: опре-
определение методом предельного угла
129
— силы 75, 119 и д.: измерение 121
и д., работа их 166
Третий закон Неютона 84 и д., 98
Трубка Пито 334
Турбины 338
Турбулентное течение 361
Турбулентность 361
Угловая скорость 42, 46: прецессии
гироскопического маятника 257
— частота: биений 400, колебаний
150, 397
Угловое перемещение тела 42
— ускорение 43
Угол атаки 351, 365: критический 368
381
Удар: абсолютно неупругий 141, аб-
абсолютно упругий 183
Ударная волна92
Узловые точки 458: нормального ко-
колебания 437
Ультразвуки 506 и д.
Упругая (силовая) связь 430
Упругие напряжения 282
— силы 75
— тела 274 и и., 279 и д.
Упругий гистерезис 293
— удар 183
Упругое равновесие 293 и д.
Упругости: модуль 283, предел 279
Уравнение: волны 452, моментов 146
и д., 250 и д.
Уравнения движения 89: твёрдого те-
тела 226 и д.
Ускорение 34 и д. и сила 78 и д., Ко-
риолиса 55 и д., 61, 102, нормальное
36, силы тяжести 107, тангенциаль-
тангенциальное 36 и д., угловое 43, центростре-
центростремительное 38, 44, 98
Установившаяся скорость 124
Устойчивое равновесие 115
Устойчивость полёта 370, 382 и д.
— равновесия тел 115 и д.
— упругого равновесия 293
Ухо 488: чувствительность 488
Фаза 397: вынужденных колебании
413

574
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Фазовая скорость воли 457
Фигуры: Лиссажу 427, Хладни 441
Физические величины 15 и д.
— законы и размерности величин 22
н д.
Физический маятник 222 и д.
Фуко опыт 91, 94, 206, 207
Хладияевы фигуры 441
Хрупкость 281
Центр инерции 216
Центрифуга 324
Центр качаний физического маятника
223
— масс 216, 217
Центробежная сила 100: инерции 197
Центростремительное ускорение 38,
44, 98
Центр тяжести 214 м д.
Циркуляционное течение (циркуля-
(циркуляция) 372 и д., 377: вокруг крыла' 377
Частота 150, 397: угловая 150, 397
Частотомер язычковый 414
Частоты колебания струны 446 и д.
— связи 431, 435: сплошной системы
442 и д.
Часы 19, 524
Число степеней свободы системы 40
Шаровой импульс 391
Шаровые волны 469
Штейнера теорема 221
Эйнштейна соотношение эквивалент-
эквивалентности массы и энергии 565
Эквивалентность массы и энергии 564,
565
— сил инерции и сил тяготения 211
Экипажи самодвижущиеся 241 и д.
Энергия 163 и д.
— звука 484 и д.: поглощение 4S3
н д., рассеяние 48S и д., средняя
485 и д.
— кинетическая 171, колебаний 402
— потенциальная 167 и состояния
равновесия 170, упругой дефор-
деформации 290 и д., 302
Энергии течение 182, течение в уп-
упругом теле 300 и д.
Эрг 164
Эталоны физических величин 15 и д.
Эхолот 508
Юнга модуль 283, 289
Язычковый частотомер 414

Опечатки
Стр.
157
159
161
161
196
243
243
570
399
400
461
484
486
486
551
551
551
Строка
14 сн.
12 св.
14 сн.
—
13 св.
23 си.
—
Зсн.\
3 cb.j
3—4 св.
17 св.
8 св.
12 свЛ
12 сн.
10 сн.
2 св.
13 си.
4 сн.
Напечатано
Должно быть
На рис. 116 поменять местами буквы X к X1
момент М' силы R'
A0.14)
A0.16)
момент М" силы R'
A0.16)
A0.18)
На рис. 142 вектор mg должен быть уменьшен
так, чтобы вектор /и<о2г был направлен горизон-
горизонтально
A3.42)
Рис. 166
A3.46)
Рис. 179
На рис. 303b стрелки должны быть перпендику-
перпендикулярны к пунктирной линии
смещения, скорости и де-
деформации
ТТЛ»
и линейки L в системе К
(рис. 447)
(рис. 448)
„„„ Щ — «»2 t
смещения и скорости
Ад»
и линейки L в системе К
(рис. 448)
(рис. 447)
По
чьей
вине
Ред.
»
Авт.
Ред.
»
Авт»
»
Ред.
•
Тир.
Ре*
*
С. Э. Xайкни