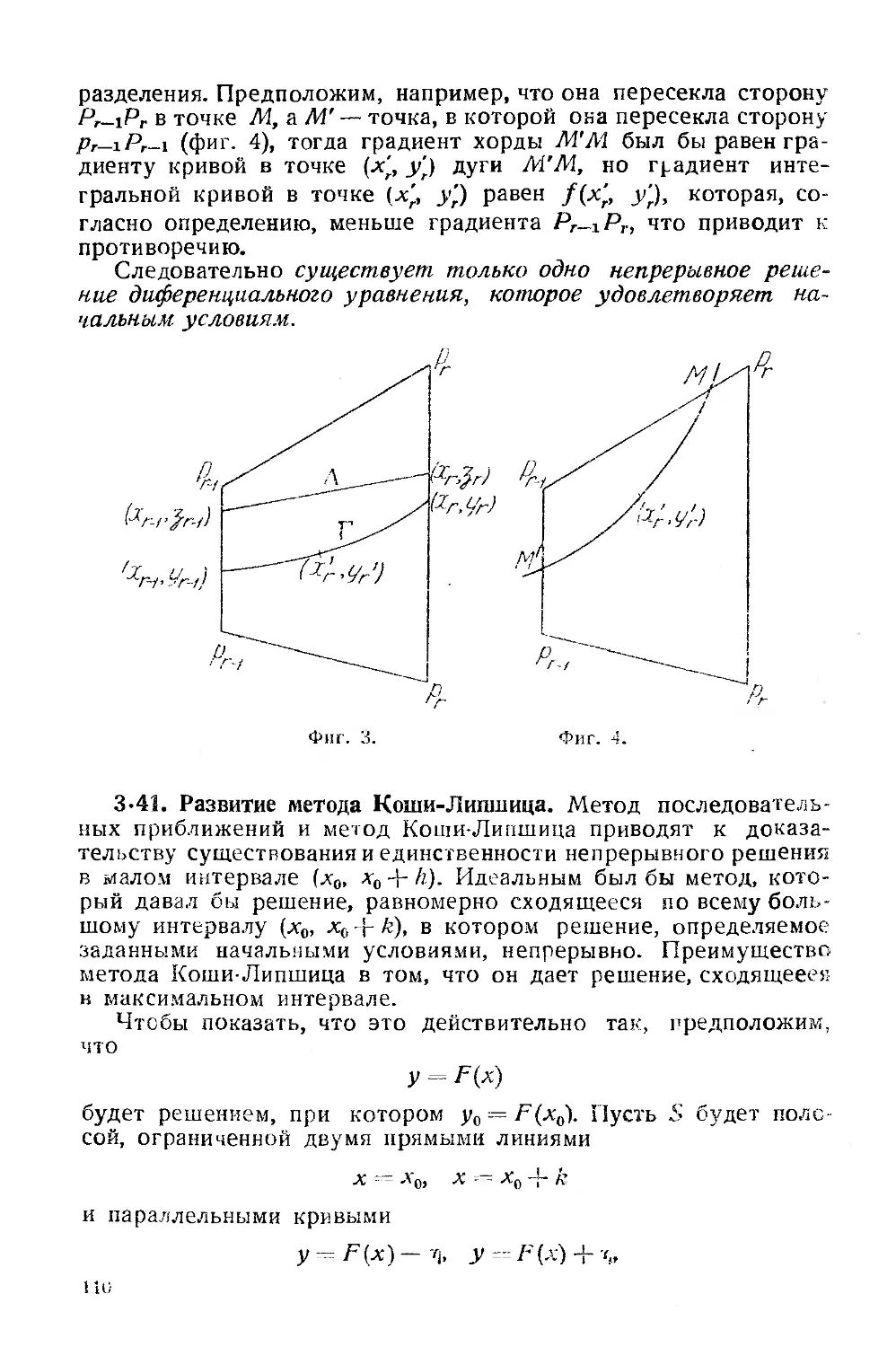
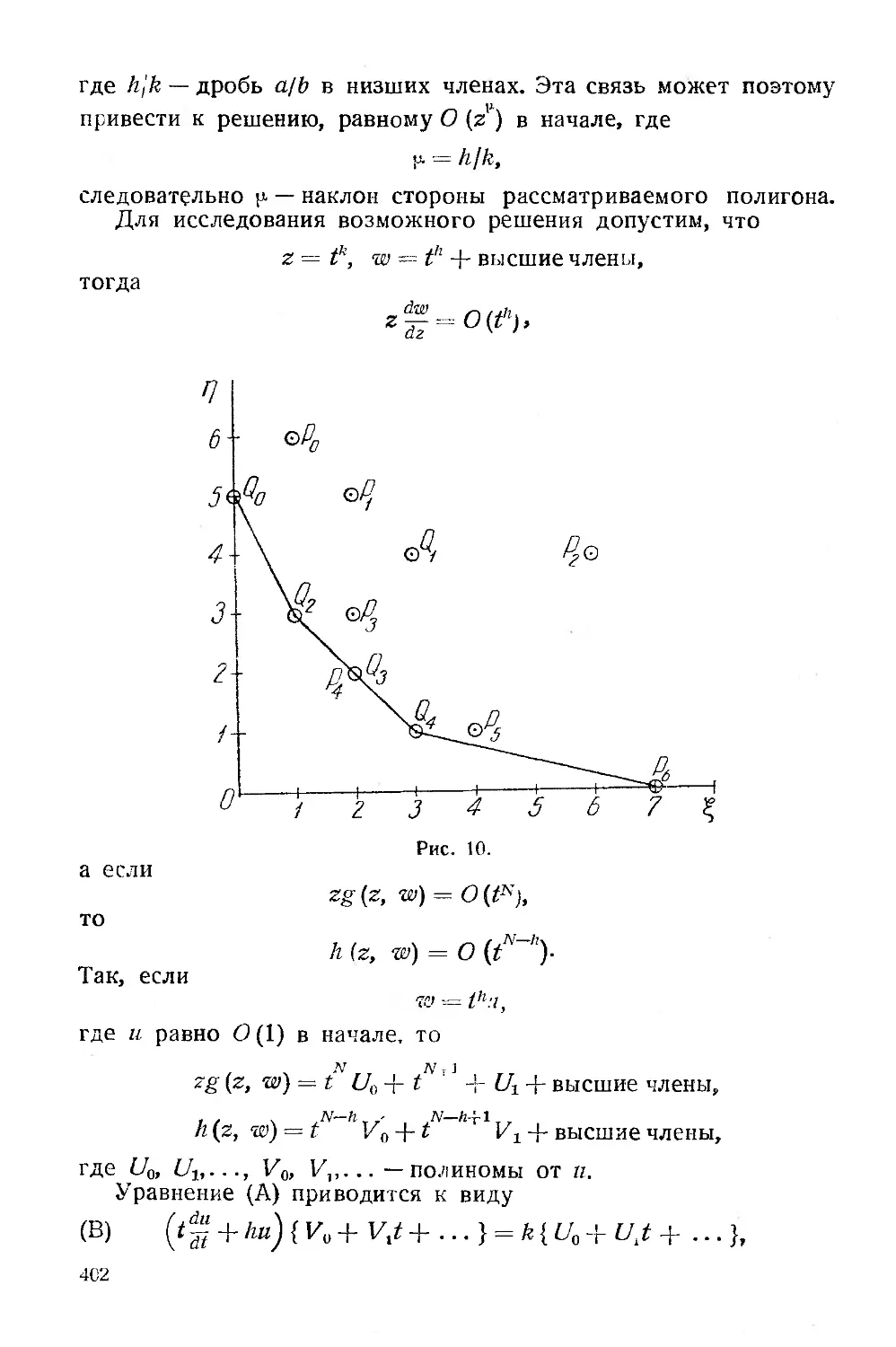
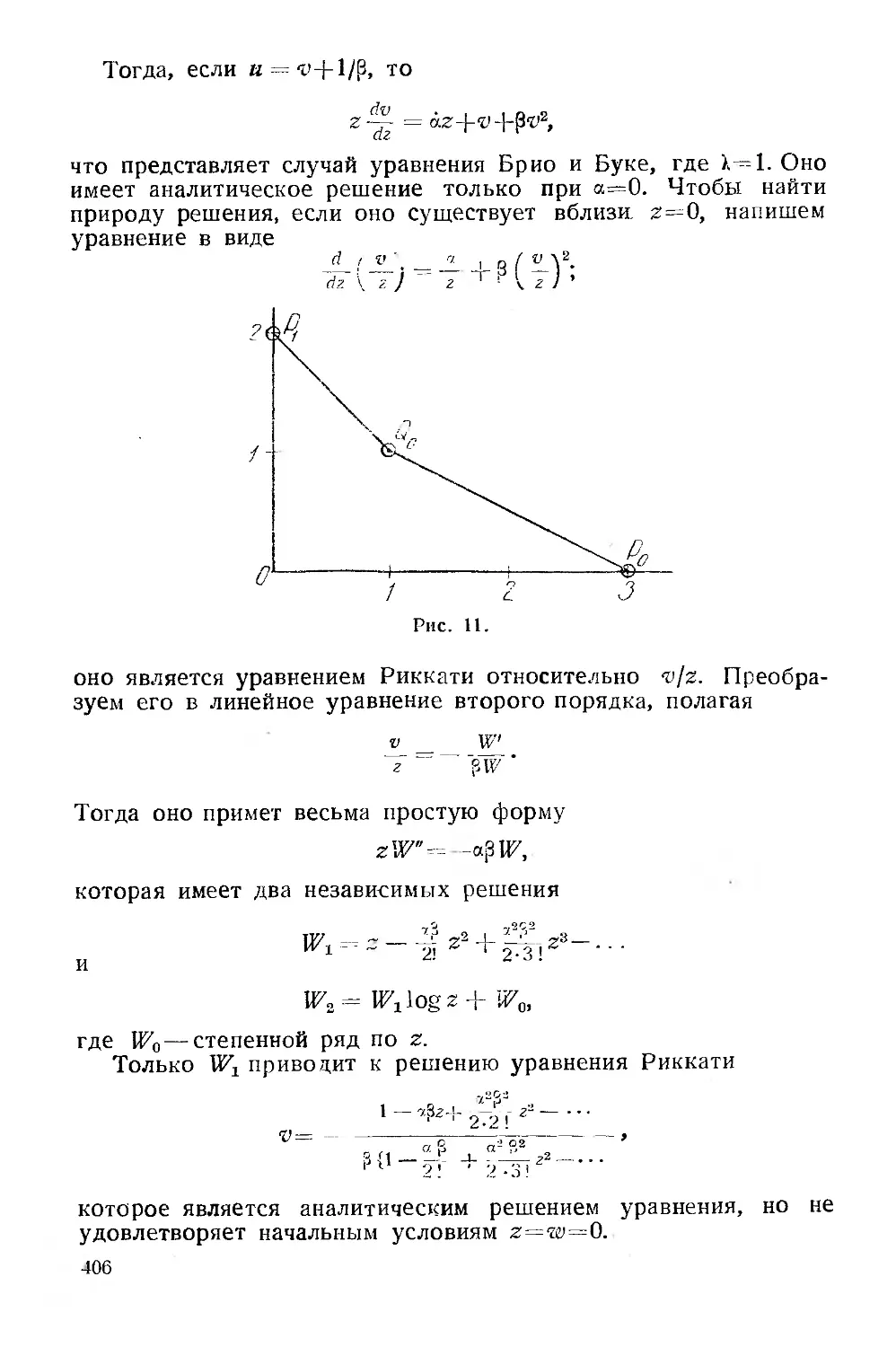
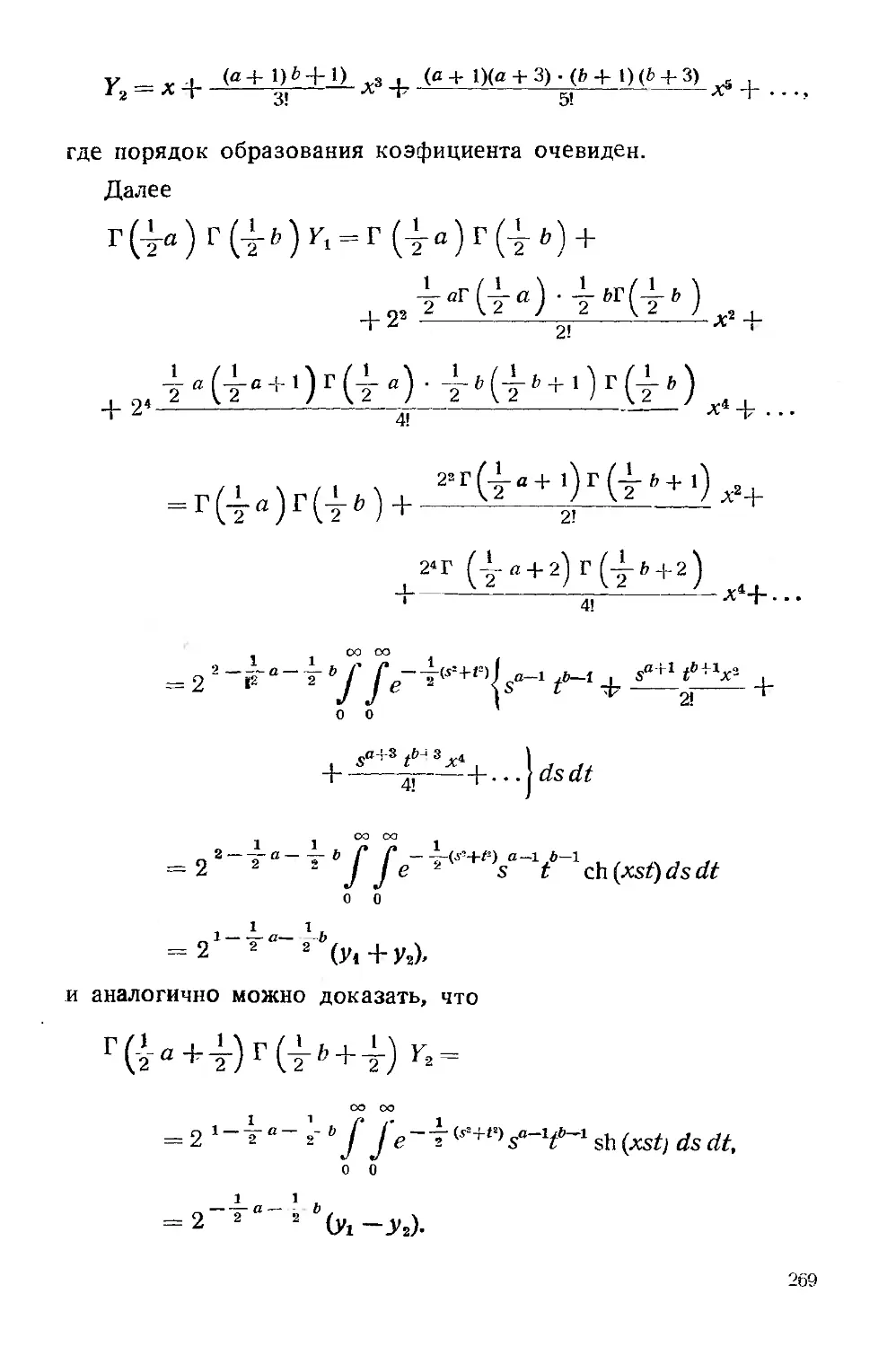Текст
Проф. Э. Л. АЙНС
ОБЫКНОВЕННЫЕ
ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРЕВОД С АНГЛИЙСКОГО
ПОД РЕДАКЦИЕЙ
А. М. ЭФРОСА
ОНТИ ГОСУДАРСТВЕННОЕ НКТП
НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО УКРАИНЫ
ХАРЬКОВ
Библиографическое описание
этого издания помещено в
„Летопнсн Укр. печати"
Ответственный редактор — А. М. Эфрос
Литредактор — С. Б. Бенгис
Техредактор — О. А. Кадашевич
Корректор С. Г. Власова
ДНТВУ. Уполномоченный Гяавлита № 683. Сдано в набор 3/V11 1938 г. Под-
Подписано к печати 20/XI 1938 г. Формат бумаги 62x94см.2 Vie Вес метр, стопы
36 кг. На одном печечагном листе 65 000 знаков. Объем 45 печатных листов,
авторских листов 42,2. Зак. № 133. Тираж 3.000 экз.
Типография Оборонгиза. Киев, Крещатик, 42.
ПРЕДИСЛОВИЕ РЕДАКТОРА
Выпускаемая в русском переводе книга Айнса (Е. L. Ince)
представляет ценный вклад в нашу математическую литературу.
Книга состоит из 21 главы и разделена на две части. В первой
части рассматриваются диференциальные уравнения в вещест-
вещественной области, во второй—в комплексной области. Начинается
книга с рассмотрения элементарных методов интегрирования,
после чего следуют две главы о существовании и природе ре-
решений и непрерывных группах преобразований. Далее после
изложения общей теории линейных диференциальных уравнений,
автор переходит к алгебраической теории линейных диференци-
диференциальных систем, теории Штурм-Лиувилля и связанной с ними
общей теории граничных проблем. В этих главах с большой
полнотой изложены наиболее существенные результаты, полу-
полученные в столь важных для физики и техники вопросах, как
вопросы теории собственных чисел и решений. Основные работы
Штурм-Лиувилля, Биркгоффа и Бохера изложены исчерпывающе.
Первые 3 главы второй части посвящены теоремам существо-
существования и особенностям нелинейных диференциальных уравнений.
Остальные 7 глав содержат чрезвычайно обширный материал
по линейным уравнениям в комплексной области. Рассматрива-
Рассматриваются: решение уравнений при помощи рядов, уравнения с нере-
нерегулярными особыми точками, системы уравнений. Кончается
книга главами об интегрировании при помощи контурных инте-
интегралов и классификацией линейных уравнений второго порядка
с рациональными коэфициентами. Классические результаты Пу-
Пуанкаре, Фукса, Клейна, Фробениуса, Пенлеве, Гамбургера изло-
изложены в этой части с достаточной полнотой. Значительное внимание
уделено в книге специальным функциям (Ляме, Матье, Бесселя
и др.). Целый ряд весьма ценных результатов и методов в этой
области (функцин Матье) принадлежат автору. В частности, Айнсом
составлены прекрасные таблицы функций Матье, вышедшие
в 1935 г. в русском издании. В книге приведено огромное коли-
количество литературных ссылок, охватывающих все наиболее суще-
существенное в области диференциальных уравнений за последние
200 лет. В конце каждой главы приложено большое количество
упражнений и задач. По своему содержанию и характеру изло-
изложения, книга является одной из наиболее полных и серьезных
книг по обыкновенным диференциальным уравнениям в мировой
литературе. К некоторому недостатку книги относится краткость
и скупость языка, значительно затруднявшая перевод книги.
Эта книга рассчитана на студентов старших курсов математи-
математических, механических и физических отделений университетов,
аспирантов тех же специальностей и на инженеров-теоретиков.
Можно надеяться, что появление этой содержательной книги
будет способствовать повышению уровня математической куль-
культуры.
А. ЭФРОС.
Харьков 1938 г.
ЧАСТЬ I
Диференциальные уравнения
в вещественной области
ГЛАВА I
ВВЕДЕНИЕ
1-1. Определения. Термин aequatio differentialis или диферен-
диференциальное уравнение был впервые введен Лейбницем (Leibniz)
в 1676 г. для обозначения зависимости между диференциалами
dx и dy двух переменных х и у. Эта зависимость содержит
переменные х ну вместе с другими символами а, Ь, с,..., которые
являются постоянными.
Такое ограниченное применение термина было вскоре заме-
заменено другим; в настоящее время под диференциальными урав-
уравнениями понимаются любые алгебраические или трансцендентные
равенства, содержащие диференциалы или производные. Однако
при этом подразумевается, что диференциальное уравнение не
является тождеством '.
Диференциальные уравнения классифицируются соответствен-
соответственно числу содержащихся в них переменных. Обыкновенное дифе-
диференциальное уравнение выражает зависимость между независимой
неременной (аргументом), зависимой переменной (функцией) и
одной или более производными функции. Диференциальное
уравнение в частных производных содержит одну зависимую и
две или более независимых переменных вместе с частными про-
производными зависимой переменной относительно независимых.
Диференциальное уравнение в полных диференциалах содержит
две или более зависимых переменных вместе с их диференциа-
диференциалами или производными относительно некоторой независимой
переменной, которая может входить или не входить в уравнение.
Порядок диференниального уравнения определяется порядком
высшей входящей в него производной. Если уравнение пред-
представлено в виде полинома от производных, то степень, в которую
возводится высшая производная, называется степенью уравнения.
Если в уравнении в обыкновенных или частных производных
зависимая переменная и ее производные входят только в первой
1 Примером диференциалыюго тождества является
/ dx у cPv
)
I dy у dsx d2y d2x __
+\dx) ' dy3+ dx*' dys '
\~dy~) dx3+\dx) ' dy3+ dx*' dys
а это в свою очередь эквивалентно
dx ' dy
степени и не встречаются в более высоких степенях или про-
произведениях, уравнение называется линейным. Следовательно
коэфицненты линейного уравнения представляют собой посто-
постоянные или функции независимой переменной или переменных.
Так, например
является обыкновенным линейным уравнением второго порядка ;
— обыкновенное нелинейное уравнение первого порядка первой
степени;
3
— обыкновенное уравнение второго порядка, которое, при осво-
освобождении от иррациональности, возведением в квадрат обоих
членов, представляет собой уравнение второй степени;
Х-х +V-J Z==0
дх ' у ду
— линейное диференциальное уравнение в частных производных
первого порядка с" двумя независимыми переменными;
d*V
dV dV __n
дх* + ду* "г" Ьг°- ~~
— линейное диференциальное уравнение в частных производных
второго порядка с тремя независимыми переменными;
дх* ду* V
— нелинейное диференциальное уравнение в частных производ-
производных второго порядка и второй степени с двумя независимыми
переменными;
udx + vdy + wdz = О,
где и, v, w — функции л;, у, z, — диференциальное уравнение
в полных диференциалах первого порядка первой степени, а
з?йхх + 2x.ydx.dy + y2dy- — zW = О
— диференциальное уравнение в полных диференциалах первого
порядка второй степени.
В случае диференциального уравнения в полных диферен-
диференциалах, любая из переменных может рассматриваться как незави-
независимая, а остальные как зависимые переменные. Так, полагая х
независимой переменной, уравнение
udx -f- vdy -f- wdz — 0
может быть переписано в виде
e+v.fiL + w*L = О
1 их dx
или в уравнение можно ввести вспомогательную переменную t,
а первоначальные., переменные рассматривать как функции t,
тогда
dx , (iv , az „
u di+vtt +wlu=0-
1 • 2. Генезис обыкновенного диференциального уравнения. Рас-
Рассмотрим уравнение
(А) / (х, у, с±, с2,..., сп)=0,
где л: и у— переменные, а с,, с2>---> сп — произвольные незави-
независимые постоянные. Это уравнение служит для определения у
как функции х. Так определяется последовательность функций,
аричем каждая функция соответствует определенному произволь-
произвольному значению съ с2,...,сп. Можно образовать такое обыкно-
обыкновенное диференциальное уравнение, которое удовлетворилосьбы
любой из этих функций. Диференцируем заданное уравнение
последовательно п раз относительно л;. Тогда мы получим п
новых уравнений, именно
дх*+ Z дхдуУ ^ ду*У + ду
дх" ду
.где
, dy „ а?у
у =¦?* у =^--^
Каждое уравнение существенно отличается от предшествую-
предшествующего *; из всех п +1 уравнений п произвольных постоянных
съ с2,. ..,сп могут быть исключены алгебраически, после чего по-
получим диференциальное уравнение я-го порядка:
Из самого способа образования этого диференциального
уравнения ясно, что оно удовлетворяется любой фУнкЦией
у — ч (х), определяемой зависимостью (А). Эта зависимость на-
называется интегралом диференциального уравнения, а каждая
функция у — у {х), удовлетворяющая диференциальному уравне-
1 При эгом принимается, конечно, что имеются все частные производные
/, и что g - не равно нулю.
нию, его решением1. Решение, включающее некоторое число
существенно различных произвольных постоянных, равное по-
порядку уравнения, называется общим решением2. Эта термино-
терминология оправдана, как будет показано в главе III, где приводится
доказательство, что для заданного значения л;, и различным
условиям удовлетворяет одно и только одно решение уравнения
и-го порядка. Возможность удовлетворения этим и условиям
зависит от наличия решения, содержащего к произвольных
постоянных.
Было принято, что интеграл содержит п постоянных сх, с2,
...,?„• Однако, если имеются только п кажущихся постоянных,
т. е., если две или больше постоянных могут быть заменены
одной постоянной без существенного изменения интеграла, то
порядок результирующего диференциального уравнения будет
меньше п. Например, предположим, что интеграл имеет вид
/{*, У, 9 («,&)}= О,
тогда он, повидимому, зависит от двух постоянных а и Ь, но
в действительности он зависит только от одной постоянной,
именно с = у(а,Ь). В данном случае результирующеедиференци-
альное уравнение первого, а не второго порядка.
С другой стороны, если интеграл приведен, т. е., если функ-
функция /(х,у,си..., сп) разложена на два множителя, каждый из
которых содержит у, то порядок результирующего диференци-
диференциального уравнения будет меньше к, так как если ни один мно-
множитель не содержит всех постоянных, то каждый из них при-
приведет к образованию диференциального уравнения порядка
менее п, и возможно, что эти два диференциальных уравнения
будут тождественны или что одно из них допускает все реше-
решения другого и следовательно удовлетворяется самим интегралом.
Пусть интеграл имеет вид
он может быть приведен и эквивалентен двум уравнениям
у — ах = 0, у — Ъх =0,
каждое из которых, следовательно и интеграл, удовлетворяет
диференциальному уравнению
у — ху' = 0.
1 Вначале применялись термины интеграл [Джемс Бернулли (James Bernoulli
1689)] н частный интеграл [Эйлер (Euler, Inst. Calc. Int., 1768)]. Термин
решение был введен Лагранжем (Lagrange 1774) и установлен главным образом
благодаря Пуанкаре (Poincard). Термин частный интеграл применяется в на-
настоящее время в очень ограниченном смысле (см. гл. VI).
2 Известное прежде как полный интеграл или полное интегральное
уравнение (Эйлер). Термин интегральное уравнение имеет в настоящее время
•совсем иной смысл (см. § 3-2), которого и следует придерживаться.
10
1 • 20. Диференциальное уравнение семейства конфокальных кони-
конических сечений. Рассмотрим уравнение
-*1. 4-
ва+Х '¦
где а и b— определенные постоянные, a X — произвольный
параметр, который может принимать все действительные зна-
значения. Это уравнение представляет семейство конфокальных
конических сечений. Диференциальное уравнение, решением
которого оно является, получается исключением >. между ним
и производным уравнением
2х Ъуу'
аа+>. ^ 6а+). ~~ и-
Из решения и производного уравнения найдем, что
и, исключая X, получим
поэтому искомое диференциальное уравнение будет
хуу'2 + (л:2 —У — а2 + й2)^' —-«У = 0,
это уравнение первого порядка второй степени.
- Производную у' можно изобразить символом р. Тогда ди-
диференциальное уравнение семейства конфокальных конических
сечений можно написать в виде
ху{р?—1) + (х2 —у2 — с2 + Ь2) /9=0.
1-21. Образование уравнений в частных производных исключе-
исключением произвольных постоянных. Пусть х1г х2, ..., хт — независи-
независимые переменные, a z — зависимая переменная, определяемая
уравнением.
/\хх, x.it ..., хт; z', съ с2, ..., сп) = О,
где съ с3,..., сп — п произвольных постоянных. К этому урав-
уравнению могут быть присоединены т уравнений, полученных ди-
ференцированием относительно каждой из переменных хъ х^,...,
хт последовательно, именно
д? 4- V • А. = 0 -^- 4- -^- • -д- =0
"^1 дг~ d*i г'"'дхт ^ дг дхт
Если k>n, то для исключения постоянных сх, cz,...,спимеется
достаточно уравнений. Если т<п, то присоединяются также
И
И
—/re (/n + 1) вторых производных уравнений; они имеют вид
. dz ¦
dz j^ d2f dz
dxr ' dz* dxr
Этот процесс продолжается до тех пор, пока будет полу-
получено достаточное число уравнений для проведения исключения.
После этого у нас будет больше уравнений, чем подлежащих
исключению постоянных, поэтому решение может привести не
к одному уравнению в частных производных, но к системе сов-
совместных диференциальных уравнений в частных производных.
1-211. Диференциальное уравнение в частных производных пло-
плоскостей и сфер. Рассмотрим случай, когда интегралом является
уравнение
z = ax -f by + с,
где а, Ь, с, — произвольные постоянные. При соответствующем
подборе этих постоянных, уравнение может представлять лю-
любую плоскость в пространстве, за исключением плоскости, па-
параллельной оси z. Первые производные уравнения имеют вид
dz_ _ dz_ _ ,
дх ' ду
Они недостаточны для исключения а, Ь и с, поэтому состав-
составляем вторые производные уравнения, именно
^ = 0 0 ^ = 0
Эти уравнения не содержат произвольных постоянных и пред-
представляют следовательно искомые диференциальные уравнения.
Обычно пишут
Р "~ их ' Ч ~ ду ' г ~ дх- '
Таким образом любая плоскость в пространстве, не параллель-
параллельная оси z, удовлетворяет одновременно трем уравнениям
г = 0, s = 0, ? = 0.
Далее, рассмотрим уравнение, удовлетворяющее наиболее
общим уравнениям сферы вида
(х — аJ + (у - бJ + (г — с)* = г*,
где а, &, с и г—произвольные постоянные. Первые производ-
производные уравнения имеют вид
(х — a) + (z — c)p = o, (y~b) + {z-c)q=G,
12
а вторые производные уравнения
При исключении z—с получим искомые уравнения, именно
1 4- р2 pq I + q2
следовательно имеем два независимых уравнения. Пусть л — зна-
значение каждого из членов этих уравнений, тогда
Если рассматривать только действительные сферы, то долж-
должно быть удовлетворено дополнительное условие
rt>s2.
1 • 22. Свойство якобианов. Покажем, что интеграл диферен-
циального уравнения в частных производных представляет со-
собой зависимость, в которую входят произвольные функции пере-
переменных. Исследование, которое приводит к этому результату,
зависит от свойств функциональных детерминантов или якобианов.
Пусть иъ «2.---J ит являются функциями независимых пере-
переменных л^, х2,...,хп. Рассмотрим ряд частных производных, рас-
расположенных следующим образом
дхг '
дщ
дх, '
дит
дх± '
диг
dxs '
diu
дх2 '¦
дит
дх, '¦
dUi
'' '"» дхп
ди2
'' ' '' дхп
дит
ил„
Тогда детерминант порядка р, элементы которого совпадают
с элементами р строк и р колонн приведенной схемы, называ-
называется якобианом1. Предположим, что все возможные якобианы
построены; тогда, если якобиан порядка р, например
дщ
дхр
ди,, дир_
дхг ' ' дхр
'Scott and Mathews, Theory of Determinants, гл. XIII.
13
не равен нулю для выбранного ряда значений х1=^1,.. .,хп = $„ и
если каждый якобиан порядка р+1 тождественно равен нулю,
то функции иг, «2,..., Up — независимы, а остальные функции
uPri,...,um могут быть выражены в зависимости от иг,..., ир.
Предположим, что для значений хи..., хп в соседстве
с ^1,.--Лп функции %,..
существует соотношение
Тогда уравнения
ир не являются независимыми, но
диг дхг ' ¦¦¦"!"
-~ =
= О
дщ Ъхр ''' дир
Clip
дхр
= 0,
удовлетворяются тождественно, и поэтому выражение
д(и,...,ир) _
иг да,
xi ' ' '' дхр
дию
ди,:
i'"'* Охр
обращается в соседстве с ?f,..., ln B нуль, что противоречит
принятому условию. Следовательно первая часть теоремы, именно,
что «!,...,Up независимы, верна.
Пусть в Ир+1,.. .,ит переменные xlt.. .,хр, хр и.. .,хпзаменены
новым рядом независимых переменных и,,.
UP> XP+U
Л'п
Докажем, что если иТ представляет какую-либо функцию*
ир+1,..., um, a xs—любую из переменных хр+1,..., хп, то иТ совер-
совершенно не зависит от xs, т. е.
Предположим, что
Ux =/, (A'j,.
oxs
п),..., llm —/га(Х,,. . ., Хп),
и пусть вместо xlt..., xp будут подставлены их выражения
в функции от новых независимых переменных ult.. ,,ир,хр±и.. .,лРу
тогда, диференцируя обе стороны каждого уравнения по xs.
получим
0
О _ ЙЛ?. ?*?i т . dfp _ дхр ( dfp
)ыг _ dfr дхг . dfr дхр dfr
14
1,..., ОТ).
Исключение выражений
дает
dfr
dxt>°
dtp
dxt''
dfr
dx
dx
• • t
I
) • * "
S
dfi
dXp'
dfP
d*p'
\dfr
dxP
' dxs
df,
dxs
dfP
dxs
dfr
= 0
или
к'' ' '' dxp' dxs dxs
d (Л fp,fr) = dur m d(fx
.., xP, xs) dxs
Поскольку, согласно условию
d Ун- ¦ ¦> flh /f) rv
ф0
ТО
l,..., я).
Следовательно каждая из функций иРг\,..., ит может быть
выражена в зависимости от функций и,х ир, что и требовалось
доказать.
1-23. Образование диференциального уравнения в частных про-
производных исключением произвольной функции. Предположим, что
зависимая переменная z связана с независимыми переменными
xv..., xn уравнением вида
F(uuu2,..., un) = 0,
где F—произвольная функция аргументов uv щ,..., ип, которые,
в свою очередь, являются данными функциями х%,..., хп и z.
Если вместо z подставить его значение в зависимости от
xv..., xn, то равенство превращается в тождество. Поэтому,
если DrUs—частная производная us по хп когда вместо z под-
подставлено его значение, то
ЭЛ)..., Dnux =0.
>,«n,..., Dnun\
Но
dz 'dx~r'
поэтому диференциальное. уравнение в частных производных,
удовлетворяемое 2, имеет вид:
дщ дщ дг диг ^_ дщ dz
дх± ' дг dXi ' ' '' дхп ' dz ' дхп
i дхг "т" йг " djcj'' ' "' длс„ ' йг
i дхг
длс„
0.
1 - 231- Диференциальное уравнение поверхности вращения.
Уравнение
представляет поверхность вращения, ось которой совпадает
с осью z. В обозначениях предыдущего параграфа
хг = х, л2 =у, иг = 2, «г = л:2 + з;2,
поэтому z удовлетворяет диференциальному уравнению в ча-
частных производных
йг_ дг_
дх' ду
2х, 2у
= 0
или
Л " Л ^-
Это уравнение удовлетворяется выражением
Z = W (Л2+У2),
где (р —произвольная функция его аргументов; оно является
поэтому диференциальным уравнением всех поверхностей вра-
вращения, имеющих общую ось х = 0, у — О-
1-232. Теорема Эйлера об однородных функциях. Пусть
Z = (р (X, у),
где ®(х, у) — однородная функция х и у степени п. Функция
<?(.*:, у) может быть написана в виде
откуда следует, что
В обозначениях § 1*23
Х^ Ху Лд у,
F{ut,
(?)•
•*-.-<,{?).
поэтому z удовлетворяет диференциальному уравнению в част-
частных производных
dz
дх
О,
— пх
которое приводится к
Аналогично, если и — однородная функция трех переменных
х, у и 2 степени п, то
ди , ди . ди
Y I *1 —1- •? till
дх ду дг
Эта теорема может быть распространена на любое число пере-
переменных.
1-24. Образование диференциального уравнения в полных дифе-
ренциалах с тремя переменными. Уравнение
<р (х, у, г) = с
представляет семейство поверхностей; предположим, что каж-
каждому значению с соответствует только одна поверхность се-
семейства. Теперь пусть (х, у, z) будет точкой на какой-либо
поверхности а (х-\-Ъх, у -\-Ъу, z-^-bz) — соседней точкой на той
же поверхности, тогда
Полагая, что частные производные
д'з д'э д®
дх ' ду' дг
существуют и непрерывны, это уравнение можно написать так
I ду(х, у, z) _
\ дх ~*"
где е1г ?2, е3-^0, когда ох, Ьу, cz-^O.
Теперь пусть еъ е2, е3 стремятся к нулю, и вместо ол, оу, 8г
напишем соответственно dx, dy, dz. Тогда получим диференци-
альное уравнение в полных диференциалах
дч> , , д'-f j , д'х> j „
Э. Айне—133—2 17
Если все три частные производные имеют общий множи-
множитель {а, т. е.
ду „ дъ у-, д'-р д
дх ' ду ""> dz ' »
то, исключив его, приведем уравнение к виду
Pd* + Qdy + Rdz = 0.
Возможность применения диференциалов dx и т. д. может
быть установлена из уравнения с двумя переменными, именно
у—fix) = с.
Этот процесс приводит к уравнению в полных диференциалах
dy—f'(x)dx = 0,
следовательно частное диференциалов dy, dx является произ-
производной dy/dx.
• Пример. Интеграл
(х + z) (у + г)
приводит к диференциальному уравнению в полных диферен-
диференциалах
У2-22 л„ , *2-*2 л., i 2г+х+У и^-п
которое после умножения на {х+у)г примет вид
{у2 — z2)dx + (л:2 — г2) dy + Bz + х +у)(х +у) dz = 0.
1*3. Решения обыкновенного диференциального уравнения. Если
известно, что обыкновенное диференциальное уравнение было
выведено процессом исключения п произвольных постоянных из
интеграла, то очевидно оно имеет решение, зависящее от п
произвольных постоянных. Возможность получения обыкновен-
обыкновенного диференциального уравнения порядка п из такого инте-
интеграла не очевидна, поэтому не следует считать, что данное
диференциальное уравнение имеет решение, зависящее от п
произвольных постоянных. При образовании диференциального
уравнения из заданного интеграла необходимо принять некото-
некоторые условия диференцируемости и непрерывности производных.
Аналогично, в обратной задаче интегрирования (переход от за-
заданного диференциального уравнения к его интегралу) необхо-
необходимо принять, что соответствующие условия удовлетворены.
С чисто теоретической точки зрения, первой возникает проб-
проблема получения ряда возможно более простых условий, которые
при их удовлетворении обеспечили бы существование решения.
Эта проблема будет рассмотрена в главе III, где будет дока-
доказана принимаемая здесь без доказательства теорема существо-
существования, именно, что при удовлетворении ряда возможных условий
18
уравнение порядка п действительно имеет единственное реше-
решение, зависящее от п произвольных начальных условий. Из этой
теоремы следует, что наиболее общее решение обыкновенного
уравнения порядка п содержит п произвольных постоянных.
Однако отсюда не следует, что не существует решения, ко-
которое не было бы лишь частным случаем общего решения.
Чгобы пояснить это, рассмотрим диференциальное уравнение,
полученное исключением с из интеграла
Ч (•*, У, с) = 0
и производного уравнения
Производное уравнение вообще содержит с. Пусть, например,
интеграл решен относительно с, и полученное значение с под-
подставлено в производное уравнение, — тогда производное урав-
уравнение становится диференциальным уравнением
где скобки указывают на исключение с. В общей форме это
уравнение может быть написано в виде
Пусть х, у, и с изменяются одновременно, тогда
Txdx+rydy+jcdc = 0.
Если с исключить, то это уравнение примет вид
1^1 *>+[«]*+ИЗ*-о.
поэтому, принимая во внимание предыдущее уравнение,
Таким образом могут быть два случая: или с — постоянная,
что приводит нас опять к интегралу
<р (х, у, с) = 0,
или
Последнее соотношение между х и v может представлять или
не представлять решения диференциального уравнения; если оно
представляет решение и не является частным случаем общего
решения (интеграла), оно называется особым интегралом (ре-
(решением).
19
Рассмотрим, например, интеграл
с2 + 2су + а~ — Xs = О,
где с — произвольная, а а — определенная постоянная. Производ-
Производное уравнение имеет вид
с dy — xdx = 0;
после исключения с оно становится диференциальным уравнением
[—у +(л2 + у"- — a?)T]dy — ля?* = 0.
Уравнение в полных диференциалах, полученное одновременным
изменением х, у, и с, будет
[с -\г у) dc + cdy — xdx = 0,
или, исключая с
(х« + / — а2) !"й?с + [ — _у +(л;2 + у — а2)F] rfy — лил; = 0.
Таким образом, кроме общего, существует еще и особое реше-
решение
х2 + у2 = а8,
которое, очевидно, удовлетворяет диференциальному уравнению.
Диференциальное уравнение первого порядка может рассма-
рассматриваться как удаленное только на одну ступень от его интег-
интеграла. Уравнение высшего порядка более удалено от своего ин-
интеграла и поэтому его интегрирозание является процессом,
в котором порядок производных последовательно понижается,
причем каждое понижение порядка на единицу сопровождается
введением произвольной постоянной. Если данное уравнение
порядка п, а при помощи процесса интегрирования получается
уравнение порядка п— 1, содержащее произвольную постоянную,
то оно называется первым интегралом данного уравнения.
Пусть дано уравнение вида
У"=/<У),
где f(y) не зависит от х. Уравнение может быть проинтегриро-
проинтегрировано, если оба члена умножить на 2у'. Следовательно
2УУ = 2/(у)У
к его первый интеграл равен
где с—произвольная постоянная интегрирования.
1 • 4. Геометрическое значение решений обыкновенного диферен-
циального уравнения первого порядка. Поскольку интеграл обык-
обыкновенного диференциального уравнения первого порядка явля-
является зависимостью между двумя переменными х и у и парамет-
параметром с, говорят, что диференциальное уравнение представляет
собой семейство плоских кривых, зависящее от одного параметра.
20
Каждая кривая этого семейства называется интегральной кри-
кривой диференциального уравнения.
Пусть уравнение имеет вид
и пусть D — область в плоскости (х, у~), в которой функция
f {х, у) однозначна и непрерывна, а(хо,уо) — точка, лежащая вну-
внутри D. Тогда уравнение связывает с (х0, у0) соответствующее
значение dy/dx, скажем р0, и определяет таким образом линей-
линейный элемент1 (х0, у0, рй), исходящий из точки (х0, у0,). Выберем
на этом линейном элементе соседнюю точку (я,, уь) и построим
линейный элемент (х1г уь /7,). Продолжая непрерывно этот про-
процесс, получим ломаную линию, которая может рассматриваться
как приближение к интегральной кривой, проходящей через
(*о, Уо)-
Этот метод приближения к интегральным кривым диферен-
диференциального уравнения иллюстрируется образованием силовых
линий под действием стержневого магнита при помощи желез-
железных опилок. На тонкий лист картона, помещенный горизонтально
и непосредственно над магнитом, насыпаются железные опилки.
Каждая железная частица намагничивается и стремится распо-
расположиться в направлении результирующей силы, и если распре-
распределению опилок помочь легким постукиванием о картон, то они
расположатся приблизительно вдоль силовых линий. Таким
образом каждая отдельная железная частица символизирует
элемент через ее среднюю точку.
Предположим, что стержневой магнит состоит из двух
отдельных полюсов противоположной полярности, расположен-
расположенных в А и В, и пусть Рбудет любой точкой на картоне. Тогда,
если координаты А, В и Р равны соответственно (— а, 0),(а, 0),
(х, у), если г a s являются соответственно длинами АР и ВР
и если X, Y — составляющие напряженности магнитного поля
в точке Р, то
У _ у _у у _ х_ +_« х — а
73~ s3' г* s*
Направление результирующей силы в точке Р равно
их X
- У
а -—. ;.
Г3 — S3
что представляет собой диференциальное уравнение силовых
линий, которое имеет решение вида
х + а х — а ,
— - = const-
1 Линейный элемент быть определен с достаточной точностью, как линия,
соединяющая точки (хв, ус) и (х„+Ъх, у„+Ьу), где Ьх и йу малы, a Zyjbx =рв-
21
Сообщая соответствующие значения постоянной, можно вычер-
вычертить силовое поле. Интегральные кривые представляют силовые
линии, приближенно изображенные железными опилками.
Поскольку было принято, что/(х,у) непрерывна и однозначна
в каждой точке D, — через каждую точку пройдет только одна
интегральная кривая. Вне D могут быть точки, в которых/(л:, у)
не будет непрерывной и однозначной; в таких точках, известных
как особые точки, поведение интегральных кривых может быть
особенным.
Аналогично, если уравнение второго порядка может быть
написано в виде
у'=Пх, у, у'),
где / (х, у, у') непрерывна и однозначна для некоторого диапа-
диапазона значений* ее аргументов, значение у' в точке (х0, у0) может
быть выбрано произвольным, в некоторых пределах, и таким
образом через точку (х0, у0) будет проходить бесконечность
(первого порядка) интегральных кривых. Общее решение содер-
содержит две произвольные постоянные, поэтому совокупность
интегральных кривых образует семейство, зависящее от двух
параметров.
Вообще, интегральные кривые обыкновенного уравнения
порядка п образуют семейство, зависящее от п параметров, а
через каждую неособую точку проходит бесконечность порядка
(п—1) интегральных кривых.
1 • 5. Совместные системы обыкновенных диференциальных урав-
уравнений. Часто возникают проблемы, которые приводят к системе
совместных диференциальных уравнений с одной независимой
и несколькими зависимыми переменными. Так например, пред-
предположим, что
<р {х, у, z, сх, с2) = О,
Ь(х,у, z, с„ с2)=0
являются двумя уравнениями относительно х, у и г, причем
каждое из них содержит по две произвольных постоянных с1
и с2. Тогда между этими двумя уравнениями и парой уравнений,
полученных путем их диференцирования по х, постоянные сг и
с2 могут быть исключены, и мы получим в результате два
совместных обыкновенных диференциальных уравнения первого
порядка
Ф {х, у, у, z, z') = О,
4" {х, у, v', z, z') = 0.
Введением достаточного числа новых переменных можно
заменить одно уравнение любого порядка системой совместных
уравнений, так, чтобы каждое уравнение содержало одну произ-
22
водную первого порядка. Эта теорема может быть доказана для
наиболее важного случая, а именно, для уравнения видаг
^ -f(x v ^ ~-Л
В этом случае вводятся новые переменные yv ys,..., уп, так
что
йУ1_ dys__ dyn-i^
d~x~~y2' dx~-~ys''--> dx "У"'
где Vj =j/. Эти уравнения вместе с уравнением
dJ? = F{x, yv у2,..., уп)
образуют систему, эквивалентную первоначальному уравнению
из п совместных уравнений, каждое из которых первого порядка.
В частности, очевидно, что если первоначальное уравнение
линейное, то уравнения эквивалентной системы также будут
линейными.
Примеры.
1. Найдите обыкновенные диференцнальные уравнения, которым удовлет-
удовлетворяют следующие интегралы
(I) у = Ахт + Вхп, (VI) у = х" (Л + В log х),
(U) у = Аетх 4- Вепх, (VII) у = е тл (А + Вх),
(III) у = A cos их + В sin пх, (VIII) у = (А + Вх) cos пх + (С + Dx) sin их,
(IV) у= emx(Acosnx+Bsmnx), (IX) j - етдг{(Л +Вх) cosnx+ (C+Dx)sin«je);
(V) v = A ch (х/Л), (X) у = Ах cos (п/х + В),
где Д fi, С, Л —произвольные постоянные, а /л и п — фиксированные постоян-
постоянные.
2. Докажите, что если
ах-х- Ь
У = oc + d'
то
2)-У" = ЗУ'2,
а если а 4- d = 0. то
(у_.г)У-2уA + v'). [Math. Tripos, I, 1911].
3. Докажите, что если у3 — Зак2-{-х3 = 0, то
d-y 2«x
rfx^ + ТЕ~
Покажите, что кривая, заданная этим уравнением, вогнута по всей своей длине
к осн х и что имеется точка перегиба при х = За. [Math. Tripos, I, 1912].
4. Докажите, что если
х A _ д-) dly.n — D - 12х) ^ — 36>» = 0,
v 7 rfx2 v dx
D'Alembert, Hist. Acad., Berlin, 4 A748), 289.
23
то
Отсюда, пользуясь теоремой Маклорена, докажите, что значение у, исчезающее
при х = 0, таково, что его пятая производная, равная единице при х = 0, мо-
может быть выражена в виде
|; {l26x5 — 84.«6 + 36л? —9л;8 + х° }. [Math. Tripos, I, 1915].
5. Покажите, что диференциальное уравнение всех окружностей в одной
плоскости имеет вид
6. Любое коническое сечение, не имеющее асимптоты, параллельной оси
может быть написано в виде
- с.
Отсюда покажите, что диференциальное уравнение всех таких конических сече
ний будет
или
(*У\'_ 45
•*) dx* ~ "¦
В частности, покажите, что диферециальное уравнение всех компланарных
парабол имеет вид
~dx*
или
7. Покажите, что если
то
_
дудх' дх2 ду2 ~~ \дхду )
8. Докажите следующее развитие теоремы Эйлера. Если / — однородная
функция степени т от хг, х2 н однородная степени п от уи у2, то
/ д б \ ( df df\/d д \ г df df\
V1 дх\+У2 WJ \XlWi + X2W2J~\XlWi + XidyJ V1 dx~i + Уг dx~2J =
= («—»!)/.
9. Докажите, что если семейство интегральных кривых линейного диферен-
цнального уравнения первого порядка
пересекается линией х =;, то касательные в точках пересечения пересекаются
в одной точке или параллельны.
Для кривых, удовлетворяющих уравнению
dx x jc3'
покажите, что при изменении 5 геометрическое место точек пересечения каса-
касательных представляет собой прямую линию.
ГЛАВА 11
ЭЛЕМЕНТАРНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
2 • J. Точные уравнения первого порядка первой степени. Обык-
Обыкновенное диференциальное уравнение первого порядка первой
степени может быть выражено в форме уравнения в полных
диференциалах
Pdx + Qdy = О,
где Р и Q —функции х ну и не содержат р. Если диференциал
Pdx 4- Qdy может быть выражен непосредственно, т. е. без
умножения на какой-либо множитель в виде du, где и — функ-
функция х и у, то уравнение называется точным1.
Если уравнение
Pdx + Qdy = 0
точное и имеет общий интеграл вида2
и = с,
то оба выражения для du, именно
Pdx + Qdy и .*Ldx+^dy
должны быть тождественны, т. е.
^~ дх' Ч- ду-
Тогда
ГА1 ?Р _ dQ
^> ду " дх'
если эквивалентное выражение -т—^— непрерывно. Следователь-
Следовательно условие интегрируемости (А) необходимо. Остается дока-
доказать, что это условие достаточно, т. е., если оно удовлетво-
удовлетворено, то уравнение точное и его общий интеграл может быть
найден в квадратурах.
1 В советской литературе более употребителен термин .диференциальное
уравнение в полных диференциалах", однако, следуя оригиналу, будем писать
точное уравнение. Прим. ред.
2 Во всей этой главе с и С обозначают постояниые интегрироваиия. Любые
другие значения этих букв будут очевидны из контекста.
25
Пусть и (х, у) определяется выражением
где л0—произвольная постоянная, а <р (у)— функция у, которая
является в данный момент также произвольной. Тогда и = с
будет полным интегралом
Pdx + Qdy = 0,
если
_ди_р ди^ _ п
дх " ' ду ~~ Ч-
Первое условие удовлетворено; второе определяет <? (у) сле-
следующим образом
следовательно
где j'o — произвольно.
Следовательно условие достаточно, потому что уравнение
точное и имеет общий интеграл
х у
/ Р (х, y)dx + /Q (ль, у) dy = с.
х0 у„
Постоянные хй и у0 могут быть выбраны по желанию. Вообще
имеется только одна произвольная постоянная, так как измене-
изменение хй или у0 эквивалентно прибавлению постоянной к левой
части интеграла. Произвольность очевидна в отношении у0; что
касается х0, то она является следствием условия интегрируе-
интегрируемости.
В качестве примера рассмотрим уравнение
26
Условие интегрируемости удовлетворено, поэтому общий инте-
интеграл будет
hy±*.d т
Ус О
Очевидно, преимущественным является условие л:0 = 0, так как
второй интеграл ^содержит log у, то у0 может быть принят рав-
равным единице." Тогда
т. е.
[log (л* + у>) - arc tg ±]*=* + 2 log^ = с,
что может быть приведено к виду
log (л2 + у2) — arc tg -j- = с.
2-11. Разделение переменных. Частный случай точного урав-
уравнения получается, когда Р является функцией одного х, a Q —
функцией одного у. В этом случае вместо Р можно написать X,
а вместо Q—Y. Тогда говорят, что уравнение
Хйх + Ydy
содержит разделяющиеся переменные; его общий интеграл имеет
вид
/Xdx + /Ydy = с.
Если Р может быть представлено в виде произведения функ-
функций X от х и Yx от у, и аналогично Q в виде произведения X,
на Y, то говорят, что переменные разделяются, так как урав-
уравнение
(I)
может быть написано в форме
(II) 4Ac+-p-rfy = 0.
Л1 71
Однако нужно отметить, что при делении уравнения на XtYt ряд
решений теряется. Если, например, х = а является корнем урав-
уравнения Хх = 0, то оно даст решение для уравнения (I), но не
обязательно для уравнения (II).
Пример:
{х* + 1) (У — 1) dx + xydy = 0.
Переменные могут быть отделены следующим образом:
27
Интегрируем
л:2 + log Xя + log {у2 — 1) == с
или если с = log С, то
Кроме того, действительными решениями данного уравнения
являются х = 0, у = 1, у = — 1. В общее решение входят только
два последних решения.
2 • 12. Однородные уравнения. Если Р и Q являются однород-
однородными функциями хну одной и той же степени [п, то уравне-
уравнение может быть приведено подстановкой1 у = vx к уравнению
с разделяющимися переменными. Так как
то уравнение
примет вид
или
где
{P(l,<i>) + <y Q A,<у)}dx + x Q A, v)d-o = 0
- - = О
Получаем решение вида
Пример:
Пусть у = -у
или
(У — 2л:3.у) й?л + (л;4 —
тогда
(•у4 + -у) fiU — A — 2i>3) xrfi) = О
3»*
откуда
или ,
log л = log -у — log A -f -у3) + log с
1 Впервые введено Лейбницем в 1691 г.
28
Таким образом получим общий интеграл вида
xs+ys = сху.
Если уравнение
Pdx + Qdy = 0
является однородным и точным, то оно непосредственно инте-
интегрируется без приведения к квадратуре, при условии, что его
степень однородности п не равна — 1; его интеграл может быть
записан в виде
Px + Qy^ с.
Пусть и = Рх + Оу, тогда
дх ' дх ' J ax
г, , дР . дР
Р + Х+У
согласно теореме Эйлера (§ 1-232); аналогично пишем выра-
ди
жение для -^~
Следовательно
dudx +
поэтому
Отсюда, если иф— U то общий интеграл будет
Рх + Qy = с
Пример:
х {х* + Зу2) dx + y (у2 + Зх2) dy = 0.
Решение:
х* + 6х2у~ + у* = с.
При и = — 1 интегрирование может быть приведено к квад-
квадратуре. Интересно отметить, что однородное уравнение
fdx±Qdy__n
Px + Qy ~ U
является точным, потому что условиеv интегрируемости, именно
ду \.Рх + Qy I дх \Рх + Qy
•39
приводится к виду
дР , дР
что верно, согласно теореме Эйлера, поскольку Р и Q однород-
однородны и одинаковой степени. Таким образом любое однородное
уравнение может быть сделано точным посредством введения
интегрирующего множителя l/(Px + Qy). Степень однород-
однородности этого точного уравнения равна — 1, так что интегрирова-
интегрирование однородного уравнения может быть вообще проведено в
квадратурах.
Уравнение типа
йу р i Ах + Ву+С \
dx \ ах + by + с J *
где А, В, С, а, Ь, с — постоянные, причем АЪ — абфО, может
быть приведено к однородной форме при помощи линейных
преобразований переменных. Пусть
х — h ~\~" v — k ~\~ 7]
где % 1] — переменные, a h, k — постоянные, так что
Ah + Bk + С = О,
Уравнение примет вид
*а - f (м + gv]
ft \ aZ + b-ц
где F — однородная функция S, ч\ нулевой степени. Постоян-
Постоянные h, k являются определенными, поскольку АЪ — аВ=?0.
Если АЪ — аВ = 0, пусть t\ будет новой зависимой перемен-
переменной, определяемой через
7} = х + By А — х + byja,
тогда
йЛ. = 1 + — F
dx 'a \at] \-c) '
Переменные опять разделяются.
Пример:
(Зу — 7х + 7) dx + Gу — Ъх + 3) dy = 0.
Подстановка
приводит это уравнение к однородному
C-/) — П) dl + Gtj — 3?) йщ = 0.
Преобразование г, = vZ приводит его к виду
G-D — 3) Ы-v + {7v2 — 7) rf; = 0
30
или
откуда
{v— 1)*(да + 1M6' = с
где с — постоянная интегрирования, т. е.
(Ч — ?)* (Ч + ?)» + с.
Общий интеграл поэтому будет
(у—л
2-13. Линейные уравнения первого порядка. Наиболее общим
линейным уравнением первого порядка является уравнение типа
где о и ф— функции одного л. Сначала рассмотрим однородное
линейное уравнение1
Его переменные разделяются поэтому
а решение будет
= се '
где с — постоянная.
Подставим теперь в неоднородное уравнение выражение
где г< — функция я, введенная вместо постоянной с. Уравнение
примет вид
— ? J = ф,
ах '
откуда
П) -=1
1 Термин однородное прилагается к линейному уравнению, если оно не
содержит члена, не зависящего ст у и ее производных. Это применение тер-
термина необходимо различать от его применения в предшествующем параграфе.
где уравнение (вообще нелинейное) называлось однородным, если Р и О были
однородными функциями х и у одной и той же степени.
31
Решением общего линейного уравнения будет выражение
содержащее две квадратуры.
Принятый здесь метод нахождения решения уравнения,—
рассматривая параметр или постоянную интегрирования с реше-
решения более простого уравнения как переменную и определяя ее
таким образом, чтобы удовлетворилось более общее уравнение,—
является частным случаем метода изменения параметров (вари-
(вариации произвольных постоянныхI.
Нужно отметить, что обшее решение линейного уравнения на-
находится в линейной зависимости от постоянной интегрирования С.
Диференциальное уравнение, полученное исключением С из урав-
уравнения
и производного уравнения
y'=*Cf'{x)+g'(x),
линейно.
Если какое-либо частное решение линейного уравнения из-
известно, то общее решение может быть получено одной квадра-
квадратурой. Пусть _ул будет решением, тогда соотношение
удовлетворится тождественно. При помощи этой зависимости
ф может быть исключена из данного уравнения, которое будет
иметь вид
Это уравнение теперь однородно относительно j> —yt и его решение
имеет вид
где С — постоянная интегрирования.
Если известны два отдельных частных решения, то общее
решение может быть выражено непосредственно через них. Об-
Общее решение имеет вид
у = Cf(x) + g(x)
и можно получить любые два частных решения у1 и у2, если
произвольной постоянной С придать частные значения С, и С2.
1 См. § 5-23. Применение этого метода для решения линейных уравнений
было впервые введено Дж. Бернулли, (Acta Enid., 1697, стр. ИЗ), но решение
в квадратурах было известно Лейбницу несколькими годами раньше.
32
Таким образом получим
y2 = C2f(x)+g(x),
следовательно
у - v, = С—_ Су
У-2—Vi ~ С2—Q'
/7/?иже/ш.
(I; у' —ау = етх {акт— постоянные, т Ф а).
Решением однородного уравнения
у' — ау — О
будет у = Сеах. Пусть в первоначальном уравнением
где ¦у — функция л, тогда
или
(«Л — С1)Х
Таким образом общее решение примет вид
У = Се**
„,_
(II) У — ау=еах.
Решение:
у = Сеах +хеах.
(III) v' о-^—.у — 2х{х2 -\- 1)-
Решение:
(IV) У cos л; + у sin л; = 1.
Решение:
у = С cos л + sin л:.
2-14. Уравнения Бернулли и Якоби.
Уравнение
где tp и ф — функции только л, называется уравнением Бернулли1.
Оно может быть приведено к линейной ф°Рме путем замены
зависимой переменной. Пусть
1 James Bernoulli, Acta Ertid. 1695, 553 (Opera 1, 663). Метод решения был
найден Лейбницем, Acta Erud. 1696, 145 [Math. Werke. 5, 329].
э. айнс—133—з 33
тогда
dz .. л ay
— = A —ti) y — n -/-
ax v /-л dx
и следовательно, если данное уравнение переписать в виде
то оно примет вид
;: будет линейным относительно 2.
Уравнение Якоби1
(Oj + й,х + с,,у) (xdy — ydx) — {a2 + b2x + c2y)dy +
+ («з + ^з^ + сзУ) ^л = О,
где коэфициенты а, Ь, с — постоянные, тесно связано с урав-
уравнением Бернулли. Произведем подстановку
х = X + а, у = Y + р.
где а, р — постоянные, которые необходимо определить, таким
образом, чтобы сделать коэфициенты при XdY — YdX,dY и dX
отделяющимися и однородными относительно X и К Когда эта
подстановка будет произведена, то уравнение расположится так,
чтобы коэфициент при XdY — YdX был однородным и первой
степени
(ЬгХ+ cj) {XdY— YdX) —
— {А2 + b.X + ctY—a(At-t?biX + cJY) — AiX}dY +
+ {Аь + ЬЪХ + c3Y-? {A, + bxX + ClY) — A.Y}dX = 0,
где
А г = аг + bra + сг3 (/- = 1,2,3).
Коэфициенты при dY и dX также будут однородными, если
аир так подобраны, что
А2 — аА1 = О, Л3 —рл4 = О
или более симметрично, если
А1 = К Аг = л1, Л3=рх,
т. е. если
(Л) «1 — X + V + Ci? = «2 + {р2 — I) а. + с$ = а3 + Ь3л +
определяется
кубическим
аг —
а2, Ъ
а3, Ъ
уравнением
X, Ьь сх
з> ^з — ^
= 0;
1 Jacobi, J. fiir Math. 24 A842) 1 (Ges.Werke4, 256) См. также уравиевие Дарбу,
§2-21.
34
когда I таким образом определена, а и 8 представляют собой
решения любых двух ураинений (Л).
Это уравнение может быть написано так
XdY-
Подставляя Y = Хи, приведем его к уравнению Бернулли
где Ui и иг — функции одного и.
Ниже (§ 2-21) мы покажем, что если тремя корнями уравне-
уравнения, определяющего )>, являются \ь Х2 и Х3 и все они существенно
различны1, то общее решение уравнения Якоби будет вида
[/*. -'»У>. - >¦. Wl> - *• = const,
где U, V, W—линейные выражения относительно х и у.
2 ¦ 15. Уравнение Риккати. Уравнение
где (рг. '-Р и 1 — функции х, называется обобщенным уравнением
Риккати2. Оно отличается от предшествующих уравнений этого
параграфа тем, что в общем случае оно не интегрируется в квад-
квадратурах.
Поэтому это уравнение определяет семейство трансцендент-
трансцендентных функций, которые существенно отличаются от элементар-
элементарных трансцендентных функций-".
Если какое-либо частное решение у —yt известно, то общее
решение может быть получено при помощи двух последователь-
последовательных квадратур- Пусть
У=Уг + г,
тогда уравнение будет
1 Случай, когда они не различны, рассмотрен Серре (Serret, Calc. Diff. et
Int., 2, 431).
2 Риккати [Riccati, Acta Erud. VIII A724)], исследовал уравнение у' + ay3 =
=> Ъхт, которое связывается обычно с его именем. Обобщенное уравнение бы-
было исследовано Даламбером (d'Alembert), см. § 12 • 51.
3 Элементарными травсцендентными функциями называются функции, кото-
которые могут быть получены интегрированием алгебраических функций, и обрат-
х
вые этих функций. Так, логарифмическая функция определяется kzkJ" x~~l dx;
1
ее обратной является экспоненциальная функция. Из экспоненциальных функ-
функций рациональным процессом выводятся тригонометрические и гиперболические
функции.
35
и, поскольку у=уг является его решением, оно приводится к
виду
Это уравнение является частным случаем уравнения Бер-
нулли: оно приводится к линейному подстановкой
z = 1/и,
после чего наше утверждение об интегрируемости доказано.
Пусть уи у2, Уз — три отдельных частных решения уравнения
Риккати, а у — его общее решение. Тогда
1 1 1
_ 1 _ 1
У—У Х У —У' 2
У—Ух Х У г —Ух' 2 Ув-Ух
удовлетворяют одному и тому же линейному уравнению и сле-
следовательно
И —Hi _^ q
н2 — их ' '
где С—постоянная. Если и, ut и и2 выразить через у, ух и у2,
то это соотношение может быть написано в виде
q
У— Ух Уъ — Ух'
Отсюда видно, что общее решение уравнения Риккати может
быть выражено через любые три отдельные частные решения,
а также, что ангармоническое отношение любых четырех реше-
решений постоянно. Формула также показывает, что общее решение
является рациональной функцией постоянной интегрирования.
Любая функция типа
у с/
где/„/2,/3,/4 — заданные функции х, а С — произвольная по-
постоянная, удовлетворяет уравнению Риккати, что можно легко
доказать, исключая С из выражения для у и его производного
для у'.
Если ф равно нулю, то уравнение Риккати может быть при-
приведено к линейному уравнению; если ф не равно нулю, то
уравнение может быть преобразовано в линейное уравнение
второго порядка. Пусть ю — новая зависимая переменная, опре-
определяемая выражением
у = 1>!Ф,
тогда уравнение примет вид
dv
dx ~"~ ' ^ '
где
Подстановкой
V = ll'jll
35
приводим уравнение к искомой форме, именно
dx- ' dx ^~
В частности, первоначальное уравнение Риккати, именно
где а и й — постоянные, примет вид1
.—„ — abxmu = 0.
Лс2
2-16. Уравнение Эйлера. Весьма важными являются уравнения
с разделяющимися переменными вида2
dx . dy _n
где
A' = a0 x4 + ax xs + a2 x~ -f a3 x тЬ- a4
Г - a0j/4 + fll>i3 + a2у + a3 jc + a4.
Рассмотрим частное уравнение
V i -
решением которого является3
arc sin л; + arc sin j = c.
Это уравнение имеет также решение
г /l —^ = С.
Поскольку, как будет показано в главе III, диференциальное
уравнение имеет лишь одно явное решение, оба решения должны
находиться между собой в определенной зависимости. Эта зави-
зависимость выражается уравнением
С=/(с).
Теперь пусть
х = sin и, у — sin-у,
1 Решение этого уравнения может быть выражено в функциях Бесселя (§7- Л).
2 Eider, lust. Ca!c. Int., I, V, VI.
X _ !
3 Функция arc sin х определяется как J' A — t-) - dt; sin x определяется
и
как обратная arc sin х, так что sin 0 = 0; cos х определяется как (I — sii.2*J,
при условии, что cosO= 1. Никакие другие свойства тригонометрических функ-
функций не используются.
Тогда
U тг V = С,
sin и cos г» + sin <v cos и = f(c)
= f(u + v).
Пусть
-у ==0,
тогда
sin и =/(и),
следовательно
sin и cos i> + sin v cos и = sin {и + i>).
Таким образом получим формулу сложения для синусоидальной
функции.
Аналогично, диференциальное уравнение
имеет решение
arg sn x + arg sn у = с,
где argsn* — обратная эллиптическая функция Якоби1 — опреде-
определяется уравнением
/At
_ ___•
о A — РJ~ (\ —k*t*)b
Пусть
х = sn и, у = sn v,
тогда
и -\- ю — с.
Второе и эквивалентное решение может быть найдено следу-
следующим образом: согласно определению
du
следовательно
Аналогично
^==— ^ = — A— J2J A — ky2) ¦
d*y d*y _ . , „ 2^ iS
1 Уиггекер и Ватсон, Курс современного анализа, гл. XXII.
38'
откуда следует, что
_ I dy , dx\ 2k*xy
~ \ X du ~*~ У d~u)
Следовательно
Хdip Уйи*_ I
dy __ -dx ~ \ X du * У du) \—
Xdu У du
Это уравнение непосредственно интегрируется; получим ре-
решение вида
хЧи - у ш)= const +log A ~ **&
или
dv ' ¦* du
т. е.
snH sn'-y тЬ sirysn'M =/(c) A —^2 sn2 и sn2 v).
Полагая v = 0, найдем, что /(к) = sn и, следовательно
. . sn u sn' v Л- sav sn' н
что является формулой сложения для эллиптической функции
Якоби sn и.
Тот же процесс интегрирования" может быть приложен и
к общему уравнению Эйлера1. В частности, следует отметить,
что при ао = О линейное преобразование приводит это уравнение
к виду
dx ] rfy. q
VAX? — g2x — gs Y^y^ — gzy — gs
Если <@(z)—эллиптическая функция Вейерштрасса, определяемая
уравнением
DO I
z=f{W-gkt-gt) 2dt,
где х = р{и), у = #>(<а), — то общим решением уравнения будет
н -f-г; = с
или
1 g3) 2 - Dу3 —fty —ft-)a } =
1 Cayley, Elliptic Functions, XIV.
39
Таким образом можно показать, что формула сложения для
— функции имеет вид
2 • 2. Интегрирующий множитель. Пусть
Pdx + Qdy = 0
будет диференциальным уравнением, не являющимся точным.
Теоретически метод интегрирования такого уравнения состоит
в определении функции р(х, у) так, чтобы выражение
V- (Pdx + Qdy)
было полным диференциалом du. Когда и найдено, проблема
приводится к квадратуре.
Возникает вопрос, существуют ли интегрирующие множители.
На основании допущения, что уравнение имеет только одно
решение 1, которое зависит от одной произвольной постоянной,
докажем, что существует бесконечное множество интегри-
интегрирующих множителей.
Пусть общим решением будет
<в (х, у) = с,
где с — произвольная постоянная, тогда его диференциал будет
иметь вид
~ dx + -,- dy = 0
дх ду *
ИЛИ
4xdx + 4vdy = 0.
Поскольку
Ч(х,у) = с
является общим решением
Pdx + Qdy = 0,
соотношение
должно обратиться в тождество, откуда следует, что функция
р существует и имеются соотношения
Чх = !'• Р, Чу = [>¦ Q-
Следовательно
1 Это допущение будет дсказано в следующей главе.
40
Пусть F(tp) будет любой функцией <р, тогда выражение
I* F(<s>) {Pdx + Qdy} = Д<р) dy
точное. Следовательно, если \>- — любой интегрирующий множи-
множитель, приводящий к решению ш = с, то u. F(w) также будет инте-
интегрирующим множителем. Поскольку Д<р) является произвольной
функцией ш, существует бесконечная последовательность инте-
интегрирующих множителей.
Так как уравнение
у. (Pdx + Qdy) = О
точное, то интегрирующий множитель удовлетворяет соотно-
соотношению
Ц?1 = ^91
ду дх
ИЛИ
dy ^dt^Wj дх)
Таким образом у. удовлетворяет диференциальному уравне-
уравнению в частных производных первого порядка. Непосредственное
определение у- зависит от уравнения более сложного характера,
чем рассматриваемое обыкновенное линейное уравнение. Однако
нужно отметить, что любое частное решение диференциального
уравнения в частных производных (не обязательно общее) до-
достаточно для нахождения интегрирующего множителя. Более
того, во многих частных случаях диференциальное уравнение
в частных производных имеет очевидное решение, которое дает
требуемый интегрирующий множитель.
Предположим, что и. — функция одного х, тогда
^Ф _ j /дР сю^
I* dx~ О \ду~ дх }¦
Следовательно необходимо, чтобы правый член этого уравнения
не зависел от у. В этом случае и получается непосредственно
квадратурой. Предположим также, что Q равно единице, тогда
Р должно быть линейной функцией у. Таким образом уравнение
примет форму
d + (
где р и q — функции одного л; поэтому уравнение линейно;
интегрирующий множитель определяется уравнением
dp.
? =-- ^
и равен
i pdx
а =¦ е'
(см. §2-13).
Примером уравнения, в котором интегрирующий множитель
может быть легко получен, является
axdy + tydx + хту" (axdy + bydx) = 0.
Рассмотрим сначала выражение axdy + $ydx; интегрирующий
множитель равен х'^у'—1, и так как
= d
то более общее выражение
*-1 ф (х$ у)
также будет интегрирующим множителем. Аналогично
xb-m-lya~n-l P(xbya)
является интегрирующим множителем для х'пу" (axdy-\-bydx).
Если Фи/7 могут быть определены так, чтобы
xv-iy,«-i ф (Х?у«) = xb-m-1ya-"-1F(xby"),
то интегрирующий множитель первоначального уравнения мо-
может быть найден. Пусть
тогда x'-yv будет интегрирующим множителем, если
Х = (Р + 1)Р-1 = (г +ць — т — 1,
и = (р + 1)а —1 = (г + 1)а — п— 1.
Эти уравнения определяют риг, следовательно и X и и, если
«Р — 6а ф 0. С другой стороны, если а = Ы, Ъ = Щ, то первона-
первоначальное уравнение примет вид
A + kx'n vn) (ajcdy + $ydx) = 0.
Получим интегрирующий множитель вида
. 2-21. Уравнение Дарбу. Дарбу исследовал следующий тип
уравнения1
Ldy + Mdx + N(xdy -ydx) = 0,
где L, M, N—полиномы относительно х иу степени не выше т.
Покажем-, что если некоторое число частных решений формы
f(x, У) = 0,
где f(x, у) — неприводимый полином, — известно, то уравнение
может быть проинтегрировано.
1 Darboux, Bull. Sc. Math. B), 2 A&78), 72:
42
Пусть общее решение имеет вид
и (х, у) = const,
тогда данное уравнение эквивалентно
поэтому
L дх + М ~dj — ™\х~дх+У WJ °-
Заменим х на ~ и у на у, где г — третья независимая пере-
переменная, тогда и [~, -у) будет однородной рациональной функ-
функцией х, у, z степени нуль и, согласно теореме Эйлера, (§ 1 • 232)
ди , ди . ди г.
Более того, и ( —, — J удовлетворяет соотношению
, ди , я. ди . »г ди „
где L, М, N — однородные полиномы от х, у, z степени т.
Эти соотношения имеют место вследствие того, что
и {х, у) = const
является решением данного уравнения; и (-^-, -у) однородно
степени нуль и удовлетворяет соотношению А (и) = 0.
Теперь пусть
fix, у) = 0
будет любым частным решением, где f(x, у) — неприводимый
полином степени h, и пусть
Тогда, поскольку g однородно и степени h,
дх ' ¦* ду дг fe
Аналогично
A(g)=L^ + MM+NM-
дх
43
поскольку решением является /=0. Это соотношение может
быть написано в форме
так как A (g) — полином степени m-\-h — I, g— полином степени
h, а К—полином степени т—1.
Оператор А имеет следующее свойство: если F—любая функ-
функция и, v, w,..., где и, v, w,... являются функциями х, у, z, то
Пусть
Мх, У) = О, /,(*, у) = 0,..., fp{x, у) = О
будут частными решениями данного уравнения, где f{x у) —
неприводимый полином степени !гГ. Пусть
Рассмотрим функцию
р
и(х, у, z) =
г а
где а„ я,....,з.г — искомые постоянные, тогда
V
т =1
где /G- — полино!И степени m—1 для любого значения г. Ана-
Аналогично и(х, у, z) является полиномом от х, у, z степени Л,а,,
Л2а2 +...-{- hpCLp. Если и (х, у, z) должно дать искомое решение
при 2=1, оно должно быть полиномом от х, у, z нулевой сте-
степени, а также должно удовлетворять соотношению А (и) = О,
откуда
ftp, + /г3а2 +... + hpzp = О,
Kfa + К&ъ +... +Драр = 0.
Каждый полином Кт содержит не больше -„- m(m + 1) членов,
так что последнее уравнение, являясь тождеством относительно
х, у, 2, эквивалентно не больше, чем -,-; m(m + l) соотноше-
соотношениям между постоянными аъ а2,...,кр. Следовательно, между р
44
неизвестными постоянными а имеется не больше
уравнений. Поэтому для этих постоянных могут быть даны
соответствующие значения, если число р превосходит число
уравнений, т. е. если
Если т(т f- l) + 2 частных решений известны, то общее
решение может бить получено без квадратур.
Если р —---/и (/и -f 1) + 1, а дискриминант уравнения равен
нулю, то мы получим тот же результат. Пусть р=2 m (m +
4-1) + 1, а дискриминант не равен нулю. В этом случае постоян-
постоянные определяются уравнениями
h&x + КчЛ- •¦¦ + hpa.p — — т — 2,
г> I is i i т/ dL дМ dN
КЛ + К2а,+... +КР^ = ьт — ду — -ь ¦
Мы теперь имеем ум (т + 1) + 1 неоднородных уравнений,
определяющих постоянные а. Это определение постоянных при-
приводит к образованию функции и (х, у, г), так что
ди . да . ди , . оч
X+y+Z(m + 2)^
A(u) E if- +/И^ + /V^- =- (f-+^+ ™Г- и.
¦ ' ах dv dz \ дх ду дг
Исключая из этих уравнений ^-, получим
+ (т + 2) и W = 0.
Но, поскольку N однородно и степени ш, то
dN . dN . dN
dN
следовательно, исключая -^—, получим
х ж -
dN
'У-л..
45
Пусть 2=1, тогда и(х, у) удовлетворяет уравнению
Но это точно соответствует условию, что и(х, у) должно быть
интегрирующим множителем для уравнения
Ldy + Mdx + N(xdy — ydx) = 0.
Следовательно если -o-m(m+ l)-f 1 частных решений из-
вестны, то интегрирующий множитель может быть найден.
Вернемся к уравнению Якоби (§ 2-14;
(а, + bxx -f qv) (хя'у —j,-rfA;) — (а2 + f2^
+ (о3 + й3л: + c3v) dx = 0;
в этом случае /я = 1. Уравнение имеет решение линейной формы
ад: + ЗУ + Т ~ const.
А (/") е (a2z + b.2x + с,у) ^ + (azz + Ь3к + с3у) -?¦ +
где X — постоянная, a f = ах + Ъу+iz. Это приводит к трем урав-
уравнениям между а, р, у, л, именно
7 iai — X) -]- *о2 + р^з = 0, Y^i ~Ь а (^2 — ^) "г" ?Ь3 = 0, ','ci ~Ь" ас2 "Г"
откуда
| «! — >•, а2, а3 i=0-
Допустим, что это уравнение имеет три разных корня Х„ Х,2 Х3,
которым соответствуют три значения /, именно U, V, W, тогда
?/V'U?fc= const
будет общим решением при г равном единице, если
Достаточно взять i = Х2 — Х3, у = Х3 — >.lt Л = )., — Xjj. Общее
решение будет иметь вид
L,-». - >-^>-s - х. ^>. - >, ^ const.
4:5
2 • 3. Ортогональные траектории. Уравнение
Ф {х,у, с) = О,
где с —параметр, представляет семейство плоских кривых. С этим
семейством кривых связано второе семейство, именно, семейство
ортогональных траекторий или кривых, пересекающих каждую
кривую данного семейства под прямым углом. Возвращаясь
к случаю, приведенному в § 1-4, первое семейство кривых
можно рассматривать, как силовые линии данного плоского
магнитного или электростатического поля. Семейство ортогональ-
ортогональных траекторий будет тогда представлять эквипотенциальные
линии в данной плоскости.
Пусть
F{x,y,p) = 0
будет диференциальным уравнением данного семейства кривых;
оно определяет градиент р любой кривой этого семейства,
проходящей через точку (л:, у). Градиент ш ортогональной кри-
кривой через (х, у) связан с р соотношением
рй = — 1,
следовательно диференциальное уравнение семейства ортогональ-
ортогональных кривых будет иметь вид
Так как диференциальное уравнение данного семейства полу-
получается исключением с из двух уравнений
то диференциальное уравнение ортогональных траекторий обра-
образуется исключением с из уравнений
Примеры.
(I) Семейство парабол
у2 = 4сх,
где с — параметр, — представляет собой интегральные кривые
диференциального уравнения
Следовательно диференциальное уравнение ортогональных траек-
траекторий имеет вид
2х + ру = О,
а сами траектории являются кривыми
47
они составляют семейство подобных эллипсов, оси которых рас-
расположены вдоль координатных осей.
(II) Семейство конфокальных конических сечений
X2
х
где >- — параметр,— является интегральными кривыми диферен-
циального уравнения
(л + ру) (у — рх) +" fa2 — Ьг)р = 0.
Это уравнение не изменяется при подстановке — р—1 вместо р,
следовательно данное семейство образуется взаимно ортогональ-
ортогональными кривыми.
2 • 31. Изогональные траектории. Изогональной траекторией на-
называется кривая, пересекающая кривые семейства под некоторым
определенным углом. Пусть этот угол равен arc tg /га, тогда,
если р и ш соответственно представляют градиенты кривой дан-
данного семейства и траектории в точке их пересечения, то
Если диференциальное уравнение данного семейства имеет вид
то диференциальное уравнение семейства изогональных кривых
будет
Пример. Рассмотрим семейство концентрических окружностей,
их диференциальное уравнение имеет вид
х-\-ур=0.
Семейство кривых, пересекающих окружности под углом arc tg /га,
дается поэтому уравнением
или
(тх + у)р + х— ту= 0.
Это уравнение однородно и дает решение вида
log yr x% -f у2 + /я arc tg — = const.
В полярных координатах уравнение траектории может быть на-
написано так
г=Се тЬ-
следовательно, кривые являются спиралями.
48
2 • 32. Конформное отображение поверхности на плоскость. Дру-
Другим важным приложением диференциальных уравнений первого
порядка является их применение для конформного отображения
алгебраической поверхности на плоскость.Действительная квадра-
квадратичная форма
dS* = Edtf + 2Fdu dv + Gdv2 {EG
представляет собой элемент поверхности. Поскольку она су-
существенно положительна, ее линейные множители
adu + bdv, a'du -f b'dv
таковы, что а и Ь являются комплексными функциями и и v,
а а' и Ь' — соответственно комплексными сопряженными функ-
функциями.
Пусть и. (и, v) будет интегрирующим множителем для adu-\-
+ bdv, тогда сопряженный множитель у.' будет интегрирующим
множителем для a'du-{-b'dv.
Если
I* {adu -г/ bdv) = dV, u' (a'du+ b'dv) = dV,
то V и V будут комплексными сопряженными функциями и
Определим х и у как новые переменные уравнений
V ~х-\- iy, V = x—iy,
и пусть
тогда
dS- = i.2 {dx- -f- dy2)
= i,2 rfs2.
Следовательно поверхность (и, ¦у) может быть конформно отоб-
отображена на плоскость {х, у)х.
Пример. Рассмотрим отображение сферы
dS2 = a2 du2 + a2 sin2 и с?*>-
на плоскость
= a2 {du + I sin и dv) {dv. — i sin и dv)
= a? sin* и (cosec a du + idf) (cosec и du — id*)).
Пусть
cosec и du = dy, dv = dx,
т. e.
y = \ag\ig~u,x = v,
тогда
dSi = 4a rf
1 Общую теорию конформных отображений см. Forsyth, Theory of Functions.
э. айнс— 133—4 49
Это соответствие между сферой и плоскостью называется
проекцией Меркатора1. Меридианы на сфере представляются ли-
линиями, параллельными оси у на плоскости, а параллели широты —
линиями, параллельными оси х. Вся сфера отображается на по-
полосу плоскости, лежащую между х = -~ я и * = + я. Любая пря-
прямая линия на плоскости представляется локсодромической кри-
кривой на сфере, т. е. кривой, пересекающей все меридианы под
одним углом.
2 • 4. Уравнения первого порядка, не первой степени. Уравнение
первого порядка степени т может быть написано в виде
где Plt..., Рт — функции х и у. Теоретически уравнение может
быть разложено на множители
(?-*)(?-*¦)••• (?-*)-«•
где р1г р2, рт — функции х и _у.
Пусть
будет общим решением уравнения
оно является также решением данного уравнения. Если
Ф(х,у,С) = 0
решение данного уравнения, то оно должно удовлетворять од-
одному из уравнений
2-^ = 0. {г=\1,2,...,т)
Отсюда следует, что любое решение (А) содержится в решении
Ь (Х.У, с>) Ъ (х. У, с)... «pm (х, у, с) = 0j
которое является общим решением. Имеющаяся произвольная
постоянная с достаточна для полного обобщения, потому что
частное решение определяется одним из уравнений типа
<fr (x,y, с) = 0,
где с имеет любое численное значение.
Пример:
1 Гергард Кремер (Gerhard Kremer, no латыни Mercator) опубликовал свою
карту мира в 1538 г. Основные математические принципы были впервые объяс-
объяснены Эдвардом Райтом (Edward Wright) в 1594 г.
50
После разложения на множители уравнение примет вид
а оба множителя дают решения
у = sh (с ± х),
где с — постоянная; следовательно общее решение будет иметь
вид
,,2 ——1рС — Х /з—С—Х\(рС—X С—С-Х\
- 4 ^ -г е е е )
где: С -= ch 2с.
2*41. Геометрическая трактовка. Диференциальное уравнение
можно рассматривать и с геометрической точки зрения. Заменим
dv ,
j-x на z и будем рассматривать 2 как третью прямоугольную ко-
координату в пространстве. Тогда уравнение
будет представлять поверхность S.
Пусть
у = Ч{х)
будет любым решением диференциального уравнения, тогда два
уравнения
у = ф (л), z = <f' (х)
будут представлять пространственную кривую Г, которая, по-
поскольку
F{()
лежит на поверхности 5. Решений диференциального уравнения,
которые соответствовали бы каждой кривой, лежащей на S,
нет, — они соответствуют лишь тем кривым, во всех точках ко-
которых удовлетворяется диференциальное соотношение
dy — zdx = 0.
Пусть
x^x{t),y=y{t),z = z(f)
будет параметрическим представлением кривой Г на S, для ко-
которой соотношение
dy — zdx = 0
51
удовлетворено. Проекцией Г на плоскость (я, у) будет кривая С
x = x(t), у = v{t)
или
У = Ч(х).
Поскольку во всех точках кривой Г уравнение
F(x,y.2)=0
принимает вид
F{x,4{x),*'(x)}=0.
кривая С или
у = <р (а)
будет интегральной кривой уравнения
/Ч*. У,/) = 0.
Пусть параметрическим изображением поверхности 5 будет
л =/(и, f), v = о- (н, г»), г = Л (и, •&),
тогда соотношение
dy — zrf д: = О
примет вид
или
Любое решение этого диференциального уравнения представляет
собой зависимость между миг), которая определяет кривую Г на
поверхности 5 так, что проекция этой кривой на плоскость {х, у)
является интегральной кривой диференциального уравнения.
Рассмотрим уравнение, которое может быть написано в виде
Соответствующая поверхность 5 может быть параметрически
представлена в виде
х = х, y = g{x, p), z=p,
и соотношение dy — zdx = 0 примет вид
Это соответствует диференциальному уравнению вида
общим решением которого будет
1(х, р, с) = О,
52
тогда интегральные кривые будут проекциями на плоскость (х, у)
пересечения поверхности
y — g{x, z) = 0
с семейством цилиндрических поверхностей
/ (х, z, с) ~ О
следовательно, если исключить р из двух уравнений
y=g(x,p), 1{х, р, с) =0,
получим общее решение данного уравнения.
2-42. Уравнения> в которые х или у явно не входят. Если ка-
какое-либо из уравнений
F(x, р) = 0, F(y, p) - 0
может быть решено относительно р, то его можно проинтегри-
проинтегрировать в квадратурах. Иногда уравнение легче решить относи-
относительно х (или у). Пусть решение имеет вид
*=№,
тогда, диференцируя по у,
откуда
y = c+fpf(p)dp
следовательно уравнения
x = f(p), y =
можно рассматривать как параметрическое представление ре-
решения. Решение можно получить исключением р из обоих урав-
уравнений.
Если уравнение не содержит л, то его нужно решить отно-
относительно у, а затем диференцировать по х. Решение получится
в параметрической форме
У=/(Р)> x = c+g{p),
где
g(p)=fp~1f(p)dp.
Более общее уравнение
F(x,p) = 0
можно выразить параметрически в виде
x = u(f), p = v(t),
тогда, диференцируя по t,
J
р dt ~u
53
откуда
y = c+fv(t)u'(t)dt.
Решение получится путем исключения t из выражений для л; и
у. Уравнение
F(y,p)=O.
которое может быть выражено в форме
y = u(t), p = v(t),
решается исключением t из
y = u{t) и x = c +
Пример. Рассмотрим уравнение
Это уравнение может быть представлено параметрически в виде
Диференцируя первое уравнение по t, получим
— -= 1 — 3^'
откуда
х = с 4- I -Т—7Г dt = с + 3t~
Таким образом хну могут быть представлены в функциях па-
параметра t.
2»43. Уравнения, однородные относительно х и у. Однородное
уравнение степени т относительно х, у может быть написано
в виде
Если оно решается относительно р, то могут образоваться урав-
уравнения типа
уже рассмотренные в § 2 • 12. Следовательно этот случай не
представляет для нас ничего нового. Рассмотрим случай, в ко-
котором уравнение может быть решено относительно ~.
Так
или
у = xf{p).
54
Диференцируя это уравнение по х, получим
Пусть р будет независимой переменной, тогда в этом урав-
уравнении переменные разделятся и оно будет иметь решение
\
р—А
или
Эти совместные уравнения
дают общее решение уравнения.
Пример:
Решим это уравнение относительно х
диференцируя по у, получим
- = -i я «/Lj-ll*
/) р ' J \ p- ay
ИЛИ
Ф р_
d7 у '
откуда
РУ = ^.
Исключая р из первоначального уравнения, получим искомое
решение
.у2 = 2сх + с-.
2 44. Уравнения линейные относительно х ну. Общим типом урав-
уравнения, решение которого может быть получено в параметриче-
параметрической форме дифереицированием, является
Производное уравнение имеет вид
Если х рассматривать как зависимую переменную, а р как
независимую, то при р — <ь(р):'О уравнение может быть напи-
написано в виде
d/> {)~ ' р ?(р)
и будет линейным уравнением в обычном смысле. Его решения
содержат две квадратуры; пусть решение будет
тогда из первоначального уравнения можно исключить х и
получить выражение для у в виде
следовательно общее решение может быть выражено параметри-
параметрически через р.
Рассмотрим теперь частные значения р, например, р„ р2,--.,
для которых
Р-г(р)^0-
для этих значений р
t „ Q
Таким образом возникает некоторый ряд изолированных интег-
интегральных кривых вида
Они представляют собой прямые линии, так что, если интег-
интегральная кривая общего семейства встречается с одной из них,
то они будут иметь общую точку перегиба. Прямые линии дают
пример особых решений, т. е. решений уравнения, не входящих
в общее семейство интегральных кривых, которые не могут
быть получены из общего решения путем придания специаль-
специального значения постоянной интегрирования.
Пример:
Производное уравнение имеет вид
откуда, если р ф О,
dp ' р
Решение этого линейного уравнения имеет вид
которое вместе с первоначальным уравнением дает искомое
решение. С другой стороны, при р — 0, получим решение
у = 0.
2 • 45. Уравнение Клеро. Уравнение Клеро
1 Clairaut, Hist. Acad., Paris A734), 209
56
не входит в класс уравнений, рассмотренных в предыдущем
параграфе, потому что в принятых обозначениях
? (Р) = Р
тождественно, следовательно, метод не дает требуемых резуль-
результатов.
Производное уравнение имеет вид
и удовлетворяется при р — с (постоянной) или
х+Ь'(Р) = О-
Значение р = с приводит к общему решению
у г= сх + 'Ь (с).
Далее мы получим частное решение посредством исключения р
из уравнений
У=рх + Ъ(р),х + ?(р)^0.
Оно не содержит произвольных постоянных и не является
частным случаем общего решения, следовательно оно будет
особым решением.
Известно, что огибающая семейства прямых линий
у = сх + ф {с)
получается путем исключения с из этого уравнения и из урав-
уравнения
О = х + <1/ (с)
и идентична кривой, дающей особое решение. Следовательно
в случае уравнения Клеро особое решение представляет огиба-
огибающую семейства интегральных кривых.
Семейство касательных к кривой
y=f{x)
удовлетворяет уравнению формы Клеро, так как, если
у = ах + ?
является касательной, то
SU + 3 =/(*), а =/(*).
Исключая х из этих уравнений, получим соотношение
Р = ф(о)
поскольку на касательной а = р имеем
у = рх
Пример:
y = px + ljp.
57
Диференцируя, получим
' UX
откуда или р = с, что дает общее ре шение
у = ex -f- 1/с
или />2 = \\х.
Особое решение получится путем исключения р из
р2 = 1 /х и у — рх + \ р
и равно
уг --= 4.V.
2-5. Принцип двойственности (дуальности). Существует преоб-
преобразование, найденное Лежандром (Legendre), при помощи кото-
которого между двумя уравнениями' первого порядка может быть
установлена двойственная зависимость. Пусть Л!"и Гбудут новыми
переменными, определяемыми соотношениями
X = р, Y = хр —у
я пусть
dY
' аХ '
Полагая, что ~ фО, получим
dX = dp, dY — xdp + pdx — dy
— xdp
v ¦--- xp— Y
следовательно
Аналогично
Таким образом преобразования
X = p, Y = xp—y
эквивалентны
a: = P, у = А'Р— Г,
следовательно они находятся в обратной зависимости друг
к другу1.
При подстановке любое из уравнений
F (х, у, ру= О, F(P, XP~ Y, X) - О
может быть преобразовано в другое; в этом смысле между ними
1 Если (х, у) и (Л", Y) рассматривать как точки в плоскости переменных
u, v, то геометрическое место точек (х, у) будет полярно-инверсным геометри-
геометрическим местом точек (X, Y) относительно параболы иг — 2v, и наоборот.
существует двойственная зависимость. Если одно из этих урав-
уравнений может быть проинтегрировано, другое может быть про-
проинтегрировано чисто алгебраическими способами.
Например, пусть
?(*, Г)-О
будет решением второго уравнения, тогда, диференцируя по X,
получим
дХ ' дУ ^ - и-
Теперь X, У, Р может быть исключено из этих двух уравнений
и выражении
х = Р, у = А'Р— Г,
что дает решение уравнения
F(x, j;, р) = 0.
В частности, уравнение
Ф{
примет вид
Переменные X и Y теперь разделяются и уравнение интегриру-
интегрируется в квадратурах.
Пример:
(У—рх)х=у.
Преобразованное уравнение имеет вид
у
Р =
У + X'
оно однородно и имеет решение
log Y —у — const.
Диференцируя по
откуда
следовательно
X,
получим
Р Y—XP
у Y-XP
У Р
0,
у
.к
Таким образом решение первоначального уравнения имеет вид
или
у =
Примечание. В случае уравнения Клеро, условие ^ф О нару-
нарушено для общего решения; этот метод приводит поэтому только
к особому решению.
2 • 6. Уравнения порядка выше первого. Простейшим диферен-
циальным уравнением общего порядка п будет
-в
Его решение является процессом п-кратного интегрирования
и может быть проведено следующим образом.
Пусть х0 постоянная, выбранная произвольно, тогда
X
d у- ff(x)dx~Cri,
dx"-1
X X
dn~2v
dx'
3 = / dxjf(x) dx + Со (х - хс) + С,
у = fdxfdx.. J'f(X)dx + Со L±-J^L1+... +C^U
л,
где Со, С,, —, С„_1—произвольные постоянные.
Однако многократный интеграл может быть замещен простым
интегралом. Пусть
тогда
li я
iixn~l
откуда
Следовательно Y является решением, которое вместе с ег о
первыми (и—1) производными исчезает при х = х&. Общим ре-
60
тением будет
Независимо от этого простого случая и случая линейного
уравнения с постоянными коэфициентами, который мы будем
рассматривать в главе VI, имеется лишь небольшое число урав-
уравнений порядка выше первого, которые поддаются элементарному
исследованию. Однако в ряде очень специальных случаев поря-
порядок уравнения может быть понижен посредством соответствую-
соответствующих преобразований переменных, комбинируемых с одной или
более квадратурами. Основные случаи этого рода мы рассмотрим
з трех последующих параграфах.
2 • 61. Уравнения, не содержащие зависимой переменной. Рас-
Рассмотрим уравнение
-d*-V. f l-v ?У\ = о
dxk' dxk 1>- '"' dxn)
где у и его k — 1 производных отсутствуют. Преобразование
приводит это уравнение к уравнению порядка п — к, содержа-
содержащих г>. Если это уравнение может быть проинтегрировано и
его решенир получится вида v = v{x), то остается только про-
проинтегрировать уравнение
которое мы разобрали в предыдущем параграфе.
Однако приведенное уравнение чаще имеет решение вида
которое трудно решить относительно v. Чтобы сделать метод
практически удобным, необходимо х и v выразить через пара-
параметр t следующим образом
= v{t), х = x(t),
тогда
dy(k-i> = v ф dx = v (t) x' (t) dt,
что после интегрирования дает з'(*~)- Этот процесс повторяется
k раз до получения искомого решения.
Важным частным случаем является уравнение вида
„ "—1.
dxn J\dxn-X)'
такие уравнения интегрируются в квадратурах.
61
2 • 62. Уравнения, не содержащие независимой переменной. Если
уравнение имеет форму
dv
его порядок может быть приведен к л — 1 заменой переменных.
Пусть у — новая независимая переменная, а р — зависимая пере-
переменная. Формулы преобразования имеют вид
йу d-v _ dp d3y d I dp\
~ax~ ¦ P' Jx* ' P ay ' ax3 ~~ P ay'[P dyj'
Данное уравнение приводится к уравнению вида
?!*
-' dyn-
Предположим, что это уравнение может быть проинтегрировано
и что его решение может быть выражено в параметрической
форме
f(t) p = g(t),
где / и g — функции вспомогательной переменной t и зависят
также от п—\ постоянных интегрирования, тогда при помощи
квадратуры получим х, выраженное через t
J ~g'O)
В частности, уравнение второго порядка, не содержащее
именно
преобразуется в уравнение
F(y. Р, Р%)=0
первого порядка.
Уравнение вида
ах" \dxn
приводится подстановкой
dx*
С2
-f(v).
dv
сли-i—=/?, то последнее уравнение примет вид
ткуда
ледовательно
Чтобы получить у, v должно быть выражено через х; реше-
ше завершается п — 2 квадратурами.
2 • 63. Уравнения, показывающие однородность формы. Рассмот-
Рассмотрим два класса уравнений. Первый класс включает уравнения
зднородные относительно у, у, у",.-., у01' и содержащие х.
Сравнение этого класса, со степенью однородности т, может
эыть написано в виде
vmF х~ , —,...." — ) = 0.
\ у у У I
Пусть и — новая зависимая переменная, определяемая соотноше-
соотношением
J lldx
тогда
где Un—-полином от и, и',..:, и'"~^. Замена зависимой пере-
переменной у на и понижает порядок уравнения л до (п — 1).
Второй класс содержит уравнения, однородные относительно
у, ху'х2, у",. ..,хпу^, но не содержащие отдельно х. Уравнение
является типичным. Произведем подстановку
х = е1,
тогда
ХТ
у У
dx
dry =
,1УГ
dy
dt
9 X
d
~dT ~
d1y
dx-
-П .
rf2v
dt*
-¦{¦ж-
dy
at
— r
o*
Таким образом преобразованное уравнение примет вид
,1. .-.. аУ а'У d"y
и не содержит отдельно х, следовательно оно переходит в урав-
уравнение, рассмотренное в § 2 • 62.
Уравнение, соответствующее последнему классу, которое не
может быть проинтегрировано более простым методом, имеет
вид г
F{y",y'-xy",y-xy' + -|**У) - 0.
Производное уравнение будет
/".(/V
где FX,F2,F3— частные производные F относительно первого,
второго и третьего аргументов соответственно. Оно удовлетво-
удовлетворяется у"' = 0 или
v= А + Вх + ±
где А, В, С — произвольные постоянные. Это является общим ре-
решением первоначального уравнения, если
F(C, В, А) = 0.
2 • 7. Совместные системы с тремя переменными. До разбора об-
общей теории интегрирования совместных систем диференциальных
уравнений рассмотрим простой случай, в котором уравнения ин-
интегрируются методами, подробно рассмотренными в предшест-
предшествующих параграфах этой главы.
Рассмотрим систему
dx dy dz
где ?, iQ и ч — функции х, у и z. Специальным и важным является
случай, когда S и -ц не зависят от z. Тогда уравнение
dx dy
содержит только хну. Предположим, что это уравнение может
быть проинтегрировано и имеет решение
Ф (X, у, а) = 0,
где а — постоянная интегрирования. Пусть также это уравнение
решено' относительно у, тогда
j> = <?(•*> а),
и пусть с,г и ?, соответствуют S и С при подстановке <р (х, а)
вместо у, тогда уравнение
dx dz
IT "С
1Dixon, Phil. Trans. R. S. (A), 186 A894), 563. Обобщение для любого по-
порядка очевидно. См. также Raffy, Bull. Soc. Math. France, 25 A897), 71.
64
не будет содержать у, а его решение
й (х, z, а, р) = О,
где р—постоянная интегрирования.
Если из обоих решений
Ф (л, у, а) = О, У (дс, г, а, р) = О
исключить а, то решения примут вид
Ф{х,у,а) = 0, * (х, у, z, P) - 0.
2-701. Интегрирование совместной линейной системы с посто-
постоянными коэфициентами. Система
их dy __ dz
Г " г, ¦ с '
где
j= а2 л + 62у + с2 z 4- d2,
+ csz + ds,
не была разобрана в предшествующем параграфе. Она может
рассматриваться аналогично после линейного преобразования
переменных. Для упрощения введем новую переменную t, чтобы
их v dz dt
Т=Т=~Г= t '
тогда, независимо от постоянных /, т, п,
dt Ux + mdy + ndz
t l? + /иг) + nZ
Пусть /, m, n выбраны так, что
/a, + ma2 + nas = /p,
lbx -f- mb2 -f- nb3 = mp,
lcx + mc2 + псг = яр,
тогда
dt _ rf (/x + my + яг)
^ p (Ix + «у + nz+ r)'
где rp = ldx-\-md^-\-ndz. Этот выбор/, m, п возможен, если р
является корнем уравнения
j ai P> a2« Q3 — 0.
|
i Cl» C2» C3 P
Предположим, что корни этого уравнения равны —. j-f у и со~
Э. Айне—133—5 65
ответствующие значения /, т, п, г равны
/,-, mi, tit, rt (i = 1, 2, 3),
тогда
dt li d (liX + miy + «jz)
t lix -r miy + n;z + i'i '
откуда
t = C- (Zvt 4- /н v ~Ь я-z -\- r V'/
следовательно решение этой системы получится вида
= Cs (/sx +msy + я3г -f rs);-
и будет содержать три постоянных интегрирования С,, С2, С3,
две из которых произвольны.
2*71. Эквивалентное диференциальное уравнение в частных про-
производных. Рассмотрим л и у как независимые переменные, a z
как зависимую. Пусть р и q будут частными производными z по
х и у соответственно, тогда
будет линейным диференциальным уравнением в частных про-
производных первого порядка; оно назыьается линейным уравнением
Лагранжа. Если
г =/(х. У)
является решением этого уравнения, то
для всех значений х, у. Это решение представляет поверхность,
называемую интегральной поверхностью диференциального урав-
уравнения в частных производных. Поскольку направляющие коси-
косинусы нормали к поверхности z=f(x, у) пропорциональны
0L Ж. _1
дх' ду' '
диференциальное уравнение выряжает отличительное свойство
касательной плоскости к интегральной поверхности.
Рассмотрим теперь систему совместных диференциальных
уравнений
dx dy dz
6 ' г, = С
и примем, что ее решения могут быть выражены относительно
постоянных интегрирования так
и{х, у, z) = a, v(x, у, z) = p.
Эти решения представляют семейства кривых в пространстве,
зависящие от двух параметров, и называются характеристиками
66
системы. Если S, ч, С существуют и однозначны в точке (д-0, ул, z0)
и по крайней мере одно из них не равно нулю при (х0, у0, ze),
то через эту точку будет проходить только о ша характеристика.
Покажем теперь, что характеристики совместной диференци-
альной системы тесно связаны с интегральной поверхностью ди-
ференциального уравнения в частных производных. Сначала до-
докажем, что если интегральная поверхность проходит через
(х0, ув, z0), то она содержит характеристику, проходящую
через эту точку. Пусть интегральная поверхность, проходящая
через (Хп, у0, z0), будет выражена через
z=f(x, УП
полагая, что S не исчезает при (х0, у0, z0), рассмотрим диферен-
циальное уравнение
dy __ vj
их ~ ?'
в котором г заменено на f(x, у). Уравнение определяет у как
функцию х и является, следовательно, диференциальным урав-
уравнением семейства цилиндров, образующие которых параллельны
оси z. Цилиндр че^ез (а0, у0, 0) пересекает инте!ральн>ю по-
поверхность по кривой, проходящей через (х0, у0, z0). Вдоль этой
кривой
их dy rdx + qdy dz
5 ^Г~ /? + qrt ~ С '
Определенная таким образом кривая является характеристикой,
следовательно, теорема доказана. Непосредственное следствие
этой теоремы: каждая интегральная поверхность является геомет-
геометрическим местом характеристик. В частности, при проведении
любой нехарактеристической кривой в пространстве, характери-
характеристики, проходящие через точки этой кривой, образуют инте-
интегральную поверхность.
Обратная теорема также верна, именно, любая поверхность,
являющаяся геометрическим местом характеристических кри-
кривых, является интегральной поверхностью диференциалъного
уравнения в частных производных*. Касательная линия к характе-
характеристике в любой произвольной точке (х0, Уо, zfl) дается выраже-
выражением
X
5.
где So, Tjo> Со — значения S, 7), С при (л, уй, z0). Уравнение касатель-
касательной плоскости в точке (хй, у0) z0) к поверхности огибающей харак-
характеристики имеет вид
(х — xQ)p0 + {y—
1 Этот специальный случай может возникнуть, если поверхность имеет каса-
касательную плоскость, параллельную оси z, потому что тогда р и г/ становятся
бесконечными и доказательство оказывается несостоятельным.
67
где р0 и q0— соответственно значения ^-, ^ на поверхности при
(¦«о» Joi zo)- Поскольку характеристика лежит на поверхности, ка-
касательная линия лежит в касательной плоскости, поэтому
Но (л0) _у0, z0) является любой точкой на поверхности; следова-
следовательно последняя будет интегральной поверхностью диферен-
циального уравнения в частных производных
lp -f щ = С.
2 ¦ 72. Образование интегральной поверхности. Совокупность
характеристик образует семейство конгруентных кривых, завися-
зависящее от двух параметров. Аналогично тому, как плоская кривая
образуется выбором, согласно определенному закону, бесконеч-
бесконечной совокупности точек из бесконечности (второго порядка) то-
точек на плоскости, так и интегральная поверхность образуется
выбором бесконечности конгруентных кривых. Пусть
и(х, у, г) = а, v(x, у, z) = ,3
будет совокупностью характеристик, из которых выбирается
бесконечность первого порядка путем установления некоторой
зависимости между аир, например
Q(a, р) = 0.
Следовательно уравнение интегральной поверхности будет иметь
вид
Q(u, v) = 0,
и это уравнение, где функция Й произвольна, является общим
решением диференциального уравнения в частных производных.
В теории обыкновенных дйференциальных уравнений первого
порядка часто требуется найти интегральную кривую, проходя-
проходящую через данную точку плоскости. Соответствующая задача
в случае диференциального уравнения в частных производных
состоит в нахождении интегральной поверхности, проходящей
через данную (нехарактеристическую) базисную кривую в про-
пространстве. Эта проблема в ее общей форме известна как проб-
проблема Коши.
Пусть
<р {х, у, z) = 0, <]> (х, у, z) = О
представляет базисную кривую и пусть
«(¦*> .V. z) = а» v (Л У> Щ = Р
будут характеристиками. Если из этих четырех уравнений
исключить х, у, z, то получим соотношение между аир, пока-
показывающее, что характеристики и базисная кривая имеют общие
точки. Пусть это соотношение имеет вид
68
Ф (а, Р) = О,
тогда
Ф (и, v) = О
— искомая интегральная поверхность.
Пример. Рассмотрим диференциальное уравнение в частных
производных
(су — Ьг)^ + (аг — ел) ^ = Ьх — ау.
Дополнительная диференциальная система имеет вид
dx dy dz
су — bz az — ex bx — ay'
Эта система эквивалентна системе
I adx + bdy + cdz = 0,
! xdx + ydy + zdz = 0,
следовательно уравнения характеристик должны иметь вид
j ax -{- by -{- cz = я,
где а и р — произвольные постоянные. Характеристики представ-
представляют собой точки пересечения всех сфер, центр которых лежит
в начале с плоскостями, параллельными прямой
(/) -*_ = Z ^ z
^ я ~Т V'
т. е. они представляют совокупности окружностей, плоскости
которых перпендикулярны к этой прямой и центры которых
лежат на ней.
Уравнение интегральных поверхностей имеет вид
х2 + у2 + г2 =f(ax + by + cz)
и представляет поверхности вращения с линией (/) в качестве
оси симметрии.
Рассмотрим теперь интегральную поверхность, имеющую ось у,
которая образована характеристическими кривыми, проходящими
через эту же ось. Получим характеристики, для которых а. и 3
таковы, что уравнения
ах + by -Ь cz = а, хг + /- + z2 = 3, л; = 0, 2 = 0
совместные. Условие их совместимости получается исключением
у из
by = я, у2 = ?
и поэтому
fc8P=o2.
Искомой интегральной поверхностью будет
&г (л2 -f >/- + z3i = Гал 4- by + czf
или
(я2 — Ъг) хг + {с* — b'1) z- + 2abxy + ЧЪсуг + 2cazx ~= 0.
2 • 73. Однородное линейное уравнение в частных производных.
Если ч равно нулю, то уравнение принимает так называемую
однородную форму
Ьр + щ *= 0.
Уравнения характеристик принимают вид
dx __dy dz
е " h о "
Последнее уравнение сразу же дает
2 = а,
следовательно характеристики являются плоскими кривыми,
плоскости которых перпендикулярны к оси г.
Важнейшим является случай, когда ? и •*] не зависят от Z;
уравнение характеристик тогда принимает вид
Z = а, и (>", у) = р
и уравнение интегральной поверхности может быть написано
в виде
* = /(«)•
Рассмотрим теперь уравнение
где ;, г), ; — функции х, у, г. Если
f{x, у, z) = с,
где г — постоянная, является решением диференциального урав-
уравнения в частных производных, то
dfB^dx + ?dy+?dz = O,
J дх ду ¦* dz
следовательно / (а, у, z) ^ с является решением совместной
системы
дх ду _ dz
Обратное также верно, так как, если
и {х, у, z) = a
любое решение совместной системы, то
, ди , , да , . ди , Л
du=dx+dv+dz 0
7A
и следовательно
ди
ди
Предположим, что
(л;, у,
будет вторым и явным решением совместной системы; оно
также будет решением диференциального уравнения в частных
производных, так что
. dv , dv dv _
+ Ч + 0
Если любое другое решение
да (х, _у, г) = у
существует, то
dwbr dw
исключая ^, Г|, ,, получим
д (и, V, ш) __ ди ди ди_ _ _
v dv д
dw dw dw
| дх ду dz
Следовательно w является функцией и н v (§ 1-22) и поэтому
диференциальное. уравнение допускает два независимых решения.
Из трех уравнений
и(х, у, z) = a, v(x, v, 2) = Р, та(х, .v, z)=t
две переменные, например хну, можно исключить, тогда
получим
w = <р (н, «и, z).
Теперь
р. f) («, V, W) _ f) (Н, f, '5) Й (И, f, Z)
~ 3 (jc, _y, z) ~ д (и, v, z)' д (х, у, z)'
d(u,v)
Первый детерминант справа равен -Д второй / . Второе
выражение не равно нулю, поскольку а и v предполагаются
независимыми, следовательно
dz
= 0,
i. e. ф независимо от z, или, иначе говоря, к1 является функцией
ТОЛЬКО U И "О.
71
Общее решение диференциального уравнения в частных
производных
- дх ^ ^ ду ^ * dz ~~ U'
будет
2 (и, v) = const,
где Q — произвольная функция его аргументов, а
11 = 0., V = Р
— любые два независимых решения дополнительной системы
дх ду dz
~Т~ ~ " == "?"*
5 1 *
Распространение предыдущих выводов на случай « переменных
очевидно. Мы получим специальный случай, если S, vj, С будут
иметь общий множитель. Результат приравнивания этого множи-
множителя нулю дает специальное решение диференциального урав-
уравнения в частных производных, которое может быть включено
в общее решение.
В качестве примера рассмотрим уравнение
Дополнительная система
dx dy dz
х~ ху г'1
имеет два независимых решения
V Z — X
х-=а> -«-
Общее решение имеет вид
2 • 8. Диференциальное уравнение в полных диференциалах.
Алгебраическое уравнение с тремя переменными вида
<р (х, у, z) = с,
где с — постоянная, приводит к диференциальному уравнению
в полных диференциалах
да , . до , . да , „
,-, <3ср бэ до .,
Если -^-, -j-, -^— имеют общий множитель ix и если
д'Х> ,-, до ,-. d<c ,-.
дх * ' ду ' ^' dz ' '
72
то диференциальное уравнение в полных диференциалах мо-
может быть написано в виде
Pdx + Qdy + Rdz = 0.
С другой стороны, если Р, Q, R — произвольные функции
Л", у, z, то уравнение в полных диференциалах не обязательно
соответствует общему интегралу вида
Ч (х, у, г) = с.
Если такой интеграл существует, то Р, Q, R должны быть
соответственно пропорциональны трем частным производным
функции 'f {x, у, z), что несправедливо в общем случае. Здесь
возникает следующая проблема — найти необходимое и доста-
достаточное условие интегрируемости данного диференциального
уравнения в полных диференциалах, выведенного из интеграла
рассмотренного вида.
Необходимо, чтобы функции tp (х, у, z) и у-{х, у, z) были
такими, чтобы условия
д® ?j ffe ,-. cte q
дх ¦* ' dv ' dz '
были удовлетворены, тогда1
ду '' ' дудх
т. е.
и аналогично
дО dR 1 „ др. Г) dv
дг ду ) ду дг '
dR Э/5 | _ р _й|А р д_р
J дг дх
Неизвестная \>. исключается из этих трех уравнений умноже-
умножением их на R, P, Q и последующим сложением. Результирую-
Результирующее уравнение
р ( дО dR | . -. г dR дР 1 . р ( дР dQ
I дг ду J ~г ^ I дх dz J I ду ду
является необходимым условием интегрируемости2.
Из данного представления очевидно (это можно легко дока-
доказать и независимо), что если I — функция х, у, z и
Pi = IP, Q, = XQ, Rt = IR,
то условие интегрируемости удовлетворяется Р„ Q,, Ru
1 При этом принимается, конечно, что изменение порядка диференцирова-
нин допустимо.
2 Enler, lust. Calc. Int., 3, A770), 1.
Докажем теперь, что условие интегрируемости является до-
достаточным, т. е. если оно удовлетворено, то существует реше-
решение, содержащее произвольную постоянную. Кроме того, дока-
доказательство дает также мегод получения решения, если условие
интегрируемости удовлетворено.
Допустим, что одна переменная является в данный момент
постоянной. Если этой переменной будет z, то уравнение при-
приводится к виду
Pdx + Qdy = 0,
где Р и Q должны рассматриваться как функции х и у, в ко-
которые z входит в качестве параметра. Это уравнение имеет
решение
и {х, у, z) — const,
где, если 1(х, у, г) — интегрирующий множитель, то
но из этого не следует, что
Пусть
Rx — \R — dz + S,
тогда, согласно предположению,
dRA , ~ fdR1 __ dPA- . ,-
I dz dy \ \dx dz (' \ dy dx
Отсюда следует, что
dS du dS du „
dx dy dy , dx
Это соотношение не удовлетворяется выражением
и(х, у, z) = const
и является тождеством. Соответственно S и и, которые рас-
рассматривались как функции х и у, находятся в функциональной
зависимости. Однако функциональная зависимость между ними
содержит также и третью переменную z, таким образом 5" мо-
может быть выражена только через и и z.
Теперь
X i Pdx + Qdy + Rdz) = fx dx + ^" dy + ff dz -f Sdz
— du-\- Sdz.
Первоначальное уравнение следовательно эквивалентно
du + Sdz = 0.
Пусть '>Ли, z) — интегрирующий множитель, тогда
X\j. (Pdx -г Qdy -f- Rdz) — u. (du + Scfe)
будет точным диференциалом db. Интеграл имеет вид
если вместо и подставить его значение в функции от х, у, z,
то интеграл примет вид
Ч(х,у. z) = c.
Аналогично можно доказать, что для того, чтобы уравнение
с п переменными
Х^хх + X2dx2 +••'•+ Xndxn = 0
имело интеграл вида
'¦ь (х1У хг, ..., хп) = с
необходимо и достаточно, чтобы ряд уравнений
(X, м., v = 1, 2, .. . , и),
удовлетворялся совместно и тождественно. Общее число таких
уравнений равно Р-п(п — 1) (я — 2); из ннх -^- (п — 1)(п — 2) не-
зависимы. Покажем этот процесс интегрирования на следую-
следующем примере
уг (у -f z) dx + zx (z -r x) dy + xy (x -~y)dz^= 0.
В этом случае
P = yz(y + z), Q = zx(z+x), R =
и условие интегрируемости удовлетворено.
Если z рассматривать как постоянную, то уравнение приво-
приводится к виду
yz (у + z) dx + zx (z + x)dy = 0,
и это приведенное уравнение имеет решение
и = <*±А?±У) = const.
Теперь
_(}iL = . ZfcL^l = L_ p
дх х~у .ггу2 '
дп ^ z (z + х) 1 g
75
Аналогично
ди
О -= л/\ — -,
х + v 2z-fx+v __ „ х + у + z
.ху ху
= _2-?L=:
следовательно
>, (Pdx + Qdy + Rdz) --= du — 2 - -- dz.
Интегрирующий множитель равен м. = г~2, а
Rdz) = f 2(B-1)<te
Следовательно общий интеграл имеет вид
-гг- - с
или, подставляя вместо и его значение в функции от х, у, z,
х + у + z
XVZ
2 • 81. Геометрическая интерпретация- Если /? не равно нулю,
то диференциальное уравнение в полных диференциалах может
быть написано в виде
dz = — -?- d,v ^- d v
или
dz = ?7d;c +
Поскольку
dz—pdx-
диференциальное уравнение в полных диференциалах эквива-
эквивалентно двум совместным уравнениям в частных производных
р = U (х, у, z), q = V (х, у, z).
Уравнение касательной плоскости в точке (х0, у0, z0) к инте-
интегральной поверхности, проходящей через (хп, у0, z0), имеет сле-
следовательно вид
z — z0 = Uo (х — х0) + Vo (у—у0),
где и„ и Ко — соответственно значения U и V в точке (л;0,
Проблема интегрирования эквивалентна поэтому нахожде-
нахождению такой поверхности, у которой направляющие косинусы ее
нормали в каждой точке (х, у, z) пропорциональны
Щх, у, z\ V{x, у, z), — 1.
Эта проблема в общем случае неразрешима; чтобы сделать ее
разрешимой, должно быть удовлетворено условие интегрируе-
интегрируемости
6U ., dU _ 6V j, dV
ду + V ~~dz~~ ~ dx^U dz •
Общее решение каждого из диференциальных уравнений в
частных производных
1х ' ду ~~ V
представляет семейство поверхностей таким образом, что через
каждую кривую в пространстве проходит только одна поверх-
поверхность каждого семейства '. Их общее решение представляет се-
семейство пространственных кривых
и (х, у, z) = a, v (х, у, z) = р,
зависящее от двух параметров о и Р; через каждую точку в
пространстве проходит только одна интегральная кривая.
Интегральная поверхность диференциального уравнения в
полных диференциалах пересекает каждую кривую этого се-
семейства ортогонально, т. е. касательная плоское !Ь в любой
точке Р интегральной поверхности должна содержать нормали
к Р обеих поверхностей и = а, г» = 1е, которые проходят через
точку Р. Отсюда
да , да ди „
Р'сЬГ+Ч-дУ DT = 0'
dv . dv dv ,.
P-fc +Ч-ду -iff-0-
Эти два уравнения определяют
р = U(x, у, z), q = V[x, у, 2).
Они связаны только тогда, когда
т. е. если условие
удовлетворено.
др
_ dq
ду дх '
интегрируемости
dU . w dU dV ,
r dz
дх '
I) dV
dz
1 Эго объясняется тем, что диференциальное уравнение в частных произ-
производных имеет то1ько одно решение, удовлетво >яющее принятым начальным
условиям. Теорема существования принимается здесь без доказательства.
77
2 • 82. Метод интегрирования Майера. Метод интегрирования,
развитый в § 2 • 8, зависит от интегрирования двух последова-
последовательных диференциальных уравнений с двумя переменными.
В методе Майера необходимо только одно интегрирование. Пусть
(хо> Уо) — любая выбранная пара значений (х, у), a zlt — произ-
произвольное значение z, так что четыре производных
dU dL[ JV_ dV_
ду ' dz ' ~длГ' ~dz
существуют и непрерывны в соседстве с {х0, ут z0). Тогда, если
уравнение интегрируется, то его решение будет полностью
определено начальным значением zn. Значение z в точке (х, у)
может быть получено, следуя от его начального чняч^ния zb,
соответственно перемещению точки Р прямолинейно в плоско-
плоскости (* ,у) от (хм _у0) к (х, у).
Примем, не нарушая общности, что точка (л:0, у0) является
началом. На прямой линии, соединяющей начало с (х, у),
у = 7.x, dy - y.dx,
где ¦/. — постоянная; поэтому уравнение примет вид
где при подстановке 7.x вместо у Ut и V, соответственно равны
О и V. Это уравнение с двумя переменными х и z имеет ре-
решение вида
(о (х, z, у.) = const,
или, поскольку z = z0 при х — О,
<р {X, Z, х) == <с (О, 2С, У-)-
Подставляя у/х вместо "/., решение
'f (х, z, У/х) = <? @, z0, yjx)
показывает его зависимость от произвольной постоянной z0.
Пример. Рассмотрим уравнение
1 -j- ху ' i + ху ''
коэфициенты dx и dy непрерывны в соседстве с х =-- О, у = О,
z = Zo так же, как и частные проигодные.
Пусть
у = хх, dy — y.dx,
тогда уравнение приводится к виду
dz 2хл; , I — xv2
IF = ' Z ' 1 +г.х2 '
1 Mayer, Math. Ann., 5 A872), 448.
78
оно линейно и имеет решение
Z = X + Z0{\ +ХХ2).
Решение данного уравнения имеет поэтому вид
Z = X + 20A + Ху).
2 • 83. Проблема Пфаффа. Если условие интегрируемости не
удовлетворено, то диференциальног уравнение в полных ди-
диференциалах не может быть производным частного интеграла,
поэтому такое уравнение считалась не имеющим смысла1.
Однако дальнейшие исследования показали, что диференциаль-
диференциальное уравнение в полных диференциалах эквивалентно двум
алгебраическим уравнениям -, известным как его интегральные
эквиваленты. Вообще говоря, если условие интегрируемости
для всех уравнений не удовлетворено, то диференциальное
уравнение в полных диференциалах с In или 2«—-1 перемен-
переменными эквивалентно системе, содержащей не более п алгебраи-
алгебраических уравненийs. Проблема определения интегральных экви-
эквивалентов любого данного диференциального уравнения в пол-
полных диференциалах известна как проблема Пфаффа. Укажем
кратко метод решения в случае tj ex переменных4.
Необходимо показать, что диференциальное выражение
Pdx + Qdy + Rdz
может быть приведено к виду
du -f- vdw,
где и, v, w — функции х, у, z. Обе формы идентичны, если
... г, ди . dw .-. ди , dw г-. ди , dw
,А) P = -JL+v--t Q = _7 + ^7, ц=1Гх. + 9-?..
Пусть
р, _ j)Q dR_ n, dR_ дР р, дР __ dQ
Н ' Oz ду ' Ч 'дх dz ' ** ду~ 'дх '
тогда
™ dv dw dv dw
~~ dz ду ду dz '
,-., dv dw dv dw
^ дх ' dz dz ' дх '
д, d> dw dv dw
" ^ ~ду~ ' Ох' ЛГ ' ~lhT "
1 Euler, Inst. Calc. Int., 3A770), 5.
3 Monge, Mem. Acad. Sc. Pans A784), 535.
:! Pfaff. Abh Akjd. Wiss Berlin A814), 76.
4 Расширенную трактовку общего случая см. Forsyth, Theory of DUieren-
lial Equations, Part J; Gouisat, Legons sur le Probleme de Pfaff.
79
Отсюда следует, что
дх ' ду ' дг '
Р' dw л- П' ди> Л- Р' &W - - П
Таким образом v и w являются решениями одного и того же
линейного диференциального уравнения в частных производ-
производных; эквивалентная совместная система имеет вид
dx dv dz
~Р'~ гг ~Qr " ~/Г'
Пусть
о.(х, у, z) — const, 8 (х, у, Zj =•= const
будут двумя независимыми решениями совместной системы
тогда v и w — функции а и 3.
Возвратимся к переменной и; так как
I p^ JJL\ p'+ S о ..д±\ с '+ S R _ J>!L\ /?' =
= Ф Г р' _^ 4-П' -^ + /?'-—\ = О
ТО
Выражение
РР' + QQ' + RR' =-¦ О
дает условие интегрируемости. Вообще « не удовлетворяет
тому же диференциальному уравнению в частных производных,
что v и w.
w может быть любой функцией а и 8. Для простоты пред-
предположим
w = а,
тогда, если между переменными х, у, z имеется соотношение
а(х, у, z) = a,
где а — постоянная, то диференциальная форма Pdx-\-Qdy-\-Rdz
приводится к dw и следовательно становится точным диферен-
циалом. Таким образом соотношение а (х, у, z) = a применяется
для выражения любой переменной, например z, и ее диферен-
циала dz через две другие переменные и их диференциалы, а
когда эти выражения подставлены вместо z и dz в PdxJrQdy+
-f- Rdz, то последнее становится полным диференциалом
d<i{x, у, ajz). При замене а на а (х, у, z), этот дифе^енциал ста-
становится равным du. Тик получаем и, а поскольку и и w известны,
вывести v можно алгебраически из уравнений (А). Диферен-
циальное уравнение в полных диференциалах
Pdx + Qdy + Rdz = О
4A
приводится к канонической форме
du + vdw = 0.
Каноническое уравнение может быть удовлетворено различно,
например
(I) и = const, w = const
(И) и = const, v = 0.
В более общем случае, если ф (и, w) некоторая произвольная
функция и и w, то интегральный эквивалент будет
(III) 4 (и, а;) = 0, «-х^- —-Jr- = O.
Зависимость (III) содержит (И), но не содержит (I). В любом
случае интегральный эквивалент состоит из двух алгебраиче-
алгебраических уравнений.
В качестве примера рассмотрим уравнение
ydx + zdy -|- xdz = 0.
В этом случае
Р=У, Q = z, R = х, Р> = Q' = R' = 1,
следовательно
РР' +QQ'+^'=t0,
т. е. условие интегрируемости не удовлетворено.
Совместная система имеет вид
dx = dy = dz;
одним решением его является
а ^5 х— у = а.
Допустим, что w = а и исключим л; из данного уравнения, ко-
рое тогда примет вид
(у -\- z) dy -f- (j; -\r a) dz = 0.
Это приведенное уравнение непосредственно интегрируется и
его решение будет
ip Е -у д>3 + .yz + az = const.
Если заменить а на х —у, tp приводится к и, так что
Э. Айне—133—6 81
Наконец, v получается следующим образом:
" дх ~' дх
т. е.
V = у — Z.
Так
ydx + zdy -
где
Следовательно интегральные эквиваленты будут иметь вид
(О -^-уг + хг = const, х -—у = const,
(II) -±-у*+хг= const, j/ — z = 0.
(ШN(«, «,) = <>. «-Ц---**- = а
Другие интегральные эквиваленты получаются циклической пе-
перестановкой л, j;, г.
2-84. Приведение интегрируемого уравнения к канонической
форме. Приведение к канонической форме может быть одина-
одинаково хорошо произведено и для интегрируемого уравнения, на
поскольку
PP'+QQ' + RR' = 0,
и удовлетворяет тому же диференциальному уравнению в ча-
частных производных, что v и w, следовательно и, v и w явля-
являются функциями а и р.
Отсюда следует, что
du + vdw = Ada- + Bd$,
где А и 5—функции только аир. Если о и Р определены, то
А я В могут быть выведены алгебраически пз любых двух или
трех совместных уравнений
P = A+B-f-, Q = A%- + Bf-. R=,Ap+B^.
дх ' d* ' ^ ду ' ду йг ' dz
Таким образом диференциальное уравнение в полных дифе-
ренциалах преобразуется в обыкновенное уравнение с двумя
переменными а и р.
Это приводит к практическому методу решения интегрируе-
интегрируемых уравнений, как видно из следующего примера (см. 2-8)
yz {у + z)dx + %х (z + x) dy -f xy {x +y)dz = 0.
Здесь
Р' = 2x{z-у), Q' = 2y(x-z), R' = 2г{у-х),
82
и условие интегрируемости удовлетворено. Совместная система
dx dy dz
x(z—~y) ~ у(x — z) ~~ z(y — x)
эквивалентна системе
j / . . ч _ dx , dy . dz n
d (x + y + z) = 0, — -b -f- + — = 0
и имеет решение
a E x+y +z = const, р = xyz — const.
Таким образом данное уравнение приводится к виду
Ada. + Bd§ = 0,
где
yz (у + г) = А + Byz,
zx(z -\-х) = А+
-^ (х + У) = ^ +
Отсюда
Л = — xyz, В = х+у + z,
т. е. уравнение принимает вид
си/р — рс?а = 0
и имеет решение
а _ X+у + Z ,
Т = const
I. Проинтегрируйте следующие уравнения:
_i 1
(I) A _^2}^х + (, _у2)гdy „ 0.
(II) x(l+y2JdJC + >'(H- x3J dy = 0; (XIV) хр — у = x2sinx;
(Ш) (*2+2<у— y2)dx — (jc2—2xy—ys) dy=0; (XV) р + 2xy = xe~-*2;
(IV) (V2 — xy) dx—(x2 — xv) dy = 0; (xvi) p sin x cos .к — у = sinsx;
(V) х^йа: + (xs— y*)dv = 0; (xvii) ^2—xy)dx+{x+\)uy=0;
(VI) (x + y) dx — Bx — у — 1) dy = 0; (XVIII) (У — xpf = 4p;
(VII) (x + 2y + 1) dx — Bx + Ay + 3) dy = O, (XIX) у — рл: + p (p - 1) = 0;
(VIII) Bx*+6xy±y*) dx+l3x-+2xy+4yz) flj>=0; (XX) xyp* + (x*+ y*)p + xy=Q
(IX) (x2 + у2) dje + x>'dy = 0; (XXI) 3'jf2 + 2px — у = 0;
(X) A +х*)р + ду=1; (xxii)
(xi) p+y tgx=sin2x; (xvni)
(xii) p+_ycosA:=e2-*; (xxiv) j^ — 2px +p2= 0.
83
2. Определите п так, чтобы уравнение
ах2 + 2Ъху + су2
^—- (ydx — xdу) = О
(X2 -4- V2)
было точным.
3. Покажите, что уравнение
(V4 — 2у2) dx + (Зху3— 4ху + у) dy = О
имеет интегрирующий множитель, который является функцией ху2, и решите
уравнение.
4. Покажите, что cosx cos_y является интегрирующим множителем урав-
уравнения
Bх tgy sec x + у2 secy) dx + Bу tg x secy -f- x2 sec a-) dy
[Edinburgh, 1915].
и проинтегрируйте полученное выражение.
5. Из соотношения
А (х2 + у2) — 2Вху + С = О
выведите диференциальное уравнение
dx dy
— -4- = О
у х2— с2 Yy2 — с2
где с2 = АС (В2 — А2). Выведите теорему сложения для гиперболического коси-
косинуса.
6. Покажите, что решением
dx dy
YY+l^d== Vi +y3
является
x2y2 + 2axy (x + y)+ a? {x —yJ — 4 (x + y) -f- 4a = 0,
где а — произвольная постоянная. В какой связи находится полученный резуль-
результат с теорией эллиптических функций?
7. Найдите кривые, для которых
(I) поднормаль постоянна и равна 2а;
(II) подкасательная равна удвоенной абсциссе в точке касания;
(III) перпендикуляр из начала к касательной равен абсциссе в точке ка-
касания;
(IV) подкасательная равна средней арифметической абсциссы и ординаты;
(V) отрезок нормали на оси х равен радиусу-вектору;
(VI) отрезок касательной на осн у равен радиусу-вектору.
8. Р — точка (х, у) на плоской кривой, С—.соответствующий центр кри-
кривизны, Т — точка, в которой касательная в Р встречается с осью х. Если линия,
проведенная через Т паралельно оси у, пересекает пополам PC, покажи те, что
2уу" = У'2 A + У2),
также покажите, что кривая является циклоидой.
[Paris, 1914].
9. Докажите, что каждая кривая, ордината которой рассматривается как
функция ее абсциссы, удовлетворяет дифергнциальному уравнению
(ху'-у?=а
84
где а—постоянная, и имеет следующее свойство: если Н—основание перпен-
перпендикуляра из начала О иа касательной в любой точке Р кривой, a Q — основа-
основание перпендикуляра из Н на ОР, то Р лежит на окружности центра О и ра-
радиуса а.
Измените переменные подстановкой
х— г cos6, у — г sin 6
и проинтегрируйте полученное уравнение.
[Paris, 1917].
ГЛАВА III
СУЩЕСТВОВАНИЕ И ПРИРОДА РЕШЕНИЙ ОБЫКНОВЕННЫХ
ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
3 • 1. Постановка проблемы. Уравнения типа
-2-я* л
решения которых были найдены в предыдущей главе посред-
посредством элементарных процессов, интегрируются потому, что они
относятся к некоторым простым классам. Однако уравнение
рассматриваемого типа не поддается элементарному рассмотре-
рассмотрению, и во многих случаях исследователь вынужден обращаться
к методу числовых приближений. Здесь возникает теоретиче-
теоретический вопрос: существует ли решение в общей форме или при
некоторых ограничениях. Исследования в этой области привели
к группе теорем, известных как теоремы существования, наи-
наиболее важные из которых рассмотрим в настоящей главе1.
Пусть (х0, у0) будет некоторой парой значений действитель-
действительных переменных (х, у), такой, что в пределах прямоугольной
области D, окружающей точку (х0, у0) и определяемой нера-
неравенствами
|jc-jCoKa, \y—yo\<b,
f(x, у) является однозначной непрерывной функцией2 х и у.
Пусть М будет верхней границей \f(x, y)\ в области D и пусть
h будет меньше, чем а и bjM. Если h меньше а, то на х на-
налагается более строгое ограничение
| X Ао | ^ П.
Функция f{x, у) должна удовлетворять еще одному усло-
условию, именно, если (х, у) и (х, Y) —две точки внутри области D
на той же абсциссе, то
!/(*, Y)-f{x,y)\<K\(Y~y)\,
где К—постоянная. Это известно как условие Липшица3.
1 См. также главу XII, где этот вчпрос рассматривается с точки зрения
теории функций комплексного переменного.
2 / {х, у) является непрерывной функцией х и у в области D, если при
заданном произвольно малом и положительном е, значение В может быть опре-
определено так, что \f(x+h, y+k)—f(x, у) | < е, при условии, что (х, у) и (<+/г,
y+k) находятся в области D и |Л|<5, | k \ <6. Важно отметить, что h и k
изменяются независимо.
3 Ниже мы покажем, что необходимо только, чтоэы условие Липшица оста-
оставалось справедливым в меньшем промежутке \х — х0 \ < h, \y— _Vo 1 < М I х—ха\.
86
Если эти условия удовлетворены, то существует некоторая
единственная непрерывная функция х (например у (к), опреде-
определенная для всех значений х так, что \х— xo\<.h), которая
удовлетворяет диференциальному уравнению и приводится к у0
при х = х0.
Мы приведем сейчас два совершенно различных доказатель-
доказательства этой теоремы существования, известных соответственно как
метод последовательных приближений и метод Коши-Лип-
Коши-Липшица.
3-2. Метод последовательных приближений1. Предположим, что
известно решение у (х), которое приводится к у0
Это решение очевидно удовлетворяет соотношению
w
(t)) dt,
которое является интегральным уравнением11, содержащим за-
зависимую переменную под знаком интеграла. Будем рассматри-
рассматривать функцию у(х) как известную, тогда интегральное уравне-
уравнение может быть решено методом последовательных прибли-
приближений.
1 Этот метод, известный повидимому еще Komi, был впервые опубликован
Лиувиллем [Liouville, J. de Math., (I), 2 A838), 19; A), 3 A838) 565], который
применил его к однородному линейному уравнению второго порядка. Распро-
Распространения метода на линейное уравнение порядка п даны Каке, [Cique, J. de
Math., B), 9 A864), 185J, Фуксом (Fuchs, Annali di Mat, B) 4 A870), 36
{Ges. Werke, 1,295] и Пеано [Peano, Mith. Ann. 32 A888), 430] Внжбочее
общей форме метоп, был разработан Пикаро.м [Picard, J de Mith., D), 9A893),
217: Traite d'Analyse, 2, 301; B изд.): 2, 34J] и Бохером {So:her, Am. J.
Math., 24 A902), 311].
- Bocher, Introduction to the Theory of Integral Equations; Уиттекер и Ватсон,
Курс современного анализа, гл. XI.
87
Допустим, что х лежит в интервалех (х0, х0 + К) и рассмот:
рим последовательность функций yl{x), у2{х),... , уп(х), опре-
определенных следующим образом
л
УЛх)=У0 + f f{t,yo}dt,
X
Уп <х) = у0 + // {t, yn_ i {t)} dt.
Докажем теперь, что
(a) с неограниченным ростом п, последовательность функций
уп (х) стремится к пределу, который является непрерывной функ-
функцией х;
(b) предельная функция удовлетворяет диференциальному
уравнению;
с) найденное таким образом решение принимает значение
у0 при х = х0 и является единственным непрерывным* решением,
которое обладает этим свойством.
Сначала докажем методом индукции, что если х лежит в рас-
рассматриваемом интервале, то \уп{х)—у0\^СЬ. Предположим, что
\yn+i(x)—Уо\<Ь; отсюда следует, что \f{t, yn-i{t)} | < М,
поэтому
X
хо
<Mh,
Очевидно
\Уг(х)-уо\<СЬ,
следовательно
\Уп(х) -у0] < b
для всех значений п. Отсюда следует, что / {х, уп (х) }<Л1 при
х0 < х < jc0 тЬ h.
Аналогично докажем, что
\Уп (X) - Уп-t (X) | < '^^ (X - *„)".
Если мы предположим, что хо-^х*С хо-\-h, то
| у„-1 (х) — jn_2 (х) | < (^1Гп! (х~ xo)"~lj
1 Это ограничение введено исключительно для удобства, оно не является
необходимым и будет вскоре исключено.
откуда, согласно условию Липшица,
X
Уп (X) - ;/„_! (X) | < / | / ( t, Уп-Л if) }—f[t, Уп-2 (t) j | dt
X
< J К jyn -i @ — Уп-2 [t) I dt,
так что
мкп-л ,
n—l
dt
= „| \X—Xo\ .
Неравенство, справедливое при п=\, действительно также
для всех значений п. Аналогично можно доказать его справед-
справедливость при х0—h^.x^Cx0, следовательно оно верно для
\x — xo\<h.
Отсюда следует, что ряд
абсолютно и равномерно сходится при \х — xo|</z и более
того — каждый член является непрерывной функцией х. Но
следовательно предельная функция
у(х)= Птуп(х)
п—>оо
существует и является непрерывной функцией х в интервале
{xo~h, xo + h)\
Теперь, если соотношение
л
llm yn (x) =yo + lim ff { t, yn-i (t) \ dt
л
= уо+ f lim fit, yn-i(t)}dt
Bromwich, Theory of Infinite Series, § 45.
верно, отсюда следует, что у [х) будет решением интегрального
уравнения
y(x)=yo+ff{t,y{t)]dt.
Х„
Законность перемены порядка интегрирования и перехода к пре-
пределу может быть доказана следующим образом:
| J [/{t у (t)} -f{t, уп-i (t)}]dt\<Kf\y(t) -yn-At) | dt
где sn не зависит от х и стремится к нулю, когда п стремится
к бесконечности.
Функция /{ t, y{f)} непрерывна в интервале л0— h <
следовательно
X
dy(x) d
=f[x,y(x)}.
Отсюда следует, что предельная функция у (х) удовлетворяет
диференциальному уравнению; она также приводится к Уо,
когда х принимает значение х0.
Остается доказать, что это решение у (х) единственное.
Предположим, что К(д;)яв яется решением, отличным от_у(л:),
удовлетворяющим начальному условию Y (х0)=у0 и непрерыв-
непрерывным в интервале (л;0) яо+/г'), где К ^ h, a h! таково, что условие,
\Y(x)-yo\<b
удовлетворяется для этого интервала. Тогда, поскольку Y(х)
является решением данного уравнения, оно удовлетворяет инте-
интегральному уравнению
y(x)=yo+ff{t,Y(f)}dt
и следовательно
У(х) -Уп (а-) = /[/{t, Y (t) }-f\t, Уп-г (О}] dt.
Пусть п = 1, тогда
Y(x)~yi (х) = J [/(t, Y(t) } -f{t,y0}] dt,
X
и из условия Липшица следует, что
\Y(x)-y1{x)\<Kb(x — x0).
90
Аналогично при п — 2
\Y{x)- y% (x)\<\ f [/{t, Y(t) }~f[t, y\ it)}] dt
KJ\Y(t)-yi{t)
dt
X
< К fKb (t - x0) dt=~ K2b (x
Xo
и в общем случае
откуда
Г {х) =у{х)
для всех значений л в интервале (х0, х0 + Л'), поэтому получен-
полученное новое решение тождественно предыдущему. Следовательно
имеется только одно непрерывное решение диференциального
уравнения, которое удовлетворяет начальным условиям.
3-21. Замечания к методу последовательных приближений. Оба
основных допущения, которые были сделаны относительно по-
поведения функции f [х, у) в области D, именно предположение
непрерывности и выполнения условия Липшица, совершенно не-
независимы. Возникает вопрос о необходимости этих допущений.
Непрерывность f(x, у) не является необходимой для суще-
существования непрерывного решения; предыдущее исследование
требует только, чтобы f (х, у) была ограничена и чтобы суще-
существовали интегралы типа
f\f\t,yn{t)}
dt.
В частности, f(x,y) допускает конечное число точек разрыва,
причем все они первого рода К
Например, диференциальное уравнение
-?^ =уA—2х) при ДО О,
= уBх—4) при ЖО
допускает непрерывное решение, удовлетворяющее начальному
1 Они могут быть дискретными точками или линиями, параллельными оси у;
любые другие линии разрывов означают нарушение условия Липшица по всему
конечному промежутку. Ми [Mie, Math. Ann., 43 A893), стр. 553] показал, что
решения существуют всегда, когда / (х, у) непрерывна относительно у и пре-
прерывна, но ннтегрируема (в смысле Рнмана) относительно х.
91
условию у = 1 при х = 1. Это решение имеет вид
У = ?*-•»' при х>0,
и справедливо для всех действительных значений х, более того—
оно единственное.
С другой стороны, для обеспечения единственности реше-
решения должно быть принято условие Липшица или аналогичное
условие. Нетрудно построить уравнение, для которого условие
Липшица не удовлетворяется и которое допускает больше
одного непрерывного решения, удовлетворяющего начальным
условиям \ Так например, в уравнении
условие Липшица нарушено в области, содержащей линию j/=0.
Уравнение допускает два действительных непрерывных реше-
решения, удовлетворяющих начальным условиям х = 0, у = 0, именно
(Г) у = 0,
B°) у = -- хг при х > О,
= —— л2 при л < 0.
Другой пример дается уравнением
где
f^x>y)~-cr~k ПРИ л и J'» не равных нулю,
= 0 при л = у = 0.
Легко доказать, что / (х, у) является непрерывной функцией
х и у. С другой стороны
Если у = рх?, Y — qx2, то
1— РЯ
U+P2)+ 0+Q2)
следовательно условие Липшица не удовлетворяется ни в одной
области, содержащей начало.
Уравнение допускает решение
у = с2 —
1 Реапо, Math. Ann., 37, A890), 182, Mie, loc. cit.; Perron, Math. Ann.
76 (Ш15), 471.
92
где с —произвольная действительная постоянная, следовательно
существует бесконечное число решений, удовлетворяющих на-
начальным условиям х = 0, у = 0.
Этот вопрос был подробно исследован Осгудом \ который
доказал, что если / (х, у) непрерывна в соседстве с {х0, у0),
то существует однократная бесконечность решений, удовлетво-
удовлетворяющих начальным условиям. Эти решения целиком лежат
в пределах площади, ограниченной двумя крайними решениями
Для существования и единственности решения необходимо
и достаточно, чтобы Yy (л) и F2 (л) были тождественны. Это
возможно, если удовлетворено условие Липшица, а также, если
условие Лилшица заменено каким-либо из менее ограничиваю-
ограничивающих условий
. Y)-f(x, у) \<КХ I Y- y\ log гу±—
\f(x, Y) -f (x,y)\<K*\Y-y\ log (T^- log log ry±-y?
где AT,, K2, ... — постоянные.
Постоянная К, которая входит в условие Липшица, опреде-
определяет для любого данного значения х быстроту сходимости срав-
сравниваемого ряда
\хх\
и следовательно показывает законность применения ряда
Уо S
являющегося приближением к предельной функции у (х). Таким
образом, если К мало, то уп{х) будет стремиться к пределу
у (х) быстрее, чем если бы К было велико. В большинстве
встречающихся на практике случаев К является верхней гра-
границей
dfjx, у)
ду
в области D. Чтобы воспользоваться этим, рассмотрим семей-
семейство кривых
f(x.y)=C
для всех значений постоянной С. Типичная кривая этого семей-
семейства пересекает каждую интегральную кривую в точке, в ко-
которой градиент последней равен С. Эти кривые называются
Osgood, Monatshr. Math. Phys. 9A898), 331.
93
изоклинами1. Пусть изоклинальные линии будут нанесены для
последовательности дискретных значений С, расположенных на
одинаковом расстоянии друг от друга (например целых) и пусть
будет проведена линия параллельно оси_у. Тогда интервалы вдоль
этой линии, в которых точки пересечения с изоклинальными
линиями густо расположены, соответствуют большим значе-
значениям К, в то время, как интервалы, в которых точки пересечения
расположены реже, соответствуют 'меньшим значениям К. Это
объясняет, почему метод последовательных приближений наибо-
наиболее успешно применяется как практический метод вычисления
в областях, где изоклинальные линии проходят более или менее
параллельно оси у2.
Метод последовательных приближений приводит к решению,
которое, как было показано, сходится в интервале | х—.fol</2,
где h — меньше а и bjM. Но выше было отмечено, что сделан-
сделанное в самом начале допущение о том, что некоторые условия
удовлетворяются по всей области \х— хо|<а, \у—_vo|<^ —
было излишне ограничивающим. Если область \х— xQ | < k,
\у—)'0|< М\х — х0 j может быть такой, в которой f(x, у) удо-
удовлетворяла бы необходимым условиям в этой области, а М
была бы верхней границей \f(x,y)\, то k конечно будет не
меньше, а может быть даже значительно больше, чем h. Неко-
Некоторым исследователям3удалось расширить область, в которой
решение сходится, но общий метод определения точных границ,
интервала сходимости до настоящего времени еще не найден.
3-22. Изменение начальных условий. Пусть данное начальное
условие у = у0 ПРИ х = х0 заменено новым условием у = уо + "Ч
при х = х0, где (х0, yo + 'q) — точка в области D, так что ('п)-^Ъ.
Тогда вместо последовательности функций
определенных в § 3-2, получим последовательность
Yi(*), Y2{x),...Yn(x),
определенную следующим образом
X
t, v0 + '1} dt,
1 Термин этот был впервые введен Кристалем [Chrystall, Wedderburn, Proc.
Roy. Soc. Edin, 24A902), 400].
2 Практические методы приближенных вычислений, основанные на методе
последовательных приближений, были предложены и описаны Северини [Seve-
rini, Rend. 1st. Lomard. B), 31 A898) 657, 950] и Коттоном [Cotton, С. R. Acad.
Sc Paris, 140 A905), 4S4; 141 A905, 177; 146 A908), 274, 510: Math. Ann. 31
A908), 107].
3 LindeOf, С R. Acad. Sc. Paris, 118 A894), 454; J. de Math. 4, A0), 1894,
117; Picard, Tralte d'Analyse, 3, 88; B nd ed.) 340; см. таьже § 3-41.
94
f У„-г(t)} dt.
Существование и единственность решения
получается, как и в предыдущем случае. Теперь
— хо
и по индукции
так что в пределе
следовательно при | х — хв ] < h решение равномерно непрерывно
при начальном значении у0. Чтобы покааать это, его можно на-
написать
У С*. У о) или У(х — хо,уо).
Более того,
. 1 „,, ,„
... +-/7[ Кп\ х - х01»
следовательно
дуп х, у»)
1 -{- K\x — л01 -{-... -f" -^y K"\x -
откуда можно вывести, что ряд
со
ду(х,у0) , , V д{Уп(х'У»)—Уп-Лх<У<й
_ . —— J^ _L_ ^ 1 —
ЧУо ^» ^'о
я=1
абсолютно и равномерно сходится; поэтому у{х,у0) равномерно
диференцируется по у0 при | х — л:0 | < h.
Из доказательства, аналогичного предыдущему, видно, что
если диференциальное уравнение содержит параметр X, т. е. если
^ —fix, у; I),
где функция f(x, у; I) однозначна и непрерывна и удовлетворяют
условию Липшица равномерно в области D при А4^;Х<;Л2,
то решение непрерывно относительно I и равномерно диферен-
цируемо по X при | х — хо\ < h.
3 • 23. Особые точки. Особая точка может быть определена
как точка плоскости (х,у), в которой одно из условий, необ-
необходимых для установления теоремы существования, перестает
быть справедливым.
Действительно, если для двух начальных значений (х0, у0) ре-
решение (а) прерывно, (Ь) не единственное и (с) не существует,
то (хо,уо) является особой точкой уравнения. Для иллюстрации
решения уравнения в особой точке или в соседстве с ней
можно привести следующие примеры:
A=) ЁУ = ±.
у ' ах х
Условия, необходимые для существования единственного
и непрерывного решения, удовлетворяются, за исключением со-
соседства с х = 0. Решение, соответствующее двум начальным
значениям (я0, у0), имеет вид
где ХофО. Если х0 = 0 и ^0^:0, то решение приводится к виду
х--=0.
Единственным исключением является случай, когда л:0=у0=0;
единственной особой точкой в конечной части плоскости (л;, у)
является начало. Теперь каждая интегральная кривая прохо-
проходит через начало, которое является узлом интегральных кривых
B-) ?—4-
В этом случае также единственной особой точкой является
начало. Любой другой точке {хо,уо) соответствует решение
Семейство интегральных кривых, соответствующее всем воз-
возможным значениям ixo,yo) касается оси х в начале, если т> 1
и оси у в начале, если 0<от<1. Таким образом, если /га>0,
каждая интегральная кривая проходит через начало.
96
С другой стороны, если т < 0, например /га = — р, то реше-
решение будет иметь вид
Семейство интегральных кривых имеет асимптотами оси х и у.
Вырожденная кривая
= 0
проходит через начало. Начало называется седлом, потому что
в соседстве с ним интегральные кривые походят на контуры
перевалов через горы.
/оо, аУ _ X + У
(Л> dx~~ ~х—
Начало является единственной особой точкой; любой другой
точке (хо,уо) соответствует решение
Начало является узлом интегральных кривых
Решение в общем случае имеет вид
Никакая действительная интегральная кривая, за исключением
вырожденной кривой л:г+_у2 = 0, не проходит через начало, ко-
которое называется фокальной точкой (фокусом).
/t-оч dy х + у
& > dx= -x~=y~'
Это уравнение наиболее эффективно решается преобразова-
преобразованием к полярным координатам.
X = Г COS 6, V = Г Sin 6;
после преобразования оно примет вид
dr
db = Г-
Интегральные кривые образуют семейство логарифмических
спиралей
г = се".
Каждая кривая семейства проходит через каждую точку плос-
плоскости, за исключением начала. Но ни одна интегральная кри-
кривая не проходит через начало, которое является фокусом каж-
каждой кривой семейства.
Э. Айне—133—7 91
Нужно отметить, что все эти примеры являются частными
случаями общего уравнения
йу ах-\- by
dx ex 4- dy *
которое может быть проинтегрировано методом §2-12. Мы
найдел5, что с точки зрения поведения интегральных кривых
в соседстве с началом уравнение получится одного из трех ос-
основных типов
I (* - cf + 4ad > 0,
II [Ь- cf
III (ft - cf + Aad ^ 0.
В случае I начало представляет собой узел, если ad — be < 0,
и седло, если ad — bc> 0; в случае II начало является фокусом,
а в случае III — узлом.
3 • 3. Распространение метода последовательных приближений на
систему уравнений первого порядка. Пусть система уравнения
имеет вид
?х = /i(•*•>У\>Уч>- ¦ • >_Vm),
'J^ ~~ >2\х> У1 >Уъ »• • • >3'm/i
dy
dx ~~ J Х' Уу' - '2>' ' ' > У''
тогда, при указанных ниже условиях, существует единственная
последовательность непрерывных реш ний этой системы урав-
уравнений, которые принимают данные значения y%yl, . ..,\Лт при
х = х0. Приведем кратко доказательство этого; метод точно со-
соответствует данному в предыдущем параграфе.
Функции/j, /а,...,/щ полагаем однозначными и непрерыв-
непрерывными относительно их /и+1 аргументов, если эти аргументы
ограничены в области D, определяемой условиями
\х-хо\<а, \У1-уЦ,сЬ,..., \ут-\*\<Ьт
Пусть наибольшая из верхних границ /, ,/2,.. .,/„, в этой области
равна М; если h меньшее из a, b J М, ..., bm | M, то х может быть
более ограничен, если это необходимо, условием j х — д-01 < h.
Необходимо ввести условие Липшица
\fr(x, Y^V.,,..., Ym)-fr(x,y,,y2,... ,vJi <h\\ У\ — у1\-\-
..,m.
9*
Теперь определим функции у"(х)> У"(х)> ¦ ¦ ¦ > Ут С*) соотноше-
соотношениями
У" W = Гг
тогда методом индукции молено доказать, что
а существование, непрерывность и единственность последова-
последовательности решений следует непосредственно. Поскольку дифе-
ренциальное уравнение порядка т
^ У I ¦ civ
(ix'n ~ J\X'y*dx''"'
эквивалентно последовательности т уравнений первого порядка
"Бс - Уи \:х = У* ¦¦¦ ' d'x" Ут-1.
отсюда следует, что если/—непрерывно и удовлетворяет ус-
условию Липшица в области D, то уравнение допускает единст-
единственное непрерывное решение, которое вместе с ее первыми т—\
производными, также являющимися непрерывными, примет про-
произвольную последовательность начальных условий для началь-
начального значения х = хй.
3 • 31. Применение к системе линейных уравнений. Рассмотрим
последовательность т линейных уравнений
dy.
^РУ \РУ +
ах
+pimУт + П 'A=1, 2... .,т),
где коэфициенты рц и rt непрерывные функции х в интервале
а<х<,Ь.
Правый член уравнения поэтому непрерывен для всех значе-
значений ух, у2,..., ут, когда х меняется в интервале (а,Ь). Никакие
дальнейшие ограничения не нужны; последовательность непре-
непрерывных решений
,. .., ут{х)
существует и является единственной в интервале (а, Ь).
Если же козфициенты непрерывны для всех положительных
и отрицательных значений х, то последовательность решений
будет непрерывна для всех действительных значений х. Это
имеет место, например, когда все функции рц и rt, представлены
в виде полиномов от х.
99
ДОПУСТИМ, ЧТО КОЭфиЦИенТЫ pij И rh ПОМИМО ТОГО, ЧТО ОНИ
являются непрерывными функциями х в интервале {а, Ь), пред-
представляют собой еще и аналитические 1У функции параметра X.
в области Л. Модули (р,,) следовательно ограничены.
Пусть Л" (число, не зависящее от X) будет их верхней границей.
Тогда интегралы, например
у? (х, 1)=у°+ /{раif)у?-1 (t, X) +... + pUtW1 (t,X) + п(t)} dt
непрерывны относительно х и аналитические относительно X.
Аналогично
\у?(х,).) - у»-* (*, X) | < ^рЦ л - л01».
Таким образом сравнение ряда
со степенным рядом
показывает, что функции у? (х,X) стремятся соответственно
к пределам у^х, X) равномерно относительно (л:, X) при а^.х^Ь
и X в области Л. Следовательно решения _у? (х, X) непрерывны
относительно а; и являются аналитическими относительно /-.
В частности, если коэфициенты являются целыми функциями
(или полиномами) от X, то решения yt (x,l) будут также целыми
функциями X и могут быть написаны в виде ряда
Уг(х,\) = иго-ЬЫ( tX -{r... + Uir lrjr... (/=1, 2...,т),
который равномерно сходится для всех значений X при a<x<&-
Если начальные условия не содержат параметра X, одно к,-0
должно удовлетворять соответствующим начальным условиям,
в то время как ua(j>0) приводится к нулю для начального
значения х.
Часто для получения решения уравнения или последователь-
последовательности уравнений, содержащих параметр X в виде ряда, удобно
принять решение в этой форме, а затем продолжать методом
неопределенных коэфициентов2.
1 Неудобно ограничивать разбор действительными значениями X, так как
приходится часто рассматривать мнимые или комплексные значения. Пусть X
будет комплексным числом, ограниченным в области А диаграммы Арганла (или
в плоскости а), с коэфициентамн аналитическими относительно X, т. е. X одно-
однозначна, непрерывна и имеет единственную производную (независящую ог на-
направления криближения) в каждой точке области Л.
2 См. Poincare, Les Mcthodes nouvelles de la Mecanique celeste I и Н.
100
3 • 32. Теорема существования для линейного диференциального
уравнения и-го порядка. Как мы уже указывали выше (§ 1 • 5),
линейное диференциалыгое уравнение
эквивалентно системе п линейных уравнений первого порядка
^ - v <iVl = v йУп-2 - v
r(x)
dx po(x) po(x) y P(,(x) Уг ¦'¦ pB(x)
Из предыдущего раздела следует, что еслиро(х), pv(x),.. .,рп (х)
и г (х) являются непрерывными функциями х в интервале a^Cx^Cb,
а ро(х) не обращается в нуль в любой точке этого интервала,
то диференциальное уравнение допускает единственное реше-
решение, которое вместе с ее первыми in—1) производными непре-
непрерывно в интервале (а, Ь) и удовлетворяет начальным условиям
У(*о) = З'о, у'(-*о) = У о. • • •, У^ (¦*<>) = У(Г1} >
где х0 — точка в интервале (а, Ь).
Приведем прямое доказательство этой теоремы, но для того,
чтобы сократить работу, ограничимся уравнением второго по-
порядка
связанным с начальными условиями
здесь с —- внутренняя точка в интервале (а, Ь), где р, q и г не-
непрерывны.
Предварительно рассмотрим уравнение
решение, удовлетворяющее начальным условиям, имеет вид
х
у = fix- t) v{t)dt + Y(x -c) + •;,
с
и это решение единственное.
Пусть уо(х) и З'д(х) будут непрерывными функциями х в ин-
интервале (а, Ь) и образуем уравнение
d2y
j~± = r(x) - qyo(x) - py'0(x).
101
Пусть у = j'i(x) будет решением этого уравнения, удовлетворя-
удовлетворяющим начальным условиям уг{с) — у, _у,'(с)=т' и следовательно
уравнению
решение которого, удовлетворяющее начальным условиям, обо-
обозначим уа(х).
Продолжая процесс, получим последовательность функций
yi{x),yz{x),...,yn{x), ...
непрерывных и диференцируемых в интервале (а, Ь) так, что
Докажем теперь, что эта последовательность имеет предел
и что предельная функция является искомым решением. На-
Напишем
ип(х) =Уп(х) -у„-!{х),
тогда
dzun(x)
и
то
поскольку
11 IV
ип{с) =
Л"
с
X
0, и» =
H)-P(t)u
о,
} (х -1) dt,
< M = J{~Q {t)Un~x (t) - p{t)un_x Щ dt.
С
Коэфициенты р(х) и q{x) конечны в интервале (af h)f так что
\p{x)\ + \q(x)\<M;
существует такое число А, что
|Иг(л)|<А, ]ui(x)\<A.
Пусть L будет больше 1 и Ь — а, тогда методом индукции по ¦
лучим
AM"-1 L3n~2
а \и'п(х)\ будет удовлетворять тому же неравенству.
Ряды
Уо(х) + {у^х) - j;0(jc) ]+...+ {уп(х) - j'/i_1 (х)}+...
и
^»+ [у№ - y'JLx)} -г - • • -г {.V» - >;_! (л)} -f...
102
поэтому абсолютно и равномерно сходятся в интервале (а, Ь).
Следовательно функции
у(х) = limyn(x), У(х) =
существуют и непрерывны в интервале (а,Ь). Теперь
поскольку ряд, представляющий у"(л:), равномерно сходится
в интервале (a, t).
• Следовательно, предельная функция у(х) удовлетворяет ди-
диференциальному уравнению; остается доказать, что это единст-
единственное решение, удовлетворяющее всем указанным условиям.
Предположим, что два таких решения у(х) и Y (х) существуют,
и пусть
()У()
Тогда v(x) удовлетворило бы однородному диференциальному
уравнению
вместе с начальными условиями
v(c) = 0, г)'(с) = 0.
Это невозможно, потому что ^(л) и г>2(я) являются любыми
двумя явными решениями однородного уравнения, следовательно
^i(^) («;(v) + p(x)v'z (л) + 9 (х) v(х)} - v2(х) {v\ (х) +
откуда
ТЛ^ (хУ°г(х) - г'^хУаЦх)} + р(х) {v^xp'Jix) - v%(x)v\{x)} = 0
линейное диференциальное уравнение первого порядка, общее,
решение которого имеет вид:
X
—fp(x)dx
v,(x)v'2 (x) - ¦», (л)г)',(л:) = Се с
гле С — постоянная, определяемая начальными значениями f,(x),
v.Jx), v\{x\ vl,(x). Это известно как тождество Абеля1.
1 Abel J. fiir. Math., 2 A827), 22 [CEuvres completes A839I, 93; A881), 1 251].
108
Теперь пусть v^x) будет решением, удовлетворяющим на-
начальным условиям
г\{с) = v\(c) =0,
тогда С = 0 и
Vj{x)v't(x) - Vt(x)v[{x) =0
тождественно. Если функция vt(x) не равна нулю, то это тож-
тождество может быть написано в виде
следовательно v2(x) постоянная, умноженная на vt{x), откуда
решения vx(x) и va<x) не являются независимыми. Это доказы-
доказывает, что vt(x) тождественно равно нулю, следовательно реше-
решение у{х) единственное.
Если коэфициенты р (х), q(x), г(х) зависят от вещественного
параметра X и являются непрерывными для всех значений х
в интервале {а, Ь\ при X, лежащих между Л, и Л2 то можно
доказать, что у(х) непрерывная функция от X, если X лежит
в пределах замкнутого интервала внутри (Л, и Л2). Достаточно
придать М такое значение, чтобы неравенство
было справедливо для всех значений \ в интервале (\lt Л2),
тогда последующие неравенства доказывают равномерную схо-
сходимость ряда
Уо(х) + {УМ — Уп(х)}+... + {уп(х) - у„-л (х)} + • • -
и его производной для всех значений х в а<х<& и для лю-
любого замкнутого интервала >. в интервале (\, Л2). Из этого не-
непосредственно следует существование и равномерная непрерым-
ность предельных функций у(х) и у\х). Слегка изменив теорему,
ее можно распространить на случай комплексного параметра "/..
3-4. Метод Коши-Липшица. Этот метод доказательства суще-
существования решений диференциального уравнения или системы
уравнений значительно отличается от метода последовательных
приближений. Он действительно является улучшением не вполне
строгой теоремы существования, данной Коши 1-
1 Первоначальный метод был разработан Коши в его лекц иях в Ecole Ро-
lytechnique между 1820 и 1830 гг.; он приведен в Sur l'integration des equations
differentielles, Prague, 1835, и в Exercises d'Analyse, 1840, 327 [CEuvres completes,
B), 11, 399]. В более полной форме он дан Муаньо [Moigno, Legons de calcul.
2A844), 385, 513]. Сущность метода дава была еще Эйлером [Inst. Calc. Int,
1A766). 493]. Улучшение метода, сделанное Липшицем, дано в Bull. Sc. Math.,
10A876), 149.
104
Пусть (х0, у0) — начальные значения, которые должны удов-
удовлетворяться решением уравнения
разделим интервал (хо,х) на я частей
таким образом, что
Хо < Хг < Х2 ¦ . ¦ < -^л_1 < Л,
и рассмотрим последовательность ут ух, уй,..., уп~г, у„, опре-
определяемую следующим образом
У\ — Уо т~ f{xo,yo) (л, — л0),
Уп = v«_i -г/(л;п_1, j;n_i) (л- —
Тогда сумма
аналогична сумме, которая приводит к выражению Коши для
определенного интеграла. Мы эту сумму сейчас обобщим чтобы
показать наиболее близкую возможную аналогию с более общим
определением Римана1.
Рассмотрим треугольник ABC (фиг. 2), образованный тремя
прямыми линиями
X^=xo + h, Y = yo + M(X-xo), Y = yo-M{X-xo),
где h — соответствует определению, приведенному в § 3-2. Тогда,
если существует непрерывная интегральная кривая, проходящая
через вершину А, то она будет лежать ниже АВ и выше АС>
потому что для любого х при х0 < х < х0 + h градиент интег-
интегральной кривой меньше градиента АВ и больше градиента АС.
Разделим треугольник на полоски линиями X = х1г X = л2,...,
X = хп, параллельными ВС. Первая из этих полосок представ-
представляет собой треугольник А Ьхсх, вторая. — трапецию схЬгЬ2с2 и т.д.
Пусть верхняя и нижняя границы функции f(x,y) в треуголь-
треугольнике АЬхсА равны Мх и mv тогда
— М < т, < М1 < М.
1 Это обобщение было введено Гурса [Goursat, Cours d'Analyse, 2 B изд.).
375]. Обобщение другим методом дано Коттоном [Cotton, Acta Math., 31 A908),
107J.
1С5
Предположим что Рх и рг — точки на линии X = хи ординаты
которой равны соответственно К, = у0 + ^i(-*i ~ Ло) и У\ =-Уе +
Проведем'PjO2 и р^8 параллельно Д5 и АС, соответственно
до пересечения с линией X = я.3 в точках Q2 и o2. Пусть М^ и mg
будут верхними и нижними границами функции /{х,у> в трапе-
трапеции /»,PiQ2(?2'. тогда, поскольку эта трапеция лежит целиком
У
0
t
y^L-
р.
*2 "п к———
X, J, \^ Х^
On
P.n
k
/9
Фиг. 2.
внутри трапеции сф^с^ отсюда следует, что -М < /«2< Ж2< Ж.
Пусть Я, и рг — точки на линии >Y==a2 с ординатами Гг =- Y
М + (х) соответственно Про
у
Мгхг
х
г точки на линии >Y2 рд г i
+ Мгхг-хх, и у2=у,+т2 (Ла-х,) соответственно. Процесс
будет продолжаться от одной трапеции к следующей до тех
пор. пока будут достигнуты точки Рп и р„ на линии X = х, ор-
ординаты которых
Г„ = Гя_( + Л*„ (X - Л'„_1) И уа == ^я-i -Г /И„ (Л - ^n-l).
Таким обрачом определены два полигона Д/у^ •••» Рп и
Ар,рг,...,рп, которые лежат целиком внутри угла CAB.
Суммы
соответствуют суммам S, и s, в классической теории интегри-
103
рования Римана1. Чтобы полностью воспользоваться этой ана-
аналогией, напишем Sn для Yn и sn для уп. Тогда, если S, и s, -
соответствующие суммы, возникающие из нового способа под-
подразделения той же области (л0, х) на v интервалов, то
При увеличении числа подразделений п или v введением
новых точек подразделения, Sn и Sv не увеличиваются так же,
как и sn и sv не уменьшаются. Пусть нижняя граница Sn и
верхняя граница sn равны соответственно Уну, тогда
Sn>Y, sn<y, Y>y.
Следовательно
Sa -sn = (Sn-Y) + (Y- у) +(у- sj,
и каждый из трех взятых в скобки членов положителен или
равен нулю. Отсюда, если доказать, что при л—* со
Sn-*Y, sn-*y, Y=y,
поскольку Y и у не зависят от п, следовательно
lim Sn и Hm sn
существуют и равны.
Остается доказать, что при заданном е можно определить
Л' так, чтобы
Sn ~~ sn < е при п > N.
Это верно, если в ABC
(I) / (л, у) является равномерно непрерывной функцией от х,
т. е. при заданном произвольно малом а число о, не зависящее
от x'vi у, может быть определено так, что
I №, JO -/(¦*". -У) I < * ПРИ | Л' - Л* | < а;
принимается, что число подразделений (х0, л:) настолько велико,
что длина каждого интервала л,_1 хг меньше з;
(II) условие Липшица
удовлетворяется для всех пар точек в треугольнике ABC, ле-
лежащих на лийиях, параллельных ВС.
Пусть при любом данном способе подразделения при заданном
значении X
or = Yr - у г,
1 Подробное объяснение метода, кратко рассмотренного здесь, см. Уиттекер
и Ватсон, Курс современного анализа, § 4-11.
107
тогда
or = 8r_i + Шг~ tnr) (xr — xr-i).
Ho
Mr-mr =/(*;, y'r)-f(x'r, y'r)
= {f(K- y'r)-ПК> y')} + {f(K> y'r)-flK> у'Л
где {x'r, y'r) и (x"r, y"r) — координаты любых точек в трапеции
Рг-гРг-lQrqr.
Отсюда следует, что
Мт — тт < X + К | у; — у'г 1,
но
I у'т - уг I < )
следовательно
Л1, — /я, < X + )
Пусть интервалы взяты настолько малыми, что
2МК{хГ — Xr-i)<.l
для г= 1, 2, ..., п, тогда
УИГ — mr < 2Х + /<3,._ь
откуда
S S {1 /
следовательно
Отсюда
. . 2X . 2X
т. е.
< f [^ 1} < е,
при условии, что X и а достаточны малы; а произвольна; поэ-
поэтому, если л достаточно велико, а каждый интервал достаточно
ЮН
мал, то
э не зависит от х, следовательно число N, не зависящее от Л",
существует, и это неравенство справедливо для п> N и для
всех значений х в интервале (х0, л0 + h). Выражения Sn и sn
поэтому равномерно стремятся к общему пределу F(x). Про-
Продолжим два полигона АРхРо.. .Рп и Ар,р.3.. ,рп вправо к линии ВС
и примем Р(х) ординатой точки на верхней дуге, a Q(x) — ор-
ординатой соответствующей точки на нижней дуге. Тогда
P(X)-Q(X)<2.
Оба полигона будут стремиться равномерно к предельной кри-
кривой Г, а именно к кривой
V
Нт Р(х) и Q(x) непрерывны, следовательно непрерывна и F(x)
я Г является также непрерывной кривой.
Любой другой непрерывный полигон, который лежит ниже
АРГР.2 ... и выше Aprf* ... имеет ту же предельную кри-
кривую Г. В частности, полигон А, угловые точки которого имеют
ординаты, определяемые соотношением
zr = гг_! -\-f(Xr-i, zr-x) (xr — Xr-i),
расположен так, как указано на фиг. 3, и его пределом явля-
является кривая Г. Если (х'г, у'г) будет любой точкой на кривой Г,
лежащей на трапеции pr—\ Pr—^ Prpr, то разности
могут быть сделаны произвольно малыми, подходящим выбором
верхней границы
-Xj Xq Хч Л], ¦ • •, X,. Хг—1,
следовательно
I /К, У'г) -f(Xr-l, Zr-i) |
могут быть сделаны произвольно малыми. Далее градиент Г
в точке (х', у') равен f(x',y'), и поэтому Г является интегральной
кривой диференциального уравнения. Более того, Г проходит
через точку (х0, у0). Таким образом предельная функция
у - F(x)
язляе/пся решением диференциального уравнения и удовлетво-
удовлетворяет начальным условиям.
Интегральная кривая Г является единственной непрерывной
интегральной кривой, которая проходит через точку А. Если бы
существовала какая-либо другая интегральная кривая, то под-
подразделение интервала (х0, х0 + h) можно было бы продолжить
до тех пор, пока эта интегральная кривая не пересекла бы ка-
какой-либо из полигонов, соответствующих этому способу под-
109
разделения. Предположим, например, что она пересекла сторону
Pr-iPr в точке М,г.М' — точка, в которой она пересекла сторону
Pr—iPr-i (фиг. 4), тогда градиент хорды ММ был бы равен гра-
градиенту кривой в точке (х'г, у'г) дуги М'М, но градиент инте-
интегральной кривой в точке (х'г, у'г) равен f(x'r, y'r), которая, со-
согласно определению, меньше градиента Pr-iPT, что приводит к
противоречию.
Следовательно существует только одно непрерывное реше-
решение диференщального уравнения, которое удовлетворяет на-
начальным условиям.
Фиг.
Фиг. 4.
3-41. Развитие метода Коши-Липшица. Метод последователь-
последовательных приближений и метод Коши-Липшица приводят к доказа-
доказательству существования и единственности непрерывного решения
в малом интервале (х0, х0 + /г). Идеальным был бы метод, кото-
который давал бы решение, равномерно сходящееся по всему боль-
большому интервалу (х0, х0 -}- k), в котором решение, определяемое
заданными начальными условиями, непрерывно. Преимущество
метода Коши-Липшица в том, что он дает решение, сходящееся
н максимальном интервале.
Чтобы показать, что это действительно так, предположи?.?,
что
y = F(x)
будет решением, при котором у0 = F(xo\ Пусть S будет поле-
сой, ограниченной двумя прямыми линиями
X —
X - -
-р К
и параллельными кривыми
но
где t\ — произвольно малое положительное число. Допустим,
что k таково, что F(x) непрерывна в интервале (х9, х0 -f- k) и
что Tj настолько мало, что условие Липшица удовлетворяется
функцией f(x, у) по всей полосе S.
Предположим, что интервал (xo,xo-\-k) подразделен точками.
абсциссы которых следующие
-^о> -^i» • - * > Хп—1, Хп,
где
Хп = Хо | к •
Пусть
_Уо> У1> • • •> Уп-и Уп
— соответствующие ординаты интегральной кривой Г, а
— соответствующие угловые точки полигона А, определяемые
рекуррентной формулой
ZT = Z,—- -\-f(xr-u Zr-i) (Xr — Xr-i)
с 2r0 ¦= у0 (фиг. 3).
Докажем теперь, что если подразделение интервала Ос0, х + k)
достаточно мало, то полигон А будет проходить целиком внутри
полосы S, а если dr= | zr —уг \, то dT < г, где е произвольно мало.
Допустим, что угловые точки до точки {хг^л, 2r_~v) и включая ее
находятся внутри полосы S, тогда при помощи теоремы о сред-
среднем значении
у г = д/г_5 +/(а;, j;;) (ay — *,_,),
где (л^, j'^)— точка на кривой Г, лежащая между точками.
(xr_i, j;r_i) и (Xr, yr).
Следовательно
2Y*— yr = zr-i — уг_3 + {/ Uv-i, гг_г) —f(x'r, y'r)} (xr — xr^lS,
HO
и согласно условию Липшица, поскольку обе точки (xr_1} zr-i),
(xr-,, yr-i) находятся в S,
Поскольку функция f(x, v) непрерывна в S, она представ-
представляет собой также непрерывную функцию х вдоль Г, и следо-
следовательно, если >. имеет произвольное значение, то о может быть
выбрана достаточно малой, так чтобы
\/(хг-ь yr-i)—f{x'r, y'r)\ <2>., если j xr — xr-\ ¦ < с.
11!
Таким образом, если подынтервал {xr, xr—i) достаточно мал, то
dT < dr—л + (xr — xr-i) B1 4
откуда, как и в предыдущем параграфе,
Следовательно, если \ выбрано так, что
Kk
2Це -1)</Сг„
то по индукции получим
| dx | < ц, ..., j dn\ <т„
т. е. все угловые точки А лежат внутри полосы S.
Пусть Л' обозначает полигон, образованный соединением
последовательных точек с абсциссами х0, хг хп интеграль-
интегральной кривой Г, и пусть Р(х) будет ординатой любой точки Л,
a Q(x) — ординатой соответствующей точки А'. Тогда, если раз-
разница между наибольшим и наименьшим значением F(x) в каж-
каждом подинтервале (xr—i, хг) менее -у е, то
1
— произвольна; пусть -ц < -у г, тогда
Q(x)-F(x)
1
-ц < -у г, т
P(x)~Q(x)
и поскольку
Р(х) ~F(x) = {Р (х) - Q (х)} + {Q И - F(jc)},
отсюда следует, что по всему интервалу (х0, х0 + k)
\P(x)-F(x)\ <е.
Таким образом, если уравнение имеет решение
У = F (х),
непрерывное в интервале (х0, х0 + k), a e произвольное поло-
положительное число, то метод Ноши-Липшица определяет, при
достаточном числе подразделений, функцию Р(х) так, что
| Р(х) - F(x) | < г
для
хос х -схо + к.
§ 3-5. Рассмотрение теоремы существования для уравнения не
первой степени. Рассмотрим диференциальное уравнение вида
112
где функция F полином от -^ и однозначна относительно х
и у. Пусть (хт у0) будут начальными значениями (х, у), тогда,
если уравнение
F(x, у, р) = О
имеет некратный корень р = р0 при х = х0, у = Уо, то оно будет
иметь только один корень
P=f(x, У)>
который приводится к р0 при х = х0, у =.у0, a f(x, у) будет од-
однозначна в соседстве с (х0, у0).
Если функция f(x, у) непрерывна и удовлетворяет условию
Липшица по всему прямоугольнику, окружающему точку (х0,у0),
то уравнение
g-/(*>)
будет иметь единственное решение, непрерывное для зна-
значений х, достаточно близких к х0, и удовлетворяющее за-
заданным начальным условиям. Это решение вполне удовлетво-
удовлетворяет первоначальному уравнению для тех же значений х, сле-
следовательно проблема в данном случае не представляет ничего
нового.
С другой стороны, если данное уравнение
F{x, у, р) = 0
имеет кратный корень р = р0 для х=х0, у = _у0, то р будет не-
неоднозначной функцией (л;, у) в любой области, содержащей
точку (х0, у0), следовательно теорема существования непри-
неприменима.
Если р = р0 является корнем кратности р в (х0, у0), то
р/
Таким образом, если
х = х0 + X, у = у0 ф V, р = р0 + Р,
то уравнение /^(x, >/, р) = 0 примет вид
* + Гф+ О
Пусть
тогда
следовательно
Э. Айне—133—8 ИЗ
Поскольку X и Р малы, Yt высшего порядка, чем X. Таким
образом, удерживая только члены низшего порядка
(dF |„ dF
и принимая
получим
0^ =
где /С— постоянная, не равная нулю.
Из этого следует, что
где Кг зависит от К и и- и не равно нулю. Таким образом, если
уравнения
0, — Ф0,
удовлетворяются совместно при
х = х0, у = у0, р = ро,
то решение, которое принимает значение у0 при х = х0, в со-
соседстве с (хт у0) будет
1
оно является функцией, имеющей р значений, которые будут
равны при х — х0.
Наиболее общим случаем, в котором /7=0, Fp = 0 удовле-
удовлетворяются совместно, является тот, когда F=0 имеет двойной
корень р= ро для х = х0, у = у0 и у, = 2. В этом случае решение
имеет вид
~ ^о)}2 = А(х~ xof+...,
следовательно в наиболее общем случае интегральная кривая
имеет точку пересечения в (х0, у0).
3-51. р-дискриминант и его геометрическое место точек. Три-
Триада (х0, у0, р0), для которой
F = 0, Fp = 0,
называется особым линейным элементом. Соответствующие зна-
значения (х0, у0) должны удовлетворять уравнению, полученному
исключением (элиминированием) р из
F {^, У, Р) = О, FP (x, у, р) = 0.
114
Полученное выражение (результантI называется р-дискрими-
Нантом2 диференциального уравнения и обозначается
bpF{x, у, р);
кривая, которую определяет уравнение
bpF{x,y, p)=0,
называется геометрическим местом точек рт дискриминанта
(р- discriminant locus).
Принимая, что х0 = О, у0 = О, можем написать диференциальное
уравнение в виде
F(x, у, р) = Uo + О, {р -р0) +... + Um (р—рь)" = О,
где коэфициенты могут быть разложены в ряд по возрастающим
целым степеням х и у. Поскольку F(x, у, р) второго порядка
относительно р — р0 при х = 0, у = О, О0 и Ux должны быть вида
Uo = «од;
Приближение к /7-дискриминанту в начале есть р = р0, так как
*оХ + ,80V = 0.
Но интегральная кривая определяется уравнением
следовательно в общем случае она не будет касательной к гео-
геометрическому месту точек р-дискриминанта (фиг. 5).
Фиг. 5.
(/^-дискриминант показан пуктиром; интегральная кривая,
встречающая /^-дискриминант в начале — сплошной линией)
Вообще геометрическое место точек р-дискриминсшта яв-
является геометрическим местом точек пересечения интеграль-
интегральных кривых диференциального уравнения.
1 Необходимо отметить, что в процессе исключения ни один изменяемый
множитель не должен отбрасываться. Следует рекомендовать применение общего
метода, например, метод исключения Сильвестра (Sylvester's dialitic method) Cus-
cott and Mathews, Theory of Determinants, X, § 10.
2 Cm. § 3-6.
В точке на геометрическом месте jo-дискриминанта уравнение
F(x,y, p) = 0
имеет не меньше двух одинаковых корней р. Это получается
вследствие пересечения интегральной кривой в рассматриваемой
точке. Если имеется больше двух одинаковых корней р, то
имеется и некоторая кратная точка с совпадающими касатель-
касательными. Предыдущая теорема будет еще более общей, если под
термином геометрическое место точек пересечения понимать
геометрическое место кратных точек, в которых совпадают каса-
касательные.
Однако геометрическое место точек /^-дискриминанта не яв-
является только геометрическим местом точек пересечения, потому
что равные корни р могут появиться и при других обстоятель-
обстоятельствах. Наиболее важным является случай, когда последовательные
члены семейства интегральных кривых имеют одну и ту же ка-
касательную, именно в точках на огибающей семейства интегральных
кривых; поэтому р-дискриминант содержит огибающую во всех
случаях, когда она существует. Более того, огибающая является
интегральной кривой, так как ее линейные элементы совпадают
с линейными элементами интегральных кривых в точках сопри-
соприкосновения. Таким образом огибающая составляется из непре-
непрерывных линейных элементов, удовлетворяющих диференциаль-
ному уравнению; но линейные элементы на р-дискриминанте
являются, согласно определению, особыми; поэтому огибающая
называется особой интегральной кривой. Пример, когда оги-
огибающая была особым решением, рассмотрен в § 2 • 44 (уравнение
Клеро).
Однако особая интегральная кривая не всегда бывает оги-
огибающей; исключительный случай возникает, когда особая инте-
интегральная кривая касается каждого члена семейства интегральных
кривых в общей для всех кривых точке. В этом случае особая
интегральная кривая будет членом общего семейства интеграль-
интегральных кривых; ее можно получить, если параметру семейств при-
придать частное значение. Она называется частной кривой.
В качестве примера рассмотрим уравнение
Bх—pf + х (у — xf Bx—p) — {y — x*f = О,
решение которого имеет вид
v = х2 + с2
у х ^1 + сх
Несмотря на то, что /^-дискриминант этого уравнения (с-ди-
скриминант его решения) содержит множитель у— х2, кривая
у=х2 не является огибающей. Эта кривая не имеет никакой
конечной точки, общей с интегральной кривой, для которой
с ф О, следовательно она является частной кривой, соответствую-
соответствующей с = 0.
Имеется еще одна возможность, именно: две непоследователь-
непоследовательные интегральные кривые имеют общую касательную в точке на
геометрическом месте р-дискриминанта. Такая точка называется
точкой совпадения (tac-point). Общая касательная к интеграль-
интегральным кривым не является касательной к геометрическому месту
точек р-дискриминанта, следовательно геометрическое место то-
точек совпадения, как и геометрическое место точек пересечения, за
исключением весьма специальных случаев, не будет интегральной
кривой диференциального уравнения.
3-52. е-дискриминант. Если диференциальное уравнение может
быть проинтегрировано, а его решение будет иметь вид
Ф (х, у, с) = О,
то огибающая, если она существует, дается уравнением (так
называемое с-дискриминэнтиое уравнение)
которое получается путем исключения с из уравнений
Как мы сейчас докажем, с-дискриминант дает не только одну
огибающую.
Пусть уравнения Ф = О, ФС = 0, решены для хну, представим
с-дискриминант в параметрическом виде
направление касательной в любой точке геометрического места
точек с-дискриминанта будет
Поскольку
дф , лф
касательная в любой точке интегральной кривой с = с0 имеет
направление
дФ (х, у, с0) / дФ (х, у, с0)
дх / ду
Пусть {х0, у0) будут координатами точки пересечения обеих
кривых
Ф (х, у, с0) = 0, 5? = 0;
ис0
если функции ф и 6 многозначны, пусть они будут так опре-
определены, что
117
тогда параметрические уравнения
будут представлять ветви геометрического места точек с-дис-
криминанта через (х0, уа).
Теперь в любой точке геометрического места с-дискрими-
нанта
дФ дх_ дФ ду _ ~
дх' dc ' ду дс '
следовательно в точке (л:0, j-0)
Таким образом интегральн ш кривая через (х0, у0) и геомет-
геометрическое место с-дискриминанта имеет общую касательную,
если только
(дФ} -АО ( — ^=Ь0
т. e. если интегральная кривая не имеет особой точки в {х0, у0).
Таким образом ветвь геометрического места точек с-дискри-
с-дискриминанта через (х0, у0) представляет собой огибающую или гео-
геометрическое место особых точек. Геометрическое место точек
с-дискриминанта разбивается на две отдельных части, одна из
которых образует огибающую, а другая — геометрическое место
особых точек. В наиболее общем случае особыми являются точки
пересечения и узлы, так что геометрическое место с-дискри-
с-дискриминанта содержит геометрическое место точек пересечения и
узлов.
Геометрические места точек с- и jo-дискриминантов имеют
общую огибающую, общее геометрическое место точек пересече-
пересечения, а возможно также и общую частную кривую.
Вследствие того, что явное общее решение уравнения не
всегда можно получить, необходимо исследовать критерии для
распознавания различных кривых, которые могут возникнуть в
геометрическом месте р-дискриминанта, не прибегая к его ре-
решению.
3-521. Примеры геометрического места точек дискриминантов.
(I) Кривые семейства
где с — параметр семейства, а а и C — постоянные C>а>0),
являются интегральными кривыми диференциального уравнения
4р2х (х — а) (х — р) = { Зх2 — 2 (а + р> х + о? }2.
Уравнение р-дискриминанта имеет вид
х{х — а)(х — Р) = {3х2 — 2(а + р)х+(#}* = О,
118
а уравнение с-дискриминанта
х(х — а){х — р) = 0.
Все три линии
х = О, х = а, л; = р
являются общими для обоих геометрических мест точек, при-
причем каждая линия касается каждого члена семейства, следова-
следовательно все три линии образуют огибающую. Остальная часть
геометрического места точек разбивается на две пары совпа-
совпадающих прямых линий
3* = а + р + / о? — аЗ + р ,
Ъх = а + р — / а- — сфТрг.
Они представляют собой геометрические места точек совпадения
первое уравнение является геометрическим местом мнимых то-
точек, а второе — действительных точек соприкосновения непо-
непоследовательных кривых семейства.
(II) Пусть
Р = а > 0;
диференциальное уравнение семейства
(y + cf = x(x — <ty
имеет вид
= Cх — аJ;
уравнение р-дискриминанта
х{3х—а)г = 0,
а уравнение с-дискриминанта
Общее геометрическое место точек х — 0 является огибаю"
щей. Геометрическое место точек р-дискриминанта также со"
держит линию х = у а, которая является геометрическим местом
точек совпадения, а геометрическое место точек с-дискрими-
с-дискриминанта содержит линию х = а, которая является геометрическим
местом узлов.
(III) Пусть
р = а = С;
диференциальное уравнение семейства
имеет вид
4р2 = 9х.
Геометрическим местом р-дискриминанта является х = 0, а
геометрическим местом с-дискриминанта—л3 — 0. Каждый член
119
семейства интегральных кривых имеет точку пересечения на оси
у, которая является следовательно геометрическим местом то-
точек пересечения.
3-6. Особые решения. Если непрерывная последовательность
особых линейных элементов образует интегральную кривую
уравнения, то эта интегральная кривая называется особой, а
соответствующее решение называется особым решениемi. По-
Поскольку особые линейные элементы существуют, согласно опре-
определению, только в точках геометрического места р-дискрими-
нанта, особая интегральная кривая должна быть ветвью гео-
геометрического места р-дискриминанта.
Для получения направления касательной в любой точке гео-
геометрического места р-дискриминанта, диференцируем уравнение
F{x, у,р) = 0
по х, тогда
dF_clF ay dF dp __ n
дх ду ' dx "^ dp ' dx ~~ U"
Но в любой точке на геометрическом месте р-дискриминанта
следовательно направление касательной определяется из урав-
уравнения
dF.dF ^У_п
дх "•" ду ' dx
Поскольку касательная к геометрическому месту р-дискри-
минанта совпадает с касательной к интегральной кривой
для существования особого решения необходимо, чтобы урав-
уравнения
F{x, у, р) = О,
dF(x, у, р)
dp
dF(x,y, p) . „ dF(x, y,p)
¦ = о,
дх ~*~Р ду
1 Примеры особых решений были впервые даны Бруком Тэйлором (Brook
Taylor) в 1715 г. Первые попытки систематической трактовки предмета [La-
grange, Mem. Acad. Sc. Berlin, 1774, (Oeuvres, 4, 5)]j De Morgan, Trans. Ornb. Phil.
Soc. 9A851), 107; Darboux, C. R. Acad. Sc. Paris, 70A870), 1331; 71, 267; Bull.
Sc. Math, 4. A873), 158; Mansion, Bull. Acad. Sc. Belg. 34A872), 149; Cayley,
Mess. Math. 2 A873), 6; 6 A877), 23 [(Coll. Math. Papers, 8. 529; 10, 19); Glaisher,
ibid., 12, A882), 1; Hamburger, J. fur. Math., 112 A893), 205], не вполне удовле-
удовлетворительны. Первая полная трактовка р-дискриминавта дана Кристалем [Trans.
Roy. Soc. Edin., 38 A896), стр. 803]. Следует упомянуть еще статьи: Hill, Proc.
London, Math. Soc. (I) 19 A888), 561; 22 A891), 216; Hudson, ibid. 33 A901), 380.
Petrovich, Math. Ann. 50 A898), 103; Bateraan, Differential Equations, IV. Теория
была распространена на уравнения с трансцендентными коэфициентами, см. Hill
Proc London Math. Soc. B), 17 A918), 149.
120
были удовлетворены совместно для непрерывной последова-
последовательности значений (х, у).
Предположим, наоборот, что
F(x, у, X) = О,
_dF[x. уЛ)_ = 0
dF(x, у, '/.) ^ dF(x, у, а) _ п
дх h Л Ъу ~U>
где X — параметр, представляют кривую. Диференцируя первое
уравнение и упрощая его при помощи второго уравнения, по-
получим направление касательной (р) в любой точке кривой
dF(x, у. У.) dF(x, у, л) __ _
д х + Р "ду и-
Воспользовавшись третьим уравнением, получим
Следовательно, если Fg не равно нулю во всех точках кри-
кривой, то
1=р,
поэтому кривая является интегральной кривой диференциаль-
ного уравнения
F{x, у, р) = 0.
Таким образом условия
вместе с условием /^ФО достаточны для существования осо~
бого решения1.
3-61. Условия для геометрического места точек совпадения- Иг
§3-5 мы знаем, что если
dF . dF
в конечном числе точек ветви геометрического места р-дискри-
минанта, то ветвь эта является геометрическим местом пере-
пересечения кратных точек. В любой точке, в которой
дх ^ оу '
две различные интегральные кривые касаются друг друга. Если
в обозначениях предыдущего параграфа '¦'фр, то интегральные
кривые не соприкасаются, следовательно они отличаются от
1 Примеры §3-521 показывают, чго огибающая может существовать при
F,, = 0.
Jt
геометрического места р-дискриминанта или, иначе говоря, полу-
получается точка совпадения. Необходимыми условиями для точки
-совпадения поэтому являются
дх
ду
это означает, что точка совпадения является двойной точкой
геометрического места /^-дискриминанта.
Чтобы /^-дискриминант мог образовать геометрическое место
точек совпадения, необходимо, чтобы каждая точка некоторой
определенной ветви была двойной, что невозможно, если только
эта ветвь не будет двойной линией; поэтому /^-дискриминант
должен содержать [как и § 3-521 (I) и (II)] квадратичный множи-
множитель, который, будучи приравнен нулю, дает уравнение геометри-
геометрического места точек совпадения.
Отсюда следует: чтобы р-дискриминант бы i геометрическим
местом точек. совпадения, необходимо, чтобы все четыре урав-
уравнения
F{x,y,p) = 0, Fp=0, Fx = 0, Fy = 0
¦были удовлетворены для непрерывной последовательности зна-
значений (х, у).
Поскольку эти уравнения удовлетворяются в каждой точке
геометрического места точек совпадения
Fppdp + Fpxdx + FplJdy = О,
Fpxdp -f- Fxxdx -f- FxOdy = 0,
Fp!Jdp -f- Fxydx + Fmdy = 0,
условие для геометрического места точек совпадения прини-
принимает вид
РТ"
pxi
РУ'
F
1 рх>
Fpg
Fm,
= 0.
3-611. Вывод из симметрии условия для геометрического места
точек совпадения. Из симметричности условий для геометрического
места точек совпадения следует, что если р-дискриминант урав-
уравнения Fix, у, р) = 0 дает геометрическое место точек совпадения,
то это справедливо и для уравнений
F(y, х, р) = 0, F[x, p, у) = 0, F(y, p, х) = 0,
F(p, х, у) = 0, F(p, у, х) = 0.
Однако, в частных случаях геиметрическое место точек совпа-
совпадения может быть приведено к одной точке совпадения.
122
Рассмотрим, например, уравнение1
F С*. У. Р) = (х* ~ о2) Р2 — 2хур — х- = 0.
условиями геометрического места точек совпадения являются
хрг —ур — х-=0, хр ¦=-- 0, {х2 — а'1) р — ху — С,
откуда
л-0, у=у, р = 0.
Геометрическим местом точек совпадения будет х = 0. Если
F(y, х. р) е (у*~ «2)р2 — 2хуР~у> =о,
то
л: = л, >» = 0, р — 0,
а геометрическим местом точек совпадения будет у — 0. Но
в уравнении
^(^. Р, У) = № — а2) У1 — 2хру — х* = 0
условиями являются
геометрическое место точек совпадения отсутствует, имеется
только одна точка совпадения в начале.
3-62. Геометрическое место точек перегиба. Интегральная кри-
кривая может рассматриваться как геометрическое место ее точек
или как огибающая ее касательных. Аналитические условия для
точки пересечения двух кривых в точечных координатах фор-
формально тождественны с аналитическими условиями для перегиба
в линейных координатах. Вследствие того, что семейство инте-
интегральных кривых имеет геометрическое место точек пересечения,
оно будет иметь в общем случае также и геометрическое место
перегибов.
Поскольку
дх + ~ду Р+ др ' дх " U
и в точке перегиба -—- = 0.. геометрическое место перегибов
дается исключением р из уравнений
F(x, y,p) = 0, Fx+pFy = 0.
В общем случае -,~г является конечной в геометрическом месте
перегибов, но
дх* Г лр дхду ГР ду*^ dp dx* '
следовательно необходимо, чтобы
Glaisher, Mess. Math., 12 A882), 0.
3.7. Разбор специального диференциального уравнения. Рассмо-
Рассмотрим уравнение'
F{x, у, р) = ау + Зхг + ixp + р* = 0.
Докажем, что если уравнение имеет особое решение (огиба-
(огибающую), то его интегральные кривые будут алгебраическими.
Если уравнение решается относительно р, то
р=-\ hx = /Т-'л* -'4рТ8 — 4ау"}.
Пусть у = vx2, тогда
xv' + 2v =yhi V f — 43 -
и, принимая a —_-. 0, напишем
и2 = f — 4p - 4ccy.
Уравнение теперь рационально, его переменные разделяются,
вследствие чего
ийи dx р.
Условия FP = Q, Fx-\-pFv =0 для особого решения равны
соответственно
¦{X + 2р = 0, 23х + V + р« = 0,
откуда, исключая р,
При этом условии, уравнение относительно и и а; приводится к
им , dx „
гг + а "*" х
и имеет общее решение
х (и ± a) const,
или
ах ± V— о.\хг — 4ау = с,
где с — параметр семейства интегральных кривых. В рациональ-
рациональной форме решение принимает вид
а интегральные кривые составляют семейство парабол, огибаю-
огибающая которых является параболой
4у + ул* = 0.
Таким образом, если существует особое решение (огибающая),
то интегральные кривые будут алгебраическими. Обратное, од-
однако, неверно. Чтобы получить условие, когда общее решение
1 Это уравнение является первым приближением, в соседстве с началом,
к уравнению F(x, у, р)= 0, когда оси так выбраны, что интегральная кривая
касается оси х в начале [Chryslal, Trans. Roy. Soc. Edin., 38 A896), 813].
124
алгебраическое, напишем уравнение в виде
udu . dx _
(и — >.)<« — р.) + Т ~ и>
где
(и — X) (к — и.) = н2 ± аи — а- — f + 4В.
Пусть _ _
2Х = ± а + / k, 2u = ± а — / /fe,
тогда
a2_? =4(— а^ — 72 + 4;3),
т.е. ?=(а + 2-гK — 16Р).
Решение имеет вид
откуда _
(и —/.) (и — ]i) х2 = с2,
и —
где
к = ± v^T2 ~ 413 —
Таким образом (принимай, что а, р и ^ — рациональные числа)
для того, чтобы общее решение было алгебраическим, необхо-
необходимо и достаточно чтобы k или
было квадратом рационального числа.
Но если это условие удовлетворено, то условие для огиба-
огибающей именно
щЛ-f — 4Р = 0,
может быть не удовлетворено. С другой стороны, если это
условие удовлетворено, то
(а + 2?J — 163 = (а + 2т)' — 4 (аТ — f)
и общее решение является алгебраическим.
Уравнение
3y±-Lx*-l-xp + p* = Q
имеет алгебраический интеграл, именно
(х2 + 12у) с2 — 2х (х2 + 9у)с + (ха -Ь ЗуJ = 0.
с- и р-дискриминанты равны ys и у соответственно.
Отрицательная половина оси у является геометрическим ме-
местом действительных точек пересечения. Правильной огибаю-
огибающей не получается потому, что точка пересечения последова-
последовательных кривых одна и та же, именно начало для всех кривых
семейства.
125
Примеры
1. Измените мегоя последовательных приближений так, чтобы можно было
доказать следующую теорему существования: если х0, у0, a, b и К имеют зна-
значения, принятые в § 3-1, а М — верхняя граница \f(x, vo\ для значений х в ин-
интервале (л'о, х(, + <?), то существует единственное решение уравнения
У =/(*, У).
которое приводится к у0 при х = х0 и непрерывно в интервале (хе, хв -j- р).
где р— меньшее из двух чисел а и К~х log A + KbM~1) [Lindeof, J. de Math.
D). 10 A894), 117].
2. Исследуйте поведение вблизи начала решений уравнений
(I) У'=У2; (И) х*у' = у;
(Ш) у =——г-о---.-; (IV) v'
(Vi xj»4->'2 = 0; (VI) х-:
3. Рассмотрите р- и с-дискриминанты уравнений
(I) Зх_у = 2рх- — 2р2, Интегралы: (Лу +2сJ = 4cxs;
(II) р3 — Ххур + 8у3 = 0, у = с (х — сJ;
(II Г) хр2 — 2ур + 4х = 0, О' = с2х2 -ь 1;
(IV) jD2B— ЗуJ = 4A — у), у2 — у3 = (х — сJ:
(V) да2 — 4*р + з' - О, У6 — 3jtV + 2сл C_у'' — 8д:2) -f с3 =0.
(VI) 8р3х = у (\2р- — 9), Зс>»2 = (х + сK.
4. Проинтегрируйте уравнение (у + рхJ = 4х2р и рассмотрите дискрими-
дискриминанты.
5. Покажите, что уравнение
A-л2)р3 =1— J*2
представляет семейство конических сечений, касающихся четырех сторон ква-
квадрата.
6. Пусть 4 (х, у, с) = 0 будет общим семейством интегральных кривых,
тогда Ф (х, у, г) =0 будет представлять поверхность, а геометрическое место
точек с-дискриминаитов — ортогональную проекцию на плоскости х, у кривой
пересечения поверхностей
Ф<*. У, *)=0, ^=0.
Рассматривая сечение Ф = 0 плоскостью, параллельной оси г, докажите, что
в общем случае
\Ф(х,у, с) = Е№-С\
где Е = 0 — огибающая, TV = 0 — геометрическое место узлов, а С = 0 — геоме-
геометрическое место точек пересечения.
[Cayley, Hill, Hudson; Salmon, Higher, Plane Curves, 3 изд., 54].
7. Покажите, что геометрическое место точек перегибов ортогональных
траекторий F(x, у, р) = 0 является вегвью кривой
-F(x,y, p) = 0, PFx-Fy = 0.
Разберите случай, когда эта кривая имеет ветвь, общую с
F(x,y,p) = 0, Fx—pFu=0. [Chrystal]
8. Покажите, что неприводимое дифереициальное уравнение первого по-
порядка, являющееся полиномом от х, у и р, степень которого относительно х, у
и р не превышает второй, не может иметь геометрического места точек совпа-
совпадения. [Chrystal}
ГЛАВА IV
НЕПРЕРЫВНЫЕ ГРУППЫ ПРЕОБРАЗОВАНИЙ
4-1. Теория диференциальных уравнений Ли. Первоначальные
исследования в области диференциальных уравнений были по-
посвящены проблеме интегрирования, т. е. проблеме нахождения
способов, при помощи которых отдельные уравнения или классы
уравнений могли быть решены непосредственно или приведены
к более удобной для решения форме. Затем были исследованы
теоремы существования, послужившие критерием для выяснения
вопроса о существовании решений уравнений, которые не ин-
интегрируются элементарными методами. Таким образом, суще-
существует ряд, повидимому, не связанных методов интегрирования,
действительных только для отдельных классов уравнений, в то-
время как теоремы существования показывают, что, за исклю-
исключением некоторых очень неестественных уравнений, каждое
уравнение имеет одно или несколько решений.
Было показано1, что более старые методы интегриро-
интегрирования основаны на общем принципе, который, в свою очередь,
оказался эффективным для нахождения новых методов. Ниже
этот объединяющий метод будет объяснен в своей простейшей
форме только для уравнений первого порядка с одной незави-
независимой и одной зависимой переменной.
4-11. Группа преобразований от одного параметра. Рассмотрим
преобразование
(Т) х1 = ч(х,у), у1 = Ъ{х,у),
при помощи которого точка {х, у) переносится к новому поло-
положению (xlt vj в той же плоскости и относится к той же паре
прямоугольных осей. Если уравнения, представляющие преобра-
преобразование, решены для х и у через хг и ух:
х = Ф (хь ух), y = W (х1г у&
то они представляют собой обратное преобразование (Т4), именно
операцию переноса точки {xlt yt) обратно к своему первона-
первоначальному положению (х, у). В результате преобразования ТиТ,
1 Klein and Lie, Math. Ann., 4 A871), 80; Lie. Forhand, Vid.-Selsk. Christiania
A874). 198; A875), 1; Math. Ann., 9 A876), 245; 11 A877), 464; 24 A884),
537; 25 A885), 71 [Lies Ges. Abhandlungen, III, IV]; Lie — Scheffers, Vorlesungen
uber Differenlialgleichungen mit Bekannten Infinitesimalen Transformationen A891):
Page, Ordinary Differential Equations A896).
127
последовательно в любом порядке получим тождественное пре-
преобразование
Xi = x, уг=у.
Рассмотрим совокупность преобразований, включенных в се-
семейство,
х1 = -ф{х, у; а), уг = <Ь(х, у; а),
где а — параметр, который может непрерывно изменяться в дан-
данном интервале Ч Любое частное преобразование семейства
получается при частном значении а. Теперь в общем случае, ре-
результат применения двух последовательных преобразований се-
семейства получается не тождественным с результатом применения
третьего преобразования семейства, потому что в общем слу-
случае а3 не может быть такой, чтобы
<р(*> у; а3) =<р {?(¦*! у; а{), 6 (х, у; aj; a2}
или, в частности, принимая
(f(x, у; а) =а — х, Ь(х, у; а)=у,
<я3 не может быть такой, чтобы для всех значений х
as — х = а2 — (аг — х).
Однако, если любые два последовательных преобразования
семейства эквивалентны одному преобразованию семейства, то
преобразования образуют конечную непрерывную группу. При-
Примем, что каждая рассматриваемая группа содержит обратное
этим преобразованиям, а также и тождественное преобразование.
Преобразования образуют группу, зависящую от одного пара-
параметра а; обозначим ее Gt.
4 «111. Примеры Gj.
(a) Группа переносов, параллельных оси х
х1=х + а, yt=y.
В результате последовательных преобразований параметров
•at и а2 получим
xl = x + a1+ а2, ух = у,
что представляет собой преобразование параметра а, -^ а2. Об-
Обратное преобразование параметра аг имеет вид
х1=х — а1. у1=у;
его параметром является —at.
(b) Группа вращений вокруг начала
хх = х cos а —у sin с, у, = х sin с + у cos a.
1 Принимается что о и ty диференцируемы относительно а в данном
интервале.
128
В результате последовательных преобразований параметров at
и а2 получим
х\ — (х cos аг—У sin аг)cos ai — (х sin аг + У cos c2) sin Oj
= х cos (ax + а2) — _у sin (а4 + а2),
у, = (a; cos а, —j/ sin а2) sin ot + U sin a2 + у cos c2) cos аг
= x sin (c, + a2) + У cos (a, -f as),
что представляет собой преобразование параметра at + o2. Об-
Обратное преобразование параметра аг будет
,х, = a; cos a, +.ysina1, yt = — jcsinc, +3'cosaj>
его параметром будет —с,,
(с) Группа
.*! = ах, yt = агу.
Преобразования параметров ах и а.2 последовательно эквива-
эквивалентны преобразованию параметра ata2. Обратное преобразование
параметра с, представляет собой преобразование параметра 1/Cj.
4-12. Бесконечно малые преобразования. Пусть а0 будет значе-
значением параметра с, соответствующим тождественному преобра-
преобразованию, так что
у; °о) = х, Ф (Л» У> ао
тогда, если е мало, то при преобразовании
A;t будет бесконечно мало отличаться от х, а уу от >»; следова-
следовательно, это преобразование отличается только на бесконечно
малую величину от тождественного преобразования и называется
бесконечно малый преобразованием.. Покажем, что каждая
группа G, содержит бесконечно малое преобразование^.
Пусть а будет любым фиксированным значением параметра а,
а E — параметром соответствующего обратного преобразования.
Таким образом
Пусть oi будет мало. Рассмотрим преобразование
*' = <р { <р (*, у; а); <1> (¦*, ^ а); р + 8f},
у = Ф {«Р {х, у, а), <1> (^. у; «); Р +8^}.
1 Ниже мы докажем, что Gx никогда не содержит больше одного бесконечно
малого преобразования.
э- айнс—133—а 129
Согласно теореме конечных приращений, если 6, и 62 поло-
положительны и меньше единицы, то
<¦ , ч , , 1 о, , дэ {»(•*. V; а), <1(Х,у; а); p-f 6^},,
x = и; { tp (л, j;, aj, 9 (x, y, a;, p ) -\ -^ or
. , . . , , . „, . Sits (x, у; a), i> (х, у; а); S -4- Ь.л1} Л,
У = ф { f (х, j»; а), ф (х, у, а); р } + -^^^^-^-^ ^ ^ ot
= y + fi(x,y; a)ot,
где S(x, у; а), ч}(х, у; а) не исчезают тождественно и независимы
от 8?, если члены второго и высших порядков не принимаются
во внимание. Эти уравнения представляют бесконечно малые
преобразования, поэтому каждая группа Gx с двумя переменными
содержит бесконечно малое преобразование; этот метод очевидно
применим (с тем же результатом) также к любому числу пере-
переменных.
Геометрически, бесконечно малые преобразования представ-
представляют малые смещения длины
в направлении 6, где
cos 6 = S//P + if, sin 6 = 7j,'/cTHHf •
Две группы преобразований называются подобными, если они
могут быть выведены одна из другой при помощи изменения
переменных и параметра. Ниже мы покажем, что каждая группа Gt
с двумя переменными аналогична группе переносов. Чтобы до-
доказать эту теорему, напишем уравнения бесконечно малого
преобразования в виде
ох = ; (X, У) 'Л, оу = 7) (Л, V) U,
тогда конечные уравнения группы могут быть найдены интегри-
интегрированием уравнений
йх = Ж- - dt
Ч*.у) ч{х,у)
Решения могут быть выражены в виде
F1{x,y) = Cl, F2(x,y)=C2 + t,
где Сх и С2 — постоянные. Пусть t — 0 соответствует тождест-
тождественному преобразованию, тогда
^i (•«„ у,) = Л (х, у), F2 (хи уг) = F2 (х, j/) + i.
Предположим, что и = F, (x,^), f = /^ (-^, Д') — новые переменные,
тогда
ul = и, vt = V + t
Таким образом данная группа приведена к группе переносов.
130
Ясно, что эта группа имеет только одно бесконечно малое пре-
преобразование, именно Ъи = О, bv = Ы. Поскольку с и ч\ определя-
определяются через и и v, первоначальная группа Gt имеет только одно
бесконечно малое преобразование.
4-121. Примеры, (а) Тождественное преобразование группы
вращения, определяемое формулами
x1 = xcosa—у sin а, ух = xsina +у cos a,
дается при а = 0, следовательно будет бесконечно малое пре-
преобразование
xv = x qosU—_у sin§? уг = xsinU + у cosU
или, заменив cos Ы и sin Ы приближенными значениями для ма-
малых U, получим
xi = х -y*t, S\ = У Ы
Это преобразование представляет вращение в положительном
направлении на малый угол 3?.
(Ь) Уравнения
хг = ах, j/j = а2у
определяют группу; тождественное преобразование соответствует
а = 1. Поэтому бесконечно малое преобразование будет
или, ограничиваясь малыми величинами первого порядка, получим
Для приведения этой группы к группе переноса, необходимо
решить уравнения
dx dy ,,
х 2у '
откуда
х\ х*
Искомыми новыми переменными поэтому будут
и = yjx2, v = log х.
4 • 13. Обозначения для бесконечно малых преобразований. Рас-
Рассмотрим изменение некоторой функции f(x,y) если к перемен-
переменным х,у применено бесконечно малое преобразование
xt = х -f ox = х +1 (x, у) U,
Изменение значения f(x, у) равно
Z-f ( у «Л — ft у it \ f{y v\
J \*S У) J \Л1>^'1^ / 'Л» У II
= fix + Sx, у + by) - f{x, у),
131
удерживая только малые величины первого порядка. Если, на-
наоборот, приращение 8/(я,у), которое данная функция f(x,y)
принимает при бесконечно малом преобразовании группы Gt
известно, то ?{х,у) и т\(х,у) известны, следовательно, известно
и само бесконечно малое преобразование. Таким образом бес-
бесконечно малое преобразование может быть полностью пред-
представлено выражением
Так, например, символ
представляет собой бесконечно малое вращение
*!==*—уЫ, yt =y
В частности
так что
Очевидно, если в группе Gt, действующей на переменные
х, у заменить эти переменные на х', у', где х', у' — любые функ-
функции х, у — то свойство группы удерживается.
Далее
^l _ df (х', у') дх' , df(x\y') д^
дх "" дх' ' дх ~*~ ду' дх"
df(x',y') df(x'.y') дх' df{x',y') ду'
ду дх' " ду "*¦ ду' ' ду '
Отсюда следует, что
дх> I df дУ
-Тх- + -дУ'~дх
df дх' 4 df
df
дх' ¦ у ду' '
Теперь пусть конечные уравнения группы Gt будут
и пусть ? = 0 дает тождественное преобразование, тогда функция
/(¦*и Vt) может рассматриваться как функция х, у и t; фиксируя
хну, разложим функцию в ряд Маклорена по t так, что
, Ух) = /о +/о t + \ /о * + • • •
132
где
/о =
Jo [at j,=c ~~ L dx1 ' dt t" ay, " dt [,=0
= -^j 5 (л, v) ф -|- v)(л,у) = ?//(дс,у),
U*f(x,y).
Следовательно разложение f[xlty^) имеет вид
f{Xy)f(x) +
где Unf—результат n-кратного воздействия оператора
на f{x, у).
В частности
представляют собой конечные уравнения группы. Можно легко
доказать, что рассматривая х и у как фиксированные величины,
к которым приводятся л, и yt при t = 0, эти уравнения дают
решение совместной системы
d d
Поэтому бесконечно малое преобразование определяет группу,
которая может соответственно рассматриваться как группа iff.
4 • 131. Примеры получения конечных уравнений из бесконечно
малых преобразований.
(а) Дано бесконечно малое преобразование
Необходимо найти соответствующую группу Qv Можно дока-
доказать, что
U х ¦= — у, U у = х,
Usx = j/, ?/3j/ = — л,
/74л = а:, U*y=y,
133
Таким образом U является циклическим оператором периода 4
относительно х и у. Отсюда следует, что
t i1 ts /4
= х cos t — у sin t,
= х sin t -\-y cos t.
Таким образом G± является группой вращения.
(Ь) Аналогично, если
"J - л дх ~т~ у ду>
то мы найдем} что
/ /2 ^з
= У + Т\У + Y\ У + ТГ-
... =xet,
Если вместо е* подставить новый параметр а, то уравнения при-
примут вид
xt = ах, ух = a_v
и определят группу равномерных усилений.
4 • 2. Функции, инвариантные относительно данной группы.
Предположим, как и выше, что конечные уравнения группы
•*i = <Р (*..У; 0» J'i = Ф (¦«• J'J О
таковы, что тождественные преобразования соответствуют t = О,
и пусть
обозначает бесконечно малое преобразование группы.
Функция Q(x,y) называется инвариантной, если хг,у1г образу-
образуются из х, у операциями данной группы
для всех значений L
134
Разложение Q(xlt yj по степеням t может быть представлено
в виде
Следовательно, если функция Q (х,у) инвариантна относи-
относительно группы, то это выражение должно быть равно Q(x,y)
для всех значений t в данном интервале. Для этого необходимо
и достаточно, чтобы UQ било тождественно равно нулю, т. е.
; ОН dQ _ п
дх ' ' ду
Функция z = Q(x,y) является поэтому решением диференциаль-
ного уравнения в частных производных
дх ' ' ду '
следовательно,
Q (х, у) = const
является решением эквивалентного обыкновенного диференци-
ального уравнения
dx dy
Так как это уравнение имеет только одно решение, завися-
зависящее от одной произвольной постоянной, то каждая группа Gt
с двумя переменными имеет только один независимый инвариант.
Иначе говоря, существует один инвариант, через который могут
быть выражены другие инварианты.
4.201. Инварианты группы вращений. Бесконечно малое пре-
преобразование группы Gt вращений имеет вид
Уравнение, определяющее Q, будет
— 4--^- = 0-
у х '
оно имеет решение хг -\-у2 = const, откуда
Q (л-, у) = х2 +у.
Геометрически очевидно, что окружности, центры которых нахо-
находятся вначале, инвариантны относительно группы. Для анали-
аналитической проверки этого заметим, что конечные уравнения
группы имеют вид
xt = х cos t — у sin t, yv = x sin t + у cos t,
тогда
2 (Xi, Уг) =x\ +y* --= (x cos ^ — у sin ^J + {x sin ^ + v cos tf
= Q(x,y)
135
независимо от значения t. Следовательно инвариантность х2 ф
Фу2 установлена. Любой другой инвариант относительно группы
должен быть функцией х* -\-у2 и, наоборот, любая функция
я2 + у2 инвариантна относительно группы.
4-21. Инвариантные точки, кривые и семейства кривых. Если
в любой точке плоскости (х, у) функции Z(x,у) и т\(х, у) равны
нулю, то эта точка является фиксированной относительно беско-
бесконечно малого преобразования
и, следовательно, является фиксированной относительно всех
преобразований группы. Такие точки называются абсолютно
инвариантными относительно группы.
Точка (ХоуУо), не инвариантная относительно группы, пере-
переносится при помощи бесконечно малого преобразования к со-
соседней точке (л;0 + Ъх, у0 -fr 3y0) так, что
J!L = -2L
Ьх S '
Если бесконечно малое преобразование повторять неопреде-
неопределенное число раз, то точка Р, первоначально совпадающая
с точкой {Хо,у0), опишет кривую, являющуюся одной из интег-
интегральных кривых уравнения
dv _ г,
1БсТ= Т"
Семейство интегральных кривых
Q (•*> У) = const
таково, что каждая кривая инвариантна относительно группы.
Семейство кривых может быть также инвариантно в том
смысле, что каждая кривая преобразуется в другую кривую
того же семейства при соответствующих операциях над груп-
группой. Таким образом семейство кривых может быть инвариант-
инвариантным в целом, хотя отдельные кривые семейства могут не быть
инвариантными относительно группы. Пусть
Q С*. У) = const
будет таким семейством кривых. Если при любом преобразова-
преобразовании группы (я, .у) переходит в (л;,,^), то
^ (хг, j/t) = const
должно представлять то же семейство кривых. Но
поэтому, если оба семейства кривых
2 (хъ yi) — const, Q {х, у) = const
136
тождественны, то выражение
должно быть постоянно для любого фиксированного значения t,
т. е. для каждой кривой семейства
UQ = const.
Таким образом для того, чтобы Q (х, у) = const представляло
семейство кривых, инвариантных в целом относительно группы,
необходимо и достаточно, чтобы UQ = const представляло то же
семейство кривых, т.е. UQ должно быть некоторой функцией 2,
например F(Q). Если F(Q) = 0, то отдельные кривые семейства
инвариантны.
Так, например, относительно группы вращения
хх = х cos t — у sin t, yt = у cos t + x sin t,
семейство прямых линий
принимает вид
где аир — параметры семейств, но
Л] xcost—jjsini x ' \ ' х-J ' \ x ' x''
Если семейство -~ = а инвариантно, то семейство
i + 4- = т
должно быть тождественно ему. Это в действительности и на-
наблюдается. Параметры а и \ связаны зависимостью
7 = аа + 1.
Теперь
Это является формой, которая принимает в данном случае
условие UQ = F(Q).
4 • 3. Распространение на случай п переменных. Группа 6\ с п
переменными хи х2, ..., хп определяется преобразованиями
х\ = iff (хъх2, . . .,лп; а) (/ = 1, 2, ... , и);
может быть доказано, как и выше, что она эквивалентна един-
t37
ственному бесконечно малому преобразованию
/7/7v х х \ =? (х х х \У- 4- 4-Р (у х у \df
lyJ \Л1> Л2) •••! ЛШ ->11Л1' Л2» •••> лп) ^к Т • • ¦ Т ч \Л1» Л2» * • Ч лп/ §^~•
Пусть t — параметр группы, при котором бесконечно малое
преобразование имеет вид
тогда, если F (хи л2,..., хп) функция, диференцируемая любое
число раз относительно ее аргументов, то
* д "-1 j "-э* • • * > и/ — v 1* 2' " * ¦ > п' I *** Г" ^^^ "Т" о i~ ^^^ I ¦ • • ¦
Будем рассматривать хх, х.г, ..., хп как координаты точки
в пространстве п измерений, a t как параметр, не зависящий
от этих координат; t можно рассматривать, например, как время.
С изменением t, точка {х[,х'2, .. .,х'п) опишет траекторию, начи-
начинающуюся в точке (xv xit..., хп), Каждая траектория очевидно
будет инвариантной относительно группы.
Как и выше, для того, чтобы функция 2 {хъ xs, х„) была инва-
инвариантной, необходимо и достаточно, чтобы UQ была тожде-
тождественна равна нулю. Кривая 2 = 0 является траекторией и сле-
следовательно инвариантна, если UQ = 0. Семейство кривых
2 = const
инвариантно, если UQ — определенная функция 2.
Наконец, уравнение
инвариантно, если ?/2 равна нулю или тождественна 2 = 0.
В первом случае уравнение 2 = а инвариантно, а в последнем
случае не инвариантно для всех значений постоянной а.
В качестве примеров инвариантных уравнений могут быть
приведены следующие.
(а) Уравнение 2 = х2+у* — с2 ¦= 0, где с —любая постоянная,
инвариантно относительно группы вращения, так как
(Ь) Уравнение 2 ~ у — х = 0 инвариантно относительно группы
¦> дх ' - ду '
так как
ш = [хш +у w) (у~х) = ~х+у = Q-
С другой стороны, уравнение у — л: + с = 0, где с — любая
не равная нулю постоянная, не инвариантно относительно группы.
138
4 • 4. Определение всех уравнений, допускающих данную группу.
Говорят, что уравнение допускает данную группу, если оно
инвариантно относительно этой группы. Пусть группой будет
Uf — ciC^nх2,..,, л:п) -^——f- ... -f- $n (Xi, -x2, .. •, лп) ~^~
и пусть
QC^,^, ...,л;п) = О
будет уравнением, допускающим группу, при которой UQ = 0.
Примем, что 2 не является множителем, общим для всех функ-
функций Si,.. .,5m пусть Sn, например, не равна нулю при S = 0, тогда,
если
= 0, и следовательно Q инвариантна относительно группы Vf.
Пусть уг,у2, ¦•-, уп_г — независимый ряд решений диферен-
циального уравнения в частных производных
Vf=O;
поскольку они являются также решениями Uf=0, они являются
и функциями первоначальных переменных х1,х2, .. .,хп. Присое-
Присоединим к у у у%>.. .,Уп_г функцию хп; полученные таким образом
функции ряда также независимы, так как в противном случае
существовала бы зависимость вида
и следовательно хп было бы решением линейного диференциаль-
ного уравнения в частных производных Vf — О, которое оче-
очевидно неверно.
С другой стороны xltxit.. .дяЧ могут быть выражены через
п переменных Ух,у2, ¦ ¦ -,_V-i и х"- Пусть при этом изменении
переменных инвариантное уравнение 2 = 0 примет вид
Кажется, что W должно содержать хп; в действительности это
неверно, так как если а — любая постоянная, то
У»
Поскольку VW (yvy2, .. .,yn_va) тождественно равно нулю и
^^'(У^Уг» • • •iJ'/i—i» -^n) = 0 тождественно или согласно уравнению
Ч?" = 0, отсюда следует, что
139
т. е. что W существенно независимо от хп. Таким образом \р
и соответственно Q могут быть выражены только через уъ
У.. ¦••.>_,.
Следовательно, если уравнение й = 0 инвариантно, то й мо-
может быть выражено через п— 1 независимых решений дифе-
ренциального уравнения в частных производных Uf=O. Иначе
говоря, каждое инвариантное уравнение 2 = 0 является частным
интегралом уравнения Uf=0.
В частности, если и и v-—два независимых решения уравнения
то наиболее общим решением, инвариантным относительно
группы Uf, будет
Q (и, v) = 0
или
•о - F{u) = 0.
4 • 5. Расширенная группа. Пусть
л, = <? (х,у; a), yt = ф (л, у; а)
определяют группу Gj с двумя переменными. Будем рассматри-
рассматривать диференциальный коэфициент р как третью переменную,
которая, относительно группы, превращается в р„ где
dxt dtp
дх
д®
die
два частных
+ дуР
+ -^Р
ду "
значения
= '/.(х,у,
а, так
,р; <
что
Пусть а и
тогда результирующее преобразование
будет результатом исключения л^, yt из уравнений двух состав-
составляющих преобразований. Аналогично
будет результатом исключения ух из
140
Таким образом в общем случае, преобразования
xi = <Р {х,у; а), ух = ^ (х,у; а), рх = \ {х,у, р; а),
действующие на линейный элемент (х, у, р), образуют группу,
которая называется расширенной группой.
Конечные уравнения данной группы могут быть представ-
представлены в виде
t , ч . Р (*. dri
следовательно,
Если функция Z, (х, у, р) определена таким образом, то беско-
бесконечно малое преобразование расширенной группы будет:
Группа может быть расширена аналогично, полагая высшие
производные .у" ,..., у(п) новыми переменными.
4 • 6. Интегрирование диференциального уравнения первого по-
порядка с двумя переменными. Выше (§ 2*1) мы показали, что
точное диференциальное уравнение первого порядка с двумя
переменными непосредственно интегрируется в квадратурах. Если
уравнение не является точным, то для его интегрирования
необходимо прежде всего определить интегрирующий множи-
множитель. Покажем, что если уравнение инвариантно относительно
известной группы, то интегрирующий множитель может быть
найден, по крайней мере, теоретически, и уравнение интегри-
интегрируется в квадратурах.
Предположим, что диференциальное уравнение
. У, Р) = О
инвариантно относительно расширенной группы
выведенной из
141
тогда необходимое и достаточное условие для этой инвариант-
инвариантности удовлетворено, именно, что выражение U'F равно нулю
само или согласно уравнению F = 0.
Допустим, что нам нужно определить и проинтегрировать
наиболее общее диференциальное уравнение, допускающее
данную группу U'f. Следовательно нужно определить два неза-
независимых решения диференциального уравнения в частных про-
производных
f df . df , r df
+ ri-f+ = 0
которое зависит от нахождения двух явных решений совместной
системы
dx civ dp
т -1= т •
Пусть и — я будет решением уравнения
dx dy
5 ¦'/
тогда, поскольку Ей ч не зависят от р, и также не будет зависеть
от р. Пусть v = ,3 будет решением
dx dy dp
отличным от и=а; очевидно ч) должно содержать р. Если И (и) —
произвольная функция и, то f=v — Н{и) удовлетворяет ;ди-
ференциальному уравнению Uf — 0, т. е.
U'{v-H(u)} = 0.
Следовательно
v-H(u) = O
будет наиболее общим обыкновенным диференциальным уравне-
уравнением первого порядка, инвариантным относительно W.
Покажем, что если и известно, то v может быть определено
в квадратурах. Известно, что любая группа может быть приведена
к группе переноса. Пусть изменение переменных с значения
(х, у) к (хг, y/j) приведет Uf к группе переносов, параллельной
оси уъ именно Utf, тогда
откуда следует, что
Таким образом хь уг определяются как функции х, у при по-
помощи уравнений
142
Первое уравнение имеет решение
л:, = и (л, у) ,
второе уравнение эквивалентно совместной системе
dx dv ду1
Одним решением этой системы является
и {х, у) = я .
Если это решение применить для исключения л; из уравнения
то ух получится в функции от х и а в квадратурах. Исключая а,
получим _ух в функции от а; и у- Таким образом необходимое
изменение переменных найдено.
Можно показать, что ?Л /, являясь расширенной груп-
группой Ult f, тождественна их /. Наиболее общее уравнение, ин-
инвариантное относительно и[ /» находится решением совместной
системы
дху _ дуг = ф;
О I 0 '
Поскольку двумя решениями этой системы являются
*! = const, /?!= const,
то наиболее общее инвариантное диференциа.1ьное уравнение
первого порядка может быть написано в виде
и интегрируется в квадратурах. В первоначальных переменных
это уравнение имеет форму
но поскольку хг — и, рх — функция одного v, а так как Н —
произвольно, мы не потеряем в общности, если примем рх = v»
Таким образом, если одно решение уравнения
dx dy
известно, то можно построить наиболее общее диференци-
альное уравнение первого порядка, инвариантное относительно
группы
J Ox ' ' ду
и это уравнение может проинтегрироваться в квадратурах.
143
4-61. Интегрирование диференциального уравнения, январи»
г о относительно группы G. Пусть данное диференциальное
уравнение будет иметь вид
dx dy
х, у) " Q(x,y)
и пусть
<р (X, у) = С
будет его решением, тогда <р (х, у) будет интегралом дифе-
диференциального уравнения в частных производных
дх~ ^ ду
Примем, что по крайней мере для одного, значения с интеграль-
интегральная кривая <р (х, у) = с не инвариантна относительно группы.
Однако интегральные кривые, как семейство, инвариантны, так
что
где F[y) — определенная функция (р не равная тождественно
нулю. Если Ф функция одного <р, то семейство кривых Ф = С
тождественно семейству ш = с. Пусть
тогда
Таким образом Ф является интегралом двух диференциальных
уравнений в частных производных
дх ^^ду
•. дФ дФ
'' дх ' ' ду
= 1,
откуда найдем, что
дФ _ — q дФ _ Р
дх Рт; — Q *' 6>Г Ptj — Q 5 '
следовательно
с?Ф = -д— dx+ х-1 rfv
Pdy — Qdx
~~ Pr,— Ql~'
Таким образом -^ 777 является интегрирующим множителем
для диференциального уравнения
Pdy - Qdx = 0 .
144
Решение уравнения
их dy
поэтому будет
С Pdy — Qdx „
J ~~Pr\~ QZ ~ '
где К— постоянная.
Если каждая отдельная интегральная кривая инвариантна
относительно группы, то выражение ?/<р тождественно равно
нулю, т. е.
^ дч> . дъ _
следовательно
Бесконечно малое преобразование принимает форму
и, наоборот, если оно имеет эту форму, то из нее нельзя получить
интегрирующего множителя уравнения
Pdy— Qdx = O.
Такой интегрирующий множитель называется тривиальным от-
относительно рассматриваемого уравнения.
4 • 62. Диференциальное уравнение первого порядка, инвари-
инвариантное относительно группы переносов. Исследуем наиболее общие
диференциальные уравнения, инвариантные относительно част-
частных групп элементарного характера. Сначала рассмотрим груп-
группу йг переносов параллельных оси а;
' дх
В данном случае расширенная группа U'f тождественна Uf.
Следовательно рассматриваемая совместная система
dx dy dp
1 б (Г
имеет решения
у = const, p = const.
Наиболее общим диференциальным уравнением, инвариантным
относительно группы, поэтому будет
где F—произвольно.
Аналогично, наиболее общим уравнением, инвариантным отно-
относительно
UJ- ду'
Э. Айне—133—10 145
будет
р = F{x) ¦
В этих двух случаях переменные разделяются.
Общая группа переносов имеет вид
UJ - а ' Ох Ь ду '
где а и b — постоянные. U'f снова тождественно Uf. Совместная
система имеет вид
adx = — bdy = ~ ,
следовательно наиболее общим диференциальным уравнением
относительно группы является
р =-F(ax + by);
оно может быть проинтегрировано, полагая ах + by новой не-
независимой переменной.
4 • 63. Диференциальные уравнения первого порядка, инвари-
инвариантные относительно афинной группы х
В данном случае Z=x, tq = О, С= — р, следовательно распро-
распространенная группа имеет вид
Совместная система
их йу dv
х 0 — р
имеет решения
хр = const, у = const.
Наиболее общим уравнением, допускающим группу, поэтому
будет
Аналогично найдено, что общее диференциальное уравнение,
допускающее афинную группу
1 Афинное преобразование представляет собой проективную коллинеацию,
преобразующую эвклидову плоскость в самое себя. Оно сохраняет параллель-
параллельность прямых линий н может быть представлено в виде
*!= ах + Ьу + с, j/, = а'х + Ь'у + с'. {ab' — a'bjzG).
Афинной группой называется группа таких преобразований; она является груп-
группой от одного параметра, если а, Ъ, с, а' V с' — функции от одного параметра
(Euler, 1748; K'ein. Erlanger Programm, 18).
146
меет вид
p=yF(x).
В обоих случаях переменные разделяются.
4>64. Диференциальные уравнения первого порядка, инвариантные
относительно группы усиления '.
Здесь р = 0, a U'f тождественно с Uf. Совместная система
dx dy dp
~х у~ " О
имеет решения
р == const, — == const,
следовательно инвариантное диференциальное уравнение общей
формы будет
оно является однородным (§ 2-12).
Если уравнение написано в виде
то его интегрирующим множителем будет
Пример:
(У—2х3у) dx + (х4 - 2xy*)dy = 0 .
Интегрирующим множителем будет
(/ - 2х*у) х + (л* -2xf)y = - (х*у + ху*),
теперь
(у4 — 2х3у) dx + (хй — 2xys) dy _ d (x*y + xy*) __ „ d(xs+yl)
x*y+xy* ~~ x*y -i- хуг лч + >-3 '
поэтому решением будет
х*у + ху* ,
(xT^W ~~ consl
ИЛИ V ' У'
X3 +У3 = с-ЧУ.
Рассмотрим теперь более общую группу
Ш = -^ • *L + -L . К
UJ - а дх~ Ъ ду '
1 Или группы перспективных преобразований.
147
Распространенной группой является
JL
а
-У-
Ь
ab P др'
Совместная система
имеет решения
adx bdy abdp
x ' у ~ (a— b)p
Т \
где аир — постоянные. Типичное инвариантное диференциаль-
ное уравнение имеет следовательно вид
p = X ° Г
Приведем частные примеры:
(II)
дх
дх
(Ш)
ОХ
Аналогично
(IV) Uf = -f- + 2- ¦ —
х дх х ду
(V) У/Е
дх " dv
Уравнение: xdy = F(xy)ydx,
Интегрирующий множитель: ху.
Уравнение: ydy = F(¦*-) dx,
\ х )
Интегрирующий множитель:
Уравнение: dy = x
Интегрирующий множитель:
1
y — x^l-^-
Уравнение: р = JL + xF ( JL
х \ х
Интегрирующий множитель:
Уравнение: хр — у = F (-1-\
\ х /
Интегрирующий множитель:
148
4 • 65. Диференциальные уравнения первого порядка, инвариант-
инвариантные относительно группы вращения
Распространенной группой является
Первое уравнение совместной системы
?,,=_,.«+**+(,+,,,?.
— у
имеет решение
где а — постоянная. Последнее уравнение может быть написано
в виде
dy dp
его решением будет
arc sin — — arc tg p = C
где P — вторая постоянная. Это решение эквивалентно
arc tg —~==г — arc tg р — В
или
arc tg —— arc tg p = p
поэтому может быть написано в виде
Наиболее общим диференциальным уравнением, допускающим
группу, будет поэтому
Если это уравнение написать в виде
(х — у F)dy — {у + х F)dx = 0,
то оно допустит интегрирующий множитель
1_
х2 + у%
Примеры
(О uf = y%
Уравнение:
или [х — F (у)} dy — ydx = О.
Интегрирующий множитель: —г
(И) Uf^
Уравнение: хр — у — F(x)
или
Интегрирующий множитель: —.
4-66. Диференциальные уравнения первого порядка, инвариантные
относительно группы
Распространенной группой является
Совместная система имеет вид
dx dv _ dp
0 1 9W'
одним решением ее является
х = а,
где а — постоянная. Вследствие этого решения, последнее урав-
уравнение принимает вид
dy dp
1 ? (а)'
откуда
р—
где 3 — вторая постоянная. Инвариантным уравнением поэтому
будет
p—yy(x) = F(x),
т. е. линейное уравнение первого порядка. Если его написать в
виде
dy — {у* (х) + F{x) }dx = 0,
то оно будет иметь интегрирующий множитель
4-7. Интегральные кривые, инвариантные относительно группы
уравнения. Семейство интегральных кривых инвариантно в целом
относительно любой группы, которую это диференциальное
уравнение допускает, но если эта группа не тривиальна, то
все отдельные кривые семейства не инвариантны относительно
группы. Однако отдельные интегральные кривые могут быть
инвариантными, поэтому важно отметить специальные свойства
этих кривых.
Если
Q(x,y, p)=0
диференциальное уравнение, инвариантное относительно группы
и если любая интегральная кривая также инвариантна относи-
относительно группы, то ее градиент в любой точке (х, у) будет ра-
равен vj/5. Отсюда любая интегральная кривая находится подста-
подстановкой vj/S вместо р в самом диференциальном уравнении; все
такие кривые, если они существуют, входят в уравнение:
Это уравнение может содержать кривые, инвариантные относи-
относительно группы, и иметь решения диференциального уравнения,
не являющиеся частными интегральными кривыми. Можно при-
привести пример, когда интегральные кривые имеют огибающую;
сама огибающая, инвариантная относительно группы, преобра-
преобразующей семейство интегральных кривых в самое себя, имеет
уравнение, удовлетворяющее диференциальному уравнению, но
не является частной интегральной кривой. Уравнение такой кри-
кривой будет особым решением диференциального уравнения.
Пример. Диференциальное уравнение
ур 8у2 = 0
допускает группу
¦> ох ' -' ду
Если особое решение существует, то оно получается подста-
подстановкой Зу/х вместо р в диференциальное уравнение, которое
принимает вид
откуда у = 0 или 27'у = 4л:3.
Общим решением уравнения будет
у = с {х — сJ,
таким образом у = 0 будет частным решением, а 27у = 4л;3 бу-
будет уравнением огибающей.
151
Примеры
1. Найдите общие диферевциальные уравнения первого порядка, инвари-
антвые относительно группы
го W=,g + $ % g
и определите соответствующие интегрирующие множители.
2. Покажите, что каждое из уравнений
(I) 2хур + х - V2 - 0, (IV)p« - х* - у = О,
(Щхр — У — хт=0, (V) р* — 4у (хр - 2yf = О,
(III) у + хр — л*р°- = О, (VI) р2 — 2х*р — 4х*у = О
допускает группу вида
?//=«* f + bv^f.
J — дх ' ду
Проинтегрируйте уравнения и найдите особые решения.
3. Покажите, что если
гК + ъК + г + ^r^
? дх+п ду+ ' Эу + "" ' ' djf(»)
является /г раз расширенной группой
то
^Et^yr^t (г =1,2,...,/,)
4. Докажите, что если « = а, г» = р, да = ¦; (а, р, •» постоянные) — независи-
независимые решения системы
dx _ йу dy' dV'
е ~ ч "V ~ а?"
при которой и содержит только хну, v содержит у', но не содержит у", а
ш содержит у", то наиболее общее диференциальное уравнение второго порядка'
нввариантное относительно дважды расширенной группы
будет
w = Ф (и, v),
где Ф — произвольная функция аргументов.
Докажите, что если w = dvjdu, то мы не потеряем в общности, следовательно
уравнение второго порядка w = Ф (и, v) будет эквивалентно уравнению пер-
первого порядка
Проверьте эту теорему для следующих групп и соответствующих инвари-
инвариантных диференциальных уравнений н покажите в каждом отдельном случае,
152
как может быть получен первый интеграл
(I) ?//=—-, V"=F (У, У'У,
(HI) (//Eip xy" ~y'F(y, xy'y,
(V) Uf=x^+yjj?. xy> =
(VI) (J/ET(x)i?, у -= p (x)jf + g(x)у + r(x).
(Page, Ordinary Differential Equations, IX).
ГЛАВА V
ОБЩАЯ ТЕОРИЯ ЛИНЕЙНЫХ ДИФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
5-1. Свойства линейного диференциального оператора.
Наиболее общее линейное диференциальное уравнение типа
. , d" v , , N d"~1y . , . ч du , , . . ч
Ро(х) -~п- + pt(x) ~i+ • • • +Pn-i U) аГ+Рп{х)у = г(х)
может быть переписано символически в виде1
(A) L (у) = {PoD" + PlD»-* + ... + pn^D + рп}у = г (х).
Примем, что коэфициенты р,„ р,,...,р„ и функция г (х) не-
непрерывные однозначные функции х в пределах интервала а<
<jc<;b и что р0 не обращается в нуль ни в одной точке этого
интервала, тогда основная теорема существования § 3 показывает,
что существует единственное непрерывное решение у (х), до-
допускающее данное значение ус в любой точке х0 в пределах
интервала (а, Ь), первые п — 1 производных которого непре-
непрерывны и принимают соответственно значения _у0', у", ..., у{"~~г>
при х0.
Выражение
L = p0D» + p.D"-^... +р„_! D + р„
называется линейным диференциальным оператором порядка п.
Диференциальное уравнение
(В) L(u) = 0
называется однородным уравнением, соответствующим (А); на-
называется оно так потому, что L(u) является однородной линей-
линейной формой относительно и, и',..., и{п>.
Следующие элементарные теоремы ясно показывают природу
оператора L.
I. Если и = иг — решение однородного уравнения (В), то и —
= Cut, также является решением, где С—любая произвольная
постоянная.
1 Понятие символического оператора было впервые введено Бриссоном
[Brisson, J. Ее. Polyt. (I) Cah., 14 A808), 197]. Его применение было расширено
Коши.
15-4
Это следует из того, что
DrCux = CDruu
таК как тогда
п
n-rut = CL{ux) = 0.
г -О
II. Если и = и1, и2,..., ит — т решений однородного уравне-
уравнения (В), то м = Ci«1+C2,m2+ ... + Cmtim также будет реше-
решением, где Сг, С2,..., Ст — произвольные постоянные.
Аналогично это следует из того, что
D' {С,»: + С2м2 + ... + Cm«nJ = Cjyui + С5ЛЛи2 + • • • + Cjynni.
Если /г линейнонезависимых'решений м„ м.2>..., н„ однород-
однородного уравнения известны1, то решение
и U) = С1гг1 + С2и2 + • • • + Спип,
содержащее п произвольных постоянных, является полным инте-
интегралом однородного уравнения. Постоянные С1з С2,..., Сп могут
быть определены только единственным образов, так что
(С) и (х0) = у0, и' (хо) - у0',.. ., at»-1) (*о) = У'оп-Ц.
III. Пусть у = уо(х) — любое решение неоднородного уравне-
уравнения (А), тогда если и(х) -полный интеграл (В), mo J'=Vo(X) +
-rii(x) будет наиболее общим решением (АJ.
Поскольку оператор Dr дистрибутивен, L также дистрибу-
дистрибутивно, т. е.
L {У0 (х) ¦+¦ и (х)} = L {у0 (Х)} + L {и (х)} = г (х),
так как
х)} = г(х), L{u(x)} = 0.
Но решение
содержит п произвольных постоянных и является следователь-
следовательно наиболее общим решением (А).
Если и (л;) так подобрано, что удовлетворяет условиям (С),
а Уо(х) таково, что
M(x) = 0,
1 Условия для линейной независимости см. § 5-2.
- d'Alembert, Misc. Taitr., 3 A762 — 65), 381.
а это возможно при условии, если г(х) не равно тождественно
нулю, то решение
>= Л (¦*)+«(*)
удовлетворяет также условиям
У (¦*>) = Уо>
Это общее решение (А) может рассматриваться как состоя-
состоящее из двух частей, именно:
1°. Из полного интеграла соответствующего однородного урав-
уравнения, имеющего форму
и{х) = Схщ-\- С3иг+ ... +Сп ип
и содержащего п произвольных постоянных, — оно называется
иногда дополнительной функцией.
2°. Из частного интеграла, который не содержит произволь-
произвольной постоянной и может быть частным решением (А). Возможно,
что решение (А) вместе с его первыми п — 1 производными об-
обращается в нуль в точке х0 в интервале (а, Ь).
Так, если рассматриваемое уравнение имеет вид
то дополнительной функцией будет A cos x + В sin x, где А и В —
произвольные постоянные; частный интеграл равен у = х. Об-
Общее решение поэтому
у — A cos х -f- В sin x -f- x.
Любое специальное решение получится, если придать А и В оп-
определенные числовые значения.
5 • 2. Вронскиан. Пусть ult u2l..., ип будут п решениями одно-
однородного уравнения порядка
?(и) = 0,
тогда наиболее общим решением или полным интегралом этого
уравнения будет
и = Cj м, -f- С2 Но -{- ... + С„ ип
при условии, что решения м1э и2,...,ип линейно независимы.
Получим условия, что п функций
их(х), и%(х), ...,ип{х),
которые приняты диференцируемыми п— 1 раз в интервале (а, Ь),
линейнонезависимы.
Если эти п функций не являются линейно независимыми, то
постоянные С„ С2, ..., Сп могут быть определены таким образом,
что
156
тождественно. Поскольку это соотношение удовлетворяется тож-
тождественно в интервале (а, Ь) оно может быть п—1 раз дифе-
ренцируемо в этом интервале, так что
С.И1 + С2и'2+ ... +Спи'
+
+ ... +
= 0.
Таким образом мы получили п уравнений, определяющих иосто-
янные С„ С2, ..., Сп. Если эти уравнения совместны, то
lt щ,..., ип) =
и„
0.
(п—1)
1 ,
(п—1)
2 ',
(л—1)
Этот детерминант называется вронскианом1 функций uit и2)..., ип.
Его тождественное обращение в нуль является необходимым ус-
условием для линейной зависимости uit иъ... , ип; поэтому его не-
неравенство нулю достаточно для линейной независимости щ,
и2,... , и„.
Предположим, наоборот, что Д тождественно равно нулю.
Может случиться, что вронскиан меньшего числа функций, на-
например, иг, и2,..., Ufa также будет тождественно равен нулю. До-
Докажем, что если ut, и%,... ,Uk—решения диференциального урав-
уравнения, то они линейно зависимы.
Пусть и^х), и2(х),..., ик(х) — функции, первые k — \ произ-
производных которых конечны в интервале а^х-^b и такие, что
их вронскиан равен нулю в интервале (а, Ь). Тогда, если врон-
вронскиан ut{x), w2(я) Uk-i(x) не обращается тождественно в
нуль, то существует тождественная зависимость вида
Uk (Л) = CjMj (х) + C2UZ {X)+... + Ck-iUk-l (Х),
где су, с2,..-, Ck—-i — постоянные2. Чтобы доказать эту теоре-
теорему, обозначим миноры элементов последней строки вронскиана
i, Щ ик
я,,
и2, ¦. ¦,
Ml ,
(ft-и
соответственно через Uu ?/,,,..?4, тогда получим k тождеств
) № (г = 0, 1,..., k - 1)
1 Введено Г. BponcKHVf (H. Wronski) в 1821 г. Тождественное обращение
ьронскиана в нуль не является достаточным условием для линейной зависимости
п функций. См. Peano, Mathesis, 6П889), 75, 110; Rend. Accad. Lincei E), 6 A897).
413; Bortoloiti, ibid., 7 A89S), 45; Vivanti, ibid, 7. 194; Bocher, Trans. Am. Math.
Soc. 2 A901), 139; Curtiss, Math. Ann. 65 A908), 282.
2 Frobenius, J. fur Math., 76 A873), 238.
157
Если мы каждое из первых k— 1 этих тождеств продиференци-
руем, а следующее тождество вычтем из результата, то полу-
получим
UWP + U'zuP + ... + U'ku'P = О (г = 0, 1 ...,k- 2).
Умножим r-ое из этих k—\ тождеств на сомножитель и^^^
в детерминанте Uk и сложим произведения, тогда
и[ик - вд = о,
и поскольку Uk не равно тождественно нулю в интервале (а, Ь),
то
Аналогично можно доказать, что
U2 =~
Поэтому из тождества
игщ + U2u2 +. .. + Ukuk =-- 0
следует
Uk {— с1и1 — с2щ —... — ск _ j ик-1 + «a-} = 0,
что и требовалось доказать.
Теперь пусть и1г и2,..., ип будут таковы, что их первые (п — 1)
производных конечны в интервале (а, Ь) и ни одно не равное
нулю выражение вида
гДе g\> Sf ' ->gn— постоянные, не обращается в нуль вместе с
его первыми (п—1) производными ни в одной точке интервала
(а, Ь). Если вронскиан ult uit..., ип обращается в нуль в любой
точке р интервала (а, Ь), то эти функции будут линейно зави-
зависимы1, так как обращение в нуль вронскиана для х = р означает,
что постоянные си с2)...,сп, не все равные нулю, могут быть
найдены таким образом, что
^4° (Р) + с2и?(р)+... + cnuV (р) = 0 (г = 0, 1, ...,п- 1),
т. е. функция
ctu, {xj + с2и2 (х) -f ... + спип (х)
обращается в нуль вместе с ее первыми п — \ производными
при х = р и следовательно тождественно равна нулю. Таким
образом теорема доказана.
Пусть и,, иг,...,ик— функции х, которые в любой точке ин-
интервала (а, Ь) имеют конечные производные до в — 1 порядка
1 Эта и следующая теорема были даны Бохером, loc. cit.
158
(n~>k). Далее ни одна функция вида
где glt g2,---,gk — постоянные не исчезает вместе с ее первыми
п—1 производными ни в одной точке интервала (а, Ь). Тогда,
если вронскиан их, и2,...,ик обращается в нуль тождественно,
то функции линейно зависимы.
Чтобы доказать это, рассмотрим первый случай, когда врон-
вронскиан и„ «2,...,«ft—1 не равен нулю в интервале (а. Ь). Пусть
р будет точкой интервала, где вронскиан не обращается в нуль.
Тогда, поскольку вронскиан непрерывен, он не обратится в нуль
в непосредственном соседстве с р, а из того, что было уже
сказано выше, следует, что постоянные си с2,...,с]; будут та-
таковы, что функция
схих + с2и2 + • • • + ск ик,
будет равна нулю в соседстве с р. Поэтому первые п — 1 про-
производных этой функции также обратятся в нуль в соседстве с р,
и следовательно, согласно условию, функция должна бвгть
тождественно равна нулю.
Рассмотрим теперь общий случай. Предположим, что врон-
вронскиан и,, и2). ..,ит обращается тождественно в нуль при A <
< m < &), в то время как вронскиан их, и2,..., w,n_i не обра-
обращается тождественно в нуль в интервале (а, Ь). Отсюда следует,
что ии и2,..., ит линейно зависимы и следовательно теорема
доказана.
Эти теоремы могут быть приложены к решениям
«iD иг(х),..., ип{х)
диференциального уравнения. Так как любое решение, которое
вместе с ее первыми п — 1 производными обращается в нуль
в любой точке интервала (а, Ь), тождественно равно нулю,
отсюда следует:
/. Если вронскиан их, и2,..., н„ равен нулю в любой точке
(а, Ь), то эти п решений линейнозависимы.
II. Если вронскиан k решений м„ м2> - • •> uk(k < n) равен нулю
в интервале (а, Ь), то эти k решений также линейно зависимы.
Если vv v%,..., vn выведены из ы,, м2,..., ип при помощи
линейного преобразования
vr = ari ux + аГ2и2+ . .. +агпип (г = 1, 2,..., п),
то легко показать, что
д (if,, v%,..., <vn) = ЛД {иь щ,..., «„),
где А — детерминант |ars|. Следовательно выражение
v2,..., vn) не равно нулю, поэтому юъ v2,..., vn линейно неза-
независимы, при условии A°), что детерминант А не равен нулю,
159
т. е. преобразование обыкновенное, и B°), что иии2,..., м„ ли-
линейно независимы.
Пусть н„ м2,..., ип представляют п линейно независимых
решений уравнения
Ци)=О,
тогда вронскиан A(elf н2,..., м„) может быть выражен в простой
форме, которую мы сейчас получим:
иъ
и/.
(Л—2)
<")
Hi ,
м2,.
«/,
н(л-
М» ,
-2)
• ¦ »
ц(я)
так как все другие детерминанты, возникающие при диференци-
ровании, имеют по два одинаковых ряда, и поэтому обращаются
в нуль. Поскольку
—pt «<"-') — ... — рп-1 И/ — р„ Mr,
отсюда следует (после небольших преобразований), что
X
Д =Д0 ехр{—f^dx}, [ехр л-= ег],
где Др — значение, к которому Д приводится при х = а:0. Это соот-
соотношение называется тождеством Абеля (§ 3-32). Оно показы-
показывает, что если ро{х) не обратится в нуль в интервале {a, b), a
До исчезает при х0, то Д тождественно равна нулю. Если До не
равна нулю, то Д не будет равна нулю нигде, за исключением
особой точки, т. е. точки, в которой pjpo становится бесконеч-
бесконечным. Такие точки исключаются, полагая, что коэфициенты L (и)
непрерывны, а р0 не обращается в нуль в интервале (а, Ь).
5- 21. Фундаментальная последовательность решений. Некоторая
линейно независимая последовательность п решений иг, и2)..., ип
уравнения
L(u) = О
образует так называемую фундаментальную последовательность,
или фундаментальную системуА Чтобы данная последователь-
последовательность п решений была фундаментальной, вронскиан п решений
1 Термин фундаментальная система был введен Фуксом [Fuchs, J. fur
Math., 66 A866), 126 (Ges. Math. Werke, I, 165)].
160
не должен быть равен нулю. Общее решение уравнения будет
иметь вид г
и=С1и1+С^и2+ ...+Спип
и не может обратиться в нуль, если все постоянные Си С2, ....
Сп не будут равны нулю.
Очевидно, существует бесконечное число возможных фунда-
фундаментальных последовательностей решений, но одна частная по-
последовательность имеет большое значение вследствие ее про-
простоты.
Пусть при и, (х)
«1 t*o) = 1. «i (•*(>) = «I (*о) = • • • = и/"-11 (х0) = 0.
Определим ит(х), где г = 2, 3,... , п, как частное решение, удов-
удовлетворяющее начальным условиям
и (х0) = а' (х0) =...= iH'-v (х0) = 0,
«*-"(*„) = 1,
и^ (х0) = «С-+1) (лс) =...== н"^-1 ^0) = С.
иг {х), Uz(x),— ,an (х) образуют фундаментальную последователь-
последовательность; значение их вронскиана при х = х0 vaBHo единице.
Единственное решение
удовлетворяющее начальным условиям
и (х0) = у0, и' (х0) = >-;..., «("-'> (х0) = Уо'"-1",
имеет вид
и (х) = у0 «х (х) +у'о в, (л) + ... +3'и("~л «п (¦«).
Любая фундаментальная последовательность решений
«iU), «2 (а),... , и„(л;)
может быть переписана так
«1 (*) = ^i. «2 W = Vifv, dx, и3 (л-) = г»! / г»а / ®з (rf*)
и в общем случае
иг (л) = ©! / va f.../v, {dxy-\
где
!1 / L ^L L
г dxlvr_1 dx \vr__2 dx " ' v3 их \uj\[
Однородное диференциальное уравнение, имеющее фундамен-
фундаментальную последовательность решений в виде п функций
ки и2,... , ип
1 Lagrange, Misc.Taur., 3 A762—(.5), 181 [CEnvres, 1, 473].
Э. Айне—133—11 161
получается исключением п произвольных постоянных С из п -\-1
уравнений
и = Сх щ + С2 «2 + • • • + Сп ип,
u(») = С, в/") + Q к2<«> + ... + С„ «п »',
поэтому
Д(и, и„ и2> ... ,«„) =0,
где Д — вронскиан н, и,, и2,... , ип. При разложении детерминанта
коэфициент и'т равен Д(гг2, гг2.- • •, ип) но не равен нулю, посколь-
поскольку к„ и,,... , и„ образуют фундаментальную последовательность.
Можно написать
V ' Д(Н1,Н2,...,Н„)
так что коэфициент при ип) в L (и) равен единице.
Уравнение получается вида
... аи, аи, , аи , - „
L («) Е "d^ + ?! -^=4" + • • • + P»-l Ji + Р" В = °.
где
Рг = — ДгМ.
а ^г получается из Л подстановкой и{-п) вместо Ui"~r\ u?") вместо
u2in~r) и т. д.
Чтобы выразить оператор L в виде произведения п операто-
операторов первого порядка, напишем
UT = Д(к, гг„и2, -.., ит),
тогда1
Повторяя этот процесс, найдем, что
f(v\ = (— V,"— a- A .J^L- d d ,^1.Л
К ' К ' V-i dx ' Л„Л„_3 "dx ¦¦' dx ' 12\ Ax
Л„Л„_3
где каждый диференциальный оператор действует на все по-
последующие.
1 № ir_j = Ул_1 V — U'r_1^r доказывается частичным разложением де-
детерминантов.
162
Если фундаментальную последовательность рассматривать
в виде
«1 = Vi, «2 = ^i j\dx , un=.v1 fv2f ... fvn (dx)" \
то уравнение примет вид1
j^ _d_ d _rf_, и
dx ' vndx ' vn_1ax ' ' ' va_ dx w, ~
Символически уравнение L (и) = 0 может быть написано так2
InLn-\ ¦•¦ L2L1{iij =0,
символ Z.,- представляет оператор D — а,-, где
Это следует из того, что
A: d
Необходимо отметить, что порядок последовательности мно-
множителей (D — а,) должен быть сохранен, так как неверно, что
для любых двух индексов г и;
(D - a,) (D - a,) = {D- ay) (D - at).
Иначе говоря, множители диференциального оператора в общем
не коммутативны.
5 • 22. Понижение порядка уравнения. Если г независимых ре-
решений уравнения порядка п
L (в) = 0
известны, то порядок уравнения может быть приведен k п — г.
Пусть
ut,uz,...,ur
будут известными решениями и пусть
d / vr\ d [
и т. д., как и раньше. Тогда, поскольку известно, что уравне-
уравнение имеет форму
d d d d d и _
dx ' vn dx vT лах' vr dx ' ' ' v2 dx ' vx '
1 Frobenius, J. fur Math., 76 A873), 264; 77 A874), 256.
2 Floquet, Ann. Ёс. Norm., B) 8 A879), 49.
163
оно может быть написано в виде
P{v) = 0,
где
д _ d d _ _jL_ if_
' ~~ vrdx' vT_xax " ' v2dx ' v, '
а Я — линейный оператор порядка n — r.
Если некоторое решение Р (v) = О известно, то соответству-
соответствующее значение и может быть получено из выражения (А) по-
посредством г квадратур.
Приведем пример уравнения второго порядка
(в) ? + /-?+«-=«•
Предположим, что одно решение этого уравнения известно;
обозначим его у1 и напишем
тогда
у"г Judx -f 2у3 и -f у, к' -f jo {у'\ /ийл + ^,гг} -f qyi f udx = О,
что приводится к
у, к' +Bу|+ру,)и==0.
Это является линейным уравнением первого порядка относи-
относительно и, решение которого имеет вид
u = Cy-2e-fpd*
и поэтому оба независимых решения (В) будут
5 • 23. Решение неоднородного уравнения. Рассмотрим общее
уравнение
(A) L(y)
при условии, что фундаментальная последовательность решений
и, (л), и% (л), ..., ип (х) приведенного уравнения
L (и) = О
известна.
Тогда общее решение приведенного уравнения будет иметь
вид
и = С1и1 + С2гг2 -f ... + С„и„,
где С,, С2, ..., Сп — произвольные постоянные. Теперь, так же,
как и в случае линейных уравнений первого порядка (§ 2 • 13),
для определения общего решения рассматриваемого уравнения
164
может быть приложен метод вариации параметров1. Пусть
у = Vxut + V2u2 +...+ Vnun,
где Vv V2,...,Vn — неопределенные функции, х удовлетворяет
уравнению (А). Задача — найти функции V. Поскольку само ди-
ференциальное уравнение эквивалентно единственному соотно-
соотношению между функциями V и г(х), то ясно, что п—1 других
соотношений могут быть установлены при условии их взаимной
совместности. Последовательность п—1 соотношений будет
V1'u1+Vi'ui+... + Vn'ua = 0,
Vx%' + V2'u2' +...+ Vn'un' = О,
/ux(»- 2> + v/ii2 <» L 2> + ... + Vn'un (»-*) = 0.
Отсюда следует, что
У' = Vxiit' + V2u2' +...+ Vnun',
у" = FlHl" + V.2u2" + ...+ Vnun\
у (я - « = к.В! (nl i *'
в то время как
Таким образом выражение
_y = К,«! + V'aKa + ... + Кпгг
удовлетворяет диференциальному уравнению
где коэфициент при j/" принят равным единице, если
(С) V,'ux («-!> + К2'и2 (» -1) + ... + !/„'«„ о. - о = г (л
Поскольку решения ^(л), и2(л),..., ггп Га;) образуют фунда-
фундаментальную последовательность, п уравнений (В) и (С) достаточны
для определения V{', V2',..., Vn' исключительно через их, м2,...,
ип и г(х). Тогда V,, V2,...,Vn получаются в квадратурах.
В частности, если уравнение второго порядка, то
dx
, V2= f-r^-r r(x) dx,
где &(щ, и2) — вронскиан и, и и2.
5*3. Сопряженное уравнение. Понятие интегрирующего мно-
множителя, которое играет такую большую роль в теории линей-
1 Lagrange, Nouv. Mem. Асгсц Berlin, 5 A774), 201; 6A775), 190 [CEuvres, 4,
9, 159].
ных уравнений первого порядка, может быть использовано в те-
теории линейных уравнений высшего порядка и приводит к важным
результатам.
Пусть
(А) ^?± *
и пусть функция v предположена такой, что vL (и) dx будет
полным диференциалом, тогда формула
приложенная к vL(u) в ее распространенной форме, дает
u)~ {и «-« pov - н(«-3> (po-yj' -1- ... + (- 1 V^a
• ~ {u'pn-2 v — u (pn-2 v)'}
dx
где
(С,
Диференциальное выражение L (v) называется сопряженным
с L (ii), a
L И = О
также называется сопряженным уравнением1, соответствую-
соответствующим
Соотношение (В) может быть выражено в форме
vL{u)-uL(v) = ?{P(u, v)};
оно называется тождеством Лагранжа. Вьфажение Р(и, г1),
1 Lagrange, Misc. Taur., 3 A762—65), 179 [CEuvres, 1, 471]. Термин был впер-
впервые введен Фуксом [J. fur Math]., 76 A873), 183 [Ges. Math. Werke, 1, 422].
166
линейное и однородное относительно
и,и',..., и "-1)
называется билинейной последовательностью.
Чтобы v могло быть интегрирующим множителем для L (и),
необходимо и достаточно, чтобы v удовлетворяло сопряжен-
сопряженному уравнению L(f) = 0. Если v — решение этого уравне-
уравнения, то уравнение
L (и) = О
приводится к линейному уравнению порядка п—1
Р{и, v) = С,
где С—произвольная постоянная.
Если г независимых решений сопряженного уравнения,
например
Vt, V2,..., Vr,
известны, то мы получим г независимых уравнений
Р (и, г»0 = Си Р {и, v2) = С2,..., Р (и, vr) = Сп
каждое порядка п—1. Из этих г уравнений можно исключить
г—1 значений и(п), и*"-2',..., и<-"~г+1); уравнение, полученное
путем исключения будет линейным уравнением порядка п — г,
коэфициенты которого содержат г произвольных постоянных
С,, С.г,..., СГ. В частности, если г = п, то все производные
M(n—D^ и(п~2\..., и' будут исключены, и в результате мы получим
выражение для и через vx, Vz,...,vn и Cv C2,..., Cn. Иначе
говоря, уравнение полностью интегрируется.
Докажем теперь, что соотношение между L (и) и L {v) обра-
обратимо, т. е. если L (v) является сопряженным с L {и), то L (и)
сопряженное с L{v). Предположим, что этого нет и пусть
Lt(u) будет сопряженным с А (г;). Тогда существует функция
Рх (и, v) такая, что
vL1{u)-uL(v)=~{Pl(u,'v)},
но
следовательно
- L{u)}=j~{Px(ut v)-P(u,
Р, (к, 1)) — Р(и, v) является однородным и линейным относи-
относительно v, v\..., гД"~ 1>, но v{Lt(и) — L(и)} не содержит гМп> и
поэтому коэфициент при «ус—]) в Р(и, v) — Pl(u, v) равен нулю.
167
Рассуждение может быть повторено; оно показывает, что
Pi(u, v) — P(u, v) тождественно равно нулю, следовательно
Z., (и) тождественно L (и).
Если уравнение тождественно своему сопряженному урав-
уравнению, то оно называется самосопряженным1.
Разложим L (и) на множители так же, как и в предыдуще.ч
параграфе
. . . _ d d d и
~~ vn+iax 'vndx "' v,dx ' v/
тогда поскольку 2
„.//„» Ну- v d d d и
vl (и) ax - -—- • —~~~ -——.... ¦—-
v,
f(d v \( d d , d u\d
J \ax vn+1j\vndx vn_1dx '" v^dx уг) '
f(d . v \( d rf._. .A.ibfc
J \dx vn+1 J \vndx wn_j dx " - vzdx vx J
d v \( d d d u\
J
vjlx vn+l ) \ vn_xdx vn_2dx * ' ' " v.2dx щ J
Ла . d v \( d ?L_ d -Ah ¦
dx vndx vn+1) \vn_1dx vn_2dx ' •• •' Vdx ' vj
и т. д.; если
Р(и, v)=:
Vn-ldX
\vndx vn+1) lwn_jdx vn_2dx ' ¦ ¦ • ' vjjx ' v~J
+
/_ i)"-2 (JL 'L- . . A- . JL\ (JL- .
\vsdx vtdx ' '' vnux vn+l J \vsax '
/ i уг—i I_d__ d^ __ d v \ и
*• \vzdx v^dx ' • • • ' ^Tndx ' v^^) Vi
И
; vxdx v2dx ' " * " yndx * v'
1 Один из первых примеров самосопряженного уравнения дан Якоби
[Jacobi, J. fur Math. 17 A837), 71 (Werke, 4, 44)],_который д-казал, что если
порядок оператора равен 2/л, то оператор будет РР, где Р и Р— сопряженные
оператэры порядка т. См. также Jacobi, J. fiir Math. 32 A846) 189 tWerke 2
127); Hesse, ibid. 54 A857), 230.
2 Frobenius, J. fur Math., 76 A873), 264. Thome, ibid., 76, 277; Frobenius, ibid.
77 A874., 257; 80 A875), 328.
168
то
В частности, если выражение L(u) самосопряженное, то
+ 1 = ± ^i ,
Таким образом, если L{u) = 0 — самосопряженное линейное дифе-
ренциальное уравнение четного порядка 2т, то оно может быть
написано в виде г
__ _ j^ _ q
t»idx * с^Лс ' ' ' t'mdje fm f i dx ' vmdx '' ' v«dx vt
ИЛИ
РР(м) = 0,
где P — диференциальный оператор
d d _d _ 1
fjdx t',,dx * *" vmax L '
m —1
a P—сопряженный оператор.
Аналогично, если уравнение L (и) = 0 самосопряженное и не-
нечетного порядка 2от—1, то оно может быть написано в виде
d d d d ^/ ii — 0
iTjdx w2d.x; * vm dx vm dx ' ' ' v2 dx
ИЛИ
где Р— оператор
d d
a P—ему сопряженный оператор.
5 • 4. Решения, общие для двух линейных диференцигльных урав-
уравнений. Если известно a priori что уравнение
L (в) = О
имеет решения, общие с другим однородным линейным уравне-
уравнением низшего порядка, то порядок первого уравнения может
быть понижен, даже если общие решения и ке даны в явнои
форме. Пусть
L Е дЛп + р, ?)«-' + ... +ря_1 D + р„
-1^- ... -f gm_! D
Frobenius, ibid.. 85 A878), 192.
161-
будут операторами порядка /п(от<я). Рассмотрим третий опе-
оператор
Rl = r0 D"-m + rx D»-"-1 + ... + rn_m_i D + г„_т,
где коэфициенты г должны быть такими, чтобы можно было
максимально понизить порядок оператора
Выбором коэфициентов г так, чтобы они удовлетворяли соотно-
соотношениям
А) =
rs g0 + г, { (я — от — 1) q'o + </,} +
+ г0 {- (п - т) (п—т - 1) q'0'+ (n - от) q[+ q2},
rn_mq0 + /¦„_„_! {^ё + 9i} + Гп-т-г {q + 2q[
можно определить оператор L — R^L-i через Dm, Dm+1, ..., Dn.
•Эти соотношения достаточны для последовательного определе-
определения г0, г,,..., г„-т после чего выражение L — /?,Lx приводится
<к оператору порядка не выше от — 1.
Необходимо отметить, что функции г выводятся из функций
р и q рациональными процессами сложения, вычитания, умноже-
умножения, деления и диференцирования, следовательно если коэфи-
коэфициенты А и А, рациональные функции х, то коэфициенты Rj
также будут рациональными функциями.
Так
L — JRtLj -f- Z.?)
где L% — оператор, аналогичный L и Lu но порядка не выше
т — 1. Рассмотрим случай, когда уравнения
?(«)== О, ^(«J-O
«меют общее решение. Это решение будет также удовлетворять
уравнению
1г (и) = 0.
Если бы каждое решение Lt(u) = 0 было решением L(u) = 0, a
?2 не было бы тождественно равно нулю, то уравнение L2(u) =0,
порядок которого не выше т—1, удовлетворялось бы отреше-
отрешениями Lx(u) = 0, что невозможно. L2 было бы поэтому тожде-
тождественно равно нулю, a L могло быть разложено на произведение
RiLt. Обратное также верно.
С другой стороны, если бы Lt (и) = 0 имело решения, не при-
принадлежащие L (и) = 0, то L% не было бы тождественно равно
170
нулю. Операторы R2 и Ls, где порядок L3 меньше порядка L2,
существуют таким образом, что
Zv_x = R..L + ?,+1.
В этом последнем уравнении 7.v+] тождественно равно нулю
или является оператором нулевого порядка, так как в любом
другом случае процесс мог быть продлен еще на одну ступень.
В первом случае каждое решение L, (и) = 0 является реше-
решением Z,v—1(«) = 0, следовательно также и
Z.v_,(h) = 0,..., ?, (и) = 0, ? (и) = 0.
Тогда
/г,
следовательно i разложено рациональными процессами на про-
произведение двух операторов.
Если мы изменим зависимую переменную
•v = U (и),
то уравнение Z, («) = 0 примет вид
R(*0=O,
где R—оператор порядка п — k, если k порядок Z,v.
Пусть v = V будет наиболее общим решением, содержащим
п — k произвольных постоянных для R("o) = 0, тогда общее
решение
L {и) = 0
получится полным решением неоднородного уравнения
U (и) = V;
это решение будет содержать п произвольных постоянных.
Во втором случае Z.v;-i — функция х или постоянная, не равная
нулю. Это показывает, что
L4-i {и) = 0, L, (и) = 0
не имеют общего решения, не равного тождественно нулю.
Если уравнение с рациональными коэфициентами не имеет
решения, общего с любым другим уравнением низшего порядка,
коэфициенты которого также рациональны, то оно называется
неприводимым. Эти рассуждения могут быть значительно раз-
171
виты, применяя понятие области рациональности. Независимая
переменная х и некоторая иррациональная или трансцендентная
функция х берутся как элементы или основания области [R].
Тогда любая функция, выведенная при помощи рациональных
процессов1 из эгих элементов, будет рациональной в области
[/?]. Если уравнение, коэфициенты которого рациональны в [И],
не имеет решения, общего с уравнением низшего порядка,
коэфициенты которого также рациональны в [/?], то уравнение
неприкодимо в области \R].
5*5. Коммутативные линейные операторы. Любое диференци-
альное уравнение типа
может быть разложено на множители и выражено в виде
так как необходимо только определить функции аг и я2 при
помощи уравнений
аг (х) + «2 {х) = 2р, «х (л:) а2 {х)+я\ (х) = q;
которые могут быть, по крайней мере теоретически, решены 2.
Данное уравнение поэтому удовлетворяется общим решением
но не удовлетворяется, за исключением очень специальных слу-
случаев, общим решением
Оно будет удовлетворено общим решением последнего урав-
уравнения так же, как и решением первого уравнения, если оба
оператора
D + 4{x)u D + «2(*)
будут коммутативны, т. е. если
{D + Ч {х)} {D + аа [X)} и = {D + a2 (x)} {D + Ч (х)} и
независимо от значения диференцируемой функции и. Для того,
чтобы операторы были коммутативны, необходимо и достаточно,
чтобы
я; (а) = а[ (л)
ИЛИ
Яа (JC) = ах (JC) +Л,
где Л — произвольная постоянная. Диференциальное уравнение
поэтому будет иметь вид
1 Рациональные процессы содержат также и диференцирование.
2 Cayiey, Quart. J. Math., 21 A886), 331 ICoII. Math. Papers, 12, 403].
!72
где Р — оператор D+a^x). Уравнение
•& + *¦&+&>¦+/''-<*>*-а
где а произвольная постоянная, может быть разложено на мно-
множители
и полностью интегрируется.
Нетрудно доказать, что оператор
можно переставлять с оператором второго порядка
Л2 + 2р?> + q,
если только последний может быть выражен в виде
{D + «{.х) + AJ {D + a {х) + Л2},
где Ах и Л2 — постоянные. Вообще, если Р и Q — операторы по-
порядка тип соответственно, то Р и Q коммутативны, если
..{D + a(x)+ Am+n},
но это условие, хотя и достаточное, но не обязательно. Так
операторы
2
Z>3 — 3x~~2D + 3x~s
коммутативны, но не могут быть выражены в форме произведе-
произведения. Поэтому возникает проблема определения необходимого и
достаточного условия для того, чтобы операторы Р и Q можно
было переставлять, если эти два оператора не могут быть сами
выражены в виде полиномов от диференциального оператора R
низшего порядка.
5-51. Условия коммутативности1. Допустим, что Р и Q — ли-
линейные операторы порядка тип, тогда, если Р и Q ком-
коммутативны, а /г — произвольная постоянная, то
(P-h)Q = Q(P-h).
Следовательно, если
Уъ У-2,---, Ут
фундаментальная последовательность решений уравнения
(A)
1BurchnaII and Chaundy, Proc. London Math. Soc. B), 21.
173
то
Q&i). QD1.),-.-, QW
также являются решениями (А) и существуют соотношения вида
Q СУ,) = «nJi + «и Уа т • - • + а,^го
Q Ы = «21 Jl + «22.У2 + • • • + ОатУт,
Q (Ут) = amlyt 4- ат.гу.г + ... + атт ут.
Пусть
У + + +
тогда
при условии, что k и постоянные с удовлетворяют уравнениям
kcr = ап сг + ап с2 -f ... + crracni (r = 1, 2,.... mj.
Чтобы эти уравнения были совместны, необходимо, чтобы k
было определено соотношением
ап — к, а12,..., аш ! = 0.
С21' а22 п,. . ., О2т
ml' "m2> ¦ • •» &mm " \
Таким образом соответственно каждому h существуют т зна-
значений постоянной к (не обязательно явных), так что уравнения
(A) Р(у)— hy = O,
(B) Q (у) — ky = О
имеют общее решение.
Соответственно каждому к в выражении (В), существуют п
значений h в выражении (А) таким образом, что (А) и (В) имеют
общее решение. Так, если (А) и (В) имеют общее решение, то h
и k относятся друг к другу согласно алгебраическому уравнению
F(h,k) = 0
степени п относительно h и степени т относительно к. Это
выражение может быть получено исключением
У г У ¦> • • • г У '
из т -\- п уравнений
DP (у) — hy' = Q, DQ <у) - ky' = О,
Г)п—1 р (,Л liyin—l) — П Г)т~1 О (v\ kvl.'n—l) — О
174
Поскольку
P(y)-hy = 0
F(P, Q)y = F(h, k)y = 0,
и следовательно у является решением уравнения
L(y) = F(P, Q)v = 0
порядка /ига.
Пусть числа
hx, h2,..., /гг
будут независимыми и пусть
будут общими решениями
PQ0— Л^ = 0, QO') —*У = 0
для данных значений /г и соответствующих значений k. Эти
функции К^ Г2,..., Уг линейно независимы, так как если бы
существовала тождественная зависимость типа
то, действуя на левую часть этого тождества при помощи Р,
Рг,..., Рг—г, мы получили бы соотношения
С^! Ух + C2h2 Y2 + ... + Crhr Yr = 0,
Ci V ^i + Q /г/-1 Г2 + ... + Cr /г/-1 Yr = 0.
Но эти соотношения не являются совместными, если только Сг*
С2 Сг не равны нулю. Это верно, независимо от числа
выбранных независимых чисел /г.
Таким образом существует неограниченная последователь-
последовательность линейно независимых функций F,, F2,... , удовлетворяю-
удовлетворяющих уравнению
Но порядок этого уравнения равен тп, и следовательно оно не
может обладать более чем тп линейно независимыми решени-
решениями. Отсюда следует, что
F{P, Q) = 0
тождественно.
Это приводит к основной теореме, что, если Р и Q явля-
являются коммутативными операторами порядка т и п соответ-
соответственно, то они тождественно удовлетворяют алгебраическому
соотношению вида
F(P,Q) = 0
степени га относительно Р и степени т относительно Q.
175
Так например, если
Р = D* — 2хг-,
Q = D3 —
то
РЗ = Q-2
и уравнения
(P — h)y = 0, {Q~k)y
имеют общие решения, если
/г3— /г2 = 0.
1. Если уравнение
S+
преобразовано подстановкой л: = С (?) в
докажите, что
и проинтегрируйте уравнение
2. Докажите, что Xs и л~8 являются решениями
rf2y 6
и получите частный интеграл
6
. 5- v = X log
* х2 - 6
Проинтегрируйте уравнение
при условии, что приведенное уравнение имеет частное решение вида у = х"-
4. Покажите, что любое однородное самосопряженное уравнение порядка 1т
может быть написано в виде
,т ,т—1
-V К/"*} + ~-т_, {Аг/т-»} + ... + Ату = 0.
dx dx
Исследуйте соответствующую теорему для уравнения порядка Ъп + l.[Bertand>
HesseJ.
5. Докажите, что если общее решение и = и (х) уравнения
известно для всех значений h, и любое частное решение для частного значения
176
hx равно и = f(x), то общее решенне уравнения
для /г ф hx имеет вид
[Darboux, С. R. Acad. Sc. Paris, 94
A882), 1456;Thfeorie des Surfaces, II, 2101-
6. Принимая начальное уравнение
-т-2= Ли
ЙЛ.2
ири Aj = 0, проинтегрируйте уравнение
Повторяя процесс, проинтегрируйте
fy_ (т(т- 1) )
их2"" { х3 ' I '
[Darboux]
где т — целое число.
7. Принимая то же начальное уравнение, но при h± = — I, проинтегрируйте
?у _ fm(m-l) п(п~\) , )
dx* ~ | sn2x + cos2* T ,'
[Darboux].
где т и и — целые числа.
О. Лине-.1Я3—12
ГЛАВА VI
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФИ-
ЦИЕНТАМИ
6-1. Линейный оператор с постоянными козфициентами. Одно-
Однородное линейное диференциальное уравнение с постоянными
коэфициентами
dx
— первое уравнение общего типа, которое бкло полностью
решено1. Но, независимо от его исторического значения, уравне-
уравнение имеет ряд важных практических приложений и представ-
представляет теоретический интерес вследствие простоты своего общего
решения. Соответствующее неоднородное уравнение2
- Al ,-r-f + ¦ • • + Д1-1 йг + Anv = fix)
также имеет ряд важных приложений.
Предположим, что Ло не равно нулю; остальные коэфи-
циенты могут быть равны нулю. Уравнение (А), может быть
переписано в виде8
F(D)y E (A0D- + A.D"-1 +... + An-i D -f Ajy = 0,
и имеет оператор, который может быть разложен на множители
A0{D-al)(D-as)...(D-an),
где а,, а2, ..., а„ — постоянные, именно корни алгебраического
уравнения
(С) ло=» + л.Г-1 +... + л„_,р; + д, = а
Множители
D — alt D — a.z, ..., D—an
коммутативны; отсюда следует, что данное однородное урав-
1 Это решение было известно Эйлеру и Даниэлю Бернулли еше в 1739 г.
Впер.чые опубликокано Эйлером [Misc. Berol, 7 A743), 193].
2 D'Alembert, Misc, Taur., 3 f 1762 —65), 381.
3 Обозначение F(D) было введено Коши. см. Ечег bes math., 2 A827) 159
[CEuvres B) 7, 198].
178
пение удовлетворяется решением каждого из уравнений первого
порядка '
6-11. Решение однородного уравнения. Пусть уг будет общим
(D-ar)y = 0,
решением
тогда
следовательно общее решение (А) будет иметь вид
где Clf С2> ..., С„—произвольные постоянные; а„ а2, ..., а„
приняты неравными. Случай, когда алгебраическое уравнение (С)
имеет одинаковые корни, мы сейчас рассматривать не будем.
Предположим, что коэфициенты Ао, Л„ ..., Ап — вещественны,
так что а„ ..., ап будут вещественными или сопряженными
мнимыми числами. Приведенное решение соответствует случаю,
когда аъ ..., ап в щественны, но требует некоторого измене-
изменения при одной или больше пар сопряженных комплексных ве-
величин. Например, пусть аг й as будут сопряженными комплекс-
комплексными числами
ат — о. -f i3, as — i ~ $,
тогда
может быть написано в виде
Сге{а :i})x + С^"-'3) х - = е"х {С,, (cos $x -f i sin р
+ Cs (cos ,8л: — i sin ,3л:)}
-= p"v {G cos ,8л + C'ssin,8л},
где
Cr = Cr -f- Cb) Cs = i f Cr — Cs).
Число прсизвольных постоянных останется поэтому прежним.
В виде примера рассмотрим уравнение
Корни
?з д. |2 _ 7; _ 15 = q
равны
3, - 2 -f /, - 2 - i,
следовательно общее решение будет иметь вид
у — Сге3х -f" е~'х (С2 cos л + С3 sin л).
179
6-12. Кратные множители. Пусть оператор
Л0О" + AxDn~ '+... + Ап-, D + Ап'
будет иметь кратный множитель, например
(D~a)p.
тогда общее решение
(D-afy = 0
будет включено в общее решение (А). Одно решение, соответ-
соответствующее этому множителю, известно, именно
где С — постоянная. Чтобы найти общее решение, применяют
метод вариации параметров. Напишем
где V — искомая функция, тогда
(D - af еах V = {D- а)р~' еал DV
= (D - af-~ eax EPV
= ...= enxDpV,
Следовательно у — е"х V будет решением
(D-afy = O.
если V — решение
D" V = О,
отсюда V — произвольный полином от х степени р—1. Таким
образом искомое решение будет иметь вид
у -.= (С, + С,х +... + СрхГ-1)е'х
и содержит р произвольных постоянных.
Наконец, при двух сопряженных мнимых числах в множителе,
повторяемом р раз, например
(D - а + %f (D - о. - #/',
соответствующее решение будет иметь вид
у =г. (Q + С«х +... + Срх"~1)е"х cos $x f
+ {С[ + С*х + ... +С'Р х"-1) е" sin Bx),
при соответствующем числе 2р произвольных постоянных.
180
Так, общим решением
будет
у = (С4 + С^х) cos л; + (С, + С4л) sin л.
6-13. Дополнительная функция. Дополнительная функция лю-
любого линейнего уравнения была определена как общее решение
соответствующего однородного уравнения. Теперь, когда все
случаи, которые могут возникнуть при постоянных коэфициен-
тах, были рассмотрены, важно определить, является ли полу-
полученное решение наиболее общим.
Сначала рассмотрим случай, когда
v -- Сгещх + аеа"-х + ... + С„еа» *
и числа аг, а2, ..., аш которые могут быть вещественными или
комплексными, различны. Если
= а, + а.2 + • • - + ап
то вронскиан решения будет иметь вид
1, 1, ..-, 1
ал а., .... а„
esx
III • ^о у • • • > "п
он не может быть равен нулю, поскольку а;:| а,, Полученные я
функций
С I fc , . . . , С
поэтому линейно-независимы, а
V = С,еа л 4- Сов"**-\- . •. -\-С„е"п Л
является общим решением.
Рассмотрим теперь крайний случай, когда все значения а
равны, тогда
у = (C1 + Csx+...-\-Cnx"-1) е"х.
Если для любых частных значений постоянных С у тожде-
тождественно равен нулю, то выражениеС1 -j- С%х +•.. + Спхп~1 также
будет тождественно равно нулю, что возможно только при С, =
^=С2 = .. . = С„ = О. В этом случае решение также будет общим.
В любом другом случае решение получится вида
р ра'х _l р Ра'-Х I 4- Р р°тХ
где Р,, Р«, ..., Рт — полиномы от х, а числа аг, а2, ..., ат —
181
различны. Покажем, что функция такого рода не может быть
тождественно равна нулю, если только полиномы Р не равны
тождественно нулю. Примем, что
РгеХ И- Р,еа'х -J-... -f Ргое0<пЯ -= О
тождественно. Пусть
bk -ak — alt
тогда тождество может быть написано в виде
Рх + Р°/"-Х -г ¦ • • + РУ' = 0.
Пусть Tj будет степенью полинома Р„ тогда, если тождество
продиференцировать гх 4-1 раз, оно примет вид
Q2e6**+-... +<?„/** = 0,
где Q2( ..., Qm—полиномы, степени которых равны степе-
степеням Р2. ..., Р„, соответственно, а числа &,. ..., Ьт неравны.
Если мы этот процесс будем продолжать, то достигнем сту-
ступени, при которой
/?„/-* = 0
тождественно, где Rm — полином, степень которого равна степени
Рт. Отсюда, Rm должен тождественно обратиться в нуль, что не-
невозможно. Следовательно
Рг€а^ Л- р р"'х Л- _'_ О рат*
i Т ' 2е i • • • i "тУ
не равно тождественно нулю.
Исследование дополнительной функции может поэтому счи-
считаться полным.
6-14. Кратные множители как предельный случай. Весьма хо-
хороший метод решения, когда оператор
Л0О« + AxDn~l -f... -Ь А_, D + Ап,
имеет кратный множитель, принадлежит Д'аламберу1. Так как
применение этого метода не ограничивается случаем, когда ко-
эфициенты постоянны, допустим, что уравнение имеет вид
d"y . dn~lv , dv , „
Ро dxn + Pi ~^=i f ¦ • - -7-Pn-i ^ + Р«У = °.
где ро, />„ ..., /7„ зависят от некоторых параметров
а„ а.2, ..,, a;i.,
и возможно также и от л.
Пусть функция f(x, г) для некоторых значений г, завися.щих
от параметров гь а2, .... я„ будет удовлетворять уравнению и
1 Hist. Acad. Berlin, 1748, 283.
182
пусть
будет последовательностью значений г, выбранных таким обра-
образом, что функции
f(x, гг), fix, г2), ..., f(x, г.)
в общем случае независимы. Эти функции представляют собой
следовательно последовательность v частных решений уравне-
уравнения. Для частных значений а1з а2, ..., а„. два или больше зна-
значений г, например гх и г.2, и соответствующие функции f(x, гг)
и f(x, i"s) будут равны, поэтому число решений уравнения, пред-
представленного функциями f(x, r), уменьшится. В данном случае
предельное значение
fix, rj)-fO±rd
если предел существует, будет решением уравнения. Этот предел
имеет вид
г)-
\df(x, г)
L дг
Случай, когда г„ г.2, и г3 равны, может рассматриваться ана-
.логично. Функция
удовлетворяет уравнению, и если существует предел этого вы-
выражения, т. е. .
то он будет решением уравнения.
Вообще, если для частных значений параметров %, я2, ...,a,i.
то уравнение имеет и решений
f(x г ) Г df(x' r) I
Рассмотрим уравнение
Заменим его более общим уравнением
последнее уравнение при я21^62 имеет общее решение
у — Ах cos ах -f Аг cos 6л -j- Л3 sin ял + .44 sin рл.
183
При а = ,8 — 1 это решение перестагт быть общим и приво*
дится к
у = С, cos л; + С3 cos л;,
но функции
U-cos ах xsn h
= —xsinx, hp sin зл:
являются частными решениями, которые не могут бэ1ть полу-
получены ни при каких значениях С,, и С3. Следовательно общее
решение данного уравнения будет иметь вид
у == (Q + С2х) cos х -f (С8 + С4л) sin л:.
6-2. Неоднородное уравнение. Определение частного интеграла
неоднородного уравнения зависит от свойств операторов, об-
обратных D, D— а и т. д., так как задача состоит в определении
значения выражений *
Оператор, обратный D, равен D~~l и представляет операцию
простого неопределенного интегрирования; аналогично D~~pяв-
D~~pявляется операцией /7-кратного интегрирования. Нужно теперь
.найти значение операторов (D — af и (D — dj~p, где а — по-
постоянная, не равная нулю.
Чтобы сделать эти операторы возможно более определен-
определенными, исключим вводимый ими элемент произвольности. Так же
как воздействие оператором D~l вводит произвольную аддитив-
аддитивную постоянную, а (в более общем случае) воздействие опера-
оператором П~р вводит произвольный элемент С, + Csx + ... +
-j- CpxF~l, так и (D — с) вводит произвольный элемент Сеах, а
Ц) — а)~р вводит еах {Сх + С2х +... + Срхр~1.) Эти выражения
входят в дополнительную функцию, поэтому они не будут рас-
рассматриваться при определении частного интеграла.
Если f(x) — функция простого типа, то эффект воздействия
на f(x) оператором (D — ay1 или (D — a)~p получается следую-
следующий2.
1°. Пусть
f(x) = ekx, k = const.
Воздействуем на обе стороны тождества
(D - с) ekx =(k-a) ekx
1 Lobatto, Theorie des caracleristiques (Amsterdam, 1837); Boole, Camb.
Math-J, 2 A841), 114.
2 Ниже оператор D непосредственно воздействует на функции независи-
независимого переменного х, что в общем случае недопустимо. Прим. ред.
184
оператором (D — a) l {k — a) i, получим
(D - a) ekx = [k - a) ekx
если кфа. Случай k = a будет разобран ниже.
Аналогично
(D - а)-1 ... (D - a,,)-1 е** - (А - д.) .. . (Л - с,,)-1 <>**
при условии, что G] ..., ар отличны от к. В частности
(В-аГРекх = (к-аГРекх.
Если /^(D) — полином от D, так что F(k)zf-.O, то
где Z7 (D) — оператор, обратный F(D).
2°. Пусть
*
В тождестве
(D - a)e*v^ --= е"'(D + k-a)X,
где X — произвольная функция от х, напишем
(D+k-a)X-=<t(*).
тогда
(D - a) ekx(D + k - a) ? (x) - ех ш (х),
следовательно
(D - с)" * екх <р (л) = е*Л (D + Л - с) <р (л).
Аналогично можно доказать, что в общем случае
(D - at)-j... (D - аРГ> екху (л) = ех (D + k - а,)'1...
...(D + k — ap)~\(x)
или
F-1 (D) е"ч (х) = екхF'* (D -f k) ш (х).
В частности, принимая k = a, = a2 = ... = ар = a, '.c(.v) — I,
получим
(D — a)-p(fx = eaxD-p- 1
следовательно специальный случай учтен
3°. Пусть
/(х) = sina-x.
Если /^D)—четный полином от D, напишем F(D) = Ф (D^) так,
чтобы Ф(О2) был полиномом от D2, тогда
Ф (D2) sin ах = Ф (— a2) sin ал,
откуда
г—1 ,r*.\ . Sill ЯЛ*
/=• (D)sin ал - ф-.-^--
В наиболее общем случае полином ^(D) нечетный; если он
имеет четный полиномиальный множитель G(D), то F(D) =
G(D)H(D), тогда
F-1 (D) sin ex = -щщ^щ sin ал
G (D) h (D) НЧ— D)
sin ал-.
Теперь G (D) И (D) Н(—D) — четный полином от D и может
быть выражен через K(D2) следующим образом:
F-1 (D) sin ax = -?=$- sin ax
H(—D) .
следовательно F~x (D) sin ел и аналогично F (D) cos ax могут
быть вычислены при условии, что К{—а'*)фО.
Комбинируя данный случай с предыдущим, можно вычислить
частные интегралы вида
f-1 (D) e" sin ax, F~l (D) ekx cos ax.
Пример:
CD2 + ID — 8) v - 5 cos л.
Частным интегралом является
_ 5
У ~ ~3D*~+2D^^ COS X
5'3?>2 — 2D — 8)
\3D*'+~2D~—"8)"C752 — 2Z? — 8) COS Л
5(ЗД2— 2D — 8)
QDi — 52D2 + 64 C0S X
5 CD2 — 2D—8)
г,-,--- COS Л
S + 52 + 64
= ^ {CD* - 8) — 2D J cos л - ^ B sin x— 11 cos *).
4\ Пусть
1?S6
тогда
(D — a)xn = nxn-v— ax",
)nz n(n \)n
X a X
r\ n(ti-l)...3 2 nl л<я-1)...3.2
,„ . га! и!
(D-a) j = - ;_, .
Отсюда
следовательно
Этот результат может быть получен формальным разложе-
разложением оператора (D — а)" по возрастающим степеням D. Отсюда
следует, что если X— полином от х степени п, то
F-1 (D)X -= (а0 + a,D + ... + anDn) X,
где
первые n -f-1 членов F~X(D).
Обратный диференциальный оператор /;~1(D) может быть
разложен на простейшие дроби как выражение, обратное поли-
полиному. Следовательно указанного достаточно для определения
частного интеграла в случаях, когда функция f{x) является
суммой членов или произведений членоЭ вида х", и ekx, sin ax
и cos ax. Члены, содержащие синусы и косинусы, могут быть
выражены также в экспоненциальной форме.
6-21. Определение частного интеграла в квадратурах. Если функ-
функция f(x) такова, что f{X) и e^axf(x) интегрируются, то частный
интеграл может быть определен в квадратурах. Предположим,
что F(D) не имеет кратных множителей. Тогда оператор F~1(D)
может быть разложен на простейшие дроби
m— a,-
г- 1
187
Частный интеграл получается вида
у = Уго^
г = 1
r=l
Нижний предел интегрирования может быть произвольным,
так как член, полученный при постоянном нижнем пределе
интегрирования, равен постоянной, умноженной на еа>"х ,исле-
довательно входит в дополнительную функцию.
Рассмотрим случай, когда F(D) содержит множитель (D — a)f>.
Часть выражения F (D) в простейших дробях, соответствую-
соответствующая этому кратному множителю, имеет вид
и соответствующим добавочным выражением к частному инте-
интегралу будет
V
Пример:
-g—
Дополнительной функцией будет Ле2* -ffie-2v. частный инте-
интеграл может быть написан в виде
^ Л
_ i_
}8s
— 2 D+2)
¦X
2tdt — 4е ¦-*$№ udt.
Нижние пределы интегрирования выбраны такими, чтобы воз-
возможно больше упростить частный интеграл. Интегрируя по
частям, получим
у = е*х%.
6-3. Линейное уравнение Эйлера. Уравнение типа
где Ао, Аь ..., Ап~ постоянные, называется уравнением Эйлера].
Оно может быть преобразовано в линейное уравнение с по-
постоянными коэфициентами подстановкой х = ez, тогда
Х их ~Тг-
где D обозначает ~^-, и аналогично
dz" dz
xn~y-~ = D{D - 1) ... (D - tl + 1)y;
dx"
уравнение таким образом приводится к виду
F(D) у = (A0D" + A'.D'-1 +...+ A'n^D + Ап) у =-./(* ) ¦
и может быть решено приведенными выше способами.
Простой множитель (D — а) оператора F(D) приводит к члену
дополнительной функции вида
Сеа~ = Сх",
в то время как кратный множитель (D — a)p приводит к
у - е°* (С, + C2z +... + CPzP~i)
¦= х" {Ct + С: log x + ... + Cp{ log я)"-*}.
Это решение особенно важно; оно может быть получено и при
помощи метода Даламбера. Так как у == ха — решение однород-
однородного уравнения, соответствующее р-кратному множителю отно-
1 Его общее решение было известно Джону Бернулли еще в !700 г. Иссле-
Исследование этого уравнения Эйлером было проведено приблизительно в 1740 г.;
опубликовано в Inst. Calc. Int. A769), 2. 483. Более позднее исследование про-
проведено Коши: см. также Мальшшен [Malmsten, J. fiir Math., 39, A850), 99].
1S9
сительно F(D), то
У л -= \ 4-ха \ -=-- \ 4-е"log х] "= х° log х,
I ' J а-¦«
также являются решениями однородного уравнения.
Аналогично, уравнения типа!
I О
(где а, Ь, А,- (а ф 0) — постоянные) можно решить подстановкон
ах + b =--= ег.
Частный интеграл может быть получен в квадратурах мето-
методом, аналогичным принятому для уравнения с постоянными коэ-
фициентами.
Пусть ft обозначает оператор х--, тогда, поскольку2
оператор
А .
1, +
может быть написан в виде
F{b) = А0Ъ« + А'^-Ч- • • • + А';1, J + Л,, ¦
а функция F(b) может быть разложена на линейные множители
(Ь) = Ао($ - а,)(Ь - а.2) ...(»- ап).
Теперь
Лт — л? = ]Л (;i — 1) . . . (и — т + 1
так что
F (») л* = ;№/по-
;№/последовательно если а таково, что /7(а) = 0, то
у =- Аха
является решением однородного уравнения
1 Lagrange. Misc. Taur., 3A702 — 65), 190 (CEuvres, I, 4«1].
- Если .-с = ^г , 8 = x — и D - -^-, то » = ?)
Aа- йг
19U
Так же, если X является функцией от х, то
И
Ътх* X = х» @ +
откуда следует, что
Подставляя у(х) вместо /7@-|-а)Л' и воздействуя оператором
F~J (&) на обе стороны этого тождества, получим
F > ((Оя* ъ (х) - дс"^-1 @ + р)«Р (л).
Если /^@) не имеет кратных множителей, то обратный опе-
оператор F~% ф) может быть разложен на простейшие дроби
n
1
так как ^аг(8 —ar) \ будучи умножено на F($), равно еди-
единице. Частное решение неоднородного уравнения следовательно
будет
"'f(x)}
г I
Если Z7^) имеет кратный множитель, например D — а/, то
соответствующая часть рациональной дроби /•"~| @J получится
вида
7-1
Соответствующими членами частного интеграла будут
р
= 'S^
p
= V
r i
?rxab-'+i
X
t
\...
1 af{t)
t
- /r'
—g j:/j
t г a.
)de
f{t)df
Пример:
dxl dx '
Это уравнение может быть переписано так:
(» - 2J j/ = 2дсэ;
дополнительной функцией будет
Частный интеграл получится вида
1
Л'
1 log л:
= 2x*jjr1 log tdt = {x log xJ.
i
6-4. Системы совместных линейных уравнений с постоянными
коэфициентами. Выше (§ 1-5) мы отметили, что одно линейное
диференциальное уравнение может быть заменено системой со-
совместных уравнений порядка ниже п, в частности системой п
совместных уравнений первого порядка. Возникает вопрос: яв-
является ли система совместных линейных уравнений эквивалент-
эквивалентной одному линейному уравнению, в том смысле, что общее
решение системы содержит таксе же число произвольных посто-
постоянных, что и полное решение одного уравнения. Этот вопрос
мы здесь разберем, предположив, что рассматриваемые уравне-
уравнения имеют постоянные коэфициенты К Такие уравнения встре-
встречаются во многих задачах динамики и имеют следовательно
и теоретический и практический интерес.
1 Первоначальное рассмотрение проблемы, проведенное Якоби, было недо-
недостаточным; тщательное исследование эквивалентности двух систем совместных
линейных уравнений было проведено Кристалем. Trans. Roy. Soc. Edin., 38
A895), 163.
192
Суть проблемы станет ясной, если рассмотреть систему
трех однородных линейных уравнений с тремя зависимыми пере-
переменными
Fit
F»
FSl
(D)y1 -
{D)y1-
(D)yx-
rF12
±FS2
(D)y2-
(D)y2 -
(D)y2-
^FiS
f^83
ФK'з = 0,
(D)ys = 0,
где Frs{D) — полиномы относительно оператора D с постоянными
коэфициентами, а х — независимая переменная.
Переменная ys может быть исключена из этих уравнений про-
процессом, аналогичным алгебраическому исключению, как если бы
операторы Frs(D) были постоянными. В результате получим
или
Fv.
F2l
Fsl
ID),
(D),
(D:,
F12
F22
' 32
(D),
(D),
(D),
F(D)yt
F»
F23
FS3
= 0
(D)
(D)
(D)
Это уравнение существует, если F(D) не равно нулю, т. е.
если все три уравнения данной последовательности действи-
действительно различны. Аналогично
F{D)ys = 0.
Выражение F(D) может быть постоянным, тогда единственно
возможным решением будет
или, иначе говоря, уравнения несовместимы. В общем случае F(D)
является полиномом от D степени т. Пусть множителями F(D)
будут
D — au D — a2,..., D — am
и предположим, что ata2 ат все различны. Решение F(D)y1=0
будет иметь вид
уг = Спеа>х + С12еа'-Х +... + С1теа™х
и, аналогично, решениями F{D)y2 = 0 и F(D)y3 = 0 будут
Уз = Csleax + Съ2еа>х +... + С3те"™х
соответственно. Всего в эти решения входят Зт постоянных,
но эти постоян".ле не все независимы. Так как уи у2,у3 должны'
удовлетворять данной системе, то эти постоянные связаны
Э. Айне—133—13 J93
соотношениями
CvFn
CirF21
ClTF3l
(ar) + С
{ar)+C
irFn(ar)-\-
Г1 F In } —
¦CtrFn(ar) =
- CsrFSs (ar) =
c,
0,
0
(r = I, 2,...,m), и если этих уравнений достаточно для опреде-
определения всех отношений С1Г: С%г • Сзг, то число постоянных умень-
уменьшится до т. Порядок системы, равный числу независимых
постоянных в его общем решении, всегда равен порядку харак-
характеристического детерминанта F(D), однако сделанные допу-
допущения не всегда действительны. Трудность заключается в том,
что если ух, у2, ys образуют общее решение системы, то может
случиться, что ни одна из функций уи у2, у3 не будет удовле-
удовлетворять характеристическому уравнению
F(D)y = 0.
Перейдем к строгому доказательству теоремы, что порядок
системы равен порядку характеристического уравнения. Сна-
Сначала установим необходимое и достаточное усло'вие для экви-
эквивалентности двух систем линейных уравнений, не обязательно
однородных и с постоянными коэфициентами.
В виде примера рассмотрим систему
U ~ (D* + l)yt + (D* + D + l)y, = х,
Ее характеристический детерминант приводится к постоянной,
откуда следует, что решение системы не должно содержать
произвольных постоянных. Рассмотрим производную систему
U—DV = x — ex;
Эта система приводится к
откуда
Это является решением данной системы. Исследование пока-
показывает, что если детерминант системы множителей, равный
в этом случае
1, -D
D, — D»—1
постоянный, то данная система и производная система эквива-
194
ленты и имеют одинаковые решения. Следовательно, в этом
случае общее решение не имеет произвольных постоянных.
6-41. Условия эквивалентности двух систем линейных уравне-
уравнений. Пусть
Fr s (D) у, + />, (D) у, + ...+ FTn (D)yn = fr (x)
(r= 1, 2,..., m),
On №)У1 + Gr2 (D)y,+ - ¦¦ + Grn (D)yn = gr (x)
(r = 1, 2,..., m)
будут двумя системами линейных уравнений с и зависимыми
переменными
У г, Уъ---> Уп,
где п > те. Предположим, что т уравнений каждой последова-
последовательности линейно-независимы, а операторы F(D) и G(D)—по-
G(D)—полиномы от D с постоянными коэфициентами. Обе системы могут
быть выражены соответственно в виде
(U) ?/, = 0, ?/а = 0,..., Um = О,
Если каждое решение (U) удовлетворяет (V), то система (V)
называется производной от системы (U). В этом случае любое
уравнение (V) может быть получено воздействием на уравне-
уравнения (U) полиномов от Пи сложением полученных результатов.
Так
Последовательность операторов lTS, при помощи которой си-
система (Vj выводится из системы (U), называется системой мно-
множителей, а детерминант
* __
ее модулем. А не может быть равен нулю, так как уравнения (V)
линейно-независимы.
Если (V) — производная система от (U) и каждое решение (V)
удовлетворяет (U), то системы называются эквивалентными.
Докажем, что для того, чтобы две системы были эквивалентны,
необходимо и достаточно, чтобы их модуль был постоянным.
Пусть детерминант
> "ram
195
будет обратным Д, тогда Ult... Um могут быть выражены че-
через VXl..., Vm в виде1
отсюда любое решение (V) удовлетворяет системе
Следовательно, если Д — постоянная, то каждое решение (V)
удовлетворяет (U). Указанное условие поэтому является доста-
достаточным. Чтобы доказать, что оно необходимо, примем, что си-
система (Uj — производная от системы (V). Тогда будет существо-
существовать последовательность полиномов от D, например 3ri, таким
образом, что
Замещая значения Vi,..., Vm через ?/,,..., Um, найдем, что
Ur = Ki (8u иг+... + Ьшит) +... +Km(lmlU1+.. . -r
+ <mUm) (r=l,2,..., m).
Ho Ut..., Um линейно-независимы, следовательно
Kl 4s+ ¦ . ¦ +Km bms = 0 (Г ± s),
Для каждого значения г для определения <СЬ..., S,m имеется
/га уравнений; их решение будет
следовательно, если Д'— модуль системы множителей 8,Л то
Л' =
hi,. •., \
Д\ j
1т, • • •, ^тт \
где Д и Д' — полиномы от D. Тождество
ДД' = 1
не может быть удовлетворено, если Д и Д' не зависят от D
т. е. если Д и Д'—постоянные. Следовательно это условие явля-
является необходимым и достаточным.
1 Scott and Mathews, Theory of Determinants, VI и XI.
196
6-42. Другая форма условий эквивалентности. Приведенная
форма теоремы эквивалентности полностью содержит систему
множителей; другая форма этой теоремы, не требующая непо-
непосредственного вычисления системы множителей, может быть
выведена следующим образом. Поскольку
Ur a Fri iD)yt 4- -.. -г Frn(D)yn—Mx),
1/, = Gn (D) у, +. .. -f GPH (D) Vn~gr (x)
и
Vr — on L'j-f-.. . +orm ?/m,
то, сравнивая операторы от ylt..., yn и подставляя Frs и Grs
вместо /у>(??) и Grs(D), получим
Gr, — Sri F, j +... o-orraFnni
f» — °п ' m"t" • • • T°rm 'mm
Из этих уравнений получим
1 "Ml
в том смысле, что каждый детерминант х порядка /я, столбцы
которого являются столбцами первой матрицы, равен соответ-
соответствующему детерминанту второй матрицы, умноженному на по-
постоянную Д. Это условие необходимо и достаточно для экви-
эквивалентности систем.
В частности, если имеется столько же уравнений, сколько
независимых переменных, именно и, то
n,..-, G,n| = Д Fn,..., Fin
И щ> ¦ • ¦ t ' nn I
Поэтому для того, чтобы две однородные системы п уравнений
с п независимыми переменными были эквивалентны, необходимо
и достаточно, чтобо1 детерминанты операторов обеих систем
были равны, будучи умножены на постоянную. Если системы
не однородны, то это условие является также и необходимым;
остальные требования, необходимые для достаточной последова-
последовательности условий, легко могут быть найдены.
1 Нужно отмртшь, что при вычислении детерминантов, содержащих f(x) и
g(x), операторы F и G умножаются на f(x) и g x), а не воздействуют на них.
Так, общий член разложения детерминанта первой матрицы равен
G21 CM G42,..., а не G.21 G34 G42... gt (x).
197
6-5. Приведение системы линейных уравнений к эквивалентной
диагональной системе. Система линейных уравнений вида
ы(D)y, -f Нл(D)y9+... + Hln{D)уп = hx[x),
г2 (D) у, + Нгз (D)y3 + ...+ Иы (D) у г. =1к(х),
^зз (D)ya+... + HSn {D)yn = А, (л),
где первое уравнение содержит _у„ второе уравнение содержит
у2, но не содержит у1г третье уравнение содержит j/3, но не со-
содержит yt и у2, а последнее уравнение содержит только уп,—
называется диагональной системой1. Операторы HutD), H22{D),
• - •, Нпп (D) называются диагональными коэфициентами. Каж-
Каждая зависимая переменная связана только с одним диагональ-
диагональным коэфициентом; форма этой связи называется диагональным
порядком.
Докажем теперь, что каждая система детерминантов ли-
линейных уравнений с постоянными коэфициентами может быть,
приведена к эквивалентной диагональной системе, в которой
зависимые переменные имеют определенный диагональный по-
порядок. Предположим, что диагональный порядок является по-
порядком возрастающих индексов, как в приведенной выше схеме.
В качестве предварительной леммы докажем, что если
*Л = Fu (Diyi + ... + Fln (D) у„ -Л (х) = О,
U» = Fai (D,yi +... + FZn (D)yn -U (x) = О
— два уравнения, содержащие некоторую зависимую перемен-
переменную, например уг, то они могут быть заменены эквивалентной
парой уравнений, одно из которых не содержит у,. Если такая
эквивалентная пара уравнений существует, то она будет иметь
вид
где L, M, L', М'—полиномы от D с постоянными коэфициен-
коэфициентами, так что
LM' — L'M
будет постоянной. Пусть Г будет наибольшим делителем Fn (D)
и F21 (D), тогда
FU(D) =ГФ. Ftl(D) = F?
где Ф и W — полиномы от D, не имеющие общего множителя
Пусть
L = W, Ж-—Ф,
, гО, t z/- k
1 Обычно диагональной системой называют систему вида: Mik = 1 ^. ?-_^
Прим. ред.
19S
тогда в
не будет члена, содержащего yt. Поскольку L и М являются
взаимно простыми относительно D, полиномы L' и М могут
быть определены1 таким образом, что
LM' - L'M
будет постоянной, не равной нулю. Следовательно лемма уста-
установлена.
Теперь, пусть данная система
?/, = 0, .... Un=0
будет расположена таким образом, что любые уравнения, не
содержащие ylt будут находиться в конце системы. Пусть Ur =
=0 будет последним уравнением, содержащим уи тогда Ur-i —
= 0и Ur—0, могут быть заменены эквивалентной парой уравнений
Ur-i = 0 и Ur — 0, второе из которых не содержит ух. Анало-
Аналогично, Uг—г = 0 и U,-\ = 0 могут быть заменены эквивалентной
парой Ur-2 = 0 и иг—г = 0, из которых второе не содержит
_у,. Этот процесс может быть продолжен до приведения к экви-
эквивалентной системе
V, = 0, ..., Va = 0,
где только V1 содержит у1. Vx должно содержат Vn поскольку
первоначальная система является определенной. Исключая Vx=
— 0, получим систему
к2 = о,.... va = о,
которая содержит все остальные переменные у2,—,Уп', она ре-
решается аналогично относительно у2 и может быть приведена
к системе
W2 = 0, .... Wn=0,
где только W2 содержит у2, Процесс повторяется до достиже-
достижения конечной диагональной системы.
6-501. Пример приведения к диагональной системе. Рассмотрим
однородную систему
(D - l)jf, + Dy2 + (D - 1) y3 = 0,
Ух +3'2+ 1>Уз =0.
При помощи системы множителей
I-X.D Ч
V— 1, D—V
1 Chrystai, Algebra, I VI. § 11.
199
последние два уравнения могут быть замещены двумя эквива-
эквивалентными уравнениями, одно из которых не содержит у1г таким
образом система примет вид
(D + 1)уг = D*y2 + (D + l)j/, = О,
Воздействуя на первые два уравнения этой эквивалентной пос-
последовательности системой множителей
1—1, D + 1.
последовательность уравнений примет вид
- Vi - D*y2 + (D3 - D3 - 1) v3 = 0,
Наконец, применяя систему множителей
/ 0, IX
V— 1, D4
к последней паре уравнений, получим диагональную систему
- 0,
(D4- 3D3 + D* + D)y3 ¦= 0
Последнее уравнение легко решить относительно у3, после чего
второе и первое уравнения дадут соответственно уг и уг.
6-51. Свойства диагональной системы. Доказательство фундамен-
фундаментальной теоремы. Пусть t/1==0, ..., Un = 0 будет диагональной
системой. Очевидно произведение диагональных коэфициентов
будет ее детерминантом. Это произведение равно постоянной,
умноженной на детерминант системы, эквивалентной данной
диагональной системе.
Диагональная система может быть решена непрерывным
приложением методов, приведенных в предыдущих параграфах
настоящей главы, для решения отдельных линейных уравнений
с постоянными коэфициентами. Пусть «>, будет степенью диаго-
диагонального коэфициента уг в D. Последнее уравнение системы
дает общее значение ддяуп, с определенным числом ш„ произ-
произвольных постоянных. Если мы подставим значение для уп в пред-
предпоследнее уравнение и пешим это уравнение для уп—х, то мы
200
введем некоторое число ш„_х дополнительных произвольных по-
постоянных. Этот процесс затем повторяется; в общем случае
выражение для у, введет шг новых произвольных постоянных,
в дополнение к некоторым или ко всем произвольным постоян-
постоянным, которые входят в уравнение для уг , вследствие того, что
это уравнение может содержать полученные ранее выражения
Поскольку шг постоянных, введенных процессами интегриро-
интегрирования относительно уг, являются новыми постоянными, совер-
совершенно отличными от постоянных, содержащихся вуг+ъ..., у„,
общее решение системы будет содержать" шх +ю2 + .. .ш„ посто-
постоянных, ни одна из которых не будет лишней. Общее число не-
независимых произвольных постоянных в полном решении системы
следовательно равно степени ее детерминанта.
Отсюда следует основная теорема, которую нужно было
установить, именно, что порядок любой определенной системы
линейных уравнений с постоянными коэфициентами равен по-
порядку характеристического уравнения.
6-52. Эквивалентные диагональные системы. ПустьЬг,г.... Ь„
будут полиномами от D с постоянными коэфициентами, тогда
любая последовательность решений Urn = 0,.. .,Un = О будет
удовлетворять уравнению
Lr+i Ur !+... + ?„?/„=().
Следовательно, если выражение вида Lr^iUr+i + ¦ • ¦ +Ln Un при-
прибавить к левому члену любого уравнения ?Л=0, то измененная
система будет иметь все решения старой системы. Однако диа-
диагональные коэфициенты результирующей системы точно соот-
соответствуют диагональным коэфициентам первоначальной системы.
На эквивалентность диагональной системы этот процесс следо-
следовательно не влияет, но он более простой.
Если диагональный порядок зависимых переменных известен,
то диагональные коэфициенты могут быть определены единст-
единственным образом, однако недиагональные коэфициенты не могут
быть так определены. Более того, диагональный коэфициент
любой переменной определяется единственным образом, если
совокупность переменных, которые следуют в диагональном по-
порядке, известна. Так, пусть за переменной у, следует в любом
порядке п — г переменных—jVn,..., у„ . Предположим, что ди-
диагональный коэфициент уг и последующие переменные имеют
вид
Кг, Ktif-, Кп
в одном порядке и
К> K+i>- ¦¦¦> К'п
в другом,тогда поскольку обе системы эквивалентны,
Но в обоих случаях последние п—г уравнений, с переменными
201
Уг~ъ.. ¦, Уп, образуют эквивалентные системы, следовательно
откуда
т. е. диагональный коэфициент достается неизменным, если
последовательность переменных, следующих за уг, остается не-
неизменной.
Предположим, что уг содержит в полном решении vr произ-
произвольных постоянных; тогда, если диагональная система распо-
расположена таким образом, что уг встречается в последнем уравне-
уравнении, то диагональный коэфициент уг будет степени vr от D.
Пусть система будет преобразована таким образом, что ут
будет встречаться в качестве диагонального члена в предпос-
предпоследнем уравнений. Поскольку полное решение уг все еще со-
содержит vr произволышх постоянных, степень диагонального
коэфициента уг не будет превышать vr; в действительности она
может быть меньше vr на степень диагонального коэфициента
последнего уравнения системы.
Степень диагонального коэфициента jv может быть еще более
понижена преобразованием системы, при котором уг должно
входить в диагональный член третьего с конца уравнения так,
чтобы диагональный коэфициент для любой данной переменной
был наименьший, если эта переменная первая в диагональном
порядке; он увеличивается при продвижении переменной в диа-
диагональном порядке и достигает максимума при последней пере-
переменной.
Если переменная последняя в диагональном порядке, то сте-
степень ее диагонального коэфициента равна общему числу про-
произвольных постоянных в полном выражении для этой переменной;
если переменная первая в диагональном порядке, то степень
ее диагональных коэфициентов равна числу произвольных по-
постоянных, которые входят только в нее. Диагональные к оэфици-
енты в этих двух случаях имеют следовательно большое зна-
значение; ниже мы приведем правила для вычисления диагональных
коэфициентов любой частной переменной, когда переменная
занимает первое или последнее место в диагональном порядке.
Пусть данной системой будет
(U) ?/, = 0, *У2 = 0, ...Un = 0,
где
Ur=Fny1-\- ... + Frnyn —fr(x),
и пусть
(V) Vt=0, V8 = 0, ..-, Vn = 0,
где
Vr = Нтгуг + .. ¦ + Hrn yn — hr (a)
202
— эквивалентная диагональная система. Пусть
будут системами множителей, которые преобразуют (U) в (V)
и (V) в (U) соответственно. Поскольку
отсюда следует, что
#п = 8u F\i + • • • + 8in fin,
а поскольку
Ur = KlV1 + ...+o'rnVn (г = 1,2,... я)
то
/Vi=8rt//U (r=l,2, ... л).
Следовательно //а должен быть общим множителем относительно
D в
F F
Ml» »' щ.
Отсюда, независимо от постоянного множителя, Нп должен
быть наибольшим общим множителем Ftl, ..., Fni. Это является
правилом для вычисления диагонального коэфициента уг (когда
он первый в диагональном порядке). Диагональный коэфициент
уг должен быть постоянным, кратным наибольшему общему
множителю ifr
F F
1 1Г, • • • , I ПГ-
Ипп, т. е. диагональный коэфициент уп (когда он последний
в диагональном порядке) вычисляется следующим образом. По-
Поскольку
^n = 8nlf/1 + ...+8imt/R,
отсюда следует, сравнивая коэфициенты при^!, .... уп— и уп, что
°ni ' in—1 "T • • • "Г ЬппГп, n_j — 0,
I —1~* —i — Q Г1 ; f—f
Предположим, что Grs будет сомножителем Frs в характеристи-
характеристическом детерминанте
- -р F 1
'11» • • • , ГМ I »
_' in» • • •» * nnj
а Гп будет наибольшим общим множителем Gln ..., Gnv и
Gm = Gin Г뻦 • •, Gnn = Gnn I n-
203
Отсюда
где X определяется соотношением
и, поскольку Gjn,..., G'nn взаимно простые числа, \— постоян-
постоянная или полином от D.
Так как обе системы эквивалентны, то модуль
ц> • • •> пп
должен быть постоянным. Этот детерминант очевидно имеет
множитель X, поэтому X — постоянная.
Отсюда следует, что
Нпп = X (Fm Gin + • • • + Fnn Gin)
*¦ (p Cj J_ -Л- F П \ — ~K—
— г \* in L/in ~T~ • • • i * nn ^nnj г *
1 n l n
В более общем случае, когда член уг последний в диагональном
порядке, его диагональный коэфициент будет постоянным мно-
множителем FITт, F — характеристический детерминант системы,
Гг — наибольший общий множитель
r,. •., G
nr,
a Gmr — минор FmT в характеристическом детерминанте.
Диференциальные уравнения, определяющие отдельно у1г... ,уп
имеют вид
~г~У\ ~~ у /l (х) "Т" • • • i In '-x)j
1 1 1 11 ! 1
f- Уп = -p-fi (х) + ...+ ^fn (х).
in l n l n
Необходимо отметить, что эта последовательность уравнений
полностью определяет уи .. .,уп.
6-53. Простые диагональные системы. Первообразные1 системы.
Из общего числа зависимых переменных некоторые переменные
могут целиком определиться недиференциальными уравнениями,
следовательно они не содержат произвольных постоянных.
Если это имеет место, то можно предположить, что рассмат-
рассматриваемые переменные устранены из системы и замещены там,
где они встречаются, их действительными значениями; тогда
система не будет содержать зависимой переменной, которая бы
могла быть определена без интегрирования диференциального
уравнения.
1 Термин первообразный следует понимать в алгебраическом смысле
Прим. ред.
204
Предположим, что в ограниченном таким образом решении
имеется только одно диференциальное уравнение. Это уравне-
уравнение должно быть последним уравнением системы, так как в про-
противном случае последняя зависимая переменная в диагональном
порядке была бы определена недиференциальным уравнением.
Пусть последней переменной будет уп, которая может быть
определена из уравнения
НппУп = О,
порядок которого равен порядку системы, так что выражение
для уп будет содержать все произвольные постоянные пол-
полного решения системы. Остальные диагональные коэфициенты
//„_!,„_!,..., Htl будут постоянные; соответствующие перемен-
переменные уп-1,¦•¦, y>i зависят от некоторых или всех постоянных,
входящих в выражение для уп, но не содержащих кроме них
никаких других произвольных постоянных. Такая система назы-
называется простой диагональной системой.
Рассмотрим условия, при которых любая данная система
может быть приведена к простой диагональной системе.
Если F—детерминант данной системы, то
Г = Пц /722 • • • ПпП,
и поскольку операции, при помощи которых Нп, //22,..., Нпп
получаются из коэфициентов первоначальной системы, являются
рациональными, отсюда следует, что Ни, #22,..., Нпп будут
также рациональными относительно коэфициентов Frs начальной
системы. Следовательно, если F не имеет множителя низшего
порядка относительно D, то //u,...,//,,_bn-i приводятся к посто-
постоянным, а эквивалентная диагональная система будет простой.
Как и выше, пусть Grs обозначает сомножитель Frs характе-
характеристического детерминанта F. Рассмотрим матрицу
Предположим, что составные элементы любого столбца являются
взаимно простыми (первообразный столбец,). Тогда, в обозна-
обозначениях предыдущего параграфа, Гг — постоянная, и следова-
следовательно, если уТ последняя по порядку в эквивалентной диаго-
диагональной системе зависимая переменная, то коэфициент уг в пос-
последнем уравнении диагональной системы будет постоянным
множителем самого F. Полученная диагональная система является
простой. Таким образом для каждого первообразного столбца
в обратной матрице данной системы может быть образована
эквивалентная диагональная система, в которой соответству-
соответствующая переменная будет последней в диагональном порядке.
В частности, если каждый столбец обратной матрицы будет
первообразным, то каждая эквивалентная диагональная система
205
будет простой, а выражение для каждой зависимой переменной
будет содержать все произвольные постоянные.
Система, каждый столбец характеристического детерминанта
которой является первым, называется первообразной системой.
Любая данная система может быть преобразована в простую сис-
систему, для которой "{г — наибольший общий множитель Fv,. ..,Fnr;
необходимо ввести только новые зависимые переменные и1У
и2,..., ип, где '
Характеристическим свойством первообразной системы яв-
является то, что в любой эквивалентной диагональной системе
первое уравнение недиференциальное.
Однородная система
(D - If у, +
= О,
(D - l)ys = 0,
приводится преобразованием
к первообразной системе
(D + 1) th
«2 =
и3 = Уз
D*u2 + (D + 1) «з = О,
(D-1K + D«2+(D- 1)иа=0,
«, + «2 + Dua = О,
приведение которой к эквивалентной диагональной форме было
произведено в § 6-501.
Пример:
BD - 2)уг + {D3 - D + 2) уа - g-*,
(D3 + 3D2 + 5D - 1)у, + (-3D2 -4D + \)у2 = 0.
Характеристическим детерминантом является
2D - 2, D3 - D + 2
D3 + 3D2+5D-1, -3D2-4D + 1
а характеристическое уравнение имеет вид
Обратная матрица получается в виде
/ — 3D» — 4D + 1, - D3 - 3D8 - 5D + 1
\- Ds + D — 2, 2D-2
206
причем оба ее столбца являются простыми. Таким образом в
любой эквивалентной диагональной системе первое уравнение
является недиференциальным, а так как в систему входят только
два уравнения, то система следовательно будет простой. Система
множителей
L , М \
Z>3-J-3D2 + 5D-1, -2D+2/
преобразует данную систему в эквивалентную диагональную
систему, в которой у% будет последним в диагональном порядке,
если L и М выбраны таким образом, что
L BD - 2) + М (D3 + 3D2 + 5D - 1)
— постоянная величина.
L и М легко определяются следующим образом. Пусть
и = 2D - 2, v = L
тогда, исключая D3, получим
D2« — 2v = — 8D2 - 10D + 2,
исключая D2 из выражений для D2« — 2v и и, получим
(D2 + 4D)« - 2v = - 18D + 2
и, наконец, исключая D из этого выражения и выражения для и,
получим «
(D2 + 4D + 9) и — 2<у = — 16.
Таким образом L и М должны иметь следующие значения:
L = D* + AD + 9, М = —2.
Система множителей
/D4 + 4D + 9 , - 2
)— 1, —2D + 2
приводит данную систему к эквивалентной диагональной си-
системе
— 16у, + (D" + Wl + 8D3 + 4D2 + 7D + 16) л = 6е~\
D{D + If (D2 + l)y2 =— 4е~Л.
Общее решение уравнения для j'2 имеет вид
У» = Q + (С2 + С3* + Qx2) fe-* + С5 cos а; + С6 sin л + у л?е~х.
Поскольку уравнение для у^ не является диференциальным,
207
получим
yi = Ct + \ {BC, + ЗС3 - 3Q) + BС3 + 6С4) л + 2С4л2}
C6sinх~^ (l + 6x — 6л2 — -|- л3)
6-6. Поведение в бесконечности решений линейной диференци-
альной системы с ограниченными коэфициентами. Здесь удобно
расширить цели исследования для того, чтобы рассмотреть
поведение решений систем при больших значениях независимой
переменной. Коэфициенты этих систем ограничены и не явля-
являются обязательно постоянными К
Примем следующую лемму. Пусть f(x) будет функцией,
ограниченной при хо<х<С<х> и пусть Xj и Х2 будут такими
двумя вещественными числами, что eXt*f(x) стремится к нулю,
a ek*xf{x) не стремится к нулю при х—»оо. Тогда в интервале
(ки X,) будет существовать число 10<Ъя таким образом, что
если г — малое положительное число, то е®*-^хf (х) стремится
к нулю, а еа° + е)х/(х) стремится к бесконечности, когда х—>оой.
Аналогично, если
— функции, определяемые в интервале (л:0, со), а X, и Х2 таковы,
что каждое произведение e4Xfr(x) стремится к нулю, в то время
как не все произведения e'-xfr(x) стремятся к нулю, когда
л—>со, то будет существовать некоторое число \,(Хх < 10< 12)
такое, что каждое произведение e<^°~~*)xfr{x) стремится к нулю,
хотя, по крайней мере, одно из произведений е(-1»+^х fr(x) не
ограничено. Число 10 называется характеристическим числом
системы рассматриваемых функций.
Рассмотрим теперь систему
ji = aiXyx + a22y2 + 1- a2nyn,
ЁГ = flniyi + апгу1 + ¦¦• + a
где все коэфициенты а — вещественные функции х, ограничен-
ограниченные в интервале (х0, со). Пусть
уг =
1 Ляпунов, Comm. Math. Soc, Харьков A892); Ann, Fac. Sc. Toulouse B), 9
A908)-
2 Эта теорема доказывается повторным подразделением интервала (Х1? Х„).
208
где X—произвольное вещественное число, тогда
^ = («1, — )•) i\ + a12v2 + ... + amvn,
rf- = «21^1 + (a2i — I) v% + . .. + ainvn.
~ = атг\ + an2v2 + ..."+ («„„ — X) -yn.
Если эти уравнения умножить соответственно на vu г>2,..., >ип,
а затем сложить вместе, то результирующее уравнение будет
иметь вид
Если ). достаточно велико, то квадратическая форма в пра-
правой части этого уравнения будет определенной и отрицатель-
отрицательной, и следовательно, если для X возьмем достаточно большое
положительное число я, то получим
~rf7~ " <U
для всех значений х в интервале {х, со). Таким, образом поло-
положительная функция v\ + v\ + ... + г'1 уменьшается с увеличе-
увеличением х, следовательно vlt щ,..., юп строго ограничены; отсюда
имеем, что
\1 О 'IX «t р 3.V <f р 7.V
У\к j >2е • • ¦ ¦ 1 УпЧ
ограничены в интервале д-0<а-<оэ; очевидно, я может быть
такой, чтобы предельное значение каждого произведения рав-
равнялось нулю.
Аналогично, если л =—,3, где р — достаточно большое поло-
положительное число, то
dx "" -^ U'
следовательно предельное значение v\ -f- <v\ + .. . + vl не равно
нулю.
Таким образом, по крайней мере один из членов
не стремится к нулю при п—><х>.
Отсюда следует, что любая система решений
\\, У*,---, Уп
Э. Айне—133 —14 2!i9
не равных тождественно нулю, допускает, характеристиче-
характеристическое число X, а также, что существует такое вещественное
число %, что
стремятся совместно к нулю при х—-»0.
Соответствующая теорема для одного линейного диферен-
циального уравнения порядка п может быть выражена следу.
ющим образом: если коэфациенты рТ уравнения
ограничены в интервале (О, со^, то существует число /. таким,
образом, что, если у — любое решение уравнения, то все
уеАХ,
стремятся к нулю при п—>оо.
Примеры
1. Проинтегрируйте следующие уравнения
rf3v , d2v „ dy
(Ш) ^3 -> - ch x; (IV) _*- _ з _
(V)H? + 4-v = fi:rsin2xcosx; <VI) rf^ + 2d^
d8y dsv d?v dv
^ + "^ = ^ C0S X; mII) tx? " 5 ±fl + S Ш
OX) ^ — 2 -f- + 4y = ег cos л;; <x> л;3 ^-'.,+Зл:2 —% + x -f = 24л--
2. Найдите решение уравнения
которое удовлетворяло бы условиям
dv
v = ^- =0 при х
3. Докажите, что частное решение уравнения
dv d2y
= ^- =0 при х = 0, 3»=^ = 0 при .y= /.
210
имеет вид
-V А
у = т sail mx J f(x) cos mx ах — т cos mx I f(x) sin mx dx [Fourier],
о о
4. Проинтегрируйте системы
W — + ах — by=et , -2- — ay -^ Ьх ~ et (в2 — Ь- = 1):
<П) ^ + п-у = 0, j* - п*х = 0;
5. Решите систему
при условии, что при t = 0
~-Зх-4у+3 = 0. ^
й'а: о>
0. Проинтегрируйте систему
7. Приведите к диагональным системам и проинтегрируйте
ИЬ- =0;
1 Dx + i
|
(D - 1)гд: + 4?>у + (D — 3) г = 0,
CD — D3).»; — 2Dy -^ (О — 1) г = 0,
где
ГЛАВА VII
РЕШЕНИЕ ЛИНЕЙНЫХ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В НЕОПРЕДЕЛЕННОЙ ФОРМЕ
7-1. Недостаточность элементарных методов. Кроме уравнений с
постоянными коэфициентами и уравнений, которые могут быть по-
получены из них путем замены независимой переменной, неизвестны
линейные уравнения порядка п, которые могли быть точно про-
проинтегрированы в элементарных функциях. Если возникает урав-
уравнение, которое не может быть приведено к одному из общих
типов, рассмотренных в главе VI, то почти всегда решение мо-
может быть выражено в неопределенной форме, т. es в виде бес-
бесконечного ряда, бесконечной непрерывной дроби или опреде-
определенного интеграла. Таким образом в большинстве случаев
уравнения, возникающие при решении задач прикладной мате-
математики, которые не могут быть приведены к уравнениям с по-
постоянными коэфициентами, имеют в качестве своих решений
новые трансцендентные функции. Следует отметить, что транс-
трансцендентные функции могут быть подразделены на два класса:
1) на функции, которые являются решениями обыкновенных ди-
ференциальных уравнений (например, функции Бесселя), и 2) на
функции, которые не удовлетворяют обыкновенным диференци-
альным уравнениям конечного порядка (например, дзета - функ-
функции Римана).
В настоящей главе мы будем рассматривать процесс выра-
выражения решения линейного диференциального уравнения в виде
бесконечного ряда или непрерывной дроби. Решения в виде
определенных интегралов мы рассмотрим в следующей главе.
В главе III было доказано, что если все коэфициенты урав-
уравнения
L (у) = р0 (х) -—¦ +pt (*)—--? -r...+pn-i(x)^ + pa(x)y - 0
конечны, однозначны и непрерывны в интервале а < х < Ь, то
¦единственными особыми точками, которые могут встретиться
в пределах этого интервала, будут корни коэфициента ро(х).
С точки зрения задачи разложения решений уравнения в бес-
бесконечные ряды, различие между обыкновенными и особыми
точками является основным. Ниже мы постараемся объяснить
различие между решениями, относящимися к обыкновенной точке,
и решениями, относящимися к особой точке.
212
7-2. Решения, относящиеся к обыкновенной точке. Фундамен-
Фундаментальные теоремы существования показывают, что если х0 — не
особая точка диференциального уравнения, то существует един-
единственное решение у (х) такое, что оно и его первые п — \ про-
производных принимают ряд произвольных значений
У0) У о , • • •, У о
при х = хф и у (х) может быть разложено в ряд Тэйлора, кото-
который сходится в некотором интервале (х0 — h, xo + h). Известно
также, что если Y^x), Y2 (x), ... ,Yn (х) — частные решения,
определяемые условиями
, (л-0) - 1, Y\' (х0) - 0,..., Yx"' -
2 (л0) = 0, }V (х„) = 1, ..., \\}п ~х) (Хо) = 0,
Yn (x0) = 0, Yn' (x0) =-= 0, . . ., У„(л ~ lj (Xo) = 1,
TO
Следовательно, чтобы образовать общее решение уравнения
или частное решение, удовлетворяющее заданным условиям-,
достаточно вывести п фундаментальных решений У, (х), Yz(x),...,
Yn(x). Для выражения Yr г(х) характерно, что его общий член
равен (х—хо)г/г\ и что оно не содержит членов (х — хо)г^г,
(Х — х„)г + 2,..., (х — хо)"~1- Однако удобнее принять коэфициент
общего члена равным единице и. постараться удовлетворить
уравнению рядом вида
y
ar, (x —
Поскольку
вронскиан последовательности решений у1{х), у2(х),.. .,уп{х)
не обращается тождественно в нуль, следовательно, последова-
последовательность фундаментальна.
Метод решения состоит в подстановке ряда в левую часть
диференциального уравнения, расположении полученного выра-
выражения по возрастающим степеням х — х0 и в последующем при-
приравнивании нулю коэфициентов последовательных степеней х — х0.
После этого между коэфициентами аГ1, аг2, аг,, ... , получится
последовательность линейных алгебраических соотношений (ре-
(рекуррентных). Таким образом коэфициенты определяются алгеб-
алгебраически.
213
7«201.Уравнение Вебера. В уравнении Вебера 1
точка х = 0 является обыкновенной точкой, и оба фундаменталь-
фундаментальных решения могут быть разложены по возрастающим степе-
степеням х. Однако более выгодно сделать предварительное преоб-
преобразование
I
где новая зависимая переменная удовлетворяет уравнению
d?v dv , _
—2 — х -.- 4- nv — 0.
etx2 dx '
Теперь, если мы примем v в форме
v = а0 + а4л + а2х2 -f ... -|-аГх~ -\- ...,
то оба фундаментальных решения vt и v2 получатся при условии
а0 = 1, ах = 0 или а0 = 0, а, = 1.
Рекуррентное соотношение, которому должны удовлетворять
коэфициенты, будет
(г + 1) (г + 2)аг, 2 == (г — я) аГ) (г = 0,1,2, ...),
следовательно
Я, _ 1 i.2, n{n-2) 4 «(Я-2ИП--4] 6 _l
1 ~ 2! ' 4Г 6!
/г-1 (П-1)(Я_3) 5 (п-1)(и-3)(/г-5) 7 ,
U2 — Л д| Л -| gj Л 7, Л , - • •
Обычные признаки показывают, что эти ряды сходятся для
всех конечных значений \х\.
7 • 21. Решения, относящиеся к особой точке. Пусть точка хй,
которую для удобства примем началом, не будет обыкновенной
точкой. Тогда можно предположить, что имеется решение вида
у = хг (а0 + а, х + ... -f av X' + ...) (я0Ф0),
хотя в этом случае г может и не быть положительным целым
числом.
1 Weber, Math. Ann., I A869), 29. Уравнение относительно v было ранее ис-
исследовано Эрмитом, С. Я Acad. Sc. Paris, 58A864), 93, 266 (CEuvres II. 293). Функ-
Функции определяемые этим уравнением, были стандартизованы Уиттекером, Ргос.
London Math. Soc. A), 35 A903), 417. См. также Уиттекер и Ватсон, Курс сов-
современного анализа, § 16-5—16-7.
214
Для исследования возможности существования таких реше-
решений, подставим ряд вместо у в L (у) и приравняем нулю коэ-
фициент члена наименьшей степени х. Этот коэфициент будет
или независимым от г или полиномом Р(г) от г, степень кото-
которого не будет превышать порядка уравнения1. В первом слу-
случае решение рассматриваемого типа не существует, и особен-
особенность х = 0 называется нерегулярной. В последнем случае, если
Р(г) степени п, особенность называется регулярной, а если
степень Р(г) меньше п — нерегулярной. Примем, что в данном
случае особенность регулярная; тогда уравнение
которое называется определяющим уравнением, будет иметь п
корней, из которых все или несколько могут быть равны. Если
уравнение.-лтривести к виду
то, чтобы Р{г) могло'быть степени п, необходимо и достаточно,
чтобы2
рг = О{х-г) <г=1,2,...,п).
Корни определяющего уравнения известны как показатели,
относящиеся к рассматриваемой особой точке. В качестве об-
общего принципа, который будет доказан несколько ниже при
помощи теории комплексных переменных (см. главу XV), можно
указать, что если показатели являются разными и ни один из
них не отличается от другого на целое число, то существует п
линейно-независимых решений рассматриваемого типа8. Если же
два или больше показателей равны или различаются на целое
число, то число решений рассматриваемого типа в общем слу-
случае меньше п, а остальные решения фундаментальной последо-
последовательности имеют менее простой характер.
7 • 22. Точка в бесконечности как регулярная особая точка. Во-
Вопрос о том, является ли какая-либо конечная особенность ре-
регулярной или нерегулярной, может быть разрешен почти сразу;
определить природу точки в бесконечности немного труднее.
Преобразование
х = z~1
1 Очевидно, Р(г) не будет зависеть от коэфициентов av a2,..., и будет
содержать а0 в качестсе множителя.
2 Символ О (л—-О будет часто встречаться ниже. Он определяется следую-
следующим образом: если функция / (х) такова, что при х -*- 0 (или со), | xr /(.v) | < А",
где К — положительное, число, независящее от х и неравное нулю, то говорят,
что / (х) порядка х—г или f(x)= О (х~г). Вообще, из контекста будет ясно,
имеет ли место предельный процесс для х-*0 или для х—>эг>. Если
Нт | xr f(x) I = 0, то все определяется вьюажением f(x) = О (х—г).
Точное ' доказательство, что рг = 0{х—г) — необходимое и достаточное
условие для регулярной особенности, будет дано ниже (§ 15-3).
3 Решение в виде ряда.
215
переносит точку в бесконечности к началу, и критерии для
обыкновенной точки регулярной и нерегулярной особенности
могут быть приложены непосредственно.
Рассмотрим уравнение второго порядка
после преобразования подстановкой х — z~\ оно примет вид
dz* + \ z z* | az + г* -V U-
Если первоначальное уравнение имело обыкновенную точку
в бесконечности, то преобразованное уравнение будет иметь
обыкновенную точку в начале, поэтому условия
должны быть верны при z—»0. Соответствующими условиями
для первоначального уравнения будут
При X—> со.
Условия для регулярной особенности имеют вид
при г—»0, и
при л-^оэ. Пусть
тогда определяющее уравнение, относящееся к особенности
2 = 0, будет иметь вид
г2 + A - Ро) r + q~- 0;
его корнями будут а и ,3. В общем случае, при а и р нерав-
неравных и не различающихся на целое число, будут существовать
216
два решения первоначального уравнения, относящиеся к осо-
особенности х = со, именно
j/, = х—'-(\ + al х~г + flg-* +•••),
У2 = -V3 A + kt х-1 -f- fc3 -х-2 +•••),
и эти разложения будут сходиться для достаточно больших
значений \х\.
Необходимо отметить, что показатели, относящиеся к точке
в бесконечности, будут равны а, ,3, а не — а, — В.
Для иллюстрации приведенных общих принципов рассмотрим
особо важное уравнение, известное как гипергеометрическое.
7 • 23. Гипергеометрическое уравнение. Гипергеометрическое
уравнение1
имеет три особых точки: х = О, л = 1 и х = со. Показатели,
относящиеся к л — 0, равны 0 и 1 — у, относящиеся к х = 1
равны 0 и *[ — a — В, а относящиеся к х = со равны а и р. Чтобы
показать это, наиболее общее решение уравнения может Оыть
написано в символической форме, данной Риманом2
= Р
правая часть этого соотношения называется Р-функцией Римана.
Решение, относящееся к особенностям х = 0 и показателю О,
.может быть разложено в ряд
,.,0 г, {~ _) 1 \ О /О _|_ 1 \ ,., /„ l_ I \ (п _1_ О\ О /О _i_ 1 \ /О ' *">\
+ i. , ^ + зГ-7 (v + 1) ^ Х ~] 3! 7 (Т + 1) (Y 1- 2) *'+••¦
и обозначается че|.ез F (а, р; у; л). Можно показать, что ряд
сходится при \х\ < 1 для всех конечных значений а и В и для
всех конечных значений у, за исключением отрицательных
целых чисел, и расходится при \х\ > 1. Если а, 3 и ? вещественны,
то ряд сходится при л = 1и7>а-т-Ви расходится при f <^a -J- 3;
ряд сходится также при х — — 1, если т + 1>а~ЬР> и расхо-
расходится, если т + 1 < я + р.
Рассмотрим решение, относящееся к особенности х = О,
с показателем 1—¦[. Принимая решение в виде ряда
v = л-1-' A -f ахх + а.2хг +...+я,г+ ...),
найдем, что
(у + 1)(V - т -f 2)a.,,i - (v + я - 7 + 1) (v + ? —7 + *)«*
1 Gauss, Comm. Gott., 2 A813) [Werke, 3, 123, 207]. Подробное исследование
гипергеометрического уравнения см. Уиттекер и Ватсон, Курс современного
анализа, гл. XIV; там же дана библиография.
2 Riemann, Abh. Ges. Wiss- Gott., 7 A857) [Math. Werke, 2 изд., 67].
217
для v = О, 1, 2, ..., при а0 = 1. Отсюда получим
y^xl-iF(a — т + 1, р —Y + 1; 2 — г, х).
Аналогично найдем два решения, соответствующие особен-
особенности х = 1,
— a, ? —8; 7 — a — P + l; 1—JC).
и два решения, соответствующие точке в бесконечности
у = x~*F(a, а —т + 1; а —р + 1; -*).
у = х-з F(p, р _ y + 1; р — a + 1; х-1).
Интервал сходимости ряда относительно 1-х равен 0<х<2,
а ряда по степеням л;—1 равен |х|>-1. Таким образом мы полу-
чилл шесть решений1; так как не больше двух решений могут
быть линейно-независимы, то между всеми решениями должна
существовать линейная зависимость.
7 • 231. Линейная зависимость между решениями в виде ряда.
Сначала докажем, что если 7>а+Р и Т не являются отрица-
отрицательными и целыми числами, то
r(?, P, Ъ ^
Поскольку при 0 < х <С 1 функция F(a, ,8; 7; х) удовлетворяет
тождеству
= apF(a, р; v; Л)_ЛA_Л)/-'(Я, р; т; л)
и поскольку, как может быть проверено на самом ряде, F"(«,
р; Y5 1) является конечной величиной, то отсюда следует, что
(T_a_p_l)P(a, 3; Т; l) = $F{a, ft T; 1).
Сравнением коэфициентов одинаковых членов можно также
показать, что
F{a, 3; т + 1; x)-F{z, Р; Т; л) = - .^-^ F(a + 1, Р + 1; V + 2; х)
= ~~F'{a, P; -- + 1; л),
I
следовательно
F(*, Р; Y + з; 1)-^(«, Р; т; 1)--^^'(». ?; т + 1; 1)
= — -,- ^—^ F(a, Р; -; + 1; 1).
1 Kummer, J. iur Math., 15 A836), 39. 127. См, также Уиттекер и Ватсон,
Курс современного анализа, Ioc. cit.
218
Таким образом мы получим
Повторным применением этой формулы найдем, что
^(а, 8; y; 1) --= Hm < Пр—~TT~zrhz~^~~''l^(<*¦• Pi 7+я; 111.
Но согласно хорошо известной теореме *, предельное значение
бесконечного произведения равно
(т)(тР)
и поскольку
F(d, p; Y-r«; 1)=1 + ~„^ш
7 -t-«
где Lfn — сходящийся ряд, положительный и уменьшающийся с
увеличением п, то
lim/^a, р; v+л; 1) = 1,
и следовательно теорема доказана.
Поскольку любое решение может быть линейно выражено
двумя независимыми решениями, мы получим тождественное
соотношение вида
/=•(<*, Р; v; х) ^ AF{7, 3; а + р - т + 1; 1 — *) +
л)т-«-PF(T —о, Т-Р; т —а-р + 1; 1-х),
где А и В—подлежащие определению постоянные.
Чтобы все ряды сходились в общем интервале
примем, что2
1 > 7 > * + Р-
Принимая последовательно л = 1 и д; = 0, получим
3; a^3 ¦¦ + 1; 1)+^,'т-я, v_p; ^ L а —р + 1; 1).
Отсюда получим значения А и В. Результирующее соотношение
будет иметь вид
F(a, 3; y; л)-=^1^~:-§Г(а, 8; a + 8^ Y + 1; 1
1 Уиттекер и Ватсон, Курс современного анализа, § 12 — 13.
2 Это строгое ограничение несущественно для результата; оно лишь при-
присуще данному методу.
21»
7 • 232. Случай, когда разность показателей является целым
числом. Оба решения, соответствующие особенности х — О, именно
У1 = F[a, р; Г, х). у, -¦= xl-'F{i - т + 1; р - ¦; + 1; 2 - Т; х),
независимы, если разность показателей 1—-f неравна нулю или
отрицательному целому числу. При "у = 1 оба решения тождест-
тождественны, при 7 = 2, 3, 4,..., решение у2 становится неверным,
вследствие обращения в нуль знаменателя в коэфициентах бес-
бесконечного числа членов ряда. Тем не менее, 'решение _у2 имеет
смысл при -[ — т (т — положительное целое число), если умно-
умножить его на соответствующий постоянный множитель. Рассмот-
Рассмотрим решение
B —;¦)...(т — ",)-(т- 1)!
Это решение остается конечным при *{, равной т, первые
т — 1 членов разложения ряда обращаются в нуль и остается
решение
1 "' 1!тЛ+ ' Тт{т+ 1) Х" ' ^ '3' т; Х^
Таким образом, если ",' — положительное целое число или нуль,
то оба решения ух и j/2 будут практически одинаковы. Общий
методг получения другого решения, существенно отличный от
приведенного выше, будет рассмотрен в главе XVI. Приведем
простой пример, иллюстрирующий общий случай.
Рассмотрим уравнение
d'-y
clx2
х = 0 является регулярной особой точкой, которой соответствует
определяющее уравнение
корни которого равны. Одно решение получается непосредст-
непосредственно, именно
.Г .' г- у4 ^
— I 1 I I I ! *
У!=Х [I + ? +4ГГ^-+ •••¦''
второе решение получается подстановкой
где г» — новая зависимая переменная. Уравнение для v, именно
f + 2y[4f = 0,
1 Lindeiof, Acta Soc. Sc. Fenn., 19 A893), 15.
220
имеет решение
dx Г dx
f {
I л + 0 (x*)\ dx = log x - I
f { —I л + 0 (x)\ dx = log x I x + O(x).
Следовательно второе решение у2 будет иметь вид
j/2 = v, log л—jc * [jg- л2 + О (л4) ;¦ •
7 - 24. Уравнение Лежандра. Диференциальное уравнение
называемое уравнением Лежандра, имеет большое значение в фи-
физических задачах; его решения известны как функции Лежан-
Лежандра1. Уравнение имеет регулярные особенности в точках + 1 и
в бесконечности и определяется схемой
J—1 со +1
j у=Р\ 0 я|1 0 х
I 0 —п О
или эквивалентной схемой
jO оо 1
j/=P'tO л+1 0 4"— тх\.
Ю — п 0 " )
Наиболее удобным является решение, расположенное по убы-
убывающим степеням х и соответствующее особенности в бесконеч-
бесконечности. Уравнение удовлетворяется двумя рядами
J^tM"-2 "i"-)A'L-^i^^3) v/i-i —
24 BтРГ)Bи 3)" "*'
x 4 ^
2-Bи— Г) ^ 2-4- BтР-Г)Bи — 3)
+ <?±У ('i ± 2) <?
¦j2 + 2'.'BяТ3) ¦¦2"-^.Bй + 3)Bи-Ь5Г +1-"
которые сходятся «ри \х[>1.
Пусть п будет целым числом (так как никаких дальнейших ог-
ограничений этим не вводится, будем рассматривать га, как поло-
положительное целое числоJ. В этом случае решение у% будет поли-
полиномом степени п, а после умножения на
_Bи)!
2" («!)°
1 Legendre, Mem., Acad. Sc, Paris, 10 A785); см. Уиттекер и Ватсон, Курссо-
временного анализа, гл. XV.
2 В общем случае, при п вещественном, достаточно рассматривать значения
1
221
будет обозначаться Рп (х). Этот специальный выбор множителя
должен быть сделан так, чтобы для всех значений п выражение
Рп A) = 1. Определенные таким образом полиномы называются
полиномами Лежандра; они играют основную роль в теории сфе-
сферических функций.
Первые шесть полиномов Лежандра имеют вид
Ро(х)=1; Рх (х) = х; Р2(х) = ±- (Зх* —\у,Рь(Х)=\Eл8— Ъх);
Pi (*) = g C5л' - -30л2 + 3); Р5 (л) = | F3;с — 70л8 + 15л).
Можно доказать непосредственно, что если п — положительное
целое число, то
Этот результат известен как формула Родрига.
Рассмотрим теперь второй ряд ys; поскольку этот ряд не за-
заканчивается при п > — 1, нет оснований ограничивать п целым
числом. Это решение в виде ряда, при умножении на1
1
¦к 2 Г {п + 1)
обозначается Qn (x). Сравнением ряда_у2с гипергеометрическим
рядом относительно х~2 легко доказать, что при х > 1
** п 1л1 —
2n+i г (я
+
Определенная таким образом функция Qn (x) может быть при-
принята в качестве второго стандартного решения уравнения Ле-
Лежандра и известна как функция Лежандра второго рода.
1 На основании формулы удвоения, для гамма-функции
22г-1Г(г)Г
этот множитель может быть выражен в виде
2«{Г(я+1)}2/ГB/г + 2);
а при п положительном целом числе он приобретает значение
Bй -f- 1,! "
222
Ряд ух не будет существенно отличаться от у2, когда 2и рав-
равно — 1 или любому положительному нечетному целому числу,
поэтому он не подходит в качестве стандартного решения. Те-
Теперь из второй схемы, при помощи которой может быть опре-
определено уравнение Лежандра, непосредственно следует, что ги-
гипергеометрический ряд
~ х)
удовлетворяет уравнению Лежандра и принимает значение 1 при
дс = 1. Более того, он является полиномом при п целом, и по-
поскольку при п > 0 только одно решение Рп (л) является поли-
полиномом, отсюда следует, что
+ l, —л; 1;4 \г
Это решение действительно для всех значений п и соответст-
соответственно принимается в качестве стандартного. Так как гипергео-
гипергеометрическая функция была определена только как ряд, который
сходится при — 1 <~2 9~ х<1, отсюда следует, что если п
не является целым числом, то разложение в виде ряда Рп (х)
имеет смысл только в интервале — 1 < х <3. Таким образом ре-
решения в виде рядов Рп (л) и Цп (л) существуют в общем ин-
интервале 1 < х < 3 К
7-241. Второе решение, когда п целое число. Поскольку показатели,
относящиеся к особенностям х = ± 1 равны, дополнительное ре-
решение к у = Рп (а;) должно содержать логарифмические члены.
Пусть предполагаемым решением будет
у = иР„ (х) — ч),
тогда
{A - х2) и" - 2хи'} Р„ (х) + 2 A - л2) и'Р'„ (х) -
- {A - х1)v" -2хч/ + n(n + l)v} = О,
и к будет таким, что
(I — х2) и" - 2хи'= О
ИЛИ
Число—1 в качестве постоянной интегрирования взято для
того, чтобы облегчить последующее отождествление полученного
решения, тогда
и v определяется уравнением
A-х2) v" - 2X1/ + n{n + \)v = 2P'n(x).
1 Представление решений в форме определенных интегралов расширяет об-
области их применимости.
223
Отсюда непосредственно можно показать, что
Р'п(Х) ~ Р'п-2 (*) = BЛ - 1) Рп_! (X),
следовательно
Р'п (х) = Bл - \)Рп-г (х) + Bл - 5) Рп-з(х)+Bп - 9) Рп^{х) +...:
последний член ряда равен ЗР, (х) или Р0(х), в зависимости от
того, является ли л четным или нечетным. Соответственно v
может быть определено из уравнения
~~ {A - х-) v'} + п (и + 1) "о - 2 V Bл - 4r -L- 3) Р„_2Л_. х[х),
где Л/ равно --^-л или -^ (л + 1), в зависимости от того, является ли
л четным или нечетным. Но частное решение уравнения
/х [ A — л2) г.'} + л (л + 1) _ -= 2 Bя — 4г - 3) Р„_„ j (л:)
имеет вид
2/; —4/" 4-3
Bг-1)_(л-г+ 1) n -' J '
.ледовательно
г 1
Таким образом искомым решением будет
^2" ^п w lus Зс^-" Г I Гя~ ~ ^ ^ ' з• (и~
2л-9 р , ,
последний член равен
з
\ (х) или "у Ро (л],
соответственно тому, будет ли л четным или нечетным. Реше-
Решение очевидно действительно для всех значений л; при 1л|>1.
Обозначим полученное решение Sn (x); тогда, поскольку
Рп 1х) и Qn (x) — явные решения,
Sa{x) = АРп (л) + BQn(X),
где А и В — постоянные. Для больших значений х!
Р„ (х) = О (а» ), С„ U) - О (л-*-1).
И ПОСКОЛЬКУ
lQg i + + +
224
Sn (x) не больше О (л"). Следовательно А = О, a Sn (x) равна
постоянной, умноженной на Qn(x), тогда
= ~Рп(х) lOg X^\~
где Rn(x) —полином степени п—1.
Разделим обе части уравнения на Рп(х) и продиференцируем
относительно х, тогда
я d J 9йМ \
«х \pn(x)j
где Тп(х) — полином степени 2л — 2 (максимум).
Поскольку
n (х) = О,
то умножением этих уравнений соответственно на Qn(x) и на
Рп(х) и вычитанием одного из другого получим
откуда, интегрируя, получим
где С — подлежащая определению постоянная. Теперь, так как
общие члены Рп (х) и Qn (x) соответственно равны
И *
2" (я!)- Bяг1)!
то мы найдем, что С=1. Следовательно
«гЯ„ (a) dQn (х) 1
или
Отсюда следует, что
Э. Айне—133—15 225
или
Пусть х — \, тогда, поскольку /3„A)=1, а Тп(\) конечно,
= 1.
Следовательно
О (х)= ' Р
N
^ B 1НГ + 1)
Р
^ Bг - 1НгГ-г + 1) п-гг , 1
.••=1
В частности
Qo (л-) = \ log
Q2 (JC)= -L P2 (*) log ^| - -f л;
Qs (*)= J- P3 (л) log ^±1 - |- л2+ -2-.
7-3. Точка в бесконечности как нерегулярная особая точка. Часто
встречаются уравнения, решения которых нерегулярны в бес-
бесконечности; в качестве примера таких уравнений можно при-
привести линейные уравнения с постоянными коэфициентами. Изу-
Изучение поведения решений таких уравнений для численно боль-
больших значений, х является поэтому достаточно важной задачей,
которая может быть разрешена только при помощи теории
функций комплексной переменной1.
Однако можно дать довольно грубые указания относительно
поведения решений, нерегулярных в бесконечности, примене-
применение которых, несмотря на их неточность, имеет некоторую
ценность.
Рассмотрим уравнение второго порядка
где хотя бы одно из условий для регулярной особенности в бес-
бесконечности, именно
р {х) = О (лГ~!)> Ч (*) =-- О (х~2)
при х — -"¦ оо нарушено. Предположим, что коэфициенты р(х)
и q (x) могут быть разложены в ряд по убывающим степеням х
Тогда, поскольку точка в бесконечности нерегулярна) одно или
оба неравенства
t, \ 1 о -^ о
должны быть удовлетворены.
1 См. гл. XVII — XIX.
226
Рассмотрим возможность удовлетворить уравнению при по-
помощи функции, которая для больших значений х имеет вид
где Р(х) — полином от х, а "V (х) = О A) при х —> со. Пусть Хл' бу-
будет общим членом Р{х), тогда, подставляя приведенное выше
выражение в уравнение и вычитая преобладающую часть каж-
каждого члена, получим
Следовательно v дается уравнением
v = а -|- 1 или Ъ — р + 2,
в зависимости от того, какое из них дает большее значение v.
Так как 2v — положительное целое число, то для упрощения
предположим, что v также положительное целое число.
Примем решение вида
где
а постоянные X, «,-.., «, з, rtx, а2, .. . определяются последова-
последовательно.
Когда решение этого типа существует, оно называется нор-
нормальным и имеет значение v. К сожалению, если ряд ю (х) не
заканчивается, он расходится в общем случае и решение по-
поэтому неверно. Тем не менее можно показать, что хотя ряд
и расходится, все же он является асимптотическим *, и, следователь-
следовательно, имеет значение для практических вычислений. Теперь при
помощи метода последовательных приближений покажем прак-
практическое значение расходящихся рядов, причем приведем при-
пример из теории функций Бесселя.
7-31. Асимптотическое разложение решений. Рассмотрим линей-
линейное уравнение второго порядка
где р и q — вещественны и ограничены на бесконечности. Разло-
Разложим р и q в сходящийся ряд
Р (*) =
q {х) = >q0+q1x~1+qix~2+ ...
3 Уиттекер и Ватсои, Курс современного анализа, гл. VIII.
227
При подстановке у =-= е'л v уравнение преобразуется в
S+ B). + Р) ~
если X — корень уравнения
'¦2+>-А>+<7о = О,
то постоянный член коэфиииента v обратится в нуль, а урав-
уравнение примет вид
Пусть
тогда, если
<V- + р, = О,
член, содержащий х~: в коэфициенте v исчезает.
Главный член коэфициента ,- равен й0 и вещественен при >.
i-.ещественном. Предположим, что &0 отрицательна1, тогда при
умножении независимой переменной на положительное число
(~"йо)~' вместо &0 получим—1.
Таким образом уравнение примет вид
dHi
dx-'
Найдем решение, принимающее значение т, при х = + со. Поло-
нсим «! = ¦»] и определим последовательность функций (ип) из
соотношений
dx- dx \ х ~*~ -2 ' ' " * J dx у xs * х3 I "
тогда2
1 Разберите случаи, когда »0 положительный коэфициент, а >. мнимы и
Пример последнего дан в следующем параграфе.
2 Решение
d-u du
dx ~Ш~~Пх)ш
которое приводится к т, при х == + со, имеет вид
и = т. + j (е '—
X
при условии существования интеграла.
228
где aj, aa,..., ,32, ps,... могут быть выражены через аь a2,...,
fc2. &,,
Отсюда следует, что
Предполоншм, что |un_i—и„_2| ограничен для х>а, и его
верхняя' граница равна Л1п_г, тогда |«n —un_i| будет ограниче-
ограничена в том же интервале, а его верхняя граница Мп удовлетворит
неравенству
где /С— постоянная, независимая от п. Ж2 ограничено для доста-
достаточно больших значений х, следовательно неравенство верно для
всех значений п. Сравнивая, получим, что ряд
и -=Kj + («2 - "j) + • • • + Ц1„ — нп_ i) + -.
сходится для достаточно больших значений х. Более того, его
сумма является решением диференциального уравнения относи
тельно и.
Теперь
е s, —> 0 при х -ъ ее. .
Аналогично
22V
и, наконец, если /и>«,
_v
'л—1 I | ™т — 1 | "т
„-! + ••¦ ' :vffl-_:i -< -хт
где е„ _ t —»О при л- —»с» .
Следовательно
«1 + («а — «i) + • • • + («п - «п-О =-
+ Cj . Со , , С/77 — 1 I С//; -р 3
где е—*0 при х—>ю. С другой стороны
I (и„ г —и„) + («„_- - «n + ij + ... |
где //—постоянная для достаточно больших значений х
Отсюда следует, что
где ",'п-^О при л ->сс.
Следовательно данное диференциальное уравнение допускает
решение вида
Ряд ИС7.л: —г может быть конечным; в этом случае представление
точно. Но если ряд не конечйый, то он обычно расходится ].
При т фиксированном и Sm, обозначающем сумму ряда
если ? произвольно мало, то
I хт (у - Sm) | < г
для достаточно больших значений \х\. Следовательно ряд дает
асимптотическое представление решения, а знак равенства за-
заменяется знаком асимптотической эквивалентности
1 Это может быть доказано рассмотрением уравнения
ay _dy
y _dy_ $
dx2 dx ' jc* > - u •
230
7-32. Уравнение Бесселя. Если п не целое число, то уравне-
уравнение Бесселя г
удовлетворяется двумя независимыми решениями
yl=Ju{x), v2 = ./_„(»,
где
Если п целое число, то эти два решения перестают быть неза-
независимыми. Второе решение, когда п целое число, логарифмиче"
ского типа -.
Рассмотрим решения, соответствующие нерегулярной особен-
особенности в бесконечности 8. Подстановкой
_ 1
У — X' 2 И
исключим из уравнения второй член, после чего оно примет вид
dhi
+ I 1 + ^— } а = 0 .
Для больших значений |л| это уравнение переходит в и" + к=0,
что предполагает подстановку4
Уравнение теперь принимает вид
1
dx2 ' dx
формально оно удовлетворяется рядом по убывающим степеням
л, именно
22. 2,-
+ ^ 4 " '^"-'-
4!-
Этот ряд расходится для всех значений х, но он асимптоти-
асимптотического типа. Так, если |л:| велик, то первые члены быстро
уменьшаются с увеличением степени и, как будет показано ниже,
можно получить важный метод для вычисления Jn{x) при х
большом.
1 Bessel, Abh. Acad. Wiss. Berlin, 1824, 34. Исторический обзор и связанные
уравнения см. Watson, Bessel, Functions, I.
2 Это решение будет полностью приведено ниже (§ 16-32).
3 Подробно см. Watson Bessel Functions, VII.
4 Другой метод решения-при я = 0, см. Stokes, Trans. Camb. Phil. Soc, 9
A850k 182; [Math. and. Phys. Papers, 2, 350j.
231
Комбинируя полученный ряд с рядом, полученным подста-
подстановкой — I вместо /, получим два асимптотических соотношения
_ i^
уг ~ х 2 (U cos х + V sin x),
у2 ~ х 2 (U sin х — V cos x),
где ?/ и V — соответственно четный и нечетный ряды
1 _ (т-)(т-*2) ц (т-"¦) (т-*) <т ~ *) 1т~ *)_
2г-2!.л:г
J_ _ „«
4
(X - „«) A. _ „«) (р _ „2)
к ч_4 Ч ' ч 1 '_ _1_
2х ~~ 23 ¦ 3! • Xs "Г • •
Связь между функцией J0{x) и соответствующим асимптоти-
асимптотическим рядом может быть выведена из соотношения*
т; Jo (л) = f cos (л- cos 6^6.
Пусть
Jo (а) = Аух + Вуг,
тогда при х —> оо
lim а 2 Уо (х) = A cos л + Б sin л',
lim а2 Л (л) = -Л sin л' + Б cos x.
Таким образом
j
А — lim х ' {Jo (a) cos a — f0 (a) sin a }
1 я
X 2 Г
= lim - -__ / j cos a cos (л cos 6) -f- sin x cos 6 sin (x cos 6) ] db
о
1 с
— lim x- I cos Bлsin2 -^-b) cos2 -4-
71 в/ Ч ^ / ^
0
+ lim-^— / cos f 2x cos2 -^- 6 J sin2 -9-
0
Пусть
v^xsin -л-е=ф.
1 Эквивалентное соотношение будет установлено в следующей главе (§ S- 22).
232
тогда
1
lim ~~ J cos Bx sin24,- б) cos2 -~- 0 rfO ==
i V~2x 1
9 2 Г 2 —
= llm — / A — ^-}2 cos Ф2 <i<p=
0
J со
J
2 2' /"
= — f cos
1
0
Второй интеграл имеет тот же предел, следовательно
_ J_
Аналогично В = к 2 , откуда
2 в .2! . _jc2 212-4!-.t4
• х3 29 • 3! • хв
7-321. Применение асимптотического ряда для числовых вычи-
вычислений. Значение асимптотического ряда может быть проиллю-
проиллюстрировано вычислением частных значений J0(x). Если для вы-
вычисления /0B) применять ряд по возрастающим степеням
/ /v-1 1 j-ll _i _i_ л \ 5 л |_
Jo \л> -1 22 ' 26 28 • З2 210 • З2 • 42 12 • З2 • 42 • 52 • ¦ "»
а последним взять член с х1е, то
/0B) = 0,22389077914
с точностью до одиннадцатого знака. Но если х = 6, а члены
взяты до Л'° включительно, то
Л F) = 0,15067
с точностью только до четвертого знака; последний член имеет
значение 0,00026, что влияет на четвертый знак. Таким образом
даже для относительно небольших значений х ряд по возра-
возрастающим степеням непригоден для практических вычислений.
Рассмотрим теперь асимптотическое представление Уо F)
Уо F) = ¦— { (sin 6 + cos 6) U + (sin 6 cos 6) V j,
где
// — 1 _ 1~ 'У~ 4- 12-3ll5' - Т~ _ 1- -З2- 5J- 72 ¦ 9
2е • 2! • 6а "*~ 212 • 4! • б4 21* -'б! • 6е
= 1 0,00195 + 0,00009 — 0,00001 + • ¦ •
= 0,99812,
хг I2 I2 • 32jJ>- , I2 • З2 ¦ 52 • 72 • 9'- _
'•' " ' 23"б 29^~ЗГ^6-! "" " 1" ¦ 5! ¦ 6-" "
=- 0,02083 — 0,00034 + 0,00003
= 0,02052.
Поскольку 2к — 6 = 0^28318, по таблицам Барроу найдем:
sin 6 = 0,27941, cos 6 = 0,96017, следовательно
Уо F) = 0,23033 @,67948 — 0,02544)
= 0,1Е054,
с точностью до пятого знака. Таким образом при помощи
асимптотического ряда более правильный результат получится
значительно быстрее, чем при применении сходящегося ряда
по иозрастающим степеням.
7-322. Большие корни функций Бесселя. Можно доказать,
как в § 7-32, что
+ Vnsinfx — -_- nv. j*)}.
где
2x
Следовательно \ — корень Jn(x), где l определяется соотноше-
соотношением
ctg (?- i- пъ - -i- -) 2Y-* •..
Если корень $ имеет большое абсолютное значение, а и не
очень велико, то S приближенно определяется уравнением
234
или
где т велико'.
Отсюда непосредственно следует, что большие корни после-
последовательных функций Бесселя отделены друг от друга 2, т. е.
между двумя большими корнями Jn (х) лежит только один ко-
корень У„м (л:).
7 ¦ 323. Дальнейшее рассмотрение применения асимптотических
Рядов. Диференциальное уравнение
dv . 1
формально удовлетворяется рядом:
_' _| :_:. i _-•_ г -L- — 4-
X ~ X* ^ X" ~ ' ' ' *~ хпт1 > ¦ ¦•>
который очевидно расходится для всех значений х.
Уравнению удовлетворяет частный интеграл
х
у = е~х
х
х f х~* е'dx,
¦—оо
который сходится при х отрицательном.
Повторным интегрированием по частям найдем
х
где
Л'
#„ - (я + 1)! е~х f х-"-2 exdx
—ос
Тепер при х<^0
А'
!/?,,(< <п + 1I ех' х-"'-; У ev^ - ! л"~ 21-
—со
Следовательно ошибка, заключающаяся в том, что рассматрива-
рассматриваются первые п членов ряда, численно меньше члена (я + 1). По-
Поэтому ряд является асимптотическим и может быть использо-
использован для рычисления интеграла.
Функция, определяемая интегралом
1 Метод введен Стоке ом [Stokes, Trans. Carab. Phil. Soc. 9A850), 184];
[Math, and Phys. Papers, 2, 352]. Полную разработку метода см. Watson, Bessel
Functions § 15 - 53.
2 Эта теорема верна для всех корней. Общая проблема распределения кор-
корней решения диференциального уравнения второго порядка будет рассмотрена
в главе X.
235
называется экспоненциал-интегральной функцией и обозна-
обозначается Ei(x).
7-4. Уравнения с периодическими коэфициентами; уравнение
Матье. Если коэфициенты диференциального уравнения одно-
однозначны, непрерывны и периодические, например, с периодом я,
то общее решение не обязательно должно также иметь период я.
Уравнение может не допускать (и обычно не допускает) такого
периодического решения.
Так, уравнение
не имеет периодического решения, если только а не равно ну-
нулю, и хотя уравнение
-i-r, 4- п2у = О
dx2 ' -'
всегда имеет периодическое общее решение, период не равен
ъ, если только п не четное целое число.
Общий случай мы рассмотрим несколько ниже (см. гл. XV);
здесь мы разберем частное уравнение, имеющее'ряд важных
практических приложений, именно, уравнение Матье1
j% + (а - 26 cos 2х)у = 0.
Это уравнение не имеет конечных особых точек, следовательно
его решения действительны для всех конечных значений х. Бо-
Более того, если G(x) — решение, не четное и не нечетное, то
G(—х) будет независимым решением
— четным решением, не равным тождественно нулю, а
±.{G(x)-G(-x)}
— нечетным решением, не равным тождественно нулю. Таким
образом достаточно рассмотреть только четные или нечетные
решения. Теперь, если бы уравнение имело два независимых
четных решения, то не существовало бы решения, удовлетворя-
удовлетворяющего начальным условиям
у@)=0, У'0@)=1,
а это противоречит условию, что начало является обыкновен-
обыкновенной точкой. Таким образом два независимых четных решения
и аналогично два независимых нечетных решения не могут су-
1 Mathieu, J. de Math. B), 13 A868), 146; Уиттекер и Ватсон, Курс современ-
современного анализа, гл. XIX ; Humbert, Fonctions de Lame et Fonctions de Mathieu.
236
шествовать. Следовательно одно фундаментальное решение
должно быть четным, а другое нечетным.
Допустим, что четное периодическое решение с периодом
2и существует и допускает разложение1
со
С0(х) = "Sj сг cos Bг + 1) х.
г О
Подставляя этот ряд в уравнение и сравнивая коэфициенты
аналогичных членов, получим последовательность рекуррентных
соотношений, связывающих коэфициенты ст, именно
(я-1-б)со-вС1 = О,
{Bг + IJ — о} сг + G (Cr+i + Cr-i) = О
(r= 1,2,3, ...)•
Эти уравнения должны быть совместными; условием их совмест-
совместности будет
Д(а, 6) = | о. — 1 — е, — 9 0, 0, ... i = 0.
! — 0 а — 9 — 6, 0. . . . [
0, - 6 а - 25, - Ь, ...
\ 0, 0, -0, а—49,..
Таким образом для того, чтобы периодическое решение рас-
рассмотренного типа существовало, постоянная а должна иметь одно
из значений, определяемых определяющим уравнением2
Ца, 6) = 0.
Эти значения называются характеристическими; когда а опре-
определенно, коэфициенты сТ могут быть получены из рекуррентных
соотношений, и определяются единственным образом, независимо
от постоянного множителя.
Пусть ап будет корнем определяющего уравнения, которое
приводится к /г2 при 6 = 0. Можно доказать, что
а" = + 2A-1)+° (б4)' (л - 5,7,9,...).
1 Диференциальное уравнение не имеет конечных особых точек, поэтому
(§§ 3-32, 12-22) его решение не имеет конечной особенности, а разложение
сходится для всех значений х. См. также Уиттекер и Ватсон, Курс современного
анализа, § 9-И.
2 В данном случае детерминант не сходится; однако умножением каждого
ряда, на соответствующий множитель его можно сделать абсолютно сходящимся,
см. Уиттекер и Ватсон, Курс современного анализа, § 2-81.
237
Можно также доказать, что если а — aon+i и сп— 1, то
is
Bл — г)! I/
это, по крайней мере для малых значений | 6 |, подтверждает схо-
сходимость ряда.
Аналогично, решение типа
50(л) - V c;sinBr+ 1)л
г о
существует, где а — корень уравнения
Рекуррентные соотношения, из которых определяются коэфи-
циенты с'г, будут
(а -1+Ъ)с'о- *с\ - 6,
{Bг + IJ - а } с\. y 0 «+1 + Ci ) = ° (г ^ 1,2, 3, .. .)•
Для соответствующих значений а существуют также решения
периода ~ вида
оо
;=0
-= У, c'rsin2rx.
г 1
Рекуррентные соотношения в этих случаях равнв1 соответственно
ас0 — (ic1-^ 0,
Dг"~а)сг + гЦсг !+<;,_,) = 0, (г-1,2,3....)»
(а ~ 4) с\ - ес; - о,
Dг2 - а) с; + О (C;f j + с;_,) ¦= 0, (г = 2, 3,4,...).
Таким образом имеется четыре различных типа решений
уравнения Матье с периодом к и 2п; эти решения, умноженные
на соответствующие множители, известны как функции Матье.
Функция Матье, которая приводится к cos тх при 6 = 0 и в кото-
238
рой коэфициент при cos тх равен единице, обозначается сет{х).
Аналогично, функция, которая приводится к sin тх при 6 = 0
и в которой коэфициент при sin тх равен единице, обознача-
обозначается sem(x). Так
се-2п i (х) типа Со (х),
се=т (•*) типа Се{х),
sein+i(x) типа S0{x),
s?2n{x) типа Se(x).
7-41. Несуществование одновременных периодических решений*
Пусть а будет таким, при котором уравнение Матье имеет пе-
периодические решения типа С0{х). Тогда возникает вопрос, воз-
возможно ли при каких-либо условиях, чтобы второе решение,
а следовательно и общее решение, было периодическим. Если
Ух и _v2 —независимые решения уравнения
и следовательно
dv.2 Aуг
то отсюда следует, что если yt типа С0(х), то у2 типа S0{x)T
а не Se{x). Если уравнение допускает и решение Со (х) и реше-
решение Su(x), то уравнения
(«-l-ejCo-Gc, О,
{Bг + ])* _ с } с,. + 0 (с, ,.+ «>_,) - О,
(г == 1,2,3, ...) должны быть совместно удовлетворены. Покажем,
что это невозможно.
Исключив а из первых двух уравнений, найдем
или
г' г' I
Последние два уравнения дают
или
| СГ> СГ 1 | j СГ— 1, СГ |
г' г с' с' '
230
откуда для всех значений г
i Ст, Сг\
Но если с„ равно нулю, а 6 не равно нулю, тс остальные коэ-
фициенты сп будут равны нулю, и решение будет тождест-
тождественно равно нулю. Поэтому с0 и с'о не равны нулю. Но для того,
чтобы ряд сходился, необходимо, чтобы
с,- —^0 при г-> со,
что приводит к противоречию. Таким образом, за исключением
случая, когда Й = 0, решения типа Со(х) и 5о(л:) не могут су-
существовать одновременно. То же можно отнести и к решениям
типа Се(х) и Se(x).
7-42. Природа второго решения. Таким образом мы доказали,
что если одно решение _у, имеет период ^ или 2п, то второе ре-
решение y.z будет определенно непериодическим. Сейчас мы опре-
определим общий характер этого второго решения. Так как
где С — постоянная, то
У*=Су1 /
1 / ¦
Теперь пусть
уj = Со (л) = ^ сг cos Br -}-1} х,
г О
тогда
y'j = V) е,. cos Чгх,
и поскольку _у2 не равна нулю при х = О,
г О
Последний ряд сходится по крайней мере для достаточно малых
значений х.
Следовательно
| со \ ( оо .
у2—-С \ V с,, cos Bг + 1) д: > s g0A: + V hT sin 2rx V.
(-^. I I • r~i )
где, поскольку известно, что функция у., не периодическая,
g0 не равна нулю, и следовательно при соответствующем вы-
.боре С
у% ¦= хС0 (х) + S'o (x),
где S'^(x) — ряд того же типа, что и 50{д:).
240
Таким образом у%(х) является не периодическим, но квази-
квазипериодическим и
у2 (х ф 2тг) = у& (х) + 2ъух (х).
Природа второго решения, когда первое решение типа S0{x),
Се{х), Se(x), может быть исследована аналогично1.
7-5. Связь между диференциальными уравнениями и непрерыв-
непрерывными дробями. Частный метод решения диференциальных урав-
уравнений, который мы сейчас рассмотрим, имеет преимущество:
он прямой и не такой искусственный, как метод решения в виде
рядов. Однако он ограничен, так как применим только к линей-
линейным уравнениям второго порядка2.
Не теряя в общности, можно принять, что рассматриваемое
уравнение имеет вид
где Qo и Р, — функции от х. После диференцирования уравнение
примет вид
' Q
где
Этот процесс повторяется неограниченно, причем получается
последовательность соотношений
где п = 1, 2, 3,..., и
Таким образом
Pl
где
1 Общее решение, когда а не характеристическое число, может быть пока-
показано в различных формах; см., например, Whittaker, Proc. Edln. Math. Soc, 32
A914), 75.
2 Этот метод был впервые применен Эйлером для решения диференциаль-
ного уравнения Риккати.
Э. Айне—133—16 241
Здесь нужно рассмотреть непрерывную дробь1
_!_ -1л J3-^ Jj}
Q6+ Qi+ Q2 + '"+ Qn+'"'
если эта дробь конечна, то она будет логарифмической произ-
производной решения уравнения; если она не конечна, то возникает
вопрос о ее сходимости. Этот вопрос разрешается следующей
основной в теории непрерывных дробей теоремой2. Непрерыв-
Непрерывная дробь (А) сходится и имеет значение у'/у, если у ф 0 и (I)
Рп-ъР, Qn-^Q при п -э со, (II) корни р! и р2 уравнения р2 = Qp-f-P
имеют неравные модули и (III), если \ рг | < | рх |, то
при условии, что \ р2 { ф 0.
При |р2| = 0 последнее условие заменяется условием конеч-
конечности предела.
7-501. Пример конечной непрерывной дроби. В случае уравнения
у = —у Л—у ,
где т — положительное целое число, производные уравнения
будут
(п)= X <п+1), 1 (п+2)
У т—пу ^т-пУ (n= I, 2,...m —1),
Отсюда следует, что
У
v
т
х -
т
{-
—
X
1
т
—
X
2
"f" " '
1
' + X
Поскольку эта непрерывная дробь конечна, она может быть
точно вычислена последовательным нахождением подходящих
дробей3, и мы найдем, что
у __ тхт~х +(т — 2)a1xm-s
Т"~ ~ хт+а1хт-*+а.,х'п-4+...
где
A
2г)\'
Следовательно можно непосредственно доказать, что уравнение
имеет решение в виде полинома
У = хт+ а^-'+а^х-'^...
1 Аналогичная непрерывная дробь может быть получена не диференциро-
ваннем, а интегрированием
2 Доказательство этой теоремы см. Perron, Die Lehre von den Kettenbruchen,
3 Chrysta!, Algebra, II, XXXIV.
242
7-51. Функция j/7, (a; f; x) и присоединенная непрерывная дробь.
Функцияг
где
является решением уравнения
*У = A ~ х)у' + ху",
когда -у не целое число; независимым вторым решением будет
Ряд заканчивается, когда а равна нулю или отрицательному
целому числу; этот случай не представляет ничего нового и мы
йе будем его рассматривать. Если ряд умножить на 1/Г(т), то
его коэфициенты будут всегда конечны, а функция обратится
в нуль, только если т — а и а будут равны нулю или отрица-
отрицательному целому числу.
Пусть
У = iFj, (а; -у; *)_
тогда
л- у(п+2)
Все производные У(п) не могут обратиться в нуль, так как если бы
Г<от+1) и уС»+3) должны были обратиться в нуль при л- = х0, то
из приведенного соотношения следовало бы, что K(m), ym~x) Hj
наконец, само К превратилось бы в нуль при х = л:0. Таким
образом Y обратилось бы в нуль тождественно, что, за исклю-
исключением специальных случаев, неверно.
Можно показать непосредственно, что
Г (a; r,x) = *Y{a + l; f + 1; x),
1 Эга функция была впервые рассмотрена Куммером [Kummer, J. fur Math.,
15 A836), 139]; обозначения введены Барнсом [Barnes, Trans. Camb. Phil. Soc,
20 A906), 253j. Конфлюэнтные гипергеометрические функции родственны им;
в обозначениях Уиттекера
1 1
m — — v
— m — v" v i \
Mk> m(x)=x~ e " ¦ 1F1, — + m — k; 2m + 1; xj;
см. Унттекер и Ватсон, Курс современного анализа, гл. XVJ. Функции Бесселя
являются частными случаями, действительно
е-1*
•¦2х) Ь i I
243
и в общем случае
Yin) (а; г, ¦*) = (а)я Г (а + и; f + щ х)
Пусть /ft будет положительным целым числом
т > | а |, /ft > 21 y |,
тогда, если п> т, то
П + '«
— ill
1
и, a fortiori, если г > 1, то
а + Я + Г
¦у + и + г
Следовательно при и > /тг
- <gm> | . | (° + /И)...(а + Я-1)
Г G + /я)
¦4
'-V|l!,
поэтому | Y{n)\*n конечно. Но уравнение для р имеет вид
и р2 = 0. Отсюда следует, что непрерывная дробь1
х
1
X
а
«+ 1
ИЛИ
г 1~х + 1 , Т —х + 2 ,
"Г" а + 1 ' а + 2 ' " " '
11+ !)JL (?. + 2) дг
сходится и равна
для всех значений л, для которых последняя функция конечна.
1 Perron, Rend. Circ. Mat. Palermo, 29 A9Ю), 124.
244
Гипергеометрическое уравнение может рассматриваться при-
примерно аналогично, но полученные результаты будут далеко
не такими простыми, как в приведенном выше случае. Для дей-
действительных значений х непрерывная дробь
+¦
сходится к значению -^\ogF(a, 3; •/; х) при л:<-|- и к значе-
значению —log/"(^ P; афр — 7 + 1;1— х) при л: >-i-*.
7-511. Непрерывные дроби и функции Лежандра. Можно дока-
доказать, что если уп — функция Лежандра Qn(x) порядка п, то2
У1 — хуо+1= О,
(п jr2)yn+s— Bл + 3)хуп+1 + (п + 1)уя = 0 (и = 0, 1, 2, 3,...)
Эти рекуррентные соотношения приводят к бесконечной непре-
непрерывной дроби
1_ 1* 2а з2
Уо ~ ~Х — "Зх — ~5х — ~Ъс~" " •'
сходимость и значение которой мы сейчас исследуем.
Поскольку при я—* со
уравнение относительно р будет иметь вид
р2 == X — \Г&— 1 .
Непрерывная дробь следовательно сходится и будет иметь зна-
значение j;0 при
limjyn "<
Ух2 - 1
Поскольку
Ит
1
~2х'
1 Jnce, Proc. London Math. Soc. B), 18 A919), 236.
2 Эти рекуррентные соотношения удовлетворяются также уп = Р„ (л), за
исключением первого, которое очевидно не удовлетворяется.
245
следовательно1
lim
Таким образом, когда
х + v х2 — 1
2\x
или когда (х)>1, у0 может быть отождествлено с Q0(.x), и
следовательно
J
Л _i ^
— Зх — ох — 1х — ¦ ¦ -
Теперь (§ 7-241), поскольку
где Rn — полином степени п — 1,
Отсюда следует, что свернутыми выражениями непрерывной
дроби для Qo (*) будут
Ri(x) P2(X) SPn'(x)
Pt(x) ' Р2(Х) ' ¦"¦• Я„(Х)' *••
Этот результат дает практический метод вычисления полино-
полиномов /?„(л).
Примеры
1. Найдите ряд, удовлетворяющий диференциальному уравнению
dv
A + х) — = ту.
4 'их J
Докажите, что если /(/и) — решение этого уравнения, которое приводится
к единице при х = 0, то для всех значений х
f(m.2)=f(m1 + щ).
2. Докажите, что функция
j1 +
2.Bn-2) + 2.4Bп~2)Bя-4)
1 Bromwicli, Infinite Series (приложение I, стр. 421).
246
удовлетворяет уравнению
d*-y 3
dv i л* — 11 1
4 . ~+ [l ¦ > v = —, когда п — четное положительное целое
rtx*^ x их \ x* S x число,
= -^-, когда п — нечетное положительное це-
целое число. [Edinburgh, 1912].
3. Найдите два независимых ряда по возрастающим степеням х, удовлетво-
удовлетворяющих диференциальному уравнению
Докажите, что это уравнение удовлетворяется также асимптотическим разло-
разложением вида
е*х * V,
1. 8-
2 2 2
где |а = -—- 1х ,а г — ряд по убывающим степеням х . [Edinburgh, 1914].
4. Покажите, что гипергеометрическому уравнению удовлетворяют функции
(I) A-*)T —Pf (т-а. 7_?;т;х),
(II) х*~тA — ^"""-^(l—о, 1 -5: 2 — -(¦, х).
Преобразуйте это уравнение, принимая последовательно в качестве новых не-
независимых переменных
z—l— х, z=l/x, z=1/A~a;), z = x/(x — 1), г=(х— \)jx,
и напишите четыре решения для каждого из полученных уравнений. Покажите,
что совокупность двадцати четырех решений можег быть подразделена на
шесть классов так, чтобы члены каждого класса были равны или являлись по-
постоянными, кратными друг другу. [Kummer].
5. Докажите, что при т положительном целом числе и — 1 < х < 1 при-
присоединенное уравнение Лежандра
удовлетворяется присоединенными функциями Лежандра
-~ т ^т Р (у\ —т
— \i — х
[Ferrers].
Найдите ряд по убывающим степеням, который удовлетворял бы этому
уравнению.
6. Покажите, что если С?(х) коэфициент /г" разложения A — 2xh + h-'f'^
по возрастающим степеням Л, то С^ (х) удовлетворяет диференциальному
уравнению
<?У Bу,~1)х^ау у (у+ 2^) _
dxi+ x2—l dx x-—\y
и выразите С$ (х) в виде присоединенной функции Лежандра.
247
7. Докажите, что диференциальное уравнение для С* (х) определяется
схемой
— 1 со 1
О
Ox
Я Докажите, что диференциальиое уравнение
d3y
+ № — (оф + ft + fc + <х + Р + 7 + 1) X) ^ — сфТ = О
удовлетворяется функцией ^(а, jj, f; 0> EJ x), которая может быть разложена
в ряд
1 +
1!U ' 2! 6 F+ l)-s(e+ 1)
9. Докажите, что если п ие целое число, то
d i J_»{y\ \ — 2sinnn
-*• + ...
Jn(x)
^ sin
[Lommel].
Jn W Jt_n (X) + Jn_t (X) J_n (X) =
10. Покажите, что если п — половина нечетного целого числа, то функция
Бесселя допускает решение в конечной форме,
/ 2 \ г
J j (X) =
*+ 2
и получите общее решение для каждого случая.
11. Покажите, что общее решение уравнения
может быть выражено в виде
j_
у = Ахг J±
S
12. Покажите, что уравнение
: у хг
248
может быть проинтегрировано в функциях Бесселя, и что если т — положи-
положительное целое число, то оно допускает общее решение
y=x {x ~d-
где А и В—произвольные постоянные.
13. Найдите решения в виде рядов (асимптотических) по возрастающим и
убывающим степеням для конфлюэнтного гипергеометрического уравнения
ах [ 4 х х>- \
и покажите, что при k = О решение будет иметь вид
1
У=х*]п
14. Докажите, что если Wkm(x) — решение конфлюэнтного гипергеометри-
гипергеометрического уравнения, то функция
~? т *
удовлетворяет уравнению Вебера
Решения этого уравнения известны как функции Вебера-Эрмита или функции
параболического цилиндра и обозначаются Dn(x).
Проверьте асимптотическое соотношение
-, л ~ТХ* /i "("->) я(я-1)(и-2)(я-3)
и покажите, что D_n_i (ix)—независимое решение.
15. Рассмотрением диференпиального уравнения
ау = —ху'+ у"
покажите, что при а > 0, х > О
2 fdt
а +2 а + 3
х + х -га; -г х + '" то t
о
16. Докажите, что подстановка у = ехи преобразует уравнение
ау = G — х)У + ху"
(а — 7) И = G + X) U1 + XU"
24У
а отсюда докажите, что
1.x. (а + 1) X (i + 2)x
Y — х + 1 — х+Т~+ т — х + 2 +""
(Y — а — 2) X
~! -г х — -у -t- jv Ч- 1 — ч + * + 2 —"¦
[Perron]-
17. Покажите, что если Dn(x) — функция Вебера-Эрмита, то
D'n(x) = j^ n-1 «J72
¦
ГЛАВА VIII
РЕШЕНИЕ ЛИНЕЙНЫХ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ПРИ ПОМОЩИ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
8*1. Общий принцип. Нам нужно получить определенный инте-
интеграл вида
(A) y(x)
где х входит в качестве параметра, удовлетворяющего задан-
заданному диференциальному уравнению
(B) Lx(y) = O.
В определенный интеграл входят три независимых элемента,
которые должны быть выбраны в зависимости от условий:
(I) функция К{х, t), называемая ядром определенного инте-
интеграла,
(II) функция v(t),
(III) пределы интегрирования аир.
Допустим, что ядро К(х, t) удовлетворяет диференциаль-
диференциальному уравнению в частных производных вида1
(C) LAK) = Mt(K),
где Mt — линейный диференциальный оператор, содержащий
только t и -dj.
Тогда, если оператор Lx можно применить к определенному
интегралу у(х), то2
Lx{y{x)} = JLx{K{x,t)}v(t)dt
= JMt{K(x, t)}v(t)dt.
с.
Пусть Mt будет оператором, присоединенным к Мь тогда из
тождества Лагранжа (§ 5-3), которое в данном случае имеет
1 Bateman, Trans. Camb. Phil. Soc, 21 A909), 171.
- Это допущение принято во всей этой главе.
251
вид1
следует
Lx {у (л)} = / К(х, t) Mt (v) dt + [P{ К, vjJZl
о.
Чтобы интеграл (А) мог быть решением уравнения (В), правый
член этого уравнения должен быть равен нулю. Это имеет место
во-первых, если v[t) — решение уравнения
Д (v) = О,
и, во-вторых, если пределы интегрирования выбраны такими
при которых
И* «}]?=«
тождественно.
Этот метод допускает значительное обобщение. Так, напри-
например, предположим, что ядро К(х, f) не удовлетворяет дифе-
ренциальному уравнению в частных производных *(С), но обе
функции К(х, f) и /.(х, f) могут быть такими, что
Lx{K(x, t)} = Mt{*{x, t)};
в этом случае
р
1-х {У (х)} = / х (х, t) Mt H dt + [p{ ¦/, v)}]t=l.
а
Теперь необходимо найти функцию v(t) и пределы интегриро-
интегрирования аи^.
8»2. Преобразование Лапласа. Если т — самая большая степень
любого коэфициента в операторе Lx, а сам оператор порядка п,
то Lx можно написать в распространенной форме
где коэфициенты ars — постоянные.
Рассмотрим вместе с Lx оператор
тогда
г Билинейная последовательность Р{К, v} содержит здесь х в качестве
параметра.
252
так как каждый член этого тождества равен
п т
ext ? ? arsx* t'.
Следовательно уравнение
Lx(y) = 0
удовлетворяется определенным интегралом
(С)
при условии, что v{t) удовлетворяет диференциальному урав-
уравнению
(D) Mt (г>) = О
и что пределы интегрирования выбраны так, что
тождественно.
Уравнение (D) называется преобразованием Лапласа выраже-
выражения Lx(y) = 0, ext — ядро преобразования v(t) в у{х). Целесо-
Целесообразность этого метода для получения явного решения данного
уравнения зависит главным образом от легкости получения ре-
решения (D). В частном и очень специальном случае, когда т = 1,
т. е. когда коэфициенты данного уравнения линейны относительно
х, преобразование Лапласа представляет собой линейное урав-
уравнение первого порядка и следовательно может быть проинте-
проинтегрировано в квадратурах1.
Важная обратная зависимость2 существует между уравне.
ниями Lx(y) = 0 и Mt(у) —0; первое представляет собой преобра-
преобразование Лапласа последнего, причем ядро этого преобразования
равно e~xl. Это следует непосредственно из тождества
Поскольку
2 2
r=o j, о
достаточно доказать, что
{ 1)
1 См. пример 1, в конце главы.
2 Petzval, Integration der litiearen Differentialgleichungen, 1 (Vienna, 1851), 472.
253
а это верно, поскольку каждый член уравнения равен
x4s + \
_ r{r-\){r-2)s(s-\){s-2)
Отсюда следует, что если у и 5 соответственно выбраны, то
(Е) -v(t)
т
будет решением (D). Зависимость между (С) и (Е) дает пример
обращения определенного интеграла, т. е. определения неизве-
неизвестной функции v(t) в виде интеграла, таким образом, чтобы
определенный интеграл представлял функцию у (х), которая
предположена известной.
8-201. Пример, иллюстрирующий преобразование Лапласа. Пусть
1Лу)^xfi + tp + q+^fx
тогда
Mt{u) = t(t + \)f + {pi-(p+g)t}u,
vMt (н) — uMt (v) = &ж [t [t + 1) uv].
Уравнение Mt(rv) = 0 имеет решение
поэтому интеграл типа
будет удовлетворять уравнению Lx (у) = 0 при условии, чтобы а
и [3 были выбраны так, что
тождественно.
Вместо t удобно написать —t; тогда интеграл
э
у (х) = je~x
о:
254
будет удовлетворять Lx(y) = 0, если аир таковы, что
тождественно обращается в нуль. Соответствующие пары зна-
значений будут иметь вид
(I) a=0, р = 1 {P>0, q>0),
(II) а = О, ,8 = со (х>0, р>0),
(III) а=], р=со (х>0, q>0),
(IV) а = — со, р = 0 (х<0, />>0),
(V) а = — оо, р = 1- (х < 0, ^ > 0).
Следовательно искомые значения а и р всегда существуют, за
исключением случая, когда р и q отрицательны. В частности,
когда р, q и х все положительны, общее решение 1ж(.у) = 0
может быть написано в виде
1 со
у - Л JV-* ^ A — t)q dt + B je~xt P(\— t)" dt,
О 1
где Л и Б — произвольные постоянные.
8-21. Определение пределов интегрирования. Уравнение
M(v) — 0, которое служит для определения v{t), порядка т;
его общее решение имеет вид
v = Clv1 (t) + C2v2(t) + ... + Ст vm(t),
где vlt vг,..., <ит образуют фундаментальную последовательность
решений, а постоянные СиСя, .. .,Ст — произвольные. Эти по-
постоянные и пределы интегрирования а и Р должны быть опреде-
определены таким образом, чтобы выражение
обратилось в нуль.
Из билинейной формы (§ 5-3) видно, что для этого доста-
достаточно определить постоянные Сх, ...,Ст, аир так, чтобы
v(t),v'(t), ...,v"n-l\t)
обратились в нуль при t = а и t = р. Это может иметь место
только в том случае, если а и р — особые точки M(v) = 0. Но
если а и р — особые точки и решение v(t) существует так, что
показатель, относящийся к каждой из этих точек, больше т — 1,
то билинейная форма обратится в нуль при а и р, и следова-
следовательно пределы интегрирования могут быть приняты равными
а и р. Этот случай, показанный на примере предыдущего пара-
параграфа, имеет практическое значение. Каждая независимая пара
255
пределов, если они существуют, приводит к независимому част-
частному решению уравнения. В некоторых случаях число опреде-
определенных интегралов достаточно для получения общего решения,
в других — можно получить только частное решение.
Щ 8-22. Представление функций Бесселя в виде определенных ин-
интегралов. Вместо ext, в качестве ядра определенного интеграла
может быть принята функция
Функции е2 не2 могут быть разложены соответственно
в ряды по возрастающим степеням xt и xtr~l, которые абсолютно
сходятся для всех значений леи для всех значений t, не равных
нулю. Двойной ряд, представляющий их произведение, поэтому
сходится для тех же значений х и t и имеет вид
LmLd 2r~S rlsl
/•=0 s=Q
При n > 0 коэфициент t" получается выбором членов двойного
ряда, для которых r = n-\-s. Эти члены образуют бесконечный
ряд
где Jn (x) — функция Бесселя порядка п. Аналогично, коэфициент
t~" равен (—1 )"Jn(x), так что
При t = e№ это соотношение принимает вид
со со
т-1 ^1
Разделяя вещественные и мнимые части, получим следующие
два выражения
cos (л; sin 6) = JO(X) + 2 ^ J2m (я) cos 2/я 6,
со
sin (x sin в) = 2 ? /2ra-i (л) sin 2m—1N.
526
Подставляя -^-гс — б вместо 6, получим
cos (х cos 6) = J0(x) + 2 ? (— 1 )mhm{x) cos 2m6,
sin (л: cos 6) = 2 ? (- 1)т+1 /gm-iU) cos Bm — 1) 6.
m=l
Из первого из этих четырех соотношений следует, что
fc
cos(a;sin6)cos«6d6 = п/n(x) при и четном,
= 0 при п нечетном.
Из второго соотношения следует, что
fsm(xsinQ)sinnBdQ = r.Jn(x) при п нечетном,
о
= 0 при п четном.
Складывая, получим, что если п — любое целое положительное
число или нуль, то
Jcos (ив — х sin в) ffl = и Jn(x).
о
Следовательно обыкновенная функция Бесселя с целым индек-
индексом может быть выражена в виде определенного интеграла1.
8-3. Ядро К(х — t). Рассмотрим возможность удовлетворить
линейному диференциальному уравнению типа Лапласа
при помощи определенного интеграла вида2
= JKl(x-t)v{t)dt.
Очевидно, К(х — t) будет удовлетворять диференциальному
уравнению в частных производных вида
при условии, что К (г), рассматриваемя как функция одной пере-
переменной г, удовлетворяет обыкновенному линейному уравнению
1 Bessel. Abh. Akad. Wiss. Berlin., 1824, 34.
2 Cailler, Bull. Sc. Math., 34A899), 26; см. также Mellin Acta, Soc. Sc. Fenn.,
21A896), № 6.
Э. Айне—133—17 257
Следовательно, если v{t) — решение уравнения
левый член которого является присоединенным выражением
правого члена (А), и если пределы интегрирования могут быть
соответствующим образом выбраны, то данное уравнение будет
иметь решение, которое может быть выражено в виде опреде-
определенного интеграла указанного типа.
8-31. Преобразование Эйлера. Часто встречается ядро типа,
рассмотренного в предыдущем параграфе
К(х — t) = (x- t)~"~l .
Преобразование, ядром которого является (x — t)si, при-
применимо к любому линейному диференциальному уравнению, где
коэфициент _у(г> — полином от х степени г. Такое уравнение
может быть всегда написано в виде
ш =
-... =0
или
ГоС) - ВД + Г,(у) - ... ± Гр(у) = 0,
где
В этих выражениях Gr — полином степени и — г, а ^—посто-
^—постоянная. Принимается, что р-^-1 полиномов GO...GP достаточно.
Подставляя — v=n + (x в ядро K(x — t), получим
u-1)... (v-+r)(x-tr+^2 (-1 У
= (я + и. — 1)... (,. + г) (х — 2^ гг-1 Gr (t),
258
следовательно
п
L, {(х - tr^ } = А V (-1).
г О
где
А = (« + и- 1)(« + л - 2)...((... + 1)и.
Теперь, если
М,(и) = G0(t) ~~- + О, @ -^ +... + Gv(t)u,
то
ЛГ^11 S !'- ~ 2). ..
... (^.- г) (х - ^+r-J Gr (О
где
Б= (- \f(p + y-l)(P + v~2).
следовательно
^ж{ (^ - ^)"J ^ } = CMt {{x-t
где С = Л/Б.
Если
ТО з
р
= CJMt{(x -
и, как в общем случае, f(^) должно быть выбрано так, чтобы
подынтегральное выражение было полным диференциалом, после
чего должны быть установлены пределы интегрирования. Опре-
Определение v{t) включает решение уравнения
Л1,{у) = О,
известное как преобразование Эйлера L,t(y) = 0. При р = 1 пре-
преобразование Эйлера представляет собой линейное уравнение
первого порядка, a v(t) может быть точно определено1.
1 Полное исследование будет приведено в § IS.4.
259
8-311. Пример преобразования Эйлера. Приведем случай урав*
йения Лежандра (§ 7-24).
В обозначениях предыдущего параграфа
x) + (u + 1) G't(x) + G2(x) =«(»* 1).
Эти соотношения удовлетворяются
Qjix) = 2(ji + l)x, G,(x) = 0,
при условии
u = И — 1 ИЛИ fi = — П — 2.
В данном случае р = 1 и уравнение Л4((и) = 0 принимает вид
A-Р)^ф2(|1 + 1)*и = 0.
Присоединенное уравнение
Mt{v) = A-^)^-2(^ + 2)^ = 0
имеет решение
Пределы интегрирования d и р должны быть выбраны так
чтобы
[(х - ^A - Р)-"-1]!^ = 0
тождественно. При и = — я — 2, я + 1>0 и |х| > 1 это условие
удовлетворяется а = — 1, Р = + 1. Отсюда определенный инте-
интеграл
41
1
f(x-t)-"-l(l-fifdt
1
удовлетворяет уравнению Лежандра. Если Qn(x) — функция Ле-
Лежандра второго рода1, то
—1
1 Уиттекер и Ватсон, Курс современного анализа, § 15*3.
260
8-32. Интегралы Лапласа. Изменяя порядок интегрирования,
можно получить интегральное выражение для функции Лежан-
дра PJx) аналогично интегралу предыдущего параграфа, пред-
представляющему Qn(x). Однако это не может быть проведено без
помощи комплексных переменных, и будет поэтому рассмотрено
нами ниже (§ 18-5). Ввиду важности полиномов Лежандра мы
здесь приведем простой метод, при помощи которого они мо-
могут быть выражены в виде определенных интегралов.
Рассмотрим ветвь функции
равную 4- 1 при И = 0. При I h I, меньшем какого-либо из выра-
жений \х-\-(х~— IJ и \х — {х2 — 1)г\, функция может быть
разложена в степенной ряд относительно h
где Pdx), Pi{x), P2(x)...— полиномы от х, которые являются
полиномами Лежандра.
Уравнение
имеет корень
v =
_ 1 — V]I — 2xh i h2
который приводится к х при h = 0 и который при | h \ доста-
достаточно малом может быть представлен в виде ряда
dnv\
S
/z-l
Легко доказать, что
dh 2 ^ ' дх
и что если <р (v) — любая функция v, то
д i , . &и \ \д ( . >
Предположим, что для некоторого целого значения п
dhu дхп~ 1 \2>Л ' дх
тогда
'IZJ^ - _?!_ {J ft,» - 1)" dv\
)hU ' l AV11 1 Pit, \ * "Л>
дх
= ^L/JL(^_i)" —
дх'}
Таким образом, поскольку соотношение верно при п— 1, оно
верно для всех значений и.
Пусть h = 0, так что v = x, тогда
следовательно
Ld/г" Jo dx«-ij 2'лл ; ,
^ = л + v —. ¦ -"— -!¦ {-L(л2
Так
следовательно
" W ~~ 2"ia * ax" '
a Pnf-x) является, по формуле Родрига (§ 7-24), полиномом Ле-
жандра.
Теперь, поскольку при | b\ <|а \
о
отсюда следует, что
со
V /г"Рп (л) =
dx т.
b2' '
cosx j a-~b2
dt
т/тз
hx — h V xz—l cost
Этот интеграл абсолютно и равномерно сходится для достаточно
малых значений \h\; разлагая интеграл в ряд по возрастающим
степеням h и сравнивая коэфициенты при /?", получим полином
Лежандра в виде интеграла Лапласа
Рп (х) = — Г \х+ гА~2"~г cost}n dt.
к j i x )
о
262
Аналогичными интегралами будут
Qn(x) = f{x +/X^T Chi}-"'1 dt,
о
m)
P,7U)-= J——J^-J {x+Vxl— 1 cost}"cosmtdt,
8-4. Преобразование Меллина. Решение при помощи опреде-
определенных интегралов, в которых ядро является функцией произве-
произведения xt, были подробно исследованы Меллином1. Такие
решения могут быть получены, если рассматриваемое диферен-
циальное уравнение имеет вид
(А)
?{)
Пусть Н будет полиномом аргумента этого уравнения, а
K(z) — любым решением обыкновенного диференциального
уравнения
тогда /С(а:^) будет удовлетворять диференциальному уравнению
в частных производных
ИЛИ
Интеграл
y = fK{xt)v(f)dt
а
удовлетворяет (А) при условии, что v (t) — решение
AU(v) = 0,
где Mi — оператор, присоединенный к Ми и при условии соот-
соответствующих пределов интегрирования аир.
8-41. Приложение преобразования Меллина к гипергеометриче-
гипергеометрическому уравнению. В качестве примера возьмем гипергеометри-
гипергеометрическое уравнение
(А)
1 Mellin, Acta Soc. Sc. Fenn., 21A896), 6, 39-
263
которое после умножения на х может быть переписано в виде
Пусть
где постоянная е произвольна. K(xt) удовлетворяет диференци-
альному уравнению в частных производных
при условии, что и = K(z) — решение
z(l-z)g + {<?-(a + 6+
Уравнение
/И,^) = О
удовлетворяется
v{f) = f-1(l-f)c-e-\
и пределы интегрирования должны быть определены так, чтобы
тождественно обратилось в нуль. Если и = F(a, b; e; xt), то это
условие удовлетворяется при a = 0, р = 1, если е >0, с> е. Сле-
Следовательно при этих условиях
y(x)=f F(a, b; e;
о
удовлетворяет (А). Теперь
у @) = /Г A - ^)с-^^ =
У@) =
о
= _о6 Г (е) Г (с —¦?)
с * Г (с)
Но эти начальные условия определяют единственное решение
^t{a, b; с;
64
следовательно
i
fF(a, b; e; xt)f~\\ - tf^dt = ТЩг(^)Р{а, b; c; x).
В частности, пусть е = b, тогда, поскольку
F(a, b; b; xf) = A - xt)~",
отсюда следует, что
/A - xtT^i} - trb-ldt = Ii^=if(a, b; c; x),
о
если й > 0 и с > b.
8-42. Получение определенного интеграла при помощи гипергео-
гипергеометрического ряда. Используя свойства гамма- и бета- функций,
можно легко преобразовать выражение в виде ряда для
гипергеометрической функции в эквивалентный определен-
определенный интеграл. Поскольку
оо
Fia, b; c;x) = \ + V
г - 1
Г\ С(С+ 1)...(С + Г— 1)
/ () \1 а (а + !)... {я + г -_1)_ Г^+r) ,\
\ Г (с) Ч"? " г! 'Г(с+г) Л)'
Теперь
о
при условии, что вещественные части b -\- г и с — & положи-
положительные, следовательно
F{a, b; с; x)=.
1
) /
г!
о
1
Г (с) 1\ь-1 гл ^с-ь-1 п _xty^dt.
Г(Ь)Г(с~
о
Проведенное изменение порядка суммирования и интегриро-
интегрирования имеет смысл, когда гипергеометрический ряд равномерно
сходится, т. е. если |xj^p<l. Представление функции в виде
265
определенного интеграла имеет смысл для всех значений х, но
для компенсации этого увеличения области применимости дол-
должны быть наложены ограничения на b и с.
Порядок интегрирования можно изменить так, чтобы ин-
интеграл представлял независимое решение диференциального
уравнения.
8-5. Решение при помощи двойных интегралов. Во многих слу-
случаях, когда попытки удовлетворить данному линейному дифе-
ренциальному уравнению при помощи определенного интеграла
типа (§8-1, А) безуспешны, можно решить задачу при помощи
кратного интеграла. Метод, основанный на преобразовании Лап-
Лапласа, практически бесполезен, если преобразованное уравнение
не первого порядка; возможность решить уравнение соответ-
соответственно ограничивается. В настоящем параграфе мы кратко
изложим метод решения диференциального уравнения при по-
помощи двойного интеграла, а в следующем параграфе подробно
разберем соответствующий пример.
Пусть Lx(y) = 0 будет данным уравнением и предположим,
что функция К{х; s, i) такая, при которой
{A) LxK(x; s, t) - MSj tK(x; s, t),
где Л%. t — диференциальный оператор в частных производных
второго порядка типа
(В) Mtit = a.df.- + b^ + c^ + d,
и а, Ь,. с и d— функции s и t. Как правило, такие соотноше-
соотношения могут быть получены только подбором; общий метод их
получения неизвестен.
Рассмотрим двойной интеграл
(С) у(х) = j'JK(x; s, t)w(s, t) dsdt,
где функция w (s, t) и область интегрирования пока не указаны.
Принимая возможность диференцирования под знаком интеграла
достаточное число раз относительно х, получим
xK(x; s, t)w{s, t)dsdt,
= JJMs,tK(x; s, t)w(s, t)dsdt.
Интегрируя по частям
266
поэтому
L,y {x) = JfK{x; s, t) MSt t (w) ds dt + [P{K, w}],
где
~~пд — д- д , д , ,
— диференциальный оператор в частных производных, присое-
присоединенный к (В), а Р {К, w] — выражение, аналогичное билиней-
билинейной форме.
Тогда w(s, t) должно быть определено, как решение дифе-
ренциального уравнения в частных производных
(Е) Ms,t(w) = O.
Таким образом решение задачи зависит от высшей области
анализа, именно от теории диференциальных уравнений в ча-
частных производных. Но в большинстве случаев, имеющих прак-
практическое значение, w{s, t) имеет особую форму u(s)<o(t), и
одно уравнение в частных производных (Е) замещается парой
обыкновенных уравнений, каждое первого порядка
«^+^==0, т ш +8 = 0,
где аир — функции только s, a f и о - функции только t.
Когда ot(s, t) определено, остается выбрать область интег-
интегрирования так, чтобы интеграл (С) существовал, а выражение
[Р{/(, w}\ тождественно обратилось в нуль.
8-501. Пример решения при помощи двойного интеграла. Рас-
Рассмотрим уравнение
Lx{y)= {x*-\)% + (a + b + lug + aby = 0-
Это уравнение решается при помощи простого преобразования
Лапласа, так как первый коэфициент — второй степени. Однако
оно может быть решено при помощи двойного интеграла, ядро
которого равно exst,— форма, соответствующая ядру Лапласа ext.
В данном случае
Lxexst = {x*s?t* —sW+(a+b+l) xst + ab} exst
= {(s ? + a ) (' Ж+ь) -s
Множитель w(s, t) удовлетворяет диференциальному уравнению
и этого достаточно, чтобы написать
w(s, f) = u(s)v(t),
267
где
du
откуда
K(S) =
и
dt *¦ '
откуда
Областью интегрирования может быть взят квадрант х > О,
у > 0, при условии, что а и b — числа, вещественные части ко-
которых положительны.
Отсюда следует, что решением данного уравнения будет
о о
и аналогично
оо оо X
Я-xst — (д-—t2) а—1 Ъ—1
е 2 s t dsdt
СО СО ]
— Jist {s'+l2) a—I b—1
e г s t dsdt
О 0
являются решениями данного уравнения.
8- 502. Связь между двойным интегралом и решениями в виде
рядов. Двойные интегралы, удовлетворяющие диференциальному
уравнению предыдущего параграфа, могут быть легко выведены
из решения в виде ряда, если воспользоваться следующим свой-
свойством гамма-функции1
Двумя решениями в виде рядов четных и нечетных функций х
соответственно будут
у . йЬ 2 о (й + 2) - fc F + 2) 4 ,
м * ~г 2| •* "I 4! Л ~*~
1 + 4) к .
У" I
Вспомним, что
"и 1 du
21 z I e " t dt, принимая « = — t".
26S
у „j. \"-r Ч"~г ч хз i Vй -f 'Л" т 3) • (ft + 1) (fc + 3) .
где порядок образования коэфициента очевиден.
Далее
4 2
+ z 2!
i.(^+,)r(±a).44it+,
-j- Z — Ij
4!
О О
3 .6J 3
«+3 .6J
о о
и аналогично можно доказать, что
оо со
о о
269
Ряды К, и Y2 сходятся для любых значений а и Ь, когда
|х| < ^соответствующие интегралы существуют для всех значе-
значений х, когда вещественные части а и b положительные. Таким
образом увеличение области применения решения достигается
за счет ограничений, наложенных на параметры а и Ь,
8-6. Периодические преобразования. Предположим, что в инте-
интеграле
(A) y(x)
ядро К {л, t) удовлетворяет диференциальному уравнению в ча-
частных производных
(B) '
Тогда, если диференцирование под знаком интеграла допустимо
и если А — произвольная постоянная, то
?
U (у) + Лу =f {Lx {К) + АЩ V (t) dt
=JK(x,
Таким образом, если для любой выбранной постоянной А функ-
функция v(t) удовлетворяет диференциальному уравнению
(C) Lt (V) + Av = 0,
а пределы интегрирования выбраны так, чтобы проинтегриро-
проинтегрированная часть была тождественно равна нулю, то определенный
интеграл будет удовлетворять уравнению
(D) Lx (у) + Ау = О
для того же значения Л.
Решение уравнений вида (С) и (D) часто разделяют на две
части, включающие не только формальное определение функции,
удовлетворяющей уравнению вместе с последовательностью на-
начальных условий, относящихся к данной точке, но также и
определение постоянной А так, чтобы другие условия были
удовлетворены. Такие условия могут быть введены, полагая ре-
решение чисто периодическим (с данным периодом) или имеющим
нуль в точке, отличной от точки, к которой относятся началь-
начальные условия.
Допустим, что такие условия наложены на решение (С) и
что такое решение существует только для последовательности
270
дискретных значений Л, а когда оно существует, то определя-
определяется единственным образом, независимо от произвольного по-
постоянного множителя. Наложим точно такую же последова-
последовательность условий на ядро К (х, t), рассматриваемое как
функция переменной х с t в качестве параметра1. Тогда, если
определенная таким образом зависимость vr (t) соответствует
характеристическому значению Аг, то
Уг{х) =j K(x, t)vr(t)dt)
будет удовлетворять уравнению (D) для параметра АТ, а также
всем начальным условиям, наложенным на vr (t). Но ут (х) при
этих ограничениях единственное и является кратным vr (x). Если
vr (х) = \гуг (х), то уг (х) будет удовлетворять однородному ин-
интегральному уравнению2
а
г3
t)y{t)dt,
где л имеет характеристическое значение К-
8-601. Решение при помощи интегрального уравнения. Пусть
данное уравнение будет иметь вид
Lx{y) +Ду = A — х2) -^ + {п — т — (т + п)х} -j- +
+ {А — р (т — п) х -f- pV}y = 0,
где т, п и р — постоянные; а т > 0, и>0. Для некоторых
дискретных характеристических значений А существует един-
единственное решение, независимое от постоянного множителя и
конечно в соседстве с особыми точками х— + 1. Ядро К (х, t),
удовлетворяющее уравнению Lx (К) = Lt {К) и конечное для всех
значений t, за исключением t= ± 1 в соседстве с х = ± 1Г
равно ерл' A -f ^)m~ (I — ^)"~J. Теперь
дР{К, v) — „,(+\ г ил._ 1^/„ л л /„л
4)t}Kv I.
Если ij (f)—конечно в соседстве с ^==±1, то выражение
в квадратных скобках тождественно обратится в нуль в этих
1 Принимается возможность определения К {х, t) для удовлетворения ус-
условий тождественно относительно t.
2 Bateman, Proc. London Math. Soc. B), 4 A907) 90, 461; Trans. Camb. Phil.
Soc, 21 A909), 187; Ince, Proc. Roy. Soc. Edin., 42 A922), 43.
271
точках, если п > 0, т > 0. Следовательно решения данного
уравнения будут удовлетворять интегральному уравнению
*xt A + tI" A - t) ly(t)dt.
1. Покажите, что диференциальное уравнение
xv(D)y + ty(D)y = 0,
где фи}— полиномы с постоянными коэфициентами, удовлетворяется
где 7 @ обратна е (t), ааи р выбраны так, что для всех значений х
з
[/'+¦/ Ф W X (О й
2. Напишите общее решение уравнения
в интегральной форме (I) для положительных и (II) для отрицательных значе-
значений х.
3. Покажите, что наиболее общее решение
dny
—i. — ху — а,
dx"
где а — постоянная, будеть иметь вид
7=о °
где со" 1 = 1, а постоянные Лг связаны соотношением
^ Аг = о.
г о
4. Докажите, что уравнение
имеет частное решение
со
sin (x/v) ё~ Т v* v&v,
о
272
а уравнение
d*y
имеет частное решение
1
/-X/V V-
е з vav,
о
где л: > 0. Какое требуется изменение при х < 0?
jpetzval].
Выведите общее решение для каждого уравнения.
5. Покажите, что уравнение
имеет решение, конечное в начале
i
/ cos mccos6+ alogctg-g-
когда о вещественное. [Sharpe, Mess. Math. X].
б. Докажите, что
удовлетворяется
+1
[\Ш—1
Г A — Я)"
У =
—1
и выведите разложение в виде ряда для этого решения.
7. Докажите, что в обозначениях главы VII, пример 8
?-1 (l — ^-т-1 ds dt
и выоазите общее решение уравнения 3F2 при помощи двойных интегралов.
8. Докажите, что частный интеграл
равен
i i
о о
и получите соответствующий результат для уравнения порядка п
Э. Айне—133—18 273
9. Докажите, что если Рт (х) — полином Лежандра, a Qm (х) — соответствую-
соответствующая функция Лежандра второго рода, то
m (х) = ~f~ J -K~j dt,
Q
—l
и выведите по индукции, что если тип — положительные целые числа и
т ;> п, то
41
1
— 1
10. Найдите диференциальное уравнение четвертого порядка, которому
удовлетворяют
Рп (х) Рт (х), Рп (х) Qm (х), рт (я) Qn (х), Qm (x) Qn (x)
и докажите, что оно преобразуется само в себя при помощи преобразования
Эйлера
Найлите общий тип уравнения порядка п, инвариантного относительно этого
преобразования.
11. Покажите, что соотношение
о
может быть заменено соотношениями
/(*)¦=/ K(x-t)o(t)dt
п (s) = je~st K(t) dt; v (s) = fe~st ? @ dt; u (s) v (s) - fe~st/ (t) dt
oo о
[Borel].
Отсюяа докажите, что если Jn (x) — функция Бесселя, то
X
j Jm (x - t) jn (t) t-1 dt^n-1 Jm+n (x).
0
12. Докажите, что ядро K(,xt) удовлетворяет диференциальному уравнению
в частных производных
если и — K(s) — решение
ds J \ dsjf
и что имеется преобразование, зависящее от ядра K(xt) выражения
274
являющегося сопряженным уравнением для
Отсюда докажите, что
со
Jn (¦*) - J Лп {2 У** } Л; @ *,
О
где х — положительное, & п — вещественное и больше —
[Bateman].
ГЛАВА IX
АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ ЛИНЕЙНЫХ ДИФЕРЕНЦИАЛЬНЫХ
СИСТЕМ
9-1. Определение линейной диференциальной системы. Линейное
диференциальное уравнение
dn У dn—'.У и
L (У) = Ро (X) ~^Г + Pi (*) ^„-1 + ¦ ¦ • +Р„_4 {X) % +
взятое вместе с одним или более дополнительных условий, ко-
которым удовлетворяют для частных значений х функция у и ее
первые (я—1) производных, образуют линейную диференциаль-
ную систему. Наиболее простой является последовательность
дополнительных условий, принятых для фундаментальной теоре-
теоремы существования (§3-32), именно
=у» у' К)=у„ ¦ ¦ •, y~fW = уola--",
у0, Уо, ¦. •, Уо"~1)— п заданных постоянных. Теорема суще-
существования показывает, что если л;0 — обыкновенная точка урав-
уравнения, то система имеет только одно решение. Эта частная по-
последовательность дополнительных условий известна как одно-
одноточечная граничная задача, поскольку должно быть найдено ре-
решение диференциального уравнения, которое удовлетворяло бы
граничным условиям в заданной точке1. Такая задача, если чи-
число независимых условий равно порядку уравнения, имеет толь-
только одно решение.
В двухточечной граничной задаче диференциальная система
состоит из диференциального уравнения и некоторого числа
дополнительных линейных условий вида
Ut {у) = aty (а) + а[у' (а) + ... +а(Г1У"~1)(а) +
+ hy Ф) + Р,- /(&)+...+ frl\b) = ъ,
где числа а, р и т — заданные постоянные, а {а, Ь)—-определен-
Ь)—-определенный интервал изменения х. Допустим, что т линейно независи-
независимых дополнительных условий этого типа были заданы. Поскольку
для 2« величин не может быть больше 2и независимых линей-
1 Указанные условия чаще называются начальными условиями. Прим. ред.
27G
ных соотношений между
У («). У (а), ..., У"' (а), у {Ь), у (Ь), ....
то отсюда следует, что m < 2п.
В "фаткой форме система может быть выражена в виде
J L (Я = г(л),
I Utly) = V (i =1,2,..., m).
С данной системой тесно связана однородная система
I L (у) = О,
1 ?Л(У) = О (г =1,2, ..., и),
называемая приведенной системой.
В приведенной системе необходимо рассмотреть два случая.
(I) Система не имеет решения, не равного тоджественно нулю;
такая система называется несовместимой {incompatible).
(II) Система имеет &(-<я) линейно-независимых решений
Ух (х)> Л (•*)> ¦ • ¦
Общее решение приведенной системы может быть написано
в виде
сх Уг (х) + с2уя (х) + .. . + cjc у* (х)
и будет зависеть от & произвольных постоянных с1э сг, ..., Сь
Система в данном случае будет k-кратно совместимой (k —
указатель совместимости).
Аналогично Для неоднородной системы могут быть два слу-
случая:
(I) Система вовсе не допускает решения, что означает, что
не может быть найдено решение уравнения L(y) — r(x), кото-
которое удовлетворяло бы граничным условиям Ui(y) = ^.
(II) Система удовлетворяется частным решением у0 (х). Тогда,
если k указатель приведенной системы, то общее решение не-
неоднородной системы будет иметь вид
Уо (•*) + схуу (х) + с2у.г (х) + ... + ckyk (х),
где
(л) + с2у2 (х)-т-.".. + скук (х)
— общее решение приведенной системы. Оно аналогично допол-
дополнительной функции (§ 5-1) линейного диференциального урав-
уравнения, когда на последнее не наложены граничные условия.
В настоящей главе мы рассмотрим общий вопрос совмести-
совместимости или несовместимости линейной диференциальной системы
и покажем аналогию, существующую между теорией линейных
диференциальных систем, с одной стороны, и теорией совмест-
совместных линейных алгебраических уравнений — с другой.
277
9-2. Аналогия с теорией системы линейных алгебраических
уравнений. Линейная диференциальная система может рассмат-
рассматриваться как предельный случай системы М линейных алгебра-
алгебраических уравнений с N переменными, когда М и N в пределе
стремятся к бесконечности. Для упрощения, распространим
аналогию на линейную диференциальную систему второго по-
порядка
С<4).
at у (а) -Ь- аг / (а) + fr у F) +fr/ (b) = v
Предположим, что ро(х), рх (х), ps(x) и г (х) — непрерывные
функции вещественной переменной х по всему замкнутому интер-
интервалу а^х^йЬ, а также, что этот интервал может быть разде-
разделен на s равных частей точками
где х0 = а, xs = Ъ, и пусть
Тогда диференциальное уравнение может рассматриваться как
предельная форма уравнения в конечных разностях г
=r
где Ал; в пределе стремится к нулю. Это уравнение в конечных
разностях верно для v = 0, 1,2,..., s — 2. На основании выраже-
выражений для Дз^ и A2J\, после того как оба члена были умножены
на Ajc?, можно написать
J\+, + ^У,+8 = ^ (v = 0, 1, 2,..., s - 2),
следовательно мы получим s — 1 уравнений, связбшэющих s-f-1
неизвестных величин
J'o» Уь Уг> •••. Л-
Аналогично, каждое граничное условие
«* J' (fl) + а,у (а) + Р/Jf F) + р;/ F) = Ti
1 Портер [Porter Ann. of Math, B), 3A902), 55] доказал, что переход к пре-
пределу от уравнения в конечных разностях к диференциальному уравнению мо-
может быть проведен совершенно строго.
278
может быть выражено в виде предельной формы
которая, в свою очередь, может быть написана в виде
Ai0 у0 + А„ у г + A s_t j/s_t + Д-5 .у, = Bi;
таким образом каждое граничное условие эквивалентно линей-
линейному уравнению в конечных разностях, связывающему у0, уи
ys-t и ys.
Примененные здесь принципы являются вполне общими; так,
линейное диференциальное уравнение порядка п, коэфициенты
которого непрерывны в интервале (а, Ь), может рассматриваться
как предельный случай семейства уравнений в конечных разно-
разностях типа
^+^+1+ • • • +Рп,У,,п == Ъ 1* = 0, 1, 2, .. .,s-n)
где, как и выше, s — число равных сегментов, на которые интер-
интервал (а, Ь) может быть подразделен. Каждое граничное условие,
независимо от того, относится ли оно к одной, двум или не-
нескольким точкам в интервале (а, Ь), также приводит к уравне-
уравнению точно такого же типа. При наличии т граничных условий
получим всего s-\-m — п-\-1 уравнений между s + 1 неизвест-
неизвестными величинами
У о' .Vi. .Уз, ¦ • •, ys-
Чтобы подчеркнуть аналогию, существующую между линей-
линейными диференциальными системами и системами линейных алге-
алгебраических уравнений, рассмотрим наиболее существешше свой-
свойства последних *.
9-21. Свойства линейной алгебраической системы. Рассмотрим
последовательность М совместных линейных уравнений
atl Xt + а]8 Х% + ... + alN AV= О,
t -\- ам? Х2 -[-••• -\-e-MN Х2\ — О,
с N переменными А^,, Х2, ..., XN. Могут быть два случая:
(I) Система не допускает никаких решений, кроме
Х1 = Х2 = ... = Ajv = О,
т. е. система несовместима.
Вохер, Введение в высшую алгебр}, гл. IV.
279
(II) Система допускает несколько решений (например k)
^11» ^21» " " М
Эти соотношения могут быть линейно независимыми, если нельзя
найти постоянные с, которые не все равны нулю и при кото-
которых N уравнений
схХа + с2Хп + ... +скХ{к = О,
А-хь = О,
были бы удовлетворены совместно. Если k последовательных
решений линейно независимы, то, вследствие однородности си-
системы, общее решение будет иметь вид
Хх = сгХи + с2Х12 +..
Ха = с1 Х.1Х -\- с.гХ22 -+-..
где сг, с2,..., Си — произвольные постоянные. В данном случае
система является k-кратно совместимой.
Указатель совместимости k данной системы определяется
следующей теоремой. Если р — высший порядок детерминанта
не равного нулю, какой можно получить из матрицы
(ап, а,2,..., alN
аМ\
то k = N—р. Число р называется рангом матрицы (А).
Рассмотрим неоднородную систему уравнений
b = bt,
а вместе с ней расширенную матрицу
t а12,.
Ранг (В) по меньшей мере равен рангу (А). Для того, чтобы
неоднородная система уравнений была совместимой, необходимо
280
и достаточно, чтобы ранг (В) был в точности равен рангу (А).
В данном случае, если
-"мо» -"^2о>• • •
— любое частное решение неоднородной системы, то общее
решение будет иметь вид
^1 = ^10 + С 1
Х2 = Х20 -\- СХ
9'22. Определение индекса линейной диференциальной системы.
Пусть Vi,Уъ• • -, Уп будет фундаментальной последовательностью
решений однородного линейного диференциального уравнения
L (у) = 0.
Определение совместимости данного уравнения с m однород-
однородными линейными граничными условиями
Ut(y) = 0, {i=l,2,..., m)
эквивалентно задаче определения постоянных с„ с2,...,сп в
общем решении
У = ty\ + С*У* + ¦ ¦ ¦ + спУп
так, чтобы граничные условия были удовлетворены. Следова-
Следовательно, все зависит от совместимости или несовместимости си-
стемы гп .одновременно заданных уравнений
c*Ui {Уд + CiUt (л) +... + спиг (уп) = 0,
СлУт (Ух) + cj)m (у,) + ...+ cnUn (уп) = 0,
а также и от ранга матрицы
УЛ) и иуп)\
.
Если ранг матрицы р —, то мы получим п — р линейно незави-
независимых последовательных значений сг, с2,..., сп и каждому из
этих значений будет соответствовать одно решение диферен-
диференциального уравнения, удовлетворяющее граничным условиям.
Следовательно индекс диференциальной системы k = п — р. Та-
Таким образом для того, чтобы данная система была k-крат-
k-кратно совместимой, необходимо и достаточно, чтобы ранг ма-
матрицы (U) был равен п — /г. В частности, если ранг матрицы
равен п, (что предполагает условие т > п), то система будет
несовместимой.
Рассмотрим неоднородную систему
[Цу) =/¦(*),
\
281
Если yltyiy...,Уп образуют, как,и выше, фундаментальную после-
последовательность решений однородного уравнения и если уо~
частное решение неоднородного уравнения, то общее решение
последнего будет иметь вид
У =у0
Чтобы граничные условия неоднородной системы были удовле-
удовлетворены, необходимо определить постоянные clt с2,..., сп из
уравнений
CiUx(ух) + c2Uy (у2) +... + спиг(уп) = т4 - Ui(Уо),
+ cJUm (У'я) + • • • +CnUm(уп) = Ъп — Um (Ув).
Возможность этого определения зависит от ранга расширенной
матрицы
/ U () U ().., U, (yn), y, - Ut (у0)
Um Ож), ?Лл Ы. • • •. Um (Уп), Чт — Um (Уо)
Для того, чтобы неоднородная система была совместимой,
необходимо и достаточно, чтобы ранг матрицы (tf1) был ра-
равен рангу матрицы {U). Если р — общий ранг матриц, то общее
решение каждой системы будет зависеть от п—р произволь-
произвольных постоянных.
Отсюда можно сделать весьма важный вывод! что если
т<п, то для того, чтобы неоднородная система имела ре-
решение, необходимо и достаточно, чтобы соответствующая
приведенная система была (п — т)-кратно совместимой; при,
т = п приведенная система несовместима.
9 • 3. Свойства билинейной формы. Выражение
называется билинейной формой двух последовательностей
N переменных
Уи J2, ¦ • •, Ул',
так как коэфициент каждого х является линейной функцией
переменных, и наоборот. Необходимо различать случай, когда
детерминант
А =
282
являющийся детерминантом этой билинейной формы, равен или
не равен нулю. В пррвом случае билинейная форма называется
сингулярной, в последнем — несингулярной (обыкновенной). При-
Примем, что рассматриваемая форма несингулярна.
Заменим переменные я,, х2,... , xN новой последователь-
последовательностью N переменных Xv Хг,..., Ху. подстановкой
хх = Cji Хх -}- с12 Х2 4~ ¦ • ¦ 4~ csjq Xx,
хг = Сц Хх + с21 Х2 4" • ¦ • 4- с2у XN,
XN — СЛТ1 Хг 4" СЛ-2 Х2 + . ¦ • 4" CNN Xy;,
детерминант которой
С = \си\
не равен нулю. Поскольку С~±-. О, подстановка обратима, т. е.
переменные X определяются только через переменные л. Би-
Билинейная форма мджет быть тогда выражена в виде
Л' Л'
а соответствующий детерминант будет
D = \du\ = \ aik | | ск,-1.
- АСфО.
Следовательно билинейная форма после подстановки остается
несингулярной.
Теперь замешщ переменные yv уг,---> У&- последователь-
последовательностью Yt, Y2,...,Vjs посредством линейной подстановки
Г, = duyt +duya + ...
Y2 = d2ly1 4- d22 y2 4-... 4-
YN —
детерминант которой не равен 0. Форма следовательно приво-
приводится» к выражению
X1Y1 4- X2Y2 4~ • ¦ •XxYx,
которое можно рассматривать как каноническое представление
несингулярной билинейной формы. Это приведение может быть
проведено различно, так как переменные хх, л2,..., xN могут
быть преобразованы в новую последовательность^, Х2,...,Хх
при помощи любой линейной подстановки, детерминант которой
не равен нулю. Однако, после того как новая последователь-
последовательность переменных Хг, Х2,...,ХК была определена, соответ-
соответствующая последовательность Yv Y^...^ стала единственной.
283
Рассмотрим, какое изменение вводится в последовательность
переменных Y при изменении одного или более переменных X.
Предположим, что
Хг, Х2,• •-,Ад/, Ajvfj-i,..., Хы,
соответствуют
^i> ^2>- • •' ^Mt Ум; i>- • •) У я-
Пусть Xt, Х2,..., Хм остаются неизменными, а ХМ-ц,--, Х^ бу-
будут заменены новыми переменными ХМт\,-.-, X'N, так что
Xlf Х2,- •., Хм, Хм f 1 • • • ) Xn
образуют линейную независимую систему. Далее, пусть
У и Yi,..., Ум, Ym+1, ... Yn
будет соответствующей системой, тогда
X1Yi-\- X2Y2+.. .-\- ХМУМ + Хщ+гУмл 1 + ¦ • • + А'л Yn
= XtYj -{- X2Ys ^-. • .-\- XmYm + Xm+iYm+i-{-- ..-\-XnYn
Поскольку Х1У Х2, ..., Ху„ Хм~1,¦. •, Xn—линейно-независи-
Xn—линейно-независимые величины, выведенные из переменных xv x2,...,xN подста-
подстановкой, детерминант которой не равен нулю, то единственная
последовательность значений xv x2,..., xN может быть най-
найдена таким образом, что
Хг =... = Хм = 0, Хм -г = 1, Хм-iz = • ¦ • = Хк = 0.
Тогда, если для этих значений х„ х2,..., xN, Хм^, Хм+2,- •., Х#
становятся равными соответственно Ам+ь Ам^2,.--, А^, то от-
отсюда следует, что
Ум+\ =Am+i Ym+i + Ам-у2Ym+2-\-• • • -\-AnYn.
У'м-г-2,- ¦ ¦ .' Y'n могут быть выражены в виде линейных комби-
комбинаций Ym+i ,..., YN. Величины Yu У2,---,У'м могут рассматри-
рассматриваться аналогично. В частности, определим последовательность
значений xt, x2,..., xN, для которых
Хг — 1, Х2 = ... = Хм = Xm+i =... = Хм = 0;
пусть для этой последовательности значений Хм+i,---,
будут соответственно равны Вм i,..., ^л'; тогда
и будут найдены аналогичные выражения для Yz,- -., Ум -
9-31. Сопряженные диференциальные системы. Теория били-
билинейных форм, которая была рассмотрена в предыдущем па-
284
раграфе, имеет важное значение в развитии понятия присоеди-
присоединенной пары линейных диференциальных систем.1
Пусть
dnu
P
d"~iu
du
будет линейным диференциальным выражением, где коэфици-
енты pi — непрерывные функции вещественной переменной х в
в интервале а<х<й, первые п — i производных р( существуют
и непрерывны, a p0 не обращается тождественно в нуль ни в
одной точке замкнутого интервала (а, ЬJ.
В этом случае сопряженное выражение примет вид
а Ци) и Цю) будут связаны тождеством Лагранжа (§ 5-3;
vL{u)-
- билинейная форма
til (ti) = iP (и, v),
где Р{и,
„п—1
dn~iu
dx"-1
Детерминантом этой формы является
(-1)"-2Ро, о
О,
О
Ро 0, ... О, О
Элементы ниже второй диагонали все равны нулю, поэтому де-
детерминант равен + (/>0)п, что не равно нулю ни в одной точке
интервала (а, Ь). Билинейная форма зависит от последователь-
последовательности переменных
и, и',..., «("-»),
1 Специальная пара присоединенных диференциальных систем дана Лиувиллем
Liouville, J. de Math., 3 A838), 606. Мазои [Mason, Trans. Am. A'ath. Sec,
7 A906), 337] рассматривает системы второго перядыа; Биркхофф [Blrckhoff. ibid.,
9 A908), 373] и Бохер [B6cher, ibid., 14 A913), 403] рассматривают общий вопрос.
Распространение на i исгемы диференциальиых уравнений см. Bounitzky, J. de Math.
F), 5 11909), 65. и Eocher, loc. cit.
2 Эго означает, что уравнение не имеет особых точек ни в интервале (а, Ь),
ни в его конечных точках.
285'
Если мы тождество Лагранжа проинтегрируем между преде-
пределами а и Ь, то получим формулу Грина
ь _
f {vL (к) - uL (v)} dx = [Р (и, v)fa.
а
Правый член представляет собой билинейную форму двух по-
последовательностей 2« величин
и {а), и'(а),..., и<"-»Ча), и[Ь), и'(Ь) ,.. ,
<и{а), о'(а) ,...,«<«-»> (а), «F), tf(b) ,.... «
его детерминант имеет вид
Д(а) О
О, ДF)
и не равен нулю. Форма [Р(и, -у)]* является обыкновенной и мо-
может быть приведена к каноническому виду.
Пусть Ult U2 ,-.-, Um будут любыми 2« линейно-независи-
линейно-независимыми однородными выражениями типа
U, (и) = а,- и (а) + я,' к' (а) + .. . + о/"-*) «<"-
+ Р, и F) + pi и' f 6) + .. . + З/"-0
(й) +
где детерминант 4я2 коэфициентов не равен нулю. В этом случае
существует единственная последовательность
независимых форм, линейных относительно
v(a), v'(a),... , «("-!) (a), -v(b), v'(b),
так что
[Р(и,
Следовательно формула Грина может быть написана в виде
ь
f{vL(a) - uL{4!)}dx = UJ/\n + U2Vm^ + ... +f72nK1.
a
Если Uv U2, ... ,Um останутся неизменными при различных
Um+i ,. ¦ •, U2n, то Vt, V2,... ,V2I1-m преобразуются в новую
последовательность Vi, V2> •• •, V%n-m, представляющую линей-
линейные комбинации Vi, V2,... V2n^m. Таким образом значения
Vlt Va,... , Van-m зависят только от Ux, (J2. ..., Um.
Система
L(<v) = 0,
[V,(v)=0 (i=l,2,...,2n-m)
является сопряженной с системой
U (и) = 0
A-1,2,..., /я).
286
Симметрия формул показывает, что вторая система также будет
сопряженной относительно первой.
Если однородную линейную диференциальную систему рассма-
рассматривать как аналогию последовательности уравнений
N — О,
\ = О,
то сопряженное уравнение будет соответствующей аналогией
Оц К,+... + аМ1Км =0,
9-32. Свойство решений k- кратно совместимой системы. Формы
ит+1,---> U2n ограничены только условием, что
Ulf Uv..., Um, Um+i, ..., U2n
линейно-независимы. Однако они имеют важное свойство; если
и1г и2,..., ик образуют линейно-независимую последовательность
решений &-кратносовместимой системы
) Ui{u) = 0 (г =1,2,..., т\
то
Ui (их), Ut («а),..., Ut (нА) (i = т + 1,..., 2»)
будут линейно-независимы.
Постоянные с1? с2,..., ск могут быть найдены таким обра-
образом, что
+ c2Ut (к,) +. -. + Cftf/r (н*) = 0 (i = т + 1,. .. ,2л).
Но
f/i (CjMj + с,н2 + ...+ сА.нь) =0 (i = 1, 2,..., те),
откуда
?/,-(«) = <V
где
г = 1, 2,..., 2/г, а и = схгг, + с2п2 +... + скик.
Эти 2и независимых однородных уравнения содержат 2п
величины
и (о), и'(а),..., и{п-и(а), и(Ь), и'(Ь), .... а(|-!)F);
так как детерминант 4я2 коэфициентов не равен нулю, эти урав-
уравнения не удовлетворяются, если только каждая из этих вели-
величин не равна нулю. Однако это невозможно, поскольку тогда и
обратилось бы в нуль. Следовательно теорема установлена.
9-33. Случай, когда число независимых граничных условий
равно порядку уравнения. Случай т = п имеет большое значение
и значительно проще общего случая. Докажем, что указатель
287
совместимости однородной диференциальной системы равен
указателю сопряженной системы.
Предположим, что данная система имеет вид
J L (и) = О
I ?/,(«) = 0 (i = l, 2.....П).
Пусть k будет ее указателем, а щ, и2,..., ик — последователь-
последовательностью линейно-независимых решений. Сопряженная система
будет иметь вид
f I (v) = О,
1К,(«) = 0 (/Ф1,2 л).
Пусть -у,, ©j,..., г»„ будет фундаментальной последовательностью
решений уравнения
I (г/) = 0;
тогда формула Грина
{uL(и) -ul(v) }dx = Ul V2n + и.У2п+... +U2nVi
будет приведена к
Un+i (и) Va(vJ +->- + Uin («) V\ (vx) = 0,
Un Аи) Va(vj +.'. . + U2n(u) Vr(vj = 6,
где и —любое решение последовательности и„ й2 иь.
Эта последовательность уравнений, рассматриваемая в виде
уравнений для определения Un+i,---, Uint имеет k решений
Un+i (и.-), •• • •, Uw («О (г = 1, 2,..., fe),
а эти решения, согласно предыдущему параграфу, линейно-не-
линейно-независимы. Следовательно ранг матрицы
равен самое большое я — к. Но это точно соответствует ма-
матрице, определяющей показатель присоединенной системы. Если
он равен k', то ранг матрицы будет п — к', следовательно
п — к,' <п — к
или
k'>k.
Однако, если обе системы взаимозаменимы, то отсюда сле-
следует, что k > k', откуда k' = k, что и требовалось доказать.
Если устранить ограничение т — п, то более общей формой
теоремы будет k'=k-\-m — п. Доказательство следует из тех
288
же общих принципов. Сначала устанавливается, что k'> k-\-m — п.
Из обратимости между системой и сопряженной с ней систе-
системой можно вывести, что &> k'+Bn — т) — п или k' <. k+ m—п,
откуда непосредственно следует теорема.
9*34. Неоднородная система. Пусть данная полная система
имеет вид
\ L («) = г.
' ' \Ut(u) = b (i=1.2,...,nj,
тогда, для того чтобы эта система имела решение, необходимо
•л достаточно, чтобы каждое решение однородной сопря-
сопряженной системы
¦; \Vt{v)=O (/ = 1, 2,..., п)
удовлетворяло соотношению
ь
(С l fvr dx = Tl V2n (v) +... + Yn Vnbl (^).
a
Пусть k будет указателем однородной системы (В); если
k = 0, то теорема следует из § 9 • 22, если же k > 0, то г^, г/2,..., юк
образуют линейно-независимую последовательность решений.
Если данная полная система имеет решение и, то пусть v
будет любым решением системы (В). Если определенные таким
образом и и v подставить в формулу Грина, то уравнение (С)
следует непосредственно.
Чтобы доказать, что условие достаточно, примем, что иь
будет любым решением уравнения
L (и) = г,
тогда теорема Грина приводит к соотношению
b
J vrdx = Ux (н0) !/2п (*/)+...+ Un (н0) V,,+i {v),
а
где <о — любое решение системы (В).
Вычитая это соотношение из (С), получим
(D) {иг(кр)-Tl}V2n&)+...+ {?/„(но)-Tn) Va i («) =-- 0.
Теперь пусть мг, и2,..., м„ будет фундаментальной системой
решений однородного уравнения
L (и) = 0,
тогда, согласно теореме Грина,
?Л («0 ^2п (-"О + ...+Un (и,) К„ , (г») - 0,
(E)
?Л Ы 1"'2п (г>) +... + ?/„ (и„) Vn! 1 («) = 0.
Э. Айне—133—19 280
Таким образом всего имеется я + 1 линейных однородных урав-
уравнений с и неизвестными V2n(v),..., Kn+i(«); они удовлетворя-
удовлетворяются k решениями
V2n (v,),..., У„г , (v,) (i = 1, 2...., Щ.
которые, согласно § 9 • 32, линейно-независимы. Ранг матрицы
последовательности и + 1 уравнений (D, Е) поэтому равен не
больше п — k, но он не может быть меньше п — k, так как
ранг матрицы п уравнений (Е) в точности равен п — k. Следо-
Следовательно, ранг обеих матриц равен п — k, откуда следует, что
данная полная система имеет решение.
При тфп, для того, чтобы система
IL (и) = г
\Ut(u) = ii (i = 1,2,..., т)
имела решение, необходимо и достаточно, чтобы каждое реше-
решение v однородной сопряженной системы
Vt {v) = 0 (*= 1> 2, .. .,2n — m)
удовлетворяло соотношению
ь
I Vrdx -f-7, Vin (V) -f- ¦ . . + "im V-'n—m 1 i^)-
a
Случай, когда п > m, k — я — лг, может быть рассмотрен на
основании выводов § 9-22; доказательство аналогично приве-
приведенному.
9-4. Самосопряженная линейная диференциальная система вто-
второго порядка. Предположим, чго
_ . . d2u , du
будет однородным линейным диференциальным выражением
второго порядка. Сопряженное выражение будет иметь вид
Поэтому, для того, чтобы выражение /. (к) было тождественным
по форме с его сопряженным L(v), необходимо и достаточ-
достаточно, чтобы
р'о — Pi-
Выражение может быть тогда написано в виде
й
290
В общей форме L (и) не является самосопряженным, но вы-
выражение
рпв L [U) - dx X их \ + р0 е и
самосопряженное. Следовательно, если любое уравнение второго
порядка может быть сделано самосопряженным посредством умно-
умножения на соответствующий множитель (который не обращается
в нуль или становится бесконечным в интервале (а, Ь) при усло-
условиях § 9-31), то мы не потеряем в общности, считая самосопря-
самосопряженное уравнение
dx \Kdx) — Ш ~ Н>
известное как уравнение Штурма, общим уравнением второго
порядка. В данном случае, пусть
тогда, если и и ю — любые две функции х, первая и вторая
производные которой непрерывны в интервале (а, Ь), то
следовательно билинейная форма будет иметь вид
Р(и, v)-.r=
Формула Грина приводится в данном случае ^простому виду
ь ь
f \vL{u)- uL(v)\ dx = [K(v -d?-u -~)\
a . a
В частности, если L(u) -=¦ 0, L{%>) = 0, она приводится к формуле
Абеля
К(Ь) { v (Ь) и' (Ь) - и (b) v' (Ь)} = К {a) {v (а) и' (а) - и (a) vf (a)}.
Рассмотрим однородную диференциальную систему
j U1 (и) = Oj и (с) + я2к (b) -f а8ы' (a) -f atu' ip) — О,
I U2 (и) = p, и (а) Ь р2и (&) + Ps«' (а) + Р4»' (&) = О,
где Lr, и Lf2 — линейно-независимы. Это условие означает, что
из шести детерминантов оу = а.-З,- — а^З,-, содержащихся в мат-
матрице
не все равны нулю-
29!
Предположим, что 8^фО, тогда, пусть U3 и U4 будут такими,
что Uv U2, U3, Ок— линейно-независимы. Например, пусть
тогда, если и и г1 —любые функции х, так что L (и) и L(v) не-
непрерывны в интервале {а, Ь), то
т. е.
» (Ь) и' (Ь) - и(b) v' (Ь)} - /С(а) [v(а)и' (а) - и {щ
= {я,и (а) + а2и (й)+а3и' (а) + я4м' (&)} К
Сравнивая коэфициенты и(а),и(Ь), и'(а) и «'(б),получим четыре
уравнения
V* + o-zVi -f Wz\=-K(a)v(a)t
Из этих уравнений можно получить Vj, V2, V3 и К4
1/,(у) = Л(&)г»F) + ~ {Z2iK(a)v'(a)+ iuK(b)v'(b)},
V,(<v) = -K(a)v(a)—±- {>.nK(a)v'(a) + hwK(b) v' (b)},
^з И = -1O ( a2 /C (a)«' to) + ax К (b) v' (b)},
V, (v) = -i- { p2 /<"(fl) ^' (a) + 3,
Чтобы система была самосопряженной, необходимо и доста-
достаточно, чтобы Vx (v) и V2 (v) были линейными комбинациями U^v)
и U2{v). Поскольку "У (с) не входит в Vlt то \\ можно получить
исключением v (а) из Ul (v) и U2 (v). Отсюда Vt — кратно
S12 (v)b + ou (г;') a -f 44 (-У') 6,
следовательно
г-(&) + g^{ 813K(b)v' (a) -f ouK(b)v' (b)}.
Из сравнения с предыдущим выражением для К, можно видеть,
292
что требуемым условием будет
Аналогичное условие может быть получено вследствие того, что
V2{v) получается исключением v(b) из 111{ч)) и U2(v). Таким
образом полученное условие необходимо и достаточно для того,
чтобы рассматриваемая система была самосопряженной.
Предположим, что 813 ф 0; в этом случае независимая после-
последовательность линейных выражений U может быть получена
при
Us(u) = n{b), U,(n) = u'(b).
Легко найти, что
V, iv) = K(b)v{b) + ~- {hJ<{a)v(a) -f i>SiK(a)v'(a)},
Vs(v) = - K(b) v' (b) -f A- {818 К (a) v {a} - SM К (a) V (a)},
f i, К (a)«' (a) }f
Отсюда можно вывести, что
— необходимое и достаточное условие, чтобы данная система
была самосопряженной.
Остальные четыре случая йиф0, о^ФО, 544ф0 и 334ф0 мо-
могут быть рассмотрены аналогично; каждый случай приводит
к тому же условию самосопряженности данной системы.
9-41. Системы Штурм-Лиувилля. Система типа
а.лу(а) + azy(b) + a,y(a) + а,у'(Ь) = 0,
(А)
называется системой Штурм-Лиувилля. В интервале а < х < fe, Л,
(которое везде положительно), g и / — непрерывные функции л,
а I —¦ произвольный параметр. Условием самосопряженности дан-
данной системы является 'J2ik(a) = ZVikKb); предположим, что это
условие удовлетворено.
Специальный случай системы, в которой граничными усло-
условиями являются
| ?{a)-hy(a)=0,
\ y'(b) + Hy(b) = 0,
2йЗ
возникает в задаче распределения температуры в неоднородном
стержне1, система самосопряженная, так как в данном случае
Исключая поочередно у'{а) иу(а), граничные условия (А) мо-
могут быть приведены к виду
| Ь1зУ(а) + Ъи,у(Ь) - o3iy'(b) = 0,
I <.i3y\a) + dl2y(b) + lity'(b) = 0.
Если о13 = 0, то, поскольку система самосопряжена, о24 = 0, и гра-
граничные условия приводятся к (В). При 8,зф0 система может
быть написана в виде
(С)
У'(а) = Ъ
и условие для самосопряженности системы примет вид
В частности, система, содержащая так называемые периоди-
периодические граничные условия
\у'(а)=У'(Ь).
самосопряженная, если
k[a) = k(b).
9*5. Диференциальные системы, содержащие параметры. Харак-
Характеристические числа. Часто в однородной диференциальной си-
системе порядка п
| Цу) = О,
\U1(y)=0 li=l,2,...,n),
коэфициенты диференциального уравнения, а иногда и гранич-
граничных условий зависят от параметра X. (Такой случай был рас-
рассмотрен в предыдущем параграфе). Основным вопросом в дан-
данном случае является определение частных значений )*, для ко-
которых система становится совместимой. Такие значения X назы-
называются характеристическими числами системы, а соответству-
соответствующие им решения — фундаментальными функциями2.
Предположим, что yv y2, ..., уп — фундаментальная последо-
последовательность действительных решений уравнения
1 В этой задаче k представляет проводимость, g — удельную теплоту, а /, h
и Н зависят от излучающей способности у поверхности и концов стержня. X дол-
должна быть определена таким образом, чтобы сделать систему совместимой.
- В советской литературе употребительны термины: характеристические,
собственные, фундаментальные числа—соответственно функции. (Прим. ред.).
294
которые должны рассматриваться как функции двух веществен-
вещественных переменных (х, X) и как таковые являются непрерывными
функциями1 (х, V); они имеют производные до (п—1) порядка
относительно х, которые также являются непрерывными функ-
функциями (л,Х) при а <; х < b и X, лежащей в интервале (Л,, Л2).
Условие совместимости
.., с\(Уа) =0
Un(yi),...,Un(yn) |
можно переписать так
F(l) = 0.
Принимая, что коэфициенты (/, — непрерывные функции X,
F(\) будет непрерывной в интервале (Лг Л»). Это уравнение на-
называется характеристическим уравнением системы, a tro корни —
характеристическими числами. Для значений а, лежащих в от-
открытом интервале Л1<Х<Л2, корни характеристического урав-
уравнения изол"рованы2; конечные точки \ и А2 могут быть пре-
предельными точками бесконечного числа корней.
Характеристическое уравнение не зависит от фундаменталь-
фундаментальной последовательности выбранных решений, так как влияние
подстановки Yt вместо _у, где
Yi = Сц Уг + С,2 ,V2 + • • • + СтУп (/ = 1,2,..., Н)
выражается в умножении левого члена характеристического
уравнения на детерминант | сц |, не равный нулю, поскольку
У1,Уи, ¦ ¦ -,Уп образуют фундаментальную последовательность3.
При каждом характеристическом числе h система будет
иметь некоторый указатель совместимости, например /г,. Более
того, л*, рассматриваемая как корень характеристического урав-
уравнения, будет иметь кратность /я,, /я* может быть не равно /г,,
но в любом случае
ki < /Hi
(не следует забывать, что k% <i n). Чтобы установить это нера-
неравенство, достаточно показать, что если X — любое характери-
характеристическое число, a k — его указатель, то
FQ.) = F"(k) = ... = F'*-1^}.) - 0.
1 Определение непрерывной функции двух вещественных переменных см.
примечание к § 31; у,, v2, ..., уп и их первые (я—1) производных относи-
относительно х — непрерывные функции (х, X); это следует из теорем существования
¦§§ 3-31, 3-32.
2 См. § 9-6.
3 Коэфициенты с,/ могут быть функциями >., но тогда последовательность
Уг, У2, ¦ ¦., Yn перестанет быть фундаментальной для любых значений л, для
которых \сц\ =0. Это усложнение может быть преодолено, если принять, что
угу%, ...,уп образуют фундаментальную последовательность для всех значений
Х в интервале (Л,, Л2).
295
Функция F(r)(l) может быть получена из детерминантов, каж-
каждый из которых содержит не меньше (п~ г) неизмененных столб-
столбцов F(k), причем остальные столбцы могут быть выведены ди-
ференцированием из соответствующих столбцов. Пусть каждый
из этих детерминантов разложен, согласно формуле Лапласа *,
по минорам, содержащимся в п — г недиференцированных столб-
столбцах. Поскольку показатель \ равен k, все детерминанты порядка
п — k +1 или больше, извлеченные из матрицы (Ui(yi)), будут
равны нулю, т. е. каждый член разложения F{r) (l) будет равен
нулю при условии, если г</г — 1. Следовательно корень X кра-
кратен k, что и требовалось доказать.
9*6. Влияние малых изменений в козфициентах линейной дифе-
ренциальной системы. Предположение, что ковфициенты линейной
диференциальной системы
(A) { 1<У)-°
\ Ut(y) = 0 (/=1,2, ...,«)
зависят от параметра I, вызывает вопрос о влиянии на совме-
совместимость системы изменения величины X. В частности, важно
определить, изменяется ли при малом изменении У. "показатель
системы, если известно, что для данного значения X, например
о, система &-кратно совместима2.
Теорема I. Показатель системы не увеличивается при
любом изменении коэфициентов, которое равномерно и доста-
достаточно мало3.
Если показатель системы для характеристического числа >.о
равен k, то внутри матрицы
существует не меньше одного детерминанта порядка n — k, ко-
который не равен нулю при а = Хо § 9-22. Предположим, что для
Хо дано небольшое изменение, тогда, если число 8 (независи-
(независимое от х) существует так, что после этого изменения каждый
коэфициент L(y) и Ut(y) изменяется по абсолютной величине,
не больше чем на о, то изменение детерминанта сравнимо с о.
Достаточно малое изменение в >0 не уменьшает детерминанта
до нуля, что доказывает теорему.
1 Scott and Mathews, Theory of Determinants, 30.
2 Настоящее исследование принадлежит Бохеру, Bull. Am. Math. Soc. 21
(Ш14), 1.
3 Для каждого характеристического числа ).о существует число с, такиы об-
образом, что оно в каждом коэфициенте L{y) no абсолютной величине меньше
о для всех значений х в интервале (а, Ь). Аналогично изменение каждого коэ-
Фициента в Ux(y) no абсолютной величине меньше с.
296
С другой стороны, все дитерминанты порядка n — k + l,
полученные из матрицы, равны нулю при X = 10. Весьма вероятно,
что малое изменение, сообщенное 10, изменило бы значение
по крайней мере одного из этих детерминантов, что означало
бы, что показатель упал ниже k.
Не рассматривая вопроса во всей его полноте, разберем важ-
важный частный случай и докажем, что при равномерном доста-
достаточно малом изменении одного отдельного коефициента, именно
у в L (у), показатель может быть приведен к нулю. Доказатель-
Доказательство основано на трех предварительных леммах.
Лемма I. Пусть уь (х) будет некоторым частным реше-
решением данной системы, соответствующим характеристическому
числу 10. Тогда существует непрерывная в интервале (х, X)
функция у (х, "/>), удовлетворяющая системе (А) для значений
X в интервале А, содержащем 10, и приводимая к у0 (х) при
к = V
Чтобы придать задаче определенность, предположим, что
детерминантом, который не обращается в нуль при X = Х0, явля-
является детирминант, образованный первыми (п — k) рядами и столб-
столбцами матрицы (U). Тогда, любое решение L (v) =0, удовлетворяю-
удовлетворяющее первым (п — k) граничным условиям, будет также удовле-
удовлетворять остальным k условиям.
Такое решение дается детерминантом
(В) у(хЛ) =
= Ух, ¦•¦ -¦ Уп-ъ, c1yn-k + 1 +... +скуп |
' Ux (V,), ..., Ut(yn-b), Су U, (уп _*,.,)+... + ckL\(yn) |
Un-k {Уд' '¦-, Un-k Ь'п-k), CxUn-h Оя-Й4 i) + - . - + CkUn-k (Уп)
Тождественное обращение в нуль этого детерминанта, если бы
оно было возможно, выразило бы линейную зависимость между
фундаментальными решениями уъ у2, . • •, уп. Так как это проти-
противоречит принятым условиям, то детерминант не равен тождест-
тождественно нулю. Следовательно, формула (В) является решением
данной системы, а также, поскольку оно зависит от k произ-
произвольных постоянных, и общим решением.
Предположим, что существует интервал А, содержащий )с
таким образом, что система удерживает показатель k для всех
значений \ в пределах А. Тогда А может быть взята достаточно
малой, чтобы детерминант из (я — k) рядов, который не обра-
обращается в нуль для 1ОУ не был равен нулю для любого значения
I в А. Следовательно (В) будет общим решением системы для
всех значений X в А, а также непрерывной функцией (х, X),
если Ci постоянные или непрерывные функции I.
297
Лемма II. Пусть и (х) будет действительным решением
системы
(о ! ^;\:Г «•=!. 2....,«,,
I ?/,- (а) = О
где g—непрерывная функция х, а чз (х) — действительное ре-
решение системы, сопряженной с (А)
(U) ^ (г = 1, 2, . -., п),
\ Vt [v) ----- О
тогда
ъ
(Е) Jg-м (х) v (x) dx = 0.
Эта лемма является следствием теоремы Грина1.
Лемма III. Если данная система А совместима и имеет
показатель k>\, то при заданном произвольно малом поло-
положительном числе в существует непрерывная вещественная
функция g (x), так что 0<g(x) <e, для которой показатель
системы (С) меньше k.
Пусть у (х) будет решением системы (А) при X = 10 и пусть
v(x) будет решением (D) для того же значения I. Каку(х), так
и <v (х) не могут иметь бесконечное число корней в интервале
(а, Ь) 2. Следовательно, в интервале (с, Ь) может быть найдена
такая точка, в которой произведение у@ v (x) не равно нулю.
Более того, поскольку у (х) v (x) — непрерывная функция х,
точка с может быть включена в интервал (а', Ь'), внутри кото-
которого у (х) v (л) не обращается в нуль. Теперь определим ср
как непрерывную вещественную функцию х, которая равна нулю
вне интервала (с', Ь'), и как положительную, но меньше е, для
a'<x<b'. Из этого определения следует, что
J fy(x)v(x)dxr-0.
Определим g посредством соотношения
g =- Щ,
где v- — постоянная и 0 </. < 1. Тогда из выражения (Е) полу-
получим
a
I yu (л) v(x)dx =0.
ь
1 Подробное доказательство см. более общий случай § 10-7.
3 Если бы у(х) имело бесконечное число корней i интервале (а, Ь), то эти
корни имели бы предельную точку, например с в интервале (а, Ъ). Тогда
у (с) = у (с) =...=-. yn~i (с) = 0, что невозможно, если у (х)не равно нулю.
См. § 10 - 2.
298
Предположим, что лемма III неверна, тогда для 0 < у < 1 си-
система (С) по меньшей мере k - кратно совместима, в то время
как по теореме I ее показатель не может превышать k для
достаточно малых изменений г.. Пусть / будет ограничена зна-
значениями, достаточно малыми для того, чтобы показатель (С)
точно соответствовал k. Тогда, по лемме J, и (х) непрерывная
функция (х, *.), которая приближается к у (х) так же равномерно,
как * к нулю. Следовательно
ь ь
Г(ьм (х) v{x)dx—^ f<р_у (х) ч) (х) dx
а а
равномерно при у. —»0. Ко это невозможно, так как первый
интеграл равен нулю для всех значений k, тогда как второй
интеграл не равен нулю. Это противоречие доказывает правиль-
правильность леммы III.
Теорема II. Если положительное число г произвольно, то
существует непрерывная вещественная функция g{x), так что
0^g(x)<s и для которой система (С) несовместима.
Функция g (х) может быть равна нулю, за исключением случая,
когда она находится в произвольно малом подиитервале (а, Ь).
Функция g, которая была определена при доказательстве
леммы III, понижает показатель системы (С) не меньше, чем на
единицу. Если показатель не равен нулю, то функцию gt (x)
можно определить так, чтобы 0<^ < г, тогда показатель
системы
I. (и) = gu + gl u,
*Л(н) = 0 (/ = 1,2 , я),
будет по крайней мере на единицу меньше показателя (С), и
следовательно не менее чем на две единицы меньше показателя
(А). При продолжении процесса показатель может быть приве-
приведен к нулю. Следовательно теорема II верна.
Если к функции g (л), которая делает систему (С) несовме-
несовместимой, прибавить достаточно малую функцию х, положитель-
положительную, но не равную нулю во всех точках интервала (а, Ь), то,
согласно теореме I, система останется несовместимой. Это
рассуждение приводит к новой теореме.
Теорема III. Если положительное число е произвольно, то
существует такая непрерывная вещественная функция g (x)
(О < g [х] < г), для которой система (С) несовместима.
Примеры
1. Покажите, что система
У" + РУ' + ЯУ = г,
*i V (a) -f а,у F) -|- а3 у' (а) + aty' (b) = A,
Pt У («)+ Р« У (*) + РзУ (а) + h\>' (b) - В
299
самосопряженная, если
ь
Ч % - Ч % = iai h - Н ?i) exp J pdx.
а
2. Докажите, что если б —произвольное положительное число, a jc,-,. . ., хр
— произвольно выбранные точки в интервале (а, 6), то существует веществен-
вещественная непрерывная функция g{x), которая обращается в нуль и изменяет знак в
каждой из точек xt, но не обращается в нуль ни в какой другой точке интер-
интервала (я, 6), которая удовлетворяет условию | g (х) \ < е и делает систему
| L(a)-gu,
{ Ut (гг) = О (i=l, 'А • .- , п)
несовместимой.
ГЛАВА X
ТЕОРИЯ ШТУРМА И ЕЕ ПОЗДНЕЙШЕЕ РАЗВИТИЕ
10-1. Теория Штурма. В настоящей главе мы рассмотрим глав-
главным образом уравнения типа
где К и G (в пределах замкнутого интервала а ^ х < Ь) — не-
непрерывные вещественчые функции вещественной переменной
х. К не обращается в нуль и следовательно может быть при-
принята продолжительной; она имеет непрерывную первую произ-
производную в пределах всего интервала.
Фундаментальной теоремой существования (§ 3-32) установ-
установлено, что такие уравнения имеют только одно непрерывное
решение с непрерывной производной, которое удовлетворяет
начальным условиям
y{c) = "iv y'k) = bt
где с —любая точка в замкнутом интервале (а, Ь). Однако, не-
несмотря на ценность теоремы существования с теоретической
точки зрения, она почти не дает сведений о природе решения,
существование которого она доказывает.
С точки зрения физических приложений, а также и с теоре-
теоретической точки зрения чрезвычайно важно определить число
корней решения, имеющихся в интервале {а, Ь). Эта задача была
впервые исследозана Штурмом1; его теория основана на рабо-
работах, которые в настоящее время считаются классическими. Две
теоремы сравнения, на которых основана настоящая глава,
являются фундаментальными; они послужили базой для весьма
важных дальнейших исследований.
10-2. Теорема разделения. Ни одно непрерывное решение
уравнения не может иметь бесконечное число корней в интер-
интервале (а, Ь), если оно нр равно нулю, так как, если бы оно
имело бесконечное число корней, то эти корни, согласно тео-
теореме Больцано-Вейерштрасса 2 имели бы не меньше одной
предельной точки с. Тогда не только у (с)=0, но также и у' (с) — 0,
так как
у (г + h) = y(c) + hy' [с + О Щ, @ с 6 < 1),
1 J. de Math, I A836), 106. Наиболее полный разбг-р теории и ее развитие
см. Bocher, Lecons sur ies methodes de Sturm (Paris, 1917); Bocher, Proceedings,
Fifth International Congress (Cambridge, 1912), I, 163.
' Унттекер и Ватсон, Курс современного анализа, $ 2-21.
301
а поскольку с — предельная точка корней, h может быть при-
принято настолько малым, что
и следовательно
откуда, вследствие непрерывности у'(Л), следует, что
у'(с)=--О.
Но система
Л (у)-О,
У(с)=У'(с)=0
не имеет решения, не равного тождественно нулю. Это доказы-
доказывает теорему, которую можно распространить на линейное
•однородное уравнение порядка п.
Предположим, что ух и у2 будут любыми двумя веществен-
вещественными линейно-независимыми решениями диференциального
уравнения. Примем, что уг обращается в нуль не меньше двух
раз в интервале (а, Ь), а х1 и хг будут двумя последователь-
последовательными нулями уу в этом интервале. Тогда у2 обратится в нуль
не меньше одного раза в открытом интервале хх < х < х2.
Однако _у2 не может обратиться в нуль при xt или при х2,
так как у2 было бы в данном случае лишь кратным yv Предпо-
Предположим, что j2 не обращается в нуль в некоторой точке интер-
интервала (хъ х>); тогда функция ух\Уч непрерывна, имеет непрерыв-
непрерывную производную по всему интервалу л:1<л<лг и тождест-
тождественно обращается в нуль в его конечных точках. Следователь-
Следовательно ее производная должна обратиться в нуль, хотя бы в одной
внутренней точке этого интервала. Но
± f_y_i \ = у?.}--1
представляет собой дробь, числитель которой является врон-
вронскианом уг и у2, следовательно она не может обратиться в
нуль в любой точке интервала {х±, х2). Это противоречие дока-
доказывает, что функция уг должна иметь не меньше одного нуля
между хг и х2. Она не может иметь также и больше одного
нуля, так как при двух нулях функция у, имела бы между ними
нуль, а хг и хг не были бы последовательными нулями рх.
Теорема, которая была таким образом доказана, может
быть иначе выражена так: нули двух вещественных линейно-
независимых решений линейного диференциального уравнения
второго порядна разделяют друг, друга {перемежаются).
Эта теорема не верна, если решения не вещественны. Так, в
уравнении
302
корни вещественных решений
уг = sin х, у2= cos x
перемежаются. В более общем случае корни двух веществен-
вещественных решений
уг — A sin х -J- # cos л:, у.2 = С sin л: -J- D cos л;
перемежаются, при условии, если AD — ВС^-О; это означает,
что эти два решения линейно-независимы. Мнимое решение
у = cos л: + / sin x
не имеет нулей ни в одном интервале вещественной перемен-
переменной х.
10*3. Фундаментальная теорема Штурма. Если имеются две
функции х, например ух и у3, определенные и непрерывные в
интервале (а, Ь), и если в этом интервале у2 имеет больше
нулей, чем уъ то говорят, что у2 осциллирует быстрее,
чем уг. Так например, если т и п — положительные целке
числа и т > п, то cos /гаде осциллирует быстрее, чем cos nx в
интервале @, я), так как первый имеет /и, а второй — п корней
в этом интервале. Теорема разделения предыдущего параграфа
может быть выражена еще следующим образом: нули всех ре-
решений данного диференциального уравнения осциллируют оди-
одинаково быстро; под этим подразумевается, что число нулей
любого решения в интервале (a, J3), находящегося в интервале
(а, Ъ), не может превышать число нулей некоторого независи-
независимого решения в том же интервале больше, чем на единицу.
Если в некотором интервале решение имеет не больше одного
нуля, то говорят, что оно не осциллирует в этом интервале.
Если решения
осциллируют в интервале (а, Ь), то они будут осциллировать
быстрее при уменьшении К и G. Докажем эту теорему для
случая, когда К постоянно, а уменьшается только G.
Пусть и будет решением
a v — решением
d
dx
где G, > G2 по всему интервалу (а, Ь), но GXA: G» во всех теч-
течках интервала. Умножая первое уравнение на v, а второе на и
и вычитая одно из другого, найдем, что
откуда
X. X.
\ K(u'v — uv')\ = /(G, - G.) uv dx
xi x\
— частный случай формулы Грина.
Пусть пределы интегрирования хх и х2 являются последо-
последовательными нулями к; предположим, что v не имеет нуля в
интервале хх < х <х2. Не теряя в общности, и и v могут рас-
рассматриваться как положительные в пределах этого интервала.
Правая часть приведенного уравнения будет тогда определенно
положительной, В левой части « = 0 при л', и х2, и\ — поло-
положительна при xt и отрицательна при х2, a v — положительна
в обоих пределах. Левая часть следовательно отрицательна, что
приводит к противоречию. Отсюда v обращается в нуль не
меньше одного раза между точками хх и х2.
Если и и v равны нулю в хъ то теорема показывает, что i>
снова обращается в нуль до появления последовательного
нуля и. Таким образом v осциллирует быстрее, чем и. Напри-
Например, решения типа
¦v" + т2г< = 0
осциллируют быстрее, чем решения
и" + п2и = О
при условии, что т> п ( — тг < — л2).
10*31. Модификация Пиконе. Более общая теорема, сравнива-
сравнивающая скорость осцилляции решений двух диференциальных
уравнений
d I d
dx\ ^d
где
КгЖ2>0, Gt>Gt,
может быть доказана при помощи расширенной формулы
[Ktti'v — K2uv'] '= f(Gl — <32) wv их 4- f{Kx — К2) u'v'dx.
1 xi. Л" i
Но здесь возникает затруднение вследствие наличия произведения
и'ч)' во втором интеграле, которое было преодолено Пиконех,
заменившего приведенную выше формулу аналогичной, получен-
полученной следующим образом:
й
Тх
{ ?
1 Picone, Ann. Scuola Norm., Pisa, 11 A909), 1.
304
u h
-О2)uv -f
i — A») и v) + a>'2- (Ai + /Q ив' ?
Получим выражение
T f
-" {KiWv— Kmv')T= f(G1—G2
л.
известное как формула Пиконе.
Пусть xt и х2 будут последовательными нулями и и предпо-
предположим, что -у—не обращается в нуль в некоторой точке замкну-
замкнутого интервала хг<^.х ; л'2. При этом правая часть формулы
Пиконе будет положительной (за исключением специального
случая, указанного ниже), а левая часть будет равна нулю. Это
противоречие доказывает, что v имеет не меньше одного нуля
в интервале (xlt x2).
Теорема также верна, если v равно нулю в одной или обеих
точках хг и х^\ для этого необходимо только небольшое видоиз-
видоизменение левой части формулы Пиконе. Предположим, что v об-
обращается в нуль в точке хг, тогда неопределенная величина и\ч)
должна быть заменена ее предельным значением u'/v', имеющим
смысл, поскольку и' и 1)' не равны нулю в тех точках, где и
и v соответственно обращаются в нуль. Следовательно
iL (K.u'v - Kjiv')] = [(К1 — К2) ии']х = ,, = 0.
Иш
Таким образом, независимо от того, будет ли v равно нулю
в хг и х2 или нет, левая часть формулы Пиконе равна нулю, а
правая часть положительная,—противоречие, которое приводит
к заключению, что v имеет не меньше одного нуля в открытом
интервале хг < х < х2.
Если в некоторой конечной части интервала {хъ х2) Gx > G2,
то первый член правой части формулы Пиконе будет положи-
положительным и не равным нулю. Единственно возможный случай,
при котором правый член может обратиться в нуль, имеет место
при Gi = G2 во всем интервале (хъ х2) и при Kt = К2 в части
этого интервала, тогда как в остальной части интервала и' = 0
(т. е. Gj = 0 в этой части). В этом случае первый и второй
интегралы равны нулю, а третий равен нулю, если v пропорци-
Э. Айне—133—20 305
онально и. Заметим, что если в любой части интервала (хъ х2)
G равно нулю, то в пределах этой области К может быть из-
изменено любым непрерывным способом без увеличения осцилляции
решения, постоянного в этой области. Этот специальный случай
может быть рассмотрен, если принять, что Gx и G2 не равны
тождественно нулю ни в одной конечной части интервала (а, Ь).
10 • 32. Условия осцилляции и неосцилляции решений уравнения.
Пусть коэфициенты К и G уравнений
<» = о
непрерывны и ограничены в интервале а -<х <с b и пусть верх-
верхние границы К и G в этом интервале равны К и G, а их нижние
границы—к и g соответственно. Так, во всем интервале (а, Ь),
К>К>к>0,
G > G > g.
В качестве первого сравниваемого уравнения рассмотрим
(В)
которое может быть переписано в виде
dx* k У '
Решения уравнения (А) в интервале (а, Ь) не осциллируют
быстрее, чем решения (В). Последнее уравнение интегрируется
непосредственно; оно имеет следующее решение.
1° Если g>0, то имеется экспоненциальное решение
exp {i^g/k:х}, не имеющее нулей в интервале (а, Ь). Аналогично,
если g=0, то сравниваемое решение может быть принято равным
единице. Отсюда, если g > 0, то решения (В) не осциллируют.
Это приводит к выводу, что если G>0eoeceM интервале (а, Ь),
то решения данного уравнения (А) не осциллируют.
2°. Если g < 0, то имеется осциллирующее решение
sinf^ — g/кл:}; интервал между его последовательными нулями
или последовательными нулями любого другого решения сравни-
сравниваемого уравнения равен ъ\Г—k/g. Следовательно, если
u/ — k/g > b — a,
то ни одно решение данного уравнения не может иметь больше
одного нуля в интервале (а, Ь). Следовательно решения (А) не
являются осциллирующими, если
_ g я2
"к (ь — of-
306
Рассмотрим теперь второе уравнение
или
d*2 К У
Решения (А) осциллируют так же быстро, как и решения (С).
Пусть G будет отрицательным; тогда решения (С) являются
осциллирующими, а интервал между последовательными нулями
любого решения будет равен и/—K/G. Отсюда следует, что
для того, чтобы решения данного уравнения (А) имели не меньше
т нулей в интервале (а, Ь) достаточно, чтобы
m it у — K/G < Ь — а
или
G m-Ti-
в частности, для того, чтобы уравнение (А) имело решение,
осциллирующее в интервале (ал Ь), достаточно, чтобы
К> {Ь — аУ '
10-33. Применение к уравнению Штурм-Лиувилля. Уравнение
типично для многих классов уравнений, возникающих в задачах
математической физики1. Осцилляционный или неосцилляцион-
ный характер их решений, а в осцилляционном случае число
нулей в интервале (а, Ь) представляет существенный интерес
для приложений.
Если k>0 и g>0, то уравнение может рассматриваться, как
частный случай общего уравнения
при
K=k, G = l — lg.
В данном случае приращение X оставляет k неизменным, но
уменьшает G, следовательно увеличивает быстроту осцилляции.
Когда k > 0, / > 0 и g изменяет свой знак внутри интервала
(а, Ь), возникает другой, очевидно отличный случай. Этот случай
может быть приведен к общему типу
См. § 9-41.
307
Если |Х| увеличивается, в то время как X удерживает свой знак,
то в общем случае К и G будут уменьшаться. Если / равно
нулю, К уменьшается, a G остается неизменным. В любом
случае увеличение |Х| вызывает более быструю осцилляцию
решения.
10-4. Первая теорема сравнения. Эта теорема имеет целью
сравнить распределение нулей решения и {х) уравнения
которое удовлетворяет начальным условиям
и (а) = ¦?,, и' (а) = a'i,
с распределением нулей решения v (х) уравнения
d (r, dv \ .-, „
-г— {К2 -.— :¦ — Gjv — О,
dx \ 2 dx ) - '
удовлетворяющего условиям
v (а) = а2, v' (а) = 7.1,
когда в пределах всего интервала (а, Ь)
Kt>K2> 0, Gt > Gt.
Сделаем следующие допущения:
1°. ау и «1 оба не равны нулю и не равны х, и ги_.
2°. Если «хфО, то
^И^ /С. (о) 4
¦-:то означает, что
3°. Тождество Gx^ G2 = 0 не удовлетворяется в некоторой
конечной части интервала (а, Ь).
Исходя из первой теоремы Штурма, можно заключить, что,
если и (х) имеет т нулей в интервале а <х < Ь, то v (х)
имеет не меньше т нулей в том же интервале, а i-ый нуль
¦v (х) меньше i-го нуля и (л:).
Пусть xv Xz,..., хт будут нулями и(х), лежащими в интер-
интервале (а, Ь); если эти нули так перенумерованы, что
то фундаментальная теорема Штурма показывает, что между
каждыми двумя последовательными нулями xf и xt_i лежит не
меньше одного нуля v (x). Теорема сравнения следует непосред-
непосредственно, если можно доказать, что по крайней мере один нуль
"V {х) лежит между а и хг.
Если и (х) имеет нуль в конечной точке а, т. е. если % = О,
то v (х) будет иметь нуль между а и ху; предположим, что
cti Ф 0. Тогда, поскольку v(a) = а2ф0, может быть приложена
308
формула Пиконе
X, X,
[и2 (Кг ~-К2 7г)]*'= У (<Л~ G2) игЛк +/1
Правая часть формулы положительна; если вычислять левую
часть при условии, что v не имеет нулей в интервале (а, ху),
она может быть приведена к выражению
_ а2 (а) ( —i^i!L
о..
которое отрицательно или равно нулю по второму условию.
Это противоречие доказывает, что между а и хг имеется не
меньше одного нуля v(x). Следовательно теорема верна.
Если все нули решения диференциальной системы
=a, y'{a) = a'
отметить в их порядке на линии AS, где Л — точка х = а, а В —
точка х = b (a <b), то влияние уменьшения К и G, оставляя
я и а' инвариантными, вызовет смещение всех корней в напра-
направлении от Б к Л. Если К и G уменьшать непрерывно1, то можно
достигнуть момента, когда в отрезок АВ войдет новый нуль.
Этот новый нуль сначала появится в точке2 В; дальнейшее умень-
уменьшение К и G приведет к тому, что нуль войдет в отрезок и
направится по направлению к А.
10'41. Вторая теорема сравнения. Пусть с будет любой внут-
внутренней точкой в интервале (а, Ь), не являющейся нулем и(х)
или г> (х); тогда в открытом интервале {а, с), ч> (х) будет иметь,
согласно первой теореме сравнения, по меньшей мере столько
же нулей, сколько и и (х). Из второй теоремы сравнения сле-
следует, что если с таково, что и (х) и v (x) имеют одинаковое
число нулей в интервале а < х <с, то
К&)и'_(с)_ ^ К,(с) у'(с)
и (с) ' v(c)
1 Этот процесс наиболее легко осуществляется, если допустить, что К и G
зависят от вспомогательного параметра X, как в уравнении Штурм-Лиувилля.
2 Граничные условия предотвращают возможность появления нового нуля
в А; поскольку решение непрерывно и изменяется непрерывно с Л* и G, —
любой новый нуль во внутренней точке интервала (я, Ь) был бы двойным нулем,
что противоречит принятым условиям. Следовательно любой новый нуль должен
входить в В.
ЗОУ
Пусть xt будет ближайшим нулем впереди с; он будет не-
несомненно также нулем и(х), а не v(x), так как между а и xt
лежит не меньше чем i (согласно условию, точно i) нулей ^(л:).
Формула Пиконе, взятая между пределами xt и с, показывает,
что
Это сразу же дает искомое неравенство. Если бы н(л) и v(x)
не имели нулей в интервале {а, с), то теорема могла бы быть
доказана аналогично, рассмотрев формулу Пиконе, между пре-
пределами а и с.
Так, в системе
у (а) = а, у (а) = а.',
эффект непрерывного уменьшения К и G вызывает уменьшение
значения К(х) ^-т^ в некоторой точке интервала (а, Ь), не
являющейся нулем у (х), до тех пор, пока эта точка станет
нулем.
Следует отметить, что теоремы сравнения, которые были
доказаны для системы (А), одинаково верны и для системы
* ' I У(а)=9а, У(а)=ро',
где р — любая постоянная. Если у (л) — решение (А), то ру (х)
будет решением (В). Это вполне очевидно. Однако, если р рас-
рассматривать как произвольную, то (В) эквивалентно системе
\L(y) = O,
где оба неоднородных граничных условия заменены одним
однородным условием. Поскольку решение (С) равно ру (х), обе
теоремы сравнения действительны в случае совершенно одно-
однородной системы (С).
10 • 5. Одномерные граничные задачи. Под граничной задачей
в общем смысле подразумевается задача, в которой определя-
определяется, имеет ли данное диференциальное уравнение решения,
удовлетворяющие некоторым граничным условиям (условиям
в граничных точках); принимая, что такие условия существуют,
определяется их функциональная природа и исследуются моди-
модификации, возникающие при изменениях в диференциальном
уравнении или в заданных граничных условиях.
Одномерной граничной задачей называется видоизменение
общей проблемы, которая возникает, если уравнение является
обыкновенным диференциальным уравнением, в частности обык-
310
новенным линейным уравнением, а граничные условия устанав-
устанавливаются для решения и его последовательных производных
при некоторых частных значениях независимой переменной х.
Фундаментальные теоремы существования главы III являются
решениями одноточечных граничных задач, так как начальные
условия относятся к отдельной точке х0. Ниже мы разберем
более обстоятельно двухточечную граничную задачу, в которой
граничные условия относятся к двум конечным точкам интервала
а < х < Ь.
Предположим, что коэфициенты диференциального уравне-
уравнения, а также и коэфициенты, входящие в граничные условия,
зависят от параметра X. Так, предположим, что
где/С и С?-^-непрерывные функции (л, X) приа<;л;< Ь, ЛХ<Х < Л2,
К— положительно и равномерно диференцируемо относительно х,
причем его производная непрерывна в интервале (а, Ь)х. Допу-
Допустим также, что и коэфициенты граничных условий являются
непрерывными функциями X при Аг < X < Л2. В этом случае
возникают вопросы двух видов.
1°. Вопросы существования. Для каких значений X существует
решение, удовлетворяющее всем условиям задачи?
2°. Вопросы осцилляции. Если решение существует, то сколько
оно имеет нулей в интервале (а, Ь)?
Для одноточечной граничной задачи первый вопрос удов-
удовлетворяется фундаментальной теоремой существования, из
которой следует, что для каждого значения X в интервале (Alt Л2)
решение существует и является непрерывной функцией {х, X).
Аналогичные вопросы мы будем рассматривать ниже2.
10 • 6. Теоремы осцилляции Штурма. Наиболее простым типом
двухточечной граничной задачи является диференциальная
система, известная как система Штурма
(А)
а!у (а) - а/ (а) = 0,
Введенные здесь частные граничные условия весьма специаль-
специального типа, так как каждое из них само по себе является
одноточечным граничным условием. Уравнение, взятое вместе
1 Возможно, что К будет иметь только одну R - производную в точке а и
одну L - производную в точке Ь.
2 Теорема осцилляции была впервые приведена в известной статье Штурма,
J. de Math., I A836), 106. Однако указанные там граничные условия — очень
специального типа. Исследование было впоследствии расширено: см. Mason,
Trans. Am. Math. Soc, 7 A906), 337; Bocher, С R. Acad. Sc. Paris, 140 A905),
928; Birkhoff, Trans. Am. Math. Soc, 10 A909), 259.
311
с первым условием, имеет только одно независимое решение,
например у = Y(x, X). Связывая это решение со вторым гранич-
граничным условием, получим характеристическое уравнение
корни которого — характеристические числа.
Предположим, что К и G — вещественные монотонно-убы-
монотонно-убывающие функции X, а, согласно условиям § 10 • 31, G не равно
нулю ни в одном конечном подинтервале (а, ?>). Верхние границы G
и К и нижние границы g и к — непрерывные монотонно-убы-
монотонно-убывающие функции X в интервале (Ах, А2).
В § 10-32 было показано, что если для любого частного
значения X уравнение
Ш = 0
таково, что
G
>
то для этого значения X уравнение допускает вещественное реше-
решение, удовлетворяющее граничному условию
и имеющее не меньше т корней в интервале (а, Ь).
Введем дальнейшее условие
— G/K—>оо при X. -> А2.
Докажем, что рассматриваемое решение может иметь любое
число сколь угодно больших нулей в интервале (а, Ь), при ус-
условии, что X приближается к Л2. Коэфициенты к и а' могут
быть функциями X; предположим, что К (а) а'/а — монотонно-
убывающая функция X.
Предположим, что X увеличивается от некоторого числа,
произвольно близкого к Ли и что рассматриваемое решение
имеет сначала i нулей в открытом интервале а<х < Ь. При
увеличении X, число нулей увеличивается, и каждый нуль стре-
стремится сместиться в направлении конечной точки а. Следователь-
Следовательно для некоторого значения X, например X = и,-, решение при-
приобретет дополнительный нуль, который появится в з конечной
точке Ь, а затем сместится, при увеличении К по направлению
к а. Для значения X = и.,- ^ 4 получается другой нуль и т. д. Та-
Таким образом существует последовательность чисел
имеющих предельную точку Л2 и таковых, что при
уравнение допускает единственное решение, имеющее точно
/и +1 нулей в интервале (а, Ь) и удовлетворяющее первому
граничному условию.
312
Более того, второй теоремой сравнения было показано, что
при изменении ). от um до рт + ь выражение
K(b)y'(b)/y(b)
будет монотонно-убывающей функцией X, которая должна умень-
уменьшаться от -)-оо до — оо, так как при X = u;n и X = um t
У (Ь) = О, НО у' ф) d~. 0.
Рассмотрим влияние второго граничного условия
Коэфициенты ,6 и ,6' могут быть функциями X; предположим,
что р не равно тождественно нулю1 и что
— монотонно-убывающая функция X.
Поскольку К (Ь)у' (Ь) у (Ь) — функция, которая при уве-
увеличении X от ут до р.т 4-1 постепенно уменьшается от+ та ДО
— оо, и поскольку — К(Ь)%'1§ постепенно увеличивается в том
же интервале, между рт и "m+i должно быть некоторое значе-
значение X, для которого эти два выражения равны, т. е. для кото-
которого второе граничное условие удовлетворяется так же, как и
первое. Для этого значения X, например Хт + 1, система совме-
совместима; она допускает решение, имеющее точно /и + 1 нулей в
интервале а <х< Ь. Полученные результаты могут быть выра-
выражены следующим образом.
Теорема I. Система (А) имеет бесконечное число вещест-
вещественных характеристических чисел, имеющих только одну
предельную точку А2. Для каждого целого числа т > / суще-
существует только одно характеристическое число Х„. и кото-
которому соответствует решение, имеющее т -f- / нулей в откры-
открытом интервале {а, Ь).
Чтобы уточнить приведенные рассуждения, допустим что
— g/k—>—со при X—>Л,.
Поскольку к положительно для всех рассматриваемых зна-
значений х и X, g в соседстве с At будет также положительно.
Рассмотрим уравнение
TxiSu = 0>
которое может быть написано в виде
и" — s2u = 0,
1 Случай Э — 0 может быть сразу исключен; второе граничное условие при-
приводится к у(Ь) = 0; следовательно, характеристическими числами являются \х,,
313
где
s2 = g/k > О
для значений X, достаточно близких к Аг.
Пусть и(х) будет решением (В), удовлетворяющим началь-
начальным условиям
(С) и(а) = а, и'(а) = а',
тогда
—s(x—a)
Для достаточно больших значений s, т. е. для значений >.,
достаточно близких к Л,, и{х) приближается к chs(x — а) и
следовательно не имеет нулей.
Пусть у(х) будет решением первоначального уравнения
которое удовлетворяет условиям (С). В этом случае условия
первой теоремы сравнения, именно
КЖ G>g,
Къ'/а > к о'/я,
удовлетворены. Следовательно у(х) не имеет больше нулей в
интервале а < х < Ь, чем и(х), и поэтому для значений К доста-
достаточно близких к Л„ у(х) не имеет нулей в интервале (а, Ь).
Отсюда следует, что г=0.
Докажем, что в интервале (Alf ^0) существует только одно
характеристическое число Хо. Поскольку для значений I в этом
интервале у(х) и и(х) не имеют нулей в а<л<&, из второй
теоремы сравнения следует, что
К(Ь)у'(Ь) ^ ки' (Ь)
У(Ь) *" и(Ь) '
Но при X—>Л„ s-^ + oo, следовательно
В'F)/И (&)->+со,
а поскольку к > О,
Таким образом с увеличением X от Л, до jv K(b)y' (b)/y(b)
постепенно уменьшается от +оо до —со. Следовательно систе-
система имеет только одно характеристическое число в интервале
( Ч> Уо)- ^се полученные результаты сформулированы в следую-
следующей основной теореме осцилляции.
Теорема II. Вещественные характеристические числа си-
системы. (А) могут быть расположены в возрастающем порядке
величины и могут быть обозначены
^о» Xj, ).2). . . ,Хт,...,
314
если соответствующими характеристическими функциями
будут
Уо» У и У2i • • • >3'т» • • ¦ >
то ут будет иметь точно т нулей и интервале а<х <Ь.
Предположим, что выражение
на котором основана теорема II, было составлено исключительно
для того, чтобы существовало характеристическое число Хо. Это
условие, хотя и достаточное, однако оно не является необхо-
необходимым для существования Хо. Другая последовательность условий,
достаточная для обеспечения существования >0, получается сле-
следующим образом.
До сих пор мы принимали, что К, G, а, а', C и C' определены
в открытом интервале ЛХ<Х<Л2. Допустим, что интервал замк-
замкнут в своей левой конечной точке, т. е. что At принадлежит
к интервалу. Пусть
Ки Glt alt a[, plf Pj
будут значениями соответствующих величин, когда Х=ЛХ; пред-
предположим также, что
gi>0, aiai'>0, рхР/>0,
но а, и а/ так же, как и рх и р/ не равны попарно нулю.
Рассмотрим теперь систему сравнения
(С)
at'H(a)—а,ы' (а)=0.
Диференциальное уравнение может быть написано в виде
u"-s2u= О,
где
Предположим, что s > 0, тогда решение системы сравнения
может быть принято равным
и (х) = аг chs (x—a) -f- — sh s (л;—a),
о
что и{х) будет существенно положительным или существенно
отрицательным для х > а.
Если v (х) — решение системы
\a1'-v(a)—a.1v'(a)=0,
315
где Kt и Gj представляют Кип при Х=Л„ то из первой теоре-
теоремы сравнения следует, что v(x) не может иметь больше нулей
в интервале (а, Ь), чем и(х); следовательно она не имеет нулей
в интервале (а, Ь), т. е. /=0. Для некоторой величины X, боль-
большей Ль именно Х=|а0, решение у (х) системы
а'у(а)—ау'(а)=0
(которое приводится к v(x) при >=А,) будет иметь нуль при
х=Ь. Поскольку и(х) и у(х) не имеют нулей в интервале (а, Ь)
при Л^Х-^^о, в данном случае может быть приложена вторая
теорема сравнения: она показывает, что
Кг(Ь)у\Ь) > _М'(*>)
при Л,<Х<и0. Правую часть неравенства можно вычислить
непосредственно; можно показать, что она положительна, откуда
следует, что левая часть также положительна. Таким образом
выражение
K{b)y'{b)ly{b),
принимающее значение Кг(Ь) -о' (b) \v (b) при Х=Л1, постепенно
уменьшается от значения > 0 до — оо при увеличении ). от \г
до V.Q. Поскольку
постепенно увеличивается от отрицательного значения при I=
= Аь мы получим точку, для которой оба выражения будут
равны, а для этого значения X [например Хо, у (х)] будет удов-
удовлетворять также второму граничному условию
Следовательно в интервале (\v \>.э) существует характери-
характеристическое число Хо, отличное от \ и \>.о (кроме случая C = О,
когда Хо = |а0), так что система (А) имеет решение, не имеющее
нулей в интервале а < х < Ь.
Рассмотрим теперь кратко специальный случай s = 0. Реше-
Решение и (л:) является здесь линейной функцией аргумента х — а.
Более того, функция и (л) существенно положительна или отри-
отрицательна в интервале (с, Ь), а выражение ku' {b)ju (b) в общем
случае положительно или равно нулю. Таким образом, как и
выше, характеристическое число Хо существует, но может (в спе-
специальном случае) совпадать с Aj. Этот случай возникает только
при
а; = р; - о, g±e о.
Теорема III. Принимая, что
g, > о, в1а; > о, р,р; > о,
зю
система (А) будет иметь бесконечную последовательность ве-
вещественных характеристических чисел
которым соответствуют фундаментальные функции
У о, Уг, Уъ---, Ут,---
таким образом, что ут имеет точно т нулей в интервале
а<х<Ь. Меньшее характеристическое число Хо отлично от
Аг кроме случая
G1 = О, а\ = О, р; = О.
10-61. Приложение к системе ШТурм-Лиувилля. Группа теорем,
известных в настоящее время как теоремы осцилляции, была
впервые доказана Штурмом1 для системы
с которой мы уже встречались (§§ 9-41, 10-33).
Предположим, что k, g и / (вещественные непрерывные
функции х при а<л<;й) не зависят от X, и таковы, что k>0,
g>0. Коэфициенты а, а', C и Р' также не зависят от ),. По-
Поскольку выражение Ge/—lg постепенно уменьшается или,
в крайнем случае, остается постоянным для любого значения х
в интервале (а, Ь) при увеличении X от \г = — со до А2 = + со,
условия, принятые при доказательстве теоремы II (§ 10- 6),
удовлетворены. В частности
при Х-^ + оэ. Следовательно, существует бесконечная последо-
последовательность вещественных характеристических чисел Хс, >.lt Х2,-..,
не имеющих предельных точек за исключением Х = + °°; если
существующими характеристическими функциями являются у0,
yv у2,..., то ут имеет точно т нулей в интервале а<х<.Ь.
Если кроме X = 0 наложены добавочные условия
/ > 0, аа' > 0, P.S' > 0,
Ах может быть принята равной нулю. В этом случае при X =0
g = min/>0,
а характеристические числа все* положительные. Этот случай
важен с физической точки зрения.
Рассмотрим случай, когда /г>0, /> 0, a g изменяет свой знак
в интервале (а,'Ь). Задача может быть разрешена так же, как и
1 J. deMath., I A836), 139,143.
317
в § 10-33. Перепишем уравнение так
d
k dy} /-Xg
dx \|X| dx] Щ
Это уравнение общего типа, если
/С= -щ-, G = -j-—g, когда X > О,
^=w-G = w+^KOr;ia^<0-
В любом случае К и G постепенно уменьшаются при увеличе-
увеличении |Х|; если условия ою'> 0, $$' > 0 также удовлетворены, то
будут постепенно уменьшаться с увеличением |Х|. До сих пор
необходимые условия были удовлетворены, но следует отме-
отметить, что поскольку g изменяет знак в интервале (а, Ь)
G > 0 и К > 0.
то
— G'K-»-co
ПрИ |Х| —> оо.
Таким образом условия теоремы I (§ 10-6) не удовлетворены;
однако отсюда не следует, что теорема неверна для рассматри-
рассматриваемого случая. Напротив, поскольку g меняет свой знак в ин-
интервале (а, Ь), можно найти такой подинтервал (а', Ь'), в котором
g > 0 в случае X > 0,
g <0 в случае Х<0.
В любом случае значения I могут быть взяты достаточно боль-
большими по абсолютному значению, чтобы обеспечить условие G<0
в интервале (а', Ь'). Следовательно необходимое условие
осуществляется в интервале (а', Ь'), когда Щ —» оо. Таким обра-
образом X может быть достаточно большой для того, чтобы реше-
решение системы
\а'у(а)~ау'(а)=0
осциллировало в интервале (а', Ъ') и a fortiori в интервале
(аг Ь). Число нулей в интервале (а, Ь) может быть увеличено
ло бесконечности, полагая I достаточно большой.
318
С другой стороны, решение системы
d с. йи'
Is-{*?}-"=*
\а'у(а)-ау'(а) = О
(при X = 0) не имеет нуля в интервале {а, Ь), если / > 0, за
исключением случая Z = 0, когда может существовать один нуль.
Предположим, что
/ > 0, а.0.' > 0, рр' > 0
и исключим специальный случай
требующий особого исследования1, тогда методы доказательства
теоремя III (§ 10 • 6) могут быть полезны при доказательстве
существования характеристических чисел, которым соответ-
соответствуют фундаментальные функции, имеющие 0, 1, 2,..., т, ...
нулей в интервале (а, Ъ). Единственной существенной разницей
является то, что случай X < 0 отличается от случая t. > 0 тем,
что получается бесконечная последовательность отрицательных
характеристических чисел с предельной точкой \— — со; это
аналогично бесконечной последовательности положительных
характеристических чисел с предельной точкой Х = «т-со. Тео-
Теорема осцилляции теперь изменяется следующим образом2.
Если g изменяет свой знак в интервале (a, b), a
/ > 0, оо' > 0, рр' > 0,
то существует бесконечная последовательность вещественных
характеристических чисел с предельными точками + °° и — оэ.
Если положительные и отрицательные характеристические чи-
числа расположить в порядке возрастающих числовых значений
и обозначить через
*0 > Mi ^2 » ¦ • ¦ > 'wi • • •>
а соответствующие фундаментальные функции обозначить
}>t, yt, yt,---, У'т,
У~а> УЧ, У-2 , • - -, Ут,
то fm и yZ будут иметь точно in нулей в интервале а < х < Ь.
1 См. Picone, Ann. Scuola Norm. Pisa, 11 A909), 39; Bocher, Bull. Am.
.Math. Soc, 21 A914), fi. T1. , ,
2 Sanlievici! Ann. Ec. Norm. C), 26 A909), 19; Picone, loc. cit; Richardson.
Math. Ann., 68 A910), 279.
319
10-7. Свойство ортогональности фундаментальных функций и ее
следствия. Рассмотрим диференциальную систему
(A)!^"' ' ь~ H0 dxn *'Ldxtl l ' "' ' Уп idx'1' " ь
где коэфициенты диференциального уравнения р0, /?,,..., /?я_.ь
рп, g и коэфициенты, входящие в выражения ?/,(«), не зависят
от параметра X. Сопряженная система будет иметь вид
Г , \ I \ — / 1 \п dn (p0V) . . л\п— 1
I "Т" • • • ^ " fix I \Гп "Г "S/ ^ — ^,
Предположим, что система (А) допускает не меньше двух
характеристических чисел, например lt и X, и 4tq соответству-
соответствующими характеристическими функциями являются н,- и «,.
Тогда система (В) совместима для h и X,; пусть характеристи-
характеристическими ФУНКЦИЯМИ будут Vi И Vj.
Формула Грина
у> i («) -нГ^)} = иу,п + u2v2n~i + ... + ад/,
(§ 9-31) верна независимо от значений и и и Пусть и = щ и
¦у = г»,; тогда правый член обратится в нуль, поскольку
и^щ) = U2 (и,) =...=Un («,) = О,
Следовательно
/ {%! («О — UiL (Vj)} dx = О,
a
откуда
(X, —X,-)/gUiVjdx = 0;
а
поскольку /.г и >7 различны
ь
= 0.
В частности, если система (А) самосопряженная, то
b
fguiul-dx = 0
а
320
Последовательность функций
Wj, lla, . . ., Ulf • ., Uj, . . .,
таких, что при заданной функции g
называется ортогональной относительно функции g; кроме того,
при g>О
ь
fguf dx > 0;
а
поэтому каждая функция н,- может быть умножена на некото-
некоторую постоянную, так что
ь
fgaj dx = I.
В этом случае функции называются нормированными. Характе-
Характеристические функции системы (А), когда последняя самосопря-
самосопряженная, образуют ортогональную последовательность. В неко-
некоторых случаях, в частности, когда g>0, они также могут быть
нормированы.
Из свойства ортогональности получаем следующую важную
теорему: если g > 0 во всем интервале (а, Ь), то все характе-
характеристические числа вещественны. Предположим, что X,- = а -|- к —
комплексное характеристическое число, тогда, поскольку коэфи-
циенты системы все вещественны, среди остальных характери-
характеристических чисел имеется число, сопряженное с а,, например
Х7-= з — ii. Если характеристическая функция щ равна s -j- it, то
щ равна s — it. Тогда
b Ь
j;gut щ dx=fg(s° -f t)dx;
и а
это выражение равно нулю только при s = t = 0. Следовательно,
если g>0, то допущение существования комплексных характе-
характеристических чисел приводит к противоречию, что доказывает
теорему. Условие g > 0 можно заменить менее ограничивающим
условием g > 0, принимая, что равенство недействительно для
всех точек некоторого конечного подинтервала (а, Ь).
10-71. Приложение к системам Штурм-Лиувилля. Приведенное
исследование может быть непосредственно приложено к системе
Штурм-Лиувилля
(A> я'у (а) — а у (а) - О,
В'3'0)+РУ(&)=О,
Э. Лйнс—133—21 321
если знак g постоянен по всему интервалу (а, Ь), то каждое
характеристическое число — вещественно1.
С другой стороны, если g изменяет свой знак в интервале
(а, Ъ), то можно доказать, что все характеристические числа
будут вещественными при
k > 0, 1> 0, 7л' > 0, 83' > О
(см. § 10-61). Предположим, что /^ — комплексное характеристи-
характеристическое число, например а + h; соответствующая характеристи-
характеристическая функция y>i будет комплексной, скажем s -f it
Тогда уравнение
удовлетворяется тождественно. Вещественная и мнимая части,
равные каждая в отдельности нулю, дают соответственно
Из этих уравнений следует, что
ь ь
f(sS + tT) dx = [k (ss' + tt')fa — J'k (s'H f-) dx +
b b
a a
Вследствие ограничений
k>0, та'>0, РР'>О
получим
поскольку /г > 0 в интервале (a, ft), as' и f не равны тождествен-
тождествен2
у
но нулю2
наконец
1 Эта теорема была известна еще Пуассону (Poisson, Bull. Soc. Philomath.,
Paris, 1826, 145).
2 *' =/' = 0 означало бы, что (а+ i' g—lzEzO, следовательно т^=^0, по-
поскольку тфО; gE=O, что противоречит сделанному допущению, что g изменяет
знак в интервале (а. Ъ).
322
Из вытекающего непосредственно отсюда противоречия видно,
что комплексные или мнимые характеристические числа в рас-
рассматриваемом случае существовать не могут. Можно доказать
также, что если yt любая характеристическая функция, то
b
fgy't dx ф 0.
а
Пусть Аг — характеристическое число, которому соответствует
у Г, тогда
Если это тождество почленно умножить на yt и проинтегри-
проинтегрировать между пределами а и ft, то получим соотношение
ь ь ь
h fgyt dx =/lyj dx +J'ky? dx — [kyt y't\ba.
a a a
Первый член правой части выражения положителен или равен
нулю, второй — определенно положителен, а третий — положи-
положителен или равен нулю. Отсюда
ь
fgyfdx>0, если Х,->0,
а
<0, если >.; <0.
В обозначениях § 10-51 характеристические функции у{ и уТ
могут быть умножены на соответствующие вещественные посто-
постоянные, так что
ь
fg{y\ )*dx = + l,
Рассмотрим теперь более общую систему1
[
(В) | &1у (а) + а2у (Ь) + а3у' (а) + а4у' (Ь) - 0,
1 (а) + hy Ф) + %У' (а) + hv' (Р) = 0
(см. § 9-41). Предположим, что по меньшей мере два из соотно-
соотношений
я„ а„ at
, _— , —— , ——
Pi Ps Ps pi
! Mason. Trims. Am. Math. Soc. 7 A906), 337.
не равны. Если
Р.
то система приводится к (А). Этот частный случай был уже
нами разобран, поэтому здесь мы его рассматривать не будем;
в любом другом случае граничнв1е условия могут быть приве-
приведены к системе
| У(а) = ъУ(Ь) + ЪУ'(Ь),
I у'(а) = Ъу(Ь) + ъ/(Ь).
Допустим, что условие самосопряженности системы
(D) i
удовлетворено, тогда соотношение
¦ ль " b
[k {ss' + tt')\ —j"k (s'a + tn) dx—fl (s2 +1*) djc = 0,
a a
вытекающее из предположения, что система (В) допускает
комплексное характеристическое число, нарушается, когда k > 0,
/>0 при
т. е. при
k (a) s (a) s' (a) — k(b)s (b) s' (b) > 0,
k (a) t (a) f (a) — k(b)t {b) t' (b) > 0.
Из (С) следует, что эти два неравенства удовлетворяются, если
k(а) { TlS + 7iЧ }.{ Та-- + Т.Ч } — * (^ S4 > 0,
где % = s(b), fi = s'(b) или S = ^F), -q-=t'(b). При помощи (D)
это неравенство может быть приведено к
что может быть переписано в виде
Из условия (С) вытекает, что ^iYs ~~ и Tz > 0; отсюда следует,
что приведенные выше неравенства удовлетворяются при
т;ъ>0 и YiT2>0.
Таким образом система (В) допускает только вещественные
характеристические числа.
Эти условия удовлетворяются в случае периодических гра-
граничных условий
у(а)
324
Следовательно, если k > О, / > 0, k (о) = k (V), характеристические
числа системы все вещественны.
10 • 72. Индекс и кратность характеристических чисел. Рассмот-
Рассмотрим снова простую систему Штурм-Лиувилля
a'v (a) — a/ (a) --= 0,
Если для любого частного значения ). индекс системы равен 2,
то наиболее общее решение уравнения должно удовлетворять
первому граничному условию, что невозможно. Индекс системы
для каждого характеристического числа равен поэтому единице.
Пусть у(х, X) будет решением диференциального уравнения,
удовлетворяющим первому граничному условию, тогда второе
граничное условие, которое удовлетворяет у (х, X), даст харак-
характеристическое уравнение
Пусть Xf будет характеристическим числом, ау(х, ).,•) — соот-
соответствующей характеристической функцией, тогда
d I. d
-Тх \k ЧкУ^- ^ I + &g-i)y (х, V = о,
d t, d , , ч I , ,. ., . . . л
dx\ dx' v ' " J v ь ''v ' ''
Исключая / из этих уравнений, а затем интегрируя полученное
выражение между пределами а и Ь, получим соотношение
[k { у (X, ).) у' (X, ).,) - у' (X, А) у (X, А,)]' +
ь
+
которое, поскольку функции у {х, X) и у (х, X,) обе удовлетворяют
первому граничному условию, а у (х, л,) удовлетворяет также и
второму граничному условию, приводится к виду
ь
?' jgy (х, аду (х, l)dx^k (b) v' (b, X.) { p> (b, >.) + Py' (&, X) }. (X - X,-),
-~k(b)y'(b- i.t)F(\)l(k-h).
Теперь, когда Х-»>,,-
F().)/fA — a,-) -¦ 71' (h), поскольку F A,) = 0,
x, X,)
325
равномерно, поскольку у (х, ).) — целая функция X. Следовательно
в пределе
ь
Pfg { У (¦*- >•¦) Y2dx = k (Ь)? (Ь, ).,) F' (),).
с
Если ,3'=t=0, то левый член уравнения также не равен нулю.
Следовательно, F' (if) ф 0, т. е. "t-t — простой корень характери-
характеристического уравнения.
При Р' = 0 модификация метода приводит к тому же резуль-
результату, с тем возможным исключением, как и в случае, когда g
изменяет свой знак в интервале (а, Ь), I равно нулю, а а' = |3' = 0.
В данном случае характеристические числа могут быть двой-
двойными корнями характеристического уравнения.
10 • 8. Периодические граничные условия. Рассмотрим теперь
следующую систему1
(А)
у(а)=у(Ь),
где условие самосопряженности системы, именно К(а)=К(Ь),
удовлетворено. Как наиболее важный, система содержит ча-
частный случай, когда К и G — периодические функции периода
(Ь-а).
Допустим, как и выше, что К и G — непрерывные функции
(х, X) при а <; х < Ь, Л, < X < Л,, и что обе эти функции убывают
с увеличением L Кроме того, введем также несколько более
ограничивающее условие
дк <и'
что не исключает наиболее важного случая Штурм-Лиувилля,
когда G — I — lg, g>0. Допустим также, что
lim —g _ lim —G
g _ ,
Пусть yl (x, ).) и v2 (x, ).) — два фундаментальных решения
диференциального уравнения, выбранные таким образом, чтобы
они удовлетворяли начальным условиям
yt(a, ).)-- 1, у, [а, X) =0,
v/(a, X) = 0, у»'(а, >.)- 1,
1 Tzitzeica, С. R. Acad. Sc, Paris, 140 A905). 223: Bocher, ibid.. 92». Mason.
ibid., 1086; Math. Ann.. 58 A904Л 52 °; Trans. Am. .v.ath. Soc, 7 fiSiW»' 337: см I
также Picard, Traite d'Analyse, 3 П и (Д.), 140. Распространение на обычную са-
самосопряженную линейную систему второго порядка см. Birkhoff, Trans. Am.
Math. Ьос, 10 0909), 259 и Ettlinger, ibid., 19 A918), 79; 22 A92!), ГАЗ.
326
тогда, согласно формуле Абеля (§ 9 • 4), выражение
(B) у, (Ь, X) у./ (Ь, X) - ys (b,l) у,' (b, X) = K{d)/K(b) = 1,
будет удовлетворяться тождественно для всех значений X.
Характеристическое уравнение имеет вид
] Уг(а, X) ~У1 (Ь, I), у3(а, X) -у2 {Ъ, X) | = О,
,ух'{а, l)-yt'(b. X), у/(а, 1)-уг'{Ь, X) !
или
что, согласно тождеству (В), приводится к уравнению
(C) Р(Ь) = уЛЬ, *) +>-2'(Л X) -2 = 0.
Число X, которое определяется уравнением .FfX.) = O так, что не
все элементы характеристического детерминанта равны нулю,
называется простим характеристическим числом. Если все эти
элементы равны нулю, то получим два линейно независимых
решения системы (А). Такое значение X, для которого
У ЛЬ, >•) = !, Vi(p. *)=0,
называется двойным характеристическим числом.
Теперь нам нужно доказать, что при указанных условиях
корни характеристического уравнения образуют бесконечную
последовательность вещественных характеристических чисел1.
Эта задача разрешается косвенно путем исследования знака
функции F (X) для различных значений X, соответственно кото-
которым решения уравнения L(y) = 0 обладают известными свой-
свойствами.
Пусть }. = ;.>-,• будет характеристическим числом системы
U(«) = o,
1 ; 1 и (а) = и (Ь) = 0.
Эта система типа Штурма — частный случай более общей
системы (§ 10 • 6, А), в которой т. = 3 =0. Следовательно она
имеет бесконечное число характеристических чисел ;j-i (?^>1),
при которых каждая соответствующая характеристическая функ-
функция щ (х) имеет в интервале 2 а *;л < Ъ некоторое число ну-
нулей, равное индексу L
1 Методы, изложенные в предыдущем параграфе, могут быть использованы
для доказательства того, что но многих случаях система не имеет комплексных
характеристических чисел.
2 Первая конечная точка а входит в интервал, а вторая конечная точка b
исключается, так как и (Ь) = и {а); характеристическое число jj.o отсутствует, по-
поскольку каждая функция щ (х) имеет нуль при х - а.
327
Характеристические числа ^ системы (D) не являются в обшем
случае корнями характеристического уравнения (С). Функция
щ (х) может быть отождествлена с функцией уг (х, и,,-).
Поскольку в данном случае
У2 (Р, i>t) = О,
тождество (В) приводится к
откуда
Jx (*» pf) У3 (*.»«)
Следовательно
/•"(»,) > 0, когда }\ (b, v-t) > 0, ноФ 1,
или когда у\ {b, jj., ) > 0, но ф 1,
Ffa) = 0, когда ух (&,;..,) = у2ф, \н) == 1,
F{\>i) < 0, когда j/j (b,!-,) или ^ (ft, и.,-) <.
Поскольку Уа(а, и,-)=1 и у2 (&,1>.,)=>'2(а.^)==0,функция ^(&,;-,)
будет положительной или отрицательной соответственно тому,
имеет ли^2(дг,о,) четное или нечетное число нулей в интервале
а<х<Ь. Поэтому, когда / четное, то F(a,)>0, следовательно
и,- может быть корнем характеристического уравнения (С); когда
i нечетное, то F(pi) < 0, и и,- не будет корнем (СI.
Знак функции F(\) в точках и,, ;«.8, ^3, • • • может быть пред-
представлен графически (фиг. 6).
^ А А А А, /^•••Аг
1 1 1 1 )_Г 1
Фиг. 6.
Таким образом характеристическое уравнение /?(Х) = 0 имеет
четное число корней2 в каждом интервале (на,Уз). (V'-з» Fs). • - •
Очевидно, существует бесконечная последовательность вещест-
вещественных характеристических чисел системы (А).
Рассмотрим систему
она допускает бесконечную последовательность характеристи-
1 Весьма небольшое изменение аргумента показывает, что при нечетном
/F<w)-=-4.
2 Возможный двойной корень считается дважды.
328
ческих чисел v,(/>0), так что каждая характеристическая функ-
функция Vi(x) имеет / нулей в интервале а <; х < Ь. Отождествляя
Vt{x) с ух (к, v,-), найдем, как и выше, что
Следовательно
/"¦(v,-) > 0, когда у\ (b, v/) > 0, но Ф 1,
Fiyd = 0, когда \\ (b, v,-) = 1,
/=• (v,) < 0, когда J-! (&, vj) < 0.
Теперь функция j/, (л% v,) имеет четное или нечетное число ну-
нулей в интервале а < х < ft, соответственно тому i четное или
нечетное. Поскольку ^(a.v,-) = 1, отсюда следует, что _>>,(&,*,-)
положительно или отрицательно, соответственно тому i четное
или нечетное. Поэтому, когда i четное — /7(v,)>0 и v; может
быть корнем характеристического уравнения (С), а когда / не-
нечетное—-F(Vi)<0 и v,- не будет корнем (С).
Л = Л, i/ff U 1>г Vj ¦ ¦ - Л^,
" 1— 1-^ Ь 1 1 1
^0 <0 >0 <0 ¦ ¦
Фиг. 7.
Знак FQ.) может быть выражен следующим образом (фиг. 7>
Функция F(a) имеет следовательно четное число корней в
каждом интервале (Л1? v,), (vj, v3). (v3, v5), ....
Очевидно, что
так как увеличение числа нулей в интервале а <:.*< Ъ озна-
означает увеличение значения X. С другой стороны, ничего неиз-
неизвестно об относительных величинах \н и v,-. Полагая, что \>t < vb
изменение знака FQ) можно выразить в виде фиг. 8.
Л= A v и у и v? Ai, vi ¦
,_L__i±—LJ. ni—UjL ^—LA ?
F(\) ^0 <0 <D >0 >0 <0 <(]¦¦¦
Фиг. 8.
Следовательно мы доказали, что при указанных условиях
для системы (А) в каждом интервале (u,-, ^i-fi), (v*, v,-+1) сущест-
существует не меньше одного характеристического числа.
Покажем далее, что для системы (А) в каждом интервале
:•-(, Уч i) или (v,-, vi+1) имеется только одно характеристическ ое
329
число. Для этого достаточно доказать, что функция F'(k) имеет
тот же знак при каждом корне F(x) =0 в любом интервале.
Поскольку восходящие и убывающие узлы должны следовать
друг за другом в графике непрерывной функции, результат
получается немедленно. Для упрощения примем, что К(х) не
зависит от X, тогда
следовательно
Предположим, что и (х, X) будет единственным решением си-
системы
f /,(«) = О,
1 и (а) = а, и' (а) = а\
где а и а' —вещественные числа, не зависящие от X. Очевидно,
-,-.- удовлетворяет неоднородному уравнению
^(кг<^[^и\\ с ди dG
dx \ dx \ EX У j дК д\
Но, как известно, соответствующее однородное уравнение
имеет два фундаментальных решения
dv . .. dv , , -,
ди д I du\
откуда --,,- и -зт- (-т—1 можно определить методом вариации пара-
параметров (§ 5-23) так, что1
Ж
Следовательно, полагая л: = ft и « =3^х в выражении
1 Не следует забывать, что
и (а, X) = -/., и' (а, '/.) = 7-'
для всех значений л, следовательно
ззп
ди „
для -^г-, найдем
, д /йи\
и полагая л; = о и и ~ у2 в выражении для -~^l w~~J> аналогично
найдем, что
)}
откуда
Л
/^21 (й 1Ь] uV + [у: (ь, '¦) -
-у\(Ь. ),)]y\it, \)v2(t, \)—y\{b, \)y\it, >-)}df.
Поскольку К (а) > 0, а сд1 < 0, знак при F (X) будет проти-
противоположен знаку при квадрической форме
где Н = уг(^, >.), ¦*1=^2(^Л)- Дискриминант этой формы равен
и, согласно формуле Абеля
>'i(^, Vy},(b, 1)—уа(Ь, Цу\(Ь, А) = 1,
он приводится к виду
следовательно для значений I, при которых характеристическое
уоавнение
Ух ('о, к) + у[, (Ь, 1) ^ 2
удовлетворяется, дискриминант равен нулю. Для таких значе -
ний I квадратическая форма может быть написана в виде
3'»5+ г<Уг-У*
V, F, >•)
331
При простом характеристическом числе X выражения
У-Л + ~2 (У2 — У iK ЛТ1 — A — Vi) Н
не могут быть равны нулю. Отсюда следует, что функция F'(l)
не равна нулю и ее знак соответствует знаку у[(Ь, X) или j/2(b, X).
Следовательно, функция FQ*) изменяет свой знак при простом
характеристическом числе X.
Если для любого частного значения X.
то формула Абеля приводится к виду
а из характеристического уравнения
Угф, 1)+У'2(Ь, Ц = 2
получим, что
УЛЬ, V = y'2(b, Х)=-1.
Рассматриваемое значение X является двойным характеристиче-
характеристическим числом и для такого значения
Аналогичным принятому при нахождении F'(к) методом можно
доказать, что
Поскольку у± и у2 — независимые решения диференциального
уравнения, a s и ? —независимые переменные, то выражение
не равно тождественно нулю. Функция F" (I) отрицательна для
двойного характеристического значения X, поэтому она находится
в соседстве с двойным характеристическим числом; F(l) сохра-
сохраняет постоянный отрицательный знак.
Поскольку функция F(\) отрицательна при j»2m-i и при u2m . t
и положительна или равна нулю при \мт, в двойном интервале
{у-2т—и \>-2т\ i) должно существовать не меньше двух простых
характеристических чисел Хр и \ч или одно двойное характери-
характеристическое число ).р — )q так, чтобы
1 < >-р С ^2m <S \ <'\'-2т 1-
В этом интервале, кроме точки ^2т. не может лежать ни одно
332
двойное характеристическое число. Если в интервале (\>-%т—и
[).2т) имеются еще другие дополнительные характеристические
числа, то они должны быть простыми, а число их четным. Но
для этих значений X функция Г' (X) имеет знак противоположный
Уг (Ь> а), что невозможно, поскольку _у2 {Ь, I) не меняет знака
в некоторой внутренней точке интервала. Следовательно в двой-
двойном интервале {мт—и vim 1), кроме lp и lq, нет никаких других
характеристических чисел. Аналогично можно доказать, что
в двойном интервале (v2m_i, vjn.-i) имеются только два характери-
характеристических числа; очевидно, этими характеристическими числами
являются Хр и У-q, поэтому
Отсюда непосредственно следует, что в открытом интервале
(^2т, >2т) или в замкнутом («••>«+ь Vom_j) характеристические
числа лежать не могут. Аналогично можно доказать, что в ин-
интервале A1<fc<v0 функция F(k) > 0 и, следовательно, характе-
характеристические числа отс>тствуюг.
Поскольку ).р и Хд — внутренние точки двойного интервала
(y-zm-i, v-гт , i), соответствующие характеристические функции ур
и yq не могут иметь меньше 2т — I или больше 2т + 1 нулей
в интервале а с х < Ь. Однако, вследствие периодических гра-
граничных условий число нулей в интервале должно быть четным.
Следовательно yv и yq имеют только по 2т нуля в интервале
а < х < Ъ.
Фиг. 9.
Обозначим интервал (.Vlt v0) через (-/.0), а интервалы (и^ >]_),
О'-2. v2),...через (v.j), (-/2),.. .(фиг. 9). В данном случае ни одно
характеристическое число не может быть внутренней точкой
любого интервала (/;). С другой стороны, между двумя после-
последовательными интервалами (у.*) и (yi:i) лежит только одно ха-
характеристическое число1; обозначим его через \ и пусть j/; (x)
будет соответствующей характеристической функцией. Тогда
у0 (х) не обратится в нуль в интервале а <• х < Ь, уг {х) и у2 (х)
обратятся в нуль два раза, ys (х) и yt (х) — четыре раза и т. д.
Это приводит к следующей теореме осцилляции.
Для системы (А) существует бесконечная последователь-
последовательность характеристических чисел Хр, \, Х2)...,'/,-,..., так что
если соответствующие характеристические функции обозна-
обозначить через у0, \'х, У«,- ¦ ¦, Vi,- ¦., то г,- б\дет иметь в интервале
а<.х<Ь четное число нулей, именно г или i-\-\ нулей.
1 Очевидно, при наличии двойных характеристических чисел это утвержде-
утверждение неверно.
10 • 81. Уравнения с периодическими коэфициентами. Наиболее
важное применение теории систем с периодическими гранич-
граничными условиями относится к случаю, когда коэфициенты дифе-
ренциального уравнения являются периодическими функциям х
с периодом, соизмеримым с (Ь — а). В частности, пусть К и G
будут четными периодическими функциями, с периодом к и пусть
граничными условиями будут
тогда из диференциального уравнения найдем, что если \\ —
любая характеристическая функция, то уТ'(— я) ^у'Р (ъ), следо-
следовательно характеристические функции будут чисто периодиче-
периодическими с периодом 2и,
Основные решения ух(х, к) и у2(х, >.) удобно выразить сле-
следующим образом
У1@, а) = 1, у2ф, I) = 0,
Х@, 1) = 0, у'2@, 1)=1;
тогда ^(х, X) будет четной, а _у2(л, ).) — нечетной функцией от х.
Если бы, например, функция уг(х, I) не была * четной, то
УЛХ)^) — Уг(~л> ^) было бы решением уравнения, которое обра-
обратится в нуль вместе с его первым производным для х = 0, что
невозможно.
Если для любого значения *Х выражение уг(— s Ц = 0, то
^(л, ).) будет иметь четное число нулей в интервале— тс<л;-^7:,
что противоречит условию у'( — к)=у'(т<:), следовательно это
значение X не было бы характеристическим. Для любого дру-
другого значения л функция yt(x, л) удовлетворяет условию
v(— «) = jf
Дальнейшее условие
У(-*)-УA0 = 0
удовлетворяется при к — v2m.
Аналогично, для всех приемлемых значений X функция у2(х, *.
удовлетворяет условию
а также условию
У(-к)=У(к) = 0
при X = \).2т. В данном случае Х? должна быть отождествлена
с V,-, когда i четное, и с \н+и когда i нечетное.
Весьма важно распространение приведенного выше случая на
периодические решения второго рода, т. е. когда у(ъ) и у'(~)
не равны, а только пропорциональны у(— -) и У(—я). Оба ли-
линейных граничных условия заменены теперь одним квадратич-
квадратичным граничным условием, именно
ЗН4
Как мы увидим ниже, эта система имеет всегда только одно
решение, а в общем случае для всех значений X — два линейно-
независимых решения.
10 • 9. Теорема осцилляции Клейна. Мы сейчас приведем при-
пример теоремы осцилляции, формулировка которой значительно
шире теорем Штурма. Она указывает пути обобщения проблемы.
Рассмотрим так называемое уравнение Ляме1
. </2-v_ j_ I (._L_ j_ _L_ 4- _J__1 dJ- Ax + B v = о
где e-^ < e2 < ея. Возьмем два замкнутых интервала (av bj), (a2, ?2);
нужно, чтобы каждый интервал целиком лежал внутри какого-
либо открытого интервала (е , е2), (е2, е3), (ея, со). Таким образом,
обеспечивается непрерывность коэфициентов диференциального
уравнения в интервалах (alt bj и (а2, Ь2).
Постоянные А и В должны рассматриваться как параметры;
задача, соответствующая физическому исследованию, состоит
в том, чтобы, если возможно, определить А и В так, чтобы
уравнение одновременно имело решение у,, удовлетворяющее
некоторым граничным условиям, относящимся к (а1У Ьг), и ре-
решение у2> удовлетворяющее некоторым граничным условиям,
относящимся к (а2, Ь2). Или, в более частном случае, нужно
так определить А и В, чтобы уравнение допускало решение Vj,
обращающееся в нуль при а, и Ьъ и имело тх корней между аг
и blt a также допускало решение у2, обращающееся в нуль при
о2 и &2, и имело т2 корней между at и Ь2. Эта задача была ис-
исследована Клейном2; его метод исследования составляет основу
значительно более общей теории, которую мы сейчас разберем.
Допустим, что в диференциальном уравнении
(А) -?-{*-
функция G имеет форму
G - 1(х) - {*0 + Х2дс -f-... +lnxn} g(x)
и следовательно зависит от п -f-1 параметров. Далее допустим.
что у нас имеются и + 1 замкнутых интервалов
<о0, Ьо), {а1у Ь,),..., (ап, Ьп),
где
ао<Ь0< а1<Ьх<... <an<bn,
1 См. Уиттекер и Ватсон. Курс современного янялиза, гл. ХХ1П,
2Math. Ann.. 18A881). 410 Gott. Nach. A890). 91, [Ges. Math. Abh.. 2, -12.
540]; Bo her, Bull. Am. Math. Soc, 4 A898), 295; 5 A889), 365. Сличай двух урав-
уравнений второго порядка с двумя параметрами рассмотрен Ричардсоном [Trans.
Am. Math. Soc. 13 (H>12): 22: Math. Ann., 73 A912), 289].
так что К, I a g—непрерывны, a g>0 для значений х, лежащих
в любом из этих интервалов1.
Теперь нам нужно исследовать возможность определения "*.<,,
>!,..., \п таким образом, чтобы можно было найти я+1 частных
решений уравнения, например у,„ \\...-, ук, где у,- удовлетво-
удовлетворяло бы двум граничным условиям
1а'гуг (а,) — а,у'г (аг) — О,
?МЬг)-%у-т(Ьг) = О (г =, О, 1,.... п)
и имело бы заданное число нулей, например mr, в интервале
(а,., Ьг).
Теорема осцилляции, которая дает полное решение указанной
задачи, может быть выражена так. Существует бесконечная
последовательность совместных характеристических чисел (>.„,
>.j,..., \n), так что каждой частной последовательности соот-
соответствует некоторая последовательность характеристических
функций. Если (п + 1) положительных целых чисел или нулей
(т0. тъ..., т J заданы, то характеристические числа, (Хо, \ъ...,
).„) могут быть выбраны единственно возможным способом так,
чтобы в каждом интервале а,- < х < br соответствующая ха-
характеристическая функция у,- имела точно тТ нулей.
Эта теорема доказывается методом индукции; она несомненно
верна при п~0, так как приводится в этом случае к теореме
осцилляции § 10-6. Предположим, что теорема верна для слу-
случая п параметров включительно; она может быть затем дока-
доказана и для случая п + 1 параметров. Если функцию G перепи-
переписать так:
G = {I (х) — \tx"g (^) ] — { '-о 4- М + ... -f In-ix"-1} g (х),
а параметр Хп принят определенным, то G можно рассматривать
как функцию, зависящую от п параметров \, У.ъ..., >«„_!. Допу-
Допустим, что эти п постоянных мсгут быть выбраны только так,
чтобы ха^ актеристические функции у0, уъ..., yn—i существовали
и чтобы каждая из них удовлетворяла определенным граничным
условиям и имела определенное число нулей в соответствующем
интервале. Найденные таким образом п характеристических чи-
чисел ).о, *!,.... >./!-i будут зависеть от ).п, следовательно, если ).„,
/¦!,..., Х„_1 выражены через Хя, то G можно рассматривать как
функцию х и параметра ли. Если теорема Штурма может быть
приложена к уравнению
ах
так, чтобы показать существование решения уп, имеющего тп
1 Относительно поведения К, I и g для значений х. не лежащих в одном из
этих интервалов, не делается никаких указаний; действительно в случае урав-
уравнения Ляме коэфициенты становятся бесконечными для некоторых значений х
(именно eL. ег. е3) вне выбранных интервалов.
336
нулей в интервале ап < х < Ьп, то теорема доказана. Поэтому
важно убедиться, что функция G (х, \п) удовлетворяет условиям,
необходимым для применения теоремы осцилляции.
Докажем, что G(x, ).„) — непрерывная функция (х, XJ для
значений х, лежащих в интервале (ап, bn). Если У.'п — некоторое
фиксированное значение параметра >-„, то разность
G(x, K)~G(x, Г)
должна обратиться в нуль по крайней мере для одного значе-
значения х в каждом интервале аг <;л < br(r < п — 1), так как, если бы
эта разность имела постоянно один знак в некотором интервале
(ar, br), то уг(х, 1п) осциллировала бы, согласно теореме сравне-
сравнения, более (или менее) быстро, чем ут, (х. \); это противоречит
условию, что уг имеет точно тг нулей в интервале (ar, bT).
Отсюда следует, что в каждом интервале (аг, Ьг) имеется не
меньше одной точки хг, удовлетворяющей условию
Gr {л,-, /-„) - G (хт, Г) (г = 0, 1,..., п - 1),
но
G (х, >.„) - G (х, Г) = { О; — >.о) + (>.; - \) х +... +(Х; - л„) х"
=Р ; — >-п) (л; — jc^ (jc — х,)... (л; — л:»-!) g- (л).
Следовательно, если л; лежит в интервале (сп, &п), то
G (л, ) „) - G (x,j:n) |J< | л; — Хп |! Ь„—во I |6n-fli |... | bn—an-i\ I g- (л) |,
откуда следует непрерывность функции G(x, ап). Аналогично
х-хг>0 (г = 0, 1 ге— 1),
когда л: лежит в интервале (а„, 6П), следовательно
G(x. )«)-G(jc. >4)
- - — <^ (J
для ап<л;^&п. Более точно
G (^> Лп) ->¦ — °° при /„ -» 4т сю,
GU, '/„) -г + со при "/.„-» —со.
Условия, необходимые для теоремы осцилляции Штурма,
поэтому удовлетворены. Следовательно существует только одно
характеристическое число ~i.n, так что jn допускает точно тп
нулей в интервале ап < х < Ьп. Таким образом теорема доказана.
Рассмотренные характеристические числа являются вещест-
вещественными. Возникает вопрос, могут ли существовать также и
комплексные характеристические числа, однако допущение су-
существования комплексных характеристических чисел приводит
к противоречию.
Э. Айне—133—22 337
Пусть
>.„ будет последовательностью совместных
характеристических чисел, которым соответствует последова-
последовательность характеристических функций и0, иъ..., ип. Если, как
мы допустили, по меньшей мере одно из чисел /0» Л1<•••» кп
комплексное, в то время как все другие коэфициенты дифе-
ренциального уравнения и граничных условий вещественны, то
диференциальная система допускает в качестве последователь-
последовательности характеристических чисел последовательность [>-0, Vi,..., pn,
> ~
сопряженную с >..„, ~/.ъ.
ф
рактеристических функций
иъ..., ип. Тогда
вместе
v0, vu..
с последовательностью ха-
ха., vn, сопряженных с и0,
dx
JLI i{^El \ _l {t -1-i 4- -1- x"\o- l\ — n
dx j их \
\i. — w» i,. •., /t^.
Исключая / из обоих уравнений и интегрируя полученное вы-
выражение между пределами аг и br, получим последовательность
уравнений
/ {(' о — Ы + 0-1 — y-i) х+ ... + Q.n — [j.n) л" } gurvrdx = 0
«г
(г = 0, 1,..., п).
r + 1 чисел /г —Нт не все равны нулю; предположим, что ни
одно из них не равно нулю, тогда между (п + 1) величинами
(у.г — \х.г) будут п + 1 уравнений; условием совместимости этих
уравнений является
) • • -ё" (^п) "о (Ао) г»о (л-0)... ип (хп) vn X
X {xn)dx0...dxn = О,
где
1.
1, хх, ..., х1
К
Щхг-.
Если р величин >.,. — и-,, обращаются в нуль (что означает, что
соответствующие числа >-,. вещественны), то из остальных п—р-^-1
уравнений могут быть составлены п + 1 уравнений. Условие их
совместимости может быть выражено в виде некоторого числа
уравнений вида (С), в каждом из которых порядок кратного
интеграла равен п—р+1- Доказательство в основном одина-
одинаково во всех случаях.
338
При п = 0 формула (С) принимает вид
_ ь
J gwvdx = 0.
а
Теперь в формуле (С)
Д (х0,..., хп) > 0, поскольку л:., < дс, < . . . < хп,
gr(xr)>0,
ит (xr) -vr (х,) > 0, поскольку и,, и v,- — сопряженные величины
Следовательно интеграл не может быть равен нулю — противо-
противоречие, доказывающее несуществование комплексных или мнимых
характеристических чисел.
Теория может быть распространена без особого труда на
уравнение, в котором
G = / — '-ago — 'igi — ¦ - • — >•„?„•
В кратном интеграле произведение
4(дс0,..., xn)g(x0)...g(xn)
может быть заменено детерминантом
&W, gii*»), ¦¦¦> gn(X0)
Комплексные характеристические числа не существуют, если
go» gi> • • • gn таковы, что детерминант сохраняет постоянный
знак, когда а0 < хй < Ьо, ..., ап < хп <3 &„.
1. Докажите, что вронскиан k линейно-независнмых решений линейного ди-
ференциального уравнения порядка п > k не может иметь бесконечное число
нулей в некотором интервале (а, Ь), в котором коэфициенты непрерывны.
[Bocher, Bull. Am. Math. Soc, 8 A901), 53].
2. Пусть у будет любым решением
d \,Лу
{*?•} -
a -rj и <в2 — функции х с их первыми производными, непрерывными в интервале
(а, Ь). Пусть
ф= ?1у — ?-2Ку'.
.л
"IT — G?! ¦
А
тогда, если {?,, ^а) ие обращается в нуль в интервале (а. Ь), то Ф не может
обратиться в нуль больше конечного числа раз, а Ф и Ф' не могут обратиться
в нуль ни в одной точке интервала (и, Ь).
IBocher, Trans. Am. Math. Soc, 2 A901), 430]
339
3. Если ух и у2 — независимые решения уравнения B) и если
то между любыми двумя последовательными нулями Ф.. лежит^ только одни
нуль Ф2.
[Bocher, ibid., 3 A902), 214].
4. Пусть ijjj и ^2 — Функции того же рода, что и q>i и f2, и пусть
ф = Ъу — а,КУ, Ч> = ^У - Ф2*У,
тогда, если ни одна из функций
не обращается в нуль в интервале (а, Ъ), то в любой части (я, Ь), где Ф не
обращается в нуль, Ф не обратится в нуль, больше одного раза
[Bocher, ibid, 2 A901), 430].
5. Если ни одна из функций
не обращается в нуль в интервале (а, Ъ), то между двумя последовательными
нулями Ф лежит только один нуль W, и наоборот.
[Bocher, ibid., 431].
6. Если к условиям E) дополншельно принять, что функции {(вь а2) и
Ж- Фг) разных знаков, то Ф и Ф не обратятся в нуль больше одного раза в
интервале (я, Ъ) и обратится в нуль только одна из этих функций. Рассмотрите
специальный случай ^ = 1, <Ь„ =.
[Bocher, ibid., 431]
7. Пусть %! и х2 аналогичны <Pj и с2 и пусть
ф, = 9lV — 9 2Ку', ЧГ = i,lV ~ <ЪгКу', X = /лу — ;лКу',
тогда, если ни одна нз шести функций
Wi'i — 9a^i. ^i'/.г ~ ФгХь Xi?2 — 7.2?i fe, ?2}, {<Pi, W. {'/.1.7.2}
Ее обратится в нуль в интервале (а, Ь), если последние три функции имеют
общий знак и если произведение всех шести функций отрицательно, то между
любым корнем Ф и большим корнем X лежит корень W, между любым кор-
корнем Ч? и большим корнем Ф лежит корень X, а между любым корнем X и боль-
большим корнем W лежит корень ф.
[B6cher, ibid., 432: Sturm, J. de Math., 1 A836), 165].
8. Если во всем интервале (в, Ь)
то нули у, у', у" будут следовать один за другим циклически в указанном по-
порядке, если К' > 0, и в обратном порядке, если К' < 0.
9. Положительные нули функций Бесселя Jn(x), .in+l{x), Jn^n(.x) следуют
друг за другом циклически в указанном порядке, если п> — 1, и в обратном
порядке, если п < — 1.
[Bocher, Bull. Am. Math. Soc. A897). 207; loc. cit. ante, 434].-
10. Для системы
[ JL
(l) { dx
[ Le[y(a)] = /Mo [y(b)], L, [y(a)} = Mx
340
где
Mi [у (x)] = yy (X) + ZiKy' (X) у = ,f 2)
a A1, G, at, P/, Tf,-, 8,- зависят от л, пусть при (я < х < 6), (At < л < Л2) будут
наложены следующие условия:
(Aj) К и G непрерывны и /С> 0 для всех рассматриваемых значений {х, X);
(Ап) К и G не увеличиваются с увеличением X, и для любого значения X
существует х, для которого К или G действительно уменьшаются;
(Аш) все восемь коэфициентов а,-, ..., В,- — непрерывные вещественные
функции X в рассматриваемом интервале и
I <ч I + i Р,-1 > 0, | -ji I + | Ч ] > 0;
(Aiv) Р' тождественно равна нулю или а;/р,- не увеличивается с увеличе-
увеличением X; В* тождественно равна нулю или у\щ не увеличивается с увеличе-
увеличением X;
(В) условия, обеспечивающие справедливость теоремы осцилляции Штурма
для системы
B)
(С)
"'с.
= 0;
sO.
Пусть уо(л:, ).) и ^(х, >.) обозначают два линейно-независимых решения
диференциального уравнеиия, удовлетворяющие условиям
тогда характеристическое уравнение для системы A) будет иметь вид
F 0) = Mt [у. (Ь, Щ + Мо [У1 (Ь, >.)] -2 = 0,
и для каждых двух характеристических дисел системы Штурма B) будет су-
существовать только одно характеристическое число. Если р.о, jj^, —располо-
jj^, —расположенные в порядке характеристические числа системы B), а H> 11р ••. —харак-
—характеристические числа системы A), то, принимая во внимание их кратность, воз-
возможны следующие случаи.
1а
lib А,
,*0
< А2.
<А2,
< (J.3
Условия для этих случаев будут соответственно иметь вид
1« Мг [уо(Ь, >.„)] > 0, F (At + е) > 0,
1ь Af, [у0 (*, л0)] > 0, F(A, + е) < 0,
И« Мг [уо (Ь, Хо)) < 0, F(\t + 0 > 0,
Иь Af, (у0 (&, Хо)] < 0, F(At + в) < 0.
Характеристическая функция, соответствующая характеристическому чи-
числу Хр, будет иметь р — 2. р — 1, р, р+1 или р+2 вулей в интервале а < х < Ъ.
[tttlinger, Trans. Am. Math. Soc, 19 A918), 79; 22 A921), 136].
ГЛАВА XI
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ ГРАНИЧНЫХ ПРОБЛЕМ
11-1. Одномерные функции Грина. Лучшим средством исследо-
исследования граничных проблем за пределами рассуждений предыду-
предыдущих параграфов являются так .называемые функции Грина, ко-
которые мы сейчас определим г. Рассмотрим полностью однородную
линейную диференциальную систему
0 = 1,2,..., п)
Предположим, что эта система несовместима, т. е. не допускает
решения, не равного тождественно нулю и которое вместе с ее
первыми п — 1 производными было бы непрерывно в интервале
(а, Ь). Несмотря на то, что (А) не имеет решения, может су-
существовать функция, формально удовлетворяющая системе, но
нарушающая, по крайней мере частично, условия непрерыв-
непрерывности.
Этому удовлетворяет функция Грина G(x, $), которая:
A°) непрерывна и имеет непрерывные производные до (п — 2)
порядка включительно при а^йх^Ь;
B°) такова, что ее производная порядка (п — 1) имеет раз-
разрыв в точке ? внутри интервала (а, Ь), причем скачок равен
i/(S)
o();
C°) формально удовлетворяет системе во всех точках ин-
интервала (а, Ь), за исключением 5.
Сначала докажем, что такая функция G(x, S) действительно
существует и что она единственная. Пусть
щ(х), «о (л), — ип(х)
будет фундаментальной последовательностью решений уравнения
тогда, поскольку функция О(х, ?) удовлетворяет уравнению в
интервале а*йх<^?, она может быть представлена в виде
О (л:, Е) = ахщ (х) + а.2и2 (х) + ... +апип(х);
1 Bocher, Bull. Am. Math. Soc, 7 A901), 297; Hilbert, Grundziige einer allge-
meinen Theorie derlinearen Integralgleichungen, VII — IX.
342
аналогично она может быть выражена в виде
G (х, ?) = Мх (*) + Ь.2щ (л)+... +Ьпип (х)
в интервале ? < х < Ъ. Но функция G {х, ?) и ее первые (и — 2)
производных непрерывны в точке S, следовательно
Н) + а2и2(Е) +... + апип (Щ - (Mi C) + b2u2 (S) +
... + &„«;(?)}= О,
{а1В(Г2) (?) + ам'п-~2) (?) + ... + апйп(№) (а)}
' E) +. • - + Mn" №)} = 0.
Прерывность (и—1) производной О"~1 {х, ?) при x = S при-
приводит к уравнению
— {bill i (?) + b2ti" * C) +... + bn\
Эти уравнения могут быть написаны в виде
CjUj (;) + CoU'2 (?) -I? •. • + спи'п E) = О,
где
с,- = bi—ai (i= I, 2, ..., я].
Дискриминант этих и уравнений равен вронскиану к, (х),
«2(xj, ..., и„(л) при х = Ц он не равен нулю, поскольку п
выбранных решений образуют фундаментальную последователь-
последовательность. Следовательно числа сг, с2, ..., сп могут быть опреде-
определены единственным способом.
До сих пор граничные условия системы в (А) не были ис-
использованы. Пусть ,
где члены, относящиеся к конечной точке а, сгруппированы
в выражение Ait а члены, относящиеся к Ь, — в выражении б,.
Тогда, учитывая, что G в интервале (а, ;) отличается от тако-
343
вого в интервале (?, Ь), очевидно, что
Ut (G) = a^Ai (и,) + о2Л< («j) +... + anAt (un)
+ biBt (щ) + &aSf (иа) +. •. + bnBt («„) = 0;
это может быть переписано в виде
W («l) + ВД («2) + • • • + bJUi (И„) = Mf Ы + Mi (И2) +
+ ... + с,Л(Ип) (* = 1, 2, .... и).
Детерминант | f/( (и7-)| не равен нулю, поскольку и граничных
условий линейно независимы, и система несовместима. Следова-
Следовательно уравнения достаточны для определения Ьъ Ь2 Ьп
через известные величины съ с2, ..., сп и коэфициенты Uu
Коэфициенты at и &,- определяются единственным способом, сле-
следовательно функция G (л:, S) — единственная. Далее функция
G(x, ?) и ее первые (п — 2) производных непрерывны в интер-
интервале (а, &), в то время как следующая производная разрывна,
именно
Теперь пусть Н(х, S) обозначает соответствующую функцию
Грина сопряженной системы
Разделим интервал (с, &) на три части (а, ?х)/ (?lt ?2), (?2,
и рассмотрим две функции Грина
Здесь может быть приложена формула Грина
г»
к) + и? (ф)} йд; - [Р(и, «)]» ,
если интервал интегрирования рассматривать как предельный
случай совокупности трех интервалов (а, ^ — в), (Si4-s, S2 —s)»
($2 + s, &), когда s стремится к нулю. В каждом из них
L(G) =0, 1{И) = 0
следовательно
Hm [P(G, H)]^ + lim [P(G, H)]fe + lim [P(G, «)[?.«= 0.
Поскольку, согласно граничным условиям,
при а: =^ с и л = &, это соотношение можно привести к виду
Hm [P(G, НЩ+l + lim [P(G, H)$:±i = 0.
344
Из § 9-31 следует, что единственным членом, имеющим
рыв в P{G, H), является
следовательно
Ро
[г-л-1/7 Т^Н
'7Л' _U.-*
поскольку
Г dn~l G -1 = '-'Е Г '"~1
Ро(УНт —-szr
L d*
отсюда следует, что
Эта формула была доказана для случая ;2 > ^ и может быть
также доказана для случая ?2 < q. Следовательно, если х и 5 —
любые две точки в интервале (с, Ь), то
Я (х, «)-G(E, х),
или G (S, л;) является функцией Грина сопряженной системы (В).
Более того, если данная система самосопряженная, то функция
Грина является симметричной, т. е.
G(i, x) = G{x, i).
Так как функция Грина данной системы единственная, то
отсюда следует, что система самосопряженная, если функция
Грина данной системы симметрична.
11-11. Решение неоднородной системы. Мы уже знаем, что,
поскольку однородная система
несовместима, любая соответствующая ей неоднородная система
в частности система
i=l, 2,..., л)
я ей неоднор
/В) jL(y) =r(x),
\Ut{y) = O (i=l, 2, ... л)
допускает только одно решение. Если функция Грина О(л;, S)
системы (А) известна, можно непосредственно получить реше-
решение (В), именно
b
(С) y{x) = fG(x, Z)rK)iR.
п
345
Поскольку
ум(л)= Г a'C{ir'S) r(g)tf. (v = l, 2, ...,n-2)
e
d"-2G(x,;)
и поскольку ,г—2 равномерно непрерывно в интервале
ОХ
(а, Ь), отсюда следует, что
Но интеграл теперь имеет разрыв в точке ? = л, следовательно
откуда, поскольку Z(G) — С,
L(y) =
= Г(Х).
Таким образом диференциальное уравнение (В) удовлетворено.
Так как функция G,- (у) не содержит производных от у по-
порядка выше (п — 1), отсюда следует, что
= 0 (/ = 1, 2, ...,«),
поскольку U,(G) = 0. Граничные условия в этом случае также
удовлетворены, и выражение (С) является решением системы (В).
Решение более общей неоднородной системы
\ ?Л(у) = ъ (i =1,2,
346
можно получить очень легко. Пусть Gt(x) будет единственным
решением системы
L (G,) = О,
,) = ... = ?Л_, (Qi) = Ui-л (О,) -... =i/n(Oj) = 0;
f
U^G,) = ...
I Ui{Gi)=\;
тогда непосредственно можно показать, что решением си-
системы (D) является
ь
у (a) = fG (x, i) r (I) Я + Y1G1 (^) + T2G2 (л) + • ¦ • +TnOn (x).
Пусть щ{х) и к.2(л;) будут линейно-независимыми реше-
решениями уравнения
А> (х) ~2 + А (л:) -— + р2 (a) u = 0.
Рассмотрим функцию
F{x, \) - Ащ(х) Ф 5и2(а-) +M*)Me)M*)M6)
где положительный знак взят при а <¦ л; ^з I, а отрицательный
при %<Сх^СЬ. Функция F{x, ?) непрерывна в интервале (с, Ь);
ее производная имеет скачек ljpoh) при х = ?, но непрерывна
во всех других точках. Третий член не зависит от выбранных
решений щ(х) и ^(х). Следовательно F(x, ?) имеет характер
функции Грина, а при выборе постоянных А и В так, чтобы
^t*i S) удовлетворила заданным граничным условиям, стано-
становится функцией Грина данной системы.
Примеры
I — = 0
A°) | dx"- и'
I @) AH
BО) I g-«2« = o.
| в(в)-=аA) = 0.
/* (д;, I) — Л ch ял + В sh «а + ~- sh я (; — х).
sh я« sh /г (x — 1)
/г sh n
347
(d > |и@) = иA),
F (x, ?) = A cos nx + B sin nx ± ~ sin n {I — л),
G (x, к) =¦ -^ {ctg -^- cos n (? — a;) + sin я | S — a: |}.
Этот последний пример показывает, что если система совме-
совместима, т. е. при п = 2Ы, где & — целое число, функция Грина
обращается в бесконечность.
11-12. Функция Грина системы, содержащей параметр. Преды-
Предыдущее исследование показывает, что когда X не является ха-
характеристическим числом системы
f ?(«) +Хи = г(л),
\ Ut (и) = 0 (г = 1, 2, ..., п),
то существует единственная функция Грина G(x, S; X), а реше-
решение системы имеет вид
Аналогично, решение сопряженной системы
( Z{v) +lv = r(x),
\ Vt(v) = O (/ = 1, 2, ...,я)
имеет вид
ь
го(х)=1 G(S, x; X)r(S)rfS.
Отсюда следует, что если Х( — характеристическое число од-
однородной системы
a iit (a) — соответствующая характеристическая функция, то
G(x, ?; A)«t(?)rfS.
а
Этот результат следует непосредственно из того, что диферен-
ииальное уравнение
L (и) + ли = (а — >.j) K( (х)
допускает решение щ(х).
348
Если Уг{х), у2(х), .. -,Уп(х) образуют линейно-независимую
последовательность решений однородного уравнения
то можно написать G(x, ?; /.) в виде1
G(x, с; /.) = —^у-~,
где
N(x, i; 1) =
У г (х), У* (х), -.., уп (х), g (X, \; '/.)
niVd, Un{Vz), ¦¦; Un(yn), Un (g)
Д (>.) = (— 1)"
v(
Уг
\-Л У
v (
-'2
причем положительный или отрицательный знак зависит от ве-
величины х (меньше или больше ?).
Теорема существования § 3-31 показывает, что если L(u),
г(х) и Ui (и) не зависят от /., то решения уг{х), у2{х), ..., У„(л)
являются целыми функциями >.. Отсюда следует, что G(x, к; л.)—
аналитическая функция '/. для всех значений >., за исключением
нулей Д(Х), т. е. для всех значений X, за исключением характе-
характеристических чисел5. Определим форму, которую принимает
функция G (л:, с; л.) в соседстве с простым характеристическим
числом X/, являющимся простым нулем Д(/-)«
Если А (X) имеет простой нуль "/-,-, то функция Грина может
быть написана в виде
G(x, ^).) = .Ai^L + Gf(Xj 5;-л)>
где функция G,(a;, l; ^ — аналитическая при /. = >.(.
1 Birkhoff, Trans* Am. Math. Soc, 9 A908), 377. Принимается, что коефи-
циент и*- в L (и) равен единице.
2 G (х, 6; X) является мероморфной функцией X.
349
Далее
R(x, с) = lim
>
В разложении детерминанта для функции N(x, с; лг) коэфи-
циент 5" (X ?; '-О равен нулю. Следовательно N (л, ;; >,г) и ее
первые п производных относительно х и % являются непрерыв-
непрерывными функциями (л;, I) для а < л: <¦ Ь, а < ? ^ ^?. Более того,
N (л, с; а) удовлетворяет системе
Г ^х («) + >-« = О,
для всех значений X, следовательно /? (х, с), рассматриваемая
как функция х, удовлетворяет этой системе для характеристи-
характеристического числа 'kt. Это характеристическое число простое, сле-
следовательно /? {х, S) имеет вид
CiUi (x),
где lit (л;) — характеристическая функция, соответствующая \и
a Ct зависит только от \. Но если рассматривать ее в виде
функции I, то R (x, S) удовлетворяет системе
\ Vt(v) = O; (i=l, 2, ...,и)
для характеристического числа Хь следовательно С{ будет иметь
вид
где cf — постоянная. Отсюда
остается определить только постоянную с{.
Выражение
(/.-).j)G(jc, ;; Х)-/?(Л, ?)
является аналитической функцией >., если >. достаточно близка
к^;оно непрерывно относительно х и ?, поскольку G и R непре-
непрерывны относительно х и I; аналогично
lim {(>. — >.,) G (х, ?; >.) — с,-«г (л) г-; (?)} = 0.
).-^- ).^
Отсюда следует, что
X -"; (/" ~~ '^ G (Л> S; "Л) "' ® di ~~ CiUi WiUi @ ""f (=) ^ = 0-
350
Далее
(>..— li)JG(X, с; >.) Щ (с) rf? = Mi I
следовательно
Таким образом мы установили теорему: если '/. =/.i— простой
корень характеристического уравнения, то функция Грина
имеет вид
где
а функция R(x, ?; /.) регулярна в соседстве с ~/н.
Если все характеристические числа ~м, модули которых меньше
числа Л, являются простыми корнями характеристического урав-
уравнения, то
G(x, g; Х)
где функция Е{х, I;'/.) неограничена при любых значениях j >. | < Л.
Поскольку и,- (х) и г»,-^) удовлетворяют однородным систе-
системам, они могут быть так нормализованы, чтобы
ь
/в,
откуда получим
11-2. Зависимость между линейной диференциальной системой
и интегральным уравнением. Любая неоднородная линейная дифе-
ренциальная система с числом граничных условий, равным по-
порядку уравнения п, может быть представлена в виде
( ' 1 Ui{y)—U ('- 1.2 п)
Более того, согласно основной теореме § 9-6, если система
задана, то функция g(x) может быть выбрана так, что однород-
351
ная система
Ut(u) =
будет несовместима. Однако отсюда не следует, что (А) имеет
какое-либо решение. Предположим однако, что (А) имеет реше-
решение уг(х), тогда система
f L(y) = g(x)y1(x) + r(x),
будет иметь единственное решение, и этим решением будет уг(х).
Как и в § 11-11, у1(х) удовлетворяет соотношению
ь
у (х) = /О(х,с){g(S)y (S)+r(ЬШ+ъОг (x)+bG2(x) + ... +-nGn(x),
о
где G(xb ?)— функция Грина системы (В).
Но у{х) входит под знак интеграла, следовательно соотно-
соотношение принимает форму интегрального уравнения с G(x, S)
в качестве ядра. Напишем
ь
= TiGi (х) + 7-А(х) +... +VnGn(х) +/G (л, I)r F) dS.
Эти выражения можно рассматривать, по крайней мере теоре-
теоретически, как известные. Тогда интегральное уравнение, кото-
которое было бы удовлетворено решением (А), будет иметь вид
ь
(С) у(х)= f{x) + / К(х, ?) у (=) <К:
оно известно, как уравнение Фредгольма второго рода Ч
Следовательно мы доказали, что любое решение диферен-
циальной системы (А), которая была предположена совмести-
совместимой, удовлетворяет уравнению (С).
Если у2(х) является решением (С), то
удовлетворяет системе
U(y)=g(x)yAx)'+r(x),
\U,(y) = 0.
Но в интегральном уравнении у(х) = у2(х), следовательно ди-
1 ^'иттeкep и Ватсои, Курс современного анализа § 11 • 2.
352
ференциальная система допускает решение у%(х), т. е. любое
решение интегрального уравнения (С) удовлетворяет диферен-
циальной системе (А).
Обе эти теоремы могут быть объединены следующим обра-
образом: диференциальная система и интегральное уравнение экви-
эквивалентны друг другу.
В частности, если X не является характеристическим числом
системы
f L(u) + lu = O
где L (и) и Ui (и) не зависят от I, то система
I il() O (i = l, 2,..., и),
= 1, 2,..., л)
эквивалентна интегральному уравнению
ь
(F) j/ (*) + * j G (л, g)j, (?
а
где
Следовательно, как и выше, G(x, S) является функцией Грина
системы (В); пусть Г (х, S; >) будет функцией Грина системы
1 ; \7s"(«) = 0 (г = 1,2,..., и),
сопряженной с (D). Тогда, применяя формулу Грина
{«? (и) - ul {v) }dx = [P (и,
а
найдем, как и в § 11-1, что
(Н) \jj G(x,zx)T{x, Sa; >)dx
).) lim
= Г(Н„ ea;X)_G(a2, EJ.
Функция Г (х, с; л), входящая в это соотношение, называ-
называется резольвентной функцией, или резольвентой ядра G(x, ?),
Э- Айно—133—23 353
так как в данном случае интегральное уравнение (F), а следо-
следовательно и диференциальная система (Е), имеют решения, ко-
которые могут быть выражены формулой
(I) yM=
как это видно из подстановки этого выражения в (F) и приме-
применяя (Н).
Но поскольку характеристические числа системы (G) явля-
являются полюсами функции Грига Г (л> ~; I) и поскольку полюсы
Г (х, S; X) являются характеристическими числами однородного
диференциального уравнения
(J) u(x) +
отсюда следует, что это интегральное уравнение эквивалентно си-
системе (D), а сопряженное интегральное уравнение
ь
(К) v (*) + I j G % х) -v {%) dl = 0
A
эквивалентно сопряженной системе (G).
Если решения системы (D) обозначить через щ Ur), а реше-
решения системы (G) — через г»,- (х), то, как известно из теории
сопряженных интегральных уравнений, системы щ (х), г»,- (х)
будут биортогональны, т. е.
Эти системы могут быть также нормированы. В этом случае
мы получим
Функция G(x, с), рассматриваемая как ядро однородного инте-
интегрального управления (J), может быть разложена следующим
образом
G(*,=,= ?-*?№ + ?(*. Е),
м А — '¦/
где h, Х3,..., ).„ расположены в порядке возрастающих моду-
модулей, а функция Е(х, S) — ядро, не имеющее характеристических
чисел по модулю меньших |л„|. Это совпадает с приведенным
в предыдущем параграфе разложением.
354
Если данная диференциальная система является самосопря-
самосопряженной, а функция Грина симметрической, то результаты теории
интегральньтх уравнений с симметрическими ядрами могут
быть приняты в данном случае целиком. Так, теоремы суще-
существования хотя бы одного характеристического числа и отсут-
отсутствия комплексных характеристических чисел верны и для са-
самосопряженных диференциальных систем.
Более того, можно показать, что если данная система имеет
форму (D), то функция Грина замкнута, т. е. не существует не-
непрерывной функции <f (х), такой, чтобы
f G(x, l)-?
тождественно. В данном случае всегда существует .бесконечная
последовательность характеристических чисел.
11-3. Применение метода последовательных приближений. До-
Доказательство теорем существования главы III при помощи ме-
метода последовательных приближений эквивалентно теоретиче-
теоретическому решению одноточечной граничной проблемы. При моди-
модификации метод может быть приложен к двухточечной пробле-
проблеме \ Проблема в этом аспекте ясно показывает роль, какую
играют характеристические числа.
Диференциальная система может быть записана в виде
\L (v) = Af(v) +r(x),
(А) IUt (у) = Vt (у) + ¦;,- (i = 1, 2,..., я),
где L(y) — диференциальное выражение порядка п, а Л1(У)~
диференциальное выражение порядка ниже п; Ut{y) и Vt(y) —
линейные формы от
у (а), у (о),..., у"-1 (а), у(Ь), у' (Ь),..., у("-1ЦЬ).
Коэфициент при у{т{х) в выражении L(y) равен единице,
остальные коэфициенты в выражениях L (у) и М {у) приняты
непрерывными в интервале (а, Ь).
Согласно §9-6, данная система может быть переписана в
форме (А) так, чтобы система
L (и) = 0
Ui(u) = 0 (/=1, 2,..., л)
была несовместима.
Пусть у0 будет такой функцией от х, чтобы М(у„) была не-
непрерывна в (с, Ь), а выражения для Vt{y0) — конечны. Тогда, по-
поскольку система (В) несовместима, система функций
, у„{х),..., ут (х),...
UouvUle, J. de Math., 5 A840) 356.
355
определяется только рекуррентными соотношениями
t (vr) = Vt (iv,) + т; (/ = 1,2,..., и).
Действительно, если G(л, ?) — функция Грина системы (В), то
r (л) = /G (л, 5) [Ж {у,-! (?)} + г (?)] Л + ? [ ^{ул-i И} + Yd G, (л),
'1
а '-1
так что, если
ТО
(С) Кг (л) = / G (л,
Возникает вопрос, сходится ли этот процесс, т. е. сходится ли
равномерно в интервале (а, Ь) ряд
и его первые п—1 производных, полученные почленным дифе-
ренцированием. Очевидно, в данном случае вопрос далеко не
так прост, как при одноточечной граничной проблеме.
Предположим, что А — число, равное большему из верхних
пределов
^!
\Gtix)\, \GUx)\,...,\G'r1)(x)\ (i=l,2,...,n)
в интервале (a, b).
Пусть F(x) будет суммой модулей коэфициентов M(v), Q —
суммой модулей коэфициентов всех п выражений Vt (v), a o;r —
большим из верхних пределов
\vr\, l^!,...,!^^-1)]
в интервале (а, Ь), тогда
для всех значений х в интервале (с, Ь) или
где
Таким образом, если АВ меньше единицы, то процесс сходится.
Очевидно также, что А зависит от коэфициентов L(v) и Ut(v),
356
а также от г (х) и -уь а В зависит только от коэфициентовМ (ifl
и Vt (v). Следовательно, если M(v) и Vf(v) могут быть выбраны
так, чтобы АВ было достаточно мало, то процесс сходится.
Удобнее всего рассматривать эту проблему при помощи вспо-
вспомогательной системы
(D)
где
L (у) - л {М (у) + г, (х)} + и (х),
Ui(y) = *{Vi(y) + 4i}+h
fi = 1, 2,... ,л),
При X = 1 эта система приводится к первоначальной системе (А).
Выберем функциюз>, (л) так, чтобы она удовлетворяла системе
(i = l, 2,...,л)
и пусть функции
определены последовательными приближениями из (D). Тогда
функция уг (л) не будет зависеть от X, а функция уг (х) будет
полиномом от X степени г— 1. В предельном случае этот поли-
полином становится степенным рядом от X, который сходится для
достаточно малых значений | X j. Здесь возникает вопрос, будет
ли он сходиться при X = 1.
Рассмотрим систему более общего характера, чем (D), именно
(Е)
V) = r !,X),
(w) = fr (i= 1, 2,..., пк
где г (л) и коэфициенты L(^) — аналитические функции от X в
данной области и равномерные непрерывные функции от л в
интервале (а, Ь). Аналогично C,- и коэфициенты \ii(w) — аналити-
аналитические функции X в данной области.
Формально решение этой системы имеет вид
Уъ-
w {х) т=
где w0 — решение уравнения
Уп
U, (Уг),..., U, (>»)
ии(у1),...,ил(у„)
&уъ...,уп — линейно независимые решения уравнения
357
Теперь, поскольку w0, yit. ..уп—решения уравнений, коэфи-
циенты которых являются аналитическими относительно ). и рав-
равномерно непрерывными относительно х, оба детерминанта, вхо-
входящие в выражение для w{x), сами являются аналитическими
относительно >. и равномерно непрерывными относительно х.
Отсюда следует, что функция w (л) будет также аналитической
относительно X и равномерно непрерывной относительно х, за
исключением тех значений >., для которых детерминант в знаме-
знаменателе обращается в нуль, т. е. за исключением характеристи-
характеристических значений >..
Полученный результат может быть приложен к системе (D),
мы найдем, что степенной ряд по >., представляющий предель-
предельное значение уг(х), сходится в любом круге, центр которого
лежит в точке /- = 0 и который не содержит ни одного харак-
характеристического числа системы
|1(и) =
\ Ut (и) -= IVt (и) (i ---- 1, 2,... ,п).
Отсюда следует, что метод последовательных приближений,
будучи применен к системе (А), образует сходящуюся последо-
последовательность, если система (F) не имеет характеристического
числа с модулем, меньшим или равным единице.
Теперь мы можем получить значительно более точный ре-
результат. Пусть л = >.j будет характеристическим числом одно-
однородной системы, соответствующей (Е). Тогда (>- — '/.,) будет мно-
множителем знаменателя w (x), и кратность этого множителя будет
по меньшей мере равна показателю \. Если (к — Хх) будет также
множителем числителя той же кратности, что и в знаменателе,
то решение w(x) будет существовать даже для характеристи-
характеристического числа Xv Это имеет место, например, в том случае,
когда кратность 'Kt равна его показателю k, а неоднородная си-
система (Е) имеет решение при I — >-t, так как тогда каждый ми-
минор порядка п — k, который можно отнять от числителя w(x),
будет равен нулю при X. = \ъ поэтому и числитель и знамена-
знаменатель будут содержать множитель (I — Хх), повторенный точно
k раз. Следовательно функция w(x) будет аналитической при
Х = Х1.
Этот результат показывает, что процесс сходится для |Х|-^1,
т. е. если какие-либо характеристические числа (F) лежат
внутри круга |Х|=1 или па его окружности; индекс каждого
характеристического числа равен его кратности и для
каждого такого характеристического числа система (D) сов-
совместима.
11-31. Условия совместимости неоднородной системы для харак-
характеристических значений параметра. Если характеристические числа
отсутствуют, то метод последовательных приближений несомнен-
несомненно сходится для всех значений параметра, для которых коэфи-
циенты уравнения непрерывны. С другой стороны, система, соот-
358
ветствующая двухточечной граничной проблеме, имеет в общем
случае характеристические числа, и для того, чтобы метод по-
последовательных приближений мог быть приложен, необходимо,
чтобы система оставалась совместимой, по крайней мере для
тех характеристических чисел, модули которых не превышают
некоторой определенной величины. Необходимые и достаточные
условия для существования решений неоднородной системы для
некоторого характеристического значения параметра—известны1.
В настоящем параграфе мы приведем условия для самосопря-
самосопряженной системы второго порядка
(А)
Допустим, что все встречающиеся в системе коэфициенты—ана-
коэфициенты—аналитические функции параметра л в данной области и что К, G
и R—равномерно непрерывные функции х в интервале {а, Ь).
Условием самосопряженности системы является
(B) ЪмК(а) = о13К(Ь),
где
'Jij = 2;р; — a/3/.
Пусть щ(х) и щ(х) будут решениями уравнения
Ци) = О,
такими, что
(C) ul'u2 — u3'u1
тогда общее решение уравнения
U, (у) = яцу (а) + а,у (Ь) + а3у' (а) + aj/ (b) = A,
U* (У) = hy (а) + кУ (Ь) + 3?/ (о) + РУ (Ь) = В.
будет иметь вид
х
у = cxuv + с.хиг + йху KRu2dx
а х
Постоянные сг и с2 определяются при помощи граничных усло-
условий следующим образом
ь
а
Ь
— {72их (Ь) -ь а4нх' F)} J KRu,dx,
о
(ия) = Б - {3lKi(a) + р„ия'(а)} / KRihdx -
а
Ab) }JKRu%dx.
а
1 Условия для уравнений второго порядка см. Mason, Trans. Am. Math. Soc.
7, A906), 337; условия для уравнений высшего порядка см. Dini, Ann. di Mat...
C), 12 A906), 243.
359
В данном случае все зависит от детерминанта
UM, и,{щ)
Значения X, для которых Д не равен нулю, не являются харак-
характеристическими числами; следовательно, данная система совме-
совместима. Цель настоящего исследования — нахождение условий,
которые должны быть наложены на R, А и В таким образом,
чтобы при Д, равной нулю, система допускала решение. Могут
возникнуть два случая.
(Г) Миноры Д не все равны нулю.
Приведенная система будет единственно совместимой; она
допускает только одно независимое решение. Пусть этим реше-
решением будет иг(х), тогда
но функции ?Л(и2) и ?/2(и2) не равны нулю.
Необходимым и достаточным для совместимости системы (А)
является условие
иг(«а) [ В -{ ^щ (а) + ^2'(а)} / KRuxdx -
-{ P2«i(&) + Mi'W j/KRuMx]
a J
[Ь
А — (а1и2(а) + я8в2'(о)} /KRu-^dx —
а
-{а&гФ) + «Л' Ф)} / KRu,dx 1=0.
a J
Коэфициент
может быть написан в виде
{cv<2 (а) + а3и2' (а)} {рЛ (а) + ;33%' (а)} ~ {а2и2 (Ь) +
2щ (Ь) ф р4и/ (Ь)} - {M2 (а) + рви,'(а)
} +{р2н2 (й) + Р4И2' (b)} {Чщ (Ь) +
= 81з {%' («)«2(а) - и2'(а)в, (а)} - 824 {и/ (й) иг(Ь) - иг'{Ь)щ.(Ь)} =
JJ1S ^24 __ rv
" К{а) К{Ь) ' V'
так что условие принимает вид
(D) Ul{ni)\e-{&щ(а)
360
Теперь
j ^«fh (b) + г31%' (а)+ 341и/ (b) = 0,
2l() + 32% ()+ 42/ (&) = 0,
[E) <
-
I 8!4«1(о) + ЫЩ ф) -\r bbiu± (a) = О,
левые части этих уравнений имеют вид
где i = 1, 2, 3, 4 соответственно.
При помощи соотношений (В), (С) и (Е) можно доказать, что
Г I
Ц, («2) (a4/C(a) щ (а)+
+ апК(Ь)щ(Ь)}=0,
-asK(b)u1'(b)}=0,
Л(*)»i(*)} ~ ^2 («2) {«4^ («) «i' (в) -
Функции Ux{u^) и U2(Uo) не равны нулю и, следовательно, они
могут быть исключены из уравнения (D) и любого из четырех
уравнений (F); выражение, полученное путем указанного исклю-
исключения, будет
{о>2К(а)щ'(а) +^К(Ь)щ'{Ь)} I В-^щЦа) + ^u2'(a)}
11()аа()} /j = 0;
оно может быть приведено к виду
(a2? -p2A)K(fl)Hi'(a) +Bi5 -р!ЛЖ(*)И|'(*) + ^/KRthdx - 0.
Более того, процесс обратим, т. е. полученное после исключения
выражение и первое уравнение (F) снова дают (D) за исключе-
исключением случая
а2К(а)иЛя) + ^К(Ь)щ\Ь) = 0,
ШФЛ")+Wb)ui'(b) -0,
т. е. когда 8^ == 0 или «/(а) = и-^{Ь) = 0. В последнем случае «х(а)
и %(й) не должны быть равны нулю, следовательно первое и
второе уравнения (Е) дают 312 = 0, что является исключительным
случаем. Уравнения, полученные исключением Ux(u2) и Uz(u2) из
361
уравнения (D) и четырех уравнений (F) будут соответственно
(а.2В-82А)К(а)и[
(G)
, (KRu.dx = О,
а
~ %А)К(Ъ)щ. (Ъ)+Ъа} KRujlx - О,
(У
/KRuxdx = О,
Zu f KRu.dx = 0.
Любое из этих уравнений эквивалентно уравнению (D), если
соответствующий детерминант о12, 343) д23 или SJ4 не равен нулю.
Если какие-либо три детерминанта равны нулю, то все детерми-
детерминанты о,; будут равны нулю, что невозможно, поскольку выра-
выражения Ul (и) и ?/2 (и) независимы. Отсюда следует, что по мень-
меньшей мере два из уравнений (G) имеют значение, отличное от
нуля.
Поэтому для. того, чтобы, система (А) была совместимой,
когда соответствующая приведенная система имеет только
одно независимое решение иъ необходимо и достаточно, чтобы
А, В, и R удовлетворяли одному из соотношений (G) с детерми-
детерминантом 2,7) не равным нулю.
При А и В, равных нулю, это условие принимает вид
Bсу Миноры Д все равны, нулю.
Приведенная система будет в данном случае двояко совме-
совместимой и допускает два решения: и, (х) и и2 (х). Допустим, что
6i3 = 0, тогда, согласно (В), Ьи = 0. Первое уравнение (Е) при-
примет вид
3a:«i (*) + 8*1 К(Ь) = О
и аналогично
2(Л
Но, согласно (С),
К(Ь) {и\{Ь) иа{Ь) — и2(Ь
S21 = Й41 = 0,
след овательно
И
S I
°23 = °43 =
Все детерминанты равны нулю, что невозможно; откуда следует,
что й13 и 824 не равны нулю.
Поскольку
U, (иг) = U, (н.) = U2 (»,) = Us (н.) = 0,
362
необходимыми и достаточными условиями для существования
решения системы (А) будут
ъ ь
А — {а.±и2(а) + а3и; (а)}/KRuxdx — {^щ (b) + а4 u\{b)}fKRu2dx = О,
а а
В - {plUa (ft) + .83^ (а)} fKRu.dx - {рА (/;) + Ъ>и\{Ь)}}кНигпх = 0.
Эти уравнения эквивалентны системе
^a)+b^jKRu2dx = О,
(Н) 1
PABM))AB)bt f Rdx = 0.
Кроме указанных, могут быть найдены еще и другие уравнения
того же типа, но только два из них будут независимы.
Для того, чтобы система (А) была совместимой, когда
соответствующая приведенная система имеет два линейно-
независимых решения щ и м2> необходимо и достаточно, чтобы
А, В и R удовлетворяли одному из соотношений (Н).
При А и В, равных нулю, R должно удовлетворять соотно-
соотношениям
ь ь
/KRu%dx = 0, / KRu2dx = 0.
а а
11 • 32. Разложение решения неоднородной системы. Рас-
Рассмотрим частную систему1
где k, g, I и р (х) — непрерывны, а А: не обращается в нуль при
а < х < Ь. Пусть й, и и2 будут двумя основными решениями одно-
однородного уравнения
что
тогда общее решение диференциального уравнения системы (А)
будет иметь вид
х
у = Схщ {х) + С^и2 {х) + «! (*)/«, @ /? (« Л — 1Цх)/и1 {f) p (t) dl,
Kneser, Math. Ann., 58 A904), 109.
363
где Сг и С2 произвольные постоянные. Каждый член, входящий
в это выражение, является интегральной функцией X, при
а < х < Ь.
Граничные условия (А) приводят к соотношениям
С, {и[ ф) + Нщ (Ь)} + С2 {щ (Ь) + Ни2 ф)} +
+ {«; (Ь) + Ни, ф)}/щ (t)p(t) dt —
— {и2 (b) + Hu^b)}/^ {t)p \t) dt = 0,
a
определяющим Сх и С2. Так
где w(x, X) — интегральная функция X для всех значений х в
интервале (а, Ь), а характеристический детерминант Д(Х) — инте-
интегральная функция X.
Пусть Х4 будет характеристическим числом однородной
системы
(В)
| г»' (а) - Аф (с) = V (b) + H<v (b) = 0,
a x;i(x) будет соответствующей характеристической фуккцией.
Тогда, поскольку эта система просто совместима, то для того,
чтобы неоднородная система имела решение при X = \и необ-
необходимо, чтобы
ь
(С)
Если это условие удовлетворено, то функция w{x, )/()
будет конечна при X = X,. Предположим, что это условие удов-
удовлетворено для всех характеристических функций
1\(х), Щ(х),..., vn(x),...,
тогда функция w(x, Х),'Д ().) будет конечной, когда X примет
любое из значений
*Ч> '-2» • - • > 'п> • - • »
т. е. она конечна для всех значений X, при которых Д обраща-
обращается в нуль. Следовательно, когда (С) удовлетворено для всех
целых значений i, то у (х) является целой функцией X и может
быть разложена при а < х < b в сходящийся ряд
где коэфициенты а0, aj,..., an>... могут быть определены мето-
методом последовательных приближений.
364
11-4. Асимптотическое разложение характеристических чисел и
функций. Допустим, что в уравнении Штурм-Лиувилля
d
~dx
во всем интервале а < х < ? функции k, g и I непрерывны,
k и g не обращаются в нуль, k имеет непрерывную производную,
a gk — непрерывную вторую производную. Тогда, если мы про-
произведем преобразования
где /С— постоянная, равная
то уравнение примет нормальный вид
где
1
a 6(z) и ср(г) — соответственно (?-&) 4 и llg, выраженные в виде
функций z. Интервал a <j х < Ь равен 0 < z < и. По всему этому
интервалу функция <7(z) непрерывна. Дальнейшее исследование
требует также существования и непрерывности первых двух про-
производных q{z)\
Граничные условия при этом преобразовании не изменяются;
предположим, что они равны
I и'@) — /ш@) = О,
где постоянные h и Н— вещественны.
Если мы теперь это уравнение напишем в виде
4^- + fu = q(z)u,
то его общее решение может быть символически выражено так:
u{z) = A cos pz 4- ? sin pz + (D2 + p2)~4 q(z)u(z)
г
= A cos pz + В sin pz + - / sin p (z — t)q(t)u(t)dt.
1 Условия MorvT быть значительно ослаблены применением метода Диксона
[Dixon, Phil. Trans. R. S. (A), 211 A911), 411].
365
Такая диференциальная система однородна; чтобы сделать ее
решение вполне определенным, первое граничное условие долж-
должно быть заменено неоднородными условиями
и@) = 1; и'(О) = /г.
Следовательно постоянные А и В определяются единственным
способом г и
z
h 1 /*
u(z) — cos pz ~j- — sin oz + — / sin p<z — f)q{t)u(t)dt.
о
Фундаментальная теорема сушествования утверждает, что \u(z)\
ограничен в интервале @, тс). Пусть М будет верхней границей,
тогда
i«(*)i < A+?) Ч f
Поскольку выражение \u(z)\ непрерывно в замкнутом интервале
О < х < п, оно достигает верхней границы, следовательно
(fL-f-/\Q(t)\dt,
откуда
для всех значений р, которые больше фиксированного положи-
положительного числа.
Если мы теперь введем второе граничное условие, то най-
найдем, что р определяется уравнением
где
г.
P=h + H + /"(cos p^ - f^ sin pt\ q (t) и (I) eft,
IE
p, = Hh + /-^sin p^ + j/cog ^i ^ ^ в ^ dt
о
Поскольку
M<l+O(p-!)
в интервале @, ъ), отсюда следует, что |Р| и jP'| оба меньше
конечных чисел, независимых от р.
1 Полученное таким образом соотношение является первым известным
интегральным уравнением первого рода, Liouville, J. de Math., 2 A837), 24.
366
Далее, поскольку u(t) имеет вид1
, , а(?, t)
+ - --,
где а(р, t) ограничено,
г
u{z) = cos pzjl —
1 о
+ sin P2 [ А + i /"cos Р^ (cos р/1 +
следовательно
u(z) = cos рг{1 + О(р-2)} + sin Р2 {Q (г)? + О (р
где
Z
Q(z) = h + \jq{t)dt.
о
Легко доказать, что
Р = к + Н+кг + О (р-1), Р' =
где
о
Характеристическое уравнение принимает вид
следовательно для достаточно больших значений р
или
рл = Я + СП
где с не зависит от га. Это выражение дает также новое доказа-
доказательство теоремы существования бесконечной последователь-
последовательности характеристических чисел.
Теперь
cos pnz = cos nz{\ + O(ra~2)} — sin nz {czriT1 + O(n~2)},
sin pnz = sin nz {1 + O(«~2)} + cos гаг {c2«-1 + O(n~2)},
следовательно характеристическая функция, соответствующая pnj
1 Hobson, Proc. London Math. Soc. B), 6 A908), 374.
367
имеет вид
un(z) = cos nz {1 + O(n~2)} + sin nz {офл + 0{ri~2)},
где
Нормируем характеристическую функцию и, обозначив ее
vn(z), получим
Это является асимптотическим выражением для характери-
характеристических функций; оно имеет особое значение для вычисления
характеристических функций при больших значениях п. Выра-
Выражение может быть продолжено до желаемой степени точностиг.
Следует упомянуть о двух специальных случаях, A°); когда Л
или Н бесконечно и B°), когда и h и Н бесконечны2. В первом
случае в одной определенной конечной точке и(х) равно нулю
тогда
Рп = П + у + О(П~1).
Во втором случае и(х) обращается в нуль в обеих конечных
точках,
а
Рп - П + 1+ С{П~').
11-5. Разложение Штурм-Лиувилля произвольной функции. Пусть
ио(х), иг(х),..., «„(¦*)»•••
будет последовательностью нормированных характеристических
функций системы
и'@) - hu(p) = О,
k'(ti) + Ни(к) = О,
соответствующей характеристическим числам
Ро> Pi. • - -» Рп. • • • >
где, как и в § 11 • 4,
Сначала покажем, что эта последовательность характеристи-
характеристических функций замкнута, т. е., если р(х) — любая функция,
1Ногп, Math. Ann., 52 A899) 271, 340; Scheisinger, ibid, 63 A907), 277; Birk-
hoff, Trans. Am. Math. Soc.,9 A908), 219, 373; Blumenthal, Archiv d Math. u. Phys.
C), 19 A912), 136.
2 Kneser, Math. Ann., 58 A904), 136.
368
непрерывная в интервале @, п), и если
(В) J'p(x)un{x)dx = О
о
для всех значений п, то
/>(*) = О
тождественно.
Рассмотрим систему
Jg {P()}/() = С,
| 'О ЛО) '() + Я() = 0.
Если р не характеристическое число, то эта система имеет един-
единственное решение, которое может быть выражено в виде бес-
бесконечного ряда
(D) v{x) = *
где v0, г1!,..., vn,.. .удовлетворяют уравнениям
?>= 0,
При помощи этих уравнений легко доказать, что
{ 1>ш_|_1 --~— vn—-г-?—\dx= I {ч)т1)п — cvm-iVn-i}dx.
0 \ X V j 0
Левая часть этого соотношения может быть записана в виде
и равна нулю вследствие граничных условий. Отсюда
um ~ lVn — \ил — J UmUnUX.
О и
Таким образом" общее значение этих интегралов зависит, только
от суммы индексов; обозначим ее через Wm . Теперь
f (a.vm _ i + $vm .г iJ dx = Wim _ 2a2 + 2 U?Smop + W2m | 2,32
о
не может быть отрицательным для любых вещественных значе-
Э. Айне—133—24 360
ний аир, следовательно, рассматривая а — 0, р = 0 поочередно*
получим
WW0
Более того, поскольку квадратическая форма от а, р — положи-
положительна, то
поэтому Wirn или равно нулю для всех значений т или всегда
положительно. Полагая W0>0, получим
w0 w% w2m
Из § 11-31 следует, что если система (С) имеет решение Vn(x)
при р = р0, то
fp(x) Vn(x)dx = O,
о
и наоборот. Более того, в § 11-32 было показано, что если это
соотношение верно для всех целых значений п, то система (С)
имеет решение v(x) для всех значений р, и это решение, согла-
согласно фундаментальной теореме существования, может быть пред-
представлено рядом (D), который будет сходиться для всех значе-
значений р и для всех значений х в интервале @, тс). Следовательно»
разложение
fvov(x)dx = Wo + f Wt +... + p2« Wn + ...
b
конечно для всех значений р, что невозможно вследствие нера-
неравенств (Е). Таким образом мы получим
откуда
г>0 = 0, р(х) = О
тождественно в интервале (а, Ь).
Пусть f(x) будет произвольной функцией вещественной пе-
переменной х. В теории рядов Фурье предполагается, что f(x)
можно представить в виде бесконечного ряда нормальных фун-
функций
f(x) = согго(л;) + схщ (*) + ... +спип(х) + ...
Если это разложение возможно, то вследствие свойства ортого-
ортогональности функций ип(х) легко найти, что
О
так что коэфициенты си определяются единственным образом.
Здесь возникают два основных вопроса:
370
A°) сходится ли ряд
со ъ.
~?ur(x)ff(t)ur{t)dt
равномерно в интервале @, я) и
B°) если ряд сходится, то сходится ли он к значению/(л:) или
другого какого-либо предела. Эти вопросы мы рассмотрим в
последующих параграфах
11-51. Сходимость разложения. Возьмем функцию у(х), непре-
непрерывную и имеющую непрерывные первую и вторую производ-
производные в интервале @, я). Рассмотрим ряд1
-Интегрируя по частям, получим
и,.(t) at = / р7С^-{р;-id)}«r(t)dt
г—119— dl4rAu
ь^(о" dt*
о (t)
/
Вследствие граничных условий это выражение приводится к виду
7
Поскольку функции (f(^) и ^(^) непрерывны и имеют непрерыв-
непрерывные первую и вторую производные, то
ограничены для достаточно больших значений р, например p>pv,
и для всех значений t в интервале @, я). Отсюда
I
. . / ,,. ,Л ,, V I \ Яф(и)Иг(я) . Лф@)«г@)
«, (л)j ? (Qщ го Л - 2Н (Л)ПГ+
Kneser, Math. Ann. 58 A904), 121.
371
где постоянные Аг конечны для всех значений г. Следовательно
ряд абсолютно и равномерно сходится в интервале 0 <л; < к.
Сумма ряда
является непрерывной функцией х в интервале @, я); обозначим
ее через 6 (я). Тогда, поскольку почленное интегрирование ряда
для й)(х)ип{х) оправдывается его равномерной сходимостью, то
п со ъ т.
J'b{x)un(x)dx = ? fur(x)un(lx)dxfur(t)<u(t)dt =
вследствие ортогональности функций ип(х). Таким образом оче-
очевидно, что
о
для всех значений я, следовательно
тождествено в интервале @, it). Отсюда ряд (А) абсолютно и
равномерно сходится в интервале 0 < х <: к, и его значение в
этом интервале равно f(x).
11-52. Сравнение разложения Штурм-Лиувилля с разложением
Фурье по косинусам. Предположим, что f(x) — непрерывная фун-
функция вещественной переменной х в интервале @, л); никаких
дальнейших ограничений вводить не будем. Пусть sn(x) будет
суммой первых (п + 1) членов разложения Штурм-Лиувилля
Исследуем поведение sn(x), когда «стремится к бесконечности1.
Разложение Фурье по косинусам является частным случаем
приведенного выше разложения Штурм-Лиувилля; диференци-
альная система, которой соответствует нормальная последова-
последовательность ортогональных функций
_L 1
' wr) cos*,..., (-j cos ил,...
1 Haar, Math. Ann., 69A910). 339; Mercer, Phil. Trans. R.S. (A),211 A910), 111.
372
имеет вид
I ?*' + 'Л' = О,
I ах2 ' ' '
I г;'@) = «'(«) = О.
Покажем, что разложение Штурм-Лиувилля f(x) ведет себя
во всех отношениях точно так же, как разложение Фурье по
косинусам. Пусть
зп (х) = у /(?) j— ~- ~ У .cos rx cos /•?> я?,
тогда, если
п I п \
V J ! ! 2 V I
Фп (а;, 0 = > йг (а;) йг @ —»~ + ~ > cos rx cos rrr
то
sn(x)-3 x) = f<5>n(x,t)f(t)dt.
о
При помощи этого соотношения докажем замечательную тео-
теорему, что
равномерно, когда /г—> со. Доказательство основано на двух
леммах.
Лемма 1. Существует такая постоянная М, что
\Фп(х, t)\<M
для всех значений п.
Воспользовавшись асимптотическим выражением иТ (х), можно
доказать, что
2
иг (х) иг (t) — cos rx cos rt =
1
2 \ 2 1
DJ ^ wcos rx sin r^ ~ь -3 wcos ^^sin
1
+ ? W} *L^L±« + -Ц- {p(x)-p @} -??
BяJ
Поскольку суммы рядов
*cc со
VI _siu_r (x-i- t) \ sui r (x — /)
r=l r i
ограничены, а Р(х) ограничена в интервале @, я), лемма следует
непосредственно.
373
Лемма II. Если функция »(л;) непрерывна в интервале (О, к)
и имеет непрерывные первую и вторую производные в данном
интервале, то
равномерно в интервале (О, тс), когда я—»аэ.
Если gn(x) и hn{x) представляют первые я-f-1 членов разло-
разложения Штурм-Лиувилля и ряда косинусов функции <р(х) соот-
соответственно, то
gn (*) — К (х) = /Ф„ (х, t) ? (t) dt.
о
Но ga(x) и hn{x) приближаются к ш(х) равномерно, что дока-
доказывает лемму.
Докажем теперь основную теорему.
Поскольку f(x) непрерывна в интервале @, гс), может быть
образована последовательность непрерывных функций
имеющих непрерывные первые и вторые производные, которые
стремились бы к f{x) равномерно в интервале @, я). Эти функции
могут быть, например, полиномами степени, равной индексу1,
тогда
snx — cn(х) - / Фп(х, t) {f{t) — *т(t)} di + /Ф„ (х, t) <fm(t)dt.
о о
Поскольку <fm приближается к / равномерно, т может быть
выбрано таким, чтобы для всех значений t в интервале @, я)
где М — абсолютная постоянная леммы I. Если т известно, то,
согласно лемме II, и может быть принято достаточно большим,
чтобы сделать абсолютное значение второго интеграла меньше
1
Следовательно
.|sn(x) —о„(л:)|<в
равномерно для достаточно больших значений п. Это доказы-
доказывает теорему:
Разложение Штурм-Лиувилля любой непрерывной функции
f{x) сходится или расходится в любой точке интервала @, я)
в зависимости от того, сходится или расходится ряд косину-
косинусов в этой точке. Оно сходится равномерно в любом подин-
тервале @, ъ) только тогда, когда ряд косинусов сходится
равномерно в этом подинтервале.
1 Weierstrass, Math. Werke, 3, 1.
374
Этот результат имеет очень большое значение, потому что
огромная работа, которая была проделана по исследованию схо-
сходимости разложения Фурье произвольной непрерывной функции,
относится (лишь с формальными изменениями) к разложению
Штурм-Лиувилля этой функции, когда условия непрерывности
и диференцируемости, которые были наложены на коэфициентьт
к, g и I, удовлетворены1.
Однако теорема имеет гораздо большее значение, чем это
кажется на первый взгляд. Так, пусть Sn(x) будет арифмети-
арифметическим средним
.., sn(x)
и пусть Sn(x) будег арифметическим средним
°оМ> 3iU),..., oa(x).
Тогда, поскольку
sn(x) — an(x)-^O
равномерно при л—» со, отсюда непосредственно следует, что
Sn(x)-rn(x)->0
равномерно. Разложение по косинусам непрерывной функции
всегда равномерно суммируемо методом арифметических сред-
средних2. Следовательно разложение Штурм-Лиувилля сумми-
суммируемо (С. I).
1 Предполагается также, что постоянные h и Н в граничных условиях зеща-
ственны и конечны.
2 Fejer, Math. Ann., 58 A904), 59.
ЧАСТЬ II
Диференциальные уравнения в комплексной
области
ГЛАВА XII
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ В КОМПЛЕКСНОЙ ОБЛАСТИ
12 • 1. Общие соображения. Целью настоящей главы является
распространение исследований главы III о существовании и при-
природе решений диференциальных уравнений с одной веществен-
вещественной независимой переменной на уравнения с комплексной неза-
независимой переменной. Сначала рассмотрим уравнение первого
порядка
dw
Чтобы уравнение имело смысл, должна существовать произ-
производная -~~, т. е. w должно быть аналитической функцией z.
Пусть/ (г, w) будет аналитической функцией1 от двух пере-
переменных z и w. При этом условии может быть приложен с не-
некоторыми изменениями метод последовательных приближений
§3-2. Основную теорему можно выразить так 2:
Диферещиальное уравнение допускает единственное реше-
решение w = w(z), аналитическое внутри круга (z — zo) = h, кото-
которое приводится к w0 при z = г0.
Метод Коши-Липшица может быть также распространен для
применения в комплексной области3. Однако для комплексных
1 Согласно определению Коши, / (г, w)—аналитическая функция г и да
в области D, если (I) /(z, да) — непрерывная функция г и да в области D, и (II)
df df
—jfa-,-jj— существуют в любой точке D. Предполагаем, что выполнены условия
Римана: т. е. если г = х + iy, w = и + iv, f(z, w) = F(x, у, и, v) + iQ{x,y, и, v),
T0 .EfL Л9 dP - j?2_ Jp d0L IF d9-
dx dy ' Sy ~~ dx ' du dv ' dv ~ du
(cm. Picard, Traite d'Analyse 2, IX).
Условие аналитичности для комплексных переменных аналогично условию
непрерывности функции / и удовлетворению условия Липшица в случае ве-
df
щественных переменных. То обстоятельство, что--,—-ограничено, когда/(г, да) —
аналитическая функция, заменяет условие Липшица в доказательстве теорем
существования.
2 Число h определяется здесь точно так же, как и в § 3 • 1. Пенлеве [Bull.
Soc. Math. France. 27, 152], показал, что в известных случаях радиус сходимости
может превышать h.
3 Пенлеве [Painleve, С. R. Acad. Sc. Paris, 128A899), 1505 и Пикар picard,
ibid. 1363; Ann. Ec. Norm C), 21 A904) 56] показали, что этот метод приводит
к сходящимся рядам, представляющим решение во всей области, где оно ана-
аналитическое.
379
переменных удобнее метод пределов1, который мы разберем
в следующем параграфе.
12-2. Метод пределов. В уравнении
dw r, х
-of =f(z- w)
функция f(z, w) предположена аналитической в соседстве с (z0,
w0). Однако мы не потеряем в общности, если вместо z— z0 и
w — w0 напишем z и w соответственно, что равносильно zo =
= w0 = 0.
Условия проблемы могут быть выражены следующим обра-
образом. Пусть функция f(z, w) будет аналитической при z и w,
остающихся соответственно внутри кругов С и Г радиусов а
и Ь, проведенных из начала плоскостей z и w.
Далее, пусть f{z, w) будет непрерывной на окружностях Си Г.
При этих условиях \f(Z, w)\ ограничен в пределах этой области;
пусть М будет его верхней границей, тогда
при \z\ < a, \w\-^.b.
Диференцируя уравнение найдем последовательные произ-
производные
d2w dsw drw
следующим
d2w
dz'
dsw
dzs
dzL
образом
df, df
dz ' dw
dw
dz
d*f
20i?)
dz3 '''
9
dw .
' dz "i
d»/ (
dw3 (
j * •
^ dw
< dz
¦)"
+
(fel
d-w
dz '
Необходимо отметить, что эти выражения образованы при по-
помощи сложения и умножения. Принимая соотношение
в качестве начального, последовательно определяются значения
коэфициентов ряда Маклорена
f~~ ¦ I "'"" 1 ^ii»*»*^!^ | | | И tt
(_ / dw \ г , / d2® \ г2
"~ VrfT/o T t~ V rf? Л 2!
y, С R. Acad. Sc. Paris. 9—11, 14, 15, 23 A839 — 46) passim, Oeuvres
(I). 4 — 7, 10; упрощено Brio and Bouquet С R., 36, 39, 40 A853, 55), passim;
J. Ec. Polyt., 1, 36 A856), 85, 131. Метод был повидимому независимо найден
Вейерштрассом IMath. Werke, A), 67, 75 A842)]; J. fur Math., 51 A856), I [Math.
Werke, I, 153]. Обработка Веиерштрасса была упрощена Кенигсбергом [J. fur
Math,. 104 A889), 174; L hrbuch, 25]. См. также Brio and Bouquet, Theorie des
Fonctions Elliptiques, стр. 325.
Очевидно, определенный таким образом ряд для w фор-
формально удовлетворяет диференциальному; уравнению; нам нужно
доказать, что он сходится при достаточно малых значениях z.
Пусть разложение Маклорена для функции f(z, w) в со-
соседстве с z — w — 0 имеет вид
f(z, w) ="^APgZPwq,
где
f*ж — — Г~ i" f ' •
Но1
следовательно
откуда, если
то
'\ > 1 ух qf
для всех положительных целых или нулевых значений р и q. Но
следовательно, если
"~ \d7~Jo 1 ~ ~> \ dzs'H2f "*~' '
является решением
равным нулю при г = 0, то
>
(jTW_-\ . / drw
поскольку последовательные члены ( ) образуются из коэ-
>. йгт /о
фициентов (~р-~y) > согласно тому же закону сложения и
умножения, по которому члены ( ': были выведены из коэ-
V d/ 'о
фициентов —г——
iPicard, Traite d'Analyse, 2 A изд.) 239; B изд.) 259.
381
Ряд для W следовательно является доминантным рядом для
функции w, т. е. ряд Маклорена для w сходится абсолютно и
равномерно внутри некоторого круга, концентрического и внут-
внутреннего относительно круга сходимости ряда для W. Точное
выражение для радиуса сходимости ряда для W можно легко
найти, так как, если диференциальное уравнение
^ = F{z, W)
написать в виде
dW M
A—?Л
dz г
то переменные разделяются, а решение, равное нулю при z = О
определяется формулой1
Радиус сходимости р определяется поэтому из уравнения
или
поэтому формально полученный ряд абсолютно и равномерно
сходится внутри любого круга \z\ = р — е, где 0 < е <р„ следо-
следовательно он является решением дифереьциального уравнения 2.
Поскольку коэфициенты ряда Маклорена для w получаются
посредством сложения и умножения и, поскольку разложение
Маклорена аналитической функции является единственным, —
уравнение допускает только одно решение, удовлетворяющее
принятым условиям.
12 • 21. Распространение на систему уравнений. Метод пределов
может быть распространен также и на систему т уравнении
первого порядка
dwi r t
~af- =/i(z, Wu wz,..., wm),
dw, r i ч
йг
1 Берется главное значение радикала, т. е. то, которое становится рав-
равным -j- 1 при 2=0.
2 Нужно отметить, что радиус сходимости ряда, полученного методом пре-
пределов, меньше полученного методом последовательных приближений. Кроме
того, следует также отметить, что внутри круга z\ = p, \w < b перьоначально
принятые эгим решением условия следовательно не нарушаются.
382
Далее, не теряя в общности, начальные условия могут быть
приняты такими, что w1 = wz = . .. = wm = 0 при z — 0. Допу-
Допустим, что функции fi, /о.. .,fm аналитические в области J2|<;<2,
\Wj\ < b, \w2\ < b,..., \wm\ < b, a M—^.верхний предел последо-
последовательности fv /2,..., /m в этой области. Тогда доминантные
функции могут быть взяты в качестве соответствующих реше-
решений уравнений
dWt ___ dWz _ _ dWm Л4
dz йг ' ' ' dz
Функции Wlt W2,..., Wm все равны нулю при 2=0, следова-
следовательно они все между собой равны. Последовательность может
быть поэтому заменена одной доминантной функцией W, удов-
удовлетворяющей уравнению
dW _ М
*~ ('~У('-:гГ'
или, учитывая начальные условия,
Y=b-b{l +i^L±i>^L ,Og (l-
откуда радиус сходимости равен
12-22. Теорема существования для линейного диференциаль-
ного уравнения порядка я. Ввиду весьма большого теоретиче-
теоретического и практического значения обыкновенных линейных урав-
уравнений, мы здесь приведем независимое доказательство сущест-
существования решений, удовлетворяющих начальным условиям при
z = го\
Пусть
будет однородным линейным диференциальньш уравнением по-
порядка п, в котором коэфициенты px{z) Pn(z) аналитические
во всей области D плоскости (z). В ряде Тейлора
г=0
где 20 и 2 находятся в области D, коэфициенты w^r)(z0) или со-
соответствующие коэфициенты су определены таким образом, что
, J. fur Math., 66, (I860), 121; [Math. Werke, 1, 159].
383
ряд будет формально удовлетворять диференциальному урав-
уравнению.
п начальных условий
w(z0),
могут быть выбраны произвольно; последовательные значения
wW(z0), w" ^(z0),...
могут быть определены из самого диференциального уравнения
и из уравнений, полученных его последовательным диференциро-
ванием относительно z. Таким образом постоянные w'^r-(z0) или
сг могут быть определены только одним способом: поскольку
они определяются из начальных значений только процессом
сложения и умножения, они остаются конечными, пока конечны
начальные значения.
Предположим, что рекуррентные сотношения, определяющие
¦ze/<r> (z0), имеют вид
tl).
Коэфициенты p^(z) ограничены во всей круговой области
\z — 20 | -С. а, которая предположена лежащей целиком внутри D;
пусть верхняя граница |/?v(z)| на круге Г или \z — z3\ = а бу-
будет Жч.
Тогда, поскольку
Р. (?) = Р° +
где pv(r) — значение—у • —vr— при z = z0, согласно теореме Коши
¦ dz
получим
(г) Т /* Pv (z)dz М*
2пг р (z—z0) nr
Следовательно, если Pv(z) определяется уравнением
то \pSz)\ < \рЛгЛ внутри круга Г и на его окружности.
Рассмотрим теперь диференциальное уравнение
-ыг =Pi[z) 1гП^ + ... + Pn-i{z) Tz + Pn(z)W.
384
Предположим, что ему удовлетворяет ряд Тэйлора
причем Со = \со\, Q= |Cjj,..., Сп_г — |cn_i|. Пусть рекуррентное
соотношение, определяющее Шг){г0), будет
Поскольку коэфициенты разложения Pv(z) ~ положительные ве-
вещественные числа и поскольку Brs получается из этих коэфици-
ентов и из Со, Clf..:,Cn_i путем сложения и умножения,Brs —
положительные вещественные числа и
откуда по индукции следует, что
| «)W (z0) |<;
следовательно
Круг сходимости доминантного ряда Х^Л2 —^оУ может быть
легко найден; он равен | z — z01 == а. Напишем z — z0 = а?, тогда
диференциальное уравнение, определяющее W(z), примет вид
это уравнение удовлетворяется степенным рядом 5jTrCr, причем
имеет место следующее рекуррентное соотношение
п
(и + г)\ Тп.., - г ( я + г-1)! Тп r_j =¦? (Л;+ г - s)! Ж^тш г-*.
Для того, чтобы ^'JJ было формально тождественно с
Yfr{z — zo)r необходимо > = атСг (при г = 0, 1, 2,... и — 1).
Отсюда по индукции получим, что -уг > 0 для всех значений г.
Следовательно
где 6„.г_2>0 и |PiB:)|^ AJx на окружности Г. Пусть Мх будет
таким, что Мг а > п, тогда
Э. Айне—133—25 385
для всех значений г, следовательно
при s > 2. Теперь
п
fn-r-i ~~ r+n4" Zd (п + г)! in+r-i
откуда
urn -\n гГ _ ,
Г -»ОО 'ул гг—1
Отсюда следует, что ряд ]У/^Г сходится при ?| < 1, а доми-
доминантный ряд сходится при \z — zo\<.a. Следовательно ди-
ференциальное уравнение допускает решение, которое удовле-
удовлетворяет указанным начальным условиям при z = z0 и может
быть выражено в виде степенного ряда, абсолютно и равно-
равномерно сходящегося внутри любого круга с z0 в качестве центра,
в котором коэфициенты pt(z),..., pn(z) — аналитич«ские функции
12-3. Аналитическое продолжение решения; особые точки. Метод
пределов показывает, что существует решение
W{z — z0) = w0 -J- ^/ir(.z — zoY
диференциального уравнения
dw г, ч
аналитическое в области
где
('-
Поскольку М — верхняя граница \f(z, w)\ в области|г |
| w — w01 < Ъ, очевидно, что М в общем случае зависит от вы-
выбора z0 и w0.
Полученное решение является единственным аналитическим
решением, соответствующим начальным значениям (z,,, w0). Од-
Однако неизвестно, могут ли существовать неаналитические реше-
решения, удовлетворяющие начальным условиям. Этот вопрос был
разрешен отрицательно1; для целей приведенного ниже иссле-
исследования достаточно показать, что не может быть решения,
удовлетворяющего начальным условиям, в виде ряда, отличного
от степенного ряда относительно z — г02. В данном случае вывод
очевиден, так как если бы ряд содержал отрицательные и дроб-
дробные степени переменной, то некоторые члены обратились бы
1 Brio and Bouquet; J. Ее Potyt. (i), cah. 36 A856), 133. Picard, Traite d'Ana-
lyse, 2. 314; B изд.), 2, 357; Painleve, Legons sur la theorie analytique des equa-
equations differentielles (Stockholm, 1895). 394.
2 Hamburger, J. fur Math., 112 A893), 211.
386
при z = z0 в бесконечность. Но значения jAr), полученные из ди-
ференциального уравнения и их последовательных производных,
конечны, что приводит к противоречию.
Утверждая, что только одно решение соответствует началь-
начальным значениям (z0, w0), мы предполагаем, что эти значения
действительно получены. Предположим, что ?с—*w0, когда
z-*z0 вдоль некоторой простой кривой С в плоскости z.
Поскольку описанный путь представляет простую кривую,
можно при данном е > 0 найти точку zt на кривой, так что
предполагаатся также, что существует 8 > 0 такое, что
\w — wo\<C?' при \z — 20|<s.
Пусть W будет аналитическим решением, a W+ W — неза-
независимым решением, удовлетворяющим измененным начальным
условиям, тогда
TF—»0 при z—*z0 вдоль С.
Теперь
~=f(z,W+W)~f(z, W)
= WF(z, W, W),
где F — ряд, который сходится, когда z — точка на С, так что
\z — zo\^a,
и когда
Принимая, что W^ О,
с
а если \z — zo\ йа, то |F| имеет верхнюю границу М, так что
с с
где / — длина рассматриваемого пути. С другой стороны, по-
поскольку 1У—*0, когда z-^Zq, значение
\l/dz\
может быть сделано сколь угодно большим, проведя инте-
интегрирование вдоль С, достаточно близко к z0. Это приводит к
противоречию, если / конечно1; следовательно не существует
1 Случай, когда / бесконечно, например, когда С — кривая, окружающая z no
спирали, см. Palijleve, Lemons. 19; Young. Proc. London, Math. Soc. {I), 34 A902) 234Л
387
решения указанаого типа, отличного от первоначального ана-
аналитического решения.
Пусть zx будет точкой внутри окружности \z—го| = р; тогда
все коэфициенты ряда
^i(z-Zi) = Щгг-zJ + W'(zt-z0) (z - Zl) + ... + P" (zt - z0) x
могут быть определены и конечны, а ряд Wt (z — zt) будет
иметь радиус сходимости, по меньшей мере равный р — \zx—zo\.
В секторе, общем для их кругов сходимости, Wt(z — гг) и
W(z — z0) формально тождественны. Следовательно функция
Wt{z — z1) во всех точках, где она аналитическая, является ре-
решением диференциального уравнения и единственным решением,
которое приводится к значению W(zx — z0) при z=zv Если
функция f(z, w) аналитическая внутри и непрерывна на грани-
границах области \z — z1\ = al, \w — wx\ = bl и если УИ, — верхняя
граница \f(z, w)\ внутри этой области, то функция Wx{z — zt)
будет аналитической во всей области | z — zx \ < рх, где
aJl —
р,=
Если р! > р — I z, — z01, то круг сходимости №], (г — 2Х) будет
простираться за пределы круга сходимости W(z — z0); это
является общим случаем1. Пусть z2 будет точкой внутри круга
сходимости Wx{z — 2,), но не обязательно внутри круга сходи-
сходимости W{z — z0), тогда ряд
W2(z~z2) = Wl(zi-zl) + W[{zt - ziXz-Zg)-!, ... + Hr)(z2 - %) x
будет формально тождественен с tt^Cz — zx) в области, общей
для их кругов сходимости, и следовательно будет удовлетво-
удовлетворять диференциальному уравнению. Он является поэтому ана-
аналитическим продолжением решения W(z — г0).
Этот процесс может быть повторен, давая последовательно
решения
W1(z-z1), 2(z-z2),..., Wk(z-zk),
являющиеся аналитическими продолжениями решения W(z — z0).
Решение в виде ряда W(z — z0), вместе со всеми рядами,
полученными аналитическим продолжением, определяет функцию
1 Picard, Bull. Sc. Math. B), 12 A888), 148; Traite d'Analyse, 2, 311; B изд.),
2, 351. Представление, имеющее смысл во всей области, где существует анали-
аналитическое решение, может быть получено заменой ряда Тэйлора рядом полиномов.
Миттаг-Леффлера [Mittag - Leffler, С. R. Acad. Sc. Paris, 123, A899), 1212].
388
F (z; z0, w0), где начальные значения zb, w0 являются парамет-
параметрами. Эта функция аналитическая во всех точках области1 D,
определяемой совокупностью кругов сходимости W, Wx, W2,.-., Wu.
Если z = C — такая точка, что при z = Z, w = F{?;z0, ^функ-
^функция f(z, w) не аналитическая, то точка С не является внутрен-
внутренней точкой области D. Такие точки вместе с точками, для кото-
которых функция F{L; z0, w0) становится бесконечной, а также точка
на бесконечности, являются особыми точками диференциального
уравнения. Ниже мы более подробно разберем эти особые точки.
12-4. Начальные значения, для которых функция /(z, w) беско-
бесконечна. Мы видели, что если функция f(z, w) однозначна и не-
непрерывна в соседстве с (г0) w0), то w может быть представлена
в виде сходящегося степенного ряда по (z — г0). Иначе говоря,
если (z0, w0) — обыкновенная точка функции f(z, w), то она будет
также обы ; говенной точкой решения w = F (z; z0, w^). С другой
стороны, ' ' ytyx точки, для которых условия однозначности и
непрерывности, наложенные на функцию f(z, w), не выполнены;
предположим, что функция f(z, w) становится бесконечной в
интервале (z0, w0), но так, что обратная величина l-f(z, w)
является аналитической в соседстве с этими двумя значениями.
В данном случае
А№ + A
где коэфициенты A0(z), A1(z), A2(z),... сами могут быть раз-
разложены в ряд по восходящим степеням (г — z0) и Л0B0) = 0.
Предположим2, что не все коэфициенты A (z) равны нулю
при z = z0. Для определенности примем, что
^о («о) = Аг (z0) = ... = АЛ_! (z0) = 0, Ak (z0) Ф 0.
Диференциальное уравнение может быть теперь написано
в виде
Ai. — {
dw /(г, w)'
где z — зависимая, a w — независимая переменная. Решение может
быть получено при помощи метода пределов; поскольку после-
последовательные производные
At *ii A^J-
dw' dw'-' ' tfwk
1 Но не обязательно аналитическая, если только область не является одио-
связной во всей области D. Например, функция logs аналитическая в любой
точке области, кроме 0 < Б <; \z\ <: Д.
2 Если все эти коэфициенты обращаются в нуль при z ~ zB, то можно
написать
G
где функция g(z, w) — аналитическая вблизи интервала (z0, wB), a G B) —
функция одной только точки г, которая обращается в нуль при z = zD. Точка z0
в данном случае является особой точкой уравнения, см. §§ 12-6, 12-61.
38»
равны нулю при z = z0, w = да0, в то время как —^ не равно
нулю, то уравнение допускает единственное решение, разложе-
разложение которого имеет вид
z — z0 = (та/ — w0)* 4{со + Ci(да — и»о) + ^ (^' — ^оJ +•¦•}.
где с0ф0. Отсюда следует, что функция w — ъ, может быть
представлена в виде
где Pi—степенной ряд, главный член которого первой степени
относительно аргумента. Следовательно имеются k + 1 решений,
удовлетворяющих начальным условиям, аг0- точка разветвле-
разветвления, вокруг которой эти решения переставляются.
В частности, пусть диференциальное уравнение имеет вид
dw g (г, w)
dz h (г, w) *
где g(z, w) и h(z, w) — полиномы от w, коэфициенты которых—
аналитические функции z. Пусть степень h (z, w) равна п, a z0
таково, что уравнения g(z0, я) = Ои h(z0, w) — 0 не имеют
общего корня, тогда г0 соответствует п значений иг0, так что
каждой из этих начальных пар значений (z0, w0) соответствует
последовательность решений с точкой разветвления в z0. Если
мы предположим, что точка z0 описывает кривую в плоскости z,
так что ни для одной точки z0 на этой кривой уравнения
g(z0, w) = 0, h(z0, w) = 0 не имеют общего корня, то каждая
точка на такой кривой является точкой разветвления для по-
последовательности решений. Точки разветвления могут рассмат-
рассматриваться как перемещающиеся особенности. С другой стороны,
любые другие особенности и в частности любые существенные
особенности возникают вследствие того, что коэфициенты поли-
полиномов g(z, w) и h{z, w) перестают быть аналитическими. По-
Поскольку это происходит совершенно независимо от w, такие
особенности являются фиксированными1 относительно их поло-
положения в плоскости z.
12-41. Значения г, для которых функция F(z; z0, w0) стано-
становится бесконечной. Пусть zx будет значением z, для которого
решение
w = F(z\ z0, w0)
бесконечно. Рассмотрим, каким образом функция F(z; z0, w0)
становится бесконечной, причем мы сделаем несколько предпо-
предположений в отношении поведения функции f(z, w) при z = zlt
W = CO.
390
Пусть w = W \ тогда диференциальное уравнение примет
вид
= ?(z, W).
Предположим, что функция w(z, W) аналитическая в соседстве
с z=zlt W = 0. Два начальных значения (гъ*0) относится следо-
следовательно к обыкновенной точке W, а соответствующее разло-
разложение W будет иметь вид
W = (г - 2^)*{с0 + <?i(г - гх) + А> (z - zxf + ...},
где ^ — положительное целое число (не равное нулю). Следо-
Следовательно
и; = W~l = (z - Zlrk{io + -U iz - 2,) -f ¦{, (г - 2,)» +...},
т. е. решение w = F(z;z0, w0) имеет полюс порядка к при z= zl или
Допустим, что функция tpB, IFj становится бесконечной в
интервале (га, 0), но так, что 1/<р(г, W) является функцией ана-
аналитической в соседстве с этими двумя значениями. Тогда (как
в § 12-4) будет существовать последовательность решений,
переставляемых между собой вокруг точки разветвления z — Zi
следующим образом
следовательно
i_
w = VT1 -(z - Zl)k+i {уо + Ti(^ - г,) + Т2 B-z,J + • • •}
или
откуда zt является одновременно и бесконечностью и точкой
разветвления для решения w = F(z; z0, w0). Оба типа фикси-
фиксированных особых точек, рассмотренных в настоящем параграфе,
называются регулярными.
12-5. Фиксированные и перемещающиеся особые точки. В насто-
настоящем параграфе f{z, w) — рациональная функция, например
где
g(z, w) = po{z) + p1 {z)w + ... +pm(z)wm,
h (z, w) = q0B) + qx (z) w + . .. +qn{z) w" .
1 To. что указано здесь относительно фиксированности существенных осо-
особенностей, относится только к уравнениям первого порядка; это не верно в отно-
отношении уравнений выше первого порядка.
391
Любые особенности решений диференциального уравнения, кото-
которые не входят ни в один класс функций, рассмотренных в двух
предшествующих параграфах, могут возникнуть только для
дискретных значений z, другими словами, они не зависят от
начального значения зависимой переменной w. Такие особен-
особенности могут возникнуть в точке z = zu где
(a)Zi — особая точка для любого из коэфициентов р и q;
например
dw w
имеет решение
V
(b)zx такова, что функция A{zlf w) тождественно равна нулю;
например
dw w
имеет решение
Предшествующий пример также иллюстрирует этот случай.
(с) zx такова, что уравнения
g{zlt да) = 0, h(zu w)=0
удовлетворяются совместно частными значениями2 w, например
dw _ w -f- si i (г — Zj) _
Тг ~ г — г\ '
здесь g = h = 0 при z = zlt w = 0, следовательно уравнение
имеет решение
Теперь пусть W=w * и
<Р (г, W) = -
— g1^' F)
a7B;w)'
Особенности могут возникнуть при z — zx, когда
(d) zx такова, что hx{z, -w) тождественно равно нулю,
1 Каждая особая точка исключается, если она может быть исключена умно-
умножением g(z, да) и Л (г, да) на соответствующую функцию г.
2 Уравнения ие могут быть удовлетворены совместно для непрерывной
последовательности значений да без того, чтобы g и h не имели общего мно-
множителя в г, — здесь этот множитель предположен исключенным. Особые значе-
значения г1 получаются исключением w из ^(г, да) = 0 и h (г, да) = 0.
392
ye) zx такова, что уравнения
удовлетворяются совместно частными значениями W.
Точка в бесконечности может рассматриваться и как особен-
особенность при преобразовании диференциального уравнения под-
подстановкой z = S" и при исследовании точки ^ = 0.
Возникающие в данном случае особые точки называются
фиксированными или существенно особыми точками диферен-
диференциального уравнения; они могут быть определены a priori
исследованием функции /(г, w). Предположим, что каждая
фиксированная особая точка, лежащая в конечной части плоско-
плоскости, окружена небольшим кругом, так что два круга не пере-
пересекаются, а каждый круг соединяется с точкой в бесконечности
прямолинейным отрезком так, что эти отрезки также между
собой не пересекаются. Таким образом односвязная область R
в плоскости z определяется так, что в любой точке плоскости
каждое решение F (z; г0, ^0) регулярно.
Предположим, что точка zx лежит внутри области R и пусть
переменная z будет стремиться к значению гъ тогда F{z; z0, w0)
будет стремиться к предельному значению (конечному или
бесконечному); пусть
F(z; z0, wo)—'Wl, когда z-^.
Здесь могут возникнуть четыре случая.
1°. Если функция f(z, w) аналитическая в соседстве с (zlt w-i),
то функция F{z; z0, w0) будет также аналитической в соседстве
с точкой zlt являющейся обыкновенной точкой уравнения.
2°. Если wt бесконечна, но функция <р (s, w) аналитическая
в соседстве с (zlt 0), то, как было показано в§ 12-41, функция
F(z; z0, w0) имеет полюс в точке zlt которая является регуляр-
регулярной особенностью уравнения.
3°. Если w-l ограничена, но функция /(г1э ^i) бесконечна, то,
поскольку коэфициенты р или q аналитические в соседстве с г„
функция h (zv чюг) должна быть равна нулю. Но функция g (zlt w^)
не может быть равна нулю в области R. Отсюда выражение
l//(z, w) аналитическое в соседстве с (zb wj, следовательно
гг — точка разветвления F(z; z0, w0), а также регулярная особая
точка уравнения.
4°. Если w-l и функция © (z, w) бесконечны в соседстве с (zx, 0),
то выражение l\y(z, w) будет аналитическим вблизи (zu 0).
Тогда г, — точка разветвления функции F(z; z0, w0) и регулярная
особая точка уравнения.
Остается доказать, что когда z стремится к zx, функция
F(z; г0, w0) не стремится к какому-либо определенному пределу1.
1 Painleve, Ann. Fac. Sc. Toulouse, A888). 38: Lee cms, 32; Picard. Traito d'Ana-
lyse, 2 B изд), 370.
ЗУЗ
Предположим, что перемещающаяся точка начинает двигаться
из точки z0 и затем описывает простую кривую С в области R.
Пусть zx будет первой точкой, при которой возникает сомне-
сомнение в отношении существования предельного значения F(z; z0, w0),
и пусть корни уравнения h(zu w) — О будут (%,..., шп, считая
кратные корни только один раз.
Пусть о будет произвольно малым положительным числом.
Определим область А в плоскости w, как совокупность точек,
удовлетворяющих неравенствам
\w — ">i 1 <V ¦ •> \id — u)n[ <о, | и; | > 1/8.
Предположим теперь, что когда z приближается к гх, то функ-
функция F{z; z0, w0) принимает значения, соответствующие точкам,
лежащим внутри Л. В этом случае существует некоторое поло-
положительное число s, так что для каждой точки z на кривой С,
для которой \z — гг\<г, одно из неравенств
\га — и, | <?,..., | w — иоп \ < S, \w\> l/o
удовлетворено. Но функция F(z; z0, w0) изменяется непрерывно,
когда z движется по С от z0 к zlt поэтому только одно из этих
неравенств может быть удовлетворено. Отсюда следует, что w
принимает какое-нибудь одно определенное значение и>„..., u)n, оо
при z = z1#
Можно еще предположить, что когда z приближается к zlF
то значения w — F(z; z0, w0) соответствуют точкам, лежащим
вне кругов А. Тогда при |г—г,|<-[ модуль \h(z, w)\ имеет поло-
положительную нижнюю границу, следовательно \f(z, w)\ будет огра-
ограничен.
Пусть z будет точкой С, так что \z± — z\ < ^ i, тогда, не-
независимо от того, какое число w связано с z, решение диферен-
циального уравнения в виде ряда, соответствующее начальным
условиям z=z, w=w, будет иметь радиус сходимости не меньший
некоторого определенного числа \>-, если только w лежит вне
кругов Д. Выберем на С точку г,, расстояние которой от zx
меньшее наименьшего и и ^ S, и пусть значение wb связанное
с ней, будет wx—F{zx\ z0, w0). Тогда круг сходимости разложения z,
в виде степенного ряда по z— zv будет содержать точку zlt
следовательно функция F{z; zo> w0) будет аналитической отно-
относительно zt.
Таким образом во всех случаях w=F(z; г0, w0) стремится к
определенному пределу, конечному или бесконечному в каждой
внутренней точке области R.
Особенность возникает в zx только для частных значений w,
которые в свою очередь зависят от (z0, w0). Изменение в интер-
интервале (z0, w0) перемещает, в общем случае, особенность от z,
к другой точке на плоскости г. Любая точка на плоскости z
394
может быть особенностью одного или более решений уравне-
уравнения. Возьмем, например, точку zk, и пусть wk будет любым
корнем уравнения h (zk, w) = 0. Тогда, если g(zk, wk) ф 0, осо-
особенность возникает для z=zk, w=wk. Такие особенности, кото-
которые перемещаются в плоскости z при изменении начальных
значений, называются перемещающимися или параметрическими
особенностями1. Теорема, доказанная в предшествующем пара-
параграфе, эквивалентна утверждению, что, если уравнение первого
порядка и первой степени, то перемещающиеся существенные
особенности отсутствуют.
В качестве примера рассмотрим уравнение
dw . г п
когда g(z, w)-= — z, h(z, w)=<w. Решение, соответствующее на-
начальной паре значений (z(), <w0), имеет вид
или
¦w = Vzf+ wl—z2.
Особенность, в данном случае точка разветвления, возникает
при h(z, iv) = w = 0. Любая точка zk может быть особой точ-
точкой, если z0 и w0 такие, что
4 = z'l + ffi'o-
В заключение следует отметить, что в то время как пере-
перемещающиеся особенности уравнения первого порядка являются
регулярными, а не существенными особенностями, это не всегда
верно для уравнений степени выше первой.
12-51. Обобщенное уравнение Риккати. В предыдущем параграфе
мы видели, что особенности решений уравнения
разделяются на две категории:
(a) фиксированные особые точки, т. е. точки в плоскости z,
расположение которых не зависит от начальных значений;
(b) перемещающиеся особые точки, которые зависят от на-
начальных значений и перемещаются в плоскости z при их изме-
изменении. Перемещающиеся особенности могут быть полюсами или
точками разветвления.
Здесь возникает вопрос, какие ограничения должны быть
наложены на функцию /(г, ну), если решения с перемещающи-
перемещающимися точками разветвления невозможны. Пусть z0 будет любой
1 Hamburger, J. fiir Math., 83 A877], 185, Fuchs, Sitz. Acad. Wiss., Berlin. 32
A884), 669 [Math. Werke, 2, 355].
395
точкой на плоскости г, не являющейся одной из фиксирован-
фиксированных особых точек. Тогда необходимо, чтобы не было значения w,
для которого уравнение
А Bс w)]=0
было бы удовлетворено. Но это уравнение всегда имеет корни,
если только h(z0, w) не зависит от w. Поскольку z0—любая не
особая точка в плоскости z, то отсюда следует, что h(z, w) —
функция одной только z. Иначе говоря,/(г, w)—полином от яу,
например
/ (г, w) = р0 (z» p! (z) w +... +рп (z) wn.
Аналогично
<Р(г, W)=-W*f(z, W~i)
= -Po(z)W*—Pl(z)W-Pi(z)-pa(z)W-*-...-
-pn(z)W~» *
должно быть полиномом от W, следовательно необходимо,
чтобы
Рг (г) = />4 (*)=••• =Рп (z) = °
тождественно.
При отсутствии перемещающихся точек разветвления дифе-
ренциальное уравнение получится вида
% = Pa (z)+Pi B) w + Р2 (г) '«Л
Полученное таким образом уравнение называется обобщен-
обобщенным уравнением Риккати1; когда pz(z) тождественно равно
нулю, оно приводится к линейному уравнению.
Отсутствие перемещающихся точек разветвления уравнения
приводит к важному заключению в отношении формы общего
решения. Пусть z0 и z будут двумя точками в области R (§ 12 • 5);
они могут быть соединены при помощи простой кривой, не про-
проходящей через какую-либо точку разветвления. Пусть w0 будет
начальным значением зависимой переменной, выбранной соот-
соответственно z0, и пусть w будет значением, соответствующим z,
полученным аналитическим продолжением через ограниченное
число кругов, которые полностью замыкают путь z^z. При этом
продолжении, решение и его обратная величина остаются ана-
аналитическими функциями w0; конечное значение w является так-
также аналитической функцией w0. Независимо от значения (ко-
(конечного или бесконечного), какое может иметь тг>0, w опреде-
определяется единственным способом, так как в области R отсутствуют
точки разветвления. Таким образом щ, рассматриваемая как
1 d'Alambert, Hist. Acad. Berlin, 19 A763), 242; Liouville, J. Ёс. Polyt. cah.,
^2 A833), 1; J. de Math., 6 A841), 1. Частный случай уравнения Риккати был
рассмотрен в § 2-15.
396
функция w0—однозначна, аналитическая и не имеет никаких
других особенностей, кроме полюгов, следовательно она явля-
является рациональной функцией w0.
Если рассматривать w как произвольное начальное значение,
a w0 — как значение, полученное из него аналитическим продол-
продолжением, то процес обратим, и следовательно w0 — рациональная
функция от w. Эта рациональная зависимость между w и w0
может иметь место только в том случае, если w дробно-линей-
дробно-линейная функция w0, т. е.
Awo+B
Cwc+ D'
где А, В, С и D — функции z.
Из свойств ангармонического соотношения следует, что если
wl3 w2 и wz — любые три частные значения уравнения Риккати,
то общее решение может быть выражено в виде
w — W\ __ я ws — -т\
W Wa W% W-'
где А — постоянная.
Решение может быть найдено еще следующим образом. Урав-
Уравнения
нения
' = РО + Р1®>2 + Р*И>1,
' = РО + Pi%>3 -Г Pi®l
совместны, если
\w', 1, w, w2
\wi, 1, wlt w\
\wz', 1, w2, w\
= 0.
Это условие эквивалентно следующему
'L Г W~W1 . Wz — Wy 1 _-Q
йг[гг) — w« w3—w1 J v°
откуда получим искомый результат.
12 • 52. Приведение к линейному уравнению второго порядка.
Если рг(г) тождественно равно нулю, то уравнение Риккати вырож-
вырождается в линейное уравнение первого порядка. Этот, случай мы
рассматривать не будем. Напишем
тогда уравнение Риккати примет вид
397
и будет приведено к однородному линейному уравнению вто-
второго порядка
Л (г) 0 -'X (z) + Pi B) р2 (г)} §+Р<,(г)р*2(г - 0.
0 §
Уравнение второго порядка
преобразуется подстановкой
w = и' и
в уравнение Риккати
d
Следовательно теория уравнения Риккати эквивалентна теории
однородного линейного уравнения второго порядка.
Общее решение линейного уравнения имеет вид
поэтому общее решение уравнения Риккати будет
ClUl'(z)+C2u2'(z)
,»¦_
Пример. Докажите, что все перемещающиеся особенности
уравнения Риккати являются полюсами.
12-6. Начальные значения, для которых функция f(z, -w) неоп-
неопределенна. Уравнение Брио и Буке1
характеризуется тем, что для двух начальных значений z = w = О,
производная, которая имеет форму 0/0, неопределенна. Нас здесь
интересует вопрос, могут ли существовать решения, аналитиче-
аналитические в соседстве cz = 0» равные нулю при 2=0.
Пусть ряд
w(z) = cxz + c2z* + . •. + cnz" + ...
формально удовлетворяет диференциальному уравнению; в этом
случае его последовательные коэфициенты определяются соот-
соотношениями
B — X) c2 = a20 -}- Оц^ -
(я — >.) с„ = Р„ (апо,... aOn, cv ..., с„_,),
где Рп — полином от его аргументов, коэфициенты которых
1 J. Ёс. Poiyt., 36, A856), 161; Picard, Traite d'Analyse, 3, II.
398
положительные целые числа. Таким образом последовательные
коэфициенты съ с2,..., сп... могут быть вычислены при условии,
если ). не является положительным целым числом. Если ряд w (г)
сходится для достаточно малых значений \z\, он будет представ-
представлять решение диференциального уравнения. Сходимость можно
доказать при помощи метода пределов следующим образом.
Поскольку предположено, что п — /. не равно нулю, можно
найти такое число В, при котором \п — >. |> В для всех значений
и. Пусть ряд
awz + а.гог" + anzw -f aoiw2 + ...
сходится и ограничен в пределах области \z\ = r, \w\— R и
пусть М будет верхним значением его модуля на граничной ли-
линии, тогда
- A10z -f A.iOz* + Auz W + Ac2
будет доминантной функцией этого ряда.
Рассмотрим корень уравнения
который равен нулю, когда z равно нулю; он может быть раз-
разложен в ряд Маклорена
имеющего конечный радиус сходимости, не равный нулю.
Козфициенты этого ряда определяются из соотношений
ВС, = A1Q,
>2, -— ^20 "г AtlCi -j-
n =— Нп
п—1/
где полином Рп формально равен полиному, определяющему
{п — I) сп. Поскольку
В < \п — XJ; А10 > jojol,..., Лоп > ]аоп|,
по индукции получим С„ > |с„ |.
Следовательно, если X не положительное целое число, то
уравнение допускает решение в соседстве с z — 0, которое об-
обращается в нуль при z = 0. Легко доказать, что это аналити-
аналитическое решение единственное1.
1 Брио и Буке показали, что если вещественная часть >. отрицательна, то
существует только аналитическое решение, пока г стремится к нулю вдоль пути
конечной длины. С другой стороны, если вещественная часть >. положительная,
то уравнение допускает бесконечное число неаналитических решений, которые
равны нулю прн г= 0. Представления этих неаналитических решений см.Picard.
С. R. Acad. Sc. Paris., 87A878), 430, 743; Bull. Soc. Math. France, 12 A883), 48
и Poincare, J. Ec. Polyt. 45A878), 13; J. de Math. C). 7 A881), 375; S A882), 251;
D), 1 П885), 167.
399
При X = 1 аналитическое решение получается только при
а,0 = 0. В данном случае сг может быть выбрано произвольно.
Аналогично, если Х = и>1, то существует аналитическое реше-
решение, если только между коэфициентами ars, где r-ts<in, су-
существует некоторое алгебраическое соотношение. Так при X —2
это соотношение принимает вид
а20 ОцОю + G02eitf = 0.
При ). = я коэфициент сп произвольный.
В качестве примера рассмотрим простой случай
dw
z-r—lw= az.
dz
Общее решение имеет вид
w = !L- г -f Cz'-- если >.-}--1,
I — Л
то = azlogz + Cz, если >. = 1,
где С—произвольная постоянная.
12 • 61. Обобщенная проблема Брио и Буке. Первый приведен-
приведенный тип. Проблема предыдущего параграфа может быть обоб-
обобщена и выражена следующим образом. Необходимо исследовать
существование решений уравнения
¦' dz - А (г, w)'
которые обращаются в нуль при z = 0, где
о@,0) = h @,0) =0.
Допустим, что функции g(z, w), h (г, w) могут быть разложены
в сходящийся двойной ряд по восходящим степеням z и w
вблизи начала, а также, что g и/г не делятся на некоторую сте-
степень z или w.
Пусть в функции g(z, w) член, содержащий w низшей сте-
степени и не умноженный на степень г, будет wm. Тогда пусть
г\ будет низшей степенью г, умноженной на wm~l
„г т— 2
22 • W
и zrm будет низшей степенью z, имеющей постоянный коэфи-
коэфициент.
Наличие wm и z'm обязательно, так как g не делится ни на
одну степень г или w, но любой из других указанных членов
может отсутствовать.
гъ г.2,...,гт — положительные целые числа, не равные нулю.
Если все члены порядка выше соответствующего этим индек-
индексам опущены, то g(z, w) приводится к полиному от г aw.
Аналогично, h (z, w) содержит члены вида
W'1, Zs'Wn ~ i, Z*"-W" - г,. . . ,Z~n,
400
первый и последний из которых должны существовать вместе
с членами высшего порядка.
Сейчас надо исследовать возможность решения, равного
в начале. Само уравнение (А) может быть написано в виде
, , . dw , »
h(z, w) z~^ = zg(z, w).
Построим диаграмму, аналогичную классической диаграмме Нью-
Ньютона, представляющей любой член z* w'r' в виде точки, декартовы
координаты которой равны (?, -ц). Пусть точки Р,- представляют
различные члены zg (г, w), а точки Q,- — члены выражения
h(z,w)z^, которое для целей диаграммы рассматривается как
выражение, эквивалентное wh (г, wI.
Среди всех этих точек на оси •»] имеется только одна точка
Q0@, n -f-1). Аналогично, на оси ? имеется одна точка Рт (гт -f-
+1,0) и отсутствуют точки Q. Также отсутствуют какие-либо
точки и в сегментах OQ0 и ОРт.
Приводимая ниже диаграмма (фиг. 10) иллюстрирует случай
dw [iufi, ?.w~\ г5да4, zw'°, zw~, zzw, г6]
dz [wi, z3w2, zw2, zHso, 2:lJ '
где члены низшего порядка относительно iw6, <w'3,...,w° даны
без числовых коэфициентов.
Построим полигон QoPm, известный как диаграмма Пьюизо
(PuiseuxJ. Он представляет собой ломаную линию, выпуклую к
началу, так что все точки Р,- и Q, лежат на этой линии или на
стороне, отдаленной от начала. Поскольку линия начинается в
Qo и кончается в Рт, должна быть по крайней мере одна сто-
сторона, которая содержала бы точки Р и Q. Однако мы не будем
рассматривать случаи, когда эти точки совпадают. Предположим,
что эти точки соответствуют членам
Эти члены связаны между собой, как члены одинакового поряд.
ка; при наличии каких-либо других точек на стороне рассмат.
риваемого полигона, соответствующие члены будут того же по.
рядка, а все точки, находящиеся не на этой стороне, будут от_
несены к членам высшего порядка. Теперь, поскольку
О {г" + aw> )
отсюда следует, что
та = О (z°/
1 Нужно отметить, что поскольку w= О(ги-), отсюда следует, что
2 Применение диаграммы Пьюизо к теории диференциальных уравнений
подробно рассмотрено Фа ином [Eine, Amer. J. Math., 11 A889), 317].
Э. Айне—133—26 401
где h\k — дробь ajb в низших членах. Эта связь может поэтому
привести к решению, равному О (z ) в начале, где
у. = hjk,
следовательно р — наклон стороны рассматриваемого полигона.
Для исследования возможного решения допустим, что
z = tk, w — th + высшие члены,
тогда
О
а если
то
Рис. 10.
zg (z, w) = О (tN),
h (z, w) = O (tN~")-
Так, если
W = lh:i,
где и равно О A) в начале, то
N Д[,]
zg (z, w) — t Uo -'- t rt/j-f высшие члены,
h (z, w) — t Vo +1 ^ V± + высшие члены,
где 6^, Ub..., Vo, Vu... —полиномы от и.
Уравнение (А) приводится к виду
(В) (tpt + hu) {Уи+ Vtt +...} = k{U0+ UJ + ...
402
а если
где л0 ф 0, то корни
дают начальные значения н0.
Уравнение (В) может быть написано в виде
(У 0 + Vjt + ...) t ff = F{u) + [kUl - huVx) t+ ....
В целях упрощения предположим, что и = и0— простой
корень уравнения /7(и) = 0; тогда
F(u) = (u-
где
F
Предположим также, что
при и= щ
и напишем
Vo = «о + ai (« — «о) + • • ¦
Тогда
, du (и — н0) F' (г/0) 4- (й^! -1— hu Уг) t + ...
dt г0 + а, (г? — и0) + Vxf + ...
ИЛИ
t-r. = i-i) -ф or + высшие члены,
где ф = и —• и0 и X ф 0. Уравнение называется в данном случае
уравнением первого приведенного типа. Так, за исключением
специального случая, где Х-—положительное целое число, перво-
первоначальное уравнение имеет решение
l/k I/ft
где РА (г ) — степенной ряд относительно z , первый член кото-
которого степени h.
Предположим, что и = и0 — кратный корень F(u) == 0, так что
F'(ho)=O; тогда, если, как и в предыдущем случае, и = и0 не
является корнем Vo = 0, то
dt ~ ав + «j (Н — н0) + 1/^4-...
или, если ю — и — и0, то
у dv 1
t-j. = at -\- члены второго и высших порядков.
403
Это является лишь частным случаем уравнения первого
приведенного типа, когда X = 0.
12 • 62. Уравнение второго приведенного типа. Рассмотрим
теперь случай, когда и0 — общий нуль F(u) и Vo, так что
F (н0) = 0 и а0 = 0.
Если, как и раньше, v = и — и0, то уравнение принимает вид
, dv __ a'v + %'t + ¦. .
It ~~ av + $t+ ... '
где a, 6, a', 8' — постоянные, некоторые из которых могут быть
равны нулюг. Правая часть уравнения все еще имеет неопре-
неопределенную форму в начале. Рассмотрение соответствующего
этому случаю полигона приводит к предположению, что пер-
первое приближение к решению в начале имеет вид
Напишем поэтому (принимая а'4-0)
«= (-4+«0$
уравнение примет вид
Если a'8 — ар'фО, то получим
t2 -~ = ).f х +¦ а^ + высшие члены.
С другой стороны, если а'8 — аЗ' = 0, то правая часть урав-
уравнения все еще будет неопределенной в начале. Процесс может
быть повторен и приведен к уравнению вида
^3 ~Ж = ^ + а^ ~Ь высшие члены
или к уравнению, в котором левая часть имеет форму 0/0
в начале. Можно доказать, что после конечного числа приве-
приведений правая часть перестанет быть неопределенной в начале,
и мы получим уравнение вида
/l+1dvm - , , .
t ~jj- = t.vm + at + высшие члены,
где т — положительное целое число > 1. Это уравнение второго
приведенного типа2.
1 Необходимые, но не достаточные условия для существования этого случая:
чтобы сторона рассматриваемого полигона (а) содержала по меньшей мере две
точки Р и две точки Q, (Ь) не содержала точек Р или (с) не содержала точек Q.
2 Для изучения поведения решений этого уравнения в соседстве с началом
см. Bendlxsori, Ofv. Vet. — Acad. Stockholm, 55 A898), 69, 139, 171; Horn, J. fur
Math., 118 A897), 257; 119 A898), 196, 267; Math. Ann. 51 A898), 346. 360. Даль-
Дальнейшее обобщение см. Perron, Math. Ann.. 75 A914), 256.
404
В общем случае начало представляет собой существенно
особую точку уравнения второго приведенного типа, так как,
если ХфО, т>\, то уравнение не может быть удовлетворено
рядом по восходящим степеням t с ведущим членом Р. Если
ХфО, т—1, уравнение может быть формально удовлетворено
рядом Маклорена, который однако расходится для всех значе-
значений t.
Например уравнение
имеет формальное решение
«=1
которое очевидно сходится только при 2=0.
12-63. Специальные случаи приведенных форм уравнения.
0) г
является уравнением второго приведенного типа, но оно явля-
является также линейным уравнением и следовательно может быть
проинтегрировано в квадратурах. Его решение имеет вид
w= e-'lmzm{a / е'1™ z~mdz+c).
Если 1=0, то интеграл алгебраический, но в общем случае
/-4-0, и в начале имеется существенная особенность.
(II) г2^=а2з+(^ (афО.рфО)
является частным случаем уравнения Риккати. Полигон, соответ-
соответствующий этому уравнению (фиг. 11), имеет две стороны PUQO
и QoPo-
На стороне. PxQ0 функция w° связана с z-w, что предполагает
решение w = O(z) в начале.
Пусть
W = ZU,
тогда уравнение примет вид
Уравнение, определяющее ыс, будет
F(u) = $u2--u = 0;
оно имеет не равный нулю корень и0 = 1/р.
405
Тогда, если и =
р, то
dv
что представляет случай уравнения Брио и Буке, где X—1. Оно
имеет аналитическое решение только при а=0. Чтобы найти
природу решения, если оно существует вблизи. 2=0, напишем
уравнение в виде
d : V ч_ _ а , о (
dz \ г } ~~ 1 т '¦ ч
оно является уравнением Риккати относительно v/z. Преобра-
Преобразуем его в линейное уравнение второго порядка, полагая
V
г
Тогда оно примет весьма простую форму
которая имеет два независимых решения
2!
где Wo — степенной ряд по z.
Только Wx приводит к решению уравнения Риккати
которое является аналитическим решением уравнения, но не
удовлетворяет начальным условиям z=w=0.
406
Поскольку сторона Р^о не дает аналитического решения,
исследуем сторону Q0P0. Она связывает zw с zs и предполагает
решение w=O(z2) в начале. Пусть
W = Z%U,
тогда
В данном случае
следовательно щ,= -у а. Напишем
тогда уравнение принимает вид
и является уравнением Брио и Буке первого типа, с ).= —2.
В данном случае существует аналитическое решение
11 — — /j 2 Я->•_!_
следовательно имеется одно решение первоначального уравне-
уравнения, аналитическое в соседстве с началом и принимающее там
нулевое значение, именно
Примеры.
1- В уравнении
dw Р(г, w)
dz ~ Q {г, w)
пусть
Р(г, W) = аг + fci»+ . .., Q (г, ш) = -гг + рш + .
и пусть >. = >.]//.2, где "Aj и >.,—-корни уравнения
Докажите, что если '/. и 1/V. не являются положительными целыми числами или
если >. не является отрицательным вещественным числом, то два частных реше-
решения будут аналитическими вблизи г = 0, w = 0; они имеют форму
U {г, w) = gz+frw + ... = 0, V(z, w) = ?г + -/.да Ч-... = 0,
где g/. — h'fzfzQ; общее решение имеет вид
U(z, и;)= c[V(z, да)]>- ,
где с — произвол'ная постоянная.
[Poincarel.
407
2. Если в обозначениях предыдущего примера"/. или 1/>.—положительное це-
целое число, докажите, что в общем случае существует только одно аналитиче-
аналитическое решение, при котором w = 0, когда z = 0. Пусть эгик решением будет
V(z,w), тогда общее решение будет иметь вид
где S (z, w) — аналитическая функция в соседстве с г = 0, ш = 0. Число Л за-
зависит от предшествующих коэфиииентов а, Ь,..., а, Н... относительно Р и Q. Рас-
Рассмотрите частный случай h = 0.
[Poincare, Bendixson, Horn].
3. Если >. — отрицательное вещественное число, то два частных аналитиче-
аналитических решения существуют, т^к что ш = 0 при г = 0, ио общее решение не имеет
формы, указанной в примере 1. Преобразуйте уравнение в другое уравнение
аналогичного типа, где а •= 1, Ji = о, а = 0, b — >., и, принимая
zw ~~ Л = р х ~ х, w = ге11,
докажите, что общее решение допускает разложение
о + о2 Л„ (и) + рМ3 (й) +...== const,
где Л», Л3)... является аналитическим вблизи /г = 0, а ряд сходится при | р [< 8,
|гг, < G, где G — произвольная величина, а В зависит от G и стремится к нулю,
когда G стремится к бесконечности.
[Bendixson]
403
ГЛАВА XIII
УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА НЕ ПЕРВОЙ СТЕПЕНИ
13-2. Классификация рассматриваемых уравнений. В рассматри-
рассматриваемых ниже уравнениях производная не определяется полно-
полностью через г и да, но она неявно связана1 сгив, так что
Из этого общего класса уравнений мы рассмотрим только те
уравнения, в которых левый член является полиномом от да и
-^-, Предположим, что
dw
тогда функцию F (z, w, р) можно выразить в виде ряда
A0(z, w)p'n + A1{z, 1ю)рт-г^ Mm-ite, w)p + Am(z, w),
в котором функции A (z, w) будут полиномами от w, с анали-
аналитическими коэфициентами по z. Предположим далее, что ука-
указанное выражение неприводимо, т. е., что оно не может быть
разложено на множители того же аналитического характера.
Нам нужно определить необходимые и достаточные условия
для отсутствия перемещающихся точек разветвления2 и получить
таким образом обобщения уравнения Риккати.
Пусть D(z, w) будет р-дискриминантом уравнения
F{z, w, p) = О
и полиномом от w, коэфициенты которого являются аналити-
аналитическими функциями z.
В последующем разборе мы исключим некоторые значения zt
для которых:
(a) D(z, w) = 0 независимо от w,
(b) A0(z, w) = 0 независимо от w,
(c) коэфициенты А имеют особые точки для общих значений w,
(d) корни D(z, w) = 0, рассматриваемые как уравнения отно-
относительно w, имеют особые точки.
Все эти значения z фиксированны и зависят только от коэ-
фициентов А; они соответствуют особым точкам, фиксированным
1 Предполагается, что элементарные свойства неявных алгебраических функ-
функций известны.
2 Fuchs, Sitz. Acad. Wiss. EerJin, 32A884), 669 [Math. Werke, 2, 355].
409
в плоскости z. Здесь и далее мы будем рассматривать z0 как
начальное значение z, отличное от одного , из перечисленных
особых значений, а и,'о будет соответствующим начальным зна-
значением w, нам нужно рассмотреть четыре независимых случая
(I) D(z0. дао)Ф0, ЛОBО> дао)фО,
(II) D(z0> н>о)ф0, A0(z0, wJ = 0,
(III; D{z0> wo\ = O, A0(z0, ®о)Ф0,
(IV) D [Zo, w0) = О, Ло (г,,, щ>0) = 0.
13-2. Случай (I). Если D(z, w) и AD(z, w) не равны нулю для
г = г0, w = w0, то из теории алгебраических функций следует,
что уравнение
(A) F(z,w,p) = 0
в соседстве с интервалом (g0, w0) определяет т независимых ко-
конечных значений р. Придадим w фиксированное значение w0,
тогда уравнение
F(z, ™о> /0 = 0
будет иметь р независимых корней, аналитических в соседстве
с г,,. Пусть этими корнями будут
wj, с52,.. .,йш,
тогда в соседстве с интервалом (z0, да0) окажутся т выражений
вида
Поскольку (о,- и коэфициенты С,- аналитические в соседстве с z0,
эти выражения могут быть написаны в виде
В) P = $) + Pi(z — z(>, w~w0) (I =1,2,...,m)j
где й^ — значение to,- при z = г0, ар,- обозначает двойной ряд,
который сходится для достаточно малых значений \z — zo\ и
j w— w01 и обращается в нуль при z = z0, w = w0. Следователь но
первоначальное уравнение (А) заменяется последовательностью
т независимых уравнений (В); каждое из этих уравнений имеет
только одно аналитическое решение, которое приводится к «>0
при г = г0. Следовательно уравнение (А) имеет т независимых
аналитических решений, удовлетворяющих начальным условиям.
Других решений оно не имеет.
13-3. Случай (II). Если A0(z0, wo) = 0, но D(z0, w0) ф 0, то
уравнение (А) определяет т значений р, одно из которых ста-
становится бесконечным при (г0, w0). He может быть двух значений
р, обращающихся одновременно в бесконечность, так как это
привело бы к Ах {z0, w0) = 0 и D {z0, w0) = 0. Следовательно для
р имеются т—1 независимых выражений, аналитических в со-
соседстве с (г0, w0), а они приводят к последовательности т — 1
решений уравнения, удовлетворяющих начальным условиям.
410
Чтобы исследовать корень, который становится бесконечным
в интервале (z0, к'о), предположим
Р = ^ = -L-
в этом случае уравнение
Flz, zv, Р~г)^-0
имеет корень
P = .P(z —2„, г» — <j,
обращающийся в нуль при (гс, г&0) и аналитический в соседстве
с ним. Это уравнение имеет решение
где г-<^2, поскольку
тг = 0 при w = w0.
(till1
Решение (А), соответствующее значению р и обращающееся
в бесконечность для (zOf та0), получится таким образом вида
Следовательно случай (II) всегда приводит к решению, имеющему
точку разветвления в z0, т. е. перемещающуюся точку развет-
разветвления. Это приводит к первому необходимому условию для
отсутствия перемещающихся точек разветвления.
Уравнение Ао (z, w) —0 не имеет решения iv ~ С(z), так что
D (z, W) ф 0.
13-4. Случай (Ш). Левая часть алгебраического уравнения
D (z, w) = 0
является полиномом от та с коэфициентами, аналитическими
относительно z. Пусть w = -q(z) удовлетворяет этому алгебра-
алгебраическому уравнению, тогда 7j(z) не будет аналитической функ-
функцией в особых точках D(z, z&), а также возможно и в некото-
некоторых других точках. Исключим эти точки, которые являются
фиксированными, из последующего рассмотрения.
Уравнение
F(z, т„ р) = 0
имеет не меньше одного кратного корня р, скажем р = ш; пусть
он имеет кратность >.. С другой стороны, для общих значений
zv уравнение
F(z, о, pj = 0
имеет т независимых корней. Пусть корни, которые равны друг
Другу И (О при W — ~q, будут
Ри Pz,---, Pi-
Предположим, что z фиксированно; пусть w опишет неболь-
небольшой круг вокруг точки т], соответствующей выбранному значе-
411
нию z. По завершении круга трх возвращается к своему началь-
начальному значению или к одному из значений р<>,..-,рх. После
того, как были описаны а(<Х) полных контура, рг принимает
начальное значение. Пусть последовательность значений, при-
принятых рг в течение этого процесса, будет
Ръ Р^-'-у Ра, Ръ
в этом случае говорят, что эта последовательность образует
цикл порядка &.
Если ръ рассматриваемая как функция w, имеет точку раз-
разветвления порядка а — 1 при w = ¦»], то
w — 4i= W*,
тогда р% становится однозначной функцией W. Но рг = ш, когда
w = -ц, и ограничено, когда w находится в соседстве с ч\. Следо-
Следовательно /?! может быть разложено в ряд Маклорена
коэфициенты которого зависят от г и который сходится, когда
z принимает не особые значения, a W достаточно мало. Пусть
ск будет первым из коэфициентов, который не обращается тож-
тождественно в нуль; тогда
ft к ¦ 1
следовательно w—q{z) удовлетворяет диференциальному урав-
уравнению
^ш = & __ g, + Ck {w^r()}T+{ {)
13-41. Условие для отсутствия точек разветвления в случае (II).
В частном случае а = 1, когда правая часть уравнения аналити-
аналитическая (за исключением изолированных точек) относительно z и
w — т] (г),, уравнение имеет аналитическое решение. Однако, если
а > 1, то правая часть не однозначна и тогда говорят, что р
имеет разветвленное значение. Рассмотрим сначала случай,
когда
*
йг
тождественно. Изолированные значения г, для которых йи^
равны, исключаются.
Пусть
й~ Тг = ао + aiB —г0) + й2(^- zcJ +... (аоф 0),
сТ = сТ + с™ (z - zo) + с™ (z -zof+... (r> k\,
412
тогда, если
w-r1(z) = Urf (a>2)
то
<#> (г - z0) + c'f (z - г0) +...} 1*7*
4Vi B - г(); + c'iU (г - го)г + ...} Н^+1 + • ¦.;
правая часть этого уравнения аналитическая для достаточно
малых значений г — г0 и W, следовательно
Ш = Т" ^о1 + высшие члены,
а это уравнение имеет единственное аналитическое решение вида
z-zo = Pe(W0.
Обращая это уравнение, получим
а первоначальное уравнение будет иметь решение
2 — 2„)« + if2 (s—z0) «>...}.
Следовательно параметрическая точка разветвления появляется,
когда уравнение
не удовлетворяется тождественно. Таким образом для отсутствия
параметрических точек разветвления необходимо следующее:
Если p = uu S--- —кратные корни F(z, tj, р) = 0, соответ-
соответствующие точкам разветвления р, то
ёг '1 ' " ' '
тождественно.
Рассмотрим далее условие
й = --¦-
йг
тождественно. Уравнение в данном случае примет вид
+ cVU (z - z0) + c[Prl (z - zof +...} Wk+l±....
413
Решение очевидно, именно W=0 или
•т = т] (г).
Это особое решение уравнения, возникшее в виде корня р-
дискриминанта.
Кроме указанного могут быть еще и другие решения; рас-
рассмотрим эти решения (а) при а — 1 > k и (Ь) при а—1 < k.
При а—1>& пусть a—l = k + r; уравнение может быть
разделено на Wk, тогда оно примет вид
а w С
где г > 1 и Сй0) Ф 0, когда z0 не является одной из фиксирован-
фиксированных особых точек уравнения. Так
-^vr = ~/m l^r + высшие члены
— уравнение, имеющее аналитическое решение
2 = го + Рг.1(
которое в свою очередь приводит к
откуда решение первоначального уравнения принимает вид
а поскольку г :> 1, то это решение всегда имеет перемеща-
перемещающуюся точку разветвления.
При а — 1 < k пусть
После деления на W~l уравнение принимает вид
к -д?- — Си Ws + высшие члены.
В данном случае -, аналитическая функция W и г — z0, сле-
следовательно имеется аналитическое решение
W = P1(z-z0).
Если5>0, то очевидным решением будет W = 0, а, согласно
•фундаментальной теореме существования, оно является един-
единственным решением, обращающимся в нуль при z = z0. Так,
особое решение
единственное при s > 0.
414
Если s = 0, то существует аналитическое решение
а решение первоначального уравнения будет
оно не имеет точки разветвления при z = z0.
Следовательно условие ft > а — 1 необходимо для отсутствия
перемещающихся точек разветвления.
13-5. Случай (IV). В данном случае w = 7, (z) — решение, общее
для обоих уравнений
D(z, w) = 0, A0(z, от) = 0,
а уравнение
/-"B, га, р) = О
имеет кратный бесконечный корень. Из корней />,, р2,..., р>.урав-
р>.уравнения
/^(г, щ», р) = О,
которые становятся бесконечными при го = tq (г), пусть р15 р2, ...,
р, образуют цикл порядка а(>1); тогда рг может быть вь'ра-
жено в виде
/>! - {^ - 7J (Z)} « [Со + СХ {W -К) B) } « + Са {^ - T,(Z) }Ь« + ...],
где коэфициенты с зависят от z, a ft — положительное целое
число, выбранное таким образом, что с0 не равно тождественно
нулю. Причем, как и выше, такое значение 20) для которого
Пусть
{w-yi(z)
при этом уравнение примет вид
или
= -^> 1^':+'-1 + высшие члены.
Поскольку ft тЬ a — 1 > 0, это уравнение имеет единственное ана-
аналитическое решение
415
откуда, обращая, получим
следовательно
Поскольку k > 0, решение имеет перемещающуюся точку
разветвления, что верно даже, когда а = 1; таким образом вы-
выражение для /?! однозначно.
Следовательно для отсутствия перемещающихся точек раз-
разветвления необходимо, чтобы. A0(z, w) и D(z, w) не имели об-
общего множителя вида w — т] (z).
Полученные условия могут быть сформулированы следующим
образом: для непоявления перемещающихся точек разветвления
необходимы следующие условия.
(А) Коэфициент A0(z, w) не зависит от w, следовательно
он приводится к функции только z или к постоянной
(§§ 13-3, 13-5). Уравнение может быть разделено на Ао, тогда
оно примет вид
рт + фх (z, w)pm~l +... +-Jm_i [г, wjp + фт B> w) = О,
где коэфициенты ф — полиномы от гс и аналитические, за исклю-
исключением изолированных особых точек относительно z.
(В) Если k» = tj(z)—корень O(z, to) = 0, a p=&(z) — кратный
корень F(z, t\,p)=Q, так что соответствующий корено F(z, w, p=Q,
рассматриваемый в качестве функции от w — ^(z), ограничен,
то (§ 13-41)
4
(С) Если порядок любой ветви равен а, так что уравнение
получается вида
k
= ск { w - ¦»] (z) j "¦,
то (§ 13-41) k > а — 1.
13-6. Зависимая переменная, бесконечная в начале. Чтобы рас-
рассмотреть возможность обращения зависимой переменной в точке
разветвления в бесконечность, допустим, что
и>->со, когда 2->z0.
Произведем подстановку
так, чтобы
W —?0, когда z — 20,
и напишем
j-j dW p
4S0
тогда уравнение примет вид
Рт - ^ (z, W-1) W- Р"'-1 +... + (— 1)'" <Lm (z, IF-1) Н^2'"' - 0.
Чтобы коэфициент каждой степени Р был рациональным отно-
относительно W, при коэфициенте Рт, равном единице, необходимо
(и достаточно), чтобы ^(z, w), ty2(z, w),..., <l>m(z, а;) были не
больше степени 2, 4,...,2,„ относительно w. При /и = 1, урав-
уравнение приводится к уравнению Риккати.
Таким образом, в дополнение к условию (А) предыдущего
параграфа, должны быть введены следующие условия:
(А') <ЬГ (z, w). степени не больше 2г относительно ги.
Допустим, что D'(z, w) является Р- дискриминантом преоб-
преобразованного уравнения. Если дискриминант D(z, w) первона-
первоначального уравнения имеет множитель w — rt(z), то D'(z,W) будет
иметь соответствующий множитель W—1.-t,(z), следовательно,
если условия (В; и (С) удовлетворены для первоначального
уравнения, то они будут удовлетворены и для преобразован-
преобразованного уравнения. Но в дополнение к этим множителям дискри-
дискриминант D'(z, w) может содержать также в качестве множи-
множителя W. Более точно: если условие (А') удовлетворено, то
D(z, w) не больше степени 2т (т — 1) относительно w, но может
быть и более низкой степени, например, 2т(т — 1) — s. В этом
случае ?У(г, w) будет содержать множитель W.
Этот последний случай должен быть рассмотрен отдельно;
он приводит к специальным условиям отсутствия точек развет-
разветвления х. Если Р, выведенное из преобразованного уравнения и
рассматриваемое как функция W, имеет точку разветвления со-
соответствующую W=0, то (условие В) Р = 0 при W—0. Отсюда
следует, что IT должно быть множителем члена W"|m(z,IF-1).
Но поскольку W является также множителем дискриминанта,
он должен быть также множителем предыдущего коэфициента
Отсюда следует, как и в § 13-41, что уравнение относи-
относительно Р, дает
к
Р = г*0) W а + высшие члены,
1 Необходимость специального рассмотрения для этого случая была впервые
указана Хилом и Берри [Proc. London. Math. Soc. B), 9 A910), 231]. Они даюг
следующее уравнение
" d {w —/(г)} I™ _,_ ..m/г
где т н г—целые числа, простые относительно друг друга, и г < т. Уравне-
Уравнение удовлетворяет условиям (А), (А'), (В), (С), но. как показывает решение
оно имеет перемещающуюся точку разветвления, для которой w бесконечна.
э. Айне—13з—27 417
где ci0> — постоянная, не равная нулю. Чтобы это выражение
для Р дало решение, не имеющее перемещающейся точки раз-
разветвления, необходимо, чтобы
k>a— 1.
Полученные два новых условия могут быть сформулированы
следующим образом.
(В') Если уравнение преобразовано подстановкой w — W~i и
W—множитель дискриминанта преобразованного уравнения,
то W должно быть множителем последних двух коэфиииен-
тов преобразованного уравнения, когда Р — многозначная функ-
функция W.
(С) Если порядок разветвления %, а уравнение может быть
представлено в виде
то k > я — 1.
Условия (А), (В), (С) и дополнительные условия (А'), (В'), (С)
необходимы и очевидно достаточны для отсутствия перемещаю-
перемещающихся точек разветвления.
Рассуждая аналогично § 12-5 для уравнения первой сте-
степени, нетрудно доказать, что решение уравнения
рт + &(z, w)pm~i + ... + фт_!(г, w)р + bm(z, w) = О
не имеет перемещающихся существенных особенностей1. Это
верно, независимо от того, имеет ли уравнение перемещающиеся
точки разветвления или нет.
13-7. Уравнения, в которые z входит неявно. Рассмотрим слу-
случай, когда уравнение вида 2
рт + A, (w)pm-* + ...+ Лт_! (w) р + Ат (w) = О,
где коэфициенты А — полиномы от w с постоянными коэфициен-
тами, а полином АТ — степени не выше 2г. Далее, пусть урав-
уравнение таково, что его решения не имеют перемещающихся точек
разветвления.
Уравнение не допускает фиксированных особых точек, за
исключением точки в бесконечности, так как такие точки яв-
являются особенностями коэфициентов А, а эти коэфициенты не
зависят от г.
Пусть w = w(s) будет любым решением уравнения. Тогда,
поскольку уравнение не изменится при подстановке z + с вме-
вместо z, где с — произвольная постоянная, то решение будет
иметь вид
w = y(z + с).
1 Painleve, Legons, 56. •
2 Brio and Bouquet, J. Ec. Polyt. A) 36 A856), 199.
418
Поскольку это решение содержит произвольную постоянную,
оно является общим решением.
Следовательно, так как все решения уравнения свободны от
точек разветвления и существенных особенностей в конечной
части плоскости г, такие решения имеют свойства рациональных
функций. Таким образом любое решение, продолженное анали-
аналитически от точки z0 вдоль любой замкнутой простой кривой в
плоскости z, возвращается к своему начальному значению в z0,
следовательно точка в бесконечности не может быть точкой
разветвления. Однако она может быть существенно особой
точкой.
Уравнение Риккати, когда z входит неявно, может быть
проинтегрировано элементарными методами. Пусть уравнение
будет
~ = я, + ацво + a2w*,
где а0, аи аг — постоянные; переменные разделяются следую-
следующим образом
dw ,
г^г Ц.Т'
a.w*+ a-iw + ай
Обозначим через рх и р2 корни уравнения a2w2 + а-рю -f- аш тогда,
если р2 -zh pi, то
dw ,
-_ - Hg
откуда
w — ?i = се""''~"''г
W — с., '
или при р2 —
где С — произвольная постоянная в каждом случае.
13-8. Биноминальные уравнения степени т. Рассмотрим теперь
уравнения типа1
(А) р"! + A (z, и<) - О,
которые полагаем неприводимыми. Допустим, что все ус-
условия для отсутствия перемещающихся точек разветвления вы-
выполнены. В частности, функция A(z, ze1) будет полиномом
степени не больше 2т; предположим, что степень полинома
меньше 2т и что он не может быть точно разделен на w. На-
Напишем w = W—*, тогда уравнение примет вид
1 Brio and Bouquet, Fonctions Elliptiques, стр. 388; для простейшего типа
= f(u>), см. brio and Bouquet, С. R. Acad. Sc. Paris, 40 A855), 342.
41Q
но здесь член W-mA{z, W-') степени 2т относительно W. С
другой стороны, если A(z, w) степени меньше 2/га относительно -w
к содержит множитель w, пусть а будет такой, при которой
zv— а не является множителем. Тогда, принимая w — a= W~~l,
получим уравнение, содержащее W'2. Следовательно, мы не
теряем в общности, предполагая, что A(z, w) точно степени 1т
относительно w.
Поскольку (А) имеет равные корни, если A{z, w) -Q, р-
дискриминант действительно равен A{z, те1). Пусть w — -q (г)
будет множителем A(z, w), тогда р^О будет корнем уравнения
рт + A (z, у)) = 0.
Пусть соответствующий корень (А) будет разветвленным при
w = t\{z). Тогда, согласно условию В (§ 13-5), которое здесь при-
приводится к
dz '
7j (z) — постоянная.
Далее предположим, что соответствующий, корень А (г. w)
не разветвлен. Тогда A(z, w) будет содержать в качестве мно-
множителя {w — т\ (z)}2m или { w — ¦»] (z) }т.
Если {w — у, (z) Ут—множитель, то уравнение примет вид
рт+К(г){и'-г^)У»^0
и будет приводимо, что противоречит сделанному допущению. Если
{w — vj(z)}m — множитель, а остающийся множитель может быть
написан в виде k{z){w — rji(z)}m, то уравнение также приво-
приводимо. Отсюда, если {w — i\{z)}m — множитель, то любой другой
множитель w — vj/z) может иметь место только до степени
меньше т, откуда следует, что значение р, соответствующее
w — %(z), разветвленное, следовательно %(z) — постоянная.
Рассмотрим сначала случай, когда A{z,w) не содержит мно-
множителя {w — ^(z)}'". Уравнение может быть тогда написано
в виде
где at —постоянная, и
а р может быть разложен в ряд, ведущий член которого равен
Приведем y-i/m к его низшим членам и напишем kija.t тогда, со-
согласно условию (С) (§13-5)
или
420
поскольку etj > 2, откуда
Следовательно задача нахождения всех возможных типов
биномиальных уравнений вида
pm+K(z)F(w) = O
сводится к нахождению последовательностей рациональных чи-
чисел — таким образом, чтобы
Но, поскольку
2 '
JAi ki J 1_
m a,- ^ a,-
любая часть -1—, которая меньше единицы, будет вида — -—,
где а > 2. Рассмотрим шесть случаев, когда уравнение степени
выше первой и неприводимо.
Тип L Имеется один множитель, показатель которого у*
превышает т. Пусть остальные показатели (ни один из которых
не может превышать т) имеют вид
т\
тогда
т 11 —~-!
откуда
< ~2" А",
поскольку а1; а2,..., аг—целые числа больше единицы. Следо-
Следовательно г = 1 и единственно возможным является наличие
двух множителей, показатели которых равны /и + 1 и/и — ]
соответственно. Уравнение будет иметь вид
1 рт + К (г) (w — ai)m+i (w - а,)-1 = О,
где т — положительное целое число.
Тип II. Пусть ;aj — т, тогда, если остальные показатели
такие же, как и в предт^дущем случае, то
т , J
421
откуда
Л( а., а,-
Зяесь могут возникнуть два случая: г —\ и г = 2. Если г = ],
то уравнение приводится к уравнению первой степени, именно
р + /f(z) (да — aj (га; — a2) = 0.
Но если г = 2, то
откуда аг = а2 = 2. Следовательно показатели равны т,~^-т,
~2 т, а уравнение приводимо, если только то не равно 2. Таким
образом единственным неприводимым уравнением этого типа
является
II p2 + K(z)(w — ay z(w — a.2){w — a3) = 0.
Типы, III — IV. Все показатели меньше то. Единственными
глед
будут
а— 1
последовательностями чисел вида , суммы которых равны 2,
1 J_ 1 1.2 2 2.3 3 1.5 2 1
IT' 2 ' 2 » 2 ' 3 ' 3 ' 3 » 4 ' ~4~' 2 ' 6 ' 3 ' ~-
Эти значения приводят соответственно к четырем типам
уравнений.
III р- + /< (z) (w — a,) (да - а2) (да - а3) (да - с4) = 0,
IV if + K{z)(w - aJHw - я3)*(да - fl3J = 0,
V p' + /С(г) (то - a,)\w - а.Пт - azf = 0,
VI pb + Kiz) (ic1 — a^w — az)*(w — a3f = 0,
где во всех случаях flj, a.2, a3, a4 — независимые постоянные.
Теперь вернемся к случаю, когда имеется множитель {w—r; (z)}m.
В этом случае уравнение может быть написано в виде
рт K(z) {w - г, (z)}mII (да — а,р = 0,
причем должно быть выполнено условие
U;>—ОТ.
Поскольку в данном случае цг</и, ^рг=/и, единственен^
возможным является наличие двух степеней рх и jj.2 так, чтобы
422
Но уравнение теперь приводимо, если только т не равно 2;
следовательно единственно возможным уравнением этого типа
будет
р* + К (г) {1С - tj (*) ]2 (w - я,) (да - а3) = О,
где й2]-й3. Это уравнение является обобщением типа II, к кото-
которому оно приводится, когда ij(z) становится постоянной ах,
отличной от аг и а3.
Эти шесть типов (включая в тип II его обобщенную форму)
исчерпывают все случаи, когда биномиальное уравнение
рт + A (z, w) = 0 .
(где т > 1, a A (z, w) — точно степени 2 т относительно w) имеет
решения, свободные от перемещающихся точек разветвления.
Каждому из шести основных типов уравнений соответствуют
уравнения, в которые w входит в степени не ниже 2т. Такие
уравнения получаются подстановкой W = (w — at) л , гдеит—щ
встречается как множитель в A (z, w). Можно доказать, что
приведенный ниже ряд выведенных таким образом уравнений
является исчерпывающим. Из заданного основного типа уравне-
уравнения выводятся новые уравнения.
Тип I pm + K(z)(w-a)m-l=:0,
рт + K(z)(w — a)m~ [ - 0.
Тип II р1 + К {z) (w — a,)- (w - - а,) - 0,
р- + К (г) (гс> — a,) (w - as) - 0.
Тип III p2 + К {z) (w — aj (е- — а.2) (w — а3) == 0.
Тип IV
Тип V
Тип VI
13-81. Интегрирование шести типов биномиальных уравнений.
Уравнение типа 1 может быть написано в виде
т т т ¦ 1 т—1
р ={A(z)} (w-aj (™ — а2) .
Пусть
,„, _ W- -Пх
С — ¦ t
»' — а%
тогда уравнение преобразуется в
dz т к '
423
рл
p*
рь
рй
р6
JrK(z)(w-a,
+ K(z){w-a,
+ R(z)(w — a1
+ K{z)(w~ai
+ K{z)(w-aj
+ K(z)(w — a}
,J(ze- — a,f
y*(w - o2)8
K(w — a2f
Yiw - a,I
f{w — a,K
{y(w — Й2)з
= 0.
-0,
-0.
= 0,
-0,
¦= 0.
следовательно его общий интеграл равен
\w~a
Рассмотрим теперь наиболее общее уравнение типа II, кото-
которое может быть написано в виде
f --, { A (z) }*{w—q (г)} * («> - a,) {w - о2).
Пусть
тогда уравнение примет вид
|== ±4rA{z)[al—ll(z)-{ а3-т,(г) J. ^],
что представляет собой случай уравнения Риккати.
Если y)(z) — постоянная, например г„ то, обозначив
мы приведем уравнение к виду
которое относительно t интегрируется элементарно.
Интегрирование остальных четырех типов вводит эллипти-
эллиптические функции. В этих уравнениях мы не теряем в общности,
заменяя K{z) на—1, так как, поскольку каждое уравнение имеет
вид
подстановка
оставляет члены относительно w неизменными. Мы не потеряем
также в общности, если будем рассматривать не основное урав-
уравнение любого типа, но любое эквивалентное уравнение.
Так, уравнение
может быть взято для иллюстрации типа III.
Тип IV может быть представлен уравнением
Пусть
(да - аг) (w — а2) = t3, -^ = Г1,
424
тогда, диференцируя, получим
3t2 d~ = Bто — at — а2) ^
или
w 9 / ^—-—2
Тип V может быть представлен уравнением
Пусть и/ = ^2 -J- «it тогда это уравнение приводится к
Тип VI может быть представлен уравнением
Пусть та = f8 + сх, тогда это уравнение приводится к
Следовательно в любом случае уравнение может быть приве-
приведено к виду
где Ра(^) —кубическая функция ?. Это диференциальное урав-
уравнение может быть проинтегрировано только при помощи эллип-
эллиптических функций1.
Линейным преобразованием это уравнение может быть при-
приведено к виду
§
откуда
где a — произвольная постоянная.
1 Уиттекер и Ватсон, Курс современного анализа, § 20- 22.
ГЛАВА XIV
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВЫСШЕГО ПОРЯДКА
14-1. Сущность проблемы. Изучение однозначных функций,
определяемых диференциальными уравнениями первого порядка,
частично рассмотренных в предшествующих главах, может счи-
считаться достаточно полным. Относительная простота исследова-
исследования уравнений, в которые р и w входят рационально, объясня-
объясняется отсутствием перемещающихся существенных особенностей.
В уравнениях второго и высших порядков даже простейшего
вида могут возникнуть перемещающиеся существенные особен-
особенности, что значительно усложняет задачу.
Рассмотрим простой пример: уравнение
d2w [dw\2 2w—\
dz2' r~ \dz } ' w-~+~\
имеет общее решение
w = tg {log (Az-В)},
где А и В — произвольные постоянные.
Когда 2 стремится к В{А произвольно или по определенно-
определенному пути, w не стремится к пределу (конечному или бесконеч-
бесконечному). Действительно из точки В!А, являющейся одновременно
точкой разветвления и существенной особенностью, возникает
бесконечное число ответвлений функции. Поскольку эта точка
зависит от постоянных интегрирокания, она является переме-
перемещающейся особенностью.
Нужно определить, существуют ли уравнения вида
. dzw t-., .
(А) -^г = F(z, w, р),
где функция F—рациональная относительно р, алгебраическая
относительно w и аналитическая относительно г, со всеми кри-
критическими точками (т. е. точками разветвления и существенными
особенностями) фиксированными г
Более общим является уравнение второго порядка
F(z,w,p,q) = 0 (? ?)
но это обобщение не имеет сейчас большого значения.
1 Picard. С. R. Acad Sc. Paris, 104 A887), 41; ПО A890), 887, J. de Math.
D), 5 A886), 203; Acta Math., 17 A893), 297: Painleve, C. R. 116 A8P3), 88, 173,
362,566; 117 A893), 211, 611, 686: 126 A898), 1185, 1329, 1697; 127 A898). 541,
945; 129 A899), 750, 949; 133 A901), 910; Bull. Soc. Math. France, 28 A900), 201:
Act;i Math.. 25 A902), 1; Gambier, C. R. 142 A906). 266, 1403, 1497; 143 A906),
741: 144 A907), 827, 962; Acta Math., 33 A910), 1.
426
14-11. Общее решение как функция постоянных интегрирова-
интегрирования. В уравнениях второго порядка важно различать, каким об-
образом постоянные интегрирования входят в решение. Фунда-
Фундаментальные теоремы существования показывают, что если кри-
критические точки фиксированные, a z не является критической
точкой, то решение полностью и единственным образом опре-
определяется значениями w0 и гс'о, которые зависимая переменная
w и ее первая производная w' принимают в точке z0. Решение
может рассматриваться как функция w0 и w'o, коэфициенты ко-
которых— функции z — 20.
Могут возникнуть три случая:
(I) Решение может быть алгебраической или рациональной
функцией от w(, и wn' или от эквивалентной пары постоянных
интегрирования; так например, уравнение
гю" + Зотгс' + w3 — q (z)
имеет обшее решение w — u'ju, где и — общее решение линей-
линейного уравнения третьего порядка.
и"' - q (z) и.
Поскольку
и - Ахил + А2и2 + A3ns,
где «J, н2, н3 образуют фундаментальную систему линейного
уравнения, а Аъ А.,, А3 — произвольные постоянные, общее ре-
решение уравнения для w будет иметь вид
w =- "г'+ Вщ> + Си3'
Ви, + Си
и будет рациональной функцией двух постоянных интегриро-
интегрирования В и С.
(II) Обшее решение не является алгебраической функцией
обеих постоянных интегрирования, но, тем не менее, уравнение
допускает первый интеграл, в который постоянная интегриро-
интегрирования входит алгебраически. В данном случае общее решение
является полутрансцендентной функцией постоянных интегри-
интегрирования. Так, первый интеграл
тс" -г 2'пуя1' - q (z)
равен
w' -r w°- -= f q (z) dz + A
и линейно зависит от постоянной А. Общее решение, следова-
следовательно, является полутрансцендентной функцией А и второй по-
постоянной интегрирования.
(III) (I) и (II) не выполнено. Общее решение в данном
случае является существенно-трансцендентной функцией обеих
постоянных интегрирования.
Как источники новых трансцендентных функций, т. е. функ-
функций, отличных от трансцендентных функций, определяемых
427
уравнениями первого порядка с алгебраическими коэфициентами,
могут рассматриваться только уравнения, которые входят в по-
последнюю категорию.
14 • 12. Метод решения. Уравнение (А; может быть заменено
системой
dw
или, в более общем случае, системой вида
I dii) ... ¦ ,
57 = W(z, w, и),
(В) ] dz
\
Предположим, что Н и К—функции параметра а, аналити-
аналитические относительно а во всей области D, с внутренней точкой
а = 0. Примем следующую лемму: если общее решение диферен-
цпальной системы однородно относительно z для всех значе-
значений а в области D, за исключением а = 0. то оно будет одно-
однородно также и для а — о.
Пусть w(z, a), uiz, а) будут двумя решениями системы, со-
соответствующими начальными условиям
Пусть С будет замкнутым контуром в плоскости z, начинаю-
начинающимся и кончающимся в 20. на котором ге'0(г) и u,fz) — аналити-
аналитические функции, причем
¦az'0(z) = -K>(z, 0), uo(z) u(z, 0).
Тогда, если функции w(z, а.) и u(z, а) разложить в ряды по
возрастающим степеням параметра я
w (z, a) = wo(z) 4- clw^z) + aaffi!2 (z}+...,
и (г, a) = и0 (z) + a«j (z) + а2и2 (г) -f ...,
то эти ряды сходятся для z, лежащих на С, и для достаточно
малых значений \а\ Пусть в то время как z описывает контур
С, w.Jiz) увеличится на k.t, тогда
/ 0
для 0< aj <a0) следовательно
Av =0
428
для всех значений v. Отсюда следует, что функции wo(z), wx{z),...
и аналогично uo{z), ux(z).. .однозначны1.
Решение распадается на две части. Сначала получается по-
последовательность необходимых условий для отсутствия переме-
перемещающихся критических точек, затем выводится последователь-
последовательность уравнений, удовлетворяющих этим необходимым условиям;
прямым интегрированием или каким-либо другим способом
можно показать, что общие решения этих уравнений свободны
от перемещающихся критических точек, доказывая таким обра-
образом достаточность условий. Для получения последовательности
необходимых условий в систему (В) вводится параметр а так,
чтобы новая система имела те же фиксированные точки, что
й (В), и, кроме того, была интегрируема при а — 0. Функции
-ffi'0(z), ii\{z),..., uo(z), %(s),..., определяются в квадратурах; для
отсутствия перемещающихся критических точек в данной си-
системе необходимо, чтобы все критические точки этих функций
были фиксированными.
Пусть
" --=* g (zo, «'о)
будет полюсом одной или обеих функций H(z0, w0, u),K(zQ, wo,u).
Мы не потеряем в общности, если примем, что g(z, w) равно
нулю, поскольку и — g(z, iv) может быть заменено новой пере-
переменной U. В данном случае система (В) может быть записана
в виде
и" J - Н0[г, w) + иЩг, тс-) +. ..,
ип ff - K0(z, w\ + uKlz, 10) + ...,
где хотя бы одно из чисел т, п больше нуля.
Допустим, что т<п + \, где п больше нуля, и введем па-
параметр а
z - z0 -r a"+1Z, w = w0 + a"-" 'l W, a -<xL'.
тогда система примет вид
За исключением случая % = 0, эта новая система имеет
фиксированные критические точки при фиксированных точках (В).
При а = О система принимает вид
1 Достаточно доказать, что функции w(z, a), u(z, -з.) однозначны относи-
относительно z для бесконечной последовательности зь -х.,,.. .значений а, имеющих а=0
как предельную точку.
429
и имеет решение
где А — произвольная постоянная. Решение системы при а. —- О
имеет следовательно перемещающуюся точку разветвления и,
согласно лемме, не может ' иметь фиксированных критических
точек при афО. Система (В) имеет решения с перемещающимися
критическими точками при т<п+\.
Предположим, что т>п+\. Пусть т = п + 1 и одновре-
одновременно K0{z, w) и другие функции K(z, w) равны нулю. Напишем
z —z0 -j- %mZ, и -O.U,
тогда система примет вид
""^ 4z
если
H0(zw w) -
то система приводится, при а = 0, к виду
Эта новая система может быть проинтегрирована в квадрату-
квадратурах; чтобы первоначальная система не имела критических точек,
необходимо, чтобы точки разветвления решений этой приведен-
приведенной системы были фиксированными.
Применяя эти условия ко всем полюсам H{z, w, и) и
K(z,w, и) вида u=g(z, w) или w=h(z) и к значениям и = оо и
w — со, получим последовательность условий, необходимых для
отсутствия перемещающихся точек разветвления общего реше-
решения. Тот же процесс может быть приложен и к любым значе-
значениям и = g(z), w = h (z), которые делают Н или К неопределен-
неопределенными, так же как и к особым точкам Н и К, если они имеются.
14 • 2. Применение метода. Рассмотрим уравнение
(С) ^r = R(z,w,p),
где R — рациональная функциям и р с коэфициентами, аналити-
аналитическими относительно г. Предположим, что R неприводимо и
поэтому может быть выражено в виде
430
где Р и Q — полиномы от р, не имеющие общего множителя.
Уравнение эквивалентно системе
dw
dp
dz
= R(z, w, p).
В данном случае т равно нулю; если R имеет полюс р — g(z, zz)r
то условие т > п -f- 1 не может быть удовлетворено. Отсюда
следует, что для отсутствия критических точек R не может
иметь полюса и должно быть полиномом от р; пусть оно будет
степени q.
Но (С) также эквивалентно системе
dw
~dz
w>
Z- w)
z' w)
В данном случае /га = 1, п = q — 2, следовательно неравенство
m > /г -j- 1 приводит к условию, что <7 равно максимум 2. Сле-
Следовательно, если общее решение (С) не имеет перемещающихся
критических точек, то необходимо, чтобы оно имело вид
(D)
-rf2HL _ / (Z
M(z, w)p + N(z, w),
где L, M и N — рациональные функции w с коэфициентами,
аналитическими относительно z.
Пусть
z = z0 + aZ, tw ,
тогда (D) эквивалентно системе, которая приводится, при з — 0, к
dZ
W),
а эта система в свою очередь эквивалентна уравнению
Следовательно необходимо найти уравнения вида
(Е)
dz*
решения которых имели бы только фиксированные точки раз-
разветвления.
14-21. Первое необходимое условие отсутствия перемещаю-
перемещающихся критических точек. Сначала покажем, что функция / (w)
431
имеет только простые полюсы; пусть w — w-^ будет полюсом
порядка г. Поскольку этот полюс можно заставить совпасть
с началом при помощи трансляции, что не изменяет формы
уравнения, <еог может быть принята равной нулю. Уравнение тогда
будет эквивалентно системе
( dw
\Р
где k — постоянная. Напишем
и» = а«7, /> = агА
тогда система примет вид
№ = *"*
При расположении по возрастающим степеням а, решение си.
стемы будет иметь вид
«7= IF,—V
где WS
a /¦> l. Следовательно, когда г> 1, критические точки не фикси-
фиксировании.
При г= I система принимает вид
dP гл ч
гфи 3 = 0 эта система имеет решение
_i
W = (Az+By-k при
или
которое не имеет перемещающихся точек разветвления, за исклю-
исключением
k— 1 4- п или k = \,
432
где п — целое число, положительное или отрицательное.
Уравнение
может быть проинтегрировано один раз; первый интеграл равен
При полюсе w = wl главная часть l(w) должна иметь вид
lit.
W — 1Юг
поэтому к выражению е (w> dw добавляется множитель (w—Wj) "¦.
Пусть v будет наименьшим общим знаменателем показателей
всех таких множителей, тогда, если
(F) р' = ?(оО,
функция y(w) не будет иметь других особенностей, кроме полю-
полюсов в конечной части плоскости. Преобразование w = W~l пока-
показывает, что <si(w) имеет полюс в бесконечности и является
рациональной функцией. Таким образом проблема зависит от опре-
определения уравнений типа (F), решения которых не имеют пере-
перемещающихся особых точек; этот вопрос был рассмотрен в § 13-8.
После диференцирования (F) отождествляется с (Е), если
^ ' vcp (w)
следовательно изучение типов уравнения (F), не имеющих пере-
перемещающихся точек разветвления, приводит к заключению, что
/(те») должно быть или тождественно нулю или одного из сле-
следующих типов:
v = m, I (w) = —-, г Л т г (гп > 1),
' v ' m(w — uj) ' m(w — a2) v "
J_ JL J_ J_
о о о о
v = 2, /(«;) = —= h — Ь~^ h— -—'
\ / да — Й1 ' w — a2 w —• as w — ai
2 _2_ 2
V = 3, /(^) = —~- + —^T + —Jr--»
A A J_
и // ч 4.4,2
v = 4, I (k>) = 1 ——¦ + —~— >
_ё_ 1- _L
v = 6, /(да) = —-— + ——- + —-—
433
Tun
Tun
Tun
Tun
Tun
/
III
IV
V
VI
О. Айне—133—28
Постоянные аъ а2, as, ai могут иметь любые значения. Урав-
Уравнения типа II исключаются, так как для настоящего анализа
они могут рассматриваться, как вырожденный случай типа III.
Способ получения l(w) из L(z, w) приводит к заключению,
что для того, чтобы решения уравнения
w) p -j- N (z, w)
были свободны от перемещающихся критических точек, необ-
необходимо, чтобы функция L(z, w) была тождественно равна нулю
или принадлежала к одному из пяти основных перечисленных
типов, где аи а2, а3, at должны рассматриваться как функции z.
14-22. Второе необходимое условие для отсутствия перемеща-
перемещающихся критических точек. Необходимо показать, что полюсы
М (z, w) и N (z, w), рассматриваемые как функции w, — простые
и входят в полюсы L{z, w). Пусть w — h(z) будет полюсом
порядка / функции M(z, w) и полюсом порядка k функции
N(z, w). Поскольку подстановка W = w — h (z), не изменяя
существенно уравнения, изменяет рассматриваемый полюс
в функции W = 0, можно принять, что h (z) тождественно равно
нулю. Уравнение может быть тогда написано в распространен-
распространенной форме
dz2 w IV, п ) \ wi
w
где п — положительное или отрицательное целое число, отлич-
отличное от 0 или 1, если -ziy == 0 — полюс функции L(z, w), и к= 1,
если w = 0 не является полюсом L (z, w).
Произведем следующее преобразование
w = a W, z = z0 + <*'Z, если k < 2/ — 1,
или
w = aW, z^zo + aJ(ft+1)Z, если k>2j-l,
и напишем
Тогда
d4V
еслиЛ<2у-1,
если,>2/-1,
434
Третье из этих уравнений содержит оба других, если а = О,
и если Мо или Л^о также равно нулю. Уравнение
где (при Жо = 0), 2у — 1 должно рассматриваться как символ,
принятый вместо положительного целого числа k, следовательно
2у — целое число не меньше 2 — может быть заменено системой
W
dW
dZ
Допустим, что j> 1, тогда, поскольку п — целое число,
у'Ф — . Более того, Мо и No не равны нулю, откуда следует,
что уравнение
имеет не меньше одного не равного нулю корня, например
и — их. Тогда и = их будет частным решением первого уравне-
уравнения указанной выше системы. Но второе уравнение системы,
которое принимает вид
dZ, 1VJ l
uWJ
имеет решение (поскольку j > 1) с перемещающейся точкой раз-
разветвления, следовательно общее решение не свободно от пере-
перемещающихся точек разветвления. Таким образом возможности
у>1 и k > 1 должны быть исключены. Следовательно, если
М (z, w) и N(z, w) имеют полюсы w = h(z), то эти полюсы
простые.
Предположим, что / = /г = я=1, т. е. что W— 0— простой
полюс функции М(z, w) или функции N(z, w) или обеих, ноне
является полюсом L {г, w). Тогда приведенное уравнение примет
вид
dHV _ МйР + А^о
TZ* " '
W
и будет эквивалентно системе
dZ
du
dZ
и
и (Мв +
W
Эта система при подстановке ш вместо и, iZ вместо Z в свою
435
очередь примет вид
dW
dZ
du
dZ
i
и
¦ >
аи (Мв 4- хЛ'0Н>
XV '
при решении относительно W пив виде ряда по возрастающим
степеням а, с Е<оэфициентами, являющимися функциями Z, эта
система имеет решение
"О
и = щ— Шои1 log ( Wo + ~т^°) + ° (а')> если мо Ф О,
\ "п /
или
и = йо -
« log AГ0 + ^=^) + О (Яз), если Мо = 0.
Здесь решение имеет перемещающуюся критическую точку,
так что единственно возможным будет
лф1, j = k=\,
т. е. w = h{z) может быть только полюсом Ж (г, да) или N(z, w),
если оно является также полюсом L(z, w). Таким образом
полюсы M(z, w) и N(z, w) являются простыми и входят в полюсы
L(z. w).
Возвращаясь к типам I —VI, видим, что выражение L{z, w)
может быть написано в виде jyf'z ""л, где D(z, w) не больше чет-
четвертой степени относительно w, г. \ (z, w) по меньшей мере на
одну степень ниже D. Следовательно М и Л'могут быть выра-
выражены в виде
гд? р- и v — полиномы от is, максимальная степень которых
должна быть определена. Пусть D (z, w) будет степени 8 от w.
В уравнении (D) напишем w = W~ , тогда уравнение примет
вид
Если числа а, которые входят в выражение для L (z, w), в типах
1 — VI все конечны, то {2W — L (z, W )}W будет конечно
(или равно нулю) при IF =0. Следовательно 117 = 0 не может
быть полюсом M{z, W *)или W2N(z, W ), откуда следует, что
4,-j
степень ц (z, w) относительно w не больше о, а степень v (z, w)
не больше 8 -f- 2. С другой стороны, если Z. (г, w) тождественно
равно нулю или вырожденного типа, где одно из чисел аг, а2,
а3, ai было взято бесконечным, то W=0—простой полюс
{2W—L (z, W )}' W , следовательно может быть простым
полюсом M(z, W ) и W*N (z, W ). В данном случае у. (z, w)
и v(z, w) имеют степени, не превышающие о -^j- 1 и 5-J-3 соот-
соответственно.
Следовательно в общем случае вторым необходимым усло-
условием для отсутствия перемещающихся точек разветвления
будет: если D(z, w) — наименьший общий знаменатель простей-
простейших дробей в выражении L(z, w) и степени о относительно w,
то M(z, w) и N (z, w) могут быть соответственно представ-
представлены в виде
|j. (г, w) -. (г, w)
D(z, w) D(z. w)
где fj. и v — полиномы от w степени не выше 3 + 1 или о -j- 3.
14 • 3. Приведение к стандартному виду. Если решения урав-
уравнения второго порядка не имеют перемещающихся критических
точек, то уравнение будет иметь вид
где L (г, w) равно нулю или одного из пяти основных типов,
перечисленных в § 14-21. Чтобы упростить форму L{z, w),
произведем одно из следующих преобразований:
(I) если L(z, it') имеет только один полюс w = а,, напишем
W - -±
W—
(II) если L (z, w) имеет два полюса w = аъ а2, напишем
(III) если L (z, if) имеет три полюса w = а^, а2, а3 или четыре
полюса w = аь а», а3, ait напишем1
1F==?.i3l.?'-«-
«2 «3 К» Я,
Уравнение тогда преобразуется к виду
-.- + С (г, V7),
1 В случае типа V более удобно
a, — я, w — a-.
где A (z, W) принимает одну из следующих восьми независи-
независимых форм
(III) ^—^- (rn — целое число, больше единицы),
' т W
V W— I U—Tj)
Здесь (III) возникает из типа I; (II), (IV) и (VIII) — из типа III,
(V) из типа IV, (VI) —из типа V, (VII) — из типа VI.
В (VIII)
~ g3 я,, — а4
= t
' fl2 — й3 ! 4
Эта величина может быть постоянной или может зависеть от z.
В последнем случае она может быть принята в качестве новой
независимой переменной Z.
14-31. Случай (I). В случае (I) выражение L(z, w) равно
нулю; вторая последовательность необходимых условий (§ 14-22)
показывает, что уравнение будет иметь вид
(G) -<™- = {A(z)w + B(z)}-^+C(z)w' + D(z)w* +
Проведенное исследование не разрешает вопроса о наличии
(либо отсутствии) перемещающихся критических точек в реше-
решении данного уравнения. Найденные условия являются необхо-
необходимыми, но ни в коем случае не достаточными. Поэтому, иссле-
исследование необходимо несколько продолжить, хотя и без суще-
существенного изменения метода.
Пусть
W
w = — , z = zo + 3.Z,
тогда уравнение принимает вид
JJ- = A (s0) W fz + С (г0) W3 + О (а),
а при а = 0 это уравнение эквивалентно системе
dW _ W^
dZ ' и '
I
438
где ao = A(zo), co = C(zo). При co = O приведенное уравнение
имеет первый интеграл
dZ2
dW 1
где т — постоянная интегрирования; его общее решение одно-
1
значно. Пусть с0 =? О, тогда если W заменить на W { —c(z)} 2, то
c(z) заменяется на — 1; следовательно, не теряя в общности,
можно предположить, что с0 — — 1. Система может быть те-
теперь написана в виде
dZ
du
где
Напишем
¦k = Oo, hk = 2.
и = h + sw,
тогда, если h = k, то система принимает вид
aw _ wz
~dZ ~~ 'h+av '
dv = ^2
а эта система имеет решение
v = с2 — a.c\h log (Z — с^) -f- О (я),
где сх и с2 — постоянные интегрирования. Но это решение
имеет перемещающуюся критическую точку; допущение h = k
должно быть, следовательно, отвергнуто.
Если кфк, то система примет вид
d\V
dZ
dv
и имеет решение
+ О (а),
439
Перемещающаяся особая точка Z = c1 будет точкой раз-
разветвления, если 2— /z2 не целое число п, положительное или
отрицательное (но не равное нулю, поскольку h2= 2 предпола-
предполагает отвергнутое ранее условие h — k). Пусть
К1 = 2 - п
и аналогично
k2 = 2 — п',
откуда
B
Следовательно остаются три независимых условия
AJ-и=1, 2 — я'= 4,
A1J— я = —1, 2-я'= -4,
(III) 2 - я = - 2, 2 - и' = - 2,
соответствующие
A)Л= + 1, А=±2, flo^ + 3,
(II) h— ±i, k = + 2i, a0 = + г,
(III) A = + i/ 2, Л = + i /2, a0 = 0;
в каждом случае должны быть приняты все верхние или все
нижние знаки.
Случай а0 = -\т 3 может быть выведен из случая а0 = — 3
переменой знака при wlt следовательно он не отличается от
последнего случая; в случае (II) преобразование w — ± iwt
приводит к изменению C(z) от —1 до +1 и изменению д0
на —1. Теперь, поскольку z0 произвольно, любое соотношение
вида
а0 = A (z0) = — 3
верно для всех значений г0 и следовательно A(z) — постоянная.
При А = 0, С^:0,заменив WHaW/~2~JC получим С = 2; если
А ф 0, С — 0 и IF заменим на — 2WJA, получим А =—2.
Следовательно, если в случае (I) общее решение уравнения
свободно от перемещающихся точек, то необходимо, чтобы
уравнение могло быть приведено подстановкой вида
w = I (z) W
к уравнению, в котором A(z) и С (г) имеют следующие пары
постоянных значений:
(а) А = 0, С - 0. (Ь) А = — 2, С = 0.
(с) Л = —3, С= —1. (d)A = -l,C=l.
(е) Л = 0, С = 2.
440
Более общее преобразование
не изменяет основных свойств уравнения (G), которое прини-
принимает вид
d°-W dW 1
dZ2 dZ !>' \ ' Л ?'|Т
-f {AY + ЗСХа + DX} — -f {л ^ + — + Av!
2D;i + ? — -^} ~J + {Л.м-.' + By.' + Cjj-3 + Da2
где штрихи обозначают диференцирование относительно z.
14-311. Случай 1(а). При А = С = 0 пусть X, и и v будут
выбраны так, чтобы они удовлетворяли соотношениям
^ + ^- = В, D1 = бсь'2,
7" Д1'
Если D равно нулю, то уравнение линейно. Этот простой слу-
случай мы сейчас рассматривать не будем, предположим, что D
не равно нулю. Тогда X, ш и ;•- определяются в квадратурах, а
преобразование
приводит уравнение к виду
где S (г) может быть выражено через В, D, Е и F.
Чтобы определить, свободны ли решения этого уравнения
от перемещающихся критических точек, допустим, что
где а — произвольная постоянная. Тогда
g = 6К- + a*S (a) + atuS (a) + \ a6u2S" (a) +
Это уравнение относительно V имеет решение, которое может
быть разложено в ряд по возрастающим степеням а
44!
где
v" = 6-у2,
v"r - I2vvr = ~ S(r'(a) (r = 0, 1, 2, 3).
При r > 4 полученное рекуррентное ^равнение более сложно,
в данном случае однако можно ограничиться исследованием
до г = 2 включительно.
Первый интеграл
Vя =
имеет вид
где h — постоянная интегрирования. Общее решение будет сле-
следовательно иметь вид
v = $(u — k, О, И),
где к — вторая постоянная интегрирования
Рассмотрим теперь однородное уравнение
v'r —12р (и —k, О, k)vr = 0;
его общим решением будет
где Сг и С2 — постоянные интегрирования. Неоднородное урав-
уравнение
может быть теперь проинтегрировано методом вариации пара-
параметров; его общее решение будет иметь вид
vr = Ux (и) {и р' + 2 $} -f U2 {и) g)',
где
й v ' 24
Теперь
S-^Hr{u^'(K — k) + 2p(u —,
— 2
следовательно при интегрировании ?Л и ?7, получим выраже-
выражение с log (u~k) при г =2. Отсюда следует, что для того,
442
чтобы решение было свободно от перемещающихся критических
точек, должно быть выполнено условие
S"(a)=O.
Но а — произвольная постоянная, следовательно
S"(Z) = 0,
откуда S (Z) — линейная форма pZ -J- q.
Таким образом, если решения уравнения (а) свободны от
перемещающихся критических точек, то уравнение может быть
приведено к виду
При тривиальных изменениях в переменных это уравнение
приводится к одной из трех стандартных форм
(I) 5 = 6ш2 (при р = 9 = 0),
(II) g? = 6тс= -ь 4" (при р - 0, q Ф 0),
(III)
4
6w^
Первые две из этих форм могут быть проинтегрированы при
помощи эллиптических функций; они дают соответственно одно-
однозначные решения
w = $(z—k, 0, A), w = $> (г— к, 1, И),
где кик — произвольные постоянные. Следовательно решения
представляют собой полутрансцендентные функции постоянных
интегрирования; они не имеют перемещающихся критических
точек, но имеют перемещающиеся полюсы. Третье уравнение
не интегрируется в элементарных функциях (алгебраических
или трансцендентныхI; его общим решением является сущест-
существенно-трансцендентная функция двух переменных. Это уравне-
уравнение следует рассматривать, как определяющее новый тип
трансцендентной функции, свободной от перемещающихся кри-
критических точек.
14-312. Случай I (Ь). Пусть I = 1, <р = z и 2\i.'=2D^ + E
при А = — 2, С = 0, тогда уравнение примет вид
1 Т. е. экспоненциальных, круговых или эллиптических. Далее термин
классические трансцендентные функции или классические трансцендентно-
трансцендентности будет применяться для обозначения класса элементарных трансцендентных
функций и трансцендентностей, определяемых линейными днференциальными
уравнениями.
443
Пусть
тогда уравнение можно написать так
в этой форме оно удовлетворяется соотношением
W = Wo + awx -f аги>2 + ...,
где
w'o = — 2w0 w'o,
Отсюда следует, что
е + 1
где а и с — произвольные постоянные, а
—2 As^d?
! +f{f(o + Qoo)}eJ dz.
Но
+ (Qo - Ро) w\.
и поскольку w\ имеет двойной полюс, двукратное интегрирова-
интегрирование выражения для w1 приведет к логарифмическому члену,
зависящему от а, если P(z0) не равно QB0) Для всех значений
z0, т. е. P(z) и Q(z) должны быть тождественно равны.
Уравнение таким образом приводится к виду
Оно теперь может быть проинтегрировано; его первый интеграл
dw
где
Этот первый интеграл типа Риккати, особые точки функции и
фиксированны, поэтому общее решение имеет фиксированные
критические точки.
Эквивалентная форма уравнения имеет вид
444
так как это уравнение имеет также первый интеграл
где
Общее решение, следовательно, является полутрансцендентной
функцией постоянных интегрирования.
14-313. Случай I (с). При Л = — 3, С= —1, уравнение,
общее решение которого имеет только фиксированные крити-
критические точки, имеет вид
dW
Общее решение его
.... 1 йи
где и (Z) — общее решение линейного уравнения третьего порядка
следовательно, оно является рациональной функцией постоянных
интегрирования.
14 • 314. Случай I (d). При А = — 1, С = 1 пусть
Зи + D = — 3" + ЪВ = ЗР B),
тогда уравнение примет вид
~^ = -W~ + W:i + P{Z){3d~+ W*
Решения, свободные от перемещающихся критических точек,
возникают в следующих пяти независимых случаях.
1 ° R(z) =P (z) — 2Р2 (г), S (г) = 0.
Уравнение может быть написано в виде
его решение получается следующим образом. Пусть
н >¦ ;> 1 4w- — 1 '
тогда
г: = v'jv,
где штрихи обозначают диференцирование относительно z.
445
Принимая
w = <f'(z)W, Z =
где
(
уравнение можно привести к стандартной форме
Уравнение может быть написано в виде
dlw dw
„ C7Q\
его решение получается следующим образом. Пусть
V 4и3 — 12и+ К 2 У 3
где К—произвольная постоянная;
тогда
к—Г
Если
где
уравнение приводится к стандартной форме
3°. Р (г) = |^ + ? B), Я (г) = Р' B) - 2Р* (z) - I2q* (z),
S{z)= -24qs(z).
Уравнение может быть написано в виде
-249» B);
для того, чтобы его проинтегрировать, допустим
и = е(рйг, v = -±ф V= $ (v + К, 0, 1),
где К— произвольная постоянная, тогда
w = Vs Y4VS — 1 + 2
446
При подстановке
w = u'{z)W, Z = y (z),
где
3<р' = Р(г)Ф,
уравнение приводится к стандартной форме
Ч2Г=- Ш^Ж + Wi- 12 ?° (Z' °> !> Г + 12 Р' (Z> °. *)-
4° р^- — ??^ /?Ы- 24г V^= 12
где
<7(г) = 4г' —ez"*;
далее е = 0 и х= 1 или е = 1 и х — произвольна. Уравнение
24s , 12
интегрируется следующим образом. Пусть
w i
+ К ~~ V 4г3 — гг—\ '
где К—произвольная постоянная,
тогда
а'—1
w = .
и — г
Преобразованием
W = w У 4гй — sz — a, Z=$(Z, e, а)
уравнение приводится к стандартной форме
dW = __wdW + w_l2Q{Zt e> a) w+ 12F(Zj з
5°. P(z) = 0, R(z)=—I2q(z), S{z)=\2q'{z),
где q (z) — новая трансцендентная функция, удовлетворяющая
диференциальному уравнению
q" = б?2 + z.
Решение уравнения
имеет вид
и'1г)-дЧг)
и(г)-д(г) >
где u(z) — любое решение
и" = 6йа + z,
отличное от q (z).
447
Следовательно каждое уравнение, которое входит в класс I (d)
и имеет общее решение свободное от перемещающихся крити-
критических точек, приводится к стандартной форме
^ ^ ' —12? (Z) W+
где
(а) ^ равна нулю,
или (8) ^ — постоянная, не равная нулю,
или (т и 5) g (z) — удовлетворяет уравнению
<7" = 6<72 + r, (yj =0 или 1)
или (е) ^ (г) удовлетворяет уравнению
«f = 6g2 + Z.
В (а) — (о) решение является полутрансцендентной, а в (г) — су-
существенно-трансцендентной функцией постоянных интегриро-
интегрирования.
14 • 315. Случай I (е). При А = О, С-1 предположим, что В
также равно нулю и пусть
Х = 1, 2;i = —?>,
тогда уравнение примет вид
Если /?(г) и S(z) — постоянные, например, ,3 и -{, то уравне-
уравнение интегрируется в эллиптических функциях. Если R(z) непо-
непостоянная, то для отсутствия перемещающихся критических то-
точек необходимо, чтобы были выполнены условия:
где 8 и v — постоянные. Подстановка
Z = z + 3
приводит уравнение к стандартной форме
Это уравнение не интегрируется в элементарных трансцендент-
трансцендентных функциях, однако можно показать, что его общее решение
будет свободным от перемещающихся критических точек.
Если В не равно нулю, то единственно возможным является
соотношение
При подстановке
448
уравнение приводится к стандартной форме
14 • 316. Канонические уравнения типа I. Таким образом в ка-
качестве канонических уравнений, характеризуемых L (z, w) = 0,
может быть принята такая последовательность десяти урав-
уравнений:
I. ^ = 0. И. % = 6W* III. ** 6 W + I
= 6 W + -I
IV. J^L ^
L-eW + Z. V.^ = -2Wl
. IX. ^r =
В уравнениях V и VI функция q (Z) произвольная, а в X
определяется так же, как и в § 14 • 314.
14 • 32. Случай II. Уравнение имеет вид
dz2 w \ dz ) \ *• ' w ' w ] dz
+ D(z\ws + E(z) w2 + F{z) w + G(z)-\
Пусть
w = a W, z = z0 + aZ, A (z0) = a0, D (z0) = d0,
тогда уравнение примет вид
1 / dW у, w/ dW , .
= W VdZ i + a" W 4z + J« W + ° (a>'
и будет эквивалентно при a = 0 системе
dW W*
dZ и
du ,.
dZ
При d0 = 0 решения этой системы однозначные; если do^O, то
можно доказать, как и в § 14-31, что единственно возможным
является ао — О. Отсюда следует, что Л (г) или D{z) тожде-
тождественно равно нулю. Аналогично, принимая
w =
можно доказать, как и в предыдущем случае, что C(z) или H(z)
тождественно равно нулю.
Э. Анне—133—29 449
14-321. Канонические уравнения типа II. 1°. При Л = С = О
получим три канонических уравнения
_ 1 / rfU7 \2
W\dZj'
VII d2U/ ! ArfU7Vi IV74 1 O1V72 I I B
Первый интеграл
DJ-ь+KW2>
где /^—произвольная постоянная. Интегрирование может быть
завершено в эллиптических функциях.
d*W l /dW\z l dW , 1 , ту/2 . оч . ,„„ . 6
или, если Z = ег
Это уравнение не интегрируется в классических трансцендентных
функциях.
2°. При АфО, СфО получаем одно каноническое урав-
уравнение
Первый интеграл типа Риккати
где К— произвольная постоянная.
3°. При А — 0, СфО получаем два канонических уравнения
AV- dZ2 ~ u/ Uz J ^ IF rfz + г^^ ^ ^ lz \ r{Z)\-
Первый интеграл
где К— произвольная постоянная.
Первый интеграл
Случай АФО, С — 0 можно вывести из предыдущего, под-
подставляя \\W вместо W. Общее решение каждого канонического
450
уравнения представляет собой полутраисцендентную функцию
постоянных интегрирования, за исключением уравнений XII и
XIII1, которые неприводимы.
14 • 33. Случай III. Уравнение имеет вид
т-Х /Лгу
=
dz2 mw
/Лгу | л в ( j + СЩ to
\ dz J ' [ v ' ' w ' w ) dz l
w* + F (z) w + G B) + --,-}
Пусть
тогда уравнение будет
Здесь, может быть приложен метод, использованный в §14-31,
но можно такие поступить следующим образом. Пусть
тогда при я = 0 уравнение приводится к
и" т " , и
, m -f I ,
+ +
77'2 т + 1 .,
+ 0ы + „ + е + е
Но если критические точки должны быть фиксированы, то пра-
правая часть этого уравнения при разложении на частные дроби
должна быть одной из восьми форм, перечисленных в § 14 • 3,
где W замещено и. Это приводит к нескольким независимым
условиям, именно:
(а) если т неограничено, то
A) функции А (г) и D(z) обе тождественно равны нулю или
(b) при т = 2
(I) A (z) — 0 тождественно, /-> (г) ф 0 или
(И) D(z)=-iA»(z),
(c) при т = 3
(d) при m = 5
451
Принимая w = 1/-У, первоначальное уравнение можно пре-
преобразовать так
d*v m 4-
dz'- rnv
— H{ZLP — G\
Отсюда следует:
(a) если т неограничено, то
(I) C{z) и H{z) тождественно равны нулю или
(II) Н(г)=— j^zpTy Ci B) >
(b) при т = 2,
(I) C(z) и //(г) тождественно равны нулю или
(II) С(г) = 0, а Я(г)ФО.
Рассмотрим в качестве примера случай, когда функции A(z)
и D(z) равны нулю. Если уравнение предварительно преобра-
преобразовать подстановкой
а а приравнять нулю, то уравнение примет вид
mW
Возможно, что E(z) также тождественно равно нулю. При
можно доказать, как и в§ 14-22, что единственно воз-
возможными условиями являются т — 2, т = 4, т = — 4. Анало-
Аналогично, если C(z) и H(z) тождественно равны нулю, то G(z) = 0
или т = 4.
Этот разбор ограничивает число рассматриваемых случаев1.
Продолжая исследование, найдем, что уравнения, решения кото-
которых свободны от перемещающихся критических точек, имеют
канонические формы, указанные в следующем параграфе.
14-331. Канонические уравнения типа III. 1°. При А, С,
D и Н, тождественно равных нулю, получим семь канонических
уравнений
XVIL Ш = ^mW AZJ-
1 Необходимо исследовать четырнадцать случаез, девять из которых суще-
существенно различны. Исследование в полной форме было впервые дано Гамбье.
[Gambler, С. R. Aead. Sc. Paris, 142 A900), 1403. 14U7J; предыдущее исследование,
проведенное Пенлеве, не было исчерпывающим.
452
Общее решение W = {KXZ -f K2)m рационально относительно
постоянных интегрирования Кг и К2-
xvra. &-ЖФ
Первый интеграл
Первый интеграл
(
эквивалентно
что представляет частный случай уравнения IX.
т СНГ 3 .-¦dWV,
XXI. HW^TwVdz) +
эквивалентно
XXIX. dZ2
XXII. ^: = А^
rfZ2 4W\dZJ
эквивалентно
xxin.
эквивалентно
что представляет частньтй случай уравнения XXX.
2е. Если С и И тождественно равны нулю и
+ тА2 = 0, то имеются два канонических уравнения
Решение:
m)(KtZ K2)mq(Z)d(Z)
1 / J1UT4 О О TV/ JIV JVf'i ' / JTU7
453
Решение:
W =
q
2и' + if- — -q— и — r
где u = t'lt, причем t — общее решение линейного уравнения
3 . Если А и D тождественно равны нулю и (/?г — 2IИ
4- жС2 = 0, то имеется каноническое уравнение
XXYI ,~ ==¦
где
q" = 6g
Решение:
2 или q"
W ' dZ
\
W* + \2q]
или q"
V—12q" — ~
= 6q*+Z.
где
у = —fyzz—
и
Q* — 6Q2 ли Q" = 6Q2 + "/, или Q =6Q2 + Z, но
Другие уравнения, когда А и D тождественно равны нулю,
являются частными случаями:
4е. Если т неограниченно и (т — 2JИ + тС2 = 0, то получим
ондо уравнение1. Оно имеет общую форму
mW \dz)
где /, » и tl/ — определенные рациональные функции двух про-
произвольных аналитических функций <7(Z) и r(Z) и их производ-
производных. В частном случае т — 2 каноническое уравнение имеет вид
~Zh dZ 2 +r^>w 2W
а его решением является
W = u'lu,
где
2и'" и' = гг + 2/=«'2 - и2.
1 Этот трудный сличай был особенно подробно изучен Гамбье, [Acta Math.
33A910). 51]. "
454
После диференцирования последнее уравнение становится ли-
линейным, четвертого порядка
-и.
Следовательно при т = 2 общее решение является рациональ-
рациональной функцией постоянных интегрирования.
5°. При т = 2, О=^Л и С тождественно равном нулю, по-
получим уравнение *
XXVIII.
где q и г определяются следующим образом. Пусть, Vx и V2
будут любыми двумя решениями одного из соотношений
<у" = 6-у2, -у" = 6-у2 -\-\ ил и if = 6<иг + Z,
тогда
Решение:
Я \V - у (Fx + V2)\'
где К удовлетворяет тому же уравнению, что Vx и К2. Если
и К2 равны между собой2, то
0= Ит-?—?-, г=0.
1
6е. При /я = 2, Л и С тождественно равных нулю,
имеются три канонических уравнения
1 * dZ* 2W\dZj •" 2 •
1 Этот случай был специально рассмотрен Гамбье, ibid., стр. 49.
2 В общем случае V зависит от двух параметров, например, а и C, и может
быть написано в виде V (Z, а, ?). Кц получается, придавая аи f специальные
значения аг и Pi и условия
к:-к;
где X и {J- — постоянные, отношение которых произвольно.
455
Первый интеграл
XXX. d&
Первый интеграл
(^ГJ= IF4 + 4a IF3 -f 4,3 IF8 + 4KW + f.
XXXI. ^-| = A (gJ + 3|_' + 4ZU72+ 2 (Z2_ и)^ _ |^
не интегрируется в классических трансцендентных функциях.
7°, При т — % А, С и D тождественно равно нулю, НфО
нулю получим три канонических уравнения
XXXII l = ! (У
Первый интеграл
Первый интеграл
XXXIV-
Решение:
где
О
8°. При п — 3, D= -тг А2, Н = —ЗС2 имеется каноническое урав-
4V 2 dWy I 2 TV7 2 r \dW , 2
xxxv-
где 2и: -f 5и + Г представляет 2«3, 2иг+ «и -Ь 3 или 2ип ф Zu +a;
1 Подробно см. Gambier, ibid., 32.
456
поэтому
q" = 2q* + Su + T, r = - -|- 5 - \(q' + q*).
Решение:
w—~ v-q "•
где V—любое решение
V = 2VS + SV + Т.
9°. При п = 5, D=5A2, H = —^-C2 имеем одно каноническое
уравнение
r - dW . 4 IK/. , 14
где
5 / т.;; - ivy
а Уг и V2 — решения
E = 0, 4"
Решение:
где I/ — общее решение К" = 6K+ 5.
14-34. Канонические уравнения типа IV. В случае IV имеем
четыре канонических уравнения1
XXXVII. ^ - >т + ^—j j ^ ; .
Первый интеграл
Решение:
xxxviii. ^ =
—-Л
Garabier, С. R. Acad. Sc. Paris, 143 A906), 741.
457
Первый интеграл
(dWy_
I5z У -
xxxix. ?ii- - <2W + т^лг Irfz; - z"" 52 + zr
+ Z + №'— 1
не интегрируется в классических трансцендентных функциях
rf|IT /J
[2W +W-l)UZ ) f W— \' dZ
где
s' = 2qs, f =~2rt.
Метод интегрирования. Пусть
тогда и определяется уравнением Риккати
и' + и* + 2га - -1 ?> = 4/ г' + SM-
где
г»' = ^(д — г) г>.
Нужно отметить, что если s и t не равны нулю, то
i!l = ?1 + —
следовательно v = /Cs^.
14-35. Канонические уравнения типа V. В случае (V) имеем
два канонических уравнения ~х
~ 2-\ Х л- 1- l.'rf
- 3 \W ' VF-1|Vrf
Первый интеграл
(^'=27/0UP*(И?- IJ.
Решение:
XUl fl— = -J -L + '
1 Gambier, C. R., 144 A907), 827.
458
Зг'— — г (r+s - д)
_
35'— ~
2
W— 1
где
3s = 2К„
а Уг — любое решение уравнения
V = V~ + -|^3 + 4СК2 + 2DK- -§,
где С, D и Е все равны нулю (уравнение XXIX), все постоянные
(уравнение XXX) или C = Z, D = Z2 - а, Е= ,3 (уравнение XXXI).
Если У — обшееЛрешение этого уравнения, то1
W 1 + з
F' - К/- К2 + F,2 - -2- (9 + г - *)(И-Vx)
14-36. Канонические уравнения типа VI. В случае (VI) имеем пять
канонических уравнений
dZ* ~4|W + W^=l{ V. dZj •
Первый интеграл
(j~y = 2o6K\Ws(W - 1)з.
Решение:
XLIV. az^ = ^\w
Решение:
№—1
Более подробно см. Gambier, Acta Math., 33 A910), 38.
459
где
" " >ыA — и%
' ~ W-~\
где
a Vj и К2 некоторые решения уравнения
К" = 2К3 + SV + Г
(уравнение VII, VIII или XI). Если V — общее решение этого
уравнения, то
О W- 1 = 2V— Уг'~ У*1 -АBУ-Уг- V,)
2(y-V1)(V--Vi)
^j/i4 14
— 1 j \dZ ! H^ i ^ 2(W~ \)}dZ ^
/3W" 9H'2\ 1
где
_ 9H'2\ 1 I
2№J~W—1)'
// = 2 (!/,'
a Vx — некоторое решение
VIII. K"=2K3+
Если 1/—общее решение этого уравнения, а
jr = I' ~~Vl' м у+ V
1 у ^i1'
ТО
QT2
w 2Т' + 2Т2 — DС + 4С + ЗЛ) Т + Н
YTVTI
( _ ^
460
\ __ 1 I
.' IV — 1 / '
где
Я = 2 (К/ ф К?) + Z,
a Fj- некоторое решение
IX. \Z"=2K3+Zl/ + a.
Интегрирование производится аналогично XLVI.
14-37. Канонические уравнения типа VII. В случае (VII) уравне-
уравнение имеет вид *
XLVIII. dZ-> =\Ш + 2{W\)) KdZ ) + \Л ^ +Б + W } dZ
—1)'
где
где
a Vj, K2, К3 — некоторые частные решения
К" = 6К2 + S E = 0, -i- или
Решение:
' 2 {Y'~ t'+ (Y — t) и} — {(Г— tf~ v*}'
где
X. У" = — YY' -f У3 — 12 VjY-\- 12K/.
14-38. Канонические уравнения типа VIII. В случай (VIII) вхо-
входят два типовых уравнения, в первом из которых т) — постоян-
постоянная, например а, а во втором2 -q = Z.
xfix ?f =I! | , t _i_ » \r^V
1 Gambler, С R., 144 A907), 962; Acta Math.. 33*(I910), 45.
2 Ibid., 143 A906). 741.
461
Первый интеграл
Общее решение может быть выражено в эллиптических функ-
функциях.
dW,
т d*W __ 1 / 1 , 1 . 1 ) , dWy (I 1__ ,
• dZ2 ~ 2 \ W "*" W — 1 'W—Zj \dZ > \ Z "¦" Z-~ 1 "¦" W
_4_ V(W-l)(W-Z)i IZj. f(Z—1) _ (S-l)Z(Z-l) I
"*" 2Z2(Z— IJ \ ' W2~r(lT~lJ (W —Z)z [¦
В общем случае это уравнение не интегрируется в классических
трансцендентных функциях. При а = C = 7 = 8 = О интегрирова-
интегрирование производится следующим образом. Пусть Л (и, Z) будет эл-
эллиптической функцией, определяемой интегралом
о V w (w — 1) (w — Z)
и пусть 20»! и 2о>2 будут ее периодами, которые являются функ-
функциями Z. Тогда общее решение уравнения будет иметь вид
где /Ci и Kz — произвольные постоянные '.
14 • 39. Заключение. Применение условий, необходимых для
отсутствия перемещающихся критических точек, приводит к
пятидесяти видам уравнения
(dW w
W
где функция F рациональна относительно W и W и аналити-
аналитическая относительно Z. Все эти пятьдесят видов, за исключе-
исключением шести, интегрируются в известных функциях, и общее ре-
решение их не имеет перемещающихся критических точек. Послед-
Последнее верно также и для остальных шести случаев; порядок дока-
доказательства будет дан ниже (§§ 14 • 41 и последующие). Таким
образом, когда указанные ограничения наложены на F, то сово-
совокупность условий достаточна, так же, как и необходима. Упо-
Упомянутые пятьдесят канонических видов уравнения могут быть
обобщены преобразованием
ш _ l(z)w+ m (г) 7
где /, т, р, q и «¦ — аналитические функции г, а новые типы
содержат все уравнения второго порядка, рациональные отно-
1 В общей форме уравнение L было впервые дано Фуксом [R. Fuchs, С. R.,<
Acad. Sc. Paris, 141 A905), 555]. Интегрирование при a, J3, -у и о, равных нулю,
проведено Пенлеве.
462
сительно w и w', общие решения которых содержат фиксиро-
фиксированные критические точки.
Если уравнение алгебраическое относительно w и неприво-
димо к эквивалентному уравнению, в которое w входит рацио-
рационально, то положение совершенно меняется. Это ясно из сле-
следующего примера х
! \
)\idw\2
S \)
1A —W2) 2 (\-~k-W2) 2
Можно доказать, что общее решение этого уравнения не
содержит алгебраических особенностей, кроме полюсов; значи-
значительно труднее доказать, что любое решение, которое стремится
к определенному значению, когда z стремится к z0 вдоль любого
пути, аналитическое или имеет полюс в z0. Но отсюда не сле-
следует, что решение мероморфное во всей плоскости г. Общее
решение имеет вид
'iv — sn{). \og (Az —В)} (mod k)s
где Л и В — произвольные постоянные. Точка г —В/А — суще-
существенная особенность решения; когда z стремится к В- А вдоль
некоторого определенного пути, w не стремится ни к какому
пределу.
Этот пример ясно показывает, почему необходимые условия
могут быть недостаточными, и следовательно, почему для того,
чтобы отсутствие перемещающихся критических точек было
оправдано, каждое из пятидесяти канонических видов уравнений,
полученных в предыдущих параграфах, должно рассматриваться
отдельно.
14 • 4. Трансцендентные функции Пенлеве. Из пятидесяти
упомянутых видов уравнений наиболее важными являются непри-
неприводимые 2, которые являются источником новых трансцендентных
функций. Эти неприводимые уравнения обозначены IV, IX, XIII,
XXXI, XXXIX и L; их удобно расположить следующим образом
(I) -5- - 6 к>а + z, (II) ^ - 2к-з + г«< + а,
у ' аг- ' v ' ёгг
<Pw ! /:iH!\2 1 dw . 1 , ., , о\ i 4 1*
IЛ) 17 + г
tiz* 12»тг-Т)Ь-.'гУ z
ш(» + 1)
"
r^ ш(» + 1)
г ' ~ w—i""'
1 Painleve, Bull. Soc. Math. France, 28 A900), 230.
2 Под неприводимым подразумевается уравнение, которое не может быть
заменено более простым уравнением или системой более простых уравнений.
463
2WTm-l
П
l г
dw 4- w(w— l)(w — г) („ ¦ ?z ,
' г2(г— lJ И ' к»а '
\ 4
г—1 ' z —Jti rfz ' г2(г— lJ
,7B—0 , В?(?—1I
"•"(да -IJ ^ (да —гJ> "
Новые трансцендентные функции, определяемые этими урав-
уравнениями, называются трансцендентными функциями Пенлеве1.
Решения (I), (II) и (III) не имеют точек разветвления и следова-
следовательно являются однозначными функциями z. Если в уравнениях
(IV) и (V) изменить независимую переменную преобразованием
z = е?, то' решения будут однозначными функциями z. Но в урав-
уравнении (VI) точки z = О, z = 1 и z=oo являются критическими.
Уравнение (VI) содержит первые пять уравнений, которые
мо гут быть из него получены 2.
Поскольку можно доказать, что решения (I) являются новыми
трансцендентными функциями, отсюда следует, что решения
остальных пяти уравнений (исключая специальные значения а,
8, у и й) не могут быть выражены посредством только класси-
классических трансцендентных функций.
Постепенное вырождение может быть проведено следующим
образом.
В уравнении (VI) подставим 1 + ez вместо z, ~ вместо о, -1
вместо у, и пусть е—»0. Предельной формой этого уравнения
будет уравнение (V).
о
В уравнение (V) подставим 1 + -<?' вместо к1, — 4|-вместо р,
-2- -\- ^- вместо a, vs вместо у и8е вместо В. В пределе, когда г —»0,
получим уравнение (III).
Аналогично в уравнение (V) подставим гш у 2 вместо w,
1 + ?Z у~2 вместо z, ^ вместо а, — -^ вместо 7, — i.jzi + s{! вме-
вместо й. В пределе получим уравнение (IV).
В уравнение (III) подставим 1 +?2г вместо z, 1 -\-2sw вместо
w,-rrti- вместо 7,— g вместо 8,— -6- вместо а,—Л-[-- вместо 3.
В пределе получим уравнение (И).
Аналогично уравнение (II) может быть получено (предельным
переходом) из (IV) подстановкой-^- — ^г вместо z,2~ ew+
вместо w, — g^—а вместо а, — 9 12 вместо 3.
1 Только первые три типа были найдены Пенлеве, последние три типа были
позднее найдены Гамбье.
2 Painleve, С. R. Acad. Sc. Paris, 143 A906), II!I. '"ешения (VO в соседстве
с особой точкой были исследованы Гйьнье. IGarnier. С. R., 1G2 (li.lC), 939, 163
A916), 8, 118]. '
464
Наконец, в уравнение (II) подставим e2z — TlT вместо z,ew + ~
4
вместо w, -^ вместо а, и в пределе получим уравнение (I).
14 • 41. Первая трансцендентная функция Пенлеве; отсутствие
перемещающихся точек разветвления. Рассмотрим более подробно
уравнение
(I) ?? =6 <«•+*,
которому удовлетворяет первая трансцендентная функция Пен-
Пенлеве. Докажем, что его общее решение не содержит перемещаю-
перемещающихся критических точек \ Основной принцип метода может
быть приложен к пяти уравнениям, определяющим остальные
трансцендентные функции.
Сначала покажем, что это уравнение допускает решения,
содержащие перемещающиеся полюсы, но не содержащие точек
разветвления.
В соседстве с некоторой произвольной точкой z0 уравнению
удовлетворяет ряд
+ ~zl(z-zor+...,
где h — второй произвольный параметр; этот ряд может быть
также написан в виде
z(zz2 ^Z *)"+ A(zzy +
{
Исключая z — z0 из последнего ряда и ряда для w', именно
Z0 \Z Z0) T" • • •
да д
4h (z - zoy
+ *0 zl(z-zof+...,
и принимая w = v~2, найдем, что
3
¦ну' = — 2&v y + +
гле е= +1. Принимая2
w = v~2, w'= — 2tJ-s — -^ zv — у v2 + иг,
1 Painieve, Bull. Soc. Math. France, 28 A900), 227; C. R. Acad. Sc. Paris, 133
A902), 411, 641,457,1020.
2 Можно также сделать преобразование
w = v, w' = 2v S— — zv — 1 v2 + uvs,
2 2
Э. Айне—133—30 405
уравнение (I) может быть преобразовано в систему
Aа)
Эта система имеет единственное решение, аналитическое
в соседстве с z0, и удовлетворяет начальным условиям и = ы0,
"У = 0 при z = z0.
Соответствующее решение «/(z) имеет полюс в точке z0, a
, 1
постоянная п равна -„ и0.
Таким образом общее решение имеет перемещающийся полюс
в некоторой произвольной точке z0. Ни одно решение не может
иметь алгебраической точки разветвления в некоторой точке г1з
так как если A{z — zt)r — главный член решения, имеющего ал-
алгебраическую особенность в гъ то г должно быть равно — 2, а
решение будет аналитическим в соседстве с гг.
14 • 42. Отсутствие перемещающихся существенных особенностей.
Теперь нам нужно показать, что ни одно решение уравнения (I)
не может иметь перемещающейся существенной особенности
в конечной части плоскости1. Для этого докажем ряд предвари-
предварительных теорем, относящихся к специальным решениям (I).
Пусть w{z) будет частным решением, которое принимает ко-
конечное значение w0, в то время, как w'(z) принимает конечное
значение w0' при z = z0. Эю решение аналитическое в соседстве
с z0. Пусть Г будет наибольшим кругом с центром в точке z0,
внутри которого w(z) не имеет никаких особенностей, кроме
полюсов. Если радиус Г бесконечен, то решение не имеет су-
существенной особенности (за исключением бесконечно удаленной
точки). Если бы радиус Г был конечным, то на окружности Г
была бы существенная особенность w{z). Покажем, что это до-
допущение не соответствует действительности.
Предположим, что z=a—существенно особая точка и пусть М
будет верхней границей \w(z)\ и \w'(z)\, когда z стремится к а
вдоль радиуса zoa. Далее решение w(z) таково, что М конечно.
Тогда, если z1 — точка на радиусе, w(Zj) = wv w'{z1) = w[, ae —
произвольная величина, то
\w — Wj\l< A, \w' — w'| < А, когда \z — zt\ < г, \гг — a\ < e,
ч
где А конечно. Теперь (I) может быть написано в виде системы
dw
dz
dw'
—г-
dz
1 Необходимость этого исследования видна из примеров §§ 14- 1, 14-39.
466
причем правая часть каждого уравнения этой системы ограни-
ограничена для всех конечных значений z,w и w'. Согласно фунда-
фундаментальной теореме существования (§ 12-2), должно существо-
существовать решение w{z), удовлетворяющее данным начальным усло-
условиям относительно zlt и аналитическое во всем круге \z — zj =e.
Решение будет таким образом аналитическим относительно а,
что противоречит принятому условию. Следовательно необхо-
необходимо предположить, что если а-—существенная особенность, то
\w(z)\ не ограничен вдоль zba.
Покажем теперь, что если iz>(z) — любое частное решение (I),
так что \w(z)\ не ограничен вдоль z^a, то точка а будет полю-
полюсом w(z) при условии, что существует последовательность то-
точек г{ на радиусе с предельной точкой а, так что \w(z)\ неог-
неограничен.
Возвращаясь к преобразованию
о
u{z) = ± wA J-+ ^1 + ЪФ + \ zw,
которое эквивалентно
и = v~s (w' + 2v
или
г О 1 1 ч
и = — v \w' — 2v~ —ryzv + -у'У2 ';>
где w = гГ, видим, что если w — решение, имеющее полюс
в точке с, то и в соседстве с а определяется так, что
u(z) = 7h-{-O{(z- of}.
Теперь, допустив, что для одного из значений и !«(%)! < С,
получим, что при z = zx одно из выражений
' + 2v~s + ~zv + i-я* \ , v 3 (w' - 2v~s -\zv + \-
будет иметь модуль меньше С. Предположим, что первое из
этих выражений удовлетворяет данному условию и преобра-
преобразуем (I) подстановкой
2 , _з 1 1ч
Полученная система Aа) будет иметь решение u{z), v(s), так
что u,<v принимают заданные начальные значения ult vt при z =
= zv Тогда, если е — малая величина
\и — щ] < К, '"V — Vj\ -с К при \г — г,| < е, |г, — а\ < s,
гле К— конечно; отсюда, согласно фундаментальной теореме
существования, следует, что u(z) и v(z) — аналитические во всем
круге \z — а\ = е. Следозательно w(z) имеет полюс в а.
4С7
Можно найти любое число функций U(z), имеющих такое же
свойство, что и u(z), именно: если для точек z1 на zoa с пре-
предельной точкой a \U(Zj)\ всегда ограничен, когда iwiz^l не огра-
ограничен, то w(z) имеет полюс в а. Такая функция может быть
построена и будет иметь преимущество рационального выраже-
выражения относительно z, w,isf.
Двузначная функция
и = w- (w' + -к "w~l' + 2гс|3 + — zw
такова, что если w имеет полюс в z0, то одно из двух опреде
лений и принимает произвольное значение 7Л при z = z0. Неза
висимо от того, какое определение правильно, и удовлетворяет
уравнению
W -т- 2 .ч- -h 2 Za ll . / j \ , 2 +
я
W- B + \- zw~" - uw~')} = 0.
Левая часть этого уравнения при разложении свободна от
дробных степеней w и может быть написана в виде
w'2 + 'W — 4та'3 - 22r^ + 4" + ¦ ¦ ¦ >
где опущенные члены содержат 11Г1, -w~2 и w~ , но не содер-
содержат w'. Пусть
и = w l -р -
тогда, подставляя вместо w ряд
10 и
найдем, что
При U'(z0) = 0 значительно усложняется работа. Для устра-
устранения этого пусть
V(z) = i/(z) +г,
тогда в соседстве с z0
V{z) = - 28// + z + O{{z- zof} = - Au{z) + z + O(w~J),
где и (z) — значение и, конечное в z0. Поскольку u'(z0) = 0,
V\z) = 1 + О (z - z0).
Пусть zx будет некоторым значением z, для которого \w\ не
ограничен, но \V\ ограничен; тогда соответствующее значение
¦w' будет любым корнем уравнения
w 2 -f- w w л — 4да3 — 2zw + z = V.
46S
Соответствующее значение и определяется выражением
;е>'2 + ш V - 4ws - 2zw + O(za^) = - 4м,
следовательно l^fz^j ограничен.
Поэтому, если существует последовательность точек Zy на
радиусе г„с, с предельной точкой а, так что \w{z)i не ограни-
ограничен, но |V(zi)[ ограничен, то для одного определения u(z) \u{z^)\
будет ограничен, следовательно w(z) будет иметь полюс в точке а.
14 • 421. Основное доказательство в случае, когда \w\ имеет поло-
положительную нижнюю границу. Здесь мы введем очень важное ограни-
ограничение, которое позже устраним,?именно: если w(z)-~решение, имею-
имеющее существенную особенность в точке а, то для всех точек
на радиусе zoa, \w(z)\ > р. При этом должна быть некоторая
последовательность точек zx на радиусе, такая, чтобы \V{zx)| был
не ограничен. Если бы \w{z-^\ и \У(гг)\ были ограничены, то.
согласно определению V, \ш {z^\ был бы ограничен, a w(z) была бы
аналитической относительно а. С другой стороны, если бы
1^(^I был ограничен, a |wBx) не ограничен, то, согласно заключи-
заключительной теореме предыдущего параграфа, функция w(z) имела бы
полюс в точке а. Таким образом, если а — существенная
особая точка, то последовательность точек zl3 для которых \V(zj)
не ограничен, несомненно существует.
На основании этого докажем, что существует другая после-
последовательность точек z2, имеющих а в качестве предельной точки,
таким образом, что |V(z2)l произвольно мал. Рассмотрим выра-
выражение
у 2w'w" + w~' w" — w~2w'2 — \2w*w' — 2zw' —2iv+ 1
V w'- + w~x iv'
—4w3 — 2zw + z
4w3
Если бы \W\ был ограничен на радиусе г^а, то \V[ был бы
ограничен, даже для последовательности точек z1( что не соот-
соответствует действительности. Следовательно последовательность
точек г2, произвольно близких к а, должна существовать так,
чтобы |H?(z2)| не был ограничен. Более того; \w(zz)\ также не-
неограничен, так как, если \w(z2)\ и |гу'BгI будут ограничены, то
,V(z2)l будет произвольно мал, a w{z) будет аналитической от-
относительно а; если \w(z2)\ ограничен, a |<zc'B:2)l неограничен, то
|P7(z3)j будет ограничен^что противоречит сделанному допущению.
Теперь, если мы исключим w' из выражений V и W, то
найдем, что
j_
Xi' --Vх + 0{w 2),
и поскольку для последовательности точек г2, имеющих пре-
предельную точку a, \w(z2)\ и |WB2); неограничены, |V(z2I произ-
произвольно мал. Из предыдущего параграфа следует, что w{z) имеет
полюс в точке z = а.
Случай, когда w(z) стремится к единственному пределу g,
в то время, как z приближается к а вдоль радиуса, может быть
сразу устранен, так как предыдущее исследование не изменя-
изменяется, за исключением несущественного элемента в выражении
для V, где член w' w замещается w'jw— g). В частности, до-
доказательство справедливо, если вместо того, чтобы иметь по-
положительную нижнюю границу, \w(z) был бы равен нулю при
z =¦-= а.
Выбор радиуса zoa в качестве линии приближения к а не
существен для доказательства; любая кривая конечной длины,
заканчивающаяся в а, ни одна точка которой (исключая aj не
является существенной особенностью w(z), была бы пригодна.
14 • 422. Случай, когда нижняя граница \iv(z)\ равна нулю. Вы-
Выше мы уже рассмотрели все возможные случаи, за исключением
одного, именно: на радиусе zoa существует последовательность
точек %, имеющих предельную точку а, так что |?c(zi)| < Р> и
другая последовательность точек г2, также имеющих предель-
предельную точку а, при которой* \w{z2)\ > р. Покажем, что даже в этом
случае а является полюсом ?o(z).
Пусть Х1( >.,,... будет последовательностью неперекрываю-
неперекрывающихся сегментов радиуса zoa, в конечных точках которых |!1ш(;г)|=р
и внутри которых \w{z)\ < р; пусть /j,/2,... будут длинами этих
сегментов. Существование последовательных точек г2 означает,
что число интервалов X бесконечно. Покажем, что каждый сег-
сегмент >.v может быть замещен изогнутым сегментом Л„ длины /., ,
где 1 </,,//, < Зтг, вдоль которого \w{z)\ == [>, причем в области
между X, и А, функция w(z) — аналитическая.
Если z рассматривать как зависимую, a w как независимую
переменную, то уравнение (I) принимает вид
AW-
Пусть Z', будет конечной точкой X., и пусть W-, будет соответ-
соответствующим значением w{Z), так что \w^ \ = р. Пусть z(w) будет
решением (Ib), так что
Если Z, = 0, то решением будет лишь z = Zv ; оно не содер-
содержит w и поэтому не соответствует никакому решению w(z)
уравнения (I). Следовательно можно предположить, что z'(W^)-:' 0.
Но если ?—положительное число < -}-, то может быть найдено
такое число т, при котором, если
!«¦¦ -:: р, |Z.;| < г,
470
то
где о является аналитической относительно w и Zv', а
Когда z описывает отрезок Xv, w описывает кривую С„ в пло-
плоскости да; эта кривая Cv будет лежать внутри некоторого кру-
круга Г, радиуса р, описанного вокруг точки w — 0; начальные и
конечные значения w будут соответствовать точкам на окруж-
окружности Г.,. Пусть S-, обозначает длину Cv. На радиусе zoa пусть
z = а -\-гё",
где а — постоянная, тогда
dw
где кривая Cv — путь интегрирования. Поскольку
отсюда следует, что
Теперь пусть да опишет меньшую дугу 1\ между конечными
точками С,, пусть ov будет длиной этой дуги, а /г, длиной ее
хорды, тогда
Но
т. е.
следовательно
1 < -г < Зтс.
Поскольку функция г'(да) аналитическая и не равна нулю
внутри круга 1\ и на его окружности, w(z) не будет иметь по-
полюсов в области между кривой av и сегментом 1Ч. Но так как
w(z) не может иметь никаких особенностей в этой области,
кроме полюсов, то X, может быть деформирована в Л^, не
встречая на своем пути никакой особой точки w(z). Таким об-
образом, если каждый сегмент Х„ заменить соответствующей ду-
дугой Л„, то образуется путь Л, ведущий от z0 к а, составленный
471
из бесконечного числа дуг, общая длина которых не превышает
Зтг/?, где R — длина радиуса zoa. Для -всех точек пути Л
| W{Z) | > р,
причем предполагается, что w(z) имеет в своей конечной точке а
существенную особенность. Однако в предыдущем параграфе
мы показали, что это невозможно, следовательно функция w(z)
не имеет существенной особенности ни в одной конечной
точке плоскости z.
14 • 43. Представление трансцендентной функции, как частного
двух целых функций. Пусть w(z) будет первой трансцендентной
функцией Пенлеве, тогда
если
отсюда следует, что
dz
a u(z) удовлетворяет уравнению
Поскольку единственными особыми точками w(z) являются по-
полюсы, при которых разложение принимает вид
единственные особенности vj(z) будут простыми полюсами.
Пусть
тогда функция C(z) однозначна, так как, хотя J -qdz бесконечно
многозначен, его значения различаются на 2м. Но С (г) не имеет
полюсов и следовательно является целой функцией z.
Таким образом функция w(z) может быть выражена в виде
;-г-2 ''?н
.-Т'' ( —1 '^
где числитель и знаменатель — целые функции z.
14 • 44. Произвольные постоянные, входящие в трансцендентную
функцию. Покажем, что трансцендентная функция Пенлеве явля-
является существенно трансцендентной функцией двух постоянных
интегрирования. Она не может быть рациональной функцией
двух параметров, так как в этом случае решение уравнения
dz-
472
d-w „ „ ,
2 = бтс2 -}-
полученное из (I) подстановкой a.z вместо 2 и a—2-w вместо w>
также было бы рациональным относительно постоянных инте-
интегрирования. Но при а=0 решение
«/=Hz + P, С Т)
нерационально относительно C и ?. следовательно оно нерацио-
нерационально и относительно своих параметров при аггО.
Предположим, что то>B)— полутрансцендентная функция по-
постоянных интегрирования, тогда уравнение (I) допустило бы
первый интеграл, являющийся полиномом от w и w', например
P(Z, W, w') = w'm + Qi B, W) W'm~l + ...+ Qffl-l (Z, W) W' +
Поскольку решение этого первого интеграла, т. е. трансцен-
трансцендентная функция, не имеет перемещающихся точек разветвле-
разветвления, Qt — полином w степени не выше 2г. Подставим zo + az
вместо z, a~zw вместо w и a.—3 w' вместо w', тогда
Р{г, w, w') = a-k Po (w, w') + Q (a-ft J) (k > 3m),
где P0(w, w') — однородный полином от \f w', \/w.
Ho Po = 0 — первый интеграл уравнения
w" —
следовательно
P0 = K(w'2
где К и у—постоянные. Легко доказать, что
и что соответственно Qm(z, -w) степени -~- т относительно w.
Функция w (г) имеет перемещающиеся полюсы, в соседстве
с которыми имеется соотношение вида (§ 14-41)
8 1 8
¦w' + -„ (-••• = ± Bгу а -f —л- zw 2 — 7/ггс1 ' + ...)
(h — постоянная), где целые и дробные степени w расположены
в разных частях уравнения. Для больших значений -w в такой
форме может быть выражен каждый корень w' уравнения
P{z, w, и/)=0,
следовательно
PB,W,-W') = Y
473
что невозможно, поскольку правый член не является полиномом
от w. Следовательно первая трансцендентная функция Пен-
Пенлеве является существенно трансцендентной функцией, завися-
зависящей от двух параметров.
Все же можно было бы предположить, что уравнение (I)
имеет частные решения, которые входят алгебраически или
могут быть выражены в классических трансцендентных функ-
функциях. Если бы решение w{z) было алгебраическим, то его
можно было разложить для больших значений \z\ в ряд вида
w = а/ + a^z1 х + ау_^~2+...
Если бы v было отрицательным или равнялось нулю, то w и w'
были бы конечны для z = со, следовательно уравнение не было
бы удовлетворено. При v > 0, v должно быть целым числом.
Предположим, что w (z) — классическая трансцендентная функ-
функция; она должна удовлетворять алгебраическому диференциаль-
ному уравнению, отличному от (I). Исключая высшие производ-
производные между (I) и выведенными из него уравнениями, с одной
стороны, и новым уравнением — с другой, получим, уравнение
вида
Р(г, те-, 0 = 0,
где Р— полином от те» и w'. Но мы показали, что это невозможно,
следовательно не существует частною решения, которое могло
бы быть приведено к известной функции.
14 • 45. Асимптотическая зависимость между первой трансцен-
трансцендентной функцией Пенлеве и эллиптической функцией Веиерштрасса.
Несмотря на то, что первая трансцендентная функция Пенлеве
является существенно новой функцией, все же она асимпто-
асимптотически связана с эллиптической ^-функцией1. Это свойство
аналогично свойству функции Бесселя Jn{z) при больших зна-
значениях2 \z\
¦4 ^} ~ ^j'cos^-
Уравнение
при у. = 1 не отличается существенно от уравнения, удовлетво-
удовлетворяемого трансцендентной функцией. Произведем преобразование
1 1
•7'1 = 7 W У = - Z
U. ^ W , /^ р| + | -
1 Уиттекер и Ватсон, Курс современного анализа, § 17 ¦ 5; Walson, Bessei
FuiK-tlons, §7-1.
" Boutrotix, Ann. Ее. Norm., 3 A913), 255; 31 A914), 99. Вторая трансцен-
трансцендентная функции Пенлеве (уравнение II, § 14 - 4) асимптотически связана с
эллинтическеш функцией sn (г) Якоби.
474
тогда уравнение примет вид
/г с
Последнее уравнение можно сравнить с уравнением
^-4 = 61^-6,
общее решение которого имеет вид
V = $[Z-$, 12, v;f
где |3 и Y — постоянные интегрирования. Из этого сравнения
следует, что для больших значений \Z\
W-S4Z-?, 12, т)
и что, если w{z)-—трансцендентная функция Пенлеве, то
w{z)~$D-zl~—B, 12,
\5
Этот вопрос был тщательно исследован Бутру, который
определил область, где асимптотическое соотношение для опре-
определенных значений 6 и т име.:т смысл (подробное доказательство
дано в указанной выше статье).
В заключение можно привести теорему, данную Пен-
леве; уравнение
¦w (z) = Л
имеет бесконечное число корней для некоторого значения по-
постоянной А.
14-5. Уравнения второго порядка алгебраические относительное.
Общая задача нахождения необходимых и достаточных условий
для того, чтобы общее решение уравнения
не имело перемещающихся критических точек, когда функция F
рациональна относительно р, алгебраическая относительно w
и аналитическая относительно z, требует применения теории
алгебраических функций1.
1 Нужно отметить, что если уравнение гмражеао в виде
—^-= *(г, w. к, р),
где функция Ф — рациональна относительно к1, и и р, а w и и связань: соот-
соотношением
И (г, да, н) = О,
где Н—полином о г w и и, коэфициенты которого аналитические функции г,
то род зависимости /У = 0 равен 0 или 1. Если род равен нулю, уравнение
приводимо к одному из перечисленных пятидесяти родов; если род равен еди-
единице, уравнение относится к одному из трех новых классов.
475
Независимо от перечисленных типов, имеются .еще три типа
уравнений, критические точки которых фиксированы. Они имеют
вид
v ' йгг 4да3 — g%w — gs\ dz , ^ ' dz v/r ъ- to->
йгг 4да3 — g%w — gs\ dz ,
Это уравнение эквивалентно системе
поэтому его решение является полутрансцендентной функцией
постоянных интегрирования. Изменением переменных система
может быть приведена к виду
4Z = u
следовательно она эквивалентна уравнению
QW3
dZ* 4W* — g.W — gz\ dZ
(§ 14 • 38, уравнение XLIX).
L (L + J 4 L l ( *' V
L _l (
W1 rf22 " 2 1© t да —1 + да— г/l rf2 У I г ^г— 1
. 1 Л dw , w(w — 1)
+ -^Гг) Ж + 27G-1)> =
Общее решение поэтому является существенно трансцендентной
функцией двух постоянных; оно может быть получено следую-
следующим образом. Пусть щ{г) будет любым решением
2г — I
U ; -¦
пусть функция Л {и, г) определяется инверсией
dw
/т
W(W — 1) (W — 2)
— = U
и пусть 2CO-J, 2ш2 будут ее периодами, тогда общим решением
рассматриваемого уравнения будет
и = Л (hj -f /Cjtoj + /Сьсо2, г),
476
где Кх и Кг—постоянные интегрирования. Следовательно урав-
уравнение не приводит к какому-либо новому типу трансцендентной
функции.
4w» — gzw-gs со У 4w3 — g.M> — g3\ { dz ) ' ^Z' dz
+ Г (z) V 4w" — g~w —1[з ,
где 2ш — любой период tf {и, g2, gs). Уравнение эквивалентно
системе
таким образом его решение является полутрансцендентной функ-
функцией постоянных интегрирования. Данная система может быть
преобразована в систему
dZ
dU __ Ы ,/2
dZ ~ ш '
следовательно первоначальное уравнение эквивалентно
что является простейшим уравнением этого частного типа.
Возникает другой вопрос, который здесь не может быть
подробно рассмотрен, именно: возможно ли особое решение
уравнения, критические точки которого не фиксированы1, если
общее решение этого уравнения свободно от перемещающихся
критических точек?
Следующий пример показывает, что это может иметь
место. Общее решение уравнения
•w" = —¦ wsw' -f- ww' |/ Aw' -j-
имеет вид
w = A tg (A*z + B);
особое решение __
/"~ '
З(г-С)'
где А, В и С — произвольные постоянные.
1 Chazy, С. R. Acad. Sc. Paris, 148, A909), 157.
477
14-6. Уравнения третьего и высших порядков, а-метод Пен-
леве, давший возможность полного исследования уравнений
второго порядка, может быть приложен к анализу уравнений
третьего и высших порядков1.
Как и выше, метод делится на две ступени: определение
условий, необходимых для отсутствия перемещающихся крити-
критических точек, и последующее доказательство достаточности
этих условий. Можно распространить этот метод для опреде-
определения,необходимых условий, но трудность доказательства до-
достаточности этих условий увеличивается с увеличением порядка
рассматриваемых уравнений.
1 Painleve, Bull. Soc. Math. France, 28 A900), 252; Chazy, C. R. Acad. Sc.
aris, 145 A907). 305, 1263; 149 AS09), 563; 150 AS10), 456; 151 A910), 203; 1?5
(IS12), 132: Acta Math., 34 AS11), 317; Gamier, C. R, 145 AS07), 308; 147
A908). G15; Ann. "Ёс. Norm. C), 29 A912), 1.
478
ГЛАЬА XV
ЛИНЕЙНЫЕ УРАВНЕНИЯ В КОМПЛЕКСНОЙ ОБЛАСТИ
15 • 1. Предварительное исследование особых точек- Рассмотрим
ряд уже установленных теорем, относящихся к однородному
линейному уравнению порядка п
(А) ?? + Р, (г) ^Г +... + р^ <*) t + Vn (z) w = 0.
Пусть z0 будет некоторой точкой, в соседстве с которой п коэ-
фициентов аналитические. Согласно теореме существования
§ 12-22, имеется единственное решение, которое вместе с его
п — 1 производными принимает некоторые значения при z = z0.
Это решение может быть выражено в виде степенного ряда
относительно z — z0, который сходится внутри круга с центром
в z0 и окружность которого прьходит через особую точку коэ-
фициентов, лежащую наиболее близко к z. Иначе говоря, осо-
особенностями решений могут быть только особенности уравнения,
поэтому, если уравнение линейно, то перемещающиеся особен-
особенности и даже перемещающиеся полюсы возникнуть не могут.
С другой стороны, общая теория линейных уравнений с ве-
вещественными коэфициентами, рассмотренная в главе V, может
быть полностью перенесена в комплексную область с некото-
некоторыми формальными изменениями в доказательстве. В частности,
если
wlt тс2,.. .,wn
представляют п независимых решений, образующих фундамен-
фундаментальную последовательность, то вронскиан
b(wly w2... .,wn)
не может обратиться в нуль при г = z0.
Поскольку
г
А = Доехр { — /рг(г) dz},
где До —значение А при z = z0, а путь интегрирования ограни-
ограничен в области, содержащей z0, внутри которой функция рг (z)
аналитическая,— очевидно, что Д не можег обратиться в нуль
ни в какой точке, кроме особой точки Pi{z).
Точка в бесконечности может быть или не быть особой точ-
точкой в зависимости от того, имеют ли коэфициенты уравнения,
479
полученного подстановкой
и последующим приведением его к форме (А), особенности в
начале.
Таким образом особые точки могут быть найдены рассмот-
рассмотрением уравнения. Для любой неособой точки можно найти
фундаментальную последовательность п независимых решений.
Необходимо определить, существует ли фундаментальная по-
последовательность решений, относящихся к любой данной особой
точке и, доказав существование этих решений, исследовать их
поведение в соседстве с особой точкой. Это исследование при-
приводит к так называемой теории Фукса линейных диференциаль-
ных уравнений1.
15-2. Замкнутые контуры, содержащие особые точки. Предпо-
Предположим, что коэфициенты уравнения (А) однозначны и имеют
только изолированные особые точки. Пусть
будет фундаментальной последовательностью решений и пусть
zn будет любой обыкновенной (т. е. неособой) точкой урав-
уравнения.
Проведем простой замкнутый контур -(, начинающийся и за-
заканчивающийся в z0, не проходящий через какую-либо особую
точку, но возможно содержащий внутри себя одну или несколь-
несколько особых точек. Пусть после того, как переменная z описала
контур в положительном направлении, последовательность wv
icz ,wn преобразуется соответственно в Wlt W2,---,Wn. Опре-
Определение Wv W2,.. .,Wn может быть проведено процессом анали-
аналитического продолжения с конечным числом ступеней2.
Поскольку коэфициенты рх (z), p2 (z),..., рп (z) не изменя-
изменяются при построении этого контура, уравнение в целом не изме-
изменяется, т. е. функции
W» W2,...,Wn
являются решениями (А); они могут быть поэтому выражены
линейно посредством фундаментальной системы wu wi,...,'wn
следующим образом
Wt = auw1 + О!2гг;2 +... -f alnwn.
(В)
a22w, + ... + a2nwn,
c2 -f... + annw
mi **"' П7
1 Riemann (Posthumous Fragment. 1857), Ges. Werke B изд.), 379; Fuchs. J.
fiir Math. 66 A866), 121; 68 A868), 354 (Ges. Werke, 1, 159. 205).
2 Если длина окружности равна /, а расстояние между некоторой особой
течкой до некоторой точки на окружности больше d, то число необходимых
ступеней будет не больше Л', где А'—целое число больше l/2d и ближайшее
ft UfslUX''
к нему
480
где коэфициенты а — численные постоянные.
В любой точке z на контуре
г
Л (wlt w2,.. .,wn) = До exp { — fpx (z) dz},
причем интеграл описывается от z0 к z и вдоль ветви контура,
по отношению к которой внутренняя часть контура находится
слева. Пусть Дх будет значением вронскиана, после того как
описан полный контур f. тогда
Д1 = \exp{-fp1(z)dz}
- 2пг7? '
= е д0,
где R — сумма вычетов рх (г) относительно полюсов, лежащих
внутри контура. Так
MWlt Wa,...,Wn)
не равно нулю при z = г0> и поскольку в некоторой обыкновен-
обыкновенной точке z
IFj, W2).. .,lFn образуют фундаментальную последовательность
решений.
Необходимо отметить, что
Теперь, поскольку эти предварительные результаты установ-
установлены, можно определить постоянные \, Xg,.. .,Х„ так, чтобы ча-
частное решение
U ¦= ijWt + >2гС2 + . . . + l.nWn,
после того как контур был полностью один раз описан, при-
приняло значение su, где s — численная постоянная. Пусть, после
того как контур был полностью описан, и преобразуется в U,
тогда
так что, если U = su, то
п
s (кхп\ + l2w2 + ... + ).„«'„) = ^ >.,. («,¦!«'! + araw2 +... + arnwn).
Это соотношение справедливо и следовательно
(С) sAr = кга1Г + >.2а2Г +... + Ъгагг +... + 1папГ
(г=1,2,...,л)
Э. Айне—133—31
Если из этой последовательности совместных уравнений мы
исключим неопределенные постоянные Хг, то найдем уравнение,
определяющее s, именно
\аи — s, а21,...,апХ\ = О
i ai2> а22 s,... ,ап2
Это определяющее уравнение называется характеристиче-
характеристическим уравнением выбранной системы. Оно не может иметь ну-
нулевого корня, так как в этом случае |ars| равнялся бы нулю.
что противоречит условию, что выбранная система является
фундаментальной. Некоторому значению s, удовлетворяющему
характеристическому уравнению, соответствует последователь-
последовательность постоянных \lt \,...Дп, отношения которых могут быть
вычислены из уравнений (С). Они приводят к решению и, опре-
определенному независимо от постоянного множителя, которое,
после того как точка z полностью описала контур ?, принимает
значение su.
Характеристическое уравнение инвариантно, т. е. не зависит
от первоначального выбора фундаментальной системы. Пусть
vlt v2,...,vn
будет фундаментальной системой, отличной от первоначально
выбранной; она должна быть связана линейной зависимостью
следующим образом
+ +... +cmwn,
... +c2nwn.
vn = cnlwt+ cn2w2 +... +cnnwn,
где коэфициенты crs — постоянные, так что |crs| =J= 0- Предполо-
Предположим, что после того как контур был описан, решения vlt <v2,.. .,vn
соответственно равны Vu V2,...,Vn, тогда
V2 = Ailv1 + Ai2v2 + .
Vn = Ащ?! + Anafj-b ¦ • ¦ +Лппч)п,
где Wrs|=j=O. Отсюда
л
Vr = У, Ars (CsiWj + CslW.2 + • - • + CSIlWn),
Уг = 'сп^г + cr2W2+... + cTnWn
n
= X Crs (a««>i + anwa + • ¦ ¦ + asnwn).
s=l
4S2
Следовательно, сравнивая коэфициенты при wh получим
п п (г — 1 о „\
S -= 1 5 -= i \ t == 1,2, . . M/jJ
Теперь, согласно этим соотношениям, произведение1
s,... ,an
\ ^
и произведение
I i
ЛД А с
равны между собой. Отсюда следует, что
12» ^22 о, . . - ?1п2
пп s ' п, А2,и- • -,Лц
относительно s.
15-21. Неповторяющиеся (некратные) корни характеристическо-
характеристического уравнения. Пусть характеристическое уравнение имеет п не-
неравных корней sx, s2,...,sllt тогда существует п решений йх, и2,
...,кп, которые, после того как контур был описан, принимают
значения Uv U2,...tUn соответственно, где
Uг = SjKi, f/2 = s2u2, ...,[/„ = sn«n.
Решения и^ и2,...,ип эквивалентны первоначальной последова-
последовательности и образуют фундаментальную систему.
Рассмотрим, в частности, случай, когда контур содержит
только одну особую точку2, например z = С и рассмотрим мно-
многозначную функцию (z — ?)р . После того как был описан пол-
полный контур, эта функция принимает вид е2"'9 (z — C)p. Пусть
индекс р*: выбран таким образом, что
j; =e
1 В качестве контура здесь удобно рассматривать круг \г — «|=/?, где,
если гг — ближайшая особая точка к с, то R — некоторое число, меньшее
*1-
2 i называется также точкой неопределенности.
483
тогда функция
*(z-C) = (z-C) ?kuk,
после того как будет описан полный контур вокруг точки I,
примет свое первоначальное значение; иначе говоря <f(z — С)—
однозначная функция z в области точки С
Более того, индекс р^ является неопределенным в том смысле,
что он может быть заменен на рк± т, где т — любое положи-
положительное целое число. Если рк может быть так определен, чтобы
функция Чк @) была конечна, но не равна нулю, то решение
называется регулярным. Следовательно регулярным является
такое решение, которое может быть выражено в виде
где
«p(z — C)-O(l) при z-»C
Индекс р* является k-ым показателем, относящимся к ^регуляр-
^регулярной особой точке z = С.
Если рк не может быть так определена, то функция yk(z — С)
(а следовательно и ик) имеет существенную особенность в точке
z = С; решение в данном случае называется нерегулярным. Это
имеет место, например, когда
15 • 22. Случай кратных корней. Предположим, что характери-
характеристическое уравнение имеет кратные корни, например, корень
Sj повторяется тг раз, s2 повторяется mz раз и т. д., до конца
нумерации, тогда
тх + mz+ ... = n-
Докажем1, что соответственно некоторому корню s кратности
т существует подпоследовательность и(</и) линейно независи-
независимых решений
vlt v2t... ,-Пр.,
которые, после того как был описан контур, принимают соот-
соответственно значения
SVlt S (tJ + Vj, ...,S (Vy. + V,,_ j)
Остальные решения v^ + i, ^ + 2, • • -,vm приводят к другим под-
подпоследовательностям с тем же множителем s. Иначе говоря,
нужно доказать, что последовательность п линейных преобра-
преобразований (§ 15 • 2, В) может быть заменена некоторым числом
подпоследовательностей типа
\/j = svu V2 = s(v2 + v,),...,Vx, = s(v., + v»._ 1),
где г»!, v2,.. .,-Оц —линейные комбинации щ, wz, ...,-wn. Докажем
1 Fuchs, J. fur Math., 66A866), 136 [Ges. Werke. I, 174]; Hamburger, J. fur Math.,
76 A873), 121.
484
это методом индукции, причем сначала примем, что это пра-
правильно в отношении (п — 1)-кратной системы, а затем уже
выведем его правильность для п-кратной системы.
Пусть о — некоторый корень характеристического уравнения;
тогда будет существовать решение v такое, что
V=w.
Из решений ъь\, w.2,...,wn по меньшей мере п — 1 линейно неза-
независимы относительно v; пусть это будет w2>.. .,wn. Посте того,
как был построен контур они принимают значения W2,.. .,Wn
соответственно, где
(С)
но
= b2 v
b.2nwn,
v + bn2w2 -f... + bmwn,
s, 0,...,О фС,
откуда следует, что
Напишем
тогда
(C)
Wn' =
= 2,3 .)•
W2 - bav = W2',..., Wn - bnv = \Vn',
bnnwn
— последовательность линейных преобразований п — 1 символов,
с детерминантом, не равным нулю. Согласно принятому усло-
условию следует, чтош2,. ..,wn могут быть заменены линейными ком-
комбинациями этих символов, например
иг, и.,,
которые принимают значения ?У/,
был описан контур.
Система (С) преобразуется в
— s
• -г^п — i. после того как
вместе с другими аналогичными подпоследовательностями и дает
в общем п — \ уравнений. Но если преобразование, которое
изменяет w2K...,-wn в иь.. .,ип~\, вместо системы (С) приложить
48Г;
к системе (С), то последняя примет вид
Ux =s«! + kjV, U2=s(u2 + иг) + k2v,. ...и?. = s(Up. + %_i) + ftpv,
где Ai, &2,. ..,?,,. —определенные постоянные, зависящие от не-
некоторых коэфициентов Ьг. Напишем
где /х, 12,... ,Хр. — произвольные постоянные. Пусть определен-
определенные таким образом величины vlt •v.2,..,,vll примут значения Vx,
V2,• • • > VV , когда иъ щ,.. .,Мц принимают значения иг, U2,.. .,U,^ ,
так что
LJ-i = V j ~\- ),xov, Uа = У2 -\- \r>3V,... yU^ = VV -}- Xj^ О'У,
тогда
(С») { ^ = SVl + ^ - (° - S) ^ ^ (г= 2,3,... *).
Допустим, что a=j=s; ).j, A2,...,>41J. могут быть выбраны таким об-
образом, чтобы коэфициент v был равен нулю в каждом отдель-
отдельном случае. Тогда последовательность подстановок принимает
каноническую форму
Vx = svv V2 = s (v2 + V&..., V; = s (Vf. + V»._ i).
Предположим, что o = s, тогда, если ^х=0, то Х1? Х2,... Д^ _,
могут быть выбраны таким образом, чтобы коэфициент при V
обратился в нуль, а последовательность подстановок снова при-
приняла бы показанную выше каноническую форму. С другой сторо-
стороны, если kx ф 0, то v может быть везде заменено на svj/^, а \ъ
^г>- • -»V— 1 могут быть выбраны таким образом, чтобы все ко-
эфициенты при i) во всех уравнениях, за исключением первого,
обратились в нуль. Каноническая последовательность подстано-
подстановок примет тогда вид
V = sv, Vx = s(vx + v), V2 = s(tJ + Vj),..., Vp. = s (Vy. + ^_i).
Могут возникнуть также две или больше последовательно-
последовательностей подстановок (С") с тем же множителем1 s —а. Они могут
быть приведены при соответствующем выборе постоянной X к
виду
)
= sv,,. + i + u/^ ^ - 2 = s (*v + 2
и т. д., причем принимается, что ^ФО, ^'ФО,... Как и выше, при
1 При наличии последовательности подстановок с множителем зфс специ-
специальное рассмотрение не обязательно, так как приведение каждой последователь-
последовательности к канонической форме следует непосредственно. Рассматриваемый случай:
когда s = с, йх ф 0, kx' ф 0 и т; д., является единственным, требующим специ-
специального рассмотрения.
486
подстановке svfk-^ вместо v, s вместо klt первая последователь-
последовательность, взятая вместе с подстановкой V = sv, становится канони-
канонической. Во второй последовательности напишем
тогда
имеет каноническую форму. Другие подпоследовательности рас-
рассматриваются аналогично. Следовательно первая часть теоремы
доказана, именно: если последовательность п — 1 подстановок
может быть приведена к канонической форме, то последователь-
последовательность п подстановок может быть также приведена. Но если
п—\, то теорема очевидно верна, а так как она тривиальна,
то она верна и в общем случае.
15-23. Решения канонической подпоследовательности. Мы до-
доказали, что соответственно т- кратному корню s характери-
характеристического уравнения существует последовательность т решений
1>Л, V2,...,Vm,
которые, после того как контур был описан, могут быть рас-
расположены в подпоследовательности так, что если решения
имеют вид
Vv V2,...,Vm,
то
Уг = svlt V2 = s {v2 + v^,..., Vp. = s (Vf. + fji — i),
Рассмотрим первую подпоследовательность, принимая, как
и выше, что контур содержит только одну особую точку z = г~,.
Рассмотрим природу у- решений, составляющих эту подпосле-
подпоследовательность.
Как и выше
1), =B -С)? ?1(Z -С),
где
а функция (fxB — С) однозначна в области точки С.
Теперь
т. е. ^ i»! — квазипериодическая функция г — С. Но функция
2~.log (г — !1) имеет ту же квазипериодичность, так как после
того как контур был описан в положительном направлении вок-
вокруг точки С, функция^, logB —С) примет значение—? log(z—
487
Следовательно, после того как контур был описан, разность
имеет свое начальное значение, поэтому
-Ь _ ^ log(Z - С) ^fc (*-',),
где функция 4*1 (г — 0 однозначна в области *. Отсюда
v* = (z- Q- {25 «h (^ - С) log B - С) + <ра B - С),}
где
<р2 (г - С) = <h(z — 0*i B - С).
Произведем подстановку
и пусть
tV = (г — С)? иг.
Тогда, если переменная z описывает простой контур в поло-
положительном направлении вокруг точки ?, t увеличивается до 14-1,
следовательно функции иг, рассматриваемые как функции t, удо-
удовлетворяют квазипериодическим соотношениям
ит (t + 1) = иг (t) + ur _ , (f). (г > 2)
Эти соотношения удовлетворяются, если принять щ (t) == 1,
iu(t) = t, а также если принять, что нг @ — полином
Cr*(*-l)...(*-r + 2).
Постоянная Сг должна удовлетворять соотношению
Л (r-l)Cr=Cr_l (^ = 1),
следовательно
Сг = 1(г-1)! (г>2).
Таким образом мы нашли частное решение функционального
уравнения, которое удовлетворяется и, (t). Обозначим это ре-
решение через bT{t), так что
17)
и рассмотрим функцию
ег @ = ег (о 7.J (^ + ог_1 (о х2 (^ +
где каждая функция "/.(г1) такова, что
488
Тогда
и следовательно
ar(*) = 0r(f) (г = 2,3,.
является решением системы соотношений
Возвращаясь к переменной г, видим, что функции г*!, гJ,.
имеют вид
vt = (z- Q? {6Я^ (г -") + ?з (г - Q,
+ e,_j »я (г -") + ... + ?,, B - С)},
где 9Г написано вместо
и где везде принято одинаковое определение логарифма,а фун-
функции «рг (г — С) однозначны в соседстве с точкой С.
Остальные подпоследовательности, имеющие тот же множи-
множитель, могут рассматриваться совершенно аналогично. Так, если
s — кратный корень характеристического уравнения, то в общее
решение входят члены, имеющие логарифмические множители.
Этот случай часто называется логарифмическим (см. §6-3).
Пример. Уравнение
z2(z + 1) dl, - z--rfT+ 4- Cz + 1) w = 0
имеет два линейно независимых решения
1 \_ ¦?,
W± = Z г , Wz= Z ~ log Z -f Z ~l .
Если z описывает контур в положительном направлении вокруг
начала, то эти решения соответственно принимают вид
U?i = —z« = — г»!, 1172=-г 2"(log z + 2w) —2r= -и/2-2к/и'1
Характеристическое уравнение поэтому будет иметь вид
- 1 - s, О 1 = 0
— 2та\ — 1 — s |
или
(s -Ь IJ = 0.
Любое решение вида
та = B — Qp {*• % (z - С) + Г-1 <ра (г - С) + • • • + Ът (z - Q},
где S— обыкновенная точка или полюс функций <р, называется
регулярным решением1. Если все и решений, относящиеся к точ-
точке С, регулярны, то С называется регулярной особой точкой
уравнения. Если какая-либо из функций ср имеет существенную
особенность в точке С, то С называется нерегулярной особой точ-
точкой уравнения.
15-24. Метод получения решений канонических последователь-
последовательностей. Исходя из уравнения
^ = B—^B — 0,
напишем
¦w = Vx fv12dz,
тогда v1? будет удовлетворять однородному линейному уравне-
уравнению порядка п—1, которое имеет не меньше одного однознач-
однозначного решения; пусть этим однозначным решением будет г>12.
Для корня s соответствующее характеристическое уравнение
степени п — 1 выпадает, а каноническая подпоследовательность
Уг = s-Vj, V2 =s(v.2 + i\),..., Vy. = s(v» + v^-i)
заменяется на
V19. ==
Теперь напишем
и повторим процесс. Таким образом возникает последователь-
последовательность j* решений, соответствующих канонической подпоследо-
подпоследовательности, именно (см. § 5-21)
vr = г>1/г>12/г>23.. ./^ i,r, (^г)'- (r=2,3,... )(г},
где t»12, y28,..., iv__i,r — все однозначны в области С. Поскольку
все эти функции однозначны, получим
*>г = B - С> {^ fro B - С) + ^~» fa (Z -:)+.-. +'f rr B - ;)},
где tr = log(z — С), а cpro — постоянная, кратная^!.
1 Thome, .1. fiir Math. 75A873}, 266.
490
15-3. Необходимое условие для регулярной особенности. Приве-
Приведенное выше исследование имеет теоретическое значение, по-
потому что оно выявляет характер общего решения уравнения,
относящегося к любой из его особых точек. Однако, оно мало
способствует разрешению более сложной задачи определения
явной формы общего решения. Мы достигли предела, дальше
которого практически невозможно продолжать исследование,
не налагая некоторых ограничений на уравнение или на его ре-
щения. Путь, который в данном случае нужно принять, весьма
ясно указывается следующей теоремой1.
Для того, чтобы точка z = t была регулярной особой точ-
точкой уравнения
dnw . , . d"-1®.' , , , s dw , , ч п
d/T + A(z) — -n~r + .-.+ Pn-i(z) T- + Pn(z)w = 0
необходимо и достаточно условие
pT(z) = (z-l)-rP(z), (r=h 2,- • -, n\
где функция P(z) аналитическая в соседстве с I.
Мы не потеряем в общности, если предположим, что точка
С является началом. Сначала докажем необходимость этого ус-
условия для z = 0. Выше мы показали, что всегда существует ре-
решение
и;, = г? ф (z),
где функция ср(г) — однозначна в области начала, и, принимая,
что это решение регулярно, ф@)^0. Теперь пусть
w — wl fvdz
будет решением уравнения, тогда v удовлетворяет диференци-
альному уравнению вида
если w — регулярное решение, то "и также должно быть регу-
регулярным. Но коэфициенты q могут быть выражены посредством
•wx и коэфициентов р следующим образом
dw,
Иг
dr Wl
1 Fuchs, J. fur Math,, 66 A866), 143; 68 A868), 358; Tannery. Ann. Ec. Norm.
B), 4 A875), 135.
491
Рассмотрим сначала простой случай п — 1; уравнение
dw
имеет решение
—fp,dx
¦w = Се ,
и для того, чтобы это решение было регулярным, необходимо, что-
чтобы рх приняла форму z~xfx (z), где /х (^—аналитическая функция
вблизи начала. Далее, рассмотрим случае п = 2. Уравнение от-
относительно v первого порядка, следовательно вблизи начала
q1(z)=O{z~1)
и
—_ . ^i = О (z ).
Отсюда, как и в первом случае,
где/хB)^—функция, аналитическая в соседстве с началом. Но
1 (dsw1 dw11
"- w% I dz2 "^ dz I '
I J
и поскольку вблизи начала
Q
dw'
p2 равно z /2B), где функция />(z) аналитическая в соседстве
с z = 0.
Доказательство теперь завершается, пользуясь методом ин-
индукции. Предположим, что теорема верна для уравнения по-
порядка п—1;так, в уравнении для v допустим, что
qT{z) = z-rgr{z) (r =1,2,..., п-\).
где gr (z) — функция, аналитическая в начале. Тогда из выраже-
выражений для коэфициентов р непосредственно следует, что
pr(z) = z-'f,.(z) (г =1,2,..., п— 1)
где/г (г) функция, аналитическая в начале. Остается доказать,
что pr(z) имеет указанное значение при г = п. Но это следует
402
непосредственно из уравнения
Следовательно указанное условие необходимо.
15-31. Достаточность условия для регулярной особой точки.
Докажем, что если в уравнении
все функции P(z) аналитические в соседстве с началом, то урав-
уравнение имеет фундаментальную последовательность п решений,
регулярных в начале.
Это уравнение может быть заменено системой
dw, dwn—\
v = -тс,, z - - = m, ... z = wn
UZ -J d? '
Idw
z -df- = A, (z) wl + Л2 (г) ws+...+An (z) wn,
где Лх (z),..., An B) — линейные комбинации Px(z),..., Pn{z) с
постоянными коэфициентами, следовательно аналитические
вблизи z=0.
Вместо указанной системы целесообразно рассмотреть более
общую систему
(
z 5 =
Z — - " = .
z ~d- = А„1Щ + Ano-u'o + ... + Anriiv,,,
где все коэфициенты А аналитические в соседстве с началом.
Докажем, что при наложении некоторого ограничения (которое
должно быть впоследствии устранено) существует последова-
последовательность решений этой системы, регулярных в начале, а также
свободных от логарифмических членов, именно
\t\ = ZrUy, гС'о = ZTU.2,. . ., 'cVn = ZrUn ,
где г —некоторая постоянная, а функции их, и2,..., ип все ана-
аналитические в начале. Постоянная г может быть выбрана таким
образом, что если съ с.,,,.., сп — значения щ, н2,..., и« при
2 = 0, то хотя бы одно из чисел с не равно нулю. Пусть ars
будет значением Ars при z = 0, тогда, подставляя в систему
значения Wj, w.,,..., wn и приравнивая нулю коэфициент при zr
493
в каждом уравнении, получим следующую последовательность
соотношений
{аи — г)с1 + а12с2 + ... 4- aincn = О,
а^сх + (й22 — г) с, + - - - + Й2«с„ = О,
[а„п — Г)С„ = 0.
Исключая неизвестные коэфициенты ст из этой системы, найдем
определяющее уравнение для г, именно
аи — г, а12,..., аи
= 0;
Обозначим его корни, которые могут быть не все независимые,
через
п. dwx dw2 dwn
1еперь, если мы вместо г -~, z-d*,..., z-^— подставим соот-
соответственно Wlt W2,..., Wn, то рассматриваемая система примет
вид
Wx = ailw1 + aV2w2 + ... + ainwn + О(z, w),
W., = яд + a.^w.2 + ... + a2nwn 4- О (z, w),
Wn= dni-Щ + an.2w2 + ... + annwn + О (z, w),
где O(z, w) — линейные выражения для wlt w2,..., wn, коэфи-
коэфициенты которых являются аналитическими функциями z, обра-
обращающимися в нуль в начале. Независимо от членов O(z, w) эта
последовательность линейных подстановок аналогична последова-
последовательности § 15-2, хотя она получена совершенно иначе. Если
пренебречь членами O{z, w), чо1<иг, w2,..., wn могут быть заме-
заменены комбинациями этих величин, именно ЧIз v2,..., vn так что,
если все корни определяющего уравнения неравны, то система
примет вид
V1 = rxvx, V.2 = r2v2,..., V,, = rnVn.
Производя точно такое же приведение системы при наличии
членов O(z, «'), можем заменить ее системой
V^w + Oiz, w),
V2 = r2v2 + O(z, w),
Если корни определяющего уравнения не все независимы, то
система может быть заменена некоторым рядом вспомогатель-
494
ных систем
Vi = rxvx + О (z, v) Vf. i = rs<Dy, и + О (z, v),
V.2 = г, (*/2 + *>x) + О (z, v), IV 2 = r2 (zv+s + щ^) + О (z,
^ = rx (Vy. + v^i) + О (г, W), К, = r2 (w, + г>,_!) + О (z, v)
и т. д. Так как последний случай включает также и первый, мы
рассмотрим только последний случай. Преобразуем систему
подстановкой
тогда, поскольку Vlt V2,..., Vn являются такими же линейными
комбинациями относительно W±, W2,..., Wn, как и чзъщ,..., vn
относительно wlt w.2)..., zun, отсюда следует, что
V - у dVl V - -, dVn
Система поэтому принимает вид
z A-^ = Ox\z, ср),
^ O^Z, tf),
Поскольку члены O(z, у) могут быть определены явно и они
линейны относительно <рь w2,..., wn с коэфициентами, аналити-
аналитическими относительно z и обращающимися в нуль в начале,
функции ф могут быть определены из уравнений в виде степен-
степенного ряда относительно z методом последовательных прибли-
приближений. Функции <рх (z),..., » .(z) должны быть равны нулю при
z = 0, в то время как <р^ @) может иметь некоторое произволь-
произвольное значение а. Так, если функция «р^ДО) не равна нулю, то
<РиB) должна содержать логарифмический член, что противо-
противоречит условию. Если разность г2 — гг равна положительному
целому числу, например т, то процесс определения последо-
последовательных коэфициентов в разложении <р fl {z) обрывается на
члене zm. Следовательно для того, чтобы можно было разложить
все функции <р в степенные ряды относительно 2, необходимо
ограничить разность гк — гх так, чтобы она не была положитель-
положительным целым числом (но она может быть равна нулю) для любого
значения k. Если это ограничивающее условие удовлетворено.,
то можно определить все коэфициенты в разложениях функции ф.
495
Остается только доказать, что эти разложения сходятся для
достаточно малых значений | г |. Ниже мы укажем возможный
метод доказательства этой сходимости.
Пусть е будет численной разностью между г2 — гх и ближай-
ближайшим положительным целым числом; рассмотрим систему обыкно-
обыкновенных линейных уравнений
где Qx, Q2,.-., Qn — линейные выражения относительно Лх,
62)..., фл, коэфициенты которых обращаются в нуль в начале.
Эта система может быть решена относительно функций <1> в виде
ряда по возрастающим степеням г с положительны ни коэфи-
циентами; ряды сходятся для достаточно малых значений | г \.
Если коэфициент ведущего члена ряда для каждой из функций i|>
является модулем ведущего члена ряда для соответствующей
функции <р, то модули остальных коэфициентов ряда для функ-
функций «> будут самое большее равны соответствующим коэфици-
ентам ряда для функций ф. Следовательно ряд для функций i?
сходится абсолютно и равномерно внутри определенного круга,
центр которого лежит в начале.
Отсюда следует, что система п линейных диференциальных
уравнений первого порядка имеет последовательность регуляр-
регулярных решений
wl = zr'u1, w., = zriu.z,..., wn = zlun ,
где иъ и,,..., н„ аналитические в соседстве с 2 = 0, а гг —
корень определяющего уравнения, так что разность
(где Г)-—некоторый другой корень определяющего уравнения) не
является положительным целим числом.
Если разность двух корней определяющего уравнения не
равна целому числу, то система имеет п независимых последо-
последовательностей решений указанного типа.
В случае одного уравнения порядка п, которое эквивалентно
системе, определяющее уравнение принимает вид
[>"]„ + Pi@) [/"]„_, + ...+Рп_1 @)г + Рп@) = 0,
Ип = ''(''—1).. .(г — я + 1)- Если корни этого уравнения
49-5
то диференциальное уравнение имеет решение
w = zrkuk(z),
соответствующее каждому корню гк, гце uk(z) — функция ана-
аналитическая вблизи z — 0, аик@)ф0, если ни одна из разностей
П—Гк, Г2 — Гк,..., Гп~Гк
не является положительным целым числом, хотя одна или
несколько разностей могут быть равны нулю.
15-311. Логарифмический случай. Для полноты доказательства
достаточности условий Фукса, допустим, что корни определя-
определяющего уравнения различаются на целое число. Пусть корни
различаются на целое число, а от всех других корней—на
числа, отличные от целых и пусть
Из доказательства предыдущего параграфа следует, что суще-
существует решение
wx = гГ1щ (z),
соответствующее гх. Пусть
w =
будет решением, тогда (§ 15-3) v будет удовлетворять уравне-
уравнению порядка и —1, удовлетворяющего условиям Фукса относи-
относительно z=0. Но поскольку
& ( W \
dz \ wj
корни характеристического уравнения, связанного с уравнением
относительно v, будут равны
г% — гх — \, г3 — гх— 1,..., г^ — Гу—\,
причем первые jj- — 1 из них — отрицательные целые числа.
Поскольку г2 > г3, получим решение
щ = гг^-г'-1ф(г),
где функция <b(z) аналитическая вблизи начала, а ф@)Ф0. Сле-
Следовательно существует решение
¦w, = wj" zr" ri *ф (z) dz,
которое, будучи умножено, если это необходимо, на постоян-
постоянный множитель, приводится в общем случае1 к решению
w2 = /' {иг (z) log z + «22 (z)}.
1 В специальном частном случае, когда разложение 4 (г) в виДе Ряда не
содержит члена гГг~Гг, логарифмический член в функции w, отсутствует.
Э. Айне—133—32 497
Процесс может быть повторен и дает в общем случае
¦т., = zn К (z) f + 1ы (z) f~l + ...+ и-,, B)} (v = 2,3,... ,и),
где все функции u(z) аналитические в соседстве с 2 = 0.
15*4. Уравнения типа Фукса. Уравнением типа Фукса назы-
называется такое уравнение, в котором каждая особая точка, вклю-
включая и точку в бесконечности, является регулярной особенностью.
Предположим, что у нас имеется v регулярных особых точек
аъ а.2,..., а,
в конечной части плоскости. Из теоремы Фукса непосредственно
следует, что коэфициент pm(z) имеет форму
рт (z) = (z - а,)-1 (г - аГт ¦ ¦ ¦ B - ач утРт (z);
поскольку в конечной части плоскости z нет других особых
точек, Рт (г) — целая функция z.
Рассмотрим поведение этих коэфициентов в бесконечности.
Для того, чтобы уравнение имело регулярную особенность в
бесконечности, точка в бесконечности должна быть самое боль-
большее полюсом функции pm(z). Следовательно Pm{z) — полином
от z, а функция рт (z) может быть выражена в виде
У р
р"» 4-
где Pms — постоянная1, a Qm — полином, высшая степень которого
должна быть определена. С другой стороны, pm(z) допускает
разложение
которое сходится для достаточно больших значений \z\; пусть
¦w = zr(c0 4- cxz i 4- c2z 24- ...)
будет решением уравнения, регулярным в бесконечности. Пока-
Показатель г может быть найден из определяющего уравнения
относительно точки в бесконечности; при наличии п независимых
регулярных решений это определяющее уравнение не должно
становиться порядка ниже п. Следовательно, поскольку опре-
определяющее уравнение получается путем приравнивания нулю
членов высшего порядка относительно 2, оно должно содержать
член высшего порядка относительно w(n\ равный O(zr~") и ни
один другой член не может иметь порядок выше этого. Но
главный член, возникающий из рт (z) w^m\ будет О {z°m + r~n ~ "'),
следовательно
^ P,ns=(^_ai)-'"...(«i.-(?v_1)-'"(«,-«,+ 1rm... (a, -
498
Отсюда
при т > 1, a Qi тождественно равно нулю.
Остается выяснить, какая степень определенности вводится
в уравнение при известных п показателях, соответствующих
каждой особой точке. Рассмотрим особенность z = as; если мы
примем регулярное решение
со
с?/ — IZ ".s/ ^, ^"у. \^ ^s/ )
то определяющее уравнение будет иметь вид
Ил + V Pms [r]n^m = 0.
Следовательно, если показатели
относящиеся к as, известны, то постоянные Pms определяются
единственно, именно
1 "
Pis—2 n(tl — \) = — >^ asft,
As—^-(л- 1) (л - 2)P1S + 24 ге(п - 1) (л - 2) {in - 1) = ?
/7
7\ ^skJsl уК ~j~ L/t
и т. д.
Предположим теперь, что ведущим членом в Qm(z) будет
Amzm'*—m—\ так что для больших значений z
г-"' I 5 P,,,s. + Л 1 + О (z-™-i}.
Если мы примем решение в виде
иг = г- F0 + ^г-1 + Ь&~*+ ...),
то соответствующим определяющим уравнением будет
„_„ - 0-
Показатели, относящиеся к точке в бесконечности, определя-
определяются как корни этого уравнения относительно з с измененными
знаками.
49»
Пусть показатели будут 8lt о2,..., 8П, тогда, поскольку At = О,
ft I
Но
следовательно
т. е. сумма всех показателей постоянна. Таким образом, если
у нас имеются v + 1 особых точек (включая точку в бесконеч-
бесконечности), то имеются также и n(v + l) показателей с одной
зависимостью между ними. Коэфициент рт (z) содержит
/га (v — 1) + 1 постоянных, именно v постоянных Pms umv — т — v -}- 1
коэфициентов полинома Qm{z). Следовательно уравнение содер-
содержит всего
независимых постоянных, «(v+1)—1 из которых является
следствием показателей. Таким образом в данном случае остается
4-(я— 1)(яу —я — 2)
произвольных постоянных.
Все /г решений, соответствующих каждой из v -}-1 особых
точек, изображаются Р- функцией Римана1
О, . . Мч оэ
. . z
которая показывает расположение особых точек и показателей,
относящихся к каждой особенности.
15 ¦ 5. Класс уравнений, общее решение которых однозначно.
Рассмотрим уравнение
. ч d w ¦ _ ,„\ d w . , , ч dw
Предположим
(а) что коэфициенты являются полиномами от г и что сте-
степень po(z) не меньше степени любого другого коэфициента;
1 Riemann, Abh. Ges. Wiss. Gott., 7 A857), 3 [Math. Werke B изд.), 67]; см.
§7-23.
(b) что особые точки, лежащие в конечной части плоскости г,
регулярны; точка в бесконечности может и не быть регулярной;
(c) что общее решение уравнения однозначно.
Для удовлетворения условия (с) необходимо, чтобы показа-
показатели, относящиеся к каждой особой точке, были целыми числами,
а также, чтобы решение не содержало логарифмических членов.
Докажем, что если эти \ словия удовлетворены, то общее реше-
решение уравнения будет иметь вид
w = С^Ъф + С2е1°-г R.2(z) + ... + С„е*л* Rn(z),
где Съ Сг,.. .,Cn — постоянные интегрирования, 1Ъ hz,..., ln —
определенные постоянные, которые не должны быть все неравны,
а функции R(z)— рациональны1.
Пусть аъ о2,...,а., будут конечными особыми точками и
пусть наименьшим отрицательным показателем, относящимся
к as, будет as; если показатели, соответствующие as, все поло-
положительные, то as будет равна нулю. Тогда замена зависимой
переменной
wx = (z — %)*' ... B — а,) "у w
преобразует это уравнение таким образом, что все показатели,
относящиеся к конечным особенностям, будут положительными
целыми числами или равны нулю. Пусть преобразованное
уравнение будет иметь вид
ЯоЮ^Ь + <?iB)df?l + • • • + <?-(*)$ + 9nWwt = 0.
Это уравнение обладает всеми свойствами (а), (Ь) и (с),
указанными для первоначального уравнения.
Предположим, что
В этом случае получим уравнение, в котором коэфициент при
w2 равен
X» q0 (z) + *"-» ql(z) + ...+ Цп-i (z) + qn (г),
а I может быть выбрана так, чтобы коэфициент при высшей
степени z был равен нулю. Полученное уравнение может быть
написано в виде
где, если Q0B) степени т относительно z, то Qn(z) самое боль-
большее степени т— 1, а остальные коэфициенты степени не выше т.
Теперь
v
1 Halphen, С. R. Acad. Sc. Paris. 10) A885), 1238.
501
где Yo — постоянная. Сумма показателей, относящихся к as,
равна
Но эти показатели—неравные положительные целые числа, и
их сумма поэтому не меньше
O + lf 2+ ... +(л-1) = ул(л- 1).
Следовательно ys равна нулю или отрицательному целому числу,
откуда
Предположим, что Qn(z) не равно тождественно нулю.
Покажем, что в этом случае можно построить конечную цепь
преобразований, приводящую к уравнению, в котором член,
соответствующий Qn(z), тождественно равен нулю. Пусть
тогда
Qe(z) ~~Jl + QS -""Jj1 +¦¦¦+ Qn-г (*) Wi + Qn (г) w3 = 0.
Если мы продиференцируем это уравнение относительно z, то
получим
{Ф) + Qx f z)} -^J1 + • • ¦ + Q; (z) wa = o.
Исключим w2 из последних двух уравнений; полученное урав-
уравнение имеет вид
Qo(z) Qn@ "x + Г { Q' 'z) + Q, (г)) QB (Z) -
^... =0,
и является уравнением того же типа, что и уравнение относи-
относительно w2. Пусть S' будет числом, заменяющим в этом урав-
уравнении число 5 в равнении для w2; S' — коэфициент при z~l
в разложении по убывающим степеням z
этот коэфициент равен /к для Q0'(z)'Q0(z), S для Qi(z)/Q0B:) и
не больше от —1 дм Q^ (z)/Qn (z). Следовательно
S' > S + 1.
502
Процесс может быть повторен (если коэфициент при Wx
в данном уравнении не равен нулю) определением уравнения
для W2, где
JV7 CW 1
а число S" такое, что
S" >S + 2
и т. д. Процесс однако конечен, поскольку S', S",... — отри-
отрицательные целые числа. Следовательно должен наступить момент,
когда коэфициент независимой переменной
W/ — d?Wz
будет равен нулю. Уравнение тогда будет иметь решение
Wf = const,
поэтому w2 — полином от z степени р. Так, поскольку
w
(г ~ а,р . . . (г - av )"-
данное уравнение имеет решение
где R(z) — рациональная функция z.
Для завершения доказательства нужно показать, что имеются
независимые решения этого типа, число которых равно порядку
уравнения. Примем это без доказательства для уравнения
порядка п — 1, а затем докажем для уравнения порядка п.
Указанное уравнение имеет одно решение рассмотренного
типа; предположим, что оно имеет вид
и напишем
w = w1 f udz.
Новая независимая переменная удовлетворяет уравнению
порядка п — 1, а это уравнение будет точно такого же типа,
что и для w. Следовательно оно имеет решение
где R (z) — рациональная функция z; пусть
w = w1feXzR (z) dz.
Поскольку функция w однозначна, интеграл
503
не может ввести логарифмических членов и будет поэтому равен
е'\Ш B),
где функция Ш (z) — рациональна относительно z; п — I незави-
независимых решений u(z) приводят к п — 1 решениям
wr=ekr'Rr{z) (г = 2, 3, ..., и),
которые вместе с wt образуют последовательность п независи-
независимых решений данного уравнения. Эта теорема ве^на, поскольку
она верна при п — 1.
Также верна и обратная теорема: если и функций e'^R^z),
e'*zR2(z),..., е'пг Rn{z) линейно независимы, то они удовлетво-
удовлетворяют диференциальному уравнению порядка я с коэфициентами
d"w
в виде полиномов, так что степень коэфициента при —— не мень-
меньше степени других коэфициентов уравнения.
Рассмотрим функцию
О (гI
где Р и Q — полиномы от z, тогда
следовательно коэфициент при w — полином степени не выше
степени коэфициента при -, .
Предположим, что для уравнения степени п — 1 коэфициент
dn-xw
при —^rj—полином степени не меньше степени остальных
коэфициентов.
п функций
удовлетворяют диференциальному уравнению
^<;+q,<z>s^+¦••+<?«<<=о,
коэфициенты которого полиномы от 2, умноженные на показатели.
Если
то возникает уравнение порядка п — 1 относительно и, решения
которого имеют вид
504
d [ Ri(z)\ d I R (z)\
dz Г ЯП*)!'"-' dz \e Rl(z)\>
причем каждое решение типа e>zR(z). На основании сделанного
допущения экспоненциальные множители в Q0(z),... , Qn^1(z)
исключаются, а степень Q0(z) равна самое большее степени
остальных коэфициентов. Произведем подстановку
полученное уравнение удовлетворяется, когда w порядка п
и указанного выше типа. В частности, степень коэфициента
—— не меньше степени других коэфициентов. Следовательно
обратная теорема доказана.
15*6. Уравнения, коэфициенты которых двояко-периодические
функции. Другой класс уравнений, общие решения которых,
если они однозначны, могут быть выражены посредством из-
известных функций, дается следующей теоремой \ Если коэфи-
коэфициенты однородного линейного диференциального уравнения —
двояко-периодические функции независимой переменной, то урав-
уравнение имеет фундаментальную последовательность решений,
которые, если они однозначны, являются в общем случае дво-
двояко-периодическими функциями второго порядка.
Пусть диференциальное уравнение имеет вид
и пусть коэфициенты p(z) будут двояко-периодическими функ-
функциями с периодами 2ш и 2ш'. Предположим также, что число
особых точек в параллелограмме периодов конечно и что об-
общее решение уравнения однозначно, для чего необходимо, чтобы
показатели, относящиеся к каждой особой точке, были нерав-
неравными целыми числами.
Пусть w^z), w2(z),... , wn(z) будет фундаментальной после-
последовательностью решений уравнения, тогда
wx (z -f 2w), w2{z + 2w),..., wn(z + 2u>)
также будут решениями, образующими фундаментальную после-
последовательность, причем в данном случае возникает последова-
последовательность п линейных соотношений
•w, (z -f 2w) = arlw1 [z)+ ... + arnwn (z) (r = 1, 2,..., n)
Рассуждая в основном так же, как и в § 15-2, можно дока-
доказать, что имеется не меньше одного решения ut(z), так что
1 Hermite, C. R. Acad. Sc. Paris, 85-94 A877—82) passim [CEuvres. 3, 266:
Pieard, С R. 89 A879), 140; 90 A880), 128; J. fur Math. 90 A881), 281; Mittag-
Leffler, C.R.. 90 A880), 299; Floquet, C.R, 98 A884), 38, 82; Ann. Ёс. Norm. C),
1, A884), 181, 405.
505
где s — численная постоянная. Рассмотрим теперь второй пе-
период. Все функции
ut(z), u1(z + 2*'). Kl(z + 4m'),-..
являются решениями уравнения. Поскольку уравнение имеет
только п независимых решений, существует такое число т (< п),
что иг(г + 2/гаш') может быть выражено в виде линейной ком-
комбинации
Ьхих (г) + Ь,чх (z + 2ю') + ... ¦+ Ьтих {2 + 2 (га - 1) ш'};
принимая, что яг—наименьшее целое число, для которого это
справедливо, постоянная йх не равна нулю.
Пусть
«2(z-f 2u/) = m3(z),
Mm_i (z + 2ш') = ит (z);
тогда
«m (z + 2ш') = Ьгиг (z) + fc3ii2 (z) + ... + bmum B);
функции ^(z), H2(z),... , «m(z) линейно независимы и
ur {z + 2ш) = sur (z) (r = 1, 2, ..., /n).
Существование указанной последовательности преобразований
показывает, что имеется не меньше одной функции v(z), явля-
являющейся линейной комбинацией ^(z), ..., um(z), так что
где s' — постоянная.
Следовательно уравнение имеет решение w — v (z), так что
v(z + 2o>) = sv (Z), г» (z + 2ш') = s'-y (z).
иначе говоря, ф (z) — двояко-периодическая функция второго
рода, или квази-двояко-периодическая функция.
В общем случае, если характеристическое уравнение, полу-
полученное подстановкой z ¦$- 2а> (или z + 2"/) вместо z, имеет п не-
независимых корней, то оно будет иметь последовательность п
фундаментальных решений, каждое из которых имеет квази-
квазипериодичность указанного характера.
506
В любом случае можно найти аналитическое выражение для
общего решения. Пусть
будет любым квази - периодическим решением данного урав-
уравнения; напишем
w =
тогда W будет однозначным решением уравнения порядка п —1.
Поскольку функция w[(z)/^(z) и ее последовательные производные
являются чисто-периодическими, коэфициенты этого уравнения
после почленного деления на {y{z)}n также будут чисто-перио-
чисто-периодическими. Это уравнение, в свою очередь, имеет квази-перио-
дическое решение <?2B)> следовательно
является решением первоначального уравнения. Этот процесс
может быть продолжен, и мы получим я независимых решений
wn = Uz)fuz)- ¦-/
15-61. Явная форма решения. Пусть
W = ttBJ
будет решением уравнения, так что
<f{z + 2ш) = sy(z), <рB + 2ш') = s'4-B).
Рассмотрим функцию
где X. и а — постоянные, a o(z) — сигма-функция Вейерштрассаг,
тогда
фB + 2ш) = еАш-^Цг), 6B + 2ш') = eIlo)'-fti'e ^),
1 Уиттекер и Ватсон, Курс современного анализа, § 20 • 42. Надо отметить,
что
c(z + 2") -2ii(z4 ш) °(г + 2(й>) _ _ .2г/(г f ш')
где Tj и ¦»)' — постоянные. Аналогично
так что
r,(z -f- 2co) = ?(г) + 2г], С(г +2»') = Ц(г) + 2г/,
507
и поэтому частное <f(z)/&(z) будет двояко-периодическим, если
2Ы — 2-qa — log s,
2ш' — 2г[а = logs'.
Поскольку известно, что1
г^' — cotj' = -^- та -Ь О,
эти уравнения определяют \ и а через ш, со', tj, t/, logs и logs''
Следовательно
где $ z) — эллиптическая функция.
Ограничим теперь рассмотрение уравнением второго порядка;
если корни двух характеристических уравнений неравны между
собой, то решения будут двояко-периодическими функциями
второго рода. Пусть этими двумя решениями будут u^z) и <f2(z)-
Рассмотрим сначала случай, когда оба характеристических урав-
уравнения имеют двойные корни; пусть
?,B + 2<d) = sfl<z), <pa'z + 2ш) = sxj'z),
?a(z + 2u/) = S''f.2B) +
Если г' = 0, то <fiB) и yz(z) — двояко-периодические функции
второго рода; если t' dz 0, то функция <в/г) может быть выра-
выражена в указанной выше форме. Аналогично, если
ТО
-/B+20))=-^),
Сравним полученные уравнения с функцией
AC(z) + Bz,
которая увеличивается на 2Лг, + 2Вш при увеличении z на 2ю,
и на 2At\ -f 25ш' при увеличении z на 2со'. Таким образом, если
Лт? + Вш = 0, А-ц' + Ва>' — ~^~-,
хУнт1екер и Ватсон, Курс современного анализа, § 20-41!-
508
то
будет двояко-периодической функцией z. В данном случае
где ^(z)—-эллиптическая функция, а А и ? — определенные
постоянные. С другой стороны, пусть
2м) =
<h(z + 2ш') = s'cft(z*, ?2 (z + 2ш') =
Эти выражения совместны, поскольку *{(z + 2«») + 2ш'} = ср {(z -f-
+ 2ш') + 2и)}. Теперь, как и выше, tp^z) — двояко-периодическая
функция второго рода, но в данном случае
-/B + 2ш) = х (z) + j, ;(г + 2*»')= x(z) + Р,
а постоянные Л и ? должны быть определены из уравнений
Ari+Bw = ~, кг{ + Bu/ =Уу.
Функция !f2(z) будет иметь такую же форму, как и раньше.
Уравнение третьего порядка может рассматриваться анало-
аналогично; специального рассмотрения требует только случай, когда
характеристическое уравнение имеет тройной корень. В этом
случае «^(z) и <f2(z) имеют указанные формы; третье решение «(z)
содержит члены вида
z2, z'4z) и С*B).
В общем случае, если характеристическое уравнение имеет
m-кратный корень, то решения будут содержать z и '(z) до
степени (т — 1) включительно. Это соответствует логарифми-
логарифмическому случаю уравнения Фукса.
15-62. Уравнение Ляме. В уравнении Ляме1
{Й + Я(Я+1)$>B)}да0
1 Уиттекер и Ватсон, Kypcfсовременного анализа, Гл. XXIII. Это уравнение
преобразуется в форму Якоби
—г— = {п(п + l)fe2sn- х — r,}w
посредством преобразований
Г:П9
где п — положительное целое число, a h — постоянная, особыми
точками являются начало и точки 2mw + 2т'ш'. Показатели,
относящиеся к любой особой точке, обозначим — п и я + 1.
Теория Фукса объясняет существование одного однозначного
решения, именно
wi(z) = B — 2/пеи — 2т'ш')п 1 W(z),
где W(z) — аналитическая функция в области точки 2/исо + 2/и'ш'
и не равна в ней нулю. Разность показателей равна 2л + 1, и
поскольку это положительное целое число, необходимо рассмот-
рассмотреть возможность второго решения w2(z), содержащего логариф-
логарифмический член. Поскольку
¦w2(z)w[(z) — ¦w1(z)w[(z) = О,
второе решение будет иметь вид
Г dZ
J {wi(z)Y
где С — постоянная. Отсюда видно, что 1,'{щ(г)}* — четная функ-
функция 2; ее вычеты относительно начала равны нулю, поэтому
логарифмический член не может возникнуть. В частности, пусть
п = 1, тогда уравнение будет иметь вид
Введем параметр а, связанный с h трансцендентным уравнением
тогда уравнение будет иметь решения
которые в общем случае независимы. Однако, если h равно еъ
е2 или е3, то решения не будут независимыми. Например, если h
равно еъ то а равно щ и оба решения, которые в общем слу-
случае независимы, приводятся к
510
При h = ех второе решение может быть получено в квадра-
квадратурах, однако удобнее получить решение при помощи предель-
предельного процесса, принимая, что h не равно ех, но отличается от
него лишь на бесконечно малую величину. Тогда уравнение
р(а) = h
будет иметь корни а = ш1 + е, где е — бесконечно малая вели-
величина. Рассмотрим функцию
где
e с(г)
-ZX (ш, — Е) g (Z + ">1 —
"* " о (г) •
Эта функция является решением уравнения; ее пределом будет
искомое второе решение ws.
Теперь
= Гц eel -j-. . .,
поэтому
е-й (.0.+.) = е-Ч1« A
Аналогично
откуда
отличается от Wx только знаком е, следовательно
Нужно отметить, что решение не является двояко-периоди-
двояко-периодическим, но состоит из двояко-периодической функции, умножен-
умноженной на экспоненциальный множитель. Следовательно, если а
1!
имеет одно из характеристических значений и>ъ ш2 или и>3, то
первое решение wt будет периодическим, а второе непериоди-
непериодическим.
Два независимых решения уравнения Ляме
могут быть также выражены в виде
{$ {z) — e1)i, {§> (г) - exf {Цг + «,,) + e,z).
15-63. Уравнения с двояко-периодическими коэфициентами при
однозначном отношении между любыми двумя решениями. Как и
выше, пусть уравнение будет иметь вид
dnw . . . d"~1w . . , .dw . , . „
d!n +Pi(z) ~-nzr, +¦¦¦ +Pn-i (г)ш +pn(z) w = 0
и пусть коэфициенты будут двояко-периодическими функциями
с периодами 2ш и 2ш'. Предположим, что хотя общее решение
неоднозначно, тем не менее отношение любых двух частных
решений является однозначней функцией z. Покажем, что этот
случай может быть приведен к случаю, когда общее решение
однозначно\
Пусть ах будет особой точкой; в этом случае показатели,
относящиеся к данной особенности, должны отличаться на целые
числа. Пусть
*i, Vi+^ш Vi + e12,...
будут показателями, расположенными в возрастающем порядке
величины, так что еа, е12>... будут положительными целыми
числами. Пусть аг будет вычетом px(z) относительно полюса
z = аг, тогда сумма корней этого определяющего уравнения
относительно ах будет равна
у и (л — 1) — «!,
что в свою очередь равняется сумме показателей, т. е.
и—1
S I
Предположим, что у нас имеется k особых точек
а:, я2,..., ак
в одном и том же параллелограмме периодов, тогда
п{ъ + v2 +- • • + v*> + y>ers = ~kn(n— 1) — Var.
Halphen, Mem. Acad. Sc. Paris, B), 28 A884) [CEuvres, 3, 55].
512
Но ^ аг — сумма вычетов относительно полюсов внутри па-
параллелограмма периодов,— равна нулю, следовательно
Я (V2 + V2 + . . . + VA.)
— целое число. Пусть т будет наименьшим целым числом, для
которого
т* (vx + v2 -f... -f vfc) = X
также является целым числом, и рассмотрим функцию
Поскольку
/ 2 + 2;мш \ V п, >^ / г \
о — = ? о I — I,
ТО
—X { 2г, (— ~-v.i) - гл\ +Бм {2m»j (
4J(z + 2mU)) = e ш
Отсюда следует, что логарифмическая производная ^ (г -f 2/?ш)
больше логарифмической производной ^ (г) на выражение
которое равно нулю. То же относится к периоду 2/то'. Следо-
Следовательно $'(z)/$ (г)—двояко-периодическая функция с периодами
2 2'
Произведем подстановку
тогда уравнение относительно W будет иметь двояко-периоди-
двояко-периодические коэфициенты с периодами 2тш, 2/жо'. Но в этом урав-
уравнении показатели, относящиеся к каждой особой точке,—положи-
точке,—положительные целые числа, следовательно уравнение имеет одно
однозначное решение. Однако, поскольку отношение между лю-
любыми двумя решениями уравнения относительно w однозначно,
то решение уравнения относительно W будет также однозначно.
Следовательно общее решение уравнения относительно W одно-
однозначно, что и требовалось доказать.
15-7. Уравнения с периодическими коэфициентами. Пусть коэфи-
коэфициенты в уравнении
однозначные чисто-периодические функции z с периодом 2ю,
не имеющие в конечной части плоскости z особенностей, кроме
полюсов Мы не потеряем в общности, если предположим,
что (о — положительное вещественное число. Теория уравнений
Э. Айне—133—33 513
этого типа аналогична теории уравнений с двояко-периодиче-
двояко-периодическими коэфициентами, откуда она повидимому была выведена;
обычно она называется теорией Флоке1.
Пусть w1{z), w2(z),..., wn(z) будет фундаментальной после-
последовательностью решений уравнения, тогда w1(z + 2ш), w.2(z +
+ 2<о),..., wn (z + 2ш) также будут удовлетворять уравнениям,
следовательно существует последовательность линейных соот-
соотношений
•tcv (z + 2ш) = anw1 (z) + а^щ (z) + ... + aTnwn (z) (r = 1, 2 , n)
в которой (как и в § 15-2) детерминант |ars| не равен нулю.
Задача определения решения u{z) так, чтобы
u(z -\- 2ш) = su (z),
эквивалентна приведению указанной выше последовательности
линейных соотношений к канонической форме, зависящей от
характеристического уравнения
hi — s, al2, ..., а1п =0.
Если это уравнение имеет п независимых корней slt s2,..., sn,
то можно найти такую фундаментальную последовательность п
решений н,(г), u.2(z),..., un(z), что
«1 <Z+ 2ш) = Sjttx B), . . ., Un(z+ 2ш) = snUn (Z).
С другой стороны, если st — кратный корень, то мы получим
подпоследовательность решений u1{z),..., и^(г), так что
«, (г + 2ш) = SiUj (г),
«2 (г + 2ш) = Sl { щ (z) + щ (z)},
На. (z + 2ш) = st {uv. (z) + ii(j i (z));
возможны и другие подпоследовательности аналогичного ха-
характера.
Рассмотрим аналитическое выражение решений в этих двух
случаях. В любом случае существует не меньше одного реше-
решения иг z), так что
ut (z + 2ш) == s^j B).
Теперь
е-Чг j 2ш) Ui (z + 2(ц) = ^-2»» e-«Hj (г)|
следовательно
е^и{г)
1 Floquet, Ann. Ее. Norm. B), 13 A883), 47.
514
является чисто-периодической фувкцией с периодом 2<л, если
а такая, что
Число а, удовлетворяющее уравнению
для любого частного значения г, называется характеристиче-
характеристическим показателем', его мнимая часть имеет неопределенное
значение, потому что к ней может быть добавлено любое целое
число, умноженное на та'/'ш.
Так, если п корней характеристического уравнения незави-
независимы, то существует линейно-независимая последовательность
и решений щ{г), щ{г),..., un(z), так что
иг(г) = еа'гчг{г),
где о.г — характеристический показатель, соответствующий sr,
а <рг (г> — чисто-периодическая функция с периодом 2ш.
Рассмотрим теперь случай, когда st — кратный корень. Если
мы напишем
то каноническая подпоследовательность приводится к
Таким образом
^ I JI 2 \ / i 1 \ ,
[z + 2a) = v^z) + v^i
ю^г + г») о,(г) т Х>
откуда
»! (г) 2ш
—чисто-периодическая функция г с периодом 2ш. В общем слу-
случае нетрудно доказать, что если
p. (Z) = г(г-2»)...{г-Bу-2)»}
"' Bш)%!
ТО
и,(Z) = <?*г{R-i (z) ъ (z)+P^-2{z)»2 (г)+... +Р, (г) ^
(v = 2, 3,..., :ч,
где «Pi(zr), ^2(^),..., (ftj.(z) — чисто-периодические функции с пе-
периодом 2<и.
515
15-71. Характеристические показатели. Если характеристический
показатель а — мнимое число, то соответствующее решение
остается конечным, когда z стремится к бесконечности вдоль
вещественной оси. Если же вещественная часть з не равна нулю,
модуль члена ё12 становится бесконечным для z — -f- со или для
z = — оо. В первом случае решение называется стабильным,
во втором — нестабильным.
Определение характеристических показателей обычно очень
сложно1. Рассмотренная теория, показывающая функциональный
характер общего решения, не дает практического метода полу-
получения явного решения. Задачу необходимо рассматривать кос-
косвенно.
Рассмотрим уравнение второго порядка
где p(z) — функция с вещественным периодом 2с«, аналитическая
во всей полосе — т( < у ^ ч\, с вещественной осью внутри нее.
В данном случае характеристическое уравнение будет иметь вид
s2 —As+ 1=0,
где А — постоянная, зависящая только от функции p(z). Пусть
f(z) и g{z) будут двумя решениями уравнения, так что
и пусть
f(z + 2ш] = auf{z) 4- al2g (z),
так что
g' (z + 2ш) -= a,J' (z) + a^g' (г).
Предположим, что z = 0, тогда
поскольку характеристическое уравнение имеет вид
то отсюда следует, что
1 Liapounov, Ann. Fac. Sc. Tout. B), 9 A907), 203 — 4>59 (впервые опублико-
опубликовано на русском языке, Харьков 1892), Polncare, Les Miiodes nouvelles de la
Mecanique celeste, IV; Horn, Z. Math. Phys., 48 A903), 400.
516
Вместо первоначального уравнения рассмотрим уравнение
¦^? = *<*)»;
оно имеет решения
/(Z, >.) = 1 + X/, (Z) + . . . + Х"/„ B) +. . •,
^ (г, ).) = 2 + *& B) +... + lagn (z) + -.. ,
так что функции/„(z) и gnC2) равны нулю при 2 = 0, а ряды
сходятся для всех значений I, если z лежит внутри параллельной
полоски, содержащей ось вещественных чисел.
Функции /n(z) и gn(z) удовлетворяют соотношениям
следовательно fn (z) и gn(z) могут быть вычислены из уравнений
/»(*) = fjp(z)f»-i(z)№*,
о о
о о
с начальными условиями
/O(Z)=1,
После того как функции fn(z), gn(z) были найдены, I может
быть приравнена единице и мы получим
Предположим, что функция р (z) — положительная для всех
вещественных значений z, тогда функции /n (z), gn (z) и g'n {z)
будут все положительны при z>0. Отсюда следует, что Л > 2»
следовательно все корни характеристического уравнения ве-
вещественны. Можно принять, что характеристические показатели
также вещественны, поэтому любое решение нестабильно. Таким
образом для получения стабильного решения необходимо, чтобы
функция р (г) была отрицательной для некоторых вещественных
значений г1.
1 Ляпунов (Soc. cit ) показал, что если функция р (г) отрицательная для
всех еещественных значений г, а абсолютная величина 2ю / p(z)dz — не боль-
о
ше 4, то | А | < 2, а корни характеристического уравнения — сопряженные ком-
комплексные числа с модулем, равным единице.
517
15-72. Уравнение Хилла. Предположим, что р {z) — четная
периодическая функция с периодом р. Уравнение может быть
написано в виде
~ + {60 + 29, cos 2г + 262 cos 4z + ¦ • •} w = О,
где функция р B) заменена эквивалентным рядом Фурье. Пред-
Предположим, что этот ряд сходится абсолютно и равномерно в пре-
пределах параллельной полоски, содержащей вещественную ось.
Пусть у нас имеется решение
w— e
тогда при подстановке в уравнение найдем, что коэфициенты Ьт
удовлетворяют рекуррентным соотношениям
(a+2ri,2br+ ?6v&r_v = 0
ч=—со
для всех целых значений г. Разделив это соотношение почленно
на (а + 2rif, a затем исключая коэфициенты Ъ, найдем-, что ха-
характеристический показатель d удовлетворяет сходящемуся опре-
определяющему уравнению
+ 4)*
—в, -е,
23-60'
еа - в, (&)= - fi0 — et
4s— b0 4s-Bo
Задача может теперь рассматриваться двояко: постоян-
постоянные 6 могут быть даны явно и необходимо определить а, или
же нужно найти зависимость, которая должна существовать
между постоянными 6 для того, чтобы а равнялось нулю, а
решение было чисто - периодическим с периодом к.
В первом случае задача разрешается непосредственно, так
как если мы напишем определяющее уравнение в виде
518
то найдем, что1
Д (и) = Д @)
следовательно а — корень трансцендентного уравнения
sin2( 4-««) = A@)sin2 (~к /еЛ
Во втором случае задача сводится к определению зависимости
между постояннбши G таким образом, чтобы
А @) = 0.
15-8. Аналогии с теорией Фукса. Если мы напишем ?
то уравнение типа Хилла может быть приведено к виду
4 ' dtl at ' ^. ^ь
v=0
Это уравнение имеет регулярные особенности приt = ± I, при-
причем в каждом случае показатели равны 0 и —, а ' также нере-
нерегулярную особую точку в бесконечности. При рассмотрении
уравнения в этой алгебраической форме, с точки зрения теории
Фукса, выявляются некоторые ее интересные свойства 2.
Фундаментальные решения, относящиеся к t — -\-1, могут быть
написаны в виде
-*) = /i — t
в первом случае ряд сходится внутри круга |1 —1\=2\ во вто-
втором случае значение \f\ —? вначале положительное, если —К
< t <-\г 1. Поскольку уравнение не изменится, если t заменить
на —t, то решения, относящиеся к особой точке t= —1, равны
причем ряд в этом случае сходится внутри круга ;1
Внутри области, общей для обоих кругов сходимости,
F1(l—t)= a.Fx (I + t) + $FZ A + t),
1 Hill, Acta Math., 8 A886); Уиттекер и Ватсон, Курс современного анализа,
§ 19-4 >..
2 Poole, Proc. London Math. Soc. B), 20 A922), 374.
519
где а, C, ^ и ? — постоянные. Зависимости
=7/4A-0
также должны удовлетворяться тождественно, так как в про-
противном случае /\(l+2) и /^(l + O находились бы в линейной
зависимости. Отсюда
к2 + РТ = PY + й2 = 1» Р (а + ») = Т (а + 2) = О,
причем возможны только два условия
(I) «=3=± 1, р=0, 7 = 0,
или
(II) а = - о, pY = 1 — а2-
Рассмотрим первое условие а = В = -j- 1, р = у = 0. Здесь
это соотношение справедливо в общей области сходимости
рядов, следовательно оно справедливо и вблизи начала. Но на-
начало является обыкновенной точкой уравнения, так что не может
существовать двух независимых четных решений, имеющих
смысл вблизи t = 0. Таким образом это первое условие должно
быть отклонено. Условия я = о = — 1, р = ^ = 0 подразумевают
существование двух независимых нечетных решений, действи-
действительных в начале; оно также должно быть отклонено. Следова-
Следовательно остаются только условия а = — 8, р-у = 1 — а2, которые
однако допускают частные случаи. Рассмотрим наиболее важные
из них.
(а) Пусть а = —о = + 1, ,8 = 0, так что
при 11 + t\ < 2. Это решение будет четным при а = + 1 и не-
нечетным при а= — 1; оно не имеет особенности в конечной части
плоскости. При подстановке ? = cosz, получим решение для а=
= + 1 в виде ряда четных косинусов кратных z, а для а= —1 —
в виде ряда нечетных косинусов также кратных z.
(b) Пусть а ==—3= + 1, т = 0. тогда
F2(l—0= ± /ЪA + 0
при |1 + ?|<2. Решением будет произведение \^1—t2 на целую
функцию t, которая меняет свой знак, когда t описывает малый
контур вокруг ^= + 1 или вокруг t = — 1. Эта целая функция
четная, если 3 = -}-1, и нечетная, если о = — 1. При подстановке
i = cos z, если 3 = -f- 1, решение получается в виде ряда четных
52U
синусов кратных г, а при 8 = — 1—в виде ряда нечетных сину-
синусов, также кратных г.
(с) Пусть а = Ь = 0, Py = 1, тогда
F1(l-t)=№{l+t), F2(l-t)=jrF1 (I + t)
при jl + t\ <2. Решения могут быть написаны в виде
F, A - *) = V 1 -Н ч if), F%(\-t) = / 1 - * * (-t),
где <p(?) — целая функция t. При подстановке ? = cosz они пре-
преобразуются в
Z7, = cos -,- zfiz), F2 = sin -у z/(t: — z),
где /(zj — ряд косинусов кратных z, который сходится во всей
конечной части плоскости z. Следовательно уравнение допускает
два независимых решения с периодом 4тг.
15-81. Существование периодических решений в общем случае.
Доказанное выше существование решений с периодом 4т: выдви-
выдвигает вопрос о возможности существования решений с перио-
периодом 2тп, где т — любое положительное целое число.
Рис. 12.
Рассмотрим контур на фиг. 12, имеющий форму петли, окру-
окружающей две особые точки t= ± 1. Начнем из точки А, в кото-
которой решения имеют вид
и будем следовать вдоль отрезка АВ. В точке В решения при-
примут вид
vB = ^ A + 0 +&,Р2A + t).
Следуя вдоль круга ВС, знак F2 изменится на обратный,
а знак Fx останется неизменным, так что
ис = aFt(l +t)- 3/yi + t). vc = -xFx A + t) - lFt(l 4-1).
Затем проведем отрезок CD; в точке D решения примут вид
uD = (а= - рТ) ^ A - t) + Р (а + 8) F2 (I -1),
^ = T(a-3)/:1(l-0 + (PY-»8)/?2(l-0.
Наконец, после того как мы опишем контур DA, решения при-
521
мут вид иА, vA, где
Но
следовательно
vA = -(а - i)Ft(l - t) -(8Y - 8»)
а = -8, ?Т=1-аа,
¦и =
Теперь пусть
тогда решением будет
W = аи + Ьг\
аи
bv = s (аи + / *>).
Уравнение, определяющее s, будет
2а2 — 1 — s, 2av
= 0
или
- 2ар, 2а2 — 1 — s
а2 - 1 _ S)! + 4«2 A — я2) = 0.
Это уравнение приводится к виду
-2a2) + l =0.
Если a8 > 1, то это уравнение дает два вещественных и неза
висимых значения s, которые, после того как были описаны
п контуров, приводят к двум решениям Wt и W2, равным соот-
соответственно s"W1 и s~nW2. Эти решения не периодические. С дру-
другой стороны, если а2 <1, то корни уравнения относительно s
являются сопряженными комплексными числами с модулем, рав-
равным единице. Предположим, что sm — 1, где т — положительное
целое число, тогда
/
2а- — 1 = cos —.
т
Таким образом, после того как были описаны т контуров,
возникают решения, принимающие свои начальные значения;
через переменную z они могут быть выражены в виде
W, = e-nilmf(- z),
где f(z) — функция с периодом 2т;, конечная для всех конечных
значений г. Эти решения имеют период 2ттг. С другой стороны,
если s не является комплексным корнем, равным единице, то
522
решения будут иметь вид
где 6 — иррациональное число. Решения теперь непериодические,
однако стабильные.
15-9. Линейные подстановки. Рассмотрим простой замкнутый
контур в области г, определяемый углом 0 при помощи урав-
уравнения
z = *(!»).
где (ь@) — однозначная периодическая функция 6. Предположим,
что контур не проходит через особые точки. Некоторое реше-
решение диференциального уравнения
dnw . , . d"~iw , . . .dw , . . „
¦^Г + А @^=Т +• • • + P«-t (z>dF + Л <Z>OT = °
может быть разложено (методом последовательных приближе-
приближений) в ряд, который сходится для всех значений вещественной
переменной 6. Пусть
будет фундаментальной последовательностью решений; тогда,
принимая, что коэфициенты уравнения однозначны, найдем, что
wx F + 2к), w, (9 + 2я),..., №„ F + 2тг)
также представляет фундаментальную последовательность. От-
Отсюда
wx @ + 2к) - aaw1 (9) + о12к-2 F) +... + alnwn F),
w,@ + 2«) = Oat», A) + a2,w2 F) +... + a.2nwn(Ь)
wn С + 2«) = M'i F, + «.w^2 (°)+ • • • + а,тта„ (8),
где коэфициенты a — постоянные с детерминантом, не обра-
обращающимся в нуль, который может быть вычислен из последо-
последовательности п уравнений типа
да,. F + 2тс) = anwl @) + ariw., F) +... + arnwn F),
w'r 0 + 2п) = ariw; D) + аг2те-; @) +... + amw'n Fj,
.jy("-DF 4- 2тс) = anw^'~l'> (Q) + й^а)!,"-1) F) 4-... -j- arnw^~1^ @).
Таким образом линейные подстановки, претерпеваемые после-
последовательностью фундаментальных решений, когда z описывает
простой замкнутый контур, могут рассматриваться как известные.
В частности, предположим, что коэфициенты уравнения —
рациональные функции г, которые при разложении на частные
дроби принимают вид
523
Из общих теорем существования следует, что если коэфи-
циенты Aik рассматривать как параметры уравнения, то реше-
решения w^z), w.2(z),..., wn(z) будут целыми функциями этих пара-
параметров, и следовательно коэффициенты aTS в последовательности
линейных подстановок будут мероморфными функциями этих
пара иетров1.
15-91. Группа линейного диференциального уравнения. Предпо-
Предположим, что коэфициенты уравнения однозначны относительно z,
а также, что имеется только конечное число особых точек. Если
мы заставим z описать замкнутый контур, не проходящий ни
через какую особую точку, то получим такой же результат, как
от линейной подстановки S, преобразующей и\, w2,..., wn со-
соответственно в
ailw1 + aJ2zc2+ • • • +alnwn,
а-пЩ + a^w, +... +a2nK-n,
102 + ... +annivn,
где детерминант постоянных ars не равен нулю.
Пусть S' будет линейной подстановкой, соответствующей
контуру, отличному от первого. Тогда, если мы проведем сна-
сначала второй контур, а затем первый, то получим подстановку
той же общей формы в виде произведения S'$, в общем слу-
случае отличного от SS'.
Любой контур в плоскости z, содержащий некоторое число
особых точек, эквивалентен последовательности замкнутых кон-
контуров или петель, описанных в определенном порядке и таким
образом, что каждая петля окружает только одну особую
точку.
Предположим, что у нас имеются т особых точек аи а2,. ..,ат
и пусть Sr будет простой подстановкой, полученной при про-
проведении контура вокруг точки аг в положительном направлении.
ТогдаSr~l будет обратной подстановкой, полученной при прове-
проведений того же контура, но в отрицательном направлении. Любая
произвольная подстановка может быть таким образом разложена
в последовательность простых подстановок
С*С^ С'"СР
где I, у, <6, р—положительные или отрицательные целые чи-
числа, а Spr обозначает Sr, описанную |р| раз в положительном и от-
отрицательном направлениях, соответственно тому, является ли
р положительным или отрицательным.
1 Дальнейшее развитие зависит в значительной степени от теории инвари-
инвариантов обычного линейного диференциального уравнения. См. Hamburger, J. fur
Math., 83 A877), 193; Poincare, Acta Math.. 4 A883), 212; Mittag-Leffler, Acta Math.,
15 A8S0J, 1; von Koch, Ibid., 16 A892), 217.
524
Совокупность таких подстановок называется группой урав-
уравнения1. Группа была определена относительно частной фунда-
фундаментальной последовательности решений. Рассмотрим теперь
вторую фундаментальную последовательность; она выводится
из первой последовательности при помощи определенной под-
подстановки L. Тогда, если S — любая подстановка, проведенная в
первой последовательности, то S~1S?— подстановка, проведен-
проведенная во второй последовательности. Очевидно,если подстановки
5 образуют группу, то подстановки L~iSZ также обра-
образуют группу, и эти группы между собой тесно связаны.
15-92. Проблема Римана. В качестве иллюстрации общей тео-
теории линейных диференциальных уравнений может служить сле-
следующая классическая задача. Нужно определить функцию
а
а р т z I,
a' 8' v'
Р
удовлетворяющую следующим условиям:
(I) функция должна быть однозначной и непрерывной во всей
плоскости, за исключением особых точек а, Ь, с;
(II) между любыми тремя определениями Pt, PS,P3 этой функ-
функции существует линейная зависимость
где съ с2, cs—постоянные;
(Ш) в соседстве с точкой а существуют два независимых
определения
где /i (z) и /2(г) — аналитические в соседстве с z = а и не равны
нулю в а. Аналогично, в соседстве с х = b имеются
(x-bfgl(z), (z-b
а в соседстве с z = с
Пусть Р, и Р2 будут любыми двумя линейно-независимыми
определениями искомой функции. Тогда, поскольку любое дру-
другое определение находится в линейной зависимости от Рг и Р2,
искомая функция будет удовлетворять диференциальному урав-
1 Эта совокупность называется также монодромной группой уравнения, в
отличие от группы рациональности. Нужно отметить, что последовательность
линейных подстановок образует группу, если она содержит: (а) тождественную
подстановку, (Ь) обратное выражение для каждой подстановки и (с) произведе-
произведение любых двух подстановок.
525
нению второго порядка
d2w dw
d> ~dJ> W
i . V
\PI p,,l
которое может быть написано в виде
= 0,
0.
где
, - Р,Р2
Рассмотрим поведение функции р в соседстве с особой точкой
z = а. Пусть
а = iz — a\af /2л р — (z п\*' f (~л
тогда
где <о(г) — функция аналитическая в соседстве с z = а. Отсюда
следует, что
"" z— a ' z — b ' z — с ' ^ ''
где функция и (z) будет везде аналитической. Теперь, поскольку
р -функция аналитическая в бесконечности, необходимо, чтобы
для больших значений \z\
Но
р =
l-2. +0(z
а поскольку h(z) = OA), необходимо, чтобы #(z) = 0, следова-
следовательно
где
Аналогично найдем, что в соседстве с а
526
следовательно q может быть выражено в виде
4 ~ {г—аJ ^ (г-Ъу ^ {г—cf ^ z — a ^ г—Ъ т г—с
где А, В, С — конечны для всех конечных значений z. Однако
более удобно принять эквивалентное выражение
а .- * LA__l--^-4- *-
4 (г—я) (г—Ь) (г—с) | г—а ' г-Ь "т г—с
где /., Л(, N—конечны для всех конечных значений г.
Поскольку точка в бесконечности является обыкновенной точ-
точкой для больших значений \z\, то
q(z) = O(z-4),
следовательно L, М, N — постоянные, откуда легко доказать?
что
L =г аа (а — Ь) (а —с),
М = 33'(Ь -с) (Ь-а),
Таким образом Р- функция Римана удовлетворяет диферен-
циальному уравнению J
ePw , v 1 — а — a' dW , у от' (й — 6) (й — с) W р.
п? "~ " ~ z — а * dz "" " z — я " (г —я) (г — Ь) {z—с7 '
которое называется обобщенным гипергеометрическим уравне-
уравнением. При а = 0, 6 == 1, с = со2, а' = Р' = 0 это уравнение преоб-
преобразуется в обыкновенное гипергеометрическое уравнение
Решения обобщенного гипергеометрического уравнения дают
таким образом искомые функции. Для того, чтобы они имели
обусловленную форму, необходимо, чтобы ни одна из разно-
разностей показателей
а-а', р-р', Т-Т'
не была целым числом, так как в противном случае в одно из
решений вошли бы логарифмические члены.
15-93. Группа гипергеометрического уравнения. Пусть Ра и Ра-
будут двумя решениями, соответствующими показателям « и а'
в особенности а, Рр и Яр— решениями, относящимися к особен-
особенности b, a PT и Рг-—решениями, относящимися к особенности с.
1 Это ураниение было впервые получено Папперитцом [Papperitz, Math. Ann.,
25 A885),213]. Риманввел некоторые упрощения, которые привели к обыкновен-
обыкновенному гипергеометрическому уравнению.
2 г — с замещено 1/г.
52Т
Пусть Г будет любой замкнутой простой кривой, например кру-
кругом, проходящим через точки a, b и с. Тогда внутри Г все
шесть решений будут аналитическими и между ними будут су-
существовать соотношения
'1 — -Ay P.( -f- Ау'Ну',
- ра. = л; рт + агрг,
где Л—постоянные коэфициенты. Эти постоянные не все неза-
независимы; между ними существуют соотношения, которые мы
сейчас определим.
Поскольку точка в бесконечности является обыкновенной,
контур в положительном направлении вокруг точки с эквива-
эквивалентен контуру в отрицательном направлении вокруг точек аи Ь.
Третье из указанных соотношений показывает, что первый
контур преобразует Ра в
в то время как первое соотношение показывает, что второй
контур преобразует Ра в
Следовательно
Лт е^Р, +
и аналогично
АУ^Р, + А\.е**Г Р.г = е~2пга'
Но
Лт Рт + АГРГ = АвР-,+ Аг
Исключая Р7, Р-,; Рн, Рр« из этих четырех соотношений, найдем
Л1 _ А? е~г'!" sin (* + р + V) т- __ А{
лт
лт.
е sin i
е KI':I sm
е. "¦" sir.
(«-
- р' + т') я
ЬР' + 7')«
f P1 4- 7) «
Лт- Л^ е лк' Sin (a' + \i +f) тс -Лр- е я"'81»(а'4- 3'+ -\) г.
Следовательно любое из cooiношений
Аг
А А А
3 3 * ¦* -v
известно.
528
Все четыре соотношения совместны, если
sin (а + р' + У) я • sin (а' + 3 + v') я sin (а + ft' + "О п ; sin (а' + р + -[) я
Sin (a + ^ -t- у') к ¦ S1.. (а' + У -t- у') я sln (а> + $' + ?) л • Sil! (а + 3 4- Т) я
что удовлетворяется на основании соотношения
Чтобы определить группу уравнения, достаточно рассмотреть
изменения, которые претерпевают два фундаментальных реше-
решения, например Р* и Ра>, когда точка z описывает контур вокруг
каждой из двух особых точек, например а и Ь. Контур, описы-
описываемый вокруг а в положительном направлении, преобразует
Ра и Ра' соответственно в
и аналогично, описав положительний контур вокруг Ь, Ра и Pa-
соответственно принимают значения
А ?е~^Р? + АгегтЛГРг, А^Р? + Аге2т'Р?..
Но поскольку
Ра = Ар Рр + Ар.Pp.,
/V^ApP
где
конечные формы, которые примут Р* и Ра; после обхода кон-
контура вокруг Ь, могут быть выражены через Р« и Р„- в виде
Не щ — Хе^ р е "? — е "'" р
>./ _ х ^« т >т^х ^а#-
Чтобы получить несколько более симметричное выражение,
допустим, что
и=(Х'—Х)Р„, «=Ра.,
тогда, если 5а — операция проведения положительного контура
вокруг а, то
Sau = е2™!!, Sa^ = e2™'v,
а если Sb — аналогичная операция относительно Ь, то
Э.'Айнс—133—34 529
где
_ lL — sin (a + ft' + f') л • sin (a' + ft + -Qrc
* ~~ X ~~ Sin (a' + ft' + -к') п • Sin (a + ft"+ V) л" '
Обе подстановки Sa и Sb могут рассматриваться как фунда-
фундаментальные подстановки группы; любая другая подстановка
состоит из целых степеней Sa и Sb.
Принимается без доказательства, что все решения уравнения
являются алгебраическими функциями z, и обладают корнями
алгебраического уравнения; каждое решение может иметь лишь
конечное число значений в каждой особой точке. Таким обра-
образом число независимых подстановок конечно, следовательно и
группа конечна. Очевидно, для конечности группы необходимо,
чтобы
' «, а', р, ,3', Т, Г
были все рациональными числами.
Если уравнение привести к нормальному виду путем устра-
устранения члена, содержащего ~ подстановкой
w = (z — aJ (z — b) 2 (z — с) 2 -у,
то оно примет вид
dz" ^^„ (г - a, f 4ф u
где
at = a, a2 = fe, a3 = c,
Алгебраические решения возможны в пятнадцати случаях, когда
^i» ^2> ^а принимают следующие значения1,
I % Чг % " х/2 V. Vs
Ш 2/S V8 Vs IV ^ !/, V4
v 2/3 v« V4 vi v8 V, Vs
vii «/s1/.1/. viii «)8i/Bv;
IXV22/6V.3 X3,6i/3v5
xi 7.%'Д xii ^VsVs
xiii Ve^'s xiv v.Vs1/.
XV s/5 */s Vs
[Подробное исследование линейных уравнений второго порядка,
общие решения которых являются алгебраическими, и практи-
практические методы получения таких решений см. Forsyth, Theory of
Differential Equations, 4, 176— 190].
1 Schwarz, J. fur Math., 75 A872), 293; Cay ley, Trans. Camb. Phil. Soc,
13 A881), 5 [Coll. Math. Papers, 11, 148]; Klein, Math. Ann., 11 A877), 115; 12,
167 [Ges. Math. Abhand, 2, 302,*307; Vorlesungen fiber das Ikosaeder, 115.
530
Примеры
1. Докажите, что если w удовлетворяет алгебраическому уравнению
w" 4- а.^"~2 + ... -fr ап = 0.
коэфициенты которого полиномы от z, то w удовлетворяет линейному диферен-
циальному уравнению порядка п—1, коэфициенты которого — рациональные
функции z.
2. Если и—любая функция z и
то докажите, что
d-w i / пи' и" \ dw J_ u'-
dz^ ~*~ \и*~+ 4 "" и' У dz 9 м2 -f 4 W "
3. Докажите, что диференциальное уравнение, соответствующее схеме
! 0 1 a or
Р 11 0 0" 0 з г
где
имеет вид
z — a) dz r z(z — 1) (z — я)
q — произвольная постоянная.
Если решение, относящееся к особой точке z = 0 с показателем 0, обозна-
обозначить через
W{a, q; з, т, >., |j.; z),
покажите, что возможны восемь решений вида
w=za (z— if (z — aj1 W(a, q; z'. -.', X', ;j.'; z).
[Если я — 1, g = 1 или й = 0, q = 0, то уравнение вырождается в ги-
гипергеометрическое уравнение. Можно построить последовательность из 64 ре-
решений аналогично последовательности из 24 решений гипергеометрического
уравнения. См. Heun, Math. Ann., 33 A889), 161, 180].
4. Уравнение
d'2w . aw .
—— + р — qw = 0
uz- dz
преобразуется подстановкой
1 г \
w= W • ехр | 7- I p dzj
в уравнение
d*W
где
1_ J !_ rfyw
[Это выражение называется нормальной формой уравнения. Уравнения,
имеющие одинаковую нормальную форму, эквивалентны, a I— нх инвариант].
Если z — функция s, то выражение
531
где штрихи обозначают днференцнрование относительно s, называется произ-
производной Шварца. Пусть wx и ш2 будут двумя независимыми решениями указан-
указанного уравнения относительно w и пусть s= w^wi, тогда
Докажите, что для изменения независимой переменной z на Z
5. Докажите, что для гипергеометрического уравнения
*) + U^i ±
{s, z}- zz (z —IJ z(z— i)
где X, |j., v зависят от a, ?, у.
[Связь полученного результата с построением алгебраических решений, см.
Forsyth, Theory of Differential Equations, 4, 182 — 184].,
6. Если уравнение Ляме с п = 1 выразить в виде уравнения Якоби
то его общее решение будет иметь вид
где dn3 а= Г[ — ft2.
Рассмотрите частные случаи
h = 1 + k2, I, k\
[Hermlte].
7. Покажите, что если п — положительное целое число, то уравнение Ляме
-^ - {ft + п{п 4- 1) Р {z)}w = О
имеет для соответствующих значений Л решения вида
(I) w = Ри (и = 2т),
(II) ^ = [{&(*) -е>_} {(эB) - у] 1" Pw_t (я - 2т),
(III) к- = Щг) - ej Pm-1 (я = 2т -1),
(IV! да = о\г)Рт_з (я = 2т -1),
где Рг полином степени г от у> (z), а е, , e(i —любые две постоянные е„ е2,еа.
Исследуйте соотьетствующие решения формы Якоби уравнения Ляме.
8. Проинтегрируйте уравнение
~dz* 1 srT2' г~ cn2l сГ~г ^ П^П ~^~ ^ '
[Darboux].
532
9. Найдите линейное диференциальное уравнение, решения которого явля-
являются произведениями решений уравнения
- + /„
и объясните, почему оно третьего порядка.
10. Покажите, что уравнение
О,
[Lindemann].
г 0
-^T " Т ° - 2г) iS
b)w
имеет два частных решении, произведением которых является однозначная
трансцендентная функция F(z), и покажите, что этими решениями являются
{F(z)} * • expfc I Z—r_ 1,
L J {z(i — z)} 2 F(z)i
w, = {Дг)> 2
{2A - г)} ^
где с — определенная постоянная. При каких условиях эти два частных реше-
решения совпадут?
[Math. Tripos, II, 1898].
ГЛАВА А VI
РЕШЕНИЕ ЛИНЕЙНЫХ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В ВИДЕ РЯДА
16-1. Метод Фробениуса. В предыдущей главе (§15-3) мы
показали, что если все решения линейного диференциального
уравнения регулярны в соседстве с особой точкой, то коэфи-
циенты уравнения подлежат некоторым определенным ограниче-
ограничениям. Так, если рассматриваемая особая точка является нача-
началом, то уравнение может быть написано в виде
п d"w , п — 1,-, . ч d"~ 'да . . •-, ,ч dw , •-, , , _
* ~^T+Z Pi(z)-^t+--- + zP"-i(z)Tz + P«№w = 0'
где функции Рг(г),.. .,Pn(z) аналитические в соседстве с 2=0.
В этом случае можно получить явное разложение п фундамен-
фундаментальных решений, относящихся к особенности в начале, а также
доказать, что эти разложения сходятся для достаточно малых
значений (z)l.
16 • Н. Формальное решение. Образуем ряд
со р +v
W(z, Р)= ? с, г (соф0),
v = О
где число о и коэфициенты с, должны быть так определены,
чтобы W было решением диференциального уравнения. Пред-
Представим диференциальное уравнение символически в виде
Lw = 0,
тогда
LW(z, u="C4L* + "
= ?c,z?+7(z, p+v),
где / (z, p -j- v) представляет выражение
[? -Ь- v]n + Гр + v]B _ tPt (z) +... + [p + vKP,._ , (z) + Pn (z);
символ [р + v]n заменяет (p + v)(p|v-l)...(p-J7V-n-jrl). Те-
Теперь представим f(z, p + v) — аналитическую функцию z в со-
соседстве с z = 0 — в виде степенного ряда по z
/. = 0
1 Frobenius, J. fur Math., 76 A873) 214. Модификации первоначального пред-
представления см. Fursyth, Differential Equations, 4. 78—97.
534
откуда
LW(z, р) = S {с,/о(р + v) + cv_ ,/х (р + v - 1) +... + cofi, (Р)}z* + \
Если
1'
то коэфициент каждой отдельной степени z должен быть равен
нулю. В этом случае возникает последовательность рекуррент-
рекуррентных соотношений
^/0(р + v) + с,_^(Р + v- 1)+... + с0/, (р) =0,
и т. д.
Поскольку с0 не равно нулю, первое уравнение последова-
последовательности
определяет п значений р, которые могут быть зависимыми или
независимыми. Если одно из этих значений выбрать таким об-
образом, чтобы/0(р+¦") Ф 0 для любого положительного целого
значения v, то рекуррентные соотношения определят постоян-
постоянные cv единственным образом.
г = <~ 1)v C°F'' <Р>
/o(P+l)/o(P + 2).../olp+v)'
где
/\ (p) =
i/i (P + v - 1), /я 0» + v - 2),...,/, _ 1 (р+1), /v (?)
/о (Р + V — 1), Л (р + V — 2),. . . ,/v _ 2 (р-Ы), /v_i(p)
0 !
о , о ,...,/0(р+1), Л(р)
Допуская, что ряд W(z,p) сходится для каждого выбранного
частного значения р, увидим, что если п корней определяющего
уравнения независимы, и никакие два из них не различаются на
целое число, то каждому числу р соответствует определенная
последовательность коэфициентов cv, а всего получается п не-
независимых решений, образующих фундаментальную систему.
Если п указанных значений р таковы, что два или несколь-
несколько различаются на целое число, то они могут быть расположе-
расположены в виде независимых последовательностей
POf Рх> - • -»Р«- Ь
так, чтобы величины в каждой последовательности различались
535
только на целые числа, и их вещественные части образовали бы не-
возрастающую последовательность. Только первый член каждой
последовательности дает решение рассмотренного типа, посколь-
поскольку, например, любой член ра + « последовательности pa...ft — t
равен ра или меньше его на положительное целое число. В пер-
первом случае решение, соответствующее ро + к, формально тожде-
тождественно с решением, соответствующим ра; во втором случае ре-
решение, соответствующее рс + к. не действительно вследствие на-
нарушения условия Л (р + v) =(= О ПРИ у = Р« — Ра + к.
Трудности второго случая могут быть устранены подстановкой
со/о(р<> J-K + v) вместо первоначальной постоянной с0; в этом случае
получается ряд, где все коэфициенты с, конечны, но первые v
членов обращаются в нуль, а ряд отличается от ряда для ра
только постоянным множителем и следовательно не является
независимым решением.
16 • 12. Модификация формального метода решения. Чтобы по-
получить все решения, соответствующие каждой последователь-
последовательности, необходимо видоизменить прежний метод следующим
образом.
Пусть а будет параметром, изменения которого ограничены
кругом, проведенным вокруг корня fo(p) = O с радиусом, доста-
достаточно малым для исключения всех других корней1. Предположим,
что мы получили ряд
где с0 — произвольна, a cv определяется как функция = при по-
помощи рекуррентных соотношений
,_ i/i (о + v - 1)+... + cof (с) = 0.
где функциональные операторы/0,/1;.. .,/v,.. .определены выше,
тогда, согласно рекуррентным соотношениям,
L«7(z, о) = S {c,fo(a + v) + с,_ <Д(о + v - 1)+... -f- cS № "
= Со/о(оJ'.
Мы получим предыдущее решение, полагая о = р, где р —со-
—соответствующее решение /0(з) = 0.
16 ¦ 2. Сходимость разложения. Пусть Г будет радиусом наи-
наибольшего круга, с центром в начале, внутри которого все функ-
1 /„((>)= 0 является алгебраическим уравнением относительно ? степени п;
следовательно его корни изолированы, и вокруг каждого корня (причем крат-
кратный корень считается только один раз) может быть проведен круг (с радиусом,
не равным нулю), который не содержит других корней.
536
ции Pi(z), Р2(г),...,Рп(г) — аналитические, тогда ряд
и ряд
/' (г, о + v) =У (X + 1)/>. + , (о + v)z> ,
2
X
полученный почленным диференцированием первого ряда отно-
относительно z, будут сходиться при \z\ < Г. Пусть М (а + v) будет
верхней границей 1/'(г, a + v)| на круге \z\ = R = T — s, где е —
произвольно малое положительное число, тогда согласно интег-
интегральной теореме Коши
откуда
\(к -J- 1)Д + 1 (з + v)| < — ¦
i/x ¦ 1 (a + V) | < Ж (a + v) /? ~ л (Х= 0,1,2,.-.)
Поскольку изменения а ограничены в соседстве с корнями
/о(°)=О и поскольку число таких корней конечно, положитель-
положительное целое число /V может быть выбрано таким, чтобы /(a -f v +
+ 1L=0 при v > N. В этом случае
С, + 1 = — y^-jr!—17 {^ Л C + V) + С, _ i/jj (О + V — 1) + . . . +
если вместо каждого члена подставить его модуль, получим
|C |<{^IIAC+V)l + 1C|l/'(O + V1)!+
Как следствие этого определения, получим
V + 1"l/4=TV+l)ii"l/o(a+v+r)|/< Uv'
поскольку jcv | < См, то
Q < |/0 (о + v + 1)| ¦+ |/0 (с + v +1
Выберем положительные числа Л, так, чтобы они удовлетворяли
537
рекуррентному соотношению
Л,+ 1^_ M(g + v) i/.(°+vJ|
Av " 1/оC + * + U! + '/о(= + •' г !) К '
и чтобы An = С№ тогда
IC+l| <С ;.1<А,_ 1 (V>N).
Теперь
/B, о + v) = [с + v]n -{- [о + v]B _ iP2 (г) +... -fPn (г),
откуда
/' (Z, a + v) = [а + v]B_x P; (Z) + [а + v]n_, Р; (г) + .. , +Р'п (~),
т. е,/'(г, а-O v) — полином от s + v степени п —1, коэфициенты
которого зависят только от г, следовательно
Af(o + v)= Max |/(z,o+ v)! (!«!</?)
< Мг | [о + v]n_t | + М2 S [з + vjn_21 + ... + уИп,
где
Л*г = Мах|Р;(г)| (|z|</?),
откуда, если v0 дано, то число К, независимое от а, существует
таким образом, что
М (з + v) < /TV,
если v > v0. Аналогично, поскольку /0 (a + v) — полином от а -fr v
степени п, существует число Ки независимо от а, причем
l/o(° + v
Отсюда, когда v—*со
/о (о + v + 1)
равномерно относительно о. откуда следует, что
А^. _ л
равномерно относительно а.
Отсюда1 степенной ряд
имеет радиус сходимости R, и поэтому, так как
\сл\< Аш
радиус сходимости ряда
1 Bromwich, Theory of Infinite Series, § 84.
538
не меньше /?. Поскольку Ап не зависит от а, сходимость равно-
равномерна относительно о.
16-3. Решения, соответствующие последовательности показателей
диференциального уравнения. Рассмотрим одну из последователь-
последовательностей показателей диференциального уравнения, например,
последовательность г
которая так расположена, что если х<>., то рх — р> положитель-
положительное целое число или нуль. Поскольку эти показатели не обяза-
обязательно равны, они могут быть разделены на подпоследовательно-
подпоследовательности так, чтобы члены каждой подпоследовательности были равны
между собой. Так, предположим, что р0 = Pi =.••• = p;-i соот-
соответствуют корню /0 (з) = 0 кратности i; pt = рг t = ...== p/_i со-
соответствуют корню кратности j — i; py= py+t = ... = pk_t соот-
соответствуют корню кратности k—j и т. д. до тех пор, пока ряд
не будет исчерпан.
Чтобы исключить возможность того, чтобы какой-либо из ко-
эфициентов Су, определяемых рекуррентными соотношениями
§ 16-12, стал бесконечным, напишем вместо с0
^о/о (о + 1) /о C + 2) • • • /о (а + ш) = С0 f (з),
где ш = р0 —ра_ь что равносильно умножению ряда для W{z, з)
на /(а), тогда
конечно, если изменения а ограничены в соседстве с любым
из ро, р1} .... p*-i. Аналогично
= Со/' (О) 2е ,
где F(p) — произведение /0 (з)/0 (а + 1)... /0 (а + <").
Теперь в функции /^(а) множитель /0 (а) степени i относитель-
относительно (а — ро), степени j — i относительно (а — р,-), степени k —j
относительно (а — р^) и т. д. Никакой другой множитель не со-
содержит (з —р0), но/0(о-j-р0 — pt) степени i относительно (а—р;).
Аналогично (а — р.) входит в виде множителя степени j — i
в функцию /о (а -f- p. — ру) и в виде множителя степени г
в /о (а 47 ро + Pi). Поэтому F{a) степени i относительно (з — ро\
1 Каждый показатель повторяегся некоторое число раз, равное кратности
соответствующего корня /0 (о) ==0.
539
степени j относительно (а — р;), степени k относительно (а — р^
и т. д.
Если а лежит в некоторой области в плоскости о, содержа-
содержащей точку р , где р — показатель рассматриваемой последова-
последовательности, то коэфициенты с—аналитические (в действитель-
действительности рациональные) функции з. Если | z\ < R, то ^Vvzv является
равномерно сходящимся рядом аналитических функций з и мо-
может быть поэтому продиференцирован относительно а. Более
того, операторы L и -— могут переставляться. Отсюда следует,
ЧТО
для s = 0, 1, 2, ..., т— 1, где т — степень F(о) в (? — рч), и, сле-
следовательно, для любого значения s
является решением диференциального уравнения.
Теперь
со
W (z, з) = z' V^g-v (з) z'',
V, О
где gv (з) = cv Л (з), откуда
do*
4=0
оо
= Ws B, з) + s log ZWs-i (Z, O)+ . . . + (log Z)s Щ (Z, a);
wr(z, з) равно
Рассмотрим показатель р0 в первой подпоследовательности.
В этом случае gv (р0) = с, f (p0) конечно или равно нулю для
всех значений v и g0 (p0) 4= 0. Следовательно здесь возникает под-
подпоследовательность i решений
540
W0 = w0{z, p0),
W1 = w0 (z, p0) log z + wj. (z, p0),
W2 = w0 (z, po) (log zf + 2щ (z, Po) log z + m, (z, p0),
= и>0 (z, Po) (log z); f + (i: — 1) Wi (z, p0) (log z)' 2+... +
+ Wt-i (Z, Po).
Наличие w0 (z, p0) (log z)' в Wr показывает, что эти i решений
линейно-независимы.
Рассмотрим показатель р* второй подпоследовательности.
Здесь gv(pi) — нуль порядка i, когда v = 0, 1, 2,..., р0 — р— 1
и конечно или равно нулю, когда v > р0 — р,-. Отсюда следует,
что
Ро-Р, — *
когда s = 0, 1, 2,... , г — 1; поэтому ведущий член в W{z, a)
степени о + р0 — р,- относительно г, т. е. степени р4 при ° = р,-.
Решения, соответствующие подпоследовательности индекса г,
были полностью перечислены; они соответственно равны Wo,
Wlt..., Wi—i. Поскольку решение
не содержит логарифмических членов, оно равно Wo, умножен-
умноженному на постоянную; при s < i — 1
является линейной комбинацией решений Wo, Wb ..., Ws.
Остаются j — i решений
J!
где s = i, i + 1, • • •, j — 1. Эти решения образуют подпоследо-
подпоследовательность
Wt - wo(z, Pj) (log z)i+iwl(z, P;) (log z)'~l+ ...+wt (z, Pj),
IP)_1 =W0 (Z, p,) (log Z)" + (у - 1) Wt (Z, p;) (log г/ + . . . +W,^(Z, p.),
541
где wr (z, рг) — линейная комбинация w0 (z, p0), чюх (z, p0), ... ,
wr(z,p^, если г<г— 1. Член wt (z, pt) не равен нулю, так как
ФО.
Л-
Остальные члены подпоследовательности индекса i содержат
выражение да,-(г, рг), умноженное на логарифмический множитель.
Так, Wi+r содержит член Wi (z, p;) (log z)r, следовательно члены
подпоследовательности линейно-независимы. В следующем па-
параграфе мы покажем, что они также линейно не зависят от чле-
членов первой подпоследовательности.
Аналогично можно доказать, что подпоследовательность
индекса j дает k— j решений, которые могут быть выражены
в виде
где s =у, у+1,..., k — 1 и т. д. до тех пор, пока вся последо-
последовательность показателей р0, plt.. .,p«_i не будет исчерпана.
Последовательность показателей
Pa- P.+ 1» ¦ • • РР—1
разделяется на подпоследовательности равных показателей и
рассматривается аналогично. Следовательно мы получили сово-
совокупность п решений; остается доказать, что они образуют
фундаментальную систему.
16-31. Доказательство линейной независимости решений. Рас-
Рассмотрим решения, соответствующие частной последовательности
показателей, например, последовательности р0, ръ ..., ра_ь и пред-
предположим, что эти решения связаны линейным соотношением
A0W0 + A,W, + ... + Л,_, W,-t = 0.
Расположим левую часть уравнения по убывающим степеням
\ogz, тогда совокупность членов высшей степени k относи-
относительно logz должна тождественно обратиться в нуль
ArWr + ... +^sWs = 0.
Но каждое из чисел Wr, • ¦ • , Ws получается из независимой
подпоследовательности, следовательно они соответствуют раз-
различным показателям. Коэфициент члена высшей степени дол-
должен обратиться в нуль так же, как и коэфициент второго выс-
высшего показателя, и т. д. Отсюда следует, что
Выражение A0W0 + A1W1 + ... + Aa-iWa~i теперь степени
k— 1 относительно logz; совокупность членов, содержащих
542
(logг)* i, приравнивается нулю. Можно доказать, что каждый
коэфициент, который входит в эти члены, равен нулю. Процесс
нужно продолжать до тех пор, пока мы не докажем, что
Л0 = Л1= ... =Аа-1 = 0.
Следовательно, решения любой частной последовательности не
находятся в линейной зависимости.
Рассмотрим теперь совокупность решений
Wlt W2,..., Wn
и предположим, что существует линейная зависимость вида
A, Wx -\- A W» + ... + AnWn = 0.
Поэтому совокупность членов высшей степени k относительно
logz должна обратиться в нуль
(ArWr +...+ ASWS) + (AtWt +...+AuWu) + ...=0.
где члены, заключенные в скобки, принадлежат к той же после-
последовательности. Предположим, что множители этих последова-
последовательностей, соответствующие контуру вокруг точки г, как на-
начала, равны Ьг, 8„,... Тогда после X контуров
0^ (AtWt +...+AnWu) + ...=0.
Поскольку Oji^e.,!! ..., эти уравнения для X = 0, 1, 2,... несов-
несовместны, если только мы не получим
ArWr+ ...+A,W. = 0, AtWt+... +Л„Г„ = 0,...,
что, как мы доказали, возможно лишь в случае
Рассмотрим теперь члены степени k — 1 относительно logz;
можно доказать, что их коэфициенты также равны нулю. Про-
Процесс следует продолжать по тех пор, пока мы не докажем, что
Аг = А2 = ... = Ап = 0.
Следовательно п решений линейно-независимы и образуют фун-
фундаментальную систему.
16-32 Приложение к уравнению Бесселя. Рассмотрим уравне-
уравнение Бесселя в виде1
или символически Lw = 0. Тогда, если
мы найдем, что
1 Forsyth. Differentia Equations, 4, 101.
543
€СЛИ
с, {(а + v)a — я2} + cv_2 = 0.
Корни определяющего уравнения
а2 — Я2 = О
(v > 2).
равны + л; если л не целое число, то соответствующие реше-
решения будут независимы. Решениями будут Jn(z) и ./_л(г), где
I (z\ _
1)
Рассмотрим сначала специальный случай, когда п равно
нулю. В этом случае/n(z) и У_я(г) совпадают с J0(z)
г2 г4
•Ч) \^/ * 2^ "Г '22Т4?
- 4а • б2 " ' "
Поскольку а=0 является двойным корнем определяющего урав-
уравнения, второе решение будет иметь вид
K0(z) = Hm A|V
где
Предположим, что и — положительное целое число; реше-
решение w = Jn (z) является единственным решением, не содержа-
содержащим логарифмов. Напишем
7-=1
так что
Лп—2
{(a + 2Я+2J — я3} {(з + 2n i-4J - П'
1
~ • • ¦ \ = w
544
При а = — п функция wx обращается в нуль, a w2 пропорцио-
пропорциональна функции Jn (z). Второе решение получается при помощи
выражения
.. dw
llin —х— .
Пусть
dw, ,v, .. dw, ....
тогда
я—i
СО
2
Член
оо
^ с—
который входит в W2, пропорционален Jn(z) и может быть опу-
опущен. Пусть
с
п
так что
1 f
Е=-
2п-1Г(п+1)'
тогда остальная часть решения w =W1+W2 будет иметь вид
w —
л—1
Г(п —г) / г
..|Г(г+1) \Т
/•=0
и может быть принята в качестве второго решения уравнения
Бесселяг.
16 • 33. Условия отсутствия логарифмов во всех решениях, отно-
относящихся к частному показателю. Первое решение, соответствую-
соответствующее последовательности показателей, например, решение Wo
1 Уитгекер и Ватсон, Курс современного анализа, § 17 • 61; Watson, Bessel
Functions, §3-52.
Э. Айне—133—35 545
§ 16-3, не содержит логарифмов; последующие решения пер-
первой подпоследовательности несомненно содержат логарифмиче-
логарифмические члены. Ведущее решение второй подпоследовательности,
например Wt, также содержит логарифмы, но в некоторых
случаях может не содержать их, в то время как остальные ре-
решения второй подпоследовательности всегда содержат лога-
логарифмы. Аналогично, для каждой подпоследовательности после
первой, единственным решением, которое может не содержать
логарифмов, является ведущее решение этой подпоследователь-
подпоследовательности.
Рассмотрим любую последовательность показателей
Ро> Pi> Рз» - ¦ - > Р:>¦¦> ¦ • • i
расположенных так, что
Р* — Ри
является положительным целым числом для и > *. Исследуем
последовательность условий, необходимых и дистаточных для
отсутствия логарифмических членов в каждом решении W^, со-
соответствующих показателю р^'.
Показатель р^ должен быть простым корнем определяющего
уравнения, так как кратный корень всегда вводит 'логарифми-
'логарифмические члены. Более того, поскольку каждый показатель рх,
индекс которого х меньше jt, превышает р{1. на положительное
целое число, любое решение вида
1 ^i + К Wo,
где их,..., fcp.—произвольнье постоянные, является решением,
соответствующим показателю р^ Следовательно решения Wo,
Wlt..., IF^-i не должны содержать логарифмов, а показатели
Pi> P2----J Pii должны быть независимы.
Теперь
Ioo
v=0
(о)
log z
^-lg-t (а)
+ (logz)^
2
Следовательно для того, чтобы Wv не содержало логарифмов,
необходимо и достаточно, чтобы
- о
1 Frobenius, loc. cit., 224.
546
для s = 0, 1, 2,..., \i — 1 и для всех значений v, откуда g\, (a)
должно содержать множитель (а — р^ для всех значений v. Но
«lil = /_ I v F1^> _Н ,,ч
«Ь<«0 1 ' /о(о+»/о(° + 2).../0(=+-0 п>и'
а поскольку g"o(a) = co/(a)i ёоC) содержит множитель (р — р^у.
Следовательно, необходимым и достаточным условием является
то, чтобы Ич (pp.) было конечно и равно нулю для всех значе-
значений v. Рекуррентные соотношения для gy (о) и для //„ (а) такие
же, как и для cw, именно
Н, (а)/0(о + V) + Н,-г (а)/х (а + v - 1) + . . . + Но (з)/, (а) = О,
где /У0(а) = 1. Отсюда следует, что если /^(рц), #>(р„.),...,
Яч_1 (р^.) конечны, то Л/v (р^.) будет также конечно, если только
Pp. +v не является корнем определяющего уравнения
При v = pll_1 — рц множитель /О(з + У^ в знаменателе //v (a)
имеет простой нуль а = f^. Следовательно, для этого необхо-
необходимо, чтобы
при v = Pix-i — Ра и достаточно, чтобы Fv (а) было приведено к
первому порядку при а = р^.
При v = p|j._» — Р|а два множителя в знаменателе Н-, (з) имеют
простые нули о = р^., именно
/о (з + v — Pli_2 + р„^_,) и /0 (а + v).
Таким образом необходимо и достаточно, чтобы для этого
частного значения v функция /\ C) обратилась в нуль второго
порядка при <з = Pp. или
[dF4 (о) 1
При v = рц_з — р,1 три множителя в знаменателе Н* (з) имеют
простые нули при а = р,,,, именно
/о (а + v - Р^-з + Pn-i), /о C + v — Рн-s + Pp.—г), /о (а + v),
следовательно для этого значения v функция Z7, (°) должна обра-
обратиться в нуль третьего порядка при о = р,,,. Поэтому необхо"
димо и достаточно, чтобы
где v = Pl Pi
Аналогично, при v = р^_г — р^, г множителей в знаменателе
И-, (о) имеют простые нули для a = p^, следовательно функция
547
(з) должна обратиться в нуль порядка г при з = рц. Послед-
Последф / ()
ним условием является то, что при
= po-
p,l функция /\
необходимых и
относящееся
образуют совокупность
достаточных для того,
к показателю ра, н° со-
содолжна обратиться в нуль порядка ;• для а = р^.
Но мы приняли, что решения, относящиеся к plt р2.---> р^-ь
не содержат логарифмов. Число условий, которым необходимо
удовлетворить, равно соответственно 1, 2,..., и—1, что вме-
вместе с у. условиями, относящимися к
~~ !Л (J* + 0 условий,
чтобы ни одно решение,
держало логарифмов.
16 • 4. Действительные и кажущиеся особенности. Особенности
решений линейного диференциального уравнения являются так-
также и особенностями уравнения, но обратное не всегда верно.
Если точка z = а удовлетворяет условиям для регулярной осо-
особенности, некоторые (если не все) решения содержат отрица-
отрицательные или дробные степени (z — а), а возможно также и
степени log (z — а). В этих случаях особенность называется
действительной. Но при некоторых специальных условиях
каждое решение может быть аналитическим относительно z=#;
в этом случае особенность называется кажущейся. Выведем
последовательность условий, достаточных для получения кажу-
кажущейся особенности К
Напишем уравнение в виде
daw , Рх{г) d^hv _,_ ^ р„-\ (г> dio ^ ''п(г>„л,_п
dz" 'г—а d/'
где P1(z),..., Pn{z)
г—a)" dz (г—а)п
функции, аналитические относительно
2 = а. Пусть течка г — а будет кажущейся особенностью, так
что каждое решение фундаментальной последовательности
Wb 1S)St. . ., Wn
является аналитической функцией от z— а в соседстве с осо-
особенностью.
Пусть
и\
W.
Ot-V
W-,
W,
Wn
и пусть &r{z) будет детерминантом, полученным из Д подста-
подстановкой wfn),. .. , я.'п(п) соответственно вместо и'1("~г), ...,w(""r),
тогда
(г —й)г
Л (г)
Fuchs, J. for Math., 68 A868), 378.
но по крайней мере для одного значения г Pr{z) не содержит
множителя (z — а)", следовательно для этого значения г Лг(а)/Д(а)
бесконечно, но Sr (z) аналитическая относительно z=a, откуда
()
Теперь
I dd (г) _
I (г) rtz
где функция GB —а) аналитическая вблизи z = а, следова-
следовательно
где Л — постоянная. Но так как функция A(z) аналитическая
относительно z = а, то Я, (а) должно быть отрицательным це-
целым числом.
Определяющее уравнение относительно г ~- а имеет вид
[с|„ + Ы«-1 Pi(a) + ... f pPn-i (a) + Рп (а) = 0.
Корни этого уравнения должны быть положительными целыми
числами и должны быть неравны, так как равные корни приводят
к логарифмическим членам. Наименьший корень может быть
равен нулю. Условие, чтобы показатели были положительными
целыми числами, включает условие, чтобы Pi (я) было отрица-
отрицательным целым числом; последнее условие может рассматри-
рассматриваться как предварительное,—если оно не удовлетворено, то
особенность несомненно действительна.
Наконец, должна быть введена последовательность условий,
достаточных для отсутствия логарифмических членов. Пусть
корни определяющего уравнения, расположенные в убывающем
порядке величины, будут р0, рх pn_t. Решение с показате-
показателем р0 не содержит логарифмов. Одно условие достаточно для
обеспечения того, чтобы каждое решение с показателем r,j
было свободно от логарифмов, два дальнейших условия доста-
достаточны для показателя р3 и т. д., и, наконец, п — 1 дальнейших
условий достаточны для показателя pn_i. Таким образом для
отсутствия логарифмических членов в общем решении доста-
достаточны
1+2+... + (п--1)= .' п(п-\)
условий.
Для получения кажущейся особенности достаточно, чтобы
показатели были положительными целыми числами или равны
нулю и чтобы логарифмические члены отсутствовали.
16 • 401. Пример условий для получения кажущейся особенности.
Уравнение
/. («') Е z1 d*w — Dz + lz2) й1°„ + D — -az) и- = 0
tlZ tl2
540
содержит два параметра 1, •/. Покажем, что при наличии неко-
некоторых соотношений между этими параметрами особенность
* = 0 является только кажущейся \
Принимая, как в общем методе, что
найдем, что
L(w)=c0{a-4)(o — i)z>,
если коэфициенты с\ удовлетворяют рекуррентным соотноше-
соотношениям
0 + v —4)(а +v-l)Cv = |Ua + v-l)-f-/-}c,_b
Показатели р0 = 4 и рх == 1 являются положительными целыми
числами; большему показателю соответствует решение, анали-
аналитическое относительно г = 0, именно w — сои, где
/г ^« Г1 _U -v ¦? _!_ ~ ?2 _L -4- ¦• 7V ~i- !
ы — ^ Aт и~ i i2~ i • ¦ ¦ т ;¦' * ( • • - j,
Tv j . 4 2 :5 • • • v . (v + 3) •
Решение, соответствующее меньшему показателю рх = 1; со-
содержит в общем случае логарифмы. Чтобы оно не содержало
логарифмов, должно быть введено одно условие. Поскольку
р0 — Pi = 3, необходимо и достаточно, чтобы
/?вA) = 0.
Теперь
/() (
F&) - /о (о + 1)/о (= + 2)/0 (а :- 3) -f
.-.{,(: + 2)+ «}UC + l) + tt-3+'4.
следовательно необходимые и достаточные условия приво-
приводятся к
C). + -/) B\ + /.) (X + /.) = 0.
Таким образом могут быть три случая:
(I) ¦/. = —). , если соответствующее решение w = z,
(II) v. = Zi., „ „ „ US) — Z
(III)-/ = -3)., „ „ w-
Только в этих случаях начало является кажущейся особен-
особенностью.
1 Forsyth, Differential Equations, т. 4. 119. Нужно отметить, чю Рг(а) — — 4,
поэтому особенность может быть кажущейся.
550
16 • 5. Метод решения Пеано-Беккера. Решение линейного ди-
ференциального уравнения, полученного в виде бесконечного
ряда методом Фробениуса или аналогичным образом, является
с практической точки зрения вполне удовлетворительным.
Однако с теоретической точки зрения это решение имеет недо-
недостаток: оно действительно только внутри круга сходимости,
который покрывает лишь незначительную часть плоскости не-
независимой переменной. Метод, который мы сейчас рассмотрим1,
представляет большой теоретический интерес, так он приводит
к аналитическому выражению общего решения, годному почти
во всей плоскости.
Рассмотрим систему п совместных линейных уравнений
~- = пцЩ + «12яу2 + •.. + u,nwn (i = 1, 2,..., п),
где коэфициенты иц — функции z. Предположим, что точка zo не
является особой точкой какого-либо коэфициента. Рассмотрим
звезду Миттаг-Леффлера2, огр ничейную непересекающимися
прямыми линиями, проведенными от каждой особой точки коэ-
фициентов к бесконечности. Для определенности предположим,
что эти ограничивающие линии являются продолжениями ра-
радиусов векторов, проведенных от точки z0 к особым точкам.
Предположим также, что эти коэфициенты utj аналитические
во всей звезде.
Система п линейных уравнений может быть представлена
символически в виде
dw
27 = uw>
где и представляет не одну функцию от z, а квадратную
матрицу
aw — совокупность {w^ w2, ..., wn).
Символ Qu определяет матрицу, полученную интегрирова-
интегрированием каждого элемента матрицы и от z0 до z вдоль пути, не
пересекающего ни одну составляющую звезды. Символ uQu
обозначает матрицу, полученную умножением матрицы и на
! Peano, Math. Ann., 32 A888), 455; Baker, Proc. London. Math. Soc, 34
A902), 354; 35 (!902;, 334; B), 2 A904), 293 (исторический обзор); Phil. Trans.
R. S. (A), 2!6 A915), 155. См. также Bocher, Am. J. Math., 24 A902), 311. Milne,
Proc. Editi. Math. Soc , 34 1915), 4!.
- Mittag - Leffler, С R. Acad. Sc. Paris, 128 A889). 1212.
551
интегрированную матрицу Qw1. QuQu обозначает Q(uQu)ht. д.
Теперь образуем ряд матриц
Q (и) = 1 + Qu + QuQu + QuQuQu + ...;
его суммой является матрица. Докажем, что элементы мат-
матрицы Q {и) сходятся абсолютно и равномерно в любой конечной
области D, содержащей z0 и лежащей целиком внутри звезды
Миттаг-Леффлера. В области D функции и,-,- ограничены; пусть До-
Добудет таково, что
I щ! < Mv
для всех точек Д и пусть М будет таково, что
Мц < М
для всех значений i и /. Примем
г
= /{«л (z) u[)} (z)+... + uin (z
при условии, что путь интегрирования— простая кривая, лежа-
лежащая внутри области D. Предположим, что 2, — любая особая
точка на пути (z0, z), Sj — длина пути (z0, гл), as — длина всего
пути (г0, г). Тогда
\uf(zl)\<s1Mij
<s1M,
s
f MSl (Ma -Мъ + ...+ Min) dSl
b
fs1ds1= \-nsm\
1 Произведение двух квадратных матриц и = (иц) и v = (ьц) того же по-
порядка и обра >уется согласно uv ~ (щ^рп + ... + Uinvnj) и в общем случае
отлично от vu.
Суммой двух матриц и и v является матрица (иц + f,j).
Символ 1, рассматриваемый в виде матрицы, может быть представлен
в виде
/ 1,0, ..., 0
I 0,1, .... 0
\ 0,0 !
552
в частности
Аналогично
! «f (z) I < /' «s? ^ '^ + И +
и т. д. до бесконечности. Но uSp(z) является (г, /)-ым элементом
матрицы Qu, ajp(z) является (г, /)-ым элементом матрицы QuQa
и т. д. Таким образом ряд
является главным рядом для каждого элемента матрицы й(к),
следовательно элементы Q(u) являются рядами, которые абсо-
абсолютно и равномерно сходятся во всей области D. Отсюда, если
к' = A + Qu + QuQu+. ..,w0,
где w0 — совокупность произвольных начальных значений (-k'J,
ic§, ..., -w®)t то почленным диференцированием получим
~=u(\+Qu + QuQu+...)w0
= гг-гг,1,
следовательно
является решением системы линейных уравнений, которое схо-
сходится в пределах любой области, целиком лежащей внутри
звезды и таково, что (wlt и1,, ..., да„) приводится к (та»5
¦ы>1 ..., w°) при z = z0.
16-51. Сво$*ктва матрицы Q(u). Пусть Q,7 будет элементом мат-
матрицы Q (и); если
w = Q(u)W,
где IF обозначает совокупность
(Wlt W2, ..., Wn),
то
ivi^QilW1-r... + %nW,i
553
При переводе на язык матричной симьолики, получим
dw
~
Пусть Q~l (и) будет матрицей, обратной Q(u), т. е. такой,
для которой
Q-1 (и) Q (и) - Q (и) Q-% (и) = 1.
Докажем, что если и и v — квадратные матрицы, состоящие
из я2 элементов каждая, то
Q (u + v) = Q (и) Q { S^1 (м) -v Q («)},
если детерминант матрицы 2 (и) не равен нулю.
Рассмотрим систему линейных диференциальных уравнений
и произведем в ней подстановку
то = Q (u) IF,
или, что то же
тогда
следовательно
т. е.
самое
(и
Q
, подстановку
W ¦=
-? = аг
-f-11) w =
=
Q~l (и) w,
v + Q (и) ~
= нда + Q (и)
.- i)Q (и) IV,
или
Отсюда следует, что
¦ш = Й (и) W
= 2 fн) Q {t~! (и) vQ (u)} w.
С другой стороны
¦w = 2 (я + г') гс0,
что, ввиду единственности решений системы с данными значе-
значениями, доказывает теорему.
Нетрудно вычислить детерминант Л матрицы S (и); в действи-
действительности
г
А =.-¦ exp J (нп + н22 +. .. + ипп) dz.
Но поскольку Qu — элемент Q (и), уравнение
если его написать полностью, будет иметь вид
Значение ^ может быть выражено в виде суммы и детерми-
детерминантов, каждый из которых получается диференцированием
всех элементов одного какого-либо столбца А. Применяя ука-
занвое выше выражение для производной ir,-,, можно показать,
что
откуда результат следует непосредственно.
В частности, если
Иц -Г «22 f • ¦ ¦ + Unll = 0,
А не зависит от г и равна единице.
16-52. Преобразование линейного уравнения порядка п в линей-
линейную систему. Линейное диференциальное уравнение порядка п
может быть представлено в виде системы п совместных урав-
уравнений первого порядка. Мы сейчас рассмотрим метод, связанный
с матричным представлением.
Пусть данное уравнение имеет вид
-2
a"~2 w
¦ —-- -, -_-- +... H -w.
Azu -s,, ilz" 'f n—1 ?'( <fe " ?ies---'"n
Напишем
w, ггк, = <p1
тогда
dz
у
Л
Если Нт— Л —, то уравнение эквивалентно системе
где гг — матрица
/ о, -1-, о, о,...,_ о, о \
/ о, н1г -17, о,..., о, о
! 1
| 0,0, Яо. — О» О
1 " ws
О, О, О, О,..., Я., , - -'--
Наибольший интерес представляют следующие случаи.
(а) Функции Рив- полиномы, и ни одна из функций <р не
имеет кратного множителя; линейная система будет иметь вид
где V—матрица, каждый элемент которой является полино-
полиномом z, z — as — множитель одной или нескольких функций s, а
As —- матрица постоянных.
Например, уравнение
(z + 1)z%w" - {(с2 + bjz + c2}z*w" - {(а, + &,)z -f
+ aj zto' - {(с + ft) z + с} й- =- О
приводится к эквивалентной системе
О, 1, 1 1-^-+1 0, 0, 0 1- r.-U'.
а, а1У й2 + 2 / \ &, ил, 62
55!j
(b) Функции Р и ш такие же, как и в случае (a), a <fi = <?2 =
=... = <рп == ю. Уравнение
приводится к
\-Е, \-В) *
С, О
0
(с) Функции Р— полиномы, »! = (?2 = • • • = ?«—1 = li а ?п ~ поли-
полином без кратных корней. Функции Н все равны нулю. В этом
случае уравнение
1 L + V
Г ^
приводится к
го" = J X + V -^-1 W +L + V t^-U
'¦- 1
(d) P — аналитические функции г; каждая из функций <р равна
единице или г — а, где а — не является особой точкой фУнк"
ций Р. Например, пусть уравнение будет иметь рид
где ро, р17 ..., рп-1 — постоянные, a Qo, Q,, ..., Q«_i — функции,
которые могут быть разложейы около начала по степеням г.
Эквивалентная система будет иметь вид
aw
где
V=/0, 0, ...,0
О, 1, 0,0, ...,0
о, о, ..., о , oiio о
Wo» Vi> • • -. Чп—i
О, 0, 2, 1, ...,0
Рй, Ри Ps, Рз, ¦ -чРп-х
I
I
557
16-53. Частные примеры. Рассмотрим уравнение первого по-
порядка
dw
йг
В этом случае легко доказать, что
QuQu = -1- (Qu)\ QuQuQu = -~ (Quf
и т. д. Решение будет иметь вид
w = w0 exp Qu,
что соответствует решению, полученному элементарными ме-
методами.
Теперь рассмотрим линейное уравнение второго порядка
(Pw
= VW
агг
Это уравнение эквивалентно системе
(dw dw'\ /0, 1\ , ,,
, dw -^
где w =-fe. Если мы предположим, что начальное значение ;
равно нулю, то легко доказать, что
"=? Й- ««-(S* о).
-(
Л
и т. д. Таким образом общее решение будет иметь вид
w = w0Wt + Т0о Wt,
где W1 и W2 определяются рядами
Wx = 1 + Q2v -f- Q4)Q2v -f-
W.2 = z + Q2vz + Q2vQ2vz + i
а(и/0, i^0)—значения (да, та') приz=0. Нужно отметить.что Q2iy,Q2^2,
Q2vQ2v, Q2vQ.2vz обращаются в нули порядков 2, 3, 4, 5 при z=0.
В виде частного примера рассмотрим уравнение Бессеш
у& 1,_ ^ ЗГ - .L,, B^ И^1 '7?'? ~~ О
558
Положим
г = Асе 2 , т = ~ га2,
4
где с — постоянная; тогда уравнение примет вид
d2w , t\
В данном случае
-|f - с [(^ —2y + H- 2]
+ { /n2 | + me [— 8 — 4^— t2- ~, + ef (b-it-P- -—)] -f
Эти ряды сходятся для всех значений t
Наконец, рассмотрим линейную систему
-g' = [Ао + Atz +... + A^z" + V Ст (z - ст) -1 ] w
и предположим, что новая переменная s может *быть найдена
так, чтобы log(z — ст) был однозначной аналитической функцией s
для некоторого диапазона значений s и для г= 1, 2,..., с; тогда
каждое решение линейной системы будет однозначной функ-
цией s.
Пусть
так что
z = cr-{-expd>r(s)
следовательно система будет иметь вид
~ = { Ч" (s) Ио + Л,*" + ... + Л Д-¦] + V CMs) } к
r—i '
— UW.
Члены
Qu = fwrfs, QwQm = J uds f iids....
X);-
являются однозначными аналитическими функциями s, а решение
аналитическое в соседстве с s.
Таким образом уравнение Бесселя может быть представлено
в виде системы
Z(i, oi+тЦ о) И
решение в этом случае может быть выражено в виде одно-
однозначной функции новой переменной s=logz.
Метод матриц применяется весьма широко, но его успешное
приложение требует знакомства с теоремами вычисления матриц,
которые не могут быть здесь приведены. Однако имеется про-
простое приложение, представляющее некоторый теоретический
интерес, которое мы рассмотрим в следующем параграфе.
16-54. Приложение к уравнению с периодическими коэфициен-
тами. Рассмотрим уравнение
где п — цело? число, а У." — периодическая функция г.
Напишем
тогда
^~ 4«einz {xe~i
*! =~-^п е-ш{Хе-ш- Yeinz).
Если х = 2iz, С = е", то система может быть написана в виде
В частности, пусть л— 1, ЧГ = 4а cos Az + 4b cos fo, тогда
±(X, Y) = (ap + bg)(X, Y),
где p, (? — обозначают матрицы
Решение
(
где
= l+ aQp + ^ p p
Q QqQp) + b*QqQq +...
абсолютно и равномерно сходится для всех значений г.
560
[Дальнейшее развитие этого метода, в частности исследо-
исследование стабильности решений линейного диференциального урав-
уравнения второго порядка с периодическими коэфициентами см.
Baker, Phil. Trans., 216 A915), 155].
Примеры
1. Решите следующие уравнения в виде ряда по возрастающим степеням г
(И) <2, + И)**_? -в»-IX
d*w dw „
+ w Q
2. Найдите полное решение гипергеометрического уравнения
(II) если ^ = 1: (II) если ч — отрицательное целое число.
3. Покажите, что уравнение
+ (++ + 3)г* Ш + A + р + ° + х + Г'° + от +
— (г — рот) — aw = 0
удовлетворяется функцией
(а; f, 5, т; г) - 1 + -^ г+
2 !р (р
и найдите остальные решения, относящиеся к особенности г = 0.
При а =т ,.Рз(а; р; о, т; г) приводится к 0F2(P> °! г)! докажите, что эта
функция удовлетворяет уравнению
d2w , dw
Установите зависимость между этими двумя уравнениями. [Pochhammer].
4. Покажите, что ни одно решение следующих уравнений, относящихся
к особенности в начале, не содержит логарифмов
d2w dw 2
(Н) гB — г*) ^ — (г2_4г + 2)|A— г) -^ + wj = 0.
5. Докажите, что вачало является кажущейся особенностью уравнения
Э. Айне—133—36 561
ГЛАВА XVII
УРАВНЕНИЯ С НЕРЕГУЛЯРНЫМИ ОСОБЫМИ ТОЧКАМИ
17-1. Возможность существования регулярных решений. Тео-
Теоремы, установленные в двух предыдущих главах, показывают,
что если точка г0 — регулярная особенность, то функциональ-
функциональный характер фундаментальной последовательности решений,
соответствующих г0, известен. Более того, каждое решение по-
последовательности может быть разложено в ряд по возрастаю-
возрастающим степеням z— z0, коэфициенты которого определяются по-
последовательно системой рекуррентные соотношений.
Предположим, что в соседстве с z0 все коэфициенты урав-
уравнения
(A)
аналитические, но хотя бы один из коэфициентов pr{z) имеет
полюс в z0 порядка, превышающего индекс г. Тогда, поскольку
условие для регулярной особенности нарушено, не все п реше-
решений, соответствующих точке 20, будут регулярными. Нужно оп-
определить, будут ли какие-либо' из этих решений регулярны, а
если будут, то найти для них аналитические выражения *.
Пусть м1г с52,..., ";•„ будут порядками полюсов, которые име-
имеют рх, р2,..., рп в z0. Рассмотрим числа
Лх 4- п — 1, E2 + « — 2,..., й„_, + 1, «5„.
из которых, согласно условию, по меньшей мере одно больше п.
Пусть gn-i будет наибольшим из этих чисел, исключая &п, и
предположим, что уравнение имеет регулярное решение
да B) = B — 20)?фB— 20),
где !f ф)фО, тогда, подставляя это решение в уравнение
увидим, что pn(z) имеет полюс в 20 порядка не выше gn^. Сле-
1 Thome, J. fur Math., 74 A872), 193; 75 AS73), 265; 76 A873), 273.
562
довательно для существования регулярного решения необхо-
необходимо, чтобы йп <?¦„_,.
17-И. Необходимое условие для существования п — г регуляр-
регулярных решений. Обобщим предыдущую теорему. Пусть gr будет
наибольшим из г чисел
&г-\-п — 1, Д2 + я — 2,..., йг + й — г;
тогда, если имеются п — г регулярных решений, то все осталь-
остальные числа
&г-у1 + П — Г— 1,..., <!&„_!-j-1, Йп
будут меньше gr. Докажем эту теорему методом индукции;
предположим, что она верна для уравнения порядка п—1; до-
докажем, что она верна и для уравнения порядка п.
Преобразуем уравнение подстановкой
IS!
где
= щ (z) fv dz,
wx{z) =(z — zofw(z-zo
— регулярное решение (A); v будет удовлетворять уравнению
вида
(В) -J^?- +?! B) ~Й + - - • + ^-2 B) -J + </„_! B) « = О
и, согласно принятому условию, что (А) имеет /г — г регулярных
решений, (В) будет иметь п — г—] регулярных решений. Пусть
будет порядком полюса в z0 относительно qx, q,,..., qn-\ со-
соответственно.
Функция qs{z) может быть выражена в явной форме
I (iZ
причем
+ s — n (s= 1, 2,..., л).
Следовательно каждое из чисел
о, + (л—1) —1, о8 + («—1) —2,..., =г + (п— I) — г,
не больше gr— 1
Предположение, что уравнение (В) имеет п — г—1 регуляр-
регулярных решений, приводит к тому, что числа
°|-+1 + (я— 1) — г— 1,..., ол_1
также не больше gv— 1. Тогда, возвращаясь к выражению для
qs, увидим, что
Йг+1 <С°»--1 йл—1 < °п—1,
563
откуда каждое из чисел
&r+ii-n — r—1,..., й„_1 + 1
не больше gr. Следовательно &п также не больше gr.
Таким образом теорема верна для уравнения порядка г + 1,
имеющего одно решение, регулярное в z0; следовательно она
верна для уравнения порядка г -f-2, имеющего два регулярных
решения, а также для уравнения порядка п, имеющего п — г
решений, регулярных в z0.
Из этой теоремы можно получить весьма важное следствие.
Пусть g будет наибольшим из чисел
щ + п — 1, &.z -f п —2,..., <5„_1 -\-1, й„,
а г — наименьшим целым числом, для которого
&Г + П— r = g,
тогда уравнение будет иметь не больше п — г независимых ре-
решений, регулярных в z0. Если бы оно имело п — s независимых
решений, регулярных в z0, то, поскольку s <г, --каждое из
s чисел
Wj-Ь-И— 1,..., ws+n — S
было бы не больше h<g. Но поскольку мы приняли, что име-
имеются п — s регулярных решений, то каждое из остальных чисел
&s+i + tl — S— 1,..., Й„
не больше h. В частности
что противоречит условию. Следовательно теорема доказана.
Число г называется классом х особой точки z0. Если все ре-
решения, соответствующие z0, регулярны, то каждое из чисел
(й0 = 0) меньше или равно и. Следовательно в этом случае г
равно нулю.
Если г>1, то число независимых решений, регулярных в z0,
будет не больше п—г, но может быть и меньше этого верх-
верхнего предела.
Так в уравнении
где а и b — постоянные (а ф 0), йх = й2 == 2, и рассматривая осо-
1 Общепринятым является термин характеристический индекс, но оба
термина (характеристический и индекс) уже были достаточно использованы.
Превышение числа п — г над действительным числом регулярных решений
удобно было бы назвать недостатком.
564
бенность в начале
с^ + и— 1 =[3_, E3 + п— 2 = 2.
следовательно
g" = 3, г = 1,
и поэтому имеется не больше одного решения, регулярного в на-
начале. Легко доказать, что если это регулярное решение суще-
существует, то его разложение будет иметь вид
w = A0 + A1z+ A2z2 +...+ Amzm +...,
где
(т + 1) aAm+i + {Ь + т (от — 1)} Ат = 0.
Но llm [.Am.t-i / АП(] = оо, следовательно ряд не сходится для не-
некоторого значения z, за исключением z = 0; в данном случае
решения, регулярного в начале, не существует.
17 • 2. Определяющее уравнение. Для упрощения примем, что
особая точка z0 будет началом. Вместо (А) рассмотрим эквива-
эквивалентное уравнение
где 1г = zgL. Теперь Lx может быть выражено в виде
z" Qo (z) D" + z"-1 Qt (z) D»-»+ ... + zQn-i (z) D + Pn (z),
где
Q,(z) = ze-n+*p,(z) (v = 1, 2,.... n).
Функции Q аналитические в соседстве с началом; из опре-
определений g и г следует, что если 2 = 0 не является регулярной
особенностью, то
Q0@) = Qi @) =.. - = Q,-i @) = о,
Qr @)^0,
а остальные коэфициенты Q конечны или равны нулю в на-
начале.
Предположим, что существует решение, регулярное в на-
начале, например
тогда коэфициент при г° , полученный из
zn~y Qv (z) D"-v w,
будет иметь вид
и обратится в нуль при v < г, но не при v = г. Поскольку z? —
565
низшая степень z, которая встречается в L^w), показатель р
должен удовлетворять определяющему уравнению
Q, (о) [?]„_.+ ... = о,
где опущенные члены еще более низкой степени р, чем приве-
приведенный член; следовательно степень определяющего уравнения
равна п — г.
В частности, при п = г определяющее уравнение примет вид
Qn@) = 0.
Следовательно, если левая часть определяющего уравнения не
зависит от р, то регулярное решение не может существовать.
17 • 21. Приводимость уравнения, имеющего регулярные решения.
Предположим, что уравнение (А) имеет k независимых решений,
регулярных в особой точке z = 0. Эти решения образуют фун-
фундаментальную последовательность для уравнения порядка /г,
коэфициенты которого удовлетворяют условиям Фукса относи-
относительно начала. Пусть это уравнение имеет вид
где коэфициент Dk в М равен единице; напишем M1 = zkM,
тогда
где Rt— диференциальный оператор порядка п — k (см. § 5-4).
Поскольку коэфициенты Lt и Мх конечны или равны нулю
в начале и аналитические в соседстве с началом, это относится
также и к коэфициентам Rx, следовательно уравнение L?w) = 0
и эквивалентное уравнение L{w) = 0 приводимы, если суще-
существует одно или несколько регулярных решений.
Уравнение
которое, согласно определению g, не является тождеством, яв-
является определяющим уравнением Ll(w)~0 L(w) = 0 относи-
относительно особенности z = 0. Пусть
М*) = /(A p)z?
где суммирование ведется от \ = 0. Поскольку
/о'р)=О, &(р) = 0
являются определяющими уравнениями L(w) = 0 и M(w) = 0,
566
/о(р) и So(P) не будут равны тождественно нулю. Теперь
следовательно
X ti
откуда
= vs;.(pR_x
является последовательностью соотношений, определяющей по-
полиномы А^р), Ах(р), А2(р),... В частности
что доказывает, что А0(р) не равно тождественно нулю.
Если полиномы Ах(р) вычислены, то Rt можно определить
следующим образом: степени полиномов ft(f) имеют верхнюю
границу и. а степени полиномов gfy) имеют верхнюю границу k;
следовательно верхняя граница степеней АДр) равна п — k.
Пусть п — k = m, тогда, поскольку
функция A (z, р) может быть выражена в виде
т— 1
коэфициенты и (г) определяются из формулы
S\ Us B) = [Дг A (Z, р)]р = о,
где
AAB,p) = A'z,P+l)-A(z,P),
(г, р) = ДА (г, р+1) - ДА (г, р).
Отсюда
А?1BР) = А(г,р)г?
= {[P]m«m (г) — [Р]т- 1«т _ | (г) + . . . + P
и следовательно /?2 — оператор
h2 (г) D + «о (z).
507
Теперь /о(р) степени п — г относительно р, а go(p) степени к.
Отсюда следует, что fi0 (р) степени п — г — к. Поскольку h0 (р) = 0—
определяющее уравнение для ^(w)^ О, степенью этого опре-
определяющего уравнения будет число, на которое степень опреде-
определяющего уравнения L(w) = O превышает число регулярных
решений. В частности, если /?х {w) = 0 не имеет определяющего
уравнения, то L (w) — 0 имеет точно п — г регулярных решений1.
17 - 3. Доказательство отсутствия регулярных решений в общем
случае. В §17-11 мы показали, что даже если уравнение L(w) =
= 0 имеет определяющее уравнение для особенности z = 0, со-
соответствующее формальное разложение решения может расхо-
расходиться для всех значений \z\. Это явление ни в коем случае не
является исключительным, исключительным является самый факт
существования регулярного решения.
Рассмотрим видоизмененное уравнение
= 0.
Если существует регулярное решение
W = Z? (Со + CtZ + C2Z2 + ...),
то р определяется уравнением
. /о(Р) = О.
Приравнивая нулю коэфициенты последовательных степеней
z в выражении
получим последовательность рекуррентных соотношений
Ci/b(P + l) + 'o/i(p)=O,
c*f0 (P + 2) + cxh (р + 1) + c0f.2 (Р) = 0,
^ /о(р + V) + Cv-l/x (р + V - 1) +. . . + C0f, (р) - 0.
эти рекуррентные соотношения определяют clt c2,..., с,... при
заданной с0 (см. § 16- 11).
Существенное различие между настоящим случаем и случаем,
рассмотренным в предыдущей главе, где все решения регулярны
в начале, состоит в том, что/0(р) степени п — г относительно р.
С другой стороны, имеются некоторые функции /„ (р), степень
которых равна п: первой из этих функций является /^_л(р).
Если процесс вычисления коэфициентов ev ограничить так,
чтобы выражение для w содержало только конечное число чле-
1 Floquet, Ann. Ёс. Norm. B), 8 A879), 63.
568
нов, то найденное таким образом решение будет регулярным в
начале. Вообще ряд не ограничивается; покажем, что в этом
случае он расходится.
Для некоторых значений к, например k—g — n,
lim IA(p + v — к)
|
поскольку числитель степени п, а знаменатель более низкой
степени относительно v; следовательно, для того, чтобы рекур-
рекуррентное соотношение
cv_l/i(P + M —I) cv_2/3(P + v —2) cc/v (p) _ __
+ Ь -
<\ /о(? + v) ^ с, /0(р + v) ^* * • г Cv /0(р + v)
было удовлетворено, необходимо, чтобы
lim c^— fel _q
следовательно ряд расходится.
17 • 4. Сопряженное уравнение. Если определяющее уравнение,
относящееся к нерегулярной особенности, степени п — г, то не
может существовать больше п — г регулярных решений. По-
Поскольку число регулярных решений может быть меньше макси-
максимума, нужно найти критерий, определяющий возможное число
регулярных решений. Этот необходимый критерий может быть
получен при помощи сопряженного уравненияг.
Пусть Lt будет диференциальным оператором, сопряженным
с Lx. В тождестве Лагранжа (§ 5- 3)
пусть и = z?, v= z — р —¦»-!, где р — произвольное, a v — целое
число, тогда
P(z9,z~''~v~') не содержит членовz9; из принятого условия от-
относительно коэфициентов оператора L следует, что Р не имеет
в начале никаких особенностей, кроме полюса, поэтому выра-
выражение .
не может иметь члена г.. Предположим, что
а также что
1 Thome, J. fur Math., 75 A873), 276, Frobenius ibid., 80 A875), 320.
569
Коэфициент z~* в z 9 у '/^(z9) равен /,(р), а коэфициент
z~l в zL1(z~p~*~i) равен »„ (— р — v — 1), откуда
/.(p) = <h(-p-v-l)
и аналогично
*v(p)=/,(—P —V —1).
Отсюда непосредственно следует, что степени двух опреде-
определяющих уравнений —/0(р) = 0, относящегося к L1(u) = О, и
<Ро(р)=О, относящегося к Lx (v) = 0, равны. Пусть этой степенью
будет п — г, 1 огда класс г будет одинаковым для обоих урав-
уравнений. В частности, если одно из уравнений ^(и)= 0 и L^v)—
= 0 имеет все решения, регулярные в особой точке, или вовсе
не имеет их, то то же верно и для другого уравнения.
Предположим, что /1(и)=0 имеет п — г решений, регуляр-
регулярных в начале. Тогда
где Мг(и) = 0 — уравнение, удовлетворяемое п — /регулярными
решениями, a Rt — оператор порядка г. Но если Rt и- Жг — со-
сопряженные операторы /?х и Мх соответственно, то
Определяющие уравнения, относящиеся к началу, как Lx, так и
Mlt— степени п — г, следовательно уравнение Rt (и) = 0 не имеет
определяющего уравнения; поэтому, если уравнение L (г») = 0
имеет п — г регулярных решений, то необходимо, чтобы сопря-
сопряженное уравнение L (и) = 0 было удовлетворено всеми решени-
решениями уравнения 7?(и)=0 порядка г, которое не имеет определя-
определяющего уравнения.
Это условие является также достаточным, так как, если оно
удовлетворено, то уравнение /^1(«) = 0, сопряженное Rt (v) — 0,
также не имеет определяющего уравнения. Следовательно по-
порядок уравнения Мх (и) = 0 равен степени определяющего урав-
нения, относящегося к рассматриваемой особенности, а все ре-
решения Мг(и} = 0 регулярны в начале; уравнение Lx(u)= 0 имеет
п — г решений, регулярных в начале.
Таким образом для того, чтобы уравнение порядка п име-
имело п — г решений, регулярных в ос бой точке, в которой опре-
определяющее уравнение степени п — г, необходимо и достаточно,
чтобы сопряженное уравнение удовлетворялось всеми решени-
решениями уравнения порядка г, которое не имеет определяющего
уравнения в рассматриваемой особой точке.
Если регулярные решения существуют, то точные выраже-
выражения для них могут быть найдены решением последовательности
рекуррентных соотношений, данных в § 17-3. Любые случаи,
когда корни определяющего уравнения кратные или различа-
570
ются между собой на целые числа, могут рассматриваться при
помощи общего метода, приведенного в § 16-3.
17 • 5. Нормальные решения. Следующая задача состоит в том,
чтобы получить разложения, представляющие решения, нерегу-
нерегулярные в особой точке. Сначала рассмотрим уравнение первого
порядка, для которого начало является нерегулярной особой
точкой. Рассмотрим уравнение
где
«р(г) —аналитическая функция в соседстве с началом, а <р@) = 0.
Общее решение имеет вид
w = AeQ (V Ф B),
где А — произвольная постоянная;
а г . , am— 1
Если решение написать в виде
w = eQ B) v(z),
то i)(z) будет решением (регулярным в начале) уравнения
Существенная особенность решения получается таким образом
вследствие наличия множителя eQiz), который называется опре-
определяющим множителем решения. Если решение такого вида
существует, то оно называется нормальным решением1; число р
называется показателем.
17-51. Решения, в которых точка в бесконечности является не-
нерегулярной особенностью. Если какая-либо точка является регу-
регулярной особенностью в уравнениях, возникающих в физических
задачах, то эта точка почти всегда находится в бесконечности.
Предположим, что любая частная особая точка, например z0,
перенесена в бесконечность подстановкой
При этом преобразовании мы не потеряем в общности и полу-
получим решение значительно более легкое.
1 Thome, J. ffir Math., 95 A883), 75.
571
Рассмотрим уравнение
d" ~~ iw , , , ч dw
где коэфициенты могут быть разложены в виде ряда по убы-
убывающим целым степеням z
рч (z) = z*v (aVo + a4z~i + аъг~ ~ +...)•
Если, согласно принятому условию, точка в бесконечности яв-
является нерегулярной особой точкой, то К-, > 1 — v, по меньшей
мере для одного значения v. Предположим, что
К* +v<KT + r при v < г,
К, + v < Кг + г при -I > г,
тогда степень определяющего уравнения, относящегося к точке
в бесконечности, будет равна п — г, а г будет классом особен-
особенности.
Покажем, что для существования нормального решения не-
необходимо, чтобы Кч было больше или равно нулю по крайней
мере для одного значения v. Если решение, нормальное в бес-
бесконечности, существует, то оно будет иметь вид
w = eQ {г)и (z)
где Q(z) — определяющий полином от 2, а и(г) будет иметь вид
Пусть
в —
dzm
так что
to=l, *j = Q',
в общем случае
= fm + tmQ'.
Если Q(z) — полином степени s, то в бесконечности
tm = O(zms-m).
Пусть уравнение, удовлетворяемое и(г), имеет вид
g ?>-+... + ^_l(Z) -* + 9„(Ф = 0,
тогда можно доказать, что
9, = Я + (« - v + 1&
в частности, что
Чп = Рп + *1р
572
„С
Теперь, если нормальное решение существует, то можно опре-
определить Q так, чтобы уравнение для и имело не меньше одного
решения, регулярного в бесконечности. Это условие ограничи-
ограничивает степень главного члена относительно qn. Степени главных
членов, составляющих qv , равны
К- K-i±s— 1. K_2 + 2s-2,..., v(s—1),
следовательно, если полином Q степени s, но вообще произ-
произвольный, то степень ведущего члена относительно q^ превышает
степень ведущего члена относительно «7*—t не меньше чем на
s—1. Таким образом в общем случае главный член относи-
относительно qn будет не меньше главного члена любого другого коэ-
фициента q4, а уравнение относительно и не будет иметь опре-
определяющего уравнения, следовательно и регулярного решения
в бесконечности.
Если нормальное решение существует, то соответствующим
выбором степени O(z) и ее коэфициентов можно сделать сте-
степень главного члена относительно qn по крайней мере на еди-
единицу меньше степени главного члена относительно qn-\\ только
в этом случае уравнение относительно и может иметь решение,
регулярное в бесконечности. Чтобы это было возможно, ни одно
из чисел
Кя, K^ + s-l, /С„_2 +2(s-l), .... n(s-l)
не должно быть больше остальных, т. е. из чисел
Kn~n(s-l), K^-in-lKs-1),
два наибольших числа должны быть равны между собой. Пустьg
будет наибольшим из чисел
тогда необходимо, чтобы
/С, —v(s—1)>0
для некоторого значения v, откуда следует, что
Но поскольку решение нормальное, а не регулярное l, s > 1 и
g > 0. Таким образом /С > 0 по меньшей мере для одного зна-
значения У.
у также отметить, что если точка в бесконечности является регуляр-
регулярной особенностью, то
по меньшей мере для одного значения ч, так что g> —1.
573
Например, уравнение
zw" -f w' -f w = 0
не имеют решения, нормального в бесконечности, так как К\ —
= К2 = — 1, следовательно g- = 2" < 0.
17 • 52. Вычисление определяющего множителя. Степень s поли-
полинома Q(z) ограничивается таким образом неравенством
Если g — положительное целое число или нуль, то очевидно
можно допустить, что s=g- + l, так как в этом случае
по крайней мере для одного значения v, а для всех остальных
значений v
следовательно из чисел
Кп> К^ + s — l, Кп_2 + 2(s -1), ..., n{s -1),
число n(s—1) равно большему числу последовательности.
Класс был определен как число г, так что
Кч + v < Кг + г при v < г,
А; + v < Kr + r при v > г,
следовательно при v > г
(я-v)(s— 1) + ф— г)
>^ + (n —v)(s—1).
Таким образом равенство
или
которое верно по крайней мере для одного значения v, именно г
может быть справедливым только при v < г, поэтому
ПРИ v< г
Ку = vg- при v = г
^» < VS" ПРИ v > г.
Пусть /и будет наименьшим значением v, для которого
=vg-, тогда
Кт + {n — m)(s— 1) = tf, + (л —г) (s —1) = ng-
574
и
Кч + (п — v) (s — 1) < ng при v < т или v > г.
Члены высшего порядка в qn(z) равны
Но
следовательно, главное выражение в qn(z) имеет вид
Пусть
<№) =
тогда, поскольку
условием для обращения в нуль члена высшего порядка в qn(z}
будет
As + am0Ars-m +... + ar0 = 0.
Следовательно, имеется не больше г независимых значений
постоянной As. Если значение As известно, то остальные по-
постоянные As—i,..., Ax могут быть вычислены последовательно.
Так, если s=g+l, то определяющий множитель может быть
получен.
Условие s = ^+l необходимо, когда g = 0, но если g —
положительное целое число, то возможны целые значения s,
которые меньше g" + l. Для получения допустимых значений s
применяется диаграмма Пьюзо(см. § 12- 61), которая должна быть
построена следующим образом: наносятся точки, декартовы ко-
координаты (х, з') которых равны
@, г), (Klf г-1),...(К„ 0),
и через точку @, г) в первом квадранте параллельно оси х
проводится вектор. Этот вектор вращается вокруг точки @, г)
по направлению часовой стрелки до тех пор, пока не пересечет
других точек. Затем он вращается в том же направлении во-
вокруг одной из этих точек, наиболее отдаленной от @, г), пока
не встретит других точек, и т. д. до тех пор, пока он, наконец,
не пройдет через точку (Кг, 0). Так образуется полигон, соеди-
соединяющий точки @, г) и (К*, 0), причем ни одна из точек не ле-
лежит выше или справа от этой линии.
575-
Рассмотрим любой прямолинейный отрезок этой линии и
предположим, например, что он проходит через точки
(Ка, г-о),..., (Л1, г—т);
пусть этот отрезок образует угол 6 с отрицательным направле-
направлением оси у. Если (A = tg6, точки на этом отрезке будут удовле-
удовлетворять уравнению
х + «> = С,
где С — постоянная; поэтому
К + Лг— о) = •.. = А1 + v (г—т),
если (К*, г — v) — точка не на отрезке, то
Следовательно, если р. — положительное целое число или нуль, то
S= JA+1,
причем s может иметь столько значений, сколько имеется неза-
независимых прямолинейных отрезков в полигоне, для которого \>- —
положительное целое число или нуль.
Если допустимое значение s получено, то метод получения
полинома Q(z) аналогичен показанному выше. После этого необ-
необходимо получить диференциальное уравнение для и и убедиться,
являются ли решения регулярными в бесконечности, так как
нормальное решение w(z) может существовать лишь в том слу-
случае, если u(z) регулярно в бесконечности. Существование опре-
определяющего множителя eQiz) само по себе недостаточно для су-
существования нормального решения; сходимость ряда относи-
относительно и(г) также необходима. Если нормальное решение суще-
существует, то оно называется решением порядка s, где s — степень
полинома Q(z). Рангом уравнения относительно рассматриваемой
особой точки является число h, где
Если h — целое число, то оно может быть равно s, вообще же h
больше s.
Когда полиномы Q(z) определены, нужно получить опреде-
определяющее уравнение, удовлетворяемое р. Если это уравнение имеет
одинаковые корни, или корни, различающиеся на целые числа,
то, кроме нормального решения, не содержащего логарифми-
логарифмических членов, могут существовать решения вида
eQ[z) z' Ыг) + ?l(z) log z +... +<?m(z) (log z/"}»
где функции !i(z) — аналитические в бесконечности.
17 • 53. Поднормальные решения. Для некоторого прямолиней-
прямолинейного отрезка диаграммы Пьюзо наклон jj. является рациональной
дробью. Для построения любых нормальных решений могут
576
быть выбраны некоторые нулевые или положительные целые
значения; нецелые значения должны быть опущены. Однако эти
дробные значения приводят к решениям нового типа, которые
называются поднормальными решениями1.
Предположим, что рациональная дробь \>. равна l/k и преоб-
преобразуем уравнение подстановкой
Тогда диаграмма Пьюзо преобразованного уравнения будет иметь
прямолинейный отрезок, расположенный под углом 6' к отри-
отрицательному направлению оси у, где
tg в' = /.
Если / — положительное целевое число, то преобразованное
уравнение может иметь нормальное решение; в этом случае
определяющий множитель Q (С) будет полиномам от С степени s,
где
Таким образом первоначальное уравнение может иметь ре-
решение нормального типа для переменной z'/k; такое решение
называется поднормальным. Очевидно, если существует одно
поднормальное решение для z1/k, то существует также и k—1
других поднормальных решений того же типа. Эти решения
образуют совокупность поднормальных решений.
Например, уравнение
ffiw +<> —-{—4 X-\w-0
имеет два поднормальных решения. Его общее решение имеет
вид
и; = Ае I z —z
Is 1\
где А и В — произвольные постоянные.
Если определяющий множитель Q(z4k) степени s относитель-
относительно z1'*, то поднормальное решение порядка sjk; в этом случае
Следовательно, если поднормальное решение существует, то
его порядок не превышает ранга уравнения.
17-54. Ранг уравнения, удовлетворяемого данной фундамен-
фундаментальной последовательностью нормальных и поднормальных функций.
Пусть
w1 = eQl z-'щ, w2 = eQ* гъ щ wn= e Qn zP/I un
y, These (Faculte des Sciences. Paris, 1885).
Э. Айве—133—37 ¦ 577
будут п функциями нормального и поднормального типа, рас-
расположенными таким образом, что их порядки равны соответ-
соответственно Yi. 7г» • • • > Тш тогда
г > Ъ > Тг > • • • > Тп
Диференциальное уравнение порядка п, удовлетворяемое
этими функциями, будет ранга h, не превышающего Г относи-
относительно особой точки в бесконечности1. Пусть
А =
.., wn
W2,
будет вронскианом п данных функций; допустим, что Д не
равна тождественно нулю. Пусть Дг будет детерминантом, полу-
полученным из Д подстановкой w[n) вместо Wi"~r\ wf вместоw""~^
че з д
и т. д. Тогда, если
рг = — Дг/Д,
то диференциальное уравнение, удовлетворяемое wt, w2>...,wn,
будет иметь вид
dnw
dzn
+А
dw , _.
щ + PnW = 0.
Ранг этого уравнения зависит от порядка коэфициентов рт
в бесконечности.
Теперь из
следует, что
ж. —
где ^ — аналитическая функция, не равная нулю в бесконечно-
бесконечности. Теперь '
(
. • . , Z
-1)(Г -1)
(„_r)(r _1
,Z V-
. ...„-D
Poincare, Acta Math., 8 A886), 305.
578
Если детерминанты разложить соответственно элементам
п — г -f-1 - го ряда, то рг принимает вид
1,?!—7
где ?/,,..., Un — функции, аналитические в бесконечности;
примем, что числа аг,.... з„ выбраны так, что Ult..., Un не
равны нулю в бесконечности.
Следовательно, если
то /ег будет наибольшим из чисел
г(Ъ - 1) + =4 — яи, ¦ • ¦ , г(•/„,- 1), .... г (-/„ - 1) + а„ — аш,
которые, в свою очередь, не меньше
г(ъ - 1), ... , r(Tfm - 1)...., г(т„ - 1),
из которых самое большое равно г(^ — 1).
Таким образом для всех значений г
следовательно
Если все данные функции нормальные, то они однозначны
относительно г и, следовательно, коэфициенты рг также одно-
однозначны относительно z. Рассмотрим случай, когда среди функ-
функций w1(z), .. .,wn(z) имеется совокупность поднормальных функ-
функций. Так, предположим, что Wi(z),...,Wk(z) образуют совокуп-
совокупность поднормальных решений. Если С = г*, то они могут быть
написаны так
где Wlt Wi, ..., Wk — нормальные функции С. Они могут быть
также расположены так, чтобы
W.2 (С) = W1 {ш С), ...,Wk(Q^
где «о* = 1.
Отсюда следует, что при подстановке шг1к вместо z!k,pr оста-
остается неизмененным, т. е. /?г однозначно относительно z. To же,
очевидно, верно и для двух и более совокупностей подкормаль-
ных решений.
Таким образом последовательность нормальных или. поднор-
поднормальных п функций и порядка, равного или меньше Г, удовле-
удовлетворяет диференциальному уравнению порядка п ранга h (не
выше Г) с однозначными коэфициентами.
579
Из этой теоремы следует, что если уравнение/.^) = 0 с одно-
однозначными коэфициентами имеет нормальные ли поднормальные
решения, то оно приводимо, так как любое число нормальных
решений или совокупностей поднормальных решений удовле-
удовлетворяет уравнению
М (w) = О
с однозначными коэфициентами. Если это уравнение не имеет
других решений, помимо удовлетворяющих L {w) — 0, то послед-
последнее уравнение может быть налисано в виде
RM (w) = О,
и, следовательно, оно приводимо.
17-6. Уравнения Гамбургера. В настоящее время неизвестна
совокупность условий, достаточных для того, чтобы уравнение
порядка п допускало нормальное решение. Эти условия уста-
установлены только в одном или двух частных случаях; из них наи-
наиболее важным является уравнение порядка п, в котором
(I) имеются только две особвте точки, именно -к = 0 и а=оо,
(II) начало является регулярной особенностью,
(III) точка в бесконечности является существенной особен-
особенностью г.
Уравнение может быть написано в виде
где рх, рг,..., рп — целые функции z; примем, что они являются
полиномами г.
Теперь, поскольку начало является регулярной особой точкой,
существует не меньше одного решения вида
где V(z) — степенной ряд, который сходится внутри некоторого
произвольно большого круга \z\ = R и 1/@)Ф0. Это реше-
решение может быть получено при помощи методов, указанных
в главе XVI.
Найдем последовательность условий, достаточных для того,
чтобы это решение было нормальным относительно особой точки
в бесконечности. Поскольку некоторое нормальное в бесконеч-
бесконечности решение имеет вид
где Q (z) — полином
1 Hamburger, J. fur Math., 103 A888), 238.
580
a U(z) — функция, аналитическая в некоторой области, не со-
содержащей начало, и не исчезающая в бесконечности. Отсюда
следует, что
где для больших значений | г | U'/U = О (z~2). Далее
F'/V можно разложить в ряд по убывающим степеням z, кото-
который содержал бы только конечное число положительных целых
степеней z. Для этого необходимо, чтобы V имело только ко-
конечное число нулей внутри любого круга Iz \ = R; пусть V
имеет k нулей, кроме нулей в существенной особенности 2 = сю.
Тогда, согласно теореме Вейерштрасса,
где Р(г) — полином z степени k, a g(z) — целая функциям. Отсюда
следовательно, g(z) является полиномом z, a /7B) является поли-
полиномом относительно z~i\ аналогично
Теперь пусть
где
— гР
Рл = ар + alZ~l + ... + а,_, z-s+i f О
тогда
w ) r dz \w
"Z.
где
В общем случае
где
Рл = -У' г}- О B~*)-
581
Заменим w'/w, w"jw,..., w{n)\w в диференциальном уравне-
уравнении, тогда полученное уравнение
sPn
-г
будет тождеством. Положительное целое число s не было огра-
ограничено; предположим, что оно настолько велико, что каждый
из полиномов z(" *)spr. (у. = 1, 2, ..., п — 1) не больше степени ns
и пусть
Определяющий множитель имеет вид
г
Q(z)=fzlv(z)dz,
и поскольку
Px=v* + O(z-'),
то v(z) получится, если взять первые s членов корня уравнения
( zsv)" + Pl ( zsv)"-1 +... +p^z'v +/»„ = 0.
В частности, уравнение, определяющее d0, будет
^ (а0) е ао + аг, s aV* +a.2, ->s a0"—2 + ... +а„, т = О,
причем а0 будет простым корнем этого уравнения.
17-61. Условия для нормального решения. Пусть
w =
тогда, если ге; — нормальное решение, то уравнение, удовлетво-
удовлетворяемое и, допускает не меньше одного регулярного решения.
Теперь
где vy_ тождественно v* в членах вида z°, z-1,..., z"^1. Саедо-
вательно
dfw
dz"
при fo— 1» ~vt — "V, поэтому диференциальное уравнение отно-
относительно и будет иметь вид
582
или
ZjZj v!(n-r-v)r dz"
/•=0 v=0
при p0 = 1.
Коэфициент и в диференциальном уравнении равен
Поскольку v получено так, как указано выше,
r=0
и поскольку s ведущих членов vn—r и юп~г совпадают, то от-
отсюда следует, что s высших членов в коэфициенте и, именно
члены z"s,... , z'-"—1^'*-1, должны обратиться в нуль, следовательно
где v и 60—известны.
Аналогично коэфициент при z -^- в диференциальном урав-
уравнении имеет вид
я—1
? (Я — Г)рг Z<"-'-]> Vn-r-i,
и поскольку я0 — простой корень уравнения
/•-==0
отсюда следует, что
Следовательно ведущий член в коэфициенте z-^- не обра-
щается в нуль, поэтому коэфициент г -^ имеет вид
^(«-«•(чо + ^г-1+ •••).
где ¦»)„ — постоянная, не равная нулю.
Если u = z°U{z), где U(z) — полином от z-\ то о должна
удовлетворять определяющему уравнению
ТHа + 60 = 0.
583
Но з = p + k, где k — положительное целое число или нуль, а р—
удовлетворяет определяющему уравнению
Ир) = [?]п + «ю[p]«-i + • • • + Ол-1,0 Р + ат = 0.
Отсюда следует, что d/гя существования нормального решения
необходимо, чтобы уравнение относительно k
имело не меньше одного корня, равного положительному це-
целому числу или нулю.
Предположим, что это условие удовлетворено и что •/.—
соответствующее значение k, тогда
и = z*(c0 + c1z~1+ ... +сж z-x)
= 2P(CX + Cx_i2+... +C0Z*).
Если это выражение подставить в диференциальное уравнение
для и, то последовательность рекуррентных соотношений
с,-2 /(р + 2) + сх_1 Gi(p + 2) + сх G2(р + 2) = 0,
где Glt G2 — полиномы от их аргументов, должна быть удовле-
удовлетворена коэфициентами сх, сх_],... Первое уравнение удовле-
удовлетворяется независимо от сх; если значение с* дано, то после-
последующие х уравнений определяют c*_i, ... , с0. Всего имеется
s(n— 1) рекуррентных соотношений, А + 1 из которых были
использованы; остальные уравнения должны быть теперь удов-
удовлетворены тождественно, соответственно определенным значе-
значениям сХ) ... , с0. Если совокупность этих соотношений удовле-
удовлетворена, то нормальное решение существует.
Если уравнение
имеет больше одного простого корня, в отношении которого
все необходимые условия удовлетворены, то мы получим соот-
соответствующее число нормальных решений диференциального урав-
уравнения.
Исследуем возможность существования п нормальных реше-
решений. Пусть plf &>, ... , р„ будут «независимыми корнями А(ао)=О
и пусть
Если нормальные решения существуют, то они будут иметь
вид
584
где Ur(z)— полином от г-1; если его степень равна х,, то
а, = Ь + х,,
где pi, р,, ... , р„ — корни /(р) = 0. Теперь
1
a S°r может быть вычислено следующим образом.
Пусть Д будет вронскианом решений ^ ,... , яу„ и
первое приближение к Д будет
и более точно
где
, ... , 2
1 ,
Pi .
РГ\
..., 1
..., Pi,
дЛ-1
фО.
С другой стороны
Таким образом мы найдем, что
В + О (z-1) = Л .
585
Аналогично
= —~sn(n— 1).
Но поскольку kx, ... , kn — положительные целые числа, это
уравнение невозможно. Следовательно, если кисла рх, ... , ,8„
неравны между собой, числа зх, ... , з„ неравны между собой,
а числа з связаны, с п независимыми корнями уравнения /(р) = 0,
то диференциальное уравнение не может иметь п нормальных
решений.
С другой стороны, если не все числа о неравны между со-
собой или если каждое число з не связано з независимым р, то
уравнение
неверно и теорема несправедлива. Можно показать, что в этих
случаях возможны п нормальных решений.
Рассмотрим случай, когда а0 —кратный корень уравнения
тогда т% = 0; поскольку
с = — %1ъ
должно быть конечным, для существования нормального ре-
решения необходимо, чтобы 60 = 0. Если исключить множитель
~(я-1дх_1 ^ то диференциальное уравнение примет вид
G, {1 + О B-*)} U + Т{1 {1+ О B-1)} 2 § +
(Г и
и в общем случае коэфициентом 2"—— будет O(zA~v-S~1).
dz
Определяющее уравнение имеет вид
6г + %з + СоЗ (з — 1) = 0 если s = 1
или
01 + т],з = О, если s> 1.
При дальнейшем исследовании получим последовательность
условий, достаточных для существования нормального решения1
v может быть равно нулю, так как O{z) также обращается
в нуль.
1 Giinther, J. fur Math., 105 A889), 1.
586
17-62. Уравнение Гамбургера второго порядка. Рассмотрим
уравнение
??
где началом является регулярная особая точка, относительно
которой определяющее уравнение имеет вид
Предположим, что регулярное решение имеет только конечное
число нулей в конечной части плоскости и что существует
нормальное решение
id = е®ю и (z),
где
тогда уравнение для и будет иметь вид
и" + 2О'и' + (Q" + Q - а - 2hz-1 - ez~2) и = 0.
Для того, чтобы это уравнение допускало решение
и =z-(l+c12-1 + caz-1!+...),
необходимо, чтобы
s=\, а* = а, п(Р = Ъ.
Коэфициенты ст удовлетворяют рекуррентным соотношениям
= о (а — 1) — с,
1)(з - г) - с}гг_, (г =2, 3, 4,...);
если бы ряд s?icrz-r не был ограничен, то он расходился бы
для всех значений \z\ и решение было бы только кажущимся.
Предположим, что ряд кончается на сх z~\ тогда
(а — у.) (а — у. — 1) — с.
Следовательно необходимо, чтобы уравнение
для ао= -\-^а или для ао= —V^a имело корень х, равный поло-
положительному целому числу или нулю; это условие очевидно
достаточно для существования одного нормального решения.
Для существования двух нормальных решений необходимы
дополнительные условия. Если оба значения о, именно
°i = + Ъ\/а, з2 = — Ь//а,
не равны нулю и если они связаны с независимыми значениями р
587
следующим образом
3i = Pi + *i. аа = р.2 + *2>
то
О = 3j + з2
= Pi + Р2 + Ч + *2 = 1 + Х1 + «2»
что невозможно, поскольку хх и х2 — положительные целые
числа или равны нулю.
С другой стороны, если
°i = з2 = О,
т. е. если t = 0 и уравнение
имеет положительный целый корень, то существуют два нор-
нормальных решения ¦
ег V^ A + ctz-J + ... +сх z~%
e~z V~a A — CjZ-1 + . . . ± Cx Z~%).
Далее, если о, и <з2 неравны между собой, но связаны с тем
же значением plt то
¦оскольку
2о! и 2а2 полжны быть целыми числами, т. е. 2b/v^a должно
быть также целым числом. Аналогично
*i + Z2 + 2р, = О,
следовательно, 2р! — отрицательное целое число, а не нуль. Но
т. е. 4с + 1 — квадрат целого числа, не равный нулю. Эти усло-
условия являются необходимыми и достаточными для существования
двух нормальных решений.
Примеры
I. Докажите, что уравнение
имеет два нормальных в бесконечности решения и получите их.
2. Докажите, что уравнения
588
(III) г*Bг + l)g + Bг* + 9г + 5) г Jf + (-2* g
+ ( — 2г2 — 5г + 3) га/ = О
имеют каждое по три нормальных в бесконечности решения и получите их.
3. Докажите, что уравнение
имеет одно нормальное в бесконечности решение.
4. Докажите, что уравнение
d2w a dw ,
имеет два нормальных в бесконечности решения, если о целое число или нуль.
5. Докажите, что уравнение
— — (ог2 + 26 + сг~2) w = О
имеет нормальное решение, если квадратное уравнение
имеет корень, равный положительному целому числу или нулю для любого
значения W Рассмотрите также следующие два случая: (I) когда оба корня —
целые числа для того же значения Y^a, и (II) когда корень уравнения — поло-
положительное целое число для обоих значений ~\Га.
6. Докажите, что уравнение
d-w dw
имеет два решения поднормального типа в бесконечности, если 2ц — нечетное
целое число.
7. Докажите, что уравнение
имеет два решения поднормального THiia в бесконечности. Выразите их посред-
посредством регулярных в начале решений.
8. Докажите, что уравнение
имеет три решения поднормального типа в бесконечности, если
'->('-¦!¦•)¦
аи — целое число, которое не делится на 3, и получите их.
[Halphen].
58»
ГЛАВА XVIII
РЕШЕНИЕ ЛИНЕЙНЫХ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
МЕТОДАМИ КОНТУРНОГО ИНТЕГРИРОВАНИЯ
18 1. Расширение области применения преобразования Лапласа.
Общий принцип преобразования Лапласа был уже рассмотрен
нами в § 8-1.
Предположим, что
г Os-=0
будет диференциальным оператором относительно г, коэфи-
циенты которого — полиномы от z степени не больше т, тогда
уравнение
Lz (w) = О
удовлетворится выражением
/
с
где функция v{C) и контур интегрирования С определяются сле-
следующим образом.
Пусть М- будет диференциальным оператором
п т
V S>rsC?>?,
а М-, будет его присоединенным выражением, тогда функция v(Z)
должна удовлетворять диференциальному уравнению
Ait (v) = О,
порядок которого равен степени полиномиальных коэфициентов
оператора Z.
Контур С выбирается таким образом, что если Р{ег\ V) —
билинейная форма преобразования, то
[Р{ел, г-}]с=О
тождественно.
Преимущество замены определенного интеграла контурным
интегралом состоит частично в увеличенной свободе выбора
пути интегрирования. Однако только это не оправдало бы от-
отдельного рассмотрения выражения решений диференциальных
590
уравнений при помощи контурных интегралов. Этот вопоос п
сматривается здесь вторично потому, что контурный интег
представляет возможность исследования решений, нерегулярных
в бесконечности, разложения которых в виде ряда расходятся
Природа коэфициентов в уравнении Lz {w) = О показывает, что
точка в бесконечности является нерегулярной особой то'чкой-
применяя контурные интегралы в решениях уравнения, можно
исследовать поведение этих решений в соседстве с особой точкой
18-11. Уравнения, коэфициенты которых первой степени. Если
коэфициенты данного уравнения первой степени, то уравнение
которому удовлетворяет функция v(Q, также первой степени*
Пусть данное уравнение имеет вид
+ ifh* + Ь)™ +...¦*¦ (anz + bn)w = О,
тогда функция г/(С) будет удовлетворять уравнению вида
где функции РA) и Q (С) — полиномы степени я1. Это решение
может быть выражено в виде
где «!,..., а„ —нули функции Я (С), принимаемые разными, тогда
Билинейный конкомитант будет иметь вид
(а0С+ а?п-1 +... + ааг + ап) v (Г) ez\
поэтому контурный интеграл
с
будет удовлетворять данному диференциальному уравнению*
при условии, что контур С, зависящий от z, выбран таким
образом, что
[ ^>Ч
тождественно относительно г.
Пусть вещественные части \ и Х2 больше — I, тогда
w = j eA<v (С) rfC
1 Нужно отметить, что выражение Р{С) равно, с точностью до постоянного
множителя, полиному ао?" + я^"—J+ ... .+«л_1 С+^д ; чтобы Я(С) не было сте-
степени ниже п, предположим, что аоф0. Точка в бесконечности будет тогда
нерегулярной особенностью для w первого ранга.
591
будет решением уравнения, если интегрирование производится
вдоль некоторой простой кривой конечной длины, соединяющей
ах и а2, но остающейся все время на конечном расстоянии от
любой точки яг, для которой вещественная частьпоказателя 1+Хг
отрицательное число или нуль.
Если вещественные части \,..., >*„ все больше — 1, то мы
получим не больше п—1 независимых интегралов указанного
типа, каждый из которых удовлетворяет данному уравнению.
Рассмотрим теперь случай, когда числа >. неограничены. Для
упрощения, будем считать, что точки alf..., ап находятся на ко-
конечном расстоянии от начала. В этом случае мы получим контур,
образованный совокупностью четырех петель, описанных после-
последовательно таким образом, что каждая петля начинается и за-
заканчивается в начале и содержит только одну особую точку.
Например, пусть первая петля будет проведена вокруг at в по-
положительном направлении, вторая петля — вокруг а2 также
в положительном направлении, третья петля будет проведена
вокруг ах в отрицательном направлении, а четвертая петля —
вокруг х, в отрицательном направлении. Функция
возвращается к своему начальному значению после того, как
контур был описан. Так могут быть образованы п — 1 незави-
независимых интегралов, удовлетворяющих данному уравнению.
Последовательность п независимых контурных интегралов,
удовлетворяющих уравнению, нельзя получить, не ограничивая
несколько 2. Предположим, например, что
в этом случае соответствующий контур получится, если точка С
будет перемещаться от — со вдоль линии, проведенной через ах
параллельно вещественной оси, до тех пор, пока она достигнет
расстояния г от %г, опишет вокруг ^ круг в отрицательном
направлении, а затем возвратится по прямолинейному пути. При
этом предполагается, что каждая точка на петле находится
на конечном расстоянии от я2,..., а„. Вообще существует п ин-
интегралов этого типа.
18-12. Разбор интеграла, когда R(z) велико. Рассмотрим ин-
интеграл
для больших значений R(z). Мы не потеряем в общности, если
предположим, что и. равна нулю, что равноценно подстановке z
вместо z + ]i, или что аг равна нулю, Что равноценно подста-
подстановке l, вместо С — аг, и если опустим множитель ё\г, который
должен быть впоследствии восстановлен. Контур тогда будет
состоять из следующих трех частей:
592
(I) вещественной оси от — <х> к — г;
(II) круга Y радиуса г, описанного в отрицательном направ-
направлении вокруг начала;
(III) вещественной оси от —г к —оо.
Пусть 1Х, [2, /3 будут соответствующими значениями интеграла
вдоль этих трех путей интегрирования. Если С вещественное
и меньше — г, то положительное целое число х может быть
найдено таким образом, что
поэтому, если R (z) > х, то
—оо
Следовательно,
Л-» О, когда )
и аналогично
/3—»0, когда R (z)-»Чг ос.
Остается интеграл /2, взятый по кругу i произвольно малого
радиуса г. Первая часть подинтегрального выражения может
быть разложена в виде
е« (с - :д'\.. (с - а>= е- {л0 + лхс + • • • + лтс+ RC+%
где Ии, Aj Ат — постоянные. Пусть М будет верхней гра-
границей
когда |?|<г, тогда получим положительное число р, так что
* I А> I -^ М, | Аг | < /Ир,..., | Ат | ¦«
и, следовательно,
гт+1
Теперь
Задача состоит в том, чтобы определить поведение /2, когда
R(z)—» + оо. Однако мы ничего не потеряем, если ограничим
рассмотрение вещественным z.
Рассмотрим интеграл
т
где z велико и вещественно; пусть z? = — t, тогда интеграл
будет иметь вид
Э. Айне—133—38 593
где х—круг радиуса rz, описанный в положительном направлении
около начала в плоскости t, следовательно, интеграл будет равен1
2* sin рпГ (р + 1).
Эта величина конечна, за исключением случая, когда р—поло-
р—положительное целое число.
Следовательно, когда z -» + со вдоль вещественной оси,
х + 1),
(v= I, 2 т),
| M -f^ Г (\ -jr m + 2) -»0,
поскольку г может быть выбрано таким, что гр < 1. Отсюда
за исключением случая, когда \ положительное целое число.
Множитель е* был временно опущен; восстанавливая этот
множитель, увидим, что рассматриваемый интеграл прибли-
приближается к пределу
где Ki конечно и не равно нулю, ко1да z приближается к -\? оо
вдоль вещественной оси.
18-13. Существование п линейно-независимых интегралов. Пред-
Предположим, что числа
«1, «г. • • • > ап
расположены таким образом, что их вещественные части обра-
образуют уб .шающую последовательность. Чтобы можно было про-
провести петлю, соответствующую каждой точке а, предположим,
что все мнимые части этих чисел неравны. В этом случае полу-
получим интегралы, соответствующие каждой точке а; пусть эти
интегралы будут соответственно равны
щ, w2,..., wn.
Эти интегралы линейно-независимы, так как в противном случае
мы получили бы линейное соотношение вида
C1w1 +¦ С2да2+... + Cnwn = 0.
1 Уиттекер и Ватсои, Курс современного анализа, § 12-22.
594
Но когда z—»-f- oo,
lim w, e~"lZ z*1rl = llm K-, e^"""'" zK ~Xv
-0 (v = 2, 3,..., я),
поскольку вещественная часть % — а, положительна Ч Следова-
Следовательно, соотношение неверно, если Сг не равно нулю. Анало-
Аналогично, С2,..., Сп равны нулю, следовательно, такое линейное
соотношение не существует.
18-14. Случай, когда функция Р(С) имеет кратные линейные
множители. Предположим, что какие-либо два числа а, например
аг и а2, равны между собой, тогда
так что
Чтобы получить совокупность интегралов, нужно найти два
независимых контура, относящихся к точке av Одним таким
контуром будет рассмотренная выше петля, но нас интересует
главным образом второй контур. Мы видели, что если аг и а2
независимы, то существует соответствующий контур, который
содержит эти две точки, но не проходит в бесконечность. Кон-
Контур, который дает второй интеграл относительно точки dj, яв-
является предельным случаем контура, содержащего обе точки ах
и а2, которые теперь совпадают.
В настоящем случае билинейная форма будет иметь вид
Соответствующим контуром была бы замкнутая кривая, начи-
начинающаяся в at в некотором направлении и возвращающаяся к ctj
в другом направлении. Иначе говоря, градиент контура должен
иметь разрыв в av Более того, он должен быть таким, чтобы
в то время кигда С, приближается к аг в любом из этих направ-
направлений, билинейная форма стремилась бы к нулю.
Пусть
так что
?!;=_?_,,*(?-?>
— k в
1 Если вещественные части любых двух (или больше) последовательных
чисел а равны между собой, то теорема хотя и верна, но доказать это значи-
значительно труднее.
595
тогда
X, ft
— — ¦— cos (<p — p)
Теперь p -> 0, тогда С -5 a1# Следовательно, чтобы этот экспо-
экспоненциальный множитель стремился к нулю, когда С приближается
к %, необходимо, чтобы cos(<p — Р) был положительным или
чтобы
Таким образом все возможные направления приближения к аг
будут лежать на одной стороне прямой линии, проведенной
через <*! в направлении р.
18-15. Уравнение с постоянными коэфициентами. Если метод
Лапласа приложить к уравнению
dnw , dn~lw , , dw . _
где коэфициенты а — постоянные, то он очевидно не даст ре-
решения. Если уравнение удовлетворяется интегралом *вида
то должно быть только удовлетворено условие, чтобы
тождественно, где
<р (С) = ajT-b а?п-1 +... ф a^-iC + an.
Таким образом ни одно диференциальное уравнение не удовле-
удовлетворяется i'(C); единственным необходимым условием является
то, чтобы функция
была аналитической в области плоскости С, тогда можно будет
принять, что контур С находится в этой области.
Рассмотрим случай, когда С = a — корень кратности т харак-
характеристического уравнения
?@ = 0;
пусть контур С содержит этот корень, но не содержит каких-
либо других корней уравнения. Выберем фунцию/@ так, чтобы
где функция <]> (Q аналитическая внутри С; постоянные А зависят
596
от выбора /(С), следовательно, они произвольны, тогда
Если мы вычислим этот интеграл, то найдем, что w равно (см.
§6-12)
e-.*{C1 + Caz+...+ Cm«»-i}-
18 • 2. Рассмотрение преобразования Лапласа в более общем слу-
случае. Отбросим ограничение, что коэфициенты диференциального
уравнения первой степени. Пусть уравнение будет иметь вид
L (W) E PO{Z) -^r + Px B) &n_! +• • • +
где P0B) — полином от z степени р, а остальные коэфициенты
полиномы степеней не выше р1. Пусть
Pr(z)^arzp + ... (г=1, 2,..., п).
Тогда, если
с
Повторным интегрированием по частям можно доказать, что
следовательно,
1 Ранг особой точки в бесконечности поэтому не больше единицы.
597
где /? — ряд членов вида
dp
коэфициенты которого полиномы от z.
Таким образом, если интеграл W является решением данного
диференциального уравнения, то необходимо, чтобы функция
"v(z) удовлетворяла диференциальному уравнению
Следовательно, определение контурного интеграла, удовлетво-
удовлетворяющего данному диференциальному уравнению, зависит (I) от
решения присоединенного уравнения порядка р и (II) от опре-
определения контура С таким образом, чтобы [R] было равно тож-
тождественно нулю относительно 2. Докажем, что п независимых
интегралов рассмотренного типа действительно существуют1.
Пусть аь а2, ..., ап будут корнями уравнения
тогда С=аъ а2>..., ап — особые точки диференциального урав-
уравнения относительно v. Каждая из этих особых точек регулярная,
и отн< сительно каждой особенности аг имеются п — 1 решений,
аналитических в соседстве с этой особенностью, и одно неана-
неаналитическое решение
%
где функция <рг(С) аналитическая вблизи ar. Рассмотрим это не-
неаналитическое решение чз. Пусть z стремится к бесконечности
вдоль прямой линии /, проведенной в отрицательном направ-
направлении параллельно оси вещественных чисел. Тогда, незначи-
незначительно видоизменяя теорему Ляпунова (§ 6-6), найдем, что поло-
положительное число [>¦ существует таким образом, что
e
d"v
стремятся к нулю, когда R(C)—» — со. То же очевидно верно,
независимо от значения v, и в отношении
.ч и." dt'C A dnv .p.;
Следовательно, если R(z)—положительно и достаточно велико,
а контур С представляет собою петлю, начинающуюся и закан-
заканчивающуюся в точке на бесконечности линии /, и окружающую
точку аг, то [R] обратится в нуль независимо от г.
1 Poincare, Am. J. Math. 7A885), 217.
598
Таким образом существует п интегралов
так что интеграл Wr соответствует точке аг. Более того как
в § 18-2, отсюда следует, что если \,..., лп не положительные
целые числа, то
стремятся к пределам не равным нулю, когда z приближается
к +оо вдоль вещественной оси. Таким образом приведенный
анализ включает также и более общий случай.
18-21. Асимптотические представления. Контурные интегралы,
полученные в предыдущем параграфе, приводят непосредственно
к асимптотическим представлениям решений 1. Отсюда следует,
как в § 18-12, что если IF —контурный интеграл
то
We~ "У l =z+if{ А о + АЛ + ... + AmC} С еЖ +
с
¦z
с
—m—1
Вдоль прямолинейных частей контура интеграл, так же как и
его произведение на любую произвольную степень z, стремится
к нулю, когда R(z)-* + co. Важной частью контура является
малый круг if, окружающий начало в отрицательном направлении.
Теперь, если г—положительное целое число, то
2М г"г j ?+геЛО: = (- l)'2i sin ХлГ(Х + г -\- 1)
и
z JRs, e аХ <К
где К не зависит от z.
Пусть
Sm = 2i sin Хп { Л0Г(/-+!)- AjT (I + 2) 2~*+ .. - ±
тогда
когда z—» со вдоль вещественной оси. Следовательно e°zz Л Sm
1 Poincare, Acta Math., 8 A886), 295.
59
является асимптотическим представлением интеграла W, т. е.
Этот асимптотический ряд формально идентичен ряду, полу-
полученному при исследовании уравнения для получения нормаль-
нормального решения. Таким образом, если этот нормальный ряд не
ограничен и не дает нормального решения, то он дает асимп-
асимптотическое представление решения.
В предыдущем исследовании мы приняли, что г стремится
к бесконечности вдоль вещественной оси. Это ограничение было
принято только для упрощения, однако нет разницы также
в том случае, когда z стремится к бесконечности вдоль любого
луча определенного аргумента. Ряд Sm не может быть асимпто-
асимптотическим представлением функции We"~°zz1^1 для всех значений
аргумента, так как, если бы
zm {We~*zzx+i -Sm}
стремилось равномерно к нулю для достаточно больших значе-
значений \z\, то We~azzч* было бы аналитическим, а представление
в виде ряда сходилось бы, что, по крайней мере в общем слу-
случае, неверно. В действительности, когда argz увеличивается,
то решение, которое Sm асимптотически представляет, внезапно
меняется. Таким образом, если решение разложено асимптоти-
асимптотически, то существенно определить пределы argz, между кото-
которыми представление имеет смысл К
18-3. Уравнения ранга выше первого; косвенная трактовка. Выше
мы получили точное решение уравнений первого ранга при по-
помощи интеграла Лапласа. Ограничение, чтобы ранг не превы-
превышал единицы, является существенным; если уравнение выше
первого ранга, то метод совершенно неприменим. Покажем, что
уравнение порядка s больше единицы может быть заменено
уравнением первого порядка и ранга, которое, в свою очередь,
может быть решено при помощи интеграла Лапласа2. Непо-
Непосредственный метод получения решения будет дан в одном из
следующих параграфов3.
Пусть уравнение имеет вид
D dnw . D &n~yw . . n dw . D n
где коэфициенты — полиномы от z, и пусть Рг будет степени
КТ' Тогда, если уравнение имеет нормальные решения порядка
1 См. пример § 18-61 и сравни с §§ 19-5, 19-6.
* Пуанкаре [Acta Math., 8 A886), 328] впервые описал метод и подробно
рассмотрел случай уравнения второго порядка. Горн [Acta Math., 23 A900),
171] продолжил анализ в случае уравнения второго порядка и ранга р.
3 18-31, см. также §§ 19-41, 19-42.
600
s в бесконечности, то
Kr<Ko + r(s-l),
а знак равенства верен по меньшей мере один раз для г > К
Пусть
Щ(г), ГвB),..., ™n(z)
будут и независимыми нормальными решениями и пусть
Образуем все возможные произведения, каждое состоящее иа
s множителей, так, чтобы
¦v = W* (г)
где индексы а, 3, ...,\i принимают любые значения 1, 2,...,п.
Число N независимых произведений равно ns, а произведения
удовлетворяют диференциальному уравнению типа
dNv . ^ dN^*v . , _, rft; _
коэфициенты которого полиномы от г; г» — нормальное решение-
порядка s, откуда, если 6Г — степень Qr, то
ег<е0+ /¦(«— 1).
Если вместо z подставить coz, св22;,... или <os~1z, то произ-
произведения могут взаимно переставляться, поэтому уравнение оста-
останется неизмененным. Следовательно можно найти такое число ту
чтобы
QT (z) = zm-'qT (?), (r = 0,l,...,N)
где <]гB?)~ полином от zs. Уравнение относительно v можно
поэтому написать в виде
Теперь пусть 2^ = С, тогда f —~ будет линейным выражением
относительно
с постоянными коэфициентами. Уравнение, следовательно, при-
примет вид
где коэфициенты являются полинома л и от С.
601
Если т)г — степень дт в 2*, то
6Г = m — г -f s^r,
откуда
•»1г < По + г.
Теперь, степень Rr равна степени высшего члена
rNn С\ rN—1n Г\
и является наибольшим из чисел
rNn С\ rN—1n Г\ rN~rn (г\
т. е. iV + %,. Следовательно, степень каждого из коэфициентов
/?i, • • •. Rn не больше степени /?0, поэтому уравнение будет
первого ранга и # может быть выражено в виде интеграла
Лапласа.
Остается вывести w из ч). Пусть
будет искомым решением; напишем
»r(z) = ?l(z<o<t-1) (г=1, 2,...,я),
тогда уравнение относительно v удовлетворится произведением
Образуем первые N производных от г»; поскольку <f>i(iV'B:) и
высшие производные могут быть выражены при помощи пер-
первых N—1 производных, мы получим всего N-{-1 уравнений
вида
<r = 0, 1,..., /V). где коэфициенты Z — рациональные функции
от z. Если мы из этих уравнений исключим N произведений
—^- ~- ... —~, то получим диференциальное уравнение
порядка N относительно v.
Рассмотрим теперь только первые N уравнений, в которых
г имеет значения 0, 1,..., N—1. Из этих уравнений любое из
N произведений может быть выражено через v, v',...,vlN~l).
В частности
<Pl B) Ъ B) • • • Ь B) = "О, Ь B) <?2 (Z) . . . <?, (Z) = Ф,
где Ф — линейное выражение относительно v, v', ..., v{N~i), коэ-
коэфициенты которых — рациональные функции от z1. Отсюда
«pi (г) =^_
1 Случай, когда детерминант коэфициентов Z обращается в нуль, был рас-
рассмотрен Пуанкаре в указан* ой выше статье. В этом случае Ф не рациональное,
но алгебраическое выражение относительно г, V, *>',..., v^N~~l\
•602
и, следовательно, если <v известно, то ra»=«1(z) получается
в квадратурах.
18-301. Пример приведения к первому рангу. Рассмотрим урав-
уравнение
второго ранга относительно точки в бесконечности. Если w =
= tf (z) — является решением, то wx = <р (— z) удовлетворяет урав-
уравнению
Пусть v — wwx, тогда
v' = w'wx + ww[,
! -j- 2w'w'lt
-j-14z2 —
+ 4 — ^} ««»! + f 122
Исключая wwx, w'wly ww\ и «/'¦syj, найдем, что уравнение, удов-
удовлетворяемое v, имеет вид
и второго ранга. Но если мы его преобразуем подстановкой
г* = С, то оно примет вид
4C-S + 14С" 1?-<4?+К>1? ~ 1K"f "(К-1)^=0
и будет первого ранга.
18-31. Уравнения ранга выше первого. Если уравнение ранга
/>]>!, то интегральное представление решений, замещающее
интеграл Лапласа, будет иметь вид *
где Z —функция от С1( ..., Ср. Рассмотрим это представление
в случае/? = 2; более общий случай значительно сложнее.
Пусть уравнение будет иметь вид
1 Cunningham, Proc. London Math., Soc. B), 4 A906), 374. Нужно отметить
что определение ранга Куннингамом несколько отличается от принятого.
603
где коэфициенты— полиномы от г, а степень pr(z) больше сте-
степени po(z) на г. Пусть po(z) имеет четную степень1 >. и пусть
I + 2й = 2т.
Посмотрим, возможно ли удовлетворить уравнение двойным
интегралом вида
где U— искомая функция от и и t, а контуры и и t не зави-
зависят от z. Далее
+^ uz° (t + uz)Udu dt,
<gf = J J etz^ uz* {(r + hzJ + и
и в общем случае
где
сог = —^— -f- с^ш,-.!.
Нужно отметить, что шг —полином вида
+ r(r-l)(r-2)(r-3) и2аф 1И)^.+ # .
о
коэфициент (^ + uz)r~^ равен нулю, когда v нечетное, и равня-
равняется постоянной, помноженной на и2 , когда v четное.
Таким образом
znL(w) = ffetz+iruz°Il(t, и, г) Ududt,
где
П& U, Z)=Zn{wnpo+wn^iPl+ . . .-f (Oi/?n_i +/?„}.
Теперь П — полином от z степени 2т = к 4- 2п. Пусть aTS будет
коэфициентом при zx^r~s в рГ, a 5S — коэфициентом при z2m~^
в П, тогда
Во == йдои" 4- aloun~'i 4- • • • 4- «по.
Bj = t { na^u"-1 + (п — 1) alOu"-2 + ... + a«_i, 0} +
+ { aotu" 4- а11м"-1 + ... + ani},
1 Если pe{z) нечетной степени, то левую часть уравнения нужно умножить
на г.
604
и в общем случае
Вг = f {п
S- 1
где Brs (и) — полином от « степени не больше п — г
Таким образом
Простое интегрирование относительно и и t дает
где скобки обозначают разность между конечными и началь-
начальными значениями после того как был описан контур и или
контур L Простые интегралы, содержащие эти скобки, назовем
полуинтегринованными членами.
Это приведение прилагается несколько раз KznL(w), так что
последнее приводится наконец к виду
z^ 2 "*' М (U, и, t) du dt + [R],
где [R] обозначает совокупность полуинтегрированных членов.
Таким образом, для того, чтобы рассматриваемый интеграл
удовлетворял диференциальному уравнению, необходимо, чтобы
функция 0{и, t) удовлетворяла диференциальному уравнению
в частных производных
M(U, и, 0 = 0,
а также, чтобы контуры были выбраны таким образом, чтобы [R]
обратилось в нуль тождественно. Если эти условия удовлетво-
удовлетворены и интеграл существует, то он дает решение данного
уравнения.
Высшая степень z в П(?, и, z) равна z2m, она может быть при-
приведена посредством т последовательных интегрирований отно-
относительно и, добавляя, таким образом к М (U, и, t), выражение
Аналогично, член 22m—1 приводится посредством т — 1 интегри-
интегрирований относительно и и одного интегрирования относительно t
и дает выражение
BU
605
Остальные члены могут быть приведены аналогично; если про-
произвести достаточное число интегрирований относительно и, то
ни одна частная производная не должна быть порядка выше т г.
Диференциальное уравнение в частных производных, удов-
удовлетворяемое U, будет, следовательно, иметь вид
/? дти
где коэфициенты Лг5 — полиномы относительно и и t. Пусть
и —а. будет некратным корнем2 уравнения В0 = 0, тогда как и
при обыкновенном линейном уравнении точка и =а будет осо-
особой точкой решения диференциального уравнения в частных
производных. Покажем, что это уравнение допускает решение,
которое может быть выражено в виде сходящегося двойного
ряда.
18-32. Определение функции U. Поскольку и = а — простой
корень уравнения
«cow" + а1йип~1 +... + aw_ii0 и -\г ап0 = О,
отсюда следует, что если
п I /«• 1\ п—1 I I О
nciQfjO. -|- уп — I) uloa -j-. . . -f- tl/i, i,q = p,
то р ф 0. Предположим, что
aoia "г ana т • • • т &m == T>
и напишем
v = u — a, s — t -j- y/3,
тогда член в Вг, который не содержит <v, будет равен fte.
Теперь
L (w) = e J J e /УФ (s, v, г) dv ds,
где
®{s, v, z)= H(t, u, z).
Член в гЧ^з1* приводится к члену, не зависимому от z, посред-
посредством jj. или jj. -f- 1 интегрирований относительно s вместе с
-у- (х — jj.) или -— (х — ц. — 1) интегрирований относительно v, в за-
зависимости от того, у. — ^ четное или нечетное. Нужно отме-
1 Нужно отметить, что уравнение М (U, и, t) = 0 не определяется един-
единственно, так как при приведении последних членов имеется некоторая свобода
выбора в отношении того, когда произв дить интегрирование относительно и
и когда относительно /.
2 Случаи кратн то корня требует несколько утомительного анализа, и не
представляет особого интереса.
606
титъ, что поскольку Ф содержит множитель z, x по меньший,
мере равно щ у. не больше п, поэтому х — у, — положительное п?
лое число или нуль. ц
Пусть (s, я))ТзП обозначает полином степени /'относительное
и степени п относительно v, тогда диференциальное уравнение
относительно U будет иметь вид
+ ( ) ^
или, при разложении
{E, ^J,й f/}-(_ 2)
-3
м=0 |х=2
где выражения A, v)n обозначают полиномы от v степени п..
Примем решение вида
тогда, если [р]т = р(р- 1).. .(р —т+1), функции / будут удов-
удовлетворять рекуррентным соотношениям
2 [?Шо + [?U-i Р* ^ + Mm-i «о/о = О,
где a0, fli, &!, c0, ... — постоянные, входящие в диференциальное
уравнение.
Первое рекуррентное соотношение приводится к виду
и удовлетворяется соотношением
/о =s >
где
607
Второе рекуррентное соотношение тогда примет вид
s ^ + (а *
где А, и Л2 — определенные постоянные, зависящие от о. Сле-
Следовательно,
где gvts)— полином от s степени г.
Докажем, что формальное решение
сходится внутри любого конечного круга | ?> | = ? Для всех зна-
значений | s |, которые больше фиксированного числа s0. Мы не
потеряем в общности, если примем, что р = О, а = 0, так как
форма ряда ]Vjgv(s) одинакова во всех случаях. Для упрощения
предположим, что s" = t; тогда диференциалыюе уравнение
в частных производных для LJ примет вид
.id dmU ,,,, , ,,, , , дти .
Его решение может быть разложено в ряд
коэфициенты которого gr(t) — полиномы, определяемые соотно-
соотношениями вида
1
(fc) ft = 0
где Ohk и &№ — постоянные.
Если полиномы <рг@ определяются соотношениями
2 2
(fc) Й О
где *Ро = ?о=1» то коэфициенты фг@ будут модулями соответ-
соответствующих коэфициентов gT (t), и следовательно
608
для всех значений t. Рассмотрим также последовательность
функций tyr(t) = crf, где
(hi *=0
dt"
коэфициенты cr положительные, если с0 = 1. Если | t | > 1
и если
A*
dtn
= 0, 1, ...,r-l),
TO
1Фг1>Ы.
Поэтому, по индукции, для всех значений г и для j t \ > 1,
Но 4r = crtr, a tpr — полином степени г с положительными ко-
r , p
эфициентами, откуда
для Л == 1, 2, ..., г, следовательно
Рассмотрим теперь выражение
оно удовлетворяет диференциальному уравнению в частных
производных вида
dmV dmV \Л \Л k+i flin—k'.h у
'¦dt
где Phfc (¦у) — степенной ряд относительно г», который сходится
внутри круга | <у | = 3, где 8 — модуль нуля B0(v), ближайший
к началу. Следовательно, если vt = С, то 1/(С) удовлетворяет
обыкновенному диференциальному уравнению вида
где Qr может быть разложен в степенной ряд по С, который
сходится для | С I < U, поэтому ряд V сходится для | С | < W,
т. е, для | v | < б.
Э. Айне—133—39 609
Отсюда следует, что ряд
сходится абсолютно и равномерно, если | v | < 8 и если 11 \
конечно и больше единицы. Но поскольку коэфициенты gy (t) —
полиномы от t, ряд сходится также при | t | <1.
Таким образом функция U(v, s) может быть представлена
двойным рядом, который сходится для всех ненулевых значений s.
включая значение s = оо, и для | v | <8. Остается доказать, что
контуры в плоскостях s и v могут быть выбраны таким обра-
образом, чтобы двойной интеграл существовал, а полуинтегрированная
часть [R] обратилась в нуль.
18-33. Завершение доказательства. Ряд для V удовлетворяет
линейному диференциальному уравнению в частных производ-
производных, коэфициенты которого Phk (v) могут быть разложены
в степенной ряд по (v — с), где с не является нулем B0{v). Его
решения могут быть аналогично разложены и сходятся внутри
круга | v — с \ — vj, где t\ — расстояние от с до ближайшего
нуля B0(v). Отсюда следует, что V допускает аналитическое
продолжение в некоторой замкнутой области в плоскости v,
не содержащей нулей B^vI. To же верно и в отношении произ-
производных V относительно v и t.
Если | t | > 1, то коэфициенты разложения V являются
главными функциями, так как коэфициенты разложения для U,
следовательно и U и ее производные допускают аналитическое
продолжение.
Если мы будем рассматривать источник коэфициентов Phk(v)
в диференциальном уравнении в частных производных для V,
то увидим, что эти коэфициенты, следовательно и коэфициенты
Qr(?, t), в обыкновенном уравнении для V ограничены при
v = оо. Поэтому, если | t \ > 1, число X может быть выбрано
таким, чтобы, когда v стремится к бесконечности в опреде-
определенном направлении,
поэтому
Следовательно, если 1 < | t \ < " и если v стремится к бес-
бесконечности, так что R(i»z2) положительно, то
е 2 U->0.
Но поскольку U абсолютно сходящийся ряд положительных
степеней t, отсюда следует, что ограничение 1 < t может быть
устранено и результат будет верен для 0 < t < т, При тех же
условиях
1 ЛП- к , ,
1 Доказательство аналогично приведенному в § 12-3.
610
Следовательно, если | s | > s0 = - \ когда j v j -> оо, то
и аналогично, когда | s | —* со, то
если
R(to2)>0, R(sz)-^O.
Таким образом всегда можно найти контуры в плоскостях
v и s, окружающие точки г> = О и s = 0 и простирающиеся
в бесконечность в соответствующих направлениях, так, чтобы
двойной интеграл
Я, } . -
е 2Ь" Uciv els
существовал и чтобы полуинтегрированный член \R] обратился
в нуль в бесконечных пределах интегрирования.
Следовательно, двойной интеграл
w = e~i'J'^t~hl ( С еЛГт2v"~ ir° s~3 x
Г Г еЛГ
X {1
является решением данного диференциального уравнения вто-
второго ранга. Не учитывая экспоненциального множителя, инте-
интегральное решение состоит из членов вида
esz+ 4
jj esz+ 4 та= V'' -11-1 8—кы dvds
+r'?^-irr°-k!idld-ri (A =1,2, ...; ft < А).
Пусть контуры в плоскостях Ей») будут петлями, окружаю-
окружающими начало и проходящими в бесконечность вдоль отрица-
отрицательной вещественной оси. Тогда рассматриваемый член будет
вида
Г (р + Л) -2m-e./?-2ft- *т2 /Ь — 1 Л1»
Г(а + * + 1J 1«-1,...,я;.
Отсюда
w — е
где P(z—1) может быть формально разложено в ряд по возра-
возрастающим степеням z !. Но поскольку бесконечное число коэфи-
011
циентов
Г(р + Л)
Г(а + Й+ 1)
беспредельно увеличивается, когда h ->0, ряд в общем случае
расходится. Таким образом, если РB~1)неограничена, то раз-
разложение не даст решения уравнения. Однако можно доказать»
что оно дает асимптотическое представление решения.
18-4. Интегралы Жордана и Похгаммера. Преобразование
Эйлера (§ 8-31) дает эффективный метод исследования уравнения
типа
= Q B) ^ -К? B) -^ + ^±Л Q» (z) -??- -...
где функции Q(z) и #(z) полиномы, так что Q (z) или zR(z)
степени п, в то время как степень другой функции не превы-
превышает п.
Жордан и Похгаммер подробно исследовали контурные ин-
интегралы, возникающие при этом преобразовании1; рассматривая
различные возможные контуры интегрирования, можно в общем
случае получить п независимых частных решений, которые
вместе составили бы общее решение.
Рассмотрим интеграл
/
с
где U — функция С, определяемая преобразованием Эйлера
именно
Тогда
где
V = Z (С) Q (С) (С - 2)и = (С - zf e
и~~Ш
1 Jordan, Cours d'Analyse, 3 C изд., 1915), 251; Pochhammer, Math. Ann.,
35 A889); 470, 495; 37 A890), 500. Дальнейшее приложение метода см. Hobson,
Phil. Trans. Roy. Soc. (A) 187 A896), 493.-
6!2
а контур С должен быть выбран таким образом, чтобы
fdV = 0
независимо от z. Это условие удовлетворяется, если
(I) С—замкнутый контур, так что начальные и конечные зна-
значения V тождественны, или
(II) С —криволинейная дуга, так что V обращается в нуль
в ее конечных точках.
В качестве общего принципа можно утверждать, что если Q (г)
полином степени п с неравными нулями, то имеются п контуров
первого типа, по одному соответственно каждому нулю ц> (z),
которые дают я независимых решений в виде контурных ин-
интегралов. С другой стороны, если Q(z) степени п, но с кратными
корнями, или степени меньше п, то число возможных незави-
независимых контуров первого типа меньше п, а недостающее число
их возмещается контурами второго типа.
18-41. Контуры, связанные с нулями Q(z). Пусть нули Q(z)
равны fl], ..., ат (т < п), тогда
г 1
где в наиболее общем случае S (С) состоит из полинома от С
с членами (С — aF)~z, (¦! — а,.) 3 и т. д., следовательно,
где ^—постоянная, а функция
мероморфная во всей плоскости. Таким образом, когда С опи-
описывает простой замкнутый контур в положительном направлении
вокруг точки а,, V возвращается к своему первоначальному
значению, умноженному на е2л'*г.
Пусть О будет некоторой точкой в этой плоскости и пусть Аг
обозначает петлю, начинающуюся и заканчивающуюся в О и окру-
окружающую точку аТ в положительном направлении. Пусть AT1 обо-
обозначает ту же петлю, описанную в обратном направлении. Рассмот-
Рассмотрим теперь сложный или двойной контур ATAsA7l AT1, состоящей
из петли Аг, петли As, петель Ат и Д„ проведенных в обратном на-
направлении. Очевидно, когда С описывает этот контур, то V возвра-
возвращается к О с начальным значением. На рис. 13 схематически по-
показан двойной контур, состоящий из четырех параллельных
013
линий, проведенных отдельно для ясности, которые совпадают
на линии (ar, asI [точка О лежит на линии (ar, as)].
Пусть Wr будет значением интеграла
где
т
п c;-flr)a
Рис. 13.
для контура Аг и для определенного начального значения под-
подинтегрального выражения /„• Пусть Wrs будет значением ин-
интеграла для сложного контура ArAsA7lA7\ тогда Wrs будет ре-
решением диференциального уравнения.
Посмотрим, что добавляет каждая из четырех петель к зна-
значению Wrs. Петля Аг дает W,- и после ее обхода конечное
значение подинтегрального выражения равно е2ш"г f0. Это яв-
является начальным значением для петли As, которое поэтому
добавляет к Wrs значение e2™r Ws и дает под интегралом
е2*1 (*г~ °s' Jo. Теперь, если бы петля Ау1 была описана при
начальном значении e2'^rJo, то обход ее добавил бы— Wr и
конечное значение подинтегрального выражения было бы Jo.
Однако в действительности имеется по отношению к этой
петле начальное значение elr'n'Jr ¦ °s) Jo; следовательно, к Wrs
будет добавлено —eZmtXs ¦ Wr и конечное значение подинте-
подинтегрального выражения будет e2luas Jo. Наконец, петля Л71 доба-
добавляет — Ws к — WTS и подинтегральное выражение возвращается
к своему первоначальному значению Jo.
Все четыре петли, следовательно, дают
Таким образом
откуда
Предполагается, что другие особые точки не лежат на линии.
6 К
Аналогичный контур можно построить относительно точек
ar, z. Пусть WTZ будет значением интеграла для этого контура,
тогда
A _ е™>) Wrs = A -- е2™' ) Wsz + A - е2™*) Wrz
и поэтому все интегралы типа WTS могут быть выражены ли-
линейно через интегралы Wn. Следовательно, имеется не больше т
линейно-независимых интегралов рассматриваемого типа.
18-42. Случай целых вычетов. Если какой-либо вычет ъТ отно-
относительно R(Q/Q{Z) является целым числом, то этот метод не-
неприменим. Так, пусть
«г = к,
где k — целое число, тогда в соотношении
WK = {1- е2г/щ) WT - A - е21""') Wz
е~""г — 1 = 0, a Wr = 0, вследствие того, что подинтегральное
выражение является аналитическим на всем контуре Аг. Следо-
Следовательно, Wrz тождественно равно нулю, а число независимых
интегралов рассматриваемого типа меньше т. В этом случае
недостающий интеграл можно получить следующим образом.
В интеграле Wrz подставим к + е вместо аг. где г — малая
величина, тогда интеграл WTZ не обратится в нуль. Очевидно,
интеграл можно разложить по степеням г, и поскольку [У7Г2]е=о = О,
это разложение будет иметь вид
Диференциальное уравнение удовлетворяется выражением
I d
U О
где Wr — форма, которую принимает интеграл WT, если член
(С — аг)°г заменить на
Если число независимых интегралов меньше т, то этот ме'
тод может быть использован для нахождения интегралов и
приведения их общего числа к т.
18-43. Контуры, связанные с кратными нулями Q(z). Пусть а
будет нулем Q(zj кратности к, тогда предыдущие методы да-
дадут только одно интегральное решение, относящееся к этой
точке. Выбирая контур таким образом, чтобы V обратилось
в нуль в его конечных точках, получим дополнительную после-
последовательность к — 1 независимых интегралов.
615
Предположим, что главная часть /?(C)/Q(C), относящаяся
к'=B, равна
Р* , , В,
и напишем
тогда
' — а = р (cos <? + i sin tf),
^~- = r (cos ? + г sin t),
=l/oP°1 (cos Pi» + / sin p,ip) e'v
* ™
> ri sin i'j)
где
a l^o конечно (не равно нулю) в соседстве с ^ = а. Экспонен-
Экспоненциальный член
^rp1-* COS {/-(*- 1)8}
доминирует в функции 1/, которая стремится к нулю или бес-
бесконечности, когда р стремится к нулю, в зависимости от того,
является ли cos {t — (k — 1) <f} отрицательным или положительным.
Уравнение
— (k— l)f) =0
дает 2(^ — 1) расположенных на одинаковом расстоянии друг
от друга значений у в интервале 0 < <р < 27:. Если через точку а
провести лучи в соответствующих направлениях, то эти лучи
разделят плоскость на 2(й—1) секторов с равными углами.
Когда С стремится к а в различных секторах,
V стремится попеременно к нулю и беско-
бесконечности. Назовем сектор, в котором V
стремится к нулю, первым сектором, и про-
пронумеруем соответственно остальные секторы.
Рассмотрим простую кривую С, исходя-
исходящую из точки а в первом секторе, пересекаю-
пересекающую второй сектор на конечном расстоянии
от а и возвращающуюся к а внутри третьего
сектора (рис. 14). Поскольку V обращается
в нуль в конечной точке С, эта кривая мо-
может быть принята в качестве контура интег-
интегрирования. Не теряя в общности, можно принять что контур С
достаточно мал, чтобы не включать некоторой особой точки
уравнения. Второй интеграл может быть получен проведением
второго контура от третьего сектора к пятому и т. д., до тех
пор, пока мы, наконец, получим k — 1 новых интегралов. Таким
Рис. 14.
образом корню Q (z) кратности k соответствует k решений урав-
уравнения в виде контурных интегралов1.
18-44. Q(z) степени меньше п. Предыдущее исследование при-
приводит к независимым контурным интегралам, равным по числу
степени Q(z). Если эта степень равна п, то исследование завер-
завершено; если степень меньше п, то необходимо найти еще допол-
дополнительные интегралы для доведения общего числа их до п.
Пусть степень Q равна п—1, тогда, поскольку R степени л —1,
т
q% = >-?,_г^ + ••.+ т+Ро+?^+о (г2) (х > о,
когда С велико. Пусть
S = p(cos<p -Hsin<?;, p'~1=r(cos^ + isint),
тогда
= IV (cosaf -f isin a<p) er-X(cosюL''si"<UJ + • • •'
где
a = ax + я, + ... + am, ш = t + ).!p,
a Vo конечно на бесконечности.
Отсюда следует, что I/ стремится к нулю или бесконечности,
когда р стремится к бесконечности, в зависимости от того,
cos(? + Vf)—отрицательный или положительный. Поэтому, если
плоскость разделить на Ъ. секторов лучами, проведенными из
некоторой точки в направлениях
cos (t + Xtp) = О,
то V будет стремиться к нулю или бесконечности в зависи-
зависимости от сегментов, когда р стремится к бесконечности. Соот-
Соответствующим контуром интегрирования, следовательно, будет
кривая, начинающаяся в бесконечности в сегменте, в котором
предельное значение V равно нулю, пересекающая последующий
сегмент, а затем возвращающаяся к бесконечности в соседнем
сегменте. Следовательно, возможны X независимых кривых этого
типа, которые не содержат никаких особых точек уравнения и
которые дают X интегралов, необходимых для получения всех я
решений в виде контурных интегралов.
18-45. Группа уравнения. Для некоторых фиксированных зна-
значений z контуры могут быть деформированы непрерывным спо-
способом, не изменяя значения интегралов, если они не встречают
на своем пути какой-либо из точек аг ат, z. Аналогично,
если z изменяется непрерывно, то интегралы также будут изме-
изменяться непрерывно, если деформация контуров соответственно
1 Предоставляется доказать, что эти k интегралов линейно-независимы.
617
движению точки z не вызывает прохождения контура через
какую-либо особую точку.
Рассмотрим влияние простого обхода в положительном на-
направлении вокруг особой точки ат. Если Ат обозначает петлю,
проведенную из произвольной точки О и окружающую точку
ат, a Z— петля, окружающая точку z, то этот обход не повли-
повлияет на петли As(s^r). Петли Аг и Z, деформированы в Аг и Z
и не встречают точек z и аг (рис. 15).
Рис. 15.
Новая петля Z' эквивалентна петле Z, состоящей из двойного
контура, окружающего ат и z, т. е. эквивалентна ZЛгZЛ71Z~1,
а новая петля Аг эквивалентна двойному контуру, окружаю-
окружающему z и аг, т. е. ZArZ~l А7Х Ат или ZArZ 1.
Пусть Wz и Wr будут соответствующими добавлениями кон-
контуров Z' и Аг к значению интеграла, взятого вокруг соответ-
соответствующего двойного контура, тогда
Wz = w. + e2rAv-Wrz, W'r = ~ WK + Wr,
следовательно, интеграл Wrz, значение которого для недеформи-
рованного контура равно
преобразуется в
A - е**) Wr-(\~ e2
е2™') W'z
Wr-_
"ri wrz.
С другой стороны, поскольку петля As остается неизменен-
неизмененной, интеграл Wsz преобразуется в
G18
Рассмотрим теперь влияние обхода вокруг {сратного нуля а
на интегралы § 18-43. Контуры представляют собой простые
замкнутые кривые, начинающиеся и заканчивающиеся в с; они
могут быть сделаны произвольно малыми. Наличие множителя
(С — zf" в подинтегральном выражении приводит к тому, что,
когда z окружает точку а, точка Z, на контуре также окружается.
Влияние этого выражается, следовательно, в умножении интеграла
на множитель е~™. Циркуляция вокруг а не влияет на инте-
интегралы этого типа, относящиеся к кратным нулям, отличным от а.
Наконец, влияние циркуляции в положительном направлении,
включающем все особые точки, выражается в умножении инте-
интегралов § 18-44 на тот же множитель е2п||Х.
Таким образом фундаментальные подстановки группы урав-
уравнения известны, следовательно—известна и сама группа.
18-46. Рекуррентные соотношения и смежные функции. Чтобы
подчеркнуть зависимость интегрального решения от параметров
%,..., ят, jjl, его можно написать в виде
W(%,..., om, fj.; z).
В частности, пусть Q(z) будет степени п и пусть корни урав-
уравнения О (z) = 0 не равны между собой, тогда
W(alt..., am к z) =/(¦;-a,) ... С- a,,)'»-1 (", - z)^" <
с
где С таково, что начальные и конечные значения подинтеграль-
ного выражения равны.
Диференцируя по z под знаком интеграла, найдем
tf* W(ai..., aro y.;z) =
= (— i)" (h- +« -1). - -(и + я—*) й^(аь. •., яп. н—»-;г)-
Подставляя это выражение (с х = 1, 2,..., и) в диференциальное
уравнение, получим линейное соотношение с коэфициентами в виде
полиномов между п -\-1 функциями
Г (а,..., а„, и; г), IF fa,..., а,„ и — 1; z),...,
IFfa,..., я„, fj, — ft; z).
С другой стороны, поскольку
(С — а) = (С-г) + (г — а),
отсюда следует, что
IFaj +1, я2,..., а„, a; z) = К, а3,..., а„, (J. + 1; z)
+ (г — a) W{o.lt а2(..., ап, ;-.; z).
Рассматривая все возможные формулы этого типа, найдем,
что все функции
W fa + /?lt..., я„ + а.. ^ + 9; г),
G1S
где pt,..., рп, q — целые числа или равны нулю, могут быть
выражены в виде линейных комбинаций, с коэфициентами в
виде полиномов, через любые п из этих функций, например
W(zlt..., о.п, и. — 1; z),..., W(a^,..., а„, и- — п; г),
представляющие рекуррентные соотношения между данными
функциями.
Если один из параметров увеличить на единицу, а другой —
уменьшить на единицу, то получим смежную функцию К Соот-
Соотношения, содержащие смежные функции, просты; так, исключая
функцию
И?(!*!,...,«„, "•— 1; z)
из
+ 1, а2)..., а„, и. — 1; z) = lF(a,, o2)..., аш u; z) +
+(г-а1IР'(я1,..., о„, I*— 1; z)
я2 -f 1,..., а„, а — 1; z) = W(аъ а2>..., аш а; ^ +
+ (г — а2) Н/^,..., кп, р. —1; z),
найдем, что
(z — a2)W(a1 + I, a,,..., Яп)а —l;z)—(z— ax) l^(a1; a2 + 1,...,
^ a2,..., on, u; 2).
Другие последовательности рекуррентных соотношений могут
быть получены из формул, аналогичных
где
18-47. Решения уравнения Римана в виде контурных интегралов.
Если в уравнении Р- функции Римана (§ 15-93) произведем
преобразование
w= (z — af (z - bf (z — c)~'u,
то получим уравнение
{+ v- (',•¦ +1) Q" (z) + A* + i) #' (-)) и = о,
где
11 = _а_р_т_1==я' +
QB) = fZ_ fl)(Z — b)(Z — C),
1 Riemann, Qott. Abh. 7 A857); [Math. Werke, 67].
620
В этом случае
1
Q
Следовательно, если С — двойной контур, окружающий любые
две точки а, Ь, с, то интеграл
умноженный на (г — о/^г—й)ч(г — с)г, представляет Р- функ-
функцию Римана.
В частности, пусть этот двойной контур содержит точки
b и с и пусть z лежит в круге Г с центром в точке а, не содер-
содержащем точек b и с; в этом случае контур С может быть дефор-
деформирован, если это необходимо, так, чтобы он целиком лежал
вне Г. Тогда для всех точек С на С
\z — a\<\Z — а\.
Пусть
larg(z — с)|<я,
далее arg(a — b) и arg(a—с) имеют главные значения, а
arg(t — a), arg(C — b) и arg(?—с) определены аналогично, когда
С совпадает с точкой О. Тогда, если arg (z — b), arg (z — с) и
arg(C — z) так определены, что они приводятся соответстненно
к arg (а — b), arg (а — с), arg (С — а), когда г—* а, то
-(а +? + Y)^ + ¦¦•}'
а ряд справа сходится абсолютно и равномерно для всех значе-
значений z внутри Г и на нем, а также для всех значений С на С.
Следовательно, если Р" есть Р- функция Римана, которая
допускает разложение
(z — aT{l+c1(z-~a) + c.2(z-aY+...},
то интегральное решение1
(Ь+, с\ ,'Ь— ,с—)
(z — af (z - bf (z — cf f U (С) (С — z)~*"^ dC
1 Способ написаний этого интеграла показывает порядок и направление
образования петель, составляющих контур.
621
представляет функцию Р{а\ умноженную на
(а - bf (а - су/Т'С" '"'С ff-af—J (С- *)'+¦* >'-* Х
Аналогично, решения Р!о/>, Рф), Р<п, Р(г>, Я170 могу быть вы-
выражены в виде контурных интегралов, взятых вдоль двойного
контура \
18-471. Периоды Абелевых интегралов. Если показатели гхъ...,
ап, v все рациональные вещественные числа, то неопределенный
интеграл
/(С - fllf-1... (С - ajn'1 (С - г)"" ' dC
является Абелевым интегралом. Его значение для замкнутого
контура, когда подинтегральное выражение принимает началь-
начальное значение, называется периодом интеграла. Из .приведенного
анализа нетрудно вывести, что периоды, которые являются
функциями от z, удовлетворяют линейному диференциальному
уравнению с коэфициентами в виде полиномов от г.
Рассмотрим, в частности, эллиптический интеграл
/A -f»)(l -k42)dt
и пусть / будет одним из его периодов. Тогда, если
w=4/г * & - г> 2 ? - г>~т
и в обозначениях предыдущих параграфов
= C(C —1), п = 2, *=-\
следовательно, w удовлетворяет гипергеометрическому уравнению
. ,. d2w , /с. л, Aw , 1 „
z(z — 1)г^+ B2 — 1)^ + — ^ = 0.
Действительно, если К и К' — четверти периодов эллипти-
эллиптической функции Якоби, то2
18-5. Функция Лежандра Pn(z). Полученный ранее результат
(§ 8-311) может быть сформулирован следующим образом. Кон-
1 Случаи, когда а — я', ^ — |3' или -у — у — целые числа или равны нулю
требуют специального рассмотрения (§ 18-42).
2 Уиттекер и Ватсон, Курс современного анализа, § 22-3 и последующие.
622
турный интеграл
дает решение уравнения Лежандра
при условии, что контур С таков, что выражение
принимает свое начальное значение после обхода контура.
Пусть А будет точкой на вещественной оси справа от С = 11
и пусть в А
arg<t-l) = arg(c + l) = O; |arg(C-z)|<«.
Если "-. начинает свое движение в А, описывает положительную
петлю вокруг точки С = 1 и возвращается к А, то выражение
(» — г)""~2 CJ — 1j"t1 принимает свое начальное значение, умно-
умноженное на егг("+1>; если аналогичную петлю провести вокруг
С — г, то выражение примет начальное значение, умноженное
на г'°1 ° 2). Следовательно, если обе петли описаны, или, что
то же, если контур интегрирования начинается и заканчивается
в А и окружает точки С = 1 иС = г в положительном направле-
направлении, но не окружает точки С = — 1, то контурный интеграл
будет решением уравнения Лежандра для всех значений п.
Таким образом контурный интеграл2
__/•'* (» *)
является функцией Лежандра; при п — положительном целом
числе и 2 = 1 интеграл
приводится к единице. Во- ( , # чч -^^^ р
обще он может быть пред- \ '7
ставлей символом Pn(z),
который, если п—положи-
п—положительное целое число, пред-
представляет полиномы Ле-
Лежандра.
Контуры С и С (рис. 16)
оба удовлетворяют необхо-
необходимым условиям, но один не может быть преобразован в другой,
не встречая на своем пути особой точки С = — 1. Следовательно,
1 Если г вещественно и больше единицы, то А должно быть справа
? = г.
2 Schafli, Uber die zwei Heine'schen Kugelfunctionen, Bern, 1881.
623
если п не целое число, то Pn(z) не будет однозначной функ-
функцией z. Для того, чтобы сделать эту функцию однозначной,
необходимо разрезать плоскости С иг вдоль вещественной оси
от — 1 до — со. Во всей разрезанной плоскости г функция
Pn(z) аналитическая.
18-51. Функция Лежандра Qn(z). Контур, который приводит
к функции Лежандра второго рода Qn(z), образуется следующим
образом1. Пусть z не будет веществен-
вещественным числом, лежащим в интервале
(— 1, + 1); построим эллипс с фокусами
в точках + 1 таким образом, чтобы
точка z лежала вне его. Из правого
конца главной оси А опишем контур С
„.,'' в виде восьмерки, окружающей точку
+ I по часовой стрелке, а точку—1
•7. против часовой стрелки и лежащей
внутри эллипса (рис. 17), тогда выра-
выражение (? — z)~"~2 (С2—I) примет свое начальное значение,
когда С возвратится к начальной точке А.
Пусть |argz| < я, |arg(z — С)|—»argz, когда ?—»0 да контуре,
и в А пусть arg (С— 1) = arg (С + 1) = 0, тогда
п (у\ _ ' Г (S2-l)"
Wn[Z)— 4isinnnJ 2«(г_уп
будет решением уравнения Лежандра, справедливым, если п не
целое число, и аналитическим во всей плоскости г, разрезан-
разрезанной вдоль вещественной оси от 1 до —со.
Предположим, что R(n+l)>0 и рассмотрим контур, состав-
составленный из:
(I) малого круга, описанного вокруг +1 в отрицательном
направлении,
(II) малого круга, описанного вокруг — 1 в положительном
направлении,
(III) линий (+1, -1) и (—1, +1).
Поскольку R(/z4-l)>0, интегралы вдоль (I) и (II) стремятся
к нулю при уменьшении кругов.
Интеграл вдоль линии (+1, —1) равен
-ri
вдоль линии (— 1, -J- 1) равен
—1
1 У штекер и Ватсон, Курс современного анализа, § 15-3.
624
Оба значения дают
Qn (z) = ~^+ij
ч i
1 A ~ ff dt.
—i
Эта формула справедлива, когда Щп + 1) > 0 и включает случай,
когда п положительное целое число или нуль (§ 8-311). Если
подинтегральное выражение разложить в степенный ряд по z~\
то получим ряд для Qn<z) (§ 7).
18-6. Конфлюэнтные] гипергеометрические функции. Уравнение
конфлюэнтных гипергеометрических функций Уиттекера2 выво-
выводится из Р- уравнения Римана, являющеюся гипергеометриче-
гипергеометрическим уравнением, при помощи следующего предельного процесса.
В Р-уравнении
Осос
у + от — с с — k z 1
^-т О
\
пусть с —» со, тогда уравнение примет вид
¦ + ¦
I w =
Видоизменим это уравнение, приняв
получим для W уравнение
Из предельной формы контурных интегралов следует, что этому
уравнению удовлетворяет решение вида
W=e
при соответствующем выборе контура С.
1 Б советской литературе принят термин „вырожденная" г. ф.
* Уиттекер и Ватсон, Курс современного анализа, гл. XVI.
Э. Айне—133—40
625
Легко доказать, что этот интеграл является решением кон-
флюэнтного гипергеометрического уравнения, если
а это условие удовлетворяется, если контур представляет собой
простую петлю, проведенную из бесконечности в направлении,
асимптотическом к положительной вещественной оси, окружаю-
окружающей начало в положительном направлении, но не окружающей
точки С = — z и возвращающейся в бесконечность по положи-
положительной вещественной оси.
Стандартное решение конфлюэнтного гипергеометрического
уравнения дается в виде
Wu, т (г) =
причем argz имеет главное значение, | arg(— С)|<С« и
argA + rJz) -»0, когда С—>0 вдоль простого пути внутри кон-
контура. Конфлюэнтная гипергеометрическая функция Wk, m (z) будет
тогда аналитической во всей плоскости, разрезанной вдоль от-
отрицательной вещественной оси.
Указанное определение Wkt m (z) перестает быть справедли-
справедливым, если т — ^ + —положительное целое число. Но если
R(»z — к + yj > 0, то контурный интеграл может быть преоб-
преобразован, как было показано в последнем параграфе, в опреде-
определенный интеграл
(г) = -^Vt /A + 4 I'""' 4 t -*- 4 в'1 at.
f )J
что также справедливо, когда т — к + у — положительное це-
целое число.
Функция W—k, m{ — z) также является решением данного
уравнения, годным при |arg( — z)|<tt. Но поскспьку в соот-
соответствующих областях существования
Wh,m(z) = e-i zz"{l + О{г~Щ
626
отношение этих двух решений не будет постоянным, следова-
следовательно они образуют фун 1аментальную последовательность.
18-61. Асимптотическое разложение Wk, m(z). Чтобы получить
асимптотические раз южение контурного интеграла для WjCjm(z)
воспользуемся формулой1 '
а
где
a I = к -f m — ^.
Подставляя этот ряд в контурный интеграл для Wfc, m(z) и
интегрируя почленно, найдем, чго (г+1)-ый член разложения
равен
LL— О- - L±Ji-y
г!
УЧ о ; &
и поскольку
это приводится к
1 '0+)
г. ^ + m л- + 2 J Г ( »г
т. е. к
Если л настолько велико, что Rf п — k + »г —^) > 0» тО послед-
последний член может быть выражен в виде определенного интеграла
/ t Rn{t, z)e dt.
См. Jacob! (Diss. Berlin, 1825), Ges. Werke, 3, 1—44.
627
Предположим, что а = k + т — -у вещественно, | z | > 1 и
|arg г | -< я — а, где а > 0, тогда
1 :: 11 + tz-11 il + t, когда R (z) > 0,
1 + tz~l | > sin а, когда Rfzi <0,
следовательно в любом случае, если р = | X | и г = j tz~~l j, то
А (X —
X —1) ...(X —л) /1 4-Л? Г „п ,
~и| I Is1"«/ J " ( К
о
L± j у
— П)
1+tf
п+1 •
Поэтому, если |z[>l, последний член по абсолютной вели-
величине будет меньше
a. \г\~п~1\ /A +^J? tm~k + n + -Te~t dt\,
где Л не зависит от 2, а поскольку интеграл сходится, то пос-
последний член будет порядка
cosec? a z — "-,
в частности, если a>ao>0 порядка z~n~1.
Следовательно для |z|>l и |argzj< п — я< п,
X
1
и! г"
Если k — у + т — положительное целое число, то ряд ограни-
ограничен и поэтому дает точное представление функции.
18-7. Функции Бесселя. Функции Бесселя целого порядка п мо-
могут быть определены1 (см. § 8-z2) как коэфициенты при С"'в раз-
ложении Лорана (Lorent) для функции е -2
@+)
. Следовательно
где контуром является некоторая простая замкнутая кривая,
окружающая начало в положительном направлении.
1 Schlomilch, Z. Math. Phys. 2 A857), 137.
628
При подстановке С = 2tjz, интеграл преобразуется в
@+)
здесь контуром снова будет некоторая замкнутая кривая, окру-
окружающая начало в положительном направлении; это может быть
круг |?| = 1, описанный против часовой стрелки.
Рассмотрим теперь, как должен быть изменен контур для того,
чтобы интеграл Jn (z) для любого значения п удовлетворял урав-
уравнению Бесселя
2 d?~ + z dF + <2 ~~ n) w = °-
Легко доказать, что контур С должен быть таким, чтобы
с
тождественно для всех г. Если п целое число, то функция
f — ri-i gXp (t — z^j^t)
примет свое начальное значение после того, как точка
С описала круг |?| = 1; если п не целое число, то эта функция
не однозначна на круге. Соответствующим контуром является
такой, на котором t—"—1 exp (t — z^jU) обращается в нуль в
конечных точках, что представляет петлю, начинающуюся на боль-
большом расстоянии вдоль отрицательной вещественной оси, окру-
окружающую начало в положительном направлении и возвращаю-
возвращающуюся к начальной точке. Так, для всех значений п функция
Jn(z) определяется интегралом
,—я—1
Ui) J
где arg z имеет свое главное значение, a |arg ?|<lrc на контуре.
Определенная таким образом функция, аналитическая для
всех значений г, она допускает разложение в виде ряда
-п.-/-
V/ 1 у +
- / )
Для всех значений п контурный интеграл может быть пре-
преобразован в определенный интеграл, где |argz| <-^-п1. Фор-
мула
1 Schlafli, Math. Ann., 3 A871), 148. Аналогичный результат, действитель-
действительный при -^-я< j arg z | <7t, был дан Сониным, ibid. 16 A880), стр. 14.
029
действительна для всех значений п, если |argzj< —п. Пусть
контуром будет круг |С|=1, присоединенный к точке в беско-
бесконечности двойной линией, проведенной вдоль отрицательной
вещественной оси.
Значение интеграла вдоль круга (принимая ? =eiH) равно
т.
— п i 8 + t z sin О
а вдоль линий ( — со, — 1) и ( — 1, — со) значения равны (если Z
заменить на te—'d в первом случае, и на teTi — во втором) выра-
выражению
—(и
1 *~ I/
В последнем интеграле положим t = е'6, тогда получим
9-2 sin6)de—^
о о
Если л — положительное целое число, то второй интеграл обра-
обращается в нуль и результат приводится к выражению § 8 22.
Примеры
1. Преобразуйте интеграл Шлэфли (§ 18-5) в интеграл Лапласа
г- 1
рп(г) = [- /"{ г + (г2 — I)~icos? |"df.
(Уиттсер и Ватсон, Курс современного анализа
§ 15-23].
Преобразуйте соответствующий ингеграл для Qn(z) в
2. Докажите, что присоединенное уравнение Ленсандра
chfj j
llbld. § 15-33]-
удовлетворяется
1 1
¦i-m (If..2+)
630
и преобразуйте последнее выражение в
{п+ 1)(п+ 2)...(п + т)
о
3. Покажите, что уравнение Эрмита-Вебера
удовлетворяется функцией
2й ! \
II г + (г- — 1) cos cp I cos mvd:.,
о
ЧТО
, @ + )
и что если п—положительное целое число, то
[Уиттекер и Ватсон, Курс современного анализа,
§ 16-51.
4. Докажите, что
_L ^
2я/
если | arg(—г) | < я и контур в обшем случае параллелен мнимой оси, но изо-
изогнут, где это необходимо, так, чтобы полюсы Г (С + а) Г(?+ [3) лежали слева, а
полюсы Г(—О — справа от пути ивтегрировавия. [Barnes, Proc. London Math.
See. B), 6 A908), 141]
5. Докажите, что если ¦ | arg (г) | < л, то
3
и что это выражение определяет Wfc, m(z), если л<! | arg г [ < — л.
[Barnes].
3
6. На основании примера 5 покажите, что если | arg г \ < -^- л, то
№fc, m (г) = yrj Afic, m (г), + —j Mlc, m (г),
631
где
Мк.т(г)
)
)
+l) + 2!Bm+l) Bm + 2)
[Уиттекер и Ватсон, Курс современного анализа,
§ 16-411.
7. Докажите, что
1
г ~ 2
Jn (г) = i Г7 П ^
2 с " Г(я+ 1)
и выведите асимптотическое разложение для ./„ (г).
8. Докажите, что
г(т-«) Г
JflV / B')Я 2 cos(гСvdC"
где С— контур в виде восьмерки, содержащий К, = 1 в положительном, а С = — I
в отрицательном направлении. Покажите, что если Щп + —) >0, то
1
Z ^ 6 cos (г cos 6) du.
г i
у
2)ПТ)У
[Hankel, Math. Ann., 1 A869), 467}
9. Докажите, что если n — целое число, то
{ •/„ + , (г) - (-1)» ./„ _ . (г)
tf ГI^"' ^^^'«
является вторым решением уравнения Бесселя, и выведите его асимптотиче-
асимптотическое разложение.
[Уиттекер и Ватсон, Курс современного анализа,
§ 17-6].
ГЛАВА XIX
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
19-1. Эквивалентные особые точки. Предположим, что в систе-
системе п линейных диференциальных уравнений первого порядка
~~?г = S Pts{z) щ (г= 1, 2,...,«),
коэфициенты ргх'г) являются аналитическими функциями неза-
независимой переменной z и не имеют других особенностей, кроме
полюсов. Любая конечная точка ярляется обыкновенной точкой
системы, если коэфициенты аналитические в этой точке; точка
в бесконечности также является обыкновенной точкой, если
когда z—»0. При изучении поведения решений в особой точке,
удобно перенести эту точку в бесконечность.
Вне круга iz| = R, который содержит все конечные особые
точки уравнения, коэфициенты могут быть разложены в ряд по
убывающим степеням z. Если q — наибольший показатель веду-
ведущего члена в любом из этих разложений, то число д+1, со-
согласно предыдущему определению, называется рангом особой
точки в бесконечности. При q < — 2 точка в бесконечности
является обыкновенной точкой, при q —— 1 она является регу-
регулярной особой точкой.
Предположим, что q>0; рассмотрим возможность удовлетво-
удовлетворения системы уравнений последовательностью формальных ре-
решений нормального типа
wT = eW uT (z),
где
тогда, если
Рг*(г) = аГад + О(г"-1),
то а определяется характеристическим уравнением
где
*„ = 1, &ге = 0, (r+s).
633
Если q— — 1, то это уравнение определяет показатель а в
регулярном решении
Природа формальных решений зависит от того, равны или
неравны между собой корни
яи а2>- • •» ап
характеристического уравнения, а при о= — 1, от того, разли-
различаются или не различаются они на целые числа. Но в любом
случае фундаментальная теорема существования означает, что
существует последовательность п линейно-независимых решений
Щ. = w(f, w^WiK•¦-, wn= vf? (s - 1, 2,...,n),
и что каждый элемент w(rs) аналитический для \z\ > R. Общее
решение может быть выражено в виде линейной комбинации
этих решений
wn = cxwP + c%w™ +... + cnw(nn}.
Любое линейное преобразование вида
п
Wr= ? ars (Z)W, (Г = 1, 2,. . ., Л),
где коэфициенты aTS(z) аналитические в бесконечности и такие,
что детерминант
не равен нулю для г = со, преобразует данную линейную дифе-
ренциальную систему в систему того же типа, именно
¦^r=?pr,(z)w, (r=l, 2,...,л).
Коэфициенты этого преобразованного уравнения даются фор-
формулой
я _ п j
J»rs (z) = ¦? еле (z) Ры (z) ais (z) — S) Mz) ~J7aUz) (r, s=1,2,..., л),
ft, г=1 *=i
где {Ors(z)} — матрица функции, обратная матрице {ars(z)}, т. е.
такая, при которой
ft- 1
634
Если коэфициенты преобразования аналитические в беско-
бесконечности, а также удовлетворяют соотношениям
ars (Z) = <jrs дЛЯ 2 _^ со,
то говорят, что первоначальная и преобразованная система имеют
зквивалентчхю особую точку в бесконечности. Поскольку об-
обратное преобразование также имеет это специальное свойство в
бесконечности, соотношение эквивалентности обратимо. Более
того, поскольку произведение двух таких преобразований так-
также имеет эту специальную форму, соотношение является
.транзитивным.
Из формул, выражающих коэфициенты prs(z) через коэфи-
коэфициенты prs(z), очевидно, что ранг преобразованной системы не
может превышать ранга первоначальной системы. Однако, по-
поскольку это соотношение эквивалентности обратимо, обратное
также верно, следовательно все системы, имеющие эквивалент-
эквивалентную особую точку, имеют одинаковый ранг.
Понятие эквивалентных особых точек определяет задачу
образования простейшей возможной системы, эквивалентной в
бесконечности данной системе. Эта задача разрешается теоре-
теоремой, которая будет доказана в следующем параграфе, именно:
каждая система п линейных диференциальных уравнений, с
особой точкой ранга g-fl в бесконечности, эквивалентна кано-
канонической системе вида
где коэфициенты Prs (z) — полиномы степени не выше q-\-1 К
Рассмотрим применение этой теоремы, когда точка в беско-
бесконечности регулярная, а корни яг, а2,..., ап характеристического
уравнения неравны между собой и не различаются на целые
числа; тогда каноническая система в простейшей форме будет
иметь вид
•Она имеет фундаментальную последовательность п решений
wT = о, wf -о
Следовательно первоначальное уравнение имеет фундамен-
фундаментальную последовательность решений
чюф, ..., wP (s = 1, 2,...,л),
1 Эга теорема дана Биркгоффом [Trans. Am. Math. Soc. 10A909), 436]. При-
Приведенное здесь более простое и более общее доказательство также дано Бирк-
Биркгоффом [Math. Ann., 74 A913), 134].
635
где w?= ^
1=1
Это является фундаментальной теоремой существования для
регулярной особой точки; аналогично, когда точка в бесконеч-
бесконечности является нерегулярной особенностью, решения канониче-
канонической системы приводят к решениям первоначальной системы.
19-2. Приведение к канонической системе. Доказательство тео-
теоремы предыдущего параграфа зависит от одной леммы теории
аналитических функций, которую даем без доказательства1.
Пусть {lrs(z)} будет некоторой матрицей функций, одно-
однозначных и аналитических для \z\^R, но не обязательно ана-
аналитических для z= со, и такой, что детерминант этой мат-
рицы не обращается в нуль для \z\ > R. В этом случае сущест-
существует матрица {ars(z)} функций, аналитических в бесконечности
и приводимых к единичной матрице (8rs), а также матрица
iers(z)} целых функций, детерминант которой не равен нулю
в конечной области, так что
= {ars (z)} {ers (г) z"s },
где klt k.2,.. .,kn — целые числа.
Значение этой леммы видно из рассмотрения функции l(z),
принимая R настолько большим, что l{z) не обращается в нуль
для |z| > R, тогда log l(z) — функция аналитическая, но неодно-
неоднозначная для \z\ > R. После обхода положительного контура
вокруг г — со, log/(z) принимает вид
log/(z) — 2я?г,
где k — целое число, следовательно разность
log/(z) — k\ogz
аналитическая и однозначная функция для \z\ > R, и при раз-
разложении в ряд Лорана она принимает вид
где функция A (z) аналитическая в бесконечности, А (со) = О,
a ?"(z) —целая функция. Пусть
a (z) = exp A (z), е (г) = ехр Е (г),
1 Доказательство, основанное на теории линейных интегральных уравнений
см. Birkhoff, Bull Am. Math. Soc, 18 A911), 64; Math. Ann.. 74 A913), 122. Дока-
Доказательство эквивалентной тео >емы в матричных обозначениях см. Birkhoff, Trans.
Am. Math. Sic, 10A909), 438; обобщение см. Proc. Am. Acad., 49 A913),
521. Эти теоремы вхо!ят в более < бшие теоремы Гильберта [Hllbert, G6tt.
Nach. A905), 307J и Племели [Plemelj, Monatschr. Math. Phys., 19A908), 211].
636
тогда
l(z) = a(z)e(z)z~k,
где функция a(z) аналитическая в бесконечности, #(оо)=1,
e(z) — целая функция, a k — целое число.
Пусть z опишет простую замкнутую кривую С в отрицатель-
отрицательном направлении вокруг круга \z\ = R, содержащую все конечные
особенности системы. Эга кривая эквивалентна контуру, описан-
описанному в положительном направлении вокруг точки в бесконеч-
бесконечности. Поскольку каждая конечная точка вне круга |z| =Ц яв-
является обыкновенной точкой системы, в некоторой точке кривой
С существует фундаментальная последовательность п решений
каждый элемент которых аналитический во всех точках С. Од-
Однако элементы этих решений неоднозначны, и поэтому, когда z
описывает полный контур вдоль кривой С, решения преобра-
преобразуются в новую фундаментальную последовательность
Обе последовательности решений связаны линейными соотно-
соотношениями
или в матричном обозначении
где (с'/1)— матрица постоянных с детерминантом, не равным
нулю.
В общем случае, т. е. когда корни pi, p2, ...,pn уравнения
неравны между собой1, первоначальная фундаментальная после-
последовательность решений может быть выбрана таким образом, чтобы
матрица (с^) имела простую форму (Srsps). Следовательно под-
подстановка, относящаяся к контуру, проведенному в положитель-
положительном направлении вокруг z = со, будет иметь вид
Теперь, пусть Хх, 1-2,.../ьп будут числами, удовлетворяющими
1 Строго говоря не следует принимать, что р„ p2i--->Pn неравны; правильнее
полагать, что элемеитарвые делители матрицы (eJf' — 8rsp) независимы.
637
уравнениям
X logPs E=1, 2,...,л).
Этими уравнениями Хх, л2,...,Хп определены с точностью до
аддитивных целых чисел. Для некоторого выбранного опреде-
определения ).s предположим, что
тогда каждая функция /„fz; будет однозначной и аналитической
для \z\>R, а детерминант этих функций будет иметь значение
-=cz~('¦'" • ¦ • >й ехр { / [ри B) + р22 (z) +... + p
где с — постоянная, не равная нулю для \z\ > R.
Матрица функций {lrs{z)}, следовательно, удовлетворяет усло-
условиям леммы и может быть разложена на произведение матриц
Пусть
Wt)=e
тогда, при определенных таким образом функциях ars{z), пре-
преобразование
/
связывает каждую частную последовательность
решений первоначального уравнения
с соответствующей последовательностью
решений преобразованного уравнения
s-l
й2 уравнений, удовлетворяемых элементами V&rS\ могут быть
скомбинированы в матричное уравнение
\dVCf
638
откуда, если {W^s)} i — матрица, обратная {lFr(i)}, то
Теперь
следовательно
Аналогично
~i} = (Л, (г)} {8rs г^ - %
где frs(z)— целые функции, следовательно
{Prs -z)} = {/rsBj} {SrsZ^ -i} {8rs2~^ } {ers (г)}
= г {/„ (z)} {ers Щ-К
Поскольку детерминант .|/rs(z)| не равен нулю в конечной области
{^«(z)} является матрицей целых функций, следовательно,
каждая функция __
zprs (z)
является целой функцией. Но поскольку ранг особой точки в
бесконечности равен д+1,
Prs U) = О №),
когда г —> со. Таким образом zpTS <z) — целая функция, имеющая
полюс порядка не больше q-{-i в бесконечности и является по-
полиномом степени не больше 9+1.
Следовательно данная система эквивалентна в бесконечности
канонической системе
Z4T=S Prs(z)Ws (r=l, 2,...,«),
* i
где коэфщиенты PrS(z)—полиномы, степени не больше q-\-\.
Каноническая система может быть далее упрощена подста-
подстановкой вида
Wr = y,cTSWs (r=l, 2 л).
s 1
В частности, если корни а,, а2,...,ап характеристического
уравнения
\a-rs — Ks a\=0
639-
неравны между собой, то постоянные crs могут быть выбраны
таким образом, чтобы полиномы Prs(z) имели вид1
При таком упрощении полиномов говорят, что система имеет
€тандарттю каноническую форму.
19-21. Изменение доказательства в случае вырождения. Для того,
чтобы показать изменение доказательства к случае вырождения,
когда два или несколько множителей р, соответствующих поло-
положительному контуру вокруг точки в бесконечности, равны между
собой, рассмотрим частный случай pi = р2- Если, как в общем
случае, существует фундаментальная последовательность реше-
решений, так что
для s = 1, 2,...,п, изменение метода не является необходимым.
Если это не так2, то фундаментальная последовательность ре-
решений существует, так что (см. § 15-22) для г= 1, 2,...,п,
pMs) (s=3, 4,...,л).
Как и выше, пусть
ls = —?-г log ps (s= 1, 3, ..., «);
напишем
i№ = г'1 [1Г2 B) + 2^/ /a B) log 2
^ = zA'/ra(z) (s=3,4,... , n).
Таким образом определяется матрица {/rsB)} функций, одно-
однозначных и аналитических для \z\>R, детерминант которых
не равен нулю для \z\> R.
1 Коэфициенты crs таковы, что операции
col-r=crl(coM) -\ +сГЛ(со1-и) ('"=!> 2,...,и)
преобразуют детерминант ;ars—8rsa| в ors(ar — a)|. Соответствующую теорему,
когда а„ а2,...ап не все независимы, предоставляется вывести читателю.
2 Т. е. когда элементарные делители матрицы (с^— ors p), соответствующие
Pi = Рг, раввы.
640
Тогда подстановка
преобразует данную систему в эквивалентную каноническую
систему
где коэфициенты Prs(z)—полиномы степени не выше <7 + 1, и
которая имеет фундаментальную последовательность решений
(г =1,2,..., и),
где
W? = /' { z\n (z) + -^j z\n (z) log z },
W'ts) = г*»"'-» е„ (z) = т?*еп (z) (s = 3, 4,..., я).
Как и выше, {/rs(z)} представляет собой матрицу целых функ-
функций, детерминант которых не обращается в нуль в конечной
области, a klf ..., kn — целые числа.
Случаи дальнейшего вырождения могут рассматриваться ана-
аналогично;' таким образом возможность приведения к канонической
форме устанавливается во всех случаях.
19-22. Простой пример приведения к стандартной канонической
форме. Рассмотрим линейное диференциальное уравнение вто-
второго порядка1
d-w , , х dw . , г.
+ Р№ + Ч ^ w °
где функции p(z) и q(z) аналитические для \z\>R, и в беско-
бесконечности
В наиболее общем случае точка в бесконечности является нере-
нерегулярной особенностью первого ранга. Если bL и Ь.2 — корни
квадратного уравнения
неравные между собой и если соответствующим образом вы-
выбрать постоянную с, то подстановкой
можно преобразовать данное уравнение в уравнение того же
вида, но с
р (z) = - 1 + Pxz~l + О (z-2), q(z) = O (г).
i Birkhoff, Trans. Am. Math. Soc, 14A913), 462.
Э. Апис—133—41 641
Если v = г -5j» то уравнение второго порядка может быть
заменено двумя уравнениями первого порядка
dw v dv
Два решения и\, wa первоначального уравнения могут быть
всегда найдены таким образом, что если точка z описывает по-
положительный контур вокруг точки в бесконечности, то
Щ
ИЛИ
Рассмотрим подробно первый случай; модификация метода для
второго случая будет дана ниже.
Линейная система допускает решения
где показатели \1У >2 удовлетворяют уравнениям
а функции Zu (z), /X2 B), /21 B) и lw (z) — однозначные и аналитиче-
аналитические для \z\%R. Более того, детерминант имеет значение
кх (^) 4г (z) — /12 (z) /21 (г) = z1"*1-^
— г е
и не равен нулю для | г \ > R.
Чтобы точно провести приведение к канонической форме,,
лемма § 19*2 для частного случая п = 2 должна быть изменена
следующим образом: Пусть lu(z), liz(z), /21(z) и I22(z) будут
функциями, однозначными и аналитическими для \ г \ > R {но
не обязательно аналитическими в бесконечности), так что их
детерминант ln(z), l^(z), I12(z), /2i(z) не обращается в нуль
для | г | > R. Тогда будет существовать последовательность функ-
функций ап (z), а12 (г), а21 (г), а22 (г), аналитических в бесконечности
и приводимых соответственно к 1, 0, 0, \ в бесконечности,
и последовательность целых функций eu(z), e12(z), е21(г), ?2г(г),
детерминант которых не обращается в нуль в некоторой точке
конечной плоскости, так что
hi B) = {flu (z) en (z) + а12 (z) а21 (z) } z\
кг (z) = {aix (z) e12 (z) + al2 (z) e22 (z)} zk:,
кх (z) = { ои( z) eu (z) + a22 (z) ea (z)} z\
I22 (z) = {o21 (г) e12 (z) + o22 (z) e22 B)} z*%
где kx и k2— целые числа.
642
Теперь, четыре функции lu(z),'ll2(z), /п(гХ?а(г) удовдегао
ряющие этим условиям, определяются при помощи соотношений
^i = z' /2, (г), v2 = z'a /22 B);
их определение зависит от выбора >х и 12. При соответствую-
соответствующем выборе этих показателей целые числа kt и k2 могут быть
приравнены нулю; предположим, что определенный выбор 1г
и Х2 сделан.
Произведем подстановку
w = eu B) IF + йц (z) V, -у = й21 (z) Г + a,, (z) V
и преобразуем систему в
где
Pii= "T [aA ~*?- ~ flH} - °м{ - 2^a»i + (- z7 + 4")a^ - a«}].
P>2 = 4" [°«{'?Г ~ aia } - а1г{ - ЩЯъ + (- P + -
a22-
{ T |} { ( j) 22
а детерминант
Л = auO22 — a12a21
не равен нулю.
Поскольку в бесконечности
«11 — «22 = 1» «12 = «21 = 0.
эти выражения допускают разложения вида
Рп = О {г~\ Р12 = rz~' + О <z~2),
Р21 = rz + О (z-2), Р22 = 1 + A + Pl) Z + О (*-2),
где г и s постоянные, значения которых будут определены ниже.
Решения преобразованной системы имеют вид
подставляя эти выражения в первое уравнение преобразован-
643
ной системы, найдем, что
i ^ B) е22 (г).
Поскольку eu(z), ej2(z), e2l(г), e23(z) — целые функции, а их де-
детерминант
en(z)ew<z) -ea(z)ea(z)
не равен нулю для некоторого конечного значения г, функции
Pniz) и P^(z) аналитические во всей конечной плоскости, за
исключением простого полюса в начале. Рассматривая второе
уравнение преобразованной системы, можно доказать, что то же
верно относительно функций P21(z) и P.x(z). Но все эти четыре
функции Prs(Z) аналитические в бесконечности; они, следова-
следовательно, линейны относительно z~l. Таким образом члены O(z~2)
в разложениях этих функций обращаются в нуль, и преобразо-
преобразованная система принимает простую каноническую форму1
Это приводит к теореме: если w(z) является решением
уравнения
где
р (z) = - 1 + а г + О (г), q(z) = O (г),
то w(z) и zw'(z) могут быть представлены, в виде
ч» (г) = аи (z) W + а12 (z) -i- • % z dw
где W — частное решение уравнения
ч» (г) = аи (z) W + а12 (z) -i- • % z dw^ = а31 (г) W+a* (г) z- ¦ dJ,
а функции an(z), a12(z), asl(z), a2i(z) аналитические в бесконеч-
бесконечности и приводятся при z= со к 1, 0, 0. 1, соответственно2.
Отождествим теперь постоянные г и s. Начало является ре-
регулярной особой точкой преобразованного уравнения с показа-
показателями \ и Х2. Определяющее уравнение, относящееся к этой
особой точке, имеет вид
Хя + (А-1) X-rs-O,
1 Система интегрируется в квадратурах, если г или s равно нулю.
2 При /¦ = 0 надо заменить
z dlF ,. z dW
— • -г- на hm - • -j-.
644
поэтому
h + Х2 = 1 —А. ХЛ = — rs-
В специальном случае, когда
ЧЮХ = PjWjt, ВУ2 = рх W2 + Wlt
функции ln{z), I12(z), l<zi(z), l&{z) определяются посредством со-
соотношений
2 = Z 2 { /12 B) + -2^. /u B) log
= zw'2 = zXl { /22 (z) + 2^T ^ (
где
19-3. Формальные решения. Предположим,что все корни а.,, .. .,а„
характеристического уравнения данной системы неравны между
собой, и что q > 0. Эквивалентная стандартная каноническая си-
система будет иметь вид
п
z 4/Г = y.Prs(z)W, (г = 1, 2 и),
где
Pss (z) = PJ
В этом случае для каждого значения s получим формальное
решение нормального типа
wx = t4\..., wn = Tt\
в котором
где
a ps выбрано таким образом, что постоянная Bss не равна нулю.
Чтобы сделать формальные решения определенными, придадим
Bss значение единицы.
Непосредственной подстановкой можно доказать, что
firs = 0
и что
645
Остальные коэфициенты тогда определятся в последователь-
последовательном порядке
Детерминант формального решения имеет вид
где
Следовательно формальный детерминант не обращается в нуль.
Поскольку решения первоначальной системы
связаны с решениями канонической системы соотношениями
типа
п
где каждая функция art(z), аналитическая в бесконечности, при-
приводится к о„ для z = со; отсюда следует, что система допускает
точно п формальных решений
wx = S{?,... , wn = Sf (s = 1,2,..., я),
в которых
где Qs{z) — полином, a v4rsB) —ряд по убывающим степеням г,
имеет значение brs для г = со.
19-4. Решение стандартной канонической системы первого ранга
при помощи интегралов Лапласа. При q = 0 стандартная канони-
каноническая система имеет вид
Формальные решения
Wx = 7f, ... , Wn = IT («=1,2, ... , я)
даются выражениями вида
646
где
а
Рассмотрим возможность удовлетворения этой системы по-
последовательностью интегралов Лапласа
IV/ С о rrt 1Г\ ИГ (f 1 О ..Л
WT — I в Vr(L,)u'^. \Г=1, Z, . . . , П).
Непосредственной подстановкой в диференциальную " систему
найдем, что должно быть удовлетворено условие
? рй'JV Ч is) Л = jze\z - аг) vr (С) dC =
е (С - ar) vr Щ - J е • |фр (С) + (С —.аР) -^ j Л (г= 1,2,..., и)-
Следовательно функции v1(Z), v.2(Q,..., fn (С) должны удовле-
удовлетворять преобразованной системе Лапласа
а соответствующий контур интегрирования должен быть таким,
чтобы каждый из членов
[e%-ar)vr?)] (г =1,2 п)
тождественно обратился в нуль в точке г.
Преобразованная система Лапласа имеет регулярные особые
точки в С = cij, а2, ... , ап и в бесконечности. Показатели, отно-
относящиеся к С = as, все равны нулю, за исключением одного, имею-
имеющего значение
Предположим, что этот показатель не является отрицатель-
отрицательным целым числом, тогда соответствующие решения преобразо-
преобразованной системы, именно
•О,(J) = (С - чГ>-\? (С - а,), ... , V$ = (С - а,)-^1 <> (С - о,),
где функции <р(^(' —as), аналитические в соседстве с С = o-s, при-
приводят к последовательности интегральных решений, если соот-
соответствующий контур представляет собой петлю Cs, идущую из
647
бесконечности вдоль соответствующего луча, окружающую
точку аг в отрицательном направлении и возвращающуюся
к бесконечности вдоль этого луча При этом луч не должен
встречать на cBoeivi пути никаких особых точек, кроме as, и не-
необходимо, чтобы R { z (t — as)} было отрицательно вдоль луча.
Последовательность решений может быть представлена фор-
формулой
WV = J /(С - од^1 <* ^(С - о,) dC (r= 1, 2,.... я).
Каждой конечной особой точке as соответствует последователь-
последовательность решений, т. е. мы получим всего п последовательностей
решений.
Если — us — 1 — положительное целое число, то контур вы-
вырождается в прямолиш йный путь интегрирования, простираю-
простирающийся в состветств\к.шем направлении от as к бесконечности.
Если — \xs—1 — отрицательное целое число или равно нулю, то
возникает логарифмический случай. Таким образом каждая по-
последовательность интегралов
представляет решение стандартной канонической системы
первсго ранга, действительное в различных секторах плоско-
плоскости г.
19-41. Решение системы второго ранга. Покажем, что приве-
приведенный выше процесс может быть видоизменен и расширен
таким образом, чтобы он охватывал системы ранга выше первого.
Рассмотрим сначала систему второго ранга \q = 1)
Формальные решения будут иметь вид
W1=T(\..., Wn=
где
648
В этом случае интеграл Лапласа заменяется интегралом бо-
более общей формы, именно
Wr = / (?\vro (С) + zvn (С)} dl (r = 1, 2,... ,я).
•Если это выражение для WT подставить в систему уравнений,
то найдем, что
S Ыо) + Р%* } f^Ko (9 + гг-ч С)} dZ =
s= 1
= /z V;B; - ar) {vro (') + zvn (Q} ^ +/ze* 4>а (С) а
или, перенося члены, содержащие z", из левой части уравнения
в правую, получим
--vsa Щ d: + ? pT^zfer-vn (Q tf"
= B; - ar) {i»ro (?) + ?^ (Г)} Л Ч'/гс'-Ч^ Q rfC
™SzW- vsxQa: - [^" s2: - ar) [г-го(ц) + zvn
(г = 1,2,...,и).
Интегралы в обеих частях уравнения исключаются если
2« функций vroC°) и vn (С) удовлетворяют 2и совместным
уравнениям
г.
— B-е —* ОС ") —— = 1)гл -\- "%¦ {Рг ^^1-' 1 ~4~ Р
(г = 1,2,..., и).
Конечными особыми точками этой системы являются С =»
=-т^а,,-^ а2).. .,-уЯп; они представляют собой нерегулярные осо-
бенности первого ранга. Точка в бесконечности является регуляр-
регулярной особенностью. Если в первоначальной системе произвести
преобразование
TP'r= e~^mZ W (r — 1 2 ..., ri)y
то /Vrfl) всюду заменится на рггA) — |Зт; в частности Ртт-1^ при-
приводится к нулю.
64»
Систему уравнений, при помощи которой определяются ч)л
ш vn(t), можно написать в виде
,+ ? {P
s— 1
n " A)
+ 2 aw^
г = i
(r= 1, 2,...,n)
Особенность С = ^-ят нерегулярна, если полюсы второго по"
рядка в С = у ага встречаются в коэфициентах системы; это имеет
место, когда рттA)ф0. Но поскольку указанным преобразова-
преобразованием /?ттA) может быть приведено к нулю, это делает особен-
особенность в Z, = tj- o.m регулярной. Предположим, что это преобра-
преобразование произведено.
Показатели, относящиеся к регулярной особенности С =
= -2~ami BCe равны нулю, за исключением
— у (Ли + 1). — Y^m + 2)'
Отсюда следует, что существует решение системы vr0(ty и vn (Q
вида
(Q =
2 а-
I
у а
где функции tfro(m) (^ —-j ат) и fа'т (^ ~ 4" *т) аналитические в
соседстве с : = ~2- «т.
Каждая особенность С = -7>- as должна рассматриваться от-
отдельно; она становится регулярной при помощи соответствующе-
соответствующего преобразования. Каждой особенности С = —-as соответствует
последовательность 2я функций
иуу \у/>' ' ' i ип0 \S/> vix \V> • • • > unl v>/m
650
Соответствующий контур Cs представляет собой петлю, окру-
окружающую точку C = -2-as в отрицательном направлении и прохо-
проходящую в бесконечность вдоль луча, так что R(z2 (С —^-as)l от-
отрицательно. Отсюда следует, что каждая последовательность
интегралов
^ (с —J-«
(/"=1,2,..., Л)
представляет решение стандартной канонической системы
второго ранга.
Случай, когда показатель— ^ (ivf-1) является целым числом,
легко может быть рассмотрен: второй показатель — ^ (v-s "Ь 2),
который тогда очевидно не является целым числом, просто за-
занимает его место.
19 • 42. Решение системы общего ранга q -\-1. В общем случае
формальные решения даются выражением
7У*> = е g*(l) ^s Ers + Вга(» »-'+...),
где
Q,() s
Обобщенные интегралы Лапласа
IF, = / ехр (й9 + S{v«, (С) + zvn Ь +•¦•+ z9vrq @} dl
(г=1, 2 я)
удовлетворяют системе ранга 9 4-1, если
/expC:z'+1) V) z/
/ = 1
+ ar /ехр (й« f ') z9 ь J 2 ^w (Q dC (r = 1, 2,..., я).
/-= i
Сюда входят все целые степени z до z? + * включительно. При-
Приравнивая нулю совокупность членов относительно г и zv + 9t1
для v =0,1,.. .,<7, получим последовательность• q-\-1 уравнений
cgr + l неизвестными функциями vn{?), ^n(Q,- • -,^5(С). После
651
исключения множителя zv уравнение будет иметь вид
/ехр (Ь* + ') {(<? + 1)/ + Ч Ф v} «„ (О Л =
s=l
+ ar / exp (Cz* + *) z9 + 4v (С)Л.
Однако, поскольку, интегрируя по частям,
/ ехр (lzg + l)zq + * «(Ц) Л = [exp(-V + *) и (С)] -/ехр (С29 f ldu (О,
каждое из q +1 уравнений удовлетворяется для соответствую-
соответствующего контура, если функции
*>го @. »п (С), • • • ,1>гя (Q (Г = 1, 2,. . .,Л)
удовлетворяют последовательности r(q+1) прообразованных
уравнений
=(9 + 1->)»„+ ? S V*^*
где r= 1, 2,...,n; v = 0, 1,..., 9.
Принимая последовательно v = 5, 9—l,...,0, можно напи-
написать преобразованнЕ1е уравнения в виде
dv п
- {(д + 1)С -«,}-# = »«+? Б р»*^,
?
dv n dv " do
_„]_! 4. v n (?)——4- 4- V v @)—^ =
Or) ^ -Г" >j Prs dC^'"^ 2j P™ d!.
s - 1 s— I
i = 1
где r= 1,2,..., я.
Конечные особенности этой системы имеют вид
г __ °i. аа °п
¦ «+1' 9+ 1'""' 9+1.
652
и являются нерегулярными особенностями не больше ранга q.
Точка в бесконечности — регулярная. Преобразование
для фиксированного т изменяет
соответственно в
}
где г = 1,2,...,«. Уравнения для vrQ, vn,. ¦.,ч)гЧ тогда будут иметь
регулярную особую точку1 в ? = ат''(<7 + 1)» относительно кото-
которой все n(g-f-l) показателей равны нулю, за исключением g-f'l,
именно
1). -(Л„ + 2).(9 + 1),...,-(а + q + \)\{q + 1);
существует решение вида
где функции tfrfcfm) аналитические вблизи " = 0Lm't(q + 1).
Таким образом, если Cs — петля вокруг С = as/ig + 1), так что
R[z? + 1{4 — vs/(q-\- 1)}] отрицательно вдоль луча, то каждая по-
последовательность интегралов
ft = О
представляет решение стандартной канонической системы
ранга q.
Если отношение (ys+ l)/(<7 + 1) — целое число, то оно может
быть заменено некоторым другим показателем (не целым чис-
числом). Секторы, в которых это интегральное представление ре-
решения действительно, будут более точно определены в следу-
следующем параграфе.
19 • 5. Асимптотические представления. Произведем в интег-
интегральном представлении функции WJ-s) подстановку
для каждого s, тогда
V-s + *
1 Birkhoff, Trans. Am. Math. Soc, 10, 460 Утверждение относительно показа-
показателей допускает косвенное доказ тельство принципом непрерывности; непо-
непосредственное доказательство неизвестно.
653
где Fs — петля вокруг точки t = 0. Разлагая подинтегральное
выражение, можно доказать, что если arg z — <р — луч, для ко-
которого
то должен быть сектор, для которого argz = (p будет внутрен-
внутренним лучом,
где ет—»0 для всех значений т, когда г—>со. Поскольку это
относится к первым ж + 1 членам, данное разложение совпа-
совпадает с формальным решением T/s). Таким образом Wr(s) может
быть асимптотически представлено ТГ^ вдоль луча argz = f
или символически
Луч в плоскости ?, вдоль которого контур Cs следует в бес-
бесконечность такой, что Rz9+ * {С — ois/(q -J- 1)} отрицательно; при
этом условии он может изменяться, пока не пройдет через не-
некоторую конечную особую точку, отличную от C = as/(<7 + l).
Нетрудно определить точные секторы в плоскости z, для кото-
которых соответствующие формулы действительны.
Всего имеется N = п(п—\) (д-}-1) лучей, для которых
и эти лучи определяются формулой
+ 1) ? = ctg arg (as — ar).
Принимая, что эти лучи независимы, обозначим их в возраста-
возрастающем угловом порядке через
причем т^+1 =Т! + 2я
Когда точка z проходит из какого-либо сектора (tm_i, тш)
в последующий сектор (-ст, тт+1), вещественная часть одной из
разностей (as — at) z9+1 меняет свой знак с положительного ни
отрицательный. Обозначим эту частную разность через
Рассмотрим некоторые из q + 1 значений т, для которых
Tm= s> и пусть ъ'т будет лучом, следующим в возрастающем
угловом порядке к tm, на котором вещественная часть другой
разности, например
К
654
где tm' — s, меняет свой знак с положительного на отрицатель-
отрицательный. Тогда аргумент контура Cs будет промежуточным между
последовательной парой аргументов
asm ~ as), arg («Sm. - «s),
a R[z9fl {C — ctsl(q -J- 1)}] останется отрицательным для
Интегралы
дают последовательность q-\-\ решений канонической системы*,
фиксированных выбором сектора, в котором должен лежать
луч контура Cs. Каждая последовательность действительна
для любого из q -\-1 соответствующих секторов
Для каждого луча arg г — (р, который лежит внутри любого
из этих секторов, существует фундаментальная последова-
последовательность решений
Wt = W1?, Wt = W?\.... Wn= Wis) (s = 1, 2,..., n),
так что
Wf ~ T[s\ W2S)~T?,..., WnS)~T<*\
Для первоначальной системы соответственно получим тео-
теорему1: существуют решения wlt w2,..., wn, так что
wr~s{rs) (r-1,2,..., я)
внутри любого данного сектора
tm < arg г < хт- + r./(q + 1).
19 • 6. Характеристика решений в соседстве с бесконечностью.
Решения канонической системы характеризуются следующей
теоремой: существует N = п(п — \) (q -j- 1) фундаментальных
последовательностей решений стандартной канонической систе-
системы, именно
wTL w'&,..., w%l
так что
1 Эга теорема обобщает результат, полученный Горном [J. fur Math., 133
A907). 19].
655
откуда
и наконец
В настоящем параграфе мы докажем эту теорему К
Согласно теореме предыдущего параграфа, плоскость z
можно разделить на конечное число секторов з, в каждом из кото-
которых существует фундаментальная последовательность решений
Wx = W[s\ W, = Wi',..., Wn = W$ (s = 1, 2,..., n)t
так что в рассматриваемом секторе
Wf, ~ 7f'.
Секторы могут быть выбраны таким образом, чтобы argz == хт
были внутренними лучами и чтобы внутри каждого сектора
лежало не больше одного луча. Если о — сектор, не содержа-
содержащий никакого луча т, то каждое решение канонической системы
уравнений может быть представлено асимптотически в области
з, так как общее решение имеет вид
Wr = cx Wii] + c2Wf > + ... + cnW'rn) [r = 1,2,.... w),
а это решение приводит к асимптотическому соотношению
Для больших значений \г\ относительные величины членов
в этом выражении соответствуют относительным величинам
а относительный порядок величины не меняется, за исключе-
исключением лучей
= Tx, t2,...,T.v,
поэтому не меняется ,и в некотором секторе о, не содержащем
лучат. Предположим, что для рассматриваемого сектора индексы
1, 2,. ..,п выбраны таким образом, что
RК^) > R(a3z?bl) > ... > R(ап^
и пусть
сг = с2 = ... = ей_1 =0, ск ф 0;
тогда для сектора
СкТ?\
1 Решения, к которым эта теорема относится, не являются интегральными
решениями §§ 19 -4^19 *42; решения в виде интегралов Лапласа сохраняют
свою асимптотическую форму в максимальных секторах; в настоящей теореме
секторы являются минимальными.
656
Но поскольку последовательные секторы примыкают друг
к другу, каждое решение Wlt W2,..., Wn будет иметь такое же
асимптотическое представление в последовательных секторах
до достижения сектора, содержащего луч т. Таким образом,
если сектор о и последующие секторы, до сектора, содержащего
^ч z"i+i включительно, сливаются в один сектор ат, отсюда
следует, что существует фундаментальная последовательность
решений
WP, Wf\..., W? (s = l,2,..., и),
так что во всем секторе зш
wr ~ т?К
Рассмотрим теперь характер общего решения
W1,W2,...,Wm
в секторе ат. Когда точка z пересекает луч argz = Tra, порядок
величины R { QSm (z)} и R { Qtfn (z)} меняется и
} > о
<0 (argz>xm).
Предположим, что на начальном ограничивающем луче сек-
сектора зт
расположены в убывающем порядке. Если z пересекает луч
arg2 = Tm, то относительный порядок двух частных последова-
последовательных членов, например
изменится. Однако, несмотря на это, общее решение
Wr - сМ" + с^г) + ¦ ¦ • + cnWrn) (г = 1, 2,..., «),
не сохранит свою асимптотическую форму, исключая случай,
q = С2 = . . . = Cft_! = 0, СьфО, Cfefi фО,
когда решение будет иметь асимптотическую форму
на начальном ограничивающем луче, и асимптотическую форму
на конечном ограничивающем луче сектора от.
Однако, если два частных решения IF,, и W'T могут быть
найдены таким образом, что на начальном ограничивающем
луче а/д
Wr-cJ™, W'r - с'„АЛТ?'^ (г = 1,2,..., п),
Э. Айии —133-*-42 р57
то линейная комбинация WT + AW'r этих решений может быть
выбрана такой, чтобы она сохранила свою асимптотическую
форму во всем секторе зт. Поскольку
необходимо только придать А значение — ck^jc'k:1.
Теперь, пусть
Wg, W$,..., W% (s = l, 2,..., п)
будет любой фундаментальной последовательностью решений,
так что в секторе аг
W% ~ T's).
Каждое из п независимых решений последовательности сохра-
сохранит свою асимптотическую форму во всем последующем секторе
з2, за исключением возможного решения
w 11 i и/21 ,. . ., Wni ,
но когда этот специальный случай возникает1, постоянная Аг
может быть выбрана такой, чтобы решение
сохранило свою асимптотическую форму
J 1 » '2 ,-•¦, In
во всем секторе о2. Поэтому новая фундаментальная последо-
последовательность решений
где
'% = W'l (sr|rSl),
сохраняет свою асимптотическую форму во всем секторе з*.
Аналогично фундаментальные последовательности решений
23»- - -, И'лЗ
(s = 1, 2,..., и)
1 Важно отметить, что этот специальный случай возникает только, когда
R (a^ z9+1) меняет порядок относительно остальных выражений R (а5г?+1) и
переходит в низший ранг.
658
¦определяются последовательно и сохраняют свои асимптотиче-
асимптотические формы в секторах о3,..., oN. Из последней последователь-
последовательности тот же процесс приводит к новой последовательности
сохраняющей свой асимптотический характер во всем секторе о1#
Остается доказать, что выбор начальной фундаментальной
последовательности решений может быть сделан таким, чтобы
Wr%+i = е**' W% (r, s = 1, 2,..., п)
Сначала покажем, что конечная фундаментальная последо-
последовательность решений совершенно не зависит от выбора началь-
начальной последовательности
Ц,)
Пусть
U'-s) № ?AS) (s = 1 2 n)
будет новой начальной последовательностью фундаментальных
решений, и пусть
[Hs) [J(s) [J(s) (s ___ 1 9 „. ^ _ о о Д/\
будут выведенными из нее последовательными фундаменталь-
фундаментальными последовательностями. Обозначим постоянную, соответ-
соответствующую Ат, через Вт.
Предположим, что в секторе (tlt t2)
R ip-fTfl'^) < R (ay2*'г) <R («*
г+i) _ выражение
шение, асимптот
го то Т •)
У] » ' 2 '¦ • ' л'
тогда, поскольку R(af29+1)~ выражение низшего порядка, воз-
возможно только одно решение, асимптотическое в (тх, т2):
следовательно
*уи)=И7« (г = 1,2,..., л).
Теперь каждые два выражения R(as2?+J) становятся равными
2(g-f 1) раз, когда z описывает полный контур вокруг начала;
если они равны на луче argz = T', то они также равны и на
лучах
Следовательно в секторе
т, < arg 2
где v = —«(«—1), любые два выражения R(asz?+1) становятся
равными только на одном луче. В частности, когда arg z увели-
656
чивается от х1 до \ • R (a,z^rl) постепенно возрастает и наконец
превосходит все остальные выражения R(asz9+1), откуда
Тогда, поскольку
U% = W$,
отсюда следует, что
Цй=И*? (г=1,2,..., п)
ДЛЯ /?7 ^ V.
Поскольку в (т15 т2) R(a,-z? ') является второй в возраста-
возрастающем порядке величиной, получим соотношение вида
y cW(n (r-1,2,..., л),
откуда '
для т — 2,3 6, где 6 —значение /и, для которого величина
R(*iZq "') меньше Rfo,-^-1). Теперь, поскольку
соотношение
может быть написано в виде
В секторе (-,,, те+1) R(aiz«+1) > R(oyz?~J), а поскольку мы дока-
доказали, что
отсюда следует, что
R — А г
следовательно
Но для т — Ь + 1, 0 + 2,..., v, порядок R(a72'? J) не может
быть ниже порядка какого-нибудь другого выражения R(asz?+1),
поэтому
U^=W^ (r=1.2,..., я)
для m = 6 -j- 1, 0 -j- 2,. .., v.
1 Нужно отметить, что значение R (a/г9"') может быть ниже R (а8г9 г)
только для s = i.
Аналогично, соотношение вида
справедливо для последовательных значений т. Постоянные с
и d в этом соотношении меняют свои значения только для
значений т, для которых относительный порядок трех выра-
выражений
R(a,-z« f), R^z^1). R(W^)
меняется для луча argz = -m. Если порядок первого выражения
(вначале низшего) увеличить относительно второго выражения,
то значение d может измениться. Если порядок второго выра-
выражения сделать больше третьего, то с будет равно нулю; если
порядок первого выражения будет также больше третьего, то
d будет равно нулю. Таким образом, если 0' — значение т, для
которого порядок первого выражения выше порядка треть-
третьего, то
(г = 1,2,...., п)
для /га = 0' + 1, 0'+2,..., v.
Продолжая доказательство, аналогично можно доказать, что
при фиксированном значении /«<v и выше него соотношение
^ = И^ (г = 1,2,..., п)
справедливо для каждого значения s. В частности, конечная
фундаментальная система
тождественна системе
Следовательно конечная фундаментальная система не зави-
зависит от выбора начальной фундаментальной системы, если, ко-
конечно, начальный выбор соответствует условиям теоремы. Пред-
положим, что начальная система определяется инвариантной
конечной системой соотношениями
Г?> = e^s W(s,n i (г, s = 1, 2, • • •. п).
Это определение имеет смысл, так как, поскольку Г(/> умножа-
умножается на e*"iv-s, когда точка г описывает полный положительный
контур вокруг точки в бесконечности, асимптотическое соот-
соотношение
справедливо для сектора (т1г т2).
Таким образом предложенная теорема полностью доказана.
Ее расрространение на первоначальную систему следует непо-
66!
средственно и может быть выражено следующим образом.
Существует N = га (га — 1) (д + 1) фундаментальных решений
системы
dw
йг ~~ Ь, rrs v~f ~«
ранг которых в бесконечности равен q, именно
что, если формальное фундаментальное решение имеет вид
С,'и) С(и; С,'я)
' 2 '' " '' п '
Т/я+1.
N фундаментальных решений связаны соотношениями
где для от = N
Любая последовательность функций wfy удовлетворяющих
всем этим условиям, дает решение диференциальной системы.
Поэтому говорят, что теорема дает полную характеристику
решений системы относительно точки в бесконечности.
Постоянные, определяющие природу стандартной канонической
системы, называются характеристическими постоянными и
распадаются на два класса. Экспоненциальными постоянными
являются <7+ 1 постоянных as, ps,..., ls каждого полинома Qs(z)
и показателей }is; всего число этих постоянных равно «(# + 2)
и они не зависят друг от друга. Постоянные преобразования Аг,
А,,..., AN не все независимы, так как п — 1 из них могут
быть исключены преобразованием
Wr = crWr (r =1,2,..., п),
где постоянные сг выбраны соответствующим образом. Число
существенных характеристических постоянных поэтому равно
n(q +2) + n(n-l)(q + \)-(п-\) -= пЦд+ 1) + L
662
Коэфициенты в стандартной канонической системе содержат
всего n%(q -f-1) + п постоянных, которые могут быть приведены
к «2(<7 + 1)+1 умножением Wlt W2,.--, Wn на соответствую-
соответствующие постоянные. В общем случае число постоянных уравнения
не может быть, далее приведено; эти постоянные поэтому назы-
называются неприводимыми постоянными системы. Поскольку число
характеристических постоянных равно числу неприводимых
постоянных, отсюда следует, что характеристические постоян-
постоянные не связаны каким-либо определенный соотношением.
19-7. Обобщенная проблема Римана. Проблема Римана в ее
первоначальной форме (§ 15 • 92), относится к трем особым
точкам, которые являются регулярными; эта проблема была
обобщена Биркгоффом следующим образом: нужно построить
систему п линейных уравнений с данными особыми точками
соответствующего ранга
<7i, 9_>.---> 9m. <Jm+u
и с данной монодромной группой при заданных характеристи-
характеристических постоянных для каждой особой точки.
Чтобы показать, что эта система имеет смысл, рассмотрим
совместную систему уравнений
представляющую наиболее общее уравнение, особые точки
которого гъ z.2,..., zm, со заданных рангов qx, g2,..., qm, qm4t.
Число произвольных постоянных ArsM и Brsk равно
ri*{ V qi + 'zm+l .
Теперь, пусть
iy(s) i^.s) .. ?&>{¦*¦) (s = 1, 2,.... n)
будет фундаментальной последовательностью решений, фикси-
фиксированных принятием условия, что в некоторой частной осо-
особой точке а
группа этой частной фундаментальной последовательности из-
известна.
В этом случае монодромная группа имеет т фундаменталь-
фундаментальных подстановок, соответственно каждой особой точке *. Каж-
1 Если эти подстановки равны соответственно Su S.,,..., Sm. a Sm j —
подстановка, соответствующая z = со, то
S/7i-fl Snf- SA - l.
где /—тождественная подстановка.
663
дая подстановка определяется матрицей пг постоянных, поэтому
группа содержит только тпг произвольных постоянных.
Число характеристических постоянных, относящихся к осо-
особенности Zfc, равно пг(дк + \) +1; общее число характеристи-
характеристических постоянных равно
т
Но показатели у определяются как группой, так и характери-
характеристическими постоянными, и число их равно ra(m-j-l). Следо-
Следовательно между постоянными группы и характеристическими
постоянными существует га(т+1) соотношений.
Наконец, должна быть создана зависимость в каждой осо-
особой точке между выбранной фундаментальной последователь-
последовательностью решений и каноническими фундаментальными последо-
последовательностями, определяемыми теоремой § 19-6. Эта зави-
зависимость определяется группой, обусловливающей показатели
в каждой особенности, за исключением п мультипликативных
постоянных. Таким образом в каждой особенности налагаются
п — i дополнительных условий; всего получаем (п—\)(т-\- 1)
дополнительных условий.
Общее число условий, которые должны быть удовлетворены,
равно
т 1
ятЧ-? {п2 (qk + 1) + 1} —я (m + 1) + (и — \){т + 1) =
11Л+1
lft=l
и следовательно равно общему числу постоянных.
Сформулированная таким образом проблема была разрешена
Биркгоффом '. Если удовлетворены очевидные условия суще-
существования, то существует или решение проблемы как указано,
или решение проблемы, измененное заменой показателей и.1;..., р.„
соответственно любой из особых точек на ^ + kt,...,
где k1} kn — целые числа.
Примеры
1. Система
имеет формальные решения
1 Proc. Am. Acad., 49A913), 536. Birkhoff, [Trans. Am. Math. Sot, 14 A913),
462-476].
664
W = S.,(z) V = -Z dSAz)
- r dz '
где, если Хг ~ к., = 1 —pt, >ч^2 =—гз, то
с ,,ч = |, _ ЬЬ. ,-1 о. "'I <Х1 + J> М'-а ±J) ,-2 I
2. Пусть
тогда, если р1ф1, р.,ф1, то г и 5 не равны нулю и формальные решении рас-
расходятся. Если pi = 1, то г или s может быть равно нулю и по меньшей мере
одно формальное решение ограничено.
Оба формальных решения при г = О имеют вид
а при s = 0
W=\, т/=0,
- re
Если оба формальных ряда ограничены, то и г и 5 могут быть равны нулю.
3. Определяя формальные решения s, (г) и 5, (г) уравнения
где
, dw
и применяя формальные решения 51(гM:,(гЛ покажите, что коэфициентк
в преобразовании
т = «„ (г) и?' + й13 (г) К,
г»= ва1(г) W+ «о2(г)К
могут быть разложены в степенной ряд по г, когда г ф 0.
665-
4. Два линейно-независимых решения уравнения примера 3 могут быть
¦представлены в виде
wt ==
t (г)/ в* c'-'-'d -С)~Ч?С + ВАг)J е~л С'
A - С)-^ rfsj (г = 1, 2 ,
где Ai(z) и Б/ (г)— функции, аналитические в бесконечности, которые приво-
приводятся к I и О при г =оо. Это представление не имеет места, если pt или р,
равно нулю, когда оно заменяется одним нз следующих представлений
и-1 = А{г) + В (г) ё1 г l~p' { e~~- zp'~2dz, w2 = Bi^e1 г1~р\
/•—Pi ¦ 1—Vi
e' г dz+ В (г)ех г ; w2 = А (г).
о. Если множители р2 и р2 не зависят друг от друга и не равны единице,
го коэфициепты в рядах Лораиа
представляющих разложения двух линейно-независнмых решений уравнения
примера 3, имеют вид
/Г^ + Ь + М^ + ОК !) +
+ \ «2 + fe2(>« + -H-2)}^v+2>+... (/=1.2).
где
V! (А, — Х2 + 1). . .(Ъ - >-2 + V) '
2 V! (>., — >.! + 1). ..(>.,-/-!+ У) =
а а.4 и fcv —таковы, что jcv|1/v, |*\,|1л конечны для всех значений v.
6. Если pt и р2 не зависят друг от друга и не равны единице и если функция
у ij) аналитическая в бесконечности, то для каждого решения Щг) уравнения
rfz2
существует соотношение вида
+ >h (г)} = а (г) W (г) + Ъ (г) ^
где а(г) и Ь(гу _ функции, аналитические в бесконечности.
ГЛАВА XX
КЛАССИФИКАЦИЯ ЛИНЕЙНЫХ ДИФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ ВТОРОГО ПОРЯДКА С РАЦИОНАЛЬ-
РАЦИОНАЛЬНЫМИ КОЭФИЦИЕНТАМИ
20 • 1. Необходимость систематической классификации. Прин-
Принципы абстрактной теории обыкновенных линейных диференциаль-
ных уравнений основаны на классических теоремах, подтвержда-
подтверждающих существование и определяющих природу решений в сосед-
соседстве с обыкновенной точкой. Свойства решений в соседстве
с регулярной особенностью, а также поведение решений относи-
относительно нерегулярных особых точек известны. С другой стороны,
недостаточно изучены функции, определяемые специальными
уравнениями или классами уравнений. Кроме простых уравнений,
решения которых являются элементарными функциями, единст-
единственным исчерпывающе изученным уравнением является гипер-
гипергеометрическое уравнение в общей форме или частные виды
его (например, уравнения Лежандра, Бесселя, Вебера или урав-
уравнение конфлюэнтных гипергеометрических функций). Частично
изучены уравнения Матье и Ляме, однако теория функций, опре-
определяемых этими уравнениями, разработана далеко не полностью.
В настоящей главе систематическая классификация линейных
диференциальных уравнений с рациональными коэфициентами
осуществляется подразделением их на типы соответственно
числу и природе их особых точек.
Эта систематизация базируется на исследовании Клейна и
Бохера1, которые установили, что основные линейные диферен-
циальные уравнения, возникающие в проблемах математической
физики, могут быть получены из уравнения с пятью регуляр-
регулярными независимыми особыми точками; в этом уравнении раз-
разность между двумя показателями, относящимися к каждой осо-
особой точке, равна -у. Слияние двух таких особых точек образует
регулярную особенность, разность показателей которой произ-
произвольна; слияние трех или больше точек в одной точке образует
нерегулярную особенность.
С каждым линейным диференциальным уравнением второго
порядка с рациональными коэфициентами связано определенное
число регулярных и нерегулярных особых точек. Рассматривая
1 Klein, Vorlesungen uber lineare Differenzlalgleichungen der zweiten Ordnung
<1894), 40; Bocher, Uber die Reihenentwickelungen der Potentialtheorie A894), p. 193.
667
каждую из этих особенностей, как образованную слиянием со-
соответствующего числа регулярных особенностей с разностью
показателей, равной —, можно считать, что это уравнение вы-
выведено определенными процессами из одной стандартной по-
последовательности уравнений. Таким образом могут быть иссле-
исследованы все уравнения.
20 • 2. Слияние особых точек. Здесь удобно ввести термин,
который обозначал бы регулярную особую точку с разностью
показателей, равной ~^\ назовем такую точку элементарной.
Если регулярная особая точка не определена таким образом,
примем, что разность показателей произвольна.
Наиболее общее уравнение, имеющее р элементарных особен-
особенностей, расположенных в точках
имеет вид (§ 15 • 4)
ap_v °=>
П(*-*г) 1
r 1
где показатели, относящиеся к ar, равны аг и аг -f- —-. Поскольку
пок-азатели, относящиеся к особой точке в бесконечности, также
различаются на-у,
/7—1
i— r Zi ' + 16
/-=1
Следовательно постоянная Л^—з определена; остальные р — 3
постоянных AG, Аъ Ap_i совершенно произвольны.
Предположим, что две элементарные особенности сливаются;
так пусть о2 = аъ тогда определяющее уравнение, относящееся
к особой точке z = аъ будет иметь вид
Р2 — 2(я,+ 7.3) р + ?1 ^Cj -j- —
где
,P-S
!— аР—s)
Разность показателей, относящаяся к особенности z = alf в этом
случае зависит от А, т. е. от произвольных постоянных Ао,...,
668
Ар—i, следовательно она произвольна, если р > 4. Однако осо-
особенность остается регулярной.
Если сливаются точки ар—\ и со, то пусть произвольные по-
постоянные Ао,..., Ap-i будут такими, что
где А'о..., *'_4 конечны, но вообще произвольны; поскольку
о..., *_4
конечно,
Уравнение принимает вид
/¦=1
особая точка в бесконечности регулярна с произвольной раз-
разностью показателей, поскольку Л^_4 произвольно.
С другой стороны, предположим, что любые q элементарных
особых точек сливаются, тогда, если q > 2, то полученная осо-
особенность не допускает определяющего уравнения, следовательно
является нерегулярной особенностью.
Природа нерегулярной особой точки определяется числом
элементарных особенностей, слиянием которых оно было обра-
образовано. Назовем нерегулярную особенность, образованную сли-
слиянием трех элементарных особенностей, особенностью первого
рода и определим нерегулярную особенность r-го рода, как
образованную слиянием г + 2 элементарных особенностей. Оче-
Очевидно, порядок слияния особенностей не влияет на природу
результирующей особенности.
20-21. Стандартные формы; преобразования. Умножая зависи-
зависимую переменную на соответствующий множитель, можно, не
изменяя разности показателей, придать одному показателю в ка-
какой-нибудь регулярной особой точке некоторое выбранное зна-
значение. Таким образом, если уравнение с зависимой переменной и
имеет элементарную особенность аг с показателями -j.t и ч.г -f — ,
то преобразование
и. = (z — аг) °г v
приводит к уравнению относительно v с особенностью в аг и
показателями, равными Ой-'.
С09
В более общем случае, когда уравнение относительно и
определяется схемой
а2
...а
. . .а„
TV Z
1,1
Т*г+Т ¦¦¦З
где звездочки обозначают, что точка в бесконечности является
некоторой особенностью (регулярной или нерегулярной), преоб-
преобразование
приводят к уравнению
С1
0
I
2
аг.
0 .
1
2 '
.. ат да
..0 -К-
1
• ¦ 2 "^
где природа особенности в бесконечности не была изменена.
Следовательно мы не потеряем в общности, если примем
в качестве стандартного уравнения с р элементарными особен-
особенностями с,, а2,..., ap_i, со следующее уравнение
2 \ dw
'.— аЛ йг
=
где, носкольку точка в бесконечности также является элемен-
элементарной,
л _ (Р-2) fa?--4)
ЛР-« ~ " ~ 16
Это уравнение называется обобщенным уравнением Ляме. Иногда
выгодно принять показатели в конечных особенностях равными?-^
и -Jr, так как тогда уравнение примет нормальный вид
i¦ =\
(г —
р—1
'
где
Ав^=-~Лр-2).
670
В некоторых случаях применяются два алгебраических преоб-
преобразования независимой переменной. Проективное преобразование
aj ~
преобразует особые точки ait a;- и а* в 0,1 и со соответственно,
не изменяя показателей, относящихся к этим точкам1. Следова-
Следовательно мы не потеряем в общности, если фиксируем эти три
особенности в точках 0,1 и со; при наличии больше трех осо-
особенностей, распределение остальных особенностей произвольно.
Следующим по своему значению является квадратическое
преобразование
z'* = z
с двумя фиксированными точками 0 и со. Элементарная особен-
особенность в любой из этих двух точек становится обыкновенной
точкой, регулярная особенность остается регулярной, а порядок-
нерегулярной особенности удваивается. Особенность в любой
другой точке z = а заменяется двумя совершенно аналогичными
особенностями в z' = +у/Га, и следовательно усложняет урав-
уравнение.
Наконец, трансцендентные преобразования применяются для
приведения уравнения к известной форме, например к уравне-
уравнению Матье. Их общее действие сводится к замене некоторых
элементарных особенностей нерегулярной особенностью транс-
трансфинитного типа.
20-22. Формула уравнения; неприводимые постоянные. Любое
данное уравнение характеризуется:
(а; числом а элементарных особенностей,
(S) числом Ь неэлементарных регулярных особенностей и
(?) числом с существенных особенностей всех родов.
с нерегулярных особенностей могут быть подразделены на:
(I) сг особенностей первого рода,
(II) ?2 особенностей второго рода,
(III) с3 особенностей третьего рода
и т. д. В этом случае говорят, что уравнение имеет формулу 2
[а, Ъ, сх, с2, с3,...,].
Уравнения, имеющие ту. же формулу, могут различаться
между собой: 1) расположением особых точек, 2) показателями,
относящимися к регулярным особенностям, и 3) произвольными
постоянными. Уравнение, формула которого дана, является
определенным, за исключением этих трех переменных, произ-
произвольная природа которых вводит в уравнение три категории
постоянных. Из постоянных первой категории, определяющих
1 Иногда применяется преобразование в + 1.— 1, °о.
2 При с — 0 получаем [а, Ь, 0]. Когда имеется только одна нерегулярная
особенность, формула приводится к [в, b, 1J, где * — тип.
671
положение особенностей, три должны рассматриваться как про-
произвольные. Каждой неэлементарной регулярной последователь-
последовательности соответствует произвольная постоянная, представляющая
разность показателей. Эти произвольные постоянные, вместе с
постоянными третьей кетегории, являются неприводимыми посто-
постоянными общего уравнения. Таким образом первое уравнение §20-2,
формула которого равна [р, 0,0], имеет р — 1 постоянных первой
категории (alt a.2,..., op_i), приводимых к р— 3; оно имеет
р—1 постоянных второй категории (а„ а2)..., cip_i), которые
могут быть исключены, и р — 3 произвольных постоянных тре-
третьей категории (Ло, Аъ..., Лр_4). Оно имеет следовательно
всего 2р — 6 неприводимых постоянных.
Слияние особенностей влияет только на постоянные первой
категории; каждое отдельное слияние двух особых точек умень-
уменьшает число неприводимых постоявных только на одну посто-
постоянную, при условии, что остается не меньше трех особенностей.
Однако, если число независимых постоянных приведено к двум
@ и со), то может быть использовано преобразование z' = Cz,
где С—соответственно выбранная постоянная, что приводит
одну из постоянных третьей категории к заданному численному
значению. При дальнейшем слиянии и только одной оставшейся
особенности (в со), может быть приложено линейное преобра-
преобразование, что снова уменьшает число постоянных третьей кате-
категорична единицу. Отсюда следует, что уравнение [р, 0,0] и все
другие уравнения, выведенные из него слиянием, имеют не
больше 2р — 6 и меньше р — 5 неприводимых постоянных.
20-221. Число независимых типов, которые могут быть выве-
выведены из уравнения [р, 0,0]. Легко доказать, что число независимых
типов уравнения, имеющих только регулярные особенности,
которые могут быть выведены ил [р, 0,0], равно 1,'2 р или г'2 (р—1),
соответственно тому, является ли р четным или нечетным. Любое
такое уравнение типа [р — 2г, г, 0].
Аналогично, число типов уравнения с одной нерегулярной
особенностью первого рода равно -^-р — 1 или -^- (р — 1), в за-
висимости от того, р—четное или нечетное. В более общем случае,
общее число типов уравнения с одной нерегулярной особой
точкой любого возможного рода равно
когда р четное, или
+ ... +2 + 2+1+1= -г(р-1)\
672
когда р нечетное. Уравнение с двумя и более нерегулярными
особенностями могут быть перечислены аналогично.
Если каждую регулярную особенность считать один или два
раза, в зависимости от того, равна ли разность показателей 1/2
или произвольна, а каждую нерегулярную особенность r-го рода
считать г+ 2 раз, то сумма полученных таким образом чисел будет
равна р. С другой стороны, число N независимых типов урав-
уравнений, которые могут быть выведены из уравнения [р, 0,0], равно
числу подразделений целого числа р на любое число целых
частей, каждое из которых меньше р. Полученные результаты
для частных значений р приведены в следующей таблице, где
NT обозначает число независимых типов уравнения с г нерегу-
нерегулярными особенностями, а N—общее теоретически возможное
число их. Само уравнение [р, 0, 0] не включено.
/' =
Ml
Л7.,
n:
Л",
Л'
4
2
—
—
—
4
_ " j
о
4
—
-
—
6
I»
3
6
1
—
—
10
7
л
;)
2
—
-
14
8
4
12
—
21
'.' !
л
10
8
1
_
29
10
5
20
14 '
2
—
41
11
5
25
20
5
—
55
12
<;
зо
30
9
1
76
20-3. Уравнения, выведенные из уравнения с четырьмя элемен-
элементарными особенностями. Уравнения, имеющие две или три эле-
элементарных особенности, и не имеющие никаких других особен-
особенностей, являются тривиальными; в настоящем параграфе рас-
рассмотрим уравнение с четырьмя элементарными особенностями,
а также случай их слияния.
Пусть четырьмя элементарными особенностями будут z = аг,
а2у as, со; поскольку сумма всех восьми показателей должна
быть равна 2, показатели относящиеся к каждой особенности,
могут быть выбраны между 0 и -^-. Тогда Аг равно нулю, а стан-
стандартная форма уравнения [4, 0, 0] может быть поэтому принята
в виде
1 1 l
Т . 2 , 2
d'w
_ _ _ А>
(г^ а,) (г — о,) (г — яя)
Б этом случае мы имеем две неприводимых постоянных —— 2
а3— aL
и Ао. Уравнение является частным случаем уравнения Ляме и
само по себе не имеет какого-либо особого значения.
Теперь, пусть особая точка z = а3 сливается с особой точкой
в бесконечности, и пусть
lim A0/as — п2.
Э. Лйнс—133—4 3 073
Если точки а, и а2 преобразовать в — 1 и -f 1 соответственно,
то уравнение принимает вид [2, 1, 0]
L
г + 1 т г— I j d2 z2 — 1
и содержит одну неприводимую постоянную п; оно представ-
представляет собой уравнение функции Гегенбауера1 C°(z).
Если й3—joo, о2 -5 ^ -5 0, а п1 имеет прежнее значение, урав-
уравнение принимает вид [0, 2, 0]
d-w , ! dw n-
us* +~T dz г
с одной неприводимой постоянной п. Умножение зависимой
переменной на г" приводит уравнение к стандартной форме
и rf4 + ¦|~2и dffi)- = 0
йг- г dz
Уравнение [1, 0, 1] получается посредством слияния а2 и а,
с со и имеет в бесконечности нерегулярную особенность первого
рода. Пусть а, ->0. Поскольку Ао произвольно, оно может быть
выбрано таким образом, чтобы
Нт А0'а.2а3 = — т2,
где т конечно. Это приводит к уравнению
j
d2w , 2 dw /n2 _
^~+Г^г -—ВД = 0-
Постоянная т2 неприводима; если зависимую переменную умно-
умножить на пг~2, то уравнение приводится к стандартной форме
HI &w_ I dw w __
dza- "•" ' z dz z' ~ U>
Наконец, пусть
аз -> a% —* <h ~^ °° >
и пусть
lim A0ja,a2as = m',
тогда уравнение будет иметь нерегулярную особенность вто-
второго рода в бесконечности и примет вид
?-„*,=о.
1 Уиттекер и Ватсов, Курс современного анализа, § 15-8.
674
Постоянная т1 может быть исключена, поэтому стандартная
форма [0, 0, 0, 1] или [0, 0, 12] приводится к
IV ' 5-^0.
Таким образом из уравнения [4, 0, 0] могут быть выведены
следующие четыре типа:
I [2, 1, 0] с одной неприводимой постоянной,
II [О, 2, 0] с одной неприводимой постоянной,
III [0, 1, 1] без неприводимой постоянной,
IV [0, 0, 0, 1] без неприводимой постоянной.
Нужно отматить, что квадратическое преобразование приво-
приводит тип III к IV, соответственно § 20-21.
21-31. Уравнения, выведенные из уравнения с пятью элемен-
элементарными особенностями. Стандартная форма уравнения [5, 0, ©|
имеет вид
и содержит четыре неприводимых постоянных.
Пусть а4-Hи пусть
Jim AJa4 •-¦ — h , lim Л,,а4 ~ 4 я (и -f 1).
Полученное уравнение имеет вид [3, 1, 0]
L 1
dz'1
и содержит три неприводимых постоянных -3-—а- , А и и. Это
й3 — йа
является алгебраической формой уравнения Ляме1.
В уравнении I пусть о.>-» а3—»1, а,—*0, тогда уравнение [1, 2, 0]
будет иметь вид
z " z -I I dz 4z(z — IJ '
и содержит две неприводимых постоянных.
Оно преобразуется квадратической подстановкой z = л2 в
присоединенное уравнение Лежандра
на II — х i —г-s— /л --г- -
Уиттекер и Ватсон, Курс современного анализа, § 23-4.
675
Уравнение iia имеет формулу [0, 3, 0], оно становится спе-
специальным потому, что показатели в z = - 1 такие же, как и в
z = ¦+• 1. Оно имеет две неприводимых постоянных, в то время,
как общее уравнение типа [0, 3, 0] имеет три неприводимых
постоянных (уравнение III следующего параграфа).
Первое из двух возможных уравнений, имеющих точку в бес-
бесконечности в качестве нерегулярной особенности первого рода,
получается процессом
аг —» 0, а.2 -> 1, а3 -> а,3
¦ СО
lim А01!а3ай = — а , lim A1jasai = —
Таким образом уравнение [2, 0,1] имеет вид
III
—\\dz 4z(z — 1)
и содержит две неприводимых постоянных. При помощи транс-
трансцендентной подстановки z = cos2.x, оно преобразуется в урав-
уравнение Матье
Ша ?*' + • (а + /г2 cos2 х) w = 0
Теперь, пусть
ах —j а3 —ч 0, <
lim yA0/a3a4 = — /г2, lim
тогда возникает уравнение
. 1 &w и2 +
Постоянная k исключается умножением независимой переменной
на — k~^, поэтому уравнение [0, 1, 1] имеет вид
m d2w , I dw . г - n- „
и содержит одну неприводимую постоянную. Квадратическое
преобразование z = х2 приводит его к уравнению Бесселя
IVa ^+xf
Уравнение Бесселя является частным случаем [0, 1, 0, 1].
Нерегулярная особенность в бесконечности второго рода
получается операциями
а2 -? о3 —, ai -j со , аг -* 0.
076
Образованное таким образом уравнение [1, 0, 0, 1] или [I, С, !.J
приводится к
\7 ^'W Л- ' ^W Л
оно содержит одну неприводимую постоянную. При подста-
подстановке z — х* это уравнение преобразуется в уравнение Вебера
Va -; .,- -\- {п -\-
имеющее формулу [0, 0, 14] (уравнение X следующего пара-
параграфа).
Наконец, если ах —»я., —? а3 —> а4 -i оо , то получим уравнение
[О, 0, 13], которое может быть приведено к стандартной форме
VI gL + ZK,^O;
оно не содержит неприводимых постоянных.
Уравнение VI преобразуется подстановкой
3 \з
в частный случай уравнения Бесселя, именно
Таким образом из уравнения [5, 0, 0] могут быть выведены
следующие шесть типов уравнений:
I [3, 1, 0] с тремя неприводимыми постоянными,
II [1, 2, 0] с двумя неприводимыми постоянными,
III [2, 0, 1] с двумя неприводимыми постоянными,
IV [0, 1, 1] с одной неприводимой постоянной,
V [1, 0, 12] с одной неприводимой постоянной,
VI [0, 0, 13] без неприводимой постоянной.
20-32. Уравнения, выведенные из уравнения с шестью элемен-
элементарными особенностями. Уравнение [6, 0, 0] удобно рассматри-
рассматривать в его наиболее общей форме, именно
dw .
~Ъ "Г"
i-)
А„
[г— а,У-
[
-да = 0,
677
где
Уравнение имеет шесть неприводимых постоянных, именно Ло,
Ак Л2 и ангармоническое соотношение трех групп из четырех
чисел alt а2, ... , а5.
Пусть os-^a> и пусть
Hm^o/eg^-J-C, UmAA — ~ С,, lim A,/a, Л,г(п+1),
а а, =а„ = с<з = а4 = 0. Тогда уравнение, возникающее из {4,1,0],
будет иметь вид
d? ' ' ¦ ---i^—O.
Это уравнение является обобщенной формой уравнения Ляме;
оно имеет четыре элементарных особенности и одну регуляр-
регулярную особенность в бесконечности с разностью показателей рав-
равной п -\- -7> и содержит пять неприводимых, постоянных.
Следующее уравнение [2. 2, 0] получается из уравнения I
операциями
ах —¦ 0, д» -^ а-л -* а • ai ~~~* ^
и имеет вид
1Сгг — /г (я ¦! I) »- ,-4
с четырьмя неприводимыми постоянными а, С„, Сх, п.
Предположим, что а = к~2 и произведем подстановку z —
— sn2(x, k); после чего уравнение может быть приведено к виду1
ца ^
Уравнение [0, 3, 0] наиболее удобно получить непосред-
непосредственно из [6,0,0]. Пусть <2t-->a2->0, а3->д4 >1, а5->с» и
пусть С„, Сг тл п будут иметь прежние значения. Все показа-
показатели %, а,, а3, а, могут быть выбраны произвольно; остаются
1 Hermlte, J. fur Math., 80 A88U), 9 [CEuvres. 4. 8]; Uarboux, С R- Acad. Sc.
Paris, 94 A882), 1645.
078
три неприводимых постоянных, например а, р, v, которые опре-
определяются следующим образом:
0 (+4 +(+4) + C
О = Ч (а а + т) + Ч (*j + \) + \ [Со+ 2СХ - я Г л + 1)} ,
тогда уравнение может быть приведено к обыкновенному ги-
гипергеометрическому уравнению
Ш 2A-2)
Уравнение [3, 0, 1] получается операциями
ах -? О , а2 -* а, а3 -> 1, о,3 -»а5 -» ее ,
1 . __ i . - — С
Пусть
^1 ~ ai = Я3 — U)
тогда уравнение примет вид
1 1 1
v -^-Т +1т + -2- + гЛ
dz- | 2 г — а ' г —
с четырьмя неприводимыми постоянными. Если a----k—2 и 2 =
= sn2^, /?), то уравнение примет вид
Это уравнение является обобщением уравнения Ляме.
Уравнение [1, 1, 1] является вырождением случая IV. Однако
более удобно вывести его из [6, 0, 0] следующим образом.
Пусть fl4-^fls->o, и пусть Со, Сг и С2 будут иметь прежние
значения. Пусть аг—*0 при а2 = 0 и а2—эя3—»1, образуя регу-
регулярную особенность с показателями 0 и г. Необходимыми усло-
условиями в этом случае будут
Г -
I)
G70
Уравнение тогда примет вид
1
d-w , J 2 , \—r\dw
Т + г=т] HI Щг^Т)w =
где а = Со, &2 = — 2С3; оно имеет три неприводимых постоян-
постоянных. Подстановка z = cos2^: преобразует его в присоединенное
уравнение Матье1
Va ^ + {ld?
Уравнение [0, 0, 2], имеющее две нерегулярных особенности
первого рода (одно в начале, а другое в бесконечности), воз-
возникает следующим образом. Пусть а4-»<з5—>со, Со, Q и С2
имеют прежние значения, а %-^аз—>а3—» » при ai = 4 , а-2= О,
а3 = 0; тогда уравнение примет вид
2з _^_ + 2, Л; + {Со + 2CiZ
Уравнение имеет только две неприводимых постоянных; если
независимую переменную умножить на соответствующую по-
постоянную, то уравнение может быть приведено к стандартной
форме
При помощи трансцендентной подстановки z = e2ix уравнение
может быть преобразовано в уравнение Матье
Получаем два уравнения, для которых точка в бесконечности
является нерегулярной особенностью второго типа. Примем, что
а3 -*а4-*а5-^оо, и
lim Л0/а3а4а5 = 4~ Со, lim Ах\аъа^ъ = ¦ ^ Q.
lim A2lasa4a5 = т- С2,
a
аг -»0, а2 —? 0 при а3 = а, = 0: тогда возникает уравнение [2, 0, 12]
1 J_ 1
VII cPw 2 . 2 \ dw ,CB + 2Cxz + 2С,г2 п
Ince, Proc. Edin. Math. Soc, 41 A923), 94.
содержащее три неприводимых постоянных. Преобразование
z = cos2x с последующим изменением постоянных приводит это
уравнение к виду1
Vila -U + [ a — (я +1) / cos 2х+ -~ I1 cos 4x\w--= 0.
Примем, как в предыдущем случае, что а3-эа4—»а3-» оо, и
аг ~s a, —; 0 при ах = а2 = —. Если Со = 9 4ш2, то показа-
показатели, относящиеся к z = 0, равны -^ т, -^--\-т. He теряя в
общности, можно принять, что Q = 2Л, С, = —j . Уравнение
тогда приводится к виду
(feJ ' I 4 ' г ' г2 .!
и содержит две неприводимых постоянных; оно является урав-
уравнением конфлюэнтных гипергеометрических функций ' U/ft>m(z).
Пусть а., -> g8 -> й4 -^й5 -^ °°, а «х -^0 при а, == 0. Если
lim A0iaMxaia5 — ~^- Со, Ит Л1,'о2ада!|а5= -у- Q,
lim i42/a2fl3G4a5 = ._, С2,
то уравнение принимает вид [1, 0, 13]
IV flate» . 1 dtc- : С0 + 2Сг + 2Сгг
dz- ' 2г dz '
dz- ' 2г dz ' 4г
Это уравнение имеет только две неприводимых постоянных
C02lCt и С0*1С2. Квадратическое преобразование z = х2 приводит
его к виду
!Ха % + {Со + 2Сг** + 2Ctx*} w = 0,
что является частным случаем [0, 0, 16].
Наконец, пусть элементарные особенности сливаются в бес-
бесконечности, тогда полученное лри этом уравнение [0, 0, 14]
может быть легко приведено к уравнению Вебера
v d-w , ( , 1 1 Л rx
X -d-.r + [n + -r2 T z-J w^-0
с одним неприводимым постоянным.
Таким образом из уравнения [6, 0, 0] слиянием его особен-
особенностей получаются следующие десять независимых уравнений2:
1 Whittaker, Bull. Am. Math. Soc, 10 A903), 125. Уиттекер и Ватсон. Курс
современного анализа, гл. XVI.
3 Типы I, IV, V и IX еще недостаточно подробно исследованы.
1581
I [4, 1, 0] с пятью неприводимыми постоянными,
II [2, % 0] с четырьмя „ ,,
III [0, 3, 0] с тремя
IV [3, 0, 1] с четырьмя „ „ ,
V [1, 1, 1] с тремя
VI [0, 0, 2] с двумя
VII [2, 0, 13] с тремя
VIII fO, 1, 12]с двумя
IX [1, 0, 13] с двумя
X [О, О, 14]с одной неприводимой постоянной.
20 ¦ 4. Лишние постоянные. Надо отметить, что в последова-
последовательности уравнений, выведенных из [6, 0, 0], число неприво-
неприводимых постоянных равно числу особенностей; в последователь-
последовательности, выведенной из [5, 0, 0], число особенностей превышает
число неприводимых постоянных на единицу. В общем случае,
число неприводимых постоянных в уравнении, выведенном из
[р, 0, 0], превышает число особенностей на р — 6. Рассмотрим,
как образуются эти постоянные.
Уравнение [р, 0, 0] содержит всего 1р — 6 неприводимых
постоянных, р — 3 из которых обусловливаются произвольным
положением р — 3 особенностей, а р — 3 постоянных не опре-
определены. Аналогично, в уравнении [р, q, 0] имеются p-\q— 3
произвольных постоянных, которые не обусловливаются поло-
положениями особых точек или произвольными разностями показа-
показателей относительно q регулярных особенностей. Эти постоян-
постоянные называются лишними постоянными.
Рассмотрим класс уравнений, имеющих одну нерегулярную
особенность первого типа. Любое такое уравнение [р, q, 1] мо-
может рассматриваться как образованное из [р + 1, «7+1, 0] слия-
слиянием элементарной и регулярной особенностей. В этом процессе
одна постоянная теряется, но она не является лишней посто-
постоянной. Следовательно [р, q, 1] имеет такое же число лишних
постоянных, что и [р 4-1, 9+Ь 0], именно [р + q — 1). Анало-
Аналогично, рассматривая [р, q, 12], как выведенное из \р, g-f 2,0]
слиянием двух регулярных особенностей, можно доказать, что
число лишних постоянных в [р, q, 12] равно р+ q—1. В общем
случае уравнение \р, q, 1..J имеет 2p + 3q + s — 3 неприводимых
постоянных, из которых р + q — 2 обусловливаются произволь-
произвольными положениями этого числа особенностей, q обусловлива-
обусловливаются разностями показателей, относящихся к q регулярным
особенностям, as — постоянными в определяющем множителе,
относящимися к нерегулярной особенности. Следовательно,
остаются р + q — 1 лишних постоянных.
Лишние постоянные входят в группу уравнения; соответ-
соответствующим выбором этих постоянных группа может быть упро-
упрощена. В качестве примера можно привести уравнение Матье
(§ 20 • 31, Ша), где постоянная k входит в определяющий мно-
082
житель, относящийся к нерегулярной особенности в бесконеч-
бесконечности1, а а — лишняя постоянная.
20>5. Последовательности уравнений с регулярными особенно-
особенностями.. Сравнения формул
[3, 1, 01, [4, 1,0],..., [р, 1, 0]...
образуют важную последовательность. Первое из них является
уравнением Ляме
Я (И + I )
4 1 1 (г - ar)
г - I
Только одна из постоянных аг приводима; поэтому мы не по-
потеряем в общности, если предположим, что особенности рас-
расположены так, что
dz
Преобразуем z подстановкой
х = -2- / (
1
так что z — $(x). В этом случае уравнение примет вид
Обобщенное уравнение Ляме будет иметь вид
I
,
р
4П<
г=1
:= 0
с р — 2 лишними постоянными, именно Ао, А^..., Ap-S. При
подстановке
1 /') Г1 I *~
2 г I г-1 Ч °Г 1
уравнение преобразуется в
о + A,z
-*} w = 0.
Другой важной последовательностью уравнений Фукса явля-
является последовательность, имеющая р особенностей. Независи-
Независимыми типами являются
[Р, 0, 0], \р—\, 1,0],..., [0, р, 0],
!nce, Proc. Roy. Soc. Edin. 46 A926), 386.
683
и каждое уравнение имеет р — 3 лишних постоянных. Уравне-
Уравнения р = 3 являются уравнениями Р- функции Римана, уравне-
уравнения р = 4 являются уравнениями Ляме и присоединенными
уравнениями, выведенными из уравнения Ляме обобщением его
элементарных особенностей. Уравнения для р — 5, 6, 7,... еще
не изучены.
20-51. Последовательности уравнений с одной нерегулярной
особенностью. Уравнение Вебера [0, 0, 14]
d*w I . 1 1
dz1 * \ ~^~ 2 4
может рассматриваться как частный случай [0, 0, 1,,]
с р—3 неприводимыми постоянными.
Мы показали, что уравнение [1, 0, 1,] (§ 20-31, V| преобра-
преобразуется квадратической подстановкой в [0, 0, 1 j. Более общее
уравнение [1, 0, 1,] имеет вид
с г— 1 неприводимыми постоянными. Оно преобразуется под-
подстановкой z — х2 в уравнение
и имеет теперь формулу [0, 0, 12г]. Но это уравнение не ти-
типично для этой формулы, поскольку она содержит только
г—1 вместо общего числа 2,. — 3 неприводимых постоянных.
Последовательность уравнений [1, 0, 1Г] можно поэтому не
принимать во внимание; она включается в последовательность
[0, 0, 1Р].
Уравнение [0, 0, lt] преобразуется квадратичной подстанов-
подстановкой в уравнение Бесселя, которое является частным случаем
[0, 1, 1,J конфлюэнтного гипергеометрического уравнения. Ана-
Аналогично, более общее уравнение [0, 1, \р]
Z2 _. _J_ -у „ "" _1_ / Л уР 1 А , уР —1 I | А ~ т1-\ ТР1 - ¦ О
с р неприводимыми постоянными преобразуется подстановкой
Z = X2 В
п A2W dlV
у*. . . \. у _L / J V/J t. Л Y'-iP—'it _ I I Л ь-2 tt - | Г7Я} . — |V
»л. , ., j л T" J ""j 1 /i «л ^ j •*/? 1" ~T~ • • • ""| rliA iv ) iv —¦ VJ*
что является частным случаем [0, 1, 12Р].
20-52. Уравнения с периодическими коэфициентами. Анало-
Аналогично тому как уравнение [2, 0, 1,] преобразуется подстанов-
E84
кой х --= cos- x в уравнение Матье, более общее уравнение
[2- О, 1„|
с р |- 1 неприводимыми постоянными преобразуется в
у ¦_, 4" И0 + -^l2 COS- X ~r . . + Л7, COS2/>X} U1 = 0?
которое может быть написано в виде уравнения Хилла
!'"Z. + !f)o + 2Ht cos 2л + ... -f 2 н;, cos 2рл} к» = 0,
имеющего важное значение в теории луны. При р = 1 оно при-
приводится к уравнению Матье, при р = 2 — к уравнению Vila
§ 20-32; частные свойства уравнений, для которых р>2, не-
неизвестны.
Если две элементарные особенности z = 0 и z == 1 уравне-
уравнения [2, О, 1Р] сливаются в начале, то уравнение принимает вид
[0, 1, U.
Уравнение Ляме может быть обобщено аналогично заменой
регулярной особой точки в бесконечности нерегулярной осо-
особенностью рода р — 1. Уравнение [3, 0, V-1] имеет вид
14
dz'1 ' U— а, ' г —а., ' г — а, J dz ' (J-(г—«,) (г — а.) (г— ,,3))
(l-w \ 'I , 2"' } dw . г Ло ,-Агг+ ... + Аггр ) „
с /? + 2 неприводимыми постоянными. Если ах = 0, а, = /г~2,
/г3 •= 1, то подстановка z=sn2(A:, А) приводит уравнение к
S о + A, sn2 л- + ... + Ар sn3" л) к; = 0.
Посредством операций
й, -4 0, а.2 —» со , а3 -» 1
[3, 0, lp—i] принимает вид [2, 0, 1Р], а обобщенное уравнение
Ляме вырождается в уравнение Хилла.
20 • 6. Асимптотическое поведение решений в нерегулярной осо-
особенности. Поскольку любое уравнение, имеющее нерегулярную
особую точку в бесконечности нечетного типа, может быть
преобразовано квадратичной подстановкой в уравнение с осо-
особенностью четного типа, достаточно рассмотреть последний
тип. Уравнение [0, 0, 12р] может быть написано в виде
dJ~ + {Ао + A.,z* +
гдо т -'-О. Если нормальное решение существует, то опреде-
определяющий множитель имеет вид
следовательно уравнение ранга р. Это верно даже при наличии
других особенностей.
Примеры
1. Найдите'условия, достаточные для того, чтобы уравнение [2,0, L] имело
нормальное решение. Рассмотрите возможность двух нормальных решений. Вы-
Выразите результаты через уравнение Vila (§ 20 • 32).
2. Покажите в визе таблицы, что уравнение [2, 0, 1..J так же относится
к [2, о, 'ij, как [!i; 1, !.] относипя s; [у, 1, lij
3. Напишите формулы для 14 уравнений, которые могут быть вывелены
из П, <\ 0].
ГЛАВА XXI
ТЕОРЕМЫ ОСЦИЛЛЯЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
21 1. Сущность проблемы. В главах X и XI был рассмотрен
ряд теорем, имевших целью определить число и распределение
вещественных нулей функций типа Штурм-Лиувилля. Комплекс-
Комплексные нули таких специальных функций, как гипергеометрическая
функция, функции Бесселя1 и функции Лежандра2 были иссле-
исследованы современными авторами, но до последнего времени
общие теоремы, охватывающие все функции типа Штурм-Лиу-
Штурм-Лиувилля, неизвестны. Этот пробел был восполнен Хиллом3, кото-
который применил полученные им результаты к функциям Лежандра *
и Матье5. В настоящей главе мы рассмотрим методы Хилла
и покажем их применение на уравнении
решения которого могут быть получены в функциях Бёсселя
первого порядка.
Данный метод основан на свойствах некоторых интегральных
равенств, известных как преобразования Грина, которые выво-
выводятся из рассматриваемого диференциального уравнения. Пове-
Поведение нулей частного решения уравнения отражается на поведении
соответствующего преобразования Грина. При рассмотрении мы
найдем, что существуют некоторые области в плоскости ком-
комплексной независимой переменной, известные как области, сво-
свободные от нулей, в пределах которых частное не обращается
в нуль.
21-2. Преобразование Грина. Предположим, что в самосопря-
самосопряженном линейном диференциальном уравнении второго порядка
(A) -
1 Hurwitz, Math. Ann., 33 A889), 246.
* Hille, Arkiv. for Mat.. 13 A918), № n.
з Atkiv f6r Mat., 16 A921), № 17, Bull. Am. Math. Soc, 28 A922), 2G1, 462:
Trans. Am. Math. Soc, 23 A922), 350.
* Arkiv for Mat., 17 A922). A& 22.
B hroc. London Math. Soc. B), 23 A924), 185.
G87
A'(z) и G(z)—аналитические функции в области D, в которой
К(г) не обращается в нуль. Если
то уравнение (А) заменяется двумя совместными уравнениями
первого порядка
(В)
Первое уравнение этой системы остается справедливым, если
каждый член заменить сопряженным ему выражением, тогда
dwx = w.-dz К (z).
Отсюда следует, что
интегрируя между пределами г, и z2 и принимая, что каждая
точка на пути интегрирования лежит в области D, получим
-t- j , w, Г- G (z) rfz = 0.
Это уравнение называется преобразованием Грина данного урав-
уравнения; оно играет такую же роль в исследовании комплексных
нулей, как и первоначальная формула Грина в случае вещест-
вещественной переменной.
Пусть
dz/K(z) - dK = dKx + idK»,
G (z) dz = dG = rfG, + i«/G,
где Ка, K2, G1; G2 вещественные функции, тогда преобразование
Грина примет вид
(С) [tcvk'J - j к, n-dK + /| a-, i2rfG = 0,
а если разделить вещественные и мнимые части, то получим
R [•«?№]'- J j и»2 |^Ki + j re, prfGj - 0,
(E)
21-21. Инвариантность преобразования Грина. Пусть Z будет
независимой переменной, определяемой соотношением
dz=f(Z)dZ,
088
где /(Z) —некоторая аналитическая функция. В новых перемен-
переменных система B1-2, В) примет вид
dwx = wMZjk (Z), dw.2 = —
k{Z) = K(z)lf(z), g(Z)=G(z)f(Z).
Если
dZjk (Z) = dt, g (Z) dZ = d©,
то преобразование Грина примет вид
^а ^2
/*| w212 df + f | a-j j2dC = 0
Z2
аналогично (С) и следовательно преобразование Грина инвари-
инвариантно относительно преобразования независимой, переменной.
Особого внимания заслуживают следующие три специальных
случая.
(I) Предположим, что Z = K(z) и напишем J (Z) = G (z) К (г);
тогда диференциальное уравнение и преобразование Грина со-
соответственно примут вид
[вд,«/J - J | ш»2 |2fi?Z + J | и/i |2 У (Z) rfZ - 0.
(II) Предположим, что Z = G(z) и напишем //(Z) — О(г)/С(г),
тогда
z.
z,
(III) Для того, чтобы получить симметричную форму, пред-
предположим, что
тогда
Iw,wJ - j -^ rfZ + /l ^ i2 S (Z) rfZ = 0.
Zl z, z,
21-3. Выбор соответствующего пути интегрирования. Путь инте-
интегрирования (z1, z,) еще не был определен; при выборе пути
Э. Айне—133-44 С89
интегрирования таким образом, чтобы одно из условий
rfKi = 0, dK2 = О,
u?G, = 0, dG2 = О
было удовлетворено, могут быть упрощены формулы B1-2, Е),
выведенные из преобразования Грина.
Кривые К] = const, К2 = const представляют взаимно ортого-
ортогональные семейства кривых в плоскости zu называются К-сетью.
В частном случае К= 1, К-сеть состоит из сети прямых линий,
параллельных осям хи у. Аналогично кривые G1=const, G2=const
образуют пару взаимно ортогональных семейств, и называются
G-сетью.
Рассмотрим G-сеть1. Напишем
где gt и g.2 — вещественные функции. Пусть Д будет областью
в плоскости z, для которой функция G (Z) мероморфная, и пусть а
будет внутренней точкой области А, для которой G (а) ф0.
Через а проходит только одна кривая каждого семейства G, =
= const, G2 = const. Наклоны этих двух кривых в а равны соот-
соответственно
gi {a)lga И, - g2 (a)/a (о).
Таким образом кривые семейства Gj = const имеют касательные,
параллельные оси л в точках, где они пересекают кривую^(г)=0,
и касательные, параллельные оси у в точках, где они пересекают
кривую g2{z) = 0- Обратное верно в случае семейства G2=const.
Единственными исключительными точками А являются нули
и полюсы функции G(z). Далее, пусть z = а будет нулем крат-
кратности k, тогда, если
a
Напишем
2 — a = rel\ ак = рещ,
откуда, отделяя вещественные и мнимые части, получим
г
G.fzO-G.fa) = RfG(z)dz = -^ r*+1 cos{(ft-M)t0+
а
z
G3B) - G2fa) е I j G (z)dz = -^-f r*+1 sin {(?+1N+* } +O irh+*).
1 Поскольку К-сеть становится тривиальной в наиболее важном случае,
именно в случае К= 1, мы будем рассматривать G*ceib. Результаты для К-сети
будут рассмотрены в конце параграфа.
690
Следовательно через точку z = а проходит k + 1 кривых каждого
семейства Ох = const, O2 = const. Кривые обоих семейств сле-
следуют друг за другом попеременно, а последовательные каса-
касательные пересекаются под постоянным углом тс/(&-)-1).
Теперь, пусть z = a будет полюсом порядка k, где &>1.
Если
и если принять, что член с {г — а)~1 отсутствует в выражении
G
для G(z), получим
G(г)dz = у + Й- -^-р B-Й)И+О{НJ-'},
где ^ + г'5—комплексная постоянная интегрирования. Отсюда
следует, что
г
G, (г) е R /*G (г) dz = т — -^-Ц- г1"* cos {(ft - 1) 0 - ш } + О (Г~к),
Z
G2 (г) Е I J'G (г) dz = В + ^ у г1"* sin {(ft - 1) 0 — ip} + О (г2~*;.
Поскольку при принятом условии Gx и G2 не содержат лога-
логарифмических членов, каждая кривая некоторого семейства, име-
имеющая точки в соседстве cz = u, проходит через z = а. Рассмат-
Рассматриваемые кривые, принадлежащие к семейству Glt являются
касательными к линиям
а кривые семейства G2 — касательными к линиям
arg (z - а) = {<р + vt: }/ffe — ]),
где в каждом случае v = 0, 1, 2,..., /г — 2.
Наконец, рассмотрим случай, когда z = a — простой полюс
G <z), и пусть
тогда
z
Jg (z) dz — -{ + 1ь + аг log (z - a) + O(z — a);
если Cj — a -\- ф, то
Gx (z) = r/g (z) rfz -. 7 + a log r — рв О (о,
G2 (z) E I /G (z)dz]= Ь + 8 log r — «6 -f О (г).
При ai:O, Pt^O, точка z ~a является точкой закручивания для
кривых обоих семейств; при a -/-0, р — О, кривые семейства Gx
691
вблизи 2 = а являются, приближенно, круговыми овалами, содер-
содержащими эту точку, а кривые семейства G2 имеют точку z = a
в качестве точки разветвления конечного порядка. При а = О,
р =? 0 справедливо обратное.
В случае К-сети имеем: если г — а—полюс K(z), то К-сеть
ведет себя в точке а так, как G-сеть ведет себя, когда точка
z— а является нулем G(z). Аналогично поведение К-сети,
когда z — а — нуль порядка больше единицы или порядка еди-
единицы, соответствует поведению G-сети, когда г — а — полюс G (Z)
того же порядка.
21-31. Специальный случай, когда функция G (z) является поли-
полиномом. Случай, когда функция G(z)—полином степени п,
имеет очень большое значение. Пусть
G (z) = Ао B — aj1 (z — aj'... (z — am)v- (vx -f v,+... + vm=n),
тогда из предыдущего параграфа можно сделать следующие
выводы: любая общая кривая любого из семейств G, не прохо-
проходящая через какую-либо точку alt а*,,..., ат, не имеет кратных
точек в плоскости z. С другой стороны, одна кривая каждого
семейства имеет кратную точку порядка vk +1 в ак, поэтому
каждое семейство имеет не больше т особых кривьи.
Каждая кривая пересекает линию в бесконечности в п -j- 1
независимых точках, но эти пересечения одинаковы для всех
кривых того же семейства. Асимптоты всех кривых вещественны
и независимы и пересекаются в одной точке, именно в точке
z _ _ #
Если Ао — «0, то асимптотические направления кривых Gx будут
и+1 '
а асимптотические направления кривых G,
где k—Q, 1,..., п. Асимптоты каждого семейства поэтому со-
составляют равные углы друг с другом и разрезают пополам углы
между асимптотами другого семейства.
Функции Gt (z) и G2(z) гармонические во всей конечной части
плоскости 2, следовательно они не могут иметь максимум или
минимум при некотором конечном значении z К Отсюда следует,
что кривая G не может начинаться или заканчиваться в ко-
конечной точке, а также что она не может быть замкнутой.
Таким образом путь интегрирования может быть проведен из
1 Forsyth, Theory of Functions, IV, 475.
бесконечности к любой выбранной точке в плоскости г, не пере-
пересекая рассматриваемой кривой.
21-4. Интервалы, свободные от нулей на вещественной оси.
• Пусть Xj и х2(х1 <х.2) будут любыми двумя произвольными точ-
точками в любом интервале (а, Ь) на вещественной оси, внутри
которого функция J(z) аналитическая. Если w —любое решение
уравнения
(A) -^- + J(z)w = 0
и
w = wlt W = w,, J (z) = g\ (z) + igo (z),
то формулы, выведенные из преобразования Грина, примут вид
(B) R [вд] — /| w2 \Чх + fgl (х) | wt |2 dx = 0,
"Vl X, X.
(C) I [да^г] + Jg., (х) | -а»! 'Чх = 0.
Докажем, что если во всед* интервале (a, ft)R7(z)<0 г/^г/
I7(z) не изменяет своего знака, то в этом интервале может
быть не больше одного нуля.
Предположим, что в этом интервале имеется больше одного
нуля и пусть хг и л2 будут последовательными нулями, тогда
в уравнении (В) [-zeyajj является нулем, в то время как, если
Й1(Л)-^0, то сумма остальных двух членов определенно отри-
отрицательна. С другой стороны, во втором уравнении (С), [te^toj
равно нулю, и если g%(x) неизменно по знаку и обращается
в нуль только в дискретных точках, то второй член не равен
нулю. Таким образом при любом условии предположение о на-
наличии больше одного нуля приводит к противоречию, что дока-
доказывает теорему. Отсюда следует, что двумя необходимыми усло-
условиями для осцилляции в интервале вещественной оси, свободном
от особых точек, являются условия
(a) чтобы R7(z) было больше или равно нулю и
(b) чтобы l./(z) изменило знак или обратилось в нуль.
Приведенная теорема должна быть видоизменена при наличии
какой-либо особой точки внутри или на конце интервала (а, Ь).
Предположим, что г=а— регулярная особая точка (А) с показате-
показателями \ и Ц. ()ч+^= 1); предположим также, что R (Хх) > -у- и пусть
w = w1 будет решением, соответствующим показателю Хх. Тогда,
поскольку z = а самое большее полюс второго порядка для
функции J(z), интегралы в (В) и (С) конечны, если в интервале
693
a, b) нет никаких особых точек, кроме z — а. Отсюда следует,
что если условия, ранее наложенные на J (z), действительны,
а также если ча\да2 ->0, когда г—- а, то w{w2 не обратится в нуль
в интервале а<л<?>.
21-41. Области, свободные от нулей. Пусть ^z, будет некото-
некотором прямолинейным отрезком в плоскости z, вдоль которой
функция J{z) аналитическая.
Напишем
¦У г 7. -I-
ге ,
тогда 0 — постоянная вдоль выбранного отрезка. Если w(z)—
любое решение уравнения B1-4, А), то преобразование Грина
примет вид
Пусть
«¦ jf^fiW — ifsir).
gt (z) cos 26 — -^ fZ) sin 20 = P (z, 6),
ft (z) cos 20 + a (z) sin 20 = Q (z, 0),
где /lf /2, P и Q вещественны; отделим вещественные и мнимые
части преобразования Грина, тогда
Л И - Л @) + / Q f z, е) | к» i2 dr - - 0.
о
Рассуждая так же, как и в предыдущем параграфе, получим
следующую теорему:
На отрезке ztz2 имеется не больше одно?о нуля wdw/dz,
если вдоль него (I) P(z, 01 < 0 или (II) Q (z, 0) не меняет знака.
Если, кроме (I), /х@)>0 или если, кроме (II), /3@) имеет
противоположный знак относительно знака Q (z, 0), /но произ-
произведение wdw/dz вовсе не имеет нуля на этом отрезке.
Видоизменим эту теорему, Рассмотрим пучок параллельных
линий (/)
z=zo-rre'\
где z0 рассматривается как переменный параметр. Пусть Т бу-
будет односвязной областью в плоскости z, в которой функция
J (z) аналитическая и граница которой пересекается каждой ли-
линией пучка в двух точках. Две линии пучка пересекают границу
в совпадающих точках; пусть этими точками будут аир. Гра-
Граница таким образом разделяется н&две независимые дуги, одна
6S4
эрых рассматривается как геометрическое место точек ?
веется дугой С. Отсюда следует лемма: °
из котор
и назыв::
На части каждой линии I, лежащей внутри Т, лежит не
больше одного нуля wdw/dz при условии, что в области Т
(I) P(z, Ъ)<.0 или (II) Q{z, 6)фО.
Е^сли кроме (I), R{wdw'jdr} > 0 вдоль С или кроме (II),
] {wdw.dr} имеет вдоль С противоположный знак относительно
Q (z, 6) в области Т, mo wdwjdz не имеет нулч в Т.
Теперь, пусть С будет отрезком на вещественной оси, функ-
функция wiz) будет вещественной для всех точек С, а б=-^-т:,
тогда
^^ й-^} = 0, P(z, b) = -gl{Z) = -R{J{z)}.
Эго приводит к следующей важной теореме:
Если w (z) — решение, вещественное на отрезке (а, Ь) веще-
вещественной оси, Т— область, симметрично расположенная отно-
относительно вещественной оси, каждая линия, перпендикулярная,
к вещественной оси, пересекающей эту область, также пере-
пересекает эту границу в двух точках и встречает (а, Ь) во вну-
внутренней точке и, наконец, если R { У (z)} > 0 в области Т, тогда
w(z) не может иметь комплексного- нуля или экстремума1 в Т.
В этой теореме слова вещественная ось могут быть заме-
заменены словами мнимая ось, а условие R{y(z)}>0 можно заме-
заменить на R {J(z)} < 0.
Если рассматриваемое уравнение имеет вид w" + w = 0, а
w(z) равно sinz, то теорема показывает, что sinz и cosz не
имеют комплексных нулей.
Аналогично можно вывести следующую теорему для мнимой
оси:
Если область Т такая лее, как и выше, если w(z)—реше-
w(z)—решение, вещественное на отрезке (а, Ь), если wdwldz имеет в {а, Ь)
фиксированный знак и если I{/(z)} имеет этот знак во всей
части области, лежащей выше вещественной оси, то w(z)
не может иметь комплексного нуля или экстремума в об-
области Т.
21-411. Применение. Рассмотрим диференциальное уравнение
d2w w р,
dz* 2 '
оно имеет регулярную особую точку в начале, с показателями
0 и 1, и нерегулярную особенность в бесконечности. Одно ре-
решение конечно в начале и может быть написано в виде
1 Экстремум (точка,чдля которой и>' (г) = 0) соответствует в теории ком-
комплексной переменной стационарной точке в теории вещественной переменной.
695
где Уц— функция Бесселя первого порядка. Это решение веще-
вещественно для всех вещественных значений z и имеет бесконечное
число вещественных отрицательных нулей'. Любое другое ре-
решение, не являющееся кратным E(z), содержит logz. Такое
решение может быть вещественным не больше, чем на поло-
половине оси; если оно вещественно на отрицательной половине
вещественной оси, то оно осциллирует. Решение, вещественное
для положительных вещественных значений х, может иметь не
больше одного положительного нуля или экстремума. В общем
случае, если w вещественно, то
_i
*_*+«, W{X) ^
следовательно w увеличивается по абсолютной величине бес-
беспредельно, но имеется одно специальное решение2, для кото-
которого предельное отношение равно —1 и для этого решения
¦ну—»0, когда х—*-\-оо.
Рассмотрим распределение комплексных нулей. EmhR(z)<0,
R(—l/z)>0, то согласно основной теореме предыдущего пара-
параграфа, ни одно решение, вещественное для отрицательных зна-
значений вещественной переменной х, не может иметь никаких
комплексных нулей в полуплоскости R(z) < 0. Более того
I (— 1/г) > 0, когда I (z) > 0.
Пусть w(z) будет некоторым решением; если оно имеет по-
положительный нуль или экстремум, то обозначим его через х0.
Тогда, согласно последней теореме § 21-41, w(z) не будет иметь
нуля в полуплоскости R(z)>.*o> При исключительном решении
оно не имеет нуля в полуплоскости R(z)>0.
21 42. Звезда, свободная от нулей. Рассмотрим пучок линий,
исходящих из точки z = а, в которой функция J(z) регулярная,
но не равна нулю. Напишем
z - а + ге'\
(z-aL(z) = P{z) + iQ(z).
Кривые
P(z) = 0, ( (z) = 0
пересекаются в точке а, где каждая кривая имеет двойную
точку. Направления касательных к этим кривым в точке а да-
даются выражениями
gt (a) cos 26 — g2 (a) sin 26 = 0, gv, (a) cos -6 + gi (a) sin 26 = 0
соответственно.
На луче, проходящем через а, под углом 6, отметим точку рь,
которая получается следующим образом. Перемешающаяся точка
начинает свое движение вой пересекает луч до тех пор, пока
1 О нулях функций Бесселя и родственных им см. Watson, Bessel Functions,
XV.
2 См. Wiman, Arkiv for Mat., 12 A917), № 14
696
Q изменит свой знак. Если Р было положительным или из-
изменило свой знак, то точкой, в которой Q изменит свой знак,
будет рц . С другой стороны, если Р все в^емя отрицательно',
то перемещающаяся точка будет продолжать свое движение до
тех пор, пока Р изменит знак, и тогда этой точкой будет рв.
Этот процесс повторяется для всех лучей пучка, а получен-
полученная совокупность сегментов apt называется звездой а. Если
особая точка J(z) внутри звезды, то она исключается прямоли-
прямолинейным отрезком, проведенным в направлении от а.
В соседстве с точкой а граница отрезка состоит из ответв-
ответвления кривой Q = О, лежащей в области Р > 0, и касательной к
этому ответвлению в z = fl (рис. 18).
Из первой теоремы § 21 «41 следует, чтсг если z = а — нуль
wd-w'dz, то это произведение не обращается в нуль в некото-
некоторой точке звезды, принадлежащей а, включая не-особые точки
ее границы.
Эта теорема может быть приложена к решению
w= z~JBiz
уравнения
Это решение имеет простой нуль в точке z = 0. Звезда, соот-
соответствующая этой точке, покрывает всю плоскость, за исключением
697
отрицательной половины вещественной оси. Отсюда следует,
что рассматриваемое решение не имеет нулей, кроме нулей, ле-
лежащих на отрицательной половине вещественной оси.
21-43. Стандартная область. Найдем область, свободную от ну-
нулей, и более обширную, чем звезда. Рассмотрим диференциаль-
ную систему в ее наиболее общей форме
dw. w, dw., ^ , ,
i.z K(z) dz \ / j.
и пусть функции К(z) и G(z) будут аналитическими во всей пло-
плоскости, за исключением некоторого числа изолированных точек.
Эти особые точки, вместе с нулями K(z), являются особенно-
особенностями диференциальной системы; исключим их из плоскости
некоторым числом соответственно проведенных отрезков. В плос-
плоскости с купюрами функции К и G, определяющие обе сети
кривых § 21-3, однозначны.
Определим стандартный путь интегрирования в виде кривой,
исходящей из какой-либо обыкновенной точки плоскости и удов-
удовлетворяющей следующим условиям:
(I) он не должен пересекать купюру, исключая, возможно,
конечную точку;
(II) он должен состоять из конечного числа дуг обеих сетей;
(III) вдоль пути должно удовлетворяться одно из следующих
четырех пар неравенств, именно
a) (p) . y\) (o)
dKx>0; dKx<0; dK2>0; rfK2<0.
Чтобы не получить прерывных касательных, предположим,
что в точке, в которой встречаются две различных дуги, угло-
угловая точка заменяется небольшой дугой с непрерывной касатель-
касательной. Это всегда можно произвести так, чтобы характеристиче-
характеристическая пара неравенств кривой не была нарушена.
Теперь пусть точка а будет такой, при которой если W(z) =
— -di\ (z) w2 (z), то W (a) = 0. Если b — другая точка на стандартном
пути, выходящем из точки а, то из равенств
ь ь ь
R [•ze|1'zwa] —/l^l2 dKi + Г jte'jpdG! = 0,
непосредственно следует, что W(z) не будет иметь ьа стандарт-
стандартном пути никаких нулей, кроме а..
Если мы совокупность стандартных путей интегрирования,
исходящих из точки а, назовем стандартной областью а, можно
сформулировать теорему:
Если1*?(а) = 0, то W{z) в стандартной области а не имеет
нулей, кроме z — а.
098
Аналогично можно построить стандартные пути для всех
точек непрерывной кривой С, на которой изменение знака
K{z) w± (z) w2 (z) известно. Совокупность этих стандартных путей
называется стандартной областью С относительно рассматри-
рассматриваемого решения.
21-431. Пример стандартной области. В уравнении
dbv ц> __ п
dl- ~г ~ U
имеем
К (г)-2, G(z)--logz.
Чтобы сделать функцию О (г; однозначной, плоскость разреза-
разрезается вдоль отрицательной половины вещественной оси.
Теперь, если z = ге'\ то стандартные кривые составляются
из дуг сетей кривых
х = const, у = const; г = const, 6 = const,
а четыре полученные пары неравенств будут соответственно
равны
й
(а)*г>0. ф)аг<.0, <й<0. <Ю>0,
dx > 0; Лс < 0; dy > 0; <iy < 0,
Предположим, что у нас имеется решение, при котором
W(xQ)=0, хи—-точка на отрицательной половине вещественной
оси. Стандартные кривые, исходящие из л0, могут охватить
следующие области:
Если (а) удовлетворяется, то областью является
R (г) > х0, \z\ > |jcoj.
Если (,8) удовлетворяется, то область отсутствует.
Если (-;) удовлетворяется, то область будет 1(г)>0.
Если (о) удовлетворяется, то область будет 1 (г) < 0.
Таким образом стандартная область охватывает всю плос-
плоскость, за исключением части вещественной оси, для которой
R(z)< Xq\; поэтому ни одно решение рассматриваемого урав-
уравнения, имеющее отрицательный вещественный нуль z — х0, не
имеет комплексного нуля или вещественного нуля z>W.
21-5. Асимптотическое распределение нулей. Теоремы, рассмот-
рассмотренные в предыдущих параграфах, имеют своей целью разре-
разрешение проблемы определения расширенных областей плоскости г,
свободных от нулей частного решения рассматриваемого дифе-
ренциального уравнения. Сейчас мы разберем дополнительную
проблему, именно распределение нулей в соседстве с нерегуляр-
нерегулярной особой точкой1.
1 Аналогичные проблемы были изучены Бутро в связи с трансцендентными
функциями Пенлеве [Ann. Ёс. Norm. (?), 30 A913), 255; C), 31 A914). 99] и Гар-
нье в связи с решениями линейных диференциальных уравнений Гарнье [J. de
Math. (8), 2 A919), 99|.
699
Диференциальное уравнение
(А)
преобразуется заменой независимой переменной
Z^ IV u-^l dz
в уравнение
(В) i
где
S (Z) = irG(z)K{z).
Его можно также написать в виде
(С) azF
где
Замена зависимой переменной
W = V~SjZ) w
преобразует уравнение в
(D)
где
Новая переменная Z, рассматриваемая как функция г, беско-
бесконечно многозначна. Предположим, что Z может быть так опре-
определена, чтобы функция Ф (Z) была аналитической во всей бес-
бесконечной области Д плоскости Z, обладающей следующими
свойствами:
(А1)Д является односвязной и ограниченной кусочно-гладкой
кривой,
(А 2) каждая линия, параллельная вещественной оси, пере-
пересекает границу Г области (I) на линейном отрезке, (II) в точке'
или (III) вовсе не пересекает ее.
(A3)А находится внутри сектора
Область, удовлетворяющая этим условиям, называется об-
областью типа А. Если Г пересекается каждой параллелью к ве-
вещественной оси, то область называется типа Аа, в противном
700
случае — типа Ab. Условия А обеспечивают условие, по которому
Д содержит полоску До конечной ширины, определяемой нера-
неравенствами вида
R (Z) > А > Ro, В1 > I (Z) > В2.
Предположим также, что в каждой точке Л функция Ф (Z)
удовлетворяет условию
(В) ФB)<^р.
где М и / — положительные числа.
Из теорем существования следует, что любое решение W(Z)
уравнения (D) ограничено в полоске До. Рассмотрим выражение
f(Z) = W, (Z, +j sin (Т- Z) Ф (Т) IF (T) dT,
где W0(Z) — решение уравнения
W'o + 1Г0 = О,
а путь интегрирования параллелен вещественной оси. Можно
показать, что
f(Z)+f(Z)-<b(Z)W(Z)=O,
и следовательно, если f(Z) — решение интегрального уравнения
(Е) /(Z)= W0(Z)+l &in[T—Z)Q>(T)f{J)dT,
i
то f(Z) будет также решением диференциального уравнения (D).
В этом смысле уравнение (Е) можно назвать эквивалентным
интегральным уравнением1.
21-51. Исследование интегрального уравнения. Прежде чем рас-
рассматривать интегральное уравнение, необходимо получить выра-
выражение для верхней границы интеграла
где а вещественно и
Здесь z не отрицательное вещественное число, а путь интегри-
интегрирования, параллельный вещественной оси. Пусть
1 Это интегральное уравнение типа Воьлтерра. Приведенное ниже исследо-
исследование интегрального уравнения было дано Хиллом [Trans. Am. Math. Soc, 26
A924), 241].
701
тогда
Теперь
| v -f el \-v = f 1 + 2v cos 0
J
(lH^i
При [6|<я второй множитель может быть разложен в ряд по
v/(l-\-vJ; полученный ряд для }v + e№\-v- будет равномерно
сходиться при 0 < 41 < оо.
Интегрируя его почленно и применяя формулу
Г(» + 2/г) ' ''
найдем, что
v гD-}ч-*)г(|л + а-1) ...
)
ft=o
sin2* 4-,
и, следовательно1,
/ (те;е; и)
Можно доказать2, что при 0 < 16 | < тх
1 В частности
2 Доказательство следует из формулы (§ 7-231), выражающей /^(а, р, ^; д)
через ^(а, Р; я + р —v+ 1; 1-х) И A — J^-"-? F(v — a; 7 — ?; f — а — p+ 1;
1 — jc), a также из того, что F(a, p; a; jc) = A —х)~^.
702
Поскольку каждая из гипергеометрических функций в этом
уравнении имеет положительную сумму при ^> 1, 0< |6 | < тс,
отсюда следует, что
D4)
1{ге№; у) < ^=—j—-— , г sin Ь ^.
(-f р.)
Гипергеометрическая функция в выражении для 1{ге№; «^воз-
«^возрастает с |6' при 0<|61<и, следовательно, если |6 |< -^ тг,
J(re№; u)</(re2 "'; »i)
С другой стороны, если-2-и< | 6 |<тс,
(И-ОГ (-2
При {А > }i > 1 выражение
ограничено; пусть его верхней границей будет С. Отсюда по-
получим
(G) /(Z;fi)<^L^
К (X — 1
где, если z = x + iy,
R=\z\ при 0<|argz|<-2-",
R=\y\ при -2-л< |argz| <л.
Рассмотрим теперь интегральное уравнение
оо
W{T)dT
и напишем
K{Z, r) = sinG--
70S
Методом последовательных приближений покажем, что решение
этого интегрального уравнения существует. Определим после-
последовательность функций W,(Z), ..., Wn(Z),..., где
сю
W1 (Z) = Wo (Z) + Г K{Z, T) Wo (T) dT,
7
¦и в общем случае
Wn (Z) = Wo(Z) + /K(Z, T) HV-i (T) dT (я = 1,2,3.... ),
7.
тогда
Wn.,(Zs- Wn{Z)= fK(Z,T){Wn(T)- Wn-v{T)}dT.
Пусть L будет верхней границей \W0(Z)\ в Ло; поскольку T—Z
вещественно на пути интегрирования,
Предположим, что для некоторого значения п
тогда
мат
/ C
V.2
C/W \«+i
т. е. неравенство справедливо для следующего значения п. Но
поскольку
fK(ZJ)W0(T)dr\
CML
неравенство справедливо для и = 1, а доказательство получа-
получается индукцией.
Следовательно Wn{Z) сходится равномерно в ^0 к предель-
ной функции W{Z), аналитической во всей области До, и удов-
удовлетворяет интегральному уравнению. Более того, W{Z) является
704
единственным ограниченным решением интегрального уравнения
так как если бы существовало второе ограниченное решение'
то разность D(Z) удовлетворяла бы однородному интеграль-
интегральному уравнению
оо
L>(Z) = I К(Z, J)DA)аI.
z
Пусть Да будет частью До, для которой R(Z)>a, где а должно
быть определено. В этом случае можно доказать, что если
ра — верхняя граница \D(Z)\ в Д«, то
СМ
Следовательно, если а выбрано так, что а1 > СУИ/'v2, то это не-
неравенство приведет к противоречию (если только ^а не равно
нулю), что доказывает, что D(Z) должно быть тождественно
равно нулю.
Доказательство справедливо для любой полоски типа До,
которую может содержать Д. Отсюда следует, что интеграль-
интегральное уравнение имеет в части Д, которая лежит в полуплоскости
R(Z)>0, единственное аналитическое решение. Рассмотрим
полуплоскость R(Z)<0, и предположим, что b — произвольно
большое положительное число. В этом случае положительное
число Мь существует и в Д
Для завершения доказательства в данном случае необходимо
ввести изменение, вследствие измененной формы неравенства
(G). Отсюда следует, что единственное решение существует
также в той части Д, которая лежит на отрицательной стороне
мнимой оси, если
R(Z)>~b,
Пусть D будет частью Д, в которой I(Z) ограничено, R(Z)
ограничено снизу, а |1 (Z) | > р, когда R(Z)<0. Пусть Л будет
верхней границей \W(Z)\ в D и пусть zx = хг -\- iyx будет точкой,
которой достигается ->тл верхняя граница, тогда, если L — верх-
верхняя граница |W0(Z)| в D, то
\ ^ т л. \ /И 7 —- - <г I У V СЛ1
где
Ri ~ \zt\, когда х1 > О,
Ri = '1Уг\> когда л, <0.
Э. Айно—133—45 "*05
1_
Теперь, если D выбрать таким, что R[> 2C/W/vs , то Д < 2/. и
= |^ или |F|, соответственно тому, X больше или меньше
нуля.
Нетрудно получить аналогичные равенства, справедливые
в той части Л, в которой I(Z)>Z?2, так как интегральное урав-
уравнне
W-(Z) = Wt{Z)+f K+[Z.T) W+(T)dT,
z
нуля
Н
в то
нение
где
Wo+(Z) = eiZW0(Z), K+ (Z, T) = eKZ~T)K(Z, T),
удовлет воряется
и можно доказать, что |W"(Z)| ограничен для I (Z) > В2. Соот-
Соответствующим выбором В2 верхняя граница | W (Z)j в рассматри-
рассматриваемой области может быть значительно меньше верхней гра-
границы /Л" выражения |Wo"(Z)| в этой области. Отсюда следует,
что
\eiZ{ W{Z) - Wo (Z) }|
где R имеет такое же значение, как и выше. Аналогичная фор-
формула может быть получена для той же части Л, для которой
l(Z)B
Ввиду этих неравенств W(Z) называется асимптотическим
выражением относительно W0Zy, можно доказать, что W (Z)
асимптотическое выражение относительно W0(Z).
21*52. Усеченные решения. Пусть H^i(Z) будет решением-
асимптотическим относительно eiZ, тогда интегральное уравне-
уравнение
DO
U(Z)=\ +±f{e*(T-Z)- 1 }<P(T)U{T)dT
z
будет удовлетворяться функцией U(Z) =e~iZ Wt (Z). Из этого
интегрального уравнения видно г, что Wx (Z) — аналитическая
функция в секторе
— п -{- е < arg Z < 2п -f- е, \г\ > р
1 Доказательство, справедливое при v = 1, см. НШе, Proc. London Math. Soc,
23 A924Л §2-24.
706
и что
где \Qi(Z)\ ограничен в секторе. Аналогично, если решение W(Z)
асимптотическое относительно е'2, то
& w2 (Z) = 1 +
Из этих формул следует, что решения WX(Z) и W2(Z) не
имеют нулей вне достаточно большого круга; они называются
усеченными в Д. То же верно и для производных W[{Z)vi W?Z).
Теперь, если область Д типа Аа, в которой каждая линия,
параллельная вещественной оси, пересекает границу, W1(Z) и
W2(Z) являются единственными решениями, усеченными в Д.
Другое решение может быть написано в виде
W(Z) = CMZ) + C2W2(Z). (ОД ф %
и будет асимптотическим относительно
Не теряя в общности, решение W0(Z) можно представить в виде
sin(Z—а); его нули равны ап = а + пп. Теперь, поскольку об-
область типа Аа, полоска До может быть выбрана так, чтобы она
содержала все нули W0(Z) при определенном значении п, напри-
например Л^о- Обозначим части А, которые лежат выше и ниже До,
через Дх и Д_х соответственно, тогда в До
eiZW(Z) = eiZ sin (Z — ct) + *Щ\
а в Д2
n ,(Z)
e-« li7|(Z) = e-'zsin (Z - a) + ~'=1->—.
В каждом случае в Дх
v2
когда
,2
где Z.v обозначает верхнюю границу |eX(Zsin(Z — a)| в Дх.
707
Теперь пусть Гп будет кругом малого радиуса е, содержа-
содержащего точку а„, тогда на Г„
2
|sin (Z — о)| > — е,
и если
|Z|>r=
то
Отсюда следует, что sinfZ — а) является главным членом
для W(Z) на любом круге Гп> который лежит в Д, и вне круга
Пусть А будет той частью Д, которая лежит вне круга
\Z\ = ?• Тогда внутри каждого круга Г„ в Л будет лежать только
один нуль W(ZI. Пусть Д* будет остатком от Д + , если уда-
удалить внутреннюю часть каждого круга Г„ в Д+, тогда W(Z) не
будет иметь нуля в А*. Аналогично можно доказать? что нули
W (Z) в А лежат по одному внутри каждого круга
где a'n = arjr-^n.
Таким образом нули W (Z) и W (Z) могуть быть обозначены
соответственно через Ап и А'п, где
Urn (Ап - ап) = 0, llm (А'п - а'п) = О,
а последовательность точек Ап называется последовательностью
нулей осциллирующего решения Wn(Z). Оба усеченных реше-
решения не имеют последовательности нулей.
Если область Д типа АЬ, существует бесконечное число реше-
решений, усеченных в Л, именно решения, асимптотические относи-
относительно функции Wo'Z', нули которой лежат вне Л. С другой
стороны, если при некотором значении п последовательность
точек ап = a -f- пк лежит в А, может быть построено решение,
последовательность нулей которого аппроксимируется форму-
формулой (an) и которое является асимптотическим относительно
U70(Z)-С sin (Z-a).
Таким образом, независимо от типа области, всегда может
быть найдено решение, нули которого аппроксимируются после-
последовательностью (a + nii), если эта последовательность лежит
в Д. Для того, чтобы показать зависимость нулей от а, напишем
Ап(а) вместо Ап и W(Z,a) вместо W(Z). Здесь возникает во-
1 Rouche, J. Ее. Polyt., 39 A862), 217.
7 08
прос, как будет изменяться Ап(а) при изменении а? Предполо-
Предположим, что а = а-{-к; придавая т постоянное значение т0, заставим
о изменяться от о0 до а0 -{- тг, тогда Ап(а) опишет непрерывную
кривую между точками Ап(а0), где ао=ао-{-й, и Ап ,(в^). г]ри
дальнейшем увеличении a /4n(«j опишет кривую, соединяющую
нули и стремящуюся к асимптоте I (Z) = т0. Эта кривая назы-
называется нулевой кривой дкференциального уравнения. Очевидно
через каждую точку в Д проходит только одна нулевая кривая
21-53. Распределение нулей в плоскости г. Полученные резуль-
результаты могут быть отнесены также и к плоскости z при помощи
подстановки
V
Z.
Эта подстановка дает конформное соответствие между плоскостями
Z и z. Односвязная область Д на плоскости Z преобразуется
в односвязную область D в плоскости z; в наиболее общем
случае преобразованная область лежит на бесконечно-многолист-
ной поверхности Римана. Любое решение w (z) будет аналити-
аналитическим во всей области D, но на границах этой области может
быть одна или несколько особых точек, соответствующих z = со.
Полученные результаты для распределения нулей в плоско-
плоскости Z могут быть перенесены на плоско*, ть г. Круг \Z\ =i со-
ответствчет кривой, разделяющей область D на две части; пусть
D+ будет частью, соответствующей Д\ Точки ап становятся точ-
точками an, a круги Гп становятся замкнутыми контурами Сп, со-
содержащими точки ап. D* определяется как часть D+, кото-
которая осталась после того, как была удалена внутренняя часть
контуров Сп. Если при некотором значении п и ьыше него точки
яп все лежат в Л, то соответствующие точки а^ будут лежать
в D. Решению W(Z, а) соответствует решение w (z, а), где
и внутри каждого контура Сп в D1 лежит только один нуль
w B, а) в то время как в D* нули отсутствуют.
Нулевые кривые в плоскости Z могут быть представлены нуле-
нулевыми кривыми © на поверхности Римана, асимптотическими
к кривым
Через каждую точку а в области D проходит только одна ну-
нулевая кривая (?(о). Отметим точки ап на ©(с) в направлении
возрастающих значений R(Z), где
W} (« = 1,2,3,...),
709
а путем интегрирования служит кривая К (а), тогда существует
решение w (z, а), нули которого Ап могут быть расположены
так, что
Пт(Ап — ап) = 0.
Рассмотрим два круга Ех и 22, проведенные в плоскости Z с ра-
радиусами Rx и R2 соответственно, где R2> Rx> R, и предполо-
предположим, что каждый из этих кругов пересекает Г (границу А), только
в двух точках. В плоскости г круговые дуги 2^ и Е2 преобразуются
в кривые Sx и S2, которые, вместе с преобразованными частями
F, заключенными между 2Х и ?2> образуют криволинейный четы-
четырехсторонник [D]. Этот четырехсторонник пересекается G(a)
в двух точках, например, гг на S, и z2 на S2. Отсюда следует,
что число нулей w{z,а) в [D] дается формулой
где путь интегрирования лежит вдоль (?(а) и — 1 <&¦<-)-1-
Аналогичные результаты могут быть получены и. в отноше-
отношении w' (z,a) из формулы
где известен только первый множитель.
21- 54. Уравнения с коэфициентами в виде полиномов. В каче-
качестве примера рассмотрим случай, когда K(z) и G(z)~ полиномы
от z; пусть
К{г) = z" + ..., G(z) = gozs+ ... (g0 ф 0).
Для того, чтобы точка в бесконечности была нерегулярной
особенностью, предположим, что g> k — 1; пусть m=g—k + 2,
так что т > 1.
Поскольку
I
Z является, в общем случае, Абелевым интегралом третьего рода.
Для больших значений z, Z имеет форму
где логарифмический член встречается только в том случае,
если т — четное число. С другой стороны
{,„8
710
_2_
где ? — двойной ряд по возрастающим степеням Z т и
который сходится для достаточно больших значений \Z\.
Далее, поскольку
FG\ - G(г)К'(г)+G' (г)К(г)
2{G(z)Yr{K(z)Y~
отсюда следует, что
следовательно
где ? — двойной ряд того же типа, что и выше.
Аналогично
Z{1+S},
и следовательно Ф (Z) удовлетворяет условию В при v = 1 в не-
некоторой области вне достаточно большого круга \Z\ = R, где
argZ ограничен. Пусть Д будет областью
\Z\>R, R(Z)^O.
Для достаточно больших значений R эта область может быть
конформно отображена на секторную область Ц* плоскости г,
в которой
^ - 60} - 8 <argz < ^{B^ + 1)тг-Л} + 8,
здесь с — малое положительное число, 60 = arggOl а ^ = 0,1, ...,
m — 1, соответственно выбранному значению Z1"™.
Если z = reA, то асимптотические нулевые кривые в плоско-
плоскости z имеют вид
1
2~т 1
г sin ~2 (m 9 + 60) + низшие члены = const,
а их асимптотическими направлениями будут
В общем случае решение w {г, а) неоднозначно в соседстве
с бесконечностью, но если © представляет часть поверхности
Римана для log z, которая лежит вне достаточно большого круга,
то w(z, а) однозначно на Ф. Нули w(z,a) образуют таким обра-
образом т последовательностей, асимптотических к направлениям 6р.
711
в каждом листе Ф. Если Л/(г) обозначает число нулей в последо-
последовательности, лежащей внутри круга \z\ = г, то когда г->со,
— ¦—т
22
Результаты § 21-52 показывают, что существуют два реше-
решения, усеченные в направлении 6^, откуда следует, что общее
число усеченных решений не преьышает 2 т. Покажем, что
действительное число усеченных решений равно т.
Рассмотрим область Д', границей которой является дуга круга
\Z\=R, _^7t + 8<argZ<^-8,
и касательные, пров денные к конечным точкам этой дуги и
простирающиеся на бесконечность в полуплоскости I(Zj<CO.
Определенная таким образом плоскость — типа А; в ней <D(Z)
удовлетворяет условию В. Пусть W1(Z) и IF2(Z) будут усечен-
усеченными решениями, асимптотическими относительно eiZ и е~а со-
соответственно. Теперь W X{Z) асимптотически стремится к eiZ в бо-
более расширенной области
— v < argZ<27i;
как это видно из рассмотрения области, симметричной А' отно-
относительно мнимой оси, W2(Z\ также асимптотически стремится
к e~iZ в расширенной области
— 2 я < arg Z < it.
Следовательно, если |I(Z)|—>оо, то
Wx(Z)—>0 в верхней половине А',
IF2(Z)—>0 в нижней половине А',
и вследствие свойств интегрального уравнения, удовлетворяемого
W(Z), эти условия достаточны для определения Wx(Z)n W2(Z)
соответственно.
В плоскости z существует т независимых областей D' со-
соответствующих A', a D'^ таково, что
rv_i + s < argz < 6^ ! — е (и = 0, 1, ... /га—1).
область Up., где
Последовательные области D'{x и D^+1 имеют общую часть, именно
&,, + ?< arg г
Имеется одно решение, усеченное в D', которое стремится к нулю
в Uf., и решение, усеченное efl'f v которое также стремится
к нулю в Up. Однако, поскольку только одно такое решение
может стремиться к нулю в U^, оба рассматриваемые решения
712
должны быть тождественны. Число усеченных решений таким
образом приводится к т; это можно показать исследованием
уравнения
5
Если wv.(z) — решение, которое стремится к нулю в f/^, тс это
решение, усеченное в примыкающих направлениях 6Р и 0^. [,
сохраняет то же асимптотическое представление в трех примы-
примыкающих областях L^-i, Uv. и и^-\.
Примеры
1. Докажите формулу
2, Рассматривая динамическую систему
(P-V
dF = —Siy
где gt и Го rtviri'HH ?, используйте результаты § 21-4 для того, чтобы дока-
доказать, что частица, начиняющая двигаться из начала в момент tr с заданной ско-
скоростью, будет продолжать удаляться от начала до тех пор, пока gi@^0, a
знак g2(t) остается неизменным.
3 Распространите ре!ультаты §§ 21-4, 21-41 на случай самосопряженного
уравнения второго порядка.
4. Пусть функция F(z) будет вещественной и положительной, когда г веще-
вещественно и больше xlt аналитической во всей области D, включающей веще-
ственвую ось с R (г) > xt и такой, что
R{F(z)}>0 или 1
в D; пусть W(z) будет решением уравнения
так что W(z)~>0, когда Z—>со в D вдоль параллели к вещественной оси. Дока-
Докажите, что W(z) не имеет нуля или экстремума в D.
5 Постройте стандартную область для решения уравнения
d2w w
имеющего комплексный нуль г = a + ib.
6. Докажите, что если ф\нкиия <J>(Z) — аналитическая и удовлетворяет
условию В в полуплоскости Г, I(Z)>-B2, то каждое решение будет асимпто-
асимптотическим к синусоидальной функции в Г — крайней правой части области, и
асимптотическим к другой синусоидальной функции в Г~ — крайней левой ча-
части области. Исследуйте нули этого решения.
7. При заданной функции sin (Z — a) существует одно решение W" {Z),
асимптотическое к ней в Г ¦", и другое решение W~(Z), асимптотическое отно-
относительно этой функции в Г . Но если ¦: = I (а) велико, то существует реше-
713
ние W(Z), асимптотическое к sm{Z-~a) во всей полуплоскости Г, а последо-
последовательности нулей в Г+ и Г~ сливаются в одну последовательность. Выше
этой последонатетьности нули отсутствуют и только конечное число нулей име-
имеется ниже ее в Г.
8. Асимптотические нулевые кривые уравнения
являются параболами с фокусом в начале и отрицательной вещественной осью
в качестве оси. Найдите распределение нулей в соседстве с асимптотической
параболой.
9. Общее решение уравнения
где О(г) — полином от г, может быть представлено н виде
w = wl (г) — ).w2 (г),
где и»! (г) и w2{z) — линейно-независимые решения, аХ—комплексный пара-
параметр. Покажите, что для того, чтобы решение было усеченным, необходимо и
достаточно, чт бы , было одчим из асимптотических значений -мероморфной
функции \ (г) = wl (z)lw.2 B).
[Примечание. Число а называется асимптотическим значением целой или
мероморфной функции /(г), если имеется простая кривая, стремящаяся к беско-
бесконечности, вдоль которой /(г)-у а].
СПИСОК ЖУРНАЛОВ, УКАЗАННЫХ В ПРИМЕЧАНИЯХ
Abh. Akad. Wiss., Berlin . . . Abhandlungen der koniglichen Akademie des Wls-
senschaften in Berlin.
Abh. Ges. Wiss., Gott Abhandlungen der koniglichen Gesellschaft der
Wlssenschaften zu Gottingen (continuation of
Comm. Gott).
Acta Erud Acta Eruditorum publicata Lipsiae.
Acta Erud. Suppl Acta Eruditorum quae Lipsiae publicantur Supple-
menta.
Acta Math Acta Mathematica, Stockholm.
Acta Soc. Sc. Fenn Acta Societatis Scientiarum Fennicae, Helsingfors.
Am. J. Math The American Journal of Mathematics, Baltimore, Md.
Ann. di Mat Annali dl Matematica pura ed applicata, Rome and
Milan.
Ann. Ec. Norm Annales scientifiques de l'Ecole Normale superieure,
Paris.
Ann. Fac. Sc, Toulouse .... Annales de la Faculte des Sciences de Toulouse.
Ann. of Math . Annals of Mathematics, Princeton, N. J.
Ann. Scuola Norm., Pisa . • . Annali della R. Scuola Normale superiore di Pisa.
Archiv d. Math. u. Phys. . . . Archiv der Mathematik und Physik (Grunert's Ar-
chiv), Greifswald und Leipzig.
Archiv for Math • . Archiv for Mathematik og Naturvidenskab, Christi-
ania (Oslo).
Arkiv for Mat Arkiv for Matematik, Astronomi och Fysik, Stock-
Stockholm.
Bibl. Math Bibliotheca Mathematica, Stockholm und Leipzig.
Bull. Am. Math. Soc Bulletin of the American Mathematical Society,
Lancaster, Pa. and New York.
Bull. Acad. Sc. Belg Bulletins de 1'Academie royale des Sciences de
Belgique, Brussels.
Bull. Sc. Math Bulletin des Sciences mathematiques, Paris.
Bull. Soc. Math. France , . . . Bulletin de la Societe mathematique » de France,
Paris.
Bull. Soc. Philomath., Paris . . Bulletin de la Societe philomathique de Paris.
Camb. Math. J The Cambridge Mathematical Journal.
Comm. Acad. Petrop Commentarii Academiae Scientiarum Imperialis Pet-
ropolitanae (Continued as Novl Comm.).
Comm. Gott Commentarii Societatis Regiae Scientiarum Gottin-
gensis (Continued successively as Novi Com-
Commentarii, Commentationes and Commentationes
recentiores.)
Comm. Math. Soc, Kharkov . . Communications and Proceedings of the Mathema-
Mathematical Society of the Imperial University of Khar-
Kharkov.
С R. Acad. Sc, Paris .... Comptes Rendus hebdomadaires des Seances de
l'Academie des Sciences, Paris.
Forhand. Vid. -Selsk., Christi-
anla Forhandlinger i Videnskabs-Selskabet i Chrlstiania
(Oslo).
Gott. Nach Nachrichten von der koniglichen Gesellschaft der
Wissenschaften zu Gottingen.
715
Hist. Acad., Berlin Histoire de l'Academie royale des Sciences et des
Belles-Lettres de Berlin.
Hist. Acad., Paris Histoire de l'Academie royale des Sciences, Paris.
J. de Math Journal de Mithematiques pures et appliquee (Liou-
ville), Parisr
J. Ёс. Polyt. Journal de l'Ecole Polvtechnique, Paris. (Reference
is made to the Cahier, each of which is separa-
separate у paged. The number of Cahiers to the volume
is irregular..
J. fur Math Journal fiir die reine und angewandte Mathematik
(Crdle'- Journal), Berlin.
Math. Ann. Maihematischt: Annalen, Leipzig.
Mathesis Mathesis, Recueil Mathematique, Gand and Paris.
Mem. Acad. Sc, Paris .... Memoires de l'Academie des Sciences de l'lnstitut
de France: since Ifc(j5, Memoites presentes par
divers savants-
Mess. Math The (Messenger of Mathematics, London and Cam-
Cambridge.
Misc. Berol. Miscellanea Berolinensia, Berlin.
Misc. Taur Miscellanea Taurinensia, Turin.
Monatsh. Math. Phys. ..... MonaUhefte fiir Mathematik und Physik, Wien.
Nouv. Mem. Acad., Berlin . . Ntuveaux Memoires de l'Academie ro\ale des
Sciences et Be les-Lettres, Berlin. (Continuation o)"
Hist. Acad, l-erlin).
Ofv. Vet., Al,ad Stockholm . . Ofversigt af Konglitja Vetenskaps-Akademiens For-
hand ingar, Stockholm.
Phil. Trans. R. S . Philosophical Transactions of the Royal Society of
London.
Proc Am. Acad Proceedings of the American Academy oi Arts and
Sciences, Boston, Mass.
Proc. Camb. Phil. Soc Proceedings с f the Cambridge Philosophical So-
Society.
Proc. Edin. Math. Soc Proceedings of the Edinburgh Mathematical So-
Society.
Proc. London Math. Soc. . . . Proceedings of the London Mathematical Society.
Proc. Roy. Soc. Edin. ..... Proceedings of the Royal Society of Edinburgh.
Quart. J.'Math ¦ The Quarterly Journal of Pure and Applied Mathe-
Mathematics, London.
Rend. Accad. Lincei ..... Atti della R. Accademia dei Lincei, Rendlconti,
Rome.
Rend. Circ. Mat., Palermo . . . Rendic<>nti del Circolo Matematico di Palermo.
Rend. 1st. Lombard ... ... Reale Istituto Lombardo di Scienze e Letter'e, Ren-
diconti, Milan.
Sitz. Akad. Wiss. Berlin .... Sitzungsberichte der koniglichen preussischen Aca-
demie der Wissenschaften. Ber in.
Trans. Am. Math. Soc Transactions of the American Mathematical Society,
Lancaster, Pa. and New York.
Trans. Camb. Phil. Soc Transactions of the Cambridge Philosophical So-
Society.
Trans. Roy. Soc. Edin Transactions of the Royal Society of Edinburgh.
Z. Math. Phys Zeitschrift fiir Mathematik und Phytik, Leipzig.
СПИСОК ЛИТЕРАТУРЫ
I. Учебные пособия
<1) Fursyth, A- R,, Theory of Differential Equations, Cambridge, 19C0—1902, six
volumes, of which the first four deal with ordinary differential equations, na-
namely:
Vol. 1. Exact Equations and Pfaff's Problem.
Vosl. II, 14. Ord nar/ Equations, not Linear.
Vol. IV. Ordinary Linear Equat ons.
B) Craig, Т., Treatise on Linear Differential Equations, New York, 1889.
C) Page, J. M., Ordinary Differential Equ,iti us, with an Introduction to Lie's
Theory of Groups of One Parameter, L< ndon, 1897.
D) Bateman, H., Differential Equations. London, 1918.
E) Goursat, E., Cours d'Analyse mathematique, Paris, Tome II Dth ed. 1924) and
Tome III. Crd ed. 1922).
Ea) A Course in Mathematical Analysis, translated by E.R. Hendrick and O. Dun-
kel, Vol. П., part 2, Boston, 1917.,
F) Jordan, C, Cours d'Analyse de 1'EcoIj Polytechnique, Paris, Tome III. Crd
ed. 1915).
G) Picard, ?., Traite d'Analyse, Paris, Tome !I Crd ed. 1926). Tome III. Bnd. ed.
1908).
(8) Schlesinger, L., Einfuhrung in die Theorie der Differentialglelchungen auf funk-
tiontheoretischer Grundiage, Berlin und Leipzig Crd ed. 1922; a revised ver-
version ff Sammlung Schubert XIII).
(9) Schlesinger, L., Handbuch der Theorie der linearen Differentialgleichungeti,
Leipzig, Band I, 1895, Band IIlf 1897, Band II», 1898.
A0) Schlesinger, L., Vorlesungen uber lineare Differentialgleichungen, Leipzig
und Berlin, 1908.
A1) hOnigsberger, L., Lehrbuch der Theorie der Differentialgleichungen, Leipzig,
1889.
A2) Heffter. L, Einleitung in die Theorie der linearen Differentialgleichungen
mit elner unabhangigen Variabeln, Leipzig, 1894.
A3) Horn J., Gewohnliche Differentialgleichungen beliebiger Ordnung, Leipzig
1905 (Sammlung Schubert L ).
A4) Bieberbach, L. Theorie der Differentia'gleichungen, Berlin, 1923.
A5) Смирнов, В. И.. Курс высшей математики, том И и III.
A6) Стеклов, А. Курс диференциадьных ураьнений.
A7) Степанов, В. Курс дифереьциальных уравнений.
II. Монографии
A) Enzyklopadie der Mathematischen Wissenschaften, Leipzig:
II. А да. Painleve, P., Gev-ohnliche Differentialgleichungen; Existenz der
Losungen, 1900.
II A 4b. Vessiot, E., Gewohnliche Differentialgleichungen; Eleraentare
lntegrationsmethoden. 1801.
(These are reproduced, in an improved form, in the Encyclopedie des
Sciences matheniat ques, Paris and Leipzig. Tome II, vol. 3, fasc. I. 1910).
II. A 7a. Bdcher, M., Randwert<iufg..ben bei gewohulichen Differential-
Differentialgleichungen, 1900.
II. В 5. Hilb, E., Lineare Differentialgleichungen im komplexen Gebiet,
1915.
717
II. В 6. Hilb, E., Nichtlineare Differentialgleichungen, 1921.
III. В 8. Liebmann, H., Geometrische Theorie der Differentialgleichungen,
1916.
B) Klein, P., Ober lineare Differentialgleichungen der zweiten Ordnung. Gottingen,
1914 (autographed; a printed edition is said to be in preparation).
C) Bdcher, M., Ober die Reihenentwickelungen der Potentialtheorie, Leipzig,
1894-
D) Painleve, P., Lemons sur la theorie analytique des equations differentielles,
professees a Stockholm, Paris, 1897 (lithographed).
E) Boutroux, P., Lecons sur les functions definies par les equations differentielles
de premier ordre, Paris, 1908.
F) Bdcher, M., Legons sur les methodes de Sturm dans la theorie des equations
differentielles lineaires et Ieurs developpements modernes, Paris, 1917.
ОГЛАВЛЕНИЕ
Часть I
Диференциальные уравнения в вещественной области
стр.
Глава I Введение -7
Глава И Элементарные методы интегрировавия 25
Глава III Существование и природа решений обыкновенных диференци-
альных уравнений '. . 86
Глава IV Непрерывные группы преобразований 127
Глава V Общая теория линейных диференциальных уравнений 154
Глава VI Линейные уравнения с постоянными коэфициентами 178
Глава VII Решение линейных диференциальных уравнений в неопределен-
неопределенной форме . 212
Глава VIII Решение линейных диференциальных уравнений при помощи
определенных интегралов • 251
Глава IX Алгебраическая теория линейных диференциальных систем . . . 276
Глава X Теория Штурма и ее позднейшее развитие 301
Глава XI Дальнейшее развитие теории граничных проблем 342
Ч а с г ь II
Диференциальные уравнения н комплексной области
Глава XII Теоремы существования в комплексной области 379
Глава XIII Уравнения первого порядка не первой степени 409
Глава XIV Нелинейные уравнения высшего порядка 426
Глава XV Линейные уравнения в комплексной области 479
Глава XVI Решение линейных диференциальных уравнений в виде рядов 534
Глава XVII Уравнения с нерегулярными особыми точками 562
Глава XVIII Решение линейных диференциальных уравнений методами кон-
контурного интегрирования . , 590
Глава XIX Системы линейных уравнений первого порядка 633
Глава XX Классификация линейных диференциальных уравнении второго
порядка с рациональными коэфициентами 667
Глава XXI Осцилляционные теоремы в комплексной области 687
Список журналов, указанных в примечаниях 715
Список литературы 717