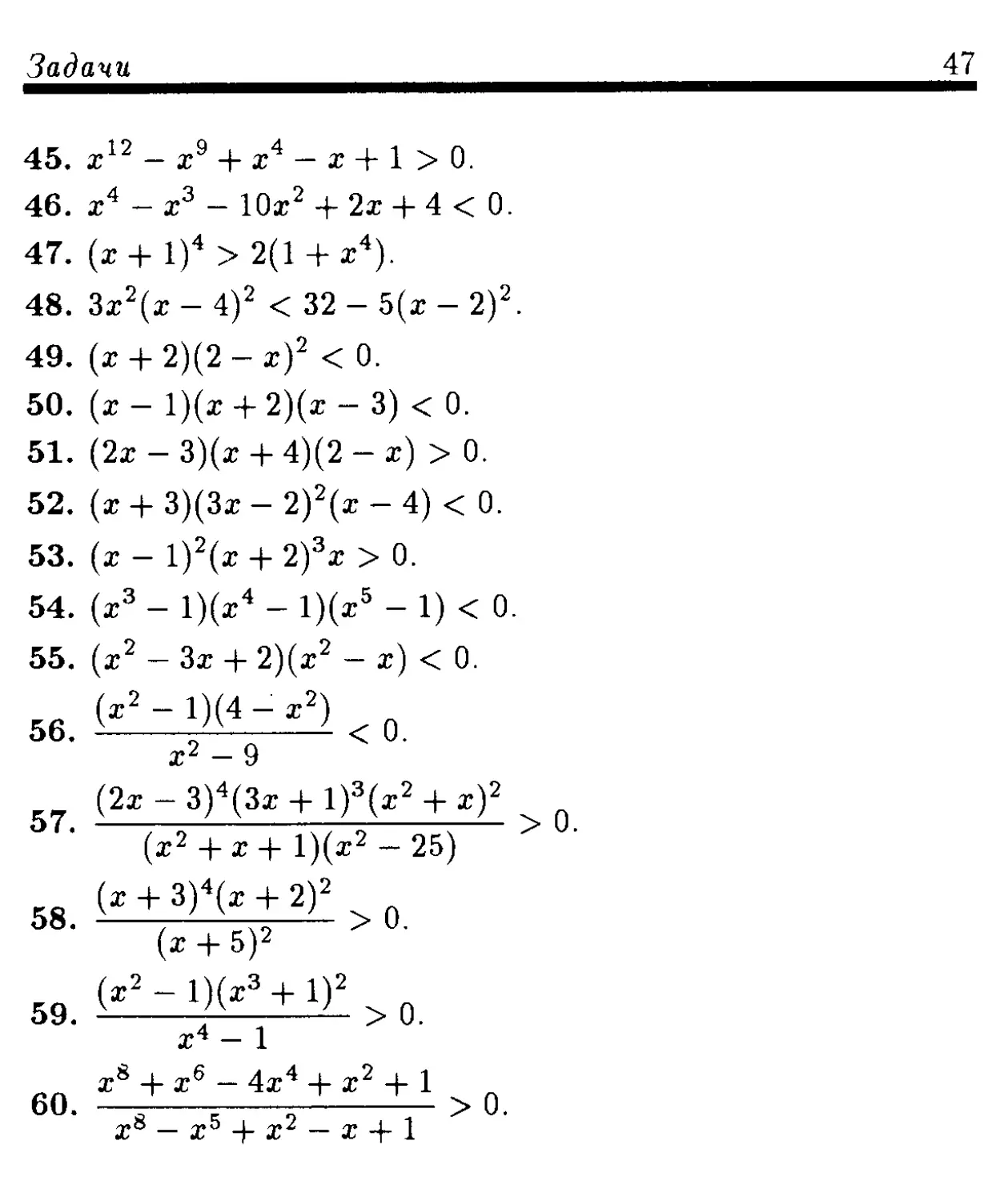С.Н.Олехник, М.К.Потапов, П.И.Пасиченко
УРАВНЕНИЯ И НЕРАВЕНСТВА.
НЕСТАНДАРТНЫЕ МЕТОДЫ РЕШЕНИЯ: СПРАВОЧНИК.
Справочник посвящен задачам, которые для школьников считаются задачами
повышенной трудности, требующим нестандартных методов решений.
Приводятся методы решений уравнений и неравенств, основанные на
геометрических соображениях, свойствах функций (монотонности,
ограниченности, четности), применении производной. Книга ставит своей целью
познакомить школьников с различными, основанными на материале программы
общеобразовательной средней школы, методами решения, казалось бы трудных
задач, проиллюстрировать широкие возможности использования хорошо
усвоенных школьных знаний и привить читателю навыки употреблять
нестандартные методы рассуждений при решении задач. Для школьников,
абитуриентов, руководителей математических кружков, учителей и всех
любителей решать задачи.
Справочное издание
Оглавление
От авторов	7
Глава I. Алгебраические уравнения и неравенства	8
1.1.	Разложение многочлена на множители	8
1.1.1.	Вынесение общего множителя	8
1.1.2.	Применение формул сокращенного умножения	9
1.1.3.	Выделение полного квадрата	10
1.1.4.	Группировка	10
1.1.5.	Метод неопределенных коэффициентов	10
1.1.6.	Подбор корня многочлена по его старшему и свободному	11
коэффициентам
1.1.7.	Метод введения параметра	13
1.1.8.	Метод введения новой неизвестной	13
1.1.9.	Комбинирование различных методов	14
1.2.	Простейшие способы решения алгебраических уравнений	15
1.3.	Симметрические и возвратные уравнения	19
1.3.1.	Симметрические уравнения третьей степени	19
1.3.2.	Симметрические уравнения четвертой степени	20
1.3.3.	Возвратные уравнения	22
1.3.4.	Уравнения четвертой степени с дополнительными условиями на	25
коэффициенты
1.4.	Некоторые искусственные способы решения алгебраических уравнений 27
1.4.1. Умножение уравнения на функцию	27
1.4.2.	Угадывание корня уравнения	29
1.4.3.	Использование симметричности уравнения	32
1.4.4.	Использование суперпозиции функций	33
1.4.5.	Исследование уравнения на промежутках действительной оси	34
1.5.	Решение алгебраических неравенств	35
1.5.1.	Простейшие способы решения алгебраических неравенств	3 5
1.5.2.	Метод интервалов	38
1.5.3.	Обобщенный метод интервалов	41
Задачи	45
Глава II. Уравнения и неравенства, содержащие радикалы, степени,	48
логарифмы и модули
2.1.	Уравнения и неравенства, содержащие неизвестную под знаком корня 48
2.1.1.	Возведение в степень	48
2.1.2.	Уравнения вида д//(х) ± y]g(x) = h(x)	51
2.1.3.	Уравнения вида ^//(х) ± %] g(x) = (р(х)	53
2.1.4.	Умножение уравнения или неравенства на функцию	56
2.2.	Уравнения и неравенства, содержащие неизвестную в основании	59
логарифмов
2.2.1.	Переход к числовому основанию	59
2.2.2.	Переход к основанию, содержащему неизвестную	64
2.2.3.	Уравнения вида log9W h(x) = log9W g(x), log/(x) (р(х) = logg(x) (р(х)	65
2.2.4.	Уравнения вида log/(x) g(x) = а	66
2.2.5.	Неравенства вида к^ф(х) /(х) > к^ф(х) g(x)	68
2.3.	Уравнения и неравенства, содержащие неизвестную в основании и 70
показателе степени
2.4.	Уравнения и неравенства, содержащие неизвестную под знаком	75
абсолютной величины
2.4.1.	Раскрытие знаков модулей	75
2.4.2.	Уравнения вида |f(x)|=g(x)	77
2.4.3.	Неравенства вида |f(x)|<g(x)	78
2.4.4.	Неравенства вида |f(x)|>g(x)	79
2.4.5.	Уравнения и неравенства вида |f(x)|=|g(x)|, |f(x)|<g(x)	81
2.4.6.	Использование свойств абсолютной величины	82
Задачи	84
Глава Ш. Способ замены неизвестных при решении уравнений	87
3.1.	Алгебраические уравнения	87
3.1.1.	Понижение степени уравнения	87
3.1.2.	Уравнения вида (х + а)4 + (х + Р)4 = с	88
3.1.3.	Уравнения вида (х-а)(х-р)(х-У)(х-8)=А	89
3.1.4.	Уравнения вида (ах2 + Ьрс + с)(ах2 + Ь2х + с) = Ах2	90
3.1.5.	Уравнения вида (х-а)(х-р)(х-У)(х-8)=Ах^	91
3.1.6.	Уравнения вида а(сх2 + дх + q)2 + b(cx2 + р2х + q) = Ах2	92
3.1.7.	Уравнения вида Р(х)=0, Р(х)=Р(а-х)	93
3.2.	Рациональные уравнения	95
3.2.1.	Упрощение уравнения
3.2.2.	Уравнения вида ———I———I-... ч——— = А
х + р! Х + р2	Х + рш
3.2.3. Уравнения вида
а,х + а,	а2х + а2	а„х + а„
1	1	।	Z Z	।	।	и и	_
х +by	x + b2	Х + Ь„
~ _ . ,,	ciyX + by	a2x + b2	ax + b .
3.2.4.	Уравнения вида----------+-----£-------+ - +-------------= А
РуХ +qyX + Ky р2х +q2x + r2 рпх +qnx + rn
„ „ ,	ауХ2 +ЬуХ+ Су а2х2 + Ь2х + с2 ах2+Ьх + с
3.2.5.	Уравнения вида —!;L + —---------------- +... + — -------- = А
oqx + Pj ос2х ч-(32	оспх + Р„
_ _ ,	АуХ	А2х	Ах
3.2.6.	Уравнения вида —2—1-----1--2— -----1-... Ч-2— ------= В
ах +ЬуХ + с ах +Ь2х + с ах +Ьпх + с
3.3.	Иррациональные уравнения
3.3.1.	Уравнения вида y/ax + b ± y/cx + d = /(х)
3.3.2.	Уравнения вида \!а- х ±Mx-b = d
3.3.3.	Сведение решения иррационального уравнения к решению
тригонометрического уравнения
3.4.	Уравнения вида
aof" (х) + ау/п~1 (х)#(х) +... + an_if(x)g"~i (х) + angn (х) = О
3.5.	Решение некоторых уравнений сведением их к решению систем
уравнений относительно новых неизвестных
Задачи
Глава IV. Решение уравнений и неравенств с использованием свойств
входящих в них функций
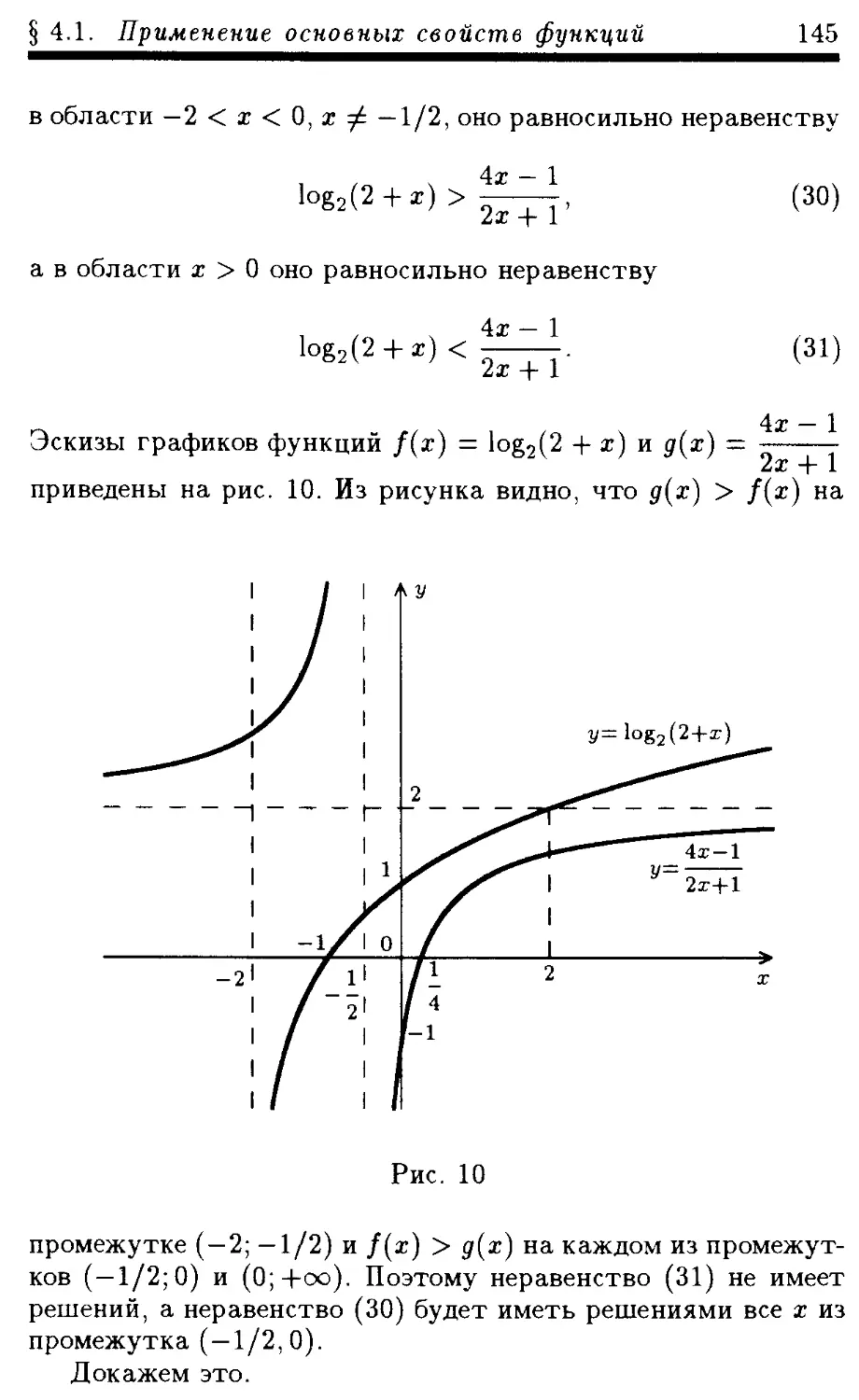
4.1.	Применение основных свойств функций
4.1.1.	Использование ОДЗ
4.1.2.	Использование ограниченности функций
4.1.3.	Использование монотонности
4.1.4.	Использование графиков
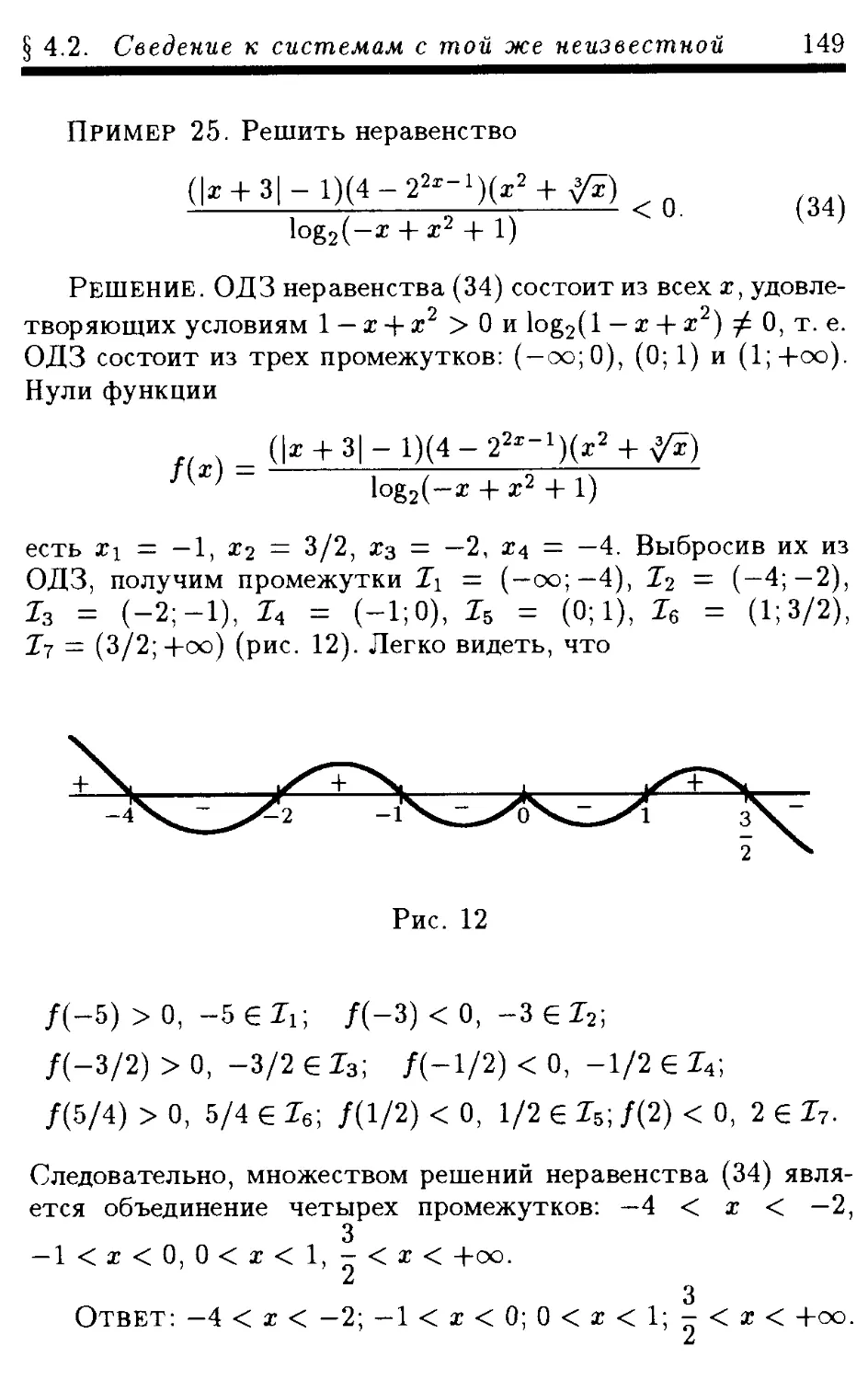
4.1.5.	Метод интервалов для непрерывных функций
4.2.	Решение некоторых уравнений и неравенств сведением их к решению
систем уравнений или неравенств относительно той же неизвестной
4.2.1.	Уравнения вида
Л2(Х) + /22(х) +... + Л2(х) = о, I Л(х) | +1 л(х) | +...+ | А(X) 1= О
4.2.2.	Неравенства вида
л2(х) + /22(х)+... + л2(х) > о, I л(х) | +1 л«I ++1Ш 1> о
4.2.3.	Использование ограниченности функций
4.2.4.	Использование свойств синуса и косинуса
4.2.5.	Использование числовых неравенств
4.3.	Применение производной
95
96
99
100
102
103
104
104
107
111
114
120
127
131
131
131
134
138
141
147
149
150
151
153
155
158
160
4.3.1.	Использование монотонности	160
4.3.2.	Использование наибольшего и наименьшего значений функции	162
4.3.3.	Применение теоремы Лагранжа	166
Задачи	166
Ответы	172
Дополнение 1
Некоторые задачи из вариантов вступительных экзаменов по математике в 176
МГУ им. М. В. Ломоносова
Дополнение 2
Образцы вариантов письменных работ, предлагавшихся на вступительных 184
экзаменах по математике в МГУ им. М. В. Ломоносова в 1992—1994 гг.
Ответы к дополнению 2	212
Оглавление
От авторов...................................... 7
Глава I. Алгебраические уравнения и неравенства 8
1.1.	Разложение многочлена на множители......... 8
1.1.1.	Вынесение общего множителя............ 8
1.1.2.	Применение формул сокращенного умножения 9
1.1.3.	Выделение полного квадрата .......... 10
1.1.4.	Группировка.......................... 10
1.1.5.	Метод неопределенных коэффициентов .... 10
1.1.6.	Подбор корня многочлена по его старшему
и свободному коэффициентам.................. 11
1.1.7.	Метод введения параметра............. 13
1.1.8.	Метод введения новой неизвестной..... 13
1.1.9.	Комбинирование различных методов..... 14
1.2.	Простейшие способы решения алгебраических
уравнений...................................... 15
1.3.	Симметрические и возвратные уравнения .... 19
1.3.1.	Симметрические уравнения третьей степени 19
1.3.2.	Симметрические уравнения четвертой степени 20
1.3.3.	Возвратные уравнения................. 22
1.3.4.	Уравнения четвертой степени с дополни-
тельными условиями на коэффициенты ... 25
1.4.	Некоторые искусственные способы решения
алгебраических уравнений....................... 27
1.4.1.	Умножение уравнения на функцию....... 27
1.4.2.	Угадывание корня уравнения........... 29
1.4.3.	Использование симметричности уравнения 32
1.4.4.	Использование суперпозиции функций .... 33
1.4.5.	Исследование уравнения на промежутках
действительной оси.......................... 34
1.5.	Решение алгебраических неравенств ........ 35
1.5.1.	Простейшие способы решения алгебраиче-
ских неравенств............................. 35
1.5.2.	Метод интервалов..................... 38
1.5.3.	Обобщенный метод интервалов.......... 41
Задачи......................................... 45
4
Оглавление
Глава II. Уравнения и неравенства, содержащие
радикалы, степени, логарифмы и модули . . 48
2.1.	Уравнения и неравенства, содержащие
неизвестную под знаком корня.................... 48
2.1.1.	Возведение в степень.............................. 48
2.1.2.	Уравнения вида у/f(x) ± \/д(х')	=	h(x)	...	51
2.1.3.	Уравнения вида \/f(x) ± у/д(х)	—	>р(х)	...	53
2.1.4.	Умножение уравнения или неравенства на
функцию...................................... 56
2.2.	Уравнения и неравенства, содержащие
неизвестную в основании логарифмов.............. 59
2.2.1.	Переход к числовому основанию..................... 59
2.2.2.	Переход к основанию, содержащему
неизвестную......................................... 64
2.2.3.	Уравнения вида log^) Л(ж) = log^,^) д(х),
............................................. 65
2.2.4.	Уравнения вида log^^j д(х) =	а. 66
2.2.5.	Неравенства вида log^j f(z)	> log^(l.) д(ж) . 68
2.3.	Уравнения и неравенства, содержащие
неизвестную в основании и показателе степени 70
2.4.	Уравнения и неравенства, содержащие
неизве	стную под знаком абсолютной величины . . 75
2.4.1.	Раскрытие знаков модулей.......................... 75
2.4.2.	Уравнения вида |f(z)| = д(х) ..................... 77
2.4.3.	Неравенства вида |/(z)| < д(х) ................... 78
2.4.4.	Неравенства вида |/(z)| > д(х) ................... 79
2.4.5.	Уравнения и неравенства вида
|/(х)| = Ш1, |f(z)| < Ж1..................... 81
2.4.6.	Использование свойств абсолютной величины 82
Задачи...................................................... 84
Глава III. Способ замены неизвестных при
решении уравнений............................ 87
3.1.	Алгебраические уравнения............................... 87
3.1.1.	Понижение степени уравнения....................... 87
3.1.2.	Уравнения вида (х + о)4 + (х + З)4 = с ... 88
3.1.3.	Уравнения вида (х — а)(х — 0)(х- у)(х — ё) = А 89
3.1.4.	Уравнения вида
(ах2 + bix + с)(ах2 + Ь?х + с) = Ах2................ 90
Оглавление
5
3.1.5.	Уравнения вида
(х — a)(z —	— 7)(z — <5) = Ах2 ...... 91
3.1.6.	Уравнения вида а(сх2 + pix + д)2 + Ь(сх2 +
+ р2х + д)2 = Лаг2..................... 92
3.1.7.	Уравнения вида Р(х) = 0, где Р(х) = Р(а — х) 93
3.2. Рациональные уравнения..................... 95
3.2.1. Упрощение уравнения ................ 95
а?	ат
3.2.2. Уравнения вида--—|---—+• • -Ч---— = А 96
Х+/31. х + /32	х+(Зт
а^х + di а2х + а2
3.2.3. Уравнения вида-----;---1-----;----(-••• +
х + bi х + b2
I &пХ “Ь ___ ]-)
х + Ьп
3.2.4. Уравнения вида
а^х + 61	। ct2^ + 62	।
pix2 + qix + ri р2х2 + q2x + г2
। Пп х + Ьп _______
pnx2 + qnx + rn
99
100
3.2.5. Уравнения вида
aix2 + bix + ci а2х2 + b2x + с2
оцх + fii	a2x +
anx2 + bnx + cn _ A
anx + (3n
102
3.2.6. Уравнения вида
— + ...+ _^И— = в .103
axO + bix + с	ах2 + b^x + с
3.3. Иррациональные уравнения ................104
3.3.1. Уравнения вида у/ах Ab ± у/ex A d — f(x) . . 104
3.3.2. Уравнения вида — х ± х — b = d.......107
3.3.3. Сведение решения иррационального
уравнения к решению тригонометрического
уравнения................................111
3.4. Уравнения вида aofn(x) + ai/n-1 (z)g(z) + • • • +
+ an_1f(z)g"-1(z) + апдп(х) = 0 ............114
3.5. Решение некоторых уравнений сведением их к
решению систем уравнений относительно новых
неизвестных...................................120
Задачи..........................................127
6
Оглавлент
Глава IV. Решение уравнений и неравенств с
использованием свойств входящих в них
функций....................................131
4.1.	Применение основных свойств функций.....131
4.1.1.	Использование ОДЗ..................131
4.1.2.	Использование ограниченности функций . . . 134
4.1.3.	Использование монотонности ........138
4.1.4.	Использование графиков.............141
4.1.5.	Метод интервалов для непрерывных функций 147
4.2.	Решение некоторых уравнений и неравенств
сведением их к решению систем уравнений или
неравенств относительно той же неизвестной . . . 149
4.2.1. Уравнения вида
Л (*) + /г (ж) + • • • + Л2 И = о,
I/1MI + 1ЛИ + • • • + \Ш\ = 0........150
4.2.2.	Неравенства вида
/1 W + /г (Ж) + •  • + /пО) > °,
l/1MI + l/2WI + ---+l/nMI>0..........151
4.2.3.	Использование ограниченности функций . . . 153
4.2.4.	Использование свойств синуса и косинуса . . 155
4.2.5.	Использование числовых неравенств...158
4.3.	Применение производной..................160
4.3.1.	Использование монотонности ........160
4.3.2.	Использование наибольшего и наименьшего
значений функции..........................162
4.3.3.	Применение теоремы Лагранжа........166
Задачи.......................................166
Ответы ...................................... •	172
Дополнение 1
Некоторые задачи из вариантов вступи-
тельных экзаменов по математике в МГУ
им. М. В. Ломоносова......................176
Дополнение 2
Образцы вариантов письменных работ,
предлагавшихся на вступительных
экзаменах по математике в МГУ
им. М. В. Ломоносова в 1992—1994 гг. . . . 184
Ответы к дополнению 2..........................212
От авторов
Имеется много уравнений и неравенств, для решения ко-
торых применимы необычные для школьника рассуждения.
В данной книге приведены некоторые нестандартные методы
решения уравнений и неравенств.
В книге считаются известными основные определения
и факты из теории уравнений и неравенств: равносиль-
ность уравнений, уравнение-следствие, совокупность уравне-
ний и т. д. Желающим освежить эти сведения рекомендуем
следующие книги, где эти понятия содержатся:
1.	Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи
вступительных экзаменов по математике. М.: Наука, 1986.
2.	Потапов М. К., Александров В. В., Пасиченко П. И. Ал-
гебра и анализ элементарных функций. М.: Наука, 1980.
3.	Вавилов В. В., Мельников И. И., Олехник С. Н., Паси-
ченко П. И. Задачи по математике. Уравнения и неравенства.
М.: Наука, 1987.
Глава I
Алгебраические уравнения и
неравенства
В этой главе рассматриваются алгебраические уравнения
степени п, т. е. уравнения вида
РпИ = О	(I)
и алгебраические неравенства степени п, т. е. неравенства ви-
да
Рп(х) > О	(II)
И
РпИ < О,	(III)
где Рп(х) — многочлен степени п, т. е.
Рп(х) = аохп + aizn-1 + • • • + an-ix + ап, а0 # 0. (IV)
При решении алгебраических уравнений и неравенств ча-
сто приходится разлагать многочлен Рп(х) на множители, по-
этому § 1.1 посвящен этому вопросу.
§ 1.1. Разложение многочлена на множители
Разложить многочлен на множители — это значит пред-
ставить его в виде произведения двух или нескольких мно-
гочленов. В этом параграфе приводятся некоторые методы
разложения многочленов в произведение множителей первой
и второй степени, поскольку знания такого разложения доста-
точно для решения алгебраических уравнений и неравенств.
1.1.1. Вынесение общего множителя. Если все чле-
ны многочлена имеют общий множитель, то, вынося его за
скобки, получим разложение многочлена на множители.
§ 1.1. Разложение многочлена на множители
9
Пример 1. Разложить на множители многочлен
х3 — За:2 4- 4х.
РЕШЕНИЕ. Все члены данного многочлена содержат общий
множитель х. Вынося его за скобки, получим разложение дан-
ного многочлена на множители
х3 — За:2 4- 4а: = х(х2 — За: 4- 4).
1.1.2. Применение формул сокращенного умноже-
ния. Иногда многочлен Рп(х') можно разложить на множите-
ли, используя формулы сокращенного умножения:
а2 —	62	=	(а —	b)(a + b),
а3 +	Ь3	=	(а +	6)(а2 — ab 4- 62),
а3 —	Ь3	=	(а —	6)(а2 4- ab 4- Ь2),
а4 —	Ь4	=	(а2 — 62)(а2 4- 62) = (а	—	6)(а	4- 6)(а2 + 62),
а5 —	65	=	(а —	6)(а4 4-а36 4-а262	4-аб3	4-i»4),
ап — bn = (а-6)(ап-1+ап-26 + ап-3г>24---4-
4- а2Ьп~3 4- abn~2 4- 6n-1), п 6 N.
Пример 2. Разложить на множители многочлен
(а:2 4- 2а:)2 — (яг 4- I)2.
Решение. Применяя формулу а2 — Ь2 = (а —6)(а4-6), имеем
(х2 4- 2а:)2 — (х 4- I)2 = (х2 + 2х — х — 1)(а?2 4- 2х 4- х 4- 1) =
= (х2 + х — 1)(а?2 4- Зх 4- 1).
Пример 3. Разложить на множители многочлен
(4а: - З)3 - (2а: - I)3.
Решение. Применяя формулу a3 — b3 = (a — b)(a2 +ab + b2),
имеем (4а: — З)3 — (2а: — I)3 = ((4а: — 3) — (2х — 1))((4а? — З)2 4-
+ (4а: - 3)(2а: - 1) 4- (2а: - I)2) = (2ж - 2)(16ж2 - 24ж + 9 + 8ж2 -
— 6х — 4х 4- 3 4- 4х2 — 4х 4- 1) = (2х — 2)(28х2 — 38a: 4- 13).
10
Алгебраические уравнения и неравенства
1.1.3.	Выделение полного квадрата. Иногда много-
член можно разложить на множители, если воспользоваться
сначала методом выделения полного квадрата, а затем, как
правило, формулой разности квадратов.
Пример 4. Разложить на множители многочлен
х4 + 6а:2 — 10.
Решение. Выделяя полный квадрат, а затем применяя
формулу разности квадратов, имеем х4 + 6z2 — 10 = (а?2)2 +
-|-2-3-a:2 + 32 - З2 - 10 = (х2 + 3)2 - 19 = (а:2 + 3)2 - (У1э)2 =
= (а:2 + 3 - л/1э) (а:2 + 3 + ^19).
1.1.4.	Группировка. Этот способ применяется чаще
всего в сочетании со способом вынесения за скобки общего
множителя. Суть его состоит в перегруппировке слагаемых
в многочлене и дальнейшем объединении в группы таким
образом, чтобы после вынесения (если это можно) общего
множителя из каждого слагаемого в данной группе в скоб-
ке получилось выражение, являющееся в свою очередь общим
множителем уже для каждой группы.
Пример 5. Разложить на множители многочлен
а:4 — 5а:2 + х3 — 5х.
Решение. Объединим в одну группу первое и второе сла-
гаемые, а в другую — третье и четвертое слагаемые. Тогда
имеем х4 — 5х2 + х3 — 5х = (х4 — 5z2) + (х3 — 5z). Вынося из
первой скобки множитель х2, а из второй скобки х, получаем
(х4 — 5z2) + (z3 — 5а:) = х2(х2 — 5) 4- х(х2 — 5). Наконец, вынося
за скобку общий множитель х2 — 5, получаем, что х2(х2 — 5) +
+ х(х2 — 5) = (z2 — 5)(z2 + а:), и, наконец, вынося за скобки
множитель х, получим, что
а:4 — 5а:2 + х3 — 5х = (х2 — 5)(z + l)z.
1.1.5.	Метод неопределенных коэффициентов. Суть
этого метода состоит в том, что заранее предполагается вид
§ 1.1. Разложение многочлена на множители
И
множителей — многочленов, на которые разлагается данный
многочлен. Этот метод опирается на следующие утверждения:
1)	два многочлена тождественно равны тогда и только то-
гда, когда равны их коэффициенты при одинаковых степе-
нях X]
2)	любой многочлен третьей степени разлагается в произ-
ведение линейного и квадратного множителей;
3)	любой многочлен четвертой степени разлагается в про-
изведение двух многочленов второй степени.
Пример 6. Разложить на множители многочлен
х3 — 5z2 + 7х — 3.
РЕШЕНИЕ. Будем искать многочлены х — а и 01Х2+0?х+0з
такие, что справедливо тождественное равенство
х3 - 5х2 + 7х — 3 = (х - «)(/?!х2 0?х + /?3).	(1)
Правую часть этого равенства можно записать в виде
0\х3 + (/?2 - а/?1)ж2 + (& -
Приравнивая коэффициенты при одинаковых степенях х в ле-
вой и правой частях равенства (1), получаем систему равенств
для нахождения а, /31, /?2, 0з-
' Л = 1,
02 ~ <*01 = -5,
0з~<*02 = 7,
. а/Зз - 3.
Легко видеть, что этим равенствам удовлетворяют числа
0i = 1, 02 = —2, 0з = 1, а = 3, а это означает, что мно-
гочлен х3 — 5х2 + 7х — 3 разлагается на множители х — 3 и
х2 — 2х 4-1.
1.1.6. Подбор корня многочлена по его старше-
му и свободному коэффициентам. Иногда при разложе-
нии многочлена на множители бывают полезными следующие
утверждения:
12
Алгебраические уравнения и неравенства
1) если многочлен ап +an-iar + - • - + aoa:n, ао / 0, с целыми
коэффициентами имеет корень хо = p/q (где p/q — несокра-
тимая дробь), то р — делитель свободного члена ап, а q —
делитель старшего коэффициента ао;
2) если каким-либо образом подобран корень х = а много-
члена Рп(х) степени п, то многочлен Рп(х) можно представить
в виде Рп(х) = (х — а)/3п-1(ж), где Pn_i(x)— многочлен сте-
пени п — 1.
Многочлен Рп_]_(х) можно найти либо делением многочле-
на Рп(х) на двучлен (о: — а) “столбиком”, либо соответству-
ющей группировкой слагаемых многочлена и выделением из
них множителя х — а , либо методом неопределенных коэффи-
циентов.
ПРИМЕР 7. Разложить на множители многочлен
х4 — Ьх3 + 7х2 — Ьх + 6.
Решение. Поскольку коэффициент при х4 равен 1, то ра-
циональные корни данного многочлена, если они существу-
ют, являются делителями числа 6, т. е. могут быть целыми
числами ±1, ±2, ±3 и ±6. Обозначим данный многочлен че-
рез Р4(х). Так как Р4(1) = 4 и = 23, то числа 1 и -1 не
являются корнями многочлена Р^х). Поскольку 7?4(2) = 0, то
х = 2 является корнем многочлена Р4(х), и, значит, данный
многочлен делится на двучлен х — 2. Поэтому
х4 — 5a:3 + 7 a?2 — Зх 4- 6	х — 2
х4 ~ 2х3 х3 - Зх2 + х - 3
— Зх3 + 7 a:2 — 5a: + 6
— Зх3 + 6a:2
х2 — 5х + 6
х2 — 2х
_ — Зх + 6
— Зх + 6
О
Следовательно, Р4 = (х — 2)(х3 — Зх2 + х — 3). Так как х3 — Зк2 +
+ х - 3 = х\х - 3) + (х - 3) - (х - 3)(о?2 + 1), то х4 — Зх3 +
-|- 7х2 — 5х + 6 = (а: — 2)(а? — 3)(а?2 + 1).
§ 1.1. Разложение многочлена на множители
13
1.1.7.	Метод введения параметра. Иногда при разло-
жении многочлена на множители помогает метод введения па-
раметра. Суть этого метода поясним на следующем примере.
Пример 8. Разложить на множители многочлен
х3- (УЗ+1) z2+ 3.
РЕШЕНИЕ. Рассмотрим многочлен с параметром а
х3 — (а + 1)аг2 + а2,
который при а = д/з превращается в заданный многочлен.
Запишем этот многочлен как квадратный трехчлен относи-
тельно а:
а2 — ах2 + (г3 — х2).
Так как корни этого квадратного относительно а трехчлена
2	2
есть ai = г и ^2 = z — z, то справедливо равенство а —
— ах2 + (а-3 — х2) — (а — х)(а — х2 + х). Следовательно, много-
член х3 — (д/з + 1) х2 + 3 разлагается на множители а/з — х
и д/з — х2 + х, т. е.
х3 — ^д/З + 1) х2 + 3 = (х — д/з) (х2 — х — д/з) •
1.1.8.	Метод введения новой неизвестной. В неко-
торых случаях путем замены выражения f(x), входящего в
многочлен Рп(х), через у можно получить многочлен относи-
тельно у, который уже легко разложить на множители. Затем
после замены у на /(аг) получаем разложение на множители
многочлена Рп(х).
Пример 9. Разложить на множители многочлен
х(х + l)(z + 2)(z + 3) — 15.
РЕШЕНИЕ. Преобразуем данный многочлен следующим
образом:
х(х + l)(ar + 2)(аг + 3) — 15 =	+ 3)][(z + 1)(х 4- 2)] — 15 =
= (х2 + 3z)(z2 + За-+ 2) - 15.
14
Алгебраические уравнения и неравенства
Обозначим х2 + За: через у. Тогда имеем
у{у + 2) - 15 = у2 + 2у - 15 = у2 + 2у + 1 - 16 =
= (у + I)2 - 16 = (у + 1 + 4)(у + 1 - 4) = (у + 5)(г/ - 3).
Поэтому
х(х + 1)(г + 2)(х + 3) - 15 = (х2 + 3х + 5) (а?2 + За: - 3).
Пример 10. Разложить на множители многочлен
(о:-4)4 + (а: + 2)4.
х — 4 4- я -Ь 2
Решение. Обозначим ---------------- = х — 1 через у.
Тогда (х - 4)4 + (х + 2)4 = (у - З)4 + (у + З)4 =
= у4 - 12г/3 + 54г/2 - 108г/ + 81 + у4 + 12г/3 + 54г/2 +
+ 108г/ + 81 = 2г/4 + 108г/2 + 162 = 2(г/4 + 54г/2 + 81) =
= 2[(у2 + 27)2 - 648] = 2 (у2 + 27 - Уб48^ [у2 + 27 + Уб48^ =
= 2 ((а: - I)2 + 27 - Уб48^ ((а: - I)2 + 27 + Уб48) = 2^х2 -
- 2а: + 28 - I81/2) (*2 - 2а: + 28 + 18л/г) .
1.1.9.	Комбинирование различных методов. Часто
при разложении многочлена на множители приходится при-
менять последовательно несколько из рассмотренных выше
методов.
Пример 11. Разложить на множители многочлен
х4 — За:2 + 4а: — 3.
РЕШЕНИЕ. Применяя группировку, перепишем многочлен
в виде
а:4 — За:2 4- 4х — 3 = (а:4 — 2а:2) — (а:2 — 4х + 3).
Применяя к первой скобке метод выделения полного квадрата,
имеем
х4 - За:2 + 4а:- 3 = (х4 - 2-1-х2 + I2) - (а:2 -4а: + 4).
§ 1.2. Простейшие способы
15
Применяя формулу полного квадрата, можно теперь запи-
сать, что
х4 — За:2 4- 4х — 3 = (ж2 — I)2 — (х — 2)2.
Наконец, применяя формулу разности квадратов, получим,
что
х4 — За?2 + 4х — 3 = (х2 — 1 + х — 2)(х2 — 1 — х 4- 2) =
= (х2 4- х — 3)(ж2 — х 4-1).
§ 1.2.	Простейшие способы решения
алгебраических уравнений
В случае п = 1 уравнение (I) обычно записывается в виде
ах 4- Ь = 0, а 0,	(1)
и называется уравнением первой степени. Уравнение (1) име-
ет единственный корень xq = —Ь/а.
В случае п — 2 уравнение (I) обычно записывается в виде
ах2 +Ьх + с, а ф 0,	(2)
и называется квадратным уравнением.
Хорошо известно, что если дискриминант D = Ь2 — 4ас
квадратного трехчлена ах2 4- Ьх 4- с:
а)	отрицателен, то уравнение (2) не имеет корней;
б)	положителен, то уравнение (2) имеет два различных
корня
— 6 4- л/62 — 4ас	—Ь — у/b2 — 4ас . .
«1 = ------7------, х2 = --------------;	(3)
2а	2а
в)	равен нулю, то уравнение (2) имеет единственный ко-
b „
рень хо =----. Иногда в этом случае говорят, что уравне-
2а	ь
ние (2) имеет два совпадающих корнях х\ = х? = —. Легко
2а
видеть, что они также отыскиваются по формулам (3).
16
Алгебраические уравнения и неравенства
При п — 3 и п — 4 существуют формулы для нахожде-
ния корней алгебраических уравнений третьей и четвертой
степеней, однако в силу их громоздкости они применяются
редко.
В общем случае не существует формул для нахождения
корней любого алгебраического уравнения более высокой сте-
пени, чем четыре. Тем не менее достаточно часто приходится
решать алгебраические уравнения степени большей, чем два.
Если многочлен записан в виде произведения много-
членов первой и второй степени, то уравнение (1) равносиль-
но совокупности соответствующих уравнений первой и второй
степени, формулы решения которых приведены выше.
Пример 1. Решить уравнение
(х - 2)(z2 + Зх + 2) = 0.
РЕШЕНИЕ. Данное уравнение равносильно совокупности
уравнений х — 2 = 0 и х2 + Зх + 2 = 0. Решение первого
из этих уравнений есть Х{ = 2. Решения второго уравнения
есть Х2 = —2, ж.з = —1. Следовательно, решения исходного
уравнения есть Ху = —2, х? = — 1 и х3 = 2.
Ответ: xi = -2, х2 = -1, х3 = 2.
Если многочлен Рп(х) имеет степень большую, чем 2, и
не разложен на множители первой и второй степени, то его
сначала надо каким-либо способом разложить на такие мно-
жители, а затем заменить уравнение (I) равносильной ему со-
вокупностью уравнений.
Приведем решения некоторых алгебраических уравнений
Рп(х) = 0, основанные на разложении его левой части —
многочлена Рп(х) — на множители методами, изложенными
в предыдущем параграфе.
Пример 2. Решить уравнение
х4 - 2х2 - 12ж — 8 = 0.	(4)
Решение. Поскольку
х4 — 2х2 — 12х — 8 = х4 + 2х2 + 1 — 4а:2 — 12ж — 9 =
= (х2 + I)2 - (2х + З)2 = (ж2 + 1 - 2х - 3)(ж2 + 1 + 2х + 3),
§ 1.2. Простейшие способы
17
то данное уравнение равносильно совокупности двух уравне-
ний
х2 — 2х — 2 = 0 и z2 + 2z + 4 = 0.
Второе уравнение этой совокупности решений не имеет, ре-
шения первого есть xi = 1 + а/З и Х2 = 1 — а/З. Эти числа и
являются решениями уравнения (4).
Ответ: хг = 1 + х/з, ж2 = 1 - а/з.
Пример 3. Решить уравнение
х3 + Зх + 5а/2 = 0.
Решение. Будем искать многочлены х + а и /?iz24-/?2^ + /?3
такие, что справедливо тождественное равенство
(х + a)(0i х2 + 02х 4- /?3) = х3 + Зх + 5у/2.
Тогда, приравнивая коэффициенты при одинаковых степе-
нях неизвестного х в левой и правой частях этого равенства,
имеем систему равенств
= 1,
+ a/?i = 0,
/?2а + /?з = 3,
, а/33 = 5а/2.
Этой системе равенств удовлетворяют числа 01 = 1, 02 =
= — а/2, 0з = 5, а — а/2. Поэтому справедливо разложение
многочлена на множители:
х3 + Зх + 5а/2 =
откуда следует, что исходное уравнение равносильно совокуп-
ности уравнений
х + а/2 = 0 и х2 — а/2х 4-5 = 0.
Эта совокупность имеет единственное решение х = — а/2.
Ответ: х = -а/2.
1<S
Алгебраические уравнения и неравенства
Пример 4. Решить уравнение
х3 + За:2 — 2х — 2 = 0.
РЕШЕНИЕ. Поскольку коэффициенты многочлена — целые
числа и старший коэффициент равен 1, то рациональные кор-
ни многочлена, если они есть, могут быть только среди чи-
сел ±1 и ±2. Легко проверить, что х — 1 есть корень многочле-
на. Значит, данный многочлен делится на х — 1. Произведем
деление многочлена х3 + За:2 — 2а: — 2 на двучлен х — 1 “стол-
биком” :
х3 4- За:2 - 2а: - 2 х - 1
~х3 ~ z2 х2 + 4z + 2
_4z2 -2а:-2
4z2 — 4z
_2х - 2
2х - 2
0
Следовательно, х3 + За:2 — 2х — 2 = (х — 1)(х2 4- 4х 4- 2),
и исходное уравнение равносильно совокупности уравнений
х — 1 = 0 и я?2 4- 4а: 4- 2 = 0, откуда получаем, что решения
исходного уравнения есть х} = 1, ж2 = —2 4-д/2, х3 = —2 —д/2-
Ответ: xi = 1, х2 = -2 4- у/2, х3 = -2 - у/2.
Пример 5. Решить уравнение
х4 - 2>/За:2 - х 4- 3 - д/З = 0.	(5)
Решение. Обозначим Уз = а и рассмотрим уравнение с
параметром: х4 — 2ах2 — х 4- а2 — а = 0.
Рассматривая это уравнение как квадратное относитель-
но а, разложим его левую часть на множители
х4 — 2ах2 — х + а2 — а = (а — х2 + х)(а — х2 — х — 1).
Значит, уравнение (5) равносильно совокупности уравнений
х2 — х — а/з = 0 и х2 4- х 4- 1 — а/З = 0.
§ 1.3. Симметрические и возвратные уравнения
19
Множество решений первого уравнения есть
1 + \/1 + 4л/з	1 - х/1 + 4л/3
Xi = ---------------- и х2 = -----------------
Множество решений второго уравнения есть
-1 + v4\/3 - 3	-1 - д/4л/3- 3
1'3 = --------------- И Х4 - -----------------------
Следовательно, исходное уравнение имеет четыре корня:
Z1, х2, хз и z4.	_________ _______________________
1 + а/1 + 4^3	1 - х/Г+ 4^3
Ответ: хг =--------------------, z2 = -----------------,
J 2 J 2
-1 +	- 3	-1 -	- 3
Е.З = -----=-----, Х4 - ----------------.
§ 1.3. Симметрические и возвратные
уравнения
1.3.1. Симметрические уравнения третьей степе-
ни. Уравнения вида
ах3 4- Ьх2 + Ьх + а = 0, а ф 0,	(1)
называются симметрическими уравнениями третьей степе-
ни. Поскольку ах3 4- Ьх2 + Ьх + а = а(х3 + 1) + bx(x 4- 1) =
= а(х + 1)(х2 — х 4- 1) + Ьх(х 4- 1) = (х 4- 1)(аг2 4- (6 — а)х 4- «),
то уравнение (1) равносильно совокупности уравнений
х 4- 1 = 0 и ах2 4- (Ь — а)х 4- а = О,
решить которую не представляет труда.
Пример 1. Решить уравнение
Зт3 4-4г2 + 4т 4-3 = 0.	(2)
Решение. Уравнение (2) является симметрическим урав-
20
Алгебраические уравнения и неравенства
нением третьей степени. Поскольку Зг3 4- 4г2 4- 4х 4- 3 =
= З(т34-1)4-4х(х4-1) = (т4-1)(3г2 —3х4-34-4х) = (т4-1)(3т24-
4-14-3), то уравнение (2) равносильно совокупности уравнений
х 4- 1 = 0 и Зх2 4- х 4- 3 = 0.
Решение первого из этих уравнений есть х = — 1, второе урав-
нение решений не имеет.
Ответ: х = -1.
1.3.2. Симметрические уравнения четвертой сте-
пени. Уравнения вида
ах4 4- Ьхэ 4- ст2 4- Ьх 4- а = 0, а ф 0,	(3)
называются симметрическими уравнениями четвертой сте-
пени.
Поскольку х = 0 не является корнем уравнения (3), то,
разделив обе части уравнения (3) на х2, получим уравнение,
равносильное исходному (3):
n а	, b
ах2 4—+ Ьх 4---------h с = 0.
х1	х
(4)
Перепишем уравнение (4) в виде
4- 6 | х 4- — ) 4- с = 0.
\ х)
1
В этом уравнении сделаем замену х 4— = у, тогда получим
х
квадратное уравнение
ау2 4- by 4- с — 2а = 0.	(5)
Если уравнение (5) имеет два корня у\ и у?, то исходное
уравнение равносильно совокупности уравнений
т2 — хух 4-1 = 0 и х2 — ху2 4-1 = 0.
Если же уравнение (5) имеет один корень у0, то исходное
уравнение равносильно уравнению х2 — уох 4- 1 = 0,-
§ 1.3. Симметрические и возвратные уравнения
21
Наконец, если уравнение (5) не имеет корней, то и исходное
уравнение также не имеет корней.
Пример 2. Решить уравнение
ж4 — 5х3 4- 8х1 2 3 — 5х 4- 1 = 0.	(6)
Решение. Данное уравнение является симметрическим
уравнением четвертой степени. Так как х = 0 не является
его корнем, то, разделив уравнение (6) на х2, получим равно-
сильное ему уравнение
7	1
х'1 - 5х 4- 8--1—7 = 0.	(7)
х хл
Сгруппировав слагаемые, перепишем уравнение (7) в виде
, 1	(	1\
х2 4- — — 51x4- — I 4-8 = 0
х*	\	х)
или в виде
( х 4— ) — 5x4— 4-6 = 0.
\	х /	\ х /
Положив х 4- — = у, получим уравнение
х
у2 - 5у + 6 = 0,
имеющее два корня у\ = 2 и у2 = 3. Следовательно, исходное
уравнение равносильно совокупности уравнений
1	1	„
х 4— = 2 и х 4— =3.
х	х
Решение первого уравнения этой совокупности есть ягi = 1,
3 + 75	3-75
а решения второго есть х2 = —-— и хз = —-—.
Следовательно, исходное уравнение имеет три корня:
Xi, х2 И Хз.
3 4-75	3-75
Ответ: xi = 1, х2 = —-—, х3 = —-—.
Алгебраические уравнения и неравенства
1.3.3. Возвратные уравнения. Уравнения вида
a0z2n+1 + aix2n 4- агх2п 1 4- • • • 4- а.пхп+1 4“
4- Хапхп 4- АЧ.-тж”-1 +    4- а0А2п+1 = 0, U
аох
2п 1 4- Я2Т2п 2 4-  •  4- an_izn + 1 4- м" 4-	...
+ Хап_-[Хп 1 4- А2ап^2Хп 2 4- • • • 4- Апао = 0,
где А — фиксированное число и ао ф 0 называются возврат-
ными уравнениями.
При А = 1 уравнения (8) и (9) являются симметрически-
ми уравнениями соответственно нечетной и четной степеней.
Возвратное уравнение нечетной степени (8) всегда имеет ко-
рень х = —А, поскольку это уравнение можно переписать в
виде
Z7„f-r2n + 1
2n —1 । \2п — 1
*г Л
и при х = —А выражения в каждой скобке обращаются в нуль.
Выделив множитель х 4- А из каждой скобки, можно доказать,
что уравнение (8) равносильно совокупности уравнений: урав-
нения х 4- А = 0 и некоторого возвратного уравнения четной
степени.
Для решения возвратного уравнения четной степени по-
ступают следующим образом.
Поскольку х = 0 не есть
делив уравнение (9) на хп и
уравнение
корень уравнения (9), то, раз-
сгруппировав члены, получим
ПО
А\п\	/
-	4-01 г
х) 1	\
/А
+ I ~
\ х
( *
+ Яп-1 I х 4—
\ X
(Ю)
= 0.
Положим г 4— = и, тогда имеем
х
/А\2
г2 + /	= u2 — 2А,
3	,, ( Х\ 3 ох
аг 4- — ) = г 4— ) — ЗА | г 4— ) = н3 — ЗАн,
\х /	\ х )	\ х
§ 1.3. Симметрические и возвратные уравнения
23
/ \ \ 4	/	\ \ 4	/	\2\
г4+( —) =(z4-— | — 4А ( z2 + — ) — 6А2 =w4— 4Aw2+2A2
\х }	\	х J	\	х )
и т. д., и уравнение (10) степени 2п относительно х запи-
шем в виде алгебраического уравнения степени п относитель-
но и. Таким образом, мы от уравнения степени 2п перешли к
уравнению степени п. Если теперь удастся решить получен-
ное уравнение степени п, то найдутся все корни уравнения (9).
Пример 3. Решить уравнение
2т4 4- Зх3 — Зх2 — Зх + 2 = 0.
(И)
РЕШЕНИЕ. Уравнение (11) является возвратным уравнени-
ем четвертой степени (А = — 1). Поскольку х — 0 не является
корнем этого уравнения, то оно равносильно уравнению
,	3	2
2х2 + Зх - 3---+ — = 0.
X X1
Последнее уравнение перепишем в виде
2(r2 + -^)4-3(z — — ) — 3 = 0
\ х1)	\	х)
или в виде
(	1\
4- 3 г--1—3 = 0.
\	х /
(12)
Положив х — — = у, запишем уравнение (12) в виде
х
2у2 4- Зу 4- 1 = 0. Корни этого уравнения есть у\ = — 1 и
1/2 = -1/2. Следовательно, исходное уравнение (11) равно-
сильно совокупности уравнений
Решения первого уравнения этой совокупности есть
-14-75	— 1 — >/5
Xj = --------- и х? = -----------, а решения второго
24
Алгебраические уравнения и неравенства
-1 + У17	_1-У17
хз = -------- и Х4 = ---------. Следовательно, эти че-
4	4
тыре корня и являются решениями исходного уравнения.
-1 + V5 -1-х/5	-1 + УП
Ответ: xi = -------, т2 = --------, г3 = -------,
-1 - V17
z4=—г—
Пример 4. Решить уравнение
х5 + 3т4 - х3 + 2х2 —24т -32 = 0.	(13)
Решение. Уравнение (13) является возвратным уравне-
нием степени 5 (А = — 2), так как его можно записать в
виде
х5 + Зх4 - х3 - т2(—2) + Зх(—2)3 + (—2)5 = 0.
Так как по сказанному выше х — 2 является его корнем, то,
сгруппировав члены уравнения, перепишем его в виде
(т5 - 32) + Зт(т3 - 8) - х2(х - 2) = 0.	(14)
Применяя формулы разности пятых и третьих степеней и вы-
делив множитель (х — 2), перепишем уравнение (14) в виде
(т-2)(Ж4 + 22:3 + 4т2 + 8т+16) +
4- Зх(х — 2)(х2 4- 2х + 4) — х2(х — 2) = 0.
Уравнение (15) равносильно совокупности уравнений
х - 2 = 0,
х4 4- 2z3 4- 4z2 4- 8х + 16 4- 3x(x2-f-2x+4) — х2 — 0.	(16)
Уравнение (16) запишем в виде
х4 4- 5г3 4- 9т2 4- 20т + 16 = 0.	(17)
Уравнение (17) является возвратным уравнением четвертой
степени (А = 4). В самом деле, уравнение (17) можно записать
так:
х4 4- 5г3 4- 9х2 4- 5-г-4 4- 42 = 0.	(18)
§ 1.3. Симметрические и возвратные уравнения
25
Так как х = 0 не является корнем уравнения (18), то, разделив
9
его на х и сгруппировав члены, получим уравнение
42 \	/	4 \
X2 + — I + 5 X + - ) + 9 = 0,
ХлJ	\	X /
(19)
равносильное уравнению (18).
• 4
Положим х 4— = у, тогда уравнение (19) перепишется в
х
виде у2 — 8 + 5у + 9 = 0.
- 5 + /21
Решения последнего уравнения есть y-L = ----------- и
-5 - /21
у2 = --------. Следовательно, уравнение (16) в свою оче-
редь равносильно совокупности уравнений
Первое из этих уравнений решений не имеет. Решения второго
уравнения есть
-5 -/21 +/10/21 - 18
-5 - /21 - /10/21- 18
Итак, исходное уравнение (13) имеет три корня: Xi, г2 и хз.
-5 - /21 + /10/21-18
Ответ: 24 = 2, х2 =----------------,
_ -5 - /21-/10/21- 18
1.3.4. Уравнения четвертой степени с дополни-
тельными условиями на коэффициенты. Рассмотрим
уравнение четвертой степени
ах4 + Ьх3 + сх2 + dx + f = 0,
(20)
26
Алгебраические уравнения и неравенства
d2a
где а^О, 6^0, с/^Ои / =
tA
Так как как х = 0 не есть корень этого уравнения, то,
разделив его на х2, получим уравнение
2 f	d
ах2 4—, 4- 6т 4---h с = 0.
хА	х
d
Обозначив ох 4— = у и учитывая, что
X
7 f	ci	(**> *>	d \	а	( d\	«» •
ах2 +	=	75	6 V	+	-=•	=	т=	(Ьх + -	—	2bd	=
xz	tr	\	xl)	bl	\ x )
= J(y2 - 2M),
tr
перепишем уравнение в виде
а >	d
+у + с - 2а— = 0.
о	о
После нахождения решений этого уравнения мы найдем реше-
ния исходного уравнения.
ПРИМЕР 5. Решить уравнение
х4 + 2z3 - 11т2 4- 4х 4- 4 = 0.	(21)
Решение. В данном уравнении а = 1, b = 2, d — 4,
ad2
f = 4. Поскольку а ф 0, b 0, d ф 0, f = ——, то это
о2
уравнение рассматриваемого типа. Поскольку х = 0 не явля-
ется корнем уравнения (21), то, разделив это уравнение на х2
( 2V
и сгруппировав его члены, получим уравнение г 4—	4-
\ х /
/	2\
4-2 г 4— I — 15 = 0, равносильное уравнению (21). Так как
\ х)
решения уравнения у2 4- 2у — 15 = 0 есть yi = —5 и у^ = 3, то
исходное уравнение (21) равносильно совокупности уравнений
2	2
х 4— = 3 и х 4— = —5,
X	X
§ 1.4. Некоторые искусственные способы
27
решения которой есть zi = 2, х2 = 1, хз
-5 - V17
Хл — --------
2
Ответ: хг = 2, х2 = 1, <з =
-5 + VI7
----п---- *4 =
§ 1.4. Некоторые искусственные способы
решения алгебраических уравнений
В этом параграфе будут приведены некоторые нестандарт-
ные способы решения алгебраических уравнений.
1.4.1. Умножение уравнения на функцию. Иногда
решение алгебраического уравнения существенно облегчает-
ся, если умножить обе его части на некоторую функцию —
многочлен от неизвестной. При этом надо помнить, что воз-
можно появление лишних корней — корней многочлена, на
который умножали уравнение. Поэтому надо либо умножать
на многочлен, не имеющий корней, и получать равносильное
уравнение, либо умножать на многочлен, имеющий корни, и
тогда каждый из таких корней надо обязательно подставить
в исходное уравнение и установить, является ли это число его
корнем.
Пример 1. Решить уравнение
г8 — х6 + х4 — х2 + 1 = 0.	(1)
РЕШЕНИЕ. Умножив обе части уравнения на многочлен
х2 + 1, не имеющий корней, получим уравнение
(х2 + 1)(г8 - х6 + х4 - х2 + 1) = 0,	(2)
равносильное уравнению (1). Уравнение (2) можно записать
в виде
х10 + 1 = 0.	(3)
Ясно, что уравнение (3) не имеет действительных корней, по-
этому и уравнение (1) их не имеет.
Ответ: нет решений.
28
Алгебраические уравнения и неравенства
Пример 2. Решить уравнение
6г3 - х2 - 20г + 12 = 0.	(4)
РЕШЕНИЕ. Умножив обе части этого уравнения на много-
член х 4- 1/2 , получим уравнение
41
6г4 + 2г3 - — х2 + 2х + 6 = 0,	(5)
являющееся следствием уравнения (4), так как уравнение (5)
имеет корень х = —1/2, не являющийся корнем уравнения (4).
Уравнение (5) есть симметрическое уравнение четвертой
степени. Поскольку х — 0 не является корнем уравнения (5),
то, разделив обе его части на 2г2 и перегруппировав его чле-
ны, получим уравнение
/	1 \	(	1 \	41
3 И + -у + *+ - - У =°-	6
\	х2 J	\	xj	4	.
равносильное уравнению (5). Обозначив у = z + —, перепишем
х
уравнение (6) в виде
„	65
Зу2 + у-Т = 0.	(7)
Уравнение (7) имеет два корня: yi — —5/2 и у2 = 13/6. По-
этому уравнение (6) равносильно совокупности уравнений
1	13	15
z + - = — И х + - = --.
х	6	х 2
Решив каждое из этих уравнений, найдем четыре корня урав-
нения (6), а тем самым и уравнения (5):
2	3	1
*1 = j, х2 = х3 = -2, хА = --.
Так как корень х^ = — 1/2 является посторонним для урав-
нения (4), то отсюда получаем, что уравнение (4) имеет три
корня: xi, х2, хз.
Ответ: хх = 2/3, х2 = 3/2, хз = -2.
§ 1.4. Некоторые искусственные способы
29
Замечание. Прием, рассмотренный в примере 2, можно
применять к уравнениям, которые после умножения на неко-
торый многочлен превращаются в возвратные или симметри-
ческие уравнения.
Например, таким образом можно решать уравнения вида
аг3 4- Ьх2 + сх 4- d = 0,	(8)
где а ф 0, d 0, с ф а, а(с — а) = d(b — d). В самом деле,
а
умножив это уравнение на многочлен х 4- получим симме-
а
трическое уравнение четвертой степени, среди корней кото-
а
рого содержится и корень х = —Отметим, что этот корень
а
может быть посторонним корнем для уравнения (8).
1.4.2. Угадывание корня уравнения. Иногда внеш-
ний вид уравнения подсказывает, какое число является корнем
уравнения.
Пример 3. Решить уравнение
х3 4-Зя - 123 - 312 = 0.
Решение. Из внешнего вида этого уравнения очевидно,
что х = 12 есть его корень. Для нахождения остальных корней
преобразуем многочлен
х3 + Зх - (123 4- 3-12) = (х3 - 123) 4- 3(х - 12) =
= (г - 12)(х2 4- 12г 4- 122 4- 3) = (х - 12)(х2 4- 12г 4- 147).
Так как многочлен х2 4- 12г 4-147 не имеет корней, то исходное
уравнение имеет единственный корень х = 12.
Ответ: х = 12.
Пример 4. Решить уравнение
х3 — Зг = а3 4- Дт,	(9)
ал
где а — отличное от нуля число.
Решение. Так как
3	1	(	1Vo21o1	( 1V Q /	1\
а 4~ —— I а 4- — ) — За--За - —у — I а 4- — 1 — 3 I а 4- —1 
а3 \ а ) а а* \ а )	\ а)
30
Алгебраические уравнения и неравенства
1
то отсюда заключаем, что х\ = а 4- - есть один из корней
а
исходного уравнения. Разделив многочлен х3 — Зх — а3-= на
аЛ
1
двучлен х — а---, получим, что
а
х3 — Зх — f а3 4—х
\ аЛ
х —
т. е. остальные корни уравнения (9) совпадают со всеми кор-
нями уравнения
/	1 \	/	1 \2
х2 4- х ( а 4— I 4- ( а 4— ) —3 = 0.	(10)
у	а]	\	а/
Дискриминант квадратного уравнения (10) есть
a)	D > 0 быть не может.
б)	D = 0 лишь при а = 1 и при а — —1.
Итак, уравнение (10) не имеет корней при а2 ф 1, имеет
единственный корень х = — 1 при а = 1 и единственный ко-
рень х = 1 при а = — 1. Добавляя еще корень х = а + 1/а,
находим все корни исходного уравнения.
Ответ: при а = 1 два корня х\ = 2, z2 = —1;
при а = —1 два корня 24 = —2, х2 = 1;
при а2 ф 1 и а ф 0 один корень = а 4- 1/а.
Пример 5. Решить уравнение
х(х2 — а) = т(х2 4- 2тх 4- «),	(П)
где а и т — данные числа.
§ 1.4. Некоторые искусственные способы
31
Решение. Из внешнего вида уравнения очевидно, что
х = —т является корнем.
Для нахождения остальных корней уравнения перенесем
все его члены в одну сторону и разложим полученный много-
член на множители. Тогда получим, что уравнение (11) мож-
но записать в виде
(х + m)(z2 — 2тх — а) = 0.
(12)
Уравнение (12) равносильно совокупности уравнений
х 4- т — 0 и х2 — 2тх — а = 0.	(13)
Первое уравнение совокупности (13) имеет единственный
корень = — т, а второе уравнение имеет решения в зависи-
мости от дискриминанта:
а)	если т2 4- а > 0, то будет два корня,
б)	если т2 + а = 0, то будет один корень,
в)	если т2 4- а < 0, то корней нет.
Отсюда легко находятся корни уравнения (11).
Ответ: при т2 4- а	<	0	х^	=	— т;
при т2 + а	=	0	Xi	—	—т, х? — т;
при т2 4- а	>	0	х^	=	—т, х% = т —	\/т2 4- а,
г3	.=	т 4- у/т2 + а.
Пример 6. Решить уравнение
х(х	+	1)	+	(я	+	1)(г	4-	2) 4- (х	4-	2)(а: 4-	3) 4- (х 4-	3)(г + 4)	+
4-	(х	4-	4)(г	4-	5) 4- (г	4-	5)(г 4-	6) 4- (я 4-	6)(г 4- 7)	4-
+	(г	+	7)(х	4-	8) 4- (х	4-	8)(г 4-	9) 4- (х 4-	9)(г 4- 10) =
=	1-2	4-	2-3 4-	3-4 4- 4-5	4- 5-6 4- 6-7 + 7-8 4- 8-9 4- 9-10.
Решение. Легко заметить, что xi = 0 и х? = —10 являют-
ся решениями этого уравнения. После раскрытия скобок это
уравнение перепишется как квадратное. А это означает, что
оно может иметь не более двух корней. Так как два корня
этого уравнения найдены, то тем самым оно и решено.
Ответ: ху = 0, г2 = -10.
32
Алгебраические уравнения и неравенства
1.4.3. Использование симметричности уравнения.
Иногда внешний вид уравнения — некоторая его симметрич-
ность — подсказывает способ решения уравнения.
Пример 7. Решить уравнение
(ж2 — х 4- I)3 х2(х — I)2
(5-V5 + 1)3	5(х/5-1)2'
(И)
Решение. Очевидно, что внешний вид уравнения подска-
зывает, что один из корней уравнения (14) есть х^ = з/б. Од-
нако для нахождения остальных корней этого уравнения при-
ем, предложенный в предыдущем пункте (разложение много-
члена на множители), здесь мало поможет. Перепишем урав-
нение (14) в несколько ином виде.
Поскольку справедливы тождественные равенства
то уравнение (14) можно переписать так:
(5-х/5 + 1)3	5(х/5-1)2
(15)
Теперь очевидно, что если хо — корень уравнения (15), то
Xi = 1 — го также корень уравнения (15), поскольку
zi----
\	2/
Покажем, что если Xi, rj 0, х\ 1, есть корень урав-
/ ч	1
нения (14), то xi = — также есть корень этого уравнения.
*1
§ 1.4. Некоторые искусственные способы
33
Действительно, так как
м_______L Л3
(х% ~х2 + I)3	\,х2	+ /
x22(x2-iy ~ _l_/j__\2
2 \ I
- U ~ Zi + ж1)3 _ (ж1 — до +1)3
Х1
то отсюда и вытекает это утверждение.
Итак, если Xj, х± У 0, Xi У 1, — корень уравнения (14), то
оно имеет еще корни
1 111
— , 1-Т1, ------, 1-----, ----
Z1	1-2-1	2Г1	1 -
т. е. уравнение (14) имеет корни
Поскольку уравнение (14) есть алгебраическое уравнение ше-
стой степени, то оно имеет не более шести корней. Таким обра-
зом, мы нашли все корни уравнения (14).
Ответ: х\ = з/5, х2 =
_ , 1 1
2:5-1	/т, х6 —	1 •
т-75
1	г	1
—Хя = 1 — 3/5, Х4 = -----------------7=,
у/5	1 — у5
1.4.4. Использование суперпозиции функций. Ино-
гда можно найти корень уравнения, если заметить, что функ-
ция, находящаяся в одной из частей уравнения, является су-
перпозицией некоторых более простых функций.
Пример 8. Решить уравнение
(ж2 4- 2х - 5)2 + 2(г:2 + 2х - 5) - 5 = х.
(16)
34
Алгебраические уравнения и неравенства
Решение. Обозначим /(г) = х2 4- 2х — 5, тогда уравне-
ние (16) можно переписать в виде f (/(г)) = х. Теперь оче-
видно, что если хо — корень уравнения /(г) = х, то г0 и
корень уравнения f (/(г)) = х. Корни уравнения х2 4- 2г - 5 =
-14->/21	-1 - У21 „
= х есть xi = -------- и х2 = --------. Следовательно, и
уравнение (16) имеет эти корни. Переписав уравнение (16) в
виде
х4 + 4г3 —4г2 - 17г + 10 = 0	(17)
и разделив многочлен х4 4- 4г3 - 4х2 - 17г 4- 10 на многочлен
(г —Г1)(х —х2), получим, что уравнение (17) можно записать в
виде (х24-х — 5)(г24-3х — 2) = 0. Следовательно, корнями урав-
нения (16) наряду с 11 и г2 являются также корни уравнения
17
— И Х4 —
х2 4- Зг — 2 = 0, т. е. числа хз =
Ответ: хг =
2
2
'21
—, х2 = ----------, Хз =
-3 - V17
г4 =
-3 - >/17
2	'
-3 4- л/17
2
2
2
1.4.5. Исследование уравнения на промежутках
действительной оси. Иногда решения уравнения можно
найти, исследуя его на разных числовых промежутках.
Пример 9. Решить уравнение
2г9- х5 + х -2 = 0.	(18)
Решение. Перепишем уравнение в виде 2(z9 — 1) —
— х(х4 — 1) = 0 или, используя формулу разности
ап - Ьп = (а - 6)(ап-1 + ап~2Ь + • • • 4- аб""2 4- б”'1),
в виде
(г - 1)(2х8 4- 2г7 4- 2х6 4- 2г5 4- х4 4- г3 4- х2 4- х 4- 2) = 0.
Отсюда видно, что один из корней данного уравнения есть
х = 1. Докажем, что уравнение
2г8 4- 2г7 4- 2х6 4- 2х5 4- х4 4- г3 4- г2 4- г 4- 2 = 0	(19)
§ 1.5. Решение алгебраических неравенств
35
решений не имеет.
Разобьем числовую ось на промежутки (—оо; -1],(-1;0]и
(0; Too).
Для любого х из промежутка (0;4-оо) имеем, что левая
часть уравнения (19) положительна, поэтому на этом проме-
жутке уравнение решений не имеет.
Поскольку
2х& + 2r7 + 2z6 + 2г5 + х4 + х3 Т х2 Т х Т 2 =
= 2г8 + 2r6(r + 1) + 2r4(r + 1) +
Т х2(х + 1) + (г + 1) + (1 - г4),
то для любого х из промежутка (—1; 0] этот многочлен по-
ложителен. Это означает, что на промежутке (— 1; 0] уравне-
ние (19) также не имеет решений.
Поскольку
2г8 + 2г7 + 2г6 Т 2г5 Т х4 + х3 + х2 Т х Т 2 =
= 2г7(х + 1) + 2r5(r Т 1) Т х3(х + 1) + х(х + 1) 4- 2,
то для любого х из промежутка (—оо; —1] этот многочлен по-
ложителен. Следовательно, и на промежутке (—оо;—1] урав-
нение (19) не имеет решений.
Итак, данное уравнение (19) имеет единственное решение
х - 1.
Ответ: х = 1.
§ 1.5.	Решение алгебраических неравенств
1.5.1.	Простейшие способы решения алгебраиче-
ских неравенств. Так как, умножая неравенство (III)
на ( — 1), его можно привести к виду (II), а умножая неравен-
ство (II) на (—1), его можно привести к виду (III), то дальше
будем считать, что в неравенствах (II) и (III) положителен
коэффициент при старшем члене, т. е. что а о > 0.
Таким образом, в этом пункте рассматриваются только
неравенства вида
аохп + air”-1 Т •  • Т ап > 0	(1)
36
Алгебраические уравнения и неравенства
и
аохп 4- aixn 1 4- • • • 4- ап < 0,	(2)
где а0 > О.
В случае п = 1 неравенства (1) и (2) обычно записывают
в виде
ах + Ь > 0, а > 0,	(3)
ах + Ь < 0, а > 0,	(4)
и называют неравенствами первой степени.
Множество решений неравенства (3) есть промежуток
( b	\
— ;4-эс , множество решении неравенства (4) есть проме-
\ a	J
(	ъ\
жуток — оо; ).
\	а /
В случае п = 2 неравенства (1) и (2) обычно записывают
в виде
ах2 4- Ьх 4- с > 0, а > 0,	(5)
ах2 4- Ьх 4- с < 0, а > 0,	(6)
и называют квадратными неравенствами.
Решения неравенств (5) и (6) зависят от знака дискрими-
нанта D = Ь2 — 4ас квадратного трехчлена ах2 4- Ьх 4- с и
приведены в таблице.
В случае п 3 многочлен (IV) надо сначала разложить
на множители и затем либо заменить неравенство равносиль-
ной ему совокупностью систем неравенств, либо применить
изложенный ниже метод интервалов.
Отметим, что при разложении на множители, конечно,
можно пользоваться всеми теми же методами, которые бы-
ли изложены при решении уравнений.
Пример 1. Решить неравенство
х3 - 3z2 4-Зг - 2 > 0.	(7)
Решение. Разложим методом группировки на множители
многочлен, находящийся в левой части неравенства
х3 — Зг2 4- Зх — 2 = х2(х — 2) — х(х — 2) 4- (х — 2) =
= (а: — 2)(т2 — х 4- 1).
§ 1.5. Решение алгебраических неравенств
37
Таблица
Неравенство	Дискриминант D и корни	Множество решений и график квадратного трехчлена ах2 4- Ьх 4- с	
аг2 + Ьх 4- с > 0, а > 0	Л V I н о кэ - 		А|	/{ —оо<г<з?1 }и / U{r2<r<+oo} ЛнИИИИИИИ') *^Т2	X
	0 = 0, го = Х1 = Ь = Х2 = - — 2а	1 У 1 го	. 1 / {-оо<г<г0}и / U{r0<r< + <x>) 0 X
	D < 0, корней нет		/ {-<Х><Г<+оо} 0	X
ах2 4- Ьх + с < 0, а > 0	D > 0, а?1 < Х2		Г/<< /11 <1<Х2 —> *^Х2 X
	0 = 0, Го = Z1 = Ь = Х2 = - — 2а	XQ	/ решений нет 0	х
	D < 0		1 решений нет 0	х
Тогда неравенство (7) можно переписать в виде
(х — 2')(х2 - х + 1) > 0.
(8)
Так как х2 — х + 1 > 0 для любого х, то неравенство (8)
равносильно неравенству х — 2 > 0.
Решения этого неравенства, а значит, и исходного, есть
все х > 2.
Ответ: 2 < х < +оо.
38
Алгебраические уравнения и неравенства
1.5.2.	Метод интервалов. В основе этого метода лежит
следующее свойство двучлена х — а: точка а делит числовую
ось на две части — справа от точки а двучлен х — а положи-
телен, а слева от точки а — отрицателен.
Пусть требуется решить неравенство
(х - oi)(x - а2).. .(х - ап) > 0,	(9)
где оц, 02,-  , an-i, <*п — фиксированные числа, среди кото-
рых нет равных, причем такие, что см < о2 < ... < on_i < ап.
Рассмотрим многочлен
P(r) = (х - at)(x - а2)... (х - ап).	(10)
Для любого числа г о такого, что г о > ог1. соответству-
ющее числовое значение любого сомножителя в произведе-
нии (10) положительно, а значит, P(xq) > 0. Для любого
числа xi, взятого из интервала (on_i,an), соответствующее
числовое значение любого из множителей, кроме множителя
(г — ап), положительно, поэтому число P(xi) < 0 и т. д.
На этом рассуждении и основан метод интервалов, состоя-
щий в следующем: на числовую ось наносят числа см, а2,...,
ап; в промежутке справа от наибольшего из них, т. е. чи-
сла ап, ставят знак плюс, в следующем за ним справа налево
интервале ставят знак минус, затем — знак плюс, затем —
знак минус и т. д. Тогда множеством всех решений неравен-
ства (9) будет объединение всех промежутков, в которых сто-
ит знак плюс, а множеством решений неравенства
(г - ai)(x - а2).. \х - ап) < 0,	(И)
где см < а2 < ... < а„, будет объединение всех промежутков,
в которых стоит знак минус.
Пример 2. Решить неравенство
(х + 3)(r - 4)(2z + 5) < 0.	(12)
Решение. Перепишем неравенство в виде
2(г — (—3))(г — (—5/2))(г — 4) < 0.
§ 1.5. Решение алгебраических неравенств
39
Рис. 1
Отметим на координатной оси числа (—3), (—5/2) и 4 и рас-
ставим знаки плюс и минус так, как указано на рис. 1.
Решениями неравенства (12) будут все х из объединения
промежутков (—ее;—3) и (—5/2;4).
Ответ: —оо < х < —3; —5/2 < х < 4.
Пример 3. Решить неравенство
х7 + 8z4 - х3 - 8 > 0.	(13)
Решение. Перепишем неравенство (13) в виде
(х4 - 1)(г3 + 8) > 0
ИЛИ
(х - 1)(ж -|- l)(z2 + l)(z + 2)(z2 - 2х + 4) > 0.	(14)
Поскольку х2 + 1 > 0 и х2 - 2х + 4 > 0 для любого дей-
ствительного х, то неравенство (14) равносильно неравенству
(ж — 1)(ж + 1)(ж-|-2) > 0. Применяя метод интервалов, находим
решения последнего, а значит и исходного, неравенства: это
будут все х из двух промежутков — 2 < х < — 1, 1 < яг < 4-оо
(рис. 2).
Ответ: -2 < х < -1; 1 < х < +оо.
Метод интервалов можно применять и при решении нера-
венств вида
х)
-2 > °,	15
х)
где Р(ж) и <?(ж) — многочлены, если заметить, что на множе-
стве всех действительных чисел неравенство (15) равносильно
неравенству P(x)-Q(x) > 0.
40
Алгебраические уравнения и неравенства
Рис. 2
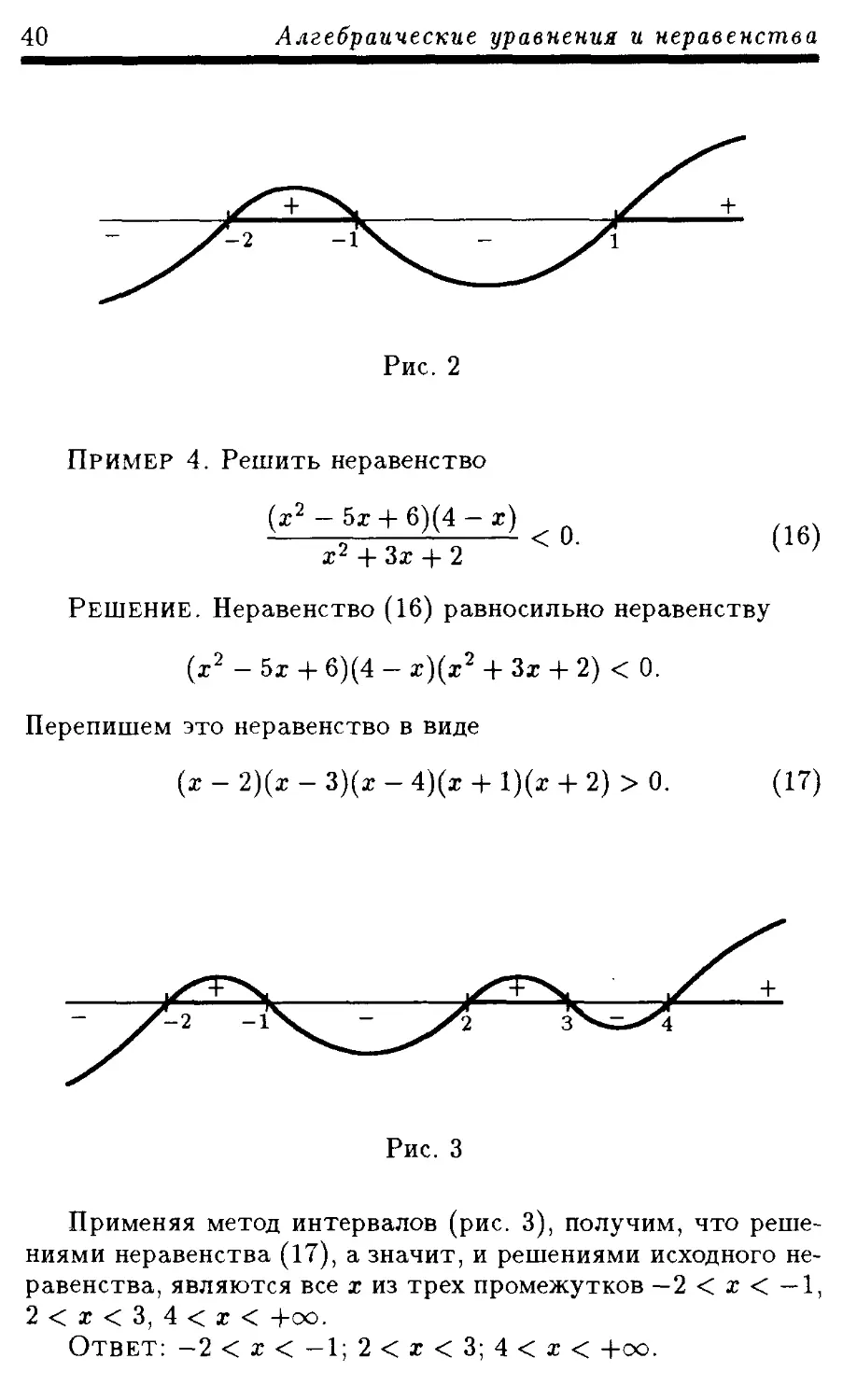
Пример 4. Решить неравенство
(ж2 - 5г + 6)(4 - ж)
z2+3z + 2	'	'
Решение. Неравенство (16) равносильно неравенству
(г2 — 5г + 6)(4 — z)(r2 + Зг + 2) < 0.
Перепишем это неравенство в виде
(х — 2)(z — 3)(z — 4)(r + l)(z + 2) > 0.	(17)
Рис. 3
Применяя метод интервалов (рис. 3), получим, что реше-
ниями неравенства (17), а значит, и решениями исходного не-
равенства, являются все х из трех промежутков —2 < х < — 1,
2 < г < 3, 4 < х < +оо.
Ответ: -2 < х < -1; 2<r<3;4<z< +оо.
§ 1.5. Решение алгебраических неравенств
41
1.5.3.	Обобщенный метод интервалов. Иногда алге-
браические неравенства степеней более высоких, чем два, пу-
тем равносильных преобразований приводятся к виду
(х - a{)kl(x - а2)*2 ...(х- an_i)t’-I(z - an)kn > О,
где fci, fc2,..., кп — целые положительные числа; сц, а2,...,
ап — действительные числа, среди которых нет равных, та-
кие, что < а2 < • • • < ап-1 < ап.
Такие неравенства могут быть решены с помощью так на-
зываемого обобщенного метода интервалов.
В основе его лежит следующее свойство двучлена (х — о)п:
точка а делит числовую ось на две части, причем:
а)	если п четное, то выражение (х — о)п справа и слева от
точки х = а сохраняет положительный знак,
б)	если п нечетное, то выражение (х — о)п справа от точки
х = а положительно, а слева от точки х = а отрицательно.
Рассмотрим многочлен
Р(г) = (ж - ai)**(a: - а2)к2 ...(х- an_1)kn~1 (х - ап)кп, (18)
где Qi < а2 < ... < ап.
Для любого числа Хо такого, что xq > ап, соответствую-
щее значение любого сомножителя в (18) положительно, по-
этому числовое значение Р(ж0) также положительно.
Для любого Xi, взятого из интервала (on_i,an), соответ-
ствующее значение любого сомножителя в (18), кроме послед-
него, положительно, а соответствующее значение последнего
сомножителя положительно, если kn — четное число, и от-
рицательно, если кп — нечетное число. Поэтому число -P(zi)
положительно, если кп — четное число, и -P(zi) отрицатель-
но, если кп — нечетное число.
Аналогично показывается, что если известен знак Р(х) на
интервале (а,-, 0,4.1), то на промежутке (o,_i,o,) знак -Р(ж)
определяется по следующему правилу. Многочлен Р(х) при
переходе через точку а,-:
а)	меняет знак на противоположный знаку Р(х) на
(а,-, 0,4.1), если ki — нечетное число;
б)	не меняет знака (тот же знак, что у Р(х) на (a,-, Oj^i)),
если ki — четное число.
42
Алгебраические уравнения и неравенства
На этом рассуждении и основан обобщенный метод интер-
валов: на числовую ось наносят числа «1, а2,...ап-, в про-
межутке справа от наибольшего из корней многочлена ста-
вят знак плюс, а затем, двигаясь справа налево, при переходе
через очередной корень а, меняют знак, если kt — нечетное
число, и сохраняют знак, если kt — четное число.
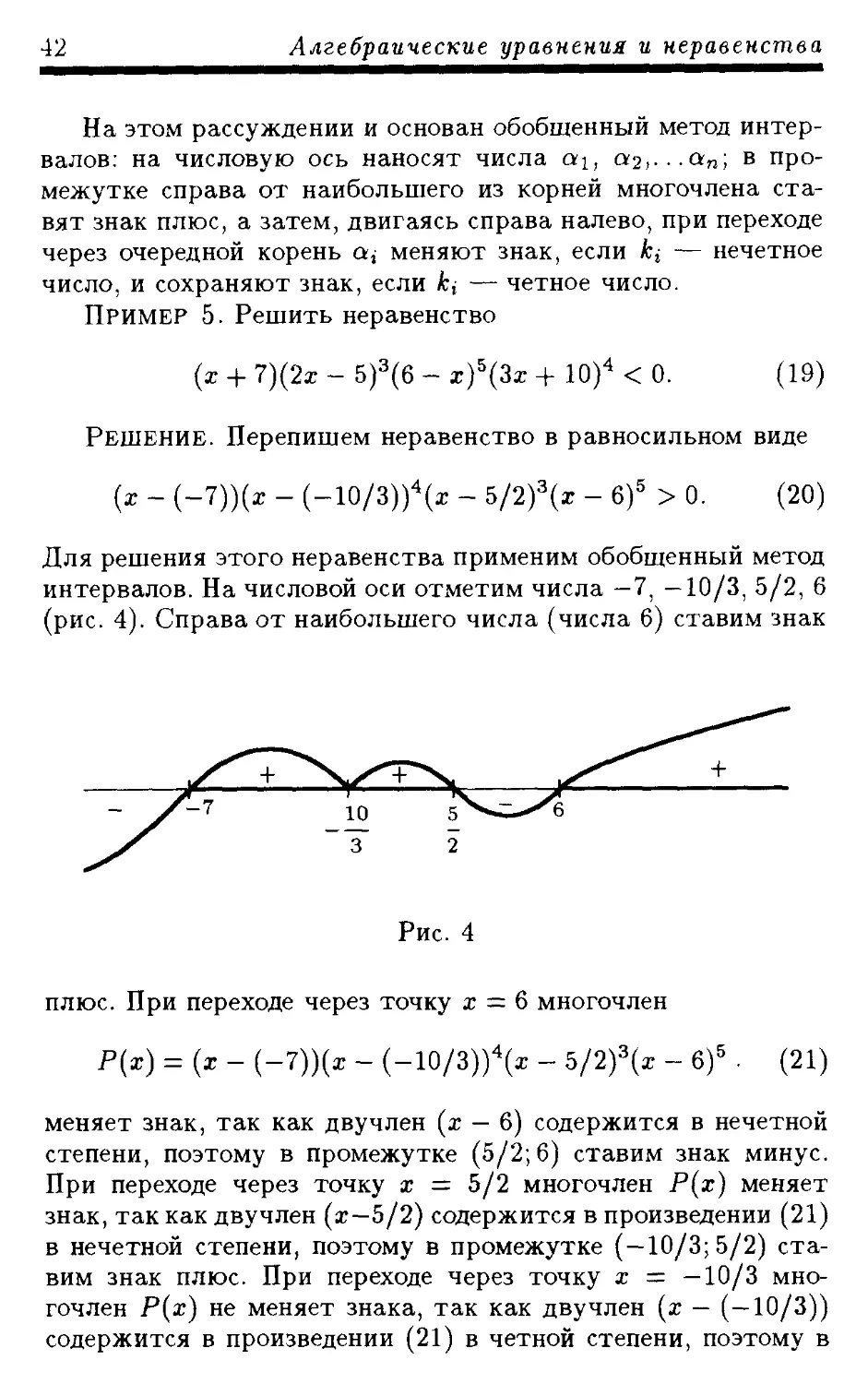
Пример 5. Решить неравенство
(х + 7)(2ж - 5)3(6 - r)5(3z + 10)4 < 0.
(19)
Решение. Перепишем неравенство в равносильном виде
{х - (-7))(z - (-10/3))4(z - 5/2)3(r - 6)5 > 0.	(20)
Для решения этого неравенства применим обобщенный метод
интервалов. На числовой оси отметим числа — 7, —10/3, 5/2, 6
(рис. 4). Справа от наибольшего числа (числа 6) ставим знак
+
-7	5Х-------
2
Рис. 4
плюс. При переходе через точку х = 6 многочлен
Р(х) = (х- (—7))(х - (- 10/3))4(z - 5/2)3(z - 6)5 •	(21)
меняет знак, так как двучлен (х — 6) содержится в нечетной
степени, поэтому в промежутке (5/2; 6) ставим знак минус.
При переходе через точку х = 5/2 многочлен Р(г) меняет
знак, так как двучлен (г—5/2) содержится в произведении (21)
в нечетной степени, поэтому в промежутке ( — 10/3; 5/2) ста-
вим знак плюс. При переходе через точку х = —10/3 мно-
гочлен Р(х) не меняет знака, так как двучлен (х — (—10/3))
содержится в произведении (21) в четной степени, поэтому в
>l 1.5. Решение алгебраических неравенств
43
промежутке (—7;—10/3) ставим знак плюс. Наконец, при пе-
реходе через точку х = —7 многочлен Р(х) меняет знак, так
как двучлен (х + 7) содержится в произведении (21) в первой
степени, поэтому в промежутке (—се; 7) ставим знак минус.
Решением неравенства (20), а значит, и равносильного ему
исходного неравенства будет совокупность промежутков, где
стоит знак плюс, т. е. объединение множеств — 7 < х < —10/3,
— 10/3 < х < 5/2 и 6 < х < -|-оо.
Ответ: -7 < х < -10/3; -10/3 < х < 5/2; 6 < х < 4-оо.
Замечание 1. Обобщенный метод интервалов можно при-
менять и при решении неравенств
где Р(х} и <?(ж) — многочлены, если заметить, что на множе-
стве всех действительных чисел неравенство (22) равносильно
неравенству
P(r)Q(r) > 0.
Пример 6. Решить неравенство
(г2 4- 1)(^2 — 1)2(ж ~ З)4
(а: 4-2)2(2г — З)5	< '
Решение. Неравенство (23) равносильно неравенству
(а:2 4- l)(z2 - l)2(z - 3)4(r 4- 2)2(2z - З)5 < 0.
Поскольку z2 4- 1 > 0 при любом а:, то последнее неравенство
равносильно неравенству
(х - l)2(z 4- l)2(z - 3)4(z 4- 2)2(z - 3/2)5 < 0.
Применим обобщенный метод интервалов. На числовой оси
отметим точки —2, —1, 1, 3/2 и 3 и расставим знаки, как
указано на рис. 5. Те промежутки, где стоит знак минус, и
дадут все решения неравенства (23).
Ответ: -2 < х < -1; -1 < х < 1; 1 < х < 3/2.
44
Алгебраические уравнения и неравенства
Замечание 2. Обобщенный метод интервалов можно при-
менять и так:
1)	найти все различные корни од, а?,.	а*,; от <	<
< .. . < ajt (к п) многочлена Pn(z);
2)	выяснить знак многочлена Рп(х) на каждом из интер-
валов (ai,a,+i), i = 1, 2,..., к — 1, (—оо,ат) и (а*,, +оо),
подставляя в Рп(х) вместо х любое число из этого интервала.
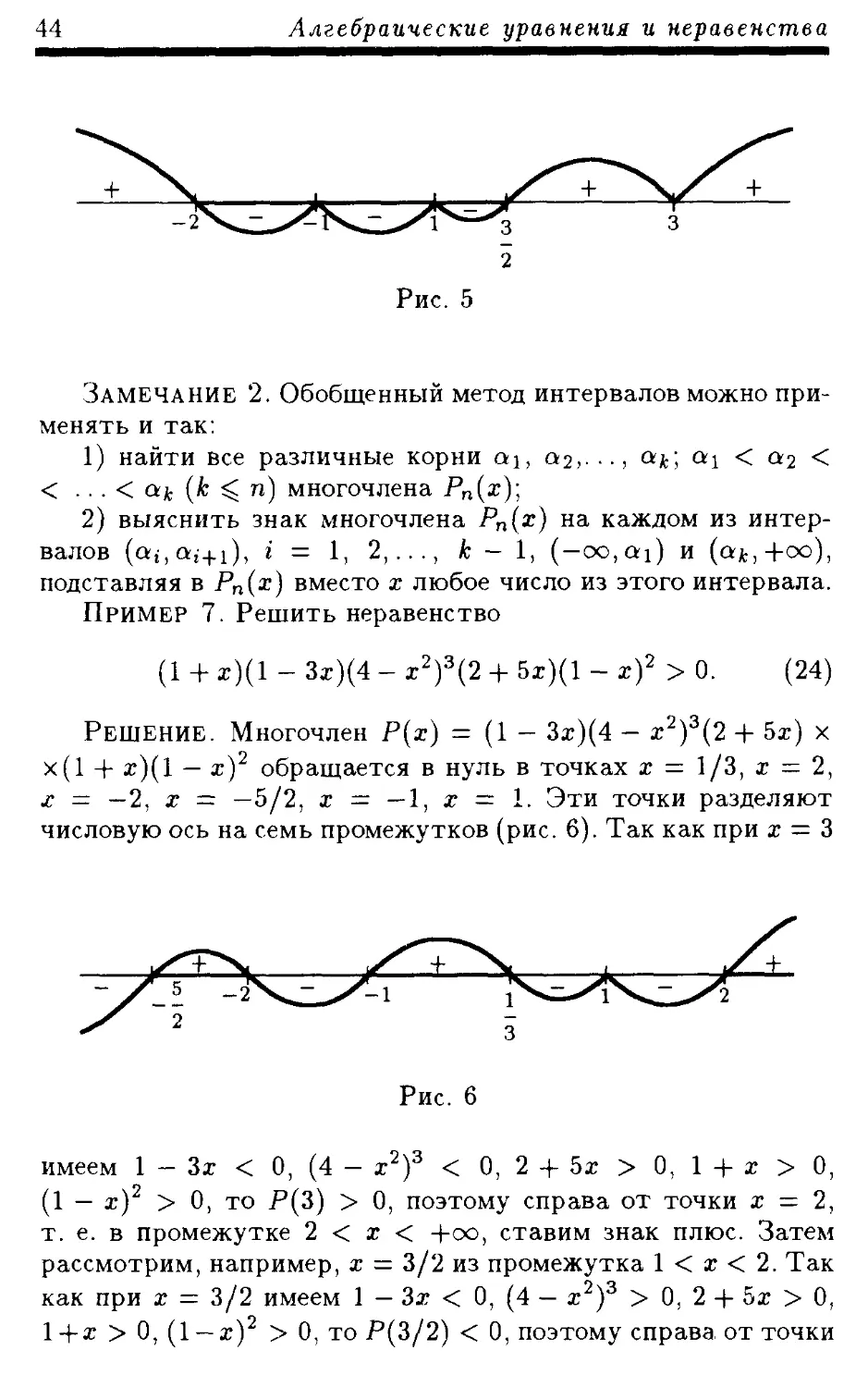
Пример 7. Решить неравенство
(1 + z)(l - 3z)(4 - r2)3(2 + 5х)(1 - ж)2 > 0.	(24)
Решение. Многочлен Р(х) = (1 — 3z)(4 — z2)3(2 + 5z) х
х(1 + z)(l — z)2 обращается в нуль в точках х = 1/3, х = 2,
х = —2, х = —5/2, х = —1, х ~ 1. Эти точки разделяют
числовую ось на семь промежутков (рис. 6). Так как при х — 3
Рис. 6
имеем 1 — Зх < 0, (4 — г2)3 < 0, 2 + Зх > 0, 1 + х > 0,
(1 — т)2 > 0, то Р(3) > 0, поэтому справа от точки х — 2,
т. е. в промежутке 2 < х < -|-оо, ставим знак плюс. Затем
рассмотрим, например, х — 3/2 из промежутка 1 < х < 2. Так
как при х = 3/2 имеем 1 — Зх < 0, (4 — z2)3 > 0, 2 + Зх > 0,
l-l-z > 0, (1 — х)2 > 0, то Р(3/2) < 0, поэтому справа от точки
Задачи
45
х = 2 в промежутке 1 < х < 2 ставим знак минус. Поступая
аналогично, расставим знаки плюс или минус, как указано на
рис. 6.
Решением неравенства (24) будет объединение всех тех
промежутков, в которых поставлен знак плюс, т. е. это бу-
дет объединение промежутков 2 < х < +оо, — 1 < х < 1/3,
-5/2 < х < -2.
Ответ: 2 < х < +оо; -1 < х < 1/3; -5/2 < х < -2.
Задачи
Решить уравнение
1.	г3 - 2х2 - 9 = 0.
2.	6z3 - х2 - 20г + 12 = 0.
3.	х3 - 6г2 + 5г + 12 = 0.
4.	(х - I)3 + (2г + З)3 = 27z3 + 8.
5.	х3 - (л/2-|- 1) х2 + 2 = 0.
6.	9z3 - 13z - 6 = 0.
,	27	1
7.	x3---= 4-х.
8	2
8.	4л/2ж3 - 22х2 + 17\/2z -6 = 0.
з	1
9.	х3 — Зх = 64 4--.
64
10.	х(х + 1) + (х + l)(z + 2) + (г + 2)(z + 3) + (г + 3)(z + 4) +
+ (х + 4)(г + 5) = 1-2 + 2-3 + 3-4 + 4-5.
12.	х4 + 2z3 - х = 2.
13.	х4 + Зх3 + 4ж2 + 6х + 4 = 0.
14.	10? + Зх3 + 5z2 + 5z + 8 = 0.
15.	4х4 + 4z3 + 3z2 — х — 1 = 0.
16.	х4 - х3 - 2х2 + Зх - 3 = 0.
46
Алгебраические уравнения и неравенства
17.	х4 — 6 а:3 + 7х2 + 6х — 8 = 0.
18.	а:4 — 2а:3 — а:2 — 2а: + 1 = 0.
19.	х4 + х3 — 15а:2 — 10а: + 50 = 0.
20.	х4 - 22а:2 - 5х + 2 = 0.
21.	а:5 — За:4 — а:3 + 5х2 + х — 1 = 0.
22.	а:5 - 2а:4 - 6а:3 + 12а:2 + х - 2 = 0.
23.	а:6(1 - х) - а:3(1 - х2) + х - х2 = 0.
24.	а:6 - 6а:4 + 8а:2 = -3.
25.	(х + I)4 = 2(1 + а:4).
26.	6(1 + а:2)2 = 25(1- а:2).
27.	а:4 - 2л/2а:2 - х + 2 - У2 = 0.
28.	(2а:2 - За: + 1)(2а:2 + 5х + 1) = 9х2.
29.	(х + З)4 + (а: + 5)4 = 16.
30.	х4 + 4х - 1 = 0.
31.	х4 — 4х3 - 1 = 0.
Решить неравенство
32.	х3 — 6а:2 + 12а: - 10 > 0.
33.	(а:2 + х + 1)(а:2 + х + 2) < 12.
34.	х3 - х > 336.
35.	2а:3 + а: + л/2 > 0.
36.	х3 - (л/З - 1) х2 - 3 < 0.
37.	х4 - 2х2 - 8а: - 3 > 0.
38.	х4 -х2 + 2х - 1 > 0.
39.	а:4 - 4х + 3 > 0.
40.	х4 + 1 — За:3 + Зх > 0.
41.	(5 - а:)4 + (2 - а:)4 > 17.
42.	(х - 1)(а: - 3)(а: - 4)(а: - 6) > 17.
43.	(6а: + 5)(3а: + 2)(х + 1) < 29.
44.	(х2 — х)2 + 3(х2 — х) + 2 > 0.
Задачи
47
45.	z12 — х9 + х4 — х + 1 > 0.
46.	х4 — х3 — Юг2 + 2х + 4 < 0.
47.	(х + I)4 > 2(1 + х4).
48.	3z2(z - 4)2 < 32 - 5(z - 2)2.
49.	(л + 2)(2 - л)2 < 0.
50.	(х - l)(z + 2)(z - 3) < 0.
51.	(2z - 3)(z + 4)(2 - х) > 0.
52.	(г + 3)(3z - 2)2(z - 4) < 0.
53.	(х - 1)2(z + 2)3z > 0.
54.	(х3 - l)(z4 - l)(z5 - 1) < 0.
55.	(z2 — 3z + 2)(z2 — x) < 0.
(z2 — 1)(4 — z2)
56.	1< 0.
z2 — 9
(2z-3)4(3z + 1)3(z2 + z)2 .
(x2 + x + l)(z2 — 25)
(z + 3)4(z + 2)2
58‘ (z + 5)2	> °'
(r2-l)(z3 + l)2
ЭУ. ----------------- u.
X4 — 1
xs + x6 — 4x4 + x2 + 1
60. -j-----------------— > 0.
Xs — X5 + X2 — X + 1
Глава II
Уравнения и неравенства,
содержащие радикалы, степени,
логарифмы и модули
§ 2.1. Уравнения и неравенства, содержащие
неизвестную под знаком корня
2.1.1. Возведение в степень. Основным методом реше-
ния уравнений и неравенств, содержащих радикалы, является
возведение, возможно даже неоднократное, обеих частей урав-
нения или неравенства в соответствующую степень.
При возведении обеих частей уравнения или неравенства
в степень надо следить за равносильностью преобразований.
Для уравнений можно не следить за равносильностью, то-
гда в конце решения надо делать проверку найденных корней.
Пример 1. Решить неравенство
\/8т + 7 — д/х + 2 <	+ 3.	(1)
РЕШЕНИЕ. ОДЗ1 неравенства состоит из всех х, удовле-
творяющих одновременно условиям
8т + 7	0, х + 2	0, т + 3 О,
т. е. ОДЗ есть все х из промежутка [— 7/8; +оо). Перепишем
неравенство (1) в виде
V&X + 7 < д/х + 2 + \/г + 3.	(2)
На ОДЗ обе части неравенства (2) неотрицательны, поэтому,
возводя обе части этого неравенства в квадрат, получим на
ОДЗ исходного неравенства равносильное ему неравенство
6г + 2 < 2у/(х + 2)(х + 3).	(3)
1 Под знаком ОДЗ (область допустимых значений) уравнения /(г) =: О
(неравенства f(x) > 0) будем понимать множество всех значений хо, для
каждого из которых выражение f(xo) имеет смысл.
§ 2.1. Неизвестная под знаком корня
49
На ОДЗ неравенства выражение 6х 4- 2 принимает как поло-
жительные, так и отрицательные значения, поэтому разобьем
ОДЗ на два промежутка [—7/8; —1/3] и ( — 1/3; 4-оо). Для любо-
го х, принадлежащего'промежутку [—7/8; —1/3], левая часть
неравенства (3) неположительная, а правая — положительная.
Это означает, что для каждого из таких х неравенство (3) вы-
полняется.
Если х принадлежит промежутку (—1/3; +оо), то обе ча-
сти неравенства (3) положительны и оно на этой области рав-
носильно неравенству
(3r+ I)2 < (х + 2)(г + 3),
т. е. неравенству
8г2 4- х — 5 < 0.
(4)
Решениями неравенства (4) являются все х из промежутка
—1 — >/ТбТ	— 14-х/1бТ „
--------- < х < ------------. Для х из этого промежутка
16	16
условию —1/3 < х < 4-ое удовлетворяют только х из проме-
жутка
1
3
-1 -ь УТбТ
16
Объединяя полученные решения в каждом из двух случа-
ев, получаем, что решениями исходного неравенства являются
7	-1 4-л/ТбТ
все х из промежутка — - х < ----—----.
7
Ответ: -- < х <
8
-14- УТбТ
16
Пример 2. Решить уравнение
\/т 4- 2 4- y/z 4- 1 = 7.
(5)
Решение. ОДЗ уравнения (5) есть все х —1. На ОДЗ обе
части уравнения (5) положительны, поэтому после возведения
в квадрат получим уравнение
х 4- 2 4- 2\/(г 4- 2)(z 4-1) 4- х 4- 1 — 49,
(6)
50
Радикалы, степени, логарифмы и модули
равносильное для х — 1 уравнению (5). Перепишем уравне-
ние (6) в виде
x/(z + 2)(z+ 1) = 23 - х.	(7)
Для любого х > 23 левая часть уравнения (7) положитель-
на, а правая отрицательна. Следовательно, среди х > 23 нет
решений уравнения (7).
Для —1 х 23 обе части уравнения (7) неотрицательны,
поэтому после возведения в квадрат получим уравнение
(z + 2)(z + l) = (23 —г)2,	(8)
равносильное для этих х уравнению (7). Уравнение (8) имеет
527 m
единственный корень а: о = Так как это число х0 удо-
влетворяет условию —1 х 23, то Xq является корнем
уравнения (5), равносильного уравнению (8) для этих х.
Ответ: х = 527/49.
Пример 3. Решить уравнение
л/8г + 1 + -/За: — 5 = у/7х + 4 + i/2r — 2.	(9)
Решение. Перепишем уравнение (9) в виде
x/8r + 1 - >/2х - 2 = х/7т + 4 - у/Ъх - 5.	(10)
Возводя обе части уравнения (10) в квадрат, получим
уравнение
8z -|-1 4- 2х — 2 — 2л/8г 4- 1-У2г — 2 =
= 7x + 4 + 3x-5- 2\/7z 4-4V3Z -5,
являющееся следствием исходного уравнения (9). Последнее
уравнение можно переписать в виде
\/8х 4- 1 x/2z — 2 — у/7х 4- 4\Z3z — 5.
Следствием этого уравнения является уравнение
(8z 4-1)(2ж — 2) = (7z4-4)(3z - 5).	(11)
§ 2.1. Неизвестная под знаком корня
51
Решения уравнения (11) есть X'L — 3 и х% = —6/5. Так как
уравнение (11) — следствие уравнения (9), то надо проверить,
являются ли Xi и х? его корнями. Подставляя эти значения х
в исходное уравнение, получаем, что х = 3 является его ре-
шением, а х = —6/5 не является.
Ответ: х = 3.
Замечание. Если уравнение (5) решать переходом к след-
ствию, то проверка найденного корня была бы затруднитель-
на. Если уравнение (9) решать с помощью равносильных пре-
образований, то его решение будет намного сложнее, чем при-
веденное выше.
Поэтому при решении уравнений с радикалами надо уметь
пользоваться любым из этих способов.
2.1.2.	Уравнения вида д//(ж) ± \/ff(z) = h(z). Уравне-
ние
V7(z) ± \/ff(x) = h(x)	(12)
можно решать при помощи описанного в пункте 2.1.1 основно-
го метода, но иногда их можно решить следующим образом.
Рассмотрим решение уравнения типа (12) на множестве
М — тех значений х, для которых /i(z) У 0.
Пусть Xq — корень уравнения
уТИ +	= Кх)	(13)
и й(го) 0. Тогда справедливо числовое равенство
\/f(xo) + V9(xo) = h(xo).	(14)
Найдем разность чисел
f(x0)-g(x0)=a(x0)	(15)
н запишем равенство (15) в виде
(VfM ~ \А(*о)) (VfM + \А(*о)) = а(ж0).	(16)
Используя равенство (14), запишем равенство (16) в виде
=	(17)
Л(*о)
52
Радикалы, степени, логарифмы и модули
Равенство (17) означает, что число г о есть корень уравнения
77—	/7777 _ /(*) “ 9(х)
f(x) - V9(x) = ---J7-7----
(18)
Таким образом, уравнение (18) является следствием уравне-
ния (13) на множестве М.
Складывая уравнения (13) и (18) и умножая полученное
уравнение на h(x'), получим уравнение
2У/(х)/г(т) = f(x) - g(x) + /i2(z),	(19)
также являющееся следствием уравнения (13) на множе-
стве М. Возведя уравнение (19) в квадрат и решив получен-
ное уравнение, надо сделать проверку найденных корней, т. е.
проверить, являются ли его корни корнями исходного уравне-
ния (13).
Замечание. Если zj — корень уравнения (13) и h(xi) = О,
то xi также есть корень уравнения (19). Следовательно, урав-
нение (19) есть следствие уравнения (13).
Отметим, что точно так же показывается, что уравне-
ние (19) есть следствие уравнения
V7(z) -	= h(x).
Пример 4. Решить уравнение
л/Зж2 - 5z + 7 + \/3z2 - 7z + 2 = 3.	(20)
Решение. Поскольку разность подкоренных выражений
3z2 — 5х + 7 и 3z2 — 7z + 2 есть 2х + 5 и
(УЗг2 - 5z + 7) 2 - (\/3z2 -7z + 2)2 =
= (у/Ъх2 — 5z + 7 — \/Зг2 — 7z + 2^ х
х (\/3z2 — 5z + 7 + \/3z2 — 7z + 2^ ,
то уравнение
.	. 	г - ... О
V3z2 — 5г + 7 — v3z2 — 7х + 2 = —-—	(21)
§2.1. Неизвестная под знаком корня
53
является следствием исходного уравнения. Тогда, складывая
уравнения (20) и (21), получим уравнение
.---------- 2 т -I- 14
2л/3ж2 - 5т + 7 = —у—,	(22)
также являющееся следствием уравнения (20). Возводя обе ча-
сти уравнения (22)в квадрат, получим уравнение
являющееся следствием исходного уравнения. Решения урав-
нения (23) есть Zj = 2 и а?2 — 7/26. Проверкой убеждаемся,
что оба эти числа являются корнями исходного уравнения.
Ответ: xi = 2, х2 = 7/26.
2.1.3.	Уравнения вида \/f(x)± \/g(x} = <f>(x). Уравне-
ние
\/f(x) +	= 4>(х)	(24)
можно решать следующим методом.
Пусть го — корень уравнения (24). Тогда справедливо чи-
словое равенство
У/(*о) + УЛ^о) = ¥>(жо).	(25)
После возведения равенства (25) в куб получим равенство
/(т0) + Зл/ЛМx/fl^o) (У/(*о) + УЛ^о)} +<?(®о) = v3(*o),
откуда в силу (25) имеем равенство
зУ/(хо)Ур(хо)у>(^о) = У(*о) - /(*о) - д(хо). (26)
Равенство (26) означает, что г о есть корень уравнения
3 \//(ж)	= ^У) “ /(ж) ~	(27)
Таким образом, уравнение (27) есть следствие уравнения (24).
Возведя уравнение (27) в куб и решив полученное уравнение,
54
Радикалы, степени, логарифмы и модули
надо проверить, являются ли найденные корни корнями ис-
ходного уравнения.
Пример 5. Решить уравнение
У2х - 1 + Ух - 1 = 1.	(28)
Решение. Возведя обе части уравнения в куб, получим
уравнение
Зх - 2 + </(2х - 1)(х - 1) (У2х - 1 + Ух - 1) = 1,
равносильное исходному. Подставляя вместо выражения
у2х — 1 + Ух — 1 единицу, получаем уравнение
Зх - 2 + 3 У(2т - 1)(х - 1) = 1,	(29)
являющееся следствием исходного уравнения.
Уравнение (29) перепишем так:
У(2х - 1)(х - 1) = 1 - х.	(30)
Возводя обе части уравнения (30) в куб, получаем уравнение
(2х - 1)(х - 1) = (1 -х)3,	(31)
равносильное уравнению (30). Решения уравнения (31) есть
Xi — 0 и х? — 1. Проверка показывает, что х^ = 0 не является
корнем исходного уравнения, а х^ = 1 является его корнем.
Ответ: х = 1.
Частным случаем уравнения (24) является уравнение вида
Уравнение (32) после возведения обеих его частей в третью
степень и замены выражения УТУУУдУ) на <А(7)+ УЙУ),
приводится к уравнению
/(г) 4- g(x) — h(x) — г(х) =
= 3 (yh(x)r(x) - УКх)д(х)) + Уф)) , (33)
§ 2.1. Неизвестная под знаком корня
55
которое есть следствие исходного уравнения. В некоторых
случаях уравнение (33) можно решить и тем самым найти
числа, среди которых содержатся корни исходного уравнения.
Подставляя их в исходное уравнение (32) и отбирая среди них
те, которые являются его корнями, получим решение уравне-
ния (32).
Пример 6. Решить уравнение
у/х + Уг:3 — г + 1 = ’Уж + 1 + у/х3 — х. (34)
Решение. Возводя обе части уравнения (34) в третью сте-
пень, имеем уравнение
х + х3-х + 1 + 3 у/х /х3 - х + \ \[х + Уг:3 - г + 1J =
= а: -|- 1 -|- z3 — а: + 3 у/х /х3 — х у/х + / х3 — х/} ,
_________________________________________________(35)
равносильное исходному. Заменяя выражение /х+/х3 — х+1
выражением /х + 1+ ух3 — х, получим уравнение, являюще-
еся следствием исходного
(/х /х3 — х + 1 — /х + 1 /х3 — х^ ( /х + 1 + у/х3 — х} ~ 0.
(36)
Уравнение (36) равносильно совокупности двух уравнений
\fx\Jx3 — г + 1 — /х + \ / х3 — х — О
(37)
+ 1 + / х3 — х — 0.
Решения первого уравнения совокупности (37) есть х = 0,
х — у/7! и х = —у/2. Решение второго уравнения совокупно-
сти (37) есть х = —1.
Проверка показывает, что х = 0, х = — л/2, х = у/2 и
х — — 1 являются корнями исходного уравнения.
Ответ: х = -л/2, х = -1, х — 0, х = у/2.
Замечание. Уравнение вида
УЖ -	+ УЖ =	(38)
можно решать следующим образом.
56
Радикалы, степени, логарифмы и модули
Умножая обе части уравнения на +^(х), перейдем
к уравнению
f(x)+g(x) = (<//(х) + \/ф)) р(х),	(39)
являющемуся следствием уравнения (38). Далее уравне-
ние (39) можно решать так, как это предлагалось в этом пунк-
те. Только надо помнить, что уравнение (39) есть следствие
уравнения (38).
2.1.4. Умножение уравнения или неравенства на
функцию. В некоторых случаях полезно умножение обеих
частей уравнения или неравенства, содержащих радикалы, на
некоторую функцию /(ж), имеющую смысл на их ОДЗ.
При решении уравнения этим способом надо либо следить
за равносильностью преобразований на ОДЗ исходного урав-
нения, либо в конце решения надо делать проверку, так как
могут появиться посторонние корни.
При решении неравенства надо следить за равносильно-
стью преобразований неравенства на его ОДЗ, и поэтому
можно умножать обе части неравенства на функцию, прини-
мающую на ОДЗ неравенства только значения одного знака
либо разбивать ОДЗ на промежутки, на которых функция зна-
копостоянна, и делать равносильные преобразования на этих
промежутках.
Пример 7. Решить уравнение
х — (уН + х + 1) (х/1 + х + х2 + х — 7) .	(40)
Решение. Умножив обе части уравнения на функцию
V 1+т — 1, получим уравнение
х (у/1 + х — 1) =• х (уД + z + х2 + х — 7) ,	(41)
являющееся следствием уравнения (40). Перепишем уравне-
ние (41) в виде
х (—\/1 + х + 1 + у^1 + z + х2 + х — 7) = 0.	(42)
Следствием уравнения (42) является уравнение
х(х2 + х — 6) = 0.	(43)
§ 2.1. Неизвестная под знаком корня
57
Решениями уравнения (43) являются Ху — 0, а?2 = 2 и т3 = —3.
Проверка показывает, что х? = 2 является корнем исходного
уравнения, аг = 0 и г = -Зне являются его корнями.
Ответ: х - 2.
Пример 8. Решить уравнение
^(т + 2)(2т-1)-ЗУГ+6 =
= 4 - У(т + 6)(2т - 1) + 3\/7Т2.	'
Решение. ОДЗ уравнения состоит из всех х, удовлетво-
ряющих одновременно условиям г + 2 2> 0, а: + 6 2> 0,
(х + 6)(2т — 1)	0, (х + 2)(2х — 1)^0, т. е. ОДЗ есть все
х 2> 1/2. На ОДЗ уравнение (44) можно переписать в виде
у/х + 2у/2х — 1 — Зу/х 4- 6 = 4 — у/х + 6л/2т — 1 + Зу/х + 2
или в виде
(у/х+ 2 + у/х + б) (у/2х - 1 - 3) = 4.	(45)
После умножения обеих частей уравнения (45) на функцию
у/х + б — у/х + 2, принимающую на ОДЗ уравнения (44) толь-
ко положительные значения, получим уравнение
V2x - 1 - 3 = у/х + б - у/х+ 2,	(46)
равносильное исходному на его ОДЗ. Поскольку выражение
у/2х — 1 — 3 обращается в нуль при х = 5, то разобьем мно-
жество х 1/2 на два множества: 1/2 х <2 5 и х > 5.
Для любого х Е [1/2; 5] левая часть уравнения (46) неположи-
тельна, а правая положительна. Значит, ни одно из этих х не
может быть решением уравнения (46), а значит, и исходного
уравнения.
Для любого х 6 (5; 4-оо) обе части уравнения (46) положи-
тельны, и оно на этом множестве равносильно уравнению
2х — 1 + 9 — 6д/2т — 1 =х+б+х+2— 2у/х + бу/ х 4- 2,
т. е. уравнению
Зд/2т — 1 = у/ х + бу/ж 4- 2.
(47)
58
Радикалы, степени, логарифмы и модули
Уравнение (47) на множестве х > 5 равносильно уравнению
9(2z - 1) = z2 + 8z + 12,
т. е. уравнению
г2 - 10z + 21 = 0.	(48)
Решения уравнения (48) есть Xi = 7 и х% = 3. Из этих зна-
чений х условию х > 5 удовлетворяет только х = 7, оно и
является решением исходного уравнения.
Ответ: х = 7.
Пример 9. Решить неравенство
\/4 — а?2 — х — | а: | — 1>0.
(49)
Решение. ОДЗ неравенства (49) состоит из всех х, для
которых —2 С х 2. Поскольку на ОДЗ \J 4 — х'1 + х +
+ |z| + 1 > 0, то, умножив неравенство (49) на функцию
^/4 — а?2 + х + |х| + 1 > 0, получим неравенство
(4 — х2) — (х + |z| + I)2 > 0,	(50)
равносильное исходному на множестве — 2	х 2.
При 0 < х 2 имеем |z| = х и неравенство (50) перепи-
шется в виде
4 — х2 — 4z2 — 4х — 1 > 0.	(51)
Решения неравенства (51) составляют промежуток
—2 — з/19	—2 + ^/19
--------- < х < ----------. Поэтому для этих
неравенства (50) составляют промежуток 0 < х <
х решения
- 2 + л/19
5
При —2 х 0 неравенство (50) перепишется в виде
4 — х2 — 1 > 0.
(52)
Решения неравенства (52) составляют промежуток
—э/з < х < э/з. Поэтому для этих х решения неравенства (50)
составляют промежуток — з/з < х 0. Следовательно, мно-
§ 2.2. Неизвестная в основании логарифма
59
жеством решений неравенства (49) является объединение про-
межутков
- V3 < х О,
т. е. интервал
—Уз < х <
л/19 — 2
5
Ответ: -V3 < х < ------
§ 2.2.	Уравнения и неравенства, содержащие
неизвестную в основании логарифмов
В этом параграфе рассматриваются уравнения и неравен-
ства вида
log^/Cz) = log^ffCz),	(1)
^(г)/(х) > log^(r)ff(z).	(2)
При решении таких уравнений и неравенств надо учиты-
вать, что их ОДЗ определяется из условий:
1)	на ОДЗ все функции /(ж), д{х), у>(х) и ф(х) имеют
смысл;
2)	на ОДЗ основания логарифмов, т. е. функции ‘р(х) и
ф(х), должны удовлетворять условиям ip(x) > 0, ф(х) > О,
/ 1, ф(х) £ 1;
3)	на ОДЗ функции, находящиеся под знаком логарифма,
должны быть положительны, Т. е. на ОДЗ должны выпол-
няться неравенства /(ж) > 0, д(х) > 0.
2.	2.1. Переход к числовому основанию. Одним из
основных способов решения уравнений и неравенств вида (1)
и (2) является следующий.
1.	Найти ОДЗ уравнения или неравенства.
60
Радикалы, степени, логарифмы и модули
2.	Перейти в логарифмах к некоторому основанию а, где
а — фиксированное число, а> Он а 1, т. е. заменить урав-
нение (1) равносильным ему на ОДЗ уравнением
l°ga /(g) _ logag(g)
loga^(z) loga^(*)’
(3)
а неравенство (2) — равносильным ему на ОДЗ неравенством
loga > loga g(g)
loga^(g) logaV>(z)'
(4)
3.	Решить полученное стандартное по внешнему виду
уравнение (3) (или неравенство (4)) на ОДЗ исходного урав-
нения (или неравенства). Его решения и будут решениями ис-
ходного уравнения (или неравенства).
Заметим, что ОДЗ уравнений (1) и (3) и неравенств (2)
и (4) совпадают, поэтому можно сразу переходить от уравне-
ния (1) к уравнению (3) и от неравенства (2) к неравенству (4)
и решать их на своей ОДЗ.
ПРИМЕР 1. Решить уравнение
Iogr(2z+ 1) = log2r3+r2(4z3+4т2 + z).
(5)
Решение. ОДЗ уравнения (5) состоит из всех х, одновре-
менно удовлетворяющих условиям х > 0, х 1, 2х + 1 > 0,
2х3 + х2 > 0, 2х3 + х2 / 1, 4х3 + 4ж2 + х > 0, т. е. ОДЗ состоит
из двух промежутков 0<г<1и1<х< +оо. Переходя в (5)
к логарифмам по основанию, например, 2, получим уравнение
log2(2z + 1) _ log2(4x3 + 4z2 + ж)
(6)
log2 х	log2(2g3 + x2)
равносильное уравнению (5) на ОДЗ. Поскольку для этих х
имеем log2(4x3 + 4х2 + х) = log2 х + 21og2(2x + 1) и
log2(2x3 + x2) = 2 log2 х + k>g2(2g + 1), то уравнение (6) можно
записать в виде
log2(2z + 1) _ log2 х + 2 log2(2x + 1)
log2 x 2 log2 x + log2(2x + 1)
§ 2.2. Неизвестная в основании логарифма
61
или, так как на ОДЗ log2 х / 0, в виде
х 21og2(2x + 1)
log2(2z + 1) _ _____log2z
log2x 9 , bg2(2z+l)
+ log2x
rv-	log2(2z + 1)
Обозначим ------------- через t, тогда уравнение (7) можно
log2x
.	1 + 2/ о
переписать в виде t = —. Решения последнего уравнения
есть /1 = 1 и О = —1. Следовательно, уравнение (7) равно-
сильно на ОДЗ исходного уравнения совокупности уравнений
log2(2z + 1) _ 1 и log2(2x + 1) _
log2z	log2x
Первое из уравнений этой совокупности не имеет решений, а
решение второго уравнения есть х = 1/2. Это число принад-
лежит ОДЗ исходного уравнения и, следовательно, является
единственным его решением.
Ответ: х = 1/2.
ПРИМЕР 2. Решить неравенство
logr(2 + х) > logjr2(x2 + 2х).	(8)
РЕШЕНИЕ. ОДЗ неравенства (8) состоит из всех х, одно-
временно удовлетворяющих условиям 2 4- х > 0, х2 + 2х > О,
х > 0, х / 1, х2 > 0, х2 / 1, т. е. ОДЗ состоит из двух
промежутков: 0<х<1и1<г< +оо.
Перейдем в логарифмах неравенства (8) к логарифмам по
основанию, например, 2. В результате получим неравенство
log2(2 + х) > log2(r2 + 2х)
log2 х	log2 х2
(9)
равносильное исходному на его ОДЗ. Поскольку на ОДЗ ис-
ходного неравенства имеем log2(x2 -f- 2r) = log2 х + log2(2 + х)
62
Радикалы, степени, логарифмы и модули
и log2 х2 = 2 log2 х, то неравенство (9) для этих х можно пе-
реписать в виде
log2(2 + х) > log2 х + log2(2 + х)
log2 х	2 log2 х
или в виде
log2(2 + ж) - log2 х > о
log2 х
или, наконец, в виде
log2 X
> 0.
(Ю)
т 2 + х 2	пт
1ак как ----- = —f- 1, то на ОДЗ исходного неравенства
х х
“2 + х	2 + х
	 > 1, следовательно, log2	 > 0. Поэтому неравен-
х-------------------------------х
ство (10) равносильно неравенству log2 х > 0. Решения по-
следнего неравенства есть все х > 1. Поскольку все х > 1
входят в ОДЗ исходного неравенства, то все они являются его
решениями.
Ответ: 1 < х < +оо.
Отметим, что иногда при решении уравнений и нера-
венств вида (1) и (2) нецелесообразно переходить к некоторо-
му постоянному основанию, так как это может сделать более
громоздкой запись уравнения (или неравенства) и не облегчит
процесс его решения.
Пример 3. Решить уравнение
!°gi-2г(6а;2 - 5а: + 1) - Iog1_3j,(4z2 - 4х + 1) = 2.	(11)
Решение. Поскольку 4х2 - 4х + 1 = (2х - I)2 = (1 - 2х)2,
6х2 — 5х + 1 = (1 — Зж)(1 — 2х), то ОДЗ исходного уравнения
состоит из всех х, одновременно удовлетворяющих условиям
1 - 2х > 0, 1 - 2х / 1, 1 - Зх > 0, 1 - Зх / 1,
т. е. ОДЗ состоит из двух промежутков: —оо < х < 0 и
0 < х < 1/3. Легко видеть, что переход в логарифмах к не-
которому основанию а приведет к громоздким выражениям.
§ 2.2. Неизвестная в основании логарифма
63
Поэтому поступим иначе: преобразуем уравнение на его ОДЗ.
Исходное уравнение на своей ОДЗ равносильно уравнению
l°gi_2r( 1 - Зх) 4- logj_2г( 1 - 2х) - 2 log1_3l(l - 2х) = 2,
т. е. уравнению
logl_2r(l - Зх) - 2 logl_3r( 1 - 2х) = 1.	(12)
Обозначим log1_2r(l — Зх) через z. Тогда поскольку на ОДЗ
logi-згО * 2^) = г----------—,
*°gl-2r(l - Зх)
то уравнение (12) можно переписать в виде
Это уравнение имеет корни z\ = — 1 и z2 = 2. Следовательно,
исходное уравнение на своей ОДЗ равносильно совокупности
двух уравнений:
logi-ZrC1 - Зх) = -1 и logj.^tl - Зх) = 2.	(13)
Первое из этих уравнений равносильно на рассматриваемой
области х < 1/3, х / 0, уравнению
logi_2l(l - Зх) = logl_2l -Д—,
1 — 2х
т. е. уравнению
Это уравнение имеет два корня: Xj = 0 и х2 = 5/6, из которых
ни один не входит в рассматриваемую область, и поэтому не
является решением исходного уравнения. Второе уравнение
совокупности (13) равносильно на области х < 1/3, х / О,
уравнению 1 — Зх = (1 — 2х)2, решения которого есть Хз = 0 и
х4 = 1/4. Из этих значений только х4 — 1/4 входит в рассма-
триваемую область и потому является единственным корнем
исходного уравнения.
Ответ: х — 1/4.
64
Радикалы, степени, логарифмы и модули
2.2.2.	Переход к основанию, содержащему неиз-
вестную. Иногда при решении уравнений и неравенств ви-
да (1) и (2) переходят к логарифмам по другому основанию,
содержащему х. При этом надо помнить, что может произой-
ти сужение ОДЗ, а следовательно, и потеря корня. Поэтому
при переходе в уравнении (или неравенстве) к логарифмам
по некоторому основанию h(x), содержащему х, вначале на-
до проверить, что h(x) > 0 для рассматриваемых х, а также
проверить, не являются ли значения х, при которых А(х) = 1,
решениями исходного уравнения, после чего уже переходить
к основанию h(x), но уже для тех х, для которых h(x) > 0 и
h(x) / 1.
Пример 4. Решить уравнение
logx х1 - log8, х3 = 0.	(14)
Решение. ОДЗ этого уравнения состоит из всех х, удовле-
творяющих условиям х > 0, х ф 4, х ф 1/8.
Будем решать это уравнение, переходя к логарифмам по
основанию х. Прежде чем сделать этот переход, проверим,
является ли х = 1 корнем исходного уравнения. Подставляя 1
вместо х в уравнение (14), получаем, что х — 1 есть его ко-
рень. Перейдя теперь в уравнении (14) к логарифмам по осно-
ванию х (учитывая, что х > 0, х ф 1, х / 4, х / 1/8), получим
уравнение
log* х2 _ log,, х3
log £ log, 8z
(15)
равносильное исходному уравнению на множестве х > 0,
х 4, х 1/8 их / 1. Уравнение (15) для этих х можно
переписать так:
2	3
1 - log* 4 log, 8 + 1
(16)
Поскольку 1 — log, 4 / 0 и 1 + log, 8/0 для рассматривае-
мых х, то уравнение (16) равносильно уравнению
2(1 4-log, 8) — 3(1 — log, 4) = 0
§ 2.2. Неизвестная в основании логарифма
65
или уравнению
121ogr2 = 1,
имеющему единственный корень х = 212. Так как этот корень
входит в рассматриваемое множество х > 0, х / 1, х / 4,
х / 1/8, то он и является решением исходного уравнения на
этом множестве.
Ответ: х = 212, х = 1.
2.2,3.	Уравнения вида log^) /i(x) = log^j </(х),
l°g/(r)	= logj(r) ^(х)- Уравнения
log^) Л(х) = log^^x),	(17)
log/(r) = logs(l) V(x)	(18)
можно решать и таким способом:
1.	Перейти от этих уравнений к их следствиям, т. е. от
уравнения (17) к уравнению
/i(x) = д(х),	(19)
а от уравнения (18) к совокупности уравнений (20)
/(х) = </(х) и у>(х) = 1.
2.	Решить уравнение (19) или совокупность уравне-
ний (20).
3.	Проверить, какие из найденных корней будут корнями
исходного уравнения.
Пример 5. Решить уравнение
logi+l+sin Л*2 + х - 1) = l°g1+l+sinl(3z + 2).	(21)
Решение. Уравнение
х2 + х - 1 = Зх + 2	(22)
является следствием уравнения (21). Переписав уравнение (22)
в виде х2 —2х —3 = 0, находим его корни xj = 3 и х? = —1- При
х2 = — 1 функция, находящаяся в основании логарифмов, при-
нимает отрицательное значение 1 -f- х2 + sinx2 = — sin 1 < 0,
66
Радикалы, степени, логарифмы и модули
т. е. Х2 не удовлетворяет уравнению (21). При х^ = 3 функ-
ция, находящаяся в основании логарифмов, принимает значе-
ние, большее нуля и не равное 1, так как 1 + Xi + sinri =
= 4 + sin 3 > 4, т. е. zi удовлетворяет уравнению (21).
Ответ: х = 3.
Пример 6. Решить уравнение
loSsinx+cos2 r+^/cosr
l°8sin r+l+ycosr
(23)
Решение. Совокупность уравнений
sin х + cos2 х + -уcos х = sin x + 1 + -/cos x,
1 — yj x"1 — x — 1,
(24)
является следствием уравнения (23). Ясно, что все решения
первого уравнения совокупности (24) есть решения уравнения
cos х = 1, т. е. хъ = 2тгАг, t EZ. При любом х^ — 2ттк, tgZ,
функция sin х + cos2 х + -Уcos ж равна 2, т. е. при этих хь осно-
вания логарифмов в уравнении (23) равны 2. Поэтому реше-
ниями уравнения (23) будут те s*, = 2?rfc, к G Z, для которых
1 — у] х^ — х^ > 0. Легко видеть, что только то — 0 удовле-
творяет этому условию, а следовательно, является решением
уравнения (23).
Решения уравнения 1 — у/х? — х = 1 есть х' = 0 и х" = 1.
Так как sinl > sinTr/4 = х/2/2, cos 1 > costt/3 = 1/2, то
/---------------- 2	/--- у/2	1
sin 1 + 1 + V cos 1 > 1, Sin 1 + cos 1 + V cos 1 > —-h - +
y/^
-I—— > 1. Значит, x" = 1 удовлетворяет уравнению (23).
Следовательно, решениями уравнения (23) являются х' = 0 и
х" = 1.
Ответ: х — 0, х — 1.
2.2.4.	Уравнения вида logy^) g(x) = а. Если в уравне-
нии
bg/(r) ЭЮ = а.	(25)
§ 2.2. Неизвестная в основании логарифма
67
а = п, где п — натуральное число, то следствием уравне-
ния (25) является уравнение
S(z) = [/(х)]~.	(26)
Если же а = 0, то следствием уравнения (25) является урав-
нение
!?(*) = 1.	(27)
Уравнение вида (25) можно решать, следовательно, так:
1.	Перейти от этого уравнения при натуральном п к урав-
нению (26), а при п — 0 к уравнению (27).
2.	Решить уравнение (26) или уравнение (27).
3.	Проверить, какие из найденных корней будут корнями
исходного уравнения.
Замечание. Конечно, можно считать, что при любом
действительном числе а следствием уравнения (25) являет-
ся уравнение
<№) = [/(*)]“>
но тогда надо уточнять, что понимается под функцией [/(я)]а.
Пример 7. Решить уравнение
log2l_i(2z2 + 4z+l) = 2.	(28)
Решение. Уравнение
2z2 + 4z+ 1 = (2z - I)2	(29)
является следствием уравнения (28). Переписав уравнение (29)
а виде 2т2 — 8я = 0, находим его корни х^ = 4 и Х2 = 0. Легко
видеть, что Xi = 4 является корнем уравнения (28), а х^ = 0
не является его корнем.
Ответ: х = 4.
Пример 8. Решить уравнение
logrcosa’ = 0.	(30)
Решение. Следствием уравнения (30) является уравнение
cos х — 1, решения которого есть x = 2як, к £ Z. Ясно, что
из этих х уравнению (30) будут удовлетворять лишь х = 2як,
ке^.
Ответ: х = 2тгк. к £ N.
68
Радикалы, степени, логарифмы и модули
2.2.5. Неравенства вида log^/(®) > log^j Со-
гласно общему методу решения неравенств, содержащих не-
известную в основании логарифмов, неравенство
log^)	g(x)	(31)
равносильно при а > 1 неравенству
loga > loga g(x)
loga loga ’
которое можно переписать в виде
loga Л*) ~ l°gq 9(х) > 0
loga <Р(Х)
Последнее неравенство равносильно совокупности систем не-
равенств
Г loga f(x) - loga 9(х) > 0, и Г loga/(ж) — loga аг(аг) < О,
( loga у>(х) >0	( loga <р(х) < 0
или совокупности систем неравенств
/(х) > д(х) >0,	( 0 < f(x) < g(x),
ip(x) >1	I 0 < (p(x) < 1.
(32)
Поэтому неравенство вида (31) можно решать следующим
образом:
1. Перейти от неравенства (31) к равносильной совокупно-
сти неравенств (32).
2. Решить совокупность неравенств (32), ее решения и бу-
дут решениями неравенства (31).
Пример 9. Решить неравенство
logr2(x2 - 4х + 3) > logr2 х2.	(33)
Решение. Неравенство (33) равносильно совокупности
двух систем неравенств:
ж2 > 1
z2_4z + 3>z2>0j	С34)
§ 2.2. Неизвестная в основании логарифма
69
О < х2 < 1,
О < х2 — 4х 4- 3
х2.
(35)
Система (34) равносильна совокупности двух систем:
х > 1,
—4х 4- 3 > О
х < — 1
—4х 4- 3 > О,
из которых первая не имеет решений, а решения второй со-
ставляют промежуток —оо < х < —1.
Система (35) равносильна совокупности систем нера-
венств
' 0 < х < 1,
< х2 — 4х -|- 3 > О,
—4х 4- 3 < О
' -1 < х <0,
< х2 — 4х 4- 3 > О,
—4х 4- 3 < 0.
и
Решения первой системы этой совокупности есть множество
3
- < х < 1, а вторая система решении не имеет.
4
Следовательно, решениями исходного неравенства явля-
ются все х из объединения двух промежутков —оо < х < — 1
3
и - < X < 1.
4
3
Ответ: —оо < х < —1: - < х < 1.
4
Процесс решения неравенства вида (31) иногда оформляют
следующим образом:
1.	Находят ОДЗ неравенства (31).
2.	Разбивают ОДЗ неравенства (31) на два множества
Му и М2: Mi — та часть ОДЗ, где <р(х) > 1, М2 — та часть
ОДЗ, где 0 < <р(х) < 1.
3.	На Mi решают неравенство f(x) > д(х), равносильное
на Mi исходному неравенству.
4.	На М2 решают неравенство f(x) < д(х), равносильное
на М2 исходному неравенству.
Объединяя решения, найденные на Mi и Л12, получают все
решения исходного неравенства.
Пример 10. Решить неравенство
logr
Зх 4- 2
х 4- 2
> 1.
(36)
70
Радикалы, степени, логарифмы и модули
Решение. ОДЗ неравенства (36) определяется из условий
Зж + 2
х > 0, ---- > 0, х 1, т. е. ОДЗ состоит из двух проме-
х 4- 2
жутков: х>1и0<ж<1.
а)	Пусть х > 1. Для этих х исходное неравенство равно-
сильно неравенству
Зт + 2
14-2
(37)
Так как ж 4-2 > 0 для рассматриваемых х, то неравенство (37)
равносильно неравенству Зх 4- 2 > х(х 4- 2), которое можно
записать в виде
х2 — х — 2 < 0.
(38)
Решениями неравенства (38) являются все х из промежутка
— 1 < х < 2. Из этих х условию х > 1 удовлетворяют х из
промежутка 1 < х < 2.
Следовательно, в случае а) решения исходного неравенства
составляют промежуток 1 < х < 2.
б)	Пусть 0 < х < 1. Для этих х исходное неравенство
равносильно неравенству
3x4-2
х 4- 2
< х.
(39)
Так как г 4-2 > 0 для рассматриваемых х, то неравенство (39)
равносильно неравенству Зх 4- 2 < х(х 4- 2), которое можно
переписать в виде
х2 — х — 2 > 0.	(40)
Решениями неравенства (40) являются все х из двух проме-
жутков —оо < х < — 1 и 2 < х < 4-оо. Ни одно из этих х не
удовлетворяет условию 0 < х < 1. Следовательно, в случае б)
исходное неравенство не имеет решений.
Ответ: 1 < х < 2.
§ 2.3. Неизвестная в основании и показателе степени 71
§ 2.3. Уравнения и неравенства, содержащие
неизвестную в основании и показателе
степени
В этом параграфе рассматриваются уравнения и неравен-
ства вида
f(xy^=g(x)h^\	(1)
> g(x)h^,	(2)
в том случае, когда обе функции /(ж) и д(х) положитель-
ны на общей части (пересечении) областей существования
функций f(x), д(х), р(х) и h(x) и хотя бы одна из двух функ-
ций <р(х) или h(x) не является числом.
Общим способом решения таких уравнений и неравенств
является следующий.
1.	Отыскивается множество М — общая часть (пересече-
ние) областей существования функций /(х), д(х), <р(х) и h(x).
2.	Проверяется, что на множестве М функции f(x) и д(х)
положительны.
3.	Затем путем логарифмирования левой и правой ча-
стей уравнения или неравенства по некоторому основанию а
(а > 0, а / 1) уравнение (1) заменяется равносильным ему
на М уравнением
*’(«) loga f(x) = h(x) loga g(x),	(3)
а неравенство (2) — равносильным ему на М неравенством
V>(x) l°ga /(*) > Л(«) loga 9(х)> а>1'	(4)
4.	На множестве М решается стандартное по внешнему
виду уравнение (3) или неравенство (4).
Пример 1. Решить уравнение
—£== = (3z-5)1°gA(2+5r-r2).
у/Зх — 5
Решение. Множество М — общая часть (пересече-
ние) областей существования функций f(x) =	..,
y3z - 5
72
Радикалы, степени, логарифмы и модули
д(х) = Зх — 5, h(x) = log^sC^ 4- 5х — ж2) — состоит из всех х,
одновременно удовлетворяющих условиям
( Зх - 5 > О,
[ 2 4- 5х — х2 > 0.
. Пользуясь формулами
Решая эту систему неравенств, находим, что множество М
5	5+ л/33
есть интервал - < х < --------
3	2
1о81/25г = ~21оё5г и
.	= (Зх-5)'1/2,
^Зх - 5 v ’
перепишем исходное уравнение в виде
(Зх - 5)"1/2 = (Зх - 5)-1/21о85(2+5г-г2)
Логарифмируя это уравнение, например, по основанию 2, по
лучим уравнение
l°g2(3x - 5) = log5(2 + 5х - х2)-log2(3x - 5),	(5)
равносильное исходному уравнению на М.
Уравнение (5) можно переписать в виде
log2(3x - 5)-(log5(2 4- 5х - х2} - 1) = 0,
откуда следует, что оно равносильно на М совокупности двух
уравнений
log2(3x — 5) = 0 и log5(2 + 5х — х2) = 1.
Первое уравнение имеет единственный корень х± = 2, ко-
торый входит в множество М. Второе уравнение равносильно
на М квадратному уравнению 2 4- 5х — х2 = 5, которое име-
5 4- У13	5 - У13 „
ет два корня х? — -------- и х3 = --------. Из этих чисел
5 4-х/Тз
в М лежит только х2 = ----------• Следовательно, исходное
уравнение имеет два корня Xi иг?.
§ 2.3. Неизвестная в основании и показателе степени 73
Ответ: х^ = 2, х2 = —-—.
ПРИМЕР 2. Решить уравнение
х2 + х + 1)*-5>А+б = (я + з)*-5>А+б
РЕШЕНИЕ. Множество М— общая часть (пересечение)
областей существования функций f(x) = х2 + х + 1,
д(х) = х + 3, <р(х) — х — 5 у/х + 6 есть все х 0. На мно-
жестве М функции /(х) и д(х) положительны. Поэтому ло-
гарифмируя обе части уравнения, например, по основанию 2,
получим уравнение
(х — зу/х + 6) log2(x2 + х + 1) = (х — 5т/х + 6) log2(x + 3),
равносильное исходному на М.
Полученное уравнение можно переписать в виде
(х - 5д/х + 6)(log2(x2 + х + 1) - log2(x + 3)) = 0,
откуда следует, что оно равносильно на М совокупности двух
уравнений
х — Ьу/х -р6 = 0 и log2(x2 + х + 1) — log2(x + 3) = 0.
Первое уравнение имеет два корня х4 = 4 и х2 = 9, входя-
щие в М. Второе уравнение равносильно на М уравнению
х2 + х + 1 = х + 3, имеющему два корня х3 = у/2 и х4 = — у/2,
из которых в М входит только х3 = у/2. Итак, решениями
исходного уравнения являются Xi = 4, х2 — 9 и х3 = у/2.
Ответ: xi = 4, х2 = 9, х3 = у/2.
Пример 3. Решить неравенство
zlog2y^ < 22+l1Og2r
(6)
Решение. Множество М— общая часть (пересечение)
областей существования функций /(х) = х, <p(x) = log2 у/х,
/г(х) = 2 + - log2 х — состоит из всех х из промежутка
0 < х < +оо. На этом множестве М положительны функции
74
Радикалы, степени, логарифмы и модули
f(x) = х и д(х) = 2. Поэтому, логарифмируя неравенство (6)
по основанию 2, получим равносильное ему на М неравенство
log2 у/х log2 х
1	9
<2 + - log2 х.
Перепишем это неравенство
в виде (log2 х)2 < 8 или в виде
—>/В < log2 х < х/8.
Решениями неравенства (7) являются все х из промежутка
< х < 2'^®. Все эти х входят в М и поэтому являются
решениями исходного неравенства.
Ответ: 2-^® < х < 2^®.
Пример 4. Решить неравенство
z + 2\r<^2
х + 1 /
X
х + 2
(8)
Решение. Множество М— общая часть областей суще-
х ~| 2	х
ствования функций f(x) = ----, д(х) = ---, <р(х) = х2 —
х + 1	х + 2
— у/х + 2 — есть все х из промежутка 0 х < сю. На этом
множестве функции f(x) и д(х) положительны, поэтому, ло-
гарифмируя неравенство (8) по основанию 2, получим равно-
сильное ему на М неравенство
/ /у» I 9 \	i
(z2 -	+ 2) log2 (——Т ) > (г2 — т/г + 2) log2 ——.	(9)
4- 1 /	х -г 2
Неравенство (9) равносильно на М совокупности
х2 — у/х + 2 > О,
< х + 2 х
< х + 1 х + 2 >
х2 — у/х -|- 2 < О,
х х + 2
> х + 2 х + 1
(Ю)
(И)
§ 2.4. Неизвестная под знаком абсолютной величины 75
Докажем, что для любого z О выполняется неравенство
х2 — у/х + 2 > 0. В самом деле, при любом х, 0 х 1,
имеем 0 у/х ^1и0^х2^1, поэтому
х2 — у/х 4-2 = х2 +1 + (1- у/х) > 0.
При любом х > 1 имеем х2 > у/х, поэтому х2 — у/х 4- 2 > 0.
Следовательно, на множестве х 0 система (11) решений не
имеет, а система (10) равносильна системе неравенств
х > 0,
< х 4- 2 х
< х 4- 1 > х 4- 2
(12)
Поскольку при х > 0 имеем х 4- 1 > 0 и i + 2 > 0, то второе
неравенство системы (12) для х > 0 равносильно неравенству
(x-j-2)2 > z(x4-1), которое можно переписать в виде 3x4-4 > 0.
Последнее неравенство справедливо для любого х > 0. Следо-
вательно, система неравенств (12) справедлива для любого
х > 0. Поэтому множество решений исходного неравенства
есть все х > 0.
Ответ: 0 < х < 4-оо.
§ 2.4. Уравнения и неравенства, содержащие
неизвестную под знаком абсолютной
величины
2.4.1. Раскрытие знаков модулей. Основной метод
решения уравнений и неравенств, содержащих модули, состо-
ит в следующем: надо разбить ОДЗ уравнения или неравен-
ства на множества, на каждом из которых каждое из выраже-
ний, стоящих под знаком модуля, сохраняет знак. На каждом
таком множестве уравнение или неравенство записывается без
знака модуля и затем решается на этом множестве. Объедине-
ние решений, найденных на всех этих множествах — частях
ОДЗ уравнения или неравенства, составляет множество всех
его решений.
76
Радикалы, степени, логарифмы и модули
Пример 1. Решить уравнение
+ 2|г-3| + 2 _ а;22|г-3|+4 + 2г-1	(!)
Решение. ОДЗ уравнения состоит из всех действитель-
ных х. Разобьем ОДЗ на два промежутка:
а)	х — 3	0 ;
б)	х — 3 < 0.
а)	Пусть х 3, тогда |аг — 3| = х — 3 и уравнение (1)
запишется на этом множестве так:
z22r+1 +21-1 = ж22г+1 +2r-1.
Это уравнение превращается в верное числовое равенство для
любого действительного х, т. е. его решениями являются все
действительные х. Из них условию х 3 удовлетворяют все х
из промежутка [3;+оо). Они и являются решениями уравне-
ния (1) в случае а).
б)	Пусть х < 3, тогда |ж — 3| = —х 4- 3 и уравнение (1)
запишется на этом множестве так:
z22r + l + 2-* + 5 _ ж22-* + 7 + 2*-1
ИЛИ
(2Г — 64-2-г)(4ж2 — 1) = 0.	(2)
Решения этого уравнения есть х^ = 1/2, х? — — 1/2, Хз = 3. Из
этих значений условию х < 3 удовлетворяют только xi = 1/2
и Х2 = —1/2. Итак, решения уравнения (1) есть Xi = 1/2,
Хз = —1/2 и все х из промежутка [3;4-оо).
Ответ: xi = -1/2; ж2 — 1/2; 3 х < сю.
Пример 2. Решить неравенство
|ж2 - ®| + |1 - x/log2(l 4- ж)| > y/log2(l 4- ж) - ж2 4- х. (3)
Решение. ОДЗ неравенства состоит из всех х, удовле-
творяющих условию х 0. Так как функции у = ж2 — х и
У = 1 - y/bg2(l + х) меняют знак на области ж 0, прохо-
дя через точку ж = 1, то разобьем ОДЗ на два промежутка:
0^ж^1и1<ж< 4-оо.
§ 2.4. Неизвестная под знаком абсолютной величины 77
а) Если 0 z 1, то ж2 — х 0 и 1— \Zlog2( 1 + z) 0.
Поэтому неравенство (3) запишется для этих х в виде
-х2 + х + 1 - x/log2(1 4- г) > yiog2(l + г) - х2 + х,
т. е. в виде
у/1оё2(1 + х) < -.
Решения этого неравенства есть 0^z<2« — 1. Все эти х
удовлетворяют условию 0 х 1, а значит, являются реше-
ниями исходного неравенства (3).
б) Если 1 < х < +оо, тох2- х > 0 и 1- y/log2( 1 4- х) < 0.
Поэтому неравенство (3) перепишется в виде
х2 - х 4- yiog2(l 4- ж) - 1 > yiog2(l 4- т) - х2 4- х,
т. е. в виде 2х2 — 2х — 1 > 0. Решения этого неравен-
1 - vz
ства составляют два промежутка: —оо < х < —-— и
1 + УЗ
—-— < х < 4-оо. Из этих х условию х > 1 удовлетво-
14-V3
ряют все х из промежутка —-— < х < 4-оо, поэтому все
они являются решениями неравенства (3). Множеством всех
решений исходного неравенства (3) будет объединение реше-
ний, найденных в случаях а) и б).
г 14- УЗ
Ответ: 0 < х < 2< - 1; ----< х < 4-оо.
’2
2.4.2. Уравнения вида |/(х)| = д^х). Уравнение
1/У)1 = И*)	(4)
можно решать основным методом. Однако в некоторых слу-
чаях полезно уравнение (4) решать следующим образом:
1. Найти ту часть ОДЗ уравнения (4), где д(х~)	0.
2. На этой области уравнение (4) равносильно совокупно-
сти двух уравнений
/О) = р(х) и -/(z)=ff(z).
78
Радикалы, степени, логарифмы и модули
Решения этой совокупности, принадлежащие рассматривае-
мой области, и дадут решение уравнения (4).
Пример 3. Решить уравнение
|2Г — cos х — 5\ = 2х 4-2 + cos х.	(5)
Решение. ОДЗ этого уравнения есть все действитель-
ные х. Очевидно, что на ОДЗ, т. е. для любого действитель-
ного х,
2х 4-2 4- cos х > 0.
Поэтому уравнение (5) равносильно совокупности уравнений
2х — cos х — 5 — 2х + 2 + cos х,
и
— (2х — cos х — 5) = 2х 4- 2 4- cos х.
Первое уравнение решений не имеет, а второе равносиль-
но уравнению 2х = 3/2, имеющему единственный корень
,	3
* = bg2-.
Ответ: х = log2 3/2.
2.4.3.	Неравенства вида	Неравенство
l/WI < sW	(6)
можно решать основным методом. Однако иногда бывает по-
лезно заменить неравенство (6) равносильной ему системой
неравенств
f /(«) < д(х),
1 -/(*) <
Пример 4. Решить неравенство
|х7 + 4х5 + ж2 + 2х — 3| < х7 4- 4х5 — х2 — 2х 4- 3.	(7)
Решение. Данное неравенство равносильно системе нера-
венств
( х7 + 4х5 + х2 + 2х — 3 < х7 + 4х5 — х2 — 2х + 3,
( —(х7 -|- 4х5 4- х2 4- 2х — 3) < х7 + 4z5 — х2 — 2х 4- 3,
§ 2.4. Неизвестная под знаком абсолютной величины 79
которую можно переписать в виде
х2 + 2х - 3 < 0,	,яч
х5(х2 + 4) > 0.	W
Решения первого неравенства системы (8) составляют про-
межуток —3 < х < 1, решения второго составляют проме-
жуток 0 < х < +оо. Следовательно, решения системы нера-
венств (8), а значит, и исходного неравенства (7) составляют
промежуток 0 < х < 1.
Ответ: 0 < х < 1.
2.4.4.	Неравенства вида |f(r)| > g(x). Неравенство
l/(*)l > g(x)	(9)
можно решать основным способом. Однако иногда бывает по-
лезно разбить ОДЗ неравенства (9) на две части иначе, а
именно:
1. Найти область, где д(х) < 0. Все х из этой области дают
решение неравенства (9).
2. Найти область, где д(х) 0 ина ней рассмотреть нера-
венство
f(x)>g2(x).
Объединение найденных решений и дает все решения нера-
венства (9).
Пример 5. Решить неравенство
\/z2 — я + 1 — 2х + 1| > \/г2 — а: 4- 1 4- 2х.	(10)
Решение. ОДЗ неравенства (10) состоит из всех действи-
тельных х.
а)	Найдем те х, для которых
\/а:2 — а: 4-1 + 2х < 0.	(11)
Перепишем неравенство (11) в виде
\/а:2 — а: 4-1 < — 2х.
(12)
80
Радикалы, степени, логарифмы и модули
Ясно, что никакое х из промежутка 0 х < +оо не явля-
ется решением неравенства (12). Пусть х < 0, для этих х
неравенство (12) равносильно неравенству
х2 — х + 1 < 4а:2.
(13)
Решения неравенства (13) составляют два промежутка:
-1-713	-1 + 713
—оо < х < ---------- и -------- < X < 4-00. Из ЭТИХ X
условию х < 0 удовлетворяют лишь х из промехсутка
— 1 — у13 _
—оо < х < ----------. Следовательно, решениями неравен-
6	,__
/in	. 1 + 713
ства (11) являются все х из промежутка —оо < х <-----,
все эти х являются решениями исходного неравенства (10).
гт	1 + 713
б)	1еперь на множестве х ----------рассмотрим нера-
венство
(7г2 — г + 1 — 2а? + 1) > (7а:2 — а? + 1 + 2а:)	(14)
Неравенство (14) можно переписать в виде
2(1 — 4а?)7 а:2 — а: + 1 > —(1 — 4а:).	(15)
Ясно, что х = 1/4 не есть решение неравенства (15). Для
любого х > 1/4 левая часть неравенства (15) отрицательна, а
правая положительна, следовательно, среди х > 1/4 нет реше-
ний неравенства (15). Для любого х < 1/4 левая часть нера-
венства (15) положительна, а правая отрицательна, следова-
тельно, любое из этих х является решением неравенства (15).
тл	-1-713
Из этих х в множество х --------- входят все х из про-
6
1 + Т1з , i
межутка--------- + х -. Все они являются решениями
6	4
исходного неравенства (10).
Объединяя решения, найденные в пунктах а) и б), получа-
ем решения исходного неравенства.
Ответ: -оо < х < 1/4.
§ 2.4. Неизвестная под знаком абсолютной величины
81
2.4.5. Уравнения и неравенства вида |f(tf)| = |^(г)|,
|/(r)| <	l?(z)|.	Уравнение
1/(*)1 =	|g(r)|	(16)
и неравенство
1/(*)1 <	Ш1	(17)
можно	решать	согласно общему	методу. Однако иногда быва-
ет полезно заменить уравнение (16) уравнением f2(x) = g2(x),
т. е. уравнением (/(ж) + ^(z))(/(z) — g(x)) — 0, равно-
сильным ему на его ОДЗ, а неравенство (17) неравенством
f2(x) < g2(x), т. е. неравенством (f(x)+g(x'))(f(x) — g(x)) < О,
равносильным ему на его ОДЗ.
Пример 6. Решить неравенство
|z3 — sin r| < |2z3 + sin x|.	(18)
Решение. ОДЗ этого неравенства есть все действитель-
ные х. Неравенство (18) равносильно неравенству
(х3 — sin х + 2r3 + sin х)(х3 — sin х — 2х3 — sin х) < О,
которое можно переписать в виде х3(х3 + 2 sin х) > 0. Решени-
ем этого неравенства является любое действительное х, кроме
х = 0. В самом деле, для любого х, принадлежащего проме-
жутку (—оо; — тг], имеем х3 < 0 и х3 + 2sinz —тг3 + 2 < 0,
поэтому х3(х3 + 2 sin х) > 0 для любого такого х. Для любо-
го х, принадлежащего промежутку (—тг; 0), имеем х3 < 0 и
sin# < 0, поэтому х3 + sin х < 0 и х3(х3 + sinz) > 0. В си-
лу четности функции х3(х3 + 2 sin г) получаем, что все х > 0
также являются решениями неравенства. Очевидно, что х — 0
неравенству не удовлетворяет.
Ответ: —оо < х < 0; 0 < х < +оо.
Пример 7. Решить уравнение
|г3 + х + 1| = |z2 + 3z — 1|.	(19)
РЕШЕНИЕ. ОДЗ уравнения (19) есть все действительные х.
Возведя обе части уравнения в квадрат, получим уравнение
(х3 + х-$-1 — х2 — Зх + l)(z3 + х + 1 + х2 + Зх — 1) = 0,
82
Радикалы, степени, логарифмы и модули
равносильное исходному. Это уравнение можно переписать в
виде (х3 — х2 — 2х + 2)(х3 + х2 + 4х) = 0, откуда следует, что
оно равносильно совокупности уравнений
х3 + х2 + 4х = 0,	(20)
и
х3 - х2 - 2х + 2 = 0.	(21)
Так как х3 + х2 + 4х = х(х2 + х + 4) и дискриминант ква-
дратного трехчлена х2 +х +4 отрицателен, то уравнение (20)
имеет единственный корень х\ = 0. Поскольку х3 — х2 —
— 2х + 2 = х2(х — 1) — 2(х — 1) = (х — 1)(х2 — 2) =
= (х - 1) (г - (г + y/2j, то решения уравнения (21) есть
х2 = 1, хз = у/2 и Х4 = — у/2.
Итак, исходное уравнение имеет четыре корня: xi = 0,
Х2 = 1, Хз = у/2 И Х4 = —у/2.
Ответ; Xi = 0, х2 = 1, х3 = у/2, х4 = —у/2.
2.4.6. Использование свойств абсолютной величи-
ны. При решении уравнений и неравенств с модулем иногда
бывает полезно решать их не по основному методу, а приме-
нять свойства модуля, в основном неотрицательность на ОДЗ
выражения, находящегося под знаком модуля.
Пример 8. Решить уравнение
|\/х2 — х — х| + |х 4- \/х| = у/х2 — х + у/х. (22)
Решение. Обозначим у/х2 — х — х через а и х + ^/х через Ь.
Тогда уравнение (22) можно записать в виде
|а| + |6| = а + Ь.	(23)
Из свойств абсолютной величины вытекает, что равен-
ство (23) возможно тогда и только тогда, когда одновременно
а 0 и J 0. Поэтому исходное уравнение (22) равносильно
системе неравенств
( у/х2 — х — х 0,
1 х + у/х 0.
§ 2.4. Неизвестная под знаком абсолютной величины 83
Решение этой системы неравенств, а значит, и исходного
уравнения есть х = 0.
Ответ: х = 0.
Пример 9. Решить уравнение
log2* 1 - loga *	+ |log^l-rio7Ta:1|-	(24) 1 l°g2 * “ 1|
Решение. ОДЗ уравнения (24) есть все х > 0, кроме х = 2.
Поскольку для любого х из ОДЗ
log^ loga*
log2 х - 1 log2 x — 1
+ log2*,
loga* _ loga*
|log2ar —1| log2 x - 1
то уравнение (24) можно переписать так:
loga*
log2 * - 1
+ |log2 *| =
log, *
1--------т + l°g2 * •
log2 x - 1
(25)
Обозначим - ^°—— через а и
loga X - 1
ние (25) можно переписать так:
log2 x через b, тогда уравне-
|a| + |&| = |a + 6|.
(26)
Из свойств абсолютной величины вытекает, что равен-
ство (26) имеет место тогда и только тогда, когда
ab 0.
Это означает, что решения уравнения (24) совпадают с реше-
ниями неравенства
т 0.	(27)
log2
log2*
Решениями неравенства (27), а значит, и исходного уравне-
ния, являются х = 1 и все х из промежутка 2 < х < +оо.
Ответ: х = 1; 2 < х < +оо.
84
Радикалы, степени, логарифмы и модули
Пример 10. Решить неравенство
|т| 4-|7 — х| 4-2|т — 2| < 4.
(28)
Решение. Для любого х 2 имеем 7 — х 5, поэтому
|т| + |7 — т| + 2|т — 2] 5, а это означает, что ни одно из х 2
не является решением неравенства (28).
Для любого х 4 имеем |х|	4, и поэтому |г| + |7 — х| +
+ 2|т — 2|	4, а это означает, что ни одно х 4 также не
является решением неравенства (28).
Для любого х из промежутка 2 < х < 4 имеем 3 < 7 — х < 5,
поэтому |7 —	> 3 и |г| > 2. Следовательно, |т| + |7 — т| +
4- 2|т — 2| > 5, а это означает, что ни одно х из промежутка
2 < х < 4 не является решением неравенства (28).
Итак, неравенство (28) не имеет решений.
ОТВЕТ: решений нет.
Задачи
Решить уравнение
1.	у/ х + 3 + у/х + 2 = 7.
2.	у/Зх + 19 + у/Зх - 2 = у/7х+ 11 + у/2х.
3.	у/2х + 1 — у/х = у/х — 3.
4.	у/11х 4- 3 — у/2 — х = у/9х + 7 — у/х — 2.
5.	у/~22 - х4 - у/10 - х4 = 2.
6.	^1 - г + ^х + 15 = 2.
7.	у/х3 — х + 5 = у/х3 + х2 — 1.
8.	у/Г^х + у/2- х = у/3 - 2х.
9.	Vx + 59 - Vx + 22 = 1.
10.	V2x + 1 + у/х = 1.
11.	у/2х+ 1 + у/х = у/2х2 +4х- 23.
12.	х + у/х + у/х 4-2 + \/г2 4- 2т = 7/2.
13.	у/2х2 4- 5х -1 - \/2х2 4- 5х - 9 = 1.
Задачи
85
14.	Ух - 1 + Ух-2 = У2х - 3.
15.	Ух2 - Ух - 1 = 1.
16.	\/4а:2 + 9а: + 5 — х/2х\ + х — 1 = \/х2 — 1.
17.	\/Зх2 + 5х + 8 — УЗх2 + 5х + 1 = 1.
18.	Ух + Ух - 16 = Ух - 8.
19.	у/Зх2 -7х + 3-х/х2 — 2 = УЗх2 -5х-1- yjх2 — Зх + 4.
20.	Ух + 1 + ^а? + 2 + \/х + 3 = 0.
21.	</(1 + г)2 - У1 -х2 + </(1 - а?)2 = 1.
22.	yjx2 = (г +
V х — 1
23.	х + 1 = (д/2 + х + 1) (V2 + а? + а?2 + х - 7) .
24.	\Jх + 3 — 4\/х —Т + \Jх -\-3 — бУх —Т = 1.
25.	Ух - 1 + ^/(х — I)3 — х + 2 = Ух + </(х — I)3 — х + 1.
2б	У2+^ + У2~^ _ 2
У2 + х - У2- х х
27.	\/х2 + х Н-1 — л/х2 — Зх + 7 = %/х2 — х + 2~Ух2 — 5а: + 8.
28.	х = (Ух+ 4 + 2) (У2х + 6 - 1) .
29.	|а?3 - 2х - 3| = |х3 - 2а: + 5|.
30.	log2 (а:4 — У х4 — 4 + а:2 + 2^ =
= log2 (а:8 - у/х4 — 4 + а:2 - io) .
31-	(log^ 2)(log2r 2)(log2 4r) = 1.
32.	log3 (y/x + \y/x - 1|) = log9 (4y/x - 3 + 4 \y/x - 1|) .
x 4 x 1	4
33.	13a:-3a:2-^==--L=i+|4-a:| = 3a:|4-a:|--7=+4.
Ух — 1 Ух — 1	Ух — 1
34.	2 log* 3 + log3r 3 + 3 log9r 3 = 0.
r2
35.	(log2 x + 2) log16r 4 = logr 4- log4 у.
36.	logyj(a: + |x — 2|) = logr(5r — 6 + 5|x — 2|).
86
Радикалы, степени, логарифмы и модули
37.	log27?_ ^+2(4г - 4л/г - 4^4- 84) = 2.
38.	log(r_2)2(4 - 4г + г2) = 2 + log(r_2)2(z + 5)2.
39.	logi_2r(6z2 - 5z + 1) - log1_3r(4r2 - 4х + 1) = 2.
40.	logi.,. х2 - 14 log16r х3 + 40 log4r Уж = 0.
41.	|х|1о8з(*2+3*) = (г2 + 3z)log3(1-;r\
42.	(2 + sin х)х ~х — (2 4- cos z)r ~х.
43.	(1 + х2 + г4 + sin2 г)2*-1 = (1 + х2 + г4 + sin2 х)2~х.
1	л —	х
44.	—===== = (1 — X2) l+*inx .
у/Г^
45.	(1 + х4 + cos z)^1-*2 = (1 + х4 + sin z)^1-*2.
Решить неравенство
46.	у/2х — 3 + >/4x4-1 > 4.
47.	у/х - 1 4- у/2х 4- 2 > 4.
48.	л/г 4- 3 > у/х — 4- у/'о — х.
49.	у/Ъх — 1 — у/х 4- 1 < >/х 4- 2.
50.	y/lx — 1 4- V3r — 2 < л/4г — 3 4- у/Ьх — 4.
51.	\/х4 4- 2х2 — 1 — у/^х4 4- г2 4-1 < \/х2 4- х.
52.	|\/х2 — х 4-1 — 2х 4-1| > \/х2 — х 4-1 4- 2х.
53.	>/х 4- 2 — у/Ъх > 4х — 2.
54.	у/х 4- 1 4- 1 < 4х2 4- у/Зх.
55.	log2(2* + 1 - х2)	log2(21'1 + 1 - х) 4- 1.
56.	logt (logr у/б — х) > 0.
57.	logr2x y/\ogx(2x3).
58.	(z2 + х + 1)^2-^+6 > (P + 2)*2~5*+6.
59.	(x2 4- l)2+r > (x2 4- I)5*-3.
2-log^r4-21ogi x 1
oil. X	*	> —.
X
Глава III
Способ замены неизвестных при
решении уравнений
Если дано уравнение
^(Л*)) = О,	(I)
то заменой неизвестной у = f (х) оно сначала сводится к урав-
нению
Ш = О,	(II)
а потом после нахождения всех решений уравнения (II)
У1, У2,--, Уп,--
сводится к решению совокупности уравнений
Л*) = J/1,	=У2,---, f(x) = уп,....	(Ш)
Этот прием достаточно хорошо известен, и поэтому в этой
главе ему уделяется мало внимания. В основном в этой главе
рассматриваются замены неизвестных для различных част-
ных случаев уравнений, не записанных в виде (I).
§ 3.1.	Алгебраические уравнения
3.1.1.	Понижение степени уравнения. Некоторые ал-
гебраические уравнения заменой в них некоторого многочлена
одной буквой могут быть сведены к алгебраическим уравне-
ниям, степень которых меньше степени исходного уравнения
и решение которых проще.
Пример 1. Решить уравнение *
(х2 + х + 2)(х2 + х + 3) = 6.
(1)
88
Способ замены неизвестных при решении уравнений
РЕШЕНИЕ. Обозначим х2 + х + 2 через t, тогда уравне-
ние (1) можно переписать в виде t(t + 1) = 6. Последнее
уравнение имеет корни С = 2 и /2 = —3. Следовательно, урав-
нение (1) равносильно совокупности уравнений х2 + х + 2 = 2
и х2 + х + 2 = —3. Решения первого уравнения этой совокуп-
ности есть Xi = О, Х2 = — 1. Решения второго уравнения есть
-1 + ^21	-1-V21 „
тз = --------, Х4 = --------. Решениями уравнения (1)
являются Х\, Х2, Хз И Г4.
,	-1 + ^1	-1-^21
Ответ: ц = 0, х2 = -1, хз =-----, z4 =---------.
Пример 2. Решить уравнение
(6z + 7)2(3z + 4)(z + l) = 1.	(2)
Решение. Умножив обе части уравнения на 12 и обозна-
чив 6x4-6 через z, получим уравнение (г + l)2(z + 2)z — 12.
Переписав это уравнение в виде
(z2 + 2z + l)(z2 + 2z) = 12	(3)
и обозначив г2 + 2г через и, перепишем уравнение (3) в виде
(и + 1)и = 12. Последнее уравнение имеет корни uj = 3 и
из — —4. Поэтому получаем, что уравнение (3) равносильно
совокупности двух уравнений г2 + 2z = 3 и z2 + 2z = —4.
Решения этой совокупности уравнений есть Zj = —3 и г2 = 1,
т. е. уравнение (2) равносильно совокупности уравнений
6х + 6 = — 3 и 6х + 6 = 1.	(4)
Решениями совокупности (4) являются Xi
они и являются решениями уравнения (2).
Ответ: п = -3/2, z2 = -5/6.
3	5
-j hz2 = -
6’
3.1.2.	Уравнения вида (z-|-a)4 + (r-|-/3)4 = с. Уравнение
(х + а)4 + (г + /З)4 = с,	(5)
где а, /3 и с — данные числа, можно свести к биквадратному
уравнению с помощью замены неизвестной
_ (х + а) + (г + /3)
У -	2
§ 3.1. Алгебраические уравнения
89
т. е. замены
Пример 3. Решить уравнение
(г- 1)4 + (т + 3)4 =82.	(6)
„	/Тс	(г - 1) + (г + 3)
Решение. Обозначим ----------------- через у, т. е. сде-
лаем замену переменных у = х 4- 1 или х — у — 1. Тогда
уравнение (6) можно переписать в виде (у — 2)4 4-(у4-2)4 = 82
или, применяя формулу (а 4-6)4 = а4 4-4а36-Ьба262 4- 4а63 4- Ь\
в виде
2у4 4-48у2 + 216 = 82.	(7)
Поскольку корни квадратного уравнения z14- 24г — 25 = 0 есть
21 = 1 и z2 = —25, то решения уравнения (7) есть решения
совокупности уравнений у2 = 1 и у2 = —25. Эта совокупность
уравнений имеет два решения j/i = 1 и уг = ~ 1- Следователь-
но, решения уравнения (6) есть х\ = 0 и х? = — 2.
Ответ: xi = 0, х2 = -2.
3.1.3.	Уравнения вида (х — а)(х — /?)(т — т)(т — <5) = А.
Уравнение
(х — а)(х — /3)(х — у)(х — 6) = А,	(8)
где числа а, /3, у, 6 и А таковы, что а</3<у<6и
(3 — а = 6 — 7, заменой неизвестных
х — а 4-х - /3 + х — 7 4-х - 6
у= --------------4--------------
сводится к биквадратному уравнению.
Пример 4. Решить уравнение
(х 4- 1)(г 4- 2)(х 4- 4)(ж 4- 5) = 10.	(9)
Решение. Сделаем замену неизвестных
т-|-1-|-г-|-2-|-г-|-4-|-г-|-5
У =
4
90
Способ замены неизвестных при решении уравнений
т. е. у = х + 3 или х — у — 3. Тогда уравнение (9) можно
переписать в виде (у — 2)(у — 1)(у + 1)(у + 2) = 10, т. е. в виде
(г/2 - 4)(у2 -1) = ю.	(ю)
Биквадратное уравнение (10) имеет два корня: у\ = — л/б и
у2 = л/б. Следовательно, уравнение (9) также имеет два кор-
ня: = —Уб — 3 и Х2 = у/б — 3.
Ответ: xi = -Уб - 3, х2 = Уб - 3.
3.1.4.	Уравнения вида (аж2Ч-61ЖЧ-с)(аж2Ч-б2^Ч-с) = Ах2.
Уравнение
(ах2 Ч- bix Ч- с)(ах2 + Ь?х + с) = Ах2,	(11)
где с/0иА/0, не имеет корня х = 0, поэтому, разделив
уравнение (11) на х2, получим равносильное ему уравнение
(аж + “ + ^1) (ar + ~ + bz'j — А = 0,
с
которое после замены неизвестной у = ах Ч— перепишется в
х
виде квадратного уравнения, решение которого не представ-
ляет трудностей.
Пример 5. Решить уравнение
(х2+ х+ 2)(х2+ 2х + 2) = 2х2.	(12)
Решение. Так как х = 0 не является корнем уравне-
ния (12), то, разделив его на х2, получим равносильное ему
уравнение
/	,	2\ (	2\
1x4-14-—)(хЧ-2-|-— 1=2.
\ х / \	х /
2
Делая замену неизвестной у = х 4---, получим уравнение
х
(у + 1)(у + 2) = 2, которое имеет два корня: у\ = 0 и у2 = — 3.
Следовательно, исходное уравнение (12) равносильно совокуп-
ности уравнений
2	2
х 4— = 0 и х Ч— = —3.
х	х
§ 3.1. Алгебраические уравнения
91
Эта совокупность имеет два корня: a?i = — 1 и rj = -2.
Ответ: arr = -1, а:2 = -2.
Замечание. Уравнение вида
ах4 + [Зх3 + 7а:2 + 8х + А = О,
у которого у = л/у и аХ > 0, всегда можно привести к
о у А
виду (11) и, более того, считая а > Ои А > 0, к виду
^у/ах2 + Va) ^yfax2 + ~^=х +	= (—У + 2-*/аА^ х2.
3.1.5.	Уравнения вида (х — а)(х — ^)(г — у)(х — 6) = Ах2.
Уравнение
(а: — а)(а: — (3)(х — т)(г — 6) = Ах2,	(13)
где числа а, /3, 7, 6 и А таковы, что а/3 = 76/0, можно
переписать, перемножив первую скобку со второй, а третью с
четвертой,в виде
(х2 - х(а + /?) + а/3)(х2 — х[у + 6) + 76) = Ла:2,
т. е. уравнение (13) теперь записано в виде (11), и его решение
можно проводить так же, как решение уравнения (И).
Пример 6. Решить уравнение
(х — 2)(а: — 1)(а: — 8)(а: — 4) - 7х2.	(14)
Решение. Уравнение (14) имеет вид (13), поэтому пере-
пишем его в виде
[(* - 2)(х - 4)][(х - 1)(г - 8)] = 7х2
или в виде
(а:2 — 6 а: + 8)(г2 — 9а: + 8) = 7а:2.
Так как х = 0 не есть решение этого уравнения, то, разделив
его обе части на х2, получим равносильное исходному уравне-
(	8А (	8\
ние а: — 6-|— ) (а: — 9 -|— =7. Делая замену переменных
\	х / \	х /
92
Способ замены неизвестных при решении уравнений
х — = у, получаем квадратное уравнение (г/ — 6)(у — 9) = 7,
х
15 + V37	15-^37
решения которого есть yi = -----и г/2 = ------• Следо-
вательно, исходное уравнение (14) равносильно совокупности
уравнений
8
х + - =
X
15 + >/37
2
8
и х + - =
X
15 - V37
2
Решения первого уравнения этой совокупности есть
Второе уравнение этой совокупности решений не имеет. Итак,
исходное уравнение имеет корни xi и х2.
Ответ:
15 + д/37 + >/30У37 + 134
15 + \/37 - \/30У37+ 134
3.1.6.	Уравнения вида а(сх2 + р^х + q)2 + b(cx2 +
+ р2х + <?)2 = Ах2. Уравнение
а(сх2 + pix + q)2 + b(cx2 + р2х + q)2 = Ах2,	(15)
где числа a, b, с, q, А таковы, что q / О, А ф 0, с / 0, а / О,
b / 0, не имеет корня х = 0, поэтому, разделив уравнение (15)
на х2, получим равносильное ему уравнение
/	q	\2	1 [	q	\ 2
a lex + - + pi + Ь ( сх -|-h р2 ] = А,
\	X	/	\	X	/
§ 3.1. Алгебраические уравнения
93
<z
которое после замены неизвестной у = сх -|— перепишется в
х
виде квадратного уравнения, решение которого не представ-
ляет трудностей.
Пример 7. Решить уравнение
3(z2 + 2х - I)2 - 2(ж2 + Зх - I)2 + 5 г 2 = 0.	(16)
РЕШЕНИЕ. Так как х = 0 не является корнем уравне-
ния (16), то, разделив обе его части на х2, получим уравнение
/	IV	(	IV
3 z + 2--	-2 г + 3--] +5 = 0,	(17)
\	X )	\	X
равносильное уравнению (16). Сделав замену неизвестной
1
х----= у, уравнение (17) перепишем в виде
3(у + 2)2 — 2(у + З)2 + 5 = 0.	(18)
Квадратное уравнение (18) имеет два корня: yi = 1 и у2 = — 1.
Поэтому уравнение (17) равносильно совокупности уравнений
х — — = 1 и х------= — 1.	(19)
х	х
Совокупность уравнений	(19)	имеет четыре корня:
Они будут корнями уравнения (16).
Л	-1 - У5 -1 + ^5	1-У5
Ответ: п = ----------, х2 = -------, х3 = —-—
£	Л/
1 + У5
Та = ----.
3.1.7.	Уравнения вида Р(г) = 0, где Р(г) = Р(а — х).
Пусть многочлен Р(х) обладает свойством: для некоторого
фиксированного числа а справедливо тождественное равен-
ство Р(х) = Р(а — х). Тогда можно показать, что существует
многочлен Q(y) такой, что справедливо тождественное равен-
94
Способ замены неизвестных при решении уравнений
2‘
ство
, при этом многочлен Р(х) должен
быть четной степени.
Поэтому уравнение Р(х) = 0 можно переписать в этом
/ а \ 2
случае в виде уравнения Q(y) = 0, где у =	— -j , степень
которого меньше степени уравнения Р(х) = 0.
Для решения таких уравнений можно поступить следую-
fl
щим образом: сначала сделать замену неизвестной х = у +
тогда получим алгебраическое уравнение той же степени 2k,
что и уравнение Р(х) = 0, но уже содержащее только четные
степени у. Делая затем замену неизвестной t — у2, получим
алгебраическое уравнение уже степени к.
Пример 8. Решить уравнение
г8 + (2 - х)8 - 48(z - 1)2(г2 - 2х + 2)2 - 32(z - I)4 = 32. (20)
Решение. Рассмотрим многочлен
P(r) = z8 + (2-z)8 — 48(х — 1)2(х2-2х + 2)2 — 32(х — I)4-32.
Поскольку легко проверить, что Р(2 — х) = Р(х), то урав-
нение (20) есть уравнение рассматриваемого вида. Сделаем
замену неизвестной у = х — 1 или х = у + 1, тогда уравне-
ние (20) перепишется в виде
[(у + I)2]4 + [(у - I)2]4 - 48у2(у2 + I)2 - 32у4 - 32 = 0. (21)
Так как (у + I)2 = у2 + 1 + 2у, а (у - I)2 = у2 + 1 - 2у,
то, подставляя эти выражения в левую часть уравнения (21)
и раскрывая четвертые степени по формуле
(а + 6)4 = а4 + 4а36 + 6а2Ь2 + 4а63 + 64,
получим, что уравнение (21) перепишется в виде
(у2 + I)4 = 16.	(22)
Уравнение (22) имеет два корня: ух = — 1 и у2 = 1- Следова-
тельно, исходное уравнение имеет также два корня: ri = 0 и
г, = 2.
Ответ: zi = 0, х2 = 2.
§ 3.2. Рациональные уравнения
95
§ 3.2.	Рациональные уравнения
Уравнения вида
<?(*)
(I)
где Н(х) и Q(x) — многочлены, называются рациональными.
Найдя корни уравнения Я(г) = 0, затем надо проверить,
какие из них не являются корнями уравнения Q(x) = 0. Эти
корни и только они будут решениями уравнения (I).
В этом параграфе приводятся некоторые специальные ме-
тоды решения уравнений вида (I).
3.2.1.	Упрощение уравнения. При помощи замены не-
известных рациональное уравнение часто сводится к алгебра-
ическому или более простому рациональному уравнению.
Пример 1. Решить уравнение
х2 + 1 2х + 3 _ 29
2г+ 3 + z2 + 1 ~ 10'
(1)
х2 + 1
2z + 3
Решение. Обозначив
через у, данное уравнение пе-
1	29
репишем в виде у + - = —. Поскольку у — 0 не есть решение
этого уравнения, то это уравнение равносильно уравнению
10у2 — 29у 4-10 = 0. Решения этого уравнения есть у\ = 5/2 и
J/2 = 2/5. Следовательно, уравнение (1) равносильно совокуп-
ности уравнений
х2 +1 5	х2 +1 2
------= - и ----------- - -.
2х + 3	2	2х + 3	5
Первое из этих уравнений на множестве всех х / —3/2 рав-
носильно уравнению
2х2 - 10а: - 13 = 0,
(3)
а второе — уравнению
5а:2 - 4а: - 1 = 0.
К)
96
Способ замены неизвестных при решении уравнений
Решения уравнения (3) есть zj = -----и х2 — -------. Ре-
шения уравнения (4) есть хз = 1 и Х4 = —1/5. Следовательно,
решениями уравнения (1) будут числа х\, х2, £з, ^4-
5 + ^51	5 — \
Ответ: хх =--------, х2 = —-
Пример 2. Решить уравнение
, Гз - 1, Т4 = -i
э
г2 48	, л ( х
V —2 ~ Ю ( ч
3 хг \ 3
4
X
х 4
Решение. Обозначим------через
3 х
перепишется в виде
и, тогда уравнение (5)
3u2 — 1 Qu + 8 = 0.
(5)
(6)
Уравнение (6) имеет два корня: щ = 2 и и2 = 4/3. Поэтому
уравнение (5) равносильно совокупности уравнений
z 4	г 4 4
----= 2 и--------= -.
3	х	3x3
Решения первого уравнения этой совокупности есть
з + уТГ з — У2Т
Zi = ------- и х2 = ------. Решения второго уравнения
есть Хз = — 2 и Х4 — 6. Следовательно, решениями исходного
уравнения (5) являются числа Xi, х2, Хз, Х4.
3 + У21	3-У21
Ответ; zi =------, х2 = —----, х3 - —2, Х4 = 6.
О1 <Х2	<*т
3.2.2.	Уравнения вида -—4----— 4----1--— = А.
z+/?i х+/32	х+/Зт
Уравнение
Q1 .	°2 +... 4. QfTi = А	(7)
х + /?1 х + /?2	х + /Зт
при некоторых условиях на числа а;, А, /?, может быть ре-
шено следующим образом. Группируя члены уравнения (7)
по два и суммируя каждую пару, надо получить в числите-
лях многочлены первой или нулевой степени, отличающиеся
§ 3.2. Рациональные уравнения
97
только числовыми множителями, а в знаменателях — трех-
члены с одинаковыми двумя членами, содержащими х, тогда
после замены переменных полученное уравнение будет либо
иметь также вид (7), но с меньшим числом слагаемых, ли-
бо будет равносильно совокупности двух уравнений, одно из
которых будет первой степени, а второе будет уравнением ви-
да (7), но с меньшим числом слагаемых.
Пример 3. Решить уравнение
11111
— 4--“Ь --4--“Ь--— 0.	(8)
х х + 1 х + 2 х + 3 х + 4
Решение. Сгруппировав в левой части уравнения (8) пер-
вый член с последним, а второй с предпоследним, перепишем
уравнение (8) в виде
1
- +
х
х + 4/	+ 1 х 4- 3/ + г + 2
(9)
Суммируя в каждой скобке слагаемые, перепишем уравне-
ние (9) в виде
2(г + 2) + 2(х + 2)	1	= 0
х2 + 4х х2 4- 4х + 3 х 4- 2
(10)
Так как х = — 2 не есть решение уравнения (10), то, раз-
делив это уравнение на 2(х 4- 2), получим уравнение
х2 4- 4х + х2 4- 4х 4- 3	2(z2 4- 4х 4- 4)	’
равносильное уравнению (10). Сделаем замену неизвестного
х2 4- 4х — и, тогда уравнение (11) перепишется в виде
1 1 1 _ 0
и + и 4- 3 "I" 2(к 4- 4)
(12)
Таким образом, решение уравнения (8) с пятью слагаемыми в
левой части сведено к решению уравнения (12) того же вида.
98
Способ замены неизвестных при решении уравнений
но с тремя слагаемыми в левой части. Суммируя все члены в
левой части уравнения (12), перепишем его в виде
5к2 + 25и + 24
2u(u + 3)(u + 4)
(13)
_	n	— LO -f V I*»»-»
Решения уравнения 5u + 25u + 24 — 0 есть щ = -----—-----
-25-У145 тт
и «2 = -----—------• Ни одно из этих чисел не обращает в
нуль знаменатель рациональной функции в левой части урав-
нения (13). Следовательно, уравнение (13) имеет эти два кор-
ня, и поэтому исходное уравнение (8) равносильно совокупно-
сти уравнений
х2 + 4х =
-25 + У145
10
и х + 4х = ----------
10
Решения первого уравнения этой совокупности есть
/15 + ^/145
V 10
Решения второго уравнения
из этой совокупности есть
Поэтому исходное уравнение имеет корни ц, х2, хз, т4.
Ответ:
Тз = -2 +
— —2 +
15 - л/145
о /15 + V145
io~
Х4 = — 2 —
10
10
§ 3.2. Рациональные уравнения
9!)
„ „ „ лл	Qix + а1 , а^Х + а2 ,
3.2.3. Уравнения вида ------;----1- ----;---F +
х + bi x + b2
otnX + an
H------;--= D. Уравнение
x + bn
“I-	।	“I- Д2 j । H-
X + bl X + b2	X + bn
= D
(14)
при некоторых условиях на числа а,. 6,, а, и D можно ре-
шить так: надо выделить целую часть в каждой из дробей
уравнения, т. е. заменить уравнение (14) уравнением
= D,
свести его к виду (7) и затем решить его способом, описанным
в предыдущем пункте.
ПРИМЕР 4. Решить уравнение
г + 4 х — 4 z + 8 х — 8	8
х — 1 z + 1 х — 2 х + 2	3'
(15)
Решение. Запишем уравнение (15) в виде
1 +
5
х — 1
+ 1 -
5
х + 1
= 1 +
10
х — 2
+ 1 +
-10
z + 2
8
3
или в виде
5
х — 1
5
X + 1 J
10
х-2
10 \
х + 2 J
(16)
Суммируя слагаемые в скобках, перепишем уравнение (16) в
виде
(17)
10 _ 40	8
z2 — 1 z2 — 4	3
Делая замену неизвестного z2 = и, перепишем уравнение (17)
в виде
10	40	8
3
и — 1 и — 4
(18)
100
Способ замены неизвестных при решении уравнений
Суммируя члены в левой части уравнения (18), перепишем
его в виде
4u2 — 65и + 16
(?z — 1)(и — 4)
(19)
Легко видеть, что уравнение (19) имеет два корня: ui = 16
и м2 = 1/4- Следовательно, исходное уравнение (15) имеет
четыре корня: Xj = 4, х2 = —4, хз = 1/2 и х4 — — 1/2.
ОТВЕТ: XI = 4, х2 = —4, х3 = 1/2, х4 = -1/2.
3.2.4. Уравнения вида
Д1Х + <>i	а?х + Ь2 +	апх + Ьп _
р4х2 + q}x + n p2x2 + q2x + r2 pnx2 + qnx + rn
Уравнение вида
ai^ + 61	a2x + 62	anx + 6n
---5----------1---r.	h • •  4	s-— A
p1x2 + q4x + r1 p2x2 + q2x + r2-----------------pnx2 + qnx + rn
(20)
при некоторых условиях на числа а,, 6,, р,, qi, г» и А можно
решать так: разложив (если это, конечно, возможно) каждую
из дробей в левой части уравнения (20) в сумму простейших
дробей
PiX2 + q,x + п х + Д х + 7.’ ’
свести уравнение (20) к виду (7), затем, проведя удобную пе-
регруппировку членов полученного уравнения, решать его ме-
тодом, изложенным в пункте 3.2.2.
Пример 5. Решить уравнение
х + 1 х + 6	_ х + 2	х + 5
х2 + 2х х2 + 12х + 35 х2 + 4х 4- 3 х2 + 10х + 24	'
Решение. Поскольку х2 + 2х = х(х + 2), х2 + 12х + 35 =
= (ж + 5)(х + 7), я2 + 4х + 3 = (х + 1)(х + 3) и х2 + 10х +
+ 24 = (х + 4)(х + 6), то, умножив числитель каждой дроби в
уравнении (21) на 2 и заметив, что 2(х+1) = х+х+2, 2(х+6) =
§ 3.2. Рациональные уравнения
101
= х + 7 + х 4- 5, 2(х + 2) = х + 1 + х + 3, 2(z + 5) = х 4- 4 + х + 6,
уравнение (21) можно записать в виде
1 1 1 1
х	х 4- 2	х + 5	х 4- 7	(99)
1 1 1 1 ^22>
х + 1 "'~х4-3"'~х4-4"'~х4-6'
Уравнение (22) имеет вид (7). Перегруппировав слагаемые в
этом уравнении, перепишем его в виде
/1 1 \ < 1 1 \
I — 4"------I 4- I --4"------ 1 —
\х	х 4- 7/	\х 4-2 х 4- 5/
/ 1 1 \ ( 1 1 \
— I -----4~------) Н- I -----4~-----)
\x4-l х 4- 6 J \x4-3 х 4- 4 J
или в виде
2х 4- 7 2х 4- 7	2х + 7	2х 4- 7
х2 4- 7х	х2 4- 7х 4- 10	х2 4- 7х 4- 6 х2 4- 7х 4- 12
Уравнение (23) равносильно совокупности уравнений
2х 4- 7 = 0
и	(24)
1 1 _ 1 1
х2 4- 7х х2 4- 7х 4-10 х2 4- 7х 4- 6 х2 4- 7х 4- 12
Для решения второго уравнения совокупности (24) сделаем
замену неизвестного х2 4- 7х 4- 6 = z. Тогда оно перепишется
в виде
1 , 1 _ 1 1
г-6 + 24-4 ~ 2 + 24-6
или в виде
,	(25)
(2 — 6)(г 4- 4)	2(2 4- 6)
Суммируя все члены в левой части уравнения (25), перепишем
его в виде
102
Способ замены неизвестных при решении уравнений
Так как уравнение z2 + Qz + 18 = 0 не имеет корней, то урав-
нение (26) их также не имеет.
Первое уравнение совокупности (24) имеет единственный
корень х = —7/2. Поскольку этот корень входит в ОДЗ второ-
го уравнения совокупности (24), то он является единственным
корнем совокупности (24), а значит, и исходного уравнения.
Ответ: х = -7/2.
3.2.5. Уравнения вида
Я1Г2 + Ь)Х -ь C1 а2х2 + Ь2х + с2
aix + fa.	а2х +/32
Уравнение
air2 + bix + ci а2х2 + b2x + с2
aiz + /?i	а2х + 02
<*пХ + Рп
^пХ "1“ Ьп X + сп _
апх + Д,
(27)
при некоторых условиях на числа a,, bi, с;, а,, Д и А после
представления каждого слагаемого в левой части в виде
aix2 + Ь{х + с.	Bi
-------— -----= ~гх + bi -|---—-
может быть сведено к виду (7).
ПРИМЕР 6. Решить уравнение
х2 + х + 1 х2 + 2г + 2 х2 + Зг + 3 х2 + 4х + 4
--------1----------------------------- — 0. (28)
z + 1 х + 2	г + 3	х + 4
Решение. Перепишем уравнение (28) в виде
12	3	4
х -|----1- х 4----х--------х-----= 0
х + 3 х + 4
х + 2
2
3
4
= 0.
(29)
или в виде
1
х + 1 ' х + 2 х + 3
Таким образом, уравнение (28) сведено к виду (7). Теперь,
группируя первый член с последним, а второй с третьим, пе-
репишем уравнение (29) в виде
—Зг	х
г2 + 5х + 4 х2 + 5х + 6
§ 3.2. Рациональные уравнения
103
Это уравнение равносильно совокупности уравнений
(30)
Последнее уравнение совокупности (30) можно переписать в
виде
2ж2-|-10ж + 11
(х + l)(z + 4)(х + 2)(х + 3)
u	-5 + х/З	—5 — Уз
Решения этого уравнения есть Xi = ----и z2 = ----------,
так как х = 0 входит в ОДЗ второго уравнения совокупно-
—5 + Уз
сти (30), то совокупность (30) имеет три корня: х\ =---,
—5 — Уз
х? = -------, Хз = 0. Все они есть решения исходного урав-
нения.
-5 +УЗ -5-УЗ
Ответ: xi =----------, z2 =-----, х$ = 0.
3.2.6. Уравнения вида
Aiz	Акх л
—z---;------1- • • • -|-;------= В. Уравнения вида
ах2 + bix + с	ах2 + окх + с
А\Х	+ Акх
ах2 + Ь^х + с	ах2 + Ькх + с
(31)
при некоторых условиях на числа а, с, 6, и А заменой неиз-
с
вестного ах Н— = у можно свести к уравнению вида
х
у +	у + Ьк
= В.
Пример 7. Решить уравнение
4х	Зх _
4z2 — 8z -I- 7	4z2 — 10z + 7
(32)
104
Способ замены неизвестных при решении уравнений
РЕШЕНИЕ. Так как х = О не является решением уравне-
ния (32), то, разделив числитель и знаменатель каждой дроби
в левой части на х, перепишем его в виде
-----—~	?------у = 1 •	(33)
42 — 8 4—	42 — 10 4—
х	х
Сделав замену переменных 4х -|—
х
ние (33) в виде
4	3
у - 8 + у - 10
= у, перепишем уравне-
= 1-	(34)
Решения уравнения (34) есть yt = 16 и у? = 9. Поэтому урав-
нение (33) равносильно совокупности уравнений
7	7
4r-|— = 16 и 4х -|— = 9.	(35)
х	х
Корни первого уравнения этой совокупности есть Х\ = - и
7 „	.
х-2 = -. Второе уравнение решении не имеет. Следовательно,
совокупность (35), а значит, и исходное уравнение имеют два
корня: х\ и 22-
Ответ: 21 = 1/2, 22 = 7/2.
§ 3.3. Иррациональные уравнения
3.3.1. Уравнения вида \/ах + b±\/cx + d = f(x). Урав-
нение	___ ________
\/ax + b4-y/cx + d = f(x)	(1)
при некоторых условиях ьа числа a, b, с, d и функцию /(2)
можно решать так: возведя уравнение (1) в квадрат, получить
уравнение
2\/(а2 4- 6)(с2 + rf) = f2(x) — (ах 4- b 4- сх 4- </),	(2)
§ 3.3. Иррациональные уравнения
105
являющееся следствием уравнения (1). Если окажется, что
/2(х) — (az-l-fe+cz + d) = (az+6)(cr+</) +А, где А — некоторое
число, то, делая замену неизвестного у = \/(ах + Ь)(сх + d),
перепишем уравнение (2) в виде
J/2 — 2у + А = 0.	(3)
Если уравнение (3) имеет решения yi и у2 (включая случай
= Уг), то совокупность уравнений
(ах + b)(cx + d) = у2, (ах + b)(cx + d} = у2
является следствием уравнения (1) и, найдя ее корни, надо
проверить, какие из них являются корнями уравнения (1).
Если же уравнение (3) не имеет решений, то не имеет ре-
шений и уравнение (1).
Отметим, что при решении уравнения (1) можно не пере-
ходить к следствиям, а на каждом этапе следить за равно-
сильностью переходов. Отметим еще, что иногда таким же
способом может быть решено уравнение вида
у/ах + b — у/ex A d — f(x).	(4)
Приведем примеры решения уравнений вида (1) и (4) перехо-
дом к следствию и равносильными переходами.
ПРИМЕР 1. Решить уравнение
у/х + 1 — У12 — г = у/ —х2 + llz — 23.	(5)
Решение. Возводя обе части уравнения (5) в квадрат, по-
лучаем уравнение
13 - Ч\/-х2 + 11г + 12 = -z2 + Их - 23,	(6)
являющееся следствием исходного уравнения. Сделав замену
неизвестного у — х2 + Их + 12 = у, уравнение (6) можно пе-
реписать в виде 13 — 2у = у2 — 35. Решения этого квадратного
уравнения есть yi — 6 и у2 = — 8. Поэтому совокупность урав-
нений
у/ —х2 + 11х + 12 = 6 и у/ —х2 + Их + 12 = — 8
106
Способ замены неизвестных при решении уравнений
есть следствие уравнения (5). Уравнение у/—x2 + llz + 12= — 8
решений не имеет. Решения уравнения у/—х2 + Hz + 12 = 6
есть Zi = 3 и Х2 = 8. Проверка показывает, что х = 8 есть
решение исходного уравнения, а х — 3 не есть его решение.
Следовательно, исходное уравнение имеет один корень х = 8.
Ответ: х = 8.
ПРИМЕР 2. Решить уравнение
у/х -\-7 — \/9 — х — у/—х2 + 2х + 63.	(7)
Решение. ОДЗ уравнения состоит из х, удовлетворяющих
одновременно условиям ж + 7	0, 9 — х 0, —х2 + 2х + 63	0,
т. е. ОДЗ есть промежуток — 7 <С х <С 9. Для х из ОДЗ, удовле-
творяющих условию х + 7 < 9 — х, т. е. для х из промежутка
—7 х < 1 левая часть уравнения (7) отрицательна, а правая
неотрицательна, значит, ни одно из этих х решением уравне-
ния быть не может.
Пусть х Е [1;9]. Для таких х обе части уравнения (7) не-
отрицательны, и поэтому оно равносильно на этом множестве
уравнению
16-2\/-х2 + 2z + 63 = (У-х2 + 2z + 63) 2 .	(8)
Сделав замену неизвестной \/ —х2 + 2х + 63 = и, перепишем
уравнение (8) в виде и2 + 2и — 16 = 0. Решения этого урав-
нения есть «1 = —1 + \/17 и «2 = -I - \/17. Следовательно,
уравнение (8) равносильно совокупности уравнений
\/-х2 + 2г + 63 = -1 - \/17	/п.
и	____________ (9)
\/-х2 +2х+ 63 = -1 + \/17.
Первое уравнение совокупности (9) решений не имеет. Второе
уравнение для х Е [1;9] равносильно уравнению — z2-f-2z-|-63 =
= 18 — 2\/17, имеющему корни х± — 1 + ^/46 + 2д/17 и х~г =
= 1 — ^46-1- 2\/17. Из этих чисел только xi попадает в проме-
жуток 1 <С х 9. Следовательно, только х^ является корнем
исходного уравнения.
Ответ: х = 1 + Л/Дб + 2-/17.
§ 3.3. Иррациональные уравнения
107
3.3.2. У равнения вида \/а — х±-^х — b = d. Уравнение
\/а — х + tfx — b = d,	(10)
где a, b, d — данные числа, а > b, d > 0, можно решать
следующим образом.
1.	Возведя обе части уравнения в квадрат, получим урав-
нение	________________________________________
у/а — х + у/х — b = d2 — 2 {/(а — х)(х — fe), (И)
являющееся следствием уравнения (10).
2.	Возведя обе части уравнения (11) в квадрат, получим
уравнение
____________ г	___________->2
а — 6 + 2л/(а — z)(z — 6) = I d2 — 2 у/(а — х)(х — 6)1 , (12)
являющееся следствием уравнения (11).
3.	Сделав замену неизвестной у = ^/(а — х)(г — 6), перепи-
шем уравнение (12)в виде
а— Ъ+ 2у2 — (d2 — 2у)2.	(13)
Уравнение (13) есть квадратное уравнение относительно у.
Если оно имеет два корня у\ и у?, то получим совокупность
уравнений
(а - т)(т - 6) = 1/1 и (а — х)(х -Ъ) = у*,
являющуюся следствием уравнения (10). Решив эти квадрат-
ные относительно х уравнения, надо проверить, являются
ли найденные корни корнями уравнения (10). Если урав-
нение (13) имеет одно решение уа, то получаем уравнение
(а — х)(х — 6) = j/д, являющееся следствием уравнения (10).
Решив это уравнение, надо проверить, являются ли найден-
ные его корни корнями уравнения (10). Наконец, если уравне-
ние (13) не имеет корней, то и уравнение (10) не имеет корней.
Заметим, что аналогично решаются и уравнения вида
у/а — х — у/х — b = d.	(14)
108
Способ замены неизвестных при решении уравнений
Пример 3. Решить уравнение
<^17 — ж + Ух + 15 = 4.	(15)
Решение. Возведя обе части уравнения (15) в квадрат,
получим уравнение
ч/17 — ж + Ух + 15 =16-2{/(17 - z)(z + 15),	(16)
являющееся следствием уравнения (15). Если возведем урав-
нение (16) в квадрат, то получим уравнение
112-32 </(17 — ж)(ж 4-15) + >/(17 - х)(х + 15) = 0,	(17)
являющееся следствием уравнения (16). Сделав замену неиз-
вестной </(17 — z)(z -|- 15) = и, уравнение (17) перепишем в
виде и2 — 32и +112 = 0. Решения этого уравнения есть щ = 4
и U2 — 28. Следовательно, имеем совокупность уравнений
{/(17 - z)(z + 15) = 4 и </(17-г)(* + 15) = 28,	(18)
являющуюся следствием исходного уравнения (15). Первое
уравнение из совокупности (18) имеет единственное решение
Zi = 1. Второе уравнение этой совокупности решений не име-
ет. Следовательно, совокупность (18) имеет единственное ре-
шение х = 1. Проверка показывает, что х = 1 есть решение
исходного уравнения.
Ответ: х = 1.
В некоторых случаях проверка найденных корней уравне-
ния-следствия затруднительна, поэтому приведем еще способ
решения уравнений типа (10), основанный на его равносиль-
ных преобразованиях.
1.	Найдем ОДЗ уравнения (10). ОДЗ есть промежуток
Ь х а.
2.	На ОДЗ обе части уравнения (10) неотрицательны, по-
этому после возведения в квадрат уравнения (10) получим
уравнение
У а — х + У х — Ъ — d2 — 2 У(а — z)(r — 6),	(19)
равносильное уравнению (10) на его ОДЗ.
§ 3.3. Иррациональные уравнения
109
3.	На области b х <С а уравнение (19) равносильно урав-
нению
/	____ _______Ч 2 Г_____________________-12
(л/а — х + у/х — b\ = d2 — 2 \/(а — х)(х — 6)1	(20)
Действительно, любое решение уравнения (19) есть решение
уравнения (20), так как при возведении в квадрат корни урав-
нения не теряются. Любое решение уравнения (20) есть либо
решение уравнения (19), либо решение уравнения
у/а — х + у/ х — b — — [d2 — 2^/(а — z)(z — 6)j .	(21)
Перепишем уравнение (21) в виде
^у/ а — х — у/х —	— ~d2.	(22)
Так как d / 0, то уравнение (22) не имеет решений, ибо
на ОДЗ левая часть неотрицательна, а правая отрицательна.
Следовательно, любое решение уравнения (20) есть решение
уравнения (19).
Итак, уравнение (20) равносильно уравнению (10) на его
ОДЗ.
4.	Обозначив у — \/(а — х)(х — 6), перепишем уравне-
ние (20) в виде
а — b + 2у2 = (d2 — 2у)2.	(23)
Уравнение (23) квадратное относительно у. Если оно имеет
два решения yi и у2 (не исключая случая у<± = 1/2), то получаем
совокупность уравнений
У(а - х)(х - b) - yi и У(а - х)(х - 6) = у2,	(24)
равносильную исходному уравнению (10) на его ОДЗ. Если
уравнение (23) не имеет решений, то и уравнение (10) не имеет
решений.
Пример 4. Решить уравнение
^17- г + tfx+ 15 = 3.	(25)
110
Способ замены неизвестных при решении уравнений
Решение. ОДЗ уравнения есть промежуток —15 х 17.
На ОДЗ обе части уравнения (25) неотрицательны, поэтому
после возведения в квадрат, получим уравнение
V17- х + у/х + 15 = 9-2</(17 - z)(z + 15),	(26)
равносильное исходному на его ОДЗ. Уравнение
(л/17^ + V* + 15) = (9 - 2 </(17 - x)(z + 15)J	(27)
равносильно уравнению (26) на его ОДЗ. Перепишем уравне-
ние (27) в виде
32 + 2л/(17- x)(z + 15) = (9 - 2 </(17 - z)(z + 15)) 2 . (28)
Сделав замену неизвестной </(17 — z)(z + 15) = г, перепишем
уравнение (28) в виде
2г2 —36г + 49 = 0.
18+^226	18-^226
Решения этого уравнения есть z\ =------и =-----------.
Следовательно, имеем совокупность уравнений
и	(29)
</(17-^ + 15)^-~2^,
равносильную исходному уравнению на его ОДЗ.
Первое уравнение совокупности (29) решений не имеет,
второе уравнение имеет два корня:
§ 3.3. Иррациональные уравнения
111
Оба эти корня входят в ОДЗ исходного уравнения и поэтому
являются его корнями.
Ответ:
Z1 = 1 +
х2 = 1 -
Замечание. Уравнение вида у/а - f(x) ± \/f(x) - b — d
заменой неизвестной у = /(z) сводится к уравнению вида (10)
или вида (14).
3.3.3. Сведение решения иррационального уравне-
ния к решению тригонометрического уравнения. За-
меной неизвестной решение иррациональных уравнений ино-
гда можно свести к решению тригонометрических уравнений.
При этом полезными могут оказаться следующие замены не-
известной.	_______
1.	Если в уравнение входит радикал у/а2 — х2, то можно
сделать замену х = a sin! или х = a cost.
2.	Если в уравнение входит радикал у/ а2 + х2, то можно
сделать замену х = atgt.	_______
3.	Если в уравнение входит радикал у/ х2 — а2, то можно
а
сделать замену х = ——.
sint
Пример 5. Решить уравнение
\Лс2 4-1 — х —
5
Чу/х2 + 1'
(30)
Решение. ОДЗ уравнения (30) есть все действительные х.
Сделаем замену неизвестной х = tgt, где можно считать, что
—тг/2 < t < тг/2. Тогда уравнение (30) запишется в виде
-------tgt = - cos t.
cost---2
(31)
112
Способ замены неизвестных при решении уравнений
Поскольку cos/ / 0 для рассматриваемых t, то уравнение (31)
для этих t равносильно уравнению
2 — 2 sin/= 5(1 — sin1 2/).	(32)
Уравнение (32) равносильно совокупности уравнений
Из решений этих уравнений промежутку —тг/2 < t < тг/2 при-
надлежит только t = arcsin(—3/5). Поэтому соответствую-
щее х есть
х — tgarcsin(—3/5) =
sin(arcsin(—3/5)) _	—3/5	_
cos(arcsin(—3/5)) yi - 9/25 ~
Ответ: x = —3/4.
ПРИМЕР 6. Решить уравнение
х 35
Z+ Vi2 - 1 ~ 12'
(34)
РЕШЕНИЕ. ОДЗ уравнения (34) состоит из всех х, удо-
влетворяющих условию |z| > 1. Ясно, что никакое отрица-
тельное х из ОДЗ не может быть решением уравнения (34).
Следовательно, все решения уравнения (34) лежат в области
1 < х < +оо. Сделаем замену неизвестной х — ——, где мож-
sm/
но считать, что 0 < t < тг/2 Тогда уравнение (34) можно
переписать в виде
1	1 __ 35
sin/	cos/ 12
(35)
Это уравнение для рассматриваемых / равносильно уравне-
нию
12(sin/ 4- cos/) = 35sin/ cos/,	(36)
которое для этих / равносильно уравнению
24(sin/ 4- cos/) = 35[(sin/ 4- cos/)2 — 1].	(37)
§ 3.3. Иррациональные уравнения
ИЗ
Делая замену неизвестной sint + cost = z, уравнение (37) мож-
но переписать в виде
35г2 - 24г - 35 = 0.	(38)
Уравнение (38) имеет корни z\ = — - и z? = -. Поэтому урав-
7	5
нение (37) равносильно совокупности уравнений
cost + sin t =—5/7 и cost + sin t = 7/5.	(39)
Первое уравнение совокупности (39) не имеет решений из про-
межутка 0 < t < тг/2, так как для любого to из этого проме-
жутка cos to + sin to > 0. Следовательно, все решения уравне-
ния (35), удовлетворяющие условию 0 < t < тг/2, содержатся
среди решений второго уравнения совокупности (39). Обозна-
чая у = sin t, это уравнение для рассматриваемых t можно
записать в виде
2/ + \/1 - У2 = 7/5.	(40)
Уравнение (40) имеет два корня: у] = 3/5 и у? = 4/5. Поэтому
уравнение (35) на промежутке 0 < t < тг/2 имеет два решения:
3	4
ti = arcsin - и t2 = arcsin -, а это означает, что уравнение (34)
5	5
имеет два корня: Xi = 5/3 и z2 = 5/4.
Ответ: xi = 5/3, х? -
ПРИМЕР 7. Сколько корней на отрезке [0; 1] имеет уравне-
ние
8z(2z2 - l)(8z4 - 8z2 + 1) = 1?	(41)
Решение. Так как искомые корни удовлетворяют усло-
вию 0 С х 1, то делаем замену неизвестной х = cost. Тогда
каждому корню хо £ [0; 1] исходного уравнения будет соот-
ветствовать ровно один корень to € [0;тг/2], где хо = costo,
уравнения
8 cost(2 cos2 t — 1)(8 cos41 — 8 cos2 t + 1) = 1,	(42)
и, наоборот, каждому корню ti £ [0; тг/2] уравнения (42) соот-
ветствует ровно один корень Xi £ [0; 1] уравнения (41). Таким
образом, задача может быть переформулирована так: сколько
корней на промежутке 0 С ! С тг/2 имеет уравнение (42)?
114
Способ замены неизвестных при решении уравнений
Поскольку 2 cos2 t — 1 = cos 2/, 8 cos4 t — 8 cos2 t + 1 = cos 4/,
то перепишем уравнение (42) в виде
8 cos t cos 2t cos 4t = 1.
(43)
Так как t = 0 не есть корень уравнения (43), то оно равно-
сильно на промежутке t G (0; тг/2] уравнению
8 sin t cos t cos It cos 4t = sin t,
или уравнению sin8/ = sin/, или, наконец, уравнению
.7/9/
sin — cos — = 0.	(44)
2	2	v '
Решения уравнения (44) есть
2	2 / тг \
/ = -irn, n G Z, и / = - —|- irm , m G Z.
7	’	’	9 K2 /
Из этих чисел условию 0 < / ^ тг/2 удовлетворяют только три
2
числа /i = -it, /2 = тг/9 и /3 = тг/З. Следовательно, исходное
уравнение (41) имеет на отрезке [0; 1] три корня.
Ответ: три корня.
§ 3.4.	Уравнения вида
aofn(x) + aifn~1(x)g(x)4-F an^if(x)gn~1 (я) + апдп(х) = 0
Уравнения вида
aofn(x) + aifn 1 (х)д(х) +   +
+ an_1f(x)gn~l(x) + апдп(х) = 0,
где ао / 0 и хотя бы один из коэффициентов ai,	ап
отличен от нуля, можно решать следующим образом.
1.	Решить уравнение
д(х) = 0.
(2)
§ 3.4. Уравнения особого вида
115
Найти те решения уравнения (2), которые являются решения-
ми уравнения /(х) = 0. Все эти решения являются решениями
уравнения (1).
2.	На множестве всех действительных чисел, исключая
найденные корни уравнения (1), его надо заменить равносиль-
ным ему на этом множестве уравнением
«0 I ' z"~\ ) + «11 /"~\ I + • • +«n-i ( ~ ч ) +«п — 0- (3)
\g(z)/ \g{x)J	\g^)J
Сделав замену неизвестной у = f(x)/g(x), переписать уравне-
ние (3) в виде
«оУп + «1УП 1 + •' • + «п-1У + «п — 0-	(4)
Алгебраическое уравнение (4) имеет не более чем п корней
У1,	Ут, где т п, найдя их, уравнение (3) заменить
совокупностью уравнений
/ \ — 2/1 >    > I \ — Ут 
Х*) д(х)
(5)
Все решения совокупности (5), принадлежащие рассматрива-
емому множеству, являются решениями уравнения (1).
3.	Объединение решений, найденных в п. 1 и п. 2, и есть
множество всех решений уравнения (1).
Приведем несколько примеров решения уравнений ви-
да (1).
Пример 1. Решить уравнение
(х2 + 4х + 8)2 + Зх3 + 14х2 + 24х = 0.	(6)
Решение. Перепишем уравнение (6) в виде
(х2 + 4х + 8)2 + Зх(х2 + 4х + 8) + 2х2 = 0.	(7)
Теперь очевидно, что уравнение (7) — уравнение вида (1).
Поскольку х = 0 не является корнем уравнения х2 + 4х + 8 = 0,
то, разделив уравнение (7) на х2, получим равносильное ему
уравнение
х2+4х + 8\2	/х2+4х + 8\
----------- I -f- о | ------- I -f- Z — и.
х j V х j
(8)
116
Способ замены неизвестных при решении уравнений
х2 + 4х + 8
Сделав замену неизвестной -----------= у, перепишем урав-
х
нение (8) в виде
у2 + Зу + 2 = 0.	(9)
Так как уравнение (9) имеет два корня: у\ = — 1 и у2 = —2, то
уравнение (8) равносильно совокупности уравнений
х2 + 4х + 8	х2 + 4х + 8
----------- = -1 и ------------= -2.
х	х
Первое уравнение этой совокупности не имеет решений. Вто-
рое уравнение этой совокупности имеет два корня: х\ = —4
и Х2 = — 2. Поэтому уравнение (8), а следовательно, и равно-
сильное ему уравнение (6) имеют два корня: ii и 1г-
Ответ: п = -4, z2 = -2.
ПРИМЕР 2. Решить уравнение
х2-1	ха-1	х2-1
4ii+*+1 + 3-6ii+*+1 = 4-9ii+*+1 .	(10)
Л2_1
РЕШЕНИЕ. Разделив обе части уравнения (10) на 9xi+*+i ,
получим уравнение
(И)
равносильное уравнению (10). Сделав замену неизвестной
х2-1
/2\ xi+*+i
( - 1	= у, перепишем уравнение (11) в виде
\ 3 j
у2 + Зу - 4 = 0.
(12)
Уравнение (12) имеет два корня: у\ = 1 и у2 = —4. Следова-
тельно, уравнение (11), а значит, и равносильное ему уравне-
ние (10) равносильны совокупности уравнений
2\
3 )
2\
3 )
4-х 4-1
= 1
и
= —4.
§ 3.4. Уравнения особого вида
117
Решения первого уравнения этой совокупности есть Zi = 1 и
Х2 = —1- Второе уравнение решений не имеет.
Ответ: xy = 1, z2 = -1.
Пример 3. Решить уравнение
log3(x2 4-z) 4-log2(х2-|-х) log4 4z-|-	(13)
+ 2 log2(x2 + х) log2 4х — 4 log4 4х = 0.
Решение. Поскольку х = 1/4 (корень уравнения log44x = 0)
не является корнем уравнения log2(x2 + х) — 0, то уравне-
ние (13) равносильно уравнению
log2(z2 + ж) + log2(r2 + х) + 2log2(x2-Ь х) _ 4 = 0	/ 14ч
log4 4х log4 4х	log4 4х
_ log2(x2 + х)
Сделав замену неизвестной —----------- = у, перепишем урав-
log4 4х
нение (14) в виде
у3 + у2 + Чу - 4 = 0.	(15)
Уравнение (15) имеет единственный корень у = 1. Следова-
тельно, исходное уравнение (13) равносильно уравнению
log2(x2 + х) = log4 4х.	(16)
ОДЗ уравнения (16) есть х > 0, поэтому на этом множестве
оно равносильно уравнению (х2 + х)2 — 4х, т. е. уравнению
х4 + 2х3 + х2 = 4х, или, наконец, поскольку х ф 0, уравнению
х3 + Чх2 + х — 4 = 0.	(17)
Уравнение (17) имеет единственный корень х = 1. Этот ко-
рень содержится в множестве х > 0. Следовательно, исходное
уравнение (13) также имеет этот же единственный корень.
Ответ: х = 1.
ПРИМЕР 4. Решить уравнение
У(2х +	+ я2)2 “ 5 \/Зх2 - 1 +	(48)
+ 6 у/ (Чх — y/l-f-z2)2 = 0.
118
Способ замены неизвестных при решении уравнений
Решение. Поскольку Зх2 — 1 = (2х + \/1-|-х2)(2х — \/1-|-х2),
то уравнение (18) можно переписать в виде
’У (2х + \/1 + х2)2 — 5 ’У (2х + л/1 + х2)(2х —\/1 + х2~) +
+ 6’У (2х — \/1 +	= О-
Так как х = 1/д/З — корень уравнения 2х — ^1 + я2 = 0 —
не является корнем уравнения 2х + \/1 + х2 = 0, то исходное
уравнение (18) равносильно уравнению

)2	..... ......-
3/2х + л/1 + х2
— Э А / --===== 4-0 = 1)
V 2х — \/1 + ж2
(19)
+ = 3 (21)
2х — д/1 + х2
/ 2х 4~ у/1 4~ «с
Сделав замену неизвестной ?/------- = у, перепишем
у 2 «с ^/1 4~
уравнение (19) в виде
У2 - 5у + 6 = 0.	(20)
Уравнение (20) имеет два корня у\ = 2 и уъ — 3. Следователь-
но, исходное уравнение равносильно совокупности уравнений
2х + \/1 + ^2
2х — у/1 + х2
Первое уравнение совокупности (21) равносильно уравнению
2х + \/1 + я2 = 8 ^2х — \/1 + х2) , т. е. уравнению
14х = 9у/1 + х2.	(22)
Уравнение (22) имеет единственный корень xi = 9/\/115.
Второе уравнение совокупности (21) равносильно уравнению
2х + \/1 + х2 = 27 ^2х — \/1 + х2 ), т. е. уравнению
13х = 7у/1 + х2.
(23)
§ 3.4. Уравнения особого вида
119
Уравнение (23) имеет единственный корень х2 = Сле-
довательно, совокупность (21), а значит, и исходное уравнение
имеют два корня: ху и х2.
Ответ: ц = 9/УТ15, х2 = 7/У120.
К уравнению вида (1) приводятся уравнения вида
A cos2 ах + В sin ах cos ах + С cos2 ах +
+ Е sin 2ах + F cos 2ах + D = О
после применения формул синуса и косинуса двойного угла:
sin2az = 2 sin аг cos az, cos2az = cos2 ax — sin2 ax и тожде-
ства D = D(sin2 ax + cos2 ai).
Пример 5. Решить уравнение
3 cos2 5z — 7 sin 10z + 4 sin2 5z = 6.	(24)
Решение. Применяя формулу синуса двойного угла и то-
ждество 6 = 6 sin2 5г + 6 cos2 5z, уравнение (24) можно пере-
писать в виде
2 sin2 5х + 14 sin 5z cos 5х + 3 cos2 5z = 0.	(25)
Поскольку те х, для которых cos Ьх — 0 не есть решения урав-
нения sin5z = 0, то, разделив уравнение (25) на cos2 5г, полу-
чим уравнение
2 tg2 5г + 14 tg 5г + 3 = 0,	(26)
равносильное уравнению (24). Сделав замену неизвестной
tg5z — z, перепишем уравнение (26) в виде
2z2 + 14z + 3 = 0.	(27)
z х	- 7 + л/43
Так как уравнение (27) имеет два корня: zi = ---------- и
—7 — д/43
z2 = --------, то уравнение (24) равносильно совокупности
уравнений
tg 5г =
-7 + V43
2
—7 - V43
----2---
120
Способ замены неизвестных при решении уравнений
Решения этой совокупности уравнений есть
1
х — - arctg
5
кк
Т’
к 6 Z,
2
1
х — - arctg
5
ТГП
Т’
п G 7L.
2
Эти решения и
Ответ:
есть решения исходного уравнения.
х —
1	( — 7 + л/43 \ як
- arctg ------------- + —, к е 7L,
5	\	2	/	5
х =
1	/ -7 - V43 \ тгп
~ arctg ---------- + —, n G Z.
5	\	2	/	5
§ 3.5. Решение некоторых уравнений
сведением их к решению систем уравнений
относительно новых неизвестных
В некоторых случаях решение уравнения можно свести к
решению системы уравнений относительно вводимых новых
неизвестных. Этот прием мы проиллюстрируем на примерах.
ПРИМЕР 1. Решить уравнение
(2 - г)5 + (г - З)5 + 1 =0.	(1)
РЕШЕНИЕ. Пусть xq — решение уравнения (1). Вводим но-
вые неизвестные и = 2 — xq, v = Xq — 3. Ясно, что и и v
удовлетворяют системе уравнений
и + v = —1,
и5 + v5 = -1.
(2)
Поскольку, как легко проверить,
и5 + v5 = (tz + т)(((и + д)2 — 2itv)2 — uv(u + v)2 + u2v2),
§ 3.5. Сведение к системам с новыми неизвестными
121
то систему (2) можно переписать в виде
( u + v = -1,
[ (u + i’)(((u + и)2 ~ 2ии)2 — ии(и 4- и)2 + и2и2) = —1. ' '
Подставляя во второе уравнение системы (3) число —1 вместо
и + v, получаем уравнение (1 — 2uv)2 — uv + u2v2 — 1, кото-
рое можно переписать в виде 5(uu)2 — 5(ии) = 0, откуда либо
UV — 0, либо UV — 1.
Таким образом, для нахождения и и v имеем две системы
уравнений:
u + v=— 1,	( U + D = — 1,
uv = 0,	1 uv = 1.
Вторая система решений не имеет. Решения первой системы
есть Ui = 0,	= -1 и u2 = —1, d2 = 0, откуда следует,
что решения уравнения (1) содержатся среди чисел т'о = 2
и х'о = 3. Проверка показывает, что оба эти числа являются
решениями уравнения (1).
Ответ: хг = 2, х2 - 3.
Пример 2. Решить уравнение
qr2
‘2 + (J77p=40-	<4>
Решение. Пусть то — решение уравнения (4). Введем но-
З^о гг
вую неизвестную уо = -----. Тогда для нахождения х0 и уо
3 + то
имеем систему уравнений
3(zo - Уо) - хоУо - О,
*о + Уо = 40.
Поскольку х2 + у2 = (zq — уо)2 + 2х0у0, то, вводя новые неиз-
вестные Uq = х0 — уо, tjq = хоУо, систему (5) можно переписать
в виде
3uo — vq = 0,
и2 + 2vo = 40.
122
Способ замены неизвестных при решении уравнений
Решения этой системы есть пары чисел uq = 4, vq = 12 и
«о = —10, do = —30, откуда для нахождения xq и уо получаем
системы уравнений
Хо - Уо = 4,
хоуо = 12,
хо - Уо = -10,
хоуо - -30.
Решения первой из этих систем есть Хо = —2, уо = — 6 и
Хо — 6, уо = 2. Вторая система решений не имеет. Итак, все
решения уравнения (4) содержатся среди чисел хо = — 2 и
х0 - 6.
Проверка показывает, что эти числа являются решениями
уравнения (4).
Ответ: ху — -2, х2 = 6.
Пример 3. Решить уравнение
— .	= = х + \/35 — х3.
Х&35-Х3
Решение. Пусть xq — решение уравнения (6). Введем но-
вую неизвестную у35 — х3 = уо, тогда х$ и уо являются ре-
шением системы уравнений
(6)
30
-------= Хо + Уо,
< хоуо
. Х1 + Уо = 35-
(П
Вводя новые неизвестные и = xq + уо, v — хоуо, перепишем
систему (7) в виде
uv = 30,
и3 — 3uv = 35.
(8)
Решения системы (8) есть и = 5, v = 6. Следовательно, для
нахождения xq и уо получаем систему уравнений
хо + Уо = 5,
хоУо = 6.
Эта система имеет две пары решений: х'о = 2, у'о — 3 и x'q = 3,
Уо = 2. Итак, все решения уравнения (6) содержатся среди
§ 3.5. Сведение к системам с новыми неизвестными
123
чисел х — 2 и I = 3. Проверка показывает, что оба эти числа
являются корнями уравнения (6).
Ответ: хх = 2, х2 = 3.
Пример 4. Решить уравнение
\^х + 45 — \^х — 16 = 1.	(9)
Решение. Пусть хо — решение уравнения (9). Введем но-
вые неизвестные i/xq 4- 45 = и, /х0 — 16 = у. Тогда и и v
являются решениями системы уравнений
и — v = 1,
и3 — v3 = 61.
Эта система равносильна системе
и — v = 1,
(и — 1>)(ы2 + UV + Г2) = 61
или системе
п = г + !,	,
(г 4- I)2 + v(v + 1) + г2 =61.
Решения системы (10) есть щ = 4, Ui = 5; v2 = —5, и2 = —4, а
это означает, что решениями уравнения (9) могут быть толь-
ко числа х'о = 80 и х'о' = —109. Проверка показывает, что эти
числа являются решениями уравнения (9).
Ответ: хг = 80, х2 = -109.
ПРИМЕР 5. Решить уравнение
у/х 4- v'x 4- 4 = 4.	(11)
РЕШЕНИЕ. Пусть Хо — решение уравнения (11). Введем
новые неизвестные хо = и2 и хо + 4 = г3, тогда и иу удовле-
творяют системе уравнений
Из первого уравнения |и| = 4 — v. Подставляя вместо |н| вы-
ражение 4 — v во второе уравнение системы (12), имеем урав-
нение v3 — (4 — г)2 — 4 = 0. Это уравнение имеет единственное
124
Способ замены неизвестных при решении уравнений
решение v = 2, но тогда xq = 4. Итак, возможное значение
корня уравнения (11) есть xq — 4. Подставляя это значение то
в уравнение (11), получаем, что оно есть его решение.
Ответ: х — 4.
Пример 6. Решить уравнение
\/10 + х2 + х + \/7 — х2 — х = 3.	(13)
Решение. Пусть т0 — решение уравнения (13). Введем
новые неизвестные ^10 + Tq + tq = и и ^7 — х2 — х0 = v,
тогда и и v являются решениями системы уравнений
и + v = 3,
u4 + V4 = 17.
Решениями этой системы являются Uj = 1, i>i = 2 и u2 = 2,
i’2 = 1, откуда следует, что xq удовлетворяет либо уравнению
^/10 + т^ + т0 = 1, либо уравнению ^/10 + т^ 4- т0 = 2. Первое
из этих уравнении решений не имеет. Решения второго урав-
нения есть х'о — 2 и т'о' = —3. Итак, решения уравнения (13)
содержатся среди чисел т'о = 2 и т'о' = — 3. Подставляя эти
числа в уравнение (13), видим, что они являются его решени-
ями.
Ответ: тх = 2, т2 = -3.
Пример 7. Решить уравнение
</87 + [log2(42r - 3-4* + 6)]2 - 5 log2(42r - 3-4* + 6) +
+ /7 + [log2(42r - 3-4* + 6)]2 - 5 log2(42r - 3-4* + 6) = 4.
(И)
Решение. Обозначим
/(т) = [log2(42r - 3-4* + 6)]2 - 5 log2(42r - 3-4Г + 6).
Тогда уравнение (14) перепишется в виде
/87 + f(x) + </7 + /(т) = 4.
(15)
§ 3.5. Сведение к системам с новыми неизвестными
125
Пусть х0 — решение уравнения (15). Введем новые неизвест-
ные \/87 + f(x0) = и, >/7 + f(x0) - v. Тогда и И V являются
решениями системы уравнений
и + v — 4,
u4 - v4 - 80.
(16)
Из первого уравнения этой системы и = 4 — г. Подставляя
вместо и во второе уравнение 4 — г, получаем уравнение v3 —
—6г2 + 16г—11 = 0. Это уравнение имеет единственный корень
v = 1, откуда следует, что zq удовлетворяет уравнению
[log2(42г - 3-4Г + 6)]2 - 5 log2(42r - 3-4* + 6) + 6 = 0. (17)
Так как уравнение у2 — Ьу + 6 = 0 имеет два корня у\ = 2 и
2/2 = 3, то уравнение (17) равносильно совокупности уравне-
ний
log2(42r - 3-4* + 6) = 2 и log2(42r - 3-4* + 6) = 3,
которая в свою очередь равносильна совокупности уравнений
42г - 3-4Г +6 = 4 и 42г — 3-4Г + 6 = 8.
Перепишем последнюю совокупность уравнений в виде
42г_3.4г+2 = 0 и 42г _ 3.4r _ 2 _ Q	(18)
Так как уравнение z1 — 3z + 2 = 0 имеет два корня: zy = 1
и Z2 = 2, то первое уравнение совокупности (18) равносильно
совокупности двух уравнений: 4Г = 1 и4г = 2, решения кото-
рой есть Xi = 0 и Х2 = 1/2. Так как уравнение z2 — 3z — 2 = 0
3 + У17	З-л/17
имеет два корня: z\ = -------- и z2 = --------, то второе
уравнение совокупности (18) равносильно совокупности двух
уравнений:
и
3 + >/17
126
Способ замены неизвестных при решении уравнений
имеющей единственное решение Х3 = log4---------. Итак,
все корни уравнения (14) содержатся среди чисел х^ = О,
,	,	3 + У17
х-2 = 1/2, хз = log4----.
Подставляя эти числа в уравнение (14), убеждаемся в том,
что они есть его решения.
,	,	3 + У17
Ответ: ц = 0, х2 = 1/2, х3 = log4 —---.
Пример 8. Решить уравнение
V^sinz — 1 4- v^sin х — 2 = 2.	(19)
РЕШЕНИЕ. Пусть xq — решение уравнения (19). Введем но-
вые неизвестные и = v2sinzo —1 и v = \/'i sin z0 — 2. Тогда
и и v являются решениями системы уравнений
( и + v = 2,
\ Зи4 - 2г4 = 1.
Из первого уравнения этой системы и = 2 — v. Подставляя
2 — v вместо и во второе уравнение, получаем уравнение
v4 — 24г3 + 72г2 - 96г+ 47 = 0.	(20)
Легко видеть, что уравнение (20) имеет корень v = 1. Разде-
лив многочлен, находящийся в левой части уравнения (20), на
г —1, получим тождество г4—24г3+72г2—96г+47 — (г—1)(г3 —
— 23г2 + 49г — 47), откуда следует, что кроме г = 1 остальные
корни уравнения (20) есть корни уравнения
г3 - 23г2 + 49г-47 = 0.	(21)
Ясно, что надо искать лишь те корни уравнения (20), кото-
рые удовлетворяют условию 0 г 2. Поскольку г3 — 23г2 +
+ 49г — 47 = (г3 — 8) — (23г2 — 49г + 39), то очевидно, что
при 0 < г 2 имеем г3 — 8 0 и 23г2 — 49г + 39 > 0. По-
этому г3 — 23г2 + 49г — 47 < 0 при любом г из промежутка
0 г 2. Следовательно, уравнение (21) не имеет корней на
отрезке 0 г 2.
Задачи
127
Таким образом, все корни уравнения (19) содержатся среди
корней уравнения
3sinx —2=1.	(22)
Перепишем уравнение (22) в виде
sin х — 1.	(23)
Уравнение (23) имеет решения х — тг/2 + 2тгАт, k G Z. Итак,
7Г
все корни уравнения (19) содержатся среди чисел х — — + 2тгк,
k G Z.
Подставляя эти числа в уравнение (19), убеждаемся в том,
что все они являются его решениями.
Ответ: х - - + 2тг&, k е 7L
Замечание. Конечно, уравнение (19) можно решить про-
ще. Действительно, поскольку 2 sin х — 1	1 и 3 sin г — 2	1,
то уравнение (19) равносильно уравнению sin х = 1.
Задачи
Решить уравнение
1.	(х2 + х + 1)(х2 + х + 2) = 12.
2.	(8х + 7)2(4х + 3)(х + 1) = 9/2.
3.	(6r + 5)2(3х + 2)(х + 1) = 35.
4.	(х2 + 2х + 7) = (4 + 2х + х2)(х2 + 2х + 3).
5.	(1 + х + х2)(6 — х — х2) = 10.
6.	(х — 1)(х + 2)(х — 3)(х + 4) = 144.
7.	х(х - 1)(х - 2)(х - 3) = 24.
8.	(х - 4)4 + х4 = 82.
9.	(х- I)4 + (х + З)4 = 626.
10.	(х2 + Зх + 4)(х2 + 4х + 5) = 2(х + I)2.
11.	(х - 1)(х - 2)(х - 4)(х - 5) = 7(х - З)2.
12.	(х2 - 16)(х - З)2 + 9х2 = 0.
128
Способ замены неизвестных при решении уравнений
13.	z4 + (1 - z)4 - (z - 1/2)2 - 25/8 = 0.
14.	(z2 - 3z + l)(z2 + 3z + 2)(z2 - 9z + 20) = -30.
15.	(2z2 - 3z + l)(2z2 + 5z + 1) = 9z2.
16.	(z + 2)(z 4- 3)(z 4- 8)(z + 12) = 4z2.
17.	z4-2z3-z2-2z + 1 = 0.
18.	z4 - 8z3 - 4z2 + 16z + 4 = 0.
19.	(z2 — 6z — 9)2 = z3 — 4z2 — 9z.
20.	(z3 + z2 + I)2 + (z3 - z2 + I)2 = 2z4.
21.	9z4 - 6z3 - 18z2 - 2z + 1 = 0.
22.	z6 - 6z4 + z3 + 9z2 - 3z - 1 = 0.
23.	(1 + z)8 + (1 +z2)4 = 2z4.
24.	1 + z5 = 2(1 + z)5.
25.	(z2 - z + l)4 - 8z2(z2 - z + I)2 + 16z4 = 0.
26.	z3 + 1/z3 + z2 + 1/z2 4- z + 1/z = 6.
27.	z3 4- 1/z3 = 6(z 4- 1/z).
„ 4z	3z
28.	1------------------= 1.
4z2 — 8z 4- 7	4z2 — lOz 4- 7
1	3	10
29.l = 
2z2 — z 4- 1	2z2 — z 4- 3	2z2 — z 4- 7
z — 1 z 4- 2 z 4- 5 z 4- 3
3 0.-----H--------—---4"----------•
z 4-2 z — 1	z4-3 z 4- 5
31 ж(а: + 1)(ж + 4)(а: + 3) + 1 о
(z 4-2)2(z 4-5)(z - 1) 4-2
32	z2 4- x 4- 1	z2 4- 3z 4- 1	5
z2 4- 2z 4- 1	+	z2 4- 4z 4- 1	6
33	z2 4- 2z 4- 2	z2 4- 8z 4- 20 z2 4- 4z	4- 6 z2 4- 6z	4- 12
x 4- 1	z	4-4	z 4-2	z	4-3
34 z2 — 8,5z 4- 15 _ 3z
z2 — 9z 4- 15 z2 — 8z 4- 15
xl 4- 2z 4- 3 z — 1	1
35. --------------1— -----= z 4—.
z—1 z2 4- 2z 4- 3 z
Задачи
129
36.	2 ( 2;C V r z2+ 	-	=5. \z — 2/
37.	,	25z2 x + 7	= n- (z + 5)2
38.	Zz4-6\/z4-4\2 Zz — 6\/z4~9\2	z2 4- 36 \z — 6/ \z — 4J ' \z4-6yyz — 9/	z2 — 36
39.	5	4	21	_ 5	4	21 z — 1	' x + 2	' z — 3 z+l	' z — 2	' z + 3
40.	2	x2 X + (1 + z)2 ~L
41.	-^— + ^— = 2 2 — z2 2 — z
42.	(z+ I)5 _ 81 z5 4-1	11
43.	z4 + 13z2 4- 36	1 z2(z4 4- 36) - 2
44.	z2 4- x 4- 1 7 z+l z2 — z 4- 1 9 z — 1
45.	2 4- \/2z 4- x'2	2 2-y/2x + x2	x2'
46.	2	3	_ z x2 4- 2z - 2 1 z2 - 2z 4- 3 - 2 '
47.	sin 2z(sin z 4- cos z) = y/2.
48.	sin3 z — cos3 z = 1 4- sin z cos z.
49.	• 3	3 sin z 4- cos z = sin z 4- cos z.
50.	X 3 COS X + sin X — tg —.
51.	5 cos 3z 4- 3 cos z = 3 sin 4z.
52.	4z2 — 1\/x2 — 2x — 8x — 3.
53. y/i - л/13 - х = \/-z2 + 13z - 35.
54. \/z 4- 6 — У10 — x = у/ —x2 4- 4z 4- 62.
55. У18 - x + y/x + 14 = 4.
130
Способ замены неизвестных при решении уравнений
56.	у/77 + х + 720-х = 5.
57.	7100 - х + 7х- 18 = 4.
58.	1.
59.	</(8 4- х)2 - </(х + 8)(8 - х) + 7(8 - х)2 = 4.
60.	</(х - 2)2 - 7(2 - х)(7 + х) + </(7 + х)2 = 3.
61.	8х2(1 — х2) + 8x71 — х2 = ^х 4- \/1 + х2^ 
62.	у/х- 1 + у/х-2 = у/2х-3.
63.	713 — х + 722 4- х = 5.
64.	у[х + yj х — у/\ — х — 1.
65.	у/2-х = 1 - 7х — 1.
66.	733 — х + у/х = 3.
67.	^/х-2 +72г-5 + Ух + 2 + 372х - 5 = 7у/2.
/--- 5х2 — 10х + 16
68.	7х - 2 = --z------—.
х2 + 6х + 4
v х2 + 34х+161
69.	87x4-5 = --!-----!----.
х 4- 9
3 4- 27х2 4- Зх — 4 2х 4- 5
70.		,	= = -----.
5 4- 37х2 4- Зх - 4 Зх 4- 8
Глава IV
Решение уравнений и неравенств с
использованием свойств входящих в
них функций
§ 4.1. Применение основных свойств функций
4.1.1. Использование ОДЗ. Иногда знание ОДЗ позво-
ляет доказать, что уравнение (или неравенство) не имеет ре-
шений, а иногда позволяет найти решения уравнения (или
неравенства) непосредственной подстановкой чисел из ОДЗ.
Пример 1. Решить уравнение
V3 - а: = log5(a: - 3).
Решение. ОДЗ этого уравнения состоит из всех х, одно-
временно удовлетворяющих условиям 3—х 0 и х—3 > 0, т. е.
ОДЗ есть пустое множество. Этим решение уравнения и за-
вершается, так как установлено, что ни одно число не может
являться решением, т. е. что уравнение не имеет корней.
Ответ: решений нет.
Пример 2. Решить уравнение
\/| sin □? | =	| sin r| + tg х.	(1)
Решение. ОДЗ этого уравнения состоит из всех х, одно-
временно удовлетворяющих условиям | sin х| 0, —|sinz| О,
7Г
х / — + тгп, n Е Z, т. е. ОДЗ есть х — тгк, к 6 Z. Подстав-
ляя эти значения х в уравнение (1), получаем, что его левая и
правая части равны 0, а это означает, что все х — тгк, к Е %,
являются его решениями.
Ответ: х = тгк, к Е 7L.
Пример 3. Решить неравенство
V1 ~ а:2 + \/а:4 — 1 < 2Г — log2(l + а:4).	(2)
132 Использование свойств входящих в уравнение функций
Решение. ОДЗ неравенства (2) состоит из всех х, одно-
временно удовлетворяющих условиям 1 — х'2	0, х4 — 1 О,
т. е. ОДЗ состоит из двух чисел = 1 и =-1. Подстав-
ляя Xi = 1 в неравенство (2), получаем, что его левая часть
равна 0, правая равна 2 — log2 2=l,T.e.xi = l есть реше-
ние неравенства (2). Подставляя х? = — 1 в неравенство (2),
получаем, что х? = —1 не является его решением, посколь-
ку левая часть неравенства (2) равна 0, а правая часть равна
2-1 — log2 2 = —1/2.
Ответ: х = 1.
Пример 4. Решить неравенство
log5 х < х/1 — х4.
(3)
Решение. ОДЗ неравенства (3) есть все х, удовлетворяю-
щие условию 0 < х <С 1. Ясно, что х = 1 не является реше-
нием неравенства (3). Для х из промежутка 0 < х < 1 имеем
log5 х < 0, а \/1 — х4 > 0. Следовательно, все х из промежутка
0 < х < 1 являются решениями неравенства (3).
Ответ: 0 < х < 1.
Пример 5. Решить неравенство
\Аг 4-3 4-	— х < х/з -
(4)
РЕШЕНИЕ. ОДЗ неравенства (4) есть все х из промежут-
ка — 3 х 9. Разобьем это множество на два промежутка
-3 а: 0 и 0 < а: 9.
Для х из промежутка — 3 х 0 имеем х/т 4- 3 0,
т/9 — х тУ9 = х/З- Следовательно, х/я 4- 3 + -У 9 — х х/3
на этом промежутке, и поэтому неравенство (4) не имеет ре-
шений на этом промежутке.
Пусть х принадлежит промежутку 0 < х 9, тогда л/х~+3 >
> х/з и У 9 — х 0. Следовательно, л/т 4- 3+ У 9 — х > х/з для
таких х, и, значит, на этом промежутке неравенство (4) также
не имеет решений.
Итак, неравенство (4) решений не имеет.
Ответ: решений нет.
Замечания. 1. При решении уравнений необязательно на-
ходить ОДЗ. Иногда проще перейти к следствию и проверить
§ 4.1. Применение основных свойств функций
133
найденные корни (соответствующие примеры уже были в пре-
дыдущих главах).
2.	При решении неравенств иногда можно не находить
ОДЗ, а решать неравенство переходом к равносильной ему
системе неравенств, в которой либо одно из неравенств не
имеет решений, либо знание его решения помогает решить
систему неравенств.
Пример 6. Решить неравенство
l°g2(2r + 1 - г2) > log2(2r-1 + 1 - х) + 1.	(5)
РЕШЕНИЕ. Отыскание ОДЗ неравенства есть непростая за-
дача, поэтому поступим иначе. Неравенство (5) равносильно
системе неравенств
’ 2х + 1 - х2 > О,
< 2r-1 + 1 — х > О,	(6)
2х + 1 - х2 > 2(2Х~1 + 1 - х).
Третье неравенство этой системы равносильно неравен-
ству х2 — 2х + 1 < 0, не имеющему решений. Следовательно,
система неравенств (6) не имеет решений, значит, и неравен-
ство (5) не имеет решений.
ОТВЕТ: нет решений.
Пример 7. Решить неравенство
Vsinx < y/l — |х| 4- sin х.	(7)
Решение. Нахождение ОДЗ неравенства (7) есть трудная
задача. Поэтому поступим иначе. Неравенство (7) равносиль-
но системе неравенств
sin х О,
< 1 — |х| + sinх 0,	(8)
sinх < 1 — |х| + sinх.
Третье неравенство этой системы имеет решениями все х
из промежутка — 1 < х < 1. Первое неравенство системы (8)
справедливо не для всех х из этого промежутка, а лишь для х
из промежутка 0 х < 1. Для всех х из промежутка 0 х < 1
второе неравенство справедливо. Следовательно, множеством
решений системы (8) является промежуток 0 х < 1.
Ответ: 0 < х < 1.
134 Использование свойств входящих в уравнение функций
4.1.2. Использование ограниченности функций. При
решении уравнений и неравенств свойство ограниченности
снизу или сверху функции на некотором множестве часто
играет определяющую роль.
Например, если для всех х из некоторого множества М
справедливы неравенства /(г) > А и д(х) < А, где А — не-
которое число, то на множестве М уравнение f(x) = д(х) и
неравенство /(z) < д(х) решений не имеют.
Заметим, что роль числа А часто играет нуль, в этом
случае говорят о сохранении знака функций f(x) и д(.х) на
множестве М.
Пример 8. Решить уравнение
sin(z3 + 2х2 + 1) = х2 4- 2х + 3.
Решение. Для любого действительного числа х имеем
sin(a:3 + 2х2 + 1)	1, х2 + 2х + 3 = (х + I)2 + 2	2. Поскольку
для любого значения х левая часть уравнения не превосходит
единицы, а правая часть всегда не меньше двух, то данное
уравнение не имеет решений.
Ответ: нет решений.
Пример 9. Решить уравнение
х3 — х — sin тгх — 0.	(9)
Решение. Очевидно, что х = 0, х = 1, х = — 1 являют-
ся решениями уравнения (9). Для нахождения других решений
уравнения (9) в силу нечетности функции /(z) = х3—х—sin тгх
достаточно найти его решения в области х > 0, х / 1, по-
скольку если xq > 0 является его решением, то и (—xq) также
является его решением.
Разобьем множество х > 0, х / 1, на два промежутка:
(0; 1) и (1; +оо).
Перепишем уравнение (9) в виде х3 — х = sin7rx. На проме-
жутке (0; 1) функция g(z) = х3 — х принимает только отрица-
тельные значения, поскольку х3 < х, а функция h(x) = sinTrz
только положительные. Следовательно, на этом промежутке
уравнение (9) не имеет решений.
Пусть х принадлежит промежутку (1;4-оо). Для каждо-
го из таких значений х функция д(х) = х3 — х принимает
§ 4.1. Применение основных свойств функций
135
положительные значения, функция h(x) = sinirx принимает
значения разных знаков, причем на промежутке (1; 2] функция
h(x) = sin тгх неположительна. Следовательно, на промежутке
(1; 2] уравнение (9) решений не имеет.
Если же х > 2, то | sin тгяг| 1, х3 — х — х(х2 — 1) > 2-3 — 6,
а это означает, что и на промежутке (2; 4-ос) уравнение (9)
также не имеет решений.
Итак, а: = 0, а: = 1 и z =-1 и только они являются реше-
ниями исходного уравнения.
Ответ: xi = 0, х2 ~ 1, х3 = -1.
Пример 10. Решить неравенство
1 — х
1 4- х
< 2*.
(Ю)
РЕШЕНИЕ. ОДЗ неравенства (10) есть все действитель-
ные х, кроме х = —1. Разобьем ОДЗ на три множества:
—оо < х < —1, — 1 < х 0, 0 < х < 4-оо и рассмотрим
неравенство (10) на каждом из этих промежутков.
Пусть —оо < х < — 1. Для каждого из этих х имеем д(х) =
1 — X
— ----- < 0, а /(х) = 2Г > 0. Следовательно, все эти х явля-
1 4- х
ются решениями неравенства (10).
Пусть — 1 < х 0. Для каждого из этих х имеем ^(х) =
2х
— 1 — ----- 1, а /(х) = 2r 1. Следовательно, ни одно из
14-х
этих х не является решением неравенства (10).
Пусть 0 < х < 4-оо. Для каждого из этих х имеем д(х) =
2z
= 1--------< 1, а /(х) = 2r > 1. Следовательно, все эти х
14-х
являются решениями неравенства (10).
Ответ: —оо < х < —1; 0 < х < +оо.
Пример 11. Решить уравнение
2?rsin х = |х — тг/2| — |х Н- тг/2|.
(Н)
Решение. Обозначим |х — тг/2| — |х 4- тг/2| через /(х). Из
определения абсолютной величины следует, что /(х) = тг при
х — тг/2, /(х) = —2х при —тг/2 < х < тг/2 и /(х) = —тг при
х тг/2. Поэтому, если х —тг/2, то уравнение (11) мож-
но переписать в виде 2?rsinx = тг, т. е. в виде sinx = 1/2.
136 Использование свойств входящих в уравнение функций
Это уравнение имеет решения х = ( —1)птг/6 + тгп, п 6 Z.
Из этих значений х условию х —тг/2 удовлетворяют толь-
ко X = (-1)птг/6 4- тгп, п = -1, —2,.... Если х тг/2,
то уравнение (И) можно переписать в виде 2Trsinr = —тг,
т. е. в виде sin г = —1/2. Это уравнение имеет решения
х = (—1)т+1тг/6 + тгт, т G Z. Из этих значений х усло-
вию х к/2 удовлетворяют только х = ( —1)т+1тг/6 4- пт.
т = 1, 2,....
Рассмотрим х из промежутка (—тг/2; тг/2). На этом проме-
жутке уравнение (11) можно переписать в виде 2Trsinr = — 2г,
т. е. в виде
sin х =---.	(12)
тг
Ясно, что х = 0 есть решение уравнения (12), а значит, и
исходного уравнения. Докажем, что других решений уравне-
ние (12) на промежутке (—тг/2; тг/2) не имеет.
Для х / 0 уравнение (12) равносильно уравнению
sin х	1
х	тг
Для любого значения х 6 (—тг/2; 0) U (0; тг/2), функция
sin х
f(x) — ------ принимает только положительные значения,
х
поэтому уравнение (12) не имеет решений на множестве
(-тг/2; 0) U (0; тг/2).
ОТВЕТ: х = 0, х = ( —1)” тг/6 + тгп, п = —1, —2,...;
х = (—1)т+1тг/6 4- тгт, т = 1, 2,....
Пример 12. Решить уравнение
sin5 х 4--= cos5 х 4-	(13)
cos' х	sin х
Решение. Пусть х0 есть решение уравнения (13), тогда
справедливы равенство
1	к	1	к	,, . ч
----	cos х0 = —=-sin х0	(14)
cos'Го-----------------------------------sin го
и неравенства |cosr0| < 1 и | sinro| < 1. Из справедливости
неравенств получаем, что левая часть равенства (14) имеет
§ 4.1. Применение основных свойств функций
137
1
тот же знак, что и   —, т. е. тот же знак, что и cosa?o, а
cos' Xq
правая часть — тот же знак, что и sin xq. Но так как sin xq и
cos zq удовлетворяют равенству (14), то они имеют одинако-
вые знаки.
Перепишем равенство (14) в виде
cos7 zq sin7 zo(sin5 х0 — cos5 го) = cos7 xq — sin7 x0.	(15)
Применяя формулу сокращенного умножения
a21+l _ 62<+1 = (a _ 6)(a2( + a2l-lb + . . . + 62()j
перепишем равенство (15) в виде
(sin Xq - cos Xo)f(xo) = 0,	(16)
где
f(x0) = (sin r0 cos z0)7(sin4 x0 + sin3 x0 cos x0 + • • • + cos4 z0) +
+ (sin6 Xq + sin5 Xq COS Xq +  • • + COS6 £())•
Так как sin^o и coszq имеют одинаковые знаки, то /(zq) > 0.
Поэтому из равенства (16) следует, что для любого решения
уравнения (13) справедливо равенство sinzo = cosi0.
Таким образом, любое решение уравнения (13) удовлетво-
ряет уравнению
sin x = cos x.	(17)
Очевидно, что любое решение уравнения (17) есть решение
уравнения (13). Следовательно, уравнение (13) равносильно
уравнению (17). Решения уравнения (17) есть х — тг/4 + Агтг,
k G 7L, они и только они есть решения уравнения (13).
Ответ: х = тг/4 + як, к € Z.
Замечание. Точно так же, как в примере 12, можно до-
казать, что уравнение
____1	 = cos2n-1 X 4	-_
cos2m-1 х_____________________sin2m 1 z ’
sin2n 1
где n, m — любые натуральные числа, равносильно уравне-
нию sin х = cos х, и затем решать это более простое уравнение.
138 Использование свойств входящих в уравнение функций
4.1.3. Использование монотонности. Решение урав-
нений и неравенств с использованием свойства монотонности
основывается на следующих утверждениях.
1. Пусть f(x) — непрерывная и строго монотонная функ-
ция на промежутке Т , тогда уравнение /(г) = С, где С —
данная константа, может иметь не более одного решения на
промежутке 1.
2. Пусть /(г) и д(х) — непрерывные на промежутке I
функции, f(x) строго возрастает, а д(х) строго убывает на
этом промежутке, тогда уравнение /(т) = д(х) может иметь
не более одного решения на промежутке Т.
Отметим, что в качестве промежутка Т могут быть
бесконечный промежуток (—оо;+оо) , промежутки (а;+оо),
(—оо;а), [а;+оо), (—со;6], отрезки, интервалы и полуинтер-
валы.
Пример 13. Решить уравнение
х_2т2 + 2т+3 _ б4	(!8)
РЕШЕНИЕ. Очевидно, что х 0 не может являться ре-
шением уравнения (18), так как тогда т-2г +2т+3	0. Для
х > 0 функция у = х-2х +2г+3 непрерывна и строго возраста-
ет, как произведение двух непрерывных положительных стро-
го возрастающих для этих х функций f = х и д = 2х +2т+3.
Значит, в области х > 0 функция у — х-2х +2г+3 принимает
каждое свое значение ровно в одной точке. Легко видеть, что
х = 1 является решением уравнения (18), следовательно, это
его единственное решение.
Ответ: х = 1.
Пример 14. Решить неравенство
2х + 3' + 4х < 3.	(19)
Решение. Каждая из функций у = 2х, у = 3х, у = 4х
непрерывная и строго возрастающая на всей оси. Значит, та-
кой же является и исходная функция у = 2х + 3х + 4х. Легко
видеть, что при х = 0 функция у = 2х + 3Х + 4Х принимает зна-
чение 3. В силу непрерывности и строгой монотонности этой
функции при х > 0 имеем 2х + 3* + 4х >3, при х < 0 имеем
§ 4.1. Применение основных свойств функций
139
2х + Зг + 4Г < 3. Следовательно, решениями неравенства (19)
являются все х < 0.
Ответ: —оо < х < 0.
Пример 15. Решить уравнение
^18 - х - у/х-2 = 2.	(20)
Решение. Область допустимых значений уравнения (20)
есть промежуток 2 х 18. На ОДЗ функции /(z) = — х/х — 2
и д(х) = -^18 — х непрерывны и строго убывают, следователь-
но, непрерывна и убывает функция h(x) = -^18 — z — -^z — 2.
Поэтому каждое свое значение функция /j(z) принимает толь-
ко в одной точке. Так как h(2) = 2, то х = 2 является един-
ственным корнем исходного уравнения.
Ответ: х = 2.
Пример 16. Решить неравенство
\/х + 2z3 + log3(z + 2) — у/1 — х < 4.	(21)
Решение. ОДЗ неравенства (21) есть промежуток
0 < х 1. На ОДЗ функция /(z) = tfx + 2z3 + log3(z + 2) —
— у/1 — х является непрерывной и строго возрастающей. Так
как /(1) = 4, то все значения z из множества [0; 1) удовлетво-
ряют исходному неравенству.
Ответ: 0 х < 1.
Пример 17. Решить уравнение
log2(|z - 1|+ 1) + </(z - I)4 = 2.	(22)
Решение. Перепишем уравнение (22) в виде
log2(|z - 1| + 1) = 2 - ^(z - I)4.
Рассмотрим функции /(z) = log2(|z — 1| + 1) и </(z) =
— — у/(х — I)4 + 2. Функция /(z) убывает на промежутке
(—оо; 1] и возрастает на промежутке [1; +оо). Функция <?(z)
убывает на промежутке [1;+оо) и возрастает на промежут-
ке (—оо; 1]. Так как на промежутке [1;+оо) функция /(z)
возрастает, а функция </(z) убывает, то на этом промежут-
ке уравнение /(z) = g>(z) может иметь не более одного корня.
140 Использование свойств входящих в уравнение функций
Легко проверить, что таким корнем является число х = 2. Так
как на промежутке (—оо; 1] функция f(x) убывает, а функция
д(х) возрастает, то на этом промежутке уравнение /(z) = д(х)
также может иметь не более одного корня. Легко видеть, что
таким числом является число х = 0. Итак, данное уравне-
ние (22) имеет два корня zi = 0, х2 = 2.
Ответ: х^ = 0, х2 = 2.
Пример 18. Решить неравенство
у/2-х2>х3 + х-1.	(23)
Решение. ОДЗ неравенства (23) есть все х из промежутка
—л/2 х л/2. Все х из промежутка —л/2 х 0 являются
решениями исходного неравенства (23), так как для каждого
такого х имеем, что функция /(г) = \/2 — z2 неотрицательна,
а функция g>(z) = z3 + z - 1 отрицательна.
Рассмотрим неравенство (23) на промежутке (0; л/2]. По-
скольку функция </(z) непрерывна и строго возрастает на этом
промежутке, а функция /(z) непрерывна и строго убывает, то,
если уравнение /(z) = </(z) имеет корень на этом промежутке,
то он единственный. Легко видеть, что таким корнем является
число z = 1.
Для каждого z из промежутка (0; 1) имеем, что /(z) =
= \/2 — х2 > 1, а д(х) =z3 + z — 1 < 1. Поэтому все z из этого
промежутка являются решениями исходного неравенства (23).
Для каждого z из промежутка (1;л/2] имеем /(z) =
= \/2 — х2 < 1, а д(х) = х3 + х — 1 > 1. Поэтому такие z
не удовлетворяют данному неравенству (23).
Итак, решениями исходного неравенства (23) являются
все z из промежутка [—л/2; 1).
Ответ: -л/2 х < 1.
Пример 19. Сколько действительных корней имеет урав-
нение
az3 + Ьх + с = 0,	(24)
если числа а и Ь одного знака?
Решение. Так как числа а и Ь одного знака, то Ь/а > О
для любого х и z2 + b/а ф 0. При с = 0 и ab > 0 очевидно,
§ 4.1. Применение основных свойств функций
141
что уравнение (24) имеет единственный корень х — 0. Пусть
с / 0. Перепишем данное уравнение в виде
1
~2 Ь'
а
(25)
Функция /(z) = 2 для каждого х Е (—оо;+оо) при-
нимает положительные значения и является непрерывной и
строго возрастающей на промежутке (—оо;0] и непрерывной
и строго убывающей на промежутке [0; +оо). Если а/с > 0, то
а
функция д(х) = —х непрерывна и строго убывает на всей
с
оси —со < х < +оо и принимает все положительные значения
для х Е (—оо;0) и отрицательные значения для х Е (0;+оо).
Поэтому уравнение (25) имеет единственный корень на про-
межутке (—со;0). Если а/с < 0, то функция д(х) =-х не-
прерывна и строго возрастает на всей оси —оо < х < +оо
и принимает все положительные значения для х Е (0; +оо) и
отрицательные значения для х Е (—оо;0). Поэтому уравне-
ние (25) имеет единственный корень на промежутке (0; +оо).
Ответ: единственный корень.
4.1.4. Использование графиков. При решении уравне-
ний или неравенств иногда полезно рассмотреть эскиз гра-
фиков их правой и левой частей. Тогда этот эскиз графиков
поможет выяснить, на какие множества надо разбить число-
вую ось, чтобы на каждом из них решение уравнения (или
неравенства) было очевидно.
Обратим внимание, что эскиз графика лишь помогает най-
ти решение, но писать, что из графика следует ответ, нельзя,
ответ еще надо обосновать.
Пример 20. Решить неравенство
\/1 — г2 < \/5 — х.
(26)
РЕШЕНИЕ. ОДЗ неравенства (26) есть все х из проме-
жутка [—1,1]. Эскизы графиков функций /(г) = \/1 — г2 и
142 Использование свойств входящих в уравнение функций
Рис. 7
д(х) = \/5 — х представлены на рис. 7. Из рисунка следует,
что для всех х из ОДЗ неравенство (26) справедливо. До-
кажем это. Для каждого х Е [—1; 1] имеем 0	/(х)	1, а
для каждого такого х имеем, что \/5 — х ^4 > 1. Значит,
для каждого х Е [—1; 1] имеем f(x) <1 1 < д(х). Следователь-
но, решениями неравенства (26) будут все х из промежутка
[-1; 1]-
ОТВЕТ: -1 х 1.
Пример 21. Решить уравнение
х2 + 2х + 3 = \/4 — х2.
(27)
Решение. ОДЗ уравнения (27) есть все х из промежутка
—2 х 2. Эскизы графиков функций /(х) = х2 + 2х + 3
и д(х) = \/4 — х2 представлены на рис. 8. Проведем прямую
у — 2. Из рисунка следует, что график функции /(х) лежит
не ниже этой прямой, а график функции д(х) не выше. При
этом эти графики касаются прямой у = 2 в разных точках.
Следовательно, уравнение не имеет решений. Докажем это.
Для каждого х Е [—2; 2] имеем \/4 — х2 <С 2, а х2 4- 2х + 3 =
= (х + I)2 + 2^2. При этом /(х) = 2 только для х = —1, а
д(х) = 2 только для х = 0. Это означает, что уравнение (27)
не имеет решений.
Ответ: нет решений.
§ 4.1. Применение основных свойств функций
143
Рис. 8
Пример 22. Решить уравнение
5 ।	з/ ^7
х + х = yj х — 7.
(28)
Решение. Эскизы графиков функций /(z) = z5 + х и
д(х') = у/х — 7 представлены на рис. 9. Легко проверяется, что
точка (—1;—2) является точкой пересечения графиков функ-
ций f(x) и д(х), т. е. х = —1 есть решение уравнения (28).
Проведем прямую у = х — 1. Из рисунка следует, что она рас-
положена между графиками функций у = /(z) и у = д(х).
Это наблюдение и помогает доказать, что других решений
уравнение (28) не имеет.
Для этого докажем, что для z из промежутка (—1;+оо)
справедливы неравенства z5 + z>z-1hz-1> v^z — 7,
а для z из промежутка (—оо;—1) справедливы неравенства
\/z — 7 > х — 1hz54-z<z — 1.
Очевидно, что неравенство z5 4-z > z — 1 справедливо для
z > — 1, а неравенство z5 + х < х — 1 для х < —1. Решим
неравенство у/х — 7 > х — 1. Это неравенство равносильно не-
равенству х — 7 > (z — I)3, которое можно переписать в виде
144 Использование свойств входящих в уравнение функций
(х 4- 1) [(х — 2)2 4- 2] < 0. Решениями этого неравенства явля-
ются все х < — 1. Точно так же показывается, что решениями
неравенства \/х — 7 < х — 1 являются все х > — 1.
Следовательно, требуемое утверждение доказано, и урав-
нение (28) имеет единственный корень х = — 1.
Ответ: х — -1.
Пример 23. Решить неравенство
6	1 4- log2(2 4- х)
2х 4- 1	х
(29)
Решение. Область допустимых значений данного нера-
венства состоит из всех х, удовлетворяющих условиям х > —2,
х / —1/2, х / 0, т. е. ОДЗ состоит из трех промежутков
—2 < х < —1/2, —1/2 < х < 0, 0 < х < 4-оо. Рассмотрим не-
равенство (29) на каждом из этих промежутков. Отметим, что
§ 4.1. Применение основных свойств функций
145
в области — 2 < х < 0, х / —1/2, оно равносильно неравенству
iog2(2+z)> (зо)
а в области х > 0 оно равносильно неравенству
4т — 1
iog2(2 + x)<—-.	(31)
lx + 1
Эскизы графиков функций /(х) = log2(2 + х) и д>(х) = -
2x4-1
приведены на рис. 10. Из рисунка видно, что д(х) > f(x) на
Рис. 10
промежутке ( — 2; —1/2) и f(x) > д(х) на каждом из промежут-
ков (—1/2;0) и (0;+оо). Поэтому неравенство (31) не имеет
решений, а неравенство (30) будет иметь решениями все х из
промежутка (—1/2,0).
Докажем это.
146 Использование свойств входящих в уравнение функций
а)	Пусть — 2 < х < —1/2. Неравенство (29) равносильно
на этом промежутке неравенству (30). Легко видеть, что для
каждого х из этого интервала справедливы неравенства
3
log2(2 4-z) < log2 - < 1,
4z - 1	3
— 2> 2
2z + 1 2z + 1
Следовательно, неравенство (30), а вместе с ним и ис-
ходное неравенство (29) не имеют решений на интервале
—2 < х < -1/2.
б)	Пусть —1/2 < х < 0. Тогда неравенство (29) также рав-
носильно неравенству (30). Для каждого х из этого интервала
/	1 \	з
log2(2 + z) > log2 ( 2 - - \ = log2 - > 0,
4х — 1
------ < 0.
2х + 1
Следовательно, любое такое х является решением неравен-
ства (30), а поэтому и исходного неравенства (29).
в)	Пусть х > 0. На этом множестве исходное неравенство
равносильно неравенству (31). Очевидно, что для любого х из
этого множества справедливы неравенства
4х - 1	3
------= 2----------
2х + 1 2х + 1
1 < log2(2 + z).
< 2,
Отсюда следует: 1) неравенство (31) не имеет решений на том
множестве, где log2(z + 2)	2, т. е. неравенство (31) не имеет
решений на множестве 2 х < +оо; 2) неравенство (31) не
4х - 1
имеет решении на том множестве, где ---- <С 1. Учитывая,
2x4-1
что в рассматриваемом случае х > 0, получаем, что неравен-
ство (31) не имеет решений на множестве 0 < х 1. Остается
найти решения неравенства (31), принадлежащие интервалу
1 < z < 2.
§ 4.1. Применение основных свойств функций
147
На этом интервале
log2(2 4- z) > log2 3,
4z - 1	3	3	7
___ = 2<2__________= -.
2х + 1 2х + 1	5	5
Покажем теперь, что справедливо числовое неравенство
log2 3 >7/5.
(32)
Действительно, поскольку З5 > 27, то 3 > 27/5, откуда и оче-
видна справедливость неравенства (32). Итак, на интервале
1 < х < 2 имеем
4х — 1
log2(2 + х) > log2 3 > 7/5 >
Значит, неравенство (31) не имеет решений на интервале
1 < х < 2. Подводя итог, получаем, что множество реше-
ний исходного неравенства есть интервал —1/2 < х < 0.
Ответ: -1/2 < х < 0.
4.1.5. Метод интервалов для непрерывных функ-
ций. Пусть надо решить неравенство /(z) > 0 (или неравен-
ство /(z) < 0). Пусть ОДЗ этого неравенства состоит из объ-
единения конечного числа промежутков!^, k = 1, 2,..., п,
занумерованных в порядке следования слева направо. При
этом, если п > 1, то 1\ и 1п могут быть соответствен-
но бесконечными промежутками (—оо;а) ((—сю; а]) и (Ь; +оо)
([6;4-оо)). Промежутки 22,..., 1п-1 соответственно могут
быть отрезками [c;d], интервалами (с; </) и полуинтервала-
ми [с; d), (с; d]. В случае же п = 1 I может быть лю-
бым из перечисленных промежутков, а также промежутком
(—оо;+оо). Предположим также, что на каждом из проме-
жутков Ik функция /(z) непрерывна и имеет конечное чи-
сло нулей. Отметим на числовой прямой нули функции /(z)
и выбросим из ОДЗ неравенства эти точки. При этом не-
которые из промежутков Ik могут разбиться на некоторое
число промежутков. На каждом из полученных промежут-
ков функция /(z) непрерывна и не обращается в нуль. Зна-
чит, на каждом из них она сохраняет постоянный знак,
148 Использование свойств входящих в уравнение функций
т. е. для каждого х из этого промежутка она принима-
ет только либо положительные, либо отрицательные зна-
чения. Выбирая в каждом из промежутков некоторую точ-
ку Zq и вычисляя знак /(zq), этот знак ставят над этим
промежутком. Тогда решением неравенства /(z) > 0 бу-
дет объединение тех промежутков, над которыми поставлен
знак плюс, а решением неравенства /(z) < 0 будет объеди-
нение тех промежутков, над которыми поставлен знак ми-
нус.
Пример 24. Решить неравенство
\/z2 — 1(4 — z) log3(3 4- z) > 0.
(33)
Решение. ОДЗ неравенства (33) состоит из всех z, одно-
временно удовлетворяющих условиям г2 - 1	0 и 3 + z > О,
т. е. ОДЗ есть объединение двух промежутков: (—3;—1] и
[1; +оо). Нули функции /(z) = \/z2 — 1(4 — z) log3(3 + z) есть
Zi = 1, z2 = — 1, Z3 = 4, Z4 = —2. Выбросив их из ОДЗ, полу-
чим промежутки (—3; —2), (—2; —1), (1;4) и (4; +оо) (рис. 11).
Определим знаки функции на каждом из этих промежутков.
Рис. 11
Поскольку /(—2,5) < 0, /(—1,5) > 0, /(2) > 0, /(5) < 0, то
на промежутке (4; +оо) функция / принимает отрицательные
значения, на промежутках (—2; —1), (1;4) — положительные
значения, а на промежутке (—3; —2) — отрицательные значе-
ния.
Следовательно, множеством решений неравенства (33)
является объединение промежутков (—2, -1), (1; 4).
Ответ: -2 < z < -1; 1 < z < 4.
§ 4.2. Сведение к системам с той же неизвестной
149
Пример 25. Решить неравенство
(|ar + 3| - 1)(4 - 22j~1)(z2 +
log2(-z-bz2 + 1)
Решение. ОДЗ неравенства (34) состоит из всех х, удовле-
творяющих условиям 1 — х + х2 > 0 и log2( 1 — х + £2) ф 0, т. е.
ОДЗ состоит из трех промежутков: (—оо;0), (0; 1) и (1;+оо).
Нули функции
(|z + 3|-l)(4-22-1)(r2 + ^)
Z	log2(-z + г2-b 1)
есть Xi = —1, х2 = 3/2, хз = —2, х^ = —4. Выбросив их из
ОДЗ, получим промежутки Ъ. = (—оо;—4), Т2 — (—4;—2),
Тз = (-2;-1), U = (-1,0), Тз = (0;1),	= (Г, 3/2),
Ту = (3/2;+оо) (рис. 12). Легко видеть, что
Рис. 12
/(-5) >0, -5еД; /(-3) <0, -3G Т2-
/(-3/2) > 0, -3/2 G 1з\ /(-1/2) < 0, -1/2 G Д;
/(5/4) > 0, 5/4 G Z6; /(1/2) < 0, 1/2 € If, /(2) < 0, 2 € Ту.
Следовательно, множеством решений неравенства (34) явля-
ется объединение четырех промежутков: —4 < х < —2,
3
— 1 < z < 0, 0 < z < 1, - < х < -|-оо.
3
Ответ: — 4 < х < —2; — l<z<0;0<z<l;-<z< -boo.
150 Использование свойств входящих в уравнение функций
§ 4.2.	Решение некоторых уравнений и
неравенств сведением их к решению систем
уравнений или неравенств относительно той
же неизвестной
4.2.1.	Уравнения вида /2(z) + f^x) + • • • + f^fx) = О,
|Л(z)| + |/2(яг)| +-1- |/*О)| = 0. Уравнения вида
/iW + /22W + --- + A2W = o,	(1)
|A(z)| + |/2(z)| + • • • + IAWI = о	(2)
равносильны системе уравнений
fi(x) = 0,
<	:	(3)
„ fk(x) = 0.
Пример 1. Решить уравнение
+ 5.4* + 4z2-2* - 2-2* + 1 = 0.	(4)
Решение. Перепишем уравнение (4) в виде
(z2 + 2-2*)2 4- (2* - I)2 = 0,	(5)
откуда очевидно, что уравнение (5) равносильно системе
уравнений
У 2г-1=0,
I z2 + 2-2г = 0.	' '
Первое уравнение этой системы имеет единственное решение
z = 0, которое не удовлетворяет второму уравнению систе-
мы (6). Следовательно, система (6) не имеет решений.
Ответ: нет решений.
Пример 2. Решить уравнение
\/z2 — 6z + 9 + ^/log2/7(z2 — 4х + 4) = 0.	(7)
§ 4.2. Сведение к системам с той же неизвестной
151
РЕШЕНИЕ. Перепишем уравнение (7) в виде
к - 3| + I log1/7(r2 - 4х 4- 4)1 = 0.
Это уравнение равносильно системе уравнений
о:-3 = 0,
l°gi/7(z2 - 4х 4- 4) = 0.	(-8'
Решение первого из этих уравнений есть х = 3. Проверка
показывает, что это число также является и решением вто-
рого уравнения системы (8). Следовательно, х = 3 является
решением исходного уравнения (7).
Ответ: х = 3.
Отметим, что к системе (3) сводится и ряд других урав-
нений. Приведем пример.
ПРИМЕР 3. Решить уравнение
log2 ^1 4- 1А4 4- z2) + log2(l -I- z2) = 0.	(9)
Решение. Для любых х справедливы неравенства
log2 (14- А4 + х2^	0,
log2(l + х2)	0.
Поэтому уравнение (9) равносильно системе уравнений
log2 (14- \А4 4- х2^ = 0,
log2(l + х2) = 0,
имеющей единственное решение х = 0.
Ответ: х = 0.
4.2.2.	Неравенства вида f2(т) + /2 (г) 4- • •  + /2(х) > О,
|/i(z)|-b|/2(a;)|4--  -4-\fn (я)! > 0. Решениями неравенств вида
Л(х) + Ш + --- + Ш>0,	(10)
|/1(z)| + |/2(z)|+---+l/n(x)| >0	(11)
152 Использование свойств входящих в уравнение функций
являются все х из их ОДЗ, за исключением тех х, которые
являются решениями системы уравнений
Л(*) = о,
fn(x) = 0.
(12)
Пример 4. Решить неравенство
(log2z-l)2 + (z-2)2 >0.	(13)
Решение. ОДЗ неравенства (13) есть все х > 0. Для на-
хождения решений неравенства (13) надо исключить из ОДЗ
все решения системы уравнений
log2 х — 1 = 0,
х - 2 = 0.
Эта система имеет единственное решение х = 2, следователь-
но, решениями неравенства (13) являются все х > 0, кроме
х = 2.
Ответ: 0 < z < 2; 2 < х < +оо.
Пример 5. Решить неравенство
| sin2 х — sin4 г | +
(14)
Решение. Перепишем неравенство (14) в виде
| sin2 х — sin4 г | +
1 4- х2
Для любого х справедливы неравенства
| sin2 х — sin4 r| 0,
2	2
X — 7Г
1 + X2
> 0.
Поэтому неравенство (14) не выполняется лишь для таких х,
что одновременно
sin2 х — sin4 х — 0,
Z2-TT2
1 + X2
= 0,
§ 4.2. Сведение к системам с той же неизвестной
153
т. е. для х = тг и х — —V.
Следовательно, решениями исходного неравенства (14) яв-
ляются все х, кроме х = тг и х = —тг.
Ответ: —оо < х < —тг; —тг <х<тг;тг<х< +оо.
Отметим, что к системе (12) сводятся иногда и другие не-
равенства.
Пример 6. Решить неравенство
1 _ cos« (^±5») + 2^- 1 > 0.	(15)
Решение. ОДЗ неравенства (15) являются все х, удовле-
творяющие условию 1 — z4 0, т. е. ОДЗ есть все х g [—1; 1].
На ОДЗ справедливы неравенства
Zz2 + z\
1 — cos4 ------—тг > 0, 2V — 1 > 0.
\	4	/
Поэтому неравенство (15) выполняется для всех х из ОДЗ,
кроме тех, которые удовлетворяют системе уравнений
Решениями второго уравнения этой системы являются Х\ = 1
и х-z = — 1. Из них первому уравнению удовлетворяет только
х = — 1. Итак, решениями данного неравенства (15) являются
все х из промежутка — 1 < х 1.
Ответ: -1 < х 1.
4.2.3.	Использование ограниченности функций.
Если при решении уравнения
/(z) = jf(z)	(16)
удается показать, что для всех х из некоторого множества М
справедливы неравенства /(z) А и g>(z) А, то на множе-
стве М уравнение (16) равносильно системе уравнений
Г /(z) = А,
1 д(х) = А.
(17)
154 Использование свойств входящих в уравнение функций
Пример 7. Решить уравнение
,	12
4z2 4- 4г 4- 17 = —--------
х1 — х 4- 1
РЕШЕНИЕ. Перепишем это уравнение в виде
/ 1\2
Г+2>)
3
1\2
х----
2 7
3
4
(18)
Очевидно, что для любых действительных х имеем
. . / 1V
у{х) = I х + - I
з
/W = ( 1V 3
И" 2) +4
Следовательно, уравнение (18) равносильно системе
НИИ
уравне-
1\2
х + 2 ) 4-4 = 4,
1\2	3	3
х---I 4— = -
2/	4	4
Эта система уравнений не имеет решений, поэтому исходное
уравнение также не имеет решений.
Ответ: нет решений.
Пример 8. Решить уравнение
(19)
Решение. ОДЗ уравнения (19) являются все действитель-
ные х. Для любых х имеем
Следовательно, уравнение (19) равносильно системе уравне-
ний
( cos2(z sin х) = 1
( logg л/я2 4- я 4- 1
(20)
§ 4.2. Сведение к системам с той же неизвестной
155
Решения второго уравнения системы (20) есть х = 0иг=-1.
Из этих значений первому уравнению удовлетворяет только
х = 0, которое, следовательно, является единственным реше-
нием исходного уравнения.
Ответ: х — о.
Пример 9. Решить уравнение
cos7 х + sin5 х = 1.	(21)
РЕШЕНИЕ. Поскольку cos2 х +sin2 х = 1, то уравнение (21)
можно переписать в виде cos7 х + sin5 х — cos2 х + sin2 х или в
виде
cos2 z(cos5 х — 1) = sin2 z(l — sin3 z).	(22)
Поскольку для любого действительного х имеем sin2 х 0,
cos2 х 0, cos5 х — 1	0, 1 — sin3 z 0, то уравнение (22)
равносильно системе уравнений
Г cos2 z(cos5 z — 1) = 0,
( sin2 z(l — sin3 z) — 0.
Система (23) равносильна совокупности систем уравнений
{cos z = 0,	( sin z = 0,
sin z = 1,	1 cos z = 1.
(23)
(24)
Решения первой из этих систем есть х = — + 2тг&, k € Z,
второй х = 2тгт, т Е Z. Все эти решения и будут решениями
исходного уравнения.
ОТВЕТ: х = 2itm, х = — + 2irk; т, k € Z.
4.2.4.	Использование свойств синуса и косинуса.
Решение большого количества тригонометрических уравне-
ний может быть сведено к решению систем уравнений. При-
мерами таких уравнений могут служить следующие:
sin ах-sin (Зх = ±1,
sin ах-cos (Зх — ±1,
A(sin ах)т 4- B(cos (Зх)п = ±(|А| + |В|),
A(sin ах)т + B(sin /?z)n = ±(|А| + |5|),
(25)
156 Использование свойств входящих в уравнение функций
где а, (3, А и В — данные действительные числа, пит —
данные натуральные числа. При решении таких уравнений
используется следующее свойство синуса: если для некоторо-
го числа zq справедливо строгое неравенство | sin ozq| < 1, то
такое число zq не может быть корнем ни одного из уравне-
ний (25). Аналогично, при решении уравнений
cos ах  cos /Зх = ± 1,
A(cos ах)т + B(cos /Зх)п = ±(| А| + |В|)
используется свойство косинуса: если для некоторого числа zq
справедливо строгое неравенство |cosazo| < 1, то такое чи-
сло Zq не может быть корнем ни одного из этих уравнений.
Пример 10. Решить уравнение
sin х- cos 4z = 1.	(26)
Решение. Если zq — решение уравнения (26), то либо
sinzo=l, либо sinzo=— 1. Действительно, если бы | sin zq| < 1,
то из уравнения (26) следовало бы, что | cos4z0| > 1, что, есте-
ственно, невозможно. Но если sinzo — 1, то из уравнения (26)
следует, что cos4zq = 1, если же sinzo = —1, то cos4zq = —1.
Следовательно, любое решение уравнения (26) является реше-
нием одной из следующих двух систем уравнений:
[ cos 4яо = 1,	v 7
|Si"a0 = _1’,	(28)
( cos 4zq = —1.	v 7
Легко видеть, что любое решение системы (27) и любое реше-
ние системы (28) есть решение уравнения (26). Следователь-
но, уравнение (26) равносильно совокупности систем уравне-
ний (27) и (28). Решим эти системы.
Первое уравнение системы (27) имеет решения
z = тг/2 4- 2тг&, i: Е Z.
Все они удовлетворяют второму уравнению этой системы, т. е.
являются решениями системы (27).
§ 4.2. Сведение к системам с той же неизвестной
157
Первое уравнение системы (28) имеет решения
х = — + 2тг/, I g Z.
Ни одно из этих чисел не удовлетворяет второму уравнению
этой системы. Поэтому система (28) не имеет решений.
Итак, решения исходного уравнения (26) совпадают с ре-
шениями системы (27).
Ответ: х = тг/2 + 2irk, k G Z.
Пример 11. Решить уравнение
3 cos4 2х — 2 sin5 х = 5.
(29)
Решение. Если хо есть решение уравнения (29), то
| cos 2z01 = 1, ибо в противном случае было бы справедливо не-
равенство | sinzq| > 1, что невозможно. Но если | cos2z0| = 1,
то из уравнения (29) следует, что sinzo = —1. Поэтому любое
решение уравнения (29) является решением системы уравне-
ний
sin z = —1,
| cos 2z | = 1.
(30)
Легко видеть, что любое решение системы (30) есть решение
уравнения (29). Следовательно, уравнение (29) равносильно
системе уравнений (30).
Первое уравнение системы (30) имеет решения
Зтг ,	, _
х = — + 2тг/, I € Z.
Все они удовлетворяют второму уравнению системы (30), т. е.
являются решениями уравнения (29).
3 тг
Ответ: х = — + 2тг/, I е Z.
Пример 12. Решить уравнение
cos3 3z + cos11 7z = —2.
(31)
Решение. Если zq — решение уравнения (31), то cos 3zq =
= — 1 (в противном случае cos7zq < —1, что невозможно).
158 Использование свойств входящих в уравнение функций
Но тогда cos7zo = —1. Следовательно, любое решение урав-
нения (31) есть решение системы уравнений
cos 3z = — 1,
cos7z = — 1.
(32)
Легко видеть, что любое решение системы (32) есть решение
уравнения (31). Поэтому уравнение (31) равносильно систе-
ме (32).
Первое уравнение системы (32) имеет решения
тг 2тгЛт ,
Хк = т- + —, к € Z.
о «5
Найдем те из этих решений, которые будут удовлетворять
второму уравнению системы (32). Это будут те Хк, для ка-
ждого из которых найдется число т € Z такое, что будет
справедливо равенство
7тг 14-тгД:
— -I-------— = тг + 2тгт.
«5	о
(33)
Перепишем равенство (33) в виде
, 3m — 2
‘ = ——
Поскольку кит целые числа, то равенство (34) справедливо
лишь тогда, когда т = 7t + 3, t € Z, но тогда к = 3/ + 1, t € 7L.
Итак, решениями системы (32) являются х^, где к — 3/ + 1,
_	тг	2тг
t € Z, т. е. х = — + 2тг/ + —, t € Z.
Ответ: х = тг + 2тг/, t G Z.
4.2.5.	Использование числовых неравенств. Иногда,
применяя то или иное числовое неравенство к одной из частей
уравнения (неравенства), его можно заменить равносильной
ему системой уравнений. Примером такого неравенства явля-
ется неравенство между средним арифметическим и средним
а +Ь	/~г	,
геометрическим —-—	vab, где а и о — положительные
числа, причем равенство здесь возможно лишь при а = Ь.
§ 4.2. Сведение к системам с той же неизвестной
159
Часто бывает полезно пользоваться следствиями из этих
неравенств, например, а + -	2 при а > 0, причем а + - — 2
а	а
тогда и только тогда, когда а = 1, а 4—	—2 при а < О,
а
1
причем а 4— — — 2 тогда и только тогда, когда а = — 1.
а
Пример 13. Решить уравнение
,--------- 4
Уж2 4-2ж 4-4 4-	= 4 - log^r2 4-ж4 4- 1). (35)
дх1 4- 2г 4- 4
Решение. ОДЗ этого уравнения есть все действительные
числа. Переписав левую часть уравнения (35) в виде
Vx2 4- 2г 4- 4	2
у 2	а/г2 4- 2г 4- 4у
замечаем, что она не меньше четырех, как сумма двух взаим-
но обратных положительных величин, и только при х = 0 она
равна четырем. В то же время правая часть при х = 0 также
равна четырем, а для всех х / 0 меньше четырех. Следова-
тельно, х = 0 есть единственное решение уравнения (35).
Ответ: х = 0.
Пример 14. Решить уравнение
( ——з--I-----) (sin8 х 4- cos2 2r) = 4 cos2 \l— x2. (36)
\sin8r cos2 2г/	V 4
Решение. Докажем, что для любых положительных чисел
а и b справедливо неравенство
4-	(а 4- Ь) 4.	(37)
В самом деле, применяя неравенство о среднем арифметиче-
ском и среднем геометрическом сначала к числам 1/а и 1/6, а
затем к числам а и Ь, имеем
160 Использование свойств входящих в уравнение функций
откуда
1 fl
2 \а + b)
1 + 1") (а + 6)	4.
a b J
Поскольку на ОДЗ уравнения (36) имеем sin8 x>Q, cos2 2х > 0,
то, применяя неравенство (37), получаем, что для любого та-
кого х левая часть уравнения (36) не меньше 4. В то же время
на ОДЗ уравнения (36) 4 cos2
4. Следовательно,
уравнение (36) равносильно системе уравнений
—з------1-----— ) (sin8 х + cos2 2т) = 4,
sin х cos2 2х )
(38)
Из последнего уравнения системы (38) находим его решения
= тг/2 и х2 = —тг/2. Подставляя эти значения в первое
уравнение системы (38), получаем, что они являются его ре-
шениями. Следовательно, хг = тг/2 и = —тг/2 являются
решениями исходного уравнения (36).
Ответ: х^ ~ тг/2, х2 = —тг/2.
§ 4.3.	Применение производной
В предыдущих параграфах были рассмотрены применения
некоторых свойств функций, входящих в уравнение, напри-
мер, свойства монотонности, ограниченности, существование
наибольшего и наименьшего значений и т. д. Иногда вопрос
о монотонности, об ограниченности и в особенности о нахо-
ждении наибольшего и наименьшего значений функций эле-
ментарными методами требует трудоемких и тонких иссле-
дований, однако он существенно упрощается при применении
производной. В этом параграфе будет показано применение
производной при решении уравнений и неравенств.
4.3.1.	Использование монотонности. В дальнейшем
будем пользоваться следующими утверждениями.
§ 4.3. Применение производной
161
1.	Если функция /(г) имеет положительную производную
на промежутке I ((а; 6), (а; +оо), (—оо; а), (—оо; +оо)), то эта
функция возрастает на этом промежутке.
2.	Если функция /(х), непрерывна на промежутке 1 ([а; 6],
[а; Ь), (а; 6] [а; +оо), (—оо; а]) и имеет внутри промежутка поло-
жительную производную, то эта функция возрастает на про-
межутке I.
3.	Если функция f(x) имеет на интервале (а; Ь) тожде-
ственно равную нулю производную, то эта функция f(x) есть
постоянная на этом интервале.
Пример 1. Решить уравнение
х5 4-г3-71-3x4-4 = 0.	(1)
Решение. Рассмотрим функцию
/(х) = х5 4- х3 — 71 — Зх 4- 4.
Область определения этой функции есть промежуток Т —
— оо; i . На этом промежутке /(х) непрерывна, внутри
его имеет производную
/'(х) = 5х4 4- Зх2 4-
3
271 - Зх ’
Эта производная положительна внутри промежутка Т. Поэто-
му функция /(х) возрастает на промежутке Т. Следовательно,
она принимает каждое свое значение ровно в одной точке. А
это означает, что уравнение (1) имеет не более одного корня.
Легко видеть, что х = —1 является корнем уравнения (1) и по
сказанному выше других корней не имеет.
Ответ: х = -1.
Пример 2. Решить неравенство
20х7 4- 28х5 4-210х — 35 sin 2х > 0.	(2)
Решение. Рассмотрим функцию f(x) = 20х7 4- 28х5 4-
4- 210х — 35sin2x. Поскольку эта функция на промежутке
1 = (-оо;4-оо) имеет производную /'(х) = 140х6 4- 140х4 4-
4- 210 — 70 cos2x, которая положительна на этом промежутке,
162 Использование свойств входящих в уравнение функций
то функция /(г) возрастает на промежутке I и потому прини-
мает каждое свое значение ровно в одной точке. Следователь-
но, уравнение /(г) = 0 может иметь не более одного корня.
Легко видеть, что таким корнем уравнения /(г) = 0 является
х = 0. Поскольку функция f(r) определена на всей прямой
и непрерывна на ней, то для х < 0 имеем f(x) < 0, а при
х > 0 имеем f(x) > 0. Поэтому решениями неравенства (2)
являются все х из промежутка (0; фоо).
Ответ: 0 < х < -|-оо.
Пример 3. Решить неравенство
ех > 1 + х.	(3)
РЕШЕНИЕ. ОДЗ неравенства (3) есть промежуток I =
= (—оо; +оо). Рассмотрим функцию /(г) = ех — 1 — х. Эта
функция на промежутке 1 имеет производную f'(x) = ех — 1.
Легко видеть, что f'(x) > 0 для любых х из промежутка
0 < х < Too. Так как на промежутке 0 Sj х < -|-оо функ-
ция f(x) непрерывна, то это означает, что на промежутке
0 х < +оо функция /(г) возрастает. Поскольку /(0) — 0, то
/(г) > 0 для любого х Е (0; +оо). Поэтому любое х Е (0; +оо)
является решением неравенства (3).
Так как /'(т) < 0 для любого х Е (—оо;0) и f(x) непре-
рывна на промежутке —оо < х 0, то функция f(x) убывает
на промежутке —оо < х 0. Поскольку /(0) = 0, то /(г) > 0
для любого х Е (—оо;0). Следовательно, любое х Е (—оо;0)
является решением неравенства (3). Поскольку /(0) = 0, то
х = 0 не есть решение неравенства (3).
Таким образом, все решения неравенства (3) составляют
два промежутка (0; +оо) и (—оо; 0).
Ответ: 0 < х < +оо; —оо < х < 0.
4.3.2.	Использование наибольшего и наименьше-
го значений функции. Справедливы следующие утвержде-
ния.
1.	Чтобы найти наибольшее и наименьшее значения не-
прерывной на отрезке [а; 6] функции, имеющей на интерва-
ле (а; Ь) конечное число критических точек, достаточно вы-
числить значения функции во всех критических точках, при-
надлежащих интервалу (а; 6), а также в концах отрезка и из
полученных чисел выбрать наибольшее и наименьшее.
§ 4.3. Применение производной
163
2.	Наибольшее (наименьшее) значение функции, принима-
емое ею на интервале I: (а; 6) ((—оо; +оо), (а; +оо), (—оо; а)),
может достигаться в тех точках интервала 1, в которых про-
изводная функция равна нулю или не существует (каждая та-
кая точка называется критической точкой).
3.	Если в критической точке хо функция непрерывна, а ее
производная, проходя через эту точку, меняет знак с минуса
на плюс, то точка го — точка минимума, а если ее производ-
ная меняет знак с плюса на минус, то xq — точка максимума.
4.	Если функция /(г) непрерывна на промежутке Т, где I
либо [а; 6], либо [а; 6), либо [а;+оо), и имеет внутри I произ-
водную и f'(x) > 0 (/'(ж) < 0) внутри I, то функция /(г)
возрастает (убывает) на 1.
Пример 4. Решить уравнение
х2 + 2х 4- 3 = (г2 + х + 1)(ж4 4- х2 4- 4).	(4)
Решение. ОДЗ уравнения (4) есть промежуток I =
= (—оо;4-оо). Так как х2 4- х + 1 > 0 для любого х, то
уравнение (4) можно переписать в виде
х2 4- 2х 4- 3
х2 4- х 4- 1
= х4 4- х2 4- 4
или в виде
х 4- 2
х2 4- х 4-1
= ж4 4-ж2 4-3.
(5)
Наименьшее значение функции /(г) = х4 4- х2 4- 3 на про-
межутке (—оо;4-оо) есть 3. Найдем наибольшее значение на
промежутке (—оо;4-оо) функции д(х) =
х 4- 2
х2 4- х 4- 1
. Так как
на промежутке (—оо;—2) функция д(х) отрицательна, а на
промежутке (—2;4-оо) положительна, то наибольшее значе-
ние функция д(х) может принимать лишь на промежутке
(-2;4-оо).
Эта функция на промежутке (—оо; 4-оо) имеет производ-
ную
х2 4- х 4- 1 — (х 4- 2)(2г 4-1) _ х2 4- 4г 4-1
(г2 4- х 4- I)2	(г2 4- х 4- I)2 ’
164 Использование свойств входящих в уравнение функций
которая обращается в нуль в точках ай = —2+\/з и г2 = — 2—у/з.
Поскольку на промежутке (—24-л/З; +оо) имеем д'(х) < 0, а на
промежутке (—2; —2 + у/з) имеем д'(х) > 0, то в силу непре-
рывности функции д(х) заключаем, что она на промежутке
[—2 + у/3; +оо) убывает, а на промежутке [—2; —2 + у/з] воз-
растает. Следовательно, в точке х? = — 2 + у/з функция д(х)
2^3 + 3
принимает наибольшее значение, причем — ---------------.
„	2\/з + 3
Поскольку ------- < 3, то для любого х справедливы нера-
венства
Z 3 > ---5--- 9\х)>
и
из которых следует, что уравнение (5) решений не имеет.
Следовательно, не имеет решений и равносильное ему
уравнение (4).
Ответ: решений нет.
Пример 5. Решить уравнение
л/г - 2 + tf4-x = 2.	(6)
Решение. ОДЗ уравнения (6) есть промежуток 2 х 4.
Рассмотрим непрерывную функцию /(г) = -У х — 2 + у/4 — х
на отрезке [2; 4]. Функция f(x) на интервале (2; 4) имеет про-
изводную
/'(х) = |(х -2)-3/4 - |(4 - х)-3/4,
обращающуюся в нуль только при х = 3. Так как функ-
ция /(г) непрерывна на отрезке [2; 4], то ее наибольшее и
наименьшее значения находятся среди чисел f(3), /(2) и /(4).
Так как /(3) = 2, /(2) = /(4) = \^2 < 2, то наибольшее зна-
чение f(x) есть /(3) = 2. Следовательно, уравнение (6) имеет
единственный корень х = 3.
Ответ: х = 3.
Пример 6. Решить неравенство
§ 4.3. Применение производной
165
Решение. ОДЗ неравенства (7) есть промежуток 1 =
= [0; +оо). Рассмотрим непрерывную функцию /(г) =
= '/г^(1 — х) на промежутке [0;+оо). Эта функция имеет
внутри промежутка (0; +оо) производную
f'(x) = ^^(l — х) — х3'2 = х1/2 (|(1 — х) — х
Эта производная внутри промежутка 1 обращается в нуль
3
только в точке xq = -. Поскольку для любой точки х, на-
5
3
холящейся слева от точки xq = имеем, что f'(x) > 0, а
5
для любой точки справа от х0 имеем f'(x) < 0, то в силу
непрерывности функции, f(x) на отрезке [0; 3/5) возраста-
г ,	3
ет, на промежутке [3/5; +оо) убывает и точка хо = - есть
5
точка максимума функции f(x). Это означает, что для любо-
го х из 1, кроме xq, справедливо неравенство /(г) < /(3/5),
2 ,--------------
/(3/5) — -х/27/125. Следовательно, решениями исходного не-
5
, .	г з\
равенства (7) являются все х из двух промежутков 0; - и
5/
/3	\
+оо .
\ 5’	J
Ответ: 0 < х < 3/5; 3/5 < х < +оо.
Пример 7. Решить неравенство
х2
ln(l + r) > х-	(8)
Решение. ОДЗ неравенства (8) есть промежуток 1 =
= (—1;+оо). Рассмотрим функцию
х2
f{x) = 1п(1 + г) — X + —.
Эта функция на промежутке I имеет производную
166 Использование свойств входящих в уравнение функций
которая обращается в нуль в точке г о = 0.
Рассмотрим функцию /(г) сначала на промежутке —
— (—1;0]. Так как /(г) непрерывна на промежутке Т\ и для
любой точки х внутри промежутка 2ц имеем f'(x) > 0, то
/(г) возрастает на Поскольку /(0) = 0, то /(г) < 0 для
любого х внутри Т\, т. е. ни одно х из промежутка не есть
решение неравенства (8).
На промежутке 2г = [0; +оо) функция /(г) непрерывна,
для любой точки х внутри промежутка Тг имеем /'(г) > 0,
поэтому f(x) возрастает на 2ц. Поскольку /(0) = 0, то
f(r) > 0 для любого х внутри Тг, т. е. любое х из проме-
жутка 0 < х < +оо есть решение неравенства (8).
Ответ: 0 < х < +оо.
4.3.3. Применение теоремы Лагранжа.
Теорема (Лагранжа). Если функция f(x) непрерывна
на отрезке [а; 6] и имеет производную на интервале (а',Ь),
то найдется такая точка с внутри интервала (а;Ь), что
f(b)-f(a) = f’(c)(b-a).
Пример 8. Решить уравнение
3-2г+2 - 7х = 17.	(9)
Решение. Заметим, что х = — 2 и х = 1 являются корня-
ми уравнения (9). Докажем, что других корней уравнение (9)
не имеет. Предположим, что уравнение (9) имеет три корня
< г2 < хз. Рассмотрим функцию f(x) = 3-2г+2 — 7х — 17.
Данная функция непрерывна на всей прямой и имеет всюду
производную. По теореме Лагранжа имеем
/(х2) - /(xi) = /'(с1)(г;2 - *1) = 0, Г1 < ci < х2,
Лжз) - Л^г) = Л(с2)(г3 - г2) = 0, х2 < С2 < х3.
Следовательно, существуют хотя бы две точки cj и с2, в кото-
рых производная функции /(г) равна нулю. Однако функция
Л(г) = 3-2г+2 In 2 — 7 имеет только один корень. Этим доказа-
но, что данное уравнение (9) имеет только два корня: х = — 2
и х — 1.
Ответ: = -2, х2 = 1.
Задачи
167
Задачи
Доказать, что следующее уравнение не имеет решений
1.	у/1 — X + у/х — 1 = 1.
2.	\/2 - г = log5(z - 2).
3.	|г - 2| + |т2 - 3| = 0.
4.	|т4 + 1| + |т2 + 4т — 5| = 1.
5.	У2т + 5 + у/х + 2 = 0.
6.	л/4 — х — у/х — 7 = 2.
7.	д/т — 4 — у/—1 — х — 0.
8.	^/х +у/х+ 5 = 2.
9.	у т + — = у/~х — 1.
10.	2r2+1 = 1 - х8.
11.	</х + 2- у/х+ 3 = 2.
12.	sin х = т2 + х + 1.
13.	log3 т — 1 +	3
Zx — 1
14.	у/х = —х2 + 8т — 15.
15.	\/10 +	+ r4V5 - х = 3.
16.	у/5 — х + у/х — 4 — (х — 1)2(т — 8).
17.	(и2 4- х + 1)(т2 + 2т + 3) = 1.
18.	log5(r + 1) + 2 log5(r - 1) = log5(l - т2) + 1.
19.	2 Iog3(4 + т2) = log2(l - (т + З)2).
20.	log4 ( г4 + 1 + - 1	) = l°g4(2 - Vx + 5).
\	x4 4-1 /
21.	sin4 x — sin2 3r + sin x = 3.
22.	(sin x + у/з cos x) sin 4x = 2.
23.	r3(log2 x — 2r) + log3 r(2r — r) + 8r(r — log2 x) = 0.
24.	x/r2 — r — 2 = log2(l — t4).
168 Использование свойств входящих в уравнение функций
25.	(г2 + 2г + 2)(г2 - х + 1) = 1.
26.	л/э — х2 — log3(| — 3) = 0.
27.	cos(sinr) = 1/2.
28.	sin2 х + sin2 у/2х + (1 + г)2 = 0.
29.	(r + 8)(4 - x)(y/x -8 + 2) = 1.
30.	\/5 — x + у/ x — 2 = (x — l)2(x — 6).
Решить уравнение
31.	cos x = 1 + x8.
32.	x2x = 8.
33.	log% cos2 x = x4.
34.	2|г|(г-2я)2 = |cosx|
35.	log5(r + 1) = x.
36.	log2 x = 3 — x.
37.	Q)' = « + 4.
38.	logi/3* = x-4.
39.	12r+ 5r = 13r.
40.	3r +4r = 7.
41.	Xх = 27.
42.	— + 2yfx = 3r(l — Inr).
43.	tyx-9 = (x- 3)3 + 6.
44.	log3(l + x3) = 2x2 — 3x.
45.	sin —= x2 — 2\[3x + 4.
2v3
46.	3r - 1 - |3* - 1| = 2log5 |6 - r|.
47.	y/x + 7 + л/ll — x — 6.
/	2 \
48.	|r- 1|+ |z-3| = 2 - f x - у j .
Задачи
169
49.
ж2	9 । 2(*-v
x4 + 25	IO
50. 4 sin Ttx = 4x2 — 4x + 5.
^>+0+1
51.
52.
х — х2 sin
ю
х
53.
* 4	4	1	4
sin x — cos x = — 1 — X .
sin X — Sin r=--(lH-Sl]
4
55.	sin5 x + cos5 x — I.
56.	sinr cos4r = 1.
57.	2 cos11 4x — sin13 9x = 3.
58.	(cos4x — cos2r)2 — sin 3r + 5.
59.	cos2 9r 4— cos2 x = cos 3x cos4 x.
4
60.	x log2(r + 1) = log1/3 x + 7.
61.	(3 - 2^2)* + (3 + 2i/2)r = 6r.
62.	sin2 4x + cos2 x = 2 sin 4x cos4 x.
63.	log2 x + (r — 1) log2 x = 6 — 2x.
64.	y/x — 2 + y/x + 1 = 3.
65.	y/x + y/2 — x +	— 3r = i/2.
66.	2cos2 X = logs(5 + *) +  /с ,
6	logsP + ^J
9tt2
67.	4|r| + -j—j— | sin x| = 12тг — 1.
Iх I
68‘	log2A/2W5^2 - 2x - 2) = io&2+j3(x2 - 2r - 3).
69.	2-|r-21 log2(4r - x2 - 2) = 1.
70.	(4x — x2 — 3) log2(l + cos2 irx) = 1.
170 Использование свойств входящих в уравнение функций
Доказать, что следующее неравенство не имеет решений
71.	Ух6 + г4 + 1 < -1.
72.	Ух + 2 - Ух+ 4 2.
73.	УГ^х + Ух - 1 > 0.
74.	|г2 — х4 + 5 sin г| < —1.
75.	|г-1|+ |2г + 3| < 0.
76. у/2 — х + у/х — 4 < 1.
77. |г2 - 1| + |г2 - 4х + 7| < 1.
	г-	 1
78.	Ух2 + X + 1+		 < 2. Ух2 + X + 1
79.	\Лг + 1 + Ул/г + 1 + з< Угл/г + и-
80.	—5				 > 1 + \/х.2 — 2х + 3. х2 — 2х + 3
81.	ог2“4г4-9	1	 1+|г-ЗГ
82.	Ух + Ух + 5 < 2,2.
83.	\/х + — > у/—2х — 1. у	X
84.	У2х2 - 4х + 3 + Ух2 - 4х + 5 < 3/2.
85.	(г2 + х + 4)(и2 + 2х + 5) < 1.
86.	2 log3(4 + г2) < log2(l - (х + 5)2).
87.	log4(2 + Ух) + log2(1 + х2 + х4) < 0.
88.	2^ + 3^ + 41+v/* < 5.
89.	У 4- х + Vr - 3 < (г - 1)4(г - 5).
90.	+ 3 + У<А — х < Уз.
91.	У4 + х + \/16 — х < 2.
92.	у/х 4- УЗ — х + Ух2 — 5х > Уз.
93.	|л/2|г| - 1| log2(2 - 2r2) > 1.
Задачи
171
94.	3 2I log2(4r — х2 — 2) > 1.
95.	2^ + 3^ + 4^+0Д < 3.
Решить неравенство
96.	х Ах > 4.
97.	5Г + 2Г > 7.
98.	Уг - 2 4- а/4 - т > ^2.
99.	у/х - 1 + Уж+ 14 > 3.
100.	у/2-х-х'1 < 2х + 1.
101.	1п(1 - х2) х + 1/4.
х2
102.	COS X 1-----.
2
х2
103.	ех > 1 + х + — .
х2
104.	1п(1 + х) — х + — > 0.
105.	у/х - 1 + х - 3	д/2(г - З)2 + 2г - 2.
106.	ех — 1 - 1п(1 + х) > 0.
107.	УГТТ -1 “ f + у > °-
108.	log2 х < 3 — х.
109.	х log3 х < 18.
110.	2^ + З^1 + 4^+2 > 20.
111.	(г + 5)(3 - х)(у/х - 4 + 2) < 0.
л/3 — х + у/х — 1 > (х — 1)4(ж — 7).
6 - 3r+1	10
х > 2х + 1
2 + log3 х 6
х — 1 2х — 1
Уж — '/х — 1	1.
112.
113.
114.
115.
Ответы
Глава I.
1. 3. 2. —2; 2/3; 3/2. 3. -1; 3; 4. 4. -1/2; -2/3; 3. 5. у/2;
1 ± 1/1 + 4\/2	1±710	3±3/5	1
------------. в. -2/3, —j—. 7. -3/2,	 8.
з
V2;	9. 17/4. 10. 0; -5. 11. ±5; ±1/5. 12. 1; -2. 13. -1;
—2. 14. Нет решений. 15. ±1/2. 16. ±7з. 17. 4; 1; -1; 2.
18. У/Д 19. ±7й;	20.	-5±^.
2	2	2	2
21. -1; 1	3±^. 22. 2; %/2 ± 1; -72 ± 1. 23. 0; ±1.
2	2
±73; ±	. 25. 1 ± 73 ± У3±2\
>/2; 1/3. 27. 1±Л5ТТ
24.
. 28.
-3; —2;
—3 ± у/7
2
2
2
2 ± 72
----— . 29. -3; -5. 30.
2
-72
-----. >- '..2.. 32. 2±
1 ± 7272 - 1
-1 ±7272-1	72
VZ ' 7272- 1 - 1 ’
72 < х < ± оо. 33. —2 < х < 1.
34. 7 < х < ± оо. 35. —1/72 < х < ± оо. 36. —оо <
< х < 7з. 37. 1 ± 72 < х < ± оо; —оо < х < 1 — Vz.
-1-75 -1±7б
38. —оо < х < --; --- < х < ± оо. 39. —оо <
2’2
1-75 г
<ж<1;1<г< ± оо. 40. —оо < х < -; 1 — v2 < х <
2
1 ± 75	/—
< —-—; 1 ± v2 < 1 < ± оо. 41. —оо < х < 3; 4 < х < ± оо.
_	7 - 713 ±4726 7 ± 713±4726
42. — оо < х < ----; --------- < х < ± ос.
173
43. —оо < х < 1/3. 44. —оо < х < + оо. 45. —оо < х <
4
<т<1;3<т< 24—49. —оо < х < —2. 50. —оо < х < — 2;
Уз
1 < х < 3. 51. -оо < х < - 4; 3/2 < х < 2. 52. -3 < х < 2/3;
2/3 < х < 4. 53. -оо < х < — 2;0<т<1;1<т< +оо.
54. — 1 < х < 1. 55. 0<г<1;1<г< 2. 56. —оо < т < — 3;
—2 < т < — 1;1<т<2;3<т< +оо. 57. —5 < т < — 1;
— 1 < т < — 1/3; 5 < т < + оо. 58. —оо <т< — 5; — 5 < т <
< — 3; —3 < т < — 2; —2 < т < + оо. 59. —оо < х < — 1;
— 1 < т < 1; 1 < т < + оо. 60. —оо < т < — 1; — 1 < т < 1;
1 < т < + оо.
Глава II.
1. 478/49. 2. 2. 3. 4. 4. 2. 5. ±Уб. 6. 1. 7. 2. 8. 1. 9. 5; -86.
10. 0. 11. 4. 12. 25/28. 13. 2; -9/2. 14. 1. 15. 0; 1. 16. -1; 5.
17. 1; -8/3. 18. 8; 4 ( 2 ±	. 19. 2. 20. -2. 21. 0. 22. -1;
-3. 23. 2. 24. 5 т 10. 25. 1; ±У2 + 1; 0. 26. ±2. 27. 1/2;
3/2. 28. -3. 29. 1. 30. ±У2. 31. 2^;	32. 0 т 1;
4. 33. 1 < х <2 4. 34. 3~4/3; 1/Уз. 35. 4; 1/4; 16. 36. 5/2;
-3± V45 —3 ± У^З
0 < т < 1; 1 < х < 2. 37. 64. 38. -----у—; -----------.
,	-	1 -з + УТз -з-УТз 3 п
39. 1/4. 40. 1; 4; У2/2. 41. -; ----; --------;	42. 0;
1; * + тгП) п е Z. 43. 0; 1. 44. 0; -тг/6. 45. ±1; тг/4. 46. 2 <
4
< т < + оо. 47. 45 - 1бУ7 < т < + оо. 48. Нет решений.
15 + У161
16
1
8
1
/2’
174
Ответы
2 х < + оо. 58. — 1<г<2;3<г< + оо. 59. —оо < х < 0;
5
0 < х < -. 60. О < х < 1/8; 1 < х < 2.
4
Глава III.
1. —2; 1. 2. -5/4; -1/2. 3.	5 ±	• 4. -1. 5.
-1 ±75
---6. 4; -5. 7. 4; -1. 8. 3; 1.
2
9. 2; —4. 10. —2;
-3. 11. 3 ± Уг(3±2>/2). 12.
13. - ± 'V7 1
__________2
14 3 ± ^29 3 ± 725 + 4730. 3 ± 725 - 4730
2	’	2	’	2
16.	_4;	_6;	~15±^.	17.
2	2
4 + 71^. 19. -1; 9;
2
7.
. 15.
. 20. -1. 21. -1; -1/3;
2
18. ±\/2;
3 ± л/б
3	'
22.
4
23. Нет решений. 24. -1. 25. " Y ". 26. 1. 27.
—3 ± Тб
--------. 28.	1/2; 7/2. 29.	-1/2; 1. 30.
2
-13/5;
-11. 31. —2 ±
-(15 + 785) ± \/114 + ЗОд/85
«5^.	...... ....... ф
14
—2 ± 1/4+--------.
V 2
15
33. 0; -5/2. 34. 2; — ;
5 ± 710. 35. -1. 36. 1; —2. 37.
18 ±>/504	г- г-
. 39. ±72; ±Тз. 40.
------. 38. 0; 6 ± 727;
- 1 ± У2У2 - 1 лп л
5	’	2	’ 41‘ 11
1±ТЗЗ ,	-Тг ± Tio
---42. 1/2; 2. 43. ±2. 44. 2. 45. ————. 46. 0;
4	2
±\/5. 47. тг/4 ± 2тгп, n £ Z. 48. (—1)”тг/4 + тг/4 + тгп, п Е Z.
2
2
4
175
49. —тг/4 ± тгп, n Е 2; тгт/2, т Е Z. 50. тг/2 ± 2л±, к Е Z;
—тг/2 ± 2тг/, I £ Z; 2 arctg 3 ± 2тгр, р Е Z. 51. тг/2 ± як, к Е Z;
( —1)п7г/6±тгп, п Е Z; (—l)m+1 arcsin ^ + ят, т Е Z. 52. 1 ±л/5;
9/4; —1/4. 53. 9. 54. 2 ±	± 2-/15. 55. 2. 56. 4; -61. 57. 99;
19. 58. ±1/2. 59. 0. 60. -6; 1. 61.	±	62. 1; 2; 3/2.
63. -14; 5. 64. 16/25. 65. 1; 2; 10. 66. 1; 32. 67. 15. 68. 3.
69. -1. 70. 5.
Глава IV.
31. 0. 32. 2. 33. 0. 34. 0; 2тг. 35. 0. 36. 2. 37. -1. 38. 3. 39. 2.
40. 1. 41. 3. 42. 1. 43. 1. 44. 0; 2. 45. Уз. 46. 1; 11. 47. 2.
48. 7г2/4. 49. у/5. 50. 1/2. 51. ±1/2. 52. 1/2. 53. 0. 54. Нет ре-
шений. 55. 7г/2±2тг&, 2тгт, к Е Z, т Е 7L. 56. тг/2±2тг&, к Е Z.
57. тг/2 (4m ± 3), т Е Z. 58. тг/2 ± 2як, к Е 1L. 59. тг/2 ± як,
к Е Z. 60. 3. 61. 1. 62. я/2 + яп, п Е Z. 63. 2. 64. 3. 65. 0.
66. 0. 67. ±Зтг/2. 68. 1 ± yil ± 4?3. 69. 2. 70. 2. 96. 1 < х <
< ± оо. 97. 1 < х < ± оо. 98. 2 < х < 4. 99. 2 < х < ± оо.
100. -2 х 1. 101. -1 < х < 1. 102. —оо < х < ± оо.
103. 0 < х < ± оо. 104. 0 < х < ± оо. 105. х = 5. 106. —1 <
< х < ±оо. 107. 0 < х < ±оо. 108. 0 < х < 2. 109. О < х < 9.
110. О < х < ±оо. 111. 4 х < ±оо. 112. 1 С х 3. 113. О <
< х < 1/2. 114. 1/2 < х < 1. 115. 1 < х < ± оо.
Дополнение 1
Некоторые задачи из вариантов
вступительных экзаменов по
математике в МГУ
им. М. В. Ломоносова
1.	Решить уравнение
а)	.	= (2х - i)i°gI/4(i+7r-2^).
у2г — 1
о	,7 + ^41
Ответ: rj = 1, х2 = -----•
б)	|х +	- r2| = >/2(2r2 - 1).
Ответ: zi = — >/2/2; х2 = ^>/б +	/4..
в)	log2(x2 + 3) + log1/25 = 21og1/4(r - 1) - log2(r + 1).
Ответ: xi = \[2.
г)	V?	- 3^) = 32^^+1-3^Z5+1+6VJ-18.
Ответ: xi =2, r2 = 9.
д) \/4 — r2(sin 2тгг — Зсозтгг) = 0.
Ответ: xi = -2, x2 = -3/2, x3 - -1/2,
x4 = 1/2, x5 = 3/2,	x6 = 2.
e)	log2//^^2 - 2r - 2) = 1оё2+Уз(г2 - 2x - 3).
Ответ: rj = 1 + ^/11 + 4а/з, x2 = 1 - \/ll + 4л/3.
ж)	log9(r2 - 5r + 6)2 = 2~‘ logyj + log3 |r - 3|.
Ответ: xi = 5/3.
з)	у/x + 2 — т/r — 1 = y/2x — 3.
Ответ: х^ = 2.
177
и)	(г + 1)-/16г + 17 = (г + 1)(8г — 23).
Ответ: ri = — 1, х? = 4.
к)	(г - 4)2 log4(r - 1) - 2 log4(r - I)2 =
= (г - 4)2logr^14 - 21ogT_1 16.
Ответ: Ху = 5/4, х? = 5, хз = 6.
2.	Решить неравенство
. д/12 + х — х2 >/12 + х — х2
а) ---------- > -------------.
’ х- 11	2г-9
Ответ: х — —3, —2
б) (г — 3)-\/г2 + г — 2	0.
Ответ: х = —2, х = 1,
х
х
л/2 — х + 4г — 3
х
х
. 3(4г2 - 9)
г) \	7 < 2г + 3.
7 УЗг2 - 3
Ответ: —3/2 sj х —1; 1 <
х
е
Ответ: — 1 < х 2, х
з | + “ (х/8х - 2z2 - 6 + 1)
Ответ: х^ = 1.
ж) (\Z14r - 2х2 - 24 + 2^ logr -
- 1
Ответ: х^ = 4.
з)	8 + 6|3 —	+ 5| > х.
Ответ: —5 х < 20.
log5(r2 - 4г - П)2 - logntr2 - 4г - И)3
И)	2 — 5г — Зг2	°'
Ответ: — 2 < х < 2 — д/5; —оо < х < — 2; 6^г< + оо.
178
Дополнение 1
3.	Доказать, что для любых действительных чисел р и t
справедливо неравенство
4(р — З)4 + 2 + (2 — 4(р — З)4) cos! О,
и найти все пары чисел (р, /), для которых это неравенство
превращается в равенство.
Ответ: (3;-тг + 2тгп), где п £ 7L.
4.	Найти все значения параметра 6, при каждом из которых
неравенство
cos2 х + 26 sin г — 2b < b2 — 4
выполняется для любых чисел х.
Ответ: 6 < — 2(1 + V2), b > 2.
5.	Найти все значения параметра а, при каждом из кото-
рых уравнение
log3(9r + 9а3) = х
имеет два решения.
Ответ: 0 < а < 1/\/зб.
6.	Найти все значения параметра а, при каждом из кото-
рых уравнение
х — а = 2 |2|г| — а2|
имеет три различных корня. Найти эти корни.
Ответ: а = -2, а = -1/2;
при а = -2:	zi = -2;	г2 = 6/5;	х3 = 10/3;
при а =-1/2: xi = -1/2; х2 = -1/5; х3 = 1/3.
7.	Найти все значения параметра а, при каждом из кото-
рых неравенство
3 — |г — а| > х2
имеет хотя бы одно отрицательное решение.
Ответ: —13/4 < а < 3.
8.	Найти все значения параметра а, при каждом из кото-
рых уравнение
2 2х 1	/-
х2 +	---+--------р 2V2 = 0
V sin a cos а
имеет единственное решение.
Ответ: а = Зтг/4 + 2тгп, п £ Z; а = тг/12 + 2тг&, k £ 7L.
179
9.	Построить на координатной плоскости множество точек,
координаты каждой из которых удовлетворяют условию
и среди точек этого множества найти все такие, в каждой из
которых координата у принимает наименьшее значение.
Ответ: ymln = — 1 при х < 0.
10.	Найти все неотрицательные числа х, при каждом из
которых из неравенств
abx 4а + 7Ь + х, а 0, b 0
следует неравенство ab 5.
Ответ: 0 < х <; л/35.
11.	Найти все значения параметра а, при каждом из кото-
рых оба неравенства
2а(а + 1) sin(x + у} — 4(а + 1) cos2(x + у) + (а + I)3 > 13(а + 1),
х2 + (а2 + I)?/2 > 2ху + а + 1
выполняются при любых X и у.
Ответ: —2\/3 < а < — 1.
12.	Найти пары чисел х и у, удовлетворяющих условиям
'(•Уз+1) (1 + cos(xy) sin(z?/)) = (Уз+1) sin2(z?/) + cos(2xy),
х2у2 - у2 + 1 = 0,
1	,	2 а
~2 + У ^6.
Xz
Ответ: (—тг/л/16 + тг2; \/16 + тг2/4) ;
(тг/%/16 + тг2; —\/16 + тг2/4) ;
(—тг/а/9 + тг2; л/9 + тг2/3) ;
(тг/л/9 + тг2; —у/д + тг2/3) .
180
Дополнение 1
13.	Найти все значения параметра s, при каждом из кото-
э Зх	9	12т
рых корни уравнении х -|---h 2s = 0 и a: -|---s = 0 не
S	S
перемежаются, т. е. оба уравнения имеют по два корня и меж-
ду двумя корнями одного из уравнений нет ни одного корня
другого уравнения.
Ответ: —'У36 < s <: —3; 0 < s < V/9/2.
14.	Найти все значения параметра а, для каждого из ко-
торых существует ровно два значения х, удовлетворяющих
системе уравнений
|х2 — 7х + 6| + х1 + 5т + 6 — 12 |х | = 0,
х2 — 2(а — 2)х + а(а — 4) = 0.
Ответ: а = 1; а = 2; 5 а 6.
15.	Найти все значения параметра а, при каждом из кото-
рых уравнение
2 ИтгхХ .------------
а — х — cos----- V8 — ах = 0
4 J
имеет на отрезке [—2; 3] нечетное число различных корней.
Ответ: a —4; а = 1; 8/3 <i а < 4; а > 4.
16.	Найти все пары чисел (х. у), удовлетворяющие условию
\Лг2 — 9 \7 sin2 х + 4 sin х cos х — 3 cos2 х — 31У15 ) =
7тг3 .	• \з /	\3
= —-----(arcsin у) — (arccosy) .
Ответ: (3;—1), (—3;—1).
17.	Найти все значения параметра а, при каждом из кото-
рых имеет хотя бы одно решение система уравнений
/	Ту
12-1 / cos----5
V	2
10 /	7
12ч / cos----7
V 2
+ 24-i/cos + 13
/. 7г(т - 2у - 1)
= 11 — \ sin------------------
V 3
2(т2 + (у - а)2) - 1 - Ч^/х2 4- (у - а)2 - 3/4.
Ответ: а = 6п — 1, а — 6п, а = 6п + 2, а = 6п + 3, п 6 7L.
181
18.	Найти все значения х, для каждого из которых выра-
жение	_______________
\/4т4 — 3 — ж8 (1 — cos(27r(2x + 21т2)))
имеет смысл и не обращается в нуль.	_______
4 г-	— 1 + \/1 + 21п
Ответ: 1 < х < V3 и х / ----——,
где п = 24, 25, 26,..., 38, 39;
уг	, -Л -1-Vl + 21m
— V 3 < х < - 1 и г i	--------,
^21
где т = 20, 21, 22,..., 32, 33.
19.	Найти все целые значения п, при каждом из которых
система уравнений
( 6х2 + 24?/(т + у) + 2(3п — 2)х + 4(3п — 2)у + 3 = 0,
[ 4(т2 + у2) + (4п + 2)у + 2п2 = 8ху + (4п + 2)х + 5/2
имеет решения. При найденных значениях решить эту систе-
му.
Ответ: п = —1;
при п = — 1 имеется четыре решения:
/1	vl уД 13	уД	73\
1э + 18+1Г’36 + Т1^12у1
/1	V? >/3 13	V?	х/з\
I 9 “	U + “б"’ 36	~ I?	“	Ну	’
Л	V? 2^.12	х/зА
I 9 +	П ~ V ’ 36	+ U	+	П у	’
Л	vl уД 13	уД	^/з\
I 9 ~	18 ~ Т’ 36	~ 1?	+	Ну'
20.	Найти все значения параметра/?, при каждом из кото-
рых уравнение
(ж - р)2 (р(т - р)2 - р - 1) = -1
имеет больше положительных корней, чем отрицательных.
Ответ: р 1.
182
Дополнение 1
21.	Найти все значения параметра а, при каждом из кото-
рых неравенство
(а3 + (1 - У2)а2 - (3 + У2)а + х2 +
+ 2(а2 — 2)ж + а > — л/2
выполняется для каждого х > 0.
Ответ: —л/2 а < 1; т/2 а < + оо.
22.	Найти все значения параметра а, при каждом из кото-
рых число решений уравнения
3(z2 + а2) = 1 — (9а2 — 2)г
не превосходит числа решений уравнения
х + (За - 2)2Зх = (8а - 4) log3(3a - 1/2) - 3z3.
Ответ: а = 2/3.
23.	Найти все решения системы уравнений
у sin х
Г+Зу ’
2	2
х । 4cos
?/sin х = log2
(бу2 + 2y)(4sin
г) = 25у2 + 6у+1,
удовлетворяющие условию |у| = 1.
Ответ: система имеет бесконечно много
решений (х' —1), где х = тг/2 + 2тгп, п£1
24.	Определить, сколько точек с целочисленными коорди-
натами находится внутри криволинейной трапеции, образо-
ванной осью абсцисс, прямыми х = 3/2, х = 129 и графиком
функции у = log2z. Точки, лежащие на границе указанной
криволинейной трапеции, не учитывать.
Ответ: 642.
25.	Пусть тип — натуральные числа, причем — —
п
правильная несократимая дробь. На какие натуральные чи-
Зп — т
ела можно сократить дробь ------, если известно, что она
5п + 2m
сократима?
Ответ: 11.
183
26.	Число Ь подобрано так, что уравнение
х — \/3 + Ь2х2 + 2Ьх (>/б —	= 6>/2 — 9
имеет решение. Найти это решение.
Ответ: х = '/З.
Дополнение 2
Образцы вариантов письменных
работ, предлагавшихся на
вступительных экзаменах по
математике в МГУ
им. М. В. Ломоносова в 1992-1994 гг.
§ 1.	Механико-математический факультет
1992
Вариант 1
1.	Решить уравнение
7 cos	+ |cos -	| ~
2.	Диагонали четырехугольника PQRS, вписанного в
окружность, пересекаются в точке D. На прямой PR взята
точка А, причем /SAD = 50°, /PQS = 70°, /RQS = 60°. Где
расположена точка А: на диагонали PR или на ее продолже-
нии? Ответ обосновать.
3.	Даны числа р и q такие, что р = logz у, q = logr у.
Найти log/ Jxyz.
4.	Один рабочий на новом станке производит за 1 час целое
число деталей, большее 8, а на старом станке — на 3 детали
меньше. На новом станке один рабочий выполняет дневную
норму за целое число часов, а два рабочих вместе выполняют
норму на старых станках на 1 час быстрее. Из какого коли-
чества деталей состоит дневная норма, если производитель-
ность рабочих одинакова?
5.	На прямой р в пространстве последовательно располо-
жены точки А, В и С такие, что АВ = 27 и ВС — 18. Найти
расстояние между прямыми р и q, если расстояния от точек А,
В и С до прямой q равны 17, 10 и 8 соответственно.
§ 1. Механика-математический факультет
185
6.	Найти все значения х, удовлетворяющие неравенству
(2 — а)т3 + (1 — 2а)х2 — &х + (5 + 4а — а2) < О
хотя бы при одном значении а, принадлежащем отрезку
1993
Вариант 2
1.	Решить неравенство
№	> l°gl7(g~ Л
l°g291 17
2.	Найти все значения параметра 6, при каждом из которых
уравнение
9х + (62 + 6)3* - Ь2 + 16 = О
не имеет решения.
3.	Решить систему уравнений
< (sin у - cos х + 1) (tg2 + ^) + tg2 (1/ + у) ) = °’
(cos х + sin ?/)(2 + sin 2у + cos у) = 0.
4.	В треугольнике PQR медиана, проведенная из верши-
3^21
ны Q, имеет длину -----. Окружности с центрами в верши-
4
нах Р и R и радиусами 5 и 1 соответственно касаются друг
друга, а вершина Q лежит на прямой, касающейся каждой
из окружностей. Найти площадь S треугольника PQR, если
известно, что 5 < 7.
5.	Точки Р, Q, R и S расположены в пространстве так,
что середины отрезков SQ и PR лежат на сфере радиуса а,
отрезки PS, PQ, QR и SR делятся сферой на три части в
отношении 1:2:1 каждый. Найти расстояние от точки Р до
прямой QR.
6.	Из пункта А в пункт В с постоянными скоростями вы-
ехали два мотоциклиста, а из В в А одновременно с ними вы-
ехал третий мотоциклист с постоянной скоростью 80 км/час.
186
Дополнение 2
Через 40 минут расстояние между первым и вторым было в
два раза меньше, чем между первым и третьим. Через 1 час
после старта расстояние между первым и вторым было равно
расстоянию между первым и третьим, а также было равно по-
ловине расстояния, которое осталось проехать третьему до А.
Через 1 час 20 минут после старта расстояние между первым
2
и вторым было равно - расстояния между первым и третьим.
5
Найти расстояние между пунктами А и В.
1994
Вариант 3
1.	Решить уравнение
4 sin х — 2 cos 2х — 1 _
cos 2г + л/З cos х — 2
2.	Решить систему уравнений
2х + 2у = 1,
Зу- бу2 = 2х-1
3.	Решить неравенство
1 ______________1_______
S(2-5x) + log2(2 — 5ar) log6(6z2 — бх + 1)
4.	В трапеции ABCD с основаниями AD и ВС диагона-
ли АС и BD пересекаются в точке Е. Вокруг треугольни-
ка ЕС В описана окружность, а касательная к этой окружно-
сти, проведенная в точке Е, пересекает прямую AD в точке F
таким образом, что точки A, D и F лежат последовательно
на этой прямой. Известно, что AF = a, AD = Ь. Найти EF.
5.	Дан куб ABCDAiBiCiDi. Сфера касается ребер AD,
DD\, CD и прямой ВС\. Найти радиус сферы, если длины
ребер куба равны 1.
6.	При каждом значении параметра а решить уравнение
2ж2 + “2ах — а2 = \/4ж + 2а + За2.
§ 2. Факультет ВМиК
187
§ 2.	Факультет вычислительной математики
и кибернетики
1992
Вариант 1
/1990	3/1991
1.	Какое из двух чисел \ --- или \ -----больше?
J V 1991	V 1992
2.	Решить уравнение
/-------- .	. ТГ
V1 + cos 4х sin ж = 2 sin —.
4
3.	Решить неравенство
log2(l 1 - х) + log2(x + 1) log2[(z + 1)(х2 + 5х - 5)].
4.	Из города А в город В выехал автомобиль. Спустя не-
которое время из В в А выехал мотоцикл. Автомобиль и мо-
тоцикл движутся по одному шоссе, их скорости на всем пути
постоянные. Автомобиль до встречи с мотоциклом находился
в пути 7 часов 30 минут, а мотоцикл до встречи ехал 3 часа.
Мотоцикл прибыл в А в 23 часа, а автомобиль прибыл в В
в 16 часов 30 минут. Найти время отправления мотоцикла из
города В.
5.	Две окружности пересекаются в точках А и К. Их цен-
тры расположены по разные стороны от прямой, содержащей
отрезок АК. Точки В п С лежат на разных окружностях.
Прямая, содержащая отрезок АВ, касается одной окружности
в точке А. Прямая, содержащая отрезок АС, касается дру-
гой окружности также в точке А. Длина отрезка В К равна 1,
длина отрезка СК равна 4, а тангенс угла С АВ равен
Найти площадь треугольника АВС.
6.	Найти все значения параметра а, при каждом из кото-
рых неравенство
4 . 9	\	. 2	.	/	2 л	ТГ \
-(X — ах) — — < sin(x — ах) + cos I 2х — 2ах 4— I
3	3	х	4 /
выполняется для всех х из отрезка [тг; 2тг].
188
Дополнение 2
1993
Вариант 2
1.	Решить неравенство
1о«У^+1-Уз(4г - х2 -	°-
2.	На отрезке 0 х тг найти все значения х, удовлетво-
ряющие уравнению
\/3 cos х — sin х
^/1 + 2 cos1 2 х — \/з sin 2х.
3.	Решить неравенство
|3Г - 4| + |ж2 - 4х + 3| <; 3r + 4х - х2 - 7.
4.	В равнобедренном треугольнике АВС с основанием АС
точка D делит сторону ВС в отношении 2:1, считая от вер-
шины В, а точка Е — середина стороны АВ. Известно, что ме-
>/23	>/23
диана CQ треугольника СЕD равна и DE =	. Найти
радиус окружности, описанной около треугольника АВС.
5.	Точка М(х'.у). декартовы координаты которой удовле-
творяют условиям
а2х — у — 2а2 — 26, х — by = 2 — 2а2,
лежит на прямой у = 2 — х. При каких а и Ь эта точка наиболее
близко расположена к точке N(3; —1)?
6.	Найти все значения а, при каждом из которых область
определения функции
1
У = ------------------7=—
3 cos х — 2 cos3 х — \/2а
совпадает с областью определения функции
__________1_________________________Л______________
sin3 х + cos3 х - а 3 cos х - 2 cos3 х - V2a
§ 3. Физический факультет
189
1994
Вариант 3
1.	Решить уравнение
8 sin 5х + cos Юг +1 = 0.
2.	Решить неравенство
|z - 7| <; 3 - у/х-4.
3.	Найти все отрицательные значения v, при каждом из
которых выполнено неравенство
log5(^) log5cost (|)
4.	В треугольнике АВС длина стороны АВ равна 18, длина
биссектрисы АЕ равна 4у/15, а длина отрезка ЕС равна 5.
Определить периметр треугольника АВС.
5.	В начальный момент лечения пациенту была произве-
дена первая инъекция: 8 единиц некоторого лекарства, а во
время каждой последующей инъекции ему вводится 5 единиц
того же лекарства. За время между инъекциями количество
лекарства в организме уменьшается в б раз. Какое количе-
ство лекарства будет содержаться в организме пациента после
25-ой инъекции?
б.	Все высоты пирамиды EFGH, грани которой являют-
ся остроугольными треугольниками, равны между собой. Из-
вестно, что FG = 17, HG = 14, a LEHG — 60°. Найти длину
ребра НF.
§ 3. Физический факультет
1992
Вариант 1
1.	Решить неравенство
8а: — 1 < 4а:2.
190
Дополнение 2
2.	Решить уравнение
8 cos х — 3 cos 2х = 5.
3.	Решить уравнение
31og3z5 = 6 + log3 х.
4.	В треугольнике АВС /.ВАС = а, /ВСА = 7, АВ = с.
Найти площадь треугольника АВС.
5.	В арифметической прогрессии девятый член в 2 раза
больше десятого, а сумма шестого и двенадцатого членов рав-
на 8. Найти первый член и разность прогрессии.
6.	Радиус окружности, описанной около треугольника
KLM, равен R. Через вершину L проведена прямая, перпен-
дикулярная стороне КМ. Эту прямую пересекают в точках А
и В серединные перпендикуляры к сторонам KL и LM. Из-
вестно, что AL = а. Найти BL.
7.	Про некоторую нечетную функцию известно, что при
х > 0 она задается формулой /(х) = 1----7=. Найти, какой
у х
формулой задается функция /(х) при х < 0. Решить уравне-
ние /(ж) = -.
8.	В конусе угол между высотой и образующей равен <р.
Боковой поверхности конуса касаются три шара радиуса г,
каждый из которых касается двух других. Шары находят-
ся вне конуса. Плоскость /?, проходящая через центры шаров,
перпендикулярна высоте конуса. Найти расстояние от верши-
ны конуса до плоскости /?.
1993
Вариант 2
1.	Решить неравенство
(1 -4х)(4-х) > 0.
2.	Решить уравнение
sin Зх = sin(3 -|- х).
§ 3. Физический факультет
191
3.	Решить уравнение
\/log5 х + 3 = 7 log5 J/x.
4.	В равнобедренном треугольнике KLM (KL = LM) угол
KLM равен <р. Найти отношение радиусов вписанной и опи-
санной окружностей для треугольника KLM.
5.	Решить неравенство
1Ж~ !| г
х + 2
6.	Через точку О проведены две прямые, касающиеся
окружности в точках М и N. На окружности взята точка К
(точки О и К — по разные стороны от прямой MN). Расстоя-
ния от точки К до прямых ОМ и МN равны соответственно р
и q. Найти расстояние от точки К до прямой ON.
7.	Число х = 5 является одним из корней уравнения
3z2 + рх + q = 0, где q < 0. Найти действительные корни
уравнения Зх4 + рх2 + q = 0.
8.	Два шара радиуса г и цилиндр радиуса 7? (7? > г) лежат
на плоскости. Шары касаются друг друга и боковой поверхно-
сти цилиндра. Цилиндр касается плоскости по своей образую-
щей. Найти радиус шара, меньшего, чем данные, касающегося
обоих данных шаров, цилиндра и плоскости.
1994
Вариант 3
1.	Решить неравенство
‘2х - 1
1---- < °-
log2 х
2.	Решить уравнение
5 cos х + 2 sin х = 3.
3.	Решить уравнение
5х-1 + 5-(0,2)г-2 = 26.
192
Дополнение 2
4.	В равнобедренном треугольнике высоты, опущенные на
основание и на боковую сторону, равны соответственно тип.
Найти стороны треугольника.
5.	Решить уравнение
2	/ X2 \
l(4ar) + log2 ( — 1=8.
2	\ О /
6.	В окружности пересекающиеся хорды АВ и CD перпен-
дикулярны, AD — т, ВС = п. Найти диаметр окружности.
7.	Для каких значений а система неравенств
—х2 + 12а? — а О,
х 2
выполняется хотя бы при одном значении х?
8.	В правильной треугольной пирамиде SABC (S — вер-
шина) угол между боковым ребром и плоскостью основания
равен а, сторона основания равна a, SH — высота пирами-
ды. Найти площадь сечения пирамиды плоскостью, проходя-
щей через точку Н параллельно ребрам 5Д и ВС.
§ 4. Химический факультет
1992
Вариант 1
1.	Решить уравнение
х + 1 + logi(-2 + 3-*) = 0.
2.	Решить неравенство
'/2 sin а: < 1.
3.	В параллелограмме ABCD угол BCD равен 150°, а
основание AD равно 8. Найти радиус окружности, касаю-
щейся прямой CD и проходящей через вершину А, а также
пересекающей основание AD на расстоянии 2 от D.
§ 4. Химический факультет
193
4.	Даны три сплава. Состав первого сплава: 55% хрома и
45% никеля. Состав второго сплава: 60% никеля, 25% хрома и
15% кобальта. Состав третьего сплава: 70% хрома и 30% ко-
бальта. Из них нужно приготовить новый сплав, содержащий
20% кобальта. Какие значения может принимать процентное
содержание никеля в этом новом сплаве?
5.	Найти все значения параметра k, при каждом из кото-
рых уравнение
2х —	— 62| = 11Л: — 3-|х 4- 4А|
1)	не имеет решений, 2) имеет конечное непустое множество
решений.
1993
Вариант 2
1.	Решить неравенство
4
(х- I)2 L
2.	Решить уравнение
(log2 х)2 + 3 logi х + 2 = 0.
3.	Решить уравнение
cos х = 1 -j- cos 2х.
4.	В квадрат площадью 18 см2 вписан прямоугольник
так, что на каждой стороне квадрата лежит одна вершина
прямоугольника. Длины сторон прямоугольника относятся,
как 1 : 2. Найти площадь прямоугольника.
5.	Найти число решений уравнения
2r+i + 21-г _ [ _ 4х_ Х1
и дать обоснование ответа.
1994
Вариант 3
1.	Решить уравнение
l"g4(.T + 1) + log4(x + 4) = 1.
194
Дополнение 2
2.	Решить неравенство
4х — 1 > 3 |ж |.
3.	Решить уравнение
Уз in 2х = \/1 — sin х — cos х.
4.	Прямоугольные треугольники имеют общую гипотену-
зу KL = 5. Вершины их прямых углов М и N лежат по
разные стороны от прямой, проходящей через точки К и L,
LM = LN = 3. Отрезок КР содержит точку М, и MP = 1.
Отрезок KQ содержит точку N, и NQ — 6. Найти разность
между площадью треугольника KPQ и суммарной площадью
треугольников KLM и KLN.
5.	Решить систему уравнений
у2 + 4у cos х + 4 — 0,
х |у|(х2 + Зу2) = 2тг3 + 24тг.
§ 5. Биологический факультет
1992
Вариант 1
1. Решить уравнение
2. Решить уравнение
(2» _ 0 \
----7 + l°g2(z2 - 14z + 40) = 2 + log2 3.
х — 4 j
3. Дана окружность, диаметр MN которой равен 16 см. На
касательной к этой окружности в точке М отложен отрезок
МР, длина которого больше чем 15 см. Из точки Р проведе-
на вторая касательная к окружности, пересекающая прямую
МN в точке Q. Найти площадь треугольника М PQ. если его
периметр равен 72 см.
§ 5. Биологический факультет
195
4. Найти все пары целых чисел р. q, удовлетворяющие од-
новременно двум неравенствам
( р2 + q2 < 18р — 20g - 166,
[ 32р — q2 > /г + 12(/ + 271.
5. Найти наименьшее значение величины
1 А 4р д \
г \ и y/l-v2) ’
где р, q, г, и, v — положительные числа, удовлетворяющие
условиям
{pv + qy1 — и2 г,
р2 + 2qr\/l — и2 д2 + г2,
/----й о 1 ~ V2 — и2 9
2qrу/1 - и2 + q2--------	г2.
С — 1
1993
Вариант 2
1.	Решить уравнение
cos 2х — 2 cos х — 3 = 0.
2.	Решить уравнение
log2(9r + 2-Зг - 5) = 1 + 21og4(3"+1 - 4).
3.	Решить неравенство
/ Г 7z - 1
51/1 - - > ------.
V z 2
4.	Даны две различные геометрические прогрессии, первые
члены которых равны единице. Известно, что сумма вторых
членов прогрессий равна 3, а сумма пятых равна 161. Найти
сумму шестых членов прогрессий.
5.	В выпуклом четырехугольнике ABCD длина отрезка,
соединяющего середины диагоналей, равна длине отрезка, со-
единяющего середины сторон AD и ВС. Найти величину угла,
образованного продолжением сторон АВ и CD.
196
Дополнение 2
6.	Найти все решения системы
' у + 2 = (3 - т)3,
< (2z - у)(у + 2) = 9 + 4j/,
х2 + г2 = 4х,
удовлетворяющие условию z 0.
1994
Вариант 3
1.	Решить систему уравнений
( 2х — у = 6,
[ 4х2 + ху + Зу2 = 48.
2.	Какое из двух чисел больше
У14 или 42 log16 ~ i§) + 1 log4 8 ?
Ответ обосновать.
3.	Найти все решения уравнения
удовлетворяющие условию - < х < 3.
4.	В трапеции ABCD даны длины оснований AD = 3,
ВС = 2 и углы А и D при основании, равные соответствен-
но arctg2 и arctg(l/3). Найти радиус окружности, вписанной
в треугольник С BE, где Е — точка пересечения диагоналей
трапеции.
5.	Найти все такие значения величины х, при каждом из
которых неравенство
(4 - 2а)х2 + (9а - 19)т + (10 - 2а) > 0
выполняется для всех а, удовлетворяющих условию
1 < а < 3.
§ 6. Факультет почвоведения
197
§ 6.	Факультет почвоведения
1992
Вариант 1
1.	Решить уравнение
2(cos 6х + sin 2х- cos 4х) = sin 6х + sin 2х.
2.	Самолет, осуществляя полет по заданному маршруту,
может лететь в метеоусловиях А, Б или В с одной и той же
скоростью, но по-разному расходуя горючее. В первый раз са-
молет находился в метеоусловиях А половину полетного вре-
мени, в метеоусловиях Б — треть времени, в метеоуслови-
ях В — 1/6 полетного времени. Во второй раз он находился
четверть времени в метеоусловиях А и 3/4 — в метеоусло-
виях В. В третий раз — по четверти полетного времени в
метеоусловиях А и Б, а половину времени — в метеоуслови-
ях В. На сколько процентов израсходует самолет полетный
норматив горючего, двигаясь весь путь в метеоусловиях В,
если в первый раз он израсходовал его на 1011%, во второй —
на 92,5, а в третий — на 97,5%.
3.	Решить уравнение
9х - 82-3* + 162 - 3*/2+2 _
З*/2 - 9
4.	Две окружности с центрами Oi и О2, лежащими на сто-
роне МN треугольника MPN, касаются друг друга и пере-
секают стороны МР и PN в точках М, D и N, С соответ-
ственно, причем МО\ = OjD = 3 и NO^ = СО? = 6. Най-
ти площадь треугольника MNP, если известно, что отноше-
ние площади треугольника МСО? к площади треугольника
OiDN равно 7^3 и PN — МР-\]2 — Уз.
5	’
5.	При каких значениях параметра а все числа из отрезка
1 х 5 удовлетворяют неравенству
Зах + 2л/3т + 1 — 6х + а — 5 < 0?
198
Дополнение 2
1993
Вариант 2
1.	Разделить число 128 на четыре части так, чтобы первая
часть относилась во второй как 2 : 3, вторая к третьей -•
как 3:5, третья к четвертой — как 5:6.
2.	Решить уравнение
sin3 х — cos3 х + sin х — cos х — 0.
3.	Решить неравенство
l°g9r*+i 37 > 1.
4.	Через точку пересечения диагоналей трапеции проведе-
на прямая, параллельная основанию и пересекающая боковые
стороны в точках Е и F. Длина отрезка ЕЕ равна 2. Опреде-
лить длины оснований трапеции, если их отношение равно 4.
5.	Найти все действительные числа а, при каждом из ко-
торых неравенство
не имеет положительных решений х.
1994
Вариант 3
1.	Решить уравнение
2(cos2 х — sin2 х) = (cos х — sin z)-(2 sin x + cos x — cos2 x).
2.	Решить систему уравнений
Г Зг-1+у = 2,
\ З2*-1 + 2у = 5.
3.	Решить неравенство
2 In ---- 4- ln(5 — 2х) j> 0.
§ 7. Географический факультет
199
4.	При каких значениях параметров а и Ь система нера-
венств
( b + cos ах 2,
[ х2 4- "2Ьх 4-9^0
имеет единственное решение?
5.	В четырехугольнике ABCD, вписанном в окружность,
диагонали АС и BD перпендикулярны и пересекаются в точ-
ке Q. Длина отрезка, соединяющего вершину С с серединой
отрезка AD, равна 3. Расстояние от точки Q до отрезка ВС
равно 1, длина стороны AD равна 2. Найти длину отрезка
AQ.
§ 7. Географический факультет
1992
Вариант 1
1.	Решить уравнение
cos 2х 4- 4 cos х 4- 3 = 0.
2.	Найти три числа а, b и с, если известно, что их сумма
равна 2, а квадратное уравнение
ах2 4- Ьх 4- с = 0
имеет единственное решение х = 2.
3.	Решить неравенство
(logx 9 - l)log3(9a-) < 3.
4.	В треугольнике АВС медиана AD и биссектриса BE
перпендикулярны и пересекаются в точке F. Известно, что
плошадь треугольника DEF равна 5. Найти площадь тре-
угольника АВС.
5.	Найти все значения параметра с, при каждом из которых
уравнение
|z2 - 2а?| 4- |z2 — За: 4- 2| = х2 — 4х 4- с
имеет ровно три различных решения.
200
Дополнение 2
1993
Вариант 2
1.	Решить уравнение
л/13 — 2х = 5 — х.
2.	Решить уравнение
3.	Найти область определения функции
4х — х2 — 4
У V я2 + х - 2
4.	В треугольник со сторонами АВ = 4, ВС = 2, АС = 3
вписана окружность. Найти площадь треугольника AMN, где
М, N — точки касания этой окружности со сторонами АВ и
АС соответственно.
5.	При каких значениях параметра а четыре корня урав-
нения
х4 4- (а — 5)ж2 +(а + 2)2 = 0
являются последовательными членами арифметической про-
грессии?
1994
Вариант 3
1.	Решить уравнение
sin 2х = V2 sin х.
2.	Сумма первых двадцати членов арифметической про-
грессии (ап) в пять раз меньше суммы первых двадцати пя-
ти членов арифметической прогрессии (6П). Найти отношение
разности прогрессии (ап) к разности прогрессии (6П), если из-
вестно, что
4а12 — &19-
§ 8. Геологический факультет
201
3.	Решить неравенство
logT(2 — х — z2) > 0.
4.	Вне прямоугольного треугольника АВС на его катетах
АС и ВС построены квадраты ACDE и BCFG. Продолже-
ние медианы СМ треугольника АВС пересекает прямую DF
в точке N. Найти длину отрезка CN, если длины катетов
равны 1 и 4.
5.	Найти все значения параметра а, при каждом из кото-
рых уравнение
а + ^/бж — ж2 — 8 = 3 + \/1 4- 2аж — а2 — z2
имеет ровно одно решение.
§ 8. Геологический факультет
1992
Вариант 1
1.	Четвертый член арифметической прогрессии равен 16,
а сумма седьмого и десятого равна 5. Найти сумму первых
восемнадцати членов этой арифметической прогрессии.
2.	Решить неравенство
у/Ь — 8 г 4- 2х 1.
3.	Решить уравнение
I bg7 3-log3 х4 — 7 log^ х2| - 41ogI49.
4.	Решить уравнение
4 cos х- cos Зх — 10 cos2 х — 16 sin х- sin Зх = 4 sin2 х 4- 3.
5.	В окружность с центром О вписана трапеция ABCD, в
которой АВ || DC, АВ = 5, DC = 1, угол АВС равен 60°.
Точка К лежит на отрезке АВ, причем АК — 2. Прямая СК
пересекает окружность в точке F, отличной от С. Найти пло-
щадь треугольника OFC.
202
Дополнение :
6.	Найти все тройки чисел (г, у, г), удовлетворяющие
уравнению
64—Зж2—zz + 14-j/24-2i/sin(7rz)=(2:z —73)(cos(7rz)-cos(27rz))2.
1993
Вариант 2
1.	Найти численное значение выражения
cty/o 4" 276v&	/—I Зу/ci -р 9v 6 \
-----------р--V а о ---------:—
Зу/а + 9V6 J \ а — 9b J
2.	Решить уравнение
15(cos 2ж)\/1 4- tg2 х = 7.
3.	На берегу озера расположены пункты А и В. Из пунк-
та Л в пункт В отправился катер, а через 1 час после этого из
пункта В в пункт А вышла моторная лодка. Еще через 1 час
они встретились и, не останавливаясь, продолжили движение.
Катер прибыл в пункт В через 2 часа 20 минут после того,
как в пункт А прибыла моторная лодка. Через какое время по-
сле начала движения произошла бы их встреча, если бы они
одновременно отправились навстречу друг другу?
4.	Решить неравенство
^l°g2S1nf(J;2) > l°g2sin г ('УЗх + 4).
5.	Точка М, лежащая вне круга с диаметром АВ, соедине-
на с точками Ап В. Отрезки МА и МВ пересекают окруж-
ность в точках С и D соответственно. Площадь круга, впи-
санного в треугольник AM В, в 4 раза больше, чем площадь
круга, вписанного в треугольник CMD. Найти меры углов
треугольника AM В, если известно, что один из них в 2 раза
больше другого.
6.	Найти все неотрицательные действительные значения
параметра а, при каждом из которых в области (у4~2)2—4ж 0
лежат ровно три точки графика функции
у = 2z(\/cos(2a7rz) — cos4(a7rz) — 1)4-2.
§ 8. Геологический факультет
203
1994
Вариант 3
1.	Какое из чисел больше 27? или 5,(29)?
2.	Упростить до целого числа выражение
7б -275 V7 -
3.	Решить уравнение
У + §7у2 + у - 6 - 6 + у2 = 0.
4.	Решить уравнение
cos 3z + cos 9х 4- cos 15т = 0.
5.	Решить неравенство
\Zllz-z2 -28# 0.
6.	Решить неравенство
6 cos х + sin Чх < 0.
7.	Геологическая информационная система поставляется
на четырех дискетах. При установке их на компьютер каждая
из дискет увеличивает объем этой системы на определенное
количество % по отношению к предыдущему объему: первая
дискета — на 10%, вторая дискета — на 12%, третья диске-
та — на 25%, четвертая дискета — на 30%. На сколько % в
результате увеличится объем этой системы?
8.	Четырехугольник ABCD таков, что в него можно впи-
сать и около него можно описать окружности. Диаметр опи-
санной окружности совпадает с диагональю BD. Доказать,
что модули разностей длин его противоположных сторон рав-
ны.
9.	Четыре бригады разрабатывали месторождение нефти
в течение трех лет, работая с постоянной для каждой брига-
ды производительностью. В течение пяти последних месяцев
второго года и первых трех месяцев третьего года работа не
204
Дополнение 2
проводилась, а все остальное время работала только одна из
бригад. Отношения времен работы первой, второй, третьей
и четвертой бригад и количества выработанной продукции
соответственно равны:
в первый год
во второй год
в третий год
4 :	5	:	2	:	1	и
2 :	3	:	1	:	1	и
1 :	2	:	2	:	4	и
17 млн. т.;
10 млн. т.;
11 млн. т..
Сколько млн. т. нефти выработали бы за 2 месяца четыре
бригады, работая все вместе?
10. Дан куб ABCDA'В'С'D', в нем через вершину С про-
ведена диагональ. Найти отношение площади сечения этого
куба плоскостью, перпендикулярной этой диагонали и прохо-
дящей через ее середину, к площади его боковой поверхности.
§ 9. Экономический факультет
1992
Вариант 1
1.	Вычислить logie | sin(7 4- тг/4)| -|- logie. | cos(37 4- тг/4)[,
/Т
если известно, что cos7 +sin7 = — \
2.	Решить неравенство
(4*-i + 41"* - 2)-1-(z2 - 5х + 4)у/7^г < 0.
3.	Фабрика получила заказ на изготовление 1005 деталей
первого типа и 2010 деталей второго типа. Каждый из 192 ра-
бочих фабрики затрачивает на изготовление 2 деталей первого
типа время, за которое он может изготовить 1 деталь второ-
го типа. Каким образом следует разделить рабочих фабрики
на две бригады, чтобы выполнить заказ за наименьшее время,
при условии, что обе бригады приступят к работе одновремен-
но, и каждая из бригад будет занята изготовлением деталей
только одного типа?
4.	В треугольной пирамиде ABCD плоские углы ВАС,
BAD и CAD при вершине А равны тг/З, Зтг/4 и тг/2 соот-
ветственно. Определить угол между гранями BAD и CAD.
§ 9. Экономический факультет
205
5.	Продолжения сторон AD и ВС выпуклого четырех-
угольника ABCD пересекаются в точке М, а продолжения
сторон АВ и CD — в точке О. Отрезок МО перпендикуля-
рен биссектрисе угла AOD. Найти отношение площадей тре-
угольника AOD и четырехугольника ABCD, если ОА = 12,
OD = 8,CD = 2.
6.	Найти все значения параметра q, при каждом из которых
число целочисленных решений неравенства х2 — 5(х — 1) 4-
4- 3|z — </| — q 0 максимально.
1993
Вариант 2
1.	Решить неравенство
logyx_g 25	2.
2.	Решить уравнение
sin Зх _
cos (х - f)
3.	Решить неравенство
3\/х4-2	6 - |х - 2|.
4.	Найти периметр плоской фигуры, заданной на коорди-
натной плоскости условиями
2|ж 4- 2| arcsin((y — I)2) $ тг(х 4- 2),
2|у - 1| - х 0.
5.	За время хранения вклада в банке проценты по нему
прибавлялись к вкладу ежемесячно сначала в размере 5% в
месяц, затем 11-%, потом 7-% и, наконец, 12% в месяц. Из-
9	7
вестно, что под действием каждой новой процентной ставки
вклад находился целое число месяцев, а по истечении срока
хранения первоначальная сумма вклада увеличилась на 180%.
Определить срок хранения вклада.
6.	Отрезки, соединяющие основания высот остроугольного
треугольника, равны 5, 12 и 13. Найти площадь треугольника.
206
Дополнение 2
1994
Вариант 3
1.	Найти все целые числа х и у, удовлетворяющие условиям
З625х3 = 9947у3,
\у\ 6.
2.	Найти область значений функции
у = \/30 - 12т-6т2.
3.	Решить уравнение
= log4((r — 14)sin х).
4.	Составить уравнение окружности наименьшего радиу-
са, внутри которой помещается множество, заданное на коор-
динатной плоскости условием
|2у+ х - 1| + |2у + 4| < 4.
5.	Предприятие производит детскую обувь и является убы-
точным. Известно, что при изготовлении т пар обуви в месяц
расходы предприятия на выпуск одной пары обуви составля-
126000	„	54000
ют не менее-------(-9— 3-------
т	т
тыс. руб., а цена реализа-
ции каждой пары обуви при этом не превосходит 18------т
4000
тыс. руб. Определить ежемесячный объем производства, при
котором ежемесячные убытки могут быть снижены до наи-
меньшего из возможных в данных условиях уровня. Вариант
полной остановки производства исключен.
6.	В выпуклом четырехугольнике KLMN отрезок MS, со-
единяющий вершину М с точкой S, расположенной на сто-
роне KN, пересекает диагональ LN в точке О. Известно, что
KL : MN = 6 : 7, КМ : ON = 2 : 1 и /.KLN + /.KMN = 180°.
Найти отношение длин отрезков МО и OS.
§ 10. Факультет психологии
207
§ 10. Факультет психологии
1992
Вариант 1
1.	Решить неравенство
3 sin 2-кх \/2 sin 4тгх + 3 cos 2тгг + -\/32.
2.	Решить систему уравнений
2*+!/ .3» ,6*+» .9* = 144
•°g(o,2l+o4«)(27r9« + 4*+*)- log5(0,2х + 0,1 у) = 2.
3.	Точки К, L, М, N, Р расположены последовательно
на окружности радиуса 2\/2. Найти площадь треугольника
KLM, если LM || KN, КМ || NP, MN || LP, а угол LOM
равен 45°, где О — точка пересечения хорд LN и МР.
4.	Найти все значения параметров а и Ь, при которых най-
дутся два различных корня уравнения
х3 — 5х2 + 7х = а,
которые будут также корнями уравнения
х3 — 8 т 4- Ь = 0.
5.	В тетраэдре ABCD на ребре АВ взята точка К, на
ребре АС — точка L, на ребре BD — точка 2V, на ребре
CD — точка М. Точки Е и G — середины ребер AD и ВС
соответственно. Прямые EG, КМ, LM пересекаются в од-
ной точке. Найти площадь четырехугольника KLMN, если
АК : КВ = 5, AD = 9, ВС = 8, а угол между скрещивающи-
мися прямыми AD и ВС равен 45°.
1993
Вариант 2
1.	Решить уравнение
ЗЗг-4
51-10
7 = 2-3 Зг-4 .
208
Дополнение ’
2.	Решить неравенство
3.	Найти все решения уравнения
—= sin2 (х Н-) + sin 3r — cos Зх —
У2 V 12/
принадлежащие отрезку [—2тг; 2тг].
4.	В остроугольном треугольнике АВС проведены высоты
CCi и АА1- Известно, что АС = 1 и LC^CAi — а. Найти
площадь круга, описанного около треугольника CiBAi-
5.	Уравнение (а — l)z2 — (2а + 1)г + 2 + 5а = 0 имеет дей-
ствительные корни Xi, х?.
1)	Найти все значения параметра а, при каждом из ко-
торых оба корня больше единицы.
2)	Найти все значения параметра 6, при каждом из ко-
торых выражение
(xi - Ь)(х2 - Ь)
не зависит от параметра а.
1994
Вариант 3
1.	Верно ли неравенство
log2 27 > у/бк^Э + 5-
(таблицами и калькулятором не пользоваться).
2.	Известно, что у = 1, z = 1 одно из решений системы
ay — bz 4- 2а = 0,
,	2	(1000тг\
(6 — 1)у2 — аг2 + 2 cos ( —-— 1=0.
Найти все решения данной системы уравнений.
§ 11. Институт стран Азии и Африки
209
3.	Из вершины С квадрата ABCD проведена прямая, пе-
ресекающая луч AD в точке К. Точка L на прямой АК равно-
удалена от прямой СК и прямой АС, причем AL на 1 м длин-
нее чем LK. Известно, что треугольник АСК тупоугольный,
а АК = 9 м. Найти косинус угла АСК.
4.	Через вершины А и В треугольной пирамиды SABC
проведена сфера, пересекающая ребра AS и BS в точках М
и N соответственно. Через точки В и N проведена вторая
сфера, пересекающая ребро SC в точках Р и Q, причем
PQ — -SC. Найти, какую часть ребра SC составляет от-
3
резок QC (QC < PC), если М — середина SA и SC = -SA.
5.	Партия деталей была изготовлена цехом в течение не-
скольких дней, причем каждый день изготовлялось одно и то
же число деталей. Когда треть продукции одного дня была
упакована в ящики, то в каждом ящике оказалось столько де-
талей, сколько ящиков понадобилось для упаковки, причем
число ящиков было равно числу дней работы цеха. После от-
сылки половины всех деталей заказчикам выяснилось, что куб
числа заказчиков был равен числу деталей, высланных каждо-
му из заказчиков. Какое минимальное число деталей мог при
этих условиях изготовить цех?
§ 11. Институт стран Азии и Африки
1992
Вариант 1
1.	Решить уравнение
2Т+5 + 2з.2*-1 _ 22 = 0.
2.	Решить уравнение
3 sin2 х — 3 cos 2х — 12 sin х + 7 г= 0.
3.	Решить неравенство
< т
2|т —6| —4 "
210
Дополнение 2
4.	Дан треугольник со сторонами 4; 8; 9. Найти длину бис-
сектрисы, проведенной к большей стороне.
5.	Решить неравенство
log1/2 | cosz|-log5(z2 - 9) < 0.
6.	При каких значениях параметра а сумма S квадратов
корней уравнения
ж2 + 2ах + 2а2 + 4а + 3 = 0
является наибольшей? Чему равна эта сумма?
1993
Вариант 2
1.	Решить неравенство
\4г2 — 5z + 8 >
3 — х '
2.	Сумма третьего и пятого членов арифметической про-
грессии равна 8. Найти сумму первых семи членов этой про-
грессии.
3.	На боковой стороне ВС равнобедренного треугольника
АВС как на диаметре построена окружность, пересекающая
основание этого треугольника в точке D. Найти расстояние
от вершины А до центра окружности, если AD = у/%, а угол
АВС равен 120°.
4.	Решить уравнение
log (Зт — 2) — 2 = 4/log2(3z — 2) + 4 logl. --- .
у	\ох — 2 /
5.	Решить уравнение
sin2 х + Зт2 cos х + Зт2 = 0.
6.	Найти все значения параметра а, при каждом из кото-
рых неравенство
х2 + 2|т — а| а2
справедливо для всех действительных х.
§ 11. Институт стран Азии и Африки
211
1994
Вариант 3
1.	Суммарный доход двух предприятий возрастет втрое,
если доход первого предприятия останется неизменным, а до-
ход второго увеличится в четыре раза. Найти отношение пер-
воначальных доходов этих предприятий и выяснить, во сколь-
ко раз надо увеличить доход первого предприятия, оставляя
первоначальный доход второго, чтобы их суммарный доход
возрос в четыре раза.
2.	Решить уравнение
gT- log3 5	—Зг   J
3.	В треугольнике АВС проведена биссектриса CD прямо-
го угла АС В; DM и DN являются соответственно высотами
треугольников ADC и BDC. Найти АС, если известно, что
AM = 4, BN = 9.
4.	Решить неравенство
2 cos х — 1	\/8 cos2 х — 8 cos х — 16.
5.	Решить неравенство
- 71 +6 7®311 -х - 7 7'^.
3
6. Найти все значения параметра а, при каждом из кото-
рых уравнение
а2х2 + 2а(>/3 - 1)х +	- 4 — 2л/з - 4
имеет решение.
Ответы к дополнению 2
§ 1. Механико-математический факультет
Вариант 1
1. —h къ, к EZ.
6
1 р -|- q -|- pq	1
2. На продолжении. 3.---------------при р ф 0; - при р = 0.
6 р 4- q — 2р</	6
4.36. 5.8. 6. (—оо; —2) U (0; 1) U (1; 4-оо).
Вариант 2
1. (1;2). 2. [—4;4].
3. (—тг/3 4- 2тгЛг; — 5тг/6 4- 2тгт); (—тг/6 4- wn; —2тг/3 4- тг(п 4- 2/));
Зх/5
к, т, п, I 6 Z. 4. ---
’ ’ ’	2
Вариант 3
5тг
1.-----1- Чтгк, к Е Z.
6
5. 9\/За. 6. 120 км.
2. х = log2 2/3, у = 1/6.
1
3
0;-
’ 5
4.	2v2 — v5. 5. х Е {0; 1} при а = 0; х =
/	2	\	(	2 \
при a G I-------т=;0 U I 0; —; х =
-1 - а- УЗа2 - 3	/	2 ’
х — ----------------- при а 6 —оо;-----
2	\	л/з]
1	х/3
< х <-----------.
2___6
1 — а + х/1 4- За2
Ч________
1 — а 4- у/1 + За2
2
2
U
§ 2. Факультет вычислительной математики
и кибернетики
Вариант 1
L vniF 2'х = + 2™’п6Z' 3 ze[2;11)-
4.11 часов. 5. -(5 4- У15). 6. а Е (2тг — 1/8; оо).
213
Вариант 2
1. 2 - \F1 < х 1; 3 х < 2 + У2. 2. О т
О
12	,
3. log34 х 3. 4. —. 5. а = b = О, b = —а2 = 1, а £ В.
Вариант 3
1. -—arcsin(2 — у/b) 4- —, п £ Z. 2. х = 4, 5 х 8.
3. v = 2тгп; п = -1, -2, -3,.... 4.44. 5. 6 + 2 (1/6)24.
6. л/247.
§ 3. Физический факультет
Вариант 1
2. 2тгА:, ± arccos - 4- 2тгЛг, к 6 Z. 3. З3^7.
О
1 ,sin(a 4- 7) sin а „	„	,	„	„ R2 „ ,	4
4. -с2—v	и------. 5. <ц = 20, d = -2. 6. —. 7.4;--.
2 sin 7	а	9
г	cos — 1
8. -!---:-------L
sin 9?
Вариант 2
тг — 3 тг 3	„
1. х > 4, х < 0. 2. —--1- -тг, - + тгп, n £ Z.
„ . у/13 + 7	тг-у>	1	а2
3. 5-------. 4. sint^tg------. 5. х < —2; х > —-. 6. —.
2	4	2	р
7 А А я f2T?VF - гд/ЗЯ + гу
7.-А/5. 8.^----------------------J.
Вариант 3
3	5
1. 1/2 < х < 1. 2. ± arccos ._4- arccos .— 4- 2тгЛ:, к £ 7L.
7	д/29	д/29
2mn	2m2
3. х = 1, х = 3. 4.	: 2-
у4т2 — пг у4т2 — пл
/------ 2 а2
5. х = 2. х — 2 7. 6. \ па1 + п2. 7. а $ 20. 8. —у=---.
9уЗ cos а
214
Ответы к дополнению 2
§ 4. Химический факультет
Вариант 1
1. —1. 2. 2ttti х < —|- 2тгтг;-Ь 2тгтг < х < тг 4- 2тгтг;
6	6
п е Z. 3. 10 ± 4д/3. 4. [15; 40] в процентах. 5. (1) (—23; 0),
(2) (—сю; —23) U (0;+оо).
Вариант 2
1. [— 1; 1) U (1; 3]. 2.2;4. 3. ± — 4- 2тгт; — 4- тг&; т, k 6 7L.
4. 8. 5. Решений нет.
Вариант 3
l.z = 0. 2. 1 < х < +оо. 3. 2тгп, j 4- 2тг&, п g Z, k g 7L,.
4.	12. 5. х = тг, у = 2.
§ 5.	Биологический факультет
3- —;—  4. 573. 5. 90°.
\ 3	8/
Вариант 1
1.	±	4- k е Z. 2.13. 3.216 см2. 4. (12;-8).
Зи 1о 6
5.	5.
Вариант 2
1.	2тгп; п g Z. 2. 1.
6.	(4; —3;0); (2;-1;2).
Вариант 3
V \ 3 ’3/
4. ------Д
35 4- 2V101 4- V^29
2. Второе больше. 3. —; —; —.
24 24 24
5. 2-Уб^х<1;4<х<24-Уб.
215
§ 6. Факультет почвоведения
— + —, & Е Z. 2.90%. 3.0.
16	4
г (	5А
5. —оо; +- .
\	з/
Вариант 1
, тг ктг
L~8 +Т’
R1
4. -(2^3-3).
Вариант 2
1.16,24,40,48. 2. п G Z. 3. (-2; 0)и(0; 2). 4.5;
5/4. 5. [-1;-| .
О
Вариант 3
1. —\-тгк, —|- тгтг, тг + 2тгт, к 6 Z, п 6 Z, т 6 Z. 2. х — 1,
4	2
2	5 + \/34	тг 2
у = 1. 3. - < х <---. 4. о = 3, а = ——тгтг, п 6
У	3	9	’33
Ь — —3, а 6 (—сю;
§ 7. Географический факультет
Вариант 1
1. тг + 2irk, к £ 7L. 2. (2;-8; 8).
4. 60. 5. 4; —.
4
Вариант 2
1. х = 2. 2. х = — + 2тгЛг, к Е
25 /—	5
4. —vl5. 5. а =------, а = —5.
64	13’
Вариант 3
±— + 2тгк, п 6 1L, к £ Z.
4
1. 7Г71,
4
5. 2 а < 3; 3 < а 4.
216
Ответы к дополнению 2
§ 8. Геологический факультет
Вариант 1
/	-1 - -У5
1. —9. 2. х £ I —оо;-------- .
3. х = 7^7+^\ х = 7Н7-^), х = 74.
1 /	4\	19>/3
4. ±- тг — arccos - 4- 7гп, п (=	5. ——.
2 \	5/	52
6. (ж = -128, у = 1, Z =	+ 384^ ,
| х = 128, у = -l,z = - 384 ).
Вариант 2
1.3. 2. х = ± arccos 5/6 4- тгп. 3. 5/4 часа.
4. -1 < х < 0; 0 < х < 4. 5. 80°, 60°, 40°. 6. 3/4 < а < 1,
1 < а < 5/4.
Вариант 3
1. 5,(29) больше.
ТГ	7Г71	ТГ	irk	„ ,	„
2.4. 3. у = -3, у = 2. 4. — + —, ±- + — , n£Z, k€%.
1 о	У	У	о
5. 4 < z < 7. 6. — + 2тгтг < х <	4- 2тгп, п 6 7L. 7. 100,2%.
9. 10 млн. т. 10. 3>/3.
§ 9. Экономический факультет
Вариант 1
1. —1. 2. х = 7; 1 < х 4. 3. 39 и 153 человек. 4. тг/4.
13	7
5. 2. 6. q = 5; — < q < -.
ч ’4^2
Вариант 2
1. log7 6 < х < 1, х > log7 11. 2. х = тг/6 4- тгп, п £ 7L.
3. —2 х —1; х = 2. 4. 10 4- 2у о. 5. 12 месяцев. 6. 195.
Вариант 3
1. (—7;—5), (0;0), (7; 5). 2. 0 < у 6.
3. — 4-2тг71,— — 4-2тгт, п £ Z, т £ TL. 4. (х — 5)2 4- (у4~2)2 = 20.
5. 12000 или 24000 пар обуви. 6. 4/3.
217
§ 10. Факультет психологии
Вариант 1
3
1. - + п, п Е Z,.
2. х = — 2 log2 3 + 41og3 2, у = 3 log2 3 — 41og3 2. 3.4. 4. а = 2,
6=3. 5. 5-Л.
Вариант 2
3 — -\/5 \	ТГ	ТГ	ТГ о
0;------ . 3.------; 2тг----. 4. — tg2a.
’	6	/	12	12	4 6
1.2. 2.
5. 1) 1; — -
\ 4
Вариант 3
; 2)
7 з
3' ~8
1
4з-
5. 41472.
§ 11. Институт стран Азии и Африки
Вариант 1
1. —2 log2 3. 2. (—1)* arcsin - + irk, к Е^-
3. (—сю; 4) U (4; 8) U [10; оо). 4. л/14.
5. ( —л/10; —тг) U (—тг; —3) U (3; тг) U (тг; л/10).
6. а = -3, S = 18.
Вариант 2
1. 1 < х < 3. 2. 28. 3. л/7. 4. 2/3 < х < 1; 1 < х 2.
5. х = 0; х = тг + 2тгп, п Е Z. 6. — 1 а 1.
Вариант 3
1. 1:2; 10. 2. х^ = 0; х? = 2. 3. 10. 4. х = тг + 2тгк, к EZ.
, « «
5. Xi = о. 6. а = ------.