Эйлеровы графы и смежные вопросы - Фляйшнер Г.

Глава II. Три столпа теории эйлеровых графов
О возможности обхода линейного комплекса без повторений и прерываний
Глава III. Основные понятия и предварительные результаты
III.3. Графы, получающиеся из заданного графа
III.4. Маршруты, цепи, пути, циклы, деревья; связность
$III.5. Совместимость, циклический порядок множества $K_v^\ast$ и соответствующие эйлеровы цепи$
III.6. Паросочетания, 1 - факторы, 2 - факторы, 1 - факторизации, 2 - факторизации, двудольные графы
III.7. Вложение графов в поверхности ; изоморфизмы
III.10. Матрицы инцидентности и смежности, потоки и напряжения
Глава IV. Характеризационные теоремы и их следствия
V.3. Двойные проходы
V.4. Пересечение границы: расщепления графов
Глава VI. Различные типы эйлеровых цепей
Глава VII. Преобразования эйлеровых цепей
VII.2. Преобразование эйлеровых цепей специального типа
VII.3. Преобразование эйлеровой цепи в орграфах
VII.4. Заключительные замечания и некоторые открытые проблемы
$III.5. Совместимость, циклический порядок множества $K_v^\ast$ и соответствующие эйлеровы цепи$
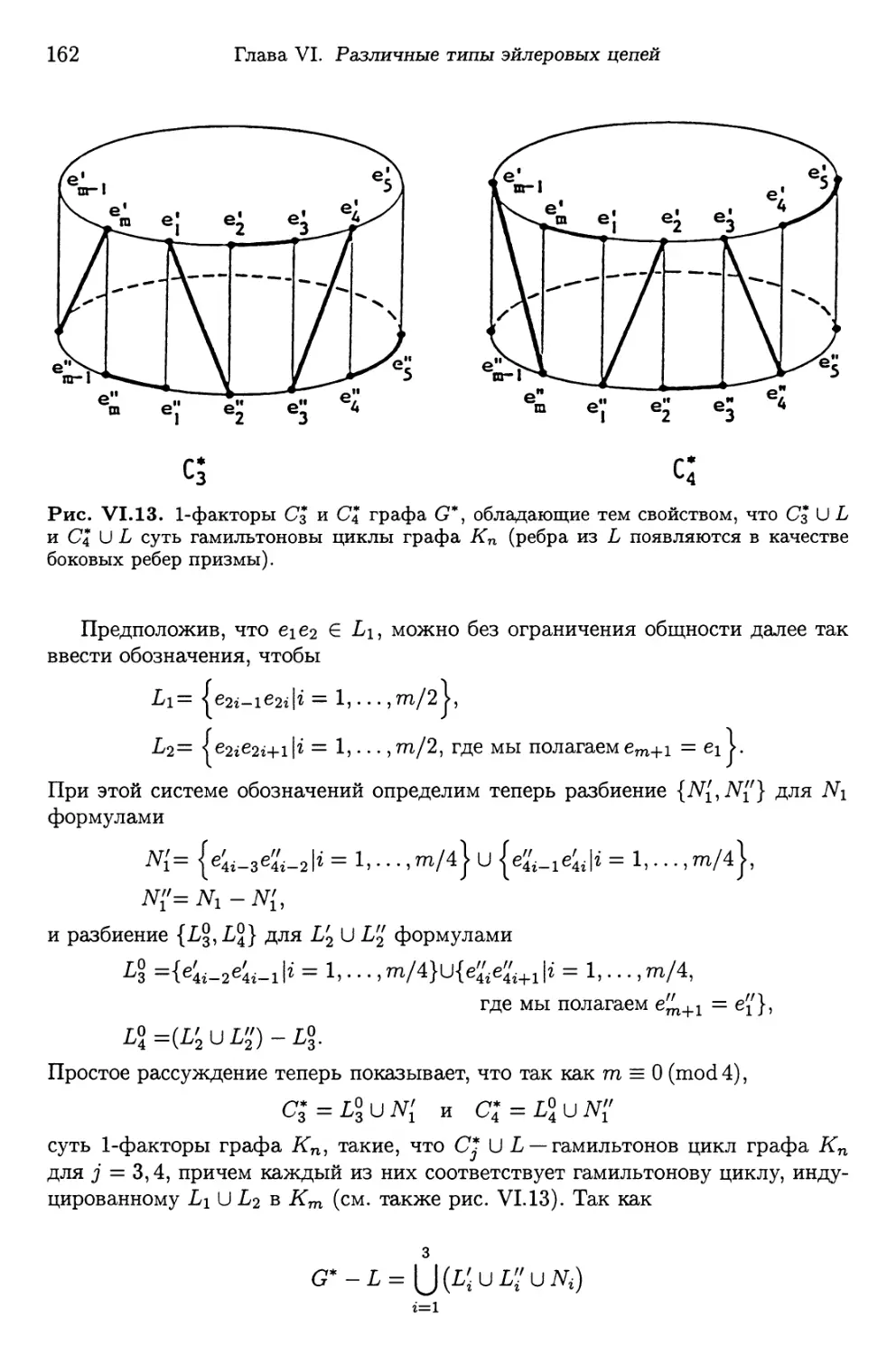
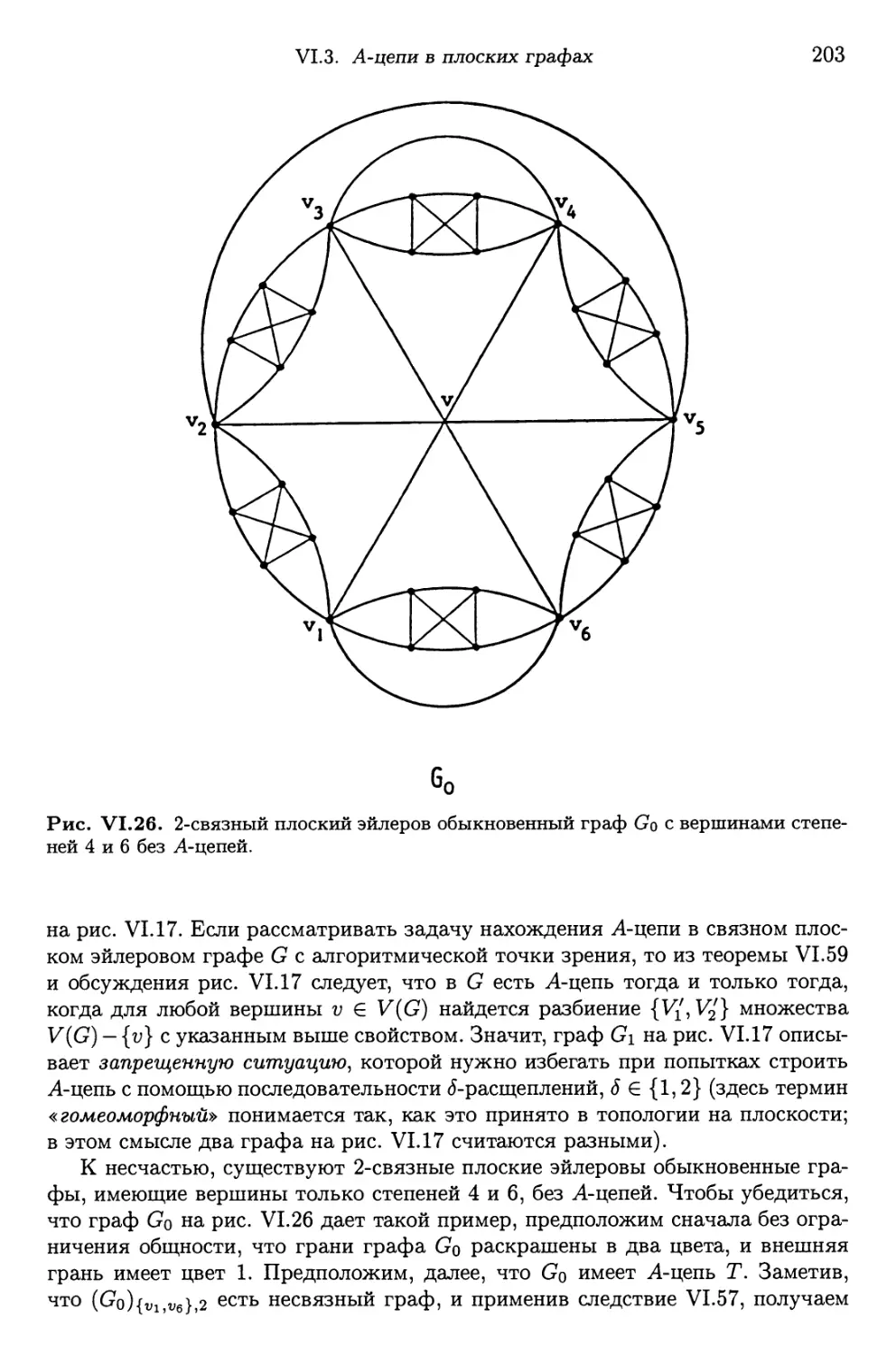
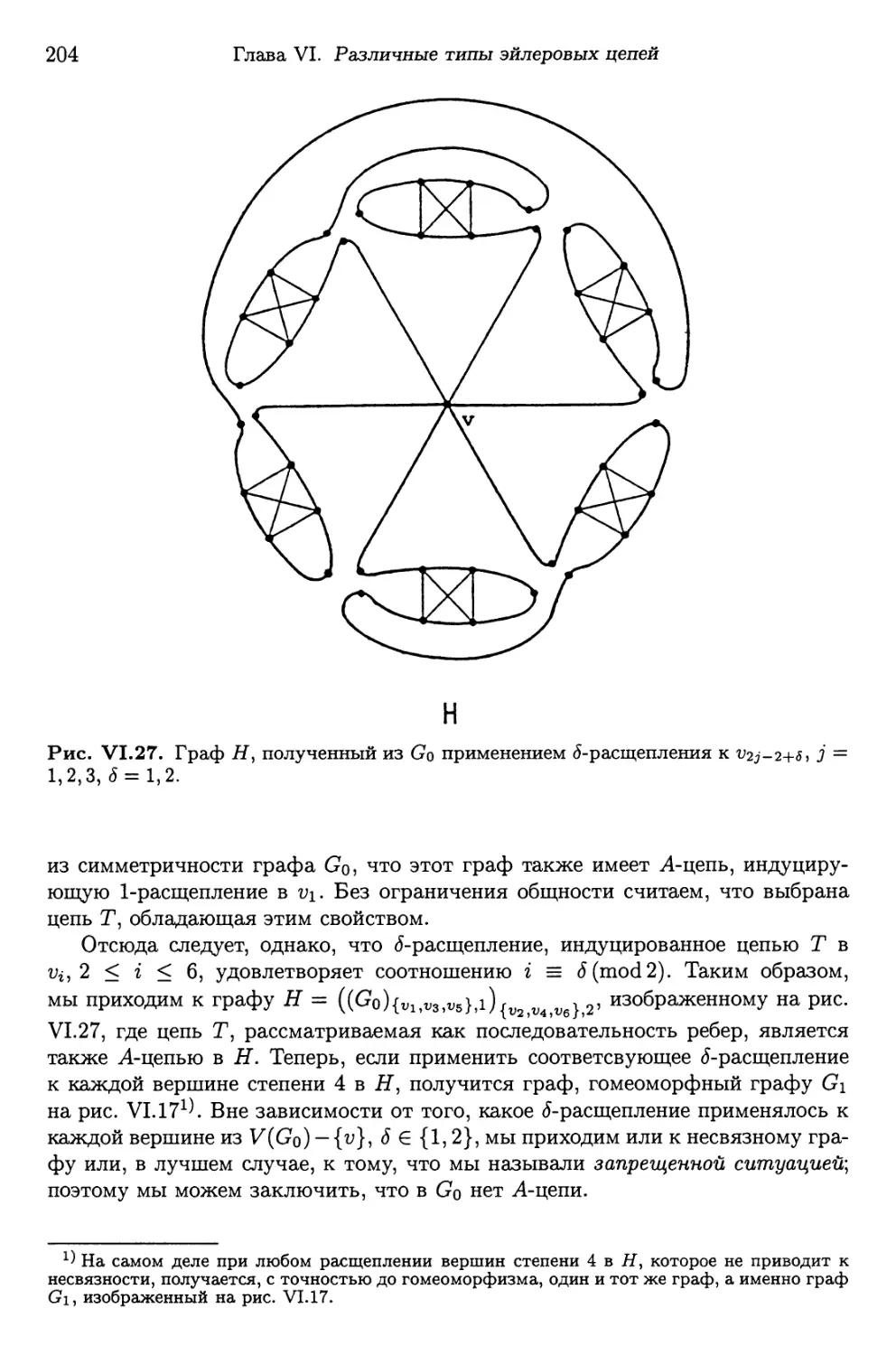
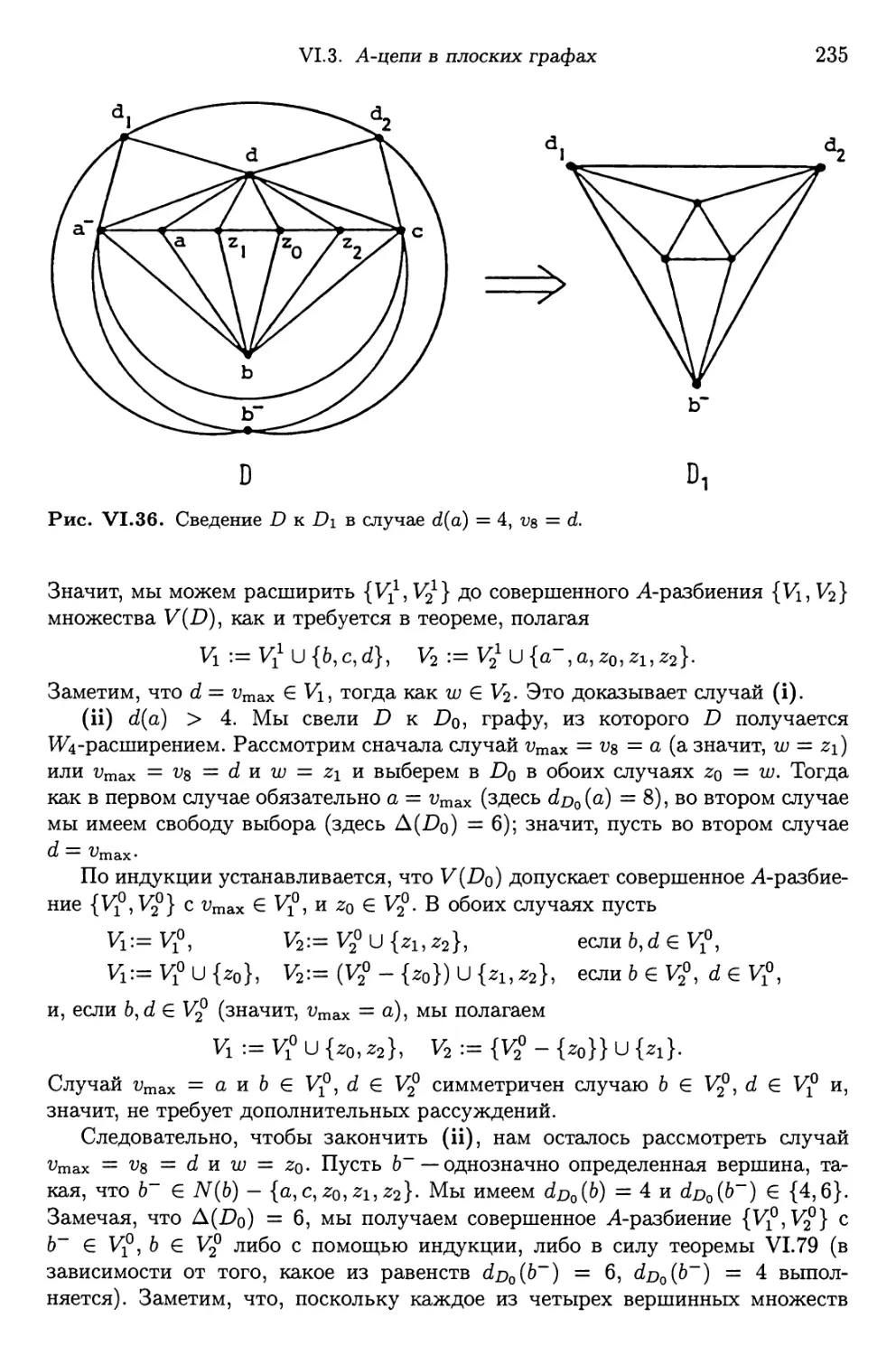
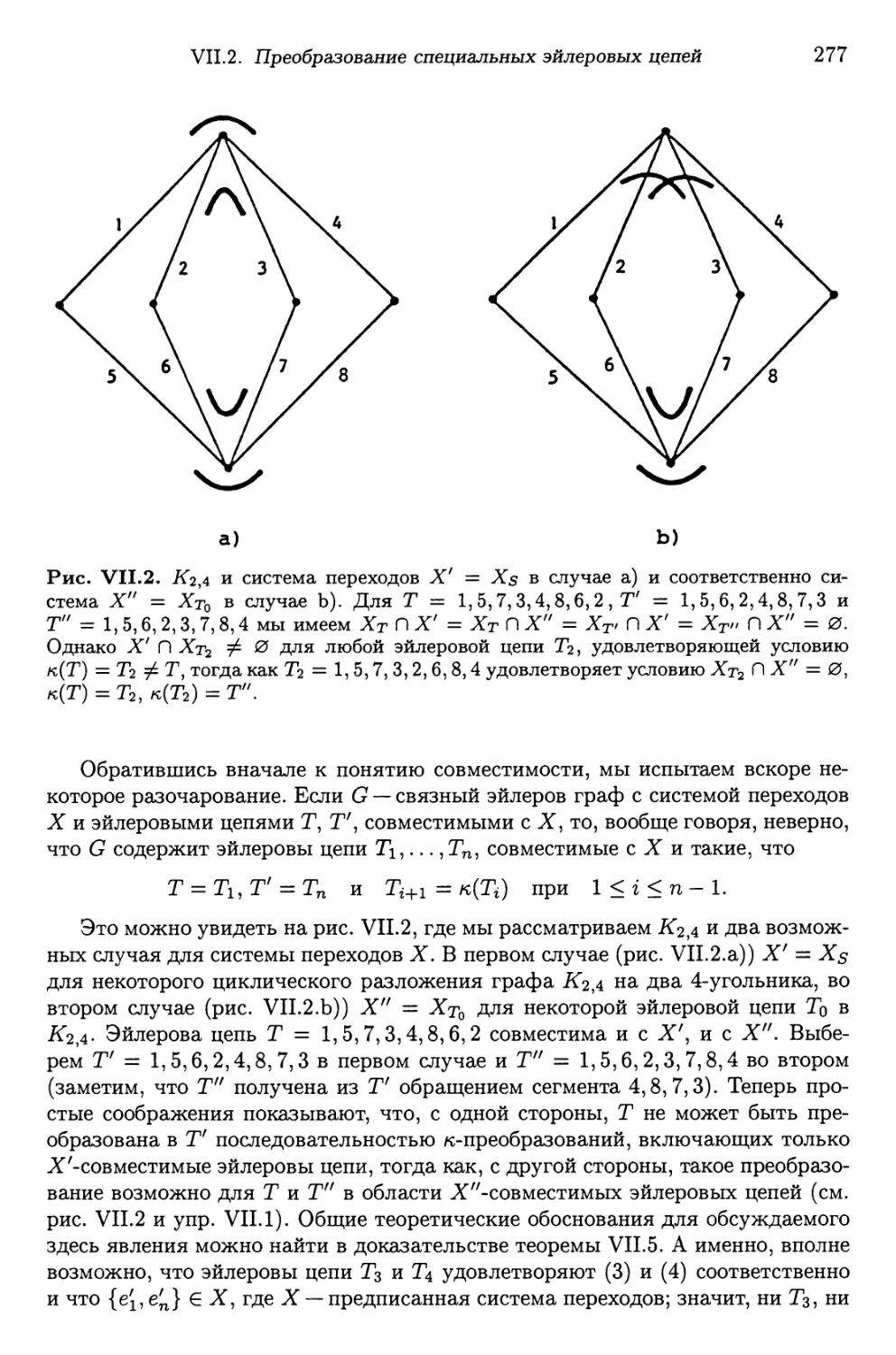
Автор: Фляйшнер Г.
Теги: комбинаторный анализ теория графов теория вероятностей математическая статистика переводная литература издательство мир
ISBN: 5-03-003115-4
Год: 1990
Похожие
Теория графов
Лекции по теории графов
Теория конечных графов Т.1
Текст
                    Г. Фляйшнер
и смежные
вопросы
Издательство «МИР

Eulerian Graphs and
Related Topics
Part 1, Volume 1
Herbert Fleischner
Institute for Information Processing
Austrian Academy of Sciences
Vienna, Austria
Ш
1990
NORTH-HOLLAND - AMSTERDAM • NEW YORK • OXFORD • TOKYO

Г. Фляйшнер
Эйлеровы
графы
и смежные
вопросы
Перевод с английского
В. А. Евстигнеева, А. В. Косточки
и Л. С. Мельникова
под редакцией
Л. С. Мельникова
Москва «Мир» 2002

УДК 519.17
ББК 22.17
Ф69
Фляйшнер Г.
Ф69 Эйлеровы графы и смежные вопросы: Пер. с англ. — М.: Мир,
2002.-335 с, ил.
ISBN 5-03-003115-4
Монография известного австрийского математика посвящена теории
эйлеровых графов — одному из интенсивно развивающихся разделов
теории графов. Это первая монография по данной теме. В книге собраны как
классические, так и современные результаты в этой области, уделено
внимание алгоритмическим вопросам, сформулирован ряд нерешенных проблем.
Изложение сопровождается большим количеством примеров и графических
иллюстраций. В книгу включена впервые переведенная на русский язык
основополагающая статья Эйлера 1736 г., посвященная известной задаче о
кенигсбергских мостах.
Книга будет полезна как специалистам в различных областях
математики, так и всем, кто применяет теорию графов.
ББК 22.17
УДК 519.17
Федеральная целевая программа книгоиздания России
Герберт Фляйшнер
Эйлеровы графы и
смежные вопросы
Зав. редакцией академик В. И. Арнольд
Зам. зав редакцией А. С. Попов. Ведущий редактор Г. М. Цукерман
Художник В. П. Григорьев
Технический редактор О. Г. Лапко. Корректор Е. Н. Клитина
Оригинал-макет подготовлен В. Н. Цлаф в пакете WT^i2?
с использованием семейства шрифтов Computer Modern с кириллическим
расширением LH
Лицензия ЛР № 010174 от 20.05.97 г.
Подписано к печати 21.03.2002 г. Формат 70 х 100/16.
Печать офсетная. Объем 10,50 бум. л. Усл.-печ. л. 27,3. Уч.-изд. л. 23,64.
Изд. № 1/9404. Тираж 3000 экз. Заказ № 5995
Издательство «Мир»
Министерства РФ по делам печати,
телерадиовещания и средств массовых коммуникаций
107996, ГСП-6, Москва, 1-й Рижский пер., 2.
Диапозитивы изготовлены в издательстве «Мир»
Отпечатано с готовых диапозитивов в
ППП «Типография Наука».
121099, г. Москва, Шубинский пер., 6.
Редакция литературы по математическим наукам
© Elsevier Science Publishers B.V.,
1990
ISBN 5-03-003115-4 (русск.) @ перевод на русский язык,
ISBN 0 444 88395 9 (англ.) издательство «Мир», 2002

От редактора перевода
Переводить книгу — хорошую и талантливую — чрезвычайно сложное дело.
Книгу нужно читать, так же как музыку надо слушать. И то, и другое
занятия рождают в человеке его собственный круг ассоциаций, не навязанный
ему насильно и рожденный в нем естественно, по его собственному уму и
сердцу. Автор посвятил эту книгу «почемучкам», для которых здесь естественно
откроются ответы на многие вопросы.
Хочется задать читателю один предварительный вопрос: что Вы знаете об
эйлеровых графах? Я задал его своим студентам и молодым коллегам. Однако
оказалось, что они не знают ничего за пределами тех двух страниц, которые
посвящены этому вопросу в известной книге Фрэнка Харари «Теория графов»
(Мир, М., 1973, стр. 83-84). В этой книге автор пытается повести нас в глубины
теории графов, что является в определенном смысле революционным шагом,
так как эта книга —одна из первых на русском языке книг по специальным
вопросам теории графов.
Эйлеровы графы — название области, с которой вообще говоря и началась
теория графов в статье Л. Эйлера, опубликованной в 1736 г. Однако тот
прогресс, который был достигнут за эти более чем два с половиной века, не очень
широко известен, особенно отечественному читателю. Исправить эту ситуацию
и предстоит этой книге. Предлагаемая читателю книга является первым томом
первой части монографии известного австрийского специалиста по
дискретной математике Герберта Фляйшнера. Не буду останавливаться на содержании
книги — достаточно ознакомиться с оглавлением. Второй том, на который
внимательный читатель найдет много ссылок, содержит многочисленные
расширения результатов данной книги. Он состоит из трех неравных по объему глав:
«Различные типы замкнутых покрывающих маршрутов» (гл. 8), «Эйлеровы
цепи —сколько их?» (гл. 9), «Алгоритмы для эйлеровых цепей и цикловых
разложений, лабиринтные поисковые алгоритмы» (гл. 10). Заинтересованный
читатель может пока обратиться к оригиналу второго тома.
Перевод этой книги имел довольно сложную судьбу, отразившую все
трудности, которые перенесла российская наука за последние годы. Хотя большая
часть перевода была сделана в 1994 г. группой сотрудников СО РАН, главным
образом из Института математики, однако мы рады тому, что, наконец она
все-таки выходит в свет. Всем принявшим участие в работе над русским
изданием этой книги и в особенности автору за его внимание и помощь я выражаю
самую искреннюю благодарность.
Нет сомнения, что книга будет полезна специалистам в различных
областях математики и студентам университетов, в том числе и технических. Она
заинтересует научных работников, занимающихся изысканиями в тех
областях, которые связаны с теоретической и технической кибернетикой, а также
с приложениями дискретной математики.
Л.С.Мельников
Новосибирск, 16 марта 2002 г.

Тем
кто
не может
удержаться
от
вопросов.
Значит,
и
моему сыну.

Портрет Леонарда Эйлера (1707-1783 гг.) работы художника из
Эльзаса Франца Бернарда Фрея (F.B.Frey) (1716-1806 гг.)
Отметим, что этот портрет, безусловно написан в годы, проведенные Л.
Эйлером в Берлине (1741-1766 гг.), поскольку он лишился одного глаза в 1735 г. (во
время первого пребывания в Санкт-Петербурге), в то время как второй глаз
он потерял в 1766 г.

Предисловие
Основной темой моих исследований с момента написания диссертации была
теория гамильтоновых и эйлеровых графов. Вплоть до 1975 г. я уделял
больше внимания гамильтоновым графам, но затем теория эйлеровых графов и
близкие к ней вопросы заняли центральное место в моей работе. Этот сдвиг в
исследовательских приоритетах (от гамильтоновых к эйлеровым графам) был
связан с задачей, которую поставил передо мной Герт Сабидусси (университет
Монреаля) летом 1975 г., когда я находился в Монреале и мы с ним
приводили совместные исследования. Тогда ни я, ни Сабидусси не могли предвидеть,
сколь широкую область применения будет иметь решение этой задачи
(называемой с тех пор гипотезой Сабидусси).
В течение 1996/97 учебного года я смог доказать некоторое обобщение
гипотезы Сабидусси для планарных эйлеровых графов (позднее названное
результатом о совместимости); начиная с 1979 г. был обнаружен ряд
приложений в теории планарных графов (частично мною самим, а частично совместно
с Биллом Джексоном, «китайским почтальоном» Гуан Мей-гу и в последнее
время Андрашем Франком). В ходе этих исследований было обнаружено, что
с помощью результата о совместимости можно в ряде доказательств избежать
применения теоремы о четырех красках (или, если хотите, предположения о
справедливости гипотезы четырех красок)1).
К сожалению, в случае непланарных графов нет простого аналога
результата о совместимости. Однако в недавней совместной работе с Биллом
Джексоном мы выдвинули гипотезу, которая содержит в качестве частного случая
эквивалентную формулировку гипотезы о двойном покрытии циклами. Это и
предыдущее утверждения показывают, почему гипотеза Сабидусси и ее
обобщения, а также ее решение в планарном случае (мы называем весь этот
комплекс гипотез и результатов проблемой совместимости) вместе с ее
приложениями и следствиями занимают доминирующее положение во второй части
этой книги.
Учебный 1977/78 год был объявлен в отделении математики Мемфисско-
го государственного университета, штат Теннесси, годом теории графов. По
приглашению Р. Фодри и Р. Шелпа я провел там осенний семестр, в течение
которого я прочитал курс по теории эйлеровых графов. В это время я был
хорошо знаком с исследованиями А. Коцига в этом направлении и помимо работы
*) Здесь уместно сделать следующее замечание: у меня нет своего мнения по поводу того,
верно ли доказательство гипотезы о четырех красках, предложенное Аппелем и Ханкеном
(устанавливающее, таким образом, теорему о четырех красках). Я предпочел бы увидеть
доказательство этой гипотезы/теоремы, полученное без помощи компьютера (но какой
специалист по теории графов не хотел бы того же?), или, по крайней мере, хотелось бы, чтобы
несколько независимых групп попыталось осуществить доказательство с помощью
компьютера по предложенной К. Аппелем и У. Хакеном схеме (но у кого же есть время и деньги на
это?).

Предисловие
9
над проблемой совместимости предпринял исследование одного специального
типа эйлеровых цепей, которое было продолжено моим первым диссертантом
С. Регнер. При подготовке материала в Мемфисском государственном
университете я впервые осознал, что как предмет эйлеровы графы представляют
собой нечто большее, чем просто скопление фактов. Мне стали ясны тенденции
развития теории эйлеровых графов. Вот почему, когда на конференции по
теории графов в Обервольфахе я узнал от Л. Байнеке и Р. Уилсона, что они
готовят книгу «Избранные направления в теории графов 2» [BEIN83a], я спросил,
не хотели бы они получить обзорную статью по эйлеровым графам. Они
выразили сомнение в том, что имеется достаточно материала, чтобы оправдать
появление такой статьи, но согласились, чтобы я попытался написать статью
для [BEIN83a]. При подготовке этой обзорной статьи я с изумлением
обнаружил, как много в действительности накопилось материала по теме «Эйлеровы
графы и смежные вопросы». За 1980 г. первый вариант обзорной статьи
«Эйлеровы графы» был подготовлен. После первых критических замечаний со
стороны редакторов сборника [ВЕШ83а] мы договорились, что я подготовлю
второй, расширенный вариант, из которого редакторы сделают сжатую
версию, которая и появилась в конце концов в [BEIN83a]. Расширенный вариант
содержал 90 машинописных страниц (из которых 10 занимала библиография,
состоящая из 124 работ).
После того как 90-страничный вариант «Эйлеровых графов»
(первоначально называвшийся «К теории эйлеровых графов») был вручен редакторам
сборника [BEIN83a], я понял что имеющегося материала достаточно для написания
книги по эйлеровым графам и смежным вопросам в четыре-пять раз большего
объема. Эта книга является результатом дальнейшего изучения литературы,
котоая стала доступной в первой полвине 80-х годов. Структура книги
частично следует структуре обзорной статьи «Эйлеровы графы» в том виде, как она
была представлена в [BEIN83a] (при этом добавлены некоторые главы и многое
переработано в остальных).
В подготовке окончательного материала для книги и при ее
перепечатывании огромную помощь мне оказала г-жа М. Венгер (она сэкономила мне
буквально сотни часов времени, которое я должен был бы потратить на
копирование, перепечатку и систематизацию материала этой книги). Г-н Эрих Венгер
выполнил большинство рисунков и написал ранее квалификационную работу
(составившую часть его квалификационной работы на получение права
преподавать в высшей школе), в которой излагал часть материала из этой книги (а
именно проблему китайского почтальона и материал по теореме Амицура и
Левицкого). Его брат Эмануил Венгер оказал мне неоценимую помощь, выполняя
функции технического организатора; будучи хорошо знаком с большой частью
моих исследований (он был моим учеником), он сделал ряд ценных замечаний.
Другие мои (бывшие) ученики, г-жа М. Масик и г-н Галамбфалви де Гегес
написали дипломные работы (как и Эрих Венгер) по произвольно трассируемым
графам и перечислению в теории эйлеровых графов соответственно. Мои
коллеги г-н Л. Димитров и г-н Р. Таллер помогли мне справиться с Техническими
трудностями при составлении указателя и внесении исправлений в некоторые
части рукописи.

10
Предисловие
Многие из моих коллег по исследовательской работе, особенно те, с кем
я предпринимал совместные исследования, внесли вклад —прямо или
косвенно—в эту книгу: ценными ли предложениями и/или замечаниями, их
собственным ли опытом в написании книг и/или статей, разъяснением ли материала, с
которым они меня ознакомили, моральной ли поддержкой, статьями ли,
которые они мне прислали, — все они помогли мне, пусть хоть в небольшой степени,
завершить книгу (которую, как бы то ни было, я должен был закончить). Я
хочу перечислить в алфавитном порядке тех, чей вклад был наиболее
значительным: Лоуэлл Байнеке, Адриан Дж. Бонди, Билл Джексон, Франсуа Же-
же, Чарльз X. К. Литтл, Криспин Ст. Дж. А. Нэш-Вильямс, Майк Д. Пламмер,
Герт Сабидусси (который обратил мое внимание на портрет Эйлера работы
Ф.Б.Фрея), Андраш Франк и Робин Уилсон. Я приношу самую теплую
благодарность им и всем остальным. Я надеюсь, книга покажет, что я должным
образом использовал их помощь.
Наконец, я хочу выразить признательность г-ну Петеру Лилли
(гражданину Великобритании, живущему в Вене), который прочитал почти всю книгу с
точки зрения стиля английского языка. Любые недостатки в этом отношении
лежат целиком на моей совести.

Глава I
Введение
Когда книга Денеша Кёнига «Theorie der endlichen und unendlichen Graphen»
(«Теория конечных и бесконечных графов») [KONI36a] впервые увидела свет
в 1936 г., она насчитывала всего 248 страниц (не считая предисловия,
оглавления и библиографии) и содержала большую часть результатов теории графов,
полученных за предшествующие 200 лет, т.е. с момента публикации статьи
Леонарда Эйлера с решением задачи о кёнигсбергских мостах.
На самом деле Эйлер представил свою статью Петербургской академии
наук в августе 1735 г., но опубликована она была только в 1741 г. в трудах
Академии «Commentarii Academiae Scientiarum Imperialis Petropolitanae» под
названием «Solutio problematis ad geometriam situs pertinentis». С другой стороны,
так как «Commentarii» датировались 1736 г., этот год может быть взят в
качестве даты рождения новой области математики, известной ныне как теория
графов.
Однако, как отметил в предисловии Д. Кёниг, при изложении теории
графов в этой книге он ограничился по существу тем, что он называл
абсолютными графами (сегодня мы бы сказали абстрактные графы), в то время как —
за небольшим исключением — топологическая теория графов (он называл ее
теорией относительных графов) и перечислительная теория графов не
рассматривались.
С момента появления книги Д. Кёнига, но в основном с конца Второй
мировой войны, теория графов развивалась все быстрее и быстрее. Это привело
к открытию все большего и большего числа журналов, специализировавшихся
на публикации статей по комбинаторным проблемам, около половины
которых (если не больше) представляли собой работы по теории графов.
Например, журнал «Journal of Graph Theory» появился в 1977 г. Этот быстрый рост
теоретико-графовых исследований выразился не только в увеличении числа
книг по теории графов, но также в том, что большая часть этих книг была
посвящена таким специальным аспектам теории графов, как топологическая
теория графов, алгебраическая теория графов и —в качестве более
современной тенденции — алгоритмическая теория графов (ориентированная на
потребности специалистов в области программирования и вычислительной техники).
Таким образом, можно сказать, что развитие теории графов шло по обычному
пути развития любой науки. Любая наука, оторвавшись сначала от более общей

12
Глава I. Введение
области исследования (книга Д. Кёнига имеет подзаголовок «Kombinatorische
Topologie der Strekkenkomplexe» («Комбинаторная топология одномерных
комплексов»), разделяется на части в соответствии с теми разными
направлениями, в которых идет развитие ее результатов и методов. В случае теории
графов это развитие было проиллюстрировано — в краткой форме — публикацией
книг «Selected Topics in Graph Theory» и «Selected Topics in Graph Theory
2» [BEIN78a, BEIN83a], содержащих 22 обзорные статьи разных авторов под
редакцией Л. Байнеке и Р. Уилсона. Третий том только что опубликован.
(Полезность теории графов для различных наук хорошо иллюстрируется книгой
«Applications of Graph Theory» («Применения теории графов») (те же
редакторы, что и выше), содержащей 12 обзорных статей1).)
Статья Эйлера о мостах города Кенигсберга (ныне Калининград) не
обрушилась на научную общественность как deus ex machina (Бог из машины). На
это совершенно ясно указывает сам Эйлер, когда в своей статье ссылается на
Лейбница:
В дополнение к той ветви геометрии, которая занимается
величинами и которой всегда уделялось самое большое внимание, существует
другая ветвь, прежде почти неизвестная, о которой впервые упоминал
Лейбниц, назвав ее геометрией положения [geometria situs]. Эта ветвь
занимается только определением положения и его свойствами] она не
включает ни измерений, ни вычислений, с ними связанных...
Эйлер заметил вскользь, что не совсем ясно, какие задачи относятся к
геометрии положения и какие методы должны использоваться для их решения, но
он определенно рассматривал кёнигсбергские мосты как именно такую задачу
в силу того, что ее решение «включало только положение и никакие
вычисления не использовались » [WILS85a].
На самом деле не позже чем в 1679 г. Лейбниц высказал следующее
утверждение в письме к Гюйгенсу (мы цитируем по [WILS85a]): Меня не
удовлетворяет алгебра в том отношении, что не позволяет получить ни кратчайшие
доказательства, ни самые красивые конструкции геометрии. Следовательно,
в силу этого я считаю, что нам нужен другой способ анализа,
геометрический или линейный, который прямо бы работал с положением точно так же,
как алгебра работает с величиной...
Введением термина analysis situs (анализ положения) он не заложил основы
новой математической области исследований, но указал общее направление, в
котором будут успешно развиваться некоторые исследования. (Читатель,
который интересуется историей термина analysis situs, должен обратиться к статье
Р. Уилсона [WILS85a].) Мы будем и в дальнейшем делать некоторые
замечания, относящиеся к истории теории графов, но нужно сказать в этой связи, что
книга Кёнига является, вероятно, самым богатым, уникальным источником по
ранней истории теории графов (под словом ранняя мы понимаем развитие
теории графов до появления в 1936 г. книги Д. Кёнига).
х) Более современные обзоры опубликованы в двухтомном издании «Surveys in Graph
Theory, I—II» (ed. G.Chartrand and M. Jacobson), Congressus Numerantum, Vol. 115-116, 1996.
Оно содержит 24 обзорные статьи. — Прим. ред.

Глава I. Введение
13
Но почему книга по эйлеровым графам? В силу того ли, что теория
графов (и, в частности, статья Эйлера) отпраздновала недавно свою 250-летнюю
годовщину? Близость времени публикации к этой годовщине есть случайное
совпадение (я планировал первоначально завершить работу над этой книгой
в конце марта 1985 г.). Однако, как уже было указано в предисловии,
имеет место не только быстрый рост числа статей по эйлеровым графам, но и
тенденция к построению теории, унифицирующей различные результаты этих
исследований. Эти два факта могут рассматриваться как необходимое условие
написания книги по эйлеровым графам и смежным вопросам] все это вместе с
интересом, проявленным многими коллегами, оправдывает ее написание. Более
того, как я отметил выше, такая книга находится в согласии с общей
тенденцией в теории графов, которая в последние двадцать лет медленно, но верно
распадается на различные части.
В следующей главе воспроизведены оригиналы трех статей, которые
образуют—по мнению большинства специалистов по теории графов — основу
теории эйлеровых графов. Большая часть книги посвящена тем результатам,
которые более или менее непосредственно относятся к концепциям,
разработанным в этих статьях. Однако, я полагаю, ограничиться этой частью теории
эйлеровых графов — это слишком сузить подход по сравнению с текущим
развитием теории графов. Эта точка зрения преобладала также в моей обзорной
статье «Эйлеровые графы», представленной в [BEIN83a]. С другой стороны,
эта точка зрения ставит проблему отбора материала для включения в книгу,
подобную этой.
Поскольку это первая книга, нацеленная на изучение эйлеровых графов, я
решил охватить так много тем, как только возможно. Некоторые темы я
рассматривал более детально, нежели другие, а иногда я лишь касался различных
аспектов, как если бы это был обзор. Это имеет, конечно, свою
отрицательную сторону, так как в некоторых случаях читатель, который захочет больше
узнать о соответствующем результате, должен будет обратиться к другим
книгам или даже к оригинальным статьям, цитируемым в этой книге. Кроме того,
иногда возникает пересечение с другими ветвями теории графов,
нашедшими отражение в книгах [BEIN78a, BEIN83a]. Это заметно в главах,
посвященных задаче о китайском почтальоне, и в тех местах, где главную роль играет
1-факторизация, а также в главах, посвященных перечислению, раскраске, и
в некоторых других местах. Но такое перекрытие — вообще говоря — более или
менее неизбежно именно из-за нынешнего состояния исследований в теории
графов.
Подбирая материал для этой книги, я просмотрел сотни статей в
поисках подходящих. Из сказанного выше ясно, что многие из статей, на которые
имеются в книге ссылки, не рассматриваются подробно. Однако одна из целей
книги — обозначить многообразие направлений сегодняшних исследований.
Таким образом, хотя у некоторых читателей может сложиться впечатление, что
библиографические ссылки излишне многочисленны по сравнению с
многообразием изложенных тем, большое число ссылок имеет то преимущество, что
помогает интересующимся читателям продвигаться в различных
направлениях за пределы этой книги. Несмотря на то, что пришлось просмотреть такое

14
Глава I. Введение
большое число статей, я надеюсь, что не пропустил ничего существенного для
теории эйлеровых графов. С другой стороны, моя обзорная статья содержала
в этом отношении некоторые погрешности.
Последнее, но не самое незначительное, замечание состоит в том, что эта
книга замкнута по материалу, потому что рассчитана на самую широкую
аудиторию. Поэтому гл. III содержит основы теории графов, включающие в
себя все, что может потребоваться в последующих главах. Я признаю, что меня
раздражают требования, предъявляемые многими монографиями,
относительно более или менее широких познаний в различных областях математики для
понимания излагаемого материала. Кроме того, утверждений типа «можно
легко убедиться», «теперь легко вывести», «легко видеть» и подобных им я
стараюсь избегать. Многие математики (включая меня самого) довольно
часто сталкивались с ситуациями в доказательствах, когда требовались бумага,
карандаш плюс полчаса или больше времени, чтобы легко убедиться в чем-
нибудь. Поэтому я, не колеблясь, включил в эту книгу множество рисунков
для иллюстрации ситуаций и различных соображений, но не использую
рисунки вместо логических соображений. Тем не менее в некоторых примерах
полные доказательства оставлены читателю в качестве нетрудных упражнений. В
силу этого настоящая книга содержит достаточно материала для организации
курсов лекций по теории графов с упором на эйлеровы графы как для
студентов, так и для аспирантов. Следовательно, ее можно читать математикам,
не слишком близко знакомым с теорией графов. Но она, несомненно,
представляет интерес и для специалистов по теории графов, поскольку содержит
много новых результатов, причем некоторые из них представляют собой лишь
частичные решения еще нерешенных более общих проблем; в книгу включено
также довольно большое число гипотез.
Несколько слов об алгоритмах и исследовании сложности. Разнообразные
проблемы (такие, как отыскание эйлеровых цепей, цикловые разложения,
обходы почтальона и маршруты обхода лабиринтов) рассматриваются также
алгоритмически. Однако я не ставлю своей целью в настоящей книге создавать на
базе теоретических исследований алгоритмы всегда, когда это возможно.
Вопрос о сложности решается аналогично. С теоретической точки зрения кажется
более важным знать, может некоторая проблема быть решена за
полиномиальное время или нет; в этой книге вопрос о том, будет сложность алгоритма
равна 0(п) или 0(п2), является вторичным. Я знаю, что многие коллеги (в
частности, специалисты по информатике или специалисты по теории графов,
имеющие склонность к таким исследованиям) будут серьезно критиковать эту
точку зрения.
Я буду чрезвычайно рад получить критические замечания
(положительные, отрицательные или смешанные) от любого читателя, поскольку это будет
способствовать улучшению моих последующих работ. Я обещаю ответить всем
моим критикам.

Глава II
Три столпа теории
эйлеровых графов
Существуют различные переводы статьи Эйлера [EULER36a] о проблеме
кёнигсбергских мостов и статьи Хирхольцера [HIER73a] о конструировании
эйлеровой цепи в связном эйлеровом графе. Однако ниже я представлю свои
собственные переводы этих двух статей1) 2\ Я решился на это, так как
переводы, которые я нашел, имели один недостаток: они были «современными»
переводами, если можно так выразиться, т. е. переводами, которые
игнорировали в большей или меньшей мере стиль, которым были написаны эти статьи
в момент их появления. Таким образом, эти переводы неточны с исторической
точки зрения и потому — неумышленно — создают искаженную картину пути
к знанию и того, как это формулировалось «в былые времена». Ясно поэтому,
что мой перевод статьи Эйлера не является ни запоздалым домашним
заданием бывшего студента, который шесть лет учил латынь, ни способом уйти от
возможных конфликтов с владельцами авторских прав.
Историческую оценку статьи Эйлера интересующийся читатель может
найти в [WILS85a, WILS86a] и [SACH86a, SACH86b].
*) Я хочу выразить благодарность X. Рейтереру из Австрийской академии наук, Вена,
который проверил мой перевод статьи Эйлера.
2) Имеется в виду, разумеется, перевод на английский язык. Что касается русских
переводов, то имеются переводы писем Л.Эйлера к Джакобо Джиованни Маринони (Marinoni,
Giovanni Jacobo, 1670-1755), итальянскому математику и инженеру, от 13 [24] марта 1736 г.,
Петербург, и к Карлу Леонарду Готлибу Элеру (Ehler, Carl Leonhard Gottlieb), бургомистру
г. Данцига, от 3 [14] апреля 1736 г., Петурбург. Первое из писем целиком посвящено задаче
о кёнигсбергских мостах, второе же — лишь в его заключительной части, где Эйлер только
напоминает основные моменты знаменитой своей статьи. [См.: Эйлер Л. Письма к ученым. —
М.: Изд-во Акад. наук СССР, 1963.] — Прим. ред.

16
Глава П. Три столпа теории эйлеровых графов
SOLUTIO PROBLEMATIS
AD GEOMETRIAM SITUS PERTINENTIS
Commentatio 53 indicis Enestroemiani
Coramentarii academiae scienliarum Petropolitanae 8 (1736), 1741, p. 128—140
1. Praeter illam geometriae partem, quae circa quantitates versatur et
omni tempore summo studio est exculta, alterius partis etiamnum admodum
ignotae primus mentionem fecit Leibnitzius1), quam Geometriam situs vocavit.
Ista pars ab ipso in solo situ determinando situsque proprietatibus eruendis
occupata esse statuitur; in quo negotio neque ad quantitates respiciendum
neque calculo quantitatum utendum sit. Cuiusmodi autem problemata ad
banc situs geometriam pertineant et quali methodo in lis resolvendis uti
oporteat, non satis est definitum. Quamobrem, cum nuper problematis cuius-
dam mentio esset facta, quod quidem ad geometriam pertinere videbatur, at
ita erat comparatum, ut neque determinationem quantitatum requireret neque
solutionem calculi quantitatum ope admitteret, id ad geometriam situs referre
baud dubitavi, praesertim quod in eius solutione solus situs in considerationem
veniat, calculus vero nuUius prorsus sit usus. Methodum ergo meam, quam
ad huius generis problemata solvenda inveni, tanquam specimen Geometriae
situs hie exponere constitui.
l) Vide epistolam a G. Leibniz (1646—1716) ad Chr. Huygekb (1629—1695) scriptam d.
8. Sept. 1679, Leibnizens Mathematische Schriften, herausg. von G. I. Gebhardt, Ersie Abt, Bd. 2,
Berlin 1850, p. 17—20, imprimis p. 19, Beilage p. 20—25. Epistola, qua Ни y a ens respondit d.
22. Nov. 1679, invenitur ibidem p. 27. Vide porro G. Leibniz, Be analysi situs, Leibnizens Matiic-
matkehc Schriflen, Zweite Abt., Bd. 1, Halle 1858, p. 178—183. L. G. D.
Lkojuuudi Eulrki Opera omnia 17 Commentationet algebraic** 1

Решение одной задачи, связанной с геометрией положения 17
2 SOLTJTIO PROBLEMATIS [129
2. Problema autem hoc, quod mihi satis notum esse perhibebatur, erat
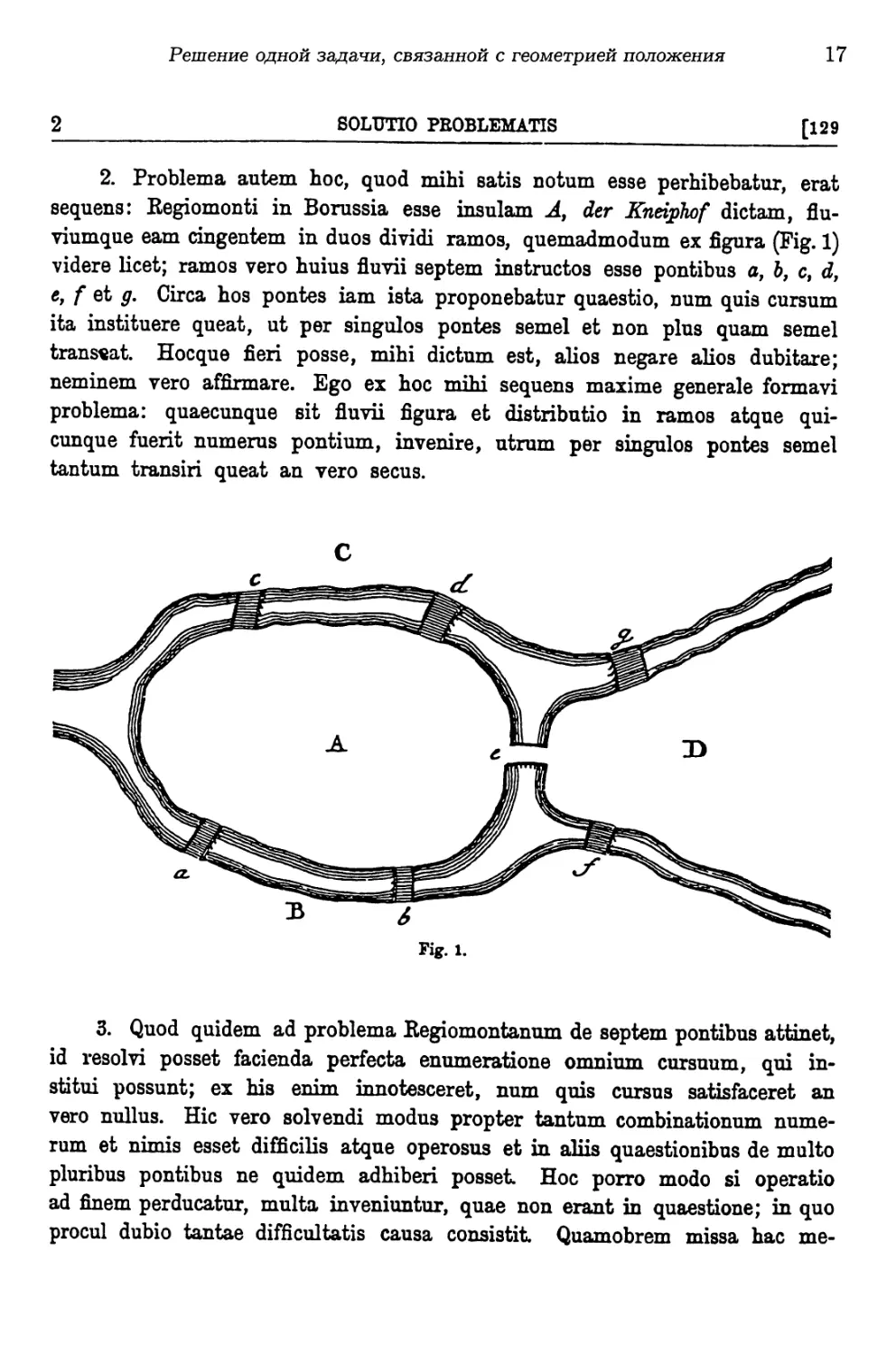
sequens: Eegiomonti in Borussia esse insulam A, der Kneiphof dictam, flu-
viumque earn cingentem in duos dividi ramos, quemadmodum ex figura (Fig. 1)
videre licet; ramos vero huius fluvii septem instructos esse pontibus a, b, c, d,
e, f et g. Circa hos pontes iam ista proponebatur quaestio, num quis cursum
ita instituere queat, ut per singulos pontes semel et non plus quam semel
trans«at. Hocque fieri posse, mihi dictum est, alios negare alios dubitare;
neminem vero affirmare. Ego ex hoc mihi sequens maxime generale formavi
problema: quaecunque sit fluvii figura et distributio in ramos atque qui-
cunque fuerit numerus pontium, invenire, utrum per singulos pontes semel
tantum transiri queat an vero secus.
Fig. 1.
3. Quod quidem ad problema Begiomontanum de septem pontibus attinet,
id resolvi posset facienda perfecta enumeratione omnium cursuum, qui in-
stitui possunt; ex his enim innotesceret, num quis cursus satisfaceret an
vero nullus. Hie vero solvendi modus propter tantum combinationum nume-
rum et nimis esset difficilis atque operosus et in aliis quaestionibus de multo
pluribus pontibus ne quidem adhiberi posset. Hoc porro modo si operatio
ad finem perducatur, multa inveniuntur, quae non erant in quaestione; in quo
procul dubio tantae difficultatis causa consistit Quamobrem missa hac me-

18 Глава И. Три столпа теории эйлеровых графов
129-131] AD QEOMETRIAM SITUS PERTINENTIS 3
thodo in aliam inquisivi, quae plus non largiatur, quam ostendat, utrum talis
cursus institui queat an secus; talem enim methodum multo simpliciorem fore
sum suspicatus.
4. Innititur autem tota mea methodus idoneo modo singulos pontium
transitus designandi, in quo utor litteris maiusculis At В, С, D singulis re-
gionibus adscriptis, quae fiumine sunt separatae. Ita, si quis ex regione A
in regionem В transmigrant per pontem a sive 6, hunc transitum denoto
litteris AB, quarum prior praebet regionem, ex qua exierat viator, posterior
vero dat regionem, in quam pontem transgressus pervenit. Si deinceps viator
ex regione В abeat in regionem D per pontem f, hie transitus repraesenta-
bitur litteris BD\ duos autem hos transitus successive institutes AB et BD
denoto tantum tribus litteris ABD, quia media В designat tarn regionem, in
quam primo transitu pervenit, quam regionem, ex qua altero transitu exit.
5. Simili modo si viator ex regione D progrediatur in regionem С per
pontem g, hos tres transitus successive factos quatuor litteris ABD С deno-
tabo. Ex his enim quatuor litteris ABD С intelligetur viatorem primo in
regione A existentem transiisse in regionem B, hinc esse progressum in
regionem D ex hacque ultra esse profectum in C; cum vero hae regiones flu-
viis sint a se invicem separatae, necesse est, ut viator tres pontes transient.
Sic transitus per quatuor pontes successive instituti quinque litteris denota-
buntur; et si viator trans quotcunque pontes eat, eius migratio per litterarum
numerum, qui umtate est maior quam numerus pontium, denotabitur. Quare
transitus per septem pontes ad designandum octo requirit litteras.
6. In hoc designandi modo non respicio, per quos pontes transitus sit
factus, sed si idem transitus ex una regione in aliam per plures pontes fieri
potest, perinde est, per quemnam transeat, modo in designatam regionem per-
veniat Ex quo intelligitur, si cursus per septem figurae pontes ita institui
posset, ut per singulos semel ideoque per nullum bis transeatur, hunc cur-
sum octo litteris repraesentari posse easque litteras ita esse debere dispositas,
ut ixnmediata litterarum A et В successio bis occurrat, quia sunt duo pontes
a et Ъ has regiones A et В iungentes; simili modo successio litterarum A
et С quoque debet bis occurrere in ilia octo litterarum eerie; deinde successio
litterarum A et D semel occurret similiterque successio litterarum В et D
itemque С et D semel occurrat necesse est

Решение одной задачи, связанной с геометрией положения 19
4 80LUTT0 PROBLEMATIS [131—133
7. Quaestio ergo hue reducitur, ut ex quatuor litteris А, В, С et D
series octo litterarum formetur, in qua omnes illae successiones toties occur-
rant, quoties est praeceptum. Antequam autem ad talem dispositionem opera
adhibeatur, ostendi convenit, utrum tali modo hae litterae disponi queant an
non. Si enim demonstrari poterit talem dispositionem omnino fieri non posse,
inutilis erit omnis labor, qui ad hoc efficiendum locaretur. Quamobrem re-
gulam investigavi, cuius ope tarn pro hac quaestione quam pro omnibus
similibus facile discerni queat, num talis litterarum dispositio locum habere
queat.
8. Considero ad huiusmodi regulam inveniendam unicam regionem A, in
quam quotcunque pontes а, Ъ, с, d etc. conducant (Fig. 2). Horum pontium
contemplor primo unicum a, qui ad regionem A ducat; si nunc viator per
hunc pontem transeat, vel ante transitum esse debuit in regione A vel post
transitum in A perveniet; quare in supra stabilito transitus designandi modo
oportet, ut littera A semel occurrat. Si tres pontes, puta а, Ь, с, in regionem
A conducant et viator per omnes tres transeat, turn in designatione eius
migrationis littera A bis occurret, sive ex A initio cursum instituerit sive
minus. Simili modo si quinque pontes in A conducant, in designatione
transitus per eos omnes littera A ter occurrere debet. Atque si numerus pontium
fuerit quicunque numerus impar, turn, si is unitate augeatur, eius dimidium
dabit, quot vicibus littera A occurrere debeat.
Fig. 2.
9. In casu igitur pontium transeundorum Regiomontano (Fig. 1), quia
in insulam A quinque pontes deducunt a, b, c, d, e, necesse est, ut in
designatione transitus per hos pontes littera A ter occurrat. Deinde littera B,
quia in regionem В tres pontes conducunt, bis debet occurrere similique
modo littera В bis debet occurrere atque etiam littera С bis. In serie ergo
octo litterarum, quibus transitus per septem pontes deberet designari, littera
A ter adesse deberet, litterarum vero Bf С et D unaquaeque bis; id quod
in serie octo litterarum omnino fieri nequit Ex quo perspicuuni est per
septem pontes Regiomontanos talem transitum institui non posse.

20 Глава II. Три столпа теории эйлеровых графов
133-134J AD GEOMETRIAM SITUS PERTIKENTIS 5
10. Simili modo de omni alio casu pontium, si quidem numerus pontium,
qui in quamque regionem conducit, fuerit impar, iudicari potest, an per
singulos pontes transitus semel fieri queat Si enim evenit, ut summa
omnium vicium, quibus singulae litterae occurrere debent, aequalis sit numero
omnium pontium unitate aucto, turn talis transitus fieri potest; sin autem,
ut in nostro exemplo accidit, summa omnium vicium maior fuerit numero
pontium unitate aucto. turn talis transitus nequaquam institui potest. Kegula
autem, quam dedi pro numero vicium A ex numero pontium in regionem A
deducentium inveniendo, aeque valet, sive omnes pontes ex una regione B,
ut in figura (Fig. 2) repraesentatur, ducant sive ex diversis; tantum enim
regionem A considero et inquiro, quot vicibus littera A occurrere debeat.
11. Si autem numerus pontium, qui in regionem A conducunt, fuerit
par, turn circa transitum per singulos notandum est, utrum initio viator cur-
sum suum ex regione A instituerit an non. Si enim duo pontes in A con-
ducant et viator ex A cursum inceperit, turn littera A bis occurrere debet;
semel enim adesse debet ad designandum exitum ex A per alteram pontem
et semel quoque ad designandum reditum in A per alteram pontem. Sin
autem viator ex alia regione cursum inceperit, turn semel tantum littera A
occurret; semel enim posita tarn adventum in A quam exitum inde denotabit,
ut huiusmodi cursus designare statui.
12. Conducant iam quatuor pontes in regionem A et viator ex A
cursum incipiat; turn in designatione totius cursus littera A ter adesse debebit,
si quidem per singulos semel transierit. At si ex alia regione ambulare
inceperit, turn bis tantum littera A occurret. Si sex pontes ad regionem A
conducant, turn littera -4, si ex A initium eundi est sumptum, quater
occurret, at si non ex A initio exierit viator, turn ter tantum occurrere debebit.
Quare generaliter: si numerus pontium fuerit par, turn eius dimidium dat
numerum vicium, quibus littera A occurrere debet, si initium non est in
regione A sumptum; dimidium vero unitate auctum dabit numerum vicium,
quoties littera A occurrere debet, initio cursus in ipsa regione A sumpto.
13. Quia autem in tali cursu nonnisi ex una regione initium fieri potest,
ideo ex numero pontium, qui in quamvis regionem deducunt, ita numerum
vicium, quoties littera quamque regionem denotans occurrere debet, definio, ut

Решение одной задачи, связанной с геометрией положения 21
6 SOLUTTO PROBLEMATIS [134-136
sumam numeri pontium unitate aucti dimidium, si numerus pontium fuerit
impar; ipsius vero numeri pontium medietatem, si fuerit par. Deinde si
numerus omnium vicium adaequet numerum pontium unitate auctum, tum
transitus desideratus succedit, at initium ex regione, in quam impar pontium
numerus ducit, capi debet. Sin autem numerus omnium vicium fuerit unitate
minor quam pontium numerus unitate auctus, tum transitus succedet in-
cipiendo ex regione, in quam par pontium numerus ducit, quia hoc modo
vicium numerus unitate est augendus.
14. Proposita ergo quacunque aquae pontiumque figura ad investigandum,
num quis per singulos semel transire queat, sequenti modo operationem in-
stituo. Primo singulas regiones aqua a se invicem diremptas litteris A, B,
С etc. designo. Secundo sumo omnium pontium numerum eumque unitate
augeo atque sequenti operationi praefigo. Tertio singulis litteris А, В, С etc.
sibi subscripts cuilibet adscribo numerum pontium ad earn regionem dedu-
centium. Quarto eas litteras, quae pares adscriptos habent numeros, eigno
asterisco. Quinto singulorum horum numerorum parium dimidia adiicio, im-
parium vero unitate auctorum dimidia ipsis adscribo. Sexto hos numeros
ultimo scriptos in unam summam coniicio; quae summa si vel unitate minor
fuerit vel aequalis num его supra praefixo, qui est numerus pontium unitate
auctus, tum concludo transitum desideratum perfici posse. Hoc vero est
tenendum, si summa inventa fuerit unitate minor quam numerus supra po-
situs, tum initium ambulations ex regione asterisco notata fieri debere;
contra vero ex regione non signata, si summa fuerit aequalis numero prae-
scripto. Ita ergo pro casu Regiomontano operationem instituo, ut sequitur:
Numerus pontium 7, habetur ergo 8.
Forties
A, 5 i 3
B, 3 2
C, 3 2
Д 3 I 2
Quia ergo plus prodit quam 8, huiusmodi transitus nequaquam fieri
potest.

22 Глава II. Три столпа теории эйлеровых графов
136] AD GEOMETRIAM SITUS PERTINENTIS 7
15. Sint duae insulae A et Б aqua circumdatae, qua cum aqua com-
municent quatuor fluvii, quemadmodum figura (Fig. 3) repraesentat. Traiecto
porro sint super aquam insulas circumdantem et fluvios quindecim pontes
a, b, c, d etc. et quaeritur, num quis cursum ita instituere queat, ut per
Fig. 3.
omnes pontes transeat, per nullum autem plus quam semel. Designo ergo
primum omnes regiones, quae aqua a se invicem sunt separatae, litteris A,
Б, С, D, Е, F, cuiusmodi ergo sunt sex regiones. Dein numerum pontium 15
unitate augeo et summam 16 sequenti operationi praefigo.
A*,
B*,
c*,
V,
E,
F*,
8
4
4
3
5
6
16
4
2
2
2
3
3
16

Решение одной задачи, связанной с геометрией положения 23
8 SOLUTIO PROBLEMATIS [137-138
Tertio litteras А, В, С etc. sibi invicem subscribo et ad quamque numerum
pontium, qui in earn regionem ducunt, pono, ut ad A octo ducunt pontes,
ad В quatuor etc. Quarto litteras, quae pares adiunctos habent numeros,
asterisco noto. Quinto in tertiam columnam scribo parium numerorum di-
midia, impares vero unitate augeo et semisses appono. Sexto tertiae co-
lumnae numeros invicem addo et obtineo summam 16; quae cum aequalis
sit numero supra posito 16, sequitur transitum desiderato modo fieri posse,
si modo cursus vel ex regione В vel E incipiatur, quippe quae non sunt
asterisco notatae. Cursus autem ita fieri potent
EaFbBcFdAeFfCgAhCiDkAmEnApBoElD,
ubi inter litteras maiusculas pontes simul collocavi, per quos fit transitus.
16. Нас igitur ratione facile erit in casu quam maxime composite iu-
dicare, utrum transitus per omnes pontes semel tantum fieri queat an non.
Hoc tamen adhuc multo faciliorem tradam modum idem dignoscendi, qui ex
hoc ipso modo non difficulter eruetur, postquam sequentes observationes in
medium protulero. Primo autem observo omnes numeros pontium singulis
litteris At В, С etc. adscriptos simul sumptos duplo maiores esse toto
pontium numero. Huius rei ratio est, quod in hoc computo, quo pontes omnes
in^datam regionem ducentes numerantur, quilibet pons bis numeretur; refer-
tur enim quisque pons ad utramque regionem, quas iungit.
17. Sequitur ergo ex hac observatione summam omnium pontium, qui
in singulas regiones conducunt, esse numerum parem, quia eius dimidium
pontium numero aequatur. Fieri ergo non potest, ut inter numeros pontium
in quamlibet regionem ducentium unicus sit impar; neque etiam, ut tres sint
impares, neque quinque etc. Quare si qui pontium numeri litteris A. B,
С etc. adscripti sunt impares, necesse est, ut eorum numerus sit par; ita in
exemplo Regiomontano quatuor erant pontium numeri impares litteris re-
gionum А, В, C, D adscripti, uti ex § 14 videre licet; atque in exemplo prae-
cedente, § 15, duo tantum sunt numeri impares, litteris D et E adscripti.
18. Cum summa omnium numerorum litteris А, В, С etc. adiunctorum
aequet duplum pontium numerum, manifestum est illam summam binario
auctam et per 2 divisam dare numerum operationi praefixum. Si igitur

24 Глава II. Три столпа теории эйлеровых графов
138-139] AD GEOMETBIAM SITUS PERTINENTIS 9
omnes numeri litteris А, Б, С, D etc. adscripti fuerint pares et eorum sin-
gulorum medietates capiantur ad numeros tertiae columnae obtinendos, erit
horum numerorum summa unitate minor quam numerus praefixus. Quam-
obrem his casibus semper transitus per omnes pontes fieri potest. In qua-
cunque enim regione cursus incipiatur, ea habebit pontes numero pares
ad se conducentes, uti requiritur. Sic in exemplo Eegiomontano fieri
potest, ut quis per omnes pontes bis transgrediatur; quilibet enim pons
quasi in duos erit divisus numerusque pontium in quamvis regionem ducen-
tium erit par.
19. Praeterea, si duo tantum numeri litteris А, В, С etc. adscripti
fuerint impares, reliqui vero omnes pares, turn semper desideratus transitus
succedet, si modo cursus ex regione, ad quam pontium impar numerus tendit,
incipiatur. Si enim pares numeri bisecentur atque etiam impares unitate
aucti, uti praeceptum est, summa harum medietatum unitate erit maior quam
numerus pontium ideoque aequalis ipsi numero praefixo.
Ex hocque porro perspicitur, si quatuor vel sex vel octo etc. fuerint
numeri impares in secunda columna, turn summam numerorum tertiae
columnae maiorem fore numero praefixo eumque excedere vel unitate vel binario
vel ternario etc. et idcirco transitus fieri nequit.
20. Casu ergo quocunque proposito statim facillime poterit cognosci,
utrum transitus per omnes pontes semel institui queat an non, ope huius
regulae:
Si fuerint plures dudbus regiones, ad quas ducentium pontium numerus est
impar, turn certo affirmari potest talem transitum non dari.
Si autem ad duos tantum regiones ducentium pontium numerus est impar,
tunc transitus fieri poterit, si modo cursus in altera harum regionum incipiatur.
Si denique nulla omnino fuerit regio, ad quam pontes numero impares condu-
cant, turn transitus desiderato modo institui poterit, in quocunque regione amhulandi
inUium ponatur.
Нас igitur data regula problemati proposito plenissime satisfit
Ьхохмхжрх Euleu Opera omnia 17 CommenUtionw algebr&ic&e
S

Решение одной задачи, связанной с геометрией положения 25
Ю SOLUTIO PROBLEMATIS AD GEOMETRIAM SITUS PERTINENTIS [140
21. Quando autem inventum fnerit talem transitum institui posse, quaestio
superest, quomodo cursus sit dirigendus. Pro hoc sequenti utor regula: tol-
lantur cogitatione, quoties fieri potest, bini pontes, qui ex una regione in
aliam ducunt, quo pacto pontium numerus vehementer plerumque diminuetur;
turn quaeratur, quod facile fiet, cursus desideratus per pontes reliquos; quo
invento pontes cogitatione sublati hunc ipsum cursum non multum turbabunt,
id quod paululum attendenti statim patebit; neque opus esse iudico plura ad
cursus reipsa formandos praecipere.

26
Глава И. Три столпа теории эйлеровых графов
Решение одной задачи, связанной с геометрией
положения1)
Study 53 of Enestroemianus' index
Труды Петербургской академии наук, 8 (1736), 1741, стр. 128-140.
1. В дополнение к той части Геометрии, которая имеет дело с количествами
и которая всегда возбуждала особый интерес, существует другая — фактически
все еще неизвестная —часть, которую впервые упомянул Лейбниц и которую
он назвал геометрией положения. Эта часть геометрии занимается именно
тем, что может быть определено только положением, а также исследованием
свойств положения; в этом смысле она не будет касаться ни количеств, ни их
вычисления. Однако виды задач, относящихся к этой геометрии положения,
и методы, используемые для их решения, были недостаточно точно
определены. Из-за этого в последнее время, когда возникала задача, которая казалась
в основе своей геометрической, но по своей природе не требовала определения
количеств и не допускала решения с помощью вычисления количеств, я был
убежден, что она принадлежит геометрии положения главным образом из-за
того, что только положение можно было использовать для ее решения, в то
время как вычисления были совсем бесполезны. Поэтому я решил объяснить
здесь метод, который разработал для решения задач подобного вида, как
пример геометрии положения.
2. Эта задача, как мне сказали, довольно хорошо известна и связана вот
с чем. В городе Кенигсберге, в Пруссии, есть остров, называемый Кнайпхоф;
река, окружающая его, делится на два рукава, что можно увидеть на рисунке2).
Рукава этой реки пересекают семь мостов а, Ь, с, d, e, / и д. В связи с этими
мостами был поставлен вопрос, можно ли совершить по ним прогулку так,
чтобы пройти по каждому из этих мостов, причем ровно по одному разу. Как я
слышал, некоторые отрицают, что это можно сделать, другие сомневаются, но
никто не подтверждает такой возможности. Исходя из этого, я сформулировал
для себя следующую общую задачу: какой бы ни была форма реки и деление
ее на рукава и каково бы ни было число мостов, пересекающих их, выяснить,
можно ли пройти по всем этим мостам, причем по каждому только один раз.
3. Конечно, можно решить кёнигсбергскую задачу о семи мостах,
составив полный список всех маршрутов, какие только можно себе представить, и
тогда станет ясно, годится ли некоторый маршрут или подходящего
маршрута нет. Однако из-за большого числа комбинаций этот способ решения задачи
представляется слишком трудным и громоздким. Кроме того, его нельзя
было бы применить к другим задачам со значительно большим числом мостов.
И даже если при таком способе решения работу можно было бы довести до
конца, возникли бы многие не относящиеся к делу обстоятельства; здесь, без
х) Отметим, что русский перевод осуществлен с английского перевода Г. Фляйшнера. —
Прим. ред.
2) См. Fig. 1 в латинском тексте. Дальнейшая ссылка на рисунки отсылают также к
латинскому тексту. — Прим. ред.

Решение одной задачи, связанной с геометрией положения 27
сомнения, лежит основная причина трудностей. Поэтому, отказавшись от этого
метода, я стал искать другой, который позволил бы только решить, возможен
ли маршрут, который удовлетворяет нашим требованиям; я подозревал, что
такой метод был бы значительно проще.
4. Весь мой метод основан на надлежащих обозначениях для отдельных
прохождений мостов. Я использую заглавные буквы А, В, С, D для
обозначения отдельных областей, на которые река разделяет сушу. Таким образом, если
некто движется из области А в область В через мост а или Ъ , то я обозначаю
прохождение моста символом АВ. Первая буква обозначает область, из
которой путешественник вышел, а вторая буква —ту область, в которую он
попадает, пройдя по мосту. Если после этого путешественник перейдет из области
В в область D по мосту /, то это перемещение может быть описано буквами
BD; однако эти два последовательных перемещения АВ и BD я обозначаю
только тремя буквами ABD, так как средняя буква В обозначает как область,
в которую попадает путешественник после первого прохождения моста, так и
область, которую он покидает, пройдя по второму мосту.
5. Точно так же, если путешественник продвигается из области D в область
С через мост #, то я буду обозначать эти три последовательных перехода
четырьмя буквами ABDC. Из этих четырех букв ABDC будет видно, что
путешественник, который вначале находился в области А, перешел в область
В, после чего попал в область D, а затем достиг области С. Заметим,
однако, что так как эти области отделены друг от друга рекой, путешественник
должен пройти по трем мостам. Далее, последовательное прохождение по
четырем мостам будет обозначаться пятью буквами, и по скольким бы мостам
ни проходил пешеход, его путь будет обозначаться буквами, число которых на
единицу больше числа мостов. Поэтому для описания прохождения по семи
мостам потребуется восемь букв.
6. При таком способе обозначения я не уточняю, какой мост проходится.
Однако если из одной области в другую можно попасть по нескольким мостам,
то неважно, каким именно мостом воспользовался путешественник, раз он
попал в нужную область. Таким образом, становится очевидным, что если можно
пройти по семи мостам, причем по каждому из них ровно по одному разу, то
этот маршрут будет изображаться восемью буквами. Порядок этих букв
должен был бы быть таким, что пара букв А и В, идущих непосредственно одна
за другой, будет встречаться в ней дважды, потому что области А и В
соединены двумя мостами а и Ъ. Точно так же пара идущих друг за другом букв
А и С будет встречаться в этой последовательности из восьми букв дважды,
пара букв А и D — только однажды и пары букв В и D, а также С и D тоже
встретятся лишь по разу.
7. Таким образом, вопрос сводится к тому, можно ли из четырех букв
А, В, С и D составить последовательность из восьми букв, в которой все эти
пары будут встречаться необходимое число раз. Но прежде чем пытаться
найти такую последовательность, нужно выяснить, можно ли так расположить
буквы, потому что если можно показать, что такое расположение невозможно,

28
Глава II. Три столпа теории эйлеровых графов
то вся работа по ее построению окажется бесполезной. Поэтому я разработал
правило, по которому можно легко решить —как для этой задачи, так и для
всех подобных задач, — может ли быть осуществлено такое расположение букв.
8. Чтобы вывести подобное правило, я рассматриваю некоторую
конкретную область А, в которую может вести произвольное число мостов a,b,c,d
и т.д. (рис. 2). Из этих мостов сначала я рассмотрю конкретный мост а,
ведущий в область А. Если путешественник пройдет по этому мосту, то он либо
находился в области А до того, как прошел по этому мосту, либо окажется в
области А после этого. Поэтому чтобы обозначить этот проход по мосту, как
описано выше, необходимо, чтобы один раз возникла буква А. Если в область
А ведут три моста, например a, b и с, и путешественник проходит по всем трем
мостам, то буква А будет встречаться в описании его движения по мостам
дважды независимо от того, начинался его маршрут из А или нет. Точно так
же, если в область А ведут пять мостов, то буква А должна встретиться при
описании его движения три раза. И когда количество мостов — произвольное
нечетное число, то если увеличить его на единицу, половина полученного числа
показывает, сколько раз должна встретиться буква А.
9. Следовательно, в случае с кёнигсбергскими мостами (рис. 1), поскольку
на остров А ведут пять мостов а, 6, с, с/, е, необходимо, чтобы буква А
встретилась в описании движения по этим мостам трижды. Кроме того, дважды
должна встретиться буква В, так как в область В ведут три моста, и буквы D
и С должны встретиться по два раза каждая. Поэтому в последовательности
из восьми букв, с помощью которой описывается рассматриваемый маршрут,
проходящий через семь мостов, буква А должна встретиться три раза, а
каждая из букв В, С, D — по два раза. Такого, однако, в последовательности из
восьми букв быть не может. Таким образом, ясно, что подобная прогулка по
семи мостам Кенигсберга невозможа.
10. Для каждого другого расположения мостов — если предполагать,
конечно, что число мостов, ведущих в каждую область, нечетно, — таким же
способом выясняется, можно или нет совершить прогулку, проходя по каждому из
мостов в точности по разу. А именно, если общее число вхождений букв равно
числу мостов, увеличенному на единицу, то такая прогулка возможна. Если,
однако, как в нашем примере, полное число вхождений букв больше, чем число
мостов, увеличенное на единицу, то прогулка невозможна. Как бы то ни было,
правило, которое я предложил для определения числа вхождений буквы А,
исходя из числа мостов, ведущих в область А, одинаково справедливо, идут ли
все эти мосты из одной области В, как это показано на рисунке (рис. 2), или
из разных областей, так как я рассматриваю только область А и выясняю, как
часто должна появляться буква А.
11. Если, однако, число мостов, которые ведут в область А, четно, то нужно
учитывать, выходит ли путешественник из А. Если в область А ведут два моста
и путешественник начал движение из этой области, буква А должна
встретиться дважды. Первый раз она будет обозначать выход из А через один мост, а
второй раз — возвращение в А через другой. Если же пешеход начал движение

Решение одной задачи, связанной с геометрией положения 29
из другой области, буква А должна встретиться только единожды: дело в том,
что, сосчитанная только один раз, она будет обозначать, в соответствии с моим
описанием таких маршрутов, как приход в А, так и уход из А.
12. Если мы предположим, что в область А ведут четыре моста и
путешественник начал свой путь из области А, то буква А должна будет встретиться
в описании всего маршрута три раза, если он переходит по каждому мосту
только один раз. Но если путешественник начинает движение в другой
области, буква А встретится дважды. В случае, когда в область А ведут шесть
мостов, буква А встретится четыре раза, если маршрут начался в области А,
но если путешественник начал движение не из области А, то буква А
встретится только три раза. Поэтому в общем случае, если число мостов четно, то,
когда маршрут начинается не в области А, половина этого числа дает число
появлений буквы А. Однако если маршрут начинается в этой самой области
А, то число появлений буквы А равно половине числа мостов плюс единица.
13. В таком маршруте начальный шаг может быть предпринят только
из одной области. Зная число мостов, ведущих в произвольную область, я
определяю, сколько раз должна появляться буква, обозначающая конкретную
область, как половину числа мостов, увеличенного на единицу, если число
мостов нечетно, но как половину числа мостов, если оно четно. Следовательно,
если число всех вхождений [букв] равно числу мостов, увеличенному на
единицу, требуемая прогулка возможна, но должна начинаться в той области, в
которую ведет нечетное число мостов. Если же число всех вхождений [букв]
окажется на единицу меньше, чем число мостов, увеличенное на единицу, то
прогулка возможна, если начать ее в области, в которую ведет четное число
мостов, потому что тогда число вхождений [букв] увеличивается на единицу.
14. Итак, обсудив произвольное расположение рек и мостов, я предлагаю
действовать следующим образом для выяснения, возможно ли пройти по всем
мостам по одному разу. Во-первых, я обозначаю области, отделенные друг от
друга водой, буквами А,В,С и т.д. Во-вторых, я беру число всех мостов и
увеличиваю его на единицу, а затем записываю его для последующего
использования. В-третьих, после того как выписаны отдельные буквы А, В, С и т. д., я
записываю рядом с каждой из них число мостов, ведущих в соответствующую
область. В-четвертых, я помечаю звездочками те буквы, рядом с которыми
записаны четные числа. В-пятых, я записываю половину каждого из этих
четных чисел рядом с ним, в то время как возле нечетных чисел я пишу половину
от этого числа, увеличенного на единицу. В-шестых, я суммирую эти
записанные последними числа; если сумма окажется меньшей на единицу или равной
числу, написанному сверху (которое представляет собой число мостов,
увеличенное на единицу), я делаю вывод, что маршрут возможен. Надо отметить,
однако, что если вычисленная сумма на единицу меньше, чем число,
записанное сверху, то маршрут обхода должен начинаться в области, помеченной
звездочкой, но если сумма равна этому числу, то маршрут должен начинаться в
непомеченной области. Поэтому для Кенигсберга указанный процесс приводит
к следующему:

30
Глава II. Три столпа теории эйлеровых графов
Число мостов равно 7; поэтому 8 — правильное значение.
Мосты
А 5 I 3
В 3 2
С 3 2
D 3 I 2
Так как суммирование приводит в числу, большему 8, осуществить искомую
прогулку невозможно.
15. Пусть А и В — два острова, окруженные водой, и четыре реки
образуют окружающие эти острова протоки, как показано на рисунке (рис. 3). Кроме
того, пусть через протоки, окружающие острова, и через реки перекинуты
пятнадцать мостов а, 6, с, d и т. д., и снова встает вопрос, можно ли пройти по всем
мостам ровно по одному разу. Во-первых, я обозначу все области, которые
отделены друг от друга водой, буквами А, В, С, D, E, F (всего имеется шесть
таких областей). Во-вторых, я увеличиваю число мостов, равное 15, на единицу
и записываю полученное число 16 сверху в следующей таблице:
А*
В*
С*
D
Е
р*
8
4
4
3
5
6
16
4
2
2
2
3
3
16
В-третьих, я записываю в виде столбца буквы Л, Б, С и т. д. и пишу рядом с
каждой из них число мостов, которые ведут в соответствующую область (таким
образом, восемь мостов ведут в А, четыре в В и т. д.). В-четвертых, я
помечаю «звездочкой» буквы, которым поставлены в соответствие четные числа.
В-пятых, я записываю в третий столбец половину от каждого четного числа,
а нечетные числа увеличиваю на единицу и записываю половину [от каждого
полученного числа в третий столбец]. В-шестых, я складываю все числа
третьего столбца и получаю 16; так как эта сумма равна числу 16, записанному
сверху (столбцов), то желаемую прогулку можно осуществить, если начать ее
в областях D или Е, которые не помечены звездочкой. Такая прогулка могла
бы проходить, например, по маршруту
EaFbBcFdAeFfCgAhCiDkAmEnApBoElD,
где я, кроме того, поместил между заглавными буквами мосты, которые
следует проходить.
16. С помощью таких рассуждений в самых сложных случаях нетрудно
решить, можно ли осуществить прогулку, проходя по всем мостам ровно по
одному разу. Однако я хотел бы предложить значительно более легкий путь
решения. Его можно будет легко вывести из предложенного выше подхода,
после того как я познакомлю читателя со следующими наблюдениями. Вначале
я отмечу, что все количества мостов, выписанные рядом с буквами А, Б, С

Решение одной задачи, связанной с геометрией положения 31
и т.д., сложенные вместе, дают удвоенное число всех мостов. Причина состоит
в том, что при таком подсчете каждый мост считается дважды, с тем чтобы
все мосты, ведущие в данную область, были учтены, ибо каждый мост ведет в
две области, которые он соединяет.
17. Из этого наблюдения вытекает, что сумма [чисел] всех мостов, ведущих
в каждую область, есть четное число, так как половина этой суммы есть в
точности число мостов. Поэтому не может случиться так, чтобы среди чисел
мостов, ведущих в любую область, в точности одно было нечетным; не может
также случиться, чтобы нечетных чисел было три, пять и т. д. Следовательно,
если числа мостов, выписанные рядом с буквами А, В, С и т. д., суть нечетные
числа, их сумма четна. Таким образом, в примере с Кенигсбергом имеются
четыре нечетных числа мостов, записанные рядом с буквами областей A,B,C,D,
что можно увидеть в пункте 14, а в последнем примере из пункта 15 имеются
только два нечетных числа, записанные рядом с буквами D и Е.
18. Так как сумма всех чисел, выписанных рядом с буквами A, JB, С и т. д.,
равна удвоенному числу мостов, ясно, что эта сумма, будучи увеличенной на
два и потом поделенной на два, дает число, выписанное сверху над
вычислениями. Поэтому если все числа, записанные рядом с буквами Д Б, С, D и т. д.,
четны и половины каждого из этих чисел воспринимаются как числа,
полученные для третьего столбца, то сумма этих чисел будет на единицу меньше, чем
число, написанное наверху. Значит, в этих случаях прогулка по всем мостам
может быть осуществлена. Действительно, в какой бы области она ни
начиналась, число ведущих в эту область мостов будет четным, как и требуется.
Таким образом, в примере с Кенигсбергом можно было бы совершить
прогулку, проходя через каждый мост дважды, ибо каждый мост можно было бы
разделить на два, и тогда число мостов, ведущих в каждую область, было бы
четным.
19. Кроме того, если только два из чисел, выписанных рядом с буквами
А, В, С и т. д., нечетны, в то время как остальные числа четны, желаемая
прогулка также возможна, но она должна начинаться в области, в которую ведет
нечетное число мостов, ибо если четные числа, а также нечетные, увеличенные
на единицу, поделены пополам, как описано выше, то сумма этих половинок
будет на единицу больше, чем число мостов, и поэтому равна числу, написанному
сверху.
Из этих рассуждений видно также, что если во втором столбце могут
встретиться четыре, шесть, восемь и т. д. нечетных чисел, то сумма чисел в третьем
столбце будет больше числа, написанного сверху, на единицу, два, три и т. д.
Поэтому прогулку осуществить нельзя.
20. Значит в каждом возможном случае следующее правило позволяет
непосредственно и без труда выяснить, можно ли осуществить прогулку по всем
мостам без повторений:
Если имеется более двух областей, в которые ведет нечетное число
мостов, можно заявить с уверенностью, что такая прогулка невозможна.

32
Глава П. Три столпа теории эйлеровых графов
Если, однако, имеются только две области, в которые ведет нечетное
число мостов, то прогулка осуществима при условии, что она начинается в
одной из этих двух областей.
Если, наконец, нет ни одной области, в которую ведет нечетное число
мостов, прогулка с требуемыми условиями осуществима, причем
начинаться она может в любой области.
Следовательно, с помощью этого правила поставленная задача может быть
полностью решена.
21. Однако, после того как выяснилось, что такая прогулка осуществима,
остается вопрос, как она должна проходить. Для этого я использую следующее
правило: мысленно удалять так часто, как это возможно, пару мостов,
ведущих из одной области в другую. Это будет существенно уменьшать в
большинстве случаев число мостов. После этого желаемый путь по оставшимся мостам
построить легко. Пары мостов, мысленно удаленные ранее, не слишком
разрушают этот маршрут. Что это именно так, становится совершенно ясно после
небольшого размышления; поэтому я не считаю необходимым останавливаться
подробнее на прокладке маршрутов.

Обход линейного комплекса без повторений
33
30 СНП. WlEHRIl.
Man vcrfolgt dabei zweckmassig die Axe des Weges statt seiner Rand-
linie. Jene Moglicbkeit beruht auf der Walirheit, dass so lange man
den Ausgang nocb nicht erreicbt hat, ein bereita durchlaufenes Stuck
der Wegeaxe nothwendig von nocb nicht beschriebenen Theilen der-
selben getroffen werden muss, weil sonst jenes Stuck in sich abge-
schlossen ware und mit dem Eingangswege nicht zusammenhinge. Man
markire sich daher den Weg, den man zurQcklegt nebst dem Sinne,
in welchem es geschieht Sobald man auf einen schon markirten Weg
stosst, kehre man um und durchschreite den schon beschriebenen Weg
in umgekehrtem Sinne. Da man, wenn man nicht ablenkte, denselbeu
hierbei in seiner ganzen Ausdehnung nochmals zurucklegen wilrde, so
muss man nothwendig hierbei auf einen nocb nicht markirten ein-
mundenden Weg treffen, den man dann verfolge, bis man wieder auf
einen markirten trifft. Hier kehre man wieder um und verfahre wie
vorher. Es werden dadurch stets neue Wegtheile zu den beschriebenen
zugefQgt, so dass man nach einer endlichen Zeit das ganze Labyrinth
durchwandem wurde und so jedenfalls den Ausgang fande, wenn er
nicht schon vorher erreicht worden ware.
Carlsruhe, December 1871.
Ueber die M6glichkeit, einen Linienzug ohne Wiederholung
und ohne Unterbrechung zu umfabren.
Yon Carl Hierholzer.
Mitgetheilt von Chr. Wiener*).
In eineni* beliebig verschlungenen Linienzuge mogen Zweige ernes
Punktes diejenigen verschiedencn Theile des Zuges heissen, auf welchen
man den fraglichen Punkt verlassen kann. Ein Punkt mit iuehrercn
Zweigen heisse ein Knotcnpuiikt, der so vielfach genannt werde, als
•) Die folgeude Uutensuchung trug der leider to frub dem Dientte der Wiseen-
tchaft durcb den Tod entritsene Pmatdocent Dr. Hierholzer dahier (gest
13. Sept 1871) einem Kreiee befreundeter Mathematiker тог. Um tie тог Ver-
gesaenhcit iu bcwahren, mutate tie bei dem Mangel jeder tcbrifllichen Aufzeicb-
nung aut dem Gcdachtnitt wieder hergestellt werden, wot icli unter Dcibilfc
meinet verehrten Collegeu Luroth durcb dan Folgende mOglichet getrcn auszu-
fuhren tnchte.

34
Глава II. Три столпа теории эйлеровых графов
Ueber eine Aufgabe der Geometria situs. 31
die Anzahl dcr Zweige angiebt, und je nach dieser Anzahl als gerad
oder ungerad genannt sein soil. Eiu gewohnlicher Doppelpunkt ware
biernach ein vierfacher Knotenpunkt, ein gewohnlicher Punkt капп
als ein zweifacher und eine freie Endigung als ein einfacher
Knotenpunkt bezeichnet werden.
Wenn ein Linienzug in einem Zuge umfaliren tccrden Jcann, ohnc
dass irgcnd tin Linienstuck mehrfach durcldaufen wird, so hat er etit-
weder keinen oder zwei ungerade Knotenpunkte. Wenn man beim Durch-
laufen irgend einen Punkt Qberschreitct, so sind dadurch zwei Zweige
eines Knotenpunktes beschrieben, und da keine Strecke zweiraal durch-
laufen werden soil, muss ein Punkt, den man im Ganzen nmal uber-
schreitet, ein 2nfacher Knotenpunkt sein. Ein Punkt kann daher
nur dann ein ungerader Knotenpunkt sein, wenn er beim Darchlaufen
einmal nicht uberschritten wird, d. h. wenn er Anfangs- oder End-
punkt isi Wenn man daher beim Durchlaufen zu dem Ausgangspuuktc
bei dem Schlusse zuruckkehrt, so konneu nur gerade Knotenpunkie
vorhanden sein; wenn nicht, so sind Ausgangs- und Endpunkt
ungerade Knotenpunkte.
Umgekehrt: Wenn ein zusammenhangender Linienzug keinen oder
zwei ungerade Knotenpunkte enthalt, so kann er in einem Zuge
umfahren werden.
Demi a) hat man irgend einen Theil des Linienzuges umfahren,
so ist jeder Knotenpunkt im noch nicht durchfahrenen Theile gerad
oder ungerad, wie er es im ganzen Zuge war; nur der Anfangs- und
Endpunkt des durchlaufenen Stucks kehren ihren Charakter um, ausser
wenn sie zusammenfalien. Denn durch das Durchlaufen eines Punktes
werden zwei Zweige, durch den Anfang und das Ende des Durch-
laufens je ein Zweig ausgeschlossen.
b) Hat man einen Linienzug in einem ungeraden Knotenpunkt zu
umfahren angefangen, so kann man nur in einem andern ungeraden
Knotenpunkte stecken bleiben. Denn in einem geraden Knotenpunkte
hat man bei jedesmaligem Durchlaufen zwei Zweige ausgeschlossen,
so dass bei erneutem Ankommen in demselben wenigstens noch ein
Zweig zum "Verlassen fibrig bleibt. Der Anfangspunkt ist aber durch
den Beginn zu einem geraden Knotenpunkte verwandelt worden, so
dass auch in ihm ein Steckenbleiben nicht moglich ist. Fangt man
dagegen einen Linienzug in einem geraden Knotenpunkte zu umfahren
an, so kann man auch in diesem stecken bleiben, indem er durch den
Beginn zu einem ungeraden verwandelt wurde.
c) Hat nun ein Linienzug zwei ungerade Knotenpunkte, so beginne
man das Umfahren in einem derselben; man wird dann nothwendig
in dem andern stecken bleiben. Der zurQckgelcgte Linienzug ist in
diesem Falle ein offener. Hat der gegebene Linienzug dagegen keine

Обход линейного комплекса без повторений
35
32 Спи. WIkner.
ungeraden Knotenpunkte, so beginne man das Umfahren in eineni
beliebigen Punkte, der also eiu gerader Knotenpunkt ist; man wird
dann nothwendig im Ausgangspunkte stecken bleiben. Der zuruck-
gelegte Linienzug ist in diesem Falle ein geschlossener.
d) Bleibt dabei ein Theil Ъ undurchlaufen, so kann derselbe nur
gerade Knotenpunkte enthalten, weil die zwei etwa vorhandenen
ungeraden Knotenpunkte durch das erste Umfahren ausgeschlossen wurden,
und die ubrigen Knotenpunkte ihren Charakter behielten. Zugleich
muss Ь mit dem schon beschriebenen Zuge a durch wenigstens einen
gemeinsamen Punkt zusammenhangen, weil sonst der Zug in mehrere
nicht zusammenhangende zerfallen wurde. Geht man beim Umfahren
des a in einem solchen Punkte P dee Zusammenhangs auf Ъ uber,
so muss man nothwendig auf Ъ in P stecken bleiben, und kann yon
da das Umfahren des a so fortsetzen, wie es friiher geschehen war.
Auf dieselbe Weise hangt man jedes noch nicht umfahrene StQck an
die schon umfahren en an und beschreibt so die ganze Linie in einem Zuge.
Es ergiebt sich noch folgender Satz: Ein Linienzug Icann nur
eine gerade Anzahl ungerader Knotenpunkte besitzen. Denn schaltet
man durch Umfahren ein Linienstuck aus, indem man in einem
ungeraden Knotenpunkte beginnt und so lauge weiter geht, bis man
stecken bleibt, was wieder in einem ungeraden Knotenpunkte geschehen
muss, und entfernt dadurch zwei ungerade Knotenpunkte; so kann man
durch Wiederholtmg die Anzahl der ungeraden Knotenpuukte auf
weniger als zwei vermindern. Dieser Rest kann aber nicht Eins,
sondem muss Null sein; denn wenn ein Zug nur einen ungeraden
Knotenpunkt besasse und man wQrde in ihm an fan gen den Zug zu
umfahren, so konnte man nie zu Eude kommen, da dies nur in einem
andern ungeraden Knotenpunkte moglich ist. Die Zahl der ungeraden
Knotenpunkte des ursprunglichen Linienzuges ist daher eine gerade.
Carleruhe, im December 1871.
Лum. der Ked. Der wesentliche Iobalt des Vorstehenden, nur in kurzerer
Darstellung, rum Theil obnc d3.1iere Ausfuhrung der Beweise, findet tich \u der
leidcr wenig bekannten Abhandlung von Listing, Vorstudien tur Topologic^
welcbe in den GSttinger Studien (Er»ter Bd., GCitingen 1847) erscbienen ist.
Vielloicht kann der vorstebende Aufsatz dazu dienen, die Aufmerksamkeit der
Geometer auf diese aacb in viclen andern Beziebnngen inbaltreicbe Arbeit wieder
hiuzulenken.

36
Глава II. Три столпа теории эйлеровых графов
О возможности обхода линейного комплекса без
повторений и прерываний
Карл Хирхольцер
Представлено Кр. Винером1)2)
В комплексе произвольно переплетенных линий3) различные части
комплекса могут быть названы ветвями точки. Вдоль них можно покидать
рассматриваемую точку. Точка вместе с некоторыми ветвями может быть названа
узлом. Число ветвей узла называют его кратностью, и в зависимости от этого
числа он либо четен, либо нечетен. Произвольная двойная точка есть,
таким образом, четырехкратный узел, обычная точка может быть описана как
двукратный узел, а свободный конец линии — как однократный узел.
Если комплекс линий может быть пройден за один прием без повторного
прохождения какой-либо его части, то он имеет либо два нечетных узла,
либо ни одного. Если при обходе проходится произвольный узел, в этот обход
оказываются включенными две его ветви, а так как ни одна линия не может
проходиться дважды, точка, которая в общем итоге проходится п раз, должна
быть 2п-кратным узлом. Точка поэтому может быть нечетным узлом, только
если она ни разу не проходится, т. е. только если она является либо начальной,
либо конечной точкой. Поэтому если при обходе происходит в конце концов
возврат в начальную точку, то могут встретиться только четные узлы; если же
возврата не происходит, то и начальная, и конечная точки суть нечетные узлы.
Обратно: если связный комплекс линий содержит два нечетных узла или
ни одного, то он может быть пройден за один прием.
Действительно: а) Если некто прошел какую-либо часть комплекса линий,
то каждый узел в еще не пройденной части имеет в точности ту же четность,
что и в целом комплексе; только начальная и конечная точки пройденной
части изменяют четность, за исключением случая, когда они совпадают.
Действительно, в прохождении через точку участвуют два ребра, но когда речь
идет о начальной и конечной точках обхода, участвует одно ребро.
Ь) Если некто начал обходить комплекс линий из нечетного узла, то он
может быть остановлен только в другом нечетном узле, ибо в каждом про-
*) Приват-доцент др. Хирхольцер, чье служение науке, к несчастью, было прервано ранней
смертью (13 сентября 1871), делал доклад о приводимом ниже исследовании в кругу коллег-
математиков. Для того чтобы уберечь эту работу от забвения, пришлось воссоздавать ее
по памяти ввиду отсутствия каких-либо записей. В предлагаемой статье я с помощью
моего уважаемого коллеги Люрота попытался сделать это настолько аккуратно, насколько это
представлялось возможным.
2) Отметим, что русский перевод осуществлен с английского перевода Г. Фляйшнера. —
Прим. ред.
3) Я использовал термин «комплекс линий» (line complex) для перевода термина Linienzug
из-за того, что вариант line system, использованный в [BIGG76a], является неточным
переводом с лингвистической точки зрения (хотя с точки зрения теории графов это, вероятно, есть
наилучший возможный перевод). Термин «одномерный комплекс» (one-dimensional complex),
который я нашел в математическом словаре, есть точный перевод термина «Linienzug»,
но он, по-видимому, не соответствует стандартной терминологии, использовавшейся во
времена Хирхольцера. На самом деле Листинг уже использовал термин «линейный
комплекс» (Linearkomplexion) более чем за двадцать лет до появления статьи Хирхольцера (см.
[LIST48a]).

Обход линейного комплекса без повторений
37
хождении четного узла участвуют два ребра, так что после повторяющихся
заходов в один и тот же узел всегда остается по крайней мере одна ветвь, по
которой его можно покинуть. Начальная точка, однако, преобразуется
началом обхода в четный узел, так что там также нельзя остановиться. Если же,
однако, некто начинает обход комплекса из четного узла, то он может быть там
остановлен, поскольку этот узел преобразуется в нечетный началом [обхода].
c) Если теперь комплекс линий имеет два нечетных узла, начнем обход в
одном из них, а закончим обязательно в другом. В этом случае покрываемый
комплекс линий есть незамкнутый комплекс. С другой стороны, если заданный
комплекс линий не имеет нечетных узлов, то начинаем обход в произвольной
точке, которая, таким образом, является четным узлом, и обход с
необходимостью завершится в начальной точке. В этом случае покрываемый комплекс
линий есть замкнутый комплекс.
d) Если некоторая часть комплекса Ъ остается непройденной, то эта [часть]
должна содержать только четные узлы, потому что два, возможно, имевшихся
нечетных узла будут участвовать в первом обходе, а оставшиеся узлы сохранят
свою четность. В то же самое время Ь должна быть связана с уже пройденной
частью а по крайней мере одной общей вершиной, так как иначе комплекс
разбивался бы на отдельные не связанные друг с другом части. Если при обходе
части а мы попадаем в 6 через связывающую точку Р, то обязательно должны
завершить обход части 6 в Р, а потом продолжать обход части а как прежде.
Таким путем можно присоединять каждую еще не пройденную часть к уже
пройденной; в итоге весь комплекс будет пройден за один раз.
Справедлива и другая теорема: комплекс линий может иметь только
четное число нечетных узлов. В самом деле, если обходить часть
комплекса линий, начинал с нечетного узла и продолжая обход так долго, как только
возможно, то остановка будет в нечетном узле; таким образом, используются
два нечетных узла. Повторяя, можно уменьшить число нечетных узлов до
менее чем двух узлов. Но один узел остаться не может, число оставшихся должно
быть нулем, ибо если бы комплекс имел только один нечетный узел и обход
комплекса начался в нем, то никогда нельзя было бы завершить обход,
поскольку завершить его можно только в другом нечетном узле. Поэтому число
нечетных узлов в исходном комплексе четно.
Карлсруэ, декабрь 1871.
Замечание редактора. Существо изложенного, но в краткой форме, иногда без
деталей доказательств, можно найти в прискорбно мало известном трактате Листинга
«Предварительные сведения по топологии» («Vorstudien zur Topologie»), который
появился в Gottinger Studien (первый том, Гёттинген, 1847)х\ Возможно, данная
статья снова привлечет внимание геометров к этой работе. Она богата по содержанию
и во многих других отношениях.
также п. 17 статьи Эйлера (Г.Ф.).

38
Глава П. Три столпа теории эйлеровых графов
Мы заканчиваем эту главу извлечением из статьи Освальда Веблена [VEBL
31а]. Хотя эта статья обычно воспринимается как одна из основных в развитии
теории графов, она содержит небольшой изъян. В общем случае неверно, что
«каждый из этих 1-циклов [из С[] совпадает с/[соответствует] 1-циклом/[1-
циклу] из Ci,...» (см. ниже). Таким образом, третий столп имеет небольшую
трещину. Однако Веблен уже в статье [VEBL12a] показал, что эта «трещина»
может быть ликвидирована: «... Действительно, начинаем с произвольного
ребра ... и описываем путь вдоль ребер ... Всякий раз, когда найдется ребро,
по которому этот путь попадает в некоторую вершину, то, поскольку число
... ребер в этой вершине четно, найдется ... ребро, по которому путь покидает
ее. Следовательно, путь может быть продолжен до тех пор, пока он не
пересечет сам себя. В этом случае часть пути образует цикл. Если его удалить, то в
каждой вершине по-прежнему останется четное число ... ребер. Потом можно
удалить другой цикл и т.д. до тех пор, пока не будут исчерпаны все ребра».
Освальд Веблен «Analysis situs» (О. Veblen, Analysis situs, pp. 15-16.)
Одномерные циклы
22. Связный линейный граф, каждая вершина которого есть конец в
точности двух одномерных ячеек, называется одномерным циклом или 1-циклом.
Согласно теоремам из § 5, разбиение любой замкнутой кривой с помощью
любого конечного множества точек превращает ее в 1-цикл. Обратно, легко видеть,
что множество всех точек на 1-цикле составляет простую замкнутую кривую.
Очевидно, далее, что любой линейный граф, такой, что каждая его вершина
является концом ровно двух одномерных ячеек, есть либо 1-цикл, либо
множество 1-циклов, никакие два из которых не имеют общих точек.
Рассмотрим линейный граф С\, такой, что каждая вершина является
концом четного числа ребер. Обозначим через 2пг число ребер, инцидентных
каждой вершине а®. Ребра, инцидентные каждой вершине а?, произвольным
образом могут быть сгруппированы в щ пар, никакие две из которых не имеют
общих ребер; пусть эти пары ребер называются парами, ассоциированными с
вершиной а®. Пусть С[ —граф, сопоставленный графу С\ таким образом, что
(1) существует точно одна точка из С[ для каждой точки из Ci, которая не
является вершиной, и (2) существуют щ вершин из С[ для каждой вершины из
С\, причем каждая из этих вершин в С[ будет инцидентна только двум ребрам
из С{, которые совпадают с некоторой парой, ассоциированной с а®.
Линейный граф С{ имеет точно два ребра, инцидентных каждой из его
вершин, и поэтому состоит из множества 1-циклов. Каждый из этих 1-циклов
совпадает с 1-циклом из Ci, и никакие два из таким образом определенных
1-циклов в С\ не имеют общей 1-ячейки. Следовательно, С\ состоит из
множества 1-циклов, которые имеют только конечное число общих 0-ячеек.
Очевидно, что линейный граф, составленный из множества замкнутых
кривых, имеющих только конечное множество общих точек, имеет четное число
1-ячеек, инцидентных каждой вершине. Следовательно, необходимое и
достаточное условие того, что С\ состоит из множества 1-циклов, у которых
общими могут быть только 0-ячейки, состоит в том, что каснсдая 0-ячейка
в С\ инцидентна четному числу 1-ячеек.

Глава III
Основные понятия и
предварительные результаты
Большую часть изложенного в этой главе можно найти в любом
вводном курсе по теории графов. Однако, так как я хочу обеспечить как
можно более широкую читательскую аудиторию, я решил начать «с азов».
Кроме того, по разным причинам, которые станут ясны по мере
изучения следующих глав, представляется удобным и даже необходимым
подходить к некоторым теоретико-графовым понятиям более
дифференцированно, чем это обычно делается (например, различать открытые и
замкнутые ребра, полуребра и т. д. — см. ниже). Этот подход требует в
качестве первого шага определить некоторые основные понятия
относительно формализованным образом. Позднее (в этой и следующих главах) мы
по возможности избегаем формализации, предпочитая более
эвристический подход к представленному в этой книге материалу по той
причине, что слишком сильная формализация слишком быстро утомляет
читателя.
Что касается этой главы, то большинство элементарных результатов
формулируются без доказательства; более опытным студентам их легко доказать,
а остальные смогут найти доказательства в любом введении в теорию графов.
Основная причина этого заключается в желании сделать настоящую главу как
можно более короткой. По той же причине многие менее элементарные
результаты будут также сформулированы без доказательств; эти доказательства
можно найти в цитируемой литературе. Я рекомендую в качестве введения в
теорию графов книги [HARA69a, BOND76a, BEHZ79a, BEIN78a, BEIN83a].
Что касается других знаний по математике, то предполагается, что
кроме теории графов читатель немного знаком с теорией множеств1), основами
алгебры и некоторыми разделами топологии поверхностей (в основном
плоскости). Что касается алгоритмов, их сложности и сложности решения проблем
распознавания, мы будем на протяжении всей книги во многих случаях
излагать соответствующий материал кратко и за подробностями отсылать
интересующегося читателя к литературе. Поэтому основные понятия теории
алгоритмов и их сложности не будут строго сформулированы. Теперь «прыгнем в
воду».
*) В этом и втором томе мы имеем дело только с конечными графами; бесконечные графы
появятся (причем в меньшем объеме) в третьем томе.

40
Глава III. Основные понятия и предварительные результаты
3) ft(jfe)
Ш.1. Смешанные графы и их основные части
Определение III. 1. Пусть даны четыре взаимно непересекающихся
множества V, К, К\ К", такие, что К, К\ К" суть равномощные множества и К = 0,
если V = 0. Кроме того, пусть даны семь отображений,
а: К'-+ К, /3: К"-+ К, /': К'-* V, д': К" -> V,
f:K-+V, g:K -> V, ft: if -> У х У U P200 U У,
где 7*2 (V) обозначает множество всех двухэлементных подмножеств из V.
Предположим, что эти отображения обладают следующими свойствами:
1) а и /3 суть биекции;
2) /(«(*')) = /'(?') и </(/?(*")) = g'{k") для А/ € К', к" € * ";
. {/(*),$(*)} «- Л(*) € 7W U 7, дая * € A •
Связи между введенными выше множествами и отображениями
иллюстрируются диаграммой на рис. III. 1.
Тогда мы назовем Н — V U К смешанным графом, ft —его функцией
инцидентности, / — его хвостовой функцией и д — его головной
функцией. Назовем смешанный граф графом, если h(K)DVx V = 0, и орграфом,
если h(K) С V х V. В большинстве случаев граф будет обозначаться через G,
а орграф — через D (понятно, что к ним будут добавляться индексы сверху и
снизу или другие символы, чтобы различать отдельные графы и орграфы).
Определение III.2. Пусть Н = V U К — смешанный граф. Назовем v € V
вершиной, V — вершинным множеством (или множеством вершин) и
используем обозначение V = V(H) (в дальнейшем мы будем использовать
символ V для вершинного множества смешанного графа Я, за исключением
случая, когда одновременно рассматриваются несколько смешанных графов).
Аналогично, полагая Е(Н) := {к G K\ h{k) ?VxV}h A{H) := {k e K\ h(K) €
V х V}, мы назовем Е(Н) реберным множеством (или множеством
ребер) смешанного графа Н, а А(Н) — его дуговым множеством (или мно-
VxVu7?(V)uV
Рис. Ш.1.

III.1. Смешанные графы и их основные части
41
жеством дуг). Если это не может привести к недоразумению, мы будем
использовать Е вместо Е(Н) и А вместо А(Н). Значит, К = Е U А. Кроме того,
для a Е А(Н) назовем /(а) хвостом дуги а и д(а) головой дуги а, в то время
как /(e) и д(е) мы называем концевыми вершинами (концами) ребра е,
если е € Е(Н). Помимо этого, для тех же самых а € А(Н), е ? Е(Н) мы будем
говорить, что а инцидентна из /(а) (или исходит из /(а)) и инцидентна
в д(а) (или заходит в #(а)), в то время, как е инцидентно обеим вершинам
/(e) и д(е). Если b € {а, е}, то будем говорить, что /(b) и д(Ь) смежны или что
Ь соединяет f(b) и/в #(Ь), в то время как Ь,с е К (Н = V U К) называются
смежными, если {/(&),#(&)} П {/(c),g(c)} ^ 0.
Далее мы выделим различные типы ребер и полуребер (дуг и полудуг
соответственно), используя определение III. 1.
Определение III.3. Пусть Н = V U EU А — смешанный граф. Будем
называть е € Е открытым ребром е и a G А открытой дугой а, в то время
как ё := {е,/(e), #(е)} назовем замкнутым ребром е и а := {а, /(а),#(а)}
замкнутой дугой а. Термин ребро (дуга) будет использоваться для
обозначения открытого либо замкнутого ребра (дуги), если явно не оговорено
противное; из контекста будет ясно, какое из понятий имеется в виду.
Аналогично, назовем {е, /(e)} ({е,д(е)}) полуоткрытым ребром е, инцидентным
вершине /(e) (р(е)); полуоткрытые дуги определим аналогично. Назовем
е' € К' (е" G К") полуребром, инцидентным вершине /'(е') (д'(е")), если
h(a(e')) ? V х V (h(f3(e")) g. V х V). Кроме того, назовем е' и е" полуребрами
ребра е, если е = а(е') = /3(е"). Однако в большинстве случаев мы
используем обозначение е' так для е', как и для е"; в тех случаях, когда мы хотим
быть более точными, мы обозначаем полуребро е' (е"), инцидентное v = f'(e')
(w = д'(е")), через e(v) (e(w)). Через Ег С К\ Е" С if" обозначаются
соответствующие множества полуребер, такие, что а(Е') = Р(Е") = Е. Аналогичные
определения вводятся для полудуг. Наконец, назовем ребро или дугу к
петлей, если /(?) = д{к), и обозначим через Av множество петель в v. Положим
А(Н) := (J Av. Если петля а является дугой, можно также говорить, что
v€V(G)
а — направленная, или ориентированная петля.
На основе предыдущих определений введем следующие обозначения для
смешанного графа Н = V U E U А:
Ev := {е е Е\ /(e) = v или д(е) = v},
Е* := {e(v) eE'\J E"\ f'(e(v)) = v и/или g'(e(v)) = v};
соответствующие множества Av С А, А* С A U А" определяются аналогично.
Однако во многих случаях мы хотим уточнить ситуацию с этими множествами
(полу)дуг. А именно, положим
А+ := {aeAv\f(a) = v}, A~ := {aeAv\g(a) =v}.
Таким образом, А~ = Av — А* тогда и только тогда, когда Av П Av = 0.
Множества полудуг (А*) и (Л*) определяются аналогично. Иногда мы
будем также говорить, что а ? A + (а € А~) начинается в и (заканчивается
в v).

42 Глава III. Основные понятия и-предварительные результаты
Основываясь на определении введенных выше множеств, введем
следующие числа (в дальнейшем мы предполагаем, что множества V и К конечны, и
используем символы | V |, | К | для обозначения числа элементов в
соответствующем множестве):
pH~\V(H)\, qH:=\E(H)\ + \A{H)\, А„:=|Л„|.
Назовем р# порядком смешанного графа Я, а <?# — его объемом.
Когда это не может вызвать недоразумения, мы сокращенно записываем
Р •= Рн и q := <?#, а если мы рассматриваем смешанные графы Hi и Н2 , то
будем писать pi := рнг , Р2 •= Ря2 и т- Д- Кроме того,
d(v) := \Е*\ + \А*\ называется степенью или валентностью
вершины г?,
8(H) := min{d(v)\v G V(H)} называется минимальной степенью
смешанного графа iJ,
A(iJ) := max{d(v)\v € V(H)} называется максимальной степенью
смешанного графа Н
следовательно, d(v) =\EV\ + \AV\ +\v , т. е. петля учитывается в d(v) дважды1).
Назовем v нечетной или четной вершиной в зависимости от четности d(v).
Таким образом, получаем следующий важный результат, содержащийся уже в
классической статье Эйлера (см. разд. 17 этой статьи в гл. II).
Лемма III.4. Для любого смешанного графа Н
2q=Y,d(v).
vev
Таким образом, число нечетных вершин в Н четно.
Классифицируя вершины смешанного графа Н по их степеням, положим
(если не оговорено противное)
Vi(H) := {v e V(H)\d{v) = г}
и назовем вершину v € У% (Н) вершиной степени i (г-валентной вершиной). В
частности, 1-валентная вершина называется висячей вершиной смешанного
графа Я", и ребро (дуга), инцидентное (инциндентная) висячей вершиной,
называется висячим ребром (висячей дугой). 0-валентная вершина называется
изолированной вершиной. Граф G с V*(G) = 0 для всех нечетных г,
называется эйлеровым графом. Кроме того, на основании леммы Ш.4 положим
а(Н):= J2 (Ф)-2) = 29-2р;
vev(H)
1) Это совпадает с (современным) общепринятым определением степени. Однако Д. Кёниг
различал два способа подсчета петель при определении d(v); см. [KONI36a, p. 163].

III.1. Смешанные графы и их основные части
43
это число будет использоваться в различных доказательствах по индукции.
Однако если Н есть орграф D = V(D) U A(D), положим для v Е V(D)
od{v)
id(v)
| (A*) |=| A* | , полустепень исхода вершины v ,
| (A*) | = | A~ | , полустепень захода вершины v ,
? (оФ)-1),
откуда следует, что cr(D) = q — р. Это равенство вытекает из такой леммы,
которая может рассматриваться как аналог леммы III.4:
Лемма III.5. Для орграфа D справедливы равенства
q= Y, od(v) = ? id(v)-
vev(D) vev(D)
Вершина v орграфа D называется источником, если id(v) = 0, и стоком,
если od(v) = 0. Заметим, что 0-валентная вершина из D — одновременно
источник и сток, но орграф не обязательно содержит источник или сток. Более того,
лемма III.5 утверждает только, что если od(v) — id(v) > 0 для некоторой
вершины v G V(D), то должна существовать некоторая вершина w E V(D) — {г?},
такая, что od(w) — id{w) < 0. Таким образом, случай, когда
id(v) = od(v) для каждой v E V(D),
является довольно частным. Назовем такой орграф эйлеровым орграфом.
К таким орграфам можно применить лемму III.5 и получить такое
Следствие Ш.5а. Пусть D — орграф, удовлетворяющий условию id(x) =
od(x) для каждой вершины х € V(D) — {v}, где v —фиксированная
вершина из D. Тогда таксисе справедливо равенство id(v) = od(v), т. е. D —эйлеров
орграф.
Орграф D называется /с-регулярным или /с-однородным орграфом
(или просто регулярным или однородным), если id(v) = od(v) = k для
каждой вершины v E У(Т)). Таким образом, /с-регулярный орграф
является эйлеровым по определению. Однако это не так для ^-регулярных или
/с-однородных графов G, которые определяются свойством d{v) = k, v E
V{G)\ они являются эйлеровыми тогда и только тогда, когда к четно. В этом
контексте и в силу лемм III.4 и III.5 мы приходим к вопросу, возможно ли в
общем случае описать степени эйлерова (ор)графа. Таких вопросов мы здесь
не затрагиваем. Достаточно сказать, что читатель сможет построить много
различных эйлеровых (ор)графов после прочтения этой главы. Тем не менее
мы отсылаем заинтересованного читателя к работам [LESN77a, RAOS79a], где
занимаются этим и подобными вопросами.
Окрестность N(v) вершины v смешанного графа Н определяется так:
N{v) := {х Е V(H) - {v}\ (Ех U Ах - Ах) П (Ev U Av - Av) ф 0}.
Положим также N*(v) := N(v) U {v}. Вершина х Е N(v) называется соседом
вершины v.

44 Глава III. Основные понятия и предварительные результаты
Если функция инцидентности h смешанного графа Н = V U E U А
инъективна (т.е. h(e) = h{a) влечет за собой е = а, е,а€^иЛ), то мы записываем
символически е = ху, если е € Е и {/(е),#(е)} = {х,у}, но если a e А и
(/(а),р(а)) = (х,у), то мы пишем а = (х,у). Однако в общем случае h не
обязательно инъективна. Тем не менее мы будем использовать эти символические
равенства, даже если h(e) = h(f) для е^еЕиеф/ или если h(a) = h(b)
для a, b € А и а ф Ь. В этом случае, однако, такие равенства следует
интерпретировать следующим образом: е (а) имеет форму ху ((я, у)). Поэтому мы
говорим о кратном ребре ху (кратной дуге (х, у)), если h(e) = h(f) = {х, у}
для е ф f {h(a) = /1(6) = (х, у) для а ф Ь). По аналогии с тем, что мы делали
для петель, положим
Аху := {е е E\h(e) = {х,у}} , Л(х>у) := {а € А|Л(а) = (х,у)} ,
А(ху) :=| Аху |, Л(х, у) :=| Л(х^) | и назовем эти числа кратностью ребра е = ху
и дуги a = (х, у) соответственно. Наконец, степенью ребра е — ху назовем
d(e) :=d(x) + d(y).
Некоторые из обсуждавшихся выше понятий продемонстрированы на рис. III.2.
н
Рис. III.2. Смешанный граф Н = УиЕиЛ с V = {?,u, u,w,z,y,z}, E =
{е, f,g,ux,zt, zz}, A = {а, 6, (ж, 2), (z,x), (?,?), (y,v), (ги,у)}. Множество висячих
вершин—это {u,v,w}, их —висячее ребро, (ги,у) и (у,г>) суть висячие дуги; А(ху) =
3, А(г,у) = 2, в то время как любое другое ребро или дуга имеют кратность 1;
Az = At = 1, A(G) = {zz, (?,?)}, где (?,?) ориентированная петля; х — единственная
четная вершина в Н.
Заметим, что мы не определили id{s), od(s) для произвольной вершины 5 Е
V смешанного графа Н = V U E U А, который не является орграфом (т. е.
для которого Е ф 0). Мы введем более общие понятия, чем понятие степени,

III.2. Связи между графами и орграфами
45
полустепени захода или полустепени исхода. Для смешанного графа Н = V U
Е U А выберем непересекающиеся множества X,Y CV и положим
E(X,Y) := {е е E\Xn{f{e),g(e)} ф 0 ф Y П {/(e),fl(e)}},
А+(Х,У) := {а € Л|/(а) € Х,$(а) € У},
Л-(Х,Г) := {а € Л|р(о) € Х,/(а) € У},
А(Х, Y):=A+ (X, У) U А~ (X, У).
Следовательно, A+(X,Y) = А~(у,Х), A~(X,Y) = A+(Y,X) и, значит,
A(X,Y) = A(Y,X); равенство E(X,Y) = E(Y,X) вытекает из определения.
Кроме того, свяжем с этими множествами числа
e(X,Y)=\E(X,Y)\, a+(X,Y)=\A+(X,Y)\ и т.д.
Однако для случая Y = V — X мы упростим эти обозначения, полагая
Е{Х) = Е(Х, V-X), е(Х) = е(Х, V - X) и т. д,
и назовем Е(Х) U А(Х) кограницей множества X. Отсюда следует, что
d(v) = e({v}) -f a+({v}) -f a~({v}) 4- 2AV. Таким образом, для х на рис. III.2
мы получаем a+({x}) — a~({x}) = 1, е({х}) — 4. Кроме того, если Н — орграф
D, не имеющий петель, то
e({v}) = 0, a+({v}) = od(v), a~({v}) = id{v) для каждой вершины v € V(D).
В большей части этой книги мы будем допускать, чтобы смешанный граф
Н имел петли и/или кратные ребра, кратные дуги соответственно. Однако
ряд результатов будет справедлив только для тех случаев, когда Х(Н) :=
^vev(H) ^v = 0 и/или Х(к) = 1 для каждого к G E(H) U А{Н).
Следовательно, назовем Н беспетельным, если Х(Н) = 0, а беспетельный смешанный
граф iJ будем называть обыкновенным, если его функция инцидентности
h инъективна. А беспетельный (смешанный) граф (орграф) с кратными
ребрами/дугами назовем (смешанным) мультиграфом (мультиорграфом).
Наконец, в большинстве случаев мы будем использовать термин «смешанный
граф» и обозначение Н тогда и только тогда, когда Е(Н) ф 0 Ф А(Н), за
исключением некоторых рассуждений этой главы и первой части гл. IX.
Ш.2. Некоторые связи между графами и (смешанными)
(ор)графами. Подграфы
Прежде чем развивать дальнейшие понятия, вернемся к определению III. 1.
Там ни одному из отображений не отдавалось предпочтения; они были
связаны между собой свойствами 1), 2), 3). Из этого определения ясно, что если
даже нам заранее дана функция инцидентности /г, это не обязательно
означает, что отображения f',gf,f,g однозначно ею определены. Действительно,
предположим, что Д : К —> V — хвостовая функция, а д\ := К —> V —
головная функция, такие, что Д(а) = /(а) и gi(a) = g(a) для а € А, тогда как для
е ? Е лишь выполняется равенство {/i(e),#i(e)} = {/(e),g(e)}, и определим
/{ : К' —> V и д[ : К" —> V так, чтобы для Д, #i, /{, д[ выполнялось свойство 2)

46 Глава III. Основные понятия и предварительные результаты
определения III. 1 (оставляя, таким образом, отображения а и /3 неизменными).
Тогда для ft,/i,#i справедливо свойство 3) этого определения. Однако если
Ы /ъ #1 заданы и обладают этим свойством 3), то Д и д\ связаны с / и д, как
описано выше. Короче говоря, для заданной функции инцидентности ft и биек-
ций а, /3 хвостовая функция и головная функция (или, эквивалентно, /' и дг)
однозначно определены с точностью до перемены их ролей на элементах из Е.
Однако для целей этой книги мы, исходя из заданного смешанного
графа Н, займемся различными изменениями функции инцидентности.
Определим их более наглядным образом. Например, если А(Н) /0и если заменить
в h(A(H)) каждую упорядоченную пару (f(a),g(a)) множеством {f(a),g(a)}
(т.е. если мы заменим каждую дугу а ребром еа, соединяющим те же самые
вершины), то получим граф, который мы назовем графом G#, лежащим в
основе смешанного графа Н. Результат обратной операции, т. е. замены ребер
е Е Е в графе G на соответствующие дуги ае, будет называться частичной
ориентацией Hq графа G, если E(Hq) ф 0, и ориентацией Dq графа G,
если Dq — орграф. Мы говорим об эйлеровой ориентации Dq графа G, если
id>DG(v) = od,DG(v) для каждой вершины v G V(Dq) = V(G)l>}. Из этого
определения следует, что граф G имеет эйлерову ориентацию, только если он сам
является эйлеровым. Наконец, если в заданном смешанном графе Н = VUEUA
мы заменим каждую пару (я, у) Е h(A) на (у,х), то назовем новый смешанный
граф противоположной или обратной ориентацией HR смешанного графа
Н. Заметим, что обратная ориентация эйлерова орграфа также является
эйлеровой. В действительности во многих случаях нам нужно будет обратить
только некоторые дуги или подмножества дуг Н. Таким образом, обобщая
введенное выше обозначение, обозначим через aR или а~ обратную дугу для а, т. е.
если а = (х,у), то aR = а~ = (у,я) =: (х,у)я, в то время как если Aq С А(Н),
то AR := {aR\a G Aq}. Кроме того, определим для Ко С К, где Н = V U К,
реберно/дугово-индуцированный (смешанный) под(ор)граф (Ко) как
(смешанный) (ор)граф Яо, такой, что V(Hq) — {v ? V\v € к для
некоторого к G Ко} и К (Но) = Хо, где соответствующая функция инцидентности fto
задана формулой ft0 := ft| (В таком контексте понятно, что
соответствующие отображения ао,/?о?/о> <7о>/о>#о определяются аналогично.) В
частности, мы используем обозначение Н — К\ := V(H) U (К — К\), где К\ С К.
Если К\ — {/с}, то будем использовать обозначение Н — к вместо Н — {к}.
Подобным же образом, для Vo С V(H) вершинно-индуцированный
(смешанный) под(ор)граф (Vo) определяется так: V((Vo)) = Vo и K((Vo)) =
ft_1(Vo x VoUT^KOuVb). To есть (Vo) содержит только те ребра и дуги из Я,
которые соединяют элементы из Vo. Определим также для V\ С V(H) смешанный
граф Н — V\ := (V(H) — Vi). To есть если мы удаляем вершину v в i7, то также
удаляем все дуги/ребра, инцидентные ей. В большинстве случаев мы будем
1' Здесь и далее индекс в Dq указывает граф, о котором идет речь. В дальнейшем мы
будем расширять эту конструкцию, отсылая к различным объектам с помощью различных
индексов и/или подиндексов всякий раз, когда это необходимо. В нескольких примерах это
будет сделано без каких-либо специальных пояснений, так как из контекста будет ясно, что
именно означают индексы, которые добавлены к различным определенным объектам
(графам, числам, параметрам и т.д.).

III.2. Связи между графами и орграфами
47
просто говорить индуцированный вместо реберно-индуцированный или дугово-
индуцированный, или вершинно-индуцированный, поскольку символы Ко и Vo
указывают, является ли индуцированный (смешанный) под(ор)граф вершинно-
индуцированным. В общем случае (смешанный) под (ор) граф Яо С Я
определяется с помощью условий V((K0)) С Vo С V(H) и Я0 := (Ко) U (Vo —
V((Ko))). А именно, граф Но получается из Н следующим образом: сначала
берется Н' := Н - К0, где К0 = К(Н) - К0, а потом Я0 := Н' - V, где V =
V(H) — Vo С Vo(Hr). Если Но — (смешанный) под(ор)граф графа Я, назовем Я
надграфом графа Яо . Для смешанного графа Я без изолированных вершин
(т. е. с Vo(H) = 0) и смешанного подграфа Н\ С Я положим H—Hi := (К(Н) —
К (Hi)) = Я — К(Н\) — Vo(H — К(Но)). То есть удаляем из Я все ребра/дуги,
принадлежащие Н\, и все вершины х из Я, для которых dn(x) = йяДх).
Таким образом, Н — Н\ также не имеет изолированных вершин. Наконец, назовем
Яо С Я суграфом или остовным подграфом, если V(Ho) = V(H). Теперь
определим для Ао С А(Н) смешанный граф (Я — Aq) U -Aq*, полученный
из Я обращением ориентации дуг из Ао, приравнивая (Я — Ао) U А§ :=
((К(Н) — Ао) U Aq*), где соответствующая функция инцидентности ^ задана
формулой hi\K(H\__A := ^\к(Н)-л ' в то вРемя как ^i(a) — ^(а)Я5 если а ^ А) •
Заметим, что Gh — СГ(я-л0)иля (см- Рис- Ш-3 и III.4).
Замечание III.6. Рассмотрение смешанного графа Н = VUEUA как
множества с некоторой структурой, наложенной с помощью функции инцидентности
/i, не является общепринятым. Однако этот подход необычайно удобен для
целей настоящей книги. С другой стороны, во многих теоретико-графовых
рассмотрениях обычно имеют дело только с обыкновенными смешанными
графами: это позволит избежать понятия функции инцидентности, просто выбирая
ECV2(V) nACVxV.
В принципе, обсуждение многих тем в этой книге можно было бы
ограничить обыкновенными графами, введя добавочные вершины степени 2 (см.
следующий раздел). Однако в большинстве рассмотрений теории эйлеровых
графов должны допускаться петли и кратные ребра/дуги, потому что
может оказаться необходимым допущение S(Я) > 2 или потому что одна из ее
очень естественных проблем требует рассмотрения смешанных графов с
петлями и/или кратными ребрами/дугами. Эти рассуждения объясняют, почему
первоначально был избран жесткий подход определения основных элементов
графа через различные отображения, а уже потом можно перейти к более
описательному подходу.
Замечание III.7. При рассмотрении множеств Ао С А(Н) и А§ мы получаем,
что AoCiAq- ф 0 тогда и только тогда, когда Ао содержит петлю вида (х, я), х G
V(H). Однако в гл. IX мы будем обсуждать возможность считать, что петлю
хх G Е можно ориентировать двумя способами. Эта возможность необходима
при использовании отображений f\g\f,g, т.е. полуребер и/или полудуг.
Замечание III.8. Использование функции инцидентности, более или
менее существенное при рассматрении смешанных графов с кратными
ребрами/дугами (см. замечание III.6), служит другой цели, которая докажет его

48
Глава III. Основные понятия и предварительные результаты
G - GH = GE
Н-Ц..
±>
HR DR
Рис. Ш.З. (Эйлеров) граф G, частичная ориентация Я графа G, которая
расширена до (эйлеровой) ориентации D графа G. Обратная ориентация DR для D получена
из обратной ориентации Яй для Я.

III.2. Связи между графами и орграфами
G
/ \
Рис Ш.4. Граф G, реберно-индуцированный подграф Gi = ({ei,e2,e3}), вершин-
но-индуцированный подграф G2 = (V(Gi)) ф Gi и суграф G3.

50 Глава III. Основные понятия и предварительные результаты
преимущество в ходе наших обсуждений: во многих рассмотрениях мы будем
получать из заданного смешанного графа Я = VUEUA смешанный граф вида
Н' — V U E U А, т. е. при некотором преобразовании графа будет изменяться
множество вершин V, но не множество К — Е U А, которое рассматривается
как множество, независимое от У, но связанное с V функцией инцидентности h
(см. определение III. 1). Этот подход к графам оказывается особенно полезным,
когда К = К(Н) задано в виде списка ребер/дуг, К = {/i, /2,..., /9}, q — <?я5
т. е. когда мы рассматриваем помеченные ребра/дуги (эти метки могут
также быть целыми числами).
III.3. Графы, получающиеся из заданного графа
Рассмотрим смешанный граф H=VuEuAn предположим, что Е U А ф 0.
Пусть Ъ € ЕU Л; для вершины z 0 V и ребер/дуг &*,Ь** ^ Еи А образуем
Ях = (Я -Ъ) U {г, 6*, 6**},
где Ъ* = xz, b** = zy, если 6 = ху, и 6* = (ж, г), 6** = (г, у), если 6 = (х,у)
(допускается случай х = у). Скажем тогда, что Hi получен из Я
подразбиением ребра/дуги Ь. Для обратной операции, т. е. замены вершины z степени
2 и Ez U Az на ребро/дугу, соединяющую элемент(ы) из N(z), предположим
сначала, что А + ф 0 ф А~ или А2 = 0 и | Е"г U Az |= 2. Тогда мы скажем,
что Я получен из Hi подавлением вершины z. Назовем два смешанных
графа Я и Я* гомеоморфными, если либо Я = Я*, либо один может быть
получен из другого при помощи непустой последовательности подразбиений
некоторых ребер/дуг и/или подавлений некоторых вершин степени 2 (мы
обозначаем это так: Я « Я*). Заметим, что если Я* может быть получен из
Я с помощью такой последовательности, то Я может быть получен из Я*
с помощью соответствующей обратной последовательности подавлений и/или
подразбиваний. Поэтому для каждого смешанного графа Я существует
смешанный граф Яо, такой, что 6(Но) > 2 и Я « Яо при условии, что каждый
2-регулярный реберно-индуцированный подграф из Gh имеет вершину,
которая не 2-валентна в Я, и a+({v}) = a~ ({v}) для каждой вершины v G ^(Я).
Если мы поразбиваем каждое b € Е U К С Н, то назовем получающийся
смешанный граф смешанным графом подразбиений смешанного графа Я и
обозначим его через S(H). Будем обозначать через Sk '= z вершину,
возникающую при подразбиении ребра/дуги /с. Отметим, что Ps(H) = Рн + <?# и
<?5(Я) — 2<?я • Кроме того, отсюда следует, что S(S(H)) —обыкновенный граф
для любого смешанного графа Я; однако в общем случае существует Hi, такой,
что Hi — обыкновенный граф, Hi « Я и рях < Ps(S(H)) • Отметим, что S(H) —
эйлеров граф, если Я —эйлеров (ор)граф. Это объясняет, почему многие
рассмотрения эйлеровых (ор)графов могут быть сведены к случаю обыкновенных
эйлеровых (ор)графов. К тому же, в принципе, элементы из ASk (ESk) можно
интерпретировать как полудуги (полуребра) дуги (ребра) к.
Для следующего понятия предположим, что Я —это граф G = V U Е или
орграф D — V U А. Реберный граф L(G) (реберный орграф L(D))
определяется так: V(L(G)) = Е (V(L(D)) = А) и е/ G E(L(G)) ((a, b) e A(L(D)))

III.3. Графы, получающиеся из заданного графа
51
тогда и только тогда, когда е,/ € Ev (a G A~,6 ? AJ") для некоторой
вершины г; ? V^(G) (г? € У(1))). Отметим, что для обыкновенного графа G граф
L{G) является эйлеровым тогда и только тогда, когда dcie) четна для каждого
е € E(G). Поэтому L(G) является (2fc — 2)-регулярным обыкновенным графом,
если G есть /с-регулярный обыкновенный граф (см. также рис. III.5).
D = Dr
D^Lffi)
Рис. III.5. Граф G, его граф подразбиений 5(G) и реберный граф L(G).
Ориентация D графа G, реберный орграф D\ = L(D) которой удовлетворяет соотношению
GDl С L(G).
Чтобы ввести следующее понятие, которое будет играть центральную роль
во многих частях книги, рассмотрим смешанный граф Н и предположим, что
существует v G V(H) с d(y) > 2 . Предположим, что К* = Е* U А* задано в
виде списка помеченных полуребер и/или полудуг; без ограничения общности
можно считать, что К* — {b[, bf2,..., 6^}, d = d(v). Для Vij 0 V(H) образуем
новый смешанный граф Hij, определенный следующим образом:
V{HUj) := V(H) U К,}, K(Hij) := К{Н),
где соответствующие отображения Д,-,5$,-,/', <?' связаны соотношениями
K'UK"
¦ЩЦ}
JtJ Уг'3\к>ик"-{ьщ} у I
?^. U A*ViJ = {Ь'^} С *Г'(Я^) иГ'(Яу).
То есть iJi,j; возникает из if, если считать полуребра/полудуги Ъ[, 6'- Е ?" * U
А* инцидентными с новой вершиной Vij, которая таким образом становится

52 Глава III. Основные понятия и предварительные результаты
вершиной степени 2 в Hij , оставляя все другие инцидентности неизменными.
Будем говорить, что Hij получается из Н отщеплением ребер/дуг bi и bj.
Кроме того, переход от Н к H^j называется операцией расщепления или
процедурой расщепления.
а)
Ч>
Ь)
Рис. III.6. а) Образование Hij из Н отщеплением bi и bj. b) Стягивание множества
Vo = {щ v,w}, дающее Яу0, и стягивание Но = ({е,/}), дающее Нн0-
Отметим, что bi = bj в том и только в том случае, когда bi = bj является
петлей; в почти всех случаях, однако, Ь[ и bj будут соответствовать различным
элементам из К. Кроме того, для чисто практических целей мы можем иногда
обозначать через Hij смешанный граф, гомеоморфный построенному выше
смешанному графу Hij и имеющий V(H) или V(H) — {v} (если d(v) = 4) в

III.4. Маршруты, цепи, пути, циклы, деревья; связность 53
качества множества вершин (т. е. мы можем рассматривать смешанный граф,
полученный из исходного Hij подавлением вершины Vij)- Из контекста,
однако, будет ясно, который из этих двух графов рассматривается. Кроме того, мы
можем обозначить — также только для практических целей — новую вершину
через г;, а не через Vij и различать исходную вершину v и новую вершину v.
Операция получения Н из Hij содержится в более общем понятии,
обсуждаемом ниже. Если d(v) = 2&, то fc-кратное применение процедуры расщепления
к v приводит к Gv (отметим, что | V^(GV) |=| V2(G) | -Ь /с). Граф Gv единствен,
только если отдельные операции расщепления указаны.
Пусть для смешанного графа Н = V U К выбрано множество Vo С V, и
пусть vq ? V — вершина. Определим новый смешанный граф Ну0 формулами
V0:=V(HVo) = V\j{v0}-Vo,
К0 := K(HVo) = K-{k€ K\{f(k),g(k)} С V0},
и пусть инцидентности в Ну0 — это оставшиеся неизменными инцидентности
для каждой вершины v Е V — Vo , в то время как /о(k) = vo (go(k) — ^о)5 если
f(k) € Vo (g(k) € Vo). Будем говорить, что Ну0 получается стягиванием Vo в
^о. В частном случае, когда V0 = {v,w} и v и w соединены ребром/дугой к G
К, будем писать #& и говорить, что Hk получен стягиванием ребра/дуги
к. Однако в некоторых случаях необходимо, чтобы некоторые (если не все)
элементы из К — К0 представлялись петлями, инцидентными вершине г/о,ив
этом случае ребро (дуга) из Н представляется (не) ориентированной петлей в
Ну0. В частности, если Н0 С (Vo)# и V(#o) = Vo, то
ЯЯо := HVo U Л0> где Л0 = K((V0)h) - К(Н0)
есть множество петель при вершине vo в Нн0- Таким образом, символ Hk
может представлять два различных смешанных графа в зависимости от того,
рассматривается ли к как открытое или как замкнутое ребро/дуга (заметим,
что в последнем случае к можно рассматривать как подграф Щ). Введенные
выше понятия проиллюстрированы на рис. III.6.
III.4. Маршруты, цепи, пути, циклы, деревья; связность
Понятия и результаты этого раздела существенны в целом для теории графов,
а не только для целей этой книги.
Определение III.9. Пусть Н = V U E U А — смешанный граф, К — Е U А.
Чередующаяся последовательность вершин и ребер/дуг
W := t;0,6i,... ,bi,Vi,bi+i,... ,Ьп»ип,
такая, что Vi € V для г = 0, ...,тг, 6* € К для г = l,...,n, {f(bi),g(bi)} =
{vi-i,Vi}, 1 < г < п, называется реберной/дуговой
последовательностью. Обозначим через E(W) (A(W)) множество ребер (дуг), которые
появляются в W, и пусть Xw(b) обозначает число появлений b € К в W. Положим
K(W) = E(W) U A(W), V(W) = {vi\ i = 0,..., n}. Секцией
последовательности W называется подпоследовательность вида fr^i^&i+i, 1<г<п — 1,аее
сегментом — подпоследовательность вида 5r,s = г>г, fcr+i, • • •, &s> vs, такая, что

54 Глава III. Основные понятия и предварительные результаты
vr = ys и каждая секция сегмента 5r?s является секцией последовательности
W. Для сегмента Sr?s из W назовем подпоследовательность &r,?V)S,&s+i из W
расширенным сегментом.
Рис. III.7. Граф G с гамильтоновым циклом С, определенным множеством Е(С) =
{/ci,/c2,/сз,е,/,/с4}. Если мы заменим е и / на д, то получим доминирующий цикл
графа G.
1) Последовательность W называется маршрутом, если f(bi) = vi-\ (и,
таким образом, g(bi) = Vi) всякий раз, когда bi € А, 1 < г < п. Также говорят,
что W начинается в vo и оканчивается в vn (или что W соединяет vq и vn) и
используют обозначение W — W(vo,vn). В случае когда K(W) = A(W), можно
также говорить об ориентированном марп1руте. Назовем маршрут
замкнутым (открытым), если v0 = vn {vq ф vn). Будем говорить о
покрывающем маршруте, если K(W) = К, тогда как У(#)-покрывающий марп1рут
удовлетворяет только условию V(W) = V(H). Покрывающий маршрут
называется двойным проходом или двойной трассировкой, если \\у(Ь) — 2 для
каждого b G К. Назовем п длиной выписанного выше маршрута W и
обозначим эту длину через l(W). Маршрут W называется более коротким, чем W,
если l(W) < l(W).
2) Маршрут называется цепью, если bi ф bj при i ф j, 1 < г, j < п. Замкнутая
покрывающая цепь называется эйлеровой цепью.
3) Открытая цепь W, удовлетворяющая условию l(W) =| V(W) | — 1, есть
путь. Замкнутая цепь называется циклом, если l(W) =\V(W) |; в этом случае
п > О1). У(#)-покрывающий цикл (путь) называется гамильтоновым
циклом (путем). Следовательно, граф Н называется гамильтоновым, если он
имеет гамильтонов цикл, и реберно-(дугово-)гамильтоновым, если каждое
его ребро (дуга) принадлежит некоторому гамильтонову циклу. Цикл С
называется доминирующим, если К(Н — V(C)) = 0. Доминирующие цепи
*) В англоязычной литературе для циклов (в оригинале «cycles». — Ред.) иногда вместо
термина «cycles» используется термин «circuits», а для замкнутых цепей —термин «cycles».
Заметим, что цикл (cycle) должен иметь по меньшей мере одно ребро/дугу.

III.4. Маршруты, цепи, пути, циклы, деревья; связность 55
определяются аналогично. Доминирующий цикл в 3-регулярном графе
называется циклом Татта. Путь, состоящий только из одной вершины и без ребер
(дуг), называется тривиальным путем.
4) Расстояние d(x, у) между х, у ? V(H) определяется как длина
кратчайшего пути, соединяющего х и у, если такой путь существует; в противном случае
d{x,y) := со.
Рис. III.8. Граф G, в котором замкнутый покрывающий маршрут v,ei,
r,e21s,e3,v,e4,t,e5)U,e6,v является эйлеровой цепью. S = {С\, Сг} — цикловое
разложение графа G для С\ = v,ei,r,е2,5,ез,г; и Сг = v,e4,t,es,u,еъ,у.
Определение ШЛО. Система из не обязательно различных циклов S =
{Ci,..., Cm}, m > 1, в смешанном графе Н = V U К называется цикловым
покрытием графа Н (или К(Н)), если K(S) := (J^i K(Ci) = К. Цикловое
покрытие, удовлетворяющее условию K(Ci) П K(Cj) = 0, 1 < г < j < га,
называется цикловым разложением смешанного графа Н (или К(Н)).
Для практических целей мы будем называть S = 0 цикловым
разложением смешанного графа Н тогда и только тогда, когда К{Н) = 0.
Путевым/цикловым разложением смешанного графа Н (или К(Н)) называется
множество S попарно дугово/реберно-непересекающихся путей/циклов графа
Н, такое, что каждая дуга (каждое ребро) к € К принадлежит точно одному
элементу из 5. Цепное разложение определяется аналогично. Множество
попарно вершинно-непересекающихся циклов называется параллельным
классом циклов.
Далее мы изложим некоторые простые результаты.
Лемма IIIЛ1. Пусть W —маршрут в Н, начинающийся в vq и заканчиваю-
щийся в vn. Тогда существует путь P(vo,vn), начинающийся в vq и
заканчивающийся в vn.
Лемма 111.12. Если W(x,у) —маршрут, начинающийся в х = Уо и
заканчивающийся в у = vn, и если W(y,z) —маршрут, начинающийся в у = v'0 и
заканчивающийся в z = vfm, то W := W(x,y), W(y, z) —маршрут,
начинающийся вх и заканчивающийся в z, где в конкатенации этих двух маршрутов,

56 Глава III. Основные понятия и предварительные результаты
разумеется, у = vn — vfQ записывается только один раз. Кроме того,
понятно, что элементы из W(y, z) перепомечены так, чтобы представить W как
маршрут в соответствии с определением III.9.1).
Заметим, что в общем случае лемма III. 11 не может быть усилена до вывода
о том, что если W\ —замкнутый маршрут, начинающийся и заканчивающийся
в v := vo = vn, то Н содержит цикл, начинающийся и заканчивающийся в v.
Действительно, если Н = G есть граф, то обратная последовательность W~l к
маршруту W также есть маршрут. По лемме III. 12 W\ = W, W~l начинается
и заканчивается в одной и той же вершине. Следовательно, если W — путь, то
W\ — W,W~X не может содержать никакого цикла. Однако если Н = D есть
орграф, то указанное выше усиление леммы III. 11 верно. Но также мы имеем
следующее утверждение.
Лемма III. 13. Если W — замкнутая цепь в Н, начинающаяся и
заканчивающаяся в v = vo = vn, и K(W) ф 0, то в W существует
подпоследовательность С, являющаяся циклом, который начинается и заканчивается в v.
Леммы III. 11 и III. 12 порождают следующие определения и замечания.
Определение III. 14. Граф G называется связным, если для произвольных
я, у ? V(G) существует маршрут W(x,y) и, таким образом, по лемме III. 11
путь Р(х, у), соединяющий х и у. Орграф D или смешанный граф Н
называется слабо связным, если граф Gd или G# соответственно является связным.
В дальнейшем для смешанных графов Н с А(Н) ф 0 вместо термина слабо
связный будет использоваться термин связный, при условии, что это не
вызовет путаницы. Смешанный граф, который не является (слабо) связным,
называется несвязным. D (Н) называется сильно связным, если для любых
х,у € V(D) (x,y € V(H)) существуют пути Р(х,у) и Р(у,х). Максимальный
связный (слабо связный) (смешанный) под(ор)граф графа G (смешанного
графа Н соответственно) называется (связной) компонентой (слабо связной
компонентой) в G (D,H соответственно). Сильно связной компонентой
орграфа D является максимальный сильно связный подорграф из D (см.
также рис. III.9).
Однако для того чтобы проверить (сильную) связность (ор)графа, нам не
обязательно рассматривать все пары вершин.
Лемма III.15. Пусть G (D) —{ор)граф, V = V{G) (= V(D)), и пусть
выбрана фиксированная вершина v E V. Граф G (орграф D) является (сильно)
связным тогда и только тогда, когда для каждой вершины w ? V — {v} в G
(в D) существует (существуют) путь P(v,w) (пути P(v,w), P(w,v)).
В действительности каждый граф G (D,H) является объединением своих
непересекающихся (слабо связных) компонент.
Таким образом, число c(G) (c(D),c(H)) (слабо связных) компонент графа G
(орграфа D, смешанного графа Н) однозначно определено, так же как и число
сильно связных компонент орграфа. Более того, Н несвязен в том и только в
том случае, когда с(Н) > 1.

III.4. Маршруты, цепи, пути, циклы, деревья; связность 57
^—<сД
D = DG
Рис. III.9. Связный граф G и ориентация D графа G. Сильно связные компоненты
орграфа D являются слабо связными компонентами С\ и Сч орграфа D — ае. Граф
G — е является несвязным.
Замечание III.16. Пусть W — маршрут в Н. Рассмотрим
подпоследовательности W\ и W2 , состоящие исключительно из ребер/дуг маршрута И^ииз его
вершин соответственно,
Wl = 6i,62, - - - ,ЬЛ , W2 = v0,ui,...,un .
Из определения III.9.1) следует, что W может быть восстановлен, если известна
только последовательность W\, и то же самое справедливо для W2, если Н —
обыкновенный граф. Однако даже если Н не обыкновенный граф, но является
орграфом, может иногда оказаться достаточным рассмотреть произвольную
дугу а вида (ifi,Vi+i) вместо фиксированной дуги, соединяющей Vi с V{+\ • В
любом случае мы также будем говорить о последовательности W\ или W2j
определенной выше, как о маршруте, и то же самое относится к специальным
типам маршрутов, таким, как цепи, пути, циклы и т.д. Например, это дает
возможность рассматривать цикловое разложение как разбиение множества
К(Н) при условии, что элементы из W\ и К(Н) рассматриваются
одновременно как замкнутые (открытые) ребра/дуги. Подобным же образом, мы не
будем различать цикл С или путь Р из определения III.9.3) и смешанный граф
(К(С))н или (К(Р))н соответственно1). Хотя это соглашение может снизить
уровень строгости доказательств, оно определенно не уменьшает их ясности.
Аналогично, если выписанная выше последовательность W2 соответствует
пути, будем иногда обозначать этот путь через (И^) (а иногда пойдем и дальше,
используя запись W2 для неупорядоченного множества, когда это не вызывает
путаницы). В случае цикла используем обозначение {W2 — {vn}) вместо (W2).
Определение III. 17. Пусть для смешанного графа Н = VUK заданы Vq С V
и К0 С К.
1) Назовем Vb (Ко) разделяющим вершинным (реберным/дуговым)
множеством, если с(Н — Vo) > с(Н) (с(Н — Ко) > с(Н)). Будем также
говорить, что Vo (Ко) разделяет Н и что пустое множество разделяет iJ, если
х) Большинство авторов не различают цикл (путь) и граф, индуцированный этим циклом
(путем).
V

58 Глава III. Основные понятия и предварительные результаты
Н несвязен. Мы можем также использовать более короткий термин —
вершинный разрез—для Vo и реберный разрез или разрезающее множество
для Ко. Минимальное разрезающее множество Ко С К в Н
определяется следующими свойствами: Ко — разрезающее множество, но никакое
собственное подмножество из Ко не является разрезающим множеством.
Наименьшим разрезающим множеством называется разрезающее множество
наименьшей мощности (таким образом, наименьшее разрезающее множество
является минимальным разрезающим множеством, в то время как обратное
неверно). В случае когда с(Н — (Vo U К0)) > с(Н) и Vo Ф 0 Ф Ко, назовем
Vo U Ко смешанным разрезом (слово «смешанный» относится к Vo U Ко,
содержащему одновременно вершины и ребра/дуги). Разрезающее множество
мощности п называется n-разрезом. Заметим, что непустая кограница
является разделяющим реберным/дуговым множеством.
2) В частном случае, когда | К0 |= 1 и К0 разделяет Я, назовем элемент из К0
перешейком. Подобным же образом, если Vo = {vo} разделяет Н или если
О < \VQ ф d(vo) — 1, то назовем vo точкой сочленения или разделяющей
вершиной (заметим, что если AUo = d(vo) — 1, то vo —либо висячая вершина,
либо инцидентная петле вершина степени 2).
3) Смешанный граф называется неразделимым, если он не содержит
точек сочленения1). Максимальный неразделимый (смешанный) под(ор)граф В
смешанного графа Н называется его блоком. Число блоков, содержащих и,
называется блоковым числом вершины v и обозначается через bn(iJ, v);
число блоков из Н называется блоковым числом для Н и обозначается через
Ьп(Я). Наконец, если блок В С Н содержит точно одну точку сочленения из
Я, то назовем его висячим блоком смешанного графа Н. Если Н неразделим,
можно также назвать его блоком.
Перешейки и точки сочленения могут быть охарактеризованы следующим
образом.
Теорема III. 18. Для смешанного графа Н = V U К справедливы следующие
утверждения:
1) k G К является перешейком тогда и только тогда, когда ни один цикл из
Gh we содержит е^ G E(Gh) (e-k = k, если k e E С К).
2) к € К — перешеек тогда и только тогда, когда V(H) может быть
разбито на два класса V и V" так, что для произвольных вершин v' G V, v" e
V" каждый путь P(v\v") в Gh содержит е^ G E{Gh) {^k = k, если
k G E С К). Кроме того, если к — перешеек, Н — к имеет точно две
(слабо связные) компоненты С',С", такие, что V — V(C'), V" — V(C").
3) Концевая вершина v перешейка является точкой сочленения в том и
только том случае, когда d(v) > 1. Следовательно, висячее ребро
является перешейком, тогда как перешеек не обязательно является висячим
ребром.
1) Заметим, что неразделимый подграф В из Н может содержать вершины, которые
являются точками сочленения смешанного графа Я, в то время как они не являются точками
сочленения подграфа В по определению.

III.4. Маршруты, цепи, пути, циклы, деревья; связность 59
х
2
х3^
х1
X
4
Рис. 111.10. Граф G с 2-разрезом Ео = {е, /} и перешейком д. Разрез Ео
является минимальным, но не наименьшим разделяющим множеством графа G. Точки
сочленения графа G суть и и v) блоки графа G суть В\ = ({А}),?2 = ({д}),Вз =
({х\,Х2,хз,Х4,и}). В\ и Вз являются висячими блоками, а Бг нет.
4) Вершина v является точкой сочленения тогда и только тогда, когда
Ьп(Я» > 1.
5) Если Н — смешанный граф без петель, то вершина v является точкой
сочленения тогда и только тогда, когда V{H) — {v} может быть
разбито на два класса V, V", такие, что для произвольных v' Е V, v" E V"
каждый путь P(v',vf/) в Gh содержит v.
6) v E V(H) является точкой сочленения в том и только том случае, когда
Н содержит {смешанные) под(ор)графы Н\,Н2, такие, что
H = HlUH2, ЯхПЯз^М и dHl(v)^0^dH2(v).
Блоки также обладают рядом интересных свойств и связаны с перешейками
и точками сочленения согласно следующему результату.
Лемма III. 19. Пусть Н — смешанный граф, имеющий по меньшей мере два
блока, и пусть В и В' —различные блоки из Н. Тогда имеют место
следующие утверждения:
1) В — (V(B))h , тп. е. блоки суть максимальные вершинно-индуцированные
подграфы без собственных точек сочленения, если Н — смешанный граф
без петель.
2) Если \К(В) |> 1, то каждое ребро из Gb принадлежит циклу графа Gb-
Если | К {В) |=1, то элемент из К (В) есть либо перешеек, либо петля
вН.
3) ВПВ' = 0 или BOB' = {v} uv— точка сочленения смешанного графа Н.
4) Каждое ребро {дуга) k E К{Н) принадлежит некоторому блоку в Н.
Таким образом, множество блоков покрывает Н.
Далее мы определим один важный класс графов (см. также рис. III. 11).

60 Глава III. Основные понятия и предварительные результаты
T = G DT = DG
Рис. 111.11. Каркас Т графа G. Т соответствует дереву Dt из корня х для
ориентации Dg графа G.
Определение III.20. Пусть if —смешанный граф.
1) Если Н не содержит циклов, то назовем его ациклическим. Если Gh не
содержит циклов, то назовем Н лесом. (Слабо) связный лес является
деревом. Если Но С Н является суграфом в Н (т. е. V(Ho) = V(H)) и деревом, то
назовем Но каркасом (остовным деревом) смешанного графа Н.
2) Предположим, что Н = D — орграф. Дерево Т С D называется
выходящим или растущим из корня г;о (входящим или растущим в корень vo)
(или коротко деревом из корня v0 (деревом в корень u0))j если для
некоторой вершины vq ? V(T) С V(D) путь P(v0,v) (P(v,vq)) в Г существует для
каждой вершины v Е V(T) — {vo}. Если (op)дерево Т в корень или из корня
г>о является суграфом в iJ, то мы говорим, что Т есть каркас, входящий в
корень или выходящий из корня vq.
Относительно каркасов (в корень или из корня) имеется следующий
классический результат.
Теорема III.21. Каждый связный смешанный граф имеет каркас. Каждый
сильно связный орграф D имеет каркас в корень (из корня) vq € V(D), где
vo — произвольная заданная вершина.
Теорема 111.21, в частности, применима к слабо связным эйлеровым
орграфам, так как они являются сильно связными. Конечно, не каждый сильно
связный орграф D является эйлеровым, так как Gd может не быть эйлеровым
(см. разд. Ш.2). Однако для ориентации графов верно следующее утверждение
[ROBB39a].
Лемма III.22. Граф G имеет сильно связную ориентацию Dg тогда и
только тогда, когда он связен и не имеет перешейков.
Доказательство. Если Dg сильно связен, то G — связный граф. Мы
утверждаем, что он не может иметь перешейков. В противном случае и Dq — o.^ и G—е
несвязны для некоторого перешейка е в G. По теореме Ш.18.2) существуют
такие вершины х,у G V(G) = V(G — е), что каждый путь Р(х,у) содержит е.

III.4. Маршруты, цепи, пути, циклы, деревья; связность 61
Отсюда следует, что Dq не может содержать никакого пути из а: в у или не
может содержать никакого пути из у в х. Следовательно, G должен не иметь
перешейков. Это завершает первую часть доказательства.
Построим сильно связный орграф D, в основе которого будет лежать граф
G, следующим образом. Так как G — граф без перешейков, то каждое его ребро
принадлежит циклу, т. е. G имеет цикловое покрытие (случай qc = 0, pg = 1
тривиален)
S = {Ci,..., Cm}.
Так как G связен, будем предполагать без потери общности, что индексы в
S выбраны таким образом, что
( U СП П С*+1 # Я. 1 < * < ™ - 1- (!)
Пусть D\ —орграф, в основе которого лежит граф Ci, где С\ преобразован
в ориентированный цикл Cf. Орграф А сильно связен. Предположим теперь,
что для г > 1 уже построен сильно связный орграф Di с Gdi — \Sj=i^j-
Преобразуем Ci+i € 5 в ориентированный цикл С^.г (выбирая одну из двух
возможных ориентации произвольно). Теперь положим
г
А+1 = A U К € А{СЦг)\е ? (J E(Cj)}
3=1
и допустим, что существует вершина v Е V(Di+i) — V(Di); в противном случае
Di+i сильно связен по аналогии с А- В любом случае ZVn слабо связен
согласно (1). По лемме III. 15 достаточно показать, что для каждой вершины w ф v
(v та же, что и выше) существуют пути P(v,w),P(w,v) в ?>г+ь соединяющие
v и ty, w и v соответственно. Мы ограничимся доказательством
существования пути Р(г?,гу), так как доказательство существования пути P(w,v) можно
провести подобным же образом.
Пройдем в С?+г из v в х, первую вершину, тоже принадлежащую Di, и
обозначим этот путь через P(v,x) С С?+г. Если w € V(C^_X) — V(Di), то пройдем
в Di из х в последнюю вершину у, содержащуюся в V^C^) П V(Di) и в
единственном пути из v в к; в орграфе С^ (возможно, х = у), а затем продолжаем
идти по Cf+x изуъи), тем самым строя путь Р(х, гу). Если w ? V{C^.l) — V{Di)^
то {x,w} С V(25i), и путь P(x,w) существует по индукции. Таким образом, в
любом случае
W(v,w) := P(v,x),P(x,w)
является открытым маршрутом в ?Vfi из г; в гу, который содержит требуемый
путь P(v,w) по лемме 111.11. Лемма 111.22 доказана.
Однако мы будем также рассматривать (ор)графы, которые лежат, в
некотором структурном смысле, между определением 111.20 и леммой III.22. А
именно, назовем граф унициклическим, если он имеет точно один цикл, и
назовем Dq циклической ориентацией графа G, если Dq содержит по
крайней мере один цикл.

62 Глава III. Основные понятия и предварительные результаты
Лемма III. 19 не полностью описывает структуру смешанного графа Я в
отношении его блоков и точек сочленения. Определим граф блоков и точек
сочленения be (Я) следующим образом:
V(bc(H)) = {B,v\B — блок смешанного графа Я, г; —его точка сочленения},
ху Е Е(Ъс(Н)) тогда и только тогда, когда {х,у} = {B,v} и v ? V(B) для
некоторой точки сочленения v и некоторого блока В из Я.
Предложение III.23. Граф Ьс(Я) ациклический. Он является деревом
тогда и только тогда, когда Я слабо связен.
Однако предложению III.23 должно соответствовать какое-то утверждение
об орграфах и их сильно связных компонентах. В отличие от графов не верно,
что каждая дуга орграфа принадлежит одной из его сильно связных
компонент. Суммируем некоторые свойства орграфов.
Предложение III.24. Пусть D —орграф с V(D) ф 0. Имеют место
следующие утверждения:
1) Если D ациклический, то он имеет по крайней мере один источник и по
крайней мере один сток.
2) Если S := {Di,..., Dr} — множество сильно связных компонент Di из D,
то {V(Di),..., V(Dr)} является разбиением множества V(D) (заметим,
что Di может состоять из единственной вершины, и в этом случае мы
назовем компоненту Di тривиальной).
3) Пусть S определено так же, как в п. 2), и A(S) := Ui=i A(Di). Дуги из D,
не принадлежащие циклам из D, являются элементами из A(D) — A(S).
4) Пусть S определено, как в п. 2), V1 := V(Di), 1 < г < г, и A(S) определено
так же, как в п. 3). Положим Н~ := Н — A(S) и образуем
A-ed :=(-.. ((Ну1)у2) . . .)уг.
DTed) редуцированный орграф, является ациклическим. Его
определение не зависит от последовательности, в которой совершаются
стягивания множеств Vх, 1 < г < г.
5) Согласно пп. 1) и 4), D содержит сильно связные компоненты D\D",
такие, что a+(V(D')) = 0 = a~(V(Dff)). Они нетривиальные, если D не
имеет ни источника, ни стока.
6) Если D имеет точно одну сильно связную компоненту D', такую, что
а+ (V(D')) = 0, то D имеет каркас в произвольную, но фиксированную
вершину v G V(D').
Граф be (Я) напоминает другой граф, используемый для описания
некоторых структур (но не является его частным случаем). Пусть S =
{Mi,...,Mfc}, k > 1, —конечная система (не обязательно различных)
множеств Мг, г = 1,..., к. Определим граф пересечений I(S) с помощью
формул
V(7(5)) = 5, EMi П EMj П E(I(S)) ф 0 <-> (г ф j Л М, П М, ф 0),

III.4. Маршруты, цепи, пути, циклы, деревья; связность 63
предполагая, что \Ем{ П Ем3\ < 1- Таким образом, 7(5) по этому
определению—обыкновенный граф. В некоторых случаях будем допускать, что I(S) —
мультиграф. В этом случае мы предположим, что \Mi П Mj |< oo, и положим
Kei,j) =\МгП Mj | для eij e EMi П EMj, гф 3-
Для графов пересечений верно следующее утверждение:
Предложение III.25. Для смешанного графа Н пусть S = {i?i,... ,Нт} —
система слабо связных подграфов Hi С Н, т > 1. Если |j?Li Hi = Н (т. е.
S покрывает Н), то существует взаимно однозначное соответствие
между слабо связными компонентами из Н и компонентами из I(S). Это
утверждение остается верным при любом из двух возможных определений
графа /(5).
Заметим, кстати, что реберный граф обыкновенного графа G можно
интерпретировать как (обыкновенный) граф пересечений для Mi := {ё*}, где
E(G) = {eu...,eq}.
Следующий результат довольно часто используется различными авторами;
он будет важен в этой книге. Первое его доказательство дано в [FLEI76a, Satz l]
для случая графов.
Лемма III.26 (лемма о расщеплении). Пусть Н — (слабо) связный
(смешанный) (ор)граф без перешейков. Предположим, что существует v € V(H) с
d(v) > 3. Образуем Hi ? иН\^ отщеплением Ъ\ ,62 ? Kv 1161,63 €
Kv
соответственно (см. разд. III.3) и предположим, что Ь\ и 6з принадлежат различным
блокам, если v —точка сочленения в Н. Тогда либо #i,2, либо Н\^ является
(слабо) связным и не имеет перешейков. В частности, если v — точка
сочленения, то Я^з обладает этим свойством. Наконец, если В С Н —блок,
такой, что {61,62,63} С Ку П К (В), то и Н\$, и #1,з связны.
Доказательство. Согласно определениям понятий, использованных в этой
лемме, достаточно рассмотреть случай, когда G = Н — граф; положим е^ :=
6г, 1 < г < 3. Если какое-либо из этих ребер — петля Л, то образование Gij для
j = 2 или j = 3 равносильно подразбиению в G—А другого ребра, участвующего
в процедуре расщепления. Однако удаление висячего блока или подразбиение
ребра в связном графе без перешейков приводит к связному графу без
перешейков (ср. предложение III.23), и петля — висячий блок. Таким образом, можем
предположить без ограничения общности, что е» 0 Л(С), г = 1,2,3. Кроме
того, так как удаление и/или добавление петель в G или Gij не создает
перешейков, не изменяет число перешейков и ни влияет на (не) связность G и G\j ,
можно предполагать без ограничения общности, что A(G — {б1,е2,ез}) = 0.
Таким образом, A(G) = 0 согласно предыдущему рассуждению. Каждое
ребро е € E(G) содержится в некотором цикле С(е) С G, так как G не содержит
перешейков (теорема Ш.18.1)). Для е = в\ это означает, что С\ := С(в\)
преобразуется в путь Pi, соединяющий vij и v в G\j, j € {2,3}, тогда и только
тогда, когда ej ? С\. Выведем несколько заключений из этого факта.
1) Существование Р\ С Gij гарантирует связность графа Gij: связность
графа G означает, что для произвольной вершины х ? V(G) — {v} существует

64 Глава III. Основные понятия и предварительные результаты
путь P(x,v) С G, который также является путем, соединяющим х и v в Gij ,
или P(x,v) U Pi содержит такой путь (см. леммы III. 11, IIL12, III. 15).
Из 1) следует 2):
2) Либо Gi,2 связен, либо vi^ и v принадлежат различным компонентам
графа Gi,2 и ei,e2 не являются перешейками этого графа (заметим, что в
этом случае ei,e2 E Gi, и применим теорему Ш.18.1)). Однако {е^ег} есть
2-разрез в G тогда и только тогда, когда Gi,2 несвязен.
3) Граф Gi,3 связен в любом случае. Если бы это было не так, {ei, ез} было
бы 2-разрезом в G (см. последнее предложение в 2)), откуда следовало бы, что
г? — точка сочленения из G, содержащаяся в блоках В\ D {ei, ез} и В^ D {ег}, в
противоречие с выбором е\ и ез (см. теорему Ш.18.4), 5) и первое предложение
в приведенном выше заключении 2)).
Еще одно свойство графа G\j выражается следующим образом:
4) Если G\j является связным, но имеет перешейки, то каждый путь
P(vij,v) содержит все перешейки графа Gij : если это не так для некоторого
PQ = P(vij,v), то каждый перешеек из Gij, не содержащийся в Р0, также
является перешейком в G (см. теорему III. 18.2); заметим, что стягивание vij
и v дает граф G и преобразует Pq в цикл графа G). Однако G —граф без
перешейков.
Оставшаяся часть доказательства разделяется на два основных случая.
I) Пусть г; —точка сочленения графа G. Граф Gi,3 связен (см. 3)), е\ и ез
принадлежат различным блокам графа G по предположению, и существуют
циклы С\ D {ei}, G3 D {ез}. Из теоремы Ш.18.5), леммы Ш.19.3) и
предложения 111.23 следует, что С\ П G3 = {v}. Поэтому Ст соответствует пути
Рг в Gi,3, г = 1,3 (см. рассуждение, предшествующее заключению 1)), и
Рх п Рз = {vi,jiv}- Теперь из 4) следует, что Gi,3 не имеет перешейков,
откуда вытекает справедливость леммы, если v — точка сочленения.
II) Пусть V — не точка сочленения. Из 2), 3) и теоремы Ш.18.6) следует,
что оба графа Gi,2 и Gi,3 связны. Из теоремы Ш.18.6) также следует, что G — v
связен. Поэтому для Vi E h(ei) — {г?}, г = 1,2, существует путь Р(г;х,г;2) С G—v\
таким образом, P(vi, V2) U {ei, ег} есть цикл Gi,2 как в G, так и в Gi,2 • Теперь
предположим, что Gi52 имеет перешеек. Рассмотрим путь Р = P(vi^^v) в Gi52 •
Согласно 4), он содержит все перешейки из Gi,2 • Начинаем проход по Р в vij.
Пусть z есть последняя вершина, инцидентная некоторому перешейку из Gi,2 ;
обозначим этот «последний» перешеек через ez. Ясно, что z ф v: в противном
случае образуем граф Gi}2 — ez, который имеет точно две компоненты, скажем
С и С", такие, что vij2 € V{Cf), v € V(C") (см. теорему Ш.18.2)). Однако,
рассматривая в G подграфы G\ = {E(Cf) U {ez}) и G2 = {E{C")), из теоремы
Ш.18.6) получаем, что г; —точка сочленения, в противоречие с
предположением. Снова рассмотрим компоненты С' D {vi^} и С" D {v} графа Gi,2 — ez • Мы
утверждаем, что ез € Е(С") не является перешейком в G", иначе по
аналогии с предыдущим рассуждением (но с ез вместо ez) можно снова заключить,
что v есть точка сочленения. Поэтому, так как ез —не перешеек в С", в С"
существует цикл С$ D {ез}; он также является циклом в Gi,2 и G. Однако
G' := {E{C'))G и G" := (E{C"))G удовлетворяют условию G' П G" = {v}; та-

III.4. Маршруты, цепи, пути, циклы, деревья; связность 65
ким образом, С\ := Gi,2 С G' и Сз С G" удовлетворяют условию С\ ПСз = {v}.
Теперь продолжаем, как в случае I). Лемма справедлива, так как случай I)
доказан, а последняя часть леммы есть прямое следствие заключения 2).
Однако неверно, что если Н = D сильно связен, то D\^ или Di,3 также
является сильно связным (и, таким образом, слабо связным и не имеет
перешейков). Это становиться ясным, если {а1,а2,аз} С А+ (С А~), когда v\$
является источником (стоком) и в J5i,2j и в -Di,3. Но даже если a± Е A+ и
а2,аз ? А~, то ни Г>1,2> ни ?>1,з не могут быть сильно связными. С другой
стороны, так как слабо связный эйлеров орграф в действительности является
сильно связным, то приведенное выше рассмотрение не будет иметь никаких
отрицательных последствий.
Нам также понадобится еще один результат, когда происходит отщепление
дуг в орграфах. Здесь символ Dij будет означать, что нами отщеплены а~ Е
А- иа+ Е А+.
Лемма III.27 (лемма о двойном расщеплении). Пусть D — слабо связный
орграф без перешейков, имеющий вершину v с d\ := id(v) > 3 и d2 := od(v) > 3.
Пусть А~ — {aj~,..., a^}, A + = {af,..., aj2}; и предположим, что оба графа
?>1?з и Di^ не имеют перешейков и слабо связны1^. Если оба графа (?>1,з)4,2
и (-^1,3)2,4 несвязны, то по крайней мере один из графов (1)1,4)2,3 м (#1,2)4,3
слабо связен и не имеет перешейков.
Доказательство. Для того чтобы по возможности сократить доказательство,
мы применим части доказательства леммы III.26. Для этой цели рассмотрим
G := Gd , Gi,3 := (Gd)i 3 » ег := ea-, fj = еа+ и т.д. Предположим, что оба
графа (Gi,3)4,2 и (61,3)2,4 несвязны. Рассуждая так же, как в доказательстве
леммы III.26, мы можем предположить без ограничения общности, что G не
имеет петель, и из заключения 2) доказательства этой леммы следует, что
{^45/2} и {ег,/*} являются 2-разрезами в Gi,3 . Можно даже сделать вывод,
что блоки #4,2 Э {е4, /2} и ?2,4 D {б2, /4} графа G\$ различны: а именно, они
соответствуют блокам В'42 '-= {Е(В^2)) и В'24 :— (Е(В2^)) в обоих графах
(61,3)4,2 и (Gi,3b,4- Вспомним теперь определение Ш.17.3) и заметим, что
соотношение c((Gi,3)4,2) = c((Gi,3)2,4) = 2 влечет за собой В'А2 П В24 = 0
в обоих графах (61,3)4,2 и (61,3)2,4 и, таким образом, ?4,2 П J92,4 = {v} в графе
Gi,3- Однако в силу последнего равенства и леммы III.19.3) ?4,2 Ф Дм и v
является точкой сочленения. Кроме того, Gi,3 не имеет перешейков и петель.
Из этого и из леммы Ш.19.2) следует, что #4,2 (Дм) содержит цикл 64,2 Э
{е4, /2} (G2,4 Э {е2, /4}), такой, что G4,2 П G2,4 = {v} в графе Gi,3 •
Теперь рассмотрим в Gi,3 блок Bi^ D {еь/з} и сравним его
положение в bc(Gi,3) с положением блоков ?4,2, #2,4 и вершины v. Для этой
цели образуем F := bc(Gi,3) — {vB2^}, где г>В2,4 Е ?"(bc(Gi,3)) соединяет г>,
#2,4 ? V(bc(Gi,3))- Согласно предложению III.23, bc(Gi,3) —дерево, которое
является ациклическим графом, из чего следует, что vB2^ — перешеек и по-
х) Согласно лемме о расщеплении, можно предположить, что если какой-либо D\j несвязен
или имеет перешейки, то j = 2.

66 Глава III. Основные понятия и предварительные результаты
тому F является лесом с точно двумя компонентами Т\ и Т2 . Без
ограничения общности можно предполагать, что В2,± € ^(Гг); тогда ?4,2 € V(Ti),
так как vB^^ ? E(F), в то время как г? и #2,4 принадлежат различным
компонентам леса F (ср. теорему III.18.2)). Однако мы могли бы рассмотреть
vB±? вместо t>i?2,45 так как В2,± и ^4,2 играли до сих пор симметричные
роли. В любом случае можно предположить без ограничения общности, что
#1,з € V(Ti). Мы получили, что В^з Ф ?2,4, но равенство ??1,з = ?4,2 мож^т
выполняться. В любом случае В\$ содержит цикл 61,3 ^ (еь/з}> такой, что
Ci,3 П Сг,4 Q {^}> где равенство достигается, только если v € V(Bi^)- Заметим
также, что dB2t4(v) = dB4,2(v) = ^в1)3(^1,з) = 2> так ка* fa, ft} и {е4,/2} суть
2-разрезы.
ДЛЯ V0 = {^2,4,^1,3} С V((Gij3)2,4) ПОЛОЖИМ Go := ((<?1,з)2,4)у0 (^2,4 —
новая вершина, полученная отщеплением в2 и /4). В самом деле, bc(Go)
удовлетворяет равенству bc(Go) = FU {г>о,г>о #1,3 ^0^2,4}, где vq есть вершина,
полученная стягиванием Vo, и обозначения для блоков сохраняются при переходе
от Gi,3 к Go • По построению Т\,Т2 С bc(Go); таким образом, каждая вершина
из Т\ может быть соединена с v путем. Это верно и для vo, так как
присоединение vq,vqBi? к пути P{Bi^,v) дает требуемый путь. Так как В2^ ? ^№), то
каждая вершина из Т2 может быть соединена вТ2 с 1?2,4 путем, который может
быть продлен с помощью vq и P{Bi$,v) до пути, оканчивающегося в v. Таким
образом, bc(Go) связен (ср. лемму 111.15), и реберные множества блоков — одни
и те же в Gi?3 ив Go (только положение блоков изменено).
Однако образование (61,4)2,3 теперь равносильно расщеплению vo
соответственно в ui,4 и ^2,з? так что EVl4 = {ei, /4}, EV2Z = {е2, /з}- Для простоты
сохраним обозначения для объектов, рассматривавшихся до сих пор. Таким
образом, в Go мы имеем Сг^ПСх.з = {^0}? так как B2^Bi^ = {^о}- Поэтому
образование графа (Go)i,4 = (61,4)2,3 (операция расщепления применяется к vq)
преобразует G2,4 и Ci,3 в два пути Р2,4 и Pi,3, такие, что P2,4nPi,3 = {^1,4, ^2,3}-
Теперь из заключения 2) в доказательстве леммы о расщеплении следует, что
(61,4)2,3 связен. Этот факт, последнее равенство и заключение 4) из
доказательства леммы о расщеплении устанавливают, что (Go)i,4 = (61,4)2,3 не имеет
перешейков. Это завершает доказательство.
Определим другой смешанный граф в связи с множествами разрезов.
Определение III.28. Пусть Н = V U К — слабо связный смешанный граф, и
пусть Ко —разрезающее множество вида Ко = К(Х) для некоторого X с V.
Образуем Н0 := Н — К0, и пусть Н[ = (Х)н0,Н2 = (V — Х)н0 (отметим, что
каждая компонента смешанного графа Но инцидентна в Н по меньшей мере
одному к € Ко, а это означает, что любая компонента из Но принадлежит
целиком Н[ или целиком Н2). Определим для г = 1,2 и Zi ? V(H) смешанный
граф
Щ := (У(Щ) U {*}) U (К(Щ) U Ко)
с теми же инцидентностями на V(H[), что и в Я, и с KZi = Ко (отметим,
что Щ слабо связен, как и Н). Назовем Н\ U Н2 перевязью Н(Ко) графа Н
относительно Ко (см. также рис. IV.2 ниже).

III.4. Маршруты, цепи, пути, циклы, деревья; связность 67
Перейдем к характеризации деревьев. Для этой цели назовем Н = V U К
пустым графом, если V = К = 0, и тривиальным графом, если К = 0,
V — {v}. По определению с(0) = 0.
Теорема III.29. Для непустого смешанного графа Т следующие
утверждения эквивалентны:
1) Т — дерево.
2) Т слабо связен и qr = Рт — 1-
3) Т слабо связен и каждое k G АГ(Т) является перешейком в Т.
4) Либо qr = Рт — 1> И) СО = 0 ^ с(Г — fc) = 2 для каэюдого k G К(Т), либо
Т — тривиальный граф.
5) Т слабо связен и с(Т — v) = d(v) для каждой вершины v G У{Т).
6) Л(Т) = 0 и для любой фиксированной вершины vq G V(T) и произвольной
вершины v G V(T) — {vo} существует единственный путь P(vo,v) С Gt •
Теорема Ш.29.2) дает такое
Следствие III.30. Если F —лес, то qp = Pf — c(F).
Деревья в корень и из корня характеризуются следующим образом.
Теорема III.31. Пусть Т — слабо связный орграф. Следующие утверждения
эквивалентны:
1) Т — дерево в корень (из корня) vq.
2) od(v) = 1 (id(v) = 1) для каждой вершины v G V(T) — {vo}, тогда как
od(v0) — 0 (id(vo) = 0) для (корня) v0 G V(T).
3) Т — ациклический орграф и существует точно одна вершина vq G V(T),
такая, что для каждой вершины v G V(T) — {vo} существует
единственный путь P(v,v0) С Т (P(v0,v) С Г).
Сравнивая деревья с неразделимыми смешанными графами, мы можем
сказать, что неразделимые графы имеют более высокую степень связности, чем
деревья; за исключением случая |V|<2h|jRT|<1, каждое дерево Т содержит
точку сочленения, тогда как неразделимый смешанный граф Н на том же
самом множестве вершин точек сочленения не содержит. То есть граф Т — v
несвязен, в то время как Н—v связен для каждой вершины v G V(T) — V\(T). To
же самое происходит при удаление единственного k G К(Т), к G К(Н)
соответственно. Мы имеем даже более сильный результат в этом направлении. Для
того чтобы сформулировать его, введем понятие блочной цепи, означающее
такой смешанный граф #, что Ъс(Н) является (возможно, тривиальным) путем.
Теорема III.32 [DIRA67a, Theorem 1]. Если Н — VUK — неразделимый
смешанный граф с \К\ > 1, то Н — к —блочная цепь для каэюдого k G К. Если
Ръс(Н-к) > 1? то концевые вершины ребра/дуги к принадлеэюат различным
висячим блокам из Н — к и не являются точками сочленения в Н — к.
Но даже среди неразделимых смешанных графов можно выделить
различные степени связности. Полные графы Кп, полные двудольные графы
Кш,п и полные симметрические орграфы if*, п > 1,ш > 1, суть —в
известном смысле —те (ор)графы, которые можно рассматривать как графы с

68 Глава III. Основные понятия и предварительные результаты
наивысшей степенью связности. Они определяются следующим образом (из
практических соображений множества вершин не указываются):
Кп : Ркп = n, qKn =(?), h(E{Kn)) = V2{V{Kn)) .
if*:p^=nl№. =2Q),
h(A(Kn)) = V(K*n) x V{K$ - {(x,x)\x e V(Kn)} .
Km,n : V{Km,n) = V'U V", V'nV" = 0, \ Vr |= m, | У |= n
QKm,n = mn, h{E(Km,n)) = {{x,y}\x eV',y? V"} .
Отметим, что множество блоков графа G на рис. III.9 состоит из одного
экземпляра К2 и двух экземпляров К% , тогда как граф G с рис. III. 11 есть
(экземпляр) К±.
В этом контексте назовем граф G дополнением графа G (с п вершинами),
если E{G) П E(G) =0,GuG = Knn V(G) = V{G) = V(Kn). Отсюда следует,
что и G, и G суть обыкновенные графы и G = G.
В любом случае мы подошли к следующему определению.
Определение III.33. Обыкновенный смешанный граф Н = V U К с р
вершинами называется к-связным, если /с < р и iJ — V7 связен для каждого
подмножества V С V с | V7 |< /с. Будем говорить, что iJ имеет связность А:,
обозначая это через к(Н) = /с, если Н /с-связен, не (А: + 1)-связен. Если,
однако, Н не обыкновенный граф, то положим к(Н) = 1, если Н имеет петлю, и
/c(G) = 2, если G является мультиграфом.
Из этого определения следует, что если Н несвязен, то к{Н) = 0; если
Н связен, то он 1-связен; к(Т) = 1, если Т — нетривиальное дерево; если Н
неразделим и не имеет перешейков, то к{Н) > 2. В частности, к(Кп) = к{К^) —
п — \ и к{Кш^ — min{ra, n}. Кроме того, отсюда следует, что если к(Н) =
к > 2, то существует вершинный разрез Vc мощности А:, или, иначе, G# 2
-Kfc+i, к + 1 = рн • Таким образом, связность может быть определена через
вершинные разрезы наименьшей мощности. Для следующего результата нам
нужны дополнительные понятия.
Определение III.34. 1) Два пути Р\ и Р2 называются внутренне
непересекающимися или просто непересекающимися (или независимыми), если
¦Pi П Р2 С Vi(Pi) П V\(P2). Они называются тотально непересекающимися,
если РгГ)Р2 = 0.
2) Пусть х,г/ — две несмежные вершины смешанного графа Н (т.е. Кр %
Gh для р — рн)- Локальная связность к(х,у) определяется через
наименьший вершинный разрез Ус, такой, что х и у принадлежат различным
компонентам из Н — Vc. Будем также говорить, что Vc отделяет х от у.
Следующая теорема играет центральную роль в теории графов.
Теорема III.35. Для обыкновенного смешанного графа Н uk € N, k < р# —1,
верны следующие утверждения.
1) Для каждой пары несмежных вершин х, у Е V(H) к{х,у) есть
наибольшее число попарно непересекающихся путей в Gh, соединяющих х и у, и
к(х,у) > к(Н) (теорема Менгера [MENG27a]).

III.4. Маршруты, цепи, пути, циклы, деревья; связность 69
2) Граф Н k-связен тогда и только тогда, когда для любых х,у Е V(H),
х фу, существует к попарно внутренне непересекающихся путей в Gh,
соединяющих х и у [WHIT32a]1).
Существует несколько доказательств теоремы Менгера; мы отошлем
заинтересованного читателя к [DIRA66a] и [McCU84a]. Заметим, что в первой
работе перечислено несколько ранних доказательств этой известной теоремы,
а в последней содержится очень короткое доказательство этой теоремы для
орграфов, из которого исходную теорему легко получить (в контексте
орграфов, однако, определение множества вершин, отделяющих х от у, данное в
[McCU84a], отличается от определения Ш.34.2)).
Однако мы будем также использовать и другие типы связности.
Определение III.36. 1) Пусть Н — смешанный граф, и пусть ?s — множество
реберных/дуговых разрезов в Н. Положим
X(H):=mm{\Ks\\Kse?s}
и назовем это число реберной связностью графа Н. Кроме того, будем
говорить, что Н /с-реберно-связен, если Х(Н) > к. Кроме того, А (ж, у)—
локальная реберная связность — есть мощность наименьшего К3 € ?3,
отделяющего х от у (т. е. х и у принадлежат различным компонентам из Н — Ks).
2) Для таких жеЯи^, как в п. 1), назовем Кс € ?s циклическим
реберным/дуговым разрезом или циклическим разрезающим множеством,
если Gh-kc имеет две компоненты, каждая из которых содержит цикл. Для
?с := {Кс € ?s\Kc есть циклическое разрезающее множество} положим
Ас(#) := {min{|i^c| \KC G ?с} если ?с ф 0;
в противном случае
( min{|ii:s| \К8е?аиН-К8
. (и. I имеет две нетривиальные
с^ I компоненты}, если такие Ks существуют,
I А(Я"), если таких Ks нет,
и назовем это число циклической реберной связностью2). Аналогично,
назовем Н циклически fc-реберно-связным, если ХС{Н) > к.
Минимальная степень, связность и реберная связность подчиняются
следующим неравенствам:
Лемма III.37. Для любого смешанного графа Н
к(Н) < А(Я) < 5(H) и А(#) < Ас(#).
Однако вполне может выполняться неравенство Ac(i7) > 5(H). С другой
стороны, в случае 3-регулярных графов (которые также называются куби-
*) Неравенство в утверждении 1) обычно опускается, так как оно —прямое следствие
определений III.33 и III.34. Кроме того утверждения 1) и 2), как, впрочем, и определения III.33
и III.34, формулируются обычно только для графов. Это ограничение, однако, не приводит
к потере общности.
2) См. [FLEI89a]. Заметим, что ?с = 0 тогда и только тогда, когда V(C\) П V(C2) ф 0 для
любых циклов С\, Сг С Gh •

70 Глава III. Основные понятия и предварительные результаты
ческими графами) логичная верхняя оценка для ХС(Н) есть обхват #(G#)
графа G# , т. е. длина наименьшего цикла (графа G#).
Для того же класса графов мы имеем даже следующее утверждение:
Лемма III.38. Пусть G есть Z-регулярный граф, такой, что «(G) < 3. Тогда
/c(G) = A(G) = Ac(G).
Доказательство. Если G несвязен, то каждая его компонента является
3-регулярной и, таким образом, имеет цикл. Отсюда следует, что 0 = «(G) =
A(G) = AC(G).
Если «(G) = 1, то каждая точка сочленения vc графа G инцидентна
перешейку из G. Это очевидно, если один из блоков, содержащих vc, есть петля.
В случае когда G — vc имеет две или более компонент, для по крайней
мере одной из них, скажем Ci, точно одно е € EVc соединяет vc с С\ в G. То
есть е отделяет С\ от G — V{C\). Отсюда следует, что A(G) = 1. Кроме того,
ни одна из компонент из G — е не является деревом: в противном случае
такое дерево было бы нетривиальным и, таким образом, имело бы две висячие
вершины, которые были бы соединены с G — V{C\) четырьмя ребрами, —
очевидное противоречие. Таким образом, каждая компонента из G — е имеет цикл
и 1 = k(G) = A(G) = AC(G).
Наконец, предположим, что «(G) = 2. Отсюда следует, что G не имеет
петель и имеет вершинный разрез {х, у}. Компонента С из G — {х, у} соединена в
G с обеими вершинами х и у, так как «(G) > 1. Таким образом, С «всасывает»
по крайней мере два ребра из ExUEy. Пусть С' — компонента из G — {х, у} — С.
Если С или С' соединены двумя ребрами с х и у, то эти два ребра образуют
2-разрез Ес. Предполагая, что обе компоненты СиС соединены по меньшей
мере, а значит, и точно тремя ребрами схиу, можно заключить без
ограничения общности, что С соединена с х точно одним ребром еиС соединена
с у точно одним ребром /. Тогда {е, /} есть 2-разрез ЕС1 такой, что х и у
принадлежат различным компонентам из G — Ес. Значит, 2 = «(G) = A(G).
Однако ни одна компонента Со из G — Eq не является деревом, где Е$ есть
произвольный 2-разрез; в противном случае мы можем заключить, как и
прежде, что Go соединяется с G — V(Co) по меньшей мере четырьмя ребрами —
снова противоречие. Таким образом, A(G) < AC(G) < 2 , из чего следует, что
2 = «(G) = A(G) = AC(G). Это доказывает лемму.
Попутно заметим, что лемма III.38 будет не верна, если мы заменим 3 на 4.
Пример приведен на рис. 111.12.
Интересно, что теорема III.35 имеет аналог для реберной связности (см.
[HARA69a, теорема 5.11] о ее независимом открытии различными авторами).
Теорема III.39. Пусть Н — смешанный граф. Справедливы следующие
утверждения:
1) Для x,yG У(П) число \(х,у) есть наибольшее число попарно реберно-
непересекающихся путей в Gh, соединяющих х и у, и А(х,у) > Х(Н).
2) Граф Н является k-реберно-связным тогда и только тогда, когда каэюдая
пара его вершин может быть соединена в Gh по крайней мере к реберно-
непересекающимися путями.

III.4. Маршруты, цепи, пути, циклы, деревья; связность 71
Рис. 111.12. 4-регулярный граф G с k(G) = 3, X(G) = 4, AC(G) = 6.
Мы завершаем этот раздел неравенством, связывающим реберную
связность и наибольшее число попарно реберно-непересекающихся каркасов.
Следующее утверждение, опирающееся на работы Татта и Нэш-Вильямса
[TUTT61a, NASH61a] (см. также [NASH64a] об обобщении на случай
наибольшего числа попарно реберно-непересекающихся лесов), доказано в [KUND74a,
Theorem 2].
Лемма III.40 (лемма Полесского—Кунду). Пусть к € N, u пусть G есть
к-реберно-связный граф без петель. Тогда число попарно
реберно-непересекающихся каркасов графа G больше или равно |~^у^] {\х~\ обозначает наименьшее
целое число, не меньшее чем х).
Доказательство. Основой для доказательства является следующий
результат Татта и Нэш-Вильямса (см. [TUTT61a, NASH61a]). Для графа G без петель
пусть Р = {V, V",..., \ДГ)} — разбиение множества V(G). Положим qp = qcp,
где Gp = (... (Gv)v" • • -)у(г) считается графом без петель. Тогда G имеет к
реберно-непересекающихся каркасов в том и только том случае, когда
qp > k(r — 1) (*)
для каждого разбиения Р множества V{G) (г =| Р | может изменяться, когда
изменяется Р).
Теперь пусть nr(G) обозначает наибольшее число попарно
реберно-непересекающихся каркасов графа G. Придавая иную интерпретацию неравенству
(*), можно сказать, что должно существовать разбиение Ро множества V(G) с
г0 :=|Р0|, такое, что
№0<(MG) + l)(r0-l)-l. (**)

72 Глава III. Основные понятия и предварительные результаты
Рассматривая Gp0 и применяя лемму III.4, получим
2№о = ]Г d{x) < 2((nT(G) + 1)(г0 - 1) - 1) =: *о- (1)
яеП^Ро)
Следовательно, Gp0 имеет вершину хо, степень которой не превосходит
До = 5й. Согласно определению Gp0, -E^q ^- -^(^Ро) можно интерпретировать
как кограницу Е(У^) С E{G), где Jro соответствует хо , и
k <\E{V^)\=\EXQ\< Ы, (2)
так как G /с-реберно-связен. Используя (1) и (2), получим
к < ^ = 2(nr(G) + 1) • !:LZ^ - - < 2(nr(G) + 1),
го го г0
т.е. ut{G) > | — 1. Лемма доказана.
III.5. Совместимость, циклический порядок множества
К* и соответствующие эйлеровы цепи
Понятие совместимости, одно из центральных понятий этой монографии,
занимало значительное место в моих исследованиях с 1975 г. Некоторые коллеги
(например, Джексон, Жеже, Буше) также были увлечены этим предметом.
Это понятие восходит к вопросам, поднятым и исследовавшимся впервые Ко-
цигом (эйлеровы цепи) и затем Сабидусси (цикловые разложения). Термин
совместимый, разъясненный далее, принадлежит Сабидусси1).
Определение 111.41. 1) Рассмотрим множество К* в смешанном графе
Н = V U К, v ? V(H). Разбиение P(v) некоторого множества М* С К*
называется (частичной) системой разбиения в v, если М* = К* (М* ф К*).
Далее, Р{Н) := \Jvev(H) P(v) называется (частичной) системой разбиения
графа Я, если М* = К* для каждой вершины v € V(H) (M* ф К* для по
крайней мере одной вершины v € V(H)), где М* = \JaeP(v) ^* Если каждый
класс в P(v) имеет точно два элемента, то будем говорить о (частичной)
системе переходов Х(у) в г; и соответственно назовем Х(Н) := UveV(H) X(v) —
(частичной) системой переходов графа Н.
2) Две (частичные) системы разбиения Pi(H),P2(H) назьгоаются
совместимыми, если для каждой вершины v € V(H) и {i,j} = {1,2}
выполняется соотношение Сг % Cj для каждого d ? Pi{v) С Рг(Н) и каждого
Cj <Е Pj(v) С Pj(H). Если предпочтение отдано Pi (Я), то будем говорить, что
Р2(Н) является Р1(Я)-совместимым, вместо того чтобы говорить, что Р\{Н)
и P<i (Н) являются совместимыми (это будет уместно в тех случаях, когда Н —
(ор)граф и Pi{H) соответствует его эйлеровой цепи (см. ниже).
*) Некоторые коллеги считали, что лучше подходит термин ортогональный. Однако
Сабидусси, я сам и другие решили сохранить термин совместимый — возможно, в силу явной
инертности, возможно, из-за недостатка воображения.

III.5. Совместимость, циклический порядок, эйлеровы цепи 73
Заметим, что по определению III.41.2) две (частичные) системы
переходов Xi(H),X2(H) являются совместимыми тогда и только тогда, когда
Xi(H) П Хг(#) = 0, так как t\ С ?2 влечет за собой ti = t2, где t\ € X\(v)
и t2 € X2(v). На самом деле это обычный способ определения
совместимости для систем переходов. Отметим, что из существование системы переходов
Х(Н) следует, что d(v) = 0 (mod 2), т.е. G# — эйлеров граф. Кроме того,
заметим, что существует взаимно однозначное соответствие между системами
переходов Х(Н) и цепными разложениями S графа Gh] а именно, t Е Х(Н)
тогда и только тогда, когда t соответствует секции некоторого элемента из
S. Таким образом, когда мы говорим о цепном разложении S графа G#, то
обозначаем соответствующую систему переходов через Xs- Кроме того, будем
называть Si, S2 совместимыми цепными разложениями, если Xs1 и Xs2
совместимы. В наших исследованиях совместимости мы будем фокусировать
внимание на случае (ор)графов, причем либо
a) Si, i € {1,2}, имеет точно один элемент (т.е. Т € Sz — эйлерова цепь
(ор)графа G (D), и в этом случае мы используем обозначение Хт вместо Xsi),
либо
b) элементы из Si суть циклы и/или пути в G (D).
Если 6(H) = 2, совместимых цепных разложений графа Gh не может
существовать просто потому, что система X(v) для v Е У2(Н) однозначно
определена. Следовательно, будем либо предполагать, что 6(H) > 2, либо считать,
что системы переходов (или разбиения) определены на V(H) — V2(H) (они
являются, строго говоря, частичными системами переходов (разбиения)), либо
молчаливо предполагать, что V(H) — V^i?) есть область определения
системы Х(Н). Кроме того, если X = Xs — частичная система переходов, где S —
цепное разложение графа Gh > и если S' С S (Н' С Н), то обозначим через
X\s' (X\w) ограничение системы X на S' (на Нг), т.е. X\s> = X П Xs*
(Х\н< = {t Е X\t С ?*(#') U А*(Н')}).
Для того чтобы ввести другие классы эйлеровых цепей, нам необходимо
еще одно понятие.
Определение III.42. Рассмотрим v Е V в смешанном графе Н = V U К.
Предположим, что К* ф 0. Для d =\K* |= d(v) пометим элементы К*
произвольным (но фиксированным образом), К* = {Ь[, Ъг2,..., bd}, и назовем любой
d-набор
0+(K*v) :=0+(v)&{(b'ilb^1,...,b'd+i_1)\i = l,...,d,
причем считается, что d + 1 = 1}
(положительным) циклическим упорядочением полуребер и/или
полудуг, инцидентных v. Назовем Ь[ и bfi+l соседями в 0+(v), г = l,...,d.
Обычно мы будем писать 0+(v) = (Ь[,Ь2,... ,bd). Для заданного 0+(v) =
(Ь'ц b'2, • • •, bd) определим отрицательное или обратное циклическое
упорядочение множества К*, полагая 0~(v) = (b[, bd,..., bf2). Пусть
Q+(ff) := {0+(v)\v Е У(Я)} , О"(Я) := {0~(v)\v Е У(#)}1}.
*) 0+(G)— это по существу тоже самое, что и классическое понятие вращательной схемы
вложения; см. [BEHZ79a, p. 104] для определения и ссылок.

74 Глава III. Основные понятия и предварительные результаты
е4
а) X Ь)
е2/ ^з *г/ \*з
Рис. III.13. Вершина степени 4 v с О4"(г;) = (ei,e2, e^e^) и а) непересекающиеся
переходы {ei,e2}, {e^e^}, b) пересекающиеся переходы {е^ез}, {е^е^}.
Понятие 0+(Я), будучи полезным инструментом при исследовании графов,
вложенных в поверхности (и для этого я использовал его сначала), может
также служить основой для определения двух различных типов эйлеровых
цепей.
Определение III.42.а. Пусть Т = vo,ki,vi,..., kn,vn, vn = vq, — эйлерова
цепь смешанного графа Я, и предположим, что задано 0+(Я). Назовем Г
А-цепью, если для каждой вершины v Е У(Н) и каждого t € X{v) С Хт
выполняется равенство t = {Ь^,&^+1}, где bj является j-м членом в 0+(г;), т.е.
последовательные ребра/дуги в Т (инцидентные вершине v) соответствуют
соседям в 0+(v). Назовем Т непересекающейся эйлеровой цепью, если для
любых v e У(Я), ti,t2 € X(v) С Хт, где tx = {6-,6J} ^ *2 = {K,Va} (&•
является г-м членом в 0+(г?)) и, что не ограничивает общности, г < j, г < s и i < г,
мы имеем либо s < j , либо j < r, I <i,j,r,s < d = d(v). Соответственно, если
два перехода ?i, ?2 обладают этим свойством, то назовем их
непересекающимися переходами, в противном случае — пересекающимися переходами
(см. также рис. III. 13).
Заметим, что если 0+(Н) задано и если А(Я) = 4, то А-цепи и
непересекающиеся эйлеровы цепи эквивалентны] действительно, если d = d(v) = 4, то
мы обязательно имеем либо i = 1, j = 4, г = 2, 5 = 3, либо г = 1, j = 2, г = 3,
5 = 4. Отсюда следует, что как Ь\ и Ьр так иЬ'ги bfs являются соседями в 0+(v).
В случае d = 2 существует только один переход, и в 0+(г;) = 0~(v) два члена
суть соседи по определению. Мы также заметим, что в том же самом случае
Д(Я) = 4 можно определить А-цепи (непересекающиеся эйлеровы цепи) как
Р(Я)-совместимые эйлеровы цепи при условии, что 0~*~(Н) задано. А именно,
если d(v) = 2, К* = {e(v), f(v)}, то пусть {е(г>)}, {f{v)} Е Р(Н), тогда как если
d(v) = 4 и 0+(г>) = (6^,63, b'3, ^)> пусть {6'15 63}, {62> ^4} € Р(Н)\ таким образом,
Р(Я) — корректно определенная система разбиения.
Мы заканчиваем этот раздел замечанием, что в случае обыкновенного
графа Я определения Р(Н),Х(Н),0+(Н) не требуют использования
полуребер/полудуг. В таких случаях мы можем время от времени обращаться к
определению этих понятий через разбиения и циклические упорядочения множе-

III.6. Паросочетания, факторизации, двудольные графы 75
ства Kv , v G V(H). Однако уже в случае, когда e,f ? ЕХГ)ЕУ (т. е. когда
существуют кратные ребра), может иметь место включение {е, /} Е Х(х)Г)Х(у). Это
может усложнить некоторые рассуждения. Из-за этого и потому что мы
допускаем в общем случае петли и кратные ребра, использование полуребер/полудуг
в приведенных выше определениях очень удобно.
Ш.6. Паросочетания, 1-факторы, 2-факторы,
1-факторизации, 2-факторизации,
двудольные графы
Определение III.43. Пусть Н = V U К — смешанный граф. Множество
М С К или М С V называется независимым, если никакие два элемента
из М не являются смежными (мы можем также говорить о множестве
независимых ребер или вершин). Независимое множество ребер/дуг называется
паросочетанием. Паросочетание М является максимальным паросочета-
нием, если не существует паросочетания М' со свойством М С М' С К\ М —
совершенное паросочетание, если V((M)) = V(H). Если Н = G — граф и
М — совершенное паросочетание, то назовем М 1-фактором или линейным
фактором. В общем случае fc-фактором графа Н = G или орграфа Н = D
является fc-регулярный остовный под(ор)граф Н. Для смешанного графа Н
fc-факторизацией называется его разложение (т.е. разбиение множества
К(Н)) на А;-факторы; граф Н тогда называется fc-факторизуемым.
Отметим, что 2-факторизация в графе (1-факторизация в орграфе) —это
специальный тип циклового разложения и что гамильтонов цикл графа G
(орграфа D) есть 2-фактор графа G (1-фактор орграфа D). Следующие два
результата являются «классическими» [РЕТЕ91а]. Первая теорема может быть
доказана с помощью леммы о расщеплении (лемма 111.26).
Теорема III.44. Каэюдый 3-регулярный граф без перешейков имеет
1-фактор.
Доказательство. Докажем несколько более сильный результат, а именно:
если задано произвольное / G E(G), где G — кубический граф без перешейков,
то существует 2-фактор Q с G, такой, что / G Q (следовательно, E(G) — E(Q)
является 1-фактором графа G). Этот результат, безусловно, верен, если G —
мультиграф на двух вершинах. Поэтому предположим, что р := рс > 2. Если
/ € ЕаГ\Еи для некоторых а, и G V(G), то существует такое ребро е € Еи C\EV,
что v G V(G) — {а, и}. Образуем С := Ge, стягивая е на vq 0 V(G). Степень
d>G'{vo) равна 4, тогда как другие вершины графа Gf остаются все еще
вершинами степени 3; кроме того, EVo = Еи U Ev — {e}. Граф G' связен и не имеет
перешейков, но vq может быть точкой сочленения. Пусть теперь / = Ъ\ € EVo
и {^2,63} = Evo П Ev. Если vq —точка сочленения в С, то никакой блок из G'
не содержит всех ребер 61,62563- Поэтому применение леммы о расщеплении
(лемма 111.26) гарантирует, что по крайней мере один из графов G[ 2 »Gi 3 свя"

76 Глава III. Основные понятия и предварительные результаты
_^.
\ S
G'= G„
Г
_^V_
6J.:
ИЛИ
л
Рис. III. 14. Расщепление ребра е двумя возможными способами: сначала
стягивание е, чтобы получить G\ затем расщепление vo подходящим образом.
зен; без ограничения общности можно считать, что этим свойством обладает
G'12 (см- также рис. III.14)1).
По индукции можно показать, что G[ 2 имеет 2-фактор Q' э {&i,2}5 где
&i,2 — ребро, возникающее из &i и b%. Если Q' не содержит единственного ребра
gf € E(G'l2) — (E{G)U{bi^}), то Q' соответствует 2-фактору Q графа G, такому,
что /, е,&2 € Q. В оставшемся случае рассмотрим С' —цикл в Q\ содержащий
*) Прямой переход от G к G\,i с помощью расщепления ребра е (которое можно
интерпретировать как комбинацию реберного стягивания с процедурой расщепления), где G[ 2 —
связный граф без перешейков, составляет сущность теоремы Фринка (см. [KONI36a, p. 182-
186]).

III.6. Паросочетания, факторизации, двудольные графы 77
bi,2 и д'. В зависимости от структуры цикла С либо С соответствует циклу
С в G, такому, что EVo С Е(С), либо он преобразуется в два цикла С\ и Сг,
такие, что / € Е(С\), {62,63} С Е(С2). Положим Q\ = {С} в первом случае и
Qi = {Ci,C2} во втором, и пусть Q = (Qf — {C'})\JQ\. Это в действительности
2-фактор графа G, содержащий / (но не е). Этим завершается доказательство
теоремы.
Теорема III.45. Каждый 2к-регулярный граф имеет 2-факторизацию.
К сожалению, теорема 111.45 оказывается неверной, если заменить 2 на 1.
Однако в одном важном случае она будет верна. Для дальнейшего вспомним
определение Кт,п.
Определение III.46. Смешанный граф Н = VUK называется двудольным,
если V = ViUV2, V\C\V2 = 0, K({V{)) = K((V2)) = 0 для некоторых Vu V2 С V.
По аналогии с нашим определением дополнения графа назовем граф G\
двудольным дополнением двудольного графа G, если E{G\) П E(G) = 0,
Gi U G = Кт,п, V{G{) = V(G) = V{Km,n).
Двудольные смешанные графы можно охарактеризовать следующим
образом.
Теорема III.47. Смешанный граф Н двудолен тогда и только тогда, когда
каждый цикл Gh имеет четную длину.
Следующий результат также является «классическим» и принадлежит
Кёнигу [KONI16a] (см. также [КОМЗба, р.170-171].
Теорема III.48. Каждый k-регулярный двудольный граф имеет 1-фактори-
зацию.
Рис. III. 15. Граф Петерсена Р$.
Кроме того, заметим, что уже Петерсен сам показал, что не каждый 3-ре-
гулярный граф 1-факторизуем. Граф Петерсена Р5 является наименьшим
примером этого типа (см. рис. III. 15).

78 Глава III. Основные понятия и предварительные результаты
На самом деле теорема III.45 и теорема III.48 эквивалентны; мы их
докажем во второй части этой книги. Однако мы разовьем специальные типы
1- и 2-факторизаций в полных графах (см. [KONI36a, p. 157-163], где также
содержатся отсылки к литературе по поводу двух следующих теорем, включая
[LUCA83a]; см. также [HARA69a, теоремы 9.1, 9.6]).
Теорема III.49. Для любого целого п > 1 полный граф К2П имеет 1-фак-
торизацию С = {Lo, Li,..., ?271-2}, такую, что Li U Lj является гамильто-
новым циклом всякий раз, когда 1 < |г — j\ < 2 или г ? {2п — 2, 2п — 3} и j = О,
или i = 2n — 2uj = l.
Доказательство. Обозначим вершины из К^п через
2тг - 1,0,1,2,..., п - 1, -(п - 1),..., -2, -1 (*)
и определим 1-фактор Lo, полагая
L0 := {(2n - 1)0} U {г(-г)/1 < г < п - 1}. (**)
Оставшиеся 2п — 2 1-факторов получаются с помощью циклического вращения
нумерации вершин, показанной в (*), за исключением вершины 2п — 1:
вообразите, что все вершины, кроме 2п — 1, представленны вершинами правильного
(2п — 1)-угольника С^п-х, упорядоченными по часовой стрелке, как показано
в (*). Вершина 2п — 1 может быть помещена внутрь С<т-\ как точка
евклидовой плоскости, которая не принадлежит ни одной диагонали многоугольника
C2n-i- Таким образом, мы получим всего 2п — 1 1-факторов Lo,... , L2n-2,
каждый того же вида, что и в (**). Сначала покажем, что Li П Lj = 0 для
г ф j; без ограничения общности можно считать, что i = 0. Следовательно,
1 < j < 2n - 2.
Предположим, что ребро е = r(—r) G Lo также принадлежит Lj, r >l,j >
1. Вершина г Е V((Lo)) имеет в V({Lj)) метку г + j, если г -f j < n — 1; в
противном случае она имеет метку — (2(тг — 1) — (г + j — 1)) = г + j + 1 — 2п.
Аналогично, (—г) G ^((Lo)) имеет в F((Lj)) метку — r + j, если —r + j < п — 1;
в противном случае она имеет метку — (п — 1 — (—г + (j — n))) = j — г + 1 — 2п.
Так как е € Lo HL^, то е имеет в Lj форму k(—k) (отметим, что каждое ребро,
инцидентное 2п — 1, принадлежит точно одному L^, 0 < г < 2п — 2). Отсюда
следует, что либо
г + j = —(—г + j) = г — j, либо
г + j + 1 - 2п = -(j - г + 1 - 2п) = г - j - 1 + 2п.
Эти равенства дают j = 0 или j = 2n — 1, в противоречие с 1 < j < 2n — 2
(отметим, что другие две возможные комбинации для к и (—к) приносят
арифметически ложное утверждение 2j = 2n — 1). Получаем, что С = {Lo, Li,..., L271-2}
есть 1-факторизация графа i^2n-
Теперь мы докажем существование гамильтоновых циклов, описанных в
утверждении теоремы. Для этой цели достаточно рассмотреть LoULi и Lin-i^^i
в силу вращательной симметрии, с помощью которой 1-факторы в С связаны
друг с другом. Рассмотрим сначала Lq U Li: пусть Рц_<5, S = 0,1, —путь в

III.6. Паросочетания, факторизации, двудольные графы 79
Lo U Li, начинающийся в 2п — 1 вдоль ребра (2п — 1)6 и следующий
«зигзагу», индуцированному описанной выше геометрической интерпретацией графа
К2п • Записывая Pi+<5 как последовательность вершин, 5 = 1,2, получим
Рх=2п- 1,0,2, -2,4, -4,..., -(п - 3), п - 1, -(п - 1),
Р2 = 2п- 1,1, -1,3, -3,5,..., п - 2, -(п - 2),
если п нечетно, тогда как для четного п
Р1=2п- 1,0,2, -2,..., -(п - 4), п - 2, -(п - 2),
Р2 = 2п - 1,1, -1,3,..., (п - 3), -(п - 3), (п - 1), -(п - 1).
Однако так как (тг — 1)(—(п — 1)) G Lo, то (—(п — 1))(—(п — 2)) € 1а. Теперь
получаем, что Pi,P2_1 —вершинные последовательности гамильтонова цикла
графа if2n для произвольного п > 1.
Наконец, рассмотрим L2n_2ULi. Опять определяем пути, следующие
«зигзагу». Однако теперь рассмотрим четыре пути: Р\ и Р2 начинаются в 0, их
первые ребра суть 02 и 0(—2) соответственно, Рз и Р* начинаются в 2п — 1, их
первые ребра будут (2п — 1)1 и (2п — 1)(—1) соответственно. В зависимости от
вычета n (mod 4) мы различаем следующие два главных случая.
Случай 1. Положим гп = 1, если п = 1 (mod 4), и гп = —1, если п = 3 (mod 4).
Снова записывая пути как последовательности вершин, имеем
Р1 = 0, +2, -4, +6,..., (-rn)(n - 1),
Р2 = 0, -2, +4, -б,..., (+гп)(тг - 1),
Р3 = 2п - 1, +1, -3, +5,..., {-rn)(n - 2),
Р4 = 2п - 1, -1, +3, -5,..., (+rn)(n - 2).
Замечая, что (п — 1)(—(п — 1)) € Lo, получаем, что (п — 2)(п — 1) € 1/2П-2 и
(—(п —1))(—(п — 2)) € Li, откуда следует, что Pi, Р3-1, Р4, Р2-1 — вершинная
последовательность гамильтонова цикла графа К2П независимо от величины гп.
Случай 2. Положим sn = 1, если п = 0 (mod 4), и sn = —1, если п = 2 (mod 4).
Теперь имеем
Рх = 0, +2, -4, +6,..., (+s„)(n - 2),
Р2 = 0, -2, +4, -6,..., {-sn)(n - 2),
Р3=2п- 1, +1, -3, +5,..., (-5п)(п - 1),
Р4 = 2тг - 1, -1, +3, -5,..., (+sn)(n - 1).
Согласно рассуждениям, аналогичным случаю 1, можем заключить, что
Pi,P4~1,P3,P2~1 определяет гамильтонов цикл графа K<in для каждого sn G
{1,-1}. Теперь теорема доказана.
Теорема III.50. Для любого п > 1 граф К.2П+\ имеет 2-факторизацию,
элементы которой являются гамильтоновыми циклами {или, что
эквивалентно, K2n+i разлагается на п гамильтоновых циклов).
Доказательство. Для п = 1 теорема справедлива тривиально; значит,
предположим, что п > 2. Пометим вершины графа i^2n+i числами 1,-1,2,—2,...,

80 Глава III. Основные понятия и предварительные результаты
тг, —тг, 2тг 4-1 и рассмотрим гамильтонов путь Pi графа i^n+i — {2гг + 1}
(записанный как вершинная последовательность)
Рх = 1,-1,2, -2,..., тг, -тг. (*)
Как и в доказательстве теоремы 111.49, будем считать вершину 2п + 1
лежащей внутри правильного 2тг-угольника С2П? вершины которого помечены по
часовой стрелке числами 1,2,..., тг, — тг, —(гг — 1),..., —2, —1. С помощью п — 1
вращений вершинных меток цикла Cin (г-е такое вращение будет полностью
определяться соответствием 1 —* г, 2 < г < гг), получим еще п — 1
гамильтоновых путей из i^2n+i — {2п +1}, каждый из которых будет иметь вид (*). Все
эти тг путей преобразуются в гамильтоновы циклы графа i^2n+i
присоединением к fc-му пути, обозначим его Рь (который начинается в к и заканчивается
в -(тг - к + 1)), ребер (2тг + 1)/с и (2п + 1)(-(п - /с + 1)), 1 < /с < п. Если
два из этих тг гамильтоновых циклов имеют общее ребро, то соответствующие
гамильтоновы пути Pi и Pj имеют общее ребро. Без ограничения общности
можно считать, что г = 1 в силу симметрии. Таким образом, 2 < j < п.
Предположим, что е = г (—г) Е Е{Р\) или / = (—(г — 1))г G S(Pi) также является
ребром из Pj , 1 < г < п или 2 < г < п соответственно. Вершина, помеченная
г в Pi, имеет в Pj метку г — j + 1, если j < г; в противном случае она имеет в
Pj метку — (j — г). Соответственно вершина —(г — 5) Е V(Pi) имеет в Pj метку
— (r + j — 1 — б), если r + j — 1 — ?<п;в противном случае она имеет в Pj метку
2n-{r + j -2-5), 5 = 0,1.
Предполагая, что g € {е,/} П E(Pj) существует, и замечая, что g имеет в
Pj вид к(—(к — 5i)), ?i €{0,1}, мы можем заключить, что либо
г—j + l = r + j — 1 — 6 + 6i, либо
j - г + ?i = 2n - г - j + 2 + &
Первое равенство дает j < 2, тогда как второе равенство дает j > n, причем оба
противоречат тому, что 2 < j < п. Отсюда следует, что п гамильтоновых
циклов, построенные выше, являются попарно реберно-непересекающимися,
откуда вытекает справедливость теоремы.
Теорема III.51 [TILL80a]. Для любого п > 1 граф К? имеет п—1 — е попарно
дугово-непересекающихся {ориентированных) гамильтоновых циклов, где е =
1 для тг = 4,6 г*б = 0 в противном случае.
Отметим, что теория паросочетаний сама по себе представляет тему
исследований (см. монографию Ловаса и Пламмера [LOVA86a]) и что известны
другие классические результаты о существовании 1-факторов в произвольных
графах (теорема Татта об 1-факторах) и в произвольных двудольных графах
(теорема Холла). Мы рассмотрим эти результаты во второй части настоящей
монографии.
С другой стороны, необходимо сейчас отметить, что эти теоремы также
составляют корни теории факторов графов. Подграф G\ С G называется
фактором, если V(Gi) = V(G), и теория факторов занимается существованием
факторов, вершины которых имеют предписанные степени. В этом контексте
отметим статью Татта [TUTT81a], а также [BER084a]: в последней статье по-

III.7. Вложение графов в поверхности; изоморфизмы
81
лучены некоторые результаты относительно /с-факторов из теоремы Татта об
/-факторе (см., например, [TUTT81a, 6.1]).
Наконец, определим другие специальные типы стягиваний графа G.
Предположим, что G имеет 1-фактор L = {ei,...,er}, г = \рс > и 2-фактор
Q = {Ci, • • • , G5}, s > 1. Пусть Vi = /i(et) для e* € Ls г = 1,... ,r, и Wj = V(Cj)
для Cj € Q, jf = 1,..., 5. Теперь положим
G/L :=(... (GVl) • • •)vP и G/Q :=(... (GWl)...)Ws
и назовем G/L (G/Q) стягиванием фактора L (Q).
III. 7. Вложение графов в поверхности;
изоморфизмы
Изучение графов, вложенных в поверхности, составляет один из разделов то-
пологической теории графов, и недавняя монография [GROS87a] показывает,
что эта область исследований стала самостоятельной ветвью теории графов.
На самом деле топологическая теория графов —один из старейших разделов
теории графов, поскольку проблему четырех красок можно рассматривать как
один из ее корней. Однако хотя топологическая теория графов и (вершинная,
реберная, граневая) раскраски графов (которые рассматриваются в
следующем разделе) пересекаются значительно, ни одна из них не должна
рассматриваться как часть другой. Для того чтобы ограничиться более наглядным
подходом к вложениям графов в поверхности, мы также отошлем читателя к
[BEHZ79a].
Под поверхностью мы понимаем (в топологическом смысле) замкнутую
связную поверхность Т, ориентируемую или неориентируемую. Назовем граф
G вложенным в Т, если его вершины являются точками поверхности F, а
его открытые ребра С С Т — гомеоморфными образами открытого интервала
(0,1), причем
a) V(G) = UceE(G) ^ (^)» гДе kd (С) := дС = С - С (С обозначает
(топологическое) замыкание ребра С).
b) С Г) С' = bd (С) П bd (С) для произвольных С,С € ?(G), С ф С, т.е. два
замкнутых ребра пересекаются, самое большее, в одном или обоих из их
концов.
Другими словами, G нарисован на Т так, что два ребра из G пересекаются,
самое большее, в вершинах графа G.
Граф G вложим в J7, если существует граф G\, вложенный в Т, и биекции
<p:V(G)->V(Gi), tf> : ВД-> ВД),
такие, что (p(h(e)) = /ii(-0(e)), где h и hi — функции инцидентности графов G
и Gi соответственно, и <р({х,у}) := {<?>(х),(/?(у)}.
В общем случае, если Си Gi —графы, а <р и ф — биекции, определенные
выше, то назовем (<?,z/>) изоморфизмом из G на G\\ будем также говорить,
что G и Gi изоморфны, и обозначать это так: G ^ Gi. Если G = Gi, мы на-

82 Глава III. Основные понятия и предварительные результаты
зовем изоморфизмы автоморфизмами. Замечая, что (</?, ф) можно заменить
биекцией <р : V(G) U E{G) -> V(Gi) U -E(Gi), такой, что
<p(V(G)) = Vid), ip(E(G)) = Е(Сг) и ф(е)) = fti(V(e)),
можно также говорить об изоморфизме (/?.
Комбинируя понятия изоморфизмов и реберных/дуговых стягиваний,
будем говорить, что смешанный граф Н стягиваем на другой смешанный граф
#о, если существует последовательность ребер/дуг, скажем /ci, fe,... ,/сг Е
К(Н), такая, что (... ({Hk1)k2) • • -)kr — Дэ- Отметим, что в случае графов
стягивания и изоморфизмы можно рассматривать как специальные типы
гомоморфизмов, которые, как и выше, определяются как пары отображений
(<р, ф), за исключением того, что <р и ф не обязаны быть биективными. В
случае графа G\ без петель, однако, надо требовать, чтобы ip(x) Ф <р(у), если х
и у смежны, либо рассматривать ограничение отображения ф на E(G) -{eG
E(G)\ | ip(h(e)) |= 1}. Гомоморфизм называется эпиморфизмом, если и ip, и
i/> суть отображения wa, и в этом случае назовем G\ гомоморфным образом
графа G и будем писать G ~ G\.
В случае когда Т— сфера (или, что эквивалентно, плоскость), назовем
граф, вложенный в Т, плоским графом, а если он вложим в Т", то
назовем его планарным.
Кроме вершин и ребер, граф G, вложенный в некоторую поверхность Т,
имеет грани. Грань —это максимальное связное множество точек F на
поверхности Т, такое, что F ПС = 0. Однако F определяет единственный
подграф графа G, называемый границей грани F и обозначаемый через bd(F).
На самом деле bd(F) —топологическая граница dF, а именно bd(F) = F — F.
Назовем вложение графа G в поверхность Т 2-ячеечным вложением, если
каждая грань F графа G гомеоморфна открытому кругу. Особый интерес
представляют внешнепланарные графы, которые по определению могут быть
вложены в плоскость так, что V(G) — V(hd(F)) для некоторой грани F Е F(G)
(F(G) обозначает множество граней вложенного графа G); в этом случае будем
говорить об внешнеплоском вложении графа G.
В добавление к граням и их границам граф G, вложенный в Т,
определяет некоторое упорядочение 0+(G), которое задается (обычно)
циклическим упорядочиванием против часовой стрелки (вложенных) ребер в
каждой вершине. С другой стороны, если G вложим в Т и если G\ и G<i —
его вложения в Т (т. е. G\ и G2 — графы, вложенные в f, и Gi ~
G ~ G2), то может часто случиться, что 0+(Gi) ф 0+(G2). Поэтому
назовем G\ и G2 — вложения графа G в Т — 0~*~-изоморфными (О--
изоморфными), если G\ ~ G2 и если 0+(v) = (ei(t>),... , е^(г;)) Е 0+(Gi)
влечет за собой 0+(</?(г>)) = (^(ei(u)),... ,^(е^(г>))) Е 0+(G2) (0~(<p(v)) =
(/0(^i(t;)),... ^(ed(v))) Е 0~(Сг)) для каждой вершины v Е V(Gi). В этом
случае мы используем символическую запись Gi ~фСг (G\ ~©G2). Кроме
того, назовем граф G однозначно вложимым в J7, если для любых двух
вложений Gi и G2 графа G в J7 выполняется G\ ~ 0 G2 или G\ ~ © G2.
Отметим, что в общем случае неизвестно, какие графы однозначно вложи-
мы в заданную поверхность Т. Тем не менее для случая плоскости эти графы

III.7. Вложение графов в поверхности; изоморфизмы
83
могут быть точно описаны [FLEI73a, Theorem 3.5]. Кроме путей, циклов и
других тривиальных классов графов, существует только один нетривиальный
класс, указанный в следующей теореме.
Теорема III.52. Каждый Ъ-связный планарный граф однозначно вложим в
плоскость1^.
Теорема III.52 не нова; она была доказана Уитни в [WHIT32a] и оттуда
получила название теоремы о (комбинаторно) двойственном графе (не путать с
(геометрически) двойственным графом; см. ниже). Действительно, Уитни
показал, что для любых двух плоских вложений 3-связного планарного графа
их (комбинаторно) двойственные графы изоморфны, и этот изоморфизм был
основой для определения однозначной вложимости. Однако Уитни также
показал, что (комбинаторно) двойственные графы существуют только для пла-
нарных графов. Таким образом, понятие однозначной вложимости,
представленное выше, является более общим, чем однозначная вложимость в смысле
Уитни, так как оно применимо к произвольным поверхностям.
Еще одну интерпретацию теоремы 111.52 можно получить, говоря, что
множество {0+(G), 0~{G)} однозначно определено относительно плоских
вложений. Конечно, граф, вложенный в некоторую поверхность, можно
рассматривать «снаружи» или «изнутри» этой поверхности, и 0+(G) переходит в 0~(G),
если мы переходим от взгляда снаружи к взгляду изнутри поверхности. Это
наблюдение также объясняет, почему определение однозначной вложимости
включает в себя 0+- и 0~-изоморфизмы.
Тем не менее, если мы имеем вложение G\ планарного 3-связного графа G
в тор, соответствующее упорядочение 0+(Gi) может удовлетворять условию
0+(G) ф 0+(Gi) ф О (G), где 0+{G) и 0~{G) относятся к произвольному
плоскому вложению графа G. В действительности G не является однозначно
вложимым в тор. Отсюда возникает вопрос, какие циклические упорядочения
для El могут быть получены из вложений графа G в различные поверхности.
Общий ответ дан следующей теоремой (см. [BEHZ79a, Theorem 5.11]).
Теорема III.53. Пусть задан нетривиальный связный граф G вместе с
0+{G). Тогда существует поверхность Т и 2-ячеечное вложение G\ графа
G в Т, такие, что G ~ ф G\.
При рассмотрении плоских графов мы будем часто использовать
следующий результат:
Лемма III.54. Пусть G — плоский граф. Имеют место следующие
утверждения:
1) Если G 2-связен, то каждая граница грани графа G есть цикл в G.
2) Если k(G) = 1, то bd(F) связен для любой грани F из G и существует
грань Fo, такая, что каждый покрывающий маршрут Wq графа bd(Fo)
проходит через некоторую вершину по меньшей мере дважды. Такая
вершина есть точка сочленения графа G. Если Wo проходит е € E(bd(Fo)) no
х) Отметим, что планарный граф также вложим в тор; в общем случае, если G вложим в
сферу с р ручками, то он вложим в сферу с q ручками для q > р.

84 Глава III. Основные понятия и предварительные результаты
меньшей мере дважды, то е — перешеек графа G. Обратно, если v (е) —
точка сочленения (перешеек) графа G, то существует некоторая грань
Fo, такая, что v ? V(hd(Fo)) (е 6 E(hd(Fo))) и каждый покрывающий
маршрут графа bd(Fo) проходит v (е) по меньшей мере дважды.
3) k(G) = 0 тогда и только тогда, когда существует грань Fo, такая, что
bd(Fo) несвязен.
Отметим, кстати, что лемма III.54 не может быть распространена на
тороидальные графы (т.е. графы, вложимые или вложенные в тор).
Будем говорить, что граф G имеет ориентируемый род г (неориенти-
руемый род г), если он вложим в сферу с г ручками (г листами Мебиуса),
но не вложим в сферу с s ручками (s листами Мебиуса) для s < г. Обозначим
ориентируемый род графа G через 7(G), а неориентируемый — через 7(G). В
действительности каждый граф имеет как ориентируемый, так и
неориентируемый роды. Планарные графы, т. е. графы, для которых 7(G) = 7(G) = О,
характеризуются следующим образом.
Теорема III.55 (теорема Куратовского). Граф G планарен тогда и только
тогда, когда он не имеет подграфов, гомеоморфных К^,з или К$.
Мы отсылаем читателя к статье [ТНОМ81Ь], которая содержит короткие
доказательства этой теоремы, а также много ссылок на различные другие
доказательства и различные другие характеризации планарных графов; см.
также [ROSS76b, HOLT81a, CHEN81a]. По поводу усовершенствований теоремы
Куратовского см. [ТНОМ84а].
В общем случае пусть G — связный граф, 2-ячеечно вложенный в некоторую
поверхность Т, имеющую точно г ручек, но без листов Мебиуса (мы пишем
l(T) = г) или имеющую точно г листов Мебиуса, но без ручек (пишем i(T) =
г). Тогда числа pg,Qg и /g (= число граней графа G) связаны формулой
Эйлера для многогранников.
Теорема III.56. Пусть G — связный граф, 2-ячеечно вложенный в
поверхность Т, удовлетворяющую условию i(F) — Т или l(^) — г- Тогда
, г Г 2 — 2г, если Т ориентируема,
PG-QG + /g = i о т
[ 2 — г, если F неориентируема.
Число 2 — 2г (2 — г) называется эйлеровой характеристикой x(F)
ориентируемой (неориентируемой) поверхности Т. Положим Xt(G) := x(F)
для 2-ячеечного вложения графа G в Т и отметим, что x(F) > 0 в точности
для четырех поверхностей: сферы и тора, которые являются ориентируемыми,
а также для проективной поверхности (один лист Мебиуса) и бутылки Клейна
(два листа Мебиуса), которые являются неориентируемыми.
При любых обстоятельствах формула Эйлера для многогранников (теорема
111.56) и 2-ячеечные вложения G связного графа Go в поверхность Т в общем
случае позволяют нам вывести важные следствия. А именно, рассматривая
множество кратчайших покрывающих маршрутов W(bd(F)) границ граней F
графа G, мы видим, что каждое ребро е используется дважды: либо потому
что оно принадлежит bd(Fi) и bd(F2), F\ Ф F2 , и, таким образом используется

III.7. Вложение графов в поверхности; изоморфизмы
85
точно по одному разу в каждом из маршрутов W(bd(Fi)), W(bd(F2)), либо,
скажем, F лежит по «обе стороны» ребра е, и в этом случае е используется
дважды в W(hd(F)). Поэтому, если обозначить через F(G) множество граней
графа G и положить F{ := {F G F(G)\l(W(bd(F))) = г}, fi :=|Ff |, то
оо оо
г=1 г=1
(отметим, что в этих суммах fi ф 0 только для конечного множества индексов
г, так как G конечен). Грань F € Fi называется г-угольной гранью. Можем
иногда использовать обозначение o~i вместо fi. Теперь, если 5(G) > 3 и fi —
О, 1 < % < б, то для р := pG, q := qG, f := /G
оо оо
Зр< ]Г Ф) = 2$ = Х>Л>7]?Д = 7/.
v€V(G) г=1 г=1
Применяя теперь теорему III.56, получим
21xAG) = 21р - 21д + 21/ < Uq - 21q + 6q = -g,
что невозможно, если x^(G) > 0, и откуда следует, что <? < 21 \xf(G) |, если
X^-(G) < 0. Аналогичные рассуждения показывают, что если 5(G) > 3, x.f(G) >
0 и fi = 0, 1 < г < 5, то x^(G) =0, / = fe и Зр = 2д, т.е. G 3-регулярен.
Суммируя части этих рассмотрений, получим такое
Следствие III.57. Пусть Т — поверхность и х(^) ~~ ее эйлерова
характеристика. Существует только конечное мносисество связных графов Go с
5(Go) > 3 (возможно, ни одного), таких, что 2-ячеечное вложение G
графа Go в Т не имеет г-угольной грани, 1 < г < б. В частности, если x(F) > 0>
то G должен иметь г-угольную грань для некоторого г е {1,2,3,4,5,6}, и,
более узко, если x(F) > 0, то G должен иметь г-угольную грань для некоторого
г €{1,2,3,4,5}.
Однако некоторые из предыдущих рассмотрений, примененные к связным
3-регулярным графам G, приводят к формуле
оо
6xAG) =6p-6q + 6f = -2q + 6/ = ?(6 - i)fi.
г=1
To есть даже если xt(G) и все fi,i ф б, известны (со всеми кроме одного
fi,i ф б, и x^(G), определяющими оставшееся /^,г ф 6), это равенство не
дает нам ключа к определению числа /б. В действительности верно следующее
утверждение:
Лемма III.58. Пусть Т — ориентируемая или неориентируемая
поверхность рода г, и пусть 0з(^) —множество всех связных Ъ-регулярных
графов без перешейков, 2-ячеечно вложенных в Т. Тогда существует бесконечное
подмножество Q^(P) С Gz(^F), такое, что для любых G\,G2 € ?3, G\ Ф G2,
имеем G\ ф G2, в то время как число г-угольных граней в обоих графах G\ и
Gi одно и тоже для любого г ф б.

86 Глава III. Основные понятия и предварительные результаты
Набросок доказательства. Заменим каждое ребро е = ху на шестиугольник
Се, вершины которого помечены против часовой стрелки: ?i, х,Х2, yi,у, У2 , где
Xi,Ui & V(G)i г = 1,2, и Gi := G Е бзС?7) выбран произвольно. Рассматриваем
ребра в Се, соединяющие ?г с yi+i ? г = 1,2 (полагая 3 = 1), как «длинные»
ребра, а остальные — как «короткие» ребра. Для е, f ? Ех отождествим х Е Се
с х Е C-f и отождествим точно одну ?$ Е Се с Ej+i ? С-^, г = 1,2 (полагая
3 = 1). Соответствующие ребра из Се и С^ также отождествим.
Получающийся граф G2 3-регулярен, и существует взаимно однозначное соответствие
между г-угольными гранями из G\ и г-угольными гранями из G2 для любого г ф 6.
В действительности б-угольная грань из G\ (если такая грань существует)
соответствует в Gi б-угольной грани, отличной от любой из этих Се, е Е E{G\).
Также имеем G\ qk G2, так как р<з2 = 4рсч • Повторением приведенной выше
процедуры легко можно построить множество Q® (F), описанное в
формулировке леммы (отметим, однако, что могут существовать и другие конструкции).
Формула Эйлера для многогранников, а также числа di :=| Vi(G) | и
fu 1 < г < 00, наводят на мысль о двойственности, что приводит к
следующему определению.
Определение III.59. Пусть G — граф, вложенный в поверхность Т.
Определим геометрически двойственный (или просто двойственный) граф
D(G), тоже вложенный в J7, следующим образом. Существуют биекции a :
V(D(G)) -> F(G) и /3 : E(D{G)) -> E(G), такие, что
a) vp Е F, если a(vp) — F\
b) I epF1 П ё |=| eFF' П (ё — /i(e)) |= 1, если P(eFF') = e, в то время как если
/3(eFF') ф е, то e^F' Пё = 0, где /3 такова, что eFF' Е J5VF П-Е^, тогда и только
тогда, когда /3(eFF') Е ?(bd(F) П bd(F')). Это включает случай, когда F = F'
лежит по обе стороны от е, а в этом случае eFF — петля.
Из этого определения следует, что G ~®D(D(G))\ таким образом, просто
пишем G = D(D(G)). В частности, а такова, что г-валентные вершины графа
D(G) соответствуют г-угольным граням графа G. Таким образом, j-угольные
грани графа D(G) соответствуют j-валентным вершинам графа G. Это не
препятствует тому, чтобы граф D(G) обладал петлями и/или кратными ребрами,
хотя G может быть обыкновенным графом. Тем не менее если G — плоский
3-связный граф, то D(G) обыкновенный. Если G ф К± —связный плоский
3-регулярный граф и рс > 2, то k(D(G)) = AC(G). Заметим, что vf Е V(D(G))
довольно часто называется столицей грани F. Также отметим, что G ~ D{G)
для G = К±\ таким образом, назовем G самодвойственным, если G ~ D(G).
Нам будет нужен другой (вложенный) граф, получающийся из вложенного
графа.
Определение III.60. Пусть G — граф, вложенный в некоторую поверхность
Т так, что каждая граница грани есть цикл. Определим радиальный граф,
обозначенный через R(G) и также вложенный в J7, следующим образом:
V{G) С V{R(G)) и существуют биекции a : V(R(G)) -» V(G)UF(G) и 0F :
EVF —+ V(bd(F)) для каждой грани F Е F(G), такие, что

III.7. Вложение графов в поверхности; изоморфизмы
87
Ф
w5 w6
Рис. III.16. 5-колесо и 6-колесо. Отметим, что W$ = К*.
a) a(v) = v для v € V(G) и vp € F, если а(г;/?) = F;
b) для ^f, удовлетворяющей условию ol{vf) = F, и е ? i?UF имеем Нл(е) =
{^F,/?F(e)} (/г я обозначает функцию инцидентности для R(G)). To есть vf
соединяется точно одним ребром с каждой вершиной v € V(bd(F)).
Отметим, что в любом случае R(G) —двудольный граф.
Введем некоторые дополнительные графы. Граф G, вложенный в
поверхность Т, называется триангуляцией поверхности J7, если F^(G) = F(G).
Отметим, что даже триангуляция плоскости не обязательно является
обыкновенным графом. Кроме того, триангуляции являются двойственными к
кубическим графам, и эйлерова триангуляция плоскости является
двойственной к кубическому двудольному плоскому графу. Мы отождествляем любое
плоское вложение 1-скелета любого из пяти Платоновых тел (тетраэдра, куба,
октаэдра, додекаэдра, икосаэдра) или любого другого трехмерного
выпуклого многогранника с соответствующим выпуклым многогранником. Это
допустимо согласно теореме Штейница и Радемахера (см., например, [HARA69a,
теорема 11.6] или [BOND76a, p.135]). В частности, заметим, что К^ — граф
тетраэдра. Обозначим через Ое граф октаэдра (см. рис. Ш.З), через Wn — граф
п-угольной пирамиды и заметим, что Wn также называется п-колесом (см.
рис. III. 16). Аналогично, будем говорить о графе n-угольной двойной
пирамиды и отметим, что Ое есть 4-угольная двойная пирамида. Наконец, цикл
С длины п, вложенный в плоскость, называется n-угольником, и плоский
граф G является триангуляцией n-угольника С, если С = bd(Fo) для
некоторой грани F0 € F(G) и F3(G) = F(G) - {F0}. Таким образом,
триангуляцию плоскости можно рассматривать как триангуляцию
треугольника, и отметим, что n-колеса являются специальными типами триангуляции
п-угольников.
Многие рассуждения относительно плоских графов (и некоторые
предшествующие результаты) явно используют следующий (топологический)
результат, к которому мы будем обращаться в различных случаях.

88 Глава III. Основные понятия и предварительные результаты
Теорема III.61 (теорема о жордановой кривой). Каждая простая
замкнутая кривая С в евклидовой плоскости Е2 разбивает Е2 в точности на три
множества,
Е2 = CUintCUextC,
такие, что int С (ext С) —ограниченная {неограниченная) область иС\ПС ф 0
для каждой (непрерывной) кривой С\, соединяющей х Е int С с у Е ext С.
Следовательно, если G — двусвязный плоский граф, то все кроме одной
грани графа G — ограниченные области; оставшаяся грань называется
неограниченной гранью и обозначается через F^. Однако каждый плоский граф
обладает этим свойством. В случае внешнеплоских графов будем предполагать
в большинстве случаев, что V(G) = V(hd(FOQ)).
Следствие Ш.61.а. Пусть С — цикл плоского графа G uv E V(G) и
предположим, что открытые ребра е, f E Ev лежат по разные стороны цикла С.
Тогда е и f принадлежат различным границам граней графа G.
Определение III.62. Назовем цикл С графа G разделяющим циклом,
если либо V(C) — вершинный разрез, либо G вложен в плоскость и как int С,
так и ext С содержат открытое ребро графа G (отметим, что С может
рассматриваться как простая замкнутая кривая). Если С — простая замкнутая кривая
в плоскости, такая, что С П G С V(G), и если как int С, так и ext С содержат
открытое ребро графа G, то мы также будем называть С разделяющим
циклом.
Отметим, что для плоского 2-связного графа G каждый цикл С С G,
удовлетворяющий условию С ? {bd(F)\F E F(G)}, является по этому
определению разделяющим циклом.
Завершим этот раздел рассмотрением плоских триангуляции.
Предложение III.63. Пусть G — триангуляция плоскости и {Vi, V2}
—разбиение множества V(G). Верны следующие утверждения:
1) Оба графа (Vi) и (V*j) являются ациклическими тогда и только тогда,
когда они являются деревьями.
2) Если (Vi) несвязен, то (Т^) содержит разделяющий цикл.
Доказательство. Предположим, что (Vi) несвязен. Рассмотрим компоненту
G\ графа (Vi). Рассматривая ее, в свою очередь, как плоский граф, можно
заключить, что граница С его неограниченной грани корректно определена.
Теперь рассмотрим V С V(G), множество вершин, смежных с элементами
из V(Gi). Так как G\ — компонента графа (Vi), то V С V2. Так как G
конечен, G\ можно выбрать так, чтобы (Vi) — Gi С extCi, где С\— жор-
данова кривая, удовлетворяющая условиям G\ С int С\ и С\ П V(G) — 0.
Эта кривая может быть выбрана так, чтобы она была циклом графа jD(G),
таким, что если е Е Е(С\), то е Е E(hd(FVl)) П E(hd(FV2)) для некоторых
vi E V(Gi), v2 E V. В силу этого выбора С±, если Л = bd(FA),FA E F(G),
удовлетворяет условию С\ П Л ф 0, то С\ П F& — незамкнутая кривая Сд,
концы которой лежат на элементах из -Б(Д), и 1 <| V(A) П V |< 2. Теперь

III.8. Раскраска плоских графов
89
будем непрерывно преобразовывать Ci, одновременно двигая кривые Сд до
тех пор, пока Сд либо стянется в единственную вершину из V(A) П V,
либо преобразуется в единственный элемент из Е(А) П E((V')). Таким образом,
С\ преобразуется в подграф G<i С (V7). Однако в силу выбора С\ это
преобразование может быть проделано таким образом, чтобы (здесь Gi
рассматривается как плоский граф) одна из граней графа G2, скажем F\, содержала
точно (V(G) П intCi) U {е = ху € E(G)\x e V(Gi),y € V П VXbdCFi))} (эти е
рассматриваются как открытые ребра). Отсюда следует, что G2 должен иметь
вторую грань i<2 (Ф i*i), содержащую компоненту G[ графа (Vi) — Gi, так
как (Vi) — Gi С extGi. To есть Gi не может быть ациклическим. Отсюда
следует, что цикл (один из циклов) графа bd(F2), обозначим его Сз,
обладает тем свойством, что G\ и G[ лежат по разные стороны от Сз- Однако
Сз С G2 С (Vf) С (у2). То есть Сз есть цикл в (V2), который разделяет
компоненты Gi,G[ С (Vi). Это доказывает п. 2) предложения. Отметим, что в
приведенных выше рассуждениях была неявным образом использована
теорема 111.61.
Пункт 1) теперь является легким следствием. Если и (Vi), и (Уг) —деревья,
они тривиально ациклические. Если (Vi) ациклический, но несвязный, то (V^)
содержит цикл, разделяющий две компоненты графа (Vi) (см. доказательство
п. 2)). Таким образом, если и (Vi), и (V2) ациклические, то (Vi) также является
связным и, аналогичным образом, связным является (V^); значит, (Vi) и (V?) —
деревья. Это завершает доказательство предложения.
III.8. Раскраска плоских графов
Проблемы раскраски занимают умы специалистов по теории графов с тех пор,
как проблема четырех красок и — вскоре после этого — проблема Хивуда
раскраски карт были «выложены на стол». Обе проблемы теперь решены, но
существует еще много нерешенных проблем раскраски. Проблемы раскраски,
связанные с эйлеровыми графами, будут рассмотрены во второй части этой
монографии. В настоящий момент нам необходимы только некоторые
свойства раскрасок планарных графов. Но сначала дадим общее определение. Без
потери общности мы можем ограничиться только графами.
Определение III.64. Пусть G — граф. Рассмотрим разбиение множества
V(G)
V(V(G)) = {Vu...,Vk}, fc>l,
такое, что E((Vi)) = 0 для i = 1,..., k.
Тогда V(V(G)) мы назовем (вершинной) fc-раскраской графа G, a V^ —его
г-м цветовым классом, для которого вершина v € Vi имеет цвет г. Число
x(G) := mm{k\G имеет fc-раскраску}
называется хроматическим числом графа G. Аналогично могут быть
определены реберная /с-раскраска и хроматический индекс x'(G)i HO можно
также ввести эти понятия с помощью вершинных раскрасок графа L(G), по-

90 Глава III. Основные понятия и предварительные результаты
лучая (или определяя) x'(G) = x(L(G)). Аналогичным образом, если G
вложен в некоторую поверхность Т так, что каждое ребро е € E{G)
принадлежит двум различным границам граней, определим граневую /с-раскраску
через fc-раскраску графа D(G) и определим граневое хроматическое
число Xf(G) := x(D(G)). В заданной граневой /с-раскраске графа G назовем
F € F(G) г-гранью, если F имеет цвет г.
Тогда проблема/теорема о четырех красках утверждает, что каждый
плоский граф G удовлетворяет условию max{x(G),XF(G)} < 4. В
действительности, относительно x(G) достаточно ограничиться триангуляциями плоскости,
или, что эквивалентно, плоскими кубическими графами относительно гране-
вых раскрасок. В этом случае имеется важный результат, не зависящий от
теоремы четырех красок.
Теорема III.65 (теорема эквивалентности Тэйта). Для плоского кубического
графа следующие утверждения эквивалентны:
1) G имеет граневую 4-раскраску.
2) G имеет реберную 3-раскраску.
3) G имеет 1-факторизацию.
Интересно, что на основании следствия III.57 довольно легко доказать
следующее утверждение:
Теорема III.65.а (теорема о пяти красках). Для любого плоского 2-связного
кубического графа имеет место неравенство Xf{G) < 5.
Пример тетраэдра К^ показывает, что в общем случае неравенство
Xf(G) < 4 не выполняется. С другой стороны, плоские кубические графы G с
Xf(G) = 3 легко охарактеризовать.
Теорема III.66 (теорема о граневой 3-раскраске). Плоский кубический граф
имеет граневую Ъ-раскраску тогда и только тогда, когда он двудольный.
Отметим, что плоский кубический двудольный граф G должен иметь
2-угольную или 4-угольную грань по следствию III.57 (ее границу назовем
двуугольником или четырехугольником соответственно). Кроме того,
такой граф G не должен иметь перешейков, потому что он 1-факторизуем по
теореме III.48, и поэтому любые два непересекающихся 1-фактора определяют
2-фактор. Это и теорема III.65, однако, не обнаруживают специфической
связи между граневой 3-раскраской и какой-либо реберной 3-раскраской графа
G. Однако, начиная с некоторой граневой 3-раскраски V(F(G)) = {F1, F2, F3}
графа G и предполагая, без ограничения общности, что k(G) > 0, получаем,
что V(F(G)) однозначно определена с точностью до перестановки цветовых
классов из V(F(G)). Определим естественную 1-факторизацию графа G,
С := V(E(G)) := {Li,L2,I/3}, полагая е ? Li тогда и только тогда, когда
две грани F' и F", для которых е € bc^F') П bd(F"), удовлетворяют
условию {F',F"} С Fj U Fk и {г, j,k} = {1,2,3}. Таким образом, если F G Fj,
то E(bd(F)) — цикл, в котором ребра из Li и L& чередуются. Так как гра-
невая 3-раскраска V(F(G)) может быть определена с помощью естественной
1-факторизации графа G, мы приходим к следующей теореме.

III.8. Раскраска плоских графов
91
Теорема III.67. Для плоского связного кубического двудольного графа G
эквивалентны следующие утверждения:
1) G имеет граневую 3-раскраску (он должен ее иметь по теореме III.66).
2) G имеет естественную 1-факторизацию.
3) G имеет 2-фактор Q, такой, что каждый С Е Q есть граница грани и
1(C) четно.
4) D(G) имеет 3-раскраску.
Мы также охарактеризуем плоские графы G с xf(G) = 2.
Теорема III.68 (теорема о граневой 2-раскраске). Плоский граф гранево
2-раскрашиваем тогда и только тогда, когда он эйлеров.
Теорема III.68 вытекает, например, из того, что для плоского графа G
граф D(G) двудолен тогда и только тогда, когда G эйлеров, и что
вершинные 2-раскраски эквивалентны свойству быть двудольным. Кроме того,
теорема 111.68 и теорема III.66 эквивалентны. Это следует из теоремы III.67
и конструкции графа G/Q, который является плоским эйлеровым графом,
если G — плоский двудольный кубический граф и Q = Li U Lj, г ф j, где
Li,Lj G С = {Li,L2,Ls} и С — естественная 1-факторизация графа G
(отметим, что обратная операция, которая находит G по G/Q, дает плоский
двудольный кубический граф, если G/Q — плоский эйлеров граф). В этом контексте
G/Q или G/L (где G — плоский граф и Q — его 2-фактор, элементами
которого являются границы граней, a L — его 1-фактор) определяются очевидным
образом, подсказанным топологией плоскости и определением упорядочения
0+(u), v € V(G). Вместо того чтобы приводить формальное определение,
отошлем читателя к рис. III. 17.
В действительности теорема 111.68 позволяет построить специального
типа эйлерову ориентацию в плоских эйлеровых графах. Пусть G — плоский
эйлеров граф, и предположим, что задана такая граневая 2-раскраска, что
неограниченная грань имеет цвет 1. Грани F, принадлежащие второму
цветовому классу ^(G), все являются, таким образом, ограниченными гранями
и S = {bd(F)|F € F2(G)} — цепное разложение графа G, так как каждое
е Е E(G) принадлежит точно одной bd(F), F Е ^(G). Заменим е на дугу
ае, такую, что когда мы проходим ае от ее хвоста к голове, грань F лежит по
левую сторону. Проделаем это с каждым ребром е Е E(G) и получим
ориентацию против часовой стрелки каждой границы bd(F), F € i*2(G), и, таким
образом, ориентацию Dq графа G. Тогда Dq эйлеров, потому что для
каждого t = {е',/'} € X(v) С Х$ вершина г? —голова дуги ае тогда и только
тогда, когда v — хвост дуги а/ . Кроме того, из определения Dq следует, что в
0+(v) = (ei(v),e2(u),..., ed(v)), d = d(v), v — голова дуги ei(v) тогда и только
тогда, когда г; —хвост ei+i(v), г — 1, • • •, d (полагаем d Л- 1 = 1). Таким
образом, в 0+(г>) Е 0~*~(Dg) заходящие и исходящие полудуги чередуются. Будем
называть Dq (соответственно Dq) канонической ориентацией графа G.

92 Глава III. Основные понятия и предварительные результаты
Ы\
V
г
v. У
а)
v
ь) ч/
G/C ье
Рис. III.17. Стягивание а) границы грани С, Ь) ребра е в плоском графе G.
Ш.9. Гамильтоновы циклы
Начнем со связи между гамильтоновыми циклами и доминирующими циклами.
Для этой цели назовем граф К\%п n-звездой (или просто звездой).
Лемма III.69 [HARA69a]. Граф G без петель имеет нетривиальную
доминирующую цепь тогда и только тогда, когда L(G) гамильтонов и G не явля~
ется п-звездой для п = рс — 1.
Гамильтоновы циклы — это еще одна центральная тема исследований в
теории графов. Вследствие ошибочного предположения Тэйта на поиски гамиль-
тоновых циклов в планарных графах сильно повлияли поиски доказательства

III.9. Гамильтоновы циклы
93
гипотезы четырех красок. На самом деле Тэйт считал, что каждый планарный
3-связный кубический граф G имеет гамильтонов цикл Н (гипотеза Тэйта).
Если бы гипотеза Тэйта была верна, то она бы положительно решала
проблему четырех красок. Действительно, если Н — гамильтонов цикл планарного
кубического графа G, то G имеет 1-факторизацию С = {Li,L2,Ls}, такую,
что L\ U Z/2 = Е(Н) и Ls = E(G) — Е(Н) (отметим, что рс должно быть
четным в силу леммы III.4 и 3-регулярности графа G). Таким образом, по
теореме эквивалентности Тэйта (теорема 111.65) любое вложение графа G в
плоскость является гранево 4-раскрашиваемым. Отметим, что существование
гамильтоновых циклов и 1-факторизаций не зависит от вложения, в то время
как граневая раскраска зависит от конкретного вложения.
Однако гипотеза Тэйта была опровергнута в 1946 г. Таттом, который
впоследствии доказал, что каждый 4-связный планарный граф гамильтонов1).
Этот результат есть прямое следствие более общей теоремы, для которой нам
нужно некоторое дополнительное понятие. Рассмотрим граф G, не
являющийся лесом, и пусть С —цикл графа G. Образуем G\ := G — V(C), и для каждой
компоненты В\ С G\ пусть
B:={E{B1)^E{V{Bl))).
То есть В возникает из В\ при добавлении всех вершин цикла С, смежных
с некоторой вершиной из В\, и всех ребер, соединяющих эти добавленные
вершины с V(Bi). Назовем v € V(В) П V(C) = V(B) - V{B\) вершиной
С-прикосновения (или просто вершиной прикосновения, если это не
приводит к недоразумению) и назовем В С-мостом (или просто мостом)2\
Отметим, что для двух С-мостов В\ и Да мы имеем Е(В\)С\Е(В2) = 0 и каждая
вершина v € В\ П B<i (если такая вершина v существует) является вершиной
прикосновения. Хорду, или диагональ, цикла С, т.е. ребро е ^ Е(С),
такое, что /г(е) С V{C) (ft — функция инцидентности графа G), также называют
С-мостом. Наконец, рассматривая е € E(G) и грани Ff,F" с е € bd(i?/) П
bd(F//), мы назовем цикл Со терминальным циклом ребра е относительно
F' (F"), если а) е G Е(С0), Ъ) F' € intC0 и F" E extC0 или F" G intC0 и
F1 € ext Со, с) «сторона» цикла Со, содержащая F' (F"), т. е. int Co или ext Co,
содержит как можно меньшее число граней. Отметим, что если С 2-связен, то
такой цикл Со —не что иное, как bd(i7'/) (bd(F")).
Следующий результат — это сущность того, что довольно часто
называют «теоремой о мостах» Татта (см. [TUTT77a, Theorem I]. Эта статья —
осовремененная версия работы [TUTT56b], которая уже содержала следствие
III.71, приведенное ниже).
*) С тех пор различными авторами было построено много планарных 3-связных кубических
графов без гамильтоновых циклов. Мы отсылаем к статье [ZAKS82a] относительно работ по
рассматриваемой теме и отметим, что в этой статье построен такой граф указанного типа,
что он содержит только границы граней длины, не превышающей 7.
2) Из контекста будет ясно, что С-мосты = мосты (bridges) не имеют ничего общего с
перешейками (bridges), определенными ранее. Терминология Татта приносит некоторым
специалистам по теории графов (и мне в том числе) головную боль. Наилучшее лекарство от
этой головной боли, однако,— его замечательные результаты. (Примечание связано с тем,
что по-английски в обоих случаях используется термин «bridge». — Ред.)

94 Глава III. Основные понятия и предварительные результаты
Теорема III.70. Для каждого ребра е, содерэюащегося в некотором цикле
планарного графа, существует цикл С, такой, что
1) С содержит е;
2) каждый С-мост имеет не более трех вершин прикосновения;
3) если Е(В) П Е(Со) ф 0 для С-моста В и терминального цикла Со ребра
е, то В имеет точно две вершины прикосновения.
Кроме того, из этой теоремы можно легко вывести следующие результаты,
которые вполне уместны в контексте этой книги.
Следствие III.71. Каждый (обыкновенный) планарный 4-связный граф G
имеет гамильтонов цикл Н.
Доказательство. Пусть С —цикл, описанный в теореме III.70, и допустим,
что некоторый С-мост В не является хордой цикла С. Тогда В Г) С есть
вершинный разрез V3 с | Va |< 4, за исключением случая, когда В П С = V(C),
и каждое е € E(G) — (Е(С) U Е(В)) есть хорда цикла С (теорема III.70.2)).
По предположению С — треугольник, две границы С' и С" граней графа G,
содержащие е, являются терминальными циклами и выполняется условие
(Д(С') П Е(В)) U (Е(С") П Е(В)) ф 0.
По теореме III.70.3) В имеет точно две вершины прикосновения, откуда
следует, что С содержит двуугольник, что противоречит тому, что G —
обыкновенный граф. Отсюда вытекает, что каждое е € E(G — С) есть хорда цикла С,
откуда следует, что Н := С — гамильтонов цикл графа G.
Следствие III. 71 обобщает такой результат, принадлежащий Уитни
[WHIT31a]:
Следствие III.72. Пусть D — обыкновенная триангуляция плоскости,
такая, что каждый треугольник этой триангуляции является границей
некоторой грани. Тогда граф D гамильтонов.
Отмечая, что условия этого следствия равносильны тому, что k(D) > 4 для
D ф К±, и замечая, что D = D(G) для некоторого планарного кубического
графа G с AC(G) = k(D) > 4, если G ф К±, мы перефразируем следствие III.72
и применим следствие III.71 вместе с леммой III.69 для того, чтобы получить
следующий результат (отметим, что для кубического графа G выполняется
равенство k(L(G)) = AC(G), если k(L(G)) < 4).
Следствие III.73. Пусть G — планарный кубический граф с AC(G) > 4. Тогда
оба графа D(G) и L(G) гамильтоновы и G имеет цикл Татта.
Хотелось бы отметить, что предшествующие результаты (включая теорему
о мостах Татта) также следуют из более общего результата Томассена,
который, в свою очередь, обобщает следствие 111.71 (см. [ТНОМ83а] и [СНЮ8ба];
в последней статье исправляется погрешность первой).
Следующий результат, имеющий лишь устное хождение, связывает
гамильтоновы циклы в плоском кубическом графе с деревьями в D[G).

III.9. Гамильтоновы циклы
95
Лемма III.74. Для плоских кубических графов G эквивалентны следующие
утверждения:
1) G гамильтонов;
2) V(D{G)) имеет разбиение {Vi,V^}, такое, что и (Vi), и (V2) являются
деревьями.
Кроме того, если заданно разбиение, описанное в п. 2), и F' := {Fv G
F(G)\v G Vi}, то ребра графа G, принадлежащие границе точно одного
элемента из F', определяют гамильтонов цикл графа G.
Доказательство. Из п. 1) следует п. 2). Пусть Н С G — гамильтонов цикл.
Будем рассматривать его как жорданову кривую. Таким образом, Н
определяет разбиение множества хорд,
E(G)-E(H):=EbUEu,
такое, что каждое ребро е G Еь лежит в int Н, а каждое ребро / G Еи лежит
в extH (здесь е и / рассматриваются как открытые ребра). Аналогично, Н
определяет разбиение множества граней,
F(G) = FbUFu,
где индексы имеют тот же смысл, что и выше. Пусть V\ С V(D(G))
—множество вершин, соответствующее Fb С F(G), a V^ — множество вершин,
соответствующее Fu, и рассмотрим (Vi),(V^) С D(G). Без ограничения общности
можно считать, что если один из этих графов содержит цикл С, то это (Vi).
Однако, поскольку граф D(G) построен на плоскости (см. определение 111.59), С
можно рассматривать как жорданову кривую, составленную из столиц
некоторых элементов из Fb и (топологических) дуг eFF>, соответствующих некоторым
элементам из Еь. По определению eFF> П е ф 0 тогда и только тогда, когда
е G E(hd(F)) П E(bd(F')) П Еъ, и в этом случае | eFF> П е |=| eFF> Пё\= 1. Из
этого равенства и теоремы 111.61 следует, однако, что вершины х и у,
инцидентные е, лежат по разные стороны цикла С (отметим, что V(G) C\D(G) = 0
по определению). Без ограничения общности можно допустить, что х G int С
Однако, поскольку V(H) = V(G) D {х,у}, существует путь Р, соединяющий
х и у в Н. Следовательно, Н П С ф 0 по теореме III.61. С другой
стороны, согласно определению графов D(G) и (Vi), С С int Я. Это включение и
условие С П Н ф 0 не могут выполняться одновременно. Отсюда следует, что
(Vi) ациклический. Аналогичным образом устанавливается, что (V^)
ациклический. Так как G — кубический граф, то D(G) —триангуляция плоскости. Из
предложения III.63.1) теперь следует, что (Vi) и (V^) являются деревьями. Это
доказывает рассматриваемую импликацию.
Из п. 2) следует п. 1). Предположим, что (Vi),^) С D(G) суть
деревья для некоторого разбиения {Vi,Vb} множества вершин V(D(G)). Пусть
F' С F(G) определяется, как в формулировке леммы. Прямыми
рассуждениями по индукции (которые мы для краткости опускаем) получаем, что F'
определяет цикл Н С G, такой, что е G Е(Н) тогда и только тогда, когда
е G E(bd(Fv)) точно для одной грани Fv G F',v G Vi. Снова
рассматриваем Н как жорданову кривую и допустим, без ограничения общности, что

96 Глава III. Основные понятия и предварительные результаты
(Vi) С mtH (отметим, что для каждой грани Fv G F' условие Fv П intiJ ф 0
выполняется тогда и только тогда, когда Fv П (ext Н U Н) — 0, причем в этом
случае Fv С intiJ). Предположим, что Н не является гамильтоновым циклом.
Из построения Н и по предположению существует х G (V(G) — V(ff)) П ext Я
(замечание: Go := (\JF eF, E(bd(Fv))) есть 2-связный внешнеплоский граф).
Поэтому х G V(bd(Fw)) для некоторой вершины w G V2 . Действительно, так
как Fv С int Н для каждой вершины v G Pi, то каждая грань Fw, такая, что
х G V(hd(Fw)), удовлетворяет условию Fw С ext Я и w G V2. Это означает,
однако, что ({w G V^z G V(bd(Fw))}) содержит цикл, который является
циклом из (V2). Это противоречит предположению о том, что (V2) есть дерево.
Следовательно, Н — гамильтонов цикл. Лемма доказана.
Обратимся теперь к гамильтоновым циклам в произвольных обыкновенных
графах. Сначала мы сформулируем известную теорему Оре, которая
обобщает результат, установленный ранее Дираком, и оказала сильное влияние на
теорию гамильтоновых графов.
Теорема 111.75 (теорема Оре). Если G — обыкновенный граф порядка р,
такой, что d(x) + d(y) > р, когда х и у несмежны, то G гамильтонов.
Доказательство. Теорема верна, если G ~ Кр. Предполагая противное,
рассмотрим граф G с максимальным qc {pg — V фиксировано), для которого
теорема неверна. Следовательно, существуют х,у € V(G), такие, что ЕХПЕУ = 0,
откуда следует, что G\ = G U {ху} — обыкновенный граф; он имеет
гамильтонов цикл Hi D {ху} по предположению и выбору G. Записывая Р := Hi — {ху}
как последовательность вершин (в которой х = vi,у = %),
Р = Vi,v2...,vp,
получаем, что vpVj ? E(G), если viVj+i G jE(G),1 < j < p — 1. В противном
случае ((Е(Р — {vjVj+i}) U {viVj+i,vpVj}) —гамильтонов цикл графа G, что
противоречит выбору G. Поэтому d(vp) < p — l — d(vi), откуда d(vi)-\-d{yp) < p.
Это противоречие предположению влечет за собой справедливость теоремы.
Тем же методом, которьш использовался для доказательства теоремы 111.75,
мы получаем результат о гамильтоновых циклах в двудольных графах.
Следствие III.76. Пусть G — обыкновенный двудольный граф с разбиением
{VUV2} (т. е. E((Vi)) = E((V2)) = 0), таким, что | Vi |=| V2\= k > 1.
Предположим, что существует такое a G N U {0}, что к > 2а и 5(G) > к — а.
Тогда G гамильтонов.
Доказательство. Проводим доказательство от противного. Так как следствие
справедливо, если G ~ К^к > пусть G выбран так, что qc максимально и
следствие не верно для G. Рассмотрим несмежные вершины v\ G V\, v2 G V2 и
образуем Gi := Gu{viv2}. Из выбора G следует, что Gi гамильтонов и каждый
гамильтонов цикл графа Gi содержит viv2 . Таким образом, G имеет
гамильтонов путь, который может быть записан как последовательность вершин
Р = Vi,b V2,l, Ui|2, l>2,2, • • • > vl,*, v2,fc,

ШЛО. Матрицы инцидентности и смежности
97
где vi = г>1д,г>2 = t>2,fc и Vij G V*, 1 < j < /с, г = 1,2. Отсюда следует, что
{viV2,j,V2t;ifj} ? 25(G); в противном случае (Е(Р) - {г^,^,.?}) U {г^г^,^^}
определяет гамильтонов цикл графа G, что противоречит выбору G.
Следовательно,
2k-2a< d(vi) + ф2) < dfai) + (& - Ф1)),
т.е. к < 2с*2, что противоречит предположению. Следствие доказано.
Существует аналог теоремы III. 75 для гамильтоновых циклов в орграфах
[MEYN73a]; короткое доказательство этого результата дано в [BOND77a].
Теорема III.77 (теорема Мейниля). Если D — сильно связный обыкновенный
орграф порядка р и если d(x) + d(y) > 2p — 1 для каоюдой пары, несмежных
вершин я, у G V(D), mo D гамильтонов.
Следствие III.78. Если D — обыкновенный орграф порядка р, такой, что
d(x) + d(y) > 2р — 3, когда х и у несмежны, то D имеет гамильтонов путь.
За обзором теории гамильтоновых графов отсылаем заинтересованного
читателя к статье Бермонда в [BEIN78a, Ch. б].
ШЛО. Матрицы инцидентности и смежности,
потоки и напряжения
Существуют различные связи между теорией графов и другими ветвями
математики, а также другими науками (см., например, [WILS79a]). Для целей
этой монографии (особенно гл. VIII и IX, которые содержатся в т. 2) особый
интерес представляют некоторые связи с линейной алгеброй и линейным
программированием (ЛП), причем не только в связи с реализациецй алгоритмов
на графах, но также для доказательства результатов в теории графов.
Ограничим рассмотрения графами и орграфами и начнем с представления графов
матрицами.
Определение III.79. 1) Пусть G — граф, множества вершин и ребер
которого заданы в виде списков, V(G) = {vi,.. .,vp}, E(G) = {ei,... ,eg}. Пусть
B(G) есть p x (^-матрица, такая, что r-я строка представляет vr, 1 < г < р,
5-й столбец представляет es, 1 < s < g, и 6r?s = 1 тогда и только тогда,
когда es G EVr\ в противном случае 6r,s = 0. Аналогично, если D — орграф без
петель, V(D) = {vi,..., vp}, A(D) = {ai,..., ag}, то 6Г?5 = 1 в р х д-матрице
B(.D) тогда и только тогда, когда as G А+г, ЬГ}3 = — 1 тогда и только тогда,
когда as G A~r\ в противном случае ЬГу3 = 0. Назовем B(G) (В(J?)) матрицей
инцидентности (ор)графа G (D).
2) Пусть G, D заданы, как в п. 1), но теперь D может иметь петели. Пусть
A(G) и A(D) суть р х р-матрицы, в каждой из которых г-я строка и г-й столбец
представляют Vi; соответствующие элементы этих матриц определяются
формулами aij(G) =| EVi П EVj | и aij(D) =| A J. П А~ |, если г =^ j, 1 < i,j < р, в то
время как ^(G) = a^i(D) = Av. . Назовем A(G) (А(Г))) матрицей
смежности (ор)графа G (D).
Сделаем следующие элементарные замечания.

98 Глава III. Основные понятия и предварительные результаты
1) Сумма элементов г-й строки матрицы B(G) (B(D)) равна d(vi) (od(vi) —
id(vi)), 1 < г < p, тогда как сумма элементов j-ro столбца матрицы B(G)
(B(D)) равна 2 (0), если G (D) не имеет петель, 1 < j < q.
2) A(G) — симметрическая матрица, в то время как A(D) удовлетворяет
равенству A(D) = (A(DR))T, где верхний индекс Т обозначает
транспонирование матриц. Поэтому в A(G) сумма элементов г-й строки равна сумме
элементов г-ro столбца, а именно, d(vi) — \Vi (так как петля учитывается только
один раз как в A(G), так и в А (?>)), в то время как в A(D) сумма элементов г-й
строки равна od(vi), а сумма элементов г-ro столбца равна id(v{) (здесь a ? AVi
учитывается один раз в г-й строке и один раз в г-м столбце).
Далее рассмотрим орграфы, дугам которых приписаны веса —
действительные числа.
Определение III.80. Пусть D — орграф.
1) Отображение <р : A(D) —> R называется потоком, если ^2a€A+ </Ка) =
YlaeA~ ^(а) для каждой вершины v € V(D).
2) Отображение фу : V(D) —> R называется потенциалом. Для заданного
потенциала фу определим ф : A(D) —> R формулой ф(а) = фу(д(а)) — фу(/(а))
(д — головная функция, / — хвостовая функция орграфа D). Назовем такое
отображение ф потенциальной разностью или напряжением. Для
дальнейшего рассмотрим С С D, такой, что Gc Q Go является циклом. Пусть
Со — ориентированный цикл, такой, что Gc0 = Gc • Положим А+(С) :=
А(С) П А(Со), А-(С) := A(CR)nA(C0).
Лемма III.81. Пусть D — орграф, и пусть заданы отображения (р,ф :
A(D) —> R. Отобраоюение ср является потоком тогда и только тогда, когда
2а€А+т ^(а) = ]Са€А-(Х) ^(а) для к°>ждой кограницы А(Х), X С V(D), в то
время как ф есть напряжение тогда и только тогда, когда J2aeA+(C) ^(а) =
23а€А-(С) ^(а) для каждого С С D, такого, что Gc есть цикл.
Между потоками и напряжениями существует тесная связь, на которую
указывает лемма III.81. Обозначим дуги орграфа D через ai,..., aq и
зафиксируем это обозначение, и пусть </?д, Фа € R9 таковы, что их г-я компонента
есть (р(а{),ф(а,1) соответственно. Пусть Я<р,11ф С R9 обозначают
соответствующие множества всех указанных векторов ^и Фа, представляющих потоки
<р и напряжения ф.
Теорема III.82. R^ и Лф являются подпространствами в R9, и Иф —
ортогональное дополнение к R^.
Однако во многих теоретических и практических вопросах (например, в
исследовании операций) основной интерес представляют не произвольные
потоки и напряжения, а те, которые удовлетворяют некоторым заданным
граничным условиям. Для этой цели введем другое понятие. Для краткости
будем писать а < /3 (а < /?), если a,/3 : A(D) —> R удовлетворяют условию
а(а) < /3(a) (а(а) < (3(a)) для каждой дуги a G A(D).

ШЛО. Матрицы инцидентности и смежности
99
Определение III.83. Пусть D — орграф, и пусть заданы отображения а, (3 :
A(D) —* Д, такие, что a < (3. Назовем поток <р : A(D) —> R (а,
/^-допустимым, если а < <р < (3. Если а(а) = 0 для каждой дуги a E A(D),
назовем /3(a) ее емкостью; в этом случае <р называют /3-допустимым, а не (а, /?)-
допустимым.
Будем применять следующую теорему Хоффмана.
Теорема III.84 (теорема Хоффмана). Пусть D—орграф, и пусть заданы
отображения а,(3 : A(D) —+ R, такие, что а < (3. Тогда (а, (3) -допустимый
поток в D существует в том и только том случае, когда следующие
неравенства выполняются для каждой кограницы Ах '= А(Х), X С V(D):
Y, а(а) < Y, 0(<О. ? а(а) ^ Е ^'
а€А? аЕА^ё a^A^ а€А^
Предположим, что орграф D и отображения а,/3 обладают следующими
свойствами: (i) существует такая дуга а$ ? A(D), что /(ao) является стоком,
а ^(ао)—источником в D — ao ; (ii) а(а) = 0 для каждой дуги а ? А(?>);
(iii) (3(ао) > J2a€A(D)-{a0} Р(а)- Тогда назовем D сетью1). В силу (ii)
тривиальный поток (f = 0 также является /3-допустимым; таким образом,
предпочтительнее искать (3-допустимый поток <р, такой, что <р(ао) является
наибольшим. Это называется проблемой максимального потока. Для того чтобы
охарактеризовать максимальный поток, рассмотрим множество V С V(-D),
такое, что /(ao) G V7, g(ao) ? V, и назовем A~(Vr) сетевым разрезом. Тогда
/3(A~(V')) := Yl/aeA-iV) ^(a) называется величиной или емкостью
сетевого разреза.
Теорема III.85 (теорема о максимальном потоке и минимальном разрезе
Форда—Фалкерсона). Если D — сеть, то максимальный поток tp(ao) равен
наименьшей величине всех возможных сетевых разрезов.
Для целей этой монографии следующее замечание выражает важную
характерную черту теории потоков; оно непосредственно получается из теоремы
111.85.
Следствие III.86 [WILS79a, р. 243]. Пусть D — сеть, такая, что (3(a) €
N U {0} для каждой дуги а € A(D). Тогда максимальный поток ip(ao) есть
целое число.
Рассмотрим частный случай, где D\ = D — {/(ао),р(а0)} —двудольный
орграф, V(Di) = Vi U V2 и Vi П V2 = 0, такой, что (ti) N(g(a0))C)D1 = Vu
N(f(a0)) П Di = V2\ (t2) a G A(Di) влечет за собой f(a) € Vi, g(a) G V2\
(t3) a € A(D) — (A(Di) U {ao}) влечет за собой (3(a) > 0; (t4) a € A(D{) влечет
x) Определение сети не совсем устоялось; приведенное здесь совпадает с определением в
[BERG62a, р. 191] за исключением условия (iii). Там (3(ао) не определено, в силу чего (р(ао)
может быть произвольно большим. С другой стороны, ip(ao) < Ea€A(D)-{a0}
/5(a)—тривиальное условие, так что (iii) формулируется просто для определения f3 на всем множестве
A(D).

100 Глава III. Основные понятия и предварительные результаты
за собой /3(a) > YlbGA+ ил~ Р(Ь) и Р(ао) такое же, как в (iii) (см. выше)1^.
д(а0) /(а0)
Кроме того, пусть задана функция стоимости с : A(D) — {ао} —* R+. Цель
в этом случае состоит в нахождении /3-допустимого максимального потока </?,
такого, что <р(а) = /?(а), если а е А+(ао) U А~{ао) и сумма T,a?A(D)-{a0} c(aMa)
минимальна.
Эта ограниченная проблема максимального потока называется
транспортной проблемой или проблемой Хитчкока [BERG62a, p. 207], частным
случаем которой является проблема о назначениях, сформулированная в
[РАРА82а, р. 248]; эти проблемы будут рассмотрены в гл. VIII. Отметим, что
проблема максимального потока может быть распространена на случай, когда
а(а) > 0, а Е A(D) — {ао}; она может быть сведена к проблеме
максимального потока в том виде, как она была сформулирована ранее (см. [BERG62a,
р. 204-205]).
Читателей, интересующихся потоками и напряжениями (особенно в связи
с исследованием операций), мы отсылаем к [BERG62a, FORD62a, EVEN79a]
и обзорной статье Авондо-Бодино в [WILS79a]. Отметим, однако, что все эти
проблемы максимального потока могут быть сведены к проблемам Л П. В
большинстве примеров последние будут формулироваться, но не будут обсуждаться
подробно.
III. 11. Алгоритмы и их сложность
За прошедшие 25 лет алгоритмы на графах и изучение их сложности стали
постоянно развивающейся темой. Опубликовано мало книг, которые были бы
целиком посвящены этой теме или рассматривали ее как одну из своих главных
тем. Но, хотя мы развиваем алгоритмы в различных главах (не только в гл. X)
и изучаем (или, по крайней мере, указываем) их сложность, это не является
одной из главных задач нашей монографии. Поэтому, чтобы сократить эту
главу, отсылаем заинтересованного читателя к обзорной статье Рида в [WILS79a]
и к [EVEN79a, PAPA82a, JUNG87a]. Эти работы содержат более или менее
явные рассмотрения сложности, включая введение в теорию TVP-полноты. Тем не
менее читателей, заинтересованных в серьезном изучении TVP-полноты, мы
отсылаем к «классике» [GARE79a]. Следовательно, хотя никакого ясного ответа
на шекспировский вопрос («в Р или в NPC? Вот в чем вопрос!»)2) не может
быть получено из результатов, помещенных в этой монографии, с настоящего
момента мы считаем, что читатель знаком с классом NP и его подклассами
Р (хорошие парни) и NPC (в настоящее время не слишком хорошие парни,
для которых существует маленькая надежда стать хорошими) в том виде, как
они определяются в [GARE79a, EVEN79a, PAPA82a]. Отметим, однако, что
С. Эвен также упоминает два других понятия АГР-полноты, принадлежащие
Куку и Ахо—Хопкрофту—Ульману.
х) Снова для таких дуг а обычно допускается бесконечная емкость. Нижняя оценка для
/3(a), приведенная здесь, не дает никаких ограничений на произвольный поток.
2) В оригинале игра слов: «to P or to NPC* напоминает шекспировское «to be or not to
be». — Прим. ред.

111.11. Алгоритмы и их сложность
101
В дальнейшем суммируем (без доказательств) некоторые проблемы
распознавания на графах, каждая из которых лежит в Р. Что касается проблем из
NPC, мы упоминаем их по мере того, как они «проходят» в контексте этой
монографии. Явная сложность полиномиальных алгоритмов будет также
упоминаться в соответствующих местах.
Теорема III.87. Пусть Н — смешанный граф. Существуют
полиномиальные по времени алгоритмы для
a) определения к(Н), Х(Н);
b) определения, является ли Н сильно связным {если Н, скажем, орграф);
c) отыскания каркаса;
d) отыскания дерева в корень vo G V(H) или дерева из корня vo G V(H), если
Н = D — сильно связный орграф.
В дальнейшем, если Q — некоторое множество действительных чисел, то
Q+ := {г G Q\r > 0}.
Теорема III.88. Пусть G — граф, и пусть задано отображение f : E(G) —>
R+ U {0}. Для Eq С E(G) положим f(Eo) = YleeE0 f(e)- Существуют
полиномиальные по времени алгоритмы для определения
a) расстояний между всеми парами u,v G V(G) (т.е. путей Р — P(u,v),
таких, что значение f(E(P)) минимальное)1^;
b) каркаса наименьшей стоимости (т. е. дерева Т, такого, что значение
f(E(T)) минимально);
c) совершенного паросочетания наименьшей стоимости, если в G вообще
существует хотя бы одно совершенное паросочетание (т. е. 1-фактора L
такого, что значение f(L) минимально)2'.
Отметим, что такие проблемы, как определение, является ли заданное
множество ребер/дуг и вершин разделяющим (и, таким образом, в частности,
является ли k G К(Н) перешейком или v G V(H) точкой сочленения),
могут быть сведены к выяснению связности в соответствующем подграфе. Таким
образом, be(H) может быть построен за полиномиальное время.
Что касается решения потоковых проблем, перечисленных в предыдущем
разделе, отметим, что они все могут быть решены полиномиальными по
времени алгоритмами, даже если емкости оказываются иррациональными числами
и, значит исходный алгоритм Форда—Фалкерсона не работает (см., например,
[EVEN79a, p. 96-97]).
Этот раздел мы завершаем рассмотрением планарных графов. Сошлемся
на [NISH 88а] как на главный источник по этой теме.
*) Первый такой алгоритм, называемый поиском в ширину (breadth first search technique),
был в основном развит Муром [MOOR59a]. Однако не хотелось бы, чтобы читатель был
введен в заблуждение заголовком этой статьи «Кратчайший путь через лабиринт», так как
в этом контексте лабиринт (maze) есть не что иное, как известный граф, в то время, как тот
же термин используется в гл. X этой монографии для графов, для которых известна только
локальная информация в каждой вершине.
2) Алгоритм, имеющий сложность 0(р3) и решающий, имеет ли G подграф с указанной
степенью для каждой вершины, построен в [ANST85a].

102 Глава III. Основные понятия и предварительные результаты
Теорема III.89. Существуют линейные по времени алгоритмы,
решающие, является ли данный граф а) планарным, Ъ) внешнепланарным (см.
[WIEG87a]).
Теорема III.90. Пусть G — планарный граф, и пусть G\ — его вложение в
плоскость. Существуют линейные по времени алгоритмы,
a) производящие плоское вложение графа G (даже если требуется, чтобы
ребра представлялись в виде прямолинейных отрезков, а все границы
граней—в виде выпуклых многоугольников] см. [СН1В84а]);
b) определяющие 0+(Gi)1^;
c) определяющие границы графа граней G\, если он не имеет перешейков]
d) производящие D(G{) из G\]
e) расширяющие G\ путем вложения планарного графа Go в некоторую грань
F ? F(Gi) и отождествления определенных вершин в bd(F) с
определенными вершинами в bd(Foo) С Go .
В действительности, даже если ориентируемый или неориентируемый род
графа G равен 1 (т.е. он вложим в тор или в проективную плоскость),
существуют не более чем полиномиальные по времени алгоритмы для нахождения
вложений (см. [PERU84a] по поводу результатов и литературы).
Теорема III.91. Пусть G — связный плоский граф. Следующие проблемы
раскраски могут быть решены за полиномиальное время:
a) граневая 2-раскраска, если G эйлеров;
b) граневая 3-раскраска, если G двудольный и кубический]
Ь') вершинная 3-раскраска, если G — эйлерова триангуляция плоскости (эта
задача эквивалентна задаче Ъ) по двойственности);
c) граневая Ъ-раскраска, если граф G кубический.
Поэтому каноническая ориентация связного плоского эйлерова графа
может быть построена за полиномиальное время.
III.12. Заключительные замечания
Дальнейшие определения и результаты, которые не связаны напрямую с
эйлеровыми (смешанными) (ор)графами, будут излагаться по мере того, как мы
будем продолжать изучение тем, так или иначе связанных с эйлеровыми
(смешанными) (ор)графами. В некоторых примерах мы будем напомнить
определения и результаты, уже сформулированные в этой главе. Поначалу мы будем
часто ссылаться на различные определения и результаты, представленные в
этой главе; однако в дальнейшем количество таких ссылок будет
уменьшаться, так как предполагается, что читатель постепенно освоит этот материал.
Кроме того, главные темы этой монографии — эйлеровы цепи и
замкнутые покрывающие маршруты, с одной стороны, и цикловые разложения и
*) Линейный по времени алгоритм для вложения графа G при условии, что 0+(G)
известно, был построен в [READ86a]. Относительно справедливости теоремы III.89 и первой части
теоремы Ш.90.а) см. [VOKI85a].

III. 12. Заключительные замечания
103
цикловые покрытия, с другой. Общие рассмотрения этих тем поглощают так
много пространства, что в большинстве случаев эйлеровы свойства
специальных классов графов (кроме планарных) мы не будем рассматривать. Тем не
менее статьи [WALL69a, LEWS72a, MITC72a, JOLI73a, JOLI75a, HAMA76a,
BOUC78a, AKIY79a, KULL80a] являются относительно свежими примерами
изучения эйлеровых (и других) свойств для специальных классов графов. В
то время как отсутствие места не позволяет уделить им отдельного внимания,
упоминание этих статей еще раз подчеркивает интерес, который проявляется
к эйлеровым графам. Применимость эйлеровых орграфов в изобразительных
процессах демонстрируется, например, в [FUCH77a].
Кроме того, многие из ссылок, приведенных в этой главе, призваны
скорее осветить «положения дел», чем помочь читателю, начинающему изучение
теории графов, расправить крылья.

Глава IV
Характеризационные теоремы
и их следствия
IV.1. Графы
Первая характеризационная теорема суммирует сущность того, что изложено
в статьях Эйлера, Хирхольцера и Веблена.
Теорема IV. 1. Для связного графа G любые два из следующих утвероюдений
эквивалентны:
1) d{v) четно для любой вершины v € V(G), т. е. G —эйлеров граф;
2) G обладает замкнутой эйлеровой цепью Т.
3) G имеет цикловое разложение S.
Доказательство. Из 1) следует 2). Проведем индукцию по
(7(G)= Y, (d(v)-2) = 2q-2p.
vev(G)
Если cr(G) = О и q > О, то каждая вершина 2-валентна и граф G является
циклом G, так как он связен. Начиная обход по С в любой вершине вдоль
одного из двух инцидентных ей ребер мы получаем замкнутую эйлерову цепь.
Если cr(G) = 0 и g = О, то G = Ki = {v} иТ = v — единственная эйлерова цепь
графа G.
Если <r(G) > 0, то рассмотрим произвольную вершину v с d(v) > 2. Пусть
ei,62,ез— три ребра, инцидентных вершине v. По лемме о расщеплении по
крайней мере один из графов G\^ и G\$ связен; скажем для определенности,
что Gi,2 связен. Так как cr(Gi,2) < &{G) и G\^ также является эйлеровым, по
предположению индукции заключаем, что Gi,2 содержит некоторую
замкнутую эйлерову цепь Т\^.. Так как E{G\$) = E(G) и любая пара смежных ребер
графа Gi?2 является также парой смежных ребер графа G, то Ti}2 индуцирует
замкнутую эйлерову цепь Т графа G. Следовательно, 1) влечет за собой 2).
Из 1) следует 3). Проведем это доказательство индукцией по cr(G), как в
приведенном выше доказательстве, пока не достигнем Gi,2 (если G = ATi, то
S = 0 есть единственное цикловое разложение графа G). По предположению
индукции Gi,2 имеет цикловое разложение 51,2- Каждый цикл С Е 5i?2, не
содержащий г;^, является также циклом в графе G. Пусть Gi,2 € Si,2
обозначает цикл с г>1,2 € V(Ci,2). Если v $ V(Ci,2), то Ci,2 соответствует в графе
G циклу С[2 eve V(C'l2)- В противном случае V(Ci,2) Э {^1,2,^} и Gi,2
соответствует подграфу Н графа G, в котором v есть 4-валентная вершина, а
другие вершины 2-валентны. Следовательно, Н может быть разложен на два

IV. 1. Графы
105
цикла Gi,G2 с ei € Е(Сг), г = 1,2 (начнем обход в v вдоль е\ и остановимся,
когда снова попадем в v\ это дает Ci, а G2 — Н — С\).
Следовательно, мы получаем цикловое разложение графа G, полагая в
случае v # V(Ch2)
5:=(5if2-{Cij2})U{Cli2},
а в случае v ? V{C\^)
5:=(51,2-{С1,2})и{С1,С2}.
Из 2) следует 1). Рассмотрим обход по фиксированной замкнутой
эйлеровой цепи Т, начинающийся в v € V(G). Для Т — v имеем G = i^i, и в этом
случае импликация верна. Следовательно, допустим, что q > 0. Для каждой
вершины х € V(G), х ф v (если такая вершина х существует), каждый раз,
когда в этом обходе мы достигаем вершины х вдоль некоторого ребра, мы
покидаем ее вдоль некоторого другого ребра. Так как Т использует каждое ребро
графа G точно один раз, то мы получаем разделение инцидентных вершине х
ребер на пары, где каждая пара состоит из заходящего и исходящего ребер.
Поэтому d(v) четно. Но для вершины v мы также имеем разделение
инцидентных ей ребер на пары: одна пара состоит из первого и последнего ребра при
прохождении по Т, другие пары определяются так же, как они определялись
выше для х ф v.
ИзЗ) следует 1). Пусть S = {Gi,..., Ct} — фиксированное цикловое
разложение графа G (возможно, 5 = 0). Для каждой вершины v E V(G) и любого
г = 1,...,? имеем dc{{v) — 0 или 2 в зависимости от того, принадлежит v
множеству V(Ci) или нет. Следовательно, так как
t
E(G) = [J E(d),
г=1
то мы имеем
t
d(v) = ^dCi{v) = 0(mod 2).
г=1
Это завершает доказательство теоремы IV. 1.
Отметим, между прочим, что в доказательствах двух предыдущих
импликаций петля w или хх учитывалась дважды, что согласуется с принятым
определением степени вершины, когда петля считается дважды.
Также отметим, что если G —несвязный граф, то он является эйлеровым
тогда и только тогда, когда он имеет цикловое разложение (см. упр. IV.1).
Таким образом, понятие циклового разложения является на самом деле более
общим по сравнению с понятием эйлеровой цепи. С другой стороны, если G
связен, то эквивалентность этих двух понятий проявляется в каждом его блоке
(см. упр. IV.l.b) и с)).
Следующие две характеризации эйлеровых графов могут быть получены
рассуждениями, подобными тем, которые использовались в доказательстве
теоремы IV. 1; поэтому их доказательства мы оставляем читателю в качестве
упражнений.

106 Глава IV. Характеризационные теоремы и их следствия
Следствие IV.2 (см. также [KOTZ68a, Lemma 1]). Граф G является
эйлеровым тогда и только тогда, когда он обладает разложением на замкнутые
цепи.
Следствие IV.3. Граф G эйлеров тогда и только тогда, когда он имеет
эйлерову ориентацию.
Другие критерии легко доказать, используя тот факт, что число нечетных
вершин в графе всегда четно (см. упр. IV.4).
Следствие IV.4. Граф G эйлеров тогда и только тогда, когда каждое его
разрезающее множество имеет четную мощность.
Следующие характеризации эйлеровых графов есть результат более
поздних независимых исследований Тойды [TOID73a] и Макки [МсКЕ84а].
Представленное здесь доказательство не использует эти работы. Другое
доказательство этой теоремы см. в [WOOD88a].
Теорема IV.5. [FLEI89b] Граф G эйлеров тогда и только тогда, когда
каждое его ребро принадлежит нечетному числу циклов этого графа.
Доказательство. Достаточность. Предположим, что каждое ребро е графа
G принадлежит нечетному числу циклов; обозначим это число через 7е-
Предположим, что граф G не содержит петель, потому что петля
принадлежит точно одному циклу и удаление петель не изменяет ни четности какой-
либо степени, ни четности числа циклов, которым ребро uv [и ф v)
принадлежит.
Пусть 5 = {Ci,..., Cm} — множество циклов графа G. Теперь заменим в
графе G каждое ребро е на 7е ребер и заменим ребро е в каждом из содержащих
его циклов на одно из 7е новых ребер. Таким образом, мы получаем новый
граф Go и множество So = {С?,..., С^} циклов, которое является на самом
деле цикловым разложением графа Go согласно приведенной выше процедуре
замены.
По теореме IV.l Go—эйлеров граф, т.е. d,G0(v) = 0(mod 2) для каждой
вершины v e V(G0) = V(G).
Однако для Ev = {ei,..., е^} С E(G) по условию имеем
7ei = 1 (mod 2) для г = 1,..., d,
в силу чего
d
0 = dGo(v) = J27е, = d (mod 2).
г=1
Следовательно, d = d(v) четно для каждой вершины v G V(G), т.е. граф G
эйлеров.
Необходимость. Предположим, что G эйлеров. Проведем доказательство
индукцией по р =| V(G) |. Если р = 1, то каждое ребро является петлей и
принадлежит ровно одному циклу, т. е. нечетному числу циклов. В дальнейшем
мы предполагаем без потери общности, что G связен.
Предположим, что р > 1. Так как G связен, то существует ребро е = ху с
х ф у. Пусть Л(е) > 1 обозначает кратность ребра е. Образуем эйлеров граф

IV. 1. Графы
107
Е2(х)
г
<
V
Е2(ху)
Л
>
Е ,(У)
J
Рис. IV.1. Граф Ge.
Ge, стягивая ребро е и обозначая вершину графа Ge, заменяющую вершины
х,у е V(G), через z. Ребра, инцидентные вершине z в Ge, можно разбить на
три класса Ez(x),Ez(y),Ez(xy), где JEz(a;) состоит из ребер графа G,
инцидентных вершине х, но не вершине у, ?2(у) определяется аналогично, a Ez(xy) —
множество петель, соответствующих в G Л—1 ребрам, инцидентным вершинам
а; и у, но отличным от е (см. рис. IV. 1).
Теперь заметим, что любой цикл С(е) графа G, содержащий е,
соответствует в Ge либо петле из Ez(xy), либо циклу, содержащему некоторое ребро
из Ez{x) и некоторое ребро из Ez(y). Обозначим цикл последнего типа
через C(ei,Ez(y)), где е^ € Ez{x). Пусть, кроме того, к — \Ez(x)\, C(ei,ej)
обозначает цикл графа Ge, содержащий два различных ребра е^е^ € Ez(x), и
7g(c) (7<зе(ег)) обозначает число циклов графа G (Ge), содержащих ребро е
{аеЕг(х)).
По условию
fc + А = dG(x) = 0 (mod 2),
а по предположению индукции
7Ge(ei) = l(mod2).
Поэтому получаем (отмечая, что \Ez{xy)\ = А — 1)
к
yG(e)=Y,\{C(ei,Ez{y))}\ + \E,(xy)\
г=1
А-1 + ]Г7Се(е,)- ? |{С(е,,е,-)}|
г=1
= А - 1 + /с = 1 (mod 2)

108 Глава IV. Характеризационные теоремы и их следствия
(заметим, что в Х^=17с?е(ег) каждый цикл C(ei,ej) учитывается один раз в
7с7е(ег) и один раз в 7Ge(ej))- Следовательно, число циклов графа G,
содержащих е G E(G), нечетно. Это завершает доказательство теоремы.
Теорема IV.5 дает нам возможность доказать другую характеризацию
эйлеровых графов в виде результата о четности числа цикловых разложений
эйлерова графа (см. также [BOND86a, Corollary 3.4]).
Следствие IV.6. Граф является эйлеровым тогда и только тогда, когда он
имеет нечетное число цикловых разложений.
Доказательство. Если граф G имеет нечетное число цикловых разложений,
то он имеет по меньшей мере одно такое разложение и потому по теореме IV. 1,
примененной к каждой компоненте графа G, он эйлеров. Следовательно,
допустим, что G эйлеров; пусть е Е E{G) выбрано произвольно, и пусть С\,..., СТ —
циклы, содержащие е. Согласно теореме IV.5, г = 1 (mod 2). Проведем
индукцию по q = \E(G)\.
Если g = 0, то 5 = 0 — единственное цикловое разложение графа G;
следовательно, предположим, что q > 0.
Если d = G — С{ — 0 для некоторого г, то г = 1 и G есть цикл с S = {Ci}
в качестве его единственного циклового разложения. Допустим поэтому, что
Gi^0, 1 < г < г. По предположению индукции Gi имеет нечетное число
цикловых разложений (отметим, что граф Gi не обязательно связен, даже если G
связен). Это дает нечетное число цикловых разложений графа G, содержащих
Ci. Обозначим это число через s(Ci) и обозначим через s(G) число цикловых
разложений графа G. Тогда
г
5(G) = ]Г s(Ci) = г = 1 (mod 2).
г=1
Теперь следствие IV.6 доказано.
Я хотел бы отметить, что о статьях [TOID73a, McKE84a] мне стало
известно из статьи [LESN86a]. To же самое относится к следующей характеризации
эйлеровых графов, которая принадлежит Шенку [SHAN79a]. Доказательство,
предложенное здесь, — это не доказательство Шенка.
Теорема IV.7. [FLEI89b] Связный граф G является эйлеровым тогда и
только тогда, когда число подмножеств из E(G) (включая пустое множество),
каждое из которых содержится в некотором каркасе графа G, нечетно.
Доказательство. Пусть G — произвольный связный граф. Пусть tq
обозначает число, определенное в формулировке теоремы, и пусть тс(е) обозначает
число соответствующих подмножеств из E(G), содержащих е. Проведем
индукцию по q =| 1?(G) |. Так как петля есть цикл, она не может содержаться ни
в каком каркасе графа G. Следовательно, предположим без ограничения
общности, что G не содержит петель. Значит, если р =| V(G) \= I, то G = Ki, q = 0
и E(G) = 0 — единственное подмножество, содержащееся в единственном
каркасе G = К\. Поэтому мы предположим, что р > 1,д > 0 (заметим, что К\
эйлеров).

IV. 1. Графы
109
Пусть е = ху — произвольное ребро. Образуем Ge, стягивая е в вершину
z E V(Ge) — V(G), заменяющую х и у. Граф Ge имеет меньше ребер, чем G,
так же как и G — е. Граф Ge связен, так как G связен, и G — е несвязен тогда
и только тогда, когда е есть перешеек графа G.
Подмножества из E(G), каждое из которых содержится в некотором
каркасе графа G, разбиваются на два класса: в первом классе лежат те
подмножества, которые содержат е, а во втором те, которые не содержат е.
Множество из первого класса, скажем М, соответствует М' := М — {е} в
Ge, где М' содержится в некотором каркасе графа Ge, a M' С E(Ge),
принадлежащее каркасу графа Ge, соответствует М = М' U {е}, где М принадлежит
первому классу. Отметим также взаимно однозначное соответствие между
каркасами графа G, содержащими е, и каркасами графа Ge- Следовательно, в силу
установленного выше с помощью индукции получаем
т:=тСе=тс(е), (1)
причем
т = 1 (mod 2) тогда и только тогда, когда Ge эйлеров. (2)
Кроме того, если N С E{G) принадлежит второму классу, то N
принадлежит каркасу графа G — е тогда и только тогда, когда G — е связен, т. е. тогда
и только тогда, когда е не является перешейком графа G. Таким образом, мы
различаем два случая.
1) Ребро е не является перешейком графа G. Тогда из установленного выше
мы заключаем, что
TG = TGe + TG-e- (3)
2) Ребро е является перешейком графа G. Тогда е содержится в каждом
каркасе графа G (см. теорему Ш.18.2 и теорему 111.21) и любое
подмножество N С E(G), принадлежащее второму классу, является подмножеством
N' С E(Ge), содержащимся в каркасе графа Ge, и наоборот. Таким образом,
в этом случае
rG = 2rGe. (4)
Следовательно, в случае 2) мы имеем rG = 0 (mod 2) в соответствии с
утверждением теоремы, так как G не может быть эйлеровым (эйлеров граф не имеет
перешейков согласно следствию IV.4) вне зависимости от того, является граф
Ge эйлеровым или нет.
Для того чтобы закончить доказательство теоремы, рассмотрим случай 1) и
допустим сначала, что G эйлеров. Тогда Ge также эйлеров, но G —е не эйлеров.
По предположению индукции и в силу (2) и (3) мы тогда имеем
rG = 1 + 0 = 1 (mod 2)
в соответствии с утверждением теоремы.
Наконец, допустим, что G не эйлеров. Если ни один из графов Ge и G — е
не является эйлеровым, то предположение индукции плюс (2) и (3) дают
rG = 0 + 0 = 0(mod 2).

110 Глава IV. Характеризационные теоремы и их следствия
Если, однако, один из графов Ge и G — е эйлеров, то они оба являются
эйлеровыми; в самом деле, в этом случае х и у — единственные нечетные вершины
графа G. Поэтому
rG = 1 + 1 = 0 (mod 2);
т.е.
tq = 0 (mod 2), если G не эйлеров.
Это завершает доказательство теоремы.
Заметим, что теорема IV.5 и следствие IV.6 установлены в [BOND86a] в
более общей постановке, где подсчитываются некоторые пути и циклы. С
другой стороны, теорема IV.5 может быть получена из результата о матроидах;
это было сделано в [МсКЕ84а ]. Тойда, доказав в [TOID73a] только
необходимость условия теоремы IV.5, вывел свой результат из результата о путях
в связных графах с точно двумя нечетными вершинами. В следующей
главе мы получим этот результат как следствие теоремы IV.5: Уэлш [WELS69a],
рассматривая характеризацию эйлеровых графов с помощью цикловых
разложений, распространяет это понятие на бинарные матроиды и показывает,
что бинарный матроид является эйлеровым тогда и только тогда, когда его
двойственный матроид двудолен.
IV.2. Орграфы
Теперь обратимся к характеризации эйлеровых орграфов. Наша следующая
теорема является аналогом теоремы IV.1 (см. [КОГШба, р. 29 ].
Теорема IV.8. Для слабо связного орграфа D любые два из следующих
утверждений эквивалентны:
1) id(v) = od(v) для каждой вершины v € V(D) (т. е. D —эйлеров граф)]
2) D имеет {замкнутую) эйлерову цепь Т;
3) D обладает цикловым разложением S.
Доказательство. 1) влечет за собой 2). Проведем индукцию по
a(D)= J2 (od(v)-l) = q-p.
veV(D)
Сначала отметим, что если cr{D) < 0, то D = К\ или D есть цикл С, так как
D слабо связен; если мы начинаем в произвольной вершине v G V(jD), to либо
Т = v, либо обход вдоль С однозначно определен ориентацией цикла С и этот
обход определяет эйлерову цепь Т орграфа D. Следовательно, допустим, что
o~(D) > 0; рассмотрим любую вершину v G V(D), такую, что id(v) = od(v) > 1,
и пусть а\ = (у\, v) — произвольная дуга, инцидентная в вершину v, и пусть
а<ь = (г;,г>2), as = {у,у$) —любые две дуги, инцидентные из вершины v. Оба
орграфа Di52 и ?>1,з эйлеровы, и по лемме о расщеплении по крайней мере один
из них слабо связен; скажем, это ?>1,2- По предположению индукции, так как
0"(?*i,2) < &(&), .Di,2 имеет эйлерову цепь Ti52, которая индуцирует эйлерову
цепь орграфа D таким же способом, как и в неориентированном случае.

IV.2. Орграфы
111
1) влечет за собой 3). Опять мы проводим индукцию по cr(D). Так как
случай cr(D) = О можно рассмотреть так же, как и в доказательстве
предыдущей импликации (с 5 = 0, если A(D) = 0), предполагаем, что c(D) > 0. Как
и в доказательстве предыдущей импликации, применим лемму о расщеплении
и без ограничения общности допустим, что Di,2 слабо связен. Пусть Si,2 —
цикловое разложение орграфа ?>i,2- Рассуждая, как в доказательстве
теоремы IV. 1, мы заключаем, что цикл С[ 2 € Si,2 соответствует в орграфе D либо
циклу Ci,2, либо подорграфу орграфа jD, который представляет собой
объединение двух дугово-непересекающихся циклов С\,С<2,- Следовательно, для
орграфов мы также получим цикловое разложение S, полагая
S = (Si,2 - {С{,2}) U {Cli2} или 5 = (5i,2-{CJi2})U{C1>C2}
в зависимости от того, соответствует С{ 2 циклу в орграфе D или нет.
Для того чтобы доказать, что 2) влечет за собой 1) и 3) влечет за собой
1), можно провести те же рассуждения, что и в доказательстве теоремы IV. 1.
Поэтому мы оставляем читателю завершение доказательства теоремы IV.8
(упр. IV.5.).
Отметим, между прочим, что следствие IV.2 тоже может быть
переформулировано для орграфов, в то время как для следствия IV.3 в общем случае
это не так; действительно, любой 4-реберно-связный эйлеров граф G можно
ориентировать таким образом, что соответствующий орграф D не является
эйлеровым, хотя D сильно связен (просто взять эйлерову ориентацию графа
G и обратить ориентацию точно одной дуги; см. также упр. IV.6). Докажем
теперь результат, который аналогичен следствию IV.4.
Следствие IV.9. Орграф D является эйлеровым тогда и только тогда,
когда каждое разрезающее множество Ао С A(D) с разбиением V\,V2
содержит столько же дуг, инцидентных из V\, сколько дуг, инцидентных из Vi
(другими словами, a+(Vi) = a~(Vi) для г — 1,2).
Доказательство. Предположим, что условие, сформулированное в
следствии, справедливо для произвольного Aq. Тогда оно должно быть также
справедливо для Ао = Av — Av, т. е. для случая, когда V\ = {v} или V2 = {v} для
произвольной вершины v G V(G). Скажем, V\ = {v}.
По условию существует столько же дуг в Av — Av, исходящих из v, сколько
существует дуг в Av, инцидентных из V(D) — {v}, т.е. заходящих в вершину
v. Таким образом, od(v) = id(v) для произвольной вершины v € V(D), т.е.
D — эйлеров орграф (отметим, что петля в v дает вклад единица и в id(v), и в
od(v)).
Обратно, если D эйлеров, то рассмотрим произвольное разрезающее
множество Ао. Так как условие выполняется тривиальным образом, если Aq = 0,
предположим, что А0 ф 0. Образуем D(Ao), перевязь орграфа D относительно
множества Aq (см. рис. IV.2.).
Для г — 1,2 из равенств odn^v) = odry(v) — idr)(v) = idoiiv) для каждой
вершины uGK следует, что также выполняется равенство odDi(zi) = idry^Zj)
(см. следствие Ш.5а). Так как дуга из Ао инцидентна из Vi
(соответственно инцидентна в Vi) тогда и только тогда, когда соответствующая дуга в AZi

112
Глава IV,
. Характеризационные теоремы и их следствия
г^
к^
D ",
Рис. IV.2. Эйлеров орграф D и его перевязь D(Aq).
обладает этим свойством, мы заключаем, что А$ содержит столько же дуг,
инцидентных из Vi, сколько дуг, инцидентных в1^,т.е. idn^Zi) = о^оДз*), г = 1,2
(отметим, что это равенство не зависит от г, потому что ido1{zi) = od,D2(z2)).
Это завершает доказательство следствия IV.9.
Теорема IV.8 имеет еще одно следствие, доказательство которого мы
оставляем читателю в качестве упражнения:
Следствие IV. 10. Каждый слабо связный эйлеров орграф является сильно
связным.
Однако теорема IV.5 не имеет аналогов в орграфах. Это видно на примере
произвольной эйлеровой ориентациии графа K<i^T » т > 1- Те же самые
орграфы показывают, что для орграфов не существует и аналога следствия IV.6, так
как они имеют четное число цикловых разложений (см. упр. IV.7 и IV.8). Что
касается аналога теоремы IV.7 для орграфов, то обсудим орграфы на рис. IV.3.
Для обоих орграфов D\ и L>2 рассмотрим каркасы, выходящие из корней
v, гу, х соответственно, и подсчитаем число Т?>. (?) подмножеств из A(Di),
содержащихся в некотором каркасе, выходящем из корня t ? {v,w,x},i = 1,2. Для
t = v имеем в D\ соответствующие подмножества
Ф, if}, Ш, {«?'}, {h'h if, 9}, {/, h'}, {Л', g1},
а в D<i — подмножества
Ф, {/}, {9}, if"}, if)"}, if, 9}, if, 9"}, if", 9}, if", 9"}-
To есть
tDi (v) = rD2 (v) + 1 = 0 (mod 2).
Следовательно, по симметрии для произвольной вершины t € {v,w,x} и
г = 1,2
rDi(t)=i + l{mod2).

IV.3. Смешанные графы
113
Di D2
Рис. IV.3. Два эйлеровых орграфа.
Для того чтобы определить для i = 1,2 четность числа тг)г подмножеств,
содержащихся в некотором каркасе, выходящем из корня, заметим, что не
существует подмножеств мощности по меньшей мере три, которые учитывались бы
в TDi, и не существует подмножеств мощности два, учитывающихся в r^i (?), t G
{v,w,x}, которые учитывались бы также в т^(?'), ^ ^ {viwix)-> *' Ф *•
Поэтому в Г?)1 учитывается девять подмножеств мощности два, а в Т?>2 — двенадцать
таких подмножеств. Так как в T?>i должны быть учтены все одноэлементные
подмножества и пустое множество, то получим для i = 1,2
Tj^i = i-\-1 (mod 2).
Отсюда мы заключаем, что не существует простого аналога (если вообще
какой-либо существует) теоремы IV.7 для орграфов. Интересно отметить,
однако, что число подмножеств (включая пустое подмножество) из A(Di)(i = 1,2),
каждое из которых содержится либо в каркасе, выходящем из корня, либо в
каркасе, входящем в корень, орграфа А, равно (ф — 3) -Ь 7 = 19. Но при
том же самом условии то же самое число достигается для любого неэйлерова
орграфа, полученного из Di переменой ориентации дуг. Отметим уже сейчас,
что орграфы на рис. IV.3 отличаются друг от друга и в другом отношении, а
именно: число каркасов, выходящих из корня t € {г>, ги, я}, равно 3 для D\ и 4
для Дг- Этот факт будет играть важную роль в вопросе о том, как перечислять
эйлеровы цепи в графах.
IV.3, Смешанные графы
Обращаясь теперь к смешанным графам, сформулируем следующий результат
(в [FLEI83b] я приписал его Батагелю и Писански [ВАТА77а]; они, так же
как и я, не знали, однако, в то время, что этот результат уже опубликован

114 Глава IV. Характеризационные теоремы и их следствия
в книге Форда и Фалкерсона [FORD62a, Theorem 7.1, p. 60]; на эту ошибку
цитирования мне указали после того, как статья [FLEI83b] была опубликована
в [ВЕШ83а]).
Теорема IV.11. Пусть Н — слабо связный смешанный граф. Тогда любые два
из следующих утверждений эквивалентны:
1) для любого X С V(H) число /н(Х) := е(Х)— \а+(Х) - а~(Х)\ является
неотрицательным четным целым числом;
2) Н имеет (замкнутую) эйлерову цепь Т;
3) Н обладает цикловым разложением S.
Доказательство. Пусть Т — эйлерова цепь графа Н, начинающаяся, скажем,
в v, или пусть S — цикловое разложение графа Н. Обход по Т или по любому
циклу С ? S вводит ориентацию на элементах из Е(Н),Е(С) соответственно
(в случае, когда А(С) — 0, выберем произвольно одну из двух возможных
ориентации). Проделывая это для каждого цикла С Е 5, мы получаем по теореме
IV.8 либо из Т, либо из S эйлеров орграф D\ с А(Н) С A(Di). В D\ мы имеем
af(X) = а^(Х) (индекс 1 отсылает к D\ для того, чтобы избежать путаницы с
а+(Х), а~(Х) соответственно) для любого X С V(D\) = V(H). Таким образом,
а+(Х) = а+(Х) + е'(Х) = а^(Х) = аГ{Х) + е"{Х),
где е'(Х) + е"(Х) = е(Х)\ следовательно,
0 = af(X) - а~(Х) = а+(Х) - а~(Х) + е{Х) - 2е"(Х)
= ai (X) - <4(Х) = а~(Х) - а+{Х) + е(Х) - 2е'(Х),
откуда
0 < 2е"(Х) = е{Х) - (а~(Х) - а+(Х)).
и
0 < 2е'(Х) = е{Х) - (а+(Х) - а~(Х)).
Поэтому е(Х)— |а+ (X) — а~(Х) \ есть неотрицательное четное целое число.
Таким образом, мы показали, что 2) влечет за собой 1) и 3) влечет за собой
1). С другой стороны, если Н имеет эйлерову цепь Т (или цикловое
разложение 5), то мы получим из Т (5), как выше, эйлеров орграф Dt iPs), в
котором исходная цепь Т (цикловое разложение S) индуцирует эйлерову цепь
То (цикловое разложение Sd)- По теореме IV.8. наличие Тр (So) эквивалентно
существованию циклового разложения S(D) (эйлеровой цепи T(D)), которые,
в свою очередь, индуцируют в Н цикловое разложение St (эйлерову цепь Ts)
просто потому, что А(Н) С A(D) для D € {Dt,Ds}- Следовательно, нами
доказана эквивалентность 2) и 3).
Для того чтобы завершить доказательство теоремы, достаточно показать,
что, начиная с 1), можно получить эйлеров орграф D, ориентируя элементы из
Е(Н) таким образом, что А(Н) С A(D). Применение теоремы IV.8 к D тогда
дает эйлерову цепь Т или цикловое разложение 5 в Н тем же самым способом,
как и в предыдущем абзаце.
Предположим, что существует смешанный граф Н (не обязательно
связный), удовлетворяющий сформулированному в 1) условию, который не может

IV.3. Смешанные графы
115
быть преобразован в эйлеров орграф D с А(Н) С A(D). Среди всех возможных
контрпримеров пусть Я выбран таким образом, что число | V(Я) | -f | Е(Н) \ —
наименьшее из возможных.
В дальнейшем назовем разрезающее множество Сх, соответствующее X С
У (Я), критическим, если /н{Х) = 0; будем говорить, что оно тривиально,
если min{| X |, | V{H) — X |} = 1. Назовем также утверждение 1) теоремы IV. 11
условием разреза.
Без ограничения общности можно считать, что Я не имеет петель, так как
по определению разрезающее множество не может содержать петель, а по
выбору Я петли лежат в А(Н)\ следовательно, если получена эйлерова
ориентация Do графа Я — Л(Я), то Д) U Л(Я) — эйлерова ориентация графа Я. Таким
образом, если р = \V(H)\ = 1, то Е(Н) = А(Н) = 0 и Я = К\ является
эйлеровой ориентацией самого себя. Следовательно, можно считать, что р > 1.
Далее отметим следующие факты относительно произвольного смешанного
графа Я*:
a) /н*(Х) = /н*(У(Н*) — X) для любого X С V(H*); это вытекает из
условия разреза. Следовательно, в дальнейшем мы можем без потери общности
предполагать в случае критического разрезающего множества Сх, что X не
содержит предписанной вершины.
b) Если Я* удовлетворяет условию разреза и имеет критическое
разрезающее множество Сх, тпо ориентация элементов из Е(Х) однозначно
определена в каждой эйлеровой ориентации D графа Я (если такая ориентация D
существует). Действительно, так как Е(Х) ф 0, то а+(Х) ф а~(Х), и если
а*(Х) > а~(Х), то каждое ребро е € Е(Х) соответствует в D дуге,
инцидентной в X] в противном случае е соответствует дуге, инцидентной из X.
Следовательно, если Я* и Щ суть два непересекающихся (смешанных) (ор)графа,
получающихся при переходе к перевязи графа Я* (см. также рис. IV.2)
относительно критического разрезающего множества Сх графа Я*, и если Я* имеет
эйлерову ориентацию D*,i = 1,2, то эйлерова ориентация графа Я*
индуцируется естественным путем ориентациями D\ и D\ (см. также упр. IV.9).
Отметим, что для {z*} = V(H*) — V(H) имеет место равенство /#;(>?*) = /#*(Х)
(даже если Сх не критическое).
c) Если Я* удовлетворяет условию разреза, то граф G*, лежащий в
основе смешанного графа Н*, является эйлеровым] поэтому граф G*, лежащий
в основе Я*,г = 1,2, эйлеров; следовательно, /н*(У) четно для любого Y С
Теперь докажем, что
Я не имеет нетривиальных критических разрезающих множеств. (1)
Предположим противное. Тогда существует X С V(H), такое, что \Х\ > 1,
\V{H)-Х\ > 1 и fH(X) = 0. Пусть Щ с {zt} = У(Щ)-У(Н) суть (смешанные)
(ор)графы из перевязи относительно Сх, г = 1,2.
Предположим, что /нг(У) < 0 для некоторого Y С У(Щ), такого, что Zi ? Y
(см. а), с)), г ? {1,2}. Тогда Y с V(H) и Су также является разрезающим
множеством графа Я по определению множества Сх и перевязи и, кроме того,
Ih{Y) = fHi{Y) > 0. Это противоречие показывает, что Ях и Яг удовлетво-

116 Глава IV. Характеризационные теоремы и их следствия
ряют условию разреза. Так как Сх нетривиально, то | V(Hi) \<\V(H) |, г = 1,2;
согласно выбору #, эйлеровы ориентации D\ графа Н\ и D<i графа #2
существуют и индуцируют, согласно Ь), эйлерову ориентацию графа #. Это
противоречие устанавливает (1) (если #i, скажем, не является смешанным
графом, то он должен быть эйлеровым орграфом по условию разреза и поскольку
Сх критическое; см. также замечания, следующие за доказательством
теоремы) .
Наш следующий шаг —показать, что
fif(v) = 0 для каждой вершины v ? V{H). (2)
Предположим, что существует х ? V(H) с }н{х) ф 0; по условию
разреза имеем /н(х) > 2, т.е. существуют в\ = их,еч — wx ? Ех. Образуем
#1,2 с помощью отщепления ребер ei,e2 от вершины х с помощью вершины
{#1,2} = У{Н\^) — V(Н), если |AxUjE^x| > 2; в противном случае пусть Н\^ = #
с х\л2 = х. Пусть Но = (#i,2 — 2:1,2) U {uw}. В силу выбора Н достаточно
показать, что Но удовлетворяет условию разреза: эйлерова ориентация графа
Но соответствует естественным образом эйлеровой ориентации графа #i,2 и,
следовательно, эйлеровой ориентации графа #, и V(H0) < V(H),\E(Ho)\ =
|ВД|-1.
Неравенство Jh{x) > 2 влечет за собой /я0(я) > 0, если х ? V(#o); но
предположим, что существует X С V(Ho) с х ? X, такое, что /н0(Х) < 0 (см.
а); заметим также, что в любом случае /#0(Х) четно). Пусть Сх обозначает
соответствующее разрезающее множество в #0.
Если uw ? Сх, то Сх = Сх' также является разрезающим множеством
графа #1,2 с /я1,2РО < 0? гДе X' — X или Xf = X U {?1,2} в зависимости от
того, выполняется равенство | {u, w} П X |= 0 или равенство | {и, w} П X |= 2.
Если uw ? Сх, то без ограничения общности можно считать, что и ?
X, w 0 X, а С'х = (Сх — {uw}) U {их\^} — разрезающее множество графа
#1,2 с /нг,2(Х) < 0 (в этом случае xi,2 &X' = Х).
Следовательно, в обоих случаях получаем X' С V(H), определяющее
разрезающее множество с $н(Х') < 0, за исключением случая, когда uw ? Сх' и
?i,2 ? X'. Мы теперь заключаем, что и, w ? X, X' — {?1,2} определяет в #
разрезающее множество С = Сх U {их, wx} и, таким образом, /#(Х; — {?1,2}) < 0.
Поэтому /#(Х' — {xi52}) = 0. Следовательно, С критическое. Так как u,w G X,
х ? V(H)— X, то из (1) следует, что {х} = V(#) — X. Это и а) дает /н{х) — 0 —
противоречие, которое завершает доказательство (2).
Поэтому критические разрезающие множества графа # суть множества
C{v}, где г> ? V(#) —произвольная вершина. Так как Е(Н) ф 0, то должна
существовать такая вершина х ? V(H), что ?"х ^ 0. Так как С{х}
критическое, в эйлеровой ориентации графа # ориентация каждого е ? Ех
определяется с помощью ос1н(х) — го1н{х) (см. Ь)). Соответственно заменим е = ху на
а ? {(х, у), (у,х)} для фиксированного е ? i5x, получая, таким образом, Н' с
У(#') = V(H) и |?(#')|<|?(#)|.
Допуская, что для #' нарушается условие разреза, находим такое
множество X С V(Hf) = У(#), что /н'(Х) < 0 и а ? Сх ; в противном случае

IV.3. Смешанные графы 117
fn{X) = fH'(X) < 0 — противоречие. Однако, так как $н'(Х) четно,
-2 > fw(X) = еН'{Х)- \а+,(Х) - оГн,{Х) \
и по условию
О < MX) = ен(Х)- \а%(Х) - аГн{Х) |
(с индексами Н,Н\ указанными, чтобы избежать путаницы). С другой
стороны, включение а € Сх дает е#(Х) = ен'(Х) -f 1 и | а^(Х) — а^(Х) \>
\аиХ)-а^,(Х)\-1.
Суммируя все это, получаем
О < /яРО < ен,(Х) + 1- \а+,(Х) - а~н,{Х) | +1 = fH,(X) + 2 < О,
т.е.
MX) = о.
Следовательно, (Сх — {&}) U {е} — критическое разрезающее множество в Н.
Предполагая без ограничения общности, что \Х\ < \V(H) — X\, мы заключаем,
что \Х\ = 1, согласно (1), т. е. X — {t} для некоторой вершины t ? V(H).
Согласно (2) и по построению графа Н! (см. выше) /#>(Х) = /яРО = 0 для
X = {t},t ф у. Поэтому с необходимостью X = {у}.
В силу неравенства /я' (у) < 0, а также формулы (2) и по построению Нг
имеет место равенство /н'(у) = —2. Предположим, что (х,у) Е А(Н'). Это
вместе с равенствами /я' (ж) = 0 и /я' (у) = —2 дает
ен(х) = а^(х) - а%(х), ен(у) = а^(у) - а^(у).
Так как
ая({х> У}) - ая(К 2/}) = ан(х) + ая(2/) ~ ая(я) ~ аяЫ>
ея({я, 2/}) < ен(х) + e#(y) - 2,
окончательно получаем /я({я5у}) < —2 в противоречие с тем, что Н
удовлетворяет условию разреза. Так как аналогичное противоречие получается из
предположения, что (у,х) € A(fT), то равенство /я'(у) — 0 должно быть
справедливым в любом случае. Таким образом, Нг удовлетворяет условию
разреза. Отсюда заключаем, что Н' имеет эйлерову ориентацию D (D = Н', если
Е(Н') = 0), которая является, однако, также эйлеровой ориентацией графа
Н. Это противоречие завершает доказательство теоремы IV.11.
Главная часть представленного здесь доказательства теоремы IV. 11
существенно отличается от изложенного в [FORD62a, BATA77a], но я не знаю, не
было ли подобного доказательства у кого-нибудь еще.
Заметим, что условие разреза теоремы IV. 11 сводится к тому, что
каждое разрезающее множество имеет четную мощность, если Н — граф, и что
а+(Х) = о>~(Х) для каждого разрезающего множества Сх, если if— орграф.
Следовательно, если мы положим X = {х},х € V(H), то это означает, что Н
является эйлеровым, если Н — граф или орграф. Поэтому теорему IV. 11 можно
рассматривать как обобщение одновременно теорем IV. 1 и IV.8, а также
следствий IV.4 и IV.9. С другой стороны, в теоремах IV. 1 и IV.8 достаточно, чтобы

118 Глава IV. Характеризационные теоремы и их следствия
для G (соответственно D) выполнялось условие разреза для X = {х}, х Е V(G)
(соответственно х Е V(D)), для того чтобы получить существование
эйлеровой цепи или циклового разложения. Поэтому хотелось бы думать, что в
теореме IV. 11 также достаточно ограничить условие разреза такими
множествами X, что \Х\= 1. Однако смешанный граф на рис. IV.4 (лежащий в его
основе граф изоморфен графу октаэдра) показывает, что этого ограниченного
условия недостаточно для существования эйлеровой цепи. Это отметили
также Батагель и Писански в [ВАТА77а], где они показали с помощью другого
примера, что соответствующая теорема, опубликованная в [С01С71а], не
верна. Что касается их доказательства теоремы IV.ll, [BATA77a, Theorem 4], то
сначала они доказывают, что если е — ху — ребро графа Н, такое, что никакой
критический реберный разрез не содержит е, то при построении эйлеровой
ориентации графа Н ребро е может быть заменено произвольно дугой (х,у)
или (у, х). Далее отмечается, как это мы делали в Ь), что если е Е Е(Х)
и Сх критическое, то ориентация ребра е в произвольной эйлеровой
ориентации D графа Н определяется условием разреза. Вместе с X
рассматривается другое критическое разрезающее множество Су с е ? Су, потому что
при построении орграфа D вынужденная ориентация ребра е может вызывать
проблемы только для таких Су. Это похоже на способ, который мы
применяли для Н! в последней части доказательства теоремы IV.11, и на этом
сходство между двумя доказательствами заканчивается. В самом деле на
следующем шаге Батагель и Писански рассматривают шесть вершинных множеств
X,Y, А = XnY,В = Х-А,С = Y-A,D = V(H)-(XUY) и устанавливают
систему из шести линейных уравнений, исходя из условия разреза для упомянутых
выше шести множеств, что дает соотношения /я(^Г) = /#00 = 0? Ih(F) > О
для F — A,B,C,D. Затем они исследуют влияние ориентации ребра е
(нарушающее условие разреза либо для X, либо для Y) на эту систему уравнений.
Приведением к противоречию они затем достигают окончательного
заключения о том, что если Сх,Су— два произвольных критических разрезающих
множества с е Е Сх П Су, то е может быть ориентировано таким образом,
что для Н' = (Н — {е}) U {а}, где а —дуга, заменяющая е, условие разреза не
нарушается.
Доказательство теоремы IV. 11, приведенное Фордом и Фалкерсоном в книге
[FORD62a, Theorem 7.1, p. 60], отличается от приведенного здесь с самого
начала. Они используют потоки в орграфах и применяют теорему Хоффмана
(см. теорему III.84) следующим образом:
Сначала каждое ребро е = ху Е Е(Н) заменяется парой дуг (х, у), (у, х), и,
таким образом, из Н получается орграф Do.
Определим интервалы [l(u,v),c(u,v)] (где /обозначает нижнюю грань, а с
обозначает емкость) для каждой дуги (и, v) G A(Dq), полагая c(u,v) = 1 и
l(u,v) — 1, если [и, v) ? А(Н), и l(u, v) = 0 в противном случае. С помощью
этого определения условие разреза преобразуется в условие теоремы
Хоффмана. Отметим, что для потока <р в D0 мы имеем <р(а) = 1 для а ? А(Н), и <р
можно считать целым числом; таким образом, (р(Ь) € {0,1} для b € A{Dq).
Ребро е = ху G Е(Н) заменяется на (х, у) тогда и только тогда, когда <р(х,у) = 1
и <р(у,х) = 0. Проделав это для каждого е € Е(Н), мы приходим к Щ, ко-

IV.4. Упражнения
119
А
Рис. IV.4. Смешанный граф, удовлетворяющий условию разреза в вершинах,
который не имеет эйлеровой цепи.
торый является либо эйлеровым орграфом (и поэтому эйлеровой ориентацией
графа Я), либо смешанным графом, таким, что Щ —Е(Щ) —эйлеров орграф.
В последнем случае из условия разреза вытекает, что Go = (Е(Щ)) —эйлеров
граф. Используя любую эйлерову ориентацию графа Go, можно продолжить
эйлерову ориентацию Щ — Е(Н'0) графа Н — Е(Щ) С Н до ориентации всего
графа Н.
Другая идея (а именно, сведение задачи нахождения эйлеровых цепей в
смешанных графах к транспортной задаче) была развита в [SERD76a, теорема
1], в то время как в теореме 2 указанной статьи также рассматривается эта
задача в терминах максимальных потоков (хотя не так, как это делалось выше).
Эти результаты приводят к полиномиальному по времени алгоритму порядка
0(pq), порядка, который может быть получен для максимальных потоков в
общем случае1).
IV.4. Упражнения
Упражнение IV. 1. Доказать, что
a) граф G имеет цикловое разложение тогда и только тогда, когда каждая его
связная компонента имеет цикловое разложение;
b) граф G имеет цикловое разложение тогда и только тогда, когда каждый
его блок имеет цикловое разложение;
c) связный граф G имеет эйлерову цепь тогда и только тогда, когда каждый
его блок имеет эйлерову цепь.
Упражнение IV.2. Доказать следствие IV>2.
*) Тогда как, также обсуждая ошибку в [COIC71a] (см. выше), А. И. Сердюков предполагает
(на основании своих результатов), «что в случае смешанных графов таких простых условий
не существует» (по сравнению с условиями существования эйлеровых цепей в графах и
орграфах) — ошибка, возможно, вызвана тем, что он не знал о книге [FORD62a, Theorem 7,
p. 60].

120 Глава IV. Характеризационные теоремы и их следствия
Упражнение IV.3. Доказать следствие IV.3.
Упражнение IV.4. Доказать следствие IV.4.
Упражнение IV.5. Завершить доказательство теоремы IV.8.
Упражнение IV.6. Доказать, что если D — эйлерова ориентация 4-реберно-
связного эйлерова графа G и D\ получается из D заменой дуги (щ v) на дугу
(г>,и), то D\ сильно связен.
Упражнение IV.7. Используя эйлерову ориентацию графа К^^т ,
попытаться построить бесконечное семейство эйлеровых орграфов, для которых не
существует аналога теоремы IV.5.
Упражнение IV.8. Доказать или опровергнуть следующее утверждение:
если D — эйлерова ориентация графа i^2,2m, то число цикловых разложений
орграфа D сравнимо с 0 (mod 2), кроме случая, когда га = 1.
Упражнение IV.9. Доказать следствие IV. 10.
Упражнение IV. 10. Пусть Сх —критическое разрезающее множество слабо
связного смешанного графа Н,X С V(H) и Е(Х) Ф 0. Пусть Н\,Н2— два
графа из перевязи графа Н относительно Сх- Показать, что если Di—
эйлерова ориентация графа Н{, то Н имеет эйлерову ориентацию, сохраняющую
ориентацию, установленную на каждом ребре е ? Е(Х) при построении Di
(г = 1,2).

Глава V
Некоторые возможные
обобщения
V.I. Разложения на цепи, путевые/цикловые разложения
Имея за плечами гл. IV, вернемся еще раз к работам Эйлера и Хирхольцера.
Фактически они доказали (Эйлер сформулировал, а Хирхольцер доказал)
больше, чем просто эквивалентность утверждений 1) и 2) теоремы IV. 1. А именно,
они доказали (в наших терминах), что: связный граф G обладает открытой
или замкнутой покрывающейся цепью тогда и только тогда, когда он имеет
не более двух вершин нечетной степени. Теорема IV. 1 же относится только
к случаю, когда G не имеет нечетных вершин. Однако случай двух нечетных
вершин легко следует из теоремы IV. 1 (заметим, что по лемме III.4, граф G не
может иметь одну нечетную вершину).
Следствие V.I. Граф G обладает открытой покрывающейся цепью Т тогда
и только тогда, когда он связен и имеет ровно две нечетные вершины; эти
нечетные вершины и будут концами цепи Т.
Доказательство. 1) Пусть у G есть открытая покрывающая цепь Т с
концами и и v. Добавим к графу дополнительное ребро ео = uv (независимо от
того, есть ли уже в G такое ребро). Мы получим граф Go = GU{eo}, имеющий
замкнутую покрывающую (т.е. эйлерову) цепь То = Т,ео,гх. По теореме IV. 1
граф Go эйлеров и, следовательно, у графа G = Go — {ео} ровно две
нечетные вершины, и и v, и они являются концами цепи Т. Далее, так как каждая
вершина х из G достижима из и вдоль Т, в G существует путь Р(и,х) для
выбраной вершины и и произвольной вершины х, u, x € V(G). По лемме III.15
G связен.
2) Пусть G связен и имеет ровно две нечетные вершины и и v. Построим
эйлеров граф Go, как выше. По теореме IV. 1 в Go есть эйлерова цепь Г0. Так
как То замкнута, ее можно обойти, начиная с любой вершины х и с любого
ребра еж, инцидентного х. Поэтому, выбрав х = v и ех = ео, мы сможем записать
То = г?,ео,Т, где Т — подпоследовательность в То с началом в и и концом в v,
не содержащая ео- Итак, Т —открытая покрывающая цепь в G с началом в и
и концом в г>, и ее концами являются нечетные вершины графа G.
Следствие V.1 имеет естественное обобщение в виде следствия V.2,
приведенного ниже; оно принадлежит Листингу и Люка [LIST48a, LUCA82a]
(Листинг сформулировал его, а Люка дал доказательство).

122
Глава V. Некоторые возможные обобщения
Следствие V.2. Пусть ui, ¦ • • , i>2m5 m > ®, ~ все нечетные вершины
связного графа G. Тогда найдется разложение мноэюества E(G) на т открытых
цепей Ti, • • ¦ ,ГШ, концы каждой из которых лежат в {v\, • ¦ • , V2m}, и любое
разложение множества E(G) на открытые цепи состоит из не менее т
таких цепей. Далее, каждая вершина Vi, 1 < г < 2т, есть нечетная вершина в
ровно одной из Tj, 1 < j < т.
Доказательство. Рассмотрим граф Go = G U ?Ь, где Е0 — {г>2г-1^2г|1 < i <
га} и Е0 П E{G) = 0. По построению Go эйлеров и поэтому имеет по теореме
IV. 1 эйлерову цепь То. Удалив ребра, принадлежащие Ео, из То, мы получим
последовательность из т открытых подцепей Т\, • • • , Тш цепи То. Их концы
лежат в {^i,--- ,^2m} (так как ребра в Ео попарно независимы). Множество
{J3(Ti),--- ,E(Tm)} образует разбиение множества E(G), поскольку E(Tq) =
E(G0) = E0 U UHi ??№) и Е0 П E(G) = 0. С другой стороны, если E(G)
разбито на г открытых цепей, то каждая вершина Vi, 1 < г < 2т, должна быть
концевой вершиной хотя бы одной из них. Отсюда г > т, и следствие V.2
доказано.
Если E(G) разложено на открытые цепи Ti, • • • ,Tm (мы предполагаем, что
G связен или, в более общем случае, каждая компонента графа G содержит
нечетные вершины), то мы можем разложить каждую цепь Т^, 1 < г < т, на путь
Рг, соединяющий две нечетные вершины графа G, и множество Si реберно-
непересекающихся циклов (Si может быть пустым), так как Ti — Pi эйлеров
(и, следовательно, имеет цикловое разложение). Итак, UHi(^ U {Pi}) есть
путевое/цикловое разложение графа G. Если G — произвольный граф, имеющий
эйлерову компоненту, то эта компонента имеет цикловое разложение, а
ациклическая компонента графа G (т. е. дерево) имеет путевое разложение. Так
как оба этих типа разложений есть частные случаи путевого/циклового
разложения, мы получаем такое
Следствие V.3. Каснсдый граф G имеет путевое/цикловое разложение, в
котором количество путей равно половине числа нечетных вершин графа G.
Как мы позже увидим, для планарных графов существуют разложения на
пути и циклы, удовлетворяющие неким дополнительным требованиям.
Прежде чем продолжить наши теоретические изыскания, скажем несколько
слов о работе Листинга. Его монографию «Vorstudien zur Topologie» [LIST48a]
можно считать одним из краеугольных камней в развитии теории графов.
Однако вклад этой книги в развитие теории эйлеровых графов не столь
значителен, как вклад любого из «трех столпов». (Подробнее о вкладе Листинга в
теорию графов можно узнать из книги Кёнига [KONI36a] и из более поздних
статей Р.Дж.Уилсона [WILS85a, WILS86a].)
V.2. Результаты о четности
Еще одно свойство графов из следствия V.1 дает такой результат, который
является следствием из теоремы IV.5 ([TOID73a, Theorem I]):

V.2. Результаты о четности
123
Следствие V.4. Пусть G — граф, имеющий ровно две нечетные вершины и
и v. Тогда число путей, соединяющих и и v, нечетно.
Доказательство. Образуем граф Go = G U {во}, где ео = uv $ E(G) (даже
если и и v уже смежны в G). Так как граф Go эйлеров, число циклов С в
Go, содержащих ео, нечетно (теорема IV.5). P(u,v) — С — {ео} есть путь,
соединяющий и и v, для каждого из этих циклов G, и, наоборот, P(u,v) U {ео}
для каждого пути P(u,v) в G есть цикл в Go, содержащий ео- Поэтому число
путей, соединяющих и и v в G, нечетно.
Отметим, что Тойда доказал сначала следствие V.4, а затем вывел из него
необходимое условие эйлеровости графа из теоремы IV.5.
Теперь мы можем доказать еще одну характеризацию эйлеровых графов
(см. также [TOID73a, Theorem III] и [BOND86a, Corollary 3.4]).
Следствие V.5. Граф G эйлеров тогда и только тогда, когда для каждой
пары вершин u, v E V(G) число путей, соединяющих и uv, четно.
Доказательство. 1) Предположим, что G эйлеров. Пусть и, v E V(G)
выбраны произвольно, и пусть Go = G U {ео}, где ео = uv ? E(G), как и выше. В
Go только две нечетные вершины, и и v. По следствию V.4 вершины и и v
соединены нечетным числом путей, один из которых —это и, ео,и. Поэтому и
и v соединены в G четным числом путей.
2) Если каждая пара вершин графа G соединена четным числом путей,
то это верно и для каждой пары смежных вершин. Значит, для любого ребра
е = ху Е E(G) число путей в G, соединяющих х и у и не содержащих е, нечетно.
Каждый из этих путей вместе с е образует цикл, содержащий е; поэтому е
лежит в нечетном числе циклов графа G, и по теореме IV.5 граф G эйлеров.
Следствие V.5 доказано.
Пусть w(G) обозначает общее число путей в G (включая пути длины 0).
Следствие V.5 дает нам еще один результат о четности для эйлеровых графов
[BOND86a, Corollary 2.7].
Следствие V.6. Пусть G — эйлеров граф с p(G) вершинами. Тогда w(G) =
p(G)(mod2).
Доказательство следствия V.6 мы оставляем читателю (упр. V.1).
Работа [BOND86a] содержит, конечно же, много не упомянутых здесь
результатов. Так, помимо эйлеровых графов, в ней доказано и много результатов
о четности для графов, имеющих только нечетные вершины. Для их
доказательства используются методы, обобщающие методы, разработанные Томасо-
ном [ТНОА78а].
Замечание V.7. Многие авторы, возможно, по причинам, указанным в
начале этой главы, определяют эйлеров граф как связный граф с 0 или 2
нечетными вершинами или, запрещая нечетные вершины, все-таки требуют связности.
В таких случаях графы, эйлеровы по определению из этой книги, называют
четными графами. Все же следует отметить, что наше определение эйлерова
графа —не каприз автора, а определение, данное самим Кёнигом [КОШЗба,
р. 19].

124
Глава V. Некоторые возможные обобщения
V.3. Двойные проходы
Следующий результат также восходит к статье Эйлера (см. разд. 18 этой статьи
в гл.П.). Он доказан —судя по всему, впервые,— в книге Кёнига [KONI36a,
р. 23].
Следствие V.8. У всякого связного графа есть замкнутый покрывающий
маршрут, проходящий через каждое ребро в точности дважды.
Для доказательства Кёниг удваивает каждое ребро #, создавая тем самым
эйлеров граф, и рассматривает эйлерову цепь в этом графе. Эта цепь
соответствует требуемому маршруту в первоначальном графе.
Аналогичной редукцией, но к теореме IV.8, доказывается следующий
более сильный результат; подробности доказательства мы оставляем читателю
(упр. V.4).
Следствие V.9. У всякого связного графа есть замкнутый покрывающий
маршрут, проходящий через каждое ребро по одному разу в каждом из двух
направлений.
Этот результат позднее возникнет еще раз при рассмотрении алгоритмов
обхода лабиринтов (см. гл. X); в таком контексте он был доказан Тремо и
Тарри.
Интересно, что после доказательства следствия V.8 Кёниг формулирует и
доказывает характеризационную теорему Веблена и затем переходит к
обсуждению задачи о кёнигсбергских мостах и задачи о домино. Он не задается
вопросом, существует ли аналог следствия V.8, относящийся к характеризаци-
онной теореме Веблена так же, как следствие V.8 относится к характеризаци-
онной теореме Эйлера-Хирхольцера. То есть Кёниг не задает такого вопроса:
верно ли, что для любого графа без перешейков найдется цикловое
покрытие, использующее каждое ребро в точности дважды? Попытки Сеймура
[SEYM79a, Conjecture 3.3] и в особенности Жеже [JAEG85a] установить, кто
первым поставил этот вопрос, были безуспешны, как и мои. С другой стороны,
в свете теоремы IV. 1 и следствия V.8 этот вопрос возникает вполне естественно,
и очень странно, что его так долго никто не ставил1).
Вот нам уже и встретилась нерешенная проблема, занимающая многих
исследователей в последние двенадцать лет. Мы еще вернемся к ней и подробно
обсудим ее и связанные с ней гипотезы и результаты.
V.4. Пересечение границы: расщепления графов
В серии статей [NASH79a, NASH85a, NASH85b, NASH87a] Нэш-Вильямс,
обобщая понятие отщепления пары ребер от вершины (в этой книге: операция
х) Книга Кёнига содержит множество замечаний и комментариев об истории различных
результатов и гипотез в теории графов, но там нет и следа этой проблемы. А У. Т. Татт
(один из главных авторитетов в подобных вопросах) пишет в ответ на мой вопрос: «Я тоже
не раз пытался найти первоначальную ссылку [на эту гипотезу]. Видимо, эта гипотеза —из
тех, что давно существовали в математическом фольклоре, но никому не приходило в голову
их опубликовать».

V.4. Пересечение границы: расщепления графов
125
получения Gi,2 из G), определяет расщепление (detachment) графа. Начинает
он с того же, что и мы (см. также доказательство теоремы IV. 1): если G —
эйлеров граф, то, произведя последовательность отщеплений так, что на
каждом шаге получающийся граф связен (см. лемму о расщеплении), мы получим
в конце концов цикл, соответствующий некоторой эйлеровой цепи графа G. И
наоборот, если Т — эйлерова цепь в G, то, совершая отщепления в соответствии
с переходами цикла Т, мы получим в результате некоторый цикл G, причем
такое соответствие между эйлеровыми цепями Т графа G и циклами G,
получаемыми из G последовательностью отщеплений, есть биекция. Сформулируем
эти соображения в виде следствия:
Следствие V.10. Граф G имеет эйлерову цепь Т тогда и только тогда,
когда G может быть преобразован в цикл С последовательностью отщеплений
от вершин степени, большей 2. Более того, число эйлеровых цепей графа G
равно числу различных помеченных циклов, которые моэюно получить из G
таким образом.
Обратимся теперь к четырем упомянутым статьям Нэш-Вильямса, в
которых предложен, без сомнения, интересный подход к теории графов. Этот
подход применим не только к эйлеровым графам, но и к гораздо более общим
классам графов.
Определение V.11. Пусть F и G —некоторые графы. Назовем F
расщеплением графа G, если E(F) = E(G) и существует отображение 7г из V(F)
на V(G), сохраняющее смежность (т.е. е = ху Е E(F) влечет за собой е =
ФМу) € E(G)).
Замечание V.12. Определение V.11 допускает, что для х ф у может быть
7г(х) = 7г(у); в частности, обычное ребро графа F может соответствовать
петле в G (заметим, что так как E(F) = E(G), то продолжение 7г на E(F) есть
тождественное отображение на E(F)). Если G —граф без петель, то для
всякой вершины v Е V(G) прообраз 7г-1(и) есть независимое множество в V(F).
В любом случае можно сказать, что 7г есть специального вида гомоморфизм
графа F на G, взаимно однозначный на множествах ребер графов F и G.
Используя понятие расщепления, мы можем переформулировать следствие
V.10 так:
Следствие V.13. Граф G имеет эйлерову цепь тогда и только тогда, когда
некоторое его расщепление есть цикл.
Иллюстрацией к следствиям V.10 и V.13 служит рис. V.1 (Метки на
ребрах графа G указывают, в каком порядке они проходятся в эйлеровой цепи
графа G.)
Нэш-Вильямс применяет понятие расщепления не только к конечным, но
и к бесконечным графам. Чтобы проиллюстрировать одно из направлений
его исследований, [NASH79a, NASH85a, NASH85b, NASH87a], процитируем
[NASH85b, Corollary 8.0].
Следствие V.14. Пусть к—четное натуральное число, и пусть G есть
к-реберно-связный граф. Пусть для каждой вершины v € V(G) задана по-

126
Глава V. Некоторые возможные обобщения
Рис. V.I. Граф G с некоторой эйлеровой цепью и его преобразование в цикл F или,
иначе, цикл F, являющийся расщеплением графа G (определяющий, таким образом,
эйлерову цепь в G).
следователъностъ fv натуральных чисел, fv = щ, • • • , щ^, такая, что щ >
/с, 1 < г < 1(у), и Y?f=l Щ = degG(v). Тогда G имеет такое к-реберно-связное
расщепление F, что 7г-1(г>) = {v\, • • • ,уцу)} и degF(vi) = щ, 1 < г < l(v), для
каждой вершины v G V(G).
Заметим, что следствие V.13 выводится из следствия V.14, если положить
к = 2, l(v) = |degG(v) для всех v € V(G) и щ = 2 при 1 < г < l(v).
V.5. Упражнения
Упра^снение V.I. Доказать следствие V.6 с помощью следствия V.5.
Упражнение V.2. Сформулировать и доказать аналоги следствий V.l, V.2 и
V.3 для орграфов. Попробовать сделать это для смешанных графов.
Упражнение V.3. Построить пример, показывающий, что следствие V.4 не
верно для произвольных орграфов.
Упражнение V.4. Доказать следствие V.9.

Глава VI
Различные типы
эйлеровых цепей
Рассмотрим доказательство теоремы IV. 1, где мы применили лемму о
расщеплении для установления того факта, что связный эйлеров граф G имеет
эйлерову цепь Т. Последовательно применяя лемму о расщеплении, мы можем
создать такую цепь Т (см. главу об алгоритмах для нахождения эйлеровых
цепей, а также следствие V.13). Однако из леммы о расщеплении можно
извлечь больше, а именно, что мы не слишком ограничены на любом шаге
порождения эйлеровой цепи, откуда мы заключаем, что G должен иметь много
эйлеровых цепей и что можно наложить ограничения (кроме естественного
ограничения, выражаемого леммой о расщеплении) на направление некоторой
эйлеровой цепи в G. В этой главе рассматривается именно вопрос о том, какой
тип ограничений может быть наложен.
VI. 1. Эйлеровы цепи, избегающие некоторых переходов
В этом разделе мы займемся вначале ограничением, которое действует, так
сказать, локально и является чисто теоретико-множественным. Рассмотрим
множество Е* для произвольной вершины v связного эйлерова графа G. Как много
переходов {е(г;), f(v)} может быть выбрано в качестве запрещенных переходов
в v , где е и / — произвольные элементы из Ev? Другими словами, каково
необходимое и достаточное условие существования эйлеровой цепи Т в
графе G, которая избегала бы любого из заданных переходов? Коциг [KOTZ68a,
Theorem 1] дал ответ на этот вопрос в следующей теореме, для формулировки
которой надо вспомнить определение 111.41.
Теорема VI.1. Пусть G — связный эйлеров граф, и пусть P(v) —разбиение
мноэюества Е* для каэюдой вершины v € V(G). Следующие утверэюдения
эквивалентны:
1) G имеет P{G)-совместимую эйлерову цепь]
2) \С\< \dc{v) для каэюдой вершины v ? V(G) и каждого класса С € P{v) С
P(G).
Доказательство. 1) влечет за собой 2). Пусть Т есть Р(С)-совместимая
эйлерова цепь графа G. Рассмотрим для произвольной вершины v € V(G) и
любого класса С ? P(v) все секции е, v, f цепи Т, для которых выполняется

128
Глава VI. Различные типы эйлеровых цепей
условие С С) {e(v), f (v)} ф 0. Так как Т P(G)-совместима, мы заключаем, что
e(v) € С тогда и только тогда, когда f(v) & С, т.е. \С П {e(v),f(v)} |= 1. Так
как каждое ребро графа G встречается в Т в точности один раз, мы делаем
вывод, что \С\< \do{v).
2) влечет за собой 1). Проведем индукцию по cr(G), замечая, что
импликация верна для cr(G) = 0. Действительно, a(G) = 0 влечет за собой \С\ = 1
для каждого С € P{G), откуда вытекает, что проход по циклу G обязательно
Р(С)-совместим. Следовательно, можно предположить, что a(G) > 0.
Выберем теперь вершину v G V(G), do(v) > 2, и класс С\ G Р(г>), такие,
что |Ci| = max{|G||G € P(v)}. Возьмем любое e\(v) € С\. Пусть е2(г>),е3(г>) —
любые два различных элемента из ?* — С\\ они существуют в силу
выбора г>, и \С\\ < \dc{v). Применяя лемму о расщеплении, мы заключаем без
ограничения общности, что Gi,2 связен (см. заключение 2) из доказательства
этой леммы). Пусть G2 € P{v) обозначает класс, содержащий е2(г?), и пусть
P~(v) := P(v) - {Ci,C2}. Положим
P'{w) := Р(ги) для каждой вершины го Е V(Gif2) — {^,^1,2},
P,K2):={{ei(t;)}>{e2(t;)}},
P~(v) U {d - {в!(«)}, С2 - {е2(и)}}, если |С2 |> 1,
P~(v) U {Ci - {ex(v)}}, если |СХ |>|С2 |= 1,
P~(v), если |Ci |=|C2|= 1,
P(Gia)= (J Р'(х).
xev(Gli2)
Отметим следующие факты, касающиеся G и P(G); они вытекают из
утверждения 2) и выбора v, ei, e2.
a) Для каждой вершины го € V(C?ij2) — {v, i>i,2} и каждого класса С € Р(ги) С
P(G) имеем \С'\< \dG{w) = §dGl 2(w).
b) Если | С" \>\ Ci - {ex(и)} | для некоторого С" € Р'(и), то С" € Р(и) и
|С2|<|С"|=|С1|<|^(г;)-1 = |^11а(«).
На основании этих фактов мы заключаем, что утверждение 2) справедливо в
отношении Gi,2 и P(Gi,2). Кроме того, g{G\^) < o-(G). Справедливость
теоремы теперь вытекает из предположения индукции.
Замечание. Коциг говорит в [KOTZ68a], что его теорема 1 (т. е. теорема VI.1)
есть ответ на вопрос, поставленный Нэш-Вильямсом на Коллоквиуме по
теории графов, проходившем в Тихани в 1966 г. Однако труды этого
коллоквиума не содержат упоминания этой или подобной проблемы, поставленной Нэш-
Вильямсом (частным образом он сообщил автору этой книги, что не помнит,
ставил ли он эту проблему). Но в данном случае важно не кто поставил
проблему, а те различные направления, которые эта теорема указывает, если делать
специальные предположения о G и P(G).
P'(v) :=

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 129
Следующий результат [KOTZ56a] частично является следствием теоремы
VI. 1, а частично — обобщением метода Петерсена доказательства того, что
4-регулярный граф имеет 2-факторизацию [РЕТЕ91а]. Этот результат был
первоначально доказан без использования теоремы VI. 1 (которая была
опубликована несколькими годами позже), точно так же, как первоначальное
доказательство теоремы VI. 1 не использует леммы о расщеплении.
Следствие VI.2. Пусть G есть связный эйлеров граф с четным числом
ребер. Тогда справедливы следующие утверждения:
1) Если Т есть эйлерова цепь графа G, то существуют два реберно-
непересекающихся остовных подграфа графа G, скажем Gr и Gb , такие,
что
GT U Gb = G, dar{v) = dcb(v) для каждой вершины v ? V(G)
и ребра подграфов Gr и Gb чередуются в Т.
2) Если G есть объединение двух реберно-непересекающихся подграфов Gr и
Gb с dcr(v) = dcb(v) для каждой вершины v € V(G), то G имеет эйлерову
цепь, в которой ребра подграфов Gr и Gb чередуются.
Доказательство. А) Раскрашивая ребра цепи Т во время ее обхода
поочередно в цвета г (красный) и Ь (голубой), получаем подграфы Gr и G&, описанные в
1) (для г>о, начальной и конечной вершины цепи Т, мы имеем dGr(vo) = dGb(vo)
в силу того, что \E(G) | четно).
В) Часть 2) следствия вытекает из теоремы VI. 1, если заметить, что каждое
разбиение P(v) состоит из двух классов одинакового размера.
Из части А) доказательства следствия VI.2 мы выводим
непосредственно один важный результат, содержащийся в знаменитой статье Петерсена
[РЕТЕ91а].
Следствие VI.3. Каждый 2к-регулярный граф, имеющий четное число
ребер, может быть разложен на два к-фактора. Следовательно, каждый
4-регулярный граф может быть разложен на два 2-фактора.
Теорема VI. 1 может быть обобщена способом, похожим на то, как теорема
IV.1 была обобщена до следствия V.2. Это было также сделано в [KOTZ68a].
Следствие VI.4. Пусть G — граф, такой, что каждая его связная
компонента содержит по крайней мере одну нечетную вершину, и пусть P(v) есть
разбиение множества Е* для каждой вершины v € V(G). Следующие
утверждения эквивалентны:
1) G имеет P(G)-совместимое разложение на р открытых цепей {где 2р
есть число нечетных вершин в G);
2) | С |< |(1 + da(v)) для каждой вершины v ? V(G) и каждого класса С ?
P(v)cP(G).
Доказательство. Так как по предположению каждая компонента графа G
содержит нечетные вершины, достаточно доказать следствие VI.4 для связных
графов с нечетными вершинами.

130
Глава VI. Различные типы эйлеровых цепей
Как и в доказательстве следствия V.2, образуем из G эйлеров граф Go,
соединив каждую пару нечетных вершин дополнительным ребром. Положим
P0(v) = P(v) для четных вершин v графа G, а для нечетных v положим
P0(v) = P(v) U {{eo(v)}}> где eo(v) соответствует ребру е0 Е E(Go) - E(G),
соединяющему v и некоторую другую нечетную вершину графа G.
P(Go) = UV?V(G) Po(v) удовлетворяет утверждению 2) теоремы VI. 1 тогда
и только тогда, когда P(G) удовлетворяет утверждению 2) следствия VI.4. С
другой стороны, Р(Со)-совместимая эйлерова цепь Т графа Go соответствует
Р(С)-совместимому разложению S графа G на р открытых цепей, и обратно.
Эти эквивалентности и справедливость теоремы VI. 1 влекут за собой
справедливость следствия VI.4.
К несчастью, параллелизм между теоремой IV. 1 и теоремой VI. 1, а также
между следствием V.2 и следствием VI.4 не может быть расширен до
утверждения о Р(С)-совместимых путевых/цикловых разложениях, вытекающего из
следствия V.3. Это так, даже если P(G) = X(G) есть система переходов.
Позднее при подробном рассмотрении совместимости (см. третий том этой
монографии), мы обсудим некоторые примеры.
Далее для связного эйлерова графа G без вершин степени 2 мы
предполагаем, что P(G) есть система переходов X(G) (см. определение III.41). Таким
образом, мы получаем следующий результат, тривиально вытекающий из
теоремы VI. 1; его можно, однако, доказать простым использованием леммы о
расщеплении (т.е. не прибегал к теореме VI. 1).
Следствие VI.5. Пусть G — связный эйлеров граф без вершин степени 2, и
пусть X = X(G) —система переходов графа G. Тогда в G существует
эйлерова цепь Т, которая совместима с X.
В частности, Т существует, если X = Хт> есть система переходов,
индуцированная эйлеровой цепью Т" графа G. Следовательно, мы можем утверждать,
что если 5(G) > 2, то G имеет по крайней мере две взаимно совместимые
эйлеровы цепи. Но каково наибольшее число взаимно совместимых эйлеровых
цепей в связном эйлеровом графе G с 6(G) > 2? Мы займемся этим вопросом
в следующем разделе этой главы.
В дальнейшем мы будем предполагать, что G есть 4-регулярный граф,
вложенный в некоторую поверхность J7, и что X(v) С X(G) есть пара
пересекающихся переходов для каждой вершины v € V(G) (см. определение Ш.42а).
Следствие VI.6. Если G — связный ^-регулярный граф, вложенный в
некоторую поверхность Т, то G имеет А-цепь.
Доказательство. Выберем X(G) в качестве системы пересекающихся
переходов (см. выше) и применим следствие VI.5.
Последовательность ребер 1,2,..., 12 на рис. VI. 1 дает пример А-цепи
октаэдра.
Однако следствие VI.6 может быть доказано не только прямым
применением леммы о расщеплении (упр. VI.3), но оно также вытекает из следующего
результата, в свою очередь получаемого применением леммы о расщеплении
(упр. VI.4).

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 131
Лемма VI.7. Пусть G — связный эйлеров граф, вложенный в некоторую
поверхность Т. Тогда G имеет непересекающуюся эйлерову цепь.
Из определений А-цепи и непересекающейся эйлеровой цепи (см.
определение Ш.42а) следует, что эти два понятия совпадают в случае 4-регулярного
графа (или, более общо, в случае, если G — эйлеров граф с Д(С) < б). Однако,
как мы увидим в разделе, посвященном А-цепям, существуют 2-связные
плоские графы, имеющие вершины только степеней 4 и б, без А-цепей (но имеющие
непересекающиеся эйлеровы цепи по лемме VI.7).
Заметим, что следствие VI.6 и лемма VI.7 для плоского случая
представляют собой известные результаты (см., например, [TUTT41a], [KOTZ68c,
Theorem 10] и [HARA69a, упр. 11.2]). Для графов, вложенных в некоторую
произвольную поверхность Т, Белый [BELY83a] доказал один результат,
который опирается не на вложение в поверхность как таковое, а на предписанный
циклический порядок на множестве Е* для каждой вершины v 6 V(G) (это
неявно содержится в статье Белого, хотя сам Белый об этом не упоминает —
поэтому его определения не совсем четки). Однако и следствие VI.6, и лемма
VI.7 суть тривиальные следствия леммы о расщеплении, как и следующая
лемма (из которой непосредственно вытекают оба упомянутых выше результата),
составляющая суть статьи Белого (см. [BELY83a, теорема 1]); мы оставляем ее
доказательство читателю (см. упр. VI.4).
Лемма VI.8. Пусть G — связный эйлеров граф с предписанным порядком
0~*~(Е*) полуребер, инцидентных v, для каждой вершины v G V(G). Тогда
G имеет непересекающуюся эйлерову цепь.
Замечание. Отдавая дань истории, заметим, что Коциг, очевидно, не
подозревал о работе [TUTT41a], доказывая следствие VI.б для случая, когда Т есть
плоскость (называя о-линией то, что здесь называется А-цепью), с помощью
следствия VI.5, ограниченного на 4-регулярные графы (см. [KOTZ68c, Theorem
3]). С другой стороны, статья [TUTT41a] начинается с такого утверждения:
«Рассмотрим плоскую сеть v, в каждом узле которой сходятся в точности
по 4 линии. По теореме Эйлера в такой сети можно найти уникурсальные
пути, которые не самопересекаются ...» (сеть = граф, уникурсальный путь
= эйлерова цепь. Г.Ф.). Это утверждение, несмотря на свою корректность (см.
следствие VI.б), не следует автоматически из теоремы IV. 1 (см. также
оригинальную статью Эйлера).
Лемма VI.8 допускает также обобщения на произвольные графы; мы
оставляем их доказательства в качестве упражнений (их формулировки в
[BELY83a] менее общи, нежели представленные здесь, но очевидно, что автор
имел в виду более общие утверждения — см. его определения 6 и 7).
Следствие VI.9. Пусть G — связный граф, имеющий в точности две
нечетные вершины, и пусть 0+(Е*) определен, как в лемме VI.8. Тогда G имеет
непересекающуюся открытую покрывающую цепь.

132
Глава VI. Различные типы эйлеровых цепей
Рис. VI. 1. А-цепь орграфа ?>2,4, где заходящие и исходящие дуги не чередуются в
вершинах хну.
Следствие VI.10. Пусть G — связный граф, и пусть 0+(?*) определен, как
в лемме VI.8. Тогда G допускает разложение на п взаимно непересекающихся
открытых цепей {где 2п есть число нечетных вершин в G).
Определения Белого несколько туманны, так как он не использует никакого
порядка 0+(?"*), а просто говорит о вершинах vi,...,vn, инцидентных
вершине v в G (в его определении 1 он заменяет v n-угольником vlv2 ... vn и считает
Vi смежной с г>г, что проблематично, тем более, что он допускает
существование в G петель и кратных ребер). Следовательно, его теорема 2 неверна для
неплоского случая: пытаясь получить аналог леммы VI.8 для эйлеровых
орграфов, он требует, чтобы такие графы имели непересекающуюся эйлерову цепь
тогда и только тогда, когда в каждой вершине v дуги, заходящие в v,
чередуются с дугами, исходящими из v. На рис. VI. 1 показана эйлерова ориентация
Аг,4 графа if2,4, которая, будучи вложенной в тор или проективную плоскость,
обладает непересекающейся эйлеровой цепью, что противоречит утверждению
Белого.
VI.1.1. Р(?))-совместимые эйлеровы цепи в орграфах
Попытаемся теперь переформулировать некоторые из предыдущих
результатов для случая орграфов. Орграф D2,±, представленный на рис. VI. 1,
показывает, что теорема VI. 1 не имеет простого аналога для орграфов: действительно,
если мы положим
P(D2A) = X(D2A) = {{1,8}, {4,5}, {2,7}, {3,6}},
то в D2,4 не существует эйлеровой цепи, совместимой с X(D2A). Это, однако, не
должно удивлять, так как, вообще говоря, для каждой дуги е, заходящей в
некоторую вершину v связного эйлерова орграфа D, найдутся id(v) — 1 = \d(v) — l
дуг, которые не могут (непосредственно) следовать за е ни в какой
эйлеровой цепи в D (а именно, это те дуги, которые заходят в вершину v и
отличны от е). Это означает, что тот факт, что D есть орграф, а не граф, сам
по себе задает некоторое разбиение P(v) множества Л* для каждой вершины

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 133
Рис. VI.2. 3-регулярный орграф вместе с системой переходов X (помеченных
маленькими дугами), не имеющий эйлеровой цепи, совместимой с X.
v € V(D) —это как раз разбиение, состоящее из двух классов, один из
которых—это (А*)+, а другой —это (<А*)~. Для этого «естественного» разбиения
P(v) и соответствующего разбиения P(D) P(D)-совместимая эйлерова цепь
есть просто произвольная эйлерова цепь графа D.
С другой стороны, для произвольного P(D) существование Р(?>)-совмести-
мой эйлеровой цепи влечет за собой справедливость утверждения 2) теоремы
VI. 1 (с заменой в этом утверждении G на D). Рисунок VI.2 показывает, однако,
что справедливости этого утверждения недостаточно для существования P(D)-
совместимой эйлеровой цепи.
Рассмотрим произвольную систему разбиения P(D) орграфа D. Располагая
леммой о расщеплении (примененной к D, так что Dij и Di,3 эйлеровы, где е\
есть дуга, заходящая в вершину -и, а следовательно, ег, в% — дуги, исходящие
из и), мы можем подумать, что если для каждой вершины v € V(G) и
произвольной полудуги е~ € С~ € P(v) С P(D) (где е~ заходит в v) существуют
две полудуги e^ef € С+ € P(v) (где e^ej" инцидентны из v) и С+ ф С", то
D имеет Р(?>)-совместимую эйлерову цепь. Другими словами, если P(D)
предоставляет в каждой вершине v для каждой полудуги е~ G (А1)~ (по крайней
мере) две возможности определить переход {е~,е^},г = 1,2, то будет ли этого
достаточно для существования Р(1))-совместимой эйлеровой цепи в D1 Ответ
на этот вопрос отрицательный, в чем можно убедиться на примере орграфа на
рис. VI.2 методом проб и ошибок.
Однако следующий результат для орграфов (который представляется мне
новым) может рассматриваться как аналог теоремы VI. 1.
Теорема VI.11. Пусть D —связный эйлеров орграф и для каждой его
вершины v € V(D) пусть P(v) есть разбиение множества А*. Если D имеет
P(D)-совместимую эйлерову цепь, то
1) |С|< \do{v) для каждой вершины v G V(D) и каждого класса С € P(v) С
P(D).

134
Глава VI. Различные типы эйлеровых цепей
Если утверждение 1) верно и если P(D) удовлетворяет следующему
условию:
2) \P(v) \> ^dn(v) + 2 для каждой вершины v Е V(D) с do(v) > 2,
то D имеет P{D)-совместимую эйлерову цепь.
Доказательство. Как следует из рассуждений, предшествующих рис. VI.2,
достаточно доказать, что из утверждений 1) и 2) следует существование P(D)-
совместимой эйлеровой цепи в D.
Рассмотрим произвольную вершину v Е V(D) с do(v) > 2. В силу
утверждения 2) даже для самого большого класса С\ Е P(v) выполняется неравенство
\С\ |< \<Id(v) (следовательно, утверждение 1) существенно только для вершин
степени 2). Поэтому если С\ не затрагивался процедурой расщепления при
построении ?>i,2, то мы все еще имеем для С\ Е P'{v) С P(D\^) неравенство
I С\ |< \dr>{v) — 1 = ^dDli2(v) (СР- это обозначение с обозначением,
использованным при доказательстве теоремы VI.1). Кроме того, из утверждения 2)
вытекает, что для такой вершины v Е V(D) имеет место неравенство | P(v) |> 4.
Поэтому мы можем вывести следующее свойство:
3) Если di)(v) > 4 для некоторой вершины v Е V(D), то либо
a) для каждого класса С Е P(v) соотношение Сп(А*)+ ф 0 выполняется
тогда и только тогда, когда С П (А*)~~ = 0,
либо
b) существуют С0, С", С" Е Р(у), такие, что С0 П (А*)+ ф 0 ф С0 П (А*)~
«СП (А$)+ = С" П (А*)+ = 0 (заметим, что \ (A*v)+ \= \dD(v) и
\P{v)\>\dD{v) + 2).
Теперь мы предположим, что теорема неверна, и построим контрпример D
с наименьшим o~(D) > 0. Исследуя случай cr(D) = 0 таким же образом, как
и при доказательстве теоремы VI. 1 (просто заменив букву G буквой D), мы
заключаем из возникающего противоречия, что некоторая вершина v Е V(D)
не 2-валентна. Выберем такую вершину v и рассмотрим для P(v) два случая,
соответствующие 3)а) и 3)Ь), приведенным выше.
В первом случае мы просто многократно применяем лемму о
расщеплении, пока v не будет замещена k = \dz>(v) 2-валентными вершинами, и
полученный орграф D' будет связным и эйлеровым. Выберем обозначения
таким образом, чтобы для этих к 2-валентных вершин мы имели Р'(уц) =
{{а<(у)},{а+(у)}} с а~(v) Е (А*)" и af(v) Е (А;)+ при i = 1, • • • , к. Так
как <t(D') < a(D), то для P(D') = (P(D) - P(v)) U \JLiP'{Vn) B D'
существует Р(1)/)-совместимая эйлерова цепь, соответствующая Р(?))-совместимой
эйлеровой цепи в D по построению P(D').
Во втором случае пусть a\(v) Е С0 П (А*)+, а2(у) Е С" П (А*)", аз(v) Е
С" П (А*)~" —произвольно выбранные вершины. Из доказательства леммы о
расщеплении следует, что D\^ или D\^ связен (в любом случае оба они
эйлеровы); без потери общности предположим, что Z?i,2 связен. Пусть P'(w) для
w ф v, vi2,Pf{vi,2),P'(v) и P(Di^) определены так же, как при доказательстве

VI. 1. Эйлеровы цепиу избегающие некоторых переходов 135
Do Во
Рис. VI.3. Do и P(Do) (где различные классы разбиения P(v) представлены
различными числами для каждой вершины v Е V(Do)) и их единственное преобразование в
D'o и P{D'o) в соответствии с Р(Do)-совместимостью. D0 не имеет Р(Г>о)-совместимой
эйлеровой цепи; поэтому Do не имеет P(Do)-совместимой эйлеровой цепи.
теоремы VI.1. Из рассуждений, предшествующих свойству 3), мы заключаем,
что P(Di^) удовлетворяет утверждению 1), а в силу выбора Со
\P'(v) \>\P(v) I -1 > \dD(y) + 1 = UDlt2{v) + 2,
т. е. P(Di^) также удовлетворяет утверждению 2) (заметим, что 3)Ь) влечет за
собой dn{v) > 6). Отсюда и из неравенства a(Di^) < <r(D) мы заключаем, что
существует Р(?>1,2)-совместимая эйлерова цепь в Д^, которая по построению
соответствует Р(/})-совместимой эйлеровой цепи в D.
В обоих случаях 3)а) и 3)Ь) мы получили в D Р(1))-совместимую эйлерову
цепь, что противоречит выбору D. Теорема VI. 11 доказана.
Нижняя граница в неравенстве из утверждения 2) теоремы VI. 11 есть
наилучшая из возможных; это показывают орграф Dq на рис. VI.3 и его сведение
kD'0.
Пусть v — произвольная вершина степени 4 в Do. Ясно, что для \P(v) \= 3
расщепление вершины г>, удовлетворяющее условию Р(Д))-сювместимости,
определяется единственным образом. И это основная причина невозможности
улучшить нижнюю границу в утверждении 2) без дальнейших предположений
относительно структуры некоторого произвольного орграфа D и относительно
P(D). Итак, с помощью последовательности процедур расщепления, согласно
лемме о расщеплении, можно прийти к связному эйлерову орграфу в
точности с двумя вершинами степени 4 и остальными вершинами степени 2 и
системе переходов, аналогичной системе X(D2,a), определенной в начале разд.
VI.1.1. Из сказанного выше следует, что замена {4,5} парой {4}, {5} и {3,6}
парой {3}, {6} в X(Дг,4) не изменяет задачу. И если мы изменим Р(х) на рис.
VI.3, положив С[ = Ci U Сз, С2 = С2 Г) (А*)", С'ъ = С2 П (А*)+, С? = С4 и

136 Глава VI. Различные типы эйлеровых цепей
Р'(х) = {С'^С^С^С^} (где d изображается на рис. VI.3 дугами с меткой г),
то для
P'(D) = (P(D)-P(x))l>P'(x)
также не существует Р'(#)-совместимой эйлеровой цепи в D.
Итак, сделаем дополнительные предположения о строении орграфа D и
структуре P(D).
Определение VI. 12. Пусть D — орграф с заданной системой разбиения
P(D). Мы будем называть P(D) почти переходной, если для каждой
вершины v G V(D) и каждого класса С G P(v) С P(D) справедливо неравенство
\С\ < 2. В этом случае мы будем писать X*(D) вместо P(D) и X*(v)
вместо P{v).
Следствие VI. 13. Если заменить в теореме VI. 11 P(D) на X*(D) (где
X*(D) —почти переходная система разбиения) и условие 2) на условие
2х) каоюдая точка v G V(D) с do(v) > 2 удовлетворяет неравенствам
dD(v) >8 u\X*(v)\> %dD(v) + l,
то получится верное утверждение.
Доказательство следствия VI. 13 может быть сведено к применению теоремы
VI. 11 (если применить лемму о расщеплении к каждой вершине v с do(v) > 2);
поэтому оно предоставляется читателю (упр. VI.7). Более того, с помощью тех
же аргументов, что используются в упр. VI.7, можно понизить нижнюю оценку
в 2') до \do{v) в случае, когда каждая вершина v удовлетворяет условию
do{y) > 8, если только она не 2-валентна. Таким образом, мы получает еще
одно следствие.
Следствие VI.14 Если заменить в следствии VI. 13 условие dp (и) > 8 на
do(v) > 8 и условие \X*(v) |> \dn(v) + 1 на \X*(v) |> ^dpty), то получится
верное утверждение.
С помощью дальнейших предположений о do(v) и P(D) мы получаем
другой результат.
Следствие VI. 15. Пусть D —связный эйлеров орграф, и пусть задана
система переходов X(D). Если 5(D) > 6, то D имеет эйлерову цепь,
совместимую с X(D).
Доказательство. По следствию VI. 14 достаточно подходящим образом
заменить каждую вершину степени 8 четырьмя вершинами степени 2. Применение
следствия VI. 14 к получаемому таким образом орграфу завершает
доказательство следствия VI. 15.
Если D не имеет вершин степени 8, то D и X(D) удовлетворяют условиям
следствия VI. 14 и следствие VI. 15 доказано. Если, однако, D имеет хотя бы
одну вершину v степени 8, то пусть af G (А*)+ и а~ G (А%)~ таковы, что
без ограничения общности можно считать, что X(v) = {{а~, а^"}, г = 1,2,3,4},
а ?>1,з и Di,4 связны. Если (?1,3)2,4 и (#1,3)4,2 оба несвязны, то по лемме о
двойном расщеплении (лемма 111.27) по крайней мере один из графов (#1,4)2,3

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 137
а.
_^
32
D D,
Рис. VI.4. 3-регулярный орграф D\, построенный из 3-регулярного орграфа D
и (?1,2)4,3 связен; пусть, например, связен (^1,4)2,3- Кроме того, по лемме
о расщеплении либо ((?1,4)2,3)3,1, либо ((?1,4)2,3)3,2 связен; пусть это будет,
скажем, Я = ((?1,4)2,3)3,1- Но тогда Я —связный эйлеров орграф,
получаемый из ? заменой v четырьмя вершинами степени 2, причем такой, что
каждая (X(D) - Х(г>))-совместимая эйлерова цепь в Я соответствует X(D)-
совместимой эйлеровой цепи в ?. Если, однако, (?1,3)2,4 или (?1,3)4,2 связен,
то дальнейшее применение леммы о расщеплении приводит к тому же
самому заключению (заметим, что эйлеровы орграфы не содержат перешейков по
следствию IV.9). Применяя это построение к каждой вершине степени 8 графа
?, мы получаем эйлеров орграф, к которому может быть применено следствие
VI. 14. Следствие VI. 15 доказано.
Рисунок VI.2 показывает, что следствие VI. 15 — наилучшее из возможных в
отношении ограничений на минимальную степень (исключая степень 2);
существует бесконечно много примеров, демонстрирующих этот факт. Чтобы
увидеть это, возьмем любой 3-регулярный орграф ? и подразобьем любые две
дуги ai,a2. Потом соединим две подразбивающие вершины si,S2 двумя
дугами вида (5i,52) и двумя дугами вида (s2,si) и определим X(si) и -Х"(5г), как
указано на рис. VI.4. Мы предлагаем в качестве упражнения проверить, что
?i имеет эйлерову цепь, совместимую с X(Di) = X(D) U X(si) U X(s2), тогда
и только тогда, когда D имеет эйлерову цепь, совместимую с данным X(D).
Следовательно, если D есть орграф на рис. VI.2 или любой 3-регулярный
орграф, получаемый из этого орграфа многократным применением расширения,
указанного на рис. VI.4, и если X(D) определено соответствующим образом, то
D не имеет Х(?>)-совместимой эйлеровой цепи. Однако если X(D) = Хт есть
система переходов эйлеровой цепи Т в графе Д то мы получим несколько
более сильный результат, который может рассматриваться как аналог следствия
VI.5 для орграфов.

138
Глава VI. Различные типы эйлеровых цепей
Следствие VI.16. Если D — связный эйлеров орграф с 5(D) > 4 и Т
—эйлерова цепь в D, то в D существует Т-совместимая эйлерова цепь Т'.
Доказательство. С учетом следствия VI. 15 достаточно построить из D
связный эйлеров орграф D' без вершин степеней 4 и б с системой переходов X(Df),
индуцированной Хт, такой, что ни один переход цепи Т в вершине степени б
в D не определяет А*, где х имеет степень 2 в D'.
На самом деле мы можем сделать лучше, строя D' таким способом, что
X(D') определяет эйлерову цепь в D'. С этой целью мы предположим, что D
имеет вершину v степени б (в противном случае по следствию VI. 15 нечего
доказывать). Запишем Т в виде
I = х, • • • , е± , т;, е1 , • • • , е2 , v, е2 , • • • , е3 , г>, е3 , • • • , х,
где X(v) = {{е^)",е<(г;)+}|г = 1,2,3} С Хт и ф)~ <= (^)", ф)+ € (А*)+,
г = 1,2,3. Тогда
II = х, • • • , е^ , и, е2 , • • • , е3 , f, е1 , • • • , е2 , v, е3 , • • • , х
есть эйлерова цепь в ?>, которая совпадает с Т везде, исключая вершины v,
где она ведет себя как Т-совместимая эйлерова цепь в D. Проделывая это шаг
за шагом для каждой вершины степени б в D, мы в конце концов получим
эйлерову цепь Т', которая совпадает с Т везде, кроме вершин степени б; в этих
вершинах она ведет себя как Г-совместимая эйлерова цепь в D. Обозначив
через D' орграф, получаемый из D заменой каждой вершины степени б тремя
вершинами степени 2 так, что X" соответствует эйлеровой цепи в jD', мы придем
к эйлерову орграфу без вершин степени 4 и б с системой переходов X(D/)1
индуцированной Т и определяющей эйлерову цепь в D'. По построению D' и
соответственно X(D') любая эйлерова цепь в D', получающаяся применением
следствия VI.15 к D', соответствует Т-совместимой эйлеровой цепи в D. Тем
самым следствие VI. 16 доказано.
Ясно, что следствие VI. 16 не может быть так обобщено, чтобы включить
эйлеровы орграфы с вершинами степени 4 (см. рассуждения, предваряющие
определение VI. 12). Остается неясным, какие 2-регулярные орграфы имеют
эйлерову цепь, совместимую с данной эйлеровой цепью; близкая проблема будет
рассмотрена в разд. VI.1.2.
Мы продолжим наш поиск результатов об орграфах, аналогичных
результатам, полученным ранее для графов. Что касается следствия VI.2, то ясно, что
если мы будем действовать, как при доказательстве этого следствия, то
сможем записать D = DrU Db (Dr и Db являются дугово-непересекающимися), в
то время как условие на степень преобразуется в условие
1') id>Dr(v) = odDb(v), odor(v) — idDb(v) для каждой v € V(D)
(любая «красная» дуга, заходящая в v, обладает парной ей «синей» дугой,
исходящей из v, и наоборот). Однако утверждение 2) следствия VI.2 для
эйлеровых орграфов уже несправедливо: чтобы увидеть это, рассмотрим любой
связный эйлеров орграф D с четным числом дуг и с точкой сочленения х
степени 4 (такие орграфы существуют (см. упр. VI.9)!). Тогда мы можем написать
D = D\ U D2, Di П D2 = х и Di связен для г = 1,2.

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 139
Таким образом, idDi(x) = id&2(x) — od,D1(x) = odry2(x) = 1. Рассмотрим
произвольную красно-синюю раскраску дуг в соответствии с эйлеровой цепью в
D и поменяем цвета цветовых классов в Д^. Теперь предположим, что D был
выбран так, что | A(Di) |= 0 (mod2), г = 1,2, и без ограничения общности
будем считать дугу, заходящую в х в D\, красной. Тогда условие 1') (см. выше)
остается справедливым для этой новой красно-синей раскраски, но теперь
idDrnDxix) = 1, odDbnD2(x) = 0>
т. е. каждая эйлерова цепь в D, достигающая х по красной дуге в Z?i, должна
продолжаться из х по красной дуге в IV
Вообще говоря, мы встретились с (несколько более общей) проблемой
необходимости определить P(v) для любой вершины v Е V(D), где P(v) состоит
из двух классов: синие полудуги, заходящие вуи исходящие из v, образуют
первый класс, аналогичные красные полудуги — второй; кроме того, P(v)
удовлетворяет условию 1/). Пусть P(D) = \JP(v). Вопрос: когда D имеет P(D)-
совместимую эйлерову цепь?
Ответ на этот вопрос дается в следующей теореме, для формулировки
которой нам понадобятся некоторые понятия.
Пусть D — эйлеров орграф, и для каждой вершины v € V(D) пусть P(v)
есть разбиение множества А* на два класса,
P(v) = {P1(v),P2(v)}.
Более того, для г = 1,2 пусть Pi(v) записывается в виде
Pi(v) = PiAv) UPil2(t;), Pifi(tO nPi|2(tO = 0,
где Pi,i(v) содержит в точности те полудуги из Pi(v), которые заходят в
v (следовательно, Рг,2 содержит только полудуги, исходящие из v). Пусть
¦P(-D) = Uv€V(D) P(v)i и ПУСТЬ новый орграф Dp получается из D
следующим способом: каждая вершина v € V(D) заменяется двумя вершинами vi^ и
г?2д, а инцидентность в Dp определяется соотношениями
А^шЯ = Pi,i(v) UP2,2(v), Al21(v) = Plt2(v) UP2<1(v).
Теорема VI.17. Пусть D —связный эйлеров орграф, и пусть P(D)
определен, как выше. Тогда следующие утверждения эквивалентны:
1) D имеет P(D)-совместимую эйлерову цепь;
2) Dp имеет эйлерову цепь.
Доказательство. Если D имеет Р(1))-совместимую эйлерову цепь Т, то по
определению Р(?>), если Г достигает произвольной вершины v G V(D) по
полудуге, принадлежащей Pi (v), то эта полудуга принадлежит Piyi (v) и Т должна
покидать v по полудуге, принадлежащей Pi+i^(v), где мы полагаем г + 1 = 1
для г = 2. Следовательно, согласно определению инцидентности в Dp, Т
определяет единственную эйлерову цепь в Dp.
Обратно, если Dp имеет эйлерову цепь Тр, то Тр определяет единственную
эйлерову цепь Г в D по определению орграфа Dp. Более того, из этого
определения следует, что полудуги, определяющие переход цепи Тр в vi^ или т^д,

140
Глава VI. Различные типы эйлеровых цепей
принадлежат различным классам системы P(v) для любой вершины v € V(D).
Это означает, что цепь Т Р(?))-совместима.
Однако следствие VI.3 имеет аналог для орграфов.
Следствие VI.18. Пусть D есть к-регулярный орграф, имеющий четное
число дуг. Тогда он может быть разбит на два дугово-непересекающихся
подграфа D\ и D2, таких, что duiiv) = к для каждой вершины v ? V(D)
иг = 1,2. В частности, если к = 2, то D есть прямая сумма двух дугово-
непересекающихся 1-факторов.
Доказательство. Первая часть следствия тривиальна — просто мы
используем красно-синюю раскраску дуг в D, как это описано выше. Что касается
второй части, то расщепим каждую вершину v на две 2-валентные вершины
v" и v+ так, что od,DQ(v~) = гй#0(г>+) = 0 в полученном таким способом
орграфе D0. При таком определении Do представляет собой двудольный граф, так
как каждая вершина в Do есть либо источник, либо сток. Следовательно,
каждая компонента орграфа D0 имеет четное число дуг. Отсюда следует, что дуги
могут быть 2-раскрашены в синий и красный цвета так, что ни одна вершина
в Do не инцидентна двум дугам одного и того же цвета. Рассматривая эту
раскраску дуг в D, мы замечаем, что idcb{v) = odcb{v) — idcr{v) — °dGr(v) = 1
для каждой вершины v € V(D). Это означает, что каждый из графов Gb и Gr
есть 1-фактор в D.
Заметим попутно, что обобщение использованной здесь идеи будет
применено в следующем разделе.
Следствия VI.6 — VI.8 могут быть также переформулированы для
орграфов, в которых ориентации дуг в 0+(А*) чередуются. Мы лишь сформулируем
наиболее общий результат, оставив его доказательство в качестве упражнения
(упр. VI.10).
Следствие VI. 19. Пусть D — связный эйлеров орграф с предписанным
упорядочением 0+(А*) полудуг, инцидентных вершине v, для каоюдой вершины
v G V(D), таким, что два последовательных элемента в 0+(Л*) не
являются оба заходящими в (соответственно исходящими из) v. Тогда D имеет
непересекающуюся эйлерову цепь.
Замечание. Проблема переформулировки некоторых из предыдущих
результатов для смешанных графов может быть интересной исследовательской
проблемой. Далее, на базе полученных к данному моменту результатов было бы
не слишком трудно сформулировать для орграфов все, что было сказано
относительно открытых цепей, разложений на цепи, а также путевых/цикловых
разложений в графах. Мы не углубляемся в детали, так как хотим
сконцентрировать внимание на неориентированных графах.
VI. 1.2. Антиэйлеровы цепи в биэйлеровых орграфах
и биэйлеровы ориентации графов
Определение VI.20. Пусть D — связный орграф, степени вершин которого
четны, и пусть Tq — эйлерова цепь графа G, лежащего в основе орграфа D.

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 141
Последовательность То в D, соответствующая Т<з, называется
антиориентированной эйлеровой цепью или, кратко, антиэйлеровой цепью, если
для каждой секции a,i,Vi+i,ai+i цепи То дуги а* и a$+i либо обе заходят в
Vi+i, либо обе исходят из vi+i. Орграф D называется антиэйлеровым, если
в нем есть антиэйлерова цепь. Если D эйлеров и имеет антиэйлерову цепь, то
он называется биэйлеровым орграфом.
Следующее утверждение есть непосредственное следствие определения
VI.20.
Следствие VI.21. Если D — биэйлеров орграф, mo idjo(v) = odr)(v) =
О (mod 2) для каждой вершины v Е V(D) и, следовательно, \A(D) |= 0 (mod 2).
Заметим, что если D просто антиэйлеров, то первая часть следствия VI.21 в
общем случае неверна, в то время как вторая часть, | A{D) |= 0 (mod 2), остается
верной.
Как обобщение конструкции орграфа Dq в доказательстве следствия VI. 18,
мы определим для произвольного орграфа D орграф D+, получаемый из D
расщеплением каждой вершины v € V(D) на v~,v+ ? V(jD^), так, чтобы
г7~,г>+ были инцидентны элементам из (А*)~,(А*)+ соответственно.
Теорема VI.22. Пусть D — эйлеров орграф. Следующие утверждения
эквивалентны:
1) dr)(v) = 0 (mod4) для каждой вершины v € V(D) и D+ связен;
2) D биэйлеров.
Доказательство. Если dr>(v) = 0 (mod4), то id^iv) = odo{v) = 0 (mod 2);
следовательно, G+, т. е. граф, лежащий в основе орграфа D+, эйлеров по
определению D+. Так как D+ связен по предположению, то связен и G+. Эйлерова
цепь в G+ соответствует антиэйлеровой цепи в D+ и антиэйлеровой цепи в D
по определению D+. Следовательно, D — связный эйлеров орграф и в нем есть
эйлерова цепь. Это значит, что в нем есть как антиэйлерова, так и эйлерова
цепи, т. е. D биэйлеров.
Обратно, если D биэйлеров, то doiv) = 0 (mod4) для каждой вершины
v Е V(D) по следствию VI.21. По определению D+ антиэйлерова цепь в D
соответствует антиэйлеровой цепи в D+; следовательно, D+ связен. Это
завершает доказательство теоремы.
Пример 2-регулярного орграфа на двух вершинах показывает, что условие
связности орграфа D^_ в утверждении теоремы VI.22 не может быть опущено.
На самом деле теорема VI.22 есть частный случай следующего результата.
Теорема VI.23. Пусть D —эйлеров орграф с do^v) = 0 (mod4) для каждой
вершины v Е V(D). Тогда D имеет единственное разложение San wa
максимальные антиэйлеровы подграфы графа D и \San |= c(D+).
Доказательство. Рассмотрим D+ и обозначим его компоненты через Gi,...,
Gfc,fc > 1. Для любого г Е {1,...,/с} пусть Gi есть граф, лежащий в
основе орграфа Ci. Так как D эйлеров и doiy) = 0 (mod4) для каждой вершины

142
Глава VI. Различные типы эйлеровых цепей
v € V(D), то d(v+) = d(v~) = О (mod 2) в D+ для каждой пары г>+, v~ € V(D+).
Следовательно, Gi эйлеров и эйлерова цепь в Gi соответствует
антиэйлеровой цепи в Сг по определению D+. Следовательно, если D\,... ,-Dfc — подор-
графы орграфа D, соответствующие Ci,...,Ca;, to San = {?>!,... , ?>&} есть
разложение орграфа D на антиэйлеровы подорграфы (заметим, что
существует взаимно однозначное соответствие между антиэйлеровыми цепями в Сг и
антиэйлеровыми цепями в D^ 1 < г < к). Более того, именно из-за
определения ?>+ и в силу того, что Ci,... ,Cfc суть его компоненты, 5ап определяется
однозначно и Di есть максимальный антиэйлеров подорграф орграфа D для
i = 1,..., к. Следовательно, | San |= c(D+). Это завершает доказательство
теоремы.
Заметим, что если D 2-регулярен, то антиэйлеровы подорграфы орграфа
D обязательно являются максимальными антиэйлеровыми подорграфами
орграфа D просто из-за того, что вершины в D+ имеют степень 2.
Какие 4-регулярные графы имеют биэйлерову ориентацию, т. е.
эйлерову ориентацию, допускающую антиэйлерову цепь? Ответ, который мы
предлагаем, выглядит не очень хорошо с алгоритмической точки зрения, но он
связывает 4-регулярные и 3-регулярные графы таким способом, который
будет играть важную роль в контексте проблемы совместимости. (Отметим, что
поставленной выше вопрос был впервые сформулирован в [BERM78b].)
Теорема VI.24. ^-регулярный граф G± имеет биэйлерову ориентацию тогда
и только тогда, когда найдется гамилътонов двудольный Ъ-регулярный граф
Gz с гамильтоновым циклом Н, такой, что G± ~ G-$/L, где L = E(Gs) —
Е(Н).
Доказательство. Если G± имеет биэйлерову ориентацию, то зафиксируем
такую ориентацию, обозначим ее через D± и построим двудольный орграф D+,
как это описано выше. Антиэйлерова цепь в D± гарантирует, что D+
связен. Поэтому для цикла Н графа Go, лежащего в его основе, граф Сз =
Go U {v+v~\v ? V(?>4)} есть 3-регулярный граф с гамильтоновым циклом
Н] по построению D+ и G% последний также двудольный и G4 — Gs/L, где
L = {v+v~\v € V(D4)} = E(G3) - Е(Н).
Обратно, если G± — G3/L и если Н = G% — E(L) — гамильтонов цикл в
3-регулярном графе G3, то ориентируем ребра в Н так, чтобы Н не содержал
пути длины 2, т.е. чтобы орграф Do, полученный таким образом из Н, имел
только источники и стоки. Биразбиение множества У(Д>), определенное
источниками и стоками соответственно, совпадает с биразбиением множества 1^(С?з)>
так как Do связен. Таким образом, каждое ребро е G L соединяет источник со
стоком, так как Сз — двудольный граф. Следовательно, орграф D4,
полученный из Do отождествлением тех же самых пар вершин, что и при образовании
G^/L из Сз, 2-регулярен и обход вдоль антиэйлеровой цепи в Do соответствует
антиэйлеровой цепи в D±. Следовательно, так как G± есть граф, лежащий в
основе орграфа D± по предположению и по построению, G± имеет биэйлерову
ориентацию. Теорема доказана.

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 143
Таким образом, двудольность графа Сз существенна для наличия у G±
биэйлеровой ориентации. Однако G± не должен быть двудольным, если он
имеет такую ориентацию. Этот факт подкрепляется следующим результатом (см.
также [BERM79d]).
Предложение VI.25. Если G — двудольный граф с dc(v) = 0 (mod4) для
каждой вершины v Е V{G), mo он не имеет биэйлеровой ориентации.
Доказательство. Предположим, что ориентация D графа G имеет
антиэйлерову цепь То, начинающуюся, скажем, в вершине v E V\ вдоль дуги (v,w), где
w E Vi и {Vi, V2} — биразбиение множества V(G) = V(D). Тогда следующая
дуга в Td имеет вид (ж,ги), где х Е V\. Дуга, следующая за (ж,ги) в Td, имеет
вид (х,у), где у Е V2, и т. д. Следовательно, первая компонента дуги из D
всегда принадлежит Vi, в то время как вторая компонента лежит в 1^. Это
означает, что D не является эйлеровой ориентацией графа G и поэтому G не
может иметь биэйлерову ориентацию.
С другой стороны, для класса связных эйлеровых графов G, у которых
каждый цикл есть блок в G, мы имеем следующий сильный результат. Хотя
это сравнительно узкий класс графов, он играет важную роль в следующих
двух разделах этой главы.
Теорема VI.26. Если G — связный граф с dc(v) = 0 (mod4) для каждой
вершины v E V(G), циклы которого суть блоки в G, то каждая эйлерова
ориентация графа G биэйлерова.
Доказательство. Будем доказывать это индукцией по числу bn(G) блоков в
G. Заметим, что в любом случае bn(G) > 2.
Если bn(G) = 2, то по предположению G имеет в точности одну вершину,
инцидентную в точности двум петлям. Ориентируем каждую из них
произвольно в одном из двух возможных направлений. Это дает эйлерову ориентацию
D графа G; проходя одну петлю в соответствии с ее ориентацией, а другую —
против ее ориентации, получаем антиэйлерову цепь в D. Следовательно, для
bn(G) = 2 теорема справедлива.
Для bn(G) > 2 рассмотрим висячий блок В\ графа G и его единственную
вершину v (G не может иметь вершин степени 2 по предположению, так что
каждый висячий блок в G есть петля). В зависимости от степени вершины v
мы различаем два случая.
1) dc{v) = 4. Рассмотрим граф Gi, получаемый из G — В\ подавлением в
G — В\ вершины v степени 2 (см. рис. VI.5).
Этот граф удовлетворяет условию теоремы и имеет меньше блоков, чем
G. Пусть D — произвольная эйлерова ориентация графа G, и пусть D\ —
эйлерова ориентация графа Gi, индуцированная ориентацией D. По
предположению индукции Di биэйлеров. Предполагая без ограничения общности, что
(x,v) Е A(D), имеем (v, у) Е A(D) и (х,у) Е A(Di). Рассматривая теперь
любую антиэйлерову цепь 7\ вД, мы видим, что 7\ может быть расширена до
антиэйлеровой цепи Т в D заменой дуги (х, у) цепью (х,г>),г>, A(i?i)~,t>, (v, у),
где А{В\)~ означает, что мы проходим В\ против его ориентации (без
ограничения общности считаем, что в Т\ дуга (х,у) проходится от х к у. Заметим,

144
Глава VI. Различные типы эйлеровых цепей
х ух у
G ^
Рис. VI.5. Граф Gi, получаемый из G удалением петли В\ и подавлением вершины
v степени 2 в G — В\; возможен случай х = у.
что для антиэйлеровой цепи обратная последовательность есть также
антиэйлерова цепь).
2) dc(v) > 4. Так как случай 1) уже разобран, мы предполагаем без
ограничения общности, что ни одна вершина степени 4 в G не инцидентна петле
в G. Следовательно, если мы возьмем граф блоков и точек сочленения bc(G),
то ни одна его висячая вершина не смежна с его вершиной степени 2.
Следовательно, так как bc(G) есть дерево, то существует точка сочленения z в G,
такая, что все блоки, содержащие z, являются петлями, за исключением,
возможно, одного из них. Не ограничивая общности, положим z — v. Поскольку
8 < dc{v) = 0 (mod4), v инцидентна двум петлям, скажем В\ и В2. Образуем
теперь
Gi = G-(B1UB2).
Gi удовлетворяет условию теоремы, так как 4 < dc{v) — 4 = dcx (v). Пусть D —
эйлерова ориентация графа G, как в случае 1), с (x,v) € A(D). Ориентация
D\ графа Gi, индуцированная ориентацией D, эйлерова; по предположению
индукции D\ даже биэйлеров. Заменим в любой антиэйлеровой цепи 7\ в D\
дугу (x,v) цепью (x,v),v,A(Bi)~~1v,A(B2), получая таким образом
антиэйлерову цепь в D (A(Bi)~ означает, как и выше, что мы проходим В\ против ее
ориентации, в то время как А(В2) показывает, что В2 проходится в
соответствии с ее ориентацией; здесь мы также можем предположить без ограничения
общности, что в Т\ дуга (я, v) проходится отхки). Это завершает
доказательство теоремы.
Предложение VI.25 и теорема VI.26 описывают классы графов,
представляющие экстремальные случаи, связанные с биэйлеровыми ориентациями
4-регулярных графов (нет биэйлеровых ориентации вообще, каждая эйлерова
ориентация биэйлерова). Предложение VI.25 описывает не все 4-регулярные
графы без биэйлеровой ориентации. Например, если G получается из двух
4-регулярных графов Gi подразбиением ребра е* с помощью одной вершины
Vi,i = 1,2, и последующим отождествлением двух вершин vi и v2 степени 2,

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 145
то G есть 4-регулярный граф с точкой сочленения v, появляющейся в
результате отождествления v\ и^. Непосредственно видно, что G имеет биэйлерову
ориентацию тогда и только тогда, когда G\ и G2 имеют такие ориентации. На
самом деле можно доказать справедливость следующего утверждения.
Лемма VI.27. Связный 4-регулярный граф G имеет биэйлерову ориентацию
тогда и только тогда, когда для каждого блока В С G, гомеоморфного
некоторому ^-регулярному графу Б*, В* имеет биэйлерову ориентацию.
Аналогичным образом можно доказать справедливость следующей леммы.
Лемма VI.28. Для связного 4-регулярного графа G каждая эйлерова
ориентация является биэйлеровой тогда и только тогда, когда для каждого блока
В графа G, гомеоморфного ^-регулярному графу В*, В* обладает тем
свойством, что каждая его эйлерова ориентация является биэйлеровой.
Доказательства лемм VI.27 и VI.28 мы оставляем читателю в качестве
упражнения (упр. VI. 11).
Замечание. Обращаем внимание, что в утверждениях предыдущих двух
лемм граф G может содержать циклы, являющиеся блоками в G; для них
не существует гомеоморфного 4-регулярного графа.
В силу лемм VI.27 и VI. 28, если мы хотим определить все 4-регулярные
графы, которые имеют биэйлеровы ориентации и/или обладают тем
свойством, что каждая эйлерова ориентация биэйлерова, достаточно рассматривать
2-связные графы. В приведенном выше примере граф вообще не имеет
биэйлеровой ориентации, но, однако, имеет точку сочленения; в [BERM79d]
приводится пример 2-связного 4-регулярного графа, не имеющего биэйлеровой
ориентации. Чтобы увидеть, что теорема VI.26 также не охватывает всех графов, у
которых эйлерова ориентация обязательно биэйлерова, мы рассмотрим
произвольную эйлерову ориентацию D^ графа К$. Довольно стандартная работа —
проверить, что D$ имеет гамильтонов цикл1) (фактически, как мы увидим
позднее, каждая эйлерова ориентация полного графа с нечетным числом
вершин есть гамильтонов орграф). Таким образом, если мы нарисуем такой
гамильтонов цикл в качестве внешнего пятиугольника, то формально
существуют только два способа выбрать ориентацию внутренней пентаграммы (см. рис.
VI.б). Эти две эйлеровы ориентации изоморфны, и последовательность
вершин 1,3,2,4,3,5,4,1,5,2,1 определяет антиэйлерову цепь, соответствующую
этим ориентациям. Таким образом, К*> имеет эйлерову и тем самым
биэйлерову ориентацию, единственную с точностью до изоморфизма. Однако если
мы пометим вершины графа К$ заранее, то такой граф К$ будет иметь
несколько эйлеровых ориентации, которые, однако, тоже биэйлеровы. На самом
деле число биэйлеровых ориентации любого 4-регулярного графа, содержащего
предписанную дугу (я, у), четно [BERM79d, Theorem 6.2].
Как мы видели в следствии VI. 18, каждый 2-регулярный орграф может
быть разложен на два 1-фактора. В общем случае может быть более чем од-
*) Отметим, что в русскоязычной литературе в случае орграфов вместо термина «цикл»
используется также термин «контур». — Прим. ред.

146 Глава VI. Различные типы эйлеровых цепей
Рис. VI.6. Для заданной циклической ориентации внешнего пятиугольника графа
Къ два возможных выбора ориентации внутренней пентаграммы дают изоморфные
эйлеровы ориентации графа Къ\ изоморфизм указан метками вершин.
но такое разложение. Следовательно, возникает вопрос: каково необходимое
и достаточное условие того, что 2-регулярный орграф имеет единственную
1-факторизацию? Ответ на этот вопрос получается как следствие такого
утверждения:
Предложение VI.29. Пусть D есть 2-регулярный орграф. Тогда
существует взаимно однозначное соответствие между 1-факторами в D и
максимальными независимыми множествами дуг в D7.
Доказательство. Если F есть 1-фактор в D, то oUf(v) = idp(v) = 1 имеет
место для каждой вершины v ? V(D). Это значит, что одна из дуг,
инцидентных v в F, исходит из г;+, другая заходит в v~ (если компонентой подграфа F
служит петля, то эти две дуги совпадают). Следовательно, F соответствует в
D+ независимому множеству дуг, покрывающему все вершины орграфа ?>+,
т.е. максимальному независимому множеству дуг в D+. Это множество дуг
определяется однозначно конструкцией орграфа D+.
Обратно, пусть М — максимальное независимое множество дуг в D+. Мы
имеем \А(С)\ = 0 (mod2) для каждого цикла С в GD- в силу того, что D+
есть двудольный орграф по построению. Более того, так как D 2-регулярен,
все вершины в D+ имеют степень 2. Отсюда следует, что М покрывает все
вершины орграфа D+. Следовательно, для каждой вершины v ? V(D)
найдется в точности одна дуга в М, исходящая из г;+, и в точности одна дуга в М,
заходящая в v~. Это значит, что М соответствует однозначно определяемому
подграфу F орграфа Д удовлетворяющему условию idp{v) = odp(v) = 1, т.е.
F является 1-фактором орграфа D. Предложение VI.29 доказано.
Если D есть 2-регулярный орграф с 1-фактором F, то D - F также есть
1-фактор F' графа D, а М' = A(D+) - М есть максимальное независимое
множество дуг в D^, если таковым является М, и если М соответствует F,
то М' соответствует F'. Это следует из определения орграфа D+. Кроме того,

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 147
если D+ имеет по крайней мере две компоненты, одна из которых есть, скажем,
С, то для определенных выше М и М' получаем, что
М" = (М П А(С)) U (М' П (?>+ - С))
есть максимальное независимое множество дуг в D+, отличное от М и Мг.
Эти рассуждения вместе с предложением VI.29 дают следующее соотношение
между понятием 1-факторизации и понятием биэйлеровости.
Следствие VI.30. ^-регулярный орграф имеет единственную 1-факториза-
цию тогда и только тогда, когда он биэйлеров.
Отметим, кстати, что предложение VI.29 есть просто другой способ
формулировки и доказательства известного результата из [BERM78b, Theorem 2.2];
следствие VI.30 встречается как утверждение во введении к работе [BERM79d],
но оно также следует из [BERM78b, Theorem 2.3 и 2.4]. Последние мы
объединим следующим образом.
Следствие VI.31. Пусть D есть 2-регулярный орграф. Тогда число 1-фак-
торов в D равно 2C^D+' и, следовательно, число 1-факторизации орграфа D
равно 2c(D+)_1.
Следствие VI.31 легко выводится из доказательства предложения VI.29 и
последующих рассуждений; поэтому его доказательство мы оставляем в
качестве упражнения.
Статья [BERM78b] заканчивается вопросом: действительно ли граф
степени 4 с нечетными циклами можно так ориентировать, что он станет
антиэйлеровым? На этот вопрос есть тривиальный положительный ответ.
Действительно, если G — произвольный связный эйлеров граф с четным числом
ребер, то пусть Т — любая эйлерова цепь в G; ориентируем ребра графа G
чередующимся образом, следуя ориентации, индуцируемой цепью Т, или в
противоположном направлении. Это дает антиэйлерову ориентацию графа G.
Очевидно, что в приведенном выше вопросе слово антиэйлеров может быть заменено
словом биэйлеров. Но тогда ответ будет отрицательным, как показывает
следующий пример: возьмем три экземпляра любого 4-регулярного графа G, не
имеющего биэйлеровой ориентации (например, по предложению VI.25 G может
быть выбран двудольным). Разобьем в каждом из трех экземпляров некоторое
ребро. Таким образом, мы имеем три графа Ga,Gb,Gc, каждый из которых
имеет по одной вершине степени 2, скажем а,Ь,с соответственно, а остальные
их вершины имеют степень 4. Следовательно, G+ = Ga U Gb U Gc U {аб, Ьс, ca}
есть граф степени 4, имеющий треугольник (т. е. нечетный цикл); но G+ не
может иметь биэйлерову ориентацию в силу того, что Ga не имеет биэйлеровой
ориентации (см. лемму VI.27).
VI.1.3. Do-ведомые эйлеровы цепи в орграфах
В заключение этого раздела рассмотрим другой тип ограничений на эйлеровы
цепи в орграфах (см. [BERK78a]).

148
Глава VI. Различные типы эйлеровых цепей
Определение VI.32. Пусть D — связный эйлеров орграф, и пусть Д) —под-
орграф орграфа D. Эйлерова цепь Т орграфа D называется Do-ведомой,
если для каждой вершины v е V(D) цепь Г проходит каждую дугу графа Do,
исходящую из v, прежде чем она пройдет какую-нибудь дугу из D\ := D — Do,
исходящую из v.
Конечно, каждый связный эйлеров орграф D может быть записан в виде
D = Do U Di, где A(D0) П A(Di) — 0; например, положим D\ = D, V(D0) =
V(D) и A(Do) = 0. В этом случае любая эйлерова цепь в D является Do-
ведомой1). Итак, определение VI.32 означает, что существование Do-ведомой
эйлеровой цепи Т может зависеть от выбора начальной вершины для Т.
Мы докажем две теоремы о существовании Do-ведомых эйлеровых цепей,
зависящих от структуры орграфа Di := D — Do (см. предложение 111.24).
Теорема VI.33. Пусть D — связный эйлеров орграф, и для данной верши-
ни v ? V(D) пусть Do С D выбран так, что D\ = D — Do есть каркас в
D, входящий в корень v. Тогда существует Do-ведомая эйлерова цепь,
начинающаяся (и заканчивающаяся) в v. Обратно, если Т —эйлерова цепь в D,
начинающаяся (и заканчивающаяся) в v, и если мы помечаем в каждой
вершине w E V(D), w ф v, последнюю дугу цепи Т, исходящую из w, mo D\,
подорграф графа D, индуцированный помеченными дугами, есть каркас,
входящий в корень v (и, следовательно, Т есть (D — Di)-ведомая эйлерова цепь
eD).
Доказательство. Пусть Do С D выбран так, что Di = D — D0 есть каркас
в D, входящий в корень v. Построим Т, начиная с вершины v и любой дуги
(и, ж), а затем выбирая любую дугу из D0, исходящую из ж, если такая дуга
существует, и дугу из Di, исходящую из х, в противном случае. Продолжаем эту
процедуру, пока она не закончится в некоторой вершине у G V(D). Тогда у = v\
в противном случае Т содержит больше дуг, заходящих в у, чем дуг, исходящих
из у, что противоречит эйлеровости D. Предположим, что Т содержит не все
дуги из D. Пусть тогда z — вершина, инцидентная дугам, не содержащимся в
Т. Так как D эйлеров и Т —замкнутая цепь, то 1й^-т{^) = ooId-t(z) ф 0.
Кроме того, z ф v по самому построению цепи Т. По определению D\ существует
путь P(z,v) С Di, соединяющий z с v. Запишем
Р(г,v) = z, (z,ui),uu ...,uk, (uk, v),v\
вполне возможно, что z = uk и и\ = v (т. е. P(z, v) может содержать в
точности одну дугу). По построению Г дуга (z,ui) не содержится в Г;
поэтому и (ui,U2) также не содержится в Т (заметим, что (wi,it2) может
содержаться в Т только тогда, когда все дуги, заходящие в щ, содержатся в Т),
и т. д. В частности, (uk,v) не содержится в Т, что противоречит равенству
idr(v) = odr(v) = ido{v) = odn(v). Таким образом, Т содержит все дуги из D.
х) Это наблюдение содержится в [BERK78a], где автор приписывает теорему IV.8 Гуду;
корни этой ошибки тянутся из [KNUT73a, p.374], а также из [AARD51a]. Приходится
сожалеть, что работа [KONI36a] была переведена на английский язык только недавно или что
Кёниг не написал ее сразу по-английски, или что ...

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 149
Отсюда и из построения цепи Т следует, что Т есть Д)-ведомая эйлерова цепь
в?>.
Предположим далее, что Г —эйлерова цепь в D, начинающаяся в
некоторой вершине v. Для каждой вершины w ф v пометим последнюю дугу пути Т,
исходящую из w, и обозначим через D\ подорграф, порожденный этими
помеченными дугами. Из определения D\ следует, что Г есть Do-ведомая эйлерова
цепь в D для Do = D — D\. Нам осталось лишь показать, что D\ является
каркасом, входящим в корень v.
Во всяком случае D\ обладает следующим свойством:
odrjiiw) = 1 для каждой w ? V(D) — {г>}, odD1(v) = 0. (*)
Следовательно, достаточно показать, что Di связен (см. теорему 111.31).
Предположим, что это не так. Тогда существует компонента В\ орграфа Z?i,
которая не содержит v, и по (*) odBx (w) = od^ (w) = 1 для каждой вершины
w € V(Bi). Из конечности орграфа D следует, что В\ содержит цикл, а
значит, и нетривиальную сильно связную компоненту. По лемме III.24.5) В\
даже содержит нетривиальную сильно связную компоненту Ci, такую, что В\
(и, следовательно, D\) не имеет дуг, исходящих из С\. Теперь если г
—последняя вершина из С\ в Т, такая, что г, (r,s),s есть секция цепи Т, причем
(г, s) G A{D\), то из выбора компоненты С\ следует, что s ? V(Ci), а из выбора
г —что Т заканчивается в s. Так как Т — эйлерова цепь, s = v, что
противоречит выбору В\ С D\ — {v}. Следовательно, Di связен, откуда следует, что D\
есть каркас, входящий в корень v. Теорема доказана.
Теорема VI.33 будет играть существенную роль в установлении факта,
который теперь известен как BEST-теорема, дающего формулу для числа
эйлеровых цепей в эйлеровых орграфах: [AARD51a]. Первая часть доказательства
теоремы VI.33, представленного здесь, следует линии доказательства,
изложенного в [KAST67a, p.76-77], а также в [AARD51a, Theorem 5b]; вторая часть
частично заимствована из доказательства теоремы 1 в [BERK78a, Theorem l].
Фактически эта вторая часть является более общей и несколько длиннее,
нежели соответствующие (в принципе идентичные) доказательства в [AARD51a,
KAST67a], но она позволяет сократить доказательство следующей теоремы.
Тем не менее я полагаю, что набросок доказательства, представленного в этих
работах, уместен, так как он имеет отношение к BEST-теореме. Оно проходит
так:
После того как (*) установлено, достаточно показать, что D\ не содержит
циклов. Предположим, что ребра в D помечены числами 1,2,..., |A(D)| в
соответствии с порядком, в котором они встречаются при прохождении цепи Т.
Отсюда следует, что если (г, s) и (s, t) суть дуги из Di, то метка у (г, s) меньше,
чем у (s,?) ((s,?) есть последняя дуга в Т, исходящая из 5, и, следовательно,
может быть пройдена только после всех дуг, заходящих в 5, одной из которых
является (г, s)). Значит, в D\ не может быть никакого цикла; в противном
случае в такой цикл должны входить дуги (г', s') и (s', t'), такие, что (r;, s') имеет
большую метку, нежели (s',tf).
Мы можем обобщить теорему VI.33, приняв во внимание выбор Dq.

150
Глава VI. Различные типы эйлеровых цепей
Теорема VI.34. Пусть D — связный эйлеров орграф. Пусть D\ С D выбран
так, что od,Dl(v) > 1 для каждой вершины v Е V(D\) С V(D), и пусть
Do = D — D\. Тогда следующие два утверждения 1) и 2) эквивалентны:
1) D имеет Do-ведомую эйлерову цепь]
2) Di имеет в точности одну (нетривиальную) сильно связную компоненту
С\, такую, что ни одна дуга из D\ не исходит из С\\
3) более того, каждая Do-ведомая эйлерова цепь в D должна
начинаться в некоторой вершине из С\, и для любой вершины из С\ найдется
Do-ведомая эйлерова цепь орграфа D, начинающаяся в этой вершине.
Доказательство. Из условия теоремы и из конечности орграфа D следует,
что D\ имеет по крайней мере один цикл; способом, аналогичным тому,
который был применен во второй части доказательства теоремы VI.33 (см.
рассуждения после (*)), мы выводим, что любая Do-ведомая эйлерова цепь Т в графе
D начинается в некоторой вершине из С\, где С\ — сильно связная компонента
в D\, такая, что ни одна дуга из D\ не исходит из С\. Повторяя эти
рассуждения, мы заключаем, что D\ имеет в точности одну такую сильно связную
компоненту С\. Следовательно, мы не только убеждаемся в том, что 1) влечет
за собой 2), но и в справедливости первой части утверждения 3).
Обратно, предположим, что утверждение 2) справедливо, и пусть г;
—любая вершина из С\. Мы хотим показать, что D имеет Do-ведомую эйлерову
цепь Т, начинающуюся в v. Для того чтобы можно было воспользоваться
первой частью построения Т из доказательства теоремы VI.33, заметим, что в
силу структуры орграфа Di в нем существует каркас DJ, входящий в корень
v (см. предложение Ш.24.6)). Запишем
A(D) = K1UK2UKZ, где К{ П К, = 0 для i ф j, г, j € {1,2,3},
где
Кг = A(D[), K2 = A(D,) - A(D[), K3 = A(D) - A(DX),
и положим
Ко = К 2 U К$.
Ясно, что (К$) = Do'-, положим (Ко) = DfQ.
Конечно, D[ может не быть входящим остовным деревом в D. Если
существует некоторая вершина х € V(D) — V(D[), то все дуги орграфа D,
инцидентные х, принадлежат К$ С Ко, поскольку V(D[) = V(D\). Применяя
неоднократно лемму о расщеплении, мы можем заменить каждую такую
вершину х вершинами степени 2, а подавляя эти вершины степени 2, мы приходим
к связному эйлерову орграфу D' с Кх 1)К2 С A(D') и V(D[) = V(D'), т. е. D[ —
каркас в Dx, входящий в корень v. Если V(D) = V(D[), то положим D' := D.
По теореме VI.33 D' имеет (D' — Dl)-вeдoмyю эйлерову цепь Г;, которая
соответствует естественным образом Do-ведомой эйлеровой цепи Т в D.
Однако Т может не быть Do-ведомой, но построение Г', как оно проводилось в
доказательстве теоремы VI.33, дает нам большую степень свободы при выборе
порядка прохождения дуг из D'—К\. А именно, для любой вершины w € V(D'),
достигнутой при построении X", можно выбрать любую дугу a G A(D') — К\,

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 151
Рис. VI.7. Эйлеров орграф D*, не имеющий Do-ведомой эйлеровой цепи (дуги из
Di помечены метками г, i = 0,1).
исходящую из w и еще не пройденную, в качестве следующей дуги, проходимой
цепью Т". Это значит, что мы можем наложить дополнительное ограничение,
требующее, чтобы в вершине w цепь Т' проходила вначале дуги из D' — D\,
исходящие из w, а потом дуги из Кч, исходящие из w, прежде чем она
пройдет какую-нибудь дугу из К\. Следовательно, если Т' построена именно таким
способом, то Т есть Д)-ведомая эйлерова цепь в D. Теорема доказана.
Теорема VI.34 есть не что иное, как легкое обобщение теоремы 1 из
работы Берковица [BERK78a], где равенство V(Di) = V(D) есть часть условия
теоремы (как мы видели, не необходимая). Более того, доказательство
теоремы VI.34 в основном следует линии доказательства результата Берковица,
за исключением того, что в представленном здесь доказательстве некоторые
технические детали не развернуты подробно из-за возможности использовать
части доказательства теоремы VI.33 и саму эту теорему. С другой стороны,
из сравнения доказательств теорем VI.33 и VI.34 становится очевидным, что
теорему VI.33 можно вывести из теоремы VI.34 почти тем же самым способом,
каким мы вывели теорему VI.34 из теоремы VI.33.
Какова наиболее общая структура, которую может иметь подорграф D\
связного эйлерова орграфа D для того, чтобы обеспечить существование (D —
?>1)-ведомой эйлеровой цепи Г? Исследование доказательств предыдущих двух
теорем показывает, что D\ не должен содержать более чем одну нетривиальную
сильно связную компоненту Ci, такую, что ни одна дуга из D\ не исходит из
С\. Но этого условия недостаточно, даже если D\ связен; это можно увидеть
на примере орграфа D* на рис. VI.7. С другой стороны, если мы положим
D'0 — (Do — {(e,d)}) U {(d, е)}, то D* имеет ^-ведомую эйлерову цепь Т*,
начинающуюся либо в а, либо в Ъ. Надо заметить, однако, что при построении
Т* нет больше свободы в выборе дуги из D'0, исходящей из d. На самом деле
Т* обязательно имеет вид
Т* = .. .с, (с,d),d, (d,e),e, (e,<f),d, (d,с)... .
Итак, по какой причине D* имеет ^-ведомую, но не Do-ведомую эйлерову
цепь? Снова обратившись к доказательству теорем VI.33 и VI.34, мы
обнаруживаем эту причину: в этих доказательствах мы вначале строили замкнутую
цепь Т, начинающуюся в г?, и как побочный результат получали вершину z и
путь P(z,v) С Di, такие, что ни одна дуга из P(z,v) не принадлежит Т; мы
получили, таким образом, противоречие. Кроме того, при доказательстве
теоремы VI.34 мы брали в расчет только подграф D[, а не весь граф Di. А что если
мы пойдем другим путем? То есть можем ли мы, вообще говоря, для данного

152 Глава VI. Различные типы эйлеровых цепей
связного эйлерова орграфа D и D\ С D найти такой, что
D имеет (D — ?>f)-ведомую эйлерову цепь Т+, которая индуцирует (D — D{)-
ведомую эйлерову цепь Т? Применяя это рассуждение к упомянутым выше D*,
?>i, D[ = D* - Dq соответственно, мы видим, что {D[)+ :— D[ U {(d,c)}
удовлетворяет условиям и утверждению 2) теоремы VI.34. (D* — (Х)[)+)-ведомая
эйлерова цепь Т+ в D* (с корнем в а или Ь) существует и порождает Г*,
как это описано выше. Как и для описанного выше орграфа D\ С D*, для
?)++ := Dx и {(е, d), (d, с)} также существует (D* — 1)^+)-ведомая эйлерова
цепь в D*\ существует, однако, .D* := D\ U {(e, d)} с D\ С -D* С -Di~+, такой,
что jD* имеет две нетривиальные сильно связные компоненты, из которых не
исходит ни одна дуга, принадлежащая D* • Отсюда следует, что в D* не
существует (D — Df )-ведомой эйлеровой цепи (см. рассуждения, предшествующие
рис. VI.7); следовательно, в D* не может быть никакой Do-ведомой эйлеровой
цепи, поскольку переход от D? = D — D^ к Dq не затрагивает никакой дуги,
исходящей из d.
Предыдущее обсуждение и теорема VI.34 приводят к следующей теореме,
дающей ответ на исходный вопрос.
Теорема VI.35. [FLEI89c] Пусть D — связный эйлеров орграф, и пусть D\ —
произвольный подграф графа D. Тогда любые два из следующих утверждений
эквивалентны:
1) D имеет {D — Di)-ведомую эйлерову цепь]
2) существует орграф Df, такой, что Dx С D* С D и для каоюдой вершины
v e V(D)
a) odD+ (v) = ocIdi (v) тогда и только тогда, когда od^1 {v) Ф О,
b) в противном случае odD+ (г?) = 1 и Df имеет в точности одну
нетривиальную сильно связную компоненту С\, причем ни одна дуга из D*
не исходит из С\\
3) существует орграф D*, такой, что Di С Df CD и
a) D имеет (D — D^)-ведомую эйлерову цепь,
b) для каждого D[ с Dx С D[ С Df, если (я, у) € A(D[ — Di), то
odDl (ж) = 0;
4) D\ содержит остовный входящий лес D^, такой, что
a) для некоторой вершины vq ? V(D\) и для каждой вершины х Е V(D{) —
{vq} равенство odD-(x) = 0 имеет место тогда и только тогда, когда
odo1 (х) = 0 и odD- (vo) = 0;
b) D имеет остовное дерево В, входящее в корень vq, и Df С В.
Доказательство. 1) влечет за собой 2). Пусть Т есть (D — .О^-ведомая
эйлерова цепь, начинающаяся в w. Если odcf1(v) > 1 для каждой вершины
v G V(D), то выберем D* = D\\ в противном случае пометим последнюю дугу
в Т, которая исходит из v, и пусть D* состоит из D\ плюс помеченные дуги. В
любом случае D\ С D* и Df удовлетворяет условиям, налагаемым на степени
в утверждениях 2а),Ь). Более того, Т есть (D — ?>^)-ведомая эйлерова цепь в

VI. 1. Эйлеровы цепи, избегающие некоторых переходов 153
силу выбора элементов из A(Df) — A(Di). Согласно теореме VI.34, Df имеет
в точности одну нетривиальную сильно связную компоненту С\, из которой не
исходит никакая из дуг орграфа Df. Импликация доказана.
2) влечет за собой 3). Возьмем орграф D^, определенный в 2)а),Ь). По
теореме VI.34 Df удовлетворяет утверждению 3)а). Теперь рассмотрим любой
орграф D[ с Di С D[ С D* и предположим, что A(D[ — D\) ф 0; пусть
(ж,у) € A(D[ — D\). По определению орграфа D* в 2) а),Ь) дуга из Df — D\
обязательно исходит из вершины z с odr>Y {z) = 0. Следовательно, если (ж, у) €
A(D[ — Di), то odo^x) = 0; таким образом, 3)Ь) справедливо.
3) влечет за собой 4). Возьмем D*, как описано в 3), и рассмотрим (D —
D^ )-ведомую эйлерову цепь Т+ в D. Если существует вершина w € V(D),
отличная от начальной вершины vo цепи Т+ и такая, что последняя дуга в Т+,
исходящая из ги, не принадлежит ?)+, то пометим эту дугу. Заметим, что в
этом случае ни одна из дуг, исходящих из w, не принадлежит D*.
Положим
jDf+ = D*, если такой вершины w не существует;
в противном случае положим
?)++ = (A(Df) U {а € A+\odD+(w) = 0 и а помечена}).
В любом случае, согласно определению орграфа D*+, Т+ есть даже (D—jD*4-)-
ведомая эйлерова цепь в D и D^+ удовлетворяет 3)Ь). Кроме того, V(Df+) =
V(D).
Помечая для каждой вершины v ф vq последнюю дугу в Т+, исходящую
из v, получаем каркас В орграфа D, входящий в корень vq (теорема VI.33),
а включение В С -Df4" следует из самого определения D*+. Определим Df
следующим образом: V(D^) = V{D{) и A(D^) = А(В) П A(Di); тогда L>f
есть остовный входящий лес в D\. Пусть (ж,у) —произвольная дуга из В, не
принадлежащая D±; тогда х ф vq. Если (ж, у) 0 A(Df), то из определения
орграфа D^+ и из включения D±+ 2 ?>i следует, что odD+(x) = 0 = odr)1(x).
Если (ж, у) € -A(-Di'), то (ж, у) ^ A(Z?i) по определению .Df, а из 3)Ь) с D[ =
D^ вытекает odo1 (x) — 0. Суммируем сказанное: D± есть остовный входящий
лес bDi, и если х, х ф vo для некоторой вершины vo ? V(D^) (которая на
самом деле есть корень дерева В), удовлетворяет условию odD-(x) = 0, то
odo1(x) = 0 (действительно, поскольку ж не является корнем дерева В, то
(ж,у) € А(В — A(D^)) для некоторой вершины у). Так как odr)1(x) = 0 в
любом случае влечет за собой odD- (ж) = 0 и odD- (vo) = odB(vo) = 0, а также
в силу того, что D^ С В с V(B) = V(D), то доказательство этой импликации
закончено.
4) влечет за собой 1). Пусть D^~ С D\ выбран, как описано в 4)а), и пусть
В — каркас в D, входящий в корень г>о, и D± С В. Применяя теорему VI.33, мы
получим эйлерову цепь Т в D, начинающуюся в vo и такую, что для каждой
вершины v Ф vq последняя дуга цепи Т, исходящая из v, принадлежит В. В
силу свободы выбора порядка, в котором дуги из А+ — А(В) встречаются в Т

154
Глава VI. Различные типы эйлеровых цепей
для каждой вершины v € V(D) и который мы использовали в доказательстве
теоремы VI.34, мы в состоянии построить Т так, что дуги из A+C)(D—Di) будут
встречаться в Т прежде, чем какая-либо дуга из A+nDi. Это справедливо даже
в том случае, когда дуга (х, у) ? В не принадлежит D\\ действительно, в этом
случае odD-(x) = ос1ог(х) = 0 в силу 4)а), т.е. А+ П A(Di) = 0, а значит,
А+ С D — D\. В случае вершины г>о, если А+0 П A(D\) ф 0, то мы строим Т,
начиная ее дугой из A+Q П A(D—D\), и всякий раз, попадая в г;о, мы продолжаем
ее дугой из А+0 C\A(D — Di), не проходившейся прежде, и делаем это, пока такие
дуги существуют. Следовательно, Т есть (D — Б^-ведомая эйлерова цепь в D.
Тем самым доказательство импликации завершено. Теорема VI.35 полностью
доказана.
Заметим, что для орграфа D* на рис. VI.7 и его подорграфов Di, D[ =
D* —Dq утверждение 4) а) справедливо как для D\, так и для D[, в то время как
утверждение 4)Ь) справедливо только для D[. Проверку деталей мы оставляем
в качестве упражнения (упр. VI. 12).
Конечно, определение VI.32 можно было бы сформулировать в более общем
виде, чтобы включить в него графы и смешанные графы. В случае графов,
например, можно было бы столкнуться с таким вопросом: имеет ли G эйлерову
ориентацию D, такую, что каркас графа G соответствует каркасу орграфа
D, входящему в корень v для некоторой вершины v ? V(G) = V(D)? Я не
нашел ни одной работы в этом направлении. Однако можно по крайней мере
сказать, что ответ на этот вопрос может быть дан за полиномиальное
время. А именно, выберем в каркасе В С G произвольную вершину v в качестве
корня и ориентируем В так, чтобы он превратился в дерево Db, входящее в
корень v. Теорема IV. 11 позволяет тогда установить существование эйлеровой
ориентации Dq для G, такой, что Db С Dq'- берем единственный смешанный
граф Я, в основе которого лежит граф G и дуги которого суть элементы из
A{Db)- Фактически именно доказательство теоремы IV.11, как оно
представлено в [FORD62a, Theorem 7.1, p. 60], показывает, что существование Dq может
быть выяснено за полиномиальное время. Повторяя этот процесс для каждой
вершины v € V(B) = V(G), устанавливаем, что ответ на поставленный выше
вопрос получается за полиномиальное время1).
Другой интересный вопрос (хотя и не относящийся к предыдущей
проблеме) состоит в следующем. Пусть G — связный эйлеров граф, и пусть дано
упорядоченное множество {ei, в2,..., ет} С E(G). Существует ли некоторая
эйлерова цепь Т, которая может быть записана в виде
Г = ...,ei,...,e2,...,e3,...,em,...?2)
На этот вопрос имеется положительный ответ, если A(G) > т — 1, а если A(G) >
2m, то можно даже предписать направление, в котором эти т ребер проходятся
х) На это мне указал проф. Цай Маочен (Пекин) во время моего визита в Китай летом
1987 г.
2) Это вопрос поставил проф. Ли Киао, Хэфэй (провинция Аньхой) во время того же визита.
Недавно тот же вопрос задал мне Г. Сабидусси.

VI.2. Попарно совместимые эйлеровы цепи
155
в цепи Т. Эти и более общие результаты содержатся в [СА1М89а]; они получены
использованием теоремы 1 из [JACK88d, Theorem l].
VI.2. Попарно совместимые эйлеровы цепи
Как мы видели в следствии VI.5, если G — произвольный связный эйлеров граф
без вершин степени 2 и X — произвольная система переходов этого графа, то
существует эйлерова цепь Т в G, совместимая с X. Это справедливо, в
частности, когда X = Хт> — система переходов, индуцированная эйлеровой цепью Т'
графа G. Возникает следующий вопрос: каково наибольшее число попарно
совместимых эйлеровых цепей в связном эйлеровом графе G? Этот вопрос был
впервые поставлен А.Дж.У. Хилтоном и Б. Джексоном, которые позднее
доказали, что если 5(G) = 2/с > 2, то существуют по крайней мере max{2, /с — 1}
попарно совместимых эйлеровых цепей [JACK87b]. В этой же самой статье
Джексон выдвинул следующую гипотезу, которая послужила отправной
точкой для результатов этого раздела и их обсуждения.
Гипотеза VI.36. Если G — связный эйлеров граф с 5(G) — 2/с > 2, то он
содержит по крайней мере 2к — 2 попарно совместимых эйлеровых цепей.
Эта гипотеза была проверена в [FLEI86a] для класса эйлеровых графов G,
у которых каждый блок есть цикл. Эти графы показывают, что оценка 2к — 2,
указанная в гипотезе, в общем случае является наилучшей из возможных: так,
если ребро е инцидентно точке сочленения v и d(v) — 2/с и если / есть
единственное другое ребро, инцидентное v и принадлежащее тому же самому блоку,
что и е, то {е(г>), f(v)} есть разделяющий переход и, таким образом, не может
содержаться в Хт, где Т — произвольная эйлерова цепь в G. Следовательно,
в этом случае существует, самое большее, 2/с — 2 возможностей для выбора
e(v) для образования перехода с другими полуребрами, инцидентными v. Но,
конечно, существуют примеры графов, которые содержат 2/с — 1 попарно
совместимых эйлеровых цепей. Для к— 2 это иллюстрирует рисунок VI.8.
(0)
v
Рис. VI.8. Граф G с 5(G) — 4 и тремя попарно совместимыми эйлеровыми цепями
Т\ = г;, 1, ги, 2, v, 3, w, 4, V] Т2 = г>, 1, w, 3, v, 4, w, 2, v; T3 = v, 1, w, 4, v, 2, w, 3, v.

156
Глава VI. Различные типы эйлеровых цепей
На самом деле можно предположить, что если усилить предположения в
гипотезе VI.36, потребовав дополнительно, чтобы G был двусвязен, то
можно даже найти 2к — 1 попарно совместимых эйлеровых цепей. Рисунок VI.8
указывает на это. В случае когда G = -FGfc+i > такая гипотеза была уже
сформулирована Коцигом [KOTZ79a]. Однако 4-регулярный граф, получаемый из
4-цикла С4 дублированием его ребер, противоречит этой возможности
усиления гипотезы VI.36. Кажется, однако, что если увеличить связность как
функцию от 5(G), то такое увеличение наибольшего числа попарно совместимых
эйлеровых цепей возможно. Фактически Билл Джексон дал характеризацию
4-регулярных графов, которые допускают три попарно совместимые эйлеровы
цепи [JACK88a, JACK88b]. Таким образом, он разобрался с частным случаем
гипотезы 1.1 из [JACK88a], которая указывает на это направление.
Впоследствии А. Буше разработал полиномиальный по времени алгоритм, который
дает три такие эйлеровы цепи [BOUC88b]. Заметим, что эти статьи основаны
на исследовании так называемых изотропных систем, которые были введены
Буше несколько лет тому назад (см., например, [BOUC87a]).
Рассмотрим гипотезу VI.36 для случая, когда G состоит точно из одной
вершины v и т > 2 петель ei,..., em. Как мы убедимся, хотя этот граф
совершенно тривиален во многих отношениях, доказательство гипотезы VI.36 даже
в этом «тривиальном» случае требует нетривиальных усилий.
Для простоты будем рассматривать G' = 5(G) вместо G; таким образом,
не нужно будет говорить о полуребрах, что упрощает обсуждение. Заметим,
однако, что понятие совместимости должно быть сужено на у, единственную
вершину, имеющую степень, превосходящую 2. ВС выберем обозначения для
ребер таким способом, чтобы е\ и е" соответствовали е^ в G, г = 1,...,т.
Вместе с G' рассмотрим его реберный граф L(Gf), который изоморфен К^ d =
d(v). Эта ситуация иллюстрируется рис. VI.9 для т = 3.
Конечно, какова бы ни была конфигурация эйлеровой цепи Г в G', ни
один из переходов {е[(у), е"(v)} не может определить секцию е?,и,е" цепи
6' L(G')
Рис. VI.9. Эйлеров граф G' и его реберный граф L{G'). «Невозможные» переходы
{e'i(v),e"(v)}, г = 1,2,3, в графе G' определяют 1-фактор L = {eie", e^e'i, e'ze'i} в
L(G')-#6.

VI.2. Попарно совместимые эйлеровы цепи
157
Т, г = 1,... ,т, просто потому, что каждый из этих переходов разделяет G'.
Это «невозможные» переходы; в L(Gf) они определяют 1-фактор L = {е\е"\1 =
1,..., га}. Конечно, любой другой переход вив графе G' определяет секцию
некоторой эйлеровой цепи в С. В L(Gf) переход, отличный от «невозможного»,
определяет ребро, не принадлежащее L. Мы можем сказать даже больше:
Эйлерова цепь в G' соответствует гамильтонову циклу Н
графа L(Gf) с Е(Н) D L, и наоборот. (*)
Итак, из приведенных выше рассуждений вытекает, что эйлерова цепь в G'
(записываемая в виде последовательности ребер) должна иметь вид
Т _ Jl Jl+l J2 fc + 1 *i 6j + l Jm Jm + l
где мы предполагаем, что Т начинается в г> и что обозначения выбраны таким
образом, что {е?',е?"+1} = {е^.,е?}для.7 = 1,... ,гаи {гь ... ,гт} = {1,...,га}.
Эта последовательность, интерпретируемая как последовательность вершин из
L(Gf), определяет не что иное, как гамильтонов цикл Н в L(Gf) с L С Е(Н).
По тем же соображениям гамильтонов цикл Я в L(G') с L С Я(Д") определяет
эйлерову цепь в G'.
Теперь если Т\ и Тч —две совместимые эйлеровы цепи в С, то
соответствующие гамильтоновы циклы Н\ и Щ графа L(G') обязательно удовлетворяют
соотношению
Е(Н1)ПЕ(Н2) = Ь. (**)
Это следует из предыдущих рассуждений и из того факта, что Х^ П Хт2 — ®
по определению совместимости.
Замечая теперь, что если Н — гамильтонов цикл в L(Gr), соответствующий
эйлеровой цепи в С, то из (*) вытекает, что E(H) — L есть 1-фактор в L(Gf), и
принимая во внимание (**), мы приходим к следующей теореме, эквивалентной
справедливости гипотезы VI.36 в случае, когда G состоит в точности из одной
вершины и га > 2 петель [FLEI86a].
Теорема VI.37. Пусть п = 2га > 2 — полооюительное четное целое число, и
пусть L есть 1-фактор полного графа Кп. Тогда существует 1-факторизация
С = {Li,..., Ln_i} графа Кп, такая, что L — L\ и L U Li является гамиль-
тоновым циклом графа Кп для г = 2,..., п — 1.
Доказательство. Для того чтобы получить 1-факторизацию, существование
которой утверждается в теореме, рассмотрим граф Кт, полученный из Кп
стягиванием ребер 1-фактора L = {ei,... ,em} С Кп. Пусть обозначения
выбраны таким образом, что е* = е[е", г — 1,..., га, и, значит, V(Kn) = {е[, e"\i =
1,..., га}; для простоты положим V(Km) = {ei,..., em} (заметим, что эта
система обозначений согласуется с обсуждением, предшествующим формулировке
теоремы VI.37).
Пусть е = е^ вг2 — фиксированное ребро графа Кт. Согласно
предыдущему выбору обозначений, в Кп имеем тождества е^ = е^е^, ei2 = e^2e"2 и
^ii , &i2 € L. Таким образом, е соответствует множеству Не из четырех ребер в
Кп, Не = {e'he'i2, e'l е?, е\ е'( , е'( е[2} (см. рис. VI.10), и это соответствие между

158
Глава VI. Различные типы эйлеровых цепей
ei.-
'е. ¦< > е. €L
Km
Ll
Кп
Рис. VI. 10. Ребро е ? Е{КШ), соответствующее Не С Е(КП).
е ? E(Km) и Не С Е(КП) определяет биекцию между ребрами е графа Кш и
подмножествами Не графа Кп, такую, что НеП Hf = 0 для е ф /.
В зависимости от четности га мы различаем два случая:
1) га = 1 (mod 2). Тогда iiTm имеет разложение
^={яг|г = 1,.
m — 1'
на (га — 1)/2 гамильтоновых циклов Hi,..., #(m-i)/2 (см. теорему III.50).
Рассмотрим произвольный, но фиксированный цикл Н ?Н.
Биекция е <^> Не позволяет описать 5-регулярный подграф Pfj =
(Uee?(tf) HeU L) С lfn (где Uee?(#) ^e есть расширение приведенной выше
биекции на Е(Н)) следующим образом (см. рис. VI. 11):
Возьмем га-угольную призму, боковые ребра которой суть элементы из L, и
добавим диагонали боковых граней. Определим обозначения в Р? таким
образом, чтобы {fj\j = 1,..., га} = {е[\1 = 1,..., га} было вершинным множеством
Рис. VI. 11. 5-регулярный граф Р#, определяющий га-угольную призму вместе с
диагоналями каждой боковой грани.

VI.2. Попарно совместимые эйлеровы цепи
159
границы «верхней» грани, a {fj\j = 1,... , га} = {e"\i — 1,... , га} было
соответствующим множеством «нижней» грани и L = {fjfj\j = 1,.. •, га}.
Мы хотим показать, что Р^ имеет цикловое покрытие четырьмя гамильто-
новыми циклами Ci, C2, С3, С4, такими, что Ci f)Cj = L для г ^ j, 1 < г, j < 4.
Для того чтобы достичь этого, сначала разложим E(P^) — L на четыре класса:
Mi = {/,7;+1|j = l,...,m},
М2 = {/;/;+i ij = i,...,m},
Мз = {/;/;+i |i = l,...,m},
M4 = {/j7i+ili = l,---,m},
где нижние индексы берутся по mod га.
Следующий шаг состоит в определении для г = 1,2 разбиения Мг на два
класса,
мг- = мг,0имгД,
где
Ma = {/ji}/SiUe{l,...,ra}, j ее A; (mod2)}, fc = 0,l,
fjl) = fj и /j2) = /" (т. е. Afi,0 содержит /?/?, /J/?,..., /^.f^, М1Л содержит
/17^ЛЛ,-..,Л*Лит.д.).
Теперь положим
с[ = (мм - {/^Л» и м2,о и {/;/{'},
с^ = (м2Д - {/?/{'» и (м1|0 - {/;_!/^}) и {/;_X, /^Л},
cj = м4.
В любом случае из самого определения классов Mi и Сг', г = 1,2,3,4,
следует, что {С{,С2, Сз, С4} есть 1-факторизация множества Е(Р^) — L. Для того
чтобы убедиться, что С* = С[ U L есть гамильтонов цикл в Р? для г = 1,2,3,4,
заметим, что С* есть 2-фактор графа Р? для г — 1,2,3,4, который для г = 1,2
не может иметь более одной компоненты, потому что га ее 1 (mod 2), в то время
как для г = 3,4 Сг есть цикл, независимо от того, что га ее 1 (mod 2).
Поэтому Сi — гамильтонов цикл для г = 1,2,3,4. Эти четыре гамильтоновых цикла
описаны на рис. VI. 12.
В силу указанной выше биекции е <-> Не, удовлетворяющей условию
Не П Hf = 0 для е/J, и потому, что 7i есть цикловое разложение графа
Кт на гамильтоновы циклы, гамильтоновы циклы d,Cj, 1 < i,j < 4,
соответствующие Н,Н* еН, также удовлетворяют условию С{Г\С^ —L. Поэтому
если мы положим С'г{Н) := С[ для г = 1,2,3,4 и произвольного Н € W, то для
?' = {СЯЯ)Д = 1,2,3,4; Я еН}
получаем
| ?' | = 4 • | И | = 4 • т~-^ = 2 га - 2 = п - 2;
следовательно, С = ?' U {L} есть 1-факторизация графа jFfn, что и требуется.
Это завершает случай га ее 1 (mod 2).

160 Глава VI. Различные типы эйлеровых цепей
2) m = 0 (mod 2). Замечая, что единственная 1-факторизация графа К±
удовлетворяет теореме, мы можем считать, что m > 4.
Согласно теореме III.49, Кт имеет 1-факторизацию С* = {Li,... , Lm_i},
такую, что Li U Lj есть гамильтонов цикл графа Кт для j = z + l,2 + 2, 1 <
г < т — 1, где мы полагаем Lm = Li, Lm+i = ?2- Пусть
7Y* = |Я/с := L2k UL2fc+i|2 < k < —-—, L2k,L2k+i € ?*|.
Так же, как в случае т = 1 (mod 2), рассмотрим для фиксированного Н € Н*
соответствующий 5-регулярный подграф P# = (Uee?(#) He\J L) С Кп\ пусть
четыре класса М*, г = 1,2,3,4, и разбиение Mi = Mj$ U М^\ для j = 1,2
определены, как выше.
Так как га четно, мы имеем, однако, более простое определение для Сг', г =
1,2,3,4, а именно,
С[ = AfifiUM2|o,
С2 = Mi,0UM2,i,
С3 = М3,
С? = М4.

VI.2. Попарно совместимые эйлеровы цепи
161
Снова из определения М{ и С[, i — 1,2,3,4, следует, что {С^С^С^С^}
есть 1-факторизация графа Р? — L, и, согласно даже более простым
соображениям, Сi = C[ U L — гамильтонов цикл графа Р#: для i = 1,2 конфигурация
верхнее ребро, L-ребро, нижнее ребро, L-ребро дает гамильтонов цикл в
точности потому, что га четно (ср. это с рис. VI.12), в то время как для г = 3,4
d — гамильтонов цикл, вне зависимости от четности га (ср. это с построением
С± в случае га = 1 (mod 2)).
По только что описанному построению мы получаем множество С попарно
непересекающихся 1-факторов С[{Н) графа Кп (с С[(Н), определенным, как
в случае га = 1 (mod 2)),
?' = {С1(Н)\1 = 1,2,3,4,Н €Н*},
но теперь
77? — 4
|?'| = 4-|И*| = 4-^т-^ = п-8.
Li
Для того чтобы получить нужную 1-факторизацию С графа Кп, остается
показать, что 7-регулярный подграф G* графа Кп с L С E(G*), соответствующий
L\ U Z/2 U1/3 С Е(Кт), имеет 1-факторизацию L" — {L, L\,..., L%\, такую, что
Lj U L — гамильтонов цикл графа Кп для j = 1,..., 6. Тогда С = С" U С будет
1-факторизацией графа Кп, что и требуется; это следует из биекции е <-* Не
с Не П Я/ = 0 для е / /, уже использованной в случае га = 1 (mod 2), и
того факта, что Н* U {L\ U L<i U L3} есть разложение графа -/^г^; кроме того,
|?|= п-8 + 7 = п-1.
Пусть Н — гамильтонов цикл графа Кш, индуцированный 1-факторами L\
и L2, и рассмотрим 5-регулярный подграф Pfa D L графа ifn, как выше
(см. рис. VI. 11). Тогда G* получается из Р# добавлением для каждого
ребра е = eiej € L3 элементов из Не = {e^e'j,е"е", е[е",е"е'^}. Предполагая без
ограничения общности, что в\е2 € Li, классифицируем ребра графа G* — L
следующим образом:
если eres e Li для г = 1,2,3, то
e^e'.eLj, e'le'^L'l, e;e's',e% e JV«.
По определению {Z^,L", А^|г = 1,2,3} есть разбиение множества E(G*) — L.
Это разбиение составляет основу для построения 1-факторов 1Л, 1 < j < 6,
которые нам требуются. Выделим два случая.
а) га = 0 (mod 4). Рассмотрим гамильтонов цикл Н' графа Кт,
индуцированный L2 и 1з, и соответствующий 5-регулярный подграф Р?, графа Кп с
L С Е(Р^,). Опять можно считать, что граф Р^, получен из га-угольной
призмы (где граничные ребра верхней (нижней) грани суть в точности ребра из
L2 UL3 (^2 U ^3)5 в т0 время как боковые ребра призмы суть ребра из L)
добавлением диагоналей боковых граней. Эти добавленные ребра есть в точности
ребра из N2 U Щ.
Теперь разобьем A^UA^ на два 1-фактора С\, С2 графа Кп так, что С{ UL и
Сз UL суть гамильтоновы циклы графа ifn (см. построение С± = С[ UL с С'А =
М± в предыдущих случаях, например, см. рис. VI.12. Кроме того, заметим, что
N2 U N3 есть объединение двух непересекающихся четных циклов).

162
Глава VI. Различные типы эйлеровых цепей
Рис. VI.13. 1-факторы Сз и С\ графа G*, обладающие тем свойством, что С% U L
и С\ U L суть гамильтоновы циклы графа Кп (ребра из L появляются в качестве
боковых ребер призмы).
Предположив, что е\в2 € Li, можно без ограничения общности далее так
ввести обозначения, чтобы
L\= le2i-ie2i\i = 1,..., га/2 j,
1,2= I e2ie2i-\-\\i = 1,... ,ra/2, где мы полагаемem+i = ei \.
При этой системе обозначений определим теперь разбиение {N[,N"} для N\
формулами
#1 = {е«-3е«-21< = 1» • • • 1 ™/*} и {*«-1<41* = 1,• • •, V*},
и разбиение {Ljj,!^} для L'2 U I^' формулами
^з =Ki-2<4-iK = 1, ¦ • •. ^/4}и{е^е^+1|г = 1,... ,ш/4,
где мы полагаем е^+1 = е"},
L2=(^ULJ')-L§.
Простое рассуждение теперь показывает, что так как га = 0 (mod 4),
C;=L°3UN[ и Cl=L°4UN[f
суть 1-факторы графа Кп, такие, что С? U L — гамильтонов цикл графа ifn
для j = 3,4, причем каждый из них соответствует гамильтонову циклу,
индуцированному L\ U1/2 в ifm (см. также рис. VI. 13). Так как
з
G*-L={J{L'i\JL'(uNi)
г=1

VI.2. Попарно совместимые эйлеровы цепи
163
и
\Jc;=({jNz)uL'2ULl
г=1 4=1 /
единственными еще не рассмотренными ребрами из G* — L являются ребра из
L[ U L'l UL'3U Ц.
Рассматривая эти ребра в качестве граничных ребер верхней и нижней граней
m-угольной призмы и рассуждая практически так же, как и при построении
С[ и С2 в начале этого случая 2), заключаем, как и выше, что
С*5=Ь[иЦ и C;=L'{UL'3
суть 1-факторы графа Кп, такие, что С? U L и С? U L являются гамильтоно-
выми циклами графа Кп. Таким образом, для L!- = С?, 1 < j < б, мы нашли
1-факторизацию С" — {L, L\,..., Lq} графа G*, как и требовалось, при
условии, что га = 0 (mod 4).
b) га = 2 (mod 4). Имеем га > б, так как в любом случае га > 4. Из
построения Cj, 1 < j < б, в случае а) ясно, что С? для j = 1,2 есть 1-фактор графа Кп
независимо от четности га, в то время как для j = 5,6 С? является 1-фактором
графа Кп при условии, что га = 0 (mod2). Но если га ф 0 (mod4), C3,C% не
являются больше 1-факторами графа Кп. Действительно, если строить С?, С%
шаг за шагом, начиная с е[е2, е'{е'2 соответственно, как в случае а), то мы
обязательно получим dc*(e[) = dcz(e'{) = 2 и dc*{ef{) — dc*{e[) = 0. Тем не менее
с помощью локального преобразования, затрагивающего С?, 1 < j < 6,
построенные в случае а), и включающего 12 ребер, смежных с е[е" в G*, мы добьемся
успеха и в этом случае. Таким образом, в дальнейшем пусть С*, 1 < j < 6, —
такие же множества ребер, как и выше, модифицированные следующим
образом в отношении верхних границ для индексов г при определении N[ и L®, а,
именно: в первом члене каждого из N[ и Lg га/4 заменяется на (га -I- 2)/4, в
то время как во втором члене каждого из этих множеств га/4 заменяется на
(га — 2)/4 (конечно, в этом модифицированном определении L® мы полагаем
em+i = ei)-
Рассматривая ребро eqem € Е(КП), допустим без ограничения общности,
что ребро е'^е'т принадлежит С\ (заметим, что в силу обозначений, выбранных
в случае а), е^е^ G iV3 С С{ U С2). В силу этого допущения е^е^е'/е^ G С]*,
где emei € L2 и е\еТ € L3; следовательно, efqef^efme'{,е[е" ? С2. Кроме
того, по-прежнему имеем е[е2 ? С%, и, согласно приведенной выше
модификации верхних границ индексов г, мы также имеем е^^е^е^е^ Е С%.
Поэтому ^"е^е^^е^е^е" Е С|. Что касается С| и Q, то е[е2,е"е" G С5* и
II II I I (- S4*
Оставляя С2 и С? неизменными, мы сначала положим
С** /О* /О** /Of*
2 — °2 » °5 ~ °5 •

164
Глава VI. Различные типы эйлеровых цепей
Для того чтобы получить оставшиеся четыре 1-фактора С** графа G*, г =
1,3,4, б, заменим некоторые ребра, инцидентные е[, на ребра, инцидентные е",
и наоборот; а именно:
сг = (сг
сг = (с;
с;* = (с4*
св" = (с;
Заметив, что в этом случае {С*|1 < г < 6} есть разбиение, но не 1-фак-
торизация множества E(G*) — L, мы заключаем из определения С**, 1 < г < б,
и того факта, что га = 2 (mod4), что ?" = {L, L^,... , L?} Для ^Г = С**, 1 <
г < б, есть 1-факторизация графа G*. Кроме того, именно потому что LUC* —
гамильтонов цикл графа G*, если га = О (mod 4), из определения С** следует,
что L U С** —гамильтонов цикл графа G*, если га = 2 (mod4). Это
заключительное наблюдение завершает случай Ь).
Следовательно, в обоих случаях га = 0 (mod 4) и га = 2 (mod 4)
нами найдена 1-факторизация Ч" графа G*, такая, что С — С! U С" есть
1-факторизация графа Кп, что и требовалось (что касается /У, см. обсуждение
случая 2), предшествующее случаю а)). Это устанавливает теорему в случае
га = 0 (mod 2), а поскольку случай га = 1 (mod 2) полностью разобран ранее,
теорема VI.37 доказана.
Теорема VI.37 дает нам теперь возможность проверить гипотезу VI.36 для
эйлеровых графов G, циклы которых являются их блоками (см.
обсуждение, следующее за формулировкой гипотезы VI.36 и предшествующее
теореме VI.37).
Теорема VI.38. Пусть G — связный эйлеров граф с 5(G) > 2. Предположим,
что каждый цикл графа G является его блоком. Тогда G содержит 5(G) — 2
попарно совместимых эйлеровых цепей, и среди любых 5(G) — 1 эйлеровых
цепей графа G существует по меньшей мере две цепи, которые не совместимы
друг с другом.
Доказательство. Вторая часть заключения теоремы следует из обсуждения,
расположенного сразу же после формулировки гипотезы VI.36; следовательно,
достаточно показать, что при указанном предположении G содержит 5(G) — 2
попарно совместимых эйлеровых цепей. Доказательство проведем индукцией
uop=\V(G)\.
Предположим, что р = 1. Поскольку 5(G) > 2, единственная вершина v
графа G инцидентна га > 2 петлям. Таким образом, мы имеем ситуацию,
обсуждавшуюся после рис. VI.8 и перед формулировкой теоремы VI.37. Было
показано, что случай р = 1 эквивалентен теореме VI.37. Следовательно,
теорема VI.38 справедлива для р — 1.
Для р > 1 действуем алгоритмически с помощью многократного
применения теоремы VI.37. Начнем с эйлеровой цепи Т эйлерова графа G с
| V(G) |= р > 1 и 5(G) > 2 и рассмотрим цикл Со с E(Cq) = E(G), обход кото-
-{Cei,ei4})U{e^ei'>e'1e;},
-К4'})иК4'},
-K^',eie;})U{eiei',ei'e;}.

VI. 2. Попарно совместимые эйлеровы цепи
165
рого в одном из двух возможных направлений соответствует То = Т. Положим
V{G) = {vu...,vp).
Пусть G\ получен из Со с помощью отождествления вершин г>1д,... , г?!^
цикла Со, где 2ki = d(v\) > 5(G) и где эти к\ вершин соответствуют замене
вершины v\ ? V(G) на fci 2-валентных вершин в соответствии с То.
Следовательно, Gi имеет точно одну вершину степени больше 2, а именно v\. Отметим,
что из самой структуры графа G (каждый цикл графа G является его блоком)
следует, что для г — 1 (с Gij = Gi)
два полуребра, инцидентные вершине vi, принадлежат одному
и тому же блоку из Gij тогда и только тогда, когда эти
полу ребра принадлежат одному и тому же блоку графа G. (*)
Перефразируем утверждение (*) более кратко, говоря, что Gij и G имеют
одно и то же блочное распределение в Vi.
Согласно обсуждению перед теоремой VI.37 и по самой этой теореме G\
имеет эйлеровы цепи Т\г\^Т\^ • • • ^Т^А^-г? которые обязательно определяют
одинаковые переходы в V(G) — {vi} (поскольку эти вершины
соответствуют множествам 2-валентных вершин в Gi), тогда как в vi они ведут себя
совместимым образом (т.е. пара полуребер, смежных в vi, определяет
переход, самое большее, для одной цепи Tij, 1 < j < 2ki — 2). Для п = 5(G)
пусть Тхд,..., TiiTl_2 — первые п — 2 эйлеровых цепей, построенных выше (если
2/ci = п, то возьмем их все), и для j = 1,..., п — 2 пусть Cij обозначает цикл,
соответствующий Tij.
Для каждого j Е {1,... ,п — 2} построим G2j из Cij при помощи
отождествления вершин ^д,.. .,г?2,^2, где 2&2 = с?(иг) > 5(G) = п (см. построение
Gi из Со выше). Мы заключаем, что утверждение (*) справедливо также для
i = 2, т.е. G2j и С имеют одно и то же блочное распределение b^5h
поэтому все эти п — 2 графов G2j имеют одно и то же блочное распределение в
V2 (заметим, что циклы из С, содержащие vi, соответствуют одному циклу в
каждом G2,j). Следовательно, если мы рассматриваем К2к2-> т0 пары
полуребер, инцидентных вершине V2 и определяющих блоки графов G2j, суть одни
и те же для любого j € {1,... ,п — 2} и поэтому определяют единственный
1-фактор L графа К2к2- Поэтому применение теоремы VI.37 плюс
обсуждение, предшествующее этой теореме, дают п — 2 < 2&2 — 2 = d(v2) — 2 эйлеровых
цепей Тгд,... ,Т2,п-2 графа G, которые определяют одни и те же переходы в
V{G) ~~{^ъ ^2} (^ именно, переходы из То), но ведут себя совместимым образом
в {vi,v2}l).
Далее рассмотрим циклы C2,j, соответствующие цепи Тг,-/, и
соответствующим образом построим графы Gsj из C2J, j = 1,..., п—2. Теперь утверждение
(*) справедливо для г = 3, т. е. все графы Gsj имеют одно то же блочное
распределение в ^з. Следовательно, мы получаем эйлеровы цепи Тзд,... ,Тз,п_2,
х) Точнее, можно было бы сначала рассмотреть T2j как эйлерову цепь графа G^j, которая
выбрана из 2&2 — 2 попарно совместимых эйлеровых цепей графа G2,j-> который в свою
очередь был получен применением теоремы VI.37 к Сг,^, j = 1,... ,п — 2. Однако начинать
следует с фиксированной 1-факторизации графа К^к2» удовлетворяющего теореме VI.37.

166
Глава VI. Различные типы эйлеровых цепей
которые ведут себя, как цепь Т0 в V(G) — {ui, г>2, г>з}, но ведут себя совместимым
образом в {г>1,г>2,г>з}.
Если р = 2 или р = 3, то теорема следует из доказанного выше. Для р >
3, мы получаем многократным применением приведенных выше рассуждений
эйлеровы цепи Гр_1д,... ,Tp_i,n_2 графа G, которые ведут себя совместимым
образом точно в V(G) — {vp}, в то время как в vp они еще ведут себя, как
Г0. Строя Gpj из цикла Cp_ij, соответствующего Tp-ij, j = l,...,n-2, и
замечая, что эти п — 2 графов имеют одно и то же блочное распределение в vp,
применим теорему VI.37 к соответствующему графу К2кр, где 2кр — d(vp) >
5(G) — п, для того, чтобы получить эйлеровы цепи Трд,... , TPjn_2 графа G,
которые теперь совместимы во всех вершинах из V(G). То есть Трд,..., Тр,п_2
суть 6(G) — 2 эйлеровых цепей графа G, которые попарно совместимы. Это
завершает доказательство теоремы.
Следует отметить, однако, что давно стоящая гипотеза Коцига [KOTZ64a,
KOTZ64b], а также другие гипотезы утверждают, что Kim имеет 1-фактори-
зацию {Li,..., L2m_i}, такую, что Li U Lj — гамильтонов цикл для г ф j, 1 <
г, j < 2m — 1. Отсюда непосредственно получается, что справедливость этой
гипотезы влечет за собой теорему VI.37: из-за симметрии графа Kim
утверждение о том, что 1-факторизация содержит предписанный 1-фактор, как это
выражено в формулировке теоремы VI.37, не является реальным
ограничением на 1-фракторизацию. Приведенная выше гипотеза, тем не менее, доказана
пока только для некоторых частных случаев: для случаев, когда 2га — 1 —
простое число, га —простое число [KOTZ64a] или 2га = 16,28,36,50,244 или 344
(подробнее по этому вопросу см. [MEND85a, SEAH87a, STIN87a]; для 2га = 12
все неизоморфные решения этой проблемы можно найти в [PETRSOa])1). С
другой стороны, доказательство теоремы VI.38, которое представлено здесь,
показывает, что теорема VI.37 и теорема VI.38 эквивалентны (см. также
утверждение, предшествующее теореме VI.37).
Теперь обратимся к вопросу, всегда ли возможно использовать подход,
примененный в доказательстве теоремы VI.38, для того, чтобы доказать гипотезу
VI.36 целиком. Возьмем эйлерову цепь То связного эйлерова графа G без
вершин степени 2 и рассмотрим цикл Со, соответствующий То; построим G\ , как
в доказательстве теоремы VI.38, применим теорему VI.38 к G\ и т. д.
Проблема, однако, состоит в том, что п — 2 графов Gij для некоторого г > 2 могут
больше не иметь одно и то же блочное распределение в vi (см. доказательство
теоремы VI.38). Эту проблему можно проиллюстрировать с помощью графа
на рис. VI.8 и его эйлеровых цепей Т\ и Т2: начиная с эйлеровой цепи Ti,
которая принимает на себя роль цепи То из доказательства теоремы VI.38, и с
цикла Со, соответствующего Ti, мы получаем из Со граф G\ с v\ = w в
качестве единственной вершины валентности, превышающей 2. Граф G\ имеет две
эйлеровы цепи, которые совместимы в го, а именно
7\,i = uij4,1, гу, 2, и2,з, 3, гу, 4, г>м
1) А. Роса информировал меня недавно, что гипотеза Коцига решена разными авторами
для 2т = 126,170, 730,1332,1370,1850, 2198, 3126, 6860.

VI.2. Попарно совместимые эйлеровы цепи
167
и
7i,2 = г>м, 1, гу, 3, г>2,з, 2, ги, 4, г>м
(^1,4 и г^2,з обозначают вершины степени 2, отвечающие расщеплению v в
соответствии с Т\). Из 7\д и Ti52 получим графы Gi,i и Gi,2, единственной
вершиной степени, превышающей 2, которых является v. Но в Gi,i блоки
определяются реберными множествами {1,2} и {3,4}, в то время как в G\^ блоки
определяются реберными множествами {1,3} и {2,4}. Следовательно, Gi,i и
Gi,2 имеют различные блочные распределения в v.
Тем не менее только что обсуждавшаяся проблема приводит нас к
следующей гипотезе (впервые выдвинутой в [FLEI86a]), справедливость которой
доказывала бы гипотезу VI.36 и которую можно рассматривать как обобщение
теоремы VI.37.1)
Гипотеза VI.39. Пусть п = 2га > 2 — положительное четное целое число, и
пусть Lo, I/,..., l/n~2) суть 1-факторы графа Кп, такие, что LqUL^ — гамиль-
тонов цикл графа Кп для i = 1,... ,п — 2. Тогда существует 1-факторизация
{Li,... ,Ln_i} графа Кп, такая, что Li U L^ — гамильтонов цикл для г =
1,...,п-2.
Заметим, что в формулировке гипотезы VI.39 1-факторы L№, 1 < г < п — 2,
не обязательно все различны и из L^ ф L^\ 1 < i < j < n — 2, не следует, что
L^ П L^ = 0. Здесь учитывается тот факт, что в доказательстве гипотезы
VI.36, аналогичном доказательству теоремы VI.38, для некоторого г > 2 два
графа Gij-L и dj2 могут иметь, а могут не иметь одно и то же блочное
распределение, а если они имеют различные блочные распределения, то они еще
могут содержать некоторую одинаковую определяющую блок пару полу ребер,
инцидентных г^.
Если I/ = ... = L(n~2\ то гипотеза VI.39 сводится к теореме VI.37 с
L — V — Ln-\. Заметим, что в этом случае 1-фактор Lo становится
несущественным: он не играет никакой роли в заключении гипотезы VI.39; таким
образом, сказать, что Lo образует гамильтонов цикл вместе cL — L' — Ln_i, —
это все равно, что сказать «пусть L — произвольный 1-фактор графа Кп».
Для того чтобы убедиться, что справедливость гипотезы VI.39 влечет за
собой справедливость гипотезы VI.36, вернемся к обсуждению,
предшествовавшему формулировке гипотезы VI.39, используя терминологию
доказательства теоремы VI.38: замечая, что для г = 1 утверждение (*) в доказательстве
этой теоремы остается справедливым, получим эйлеровы цепи 7\д,... ,Tijn_2,
ведущие себя совместимым образом точно в v\, а из соответствующих циклов
Gi,i,..., Gi?n_2 получим G2,i,..., G2,n-2- Пусть г > 2 — наименьшее целое
число, для которого п — 2 графов Gij,j = l,...,n — 2, не удовлетворяют (*),
т. е. у этих п — 2 графов не одно и то же блочного распределение. Если
такого г < р не существует, гипотеза VI.36 устанавливается для этого G при
помощи р-кратного применения теоремы VI.37. Если, однако, такое i < p
существует, заметим следующее: переходы цепи То в Vi одни и те же для каждого
Gi,j, j = 1,..., n —2 (см. определения графов G\ и Gij для г > 2), и эти перехо-
х) Некоторые другие гипотезы, похожие на гипотезу VI.39, были выдвинуты в [FLEI86a].

168 Глава VI. Различные типы эйлеровых цепей
ды соответствуют 1-фактору Lq графа Kni, где п < щ = d(vi). Аналогично, для
каждого j = 1,..., п — 2 блоки из Gij определяют 1-фактор L^ графа Kni,
такой, что LqUL^ является гамильтоновым циклом графа Кп (см. утверждение
(*), предшествующее теореме VI.37). То есть условие гипотезы VI.39
выполняется (если п < щ, то L^ = Z,(n~2) для n — 2<j<rii — 2). Допуская
справедливость этой гипотезы, получаем 1-факторизацию С = {Li,... ,Lni_i} графа
Kni, такую, что Lj U L^ — гамильтонов цикл графа KUi для j = 1,..., щ — 2.
Значит, Lj определяет эйлерову цепь Tij графа Gij для j = 1,... ,п — 2, и,
поскольку С есть 1-факторизация, эти п — 2 эйлеровых цепей Tij ведут себя
совместимым образом точно в i>i,...,г^. Для г < р получим из этих цепей Tij
соответствующие циклы dj и, следовательно, графы G^+ij, j = 1,... ,n — 2.
Тогда повторяем приведенные выше соображения с г +1 вместо г и т. д. Таким
образом, справедливость гипотезы VI.39 влечет за собой справедливость
гипотезы VI.36. Приведенное выше обсуждение показывает, что, с другой стороны,
из справедливости гипотезы VI.36 следует некое утверждение относительно
1-факторизаций графа Kn, n = 0 (mod 2). Тем не менее неясно, является ли это
«некое утверждение» настолько же сильным, как гипотеза VI.39, т. е.
являются ли эти две гипотезы эквивалентными. Действительно, неясно даже, имеем
ли мы дело при доказательстве гипотезы VI.36 со всеми возможными
системами блочных распределений, как сформулировано (в иной, непрямой, форме) в
условии гипотезы VI.39. Отметим, что теорема 1 из [JACK88a] решает
гипотезу VI.36 для случая к = 3, используя изотропические системы, а не на гипотезу
VI.39.
Итак, поскольку мы не можем в настоящий момент доказать ни одну из двух
этих гипотез, можно попытаться заменить в гипотезе VI.36 величину 2к — 2 на
функцию f(k) и, зная, что 2к — 2 является верхней оценкой для f(k) (см.
теорему VI.38), поинтересоваться «приличной» нижней оценкой. В самом деле, в
результате Джексона (см. обсуждение, предшествующее гипотезе VI.36)
утверждается, что f(k) > max{2, к — 1}. Этот результат непосредственно вытекает из
обобщения следствия VI.43 (см. теорему VI.42 и следствие VI.43 ниже). Но
прежде чем формулировать эти результаты, нам нужно исследовать другие связи
между системами переходов в связном эйлеровом графе и гамильтоновыми
циклами, содержащими заданный 1-фактор некоторого связанного с ними графа.
Пусть G — связный эйлеров граф с 5(G) = 2к > 2, и пусть заданы г систем
переходов Xi,...,Xr графа G. Рассмотрим произвольную вершину v € V(G), и
пусть Xo(v) —произвольная система переходов в v, если v — яе точка
сочленения; в противном случае пусть система переходов в v, Xo(v), определена таким
образом, что она индуцирует систему переходов в г; в каждом блоке,
содержащем v (поскольку G эйлеров, каждый блок, содержащий г;, имеет четное число
полуребер, инцидентных г>; следовательно, Xo(v) может быть определена, как
выше). Пусть Х0 = \Jvev(G) -^o(v), и пусть Xi(v) С Хи г — 1,..., г, —
соответствующие системы переходов в v.
Теперь пусть е^,... ,е^, d = d(v) = 0(mod 2), —полуребра, инцидентные v,
и рассмотрим полный граф К^ с V(Kd) = {e[\l = 1,... ,d}. Аналогично тому,
что было сказано в обсуждении, предшествующем теореме VI.37, заключаем,

VI.2. Попарно совместимые эйлеровы цепи
169
что система переходов в v соответствует 1-фактору L(v) графа К&. Пометим
в Kd ребра 1-фактора Lj(v), соответствующие Xj(v), j = 0,... ,г.
Нам известно, что построение эйлеровой цепи Т графа G равносильно
замене шаг за шагом каждой вершины v графа G на t = \d(v) вершин v\,..., vt
степени 2 так, что на каждом шаге получающийся граф Gv связен. Теперь, если
цепь Т совместима с Х{, то Xt(v) f)Xi(v) = 0,г = 1,...,г. Следовательно,
Xt(v) соответствует 1-фактору Lt(v) в Kd с
LT(v) П Li(y) = 0, г = 1,..., г. (о)
Это необходимое условие для существования цепи Т, совместимой с Х^ г =
1,...,г. Но оно не является достаточным, потому что не учитывает, что Gv
должен быть связным (заметим, что элементы из Xt(v) суть в точности
множества ??., j = 1,...,?). С другой стороны, рассмотрение утверждения (*),
предшествующее теореме VI.37, плюс наблюдение, что Xo(v) однозначно
определена тогда и только тогда, когда каждый блок графа G, содержащий v,
содержит точно два полуребра, инцидентных вершине г;, приводит к следующему
заключению:
Если Lt(v) U Lo(v) — гамильтонов цикл графа Kd, то Gv связен. (оо)
Суммируя (о) и (оо), мы, казалось бы, сталкиваемся со следующим вопросом:
верно ли, что Kd (с 4 < d = d{v) = 0 mod 2)) содержит 1-фактор L, такой,
что Li(v) П L = 0, г = 0,..., г, и Lq(v) U L — гамильтонов цикл? Рассмотрим
случай г = 1. Если d = 4, то К± имеет единственное разложение на 1-факторы,
любые два из которых дают гамильтонов цикл в К±\ поэтому, вне
зависимости от того, является множество L\{v) П Lo(v) пустым или нет, К± содержит
1-фактор L с Li(v) П L = 0, такой, что Lo(v) U L — гамильтонов цикл в К±
(отметим, что в этом случае L\(v) ПL0(v) ф 0 дает L\{v) — L0(v)). Если d > 4,
то d > б, и, согласно теореме VI.37, Kd имеет 1-факторизацию {Li,..., Ld-i},
такую, что Lo(v) = L\ и Lq{v) ULi — гамильтонов цикл для г = 2,..., d— 1. Так
как d > 6, то \d < d—2, т. е. 1-фактор Li(v) (который имеет \d ребер)
удовлетворяет условию L\{y) f)Li = 0 по крайней мере для одного H3zG{2,...,d—1}.
Отсюда мы заключаем, что поставленный выше вопрос имеет положительный
ответ, если г — 1 (отметим, что того же самого мы могли добиться без
применения теоремы VI.37, используя а) результаты о совместимости из разд. VI. 1,
Ь) лемму о расщеплении и с) структуру Lo(v)).
Итак, проблема, с которой мы в действительности столкнулись, такова
(положим Li = Li(v)):
Пусть заданы г + 1 1-факторов Lo, Li,..., Lr графа Kd, где d > 2
является четным целым числом. Насколько велико может быть г,
чтобы Kd имел 1-фактор L с L П Li = 0, i = 0,..., г,
и объединение LU Lq было гамильтоновым циклом? (о о о)
Ответ на вопрос (ооо) вытекает из следующего результата (см. [HAGG79a]).
Заметим, что граф четного порядка, удовлетворяющий теореме Оре (теорема
III.75), содержит 1-фактор, поскольку он имеет гамильтонов цикл (обобщение
следующей теоремы см. в [BERM83a]).

170
Глава VI. Различные типы эйлеровых цепей
Теорема VI.40. Пусть Н — обыкновенный граф четного порядка d > 4,
такой, что йн(х) + dn(y) > d + 1 для каждой пары несмежных вершин из Н,
и пусть L — произвольный 1-фактор из Н. Тогда L содержится в некотором
гамильтоновом цикле графа Н.
Доказательство. Мы действуем от противного. Поскольку Kd тривиально
удовлетворяет условию теоремы и поскольку указанный 1-фактор L С E(Kd)
содержится в некотором гамильтоновом цикле Kd по теореме VI.37, мы можем
выбрать граф Н, обладающий следующими свойствами:
a) Н есть собственный подграф графа Kd, удовлетворяющий условию
теоремы,
b) H имеет 1-фактор L, не содержащийся ни в одном гамильтоновом цикле Я,
c) | Е(Н) | наибольшее из возможных.
Следовательно, если х и у— любые две несмежные вершины из Н, то Ни {ху}
имеет гамильтонов цикл С, содержащий L. Ребро ху принадлежит Е(С); в
противном случае Н не является контрпримером к теореме. Записав С как
последовательность вершин с х = xi, у — Xd,
С = Х\ , Х2, • • • , Xd—l ,Xd<>Xi,
мы заключаем, что
L = {Х1Х21Х3Х4,... ,Xd-iXd}.
По тем же соображениям, которые использовались при доказательстве
теоремы Оре, мы заключаем, что из d{x)+d(y) > d+1 следует существование вершин
Х{ и Хг+ь таких, что xiXi+i,XdX{ € Е(Н), 2 < г < d — 2. Если XiXi+i g. L, то
цикл С\ с
Е{С\) = (Е(С) — {xiXd,XiXi+i}) U {xixi+i,XdXi}
(см. доказательство теоремы Оре) является гамильтоновым циклом в iJ,
содержащим L в противоречие с выбором Н. Значит,
XiXi+i G L и i нечетно. (*)
Чтобы получить противоречие, касающееся выбора iJ, удовлетворяющего (*),
разложим Н на два подграфа Hi и Hi, где Hi —двудольный граф с L С E(Hi)
и среди графов с этим свойством | E(Hi) \ наибольшее из возможных, иЯ2 =
H—Hi. Следовательно, V(Hi) = V(H). Далее, пусть Н[ = Hi—L. Заметим, что
Hi связен по условию теоремы; значит, разбиение множества вершин V(Hi) на
два множества {А±, Bi) однозначно определено и | Ai |=| Bi |= |d, поскольку
L С E(Hi). Без ограничения общности можно считать, что xi G А\. Выведем
некоторые свойства графа Hi.
Рассмотрим произвольное е = XjXj+i € L\ без ограничения общности
можно считать, что Xj G Ai (в противном случае заменим индекс j¦ + 1
на j — 1). Определим теперь новый двудольный граф Щ с биразбиением
V(H{) = А\ U BI следующим образом:
А\ = (Ai - {Xj}) U {xJ+1}, BI = (Bi - {xj+i}) U {Xj}>
E(H{) = {uv e E{H)\u eA^ve B*}.

VI.2. Попарно совместимые эйлеровы цепи
171
Заметим, что
\Е(Н*)\=\ ВД)| +dH2(e)-dHl(e).
Используя тот факт, что L С Е(Щ) по определению графа Щ, мы можем
заключить из выбора Hi, что | E(Hi) \<\ E{Hi) |. Этот факт и равенства,
приведенные выше, дают
Зщ (б) > d>H2 (e) для произвольного е ? L. (**)
Следовательно, если е = XjXj+i, f = XkXk+i ? L, то
dH[ (e) + dH{ (/) > dH2 (e) + dH2 (/).
Это неравенство вместе с ^я(е) = d#j (e) + d#2 (е) Н- 2 для любого е ? L дают
2яЦ (е) + 2dH[ (/) > йл(е) + <*я(Л - 4.
Теперь, так как е = XjXj+i, f = х^х^_[_1 и без ограничения общности можно
считать, что Xj,Xk ? -Ai, мы получаем из предыдущего неравенства и выбора
Hi, что
сгЯ((е) + сЦ(Я > d - 1, если XjXk+i,xkXj+i ? Е{НХ). (* * *)
(отметим следующее: из максимальности величины \E[Hi)\ следует, что
XjXk+i,XkXj+i $. Е(Н), тогда как dn{xj) -f dn(xk+i) > d+1 no условию).
Построим из Hi орграф D следующим образом: заменим каждое ребро
ху ? E(Hi) на дугу (у,х), где х ? А\\ по полученному орграфу Dhx построим
орграф D := Dhx/L (где L означает множество дуг в 2}#13 соответствующее
множеству L в Hi). Из практических соображений пометим вершины в D
метками элементов из L С E(Hi) в соответствии с процедурой стягивания. Это
дает
dD(e) = (1щ(е).
Поскольку е, / ? V(D) не смежны для введенных выше e,f ? L тогда и
только тогда, когда XjXk+i,XkXj+i 0 E{Hi) (напомним, что Hi двудольный!), и
поскольку d = 2 | VX-D) |, мы получим из (* * *) неравенство
^я(е) -f ^d(/) > 2 | V(D) | —1, если e,f? V(D) несмежны. (****)
Однако поскольку мы в этот момент не знаем, является ли D строго
связным, теорема Мейнеля пока не может быть применена к D (заметим, что D
не содержит кратных дуг по определению орграфа Дн-J. Но для применения
следствия III.78 строгой связности не требуется. Значит, мы можем заключить,
что D содержит гамильтонов путь Рр, который мы запишем как
последовательность вершин,
где га = \d =| V{D) | и {е^,..., е^} = V(D) = L. Из построения ориентации
Dhx графа Hi следует, что Рр соответствует обратному гамильтонову пути в
Dhy; значит, Pd соответствует гамильтонову пути Р в Hi, содержащему L.
Если концы пути Р связаны ребром е в Н, то Р U {е} — гамильтонов цикл
в Я, содержащий L, в противоречие с выбором Н. Без ограничения
общности можно поменять метки вершин из Р так, чтобы Е(Р) = Е(С) — {xdXi},

172
Глава VI. Различные типы эйлеровых цепей
и, значит, Pd = ei, ег,..., em для е\ — Xii-\X2i,i = 1,..., m. Из условия
следует (см. рассуждения, предшествующие (*)), что x\Xi+\,x&Xi G Е{Н), а по
(*) г нечетно. Кроме того, поскольку Р С Н\ и по предположению xi G Ai,
мы имеем Ai = {22.7-1 |j = 1,..., |d}, Si = {x23\j = l,...,|d}. Это дает
X\Xi+\,XiXd G E(H\), так как г нечетно. Таким образом, (xi+i,xi),(xd,Xi) G
A(jDhJ по определению орграфа D#15 и эти две дуги соответствуют дугам
(ej,ei),(em,ej) G A(D), где е^ = ?г?г+1 и j = (i + l)/2, откуда мы
заключаем, что Pd U {(e^, ei), (em, е^)} есть строго связный остовный подорграф из L>,
т.е. D строго связен. По теореме Мейнеля D имеет гамильтонов цикл Cd- Мы
заключаем, как и выше в отношении связи между Pd и Р, что Cd
соответствует гамильтоновому циклу Со из Нi с L С E[Cq). Поскольку V(Hi) = V(H),
мы получаем заключительное противоречие с выбором Н. Теорема полностью
доказана.
Теперь мы в состоянии ответить на вопрос (о о о), сформулированной перед
теоремой VI.40. Этот вопрос эквивалентен вопросу, имеет ли граф Н = (Kd —
U[=o Li)VJLo гамильтонов цикл, содержащий Lq. По определению Н и потому,
что для некоторых i ф j, 0 <i,j < г, может выполняться условие LiDLj ф 0,
мы имеем (Ih(v) > (d — 1) — (г + 1) + 1 = d — г — 1 для произвольной вершины
v G V(H). Значит,
dH(x)+dH(y) > 2d-2т-2, если x,yeV(H) и ху <? Е(Н).
Следовательно, если 2d — 2т — 2 > d + 1, то теорема VI.40 гарантирует
существование гамильтонова цикла С в Н с Lo С Е{С). Тогда, поскольку
2d — 2т — 2 > d -f 1, если и только если г < -{d — 3),
z
и поскольку г целое, первым ответом на вопрос (о о о) является такой: т
может быть так же велико, как \d — 2. Кроме того, предшествующее (о о о)
обсуждение показывает, что всегда можно предположить, что г > 1. Мы
объединим эти доводы в следующий результат, который, таким образом, вытекает
из теоремы VI.40.
Следствие VI.41. Пусть d — четное целое число, большее 2, и пусть т —
положительное целое ст < max{l, \d—2}. Пусть Lo,Zq,...,Lr суть 1-факторы
полного графа Kd- Тогда граф Н := (Kd — Ul=o -^г) U Lo имеет гамильтонов
цикл С, содержащий Lq.
Пусть С и Lo те же, что и в следствии VI.41, и пусть Lt — С — Lo; это
1-фактор графа Н. Это значит, что в Kd имеется 1-фактор Ьт с Ьт П Li = 0
для г = 0,..., г и Lt U Lo — гамильтонов цикл. Теперь, учитывая утверждения
(о) и (оо), которые и привели нас к вопросу (о о о) и, следовательно, к теореме
VI.40 и следствию VI.41, и интерпретируя Lt и L^, 0 < г < г, в терминах
систем переходов, мы можем сформулировать такое утверждение:
Пусть G — связный эйлеров граф с Д(С) > 4? и пусть v — любая
вершина из G с d(v) > 2. Возьмем положительное целое число г,
такое, что т < max{l, kv — 2}, где 2kv = d(v). Пусть Xi(v), 1 < г < г, —

VI.2. Попарно совместимые эйлеровы цепи
173
произвольные системы переходов в v, a Xq(v) — система переходов в
у, ни один из элементов которой не состоит из двух полу ребер,
принадлежащих разным блокам графа G. Тогда существует система
переходов в и, Xt(v), такая, что Xt(v) П Xi(v) = 0 для г = 0,..., г,
и Gv связен, где инцидентности в вершинах степени 2 из
V(GV) — V(G) определены элементами из Хт(и). (I)
Пусть теперь G — связный эйлеров граф без вершин степени 2. Положим
k = \5(G), т.е. fc = minl/c^l?; ? V(G)}, и пусть г < max{l, fc-2}. Обозначим
вершины из G через vi,..., vp, p = \V(G) |, и положим Go := G, Gj = (Gj-i)Vj-, j =
l,...,p. Для данных систем переходов Хг графа G, 1 < г < г, которые
индуцируют системы переходов Xi(v) в вершинах г; = Vj, j = 1,... ,р (см. (I)),
мы имеем Xi = U?=i Xi(vj). Делая в (I) шаг за шагом замены G = Gj-i и
г; = Vj и определяя Хо(и^) для Vj ? V(Gj_i), j = 1,...,р, мы придем
после р-кратного применения (I) к связному эйлерову графу Gp, который имеет
лишь вершины степени 2, т.е. является циклом. Значит, Хт = Uj=i Xt(vj) —
система переходов, определяющая эйлерову цепь Т; далее, Хт П Xi = 0, т.е.
Т совместима с Х^, г = 1,... ,г. (Заметим, что Хо = U?=i -^o(^j) играет, так
сказать, вспомогательную роль только потому, что она не может быть
определена заблаговременно). Итак, мы получили главный результат из [JACK87b],
который может быть выражен следующей теоремой.
Теорема VI.42. Пусть G — связный эйлеров граф с 5(G) = 2k > 2, и пусть
г < max{l,fc — 2} —положительное целое число. Пусть даны системы
переходов Х\,..., ХТ. Тогда в G существует эйлерова цепь, совместимая с
Xi, i = l,...,r.
Следствие VI.43. Связный эйлеров граф G с 5(G) = 2/с > 2 имеет не меньше
max{2, k — 1} попарно совместимых эйлеровых цепей.
Доказательство следствия VI.43 вытекает из теоремы VI.42; поэтому мы
оставим его в качестве упражнения.
Заметим, что теорема VI.42 была доказана для четного k Джексоном и
Уормалдом [JACK88c ]. Они показали, что достаточно, чтобы г < к — 1. Более
того, они показали, что если 5(G) = 2k > 2, то G имеет k попарно
совместимых эйлеровых цепей. Следующие соображения показывают, что в последнем
результате невозможен произвольный выбор попарно совместимых эйлеровых
цепей.
Неравенство г < {l,fc — 2} в теореме VI.42 — наилучшее из возможных, в
чем можно убедиться на следующем примере (см. также рис. VI. 14): пусть Н
есть 2-связный б-однородный граф. Рассмотрим две совместимые эйлеровы
цепи Г^Гз'вЯи возьмем три экземпляра графа Я. Подразобьем в каждом из
них ребро и отождествим разбивающие вершины, получая таким образом граф
G с точкой сочленения v (см. рис. VI. 14). В каждом из трех блоков графа G
имеются цепи Т[, Т'2\ эти эйлеровы цепи могут быть продолжены до двух
совместимых эйлеровых цепей Т\ и Т2, как показано на рис. VI. 14. G не содержит
эйлеровой цепи Т, совместимой с Т\ и T<i\ в противном случае начальная секция
цепи Т, начинающаяся с прохода по в\ к v (что не ограничивает общности),

174
Глава VI. Различные типы эйлеровых цепей
' \
е I 'е
.-ДА
G
Рис. VI. 14. б-однородный граф G с двумя совместимыми эйлеровыми цепями Т\ —
ei, г>,ег,... ,ез,^,в4,... ,65, v,ее,... и Гг = ei, v, в4,.. • ,es, v, ег,... ,ез,г>,ев, — В G
не существует эйлеровой цепи, совместимой с Ti и Тг.
должна иметь вид ei,v,ез или ei,v, es- В первом случае следующей
содержащей v секцией должна быть ег, v, б4 (чтобы не нарушить совместимости), а во
втором случае следующей такой секцией должна быть е±, г>, ег- Но тогда третья
секция, содержащая и, в Т должна либо иметь вид e*>,v,eQ (в первом случае),
либо вид ез,г>,ев (во втором случае). Значит, Хт ^Хтг ф 0 в первом случае
и Хт П Хт2 ^ 0 во втором случае. Следовательно, G не содержит
эйлеровой цепи, совместимой с 7\ и Т2. Этот пример также показывает, что решение
гипотезы VI.36, использующее «жадный» алгоритм, невозможно. Этот факт,
однако, был установлен уже эквивалентностью теорем VI.37 и VI.38.
Существует другой подход к решению гипотезы VI.36. Первоначально
предложенный А. Дж. Хилтоном, он изложен в [FLEI86a] (хотя и в виде, отличном
от представленного ниже). Мы назовем его подходом сверху вниз в
противоположность к подходу снизу вверх, описанному в обсуждении, приведшем к
формулировке гипотезы VI.39.
При подходе сверху вниз мы начинаем со связного эйлерова графа G с
6(G) > 2, где vi,... ,г>?, t > 1, суть вершины степени, большей 2. Теперь
построим множество Q\ из d(v\) — 2 связных эйлеровых графов расщеплением
вершины vi на вершины степени 2 d(v{) — 2 способами таким образом,
чтобы ни одна пара ребер, инцедентных v\ в G, не появлялась в качестве пары
смежных ребер более чем в одном элементе из Q\. Теорема VI.37 гарантирует,
что Q\ существует. Действительно, если мы соединим в пары ребра,
инцидентные v\ в G, таким образом, что это спаривание индуцирует соответствующее
спаривание в каждом блоке, содержащем v\, то построение Q\ является в
точности применением теоремы VI.37 к Kd(v{) с L С iQ(Vl), представляющим это
спаривание. Конечно, теорема VI.37 может давать не одну 1-факторизацию
для Kd(Vl) — L, и, значит, Q\ не обязательно определено единственным
образом. Хотя элементы G\,i в Q\, 1 < г < d(v\) — 2, могут быть не изоморфными,
графы Gi,i — V2(Gi,i)j однако, изоморфны. Применим, далее, теорему VI.37
к V2 в каждом из Gi^, 1 < г < d(v\) — 2, или, другими словами, произведем
в каждом Gn d(v2) — 2 попарно «совместимых» расщеплений в вершине V2-

VI.2. Попарно совместимые эйлеровы цепи
175
Тогда мы получим для каждого г, 1 < г < d(v\) — 2, множество ?/2,г из d(v2) — 2
элементов С2,г,ь обладающее тем свойством, что графы G2,i,k — ^(С2,г,&)
изоморфны, 1 < к < dfa) — 2. Это верно даже для элементов, принадлежащих к
различным С/2,г- Далее, попытаемся построить множество Q2, беря в точности
по одному элементу из каждого из 2к — 2 множеств среди множеств С/2,г так,
чтобы ни одна пара ребер, смежных с V2 в G, не являлась парой смежных
ребер более чем в одном из таких элементов. Из сказанного выше мы
получаем, что Н\ — Vi(H\) — Н2 — ^(#2) для i2i,#2 ? Qi- Если это множество
С/2 может быть построено, то поступим с G2, как выше поступали с Qi, но
с вершиной Уз вместо V2- Но существует ли (?2? Может быть, следует более
аккуратно выбирать 2к — 2 графов при попытке образовать Qi; возможно,
следует рассматривать все возможности выбора при формировании Gi (т. е. все
возможные 1-факторизации, возникающие при применении теоремы VI.37 к
Kd(vi) — L). В настоящее время это неизвестно. Но эти попытки приводят нас
к следующему вопросу: если G\,..., G2I1-2 суть графы на некотором
множестве вершин V, такие, что Gi — l^(Gj) — Gj — ^(Gj) для l<i,j<2k — 2,u
2k < min{d(v)\v € V(G) — V2(G)}7 то возможно ли произвести для каждого
i, 1 < i < 2k — 2, расщепление некоторой вершины v € V(G) — V«2(G) в
каждом Gi так, чтобы любые е, f, инцидентные v в Gi, оказались смежными не
более чем в одном из 2к — 2 графов, полученных таким образом?
Положительный ответ на этот вопрос, однако, равносилен доказательству гипотезы VI.39.
Заметим, что если мы опустим требование, чтобы графы G2,z,fc, построенные
выше, были связными, чтобы они могли принадлежать С/2, то С/2 существует.
Это гарантируется теоремой VI.37. Тогда оба подхода — сверху вниз и снизу
вверх — вместе с применением теоремы VI.37, дают нам следующий результат
(см. [FLEI86a, Theorem 2]; там приведены два доказательства теоремы 2,
представляющие соответствующие подходы): если G — эйлеров граф с 5(G) > 4, то
существует 5(G) — 1 попарно совместимых цепных разложений. Хотя этот
результат, в сущности, не что иное, как перевод теоремы VI.37 на язык
совместимости в эйлеровых графах, возникает интересный вопрос, получается ли
верное утверждение, если заменить в этом результате «цепь» на «цикл».
Следует заметить, что в случае G = Агт+ь пг > 2, проблема была рассмотрена
Коцигом, который интересовался, имеет ли i^2m+i 2m — 1 попарно
совместимых разложений на гамильтоновы циклы [KOTZ79a, Definition 2, Problem 4]
(Коциг использовал термин «совершенный» (perfect) вместо «совместимый»).
VI.2.1. Попарно совместимые эйлеровы цепи в орграфах
Рассмотрим проблему нахождения максимального числа попарно совместимых
эйлеровых цепей в орграфах и предположим сначала, что каждый блок в
связном эйлеровом орграфе D является циклом и что 5(D) > 2. Рассмотрим
вершину v. Как и в обсуждении, ведущем к формулировке теоремы VI.37, мы
построим новый граф, вершинами которого являются полудуги, инцидентные
у, где, как и раньше, пары полудуг, принадлежащих одному и тому же блоку
D («невозможные» переходы) определяют 1-фактор L нового графа и каждое
другое ребро нового графа соединяет полудугу, заходящую ви,с выходящей из

176 Глава VI. Различные типы эйлеровых цепей
Рис. VI.15. i^4,4 не может быть разложен на 1-факторы I/o,I/i, 1/2,?з, такие? что
Lo = L = {ii'\i = 1,2,3,4} и L U Lj — гамильтонов цикл, j = 1, 2,3.
v полудугой. Следовательно, этот новый граф есть Kd,d-> гДе d — id{v) = od(v),
и, как и раньше, мы получаем, что эйлерова цепь Т орграфа D соответствует
гамильтонову циклу Н графа Kd,d с L С Е(Н), а если Т\,Т2 суть две
совместимые эйлеровы цепи графа D, то соответствующие гамильтоповы циклы
Hi,H2 удовлетворяют условию E(Hi) П Е(Н2) = L. Итак, вопрос состоит в
следующем: может ли Kd,d быть так разложен па 1-факторы L\,...,Ld,
что Li = L и L U Li —гамильтонов цикл в Kd,d для г = 2,...,d?
Попытаемся ответить на этот вопрос, действуя, как и в неориентируемом случае.
Стянем в Kd,d 1-фактор L, чтобы получить Kd (см. доказательство теоремы
VI.37). Гамильтонов цикл Н' в Kd соответствует в Kd,d 3-однородному графу
Р^,, который можно считать полученным из d-угольной призмы
добавлением диагоналей в боковые грани и удалением ребер, ограничивающих верхнюю
и нижнюю грани. Элементы множества L — это боковые ребра призмы.
Значит, Р?, можно разложить на три 1-фактора Cq, C{, С2, где Cq = L и L U С[
является гамильтоновым циклом графа Kd,d-> г = 1,2 (см. определение С'г и
С^ в случае 2) доказательства теоремы VI.37). Отсюда мы делаем вывод, что
поставленный выше вопрос имеет положительное решение, если d нечетно
(заметим, что Kd для нечетного d имеет разложение на гамильтоновы циклы).
Однако если d четно, то ответ на этот вопрос будет, вообще говоря,
отрицательным; это можно установить методом проб и ошибок с помощью рис. VI. 15,
где d — 4.
Теоретическое обоснование этой проблемы (которое возникает из
выбранного подхода, как мы увидим позднее) можно частично найти, изучая
доказательство теоремы VI.37. Пусть {Li,... ,L^-i} есть 1-факторизация графа
Kd, такая, что L* U Lj является гамильтоновым циклом графа Kd, 1 < i,j <
d, 1 <\ г — j |< 2, где Ld = la, а Li U L»+i, г = 4,... ,d — 2, г = 0 (mod2),
определяет Р#,, как выше, и дает снова два гамильтоновых цикла Щ^Щ+\
в Kd,d с Щ П Hi+i = L. Но если мы посмотрим на 4-однородный граф
G4 Э L, определенный с помощью G3 = (la U L2 U Дя), то
доказательство теоремы VI.37 указывает, что в общем случае G± неразложим на четыре
1-фактора L = Cq, С{, С2, С'ъ так, чтобы L U С[ был гамильтоновым циклом в

VI.2. Попарно совместимые эйлеровы цепи
177
G3=Kd
G4=K,
d,d
D4
Рис. VI. 16. Гамильтоновы циклы L\ U L2, L\ U L3, Li U L3 из Сз (где числом i
помечены элементы из Li) соответствуют гамильтоновым циклам Hi, if2, Hz из Ga (ребра
которых, не принадлежащие L, помечены числами 12,13,23 соответственно),
которые, в свою очередь, соответствуют ориентированным гамильтоновым циклам в
орграфе Da. Последние определяют разложение орграфа De на три ориентированных
гамильтоновых цикла. Ребра (дуги) из L в Ga {Da) помечены 0. Индексы t и Ь
означают «верх» и «вниз».
Kd,d, i = 1,2,3 (несмотря на то, что Li U Lj является гамильтоновым циклом
BKd, 1фэ,1<г,з<Ъ).
Предположим теперь, что G± имеет такое разложение. Ориентируем
гамильтоновы циклы Hi = L U C-, г = 1,2,3, таким образом, чтобы ребра из L
проходились всегда в одном и том же направлении, скажем, сверху вниз. Это
возможно, так как G± —двудольный граф (см. рис. VI. 16). Таким образом, Ga
преобразован в двудольный орграф D±.
По определению графа G± орграф D± определяет 3-однородный орграф
Dq, причем можно считать, что он получен из Gs заменой каждого ребра
ab € E(Gs) на две дуги (а, 6), (6, а) € A(Dq); орграф Dq разлагается на три
ориентированных гамильтоновых цикла Щ,Щ,Щ, соответствующих
исходным гамильтоновым циклам L\ U L<i,L\ U Z/3^2 U L3 из Gz (см. рис. VI.16).
Далее мы определим эйлерову цепь Т в Dq следующим образом: начиная с
u ? V(Dq) = VXG3), например, мы проходим весь цикл Щ; снова достигнув
и, мы продолжаем идти вдоль Щ; полностью пройдя Щ, мы проходим дуги

178
Глава VI. Различные типы эйлеровых цепей
из Щ. Следовательно, Т соответствует замкнутому покрывающему маршруту
W в графе Сз, который начинается в вершине u E V(Gs) и следует сначала
по элементам из 1/2 U Li, что соответствует прохождению по Щ в Т, затем
продолжается вдоль элементов из L$ U L<i и, наконец, проходит по элементам
из L\ U Ls в соответствии с прохождением через Щ,Щ соответственно. То
есть W обладает следующими свойствами: W проходит каэюдое ребро из Сз
точно один раз в каждом направлении, и ни одно ребро из G% не проходится
во второй раз сразу же после того, как оно было пройдено в первый раз. Как
мы увидим в гл. VIII (см. теорему VIII.4), наличие замкнутого покрывающего
маршрута в(?з с этим свойством означает, что | V(Gz) |= 2(mod4)1). Мы
утверждаем, что граф Gz двудольный. Чтобы убедиться в этом, рассмотрим Dq и
удалим следующие дуги: если ab E Li, удалим из Щ дугу, соединяющую а и 6;
если аб Е 1^2, удалим соответствующую дугу из Н±; если ab Е ?з > удалим
соответствующую дугу из Щ (на рис. VI. 16 это соответствует удалению в Dq дуг,
исходящих из и). Полученный таким образом подорграф D3 С Dq является
такой ориентацией графа Сз, что каждая вершина является либо источником,
либо стоком: т. е. Ds двудолен и таков же Сз (заметим, что по предположению,
если об одной из дуг, инцидентных и Е V(Dq), известно, что она принадлежит
#*, г Е {1,2,3}, то и о каждой из оставшихся пяти дуг известно, к какому
множеству Щ она принадлежит; см. рис. VI.16).
С другой стороны, D± можно получить из Dq , заменив каждую вершину
v E V(Dq) на vt и уь, добавив дугу (vt^Vb) и превратив дуги, заходящие в
v (исходящие из v) в дуги, заходящие в vt (исходящие из Уь). Кроме того,
если Dq имеет разложение на три гамильтоновых цикла, то можно заключить,
используя ?>4, что G± имеет 1-факторизацию {Cq, C{, С^, С'3}, такую, что Щ =
L U Сг', г = 1,2,3, для L = Cq является гамильтоновым циклом в G±.
Кроме того, поскольку гамильтоновы циклы Щ,Щ,Щ в Dq индуцируют
ориентацию гамильтоновых циклов L\ U L<i,L\ U Z/3^2 U L3 в (?з, такую, что
каждое ребро в Сз проходится этими гамильтоновыми циклами в точности по
одному разу в каждом из направлений, то мы можем заключить, что
направление стрелок на рис. VI. 16 можно также заменить на противоположное. Иначе
говоря, мы имеем следующий результат.
Предложение VI.44. Пусть Сз и G± такие же, как выше, причем G%
имеет 1-факторизацию {Li,!^,!^}? такую, чтоLiUl^ZaUZ^^ULs
—гамильтоновы циклы в Сз- Тогда G± имеет 1-факторизацию {Ь^С^^С^С^}, такую,
что L{JC[ является гамильтоновым циклом в G±, г — 1,2,3; тогда и только
тогда, когда указанные выше гамильтоновы циклы в G% имеют циклическую
ориентацию, такую, что каждое ребро в Сз проходится по одному разу в
каждом направлении двумя гамильтоновыми циклами, которым оно
принадлежит.
Если Сз — двудольный 3-однородный граф, то он имеет 1-факторизацию
{Li,L2,?3} (см- теорему 111.48). Если {Vi,^} —разбиение V(G$) на доли
(которое определено единственнным образом тогда и только тогда, когда Сз свя-
1^ Теорема из [AUBE82b] верна по тем же соображениям. Однако теорема VIII.4 в этой
работе не используется.

VI.2. Попарно совместимые эйлеровы цепи
179
зен) и если мы заменим каждое ребро v\v2 € L\ U L2 на дугу (^ь^), где
v\ G V\ и v2 € V2, а такое ребро из L3 заменим на дугу (^2,^i), то 2-факторы
Li UL3,1/2 U1/3 станут 1-факторами i7^, -F3 полученного так орграфа D%.
Следовательно, если обозначить через F2R обратную ориентацию фактора F2 и если
F\ означает циклическую ориентацию цикла L\ U L2, индуцированную дугами
из ?>з, соответствующими Li, то Fi,F2R^Fs определяют циклическую
ориентацию циклов L\ U L2, Li U1/3 и Z/2 U L3 соответственно, так что каждое ребро е
из Сз проходится двумя 2-факторами, содержащими е, в точности по одному
разу в каждом направлении. Учитывая приведенные выше соображения, мы
получаем следующий результат:
Предложение VI.45. Пусть G$ есть ^-однородный граф, имеющий такую
1-факторизацию {Li,L2iLs}, что Hi = Li ULi+i» ^ — 1,2,3 {где мы полагаем
L± = Li) является гамильтоновым циклом в Gs- Следующие утверсисдения
эквивалентны:
1) | У(Сз) |= 2 (mod4) и G — двудольный граф;
2) #г, г = 1,2,3, можно циклически ориентировать так, что каждое ребро
проходится однажды в каждом направлении двумя соответствующими
циклами Hi.
В силу предложений VI.44 и VI.45 и обсуждения, предшествующего им, наш
первоначальный подход к 1-факторизации {Li,..., Ld] графа K^d с LiULi, ^ —
2,...,d, являющимся гамильтоновым циклом в Kd,d, приводит к следующей
проблеме:
Найти положительное целое число d > 2, такое, что d = 2 (mod 4), для
которого Kd имеет 1-факторизацию {Li,..., Ld-i} с такими свойствами:
a) Li U I/i+i, i = 1, • •., d — 2, и L\ U L3 суть гамильтоновы циклы в К&\
b) (Li U L2 U L3) — двудольный граф.
Несложно показать, что должно выполняться неравенство d > 10:
действительно, в случае графа К$ граф (L\ U L2 U L3) с этими свойствами
определен однозначно с точностью до изоморфизма, и из этого следует, что
Kq — {Li U I/2 U 1/з} — несвязный граф, состоящий из двух
пересекающихся треугольников, который, следовательно, не может быть разложен на два
1-фактора.
Однако положительным итогом и непосредственным следствием нашего
обсуждения является такая теорема.
Теорема VI.46. Пусть задан 1-фактор L С Kd,d> d > 2. Тогда существует
1-факторизация {L,L2,... , !/<*} графа Kd,d> обладающая следующими
свойствами:
a) L U Li — гамильтонов цикл графа Kd,d для г = 2,..., d — 1;
b) если d нечетно, то L U Ld таксисе является гамильтоновым циклом]
c) если d = 0 (mod 4) или d = 6, то LU Ld не гамильтонов цикл.
Теорема VI.46 дает нам некоторую информацию, касающуюся
максимального числа Nt попарно совместимых эйлеровых цепей орграфа D, а именно,

180
Глава VI. Различные типы эйлеровых цепей
d — 2< Nt < d— 1 для d = ^S(D) > 2, в то время как Nt = d—l для нечетного
d и Nt — d—2 для d = 4 (см. рис. VI.15). Но мы не смогли получить наилучший
возможный результат для Nt просто потому, что потеряли часть информации,
использовав тот же подход, что и в неориентированном случае.
Вернемся к рассмотрению исходной проблемы 1-факторизации графа Kd,d-
Пусть L = {viVi\i = 1,..., d} обозначает 1-фактор графа Kd,d, гДе V := {vi\i =
1,..., d}, V := {v[\i = 1,..., d} и {V, V'} — разбиение вершин графа Kd,d на
две доли. Ориентируем ребра из K^d так> что элементы из L направлены из
V в У, тогда как элементы из E(Kd,d) — L направлены из V в V7; пусть Kd d —
орграф, полученный таким образом. Теперь каждый гамильтонов цикл из Kd,d<>
содержащий L, является гамильтоновым циклом в Kdd (и наоборот), и если
мы стянем в Kd d дуги (г^, ^), г = 1,..., d, то получим полный симметричный
орграф Kd, гамильтоновы циклы которого находятся во взаимно
однозначном соответствии с гамильтоновыми циклами орграфа Kd d (и, значит, также
с гамильтоновыми циклами в Kd,d, содержащими L). Итак, исходная задача
1-факторизации графа Kd,d (поставленная в начале этого раздела)
эквивалентна вопросу, может ли Kd быть разложен на гамильтоновы циклы. По теореме
III.51 это возможно для значений d> 1 и dy? 4,6. Значит, мы получили
следующий результат.
Теорема VI.46.а. Пусть L есть 1-фактор графа Kd,di где d > 2. Тогда
существует 1-факторизация {L, L2,..., Ld}, такая, что L U Li — гамильтонов
цикл графа Kd,d для г = 2,..., d, где d^ 4,6.
В силу того, что было сказано в начале нашего обсуждения, следующий
результат есть прямое следствие теоремы VI.46.а.
Теорема VI.47. Пусть D — связный эйлеров орграф, каэюдый цикл которого
является блоком в D. Тогда при d = \5{D) > 2 число Nt удовлетворяет
следующим условиям:
NT=d—l, если d /4,6,
Nt —d — 2, если d =4,6.
(Заметим, что из теорем VI.46 и VI.46.a следует, что при d! > d граф Kd>,d'
имеет хотя бы d — 1 непересекающихся 1-факторов, каждый из которых
определяет гамильтонов цикл, содержащий предписанный 1-фактор L.)
Чтобы получить для эйлеровых орграфов результаты, аналогичные теореме
VI.42 и следствию VI.43 соответственно, мы естественным образом приходим
к формулировке и доказательству результата о двудольных графах,
аналогичного теореме VI.40 (см. также [BERM81b, Theorem 3.1]).
Следствие VI.48. Пусть двудольный обыкновенный граф Н с 2d > 2
вершинами и с разбиением вершин {А, В} на две доли имеет 1-фактор.
Предположим, что dn{a) + dn(b) > d + 2 для любых а € А и b € В, где ab 0 Е{Н).
Тогда каэюдый 1-фактор из Н содержится в гамильтоновом цикле графа Н.
Доказательство. Мы следуем доказательству теоремы VI.40. Во всяком
случае | А |=| В |= d, поскольку Н имеет 1-фактор. Заметив, что следствие VI.48

VI.2. Попарно совместимые эйлеровы цепи
181
верно для Kd,d по теореме VI.46 и предположив, что оно не верно в общем
случае, выберем контрпример Н с максимально возможным | Е(Н) | при условии,
что | V(H) | наименьшее из возможных. Отсюда мы заключаем, что d > 2 и
что Н U {ab} имеет гамильтонов цикл С, содержащий произвольный
предписанный 1-фактор L, для произвольных несмежных a Е A, b G В. Тогда мы
можем записать
С — {ab} = ai,aibi,bi,&ia2,a2,a262, • • • ^d^dbd^bd,
где a = ai,6 = 6dHL = {а^г = 1,... ,d}.
Поскольку Я двудольный и a±bd & Е(Н), из условия на степени
dH(ai)+dH(bd) >d + 2
следует существование такого ic2<i<d— 1, что
aibi.aibd G ?(#)
(заметим, что С — {aft} содержит d ребер вида ej := a,jbj). Кроме того, для
ej = ajbj,ek = dkbk ? L, таких, что ajbk.akbj 0 Е(Н), мы получаем
dH(ej) + dH{ek) = dH(aj) + dH(bj) + d#(afc) + MM > 2d + 4.
Теперь пусть ?># и D := Dh/L определены, как в доказательстве теоремы
VI.40 (с Н вместо Н\). Тогда из предыдущих неравенств для каждой пары
ej, ек несмежных вершин из D мы получаем
dD(ej) + dD(ek) >2d = 2\V(D)\ .
(Заметим, что ^я(^) = do(ej) + 2.) Кроме того,
АР := {(е*, e<+i)|i = 1,..., d - 1} С A(D),
поскольку (6i,af+i) € A(D#) для г = l,...,d— 1. Значит, Pd '•= (Ар)—
гамильтонов путь в D. Далее, если a\bi,aibd E Е{Н), то (6i,ai), (bd,a>i) ?
D#, откуда мы заключаем, что (ei,ei), (e^e*) G A(D). Следовательно, Pd U
{(ег, ei), (e^, е^)} — сильно связный остовный подорграф в D. Это означает, что
D сильно связен. Этот факт и последнее неравенство позволяют примерить
теорему Мейниля. По самому определению орграфов D и Dh гамильтонов цикл
в D соответствует гамильтонову циклу в Н, содержащему L. Это противоречие
доказывает справедливость следствия VI.48.
Следствие VI.49. Рассмотрим Kd,d для d > 3, и пусть Lq. Li, ..., Lr суть
l-факторы из Kd,d, г^е r < (d — 2)/2. Тогда (Kd,d — Ui=o -^*) ^ ^о имеет
гамильтонов цикл, содержащий Lq.
Доказательство. Положим L = Lq и Н = (Kd,d — Ui=o ^*) ^ ^о- Мы имеем
d# (v) >d-(r + l) + l = d-r.
Значит,
йя(а) + d#(6) > 2d - 2r > d + 2, если afc ? ?(#).
Следствие VI.49 теперь вытекает из следствия VI.48.
Заметим, между прочим, что если мы заменим в следствии VI.49
ограничения на d и г на следующие: d > 3 и г < тах{1, (d — 2)/2}, то его заключение

182
Глава VI. Различные типы эйлеровых цепей
неверно уже для d = 3. Достаточно лишь выбрать L\ с | Lq П Li |= 1. Если,
однако, Lo П L\ — 0, то эти более слабые ограничения приводят к тому же
самому заключению, что и в следствии VI.49.
Основываясь на предыдущих соображениях, мы выведем теперь
следующий результат из следствия VI.49 аналогично тому, как мы получили теорему
VI.42, применив следствие VI.41.
Теорема VI.50. Пусть D — связный эйлеров орграф с 5(D) > 6, и пусть
Х±,... ,ХГ —любые г систем переходов, где г < (5(D) — 4)/4. Тогда D
имеет эйлерову цепь, совместимую с Хг, г = 1,..., г.
Эта теорема и замечание после следствия VI.49 дают аналог следствия
VI.43.
Следствие VI.51. Пусть D —связный эйлеров орграф с 5(D) > 6. Тогда D
имеет не меньше max{2,5(D)/4} попарно совместимых эйлеровых цепей.
Эта нижняя оценка максимального числа попарно совместимых эйлеровых
цепей в общем случае является наилучшей из возможных (см. упр. VI.4).
Однако, учитывая теорему VI.47, мы высказываем следующую гипотезу (мы не
станем, однако, формулировать гипотезу об 1-факторизациях в Kd,d,
соответствующую гипотезе VI.39, из справедливости которой следует справедливость
гипотезы VI.52).
Гипотеза VI.52. Максимальное число попарно совместимых эйлеровых
цепей в связном эйлеровом орграфе D с 5(D) > 4 не меньше, чем \5(D) — 2.
Заметим, кстати, что большинство предыдущих результатов опубликовано
в [FLEI90a].
Конечно, можно попытаться применить обсуждения из этого раздела и к
смешанным графам. Однако в случае, когда каждый блок является циклом,
не нужно больше искать 1-факторизацию для i^d или Kd,d специального
типа, но теперь следует искать максимальное число г попарно непересекающихся
1-факторов L\,..., Lr в графе Н с 2d вершинами, таких, что Li U L — гамиль-
тонов цикл и L — предписанный 1-фактор Н, i = 1,..., г. Действительно, Н в
общем случае уже не является однородным, однако Kd,d Q Н С if2d- Эти
включения являются строгими, если и только если смешанный граф имеет хотя бы
один блок, содержащий дугу, и хотя бы один блок, содержащий только ребра;
действительно, если блок содержит дугу, то она задает ориентацию ребер
этого блока по условию разреза (теорема IV. 11). Для произвольных смешанных
эйлеровых графов положение сложнее: действительно, в случае, аналогичном
следствиям VI.41 и VI.49, гамильтонов цикл, содержащий Lq (соответствующий
замене вершины v степени 2d на d вершин степени 2), дает преобразование
некоторого связного эйлерова смешанного графа М в связный смешанный граф
Mv. В Mv условие разреза еще выполняется для каждой вершины, но оно
может не быть верным глобально. Поэтому нельзя автоматически утверждать,
что Mv имеет эйлерову цепь (ср. с утверждением (I) после следствия VI.41).
На самом деле эта проблема может возникнуть, даже если каждый блок в М

VI.3. А-цепи в плоских графах
183
является циклом. Таким образом, не ясно даже, как решать проблему
нахождения максимального числа попарно совместимых эйлеровых цепей в смешанных
графах.
Мы завершаем этот раздел замечанием о том, что проблемы эйлеровых
цепей специальных типов сводятся к проблемам гамильтоновых циклов
специальных типов (причем решения некоторые из последних проблем дают
решения некоторых из первых). Это наиболее общий способ описания подхода,
примененного в этом разделе. В следующем разделе мы пойдем другим путем,
изучая проблемы, связанные с эйлеровыми цепями специального типа в
плоских графах, и показывая, как эйлеровы проблемы связаны с гамильтоновыми.
VI.3. А-цепи в плоских графах
Как мы видели в разд. VI. 1, для связных ^-однородных графов (а таксисе для
связных эйлеровых графов с A(G) < 4) понятия непересекающейся
эйлеровой цепи и А-цепи совпадают. Тем не менее, в то время как каждый связный
эйлеров граф, вложенный в некоторую поверхность Т, имеет
непересекающуюся эйлерову цепь (лемма VI.7), аналогичное утверждение об А-цепях неверно,
даже если .Т7 — плоскость (или, что то же самое, сфера). Этот факт
иллюстрируется следующим рисунком, который также показывает, что существование
А-цепи может зависеть от конкретного вложения планарного графа.
На рис. VI.17 (единственная) А-цепъ в G2 определена переходами {1',2'},
{3', 4Л}, {5/, 6'} (помеченными на рисунке маленькими дугами ), где {i'\i =
1,... ,6} = Е*. Те же переходы определяют непересекающуюся эйлерову цепь
Т\ в G\. Но Т\ не является А-цепью в Gi. В самом деле, если начать
поиск А-цепи в Gi с прохождения ребра 1 по направлению к и, то неизбежно
следующим будет переход {1',2'} (поскольку выбор другого перехода, {1',6'},
разделяет граф). Значит, {3',4'} должен быть следующим переходом в v (в
Рис. VI. 17. Два вложения G\ и (?2 одного и того же планарного графа: Gi не имеет
А-цепи, (?2 имеет, но и Gi, и Сг имеют непересекающиеся эйлеровы цепи.

184
Глава VI. Различные типы эйлеровых цепей
противном случае {3', 6'} отсекает «внутренний» треугольник от оставшейся
части графа); таким образом, X(v) = {{1/, 2'}, {3',4'}, {5', 6'}}. Так как 5' и 6'
не являются соседними в циклическом упорядочении ребер, инцидентных v,
то X(v) определяет не А-цепь, но непересекающуюся эйлерову цепь Т\
(которая «близка насколько возможно» к А-цепи). Следовательно, в G\ вообще нет
А-цепи.
Рисунок VI. 17 также указывает, как можно избежать наличия А-цепи в
связном планарном эйлеровом графе G с вершиной v и тремя или более
блоками, содержащими v. Пусть В\, В2, Вз — три таких блока. Мы вложим G в
плоскость так, чтобы
ВД) П bd(Foo) ф 0 ф Е(В2) П bd(Foo), но Е{ВЪ) П bd(Foo) = {v}
и чтобы существовала такая граница грани bd(F), что
bd(F) П Е(В2) ф0ф bd(F) П Е(В3) и Е„ П bd(F) П bd(Foo) ф 0.
Тогда рассуждения, аналогичные использованным при обсуждении рис.
VI. 17, показывают, что полученное так вложение графа G в плоскость не
допускает А-цепи. Дальнейшее обсуждение, связывающее А-цепи со специальными
расщеплениями вершин, даст теоретический ответ относительно
несуществования А-цепей в G\ на рис. VI. 17 и в только что обсуждавшемся вложении
графа G в плоскость.
В дальнейшем G — это связный эйлеров плоский граф. Поскольку G
плоский, то для любой вершины v € V(G) его вложением в плоскость задано
циклическое упорядочение инцидентных ей ребер против часовой стрелки, которое
мы обозначим 0+ (v) = (e'1? е2,.. •, е^), где d = d(v).
Лемма VI.53. Допустим, что эйлеров плоский граф G с A(G) > 2 имеет
А~цепъ Т. Пусть v Е V(G) — произвольно выбранная вершина с d = d(v) > 2
и {е[,е2} —первый переход, определенный А-цепью Т в v. Можно считать,
что Т = ... ,ei,v, е2, Тогда
Т = ..., еь v, е2,..., е3, и, е4,..., ed-i,v, ed,...,
где
0+(v) = (е/1,е2,...,е^_1,е^) или 0+(<и) = (е^е^,... ^е^)
и е2г = в2г+1, еа/ш и только если e2i — петля, г ? {1,..., \d} (мы полагаем
ed+i = ei).
Доказательство. Допустим, что Т содержит расширенный сегмент X" вида
X" = е2г-1,и,е2г,...,/,г;,?,
где из ребер, входящих в Т", только е2г-1,е2г,/, # инцидентны v и f ф e2;+i
(соответственно f ф е± при 2г = d). Можно считать (сдвинув индексы в
0+(г;), если потребуется), что г = 1, откуда следует, что / = ej для
некоторого j € {4, ...,d}. Тогда Т' содержит подпоследовательность С, которая
является циклом, начинающимся и заканчивающимся в v и проходящим по
е2 и е^. Следовательно, если s(ek) — подразбивающая точка ребра е&, к = 1,3,

VI.3. А-цепи в плоских графах
185
то s(ei) лежит вне С тогда и только тогда, когда 5(ез) лежит внутри С.
Теперь, поскольку г = 1, благодаря возможности циклического сдвига начальной
вершины в Т мы можем без ограничения общности представить Т в виде
где Тп — подпоследовательность в X", начинающаяся и заканчивающаяся в v
и не содержащая е\ и д, а Т'" — оставшаяся часть цепи Г, т.е.
подпоследовательность в Г, у которой первое ребро есть д, а последнее ребро есть е\.
По построению ез € Т'". Значит, рассматривая Т"' как замкнутую кривую,
начинающуюся и заканчивающуюся в v, мы заключаем из сказанного выше,
что Т'" содержит незамкнутую кривую То с концами s(ei) и s(e^). По теореме
Жордана (теорема 111.61) найдется такая вершина w на С, что хотя бы одна
секция /г,гу,/г+1 А-цепи Т является секцией в Г"', а подразбивающие точки
5(/г), s(fi+i) лежат по разные стороны от С. Но тогда fa и /i+1 не лежат на
границе одной грани в G (см. следствие III.61а). Из этого противоречия вытекает
справедливость леммы VI.53.
Из леммы VI.53 следует, что, зная один переход А-цепи Т в v ?
V(G), мы знаем уже и все другие ее переходы в v, т.е. если {е^е^} €
XT(v) и 0+{v) = (ei,e?,...,e^) или О" (и) = (е[,е'2,... ,<,), то Xr(v) =
{{ei'e2}'{e3'e4}'- • • >{ed-i>ed}}- Следовательно, мы можем сформулировать
более общее утверждение:
если Т есть А-цепъ в эйлеровом плоском графе G с A(G) > 2 и если
0+(v) = {ei,e!2,...,e,d_l,erd) для произвольно выбранной вершины v € V(G),
то
либо Xr(v) = {{ei,e^},...,{ei_1,ei}},
либо XT(v) = {{e2,e3>,...,{ed>ei}}-
Заметим, что справедливость (I) основана (неявно) на теореме Жордана,
которая неверна для поверхностей рода больше чем 0. Тем не менее понятие
А-цепи можно определить для графов G, вложенных в любую поверхность.
Фактически любая А-цепь в G дает одну и ту же локальную информацию,
выраженную утверждением (/).
С другой стороны, (/) — более слабое утверждение, чем лемма VI.53, так как
в лемме VI.53 утверждается, что А-цепь Т «подбирает» ребра, инцидентные
v, либо по часовой стрелке, либо против в их циклическом порядке,
индуцированном вложением графа G. Которая из этих процедур будет иметь место в
Т, зависит, конечно, от направления, в котором проходится Т. Так или иначе,
как только на Т выбрана ориентация фиксацией начальной вершины и
начального ребра, Г определяет разбиение множества V — V(G), V = V+ U V", где
V+ (У~) содержит в точности те вершины v, при которых Т «подбирает»
инцидентные им ребра согласно 0+(v) (0~(v)). Если Т проходится в обратном
направлении, то, естественно, множества V+ и V~ меняются ролями. То есть
разбиение {У+, V~} множества V(G) однозначно определяется А-цепью Т, где
смысл V+ и V~ зависит от направления прохождения цепи Т. Возникает
вопрос, возможно ли получить это разбиение вне зависимости от ориентации Т

186
Глава VI. Различные типы эйлеровых цепей
и без использования 0+(г>) и/или 0~(г>)? Чтобы убедиться, что это возможно,
мы воспользуемся теоремой 111.68.
Для плоского эйлерова графа G с A(G) > 2 рассмотрим граневую
2-раскраску (цветами 1 и 2), и пусть Т есть А-цепь в G. Выберем
произвольно v Е V(G) с d = d(v) > 2 и пометим полуребра, инцидентные v,
символами е^, е2,..., e'd так, что 0+(v) = (е[, е2,..., e'd). Предположим далее, что
грань, граница которой содержит е\ и е2, окрашена цветом 1. Тогда грани
F2i-i (F2i) с {е2»-1,е2»} С E(bd(F2i-i)) {{e2iye2i+1} С E(bd(F2i))) окрашены
цветом 1 (2), г = l,...,|d. Теперь, если мы расщепим v на к = \d
вершин степени 2 т/1),..., i/fc), придерживаясь Xt(v) (т. е., {?"*(г) |г = 1, ...,&} =
Xt(v))> так что полученный граф Gv будет плоским, то, согласно (/), грани
^2г-2+(55 i = l,...,fc, входят (гомотопически) неизменными в Gv, в то время
как грани F2i+is,i = 1,..., fc, сливаются в Gv в одну грань, где J = 1 или
5 = 2 в зависимости от структуры Xt{v) (см. рис. VI. 18). Таким образом, мы
приходим к следующему определению (напомним, что 1-грани и 2-грани —это
грани, окрашенные цветами 1 и 2 соответственно в граневой 2-раскраске).
а) 1-расщепление
Ь) 2-расщепление
Рис. VI. 18. Граф Gv, полученный из G применением б-расщепления к v 6 V(G),
J = l,2.

VI.3. А-цепи в плоских графах
187
Определение VI.54. Пусть зафиксирована граневая 2-раскраска плоского
эйлерова графа G с A(G) > 2, и пусть произвольно выбрана вершина v ?
V(G) с 2k = d(v) > 2. Выберем обозначения так, что 0+(v) = (е[,е'2, ..., e'd) и
е[,е2 лежат на границе некоторой 1-грани. Для 6 ? {1,2} определим X$(v) =
{{е2г-2+(5' е2г-1+ЛК = 1» • • • > &} (полагая е'2к+1 = е[) и построим плоский граф
Gv так, что E*{i) = {e2i_2+6, е2г-1+<5}> г = 1,..., /с, и bd(F) для любой 5-грани F
в G является ее границей и в G, и в Gv. Тогда мы скажем, что Gv —результат
(6 + 1)-расщепления, примененного к вершине v ? V(G), где мы полагаем
5+1 = 1 при 6 = 2 (см. рис. VI.18)1).
Учитывая определение VI.54 и предшествующий ему абзац, мы можем
сказать, что любая А-цепь Т в плоском эйлеровом графе G без вершин степени 2
порождает такое разбиение {Vi, V2} множества V(G), что v ? V$, если и только
если Xt(v) = Xs+i(v) (мы полагаем 5 + 1 = 1 при 6 = 2). Значит, Vs
содержит в точности те вершины, в которых Т индуцирует 5-расщепление, 6 = 1,2.
Конечно, возможен случай \\ = 0 или V2 = 0; то же самое можно сказать о
разбиении {V4", V""} (см., например, G2 на рис. VI. 17).
Заметим, что в определении VI.54 0+(v) использовалось только для
практических целей. Как показывает рис. VI. 18, 5-расщепление можно определить
только по плоскому эйлерову графу G и фиксированной 2-раскраске его граней
(см. [FLEI74a, Definition 2 ]).
Следствие VI.55. Пусть G—плоский эйлеров граф без вершин степени 2
с фиксированной граневой 2-раскраской, в котором есть А-цепь Т, и пусть
{V+,V~}, {^15^2} —два разбиения множества V(G), индуцированные цепью
Т (см. выше). Тогда {VUV2} = {V+,V~}.
Доказательство. Выберем для Т начальную вершину х и начальное ребро
е = ху, задав тем самым ориентацию цепи Т. Цвет грани, расположенной
справа от е при проходе ребра е от х к у, без ограничения общности полагаем
равным 1. После такого выбора ориентации мы сразу получаем следующие
свойства (см. также лемму VI.53 и рис. VI. 19):
1) для любого 0+(v) = (е[,е2, ...,е^), d = d(v), ребро е\ проходится по
направлению к v, если и только если e'i+l проходится по направлению из v
(мы полагаем e'd+l = e[).
2) для любого f = uw ? E(G), если / проходится по направлению из и к w,
то цвет грани справа от / есть 1.
*) Учитывая определение VI.54 и предшествующее обсуждение, мы можем сказать, что
для точки сочленения v графа G граница bd(F2i-2+<0 может быть циклом в Gv, хотя она
и не является циклом в G, но есть взаимно однозначное соответствие между
маршрутами по компонентам границы bd(F2i-2+5) в Gv и соответствующими маршрутами в G, т.е.
c<3(bd(F2i_2+<0) = cGv(hd(F2i-2+s))- Аналогично, если v — точка сочленения в G, то F2i+i_<5
могут оказаться одной и той же гранью в G для г = 1,..., fc, и эта грань становится также
одной гранью в Gv; но в этом случае CG(bd(F2;+i-<s)) < CGv(bd(F2i+i-s)). Таким образом, с
топологической точки зрения можно сказать, что переход от G к Gv не меняет
гомотопических свойств граней F2j-2+<b г = 1,..., fc, но он меняет эти свойства, если F2i+i-s = F2J+1-8
при j Ф i, 1 < г, j < k. Однако такие рассмотрения нужны, только если v — точка сочленения
bG.

188
Глава VI. Различные типы эйлеровых цепей
\ -- -. /
Рис. VI. 19. Задание ориентации на А цепи Т; для любой дуги цвет расположенной
справа от нее грани есть 1.
Следовательно, Т индуцирует в v 1-расщепление, если и только если v e V~
(и, значит, индуцирует в v 2-расщепление, если и только если v G У+). Тем
самым следствие доказано.
Определение VI.56. Пусть G — плоский эйлеров граф с 5(G) > 2 с
фиксированной граневой 2-раскраской. Разбиение {V, Vй} множества V(G) назовем
А-разбиением, если в G есть такая А-цепь Т, что индуцированное ею
разбиение вершин {Vi, V2} удовлетворяет равенству {V, V"} = {Vi, V2}.
Рассмотрим теперь разбиение {V\V'r} множества V(G), где G — граф из
определения VI.56. Как можно узнать, является ли {V', V"} А-разбиением?
Другими словами, мы хотим охарактеризовать А-разбиения графа G. Для
этого введем несколько обозначений. Пусть вершина v € V(G) выбрана
произвольно. Обозначим через GV}$ граф Gv, полученный из G применением к v
5-расщепления (см. рис. VI.18), 5 Е {1,2}. Для Ц> — {i>i,... , г^} С V(G) мы
положим GVq,s = (... {{GVlls)v2ts) ••¦)«*,*' S G i1»2)- Если vo - 0> т0 бУДем
считать, что Gy0,6 = G. В этих обозначениях из следствий V.10 и V.13 мы
сразу получаем такой результат.
Следствие VI.57. Пусть G такое, как в определении VI.56, и пусть
{V\V"} —разбиение множества V(G). Следующие утверждения
эквивалентны:
1) {V\Vff} есть А-разбиение]
2) хотя бы один из графов (Gv,i)v",2 и (Gv jl)v" ,i является циклом.
Конечно, (Gw)y",2 может быть циклом, хотя (Gv\2)v\i и не цикл.
Примером служит граф октаэдра, что видно на рис. VI.20.a). Однако мы назовем
А-разбиение {V7, V7'} совершенным, если и (Gv,i)v",2, и (Gv,2)v",i
—циклы. Пример совершенного А-разбиения дан на рис. VI.20.b). Заметим
попутно, что в [FLEI74a] А-разбиение — это то, что здесь мы называем совершенным
А-разбиением.

VI.3. А-цепи в плоских графах
189
а) Ь)
Рис. VI.20. а) Граф октаэдра с несовершенным А-разбиением. Ь) Тот же граф с
совершенным А-разбиением (элементы из V {V") помечены символами vf (v")).
На самом деле при проверке, является ли данное разбиение {V, V"}
множества V(G) А-разбиением (соответственно совершенным А-разбиением), не
требуется обязательно выяснять, связен ли граф (Gv,i)v",2 или (Gv\2)v",i
(соответственно связны ли они оба), поскольку оба эти графа 2-однородны.
Чтобы убедиться в этом, сформулируем сначала лемму, доказательство
которой оставляем читателям в качестве упражнения (упр. VI. 15).
Лемма VI.58. Если G — наделенное граневой 2-раскраской вложение в
плоскость связного графа, каждый блок которого есть цикл, имеющий общее
ребро с границей неограниченной грани графа G, то в G есть А-цепь Т. Кроме
того, если внешняя грань графа G окрашена цветом 1 (2), то Т индуцирует
2-расщепление (1-расщепление) в каждой вершине v ? V(G) — V2{G) и, таким
образом, Т однозначно определена.
С помощью леммы VI.58 мы получаем следующую характеризацию плоских
графов, имеющих А-цепь.
Теорема VI.59. Связный плоский эйлеров граф G с фиксированной граневой
2-раскраской имеет А-цепь, если и только если для некоторого мнооюества
Vo С V(G) и 5 = 1 или 6 = 2 граф Gy0,<5 связен и является внешнеплоским,
так что каждый его блок является границей грани1).
Доказательство. Допустим, что в G есть А-цепь Т. Тогда пусть {Т^,^} —
разбиение множества V(G) — V^(G), индуцированное цепью Т, где Vs
содержит в точности те вершины, в которых Г порождает ^-расщепление, S = 1,2
(см. обсуждение, следующее за определением VI.54). Допустим без
ограничения общности, что внешняя (неограниченная) грань графа G есть 1-грань, и
^ G\r0,6 есть ВИД деревьев Хусимщ которые определяются как связные графы, где каждое
ребро принадлежит не более чем одному циклу (см., например, [HARA53a], где рассмотрение
таких графов связывается с именем Хусими [HUSI50a]).

190
Глава VI. Различные типы эйлеровых цепей
рассмотрим Н := Gvlti- Так как для каждой вершины v G V\ цепь Т
индуцирует 1-расщепление, примененное к и, то А-цепь Т соответствует
некоторой А-цепи Тн в Н (на самом деле, если Т и Тн записаны как
последовательности ребер, то Г = Тн)- Значит, Н связен. Если Н не внешнеплос-
кий или если в нем есть блок, не являющийся границей грани, то в нем
есть 1-грань Fi, отличная от внешней грани. Поскольку цепь Тн индуцирует
2-расщепление в каждой вершине w ? V(H) — ^(Я), то она соответствует
некоторой А-цепи Т\ в #1 = #v12,2, гл-е ^12 — ^(bd(i*\)) П V2. С другой
стороны, так как 2-расщепления не меняют границы (рассматриваемые как
последовательности ребер) 1-граней (см. рис. VI.18.b)), то F\ есть 1-грань графа
Hi, отличная от внешней грани, и bd#i(-Fi) — цикл с (1нг(х) = 2 для
любых х е V(bdHiCFi))- Значит, bdtf^Fi) является нетривиальной
компонентой в #1, т.е. Hi несвязен, что противоречит наличию эйлеровой цепи 7\
в Hi. Таким образом, Н внешнеплоский и каждый из его блоков есть
граница грани, и при Vo = Vi и 8 = 1 граф Gv0,s обладает требуемыми
свойствами.
Обратно, предположим, что для некоторого множества Vo С V(G) и S G
{1,2} граф Gv0,6 связен, внешнеплоский и каждый из его блоков есть
граница грани. По лемме VI.58 граф Gv0,s имеет А-цепь То, которая соответствует
эйлеровой цепи Т в G, индуцирующей ^-расщепление в каждом из элементов
множества Vo- Тогда Т порождает 1- или 2-расщепление в каждой из вершин
графа G кроме вершин степени 2. Следовательно, Т есть А-цепь в G. Теорема
VI.59 доказана.
Мы не можем заключить из второй части доказательства, что А-цепь Т в
G индуцирует 1-расщепление для элементов из Vo, если внешняя грань графа
Gv0,s окрашена цветом 1, так как, возможно, G сам удовлетворяет условиям
леммы VI.58 и тогда Т индуцирует 2-расщепление всех элементов из V(G) —
V2(G).
Рисунок VI.21 показывает, что существуют связные внешнеплоские
эйлеровы графы без А-цепей.
На самом деле, если мы предположим, что внешняя грань графа Н на
рис. VI.21 есть 1-грань, то треугольник (а,6,с) —тоже граница 1-грани Fi. И
1-расщепление в любой из вершин a,b,c приводит к несвязному графу,
одна из компонент которого — треугольник, а Я{адс}?2 содержит E(bd(Fi)) как
множество ребер некоторой нетривиальной связной компоненты. Значит, Н не
может иметь А-цепи. Мы оставляем в качестве упражнения доказательство
(как обобщение идеи, использованной на рис. VI.21) того, что если G — граф,
удовлетворяющий условиям леммы VI.58, то найдется связный внешнеплоский
обыкновенный эйлеров граф Н без А-цепи, содержащий подграф, гомеоморф-
ный (в топологическом смысле) графу G (упр. VI.16).
Неудивительно, что графы, рассматривавшиеся при обсуждении рис. VI.21,
имели точки сочленения, поскольку в [REGN76a] было показано, что любой
2-связный внешнеплоский обыкновенный эйлеров граф имеет А-цепь. В
дальнейшем мы называем элементы из E(G) — E'(bd(F00)) внутренними ребрами
внешнеплоского графа G, внешней гранью которого является F^.

VI.3. А-цепи в плоских графах 191
и
Рис. VI.21. Связный внешнеплоский обыкновенный эйлеров граф без А-цепей
(заметим, что в Н есть вершины только степеней 2, 4 и 6).
Кроме того, мы будем использовать следующие леммы. Для краткости мы
распространим понятие J-расщепления на вершины степени 2, говоря, что Т
индуцирует в такой вершине J-расщепление, где 5=1 или S = 2, и в этом
случае выбираем 6 € {1,2}, как это нам удобно.
Лемма VI.60. Пусть Н — плоский эйлеров граф с фиксированной граневой
2-раскраской, являющийся (нетривиальной) блочной цепью, внешняя грань
Fqo которого есть 1-грань, и пусть В\,... ,ВГ —блоки графа Н,
занумерованные так, что BiCiBj ф 0, если и только если \i — j\ < 1. Допустим далее,
что E(bd(Foo)) П Е(Вг) ф 0 для г = 1,... ,г. Тогда в Н есть А-цепь, если и
только если в Bi есть А-цепь, индуцирующая 2-расщепление в каждой точке
сочленения графа Н, лежащей в Bi.
Доказательство. Обозначим через Хг,г+1 точку сочленения графа iJ, для
которой {ач,*+1} = Bi П Bi+i, г = 1,..., г — 1. Пусть ей fi, 9иЫ € E(Bi) — ребра,
удовлетворяющие условиям
ей fi € Ex._lti П bd(Foo), gu Ы ? EXiti+1 П bd(Foo), г = 2,..., r - 1,
9uhi € EXl2 nbd(Foo), er,/r e EXr_1>r Obd^)
и такие, что 0+(zi-i,i) = (е-,#•_!,...,/*•_!,/г;,...), г = 2,...,г (последнее
условие не ограничивает общности). Отсюда мы заключаем, что g^-i и е*, а также
hi-i и fi являются соседними в обходе по bd(Foo).

192
Глава VI. Различные типы эйлеровых цепей
Теперь предположим, что в Н есть А-цепь Т. В силу выбранных
обозначений и предположений и поскольку без ограничения общности можно считать,
что Т начинается в х\$ вдоль ребра 0i, цепь Г имеет вид
Г = pi,...,/ii,/2, • • •,/12>/з? • • • ihr-iifr,... ,ег,
<7г-ь- • • »er-i,... ,ез,02,- • -вг.
Заметим, что так как Т есть А-цепь в плоском графе, то Т пройдет по всем
ребрам из Si, прежде чем пройти хотя бы одно ребро из Bi, 2 < г < г, и
аналогично пройдет (после /г) по всем ребрам из Вг, прежде чем пройти хотя
бы одно ребро Вг, 2 < i <г — 1; для г = 2,..., г — 1 цепь Т проходит ребра из Bi
в двух подцепях, а именно /*,..., hi и д^ ..., е*. Следовательно, Т индуцирует
А-цепи Тг в Д, г = 1,..., г, следующим образом:
Ti = pi,... ,fti, Tr = /r,... ,er,
Г» =/i,...,ftt,0t,...,ei для 2 < г < г - 1.
Таким образом, Tj индуцирует 2-расщепление в Жг-1,г>#г,г+1 € V(Bi) (в
случаях, когда с!вД#г-1,г) = 2 или dBi(^i,z+i) = 2, мы тоже можем считать, что Ti
индуцирует 2-расщепление).
Обратно, если Ti есть А-цепь в Вг, порождающая 2-расщепление в
точках сочленения графа Н, принадлежащих Вг, г = 1,..., г, то без ограничения
общности это можно выразить так, как мы это делали выше, и, как и выше,
можно построить Т, разлагая Ti, г = 2,... ,г — 1, на две подцепи, причем Т
будет А-цепью в Н. Лемма доказана.
Изучим некоторые свойства внешнеплоских графов.
Лемма VI.61. Пусть G есть 2-связный внешнеплоский эйлеров
обыкновенный граф (не являющийся циклом), внешняя грань Fo которого есть 1-грань.
Пусть, далее, Н := Gv,i для некоторой вершины v ? V(G) с d(v) > 2. Тогда
Н обладает следующими свойствами:
1) если jFi ф Fq есть 1-грань в G с v G V(bd(Fi)), то любая вершина w G
V(bd(Fi)) — {v} есть точка сочленения графа Н\
2) точки сочленения графа Н —это в точности вершины, описанные el);
3) Н есть нетривиальная блочная цепь.
Доказательство. Для доказательства свойства 1) мы заметим, что,
поскольку G — внешнеплоский граф, v,w G V(bd(Fi)) П V(bd(F0)). Другими словами,
на плоскости найдутся две такие незамкнутые кривые Cq,C\, что
a) dnG = {v,w}, i = 0,1,
b) Ci — {v, w} лежит внутри грани Fi, i = 0,1
и, следовательно,
c) С := Со U С\ — простая замкнутая кривая на плоскости и С П G — {у, w}.
По построению и по теореме Жордана С делит Fi — С, г = 0,1, на две части,
лежащие по разные стороны от С. Отсюда и из того факта, что F0 и F\ суть
1-грани, можно заключить, что с каждой стороны от С есть положительное

VI.3. А-цепи в плоских графах
193
четное число ребер, инцидентных вершинам v и w соответственно. Поскольку
G — обыкновенный граф, то с каждой из двух сторон от С должна лежать хотя
бы одна вершина графа G. Значит, v и w — вершинный разрез графа G. Точнее,
мы можем представить G в виде
G = G'UG", где G'nG" = {v,w}
и
d,G'{v) = d,G'(w) = d,G"{v) = dc"(w) = 0 (mod 2). (*)
Следовательно, Gf и G" лежат по разные стороны от С (исключая, конечно,
v и w, которые лежат на С). Значит, если мы построим плоский граф Hi
расщеплением v на две вершины vf и v" таким образом, что Ev> = Ev П E(Gf) и
Ev» = EVD E(G"), a vf (v") лежит по ту же сторону от С, что G' (G"), то
Нг^ЩиЩ, где Н[ П Щ = {w},
а Н[, Н" и Hi связны и эйлеровы по (*). Более того, w — единственный элемент
из Hi, лежащий на С (поэтому Н[ и Н" лежат по разные стороны от С, за
исключением вершины w), и по построению w является точкой сочленения
в Hi. Также по построению имеем
Н := Gv,i = ((Hi)v<,i)v„v
и Н можно записать в виде
tf = #,U#", где Н'Г\Н" = {<ш}
и
Н = (Нг )v>,i, H =(Я1)^д.
Таким образом, Н' и Н" лежат по разные стороны от С за исключением w.
Поэтому w является точкой сочленения и в графе Н.
Вернемся к доказательству свойства 2).
Заметим сразу, что вершины v^ степени 2, i = 1,... ,fe, k = \dc{v),
возникающие при 1-расщеплении вершины г;, не могут быть точками сочленения
в Н] в противном случае Ev{i) состояло бы из двух перешейков графа Н, что
противоречит эйлеровости этого графа.
Рассмотрим теперь путь
P0:=hd(F0)-vCHnG,
и пусть х € V{Po) выбрана так, что х ? V(bA(Fi)), если Fi ф Fo является
1-гранью в G и v G V(bd(Fi)). С учетом доказанного выше и свойства 1)
достаточно показать, что х не является точкой сочленения вН.В любом случае
по выбору х имеем vx 0 Ev — {ei, e<f}, где {ei, e^} = Ev П ?'(bd(Fo)).
Пусть пути Pi и Рч таковы, что
Po=PiUP2,PinP2=x
(возможно, E(Pi) = 0 или Е(Р2) = 0). Рассмотрим два случая.
а) Допустим, что существует такая вершина Xi E V(Pi) — {х}, г = 1,2, что
или xi^2 G Е(Н), или xiu^, жг^;^ € -Е'(Я) для некоторого j € {1,..., к}. Пусть

194
Глава VI. Различные типы эйлеровых цепей
Р3 = P3(xi,x2) — путь, соединяющий х\ и х2 в Р0. Тогда х € У(Р$) - {xi,жг}-
Пусть цикл Cj в Н определен следующим образом:
Cj = (Е(Р3) U {xix2}), если xix2 G Р(#),
Cj = (Е(Рз) U Sv(j)) в противном случае
(заметим, что {x\v^\x2V^} = Evu), если x\x<i 0 Е(Н)). Во всяком случае
ffO') := (V(Cj)) есть 2-связный подграф в Н. На самом деле Cj С bd(Poo),
где Роо — неограниченная (внешняя) грань в Н. Поскольку Н и Н^ С Н
также внешнеплоские и Cj —граница внешней грани в Н^\ мы заключаем, что
Еи С Е(Н^) для любой вершины u € V(Cj) — {xi^X2,v^} (отметим, что
элементы из Еч П Р(Рз) являются последовательными элементами в 0+(и)).
Следовательно, и не может быть точкой сочленения в if, так как Н^
является 2-связным подграфом графа Н и, тем самым, подграфом некоторого блока
в Н. Замечая, что
V(Cj) - {xux2,vW} = V(P3) - {хьх2},
приходим к выводу, что х является одной из этих вершин и и, таким образом,
х не есть точка сочленения в Н.
Ъ) Допустив теперь, что не существует х* Е V(Pi)—{х}, г = 1,2, со
свойствами, описанными в а), мы сразу выводим справедливость следующих равенств:
E{G) = E1 U Е2 , Ei П Е2 = 0,
Ег = Е((У(Рг)и{у})), г = 1,2.!)
Следовательно, из допущения, что P(Pi) Ф 0 # Е{Р2), следует, что
г; и х разделяют G. Кроме того, из этих двух соотношений следует даже,
что в G есть грань F ф F0 с v,x Е V(bd(P))2\ Согласно выбору х, Р не
может быть 1-гранью; значит, это 2-грань и в G, и в Н. Таким образом,
vti) ^ V(bd(P)) П V(H) для некоторого j Е {1,...,/с}. Аналогично случаю
а) пусть Рз = Рз{хг,Х2) С Pq обозначает путь, содержащий х, такой, что
{у(^Х1,у(^Х2} = Evu). Используя те же символы, определим Cj и Н^\ как
в случае а); снова Cj С bd(Poo) и Cj— цикл и в G, и в Я. Продолжая
рассуждения, как в случае а), мы можем заключить, что х не есть точка
сочленения в Н, если х = и для некоторого и Е V(P$) — {xi,x2}. Ввиду этого и
так как vx 0 Ev — {ei,e^} по выбору х, мы приходим к следующим выводам:
х Е {xi, х2}, а значит, vx Е Ev С E(G), откуда следует, что г?х € {ei, e^}. Таким
образом, или E(Pi) = 0, или Р(Р2) = 0. Без ограничения общности можно
считать, что vx — е\. Пусть х' — элемент множества V(G) — {v}, инцидентный
ребру е2, которое выбрано с помощью 0+(v) = (е^, е2,..., efd), и пусть в этом
случае Рз = Рз(х,х') С Ро — путь, соединяющий х и х' в Pq. Снова используя
те же обозначения и замечая, что в этом случае j = 1, мы определяем так
*) Заметим, что в определении Pi не сказано, является Pi путем в Ро «влево» или «вправо»
от х; значит, мы без потери общности можем писать один и тот же индекс г в обеих частях
последнего равенства.
2) Этот вывод справедлив для любой разделяющей пары вершин в 2-связном плоском
графе.

VI.3. А-цепи в плоских графах
195
же, как и выше, цикл С\, являющийся границей внешней грани в Н^\ где,
как и выше, Р^1) := (V(Ci)) есть 2-связный внешнеплоский подграф графа
Н. Но, кроме того, в этом случае Ех С Е(Н^). Действительно, С\ можно
представить в виде
d = Р3' U {е2}, где Р3' = ^з U {v,vx}.
Это дает ситуацию случая а), где v и хг играют роли rci и^. Таким образом, х
не есть конечная вершина пути Р3'; поэтому, как и выше, Ех С Е(Н^) и,
следовательно, х не является точкой сочленения в Н. Это завершает доказательство
свойства 2).
Чтобы увидеть, что Н есть нетривиальная блочная цепь, еще раз
рассмотрим путь Ро, определенный в начале доказательства свойства 2), и пусть
х\,х,Х2— три различные вершины, лежащие на Ро в указанном порядке. Мы
утверждаем, что х не есть точка сочленения в Р, если х\ и х^ принадлежат
одному и тому же блоку В С Н.
Блок В 2-связен, поскольку Н — обыкновенный эйлеров граф. Значит,
найдется цикл С С В с ii,i2 G V(C). Используя путь Рз = РзОеъяъ) ^ ^о5
построим 2-связный подграф Pi графа Н по правилу
Pi := С U Рз
(возможно, Pi — С\В\ ф Р, если В\ ф С). Тогда Pi С Р, поскольку С С
Р и «(Pi) > 2. Кроме того, х ? V(B\), так как х € ^(Рз); следовательно,
? € V(P). Далее, из включения Рз С Р следует, что Рз С bd(P*), где Р* —
неограниченная (внешняя) грань внешнеплоского графа Р. Заметим, что, как
и выше, элементы из Ех П Р(Рз) следуют один за другим в 0+(х). Значит,
Рх С Е(В), т.е. х не есть точка сочленения в Н. Таким образом, поскольку
иО), j = 1,..., fc, тоже не есть точка сочленения в Я и V(Po) = V(H) — {v^ \j =
1,..., А:}, то любой блок графа Н содержит не более двух точек сочленения
графа Н. А поскольку Н связен, но не 2-связен и является обыкновенным
графом, то любая точка сочленения графа Н принадлежит двум его блокам,
т.е. Ьс(Р") является нетривиальным путем. Отсюда следует справедливость
свойства 3), и доказательство леммы VI.61 закончено.
Наконец, докажем одно свойство 2-связных внешнеплоских графов.
Лемма VI.62. Пусть В есть 2-связный внешнеплоский обыкновенный граф
с внешней гранью F^, и пусть В~ := В — е для некоторого ребра е = ху €
P(bd(Poo)). Обозначим через F^ Ф Роо другую грань в В с е Е P(bd(P2)). Тогда
В~ обладает следующими свойствами:
1) V(bd(F2)) — {х,у} есть множество точек сочленения в Р~;
2) Р~ есть {нетривиальная) блочная цепь, в которой х и у принадлеоюат
разным концевым блокам в Р~, и они не являются точками сочленения
графа Р".
Доказательство. Лемма, очевидно, справедлива, если Р —цикл, т.е. если
Р~ — путь. Допустим поэтому, что В не является циклом. Любая вершина
w € V(bd(F2)) — {#, у} есть точка сочленения в Р~: это вытекает из того
факта, что w ? V(bd(F2)) П y(bd(Poo)) и ху € P(bd(P2)) П P(bd(Poo)), откуда

196
Глава VI. Различные типы эйлеровых цепей
следует, что найдется плоская обыкновенная замкнутая кривая С,
пересекающаяся с В лишь по w и в точности одной точке ребра ху (ху рассматривается
как топологический образ открытого единичного отрезка (0,1)). Таким
образом, х и у лежат по разные стороны от С. Значит, любой путь из а: в у в
графе В~ проходит через w, т. е. w есть точка сочленения в В~. Заметим, что
V(bd(i*2)) — {х,у} ф 0, поскольку G есть обыкновенный граф.
Пусть теперь z — произвольная точка сочленения в В~. Так как В 2-связен,
а В~ не 2-связен, то по теореме III.32 В~ есть нетривиальная блочная цепь,
причем х и у принадлежат различным концевым блокам в В", и они не
являются точками сочленения в В~. Тогда любой путь Р(х,у) С В~ содержит z,
и любой цикл в В, содержащий ху, содержит также и z. Поскольку bd(i*2)
является таким циклом, а х и у не являются точками сочленения в В-, то
z € V(bd(F2)) — {x,y}. Лемма доказана.
Обратимся теперь к результату Регнер об А-цепях во внешнеплоских
эйлеровых графах.
Теорема VI.63. Пусть G есть 2-связный внешнеплоский обыкновенный
эйлеров граф. Рассмотрим граневую 2-раскраску в G, такую, что внешняя грань
Fq есть 1-грань. Пусть вершина v € V(bd(Fo)) с d(v) > 2 выбрана
произвольно (если такая v найдется). Тогда в G есть А-цепь, индуцирующая
1-расщепление в v.
Доказательство. Если в G есть только вершины степени 2, то это цикл;
обход этого цикла есть А-цепь; поэтому мы можем предполагать, что в G
имеется хотя бы одна вершина степени, большей 2. Заметим, что, поскольку G есть
2-связный обыкновенный граф, в этом случае в G имеется не менее трех
вершин степени, большей 2. Следовательно, наименьший граф G0, не
являющийся циклом и удовлетворяющий условиям теоремы, имеет ровно три
вершины степени 4 и три вершины степени 2; его можно получить из вложения в
плоскость октаэдрального графа удалением всех ребер границы внешней
грани (см. рис. VI.22). 1-расщепление в v дает граф G!^, имеющий ровно две
вершины х,у степени 4, которые обязательно являются точками сочленения
графа С°д. В самом деле, G® х удовлетворяет условиям леммы VI.58 и
потому можно считать, что в G0 есть А-цепь Т0, индуцирующая 1-расщепление в
вершине v и 2-расщепление в каждой из вершин х и у. Используя те же
рассуждения, заключаем, что если G есть внешнеплоский граф, гомеоморфный
G0, то в G есть А-цепь Т, порождающая 1-расщепление в выбранной вершине
v и 2-расщепление в двух других вершинах степени 4.
Теперь мы можем применить индукцию. Рассмотрим граф G,
удовлетворяющий условию теоремы и имеющий п > 3 вершин степени, большей 2, и
допустим, что теорема верна для всех соответствующих графов Н с не более
чем п — 1 такими вершинами.
Рассмотрим в G выбранную вершину v и 0+(v) — (е^е^,... ,е^), где d =
d(v) > 2, и без ограничения общности допустим, что e\,e<i € E'(bd(Fo))5 где Fq
есть внешняя грань в G. Теперь образуем Н = С„д и положим Р0 = bd(F0) — v.
Во всяком случае Н связен, эйлеров и внешнеплоский.

VI.3. А-цепи в плоских графах
197
v
@
G0
Рис. VI.22. 2-связный внешнеплоский эйлеров граф G0 с Л-цепью То, которая
индуцирует 1-расщепление в v.
Если мы обозначим точки сочленения в Н через xi,..., хг в том порядке, в
котором они появляются в Ро> то из рассуждений, использованных при
доказательстве свойства 3) леммы VI.61, следует, что х* и Xj принадлежат одному и
тому же блоку графа Н, если и только если | i — j |= 1. Значит, мы можем
обозначить блоки графа Н через ?ь ..., -Br+i, так что х\ ? V{B{), xT ? V(Br+i)
и Xj_i,Xi € ^(?г) при 2 < г < г. Что касается распределения вершин
г/.?), j = 1,..., /с, d(i;) = 2fc, в этих блоках В*, г = 1,..., г + 1, то
|{v(1\t;W}nV(Bi)|=|{^1\t;W}nVr(Br+i)|=l1
так как G 2-связен и в силу определения вершин v^\ j = 1,..., к. Без
ограничения общности можно считать, что г/1) € V(Bi), v^ ? V(Br+i) (заметим,
что обозначения для J5^, г = 1,...,г-Ь 1, можно выбирать или «слева направо»,
или «справа налево»). Для j = 2,..., к — 1 пусть ij обозначает такой индекс,
что у(^ € V(Bij). Конечно, могут найтись блоки графа Н, не содержащие
никаких v^\ j = l,...,fc, но при j ф m мы имеем ij ф im, поскольку
среди четырех вершин из Ро, инцидентных элементам из Evu) U Ev(m), найдутся
две точки сочленения в Я, каждая из которых отделяет оставшиеся две
вершины друг от друга (см. доказательство леммы VI.61, свойство 3), и учтем,
что G есть обыкновенный граф и вершина из Р$, инцидентная некоторому
ребру е G Ev — {б1,е^}, является точкой сочленения графа Н по лемме VI.61,
свойство 1)). Из внешнеплоского вложения графа G и определения вершин
VU), j = 1,..., /с, следует, что если j < га, то ij < гт. Кроме х*, г = 1,..., г, мы
введем хо и xr+i в G, определенные условиями vxq = е\ и vxr+i = ед. Таким
образом, Bi П {xj\j = О,... ,г + 1} = {xi-i,Xi}. Рисунок VL23 иллюстрирует

198
Глава VI. Различные типы эйлеровых цепей
G Н
Рис. VI.23. Графы G и Я = GvA.
структуру графа Н, которая вытекает из леммы VI.61 и приведенных выше
рассуждений.
Внешняя грань Foo блочной цепи Н является 1-гранью, и Pq С bd(Foo).
Кроме того, bd(F00)n^(Bi) ф 0 при г = 1,... ,г + 1, поскольку ?(#г)П?(Р0) 7^
0. Это и выбранные обозначения позволяют применить лемму VI.60. Таким
образом, А-цепь в G, индуцирующая 1-расщепление в г;, обязательно
индуцирует 2-расщепление в каждой из вершин xi,...,xr. С другой стороны, если
мы можем показать, что в Bi есть А-цепь, индуцирующая 2-расщепление в
Xi-i и Xi, i = 1,... ,г + 1, то по лемме VI.60 в Н есть А-цепь, а это
эквивалентно утверждению, что в G есть А-цепь, индуцирующая 1-расщепление в v.
Значит, для завершения доказательства теоремы достаточно показать, что в
(Bi){xi-i,xi},2 имеется А-цепь при г = 1,...,г + 1. Итак, зафиксируем
произвольное г€{1,...,г + 1}и рассмотрим Bi. В зависимости от положения Bi в
Н и его структуры мы рассмотрим следующие случаи:
(I) V(Bi)n{t;«)|j = l,...,fc} = 0.
Для краткости положим В = Bi, х = Xi-i и у = Х{. Пусть Ai = (ж,u,?i),
Л2 = (у, t;,^) — два треугольника с ti, ^2 & V(G). Построим вложение в
плоскость планарного графа
?+ = ?U AiU Д2,
такое, что t\ и t<i имеют степень 2 в В+ и лежат на границе неограниченной
грани В+ (см. рис. VI.24). Заметим, что для неограниченной грани F^ графа В
V(bd(FU)) = V(P(x,y)), где P(x,y) = bd(OnPo;
в противном случае Ро U {ei,e<f} = bd(F0) есть цикл в G, содержащий
некоторую вершину цикла bd(F^) в своей ограниченной (но не в
неограниченной) области, а это противоречит тому факту, что G внешнеплоский. Таким
образом, вложение графа В+, описанное выше и проиллюстрированное на

VI.3. А-цепи в плоских графах
199
Рис. VI.24. Построение внешнеплоского графа Б+ из внешнеплоского графа В
добавлением треугольников Ai и Аг.
рис. VI.24, действительно внешнеплоское. Более того, поскольку В 2-связен,
мы можем заключить из тех же соображений, что Р'(х, у) := bd(i^) — P(x, у)
не содержит ребер, кроме ху (см. рис. VI.24).
Теперь предположим, что в В есть не более п — 2 вершин степени, большей
2; тогда в В+ есть не более п—1 таких вершин. Значит, применяя теорему к J3+,
мы получаем А-цепь Т+ в В+, индуцирующую 1-расщепление в v (граневая
2-раскраска графа В+ порождена граневой 2-раскраской графа G с помощью
граневой 2-раскраски графа В). Замечая, что цепь Т+, прочитанная как
последовательность ребер, может также рассматриваться как А-цепь в -В?1? мы
заключаем, что по лемме VI.60 в В есть А-цепь Т, такая, что расщепления
вершин, определенные с помощью Хт{х) и Хт(у), суть 2-расщепления.
Однако если в В есть в точности п — 1 вершин степени, большей 2, то к
В+ нельзя применять индукцию, как это было сделано выше. В этом случае
мы поступим по-другому. Рассмотрим 2-грань i<2 в В (которая фактически
является также 2-гранью в G) с ху € bd(F2) и построим В~ = В — {ху}.
По лемме VI.62 мы можем записать блочную цепь В~ как объединение этих
блоков,
в~ = в~и...ив-,
где t =\ F(bd(F2)) | —1 и В~ П BJ ф 0, если и только если | i — j |= 1.
Далее, мы можем положить для j = 1,..., t — 1
{Wj} = B-nB-+1,
где Wj € V(bd(F2)) — {я, у} по лемме VI.62. Наконец, положим w$ = х и wt = у
(без ограничения общности можно считать, что х Е В^,у Е В^). Отметим,
что, поскольку
dB- (z) = 1 (mod2), если и только если z € {х, у},

200
Глава VI. Различные типы эйлеровых цепей
В- В±
Рис. VI.25. Блок В = Bi графа Я, неэйлеровы блоки В~ в В — {ху}, i G J, и
эйлеровы блочные цепи i^- в Д~ — {wj-iWj}, j G Jo-
мы имеем для j G J:={l,...,t}
rfs-(^_i) = dB-(wj) = l(mod2),
j 3
dB- (u) = 0 (mod 2), если и ф Wj-i, Wj.
Поскольку В внешнеплоский и V(bd(F2)) = {wj\j = 0,... ,?},
E(hd(F2)) - {xy} = {wj^wjlj G J}.
Значит, Wj-iWj G E(B~) при j G J и, согласно сказанному выше, 5'- :=
В~ — {wj-iWj} эйлеров. Конечно, равенство E(Bj) = 0 может быть верным
для некоторых (но не для всех) j G J. Рассмотрим J0 := {j G J\E(Bj) Ф 0}
и заметим, что, поскольку В~ есть блок в В", граф В~ 2-связен при j G Jo-
Значит, Bj есть связный эйлеров внешнеплоский граф. Из тех же
соображений, что и при доказательстве леммы VI.62, мы можем заключить, что Bj
есть нетривиальная блочная цепь, а значит, она содержит точку сочленения и
Wj-i,Wj принадлежат различным концевым блокам в Bj и не являются
точками сочленения в Bj.
Суммируя приведенные приложения леммы VI.62, мы можем представить
В в следующем виде:
? = bd(F2)U (J В'у
JZJo
где Bj — нетривиальная эйлерова блочная цепь при j G Jo; любые две из этих
блочных цепей имеют не более одной общей вершины, и эта вершина
принадлежит Vr(bd(F2)).
Рисунок VI.25 иллюстрирует эту структуру графа В.
Теперь наша цель —для каждого j G Jo найти две подцепи,
покрывающие Bj, и так скомбинировать их с циклом bd(i<2), чтобы получить требуемую

VI.3. А-цепи в плоских графах
201
А-цепь в В. Пусть Cj — произвольная точка сочленения в Bj . Так же как мы
определяли В+ по В (см. рис. VI.24), мы можем теперь построить для
каждого j ? Jo 2-связный внешнеплоский эйлеров граф В^ добавлением к Bj
двух треугольников А^ = (wj-i,p,ti), Д2 = iwj,P,t2) B вершинах Wj-i,Wj
соответственно, где р, ?i,^2 0 V(G) и ti,t2 имеют степень 2 в Bj~. Теперь, если
мы сравним эту конструкцию с имеющейся на рис. VI.24, то у нас будет Wj-i
вместо я, Wj вместо ?/, р вместо v и Bj вместо В. Тот факт, что В 2-связен, а
Bj есть блочная цепь (и, следовательно, не может содержать Wj-iWj), не имеет
значения.
Во всяком случае в В^ есть rij < п вершин степени, большей 2; это
выводится из того факта, что В~ есть нетривиальная блочная цепь. Теперь по
индукции мы можем заключить, что в B~j имеется А-цепь Х^~, индуцирующая
в Cj некоторое 1-расщепление. По лемме VI.60 Т* индуцирует 2-расщепление
в Wj-i,Wj ир (заметим, что (Bj~)Cjд есть блочная цепь, где Wj-i,Wj,p — три из
ее точек сочленения). Значит, мы можем записать Т* как последовательность
ребер следующим образом:
Т+ = pWj-i, Т[3), Wj-\ti, tip, pt2, t2Wj, Т2Ы , WjP,
где Т± и Т2 — реберно-непересекающиеся замкнутые цепи, покрывающие Bj.
Цепь Т^ индуцирует 2-расщепление в Wj-i, а Г2 —в Wj. Поскольку Т^ и
Т2 являются А-цепями соответствующих компонент в (Bj)Cjii, то два ребра,
инцидентные u Е V(Bj), которые не являются последовательными в 0+(ii), не
смогут образовать переход, определенный какой-либо из цепей 7^ , Т2.
По аналогии с доказательством леммы VI.60, мы можем теперь выбрать для
каждого j € J0 ребра е,, ft,gj, hj с е-,-, ft G EWj_1 П E(B,j)igjJ hj € EWj П E(Bj)
так, что цепи Т^ и Т2 (рассматриваемые как последовательности ребер)
можно записать в виде
7\ = ej, T\ j, ft и Т2 = /ij, T2j, pj.
Рассмотрим вершины Wj, j € J U {0}. Если j,,; -h 1 0 Jo, то (Ib(wj) = 2; если
J' ? Jo, j' + 1 ?¦ Jo, то T2 содержит ребра Е^., а T^ ' не существует; если
j ^ Jo, J -Ь 1 € Jo, то Т\° ' содержит ребра EWj, а T2 не существует; если
j,j -Ь 1 € Jo, то и Т2 , и Ti существуют и содержат ребра из JS^.. Кроме
того, если мы посмотрим на 0+(wj) в В, то либо
0+(ги,) = (wj+iWj,WjWj-i),
либо
0+(го,) = {wj+1Wj,WjWj-Ugj,... ,ftj),
либо
0+(^) = (wj+iWjiWjWj-xJj+u..., ej+i),
либо
0+(^) = {wj^Wj.WjWj-^gj,..., Л,, /j+i,...,e^+i),

202
Глава VI. Различные типы эйлеровых цепей
в зависимости от того, который из перечисленных выше четырех случаев
относительно j,j + 1 € J имеет место (wj-i = wt, если j = 0). Положив для i = 1,2
и j е J
ST^j) = T[j\ если j € Jo, и <57;(i) = 0, если j e J - J0,
и принимая во внимание приведенные выше равенства с TJj и 0+(wj), мы
заключаем, что
Гв = w0wt, ST^\wtwt-i, «Я1/**, 5Т^~г\ wt-iWt-2, • • •, гу2гУь
есть А-цепь в Б, индуцирующая в Wj, j € JU{0}, и, таким образом, в гУо = Яг-i
nwt = Xi 2-расщепления. Другими словами, в (Вг){ж»_1,ж»},2 есть А-цепь. Этим
доказан случай (I).
(II) У(ВОП{^)|^ = 1,...,*;}#0.
Тогда существует в точности одно такое j е {1,...,/с}, что v^ G V(Bi)
(см. обсуждение, предшествующее рис. VI.23). Снова положим для краткости
В = Вг,х = я*-ьг/ = ^г5 положим v = v^\ и пусть Р(х,у) = bd(F^C)) П Ро
определено, как в случае (I).
В любом случае в В меньше вершин степени, большей 2, чем в G. Поэтому
если ху ? Е(В), то мы подавим вершину и, чтобы получить В* рассмотренного
в (I) вида; любая А-цепь в В* соответствует некоторой А-цепи в В и наоборот.
Так как ху ? Е(В), то примененная к В* индукция дает требуемую А-цепь
графа В. Поэтому мы предполагаем, что ху € Е(В): В содержит треугольную
2-грань Л = (и,ж,у).
Если Д = В, то обход по Л есть, как и требуется, А-цепь в В в силу нашего
дополнительного определения <5-расщепления в вершинах степени 2. Поэтому
предположим, что Л ф В. В этом случае мы имеем в точности ситуацию,
иллюстрируемую рис. VI.25 с t = 2, Jo = {2}, v вместо iuo, х вместо w\ и
таким же у, что и на рис. VI.25.
Заметим, что В — v есть 2-связный внешнеплоский обыкновенный граф;
значит, В~ := (В — v) — {ху} = В — А есть нетривиальная блочная цепь по
лемме VI.62. Как и в случае (I), мы находим вершину с Е Р(х,у) — {ж,у},
которая является точкой сочленения в В~, и по индукции А-цепь Те в В,
которая индуцирует 1-расщепление в с и, следовательно, 2-расщепления вхи
у. Таким образом, при всех возможностях мы свели случай (II) к случаю (I).
Теорема VI.63 доказана.
Возникает подозрение, что в условиях теоремы VI.63 можно не требовать,
чтобы граф G был внешнеплоским, и получить более общее утверждение.
Или, более осторожно, можно спросить: верно ли, что любой обыкновенный
2-связный эйлеров плоский граф имеет А-цепъ? Действительно, когда я
впервые рассматривал задачу нахождения А-цепей в плоских эйлеровых графах,
то думал, что 2-связности будет достаточно, чтобы плоский эйлеров граф G
допускал такое разбиение {V[, V^} множества V(G) — {v} для некоторой
вершины v G V(G), что (Gv\i)v\2 не содержит подграфа, гомеоморфного графу G\

VI.3. А-цепи в плоских графах
203
Рис. VI.26. 2-связный плоский эйлеров обыкновенный граф Go с вершинами
степеней 4 и б без А-цепей.
на рис. VI. 17. Если рассматривать задачу нахождения А-цепи в связном
плоском эйлеровом графе G с алгоритмической точки зрения, то из теоремы VI.59
и обсуждения рис. VI. 17 следует, что в G есть А-цепь тогда и только тогда,
когда для любой вершины v € V{G) найдется разбиение {V/, V^} множества
V{G) — {v} с указанным выше свойством. Значит, граф G\ на рис. VI. 17
описывает запрещенную ситуацию, которой нужно избегать при попытках строить
А-цепь с помощью последовательности 5-расщеплений, 5 € {1,2} (здесь термин
«гомеоморфный» понимается так, как это принято в топологии на плоскости;
в этом смысле два графа на рис. VI. 17 считаются разными).
К несчастью, существуют 2-связные плоские эйлеровы обыкновенные
графы, имеющие вершины только степеней 4 и 6, без А-цепей. Чтобы убедиться,
что граф Go на рис. VI.26 дает такой пример, предположим сначала без
ограничения общности, что грани графа Go раскрашены в два цвета, и внешняя
грань имеет цвет 1. Предположим, далее, что Go имеет А-цеиъ Т. Заметив,
что (Go){Ul,V6}>2 есть несвязный граф, и применив следствие VI.57, получаем

204 Глава VI. Различные типы эйлеровых цепей
н
Рис. VI.27. Граф #, полученный из Go применением (5-расщепления к V2J-2+5, j =
1,2,3,(5 = 1,2.
из симметричности графа Go? что этот граф также имеет А-цепь,
индуцирующую 1-расщепление в v±. Без ограничения общности считаем, что выбрана
цепь Т, обладающая этим свойством.
Отсюда следует, однако, что ^-расщепление, индуцированное цепью Т в
Щ, 2 < г < б, удовлетворяет соотношению i = 6 (mod2). Таким образом,
мы приходим к графу Я = ({Go){VuV3,V5}a){v2iV4iV6}^ изображенному на рис.
VI.27, где цепь Т, рассматриваемая как последовательность ребер, является
также А-цепью в Н. Теперь, если применить соответсвующее J-расщепление
к каждой вершине степени 4вЯ, получится граф, гомеоморфный графу G\
на рис. VI.171). Вне зависимости от того, какое J-расщепление применялось к
каждой вершине из V{Gq) — {г>}, д € {1,2}, мы приходим или к несвязному
графу или, в лучшем случае, к тому, что мы называли запрещенной ситуацией;
поэтому мы можем заключить, что в Go нет А-цепи.
х) На самом деле при любом расщеплении вершин степени 4 в Я, которое не приводит к
несвязности, получается, с точностью до гомеоморфизма, один и тот же граф, а именно граф
Gi, изображенный на рис. VI. 17.

VI.3. А-цепи в плоских графах
205
Рис. VI.28. Граф Go\ полученный из графа Go, изображенного на рис. VI.26,
изменением лишь вложения ребра v\vq: v\Vq принадлежит в Go границе внешней грани,
а в Gq1 — границе 2-грани, содержащей v. В Gj есть А-цепь, а в Go —нет.
Интересно отметить, что небольшое изменение вложения графа Go дает
плоский граф Gq\ в котором есть А-цепь Г (см. рис. VI.28); проверку этого
утверждения мы оставляем читателю в качестве упражнения.
Значит, наличие А-цепи в 2-связном плоском эйлеровом графе может
зависеть от вложения лежащего в его основе (абстрактного) планарного
графа. Аналогичный факт уже отмечался для 1-связных графов (см. рис. VI. 17,
VI.26 и VI.28). Теперь можно было бы спросить, существует ли для
данного 2-связного планарного эйлерова графа G такое вложение Н этого графа в
плоскость, что в Н есть А-цепь. Однако С. Регнер (с помощью автора)
построила 3-связный планарный эйлеров граф, в котором нет А-цепей.
Поскольку для любых двух вложений #i,#2 такого графа либо O^(G) = G#2(G),
либо O^(G) = 0]j2(G) (см. теорему III.52), мы можем заключить, что в
случае 3-связного планарного эйлерова графа наличие или отсутствие в нем
А-цепи не зависит от выбранного вложения. С другой стороны, ввиду
леммы VI.60, если имеется планарный 3-связный эйлеров граф G без А-цепей,

206
Глава VI. Различные типы эйлеровых цепей
то в планарном эйлеровом графе Hi = G' U G", где G' и G" суть
экземпляры графа G и G1П G" = {и} € V(Hi) (а значит, «(#i) = 1), нет А-це-
пей ни при каком вложении в плоскость Н\. Далее, если Я2 = G' U G",
где G1 ,G" те же, что и выше, и G' П G" = {v,w} € ^(Я2) (а значит,
ю(Яг) = 2), то тоже ни в каком вложении графа Я2 в плоскость нет А-цепей.
Это заключение сразу вытекает из следующей леммы (см. также [REGN76a,
Bemerkung 3.2]). Обозначим через G? граф, построенный из G& тем же
способом, которым Я+ был построен из Я в доказательстве теоремы VI.63 (см.
рис. VI.24).
Лемма VI.64. Предполоэюим, что плоский 2-связный эйлеров граф G можно
представить в виде
к
G=(jGi, E(Gi) П E(Gj) = 0 для г ф j, 1 < г, j < к, к > 2,
г=1
так, что Gi эйлеров, n(Gi) > 2 и Gi П G^+i = г>г,г+1 ? ^(G),
Gi П Gj = 0, еа/ш г + 1 < j < fc, г = 1,..., /с,
(мы считаем, что к + 1 = 1; еслгл к = 2, то \G\ П G2 |=| {^1,2,^2,1} |= 2).
Предполоэюим, далее, что грани графа G 2-раскрашены, причем внешняя грань
Fqo имеет цвет 1, и что Я(Ь(1(^оо)) П E(Gi) ф 0 прг* г = 1,..., к. Следующие
утверждения эквивалентны:
1) G имеет А-цепь;
2) обозначения можно выбрать так, что:
либо в Gi,Gfc есть А-цепи, индуцирующие 1-расщепление в Vk,i и 2-рас-
щепление в t>i,2>^/c-i,fc соответственно, а при г = 2,..., к — 1 в Gi есть
А-цепь, индуцирующая 2-расщеплениия в ^-i,z^i,z+i;
либо в Gi есть А-цепь, индуцирующая 2-расщепления в ^г-1,г?^г,г+1 Щи
г = 1,..., к — 1 (полагаем иод = Vk,i), и в G^ есть А-цепь, индуцирующая
2-расщепление в каждой из вершин Vk-i,k,Vk,i,v, где {v} = Va(G~^) — V±(Gk)-
Доказательство. Заметим сначала, что есть в точности две грани,
границы которых содержат все вершины иг,г+ь i = 1,-..,&, а. именно i7^ и еще
одна 1-грань, назовем ее F\. Это непосредственно следует из условия
леммы. Значит, при i Ф j, I < i,j < к, Н = G{Vii+ljV. .+1}д есть несвязный
граф: чтобы убедиться в этом, рассмотрим простые незамкнутые кривые
С\ С F\ U {vi.i+ijUjj+i} и Coo С -^оо U {^i+b^j+i}? каждая из которых
соединяет uifi+1 и ^,J+i. Тогда Ci ПС2 = {vt,t+ii Vj^+i}; значит, С = Ci UCoo есть
простая замкнутая кривая, содержащая открытые ребра графа Сив своей
ограниченной, и в неограниченной областях. В силу этого и поскольку каждый
из графов Gi эйлеров, г = 1,..., к, граф Я можно построить (топологически)
так, чтобы С также содержала открытые ребра графа Я и в своей
ограниченной, и в неограниченной областях и С П Я = 0. Таким образом, мы можем
заключить, что Я несвязен (ср. доказательство свойства 1) леммы VI.61). Из
этих рассуждений вытекает, что если G имеет А-цепь Т или если такую цепь

VI.3. А-цепи в плоских графах
207
Т надо построить из соответствующих А-цепей в Gi, z = l,...,fc-l, G?
соответственно, то цепь Т или построение цепи Т индуцирует 2-расщепление во
всех, кроме, может быть, одной, вершинах v^i+i, г = 1,..., fc.
Теперь предположим, что G имеет А-цепь Т, индуцирующую 1-расщепление
в некоторой вершине v^i-\-i - Без ограничения общности мы можем
предположить, что обозначения выбраны так, что г = fc (если необходимо,
применив циклическую перестановку индексов, чтобы получить г = fc). Построим
плоский граф Нху из G, заменив v^i на две вершины х, у ? V(G), так что
Ех = EVklC\E(Gi), Ey = EVkinE(Gk)> Значит, Нху есть нетривиальная
эйлерова блочная цепь, блоки Hi которой определены с помощью E{Gi), г = 1,..., fc,
а точки сочленения — вершины г>г,г+ь г = l,...,fc — 1. Другой способ
получить Нху — отождествить те вершины степени 2 в GVfcl,i, которые
инцидентны ребрам из G\ (Gfc), и ввести новую вершину х (у). Отсюда следует, что
(НХу)г уг — GVfcjlji. Перенося граневую 2-раскраску графа G на Нху, мы
можем заключить из леммы VI.60, что любая А-цепь Тн из Нху индуцирует
А-цепь Тг в Hi = (E(Gi)), i = 1, • • •, fc, так что Ti индуцирует 2-расщепление
в вершинах из Hi, которые являются точками сочленения в Нху. Если
рассматривать Т как последовательность ребер, то она также является А-цепью в
Нху и (Нху), у . Следовательно, в этом случае из существования А-цепи Т в
G следует, что Gi имеет А-цепь, индуцирующую 2-расщепление в Vi-i^v^i+i
для г = 2, ...,fc — 1, и оба графа G\ и Gk имеют А-цепь, индуцирующую
1-расщепление в Vk,i и 2-расщепление в vi,2,Vk-i,k соответственно.
Обратно, если Gi имеет описанную выше А-цепь, построенный выше граф
Нху имеет А-цепь Тн по лемме VI.60, и Тн индуцирует 1-расщепление в я и
у. Поскольку {Нху)г уг= GVfc|1,i, из этого следует, что GVfcflji также имеет
А-цепь, т.е. G имеет А-цепь, индуцирующую 1-расщепление в г^д.
Теперь предположим, что G имеет А-цепь Т, индуцирующую 2-расщепление
в г>г,г+ь г = 1,..., fc. Используя обозначения, подобные тем, которые
использовались в доказательстве леммы VI.60, мы можем выбрать ребра ei,fi,gi,hi €.
E{Gi), г = 1,..., fc, так, чтобы
ег е Еь._1ш. П ?(bd(Foo)), ft ? EVi_lti П ?(bd(Fi)),
9i € Я„м+1 П ?(bd(Foo)), Ы e EViti+1 n JS(bd(Fi));
без ограничения общности мы можем предположить, что обозначения при
определении графа G были выбраны так, что 0+(^,i+i) = (е^+1,<^,... ,Л?,
Л+1' • • •)•
Рассмотрим теперь поведение цепи Т в фиксированных Gi, 1 < г < fc.
Поскольку Т есть А-цепь, единственными переходами цепи Т, содержащими в
точности одно полуребро из Gi, являются {eJ,ftLi},{/i.fci-i}>{ft^ei+i}.{fti»/i+i}-
В силу этого и так как граф G плоский, Т не может иметь вид
1 = ..., ei, ±i, hi,..., gi, ±i , /i,... , (1J
где ВД) U ?(Г/') = E{Gi) - {eh fu gu Ы}.
Следовательно, Т должна либо иметь вид
1 =...,ei,i^ , Qi,..., hi, ±i , ji,... [2)

208
Глава VI. Различные типы эйлеровых цепей
(где {g^h[} 0 Хт, поскольку Г не индуцирует 1-расщепления в г^+i), либо
вид
1 = ..., ti, 11 , ji,..., hi, i^ , gi,... , (оJ
где JS(IT) U E(T~) = Е(Т*) U ВД**) = E{Gi) - {еи^,д{,Ы} (мы можем
предполагать без ограничения общности, что е* есть первое ребро из Gi в Т).
Таким образом, если Т имеет вид (2), то
•L г •= &г» -а г i 9ii ^i, 1 ^ , /i
является А-цепью Gi, индуцирующей 2-расщепление в каждой из вершин
Vi-i,i,Vi,i+i- Если Г имеет вид (3), то
Т+ := vx, euT*, fi,xtutiv, vt2,t2y, huT**,ghyv, (4)
где х := Vi-ij, У '•= Щ^+i и v,ti,t2 0 V(G), есть А-цепь из Gf, индуцирующая
2-расщепление в каждой из вершин v, Vi-i,i, Vi,i+i (см. рис. VI.24 с Gi вместо В).
Чтобы убедиться, что Г должна иметь вид (2) для всех, кроме одного, Gi и
что она должна иметь вид (3) для оставшегося G^, i € {1,..., fc}, мы заметим,
что Г не может иметь вид (2) для всех г = 1,..., /с; в противном случае мы
имели бы
Г = ei,T^,д1, е2,Т^Г,д2,..., ек,Тк ,дк;
т. е. Т не покрывает все E(G), поскольку {gfk, e[} Е Хт (заметим, что {д[, efi+1} E
Хт, г = 1,..., fc). Значит, мы можем заключить, что Т должна где-то
«повернуть назад», но, поскольку Т индуцирует 2-расщепление в каждой вершине
Vij+i, г = l,...,fc, этот «поворот» должен иметь место внутри некоторого
Gj, j € {1,..., fc}. Без ограничения общности мы можем предполагать, что
первый «поворот» происходит для j = fc, если Г начинается cei,zE{l,...,fc — 1}.
Значит, Т имеет вид
Г = е»,Т~,ди ..., ek-i,Tfc"_1,gk-i, ек,Т?, Д, /i^-i,^"_"i, Л-i,
^^ _ (5)
• • • »^г,Г^ ,Л,. • .,fi,hk,Tj!*,gk,ei,... ,ег-1,Ти,^_ь
Но тогда
Т~ :=е», Г/", (fc,...,efc_i, Т?_х, дк-\, ftfc-ъ Tj^[, ,„ч
_ (о)
Д-1, • • • ,Ы,Т{ , /j,..., /i, ei,..., ei_i, ^_1? <7i_i
есть А-цепь в G~ := G — Gk. Так как по определению G~ является блочной
цепью в G, если fc > 3, в то время как по предположению он 2-связен при к = 2,
то в силу леммы VI.60 для к > 3 и формулы (б) для к = 2 соответственно цепь
Г индуцирует А-цепь Т* в G*, такую, что Т^ индуцирует 2-расщепление в точках
сочленения графа G~ и в силу (б) также в вершинах vk-i,k и vkli- Кроме того,
цепь Т?", определенная как Т* в формуле (4), является А-цепью в Gj, как и
требуется в лемме.
Чтобы завершить доказательство, достаточно доказать, что если Ti
является А-цепью в Gi для г = 1,...,А:-1и если Т? является А-цепью в GjJ", о
которой идет речь в заключении леммы, то G имеет А-цепь.

VI.3. А-цепи в плоских графах
209
Определим G~, как выше, и применим лемму VI.60 к G~. В результате мы
получим А-цепь Т~ в G-, которая индуцирует 2-расщепление и в Vk-i,k> и в
Vk,i- Выбрав те же обозначения для определения А-цепи Х^ в G^, что и выше,
мы можем выписать цепь Т~, как в (6), и Г^", как в (4) (заменив индекс г на
индекс к). Такую цепь Т, как цепь в формуле (5), можно теперь получить,
вставив в (б) соответствующую подцепь из (4), и это будет А-цепь в G. Лемма
VI.64 доказана.
На самом деле лемму VI.60 можно обобщить, но лишь в одном направлении.
Это обобщение является естественным обобщением упр. IV. 1.с), но тоже только
в одном направлении.
Лемма VI.65 (cM.[REGN76a, Lemmal.4]). Если связный плоский эйлеров граф
G имеет А-цепь, то в каждом его блоке есть А-цепь.
Доказательство леммы VI.65 и построение примера, показывающего, что
обратное утверждение к утверждению леммы VI.65 не выполняется, мы
оставляем читателю в качестве упражнения.
Прежде чем мы обратимся к построению планарного 3-связного эйлерова
графа без А-цепей, мы должны изучить А-разбиения. Для этого введем
несколько понятий.
Определение VI.66. Пусть Fi,...,Fm, т > 1, суть т различных граней
плоского эйлерова графа с заданной граневой 2-раскраской, такие, что i^,
г = 1,...,т, является 5-гранью для фиксированного 5 G {1,2}.
Предположим, что существуют различные вершины ^i,2, ^2,з>-• • >^т,ь гДе vi,i+i €
bd(Fj) П bd(i^+i), г — 1,..., т (где нижние индексы надо понимать по модулю
т). Тогда мы назовем R = {Fi,..., Fm} одноцветным кольцом граней
графа G, a Lr := {^1,2, • • • ,%д}-полным множеством связей этого кольца
(если т = 2, то vi^ ф Щ,\)-
Следующие результаты связывают А-разбиения с кольцами граней и
полными множествами связей (см. [FLEI74a, Theorem 1, Corollary 1]).
Теорема VI.67. Пусть G есть 2-связный плоский эйлеров граф без вершин
степени 2 с граневой 2-раскраской, и пусть {Vi,^} —разбиение множества
V(G). Тогда следующие утверждения эквивалентны:
(1) в G есть А-цепь, которая индуцирует А-разбиение {Vi,^};
(2) пусть R — любое одноцветное кольцо граней графа G и Lr — произвольное
полное множество связей кольца Д; тогда если элементы из R являются
5-гранями, то Lr <?. V$, 6 G {1, 2}.
Кроме того, если мы в (1) заменим «А-разбиение» на «совершенное
А-разбиение», а в (2) заменим «Lr ? V$» на «V\ ~? Lr <?. V2», то эти
более сильные утверждения также будут эквивалентны.
Доказательство. (1) влечет за собой (2). Предположим, что Lr С Vs,
5 G {1,2}, для некоторого одноцветного кольца граней R графа G,
элементы которого являются 6-гранями, и некоторого полного множества связей Lr.

210
Глава VI. Различные типы эйлеровых цепей
Можно без ограничения общности предполагать, что 6=1. Мы утверждаем,
что Н := Glra несвязен.
Поскольку R — одноцветное кольцо граней графа G и 5 = 1, существуют
различные 1-грани Fi,..., Fm графа G, такие, что
R = {Fi,..., Fm}, 0 ф bd(F,) П bd(Fi+1) С V{G), г = 1,..., m,
и по определению
LH П (bd(Fi) П bd(Fi+i)) = Ki+i}, i = 1,..., m.
Пусть теперь Сг С i*i Ubd(Fi) —простая незамкнутая кривая, такая, что С* П
bd(Fi) = {г>г-1,г, ^,-u+i}. Тогда С = \Ji=i ^г~простая замкнутая кривая.
Поскольку Fi является 1-гранью, г = 1,... ,т, С содержит и внутри себя (в ор-
ганиченной области кривой С), и вне (в неограниченной области кривой С)
положительное четное число открытых ребер из EVii+1, г = 1,...,га (в
противном случае С{ и C^+i лежали бы в гранях разных цветов или выполнялось
бы равенство Ci = Сг+ъ откуда следовало бы, что Fi = i*i+i)- Кроме того, по
предположению CC]G = LrCVi.
Без ограничения общности мы можем предположить, что обозначения
выбраны так, что при 0+(viti+i) = (ei,e2, • •. ?е^), d* = d(t^,i+i) > 2 внутри
кривой С лежат именно открытые ребра ei, ег,.. •, eni. Тогда из предыдущего
абзаца следует, что 2 < щ = 0(mod2) и di — щ > 2. Далее, мы можем
произвести 1-расщепление в вершине г>г,г+ь i — 1, • • •, тп, так, что г/1), ..., у^ш^ все
целиком лежат внутри С, а г/т*+1),..., v^ лежат целиком вне С, где га* = |пг
и ki = \&i (см. рис. VI.18). Следовательно, так как С П G = L# С Vi, то мы
можем заключить, что Н несвязен.
Поскольку Н несвязен и Lr С Vi, граф Gvi,i несвязен и, далее, несвязен
граф (Gv1,i)v2,2- С другой стороны, так как {Vi, V2} есть А-разбиение,
соответствующее А-цепи Т графа G, такое, что V$ содержит в точности те вершины,
в которых Т индуцирует 5-расщепление, 5 = 1,2, то (Gvui)v2,2 — цикл (ср. со
следствием VI.57). Это противоречие доказывает, что из (1) следует (2).
(2) влечет за собой (1). Рассмотрим Н = (Gv1,i)v2,2- Это 2-регулярный
граф. Если Н связен, то, согласно следствию VI.57, {Vi, V2} есть А-разбиение,
полученное из некоторой А-цепи Т, индуцирующей 5-расщепление в точности
в элементах из V$, 5 = 1,2. В этом случае доказываемое утверждение
справедливо. Следовательно, предположим, что Н несвязен. Выберем Vo С V(G) столь
малым, сколь это возможно, так, чтобы Hq := (Gy',i)v",2 был несвязным, где
Vq = Vo П Vi, Vq = Vo П V^. Отсюда следует, что Но имеет грань Fq, такую, что
bd(Fo) несвязна; без ограничения общности можно считать Fo неограниченной
гранью графа Но. Кроме того, так как мы не делали никаких предположений
относительно граневой 2-раскраски графа G, мы теперь можем предполагать,
что Fo есть 1-грань.
Далее, если Vq ф 0, рассмотрим w € vf0. Мы утверждаем, что уже
Hi := (Gv^^v^'-iw}^ обладает несвязной границей грани (откуда следует, что
Hi несвязен). Действительно, Hq = (#i){™},2 и по определению 5-расщепления,
6 ? {1,2}, 1-грани графа Hi (гомотопически) инвариантны относительно
применения 2-расщепления к некоторой вершине этого графа (см. подстрочное

VI.3. А-цепи в плоских графах
211
примечание в конце определения VI.54), т.е. bd(Fo) несвязна уже в Hi. Это
противоречит выбору множества Vq. Следовательно, V? = 0 и, таким образом,
Vo С Vi. Снова в силу выбора Vo и в силу связности графа G имеет место
включение Vo С Vp0 для Vp0 := У((Е(Ъ<1(Ро)))с), так как из включения Vo С Vi и
несвязности графа Щ следует несвязность внешней грани графа GV0nvFo,i-
Рассмотрим Ci, связную компоненту границы bd(Fo), и пусть Сг :=
bd(Fo) — Ci. Пусть С —простая замкнутая кривая, лежащая в F0 и такая,
что intС D Hi, extС D Но — Hi, где Hi — связная компонента графа Но,
такая, что Hi э С±. В силу выбора Vo для каждой вершины v ? Vo
некоторые из вершин v^ лежат в int С (т.е. в Hi), а некоторые —в ext С (т.е.
в Но — Hi), г = 1,.. .^dc(v); в противном случае С П GvQ-{v},\ — ® и
int С П Gv0-{v},i ф 0 Ф ext С П GV0-{v},i Для некоторой вершины v ? Vo. Без
ограничения общности мы можем предполагать, что С инвариантна
относительно перехода от Но к G, рассматриваемого как топологическая процедура
(т.е. предполагать, что С —простая замкнутая кривая и в G тоже; ср. с рис.
VI. 18), и С П G = Vo, а (С - V0) П F^ = 0 для любой 2-грани F^ графа G.
Так как С П G = Vo, то мы можем представить Vo следующим образом:
Vo = {vi,2,^f3,...,vmji}, (ii)
где вершины Vi-ij и v^i+i делят С на две простые незамкнутые кривые С[
и С", такие, что Сг' П Vo = {г>г-1,г, Vi,t+i}- Кривая Сг' - {^-1,г, ^м+i} лежит в
однозначно определенной 1-грани; обозначим ее Fi, i = 1,..., га. В силу выбора
множества Vo
Fi ф Fj для i ф j, 1 < i,j < га, (г2)
и
bd(Fi) П bd(Fj) ф 0 тогда и только тогда, когда |г - j\ ? {1, m — 1}, (г3)
где
bd(Fi) П hd(Fi+i) = {г^+i} (мы считаем, что га + 1 = 1). (г4)
В противном случае можно нарисовать на плоскости простую замкнутую
кривую С", такую, что C~C\F^ = 0 для любой 2-грани графа G, C~nG = V?~ С Vo
и (С~ — VJ)"") П ^ = 0 для хотя бы одного, но не для всех г ? {1,...,т}.
Используя соображения, аналогичные тем, которые применялись при
доказательстве того, что из (1) следует (2), можно показать, что эти свойства кривой
С~ гарантируют несвязность графа G^- Л • Следовательно, если имеет место
(ii) — (и), то R = {Fi,..., Fm} является одноцветным кольцом граней, a Vo —
полным множеством связей этого кольца. Поскольку R состоит из 1-граней и
И) Q Vi, утверждение (2) выполняться не может. Следовательно, Н должен
быть связным.
Чтобы завершить доказательство теоремы, предположим теперь, что
А-разбиение из утверждения (1) является совершенным и что в (2) множество
Lr удовлетворяет более сильному условию Vi ^ Lr <?. Vz. Будем обозначать
соответствующие утверждения через (1') и (2/).
Если {Vi,V?} — совершенное Л-разбиение, то по определению (Gy1,i)v2,2
является циклом (который соответствует цепи Т) и, значит, (Gv2,i)vi,2
—тоже цикл. Через Г* обозначим Л-цепь в G, соответствующую этому второму

212
Глава VI. Различные типы эйлеровых цепей
циклу, и положим Vi := V2, V% '= V\- Поскольку (1) влечет за собой (2),
двукратное пременение этой импликации дает соотношения V? ^ Lr <?. Vs для
любого одноцветного кольца граней R и любого полного множества связей Lr.
Таким образом, Lr <? Vs, 5 = 1,2. Значит, (1/) влечет за собой (2'). Заметим,
что {Vs,V?} = {14)^2} независимо от выбора 6 € {1,2}. Следовательно, нам
не надо указывать цвет элементов одноцветного кольца граней R.
Предположим, что выполняется (2'). Определим V^*, как выше.
Поскольку из (2) следует (1), из доказательства этого факта мы получаем, что и
(Gvi,i)v2l2, и (Gv*,i)v2*,2 = (GV2li)vlf2 являются циклами, т.е. {Vi,V2} —
совершенное А-разбиение. Теорема VI.67 полностью доказана.
Эта теорема показывает, что граф Gs = (Vs) С G, 5 = 1,2, где {Vi, V2} есть
А-разбиение и G удовлетворяет предположениям теоремы, должен обладать
очень специальной структурой. Чтобы ее выяснить, рассмотрим
произвольный цикл С из G, который не является границей грани. Тогда и int С, и ext С
содержат (открытые) ребра графа G (здесь мы рассматриваем С как простую
замкнутую кривую на плоскости). Кроме того, и int С, и ext С содержат также
1-грани и 2-грани. В частности, каждое ребро е € Е(С) принадлежит
некоторой границе bd(F«5), где Fs есть J-грань, 5 = 1,2. Следовательно, рассматривая
R6 = {Fs\E{hd(Fs)) П Е(С) ф 0, F5 есть 5-грань}, 5 = 1,2,
мы получаем, что Rs — одноцветное кольцо граней с полным множеством
связей LR С V(C), 5 = 1,2. Согласно теореме VI.67, V(C) <? V5 и, значит, С <? Gs,
5 — 1,2. Поэтому
если Gs содержит цикл К, то К — граница некоторой 5-грани. (*)
Если мы предположим, что G — плоский эйлеров граф с «(G) = 1 и,
возможно, вершинами степени 2, наделенный граневой 2-раскраской, то утверждение
(*) для него верно. Действительно, А-цепь в G индуцирует А-цепь в каждом
блоке графа G (см. лемму VI.65) и любой цикл из Gs обязательно содержится
в некотором блоке графа G. Кроме того, если цикл С С G содержит вершину
степени 2 графа G и не является гранью 5-грани, то, как и выше, можно
построить одноцветное кольцо граней Rs с Lr С {v e V(C)\<Ig(v) > 2} в качестве
его полного множества связей, 6 е {1,2}. В этом случае Lr <? Vs, 5 € {1,2}, по
теореме VI.67; следовательно, (Lr)c ? Gs и, кроме того, С ? Gs-
Подводя итог этих рассуждений, мы приходим к следующему результату
[REGN76a, Satz 2.1].
Следствие VI.68. Если Т — некоторая А-цепъ связного плоского эйлерова
графа G с заданной граневой 2-раскраской и если {Vi, V2} — соответствующее
А-разбиение графа G, то Gs = (Vs) содержит, некоторый цикл С, только если
С является границей 8-грани, 6 ? {1,2}.
Отметим, однако, что графы G\ и G2 не обязательно связны. Этот факт
продемонстрирован на рис. VI.29. Кроме того, утверждение, обратное к
следствию VI.68, неверно, даже если Gs ацикличен. Другими словами, граф G
может иметь вершинное разбиение {Vi, Vi}, такое, что Gs = {Vs) ацикличен, но
не иметь А-цепи. В этом можно убедиться, рассмотрев граф Go на рис. VI.26.
Мы оставляем это читателю в качестве упражнения.

VI.3. А-цетт в плоских графах
213
^
"1
1С
Ц
Л
а)
Ь)
с)
Рис. VI.29. а) Четырехугольная антипризма Я, Ь) А-цепь Т в Н и с) подграфы,
индуцированные А-разбиением, соответствующим цепи Т. Заметим, что Н 4-однороден
и помимо двух четырехугольных граней имеет только треугольные.
Следующий результат, однако, показывает, что результат, обратный к
лемме VI.68, верен, если граф Gs связен. Но чтобы это установить, нам
понадобятся некоторые результаты об одноцветных кольцах граней.
Рассмотрим одноцветное кольцо граней R = {i*i,i<2,... ,Fm}, m > 2,
2-связного плоского эйлерова графа G с граневой 2-раскраской. Пусть
bd(Fi) nbd(Fj) = 0 для \i-j\>l, 1 < м < m,
за исключением случая {i,j} = {1,га}.
(*)
Поскольку G является 2-связным, bd(Fj) —цикл для г = 1,...,га. Выберем
обозначения, как в доказательстве теоремы VI.67. Пусть Lr — полное
множество связей. Сопоставим ему простую замкнутую кривую С = C(Lr), как в
первой части доказательства теоремы VI.67, где С = Ц™ i Cu Ci С F* и CflG = Lr.
Разумеется, С зависит не только от выбора кривых С* С F*, но в большей
степени от выбора множества Lr, которое определено однозначно тогда и только
тогда, когда |bd(i^) П bd(Fi+i)| = 1, г = 1,..., га (например, когда G является
3-связным). Среди всех возможных выборов для Lr и соответствующей
кривой C(Lr) остановимся на таких LR и Со = C(LR), чтобы для любого полного
множества связей L'R выполнялось условие
int С0П1/Я = 0.
(**)
Заметим, что если bd(i^) Dbd(Fi+i) D {^M+b^i+i}' т0 из любого полного
множества связей L'R, такого, что i^+i € L'R, можно получить другое полное
множество связей, полагая L*R = (L'R — {v^i+i}) U {v*i+1}. Отсюда следует,
что выбор LR и Со, удовлетворяющих условию (**), возможен. Заметим, что
множество LR определено однозначно. Аналогично, пусть LR — однозначно
определенное полное множество связей, такое, что С\ = C(RR ) и
ext С\ П LR = 0 (* * *)

214
Глава VI. Различные типы эйлеровых цепей
для любого полного множества связей L'R. В силу (*) и 2-связности графа G
существуют циклы Co,Ci С G, задаваемые формулами
m 77i
Со := U<intCbn??(bd(Ji))>, d := (J(extCi nB(bd(F0)>. (****)
г=1 г=1
Теперь мы можем представить еще один результат из диссертации С. Регнер
(см. [REGN76a, Satz 2.2]). Ее исходное доказательство содержит
незначительный дефект; представленное здесь доказательство в деталях заметно
отличается от него.
Следствие VI.69. Рассмотрим разбиение вершин {VI, V2} плоского 2-связ-
ного эйлерова графа G с граневой 2-раскраской. Если Gs := (Vs), 6 = 1,2,
связен и если каждый цикл из Gs есть граница 5-грани, то {Vi, V^} есть
А-разбиение.
Доказательство. Ввиду теоремы VI.67 достаточно показать, что если
элементы каждого одноцветного кольца граней Д являются 5-гранями, то Lr % V$
для каждого полного множества связей Lr, 5 Е {1,2}.
Будем действовать следующим образом. Выберем одноцветное кольцо
граней Д с минимальным | Д |, элементы которого суть 5-грани, такое, что Lr С V$
для некоторого полного множества связей Lr, 6 ? {1,2}; предположим без
ограничения общности, что 5=1. Выпишем явно Д = {Fi,... ,Fm},m > 2, и
Lr = {^1,2, • • • ,Vm,i}- Мы имеем bd(Fi)nbd(Fj) = 0 для \i—j |> 1, 1 < г, j < m,
за исключением {i,j} = {l,m}; это следует из выбора Д.
Теперь выберем кривую С{, 1 < г < ш, и определим простую замкнутую
кривую С, такую, что С f)G = Lr С Vi, как и в первой части доказательства
теоремы VI.67. Поскольку С nG = Lr С Vi и G2 связен, то
либо int CnV2 = 0, либо ext CnV2 = 0,
ибо, применив теорему о жордановой кривой, получим, что каждый путь
Р(х,у) в G, соединяющий х € int С с у € ext С, удовлетворяет условию
Р(х,у) DLr^ 0. Без ограничения общности можно считать, что
intCnV2 = 0. (1)
Используя рассуждения, предшествующие формулировке следствия VI.69, и
равенство (1), мы можем даже допустить, что Lr и С были выбраны так, что
Lr = L^ и С = Со, а значит, удовлетворяют (**). Пусть Со—цикл,
определенный в (****). По (1) и определению Со и поскольку по предположению
Lr С Vi, мы заключаем, что Со С (Vi). Теперь, поскольку каждое ребро из
Со есть граничное ребро некоторого элемента из Д и некоторой 2-грани и
поскольку Д содержит, самое меньшее, два элемента, Со не может быть границей
1-грани. Это противоречие с предположением завершает доказательство
следствия.
Значит, применив следствия VI.68 и VI.69, можно заключить, что разбиение
{Vi,V2} множества V{G), где G есть 2-связный плоский эйлеров граф,
является совершенным А-разбиением, только если (Vi) и (У2) ациклические, а если
(Vi) и (V2)—деревья, то это разбиение является совершенным А-разбиением.

VI.3. А-цепи в плоских графах
215
Заметим, что А-разбиение графа на рис. VI.29 совершенно, но
соответствующие графы (VI), (V2) суть оба несвязные леса, тогда как граф на рис. VI.26,
хотя и не имеет А-цепей, но допускает такое разложение множества вершин
(см. упр. VI.20). Заметим, что граф на рис. VI.29 имеет только две 4-угольные
грани, а другие его грани треугольные.
Однако, если G — эйлерова триангуляция плоскости, вершинное разбиение
{V^, V2} индуцирует ациклические подграфы (Vi),(l^) тогда и только тогда,
когда эти подграфы суть деревья (см. предложение III.63). Итак, мы пришли
к следующему результату.
Теорема VI.70. Разбиение вершин {Vi, V2} эйлеровой триангуляции
плоскости является совершенным А-разбиением тогда и только тогда, когда (Vi)
и 0^) суть деревья.
Мы можем переформулировать теорему VI.70, не используя понятия
А-разбиения или совершенного А-разбиения соответственно. Чтобы убедиться
в этом, рассмотрим следствия VI.68 и VI.69 для случая эйлеровой
триангуляции плоскости. Тогда эти два следствия взаимно обратны, ибо если (Vi)
несвязен, то (Vj) имеет цикл, не являющийся границей грани (см. предложение
111.63 и [FLEI74a, Corollary 2]), {г, j} = {1,2}.
Пусть теперь D — эйлерова триангуляция плоскости, заданная вместе с ее
граневой 2-раскраской; предположим, что D имеет А-цепь Т и {Vi,V^}
—разбиение вершин, соответствующее Т. Предположим, что (Vs) содержит цикл
Л, 5 € {1,2}; Д есть (треугольная) граница 5-грани по следствию VI.68.
Положим Е(А) = {ei,ег,ез}. По определению Т индуцирует 5-расщепление во всех
вершинах из V(A), т. е. {{е^, е^}, {е^, е^}, {ез, е'{}}Г\Хт — 0. Другими словами,
любые два ребра из Л не являются последовательными в Т. Мы скажем, что Т
разделяет ребра границы Л. Аналогично, мы назовем А-цепь Т неразделя-
ющей, если Г не разделяет ни одну границу грани в D. С другой стороны, если
Т разделяет ребра некоторой границы грани из D, соответствующий граф (Vs)
содержит цикл (являющийся треугольником). Значит, мы можем
переформулировать теорему VI.70 следующим образом.
Теорема VI.70.а. Для разбиения вершин {Vi,T^} эйлеровой триангуляции
плоскости D следующие утверждения эквивалентны:
1) (Vj) есть дерево для г = 1,2;
2) D имеет неразделяющую А-цепь.
Заметим, что для определения неразделяющей А-цепи не обязательно
начинать с граневой 2-раскраски; можно начать также и с разбиения вершин
{У+, У~}, связанного с 0+(Г>), 0~(D) соответственно (см. лемму VI.53).
Теоремы VI.70 и VI.70.a хорошо известны. Мы знаем, что 2-связный
плоский кубический граф Сз имеет гамильтонов цикл тогда и только тогда, когда
двойственный к нему граф D = D(Gz) имеет такое разбиение вершин {Vi, V2},
что оба графа (Vi) и (V2) суть деревья (лемма III.74). А если Сз также
двудольный, то D = D(Gs) —эйлерова триангуляция плоскости, причем D имеет
кратные ребра тогда и только тогда, когда /с(Сз) = 2. Значит, мы пришли к
следующей эквивалентности относительно гамильтоновых циклов и А-цепей
[FLEI74a, Theorem 2].

216
Глава VI. Различные типы эйлеровых цепей
Теорема VI.71. 2-связный плоский кубический двудольный граф имеет га~
милътонов цикл тогда и только тогда, когда двойственный к нему граф
имеет неразделяющую А-цепь.
Существует много прямых доказательств теоремы VI.71. Наилучшее,
насколько я знаю, до сих пор не опубликованное, доказательство я приписываю
Татту1). Поскольку оно элегантно и относительно кратко, мы изложим его
подробно (суть доказательства принадлежит Татту, изложение — автору).
Доказательство Татта теоремы VI.71. Пусть Н — гамильтонов цикл
2-связного плоского кубического двудольного графа G$. С топологической
точки зрения Н представляет собой простую замкнутую кривую на плоскости,
такую, что некоторые открытые элементы множества L := E{G%) — Е{Н)
лежат в extiif, а некоторые в intif. Запишем Н как последовательность
ребер, Н = ei,e2,.. • ,e2fc, обозначим через s(ej) точку открытого ребра
е^, j — 1,..., 2/с, и построим простую замкнутую кривую С следующим
образом: для г = l,...,fc пусть Сч%-\ —простая открытая кривая, соединяющая
s(e2i-i) и s(e2i), такая, что
C2i-i - {s(e2i-i),s(e2i)} С int#
(и лежащая достаточно близко к секции цикла Н, содержащей вершину,
инцидентную e2i-i,e2i). Аналогично, для г = 1,..., к пусть С2г — простая открытая
кривая, соединяющая s(e2i) и s(e2i+i), такая, что
C2i - {s(e2i),s(e2i+i)} С ext#,
(мы полагаем e2k+i = е\). Без ограничения общности можно считать, что
I Cj П е \< 1 для е G L и j = 1,..., 2к. Кривая
2к
обладает следующим свойством: каждое е G E(Gs) имеет в точности одну
общую точку с С: для е Е Е(Н) это следует из определения кривой С, а для е Е L
это следует из неравенства |Cj-ne| < 1 и того факта, что Сз —двудольный граф:
заметим, что е — ху делит Н на два пути Р\ (я, у),Р2(х, у) так, что Pi (ж, у) U{e}
и Р2(х, у) U {е} суть четные циклы, и при обходе по С, если некоторая вершина
из Н лежит слева от С, то следующая вершина из Н лежит справа от С.
Для каждого j E {1,...,2/с} существуют грани Fj и F" из Сз, такие, что
Cj HF- ф0ф Cj П Fj и CjDF = 0 для каждой грани F Ф F-, Fj'
и
Fj ф Fj\ если и только если Cj Г)еф 0 для некоторого е Е L.
х) Я не уверен, что Татт знает, что я знаю о том, что это доказательство принадлежит ему,
но его доказательство составляет сущность критики подхода к А-цепям, представленного
в [FLEI74a]; когда первоначальная рукопись была возвращена мне вместе с замечаниями
рецензентов, имя Татта было недостаточно хорошо стерто. Тем не менее я решил
придерживаться представленного здесь и ранее в [FLEI74a, REGN76a] подхода, ибо он оказался
достаточно плодотворным, и теория А-цепей, развитая до сих пор, возможно, будет
полезной для доказательства гипотез об А-цепях, сформулированных ниже.

VI.3. А-цепи в плоских графах
217
Это следует из предыдущего абзаца. Далее мы выберем точку v'j ? CjDFj и
точку vfj ? CjOFj', причем Vj = v'j, если и только если Fj = Fj'. Объявив элементы
множества Vr := {vpVj\j = 1,..., 2/с} вершинами, мы превратим С в плоский
(в смысле теории графов) цикл Т, открытые ребра которого — в точности
(топологические) связные компоненты из С — Vr- По построению каждое ребро
из Т имеет общую точку точно с одним ребром из Сз, и наоборот; эти точки
определены однозначно. Также по построению для каждой грани F из Сз
существует топологический диск К С F, такой, что КГ\С = {х ? VtHF}. Значит,
для каждой грани F из Сз мы можем стянуть К в точку vp таким образом, что
ни одна пара открытых ребер ни в какой деформации цикла Т (возникшей во
время процесса сжатия) не пересечется. Следовательно, поскольку Т —
плоский цикл (и, значит, может рассматриваться как А-цепь в самом себе), он
преобразуется в А-цепь графа D, вершины которого суть полученные выше точки
vf, а открытые ребра взаимно однозначно соответствуют связным
компонентам из С — Vt- Эта А-цепь графа D на самом деле является неразделяющей
потому, что Н — гамильтонов цикл графа G%. По построению Т и D имеется не
только биекция между vp ? V(D) и гранями F графа (?з, но выполняется еще
такое условие: для любых граней F' ,F" из G$ мы имеем ев — vf>vf" E E{D)
тогда и только тогда, когда существует е G E(hd(F')) П E(bd(F")) и связная
компонента из С — Vr, соответствующая е^>, имеет в точности одну общую с е
точку. Это, однако, и показывает, что D двойствен к G3.
Обратно, предположим, что D = D(G?) имеет неразделяющую А-цепь Тр>.
Рассмотрим цикл Т, полученный из Try соответствующим расщеплением
каждой вершины v € V(D) в \d(v) вершин vp степени 2, принадлежащих грани
F графа Сз, для которой v ? F. По построению каждое открытое ребро из
Т пересекает точно одно открытое ребро из Сз точно в одной точке, и
наоборот. Значит, для плоской простой замкнутой кривой С, соответствующей Т, мы
имеем С П е = {5(e)} для каждого е ? E{G$). Кривая С соответствует
плоскому циклу С с V(C) = {s(e)|e ? .Е(Оз)}, такому, что ребра из С соответствуют
связным компонентам из C — V(C). По этой причине и так как цепь Td неразде-
ляющая, для каждой вершины v ? V(G), если Ev = {ev, fv,gv} C E(Gs), то, без
ограничения общности, либо s(ev)s(fv) ? Е{С) и s(ev)s(gv),s{gv)s(fv) 0 Е(С),
либо s(ev)s(gv),s(gv)s(fv) ? Е(С) и s(ev)s(fv) 0 Е(С). Определим теперь Н
условием Е(Н) = {ev,fv\v ? V(G)}. По определению Н есть 2-однородный
остовный подграф в (?з, и поскольку С —простая замкнутая кривая, такая,
что С П е = {s(e)} для каждого ребра е ? E(Gs), граф Н связен. Значит, Н —
гамильтонов цикл в G3. Это завершает доказательство.
VI.3.1. Двойственность между А-цепями в плоских эйлеровых
графах и гамильтоновыми циклами в плоских кубических графах
После доказательства теорем VI.70, VI.70.а и VI.71 становится ясно, что
существует тесная связь между А-цепями в связных плоских эйлеровых графах
(соответственно в эйлеровых триангуляциях плоскости, что точнее) и
гамильтоновыми циклами в связных планарных кубических двудольных графах.

218
Глава VI. Различные типы эйлеровых цепей
03-{а.Ь.}
а)
Ь)
Рис. VI.30. а) Наименьший 2-связный плоский кубический двудольный негамиль-
тонов граф. Ь) Заменяя для г = 1,2,3 двуугольники (di,bi) в а) на <2з — {йг,&г}5
получим наименьший такой граф, который является обыкновенным.
Конечно, не каждый планарный 2-связный кубический двудольный граф
имеет гамильтонов цикл1). Граф на рис. VI.30a) является таким примером;
мы оставляем в качестве упражнения доказательство того факта, что это
действительно наименьший такой пример и что он однозначно определен. Если
заменить каждый двуугольник этого графа экземпляром 3-мерного куба <Эз
без одного ребра, то получится обыкновенный 2-связный плоский кубический
двудольный граф, который не является гамильтоновым (см. рис. VI.20(b)).
Независимо и почти одновременно было показано в [РЕТ081а] и [ASAN82a], что
этот обыкновенный граф представляет собой действительно наименьший из
примеров этого типа и что он определен однозначно.
Однако интерес к гамильтоновым циклам в плоских кубических
двудольных графах возник не из эквивалентности с А-цепями в эйлеровых триангу-
ляциях плоскости, сформулированной в теореме VI.71. Напомним, что Тэйт,
доказав, что проблема четырех красок эквивалентна предположению, что
каждый планарный 2-связный кубический граф имеет 1-факторизацию, высказал
предположение, что каждый планарный 3-связный кубический граф
гамильтонов (см. [KONI36a, p. 27-28]). Эта гипотеза, сформулированная в 1880 г. и
направленная на легкое доказательство проблемы четырех красок, была
опровергнута в 1946 г. Таттом, который предположил, в свою очередь, что если в
предположении Тэйта заменить «планарный» на «двудольный», то графы бу-
*) По контрасту со случаем А-цепей существование гамильтонова цикла не зависит от
конкретного вложения. С другой стороны, планапный кубический двудольный граф Сз имеет
гамильтонов цикл, если и только если для каждого плоского вложения Яз графа Gz орграф
D(Hz) имеет неразделяющую А-цепь (теорема VI.71). Это интересный факт, ибо в случае,
когда k(Gz) — 2, для двух вложений Н'Ъ,Н'Ъ' графа G3 может иметь место соотношение
D(H'3) ф. D(Hg).

VI.3. А-цепи в плоских графах
219
дут гамильтоновыми [TUTT71a]. Дж. Д. Хортон опроверг предположение Тат-
та; его первый контрпример содержал 96 (!) вершин (позднее он нашел пример
с 92 вершинами [HORT82a]). Позже М.Н. Эллингэм построил контрпример с
78 вершинами, а в совместной работе Эллингэм и Хортон построили
контрпример к гипотезе Татта с 54 вершинами (по поводу исходного графа Хортона
см., например, [BOND76a]; по поводу других контрпримеров и других
деталей см. [ELLI82a, ELLI83a]). Недавно Дж. Р. Джорджес и А. К.Кельманс
получили контрпримеры с 50 вершинами, которые циклически 4-реберно-связны
[GEOR89a, КЕЬЪШа]1).
Следующее предположение обычно приписывается Д. Барнетту. Согласно
частному сообщению Татта 1972 г., он также думал о нем. Следовательно, мы
можем назвать это предположение гипотезой Барнетта—Татта (ГБТ).
Гипотеза VI.72 (ГБТ). Каждый планарный 3-связный кубический
двудольный граф гамильтонов.
С учетом теоремы VI.71 ГБТ эквивалентна следующему предположению
(заметим, что двойственным графом к планарному 3-связному кубическому
графу является обыкновенная триангуляция плоскости, и наоборот).
Гипотеза VI.73. Каждая обыкновенная эйлерова триангуляция плоскости
имеет неразделяющую А-цепъ.
Хотя следующее предположение кажется слабее, чем гипотеза VI.73, они на
самом деле, эквивалентны [FLEI74a].
Гипотеза VI.74. Каэюдая обыкновенная эйлерова триангуляция плоскости
имеет А-цепъ.
Эквивалентность между последними двумя гипотезами (и, значит, между
гипотезами VI.74 и ГБТ) вытекает из следующего результата. Здесь мы
рассматриваем две эйлеровы триангуляции плоскости Do иД, которые связаны
друг с другом следующим образом. Для каждой границы грани Л = (а&, 6с, со)
из Do берем экземпляр плоского октаэдра минус граница внешней грани
Д0 = (а,Ь,с), вкладываем его внутрь Л и отождествляем соответствующие
вершины а, 6, с (см. рис. VI.31).
Лемма VI.75. Пусть Do —эйлерова триангуляция плоскости, и пусть D\
получена из Do описанным выше способом. Тогда следующие утверждения
эквивалентны:
1) Do имеет неразделяющую А-цепь.
2) Di имеет А-цепь.
Доказательство. Предположим сначала, что Do имеет неразделяющую
А-цепь и применим теорему VI.70.а, в силу которой мы можем записать
V(D0) = Vi U V^°, так что (1^°) —дерево, г — 1,2. Далее, рассмотрим
произвольную грань F из Do, скажем V(bd(F)) = {а,Ъ,с}. Поскольку (V®) —
1^ На эти две статьи обратил мое внимание Х.Гропп. Как он отмечал в [GROP89a],
двудольные кубические графы обхвата > б изучались еще в 1887 г., но в терминах объектов,
которые потом стали называть «симметричными конфигурациями».

220
Глава VI. Различные типы эйлеровых цепей
D0 H0 D,
Рис. VI.31. Получение эйлеровой триангуляции плоскости D\ из эйлеровой
триангуляции плоскости Do вложением в каждую грань триангуляции Do экземпляра
графа Яо (на рисунке показана эта операция только для одной грани).
дерево, г = 1,2, мы имеем V? П V(hd(F)) ф 0 ф У2° П V(hd(F)). Значит, без
ограничения общности мы можем записать а, 6 Е V^, с Е V^0, где {j, /с} = {1,2}.
Присоединим с\ к К° и ai,&i к Vjr?. Таким расширением множеств V^1 и V^0,
произведенным для каждой грани F из Do, мы получим разбиение вершин
{V]1,!^1} в D\. Из построения этого разбиение следует, что (V^1) и (V^1)
ацикличны, а значит, это деревья. По теореме VI.70.а Di имеет (неразделяющую)
А-цепь.
Обратно, если Di имеет А-цепь, то по следствию VI.68 соответствующее
А-разбиение {V/, V^1} обладает тем свойством, что (V^1) и (V^1) содержат цикл,
только если он является границей грани в D\. Значит, мы заключаем, что
если V? := V(D0) П V?, У2° := V(D0) П V2\ то {V?) и (У2°) не имеют циклов.
По предложению III.63.1) и теореме VI.70.а Do имеет неразделяющую А-цепь.
Значит, лемма верна.
Эквивалентность между гипотезами VI.73 и VI. 74 следует теперь из
леммы VI.75, поскольку они сформулированы для всех обыкновенных эйлеровых
триангуляции плоскости и D\ является обыкновенным тогда и только тогда,
когда Do является обыкновенным (заметим, что Do С D\).
Эквивалентность между этими двумя гипотезами соответствует, однако,
аналогичной эквивалентности в двудольных кубических графах.
Действительно ГБТ эквивалентна утверждению, что каждый планарный 3-связный
кубический двудольный граф имеет доминирующий цикл. Доказательство этой
эквивалентности аналогично доказательству леммы VI.75 в терминах теории
кубических графов; мы оставляем его поэтому в качестве упражнения.
В [FLEI74a] сделано предположение, что каждый планарный S-связный
эйлеров граф имеет А-цепь (следует заметить, что в этом случае нет
необходимости говорить о плоских графах, поскольку изменение вложения либо оставляет
инвариантным 0+(v), либо меняет 0+(v) на 0~(v) для каждой вершины v).
Это предположение, если оно верно, немедленно доказывает гипотезу VI.74,
поскольку обыкновенная триангуляция плоскости, отличная от К$, 3-связна.

VI.3. А-цепи в плоских графах
221
Xi-1 *?
Рис. VI.32. Граф Щ.
Чтобы построить планарный 3-связный эйлеров граф без А-цепи, как это
делала С. Регнер, можно использовать способ, подобный описанному выше
построению D\ из Д>
Начнем с негамильтонова плоского 3-связного кубического графа Сз;
такие графы существуют (см. с. 93). Рассмотрим двойственный к нему граф
D := D(Gz) и обозначим нечетные вершины графа D через v\, v2,..., v2k-i>^2fc5
k > 1. Рассмотрим множество путей Р := {Pi,2, • • • 5-p2fc-i,2fc}5 такое, что
P2j-i,2j соединяют V2j-i и V2ji 1 < J < к (см. следствие V.3).
Для произвольного, но фиксированного j, 1 < j < к, положим
Р' \- P2j-l,2j = Хо,ЖоЖ1,Х1,... ,Xt-lXuXu Где {x0,Xt} = {V2j-l,V2j},
и для г = l,...,t пусть уг означает одну из двух вершин, каждая из
которых определяет границу грани, содержащую Xi-\Xi. Пусть Д* — (треугольная)
граница грани, содержащая Xi-i,Xi,yi. Вложим теперь экземпляр графа Щ,
изображенного на рис. VI.32, внутрь Д* таким же образом, как Но был вложен
внутрь Д при получении Di из Do (см. рис. VI.31 выше). Проделав это для
г = 1,... ,?, мы получим плоский граф D', имеющий только 3- и 4-угольные
границы граней, причем D С D'. Граф D' имеет только 2к — 2 нечетных
вершин, поскольку
dD'{v2j-i) = dD(v2j-i) + 3 = dD'{v2j) = dD(v2j) +3 = 0 (mod 2),
dD'{xi) = do(xi) +6 = dD(xi) (mod2), i = l,...,t- 1,
dD'{Vi) = dD(yi) + 2 = dD(y) (mod2), i = l,...,t.
Заметим, что в D' не существует 4-угольных границ граней, содержащих ребра
из D. Значит, если мы выберем Р" € Р, Р" ф Р\ мы можем получить граф
D" из D' таким же образом, как мы получили D' из D. Конечно, вершина,
соответствующая одной из введенных выше вершин y*> может и не лежать в
V(D); но это не имеет значения, поскольку Е(Р") П E(Q) = 0 для каждой
4-угольной границы грани Q из D' (заметим, что Р" С D). Теперь Dn имеет
только 2к — 4 нечетных вершин. Значит, после к шагов мы получим плоский

222
Глава VI. Различные типы эйлеровых цепей
эйлеров граф D^k\ имеющий только 3- и 4-угольные границы граней,
причем D С D^k\ Поскольку |У(С?з)| > 2, мы имеем D ф Къ, т.е. D является
cJ-связным и, следовательно,
D(k)
также 3-связный и обыкновенный граф (это
следует из всего построения
Однако D^ может все же содержать границы граней Л, которые также
являются границами граней в D. Для таких Л действуем, как и при построении
D\ из D0 вложением графа Я0, как показано на рис. VI.31. Полученный в конце
концов граф G обладает следующими свойствами:
1) G — плоский 3-связный эйлеров граф;
2) D С G;
3) ни одна из границ граней графа D не является границей грани в G.
Из этих свойств следует, что если G имеет А-цепь, то соответствующее
А-разбиение {Vi, V^} множества вершин V(G) индуцирует разбиение
множества вершин {V{, V2) в D, которое обязательно индуцирует ациклические
графы (V[), (V2) (см. свойство 3) и следствие VI.68). Значит, поскольку D —
обыкновенная триангуляция плоскости, они являются деревьями. Поэтому (см.
лемму III.74) Сз с D = D(Gz) имеет гамильтонов цикл. Это противоречие с
выбором Сз показывает, что G не имеет А-цепи.
Однако положительным результатом этого построения графа G из D =
D{Gz) является следующее общее замечание, полное доказательство которого
содержится в приведенном ниже доказательстве теоремы VI.91.
Пусть G$ есть 3-связный планарный кубический граф. Тогда существует
плоский (даже плоский 3-связный) эйлеров граф G с D — D(Gz) С G,
такой, что ни одна из границ граней графа D не является границей грани
графа G, и Сз гамильтонов, если и только если G имеет А-цепь. (VI.А)
Кроме того, мы можем отметить следующее. В данном выше построении
плоского 3-связного эйлерова графа G без А-цепи, обладающего свойствами 1), 2),
3), можно действовать таким образом, чтобы каждая грань графа D
содержала не более одного экземпляра графа Щ, изображенного на рис. VI.32. Это
следует из теоремы 10 и ее доказательства [FLEI74c] (см. также рассуждения
о регулирующих множествах вокруг приведенного ниже рис. VI.35). Другой
путь получения G с такими свойствами опирается на приложение задачи
китайского почтальона. Это будет сделано в разделе, посвященном сложности.
Сравнивая приведенное выше построение плоского 3-связного эйлерова
графа G из плоского 3-связного кубического графа Сз с помощью D = D(Gs) с
гипотезой VI.74 и отмечая, что G имеет только 3- и 4-угольные границы
граней, мы приходим к вопросу, можно ли опровергнуть эту гипотезу (а значит,
и ГБТ). Все, что для этого нужно, —это триангуляция Дг плоскости, все
вершины которой, за исключением двух, имеют четную степень, а оставшиеся две
вершины принадлежат одной и той же границе грани и имеют нечетную
степень. Без ограничения общности можно предположить, что эти две вершины,
обозначим их Xi-i и х^ лежат на границе внешней грани bd(Foo). Тогда
граница внешней грани графа Н[ := ?)2 — bd(Foo) должна быть б-угольной, как
и в случае Щ на рис. VI.32, где единственные нечетные вершины в графе Н[
суть Xi-i и Xi и Н[ имеет только 3-угольные границы граней, за исключением

VI.3. А-цепи в плоских графах
223
внешнего 6-угольника. Приведенное выше построение, начинающееся с нега-
мильтонова графа (Зз, должно было бы привести к обыкновенной эйлеровой
триангуляции G плоскости без А-цепей. К сожалению, такой триангуляции Z?2
не существует [MOON65a, FLEI74b].
Лемма VI.76. Не существует триангуляции G плоскости, имеющей точно
две нечетные вершины х,у и такой, что ху € E(G).
Доказательство. Мы представим два доказательства, оба непрямые. Первое
доказательство дано My ном, второе доказательство найдено автором очень
давно, но не было раньше нигде опубликовано.
1) Предположим, что такой граф G существует. Тогда Н := G — {ху} —
плоский эйлеров граф с одной 4-угольной гранью Q, все остальные грани
которого 3-угольные. Рассмотрим граневую 2-раскраску графа Я, такую, что Q
есть 1-грань. Положим Т% — {F\F есть г-грань}, г — 1,2. Поскольку каждое
ребро из Н принадлежит границе точно одной 1-грани и точно одной 2-грани,
мы имеем
\Е(Н)\= ? \E(bd(F))\= J2 |?(bd(F))|.
F€JFi FeF2
С другой стороны, равенство \E(bd(F)) |= 3 для F ф Q дает
J2 |#(bd(F))|=l(mod3) и ^ \E(bd(F)) |= 0 (mod3),
что противоречит предыдущим равенствам.
2) Предположим, что G существует, и пусть Н = G — bd(Foo), где мы
без ограничения общности можем предполагать, что х,у G V(bd(Foo)).
Рассмотрим плоское вложение графа К±, и пусть V{K±) = {я1,Я2»УъУ2}> так что
{х\У1,Х2У2} есть 1-фактор графа К±. Пусть Fj—грань с хгуг € E(bd(Fi)), г —
1,2; следовательно, F\ Ф F2. Вложим теперь по экземпляру графа Н в каждую
из граней F\, F2 и отождествим Х{ с х и yi с у в соответствующем
экземпляре графа Н, i = 1,2. Далее, отождествим вершины z Ф х,у из bd(i?00) П Н в
соответствующем экземпляре графа Н с соответствующими вершинами Zi в
hd(Fi) С K±,i — 1,2 (заметим, что z\ Е {2^2,У2},^2 ? {xiiVi})- Новый граф
G\ является эйлеровой триангуляцией плоскости, так как для v ? V(K±) мы
имеем dGl{v) = 3 + dH(x) -f dH{z) = 3 + dH{x) = 3 + dH(y) = 0 (mod2).
Кроме того, x(Gi) = 3 и if 4 С G\. Поскольку x(^4) = 4, мы получили
нужное противоречие.
На языке кубических графов лемма VI.76 утверждает, что не существует
плоского (2-связного) кубического графа, имеющего точно две нечетные
границы граней с одним общим ребром.
Однако в работе Гудея имеется частичное решение ГБТ [GOOD75a]. Чтобы
сформулировать результат Гудея, рассмотрим плоский 3-связный кубический
двудольный граф Сз со следующими свойствами:
1) | E(bd(F)) |е {4, б, 8} для каждой грани F графа G3;
2) | E(bd(F)) |= 8 для не более чем одной грани F графа Сз;
3) если существует F8 с \E(bd(Fs)) |= 8, то существует и F± с |E(bd(F4)) |= 4
иЪd(F8)nЪd(F4)ф0.

224
Глава VI. Различные типы эйлеровых цепей
Пусть Во означает множество всех графов Gs, обладающих этими свойствами.
Из формулы Эйлера для многогранников следует, что Gs G Во имеет точно
шесть 4-угольных границ граней, если он не имеет 8-угольных границ граней,
и точно семь 4-угольных границ граней в противном случае (см. упр. VI.23).
Результат Гудея может быть сформулирован следующим образом.
Теорема VI.77. Пусть Gs G Во выбран произвольно, и пусть Fm&x — любая
грань, удовлетворяющая условию \E(bd(Fmax)) |= max:, такая, что
существует 4-угольная грань F± с bd(Fmax)nbd(F4) Ф 0. Тогда существует
гамильтонов цикл Н в Gs, для которого выполняется условие E(bd(Fm8iX) П bd(F4)) G
Е(Н) (заметим, что для любых двух граней F', F" в Ъ-связном плоском
кубическом графе | J5(bd(F')) П ?(bd(F")) |G {0,1}).
Наша цель — перевести доказательство Гудея теоремы VI.77 в термины
теории А-цепей. Для этого мы сначала исследуем, что это означает в терминах
J-расщеплений вершин графа D(Gs), если е G E(Gs) принадлежит гамильто-
нову циклу Н графа Gs- Временно не будем учитывать тот факт, что Gs
двудольный. По лемме III.74 Gs имеет гамильтонов цикл Н, если и только если мы
можем записать V(D) = ViUV^ и (Vi)d —дерево, г = 1,2, где D = D(Gs). Кроме
того, по той же лемме Н содержит в точности те ребра, которые соответствуют
в D элементам {^ii^l^i G Vi, ^2 G V2}. Значит, если мы рассматриваем границы
граней bd(Fj) графа Сз, соответствующие вершинам Vj G Vi для
фиксированного г G {1,2},то?(Я) = \}у.^Е^{Е^))-{д^к € ?(bd(F,)nbd(Ffc))|^,^ G
Vi} (см. доказательство леммы III.74). Теперь мы воспользуемся тем, что Gs
двудольный и, значит, D — обыкновенная эйлерова триангуляция.
Следовательно, рассматривая совершенное А-разбиение {Vi, V^} графа D,
соответствующее Н С Gs (см. теоремы VI.70, VI.70.а и VI.71), мы заключаем, что для
е* = ху, т. е. ребра, соответствующего е G Е(Н), | {ж, у}П Vi |=| {х, у} П V<i \— 1.
Кроме того, поскольку {Vi,!^} — совершенное А-разбиение, т.е. (Dv1,i)v2,2 и
(Dv2,i)vi,2 суть циклы, мы можем предположить без ограничения общности,
что х G V\,y G V2. Это означает в терминах ^-расщеплений, что если на D
задана граневая 2-раскраска, то D имеет неразделяющую А-цепь,
индуцирующую 1-расщепление в х и 2-расщепление в у.
Обозначим теперь через 7о множество всех обыкновенных эйлеровых
триангуляции D плоскости с заданными на них граневыми 2-раскрасками (такими,
что внешняя грань является 1-гранью), обладающих следующими свойствами:
1') do(v) G {4,6,8} для каждой вершины v G V(D);
2') Ud(v) = 8 для не более чем одной вершины v G V(D);
3') если существует вершина v$ G V(D) с dr)(vs) = 8, то она смежна с вершиной
степени 4bD.
Как и выше, из формулы Эйлера для многогранников следует, что D G %
имеет в точности шесть вершин степени 4, если он не имеет вершин степени 8;
в противном случае он имеет в точности семь вершин степени 4 (см. упр. VI.23).
Заметим, что оба множества Во и % бесконечны; это мы получаем из
[GRUN67a, p. 254, Theorem 2] или леммы III.58 и того факта, что
двойственность устанавливает взаимно однозначное соответствие между элементами из
Во и % ^ Значит, мы вывели следующий результат для А-цепей.

VI.3. А-цепи в плоских графах 225
Do D,
Ш (ii)
Рис. VI.33. Эйлерова триангуляция плоскости jDi, полученная из эйлеровой
триангуляции плоскости Do с помощью ^-расширения (возможно, a = с Ф d или
Ъ = <1фс).
Теорема VI.77.a. Пусть D ? Т0 выбрана произвольно, и пусть vmax € V(D) —
вершина максимальной степени, выбранная таким образом, что она смежна
с вершиной w степени 4. Тогда D имеет неразделяющую А-цепь, индуцирую-
щую 1-расщепление в г>тах и 2-расщепление в w.
До того как мы приступим к доказательству теоремы VI.77.a, следует
получить несколько других результатов. Для этого определим специальный класс
эйлеровых триангуляции плоскости.
Пусть D — триангуляция плоскости, и пусть Л = (а, Ь, с)—граница
грани в D. Вложим граф Я0, как изображено на рис. VI.31, в соответствующую
грань графа D (т. е. Л заменяется на октаэдр Об); обозначим полученный граф
через D\. Будем говорить, что Di получен из D октаэдральным
расширением (кратко Об-расширением) в треугольнике Л. Чтобы определить
вторую операцию, предположим, что существует вершина z0 e V(D)
степени 4, и рассмотрим 4-колесо W4, определенное с помощью N*(z0); положим
N(zo) = {a,6,c,d} в соответствии с порядком O+(z0) = (azo,bzo,cz0,dzo) (W4
может быть вырожденным, т. е. а = с или b = d). Определим триангуляцию
плоскости D\ соотношением
Di = (D - {az0,cz0}) U {zi,z2,azi,bzi,dzi,zoZi,cz2,bz2,dz2,zoz2}.
Будем говорить, что Di получена из D И^-расширением с вершиной z0
степени 4 в качестве центра (см. рис. VI.33).
Пусть теперь п — положительное целое число; пусть D0 = D, Dn = D' и Д
получается из A_i с помощью Ое- или И^-расширения, г = 1,..., п.
Тогда мы скажем, что D' получается из D последовательностью 06- и/или
И^-расширений. Справедливость следующих утверждений является
следствием определений введенных выше расширений:
1) триангуляция D' эйлерова, если и только если D эйлерова;

226
Глава VI. Различные типы эйлеровых цепей
2) если |V(Z?)| > 4, то D — обыкновенная триангуляция, тогда и только тогда,
когда D1 — обыкновенная триангуляция.
Условие | V(D) |> 4, однако, не может быть опущено; можно считать, что
октаэдр получен W^-расширением эйлеровой триангуляции плоскости, состоящей
из двух вершин степени 4 и двух степени 2. Если |V(D)| > 4 и если a = с или
b = d, то D имеет две пары кратных ребер: два ребра ba и соответственно два
ребра zoa или два ребра z0b. Однако только одна из этих двух пар кратных
ребер может исчезнуть при W±-расширении. Это становится яснее из следующих
рассмотрений.
Во-первых, если D{ есть результат Об-расширения триангуляции Di-\, т0
E(Di-i) С E(Di), г Е {1,..., гг}. Значит, если | V(-Di-i) |> 3, то независимо от
степеней вершин а, Ь,с в Di-i (где А = (a,b,c); см. рис. VI.31) Dj — {a,b,c}
несвязен для каждого j, г < j < п (если A-i имеет вершину х Е {a,b,c}
степени 2, то уже Dj — ({a, Ь, с} — {х}) несвязен, и если ни одна из вершин
a,b,c не является вершиной степени 2 в J3i-i» T0 d>Di(y) > б для у Е {а, 6,с},
из чего следует, что ни одна из а, Ь, с не может быть центром ^-расширения
в Dk, г < к <п).
Во-вторых, если Di получен из Г>г-1 посредством W±-расширения и если
d>Di-i (a) > 4, ^Di-x (с) > 4, то Q = (а, 6, с, б?) — разделяющий 4-угольник в
каждом Dj, г — 1 < j < п. Из условия на степень вершин а и с следует
существование вершины х 0 {а, Ь, с, d, z0} и, кроме того, E(Q) С E(Dj), г — I < j < п.
Эти рассуждения приводят нас к следующему структурному результату.
Формулируя его, мы будем следовать обозначениям на рис. VI.31 и VI.33.
Лемма VI.78. Пусть D — обыкновенная эйлерова триангуляция плоскости,
полученная из октаэдра Oq (непустой) последовательностью Oq- и/или W±-
расширений. Тогда по меньшей мере одно из следующих утверждений верно:
1) D содерэюит разделяющий треугольник А = (а,Ь,с) и Oq содерэюит А в
качестве индуцированного подграфа, такого, что Df0 := D — Но может
быть получен из Oq посредством (возможно, пустой)
последовательности Oq- и/или W±-расширений (Но := Oq — А);
2) D содерэюит (по крайней мере) две вершины z'0,Zq степени А, такие, что
соответствующие 4-колеса W±,W± обладают следующими свойствами:
dD(z[) = dD(z'2) = dD(z'{) = dD(4) = 4,
E(Wi) П E(Wif) = 0
и каждый из графов
D'q := (D — {z[,zf2}) U {a'zf0,cfz'0} и Dq (определяется аналогично )
может быть получен из Oq посредством (возможно, пустой)
последовательности Oq- и/или W±-расширений.
Доказательство. По предположению существует последовательность
эйлеровых триангуляции плоскости Do, D\,..., Dn, такая, что D0 = Oq, Dn = D и Di
получен из Di-i Oq- или W±-расширением, i = 1,..., п.
Предположим, что п = 1. Если D получен из Oq с помощью Ов-расширения,
графы по обе стороны (однозначно определенного) разделяющего
треугольника А = (а,Ь,с) изоморфны графу Н0 := Oq — А. Значит, утверждение 1)

VI.3. А-цепи в плоских графах
227
леммы справедливо. Если же D получен из Oq с помощью W4-расширения,
то он изоморфен б-угольной двойной пирамиде. Значит, мы можем найти
разбиение {У1,У1'} множества V±(D) (которое определяет б-угольное основание
этой двойной пирамиды), такое, что Р' := (VI) и Р" := (V±) суть пути длины
два. Далее, W4' := (V{ U V6(D)) и W? := (V? U V6(D)) являются 4-колесами со
свойствами, приведенными в утверждении 2) леммы (z'Q, zf0f суть вершины
степени 2 из Р', Р" соответственно и z[, z'2 (z", z'?) — висячие вершины из Р' (Р")).
Итак, мы доказали справедливость леммы для п = 1.
Рассмотрим теперь случай п > 1 и предположим сначала, что Di получен
Об-расширением из IV i для некоторого i ? {1,..., п}. Без ограничения
общности можно предположить относительно треугольника Д = (a,b,c) С IV ъ
на котором действует это Ов-расширение, что А ф bd(jFoo), где F^ —
внешняя грань графа IV-1- Следовательно, граф #о, используемый при этом
Об-расширении на Л, лежит в ограниченной области треугольника Л. Более
того, Л разделяет Di и doiix) > б для любых х Е {а,Ь,с}. Значит, каждое
Ое- или И^-расширение, произведенное после Об-расширения на Л,
происходит полностью или «вовне», или «внутри» Л.
Если не все эти последние расширения происходят по одну и ту же сторону
от Л, то рассмотрим последнее из происходящих вовне и последнее
происходящее внутри Л. Обозначим получающиеся при этом графы через Dj и Dk
соответственно, i < j,k <п.
Если каждый из графов Dj и Dk получен W4-расширением из Dj-i,Dk-i
соответственно, то утверждение 2) леммы верно для соответствующих 4-колес
W4 и W4 с Wl := W± , W'l := W4 : это следует из выбора j и к и
рассуждений, предшествующих формулировке леммы VI.78, а также из определения
последовательностей DJ,..., D^_x для D0, соответственно D?*,..., D%Li для
Dq , формулами
D*r=Dr, r = 0,...,j-l, и D** = Ds, 5 = 0,...,fc-l,
D; = (Dr+i - {z[j\4j)}) U {a^2^\c^^\ r = j,...,n - 1,
D? = {D*1-{z?\4h)})U{alkHk\clk^k)h a = *,...,n-l,
где Zq \z\* ,z<z \a,(l\cW соответствуют zo,2i,Z2,a, с на рис. VI.33 для I = j, к.
Заметим, что d,Dr(zi ) = ^?>г(г2 ) = ^ds{z{ ') = dos{z2 ) = 4 для каждого
г Е {j,..., п} и соответственно для каждого s E {&,..., п}.
Значит, мы можем предположить без ограничения общности, что Dj
получен Об-расширением из Dj-i. Обозначим через Hq ~ Н0 граф,
используемый для этого Об-расширения на треугольнике Д^. Поскольку в силу выбора
h r — h • • •» п, октаэдр Oq — AW U Hq принадлежит каждому Dr, мы
заключаем, что D'0 := D — Hq получен из Oq последовательностью Об- и/или
W4-расширений, а именно,
Do, • • .,Dj-U Dj+1 - H{0j\ ...,Dn- H^.
Поскольку мы можем использовать те же соображения, если все расширения,
следующие за Об-расширением на Л, происходят вне Л (с Л и Но вместо Д^

228
Глава VI. Различные типы эйлеровых цепей
и #о ), учитывая уже рассмотренные случаи, мы можем предположить, что
все эти последние расширения происходят внутри Л.
В частности, мы можем предположить, что Dn не получается из Dn-\
Об-расширением (в противном случае для D := Dn, D0 := Du—Hq, Hq ~ Ho
верно утверждение 1) леммы). Обозначим через W'l 4-колесо,
ассоциированное с W4-расширением, в результате которого Dn получается из Dn-i.
Возьмем теперь минимальное г € {1,...,п}, такое, что D\ получается из Di-\
Об -расширением.
Если г = 1, то Щ := Di - (Н0 U Д) ~ Я0 и, значит, Щ С Dt, t = 2,..., n;
поскольку Но U Д ~ Об, мы можем положить
D*:=H0UA и ?>*_! :=Dt-H$, * = 2,...,n,
чтобы получить D^-i = D — Щ =: Df0, применяя к Об последовательность
Ое- и/или ^-расширений.
Если г = 2, то Di изоморфен б-угольной двойной пирамиде.
Положим V±(Di) = {^1,^2,... ,^б} в соответствии с упорядочением 0+(ги) =
(wvi,wv2,.. .,1Мб), где Vq(Di) = {w,x}. Без ограничения общности эти
обозначения можно выбрать таким образом, что Д = (vs,vq,w)(= (а,Ь,с)). Но
тогда WI = ({^1,^2,г;з,гу,ж}) является 4-колесом, лежащим целиком вне Д,
и W'A С Dj, j = 1,...,гг. Значит, для W±-расширения, в результате
которого Dn получается из Dn-\ (см. выше), W'l лежит целиком внутри Д; отсюда
следует, что E(W±) П E(W±) = 0. Приписав вершинам v<z, v\, v$, vq , V4 ту же
роль, которую играют на рис. VI.33 вершины zo, z\, z2, а, с, соответственно, мы
полагаем
?>*_! := (^ - {vi,v3})U{w;2,V4W2}, j = 1,...,п.
Это дает нам Dq ^ Об, D^_1 = L>g (?)д определено в утверждении 2)
леммы), и D!- получен из Dj_x тем же расширением, в результате которого Dj+i
получается из Dj, j — 1,..., n — 1.
Для завершения доказательства леммы следует рассмотреть случай,
когда либо г > 2, либо D получен из Об последовательностью Т^-расширений.
Предположим сначала, что Dj является (4 + 2j)-угольной двойной пирамидой,
где j = г — 1, если существует i > 2, и j = п, если D := Dn получен из Об
проведением n W^-расширений. Мы либо находим W±,W'l аналогично
случаю г = 2, либо можем взять любые два реберно-непересекающихся 4-колеса
W±, W'l (4 -f 2п)-угольной двойной пирамиды. В обоих случаях W± и W±
удовлетворяют утверждению 2) леммы.
Рассмотрим, наконец, случай, когда существуют некоторые к < i, к < п
соответственно, такие, что Dj является (4-f 2<7')-угольной двойной пирамидой для
1 < .7 < к—1, в то время как Dk таковой не является. Заметим, что D\ во всяком
случае есть б-угольная двойная пирамида. Из этого следует, что Dk содержит
4-угольник Q = (w,x,vr,vr+2}, где {w,x} = V(Dk-i) - V^(Dk^i), do^fa) =
d<Dk(vs) — 2 = 4 для s € {r, r-j-2} и где мы выберем обозначения таким образом,
что vtvt+i € E(Dk-i) для t = 1,..., 2к+2 (полагая г^+з = ^i)- Без ограничения
общности можно считать, что г = 1. Тогда Q = (w,x,vi,v$) —разделяющий
4-угольник, не содержащий вершин степени 4, в Dj, j > к > 2. Значит,
каждое Ое- или И^-расширение, в результате которого Dj+i получается из

VI.3. А-цепи в плоских графах
229
Dj, j = k,... ,n — 1, происходит целиком либо внутри, либо вне Q.
Рассуждая, как выше (заменив Л на Q), мы можем прийти к заключению, что все
эти расширения происходят по одну сторону от Q. С другой стороны, v2 и
^5 являются в Dk центрами 4-колес W4 = (N*(v2)), W4 = (N*(v^))
соответственно, лежащих по разные стороны от Q. Следовательно, W4 С Dj и
I V4(W{) П V4(Dj) |= 3 для некоторого Wl € {W4(2), W4(5)} и j = k,..., п.
Обозначим через W4' 4-колесо, соответствующее W^-расширению, в результате
которого Dn получается из Dn-\. Далее, jDq, определенное соответственно,
получается из Oq с помощью последовательности Do,... ,Dn-i = Dq. Как и
для D'Q, мы введем обозначения W4 = ({zbiziiz2ib',df}) и а',с' по аналогии
с обозначениями на рис. VI.33, где {b'd!} = {^1,^3} и {о!,с'} = {w,x}, если
Wl = W[2\ и {b',df} = {w,x} и {a',cf} = {v3,v7}, если W[ = W4(5) (мы
полагаем у? = v\, если А: = 2). Теперь положим
D*:=Dj для 0<j<fe-l-5,
Dz*:=(A+i-{z[,z^})U{a,4,c^} для fc-<J<J<n-l,
где 5 = 0, если W4' = W4(2), и 5 = 1, если W4' = W4(5). Мы получим D'0 = ^_1з
действуя на Об последовательностью Oq- и/или W4-расширений, поскольку Dj
получается из Dj_1 теми же самыми расширениями, которыми Dj+i
получается из Dj, j = k — 6,..., n — 1. Заметим, что для fc = 2 и <$= 1 D{ получен
из Dq с помощью W±-расширения, и таким же образом D\ получен из Do, но
центры этих ^-расширений различны. Лемма VI.78 доказана.
Теперь мы используем эту лемму для доказательства результата об А-цепях,
который обобщает частный случай результата Гудея.
Теорема VI.79. Пусть D—эйлерова триангуляция плоскости с заданной
граневой 2-раскраской, причем D — либо октаэдр, либо получен из октаэдра
последовательностью Oq- и/или W^-расширений. Пусть А = (x,y,z) —про-
извольно выбранная граница грани с x,y,z € V(D). Тогда D имеет нераз-
деляющую А-цепь, которая индуцирует {совершенное) А-разбиение {14,1^},
удовлетворяющее условию х G Vi, у, z ? V2.
Доказательство. Без ограничения общности можно считать, что Л есть
граница внешней грани F^ графа D и F^ есть 1-грань (заметим, что совершенное
А-разбиение не зависит от граневой 2-раскраски). Если D — октаэдр, то он
имеет неразделяющую А-цепь Т; например, можно взять граф на рис. VI.20b), и,
положив Vi = V, V2 = V", мы имеем | Vi П V(A) |= 1, | V2 П V(A) |= 2.
Вследствие симметричности октаэдра мы можем поэтому предположить без
ограничения общности, что х € Vi, у, z € V2. Значит, в случае октаэдра теорема верна.
Пусть теперь D удовлетворяет условию теоремы, и предположим, что D —
не октаэдр. По построению D и по лемме VI.78 мы различаем следующие два
случая:
(1) D удовлетворяет утверждению 1) леммы VI.78. Придерживаясь
обозначений рис. VI.31 с D вместо Z>i, положим
D'0:=D-H0,
где До := (а, Ъ, с) — граница грани.

230
Глава VI. Различные типы эйлеровых цепей
В силу симметрии возможных положений Л в До U Но мы можем
предположить без ограничения общности, что если Л С До U Яо> то либо х =
аь?/ = &i?z = сь либо ж = ai,y = а,2 = ci, либо х = с,у = a,z = ci, либо
х = &i,r/ = 6, г = с.
Теперь, применив индукцию к ?>q мы получаем без ограничения общности
(в силу симметрии, если Д <? До U Я"0, или в силу свободы выбора, если Д С
До U#o), что a G V^ и 6, с € V?, {j, A:} = {1,2}, для совершенного А-разбиения
{Vj0,!^0} множества V(D'0), соответствующего некоторой неразделяющий
А-цепи в Dq. Положим
^=У/и{6ьС1}, Vk = Vk°U{ai}, {J,*} = {1,2}.
Следовательно, {V}, V&} — требуемое совершенное А-разбиение, если Д (jL До U
#о или если j = 2,fc = 1 и {я, у, z} ^ {bi, Ь, с}. С другой стороны, если
Д С ДоиЯои j = l,fe = 2, то {Vi, V2} — требуемое совершенное А-разбиение,
если {х, у, z} = {61,6, с}; в других случаях мы используем тот факт, что (V^°)
и (Vs), 6 = 1,2, суть деревья в ?>; значит, для VJ* := У2 и У2* := Vi разбиение
{Vi*, V?} — это требуемое совершенное А-разбиение. Наконец, для j = 2, А; = 1
и {х,у, z} = {61,6, с} мы определим Vi*,!^*, как и выше, чтобы получить
искомое совершенное А-разбиение {^*,У2*}. Это завершает рассмотрение
случая (1).
(2) D удовлетворяет утверждению 2) леммы VI.78. Тогда D содержит
4-колесо W^ как изображено на рис. VI.33(ii) с Д <f_ W±. Придерживаясь
обозначений этого рисунка с D вместо D\ и D'0 вместо Do, мы определим сведение
D к Df0 и применим индукцию к D'0, чтобы, как и выше, получить {VJ0,!^0}.
В зависимости от распределения a, zo,c между V± и V$ мы рассмотрим два
случая.
Если для {j, к} = {1,2} либо {a, z0, с} С V?, либо {a, z0} С V? и с € V%
(случай {с, го} С V? и a Е V% по причине симметрии не требует дополнительных
рассмотрений), то обязательно {6, d} С V?. В обоих случаях мы положим
V5:=lf и{г1>га}, Vk:=Vk°, {j,k} = {1,2},
чтобы получить требуемое совершенное А-разбиения {V},Vfc} = {^,У2} для
D.
Значит, нам необходимо рассмотреть случай {а, с} cV^zoG V?. Так как
{V®,Vf?} есть А-разбиение, то {&, d} (jL V®. Из соображений симметрии мы
можем предположить без ограничения общности, что b € V^, d € V?. Для
получения совершенного А-разбиения {V^-, VJ-} = {VI, V^} для ?>, требуемого в
теореме, мы положим в этом случае
Vr.= V?U{zo}, Vk:=(Vk0-{z0})U{z1,z2}, {j,k} = {1,2}.
Заметив, что эти рассмотрения исчерпывают все случаи, вне зависимости от
того, AnW^ = 0 или AnWi Ф 0 (в силу леммы VI.78 в любом случае Д (]L W4),
мы заключаем, что теорема доказана.
В терминах теории кубических графов теорема VI.79 —по
двойственности—эквивалентна на самом деле следующему результату о гамильтоновых
циклах (см. также рассуждения, следующие за формулировкой теоремы VI.77).

VI.3. А-цепи в плоских графах
231
Следствие VI.80. Пусть (?з — (S-связный) плоский кубический двудольный
граф, который может быть получен из куба последовательностью одной или
обеих из следующих операций:
1) замена вершины на три взаимно смежных А-угольника\
2) замена ^-угольника Q на три 4-угольника, два из которых не смежны.
Тогда для любого е G E(Gz) в Сз существует гамильтонов цикл, не
содержащий е.
Доказательство формулируемого ниже следствия непосредственно
вытекает из части доказательства теоремы VI. 79; поэтому мы оставляем его в качестве
упражнения читателю.
Следствие VI.81. Пусть Do и D\ — эйлеровы триангуляции плоскости,
такие, что D\ получается из Do последовательностью Oq- и/или W±-
расширений. Тогда Do содержит перазделяющую А-цепь в том и только том
случае, когда Di содерснсит перазделяющую А-цепь.
Мы не стали формулировать следствие VI.81 в терминах теории кубических
графов; это можно сделать таким же образом, как мы получили следствие VI.80
из теоремы VI.79.
Имеется аналогичная И^-расширению процедура создания новой
эйлеровой триангуляции плоскости Di из данной эйлеровой триангуляции плоскости
D0. А именно, пусть вершины а, 6, с, d G V(D0) заданы, как на рис. VI.33, и
предположим, что ас G E{Dq). Разобьем дополнительно ас двумя новыми
вершинами, скажем z\ и z^ , и соединим эти вершины ребрами с каждой из вершин
b и d. Полученный граф Di действительно является эйлеровой
триангуляцией плоскости. Назовем это построение D\ из Do слабым И^-расширением
(см. рис. VI.34 ниже). В терминах теории плоских кубических графов слабое
И^-расширение соответствует замене ребра е G E(Gs) на два смежных 4-уголь-
ника Qi, Q2 таким образом, что четность числа | E(bd(F)) | не меняется ни для
одной грани F из Сз- Следовательно, если Сз двудольный, то двудолен и новый
граф.
Однако если мы переформулируем лемму VI.78 для графов, полученных
из Oq последовательностью Oq- и/или слабых W4-расширений, она будет
неверна. То есть, начиная с Oq, можно получить эйлерову триангуляцию
плоскости D последовательностью слабых И^-расширений так, чтобы
соотношение N(v) П V±(D) = 0 было справедливо для каждой вершины v G Va(D)
за исключением пары смежных элементов из V±{D). (Мы оставим в качестве
упражнения построение такого примера.) Этот факт перестанет удивлять,
однако, если заметить, что в следствии VI.81 соответствие между А-цепями в
Do и А-цепями в D\ является биективным (см. также доказательство
теоремы VI.79). Это наблюдение станет неверным, если в следствии VI.81 заменить
W\-расширения на слабые W±-расширения. Действительно, хотя и верно, что
неразделяюшую А-цепь из Do можно расширить до неразделяющей А-цепи в
триангуляции D\ (полученной из Do последовательностью Oq- и/или слабых
И^-расширений), обратное может быть неверным для некоторой
неразделяющей А-цепи из D\.

232
Глава VI. Различные типы эйлеровых цепей
D0 D,
Рис. VI.34. D\ получен из Do слабым И^-расширением. Если D\ имеет совершенное
А-разбиение {VijVb}, указанное метками 1 и 2 при вершинах, то для
соответствующего разбиения {V]0, V§} множества V(D0) граф (V]0) имеет цикл, содержащий ас, в
то время как (У2°) несвязен.
Рисунок VI.34 иллюстрирует это рассуждение.
Заметим, что, начиная с Об, путем Об-, W±- и слабых ^-расширений
можно получить лишь некоторые эйлеровы триангуляции плоскости, так как,
вообще говоря, эйлерова триангуляция плоскости не обязательно содержит
смежные вершины степени 4. В самом деле, если Сз — плоский 3-связный
кубический граф с обхватом 5, можно найти независимое множество ребер ?0,
такое, что кубический граф Gg, полученный из G3 заменой каждого ребра
е Е Е0 на 4-угольник Qe, будет плоским и, вдобавок, двудольным (см. рис.
VI.35). Такое множество Е0 называется регулирующим множеством
(ребер), и каждый 1-фактор L из Сз есть регулирующее множество; так как он
задает в G% 2-фактор Q*, содержащий четные граничные циклы, а именно
Q* = {Qe\e e L с E{Gz)} (по теоремам 111.66 и 111.67 плоский кубический
граф является двудольным тогда и только тогда, когда он содержит 2-фактор,
состоящий из четных граничных циклов). С другой стороны, регулирующее
множество из G3 не обязательно есть подмножество 1-фактора L с E(Gs)1>}.
Во всяком случае в терминах эйлеровых графов переход от Сз к G? (с помощью
регулирующего множества Е0) означает преобразование графа A) := D(Gs) в
эйлерову триангуляцию плоскости. Это преобразование достигается
подразбиением каждого ребра е* = ас е E(D0), соответствующего ребру е ? Е0 С 2?(С?з),
с помощью вершины z0 и соединением z0 с обеими вершинами b и d, где а, с, b и
а, с, d суть вершины граничных треугольников, содержащих е* (см. рис. VI.34).
Кроме того, поскольку Е$ — независимое множество ребер, то ни одна пара
ребер е*, /* G 25(A)), соответствующих е, / G Е0, не принадлежит границе грани
в Аь Значит, приведенное выше преобразование графа А> может быть
проведено одновременно для всех соответствующих е*. Поэтому и приведенное
х) Заметим, что G? может быть 3-связным, хотя к(?з) = 2. Это имеет место, однако,
тогда и только тогда, когда все разделяющие множества Es размера 2 в Gz принадлежат
некоторому регулирующему множеству Е0 из (?з (заметим, что если | Es |= 2, то во всяком
случае \ЕоП Е$\^ I; один из путей доказательства этого факта, например, — дуализация
леммы VI.76).

VI.3. А-цепи в плоских графах
233
V
Т
G3 G3
Рис. VI.35. Преобразование плоского кубического графа Gz в плоский кубический
двудольный граф G% заменой ребра е из некоторого независимого множества ребер
Ео на 4-угольник Qe-
выше построение плоского эйлерова 3-связного графа без А-цепей можно
проводить таким образом, чтобы каждая грань из D содержала не более одного
экземпляра графа Щ, изображенного на рис. VI.32. Отметим, что понятие
регулирующего множества было введено и изучено в [FLEI74c]. Перенесем
теперь доказательство Гудея теоремы VI.77 в теорию А-цепей. Заметим, однако,
что наше доказательство обобщает два частных случая доказательства Гудея,
которые рассматривались в [GOOD75a] в стиле «легко видеть, что». Это
обобщение выражено в теореме VI.79.
Доказательство теоремы VI.77.а. Рассмотрим сначала общие структурные
свойства графа D, которые следуют прямо из того факта, что D есть
обыкновенная триангуляция плоскости.
а) Если Р4—путь с 1(Р±) = Зи V(P±) С V^D), то Р± — индуцированный
путь и либо V(P±) С N(v$), где d(v$) = 8, либо D есть б-угольная двойная
пирамида, D ~ Oq, соответственно.
Заметив, что теорема верна для Oq ? % по теореме VI.79, продолжаем
по индукции и различаем несколько случаев в зависимости от распределения
вершин степени 4 в выбранном графе D € %.
Случай 1. D получен О б-расширением эйлеровой триангуляции плоскости
Do. Тогда Do содержит граничный треугольник Л = (а,Ь,с), на котором
было произведено это 06-расширение. Предположим сначала, что A(D) < 8.
Тогда (1в(а) = dr>(b) = dr){c) = б и, значит, в Do — D — Но (Но изображен
на рис. VI.31) мы имеем drj0(a) = dr)0(b) = dr)Q(c) = 4. То есть Do получен
Об-расширением некоторой эйлеровой триангуляции плоскости D' и т. д.
Следовательно, D получен в этом случае из Oq последовательностью Об-
расширений. Значит, в этом случае из теоремы VI.79 вытекает справедливость
теоремы VI.77.a. С другой стороны, если A(D) = 8, то существование не-

234
Глава VI. Различные типы эйлеровых цепей
разделяющей А-цепи в D получается по индукции в силу следствия VI.81,
и доказательство теоремы VI.79 показывает, как совершенное А-разбиение
{ViiVf} множества V(Do) может быть расширено до такого же разбиения
{VI, V2} множества V(D). В частности, если v$ с (1d(vs) — 8 лежит в Л, то
без ограничения общности можно считать, что v$ = г;тах = а и w = ai (см.
утверждение теоремы VI.77.а); значит, мы получаем с помощью индукции и
соотношений dD0(a) = 6 = Д(Аз), do0(b) = 4, ах ? V(A)), что а G Vj°, b € V2'.
Поэтому мы можем определить Vi,V2 таким образом, что ai € V^, 6i € Vi и
ci G Vfc тогда и только тогда, когда с € V}, где {j,fc} = {1,2}. Следовательно,
{У\ ,V2} — требуемое разбиение.
Случай 2. D получен W^-расширением эйлеровой триангуляции плоскости
D0. По индукции и следствию VI.81 D содержит неразделяющую А-цепь,
поскольку такую цепь имеет Д), и мы знаем из доказательства теоремы VI.79,
как расширить совершенное А-разбиение {V^0,!^0} множества V(Do) до
совершенного разбиения {Vi, У2} множества V(D), если vm3^w e E(D0 — {z0}).
Если, однако, {vma,X)w} П V(W4) ф 0, мы продолжим следующим образом.
Если A(-D) < 8, то способом, подобным примененному в случае 1, мы
установим, что D получен из Oq последовательностью W^-расширений, и, значит,
в этом случае теорема VI.77.а также следует из теоремы VI.79. Однако если
Д(?>) = 8, мы совершаем различные редукции, зависящие от положения
вершин vmSiX = v$ и w в W\ U {а, с} (мы используем обозначения рис. VI.33). Так
как d(ys) = 8, то v$ ф Zi, г = 0,1,2; значит, по соображениям симметрии мы
можем предполагать без ограничения общности, что v$ € {a, d}, поскольку мы
обязательно имеем v$ € {a, 6,с,d}. По свойству а), если min{d(a),d(c)} = 4,
то vs = d, поскольку D Э Р± D {zo,zi,z2}. В силу этого мы также можем без
ограничения общности предположить, что d(a) = 4, если min{d(a), d(c)} = 4.
(i) d(a) = 4. Тогда ^тах = ^8 = d, и мы обязательно имеем ситуацию,
изображенную на рис. VI.36, где
{а"} = N(b) -{а,20,21,22,с}
(заметим, что непременно d(b) = 6), и, следовательно,
са~ е E(D), N(a-) П N(c)= {d, 6,6"},
N(d)nN(a~) = {a,c,di}, iV(d) П N(c)= {z2,a~,d2}.
Замечая, что обязательно d(a~) = d(c) = б, мы заключаем, что либо D есть
граф, изображенный на рис. VI.36, либо Л = (di,d2,b~) есть разделяющий
треугольник в D. Кроме того, для выбранной вершины w степени 4, смежной
с ^тах, мы имеем w ? {a, zo, z\, z2}. В обоих случаях мы сводим сторону
треугольника Л, содержащую zo, к октаэдру, а значит, получаем меньший граф D\
с A(Di) = б (см. рис. VI.36). Следовательно, либо D\ ~ Об, либо D\ получается
из Oq последовательностью Об-расширений (см. случай 1). Во всяком случае
можно предположить в силу теоремы VI.79, что Ь~ € V^1, di,d2 € V2 для
соответствующего совершенного А-разбиения {V^1, V2} множества V(Di—V(mtA)).

VI.3. А-цепи в плоских графах
235
D D,
Рис. VI.36. Сведение D к D\ в случае d(a) = 4, v% = d.
Значит, мы можем расширить {V^1, V^1} до совершенного А-разбиения {1^, У2}
множества ^(?>), как и требуется в теореме, полагая
Vl :=Vj;\J{b,c,d}, V2 :=У2г U {a~,a,z0,zuz2}.
Заметим, что d = г>тах G Vi, тогда как ги € V2. Это доказывает случай (i).
(ii) d(a) > 4. Мы свели D к Do, графу, из которого D получается
W4-расширением. Рассмотрим сначала случай г>тах = г;8 = а (а значит, w = z\)
или г>тах = v$=dttw = ziH выберем в Do в обоих случаях zo = w. Тогда
как в первом случае обязательно a = fmax
(здесь dDQ(a) = 8), во втором случае
мы имеем свободу выбора (здесь Д(Д)) = б); значит, пусть во втором случае
& — ^max*
По индукции устанавливается, что V(D0) допускает совершенное А-разбие-
ние {VfjVtP} с
^тах € V°, и z0 € Vj. В обоих случаях пусть
Vn= V?, V2:= V? U {zi, z2}, если 6,d 6 V?,
И:= ^i° U {zo}, V2:= (V? - {z0}) U {zuz2}, если 6 e V?, d € V?,
и, если b, d € Vj1 (значит, г>тах = а), мы полагаем
Vi:=Vfu{2b,2i}> V2:={V?-{2b}}U{zi}.
Случай vmax = а и 6 € Ц0, d G 72° симметричен случаю 6 € V^0, d € Vf и,
значит, не требует дополнительных рассуждений.
Следовательно, чтобы закончить (ii), нам осталось рассмотреть случай
^тах = vs = d и w = z0. Пусть b~ — однозначно определенная вершина,
такая, что Ъ~ е N(b) - {а,с, z0,zi,z2}. Мы имеем dD0{b) = 4 и dD0(b~) ? {4,6}.
Замечая, что Д(Д)) = б, мы получаем совершенное А-разбиение {VJ0,!^0} с
Ь~ G V]0, 6 € V^° либо с помощью индукции, либо в силу теоремы VI.79 (в
зависимости от того, какое из равенств dr>0(b~) = б, doQ(b~) = 4
выполняется). Заметим, что, поскольку каждое из четырех вершинных множеств

236
Глава VI. Различные типы эйлеровых цепей
{а,6,с,d}, {а, Ь~,с, d}, {а,6, с,zq] и {а,6~,с,^о} определяет 4-угольник, мы не
можем иметь {а, с, d} С V^° или {a,z0,c} С V^° для какого-либо г G {1,2}.
Следовательно, если {а, с} С V^°, то {zo,d} С V^, где {i,j} = {1,2}. С другой
стороны, если a GV®, cGV® для г ф j, мы можем предположить из
соображений симметрии, что a G VJ°, с G V^0. Из этого следует, что zq G Vi0, d G V?;
в этом случае мы знаем из доказательства теоремы VI.79, как расширить
{V^jVj} до совершенного А-разбиения {V^,!^*} множества V(-D), и,
положив V\ :— V2 ,V2 := V*, мы получим соответствующее А-разбиение {Т^,^}
множества V(D). Итак, нам остался случай {а, с} С V^°. Без ограничения
общности можно считать, что г = 2 (в противном случае мы поменяем
местами Vi и V^0; значит, может выполняться включение b ? V^0).
Следовательно, d,z0 € V?. Если Ъ G V?, то VI := (^° - {г0}) U {Zl}, V2 := \/20 U {гь,г2}
задают А-разбиение, требуемое в теореме. Для случая Ъ € V® мы положим
Vi := (Vi — {zo}) U {^i, z2}, V2 := V20 U {^о}, чтобы получить требуемый
результат. Это завершает рассмотрение случая (ii) и, значит, доказывает случай 21).
Случай 3. \N(w) П V±{D) |= 1. Следовательно, D получен слабым
^-расширением эйлеровой триангуляции плоскости Do- Используя обозначения рис.
VI.34, поскольку случаи 1, 2 уже рассмотрены, мы заключаем, что d(x) > 6
для х G {а, 6, с, d}\ по симметрии мы предполагаем без потери общности, что
если d(x) = 8, то х G {а, 6}. Значит, г;тах G {а, 6}, и по симметрии мы
предполагаем, что в любом случае w — z\.
Мы определим эйлерову триангуляцию плоскости Di, отождествляя Ь и d
в D — {zi,z2,ab,be} и обозначая эту новую вершину через z. Значит, во
всяком случае dD1(c) = 4, тогда как dD1(z) G {6,8}, do^a) € {4,6} зависят от
существования и положения вершины степени 8bD. Следовательно, в Di мы
обозначаем г>тах = z (либо по необходимости, либо поскольку мы имеем
свободу выбора) и выбираем w = с.
Предполагая вначале, что D\ обыкновенный, мы применим индукцию,
чтобы получить совершенное А-разбиение {Vi1, V^1} множества вершин графа D\ с
z G Vi1, с G V2. Тогда V[ := (Vi1 -{*})U{b,d}, ^ := V^1 — разбиение множества
V(D) — {zi, z2}, такое, что (У/) —лес с не более чем двумя компонентами, в то
время как (К/) —дерево. Теперь положим
Vi~ V[ U {z2}, V2:= V{ U {zi}, если b = vmax и a G V?,
Vx-Vl, V2:=VJU{zuz2}, еслиа?У{,
Vi~ V{ U {z2}, V2:= V{ U {zi}, если a = <w и a G F2'.
*) Этот последний случай vmax = v& = d, w = zo (приведенный к двойственной
форме) требует в доказательстве Гудея другого типа сведения, поскольку Гудей не
располагал двойственным вариантом теоремы VI.79. Заметим, что в этом случае мы можем иметь
dD0(b) = d?>0(b~) = 4, что не позволяет заключить по индукции, что Ъ~ G V^, Ъ Е V2°- С
другой стороны, мы должны избежать ситуации a,c,d€ V^0, 20,6 € V2°; действительно, это
обязательно дало бы d,zq G Vi, 21,22 G V2. Конечно, можно было бы в этом случае также
применить теорему VI.79, так чтобы d E Vj0, a, zq G V2°, для получения требуемого
результата, но, поскольку dD0(d) = dr>0{o) = 6, нельзя использовать в теореме VI.77.а индукцию для
получения d G Vj0, a G V2°.

VI.3. А-цепи в плоских графах
237
Во всех случаях {Vi, V2} есть А-разбиение множества V(D), которое требуется
в теореме.
Чтобы закончить случай 3, осталось показать, что Di должен быть
обыкновенным графом. Это равносильно тому, чтобы показать, что bd 0 E(D) и
что N(b) C)N(d) ~ {a,zi,z2,c}.
Предположим сначала, что bd € E(D). Тогда каждая из сторон
треугольника Л* = (6,zi,d) определяет триангуляцию плоскости D*, для которой Д*
является границей грани. Однако do*(zi) = 1 (mod 2), и, поскольку все
вершины графа D* — V(A*) имеют четную степень в D*, в точности одна из вершин
Ъ и d имеет нечетную степень в D*. Значит, D* — триангуляция плоскости в
точности с двумя нечетными вершинами и они смежны. Это противоречие с
леммой VI.76 показывает, что bd 0 E(D).
Предположим, что существует х € N(b) П N(d) — {a,zi,z2,c}.
Поскольку d имеет степень б, то либо Л = (с, d, x), либо Л = (а, d, x) является
границей грани в D. Рассмотрим Ai = (?,6,х) с Е(А) П E(Ai) = {tx},
где t G {а, с} в зависимости от того, какой случай имеет место, и
обозначим через D* триангуляцию плоскости, для которой Ai является
граничным треугольником и которая не содержит z\, z2. Тогда D* ф. К$, потому
что min{d?)(a),d?>(c)} > 4. Так как в любом случае dD*(t) = 0 (mod 2), то
dr)*(b) = dp*(x) = 0 (mod 2) по лемме VI.76. Обозначим через у вершину,
удовлетворяющую условию {?,у} — {а,с}. Поскольку d,у,zi,z2 ? V(D*), в силу
приведенных выше сравнений {dD*{b),dD*(x),dD*(t)} С {2,4}. Так как если
do*(x) = 2, то b и t разделяют ?)*, а значит, и D, мы имеем do*(x) = 4,
а поскольку d 0 V(D*), мы заключаем, что do{x) = б. По аналогичным
соображениям dn*(b) = dn*(t) = 4. Кроме того, так как г;тах € {а, 6} и
у,z\,z2 ? V(D*), то г;тах = Ь и d^(6) = 8. Поскольку di)(a) > 4, мы
имеем dr>(a) = 6. Следовательно, можно без ограничения общности считать, что
t = с. Положим {6i} = N(b) — ({a, zi,z2}UND*(b)), {di} = N(d) — {a, zi,Z2,c,x}.
В силу предыдущих рассуждений о степенях вершин b и х и поскольку
степень вершины d равна б, эти равенства вполне корректны; кроме того, если
xdi,xbi ? E(D) - E{D*) и xd <E S(Z3), то dx = Ъ\. Значит, А2 = (a,6,di) —
треугольник, и он должен быть границей грани, потому что N(b) — {a,di}
лежит по одну сторону от А2. Следовательно, doia) — 4; с другой стороны, а
и di разделяют D. Однако dp (а) > 4. Это противоречие завершает разбор
случая З1).
Случай 4. N(w)nV±(D) = 0. Используя обозначения рис. VI.33(i) с D вместо
Do, мы имеем w = zq. Можно предположить без ограничения общности, что
^тах = а; следовательно, dr)(a) € {б, 8} и dp(x) = б для х ? {&, с, d}. Определим
х) Можно было действовать по-другому, рассматривая D** := (D — D*)UA\ и D* отдельно,
применяя индукцию к D**, а теорему VI.79 к D* (заметим, что A(D*) < б и do*(s) = 4 для
s € V(Ai)) Однако в данном случае я предпочел представленный здесь подход, поскольку он
не опирается на теорему VI.79. К сожалению, Гудей не приводит соответствующую часть
своего доказательства (которое является довольно схематичным) и ограничивает рассмотрение
связности случаем, двойственным к случаю 4 (см. ниже), где он использует двойственную
форму леммы VI.76. Более того, даже его ограниченные рассмотрения являются неполными
и имеют пробел (см. подстрочное примечание в конце доказательства).

238
Глава VI. Различные типы эйлеровых цепей
Di, отождествляя Ь и d в D — {zo, ab, be}, и, как и в случае 3, обозначим новую
вершину через z. Снова D\ — эйлерова триангуляция плоскости с d^ (a) G
{4,6}, dDl(c) = 4, dDl(z) = 8.
Предположив сначала, что D\ обыкновенный, мы применим индукцию к
?>i, чтобы получить подходящее разбиение {V^V^} множества V(D{) с z G
Vi, се Vj. Подобно случаю 3, это дает разбиение {V{, V2f} множества V(D) —
{zo} с b, d G V{, с G V2'. Следовательно, если мы положим
VL-V/, ^^U{z0} при а € V{,
Vi:=Vb V2:=V{U{zo} при а G У2',
то {Vi,V2} —искомое А-разбиение множества V(D).
Значит, для завершения случая 4 и, следовательно, доказательства
теоремы VI.77.a осталось лишь показать, что D\ — обыкновенный граф. Мы
будем действовать, как в случае 3, предполагая, что существует вершина
ж G N(b) П N(d) — {a,zo,c} (показывается, как и раньше, что bd ^ E(D), где
вместо z\ используется zq).
Покажем сначала, что xt ? E(D) хотя бы для одного t G {a, с}.
Предположим противное, а именно пусть xa,xc G E(D). Тогда хотя бы один из
треугольников Дх = (ж, d, а) и Л2 = (ж, Ь, а) не является границей грани в D,
и это же верно по отношению к треугольникам Д3 = (x,d,c) и Д4 = (ж, 6,с);
в противном случае должно быть d^(a) = 4, d?>(c) = 4 соответственно.
Поскольку 6, d G Ve(-D), мы предполагаем без ограничения общности, что Дз не
является границей грани в D. Но тогда мы находим триангуляцию плоскости
D* ф К%, как и в рассуждениях о связности в случае 3, с Дз, являющимся
границей грани в D*, и zq 0 V(D*). В силу леммы VI.76 при k(D) > 3 и
поскольку 6,с G Vq(D), do(x) G {4,6}, мы имеем do*(d) = do*[с) = do*(x) — 4;
значит, dr>(x) = б. Следовательно, А2 —граница грани D и, значит, Дх
разделяет D. В частности, сторона треугольника Дх, не содержащая zq, содержит
два или четыре элемента из Еа, два элемента из Ed, но ни одного элемента из
Ех, поскольку dr>{x) = б = dn*(x) + | {xb,xa} |. Значит, and разделяют D —
противоречие.
Предположим теперь, что ха,хс ? E(D). Тогда сторона 4-угольника Qi :=
(a, 6,ж, d), не содержащая го, содержит в точности один элемент е& G ?"б и в
точности один элемент е^ G ?^, и то же самое верно для 4-угольника Q2 :=
(с, 6, x,d). Это следует из того, что 6, d G V^(D). Положим е& = fru^, е^ = dud-
Из распределения элементов из Еь и ^ по отношению к сторонам Qx следует,
что xub,xud G E(D). Чтобы убедиться, что щ = Ud, рассмотрим
триангуляцию D~ 4-угольника Q~ := (b,ж,d, zq), определенную стороной 4-угольника
Q-, не содержащей а. В силу предыдущих рассуждений d^-(b) = d^-(d) =
4, ^-(zo) = 3. Значит, с^-(ж) = l(mod2). Пусть Vb,Vd определены так же,
как мы определяли ut,Ud выше, но по отношению к Q2. Заметим, что
0+(6) = (Ьж, Ьуь, be, bz0,ba, Ьщ), 0+(d) = (dx, dud, da, dz0,dc, dvd),
и, следовательно, (b, с, Уь) и (d, с, yd) суть границы граней. Поскольку dp (с) — б
и k(D) > 3, мы заключаем, что уь Ф yd] значит, 0+(с) = (сг^, cd, cz0, cb, суь, cs)
для некоторого 5 G V(D~). Из этого и из соотношений do(x) < б и dD-(x) =

VI.3. А-цепи в плоских графах
239
1 (mod 2), в свою очередь, следует, что dD-(x) = 5. Поскольку как щ и Ud, так
и Vb,Vd лежат по разные стороны от Q-, обязательно щ = Ud- Но тогда
0+(а) — (aub,ab,azo,ad), т.е. do (а) = 4,
в противоречие с do{o) G {б, 8} (заметим, что (a, d, u^) и (а, 6, и^) суть границы
граней в D). Значит,
ха € E(D) тогда и только тогда, когда хс 0 E(D). (*)
Теперь, согласно лемме VI.76 и условию do (с) = 6, если хс ? E(D), то точно
один из Лз и Д4 не является границей грани и сторона четырехугольника
Qi — (а, 6, х, d), не содержащая zo, не имеет общих точек либо с Еь, либо с Ed
(заметим, что 6, d € V^D)). Значит, ха € E(D), a это противоречит (*). Отсюда
и следует, что обязательно ха G E(D), хс ? E(D). Если do (а) = 6, то получаем
то же противоречие симметричными рассуждениями; таким образом, dp (а) =
8. В любом случае из условий do {а) € {6,8} и ха ? E(D) следует, что точно
один из Ai = (x, d, а) и Д2 = (ж, 6, а) не является границей грани; на самом
деле из условия do(x) < б и леммы VI.76 следует, что Ai есть граница грани
тогда и только тогда, когда А2 не является границей грани. Далее проводим
рассуждения, симметричные предыдущему случаю хс Е E(D), чтобы получить
противоречие ха,хс € E(D). Значит, мы установили, что х не существует, т.е.
k{D\) > 3. Теорема VI.77.a теперь доказана1).
В порядке самокритики следует отметить, однако, что теорема VI.77.а (а
значит, результат Гудея) была сформулирована в [FLEI83b, Theorem 4.4]
некорректно, ибо та часть предположения, где требуется, чтобы вершина степени
8 была смежна с вершиной степени 4, была опущена, а заключение теоремы
было сформулировано в более слабой форме, а именно утверждалось лишь,
что D имеет Л-цепь.
К сожалению, я был не в состоянии обобщить теорему VI.77.а, чтобы
получить то же заключение, что в теореме VI.79. С другой стороны, это
обобщение будет получено, если допустить, что верна любая из гипотез VL72-VI.74.
Чтобы убедиться в этом, мы сформулируем другую гипотезу об А-цепях
(соответственно А-разбиениях) и затем покажем, что она эквивалентна гипотезе
VI.73 (и, значит, также гипотезе VI.74).
*) В своих рассуждениях о связности Гудей совершает следующую ошибку: говоря нашим
языком, он спутал пары вершин {а, с} и {Ь, <2}, утверждая, что х' ? N(a)C\N(c) — {b, zo, d} ф 0
невозможно. Его доказательство неполно, неоправданно усложнено и использует тот факт,
что граф не может иметь точно одну вершину нечетной степени (в двойственной
форме). Для того чтобы увидеть, что х' может все же существовать, рассмотрим Об с его
4-угольным основанием, обозначенным символами a,b,c,d в некотором циклическом
порядке, и обозначим «верхнюю» («нижнюю») вершину этой двойной пирамиды через zo (x')-
Применим Об-расширение к границе грани (a, d, x') и слабое W\-расширение к 4-угольнику
(а, я', с, Ъ) с диагональю Ъх'. Полученный таким образом граф D' удовлетворяет условиям
dD/(a) = 8, d,c,x' G Vq(D'). Ho dD/(b) = 4. Тогда ^-расширение графа ?)', примененное
к 4-колесу, определенному а, Ь, с и двумя вершинам степени 4, полученными при указанном
выше слабом W4-расширении, дает контрпример к рассуждениям Гудея о связности. Более
того, Гудей не рассмотрел случай х € N(b) П N(d) — {a, zo, с}. Недостаток доказательства
Гудея состоит лишь в том, что он рассматривает только случай d?)(a) = 6; формальные
аргументы корректны. Но он делает неверный вывод о несуществовании х', ибо х' может
существовать, если dn{a) = 8, как показывает наш пример. Заметим, однако, что результат
Гудея был доказан заново в [РЕТ077а].

240
Глава VI. Различные типы эйлеровых цепей
Гипотеза VI.82. Пусть D — обыкновенная эйлерова триангуляция
плоскости с граневой 2-раскраской, и пусть Л = (х, у, z) —граница грани в D. Тогда
D имеет совершенное А-разбиение {Vi, V2} с х € Vi, у,z Е V2.
Предложение VI.83 (см. также [REGN76a, Satz 3.2, 3.3]). ГипотезыУ1.82 и
VI.73 эквивалентны.
Доказательство. Поскольку понятия неразделяющей А-цепи и совершенного
А-разбиения для случая плоской эйлеровой триангуляции эквивалентны1), то
из гипотезы VI.82 следует гипотеза VI.73. Значит, достаточно показать
обратное.
Итак, пусть D и x,y,z выбраны так, как это указано в гипотезе VI.82,
и пусть Ai = (я, у, ги), w ф г, есть граница грани в Z), удовлетворяющая
условию Е(А) П E(Ai) = {ху}. Пусть D' и D" — два экземпляра графа D
с xr,yf,z' (хП,у",z"), обозначающими вершины из D' (D"), которые
соответствуют вершинам х,у, z, и положим Н' := D' — Л', Н" := D" — Д", где Л' и
Л'' суть границы граней, соответствующие Л. Вложим теперь Н' в int Л и Н"
в int Ai так, чтобы после отождествления у' с z, z' и у" сх, х' и z" с у и х" с w
полученный граф D\ был эйлеровой триангуляцией плоскости.
Следовательно, Df ~ #' U Л и jD" ~ Н" U Дь Пусть Di имеет совершенное А-разбиение
{V?,!#}. Обозначим через {V?, V?}, {V/, У2'}, W, У2"} разбиения вершин из
D,D',D" соответственно, индуцированные разбиением {Vi1, V^1}.
Из включения х, у € Vj следует, что z G I41, где {j, fc} = {1,2}. Но тогда
х" € V^', у", z" € VI", что равносильно утверждению, что D имеет совершенное
А-разбиение {Vi*, V^*} cxG V^*, ?/, z e V^*, {j, &} = {1,2}. Значит, если k = 1,
то V5 := V/, 5 = 1,2, а если k = 2, то Vi := V^* и V2 := Vi* дают совершенное
А-разбиение {Vi, V2} в D с х € Vi, у,2;б72.
Рассматривая {я, у} {? V^1, j = 1,2, мы можем предположить без
ограничения общности, что ж € Vi1, у € V21. Далее, если z eV^, то {Vi, V2} для Vi :=
Vi°, V2 := V? есть совершенное А-разбиение, что и требуется. Если, с другой
стороны, z G Vi1, то мы получаем а/ Е Vj,, у', z' G V/. Это равносильно
утверждению, что D имеет совершенное А-разбиение {^*,У2*} с у,z ? Vi*, x Е V^*;
значит, {Vi,V2}, определенное равенствами Vi := V^*, V2 := Vi*, —требуемое
разбиение. Предложение теперь доказано.
Мы оставим в качестве упражнения сформулировать гипотезу VI.82 в виде
более строгой (но эквивалентной) версии ГБТ (гипотеза VI.72).
Итак, с одной стороны, мы получили (по сути второстепенное) частичное
решение гипотезы VI.73 (или, эквивалентно, ГБТ2), гипотезы VI.74 соответ-
*' Неразделяющие Л-цепи были определены только для триангуляции плоскости, но не
составляет проблемы распространить это определение на произвольные плоские эйлеровы
графы. Эквивалентности между этими двумя понятиями в общем случае не установлено,
ибо, хотя совершенное А-разбиение определяет две неразделяющие A-цепи, вообще говоря,
неверно, далее в случае 4-однородного графа, что А-разбиение {Vi,V^}, соответствующее
неразделяющей А-цепи, — совершенное А-разбиение. Однако если (V^> связен для 6 = 1,2,
то {Vi, Уг} есть на самом деле совершенное А-разбиение (см. следствие VI.69).
2) В [HOLT85a] было показано, что ГБТ справедлива для графов с меньше чем 66
вершинами.

VI.3. А-цепи в плоских графах
241
ственно) и, с другой стороны, мы можем вывести другую эквивалентную
версию этой гипотезы, а именно гипотезу VI.82. Эквивалентность между А-цепями
в эйлеровых триангуляциях плоскости и гамильтоновыми циклами в плоских
двудольных кубических графах составила основу рассмотрений этого раздела
(и привела даже к более общему утверждению о эквивалентности (VI.А), см.
обсуждение, предшествующее лемме VI.76); эту эквивалентность можно
рассматривать как достаточную мотивацию для изучения А-цепей в
произвольных плоских эйлеровых графах. Но исторически изучение А-цепей началось с
другой гамильтоновой проблемы в плоских двудольных кубических графах.
Коциг (см., например [KOTZ62a, 64а]) изучил и определил конструктивно
такие кубические графы Gs, которые допускают 1-факторизацию {Li,L2,Ls},
такую, что Li U Lj — гамильтонов цикл в Gs для i ф j, 1 < г, j< 3; он доказал
также, что, кроме мультиграфа на двух вершинах, не существует плоского
двудольного кубического графа, который допускает 1-факторизацию указанного
выше типа [KOTZ62a, Theorem 3]. Это привело меня к следующему вопросу
(F): пусть Gs есть 2-связный плоский двудольный кубический граф, и пусть
С — {Li, L2,1/3} — его естественная 1-факторизация (см. теорему 111.67).
Когда Gs содержит гамильтонов цикл Н с L С Е(Н) для некоторого L ? С?
Чтобы ответить на этот вопрос, предположим, не ограничивая общности,
что L — Li, и пусть Q — L<i U ?3. По определению С Q есть 2-фактор графа
Сз, элементы которого —это в точности границы 1-граней из Gs в граневой
3-раскраске, лежащей в основе определения С. Образуем G := Gs/Q в
естественном топологическом смысле путем стягивания каждой границы ЬсЦ-Р) €
Q в вершину из F, не допуская пересечений открытых ребер в ходе стягивания.
Следовательно, для каждой вершины vp ? V(G) циклический порядок 0+(vf)
определяется циклическим порядком, в котором полуребра из L, инцидентные
вершинам из bd(F), встречаются в bd(F) и где vp — вершина из G,
соответствующая bd(F) С Gs- По построению и поскольку Gs двудольный, G — связный
плоский эйлеров граф. Данное выше построение G из Gs приводит к
следующему простому результату, доказательство которого вытекает из предыдущих
рассуждений, и поэтому мы оставляем его в качестве упражнения.
Лемма VI.84. Пусть Gs есть 2-связный плоский двудольный кубический
граф, и пусть С — его естественная 1-факторизация. Пусть выбран L G С
и Q :— E(Gs) — L. Пусть, далее, G = Gs/Q получен, как описано выше. Тогда
следующие утверждения эквивалентны:
1) Gs имеет гамильтонов цикл, содержащий L\
2) G имеет А-цепь.
Значит, исходный вопрос (F) эквивалентен вопросу: какие связные плоские
эйлеровы графы G допускают А-цепь? Как мы видели раньше, существуют
даже графы G с k(G) = 3, которые не допускают Л-цепей. Построенный пример
графа G имел только 3- и 4-угольные границы граней, но для v G V{G) — V±{G),
число d(v) было довольно большим. По контрасту с ним граф Go на рис.
VI.26 имеет только вершины степеней 4 и б, k(Go) = 2, но в нем есть даже
8-угольные грани. Можно уменьшить размер граней заменой 2-угольниками

242
Глава VI. Различные типы эйлеровых цепей
a) G' Ь) Gj
Рис. VI.37. а) б-однородный мультиграф G' без А-цепи, не имеющий тг-угольной
границы грани для п > 4 и имеющий точно две 4-угольные границы граней. Ь)
Кубический двудольный граф G3, такой, что G' = G'^/Qq (Qe определен границами
граней, помеченных <3б). G'$ гамильтонов, но не содержит гамильтонова цикла Н с
E(G'3)-Q6CE(H).
2-связных подграфов из Go, которые определены компонентами из Go — ^(Go)
и ребрами, связывающими их с вершинами степени б (см. рис. VI.37). Эйлеров
мультиграф G', полученный таким образом, является б-однородным и имеет
только 2-, 3- и 4-угольные границы граней. Но он не имеет А-цепи по той
причине, по которой Go не имеет А-цепи. Однако, основываясь на лемме VI.84, мы
можем представить G' в виде G' = G3 /Qq , где Qq — множество шестиугольных
границ граней из G'3; другие грани ограничены в G3 4-, б- и 8-угольниками.
Заметив, что G'3 имеет точно две 8-угольные границы граней, мы видим, что
D = D(Gf3) — обыкновенная эйлерова триангуляция с вершинами степени 4, 6
и точно двумя вершинами степени 8. Это значит, что D «почти» принадлежит
То или, другими словами, G3 «почти» принадлежит Во (см. определения % и
Во перед формулировками теоремы VI.77.a и теоремы VI.77 соответственно).
Однако, хотя G3 имеет 2-фактор Qe, каждый элемент которого —
шестиугольник, G3 не имеет гамильтонова цикла, содержащего 1-фактор E(G3) — Qq. Тем
не менее мы предлагаем следующий вопрос: имеет ли граф Сз € Во
гамильтонов цикл Н с L С Н, где L есть 1-фактор в естественной 1-факторизации
графа Сз? Можно задать тот же вопрос относительно кубических графов,
двойственные к которым встречаются в теореме VI.79. В терминах А-цепей в эй-

VI.3. А-цепи в плоских графах
243
леровом графе мы приходим к следующему вопросу: существует ли А-цепь
в 2-связном плоском эйлеровом графе G с Vn(G) = 0 для п > 6, таком, что
\E(bd(F)) |< 5 для каждой грани F и \E(hd(F')) |= 4 для не более чем одной
грани F''? Граф G' на рис. VL37(a) показывает, что нельзя допускать более
одной такой грани F''. Кроме того, этот же граф G' показывает, что детальное
рассмотрение 2-факторов Q вообще бесперспективно (в этом случае Q = Qq —
множество шестиугольников). Однако если (не обязательно планарный)
связный кубический граф Сз имеет 2-фактор Q±, каждый цикл которого есть
4-угольник, то Сз имеет гамильтонов цикл Я D E(Gs) — Qa [KOTZ68c,
Theorem 6]. Это получается применением следствия VI.6. Поэтому мы оставляем
читателю доказательство этого результата.
Поставленный выше вопрос (F) и соответственно утверждение об
эквивалентности из леммы VI.84 можно также сформулировать в терминах А-цепей
в эйлеровой триангуляции плоскости.
Теорема VI.85. Пусть Сз есть 2-связный плоский двудольный
кубический граф с его естественной 1-факторизацией С, и пусть D = D(Gs)
задан вместе с вершинной Ъ-раскраской {Сг,С2,Сз}, соответствующей
(естественной) граневой 3-раскраске графа G% (см. теорему 111.67).
Следующие утверждения эквивалентны:
1) Сз имеет гамильтонов цикл Н, содержащий L\ Е ?;
2) V(D) имеет совершенное А-разбиение {V\, V2}, удовлетворяющее
равенствам Vi = С[ U С2, V2 = С'{ U С3, С[ U С{' = d.
Доказательство. Рассмотрим Н как простую замкнутую кривую в
евклидовой плоскости. Для каждого е € Li, поскольку е € ?,(Я)ПЕ'(Ьс1(^2))ПЕ,(Ь(1(^з))
для некоторой 2-грани F2 и 3-грани F% в естественной граневой 3-раскраске
графа Сз, мы заключаем, что F2 € int H тогда и только тогда, когда F3 E ext Я.
Предположим, что для ei,/i G L\ соответствующие г-грани F',F" с в\ G
j?(bd(F')), /1 Е jE'(bd(F'/)) лежат по разные стороны от Я, г е {2,3}. Выбирая
в\ и /i лежащими на Я так близко друг от друга, как это возможно, мы можем
предположить, что в\ и Д связаны в Я ребром д. Без ограничения общности
можно считать, что д € L2 Е С. Обозначим через ез,/з Е Ь% ребра,
связывающие д с ei и Д соответственно. Открытые ребра е'3,/% не могут лежать
по одну и ту же сторону от Я; с одной стороны, E(bd(F')) П E(bd(F")) ф 0,
что противоречит тому, что обе грани F' и F" являются г-гранями. С другой
стороны, из того факта, что вд,/з лежат по разные стороны от Я, следует,
что {ез,р,Д} С E(bd(F*)) и {ei,<7,/3} С E(bd(F**)) для некоторых граней
F* и F**. Однако, поскольку в естественной реберной 3-раскраске С граница
каждой грани содержит ребра только двух классов из ?, тогда как каждая из
границ bd(F*) и bd(F**) содержит ребра из всех трех классов С, мы получаем
противоречие, из которого следует, что либо все 2-грани лежат в ext Я, либо
все лежат в int Я. Предположим, не ограничивая общности, что 2-грани лежат
в int Я. Из приведенных в начале доказательства соображений вытекает, что
3-грани лежат в ext Я. Обозначив через С[ (С") обязательно непустое
множество 1-граней, лежащих в int Я (ext Я), и положив далее V\ := V(Ti), V2 :=

244
Глава VI. Различные типы эйлеровых цепей
V(T2), где Т\ и Тч суть деревья в Г>(Сз), определенные гранями из Сз,
лежащими в int(iJ) и ext(H) соответственно, мы получим V\ = C{UC2, Vi = С"иСз,
где С[ U С" = Ci, С{ ПС" = 0 по определению. Далее, поскольку Gz
двудольный, D := D(Gs) есть эйлерова триангуляция плоскости и, значит, {VI, V2} —
совершенное А-разбиение множества V(D) по теореме VI.70.
Обратно, предположим, что совершенное А-разбиение {Vi,V^} множества
V{D) задано так, как это описано в 2), и пусть Г* = (V*), г = 1,2, —
соответствующие деревья. Для каждого г G {1,2} ребра из Сз, принадлежащие в точности
одной из границ граней среди представленных в V*, определяют гамильтонов
цикл Н в Сз, причем Н происходит как из Vi, так и из Vi.
Поскольку
Vi = C[ U С2, т. е. С3 П VI = 0,
и
Li = {е G ?(bd(F2)) П S(bd(F3))|Fj является j-гранью, j = 2,3},
мы приходим к заключению, что каждое ребро из L\ принадлежит точно
одной границе грани, представленной в Vi. Значит, L\ С Е(Н). Это завершает
доказательство теоремы.
Следовательно, вопросы существования А-цепей в плоском эйлеровом
графе можно, в принципе, трактовать как вопросы существования А-цепей
специальных типов (соответственно совершенных А-разбиений) в эйлеровой
триангуляции плоскости или, кроме того, как вопросы существования специальных
типов гамильтоновых циклов в плоском двудольном кубическом графе. Это
приводит нас к вопросу, почему надо работать с А-цепями в плоских
эйлеровых графах, а не прямо рассматривать гамильтоновы проблемы в плоских
двудольных кубических графах (в частности, в силу эквивалентности между
ГБТ и гипотезой VI.73, а также между результатом Гудея (теорема VI.77) и
теоремой VI.77.a). История вроде бы подтвердила «гамильтонов подход», и в
разд. VI.2 мы доказали результат о гамильтоновом разложении для решения
эйлеровой проблемы. Однако, как мы увидим далее в контексте разложений
на совместимые циклы, исследование некоторых проблем в эйлеровых графах
с интерпретацией соответствующих результатов на языке кубических графов
оказалось действительно очень результативным подходом. В частном случае
А-цепей, по моему мнению, «эйлеров подход» может быть столь же
плодотворным. Это мнение основывается не только на многолетнем опыте изучения
как эйлеровых, так и гамильтоновых проблем, но также и на
методологической разнице между исследованиями А-цепей и гамильтоновых циклов в
соответствующих классах графов. А именно, нахождение эйлеровых цепей любого
вида всегда затрагивает все ребра графа, тогда как нахождение гамилътонова
цикла требует подходящего расположения некоторых ребер и отбрасывания,
так сказать, оставшихся ребер. Последняя проблема представляется, таким
образом, более сложной, если рассматриваемый граф имеет лишь вершины
малой степени (в частности, если он 3-однородный). В подтверждение этой точки
зрения можно сравнить теорему Оре (теорема III.75) с ГБТ (гипотеза VI.72)).
Мы закончим этот подраздел демонстрацией отношения между
произвольными плоскими 2-связными графами и некоторыми эйлеровыми триангуля-

VI.3. А-цепи в плоских графах
245
циями плоскости, обладающими неразделяющей А-цепью [REGN76a, Theorem
5.1], соответственно, плоскими двудольными кубическими графами с гамиль-
тоновым циклом. А именно: пусть G — плоский 2-связный граф, и рассмотрим
GA :=5(G)Ui?(5(G)).
Из определения следует, что Сд — эйлерова триангуляция плоскости (заметим,
что S(G) двудольный); это обыкновенный граф, поскольку «(G) > 2. Снова по
определению вершинная 3-раскраска графа Сд (которая единственным
образом определена с точностью до перестановки цветовых классов) задана
разбиением {Т4^ ^2, V3} множества V(G/\), где
V, := V(G), V2 := V(S(G)) - V(G), V3 := V(R(S(G))) - V(S(G))
(заметим, что V\ — независимое множество уже в 5(G), V<i — независимое
множество по определению 5(G) и У$ — независимое множество, поскольку каждая
грань из S(G) содержит точно одну вершину из R(S(G))). Заметив, что V<i —
множество вершин степени 4 в Сд, мы можем заключить из теоремы VI.67, что
Н := ((Ga)vi,i)v3,2 связен и имеет только вершины степеней 2 и 4; значит, он
содержит А-цепь Тн, которую можно интерпретировать как А-цепь Т из Сд.
Из определения Т следует, что она неразделяющая. Значит, G3 := D(G&) —
гамильтонов плоский двудольный кубический граф с k,(Gs) = 3.
VI.3.2. А-цепи и гамильтоновы циклы в эйлеровых графах
Возвращаясь к обсуждению теоремы VI.85, мы сталкиваемся с вопросом, в
каком направлении следует двигаться, чтобы выяснить, какие классы плоских
эйлеровых графов допускают А-цепи. Как мы видели выше и
сформулировали эквивалентным образом, детальное изучение степеней вершин из цветового
класса в вершинной 3-раскраске эйлеровой триангуляции плоскости не
представляется перспективным, за исключением случая, когда каждая вершина
цветового класса имеет степень 4. Но имеется параметр, который играет
существенную роль во многих проблемах теории графов и особенно в теории
плоских графов — связность. Как мы видели ранее, существует 3-связный плоский
эйлеров граф, не допускающий Л-цепей. Хотя в нашем построении
триангуляция плоскости, с которой мы начинали, может быть 5-связной (поскольку
существуют негамильтоновы плоские циклически 5-реберно-связные
кубические графы), получаем мы всегда 3-, но не 4-связный плоский эйлеров граф.
Я пытался модифицировать конструкцию, чтобы получить 4-связный плоский
эйлеров граф без Л-цепей, удовлетворяющий эквивалентности в утверждении
(VI. А) (см. обсуждение, следующее за леммой VI.75), но безуспешно. Поэтому
я высказываю следующее предположение.
Гипотеза VI.86. Каждый плоский 4-связный эйлеров граф имеет А-цепь.
Неудача, о которой я сказал выше, — не единственная причина для этого
предположения. На самом деле из теоремы о мосте Татта (теорема III.70)
следует, что каждый планарный 4-связный граф является гамильтоновым
(следствие III.71). И это действительно очень сильное свойство. Кроме того,
показано, что проблема нахождения гамильтонова цикла в 4-связном планарном

246
Глава VI. Различные типы эйлеровых цепей
графе имеет полиномиальную сложность. Более точно, был найден алгоритм,
основанный на доказательстве теоремы о мосте Татта (теорема III.70),
«время и память которого ... оцениваются сверху величиной порядка 0(п3)»,
где п есть число ребер [GOUY82a, Theorem 2]. Это резко контрастирует с тем
фактом, что решение вопроса о существовании гамильтонова цикла в
плоском 3-связном кубическом графе является iVP-полной проблемой [GARE76a],
и этот факт будет играть некоторую роль в нашем исследовании сложности
задачи выяснения, имеет ли планарный эйлеров граф А-цепь. Кроме того,
нахождение гамильтоновых циклов в двудольных кубических планарных
графах—тоже iVP-полная проблема [PLES83a]; однако этот результат включает
в себя все такие 2-связные графы (которые не слишком интересны с точки
зрения ГБТ и в силу соображений двойственности не играют заметной
роли при рассмотрении А-цепей). С другой стороны, в [NISH83a] было показано,
что проблема нахождения гамильтонова маршрута (кратчайшего замкнутого
маршрута, покрывающего все вершины) в триангуляции плоскости может быть
решена за время порядка 0(р2) и что длина гамильтонова маршрута не больше
\(р—3) при р > 9 *). Значит, в случае 4-связной триангуляции плоскости можно
найти гамильтонов цикл даже за время 0(р2). Позднее в [ASAN84a] был
построен линейный алгоритм нахождения гамильтонова цикла в таких графах,
и в том же году Н. Чиба и Т. Нисизеки опубликовали такой алгоритм для
произвольного 4-связного плоского графа (см., например, [NISH88a, pp. 182-184].
Существование гамильтонова цикла в 4-связных триангуляциях плоскости
вытекает из результата Татта, но было доказано еще X. Уитни в тридцатых годах
(см. следствие III.72). Заметим, что триангуляция плоскости не обязательно
гамильтонова — стоит только применить Об-расширение к каждой грани такой
триангуляции). Эти рассуждения можно рассматривать как положительное
обоснование гипотезы VI.862).
Гамильтонов цикл Н в обыкновенном плоском графе G определяется двумя
обыкновенными 2-связными внешнеплоскими графами G\, G2,
удовлетворяющими условиям Gi UG2 = G и G\ ПСг = Н3\ Действительно, рассматривая Н
как простую замкнутую кривую на плоскости, а плоский граф — как некоторое
множество точек, можно определить G\ и G2 формулами
V(G1) = V(G2) = V(G),
E(Gi) = {ee E(G)\e П int Я = 0}, E(G2) = {/ G E(G)\f П ext H = 0}.
*' Здесь вкралась ошибка — на самом деле установлено, что за время порядка 0(р2) может
быть найден У(С)-покрывающий маршрут, длина которого не превосходит 3(р — 2)/2, в то
время как указанная проблема для таких графов АГР-полная. — Прим. автора к русскому
изданию.
2) А. Роса однажды сказал мне во время прогулки, что, по его мнению (и я надеюсь, что я
цитирую его правильно), имеется две категории гипотез: во-первых, те, о которых «каждый
знает, что они должны быть верны, но никто еще их не смог доказать», и, во-вторых, те,
о которых говорят: «удивительно, если они окажутся верными». Я полагаю, что это очень
хорошая характеристика, как математики (сколько их?) относятся к гипотезам (в моих
собственных исследованиях я сталкивался с обеими ситуациями). Что касается гипотезы VI.86,
я бы поместил ее между этими двумя категориями.
3) Конечно, в точности для одного из G\ и Gi «внешняя грань» ограничивает область,
определенную циклом Я", но не сложно заново вложить соответствующий граф Gi, г Е {1,2},
не меняя <D+(Gi), — просто начать с вложения графа G в сферу.

VI.3. А-цепи в плоских графах
247
Теперь, если оба графа G\ и G2 эйлеровы, то по теореме VI.63 они имеют
А-цепи Т\ и Тч соответственно. Значит, можно надеяться, что этого достаточно
для построения А-цепи Г в G, начиная с 2\ и Т2.
К сожалению, для 4-связного плоского эйлерова графа G наличие гамиль-
тонова цикла Н не гарантирует простого способа нахождения А-цепи в G. Это
общее утверждение иллюстрируется следующем обсуждением, в котором мы
говорим, что гамильтонов цикл Н графа G обладает А-свойством, если
любая пара ребер {е,/}, смежных в Н, принадлежит границе грани в G (или,
что эквивалентно, е' и /' — соседи в 0+(v), где е',/' € Е*; ср. [REGN76a,
Definition 4.2.1.]). Как мы увидим ниже, если G допускает такой цикл if,
обладающий А-свойством, то действительно можно скомбинировать А-цепи Т\ и
Ti в G\ и Gi соответственно, чтобы получить А-цепь в G. На самом деле
в этом случае можно начинать с произвольных А-цепей. Однако сначала мы
изучим А-разбиения во внешнеплоских эйлеровых графах. Следующий
результат [REGN76a, Theorem 4.1.2.] дает простую и точную характеризацию таких
А-разбиений (этот результат будет более уместен, однако, при выводе формулы
для числа А-цепей во внешнеплоском графе. См. т. 2, гл. IX).
Теорема VI.87. Пусть G — обыкновенный 2-связный внешнеплоский эйлеров
граф с заданной граневой 2-раскраской, внешняя грань F^ которого является
1-гранью. Тогда следующие утверждения эквивалентны:
1) G имеет А-цепь.
2) V(G) допускает разбиение {Vi, V2}, такое, что \ V(bd(F\)) П Vi |= 1 для
каждой 1-грани F\ ф F^.
Доказательство. Если G — цикл, то эквивалентность между утверждениями
1) и 2) верна из-за их бессодержательности, ибо в этом случае грани F\ ф
Fqo не существует. Значит, в дальнейшем обсуждении мы предполагаем, что
Д(С) > 2. Это значит, что существует хотя бы одна 1-грань F\ ф F^.
a) Пусть Т есть А-цепь в G, и пусть F\ ф Foo выбрана произвольно. Далее,
пусть {Vi, V2} обозначает любое А-разбиение, определенное цепью Т.
Поскольку Fi есть 1-грань, мы получаем | V(bd(Fi)) f)Vi |> 0; это следует
исключительно из того факта, что A(G) > 2; в этом случае из V(bd(Fi)) П Vi = 0 следует,
что Gv2,2 несвязен и (E(bd(Fi))) —его компонента.
Предположим теперь, что V(bd(Fi)) П Vi D {v, w}. Тогда R = {Fi,Foo} —
одноцветное кольцо граней с Lr = {v, w} в качестве полного множества связей.
Элементы из R суть 1-грани, и справедливость включения Lr С Vi следует из
предположения. В силу теоремы VI.67, однако, это противоречит тому факту,
что {Vi,V2} есть А-разбиение.
b) Предположим, что для каждой 1-грани F\ ф F^ разбиение {Vi, V2}
множества V(G) удовлетворяет условию | V(hd(Fi)) П V\ \— 1. Рассмотрим
произвольное одноцветное кольцо граней R, элементы которого суть 5-грани для
фиксированного S € {1,2}, и пусть Lr — полное множество связей кольца R.
По теореме VI.67 достаточно показать, что Lr % Vs. Предположим, напротив,
что для некоторых таких йи Lr мы имеем Lr С Vs.

248 Глава VI. Различные типы эйлеровых цепей
Предположим сначала, что 6 = 1. Так как |Д| > 1, то F\ ? Д для
некоторой грани Fi ф Fqo, и по определению |V(bd(Fi)) П Lr\ = 2. Следовательно,
|y(bd(Fi)) П Vi\ > 1, что противоречит 2).
Теперь предположим, что 6 = 2. Среди возможных выборов Д и Lr
рассмотрим такой, что | Lr | минимально, т. е. из того, что L С Lr, следует, что не
существует одноцветного кольца граней Д', для которого L было бы полным
множеством связей. Мы хотим показать, что Lr = V(bd(F*)) для некоторой
1-грани F* ф Foo.
Из минимальности Lr следует, что | bd(F') П bd(F") П Lr \g {0,1} для
различных элементов F', F" € Д. Значит, мы можем выразить Д и Lr в
следующем виде:
R = {-^Ь • • • ?-^ш}>
?д = {vi,z+i|г = 1,..., га, причем считается, что г>т,т+1 = г>тд},
где
LflHbd(Fi) nbd(Fi+i) = {viii+i} для г = 1,...,га
(считается, что Fm+i = Fuvm^m+1 = vm,i) и
bd(Fi)nbd(F7) = 0 для j - г > 1, 1 < г < j < m, {г J} ф {1,га}.
Как и в первой части доказательства теоремы VI.67, мы строим простую
замкнутую кривую С с
771
GDC = LR и C-LRc\jFi.
г=1
Неограниченная область кривой С, extC, содержит Foo, и, поскольку граф G
внешнеплоский, из этого следует, что intC П V(G) = 0. Следовательно, путь
-Рм+ь соединяющий Vi-M и г^+i в bd(Fi), открытые ребра которого лежат в
intC, должен удовлетворять условию
Рг,г+1 С intC U {Vi-l,i, Vj,i+l}»
и, значит,
V(P»,i+i) = {vi-i,i,r;i,i+i}, т.е. F(PM+i} = {vi-i.t^i+i}-
Следовательно,
(L#) С intС U Lr и (?#) —цикл.
Поэтому Л(е) = 1 (е G F(G)), и из минимальности L# следует, что
{mtC-E((LR)))nG = 0.
Это значит, что смежные ребра в {Lr) являются последовательными в 0+(v),
где г; —их общая концевая вершина. Тогда {Lr) —граница грани bd(F*).
Поскольку E({Lr)) DF(bd(Fi)) ф 0 для г = 1,..., га, из этого следует, что F* есть
1-грань, и F* ф Fqo, потому что {Lr) П extC = 0. Значит, мы нашли 1-грань
F*c
V(bd(F*)) = LRC V2, т. е. | ^(bd(F*)) П Уг \= 0.
Это противоречие с утверждением 2) завершает разбор случая 5 = 2] значит,
Lr % Ye, 6 G {1,2}, для каждого одноцветного кольца граней Д, такого, что

VI.3. А-цепи в плоских графах
249
его элементы суть 5-грани, a Lr — его полное множество связей. По теореме
VI.67 G имеет А-цепь, которая индуцирует А-разбиение есть {Vi, V2}.
Теперь докажем результат, сформулированный в конце обсуждения
предыдущей теоремы VI.87.
Теорема VI.88 ([REGN76a, Theorem 4.2.1.]). Пусть G — обыкновенный
плоский эйлеров граф с гамилътоновым циклом Н, обладающим А-свойством.
Тогда G имеет А-цепъ.
Доказательство. Мы можем считать, что G есть объединение двух 2-связных
внешнеплоских эйлеровых графов G\ и G2 с G\ П G2 = Н (см. обсуждение,
предшествующее теореме VI.87). Пусть 7\ и Т2 суть А-цепи в G\ и G2
соответственно; по теореме VI.63 7\ и Т2 существуют. (Мы начинаем с гране-
вой 2-раскраски графа G и применяем теорему VI.63 к графу G*, граневая
2-раскраска которого индуцирована граневой 2-раскраской графа G, г = 1,2.
Значит, грань из G*, граница которой содержит все вершины из G, имеет цвет
1 либо 2 в зависимости от значения г ? {1,2}.)
Поскольку Н обладает А-свойством, то для произвольной вершины v E
V(G)
dciiy) > 2, только если dc^v) =2и dc^v) = dc{v), {i,j} — {1,2}. (*)
Рассмотрим теперь {Vl,V2}, Л-разбиение, соответствующее цепи Т* в G*, i =
1,2, и положим
W) := Vf П (V(Gi) - V2(Gi)) для произвольных г J е {1,2}.
Это определение вместе с равенством VI П V2 = 0 и (*) дает
W]nWlk = 0 для 0\г)#(М), {М,МК{1,2} (**)
(заметим, что Wj С V2(Gk) для {г, к} = {1,2}).
Следовательно, {Wj\i,j = 1,2} есть разбиение множества V(G) — V2{G)\
значит, Wj := Wj U Wj, j = 1,2, определяют разбиение множества V(G) —
V2{G).
Заметим теперь, что вершина v2 степени 2 не может принадлежать
никакому полному множеству связей Lr ни для какого одноцветного кольца граней R,
ибо v2 принадлежит в точности одной <5-грани, 5 = 1,2. Значит, если мы можем
показать для таких R и Lr, что Lr % W$, при условии, что элементы из R суть
5-грани, 5 Е {1,2}, то для любого V2 С V2(G) можно получить А-разбиение
{VUV2} множества V(G), положив Vi := W1 U У2°, V2 := W2 U (V^G) - V<?) (см.
теорему VI.67).
Итак, пусть R и Lr такие же, как мы описали выше. Если все элементы из R
суть 5-грани из Gi, г G {1,2}, то из существования Т$ следует, что Lr % Wj, no
теореме VI.67, S Е {1,2}. Поскольку W^ С V2(Gi) для {г,^} = {1,2}, мы имеем
Lr % Ws- Значит, мы должны предположить, что некоторые элементы из R
суть грани из Gi, а некоторые — грани из G2 и все они — 5-грани, 5 Е {1,2}.
Далее мы сужаем ситуацию, предположив (что не ограничивает общности),

250
Глава VI. Различные типы эйлеровых цепей
что «внешняя» грань F1 (F2) графа Gx (G2) имеет цвет S (5 + 1), где мы
полагаем 5 + 1 = 1, если 6 = 2 (см. второе подстрочное примечание в
обсуждении, предшествующем теореме VI.87). Далее, пусть R = {i<\,... ,Fm;ra > 1}
и Lr = {^1,2,^2,3, • • •»vm,i} (см. доказательство теоремы VI.87, часть Ь)).
Перенумеровав, если необходимо, элементы из R и Lr, мы можем предположить
без ограничения общности, что bd(Fi) С Gx, bd(Fm) С G<i- Положим
i2 = min{z|l < i < m и bd(JFi) С G2} и i\ = i2 — 1.
Тогда мы получим в G\ одноцветное кольцо граней R', элементы которого суть
5-грани, и соответствующее полное множество связей Z/ = Lr>, положив
R' := {Fi,...,^,^1}, U = {vi,2,...,Viui2,vm,i}.
Мы имеем L' С Lr и I/ С V(Gi). Если бы мы имели L# С W$, to из этого и из
включения W| С V^(Gi) следовало бы, что I/ С Wj С У/. Но теорема VI.67,
примененная к Gx, утверждает, что из существования цепи Т\ и А-разбиения
{ViiV}} следует, что V %. V$. Значит, Lr % W$. Снова по теореме VI.67 и
приведенным выше определениям множеств V± и Vi это означает, что {Vi, V2}
есть А-разбиение для G, т. е. G имеет А-цепь. Теперь теорема VI.88 доказана.
Однако не каждую А-цепь Т графа G можно получить из А-цепей 7\ и
Т2 графов Gi и G2 соответственно, как описано в доказательстве теоремы
VI.88. А именно, некоторое А-разбиение {Х^, V2} множества V(G) может не
быть А-разбиением множества V(Gi) = V(G) для г = 1,2. Это можно увидеть
уже в случае графа Об, который мы можем считать полученным из цикла
Об = (vi,... ,г>б) добавлением Дх = (^1,^3,^5) и Дг = (^2,^4,^б)- Вложим
Дх в ограниченную область цикла Ов; значит, Л2 лежит в неограниченной
области цикла Cq. Мы предполагаем, что внешняя грань графа Об с граневой
2-раскраской есть 1-грань. Положив Н := Об, Gx := H U Л1? G2 := H U Дг и
Ух •= {^2^з5^б}> V2 := {^ъи*,^}, мы заключаем, что хотя {Vi, V2} —
(совершенное) А-разбиение множества V(G), {VbV^} не является А-разбиением ни
множества V(Gi) = V(G), ни множества T^(G2) = V(G) (заметим, что Н
обладает А-свойством). Действительно, (Gx){Vl,V5},2 несвязен, и поэтому несвязен
(Gz){v2,v6},i- Однако если А-разбиение {Vx> V2} множества V(G) является
также А-разбиением множества V(Gi), i G {1,2}, мы можем сказать, что
последнее есть индуцированное А-разбиение первого. Соответственно мы можем
сказать, что А-цепъ Ti графа Gi индуцирована А-цепъю Т графа G.
Граф на рис. VI.38 показывает эйлерову триангуляцию плоскости D с га-
мильтоновым циклом Н, так что соответствующие графы Gx, G2
удовлетворяющие условиям Gx U G2 = D и Gx П G2 = Я (см. рассуждения перед теоремой
VI.87), эйлеровы. Рассмотрим этот граф D: Н не обладает А-свойством,
поскольку (V(Gi) - V2(Gi)) П (V(G2) - V2(G2)) = {a,6,c,d,e,/}. Из теоремы
VI.63 мы знаем, что Gi имеет А-цепь Т^, г = 1,2. Покажем теперь, что
никакой выбор Т\ и Т2 не допускает расширения этих А-цепей до А-цепи Т из G
способом, подобным тому, который использовался в доказательстве теоремы
VI.88. Для этой цели достаточно показать, что Т\ не индуцирует
расщепление множества Vo := {a, 6, с, d, e, /} того же типа, что Т2. Более точно, пусть
граневые 2-раскраски для Gx и G2 получены из граневой 2-раскраски для D.

VI.3. А-цепи в плоских графах
251
Рис. VI. 38. Эйлерова триангуляция плоскости D с гамильтоновым циклом if,
определяющим два 2-связных внешнеплоских эйлеровых графа G\, G2 с D = G\ UG2, Н =
GiDG2. Граф D не имеет А-разбиения, индуцирующего А-разбиения в обоих графах
Gi и G2 (заметим, что (V{Gi) - V2(Gi)) П (V(G2) - V2{G2)) ф 0).
Среди G\ и G2 пусть G\ определен как граф, внешняя грань F^ которого
есть неограниченная область цикла Н (где Н рассматривается как простая
замкнутая плоская кривая), и предположим (без ограничения общности), что
граневая 2-раскраска графа D выбрана так, что Fqq в Gi есть 1-грань.
Значит, «внешняя» грань int H графа G2 является 2-гранью. Как и в
доказательстве теоремы VI.88, пусть {V^V^} есть А-разбиение, соответствующее
произвольно выбранной А-цепи Ti из Gi, г = 1,2. Покажем теперь, что равенства
Vo П Vi = Vo П Fj2, Vo П V2 = Vo П V% не могут иметь места.
Предположим, что а € Vj1. Поскольку d, е, / — граничные вершины 1-граней
из Gi, каждая из которых содержит также а в качестве граничной вершины,
{d, e, /} С V^1 в силу теоремы VI.87. Однако по той же теореме включение
{е,/} С V% невозможно, так как {е, /} С bd(F2) для некоторой 2-грани F2 из
G2 и так как «внешняя» грань графа G2 также является 2-гранью. Значит,
рассматриваемые равенства не верны, если a € V*.
Предположим теперь, что а € V^1 П У22. Поскольку Ь и с —граничные
вершины 2-граней из G2, каждая из которых также содержит а в качестве
граничной вершины, по теореме VI.87 мы имеем {&, с} С V?. С другой
стороны, {Ь,с} С y(bd(Fi)) для некоторой 1-грани из G\\ значит, по теореме VI.87

252
Глава VI. Различные типы эйлеровых цепей
имеем {6, с} % V± . Следовательно, и в случае a Е V^1 мы можем заключить,
что указанные равенства неверны. Однако мы оставим в качестве упражнения
проверку того факта, что D в самом деле имеет А-цепь (заметим, однако, что
k(D) = 3).
Итак, хотя в общем случае невозможно из некоторой А-цепи графа G
получить А-цепи Ti в Gi, г — 1,2 (где Gi определены, как выше, относительно
гамильтонова цикла Н), даже если Н обладает А-свойством, мы получили
следующий интересный результат [REGN76a, Satz 4.2.2]. Мы представим
доказательство, совершенно отличное от доказательства Регнер.
Теорема VI.89. Предполооюим, что плоский эйлеров граф G, снабженный
граневой 2-раскраской, имеет гамильтонов цикл Н, определяющий два внеш-
неплоских графа G\,G2, удовлетворяющих условиям G\\JG2 = G, G\C\G2 = Н
(см. выше). Если G имеет А-цепь Т, индуцирующую А-цепъ Ti в Gi, T
индуцирует также А-цепъ Tj в Gj, {i,j} = {1,2}.
Доказательство. Мы можем предположить без ограничения общности, что
Fqo, неограниченная грань графа G\ (с bd(i7'00) = Н) является 1-гранью в
граневой 2-раскраске графа G±, индуцированной граневой 2-раскраской графа G,
и что G имеет Л-цепь Т, индуцированную А-цепью Т2 в Gi- Пусть {Vi, V2} есть
А-разбиение множества V(G) — V(G2), соответствующее цепям Т,Т2
соответственно. Покажем, что {Vi,^} — также А-разбиение множества V{G\). Для
этого мы вначале заметим, что G1 := Gvl5i —связный внешнеплоский граф,
внешняя грань F^ которого является 1-гранью с j&(bd(F00)) С E(bd(F^Q)),
такой, что E(hd(F^0)) П Е(В) ф 0 для каждого цикла В из G1 (лемма VI.58,
теорема VI.59). Если мы сможем показать, что каждый нетривиальный блок
из G1 — E(G\) является висячим блоком в G1, то в G1 — (G2 — Е(Н)) имеется
точно одна нетривиальная компонента, а именно (Gi)vbi, удовлетворяющая
предположению леммы VI.58.
Рассмотрим граф
G° := (G2)Vl,iU (Eid) - Е(Н)).
G° определен корректно, так как «внешняя» грань F°° графа G2 является
2-гранью в индуцированной граневой 2-раскраске графа G2 (поскольку Fqq
есть 1-грань) и, значит, Е(Н) = E(bd(F°°)); поэтому построение G0 из (G2)Vl,i
состоит в добавлении диагоналей цикла Н, лежащих в Gi, т.е. добавлении
элементов из (Gi) — E(H). Кроме того, поскольку Т2 проходит по границе
однозначно определенной 1-грани из (G2)vbi, то по определению G0 связен.
Далее, из включения E(hd(F°°)) С E((G2)vui) следует, что
1) (G2)vi,i содержит в качестве блока (E(bd(Foc)))\
следовательно,
2) G0 имеет блок В°° э (?(bd(F°°))) с В°° ~ d;
3) каждый блок С из G0 — В°° является циклом с Е(С) С E(G2) — Е(Н),
и, значит, С — висячий блок в G0 (см. 2)).

VI.3. А-цепи в плоских графах
253
Пометим вершины из 5°° в соответствии с их исходными метками в G;
тогда мы получим В°° = G\ и изоморфизм
Gl * (GV.,1- (*)
Для каждого блока С из G0, отличного от В°° (см. 3)), мы имеем СГ\В°° С V2-
Значит, единственная вершина vq ? С П J5°° не затронута переходом от G0 к
(G°)vi,i- Поскольку каждая вершина х € V(C—vc) имеет степень 2 в G0 и,
значит, также и в (G°)vi,i, каждый блок С из G0 — ??°° — висячий блок в (G°)v1?i.
И наконец, если мы рассматриваем G\ и (G°)vi,i как непомеченные графы,
то изоморфизм (*) делается тождественным (в (*) изоморфизм может быть
выбран так, чтобы он был тождественным на E{Gl) = E((G°)v1,i)-
Следовательно, каждый нетривиальный блок в G1 — E(G\) является висячим блоком
из G1, множество ребер которого принадлежит G2 — Н. Поэтому
(G1 - E(G2 - Н)) - VoiG1 - E(G2 - Я)) = (Gi)Vlli,
и этот граф удовлетворяет предположению леммы VI.58, так как G1 также
удовлетворяет этому предположению (левая часть последнего равенства
означает лишь удаление некоторых висячих блоков из G1, которое приводит к
связному графу и оставляет неизменными свойства вложения, приведенные в
лемме). Из этого вытекает, что (Gi)vi,i имеет А-цепь. Следовательно, G\ имеет
А-цепь. Теорема доказана.
Возможно, приведенные выше рассуждения об А-цепях в плоских гамиль-
тоновых эйлеровых графах будут полезны при возможном доказательстве или
опровержении гипотезы VI.86. Я не знаю, однако, какие из плоских 4-связных,
эйлеровых графов допускают гамильтонов цикл Н, обладающий А-свойством
или хотя бы такой, что графы G\, G2, определенные как intHUН и extHUH,
эйлеровы.
Итак, рассмотрим гипотезу VI.86 для случая эйлеровых триангуляции D.
Представленные ранее конструкции (см. также рассуждения перед
гипотезой VI.86) не позволяют прийти к заключению, что А-цепи и неразделяющие
А-цепи суть эквивалентные понятия в 4-связной эйлеровой триангуляции
плоскости (ср. с гипотезами VI.73, VI.74 и дискуссией, приводящей к лемме VI.75).
Изменим гипотезу VI.86 для триангуляции плоскости, заменив в ней
выражение «А-цепь» на «неразделяющая А-цепь». Из теоремы VI.71 и соотношения
k(D(Gs)) = \с{(*з) для связных плоских кубических графов Сз Ф К±
следует, что эта модифицированная гипотеза эквивалентна ГБТ (гипотезе VI.72)
для случая циклически 4-реберно-связных планарных двудольных кубических
графов. Но что следует из существования (не обязательно неразделяющей)
А-цепи в D — T)\G%) для G3? Ответ на этот вопрос дает следующая
теорема. Вспомним, что доминирующий цикл в графе G (или цикл Татта, если G
кубический) —это цикл G, такой, что E{G — V(G)) = 0.
Теорема VI.90. Пусть Сз — связный плоский двудольный кубический граф с
разбиением {Vi^}, и пусть D(Gz) —двойственный к нему. Следующие
утверждения эквивалентны:
1) D{Gz) имеет А-цепь;

254
Глава VI. Различные типы эйлеровых цепей
2) Сз имеет цикл Tamma С, такой, что V \— Gz — V{C) удовлетворяет
следующим условиям:
a) Vi П V С int С тогда и только тогда, когда V^ П V С ext С;
b) Vi П V7 П ext С = 0 tun Vi П V П int С = 0.
Доказательство теоремы VI.90 можно получить, модифицируя
доказательство Татта теоремы VI.71; поэтому оставим его в качестве упражнения.
Заметим, что в теореме VI.90 эквивалентность между циклами Татта
специального типа вбз и А-цепями в D(Gz) не требует, чтобы Лс(Сз) = 4. С
другой стороны, теорема о мосте Татта гарантирует существование
доминирующего цикла в планарных циклически 4-реберно-связных кубических графах
(следствие III.73). Значит, в случае Ас(Сз) = 4 эквивалентность, выраженная
в теореме VI.90, сводится к вопросу, можно ли найти в непустом множестве
циклов Татта из Gz элемент, удовлетворяющий условиям а) и Ь). Заметим
также, что если рассматривать неразделяющие А-цепи, то достаточно
доказать гипотезу VI.73 для 4-связных триангуляции; это следует из предложения
VI.83 и равносильно тому, что достаточно доказать ГБТ для соответствующих
циклически 4-реберно-связных графов (см. упр. VI.25 и VI.30).
VI.3.3. Как искать А-цепи: обсуждение сложности и предложения
для некоторых алгоритмов
Хотя рассмотрение сложности является очень важной частью современной
теории графов (в частности, с учетом приложений к различным проблемам,
например в исследовании операций), она не составляет существенной части этой
книги. Тем не менее здесь и в других главах такие исследования сложности
будут представлены в зависимости от важности, которую я придаю
некоторой (решенной или нерешенной) проблеме; однако я ограничил рассмотрения
в этом разделе вопросом, является ли данная проблема (по крайней мере)
iVP-сложной или можно ли ее решить/разрешить за полиномиальное время1).
В дальнейшем мы в основном ограничимся 3-связными планарными
эйлеровыми графами. Действительно, как мы видели ранее, 2-связный планарный
эйлеров граф G может иметь плоские вложения G\ и G2, такие, что G\ не
имеет А-цепи, в то время как G<i имеет (см. рис. VI.26-VI.28). Таким образом, мы
должны были бы рассматривать также проблемы вложения; соответственно
мы должны были бы проверять все плоские вложения на предмет
существования или несуществования А-цепей. С другой стороны, 3-связные плоские
графы G единственным образом вложимы в плоскость (см. теорему 111.52);
значит (см. обсуждение перед леммой VI.64), существование А-цепи в таком
графе G, который является также эйлеровым, не зависит от конкретного
вложения графа G в плоскость (или, эквивалентно, в 3-мерную сферу). Тем не
х) Я знаю, что это очень субъективная точка зрения и предвижу разочарование и критику
некоторых моих коллег. Однако при том материале, из которого пришлось выбирать, полное
исследование сложности и/или алгоритмов заняло бы большую часть книги. К тому же я
вряд ли могу считать себя специалистом в этой области. Поэтому я предпочитаю оставить
ее более компетентным исследователям.

VI.3. А-цепи в плоских графах
255
менее для практических целей мы всегда будем рассматривать некоторое
вложение графа G.
На основании конструкции Регнер плоского 3-связного эйлерова графа без
.А-цепей (в соответствии с утверждением (VI.А), предшествующим лемме
VI.76) и в силу [GARE76a] сформулируем и докажем следующий результат:
Теорема VI.91. Проблема определения, содержит ли данный связный
планарный эйлеров граф А-цепь, NP-сложна. Это верно, даже если
ограничиться S-связными графами1^.
Доказательство. По утверждению (VI.А), если Сз — планарный 3-связный
кубический граф, то существует планарный 3-связный эйлеров граф G с
D{Gz) С G, такой, что ни одна граница грани в D(Gz) не является границей
грани в G и G имеет А-цепь тогда и только тогда, когда Gz имеет гамильто-
нов цикл. Поскольку гамильтонова проблема для Gz iVP-сложна [GARE76a],
(более чем) достаточно показать, что проблема А-цепи для G Э D{Gz)
полиномиально эквивалентна проблеме гамильтонова цикла для Gz и что G может
быть построен из Gz за полиномиальное время. Поскольку из теорем 111.89 и
III.90 следует, что определение того, является ли данный граф планарным и,
если это так, нахождение плоского вложения может быть проведено за
полиномиальное время, мы можем предполагать, что графы Gz, G на самом
деле плоские. Проблема нахождения граневой 2-раскраски для графа G может
также быть решена за полиномиальное время (теорема III.91). Значит, можно
предположить, что граневая 2-раскраска для графа G также дана.
Предположим, что в G D D{Gz) дана А-цепь Т. Простой проход по Т в
каждой достигнутой вершине v (достигнута ли она при этом проходе впервые
или нет) указывает нам, лежит v в V\ или в V2, где {Vi, V2) есть А-разбиение,
индуцированное цепью Т. Действительно, вместе с вложением графа G мы
можем определить границы граней из D{Gz) за полиномиальное время
(теорема III.90с); значит, мы знаем, принадлежат ли ребра из Ev,
последовательные в Т, границе 1-грани или 2-грани из G. Значит, {Vi,^} получено
за полиномиальное время P\(pg) из Т. Располагая V(D(Gz)), мы получим
V( \— Vi П V(D(Gz)), такое, что {V() —дерево, г = 1,2, за полиномиальное
время P2(pg)- Зная биекцию vp ? V(D(Gz)) <-> bd(i7') С Gz для каждой грани F
из Сз (которая требует лишь полиномиальной памяти и времени), мы получим
Go = {JVf?v' bd(F) С Gz- Это и удаление тех ребер из Go, которые
принадлежат bd(F') и bd(F") для F' ф F", vf'Vf" ^ ^((V/)), может быть сделано
за полиномиальное время Pz{PGz) и получен Н, гамильтонов цикл графа G3.
Поскольку рс < const-рс3 (см. ниже), P(pg3) '•= Pi(pg) + P2(pg) + P3(pg3) есть
полином от рс3 =\ V(G$) |, представляющий время, необходимое для получения
гамильтонова цикла Н графа Gz из А-цепи Т графа G.
Обратно, пусть задан гамильтонов цикл Н С G3. Тогда требуется
полиномиальное время P{(pg3), чтобы получить вершинное разбиение {V^^V^} мно-
х) Первая часть этой теоремы доказана в [BENT87a], где авторы говорят о
«непересекающихся эйлеровых цепях», которые мы называем А-цепями. Кроме того, их конструкции в
большинстве случаев включают кратные ребра и точки сочленения. Важно также отметить,
что мотивацией этой статьи служит проблематика рассечения пламени (flame cutting).

256
Глава VI. Различные типы эйлеровых цепей
жества D(Gz), такое, что (VJ) —дерево, г = 1,2 (V{ соответствует множеству
граней F из Сз с F С int Н). Чтобы получить А-разбиение {Vi, V2} множества
V(G), такое, что V( = Vi П У(??(Сз)), г = 1,2, мы выберем специальный способ
построения плоского 3-связного эйлерова графа G с D(Gz) С G, такого, что ни
одна граница грани в D{Gz) не является границей грани в G. В обсуждении
перед леммой VI.76 было отмечено, что построение графа G не единственно
и что оно может быть проведено таким образом, что каждая грань из D(Gs)
содержит точно один экземпляр либо графа Hi, изображенного на рис. VI.32,
либо графа #о, изображенного на рис. VI.31. Это построение может быть
выполнено как последний шаг доказательства; значит, предположим сначала, что
граф G с этими свойствами уже задан. Тогда рс < /g3 +5pg3 — 6р<?3» гДе второе
неравенство следует из формулы Эйлера для многогранников, а первое
неравенство обусловлено тем, что грань из D(Gs) (которая соответствует вершине
из Сз, и наоборот) содержит либо 3, либо 5 вершин из V{G) — V(D(Gz))-
Имея D(Gs) и {V^,V^}, мы можем расширить это разбиение до {Vi,^}
следующим образом:
a) Грань F из D(Gs) содержит точно три вершины; тогда она содержит Но.
Следуя обозначениям рис. VI.31, мы можем по соображениям симметрии
предположить без ограничения общности, что a, b Е V/, с € V{. В этом случае мы
считаем, что {ai, 61} С V2, с\ ? V\. Заметим, что имеется всего б возможностей
для распределения вершин а, 6, с между V{ и V{.
b) Грань F из D(Gz) содержит точно пять вершин; значит, она содержит
Hi. Мы следуем обозначениям рис. VI.32, и, снова имея шесть возможностей
распределения вершин Xi-i, Xi, г/i между V[ и V^ мы без ограничения общности
можем предположить из соображений симметрии, что либо {xi-i,Xi} С V[ и
yi ? V2, либо {xi-i,yi} С V[ и Xi € V{. В любом случае пусть вершина из
G, однозначно определенная пересечением N(xi-i) П N(yi) П F, принадлежит
V<i\ пусть вершина U из G, однозначно определенная пересечением N(xi-i) П
N(xi)C\F, принадлежит Vi, за исключением случая, когда Л = (#i-i, U,Xi) есть
граница 2-грани и yi € V^; в этом случае мы считаем, что U принадлежит V2,
и пусть соответствующая вершина из N(xi) П N{yi) П F принадлежит V\. Что
касается двух оставшихся вершин Щ-\ Е N(x{-i) к Щ е N(xi) из ^(Я"г) П F,
ТО ПОЛОЖИМ Щ-\,Щ € V2-
Поскольку (l^)—дерево, г = 1,2, и в силу способа, которым мы
расширяли {V/,^'} до {Vi,V2}, из этих рассмотрений следует, что {Vi?!^} есть
А-разбиение, которое может быть получено из {V[, V?} за полиномиальное
время РзСРСз)- Таким образом, при наличии граневой 2-раскраски графа G
мы можем выполнить переход от {VI,Х^} к циклу Т, который обозначает
А-цепь в G, при помощи пошаговой процедуры. А именно, положим Go := G и
d := (Gi-i){v.ytS, г = 1,...,pg, где V{G) = {vi,... ,vPG} и значение 5 G {1,2}
определяется условием и* € V?. Поскольку этот переход от G;_i к G2 может
быть проделан за полиномиальное время, мы получаем Т = GPG из {Vi, V2} за
полиномиальное время P3'(Pg)- Снова, поскольку рс = const.pG3, мы получаем
А-цепь Т для G из данного гамильтонова цикла Н графа Сз за
полиномиальное время P'(jpGz) = P{(pg3) + PiiPGs) +-Рз(Р<з)- Значит, проблема нахождения

VI.3. А-цепи в плоских графах
257
А-цепи в G D D(Gs) полиномиально эквивалентна проблеме нахождения га-
мильтонова цикла в Gz.
Покажем, наконец, что построение графа G, такого, что каждая грань из
D(Gs) содержит точно один экземпляр либо графа Hi, либо графа Но, может
быть произведено за полиномиальное время. Заметим, прежде всего, что
переход от Сз к D(Gz) может быть осуществлен за полиномиальное время Qi{jpG3)-
Теперь мы забежим вперед и коснемся обсуждения проблемы китайского
почтальона (СРР), которая будет подробно рассматриваться в т. 2, гл. VIII.
А именно: для любого связного графа Н существует эйлеров надграф Hi со
следующими свойствами:
1) У(ЯО = V(Я), ВД) Э Е{Н);
2) если х и у не смежны в Н, они не смежны ивЯ^
3) для каждого цикла Ci из Hi
\Е(С1)П(Е(Н1)-Е(Н))\<^1(С1).
Более наглядно, свойства 1)-3) показывают, что Hi получен из Н заменой
некоторых ребер из Н на ребра кратности 2 таким образом, что Hi эйлеров и
что для каждого цикла С из Н число ребер из С, которые заменены в Hi на
кратные ребра, не превосходит \1{С). Как мы увидим при обсуждении
проблемы китайского почтальона, построение Hi из Н может быть произведено
за полиномиальное время. Заметим, что при этом построении
d>Hi-E(H){v) = dn(v) (mod2) для каждой вершины v G V(H) = V(Hi).
Применим к построению графа G из Н = D(G$) предыдущие рассуждения,
чтобы получить, что можно пометить ребра из D(Gz) метками 0 и 1 за
полиномиальное время Q2(pg3) таким образом, что в D(Gz) для Ei := {е €
E(D(Gs))\\(e) = 1} (где Л обозначает функцию пометки)
|Ev П Ei |= d?>(G3)(v) (mod2) для каждой вершины v € V(D(Gz)) (l)
и что для каждого цикла С из D(Gz)
\Е(С)ПЕг\<±1(С). (2)
В частности, (2) выполняется для треугольной границы грани Д из D(Gz).
Значит, для каждой такой Л мы имеем | Е(А) DEi\e {0,1}. Следуя обозначениям
рис. VI.31 и VI.32, запишем V(A) := {а, 6, с}, если Е(А) П Ег = 0, и V(A) :=
{xi_i, Xi, уг}, если E(A)C\Ei Ф 0, где обозначения выбраны таким образом, что
без ограничения общности можно считать, что {x^iXi} = E(A) f)Ei. Из двух
границ граней, содержащих Xi-iXi, выберем одну и зафиксируем ее; обозначим
ее, как и выше, через Л.
Для каждой границы Л, выбранной так, чтобы Е(А) П Ei ф 0, вложим
граф Щ, изображенный на рис. VI.32, в соответствующую грань. Для каждой
другой границы грани Л = (a,b,c) вложим Но, изображенный на рис. VI.31,
в соответствующую грань. Обозначим через G граф, полученный из D(Gs)
таким образом. На это требуется только полиномиальное время Qz{pgz)-> п°-
тому что для каждой из рс3 границ граней графа D(Gs) вложение графов

258
Глава VI. Различные типы эйлеровых цепей
Яо, Щ соответственно может быть произведено за постоянное время.
Значит, полный переход от Сз к G может быть сделан за полиномиальное время
Q(PG3) = Qi(pg3) + Q2(pg3) + Q3(pg3)- Из (1) и построения G из D(G3) следует,
что граф G плоский и эйлеров; он также 3-связен, так как Сз 3-связен. Это
завешает доказательство теоремы.
Заметим, что на втором шаге доказательства теоремы VI.91 не
обязательно явно расширять {V^V^} до {14,^}. Достаточно построить связный
4-однородный граф G — (С\^д) v2',2j a затем за полиномиальное время
алгоритмически найти А-цепь для G последовательным применением, скажем, леммы
о расщеплении (см. т. 2, гл. X).
Что касается сложности проблемы А-цепей в планарных 4-связных графах,
то вполне возможно, что она сравнима со сложностью гамильтоновой
проблемы. Действительно, как мы отмечали выше, в 4-связных плоских графах га-
мильтонов цикл может быть найден за полиномиальное время. Из этого
следует, что цикл Татта в планарном кубическом графе Gz с Ас(Сз) > 4 также
может быть найден за полиномиальное время; в этом случае L{Gz) —планарный
4-связный граф (см. следствие III.73). Конечно, это не гарантирует, что цикл
Татта типа описанного в теореме VI.90 может быть найден за полиномиальное
время1). На самом деле, имеются некоторые основания для проведения такой
аналогии. В добавление к фактам, приведенным в обсуждении после гипотезы
VI.86, мы можем сделать следующее замечание (мы ограничимся наброском
доказательства, оставив детали в качестве упражнения).
1) А~цепъ в 2-связном внешнеплоском обыкновенном графе может быть
найдена за полиномиальное время.
Мы используем теорему VI.87, чтобы найти процедуру построения А-цепи в
2-связном внешнеплоском обыкновенном графе G. Предположим, что G
снабжен граневой 2-раскраской, при которой внешняя грань Foo является 1-гранью.
Процедура (можно сказать, алгоритм) состоит в том, чтобы последовательно
пометить вершины степени, превышающей 2, так, чтобы в конце концов каж-
х) С другой стороны, было объявлено, что проблема гамильтонова цикла разрешима за
полиномиальное время для произвольных реберных графов (см. [GARE79a, p. 199, [GT37]], где
авторы ссылаются на [LIUC68a]); значит, проблема циклов Татта должна лежать в Р (см.
лемму III.69). Это сообщение должно быть ошибочным. Чтобы в этом убедиться, мы сначала
рассмотрим L(Gz) для 2-связного кубического графа Gz- Далее мы введем новую вершину
vp+i для каждой вершины V{ из Gz и добавим новое ребро ViVp+i, г = 1,... ,р. Обозначим
через Н полученный таким образом граф. Наконец, рассмотрим Ь(Н) и S(Gz)UL(Gz)-
Можно считать, что последний граф получен из 5(Сз), если положить V(L(Gz)) — V2(S(Gz)) и
затем добавить E(L(Gz))- Если мы будем действовать таким образом, то графы L(H) и
S(Gz)UL(Gz) изоморфны. При этом представлении L(H) непосредственно можно показать,
что существует взаимно однозначное соответствие между гамильтоновыми циклами в Gz
и гамильтоновыми циклами в L{H). Кроме того, конструкция, которую мы описали выше,
преобразование гамильтонова цикла в Gz в соответствующий гамильтонов цикл в L(H) и
обратное преобразование могут быть осуществлены за полиномиальное время. Значит, мы
можем заключить, что проблема гамильтонова цикла для Ь(Н) является TVP-полной, даже
если Gz планарный и 3-связный (ср. [GARE76a]). Заметим, что эти соображения —
небольшая модификация рассуждений Бертосси в [BERT81a], который имел дело с аналогичной
ошибкой, касающейся проблемы гамильтонова пути [GARE79a, p. 199, [GT 39]]. Между
прочим, я не смог найти в книге Лиу (Liu) объявленный в [GARE79a] результат.

VI.3. А-цепи в плоских графах
259
дая 1-грань F\ ф F^ содержала точно одну помеченную вершину. Обозначим
через V\ множество помеченных вершин и положим V^ := V(G) — V\. Тогда
разбиение {Vi,V2} будет удовлетворять теореме VI.87 и, значит, (Gvi,i)v2,2 будет
циклом, представляющим А-цепь графа G.
Начальным этапом, тем не менее, является построение графа, слабо
двойственного графу G,
Dw(G):=D(G)-f00,
где /оо — вершина графа D(G), двойственного к G, соответствующая Fqq.
Показано [FLEI74d, Theorem l, Corollary], что DW(G) для 2-связного внешнеплоско-
го графа G является деревом. Значит, в нашем случае Tw := DW(G) —дерево,
разбиение вершин {V^, V™} которого, соответствующее граневой 2-раскраске
графа G, таково, что висячие вершины из Tw принадлежат V™. Выбираем
vo G V™ и ориентируем ребра из Tw таким образом, что Tw преобразуется в
выходящее дерево Ttf с V{T™) = V(TW) и корнем v0. Пусть для каждой
вершины v G V™ через Fv ф F^ обозначена 1-грань из G, соответствующая v, и
пусть для любой 1-грани F ф Foq из G через vp обозначается соответствующая
вершина из V™. Заметим, что следующие начальные шаги могут быть всегда
сделаны за полиномиальное время Ро(п), где n =| V(G) |:
a) нахождение границ граней в G и классификация их в соответствии с тем,
принадлежат они 1-грани или 2-грани;
b) нахождение для каждой вершины v G V(G) множества Cv 1-граней Fi,
таких, что v G V(bd(Fi));
c) построение плоского выходящего дерева Т™ с корнем v$ и разбиения вершин
Вначале пометим корень vq G V^T^). Затем пометим произвольную вершину
vi G bd(FVo), и пусть vi принадлежит V\ (заметим, что FVQ является 1-гранью
по выбору vo). Рассмотрим далее CVl и пометим vp G V™ для каждой грани F G
CVl — {FVQ}. На этом шаге, так же как и на любом последующем шаге процесса
приписывания меток, следующее свойство выполняется именно потому, что G
есть 2-связный внешнеплоский граф:
Если P(vo,w) —путь в Т™, соединяющий корень vq с вершиной
w G V™, и если w помечена, то все элементы из V(P(vq,w)) П V™
также помечены. (*)
Далее мы выберем непомеченную вершину v G V™, удовлетворяющую
условию, что
все элементы из V(P(vq,v) — v) П V™ уже помечены. (**)
Пометим эту выбранную вершину v. Из того, что G внешнеплоский и
обыкновенный, следует, что существует вершина V2 G V(bd(Fv)), такая, что
d{v2) >4u для каждой грани F G CV2 — {Fv} вершина vp G У(Т™)
еще не помечена. (* * *)
Пометим V2- Затем мы пометим в Ttf каждую вершину vp ф v для F G CV2 —

260
Глава VI. Различные типы эйлеровых цепей
Заметим, что по (*) уже помеченные элементы из V™ вместе с элементами
из V™ч смежными с этими помеченными вершинами, определяют поддерево
Т' дерева Т™ с корнем v$. Следовательно, если Т' ф Т™, то мы выбираем
вершину х ? V™, удовлетворяющую условию (**) (с х вместо и), так, чтобы
пометить х и найти v3 € V(bd(Fx)), удовлетворяющую (* * *) (с г»з вместо
г>г), и помечаем г^. Затем мы помечаем в Г^ вершину vf ф х для каждой
F ? CV3 — {Fx}. Заметим, что поддерево Т" из Т™, определенное после этого
нового шага процедуры приписывания меток таким же образом, как выше было
определено Г', удовлетворяет условию
Г С Т" С Т0™.
Значит, выбор вершины в V™, удовлетворяющей условию (**), и вершины в
G, удовлетворяющей (***), и приписывание метки последней вершине,
многократно повторенный, в конце концов приводит нас к выходящему дереву Т^,
удовлетворяющему условию
т'сГс.сг^ =т0™.
После этого г-го шага множество V\ С V(G), состоящее точно из помеченных
вершин из V(G), и V2 := V(G) — V\ определяют разбиение вершин. Заметим,
что именно в силу (* * *) выполняется утверждение 2) теоремы VI.87. Значит,
{Vi, V2} есть А-разбиение множества V(G).
Заметим попутно, что предыдущие алгоритмические рассуждения вместе с
теоремой VI.87 составляют другое доказательство теоремы VL63, не зависящее
от представленного ранее.
Что касается сложности приведенной выше процедуры приписывания
меток, то мы видим, что после j-ro шага, 1 < j < г, выбор вершины v € V™,
подчиненной (**), произволен в множестве источников из Т^ — V(T^).
Поэтому построение Т^, а также выбор и приписывание меток таким вершинам
v среди источников из Ttf — V(T^) могут быть произведены за
полиномиальное время Pi(n). Поскольку процедура приписывания меток в Т™ может
быть скомбинирована с приписыванием меток соответствующим элементам в
множествах ?v, нахождение вершины Vj+2 Е V(G), удовлетворяющей условию
(***), на (j + 1)-m шаге может быть проделано за полиномиальное время Р2(п).
Значит, время, необходимое для построения Л-разбиения {Vi, У2}, не больше
чем Po(n) +n(Pi(n) -fP2(^))- Поскольку переход от {Vi, V2} к (Gvui)v2,2 также
может быть проделан за полиномиальное время, то и нахождение А-цепи в G
может быть произведено за полиномиальное время.
На основании 1) получаем следующее утверждение.
2) Если G — обыкновенный плоский эйлеров граф с заданным гамилыпоновым
циклом Н, обладающим А-свойстпвом, то А-цепь в G может быть
найдена за полиномиальное время..
Используя обозначения доказательства теоремы VI.88, мы можем заключить
из 1), что А-цепи Т\ и Т2 из G\ и G2 соответственно могут быть найдены за
полиномиальное время (где Gi UG2 = G, G\ C\G2 — Н). Значит, и соответству-

VI.3. А-цепи в плоских графах
261
ющее А-разбиение {V^V^}, индуцированное цепью Х*, i = 1,2, может быть
найдено за полиномиальное время. Так как четыре вершины множеств
Wij:=V^{V{Gi)-V2{Gi)), ME {1,2}
можно найти за полиномиальное время, то мы приходим к Wj := WjuW?, j =
1,2, за полиномиальное время. Поскольку (Gwi,i)w2l2 может быть получен за
полиномиальное время и поскольку этот граф есть цикл (см. доказательство
теоремы VI.88), он соответствует А-цепи из G, найденной за полиномиальное
время.
Мы замечаем, однако, что приведенные выше рассуждения основаны на
данном гамильтоновом цикле Н из G. Значит, возникает вопрос: какова
сложность проблемы, имеет ли данный 4-связный планарный эйлеров граф гамиль-
тонов цикл, обладающий А-свойством? Конечно, в 2) мы не нуждаемся в
дополнительных предположениях относительно «(G) (однако «(G) > 2,
поскольку G гамильтонов), но, учитывая гипотезу VI.86 и теорему Татта о га-
мильтоновых циклах (следствие 111.71), мы ограничимся в приведенном выше
вопросе 4-связными графами. Следует заметить, что если G —любая
эйлерова триангуляция плоскости (4-связная или нет, обыкновенная или нет), то эта
проблема принадлежит Р; действительно, в таких графах G, если е, / Е E(G)
инцидентны v e V(G) и 0+(v) = (..., e(v), /(г>),...), то е и / либо определяют
единственный гамильтонов цикл Я, обладающий А-свойством, се,/ Е Е(Н),
либо Н вообще не существует (упр. VI.32). Значит, вполне может быть, что
ответ на наш вопрос также «полиномиальный». Заметим, что для триангуляции
D плоскости гамильтонов цикл с А-свойством есть специальный тип левого-
правого пути, определенного в [SHAN75a].
Мы оставляем читателю проверку сложности нахождения А-цепи в графах,
подпадающих под теоремы VI.77.a или VI.79 (упр. VI.33), и теперь рассмотрим
общий случай.
А-цепной алгоритм для произвольных плоских эйлеровых
графов. Мы начинаем с 2-связного плоского эйлерова графа Go, не
являющегося циклом, и косвенно с теорем VI.59 и VI.67. Однако вместо того, чтобы
рассматривать одноцветные кольца граней, мы сочетаем процедуру
приписывания меток вершинам с последовательностью 1-расщеплений1).
Шаг 0. Рассмотрим Go с граневой 2-раскраской, такой, что внешняя грань
Fq° графа Go является 1-гранью. Положим V^* = V(hd(Fo°)) — V^Go), и пусть
х\ € Vq выбрана произвольно. Положим г = 1.
Шаг 1. Строим Gi := (Gi-i){Xi},i- Обозначим через Ff° внешнюю грань
графа G^ и пусть граневая 2-раскраска графа Gi индуцирована граневой
2-раскраской графа Gi_i-
Шаг 2. Пометим те из еще не помеченных элементов из V(bd(F?°)), которые
являются точками сочленения графа Gi, и пусть V* обозначает множество
непомеченных вершин в V(bd(F?°)) — V2(Gi).
1) Для случая эйлеровой триангуляции плоскости этот алгоритм уже был очерчен в
[FLEI88a].

262
Глава VI. Различные типы эйлеровых цепей
Шаг 3. Если V* Ф 0, то выбираем любую вершину Zj+i G V*. Положим
г — г + 1 и переходим к шагу 1.
Если V* = 0, то продолжаем.
Шаг 4. Положим V** = {х\х <Е (?(G*) - ?(bd(i^°))) U (У(С,) - V2{Gi))\x не
помечена, если это вершина}. Если V** = 0, переходим к шагу 7.
Если V** ф 0, то продолжаем.
Шаг 5. Ищем наибольшее целое j < г, такое, что V? — {xj+i} ф 0.
Если такого j не существует, то переходим к шагу 8.
Если j существует, продолжаем.
Шаг 6. Пометим Xj+i и положим V? = V? — {xj+i}. Положим i = j и
переходим к шагу 3.
Шаг 7. Go имеет А-цепь.
Шаг 8. Go не имеет А-цепи.
На самом деле этот алгоритм делает больше, чем просто определяет, есть
ли в Go А-цепь: действительно, если V* = 0 = V** для некоторого г > 0 (что
является необходимым и достаточным условием достижения шага 7), то Gi
удовлетворяет условию леммы VI.58. Следовательно, проход по bd(Ff°)
описывает А-цепь То в Go- Более того, А-разбиение {Vj0, У20} в Go, соответствующее
цепи То, в обозначениях из алгоритма определяется так:
Vi° = {xi,...,Xi},
V? — {х G V(G)\x помечено или х € V^Go)}.
Заметим, что построение графа G* и определение множеств V*,V**
соответственно может быть сделано очень быстро. Это также верно для определения
целого j < г в шаге 5. Однако весь алгоритм очень медленный. Это становится
яснее при изучении шагов 4, 5 и 6: VJ* = 0 и V** ф 0 означают, что в этот
момент нельзя продолжать «жадный подход», выраженный шагами 1, 2 и 3,
т. е. мы зашли в тупик. В этот момент каждый блок В из G*, удовлетворяющий
условию В П V** ф 0, определяет одноцветное кольцо граней R (элементы
которого суть 2-грани) с полным множеством связей Lr := V(bd(F§?)) — V2(B),
где F§? — внешняя грань блока В (вложение которого индуцировано
вложением графа Gi) и bd(Fg°) С bd(Fi°°). Действительно, V* = 0 означает, что все
элементы из V(bd(Fg))) — V2(Gi) уже помечены; так как это и соотношение
В П V** ф 0 влекут за собой intbd(Fg°) П V** ф 0, то имеется не меньше
двух 2-граней F2 с E(bd(F2)) П E(bd(Fgi)) ф 0, откуда следует, что R
определено множеством этих 2-граней. Заметим, кроме того, что помеченная
вершина из Gi не обязана быть точкой сочленения в Gi (см. шаг 6). Шаги 5 и
б означают выход из этого тупика. Это значит, что необходимо вернуться к
некоторому графу Gj, j < г (из практических соображений следует выбрать
наибольшее j) и выбрать некоторую вершину х^+1 ? V? — {xj+i}, к которой
применить 1-расщепление, чтобы получить G^+1. С этого момента х$+\
становится помеченной вершиной, и вся работа алгоритма по созданию G;+i,..., Gi

VI.3. А-цепи в плоских графах
263
не приносит пользы. Это означает, что процедуры приписывания меток и
расщепления в таких графах не закончены. Но перемещение Xj+i из V? в
множество помеченных вершин графа Gj не говорит ничего о «конечной судьбе»
вершины xj+i в Л-разбиении {VJ0, V2} для графа Go, которое может
существовать, поскольку на более поздних шагах можно достичь f < j, и продолжение
с шага 1 для i = j' + l может привести к образованию множества Vj*, k > j',
содержащего упомянутую выше вершину Xj+i снова. Заметим, однако, что ajj+i
остается помеченной вершиной до тех пор, пока упомянутое выше V? не будет
исчерпано шагом б.
Работа нашего алгоритма (и его медленность) делается еще яснее, если
Go = D есть эйлерова триангуляция плоскости, ибо в этом случае наш
алгоритм равносилен построению связных графов D\ (порожденного
вершинами, к которым применено 1-расщепление) и D2 (порожденного помеченными
вершинами), таких, что
V(D{) U V(D2) = V(D), V{D{) П V(D2) = 0
и Ds для 5 = 1,2 имеет цикл G, только если С = bd(i*i), где F$ есть J-грань (см.
следствия VI.68 и VI.69 и последующее обсуждение). И на каждом шаге
алгоритма граф, порожденный вершинами, к которым применено 1-расщепление,
обладает этим свойством. Оставим в качестве упражнения преобразование
этого алгоритма в алгоритм нахождения гамильтонова цикла в плоском
кубическом двудольном графе (это очевидный алгоритм!).
Однако, принимая во внимание эквивалентность гипотез VI.73 и VI.74,
полученную в лемме VI.75, можно модифицировать изложенный выше алгоритм
так, чтобы он решал, имеет ли данный плоский эйлеров граф Go неразделя-
ющую А-цепь (упр. VI.34.b)). Если Go содержит такую А-цепь, результатом
этого модифицированного алгоритма будет внешнеплоский эйлеров граф G*
(для некоторого % > 0), блоки которого являются границами 2-граней F2
графа Go, таких, что bd(F2) содержит больше ребер, чем точек сочленения графа
Gi. Если ограничиться эйлеровой триангуляцией плоскости Do, это будет
означать, что
каждый блок из Di содержит не более двух точек сочленения из D{. (*)
Утверждение (*) очевидно для i = 0, а также для г = 1; значит, невольно
напрашивается предположение, что (*) может быть верно и для всех графов
Do, Di,..., Di модифицированного А-алгоритма. Это «предположение»
приводит нас к более общему предположению, где мы рассматриваем обыкновенные
эйлеровы триангуляции n-угольника на плоскости. В этом случае п = 0 (mod 3),
и для каждого такого п должна существовать триангуляция этого типа (см.,
например, [FLEI74b]: заметим, кроме того, что лемма VI.76 есть следствие
этого факта).
Гипотеза VI.92. Пусть выбрано целое положительное п = 0(mod3), и
пусть Dq — обыкновенная эйлерова триангуляция п-угольника на плоскости с
граневой 2-раскраской, такой, что внешняя грань Fq° графа Dq есть 1-грань.

264
Глава VI. Различные типы эйлеровых цепей
Тогда существуют такие (различные) вершины Xk € V(D0) — Уг(Д)), что
Dk := {Dk-i){Xk},i, к — 1,... , г, обладают следующими свойствами:
a) Xk € V'(bd(Fj^1)) — V^jD/c-i) (i^i есть внешняя грань в Dk-i)',
b) каждый блок в Dk имеет не более двух точек сочленения Dk]
c) если к = г, то каждый блок в Dk есть граница 2-грани (являющаяся
треугольником).
Таким образом, в силу свойства Ь) гипотеза VI.92 есть обобщение
гипотезы VI. 73.
VI.3.4. Заключительные замечания о непересекающихся эйлеровых
цепях и Л-цепях и другие проблемы
Как мы заметили в начале этого раздела, непересекающиеся эйлеровы цепи и
А-цепи суть принципиально различные понятия, хотя они совпадают для
графов G с Д(С) < 4. Основное различие между этими двумя типами эйлеровых
цепей можно также продемонстрировать топологически.
Напомним, что эйлерова цепь Т связного эйлерова графа может быть
определена с помощью последовательности операций расщепления вершин степени,
превосходящей 2, так что граф, полученный после последней операции
расщепления в этой последовательности, является циклом (см. также следствие
V.13). С другой стороны, связный эйлеров граф G с q ребрами можно
считать полученным из g-угольника Cq с помощью гомоморфизма, действующего
биективно на множествах ребер графов G и Cq (см. замечание V.12).
Применим эти рассуждения к произвольному связному плоскому
эйлерову графу G и неразделяющей эйлеровой цепи Т из G. Обозначим через Ст
плоский цикл, соответствующий цепи Т. Кроме того, по аналогии с операцией
5-расщепления, 6 = 1,2, мы рассмотрим при построении Ст из G /с-кратное
применение процедуры расщепления для получения к вершин v\,..., Vk
степени 2 из вершины v степени 2/с, к > 1, как одновременную процедуру по замене v
этими к вершинами степени 2. Заметим, что эта процедура замены может быть
произведена таким образом, что г>1,..., Vk лежат в (геометрической)
окружности K(v,e) с центром v и радиусом е и K(v,e) не содержит других вершин из
G, Ст соответственно, a K(v,e) П (E(G) — Ev) — 0. Заметим, что Ст
является простой замкнутой кривой, поскольку цепь Т непересекающаяся. Значит,
G можно считать полученным из правильного ^-угольника Cq(q =| E(G) \) в
плоскости следующим образом:
где
(f есть гомотопическая деформация
и
ф есть непрерывное отображение плоскости ?2 на себя,

VI.3. А-цепи в плоских графах
265
такое, что
ф{х) = v для х ? TC(v,e) kv G V[G) - V2{G),
ф : ?2 - (J K(v,e) -> S2 - V[G) биективно.
v?V(G)-V2(G)
Поскольку А-цепь является специальным типом непересекающейся
эйлеровой цепи, сказанное верно, конечно, если Т есть А-цепь. Однако если Т есть
А-цепь, мы можем предположить, что Ст обладает дополнительным
свойством, что для каждой вершины u€V(G) — V^(G)
существует 8 < ?, такое, что К (у* 5) П Ст — {^i, • • •, Vk}. (A)
Используя планарность, мы можем заменить (А) на
в точности одно из K(v,e) Г) int Ст и К(у,е) П ext Ст
является областью. (А')
Если мы рассмотрим граневую 2-раскраску на G (где F°°, как обычно, есть
1-грань) и индуцированную раскраску цикла Ст, то K(v,e) П int Ст является
областью тогда и только тогда, когда Т индуцирует 2-расщепление в v.
В случае непересекающейся эйлеровой цепи, не являющейся А-цепью, хотя
бы для одной вершины v G V(G) — V?(G) ни одно из двух определенных в (А7)
множеств не связно.
Таким образом, мы имеем способ топологического построения всех связных
плоских эйлеровых графов (ср. с [ABRH79a, Theorem 3]) и также тех из них,
которые содержат А-цепь. Проблема А-цепи может, следовательно, быть
переформулирована как проблема описания различных классов таких графов в
терминах параметров теории графов.
Заметим, что изложенные выше соображения могут в принципе быть
применены к произвольным графам, вложенным в некоторую (ориентированную
или неориентированную) поверхность J7, за исключением графов с граневой
2-раскраской. В частности, свойство (А) остается справедливым как
топологическое средство, позволяющее отличать А-цепи от других непересекающихся
эйлеровых цепей. Заметим, что понятие А-цепи было первоначально введено с
помощью 0+(i;), 0~(v) соответственно и не требовало понятия 5-расщепления.
Однако для различных непересекающихся эйлеровых цепей 7\ и Т^ в
некотором графе G циклы Стг и Ст2 могут быть негомотопны.
Что касается А-цепей в связных плоских эйлеровых орграфах D и/или
смешанных графах М, то имеет смысл рассматривать эту проблему, только если
D ориентирован каноническим образом и/или если М можно ориентировать
каноническим образом (легко выяснить, допускает ли М такую ориентацию,
ибо каноническая ориентация определяется единственным образом по одной
заданной дуге). Однако рассмотреть проблему А-цепи в канонически
ориентированном орграфе D — это все равно, что рассмотреть ее в соответствующем
неориентированном графе G, ибо если G имеет А-цепь Г, то либо Т, либо Т~1
соответствует А-цепи в D и А-цепь в D соответствует А-цепи в G. Это следует
прямо из связи между А-цепью и ^-расщеплениями, 5 = 1,2. Однако, быть

266
Глава VI. Различные типы эйлеровых цепей
может, интересно изучить (в связи с теоремой VI.33) такие входящие деревья
в D, которые соответствуют А-цепям в D.
Другая проблема (которая не рассматривалась в явном виде в этой главе)
касается произвольного связного эйлерова графа G, расположенного на
плоскости таким образом, что открытые ребра не содержат точек, соответствующих
вершинам, два открытых ребра имеют, самое большее, одну общую точку, в
которой они могут пересекать друг друга, и никакие три открытых ребра не
пересекаются в одной точке. Такое расположение графа G определяет
некоторое упорядочение 0+(G), из которого можно получить специальную систему
переходов Х0 следующим образом: t € X0(v) «-+ ? = {ef{, e'k+i}, 1 < г < к =
kv = \d(y), и v 6 V(G) выбрано произвольно. Однако Хо = Xs для некоторого
единственного цепного разложения S графа G. Отсюда возникают следующие
вопросы:
1) Существует ли для данного графа G такое его расположение на
плоскости, что Хо = Хт для некоторой эйлеровой цепи Т графа G?
2) Как много существует таких расположений графа G, что некоторая
эйлерова цепь Т из G удовлетворяет условию Хт = Хо (где Хо связано с некоторым
расположением) ?
3) Какие цепные разложения S графа G, удовлетворяющие условию Хо =
Xs, могут быть получены таким образом?
Эти вопросы были поставлены в [HARB89a], где вопрос 1) решен
утвердительно для G = К2п+1, п ? N.
VI.4. Упражнения
Упражнение VI.1. Доказать следствие VI.2, п. 2), применяя лемму о
расщеплении (т.е. не используя теорему VI. 1).
Упражнение VI.2. Построить граф G и определить систему разбиения
P{G), удовлетворяющую следствию VI.4.2), такую, что G не имеет P(G)-
совместимого разложения на пути/циклы, в котором число путевых элементов
в S равно половине числа нечетных вершин в G.
Упражнение VI.3. Доказать следствия VI.5 и VI.6, используя только лемму
о расщеплении.
Упражнение VI.4. Доказать лемму VI.7 и лемму VI.8, используя лемму о
расщеплении.
Упражнение VI.5. Доказать следствия VI.9 и VI.10.
Упражнение VI.6. Доказать, что орграф на рис. VI.2 не имеет Х-совмести-
мой эйлеровой цепи.
Упражнение VI.7. Доказать следствие VI.13 (указание: для v с do(v) > б
показать сначала, что если \X*(v) \= \do(v) +1, то существует С* € X*(v), г =

VI.4. Упражнения
267
1,2,3, с | Ci |= 2 и (А*)+ ;# (Ji=i Q <jL (A*) . Затем применить лемму о
расщеплении, как в доказательстве теоремы VI.11).
Упражнение VI.8. Показать, что D\ на рис. VI.4 имеет Х(?>1
^совместимую эйлерову цепь тогда и только тогда, когда D имеет Х(?))-совместимую
эйлерову цепь, где X(D) задана и X(Di) = X(D) U X(si) U X(s2).
Упражнение VI.9. а) Построить связный эйлеров орграф D, такой, что
V(D) содержит нечетное число вершин степени б и некоторое число вершин
степени 4.
Ь) Из двух графов описанного в п. а) типа построить эйлеров орграф с четным
числом ребер и точкой сочленения степени 4.
Упражнение VI. 10. Доказать следствие VI.19.
Упражнение VI.11. Доказать леммы VI.27 и VI.28. Определить такие графы
G, степени вершин которых кратны четырем и для которых эти две леммы
также верны.
Упражнение VI.12. Показать, что подорграфы Di и D[ = D* — Df0 орграфа
D* на рис. VI.7 удовлетворяют утверждению 4)а) теоремы VI.35, тогда как
утверждение 4)Ь) справедливо лишь для D[.
Упражнение VI.13. Доказать следствие VI.43.
Упражнение VI. 14. Построить 4-регулярный обыкновенный орграф,
содержащий две, но не три попарно совместимые эйлеровы цепи (указание:
применить рассуждения, аналогичные обсуждению рис. VI. 14).
Упражнение VI. 15. Доказать лемму VI.58.
Упражнение VI.16. Доказать, что если G удовлетворяет условию леммы
VI.58, то существует связный внешнеплоский обыкновенный граф Я,
содержащий подграф Н', гомеоморфный G, такой, что Н не содержит А-цепи. Если
исключить свойство «обыкновенный», то Н может быть построен таким
образом, что Н' содержит все его вершины.
Упражнение VI. 17. Построить 2-связный внешнеплоский эйлеров граф, не
имеющий А-цепи.
Упражнение VI.18. а) Построить А-цепъ в графе G'q на рис. VI.28.
b) Показать, что G% не содержит А-цепи, индуцирующей 1-расщепление в
vi, если во внешней грани графа G'q имеется 1-грань в граневой 2-раскраске
графа G'q.
c) Найти другое плоское вложение абстрактного графа, из которого получены
Go и G'q, допускающее А-цепи.
Упражнение VI.19. Доказать лемму VI.65 и показать на примере, что
обратное утверждение неверно.
Упражнение VI.20. Показать, что граф, изображенный на рис. VI.26
(который не имеет А-цепи), имеет разбиение вершин {Vi,V2}, такое, что (Vs)
ацикличен, S = 1,2.

268
Глава VI. Различные типы эйлеровых цепей
Упражнение VI.21. Доказать, что граф на рис. VI.30(a) является
наименьшим планарным 2-связным двудольным кубическим негамильтоновым графом
и что он определен однозначно.
Упражнение VI.22. Доказать, что следующие утверждения эквивалентны:
1) Каждый плоский 3-связный кубический двудольный граф содержит гамиль-
тонов цикл (ГБТ).
2) Каждый плоский 3-связный кубический двудольный граф содержит
доминирующий цикл.
Упражнение VI.23. а) Доказать, что если G$ (D)— плоский 3-связный
кубический двудольный граф (обыкновенная эйлерова триангуляция плоскости),
грани которого ограничены 4-, 6- или 8-угольниками (степени вершин которых
суть 4, б или 8), то (?з (D) содержит точно шесть 4-угольных граней (вершин
степени 4), если он не содержит 8-угольных граней (вершин степени 8); он
содержит точно семь 4-угольных граней (вершин степени 4), если в нем есть
точно одна 8-угольная грань (вершина степени 8).
Ь) Построить эйлерову триангуляцию плоскости с вершинами степени 4, б и
8, такую, что в ней есть в точности одна вершина v степени 8 и v не смежна
ни с одной вершиной степени 4.
Упражнение VI.24. а) Доказать следствие VI.81.
Ь) Начиная с октаэдра, построить эйлерову триангуляцию плоскости D
последовательностью слабых И^-расширений так, чтобы D имела точно одну пару
смежных вершин степени 4.
Упражнение VI.25. Сформулировать гипотезу VI.82 для кубических
графов, чтобы получить более строгую (но эквивалентную) версию гипотезы
VI.72.
Упражнение VI.26. Доказать лемму VI.84.
Упражнение VI.27. Доказать, что если Сз — связный 3-однородный граф
с 2-фактором, состоящим только из 4-угольников, то G% имеет гамильтонов
цикл Н D E(Gz) — Qa (указание: использовать следствие VI.6, опуская такие
4-угольники в Q45 которые содержат либо диагональ, либо ребра кратности 2).
Упражнение VI.28. Показать, что граф D на рис. VI.38 имеет А-цепь.
Упражнение VI.29. Доказать теорему VI.90.
Упражнение VI.30. Показать, что гипотезу VI.73 достаточно доказать для
4-связных графов (указание: применить гипотезу VI.83).
Упражнение VI.31. а) Разработать детали предложенного алгоритма для
нахождения А-цепи в 2-связном внешнеплоском обыкновенном графе (в
частности, показать, что выполняются условия (*) и (* * *) ).
Ь) Проверить в деталях рассмотрение сложности этого алгоритма (как велика
экспонента величины Pi{n) для г = 0,1,2?).

VI.4. Упражнения
269
Упражнение VI.32. Доказать следующие утверждения:
a) Если G есть (эйлерова) триангуляция плоскости и е, / Е .E(G) смежны в
границе грани графа G, то имеется не более одного гамильтонова цикла Н
в G, обладающего А-свойством, с е,/ € Е(Н), и выяснение того, существует
этот цикл Н или нет, может быть проведено за линейное время (заметим, что
G уже вложен в плоскость).
b) Используя а), показать, что проблема установления существования
гамильтонова цикла с А-свойством в (эйлеровой) триангуляции плоскости лежит в Р.
Упражнение VI.33. Изучить сложность описанного в теоремах VI.77.а и
VI.79 поиска А-цепи в D, где D есть эйлерова триангуляция плоскости.
Упражнение VI.34. а) Преобразовать А-алгоритм для произвольного
плоского эйлерова графа в алгоритм нахождения гамильтонова цикла,
соответственно цикла Татта, со свойствами, определенными в теореме VI.90, в плоском
кубическом двудольном графе (указание: использовать лемму VI.75, теорему
VI.90 и их доказательства).
Ь) Модифицировать этот алгоритм для А-цепей таким образом, чтобы он
решал, содержит ли данный связный плоский эйлеров граф неразделяющую А-
цепь.

Глава VII
Преобразования
эйлеровых цепей
В предыдущей главе мы изучали различные типы эйлеровых цепей в
произвольных эйлеровых графах и орграфах, а также в некоторых классах
эйлеровых графов. Теперь мы рассмотрим множество всех эйлеровых цепей в
произвольном эйлеровом графе G. Существует ли способ преобразования эйлеровой
цепи Т\ графа G в другую его эйлерову цепь Т2? Для этого мы должны вначале
уяснить себе, при каких условиях цепи 7\ и Т^ считаются различными.
Определение VII. 1. Две эйлеровы цепи Т\ и T<i в связном эйлеровом
(ор)графе G считаются различными тогда и только тогда, когда Хтх ф Хт2-
Другими словами, если эйлерова цепь Т" графа G получена из Т
обращением ориентации или циклическим сдвигом последовательности ребер,
представляющих Г, то Г и Т' считаются совпадающими. Определение VII. 1
соответствует подходу, который использует для различения эйлеровых цепей
большинство авторов. Кроме того, к нему естественно приводит следствие V.10.
Конечно, в случае орграфа D переориентация последовательности дуг,
образующих его эйлерову цепь Т'г, для получения эйлеровой цепи Т" этого
орграфа неприменима, так как проход дуги (v, w) от w к v в эйлеровой цепи
не разрешен.
Однако есть и другие способы различения двух эйлеровых цепей, которые
следует здесь упомянуть. Например, У. Татт считает цепи Т и X" различными,
если представляющие их последовательности ребер (и/или дуг) не совпадают.
Точнее, Т ф Т', если ГиГ' либо начинаются с различных вершин, либо для
некоторого i ? {l,...,g} г-е ребро (дуга) цепи Т не совпадает с г-м ребром
(дугой) цепи X". Сравнивая этот подход с определением VII. 1, мы видим, что
последнее задает на множестве эйлеровых цепей (ор) графа отношение
эквивалентности, каждый класс которого состоит в точности из 2q эйлеровых цепей
(из q цепей в случае орграфа), которые задают одну и ту же систему
переходов, но являются различными в смысле Татта. Для целей этой книги, однако, в
случае графа подход Татта к различению эйлеровых цепей не приносит ничего
нового, кроме указанного множителя 2q. Однако в случае орграфа
различимость в смысле Татта иногда уместна.
Существует еще один способ различения эйлеровых цепей в (ор)графе.
Предположим, что ребра (дуги) (ор)графа Н заранее помечены произволь-

VII. 1. Преобразование произвольных эйлеровых цепей 271
но символами Д,..., fq. Тогда эйлерова цепь Т графа iJ, записанная в виде
последовательности ребер (дуг),
Т = /тг(1) j /тг(2)» • • • » /тг(<?) 1
определяет некоторую перестановку 7г элементов множества {1,2,..., q}.
Эйлеровы цепи 7\ и Т2 графа Я будем считать различными тогда и только тогда,
когда соответствующие перестановки ъ\ и 7Г2 различны. Этот способ
различения эйлеровых цепей (который согласуется с точкой зрения Татта) будет
играть существенную роль в получении одного результата о четности
эйлеровых цепей в орграфах, который, в свою очередь, имеет интересное приложение
в линейной алгебре.
VII. 1. Преобразование произвольных эйлеровых цепей
в графах
Пусть G — связный эйлеров граф, не являющийся циклом. Рассмотрим в G
систему переходов Хт, заданных эйлеровой цепью Т. Пусть ti,t2 G X(v) С Хт
для v ? V(G) — V2(G) ф 0 выбраны произвольно, и положим t\ = {/{,#[}, ?2 =
{/2^/3}- Пусть Н — связный эйлеров граф, полученный из G отщеплением тех
пар ребер, которые соответствуют элементам из Хт — {^ъ^}• Тогда Uh{v) = 4
и V2(#) = V(H) — {v}. Далее, Г соответствует некоторой эйлеровой цепи 7\
графа Н и ti, ?2 G Xz\. Из структуры графа iJ следует, что /{, fy, /3 не могут
быть полуребрами из одного и того же блока графа Н. По лемме о
расщеплении, следовательно, один из графов #i,2 и Н\^ связен. Предположив без
ограничения общности, что связен #1,2, мы получаем, что ^(#1,2) = ^(#1,2),
т. е. #1,2 является циклом. Значит, проход по Н\^ задает эйлерову цепь T<i
графа Н. Согласно построению и определению VII. 1, Т\ Ф Т2. Кроме того, Т^
соответствует эйлеровой цепи Т' ф Т графа G, система переходов X' := Хт>
которой удовлетворяет равенству
X' = (Xr-{ti,t2})U{t;,^}, ВДе *i-{Л,/2},^:={/з,^}- (1)
Подытоживая эти соображения, мы получим следующий результат (см.
также [KOTZ68c, Theorem 1] и [ABRH80a, Lemma l]).
Лемма VII.2. Пусть Т — эйлерова цепь связного эйлерова графа G, где
V(G) — V2(G) ф 0, и пусть ?i,?2 —два различных перехода цепи Т в
некоторой вершине степени, большей 2. Тогда найдется эйлерова цепь графа G,
переходы которой совпадают с переходами Т, за исключением t\ ut2.
Мы можем описать эйлеровы цепи ГиГ'в терминах последовательностей
ребер следующим образом:
¦* = &1 ? • • • ? ^m—l ? &тп,П) ^n-f-1 > • • • > ?qt . .
1 = в\, . . . , em—15 ^гп,п'> еп+1 -I - - • i^qi
где ?(G) = {ei,...,eg}, 5m?n — замкнутая цепь, начинающаяся ребром ет и
оканчивающаяся ребром еп в той же самой вершине v G V(G) — ^(G), и em_i =
/ь em = pi, en = /2, en+i = /3. Значит, формулы (1) и (2) описывают одну и

272 Глава VII. Преобразования эйлеровых цепей
ту же ситуацию. Введем следующее определение, согласующееся с [ABRH80a,
SKIL83a] (см. также работу [KOTZ68c], которая исторически положила начало
исследованиям из этой главы). Мы сохраним введенные ранее обозначения.
Определение VII.3. Пусть Т и Г' —две эйлеровы цепи связного эйлерова
графа G, и пусть v € V(G) — V^(G) Ф 0. Если соответствующие системы
переходов Хр, X1 удовлетворяют (1), то мы можем говорить, что X' (X") получается
из Хт (Т) посредством /^-преобразования, которое задается
преобразованием t\ и ^2 в t[ и t2. Мы говорим также, что Т' получена из Т обращением
сегмента 5т, который начинается и заканчивается в одной и той же вершине
v (см. (2)).
Заметим, что операция, обратная к «-преобразованию, также есть
«-преобразование. Это следует как из (1), так и из (2): заметим, что (S^)-1 =
Sm^n. Если мы распространим (1) и на случай {^ь^} = {^1^2} (т- е- Т1 = Т),
то определение VII.3 позволит рассматривать тождественное преобразование
(т. е. случай Хт = X') как «-преобразование. Для краткости мы будем писать
к(Т) = X", если Т" получено из Т посредством «-преобразования1).
Определение VII.4. Пусть T(G) означает множество всех эйлеровых
цепей связного эйлерового графа G. Если Т,Х" € T(G), то цепи ГиГ'
назовем «-связанными2), если для некоторого п € N существуют такие цепи
Г0,...,ТпеТ(С),что
Г = Г0, Т' = ТП и Тг = «(Т*_1) при 1<г<п.
Значит, если Т,Г',Г" € T(G) таковы, что «(Т) = V и при этом V и Г"
«-связаны, то Т и Т" также «-связаны.
Из определения VII.4 и обсуждения, непосредственно следущего за ним,
можно заключить, что «-связанность определяет отношение эквивалентности
на множестве T{G). Это означает, что T(G) допускает разбиение V(G,«),
классы которого суть классы эквивалентности по отношению к этому разбиению.
Возникает вопрос о числе таких классов в V(G,«). Ответ на него дает
следующая теорема.
Теорема VII.5. Для любого связного эйлерова графа G имеет место
равенство \V(G, «)|= 1.
Доказательство. Если G — цикл, то \T(G)\= 1 по определению VII. 1.
Теорема верна в этом случае (T(G) = {Т}), поскольку единственным
«-преобразованием здесь является тождественное преобразование. Поэтому мы
предполагаем, что V(G) - V2(G) Ф 0, и \T(G) |> 1 по лемме VII.2.
Допустим, что Ti,T2 € T(G) не «-связаны. Положим Х\ := Хт\, X<i \— Хт2
и выберем Т\ и Т2 так, чтобы число | Х\ Г\Х2 | было наибольшим из возможных.
Теперь рассмотрим вершину v € V{G) — V^(G), такую, что Xi(v) Ф X2(v),
*' Поскольку это формальное равенство не уточняет, с помощью какого ^-преобразования
Т" получена из Т, мы имеем к(Т) = Г', к(Т) = Т" и Т" ф Т" для различных /с-пре-
образований.
2) Заметим, что ^-связанность — это то же, что и связанность в [SKIL83a].

VII. 1. Преобразование произвольных эйлеровых цепей 273
где Xi(v) С Xi, г = 1,2, —множество переходов в вершине v, индуцированное
цепью Т^ Такая вершина v должна существовать, так как Т\ фТ2. Поскольку
d(v) = 2к > 2, то из выбора вершины v следует, что xi,2(v) :=\Xi(v) Г\Х2(у) |<
к — 2 (заметим, что из xii2(v) = к — 1 вытекает x\i2(v) = к, а это невозможно
по выбору г;).
Следовательно, существуют г := k — xij2(v) > 2 переходов множества Х\(v),
не принадлежащих Х2, и наоборот. Можно так обозначить эти переходы, что
где
{гь...,гг} = {1,...,г} и ij^j для 1 < j < г.
Значит, для {e'l5/{} G Х\(у) — X2(v) существуют два различных перехода
WiJDiWnJi} ^ ^2(v) - Хг(у), где m = n и 1 = гп, 1 < ш,тг < г1).
Положим теперь
*i.i~{ei,/{}. *i,2:={e;,/;},
Применим лемму VII.2 при Т = Ti и t3 = tii3, 5 = 1,2. Тогда существует такое
Т3 G T(G), что к(Тг) =Г3и13 := ^т3 DXi- {*i,i,*i,2}- Значит, либо
Х3 = № -{tM>t1|2}) U {{el,/;},{<,/!'}},
либо
Х3 = (Хх - {tM>t1>3}) U {{<*,<}, {/{,/;}}. (3)
Определяя ?3,2 (^) по аналогии с x\^{v) и замечая, что
(Хг - {ti,utlt2})nX2 = ХгПХ2,
мы из того, что Хз D Х\ — {^д, ?1,2}, заключаем, что в первом случае x%i2{v) >
х\,2(v) и, значит, \Х$ П Х2\ > \Xi П Х2\. Из нашего выбора множеств Ti и
Т2 вытекает, что Тз и Т2 /^-связаны. Из этого и того факта, что к(Т\) = Тз,
следует, что Т\ и Т2 «-связаны, что противоречит выбору 7\ и Т2, и, значит,
Хз удовлетворяет соотношению (3).
Теперь применим лемму VII.2 при Т = Т2 и t3 = t2,s, s = 1,2. Используя
симметричные рассуждения, мы получаем существование цепи
Т4 е T(G), такой, что я(Г2) = Г4, Х4 D Х2 - {*2fi,*2,2},
и система Х4 должна удовлетворять соотношению
Х4 = (Х2 - {t2il,t2,2}) U {{е[,е'п},{/{,&}}. (4)
Сравнивая (3) и (4), мы можем убедиться в справедливости равенства
|Х3ПХ4|=|Х1ПХ2|+1 + гт,п,
*' Заметим, что эти 2т переходов соответствуют 2-фактору Q в -К"2г5 где V(i^2r) =
iejifi'\j = 1? • • ч7*} >^(-^2г) состоит из всех возможных переходов, a Q состоит только из
четных циклов по определению этих 2т переходов (см. также обсуждение после
предложения VI.36 и перед теоремой VI.37). Значит, выбор индексов ij, j = 1,... , г, может быть даже
более специфичным. Позднее мы это проделаем.

274
Глава VII. Преобразования эйлеровых цепей
где 5т,п — символ Кронекера. В силу выбора цепей Т\ и Т2 цепи Г3 и Г4
«-связаны. Однако из этого и из формальных равенств «(Т\) = Т3, к(Т2) = T4
вытекает, что и Т\ и Т2 также «-связаны. Это противоречие показывает, что
теорема верна.
Заметим, кроме того, что приведенное выше доказательство отличается от
доказательств из [ABRH80a, Theorem ] и [SKIL83a, Theorem 1].
Зная, что любой связный граф G с 2к > 0 вершинами нечетной степени
допускает разложение S на к открытых цепей, такое, что нечетная вершина
графа G является конечной вершиной точно одной цепи в S (см. следствие
V.2), можно обобщить теорему VII.5 следующим образом. Соединим новую
вершину vo 0 V(G) с каждой нечетной вершиной графа G точно одним ребром,
чтобы получить связный эйлеров граф Н. По каждому разложению S графа G,
описанному выше, можно построить эйлерову цепь графа Н. Если мы положим
S = {Т{щ, Vi)\i = 1,..., к}, где Т(щ, Vi) —тот элемент из 5, который соединяет
нечетные вершины щ,Уг G V(G), то
Тн :=T(ui, vi),vivo, v0, v0u2,T(u2, v2),v2vo,Чь
. . . , V0Ui, T(uU Vi),ViVo, . . . , T(lZfc, Vk), VkV0, Vo, УоЩ
является эйлеровой цепью графа Н. Фактически, если к > 1, то одно и тоже
разложение 5 множества E(G) определяет несколько таких цепей Г#. Кроме
того, каждая эйлерова цепь Тн из Н определяет разложение S множества E(G)
на открытые цепи. Значит, по теореме VII.5 любые два таких разложения Si, 52
множества E(G) могут быть преобразованы друг в друга последовательностью
«-преобразований, примененных к соответствующим эйлеровым цепям Т\,Т2
из Н. Формулируя эти «-преобразования в терминах обращения сегментов и
замечая, что сегмент может начинаться и кончаться в vo 0 V(G), немедленно
получаем, что в общем случае мы не можем утверждать, что Si и S2 могут
быть преобразованы друг в друга последовательностью обращений сегментов
(соответственно «-преобразований), совершаемыми только в G. На рис. VII. 1
это показано. Конечно, мы можем распространять обращение сегмента
(соответственно, «-преобразование) на произвольные графы G, ограничиваясь в
Н лишь сегментами, не содержащими элементов из EVQ (и/или ограничивая
«-преобразования элементами из Xsx — Х^Дг^о)).
Однако если к = 1 (т. е. если в G есть открытая покрывающая цепь), то
любые две такие цепи могут быть преобразованы друг в друга
последовательностью обращений сегментов. Чтобы убедиться в этом, образуем сначала Н
из G, как описано выше, и положим {u,v} = Nh{vo)- Более точно, так как
вершина vq имеет степень 2, в Н можно определить соответствие
Гя€Т(#)->г?еТо(С),
где T0(G) является множеством всех незамкнутых покрывающих
цепей в G, соединяющих нечетные вершины u, v E V(G), и где Тн определено
последовательностью ребер
Тн = vou,T%.,vvo.

VII. 1. Преобразование произвольных эйлеровых цепей 275
Рис. VII. 1. Разложение 5i множества E(G) на две незамкнутые цепи
Т(щ, vi), T(u2,V2), где малыми дугами изображены элементы из Xsi, не может быть
превращено обращениями сегментов в путевое разложение 5г := {-P(^i > ^2), P{v\, ^2)}
множества E(G).
По определению VII. 1 можно, не ограничивая общности, записывать элементы
из Т(Н) так, чтобы они начинались и кончались в vq. Значит, вьшисанное
соотношение между Тн и Tq позволяет считать наше соответствие биекцией
между Т(Н) и %(G).
Далее, рассмотрим Т,Х" Е Т(Я), такие, что к(Т) = V. Предположив, что
G есть связный граф, не являющийся путем, мы можем рассмотреть
х е V(H) - V2(H) = V(G) - (V2(G) U Vi(G)) ф 0.
Теперь мы можем записать Т как последовательность ребер вида
Т = 5i,m_i,5m,g, 2 < га < q, (*)
где 5ijm_i и Sm,q суть сегменты с началом и концом в я; значит, Т начинается
и заканчивается в х. Кроме того, га = 2 (га = q), если и только если
первое (последнее) ребро в Г является петлей. Теперь предположим, что Т ф Т".
Поскольку к(Т) = Г', то Т" получено из Т обращением некоторого
сегмента 5r,s, начинающегося и заканчивающегося в у Е V(H) — V^ff). Вследствие
(*) и определения VII. 1 можно предполижить без ограничения общности, что
у = х, г = 1, s = га — 1. Значит,
T' = srX-i,sm,q. (**)
Перейдя к обозначениям из (1) и (2), имеем теперь
*1 = {е1>етпЛ ^2 = {em-Ueg}*
Однако для
Jm,q
Tit rr q—1
— «3l,m—1» On

276
Глава VII. Преобразования эйлеровых цепей
соответствующая система переходов X" также удовлетворяет (1), где ?i, ?г> t[, t'2
суть переходы, описанные в (***). Значит,
Х" = Х\ т.е. Т" = Т'.
Таким образом, Т' может быть получена из Т обращением сегмента Sm,g
вместо Si,m_i. Другими словами, если к(Т) = Т" и Т ф Т", то Т' может быть
получена из Т обращением сегмента, не содержащего наперед заданного ребра
(см. также [SKIL83a, Lemma 1]). Обобщая это на любые две к-связанные цепи
Т,Т' ? Т(Н), мы можем сказать, что Т' может быть получена из Т
последовательностью обращений сегментов, такой, что ни один из обращенных
сегментов не содержит элементов из Е(Н) — E(G). Этот факт и теорема
VII.5 эквивалентны следующему результату [SKIL83a, Theorem 2], который
получен как итог предыдущих рассуждений.
Следствие VII.6. Пусть G — связный граф с точно двумя нечетными
вершинами, и пусть TfjTj ? %{G) выбраны произвольно. Тогда Tf и Т®
к-связаны (т. е. они могут, быть получены друг из друга
последовательностью обращений сегментов).
Если взглянуть еще раз на общий случай (когда G содержит 2/с > 2
нечетных вершин) в свете рассуждений, следующих за теоремой VII.5, то не ясно,
как приступить к проблеме классификации для 5(G), где S(G) —множество
всех разложений S множества E(G) на к открытых цепей. Следует ли
просто придерживаться концепции сегментного обращения, которая была принята
для случаев к = 0 (теорема VII.5) и к = 1 (следствие VII.6), или надо
использовать для сегментного обращения некоторые сегменты эйлеровых цепей также
и из HI Предыдущее обсуждение наводит на мысль, что надо
придерживаться такого сегментного обращения, которое использовалось в случаях к = 0,1.
Возникает следующий вопрос (см. также обсуждение рис. VII. 1): если G —
связный граф, имеющий точно 2к > 2 нечетных вершин, насколько велика может
быть мощность \V(G,k)\? Здесь V{G,k) означает разбиение множества 5(G),
индуцированное «-связанностью, которая остается отношением
эквивалентности, если рассматривать открытую цепь T(u,v) и ее обращение T(u,v)~l как
один и тот же объект (см. определение VII. 1). Является ли \V(G, к) |
функцией /(fc), зависящей лишь от к? Может ли быть /(/с) = /с? По моему мнению
эти вопросы заслуживают исследования; кажется, никто не занимается этой
задачей.
VII.2. Преобразование эйлеровых цепей
специального типа
Вместо обобщений обратимся теперь к некоторым частным случаям.
Рассмотрим в связном эйлеровом графе множество Т* всех эйлеровых цепей
некоторого специального типа и выясним, являются ли любые две из них ю-связанными
в Т*. Точнее, если Т, Т" € Т* выбраны произвольно, то существует ли такая
последовательность объектов Ti,..., Тп е Т*, что 7\ = Т, Тп = V и K,(Ti) = Ti+i
при г = 1,... ,п — 1?

VII.2. Преобразование специальных эйлеровых цепей 277
а) Ь)
Рис. VII.2. if2,4 и система переходов X' = Xs в случае а) и соответственно
система X" = Хто в случае Ъ). Для Т = 1,5,7,3,4,8,6,2, Г' = 1,5,6,2,4,8,7,3 и
Т" = 1,5,6,2,3,7,8,4 мы имеем Хт П X' = Хт П X" = Хт> П X' = Хт» С\ X" = 0.
Однако X' П Хт2 Ф 0 для любой эйлеровой цепи Тг, удовлетворяющей условию
к(Т) —Т^фТ, тогда как Тг = 1,5,7,3,2,6,8,4 удовлетворяет условию Хг2 П X" = 0,
л(Г) = Т2,л(Г2) = Т".
Обратившись вначале к понятию совместимости, мы испытаем вскоре
некоторое разочарование. Если G — связный эйлеров граф с системой переходов
X и эйлеровыми цепями Т, Г', совместимыми с X, то, вообще говоря, неверно,
что G содержит эйлеровы цепи Ti,..., Тп, совместимые с X и такие, что
Т = Тг,Т' = ТП и Ti+i=«(Ti) при 1<г<п-1.
Это можно увидеть на рис. VII.2, где мы рассматриваем i^2,4 и два
возможных случая для системы переходов X. В первом случае (рис. VII.2.a)) X' = Xs
для некоторого циклического разложения графа if2,4 на два 4-угольника, во
втором случае (рис. VII.2.b)) X" = Хт0 для некоторой эйлеровой цепи Го в
#2,4- Эйлерова цепь Т = 1,5,7,3,4,8,6,2 совместима и с Х\ и с X".
Выберем Т" = 1,5,6,2,4,8, 7,3 в первом случае и Т" = 1,5,6,2,3,7,8,4 во втором
(заметим, что Т" получена из Т' обращением сегмента 4,8,7,3). Теперь
простые соображения показывают, что, с одной стороны, Т не может быть
преобразована в Т' последовательностью «-преобразований, включающих только
Х'-совместимые эйлеровы цепи, тогда как, с другой стороны, такое
преобразование возможно для Т и Т" в области ^''-совместимых эйлеровых цепей (см.
рис. VII.2 и упр. VII.1). Общие теоретические обоснования для обсуждаемого
здесь явления можно найти в доказательстве теоремы VII.5. А именно, вполне
возможно, что эйлеровы цепи Тз и Т± удовлетворяют (3) и (4) соответственно
и что {е[, e'n} G X, где X — предписанная система переходов; значит, ни Тз, ни

278
Глава VII. Преобразования эйлеровых цепей
Т± не совместимы с X. Именно это и произошло на рис. VII.2.а). Вопрос,
однако, в том, из-за чего же в основном возникают трудности: из-за структуры
системы X, из-за структуры графа G или из-за понятия «-преобразования?
Оказывается, если подходящим образом обобщить понятие «-преобразования,
то для понятия совместимости мы получим способ дать утвердительный ответ
на поставленный в начале разд. VII.2 вопрос.
Пусть Т —эйлерова цепь связного эйлерова графа G, у которого V(G) —
V2(G) ф 0, и Хт - система переходов, соответствующая цепи Т. Выберем
ti = {f[,g[}, ti = {/2^2} € Хт{у) ДЛЯ некоторой вершины v G V(G) — V2(G) и
определим
Х':=(Хт-{Ь,Ь})и{*1&} (!')
таким образом, что
*i U t2 = t[ U *2, где *i, *2 G X»,
и
X1 не является системой переходов эйлеровой цепи.
Из этого следует, что X' является системой переходов, соответствующей
разложению множества ребер E(G) на цепи S' с | S' |= 2. Действительно, из
определения X' следует, что \Sr\> 2. Если же мы образуем Н из G так же, как в
рассуждениях, предшествующих (1), где V^ff) = V(H) — {v} и Е* = ?'х Ut2, то
расщепление v на две вершины степени 2 в соответствии с t[ и t2 приведет нас
к 2-однородному графу Л"', имеющему точно две связные компоненты. Однако
Н' есть не что иное, как 2-однородное расщепление графа G,
соответствующее X'.
Обратно, пусть G имеет цепное разложение S' = {Т^Т^} с \S'\ = 2.
Положим X' = Xs> и Х[ := Х'\т>., i = 1,2. Выберем и € V(G) так, что Ev П
Т/ ^ 0» * = 1,2. (Заметим, что существование разложения S' обеспечивает
существование такой вершины v € V(G) — V^G).) Выберем, далее, произвольно
t^ e X[(v), г = 1,2, и определим пару переходов ti, ^2, посредством соотношений
|^-П?-|=1 для г, j = 1,2 и tint2 = 0. (*)
Тогда
Xr:=(X'-{«i,^})U{ti,«2}, (1")
где ti, ^2 € Хт(^), определяет эйлерову цепь Г графа G. Это следует из (*) и
рассуждений, следующих за (1/), что, в свою очередь, показывает, что
преобразования системы Хт в X1 и/или системы X1 в Хт, определенные формулами
(1') и (1"), являются взаимно обратными операциями. Заключая эти
рассуждения, введем следующие понятия.
Определение VII.7. Пусть G —связный эйлеров граф, у которого V(G) —
^(G) ф 0, Т € T(G) и 5' —цепное разложение множества E(G), такое,
что \S'\ = 2; обозначим через Хт и X' соответствующие системы
переходов. Если для некоторой вершины v Е V(G) — V^G) найдутся такие ti, *2 €
Xr(v), ?i,$2 € -^'(u)j которые удовлетворяют соотношению (]/), то скажем,
что X1 получена из Хт посредством «-отделения; это можно формально
записать так: 5 = «'(Г). Если для некоторых объектов Хт, 5', ?$,??, г = 1,2,
Удовлетворяется соотношение (1")> то скажем, что Хт получена из X' посредством

VII.2. Преобразование специальных эйлеровых цепей 279
к-поглощения, и выразим это формально записью Г = «"(5'). Будем
говорить, что X" е T{G) получена из Г посредством ^-преобразования, если
существует такое цепное разложение S' множества -E'(G), что 5' = к'(Т) и
V — «"(5'). Для простоты запишем теперь «* — к"к' иГ = «*(Т) (что
оправдывается равенством Т' — к"(к'(Т))).
Замечание. Отметим, что в определении VII.7 равенство |5'| = 2 следует
прямо из определения «-отделения. Более того, применение «*-преобразования
означает, что соответствующее «-поглощение, быть может, применено, а быть
может, не применено к тем вершинам, к которым было применено соотвеству-
ющее «-отделение. Однако следует заметить, что в гл. X (см. т. 2) мы будем
рассматривать понятия «-отделения и «-поглощения в более общем смысле,
который подсказывается определением VII.7 (если из этого определения удалить
ограничение |5' |= 2 и рассматривать Т как другое цепное разложение).
Можно определить /^-связанность так же, как была определена
«-связанность (просто заменив « на «* в определении VII.4). Предоставим
читателю показать, что (упр. VII.2) «*-связанность также определяет отношение
эквивалентности на множестве T(G).
Для следующего результата, однако, нам необходимо скомбинировать «- и
«* -преобразования.
Определение VII.8. Пусть Т, X" Е T(G), где G есть связный эйлеров граф.
Скажем, что Т' может быть получена из Т посредством «i-преобразования,
кратко V = «i(T), если либо V = «(Г), либо Т = «*(Т).
Определим к\-связанность аналогично тому, как мы определили
«-связанность (см. определение VII.4), и оставим читателю доказательство
того факта, что «i -связанность также определяет отношение эквивалентности
на T(G).
Однако в дальнейшем обсуждении нас будут интересовать такие
преобразования эйлеровых цепей, совместимых с данной системой переходов X, при
которых не используются никакие другие эйлеровы цепи. Поэтому мы пришли
в конце концов к следующему определению.
Определение VII.9. Пусть T(G, X) — множество всех эйлеровых цепей (в
связном эйлеровом графе G), совместимых с данной системой переходов X =
X(G). Обозначим, далее, через 5г(С) множество всех цепных разложений 5
графа G с |5| = 2 и через 5г(С, X) все такие элементы из 52(G), которые
совместимы с X. Назовем эйлеровы цепи ТиГ ^х-связанными, если
существуют такие Т0,... ,ТП <Е T(G,X), что 1) Г = Г0, Г = Тп и Т{ = «i(7i_i) для
1 < г < п и 2) если Ti = «i(Ti_i) = «*(Tf_i) для некоторого г, 1 < г < га, то
из Si-г е 52(G), Si-i = «'(Тг-i), «"(u-i) = Ti следует 5,-1 € S2(G,X).
Аналогично, «х-связанность определяет отношение эквивалентности на
множестве T(G,X) (см. упр. VII.2). Это индуцирует разбиение P(G, «х)
множества T(G,X), элементы которого суть классы «х-связанности. Следующая
теорема—аналог теоремы VII.5 для эйлеровых цепей, совместимых с X.

280
Глава VII. Преобразования эйлеровых цепей
Теорема VII. 10. Для каэюдого связного эйлерова графа G и каэюдой заданной
системы переходов X этого графа \V(G, к,х) |= 1.
Доказательство. Если G — цикл, то теорема доказывается аналогично
теореме VII.5 (заметим, что в этом случае X = 0). Поэтому будем считать,
что V(G) - V2(G) ф 0. Случай T(G,X) = {Г} тривиален, так как тогда
«i(T) = к,(Т) = Г, где к означает в этом случае тождественное преобразование.
Значит, предположим, что \T(G,X)\> 1 и существуют Т\,Т2 Е T(G,X),
которые не являются «х-связанными. Будем действовать, как при доказательстве
теоремы VII.5, используя те же обозначения. Выберем опять такие Т\ и Г2, что
число | Х\ П Х2 | является наибольшим из возможных для сответствующих
систем переходов Х\ и Х2. При этом условии выберем такой граф G, что \E{G) \
минимально; тогда V2(G) = 0. Далее, если е — петля, то ее два полуребра мы
будем различать нижними индексами, а не символами е',е" (ef указывает на
то, что мы имеем дело с полудугой).
Опять имеет место Т\ ф Т2 (тождественное преобразование есть
к\-преобразование); значит, существует вершина v € V(G), такая, что d(v) = 2k и
^1,2(v) '= \Xi(v) П X2(v)\ < к — 2. Кроме того, при г := к — xi,2(v) мы опять
имеем соотношения
{e[,f{},...,{e'r,fr}^X1(v)-X2(v),
{e[J^},...,{e'r,fi}eX2(v)-X1(v), (*)
{ii,...,ir} = {!,...,г} и цФз Для 1 < 3 < г-
Учитывая импликацию
T1,T2€T(G,X)=*{{e'j,fj},{e'j,ti.}\j = l,...,r}nX = 0 (Х)
и подстрочное примечание к доказательству теоремы VII.5, без ограничения
общности можно предположить, что {e'i,fi-i} ? X2(v) — Xi(v), г = 1,... ,m,
полагая /q = frm. Следовательно, п = 2 (см. доказательство теоремы VII.5 по
поводу индекса п). Отсюда следует, что
*1Д = WiJi}> *i,2 = W2J2} e Хг(у)-Х2(у),
*2Д = {el. /m). *2,2 = {е2, Л'} € Х2(«) - Хг(ь).
Рассмотрим четыре системы переходов (см. формулы (3), (4) в доказательстве
теоремы VII.5 и равенства, непосредственно предшествующие им)
Х'3 :=№-{*!,!, t1]2}) U {{ei,/^}, {4 Л».
Х% := № -{ti,i,til2})U{{ei,e2},{/2,/i'}},
Х'А := (Х2 -{^bt^DuUeiJO^e,,/^}},
X;:=№-{t2,1,i2,2})U{{e'1,e2},{/{,/^}}.
Заметим, что при i G {3,4} из этих определений следует, что
Х[ = Х^, если и только если X" = Xs±, / ч
X" = Х^, если и только если Хг' = Хз±,
где Ti е= T(G) и 5i € 52(G); кроме того,
из Г» ? T(G, X) следует, что S* G 52(G, X). (* * *)

VII.2. Преобразование специальных эйлеровых цепей 281
Поскольку {e'2,f{} G Х2, {e[,f[} € Хь то
{ei,^a, если Х'г=ХТъ для T3gT(G) (,
{ei,/;}GX, если XJ = *т4 для Г4 € T(G). l°j
В противном случае, как и в доказательстве теоремы VII.5, получается
противоречие.
Следовательно, в силу (5) и (**)
{ei, е2} е X, только если X" = XTi для Г» G Т(<2), г = 3,4. (6)
Аналогично, {е^е^} € X", г = 3,4, и, выбрав Т\,Т2 € T(G,X), получаем, что
из Xl' = XTi,i = 3,4, следует {Г3,Т4} % T(G,X). (7)
В противном случае мы, рассуждая, как в доказательстве теоремы VII.5,
придем к противоречию.
Теперь мы можем рассмотреть три основных случая.
Случай 1. Предположим, что Х[ = XTi, X1' = Хт, для Г*, Г, € T(G).
Согласно (**), г ф j, а значит, {z,j} = {3,4}; без ограничения общности можно
считать, что г = 3 и j = 4. По (5) и (6) {е^, /2} ? X, из чего следует, что m > 2
и {е^, е^}, {/i, /2} ^ ^- Поскольку Г3 ? T{G,X), то из (* * *) вытекает, что
5з € «S2(G, X), где Xs3 = Х%. В зависимости от того, верно или нет включение
Т4 € T(G,X), различаются два подслучая.
Подслучай 1.1. Т4 G T(G,X). Положим 5з = {5е,5/}, причем ei,e2 € ??(5е)
и, следовательно, /ь/г G E(Sf). Заметим сначала, что Xi(t>) — {?1,1,^1,2} ф 0,
поскольку m > 2.
Рассмотрим, далее, проход по Г4, начиная с v вдоль е\. Поскольку Т4 € T(G)
и {е[,е2} € Хт4 = Х^, мы достигнем v вдоль в2, лишь пройдя по всем
элементам из E(G). Следовательно, поскольку для Se это не так, должна
существовать вершина w € V((Se)) П V((S/)), в которой переход {h[^g[} G Х4'
удовлетворяет условиям hi E E(Se),gi Е E(Sf). Значит, мы нашли такие /i2?#2 € JS^,
что в любом случае {h[,hf2} € Xi(w), a {^1,^2} ^ Xi(w), если ги ^ v, в то время
как, если w = и, мы полагаем ^ = /г', г = 1,2. Заметим, что {/{,/2} € Хд'. В
любом случае {{fti,/^}» {^1^2}} П Xi П Х2 — 0 по построению и вследствие
того, что га > 2 и {e'l5 е^} е Х? П Х?'.
Кроме того, при {r,s} = {1,2}
из {{fti,^},{^^i}}nX#0 следует {{fti,^}, {%,?}} ПХ = 0.
Значит, мы получаем справедливость этих равенств для некоторого выбора
г и 5, где {r,s} = {1,2}. Мы можем записать Se при некоторых j и к, где
{j,/c} = {1,2}, в виде
Se = е^,... ,/ii,/i2,... ,efc
(возможно е^ = /ii или е* = /i2, но {е7-,е&} 7^ {^1,^2}) и
S/ = gs,---,gr
(заметим, что h2 Е E(Se), поскольку hi G E(Se) и {/i^,^} € Xi(w), и что,
аналогично, #2 € E(S/)).

282
Глава VII. Преобразования эйлеровых цепей
Отсюда мы получаем
Из самого построения цепи Tj^ вытекает, что Tj^ € T(G,X).
Значит, так как к'(Тг) = S3 ? 52(G,X) и я"(53) = Г,,* € T(G,X), то Ti и
Tjtk «х-связаны. Кроме того, Т2 и Т4 также «х-связаны, поскольку Т4 €
T(G,X) и Т4 = «(Т2) = «i(T2). С другой стороны, так как {{h[, h'2}, {91,92}} П
Xi П Х2 = 0, то
из {e;,4}Gi;nIrjifc следует, что \Х% nXTjtk\>\X1nX2\ .
Из выбора Ti и Г2, и T±,Tj,k e T(G,X) вытекает, что Т4 и Т^ «х-связаны.
А тогда можно, наконец, сделать заключение о «х-связанности Т\ и Т2. Это
противоречие доказывает под случай 1.1.
Подслучай 1.2. Т4 ? T{G,X). Согласно (***), 54 ? S2(G,X), и Х<?4 = Х'4 по
(**). Это означает, что {/{, /^} € X, так как {е'1? е^} ^ X, и, значит, {е^, /^} ?
X. Кроме того, сохраняя обозначения, введенные в подслучае 1.1, положим
?3 = {5е, 5/}, как и выше, и
S; = S4 = {S*e,S}}, где еьДеВД) и e2JmeE(S}).
В этом случае, однако, S? играет ту же роль, что 5з в подслучае 1.1, a Se —
роль Т4. Рассмотрим проход по 5е, который начинается с v вдоль е\\ следуя
элементам из Х\ и не выходя из 5е, мы придем в конце концов в v, пройдя
по E(Se)i и последним ребром будет е2. Этот проход, интерпретированный
как проход некоторых элементов множеств E(S*) и E(Sf), начинающийся с
е\ ? E(S*) и заканчивающийся е2 € E(Sf), должен в какой-то вершине ги €
V((Sf)) П V((S^)) перейти из ?* в S^. Значит, аналогично подслучаю 1.1,
мы можем сделать вывод, что существуют такие {h^g^} € X^(w), что hi €
?(S*), #1 € ^(5'/)i кроме того, имеются /i2,#2 € JE^, такие, что в любом случае
{hi,h'2} € ^2(w)> a {#i,?2} € Х2(ги) для w ф v, тогда как для w = v мы
полагаем д[ = /^, д'2 = е^ ({е2>/т} € Х'А). Поскольку мы в любом случае
имеем {/ii,/i2} С E(S*) и {<7i,#2} С E(Sj), то, как и в подслучае 1.1, можем
сделать вывод, что для
S* = ei,...,^,/ifc,...,/i, где {j,fc} = {1,2},
и
Sf = ga,'.-,9r, где {5,г} = {1,2},
цепь Tjk = ei,..., Aj, 5p ftfc,..., /1 удовлетворяет условию Т^ € T(G, X), так
как {{h'j,g's}i{h'k,g'r}} П X = 0 для фиксированных {j, fc} = {1,2} и одного
из двух возможных выборов {5, г} = {1,2}. Заметим, что Sj можно выразить
аналогично для обоих выборов 5 и г.
Поскольку по построению
{h[,h'2}eX2(w)-X1(w) и {?,&}# Xdw)
в любом случае (заметим, что га > 2), в то время как
{е'1,П}€Хт1кПХ1-Х1ПХ2,

VII.2. Преобразование специальных эйлеровых цепей 283
учитывая, что Х\ П Х2 С Хт?к, мы получаем
\ХгГ\Хт* |>|Xi ПХ2| .
Следовательно, в силу выбора 7\ и Т2 цепи Т\ и T*fc являются /$х-связанными
и по построению T*fc и Т2 также /сх-связаны. Значит, и 1\ и Т2 являются
«х-связанными. Это противоречие доказывает подслучай 1.2 и, значит, весь
случай 1. Заметим, что в обоих подслучаях специальное рассмотрение случая
v = w для определения gi = /*, г = 1,2, и соответственно pi = /m и #2 =
е2 в действительности не необходимо. Однако оно показывает, как в случае
v = w можно построить Tjtki Т?к соответственно, изменяя минимальное число
элементов в исходных системах Х\, Х2.
Поскольку случай 1 завершен, нам осталось рассмотреть случаи, когда
Х[ = Хг., i = 3,4, или Х'1 = Хт„ г = 3,4.
Случай 2. Хг' = ХГ., г = 3,4. Согласно (5),{{ei,/?}, {e2,/^}} С X, так что
га > 2; кроме того, X" = -Х^ по (**), и Si e <S2(G, X), г = 3,4, по (***).
Сохранив большинство из введенных ранее обозначений, запишем
?з = {^е» 5/}, 54 = {5*, 5^},
TAe{eue2}CE(Se)nE(S;), {/i,/2} С ВД), {fi, fm} Q E(S}).
Подслучай 2.1. E(Se) Ф E(S*). Из этого предположения и того факта,
что {ei,e2} С E(Se) П E(S*), следует, что, начиная проход по S* с
вершины v вдоль ei, можно найти такой {h'^g^} G X2(w) для некоторой вершины
w e V((E(S*))), что hi G E(Se), g\ G E(Sf). Тогда, как и раньше, мы
найдем такие h2,g2 G Ew, что {/i'i,/i2} € Xi(w) в любом случае, {#i,<72} G -X"i(w),
если г> ^ w (и тогда #2 € E(Sf)), а при v = w полагаем д[ = //, г = 1,2 (см.
подслучай 1.1).
Мы сохраним обозначения, используемые в предыдущих рассуждениях, для
единства подхода и повторим рассуждения для прохода по 5е, начиная с
вершины v вдоль е\\ мы найдем {h^g^} G X\(w) для некоторого w G V((E(Se))),
так что hi G E(S*), gi G E(Sf), и найдем такие /i2,#2 € ?^, что {/i'i,/i2} €
X2(w) в любом случае и {д[,д2} € Х2(гу), если v ф w, тогда как для v = w мы
определим д[ = f[, g'2 = f!^. Заметим разницу с подслучаем 1.2,
обусловленную тем фактом, что теперь XsA = Х±.
Как и в случае 1, мы получаем по построению
{{h'i,h'2},{gfi,g'2}}nXinX2 = 0,
и Tj^.Tjk G T(G,X) для эйлеровых цепей строятся способом, аналогичным
приведенному в подслучаях 1.1, 1.2 соответственно. Мы имеем
(Хг Л Х2) U {{ei,е^}} С XTi,h П Хт-
Из этого и из выбора 7\ и Т2 следует, что T^k и T*fc /sx-связаны. Кроме того,
по построению Ti и T^k юх-связаны; то же самое имеет место и для Т2 и Т?к.
Отсюда заключаем, что Ti и Т2 «х-связаны. Это противоречие доказывает
подслучай 2.1.

284 Глава VII. Преобразования эйлеровых цепей
Подслучай 2.2. E(Se) = E{S*). Следовательно, E(Sf) = E(S}). Из этого,
из того, что fm ? E(Sj), а также из того, что {e'm,fm} G Х%, вытекает, что
ет, /т € ?(?/) = E(Sj), из чего вместе с включением {е^, /^-i} € Х^', в свою
очередь, следует em, /m_i € E(Sj) = E(Sf) (заметим, что т > 2) и т. д. Значит,
поскольку Д <Е E(Sf) = E(S*f), мы имеем Ev - {eue2} С ?(S» = #(S}).
Рассмотрим два случая.
(2.2.1) т > 3. Тогда {е?,/?} G Х?', {е?,Я} G Х%, и, поскольку {ei,$},
(е2> fm) G X и m > 3, получаем
{{е^е;.},{Л,е;.}Ь = 1,2}ПХ = 0.
В силу предыдущих рассуждений и поскольку мы можем записать
Sf = /», •.., е3, /з, • • •, fj для некоторого выбора {г, j} - {1,2}
и
5]f = /л,..., е3, /г, •. •, /z для некоторого выбора {/с, /} = {1, ш},
обе цепи
Г = /i,...,e3,5e,/3,...,/j и Г* = Л,...,ез,5*,/2,...,/г
(где мы считаем, что и 5е, и 5* начинаются cei и кончаются ег) принадлежат
T(G,X). По построению
{{e/3,ei}}U(X1nX2)=XTnXT.,
из чего следует, что Т и Т* кх-связаны вследствие выбора Ti and T2.
Из этого, а также из построения цепи Т из Ti и соответственно цепи Т* из
Т2 следует, что 7\ и Т2 кх-связаны, и мы снова получаем противоречие.
(2.2.2) т = З.ТогдаХ(^)Э{{е1,Л},{е,2,Л},{45/1/}}1)-Поскольку{е1,е2}С
E(Se) = E(S*), имеются три возможности для 5/ и 5^ при прохождении ребер
из Ev — {ei, е2}. В зависимости от этих возможностей мы можем строить Т, Т* Е
T(G,X).
(a) Sf = /1,..., /3, ез,..., /г- Заметим, что S^ не может содержать сегмента
?з,2 = ез> • • • > /г> так как {е3, /2} € -Х^', из чего следует, что Х'1 |s3,2C ^'1- Это
вместе с включением S3,2 С 5г противоречило бы тому, что 5* — замкнутая
цепь. Так или иначе, если 5/ удовлетворяет приведенному выше равенству, то
Т\ имеет вид
Т\ = ei,/i,... ,/з,ез,... ,/2,б2,...;
следовательно, с помощью «-преобразования мы получим Г € T(G,X),
Т = еь /i,..., /3, /2,..., е3, е2,....
^ Заметим, что m = 3 не означает, что d(v) = 6. Это непосредственно видно из
подстрочного примечания в доказательстве теоремы VII.5, где 2га — длина цикла в 2-факторе Q из
Kir- Кроме того, {е3, /{} 6 X{v), поскольку га = 3 и {е[, /з), {е2, /3} € -Х"(г;), а также в силу
комбинации случая 1 и (5), если мы положим ti,2 = {е3,/з}-

VII.2. Преобразование специальных эйлеровых цепей 285
(b) Sf = /1,... ,/2,ез,.. .,/з- Аналогично случаю (а) заключаем, что 5/ не
может иметь сегмент вида ез,..., /з- Здесь цепь Т2 и цепь Т* € T(G, X),
полученная из Т2 с помощью «-преобразования, имеют вид
^2 = б1,/з,. • .,е3,/2,.. • ,Л,е2,...,
21* = ei,e3,... ,/з,/2,--.,/ье2,—
(c) Или 5/ = /ь ..., е3, /з, • • •, /г, или 5^ = /ь ..., е3, /2,..., /з- Тогда для Ti и
Т2 имеем выражения
2\ = ei,/i,... ,е3,/з,.. .,/2,е2,...,
2г = ei,/3,... ,/2,е3,... ,/i,e2,—
Отсюда для цепи Т € T(G, X), полученной из 7\ с помощью «-преобразования,
имеем
Т = в1,ез,... ,/ъ/з,- • .,/2,62,. ¦ •,
тогда как из 54 = {5*, 5^} с помощью «-поглощения получаем Т* ? Т(С?,Х),
Т* = е1,е3,...,/ъ/з,...,/2,е2,
Во всех случаях (а),(Ь),(с) цепи Т и Ti, соответственно Т* и Т2, являются
«х -связанными и
Xi П Х2 С Х^, Xi П Х2 С Хт* соответственно.
С другой стороны, если сравнить любую построенную цепь Т с любой
построенной цепью Г*, то можно заключить, что
или {е[, eg} е ХтС\ Хт*, или {/2, /з} G Хт П Хт*,
или Т такая, как в случае (а), и Т* такая, как в случае (с).
Значит, при первых двух возможностях имеем | Хт П Хт* | > | Xi П Х2 | и
цепи Т и Т* «х-связаны. Цепи Т и Т* «х-связаны и при третьей
возможности, поскольку в случае (с) мы имеем {е2,/2} € Хт*, откуда следует, что
| Xi П Хт* \>\ Х\ П Х2 | и, значит, Т* и Т\ «х-связаны. Отсюда и из равенства
Т\ = к(Т) получаем, наконец, что Т и Т* «х-связаны в любом случае.
Следовательно, так как во всех рассматриваемых случаях Т = «i(Ti),T* = «i(T2),
то Ti и Т2 «х-связаны. Это противоречие доказывает подслучай (2.2.2) и,
значит, весь подслучай 2.2. Таким образом, случай 2 разобран.
Случай 3. Хг" = XTi, г = 3,4. Согласно (7), Г,- 0 T(G,X), если Tfc G T(G,X)
при любом выборе {j, fc} = {3,4}; значит, без ограничения общности считаем,
что j = 3, к = 4.
Подслучай 3.1. Т4 ? T(G,X). Тогда по (* * *) имеем Xg = Xs3i где 53 G
<S2(G,X). Кроме того, {е^,е2} 0 X, {/{,/2} G X. Заметим, что га > 2 и Т4 =
6i, • • •, /ь /тп? • • •, е2. Используя предыдущие обозначения, запишем
53 = {5е,5/}, где {e2,/i} G 5e,{ei,/2} G S/.
Теперь мы будем рассуждать подобно под случаю 1.1. Начнем проход по Т4 с v
по ребру ei ? E(Sf) и заметим, что этот проход должен закончиться ребром е2
после того, как пройдены все остальные ребра из G. Следовательно, поскольку

286
Глава VII. Преобразования эйлеровых цепей
/i,e2 G E(Se), a E(Se) С E(G), в некоторой вершине w существует переход
{Ki9i} € X2(w)-Xi(w)1 для которого hi G E(Se), 9i G E(Sf). Соответственно
пусть h2,g2 ? ¦Е'ги выбраны таким образом, что {h[,h2} G Х\ (и, значит, /i2 ?
E(Se)) и {#i,<72} € -X"i> если w Ф v, поскольку для v = w мы обозначили
д'г = е'х, д2 = /г (поэтому #i,#2 € ?(S/) в любом случае). Продолжая теперь
наши рассуждения аналогично подслучаю 1.1, получим Т^ ? T(G,X) из
5з посредством «-поглощения; таким образом, Tj,k и 7\ кх-связаны. Кроме
того, {{f[,ef2}} U Xi П Х2 С Х2 П -Xriffc по построению и в соответствии со
структурой Т4 и 5з, откуда следует, что Tj^ и Т2 «х-связаны в силу выбора
Т\ и Т2. Значит, Т\ и Т2 также «х-связаны. Это противоречие с выбором 7\ и
Т2 доказывает подслучай 3.1.
Подслучай 3.2. Г4 ? T{G,X). Поскольку случай Г3 € T(G,X) симметричен
подслучаю 3.1, нам надо лишь рассмотреть случай, когда Гз ? T{G,X). Из
(* * *) следует, что S$,S± G 5г(С,Х), где Хд = Xs3 и Х'А = Xs4. Используя
предыдущие обозначения, получим следующие выражения:
53 = {5e,S/} с {/i,e2}CJS(5e), {еь/2} С E(Sf),
54 = {S*e,S}} с {еь/^СЕ^), {е2,/ш}СЕ(5;).
Теперь мы имеем E(S*) ф E(Se) ф E(S^). Значит, мы можем рассуждать
аналогично тому, как рассуждали в подслучае 2.1, начав проход по S* с
вершины v по ребру Д. Поскольку Д G E(Se) и е\ G E(Sf), найдется такой
{^i>#i} € ^2(w) для некоторой вершины ги G V((5*)), что /ii G E(Se), д\ G
E(Sf)', аналогично, найдутся такие /i2,#2 € Ew, что {hi,/^} ^ -Xi(w) B любом
случае, и {д[,д2} G ^i(w), если w ф v, а, если w = v, то мы полагаем д[ =
ei> #2 = /г • Заметим, что {#1,02} Q #(5>) и {^,^} € Х? - Х2, так как либо
w фу, либо m > 2; кроме того, {^i,/^} 7^ {/i>e2}> поскольку {f'i,e2} G X2.
Эйлерова цепь Tj^ G T(G,X), построенная аналогично подслучаю 1.1,
удовлетворяет соотношению
(X1nX2)u{{f{,e'2}}CX2nXTi<k.
Благодаря выбору 7\ и Т2, из этого соотношения следует, что Т2 и Т^/-
«х-связаны. Из этого факта и того, что «i(Ti) = 7)^, следует, в свою очередь,
что Т\ и Т2 /сх-связаны, и вновь мы пришли к противоречию. Это доказывает
подслучай 3.2 и, следовательно, случай 3. (Заметим, что здесь построение
цепи T*fc, как в подслучае 2.1, небязательно, так как Tj^ содержит переход
цепи Т2, который не учитывался в Х\ Г)Х2, тогда как в подслучае 2.1
построение обеих цепей Tj^ и T*fc было необходимо, поскольку {е[, е2} ? Х\ U Х2).
Получив противоречие в каждом из трех главных случаев (которые
исчерпывают все возможности строения цепей Т\ и Т2), мы можем сделать
вывод, что T(G,X) не может содержать двух элементов, не являющихся
/сх-связаными. Теорема VII. 10 доказана.
Внимательно взглянув на доказательство теоремы VII.10, мы обнаружим,
что на самом деле мы доказали более сильный результат. Чтобы это
установить, мы должны рассмотреть для связного эйлерова графа G систему
разбиения P(G), частным случаем которой является система переходов X =

VII.2. Преобразование специальных эйлеровых цепей 287
X(G). В соответствии с этим мы обозначим через T(G,P(G)) множество
всех P(G)-совместимых эйлеровых цепей из G и введем множество
<S2(G, P(G)). Кроме того, мы обобщим определение VII.9, чтобы получить
понятие /cp(G)-связанности, которое вновь определяет отношение
эквивалентности на T(G, P(G)), классы эквивалентности которого определяют
соответствующее разбиение P(G, Kp(G))- Для этих более общих понятий сформулируем
теперь лемму, доказательство которой оставим читателю (упр. VII.3).
Лемма VII.11. Пусть G — связный эйлеров граф и P(G) —произвольная
система разбиения. Рассмотрим произвольную цепь Т ? T(G, P(G)) (S €
5г(С, P(G))), и пусть {ei,/{}, {e^,/^} € Хт (Xs) выбраны произвольно. Тогда
для всех К ? P(G)
либо {е^е'ъ} ? К J> {![,&}, либо {e[J^} g К 2 {е?,Д'}.
Из этой леммы следуют равенства, аналогичные (**) и (***), и
соотношения, соответствующие (5), (6), (7), также верны (просто X заменяется на
P(G); см. начало доказательства теоремы VII. 10). Эти равенства и
соотношения, однако, были в центре внимания в доказательстве теоремы VII. 10. Итак,
мы пришли к следующему результату, обобщающему теорему VII. 10, который
можно доказать так же, как и теорему VII. 10 (следует лишь заменить
символические выражения типа {е',/'} € X на {е', /'} С К ? P(G)). В качестве
упражнения оставим читателю преобразование доказательства теоремы VII. 10
в доказательство следующего результата.
Теорема VII.12. | V(G,Kp(G)) |= 1 для каждого связного эйлерова графа G
и каждой системы разбиения P{G), такой, что \ К \< \d(v) для каждого
К Е P(v) С P(G) и любой вершины v G V(G).
Заметим, что в теореме VII. 12 ограничения на размеры элементов из
P(G) необходимы и достаточны, чтобы получить T(G,P(G)) ф 0 (см.
теорему VI.1)1)
VII.2.1. Приложения к эйлеровым цепям специального
вида и к 1 -преобразования
Некоторые из следующих результатов являются непосредственными
следствиями теоремы VII. 10. Мы рассматриваем связные 4-однородные графы G или
такие эйлеровы графы G, которые вложены в поверхность, вместе с тремя
типами эйлеровых цепей. В первых двух случаях мы считаем G
вложенным в поверхность и обозначаем множество всех А-цепей и
множество непересекающихся эйлеровых цепей из G через Тд(С) и Tni(G)
соответственно. В третьем случае рассмотрим 2-факторизацию {фьфг}
х) Я решил доказать теорему VII. 10 и оставить в качестве упражнения доказательство
теоремы VII. 12 (вместо того, чтобы получить первый результат как следствие второго), так
как система переходов более наглядна, чем общая система разбиения (и, конечно, потому, что
между соответствующими доказательствами нет реальной разницы). Кроме того, теорема
VII. 10 более важна для дальнейших обсуждений, чем теорема VII. 12.

288
Глава VII. Преобразования эйлеровых цепей
4-однородного графа G (см. следствие VI.3) и обозначим через Ta{G]Qi,Q2)
множество всех эйлеровых цепей графа G, у которого ребра из Qi
и Q2 чередуются (т. е. эйлеровых цепей, совместимых с цикловым
разложением 5 = Qi U Q2)- Кроме того, для Ti,T2e7a(G)
(соответственно Ti,T2 € Tni(G), Ti,T2 € Ta{G\Qi,Q2)), удовлетворяющих условию Т2 =
/ci(Ti), мы назовем это «i-преобразование /^-преобразованием
(соответственно /^/-преобразованием, /^-преобразованием) и в соответствии
с этим определим /сд-связанность (соответственно /^/-связанность, ка-
связанность). Мы требуем, однако, чтобы если «^-преобразование
является «"-преобразованием (см. определение VII.8), то цепное разложение 5',
удовлетворяющее кЦТ\) — S' (см. определение VII.7), было получено из Т\
выбором для v ? V±(G) пары непересекающихся переходов, отличных от
Хтг(у). Аналогично, если «///-преобразование («а-преобразование) является
«"-преобразованием, то из того, что «'(Ti) = S', следует, что
соответствующая система переходов Xsf является непересекающейся (совместимой с
цикловым разложением Qi U Q2). Заметим, что если граф G плоский, то «^-
преобразование обязательно является «"-преобразованием, но это не всегда
так, если G вложим в поверхность, отличную от плоскости или сферы (упр.
VII.5a), b)). Кроме того, в случае 4-однородных графов понятия к а- и «дг/-
преобразований совпадают. Мы снова оставим в качестве упражнения
доказательство того факта, что каждое из понятий к a- k>ni- и «а-связанности
определяет отношение эквивалентности в соответствующем множестве эйлеровых
цепей (упр. VII.5.c)).
Следствие VII. 13. Пусть G — связный ^-однородный граф, вложенный в
поверхность. Тогда любые два элемента из Ta(G) КА-связаны.
Доказательство. Поскольку G вложен в поверхность, 0+(v) задано этим
вложением для каждой вершины v Е V(G). Значит, можно говорить о
пересекающихся и непересекающихся переходах. Поскольку граф G является
4-однородным, пересекающиеся переходы определены вложением G
однозначно. Пусть X — система этих пересекающихся переходов. Тогда
T(G,X) = TA(G),
и «^-связанность эквивалентна в этом случае «^-связанности. Следствие
VII. 13 вытекает теперь из теоремы VII. 10.
Другой способ построения всех элементов из Ta(G) и описания
«^-преобразований был развит в [KOTZ68c] для случая, когда граф G плоский
(и для наших целей этот случай подходит, когда мы говорим об Л-цепях). А
именно, рассмотрим граневую 2-раскраску плоского связного 4-однородного
графа G (используя цвета 1 и 2) и построим для г = 1,2 граф Mi
следующим образом: каждый элемент х € V(Mi) взаимно однозначно представляет
г-грань F(x) графа G и х,у € V(Mi) связаны | V(bd(F(x))) П V{bd(F(y))) \
ребрами, т.е. каждая вершина v ? V(G) соответствует ребру ei(v) Е Е(Мг).
Пусть % означает множество каркасов графа Mi. Следующий результат
устанавливает связь между % и Тд(С) и описывает «^-преобразования в TA(G)
(см. [KOTZ68c, Theorems 14-17]).

VII.2. Преобразование специальных эйлеровых цепей 289
Теорема VII. 14. Пусть G — плоский связный ^-однородный граф, и пусть
Mi, i = 1,2, — граф, построенный выше в соответствии с фиксированной гра-
невой 2-раскраской графа G. Тогда
1) существует биекция oti между Ta(G) и %, i — 1,2, и биекция а±^ меэюду
Т\ и 72, которые определены следующими условиями:
(i) если {Vi,V2} есть А-разбиение, соответствующее Та G Ta(G), то
аг(ТА) = ({ф) G E(Mi)\v G Vi}) G %, г = 1,2,
(ii) если Т\ G Т\ и Та G Ta(G), причем Т\ = а\(Та), то
01,2(21) = <{e2(t>) G E(M2)\e1(v) # ВД)}) = а2(ТА) € Т2,
(iii) а2 =ai,2ai;
2) для Та,Т'а € 7a(G) эквивалентны следующие утверждения:
(i) кл(Гл) = Г^ и Гл ^ ГД,
(ii) a*( Тд) U OLi(T'A) имеет в точности один цикл, г = 1,2.
Доказательство. 1) Рассмотрим Л-разбиение {Vi, Рг}, соответствующееТд ?
Тд(С), и построим плоские графы Яг-ы := Gv^i, г = 1,2 (полагая 3 = 1). По
теореме VI.59 Щ является связным внешнеплоским графом1), блоки которого
суть его циклы, которые, в свою очередь, являются границами г-граней графа
G, i = 1,2. Значит, можно определить Т* С Mi следующим образом:
V(Ti) = V(Mi),
E(Tt) = {ху е E(Mi)\x,y€ V(Ti) A (bd(FHi(x)) Dbd(FHi(y)) Ф 0)}
(где индекс Hi означает, что рассматривается соответствующая грань в Hi).
В силу структуры графов Hi для каждых х, у G V(Ti) выполняется
неравенство |bd(F#.(a;)) П bd(FHi(y)) |< 1. По определению Hi и поскольку v G V(G)
тогда и только тогда, когда еДи) G E(Mi), мы заключаем, что для г = 1,2
ху = e^f) G E(Ti) тогда и только тогда, когда
bd(FHi(x))nhd(FHi(y)) = W € Vi
(см. лемму VI.58).
Прежде всего, заметив, что
d>Hi(v) = 4, если и только если ei(v) G E(Ti), (*)
и рассматривая граф подразбиений S(Ti), из предыдущих рассуждений
получим, что
E(Ti) = {ei(v)GE(Mi)\veVi},
S(Ti) ~Ъс(Щ).
Поскольку Hi связен, be (Hi) —дерево. Из этого и из равенства V(Ti) = V(Mi)
следует, что
Ti = ({ei(v) G E(Mi)\v G Vi}) G %. (**)
Заметив, что Hi уже охарактеризован Л-разбиением {Vl5 V2}, получим из (*) и
(**), что аг(Гд) = Г* определяет биекцию между Ta(G) и%, удовлетворяющую
условию (i).
г> Более точно. Hi — планарный граф, вложенный таким образом, что некоторая (г + 1)-
грань содержит в своей границе некоторое ребро каждого блока.

290
Глава VII. Преобразования эйлеровых цепей
Чтобы убедиться, что (ii) также верно, достаточно сравнить Н\ с Яг и
7\ с Т2 (с Тг, определенным выше, г = 1,2). Вначале заметим, что Н\ и Н2
описывают одну и ту же цепь Та G 7a(G). Значит, ai (Га) = Ti, 0:2 (Га) = Г2.
Из (*) и из определения графов Н\ и #2 мы можем, следовательно, заключить,
что ei(v) G E(Ti), если и только если е2(у) & Е(Т2). Значит, ai,2(ri) = Г2
определяет биекцию между 71 и 72, которая требуется в (ii).
Справедливость (iii) теперь следует из предыдущих рассуждений.
2) Пусть «л(Га) = Т'А для Га,Гд G Ta(G). Как было отмечено выше (см.
также упр. VII.5), «а (Га) = я* (Га), т.е. «* = к"к', где «' есть «-отделение,
а «" есть «-поглощение. Тогда сушествует такая S G 52(G), что Xs содержит
только непересекающиеся переходы, к/(Га) = S и k"(S) — Т'А. Обозначим через
v (w) ту вершину графа G, в которой имеет место «-отделение («-поглощение),
и положим далее Г* := аДГЛ), IV := о^Г^), г = 1,2. Пусть {VUV2} ({V/, У2'})
обозначает А-разбиение графа G, соответствующее цепи Га (Гд). Заметим,
что v ф w тогда и только тогда, когда Гд Ф ТА. Без ограничения общности
можно считать, что г = 1 (случай г = 2 может быть разобран аналогично).
Переход от Га к 5, т. е. применение «-отделения в v, эквивалентен замене
{Vi, У2} либо на [Vi U {у}, V2 - {v}}, либо на {Vi - {у}, V2 U {у}} в
зависимости от того, у G V2 или v G V\. Следовательно (и это эквивалентно), Т\
преобразовывается либо в унициклический граф Тс := Т\ U ei(v) с ei(^),
обязательно принадлежащей однозначно определенному циклу С из Гс, либо в
лес Тр := Ti — ei(u), который имеет точно две компоненты К\ и К2 (см. l)(i)).
Однако, поскольку переход от 5 к Гд, т. е. применение «-поглощения в w,
должен дать А-разбиение {V{,V2}, соответствующее цепи Гд, мы получаем, что
либо
VI = (V, U {у}) - М, Vi = (V2 - {у}) U {w}
(т. е. у G V2 тогда и только тогда, когда w G Vi; заметим, что gTi = 9т7 = |ViI =
\V{\), либо
K = №-W)uW, vi = (v2u{y})-{w}.
Соответственно (и это эквивалентно) Т[ = ai (Гд) получается из Тс удалением
ei(w), а из Гр добавлением ei(w). В первом случае e^{w) G Е(С), во втором
случае ei(w) = х\х2, где ж^ G V^ifj), j = 1,2; это следует из того факта, что
2? €71.
Приведенное выше построение Г{ из Т\ показывает, что в любом случае
Тг П Т{ = Ti U Г/ - {ei(u), ei(u;)}
является лесом, который имеет точно две компоненты, такие, что каждое из
ei(v) и ei(w) соединяет вершины из различных компонент. Следовательно,
ai (ГА) U ax (ГА) = Тг UT{ = Тг ПГ2 U {е^у), e^w)}
содержит точно один цикл (который обязательно содержит е\ (у), е\ (w)). Таким
образом, 2)(i) влечет за собой 2)(ii).
Обратно, предположим, что а*(Га) и аг(Г^), г = 1,2, содержит точно один
цикл; обозначим его через С. Тогда Та ф TfA. Положим Ti := а* (Га), Г/ :=
ai(TA). Так как Г*,Г/ е^ип. l)(i) уже доказан, то
|ВД) - Е(Т[) |=|ВД) - ВД) |= 1

VII.2. Преобразование специальных эйлеровых цепей 291
(в противном случае либо Т» UT/ имеет более чем один цикл, либо Ti = Т/, что
противоречит Та фТ'^). Положим
{ф)} = ВД) - E(rt), {*(«;)} = ВД) - E{Ti).
Следовательно, T[ можно получить из Ti удалением сначала еДи), затем
добавлением ei{w) (а также добавлением сначала еДги), а затем удалением ei(v)).
Из первой части доказательства п. 2) следует, что переход от Ti к Ti—ei(v)
соответствует преобразованию цепи Та в 5, где 5 Е S2(G) и Xs(v) является парой
непересекающихся переходов. Следовательно, это преобразование является к-
отделением, т.е. к'(Та) = S. Аналогично, так как Т[ = (Ti — ei(v)) U {ei(w)}
является деревом, то в силу биекции из п. l)(i) и по построению построение
цепи Гд из S является «-поглощением, включающим только
непересекающиеся переходы, т. е. k"(S) = Т'А. Таким образом, Т'А = к"(к!(Та)) = «лСГа), т. е.
2)(ii) влечет за собой 2)(i). Это завершает доказательство теоремы.
Отметим, что каждый каркас связного графа G может быть получен из
любого другого каркаса графа G последовательностью процедур «ребро
удаляется—ребро добавляется», описанной выше. Это и теорема VII. 14 дают
доказательство следствия VII. 13 (ограниченного на плоские графы), независимое
от теоремы VII. 10.
На самом деле можно получить результат, аналогичный теореме VII. 14, для
произвольных связных плоских эйлеровых графов G. Существуют, однако, два
способа подойти к этой проблеме. Если мы хотим придерживаться графов, то
(при построении соответствующего графа Mi) V(Mi) не только состоит из
«столиц» г-граней, но также из V(G). В этом случае ху Е E(Mi) тогда и только
тогда, когда | {х, у} П V(G) |= 1, где х ? V(G), и у соответствует г-грани F(y) с
х € bd(F(y)). Отметим, что этот способ определения Mi соответствует S(Mi) в
случае 4-однородного графа G (см. обсуждение, непосредственно
предшествующее теореме VII. 14).
В настоящей (более общей) ситуации, однако, не существует больше
биекции oti между Ta(G) и множеством % каркасов графа Mi. Напротив, Гд е
Ta(G) с А-разбиением {Vi,!^} соответствует любому Ti € %, в котором
dTi(vj) = 1 для каждой вершины Vj G V} и dr^Vi) = \dc{vi) для каждой
вершины Vi € Vi, где {i,j} = {1,2}. Итак, каждая цепь Та € X^(G)
связана с множеством деревьев %(Та) Q %- Тем не менее, двойственность между
71 и 7г, которая выражена в п. l)(ii) теоремы VII. 14, остается справедливой
в модифицированной форме; то же самое может быть сказано о п. 2) этой
теоремы.
Однако более подходящим инструментом для описания аналога теоремы
VII. 14 для случая произвольных плоских связных эйлеровых графов G может
быть понятие гиперграфов. В этом случае V(Mi) определяется, как в случае
4-однородных графов, и соответствие между v € V(G) и ei(v) G E(Mi) тоже
сохраняется. Но теперь
ei(v) = {х е V(Mi)\F(x) естьг-грань с v G V(bd(F(x)))}.

292
Глава VII. Преобразования эйлеровых цепей
Определяя остовное гипердерево Т* гиперграфа Mi тем же способом, что и в
случае графов, можно показать, что теорема VII. 14, в том виде, как она
сформулирована выше, остается справедливой даже в этом более общем смысле.
Мы оставляем в качестве упражнения проверить детали приведенного выше
обсуждения двух возможных обобщений теоремы VII. 14 на произвольные
плоские связные эйлеровы графы (упр. VII.6). Отметим, однако, что из-за биекции
cti между Ta(G) и множеством % остовных гипердеревьев (в общем случае)
решение вопроса существования остовного гипердерева в общем гиперграфе
есть JVP-полная проблема. Построение Mi из G может быть проведено за
полиномиальное время, так же как и обратное построение при условии, что G —
плоский граф. Итак, если мы ограничимся только планарными 3-связными
эйлеровыми графами G, то границы граней таких графов однозначно
определены независимо от действительного вложения графа G (см. теорему III.52).
Следовательно, в этом случае гиперграф Mi определяется одним лишь графом
G и наоборот. Так как теперь для таких G решение вопроса о существовании
А-цепи является TVP-полной проблемой (см. теорему VI.91), то решение
вопроса о существовании остовного гипердерева Т* С Mi также является
iVP-полной. Оставим проверку деталей этих рассуждений о сложности в
качестве упражнения (упр. VII.7).
Однако нельзя не отметить, что точно так же, как теорема VII. 14
сама по себе не влечет за собой следствие VII. 13 (см. абзац, непосредственно
следующий за доказательством теоремы VII. 14), обобщение теоремы VII. 14
на произвольные плоские связные эйлеровы графы G само по себе не дает
никакой информации о классах эквивалентности множества Ta(G)
относительно /^-связанности. Конечно, /^-преобразование может включать только
4-валентные вершины, так как мы также требуем, чтобы S индуцировала 1-
или 2-расщепление в каждой вершине графа G. В самом деле, в этом случае
Т,Т' ? Xa(G) принадлежат одному и тому же классу эквивалентности
тогда и только тогда, когда соответствующие им А-разбиения {Vi, V2} и {V[, V^}
удовлетворяют равенствам
Vi - (V2(G) U Vi(G)) = Vl- (V2(G) U V4(G)), i = 1,2.
Оставим в качестве упражнения проверку того, что и в общей ситуации ка-
связанность является на самом деле отношением эквивалентности на Ta(G) и
что отмеченные выше равенства определяют классы эквивалентности
множества Ta(G) относительно /^-связанности (упр. VII.8).
Тем не менее, если рассмотреть множество T^iiG) для произвольного
связного эйлерова графа, вложенного в поверхность, то можно установить
результат, аналогичный теореме VII. 10. Доказательство этого результата будет
проще, чем доказательство теоремы VII.10, но в то же время будет
показано, что мы не имеем той же степени свободы в применении соответствующего
«1-преобразования. Для этого доказательства нам будут нужны следующие
леммы.
Лемма VII. 15. Пусть G — граф, вложенный в поверхность и имеющий
четную вершину v. Пусть X(v) — система непересекающихся переходов в v.
Тогда по крайней мере для одного t ? X(v), скажем t = {ef, /'}, e! и f являются

VII.2. Преобразование специальных эйлеровых цепей 293
последовательными в 0+(v). Кроме того, если v 0 V2(G), то существует по
меньшей мере два таких перехода.
Доказательство. Пусть 0+(v) := (е[,... , e2fc). Если к = 1, то X(v) =
{{ei?e2}}> и лемма вытекает в этом случае просто из того, что G есть
вложенный граф. Если к = 2, то либо X(v) = {{e'^e^}, {e^e^}}, либо X(v) =
{{е15е4}'{е2'ез}}' потому что X(v) является множеством непересекающихся
переходов, откуда мы можем заключить, что лемма также верна для к = 2.
Итак, рассмотрим случай к > 2 и предположим, что существует
{е|,е-}бВД, такой, что г — 1ф j фг + 1, (*)
где полагаем г — 1 = 2&, если г = 1, и г + 1 = 1, если г = 2к.
Среди всех возможных выборов для i и j, удовлетворяющих (*), возьмем
такой, для которого число \г — j\ — наименьшее среди возможных. Без
ограничения общности можно предположить, что в 0+(г>) обозначения выбраны
таким образом, что г = 1. Следовательно, 2 < j < 2к.
Именно потому, что X(v) является множеством непересекающихся
переходов, мы имеем
{ele'm} <?X(v), если 2<l<j<m<2k. (**)
Рассмотрим открытые целочисленные интервалы
h,j:=(lj) и Jii2fe := (j, 2к)
и выберем /,n ? hj, такие, что
число 11 — п | наименьшее среди возможных и t:= {e[, e'n] € X(v). (* * *)
Тогда t обладает свойствами, описанными в лемме с е' — е[, /' = е'п\ в
противном случае мы получим противоречие либо с (*) и выбором i и j, либо с
(**).
Что касается нахождения второго перехода t' € X(v), обладающего
свойством, сформулированным в лемме, то либо tf = {e2fc_i>e2fc} € X(v) (и в
этом случае ничего больше не надо доказывать), либо {вр,е2А.} G X(v), где
j < р < 2к - 1.
В последнем случае рассмотрим соответствующий открытый
целочисленный интервал 1р^к •= (р,2fc) и V\п' G /p,2fc, удовлетворяющие (* * *).
Используя то же самое рассуждение, что и выше, в силу неравенства max{Z,n} <
mm{V,п'} можно заключить, что t' = {^,,е^,} ф t и что f также обладает
свойством, сформулированным в лемме (с е' — е[,, f = efn,). Теперь лемма
VII. 15 доказана.
Из леммы VII. 15 следует, что если Хт является системой непересекающихся
переходов, соответствующей (непересекающейся) эйлеровой цепи Т связного
эйлерова графа G, который вложен в поверхность, то в каждой вершине Т по
крайней мере в одном переходе ведет себя, как А-цеиъ.
Лемма VII. 16. Пусть G — связный эйлеров граф, вложенный в поверхность.
Предположим, что Xs есть система непересекающихся переходов для
некоторого S = {Se,Sg} Е 52(G). Тогда для каждой вершины w € V((E(Se))) П

294 Глава VII. Преобразования эйлеровых цепей
V((E(Sg))) существует цепь Tw ? Tni{G), такая, что Tw получается из S с
помощью к-поглощения в w.
Доказательство. Выберем w ? V((E(Se))) П V((E(Sg))) произвольно и
рассмотрим Xs(w) вместе с 0+{w) = (h[,..., h'2k)', k > 1 из-за выбора w. Без
ограничения общности мы можем предположить, что обозначения для 0+(w)
выбраны таким образом, что hi ? E(Se). Поэтому для t\ = {h[, h'^} ? Xs(w)
имеем hj ? E(Se). Пусть t2 = {h'm, h'n} ? Xs{w) выбрано так, что hm, hn € E(Sg);
без ограничения общности можно считать, что т < п. Кроме того, j < m или
j > п, так как Xs — система непересекающихся переходов; без ограничения
общности считаем, что j < т.
Предположим, что
{h!r, hfs} 0 Xs{w), если г и s удовлетворяют j < г < т < п < s < 2k.
Тогда
Xa(w) := (Xs(w) - {tut2}) U {{К,К},ЩЛ'т}}
состоит только из непересекающихся переходов. Следовательно,
X* = (Xs-Xs(w))UXa(w)
есть система непересекающихся переходов графа G. Кроме того, из
определения Xa(w) следует, что преобразование системы Xs в X* определяет
^-поглощение в w (см. равенства (*) и (1") в обсуждении, непосредственно
предшествующем определению VII.7). То есть X* = Xtw, где Tw ? Tni(G), и
Tw получается из 5 с помощью ^-поглощения.
Если, тем не менее,
{hfr, h's} ? Xs(w) и j < г < т < п < s <2k для некоторых г и s,
то положим
t[ := {h'r,h's}, tf2 := ^2, если /ir,/is ? E(Se),
t[ := ti, tf2 := {hfr, h's} в противном случае
и повторим приведенные выше рассуждения с t'^t^ вместо t\,t<2. (отметим, что
если {h'r,h's} ? Xs{w), то {hr,hs} П E(Se) ф 0 тогда и только тогда, когда
{hr,hs} С E(Se)). Так как d{w) < оо, то для некоторого (4 ,4 } ^ Xs(w)
указанное выше «-поглощение, преобразующее S в Tw ? 7дг/(С), может быть
произведено с помощью ц\ц вместо ti,t2- Лемма VII. 16 доказана.
В соответствии с ранее использованной системой обозначений V(G, k^i) —
разбиение множества 7w/(G), индуцированное /^/-связанностью.
Теорема VII.17. \V(G, kni) |= 1 для любого связного эйлерова графа G,
вложенного в поверхность.
Доказательство. Теорема тривиально верна, если \Tjsji(G)\ = 1 (поскольку
тождественное преобразование является /^/-преобразованием). Поэтому
далее мы неявно предполагаем, что \Tni(G)\ > 1 и существуют эйлеровы цепи

VII.2. Преобразование специальных эйлеровых цепей 295
2\,Т2 € Tni(G), которые не являются /^/-связанными. Обозначая
соответствующие системы переходов через Х\ и Х2 (мы сохраняем систему
обозначений из доказательства теоремы VII. 10, когда это возможно), можно снова
считать, что Т\ и Т2 выбраны таким образом, что число | Х\ П Х2 | —наибольшее
среди возможных, но на этот раз при условии, что cr(G) := ^2vev(G)(^(v) ~2) ~~
наименьшее среди возможных. Из условия |7дг/(С) |> 1 следует, что c(G) > 0.
Пусть v — произвольная вершина, для которой Xi(v) ф X2(v). По
лемме VII. 15 существует переход t = {е',/'} € X2(v), такой, что 0+(v) =
(...,е',/',...).
Предположим, что также t € X\(v). Тогда можно образовать G', отщепляя
е и / от v таким образом, что V(G') = V(G) U {vej} и е, / суть ребра,
инцидентные vej, и G' можно считать вложенным в ту же самую поверхность,
что и G. Так как t G Х\ П Х2, то Т* соответствует некоторой эйлеровой цепи
Т[ графа G' с Х[ = Х$, где Хг' есть система переходов, соответствующая цепи
Т/, г = 1,2. Заметим, что в силу положения t в G и условия
г е Xi n х2 = х{ п х'2 (*)
любая система непересекающихся переходов графа G' соответствует системе
непересекающихся переходов в G. Поскольку a(G/) < cr(G), из выбора графа G
следует, что Т[ и Т2 являются /^/-связанными. Рассматривая различные кщ-
преобразования, использованные при преобразовании Т[ в Т2, как операции,
произведенные в G, и учитывая (*), получаем, что Т\ и Т2 также являются
/^/-связанными. Это противоречит выбору 7\ и Т2; следовательно, t ? Xi(v).
Итак, рассмотрим te = {e',^} и ?/ = {/',#2}, где te,tf ? Х\(у), и положим
для t* = {д[,д2}
x* = (x1-{te,t/})u{t,t*}, x; = x2.
Благодаря структуре t € X2(v) = X2(v) получаем, что X* есть система
непересекающихся переходов. Кроме того,
\х;пх;\>\х1пх2\+1, (**)
поскольку t € XI П Х%, тогда как t ? Х\. Следовательно, если Хх* = Хт*
для Т* ? 7/v/(G), то в силу выбора цепей Т\ и Т2 цепи Т* и Т2 являются
/^/-связанными. Отсюда и из того, что Г* = kni(Ti), однако, следует, что
7\ и Г2 являются /^/-связанными, в противоречие с выбором Т\ и Г2, а это
означает, что X]* = Xs для некоторого S € S2(G). В соответствии с системой
обозначений, использованной ранее, пусть 5 = {Se,Sg}, и без ограничения
общности можно считать, что е, / ? E(Se)] поэтому д\,д2 ? E(Sg) (это следует
из включения S ? S2(G)).
Как и в доказательстве теоремы VII. 10, рассмотрим теперь проход по Т2,
начинающийся в v вдоль е. Поскольку t € Х2, этот обход будет
заканчиваться в v сразу после прохода ребра /. Так как е, / ? E(Se), gi,g2 & E(Se)
и, следовательно, ^(^е) С ?(Т2) = ?(G), то существует вершина ги, в
которой Г2 переходит из 5е в 55, и d(v) > 4, если w = v. В любом
случае w ? V((E(Se))) П V((??(5^)>). Для t ? XI П Х? пусть G' получен (так
же, как в первой части доказательства) при помощи отщепления ребер е и

296
Глава VII. Преобразования эйлеровых цепей
f от v (отметим, что t = {е',/'}), и переопределим Х[ — X*, i = 1,2,
соответственно; но теперь Х[ = Xs* для Sf G 5г(0'), где 5' = {5^,5^} и
S(5g) = E(Se), E(Sfg) = E(Sg). Мы различаем следующие два случая.
Случай 1). X[(w)r\Xr2{w) = 0. В этом случае лемма VII.16 может быть
применена непосредственно к Gr и S' так, чтобы получить Г^ G Tni{G!), где Т^
получается из 5' при помощи «-поглощения в w. Отсюда следует, что T'w и
Т2 являются /^/-связанными (где Т2 € Tni(G') соответствует Т2), так как из
определения системы Х[ и соотношений X{(w) П -Х"2(ги) = 0 и (**) вытекает
справедливость неравенства | Хт^ П Х2 |>| Xi П Х2 |. Таким образом,
соответствующие эйлеровы цепи Tw,T<i G 7ni(G) являются «-связанными. В силу
этого и так как k/(Ti) = 5, k"(S) = Tw и Х{ есть система
непересекающихся переходов, цепи Т\ и T<i оказываются /^/-связанными. Это противоречие
устанавливает случай 1).
Случай 2). X[(w) П X'2(w) ф 0. В этом случае рассмотрим сначала 0+(w) в
G' и запишем
0+(u;) = (fti,^,...,/4fc), k>2
(отметим, что d,G'(w) > 4 вне зависимости от того, w = v или w ф v).
Рассмотрим произвольный элемент t' = {h'm, h'n} G X[(w) ПХ2(и;), где 1 < m < n < 2/c;
без ограничения обпщости можно считать, что га = 1. По самому определению
непересекающихся переходов отсюда следует, что t" — \К\, h'j} tf. X'^v^UX^w)
для г и j, удовлетворяющих условию 1<г<п<<7<2/с. Следовательно,
произвольный элемент из (X[(w) \JX'2{w)) — {t1} может лежать по любую сторону от
незамкнутой кривой Cm,n, определенной посредством h'm U h'n. Таким образом,
Cm,n определяет разбиение системы X[(w), г — 1,2,
?№)) = №и,^},х;,Ги} (***)
(возможно, X'iX{w) = 0 или X'iT{w) = 0, но Xfit(w) U -Хг'|Г(ги) # 0);
X^w) (X[r{w)) содержит в точности те переходы из X^(w), которые
лежат по левую (правую) сторону от Cm,n (где левая сторона и правая сторона
означают противоположные стороны по отношению к Cm,n). Это разбиение
(* * *) позволяет заменить вершину w на три вершины wi,wr,wt ?¦ V(G) таким
образом, что
?*,= [J t, E*Wr= (J t, E*Wt=t'.
t€X'.tl(w) t?X'ir{w)
Из определения разбиения (* * *) следует, что эта процедура замены может
быть представлена таким образом, что получающийся граф G't можно считать
вложенным в ту же самую поверхность, что и G. Кроме того, из (* * *)
следует, что S' и Т2 преобразуются в соответствующие элементы Sft G ^(GJ) и
T^t G TNi{G't). Наконец, из (* * *) и построения G't следует, что любая
система непересекающихся переходов в G't соответствует системе непересекающихся
переходов в G' и G.
Будем повторять приведенную выше процедуру, если это необходимо, до тех
пор, пока не придем к связному эйлерову графу Н со следующими свойствами:

VII.2. Преобразование специальных эйлеровых цепей 297
1) V(H)DV(Gf -w)-
2) элементы tj из X[{w) П Xr2{w) представлены в Н вершинами Wj степени
3) dH(wa) > 4 для любой вершины
wa € V(H) - (V(G' -w)U {wj/t'j G X[(w) П X'2(w)}),
и
^wci;h, < = 1,2,
где эти Xi(wa) удовлетворяют условиям
XiK)ni2W = 0,
[JXi(wa) = Хг'(г/;) — -X^+1(iu), г = 1,2 (полагаем 3 = 1),
тогда как вершины из G — w остаются неизменными в Н.
4) Н можно считать вложенным в ту же самую поверхность, что и С, и
полученным из G' таким образом, что Хг(Н) есть система непересекающихся
переходов, которую можно записать так:
Xi(H)=Xi г = 1,2
(см. 2) и 3); отметим, что переход есть пара полуребер, независимых от
инцидентности с действительными вершинами). Кроме того, каждая система
непересекающихся переходов в Н также соответствует такой системе в G'.
В силу 4) Xi(H) = XsH для разложения Sh = {Se,H,Sg,H} ? ^(Я),
соответствующего указанному выше Sf Е ^(С), и Х2(Н) = Хтн для цепи
Тн € Tni(H), соответствующей Т2 G Tj^i(Gf). Отметим, что поскольку Т2
проходит в вершине w из Se в Sg, мы можем найти некоторую вершину
wH € {wa\dH(wa) >4,wa? V(H) - V(G' - ti;)},
в которой Тн проходит из Se,# в Sg,H- Следовательно, так как X\{wh) П
X2(wh) = 0, согласно 3), мы свели случай 2) к случаю 1) с H,wh,Sh,Th
вместо G' ,w,S' ,Т2 соответственно. Таким образом, применение леммы VII. 16
дает цепь Т^ е Tni(H), которая получается из Sh с помощью «-поглощения
в wh- Рассуждая теперь так же, как в случае 1), мы можем заключить, что
Т^ и Тн являются «^/-связанными, а это все равно, что сказать, что Tw,
эйлерова цепь графа G, соответствующая Т^, и Т2 являются «///-связанными.
Кроме того, таким же образом мы можем заключить, что Т\ и Tw являются
«дг/-связанными. Следовательно, 7\ и Т2 являются «/^/-связанными —
противоречие, которое доказывает случай 2.
Получив противоречия во всех возможных случаях, мы доказали теперь
теорему.
Хотелось бы отметить, что вложения в поверхность графа G и различные
производные графы не были обязательны для формулировки и
доказательства теоремы VII. 17. Действительно важно здесь то, что 0+(v) было задано
для каждой вершины v ? V(G), и этого достаточно для определения
непересекающихся переходов. С другой стороны, доказательство, представленное здесь,

298
Глава VII. Преобразования эйлеровых цепей
Рис. VII.3. Связный плоский эйлеров граф G с эйлеровой цепью 7\ (Тг),
переходы которой помечены маленькими (пунктирными) дугами, /с-отделение цепи 7\ в
v, включающее ребра е,/, дает S ? S2{G) без пересекающихся переходов. В силу
структуры системы Xi(w), i — 1,2, последующее /с-поглощение в ги, дающее цепь
Tw e TNI(G), приводит к тому, что \XTw(w) П X2(w) \=\Xi(w) П X2(w) |= 0.
показывает, что построение различных графов, которые необходимы для того,
чтобы найти подходящие /^/-преобразования, чтобы преобразовать 7\ в Тг,
позволяют придерживаться все время одной и той же поверхности. Кроме того,
доказательство теоремы VI. 17 указывает, что обычно для того, чтобы найти
подходящие /^/-преобразования, требуется больше алгоритмической работы,
чем в случае «х-связанности. Возможно, что в случае S G 52(G) без
пересекающихся переходов никакое ^-поглощение в w не даст цепи Tw G T^/(G),
удовлетворяющей условию \Xtw ПХ2 |>|-X"i 0X2 I (см. рис. VII.3). Следовательно,
мы вынуждены получать S из Ti таким образом, чтобы S уже удовлетворяло
условию | Xs Г) Х2 \>\ Х\ ПХг |) а затем производить «-поглощение в г^, не
вовлекая никакого элемента из Х\ (w) П Х2 (w).
Наконец, обратимся к /^-преобразованиям эйлеровых цепей в связных
4-однородных графах G. Хотелось бы напомнить, что Ta(G',Q\,Q2) для
2-факторизации {Qi, Q2} графа G обозначает множество эйлеровых цепей
графа G, в котором ребра из Qi и Q2 чередуются (см. обсуждение перед
следствием VII. 13). Что касается другого приложения теоремы VII. 10, мы
получаем следующий результат, в котором V(G, ка) обозначает разбиение множества
Ta(G\Qi,Q2) на классы эквивалентности относительно /^-связанности.
Следствие VII.18. Пусть G — связный ^-однородный граф, и пусть {Qi, Q2}
есть его 2-факторизация (которая существует согласно следствию VI.3).
Тогда \V(G,Ka)\= 1.

VII.2. Преобразование специальных эйлеровых цепей 299
Доказательство. S = Q\ U Q2 есть специальный тип циклового разложения
графа G; его индуцированная система переходов обозначается через Xs- Из
самого определения S и Xs следует, что
Ta(G;Q1,Q2) = T(G,Xs).
Кроме того, понятия /^-связанности и кх3-связанности в этом случае
совпадают. Таким образом,
V(G,Ka) = V(G,KXs).
Эти замечания и справедливость теоремы VII. 10 обеспечивают справедливость
следствия VII. 18.
В случае юа-преобразований можно обобщить это понятие и следствие
VII. 18 аналогично тому, как обобщалась теорема VII. 10, что привело к
теореме VII.12. А именно, предположим, что G — связный эйлеров граф с четным
числом ребер. Тогда G может быть разложен в два реберно-непересекающихся
эйлеровых подграфа G\ и G2 с dcx(v) = dc2{v) Для каждой вершины v Е V(G)
(см. следствие VI.2).
Обозначим через Ta(G;Gi,G2) множество эйлеровых цепей, которые
поочередно проходят по ребрам из G\ и G2. Соответствующим образом обобщим
понятие /^-преобразования и /^-связанности. Тогда следующий результат
может быть получен из теоремы VII. 12 способом, который во многом похож на
тот, которым мы вывели следствие VII. 18 из теоремы VII. 10. Поэтому оставим
его доказательство читателю (упр. VII.9).
Следствие VII.19. Пусть G — связный эйлеров граф с четным числом
ребер, и пусть {Gi,G2} —разложение графа G в два подграфа с одинаковой
последовательностью степеней {d(vi),..., d(vp)}. Тогда любые цепи Т\, Т% Е
Ta{G\G\,G2) являются ка-связанными.
В случае 4-однородных графов G, однако, мы следующим образом получаем
для фиксированой цепи Т Е Ta{G\ Qi, Q2) классификацию вершин графа G на
«нечетные» и «четные» вершины. Пусть Т представлена в виде
Т = ui,ei,t;2,e2,... ,е*_1,и»,е»,... ,е^, vj+i,ej+i,... ,ед,г>ь
и предположим, что Vi = Vj+i. Рассмотрим сегмент
и эйлерову цепь Т*, полученную обращением сегмента S^, т.е.
Т* = vi,ei, — ,e»_i,iS^- ,ej+i,...,eq,vi.
Из самого определения цепей Г и Т* следует, что Г* Е Ta(G;QiiQ2) тогда и
только тогда, когда \E(Sij) |= 1 (mod2).
Рассмотрим случай, когда | E(Sij) |= 0(mod2). Тогда /^-преобразование,
захватывающее v := Vi = Vj+i, не может быть «-преобразованием. С другой
стороны,
если |ВД,,-)|=0(то<12), то V((E(Sitj))) П V((E(G) - E(Sitj))) ф {v}.

300
Глава VII. Преобразования эйлеровых цепей
В противном случае в (E(Sij)) кроме вершины v степени 2 имелись бы
вершины степени 4, т. е. (E(Sij)) был бы гомеоморфен 4-однородному графу с
нечетным числом ребер, что невозможно. Итак, вершина w € V((E(Sij))) — {v}
степени 2 существует и Т имеет вид
1 =Ui, 6i,..., 6^—1, Hi, е^,..., em—i, vm) em,..., е^, fj+i, ^j+ii
..., en_i, vn, en,..., eg,, t^i,
где гу = г>т = vn и
| {er_i, er} П -B(Qi) |=| {er_i, er} П ?(Q2) 1= 1 для г = ij + 1, m, n.
Теперь мы покажем, что из этих равенств следует существование
/^-преобразования, захватывающего вершины v и w. Для таких ка — к" к' и
5y+i,i_i := ^ч_1, e^-f-i,..., е9, vi, ei,..., e^-i, Vi можно определить
я'(Г) := S' = {5ij,5J+i,i-i},
которое совместимо с 5 := Q\ U Q2 в силу того, что | E(Sij) |= 0(mod2).
Если мы обозначим через SVn-i,™ и 5n-i,n сегменты цепи Г, полученные из
Sij , 5J+i,i-i соответственно циклическими сдвигами с тем, чтобы они
начинались и заканчивались в w, то для каждого сегмента 5^_1п ? {5n_i,n, S~^i n}
J- = *Ьт—1,тп5 ^n—l,n ^ ^V^7)5
поскольку 5' совместимо с 5, получаем, что
ТОЧНО ДЛЯ ОДНОГО &п—1,п ^ {*->n—l,n? ^n—l,nl'
То есть существует «-поглощение, захватывающее w, такое, что
k"(S') = Г*, т. е. «а(Г) = Г* для ка = к"к'.
Заметим, что вообще, если мы зафиксируем начальную вершину v\ и
начальное ребро ei цепи Т, то Т определяет для каждой вершины v € V(G)
единственное цепное разложение Sfv = {SiiV, S2,v} (каждый из элементов
которого начинается и заканчивается в v). Кроме того, |i5(G)| = 0 (mod 2), так как
G есть 4-однородный граф; следовательно,
\E(Shv)\=\E(S2,v)\ (mod 2). (1)
Это сравнение приводит к следующему более общему определению.
Определение VII.20. Пусть Т — эйлерова цепь в связном 4-однородном
графе G, начинающаяся bdo G V{G) вдоль е Е EVo, и рассмотрим для каждой
вершины v ? V(G) единственное цепное разложение Sv = {5i,v,52,u}5 которое
состоит из двух сегментов цепи Т, начинающихся и кончающихся в v. Тогда
можем назвать вершину v Т-четной или Т-нечетной, в зависимости от того,
является \E(S\iV)\ (и потому, согласно (1), \E(S2,V) |) четным или нечетным.
На самом деле в силу (1) разбиение на Г-четные и Т-нечетные вершины
для заданной эйлеровой цепи Т не зависит от выбора начальной вершина v\
и начального ребра е\ (упр. VII. 10). Следовательно, любая эйлерова цепь Т
графа G определяет разбиение V(G) на Т-четные и Т-нечетные вершины, и
это разбиение зависит только от Т.

VII.2. Преобразование специальных эйлеровых цепей 301
Рис. VII.4. Два 4-однородных графа d с эйлеровыми цепями Tij Е
Ta(Gi',Qi,i,Qi,2), i, j — 1,2, где ребра из Qz,fc помечены с помощью к, к = 1,2,
а переходы из Ti,i помечены маленькими дугами, в то время как переходы из Тг,2
помечены маленькими пунктирными дугами, г = 1,2. Так как Ti,i и Ti,2 определяют
одни и те же переходы в х Е V(G\), то х представлена двумя вершинами степени 2.
Вершина v является Ti,i-четной в 6ч, г = 1,2, в то время как ги Ti,i-нечетна в G\ и
Тгд-четна в Сг-
Из этого определения и предшествующего обсуждения следует, что
«^преобразования являются «-преобразованиями как раз в Т-нечетных
вершинах графа G, в то время как «^преобразование, которое является
«*-преобразованием, состоит из «-отделения в Т-четной вершине и «-поглощения в
некоторой (Т-четной или Т-нечетной) вершине w e V((E(SiiV)))nV((E(S2,v)))-
Однако неверно, что эта вершина w должна быть в любом случае Т-четной
(или Т-нечетной). Этот факт демонстрируется с помощью графов G\ и G2 на
рис. VII.4. Здесь эйлеровы цепи Т^ € ^(G^Q^bQi^), hj — 1»2,
удовлетворяют равенствам
к'СГа) = S'itV, K"(S'itV) = Tit2,
где «-отделение «' совершается в Т^д-четной вершине v, в то время как
«-поглощение «" совершается в w, которая является Т\^-нечетной в G\ и Тгд-четной в
G2- Следовательно, в G\ «а-преобразование, захватывающее вершину ги, может
быть таким, что
«(ri1i)=T*€re(Gi;Qi>i>Oi|2),
XT.(v) = XTlA(v), XT*{w) = XTli2H, XT*{x) = *Tlfl(*) = XTlt2{x).
Тем не менее v является Т*-нечетной. Следовательно, существует
«а-преобразование, такое, что «(Т*) = Т\^- То есть приведенное выше
«"'-преобразование, преобразующее Т\^ в Ti^, может быть заменено двумя «а-преоб-
разованиями, которые являются «-преобразованиями. Такая замена
невозможна, однако, в случае Тгд и Т2,2- Как мы сейчас увидим, это явление носит общий
характер.

302
Глава VII. Преобразования эйлеровых цепей
Определение VII.21. Пусть G — связный 4-однородный граф, и пусть
Т\,Тъ е %{G]Qi,Q>2)- Для 5 = Qi U Q2 и для некоторых вершин и, w € V{G)
предположим, что «'(Ti) = Sf € 5г(С; Xs), «"(5') — T2l где к' есть «-отделение
в v и к" есть «-поглощение в эд. Назовем «а := «"/с' сводимым или
несводимым (относительно v,w) в зависимости от того, является w Ti-нечетной или
Т\-четной (отметим, что v является Ti-четной в любом случае, так как «а есть
/^-преобразование).
Лемма VII.22. Пусть G, Ti,T2,S, S', ка — «"«', v u w —объекты,
использованные в определении VII.21. Тогда
1) «а является сводимым в том и только том случае, когда существуют
Т* ? Ta(G\ Qi, Q2) и ^-преобразования kw и kv, захватывающие w, v
соответственно, такие, что kw(Ti) =T* и kv(T*) = T2;
2) «G является несводимым в том и только том случае, когда
существует S" e S2(G,XS), такое, что к'(Тг) = S", R"(S") = T2, где «' («") есть
к-отделение (к-поглощение) в w (v).
Доказательство. 1) Предположим, что «^-преобразование сводимо.
Согласно определению VII.21, вершина w Ti-нечетна. Значит, в силу обсуждения
после следствия VII.19 и определения VII.20 существуют Т* е Ta{G]Qi,Q2) и
«^преобразование kw, которое является «-преобразованием, такие, что
kw(Ti) = Г* и Хт* - XT.(w) = XTl - XTl (w).
Мы утверждаем, что v Т*-нечетна. Это становится очевидным, если
представить 7\ в следующем виде:
Тг = vo, ei, vi, /1,..., h[, v», /1",..., fj,Vj, eJ+i,..., /i?, Vk, h'k,..., /m, vm,
где vo = Vj = vm = v и Vi = Vk = w. Кроме того, допустим без ограничения
общности, что ei, e^+i G E(Qi), Д, /j, fm € E(Q2). Это возможно, поскольку v
Т\-четна. Так как w является Т\-нечетной, то для одного из двух выборов для
г, 5, {r, s) = {1,2}, мы имеем
W,b'fc}C?(Qr), WX)CE(Qe). (*)
Значит, Г* имеет вид
Т* = vo, ei, vi, /1,..., h\,vu К,..., ej+i,Vj, fj,..., /1", и», ft^.,..., /m, vm.
To есть, начиная в v = ^o вдоль е\ ? E(Qi), мы снова достигнем v = Vj после
прохождения eJ+i G E(Qi), т. е. г> Г*-нечетна.
Следовательно, существует «а-преобразование «v, которое является
«-преобразованием, такое, что «V(T*) = Т2* € Ta(G]Qi,Q2) и Хг* — Хг*(г;) =
Хт2* — Xr2*(v). Следовательно,
XTl - (XTl (v) U XTl И) = *т2- - №у («) U Хт2. («;))
= XT2-(Xt2(v)UXt2H),
и
(XTl (и) U XTl (to)) П (Хт2. (и) U Хту («>))
= (XTl (v) U XTl (го)) П (ХТ2(г>) U ХТг (to)) = 0.
В силу этих равенств и так как Ti,Тг,Т2* е 7^(G; Qi, Q2), то Тг = Т2*.

VII.2. Преобразование специальных эйлеровых цепей 303
Обратно, предположим, что для Ti,T2 G Zi(G;Qi,Q2) существуют Т* е
7^(G;Qi,Q2) и «-преобразования «^и И «v (затрагивающие iu,v
соответственно), такие, что kw(Ti) = Г* и kv(T*) = Т2. Определение VII.20 и последующее
обсуждение показывают, что ги является Ti-нечетной. С другой стороны,
поскольку «а = «"«' есть «"-преобразование, вершина v должна быть Ti-четной
(см. определение VII.21). Следовательно, «а = «"«' является сводимым по
определению VII.21. Это завершает доказательство утверждения 1).
2) Если «а несводимо, то w также является 7\-четной. Следовательно,
используя те же самые символы с тем же самым значением, что и в первой части
доказательства п. 1), и так, чтобы выполнялись соотношения (*), получим
Т\ = v0, ei, vi, /i,..., /г-, v», h",..., fj,Vj,ej+i,...
. . . , hk,Vk, hk, . . . , fm,Vm-
Таким образом, изменяя переходы в w = V{ = vk так, чтобы не нарушать
совместимость с Xs, мы получим две реберно-непересекающиеся подцепи,
покрывающие E(G),
S",w = v*> Ki - • • i /i» ui» еЯ-ь • • •>h'ki vk,
To есть S" := {5(^,5^} € <S2(G,X5) и «'(71) = S" для некоторого «-отде-
ления к' в w.
Тем не менее с помощью сдвига можно переписать элементы из S" так,
чтобы получить
^1,1; = Ч7> eJ+li ' ' ' > ЛА;> и*> М'> • • •> /?> UJ>
^2,v = vrrf> Ci, Vi, /i, . . . , h^ Vi, hk, . . . , fm,Vm.
To есть если 5' = {S{jV, 5^}, то «'(T2*) = 5' для некоторого Т2* ? Ta(G; Qb Q2).
Поскольку S' получается из S" с помощью циклического сдвига
последовательностей, описывающих ее элементы, и так как обратной операцией к
«-отделению является «-поглощение, мы имеем R"(S") = Т2* для «-поглощения
R" в v. Теперь мы можем заключить, как и в первой части доказательства 1),
что Г2* = Т2.
Обратно, предположим, что два «^преобразования «"«' и «"«'
удовлетворяют условию «"(«'(Ti)) = «"(«'(7\)) = Т2, где к! является «-отделением в г; и
Rf есть «-отделение в w. Тогда обе вершины v и w должны быть Т\ -четными
(см. обсуждение после определения VII.20); следовательно, «а несводимо. Это
завершает доказательство 2). Лемма VII.22 теперь доказана.
Лемма VII.22 утверждает, что «^преобразование к"к,' является сводимым
тогда и только тогда, когда можно избежать использования «объезда» через
S2(G,Xs) с помощью применения двух «-преобразований kw и kv, каждое из
которых дает элемент из ^(G;Qi,(22). Этот факт, т. е. возможность
обходиться «-преобразованиями вместо того, чтобы комбинировать «-отделение с
«-поглощением, оправдывает термин сводимое. С другой стороны, если «"«'
несводимо, неважно, в которой из двух вершин v и w мы начинаем «-отделение,

304
Глава VII. Преобразования эйлеровых цепей
т. е. в этом случае произведение к"к коммутативно в том смысле, что
преобразования к/ и я", рассматриваемые как операции на системах переходов, дают
k"k'(Ti) = /cV(Ti) = Т2, где к'(Тг),к"(Тг) G <S2(G,X5), но, вообще говоря,
«ТО ф к'ТО-
Подводя итог обсуждения, проведенного после следствия VII. 19,
приходим, таким образом, к следующему результату, который основан на следствии
VII.18.
Теорема VII.23. Пусть G — связный ^-однородный граф G с 2-факторизацией
{Qi,Q2}- Для любых двух эйлеровых цепей Т,Т' Е Ta{G\Qi,Q2) существует
последовательность эйлеровых цепей То,... , jTm для некоторого тп > 1,
такая, что Го = Т, Тт = Г', Тг € Ta(G]Qi,Q2), г = 0,.. .,m, u для г = 1,... ,га
г^епъ Тг получается из T^_i с помощью применения ^-преобразования. Если
это ^-преобразование является ^-преобразованием, то оно применяется в
Ti-i-нечетной вершине. Однако если это к*-преобразование, оно является
несводимым ^-преобразованием, примененным к двум T^-i-четным вершинам
v и w, где w принадлежит двум сегментам из Ti-\, начинающимся и
заканчивающимся в v. В этом случае неважно, применяется ли к-отделение в v,
а ^-поглощение в w, или наоборот.
Здесь следует уже отметить, что теорема VII.23 будет играть центральную
роль в подходе Г. Сабидусси к проблеме, которую называют проблемой
совместимости [SABI84a]. В самом деле, теорема VII.23 может быть преобразована
в теорему (7.7) из [SABI84a,], и большая часть рассуждений, приводящих к
теореме VII.23, содержится в этой статье. Краткое описание подхода Сабидусси
к проблеме совместимости, а также обсуждение различных других подходов
и различных аспектов проблемы совместимости заинтересованный читататель
может найти в [FLEI88a].
VII.3. Преобразование эйлеровой цепи в орграфах
Точно так же, как мы использовали теоремы VII. 10 и VII. 12 для того, чтобы
получить различные результаты относительно преобразований специальных
типов эйлеровых цепей в графах, мы можем применить теорему VII. 12 для того,
чтобы получить для орграфов результат, аналогичный теореме VII.5. Для этой
цели обозначим, как и выше, через T(D) множество всех эйлеровых
цепей связного эйлерова орграфа D и определим к,-, «*-, к,\-преобразования и
/с-отделения и «-поглощения. Конечно, эти операции должны быть определены
таким образом, чтобы каждый переход виЕ V(D) всегда состоял из входящей
и выходящей полудуг, инцидентных v. Это объясняет, почему для орграфа D
«-преобразования не являются достаточно общим инструментом для того,
чтобы преобразовать Т ? T(D) в каждый другой элемент из T(D) (см. рис. VII.5).
Однако, как мы увидим ниже, к,\-преобразований достаточно для того, чтобы
установить для орграфов результат, аналогичный теореме VII.5.
Как и в случае графов, можно определить понятия к-, «*-, к\-связанности и
показать, что каждое из этих понятий определяет отношение эквивалентности
на T(jD); оставим доказательство этого в качестве упражнения (упр. VII. 11).

VII.3. Преобразование эйлеровой цепи в орграфах
305
D
Рис. VII.5. D имеет точно две эйлеровы цепи, 7\ и Тг (помеченные
маленькими и маленькими пунктирными дугами); /c(Ti) ф Тг для любых двух возможных
к-преобразований, но tt*(7\) = Тч для каждых двух возможных к* -преобразований
к* = к"к! (ср. с упр. VII.5).
Каждое из этих отношений эквивалентности на T{D) снова определяет,
конечно, разбиение T(D) на классы эквивалентности. Для наших целей мы будем
рассматривать разбиение V(D,ki).
Теорема VII.24. Пусть D —связный эйлеров орграф. Тогда \V(D,ki)\= 1.
Доказательство. Наша цель —вывести теорему VII.24 из теоремы VII. 12.
Для этого рассмотрим связный эйлеров граф G, лежащий в основе заданного
связного эйлерова орграфа D. Для каждой вершины v € V(D) пусть
PV(D):={(A*V)+,(A:)-}
является разбиением множества А* на классы полудуг, исходящих из v и
заходящих в v соответственно. Так как V(D) = V(G), то для той же вершины v
можно определить
Pv(G):={(Et)+,(K)-h
считая, что для е = vx e E(G) полуребро е' принадлежит {Е*)+
(соответственно (Е*)~) тогда и только тогда, когда для соответствующей дуги а ? A(D)
полудуга а' удовлетворяет условию о! 1_ (А*)+ (соответственно о! J_ (A*)-), т.е.
тогда и только тогда, когда а = (v,x) (соответственно а = (x,v)). Это
определение подразумевает включение кратных дуг (причем в этом случае
каждая дуга вида (и,ж), (ж,г?) соответственно должна рассматриваться отдельно
в указанном выше соответствии), а также петель (v,v) в D (в этом случае
одна полупетля принадлежит (Е*)+, а другая принадлежит (Е*)~). Наконец,
положим
P(G):= (J PV(G).
v€V(G)

306
Глава VII. Преобразования эйлеровых цепей
По определению P(G) является системой разбиения графа G, такой, что \К\=
\d{v) для каждого К € PV{G) и каждой вершины v € V(G) = V(D).
Следовательно, T(G,P(G)) ф 0 по теореме VI. 1 и \V(G,«p(g)) 1= 1 п0 теореме VII.12.
Однако в силу определения системы P(G) существует взаимно однозначное
соответствие между Р(С)-совместимыми эйлеровыми цепями графа G и
эйлеровыми цепями орграфа J9, и по тем же соображениям Tq,T'g € T(G,P{G))
являются к;р(<з) -связанными тогда и только тогда, когда соответствующие
цепи Td,T'd e T(D) являются «i-связанными. То есть | V(D,Ki) |= 1. Теперь
теорема доказана.
Заметим, что приведенное выше применение теоремы VI. 1 и биекция между
T(G,P(G)) и T(D) дают доказательство первой части теоремы IV.8.
Другой подход к тому, чтобы преобразовать произвольную цепь Т Е T(D) в
любую другую V ? T(D), избран в [Х1АХ84а]1). При этом подходе мы не имеем
дела с цепными разложениями, как в случае к,\-преобразований; на каждом
шаге мы преобразуем элемент из T(D) в другой элемент из T(D). Инструмент
для этого подхода дает следующее определение.
Определение VII.25. Пусть D — связный эйлеров орграф, и предположим,
что некоторая цепь Т € T(D) может быть представлена следующим образом:
Т = ..., щ Т(щ v), v,..., u, T'(u, v), v,...,
где T(u,v) и T'{u,v) суть дугово-непересекающиеся цепи, соединяющие и и v
(возможно, u = v); предположим также, что A(T{u,v)) U A(T'(u,v)) ф A(D)
(это всегда так, если иф v). Тогда говорят, что
Г/ = ...,и,Г/(и,и),г;,...,гх1Г(и,г;),и,...
получается из Т с помощью т-преобразования, которое меняет
местами T(u,v) и T'(u,v). Выразим это преобразование формальным равенством
т{Т) = Г.
Замечание VII.26. 1) Ксиа (Xia) называет т-преобразование Т-преобразова-
нием; но, поскольку мы используем греческую букву к для различных
преобразований и так как буква Т обычно используется для эйлеровой цепи,
использование буквы г вместо Т в названии приведенного выше преобразования
кажется разумным.
2) Из определения VII.25 следует, что не только V € T(D) для Т € T(D)
и V — т(Г), но даже Т' ф Т. Это гарантировано условием A(T(u,v)) U
A(X"(u, v)) ф A(D). To есть в отличие от различных предыдущих
преобразований т-преобразование никогда не может быть тождественнным. Поэтому
возникает вопрос: каковы орграфы, имеющие в точности одну эйлерову цепь?
Ответ достаточно простой: связный эйлеров орграф D имеет в точности
одну эйлерову цепь тогда и только тогда, когда каэюдый цикл из D является
*) Эта статья опубликована на китайском языке, а английского резюме к этой статье
недостаточно для того, чтобы понимать существо дела. Вольфганг Рупперт из Вены перевел
наиболее важные отрывки статьи, и я надеюсь их правильно воспроизвести в последующем
обсуждении. В любом случае я хочу выразить благодарность Вольфгангу Рупперту за то,
что он затратил время на перевод больших кусков статьи.

VII.3. Преобразование эйлеровой цепи в орграфах
307
блоком в D u A(D) < 4. Доказательство этого утверждения мы оставляем в
качестве упражнения.
3) Однако если Т' = т(Т), то для для той же самой пары цепей
T(u,v),X"(u, v), которая была использована при преобразовании Т в Т' (см.
определение VII.25), мы получим т(Т') = Т, т.е. т, в некотором смысле,
удовлетворяет формальному равенству т2(Т) = т(Т') — Т. Следовательно, имеет
смысл назвать цепи Т, Т' Е T{D) т-связанными, если либо Г = X", либо
существует последовательность То,..., Тт, га > 0, где Ti Е T(D) для г = 0,..., га,
такая, что Г0 = Т,Тт = V и Ti — r(Tj_i) для г = 1,...,га. Опять т-
связанность определяет отношение эквивалентности на Т(?>), которое, в свою
очередь, определяет разбиение V(D,r) (см. упр. VII.13).
Главный результат работы [Х1АХ84а] — следующая теорема.
Доказательство, представленное здесь, отличается, тем не менее, от доказательства,
данного в цитируемой статье.
Теорема VII.27. \V(D,r)\ = 1 для каждого связного эйлерова орграфа D.
Доказательство. Если |Т(?>)| = 1, теорема очевидна, так как Т Е T(D)
является единственной цепью, т-связанной с ней самой; значит, можно
предположить, что |Т(Г>)| > 1.
Пусть для D теорема неверна. Тогда существуют цепи Т, Т' Е T(D),
которые не являются т-связанными. Предположим, что ГиГ' выбраны так, что
| Хт П Хт* | является настолько большим, насколько это возможно при
условии, что cr(D) := J2vev(D)(0(^(v) ~ -0 =l A(D) I ~~ I V(D) | является настолько
малым, насколько это возможно. Для практических целей мы можем
вывести некоторое свойство орграфа D, которое должно быть связанным с этими
ограничениями:
Для каждой вершины v E V{D) или Xt(v) П Xt>(v) = 0, или d(v) = 2. (1)
В противном случае пусть г; —вершина с Хт(у) П Xt'(v) ф 0 и d(v) > 2.
Пусть t — {е', /'} Е Xt(v) П Хт>(у) и отщепим дуги е, / для того, чтобы
образовать новый эйлеров орграф D\ (отметим, что {е, /} П А+ / 0 / {е, /} П А~).
Эйлеровы цепи ГиГ' соответствуют эйлеровым цепям Т\^Т[ орграфа D\\
следовательно, D\ связен. Кроме того, Хтг = Хт, X?' = Хт>; следовательно,
\ХТГ\ХТ'\ = \XTl ПХц\. Однако g(D{) < a(D), так как \A(Di)\ = \A(D)\,
но |V(Di)| = |V(D)| -f 1. Таким образом, Т\ и Т[ являются т-связанными.
Отметим, что ни для какой цепи Т\{х,у) в Di, использованной в одном из
т-преобразований, которые применяются для преобразования Т\ в 2\', мы не
можем иметь vej E {х,у}, где vej E V{D\) — V(D), так как не существует
двух дугово-непересекающихся открытых (или замкнутых) цепей в D\,
начинающихся (или заканчивающихся) в vej. Следовательно, Т\(х,у)
соответствует цепи Г(х, у) в D, которая является открытой цепью тогда и только тогда,
когда Ti(x,y) является открытой цепью. Следовательно, т-связанность цепей
Т\ и Т[ равносильна т-связанности цепей ГиГ'в противоречие с нашим
допущением.

308 Глава VII. Преобразования эйлеровых цепей
D
Рис. VII.6. Эйлеровы цепи Т,Т' Е T(D), переходы которых помечены
маленькими (соответственно маленькими пунктирными) дугами. Возможно, v = w. Сегмент
5(е+,е~) С Т содержит д~ и д+, но ни одну из полудуг /~,/+,h~h+.
Рассмотрим теперь произвольную вершину v ? V(D) — V^D), и пусть t ?
Xt*(v) выбран произвольно. Пусть t = {е(г;)~,е(г>)+}, где е~ € А", е+ G А+,
и пусть ti,^2 G -Уг(и) выбраны таким образом, что t\ — {/(^)~,е(г?)+}, ti =
{Ди)+,ФГ}- Согласно (1), tx ф t2 и /" Е А", /+ € Л+.
Теперь проход по цепи Т, начинающейся в и вдоль е+, достигает г> вдоль е~
до того, как будет пройдена /+ или /~. Следовательно, Т содержит сегмент
5(е+,е~) С Т. С другой стороны, если также считать, что Т' начинается в v
вдоль е+, то е~ будет ее последней дугой. Следовательно, существуют
переходы ^,?4 ^ Xt'(iu) для некоторой вершины
w € V((A(S(e+, е-)))) П V((A(T) - A(S(e+, e"))»,
такие, что
*з = {рН",ЛМ+}» *4 = {^H+,/iH-},
где
д+ е А+ П А(5(е+, е")), fG^n A(S(e+, е')),
h+eA+П (A(D) - A(S(e+, e"))), Ге^П (Ар) - A(S(e+, e"))),
и tg = {g(w)+, g(w)~} G Xt(w) (см. рис. VII.6 и доказательство теоремы
VII.17).
Возможно, v = iu. Но в любом случае Г может быть выражена в виде
Г = v, 5(е+, е"), v, /+,..., /г", ги,...,/", v.
То есть в Т существует собственная подцепь, соединяющая v и w и такая, что
/+ — ее первая, a ft" —последняя дуги; обозначим эту подцепь через T'(v,w).
Заметим, что T'(v,w) не содержит ни одну из дуг из 5(е+,е~). Аналогично,

VII.4. Заключительные замечания и открытые проблемы 309
5(е+,е ) содержит подцепь T(v,w), для которой е+ является первой, а д —
последней дугами. Записывая
5(е+, е~) = T(v, w),w, T(w, v),
мы можем выразить Т в более явной форме:
Г = v, T(v, w),w, T(w, v),v, T'(v, w),w,..., /", v.
Следовательно, мы получаем Т* € T(D), T ф Г*, с помощью г-преобразования,
которое меняет местами T(v,w) и T'(v,w). Значит,
Т* = v, Т'(г>, гу), гу, Г(ги, г>), v, Г(г>, гу), гу,..., /~, v.
Возможно, Г* = V'. Тем не менее в любом случае d(v) > 2, d(w) > 2 и
?,?4 € Хт* Г\Хт' Э ХтПХт'- Это и (1) вместе с выбором цепей ТиТ' означает,
что Т* и Т' являются т-связанными (что верно также, если Т* = Т').
Следовательно, так как т(Т) = Г*, Т и X" являются т-связанными. Это противоречие
с выбором Г и Г' окончательно доказывает справедливость теоремы.
Из соображений ограниченности времени и места мы не будем продолжать
изучение преобразований «неограниченных» эйлеровых цепей в орграфах и
предлагаем заинтересованному читателю найти подходящие преобразования, с
помощью которых можно связать любую Р(?>)-совместимую (соответственно
(D — .О^-ведомую) эйлерову цепь с любой другой такой цепью. Хотя я сам не
занимался поиском таких преобразований, я верю, что к- и «"-преобразований
достаточно для того, чтобы исследовать эту проблему для орграфов
аналогично тому, как это делается для графов (отметим, что т-преобразование можно
рассматривать как комбинацию к-отделения с ^-поглощением). Что касается
преобразования антиэйлеровых цепей в орграфе D, достаточно рассмотреть
D+. Граф G+, лежащий в основе D+, является связным эйлеровым графом,
потому что антиэйлерова цепь в D соответствует антиэйлеровой цепи в D^ и,
таким образом, эйлеровой цепи в G+, и наоборот. Таким образом,
преобразование антиэйлеровых цепей в D эквивалентно преобразованию эйлеровых цепей в
G+, которое может быть сделано исключительно с помощью «-преобразований
(теорема VII.5).
VII.4. Заключительные замечания и
некоторые открытые проблемы
В предыдущих разделах этой главы мы ввели различные типы преобразований
для того, чтобы иметь возможность построить любую эйлерову цепь
специального типа, если хотя бы одна такая эйлерова цепь задана. Этот подход к работе
с целым множеством Т эйлеровых цепей вызывает следующий вопрос:
При заданных цепях Т, Т' G Т как часто мы должны применять
некоторый тип к\ -преобразований, чтобы преобразовать Т вТ' ? (*)
Другими словами, как обстоит дело со сложностью преобразования цепи Т
в X"? Отметим, что единственное ^-преобразование может быть выполне-

310
Глава VII. Преобразования эйлеровых цепей
но за полиномиальное время, даже если нужно искать вершину v, в
которой должно выполняться «-преобразование. Следовательно, построение
цепей Т\,Т[ € T(G), удовлетворяющих соотношениям 7\ = я(Т), Т[ = «(Г7) (с
«-преобразованиями, выполняемыми в v) и
|xTl nxTi/|>|xTnxT/|,
может быть выполнено за полиномиальное время (упр. VII. 15).
Следовательно, первоначальный вопрос (*) есть настоящий ключ к вопросу о
сложности «-связанности. А. Буше ответил на этот вопрос для случая связных
4-однородных графов G. Он показал, что в случае произвольных цепей Т, Т" €
T(G) требуется не более 3lj '' «-преобразований для того, чтобы
преобразовать Т в X" [BOUC90a]. Наряду с этим результатом он выдвинул гипотезу,
которая утверждает, что ' ^ можно заменить на |V(G)| 4- 1.
Однако аналогичные исследования сложности для различных типов
«1-преобразований (которые развиты для различных типов эйлеровых цепей в
графах и орграфах, рассматривавшихся до сих пор) еще не проведены. Я
ожидаю, что они все будут состоять в нахождении полиномиальных по времени
алгоритмов.
Наконец, отметим интересную структурную особенность, связанную с
«-преобразованиями. Определим граф эйлеровых цепей G(T,«) как граф,
вершины которого суть элементы из Т := T(G), и Т1Т2 ? JE(G(T,«)) тогда и
только тогда, когда «(Т\) = Т2. Отметим, что если «(7\) = Т2, то «(Т2) = 7\.
Следовательно, G(T,«) является корректно определенным графом.
Из теоремы VII.5 следует, что G(T,«) связен, так как любые две эйлеровы
цепи графа G могут быть получены друг из друга с помощью
последовательности «-преобразований. Тем не менее Жанг (Zhang) и Гуо проверили
значительно более сильный результат, который мы представляем без доказательства
(детали см. в [ZHAFSGa])1).
Теорема VII.28. Если \ T(G) \> 2, mo G(T,«) является реберно-гамилъто-
новым.
Снова (аналогично тому, как произошло с результатом Буше [BOUC90a])
мы подошли к вопросу, существуют ли результаты, подобные теореме VII.28,
если ограничиться рассмотрением специальных классов эйлеровых цепей
(таких, как Тх := T(G, X) и т. п.) и подходящих «i-преобразований, и определяем
ограниченный граф эйлеровых цепей (например, G(7x,«x))« В силу
теорем VII.10, VII.12, VII.17, VII.23, VII.24, VII.27 и следствий VII.13, VII.18,
VII. 19 эти ограниченные графы эйлеровых цепей всегда являются связными.
Но являются ли они гамильтоновыми? Как они могут быть
охарактеризованы, как может один тип ограниченных графов эйлеровых цепей отличаться
от другого? Отметим, что в [ZHAF86a] авторы анонсируют, что они нашли
результат, аналогичный теореме VII.28, для ориентированного графа эйлерова
*) Жанг (Zhang) и Гуо (Guo) говорят о графе эйлерова обхода Eu(G), который мы называем
графом эйлеровых цепей G(T, к,).

VII. 5. Упражнения
311
обхода, но не указывают, какой из типов преобразования служит в качестве
основы для определения ребер этого графа. Принимая во внимание теорему
VII. 14 и абзац, следующий за ее доказательством, имеет смысл отметить
следующее в связи с перечисленными выше вопросами. Построим древесный граф
GT графа G, где V(GT) = {Т С G \ Т есть каркас графа G] и ТгТ2 € E(GT)
тогда и только тогда, когда \E(Ti U Т2) — Е(Т\ П Т2)| = 2 (ср. это
равенство с /^-преобразованиями и множеством % каркасов из М{ при обсуждении,
приводящем к формулировке теоремы VII. 14). В самом деле, древесные
графы Gt уже рассматривались неявно в [ORE062a] и явно в [CUMM66a]. В
последней работе показано, что Gt является реберно-гамильтоновым
(короткое доказательство этого результата было дано в [SHAN68a]). Принимая во
внимание теорему VII. 14, понятно, что сходство между этим результатом о
древесных графах и теоремой VII.28 не является случайным. Действительно,
древесный граф (Мг)т графа М* есть не что иное, как G(Ta{G),ka)-
Относительно других, более ранних, исследований древесных графов мы отсылаем к
[BAR068a, BAR068b]. Что касается других структурных соображений
относительно древесных графов, упомянем [SHAN81a], где доказывается, что если
графы Gt, {Gt)t и {{Gt)t)t являются эйлеровыми, то {{(Gt)t)t)t не
является эйлеровым, за исключением случая Gt ? {К\, К^}. Наконец, отметим, что
для орграфа D растущий в корень древесный граф Dt при
фиксированном корне vo Е V(D) может быть определен подобно упомянутому выше
графу Gt- Это было сделано в [DORF74a], где показано, что Dt всегда является
связным. Завершим наши обсуждения, отметив, что графы, подобные графам
эйлеровых цепей или древесным графам, встречаются в линейной алгебре; там
мы имеем дело с перестановочными графами, вершины которых суть
некоторые т х n-матрицы (см. детали в [BRUA82a] ). Здесь мы также сталкиваемся с
вопросом о гамильтоновости (в связи с перестановочными графами). Согласно
Ли Цяо, это «большой вопрос».
VII.5. Упражнения
Упражнение VII. 1. Показать, что на рис. VII.2 не существует
последовательности Ti,...,Tn Х'-совместимых эйлеровых цепей графа К2,± с Т =
Ti, V — Тп и к(Тг) = Ti+i, 1 < г < п — 1. Описать обращения сегментов, с
помощью которых можно получить Тч из Т и Т" из Т2.
Упражнение VII.2. Показать, что каждое из понятий к*- и к\-связанности
определяет отношение эквивалентности на T{G). Показать то же самое для
понятия к,х-связанности в T{G,X).
Упражнение VII.3. Доказать лемму VII.11.
Упражнение VII.4. Превратить доказательство теоремы VII. 10 в
доказательство теоремы VII. 12.
Упражнение VII.5. а) Показать, что если ка{Т\) = Т2 для Ti,T2 ? Ta(G),
где G — связный плоский 4-однородный граф, то это /сд-преобразование
является /^-преобразованием.

312
Глава VII. Преобразования эйлеровых цепей
b) Построить пример непланарного графа G, вложенного в поверхность, для
которого это заключение неверно.
c) Доказать, что каждое из понятий юд-, «дг/- и /^-связанности определяет
отношение эквивалентности на соответствующем множестве эйлеровых цепей.
Упражнение VII.6. Распространить теорему VII. 14 на произвольные
связные плоские эйлеровы графы двумя способами так, чтобы
a) Mi являлся (двудольным) графом,
b) Mi являлся гиперграфом (см. первую часть обсуждения после
доказательства теоремы VII. 14).
Упражнение VII.7. Показать, что выяснение существования остовного
гипердерева в М{ (см. упр. VII.6.Ь)) является iVP-полной проблемой, если мы
ограничиваемся рассмотрением тех М*, которые соответствуют планарным
3-связным эйлеровым графам (см. вторую часть обсуждения после
доказательства теоремы VII. 14).
Упражнение VII.8. а) Показать, что понятие к,д-связанности,
распространенное на произвольные связные плоские эйлеровы графы, определяет
отношение эквивалентности на Ta(G).
b) Показать, что два элемента из 7a(G) принадлежат одному и тому же
классу эквивалентности относительно /^-связанности тогда и только тогда,
когда соответствующие им А-разбиения совпадают в вершинах, степени которых
превышают 4.
Упражнение VII.9. Обобщить понятие /^-преобразования на случай
связных эйлеровых графов, имеющих четное число ребер, и доказать следствие
VII.19. (Указание. Применить теорему VI. 1, следствие VI.2 и теорему VII. 12).
Упражнение VII.10. Пусть Г —эйлерова цепь связного 4-однородного
графа G. Показать, что в определении VII.20 v E V(G) является Т-четной
(Т-нечетной) независимо от выбора начальной вершины и начального ребра
цепи Т.
Упражнение VII.11. Определить «-, «*- и к\-связанность для орграфов и
показать, что каждое из этих понятий определяет отношение эквивалентности
на T(D).
Упражнение VII. 12. Доказать, что следующие два утверждения
эквивалентны:
1) D является связным эйлеровым орграфом, имеющим точно одну эйлерову
цепь;
2) каждый цикл орграфа D является блоком в D и A(D) < 4.
Упражнение VII. 13. Доказать, что т-связанность определяет отношение
эквивалентности на T(D).
Упражнение VII.14. Рассмотреть Р(?>)-совместимые эйлеровы цепи в
связном эйлеровом орграфе D и найти преобразования, с помощью которых любая

VII. 5. Упражнения 313
такая цепь может быть преобразована в любую другую такую цепь.
Исследовать ту же самую проблему относительно (D — Д))-ведомых эйлеровых цепей.
Упражнение VII.15. Пусть G — связный эйлеров граф, и пусть Т, Т' € T(G).
Показать, что
1) проблема отыскания вершины v, в которой Хт ф Хт> {v), может быть решена
за полиномиальное время;
2) построение цепей Ti,T[ € T(G), удовлетворяющих условиям Хт — Xt{v) —
Хт, - ХтМ* Хт> - XT'{v) = Хт{ - XT{(v), «(Г) = Ть к(Г) = Т{ и |XTl(t;) П
Xt[{v) \>\Xt(v) П Xt'(v) I, может быть проведено за полиномиальное время.

Список литературы1)
[AARD51a] van Aardenne-Ehrenfest, Т., de Bruijn, N.G.; Circuits and
Trees in Oriented Linear Graphs, Simon Stevin 28 (1951)
203-217.
[ABRH79a] Abrham, J., Kotzig, A.; Construction of Planar Eulerian
Multigraphs, Proc. Tenth Southeastern Conf.
Combinatorics, Graph Theory k. Computing, Florida Atlantic Univ.,
Boca Raton, April 2-6, 1979, Congr. Numer. 23 (1979)
Vol.1, 123-130.
[ABRH80a] Abrham, J., Kotzig, A.; Transformations of Euler Tours,
Ann. Discrete Math. 8 (1980) 65-69.
[AKIY79a] Akiyama, J., Harary, F.; A Graph and Its Complement With
Specified Properties I: Connectivity, Internat. J. Math. &
Math. Sci., Vol.2, No.2 (1979) 223-228.
[ANST85a] Anstee, R.P.; An Algorithmic Proof of Tutte's f-Factor
Theorem, J. Algorithms 6 (1985) 112-131.
[ASAN82a] Asano, Т., Saito, N., Exoo, G., Harary, F.; The Smallest 2-
Connected Cubic Bipartite Planar Nonhamiltonian Graph,
Discrete Math. 38 (1982) 1-6.
[ASAN84a] Asano, Т., Kikuchi, S., Saito, N.; A Linear Algorithm for
Finding Hamiltonian Cycles in 4'Connected Maximal
Planar Graphs, Discrete Appl. Math. 7 (1984) no.l, 1-5.
[AUBE82b] Aubert, J., Schneider, В.; Graphes orientes indecomposables
en circuits hamiltoniens, J. Combin. Theory Ser. В 32
(1982) 347-349.
[BAR068a] Baron, G.; Tiber den Baumgraphen eines endlichen gerichte-
ten Graphen, Arch. Math., Vol. XIX, Fasc. 6 (1968) 668-
672.
x) На стр. 328 приведены работы, имеющиеся на русском языке, а также работы,
добавленные автором к русскому изданию. — Прим. ред.

Список литературы
315
[BAR068b] Baron, G., Imrich, W.; On the Maximal Distance of Span-
ning Trees, J. Combin. Theory 5 (1968) 378-385.
[BATA77a] Batagelj, V., Pisanski, Т.; On Partially Directed Eulerian
Multigraphs, Publ. del'Inst. Math., Nouvelle serie 25 (1977)
no.39, 16-24.
[BEHZ79a] Behzad, M., Chartrand, G., Lesniak-Foster, L.; Graphs and
Digraphs (Prindle, Weber & Schmidt Int. Series, Boston,
Mass.,1979).
[BEIN78a] Beineke, L.W., Wilson, R.J. (eds.), Selected Topics in Graph
Theory (Academic Press, New York, 1978).
[BEIN83a] Beineke, L.W., Wilson, R.J. (eds.), Selected Topics in Graph
Theory 2 (Academic Press, New York, 1983).
[BELY83a] Belyj, S.B.; On Non-Self-Intersecting and Non-Intersecting
Trails, Mat. Zametki 34 (1983) no.4, 625-628.
[BENT87a] Bent, S.W., Manber, U.; On Non-Intersecting Eulerian
Circuits, Discrete Appl. Math. 18 (1987) 87-94.
[BERG62a] Berge, C., Ghouila-Houri, A.; Programme, Spiele, Trans-
portnetze (B.G. Teubner Verlagsgesellschaft, Leipzig, 1967).
[BERK78a] Berkowitz, H.W.; Restricted Eulerian Circuits in Directed
Graphs, Colloq. Math. 39 (1978) Fasc.l, 185-188.
[BERM78b] Berman, K.A.; Aneulerian Digraphs and the Determination
of those Eulerian Digraphs Having an Odd Number of
Directed Eulerian Paths, Discrete Math. 22 (1978) 75-80.
[BERM79d] Berman, K.A.; Bieulerian Orientations of 4'Valent Graphs,
Res. Report CORR 79-25, Fac. of Math., Univ. of
Waterloo (1979).
[BERM81b] Berman, K.A.; On Graphs where every 1-Factor lies in a
Eamiltonian Cycle, unpublished manuscript.
[BERM83a] Berman, K.A.; Proof of a Conjecture of Hdggkvist on Cycles
and Independent Edges, Discrete Math 46 (1983) no.l, 9-13.
[BER084a] Bermond, J., Las-Vergnas, M.; Regular Factors in Nearly
Regular Graphs, Discrete Math. 50 (1984) no.l, 9-13.

316
Список литературы
[BERT81a] Bertossi, A.A.; The Edge Eamiltonian Path Problem is NP-
Complete, Inform. Process. Lett. 13 (1981) no.4-5,
157-159.
[BIGG76a] Biggs, N.L., Lloyd, E.K., Wilson, R.J.; Graph Theory 1736-
1936 (Clarendon Press, Oxford, 1976).
[BOND76a] Bondy, J.A., Murty, U.S.R.; Graph Theory with
Applications (The Macmillan Press Ltd, London, 1976).
[BOND77a] Bondy, J.A.; A Short Proof of MeynieVs Theorem, Discrete
Math. 19 (1977) 195-197.
[BOND86a] Bondy, J.A., Halberstam, F.Y.; Parity Theorems for Paths
and Cycles in Graphs, J. Graph Theory 10 (1986) 107-115.
[BOUC78a] Bouchet, A.; Triangular Imbeddings into Surfaces of a Join
of Equicardinal Independent Sets Following an Eulerian
Graph, in: Alavi, Y., Lick, D.R. (eds.); Theory &
Applications of Graphs, Proc, Michigan 11-15, 1976, Lecture Notes
in Math. 642 (Springer, Berlin-New York, 1978) 86-115.
[BOUC87a] Bouchet, A.; Isotropic Systems, European J. Combin. 8
(1987) 231-244.
[BOUC88b] Bouchet, A.; Compatible Euler Tours and Supplementary
Eulerian Vectors, submitted to European J. Combin.
[BOUC90a] Bouchet, A.; к-Transformations, Local Complementations
and Switchings, in: Hahn, G., Sabidussi, G., Woodrow, R.
(eds.); Cycles and Rays, NATO ASI Ser. С (Kluwer
Academic Publ., Dordrecht, 1990) 41-50.
[BRUA82a] Brualdi, R. A, Li, Q.; Small Diameter Interchange Graphs
of Classes of Matrices of Zeros and Ones, Linear Algebra
Appl. 46 (1982) 177-194.
[CAIM89a] Cai, M., Fleischner, H.; An Eulerian Trail Traversing
Specified Edges in Given Order, preprint.
[CHEN81a] Chen, C.C.; On a Characterization of Planar Graphs, Bull.
Austral. Math. Soc. 24 (1981) 289-294.
[CHIB84a] Chiba, N., Tadashi, Y., Takao, N.; Linear Algorithms for
Convex Drawings of Planar Graphs, in: Bondy, J. A.,
Murty, U.S.R. (eds.); Progress in Graph Theory, Conf. on

Список литературы
317
Combinatorics, Univ. Waterloo, Ontario, 1982 (Academic
Press, Toronto, Ontario, 1984) 153-173.
[CHIB86a] Chiba, N., Nishizeki, Т.; A Theorem on Paths in Planar
Graphs, J. Graph Theory 10 (1986) 449-450.
[COIC71a] Coi, S., Chai, S.M.; Applied Graph Theory (Russian), Izdat
"Nauka" Kazah. SSR, Alma-Ata (1971).
[CUMM66a] Cummins, R.L.; Hamilton Circuits in Tree Graphs, IEEE
Trans. Circuit Theory C-T 13 (1966) no.l, 82-90.
[DIRA66a] Dirac, G.A.; Short Proof of Menger's Graph Theorem,
Mathematika 13 (1966) 42-44.
[DIRA67a] Dirac, G.A.; Minimally 2-Connected Graphs, J. Reine
Angew. Math. 228 (1967) 204-216.
[DORF74a] Dorfler, W.; Der Arboreszenzengraph eines gerichteten
Graphen, Math. Nachr. 59 (1974) no.1-6, 35-49.
[ELLI82a] Ellingham, M.N.; Constructing Certain Cubic Graphs, in:
Combinatorial Mathematics IX, Brisbane, 1981; Lecture
Notes in Math. 952 (Springer, Berlin-New York, 1982) 252-
274.
[ELLI83a] Ellingham, M.N., Horton, J.D.; Non-Hamiltonian 3-Connec-
ted Cubic Bipartite Graphs, J. Combin. Theory Ser. В 34
(1983) 350-353.
[EULER36a] Euler, L.; Solutio problematis ad geometriam situs pertinen-
tis, Commentarii Academiae Petropolitanae 8 (1736) 1741,
128-140 = Opera omnia Ser. I, Vol. 7, 1-10.
[EVEN79a] Even, S.; Graph Algorithms (Computer Science Press, Inc.,
Rockville, 1979).
[FLEI73a] Fleischner, H.; The Uniquely Embeddable Planar Graphs,
Discrete Math. 4 (1973) no.4, 347-358.
[FLEI74a] Fleischner, H.; The Importance of Being Euler, Abh. Math.
Sem. Univ. Hamburg 42 (1974) 90-99.
[FLEI74b] Fleischner, H., Roy, P.; Distribution of Points of Odd Degree
of Certain Triangulations in the Plane, Monatsh. Math. 78
(1974) 385-390.

318
Список литературы
[FLEI74c] Fleischner, H.; On Regulating Sets and the Disparity of
Planar Cubic Graphs, Canad. Math. Bull. 17 (1974) no.3,
367-374.
[FLEI74d] Fleischner, H., Geller, D.P., Harary, F.; Outerplanar Graphs
and Weak Duals, J. Indian Math. Soc. 38 (1974) 215-219.
[FLEI76a] Fleischner, H.; Bine gemeinsame Basis far die Theorie der
Eulerschen Graphen und den Satz von Petersen, Monatsh.
Math. 81 (1976) 267-278.
[FLEI83b] Fleischner, H.; Eulerian Graphs, in: Beineke, L.W., Wilson
R.J. (eds.); Selected Topics in Graph Theory 2 (Academic
Press, London-New York, 1983) 17-53.
[FLEI86a] Fleischner, H., Hilton, A.J.W., Jackson, В.; On the
Maximum Number of Pairwise Compatible Euler Cycles, to
appear in J. Graph Theory.
[FLEI88a] Fleischner, H.; Some Blood, Sweat, but no Tears in Eulerian
Graph Theory, in: Proc. 250"1 Anniversary Conf. on Graph
Theory, Congr. Numer. 63 (1988) 8-48.
[FLEI89a] Fleischner, H., Jackson, В.; A Note Concerning Some
Conjectures on Cyclically J^-Edge Connected 3-Regular Graphs,
in: Andersen, L.D. et al. (eds.); Graph Theory in Memory
of G.A. Dirac; Ann. Discrete Math. 41 (1989) 171-178.
[FLEI90a] Fleischner, H.; Jackson, В.; Compatible Euler Tours in
Eulerian Digraphs, in: Hahn, G., Sabidussi, G., Woodrow, R.
(eds.); Cycles and Rays, NATO ASI Ser. С (Kluwer
Academic Publ., Dordrecht, 1990) 95-100.
[FORD62a] Ford, L.R.,Jr., Fulkerson, D.R.; Flows in Networks
(Princeton Univ. Press, Princeton, New Jersey, 1962).
[FUCH77a] Fuchs, H., Kedem, Z.M., Uselton, S.P.; Optimal Surface
Reconstruction from Planar Contours, in: Foley, J. (ed.),
Graphics and Image Processing, Comm. ACM 20 (1977)
no.10, 693-702.
[GARE76a] Garey, M.R., Johnson, D.S., Tarjan, R.E.; The Planar
Hamiltonian Circuit Problem is NP-Complete, SIAM J.
Comput. 5 (1976) 704-714.

Список литературы
319
[GARE79a] Garey, M.R., Johnson, D.S.; Computers and Intractability,
A Guide to the Theory of HP-Completeness (W.H. Freeman
& Company, San Francisco 1979).
[GEOR89a] Georges, J.P.; Non-Hamiltonian Bicubic Graphs, J. Combin.
Theory Ser. В 46 (1989) 121-124.
[GOOD75a] Goodey, P.R.; Hamiltonian Circuits in Polytopes with Even
Sided Faces, Israel J. Math. 22 (1975) no.l, 52-56.
[GOUY82a] Gouyou-Beauchamps, D.; The Hamiltonian Circuit
Problem is Polynomial for 4-Connected Planar Graphs, SIAM J.
Comput. 11 (1982) no.3, 529-539.
[GROP89a] Gropp, H.; Configurations and the Tutte Conjecture, talk
held at the Twelfth British Combin. Conf., Univ. of East
Anglia, Norwich, July 1989.
[GROS87a] Gross, J.L., Tucker, T.W.; Topological Graph Theory (John
Wiley k Sons, New York, 1987).
[GRUN67a] Griinbaum, В.; Convex Polytopes; Pure and Applied
Mathematics, Vol. XVI (John Wiley & Sons, New York, 1967).
[HAGG79a] Haggkvist, R.; On F-Hamiltonian Graphs, in: Bondy, J.A.,
Murty, U.S.R. (eds.), Graph Theory and Related Topics
(Academic Press, New York, 1979) 219-231.
[HAMA76a] Hamada, Т., Yoshimura, I.; Traversability and Connectivity
of the Middle Graph of a Graph, Discrete Math. 14 (1976)
no.3, 247-255.
[HARA53a] Harary, F., Uhlenbeck, G.E.; On the Number of Husimi
Trees, Proc. Nat. Acad. Sci. U.S.A. 39 (1953) 315-322.
[HARA69a] Harary, F.; Graph Theory (Addison-Wesley Publ., Reading,
MA, 1969).
[HARB89a] Haxborth, H., Harborth, M.; Straight Ahead Cycles in
Drawings of Complete Graphs, to appear in Rostock Math. Kol-
loq.
[HIER73a] Hierholzer, C; Tiber die Moglichkeit, einen Linienzug ohne
Wiederholung und ohne Unterbrechung zu umfahren, Math.
Annalen VI (1873) 30-32.

320
Список литературы
[HOLT81a] Holton, D.A., Little, C.H.C.; Elegant Odd Rings and Non-
Planar Graphs, in: Combinatorial Math. VIII, Geelong
1980, Lecture Notes in Math. 884 (Springer, Berlin 1981)
234-268.
[HOLT85a] Holton, D.A., Manvel, В., McKay, B.D.; Hamiltonian
Cycles in Cubic 3-Connected Bipartite Planar Graphs, J. Corn-
bin. Theory Ser. В 38 (1985) no.3, 279-297.
[HORT82a] Horton, J.D.; On Two-Factors of Bipartite Regular Graphs,
Discrete Math. 41 (1982) no.l, 35-41.
[HUSI50a] Husimi, K.; Note on Mayer's Theory of Cluster Integrals, J.
Chem. Phys. 18 (1950) no.5, 682-684.
[JACK87b] Jackson, В.; Compatible Euler Tours for Transition Systems
in Eulerian Graphs, Discrete Math. 66 (1987) 127-131.
[JACK88a] Jackson, В.; A Characterisation of Graphs Having Three
Pairwise Compatible Euler Tours, preprint.
[JACK88b] Jackson, В.; Supplementary Eulerian Vectors in Isotropic
Systems, preprint.
[JACK88c] Jackson, В., Wormald, N.C.; Cycles Containing Matchings
and Pairwise Compatible Euler Tours, preprint.
[JACK88d] Jackson, В.; Some Remarks on Arc-Connectivity, Vertex
Splitting, and Orientation in Graphs and Digraphs, J. Graph
Theory 12 (1988), no.3, 429-436.
[JAEG85a] Jaeger, F.; A Survey of the Cycle Double Cover Conjecture,
in: Alspach, B.R., Godsil, CD. (eds.); Cycles in Graphs,
Ann. Discrete Math. 27 (1985) 1-12.
[JOLI73a] Jolivet, J.-L.; Sur le joint d'une famille de graphes, Discrete
Math. 5 (1973) 145-158.
[JOLI75a] Jolivet, J.-L.; The Join of a Family of Graphs, in: Haj-
nal, A., Rado, R., Sos, V.T. (eds.), Infinite and Finite Sets,
Vol.II, Colloq., Keszthely, 1973, dedicated to P. Erdos on
his 60th birthday, Colloq. Math. Soc. Janos Bolyai, Vol.10
(North-Holland, Amsterdam, 1975) 935-938.
[JUNG87a] Jungnickel, D.; Graphen, Netzwerke und Algorithmen (Bib-
liographisches Institut, Mannheim-Wien-Zurich, 1987).

Список литературы
321
[KAST67a] Kasteleyn, P.W.; Graph Theory and Crystal Physics, in:
Harary, F. (ed.); Graph Theory and Theoretical Physics
(Academic Press, New York, 1967) 43-110.
[KELM88a] Kel'mans, A.K.; Cubic Bipartite Cyclically ^-Connected
Graphs Without Hamiltonian Cycles, Russian Math.
Surveys 43 (1988) no.3, 205-206.
[KNUT73a] Knuth, D.; The Art of Computer Programming, Vol.1,
Fundamental Algorithms (Addison-Wesley, Reading, Mass.,
1973).
[KONI16a] Konig, D.; Uber Graphen und ihre Anwendung auf Deter-
minantentheorie und Mengenlehre, Math. Ann. 77 (1916)
453-465.
[KONI36a] Konig, D.; Theorie der endlichen und unendlichen Graphen
(Chelsea Publ. Сотр., New York, 1950, first publ. by Akad.
Verlagsges., Leipzig, 1936).
[KOTZ56a] Kotzig, A.; Euler Lines and Decompositions of a Regular
Graph of Even Order into Two Factors of Equal Orders (in
Slovak), Mat.-Fyz. Casopis. Slovensk. Akad. 6 (1956) no.3,
133-136.
[KOTZ62a] Kotzig, A.; The Construction of Hamiltonian Graphs of
Degree Three (Russian), Casopis Pest Mat. 87 (1962) 148-168.
[KOTZ64a] Kotzig, A.; Hamilton Graphs and Hamilton Circuits, in:
Theory of Graphs and its Applications, Proc. Symp. Smo-
lenice June 1963 (Publ. House Czech. Acad. Sci., Prague,
1964) 63-82.
[KOTZ64b] Kotzig, A.; Problem 20, in: Theory of Graphs and Its
Applications, Proc. Symp. Smolenice June 1963 (Publ. House
Czech. Acad. Sci., Prague, 1964) 62.
[KOTZ68a] Kotzig, A.; Moves Without Forbidden Transitions in a
Graph, Mat.-Fyz. Casopis 18 (1968) no.l, 76-80.
[KOTZ68c] Kotzig, A.; Eulerian Lines in Finite 4-Valent Graphs and
their Transformations, in: Erdos, P., Katona, G.; Theory of
Graphs (Academic Press, New-York, 1968) 219-230.
[KOTZ79a] Kotzig, A.; Proc. Tenth Southeastern Conf. on Comb.,
Graph Theory and Computing, Vol. 2, Problem Session,
Congr. Numer. 24 (1979) 913-915.

322
Список литературы
[KULL80a] Kulli, V.R., Акка, D.G.; On Semientire Graphs, J. Math.
Phys. Sci. 14 (1980) no.6, 585-588.
[KUND74a] Kundu, S.; Bounds on the Number of Disjoint Spanning
Trees, J. Combin. Theory Ser. В 17 (1974) 199-203.
[LESN77a] Lesniak, L., Polimeni, A. D., Vanderjagt, D. W.; Degree Sets
and Traversability, Rend. Math. 10 (1977) 193-204.
[LESN86a] Lesniak, L., Oellermann, O.R.; An Eulerian Exposition, J.
Graph Theory 10 (1986) no.3, 277-297.
[LEWS72a] Lewinski, K.-H.; Graphen von Graphen, Atti Accad. Sci.
Istit. Bologna CI. Sci. Fis. Rend. (12) 10, fasc.l (1972/73)
63-72.
[LIST48a] Listing, J.В.; Vorstudien zur Topologie, reprinted from
Gottinger Studien (1847) (Vanderhoeck & Ruprecht, Gottin-
gen, 1848).
[LIUC68a] Liu, C.L.; Introduction to Combinatorial Mathematics
(McGraw-Hill, New York, 1968).
[LOVA86a] Lovasz, L., Plummer, M.D.; Matching Theory, Ann.
Discrete Math. 29 (North-Holland, Amsterdam, 1986).
[LUCA82a] Lucas, M.E.; Recreations Mathematiques I (Gauthiers-
Villaxs et fils, Paris, 1882).
[LUCA83a] Lucas, M.E.; Recreations Mathematiques II (Gauthiers-
Villars et fils, Paris, 1883).
[McCU84a] McCuaig, W.; A Simple Proof of Menger's Theorem, J.
Graph Theory 8 (1984) no.3, 427-429.
[McKE84a] McKee, T.A.; Recharacterizing Eulerian: Intimations of
New Duality, Discrete Math. 51 (1984) 237-242.
[MEND85a] Mendelsohn, E., Rosa, A.; One-Factorizations of the Com-
plete Graph - A Survey, J. Graph Theory 9 (1985) no.l,
43-65.
[MENG27a] Menger, K.; Zur allgemeinen Kurventheorie, Fund. Math.
10 (1927) 96-115.
[MEYN73a] Meyniel, H.; Une condition suffisante d'existence d}un
circuit Hamiltonien dans un graphe oriente, J. Combin.
Theory Ser. В 14 (1973) 137-147.

Список литературы
323
[MITC72a] Mitchem, J.; Eamiltonian and Eulerian Properties of
Entire Graphs, in: Graph Theory & Applications, Kalamazoo,
Mich., 1972, Lecture Notes in Math. 103 (Springer, Berlin,
1972) 189-195.
[MOON65a] Moon, J.W.; Solution to E 1667 [1964, 205], Amer. Math.
Monthly 72 (1965) 81-82.
[MOOR59a] Moore, E.F.; The Shortest Path Through a Maze, Proc. Int.
Sympos. Switching Theory 1957, Paxt. II (Harvard Univ.
Press, Cambridge, Mass., 1959) 285-292.
[NASH61a] Nash-Williams, C.St.J.A.; Edge-Disjoint Spanning Trees of
Finite Graphs, J. London Math. Soc. 36 (1961) 445-450.
[NASH64a] Nash-Williams, C.St.J.A.; Decomposition of Finite Graphs
into Forests, J. London Math. Soc. 39 (1964) 12.
[NASH79a] Nash-Williams, C.St.J.A.; Acyclic Detachments of Graphs,
in: Wilson, R.J. (ed.); Graph Theory and Combinatorics,
Proc. Conf. Open Univ.; Milton Keynes, 1978, Res. Notes
in Math. 34 (Pitman, San Francisco, 1979) 87-97.
[NASH85a] Nash-Williams, C.St.J.A.; Detachments of Graphs and
Generalized Euler Trails, in: Anderson, I. (ed.); Surveys in
Combinatorics, 1985, Math. Soc. Lecture Notes Ser. 103
(Cambridge Univ. Press, London, 1985) 137-151.
[NASH85b] Nash-Williams, C.St.J.A.; Connected Detachments of
Graphs and Generalized Euler Trails, J. London Math. Soc. 31
(1985) no.2, 17-29.
[NASH87a] Nash-Williams, C.St.J.A.; Amalgamations of Almost
Regular Edge-Colourings of Simple Graphs, J. Combin. Theory
Ser. В 43 (1987) 322-342.
[NISH83a] Nishizeki, Т., Asano, Т., Watanabe, Т.; An Approximation
Algorithm for the Hamiltonian Walk Problem on Maximal
Planar Graphs, Discrete Appl. Math. 5 (1983) no.2, 211-
222.
[NISH88a] Nishizeki, Т., Chiba, N.; Planar Graphs: Theory and
Algorithms, Ann. Discrete Math. 32 (North-Holland,
Amsterdam, 1988).

324
Список литературы
[ORE062a] Ore, 0.; Theory of Graphs (Amer. Math. Soc, Providence,
Rhode Island, 1962).
[PAPA82a] Papadimitriou, C.H., Steiglitz, K.; Combinatorial
Optimization: Algorithms and Complexity (Prentice Hall, Inc., New-
Jersey, 1982).
[PERU84a] Peruncic, В., Duri'c, Z.; An Efficient Algorithm for
Embedding Graphs in the Projective Plane, in: Graph Theory With
Applications to Algorithms and Computer Science
(Kalamazoo, Mich., 1984), Wiley-Intersci. Publ. (Wiley, New York,
1985) 637-650.
[PETE91a] Petersen, J.; Die Theorie der regularen Graphs, Acta Math.
15 (1891), 193-220.
[PET077a] Peterson, D.L.; Hamiltonian Cycles in Bipartite Plane
Cubic Maps, Ph.D. thesis, Texas A& M Univ. (1977).
[PET081a] Peterson, D.L.; A Note on Hamiltonian Cycles in Bipartite
Plane Cubic Maps Having Connectivity 2, Discrete Math.
36 (1981) 327-332.
[PETR80a] Petrenyuk, L.P., Petrenyuk, A.Y.; Intersection of Perfect
1-Factorizations of Complete Graphs, Kibernetika 1 (1980)
6-8, 149.
[PLES83a] Plesnik, J.; On NP-Completeness of the Hamiltonian
Cycle Problem in Bipartite Cubic Planar Graphs, Acta Math.
Univ. Comenian. 42/43 (1983) 271-273.
[RA0S79a] Rao, S.B., Bhat-Nayak, V.N., Naik, R.N.; Characterization
of Frequency Partitions of Eulerian Graphs, in: Graph
Theory, Proc. Symp., Calcutta 1976, ISI (Indian Stat. Inst.)
Lecture Notes 4 (1979) 124-137.
[READ86a] Read, R.C.; A Method for Drawing a Planar Graph Given
the Cyclic Order of the Edges at Each Vertex, Combinatorics
& Optimization, Research Report CORR 86-14 (July 1986)
Fac. of Math., Univ. of Waterloo.
[REGN76a] Regner, S.; Zur Existenz einer speziellen Art von Eulerschen
Linien in ebenen Graphen, Ph.D. Thesis, Univ. of Vienna
(1976).

Список литературы
325
[ROBB39a] Robbins, H.E.; A Theorem on Graphs with an Application
to a Problem of Traffic Control, Amer. Math. Monthly 46
(1939) 281-283.
[ROSS76b] Rosenstiehl, P.; Characterization des graphes planaires par
une diagonale algebrique, C.R. Acad. Sci. Paris Ser. A
(Oct. 1976) 417-419.
[SABI84a] Sabidussi, G.; Eulerian Walks and Local Complementation,
D.M.S. no.84-21, Dep. de math, et de stat., Univ. de
Montreal, Nov. 1984, to appear in European J. Combin.
[SACH86a] Sachs, H., Stiebitz, M.; 250 Jahre Graphentheorie, Bin
Beitrag zur Vorgeschichte der Abhandlung Eulers uber das
Konigsberger Bruckenproblem, preprint, to appear in NTM
Schr. Geschichte Natur. Tech. Medizin 1/88.
[SACH86b] Sachs, H., Stiebitz, M., Wilson, R.J.; Euler's Konigsberg
Letters, preprint, Techn. Hochschule Illmenau, Illmenau,
DDR.
[SEAH87a] Seah, E., Stinson, D.R.; A Perfect One-Factorization for
K36, preprint.
[SERD76a] Serdjukov, A.I.; Eulersche Konturen auf gemischten Gra-
phen, Diskret. Analiz, Novosibirsk 29 (1976) 61-67.
[SEYM79a] Seymour, P.D.; Sums of Circuits, in: Bondy, J.A., Murty,
U.S.R. (eds.); Graph Theory and Related Topics (Academic
Press, New York, 1979) 341-356.
[SHAN68a] Shank, H.; A Note on Hamilton Circuits in Tree Graphs,
IEEE Trans. Circuit Theory, C-T 15 (1968) 86.
[SHAN75a] Shank, H.; The Theory of Left-Right Paths, in:
Combinatorial Mathematics III, Proc. Third Australian Conf., Univ.
Queensland, St. Lucia, 1974; Lecture Notes in Math. 452
(Springer, Berlin-New York, 1975) 42-54.
[SHAN79a] Shank, H.; Some Parity Results on Binary Vector Spaces,
Ars Combin. 8 (1979) 107-108.
[SHAN81a] Shank, H.; Consecutive Eulerian Tree Graphs, Ars Combin.
12 (1981) 69-71.

326
Список литературы
[SKIL83a] Skilton, D.K.; Eulerian Chains and Segment Reversals, in:
Koh, K.M., Yap, H.P. (eds.); Graph Theory, Proc. First
Southeast Graph Theory Colloq., Singapore , May 1983;
Lecture Notes in Math. 1073 (Springer, Berlin-New York,
1984) 228-235.
[STIN87a] Stinson, D.R., Seah, E.; A Perfect One-Factorization for
Кьо> preprint.
[THOA78a] Thomason, Andrew G.; Hamilton Cycles and Uniquely Edge
Colorable Graphs, in: Advances in Graph Theory, Proc.
Conf. Cambridge 1977; Ann. Discrete Math. 3 (1978)
259-268 (North-Holland, Amsterdam, 1978).
[THOM81b] Thomassen, C.; Kuratowski's Theorem, J. Graph Theory 5
(1981) no.3, 225-241.
[THOM83a] Thomassen, C.; A Theorem on Paths in Planar Graphs, J.
Graph Theory 7 (1983) no.2, 169-176.
[THOM84a] Thomassen, C.; A Refinement of Kuratowski's Theorem, J.
Combin. Theory Ser. В 37 (1984) 245-253.
[TILL80a] Tillson, T.W.; A Hamiltonian Decomposition ofK^m,2m >
8, J. Combin. Theory Ser. В 29 (1980) 68-74.
[TOID73a] Toida, S.; Properties of a Euler Graph, J. Franklin Inst. 295
(1973) 343-345.
[TUTT41a] Tutte, W.T., Smith, C.A.B.; On Unicursal Paths in a
Network of Degree 4, Amer. Math. Monthly 48 (1941) 233-237.
[TUTT56b] Tutte, W.T.; A Theorem on Planar Graphs, Trans. Amer.
Math. Soc. 82 (1956) 99-116.
[TUTT61a] Tutte, W.T.; On the Problem of Decomposing a Graph Into
n Connected Factors, J. London Math. Soc. 142 (1961)
221-230.
[TUTT71a] Tutte, W.T.; On the 2-Factors of Bicubic Graphs, Discrete
Math. 1 (1971) no.2, 203-208.
[TUTT77a] Tutte, W.T.; Bridges and Hamiltonian Circuits in Planar
Graphs, Aequationes Math. 15 (1977) 1-33.
[TUTT81a] Tutte, W.T.; Graph Factors, Combinatorica 1 (1981) no.l,
79-97.

Список литературы
327
[VEBL12a] Veblen, О.; An Application of Modular Equations in
Analysis Situs, Ann.of Math. (2) 14 (1912/13) 86-94.
[VEBL31a] Veblen, O.; Analysis Situs, Amer. Math. Soc. Colloq.
Publ. 5, Part II (1931) 1-39.
[VOKI85a] Vo, K.; Ranking and Unranking Planar Embeddings, Linear
and Multilinear Algebra 18 (1985) no. 1, 35-65.
[WALL69a] Wall, C.E.; Arc Digraphs and Traversability, in: The Many
Facets of Graph Theory, Proc. Conf., Western Michigan
Univ., Kalamazoo, Michigan, 1968, Lecture Notes in Math.
110 (Springer, Berlin, 1969) 287-290.
[WELS69a] Welsh, D.J.A.; Euler and Bipartite Matroids, J. Combin.
Theory 6, (1969) 375-377.
[WHIT31a] Whitney, H.; A Theorem on Graphs, Ann. Math. 32 (1931)
378-390.
[WHIT32a] Whitney, H.; Congruent Graphs and the Connectivity of
Graphs, Amer. J. Math. 54 (1932) 150-168.
[WIEG87a] Wiegers, M.; Recognizing Outerplanar Graphs in Linear
Time, in: Tinhofer, G., Schmidt, G. (eds.); Graph-Theoretic
Concepts in Computer Science, Proc. Int. Workshop WG
1986, Bernried, FRG, Lecture Notes in Computer Science
246 (Springer-Verlag, Berlin-Heidelberg-New York, 1987)
165-176.
[WILS79a] Wilson, R.J., Beineke, L.W. (eds.); Applications of Graph
Theory (Academic Press, London-New York,1979).
[WILS85a] Wilson, R.J.; Analysis Situs, in: Alavi, Y. et al. (eds.);
Graph Theory with Applications to Algorithms and
Computer Science, Proc. Kalamazoo Conf., Kalamazoo, Mich.,
1984 (Wiley Intersci. Publ., New York, 1985) 789-800.
[WILS86a] Wilson, R.J.; An Eulerian Trail Through Konigsberg, J.
Graph Theory 10 (1986) no.3, 265-275.
[WOOD88a] Woodall, D.R.; A Proof of McKee's Eulerian-Bipartite
Characterization, preprint.
[XIAX84a] Xia, X.; Transformations of Directed Euler Tours, Acta
Math. Appl. Sinica 7 (1984) no.l, 73-77.

328
Список литературы
[ZAKS82a] Zaks, J.; Non-Hamiltonian Simple Planar Graphs, Ann.
Discrete Math. 12 (1982) 255-263.
[ZHAF86a] Zhang, Pu-ji; Guo, Xiao-fong; Hamilton Cycles in Euler
Tour Graph, J. Combin. Theory Ser. В 40 (1986) 1-8.
Работы на русском языке
Здесь приведены работы из списка литературы, имеющиеся на русском языке.
[BELY83a] Белый С. Б. — Матем. заметки, т. 34, 1983, №4, 625-628.
[FORD62a] ФордЛ.,ФалкерсонД. Потоки в сетях. — М.: Мир, 1966.
[GARE79a] Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые
задачи. —М.: Мир, 1982.
[HARA69a] ХарариФ. Теория графов. —М.: Мир, 1973.
[KNUT73a] Кнут Д. Искусство программирования для ЭВМ. т. 1. Основные
алгоритмы. — М.: Мир, 1976.
[LOVA86a] ЛовасЛ., ПламмерМ. Прикладные задачи теории графов. Теория
паросочетаний в математике, физике, химии. — М.: Мир, 1998.
[ORE062a] Ope О. Теория графов. —М.: Наука, 1968.
[РАРА82а] ПападимитриуХ., СтайглицК. Комбинаторная оптимизация.
Алгоритмы и сложность. —М.: Мир, 1985.
[SERD76a] Сердюков А. И.— Дискрет, анализ, т. 29, 1976, 61-67.
Работы, добавленные автором к русскому изданию
[FLEI89b] FleischnerH. Elementary proofs of (relativly) recent characterizations
of Eulerian graphs, First Montreal Conference on Combinatorics and
Computer Science, 1987. — Discrete Appl. Math., 24 (1989), no. 1-3,
115-119.
[FLEI89c] FleischnerH., WengerE. Characterizing Directed Postman Tours, In:
Topics in Combinatorics and Graph Theory, Bodendiek R., Henn R.
(Eds.), Physica-Verlag, Heidelberg, 1990, pp. 257-263.
[POLE71a] Полесский В. П. Об одной нижней границе надежности
информационных сетей. — Пробл. передачи информ., т. 7, 1971, № 2, 88-97.

Предметный указатель
Предварительные замечания . Вместо того , чтобы составлять отдельный
указатель обозначений , я объединил обозначения с понятиями , которые они
представляют . Те обозначения , которые используются лишь в небольших
частях книги , я в указатель не включал . 1)
Автоморфизм (automorphism) 82
антиориентированная эйлерова цепь
(antidirected eulerian trail) 141
антиэйлеров орграф (aneulerian
digraph) 141
антиэйлерова цепь (aneulerian trail) 141
ациклический с . г . (acyclic mixed graph)
60
Беспетельный с . г . (loopless mixed graph)
45
биэйлеров орграф (bieulerian digraph)
141
биэйлерова ориентация (bieulerian
orientation) 142
блок (block) 58
блоковое число bn(# , u) , bn(#) (block
number) 58
блочная цепь (block - chain) 67
блочное распределение (block
distribution) 165
г - валентная вершина (г - valent vertex) 42
валентность d(v) (valency) 42
Do - ведомая цепь (Do - favoring trail) 148
величина сетевого разреза (value) 99
вершина (vertex) 40
- прикосновения (~ of attachment) 93
вершинная fc - раскраска (к - vert ex
coloring) 89
вершинно - индуцированный
(смешанный) под(ор)граф (Vo)
(vertex - induced (mixed) sub(di)graph)
46
вершинное множество V (vertex set) 40
вершинный разрез (vertex cut) 58
*' В указателе , как правило , вместо часто встречающегося словосочетания «смешанный
граф» будет употребляться сокращение «с . г . » . — Ред .
висячая вершина графа (end - vertex of а
graph) 42
висячее ребро/дуга (end - edge/arc) 42
висячий блок (end - block) 58
вложенный граф (embedded graph) 81
вложимый граф (embeddable graph) 81
внешнепланарный граф (outerplanar
graph) 82
внешнеплоский граф (outerplane graph)
82
внешняя (неограниченная) грань (outer
(unbounded) face) 189
внутренне непересекающиеся пути
(internally - disjoint paths) 68
внутреннее ребро (inner edge) 190
Гамильтонов маршрут (hamiltonian
walk) 246
- путь (~ path) 54
- с . г . (~ mixed graph) 54
- цикл (~ cycle) 54
геометрически двойственный граф
D(G) (geometrical dual graph) 86
гиперграф (hypergraph) 291
гипердерево (hypertree) 292
гипотеза Барнетта—Татта (ГБТ)
(Barnett—Taitte conjecture) 215
- Тэйта (Tait's ~) 93
голова дуги (head) 41
головная функция (head function) 40
гомеоморфные графы (homeomorphic
graphs) 50
гомоморфизм (homomorphism) 82
гомоморфный образ (homomorphic
image) 82
граневая fc - раскраска (fc - face coloring) 90

330
Предметный указатель
граневое хроматическое число xf(G)
(face chromatic number) 90
граница грани bd(F) (boundary) 82
грань (face) 82
г - грань (г - face) 90
граф (graph) 40
- Петерсена (Petersen ~) 77
- блоков и точек сочленения be (if)
(block - cut vertex ~) 62
- , лежащий в основе с . г . (underlying ~)
46
- пересечений 7(5) (intersection ~) 62
- подразбиений (смешанный) S(H)
(subdivision mixed ~) 50
Двойная трассировка (double tracing)
54
двойной проход (double tracing) 54
двойственный граф D(G) (dual graph)
86
двудольное дополнение (bipartite
complement) 77
двудольный с . г . (bipartite mixed graph)
77
дерево (tree) 60
- Хусими (Husimi ~) 189
- в корень (in - tree) 60
- , входящее в корень (in - arborescence)
60
- , выходящее из корня
(out - arborescence) 60
- из корня (out - tree) 60
- , растущее в корень (in - arborescence)
60
- , - из корня (out - arborescence) 60
диагональ (diagonal) 93
длина маршрута (length) 54
доминирующая цепь (dominating trail)
54
доминирующий цикл (~ cycle) 54
дополнение графа (complement) 68
(а , /3) - допустимый поток ((a , /3) - feasible
flow) 99
древесный граф (tree graph) 311
дуга , заходящая в вершину (arc incident
to a vertex) 41
- , инцидентная в вершину (~ incident
to a vertex) 41
- , - из вершины (~ ~ from a vertex) 41
- , исходящая из вершины (~ incident
from a vertex) 41
дугово - гамильтонов с . г . (arc - hamiltonian
mixed graph) 54
дугово - индуцированный подорграф (Vo)
(arc - induced subdigraph) 46
дуговое множество A (arc set) 40
Емкость дуги /3(a) (capacity) 99
- сетевого разреза (~) 99
естественная 1 - факторизация (natural
1 - factorisation) 90
Задача о кёнигсбергских мостах
(Konigsberg Bridges Problem) 40
замкнутая дуга (closed arc) 41
замкнутое ребро (closed edge) 41
замкнутый маршрут (closed walk) 54
звезда , n - звезда Kiyn (n - star) 92
Изолированная вершина (isolated
vertex) 42
изоморфизм (isomorphism) 81
0+/0~ - изоморфные графы 82
индуцированное А - разбиение (induced
A - partition) 250
индуцированный (смешанный)
под(ор)граф (Vo) (induced (mixed)
sub(di)graph) 46
источник (source) 43
Каноническая ориентация (canonical
orientation) 91
каркас (spanning tree) 60
- , входящий в корень (~ in - tree) 60
- , выходящий из корня (~ out - tree) 60
кограница (coboundary) 45
п - колесо (n - wheel) 87
компонента (component) 56
концевая вершина (конец) ребра
(end - vertex of an edge) 41
корень (root) 60
кратное ребро/дуга (multiple edge/arc)
44
кратность ребра/дуги A(e) (multiplicity)
44
критическое разрезающее множество
(critical cut set) 115
кубический граф (cubic graph) 70
Лемма о двойном расщеплении (Double
Splitting Lemma) 65
- о расщеплении (Splitting ~) 63
лес (forest) 60
линейный фактор (linear factor) 75

Предметный указатель
331
локальная реберная связность Л(х , у)
(local edge - connectivity) 69
- связность «(я , у) (~ connectivity) 68
Максимальная степень Д(#)
(maximum degree) 42
максимальное паросочетание (maximal
matching) 75
маршрут W(vo , vn) (walk) 54
матрица инцидентности B(G) , В(Г>)
(incidence matrix) 97
матрица смежности A(G) , A(D)
(adjacency matrix) 97
минимальная степень S(H) (minimum
degree) 42
минимальное разрезающее множество
(minimal cut set) 58
множество вершин V 40
- граней F(G) (face ~) 82
- дуг A (arc ~) 41
- петель Л„ , Л(Я) (~ of loops) 41
- ребер (edge ~) E 40
мост , С - мост (bridge) 93
мульти(ор)граф (multi(di)graph) 45
Надграф (supergraph) 47
наименьшее разрезающее множество
(minimum cut set) 58
направленная петля (directed loop) 41
напряжение (tension) 98
независимое множество ребер/дуг
(independent set of edge/arcs)) 75
независимые пути (independent paths)
68
неограниченная грань Foo (unbounded
face) 88
неориентируемый род y(G) (non -
orientable genus) 84
непересекающаяся эйлерова цепь
(nonintersecting eulerian trail) 74
непересекающиеся переходы
(nonintersecting transitions) 74
- пути (disjoint paths) 68
неразделимый с . г . (nonseparable mixed
graph) 58
неразделяющая цепь (non - separating
trail) 215
несводимое «а - преобразование
(irreducible «a - transformation) 302
несвязный граф (disconnected graph) 56
нечетная вершина (odd vertex) 42
Т - нечетная вершина (T - odd vertex) 300
Обратная дуга aR , a" (inverse arc) 46
- ориентация Hr (~ orientation) 46
обращение сегмента (reversal of a
segment) 272
обхват g(G) (girth) 70
объем qH с . г . H (size) 42
обыкновенный с . г . (simple mixed graph)
45
ограничение системы переходов X\s ,
Х\н (restriction) 73
однозначно вложимый граф (uniquely
embeddable graph) 82
(А ; - )однородный (ор)граф ((fc) - regular
(di)graph) 43
одноцветное кольцо граней (unicolored
face - ring) 209
окрестность N(v) (neighborhood) 43
октаэдральное расширение Об
(octahedral extension) 225
операция расщепления (splitting
operation) 52
орграф (digraph) 40
ориентация (orientation) 46
ориентированная петля (oriented loop)
41
ориентированный маршрут (directed
walk) 54
ориентируемый род 7(<2) (orientable
genus 84
остовное дерево (spanning tree) 60
остовный подграф (spanning subgraph)
47
« - отделение (^ - detachment) 278
открытая дуга (open arc) 41
открытое ребро (open edge) 41
открытый маршрут (open walk) 54
отщепление ребер/дуг (splitting away)
52
Параллельный класс циклов (parallel
class of cycles) 55
паросочетание (matching) 75
перевязь (tie - up) 66
пересекающиеся переходы (intersecting
transitions) 74
переход (transition) 72
перешеек (bridge) 58
петля (loop) 41
планарный граф (planar graph) 82
плоский граф (plane graph) 82
« - поглощение (« - absorption) 279

332
Предметный указатель
под(ор)граф (sub(di)graph) 47
подавление (suppressing , suppression) 50
подграф (subgraph) 46
подразбиение ребра (subdividing ,
subdivision) 50
покрывающее множество блоков
(covering set of blooks) 58
- - подграфов (~ ~ ~ subgraphs) 63
покрывающий маршрут (covering walk)
54
^(Я) - покрывающий маршрут 54
полное множество связей (complete set
of links) 209
NP - полнота (NP - completeness) 100
полный граф Kn (complete graph) 67
- двудольный граф Km , n (~ bipartite
graph) 67
- симметрический орграф К„ (~
symmetric digraph) 67
полудуга (half - arc) 41
- , заканчивающаяся в вершине (~
ending at a vertex) 41
- , начинающаяся в вершине (~ starting
at a vertex) 41
полуоткрытая дуга (half - open arc) 41
полуоткрытое ребро (half - open edge) 41
полуребро (half - edge) 41
полустепень захода id(v) (in - degree) 43
полустепень исхода od(v) (out - degree) 43
помеченное ребро/дуга (labeld edge/arc)
50
порядок dH с . г . Я (order) 42
потенциал (potential) 98
потенциальная разность (potential
difference) 98
поток (flow) 98
почти переходная система разбиения
X* (almost transitional partition
system) 136
« - преобразование (к>transformation) 272
к* - преобразование («" - transformation)
279
«i - преобразование (щ - transformation)
279
«A - npeo6pa30BaHHe(ttA - transformation)
288
tta - преобразование (/^ - transformation)
288
kni - преобразование
(/^/ - transformation) 288
т - преобразование (r - transformation) 306
проблема Хитчкока (Hitchcock problem)
100
- китайского почтальона СРР (CHinese
Postman Problemn ) 259
- максимального потока (maximal flow
~) 99
- о назначениях (assignment ~) 100
- четырех красок (Four Color ~) 81 , 89
противоположная ориентация (reverse
orientation) 46
процедура расщепления (splitting
procedure 52
пустой граф (empty graph) 67
путь (path) 54
Радиальный граф R(G) (radial graph)
86
. 4 - разбиение (A - partition) 188
разделяющая вершина (cut vertex) 58
- цепь (separating trail) 215
разделяющее вершинное (реберное/
дуговое) множество (separating vertex
(edge/arc) set) 57
разделяющий цикл (separating cycle) 88
разрез (га - разрез) (га - cut) 58
разрезающее множество (cut set) 58
раскраска (coloring) 89
расстояние (distance) 55
растущий в корень древесный граф
(in - tree graph) 311
Об - расширение (Об - extension) 225
И^ - расширение (^ - extension) 225
расширенный сегмент (extended
segment) 54
расщепление графа (detachment) 125
^ - расщепление (^ - splitting) 187
реберная /с - раскраска (Zc - edge coloring)
89
- связность А(Я) (edge - connectivity) 69
реберная/дуговая последовательность
(edge/arc sequence) 53
/с - реберно - связный с . г . (fc - edge - connected
mixed graph) 69
реберно - гамильтонов с . г .
(edge - hamiltonian mixed graph) 54
реберно - индуцированный подграф (Vo)
(edge - induced subgraph) 46
реберное множество Е (edge set) 40
реберный (ор)граф L{G) (L(D)) (edge
(di)graph) 50
- разрез (~ cut) 58

Предметный указатель
333
ребро , инцидентное вершине (edge
incident with a vertex) 41
ребро/дуга , соединяющая вершины
(joining edge/arc) 41
регулирующее множество (regulating
set) 232
(А ; - )регулярный (ор)граф ((fc) - regular
(di)graph) 43
редуцированный орграф r>red (reduced
digraph) 62
род (genus) 84
Самодвойственный граф (self - dual
graph) 86
сводимое «а - преобразование (reducible
«a~
transformation) 302
Л - свойство (A - property) 247
« - связанность (« - association) 272
«* - связанность («" - association) 279
«i - связанность («i - association) 279
«А - связанность («д - association) 288
«x - связанность («x - association) 279
«а - связанность («a - association) 288
«^ - связанность («^/ - association) 288
«р(<з) - связанность («p(G) - association)
287
т - связанность (r - association) 307
связность с . г . «(Я) (connectivity) 68
связный граф (connected graph) 56
fc - связный с . г . (fc - connected mixed graph)
68
сегмент (segment) 53
секция (section) 53
сетевой разрез (network cut) 99
сеть (network) 99
сильно связная компонента (strongly
connected component) 56
- связный граф (~ connected graph) 56
система переходов (частичная) X(v) ,
X(H) ((parial) transition system) 72
- разбиения (частичная) P(v) , P(H)
((parial) partition ~) 72
слабо двойственный граф (weak dual
graph) 259
- связная компонента (weakly connected
component) 56
- связный граф (~ connected graph) 56
слабое И^ - расширение (weak
WVextension) 231
сложность алгоритмов (compexity of
algorithms) 100 , 101
смежные вершины (adjacent vertices) 41
- ребра/дуги (~ edge/arc) 41
смешанный граф (mixed graph) 40
- разрез (~ cut) 58
совершенное Л - разбиение (perfect
A - partition) 188
- паросочетание (~ matching) 75
совместимые системы разбиения
(compatible partition systems) 72
- цепные разложения (~ trail
decompositions) 73
сосед (neighbor) 43
- в 0+(v) H 73
степень вершины d(v) (degree) 42
- ребра d(e) (~) 44
сток (sink) 43
столица (capital) 86
стягиваемый с . г . (contractible mixed
graph) 82
стягивание 1(2) - фактора (contraction of
l(2) - factor) 81
- Hv0 с . г . H (~) 53
суграф (spanning subgraph) 47
Теорема Менгера (Menger's theorem) 68
« - о мостах» Татта (Tatte's «Bridge
Theorem») 93
терминальный цикл (terminal cycle) 93
тороидальный граф (toroidal graph) 84
тотально непересекающиеся пути
(totally disjoint paths) 68
точка сочленения (cut vertex) 58
транспортная проблема (transportation
problem) 100
триангуляция (triangulation) 87
тривиальное разрезающее множество
(trivial cut set) 115
тривиальный граф (trivial graph) 67
- орграф (~ digraph) 62
- путь (~ path) 55
г - угольная грань (г - gonal face) 86
гг - угольник Wn (n - gon) 87
унициклический граф (unicyclic graph)
61
условие разреза (cut condition) 115
Фактор (factor) 80
l - фактор (1 - factor) 75
fc - фактор (k - factor) 75
fc - факторизация (fc - factorisation) 75

334
Предметный указатель
fc - факторизуемый с . г . (fc - factor able
mixed graph) 75
формула Эйлера для многогранников
(Euler's Polyhedron Formula) 84
функция инцидентности h (incidence
function) 40
- стоимости (cost ~) 99
Хвост дуги (tail) 41
хвостовая функция (tail function) 40
хорда (chord) 93
хроматический индекс x{G) (chromatic
index) 89
хроматическое число x(G) (chromatic
number) 89
Цветовой класс (color class) 89
цепное разложение (trail decomposition
55
цепь (trail) 54
Л - цепь (A - trail) 74
цикл (cycle) 54
- Татта (Tutte ~) 55
циклическая ориентация (cyclic
orientation) 61
- реберная связность Ac(#) (~ edge/arc
cut) 69
циклически fc - реберно - связный с . г .
(cyclically fc - edge - connected mixed
graph 69
циклический реберный/дуговой разрез
(cyclic edge/arc cut) 69
циклическое разрезающее множество
(cyclic cut set) 69
- упорядочение пол у ребер/полудуг
(положительное ,
обратное/отрицательное) 0+(г>) ,
0~(v) (~ ordering) 73
цикловое покрытие (cycle cover) 55
- разложение (~ decomposition) 55
Частичная ориентация (partial
orientation) 46
четная вершина (even vertex) 42
Т - четная вершина (T - even ~) 300
Эйлеров граф (eulerian graph) 42
- орграф (~ digraph) 43
эйлерова ориентация (eulerian
orientation) 46
- характеристика x{F) - > Xf(G) (Euler
characteristic) 84
- цепь (eulerian trail) 54
эпиморфизм (epimorphism) 82
2 - ячеечное вложение (2 - cell embedding)
82
G(T , «) 310
G(Tx , *x 310
Z(G) 272
T{G) 272
T(G , P(G)) 287
TA(G) 287
Ttt(G ; Qi , Q2) 288
TNI(G) 287

Оглавление
От редактора перевода 5
Предисловие 8
Глава I. Введение 11
Глава И. Три столпа теории эйлеровых графов 15
Решение одной задачи, связанной с геометрией положения 16
О возможности обхода линейного комплекса без повторений и прерываний 33
Из «Analysis situs» О. Веблена 38
Глава III. Основные понятия и предварительные результаты 39
111.1. Смешанные графы и их основные части 40
111.2. Некоторые связи между графами и (смешанными) (ор)графами.
Подграфы 45
111.3. Графы, получающиеся из заданного графа 50
111.4. Маршруты, цепи, пути, циклы, деревья; связность 53
111.5. Совместимость, циклический порядок множества К* и соответствующие
эйлеровы цепи 72
111.6. Паросочетания, 1-факторы, 2-факторы, 1-факторизации, 2-факториза-
ции, двудольные графы 75
111.7. Вложение графов в поверхности; изоморфизмы 81
111.8. Раскраска плоских графов 89
111.9. Гамильтоновы циклы 92
III. 10. Матрицы инцидентности и смежности, потоки и напряжения 97
III. 11. Алгоритмы и их сложность 100
III. 12. Заключительные замечания 102
Глава IV. Характеризационные теоремы и их следствия 104
IV.1. Графы 104
IV.2. Орграфы 110
IV.3. Смешанные графы 113
IV.4. Упражнения 119
Глава V. Некоторые возможные обобщения 121
V.I. Разложения на цепи, путевые/цикловые разложения 121
V.2. Результаты о четности 122
V.3. Двойные проходы 124
V.4. Пересечение границы: расщепления графов 124
V.5. Упражнения 126
Глава VI. Различные типы эйлеровых цепей 127
VI. 1. Эйлеровы цепи, избегающие некоторых переходов 127
VI.2. Попарно совместимые эйлеровы цепи 155
VI.3. А-цепи в плоских графах 183
VI.4. Упражнения 266
Глава VII. Преобразования эйлеровых цепей 270
VII. 1. Преобразование произвольных эйлеровых цепей в графах 271
VII.2. Преобразование эйлеровых цепей специального типа 276
VII.3. Преобразование эйлеровой цепи в орграфах 304
VII.4. Заключительные замечания и некоторые открытые проблемы 309
VII.5. Упражнения 311
Список литературы 314
Предметный указатель 329

Г. Фляйшнер
и смежные вопросы
Монография посвящена одному из важных
разделов теории графов - теории эйлеровых
графов. В ней собраны как классические, так и
современные результаты, уделено внимание
алгоритмическим вопросам в связи с различными
приложениями. Изложение сопровождается
большим количеством примеров и графических
иллюстраций, сформулированы нерешенные проблемы.
Книга удачно дополняет имеющуюся по этой
тематике литературу и будет полезна как
специалистам в различных областях математики, так и всем,
кто применяет теорию графов.
ISBN 5-03-003115-4
785030"031156