Лекции по теории графов - Тышкевич Р.И., Емеличев В.А., Мельников О.И., Сарванов В.И.

Автор: Тышкевич Р.И. Емеличев В.А. Мельников О.И. Сарванов В.И.
Теги: комбинаторный анализ теория графов теория вероятностей математическая статистика издательство наука физматлит
Год: 1990
Похожие
Теория графов
Эйлеровы графы и смежные вопросы
Теория графов
Незнайка в стране графов
Текст
                    
Лекции
по ТЕОРИИ
ГРАФОВ
Допущено Государственным комитетом СССР
по народному образованию в качестве
учебного пособия для студентов, обучающихся
по специальностям «Математика» и «Прикладная математика»
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 9 0
ББК 22.174
Л43
УДК 519.17(075.8)
Авторы: В. А. ЕМЕЛИЧЕВ, О. И. МЕЛЬНИКОВ,
В. И. САРВАНОВ, Р. И. ТЫШКЕВИЧ
Лекции по теории графов/Е м е л и ч е в В. А., Мельни-
ков О. И., Сар ванов В. И., Тышкевич Р. И.— М.: Наукам
Гл. ред. физ.-мат. лит., 1990.— 384 с.— ISBN 5-02-013992-0.
Излагаются основы теории графов, обсуждаются некоторые*
известные проблемы. Приводятся примеры сведения прикладных
задач к задачам теории графов и использования аппарата этой
теории. Отдельная глава посвящена комбинаторным алгоритмам^
связанным с поиском структурных и числовых характеристик гра-
фов. Каждая глава сопровождается упражнениями.
Для студентов вузов, обучающихся по специальностям «Мате-
матика» и «Прикладная математика».
Табл. 1. Ил. 211. Библиогр. 32 назв.
Рецензенты:
1. Кафедра математических методов исследования операций
Воронежского государственного университета.
2. Кафедра теории исследования операций Ленинградского го-
сударственного университета.
Л
1602100000—110 о.
053(02)-90
©«Наука».
Физматлит, 1990
ISBN 5-02-013992-0
Посвящается
Дмитрию Алексеевичу СУПРУНЕНКО
Предисловие
В основу настоящего учебного пособия положены кур-
сы лекций, которые читались авторами в Белорусском
государственном университете им. В. И. Ленина для сту-
дентов-математиков и в Белорусском политехническом
институте для студентов, обучающихся по специальности
«Прикладная математика». Изложение материала в кни-
ге ставит своей целью дать в руки студентов орудие,
применимое как к наукам о поведении (кибернетика,
теория информации, теория систем, теория игр), так и
к теории множеств, теории матриц, теории групп и к
другим чисто абстрактным дисциплинам. Основной зада-
чей этого учебного пособия является ознакомление сту-
дентов с теоретическими основами теории графов. Вме-
сте с тем большое внимание уделяется вопросам приме-
нения теории графов к решению прикладных задач и в
связи с этим,— построению эффективных алгоритмов.
Книга состоит из двенадцати глав.
В главе I даны основные понятия теории графов. Об-
суждается гипотеза Келли — Улама о реконструируемо-
сти, вводятся регулярные, двудольные и реберные гра-
фы, изучается группа автоморфизмов графа. Глава за-
канчивается результатами, характеризующими свойства
графов при большом числе вершин. Эти свойства отра-
жают в некотором смысле типичный случай и потому
формулируются в терминах «почти всех» графов.
Глава II посвящена деревьям и остовам. Она содер-
жит матричную теорему Кирхгофа о деревьях и теорему
Кэли о числе помеченных деревьев. В этой же главе из-
лагаются и обосновываются алгоритмы Краскала и При-
ма для решения задачи об остове минимального веса.
Глава III содержит элементарное замкнутое изложе-
ние основ теории матроидов и трансверсалей, специаль-
но приспособленное к нуждам теории графов.
Глава IV касается понятий независимости и покры-
тия. При этом понятия вершинного и реберного покры-
тий в идейном плане объединены.
1*	3
В главе V излагаются вопросы, связанные с вершин-
ной и реберной связностью графа, которые имеют непо-
средственное отношение к надежности и живучести раз-
личных сетей. Особо выделены двусвязные графы. При-
водятся новое краткое доказательство известной теоремы
Менгера (1927 г.) о вершинном разделении графа, при-
надлежащее В. Маквайгу, и критерий Уитни (1932 г.)
/с-связности графа.
В главе VI приводятся критерии планарности графа
Л. С. Понтрягина и К. Куратовского, X. Вагнера, С. Мак-
лейна, X. Уитни, разбирается задача укладки графа на
плоскости, даны некоторые характеристики непланарно-
сти графа — род, толщина, число скрещиваний, иска-
женность.
Глава VII посвящена эйлеровым и гамильтоновым
графам. Она открывается критерием существования эйле-
рова цикла в графе. Далее приводятся разнообразные до-
статочные условия гамильтоновости графа — результаты
X. Уитни (1932 г.), У. Татта (1943 г.), Г. Дирака
(1952 г.), О. Оре (1960 г.), В. Хватала (1972 г.) и др.
В главе VIII исследуются степенные последователь-
ности графов, т. е. списки степеней их вершин. Приво-
дятся два критерия графичности последовательности на-
туральных чисел — критерий Гавела — Хакими и крите-
рий Эрдёша — Галлаи. Изучается процедура построения
реализации графической последовательности с предпи-
санными теоретико-графовыми свойствами. Исследуются
классы графов, определяемые степенными последова-
тельностями,— расщепляемые графы, пороговые гра-
фы. Последний класс графов связан с минимиза-
цией числа линейных неравенств, задающих булеву
функцию.
В главе IX обсуждаются вопросы раскраски вершин
и ребер графа. Здесь рассматривается знаменитая гипо-
теза четырех красок, вводится и изучается важный класс
графов — совершенные графы, излагается теорема Визин-
га о реберной раскраске.
Глава X отведена ориентированным графам. Рассмат-
риваются обходы и базы в ориентированном графе, де-
тально исследуются пути.
В главе XI излагается теория гиперграфов, которые
являются естественным обобщением графов. Здесь рас-
сматриваются циклы в гиперграфе, независимые множе-
ства вершин гиперграфа. Особое внимание уделено зада-
чам реализации гиперграфов различными типами графов.
4
Подобные задачи возникают при проектировании интег-
ральных схем.
В главе XII вводится понятие полиномиального ал-
горитма (именно такие алгоритмы подразумеваются в
гл. I—XI при употреблении словосочетания «эффектив-
ный алгоритм»). Глава содержит изложение двух алго-
ритмов анализа графов — поиска в глубину и поиска в
ширину. Исследуются задачи нахождения кратчайших пу-
тей в графе, построения паросочетаний в двудольном
графе, поиска кратчайшего остова во взвешенном графе.
Дается введение в теорию Л^Р-полноты.
Каждая глава книги иллюстрирована примерами све-
дения прикладных задач к задачам теории графов и ис-
пользования аппарата этой теории. Обсуждается связь
теории графов с проблемами надежности, задачами со-
ставления расписаний, передачи информации, выбора
проекта, распределения оборудования, проектирования
интегральных схем и коробок скоростей и т. д. Выявле-
ны связи теории графов с другими разделами дискретной
математики, такими, например, как математическая ло-
гика, булево программирование, теория кодирования. Для
доказательства теоретико-графовых теорем используется
аппарат алгебры.
Для целей тренировки в конце каждой главы поме-
щены упражнения; все они носят учебный характер.
За последние годы теория графов развилась в столь
обширный самостоятельный раздел дискретной математи-
ки, что невозможно изложить все основные направления
этого раздела в одной книге ограниченного объема. По
этой причине очень трудно очертить круг вопросов, ко-
торые должны входить в учебное пособие для студен-
тов-математиков. Очевидно, что в содержании настоящей
книги отражены наши взгляды. Однако некоторые во-
просы теории графов, привлекательные для нас, напри-
мер, сети, транспортные сети, потоки в сетях и т. д.,
оказались за пределами этой книги, поскольку они тра-
диционно входят в другие учебные курсы — такие как
«Исследование операций», «Методы оптимизации», «Ди-
скретная математика». Мы мало касались проблемы изо-
морфизма графов, которой, на наш взгляд, должна быть
посвящена отдельная книга.
Терминология теории графов, к сожалению, еще не
установилась. Попытки ряда авторов унифицировать обо-
значения и упорядочить терминологию до сих пор не
увенчались успехом. Поэтому мы вынуждены наряду с
5
основным термином, как правило, приводить в скобках
другие, широко употребляемые в современной советской
и зарубежной литературе по теории графов.
В книге принята сквозная нумерация параграфов.
Теоремы, утверждения, леммы, следствия и рисунки ну-
меруются двумя числами: первое из них — это номер па-
раграфа, а второе — их порядковый номер, причем нуме-
рация — сквозная внутри параграфа.
Начало и конец доказательства обозначаются симво-
лами > и <1 соответственно.
Следует сделать замечание относительно авторства
приводимых теорем. В ряде случаев мы даем фамилии
авторов и годы опубликования результатов, но большая
часть теорем оказалась безымянной. Это, конечно, не оз-
начает, что мы претендуем на авторство.
На различных стадиях работы над книгой мы поль-
зовались советами и замечаниями, высказанными многи-
ми коллегами и нашими учениками. Среди них М. С. Га-
ращук, Г. М. Гутин, В. Э. Зверович, И. Э. Зверович,
С. Г. Инджеяп, А. Н. Исаченко, М. М. Ковалев, В. П. Ко-
зырев, Н. М. Корнеенко, А. Д. Коршунов, А. В. Косточ-
ка, А. П. Крачковский, А. Г. Левин, Л. С. Мельников,
В. А. Перепелица, К. Ф. Присакару, В. Л. Тюрин,
А. А. Черняк. Всем им мы выражаем искреннюю благо-
дарность.
Мы от души благодарим рецензентов — коллективы
кафедры математических методов исследования операций
Воронежского государственного университета и кафедры
теории исследования операций Ленинградского государ-
ственного университета; в частности, мы благодарны про-
фессору Н. Н. Петрову и доценту И. Б. Руссману. Их
детальная и благожелательная критика во многом спо-
собствовала улучшению первоначального текста книги.
Мы благодарим также редактора книги А. Д. Вайнштей-
на, внесшего ряд усовершенствований в текст.
Мы особенно благодарны академику АН БССР
Д. А. Супрупенко и члену-корреспонденту АН СССР
С. В. Яблонскому за постоянную помощь, ценные сове-
ты и поддержку.
Введение
Начало теории графов все единодушно относят к
1736 г., когда Л. Эйлер не только решил популярную
в то время задачу о кенигсбергских мостах, но и нашел
критерий существования в графе специального маршру-
та (эйлерова цикла, как теперь его называют). Однако
этот результат более ста лет оставался единственным
результатом теории графов. Лишь в середине XIX века
инженер-электрик Г. Кирхгоф разработал теорию деревь-
ев для исследования электрических цепей, а математик
А. Кэли в связи с описанием строения углеводородов
решил перечислительные задачи для трех типов деревь-
ев. К этому же периоду относится появление знамени-
той проблемы четырех красок.
Родившись при решении головоломок и заниматель-
ных игр (задачи о шахматном коне, о ферзях, «круго-
светное путешествие», задачи о свадьбах и гаремах и
т. п.), теория графов стала в настоящее время простым,
доступным и мощным средством решения вопросов, от-
носящихся к широкому кругу проблем. Графы букваль-
но вездесущи. В виде графов можно, например, интер-
претировать схемы дорог и электрические цепи, геогра-
фические карты и молекулы химических соединений, свя-
зи между людьми и группами людей.
За последние три десятилетия теория графов превра-
тилась в один из наиболее бурно развивающихся разде-
лов математики. Это вызвано запросами стремительно
расширяющейся области приложений. В теоретико-гра-
фовых терминах формулируется большое число задач,
связанных с дискретными объектами. Такие задачи воз-
7
никают при проектировании интегральных схем и схем
управления, при исследовании автоматов, логических це-
пей, блок-схем программ, в экономике и статистике, хи-
мии и биологии, в теории расписаний и дискретной опти-
мизации. Таким образом, теория графов становится одной
из существенных частей математического аппарата ки-
бернетики, языком дискретной математики. В значитель-
ной степени через теорию графов происходит ныне про-
никновение математических методов в науку и технику.
Все это привело к тому, что теория графов появилась
и в учебных планах наших университетов и технических
вузов.
Глава I
Начальные понятия
§ 1. Определение графа
Термин «граф» впервые появился в книге выдающе-
гося венгерского математика Д. Кёнига в 1936 г., хотя
начальные задачи теории графов восходят еще к Эйлеру
(XVIII в.).
Пусть V — непустое множество, V(2) — множество всех
его двухэлементных подмножеств. Пара (V, Е), где Е —
произвольное подмножество множества V(2), называется
графом (неориентированным графом},
В этой книге рассматриваются только конечные гра-
фы, т. е. множество V предполагается конечным, хотя в
определении графа конечность этого множества не тре-
буется. Элементы множества V называются вершинами
графа, а элементы множества Е — ребрами. Итак, граф —
это конечное множество V вершин и множество Е ребер,
Е s У(2). Множества вершин и ребер графа G обознача-
ются символами VG и EG соответственно. Вершины и
ребра графа называются его элементами. Число I VG\
вершин графа G называется его порядком и обознача-
ется через |G|. Если |G| = п, Ifi'Gl = m, то G называют
(п, тп)-графом.
Говорят, что две вершины и и v графа смежны, если
множество {и, и} является ребром, и не смежны в про-
тивном случае. Если е = {и, v} — ребро, то вершины и
и v называют его концами. В этой ситуации говорят так-
же, что ребро е соединяет вершины и и v. Такое ребро
обозначается символом uv.
Два ребра называются смежными, если они имеют об-
щий конец.
Вершина v и ребро е называются инцидентными, ес-
ли v является концом ребра е (т. е. e = uv}, и не ин-
цидентными в противном случае.
Заметим, что смежность есть отношение между одно-
родными элементами графа, тогда как инцидентность яв-
ляется отношением между разнородными элементами.
9
Множество всех вершин графа G, смежных с некото-
рой вершиной v, называется окружением вершины v и
обозначается через NQ(y) или просто N(y).
Графы удобно изображать в виде рисунков, состоя-
щих из точек и линий, соединяющих некоторые из этих
точек. При этом точки соответствуют вершинам графа,
а соединяющие пары точек линии — ребрам. В качестве
иллюстрации рассмотрим граф G, изображенный на
рис. 1.1. Это (5, 6)-граф, FG = {1, 2, 3, 4, 5}, EG = {{1,
2}, {1, 5}, {2, 3), {2, 4), {2, 5}, {4, 5}}. Вершины 1 и 2
смежны, а 1 и 3 не смежны. Вершина 1 и ребро {1, 2}
инцидентны. N(2) = {1, 3, 4, 5}.
Приведем примеры некоторых графов специального
вида.
Граф G называется полным, если любые две его вер-
шины смежны, т. е. EG = (VG)(2). Полный граф порядка
Рис. 1.3
п обозначается символом Кп, число ребер в нем равно
j	е На рПС 12 изображены графы Кп,
п 5.
Граф называется пустым, если в нем нет ребер. Пу-
стой граф порядка п обозначается через Оп.
На рис. 1.3 показаны простые циклы Сп (п = 3, 4)
и простые цепи Рп (п = 2, 3, 4). Очевидно, что К<2 =
Рис. 1.4
а £з = Сз- На рис. 1.4 приведены два изображения про-
стого цикла С5.
40.
На рис. 1.5 изображены колеса Wn (п = 3, 4, 5). За-
метим, что Жз ~ и I Wn\ — п + 1.
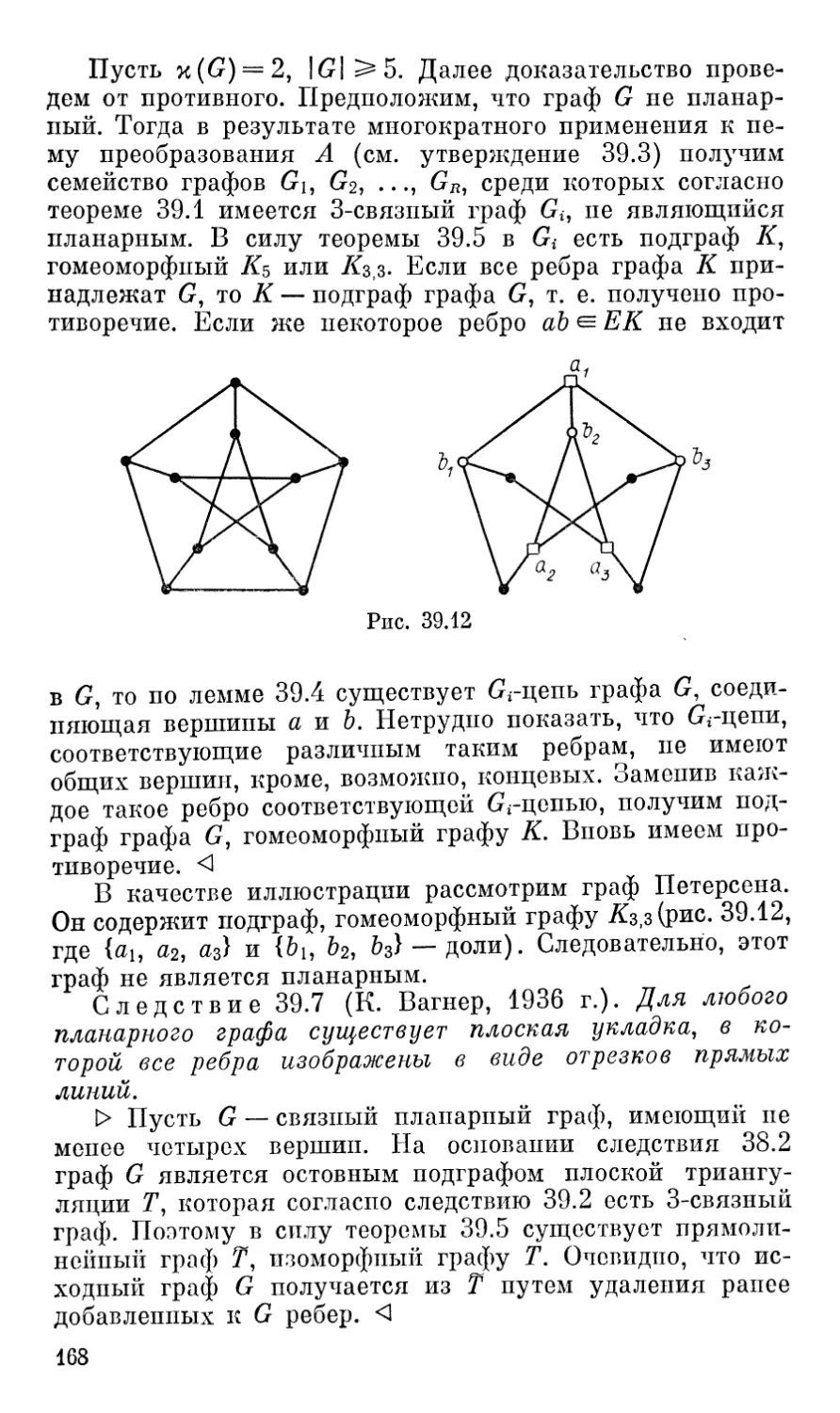
На рис. 1.6 изображен граф Петерсена.
Красивыми примерами являются графы пяти плато-
новых тел (т. е. правильных многогранников): тетраэд-
ра, куба, октаэдра, додекаэдра, икосаэдра (рис. 1.7).
Ниже неоднократно используются термины «разбие-
ние» и «покрытие». Набор подмножеств множества S на-
зывается покрытием множества S, если объединение этих
Рис. 1.5
подмножеств совпадает с S. Покрытие называется раз-
биением, если никакие два из входящих в него подмно-
жеств не пересекаются.
Граф называется двудольным, если существует такое
разбиение множества его вершин на две части (доли),
что концы каждого ребра принадлежат разным частям.
Если при этом любые две вершины, входящие в разные
доли, смежны, то граф называется полным двудольным.
Полный двудольный граф, доли которого состоят из р
и из q вершин, обозначается символом Kp>q. При р = 1
получаем звезду К\л. Очевидно, что К\,\ = Pz, K\,z =
= Рз, Kz,2 = Cj[. На рис. 1.8 изображены звезда К\$ и
полный двудольный граф ТГз.з-
Заметим, что одна из долей двудольного графа мо-
жет быть пустой. Так, О\ — двудольный граф с одной
пустой долей, Oz можно трактовать как двудольный граф
с двумя одновершинными долями или как двудольный
граф, одна из долей которого содержит две вершины,
а другая является пустым множеством.
Аналогично двудольным определяются k-дольный и
полный к-долъный графы для к = 3, 4, ... На рис. 1.9
приведен трехдольный граф.
Легко подсчитать число всех графов с фиксирован-
ным множеством вершин V. Эти графы различаются сво-
ими ребрами, и потому их число равно количеству под-
множеств в 7(2), т. е. 2V2', где п= |7|. Однако эти графы
11
Тетраэдр
Куд
Рис. 1.7
1 2
не всегда следует различать. Как в применениях тео-
рии графов, так и в самой этой теории чаще существенно
лишь то, что есть объекты (вершины графа) и связи
между объектами (ребрами). С этих позиций графы, ко-
торые получаются один из другого изменением наимено-
ваний вершин, разумно не различать. Оформим эти со-
ображения в виде следующего определения.
Пусть G и Н — графы, а ср: VG VH — биекция. Ес-
ли для любых вершин и и v графа G их образы <р(^)
и ср (г?) смежны в Н тогда и только тогда, когда и и v
смежны в G, то эта биекция называется изоморфизмом
графа G на граф Н. Если такой изоморфизм существует,
то мы пишем G = Н (тогда и Н = G) и говорим, что гра-
фы G и Н изоморфны.
Например, три графа, представленные на рис. 1.10,
изоморфны (почему?), а графы на рис. 1.11 не изоморф-
ны (почему?). Вопрос о том, изоморфны ли два данных
Рис. 1.10
графа, в общем случае оказывается сложным (см., на-
пример, [18]).
Очевидно, что отношение изоморфизма графов явля-
ется эквивалентностью, т. е. оно симметрично, транзи-
тивно и рефлексивно. Следовательно, множество всех
графов разбивается на классы так, что графы из одного
класса попарно изоморфны, а графы из разных классов
не изоморфны. Изоморфные графы естественно отожде-
ствлять, т. е. считать совпадающими (их можно изобра-
зить одним рисунком). Они могли бы различаться конк-
13
ретной природой своих элементов, но именно это игно-
рируется при введении понятия «граф».
В некоторых ситуациях все же приходится различать
изоморфные графы, и тогда полезно понятие «помечен-
ный граф». Граф порядка п называется помеченным,
если его вершинам присвоены некоторые метки, напри-
мер, номера 1, 2, ..., п. Отождествив каждую из вер-
шин графа с ее номером (и, следовательно, множество'
вершин — с множеством чисел {1, 2, ..., тг}), определим
Рис. 1.11
равенство помеченных графов G и Н одного и того же
порядка: G = H тогда, когда EG = EH. На рис. 1.12 изо-
бражены три разных помеченных графа.
При необходимости подчеркнуть, что рассматривае-
мые графы различаются лишь с точностью до изомор-
физма, говорят: «абстрактный граф». Строго говоря, аб-
страктный (или непомеченный) граф — это класс изо-
морфных графов.
Число gn непомеченных графов порядка п определя-
ется сложно. Известна формула Пойа
дающая асимптотику числа gn. Эта формула означает,
что две функции g(n)= gn и / (п) = 2V2' / п! асимптотиче-
ски равны, т. е. lim g(rt)/f(ri) = 1 (см. книгу [29],
П-^оо
где излагается целый ряд результатов, связанных с чис-
лом графов, имеющих те или иные предписанные свой-
ства).
14
Как отмечалось выше, верно
Утверждение 1.1. Число 1п помеченных графов
порядка п равно 2х .
Итак, число помеченных графов порядка п «пример-
но» в п\ раз больше числа непомеченных. Этот факт
кажется интуитивно ясным: существует ровно п\ поме-
ток множества, состоящего из п вершин. Однако послед-
нее отнюдь не означает, что из каждого непомеченного
графа получается п\ помеченных. Например, все пометки
пустого графа приводят к одному и тому же помеченно-
му графу; простая цепь Рз порождает три, а не шесть
помеченных графов (рис. 1.12). Но все же, как пра-
вило, каждый непомеченный граф приводит к п\ поме-
ченным графам.
Для произвольного графа G следующим образом оп-
ределяется дополнительный граф (или дополнение)
G: VG = VG, и любые две несовпадающие вершины
смежны в G тогда и только тогда, когда они не смежны
в G (рис. 1.13).
Очевидно, что G = G и G Я, если G = Н.
Граф, изоморфный своему дополнению, называется
само дополнительным. Например, Aj, Р4 и С5 — самодопол-
-нительные графы. Самодополнительные графы составля-
ют важный, хотя и экзотический, класс графов, опре-
деленным образом связанный с проблемой распознавания
изоморфизма графов (см., например, [18]).
Иногда приведенное выше определение графа оказы-
вается недостаточным и приходится рассматривать бо-
лее общие объекты, в которых две вершины могут сое-
диняться более чем одним ребром. Так возникает поня-
тие «мультиграф». Мулътиграф — это пара (И, Е), где
V *- непустое множество {вершин}, а £ — семейство под-
41
множеств множества V(2) (ребер). Употребление терми-
на «семейство» вместо «множество» означает, что эле-
менты множества V(2) могут в Е повторяться, т. е. до-
пускаются кратные ребра.
Дальнейшее обобщение состоит в том, что кроме крат-
ных ребер допускаются еще петли, т. е. ребра, соединя-
ющие вершину саму с собой. Псевдограф — это пара (V,
Е), где V — непустое множество (вершин), а Е — неко-
торое семейство неупорядоченных пар вершин (ребер),
не обязательно различных. На рис. 1.14 изображены
мультиграф и псевдограф.
Изучаются также ориентированные графы. Тогда мно-
жество У(2) двухэлементных подмножеств заменяется де-
картовым квадратом V2, состоящим из упорядоченных
пар элементов множества V. Итак, ориентированный
Рис. 1.16
граф (или орграф)—это пара (V, Л), где V — множе-
ство вершин, А — множество ориентированных ребер, ко-
торые называются дугами, A s V2. Если a = (v\, V2) —
дуга, то вершины щ и называются ее началом и кон-
цом соответственно. На рисунке дуги отмечаются стрел-
ками, указывающими направление от начала к концу
(см. рис. 1.15). Аналогично определяется ориентирован-
ный мулътиграф (см. рис. 1.16). Рассматриваются также
смешанные графы, у которых есть и дуги, и неориенти-
рованные ребра.
Для всех этих видов графов естественно вводится по-
нятие изоморфизма как биекции между множествами
16
вершин, сохраняющей смежность, кратности ребер, пет-
ли и направления дуг.
Графы в смысле нашего первого определения назы-
ваются еще простыми (или обыкновенными). Хотя часто
для теории несущественно, какие из этих видов графов
(простые, мульти- или псевдо-) рассматриваются, однако
главный персонаж этой книги — простой граф. Ради со-
кращения речи термин «граф» употребляется и в других
ситуациях (например, вместо «мультиграф» или «ориен-
тированный граф»), но подобные случаи либо специаль-
но оговариваются, либо ясны из контекста.
§ 2. Подграфы
Граф Н называется подграфом (или частью) графа
G, если VH VG, ЕН EG. Если Н — подграф графа G,
то говорят, что Н содержится в G. Подграф Н называ-
ется остовным подграфом (или фактором), если VH =
== VG. Если множество вершин подграфа Н есть Ur
а множество его ребер совпадает с множеством всех ре-
бер графа G, оба конца которых принадлежат U, то Н
называется подграфом, порожденным (или индуцирован-
ным) множеством U, и обозначается через G(U).
На рис. 2.1 изображены граф G и три его подграфа Н\,
Н2 и Яз, среди которых Я3 является остовным, а Ih —
порожденным.
Рассматриваются также подграфы, порожденные мно-
жествами ребер. Для Е' EG множество ребер порож-
денного подграфа G(E') совпадает с Е', а множество вер-
шин — с множеством концов ребер из Е'.
Важный класс подграфов составляют подграфы, по-
лученные в результате удаления вершин. Пусть v — вер-
шина графа G. Граф Gv = G — v получается из графа G
в результате удаления вершины v и всех инцидентных
ей ребер. Очевидно, что Gv = G (VG\v). На рис. 2.2 изо-
В. А. Емеличев и др.	17
'сражен подграф G — 5, полученный из графа G, пред-
ставленного на рис. 2.1, удалением вершины 5.
С графами Gv связана знаменитая гипотеза рекон-
-струируемости Келли — У лама. Для каждой вершины
l'g I'G построим подграф Gv = G —
(l	— v. Систему {(?„: v^VG} всех та-
X.	ких подграфов назовем колодой гра-
фа G и обозначим через P(G). На-
	 >4*__ж пример, если G = то P(G)= {Kzf
7______________2	3 Kz, О2}.
Пусть |G| = п. Перенумеруем в
Рис< 2,2	произвольном порядке вершины гра-
фа G числами 1, 2, ..., п и выпи-
шем графы, входящие в колоду P(G):
P(G) = {Gb (?2, ...» Gn}, G^G-i,
Пусть теперь H — еще один граф порядка п. Если су-
ществует такая нумерация вершин графа Я, при которой
Gi^Hi	п), то колоды P(G) и Р(Н) называются
равными'. P(G) = Р(Н). Например, Р(Яг) = Р(б?2) =
= {Oi, ОД.
Граф Н называется реконструкцией графа G, если
P(H) = P(G).
Граф G называется реконструируемым, если он изо-
морфен каждой своей реконструкции. Не все графы ре-
конструируемы: О2 и К% являются реконструкциями друг
друга. Гипотеза Келли — У лама утверждает, что это
единственное исключение.
Гипотеза реконструируемости (П. Келли,
С. Улам, 1945 г.). Все графы порядка п>2 реконструи-
руемы.
Несмотря па простоту формулировки, вот уже более
сорока лет проблема не поддается решению. Любопытно
и то, что пет единого мнения об истинности или ложно-
сти гипотезы. Подтверждена реконструируемость графов
порядка п для 3 С п С 10. Известно, что если граф G
реконструируем, то дополнительный граф G также ре-
конструируем.
Гипотезу Келли — Улама часто называют гипотезой
вершинной реконструируемости. Наряду с ней для гра-
фов, имеющих более трех ребер, существует гипотеза
Харари реберной реконструируемости (1964 г.). Она фор-
мулируется аналогично вершинной, но вместо вершины
.удаляется ребро: для ребра е графа G подграф Ge = G —
— е получается из G в результате удаления ребра е (кои-
цы ребра не удаляются, т. е. G — е является остовиым;
подграфом). Гипотеза реберной реконструируемости под-
тверждена для многих классов графов. В частности, из-
вестно, что (п, т)-граф реберно реконструируем, если
т>п(п—1)/4 (Л. Ловас, 1972 г.) или
(В. Мюллер, 1977 г.).
Пусть X — множество каких-либо элементов графа G.
Аналогично подграфу G — и определяется подграф G —
— X: из G удаляются все вершины и ребра, входящие
в X, и каждое ребро, хотя бы один конец которого при-
надлежит X. Если, например, X — {у, щ, ^1, то G — X —
= ((G — и) — ei)— е2. Порядок удаляемых элементов не-
существен, поэтому можно писать просто G — X —
— G — v — в\ — е2.
§ 3. Операции над графами
Удаление вершины или ребра, а также переход к под-
графу — это операции, с помощью которых можно из
имеющегося графа получать другие графы с меньшим
числом элементов. Известны также операции, позволяю-
щие, наоборот, получать из имеющихся графов «боль-
шие» графы. Такова, например, операция добавления*
Рис. 3.1
ребра', если вершины и и v графа G не смежны, то мож-
но определить граф G + е, где е = ии. Он получается из
графа G добавлением ребра е.
Здесь рассматриваются другие операции над графами,
нужные для дальнейшего изложения.
Одной из наиболее важных является операция объ-
единения. Граф Н называется объединением (или нало-
жением} графов F и G, если VH = VF U VG и ЕН =
= EF U EG (рис. 3.1). В этой ситуации пишут Н — F U G.
Объединение F U G называется дизъюнктным, если VF А
A VG = 0. Аналогично определяются объединение и
дизъюнктное объединение любого множества графов, при-
чем в последнем случае никакие два из объединяемых
графов не должны иметь общих вершин.
2*
Пусть Gi==(Vi, Ei) (f = 1, 2)—два графа. Произве-
дением GiXG2 = G называется граф, для которого VG =
= Vi X У2 — декартово произведение множеств вершин
Ч Щ
X •---®---•
2*
(1,0^ (1,v2)	(1,v2)
	
(2,4) (2,v2) (2,v3)
Рис. 3.2
исходных графов, a EG определяется следующим обра-
зом: вершины (ui, U2) и (щ, V2) смежны в графе G тог-
да и только тогда, когда или щ = v\, а и2 и V2 смежны
в С2, или U2 = V2, а и\ и v\ смежны в G\ (рис. 3.2).
Очевидно, что
|Gi X G2I = II • 1(?21,	\Е(Gi X бг2) I =
= \GX\ • |EG2I + |G2I • l£Gil.
G помощью операции произведения вводится важный
класс графов — дг-мерные кубы, п-мерный куб Qn опре-
деляется рекуррентно:
<21 = ^2, Cn = ^2xCn-i, n>i.
Очевидно, что Qn — граф порядка 2П, вершины которого
можно представить (0, 1)-векторами длины п таким об-
разом, что две вершины будут смежны тогда и только
(0,1) (1,1)
(0,0) (1,0)
Рис. 3.3
тогда, когда соответствующие векторы различаются ров-
но в одной координате. Поскольку каждая вершина п-
20
мерного куба инцидентна п ребрам, то число его ребер
равно п2п~х. На рис. 3.3 представлены кубы Q2 и Q3.
Еще одна важная операция — отождествление (или
.слияние} вершин. Пусть и и v — две вершины графа G,
Н = G — и — v. К графу Н присоединим новую вершину
и', соединив ее ребром с каждой из вершин, входящих
б объединение окружений вершин и и v в графе G. Го-
ворят, что построенный граф получается из графа G
^отождествлением вершин или.
Рассматривается также операция стягивания ребра.
Стягивание ребра uv означает отождествление смежных
вершин ник. На рис. 3.4
показаны граф G и граф,
полученный из G стягивани-
ем ребра {1, 2}.
Граф G называется стя-
гиваемым к графу Н, если Н
получается из G в результа-
те некоторой последователь-
ности стягиваний ребер. Легко видеть, например, что
граф Петерсена стягиваем к К$ и, стало быть, к любому
Кп с п<Ь. Очевидно, что любой непустой связный граф,
отличный от Ki, стягиваем к К%. Но уже не любой связ-
ный граф стягивается к графу Кз- Например, простая
цепь Рп не стягивается к Кз. Естественно возникает па-
раметр p(G)—максимум порядков полных графов, к ко-
торым стягивается граф G. Параметр ц(бг) называется
числом Хадвигера графа G. Это число связано с пробле-
мой четырех красок (см. § 59).
В определенном смысле двойственной к операции стя-
гивания ребра является операция расщепления верши-
ны. Пусть v — одна из вершин графа G. Разобьем ее
2	2
и w 4
4
Рис. 3.5
окружение произвольным образом на две части М и N
и выполним следующее преобразование графа G: удалим
вершину v вместе с инцидентными ей ребрами, добавим
новые вершины и и ш и соединяющее их ребро uw, вер-
21
шину и соединим ребром с каждой вершиной из множе-
ства М, а вершину v — с каждой вершиной из множе-
ства N. Полученный в результате граф обозначим сим-
волом G. Будем говорить, что G получается из графа G
расщеплением вершины и (рис. 3.5).
§ 4.	Цепи, циклы, компоненты
Чередующаяся последовательность
Щ, е\, v2, е2, ..eh vl+i	(1)
вершин и ребер графа, такая что ег = ViVi+{ (/=1, /Ц
называется маршрутом, соединяющим вершины V\ и vt+i
(или (щ, Vi+\)-маршрутом). Очевидно, что маршрут (1)*
можно задать последовательностью
Pl, Р2,	Z2/+1	(2>
его вершин, а также последовательностью
е1, е2, ..., et
ребер.
Маршрут называется цепью, если все его ребра раз-
личны, и простой цепью, если все его вершины, кроме,
возможно, крайних, различны. Маршрут (1) называется
циклическим, если = vt+\. Циклическая цепь называ-
		ется циклом, а циклическая простая
у________________цепь — простым циклом. Число I ребер
j	\у4 5	6 в маршруте (1) называется его дли-
•--ту *	• ной. Простой цикл длины I называется
/ у , 1-циклом, 3-цикл часто называют тре-
J \	* угольником. Длина всякого цикла не
7* ъд менее трех, если речь идет о простом
Рис. 4.1 графе, поскольку в таком графе нет
петель и кратных ребер. Минимальная
из длин циклов графа называется его обхватом.
Очевидно, что любую цепь графа можно рассматривать
как его подграф.
Пусть Р — некоторая цепь вида (2) в графе G, Vi
и Vj — входящие в нее вершины, i < /. Очевидно, что
часть Vi, vi+\, ..., цепи Р, начинающаяся в вершине Vi
и заканчивающаяся в Vj, сама является цепью графа G.
Эта цепь называется (v^ Vj)-подцепью цепи Р.
Обратимся, например, к графу, изображенному на
рис. 4.1. В нем (1, 2) и (1, 2, 4, 7) являются простыми
цепями; (1, 2, 4, 7, 8, 4) — цепь, не являющаяся простой;
(1, 2, 4, 7, 8, 4, 2) —маршрут, не являющийся цепью;
(1, 2, 4, 1)—простой цикл. Обхват этого графа равен 3.
22
У Цд = Vy
s'
V*
Рис. 4.2
Для ориентированного графа вводится понятие ори-
ентированного маршрута — это последовательность вида
(1), в которой е{ ~ (vt, vi+\). Аналогом цепи в этой си-
туации служит путь {ориентированная цепь). Вершина и
называется достижи-
мой из вершины и, если
существует (и, ??)-путь.
Поскольку при и
¥= v произвольный (и, и
-маршрут, не являю-
тцийся простой цепью,
превращается в про-
стую (а, и)-цепь после
устранения «лишних
кусков», то верно
Утверждение 4.1.
При u¥=v всякий (и, и)-маршрут содержит простую {и,
и)-цепь.
Аналогично получается
Утверждение 4.2. Всякий цикл содержит про-
детой цикл.
Ниже окажутся полезными следующие утверждения
4.3 и 4.4.
Утверждение 4.3. Объединение двух несовпадаю-
щих простых (u, и)-цепей содержит простой цикл.
> Пусть Р=(щ, . . ., uk) и 2 = (щ, . . ., Vi) — несовпа-
дающие простые цепи, щ = v\ =* a, uk = vt = и, иа и va —
первые, считая от а, из несовпадающих вершин этих це-
пей, и — первые из совпадающих вершин, следу-
ющих после иа и va. Тогда а > 1 и объединение (Щх-i,
щ)-подцепи цепи Р и (ра-ь пт)-подцепи цепи Q являет-
ся простым циклом
Ua— 1,	U&, . . .,	1, . . ., Pa, Utx~ 1
(рис. 4.2). <1
Утверждение 4.4. Если С и D — два несовпада-
ющих простых цикла, имеющих общее ребро е, то граф
(C[}D)—e также содержит простой цикл.
> Если е = uv, то С—ей D — е — несовпадающие
простые {и, и) -цепи. Поэтому нужное следует из пре-
дыдущего утверждения. <1
Граф называется связным, если любые две его не-
совпадающие вершины соединены маршрутом. Учитывая
утверждение 4.1, можно в этом определении заменить
маршрут цепью или простой Цепью.
21
Очевидно следующее
Утверждение 4.5. Для связности графа необхо-
димо и достаточно, чтобы в нем для какой-либо фикси-
рованной вершины и и каждой другой вершины и суще-
ствовал (и, и)-маршрут.
Всякий максимальный связный подграф графа G на-
зывается связной компонентой (или просто компонентой)
графа G. Слово «максимальный» означает максимальный
относительно включения, т. е. не содержащийся в связ-
ном подграфе с большим числом элементов. Множество
вершин связной компоненты называется областью связ-
ности графа.
Теорема 4.6. Каждый граф представляется в виде
дизъюнктного объединения своих связных компонент.
Разложение графа на связные компоненты определено
однозначно.
> Пусть G — произвольный граф. На множестве VG
определим бинарное отношение —, положив и ~ v для
вершин и и v, если и = v или в графе G существует
(и, и)-маршрут. Очевидно, что это отношение есть эк-
вивалентность. Следовательно, мы получим разбиение
множества VG на классы, отнеся в один класс все верши-
ны, эквивалентные друг другу. Пусть VG = Ц Vi—
г
такое разбиение. Очевидно, что порожденные подграфы
Gi = G(Vi) и только они являются компонентами графа
G и G = [)Gi — дизъюнктное объединение. <
i
Полезно следующее
Утверждение 4.7. Для любого графа либо он
сам, либо его дополнение является связным.
> Пусть G — несвязный граф, А — одна из его обла-
стей связности, В = VG\A. Тогда для любых а из Л и &
из В в дополнительном графе G есть ребро аЪ. Следова-
тельно, произвольная вершина из В соединена с а мар-
шрутом длины 1, а произвольная вершина из А (отлич-
ная от а) соединена с а маршрутом длины не боле_е
чем 2. Теперь из утверждения 4.5 вытекает, что G
связен. <1
С помощью предыдущего утверждения некоторые
проблемы (например, проблема изоморфизма) сводятся’
к случаю связных графов.
Полезна также и следующая
Лемма 4.8. Пусть G — связный граф, е EG. Тогда*:
1) если ребро е принадлежит какому-либо циклу гра-
фа G, то граф G — е связен;
24
2) если ребро е не входит ни в какой цикл, то граф
G — е имеет ровно две компоненты.
> 1) Пусть ребро е = uv принадлежит циклу С гра-
фа G. Заменив в каждой (х, у)-цепи, содержащей е, под-
цепь (и, е, v) (и, р)-цепью С — е, получим (х, ^-мар-
шрут, не содержащий ребра е. Следовательно, в графе G
любые две несовпадающие вершины соединены маршру-
том, не проходящим через е. Но тогда и граф G — е
связен.
2)	Пусть ребро е = uv не входит ни в какой цикл
графа G. Тогда, очевидно, вершины и и v принадлежат
разным компонентам, например, Gu и соответственно Gv,
графа G — е. Для произвольной вершины х Ф и в G су-
ществует (х, и)-маршрут. Если ребро е в этот маршрут
не входит, х е Gu. В противном случае х Gv. <1
Ниже число ребер и число компонент графа G обо-
значаются через m(G) и k(G) соответственно.
Очевидно, что число ребер в произвольном графе по-
рядка п не больше числа ребер в Кп, равного Но
сколько ребер может быть в графе порядка п с фикси-
рованным числом к компонент? На этот вопрос отвечает
следующая
Теорема 4.9. Если k(G)=k для п-вершинного гра-
фа G, то
n~k^m(G)^(n~k)(n~k+ 1)/2,	(3)
причем обе эти оценки для m(G) достижимы.
> Вначале рассмотрим верхнюю оценку. Пусть G —
граф порядка п с к компонентами и максимальным для
таких графов числом ребер. Тогда каждая его компо-
нента является полным графом. Пусть, далее, Кр и Kq —
две компоненты, р > q > 1, v — вершина из второй ком-
поненты. Удалив из графа все ребра, инцидентные вер-
шине v, и соединив v ребром с каждой вершиной из пер-
вой компоненты, получим новый граф порядка п с тем
же числом компонент и большим числом ребер. Послед-
нее невозможно, стало быть, только одна из компонент
может иметь порядок, больший 1. Он равен п — к+1,
и потому
/Г1\ (п — к+1\
2 J
(п _ к) (п - к + 1)
2
Справедливость верхней оценки (3) и ее достижимость
доказаны.
25
Перейдем к доказательству неравенства m(G)>n —/сь
Оно очевидно при m(G)=0, так как тогда к = п. Вос-
пользуемся индукцией по m(G). Пусть t?z(G)>0 и пусть,
для графов с меньшим, чем m(G), числом ребер соот-
ветствующее неравенство верно. Рассмотрим граф G —
— е, где е EG. Согласно лемме 4.8 число компонент
этого графа равно к или к + 1. Число ребер в нем равное
m(G) — 1. По индуктивному предположению в обоих слу-
чаях m(G) — 1 > п — к — 1. Следовательно, m(G)^ п — к.
Нужное неравенство доказано.
Дизъюнктное объединение G = Oh-\ U Кп_к+\ реализу-
ет равенство m(G) = п — к. <1
Из первой части приведенного доказательства вы-
текает
Следствие 4.10. При фиксированных пи к^1ъ
среди графов G порядка п с k(G)—k существует толь-
ко один граф, а именно, G = U Kn_h+\, с максималь-
ным числом ребер.
Графы с минимальным числом ребер (при фиксиро-
ванных п и к) изучаются в следующей главе.
§ 5. Степени вершин графа
Степенью (или валентностью) вершины графа G на-
зывается число инцидентных ей ребер, т. е. число вер-
шин в ее окружении. Будем обозначать степень верши-
ны v через degGp (или degp). Тем самым deg v = \N(v) L
Максимальная и минимальная степени вершин графа G
обозначаются символами A(G) и 6(G) соответственно:
A (G) == max deg v, 6 (G) = min deg v.
v^VG	v^VG
Список степеней вершин графа называется его сте-
пенной последовательностью. Порядок членов в этой по-
следовательности роли не играет.
Вершина степени 0 называется изолированной, вер-
шина степени 1 — концевой (или висячей). Ребро, ин-
цидентное концевой вершине, также называется конце-
вым. Вершина графа, смежная с каждой другой его вер-
шиной, называется доминирующей.
Рассмотрим сумму степеней всех вершин графа. Каж-
дое ребро вносит в эту сумму 2, поэтому верно
Утверждение 5.1 («лемма о рукопожа-
тиях»). Сумма степеней всех вершин графа — четное
26
число, равное удвоенному числу ребер'.
S deg!; = 2| EG\.
v(EVG
Возможная интерпретация этой леммы такова: по-
скольку в каждом рукопожатии участвуют две руки, то
при любом числе рукопожатий общее число пожатых
рук четно (при этом каждая рука учитывается столько
раз, во скольких рукопожатиях она участвовала).
Следствие 5.2. В любом графе число вершин не-
четной степени четно.
Понятие степени вершины и лемма о рукопожатиях
сохраняются для мульти- и псевдографов. При этом каж-
дая петля вносит в степень соответствующей вершины
Двойку.
§ 6. Матрицы, ассоциированные с графом
В этом параграфе вводятся три матрицы, связанные
с произвольным графом, и еще одна матрица, связанная
с двудольным графом.
На всем протяжении этой книги элемент матрицы М,
занимающий позицию (Z, /), обозначается символом Мц.
Матрица, каждый элемент которой равен 0 или 1, на-
зывается бинарной.
Пусть G — помеченный граф порядка п, VG = {1,
2, ..., п}. Определим бинарную п X гс-м атрицу A=A(G),
положив
(1, если вершины i и у смежны,
~ (0 в противном случае.
,.A(G) называется матрицей смежности графа G. Это сим-
метрическая матрица с нулями на диагонали. Число еди-
ниц в строке равно степени соответствующей вершины.
Очевидно, что соответствие G >-> A (G) определяет
биекцию множества помеченных графов порядка п па
множество бинарных симметрических п X ^-матриц с ну-
левой диагональю.
Аналогично определяются матрицы смежности А
мульти- и псевдографов: Ац равно числу ребер, соеди-
няющих вершины I и у (при этом петля означает два
ребра).
27
Так же определяется матрица смежности A(G) ори-
ентированного графа G:
И(0)у
|1, если (/, /) е AG,
10 в противном случае.
Здесь AG — множество дуг орграфа G.
Очевидно, что любая квадратная бинарная матрица
является матрицей
смежности некоторого ориентирован-
ного графа. На рис. 6.1 изображен
ориентированный граф с матрицей
смежности
"О 1 1 Г
10 11
0 0 10 *
_0 0 0 0_
Рис. 6.1	Абстрактный граф приводит к
различным матрицам смежности в
зависимости от нумерации вершин. Посмотрим, как
связаны между собой эти матрицы. Пусть G и
Н — помеченные графы порядка п и G = Н. Это оз-
начает, что G и Н различаются только нумерацией вер-
шин, т. е. существует подстановка s на множестве вер-
шин, сохраняющая смежность: вершины и и v тогда и
только тогда смежны в G, когда их образы s(u) и s(v)
смежны в Н. Положив A(G)=A, B(G} = B, получаем
Bs(i}s(j) = Ац, f=l, n, 7 = 1, n. (1>
Тем самым доказано
Утверждение 6.1. Графы изоморфны тогда и
только тогда, когда их матрицы смежности получаются
друг из друга одинаковыми перестановками строк и
столбцов.
Это утверждение верно также для мультиграфовг
псевдографов и ориентированных графов.
Из предыдущего утверждения вытекает, в частности^
что ранги матриц смежности изоморфных графов равны.
Последнее позволяет ввести для абстрактного графа сле-
дующее определение ранга: рангом графа называется
ранг его матрицы смежности. Как и в случае матриц,
ранг графа G будем обозначать через rank G.
Пусть s — произвольная подстановка, действующая
на множестве {1, 2, ..., п}. Определим бинарную пХп-
28
матрицу S, положив
|1, если s(j) = i,
г] 10 в противном случае.
Очевидно, что в каждой строке и в каждом столбце мат-
рицы 5 содержится ровно по одной единице и det S ==
=±1. С помощью прямых вычислений проверяется, что
^SAS )ij =
для любой п X ^-матрицы А. Равенства (1) теперь мож-
но переписать в виде одного матричного равенства В =»
^SAS-'.
Из последнего равенства следует, что матрицы смеж-
ности изоморфных графов подобны. Поэтому равны ха-
рактеристические полиномы этих матриц. Следовательно,
корректно определение ха-
рактеристического поли-
нома графа как характе- •	/ VK
ристического полинома __________ /	\ X.
его матрицы смежности.	•	• •	•
Спектр этой матрицы, т. е.	Рис. 6.2
совокупность корней ха-
рактеристического полинома с учетом их кратностей, на-
зывается спектром графа.
Как известно из линейной алгебры, вещественная
симметрическая матрица (а матрицы смежности графов
являются таковыми) определяется своим спектром с точ-
ностью до подобия. Тем не менее из совпадения харак-
теристических полиномов графов отнюдь не следует изо-
морфизм этих графов. Неизоморфные графы с равными
характеристическими полиномами называются коспект-
ралъными. Например, два графа, изображенные на
рис. 6.2, коспектральны, их характеристический полином
равен х^(х2 — 4).
Глубокие свойства и применения спектра графа рас-
смотрены в книге [31].
С двудольным графом удобно связать еще одну мат-
рицу. Разбиение множества вершин двудольного графа
на доли определяется этим графом неоднозначно. Часта
такие графы рассматривают вместе с фиксированными
разбиениями на доли. Если G — двудольный граф с до-
лями X и Y и множеством ребер Е, то пишут G =
= (Х, У, Е). Итак, пусть G = (X, У, Е), |Х| == m, jУ| = п.
Занумеруем вершины доли X числами 1,2,..., пг, а до-
29
ли Y — символами z/i, 7/2, •.yn- Определим бинарную
т X ^-матрицу М = М(Х, Y, Е), положив
fl, если вершины i и yj смежны,
[0 в противном случае.
Матрицу М назовем приведенной матрицей смежности
двудольного графа.
Возвратимся к произвольным графам. Вторая из мат-
риц, вводимых в общей ситуации,— матрица Кирхгофа.
Пусть G — помеченный граф порядка п, VG = {1, 2, ...
..., п}. Определим п X тг-матрицу B = B(G), положив
—
— 1, если вершины i и j смежны,
О, если i^j и вершины i и / не смежны,
deg z, если i = /.
Матрица B(G} называется матрицей Кирхгофа графа G.
Сумма элементов в каждой строке и в каждом столбце
этой матрицы равна нулю.
Утверждение 6.1 останется верным, если вместо мат-
риц смежности рассматривать матрицы Кирхгофа. Со-
храняется и прежнее доказательство.
Во второй главе этой книги используется следующее
Утверждение 6.2. Пусть В — произвольная чис-
ловая п X п-матрица, в каждой строке которой и в каж-
дом столбце сумма элементов равна нулю'.
п	___ п	____
=	1 = 1, пт,  2 Sij = 0, j=l,n.
j=l	i=i
Тогда алгебраические дополнения всех элементов мат-
рицы В равны между собой. В частности, этим свойст-
вом обладает матрица Кирхгофа произвольного графа.
> Очевидно, что гапк5<тг. Если rank 5 < я — 1,
то алгебраические дополнения всех элементов этой мат-
рицы равны 0. Пусть rank В = п — 1 и С — присоединен-
ная матрица для матрицы В, т. е. элемент Сц равен ал-
гебраическому дополнению А# элемента Вц в матрице В,
i = 1, п, /=1, п. Известно, что ВС — (detB)E, где Е —
^единичная матрица. В наших условиях det 5 = 0, ВС =
= 0 — нулевая матрица. Следовательно, для столбца
^матрицы С с номером /, 7 = 1, п, верны равенства
ВцСц; + BizCti + ... + BinCnj = 0,	i = 1, п,
30
т. е.	_____
ВцА^ + Bi2Aj2 + ... + BinAjn = 0, i = 1, n.
Эти равенства можно рассматривать как систему линей-
ных однородных уравнений с матрицей В относительна
неизвестных Ал, Aj2, • • Ajn. Так как гапк5 = тг 1Г
то все решения системы пропорциональны. Но вектор
(1, ..., 1) удовлетворяет системе, поэтому
Л л = Aj2 = ... = Ajin, j = 1, п.
Учитывая, что СВ = 0, аналогично получаем
A li = A2i ~	= АПг<) 1=1, П.
Следовательно,
.Ац = Ам, i, j, к, 1 = 1, п. <1
Наконец, определим матрицу инцидентности графа.
Пусть G — (п, т)-граф, VG = {1, 2, ..., п}, EG = {е^
е2, ..., ет}. Определим бинарную п X m-матрицу I = I(G)
условиями:
1, если вершина к и ребро ег инцидентны,
О в противном случае.
Ihl — !
Матрица I называется матрицей инцидентности графа GL
В каждом ее столбце ровно две единицы, равных столб-
цов нет. Как и выше, соответствие G -* I (G) является
биекцией множества помеченных (п, тп)-графов с зану-
мерованными ребрами на множество п X m-матриц, удов-
летворяющих описанным условиям.
Для ориентированных графов определение матрицы
инцидентности I видоизменяется:
1,
hi= -1,
О,
если вершина к является началом дуги
если вершина к является концом дуги
если вершина к и дуга аг не инцидентны..
Аналогично утверждению 6.1 получается
Утверждение 6.3. Графы (орграфы) изоморфны
тогда и только тогда, когда их матрицы инцидентности
получаются друг из друга произвольными перестановка-
ми строк и столбцов.
Пусть G — граф. Превратим каждое его ребро в дугу,,,
придав ему одну из двух возможных ориентаций. Полу-
31
чеппый ориентированный граф называется ориентацией
графа G. Непосредственно проверяется
Утверждение 6.4. Если В — матрица Кирхгофа
графа G, а I — матрица инцидентности какой-либо его
ориентации Н (нумерация вершин в Н та же, что и в G),
то В—Пт (здесь Т — операция транспонирования мат-
рицы) .
§ 7.	Регулярные графы
Граф называется регулярным (или однородным), ес-
ли степени всех его вершин равны; степенью регулярно-
го графа называется степень его вершин. Степень регу-
лярного графа G обозначается через deg G.
Все полные графы регулярны. Графы платоновых тел
также регулярны. Регулярным графом степени п являет-
ся тг-мерный куб Qn-
Из леммы о рукопожатиях вытекает, что не суще-
ствует регулярного графа, порядок и степень которого
нечетны.
Утверждение 7.1. Пусть натуральные числа п и
d, среди которых есть четное, удовлетворяют неравен-
ствам G^d^n—i. Тогда существует регулярный граф
порядка п и степени d.
>	Для d = 0 утверждение очевидно. Кроме того, если
G — регулярный граф порядка п степени d, то дополни-
тельный граф G также регулярен и deg G = п — 1 — d.
Поэтому достаточно рассмотреть случай, когда 0 < d <
^(n-i)/2.
Пусть Zn — аддитивная группа классов целых чисел
по модулю п, A cz Zn, 0 А и для х А класс — х так-
же принадлежит множеству А. Определим граф G по-
рядка п с множеством вершин Zn следующим условием:
вершины х и у смежны, если х — у^А. Очевидно, что
граф G регулярен и степень его равна |Л|. Остается
.доказать, что для любого числа d, удовлетворяющего
указанным выше условиям, существует подходящее
d-элементное множество А. При d = 2k можно взять
Л = {±1, ±2, ..±к), а при d — 2к + 1 оказывается чет-
ным п, и можно взять Л = {±1, ±2, ..., ±к, п/2} (см.
рис. 7.1, где тг = 8, d —3). <
Утверждение 7.2. Если G = (X, Y, Е) — непустой
регулярный двудольный граф, то |Х| = |У|.
>	Так как доле X принадлежит только один из кон-
цов каждого ребра графа G, то число тп его ребер равно
22
IXI deg G. Аналогично m = IУI deg G. Следовательно,
IXI deg G = | УI deg G.	Поскольку deg G 0, to
IXI = IУ1. <
Иногда, хотя и редко, граф определяется степенями
своих вершин. Например, только Оп является регуляр-
ным графом порядка п пулевой степени. Регулярный
граф первой степени имеет четный по- ___________
рядок 2m и является дизъюнктным	/К
объединением тп ребер. Этот граф обо- У \
зпачается символом тпК^. Все связные
компоненты регулярного графа второй
степени являются простыми цикла-	\ у*
ми. Однако уже кубические графы, \ /	\/
т. е. регулярные графы степени 3,	*----
устроены сложно и не определяются	Рис. 7.1
степенями своих вершин. Примером
кубического графа является граф Петерсена (рис. 1.6).
Отметим любопытное свойство спектра регулярного
графа.
Теорема 7.3. Пусть G — регулярный граф степе-
ни d. Тогда:
1)	число d является корнем характеристического по-
линома графа G;
2)	если G — связный граф, то кратность корня d
равна 1;
3)	d^ IXl для любого корня X характеристического
полинома графа G.
>	1) Пусть VG = {1, 2, .. ., п}, A (G) = А — матрица
смежности графа G, и — столбец высоты п, все элементы
которого равны 1. Поскольку в каждой строке матрицы
А ровно d единиц, то Au = du и, следовательно, и — соб-
ственный вектор, a d — собственное значение линейного
оператора А. Но каждое собственное значение является
корнем характеристического полинома. Тем самым дока-
зано, что d — корень характеристического полинома
графа G.
2)	Для произвольного собственного вектора х~(х[,
^2, • • •, %п) с собственным значением d имеем
Ах = dx, хФ 0.	(1)
Пусть х3 — координата вектора х с максимальным моду-
лем, Xj = A(/)—окружение вершины / в графе G. Из
равенства (1) для /-й координаты вектора Ах вытекает
(Ах\ = 2 xi = dxj	(2)
3 в. А. Емеличев и др.
13
и, далее,
s |^|.	(3)
ieiVj
Поскольку |7Vjl = d, то из соотношений (2) и (3) сле-
дует, что Xi = Xj для всех i из Nj. Для связного графа G
теперь получаем, что все координаты вектора х равны
между собой, т. е. размерность подпространства соб-
ственных векторов линейного оператора А, относящихся
к собственному значению с/, равна 1. Следовательно,
и кратность корпя d характеристического полинома мат-
рицы А равна 1.
3)	Пусть % — произвольный корень характеристиче-
ского полинома матрицы Л, х — соответствующий соб-
ственный вектор. Тогда Ах = %х, и в тех же обозначе-
ниях, что и выше, имеем
= S = I	2 |ХгК<7|^-|,
откуда |X| d. <
§ 8.	Метрические характеристики графа
Пусть G — связный граф, а и и v — две его несов-
падающие вершины. Длина кратчайшего (tz, v)-маршру-
та (он, естественно, является простой цепью) называ-
ется расстоянием между вершинами и и v и обознача-
ется-через d(u, v). Положим еще d(u, u)=0. Очевидно,
что введенное таким образом расстояние удовлетворяет
следующим аксиомам метрики:
1)	d(u, v)> О,
2)	d(u, v)=0 тогда и только тогда, когда и = v,
3)	d(u, v) == d(v, и),
4)	d(u, v)+d(v, d(u, w) (неравенство тре-
угольника) .
Понятие расстояния между вершинами в связном гра-
фе позволяет определить к -ю степень графа. Пусть G —
связный граф, к — натуральное число. Граф Gh имеет то
же множество вершин, что и С; несовпадающие вершины
и и v смежны в графе Gh тогда и только тогда, когда
для графа G верно неравенство d(u, v)^k. Очевидно,
что если к |G| — 1, то Gh— полный граф.
Для фиксированной вершины и величина
е(и) = max d(u, v)
34
называется эксцентриситетом вершины и. Максимальный
среди всех эксцентриситетов вершин называется диамет-
ром графа G и обозначается через d(G). Тем самым
d(G) = maxe(iz).
.иеус
Вершина v называется периферийной, если е(у) = d(G).
Простая цепь длины d(G), расстояние между концами
которой равно d(G), называется диаметральной цепью.
Для иллюстрации обратимся к графу на рис. 8.1.
Здесь d(l, 2)=1, d(l, 3)=2; е(1) = 2;
d(G)=2. Все вершины, кроме вершины
2,	являются периферийными, (1, 2, 3)—	\	/
диаметральная цепь.	\/
Утверждение 8.1. Для всякого
связного графа G верно неравенство /'Х
d(G)^rankG.	/	\
> Пусть d(G) = d и	1	4	*3
V\, V2, . . ., Vd+X	(1)
— одна из диаметральных цепей графа G. Рассмотрим
матрицу смежности -4(G), причем выберем нумерацию
вершин так, чтобы вершины (1) имели номера 1, 2, ...
..., d + 1 соответственно. Очевидно, что
^(G) =
А В
С D
— клеточная матрица, в левом верхнем углу которой
расположена матрица смежности А порожденного под-
графа G(v\, V2, ..., nd+i). Этот подграф является простой
цепью, следовательно,
“"О 1 0 ... О 0~
1 0 1 ... О О
О 1 0... О О
0 0 0 ... 0 1
„0 0 0 ... 1 0.
— симметрическая матрица порядка d+i, все элементы
которой, за исключением двух ближайших к диагонали
полос единиц, равны нулю. Мипор порядка d матрицы А,
остающийся после устранения первого столбца и послед-
ней строки, равен 1. Следовательно, гапкЛ(С)^
rank А d. <
Минимальный из эксцентриситетов вершин связного
графа называется его радиусом и обозначается через
3*	35
r(G):
r (G) min e (u) = min max d {u, v).
ueVG	uEVGveVG
Очевидно, что радиус графа не больше его диаметра.
Вершипа и называется центральной, если е (о) = г (G).
Множество всех центральных вершин графа называется
его центром. Граф может иметь единственную централь-
ную вершину или несколько центральных вершин. На-
конец, центр графа может совпадать с множеством всех
вершин. Например, центр простой цепи Рп при четном
числе вершин п состоит ровно из двух вершин, а при
нечетном — из одной; для цикла же Сп все вершины
являются центральными.
Задача нахождения центральных вершин графа по-
стоянно возникает в практической деятельности людей.
Пусть, например, граф представляет сеть дорог, т. е.
вершины его соответствуют отдельным населенным
пунктам, а ребра — дорогам между ними. Требуется оп-
тимально разместить больницы, магазины, пункты об-
служивания. В подобных ситуациях критерий оптималь-
ности часто заключается в оптимизации «наихудшего»
случая, т. е. в минимизации расстояния от места обслу-
живания до наиболее удаленного пункта. Следовательно,
местами размещения должны быть центральные верши-
ны графа.
Реальные задачи (их называют минимаксными зада-
чами размещения, см. [27]) отличаются от этой идеаль-
ной тем, что приходится еще учитывать другие обстоя-
тельства — фактические расстояния между отдельными
пунктами, стоимость, время проезда и прочее. Для того
чтобы учесть это, используют понятие «взвешенный
граф». Пусть G — граф, w: EG R+ — вещественно-
значная функция, ставящая в соответствие каждому реб-
ру е положительное (или неотрицательное) число w(e}—
вес ребра е. Пару (G, w) назовем взвешенным графом.
Под длиной (или весом} любого подграфа взвешенного
графа будем понимать сумму весов его ребер. В осталь-
ном все определения сохраняются.
§ 9. Критерий двудолыюсти графа
Д. Кёниг сформулировал простой критерий двудоль-
пости графа в терминах длин циклов.
Теорема Кёнига (1936 г.). Для двудолъности
графа необходимо и достаточно, чтобы он не содержал
циклов нечетной длины.
36	.
> Необходимость. Пусть G — двудольный граф,
С — один из его циклов длины к. Пройдем все ребра
этого цикла' в той последовательности, в какой они на
нем расположены, начиная с некоторой вершины и. Сде-
лав к шагов, вернемся в v. Так как концы каждого реб-
ра лежат в разных долях, то к — четное число.
Достаточность. Не ограничивая общности, мож-
но рассматривать только связные графы, ибо дизъюнкт-
ное объединение двудольных графов также двудольно.
Пусть связный граф G порядка п > 1 не имеет циклов
нечетной длины, v VG. Постро-
им разбиение VG = A U В следую-
щим образом: произвольную вер-
шину и графа G отнесем к клас-
су Л, если расстояние d(u, v)—
четное число, и к классу В, если
это расстояние нечетно. Остается
доказать, что порожденные под-
графы б(Л) и G(B) являются пу-
стыми. Пусть, напротив, существу-
ют две смежные вершины и и ш,
входящие в один класс. Тогда ни
Рис. 9.1
одна из них не совпадает с и, поскольку v Л, а окруже-
ние вершины v входит в класс В. Пусть, далее, U —
кратчайшая (и, г>)-цепь, W — кратчайшая (ш, у)-цепь,
V\ — последняя, считая от и, из общих вершин этих це-
пей, лежащая на цепи U (рис. 9.1). Обозначим че-
рез Хи и Yu соответственно (щ щ)- и (щ, н)-подцепп
цепи U, а через Xw и Yw—соответственно (v, v\)~
и (щ, w)-подцепи цепи W. Очевидно, что длины цепей
Хи и Xw совпадают и, следовательно, длины цепей Yu и Yw
одного характера четности. Но тогда объединение це-
пей Yu и Yw и ребра uw является циклом нечетной
длины. <1
Очевидно
Следствие 9.1. Граф является двудольным тогда
и только тогда, когда он не имеет простых циклов не-
четной длины.
Доказательство теоремы Кёнига подсказывает про-
стой способ распознавания двудолыюсти графа. Этот
способ основан на простом приеме, называемом поиском
в ширину. Поиск в ширину следующим образом припи-
сывает вершинам рассматриваемого графа номера 0, 1,
2, . . . Начиная с произвольной вершины, приписываем
ей номер 0. Каждой вершине из окружения вершины 0
37
приписываем номер 1. Теперь рассматриваем поочеред-
но окружения всех вершин с номером 1 и каждой из
входящих в эти окружения вершин, еще не занумеро-
ванных, приписываем номер 2. Рассматриваем окруже-
ния всех вершин с номером 2 и т. д., пока возможно.
Если исходный граф G связен, то поиск в ширину за-
нумерует все его вершины.
Далее, разобьем множество VG па две части — А и
В, отнеся к А все вершины с четными номерами, а к
В — все остальные вершины, и рассмотрим порожденные
подграфы G(H) и G(B). Если оба они пусты (достаточ-
но проверить, что все пары вершин с равными номера-
ми пе смежны), то G=(A, В, Е) — двудольный граф.
В противном случае граф G пе является двудольным.
Простых способов распознавания /с-дольпости графа
при к > 2 нет.
Очевидно, что с помощью поиска в ширину можно
также решить следующие задачи:
1)	разбить множество вершин графа на его области
связности;
2)	для несовпадающих вершин и и и связного графа
найти кратчайшую (и, к)-цепь;
3)	в ориентированном графе найти множество всех
вершин, достижимых из заданной вершины v.
§ 10. Реберный граф
Пусть S — непустое множество, a F = {£i, S%, ...
..., SA — его покрытие непустыми несовпадающими под-
множествами. Определим граф Q(F) следующими усло-
виями: EQ(F) = F, вершины Si и S$ смежны, если
и Si П Sj =# 0. Произвольный граф G называется графом
пересечений, если и только если существуют такое мно-
жество S и такое покрытие этого множества F, что G =
^£>(F).
Утверждение 10.1. Любой граф является графом
пересечений.
> Пусть G — граф, VG = {1, 2, ..., п}, S — множество
элементов графа G. Для i = 1, п обозначим через Si мно-
жество, составленное из вершины i и всех инцидентных
ей ребер. Положив F = {S\, S2, ..., Sn}, получим G^
^Q(F). <
Важный класс графов пересечений составляют ребер-
ные графы. Для произвольного графа G реберный граф
L(G) определяется следующими двумя условиями:
38
1) 7G(G)=KG,
2) вершины e\ и e<i смежны в Z(G) тогда и только
тогда, когда ребра ei и е% смежны в G,
Если для некоторого графа Н существует такой
граф G, что H~L(G), то Н также называется реберным
графом.
На рис. 10.1 совмещены два графа — G и L(G). Вер-
шины графа G — темные кружочки, вершины графа
Рис. 10.1
Z(G) — светлые кружки. Ребра графа G — тонкие линии,
ребра графа Z(G)— жирные линии.
Утверждение 10.2. Если d\, d%, ..., dn — степен-
ная последовательность (п, т)-графа G, то L(G) явля-
ется (m, I)-графом, где
1 = di —т.
> Очевидно, что i-я вершина графа G порождает
рл Щ-1) dl-di
\2) =-----2------------
ребер графа L(G), поэтому
I = 4- 2 di---Т di = V dl — т. <
г=1	г=1	г=1
Очевидно, что если графы G и Н изоморфны, то L(G}
и L(H) также изоморфны. В то же время справедливы
соотношения £(/<з)^ £(/<^3) = 7к3. X. Уитни доказал, что
Кз и К1(з — единственная пара несовпадающих связных
графов, имеющих один и тот же реберный граф. Если по-
рядок хотя бы одного из рассматриваемых графов меньше
пяти, то это проверяется непосредственно, а для графов
больших порядков вытекает из следующей теоремы.
39
Теорема 10.3 (X. Уитни, 1932 г.). Пусть G и Н —
связные графы, IGI >4, \Н\ > 4 и L(G) = L(H). Тогда
G — II и, более того, для всякого изоморфизма ср: L(G)->
L(H) существует единственный изоморфизм гр: G -> Н,
индуцирующий ср, т. е. такой, что ф(е) = гр(и) гр(о) для
любого ребра е = ии графа G.
>	Изоморфизм <р реберных графов L(G) и L(H) бу-
дем рассматривать как биекцию EG -* ЕП между мно-
жествами ребер графов G и II, при которой смежным реб-
рам соответствуют смежные, а несмежным — несмежные.
Лемма 10.4. Если ребра ъ (i = 1, г) составляют
звезду К\ г в графе G, то их образы (p(et) составляют та-
кую же звезду К\ г в графе Н.
>	Доказательство леммы. При г = 2 утверж-
дение леммы верно по определению изоморфизма графов.
Пусть г=3и ребра е%, е$ составляют в графе G звез-
ду К1з. Поскольку граф G связен и порядок его более
четырех, то в нем есть четвертое ребро е, смежное с каж-
дым из ребер вг или точно с одним из них. Таким же свой-
ством обладает ф(е) по отношению к ф(вг). Ребра ф(е;)
составляют в графе Н либо звезду К\$, либо треугольник.
Но ребро, смежное с каким-либо ребром треугольника,
смежно ровно с двумя из ребер. Тем самым доказано, что
ребра <р(вг) составляют звезду в графе Н. Нужное ут-
верждение доказано для г = 3. Очевидно, что для г > 3
оно просто получается по индукции. <
Поскольку отображение ср-1: L(H)~+ L(G) также яв-
ляется изоморфизмом реберных графов, то из предыду-
щей леммы вытекает следующее утверждение: ребра
(i = 1, г) составляют максимальную (относительно вклю-
чения) звезду К\ г в графе G тогда и только тогда, когда
их образы ф(Сг) составляют максимальную звезду К\}Г в
графе Н.
Итак, изоморфизм ф определяет биекцию между мно-
жествами максимальных звезд графов G и Н. Очевидно,
что в каждой из этих звезд более одного ребра, и потому
в ней есть лишь одна центральная вершина. Максималь-
ную звезду графа G с центром х обозначим через SG(x).
Очевидно, что если ф(5е (х)) = SH (х'), то соответствие
гр: х х’ является инъекцией множества всех вершин
графа G, не являющихся концевыми, в аналогичное под-
множество вершин графа Н. Из соображений симметрии
следует, что гр — биекция.
Теперь распространим действие отображения гр на
концевые вершины графа G. Пусть v — одна из таких вер-
40
шин. В графе G есть смежная с ней вершина х степени
большей, чем 1. Положим xv == е и выберем в звезде
SH(x') такое ребро е' = x'v', что ф(е) = е'. Покажем, что
deg v' = 1.	(1)
Пусть это не так. Тогда в звезде Sn(v') есть ребро е1 =
= е'. Следовательно, в звезде qr1 (SH(v')) есть ребро
ех = ф-1(4)? смежное с ребром е, но пе входящее в
SG(x). Но тогда вершина v — конец этого ребра и deg v
=# 1. Равенство (1) доказано.
Положив ф(г?) = v', получим инъекцию множества кон-
цевых вершин графа G в множество концевых вершин
графа Я. Из соображений симметрии теперь следует, что
ф— биекция.
Итак, построена биекция ф: VG -> VH. Докажем, что
эта биекция является графовым изоморфизмом. Сохраним
обозначение SG(x) и в том случае, когда deg х = 1. В этой
ситуации 5G(x) содержит одно ребро, инцидентное вер-
шине х, и не является максимальной звездой. Смежность
вершин х и у в графе G означает, что звезды SG(x) и
SG(y) имеют общее ребро. Поэтому
(ху е EG) (х'у' е ЕН).
Доказано, что ф: G -> Н — изоморфизм графов. Из опре-
деления отображения ф видно, что оно индуцирует ф, т. е.
ф(е) = х'у' = ф(^)ф(г/) Для любого ребра e = xy^EG.
Существование нужного изоморфизма ф доказано.
Остается доказать единственность. Пусть, напротив,
есть два изоморфизма ф1 ¥= фг, удовлетворяющих условию
теоремы. Тогда ф1 (а) ¥= ф2 (а) для некоторой вершины
a^VG. Рассмотрим произвольное ребро е = ах в гра-
фе G, Тогда
ф1(а)ф1(х) = ф(е) = ф2(а)ф2(я),
и, следовательно, ф2 (х) = ф1 (а). Если deg а > 1 и ау —
другое ребро G, то аналогично получаем ф2(г/) = ф1 (а) =
= ф2(^), что противоречит инъективности фг. Если же
dega = l, то из ф2(х)= ф1 (а) получаем deg х = 1, что
противоречит связности G. <1
Известно, что не всякий граф является реберным, на-
пример, звезда Я1>3 не есть реберный граф. (Характери-
зация реберных графов имеется в книге [7].) Однако
класс реберных графов достаточно содержателен. Об этом
свидетельствует, в частности, тот факт, что гипотеза ре-
41
берной реконструируемое™ произвольных графов эквива-
лентна гипотезе вершинной реконструируемости реберных
графов. Приведем без доказательства следующую теорему.
Теорема 10.5 (Р. Хемминджер, 1969 г.). Связный
граф G с более чем тремя ребрами реберно реконструи-
руем тогда и только тогда, когда реберный граф L(G)
вершинно реконструируем.
Отметим еще любопытную связь, существующую меж-
ду матрицей инцидентности графа G и матрицей смеж-
ности реберного графа L(G).
Утверждение 10.6. Если I = 1(G) — матрица ин-
цидентности графа G и А = A(L(G))—матрица смежно-
сти графа L(G), записанная при той же, что и I, нуме-
рации ребер, то
Г1 = А + 2Е,	(2)
где Е — единичная матрица порядка |/?бг|.
> Рассмотрим элемент произведения 1Т1, занимающий
позицию (k, I):
р
Последняя сумма равна числу вершин графа G, инцидент-
ных обоим ребрам с номерами к и I. При к = I это число
равно 2. Если к ¥= I, то это число по определению есть эле-
мент Ам матрицы А. Равенство (2) доказано. <
Следствие 10.7. Любой корень характеристиче-
ского полинома всякого реберного графа не меньше,
чем —2.
> Пусть G — реберный граф. Тогда для него верно
равенство (2). С другой стороны, пусть Ах = Кх для не-
нулевого вектора х. Тогда 1т1х =(Х + 2)х (в силу равен-
ства (2)). Теперь рассмотрим квадрат длины вектора 1х:
\1х\2 = хт1Чх =	+ 2)хтх = (^ + 2) Iх12.
Следовательно, Z + 2 > 0, Z > — 2. <
§ И. Группа автоморфизмов графа
Характеристикой симметрии графа является его груп-
па автоморфизмов.
Произвольная подстановка ср на множестве вершин
графа G, сохраняющая отношение смежности, т. е. такая,
что образы ф(н) и ф(р) вершин и и v смежны тогда п
только тогда, когда смежны сами вершины и и v, назы-
вается автоморфизмом графа G.
42
Иными словами, автоморфизм графа — это изоморфизм
графа на себя.
Любой граф G имеет по меньшей мере один автомор-
физм — тождественное преобразование е: VG -> VG, при
котором e(y)=v для любой вершины и. Очевидно, что
если ф — автоморфизм графа G, то и обратная подстанов-
ка ф-1 также является автоморфизмом, если же подста-
новки ф и ф обе суть автоморфизмы, то и их произведение
фг|) — автоморфизм. Поэтому верно следующее (важное,
хотя и очевидное)
Утверждение 11.1. Множество всех автоморфиз-
мов графа относительно операции умножения подстановок
является группой.
Группа автоморфизмов графа G обозначается через
Aut G.
Очевидно также
Утверждение 11.2. Всякий автоморфизм графа
G является также автоморфизмом дополнительного гра-
фа G, т. е. Aut G = Aut G.	_
Поскольку среди двух графов G и G хотя бы один яв-
ляется связным, то в силу утверждения 11.2, когда мы
имеем дело с группой автоморфизмов, достаточно рассмат-
ривать лишь связные графы.
Введем важное понятие орбиты группы подстановок.
Пусть Г — произвольная группа подстановок на мно-
жестве V. Определим на V бинарное отношение —, поло-
жив и — v для и, v е V тогда и только тогда, когда в Г
существует такая подстановка s, что s(u)=v. Очевидно,
что отношение ~ является отношением эквивалентности
и, следовательно, множество V разбивается на классы эк-
вивалентных элементов: все элементы, входящие в один
класс, переводятся подстановками из группы Г друг в
друга, а элементы из разных классов друг в друга не пе-
реводятся. Эти классы называются орбитами группы Г.
Разбиение множества вершин графа G на орбиты груп-
пы Aut G — важная задача. В сущности, применение
к графу автоморфизма означает перенумерацию его вер-
шин, причем отношение смежности должно сохраняться.
Поэтому для любого автоморфизма ф у вершины графа v
и ее образа ф(у) «все одинаково» (степени равны, гра-
фы, порожденные окружениями, изоморфны и т. д.). Так
что орбиты группы Aut G это просто классы «одинако-
вых» вершин. Более того, известно, что проблема распоз-
навания принадлежности двух вершин произвольного гра-
фа одной орбите его группы автоморфизмов и проблема
43
изоморфизма графов эквивалентны в том смысле, что лю-
бой алгоритм, эффективно решающий одну из этих проб-
лем, может быть преобразован в эффективный алгоритм
для другой (см., например [18]). К сожалению эффек-
тивные алгоритмы для решения этих двух проблем не
известны (о том, какие алгоритмы считаются эффектив-
ными, см. гл. XII).
Трудно сказать что-либо определенное о строении
группы автоморфизмов произвольного графа. Она может
быть и «малой», и «большой». Найдем, например, Aut G
Рис. 11.1
для графа G, изображенного на рис. 11.1.
Очевидно, что любой автоморфизм либо
оставляет неподвижной вершину 1, либо
переставляет ее с вершиной 3. В любой
ситуации вершины 2 и 4 либо обе непод-
вижны, либо переводятся друг в друга.
Итак, Aut G состоит из четырех эле-
ментов: с, транспозиций (1,3) и (2,4) и
произведения этих транспозиций — (1,3) (2,4).
Очевидно, что каждый из двух графов, изображенных
на рис. 11.2, имеет лишь один автоморфизм — тождест-
венный. С другой стороны, очевидно, что группой авто-
морфизмов полного графа Кп является вся симметриче-
ская группа Sn.
С 1936 г. известен следующий вопрос Д. Кёнига:
какие конечные группы являются группами автоморфиз-
мов графов? Этот вопрос можно интерпретировать двоя-
ким образом. Первый вариант: какие конечные группы
Рис. 11.2
изоморфны группам автоморфизмов графов? На этот воп-
рос почти сразу же ответил Р. Фрухт (1938 г.).
Теорема Фрухт а. Каждая конечная группа изо-
морфна группе автоморфизмов некоторого графа.
> Пусть Г — группа порядка п > 1 (для п = 1 выше
приводились примеры). Построим граф G описанным ни-
же способом. В качестве исходного множества вершин
возьмем множество всех элементов группы Г. Каждую
упорядоченную пару (u, v) несовпадающих вершин сое-
диним простой цепью Puv длины 3, добавляя всякий раз
по две новые вершины аи„ и Ь UV- Puv (W) UuV) buv^ О ). За-
44
тем к каждой из вершин auv «приклеим» простую цепь
Р(а, и, v) длины I (а, и, и), все вершины которой, исклю-
чая auv,— новые. Аналогично построим цепи Р(Ь, и, р)
длины I (&, и, v). При этом будем соблюдать следующее
условие: длины всех цепей попарно различны всегда, кро-
ме случая, когда u~rv =	и. и, v\ Г. В послед-
нем случае должно быть
Z(a, и, v)=l(a, щ, щ), l(b, и, v)=l(b, щ, V\). (1)
Построенный таким образом граф обозначим буквой G.
(На рис 11.3 показаны соответствующие графы для
п == 2 и 3. В этой ситуации Г — циклическая группа:
Г ={щ v2 = е} при п = 2, Г = {щ v2, и3 = е} при п = 3.)
Докажем, что группы Aut G и Г изоморфны. Вначале
45
фиксируем в Г какой-либо элемент w и следующим обра-
зом определим отображение lw: VG -> VG. Для х е Г
Zw(^) = wx — произведение элементов группы; вершины
цепи Р(а, и, v) переводятся в вершины цепи
Р(а, wu, wv), причем сохраняется последовательность
вершин в цепи, т. е. lw(auv) = a(wu}{wv} и т. д.; аналогично
для цепи Р(&, wu, wv). Прямая проверка подтверждает,
что lw Aut G.
Теперь докажем равенство
Aut G = {Ц-. w е Г).	(2)
Пусть ф — произвольный автоморфизм графа G. Очевид-
но, что ф все концевые вершины и, следовательно, все це-
пи PUv переводит друг в друга. Поэтому автоморфизм
ф переставляет друг с другом вершины вида auv, а также
вершины вида buv. Следовательно, и элементы группы Г
переставляются друг с другом. При этом из условия (1)
следует, что если ф(и) = щ, ф(v) — щ, то u~rv = иг 1р1 для
всех и, v е Г. Из этого равенства, положив ф(е)= ш, по-
лучим q)(x)=wx для любого х е Г, т. е. ф = lw- Равен-
ство (2) доказано.
Далее, определим отображение ф: Г -> Aut G, поло-
жив ф(я)= 1Х для любого х е Г. Очевидно, что отображе-
ние г|) является изоморфизмом групп Г и Aut G. <1
Конструкция, приведенная в предыдущем доказатель-
стве, неэкономна в том смысле, что приводит к графам
с большим числом элементов. Как правило, эти графы
можно «уменьшить». Например, при п = 2, 3 вместо гра-
фов, приведенных на рис. 11.3, можно взять графы на
рис. 11.4. Группой автоморфизмов графа, показанного на
рис. 11.5, также является циклическая группа порядка 3.
Можно указать примеры групп подстановок, которые
хотя и изоморфны по теореме Фрухта группам автомор-
физмов графов, по сами таковыми не являются. Рассмот-
рим знакопеременную группу Ап, состоящую из всех чет-
ных подстановок (и > 3). Пусть Ап s Aut G. Легко заме-
46
тить, что группа Ап дважды транзитивна, т. е. для любых
Z, 7, A, I е VG, Z ¥= /, к Ф Z, в Ап существует такая подста-
новка ф, что ф(0== к, ф(/) = Если ф — автоморфизм не-
которого графа G, то в G либо любая пара вершин смеж-
на, т. е. G = Кп, либо любая пара вершин не смежна, т. е.
G = Оп. В обоих случаях Aut G = Sn¥= Ап.
Естественно возникает неизмеримо более сложный ва-
риант вопроса Д. Кёнига. Этот, по-видимому, далекий от
решения вариант известен как
Проблема Кёнига. Установить, какие условия
необходимы и достаточны, чтобы для заданной на множе-
стве У группы подстановок Г существовал такой граф G
с множеством вершин V, что Aut G = Г.
§ 12. «Почти все» графы
В этом параграфе приводятся некоторые результаты,
характеризующие свойства графов при большом числе
вершин, т. е. в асимптотике. Эти свойства формулируют-
ся в терминах «почти всех графов» и отражают тем самым
типичный случай.
Обозначим через S? (п) множество всех помеченных
простых графов с множеством вершин V = {1, 2, ..., п}.
(П\
Как отмечалось в § 1,	(п) \ = 2К2 .
Пусть Р — некоторое свойство, которым каждый от-
дельно взятый граф из S? (п) может обладать или не об-
ладать. Через $Р{п) обозначим множество тех графов из
&(п), которые обладают свойством Р. Будем говорить, что
почти все графы {почти каждый граф} обладают свойст-
вом Р, если
lim | Р (п) |/| (п) | = 1,
П-»оо
и почти пет графов, обладающих свойством Р, если
lim | $Р (п) |/| $ (га) | = 0.
П-»оо
Ясно, что если почти все графы обладают свойством Р,
то почти нет графов, не обладающих свойством Р.
К настоящему времени получены результаты о боль-
шом количестве свойств графов в терминах «почти всех
графов». Приведем некоторые из этих результатов.
Теорема 12.1. Почти все графы связны.
> Обозначим через ^св(^) множество связных графов
из а через <3&{п)— множество тех графов из S’(n),
47
в каждом из которых имеется по крайней мере одна ком-
понента порядка в. Тогда справедливо неравенство
[п/2]
2 1^)1-	(1)
S—1
Далее рассмотрим следующий прием построения
графов:
1) множество V разбиваем па подмножества V\ и Рг,
где IVJ = s, IV2I = n — s (таких разбиений имеется п));
\5 / )
2) образуем всевозможные графы на множестве вер-
шин Vi и всевозможные графы на множестве вершин V2.
В результате второй операции получим
£ ---------------------
различных графов. Резюмируя, имеем
(2)
/п\
Так как | (м) | = 2V2 , то из неравенств (1) и (2) сле-
дует, что
[п/2]
1 - 2	(3)
8—1
где /(5) = (sj2-s(”-s).
Рассматривая отношение /($+!)//($), убеждаемся
в том, что на отрезке [1, [п/2]] функция f(s) убывает.
Поэтому
1>/2]	2
2 /(«)<!/«)-о,
8=1
откуда на основании (3) заключаем, что теорема 12.1
верпа. <
Теорема 12.2. Диаметры почти всех графов рав-
ны 2.
Для доказательства этой теоремы понадобится следую-
щее очевидное
Утверждение 12.3. Число всех графов из 3 (п),
в каждом из которых зафиксированы одни и те же г ре-
бер и одновременно отсутствуют к других фиксированных
ребер, равно 2х
48
> Доказательство теоремы 12.2. Прежде
всего заметим, что диаметр почти каждого графа не мень-
ше 2, поскольку только полный граф имеет диаметр 1.
Теперь убедимся, что диаметр почти каждого графа не
может быть больше 2. В множестве V фиксируем верши-
ну и непустое подмножество U с= V, удовлетворяющее
следующим двум условиям: 1) v\ U; 2) г=|С7|^
п — 2. Положим W = V\(U U vi) и выберем вершину
v s W. Рассмотрим множество	всех графов из
^(тг), в которых окружение вершины щ совпадает с U,
а вершина v не смежна ни с какой вершиной из U. Для
графов из этого множества есть г обязательных ребер и
п — 1 запрещенных. Согласно утверждению 12.3
|^v(n)| = 2^“r~n+1.
Для выбора вершины v в множестве W есть п — г — 1
возможностей. Если теперь
‘SuvAn)= U
1 v^W 1
ТО
—г — 1) | (тг) | =
/	4\o(2)~r~n + 1	o(2)_’r~n+1
= (n — r — 1)2V2/	<n2V2/
Пусть, далее,
W =7= U fa),
1 U 1
где в качестве U фигурирует каждое из подмножеств мно-
жества V, удовлетворяющее указанным выше условиям
1) и 2). При фиксированном r = \ U\ для выбора множе-
/ п — 1 \
ства U есть	I вариантов, поэтому
4 в. А. Емеличев и др.
49
Далее используем формулу бинома Ньютона: для лю-
бых чисел а и Ъ и натурального п верно равенство
(a + b)n= X
7=0 V ‘
^здесь (q) = 1^. Согласно этой формуле
Поэтому из (4) вытекает
Обозначив
^'(n)= U $vAn),
iy=y 1
имеем
|^'(re)|<72|^i(«)|<ZZ22^ П + 7у)П 1
Далее получаем
lim
П-»оо
I r (n)l
I (га) I
= lim re2
тг-»оо
1Г'-0
I
В то же время легко видеть, что если <S" (п)— множе-
ство графов с диаметром более 2, то	(п) • Дей-
ствительно, возьмем произвольный n-вершинный граф G,
диаметр которого не менее 3. В нем существуют хотя бы
две вершины щ и р, расстояние между которыми равно
трем. Очевидно, что G	гДе U==Ng(vi). По-
этому S" — Итак, почти нет графов с диамет-
ром более 2, что и доказывает теорему. <1
Следствие 12.4. Радиус почти каждого графа сов-
падает с диаметром этого графа и равен 2.
> Очевидно, что r(G)^d(G) для любого графа G.
Поэтому достаточно показать, что почти нет графов ра-
диуса 1. Рассмотрим множество ^'(м) графов из З’(м),
в которых степень фиксированной вершины v равна п — 1.
Имеем
|^'(п)| = 2^ 2^ = 2^2^ п+\
50
откуда получаем, что число графов из ^(п), максималь-
ная степень вершин которых равна п— 1, не превосходит
oG)-"*1 тт	у
числа пЛ . Но это означает, что почти нет графов,
среди вершин которых есть хотя бы одна доминирующая.
Поэтому почти нет графов радиуса 1, так как всякий граф
радиуса 1 содержит хотя бы одну доминирующую вер-
шину. <
Теорема 12.5. Почти все графы имеют единствен-
ную вершину максимальной (минимальной) степени.
Теорема 12.6. Группа автоморфизмов почти каж-
дого графа совпадает с единичной группой.
Доказательства этих теорем можно найти, например,
в обзоре [21].
УПРАЖНЕНИЯ
1.	Пусть G и II — два графа. Докажите, что если G Н, то
и II G.
2.	Найдите все попарно пеизоморфпые графы пятого порядка.
3.	Докажите, что три графа, изображенные па рис. 1.10, изо-
морфны, а графы па рис. 1.11 не изоморфны.
4.	Найдите число помеченных (и, тп)-графов.
5.	Докажите, что если порядок самодополпитслыюго графа
равен п, то п == 0 (mod 4) или п = 1 (mod 4).
6.	Докажите, что не все графы с тремя ребрами реберпо ре-
конструируемы.
7.	Найдите самодополнительный граф с минимальным отлич-
ным от 1 числом вершин.
8.	Докажите, что для любых натуральных чисел п, т и к, удов-
летворяющих условиям
[n — k-\-i\
i^Lk^Ln, n — k^.m^l 2 h
существует (n, m) -граф, имеющий ровно к компонент.
9.	Докажите, что если число ребер графа порядка п >* 2 боль-
(п — 1\
ше, чем I 2 I, то он связен.
10.	Докажите, что в связном графе любые две простые цепи
максимальной длины имеют общую вершину.
И. Докажите, что не существует графа, степени всех вершин
которого попарно различны.
12.	Докажите, что если 6(G) (и — 1)/2, то граф G связен.
13.	Нарисуйте все попарно неизоморфные кубические графы
восьмого порядка.
14.	Пусть Gn — граф, множество вершин которого совпадает с
отрезком натурального ряда {1, 2, ..., п}, а множество ребер оп-
ределяется следующим условием: несовпадающие вершины и и v
смежны тогда, когда числа и и v взаимно просты.
а)	Запишите матрицу смежности графа G§.
б)	Является ли граф Gn связным?
4*
51
в)	Докажите, что при т < п граф Gm является порожденным
подграфом графа Gn.
15.	Докажите, что элемент матрицы (A(G))h, занимающий по-
зицию (i, j), равен числу (г, /)-маршрутов длины к в графе G.
16.	Постройте граф, центр которого:
а)	состоит ровно из одной вершины;
б)	состоит ровно из трех вершин и не совпадает с множеством
всех вершип;
в)	совпадает с множеством всех вершин.
17.	Докажите, что два графа, изображенные на рис. 6.2, ко-
спектральпы.
18.	Матрица называется вполне унимодулярной, если каждый
ее минор равен 1, —1 или 0. Докажите, что матрицы инцидентно-
сти двудольного графа и ориентированного графа вполне упимо-
дулярпы.
19.	Докажите, что диаметр графа не превосходит его удвоенно-
го радиуса.
20.	Приведите пример графа, диаметр и радиус которого равны.
21.	Докажите, что (и, т)-граф связен, если в нем отсутст-
вуют циклы нечетной длипы и пг > (п— 1) 2/4.
22.	Является ли граф, изображенный па рис. 1.1, двудольным?
23.	Найдите расстояние d(u, и) в графе, изображенном па
рис. 1.2.
24.	Докажите, что при п > 2 звезда К^п не является ребер-
ным графом.
25.	Найдите группы автоморфизмов графа, изображенного на
рис. 11.5, простой цепи Рп, простого цикла Сп и графа Петерсена.
Докажите, что группа автоморфизмов графа Петерсена изоморфна
симметрической группе 5s.
26.	Найдите граф минимального порядка, отличного от 1, с
тождественной группой автоморфизмов.
27.	Докажите, что число помеченных графов, изоморфных не-
которому графу G порядка и, равно n!/| Aut (7|.
28.	Сколько помеченных графов порождают простая цепь Рп
и простой цикл Сп?
Глава II
Деревья
Как показано в § 4, среди графов с фиксированными
порядком и числом компонент лишь один имеет макси-
мальное число ребер. Другой крайний случай — мини-
мальное число ребер — приводит к большому классу гра-
фов. Наиболее важными среди них являются связные гра-
фы, которые называются деревьями. Класс деревьев зани-
мает в теории графов особое положение. С одной сторо-
ны, это достаточно просто устроенные графы, и многие
задачи, весьма сложные в общей ситуации, для деревьев
решаются легко. Доказано, например, что все деревья ре-
конструируемы; несложно распознается изоморфизм де-
ревьев. С другой стороны, деревья часто встречаются в об-
ластях, на первый взгляд не имеющих отношения к тео-
рии графов.
Деревья открывались независимо несколько раз. Еще
в прошлом веке Г. Кирхгоф ввел деревья и применил их
к исследованию электрических цепей, а А. Кэли, пере-
числяя изомеры насыщенных углеводоров, еще раз от-
крыл деревья и первым исследовал их свойства. Тогда же
деревья были введены и исследованы К. Жорданом как
чисто математический объект.
§ 13.	Определение дерева
Деревом называется связный граф, не содержащий
циклов. Любой граф без циклов называется ациклическим
(или лесом). Таким образом, компонентами леса являют-
ся деревья. На рис. 13.1 изображены все деревья шестого
порядка.
Существует несколько вариантов определения дерева;
некоторые из них отражены в следующей теореме.
Теорема 13.1. Для (п, т)-графа G следующие ут-
верждения эквивалентны:
1)	G — дерево,
2)	G — связный граф и m = п — 1;
53
3)	G — ациклический граф и т = п - 1;
4)	любые две несовпадающие вершины графа G соеди-
няет единственная простая цепь;
5)	G — ациклический граф, обладающий тем свой-
ством, что если какую-либо пару его несмежных вершин
соединить ребром, то полученный граф будет содержать
ровно один цикл.
> 1) => 2) Воспользуемся индукцией по п. При п = 1
утверждение тривиально. Пусть тз>1, e^EG, В дере-
ве G пет циклов, следовательно, согласно лемме 4.8, граф
Рис. 13.1
G — е имеет ровно две компоненты. и Т%, каждая из
которых есть дерево. Пусть дерево Ti является (гц, тг)-
графом, I = 1, 2. По индуктивному предположению верно
равенство
Шг = Пг — 1.	(1)
Далее имеем
Ш = 7П1 + ТП2 + 1 =(П1 — 1) + (п2 — 1)+ 1 =
= (ni + тг2) — 1 = п — 1.
2)	=> 3) Граф G связен и пг = п — 1. Нужно доказать,
что в G нет циклов. Пусть, напротив, в графе G есть цикл
и пусть е — ребро этого цикла. Тогда граф G — е связен
(лемма 4.8) и имеет п — 2 ребра, что противоречит теоре-
ме 4.9. Следовательно, G — ациклический граф.
3)	=> 4) Пусть к — число компонент графа G. Пусть,
далее, компонента Ti является (иг-, тг)-графом. Так как
Ti —дерево, то верно равенство (1). Теперь имеем
п — 1 = m = тп\ + ТП2 + ... + тк =
==(^1 - 1) + (гс2 ~ 1)+ ... +{пк - 1) =
= (пх + .. . + nk) — к = п — к,
т. е. к « 1. Итак, G — связный граф и потому любые не-
54
совпадающие вершины и и и соединены в нем простой
цепью. Если бы в G были две несовпадающие простые
(и, р)-цепи, то согласно утверждению 4.3 их объедине-
ние содержало бы цикл. Следовательно, каждые две вер-
шины соединены единственной простой цепью.
4)	=> 5) Пара несовпадающих вершин, принадлежащих
одному циклу, соединена по меньшей мере двумя просты-
ми цепями. Следовательно, граф G ациклический. Пусть
и и v — две его несмежные вершины. Присоединим к гра-
фу G ребро е = ии, В G есть простая (и, р)-цепь, кото-
рая в G + е дополняется до цикла. В силу утвержде-
ния 4.4 этот цикл единственный.
5)	=> 1) Нужно доказать, что граф G связен. Если бы
вершины и и v принадлежали разным компонентам гра-
фа G, то граф G + uv не имел бы циклов, что противоре-
чит утверждению 5). Итак, G связен и потому является
деревом. <1
Следствие 13.2. В любом дереве порядка п^2
имеется не менее двух концевых вершин,
> Пусть
di, с?2, ..dn	(2)
— стспеппая последовательность дерева. Тогда
2 di = 2(га —1)
1=1
(лемма о рукопожатиях) и все di > 0. Следовательно, хо-
тя бы два числа из последовательности (2) равны 1. <1
Пусть Н — остовный подграф произвольного графа G,
Если на каждой области связности графа G графом Н по-
рождается дерево, то Н называется остовом (или карка-
сом) графа G, Очевидно, что в каждом графе существует
остов: разрушая в каждой компоненте циклы, т. е. уда-
ляя лишние ребра, придем к остову. Остов в графе легко
найти с помощью поиска в ширину.
Следствие 13.3. Число ребер произвольного гра-
фа G, которые необходимо удалить для получения осто-
ва, не зависит от последовательности их удаления и рав-
но m(G)~\G\ + k(G), где m(G) и k(G)—число ребер
и число компонент графа G соответственно,
> Если (п\, mi)-граф Н является одной из компонент
графа G, то для превращения ее в остовное дерево нуж-
но удалить 7/71—(т71 —1) подходящих ребер. Суммируя
по всем k(G) компонентам, получим требуемое. <1
55
Число v(G) = m(G) — |G| + k(G) называется цикли-
ческим рангом (или цикломатическим числом) графа G.
Число v*(G) = 1б?1 —k(G) ребер любого остова графа G
называется коциклическим рангом графа G. Таким обра-
зом, v(G)+ v*(C?)= m(G).
Очевидны три следствия 13.4—13.6.
Следствие 13.4. Граф G является лесом тогда и
только тогда, когда v(G) = 0.
Следствие 13.5. Граф G имеет единственный цикл
тогда и только тогда, когда v(G)= 1.
Следствие 13.6. Граф, в котором число ребер не
меньше, чем число вершин, содержит цикл.
В гл. III окажутся полезными утверждения 13.7, 13.8.
Утверждение 13.7. Всякий ациклический под-
граф произвольного графа G содержится в некотором ос-
тове графа G.
> Пусть Н — ациклический подграф в G. Очевидно,
что достаточно рассмотреть ситуацию, в которой Н — ос-
товный подграф и G связен. Если теперь Н не является
остовом, то он несвязен. Пусть А — одна из областей связ-
ности графа Н. В графе G есть такое ребро аЪ, что а е А,
Ъ е VH\A. Граф Н + аЪ — ациклический остовный под-
граф графа G, имеющий меньше, чем Н, компонент. По-
вторяя аналогичное построение, доберемся до дерева, т. е.
до остова, содержащего граф Н. <
Утверждение 13.8. Если S и Т—два остова гра-
фа G, то для любого ребра е\ графа S существует такое
ребро в2 графа Т, что граф S — e\ + ez также является
остовом.
> Не ограничивая общности, будем считать граф G
связным. Граф S — е{ имеет ровно две области связно-
сти; пусть это будут А л В. Поскольку граф Т связен, то
в нем существует ребро в2, один из концов которого входит
в А, а другой — в В. Граф Н = S — е{ + е^ связен и чис-
ло ребер в нем такое же, как в дереве S. Следова-
тельно, он сам является деревом. Итак, Н — остов гра-
фа G. <
Очевидно, что два предыдущих утверждения об осто-
вах (13.7 и 13.8) сохраняются для произвольного псевдо-
графа.
Докажем еще следующую теорему.
Теорема 13.9. Центр любого дерева состоит из од-
ной или из двух смежных вершин.
> Очевидно, что концевые вершины дерева Т являют-
ся центральными только для Т = К\ или Т = К^.
56
Пусть Т — дерево порядка п > 2. Удалив из Т все
концевые вершины, получим дерево Т'. Очевидно, что экс-
центриситет Т' на единицу меньше эксцентриситета дере-
ва Т и что центры деревьев Т и Т' совпадают. Далее до-
казательство легко проводится индукцией по числу вер-
шин. <1
§ 14. Матричная теорема Кирхгофа
Как уже отмечалось, в каждом графе имеется остов.
В общем случае остов определен неоднозначно. Естествен-
но возникает вопрос: как много остовов в графе? Очевид-
но, что при ответе на этот вопрос достаточно ограничить-
ся случаем связного графа. В связном графе остовом
служит любое остовное дерево, т. е. остовный подграф,
являющийся деревом. Число остовов в связном графе
определяется в неявной форме следующей теоремой.
Теорема Кирхгофа (1847 г.). Число остовиых
деревьев в связном графе G порядка п^ 2 равно алгеб-
раическому дополнению любого элемента матрицы Кирх-
гофа B(G).
Доказательство опирается на следующую лемму.
Лемма 14.1. Пусть H — (pn+i, т)-граф, I — мат-
рица инцидентности какой-либо его ориентации, М — про-
извольный минор порядка ш матрицы I. Тогда:
1) если Н — дерево, то М = ± 1;
2) если Н не является деревом, то М = 0.
> Доказательство леммы. Прежде всего за-
метим, что можно произвольно менять нумерации вершин
и ребер графа Н, от этого рассматриваемый минор может
лишь изменить знак.
Пусть а — вершина, соответствующая строке матри-
цы I, не вошедшей в минор М. Если граф Н не является
деревом, то он несвязен. Пусть 7£ = {1, 2, . . ., к} — его
область связности, не содержащая вершины а. С помощью
подходящей перенумерации ребер графа Н матрицу I
приведем к клеточно-диагональному виду I = diag [Zj, 12],
где 7i — матрица инцидентности компоненты Н(К). Ми-
нор М содержит все первые к строк матрицы I, сумма
которых равна нулевой строке. Следовательно, М = 0.
Пусть теперь Н — дерево. Заново перенумеруем вер-
шины и ребра графа Н следующим образом. Одной из кон-
цевых вершин v, отличных от вершины а, а также ребру,
инцидентному вершине v, присвоим номер 1. Далее рас-
смотрим дерево Т\ = Н — и. Если его порядок больше 1,
то одной из его концевых вершин и, отличных от а,
а также инцидентному ей ребру присвоим номер 2. Рас-
смотрим дерево Т2 = Т\ — и. Итерируя этот процесс, по-
лучим новые нумерации вершин и ребер дерева Я, при-
чем вершина а будет иметь номер m + 1. Матрица I при
этом примет вид
-±1	0...	о”
*	± 1 ...	0
*	* ...	+	1
__ *	* ...	*_
(Здесь и в дальнейшем символом * будут обозначаться
те элементы или блоки матрицы, значения которых не
влияют на ход рассуждений.) Минор М, остающийся пос-
ле удаления последней строки этой матрицы, равен ±1. <
Еще один факт, используемый при доказательстве тео-
ремы Кирхгофа,— формула Бинэ — Коши, которую мы
приведем без доказательства. Пусть А и В — пХ тп- и
m X n-матрицы соответственно, С = АВ и п^ш. Минор
порядка п матрицы В назовем соответствующим минору
порядка п матрицы Л, если множества номеров строк пер-
вого из них и номеров столбцов второго совпадают.
Формула Бинэ — Коши. Определитель матри-
цы С равен сумме произведений каждого минора порядка
п матрицы А на соответствующий минор матрицы В.
> Доказательство теоремы Кирхгофа.
Пусть I — матрица инцидентности какой-либо ориентации
(п, т) -графа G. Согласно утверждению 6.4 верно равен-
ство
B(G) = IIT.	(1)
Поскольку G — связный граф, то т > п — 1. Если В —
подматрица, остающаяся после удаления из B(G) послед-
них строки и столбца, а С — подматрица, остающаяся по-
сле удаления из I последней строки, то в силу (1) В =
= ССТ. Алгебраическое дополнение Апп элемента, зани-
мающего в матрице B(G) позицию (п, тг), равно det В.
Из формулы Бинэ — Коши теперь следует, что Апп равно
сумме квадратов всех миноров порядка п — 1 матрицы С.
Согласно лемме 14.1 каждый такой минор М равен ±1,
если остовный подграф графа G, ребра которого соответ-
ствуют столбцам, вошедшим в М, является деревом, и ну-
лю в противном случае. Следовательно, Лпп равно числу
остовных деревьев в графе G. Поскольку алгебраические
дополнения всех элементов матрицы B(G) равны (ут-
верждение 6.2), то теорема доказана. <
58
Следствие 14.2. Для числа компонент п-вершин-
ного графа G верно равенство
k(G)=n-w&B(G).
> Если граф G связен, то в нем есть остовпое дерево.
Согласно предыдущей теореме rank B(G) > п — 1. С дру-
гой стороны, всегда det 5 (б?) =0. Следовательно,
rank 5(G) = п — 1.
Пусть теперь граф G имеет ровно к компонент. Тогда
при подходящей нумерации вершин матрицей B(G) слу-
жит клеточно-диагональная матрица diag[5i, #2, ..Bk],
диагональные клетки которой Bi являются матрицами
Кирхгофа соответствующих компонент. Учитывая уже до-
казанное, имеем rank В (G) = п — к. <
Следствие 14.3. При п > 1 число остовов в пол-
ном графе Кп равно пп~2.
> Рассмотрим алгебраическое дополнение Ац эле-
мента матрицы
В(Кп) =
п — 1	— 1 ... — 1
— 1 п — 1 . . . — 1
_ — 1	—1 п — 1_
занимающего позицию (1, 1). Оно равно определителю
п — 1	— 1 ...	— 1
— 1 п — i ... — 1
— 1	— 1 ... п — 1
порядка п — 1. Далее имеем
1	1 • • г 1
— 1 п — 1 .. / — 1
— 1	— 1 ... п — 1
Очевидно, что число остовов в Кп равно числу поме-
ченных деревьев порядка п. Поэтому предыдущее след-
ствие можно сформулировать в виде следующей теоремы,
впервые полученной А. Кэли в 1897 году.
Теорема Кэли. Число помеченных деревьев по-
рядка п равно пп~2.
§ 15. Остов минимального веса
Рассмотрим следующую задачу: во взвешенном связ-
ном графе требуется найти остов минимального веса. Эта
задача возникает при проектировании линий электропе-
редачи, трубопроводов, дорог и т. п., когда требуется за-
59
данные центры соединить некоторой системой каналов
связи так, чтобы любые два центра были связаны либо
непосредственно соединяющим их каналом, либо че-
рез другие центры и каналы, и чтобы общая длина (или,
например, стоимость) каналов связи была минимальной.
В этой ситуации заданные центры можно считать верши-
нами полного графа с весами ребер, равными длинам (сто-
имости) соединяющих эти центры каналов. Тогда иско-
мая сеть будет кратчайшим остовным подграфом полного
графа. Очевидно, что этот кратчайший остовный подграф
должен быть деревом. Поскольку полный граф Кп содер-
жит пп~2 различных остовных деревьев, то решение этой
задачи «слепым» перебором вариантов потребовало бы
чрезвычайно больших вычислений даже при относитель-
но малых п. Однако для ее решения имеются эффектив-
ные алгоритмы. Опишем два из них — алгоритмы
Дж. Краскала (1956 г.) и Р. Прима (1957 г.), примени-
мые к произвольному связному графу.
Задача об остове минимального веса
(о кратчайшем остове): в связном взвешенном
графе (G, w) порядка п найти остов минимального веса.
Алгоритм Краскала, решающий эту задачу, заключа-
ется в следующем.
1. Строим граф Т\ = Оп + ех, присоединяя к пустому
графу па множестве вершин VG ребро е\^ EG минималь-
ного веса.
2. Если граф Ti уже построен и i< п~ 1, то строим
граф Ti+x = Ti + ei+x, где ем — ребро графа G, имеющее
минимальный вес среди ребер, не входящих в Ti и не со-
ставляющих циклов с ребрами из Ti.
Следующая теорема утверждает, что алгоритм Краска-
ла всегда приводит к остову минимального веса.
Теорема 15.1. При i < п — 1 граф Ti+\ можно по-
строить. Граф Тп-\ является остовом минимального веса
в графе (G, w).
> Граф Ti имеет ровно i ребер и потому при i < п — 1
является несвязным. А так как граф G связен, то в нем
есть по меньшей мере одно ребро, не составляющее цик-
лов с ребрами графа Tit Итак, нужное ребро ei+i суще-
ствует и граф Ti+i можно построить.
Рассмотрим граф Тп-1- Поскольку Tn~i является
(п, п~ 1)-графом без циклов, то согласно теореме 13.1
это дерево. Остается доказать, что вес дерева Тп_\ мини-
мален. Предположим, что это не так, и среди всех остовов
графа G минимального веса выберем такой остов Т, ко-
60
торый имеет с деревом Тп_\ максимальное число общих
ребер. Пусть ei = ab — ребро дерева Тп-\, не содержа-
щееся в Т и имеющее минимальный номер среди ребер
дерева Тп-\, не входящих в Т (напомним, что в процессе
построения дерева Тп-\ его ребра получили номера 1,2,..
..., п— 1). В дереве Т есть простая (а, 6)-цепь. Присое-
динив к ней ребро получим цикл. В этом цикле есть
ребро е, не входящее в дерево Тп-\- Заменив в дерево Т
ребро е на получим новый остов Т' = Т — е + eit Но
Т—остов минимального веса, следовательно,	—
— w(T) + w(et)— w(e)^ т. e.
w^i)^ w(e).	(1)
С другой стороны, присоединяя ребро е к Тг—х (при i = 1
полагаем Ti-i = On), мы не получим цикла, поскольку
ребра ei, 62, ..вг-i, е входят в дерево Т, и потому, если
бы вес w(ei) был больше, чем ш(е), мы взяли бы при
построении дерева Ti ребро е вместо eit Из (1) теперь
следует, что w (е*) = w (е), w{Tf) = w(T).
Итак, Т' — остов минимального веса. Число ребер,
общих для деревьев Т' и Тп_i, больше, чем число ребер,
общих для Т и Тп-\, что противоречит выбору дерева Т.
Полученное противоречие и доказывает теорему. <1
В качестве иллюстрации рассмотрим взвешенный граф,
изображенный на рис. 15.1, а. Полагаем щ —{1, 4}, е% =
= {4, 5}. Среди оставшихся ребер минимальный вес име-
ет, например, ребро {1, 5}. Однако оно не пригодно для
построения, поскольку составляет цикл с двумя предыду-
щими ребрами. Можно взять ез = {2, 3}, 64 = {2, 5}. Итак,
ребра {1, 4}, {4, 5}, {2, 3}, {2, 5} составляют остов мини-
мального веса (рис. 15.1,6)).
Алгоритм Прима отличается от алгоритма Краскала
только тем, что на каждом этапе строится не просто ацик-
лический граф, но дерево. Именно:
1. Выбираем ребро е\ = ab минимального веса и стро-
им дерево полагая VT\ = {а, &}, ETi = {ei).
61
2. Если дерево Ti порядка i + 1 уже построено
и Кп — 1, то среди ребер, соединяющих вершины этого
дерева с вершинами графа G, не входящими в Th выбира-
ем ребро ei+i минимального веса. Строим дерево при-
соединяя к Тг ребро ei+\ вместе с его не входящим в Ti
концом.
Для этого алгоритма также верпа теорема 15.1, дока-
зательство которой аналогично приведенному выше.
В некоторых ситуациях требуется построить остов не
минимального, а максимального веса. К этой задаче так-
же применимы и алгоритм Краскала, и алгоритм Прима.
Следует только всюду минимальный вес заменить мак-
симальным.
С задачей об остове минимального веса тесно связана
задача Штейнера. Первоначально она формулировалась
как следующая
Евклидова задача Штейнера: произволь-
ное множество U точек евклидовой плоскости требуется
соединить непрерывными линиями так, чтобы любые две
точки были связаны либо непосредственно соединяю-
щей их линией, либо через другие точки и соединяю-
щие их линии, и чтобы сумма длин линий была мини-
мальной.
Множеству точек U можно поставить в соответствие
полный граф Х(С7), вершинами которого будут элемен-
ты С7, а вес каждого ребра будет равен расстоянию меж-
ду соответствующими точками.
Евклидова задача Штейнера отличается от задачи по-
строения остова минимального веса в графе K(U) тем,
что в этот граф разрешается вносить новые вершины —
точки Штейнера. Их можно добавлять столько, сколько
потребуется, чтобы дерево, их соединяющее, имело мини-
мальный вес.
Если в предыдущей задаче в качестве расстояния меж-
ду точками (яд, yi) и (^2, У2) взять величину |яд —	+
+ l^i — Z/2I, то получится прямоугольная задача Штейнера.
Эта задача сводится к следующей широко известной
задаче.
Задача Штейнера па графах. В связном
взвешенном графе G с выделенным подмножеством вер-
шин U VG требуется найти связный подграф Г, удов-
летворяющий следующим двум условиям:
1) множество VT содержит заданное подмножество Е7;
2) граф Т имеет минимальный вес среди всех под-
графов, удовлетворяющих условию 1).
62
Очевидно, что искомый подграф является деревом. Он
называется деревом Штейнера.
Очевидно также, что задача построения дерева Штей-
нера эквивалентна задаче нахождения остова минималь-
ного веса в порожденных подграфах графа G, множества
вершин которых содержат U.
Какие-либо эффективные алгоритмы, решающие зада-
чу Штейнера, неизвестны.
УПРАЖНЕНИЯ
1.	Нарисуйте все попарно пеизоморфпые деревья седьмого
порядка.
2.	Найдите дерево минимального порядка и > 2 с тождествен-
ной группой автоморфизмов.
3.	Докажите, что центр дерева состоит из одной вершины в
случае, когда диаметр этого дерева является четным числом, и из
двух смежных вершин, когда диаметр — число нечетное.
4.	Докажите, что радиус r(G) и диаметр d(G) любого дерева
G связаны соотношением
r(G) =]d(G)/2[.
5.	Верно ли, что если диаметр связного графа G равен к
(к > 2), то в G существует остовпое дерево, диаметр которого так-
же равен /с?
6.	(п, т)-граф называется сбалансированным, если никакой
его подграф пе имеет вершин степени большей, чем 2т/п. Пока-
жите, что всякое дерево при п > 2 — несбалансированный граф.
7.	Найдите остовные деревья в К$, К3,3 и в графе Петерсена.
8.	Докажите, что подграф Н графа G является в G остовом
тогда и только тогда, когда верны равенства |Я| = |G|, т(Н) =
= |G| — k(G), k(H) = k(G).
9.	Используя матричную теорему Кирхгофа, найдите число
остовных деревьев в полном двудольном графе Кт,п.
10.	Докажите, что число помеченных двудольных деревьев с
числами вершин в долях тип равно тп-1пт-1.
И. Покажите, как найти остов графа с помощью поиска в
ширину.
12.	Постройте такое множество U точек на плоскости, для ко-
торого вес дерева Штейнера был бы меньше веса любого остовпого
дерева графа K(U).
Глава III
Матроиды и трансверсали
В этой главе вводится повый комбинаторный объект —
матроид, появляющийся в результате обобщения хорошо
известного читателю понятия линейной зависимости. Хо-
тя понятие «матроид» возникло относительно давно,—
в 30-е годы нашего столетия (впервые это понятие ввел
X. Уитпи)—место теории матроидов в математике и, тем
более, в математическом образовании первоначально не
было осознано. Теперь же, когда открываются все новые
и новые классы матроидов, объединяющая роль идеи мат-
роида, позволяющая с возрастающим успехом применять
к решению комбинаторных проблем методы алгебры, ста-
новится все более ясной.
Для пас матроиды интересны, прежде всего, по двум
причинам. Первая — их связь с теорией графов. Факти-
чески, именно соответствие между некоторыми теоретико-
графовыми и алгебраическими понятиями привело к со-
зданию теории матроидов. Вторая причина состоит в том,
что задачи оптимизации па матроидных структурах ре-
шаются с помощью простого, так называемого «жадного»
алгоритма, который является обобщением алгоритма Кра-
скала для нахождения остовного дерева минимального
веса в связном взвешенном графе (§ 15). «Жадный» ал-
горитм изучается в этой главе.
§ 16. Азбука теории матроидов
Известно несколько эквивалентных друг другу опре-
делений матроида. Эти определения различаются тем, что
учитывают различные свойства независимости. Начнем
с определения, основанного на свойствах максимальных
независимых множеств — баз.
Матроидом М называется пара (Е, &), где Е — конеч-
ное непустое множество, а $ (или ^(71/)) — непустое
множество его подмножеств (называемых базами), удов-
летворяющее следующим двум условиям (аксиомы баз).
64
В.1. Никакая из баз не содержится в другой базе.
В.2. Если В\ и 52 — базы, то для любого элемента
b^Bi существует такой элемент с^52, что (5ДЬ)и с —
также база.
Элементы множества Е называются элементами мат-
роида М. Число |5| называется порядком матроида М.
Понятие матроида является естественным обобщением
понятия линейной независимости. А именно, если Е —
конечная система векторов некоторого линейного про-
странства, содержащая ненулевой вектор, то в Е суще-
ствует максимальная линейно независимая подсистема —
база системы Е. Напомним, что все базы системы Е удов-
летворяют аксиомам баз В.1 и В.2. Следовательно, всякая
такая система вместе с ее базами является матроидом.
Этот матроид называется векторным.
Очевидно, что в обозначениях аксиомы В.2 либо Ъ <= В2
и тогда можно взять с = Ь, либо с^В2\В\, иное противо-
речило бы аксиоме В.1. Поэтому совокупность аксиом В.1
и В.2 равносильна совокупности аксиом В.1 и
В'.2. Если 51, В^ $ и Ъ^ВхКВъ, то в В2\В\ сущест-
вует такой элемент с, что (В\\Ъ)\} с
Утверждение 16.1. Все базы матроида равно-
мощны.
> Пусть 51 и 52~ базы, |5i I 152| и В[ = {bi, b2,...
..., Ьр}. Согласно аксиоме В.2 в базе В2 существует такой
элемент ci, что
5'=(5i\bi)Uci = {ci, b2,	Ьр}^<
Далее, существует такой элемент с2 52, что
В" = (5'\b2) U с2 = ki, с2, Ь3, ..Ьр) е= «$.
Итерируя этот процесс, получим базу В = {ci, с2, ..ср),
являющуюся подмножеством в 52 и потому совпадаю-
щую с 52 в силу В.1. Следовательно, \В2\ = р. <
Мощность базы матроида М назовем его рангом и
обозначим через р(Л/).
Любое подмножество базы матроида называется не-
зависимым. В частности, пустое множество независимо.
Совокупность всех независимых подмножеств элементов
матроида М обозначим через 3 (М) (или просто 5^). Ни-
же множество У (М) называется набором независимых
множеств матроида М.
Очевидно, что &(М) совпадает с множеством элемен-
тов из &(М), максимальных относительно включения,
так что множества ^(М) и У (М) определяют друг друга.
5 в. А. Емеличев и др.	65
Теорема 16.2. Набор 3f {М} независимых множеств
матроида удовлетворяет следующим двум условиям {ак-
сиомы независимости).
1.1. Если Х^Я(М), Y<=X,to Y^3f{M}.
1.2. Если X, Y^J(M) и 1X1 < I У|, то в Y\X сущест-
вует такой элемент у, что X U у е= % {М).
> Справедливость условия 1.1 очевидна; рассмотрим
условие 1.2. Пусть X, Y У {М) и |Х| < |У|. Пусть, да-
лее,	Y^B\. Среди баз, содержащих X, вы-
берем такую базу В2, чтобы пересечение В\ П В2 содержа-
ло наибольшее число элементов. Докажем, что 7?2\Х^=7?ь
Действительно, если бы существовал элемент Ъ е 52\Х,
ЬФВ\, то по аксиоме В.2 в базе В\ нашелся бы такой
элемент я, что С = (B2\b) U z е= ${М). Но тогда \С ASJ >
>|В2ПВ11, что невозможно. Следовательно, В2\Х и У
содержатся в В\, причем |/?2\Х| + I У| =p(Af)— |Х| +
+ |У| >р(Л/)= I2?il. Тем самым существует г/(Т?2\Х) Я
А У. Поскольку X U у В2, то элемент у — искомый. <
Очевидно, что аксиома 1.2 эквивалентна следующей
аксиоме.
Г.2. Если X, Y^V(M) и 1X1 < |У|, то в Y сущест-
вует такое подмножество Z, что X U Z е= У (М), |Х U Z! =
= |У|.
Следующая теорема показывает, что в основу опре-
деления матроида можно положить не базы, а независи-
мые множества.
Теорема 16.3. Пусть Е — конечное непустое множе-
ство, /7 — непустая совокупность его подмножеств, удов-
летворяющая аксиомам независимости 1.1 и 1.2, $ — мно-
жество всех элементов из Sf, максимальных относительно
включения. Тогда & удовлетворяет аксиомам баз В.1
и В.2.
О Очевидно, что $ есть множество всех элементов из
3 максимальной мощности. Пусть теперь В\, В2^$,
ех^В\. Тогда В\\е\ |5i\eiI = IZ?2! — 1. Следователь-
но, существует такой элемент е2 В2, что
(В{\е1)ие2 = Вз^ЗГ, |531 = |Р21.
Из последнего равенства вытекает, что В%^$. Тем са-
мым доказано, что выполняется условие В.2. Справедли-
вость условия В.1 очевидна. <
Предыдущая теорема дает основание для нового опре-
деления матроида. Матроидом назовем пару {Е, 3f), где
Е — множество, а 3 — непустая совокупность его под-
множеств (называемых независимыми), удовлетворяю-
66
щих аксиомам независимости 1.1 и 1.2. Множество 3 на-
зовем набором независимых множеств матроида. Макси-
мальные относительно включения независимые подмно-
жества назовем теперь базами матроида. Аксиомы баз
при этом действительно будут выполняться. В этом смыс-
ле приведенные два определения матроида эквивалентны.
Определим ранговую функцию (функцию ранга) мат-
роида 71/, ставящую в соответствие каждому подмноже-
ству А Е число, равное максимальной из мощностей
входящих в А независимых подмножеств и называемое
рангом множества А: р(4) = max {|Xl: Х^А, X У (М)}.
Очевидно, что р(Е) совпадает с определенным выше
рангом р (71/). Очевидно также, что подмножество А Е
независимо тогда и только тогда, когда р(4) = [4|.
Теорема 16.4. Ранговая функция матроида удов-
летворяет следующим трем условиям (аксиомы ранга):
р.1. 0<р(4)< |41 для каждого А — Е;
р.2. р(4)^р(В), если А В Е\
р.З. р(4 U В)+ р(4 П В)^ р(4) + р(2?) для любых
А,В<=Е.
> Первые два условия очевидны, рассмотрим третье.
Пусть А,В^Е, а X — наибольшее по числу элементов
независимое подмножество в А П В. Согласно условию
Г.2 в A U В существует наибольшее по числу элементов
независимое подмножество У, содержащее X. Представим
У в виде У = X U V U ТУ, где У s А\В, W В\А. Незави-
симое подмножество X U У содержится в 4, поэтому
р(4)> IX U У|. Аналогично р(2?)> IX U W\. Следователь-
но, р(4) + р(5)> |XU 71 + |XU W\. Поскольку ХП7 =
= ХПТУ = 0, то далее имеем р(4) +р(5)^ |Х|+(|Х| +
+ 171 + IWI). Но |Х| =р(4 ПД), |Х| + |7| + |1У| =
= |У| =р(4 U В).
Итак, р(4) + р(5)>р(4 U5) + p(4 П5). <
Подмножество 4 из Е называется зависимым, если
оно не является независимым. Минимальное относитель-
но включения зависимое множество называется циклом.
Очевидно, что подмножество множества Е независимо
тогда и только тогда, когда оно не содержит циклов.
Множество циклов матроида 71/ обозначим через 8 (71/)
(или просто 8).
Теорема 16.5. Если М — матроид, то множество
8 (М) удовлетворяет следующим двум условиям (аксио-
мы циклов).
С.1. Ни один из циклов не содержится в другом
цикле.
5*	67
С.2. Если С\ и С2 — несовпадающие циклы и е & С\ П
A С2, то множество (G U С2) также содержит цикл.
> Выполнимость условия С.1 очевидна, рассмотрим
условие С.2. Пусть D = (С\ U С2) \е. Достаточно доказать,
что множество D зависимо. Прибегнем к помощи ранго-
вой функции; в ее терминах нужно доказать неравенство
p(Z))< |2?|. Но D С\ U С2, и потому p(Z>)^ p(Ci U G).
Согласно аксиоме р.З
p(G UC2)^p(C1) + p(C2)-p(C1nC2).
Очевидно, что p(G)= ICJ1 для цикла G. Так как
множество Ci А С2 независимо, то p(Ci А С2) == IG A C2I.
Итак,
p(Z))^p(C1 UC2)^ ICJ ~ 1+ 1С21 - 1- ICi АС21 =
= iCi UC2I -2
и \D\ = iCi U С21 — 1, а значит, p(Z))< \D\. <
Заметим, что совокупность аксиом р.1 — р.З (как и
С.1, С.2) можно использовать для еще одного определе-
ния матроида.
Следствие 16.6. Если М = {Е,	— матроид с на-
бором независимых множеств 3, Х^ SC у Е, то мно-
жество X U у содержит не более одного цикла.
> Пусть, напротив, в X U у есть два несовпадающих
цикла Ci и С2. Элемент у содержится в каждом из них,
и, согласно предыдущей теореме, существует третий цикл
С в множестве D =(Ci U C2)\z/. Следовательно, D — зави-
симое множество. Но D X и потому независимо. Полу-
ченное противоречие доказывает нужное утверждение. <1
Очевидно, что из предыдущего следствия вытекает
Следствие 16.7. Для любой базы В матроида и
любого его элемента е, не входящего в эту базу, множе-
ство В U е содержит ровно один цикл.
§ 17. Двойственный матроид
Пусть М = (Е,	— матроид £ множеством баз Для
произвольного X Е положим X = Е\Х. Если В то
множество В назовем кобазой матроида М. Пусть =
= {В: В е $} — множество всех кобаз.
Теорема 17.1. Множество ЗИ* удовлетворяет акси-
омам баз В.1 и В'.2.
О Справедливость условия^ В.1 очевидна, рассмотрим
условие В'.2. Пусть Bi и В2 — две кобазы, x^Bi\B2.
68
Нужно доказать существование в Z?2\7?i такого элемента
Уч что
A =(BiV)U	(1J
Так как х^В\, то согласно следствию 16.7 множество
В\ U х содержит цикл С. Поскольку цикл пе может со-
держаться в базе, то существует	Так как
то у^х. Следовательно, у^В\. Итак, у^В^ХВ}.
Теперь докажем, что верно (1). С этой целью рас-
смотрим множество А=(В\ \)х)\у. В силу следствия 16.7
С является единственным циклом, содержащимся в В\ U х.
Поэтому А не содержит циклов и, следовательно, явля-
ется независимым множеством. Далее |Л| = I5J, так что
А — база и потому А — кобаза. <
Из предыдущей теоремы вытекает, что пара (Е, ^*)
является матроидом с множеством баз Этот матроид
называется двойственным к матроиду М и обозначается
через М*. Очевидно, что #** = М.
Зависимое (независимое) множество элементов мат-
роида М* называется независимым (конезависимым) в
М. Цикл матроида ЛР называется коциклом матроида М.
Ранговая функция матроида ЛР называется коранговой
функцией матроида М и обозначается через р*. Очевид-
но, что р*(Л7)= |2?| — р(Л7).
Поскольку кобазы, коциклы и т. д. являются базами,
циклами и т. д. двойственного матроида, то для любого
утверждения о циклах, базах и т. д. матроида сущест-
вует аналогичное двойственное утверждение о двойствен-
ных объектах — коциклах, кобазах и т. д. Если одно из
этих утверждений верно для всех матроидов, то верно и
двойственное утверждение.
Очевидно, что в терминах кобаз можно следующим
образом определить зависимые множества.
Утверждение 17.2. Произвольное подмножество
элементов матроида является зависимым тогда и только
тогда, когда оно имеет непустое пересечение с каждой
кобазой.
Теорема 17.3. Непустое подмножество X элементов
матроида является циклом тогда и только тогда, когда
оно удовлетворяет следующим двум условиям:
1) IX А С\ Ф 1 для каждого коцикла С:
2) X — минимальное относительно включения непу-
стое подмножество, удовлетворяющее условию 1).
Доказательство этой теоремы основано на следующих
двух леммах.
69
Лемма 17,4. Для любого непустого независимого
подмножества X элементов матроида существует такой
коцикл С, что |Х П С\ = 1.
> Множество X содержится в некоторой _базе В.
Пусть х^Х. В силу следствия 16.7 множество В U х со-
держит некоторый коцикл С. Очевидно, что С ftB — {х} =
= спх. <
Лемма 17.5. Для всякого цикла X и любого коцик-
ла С матроида верно соотношение |Х П Cl ¥= 1.
> Пусть, напротив, X П С = {х}, Согласно утвержде-
нию 17.2 коцикл С — минимальное подмножество в Е,
имеющее непустое пересечение с каждой базой. Следо-
вательно, С — максимальное подмножество в Е, не содер-
жащее баз, и потому С U х содержит некоторую базу В.
Множество Х\х независимо и содержится в С U х. Из ак-
сиомы 1.2 теперь получаем, что существует база Z), удов-
летворяющая условию Х\я D s С U х. Но С пе содер-
жит баз, поэтому х е D, X^D. Последнее противоречит
аксиоме 1.1. <
> Доказательство теоремы 17.3. Необхо-
димость. Пусть X — цикл. Тогда па основании лем-
мы 17.5 |ХПС| тМ для каждого коцикла С. Любое под-
множество из X независимо и, в силу леммы 17.4, не
удовлетворяет условию 1).
Достаточность. Пусть X — непустое подмноже-
ство элементов матроида, удовлетворяющее условиям 1)
и 2). Согласно лемме 17.4 множество X зависимо. Все
его собственные подмножества не удовлетворяют усло-
вию 1) п независимы в силу леммы 17.5. <
§ 18.	Примеры матроидов
Рассмотрим некоторые примеры матроидов. .
1.	Пара (Е, {Е}), где Е — конечное непустое множе-
ство, является матроидом, единственной базой которого
служит само множество Е. Этот матроид называется сво-
бодным (или дискретным). Циклов свободный матроид
не имеет, всякое подмножество X Е независимо,
р(Х) = |Х|.
Двойственный к свободному — тривиальный матроид
(2?, {0}), единственной базой которого является пустое
множество. Очевидно, что 0 служит единственным неза-
висимым множеством тривиального матроида; его цик-
лы— все одноэлементные подмножества множества Е\
р (X) = 0 для любого X Е.
70
2.	Пусть L — линейное пространство над произволь-
ным полем F, Е L — конечное непустое подмножество,
3 — множество, элементами которого служат все линейно
независимые над F системы векторов из Е и пустое мно-
жество. Тогда пара (Z?, «7) является матроидом с набо-
ром независимых множеств 3 (этот факт вытекает из
известной в линейной алгебре теоремы Штейница о за-
мене). Такой матроид называется векторным матроидом,
порожденным множеством векторов Е. Базами этого мат-
роида служат все базы множества Е. Если же в Е нет
баз, т. е. если Е = {0}, то единственной базой векторного
матроида является пустое множество, т. е. он тривиален.
Ранг векторного матроида равен рангу множества Е,
т. е. размерности подпространства, порожденного мно-
жеством Е.
В частности, взяв в качестве Е множество векторов,
являющихся столбцами (строками) какой-либо матрицы
А, получим матричный матроид, или матроид столбцов
(строк) матрицы А. Ранг этого матроида равен рангу
матрицы А.
В качестве иллюстрации рассмотрим матроид М столб-
цов матрицы
“1 1
А = 0 0
1 0
1 0“
1 1
1 1
Обозначив г-й столбец этой матрицы через е{ (г=1, 4),
получим Е = {е\, е%, е3, е4}, p(Af) = rank4 = 3. Перебирая
все максимальные линейно независимые системы столб-
цов матрицы А, обнаружим, что матроид М имеет ровно
3 базы: =	е2, е3}, Z?2 = {ei, е2, е4}, Вз = {е\, е3, е4}.
Зависимых множеств 2: Е и {е2, е3, е4}, причем последнее
множество^ служит —единственным циклом матроида Л/.
Кобазы: В\ = {еД 7?2 = {е3}, Вз — {е2}. Козависимые мно-
жества: {^1} и каждое подмножество в Е, содержащее
более одного элемента. Коциклы: {ej, {е2, е3}, {е2, е4},
(е3, е4}.
3.	Пусть G — произвольный граф. Определим матро-
ид М (G) = (E, &) на множестве E = EG, объявив базами
множества ребер всех остовов графа G, т. е. & = {ЕН:
Н — остов G}. Из утверждения 13.8 вытекает, что аксио-
мы баз в этой ситуации действительно выполняются. По-
скольку каждый подграф графа G, являющийся лесом,
содержится в некотором остове (утверждение 13.7), то
независимыми множествами в M(G) служат множества
71
ребер подграфов в G, являющихся лесами, и только они.
Циклы матроида М(G)— это множества ребер простых
циклов графа G. Если n(G), m(G), k(G)— числа вер-
шин, ребер и компонент графа G соответственно, то
p(TI7(G)) = n(G)-/f(G) = v*(G),
p*(7l7(G)) = m(G)-p(TI7(G)) = v(G),
т. е. ранг и коранг матроида М (G) равны, соответствен-
но, коциклическому рангу и циклическому рангу графа G.
Если В — множество всех ребер какого-либо остова
графа G, то множество EG\B называется коостовом. Под-
множество U^EG называется разделяющим множеством
графа G, если число компонент графа G — U больше, чем
число компонент G. Минимальное относительно включе-
ния разделяющее множество называется разрезом. Коба-
зами в 717(G) служат коостовы графа G. Из утверждения
17.2 непосредственно вытекает,
е	что козависимые множества в
Jz	M(G)—это разделяющие множе-
*—-------- -------—• ства графа G, а коциклы — это
3	4 разрезы. Поэтому между свойст-
Рис. 18.1 вами простых циклов и разрезов
графа существует большая анало-
гия. Эта аналогия и явилась одной из причин возникно-
вения понятия «матроид».
Матроиды 717(G) и 717*(G) называются матроидом цик-
лов (циклическим матроидом) и матроидом разрезов (ко-
циклическим матроидом) графа G соответственно.
Рассмотрим, например, циклический матроид 717(G)
графа G, изображенного на рис. 18.1. Для этого матроида
Е = {е\, ег, вз, е±}. Он имеет ровно три базы: 2?i = {щ, вг,
£4}, Bz = {e\, е3, 04}, В3 = {е2, е3, ^4}. Единственным его
циклом служит множество {ci, е2, е3}. Кобазы: В\ = {03},
Т?2 = {^2}, В3 = {щ}; коциклы: {ei, ег), {щ, в3}, {вг, е3}, {^4}.
Очевидно, что для любого дерева Т циклический мат-
роид 717(Т) свободен, а 717*(Т) тривиален.
Вернемся к произвольным графам. Применяя уста-
новленные выше утверждения о свойствах баз, независи-
мых множеств и циклов матроида к матроидам 717(G)
и 7J7*(G), получим следующие утверждения о графах.
Каждое из них несложно доказать непосредственно, од-
нако здесь вскрывается их общая сущность.
Утверждение 18.1. Пусть F и Н — ациклические
подграфы графа G и \EF\ < \ЕН\. Тогда существует та-
72
кое подмножество X ЕЙ, что граф F' = F + X также
является ациклическим и \EF'\ = \ЕН\.
Утверждение 18.2. Если D\ и D% — несовпадаю-
щие разрезы в графе G, имеющие общее ребро е, то мно-
жество ребер (D\ U D%)\e является разделяющим.
Утверждение 18.3. Для любого непустого ацик-
лического подграфа F графа G существует разрез в G,
имеющий с F ровно одно общее ребро.
Утверждение 18.4. Число общих ребер любого
простого цикла и любого разреза графа отлично от 1.
Замечание. Очевидно, что в формулировках ут-
верждений 18.1 —18.4 может фигурировать произвольный
псевдограф, а не только простой граф.
§ 19. Изоморфизм матроидов
Пусть Мх=(Е\, $\) и М2== (Е2, ^2) —два матроида
с множествами баз и ^2, ср: Е\-+Е2— биекция. Для
Х<=Е\ положим ср(Х) = {ср (а?): х^Х}. Если для любого
имеем ср(Х)^ тогда и только тогда, когда Х^
то биекция ср называется изоморфизмом матроида
М\ на матроид М2.
В этой ситуации будем писать
ср: Mi-M2.	(1)
Для изоморфизма ср существует обратная биекция
ср-1, причем очевидно, что для любого	имеем
ср-1(У)^^1 тогда и только тогда, когда Y $2. Следова-
тельно, если (1)—изоморфизм матроидов, то и ср-1:
М2 М1 — также изоморфизм.
Если существует изоморфизм (1), то будем называть
матроиды М\ и М2 изоморфными и писать М\ =М2.
У т в е р ж д е п и е 19.1. Если ср: М\ -+М2 — изомор-
физм матроидов, то:
1)	ср(Х)—независимое множество матроида М2 тогда
и только тогда, когда X является независимым множест-
вом матроида М\;
2)	ф(Х)—цикл матроида, М2 тогда и только тогда,
когда X является циклом матроида Mi;
3)	ср(Х)—кобаза матроида М2 тогда и только тогда,
когда X является кобазой матроида М\;
4)	<р(Х)—коцикл матроида М2 тогда и только тогда,
когда X является коциклом в М\.
> 1) Пусть X—независимое множество матроида Mi.
Тогда X содержится в некоторой базе B^&i. Множество
73
ф(Х) содержится в базе ф(В)е^2 и потому независимо
в матроиде М2. Поскольку множество ф(Х) отображает-
ся на X обратным изоморфизмом ср”1, то из независимо-
сти множества ф(Х) в свою очередь следует независи-
мость множества X.
2)	Пусть X — цикл матроида М\, т. е. минимальное
относительно включения зависимое множество. Применяя
уже доказанное утверждение 1), заключаем, что ф(Х)—
минимальное относительно включения зависимое множе-
ство матроида М2.__
3)	Положим Х = Е\Х. Множество_Х—кобаза мат-
роида 71/1_тогда и только тогда, когда X — база т. е.
когда ф(Х)база матроида М2. Последнее равносильно
тому, что ф(Х)—кобаза в М2. Но ф(Х) = ф(Х).
4)	Коциклы матроида — это минимальные козависи-
мые множества. Подмножество X элементов матроида М\
козависимо тогда и только тогда, когда оно пересекается
G	Н
Рис. 19.1
с любой базой этого матроида. Последнее равносильно
тому, что множество ф(Х) пересекается с любой базой
матроида М2, т. е. ф(Х) козависимо в матроиде М2. <
Из предыдущего утверждения непосредственно вы-
текает
Следствие 19.2. Если матроиды изоморфны, то
двойственные матроиды также изоморфны, т. е. если ф:
М\-+ М2 —изоморфизм матроидов, то <р:	так-
же является изоморфизмом матроидов.
Итак, изоморфные матроиды «одинаково устроены»,
что дает основание их не различать. Поэтому любой
матроид, изоморфный векторному, также назовем век-
торным. Матроид назовем графическим, если он изомор-
фен матроиду циклов M(G) некоторого графа G, и ко-
графическим, если он изоморфен матроиду разрезов
M*(G).
На рис. 19.1 изображены два графа G и Н, цикличе-
ские матроиды которых изоморфны.
74
§ 20. Представление матроида
Стремление попять строение тех матроидов, которые
близки к векторным, т. е. если и не являются векторны-
ми, то отличаются от последних лишь незначительно,
приводит к понятию представления матроида, в опреде-
ленном смысле близкому к понятию изоморфизма.
Пусть М — матроид с множеством элементов Е, Fn —
линейное пространство столбцов высоты п над полем F.
Отображение ср: Е -> Fn называется представлением мат-
роида М над полем F, если оно удовлетворяет следующе-
му условию: для любого подмножества X = {ei, ег, ...
..., ek} множества Е система векторов cp(ei), ср(^2), ...
..., ср(^) линейно независима над полем F тогда и толь-
ко тогда, когда X является независимым множеством
матроида М.
Пусть ср: Е Fn -— представление матроида М, Е =»
= {(?i, в2, ..., е,п}. Построим пХт-матрицу
ф(£’) = [ф(е1)	ф(е2)	...	ф(ет)],
столбцами которой являются образы элементов матрои-
да М в представлении ср. Эта матрица также называется
представлением матроида М.
Утверждение 20.1. Пусть М — матроид с мно-
жеством элементов Е = {е\, вг, ..., е™), А — произвольная
п X m-матрица над полем F. Для того чтобы матрица
А была представлением матроида М, необходимо и доста-
точно выпс гнениз следующих двух условий'.
1) rank Л == р(М);
2) система любых р = р(М) столбцов матрицы А с но-
мерами h, ..., zp линейно независима тогда и только
тогда, когда множество	. .., £ip} является базой
матроида М.
> Очевидно, что Л=ср(£) удовлетворяет условиям
1) и 2). С другой стороны, пусть /гX m-матрица А удов-
летворяет этим условиям и пусть Ai, А2, ..., Ат — ее
столбцы. Тот да, положив ср(ег) = Л/, получим представ-
ление ср: Е -* Fn матроида М. <
Матроид называется представимым над полем F, если
он имеет представление над F. Как подтверждают сле-
дующие примеры, одни матроиды представимы над лю-
бым полем, другие — не над любым.
Пусть М — матроид с множеством элементов £ = {1,
2, 3}, базами которого служат все двухэлементные под-
множества множества Е. Очевидно, что этот матроид
75
представим над произвольным полем, поскольку матрица
'1 0 1'
О 1 1
служит представлением матроида М.
С другой стороны, возьмем в качестве М матроид с
множеством элементов £ = {1, 2, 3, 4}, базами которого,
как и выше, служат все двухэлементные подмножества
множества Е. Пусть матрица А является представлением
этого матроида над полем F из двух элементов. Тогда
rank А = 2 и, следовательно, столбцы этой матрицы при-
надлежат двумерному линейному пространству над F.
Двумерное линейное пространство над полем из двух
элементов — это четырехэлементное множество {а, 6,
а +6, 0). Следовательно, столбцами матрицы А являются
а, Ъ, а + 6, 0. Но поскольку любое двухэлементное под-
множество множества Е является базой матроида М, то
любые два столбца матрицы А должны быть линейно
независимы. Полученное противоречие доказывает, что
матроид М не представим над полем из двух элементов.
Если же F — произвольное поле, содержащее более
двух элементов, то, например, матрица
[j?;;]-b<sF'
является представлением матроида М над F. Итак, рас-
сматриваемый матроид представим над любым полем,
кроме поля из двух элементов.
Очевидно, что свободный матроид представим над лю-
бым полем — его представлением служит, например, еди-
ничная матрица. Двойственный ему тривиальный матроид
также представим, его представление — нулевая матрица.
Заметим, что существуют матроиды, не представимые
ни над каким полем.
Из определения представления вытекает, что оно дей-
ствует инъективно на каждом независимом множестве
элементов матроида. Однако в целом оно может оказать-
ся и не инъективным. Рассмотрим, например, матроид
М = (Е, с множеством элементов Е = {1, 2, 3, 4, 5}
и множеством баз & = {{3, 4}, {3, 5), {4, 5}}. Его цикла-
ми служат множества {1}, {2} и {3, 4, 5}. Положив
Ф(Е) =
0 0 10 1
0 0 0 1 1
76
получим представление ф матроида М над произвольным
полем. Это представление пе является инъективным.
Очевидно, что рассматриваемый матроид не имеет инъек-
тивных представлений ни над каким полем, поскольку
ф(1) = ф(2) = 0 для любого представления ф этого мат-
роида.
Легко понять, что матроид, для которого существует
инъективное представление, является векторным. В са-
мом деле, для произвольного представления ф некоторого
матроида М = (Е\ рассмотрим множество столбцов
{ф(е): е^Е}. Это множество порождает векторный мат-
роид, который обозначим через ф(7И). Если отображение
ф инъективно, то оно естественно индуцирует изомор-
физм ф' матроидов М и ф(М): ф'(е) = ф(г) для любого
элемента е матроида М. Итак, верно
Утверждение 20.2. Если представление ф мат-
роида М инъективно, то 7И~ф(/И).
С другой стороны, пусть L — n-мерное линейное про-
странство над произвольным полем F, Е L — конечное
непустое подмножество, М — векторный матроид, порож-
денный множеством векторов Е. Зафиксируем в простран-
стве L произвольный базис. Поставив в соответствие каж-
дому вектору из Е его координатный столбец в отмечен-
ном базисе, получим представление Е -*• Fn матроида М.
являющееся инъективным.
Итак, инъективные представления существуют у всех
векторных матроидов и только у них.
Теорема 20.3. Если матроид представим над полем
F. то двойственный ему матроид также представим над F.
> Для свободного и тривиального матроидов утверж-
дение теоремы очевидно. Пусть М — нетривиальный мат-
роид, не являющийся свободным, р = р(Л/), п X m-матри-
ца А — представление над полем F матроида М. Тогда
rank А = р, 0 < р < т.
Рассмотрим однородную систему
ЛХ = 0	(1)
линейных уравнений с матрицей А (здесь X — столбец
неизвестных #i,	..., хт. 0 — нулевой столбец высоты
п). Пусть Y — множество всех столбцов из Fm. являю-
щихся решениями системы (1). Как известно из алгебры,
Y — подпространство пространства Fm размерности т — р.
Выберем какой-либо базис
Уь У2, ..., Ут_р	(2)
77
подпространства Y и составим из столбцов (2) тХ
X (тп — р)-матрицу J? = [У1 У2 ... Ут-р].
Теперь докажем, что транспонированная матрица ВТ
является представлением матроида Л/*, для чего исполь-
зуем утверждение 20.1. Имеем
rank Вт = rank В = тп — р = р (М*).
Далее вспомним, что базами матроида Л/* являются до-
полнения до баз матроида М. Поэтому достаточно уста-
новить следующее: система каких-либо р столбцов мат-
рицы А линейно независима тогда и только тогда, когда
линейно независима дополняющая система ш — р столб-
цов матрицы Вт (или строк матрицы В). Слово «допол-
няющая» означает, что номера столбцов второй системы
отличны от номеров столбцов первой.
Выделим какую-либо систему р столбцов матрицы А.
Пусть, для определенности, это первые р столбцов,
и пусть С — подматрица в 4, составленная из взятых
столбцов. Теперь рассмотрим однородную систему линей-
ных уравнений
cz = o
(3)
с матрицей С (Z — столбец неизвестных zi, z2, ..., zp).
Если столбцы матрицы С линейно зависимы, то си-
стема (3) имеет ненулевое решение Z. Рассмотрим стол-
бец
’ Z ~
и = 0
о
высоты тп, полученный добавлением тп — р нулей к столб-
цу Z. Очевидно, что U — решение системы (1), т. е. U е
е У. Поскольку (2)— базис пространства У, то
U = У! + а2У2 + ... + ат_рУт_р.	(4)
Введем столбцы
^1»	•••» Yт~р	(5)
высоты тп — р, отбросив из каждого столбца (2) первые
р координат, и рассмотрим матрицу 29=[У^ Y'2 ...
... Ут—р]? столбцами которой являются векторы (5).
Это квадратная матрица, строки которой суть последние
78
т — р строк матрицы В. Из равенства (4) следует
«1Л + а2^2 + • • • + О^ти-рУ m--p = 0*	(6)
Среди коэффициентов а< в последнем равенстве есть от-
личные от нуля, поскольку U =#0. Следовательно, систе-
ма столбцов (5) линейно зависима.
Обратно, пусть система каких-либо, например, послед-
них т — р строк матрицы В линейно зависима. Тогда
(5) — линейно зависимая система векторов, и потому вер-
но равенство вида (6), среди коэффициентов а» которого
есть отличные от нуля. Определим столбец U формулой
(4). Поскольку система векторов (2) линейно независи-
ма, то £7¥=0, и U — решение системы (1). Итак, система
(1) имеет ненулевое решение вида U. Но тогда столбец
Z, который получается из U в результате удаления по-
следних т — р координат, является ненулевым решением
системы (3). Следовательно, столбцы матрицы С линей-
но зависимы.
Доказано, что из линейной зависимости каких-либо
т — р строк матрицы В вытекает линейная зависимость
дополняющей системы р столбцов матрицы А. Тем самым
доказана теорема. <3
§ 21. Бинарные матроиды
Рассмотрим более детально матроиды, представимые
над полем из двух элементов,— бинарные матроиды.
Бинарным является, например, матроид М =
с множеством элементов Е = {1, 2, 3, 4}, множество
баз которого составляют все трехэлементные подмноже-
ства в Е, содержащие 1. В самом деле, положив ф(1) =
= (1, 1, 0, 0), Ф(2) = (0, 1, 1, 0), ф(3) = (0,0,1,1), ф(4) =
“(О, 1, 0, 1), получим представление матроида М над
полем из двух элементов 0 и 1.
Пусть F = {0, 1} = Z2 — поле классов целых чисел по
модулю 2, М — матроид с множеством элементов E,m-
порядок матроида Л/, т. е. число элементов в 2?, 2В — бу~
леан множества Е (совокупность всех подмножеств мно-
жества Е). Превратим этот булеап в линейное простран-
ство над Z2, определив подходящим образом сложение
подмножеств и их умножение па 0 и 1. Именно, для
X, Y 2е положим X + Y = (X U У) \ (X А У) — сумма мно-
жеств по модулю 2 (симметрическая разность), 1-Х =
= X, 0 • X = 0. Прямая проверка подтверждает, что в 2я
79
внесена структура линейного пространства пад Z2, пуле-
вым вектором которого служит 0.
Пусть L — подмножество пространства 2Е, состоящее
из пустого множества, всех циклов матроида М и объеди-
нений попарно пепересекающихся циклов. Фиксируем ка-
кую-либо базу В матроида М. Согласно следствию 16.7
для любого е В в множестве В U е существует ровно
один цикл. Обозначим этот цикл через Се.
Теорема 21.1. Если исходный матроид М является
бинарным, то L—подпространство пространства 2Е раз-
мерности р*(Л/), базис которого составляют все циклы
из множества
{Се: е^В},	(1)
где В — произвольная база матроида М.
> Пусть п X тп-матрица А является представлением
матроида М над Z2. Для произвольного непустого под-
множества X множества Е обозначим через S (X) сумму
(по модулю 2) всех столбцов матрицы А, соответствую-
щих элементам из X.
Заметим, что непустое подмножество X Е является
элементом множества L тогда и только тогда, когда
5(Х) = 0. Действительно, пусть вначале X — цикл. Тогда
система столбцов, соответствующих элементам из X, ли-
нейно зависима над Z2, и потому для какого-либо под-
множества Y в X S(У) = 0. Но всякая часть рассматри-
ваемой системы столбцов линейно независима, следова-
тельно, Y = X. Итак, S(X) = 0 для цикла X. Очевидно,
что то же верно, если X — объединение попарно непере-
секающихся циклов.
Обратно, пусть X Е и S (X) = 0. Тогда система столб-
цов матрицы А, соответствующих элементам подмноже-
ства X, линейно зависима над Z2 и, следовательно, X —
зависимое множество. Поэтому оно содержит цикл Х\.
Если У = X\Xi ¥= 0, то 5(У) = 0, поскольку 5(Х) =
= 5(Х1) = 0 и S(X) = 5(Xi) + S(Y). Следовательно, У со-
держит цикл Х2. Через несколько подобных шагов мы
разобьем множество X па непересекающиеся циклы.
Пусть X и У — произвольные элементы множества L,
Z = X(\Y, X' = X\Z, Y' = Y\Z. Тогда Х+У^Х'иУ',
Х'АУ' = 0, 5(Х+У) = 5(Х') + 5(У'). Но 5(Х) = 0 =
= 5(Х') + 5(2), поэтому 5(Х') = 5(2). Аналогично
5(У') = 5(2). Следовательно, 5(Х + У) = 5(Z)+ S(Z) = 0.
Тем самым доказано, что L — подпространство про-
странства 2е.
80
Теперь докажем, что (1)—базис пространства L.
Если бы система векторов (1) была линейно зависимой
над Z2, то сумма каких-либо из них была бы равна ну-
левому вектору пространства 2£, т. е. пустому множеству.
Но если ei, в2, ..., ek — попарно различные элементы из
В, то
Сег + Се2 + . . . + Сек Э	вк}.
Следовательно, система (1) линейно независима.
Остается доказать, что произвольный элемент X про-
странства L является суммой по модулю 2 каких-либо
циклов из (1). Это очевидно для Х = 0. Пусть x^L и
X ¥= 0. Согласно утверждению 17.2 X А В 0. Если
X А В = {^1, е2, ..eh}, то
X = Се^Л- Се2 + ... + Cek-
В самом деле, это равенство равносильно равенству
Се± + Се2 + . . . + Cek + X = 0	(= 0).	(2)
Левую часть последнего обозначим через D. Так как
Cei П В = {^i} и ei X, то D А В = 0. Следовательно,
D — независимое множество. С другой стороны, D^L,
а каждый элемент пространства L, отличный от пустого
множества, является зависимым множеством. Итак, D =
= 0, т. е. верно равенство (2). <
Заметим, что условие бинарности в формулировке
теоремы 2.1 существенно. Пусть, например, М = (Е,	—
матроид с множеством элементов Е = {1, 2, 3, 4}, базами
которого служат все двухэлементные подмножества мно-
жества Е. Тогда {1, 2, 3} и {1, 2, 4} — циклы, а {1, 2, 3} +
+ {1, 2, 4} = {3, 4} — база. Следовательно, множество!,
не является в этом случае подпространством.
Возвратимся к бинарным матроидам. Пространство L
называется пространством циклов матроида М, а его ба-
зис (1)—базисом циклов этого матроида (относительно
базы В).
Так как двойственный матроид /И* также является
бинарным (теорема 20.3), то верна теорема, двойствен-
ная предыдущей, и возникают понятия пространства ко-
циклов и базиса коциклов. Именно, пусть Л* — подмно-
жество булеана 2Е, элементами которого служат все ко-
циклы матроида М, объединения попарно непересекаю-
щихся коциклов и пустое множество. Фиксируем в М
базу В. Тогда для любого элемента е В множество
6 В. А_. Емеличев и др.	81
В U е содержит ровпо один коцикл С*. В этих обозначе-
ниях верно
Следствие 21.2. Множество L* является подпро-
странством пространства 2Е размерности p(Af). Множест-
во коциклов
{С*е: ее=В},	(3)
где В — фиксированная база матроида М, служит бази-
сом этого пространства.
Базисы циклов (1) и коциклов (3) легко определя-
ются друг через друга. Верна следующая
Теорема 21.3. Пусть f^B, Се^ ..., Ceh] —
множество всех циклов из базиса (1), содержащих f,
Xf = {/, ei, в2, ..., ek}. Тогда Xj = С*.	__
> Согласно следствию 16.7 множество BUf содержит
ровно один коцикл. Очевидно, что Xj^BVf. Поэтому
достаточно доказать, что Xf является коциклом. По тео-
реме 17.3 множество Xf — коцикл, если выполняются сле-
дующие условия:
1) IX/ 3	1 для каждого цикла С;
2) Xf — минимальное непустое множество, удовлетво-
ряющее условию 1).
Пусть С — цикл, D — С 3 Xh Так как (1) — базис про-
странства циклов, то С однозначно представляется в ви-
де суммы циклов из (1):
с = Сч1 + • • • + C4t*	(4)
Если / s С, то / принадлежит хотя бы одному слагаемо-
му в (4), например, f^Cei- Тогда
ei^Xj, {/,	|Z)|>1.
Пусть С. Тогда либо / не входит ни в одно из
слагаемых (4), либо / входит по меньшей мере в два из
этих слагаемых. В первом случае D = 0. Во втором
пусть, например,
‘1	*2
Тогда ei2] D, |Z)1 > 1. Тем самым доказано, что
выполняется условие 1).
Пусть теперь У<=Х/. Если f&Y, то Y содержится в
кобазе и потому конезависимо. Согласно лемме 17.4 су-
ществует такой цикл С, что 1УПС1 =1. Если же j^Y,
62
но, например, У, то |У П Cei | = 1. Тем самым дока-
зано, что Xf — коцикл. <1
Ниже окажется полезным следующее
Утверждение 21.4. Если ср — изоморфизм бинар-
ного матроида М\ на матроид Мъ, а, (1)—базис циклов
матроида М\ относительно базы В, то система
{ф(Се): е^В}	(5)
является базисом циклов матроида М2 относительно ба-
зы ф(В).
> По определению изоморфизма матроидов множество
ф(В) является базой матроида М2- Для любого цикла С
матроида Mi множество ф(С)—цикл матроида М2. Если
теперь е — элемент матроида М\ и то ф(е)<^ф(В).
Согласно следствию 17.7 множество 5 = ф(5)иф(е) со-
держит ровно одип цикл. Этот цикл совпадает с ф(Се),
поскольку Се — В U е и, следовательно, ф(Се) S. Итак,
доказано, что (5)—базис циклов матроида М2 относи-
тельно базы ф(В). <
Теперь обратимся к графам. Графический и, следова-
тельно, кографический матроиды бинарны, о чем свиде-
тельствует
Теорема 21.5. Для любого непустого графа G мат-
рица инцидентности I = 1(G) является представлением
циклического матроида M(G) над Z2.
> Для произвольного подмножества ребер X обозна-
чим через ЦХ) подматрицу матрицы Z, составленную из
столбцов, соответствующих ребрам, входящим в X. До-
статочно доказать, что rankZ(X)< |Х| тогда и только
тогда, когда подграф G(X), порожденный множеством
ребер X, содержит цикл. Но ЦХ)— матрица инцидентно-
сти графа G(X). При изменении нумерации вершин или
ребер ранг этой матрицы, понятно, пе изменится. Пусть
граф (ЦХ) содержит цикл С. Перенумеруем вершины и
ребра графа G(X) так, чтобы элементы, входящие в цикл
С, имели меньшие номера. Теперь матрица ЦХ) прини-
мает вид
Z(X) =
А *
О
где А — матрица инцидентности графа С. В каждом
столбце матрицы А ровно две единицы, поэтому сумма
ее строк по модулю 2 равна нулевой строке. Следова-
тельно, det А = 0, и столбцы матрицы А, а вместе с ними
и столбцы матрицы ЦХ) линейно зависимы.
6«	83
Пусть теперь граф G(X) —ациклический. Очевидно,
что достаточно считать его деревом. Снова изменим нуме-
рацию вершин и ребер графа G(X). Одной из концевых
вершин дерева G(X) и инцидентному ей ребру припи-
шем номер 1. Теперь обратимся к дереву G(X) — 1. Од-
ной из его концевых вершин и инцидентному ей ребру
припишем номер 2 и т. д. В этой нумерации матрица
инцидентности примет вид
“10 ... О-
*	1 ... 0
•	• • • • •
*	* ... 1
*	* ... *_
ЦХ) =
ранг ее равен числу столбцов. <1
Обратимся еще раз к представлениям циклического
матроида М (G) над Z2. Пусть EG = Е и ср: Е —>Z2 —
представление. Поскольку длина цикла в графе не менее
трех, то все двухэлементные множества ребер независи-
мы. В этой ситуации, как отмечалось выше, представле-
ние ф индуцирует изоморфизм матроидов. Поэтому из
предыдущей теоремы непосредственно вытекает
Следствие 21.6. Циклический матроид M(G) не-
пустого графа G изоморфен векторному матроиду над Z2,
порожденному столбцами матрицы инцидентности 1(G).
К бинарному матроиду M(G) применима также тео-
рема 21.1, т. е. верно
Следствие 21.7. Все циклы графа G, объединения
циклов, не имеющих общих ребер, и пустое множество
относительно сложения по модулю 2 и умножения на
числа по формулам 1 X = X, 0 - X = & составляют ли-
нейное пространство над Z2 — пространство циклов графа
G, размерность которого равна циклическому рангу v(G).
Аналогичное утверждение верно для разрезов.
Базисы циклов и коциклов матроида M(G) называ-
ются базисами циклов и, соответственно, разрезов гра-
фа G.
Следствие 21.8. Каждый цикл графа однозначно
представляется в виде суммы по модулю 2 циклов, взя-
тых из какого-либо фиксированного базиса циклов. Ана-
логичное утверждение верно для разрезов.
Следствие 21.9. Любой граф G содержит не более
чем 2V(G) — 1 циклов.
Как правило, число циклов в графе значительно мень-
ше, чем число, указанное в предыдущем следствии. Од-
84
нако приведенная оценка точна в том смысле, что суще-
ствуют графы, число циклов в которых равно 2V(G) — 1.
Таковы, например, все леса и граф, изображенный на
рис. 21.1.
Следствие 21.10. Любой граф имеет не более чем
2V*(G) — 1 разрезов.
Следствие 21.11. Пусть G — граф, Н — его остов,
/ е ЕН, {С^, Се<2, ...» Сек] — множество всех циклов,
входящих в базис циклов относительно Н и содержащих f,
С* = {у,	е2) ..eky Тогда {С*: f <= ЕН] — базис разре-
зов графа G относительно остова Н.
Рассмотрим примеры.
1. Пусть G — граф, изображенный на рис. 21.2. Мно-
жество ребер {1, 2, 6, 8} порождает в G остов. Базис
циклов относительно этого остова: Сз = С(2, 3, 8), =
= G(1, 2, 4), G5 = G(1, 5, 6), G7 = G(2, 1, 6, 7), С9 =
= G(6, 1, 2, 8, 9). Каждый другой цикл однозначно раз-
лагается в сумму каких-либо из этих пяти. Например,
(7(3, 5, 9) = С3 + С5 + С9. Множество {С*, С*, С*, С*}, где
С* = {1, 4, 5, 7, 9}, С*2 = {2, 3, 4, 7, 9},	= {6, 5, 7, 9},
С* = {8, 3, 9}, является базисом разрезов графа G.
2. Найдем базис циклов графа G, заданного своей
матрицей инцидентности I. Пусть
'1 0 1 ООО-
ll 0 1 00
0 10 0 10
000111
_0 О 1 0 О 1_
Этот граф изображен на рис. 21.3, однако при отыскании
базиса циклов рисунок использоваться не будет.
85
1
2
Рис. 21.3

В силу следствия 21.6 базы системы столбцов этой
матрицы соответствуют ребрам остовов, а минимальные
линейно зависимые системы столбцов — простым циклам.
Используем два следующих утверждения из линей-
ной алгебры:
1) Пусть А' — матрица, полученная из матрицы А в
результате элементарных преобразований строк. Если ка-
кой-либо столбец матрицы А линейно выражается через
другие ее столбцы, то точно такое же
соотношение (с теми же коэффициен-
тами и номерами столбцов) верно и
для столбцов матрицы А'.
2) Всякую невырожденную матри-
цу с помощью элементарных преобра-
зований строк можно превратить в еди-
ничную.
Превратим базисную подматрицу
матрицы I (т. е. подматрицу макси-
мального порядка с отличным от нуля
определителем) в единичную, после че-
го совсем просто будет найти в графе
G остов и базис циклов. Прибавляя
поочередно ко второй строке первую,
и четвертую,
по-
к пятой — третью
(по модулю 2)
к третьей — вторую,
0“
О
О
1
0_
Итак, rank 7 = 4, первые четыре столбца составляют базу
системы столбцов. Соответствующие им ребра е\, е^, е$,
порождают в графе G остов.
Далее к первой строке прибавляем третью и четвер-
86
Линейные соотношения между столбцами последней мат-
рицы те же, что и между столбцами исходной матрицы I.
Если Ak (к = 1, 6)—столбцы матрицы /, то ^s = ^2 + ^4,
Лб = Л1 + Лз+ ^4, столбцы Лг, Л4, Л5 линейно зависимы
над Z2, причем это — единственная минимальная линей-
но зависимая система столбцов, содержащаяся в {Л 1, Л2,
Лз, Л4, Л5}. Аналогично {Л1, Лз, Л4, Л б) — единственная
минимальная линейно зависимая система столбцов, со-
держащаяся в {’Л 1, Л 2, Лз, Л 4, Л б). Ребра графа G, соот-
ветствующие столбцам матрицы /, входящим в эти мини-
мальные линейно зависимые системы, образуют в G про-
стые циклы, составляющие базис системы циклов:
Се = ^(^2» ^4’ ^б)’ Се = ^(^1? ^3’ ^4’ еб)
о	о
(см. рис. 21.3).
§ 22. Трансверсали
Пусть Е — конечное непустое множество, a S =
= (5i, 5г,.. 5m)— m-членное семейство его подмножеств,
т. е. последовательность длины т, составленная из непу-
стых (не обязательно различных) подмножеств множе-
ства Е. Подмножество Т ^Е называется трансверсалью
(или системой различных представителей) семейства 5,
если существует биективное отображение ср: Т...
..., ml, при котором для каждого t^T выполняется ус-
ловие £<=5ф(/). Это означает, другими словами, что су-
ществует такая нумерация элементов множества Т7, при
которой ti^Si (f = l, m).
Подмножество Т ^Е называется частичной трансвер-
салью семейства S, если существует инъективное отобра-
жение ф: Т -> {1, 2, ..., т), при котором для каждого
t^T выполняется условие S^. Тем самым, частич-
ные трансверсали семейства 5 — это трансверсали его
подсемейств.
Вопрос о существовании трансверсали часто возникает
на практике. В шуточной форме его можно сформулиро-
вать как следующую задачу о свадьбах: известно некото-
рое множество юношей, каждый из которых знаком с
несколькими девушками. При каких условиях можно
женить юношей так, чтобы каждый из них женился на
знакомой ему девушке?
Например, если есть четверо юношей #i, х^ х^ Х4 и
пять девушек z/i, z/2, z/з, z/4, z/5, а отношение знакомства
между ними задается таблицей 22.1, то возможно сле-
87
дующее решение: женится на г/4, #2 —на t/i, — па
Уз, ^4 — на Z/2. Если теперь Е = {у{, у2, уз, У4, У^, то рас-
смотренной таблице соответствует семейство подмножеств
S = (5ц S2, S3, S4) множества Е, где Si — множество де-
вушек, с которыми знаком юноша хь т. е. 5i = {z/i, у^, У^,
52 = {z/i}, 5з = Ы Уз, yJ, 54 = {у2, yj. Задача о свадь-
бах имеет решение, когда для соответствующего семейст-
Таблица 22.1
Юноша	Девушки, с которыми знаком юноша
	У1, У 4, Уъ
Х%	У1
	У2, Уз, У 4:
Х4	У2, У4
ва подмножеств S существует трансверсаль. В нашей си-
туации трансверсалью служит, например, множество
<i/i, г/2, Уз, /М, при этом z/4e-Si, yi^Si, ys^S3, y2^S4.
Трансверсали семейства множеств может и не суще-
ствовать. Пусть, папример, S = (5i, S2, S3, S4), Si = {1, 2},
4
S2 = {1, 2, 3}, S3 = {2, 3), S4 = {1, 3}. Тогда U Si = 3,
1=1
четыре элемента. Следо-
а в трансверсали должно быть
вательно, трансверсали нет.
Задача о существовании
Ф. Холлом.
трансверсали решена
Теорема Холла (1935 г.). Пусть Е — непустое
конечное множество, S = (S\, S2, ..., Sm)—семейство его
подмножеств. Для существования трансверсали семейства
S необходимо и достаточно, чтобы для каждого k = 1, тп
объединение 5^ U Si2 U • • • U Sik любых к подмножеств
Si содержало не менее к различных элементов.
Теорема Холла является отправным моментом теории
трднсверсалей. Известно несколько доказательств этой
теоремы. Ниже приводится доказательство более общей
теоремы, принадлежащей Р. Радо.
Часто возникает ситуация, когда вместе с семейством
подмножеств S па множестве Е определена структура
матроида М, и нужно решить вопрос о существовании
трансверсали семейства S, независимой относительно мат-
роида М, т. е. являющейся независимым подмножеством
88
элементов этого матроида. На этот вопрос отвечает сле-
дующая
Теорема Радо (1942 г.). Пусть М — матроид с
множеством элементов Е, S — (Si, S2, ..., Sm)—семейство
непустых подмножеств множества Е. Для существования
трансверсали семейства S, независимой относительно мат-
роида М, необходимо и достаточно, чтобы для каждого
k — i, m объединение любых к подмножеств Si имело
ранг, не меньший чем к.
Теоремы Холла — частный случай теоремы Радо. Дей-
ствительно, если М — свободный матроид, то ранг любого
подмножества Х^Е равен |Х|.
> Доказательство теоремы Радо. Необхо-
димость условия теоремы очевидна; если существует не-
зависимая трансверсаль семейства S, то ее пересечение
с объединением любых к подмножеств Si содержит fc-эле-
ментное независимое подмножество. Следовательно, ранг
этого объединения не менее к.
Достаточность. Вначале докажем, что при вы-
полнении условий теоремы ни одно из множеств 5, не
может содержать более одного такого элемента, удаление
которого нарушает условие теоремы. Пусть, напротив,
множество 51 содержит два таких элемента х и у. Это
значит, что существуют такие множества индексов А и
В в {2, ..., т}, что
p(.LMi и < |Л I,
Р( U Si и (5x\z/) <|5|,
иев	)
где р — ранговая функция матроида М. Положив
U Si и (SiM) = с, и Si и (5А?/) = D,
й=А	ieB
имеем
Ml + 151 > р(С) + р(5)^ р(С и D)+ р(С n D)
(см. аксиому р.З). Но
с и D = и Si, С л Я = и Si.
iGAUBUl	ieAQB
Поэтому
| Л | + | 51 р f и 5Д + рГ U 5p.
UGAUBUl / \геАГ)В )
В то же время по условию теоремы
р( и Si)>и и #1 + 1,
\teAUBUi /
р( и	Л Я|.
USAflB )
89
5' = (5U,512, ...,8
Итак, \А | + |Б| bl U В\ + 1 + \А Л 51 = \А | + |В| + 1.
Последнее противоречие доказывает нужное утверждение.
Пусть теперь какое-либо из подмножеств Si содержит
более одного элемента. Тогда из Si можно удалить неко-
торый элемент, не нарушив справедливости условия тео-
ремы. Итерируя этот процесс, придем к ситуации, в ко-
торой ISJ = 1 (г==1, т) и выполняются условия теоре-
мы. По тогда все Si попарно различны и их объединение
и есть нужная трансверсаль. <1
Понятие трансверсали можно обобщить следующим
образом. Пусть Е — конечное непустое множество, S —
= (Si, S2, . . ., Sm)— семейство его непустых подмножеств,
(Ад, /ь2, ..., кт)—последовательность целых положитель-
ных чисел. Семейство P=(Pi,	Рт) подмножеств
из Е назовем (A?i, к2, ..., кт)-трансверсалью семейства 5,
если
1)	P^Si, i = 1, m;
2)	|PJ = ki, i = 1, m;
3	) Pi Pj = 0 при i =/= j.
Очевидно, что введенная выше трансверсаль является
(1, ..., 1)-трансверсалью. Поэтому задача о свадьбах
(о существовании трансверсали) естественным образом
обобщается теперь в виде задачи о гаремах. Решение
этой задачи, т. е. условия существования (/ci, &2,..кт)~
трансверсали, легко получить непосредственно из теоре-
мы Холла. Заменим семейство S другим семейством
^21’ *^22’ • • • 1	• • •
. . . , Smi, Sm2^ • • • ’
где Sij^Si (j==l, m, j = 1, kt, t=l, m). Очевидно, что
семейство S имеет (Ад, 7f2, ..., km)-трансверсаль тогда и
только тогда, когда существует трансверсаль семейства
S'. Таким образом, верно
Следствие 22.1. Для существования (Ад, к2,..., кт)~
трансверсали семейства S = (Si, S2, ..., Sm) необходимо
и достаточно, чтобы для любого Z^{1, 2, ..., тп} выпол-
нялось неравенство
|.и	(1)
I ieZ I гЫ
Аналогично из теоремы Радо можно получить крите-
рий существования независимой (к\, к2, ..., кт) -транс-
версали.
90
Йз теоремы Радо вытекает также следующий крите-
рий существования независимой частичной трансверсали
фиксированной мощности.
Следствие 22.2. В обозначениях теоремы Радо се-
мейство S имеет независимую частичную трансверсаль
мощности I С пг тогда и только тогда, когда для каждого
k = 1, m ранг объединения любых к подмножеств Si не
меньше, чем к + t — тп.
>	Пусть D — такое множество, что |Z)| == m — t и
D(}E = 0. Построим новый матроид М' на множестве
Е U D, объявив его базами все подмножества В U D, где
В — база матроида М (очевидно, что аксиомы баз дей-
ствительно выполняются), и рассмотрим семейство
Т--=(Т}, Т2, ..., Tm), Ti = S^D, i = 1, тп.
Очевидно, что исходное семейство S имеет независимую
частичную трансверсаль мощности t тогда и только тогда,
когда семейство Т имеет трансверсаль, независимую от-
носительно матроида М'. Согласно предыдущему след-
ствию, для существования такой трансверсали необходи-
мо и достаточно, чтобы объединение любых к подмно-
жеств Ti содержало независимое относительно матроида
М' подмножество мощности к. По последнее условие рав-
носильно условию следствия. <
Взяв в качестве М свободный матроид, получим
Следствие 22.3. Семейство подмножеств S имеет
частичную трансверсаль мощности тогда и только
тогда, когда для каждого к = 1, тп объединение любых к
подмножеств Si имеет мощность не меньше, чемк + t — тп.
Произвольное семейство S = (Si, S2, ..., Sm) непустых
подмножеств множества Е определяет на Е структуру
матроида, независимыми множествами которого являются
частичные трансверсали этого семейства и пустое мно-
жество. Об этом свидетельствует следующая
Теорема 22.4 (Дж. Эдмондс, Д. Фалкерсон, 1965 г.).
Множество 3, элементами которого служат все частич-
ные трансверсали семейства подмножеств S и пустое мно-
жество, удовлетворяет аксиомам независимости 1.1 и 1.2.
>	В доказательстве нуждается только справедливость
условия 1.2. Произвольную частичную трансверсаль X =
= {х\, х2, ..., xh} семейства S, представляющую подсемей-
ство (5^, Si2, .. ., $ik), т. е. такую, что Sip, запи-
шем в виде
{(^1, и), (х2, 7*2), (Xk, ife)}.	(2)
91
Пусть
71), (j/2, /2), • • (Уь ji)}	(3)
— еще одна частичная трансверсаль и I > к. Нужно до-
казать существование среди z/i, у 2, ..., yi такого г/, что
XUy^Sf.
Если в (3) есть такая пара (г/, /), что у пе совпадает
пи с одним из х в (2), а/— пи с одним из f, то, очевид-
но, что X U у е 3.
Пусть теперь в (3) нет такой пары. Но так как 1>к,
то существует индекс /, пусть это 7*1, отличный от всех
индексов / в (2). При этом у\ совпадает с каким-либо
из х, например, у\ = х\. Теперь можно написать
{(^1, /1), (^2, г’г), ..ih)\
т. е. трансверсаль X представляет и подсемейство
при этом х\ = у\. Среди индексов 7*2, ..]i
существует индекс, отличный от каждого /г, • .h, пусть
это будет 72. Тогда у2 совпадает с каким-либо из #2,..
например, У2 = Х2. Теперь имеем
{(^1, 71)» (^2, 72)7 (^3, г’з),	(^й, г’й)},
*1 = Z/1,	^2 = Z/2.
Итерируя этот процесс, получим Xi = yi (/==1, к) (с точ-
ностью до перенумерации элементов г/г). Следовательно,
X - <Z/i7 z/2, ..z/J, X U yh+i <
Итак, (Z?, У)—матроид с набором независимых мно-
жеств 3. Этот матроид называется матроидом трансвер-
салей семейства S. Матроид, изоморфный матроиду транс-
версалей какого-либо семейства подмножеств, называется
трансверсальным.
В важном частном случае, когда исходное семейство
S является разбиением множества Е, т. е. U Si = Е,
г
и подмножества St попарно не пересекаются, матроид
трансверсалей семейства S называется матроидом раз-
биения S. Очевидно, что подмножество X Е независимо
относительно матроида разбиения S тогда и только тог-
да, когда IX П 5J 1 (/ = 1, ш).
§ 23. Жадный алгоритм
Рассмотрим следующую задачу дискретной оптимиза-
ции. Пусть Е — непустое конечное множество, w: Е ->
R+ — функция, ставящая в соответствие каждому эле-
92
менту е этого множества неотрицательное действительное
число w(e)~— вес элемента е. Для Х^Е вес w(X) опре-
делим как сумму весов всех элементов множества X:
№(Х)= 2 «^(4
Пусть, далее, 3 — некоторый набор подмножеств множе-
ства Е, т. е. 3 2е. Задача состоит в выборе в «7 под-
множества максимального веса.
Оказывается, что в случае, когда 3 является набором
независимых множеств матроида, эта оптимизационная
задача решается с помощью следующего простого алго-
ритма.
Жадный (градиентный) алгоритм.
1-й шаг. Находим такой элемент в\ е Е, что
zr(^1) = max ш(е).
{е}€=«7
к-и шаг (к >2). Находим такой элемент ек^Е, что
w(ek) = max w(e).
{ei.
1
Если такого элемента нет, то конец.
Примером жадного алгоритма служит алгоритм Кра-
скала нахождения остова максимального веса во взве-
шенном графе (см. § 15).
Очевидно, что выходом жадного алгоритма всегда яв-
ляется элемент множества «7, максимальный относитель-
но включения. Однако он может оказаться не максималь-
ного веса. Чтобы убедиться в этом, рассмотрим пример:
Е = {1, 2, 3), 3 = {{1), {1, 2), {2, 3}}, ш(1) = 3, ш(2) = 2,
ш(3) = 4. Наш алгоритм найдет множество {1, 2}, хотя
множество {2, 3} имеет больший вес.
Возникает вопрос: когда же можно гарантировать по-
лучение подмножества максимального веса, решая задачу
с помощью жадного алгоритма? На этот вопрос отвечает
следующая
Теорема 23.1. Если 3 — набор независимых мно-
жеств матроида М = (Е, 3), элементам которого припи-
саны неотрицательные веса, то жадный алгоритм находит
в 3 множество максимального веса.
> Очевидно, что жадный алгоритм строит базу; пусть
это база
Вй = {ei, е2, ер), w(ei)>ip(e2)^...>w(ep).
93
Остается показать, что вес базы Bq максимален. Пусть
это не так. Среди всех баз максимального веса выберем
такую базу В, которая имеет наибольшее число общих
элементов с Bq. Так как B=£Bq и |В| == |2?01, то Bq\B^
^0. Выберем в Bq\B элемент ег с минимальным но-
мером i. Множество BU е{ содержит цикл С. Так как ба-
за матроида циклов не содержит, то существует е е С \ Bq.
Пусть В' =(B\e)(J cit Множество В' пе содержит циклов,
поскольку С — единственный цикл в В U е, (следствие
16.7). Кроме того, |5'| = |В|. Следовательно, В' являет-
ся базой. Далее имеем
В' A Bq = (В A Bq) U е,, \В' Л В01 > |5 А Во1.
Поэтому
w(B')<w(B),	(1)
иное противоречило бы выбору базы В.
С другой стороны, w (В') = w(В) — w(e)+ w(ег), по-
этому из (1) вытекает, что w(e)> w(ei). Но последнее
неравенство неверно, поскольку на Z-м шаге алгоритм вы-
брал а не е. Полученное противоречие доказывает
теорему. <
Из приведенного выше доказательства вытекает, что
жадный алгоритм можно трактовать как следующую про-
цедуру получения базы максимального веса в матроиде:
выбираем элементы матроида в порядке невозрастания
весов, отвергая лишь те элементы, добавление которых
нарушает условие независимости получаемых множеств.
Аналогично работает жадный алгоритм и для полу-
чения базы минимального веса, только при этом элемен-
ты матроида выбираются в порядке неубывания весов.
Заметим, что приведенное здесь доказательство пре-
дыдущей теоремы буквально то же, что и доказательство
теоремы 15.1, обосновывающей алгоритм Краскала.
Оказывается, верна теорема, в некотором смысле об-
ратная предыдущей.
Теорема 23.2. Пусть F — набор подмножеств конеч-
ного множества £, обладающий тем свойством, что если
X^F, У cz X, то Y^F. Тогда, если F не является на-
бором независимых множеств матроида, то применение к
F жадного алгоритма не гарантирует получения подмно-
жества максимального веса.
t> Пусть для набора F не выполняется аксиома 1.2,
т. е. в F есть такие X = {xi, х%, ..., У = {у1, г/2, . ..
..., yk), что*не существует Xi е X\yt, для которого У U Xi е
^F. Покажем, что в этом случае можно так подобрать
94
веса, что жадный алгоритм построит множество не мак-
симального веса.	____
Пусть w?(z/i)=l (z=l, &), w\xi)==t, если Xi^X\Y,
где 0<£<1, u;(e) = 0, если Е\ (XU У). Тогда жад-
ный алгоритм построит сперва множество У. Так как от-
сутствует такой элемент х^ что У U Хг F, то далее алго-
ритм выберет элементы из E\(XU У) и закончит работу,
получив в результате множество Xq, вес которого равен
весу множества У.
Пусть |ХПУ|=р. Тогда ш(Х) = р — (к + 1 — р)t. По-
этому, учитывая, что w(Xo) = &, можно выбрать 0<£<1
таким, чтобы было w(Xq)<w(X). Тем самым жадный ал-
горитм не находит в F множества максимального веса. <
§ 24.	Объединение и пересечение матроидов
Пусть М\ и М2 — два матроида на множестве элемен-
тов Е с наборами независимых множеств «71 и «7 г соот-
ветственно. Положим
«7 = {ХиУ: X^yh
Как показывает прямая проверка, множество «7 удовлет-
воряет аксиомам независимости. Следовательно, (Е, «7) —
матроид, для которого Ft служит набором независимых
множеств. Этот матроид называется объединением мат-
роидов М[ и М2 и обозначается через М\ U М2.
Очевидно, что операция объединения матроидов ассо-
циативна, и можно говорить об объединении нескольких
матроидов.	_____
Теорема 24.1. Пусть {Me. 1, к} — семейство
матроидов, определенных на одном и том же множестве
Е, с ранговыми функциями рг- соответственно, к>1, М —
объединение всех этих матроидов. Тогда ранговая функ-
ция р матроида М определяется для любого подмножест-
ва Х^Е равенством
р (X) = min {Р1 (4) + р2 (4) + ... + pft (4) + | Х\41}. (1)
АсХ
> Рассмотрим отдельно два случая.
1. р(Х)=|Х|. В этом случае р(Л)= |Л| для любого
подмножества А^Х. Очевидно, что
р(4)<р1(4)+р2(4)+... + рЛ(4),
95
поэтому
Pl(Л) + р2(Л) + ... + рДЛ) + |Х\ЛI >р(Л) + |Х\Л| =
= |Л| + |Х\Л| = |Х|=р(Х).
При А = 0 получаем
Р1(Л) + р2(Л) + ... + р,(Л) + |Х\Л I = 1X1 = р(Х).
Равенство (1) доказано.
2. р(Х)< 1X1. Воспользуемся индукцией по к. Внача-
ле пусть к = 2. По определению р(Х)= |5|, где В — мак-
симальное независимое подмножество в X. Очевидно, что
В = (В A A) U (В А (Х\Л)) для любого А X. Так как
|ВАЛ| <р(Л)<Р1(Л)+р2(Л),
\В А(Х\Л)| |Х\Л|,
то для любого А X
р(Х)= \В\ = \В А Л| + |ВА(Х\Л)|
< Р1(Л) + р2(Л) + |Х\Л|.	(2)
Теперь получим нижнюю оценку для р(Х). Пусть
М2 — копия матроида ЛГ2, определенная на множестве
имеющем пустое пересечение с Е. Более точно: Е =
= {^1? е2, ..., еп), Е' =	е2, . . ., еп], Е П Е' = &, мно-
жество	e'im} независимо относительно матрои-
да М2 тогда и только тогда, когда	неза-
висимо относительно М2. Очевидно, что можно опреде-
лить матроид на множестве Е U Е', объявив его незави-
симыми множествами объединения X U У, где X Е
независимо относительно матроида М\, Y^E' — относи-
тельно М2. Обозначим этот матроид и его ранговую функ-
цию через М} U М2 и р' соответственно.
Пусть теперь X — произвольное подмножество мно-
жества Е. Положив <S'i=Ui, в|}, 5r = (5ri:	полу-
чим семейство S подмножеств множества Е U Е". Согласно
следствию 22.2 для любого |Х| частичная трансвер-
саль мощности t семейства В, независимая относительно
матроида Mr (J М2, существует тогда и только тогда, когда
для любых г подмножеств Si выполняется условие
p'(5{i U ... U 5ir)>r + Z-|X|, г=1,|Х|.	(3)
Объединение множеств, заключенное в скобки, предста-
96
вим в виде A U А', где А ^Е, А' — Е'. Ясно, что
р'(Л иЛ') = Р1(Л) + р2(Л)\ |Х| —г = |Х\ЛI,
поэтому условие (3) можно переписать так:
Р1 (Л) + р2(Л)> t - |Х\Л|.	(4)
G другой стороны, легко понять, что следующие два
утверждения равносильны:
1) существует частичная трансверсаль мощности t се-
мейства подмножеств 5, независимая относительно мат-
роида Мх J М2;
2) p(X)>t
В самом деле, пусть Т — такая трансверсаль и пусть,
для определенности,
Т= {г?1, .. вр, е'^!, ..et], ei<=E, e'j(=E’. (5)
Тогда
{eP .. ., ер} е= St (Мх),	(е'р+1, ..., e't] е= 3 «),
{еР+!,	е;}е.7(М2)
и, следовательно,
{еь еР+1, ..., et} U М2\	(6)
т. е. выполняется условие (2).
Обратно, если выполняются условия (2) и (6), при-
чем
{ei, ..., ер) «5^ (Л/\),
{^р+1, ..., et}^^(M2),
то множество Т, определяемое условиями (5), является
частичной трансверсалью мощности t семейства подмно-
жеств S, независимой относительно матроида J М2.
Равносильность утверждений 1) и 2) доказана.
Из предыдущего вытекает, что р(Х)^М тогда и только
тогда, когда для любого подмножества Л множества X
верно неравенство (4). Следовательно, при £ = р(Х)+1 в
X существует такое подмножество Ло, которое не удовлет-
воряет неравенству (4), т. е.
Р1 (Ло) + Р2 (Ло) < Р (X) + 1 - I Х\ЛоI,
откуда
р(Х)>р1(Ло) + р2(Ло)+1Х\Ло1.	(7)
Из (7) и (2) вытекает
р(Х) = р1(Ло) + р2(Ло)+1Х\Ло1.
7 в. А. Емеличев и др.	97
Последнее равенство в сочетании с неравенством (2) при-
водит к формуле
р (X) = min {Р1 (А) + р2 (А) + | Х\А |}.
А^Х
Для к = 2 теорема доказана.
Пусть теперь к > 2 и теорема верна для объединения
менее чем к матроидов. Если р' — ранговая функция
объединения Л1\ U М% U ... U Mh-\, то в силу доказанного
выше и индуктивного предположения имеем
р (X) = min {р' (5) + Pfc (5) + I Х\в |} =
ВсХ
= min fmin {р± (Л) + ... + pft., (Л) + | В \Л |} +
вех \л^в
+ рй(В) + |Х\5|}.
Поскольку А^В и |5\А| + |Х\В| = |Х\А|, то рассмат-
риваемый минимум достигается лишь при А = В, и пото-
му получаем
р(Х) = min{P1(A) + . .. + ph(A) + | Х\А |}. <
А^Х
Ниже через (Е, р) обозначается матроид с множест-
вом элементов Е и ранговой функцией р.
Следствие 24.2. Матроид (Е, р) имеет I попарно
иепересекающихся баз тогда и только тогда, когда для
любого А^Е верно неравенство
Zp(A)+|Al^Zp(£).	(8)
>	Пусть 1М — объединение Z экземпляров матроида
#, р' — ранговая функция этого объединения. Очевидно,
что p'(Z7l/)C Zp(7H) и М имеет Z попарно непересекаю-
щихся баз только при условии р' (1М) = Zp (71/). Теперь
нужное утверждение непосредственно вытекает из пре-
дыдущей теоремы. <
Следствие 24.3. Для представимости множества Е в
виде объединения не более чем I независимых подмно-
жеств матроида М — (Е, р) необходимо и достаточно, что-
бы любое подмножество А^Е удовлетворяло условию
|А| ^Zp(A).	(9)
>	Множество Е представимо в виде указанного объ-
единения только тогда, когда р'(1М)= \Е\. Согласно тео-
реме 24.1 _последнее равносильно неравенству I Е\ <
Zp(А) + |АI, в свою очередь равносильному неравенст-
ву (9). <
98
Применим два предыдущих следствия к циклическому
матроиду M(G) непустого графа G. В рассматриваемой
ситуации независимыми множествами матроида служат
множества ребер ациклических подграфов. Объединим
каждый такой подграф со всеми не входящими в него
вершинами G и будем считать подграф остовным. Для
любого остовного подграфа Н верно равенство р(71/(Я)) =
= n(G) — к (Н). Если II — остовный подграф с множест-
вом ребер А, то неравенства (8) и (9) превращаются в
неравенства
m(G)- т(Н)>	k(G))	(10)
и, соответственно,
m(#)<Z(n(G)-&(#)).	(11)
Поэтому верны следующие два утверждения.
Следствие 24.4. В непустом графе G имеется I
реберно непер есекающихся остовов тогда и только тогда,
когда любой его остовный подграф удовлетворяет нера-
венству (10).
Следствие 24.5. Для того чтобы непустой граф G
был объединением не более чем I своих остовов, не имею-
щих общих ребер, необходимо и достаточно выполнение
условия (11) для любого его остова Н.
Аналогично введенному выше понятию объединения
матроидов можно ввести понятие их пересечения. Пусть
Mj = (E, f/j) (/ = 1, k)—к матроидов на множестве эле-
ментов Е с наборами независимых множеств <7j. Пару
k
М = (Е, Sf), где <7 = П <7j, назовем пересечением матрои-
5=1
______________	k
дов Mj (/== 1, к) и обозначим М = f] Mj,
j-i
Разумеется, пересечение матроидов также может ока-
заться матроидом. Например, пересечение тривиального
матроида и любого матроида с тем же множеством эле-
ментов есть тривиальный матроид. Но, как правило, пере-
сечение матроидов М не является матроидом с набором
независимых множеств «7, поскольку «7 может не удов-
летворять аксиоме независимости 1.2. Например, пересе-
чение двух матроидов /1/1=(Я, .71) и 7И2 = (£', «7о), где
Е = {1, 2, 3, 4), = {0, {1}, {2}, {3}, {4}, {1, 3}, {1, 4},
{2, 3}, {2, 4}}, «72 = Ж {О, {2}, {3}, {4}, {1, 2}, {1, 4},
{2, 3}, {3, 4}}, не есть матроид, так как множество
7*	99
Z7i 0 3^2 = 101 (I), {2}, {3}, {4}, {1, 4}, {2, 3}} не удовлетво-
ряет условию 1.2.
В § 28 читатель столкнется со следующей задачей:
Задача о пересечении к матроидов. Даны
к матроидов на одном и том же множестве элементов Е.
Требуется найти в Е наибольшее по числу элементов
подмножество, являющееся независимым множеством
каждого из заданных матроидов.
Пусть, например, заданы два графа G и Я, причем
|2?б?| = \ЕН\ == т. Пусть ребра этих графов занумерованы
с помощью одних п тех же меток: EG == ЕН — {1, 2, ...
..., т}. Очевидно, что задача нахождения в Е наиболь-
шего по числу элементов подмножества, не содержащего
циклов ни первого, ни второго графов, и есть задача о
пересечении двух графических матроидов M(G) и М(Н}.
Задача о пересечении лишь двух матроидов стоит
особняком: она эффективно решается методом чередую-
щихся последовательностей (см., например, [25]). Идея
этого метода демонстрируется в § 77.
При к > 2 задача о пересечении к матроидов стано-
вится очень трудоемкой. Даже для решения ее простей-
шего варианта — задачи о пересечении трех матроидов
разбиений — не найдено, и скорей всего не существует,
эффективных алгоритмов.
УПРАЖНЕНИЯ
1.	Пусть М — матроид порядка п. Покажите, что число его баз
(п \
р(М)г а числ0 его Диклов не превосходит
/ п \
+1J-
2.	Пусть М = (Е, У) — матроид с набором независимых мно*
жеств 0^=А^Е. Пусть, далее, St' =	Xf]A==0}.
Докажите, что М' = (Z?, ^7') — матроид с набором независимых
множеств <7'. Мэ?роид М' называется сужением матроида М по-
средством А.
3.	Пусть в обозначениях предыдущего упражнения ==
= {X П А: Хе 3}. Докажите, что М" = (Еч 3") — матроид с на-
бором независимых множеств 3". Матроид М" называется ограни-
чением матроида М на А.
4.	Пусть Е — непустое конечное множество, к |1?|. Докажи-
те, что множество & всех ^-элементных подмножеств множества Е
удовлетворяет аксиомам баз и, следовательно, (Z?,	— матроид.
Его называют однородным матроидом ранга к.
5.	Пусть D — ориентированный граф, и пусть Е и Y — два не-
пересекающихся подмножества его вершин. Подмножество А Е
называется независимым, если существует |А| вершипно непе-
100
ресекающихся простых орцепей из Л в У. Докажите, что эти не-
зависимые множества задают некоторый матроид.
6.	Пусть М — матроид с ранговой функцией р. Докажите, что
для любого подмножества А его элементов
. р*(Л) - |А| + р(А)-р(М),
где р* — корапговая функция матроида М.
7.	Для каких к и п существуют однородные матроиды поряд-
ка п и ранга 7с, являющиеся матроидами циклов некоторого графа?
8.	Исследуйте циклические матроиды М(К$) и Л/(/<31з). Дока-
жите, что они не являются кографическими.
9.	Покажите, что с точностью до изоморфизма число матрои-
дов порядка п не превосходит 22 .
10.	Охарактеризуйте графы, матроиды циклов и разрезов ко-
торых изоморфны.
И. Покажите, что с точностью до изоморфизма существует
ровно 4 матроида порядка 2 и 8 матроидов порядка 3. Сколько сре-
ди них представимых над каким-либо полем?
12.	Пусть Mi и М2 — матроиды на множестве Е с ранговыми
функциями pi и р2. Докажите, что Mi и М2 имеют общее незави-
симое множество мощности к тогда и только тогда, когда pi (А) +
+ р2(А) к для любого А Е.
13.	Докажите, что каждый однородный матроид является транс-
версальным.
14.	Докажите, что трансверсальные матроиды и только они
представимы в виде объединений матроидов ранга 1.
15.	Докажите, что циклический матроид М(К^ не является
трансверсальным.
16.	Докажите, что матроид, двойственный к трансверсальному,
пе обязательно является трансверсальным.
17.	Докажите, что с точностью до изоморфизма число трапс-
нереальных матроидов порядка п но превосходит 2 .
18.	Необходимо выполнить на ЭВМ множество заданий. Все
задания требуют для выполнения одинакового времени. Каждому
из заданий присвоен крайний срок выполнения.
а)	Покажите, что набор всех подмножеств заданий, которые
можно выполнить с соблюдением сроков выполнения, образует
набор независимых подмножеств некоторого матроида.
б)	Допустим, что за каждое пе выполненное в срок задание
необходимо заплатить штраф, величина которого одинакова для
всех заданий. В каком порядке следует выполнять задания, чтобы
общий штраф был минимальным?
19.	Пусть М — матроид, элементам е которого приписаны не-
отрицательные веса w(e). Докажите, что
min max w (с) = max minw(e),
где &—множество баз матроида 7И,	— множество коциклов ма-
троида М.
101
Глава IV
Независимость и покрытия
Во многих прикладных задачах требуется найти в ко-
нечном множестве объектов максимальную систему объ-
ектов, попарно не связанных друг с другом, или же вы-
брать минимальную систему объектов, связанных со все-
ми другими. Формулировки подобных задач на языке
теории графов приводят к понятиям независимости и
покрытия.
§ 25. Независимые множества и покрытия
Множество вершин графа называется независимым
(пли внутренне устойчивым), если никакие две верши-
ны из этого множества не смежны. Иными словами, если
S VG и 5 независимо в графе G, то порожденный под-
граф G(S) является пустым. Очевидно, что если при
этом S' cz 5, то S' — также независимое множество.
Независимое множество называется максимальным,
если оно не является собственным подмножеством неко-
торого другого независимого множества. Наибольшее по
мощности независимое множество называется наиболь-
шим. Ясно, что наибольшее независимое множество яв-
ляется максимальным. Обратное, вообще говоря, неверно.
К отысканию наибольшего независимого множества
вершин в графе сводится, например, известная задача о
восьми ферзях, которую связывают с именем К. Гаусса.
Задала о восьми ферзях: требуется так рас-
ставить па шахматной доске наибольшее число ферзей,
чтобы они не атаковали друг друга.
Таких ферзей, очевидно, может быть не более восьми,
так как никакие два пз них не должны находиться па
одной вертикали или горизонтали. Рассмотрим граф, вер-
шины которого соответствуют клеткам доски, а ребра —
парам клеток, лежащих на одной вертикали, горизонтали
или диагонали. Ясно, что требуемой в задаче расстановке
ферзей соответствует наибольшее независимое множество
102
в этом графе. Одно из решений задачи о восьми ферзях
показано на рис. 25.1.
Число вершин в наибольшем независимом множестве
графа G называется числом независимости (числом внут-
ренней устойчивости, неплотностью') этого графа и обозна-
чается через ao(G).
Например, для графа G, изображенного па рис. 25.2,
ao(G) = 4, множества вершин {1, 2, 3, 7), {1, 2, 3, 8},
{2, 3, 5, 7} и {2, 3, 5, 8} являются наибольшими незавп-
симыми, а {4, 7} — мак-
симальное независимое
множество, не являю-
щееся наибольшим.
Содержанием боль-
шинства задач, связан-
ных с понятием незави-
симости,
ределение
являются оп-
числа неза-
висимости и отыскание наибольшего независимого мно-
жества. Эти задачи, как правило, очень трудны, и потому
для их решения оказываются полезными оценки числа
независимости.
Теорема 25.1. Для любого графа G верно нера-
венство
a0(G)> S (l + degy)-1-
v= VG
(1)
> Если G — полный граф, то в (1) имеет место ра-
венство. Поэтому не теряя общности будем считать, что
G^Kn.
Воспользуемся индукцией по числу вершин графа G.
В справедливости неравенства (1) для графов порядка
гс < 2 легко убедиться непосредственно. Пусть теперь
\VG\ = гс > 2 и для всех графов порядка, меньшего чем
гс, неравенство (1) верно. Выберем в графе G вершину х
минимальной степени. Так как G=£Kn, то х U N(x)^ VG.
Пусть G' ~ G — (х U N(x)). Согласно индуктивному пред-
103
положению для графа G' верно неравенство, аналогичное
неравенству (1). Пусть М' — наибольшее независимое
множество вершин графа G'. Ясно, что множество М =
= М' U х независимо в графе G, и для доказательства тео-
ремы достаточно показать, что
*51 = 2 (1 + deg^ vy~l ^5 S2 = 2 (1 + deg^ + 1-
v(=VG	v^VG'
Обозначим через Q множество вершин графа G', каж-
дая из которых смежна в G с какой-либо вершиной из
N(х) (см. рис. 25.3). Очевидно, что слагаемые в 55, соот-
ветствующие вершинам v из Q, меньше аналогичных сла-
гаемых в 5г, а слагаемые в
51 и 5з, соответствующие вер-
шинам v из VG'\Q, совпада-
ют. Стало быть, достаточно
показать, что
------------------------------1-----р
1 + degG *
+ 2 (1 + degev)-^ 1.
v^N(x)
(2)
Согласно выбору вершины
х для любой вершины у из
N(х) имеем degG х degG у.
Поэтому левая часть неравенства (2) является суммой
(l + degG3?) слагаемых, не превосходящих (l + degt?#)-1
и, следовательно, не превосходит 1. <1
Пусть
d = ТЭТ 2 de«v
1 1
— среднее арифметическое степеней графа G.
Следствие 25.2. Для любого графа G порядка п
верно неравенство

п
1> Известно неравенство Коши -- Буняковского:
для любых аг, Ъг > 0. Полагая
аг = 1 + deg Vi, Ьг = (1 + deg ^-)
Vi e VG,
104
получим
S (1 4- deg i’)'j f 2 (1 + deg p)-1) > ?i2.
reVG	J \velVG	J
Последнее неравенство вместе с неравенством (1) приво-
дит к соотношениям
2
“o(G)JL(* + degР)”1 2 (”+dog0 = i+d- <
vgVG
По существу, доказательство теоремы 25.1 дает про-
стой алгоритм построения независимого множества М та-
кого, что
|Af |> 2 (1 + degp)-1.
vsva
Это множество строится следующим образом: каждый раз
в графе выбирается вершина минимальной степени и за-
носится в множество М. Затем эта вершина и все смеж-
ные с ней удаляются из графа и процесс продолжается.
Как уже отмечалось, задача отыскания наибольшего
независимого множества вершин в графе очень трудна
для алгоритмического решения. Поэтому множество М,
построенное описанным выше способом, иногда прини-
мают в качестве ее приближенного решения. Что можно
сказать о точности такого решения, или, иначе говоря,
как далеко величина 2 (l + degp)”1 может отстоять от
reVG
czo(G)? Ниже показано, что отношение первой из этих
величин ко второй может быть сколь угодно малым чис-
лом, т. е. такое решение может оказаться плохим.
Рассмотрим граф G = Gm, для которого множества Pi,
Tz2, Уз, {и}, {р} образуют разбиение VG, [У{[=тп
_______	5
(Z-1, 3), EG = и Ei, Ei = {vx:	E2 = {xy: x^V{,
z/ezy2}, Ез = {xy^x v2, у^Уз}, E^ {их: x U 73},
E$ = {xy: x^V2, у V2, x ¥= у} (см. рис. 25.4, где изобра-
жен граф Gt). Легко видеть, что при любом тп 2 верно
равенство av(Gm) = 2m. В то же время мощность множест-
ва М в графе Gm равна трем.
Пусть снова G — произвольный граф, А = А(б?)—мак-
симум степеней его вершин. Тогда из теоремы 25.1 оче-
видно следует неравенство
a0(G)>n/(A + l), n=lGl,	(3)
105
которое, впрочем, нетрудно получить непосредственно.
Теорема Брукса (см. § 54) дает более точную оценку:
если G — связный граф, Л = A (G)	3 и G ¥= /<п, то
aQ(G)>n/A,	(4)
Эта оценка предпочтительнее оценки (1) в случае, когда
граф G — регулярный, или близкий к регулярному. Так,
I
Рис. 25.4
если G — кубический граф, то из неравенства (4) полу-
чаем ссо(G)> п/3, в то время как (1) дает только ao(G)>
п^. Легко, однако, привести примеры, в которых более
точна оценка (1).
Дальнейшее уточнение нижней оценки числа ao(G)
связано с использованием, помимо степенной последова-
тельности, дополнительной информации о графе и суже-
нием класса рассматриваемых графов. Следующая тео-
рема, приводимая без доказательства, усиливает оценки
(1) и (3) для рассматриваемых в ней классов графов.
Теорема 25.3 (Д. Григгс, 1983 г.). Пусть G — связ-
ный граф порядка п^З, пе содержащий треугольников и
не являющийся цепью либо циклом нечетной длины.
Тогда
а» >мд -Г--1Г + 2 d + deS О"1, А = А (<?)• (5)
4	' veVG
Приведенное неравенство превращается в равенство тогда
и только тогда, когда граф G является циклом четной
длины или совпадает с одним из графов, изображенных
на рис, 25.5.
106
Независимое множество вершин графа имеет естест-
венную матричную интерпретацию. Пусть Х = {щ, z>2, ...
..., vk} — независимое множество вершин графа G, А =
= A (G) — матрица смежности. Множеству X в матрице А
соответствует подматрица, элементы которой, расположен-
ные в строках и столбцах, соответствующих элементам
Рис. 25.5
множества X, равны нулю. Такое представление позво-
ляет получить верхнюю оценку числа ао(С?) с помощью
характеристических чисел матрицы А.
Обозначим через р+, р~ и р° число положительных,
отрицательных и нулевых собственных значений матри-
цы смежности графа соответственно.
Теорема 25.4 (Д. Цветкович, 1973 г.). Для всякого
графа G справедливо неравенство
a0(G)р° + min{/>~, р+}.	(6)
> Пусть ao(G) = тп. В графе G есть порожденный
пустой подграф порядка тп. При подходящей нумерации
вершин этому подграфу соответствует подматрица А' мат-
рицы Л, занимающая строки и столбцы с номерами 1,
2, ..., //г, все элементы которой равны нулю. Пусть >
> Х2	и Ц1 Ц2 ^ ... ^ Цт — собственные значе-
ния матриц А л А' соответственно. Эти числа связаны
известными неравенствами Коши
Цг

I == 1, Ш
(см. [23]). Поскольку А'— нулевая матрица, то все
Цг = 0. Отсюда получаем неравенства
0 С X/, Xn_m+i 0, I = 1, тп.
Из этих неравенств следует, что + р° > m и р~ + р° > т,
т. е. т р° + min {/?“, р+}. Неравенство (6) доказано. <
Независимые множества вершин графа имеют самые
разнообразные применения. Оставляя в стороне голово-
ломки и задачи развлекательного характера, рассмотрим
одно из применений независимости в теории информа-
107
ции. Возникающую здесь ситуацию можно упрощенно
описать следующим образом. Источник информации по-
сылает сообщения, являющиеся последовательностями
сигналов из множества X = {^i, £2, • • •, При передаче
возникают (например, вследствие помех) искажения сиг-
налов. Поэтому на принимающей станции некоторые
сигналы могут быть поняты как другие, т. е. перепута-
ны. Рассмотрим граф G, у которого VG — X и XiXj^EG,
если и только если Xi и х$ могут быть перепутаны. Тогда,
чтобы получить безошибочный код, т. е. исключить пере-
путывания, следует пользоваться сигналами из независи-
мого подмножества вершин графа G. Стремление полу-
чить максимальное количество таких сигналов приводит
к задаче отыскания наибольшего независимого множества
вершин в графе G.
Обычно одним сигналом не ограничиваются, а посы-
лают тексты в виде слов. Если все передаваемые слова
имеют длину к, то очевидно, что рассматриваемый код
содержит по меньшей мере (cco(G))ft слов, различаемых
при приеме. Но фактически их может быть больше. Рас-
смотрим пример, принадлежащий К. Шеннону. Пусть
G == С5 — простой цикл длины 5 с вершинами, пронуме-
рованными числами 1, 2, ..., 5 в порядке следования по
циклу. Тогда cco(G) = 2, {1, 3} — наибольшее независи-
мое множество вершин графа G. Это множество дает
4 слова (1, 1), (1, 3), (3, 1), (3, 3) длины 2, которые
различимы, т. е. при приеме не могут быть приняты
Йодно в качестве другого. Однако 5 слов
(1, 1), (2, 3), (3, 5), (4, 2), (5, 4)
также различимы. Максимальное чис-
ло различимых слов удобно описыва-
ется с помощью вводимых ниже тер-
минов.
Пусть G — произвольный граф, к —
натуральное число. Следующим образом
Рис. 25.6 определим граф — сильную степень
графа G. Множество вершин графа Gh
совпадает с декартовой степенью (FG)ft; несовпадающие
вершины (ui, U2,..uk) и (vi, V2,..., vk) смежны в графе
Gh тогда и только тогда, когда для каждого индекса i =
= 1, к выполняется условие Ui = или UiVi е EG. На
рис. 25.6 изображен граф G2, где G = P^.
Очевидно, что если графу G придается тот же смысл,
что и в описанной выше задаче из теории информации,
то наибольшее число различимых слов длины к равно
108
числу независимости ao(Gft). Очевидно также, что ao(Gft)>
>(ao(G))\
К. Шеннон ввел параметр
V—
0(G) = sup у aQ(Gk),
называемый теперь шенноновской емкостью графа G. Из
предыдущего следует, что 0(G) > ao(G) и что в общем
случае это неравенство не превращается в равенство.
Вычисление шенноновской емкости является очень
трудной задачей даже для графов с небольшим числом
вершин. Шенноном доказано, что если число кликового
покрытия c(G) (см. § 26) удовлетворяет равенству
c(G) = ao(G), то 0(G) = ao(G). Таковы, например, все со-
вершенные графы (см. § 61). Однако последнее равенст-
во неверно уже для простейшего графа, не являющегося
совершенным, а именно для цикла С5. Л. Ловас доказал,
что 0(С5) = Т5. Получение этого частного результата по-
требовало немалых ухищрений, развитая при этом техни-
ка позволяет находить шенноновские емкости ряда дру-
гих графов.
С понятием независимости в графе связано понятие
доминирования. Подмножество V' вершин графа G назы-
вается доминирующим, (или внешне устойчивым), если
каждая вершина из VGW' смежна с некоторой верши-
ной из У'. Иначе говоря, каждая вершина графа нахо-
дится на расстоянии не более 1 от доминирующего мно-
жества. Доминирующее множество называется минималь-
ным, если никакое его собственное подмножество не яв-
ляется доминирующим. Доминирующее множество, имею-
щее наименьшую мощность, называется наименьшим.
Иллюстрацией к только что введенным понятиям мо-
жет служить следующая занимательная
Задача о пяти ферзях: требуется расставить
на шахматной доске наименьшее число ферзей так, что-
бы каждая клетка доски была под боем.
Очевидно, что всякой такой расстановке ферзей соот-
ветствует наименьшее доминирующее множество в графе,
введенном выше в связи с задачей о восьми ферзях.
Одно из решений задачи о пяти ферзях приведено на
рис. 25.7.
Подмножество вершин графа, являющееся как неза-
висимым, так и доминирующим, называется ядром.
109
Очевидно, что независимое множество является мак-
симальным (не обязательно наибольшим) тогда и только
тогда, когда оно доминирующее. Таким образом, ядра гра-
фа — это максимальные независимые множества вершин.
С другой стороны, доминирующее множество не обяза-
тельно независимо. Например, множества вершин {1, 2,
3, 7}, {1, 2, 3, 8}, {2, 3, 5, 7), {2, 3, 5, 8}, {4, 7} являются
ядрами графа, изображенного на рис. 25.2. Наименьшее
Рис. 25.7
доминирующее множе-
ство вершин цепи со-
стоит из двух смежных
вершин.
Понятия доминирую-
щего множества и ядра
естественным образом
переносятся и на слу-
чай ориентированных
графов. Получаемые при
этом результаты более
интересны, чем в слу-
чае неориентированных
графов (см. § 67).
Отыскание в графе
наименьшего доминиру-
ющего множества явля-
ется содержанием мно-
гих прикладных задач. Типичная ситуация, в которой
возникает подобная задача, такова. Имеется множество
населенных пунктов, связанных дорожной сетью. В неко-
торых из них надо разместить предприятия обслуживания
так, чтобы расстояние от каждого из населенных пунктов
до какого-либо из предприятий не превосходило заданной
величины. Размещение следует выполнить так, чтобы обой-
тись минимальным количеством предприятий. Если поста-
вить в соответствие населенным пунктам вершины графа,
в котором две вершины смежны тогда и только тогда, ког-
да расстояние между соответствующими пунктами не пре-
вышает заданной величины, то задача очевидно сводится
к построению в графе наименьшего доминирующего мно-
жества.
Введем еще одно понятие, связанное с понятием не-
зависимости. Будем говорить, что вершина и ребро графа
покрывают друг друга, если они инцидентны. Таким об-
разом, ребро е = аЪ покрывает вершины а и Ъ, а каждая
из этих вершин покрывает ребро е. Подмножество V' VG
НО
называется покрытием (вершинным покрытием, опорой)
графа G, если каждое ребро из EG инцидентно хотя бы
одной вершине из V'. Покрытие графа G называется ми-
нимальным, если оно не содержит покрытия с меньшим
числом вершин, и наименьшим, если число вершин в нем
наименьшее среди всех покрытий графа G. Число вершин
в наименьшем покрытии графа G называется числом по-
крытия (или числом вершинного покрытия) графа G и
обозначается через Po(G).
Например, на рис. 25.2 каждое из множеств Xi = {4,
5, 6, 8}, Х2 = {4, 5, 6, 7}, Х3 = {1, 2, 3, 5, 6, 8} является
покрытием, причем Xi и Х2 — наименьшие покрытия,
а Х3 — минимальное покрытие.
Следующая теорема указывает на тесную связь меж-
ду покрытиями и независимыми множествами графа.
Теорема 25.5. Множество U вершин графа G явля-
ется (наименьшим, минимальным) покрытием тогда и
только тогда, когда U = VG\U — (наибольшее, максималь-
ное) независимое множество. Следовательно,
a0(G)+fJ0(G)= |G|.
> По определению множество U независимо тогда и
только тогда, когда в графе нет ребра, оба конца которого
содержатся в U, т. е. когда хотя бы один из концов каж-
дого ребра принадлежит U. Последнее означает, что U —
вершинное покрытие. _
_ Поскольку IU\ + |СЛ| = IGI, то, очевидно, наибольшим
U соответствуют наименьшие U и наоборот. <
С помощью этой теоремы все приведенные выше оцен-
ки числа ao(G) очевидным образом преобразуются в оцен-
ки для ₽o(G).
§ 26. Клика
Антиподом понятия независимого множества является
понятие клики. Подмножество V' вершин графа G назы-
вается кликой, если любые две входящие в него верши-
ны смежны, т. е. если порожденный подграф G(V') яв-
ляется полным. Клика называется максимальной, если
она не содержится в клике с большим числом вершин,
и наибольшей, если число вершин в ней наибольшее сре-
ди всех клик. Число вершин в наибольшей клике графа G
называется его плотностью (или клико вым числом) и
обозначается через cp(G). Как и в случае независимых
111
множеств, максимальная клика графа может оказаться
не наибольшей, и это обстоятельство делает задачи на-
хождения числа cp(G) и наибольшей клики для произ-
вольного графа G крайне трудными.
Очевидно следующее
Утверждение 26.1. Подмножество вершин графа
G является кликой тогда и только тогда, когда оно неза-
висимо в дополнительном графе G. Следовательно, ф(б?) =
= ао(<?).
С помощью этого утверждения и приведенных в § 25
оценок числа <zo(G) просто получаются соответствующие
оценки числа cp(G).
Очевидно, что все клики графа, как и все максималь-
ные клики, составляют покрытие множества вершин.
Наименьшее число клик графа G,
1	покрывающих множество VG, на-
зывается числом кликового по-
/	\ крытия и обозначается через
2А------A
/ \	\ Очевидно, что с (G) > ао (б?) для
/	любого графа G.
£ О взаимном	расположении
клик в графе можно судить по
Рис. 26.1	свойствам вводимого ниже графа
клик.
Граф пересечений максимальных клик графа G назо-
вем графом клик и обозначим через Q(G). Таким обра-
зом, вершины графа Q(G) биективно соответствуют мак-
симальным кликам графа G и две вершины смежны тогда
и только тогда, когда соответствующие клики пересека-
ются. Если для некоторого графа Н существует такой
граф G, что H^Q(G), то Н также называется графом
клик.
Очевидно, что граф Q(G) может быть как «большим»,
так и «малым». Например, Q{On) = On, Q(Kn) = К\,
Q(K1>n) = Kn, Q(Pn) = Pn^, Q(Cn)~Cn. Для графа G,
изображенного на рис. 26.1, <?(С) = ^4.
Известью, что существуют графы, не являющиеся гра-
фами клик. Таков, например, граф, представленный на
рис. 26.1. Тем не менее следующая теорема свидетельст-
вует о том, что расположение клик в произвольном гра-
фе достаточно произвольно.
Теорема 26.2. Для любого (п, тп) -графа Н сущест-
вует такой граф G порядка п + пг, что Н изоморфен не-
которому порожденному подграфу графа клик Q(G). Если
112
при этом Н не содержит треугольников, то граф G мож-
но выбрать так, что
> Пусть
VH = {1, 2, .. , п}, ЕН = {щ, е2, ..ет}.
Описанным ниже способом построим граф G с множест-
вом вершин
VG == {vi, i?2, ..vn, Е[, Е2, ..., Ет}.
Если Е (0 = еа^, ...,	— множество всех ребер
графа Н, инцидентных вершине i, то положим
Vi = Еа±, Eaz, . .
Gi = K(Vi) — полный граф с множеством вершин Vi,
G = Gi U G2 U ... U Gn.
Рассмотрим граф клик Q(G). Очевидно, что каждое из
множеств Vi служит максимальной кликой графа G. Кро-
ме этого, возможны еще максимальные клики, нс содер-
жащие вершин вида Vi. Пусть X — одна из них,
Еа, Е$ ^Х, Еае= ViWi, Е$ V^Vi. (1)
Заметим, что ЕаЕ$ EG тогда и только тогда, когда реб-
ра са и вр графа Н смежны. Поэтому из (1) следует, что
существует вершина к, инцидентная каждому из ребер
еа и ер, и потому Еа е Vh, Е$ Vh. Таким
образом, | Х| >2 и любые две вершины,
принадлежащие клике X, вместе входят
в какое-либо из множеств Vi. Посколь-
ку клика X не совпадает ни с одним
из Vi, то в ней есть три вершины Еа,
Ер, Ет такие, что Еа, Ер е Vh, Еа, Ет
V^ Е$, Е^ Vj и индексы i, j, к по-
Рис. 26.2
парно различны. Тогда ребра еа, ер,
составляют в графе Н треугольник (рис. 26.2). По-
скольку в графе II нет четвертого ребра, смежного с каж-
дым из ребер Са, Ср, ет, то Ш = 3, X = Ха₽т = {Еа, Ер, Ет}.
Очевидно и обратное: если ребра еа, ер, ег составляют
треугольник в графе II, то множество ХаРт является мак-
симальной кликой графа G.
Таким образом, если в Н нет треугольников, то
Е()(6г) = {V\, V2, ..., Vn}. Если в графе Н есть треуголь-
ники, то вершинами графа Q(G) служат все множества
Vi и все клики графа G вида Харт.
8 В. А. Емеличев и др.
113
В любой ситуации обозначим через F подграф графа
(2(G), порожденный множеством вершин F = {Fi, F2, •••
..., Vn}. Очевидно, что отображение VH V, при кото-
ром i^Vi, является изоморфизмом графов Н и F. Итак,
если в Н нет треугольников, то II^Q(G). В противном
случае граф Н изоморфен порожденному подграфу F гра-
фа ^(G). <
На рис. 26.3 изображен граф G, описанный в доказа-
тельстве предыдущей теоремы; в качестве Н взят граф,
представленный на рпс. 26.1, а на рис. 26.4 показан граф
клик (2(G).
Следствие 26.3. Всякий граф, не содержащий тре-
угольников, является графом клик.
114
Иногда полезно понятие матрицы клик. Пусть G —
произвольный граф, Q = {Q\, QP) — множество всех
его максимальных клик, VG ={vi, и2, ..., уп}. Следую-
щим образом определим бинарную р X n-матрицу С —
= C(G), строки которой соответствуют кликам из множе-
ства Q, а столбцы — вершинам графа G:
(j _ рЬ если
гз [0 в противном случае.
Матрица C(G) называется матрицей клик графа G.
Очевидно, что матрица клик определяется с точностью
до перестановок строк и столбцов.
Например, для графа G, изображенного на рис. 26.1,
rl 1 1 0 0 От
г(Гх__ 0 10 110
Ь “ 0 110 10*
0 0 10 11
§ 27. Проблемы клики, изоморфной вложимости
и изоморфного подграфа
Пусть G и G' — два графа. Требуется установить, су-
ществует ли в графе G' подграф, изоморфный графу G.
Эта проблема изоморфного подграфа является одной из
труднейших алгоритмических проблем теории графов.
Другой вариант этой проблемы — проблема изоморф-
ной вложимости: требуется установить, существует ли в
графе G' порожденный подграф, изоморфный графу G.
Проблема изоморфного подграфа превратится в про-
блему изоморфизма графов, если дополнительно поло-
жить IGI = |G'| и \EG\ — \EG'\. Аналогично проблема
изоморфной вложимости превратится в проблему изомор-
физма, если положить | Gl = IG' I.
Проблему клики часто рассматривают в таком виде:
заданы граф G и натуральное число с; установить, верно
ли неравенство cp(G)^c?
Очевидно, что проблема клики является частным слу-
чаем как проблемы изоморфного подграфа, так и пробле-
мы изоморфной вложимости: требуется установить, явля-
ется ли полный граф Кс подграфом графа G. На самом
деле эти три проблемы эквивалентны, т. е. и проблема
изоморфной вложимости, и проблема изоморфного под-
графа могут рассматриваться, в свою очередь, как част-
ные случаи проблемы клики. Этот факт первым доказал
8*	115
В. Г. Визинг, использовав свою конструкцию модульного
произведения графов. Удобнее рассматривать не само
произведение Визинга, а дополнительный к нему граф.
Именно эта конструкция ниже названа модульным про-
изведением.
Модульным произведением G<Z>G' графов G и G' на-
зывается граф, определяемый следующими условиями:
1) V (G<> G') = VG X VG' — декартово произведение
множеств VG и VG';
2) вершины (и, и') и (р, v') графа G<>G' смежны
тогда и только тогда, когда одновременно и =/= га, и =/= и' и
Рис. 27.1
либо uv^EG, uv'^EG', либо uv^EG, u'v'^EG'
(рис. 27.1).
Теорема 27.1 (В. Г. Визинг, 1975 г.). Граф G изо-
морфно вкладывается в граф G' тогда и только тогда,
когда ф (G О G')	| G |.
> Положим \G\=n. Пусть в графе G' существует
порожденный подграф Я, изоморфный графу G, if: VG ->
VH—изоморфизм графов, И(? = {1, 2, ..., п}, ф(г) = Рг
(г = 1, п). Из определения модульного произведения не-
посредственно вытекает, что вершины (1, v\), (2, р2), •••
..., (тг, Vn) попарно смежны в графе G<yG' и, следова-
тельно, (p(G<>G')^72.
Обратно, пусть cp(G<>G')^n, С — клика в графе
GOG', содержащая ровно п вершин. Тогда С = {(1, щ),
(2, р2), . •(га, Рп)}, причем вершины Vi (i=l, га) по-
парно различны. Положим H = G'(y\, р2, ..., vn). Оче-
видно, что соответствие i >-> Vi является изоморфизмом
графов G и Н. <1
Заметим, что вершины (f, Vi) с равными одноимен-
ными координатами не смежны, поэтому Ф (G ф G') га.
116
Следовательно, неравенство из формулировки предыду-
щей теоремы на самом деле является равенством.
Перейдем к проблеме изоморфного подграфа. Здесь
требуется слегка изменить конструкцию модульного про-
изведения.
Большим модульным произведением G<>G' графов G
и G' назовем граф, определяемый следующими усло-
виями:
1)	7(G<>G') = 7GX VG';
2)	вершины (и, и) и (щ v') графа G<>G' смежны
тогда и только тогда, когда и Ф v, и v' и либо uv е EG,
u'v'^EG', либо uv^EG.
Теорема 27.2. В графе G есть подграф, изоморф-
ный графу G, тогда и только тогда, когда <p(G<>G') =
= \G\.
Доказательство аналогично доказательству предыду-
щей теоремы.
§	28. Интерпретации независимых множеств
Независимые множества вершин графа связаны с са-
мыми разными вопросами, на первый взгляд кажущими-
ся далекими от теории графов. Рассмотрим некоторые из
этих связей. Поскольку клики графа суть независимые
множества вершин его дополнения, то все сказанное ни-
же о независимых множествах в равной мере относится
к кликам.
1.	Связь с многогранниками.
Пусть А — бинарная m X ^-матрица без нулевых столб-
цов. Рассмотрим многогранник
Р(Л) = {х: Ах 1, х^ 0}
— множество всех n-мерных векторов х с неотрицатель-
ными вещественными координатами, удовлетворяющих
системе линейных неравенств
Ax^l.	(1)
Здесь 1 (0)—столбец соответствующей высоты, каждая
компонента которого равна 1 (0). Нас будут интересо-
вать целые точки многогранника Р(Л), т. е. такие реше-
ния системы (1), координаты которых — целые неотри-
цательные числа. Поскольку все столбцы матрицы А не-
нулевые, то очевидно, что все решения системы (1) удов-
летворяют и системе неравенств х 1. Следовательно,
117
целыми точками многогранника Р(Л) служат все (0, 1)-
решения системы (1) и только они.
Определим граф G = GA — граф пересечений столбцов
матрицы А — положив VG = {1, 2, ..., п} и объявив вер-
шины i и / смежными тогда и только тогда, когда неиз-
вестные Xi и Xj вместе входят в какое-либо из неравенств
(1), т. е. хотя бы в одной из строк матрицы А позиции
I и / занимают 1.
Для произвольного подмножества U VG следующим
образом введем характеристический вектор хи =(#1, х%, ...
..хп):
_ (1, если i е U,
Хг (0, если i U.
Очевидно, что U хи — биективное соответствие между
подмножествами множества VG и тг-мерпыми бинарными
векторами.
Набор всех независимых подмножеств вершин графа
G обозначим через «7G. Удобно считать, что 0 т. е.
что пустое множество вершин независимо.
Теперь очевидно, что подмножество U VG является
элементом множества 3^G тогда и только тогда, когда век-
тор Хи является решением системы (1). Следовательно,
целые точки многогранника Р(А) можно трактовать как
характеристические векторы независимых подмножеств
вершин графа GA.
С другой стороны, легко видеть, что для произвольно-
го графа G существует такая матрица А, что GA~G.
В самом деле, в качестве А можно взять матрицу клик
C(G). Заметим, что матрица А определяется графом G
неоднозначно. Так, при непустом G в качестве А можно
еще взять транспонированную матрицу инцидентности
Z(G)T. В общей ситуации одному графу соответствует не-
сколько матриц А, их многогранники Р(А) могут быть
различны, но множества целых точек этих многогранни-
ков совпадают.
2.	Связь с булевыми функциями.
Другая интерпретация независимых множеств связа-
на с булевыми функциями. Пусть В = {0, 1), Вп — мно-
жество всех бинарных векторов длины п, Произвольное
отображение из Вп в В называется булевой функцией п
переменных. Положив х^у для х = (х[, х^ ..., хп), у ==
= (Z/i, У2, . .уп), если Xi у< для всех 1 = 1, п, определим
на множестве Вп частичный порядок Булева функция
118
f называется монотонной, если истинна импликация
(я у) =Н/(ж) «£/(?/)).
Пусть f — булева функция п переменных, х Вп. Если
f(x)=l, то х называется единицей функции Д Если, к то-
му же, истинна импликация (у < х)=> (/(#) = 0), то х
называется нижней единицей функции Д Аналогично
определяются пуль и верхний нуль: если /(^) = 0, то х
называется нулем функции /; если при этом истинна
импликация (у > х) (f (у) = 1), то х называется верх-
ним нулем.
Очевидно, что монотонная булева функция определя-
ется множеством всех своих нижних единиц (верхних
нулей), причем роль множества нижних единиц монотон-
ной булевой функции может играть любая система по-
парно не сравнимых элементов из Вп.
Число координат бинарного вектора, равных единице,
называется его нормой. Монотонная булева функция на-
зывается графической, если норма каждой ее нижней
единицы равна 2, либо если эта функция тождественно
равна нулю.
Пусть f — графическая булева функция п переменных.
Следующим образом определим граф Gf. Его множество
вершин УС/ = {1, 2, ..., п}; вершины i и / смежны тогда
и только тогда, когда бинарный вектор нормы 2, г-я и
7-я координаты которого равны единице, является едини-
цей функции Д Очевидно, что если хц — характеристиче-
ский вектор подмножества U VGf, то f(xu) = 0 тогда и
только тогда, когда Ut=3Gf. Следовательно, нули графи-
ческой булевой функции / можно трактовать как харак-
теристические векторы независимых подмножеств вершин
графа Gf.
С другой стороны, легко видеть, что для каждого гра-
фа G существует графическая булева функция Д удовлет-
воряющая условию Gf^G. В самом деле, /^0 для Оп;
если же G ¥= Оп, то нижними единицами подходящей гра-
фической булевой функции f служат все характеристиче-
ские векторы ребер этого графа.
3.	Связь с пересечением матроидов.
Пусть G — граф. В определенных ситуациях удобно,
чтобы множество SfG оказалось набором независимых
множеств матроида. Тогда с помощью «жадного» алгорит-
ма легко найти наибольшее независимое множество вер-
шин графа G. К сожалению, такие графы редки.
Граф, каждая компонента которого является полным
графом, назовем М-графом.
119
Утверждение 28.1. Пара (VG, 3^G) является мат-
роидом с набором независимых множеств ^G тогда и
только тогда, когда граф G есть М-граф.
> Пусть M*=(VG, ^G) — матроид с набором незави-
симых множеств 3?G. Очевидно, что циклами матроида
М служат двухэлементные подмножества смежных вер-
1	шин. Пусть теперь ab, Ъс е
^EG. Тогда {а, Ъ} и {Ъ, с} —
циклы матроида М. Согласно
аксиоме С.2, множество {а, с}
\\ /	также является циклом и,
\	следовательно, ас е EG. До-
у / s'	казано, что каждая связная
компонента графа G — пол-
7	ный граф.
Рис. 28.1	Обратное очевидно: если
G является Л7-графом, то
Z7G — набор независимых множеств матроида разбиения
множества VG на области связности графа G. <1
Поскольку граф с одним ребром является ЛЛграфом,
то очевидно, что любой граф G можно представить в ви-
де объединения
G = G1UG2U...UGM	(2)
ДЛграфов Gi с совпадающими множествами вершин. На-
зовем такое представление графа G его матроидным раз-
ложением. Минимальное число ц компонент в матроидных
разложениях графа G обозначим через ц(С) и назовем
его матроидным числом.
Рассмотрим, например, граф G, изображенный на
рис. 28.1. Этот граф можно представить в виде объедине-
ния G = Gi U G‘2 двух 7И-графов Gi и (?2, каждый из ко-
торых является дизъюнктным объединением двух полных
графов:
Gi = G(l, 2, 3, 4)UG(5, 6, 7),
G2 = G(l, 2, 5, 6)UG(3, 4, 7).
Очевидно, что G не является 717-графом, поэтому ц((?) = 2.
Если (2)—матроидное разложение графа G, то
ц
.57?= П
а=1
где «Уба —набор независимых множеств матроида Ма =
=|(7<?, являющегося матроидом разбиения множе-
120
ства VG на области связности графа Ga. Другими слова-
ми, непустые элементы множества ^Ga— это все частич-
ные трансверсали разбиения множества VG на области
связности графа Ga.
Верно и обратное. Пусть дано ц. разбиений
Vk£ U Vk2 U • • • U ^Kik = VG, к = 1, ц, (3)
множества VG. Если Gh — объединение ik полных графов
с множествами вершин V^, V%2, • •a G— объеди-
нение всех графов Gk, то независимыми подмножествами
вершин графа G служат частичные трансверсали, общие
для всех разбиений (3), и только они.
Итак, набор всех независимых подмножеств вершин
произвольного графа G при	ц можно трактовать
как набор всех частичных трансверсалей, общих для ц
разбиений вида (3). В частности, нахождение в графе
наибольшего независимого множества вершин есть в точ-
ности задача о пересечении нескольких матроидов раз-
биений.
Задача определения числа p(G) для произвольного
графа G, по-видимому, очень сложна. Тем более сложно
построение соответствующего матроидного разложения.
Определенный интерес имеет характеризация графов, для
Рис. 28.2
которых p(G) = 2. Задача определения числа независимо-
сти cco(G) для графов этого класса может формулировать-
ся как задача о наибольшей мощности трансверсали раз-
биения, независимой относительно матроида некоторого
разбиения.
Приведем без доказательства характеризацию графов
с матроидным числом, равным 2, в терминах запрещен-
ных порожденных подграфов.
Теорема 28.2. Для связного графа G, не являю-
щегося полным, следующие два утверждения равно-
сильны'.
1) H(G) = 2;
121
2) граф G не содержит простых циклов нечетной дли-
ны Z>5, звезды К\$, колеса W4 и графа W4 —е
{рис, 28.2) как порожденных подграфов.
Некоторые оценки числа p(G) см. в § 57.
§ 29. Паросочетания
Пе менее важным, чем понятие вершинной независи-
мости, является понятие реберной независимости.
Произвольное подмножество попарно несмежных ре-
бер графа называется паросочетанием (или независимым
множеством ребер), В качестве иллюстрации рассмотрим
граф, изображенный на рис. 29.1. В нем паросочетаниями
являются, например, {^2), {ej,
{^2, вб), {^1, вз, вб, £7}.
Паросочетание графа G на-
е7 зывается максимальным, если
оно не содержится в паросоче-
тании с большим числом ребер,
и наибольшим, если число ре-
бер в нем наибольшее среди
всех паросочетаний графа G,
Число ребер в наибольшем па-
графа G называется числом паросочетания и
росочетании
обозначается через cxi(G).
Ясно, что независимые множества ребер графа G на-
ходятся во взаимно однозначном соответствии с незави-
симыми множествами вершин реберного графа L{G), и,
следовательно, oci (G) = czo(L(G)). Тем не менее для на-
хождения наибольшего паросочетания в произвольном
графе существуют эффективные алгоритмы.
С понятием паросочетания тесно связано понятие ре-
берного покрытия. Реберным покрытием графа G называ-
ется такое подмножество ребер Е' EG, которое покры-
вает все вершины графа, т. е. такое, что каждая вершина
в G инцидентна по крайней мере одному ребру из Е'.
Из этого определения следует, что лишь графы с изоли-
рованными вершинами не имеют реберных покрытий. Ре-
берное покрытие графа называется минимальным, если в
нем не содержится покрытий с меньшим числом ребер, и
наименьшим, если число ребер в нем наименьшее среди
всех покрытий. Число ребер в наименьшем реберном по-
крытии графа G называется числом реберного покрытия
и обозначается через £i(G).
122
Очевидно, что [3i (G)> IGI/2. Например, в графе, изо-
браженном на рис. 29.2, множество из пяти ребер {{1, 9},
{2, 8), {3, 7), {4, 5), {5, 6}} является реберным покры-
тием, а поскольку [31(G) >4,5, то оно наименьшее.
Паросочетание называется совершенным (или {-фак-
тором). если оно одновременно является реберным покры-
тием. Иногда сам граф называют паросочетанием — тогда,
когда все ребра графа составляют одно паросочетание.
Так, граф тКъ является совершен-
ным паросочетанием. В графе, изо-
браженном на рис. 29.1, Ui, ез,
вб, ет) — совершенное паросочета-
ние. Очевидно, что если в графе
есть совершенное паросочетание,
то оно является наименьшим ре-
берным покрытием.
Читатель помнит, что число
вершин в наибольшем независи-
мом множестве и число вершин в наименьшем покрытии
графа G порядка п связаны соотношением
ao(G)+ [3o(G) = п.
Аналогичное верно и для соответствующих реберных па-
раметров, т. е. справедлива следующая
Теорема 29.1 (Т. Галлаи, 1959 г.). Для любого
графа G порядка п без изолированных вершин верно ра-
венство
ai(G)+MG) = n.
> Положим ai=ai(G), [3i = [31(G) и докажем два не-
равенства
CZ1 + [31^72,	(1)
czi+[3i>73,	(2)
объединение которых и означает гарантируемое теоремой
равенство.
Пусть 71/ — наибольшее паросочетание в графе G. Рас-
смотрим подмножество V' всех вершин этого графа, не
покрываемых ребрами из М. Очевидно, что либо У' — не-
зависимое множество вершин, либо У' = 0, иначе паро-
сочетание М не было бы наибольшим. Кроме того, |Г'| =
= п — 2аь При V' Ф 0 для каждой вершины и^-У' вы-
берем в графе G ребро, ей инцидентное. Множество
выбранных ребер обозначим через Е'. При У' = 0 поло-
жим Е' = 0. Поскольку в графе G нет изолированных
123
вершин и множество V' независимо, то IЕ' | = IУ' | =
= —2&1. Очевидно, что множество Е' U М является ре-
берным покрытием, следовательно,
pi \Ef U М\ = \Е'\ + IМ\ = (п — 2cci) + ai = п — оц;
неравенство (1) доказано.
Перейдем к доказательству неравенства (2). Пусть
Р — наименьшее реберное покрытие графа G. Рассмотрим
подграф G'~G(P), порожденный ребрами покрытия Р.
Поскольку Р является наименьшим покрытием, то в гра-
фе G' всякое ребро инцидентно вершине степени 1, т. е.
каждая связная компонента графа G' является звездой.
Пусть t — число этих звезд и — число ребер в f-й ком-
поненте, i = l, t. Выбрав в каждой компоненте по одному
ребру, получим некоторое паросочетание Р' мощности Л
Следовательно,	Поскольку в графе G' нет изоли-
рованных вершин, то
t	t
И == 2 (^i + 1) = 2	+	+
1=1	1=1
Неравенство (2) доказано. <
§ 30. Паросочетания в двудольном графе
При изучении паросочетаний основное внимание будет
уделяться двудольным графам. Для поиска паросочета-
ний в произвольном графе используются те же идеи, что
и в случае двудольных, только реализация их услож-
няется.
Самые разные задачи связаны с построением паросо-
четаний в двудольных графах. Приведем только два при-
мера. Первый из них — задача о свадьбах, упоминавшая-
ся в § 22 в связи с теорией трансверсалей. Существова-
вание решения этой задачи равносильно существованию
в специально построенном двудольном графе (X, У, Е)
паросочетания, покрывающего X. В этом графе вершины
из X соответствуют юношам, из У — девушкам, а ребро
соединяет вершины, соответствующие знакомым юноше и
девушке. На рис. 30.1 изображен граф для задачи о
свадьбах, заданной таблицей 22.1. Жирными линиями
выделены ребра паросочетания, решающего задачу.
Второй пример —задача о назначениях. Име-
ется конечное множество исполнителей {a?i, #2, ..
каждый из которых может выполнять некоторые из ра-
124
бот {yi, у2, ..упУ- Стоимость выполнения работ у^ ис-
полнителем xj равна Wij. Нужно распределить исполните-
лей по работам, т. е. назначить по одному исполнителю
на каждую работу, так, чтобы, во-первых, выполнить все
работы и, во-вторых, минимизировать общие затраты. Как
и в случае задачи о свадьбах, строится двудольный граф,
каждому ребру которого приписывается вес, равный стои-
мости выполнения исполнителем соответствующей рабо-
ты. Возможность выполнения всех работ равносильна су-
ществованию в графе совершенного паросочетания, а на-
значение, минимизирующее все затраты, соответствует
наибольшему паросочетанию с ми-
нимальным суммарным весом.
Рассмотрим условия существо-
вания паросочетаний. Для произ-
вольного подмножества Л в VG
положим
7МЛ) = Х(Л) = U
veA
Назовем NG(A) окружением под-	Рис. 30.1
множества А в графе G.
Очевидно, что если для графа G = (X, У, Е) сущест-
вует паросочетание, покрывающее X, то для любого под-
множества А в X число вершин, смежных с элементами
из Л, не меньше, чем число вершин в Л, т. е.
|Х(Л)| > |ЛI.
Оказывается, что это условие является и достаточным
для существования такого паросочетания.
Теорема 30.1. Для существования в двудольном
графе G=(X, У, Е} паросочетания, покрывающего X,
необходимо и достаточно, чтобы любое подмножество А
множества X удовлетворяло условию
1Л |	|Х(Л) I.
Ниже показано, что эта теорема является переформу-
лированной теоремой Холла о трансверсалях и потому не
нуждается в дополнительном доказательстве. Однако для
того, чтобы сделать эту главу независимой от предыду-
щей, приведем прямое доказательство теоремы о паросо-
четаниях.
> Доказательство теоремы 30.1. Необходи-
мость утверждения теоремы очевидна.
125
Достаточность докажем индукцией. Пусть G = (X, Y,
В) ~ двудольный граф с |Х| = т > 0, удовлетворяющий
условию теоремы. При т = 1 единственная вершина из X
инцидентна хотя бы одному ребру, которое и является
нужным паросочетанием.
Пусть т > 1 и теорема верна для графов, у которых
1Х| < т. Отдельно рассмотрим два возможных случая.
1. Для каждого собственного подмножества А в X
верно строгое неравенство |Л I < |2УС(Л) I. Выберем в G
произвольное ребро ху. Если G' = G — х — у, X' = Х\х,
Y' = Y\y, Е' = Е\{хи, vy. u^Y, X), то (X', Y', Е') —
двудольный граф, |Х'| = т — 1. Пусть А' — произвольное
подмножество множества X'. Так как М'| < |7VG(^4Z) I,
а из У удалена только одна вершина, то | А' |	(^4')|.
По индуктивному предположению в графе G' существует
паросочетание М, покрывающее X'. Добавив к М ребро
ху, получим нужное паросочетание графа G.
2. В множестве X существует такое собственное под-
множество 4о, что верно равенство
Mol = |Xg(40)I.	(1)
Пусть G' и G7'—подграфы графа G, порожденные
множествами вершин Ло U МДЛо) и VG\(A$ U 7VG(Z0))
соответственно. Рассмотрим подграф Gr. Для любого под-
множества А Ао имеем NG(A) = ^g' М)> и, следова-
тельно, | А |	| NG>(A) |. По индуктивному предположению
в G' существует паросочетание, покрывающее Ао.
Обратимся к подграфу G". Для любого подмножества
А Х\Л0 выполняются соотношения
I Ао I + 1 I = I Ао U | | Ng (4о U А) | =
= \NG(A0)\ + \NGff(A)\
и верно равенство (1). Следовательно, | А |	| NG„ (Л)|
и по индуктивному предположению в графе G" сущест-
вует паросочетание, покрывающее Х\4о. Объединяя это
паросочетание с построенным выше, получим паросочета-
ние в графе G, покрывающее X. <
Следствие 30.2. В любом регулярном непустом
двудольном графе существует совершенное паросочетание.
> Пусть G =(Х, Y, Е)—регулярный двудольный
граф, deg G = тп > 0, А X. Тогда число ребер, инци-
дентных вершинам из А, равно ml Al. Степени концов
этих ребер все равны тп, поэтому
|Х(Л) I > т\А\/т = IАI.
126
Согласно теореме 30.1 существует паросочетание, покры-
вающее X. Поскольку для регулярного двудольного гра-
фа G = (Х, У, Е) всегда |Х| = |У|, то в нем всякое паро-
сочетание, покрывающее X, является совершенным. <1
Следствие 30.3. Регулярный двудольный граф не-
нулевой степени является реберно непересекающимся
объединением 1-факторов.
> Пусть G — регулярный двудольный граф степени
тп > 0. При ш = 1 он является 1-фактором. Пусть тп > 1.
Согласно предыдущему следствию в G существует совер-
шенное паросочетание М. G — М — регулярный двудоль-
ный граф степени тп — 1. Проведя эту процедуру не-
сколько раз, придем к объединению Ьфакторов. <1
Заметим, что утверждение следствия 30.3 перестает
быть верным, если не требовать двудольности графа.
В частности, граф Петерсена (рис. 1.7) был впервые
введен в качестве примера кубического графа, не являю-
щегося объединением ^факторов.
Следствие 30.4. Пусть G = (X, У, Е) — двудольный
граф, t—натуральное число, |Х|. Для существова-
ния в графе G паросочетания мощности t необходимо и
достаточно, чтобы любое подмножество А X удовлетво-
ряло условию
1МДЛ)| > |Л| + t- 1X1.	(2)
> Построим новый двудольный граф G' =ДХ, Y', Е'),
добавив |Х| — t новых вершин к доле У и соединив реб-
ром каждую из них с каждой вершиной из X. Очевидно,
что существование в графе G паросочетания мощности t
равносильно существованию в графе G' паросочетания,
покрывающего X, для чего должно выполняться условие
А | NGf (Л) |. Последнее равносильно условию (2),
поскольку | Ng' (^) I = I Ng (Л) | + | X | — t. <
Для полноты картины отметим без доказательства
следующую теорему.
Теорема 30.5. В произвольном графе G совершен-
ное паросочетание существует тогда и только тогда, ког-
да для любого подмножества S VG верно неравенство
|5| > ро(^), где р0(5)—число компонент нечетного по-
рядка графа G — S.
Возвратимся к двудольным графам. Пусть G =
~(Х, У, Е)— двудольный граф с непустыми долями. Для
любого подмножества Л X положим
1| АI — |2V(4)|, если А^0,
{ > 10,.	если 4 = 0.
127
Величину
б0 = б0(Х, Y, Е) = max 6 (Л)
Ас~Х
назовем дефицитом графа G=*(X, Y, Е). Очевидно, что
О 6о < 1X1.
Т е ор е м а 30.6. Для произвольного двудольного гра-
фа G=(X, У, Е) с непустыми долями верно равенство
ai(G) = |Х| -8о.
> Перепишем неравенство (2) в виде
б(Л) = \А\- \N(A)\ С |Х| -t,	(3)
Согласно следствию 30.4 для существования паросочета-
ния мощности t необходимо и достаточно, чтобы для каж-
дого А X выполнялось условие (3). При t = 1 Х| — 8о
имеем б(Л)^ |Х| — t = бо, и, следовательно, неравенство
(3) верно. Поэтому граф G имеет паросочетание мощно-
сти IXI — бо.
Если же t = 1X1 — 8о + 1, то неравенство (3) принима-
ет вид б(Л)^ IXI — t = бо — 1 и нарушается для тех под-
множеств Ло, для которых 8(Ло)=8о. Следовательно,
граф G не содержит паросочетания мощности |Х| —
- - бо + 1. <
Следствие 30.7. Для любого двудольного графа
G=(X, Y, Е) верно равенство
|Х| - б0(Х, У, Е)~ 1 У| -б0(У, X, Е).	(4)
В частности, при |Х| = IУ|
б0(Х, У, 2Г) = 80(У, X, £).
> Для доказательства достаточно заметить, что каж-
дая часть равенства (4) совпадает с ai(G). <
§ 31. Двудольные графы и семейства подмножеств
Обсудим связь между двудольными графами и их
паросочетапиями, с одной стороны, и семействами под-
множеств и их трансверсалями — с другой.
Пусть G=(X, У, Е)—двудольный граф без изоли-
рованных вершин. Будем считать, что X = {1, 2, ..., т},
и определим семейство 5G = (5i,	Sm) непустых
подмножеств множества У условием Si = N(i) (j^l, т).
С другой стороны, пусть S = (5i, 5г, ..5т)—семей-
ство непустых подмножеств произвольного конечного
множества У. Определим двудольный граф Gs = (Х, У, Е),
128
положив X = {1, 2, ..., тп}, N(i) — (i 1, тп). Очевид-
но, что Sqs — S и соответствие G »-► Sg является биек-
цией между классом всех двудольных графов (X, У, Е)
с фиксированными долями X — {1, 2, ..., тп} и У и клас-
сом всех тп-членных семейств непустых подмножеств
множества У.
Если М — паросочетание двудольного графа G =
= (Х, У, Е), то обозначим через YM множество вершин
из доли У, покрываемых ребрами этого паросочетания, а
через T(G) — множество, элементами которого служат все
Ум, где М — произвольное паросочетание графа G, и пу-
стое множество. Как подтверждает очевидная проверка,
верно следующее
Утверждение 31.1. Если G ==(Х, У, Е) — двудоль-
ный граф без изолированных вершин и & Ф % У, то
T(G) тогда и только тогда, когда множество Z явля-
ется частичной трансверсалью семейства подмно-
жеств SG.
Поскольку все частичные трансверсали произвольного
семейства непустых подмножеств и 0 составляют набор
независимых множеств матроида трансверсалей, то верно
Следствие 31.2. Для любого двудольного графа
G =(Х, Y, Е) без изолированных вершин пара
(У, T(G))—матроид, совпадающий с матроидом транс-
версалей семейства SG. При этом число паросочетания
ai(G) равно рангу р(У, T(G)).
Итак, условие существования в графе G паросочета-
ния фиксированной мощности t совпадает с условием су-
ществования соответствующей трансверсали. Поскольку
в рассматриваемой ситуации
и и N(i) = N(A)
A	ieA
для любого подмножества A s X, то теорема Холла пре-
вращается в теорему 30.1, а следствие 22.3 — в след-
ствие 30.4.
Как показывают примеры, максимальное паросочета-
ние в графе может оказаться не наибольшим, и это сви-
детельствует о том, что совокупность всех паросочетаний
произвольного графа, вообще говоря, нельзя принять в
качестве набора независимых множеств матроида. Тем
не менее задача нахождения в двудольном графе наи-
большего паросочетания связана с матроидами. Ее мож-
но сформулировать как задачу о пересечении двух мат-
роидов разбиения, или, что то же, как задачу о выборе
9 в. А. Емеличев и др.
129
трансверсали максимальной мощности, общей для двух
разбиений некоторого множества. В самом деле, разобьем
множество ребер двудольного графа G=(X, Y, Е) на
классы, отнеся в один класс все ребра, покрывающие од-
ну и ту же вершину из X. Пусть Мх — матроид этого
разбиения. Аналогично определим матроид MY. Очевидно,,
что подмножество ребер графа G является паросочетани-
ем тогда и только тогда, когда оно независимо как отно-
сительно матроида Мх, так и относительно MY. Следова-
тельно, наибольшее паросочетание в графе G — это наи-
большее по мощности множество ребер, независимое как
относительно матроида Мх, так и относительно матроида
MY. Именно на последнем обстоятельстве основан успех
процедуры построения наибольшего паросочетания в дву-
дольном графе, приведенной в § 77.
§ 32. Паросочетания и покрытия
Как отмечалось в § 25, определение числа p0(G) и,
тем более, построение наименьшего вершинного покрытия
для произвольного графа G — сложные алгоритмические
задачи. Эффективных алгоритмов для их решения, види-
мо, не существует.
Очевидно, что для каждого графа G число вершин в
любом покрытии не меньше числа ребер в произвольном
паросочетании, в частности,
Po(G)^ai(G).
Последние два числа могут как совпадать, так и не сов-
падать. Например, Ро(^3)= 2 ¥= ai(X3)= 1. Для двудоль-
ного же графа эти числа всегда равны, т. е. верна сле-
дующая
Теорема 32.1. Для любого двудольного графа G
число вершин в наименьшем вершинном покрытии равно
числу ребер в наибольшем паросочетании:
Po(G)=ai(G).
> Пусть G =(Х, У, Е)— двудольный граф. Вначале
предположим, что в G нет изолированных вершин. Оче-
видно, что для любого подмножества А X множество
С = А(Л)и(Х\Л)	(1)
является покрытием графа G. С другой стороны, пусть
D — произвольное минимальное покрытие. Представим
130
множество D в виде
Z) = XiUyb Х^Х, У1^У,
и положим А = X\Xi. Тогда 7У(Л)^ Уь Но как замечено
выше, множество Xi U N(A) само является покрытием.
Поскольку покрытие D минимально, то D = Х\ U N(A).
Итак, всякое минимальное покрытие графа G имеет вид
(1), и потому
P0(G) = min] С| = min(| Х\Л| + |ДГ(Л)|) =
С	АсХ
= шт(|Х|-|4| + |^(Л)|) =
AQX
== | X | - шах (| А | - ] N (Л) |) = | X | - б0 (X, У, Е) =	(G).
А^Х
Для графов без изолированных вершин теорема доказана.
Очевидно, что при добавлении к графу G изолирован-
ной вершины не меняется ни Po(G), ни ai(G), так что
теорема верна и для графов с изолированными верши-
нами. <
Поскольку для любого графа G верны равенства
ao(G) + Po(G)=l 1^1 (теорема 25.5) и ai(G) + ^i(G) = IG|
(теорема 29.1), то из теоремы 32.1 вытекает
Следствие 32.2 (Д. Кёниг, 1916). Для любого дву-
дольного графа G верны равенства
a0(G)+ai(G)- IGI, a0(G)=MG).
Как показано в § 77, для построения наибольшего
паросочетания и наименьшего вершинного покрытия в
двудольном графе существуют эффективные алгоритмы.
Следовательно, и сложнейшая в общей ситуации задача
нахождения наибольшего независимого множества в клас-
се двудольных графов решается эффективно.
Как следствие из теоремы 32.1 получим один важный
факт из теории бинарных матриц, доказанный Д. Кёни-
гом в 1931 году. Под линией матрицы будем понимать ее
строку или столбец. Два элемента матрицы назовем не-
зависимыми, если они не лежат на одной линии.
Теорема Кёнига. Максимальное число попарно
независимых единиц бинарной матрицы равно минималь-
ному числу ее линий, содержащих все единицы матрицы.
> С одной стороны, произвольная бинарная матрица
А может истолковываться как приведенная матрица
смежности некоторого двудольного графа G ==(Х, У, £').
Тогда независимость двух единиц матрицы означает, что
9*	131
соответствующая им пара ребер графа G несмежна. По-
этому максимальное число независимых единиц матрицы
А равно числу паросочетания ai(G).
С другой стороны, каждой строке матрицы А соответ-
ствует вершина из X, каждому столбцу — вершина из У,
а единицам линии — ребра, инцидентные соответствую-
щим вершинам. При этом множеству линий матрицы Л,
содержащих все ее единицы, соответствует множество
вершин графа G, являющееся покрытием. Следовательно,
минимальное число элементов в покрытиях графа G рав-
но минимальному количеству линий матрицы А, содер-
жащих все ее единицы. Но согласно теореме 32.1 число
вершин в наименьшем покрытии графа G также равно
cci(G). <
УПРАЖНЕНИЯ
1.	Найдите наибольшее независимое множество вершин в гра-
фе Петерсена.
2.	Докажите, что если G— дерево, то a0(G)	п/2.
3.	Докажите, что если a0(G) = a0(G3), то граф G является
ЛГ-графом.
4.	Приведите пример графа, в котором наименьшее домини-
рующее множество не является независимым.
5.	Пусть G — граф без изолированных вершин. Докажите, что
G содержит такое доминирующее множество Z), что VG\D—тоже
доминирующее.
6.	Пусть 8(G) —мощность наименьшего доминирующего мно-
жества в графе G. Покажите, что если в G нет изолированных вер-
шин, то 8(G)	я/2. В случае, когда п — произвольное четное чис-
ло, приведите пример связного графа порядка тг, для которого
8(G) = т?/2.
7.	Приведите пример связного тг-вершипного графа G, у кото-
рого число ₽i(G) максимально среди всех графов порядка п.
8.	Верно ли, что любое паросочетание графа содержится в наи-
большем паросочетапии?
9.	Покажите, что дерево Т имеет совершенное паросочетание
тогда и только тогда, когда ро(^) = 1 для всех вершин из Г, где
ро(гл) —число компонент нечетного порядка графа Т — и.
10.	Пусть М и N — непересекающиеся паросочетания графа G,
причем |Л/| >> |А|. Покажите, что в графе G существуют непере-
секающиеся паросочетания М' и 7V', удовлетворяющие условиям
\М'\ = |Л£| —1, |А'| = |А| +1, ЛГи#7 = М (JX.
11.	Докажите, что бинарную матрицу, в каждой строке и в
каждом столбце которой ровно к единиц, можно представить в
виде суммы к бинарных матриц, в каждой строке и в каждом
столбце которых ровно одна единица.
Глава V
Связность
Связный граф был определен как граф, у которого лю-
бые две вершины соединены цепью. Так, оба графа Кп и
Сп связны, однако интуитивно ясно, что при п > 3 граф
Кп «сильнее» связен, чем Сп. В этой главе вводятся и ис-
следуются понятия, характеризующие степень связности
графа.
§ 33. Вершинная связность и реберная связность
Прежде чем ввести понятия вершинной и реберной
связности, рассмотрим одну математическую модель, воз-
никающую, в частности, при проектировании и анализе
сетей ЭВМ. Имеется сеть, состоящая из центров хране-
ния и переработки информации. Некоторые пары центров
соединены каналами. Обмен информацией между любы-
ми двумя центрами осуществляется либо непосредственно
по соединяющему их каналу, если он есть, либо через
другие каналы и центры. Сеть считается исправной, если
каждая пара центров в состоянии обмениваться инфор-
мацией. Такой сети естественно сопоставить граф: вер-
шины — центры, ребра — каналы сети. Тогда исправной
сети будет соответствовать связный граф. Важным поня-
тием является надежность (живучесть) сети, под кото-
рой обычно подразумевают способность сети функциони-
ровать при выходе из строя одного или нескольких цент-
ров или (и) каналов. Ясно, что менее надежной следует
считать ту сеть, исправность которой нарушается при
повреждении меньшего количества элементов. Оказывает-
ся, надежность сети можно измерять на основе вводимых
ниже определений.
Числом вершинной связности (или просто числом
связности') % (б?) графа G называется наименьшее число
вершин, удаление которых приводит к несвязному или
одновершинному графу.
133
Т/ч, например, x(7£i)=0, x(7£n)=ft— 1, x(Gn)=2.
Это вполне согласуется с интуитивным представлением о
том, что при п > 3 граф Кп сильнее связен, чем Сп.
Граф G, представленный на рис. 33.1, связен, но его
связность можно нарушить, удалив вершину 4. Поэтому
x(G) = 1. Если же попытаться нарушить связность этого
графа путем удаления ребер (а не вершин), то придется
удалить не менее трех ребер. Например, G распадается
на две компоненты при удалении ребер {4, 5), {4, 6}, {4, 7}.
Чтобы учесть это обстоятельство, введем еще одно опре-
деление.
Пусть G — граф порядка п > 1. Числом реберной
связности X(G) графа G назовем наименьшее число ре-
бер, удаление которых приводит к несвязному графу.
Число реберной связности графа будем считать равным
нулю, если этот граф одновершинный.
В качестве иллюстрации снова обратимся к графу G
на рис. 33.1. Здесь X(G)==s3 и, следовательно, X(G)>
>x(G). Ниже будет показано, что противоположное не-
равенство невозможно ни для какого графа.
Определим некоторые элементы графа, играющие осо-
бую роль в дальнейших рассмотрениях.
Вершина v графа G называется точкой сочленения
(или разделяющей вершиной), если граф G — v имеет
больше компонент, чем G. В частности, если G связен и
v — точка сочленения, то G — v не связен. Аналогично
ребро графа называется мостом, если его удаление уве-
личивает число компонент.
Таким образом, точки сочленения и мосты — это свое-
го рода «узкие места» графа. Граф, изображенный на
рис. 33.2, имеет три точки сочленения а, Ъ, с и один
мост аЪ.
Понятно, что концевая вершина моста является точ-
кой сочленения, если в графе есть другие ребра, инци-
дентные этой вершине.
134
Возвращаясь к рассмотренной в начале параграфа се-
ти, нетрудно заметить, что число вершинной связности и
число реберной связности ее графа отражают чувстви-
тельность сети к разрушению центров и каналов соответ-
ственно, а мостам и точкам сочленения отвечают наибо-
лее уязвимые места сети.
Если 6(G)—минимальная степень вершин графа G,
то очевидно, что Х(С)<б(С), поскольку удаление всех
ребер, инцидентных данной вершине, приводит к увели-
чению числа компонент графа.
Выясним теперь соотношение между числами x(G) и
Z(G). Если граф G не связен или имеет мост, то очевид-
но, что x(G) = %(G). Пусть G — связный граф без мо-
стов. Выберем в этом графе множество Z?i, состоящее из
2i = Z(G) ребер, удаление которых приводит к несвязно-
му графу. Пусть Е2^ЕХ, IjE^I =% — 1. Граф G — Е2 свя-
зен и имеет мост, который обозначим через uv. Для каж-
дого ребра из множества Е2 выберем какую-либо инци-
дентную ему вершину, отличную от и и v. Удалим те-
перь выбранные вершины из графа. Этим самым будут
удалены, в числе прочих, и все ребра, входящие в Е2.
Если оставшийся граф не связен, то x = x(G)<X. Если
же он связен, то ребро uv является мостом. Поэтому уда-
ление одной из вершин и или v приводит к несвязному
или одновершинному графу, а это означает, что х X.
Таким образом, доказана
Теорема 33.1. Для любого графа G верны нера-
венства
x(G)<X(G)<6(G).
Следующее утверждение показывает, что эти нера-
венства нельзя усилить.
Утверждение 33.2. Для любых натуральных чи-
сел р, q, г, таких, что р q г, существует граф G, у
которого x(G) = р, X(G) = q, 6(G) = г.
> Рассмотрим граф G порядка 2(г+1), у которого
VG = Vi U V2, где Vi={vi, v*,	(/=1,2). В мно-
жество ребер этого графа включим, во-первых, все ребра
вида (j = 1, 2; k,l = 1, г + 1, k I). Таким образом,
каждое из множеств (j =* 1, 2) является кликой в G.
Во-вторых, в множество EG включим все ребра вида
vhvh (& = 1, р) и вида VpVp+k (к = 1, q — р)(строение графа
G схематично показано на рис. 33.3). Учитывая равен-
ство	тг —11, легко убедиться в том, что построен-
ий
ный граф обладает нужными свойствами, т. е. что x(G) —
=	6(G)=r. <
Тем не менее верна следующая теорема, приводимая
здесь без доказательства (см. обзор [21]).
Теорема 33.3. Для почти каждого графа G верно
равенство
x(G) = %(G).
Граф G называется k-связным, если x(G)>&, и ре-
берно-к-связным, если X(G)^ к. Таким образом, отлич-
ный от Ki граф 1-связен (односвязен) тогда и только
тогда, когда он связен, а
2-связные (двусвязные)
графы — это связные гра-
фы без точек сочленения,
не являющиеся одновер-
шинными.
Граф G, изображенный
на рис. 33.1, 1-связен и ре-
берно-3-связен. Легко ви-
деть, что этот граф содер-
жит подграфы, являющие-
ся «более связными», чем
сам граф. Таков, например,
подграф, порожденный
множеством вершин {1,
2, 3, 4, 8). Он 3-связен.
Чтобы учесть эту и
подобные ей ситуации, естественно ввести следующее
определение: максимальный /с-связный подграф графа
называется его к-связной компонентой, или просто к-ком-
понентой.
Это определение иллюстрируется на рис. 33.4. На
этом рисунке граф Gi имеет две 2-компоненты, aft —
Рис. 33.4
две 3-компоненты. Сами графы Gi и ft являются 1-ком-
понентами графа Gi U G%. Легко заметить, что 2-компо-
ненты графа Gi имеют одну общую вершину, а 3-компо-
136
ненты графа G2 — две общие вершины. Следующая теоре-
ма показывает, что это обстоятельство не случайно.
Теорема 33.4. Две различные к-компоненты графа
имеют не более чем к — 1 общих вершин.
> Пусть Gi и С2 — различные ^-компоненты графа G
и VG\ A VG2 = X. Предположим, что |Х| > к, и докажем,
что тогда граф б? 1 U б?2 должен быть /с-связным. Для это-
го в данном случае достаточно показать, что он остается
связным после удаления любых к — 1 вершин, т. е. если
У с= F(Gi U G2), 1У1 =к- 1, то граф (<7i U672)—У свя-
зен. Положим
у. = (УСАХ) ПУ, Z = 1, 2, Уз = X А У.
Ясно, что
IУ,| к- 1, f = 1, 2, 3, У= У1 U У2и Уз.
Поскольку
I У, и У31 ^к- 1, i= 1, 2,
и графы Gi и G2 fr-связны, то графы
Я, = С1-(У^и Уз), I- 1, 2,
связны. Так как по предположению |Х| > к, то Х\У3=/=
= 0, т. е. связные графы Hi и Я2 имеют хотя бы одну
общую вершину. Следовательно, связен граф Я1 U Я2 =
==(Gi U G2) — У. Последнее означает, что граф Gi U G2
/с-связен. Поэтому, вопреки предположению, ни Gi, ни
G2 не являются /с-компонентами графа G. <1
§ 34.	Двусвязные графы
Случаям, когда к =* 2 или к = 3, в теории графов от-
ведена особая роль. Это объясняется следующими причи-
нами. Во-первых, 2- и 3-связные графы фигурируют во
многих теоретических и прикладных вопросах, в частно-
сти, ряд задач достаточно уметь решать для 2-связных
компонент. Во-вторых, при к = 3 и, особенно, при к = 2
удается дать в некоторой степени обозримое описание
соответствующих графов.
Рассмотрим вначале некоторые простые свойства
2-связных графов, вытекающие непосредственно из опре-
делений:
1)	степени вершин 2-связного графа больше единицы;
2)	если графы G\ и G2 2-связны и имеют не менее
двух общих вершин, то граф Gi U G2 также 2-связен;
137
3)	если граф G 2-связен и Р — простая цепь, соеди-
няющая две его вершины, то граф G U Р также 2-связен;
4)	если вершина и не является точкой сочленения
связного графа, то любые две его вершины соединены
цепью, не содержащей v; в частности, в 2-связном графе
для любых трех несовпадающих вершин а, Ъ, v имеется
(а, Ь)-цепъ, не проходящая через v.
Этими свойствами мы будем пользоваться без каких-
либо пояснений и дополнительных ссылок на них.
Теорема 34.1. Пусть G — связный граф и IG| > 2.
Тогда следующие утверждения эквивалентны:
1)	граф 2-связен;
2)	любые две вершины графа принадлежат простому
циклу',
3)	любая вершина и любое ребро принадлежат про-
стому циклу;
4)	любые два ребра принадлежат простому циклу;
5)	для любых двух вершин а и Ъ и любого ребра е
существует простая {а, Ъ)-цепь, содержащая е;
6)	для любых трех вершин а, Ъ, с существует про-
стая (а, Ь)-цепъ, проходящая через с.
> 1) => 2). Пусть а и Ъ — две вершины графа G. Рас-
смотрим множество всех простых циклов графа G, содер-
жащих а. Обозначим через U множество всех вершин,
входящих в эти циклы. Ясно, что £7 =/= 0. Действительно,
простой цикл, содержащий а, можно получить, объеди-
нив два ребра ах и ау (х¥=у) и простую (х, у)-цепь,
не проходящую через а (существующую согласно свой-
ству 4)). Предположим, что Ъ & U, и положим U = VG\U.
Поскольку граф С_связен, то в нем найдется такое ребро
zt, что z g U, t^U (рис. 34.1). Пусть S— простой цикл,
содержащий а и z. Так как G — 2-связный граф, то в
нем имеется простая (я, 7)-цепь Р, не содержащая z.
Пусть v —• первая, считая от t, вершина, входящая в 5,
т. е. (7, и)-подцепь цепи Р пе имеет с S общих вершин,
отличных от и. Теперь легко построить простой цикл, со-
державший а и t. Он получается объединением (в, г)-цепи,
проходящей через а и являющейся частью S, с ребром
zt и (t, v)-подцепью цепи Р (на рис. 34.1 этот цикл пока-
зан пунктирной линией). Следовательно, t^U; но это
противоречит выбору ребра zt. Таким образом, /7 = 0,
т. е. а п Ъ лежат на общем простом цикле.
2) => 3). Пусть а — вершина и zt — ребро графа G.
По условию G содержит цикл S, проходящий через вер-
шины а и z. Не теряя общности будем считать, что zt &
138
&S. Если при этом окажется, что S проходит через вер-
шину t, то требуемый цикл строится очевидным обра-
зом. Пусть S не проходит через t. Тогда рассмотрим про-
стой цикл S', проходящий через вершины t и а. Такой
цикл, по условию, существует. Частью этого цикла яв-
ляется простая цепь Р, соединяющая t с некоторой вер-
шиной v е S. Цепь Р можно выбрать так, чтобы VP А
A KS = {у}. Искомый цикл теперь строится точно также,
как в предыдущем пункте.
3)=>4). Пусть аЪ и tz — два ребра графа G. По ус-
ловию G имеет простые циклы S и S', первый из кото-
рых содержит аЪ и z, а второй — аЪ и t. Далее искомый
цикл строится так же, как в предыдущих пунктах.
4)=>5). Пусть a, b^VG, tz^EG. Будучи связным,
граф G содержит простую цепь Р =(а, х, .. ., &). Соглас-
но утверждению 4) в графе G есть простой цикл S, со-
держащий ребра ах и tz. Легко видеть, что в объединении
S U Р имеется требуемая цепь.
5)=> 6). Пусть а, Ъ, с е VG, cd^EG. По условию в
графе имеется простая (а, &)-цепь, проходящая через cd
и, следовательно, содержащая с.
6)=> 1). Пусть VG. Покажем, что граф G — v свя-
зен, т. е. любая пара а, b его вершин соединена цепью.
Действительно, согласно утверждению 6) в графе G
имеется простая (v, &)-цепь, проходящая через верши-
ну а. Эта цепь содержит (а, &)-подцепь, которая, очевид-
но, не проходит через v и, следовательно, является (а, Ь)-
цепью и в графе G — v. <
Если в формулировке теоремы 34.1 заменить всюду
слова «простая цепь» и «простой цикл» соответственно на
слова «цепь» и «цикл», то получим аналогичную теоре-
му о 2-реберно-связных графах.
Как отмечалось выше, при решении многих задач на
графах достаточно уметь решать эти задачи для каждой
139
2-связной компоненты графа. Поэтому представляет ин-
терес взаимное расположение 2-компонент в графе.
Максимальные относительно включения элементы
множества связных подграфов графа G, не имеющих то-
чек сочленения, называются его блоками. Таким образом,
каждый блок графа либо 2-связен, либо совпадает с К%
или с К\ (граф К[ — блок тогда и только тогда, когда он
является связной компонентой). Связный граф без точек
сочленения также называют блоком. Множество вершин
блока будем называть блоковым множеством.
Например, граф, изображенный на рис. 34.2, содер-
жит пять блоков Bi 1, 5) (они обведены пунктирны-
ми линиями). Среди этих блоков Bi, В% и В6— 2-связ-
ные графы, а каждый из двух оставшихся является
ребром.
Утверждение 34.2. Любые два блока графа име-
ют не более одной общей вершины. В частности, всякое
ребро графа входит только в один его блок.
Утверждение 34.3. Если блок графа содержит
вершины а и Ъ, то он содержит и всякую простую
(а, Ь)-цепъ этого графа.
Утверждение 34.4. Если вершина v входит более
чем в один блок графа G, то v — точка сочленения этого
графа.
Эти утверждения непосредственно следуют из пере-
численных в начале параграфа простейших свойств
2-связных графов и теоремы 34.1.
Следствие 34.5. Система блоковых множеств гра-
фа является покрытием множества его вершин. Каждая
пара блоковых множеств либо не пересекается, либо
имеет единственную общую вершину, и эта вершина яв-
ляется точкой сочленения графа.
Следующая конструкция дает представление о струк-
туре графа «с точностью до блоков». Пусть В {5J и
С = {ц} — соответственно множества блоков и точек со-
членения графа G. Сопоставим с G граф bc(G), у кото-
рого В U С — множество вершин и {BiCf. Bi В, Cj е С,
140
Cj e В} — множество ребер. Тем самым, ребра двудоль-
ного графа bc(G) указывают на принадлежность точек
сочленения блокам. На рис. 34.3 представлены графы G
и bc(G).
Утверждение 34.6. Если граф G связен, то
bc(G) — дерево,
> Очевидно, что из связности графа G вытекает связ-
ность графа bc(G}. Предположим, что bc(G) содержит
цикл С. Пусть этот цикл имеет вид С =	b^, cj2,
.. ., сц, Ьц, с^. Каждый из блоков Bih содержит
с^+1)-цепь и объединение этих цепей дает простой
цикл в графе G. Обозначим этот цикл через С". Ясно,
что С" содержит по крайней мере две вершины каждого
из блоков Bik. Поэтому из утверждения 34.3 следует,
что цикл С должен содержаться в каждом из этих бло-
ков. Последнее означает, что каждая пара блоков
имеет не менее I С" I > 3 общих вершин. Получаем про-
тиворечие с утверждением 34.2. <
Граф bc{G} называется bc-деревом связного графа G.
Блоки графа G, соответствующие концевым вершинам
его dc-дерева, называются концевыми блоками.
Похожее представление графа можно получить, по-
ложив в основу его максимальные реберно-2-связные
подграфы, т. е. максимальные связные подграфы, не со-
держащие мостов. Такие подграфы называют листами.
Не останавливаясь на деталях, заметим следующее. Каж-
дая вершина графа порядка п > 1 принадлежит в точно-
сти одному листу и каждое ребро, не являющееся мо-
стом, входит только в один лист. Таким образом, граф
состоит из листов и мостов, соединяющих некоторые из
них. Для описания строения графа «с точностью до ли-
стов» можно ввести граф, аналогичный графу &c(G).
Вершины такого графа биективно соответствуют листам
141
графа G и две его вершины соединены ребром в том и
только в том случае, когда соответствующая пара листов
в G соединена мостом. Можно показать, что введенный
таким образом граф является деревом, если исходный
граф связен.
На рис. 34.4 граф G имеет 5 листов Л2, Л3, L4, L5
и 4 моста, а граф G' показывает, как связаны между со-
бой листы графа G.
Приведем некоторые результаты о трехсвязных гра-
фах, которые будут использованы в главе «Планарность».
Пусть G — связный граф, Н — некоторый его под-
граф. Простую открытую цепь щ, у2, . .*4, А: > 3, гра-
фа G назовем Я-цепью, если выполняются условия
vx VH, vh VH, Vi <£VH, i =
Ребро е = uv графа G также будем называть Я-цепью,
если и & VH, v <= РЯ, е Ф ЕН.
Лемма 34.7. Пусть G — двусвязный граф. Тогда для
всякого его подграфа Н, содержащего более одной верши-
ны и отличного от G, существует Н-цепъ графа G.
> Если Я — остовный подграф, то любое ребро графа
G, не входящее в ЕН, служит Я-цепью.
Пусть подграф Я не является остовным. Рассмотрим
три попарно различные вершины и е VH, v <= VH, w Ф-
Ф VH. По теореме 34.1 в графе G есть простая (и, v)-
цепь, проходящая через w. Очевидно существование под-
цепи этой цепи, являющейся Я-цепью графа G. <1
Ниже для и, v е VG положим Guv = G — и — v.
Теорема 34.8. Во всяком 3-связном графе G есть
такое ребро uv, что граф Guv не имеет точек сочленения.
> Если |G| =тг = 4, то утверждение теоремы оче-
видно. Поэтому будем считать, что п > 5. Предположим
противное, т. е. что для любого ребра uv е EG граф Gu*
142
имеет хотя бы одну точку сочленения. Тогда из 3-связ-
ности графа G следует, что при любом выборе ребра uv е
е EG граф GUv обладает следующими свойствами
(рис. 34.5):
1)	если а — висячая вершина графа Guv, то av^-EG,
аи EG\
2)	всякий висячий блок графа Guv, не являющийся
ребром, содержит такую пару вершин сиг/, отличных от
точек сочленения графа Guv, что
ис EG, vd EG]
3)	всякий блок графа Guv, имею-	ту
щий ровно две точки сочленения и	: d
отличный от ребра, содержит такую /"/ у
вершину Z, не являющуюся точкой Л у ду
сочленения графа Gut), что ul^EG
или vl EG.	v^-—
Обозначим через Buv максималь-
ный по числу вершин блок графа МI I ix
<7UU, а через tuv — число вершин в
этом блоке. Теперь выберем ребро рис
uv так, чтобы число tuv было наи-
большим.
Покажем, что в этом случае tuv > 3. Пусть tuv = 2 и
а — висячая вершина графа Guv (являющегося деревом).
Так как п > 5, то существует ребро cd е EGUV, с =£ а,
а. Из свойства 1) вытекает, что в графе Gcd сущест-
вует цикл (u, a, v, и), т. е. tcd > tuv. Получено противоре-
чие, следовательно, tu* > 3.
Через Duv обозначим &с-дерево графа Guv и рассмот-
рим следующие случаи.
1.	Дерево Duv не является цепью. Выберем в этом де-
реве цепь, соединяющую пару висячих вершин и прохо-
дящую через вершину, соответствующую блоку Buv. Этой
цепи соответствует последовательность 51, .. ., Вр блоков
графа Guv, среди которых содержится блок Buv, причем
блоки В[ и Вр являются висячими (рис. 34.6).
Пусть В' — произвольный висячий блок графа Guv,
отличный от Bi и Вр. Из свойств 1) и 2) вытекает су-
ществование таких отличных от точек сочленения графа
Guv вершин а е VBi, b VBP, с е VB', что ис EG,
va е EG, vb е EG. Тогда в графе Guc вершины множества
р
(J VB{ U v входят в один блок и, следовательно, tuv <
г=1
< tuc. Последнее противоречит выбору ребра uv.
2.	Дерево Duv — цепь и Buv — блок графа GUVJ не яв-
143
ляющийся висячим. Пусть .., Вр — последователь-
ность всех блоков графа G, причем блоки Bi и Вр — ви-
сячие, Вг П Д+1 ¥= 0 (i = 1, р — 1), Buv = Bk (\<к<р)
(рис. 34.7). Согласно свойству 3) найдется вершина fes
е VBuv, отличная от точек сочленения графа Guv, смеж-
ная с и или с v. Пусть ub g EG. Согласно свойствам 1)
и 2) существуют такие отличные от точек сочленения
графа Guv вершины а е VB\, с VBP, что иа е EG, vc е
EG. Легко видеть, что в графе Gvc имеется блок, содер-
k
жащий все вершины множества (J J и» Поэтому
1=1
tvc > tuv, и снова получаем противоречие.
3.	Дерево Duv — цепь и Buv — висячий блок графа
Guv. Если граф Guv содержит такое ребро ху, что VBuv П
Г) {х, у} — &, то, используя свойство 2), легко показать,
что в графе Gxy есть блок, содержащий множество вер-
шин VBuv U {и, v), а, значит tuv < txy. Так как Buv — вися-
чий блок графа Guv, то последнее означает, что граф Guv
состоит из блока Buv и ребер ab\, аЪ^, ..., abt (рис. 34.8).
Из 3-связности графа G следует, что граф G — а не име-
ет точек сочленения. Поскольку в графе G — а вершина
Ъ\ смежна только с вершинами и и v, a uv е EG, то граф
Gab^ также не имеет точек сочленения, что противоречит
предположению.
Таким образом, показано, что во всяком 3-связном гра-
фе G существует такое ребро uv, что граф Gu? не имеет
точек сочленения. <
144
Следствие 34.9. Всякий 3-связный граф с числом
вершин 5 содержит ребро, стягивание которого при-
водит к 3-связному графу.
> Доказательство также проведем от противного.
Пусть, стягивая некоторое ребро х = uv 3-связного гра-
фа G в вершину х, получаем граф Gx, для которого
х(бу = 2. (Равенство z(Gx)=l
невозможно в силу 3-связности
графа G.) Тогда в графе Gx су-	Ж
ществуют две вершины, удаление \\/& \ r\\v
которых делает его несвязным. \
Одной из них должна быть х	в
(в противном случае %(G)=2). /X ; /
Удалению вершины х из Gx coot- // V /
ветствует удаление вершин и и v
из графа G. Поэтому для любого	Шу
ребра х = uv EG граф G имеет
такую вершину w, что граф G —	Рис- 3/18
— и — v — w несвязен. Вершина
w является точкой сочленения графа Guv, что противоре-
чит предыдущей теореме. <
Отметим еще без доказательства следующую теорему
(см. обзор [21]).
Теорема 34.10. Почти все графы двусвязны.
Поскольку каждый мост инцидентен точкам сочлене-
ния графа, то из этой теоремы вытекает
Следствие 34.11. Почти все графы не содержат
мостов.
§ 35. Теорема Менгера
Из теоремы 34.1 следует, что граф 2-связен тогда и
только тогда, когда любые две его несовпадающие верши-
ны а и Ъ соединены парой простых {а, Ь)-цепей, не имею-
щих общих вершин, за исключением а и Ъ. Аналогичный
критерий /с-связности справедлив при произвольном к.
Говорят, что множество вершин S разделяет несмеж-
ные вершины а и Ъ связного графа G, если в графе G — S
вершины а и Ъ принадлежат различным связным компо-
нентам. В этой ситуации множество S называют также
сепаратором или (а, Ъ)-сепаратором. Две (а, Ь)-цепи гра-
фа G называют непер ссекающимися, если у них нет об-
щих вершин, за исключением а и Ъ, и реберно-непересе-
кающимися, если у них нет общих ребер. Очевидно, не-
Ю В. А. Емелячев и др.
145
пересекающиеся цепи являются и реберно-непересекаю-
щимися, а обратное, вообще говоря, неверно.
К. Менгер доказал в 1927 году следующую теорему,
устанавливающую соотношение между числом непересе-
кающихся простых цепей, соединяющих две несмежные
вершины графа, и его связностью.
Теорема Менгер а. Наименьшее число вершин,
разделяющих две несмежные вершины графа а и Ъ, рав-
но наибольшему числу попарно непересекающихся про-
стых (а, Ь)-цепей этого графа.
Приведем доказательство, принадлежащее В. Маквай-
гу (1982 г.).
> Ясно, что если к вершин разделяют а и Ъ, то су-
ществует не более к попарно непересекающихся (а, &)-
цепей. Остается показать, что если в графе G нет мно-
жества, содержащего менее чем к вершин, разделяющих
несмежные вершины а и Ъ, то в нем имеются к попарно
непересекающихся цепей. Используем индукцию по к.
Утверждение правильно при к = 1. Предположим, что
оно верно для некоторого Л>1. Рассмотрим граф G, в
котором несмежные вершины а и Ъ нельзя разделить
множеством, содержащим менее чем к + 1 вершин. По
предположению индукции в G имеется к попарно непере-
секающихся (а, 6)-цепей Pi, Р2, ..., Pk- Рассмотрим мно-
жество вторых (считая а первой) вершин в этих цепях.
Это множество состоит из к вершин и, следовательно,
юно не разделяет вершины а и Ъ. Значит, имеется (а, &)-
цепь Р, первое ребро которой не принадлежит ни одной
из цепей Рг- (i — 1, к). Пусть и— первая, считая от а,
вершина Р, принадлежащая одной из (i = 1, к), и
пусть Pft+i обозначает (а, и) -подцепь цепи Р. Цепи
Pi, . . ., Рк, Ph+i могут быть выбраны, вообще говоря,
многими различными способами. Выберем их так, чтобы
в графе G — а расстояние от v до Ъ было минимально.
Если окажется, что v = Ъ, то Pi, Р2, . . ., Pk+i будет тре-
буемым набором из к + 1 цепей. Допустим, что и^Ъ.
Тогда в графе G— v вершины а и Ъ нельзя разделить
множеством, содержащим менее чем к вершин. По индук-
тивному предположению в этом графе имеется к непере-
секающихся (а, &)-цепей Q\, Q2, . . ., Qk, которые могут
быть выбраны разными способами. Выберем их так, что-
бы множество
\fe-hi
L = EGy^EPi
146
включало минимальное число ребер этих цепей. Иначе-
говоря, цепи Qi должны состоять «в основном» из ребер
цепей Pi. Рассмотрим теперь граф Я, состоящий из вер-
шин и ребер цепей (?i, (?2, ..., Qh и вершины v (эта вер-
шина будет в графе Н изолированной). Пусть Рг — одна
из цепей Pi (Z = 1, к + 1), у которой ребро, инцидентное
вершине а, не принадлежит ЕН. Ясно, что такая цепь
среди Pi (i = 1, к + 1) найдется, поскольку число их рав-
но &+ 1, а цепей Qi, составляющих Н, только к. Пусть,,
далее, х — первая, считая от а, вершина Рг, входя-
щая в VH.
Если х = Ъ, то, добавив цепь Рг к Q\, Qz, .. ., Qh, по-
лучим требуемый набор из к + 1 (а, Ь)-цепей. Допустим,
что х =/= Ъ, и рассмотрим другие возможности для х.
Если х = v, то обозначим через R кратчайшую
(р, Ь)-цепь в G — а. Пусть z—первая, считая от v, вер-
шина цепи R, лежащая на некоторой Qj (/=1, к). Объ-
единим цепь Рт с (v, z) -подцепью цепи R и обозначим по-
лученную (a, z)-цепь через	Цепи (Л, Qz, . . Qk,
Qk+\ обладают тем свойством, что расстояние в графе
G — а от z до Ъ меньше, чем расстояние от v до Ъ, а это
противоречит выбору Pi, Pz, ..., Ph, Ph+\-
Рассмотрим теперь последнюю возможность: х при-
надлежит некоторой цепи Qi (i = 1, к). В этом случае
(а, х) -подцепь цепи Qi имеет ребра в L, иначе бы две
цепи в {Pi, Pz, . . ., Рк, Ph+\} пересекались в вершинах,
отличных от а, Ъ, v. Заменив теперь (а, х) -подцепь Qi на
(а, х)-подцепь Рг, получим непересекающиеся (а, Ь)-це-
пи в графе G — v, и эти цепи будут использовать меньше
ребер из L, чем ()i, . . ., Qh. Снова получаем противоречие,
которое и завершает доказательство теоремы. <
Из теоремы Менгера непосредственно вытекает
Теорема 35.1 (X. Уитни, 1932 г.). Граф к-связен
тогда и только тогда, когда любая пара его несовпадаю-
щих вершин соединена по крайней мере к непересекаю-
щимися цепями.
Имеется несколько аналогов и обобщений теоремы
Менгера. Здесь мы остановимся на реберном варианте
этой теоремы.
Во многих прикладных задачах приходится рассмат-
ривать множество ребер (а не вершин, как ранее), раз-
деляющих вершины а и Ъ графа G, т. е. такое множество
ребер R, что а и Ъ входят в различные компоненты гра-
фа G — R. Минимальное относительно включения мно-
10*
147
жество R с этими свойствами называется (а, Ъ)-разрезом
графа G.
Теорема 35.2. Наибольшее число реберно-непересе-
кающихся цепей, соединяющих две вершины графа,
равно наименьшему числу ребер, разделяющих эти вер-
шины.
> Доказательство этой теоремы легко получить, ис-
пользуя теорему Менгера. С этой целью сопоставим гра-
фу G граф G', который получается из G следующим обра-
зом. Каждая вершина и е VG заменяется группой из
deg v попарно смежных вершин, а ребра графа G', соеди-
няющие вершины из разных групп, находятся в биектив-
ном соответствии с ребрами графа G (рис. 35.1). Если в
графе G нет (а, Ь)-разреза, содержащего менее чем к ре-
бер, то в G' нет множества, имеющего менее чем к вер-
шин, разделяющего какую-либо пару вершин а , Ъ' из
групп, соответствующих а и Ъ. Тогда по теореме Менгера
вершины а и Ъ' соединены в G' по крайней мере к вер-
шинно-пепересекающимися цепями, которым соответству-
ет столько же реберпо-пепересекающпхся (а, Ь)-цепей
графа G.
С другой стороны, ясно, что граф, имеющий (а, Ь)-раз-
рез из к ребер, может содержать не более к реберно-непе-
ресекающихся (а, Ь)-цепей. <
УПРАЖНЕНИЯ
1.	Докажите, что К(Кп) = п — 1.
2.	Докажите, что для всякого кубического графа G справедли-
во равенство x(G) = K(G).
3.	Докажите, что кубический двудольный граф не имеет
мостов.
148
4.	Пусть |G| ^4 и G — минимально 2-связный граф, т, е. та-
кой, который перестает быть 2-связным при удалении любого реб-
ра. Покажите, что G не содержит треугольников.
5.	Покажите, что в минимально 2-связном графе любая вер-
шина смежна с вершиной степени 2.
6.	Пусть G— связный граф и |G| > к. Покажите, *гго граф
Gk является Zc-связным.
7.	Покажите, что реберный граф L(G) любого Л:-связного гра-
фа G также является ^-связным.
8.	Докажите, что в 3-связном графе через любые три вершины
проходит простой цикл.
9.	Докажите или опровергните утверждение: всякий 2-связный
граф G, для которого 6(G) ^4, содержит два реберно-непересе-
кающихся остовных дерева.
10.	Докажите или опровергните утверждение: граф, являющий-
ся объединением двух реберно-непересекающихся остовных де-
ревьев, 2-связен.
11.	Какое наибольшее число точек сочленения может быть в
графе порядка п?
12.	Докажите, что граф, полученный из /с-связного графа уда-
лением з ребер (s < к), является (к — s)-связным.
13.	Докажите, что для любого А:-связного графа G число па-
росочетания ai(G) удовлетворяет неравенству
«i(G) > [(* + 1)/2]
([а] обозначает наибольшее целое число, не превосходящее а),
14. Пусть X — минимальное разделяющее множество вершин
графа G и Gi, G2, ..., Gk — компоненты графа G — X Докажите, что
для любых х е X и i = 1, к найдется такая вершина у е FGt-,
что ху е EG.
Глава VI
Планарность
§ 36. Плоские и планарные графы
Во многих случаях не имеет значения, как изобразить
граф, поскольку изоморфные графы несут одну и ту же
информацию. Однако встречаются ситуации, когда вaжнof
выяснить, возможно ли нарисовать граф на плоскости
так, чтобы его изображение удовлетворяло определенным
требованиям. Например, в радиоэлектронике при изго-
товлении микросхем печатным способом электрические
цепи наносятся на плоскую поверхность изоляционного
материала. А так как проводники не изолированы, то они
не должны пересекаться. Аналогичная задача возникает
при проектировании железнодорожных и других путейу
где нежелательны переезды.
Таким образом возникает понятие плоского графа.
Плоским графом назовем граф, вершины которого явля-
ются точками плоскости, а ребра — непрерывными плос-
кими линиями без самопересечений, соединяющими соот-
ветствующие вершины так, что никакие два ребра не
Рис. 36.1
имеют общих точек, кроме инцидентной им обоим верши-
ны. Примеры плоских графов даны на рис. 36.1.
Любой граф, изоморфный плоскому графу, будем на-
зывать планарным. Граф К±, изображенный на рис. 36.2,
является планарным, так как он изоморфен графам на
150
рис. 36.1, б, в. На том же основании граф на рис. 36.3, а
планарен, поскольку графы, представленные на рис. 36.3,
щ б, изоморфны.
Очевидны следующие утверждения;
1) всякий подграф планарного графа планарен\
2) граф планарен тогда и только тогда, когда каждая
<его связная компонента — планарный граф.
О планарных графах говорят, что они укладываются
на плоскости (имеют плоскую укладку). В дальнейшем
будут рассматриваться укладки графов не только на
1?ис. 36.2
Рис. 36.3
плоскости, но и на других поверхностях и в пространстве.
Поэтому дадим определение укладки графа в произволь-
ное пространство.
Прежде всего введем понятие мюрдановой кривой,
под которой будем понимать непрерывную спрямляемую
линию, не имеющую самопересечений.
Будем говорить, что граф G укладывается в простран-
ство L, если существует такое отображение вершин и ре-
бер графа G соответственно в точки и жордаповы кривые
этого пространства, что различным вершинам соответ-
ствуют различные точки, а кривые, соответствующие раз-
личным ребрам, пересекаются только в инцидентных
этим ребрам вершинах. Изображенный таким образом
граф называется укладкой графа G в пространство L.
Теорема 36.1. Каждый граф укладывается в трех-
мерное пространство Е3.
> Все вершины графа G помещаем в различные точ-
ки оси ОХ. Из пучка плоскостей, проходящих через эту
ось, выберем \EG\ различных плоскостей. Далее, каждое
ребро uv е EG изображаем в соответствующей плоскости
полуокружностью, проходящей через вершины и и v. По-
нятно, что в результате получаем укладку графа G в Е3,
так как все ребра лежат в разных плоскостях и потому
не пересекаются во внутренних точках. <
Теорема 36.2. Граф укладывается на сфере тогда и
только тогда, когда он планарен.
151
> Для доказательства этой теоремы достаточно рас-
смотреть стереографическую проекцию (рис. 36.4)».
Пусть граф G уложен на сфере. Проведем плоскость Q,
касательную к сфере, так, чтобы северный полюс N (точ-
ка, диаметрально противоположная точке касания) не
лежал на ребре и не совпадал с вершиной графа G. Те-
перь рассмотрим граф G', полученный стереографической
проекцией графа G из точки N на плоскость Q. Посколь-
ку существует биективное соответствие между точками
сферы, отличными от N, и их стереографическими проек-
циями, то граф G' плоский и изоморфен графу G. Следо-
вательно, G — планарный граф.
Обратное утверждение доказывается аналогично с уче-
том установленной биекции. <
Определения плоского и планарного графов, так же
как и теоремы 36.1, 36.2 и многие другие утверждения
этой главы, сохраняются и применительно к мульти- и
псевдографам.
Следующая классическая головоломка наводит на
мысль, что существуют не только планарные графы.
Задача о трех домах и трех колодцах. Имеются три до-
ма 1, 2, 3 и три колодца 4, 5, 6 (рис. 36.5). Каждый хо-
зяин пользуется любым из трех колодцев. В некоторый
момент обитатели домов решили проложить дорожки до
колодцев так, чтобы исключить встречи на дорожках, т. е.
чтобы дорожки не пересекались. Возникает вопрос: воз-
можно ли это, т. е. возможно ли построить плоскую ук-
ладку графа Т^з.з? Все попытки нарисовать девять непере-
секающихся дорожек, соединяющих дома с колодцами,
заканчиваются неудачей. При этом легко нарисовать
восемь непересекающихся дорожек, но девятая обяза-
тельно пересечет хотя бы одну из этих восьми. Оказы-
вается, что неудачи не случайны. Ниже будет доказано*
что граф 7^з,з не укладывается на плоскости, т. е. не яв-
ляется планарным.
152
На самом деле не только существуют непланарные
графы, но верно утверждение, приводимое ниже без до-
казательства (см. [21]).
Утверждение 36.3. Почти все графы не являются
планарными.
§ 37. Грани плоского графа. Формула Эйлера
Гранью плоского графа называется максимальное по
включению множество точек плоскости, каждая пара ко-
торых может быть соединена жордановой кривой, не
пересекающей ребра графа. Тем самым каждая точка
плоскости принадлежит хотя бы одной грани плоского
графа. Границей грани будем
считать множество вершин и
ребер, принадлежащих этой	яг^/'Хч
грани.	I з /д ySy 4
На рис. 37.1 изображен I / J X. .
граф с четырьмя гранями. От- I / JL—4 2 X.
метим, что всякий плоский 14— —X/
граф имеет одну, и притом с	h
единственную, неограниченную	Рис. 37.1
грань (на рис. 37.1 грань 4).
Такая грань называется внешней, а остальные грани —-
внутренними.
Легко видеть, что всякую внутреннюю грань плоско-
го графа G можно преобразовать во внешнюю с помощью
стереографической проекции. Для этого, воспользовав-
шись теоремой 36.1, уложим граф G на сфере так, чтобы
северный полюс оказался внутри выбранной грани. Далее
рассмотрим стереографическую проекцию G' графа G на
плоскость, касающуюся сферы в южном полюсе, т. е. в
точке, диаметрально противоположной северному полюсу.
Очевидно, что выбранная грань графа G станет при этом
внешней в G', а внешняя грань графа G — внутренней
гранью графа G', который изоморфен графу G. На
рис. 37.2 представлен граф, получающийся из графа, изо-
браженного на рис. 37.1, путем такого преобразования.
При этом внутренняя грань 1 стала внешней.
Понятие грани естественным образом распространя-
ется на псевдо- и мультиграфы (рис. 37.3).
Сформулируем несколько очевидных свойств плоских
укладок графа, которые в дальнейшем будем неоднократ-
но использовать, порой и не ссылаясь на них.
153
Свойство 1. Всякий планарный граф допускает
такую плоскую укладку, в которой любая выбранная вер-
шина (ребро) графа будет принадлежать внешней грани^
Свойство 2. Пусть граф G состоит из двух связ-
ных компонент G\ и Gz, являющихся плоскими графами*
а
9
Рис. 37.2
Рис. 37.3
и произвольным образом выбраны вершины Vi е VGi и
v2^VG2. Тогда граф G, полученный из G слиянием вер-
шин v\ и V2 в вершину v, имеет плоскую укладку. При
этом вершина и является точкой сочленения графа G
(рис. 37.4).
Аналогично можно «склеивать» два плоских графа и
по ребру.
Свойство 3. Всякие две вершины, принадлежащие
границе некоторой грани плоского графа, можно соеди-
нить простой цепью произвольной длины так, что вы-
бранная грань разобьется на две грани.
Отметим, что это свойство является следствием из-
вестной теоремы Жордана о кривой.
Свойство 4. Для любого плоского графа каждая
точка плоскости, не лежащая на ребре, входит только в
одну грань, а каждая точка ребра, не являющаяся вер-
шиной, входит только в одну грань, если это ребро яв-
ляется мостом, и точно в две грани, если оно не мост.
Далее будем пользоваться следующими обозначения-
154
ми: n, m, /—соответственно число вершин, ребер и гра-
ней плоского графа.
Теорема Эйлера (1758 г.). Для всякого связного
плоского графа верно равенство
n-m + f^2.	(1)
Равенство (1) называется формулой Эйлера.
> Пусть G — связный плоский n-вершинный граф.
Рассмотрим некоторый остов Т этого графа. Очевидно,
что дерево Т имеет одну грань (внешнюю) и п вершин.
В то же время известно (см. теорему 13.1), что число
ребер дерева Т равно п— 1. Поэтому для графа Т фор-
мула (1) верна. Теперь будем поочередно добавлять к Т
недостающие ребра графа G. При этом на каждом шаге
число вершин, естественно, не меняется, а число ребер и
число граней увеличивается на единицу на основании
свойства 3. Следовательно, формула (1) будет верна для
всякого графа, получающегося в результате таких опера-
ций (шагов), а поэтому она верна и для графа G, ко-
торым заканчивается вся эта процедура. <
Из теоремы Эйлера вытекает ряд интересных след-
ствий.
Прежде всего, рассмотрим в трехмерном пространстве
выпуклый многогранник с п вершинами, тп ребрами и f
гранями. Очевидно, что спроектировав этот многогранник
на описанную около него сферу, далее уложив его так,
чтобы северный полюс находился внутри одной из гра-
ней, и произведя затем стереографическую проекцию, по-
лучим связный плоский граф. Поэтому справедливо
Следствие 37. 1. У всякого выпуклого многогран-
ника сумма числа вершин п и числа граней j без числа
ребер тп равна двум', п + f — тп — 2.
Доказательство именно этой формулы и было впервые
опубликовано Л. Эйлером в 1758 г. в «Записках Петер-
бургской академии наук».
Следствие 37.2. Число граней любой плоской ук-
ладки связного планарного (п, тп)-графа постоянно и
равно тп — п + 2.
Другими словами, число f является инвариантом пла-
нарного (п, тп) -графа, т. е. не зависит от способа укладки
этого графа на плоскости.
Следствие 37.3. Для связного планарного [п.т]-
графа т Зп — 6 при п^ 3.
< Не теряя общности, будем считать, что G —
плоский граф. Прежде всего заметим, что всякое ребро
155
плоского графа либо разделяет две различные грани, ли-
бо является мостом (см. свойство 4). Поскольку G — граф
без петель и кратных ребер, то всякая грань ограничена
по крайней мере тремя ребрами (исключение составляет
лишь случай, когда G — дерево с тремя вершинами, но
для такого графа неравенство Зп — 6 > т справедливо).
Поэтому число 3/ является оценкой снизу удвоенного чис-
ла ребер графа G, т. е. 3/	2т. Отсюда, учитывая, что
по формуле Эйлера / == т — п + 2, приходим к требуемо-
му неравенству. <
Из этого следствия сразу же получаем
Утверждение 37.4. Граф К$ не планарен.
<1 Действительно, для графа Кз п = 5, т?г = 10. По-
этому неравенство Зп — 6 > т превращается в неверное:
9	10, т. е. граф К$ не может быть планарным. <
Утверждение 37.5. Граф Кз,з не планарен.
> Для рассматриваемого графа п = 6, т = 9. Поэто-
му, если бы он был планарным, то для любой его плоской
укладки выполнялось бы / = 5 согласно следствию 37.2.
В то же время всякая грань двудольного графа Кз,з долж-
на быть ограничена по меньшей мере четырьмя ребрами.
Следовательно, 2т т. е. 18 > 20. Полученное про-
тиворечие доказывает утверждение 37.5. <
Мы особо останавливаемся на графах К$ и Хз.з, по-
скольку, как мы увидим в § 39, эти графы являются ми-
нимальными непланарными графами и играют важную
роль во многих критериях планарности.
Из теоремы Эйлера вытекает также
Следствие 37.6. Если в связном плоском (п,т)-
графе граница каждой грани является r-циклом, г^З,
то
m(r — 2) = г(п — 2).
> Так как каждая грань графа ограничена г-циклом,
то каждое ребро принадлежит ровно двум граням, т. е.
fr — 2m. Подставляя сюда / из формулы Эйлера, получа-
ем искомый результат. <
Очевидно, что не всегда граница грани плоского гра-
фа является простым циклом (см., например, грань 2 на
рис. 37.1). Однако для 2-связных графов это так. А имен-
но, верна следующая
Теорема 37.7. Плоский граф двусвязен тогда и
только тогда, когда границей всякой его грани является
простой цикл.
156
> Необходимость. Доказательство проведем от
противного. Пусть существует плоский 2-связный граф
G, в котором некоторая грань ограничена не простым
циклом. Поскольку граф G содержит хотя бы один про-
стой цикл, то существует такой максимальный 2~связный
подграф Н графа G, что граница каждой его ^грани яв-
ляется простым циклом. При этом Н =И= G. По лемме 34.7
в G существует Я-цепь. Эта простая цепь должна разби-
вать некоторую грань плоского графа Н на две грани.
Очевидно, что каждая из этих граней ограничена простым
циклом. Однако это противоречит выбору подграфа Н.
Достаточность. Допустим, что плоский граф^
каждая грань которого ограничена простым циклом, не
является 2-связным. Тогда граф имеет точку сочленения.
Но это значит, что существует грань, ограниченная не
простым циклом. <1
Теорема 37.8. Связный граф планарен тогда и толь-
ко тогда, когда каждый его блок планарен.
> Необходимость очевидна.
Достаточность докажем индукцией по числу блоков к.
Если к =* 1, то утверждение очевидно. Пусть граф G со-
стоит из к > 1 планарных блоков. Согласно утвержде-
нию 34.6 существует хотя бы один концевой блок В,
имеющий точку сочленения и. Поскольку подграф G —
— (В — и) содержит к — 1 блоков, то по предположению
индукции он планарен. Следовательно, существует такая
его плоская укладка, что вершина v находится на внеш-
ней грани. Точно так же граф В имеет плоскую укладку
с вершиной v на внешней грани. Поэтому объединение
(G — (В — v)) U В, изоморфное графу G, имеет плоскую
укладку па основании свойства 2. <1
Из теоремы 37.8 следует, в частности, что для выяс-
нения вопросов, связанных с планарностью, достаточно
рассматривать лишь 2-связные графы.
§ 38. Плоские триангуляции
В этом параграфе изучается особый класс графов —
плоские триангуляции. Такие графы интересны тем, что
всякий планарный граф порядка п изоморфен подграфу
некоторой плоской триангуляции с п вершинами.
Грань плоского графа, ограниченную треугольником
(3-циклом), также будем называть треугольником.
Связный плоский граф называется плоской триангу-
ляцией, если каждая его грань (в том числе и внешняя)
157
является треугольником. Тем самым, плоская триангуля-
ция содержит не менее трех вершин.
Максимальным плоским (планарным) графом назы-
вается n-вершинный (п > 3) граф, который перестает
быть плоским (планарным) при добавлении любого реб-
ра. На рис. 38.1 приведены максимальный и не макси-
мальный плоские графы. Разумеется, что от добавления
Рис. 38.1
кратных ребер планарность графа не нарушается. Одна-
ко мы условились рассматривать лишь простые графы.
Теорема 38.1. Граф является максимальным пло-
ским графом тогда и только тогда, когда он представляет
собой плоскую триангуляцию.
> Необходимость. Пусть G — максимальный
плоский граф. Прежде всего заметим, что граф G явля-
ется 2-связным. Поэтому по теореме 37.7 всякая грань Г
такого графа, не являющаяся треугольником, ограничена
простым циклом (щ, V2, v$, щ, . . ., содержащим не
менее четырех вершин. Так как G — плоский граф, то он
не может одновременно содержать
ребра viz?3 и (ведь эти ребра
должны быть изображены вне гра-
ни Г, см. рис. 38.2). Предположим,
ц например, что V\V3&EG. Тогда пос-
ле добавления ребра в грань Г
граф G остается плоским, что
противоречит его максимальности
(рис. 38.2).
Достаточность. Пусть G —
плоская триангуляция. Так как G —-
связный граф, то очевидно, что вся-
добавления которого граф G остается
плоским, должно разбивать некоторую грань графа G на
две грани. Однако в плоской триангуляции всякая грань —
треугольник и, следовательно, разбить ее на две путем
добавления ребра невозможно. <3
Теорема 38.1 дает следующее важное
Следствие 38.2. Всякий плоский граф является
юстовным подграфом некоторой плоской триангуляции.
158
Иными словами, каждый плоский граф можно допол-
нить ребрами так, что он станет плоской триангуляцией.
Из теоремы 38.1 и следствия 37.6 (при г = 3) вы-
текает
Следствие 38.3. Для всякого максимального пла-
нарного (п, т)-графа т = Зп — 6.
Утверждение 38.4. Если ч^сло вершин плоской
триангуляции не меньше четырех, то степень каждой
вершины не менее трех.
> Возьмем произвольную вершину и. Пусть w —
смежная с ней вершина. Ребро viv принадлежит двум гра-
ням— треугольникам (р, w, и\) и (р, w, U2), причем
щ иг, так как число вершин графа не меньше четырех.
Таким образом, v смежна по крайней мере с тремя вер-
шинами W, U\, U2. <1
Утверждение 38.5. Всякий планарный граф с
п 4 вершинами имеет по крайней мере 4 вершины са
степенями, не превосходящими 5.
> Без потери общности будем считать граф G плос-
ким. Добавляя ребра, сделаем граф G максимальным
плоским графом G', каждая вершина которого в силу
утверждения 38.4 имеет степень не меньше 3. Поэтому,,
принимая во внимание следствие 38.3 и лемму о рукопо-
жатиях (утверждение 5.1), получаем
2 (Зп — 6) = 2m = Зп3 + 4п4 + 5п5 + . -.
> З(в3 + в4 + п5) + 6 S
1^6
где п — число вершин графа G', тп — число его реберг
а п{ — число вершин степени i в этом графе. Отсюда, учи-
тывая, что n == Vj п<, легко получаем
i>3
Пз + П4 + П5 4,
т. е. в графе G', а тем более в графе G, имеется по край-
ней мере 4 вершины со степенями, не превышающими 5. <
§ 39. Критерии планарности
Имеется несколько критериев планарности графа. Мы
рассмотрим характеризации планарности графов, данные
Л. С. Понтрягиным, К. Куратовским, К. Вагнером и
С. Маклейном. Следует заметить, что практическая про-
верка условий, которыми ниже характеризуются планар-
ные графы, не всегда является простой. Однако разрабо-
159
таны эффективные алгоритмы, позволяющие для любого
заданного графа или найти его плоскую укладку, или
установить, что граф непланарен. Один из таких алгорит-
мов приведен в § 41.
Для того чтобы сформулировать широко известный
критерий Понтрягина — Куратовского, введем понятие
гомеоморфизма графов. Нам понадобится операция под-
разбиения ребра е — аЪ графа. Она состоит в следующем:
из графа удаляется ребро е и до-
бавляются два новых ребра ei = av.
'( I )	L	Т в2 = vb, где v — новая вершина.
Ч У	V.	J Два графа называются гомео-
\	/	\ /	морфными, если оба они могут
\ /	\ /	быть получены из одного и того
\ /	\/	же графа подразбиением его ре-
V	V	бер.
Рис. 39.1	На рис. 39.1 изображены гомео-
морфные графы.
Если граф планарный, то очевидно, что любой граф,
гомеоморфный ему, также является планарным.
Исторически первым критерием планарности графов
является следующий критерий, доказанный Л. С. Понт-
рягиным (1927 г.) и К. Куратовским (1930 г.) независи-
мо друг от друга.
Теорема Понтрягина — Куратовского.
Граф планарен тогда и только тогда, когда он не содер-
жит подграфов, гомеоморфных К$ или
Тем самым можно утверждать, что многие графы не-
планарны и независимо от того, как они изображены на
плоскости, некоторые их ребра обязательно пересекаются.
Необходимость условий теоремы уже доказана, по-
скольку доказана непланарность графов К$ и Л’з.з (след-
ствия 37.4 и 37.5). Для доказательства достаточности
требуются новые понятия и теоремы. Попутно будет до-
казано, что всякий планарный граф можно уложить на
плоскости так, что каждое его ребро будет отрезком
прямой.
Ранее было показано (см. теорему 37.8), что граф
планарен тогда и только тогда, когда планарны его дву-
связные компоненты. Оказывается, будет достаточно, ес-
ли мы, касаясь вопросов, связанных с плоской укладкой
2-связного графа G. рассмотрим лишь 3-связные графы,
полученные из G специальным образом.
Пусть x(G) = 2, |G|	4. Из определения двусвязности
вытекает существование вершин a. Ъ VG. таких что
160
граф Н = G — а — Ъ пе связен. Рассмотрим следующее
преобразование А графа G. Пусть Н\, Н2, ..., Нг —
связные компоненты графа Н. Для каждой такой компо-
ненты Hi рассмотрим граф Gi, порожденный в G мно-
жеством VHi U a U Ъ и дополненный ребром если аЪ
Ф EG. В результате преобразования А получаем семей-
ство графов Gi, G2, ..., Gr, причем |GJ >3, x(Gi)^2
(j = 1, г) (рис. 39.2).
Теорема 39.1. Пусть %(G)=2, |G|>4. Граф G
планарен тогда и только тогда, когда планарен каждый
граф Gi, полученный в результате преобразования А.
> Необходимость. Если G — планарный граф,
то любой его подграф, в том числе Gi = G(T/Gi), плана-
рен. Если Gi содержит ребро аЪ, то Gi == Gi. В противном
Рис. 39.2
случае по лемме 34.7 в G существует Gj-цепь L, соединя-
ющая вершины а и Ъ. Подграф Gi U L планарен, но он
гомеоморфен графу Gi.
Достаточность. Пусть все графы Gi, G2, ..., Gr
планарны. Пусть Р{, Р2, ..., Рг — соответствующие им
плоские укладки, у которых ребро ab лежит па внешней
грани. Будем последовательно объединять графы Р\,
Р2, . •Рг. Сначала построим такую укладку объедине-
ния Pi>2 графов Pi и Р2, в которых имеется общее ребро
ab, что граф Р2 лежит на внешней грани графа Рь Затем
изобразим Pi)2 так, чтобы ребро ab оказалось на внешней
грани, и используя прежний прием, построим объедине-
ние Р1,2,з графов Pi)2 и Р3 (рис. 39.3) и т. д., пока не объ-
единим все графы Рь Р2, .. ., Рг. Полученный в резуль-
И В. А. Емеличев и др.
161
тате плоский граф Рь2, ,„>г может отличаться от исходно-
го графа G только ребром ab. <
Следствие 39.2. Всякая плоская триангуляция,
имеющая более трех вершин, 3-связна.
> Доказательство проведем от противного. Предполо-
жим, что G — плоская триангуляция и x(G)=32. Пусть
а и Ъ — такие вершины, что граф G — а — Ъ не связен.
Совершив преобразование А графа G, получим, согласно
теореме 39.1, планарные графы Gi, G2, .. ., Gr. Пусть Pb
Р2, ..Рт — соответствующие им плоские укладки, в ко-
торых ребро аЪ лежит на внешней грани. Объединим их
последовательно, как это делалось при
теоремы 39.1. При
доказательстве
этом па последнем шаге, объединив
графы Pi>2......г-i и Рг, получаем граф
Pi,2)...,r, внешняя грань которого со-
держит (поскольку IPJ >3)
смежные
d^VPr,
т. е. Pi,2,
Рис. 39.4
не-
вершины с е VP12....г_! и
с, d^{a, Ъ} (рис. 39.4),
.... г, а, следовательно, и G
не является плоской триангуляци-
ей. <
Вернемся к графу G, для которо-
го x(G) = 2, |G|>4. Если среди
графов Gb G2, ..., Gr, полученных
с помощью преобразования А, есть граф Gi? для которого
x(Gi) = 2, IGJ > 4,то к нему вновь можно применить пре-
образование А и т. д. до тех пор, пока это преобразование
будет возможным. Поэтому справедливо
Утверждение 39.3. Пусть x(G) = 2, |Gl 4. Тог-
да в результате многократного применения преобразова-
ния А к графу G будет получено такое семейство графов
162
что для любого i = 1, R либо Gi=K3, либо
Поскольку Кз — планарный граф, то из теоремы 39.1
и утверждения 39.3 следует, что вопрос о планарности
2-связных графов свелся к вопросу о планарности 3-связ-
ных графов.
Прежде чем формулировать критерий планарности
3-связпых графов, докажем лемму.
Лемма 39.4. Пусть x(G) = 2, | GI > 4. Пусть, да-
лее, G\, G%, .. ., Gr — графы, полученные в результате пре-
образования А, и аЪ — ребро этих графов, не принадле-
жащее графу G. Тогда для любого i = 1, г существует
Gi-цепъ графа G, соединяющая вершины а и Ъ.
>	Поскольку %(Gk)^2 для любого к = 1, г, то по
теореме 34.1 ребро ab принадлежит некоторому простому
циклу графа Gk. При любом к ¥= i часть этого цикла, пе
содержащая ребра аЪ, и служит искомой Gi-цепыо. <
Плоский граф назовем выпуклым прямолинейным гра-
фом, если границей каждой его грани является выпуклый
многоугольник. Напомним, что многоугольник называет-
ся выпуклым, если оп целиком расположен по одну сто-
рону от любой прямой, на которой лежит сторона много-
угольника, и никакие две его стороны пе лежат па од-
ной прямой.
Теорема 39.5. Если граф 3-связный, то он либо
изоморфен выпуклому прямолинейному графу, либо со-
держит подграф, гомеоморфный или К^.
>	Доказательство проведем индукцией по числу п
вершин графа. Для п = 4 утверждение теоремы верно,
так как граф К\ изоморфен выпуклому прямолинейному
графу (см. рис. 36.1, б), а других 3-связных четырехвер-
шпппых графов не существует.
Пусть G — 3-связный граф, IG\	и для всех
графов с меньшим числом вершин теорема верна. Соглас-
но следствию 34.9 в графе G есть такое ребро х = uv,
что граф Gx, полученный из G в результате стягивания
этого ребра, является 3-связпым. Пусть Gx содержит под-
граф И, гомеоморфный К$ (рис. 39.5, а). Покажем, что
тогда граф G содержит подграф, гомеоморфный или
Это очевидно в случае, когда И не содержит верши-
ны х, полученной в результате стягивания ребра х, или
содержит ее в качество вершины степени 2. Пусть теперь
степень каждой из вершин а, Ъ, с, d, х в Н равна четы-
рем. Тогда вершина х соединена простыми непересекаю-
11*	163
щимися цепями Zq, Z2. ^з, Еа с вершинами a, b, с, d
соответственно. В графе G этим цепям соответствуют пе-
пересекающиеся простые цепи Lj, L2,	соединяю-
щие каждую из вершин а, Ь, с, d с одной из вершин и
или и. Если одпа из этих вершин, например и, принадле-
жит трем или четырем цепям, то в G существует под-
граф, гомеоморфный (рис. 39.5, б). А если каждая из
39.5
вершин и и v принадлежит ровно двум цепям, то в G су-
ществует подграф, гомеоморфный Кз$ (рис. 39.5, в, г).
Аналогично можно показать, что если Gx содержит
подграф, гомеоморфный Кзгз, то и G содержит подграф,
гомеоморфный К3,з-
Пусть теперь в Gx нет подграфов, гомеоморфных гра-
фам Кз или КЗ'З. По индуктивному предположению суще-
ствует выпуклый прямолинейный граф Gx, изоморфный
графу Gx. Тогда Gx — х — 2-связпый плоский граф, каж-
дая грань которого, по теореме 37.7, ограничена простым
циклом.
Как обычно, через NG(v) обозначим окружение вер-
шины v в графе G. Пусть С — простой цикл, ограничи-
вающий грань графа Gx — х, которая содержит
164
Вершины из NG(v)\u делят цикл С па простые цепи
Li =(«1, ..., <22), L2 =(d2, ..., «з), ..Lh = (ah, ..., «1).
(1)
Далее рассмотрим отдельно два случая.
Случай 1. Все вершины из NG(u)\v принадлежат
одной из цепей (1). Тогда, удалив из Gx все ребра вида
(х, &), где Ь (i = 1, 7с), получим граф G', изоморф-
ный графу G — и. Ребрами графа Gf являются отрезки,
и все его грани, кроме, возможно, грани, содержащей
вершины из NG(u), будут выпуклыми многоугольниками.
Пусть вершина х принадлежит внутренней грани гра-
фа Gx. Очевидно, что всякий выпуклый многоугольник
обладает следующим свойством: для любой его вершины
существует такая ее окрестность, в которой можно пере-
мещать эту вершину (при неподвижных остальных), не
нарушая выпуклости многоугольника. Поэтому в графе
Gx существует такая окрестность О (Ж) точки х, что при
перемещении х в О (Ж) будет сохраняться выпуклость
всех многоугольников, находящихся внутри цикла С,
Будем считать, что вершины из NG(u)\v находятся па
цепи Lk и разбивают ее на части: (<2i, ..., &i), (&i, ...
..., 62), ..., (bz-i, ..., &z), (bh ..., ak). Обозначим через
Т точки плоскости, лежащие внутри кривой (цикла)
(£, bi, ..., &2, ..., bh х). Из определения выпуклого
многоугольника следует, что, поместив вершину и в лю-
бую точку области О(х)П Т и соединив и со всеми вер-
шинами из TVg(^) (считая х — v), получим выпуклый
прямолинейный граф, изоморфный графу G (рис. 39.6).
Подобным образом поступаем и тогда, когда вершина
х принадлежит внешней грани графа Gx. (На рис. 39.7 а, б
165
изображен случай, когда вершина и принадлежит внут-
ренней грани графа G', а па рис, 39.7 в, г — внешней.)
Случай 2. Не существует цепи (1), содержащей все
вершины из множества 7Vg(u)\p. В зтой ситуации
Рис. 39.7
множество всех ребер, инцидентных и п и, нельзя изобра-
зить без пересечений.
В самом деле, если
М- l(7VG(u)\z;)A(7VG(^)\zz)l > 3,
т. е. число вершин цикла С, смежных и с и, и с v, не
меньше трех, то в G существует подграф, гомеоморфный
графу К$ (рис. 39.8).
Если же М С 2, то в G есть подграф, гомеоморфный
графу Т^з.з. На рис. 39.9—39.11 изображены случаи, ког-
да М = 2, 1, 0 соответственно.<1
Следствие 39.6 (теорема Понтрягина — Ку-
ратове к ого). Граф планарен тогда и только тогда,
когда он не содержит подграфов, гомеоморфных графам
К$ или
> Осталось доказать достаточность условий теоремы.
Пусть в графе G пет подграфов, гомеоморфных
или /<з з. Если G — З-связный граф, то по теореме 39.5 оп
планарен.
166
Рис. 39.8
Рис. 39.9
Рис. 39.10
Рис. 39.11
167
Пусть x(G) = 2, |G|	5. Далее доказательство прове-
дем от противного. Предположим, что граф G не планар-
ный. Тогда в результате многократного применения к не-
му преобразования А (см. утверждение 39.3) получим
семейство графов Gj, G2, ..., GR, среди которых согласно
теореме 39.1 имеется 3-связпый граф G/, пе являющийся
планарным. В силу теоремы 39.5 в Gi есть подграф К,
гомеоморфный К$ или /€з,з- Если все ребра графа К при-
надлежат G, то К — подграф графа G, т. е. получено про-
тиворечие. Если же некоторое ребро ab е ЕК не входит
Рис. 39.12
в G, то по лемме 39.4 существует Сгцепь графа G, соеди-
няющая вершины а и Ъ. Нетрудно показать, что (?г-цепи,
соответствующие различным таким ребрам, пе имеют
общих вершин, кроме, возможно, концевых. Заменив каж-
дое такое ребро соответствующей Сгцепыо, получим под-
граф графа G, гомеоморфный графу К. Вновь имеем про-
тиворечие. <
В качестве иллюстрации рассмотрим граф Петерсена.
Он содержит подграф, гомеоморфный графу /£з,з(рис. 39.12,
где {«1, а2, аз) и {bi, Ь2, Ь3} — доли). Следовательно, этот
граф не является планарным.
Следствие 39.7 (К. Вагнер, 1936 г.). Для любого
планарного графа существует плоская укладка, в ко-
торой все ребра изображены в виде отрезков прямых
линий.
> Пусть G — связный планарный граф, имеющий пе
менее четырех вершин. На основании следствия 38.2
граф G является остовным подграфом плоской триангу-
ляции Т, которая согласно следствию 39.2 есть 3-связный
граф. Поэтому в силу теоремы 39.5 существует прямоли-
нейный граф Т, изоморфный графу Т. Очевидно, что ис-
ходный граф G получается из Т путем удаления ранее
добавленных к G ребер. <1
168
Помимо критерия Понтрягина — Куратовского есть и
другие критерии планарности графа. Приведем некоторые
из них без доказательств.
Теорема 39.8 (К. Вагнер, 1937 г.). Граф планарен
тогда и только тогда, когда в нем нет подграфов, стяги-
ваемых к графам или
Поскольку граф Петерсепа очевидным образом стяги-
вается к (для этого нужно стянуть пять ребер, соеди-
няющих вершины внутреннего и внешнего циклов), то
пепланарность графа Петерсепа с помощью критерия
Вагнера доказывается совсем просто.
Отметим здесь, что стягивая любое ребро планарного
графа, получаем вновь планарный граф.
Очевидно, что все ациклические графы планарны.
Поэтому вполне естественна формулировка критерия пла-
нарности, исключающая этот тривиальный случай. Та-
ким критерием является следующая
Теорема 39.9 (С. Маклейн, 1937 г.). Граф плана-
рен тогда и только тогда, когда в каждом его нетривиаль-
ном блоке есть такой базис циклов С\, С%, ..., Ch и такой
один дополнительный цикл Со, что любое ребро блока
принадлежит ровно двум из этих k + 1 циклов.
§ 40. Двойственность и планарность
Целью этого параграфа является получение еще од-
ного критерия планарности графа, основанного на поня-
тии двойственности.
Условимся, что всюду в этом параграфе слово «граф»
означает «псевдограф». Кроме того, видоизменим здесь
использованную выше (см. § 3) операцию стягивания
ребра e = uv <^EG, под которой теперь будем понимать
удаление ребра е и отождествление вершин и и v в но-
вую вершину, инцидентную тем ребрам графа G, которые
были инцидентны вершинам и и v, за исключением реб-
ра е (рис. 40.1). Тем самым теперь появляющиеся при
стягивании ребра кратные ребра не отождествляются,
как ранее.
Для плоского графа G построим новый плоский граф
G*, который назовем геометрически двойственным к G.
Для этого внутри каждой грани Tf графа G выберем по
одной точке и*. Эти точки — вершины будущего графа
G*. Далее, каждому ребру е EG поставим в соответствие
жорданову кривую е*, которая пересекает лишь одно реб-
ро е графа G и соединяет вершины , лежащие в гра-
169
нях, границы которых содержат ребро е (таких граней
может быть две или одна). Кривые е*—ребра графа G*.
Очевидно, что ребра графа G* можно провести так, чтобы
они не пересекались. На рпс. 40.2 сплошной линией
изображен граф G, а пунктирной — граф G*. Заметим,
что петлю в G* порождает всякий мост в G, а кратные
ребра появляются в G* тогда и только тогда, когда две
грани графа G имеют более одного общего ребра.
Из этого построения очевидно, что граф G*, геометри-
чески двойственный к плоскому графу G, определяется
однозначно с точностью до изоморфизма, причем граф G*
всегда связен. Последнее утверждение легко доказать ин-
дукцией по числу вершин графа G* (т. е. по числу гра-
ней графа G) путем стягивания ребра е* графа G*, что,
очевидно, соответствует удалению ребра е в графе G. При
этом, если ребро е — граница двух граней, то упомяну-
тые операции приводят к уменьшению числа вершин гра-
фа G* (числа граней графа G) на единицу.
Применяя формулу Эйлера, легко получить
Утверждение 40.1. Если G — плоский связный
(тг, т)-граф с f гранями, a G* — (n*, т*)-граф, геометри-
чески двойственный к нему, с j* гранями, то п* == /,
m* = m, j* = п.
Поскольку граф G* — плоский, то можно построить
граф, геометрически двойственный к G*, который естест-
170
венно обозначить через G**. Связь между графами G и
G** устанавливает следующая теорема.
Теорема 40.2. Если G —плоский связный граф, то
граф G** изоморфен графу G.
О Из утверждения 40.1 следует, что 7г** = /* = п, где
ft**=|G**l. Следовательно, каждая грань графа G* со-
держит одну вершину графа G (G**). Поэтому построе-
ние, при помощи которого граф G* получен из G, можно
обратить, т. е. получить G из G*. <
Граф, двойственный к планарному графу, определяет-
ся следующим образом: рассмотрим любую укладку это-
го графа и построим геометрически двойственный граф.
Здесь уместно отметить, что планарный граф, допускаю-
щий несколько укладок на плоскости, может иметь не
изоморфные двойственные графы (см. упр. 25).
Теорема 40.3. Пусть G—планарный граф, G* —
граф, геометрически двойственный к G. Подмножество
ребер из G образует простой цикл в G тогда и только
тогда, когда соответствующее множество ребер из G* об-
разует разрез в G*.
Для доказательства этой теоремы потребуется одна
очевидная лемма.
Лемма 40.4. Пусть Н — связный граф, множество
VH вершин которого разбито на два подмножества V\ и
V2. Множество ребер
М(V\, V2) == {б = щное ЕН • Vi Vj, V2G V2}
является разрезом тогда и только тогда, когда графы
H(V\) и Н(уг2>) связны.
> Доказательство теоремы 40.3. Не исклю-
чая общности, будем считать, что G — плоский граф.
Пусть С — простой цикл в G. Тогда он ограничивает
одну или несколько внутренних граней графа G, т. е. ог-
раничивает часть плоскости, содержащую непустое мно-
жество W вершин графа G*. Поэтому ребра из G*, пере-
секающие ребра цикла С, образуют множество М в G*,
удаление которого разделяет связный граф G* на два
подграфа с множествами вершин W и ИСАИ7 (рис. 40.3).
Индукцией по числу вершин легко доказать связность
каждого из этих подграфов. Следовательно, на основании
леммы 40.4 М — разрез в графе G*.
Путем обращения приведенного выше рассуждения до-
казывается обратное утверждение о том, что разрезу в
G* соответствует простой цикл в G. <3
171
Теорема 40.3 естественным образом приводит к сле-
дующему комбинаторному определению двойственности
графов, которое обобщает геометрическую двойственность
и позволяет сформулировать еще один критерий планар-
ности графов.
Граф G* называется абстрактно двойственным к гра-
фу G, если между множествами EG и EG* существует
биекция, обладающая тем свойством,
что подмножество ребер из G обра-
зует простой цикл в G тогда и
только тогда, когда соответствующее
ему подмножество ребер из G* об-
-- разует разрез в G*.
На рис. 40.4 изображены граф и
абстрактно двойственный к нему
граф. Соответствующие ребра обо-
Pnc 40 3 значепы одной и той же буквой.
Другой пример графов G и G* при-
веден па рис. 40.5.
Понятие абстрактной двойственности обобщает поня-
тие геометрической двойственности, так как согласно тео-
реме 40.3 справедливо
Утверждение 40.5. Граф, геометрически двойст-
венный к плоскому графу, является абстрактно двойст-
венным к нему.
Непосредственно из определения вытекает следующее
утверждение.
Утверждение 40.6. Граф Н является абстрактно
двойственным к графу G тогда и только тогда, когда ма-
Рис. 40.4
троид M(G) циклов графа G изоморфен матроиду М*(Н)
разрезов графа Н.
Теорема 40.7. Если граф G* — абстрактно двойст-
венный к G, то G—граф, абстрактно двойственный к G*.
Отметим, что здесь, в отличие от теоремы 40.2, не тре-
буется связность графа G.
172
> На основании утверждения 40.6 матроид M(G) изо-
морфен матроиду ЛР(£*). Поэтому в силу следствия
20.2 матроиды M*(G) и 7И**(бг*) также изоморфны. Но
Л/**(С*)==Л7(б?*), Следовательно, матроид M(G*) цик-
лов графа G* изоморфен матроиду M*(G) разрезов гра-
Рис. 40.5
фа G, т. е. на основании утверждения 40.6 граф G явля-
ется абстрактно двойственным к G*. <1
Таким образом, учитывая теорему 40.7, графы С и G*
можно называть двойственными.
На вопрос о том, каждый ли подграф графа, имеюще-
го двойственный граф, обладает двойственным графом,
отвечает
Теорема 40.8. Пусть G и G* — двойственные графы,
е = EG, е* =	— соответствующее ребро гра-
фа G*. Если Н—граф, полученный из графа G удале-
нием ребра е, а Р — граф, полученный стягиванием реб-
ра е* в G*, то Н и Р — двойственные графы, причем би-
екция между множествами ЕН и ЕР остается такой же,
как и между EG и EG*.
> Любой простой цикл С графа Н == G — е является
простым циклом и в графе G. Поэтому соответствующее
множество ребер С* — разрез в G*, разделяющий мно-
жество вершин VG* на два множества V\ и И2. По-
скольку е* Ф С*, то вершины иг и и2 находятся одновре-
менно либо в Vr, либо в У2. Поэтому С* — разрез и
в Р. Итак, каждому простому циклу графа И соответству-
ет разрез графа Р.
Пусть теперь С* — разрез в Р. Так как е*^С*, то
С* —разрез и в G*. Поэтому С — простой цикл графа G.
Поскольку е Ф С, то С — простой цикл и в II. Следова-
тельно, всякому разрезу в Р соответствует простой цикл
в Н. <
Принимая во внимание, что всякий подграф Н графа
G можно получить из G удалением ребер, не принадле-
жащих подграфу Я, из теоремы 40.8 выводим
173
Следствие 40.9. Если граф имеет абстрактно двой-
ственный граф, то всякий его подграф также имеет аб-
страктно двойственный граф.
Поскольку на основании теоремы 40.7 двум ребрам
графа G, инцидентным вершине степени 2 (т. е. разрезу,
отделяющему эту вершину), соответствуют два кратных
ребра (2-цикл) графа G*, то получаем еще одно следст-
вие теоремы 40.8.
Следствие 40.10. Если граф G имеет абстрактно
двойственный граф, то любой граф, гомеоморфный графу
G, также имеет абстрактно двойственный.
Теорема 40.11. Всякий планарный граф имеет
абстрактно двойственный к себе граф,
> Для доказательства достаточно рассмотреть любую
плоскую укладку G исходного планарного графа и граф
G*, геометрически двойственный к G. На основании ут-
верждения 40.5 граф G* — абстрактно двойственный
к G. <
Оказывается, не всякий граф имеет абстрактно двой-
ственный граф.
Утверждение 40.12. Граф /£з(з не имеет абстракт-
но двойственного графа,
> Доказательство проведем от противного. Допустим,
что граф Л^з.з имеет двойственный граф G, Поскольку
Кз.з имеет лишь 4-циклы и 6-циклы, то граф G не имеет
разрезов с менее чем четырьмя ребрами. Поэтому deg v >
>4 для всякой вершины VG. А из того, что граф Кз,з
не имеет разрезов, состоящих из двух ребер, следует, что
в графе G нет 2-циклов, т. е. он не содержит кратных ре-
бер. Следовательно, |G| ^5. Суммируя все полученное и
принимая во внимание лемму о рукопожатиях, выводим,
что |Z?G|	10. Но \EG\ = |2?Лдз1 =9. Полученное проти-
воречие доказывает утверждение 40.12. <
Утверждение 40.13. Граф не имеет абстрактно
двойственного графа,
> Допустим, что граф К$ имеет двойственный граф
G. Так как граф К$ не имеет циклов длины один или два,
то степень каждой вершины графа G не менее 3. В то
же время из того, что граф К$ имеет лишь разрезы, со-
стоящие из 4 или 6 ребер, следует, что все простые цик-
лы графа G имеют четную длину, т. е. G — двудольный
граф. Если бы было IGI то получилось бы \EG\ <9.
но |Z?G| = \ЕК$\ == 10. Итак, |С|^7. Поэтому граф G
должен иметь по крайней мере 1/2 X 7 X 3 > 10 ребер.
Однако это противоречит условию \EG 1 = 10. <1
174
Теперь мы можем доказать еще один критерий пла-
нарности графов.
Теорема 40.14 (X. Уитни, 1932 г.). Граф планарен
тогда и только тогда, когда он имеет абстрактно двой-
ственный граф.
> Необходимость установлена теоремой 40.11.
Достаточность докажем, показав, что неплапарный
граф G не имеет абстрактно двойственного. Согласно тео-
реме Понтрягина — Куратовского граф G содержит под-
граф Я, гомеоморфный Кз.з или К$. Если бы граф G имел
абстрактно двойственный граф, то по следствию 40.9 и
подграф Я имел бы абстрактно двойственный граф.
Но согласно следствию 40.10 это означало бы, что
граф Яз.з или Я5 должен был иметь абстрактно двойствен-
ный. Однако это противоречит утверждениям 40.12 и
40.13. Поэтому граф G не имеет абстрактно двойственно-
го графа. <
Из теорем 40.14 и 40.7 и утверждения 40.6 получаем
Следствие 40.15. Следующие утверждения эквива-
лентны.
1)	граф G планарен*,
2)	матроид циклов M(G) кографичен;
3)	матроид разрезов M*(G) графичен.
§ 41. Алгоритм укладки графа на плоскости
Рассмотренные в предыдущих параграфах критерии
планарности таковы, что если даже удалось установить
планарность графа, то нет информации о том, как стро-
ить его укладку на плоскости. В то же время при реше-
нии практических задач, о которых говорилось в начале
этой главы, недостаточно знать, что граф планарен, а не-
обходимо, как правило, построить его плоское изображе-
ние. Все это вызвало появление алгоритмов, которые не
только проверяют граф на планарность, но и одновремен-
но строят его плоскую укладку, если это возможно. Один
из таких алгоритмов (алгоритм 7) рассмотрим в этом па-
раграфе.
Алгоритм у укладки графа G представляет собой про-
цесс последовательного присоединения к некоторому уло-
женному подграфу С^графа G повой цепи, оба конца ко-
торой принадлежат G. Тем самым эта цепь разбивает
одну из граней графа G на~две. При этом в качестве на-
чального плоского графа G выбирается любой простой
175
цикл графа G. Процесс продолжается до тех пор, пока
не будет построен плоский граф, изоморфный графу G,
или присоединение некоторой цепи окажется невозмож-
ным. В последнем случае граф G не является планарным.
Поскольку связный граф планарен тогда и только
тогда, когда планарны все его блоки (теорема 37.8),
а граф К2 планарен, то будем предполагать не теряя
общности, что укладываемый граф 2-связеп.
Введем ряд определений. Пусть построена некоторая
укладка подграфа G графа G. Сегментом S относительно
G (иногда просто сегментом) будем называть подграф
графа G одного из следующих двух видов:
1) ребро e = uv^EG такое, что e&EG, u,v^VG;
2) связную компоненту графа G — G, дополненную
всеми ребрами графа G, инцидентными вершинам взя-
той компоненты, и концами этих ребер.
Очевидно, что в случае, когда граф G планарный, вся-
кий сегмент, как подграф графа G, планарен, а в случае,
когда G не является планарным, сегмент может быть как
планарным, так и не планарным.
Вершину v сегмента S относительно G будем назы-
вать контактной, если v е VG. Так как в графе G пет то-
чек сочленения, то легко доказать, что в случае, когда
граф G является 2-связным, каждый сегмент содержит пе
менее двух контактных вершин.
Па рис. 41.1 изображены граф G, его уложенный под-
граф G и все сегменты относительно G. Контактные вер-
шины сегментов обведены кружками.
Поскольку граф G плоский, то он разбивает плоскость
на грани. Допустимой гранью для сегмента S относитель-
но G называется грань Г графа G, содержащая все кон-
тактные вершины сегмента S. Через Г (S) будем обозна-
чать множество допустимых граней для S. Может ока-
заться, что Г (S) = 0.
Простую цепь L сегмента S, соединяющую две раз-
личные контактные вершины и не содержащую других
контактных вершин, назовем a-цепью. Очевидно, что вся-
кая a-цепь, принадлежащая сегменту, может быть уло-
жена в любую грань, допустимую для этого сегмента.
Два сегмента 51 и S2 относительно G назовем кон-
фликтующими, если 1) 0 == Г (51) А Г (£2)^ 0, 2) сущест-
вуют две a-цепи L\^S\,	которые без пересечений
нельзя уложить одновременно ни в какую грань Г 0.
В противном случае будем говорить, что сегменты не
конфликтуют,
176
Для графа, изображенного на рис. 41.1, конфликтую-
щими являются, например, сегменты 51 и S2, S3 и S4,
$2 И $6.
Вернемся к обсуждению алгоритма у.
Итак, на первом шаге этого алгоритма уложим про-
извольный простой цикл графа G.
Пусть, далее, G — построенная па предыдущем шаге
укладка некоторого подграфа графа G. Для каждого
5,	S2
Рис. 41.1
сегмента относительно G находим множество допустимых
граней. Теперь могут представиться только следующие
три случая.
1.	Существует сегмент, для которого нет допустимой
грани. Как мы покажем в дальнейшем, граф G в этом
случае не планарен.
2.	Для некоторого сегмента S существует единствен-
ная допустимая грань Г. Тогда очередной шаг состоит в
расположении любой a-цепи сегмента S в грани Г. При
этом, как уже отмечалось, a-цепь разбивает грань Г на
две грани.
3.	Г (5) >2 для всякого сегмента S. Тогда появляется
несколько вариантов продолжения построения укладки
графа, поскольку любой сегмент можно размещать в лю-
бую допустимую для этого сегмента грань. Поэтому воз-
никают опасения, что неудачный выбор сегмента и гра-
21 в. А. Емеличев и др,
177
ни может помешать процессу построения укладки на
следующих шагах и плоская укладка планарного графа
не будет построена. Это могло бы привести нас к невер-
ному заключению о том, что планарный граф непланарен.
В дальнейшем мы покажем, что в этом случае для про-
должения алгоритма у можно выбирать a-цепь в любом
сегменте и помещать ее в любую допустимую грань.
Теперь формально опишем алгоритм у, а затем зай-
мемся его обоснованием.
Алгоритм у.
0. Выберем некоторый простой цикл С графа G и
уложим его на плоскости; положим G=C.
1.	Найдем грани графа G и сегменты относительно G.
Если множество сегментов пусто, то перейдем к п. 7.
2.	Для каждого сегмента S определим множество
Г (S).
3.	Если существует сегмент S, для которого Г(5) =
= 0, то граф G пепланарен. Конец. Иначе перейдем к
п. 4.
4.	Если существует сегмент S, для которого имеется
единственная допустимая грань Г, то перейдем к п. 6.
Ипаче — к п. 5.
5.	Для некоторого сегмента S (Г(5)>1) выбираем
произвольную допустимую грань Г.
6.	Поместим произвольную a-цепь L^S в грань Г;
заменим G на G U L и перейдем к п. 1.
7.	Построена укладка G графа G на плоскости. Конец.
Шагом алгоритма у будем считать присоединение к
G a-цепи L.
Дальнейшее изложение посвящено обоснованию алго-
ритма у. Сначала докажем, что для планарного графа ал-
горитм у строит плоскую укладку графа. Для этого нам
понадобятся две леммы.
Лемма 41.1. Если конфликтующие сегменты S\ и
S2 относительно G таковы, что |T(Si)l >2, IГ(S2) I 2,
то r(Si)=r(S2), |Г(51)|=2.
> Сначала докажем, что Г(51) = Г(/>2). Допустим про-
тивное. Тогда по условию леммы существуют три различ-
ных грани: Г1^Г(51), Г2еГ(52), Г3 0 = Г (Si) П
АГ(52)^^. Поэтому всякая a-цепь L\^S\ укладывает-
ся в Г1, а всякая a-цепь Lz^Sz укладывается в Г2. Но
это значит, что всякая пара a-цепей	Lz — Sz од-
новременно укладывается вне Гз. Тогда опи укладывают-
ся и внутри грани Гз. Но это противоречит тому, что Si
и S2 — конфликтующие сегменты.
178
Итак, Г№) = Г(52) = 0.
От противного легко показать, что 101=2. Пусть
|0| > 3. Тогда существует по крайней мере три различных
грани Г1, Г2, Гз^О. Поэтому, повторяя предыдущие рас-
суждения, получаем противоречие. <
Построим вспомогательный граф S(G) по следующему
правилу: каждому сегменту относительно G поставим в
соответствие вершину графа S(G), причем будем считать,
что две вершины смежны тогда и
только тогда, когда соответствующие
им сегменты конфликтующие.
На рис. 41.2 изображен вспомо-
гательный граф S(G), соответствую-
щий сегментам ранее рассмотренного 2	3 J
графа G (рис. 41.1) относительно G. Рис. 41.2
При этом вершины графа S(G) обо-
значены так же, как и соответствующие им сегменты.
Частичной укладкой планарного графа G называется
такой граф, который можно получить из какой-либо
укладки графа G на плоскости путем удаления неко-
торых ребер и вершин. Тем самым во всякую частичную
укладку планарного графа G можно уложить остав-
шуюся часть, т. е. недостающие вершины и ребра
графа G.
Лемма 41.2. Если результатом некоторого шага ал-
горитма у является частичная укладка G планарного гра-
фа G такая, что IГ (S) I >2 для всякого сегмента S отно-
сительно G, то S(G) — двудольный граф,
> Доказательство проведем от противного. Пусть
граф S(G) не двудольный. Тогда на основании теоремы
Кёнига в S(G) есть r-цикл нечетной длины. Этому циклу
соответствует последовательность Р сегментов Si, S2, ...
..., Sr, Si относительно ffi, в которой каждые соседние
сегменты конфликтующие. Поэтому на основании леммы
41.1 Г(5г)={Г1, Г2} (г = 1, г). Поскольку S’ —частичная
укладка графа G, то все сегменты Si, S2, ..., Sr могут
быть уложены, а так как соседние сегменты последова-
тельности Р конфликтуют, то опи должны быть уложены
в различные грани (Г1 и Г2). Но это невозможно в силу
нечетности числа сегментов г. <1
Теорема 41.3. Если G — планарный граф, то ре-
зультатом каждого шага алгоритма у является частичная
укладка G графа G.
> Доказательство проведем индукцией по числу
шагов.
12*	179
Полученный па начальном этапе работы алгоритма у
граф G является простым циклом, который присутствует
в любой укладке графа G. Следовательно, G — частичная
укладка.
Пусть граф G, построенный на предыдущем шаге ра-
боты алгоритма у, является частичной укладкой. Пока-
жем, что граф G U L, полученный па очередном шаге при-
соединением к G a-цепи Л, также является частичной
укладкой.
Прежде всего заметим, что пе существует сегмента 5
относительно G, для которого Г(5)=0. Действительно,
если бы такой сегмент S существовал, то существовала
бы и a-цепь этого сегмента, обе контактные вершины ко-
торой не принадлежат одной грани. Поэтому укладка та-
кой цепи (и тем более сегмента 5) невозможна.
Итак, могут представиться лишь следующие два
случая.
Случай 1. Для некоторого сегмента S относительно
G существует единственная допустимая грань Г. Пусть
G' — укладка графа G, из которой путем удаления вер-
шин и ребер можно получить граф G. В этой укладке
сегмент S находится в грани Г, так как только этой гра-
ни принадлежат все его контактные вершины. Это зна-
чит, что, помещая любую a-цепь L е S в грань Г, снова
получим частичную укладку графа G.
Случай 2. IГ (5)1 ^2 для всякого сегмента S отно-
сительно G. Рассмотрим связную компоненту Н двудоль-
ного (по лемме 41.2) графа 5(ff), содержащую пе менее
двух вершин. Эта компонента также является двудоль-
ным графом, и в силу леммы 41.1 Г(5) = {Г1, Гг) для
всякого S Н.
Пусть G' — укладка графа G, из которой путем уда-
ления вершин и ребер можно получить граф G. Так как
все контактные вершины каждого сегмента принадлежат
только граням Г1 и Г2, то каждый из сегментов относи-
тельно G находится в одной из этих граней. При этом
сегменты, соответствующие вершинам каждой доли гра-
фа S(G), пе конфликтуют. Поэтому в графе G' сегмен-
ты, соответствующие одной доле, находятся в грани Гц
а сегменты, соответствующие вершинам другой доли,—
в грани Г2. Если теперь сегменты, находящиеся в Гь по-
менять местами с сегментами, находящимися в Г2, то по-
лучим граф G", который также является укладкой гра-
фа G. Это значит, что всякая a-цепь любого сегмента
S <= Н в любой плоской укладке графа G может быть рас-
180
положена и в Fi, и в Г2. Иными словами, помещая сс-цепь
L S в любую грань, допустимую для сегмента S, полу-
чаем частичную укладку графа G.
Если для некоторого сегмента S пет конфликтующих
сегментов, т. е. вершина S^S(G) является изолирован-
ной, то наше утверждение очевидно. <1
Замечание. Если граф G не является циклом, то
в процессе работы алгоритма 7 встретится случай, когда
IГ (5)1 ^2, и поэтому существуют различные укладки
графа G. На рис. 41.3 показаны две возможные укладки
графа G, изображенного на рис. 41.1.
Следствие 41.4. Если граф G планарный, то алго-
ритм ц строит его плоскую укладку.
Следствие 41.5. Если в процессе работы алгоритма
ц встретится сегмент S, для которого нет допустимой гра-
ни, то граф G непланарный.
Проиллюстрируем работу алгоритма ц на примерах.
Пример 1. Пусть граф G изображен па рис. 41.4.
Уложим сначала цикл С==(1, 2, 3, 4, 1), который разби-
вает плоскость на две грани Г1 и Г2. На рис. 41.5 изобра-
жены граф G = C и сегменты Si, S2, S3 относительно G
с контактным вершинами, обведенными кружками. Так
как Г = {Г1, Г2} (i = l, 2, 3), то любую сс-цепь про-
извольного сегмента можно укладывать в любую допусти-
мую для пего грань. Поместим, например, a-цепь L =
= (2, 5, 4) в Гь Возникает новый граф G и его сегмен-
ты (рис. 41.6). При этом Г(51)={Г3}, Г(52)-{ГЬ Г2},
F(S3) = {Г1, Г2, Гз). Укладываем цепь Л = (1, 5) в Г3
(рис. 41.7). Тогда Г(51) = {Г1, Г2}, Г(52)={ГЬ Г2}. Да-
лее, уложим a-цепь L=(2, 6, 4) сегмента Si в Г1
(рис. 41.8). В результате имеем Г (Si) = {Г5}, Г(52) =
= {Г1, Г2, Г3}. Наконец, уложив ребро (6, 3) в Гь, а ребро
181
2
®
®
4
2
®
4
^2
182
(2, 4) —например, в Г1, получаем укладку графа G па
плоскости (рис. 41.9).
Пример 2. Пусть С = Кзз (рис. 41.10).
Цикл G и сегменты относительно этого цикла изобра-
жены на рис. 41.11. При этом Г(5г) = {Гц Г2} (i = 1, 2, 3),
Рис. 41.12
Помещаем Si в грань Г2. Тогда S2 необходимо поместить
в грань Г1 (рис. 41.12). Поскольку Г (51)=^, то Хз,з —
неплапарпый граф.
§ 42. Характеристики непланарных графов
Приводимые ниже характеристики графов представля-
ют ту или иную меру неплапарпости.
Род графа. Мы уже знаем, что планарные графы и
только они укладываются как па плоскости, так и па сфе-
183
ре. Возникает вопрос: можно ли уложить пеплапарыый
граф на какой-либо другой поверхности?
Утвердительный ответ на этот вопрос получаем сразу
же, если нарисуем граф на плоскости и для каждого пе-
ресечения двух ребер, добавив к плоскости ручку, прове-
дем одно ребро по ручке, а другое — под ней. На рис. 42.1
изображена укладка графа К$ па плоскости, к которой
добавлена одна ручка, т. е. построен «мост». Тем самым
очевидно, что граф К$ (и А*з,з) можно уложить па торе,
т. е. на сфере с одной ручкой (рис. 42.2).
Графы, которые нельзя уложить на плоскости, по
можно уложить на торе, называются тороидальными.
На рис. 42.3 изображена укладка графа /<з,з на торе.
Укладку тороидального графа на торе удобно изобра-
зить с помощью прямоугольника, в котором отождествле-
ны обе пары противоположных сторон. На рис. 42.4—42.7
изображены такие укладки тороидальных графов Къ, Кз,з,
Ki, Кщ соответственно.
Определим теперь род y(G) графа G как наименьшее
число ручек, которые необходимо добавить к сфере, что-
бы можно было граф G уложить на полученной таким
образом поверхности.
Тем самым, поскольку графы Кз,з, К7, К44 пепла-
парны, то у(Т^5) = у(Хз,з) = 7(^7)== 7 (^4,4)='1. Очевидно,
что 1) y(G) = O тогда и только тогда, когда граф G пла-
нарный; 2) 7((?)=1 тогда и только тогда, когда граф G
тороидальный.
Приведем без доказательств некоторые известные ре-
зультаты о роде графа (см., например, [7], [28]):
y(G)>] (тп — 3n)/6 + 1 [, п>3,
если G — связный (п, тп)-граф (здесь и далее ]#[ — наи-
меньшее целое число t^x);
если 5i, В2, ..., Bk — система всех блоков графа G, то
k
Y(^)= 2 ?(Si);
2-1
Т(Я„) = ](п-3)(тг-4)/12[,	п>3;
T(^p,g) = ](р — 2)(7— 2)/4[,
7 (<?„)=! + (zz-4)2^3,
где Qn — тг-мерпый куб.
Число скрещиваний. Числом скрещиваний cr(G)
графа G называется наименьшее число пересечений,
184
Рис. 42.6
185
получаемых при изображении графа на плоскости (поня-
тие пересечения относится к пересечению ровно двух
ребер). Очевидно, что сг(б?) = О тогда и только тогда, ког-
да G — планарный граф.
Приведем здесь следующие известные оценки для чис-
ла скрещиваний:
причем при р 6 и любом q
£--1
2
Толщина графа. При изготовлении печатных схем
соединительные провода наносятся на одну сторону не-
проводящей пластинки. Поскольку печатные проводники
не изолированы, то они не должны пересекаться. Поэто-
му важно знать, является ли планарным граф, в котором
роль вершин играют приборы, а ребрами являются сое-
динения. Если такой граф непланарный, то возникает
вопрос: какое наименьшее число пластинок необходимо
для комплектования всей схемы (сети)? Таким образом,
мы приходим к понятию толщины графа. Толщиной t(G)
графа G называется наименьшее число его планарных
подграфов, объединение которых дает граф G. Очевидно,
что толщина планарного графа равна 1. Для толщины
связного (ft, m)-графа справедливы оценки
4 z^j3n —6[	V/ L Зп —6 J
Действительно, первое неравенство сразу вытекает из
следствия 37.3, а второе следует из первого, если учесть
легко доказываемое равенство
]а!Ъ [= [(ft + Ъ - 1)/Ь],	(1)
где ft, Ъ -— положительные целые числа.
Непосредственным следствием первого неравенства
является следующая оценка толщины полного графа
(ввиду того, что тп = К — целое число):
t{Kn)
n(n — 1)/2 4-3 (n — 2) — 1
3(га— 2)
« + 7
6 .*
186
Оказывается, что
t(Kn) =
'п + 7Л
6
если (mod 6) и п¥=9.
Известны также следующие формулы для толщины
(доказательство можно найти в [28]):
4Qn)-
п + 1
4
где Qn — n-мерный куб;
(^р,д)
PQ
2(p + q~2) I/
за исключением, возможно, тех случаев, когда p<q,
pq — нечетное и существует такое целое число к, что
q — [2к(р— 2)/(р — 2к)].
Из последней формулы, используя равенство (1), по-
лучаем формулу
№р,р) ~
~р + 5
4
Искаженность графа. Искаженностъю sk(G) графа G
называется наименьшее число ребер, удаление которых
приводит к планарному графу. Для искаженное™ полно-
го графа справедлива формула
sk (Кп) =	— Зп + 6, п > 3,
которая непосредственно вытекает из следствия 38.3.
УПРАЖНЕНИЯ
1.	При каких значениях п графы Gn (определение см. в упр. 14
гл. I) планарны?
2.	Докажите, что любой граф можно уложить в трехмерном
пространстве так, что все его ребра будут изображены прямоли-
нейными отрезками.
3.	Всегда ли планарен реберный граф L(G} планарного гра-
фа G?
4.	Нарисуйте граф, изоморфный графу, изображенному на
рис. 37.1, так, чтобы внешней стала грань а) 2; б) 3.
5.	Скольким граням может принадлежать вершина степени
d 1 плоского графа?
6.	Покажите, что формула Эйлера следующим образом обоб-
щается на случай несвязного плоского графа: п— m + f ~ k + i,
где к — число связных компонент графа, а остальные символы
имеют прежний смысл.
187
7.	Нарисуйте плоский граф (п >5), среди вершин которого
ровно 4 вершины со степенями, пе превышающими 5.
8.	Существуют ли 6-связные планарные графы?
9.	Докажите, что для связного плоского (п, тп)-графа с п 3,
грани которого но являются треугольниками, верно неравенство
т 2/i — 4.
10.	Покажите, что всякая плоская триангуляция с п 3 вер-
шинами имеет 2п — 4 грани.
11.	Все вершины плоской триангуляции раскрашены произ-
вольным образом в три цвета. Грапь будем называть правильной,
Рис. VI.1
если ее вершины окрашены в три различных цвета. Покажите, что
число правильных граней четно.
12.	Пусть в плоской триангуляции G существуют такие три
вершины «, Ъ, с, что граф G — {а, Ь, с} не является связным. До-
кажите, что тогда граф G содержит 3-цикл (а, &, с), не являющий-
ся границей грани.
13.	Для всякого связпого планарного (п, т)-графа с п 3,
обхват которого равен h 3, верно неравенство m(h — 2)^
Д(п — 2). Используя это соотношение, докажите, что граф Пе-
терсена неплапарен.
14.	Убедитесь, что реберные графы графов К5 и 2£3,з не-
планарны.
15.	Какие из графов, изображенных па рис. VI. 1, являются
планарными?
16.	При каких п графы порядка 2п, изображенные па рис. VI.2,
являются планарными?
Рис. VI.2
17.	Изобразите стереографические проекции пяти Платоно-
вых тел.
18.	Докажите, что по существует плоского графа с пятью гра-
нями, обладающего тем свойством, что любые две его грани имеют
общее ребро.
188
49. Пусть G — плоский двусвязный граф. Докажите, что мно-
жество всех простых циклов, каждый из которых ограничивает
внутреннюю грань графа G (см. теорему 37.7), образует базис цик-
лов графа G.
20. Планарный граф называется внешнепланарным, если его
можно уложить па плоскости так, что все его вершины будут ле-
жать на границе одной грани (удобно в качестве такой грани брать
внешнюю грань). Докажите, что следующие утверждения экви-
валентны:
1)	граф G впсшпеплапарсп;
2)	граф G', полученный из G добавлением повой вершины и
соединением ее новыми ребрами со всеми вершинами графа G,
планарен;
3)	каждый блок графа G внешнепланарен.
21.	Внешпепланарный граф называется максимальным внешне-
планарным, если он перестает быть внешнепланарпым при добав-
лении любого ребра. Пусть в таком графе число вершин п 3 и
а	б
Рис. VI.3
все они лежат па границе внешней грани. Покажите, что тогда
граф имеет п — 2 внутренние грани.
22.	Докажите, что любой максимальный внешпепланарный
граф G с п 3 вершинами имеет а) 2п — 3 ребра; б) по крайней
мере две вершины степени 2; в) x(G) = 2.
23.	Какое минимальное число ребер (вершин) необходимо уда-
лить из куба Q$, чтобы полученный граф стал планарным?
24.	Докажите изоморфизм графов, изображенных па рис. VI.3.
Изоморфны ли графы, геометрически двойственные к ним?
25.	Пусть плоский граф G не связен. Покажите, что тогда его
«второй геометрически двойственный» граф G** не изоморфен
графу G.
26.	Покажите, что граф, геометрически двойственный к коле-
су Wn, является колесом.
27.	Пусть планарный (п, иг)-граф G таков, что двойственный
к нему изоморфен графу G. Покажите, что тогда т = 2п — 2.
28.	Покажите, что планарный граф (без петель) является
2-связным тогда и только тогда, когда двойственный к нему
2-связен.
29.	Найдите графы, геометрически двойственные к стереогра-
фическим проекциям платоновых тел.
30.	Воспользовавшись алгоритмом у укладки графа па плос-
кости, покажите, что граф не планарный.
31.	С помощью алгоритма у постройте плоские укладки или
установите непланарность графов, изображенных на рис. VI.4.
32.	Чему равна искаженность графов К$, К3,3 и графа Пе-
терсена?
33.	Чему равно число скрещиваний графов К3, К3>3 и графа
Петерсена?
189
34.	Докажите или опровергните утверждение: ст (G) = 1 для
непланарного графа G тогда и только тогда, когда существует та-
кое ребро е, что граф G — е планарен.
1 Р7 Г	1 n + 1 ’
35.	Покажите, что I (Ap>q)> J 2 (р -|- — 2) | ’ Z (<?п) > ]	.
36.	Найдите толщину графов К5, К3>3 и графа Петерсена.
37.	Покажите, что всякий непланарпый граф гомеоморфен не-
которому графу толщины 2.
38.	Уложите куб Q4 на торе.
39.	Найдите род графа Петерсена.
40.	Приведите пример графа рода 2.
Рис. VI.4
41.	Покажите, что род графа пе превосходит числа скрещива-
ний, т. е. 7(G) ^cr(G). Приведите примеры графов G, для кото-
рых 1) y(G) < cr(G), 2) 7(G) = cr(G).
42.	Покажите, что не существует полного графа рода 7.
43.	Можно ли уложить графы К3 и К3>3 на листе Мёбиуса?
Глава VII
Обходы
Основные положения этой главы связаны с существо-
ванием в графе эйлеровых или гамильтоновых цепей и
циклов. Подобные вопросы возникли в значительной ме-
ре под влиянием головоломок и игр. Тем не менее зада-
чи, касающиеся эйлеровых и, в особенности, гамильтоно-
вых цепей и циклов, чрезвычайно часто встречаются на
практике. Это случается, например, в ситуациях, когда
качество выполнения некоторого комплекса операций
(работ, мероприятий) существенно зависит от порядка,
в котором они выполняются.
§ 43. Эйлеровы графы
Все сказанное в этом параграфе о графах в равной
степени относится к мультиграфам.
Начало теории графов как раздела математики связы-
вают с так называемой задачей о кёнигсбергских мостах.
Эта знаменитая в свое время задача состоит в следующем.
Семь мостов города Кёнигсберга (ныне Калининград)
были расположены на реке Прегель так, как изображено
Рис. 43.2
Рис. 43.1
па рис. 43.1. Спрашивается, можно ли, выйдя из дома,
вернуться обратно, пройдя в точности один раз по каж-
дому мосту?
Сопоставим плану города граф G, вершины которого
соответствуют четырем разделяемым рекой участкам су-
ши Л, В, С и D, а ребра — мостам. Этот граф (точнее,
мультиграф) изображен на рис. 43.2. Таким образом, за-
191
дачу о кёнигсбергских мостах можно па языке теории
графов сформулировать так: есть ли в мультиграфе G
цикл, содержащий все ребра этого мультиграфа?
Эйлер доказал неразрешимость задачи о кёнигсберг-
ских мостах. В своей работе, опубликованной в 1736 году,
он сформулировал и решил следующую общую проблему
теории графов: при каких условиях связный граф содер-
жит цикл, проходящий через каждое его ребро?
Цикл в графе называется эйлеровым, если он содер-
жит все ребра графа. Связный граф, в котором есть эйле-
ров цикл, называется эйлеровым графом. Такой граф мож-
но парисовать, пе отрывая карандаша от бумаги и пе
повторяя линий.
Например, граф, изображенный на рис. 43.3, является
эйлеровым, поскольку он содержит эйлеров цикл (1, 2, 3,
4, 5, 6, 4, 2, 6, 1). В этом графе есть и другие эйлеровы
циклы. Ясно, что любые два таких цикла отличаются
друг от друга только порядком обхода ребер.
Помимо задачи о кёнигсбергских мостах известен ряд
других старинных занимательных задач (головоломок),
решение которых сводится к выяснению вопроса «являет-
ся ли граф эйлеровым?». В одной из них требуется обри-
совать фигуру, именуемую саблями (знаком) Магомета
(рис. 43.4), не отрывая карандаша от бумаги и не повто-
ряя линий.
Теорема 43.1 (Л. Эйлер, 1736 г.). Связный граф
является эйлеровым тогда и только тогда, когда степени
всех его вершин четны.
> Необходимость. Пусть G — эйлеров граф. Эйле-
ров цикл этого графа, проходя через каждую его верши-
ну, входит в нее по одному ребру, а выходит по другому.
Это означает, что каждая вершина инцидентна четному
числу ребер эйлерова цикла, а поскольку такой цикл со-
держит все ребра графа G, то отсюда следует четность
степеней всех его вершин.
192
Достаточность. Предположим теперь, что степени
вершин графа G четны. Начнем цепь Р\ из произвольной
вершины щ и будем продолжать ее, насколько возможно,
выбирая каждый раз новое ребро. Так как степени всех
вершин четны, то попав в очередную отличную от v\
вершину, мы всегда будем иметь в распоряжении еще не
пройденное ребро. Поэтому цепь Р\ можно продолжить
путем добавления этого ребра. Таким образом, построение
цепи Р\ закончится в вершине щ, т. е. Р\ непременно бу-
дет циклом. Если окажется, что Р\ содержит все ребра
графа G, то это будет требуемый эйлеров цикл. В про-
тивном случае, удалив из G все ребра цикла Р\, рассмот-
рим граф Gi, полученный в результате такой операции.
Поскольку Р\ и G имели вершины только четных степе-
ней, то, очевидно, и Gi будет обладать тем же свойством.
Кроме того, в силу связности графа G графы Pi и Gi
должны иметь хотя бы одну общую вершину р2. Теперь,
начиная с вершины р2, построим цикл Р2 в графе G\ по-
добно тому, как строили цикл Р[. Обозначим через Рг и
Рг части цикла Р\ от v\ до р2 и от и2 до v\ соответст-
венно. Получим новый цикл
Р з ~ Р± U Р 2 и Рп
который, начиная с V\, проходит по ребрам цепи до
р2, затем обходит все ребра цикла Р2 и, наконец, возвра-
щается в v\ по ребрам цепи Рг (рис. 43.5).
Если цикл Р3 не эйлеров, то проделав аналогичные по-
строения, получим еще большой цикл и т. д. Этот процесс
закончится построением эйлерова
цикла. '<	( \р
Будем говорить, что набор ребер-	4 J 2
но пепересекающихся цепей (не обя- р'
зательно простых) покрывает граф G,
если каждое ребро графа G входит /	)
в одну из этих цепей. Пусть связный \	1
граф G содержит к вершин нечетной	—— -----
степени. По лемме о рукопожатиях
к четно. Рассмотрим граф G', полу- Рис* 43,5
чепный добавлением к G новой вер-
шины и и ребер, соединяющих v с вершинами графа G
нечетной степени. Поскольку степени всех вершин графа
G' четны, то G' содержит эйлеров цикл. Если теперь
выбросить v из этого цикла, то получится к/2 цепей, со-
держащих все ребра графа G, т. е. покрывающих G,
13 в. А. Емеличев и др.	193
С другой стороны, граф, являющийся объединением г ре-
берно-непересекающихся цепей, имеет самое большее 2г
вершин нечетной степени. Поэтому меньшим числом це-
пей граф G покрыть нельзя. Тем самым доказано
Следствие 43.2. Если связный граф содержит ров-
но к вершин нечетной степени, то минимальное число
покрывающих его реберно-непересекающихся цепей рав-
но к/2.
В частности, когда к = 2, граф имеет цепь, которая
соединяет вершины нечетной степени и содержит все
ребра графа. Цепь, содержащую все ребра графа, назы-
вают эйлеровой.
Из доказательства теоремы 43.1 видно, что эйлеров
граф содержит, как правило, несколько эйлеровых цик-
лов. Зная один такой цикл, получить новый можно сле-
дующим простым приемом.
Пусть С — исходный эйлеров цикл, и вершина v про-
ходится в этом цикле более одного раза. Рассмотрим
часть (подцикл) цикла С, состоящую из ребер и вершин,
проходимых между к-м и Z-м (к < Z) посещениями вер-
шины v. Это будет некоторый цикл Сь Цикл С, как и
всякий эйлеров цикл, задает некоторый порядок обхода
ребер графа и индуцирует порядок прохождения ребер
цикла С\, Если теперь порядок обхода ребер С\ изменить
на обратный, а на остальных ребрах оставить его таким,
каким он был в С, то, очевидно, получим новый эйлеров
цикл С', Например, в графе, изображенном на рис. 43.3,
можно получить новый цикл С' = (1, 2, 6, 5, 4, 3, 2, 4, 6, 1),
полагая С = (1, 2, 3, 4, 5, 6, 2, 4, 6, 1) и Сх = (2, 3, 4, 5, 6, 2).
В этом примере цикл С\ составлен из ребер, проходимых
в С между первым и вторым посещениями вершины 2.
Итак, изменив указанным способом эйлеров цикл, по-
лучаем новый эйлеров цикл. Следующая теорема, приво-
димая здесь без доказательства, утверждает, что после-
довательности таких изменений достаточно для получения
всех эйлеровых циклов из данного.
Теорема 43.3 (А. Коциг, 1980 г.). Если С и С' —
эйлеровы циклы графа G, то в G существует такая по-
следовательность эйлеровых циклов С = С\,	Ch =
= С', что Ci+i получается из Ci путем изменения порядка
обхода ребер некоторого подцикла на обратный.
Естественно возникает вопрос: как найти хотя бы
один эйлеров цикл в эйлеровом графе С, т. е. как зану-
меровать ребра графа числами 1, 2, ..., \EG\ с тем, что-
бы номер, присвоенный ребру, указывал, каким по счету
194
это ребро проходится в эйлеровом цикле? Оказывается,
это можно сделать, если нумеровать ребра, придержива-
ясь следующих двух правил:
1. Начиная с произвольной вершины и, присваиваем
произвольному ребру uv номер 1. Затем вычеркиваем
ребро uv и переходим в вершину v.
2. Пусть w — вершина, в которую мы пришли в ре-
зультате выполнения предыдущего шага, и к — номер,
присвоенный некоторому ребру на этом шаге. Выбираем
любое ребро, инцидентное вершине ш, причем мост вы-
бираем только в том случае, когда нет других возмож-
ностей; присваиваем выбранному ребру номер к + 1 и вы-
черкиваем его.
Этот процесс, называемый алгоритмом Флёри, закан-
чивается, когда все ребра графа вычеркнуты, т. е. зану-
мерованы.
> Дадим теперь обоснование алгоритма. Прежде все-
го заметим, что поскольку степень каждой вершины гра-
фа G четна, то алгоритм может закончить работу только
в той вершине, с которой начал. Поэтому он строит не-
который цикл С, и надо только доказать, что этот цикл
включает все ребра графа G. Предположим, что это не
так, и пусть G' — связная компонента графа G — EC, не
являющаяся изолированной вершиной. Рассмотрим мно-
жество А ребер цикла С, инцидентных вершинам, вошед-
шим в G'. Ясно, что А ¥= 0. Пусть а — ребро из А, полу-
чившее в процессе работы алгоритма наибольший номер,
т. е. вычеркнутое последним среди ребер 4. Тогда, как
легко видеть, ребро а к моменту вычеркивания было мос-
том в графе. Однако это противоречит правилу выбора
очередного ребра. <
Заметим, что эйлеровы графы достаточно редки. Вер-
на следующая
Теорема 43.4 (Р. Рейд, 1962 г.). Почти нет эйле-
ровых графов,
> Пусть ^i(n) —множество всех эйлеровых графов
из (п) (см. § 12), а ^2(п) — множество всех графов из
^(п), степени всех вершин которых четны. Согласно тео-
реме 43.1 имеем
(1)
Очевидно, что все графы из ^2 (я) можно получить, до-
бавляя к некоторому графу из —1) новую вершину
и соединяя ее со всеми вершинами нечетной степени.
13*	195
Так как
I <з (п -1) । =;2V 2 <
то
I^2(п)|<2^ 2^ = 2^^п+1 = о(2^2^) =0(|^(п)|).
Поэтому па основании (1) имеем l^i (п) I = о( l^(n) I),
что и доказывает теорему. <
Замечание. Запись /(тг)= o(g(n)) означает, что
§ 44. Гамильтоновы графы
Граф называется гамильтоновым, если в нем имеется
простой цикл, содержащий каждую вершину этого графа.
Сам этот цикл также называется гамильтоновым. Га-
мильтоновой называют и простую цепь, содержащую каж-
дую вершину графа. Слово «гамильтонов» в этих опреде-
лениях связано с именем известного ирландского мате-
матика У. Гамильтона, которым в 1859 году предложена
следующая игра «Кругосветное путешествие». Каждой из
двадцати вершин додекаэдра приписано название одного
из крупных городов мира. Требуется, переходя от одного
города к другому по ребрам додекаэдра, посетить каждый
город в точности один раз и вернуться в исходный город.
Эта задача, очевидно, сводится к отысканию в графе до-
декаэдра (рис. 44.1) простого цикла, проходящего через
каждую вершину этого графа.
Не все связные графы гамильтоновы хотя бы потому,
что такой граф должен быть двусвязным. Однако пример
графа, представленный на рис. 44.2, показывает, что для
гамильтоновости графа двусвязности недостаточно.
196
Любой граф, содержащий две вершины степени 3, со-
единенные тремя простыми попарно пепересекающпмися
цепями длины не менее двух, называется тэта-графом
(рис. 44.2).
Теорема 44.1. Каждый иегамилътоиов двусвязный
граф содержит тэта-подграф.
> Пусть G — негамильтопов двусвязный граф и С —
простой цикл максимальной длины в этом графе. По ус-
ловию теоремы множество S = VGWC непусто. Как под-
тверждает прямая проверка, среди двусвязных графов
порядка меньше пяти нет
негамильтоновых, поэтому
IGI >5. Из двусвязности
графа G и теоремы 34.1
следует, что \VC\ >4.
Пусть xv — такое реб-
ро графа G, что х <= ИС,
v <= S, а и Ъ — вершины
цикла С, смежные с х
(рис. 44.3). Поскольку
С — максимальный цикл,
то вершина v не смежна
ни с а, ни с Ъ (иначе можно было бы построить боль-
ший цикл). Рассмотрим теперь граф G — x, который, оче-
видно, связен.
В этом графе для каждой вершины у VC имеется
(р, у)-цепь. Выберем из этих цепей кратчайшую (р, у*)-
цепь Р*. Учитывая, что С — максимальный цикл, имеем
у* ¥= a, z/* =И= Ъ. Кроме того, Р* не содержит вершин цикла
С, отличных от г/*, так как иначе можно было бы постро-
ить более короткую цепь. Объединив цикл С и цепь Р*,
получим искомый тэта-подграф. <1
Несмотря на внешнее сходство постановок, задачи
распознавания эйлеровости и гамильтоновости графа
принципиально различны. Используя теорему 43.1, легко
узнать, является ли граф эйлеровым. В случае положи-
тельного ответа алгоритм Флёри позволяет достаточно
быстро построить один из эйлеровых циклов.
Что касается гамильтоновости, то ситуация здесь су-
щественно иная. Ответить на вопрос, является ли данный
граф гамильтоновым, как правило, очень трудно. Очевид-
но, что проблема распознавания гамильтоновости графа
есть частный случай проблемы изоморфного подграфа.
Изучение условий гамильтоновости графов — одно из
весьма популярных направлений теории графов. Основ-
197
ная масса доказанных здесь теорем утверждает, что при
выполнении определенных условий граф содержит га-
мильтонов цикл, причем метод доказательства таких тео-
рем обычно дает и эффективный алгоритм построения са-
мого гамильтонова цикла. В этом параграфе мы рассмот-
рим несколько теорем такого рода (достаточных условий
гамильтоповости).
Интуитивно ясно, что если граф содержит много ре-
бер и эти ребра к тому же достаточно равномерно распре-
делены, то граф «предрасположен» быть гамильтоновым.
В трех приводимых ниже теоремах можно усмотреть
подтверждение этому.
Напомним, что степенной последовательностью графа
называется список степеней его вершин.
Теорема 44.2 (В. Хватал, 1972 г.). Граф со степен-
ной последовательностью	.. .^dn является га-
мильтоновым, если для всякого к, удовлетворяющего не-
равенствам 1 С к < п/2, истинна импликация
(dk к) => (dni~h ^п-к).
> Теорему докажем от противного. Пусть существует
негамильтопов граф, последовательность степеней вершин
которого удовлетворяет условиям теоремы. Соединив две
несмежные вершины такого графа ребром, получим, как
легко видеть, граф со степенной последовательностью,
снова удовлетворяющей условиям теоремы. Так как пол-
ный граф гамильтонов, то отсюда следует, что существу-
ет максимальный негамильтонов граф, степенная после-
довательность которого обладает таким же свойством.
Этот граф будем обозначать через G. Таким образом, до-
бавление любого нового ребра к графу G приводит к по-
явлению в нем гамильтонова цикла. Поэтому любые две
его несмежные вершины соединены гамильтоновой цепью.
Выберем в графе G пару несмежных вершин щ и ип
так, чтобы величина deg V\ + deg vn была максимальной.
Пусть Ki, р2, ..., vn— гамильтонова цепь, соединяющая
эти вершины.
Если в графе G вершины и Vj смежны, то вершина
ип не может быть смежной с Pj-i, поскольку в противном
случае граф G содержал бы гамильтонов цикл
(Р1, Р2,	Pj-1, Vn, Vn-\, Vn-2,	Pj+1, Pl)
(рис. 44.4). Таким образом, вершина vn не смежна по
крайней мере с deg V\ вершинами, и поэтому deg vn С
198
sC n — 1 — deg V\. Отсюда получаем
deg V\ + deg vn n — 1 < n.
Для определенности будем предполагать, что deg Vi
< deg vn. Это вместе с предыдущим неравенством дает
deg v\ < п/2. Поскольку величина deg щ + deg vn макси-
мальна, то степень каждой вершины, не смежной с vn, не
U/ V2 Vj-1 Vj Vj + 1 Vn-2 Vn-1 Vn
Рис. 44.4
превосходит deg Vi. При этом таких вершин, как уже от-
мечалось, не менее чем deg щ. Поэтому выбрав /c = degKi,
получим dh^k<n/2. Следовательно, по условию теоремы
dn-h > п — к. Последнее означает, что имеется по крайней
мере к+1 вершин степени не меньше чем п — к. Такими
вершинами являются, например, вершины со степенями
dn, dn-\, ..., dn_k. Поскольку degui = /c, то Vi не может
быть смежной со всеми этими вершинами, и, значит, най-
дется такая вершина vh не смежная с щ, что degyz>
^п — к. Но тогда
deg v\ + deg vL > к + (n — к) > deg V\ + deg pn,
что противоречит выбору вершин щ и vn. <
С помощью только что доказанной теоремы можно
получить ряд других достаточных условий гамильтоно-
вости. Эти условия проще и, естественно, слабее теоре-
мы 44.2.
Теорема 44.3 (О. Оре, 1960 г.). Если для любой
пары и и v несмежных вершин графа G порядка п>3
выполняется неравенство deg и + deg v > п, то G — га-
мильтонов граф.
> Пусть
VG = {щ, V2, ..vn}, di = deg i =• 1, n,
и d\ d2 < ... < dn — степенная последовательность гра-
фа G. Согласно теореме 44.2 достаточно показать, что ус-
ловие нашей теоремы обеспечивает выполнение нера-
венств
dk>k, к=Л, [п/2-1].
Доказательство проведем от противного. Пусть для не-
которого t^{l, ..., [п/2 — 1]} выполняется неравенство
199
dt С t. Существование индексов i и / таких, что I, j и
ViVj&EG, привело бы к неравенствам
di + dj -С 2dt ^2t < п,
противоречащим условию теоремы. Следовательно, вер-
шины щ, Р2, •.vt попарно смежны. Это вместе с нера-
венствами di С t (Z =• 1, 0 означает, что каждая вершина
vL (1=1, t) смежна пе более чем с одной вершиной vm,
t+l^m^n. Далее, поскольку t<n/2, то п — t > t. По-
этому найдется вершина щ, t + 1 < j тг, не смежная ни
с одной из вершин Vi (Z=l, t). Следовательно, deg щ
п — t — 1. Но тогда для пары несмежных вершин vt и
Vj имеем неравенство deg vt + deg Vj < n, которое противо-
речит условию теоремы. <1
Из этой теоремы непосредственно вытекает следующая
Теорема 44.4 (Г. Дирак, 1952 г.). Если |б?| = п 3
и для любой вершины v графа G выполняется неравен-
ство deg v п]2, то G — гамильтонов граф.
Нетрудно заметить, что во всяком ^-вершинном гра-
фе, удовлетворяющем условиям любой из рассмотренных
выше теорем 44.2—44.4, число ребер не меньше чем
(п — 1)2/4. С другой стороны, п-вершинный планарный
граф, как мы знаем, содержит не более Зп — 6 ребер. По-
этому рассмотренные выше достаточные условия заведомо
неприменимы к планарным графам.
Легко указать 2-связный негамильтонов планарный
граф. Таким графом является, например, тэта-граф. При-
вести пример 3-связного планарного
графа без гамильтонова цикла уже
не столь просто. Такой граф, оказы-
вается, должен содержать не мепее
11 вершин. Этот факт был установ-
лен Д. Барнеттом и Е. Юковичем
(1970 г.). Найденный ими негамиль-
тонов планарный 3-связный граф с
минимальным числом вершин изо-
бражен на рис. 44.5. В том, что этот
граф пе содержит гамильтонова цикла, можно убедиться,
проделав не слишком большой в данном случае перебор
вариантов. Проще, однако, заметить, что он — двудольный
и, следовательно, пе содержит циклов нечетной длины,
в частности, гамильтоновых циклов.
Следующая теорема — один из наиболее сильных ре-
зультатов, касающихся гамильтоновых графов.
200
Теорема 44.5 (У. Татт, 1946 г.). Всякий ^-связный
планарный граф является гамильтоновым.
Весьма сложное доказательство этой теоремы здесь
опускается.
Следствие 44.6 (X. Уитни, 1932 г.). Если в мак-
симальном плоском графе G каждый 3-цикл является
границей некоторой грани, то G^—^гамильтонов граф.
пый плоский граф 3-связеп. Если же такой граф не
> Как известно (следствие 39.2), всякий максималь-
) яв-
ляется 4-связным, то
он необходимо содер-
жит 3-цикл, не являю-
щийся границей ника-
кой грани (см. упр. 12
гл. VI). <
Пример максималь-
ного планарного нега-
мильтонова графа G с
11 вершинами приве-
ден па рис. 44.6. От-
сутствие гамильтонова
цикла следует из того, что шесть вершин графа G, по-
меченных знаком «+», попарно не смежны, а на цикле
длины 11 могут лежать не более пяти таких вершин.
Согласно следствию 44.6, этот граф должен содержать
3-цикл, не являющийся границей никакой грани. Та-
кими 3-циклами являются, например, (а, Ь, с) и
(а, с, d).
Если в zz-вершиппом графе G фиксировать одну вер-
шину и обход всегда начинать с нее, то всякому гамиль-
тонову циклу очевидным образом будет соответствовать
перестановка элементов множества VG. Тем самым най-
ти гамильтонов цикл либо убедиться в отсутствии та-
кого цикла можно путем перебора (п— 1)! перестановок.
Если граф G гамильтонов, то проделать этот перебор в
полном объеме придется только в случае крайнего неве-
зения — когда нужная, т. е. отвечающая гамильтонову
циклу перестановка встретится последней в этом процес-
се. Если же G — негамильтопов граф, то действуя по-
добным образом, придется в любом случае проверить все
(п — 1)! перестановок.
На практике не пользуются столь бесхитростным спо-
собом распознавания гамильтоновости, а применяют раз-
личные алгоритмы частичного перебора. Однако и там
наблюдается такой же эффект — т. е. негамильтоновость
201
установить, как правило, труднее, чем гамильтоновость.
В этой ситуации были бы полезны необходимые условия
гамильтоновости. Такие условия нужны и для построе-
ния примеров негамильтоновых графов с заданными свой-
ствами. К сожалению, для графов общего вида необходи-
мые условия гамильтоновости неизвестны, за исключе-
нием уже упоминавшегося банального факта, что гамиль-
тонов граф должен быть 2-связпым. Иначе обстоит дело
с планарными графами.
Всякую грань плоского графа, граница которой со-
держит ровно к ребер, назовем ^-гранью.
Теорема 44.7 (Э. Я. Гринберг, 1968 г.). Пусть fk —
число к-граней плоского графа G. Если G — гамильто-
нов граф, то для каждого к^ 3 существуют такие целые
неотрицательные числа fb, fk> чпго
fk + fk = fk,
^f'k(k-2) = ^fh(k-2).	(1)
k^3	k^3
> Пусть граф G содержит гамильтонов цикл С. Этот
цикл делит плоскость на две части — ограниченную —
Di и неограниченную — Т?2. Тем самым граф G представ-
ляется в виде объединения двух графов G\ и (?2, содер-
жащихся в 51 и О2 соответственно. Ясно, что D[ — грань
графа G2, jD2 — грань графа Gx и EGx A EG% — ЕС. Пусть
fh—число Л-граней графа G\, отличных от Z)2, a fk —
число A-граней графа С2, отличных от D\. Очевидно, что
fk + fk = fk-
В графе G, изображенном на рис. 44.7, ребра гамиль-
тонова цикла С обведены жирными линиями. Граф Gx
включает, помимо цикла С, ребра ^2^8, iw,
глще, а граф G2 — ребра V7V9 и г?5^ю- В этом примере
/з — 5, /4 = 2, /5 == /б*= 1, /з = 4, А = 2, /з — /5 = /б = 1»
а остальные fk, f'k, fb равны 0.
202
Возвращаясь к доказательству, установим теперь
справедливость равенства (1). С этой целью заметим, что
удвоенное число ребер графа G\ равно 2 Л& + п, а чис-
fe>3
ло всех его граней — 2 h + 1- Поэтому, согласно фор-
Ь^З
муле Эйлера, можем написать
2 fk^ + п — 2(2 fk + Л ” 2 (п — 2).
\ь>з /
После очевидных упрощений имеем
^f'h(k-2) = n-2.
fe>3
Аналогичное соотношение верно и для графа т. е.
2A(t-2) = n-2.
fe>3
Объединив два последних равенства, получим (1). <1
Установление негамильтоновости графа путем пере-
бора всех разбиений чисел fk и последующей проверки
выполнения равенства (1) едва ли проще полного пере-
бора перестановок, о котором упоминалось выше. Польза
теоремы 44.7 в другом — иногда удается, проанализиро-
вав числа Д, сразу сделать вывод об отсутствии подхо-
дящего разбиения, т. е. вывод о негамильтоновости гра-
фа. Рассмотрим в качестве примера граф, изображенный
на рис. 44.8. Для этого графа /4 = 1, /5 = 18, /в = 4, а ос-
тальные fh равны 0. Поэтому соотношение (1) должно
иметь вид
2/4 + 3/5 + 6/8 = 2/4 + 3/5 + 6/8,
откуда следует, что /4 = /4(шос13). Это, однако, невоз-
можно, поскольку /4 + /4 =	— 1. Таким образом,
203
нужного разбиения чисел fk не существует, и значит,
граф негамильтонов.
Рассмотрим еще один класс теорем о гамильтоновых
графах. В этих теоремах утверждается, что если граф G
удовлетворяет определенным условиям, то граф, полу-
чаемый из G с помощью некоторой операции, гамиль-
тонов.
Теорема 44.8 (Ф. Харари, С. Нэш-Вильямс,
1965 г.). Реберный граф L(G) гамильтонов тогда и толь-
ко тогда, когда в графе G имеется цикл, содержащий
хотя бы по одной вершине из каждого его ребра.
Из этой теоремы, приводимой здесь без доказатель-
ства, вытекает, в частности, что если граф G является
эйлеровым или гамильтоновым, то реберный граф L(G)
гамильтонов.
Интуитивно ясно, что если граф G порядка п 3
связен, то при достаточно большом к граф Gh гамиль-
тонов (определение графа Gh см. в § 8). Кроме того,
из гамильтоновости графа Gh очевидно следует гамиль-
тоновость графа Gh+{. В связи с этим представляет
интерес наименьшее к, при котором граф Gk гамиль-
тонов.
Теорема 44.9 (Д. Караганис, 1968 г.). Если граф
G порядка п^ 3 связен, то G3 — гамильтонов граф.
> Теорему достаточно доказать для случая, когда
G — дерево. Будем доказывать следующее, несколько бо-
лее сильное утверждение: для любого фиксированного
ребра аЪ дерева G граф G3 содержит гамильтонов цикл,
проходящий через аЪ. Это утверждение легко проверить
непосредственно для деревьев с числом вершин не более
четырех. Предположим, что существуют деревья с боль-
шим числом вершин, для которых оно не верно. Выбе-
рем из них дерево Go с минимальным числом вершин.
Пусть аЬ — некоторое ребро дерева Go. При удалении
этого ребра Go распадается на два дерева G\ и G2 таких,
что а VGi, Ь VG2. По крайней мере одно из них, на-
пример Gi, содержит не менее трех вершин. Выберем
вершину v KGi так, чтобы ребро va принадлежало EG\.
Поскольку I VGi I < I VGq I, то G[ содержит гамильтонов
цикл Яь проходящий через ребро va.
Теперь рассмотрим дерево G2. Сначала допустим, что
|FG2l^3, и пусть Ьх— ребро графа G2, инцидентное
вершште Ь. Поскольку I VG?J < I FGol, то G% содержит
гамильтонов цикл Я2, проходящий через ребро Ьх. Ис-
пользуя циклы Н[ и Я2, легко построить цикл Н в графе
204
6?о> проходящий через ab. Для этого достаточно удалить
ребра av и Ъх из Н\ й Н2 соответственно и добавить реб-
ра ab и xv, т. е. положить
Н = (Я1 — va) U (IE — Ъх) + xv + ab.
Пусть теперь |УС21 =2, т. е. С?2 состоит из одного
ребра Ьс. Тогда положим
Н = (Я1 — va) + ab + be + vc.
Наконец, если G2 содержит единственную вершину Ъ,
то
Я = (Я1 — va) + ab + bv.
Итак, во всех случаях граф Gq содержит гамильто-
нов цикл Я, проходящий через ребро ab дерева Go, что
противоречит выбору Go. <1
Легко указать граф, квадрат которого негамильтонов.
Таков, например, граф, получающийся из звезды Л^з
подразбиением каждого ребра.
Следующая теорема, приводимая без доказательства,
является наиболее значительным результатом среди всех,
касающихся гамильтоновых циклов в степенях графов.
Теорема 44.10 (Г. Флейшнер, 1971 г.). Если G —
двусвязный граф порядка 3, то G2 — гамильтонов
граф.
Во многих прикладных задачах требуется строить га-
мильтонову цепь, а не цикл. Граф, содержащий такую
цепь, называется трассируемым. Задачи о гамильтоновой
цепи и гамильтоновом цикле эквивалентны в том смыс-
ле, что, умея решать одну из них, мы смогли бы решить
и другую. Эту эквивалентность можно установить с по-
мощью очень простых конструкций. Вместе с исходным
графом G, для которого надо решать обсуждаемые зада-
чи, рассмотрим новые графы G' и G" (ab). Граф G' по-
лучается добавлением к графу G новой доминирующей
вершины, a G" (ab)— добавлением к G двух вершин z
и у и пары ребер za и yb (a, b^VG). Теперь легко
видеть, что граф G является трассируемым тогда и толь-
ко тогда, когда граф G' гамильтонов. С другой стороны,
очевидно, что гамильтоновость графа G эквивалентна су-
ществованию гамильтоновой цепи хотя бы в одном из
графов G" (ab), ab^EG. Приведенные конструкции ил-
люстрируются на рис. 44.9.
Практические применения только что рассмотренного
раздела теории графов связаны прежде всего с широко
205
известной задачей коммивояжера. Она состоит в следую-
щем: коммивояжер должен посетить каждый из задан-
ных п городов по одному разу, выехав из некоторого из
этих городов и вернувшись в него же. Требуется найти
кратчайший маршрут, зная расстояния между каждой
парой городов.
Математическая постановка этой задачи выглядит
так: в полном взвешенном графе требуется найти га-
мильтонов цикл (или цепь) минимального веса. Под ве-
сом цикла понимается сумма весов составляющих его
ребер.
Например, при производстве печатных плат сверлиль-
ный станок с числовым программным управлением дол-
жен сделать большое количество отверстий в заданных
Рис. 44. 9
точках платы, переходя от одной точки к другой. Время
работы такого станка складывается из суммарного вре-
мени сверления, которое не зависит от порядка обхода
точек, и из суммарного времени переходов от одной точ-
ки к другой. Требуется задать такую последовательность
обхода точек, чтобы общее время работы станка было
минимально. Легко видеть, что это — задача коммивоя-
жера.
Представление о непосредственных применениях га-
мильтоновых цепей дает следующая ситуация: имеется
машина (станок, компьютер) и п заданий, каждое из
которых она способна выполнить после соответствующей
настройки. При этом необходимо затратить на перена-
ладку tij единиц времени для того, чтобы после выпол-
нения г-го задания выполнить /-е. В предположении, что
tn = tji, требуется найти последовательность выполнения
заданий, при которой время каждой переналадки пе пре-
восходит величины t. Если построить граф G, у которого
VG = {1, 2, ...» n), EG^lij.
20а
то наша задача сведется к отысканию гамильтоновой це-
пи в этом графе.
В заключение отметим без доказательства теорему,
отражающую типичный случай.
Теорема 44.11 (В. А. Перепелица, 1969 г.). Почти
все графы гамильтоновы.
УПРАЖНЕНИЯ
1.	Докажите, что граф является эйлеровым тогда и только тог-
да, когда каждый его блок эйлеров.
2.	Докажите, что эйлеров граф является объединением ребер-
но-непересекающихся простых циклов.
3.	Пусть G — дерево. Когда граф G2 эйлеров?
4.	Каким должен быть граф G, чтобы реберный граф L(G) был
эйлеровым?
5.	Покажите, что граф Петерсена пегамильтонов.
6.	Найдите связный граф G с минимальным числом вер-
шин, большим 2, для которого граф G2 негамильтонов.
7.	Приведите пример такого реберно-2-связного графа G, что
граф G2 негамильтонов.
8.	Граф называется гамильтоново-связным, если любые две
его вершины соединены гамильтоновой цепью. Является ли трех-
мерный куб Qs гамильтоново-связным?
9.	Негамильтонов граф G называется гипогамилътоновым, если
граф G — х гамильтонов для любой вершины х. Покажите, что граф
Петерсена гипогамильтонов.
10.	Докажите, что всякий гамильтоново-связный граф порядка
п 3 является 3-связным.
11.	Пусть тп и п — натуральные числа, G — граф решетки, т. е.
VG = {(ж, у): х = 1, тп, у — 1, п} и аЪ е EG тогда и только тогда,
когда а — (х, у), b = (z, t) и | х — z | = 1 или | у — 11 = 1. При
каких тп и п граф G гамильтонов?
12.	Пусть в плоском 3-связном графе G существует грань, име-
ющая с любой другой его гранью хотя бы одно общее ребро. По-
кажите, что граф G гамильтонов.
13.	Покажите, что связный граф является гамильтоновым, ес-
ли его группа автоморфизмов содержит полный цикл.
14.	Покажите, что регулярный граф степени 4, окружение
каждой вершины которого связно, является гамильтоновым.
15.	Для каждого п > 4 приведите пример негамильтопова
([п/2] — 1)-связного тг-вершинного графа.
16.	Приведите пример графа, для которого выполняются ус-
ловия теоремы 44.2, но не выполняются условия теоремы 44.3.
17.	Пусть тг-вершинный граф G удовлетворяет условиям тео-
ремы 44.2. Докажите, что тогда |£G| (п —1)2/4.
18.	Найдите гамильтонов цикл в графе, изображенном па
рис. 44.1.
19.	Покажите, что всякий связный граф содержит маршрут, в
котором каждое ребро графа повторяется не более двух раз.
20.	Задача Эйлера о шахматном коне. Найдите такую последо-
вательность ходов шахматного коня, чтобы, начав с произвольной
клетки, пройти через каждую клетку шахматной доски один раз
и вернуться в исходную.
Глава VIII
Степенные
последовательности
Эта глава посвящена теории степенных последова-
тельностей. Напомним, что степенной последователь-
ностью графа называется список степеней его вершин.
Часто по степеням вершин графа можно судить о его
строении. Например, граф, в котором полусумма сте-
пеней вершин (т. е. число ребер) не меньше числа вер-
шин, содержит цикл (следствие 13.6); граф, степень
каждой вершины которого равна двум, есть дизъюнкт-
ное объединение циклов; граф, степень каждой вершины
которого — четное число, пе равное нулю, является объ-
единением циклов (теорема 43.1) и т. д. В предыдущих
главах есть и другие факты, поддающиеся интерпрета-
ции подобного рода.
Естественно возникают следующие вопросы. Как свя-
заны между собой степени вершин графа? Как по списку
степеней вершин судить о свойствах графа? Какова
связь между графами с совпадающими списками сте-
пеней вершин? Можно ли построить граф с заданным
списком степеней вершин и предписанными теоретико-
графовыми свойствами и как это сделать?
Подобные вопросы особенно интенсивно изучаются в
настоящее время. Это не только продиктовано внутрен-
ней логикой развития теории графов, но имеет и прак-
тическое значение. Если в виде графа представляется
коммуникационная схема, узлам которой соответствуют
вершины графа, а ребрам — каналы связей между вер-
шинами, то возникает задача построения графа с задан-
ными степенями вершин и, например, максимально воз-
можной связностью. Такой граф соответствовал бы схеме
с заданными пропускными способностями узлов и мак-
симальной надежностью. Одна из исторически первых
задач теории графов также относится к этому кругу
проблем. Именно, в 1857 году А. Кэли, изучая насыщен-
ные углеводороды, пришел к задаче перечисления де-
ревьев, степени вершин которых равны 1 и 4.
208
§ 45. Графическая последовательность
Последовательность (di, d%, ..., d„) целых неотрица-
тельных чисел ниже называется п-последовательностью и
обозначается одной буквой d. //-последовательность d на-
зывается графической, если существует граф, степенная
последовательность которого совпадает с d. Этот граф
называется реализацией последовательности d.
Очевидно, что порядок членов в графической /г-после-
дователыюсти d несуществен, а каждый ее член di удов-
летворяет неравенствам Q^di^n — 1. Часто удобно эти
последовательности считать невозрастающими. Согласно
лемме о рукопожатиях сумма всех членов графической
последовательности является четным числом.
Назовем //-последовательность d правильной, если вы-
полняются два следующих условия:
1) п — 1 > di > d2 > ... > dn,
п
2) 2 di — четное число.
Без ограничения общности графическую последова-
тельность можно считать правильной.
Иногда последовательность d удобно записывать в ви-
1	/	kg	&Р\
де а = (^г, с2 л • • •> Ср Л где числа сг- попарно различны,
а показатель кг означает количество повторений числа Ci
в последовательности d. Так, (5, 2, 16) = (5, 2, 1, 1, 1,
1, 1, 1).
Рассмотрим последовательность d=(24, I4). Суще-
ствуют ровно пять графов, являющихся реализациями
последовательности d. Они имеют следующие компонен-
ты: 1) С4, К2 и К2, 2) Кз, Р3 и К%, 3) Рв и К2, 4) Р$ и
Рз, 5) Р4 и Р4.
В общем случае графическая последовательность име-
ет много реализаций и их число определить сложно.
В установлении связи между этими реализациями важ-
ную роль играет вводимое ниже понятие переключения.
Пусть G — граф, а, Ъ, с, d — четыре его попарно различ-
ные вершины, причем ab^EG, cd*=EG, но ac^EG,
bd^EG. Тогда говорят, что граф G допускает переклю-
чение s = (ab, cd). Полученный в результате переключе-
ния s граф обозначается через sG', граф G превращается
в sG в результате удаления ребер ab и cd и присоеди-
нения ребер ас и bd*. sG = G — ab — cd +ас + bd. Обрат-
ное переключение s"*1 = (ас, bd) применимо к графу sG.
14 в, А, Емеличев и др.	209
Тождественное преобразование ребер графа также по оп-
ределению является переключением.
Например, па рис. 45.1 изображены графы G и sG,
где $ = ({1, 3), {4, 2}).
Очевидно, что переключение пе меняет степеней вер-
шин графа. Роль переключений определяется следующей
теоремой.
Теорема 45.1. Любая реализация графической по-
следовательности получается из любой другой ее реали-
Рис. 45.1
занумерованы числами 1,
ния степеней'.
зации посредством примене-
ния подходящей цепочки
переключений.
Доказательство этой тео-
ремы основано на следую-
щей лемме.
Лемма 45.2. Пусть G —
граф, вершины которого
..., п в порядке невозраста-
FG = {1, 2, ..., п}, deg Z = йг-,
di di+\, i = 1, п — 1.
Тогда для любой его вершины i существует такая после-
довательность переключений si, ..., st, что в графе Н =
= st...s\G окружение вершины I совпадает с множе-
ством из di вершин наибольших степеней, т. е.
({1,2, . . ., di},	если di,
2, . . f — 1, i + 1, . . ., di + 1}, если i di.
Рис. 45.2
> Пусть i, j, k^VG, ]>k, ij^EG, ik<£EG. Так как
dh > dj, то существует четвертая вершина Z, смежная с k,
но пе смежная с j (рис. 45.2, где, как и всюду в этой
главе, пунктирными линиями обо-
значены ребра, отсутствующие в
графе). Следовательно, граф G до-
пускает переключение s = (ij, kl).
Если G' = sG, то ik^EG', ij^EG'.
Сделав несколько подобных пере-
ключений, придем к нужному гра-
фу Н. <1
> Доказательство теоремы 45.1. Пусть d — правиль-
ная графическая ^-последовательность. Воспользуемся
индукцией по п. Как подтверждает прямая проверка,
при п 4 каждая графическая последовательность имеет
только одну реализацию. Следовательно, для п < 4 ут-
210
верждение теоремы тривиально. Пусть п > 4 и это ут-
верждение верно для всех графических (тг — ^-последо-
вательностей. Пусть, далее, G\ и G2 — две реализации
последовательности d. Для каждого из графов Gi и G2
обозначим через v какую-либо вершину степени d\. Со-
гласно лемме 45.2 существуют такие цепочки переклю-
чений 51, ..., st и sv .. ., sri что в графах Нх = st... siGj
и Н2 = sr . .. sfi2 окружения вершины v состоят из
вершин степеней d2, d3, . .., d^+i- Поэтому степенные
последовательности графов Н\ — v и Н2 — и совпадают.
По индуктивному предположению существует такая це-
почка переключений ..., sk, что
Hl-v^sh...sl(H2-v).
Эти переключения не затрагивают вершины и, поэтому
Н\ = sh... s\H2. Далее имеем
Gt = s?1... s?1#! = S11...	=
= s?1 . . .	. . . S^r . . . S1G2. <
Иногда, хотя и редко, граф определяется своей сте-
пенной последовательностью однозначно. Если все реа-
лизации графической последовательности изоморфны,
то эта последовательность называется униграфической,
а ее реализация — униграфом. Строение униграфов из-
вестно, однако его описание слишком сложно. Унигра-
фом является, например, простой цикл С5.
§ 46. Критерии графичности последовательности
Как отмечалось выше, графическую последователь-
ность всегда можно считать правильной. Кроме того,
в ней должны быть равные члены (если длина ее п > 1),
поскольку не существует графа, степени всех вершин
которого попарно различны (см. упражнение И в гл. I).
Однако указанные условия отнюдь не являются до-
статочными для графичности последовательности. Оче-
видно, например, что последовательность (З2, I2) не яв-
ляется графической, хотя и удовлетворяет упомянутым
условиям.
Известно несколько критериев графичности последо-
вательности. Одной из важнейших теорем такого рода
является критерий Гавела — Хакимщ к изложению ко-
торого мы приступим.
211
Пусть d — правильная ft-последовательность, п > 1.
Зафиксируем индекс f, 1 i С ft, и через сг обозначим
(гс — ^-последовательность, которая получается из после-
довательности d вычеркиванием Z-ro члена. Тем самым
.	\dk. если к<Ц,
С = (с1? С2, . . . , £?г-1), Ck = \ ргтти к^> 7
если tv I.
Пусть, далее, последовательность —	/2, ...» /п-i) по-
лучается из последовательности с1 в результате умень-
шения на единицу каждого из первых di членов:
(Ck—1, если k^di,
~~ \ck, если d{.
Тогда d1 называется производной последовательностью.
Например, если cZ = (3, 3, 1, 1), то cZ1 = (2, 0, 0)=d2,
cZ3=(2, 3, l) = cZ4.
Теорема 46.1	(В. Гавел, 1955 г., С. Хакими,
1962 г.). Пусть d — правильная п-последовательность,
ft> 1. Если для какого-либо индекса 1, 1 С i С ft, произ-
водная последовательность dl является графической, то и
d — графическая последовательность. Если последова-
тельность d графическая, то каждая последовательность
d* (i = 1, ft) является графической.
> Пусть d* — графическая последовательность, Н —
ее реализация. Добавив к графу Н новую вершину и
соединив ее ребрами с di вершинами наибольших степе-
ней, получим реализацию последовательности d. Следо-
вательно, d — графическая последовательность.
Обратно, пусть последовательность d является графи-
ческой. Согласно лемме 45.2 существует такая реализа-
ция G этой последовательности, в которой некоторая вер-
шина v степени di смежна с di вершинами, степени ко-
торых наибольшие. Очевидно, что граф G — v является
реализацией последовательности dl. <
Предыдущий критерий вместе с леммой 45.2 подска-
зывают алгоритм распознавания графичности правиль-
ной последовательности и построения одной из ее реа-
лизаций. Назовем этот алгоритм 1-процедурой. Пусть d —
правильная ft-последовательность, V — ft-элементпое
множество вершин (будущего графа), каждому элемен-
ту v которого приписано неотрицательное целое число
d(y)—метка, причем d(y)<n. Пусть, далее, S(v)— под-
множество V, составленное из d(v) отличных от вер-
шины v вершин с максимальными метками (S(и) оп-
212
ределено не однозначно). Шаг 1-процедуры заключается
в следующем:
1)	фиксировать произвольную вершину v с положи-
тельной меткой (далее эта вершина называется ве-
дущей) ;
2)	фиксировать одно из подмножеств S(и);
3)	вершину v соединить ребром с каждой вершиной
из S(и);
4)	изменить метки вершины v и каждой из вершин
н, входящих в S(v), положив d(y):=0, d(u) := d(u) — 1.
Если в результате применения шага /-процедуры ка-
кая-либо из меток становится отрицательной, то говорят,
что этот шаг проваливается.
/-процедура применяется к правильной п-последова-
тельности d и заключается в последовательном выпол-
нении шагов. Берем V = {1, 2, ..., п} и первоначально
7	е rj/ /А (0) 9	9 (0)	Л
2	• (J) IЦ (2)	10)	9(0)
3 • (2) \\ (1) (ь(0) • (О)	/ V
4* (2)	• f/;	9(0)	/	\
5 • (2)	• (2) V (1)	1 (0)	4
Рис. 46.1
полагаем d(i) = di. Из леммы 45.2 и критерия 46.1 вы-
текает, что возможно одно из двух: либо мы приходим
к нулевой последовательности меток и одновременно по-
лучаем реализацию последовательности d, либо очеред-
ной шаг проваливается, т. е. последовательность d пе
является графической.
На рис. 46.1 /-процедура демонстрируется на приме-
ре последовательности (З2, 23). Каждый столбец на этом
рисунке соответствует одному шагу /-процедуры.
Отметим еще один критерий графичности последова-
тельности.
Теорема 46.2 (П. Эрдёш, Т. Галлаи, 1960 г.). Пра-
вильная п-последователъностъ d является графической
тогда и только тогда, когда для каждого к — 1, п — 1 вер-
но неравенство
k	п
2 di^ к (к — 1) + 2 min{&, dj.	(1)
Н=1
213
> Необходимость неравенства (1) проверяется легко.
Пусть G — реализация последовательности й,
___	k
VG = {1,2, ..., п}, deg i = di, i = l,n, Sk= 2 di-
i=l
Разобьем сумму Sk на две части: Sk = А + В, где А —
сумма степеней вершин порожденного подграфа G(l,
2, ..Л), а В — вклад, вносимый в сумму Sk ребрами
вида ij, где i^k, j > к. Очевидно, что
А^к(к-1),	2 min{fc,di},
i=k+l
откуда и вытекает неравенство (1).
Приведем доказательство достаточности условий тео-
ремы, принадлежащее С. А. Чоудаму (1986 г.). Пусть
d — правильная ^-последовательность, причем неравен-
ство^!) верно для каждого к == 1, п— 1. Если di = r
(г=1, п), то хотя бы одно из чисел г и п четное, по-
скольку сумма членов последовательности d — четное
число. Кроме того, rCn- 1. При этих условиях суще-
ствует ^-вершинный регулярный граф степени г (ут-
верждение 7.1). Стало быть, d—графическая последова-
тельность.
Пусть теперь среди членов di последовательности d
есть различные. Не ограничивая общности, рассмотрим
случай, когда dn 0. Воспользуемся индукцией по сумме
п
z = ^di
г=1
членов последовательности d. При S = 2 условиям тео-
ремы удовлетворяет только одна ^-последовательность
(1, 1, 0, ..., 0); эта последовательность, очевидно, гра-
фическая. Возьмем теперь S > 2 и предположим, что ус-
ловия теоремы достаточны для графичности любой пра-
вильной ^-последовательности с меньшей чем S суммой
членов. Пусть £ = minK: di>di+i}. Тогда l^^^C/z—l.
Положим
(di, i	t, Yb,
c = (cn c2, .. ., cn), Ci =	. =
и докажем, что последовательность с также удовлетворя-
ет условиям теоремы. Пусть
k	k
Sk ” ZJ dit Sk == 2 Ci9
i==l	i=l
214
Заметим, что = 5ft (/г = 1,/ —1). Нужно доказать не-
равенства
Si к (к — 1) + У, min {к, cj,	i = l,n — 1. (2)
i=fe+l
Это совсем просто при k^t. Имеем
Sh = S'fc — 1 ^Zk(k — 1) + 2 min {/г, di} — 1
i=fe+l
п
^к(к — 1) + 2 min {А;, с*},
i—h+1
и неравенство (2) верно.
Пусть теперь к < t — 1. В этой ситуации
s'h = Sh = kdh.	(3)
Если, к тому же, dh^ к — 1, то из равенств (3) непосред-
ственно вытекает
к {к — 1)^ к (к — 1) + 2 min {Л, сД,
i=fc+l
т. е. неравенство (2) верно.
Далее отдельно рассмотрим две возможности: 1)	=
= /с, 2) dh>k+i.
1) Заметим, что в рассматриваемом случае
2 йг-2>0.	(4)
i—h+2
Это очевидно при к + 2 п~ 1. Если же к + 2 = п, то
t — n — 1 и, следовательно, d = ((тг — 2)п-1, йп). Далее,
имеем S = (тг — 2) (п — 1)+ dn. Так как S — четное число
и dn > 0, то dn 2, откуда и следует неравенство (4).
Согласно (3) и (4)
5/, = /с2 Л2 — к + cZ/i+i
к" — к + cZ/i+i + dfr+z + ... + dH — 2. (5)
Для i> к имеем
di — min {к, di), di — 1 = min {к, di-x},
поэтому из (5) следует, что
Sk^.k(k—1) + У min{fc,Ci},
т. е. неравенство (2) верно.
215
2) Если dn > к + 1, то
min {Л, d) = min {к, dt_\} = к.
Поэтому
Sk = Sk к (к — 1) + 2 т*п {&> ^г} =
i—k+l
= к(к — 1)4- У min {7f,cJ,
i—/i+i
и неравенство (2) верно.
Пусть теперь dn<k+ 1. В этом случае верно нера-
венство
Sk^k(k-1) + 2 min{&, dj—-1.	(6)
i=k+l
Действительно, если, напротив, (6) неверно, то
Sh = к (к — 1) + 2 min {A:, di}.
i=»+l
Положив г = min {7: dt+i+i^k} и учитывая (3), получим
kdh = Sh = к (к — 1) + (t + г — к) к + 2	=
г=/4-г+1
— к (t + г — 1) + 2
и, далее,
= (к + 1)	= k(t + г — 1) +
п	п
4--±—	2 di>k(t + r—1) +	—
i=/4-r+l	i=f+r+l
= (к + l)k + (к + 1)(г + r-k-i) + 2 di =
i—f+r+l
= (А.Ч-1)7с+ 2 min{7;+l,di}.
i=-/i+2
Последнее противоречит тому, что последовательность d
удовлетворяет неравенствам (1). Неравенство (6) до-
казано.
С учетом (6) и (3) получаем
S'k^k{k— 1)+ 2 min{7с, dj — 1.	(7)
i=fe+l
216
В рассматриваемом случае I > к + 1, dt = dh > к + 1,
min {к, dt} =mm{fe, с J = к, min {к, сп} = сп = dn— 1,
min {к, dn} = dn, поэтому из (7) вытекает
S'k^.k(k — 1) + У min {Л, еД.
г=/г+1
Тем самым доказано, что в любой ситуации последо-
вательность с удовлетворяет условиям теоремы. Так как
сумма членов этой последовательности равна S — 2, то
она графическая по индуктивному предположению. Возь-
мем произвольную реализацию G последовательности с.
Пусть a, b<^VG, dega = ct, deg b = cn. Если вершины a
и & не смежны, то граф G + ab является реализацией по-
следовательности d и, следовательно, d — графическая по-
следовательность.
Пусть ab EG. Так как deg а == dt — 1 п — 2, то су-
ществует вершина e^VG, не смежная с а. Но deg е
deg 6, поэтому существует вершина	смежная
с е и не смежная с Ъ. Итак, граф G допускает переклю-
чение s == (а&, ef). Граф sG == G — ab ~ ef + ае + bf также
служит реализацией последовательности с, причем в нем
вершины а и Ъ не смежны. Но тогда, как доказано вы-
ше, последовательность d является графической. <
При тестировании последовательности с помощью
критерия Эрдёша — Галлаи нет необходимости прове-
рять все п — 1 неравенств (1). Пусть d — правильная
^-последовательность, k(d) = max {i: di^i}. Тогда верно
следующее
Утверждение 46.3. Если последовательность d
удовлетворяет каждому из неравенств (1) при к =
= 1, k(d), то она удовлетворяет и каждому из остав-
шихся неравенств (1).
Доказательство опускается.
§ 47. Реализация графической последовательности
с максимальной связностью
В зависимости от выбора ведущих вершин /-процеду-
ра может строить различные реализации графической
последовательности. Ее можно организовать так, чтобы
она строила реализации с некоторыми предписанными
свойствами, если, конечно, такие реализации существу-
ют. Ниже показано, как с помощью /-процедуры постро-
ить такую реализацию G графической последовательно-
го
сти, число Z(G) реберной связности которой максималь-
но среди всех реализаций.
Пусть d — правильная графическая ^-последователь-
ность. Поскольку Л (G) С 6(G) для любого графа G
(6(G)—минимальная степень вершин), то мы стремимся
построить реализацию G последовательности d с
X(G)=dn.
Вначале построим просто связную реализацию.
Теорема 47.1. Правильная графическая п-последо-
вательность d может быть реализована связным графом
тогда и только тогда, когда dn> 0 и верно неравенство
3^>2(п-1).	(1)
г=1
Если указанные условия выполняются, то 1-процедура,
на каждом шаге которой ведущей является вершина с
минимальной положительной меткой, приводит к связ-
ному графу.
Замечание. При dn > 1 неравенство (1) выполня-
ется автоматически.
> Необходимость условий теоремы очевидна. В самом
деле, связный граф порядка п не имеет изолированных
вершин и число ребер в нем пе менее п— 1. Из леммы
о рукопожатиях вытекает неравенство (1).
Достаточность докажем индукцией по длине после-
довательности d. При п ~ 2 условиям теоремы удовлет-
воряет только одна последовательность d=(l2). Реали-
зацией этой последовательности служит связный граф
К2, стало быть, для п = 2 теорема верпа. Пусть теперь
п > 2 и доказываемое утверждение верно для графиче-
ских последовательностей, длины которых меньше п. От-
дельно рассмотрим два случая: 1) dn = 1, 2) dn> 1.
1) dn~i. Так как п > 2, то из неравенства (1) вы-
текает, что d\ > 1. Рассмотрим производную последова-
тельность
dn = (/i, /2,	/п-i), /i=di-l, fi —di, i=-2, n-i.
Поскольку
n— 1	n
2 A = 2 ^i-2>2(n-2),	fi>0,
i=l	i=l
то последовательность dn удовлетворяет условиям тео-
ремы.
218
2) dn>i. Снова будем различать две ситуации:
a) ddn — 2 и б) ddn>2.
В ситуации а) из условий теоремы следует, что
= 2, с/2 = 2, d = (m, 2”-1), т > 2.
Для производной последовательности dn имеем
d"=(/b h, /„-1) = (тп-1, 1, 2я-3),
п—1
2 h =
г—1
т + 2(n-3)^2(n-2),ft>0.
В ситуации б) для производной последовательности
dn получаем
dn = (Л, /2, • • •, /п-i), /г > 1, i =
2 /г>2(п-2).
г=Ц
Итак, в любой ситуации производная последователь-
ность dn удовлетворяет условиям теоремы и по индук-
тивному предположению имеет связную реализацию //,
получаемую в результате описанной в формулировке тео-
ремы /-процедуры. Добавив к графу Н новую вершину,
смежную с вершинами степеней /1, /2» • • -ifdn, получим
связную реализацию последовательности d. <
Аналогично доказывается
Теорема 47.2. п-последователъностъ d может быть
реализована деревом тогда и только тогда, когда она не
содержит нулей и верно равенство
п
2 d{ = 2(n-l).
г=1
При выполнении указанных условий 1-процедура постро-
ит реализацию последовательности d деревом, если на
каждом шаге выбирать в качестве ведущей вершину с
минимальной положительной меткой.
На рис. 47.1 показана /-процедура, строящая дерево,
которое является реализацией последовательности d =
= (32, 2, I4).
Перейдем к графам с более высоким числом реберной
связности. Приведем без доказательства следующую тео-
рему.
Теорема 47.3 (Д. Уэнг, 1976 г.). Каждая правиль-
ная графическая п-последователъностъ d с dn> 1 имеет
219
реализацию, число реберной связности которой равно dn.
Такая реализация строится 1-процедурой, на каждом ша-
ге которой ведущей является вершина с минимальной
положительной меткой.
С числом вершинной связности дело обстоит сложнее.
Известно, что правильная графическая тг-последователь-
ность d может быть реализована графом с числом вер-
шинной связности dn или dn — 1, причем соответствую-
щую реализацию также можно получить посредством
1 • (3) Л		(2)	• (2)	X» (1)	• (1)	40)	• (0)	5<
2 43)	•	(3)	42)	/ • (2)	Л (1)	!•(()	Я (О)	Ъ
3 42)	•	(2)	•12)	•(2)	• (2)	* (1)	ь (0)	3<
4 41)	•	(1)	• (1)		40)	• (0)	• (О)	
5 41)	•	(1)	[•(1)	40)	•(0)	•(О)	• (0)	2*
6 9(1)	•	(1)	* (0)	•(О)	• (D)	• (О)	• (О)	
7 • (1)		(0)	• Ю)	• (О)	•(О)	40)	•(О)	4<
Рис. 47.1
/-процедуры. Однако доказательство этого факта и опи-
сание выбора ведущих вершин достаточно громоздки и
потому здесь не приводятся.
§ 48. Гамильтонова реализация графической
последовательности
В этом параграфе будет показано, как с помощью
/-процедуры построить реализацию графической последо-
вательности, обладающую гамильтоновой цепью или га-
мильтоновым циклом, если такие реализации существуют.
В формулировке следующего утверждения использу-
ется обозначение S(и), введенное в § 46.
Теорема 48.1 (В. Чангфейзеп, 1978 г.). Если су-
ществует реализация правильной п-последовательности d,
имеющая гамильтонову цепь с началом в вершине сте-
пени di, то к такой реализации приведет 1-процедура,
на первом шаге которой ведущей является вершина
степени di, а на каждом из последующих — вершина
с минимальной положительной меткой из множества
8(и), где v — вершина, ведущая на предыдущем шаге.
220
Доказательство этой теоремы требует перебора воз-
можных вариантов и потому громоздко; здесь оно опу-
скается.
Перейдем к построению гамильтоновой реализации.
Оно основано на следующей теореме.
Теорема 48.2 (В. Чангфейзен, 1978 г.). Для того
чтобы правильная п-последователъностъ d имела реали-
зацию в виде гамильтонова графа, необходимо и доста-
точно выполнение следующих двух условий*.
1) й>1,
2) существует реализация последовательности d, име-
ющая гамильтонову цепь с началом в вершине степени d\.
> Необходимость условия теоремы тривиальна, до-
кажем достаточность. Пусть G — реализация последова-
тельности d, имеющая гамильтонову цепь (t?i, ^2, • •vn)
с началом в вершине щ степени d\. Если vivn^EG, то
(v\, V2, .vn. v\)—гамильтонов цикл.
Пусть v\Vn<£EG. Тогда вершина vn смежна с какой-
либо вершиной где 1<1<п— 1. Рассмотрим верши-
ну Vi±i. Если Р1Рг+1 ^=EG, то
(щ, 1?2, Vi, Vn, Vn-x, ..., Vi+}, щ)
— гамильтонов цикл. Пусть теперь viVi+i&EG. По-
скольку вершина Vt смежна как с vi+], так и с vn, а вер-
шина щ не смежна пи с vi+\, пи с vn, хотя
Jt(0) *(о) *(о) *(о) •(о)
\/ \	l>(0) •(0) *(0)
: /Г \:	*(о) *(о) •(о) •(о)
• /\
’•/	\	5*(2)	*(2) \(/) ♦
6*(2) *(2) *(2)
Рис. 48.1	Рис. 48.2
> deg Vi, то существует такая вершина vh, что к Ф 2,
v\vKt=EG, ViVk^EG. Но тогда граф G допускает пере-
ключение s = (vivk, Vi^\Vi). Граф sG имеет гамильтонов
цикл
(Щ, V2, Vi, Vn, Vn-\, ZA-i-l, Vi)
(рис. 48.1). <
На рис. 48.2 показана процедура построения гамиль-
тоновой реализации последовательности (З2, 24). Полу-
чен граф G с гамильтоновой цепью (1, 3, 2, 5, 6, 4);
(1, 3, 2, 5, 6, 4, 1)— гамильтонов цикл.
221
§ 49. Расщепляемые графы
Некоторые свойства графов полностью определяются
степенными последовательностями, т. е. либо присущи
всем реализациям степенной последовательности, либо
пи одной из них. Одно из таких свойств — расщепляе-
мость.
Граф G называется расщепляемым, если существует
разбиение множества его вершин па клику п независи-
мое множество, т. е. такое разбиение
AUB = VG,	(1)
что порожденный подграф G(A) является полным,
a G(B)—пустым. Это разбиение называется полярным.
Множество А называется верхней долей графа G, а В —
нижней; одна из этих долей может быть пустой.
Как подтверждает простая проверка, все графы по-
рядка п 3 расщепляемы, по уже среди четырехвершин-
пых графов есть и расщепляемые и пе расщепляемые.
Для правильной графической последовательности d
введем параметр m(d), положив
m(d) = max {г: di^i— 1).
Например, m(d)=3 для d = (42, 22, I2).
Теорема 49.1 (П. Хаммер, Б. Симеоне, 1981 г.).
Пусть d — правильная графическая п-последователъностъ,
G — ее произвольная реализация. Граф G расщепляем
тогда и только тогда, когда верно равенство
2 d{ = m(m — 1) + 2 d^	(2)
1=1	i—m+l
где тп = m(d).
> Пусть G — расщепляемый граф. Среди всех поляр-
ных разбиений множества VG выберем разбиение (1) с
максимальным числом вершин в верхней доле. Очевидно,
что если а е А, Ъ^В и IАI = к, то deg а > к — 1, deg Ъ <
< к. Следовательно, тп = к. Поскольку б(Л) = Кт,
G (В)= Оп_т, то верно равенство (2).
Обратно, пусть для некоторого графа G VG = {1, 2, ...
..., п}, deg i = d^ Положим А = {1, 2, ..., т}, В =
= {т+1, ..., п} и сумму степеней вершин из А разобь-
ем па две части:
2 di — С + Da
1=1
222
где С — вклад, вносимый в эту сумму ребрами вида
а^А, а Р — тот вклад, который вносят ребра вида ab,
а^А, Ъ^В. Очевидно, что верны неравенства
п
C^m(ni—V),	У\	(3)
i=m + l
Равенство (2) верно только тогда, когда оба неравенства
(3) являются равенствами. Но это и означает, что Сг(Л)==
— Кт, G(B) = On_m. <
Очевидно
Следствие 49.2. Если одна из реализаций графиче-
ской последовательности расщепляема, то и все ее реали-
зации расщепляемы.
Графическая последовательность называется расщеп-
ляемой, если она имеет расщепляемую реализацию.
При доказательстве достаточности выполнения усло-
вия (2) для расщепляемости графической последователь-
ности d не были использованы ни смысл параметра m(d),
ни то, что последовательность d не возрастает. Поэтому
верно
Утверждение 49.3. Для расщепляемости графиче-
ской п-последователъности d необходимо и достаточно,
чтобы для какого-либо тп, 1 m < п, выполнялось ра-
венство (2).
Расщепляемые графы составляют важный и содержа-
тельный класс графов. В частности, оп включает в себя
все пороговые графы, рассматриваемые в следующем па-
раграфе. Некоторые задачи, сложные в общей ситуации
(например, задача построения наибольшего независимого
множества), становятся тривиальными в классе расщеп-
ляемых графов. Другие задачи для этого класса графов
столь же сложны, как и для произвольных графов. Из-
вестно, например, что проблема изоморфизма произволь-
ных графов просто сводится к аналогичной проблеме для
расщепляемых графов (см. [18]).
Характеризация расщепляемых графов в терминах
запрещенных порожденных подграфов приведена в § 62.
§ 50. Пороговые графы
Среди расщепляемых графов важный класс составля-
ют пороговые графы. Вершины произвольного графа G
порядка п занумеруем числами 1, 2, ..., п, т. с. положим
VG = {1, 2, ..., п}. Как и в § 28, обозначим через &G
223
множество, элементами которого служат все независимые
подмножества вершин графа G и пустое множество. Если
существуют такие неотрицательные вещественные числа
ai, аг, ..ап, р, что множество всех (0, 1)-решений не-
равенства
+-СС2^2 + • • •+ctn^n Р	(1)
совпадает с множеством характеристических векторов
элементов множества то граф G называется порого-
вым, а неравенство (1) — разделяющим неравенством.
Например, граф, изображенный па рис. 50.1, является
пороговым, 3^1 + 2x2 + £з + 2^4	3 — разделяющее нера-
Рис. 50.1	Рис. 50.2
венство. Очевидно, что полный и пустой графы также
являются пороговыми.
Отметим некоторые свойства пороговых графов.
Очевидно следующее
Утверждение 50.1. Любой порожденный подграф
порогового графа также является пороговым.
Лемма 50.2. Графы 2К2, и С4 не являются по-
роговыми.
> В самом деле, изобразим схематично все три рас-
сматриваемых графа на одном рисунке 50.2. Пусть те-
перь какой-либо из этих графов пороговый и
a + а2#2 + сез^з + &4<Г4 Р
— разделяющее неравенство. Тогда
ai + аг > ₽,	+ аз < Р,
аг + «4 Р,	'аз + а4 > {3.
Но последняя система неравенств противоречива. Тем са-
мым лемма доказана. <
Непосредственно из предыдущего вытекает
Следствие 50.3. Любой пороговый граф не имеет
порожденных подграфов вида 2К^ и С±.
Обозначил! через К ° G и О ° G графы, полученные из
графа G присоединением новой доминирующей и, соответ-
ственно, изолированной вершины.
Лемма 50.4. Если G — пороговый граф, то оба гра-
фа К ° G и О ° G также являются пороговыми.
224
> Пусть G — пороговый граф порядка п, (^ — разде-
ляющее неравенство. Рассмотрим граф К ° G. Пусть а —
минимальное число среди коэффициентов а» в неравенст-
ве (1); Ъ — минимальное число среди всех таких сумм
S = Ctl^l + «2^2 + . . . +	= 0, 1, i = 1, n,
что 5>Р; би у — произвольные числа, удовлетворяющие
неравенствам
₽<6<Ь,	б-а<у^6.	(2)
(В случае, когда G = On, указанного b не существует и
в (2) соответствующее неравенство опускается.) Пря-
мая проверка подтверждает, что неравенство
+ а2#2 + ... + апхп + Y^n+i б	(3)
является разделяющим для графа К° G.
Аналогично, взяв в (3) у и б, удовлетворяющие усло-
виям р < б < 6, у б — р, получим разделяющее нера-
венство для графа О ° G. <1
Как отмечалось выше, некоторые графы являются
униграфами, т. е. с точностью до изоморфизма определя-
ются своими степенными последовательностями.
Из того факта, что любые две реализации графической
последовательности получаются одна из другой с по-
мощью цепочки переключений (теорема 45.1), вытекает
Следствие 50.5. Граф G является униграфом тогда
и только тогда, когда для любого переключения s графы
G и sG изоморфны.
Ниже доказано, что пороговые графы и только они со-
ставляют простейший класс Ж униграфов — графов, во-
все не допускающих переключений, отличных от тождест-
венного. Непосредственно из определения переключения
вытекает следующая характеризация этого класса в тер-
минах запрещенных порожденных подграфов.
Утверждение 50.6. Граф принадлежит классу Ж
тогда и только тогда, когда ни один из трех графов 2К%,
Pt и Ct не является его порожденным подграфом.
Следствие 50.3 означает, что любой пороговый граф
принадлежит классу Ж.
Лемма 50.7. Если G^J£, то в графе G есть либо до-
минирующая, либо изолированная вершина.
> Пусть, напротив, G е Ж и в графе G нет ни доми-
нирующих, пи изолированных вершип, и пусть и — его
вершина максимальной степени. Тогда в этом графе су-
ществуют две такие вершины и и w, что uv е EG,
uw^EG.
15 в. А. Емеличев и др.
225
Если при этом vw^EG, то, поскольку степень верши-
ны и максимальна, существует четвертая вершина ж,
смежная с и и пе смежная с v (см. рис. 50.3). Порожден-
ный подграф G(u, v, w, х) входит в список подграфов,
запрещенных для класса JJf утверждением 50.6 (оп сов-
падает с Ра или с С4).
Пусть vw&EG. Так как в графе G пет изолирован-
ных вершил, то существует четвертая вершина х, смеж-
ная с w. Вершины и и v смежны с х, иначе порожденный
Рис. 50.3
подграф G(u, v, w,x) имел бы вид, запрещенный утверж-
дением 50.6. Так как и — вершина максимальной степе-
ни, то существует пятая вершина у, смежная с и, но не
смежная с х. Подграф б(г/, гр, х, у) снова запрещенный
(рис. 50.4).
Полученное противоречие доказывает лемму. <
Очевидны следующие два свойства графов из клас-
са Ж
1. Порожденный подграф любого графа из класса Ж
также принадлежит этому классу.
2. Если G е Ж, то оба графа К ° G и О ° G также при-
надлежат классу .
Для п > 2 положим
G\ ° G20...0 Gn — Gi ° (б?2 ° (... ° Gn)),
где Gn = K], Gi = К или Gi = О (г = 1, п— 1). Очевидно,
что из вышесказанного вытекает следующее
Утверждение 50.8. Класс Ж есть класс всех гра-
фов, имеющих вид
G\ ° G% 0... °Gn,
где Gn = Ki, п^1, а для i=l, п — 1 компоненты Gi не-
зависимо друг от друга принимают значения К или О.
Теорема 50.9. Граф является пороговым тогда и
только тогда, когда он имеет вид, описанный в утвержде-
нии 50.8.
> Требуется доказать, что класс пороговых графов
совпадает с классом Ж'. Выше отмечалось, что любой по-
роговый граф принадлежит классу JJf. С другой стороны,
226
согласно утверждению 50.8 любой граф из класса УС мож-
но построить, исходя из одной вершины, присоединяя на
каждом шаге к уже полученному графу либо доминирую-
щую, либо изолированную вершину. Одновершинный
граф является пороговым. Согласно лемме 50.4 свойство
пороговости графа сохраняется при присоединении к графу
новой доминирующей или изолированной вершины. Сле-
довательно, любой граф из класса Ж является поро-
говым. <
Следствие 50.10. Любой пороговый граф является
расщепляемым.
> Пусть пороговый граф G получается из вершины а
в результате присоединения на каждом шаге к уже полу-
ченному графу либо доминирующей, либо изолированной
(1,1,1)	(0,1,1)	(1Д1)	(1,1,0)	(0,0,1) (0,1,0)	(1Д0) (ОДО)
Рис. 50.5
вершины. Отнеся к верхней доле вершину а и все вер-
шины, присоединенные как доминирующие, а к нижней
доле — все остальные вершины, получим полярное раз-
биение множества VG. Следовательно, граф G расщеп-
ляем. <
Следствие 50.11. Для любого натурального числа
п существует ровно 2П“1 попарно иеизоморфных порого-
вых графюв порядка п.
> Очевидно, что два графа
Gi ° G2 о ... о Gn, 6^62° ... °Gm
вида, описанного в утверждении 50.8, изоморфны тогда и
только тогда, когда
п = m, Gi = Gi9 i = 1, /г — 1.
Каждая из компонент Gi может принимать два значения.
Следовательно, число неизоморфных среди таких графов
равно 2П-1. <
На рис. 50.5 показаны все 8 пороговых графов поряд-
ка 4. Из теоремы 50.9 следует, что каждый из них опре-
деляется (0, 1)-вектором (а, 0, у).
Непосредственно из теоремы 50.9 вытекает
Следствие 50.12^ Если G — пороговый граф, то и
дополнительный граф G также является пороговым.
15*	227
Графическая последовательность, имеющая пороговую
реализацию, называется пороговой. Все реализации поро-
говой последовательности изоморфны, поскольку порого-
вый граф является униграфом. Очевидно, что из теоремы
50.9 вытекает следующий критерий пороговости последо-
вательности целых неотрицательных чисел.
Следствие 50.13. При п> 1 правильная п-последо-
вателъностъ d является пороговой тогда и только тогда,
когда верно одно из следующих двух утверждений'.
1) d\*=n— 1 и производная последовательность d1 =
= (Й2—1, ..., dn —1) пороговая',
2) dn = 0 и производная последовательность dn =
= (di, d2, ..., dn-i) пороговая.
§ 51. Пороговое разложение графа
Поскольку граф с одним ребром является пороговым,
то любой граф G можно представить в виде объединения
G = Gi U G2 U ... U Gt
пороговых графов Gi с совпадающими множествами вер-
шин. Назовем такое представление пороговым разложе-
нием графа G. Минимальное число t компонент в порого-
вых разложениях графа G назовем пороговым числом
графа G и обозначим через th(G).
Параметр th(G) связан с минимизацией числа линей-
ных неравенств, задающих булеву функцию. Рассмотрим
эту связь. Пусть
ац^1 + ai2^2 + ... +а\пхп {$1,
a2i#i + а22Я2 +... +a2n£n й,
(1)
ацХ[ + а/2^2 + ... +atnxn
— система линейных неравенств с вещественными коэф-
фициентами и правыми частями, В — {0, 1), Вп — множест-
во всех бинарных векторов (х\, я2, ..., хп) длины п. Оп-
ределим булеву функцию /: Вп->В, положив /(#i, #2, ...
..., ял) = 0 тогда и только тогда, когда вектор (#i, Х2, ...
..., хп) удовлетворяет системе (1). Будем говорить, что
функция f определяется системой неравенств (1). Тем са-
мым множество нулей булевой функции, определяемой
системой линейных неравенств, совпадает с множеством
(0, 1)-решений этой системы.
228
Теорема 51.1. Любая булева функция определяется
некоторой системой линейных неравенств.
> Известно, что всякая булева функция / от п пере-
менных может быть задана своей совершенной дизъюнк-
тивной нормальной формой (совершенной д. н. ф.):
/ (^, Х2, . . . , Хп) = V ^1^22 • • •
где (oi, 02, .. оп) пробегает множество всех единиц
функции /,
о. (Xi при Oi = 1,
X •	— I —
г l^i при Oi = О
(см., например, [32]).
Легко видеть, что каждая конъюнкция g вида
/	\	^2	^71
g (з?1, Х2ч . . . , XnJ = X} х2 . .. хп
определяется одним линейным неравенством. В самом де-
ле, пусть, для определенности,
g (»^1, «^2, • • •? Х\Х2 • • . Хп.
Рассмотрим неравенство
Х[ + Х2 + . . . + Хп П — 1.
Бинарный вектор х = (х\, я2, •••, лп) пе удовлетворяет
этому неравенству только при условиях
Х\ = Х2 = . . . = хп = 1.
Но эти же условия необходимы и достаточны для того,
чтобы вектор х был единицей функции /.
Аналогично, конъюнкция
Х[ . . . Х^Х4-1 ... X п
определяется неравенством
Xi + ...+ xh — xh+\ — ... — xn^zk — 1.
Итак, каждая элементарная конъюнкция, входящая в
совершенную д. н. ф. функции /, определяется одним ли-
нейным неравенством. Очевидно, что функция / опреде-
ляется системой этих неравенств. <
Минимальное число t неравенств в системах, задаю-
щих функцию /, называется пороговым числом функции
/ и обозначается через t(f). Если функция f графическая,
т. е. / = 0 или / — монотонная булева функция, все ниж-
ние единицы которой имеют норму 2, то, как показано в
229
§ 28, этой функции соответствует граф Gf, множество ха-
рактеристических векторов независимых подмножеств вер-
шин которого совпадает с множеством нулей функции /.
Теорема 51.2. Для любой графической функции f
верно равенство
=	(2)
> Пусть / — графическая функция,
Gf = G\ U б?2 U ... U Gt
— пороговое разложение графа Gf. Тогда система «7G/
всех независимых подмножеств вершин графа Gt есть пе-
ресечение
=	(3)
a
аналогичных систем для пороговых графов Ga. Множест-
во характеристических векторов элементов системы «7Ga
совпадает с множеством бинарных решений линейного
неравенства, являющегося разделяющим для графа Са.
Из равенства (3) следует, что множество бинарных ре-
шений системы из t таких неравенств есть множество ха-
рактеристических векторов элементов из ^Gf, т. е. мно-
жество нулей функции /. Следовательно, эта система не-
равенств задает функцию /, и потому	Итак,
Обратно, пусть функция / задается некоторой систе-
мой линейных неравенств (1). Следующим образом по-
строим t графов Gk (/г = 1, t) : VGk = {1,2, ..., п}, ij е EGk
тогда и только тогда, когда i j и ahi + aw > Очевид-
но, что
G\\]G’2[] ... \}G't = Gj.	(3')
Предположим, что какой-либо из графов Gk не являет-
ся пороговым. Тогда в нем есть порожденный подграф,
запрещенный следствием 50.3; пусть это подграф, пока-
занный на рис. 50.2, где пунктирные линии означают
отсутствие соответствующих ребер. Из определения графа
Gh следует, что
Otkl + CZft2 •^>	GCfel "1” ^h3 Ph?
>ah2 + aft4 ^Рь,	> Pft.
Но последняя система неравенств противоречива, следо-
вательно, Gk— пороговый граф. Итак, (3х)—пороговое
230
разложение графа Gf. Поэтому th(G/)^^ и, следователь-
но, tli(G/)^ t(f). Равенство (2) доказано. <
Вычисление порогового числа произвольного графа G
и, тем более, построение соответствующего порогового
разложения графа — крайне трудные задачи. Пороговое
число можно оценить с помощью числа независимости
ao(G), однако последнее так же трудно вычислимо.
Теорема 51.3 (В. Хватал, П. Хаммер, 1977 г.). Для
любого непустого графа G порядка п верно неравенство
th(G)+a0(G)^n,	(4)
а если в G нет треугольников, то
th(G)+a0(G) = n.	(5)’
> Пусть S — наибольшее независимое множество вер-
шин графа G,
VG\S = {zzi, г/2, ..., uh}.
Обозначим через Ei множество ребер графа G, инцидент-
ных вершине щ (i = l,/c). Поскольку ребра, входящие
в составляют звезду, являющуюся согласно теоре-
ме 50.9 пороговым графом, то и граф Gi = (VG, Ег) поро-
говый. Но
k
U Gi = G.	(6)
i=l
Следовательно, (6) — пороговое разложение графа G. По-
этому tli(G) к = п — ao(G), т. е. верно неравенство (4).
Пусть теперь в графе G нет треугольников и пусть
G=-G\ UG2U...UGt
— пороговое разложение с минимальным числом компо-
нент. В пороговом графе Gi также нет треугольников. Из
теоремы 50.9 следует поэтому, что граф Gi является
звездой или получается из звезды в результате присоеди-
нения изолированных вершин. В любом случае в графе
Gi есть вершина нг, инцидентная всем его ребрам. Так
t
как U EGi = EG, то множество VG\{ui, U2, ..ut} не-
г=1
зависимо в графе G. Следовательно, схо(С)>/г — lli(G),
что вместе с неравенством (4) приводит к равенству
(5). <
231
Заметим, что равенство (5) может быть верным и для
графа с треугольниками. Таков, например, граф па
рис. 51.1.
Поскольку для любого тг-вершинного графа G верно
равенство ao(G) + fio(G) = п (теорема 25.5), где Po(G) —
Л число покрытия графа G, то из предыдущей
теоремы вытекает
Следствие 51.4. Для любого графа G,
не содержащего треугольников, верно ра-
венство th(G) = p0(G).
В частности, любой двудольный граф не
Рис. 51.1 содержит треугольников. Кроме того, для
двудольного графа G верно равенство
Po(G)=czi(G), где czi(G) —число паросочетания (теоре-
ма 32.1). Поэтому из теоремы 51.3 вытекает
Следствие 51.5. Для любого двудольного графа G
верно равенство th(G) = cti (G).
Таким образом, в классе двудольных графов параметр
tli (G) вычисляется несложно.
§ 52. Степенное множество графа
Степенным множеством графа называется множество
степеней его вершин. От степенной последовательности
это множество отличается тем, что в нем пе учитывается
число вершин, имеющих заданную степень, тогда как в
степенной последовательности каждое число фигурирует
।	столько раз, степенью скольких вер-
I	шип оно является.
А	Степенное множество графа G обоз-
/ \ начим через S(G). Так, для графа G,
у \ изображенного па рис. 52.1, 5(G) =
У\	={1,2, 3}.
S	Хотя степенная последовательность
Рис. 52.1 графа удовлетворяет определенным ус-
ловиям, однако степенным множеством
графа может быть произвольное множество. Об этом
свидетельствует следующая
Теорема 52.1. Любое конечное множество S нату-
ральных чисел является степенным множеством некото-
рого порогового графа. Минимальный порядок таких гра-
фов равен s +1, где s — максимальное число из мно-
жества S.
Очевидно, что из этой теоремы вытекает
232
Следствие 52.2. Любое конечное множество целых
неотрицательных чисел является степенным множеством
некоторого графа.
> Доказательство теоремы 52.1. Если S(G) =
= S, то |G| >s+ 1, так что нужно только доказать су-
ществование подходящего графа G. Утверждение триви-
ально для одноэлементного множества S, поскольку
S(Кп)={п — 1}. Пусть теперь
S = {di, с?2, ..dn), di> d2> ... > dn, n > 1,
и пусть, для определенности, п = 2р — четное число. Нуж-
ный граф будем искать в виде
G = Кх о Оу оКх °Оу о ...о Кх о Оу ,	(1)
Д У} Л2 У2	Р Мр1	' '
где КХ°Н — граф, полученный из графа Н добавлением
х доминирующих вершин, а ОУ°Н — граф, полученный
из графа Н добавлением у изолированных вершин. Лю-
бой граф вида (1) является пороговым. Попытаемся по-
добрать числа ха и г/р в выражении (1) так, чтобы вы-
полнялось равенство S(G) = S. Для этого должно быть
-1+^+^2+.. .+^_1+^р+^_1+.
“1 +z/2+-. •+Ур-1+хр+Яр~1+-. .+^=^2,
“-1+z/p_1+v^p-i+- • -+*r=dp>
^р+^р-гН • •+;ri~^p+i»
Хр-1^~' • •+;ri“c?p+2»
Очевидно, что система уравнений (2) относительно не-
известных xh Уз (Z = l,p, / = 1, р) имеет решение, все
координаты которого положительны:
х\ dn,	у 1 d\ d2,
х2 = dn-\ — dn,	y2 = d2-'d3,	(3)
Xp — dp+\ dP+2, Ур dp dP+i 4 1.
Подставив в выражение (1) числа, определяемые равенст-
вами (3), получим граф (?, для которого S(G)=S. Число
его вершин равно
Xi + х2 + ... + хр + у\ +у2 + ... + Ур = d\ + 1.
233
Для нечетного п = 2р + 1 построение аналогично, толь-
ко вместо формулы (1) используется формула
G = КХ1 о ОУ1 о кхе Оуа° ... о КХр о ОУр о КХр+1. <
УПРАЖНЕНИЯ
1.	Докажите, что при п 4 все графы порядка п являются
уииграфами, а при п > 4 среди графов порядка п есть как уни-
графы, так и не упиграфы.
2.	Найдите последовательность переключений, переводящую
один из графов, представленных на рис. VIII.1, в другой.
Рис. VIII.1
3.	Докажите что последовательность (44, З2, 23) является гра-
фической и постройте какую-либо ее реализацию.
4.	Постройте связную реализацию последовательности (6, 4,
3, 24, 1). Есть ли у этой последовательности реализации, не явля-
ющиеся связными?
5.	Постройте реализацию G последовательности (6, З4, 22) с
X(G) = 2.
6.	Докажите, что при п 3 все графы порядка п расщепляе-
мы, а при п > 3 среди графов порядка п есть и расщепляемые, и
не расщепляемые.
7.	Является ли последовательность (5, З2, 23) расщепляемой?
8.	Найдите все реализации последовательности (6, 5, 43, 2, 1).
Рис. VIII.2
9.	Докажите, что граф, изображенный на рис. VIII.2, явля-
ется пороговым. Найдите для него разделяющее неравенство.
10.	Постройте какой-либо граф, степенное множество которого
совпадает с 5 = {1, 3, 5}.
11.	Докажите, что любое конечное множество натуральных чи-
сел, содержащее 1, является степенным множеством некоторого де-
рева. Постройте дерево Г, степенное множество которого S(T) =»
- {1, 2, 3}.
12.	Докажите, что если два пороговых графа G и II пе имеют
изолированных вершин и S(G) — S(Н), то эти графы изоморфны.
Глава IX
Раскраски
Задачи раскраски вершин или ребер графа занимают
важное место в теории графов. К построению раскрасок
сводится целый ряд практических задач. Характерной
особенностью этих задач является существование объек-
тов, которые по каким-либо причинам не могут быть объ-
единены в одну группу.
§ 53. Правильная раскраска
Пусть G — некоторый граф, к — натуральное число.
Произвольная функция впда f :VG -> {1, 2, ..., к} назы-
вается вершинной к-раскраской, или просто к-раскраской^
графа G. Если позволяет контекст, то к в этом определе-
нии опускается. Раскраска называется правильной, если
/(u)=#/(v) для любых смежных вершин и и V. Граф, для
которого существует правильная /с-раскраска, называется
к-раскрашиваемым (или раскрашиваемым к цветами).
В определении раскраски вместо множества {1, 2, ..., к}
можно взять произвольное ^-элементное множество.
Правильную ^-раскраску графа можно трактовать как
окрашивание каждой его вершины в один из к цветов,
при этом смежные вершины должны получать различ-
ные цвета. Поскольку функция / пе обязательно сюръек-
тивна, то при /с-раскраске фактически может быть ис-
пользовано менее к цветов. Таким образом, правильную
/с-раскраску графа G можно рассматривать как разбие-
ние
Vi и V2 и ... и Vt = VG, l^k,
множества вершин VG на не более чем к непустых клас-
сов, каждый из которых является независимым множест-
вом. Классы этого разбиения называются цветными
классами.
Минимальное число к, при котором граф G является
/с-раскрашиваемым, называется хроматическим числом
этого графа и обозначается х(^). Если x(G) = fc, то граф
235
G называется к-хроматическим. Правильная ^-раскраска
графа G при /с = /((?) называется минимальной.
В качестве иллюстрации рассмотрим граф G, изобра-
женный на рис. 53.1, где указана одна из правильных
4-раскрасок. Меньшим числом цветов этот граф раскра-
сить правильно нельзя. Действительно, граф содержит
цикл (i?i, V2, v$, v$, vs, Vi), для пра-
вильной раскраски которого нуж-
но не менее трех цветов, а для
вершины vq требуется новый цвет.
Итак, %(G) = 4.
Рассмотрим некоторые практи-
ческие задачи, сводящиеся к пра-
вильной раскраске графов.
1.	Задача составления расписа-
ний. Предположим, что нужно про-
честь несколько лекций за крат-
чайшее время. Чтение каждой лек-
ции в отдельности занимает один
час, но некоторые лекции не мо-
читаться одновременно (например, их читает одни и
же лектор). Построим граф G, вершины которого би-
ективно соответствуют лекциям, и две вершины смежны
гут
тот
тогда и только тогда, когда соответствующие лекции нель-
зя читать одновременно. Очевидно, что любая правильная
раскраска этого графа определяет допустимое расписание:
лекции, соответствующие вершинам графа, составляющим
цветной класс, читаются одновременно. И, обратно, любое
допустимое расписание определяет правильную раскраску
графа G. Оптимальные расписания соответствуют мини-
мальным раскраскам, а число часов, необходимое для про-
чтения всех лекций, равно /(G).
2.	Задача распределения оборудования. Заданы мно-
жества У = {z?i, V2, ..., vn} и S = {si, S2, ..., .s\J работ и
механизмов соответственно. Для выполнения каждой из
работ требуется некоторое время, одинаковое для всех
работ, и некоторые механизмы. При этом никакой из ме-
ханизмов не может быть одновременно занят в несколь-
ких работах. Нужно распределить механизмы так, чтобы
общее время выполнения всех работ было минимальным.
Построим граф G, положив VG = V и объявив верши-
ны Vi и Vj	смежными тогда и только тогда, когда
для выполнения работ пг и Vj требуется хотя бы один
общий механизм. При правильной раскраске графа G ра-
боты, соответствующие вершинам одного цвета, можно
236
выполнять одновременно, а наименьшее время выполне-
ния всех работ достигается при минимальной раскраске.
3.	Задача о проектировании коробки скоростей. Короб-
ка скоростей — механизм для. изменения частоты враще-
ния ведомого вала при постоянной частоте вращения ве-
дущего. Это изменение происходит за счет того, что на-
ходящиеся внутри коробки шестерни (зубчатые колеса)
вводятся в зацепление специальным образом. Одна из
задач, стоящая перед конструктором коробки, заключает-
ся в минимизации ее размеров, а это часто сводится к
минимизации числа валов, на которых размещаются
шестерни.
Построим граф G, вершины которого биективно соот-
ветствуют шестерням. Если по какой-то причине две
шестерни не должны находиться на одном валу (напри-
мер, они могут быть в зацеплении, или их общий вес
велик для одного вала и т. д.), то соответствующие вер-
шины графа соединим ребром. Вершины, имеющие один
цвет при правильной раскраске этого графа, определяют
шестерни, которые могут находиться на одном валу,
а хроматическое число %(<?) равно минимальному коли-
честву валов, нужных для проектируемой коробки.
Для некоторых графов хроматические числа найти не-
сложно. Например, %(7£п) = п, у^(Кп — е) = п — 1, у(Кпт)=^
=•2, х(С2п) = 2, х(С2п+1) = 3.
Очевидно, что граф является 1-хроматическим тогда
и только тогда, когда он пустой, а 2-хроматическим —
когда он двудольный и непустой. Обычно 2-хроматичес-
кий граф называют дихроматическим. Поэтому теорему
Кёнига о двудольных графах можно сформулировать в
следующем виде:
Теорема 53.1. Непустой граф является дихромати-
ческим тогда и только тогда, когда он не содержит цик-
лов нечетной длины.
Задачи определения хроматического числа и построе-
ния минимальной раскраски произвольного графа явля-
ются очень сложными, эффективные алгоритмы их ре-
шения неизвестны. Рассмотрим простой алгоритм построе-
ния правильной раскраски, в ряде случаев приводящий
к раскраскам, близким к минимальным.
Алгоритм последовательной раскраски.
1. Произвольной вершине 0\ графа G припишем
цвет 1.
2. Если вершины z?i, i?2, ..., Vi раскрашены I цветами
1, 2, ..., Z, I i, то новой произвольно взятой вершине
237
vi+\ припишем минимальный цвет, не использованный
при раскраске вершин из ее окружения.
Раскраска, к которой приводит описанный алгоритм,
называется последовательной. Очевидно, что это — пра-
вильная раскраска. Для некоторых классов графов (на-
пример, полных Л-дольных) последовательная раскраска
является минимальной. В общем случае это не так.
Следующая теорема сводит задачу построения пра-
вильной раскраски графов к аналогичной задаче для
двухсвязных графов.
Теорема 53.2. Если каждый блок графа к-раскра-
шиваем, то и сам граф также к-раскрашиваем.
> Воспользуемся индукцией по числу блоков рассмат-
риваемого графа. Для графа, являющегося блоком, ут-
верждение тривиально. Предположим, что теорема верна
для графов, состоящих из Ш > 1 блоков. Пусть теперь
G — граф, имеющий ровно m + 1 блоков, В — один из его
концевых блоков, Н — объединение всех остальных бло-
ков. По индуктивному предположению оба графа В и Н
являются ^-раскрашиваемыми. Зафиксируем для каждого
нз них правильную ^-раскраску.
Графы В и Н имеют ровно одну общую вершину и.
Если ее цвета в обеих фиксированных /с-раскрасках сов-
падают, то получена правильная й-раскраска графа G.
В противном случае нужно очевидным образом переста-
вить цвета в одной из фиксированных раскрасок. <
§ 54. Оценки хроматического числа
Поскольку задачу правильной раскраски точно ре-
шить трудно, то актуальны оценки хроматического числа,
выражаемые в терминах более или менее просто вычис-
лимых параметров графа. Рассмотрим несколько оценок
хроматического числа, связанных со степенями вершин
графа.
Обозначим через 3? множество всех порожденных под-
графов графа G, а через 6(G), как обычно,—минималь-
ную пз степеней вершин графа G.
Теорема 54.1. Для любого графта G верно неравен-
ство
X(G)< 1 + max 6 (Я).
> Утверждение теоремы очевидно для пустых графов.
Пусть G — произвольный %-хроматический граф, % > 2,
238
a H — его минимальный порожденный подграф, удовлет-
воряющий условию х(Я)==/. В этом случае /(И —z?)C
% — 1 для любой вершины v графа Н.
Предположим, что degH v < х — 1. Граф II — v правиль-
но раскрасим % — 1 цветами. Окрасив затем вершину v в
один из этих цветов, не использованный при окраске
смежных с пей вершин, получим правильную (% — ^-рас-
краску графа Я. Следовательно, degH % — 1 и
X — 1^6 (Я)	шах б (Я). <]
Как и ранее, через А(С?) обозначим наибольшую из
степеней вершин графа G.
Следствие 54.2. Для любого графа G верно нера-
венство
X(G)^1 + A(G).
Некоторое улучшение последней оценки дает сле-
дующая
Теорема Брукса (1941 г.). Если G — связный
граф не являющийся полным, и A(G)^ 3, то х(^)^ A(G).
> Пусть A (G) = тп > 3. Очевидно, что максимальная
степень вершин каждого блока графа G не превосходит тп.
Поэтому, с учетом теоремы 53.2, достаточно, не теряя
общности, провести доказательство для двусвязпых
графов.
Пусть G — двусвязный граф. Сначала покажем су-
ществование в графе G таких вершин и и v, что расстоя-
ние d(u, v) равно 2 и граф G — u — v связен. Это очевид-
но, если х(С?)> 3.
Допустим, что х ((?)=-2. Пусть D —- множество всех
доминирующих вершин графа G. Поскольку G не явля-
ется полным графом, то I VG\D| > 2. Если D 0, то в ка-
честве вершип и и v можно взять любые две несмежные
вершины из VG\D.
Пусть Я —0. Выберем в графе G вершину z степени
пе менее трех. Если граф G ~ z 2-связный, то^ в качестве
вершины и возьмем z, а в качестве v — любую вершину,
находящуюся от z на расстоянии 2.
Пусть x(G —z)= l, А и Я —два концевых блока гра-
фа G — z. Существуют две вершины и А и v В, не яв-
ляющиеся точками сочленения графа G — z и смежные с
вершиной z, иначе оказалось бы, что x(G)=-l.
Легко видеть, что граф G — и — v связен. Действитель-
но, удаление вершин и и v не нарушает связности бло-*
239
ков А и В, поэтому граф G — и — v — z связен. Из того,
что deg 2^3, следует теперь связность графа G — и — v.
Итак, показано существование нужных вершин и и
р, смежных с некоторой вершиной zr. Поскольку граф
G — и — v связен, то его вершины можно так занумеро-
вать числами 1, 2, п — 2, что каждая вершина, кроме
z\ будет смежна по крайней мере с одной вершиной,
имеющей меньший номер.
Теперь окрасим несмежные вершины и и v в цвет 1.
Затем будем последовательно приписывать вершинам
zn~2, zn-3, ..., z\ один из цветов 1, 2, ..., т по следующе-
му правилу. Пусть к > 1 и верши-
ны и, V, Zn-2, Zn-3, ..zh+\ уже
окрашены. Так как zk смежна хо-
тя бы с одной из вершин с мень-
шим номером, то степень верши-
ны zh в порожденном подграфе
G (щ v, zn~2,..., zA+i, zk) меньше т.
Вершине zk присвоим любой
цвет, не использованный при рас-
краске смежных с ней вершин.
Так же поступим и с вершиной
zi. Так как degzi^zn и хотя бы
две вершины из окружения вер-
шины zi (и и v) окрашены в один цвет, то в множестве
цветов {1, 2, ..., т} существует цвет, не использованный
при раскраске вершин из этого окружения. Этот цвет и
припишем вершине zi. Очевидно, что получена правиль-
ная zn-раскраска графа G. <
Оценка, устанавливаемая теоремой Брукса, достижи-
ма. Так, для кубического графа G, изображенного на
рис. 54.1, существует правильная 3-раскраска, а пра-
вильная 2-раскраска невозможна, ибо это не двудольный
граф. Следовательно, %((?) = 3 = А (б?).
Однако теорема может дать и завышенную оценку
хроматического числа. Например, из этой теоремы сле-
дует, что %(Лл>п)^п, в то время как %(7^i>n)=-2.
Две вершины графа называются соцветными относи-
тельно некоторой правильной раскраски, если при этой
раскраске они имеют один цвет.
Следствие 54.3. При любой минимальной раскрас-
ке связного неполного графа существуют две соцветные
относительно этой раскраски вершины, расстояние между
которыми равно 2.
> Пусть G — связный неполный граф. При х = X (fi) ==»
240
— 2 утверждение тривиально, так как в этом случае G
является связным двудольным графом, имеющим не ме-
нее трех вершин.
Если х 3, то из предыдущей теоремы следует,
что граф содержит хотя бы одну вершину у, для ко-
торой deg v > /. Поэтому среди смежных с v вершин
найдутся по крайней мере две вершины, имеющие
один цвет. <1
Следующая теорема связывает хроматическое число
графа с числами его вершин и ребер.
Теорема 54.4 (А. П. Ершов, Г. И. Кожухин, 1962 г.).
Для любого связного (п, т)-графа G верны неравенства
^yfG)^ 3 + V9 + 8(m — n) j.,
(Напомним, что пара [ ] квадратных скобок означает
целую часть числа, а пара { } фигурных скобок — дроб-
ную часть.),
> Докажем только правое неравенство (доказатель-
ство левого громоздко).
Если G — полный граф, то неравенство проверяется
непосредственно.
Пусть граф G не является полным и x(G) = /. Соглас-
но следствию 54.3 при любой минимальной раскраске
граф имеет пару соцветных вершин v\ и v%, для которых
d(vi, Р2)==2. Построим граф Gi, слив v\ и в вершину и.
Граф G\ имеет на одну вершину и по крайней мере
па одно ребро меньше, чем граф G. Очевидно, что
Х(С?1) = Х. В противном случае, правильно раскрасив %i
цветами (%i < %) граф Gi, можно было бы построить и
/i-раскраску графа G. Для этого нужно было бы окрасить
вершины V\ и V2 в цвет вершины у, а для остальных вер-
шин сохранить их цвета в графе Gi.
Операции слияния соцветных вершин будем произво-
дить до тех пор, пока не получим полный граф Kt. Пусть
таких слияний потребуется 5. Так как по-прежнему
Х(^) = Х» то Z = X = 72-S.
Граф Kt имеет 1(1 —1)/2 = /(/ — 1)/2 ребер, т. е. па
т~Х(Х“"1)/2 ребер меньше, чем граф G. Поскольку
после каждого слияния число ребер графа уменьшалось
хотя бы па единицу, то имеем
zn-x(x-l)/2^s.
16 в. А, Емеличев и др.
241
Поэтому, учитывая, что % « п — $, получаем
Из последнего неравенства следует
X(G)=X<y(3+ /9 + 8(т — п)). <
Существуют графы, для которых оценки, установлен-
ные предыдущей теоремой, достигаются. Таковы, напри-
мер, полные графы.
Ниже рассматриваются оценки хроматического числа,
имеющие скорее теоретический интерес, поскольку пара-
метры графа, с которыми они связаны, вычисляются
столь же сложно, как и само хроматическое число.
Тривиальной нижней границей для хроматического
числа является плотность. Очевидно, что %(С)^ф(С)
для любого графа G. На первый взгляд может показаться,
что плотность графа тесно связана с его хроматический!
числом, и если плотность ф(б?) невелика, то невелико и
%(G). Однако на самом деле разность /(G) — ф(С) мо-
жет быть сколь угодно большим числом. А именно, вер-
на следующая
Теорема 54.5 (А. А. Зыков, 1949 г.). Существуют
графы без треугольников с произвольно большим хрома-
тическим числом.
> Для доказательства индуктивно построим последо-
вательность S— (G2, Gz, ..., G{, ... ) графов Gi без тре-
угольников, таких, что %(Gi) = i- Положим G2 = К2. Если
граф Gi уже построен, i^2 и VGi = {vi, v2, ..nJ, то
граф Gi+i определим по следующему правилу: VGi+i =
^VG{U V' Un, = [v^vi .. .,v„}, VGt-П 7'= 0,
^VGiUV'; каждую вершину Vj соединим ребрами с те-
ми вершинами из VGi, с которыми смежна щ в графе Gz;
вершину v соединим ребрами с каждой вершиной из 7'
(см. рис. 54.2 и 54.3, где изображены графы G3 и G4).
Полученный таким образом граф имеет 2п + 1 вершин.
Покажем, что Gi+\ — искомый граф. Так как вершина
v не смежна ни с одной вершиной из множества VGh
а вершины из V' попарно пе смежны, то никакой тре-
угольник в Gi+i пе может содержать вершину v. По той
же причине треугольник не может содержать более од-
ной вершины из V'. Если же треугольник образовывали
бы вершины Vj, vh, vz, то в графе Gi вершины Vj, vz
также составляли бы треугольник. Поскольку в графе
242
Gi треугольники отсутствуют, отсюда следует, что в гра-
фе Gi+i их также нет.
Теперь докажем, что x(Gi+i)=i+l. В самом деле,
любую правильную i-раскраску графа Gi легко продол-
жить до правильной (/ +1)-раскраски графа Gi+i, поло-
жив / (?4) = /(^.;) Ддя 7 = 1, и приписав вершине v
некоторый новый цвет. С другой стороны, если бы су-
ществовала правильная /-раскраска графа Gi+i, то па
Рис. 54.3
раскраску вершин из У' понадобилось бы не более i — 1
цветов (отличных от цвета вершины и). Изменив окраску
вершин графа Gi так, чтобы каждая вершина Vj получила
тот же цвет, что и vj, можно было бы построить правиль-
ную (/ —1)-раскраску графа Gi5 в то время как %(Gi) = Z.
Таким образом, доказано, что граф Gi+i не содержит
треугольников и %(Gi+i) = /+l. <
Заметим, что графы, существование которых гаранти-
руется предыдущей теоремой, являются экзотическими,
поскольку для почти каждого графа G верно следующее
утверждение: если q(G)^k, то и %(G)^k (Ф. Колай-
тис, X. Прёмель, В. Ротшильд, 1987 г.).
Как показывает теорема 54.5, графы с плотностью,
равной 2, могут иметь сколь угодно большое хроматичес-
кое число. Следующая теорема, приводимая здесь без до-
казательства, свидетельствует об отсутствии связей меж-
ду хроматическим числом и обхватом графа.
Теорема 54.6 (П. Эрдёш, 1961 г.). Для любых на-
туральных чисел lux существует х~хРоматический граф,
обхват которого превосходит I.
Оцепим хроматическое число в терминах числа неза-
висимости.
Теорема 54.7. Для любого графа G верно
n/aQ х п ~ ао + 1,	(1)
где п= IGI, ao = ao(G), х==Х(^)-
16*
243
> При любой минимальной раскраске множество VG
разбивается на % цветных классов Vi, V2, ..Vx, каждый
из которых является независимым множеством. Поэтому
если | FJ = Пг, то rii < «о для всех i = 1, х, и
%
n- 2 ?г{<Хао-
г—1
откуда следует левое из неравенств (1).
Перейдем к доказательству правого неравенства.
В графе G есть независимое множество вершин S, содер-
жащее ровно ао элементов. Так как |G — S\=n — ао, то
%(G — S)^n — ао и, следовательно, % п — ао + 1. <
Следствие 54.8. Если G — связный граф, не являю-
щийся полным, и A(G)> 3, то
a0(G)> |G|/A (G).
> Рассмотрим последовательность неравенств
a0(G)> |G|/x(G)> 1G|/A(G).
Первое из неравенств вытекает из предыдущей теоре-
мы, а второе — из теоремы Брукса. <3
Дополнением теоремы 54.7 является
Теорема 54.9. Для любых натуральных чисел п, ао
и х, удовлетворяющих неравенствам (1), существует граф
порядка п с числом вершинной независимости ао и хро-
матическим числом %.
> Рассмотрим отдельно три случая: 1) ао=1;
2) ссо > 1 и n = aol, где I — целое число; 3) п пе крат-
но ао.
1)	Из (1) следует, что х = п, и Кп— нужный граф,
так как а0(Я„) = 1 = а0, % (ТС) = 7? = /.
2)	Пусть G — полный Z-дольный граф, в каждой доле
которого ровно ао вершин. Тогда /(G)= Z = дг/ао. Фикси-
руем некоторую долю U и каждую из не входящих в эту
долю вершин будем последовательно превращать в доми-
нирующую, добавляя недостающие ребра. На каждом
таком шаге хроматическое число возрастает на 1. В ре-
зультате придем к полному (п — ао + 1) -дольному графу
F, все доли которого, кроме доли U, одновершинные. Оче-
видно, что % (F) = п — ао + 1.
3)	Если п пе кратно ао, то в качестве исходного гра-
фа берется n-вершпнный полный ([n/ao] + 1)-дольный
граф, [тг/ао] долей которого содержат по ао вершин.
244
Выбрав в качестве U одну из таких долей, дальнейшие
рассуждения проведем так же, как в случае 2. <3
Естественный интерес вызывает стремление уточнить
оценку хроматического числа, устанавливаемую теоре-
мой Брукса. О. В. Бородин и А. В. Косточка в 1977 го-
ду выдвинули следующую гипотезу, пока пе доказан-
ную и пе опровергнутую:
Гипотеза. Если Д(С?)>9 и (p(G)^A(G), то
X(G)^A(G)-1.
Приведем без доказательства теорему, дающую асимп-
тотику хроматического числа.
Теорема 54.10 (А. Д. Коршунов, 1980 г.). Хрома-
тическое число почти каждого графа G порядка п удов-
летворяет соотношению
X(G)~ и/2 log2 п.
§ 55. Хроматический полином
Поскольку f-раскраской графа G является произволь-
ное отображение вида VG-+{1, 2, ..., И, то число по-
парно различных ^-раскрасок этого графа равно числу
всех таких отображений, т. е. tn, где n=\VG\. Но если
ограничиться только правильными раскрасками, то вопрос
о числе различных среди них становится сложным. Ко-
личество попарно различных правильных ^-раскрасок
графа G называется хроматической функцией графа G
и обозначается через f(G, t).
Очевидно, что наименьшее из чисел £, для которых
/((?, t) ¥= 0, есть %(G).
Для некоторых графов хроматическая функция опре-
деляется совсем легко. Например, f(On, = так как
цвета всех вершин пустого графа можно выбирать неза-
висимо друг от друга. При правильной раскраске пол-
ного графа Кп первая вершина может иметь любой из t
заданных цветов, а для окраски каждой из последующих
вершин разрешается использовать на один цвет меньше,
чем для предыдущей. Поэтому	=
.. .(t — п + 1). Итак, имеем
(t(t — 1)...(/ — п + 1), если t п,
В общем случае, как отмечалось выше, вычисление
хроматической функции сопряжено с большими трудно-
стями. Приведем несколько утверждений, позволяющих
упрощать ее вычисление.
245
Утверждение 55.1. Если G = G\ U G2 U ... U Gk —
дизъюнктное объединение графов, то
k
f(G, *) = ПЖ,О-
г-1
>	Это утверждение вытекает из того, что раскраска
каждой из компонент Gt может выбираться незави-
симо. <1
Утверждение 55.2. Если G = G\\}G2 и графы G{
и G2 имеют только одну общую вершину, то
= (1)
>	Фиксируем какую-либо правильную раскраску j\
графа Gi. Для продолжения ее до правильной раскраски
графа G нужно взять такую правильную раскраску f2
графа G2, при которой цвет f2(v) вершины v, общей для
графов G\ и G2, равен цвету	Поскольку число
правильных 2-раскрасок графа G2, при которых цвет вер-
шины v фиксирован, пе зависит от этого цвета, то для
выбора раскраски /2 имеется f(G2, t)/t возможностей,
откуда и следует равенство (1). <
Утверждение 55.3. Пусть и и v — две несмежные
вершины графа G. Если G\ = G + uv, a G2 получается
из графа G в результате слияния вершин и и v, то
f(G, t) = f(Gh t) + f(G2, 2).
> Число правильных 2-раскрасок графа G, при кото-
рых цвета вершин и и v различны, не изменится, если
к G присоединить ребро uv. Следовательно, это число
равно /(Gi, t). Аналогично, число правильных 2-раскра-
сок графа G, при которых цвета вершин и и v совпада-
ют, равно /(С% 2). Складывая эти два числа, получим
число всех правильных 2-раскрасок графа G, т. е.
/(G,2). <
Предыдущее утверждение позволяет свести вычисле-
ние функции f(G, 2) произвольного графа G к вычисле-
нию хроматических функций графов с большим числом
ребер или с меньшим числом вершин, и следовательно,
в конце концов,— хроматических функций полных гра-
фов. К сожалению, число этих графов может оказаться
катастрофически большим.
Очевидно
Следствие 55.4. Хроматическая функция любого
графа G равна сумме хроматических функций некоторого
246
числа полных графов, порядки которых не больше,
чем IGI.
Поскольку f(Kn, £) —полином от t, то верно
Следствие 55.5. Хроматическая функция f(G, t)
любого графа является полиномом от t.
Поэтому хроматическую функцию f(G, t) обычно на-
зывают хроматическим полиномом графа, G.
Найдем с помощью утверждения 55.3 хроматический
полипом графа G, изображенного на рис. 55.1. При этом
Рис. 55.1
Рис. 55.2
вместо /(G, t) = f(Gi, £)-Ь/(С?2, t) будем писать G =
= Gi ® Сг или рисовать соответствующие графы. На пер-
вом шаге получим ситуацию, представленную на рис. 55.2.
Далее см. рис. 55.3. Итак,
/(G, t) = f(K5, t)+3f(K4, 0 + 2/(Х3, 0 =
= Z(^-l)(^ — 2)(^ — 3)(^-4) +
+ 3ф- 1) (t — 2) (t-3) + 2t(t- 1) (i-2) =
= Z5 - 7Z4 + 19£3 - 23Z2 + 10Z.
Используя утверждение 55.3, можно уточнить вид
хроматического полинома. Следующую теорему предла-
гаем доказать самостоятельно.
Рис. 55.3
Теорема 55.6. Хроматический полином любого
(п, т)-графа G, содержащего ровно к связных компо-
нент, имеет вид
j(G, t) = tn — mtn~} + an-2tn~2 — an-3tn~3 + ... + (—l)n~*ahth,
где Hi — целые неотрицательные числа.
247
Несомненный интерес представляет следующий во-
прос, ответ па который пока пе получен: каким условиям
должен удовлетворять полином, чтобы он был хромати-
ческим полиномом некоторого графа? Любопытно было
бы найти условия, при которых хроматические полино-
мы графов совпадают. Примерами таких графов являют-
ся деревья, которые можно определить в терминах хро-
матических полиномов.
Теорема 55.7. Граф G порядка п является деревом
тогда и только тогда, когда
f(G, =	(2)
> Докажем только необходимость условия теоремы,
а достаточность оставим читателю в качестве упражне-
ния. Пусть G — дерево порядка п. Воспользуемся индук-
цией по п. При п = 1 имеем G = K{, f(G, t) = t, при п==
= 2 — G = K2i f(G, t) = t(t—l). Следовательно, при п =
= 1,2 равенство (2) верно. Предположим теперь, что
это равенство верно для любого дерева G порядка ш,
2^ш< п, и рассмотрим дерево Т порядка п. Если и —
концевая, a v — смежная с ней вершины дерева Т, Т[ =
~Т{и, v), Т2 — Т — и, то
Т\=К2, f{T\,t) = t{t—l), т = т^т2,
и по индуктивному предположению j(T2, t) = t(t — i)n~2.
Применяя затем утверждение 57.2, получаем
= ±t(t - l)t(t - 1)п~2 = t(t - if-1. <1
§ 56. Раскраска ребер
Реберной k-раскраской графа G называется функция
ф, ставящая в соответствие каждому его ребру е число
ф(е) из множества {1, 2, ..., к}. Если ф— реберная рас-
краска и ф(е) = с, то говорят, что ребро е окрашено в
цвет с. Множество всех ребер, окрашенных в фиксиро-
ванный цвет, называют реберным цветным классом. Ре-
берная раскраска называется правильной, если смежные
ребра имеют разные цвета. Граф, допускающий правиль-
ную реберную fc-раскраску, называется реберно к-рас-
крашиваемым. Минимальное число к, при котором граф G
является реберно /с-раскрашиваемым, называется хрома-
тическим индексом {хроматическим классом, реберным
хроматическим числом) графа G и обозначается через
248
Рис. 56.1
%'(G). Если %'((?) = &, то граф G называется реберно
к-хр о магическим.
Поскольку ребра любого графа G смежны тогда, когда
смежны соответствующие вершины реберного графа L(G),
то X'(G) можно определить как хроматическое число
графа L(G), т. е. х'(G) = %(G(G)).
При правильной реберной раскраске каждое множе-
ство ребер одного цвета является паросочетанием. По-
этому число (G) можно рассматри-
вать как наименьшее число паросоче-
таний, на которые разбивается множе-
ство ребер графа G.
Поскольку при любой правильной
раскраске графа G ребра, инцидент-
ные одной вершине, имеют различные
цвета, то /'(G)^A(G). Легко приве-
сти примеры, когда %'(G)>A(G) (см.
рис. 56.1).
Следующая теорема, принадлежа-
щая В. Г. Визингу (1964 г.), дает
поразительно точные оценки хроматического индекса
графа.
Теорема 56.1. Для любого графа G верны не-
равенства
A(G)^x'(G)<A(G)+l.
> Как отмечалось выше, левое из этих неравенств
очевидно, остается доказать правое. Оно верно для К%.
Предположим, что в общей ситуации правое неравенство
пе выполняется. Среди всех графов, ему пе удовлетво-
ряющих, выберем граф G с минимальным числом ребер.
Пусть е\ е EG, Н = G — е\. Имеем
X'(G)>A(G)+1,	(1)
НО
х'(Я)^Д(Я)+1^ A(G)+1.
Пусть A = A(G). Зафиксируем правильную раскраску (р:
ЕН{1, 2, ..., А+1) ребер графа Я и скажем, что
цвет q^{t, 2, ..., А + 1) отсутствует в вершине v^VH,
если ф(е)=/= q для любого ребра е, инцидентного верши-
не v. Так как число возможных цветов больше чем А,
то в каждой вершине отсутствует хотя бы один цвет.
Пусть ei=xyi, a s и t\ — цвета, отсутствующие в вер-
шине х и в вершине у\ соответственно. Исходя из пары
т/i, t\, построим индуктивно две последовательности —
249
вершин z/i, z/2, . •Ук и цветов ti, tz, ..., thl— удовлетво-
ряющие следующим трем условиям:
I)	xy^e^EG	____
II)	цвет ti отсутствует в вершине z/£ (г=1, к);
III)	(p(ei+i) = ^ (г = 2,/с-1).
Пусть последовательности у\, ..., у{ и Ц, ..., ti уже по-
строены. Если существует такое ребро е = ху е ЕН, ин-
цидентное вершине х, что у&{у\, ..., т/J, ср(с) = ^, то
полагаем yi+\ = у и берем в качестве ti+\ один из цветов,
отсутствующих в вершине у. Если же описанного ребра е
не существует, то полагаем k = i. Нужные последова-
тельности построены.
Далее возможны две ситуации.
1) Не существует ребра ху^ЕН, для которого
ф(од) = 4- Переопределим функцию ф, положив ф(ег) = ti
(г=1,й) и оставив значения на других ребрах неизмен-
ными. Получена правильная раскраска ср: EG^{i, 2, ...
..., Д + 1} ребер графа G.
2) Существует ребро ху^ЕН, для которого у(ху} =
= th. Тогда это ребро совпадает с каким-либо из е£ (/ —
= 2, к). Пусть, скажем, ху = е^. Снова переопределим
функцию ср, полагая ф(е£)=^£ (i=l,y — 1). Ребро е> пока
не окрашено, значения функции ф па всех остальных
ребрах не меняются.
Рассмотрим остовный подграф F графа G, ребрами
которого служат все ребра графа G, имеющие цвет s или
th. Очевидно, что степень каждой вершины графа F пе
более двух, и потому каждая его связная компонента
является либо простой цепью, либо простым циклом,
либо Ki. Степени вершин х, yj и yh в F не более едини-
цы, следовательно, эти три вершины не могут входить
в одну компоненту. Рассмотрим отдельно два случая.
а)	Вершины х и уз находятся в разных компонентах
графа F. В этом случае в компоненте, содержащей вер-
шину г/j, переставим цвета 5 и th, т. е. положим ф(е) = $,
если было ф(е) = ^, и наоборот. Тогда цвет 5 будет от-
сутствовать и в вершине х, и в вершине у^ что позволит
положить ф(с^) = §. Вновь получается правильная
(Д + 1)-раскраска ребер графа G.
б)	Вершины х и yh находятся в разных компонентах
графа F. Положим ф(е£) = ^ (г = /, к— 1), а ребро ек
оставим пока не окрашенным. Это действие не затраги-
вает ребер графа F. Переставим теперь цвета $ и th в
250
компоненте графа F, содержащей вершину yk. Теперь
цвет s отсутствует и в вершине и в вершине ук- По-
лагаем далее cp(eh) = s. Построена правильная (Д + 1)-
раскраска ребер графа G.
Итак, в любой ситуации строится правильная
(Д + 1)-раскраска ребер графа G, что противоречит не-
равенству (1). Это противоречие и доказывает теорему. <
В частности, теорема Визинга свидетельствует о том,
что теорема 54.5 о существовании графов без треуголь-
ников с произвольно большим хроматическим числом пе-
рестает быть верной в классе реберных графов, где хро-
матическое число и плотность графа различаются не бо-
лее чем на 1. Тем не менее даже в этом случае, т. е.
в узком классе реберных графов, хроматическое число
определяется сложно: несмотря на то, что величина
%Z(G) может принимать только два значения — A(G)
или A(G)+1 — ее определение является весьма трудной
задачей.
Найдем хроматический индекс для некоторых клас-
сов графов.
Теорема 56.2. Справедливы равенства
X (Я2я+1) = А(^2я+1)+ 1 = 2п+ 1,
%\К2п) = Ь(К2п) = 2п-1.
> Докажем первое равенство. Пусть
Е\ U Е2 U ... U Ei = ЕК2п+{
— разбиение множества ЕК2п+\ на цветные классы. Так
как ребра одного класса не смежны, то
\Е<\ <[\K2n+i\/2] = n,
откуда получаем
I> I ЕК2п+11 / max I	I>| EK2n+1 \/п = 2п + 1.
Из теоремы 56.1 теперь следует, что %'(К2п+}) = I =
= 2п+1.
Перейдем ко второму соотношению. Пусть v — про-
извольная вершина графа К2п. Рассмотрим граф G =
= К2п — v = К2п-\. По доказанному выше ребра графа G
можно раскрасить 2п — 1 цветами. Так как степень лю-
бой вершины и графа G равна 2п — 2, то некоторый цвет
не будет представлен в вершине и. С другой стороны,
множество всех ребер цвета Ci образует паросочетание в
графе G. Поэтому вследствие нечетности IPGI найдется
251
такая вершина что цвет ct будет отсутствовать в
Отсюда следует, что цвета, отсутствующие в вершинах
графа G, попарно различны. Для получения требуемой
раскраски ребер графа Kzn нужно приписать каждому
ребру vui цвет, не представленный в вершине щ-. <
Теорема 56.3 (Д. Кёниг, 1931). Для любого дву-
дольного графа G верно равенство /'(G) = A(G).
> Пусть, напротив, утверждение теоремы неверно,
и G — двудольный граф с минимальным числом ребер,
для которого %'(G) = Д (G)+1. Тогда для любого ребра
e^EG справедливо равенство %' (G — е) = Д (G — е) <
^A(G). Зафиксируем ребро e = uv^EG и правильную
реберную Д (G)-раскраску ср графа G — е и обозначим че-
рез Mw множество цветов, отсутствующих в некоторой
вершине w. Очевидно, что Ми ¥= 0,	0. Если Ми А
A Mv ¥= 0, то ребро е можно окрасить в цвет, принадле-
жащий этому пересечению. Поэтому Ми A Mv = 0. Пусть
s Ми, t е Mv. Рассмотрим цепь L, начинающуюся в вер-
шине р, ребра которой попеременно окрашены в цвета
s и t и которая имеет наибольшую длину среди таких
цепей. Вершина и не входит в L, иначе (р, и)-подцепь
цепи L вместе с ребром е образовала бы в графе G цикл
нечетной длины, что невозможно в двудольном графе.
Переставив цвета 5 и t в цепи L, можно затем окрасить
ребро е в цвет $, что противоречит исходному предполо-
жению. <
Типичная ситуация отражается следующей теоремой,
приводимой без доказательства (см. обзор [21]).
Теорема 56.4. Для почти каждого графа G верно
равенство
= \(G).
§ 57. Связь матроидных разложений графов
с раскрасками
Отметим простые связи, существующие между матро-
идными разложениями графов и раскрасками. Напомним,
что матроидным разложением графа G называется пред-
ставление его в виде объединения
G = Gi U G2 U ... U G(l
ЛЛтрафов, т. е. графов, все связные компоненты которых
суть полные графы; минимальное число ц компонент в
матроидных разложениях графа G — матроидпое чис-
ло |i(G).
252
Зафиксируем правильную раскраску ребер графа G
и рассмотрим разбиение множества ребер на цветные
классы:
Е^Е2\} ...\}Eh = EG.	(1)
Очевидно, что граф Gi, для которого VGi = VG, EGi = E^
является Л7-графом, и
G = Gx U G2 U ... U Gh	(2)
— матроидное разложение. Итак, разбиение на цветные
классы (1) определяет матроидное разложение (2) гра-
фа G. Тем самым доказано
Утверждение 57.1. Для любого графа G верно
неравенство
Учитывая это неравенство и теорему 56.3, получаем
Утверждение 57.2. Если граф G не содержит тре-
угольников, то
Для любого двудольного графа G верно равенство
ji(G) = A(G).
> Если граф G пе содержит треугольников, то его
реберный граф L(fi) и граф клик (?(G) могут разли-
чаться только изолированными вершинами. Следователь-
но, если Xq(G)—хроматическое число графа (?(G), то
%Q(G) = %'((?), так что для графа G без треугольников
P'(^)==Xq(^)===X,(^)- Применяя теорему 56.3, получим
второе равенство. <
Для матроидного числа произвольного графа хрома-
тическое число его графа клик является верхней грани-
цей. А именно, верно
Утверждение 57.3. Для любого графа G справед-
ливо неравенство
h(G)^xq(G).	(3)
> Подграф, порожденный в G объединением клик,
входящих в один цветной класс при правильной вершин-
ной раскраске графа клик Q(G), является Af-графом, по-
скольку все его связпые компоненты — полные графы.
Следовательно, если
FiU72U...U Vh=VQ(G)
—- разбиение на цветные классы множества вершин гра-
фа клик, a Gi получается из порожденного подграфа
253
G(K) в результате присоединения всех вершин из 7G\7i
как изолированных, то G = Gi U G2 U . . . U Gk — матроид-
ное разложение. Тем самым неравенство (3) доказано. <
В качестве иллюстрации рассмотрим граф G, изобра-
женный на рис. 57.1; для него Q(G) = K4, Xq(G) =
= X'(G) = 4, И((7) = 3.
Утверждение 57.4. Для произвольного графа G
равенства p(G) = 2 и Xq(G) = 2 равносильны.
> Если Xq(G) = 2, то |i(G)^2. Но при pi(G)= 1 ни-
какие две максимальные клики графа G не пересекают-
ся, и потому (2(G)—пустой граф, Xq(G)=1. Итак, при
Zq(G) = 2 и p(G) = 2.
Остается доказать истинность импликации
И(С) = 2=^(£) = 2.	(4)
Доказательство основано на следующей очевидной
комбинаторной лемме.
Лемма 57.5. Пусть S — конечное множество, каждо-
му из элементов которого приписан один из двух фикси-
рованных цветов или оба эти цвета. Если для любой пары
элементов множества S существует общий приписанный
им цвет, то тогда и все элементы множества имеют об-
щий приписанный им цвет.
Пусть теперь
G = G!UG2	(5)
— матроидпое разложение графа G. Достаточно доказать,
что любой полный подграф графа G целиком содержится
•	в каком-либо из G,; если это так, то
разложение (5) определяет правиль-
/- - - \ ную 2-раскраску графа клик и истин-
пость импликации (4) доказана.
у \у \ Каждому из ребер графа G следую-
*	*	* щим образом припишем один из цве-
Рис. 57.1 тов {1, 2} или оба эти цвета. Именно,
всем ребрам графа Gi (Z = 1, 2) при-
писывается цвет i. Пусть теперь Q — клика графа G,
ei, е EG (Q).
Если ребра е{ и е2 смежны, то в порожденном под-
графе G(Q) существует третье ребро е, смежное с ними
обоими. Какие-то два из этой тройки ребер имеют общий
цвет, поскольку цветов только два. По концы этих трех
ребер вместе входят в одну из связных компонент гра-
фа Gi, являющихся полными графами, следовательно,
и третье ребро имеет тот же цвет. Итак, для любой пары
254
смежных ребер графа G(Q) существует общий приписан-
ный им цвет.
Если же ребра е\ = ищ\ и ^ = ^2^2 не смежны, то в
графе G(Q) есть еще четыре ребра сз = ищ^, £4 = ^2,
в5 = U\V2, eQ = V\U2. Для каждой пары смежных из этих
ребер существует общий цвет, откуда очевидно вытека-
ет, что существует цвет, общий для ребер ej и ер.
Доказано, что любые два ребра графа G(Q) имеют
общий цвет. В силу леммы 57.5 существует общий цвет,
например 1, приписанный всем ребрам графа G(Q). По-
следнее означает, что G(Q) содержится в одной из ком-
понент графа G\. <1
Из утверждения 57.4 вытекает
Следствие 57.6. Если %(G) = 3, то и p(G) = 3.
§ 58. Раскраска планарных графов
Проблема раскраски планарных графов является од-
ной из самых знаменитых проблем теории графов. Воз-
никшая в середине прошлого века, опа до сих пор при-
влекает внимание специалистов и любителей.
Первоначально вопрос формулировался в следующем
виде: достаточно ли четырех красок для такой раскраски
произвольной географической карты, при которой любые
две соседние страны окрашены в различные цвета? При
этом рассматриваются лишь те карты, в которых грани-
ца любой страны состоит из одной замкнутой линии,
а соседними считаются страны, имеющие общую грани-
цу ненулевой длины.
Позднее понятия карты и ее раскраски были форма-
лизованы следующим образом. Связный плоский мульти-
граф без мостов называется картой. Грани карты, имею-
щие общее ребро, называются смежными. Функция /,
ставящая в соответствие каждой грани вГ карты нату-
ральное число /(Г)^{1, 2, ..., к} — цвет грани Г,— на-
зывается к-раскраской, если цвета смежных граней раз-
личны. Карта называется k-раскрашиваемой, если для
нее существует к-раскраска.
В 1879 году британский математик А. Кэли опубли-
ковал в первом томе Трудов Лондонского географиче-
ского общества статью, посвященную проблеме раскрас-
ки карт, в которой сформулировал гипотезу четырех кра-
сок (сама задача была известна и ранее).
Гипотеза четырех красок: всякая карта 4-
р искрашиваема.
255
Часто пользуются другой формулировкой гипотезы
четырех красок: всякий планарный граф ^-раскрашиваем.
Поскольку планарный граф по определению изомор-
фен некоторому плоскому, то эквивалентность этих двух
формулировок гипотезы четырех красок вытекает из сле-
дующей теоремы.
Теорема 58.1. Карта G является к-раскрашиваемой
тогда и только тогда, когда геометрически двойственный
граф G* вершинно к-раскрашиваем.
> Поскольку граф G плоский и не имеет мостов, то
двойственный граф G*— плоский граф (без петель).
Пусть задана некоторая правильная /с-раскраска карты G,
Построим /с-раскраску графа G*, приписав каждой его
вершине цвет той грани, в которой находится эта верши-
на. Так как вершины графа G* смежны тогда и только
тогда, когда смежны содержащие их грани, то получен-
ная раскраска оказывается правильной.
Аналогичным образом можно перейти от правильной
раскраски графа G* к правильной раскраске карты G. <
Заметим, что существуют плоские графы, которые
нельзя раскрасить правильно менее чем четырьмя цве-
тами. Таков, например, граф К^.
Первоначально гипотеза четырех красок пе показалась
слишком сложной и появилось несколько ее «доказа-
тельств», в которых позднее были обнаружены пробелы.
В дальнейшем эту проблему, сбивающую с толку про-
стотой формулировки, пытались решить многие извест-
ные математики. Большой интерес к теории графов, воз-
никший в связи с гипотезой четырех красок, способство-
вал открытию многих важных результатов, поскольку
они казались полезными для решения проблемы. До сих
пор эта проблема остается мощным стимулом исследова-
ния различных свойств графов.
Сначала рассмотрим раскраски планарных графов
двумя и тремя цветами.
Согласно теореме Кёнига /(G) = 2 для непустого гра-
фа G тогда и только тогда, когда он не содержит цик-
лов нечетной длины, откуда несложно получить следую-
щее утверждение.
Утверждение 58.2. Плоский двусвязный граф яв-
ляется дихроматическим тогда и только тогда, когда гра-
ница каждой его грани содержит четное число ребер.
> Достаточно доказать, что плоский двусвязный граф,
граница каждой грани которого состоит из четного числа
ребер, является двудольным. Рассмотрим произвольный
256
простой цикл С такого графа. Этот цикл делит плоскость
на две части — внутреннюю (по отношению к циклу)
и внешнюю. Считаем, что сам цикл принадлежит каж-
дой из частей.
Пусть внутренняя часть плоскости содержит грани
Г1, Гг, ..1\ с числом ребер в их границах Zi, Z2, ..Zh
соответственно. Так как любое из чисел Ц четное, то их
сумма также четная. Но каждое ребро, не принадлежа-
щее циклу С, входит в эту сумму дважды, откуда сле-
дует, что длина цикла С четная. Из теоремы 9.1 следует,
что рассматриваемый граф является двудольным. <
Аналогичное утверждение верно и для односвязных
графов, только в этой ситуации каждый мост, входящий
в границу грани, учитывается дважды.
Утверждение 58.3. Карта G является 2-раскраши-
ваемой тогда и только тогда, когда граф G эйлеров.
>	Учитывая теорему 58.1, нужно лишь доказать, что
геометрически двойственный граф G* является двудоль-
ным тогда и лишь тогда, когда граф G эйлеров. Послед-
нее оставлено читателю. <
Теорема 58.4 (М. Крол, 1973 г.). Плоский граф
3-раскрашиваем тогда и только тогда, когда он является
подграфом плоской триангуляции с четными степенями
вершин.
>	Необходимость. Будем считать, что порядок
рассматриваемого графа более трех (для К% утвержде-
ние тривиально). Пусть вершины плоского графа G пра-
вильно раскрашены тремя цветами 1, 2, 3. Рассмотрим
произвольную отличную от треугольника грань Г этого
графа. Возможны следующие случаи.
1)	Границей грани Г является цикл четной длины,
вершины которого окрашены в два цвета, например,
1 и 2. Тогда поместим внутри Г вершину w, соединив
ее ребрами с каждой из вершин этого цикла, и окрасим
эту вершину в третий цвет 3 (рис. 58.1, а).
2)	Границей грани Г является 4-цикл C = (ki, V2, v%,
V4, щ), вершины которого окрашены в три цвета, напри-
мер, v\ — в цвет 1, V2 — в 2,	— в 3, щ— в 2. В этом
случае поместим внутри грани Г цепь L = (v\, w\, W2, Уз),
связывающую несмежные вершины цикла С, имеющие
различные цвета. Соединим W\ и W2 с вершинами этого
цикла, окрашенными в один цвет. Для получения пра-
вильной раскраски остается каждой из вершин w\ и W2
приписать цвет 1 или 3, однозначно определенный (см.
рис. 58.1, б).
17 в. А. Емеличев и др.	257
3)	Границей грани Г является Z-цикл, I > 4, верши-
ны которого окрашены в три цвета. Поместим в Г вер-
шину и?, припишем ей цвет 3 и соединим ее со всеми
вершинами цикла, имеющими цвета 1 и 2. Грань Г при
этом разобьется на несколько граней, границами которых
а	б	б
Рис. 58.1
будут треугольники и 4-циклы (рис. 58.1, в). С послед-
ними поступим так же, как в предыдущих случаях.
Проделав описанные построения для выбранной гра-
ни Г, отличной от треугольника, получим новый правиль-
но 3-раскрашенный граф, в котором Г уже разбита на
треугольники. Выполнив эти операции для всех таких
граней, придем к правильно 3-раскрашенной плоской
триангуляции, подграфом которой и будет исходный граф.
Покажем, что степени всех вершин этой триангуляции
четны. Пусть и — произвольная вершина, имеющая, для
определенности, цвет 1. Поскольку G'#=K3, то вершины,
смежные с и, образуют цикл. Так как для их раскраски
достаточно двух цветов 2 и 3, то этот цикл имеет четную
длину и, следовательно, степень вершины v четная.
Достаточность. Пусть граф G является подгра-
фом плоской триангуляции Т с четными степенями вер-
шин. Покажем, что он 3-раскрашиваем.
Поскольку Т — эйлеров граф, то согласно утвержде-
нию 58.3 его грани можно раскрасить двумя цветами,
например, красным и синим. Ориентируем ребра, огра-
ничивающие каждую красную грань, так, чтобы при
движении по ориентированному ребру грань оставалась
справа. Произвольную вершину v графа Т окрасим в
цвет 1 и для каждой вершины w рассмотрим любую
простую (и, гр)-цепь Р. Пусть а(Р) и (3(Р) —числа ре-
бер этой цепи, ориентация которых совпадает и, соответ-
ственно, не совпадает с направлением цепи от v к w.
Припишем вершине w цвет c(w) == 1 + а(Р) — £(Р) (mod 3).
258
Покажем, что выполненная таким образом раскраска
окажется правильной. Сперва докажем, что окраска лю-
бой вершины w не зависит от выбора цепи Р. Рассмот-
рим произвольный простой цикл С в графе Т, ограничи-
вающий некоторую область F. Если при движении по
ориентированному ребру,
принадлежащему С, от его
начала к концу область на-	/к\У // \
ходится справа от ребра, то -------ЬЛ / с \\/7
назовем это ребро а-ребром,	I /	/v/ к
в противном случае — b-реб-	\1
ром. Пусть а и р - числа	--
а-ребер и, соответственно,	-
&-ребер в С, а к и s — числа	Рис. 58.2
красных и синих внутрен-
них граней в области F. Каждое а-ребро принадлежит
красной внутренней грани, а &-ребро — синей внутрен-
ней грани.
Вычислим число р ребер, находящихся внутри цик-
ла. С одной стороны, они принадлежат красным граням,
поэтому р = Зк — а. С другой стороны, эти ребра принад-
лежат синим граням, так что р = 3s — 0. Отсюда Зк — а =
= 3$ — р, или а — р = 3& — 3s = О (mod 3).
Пусть Р\ и Рг-—две различные простые (р, м)-цепи.
Покажем, что ci(zz?) = c2(w), где
Ci(w) = 1 + а(Р<) — fi(Pi) (mod3),	i = 1, 2.
Вначале рассмотрим случай, когда цепи Pi и Рг не
имеют общих вершин, отличных от и и w (см. рис. 58.2,
на котором красные грани обозначены буквой К, а си-
ние — С).
Пусть С — цикл, полученный объединением цепей Pi
и Р2. Для определенности считаем, что ориентация а-ре-
бер совпадает с направлением цепи Рь Тогда С содер-
жит а(Р1)+р(Рг) a-ребер и a(P2)+fi(Pi) &-ребер. По до-
казанному выше
(a (Л) + р (Р2)) - (а(Р2) + р (Pi)) 0 (mod 3),
а (Л) - ₽ (Л) а (Р2) - р (Р2) (mod 3),
откуда вытекает, что ci(w) = c2(zz?).
Если цепи Pi и Р2 имеют общие вершины, отличные
от v и w, то объединение этих цепей разбиваем на про-
стые циклы и цепи, а далее проводим доказательство
так, как для случая одного цикла.
17*	259
Таким образом доказано, что после выбора цвета вер-
шины v остальные вершины графа Т однозначно рас-
крашиваются тремя цветами. Покажем, что эта раскра-
ска является правильной. Рассмотрим любые две смеж-
ные вершины и и w графа Т, отличные от вершины р.
Из простых (у, и)- и (v, w)-цепей выберем кратчайшую.
Пусть ею окажется (у, ш)-цепь Р. Рассмотрим также
(у, м)-цепь, полученную при присоединении к цепи Р
ребра wu. Тогда
с (w) = 1 + а (Р) - ₽ (Р) (mod 3),
с(и) = 1 + а(Р) - Р(Р)± 1 (mod3)
(знак последнего слагаемого зависит от ориентации реб-
ра wu). В случае, когда v = w, последнее соотношение
принимает вид с (и) = 1 ± 1.
Отсюда следует, что c(w)¥=c(u), и раскраска графа Т
является правильной.
Поскольку G — подграф 3-раскрашиваемого графа Т,
то он также 3-раскрашиваем. <
Утверждение 58.2 и теорема 58.4 дают необходимые
и достаточные условия существования правильной рас-
краски вершин плоского графа двумя и тремя цветами.
Однако между этими утверждениями есть принципиаль-
ная разница: условие утверждения 58.2 легко проверяе-
мо, но не известно эффективных способов проверки усло-
вий теоремы 58.4. Приведем без доказательства одно
легко проверяемое достаточное условие 3-раскрашивае-
мости плоского графа.
Теорема 58.5. Любой плоский граф, содержащий
менее четырех 3-циклов, 3-раскрашиваем.
§ 59. Проблема четырех красок
Гипотеза четырех красок привлекала внимание мно-
гих исследователей. Уже в 1880 году появилось первое
доказательство А. Кемпе. Ошибка в этом доказательстве
была обнаружена Р. Хивудом в 1890 году. Одновременно
он показал, что если в формулировке гипотезы слово
«четыре» заменить на «пять», то она легко доказывается.
Теорема 59.1 (Р. Хивуд, 1890 г.). Каждый планар-
ный граф 5-раскрашиваем.
> По-прежнему, не теряя общности, будем рассматри-
вать плоские графы. Проведем доказательство индукцией
по числу вершин графа. Теорема справедлива для гра-
260
фов с не более чем пятью вершинами. Предположим,
что она верна для графов порядка, не превосходящего п,
п > 5.
Рассмотрим произвольный плоский граф G порядка
п+\. Согласно утверждению 38.5 этот граф содержит
вершину р0, степень которой не превосходит пяти. Пусть
N = 2V(po)—окружение вершины vo в графе G. Отдельно
рассмотрим два случая.
1) I7VI ^4. По индуктивному предположению граф
G — vo 5-раскрашиваем; раскрасим его вершины пятью
цветами. Затем окрасим вершину vo в тот из пяти
цветов, который пе использован при раскраске вер-
шин из N.
2) |7V| = 5. В множестве N существуют две несмеж-
ные вершины щ и р2, иначе G(N) = K$ и граф G не пла-
нарен. Граф G', полученный из G — vQ слиянием этих
вершин в вершину v (см. рис. 59.1), является плоским
и по индуктивному предположению 5-раскрашиваемым.
Фиксируем какую-либо из его правильных 5-раскрасок.
В графе G окрасим вершины v\ и р2 в цвет вершины р,
а остальные отличные от v вершины — в те же цвета,
что и соответствующие вершины графа G'. Затем при-
пишем вершине Vq цвет, не использованный при раскра-
ске вершин из 7V.
Таким образом, получена правильная 5-раскраска
графа G. <1
Трудность проблемы четырех красок привела к появ-
лению большого числа равносильных ей формулировок.
Изучая эквивалентные задачи, исследователи пытались
доказать гипотезу четырех красок.
Теорема 59.2. Следующие три утверждения экви-
валентны:
1)	произвольный плоский граф i-раскрашиваем;
2)	любая кубическая карта i-раскрашиваема]
261
3)	хроматический индекс произвольной кубической
карты равен 3.
> Вначале докажем истинность импликации 2)=^1).
Согласно теореме 58.1 достаточно показать, что 4-рас-
краска произвольной карты определяется 4-раскраской
некоторой кубической карты.
Пусть G — произвольная карта, и — ее вершина сте-
пени 2. Замена ребер uv и uw, инцидентных вершине и,
ребром vw приводит к новой карте G. Легко видеть, что
правильная раскраска одной карты очевидным образом
переносится на вторую. Поэтому без ограничения общ-
ности можно считать, что в графе G нет вершин второй
степени.
Пусть и — произвольная вершина степени I > 4,
7V(^) = {z;i, V2, ..., vt} — окружение вершины и, причем
вершины в N(u) так занумерованы, что обход ребер в
последовательности uv^ UV2, ..., uvt происходит в на-
правлении движения часовой стрелки. Заменим вершину
и простым циклом C = (ui, иг, ..., uh щ) и соединим Ui
и Vi ребром, i = l,l (рис. 59.2). Проводя аналогичную
процедуру для каждой вершины графа G, степень кото-
рой больше трех, получим кубическую карту, которая,
Рис. 59.2
по предположению, 4-раскрашиваема. Искомая 4-раскра-
ска граней карты G получается стягиванием каждого до-
бавленного цикла в точку.
Теперь докажем, что 1)=^3). Пусть произвольный
плоский граф 4-раскрашиваем. Рассмотрим некоторую
кубическую карту G. Согласно теореме 58.1 эта карта
также является 4-раскрашиваемой. Фиксируем одну из
ее 4-раскрасок и будем считать, что выбранные 4 цвета
составляют абелеву группу А = {0, а, &, а+&}=(а)4-
262
+ (Ь)—прямую сумму двух циклических групп второго
порядка. (Это коммутативная группа, в которой а + а =
= Ь + Ь = 0.) Определив теперь цвет каждого ребра гра-
фа G как сумму цветов двух разделяемых этим ребром
граней, получим правильную раскраску ребер тремя цве-
тами а, Ь, а + Ь.
Наконец, докажем, что 3)=>2). Пусть G —-кубиче-
ская карта и %'(G) = 3. Фиксируем правильную ребер-
ную 3-раскраску графа G цветами а, Ъ и с. Рассмотрим
подграф графа G, порожденный ребрами, окрашенными
в цвета а и Ъ. Очевидно, что этот подграф является
объединением простых циклов. Припишем точкам пло-
скости, лежащим внутри циклов, цвет 1, а вне — цвет 2.
Аналогично, точкам плоскости, лежащим внутри циклов,
индуцированных ребрами, имеющими цвета а и с, при-
пишем цвет 3, а вне таких циклов — цвет 4. Таким об-
разом, каждой грани карты G окажется приписанной
одна из следующих пар цветов: (1, 3), (1, 4), (2, 3),
(2, 4). Эти пары определяют раскраску карты четырьмя
цветами, поскольку смежным граням соответствуют раз-
ные пары. <
В связи с проблемой четырех красок Г. Биркгоф в
начале века поставил вопрос: какими свойствами должны
обладать минимальные плоские графы, вершины кото-
рых нельзя правильно раскрасить четырьмя цветами?
Такие графы называются неприводимыми. Далее изуча-
лись графы, их называли приводимыми конфигурация-
ми, которые не являются подграфами неприводимых
графов.
В дальнейшем многие математики изучали гипотети-
ческие неприводимые графы и приводимые конфигура-
ции. Эти исследования позволили довести число вершип
в графах, для которых доказана их 4-раскрашиваемость,
до 96.
В 1969 году X. Хееш свел проблему четырех красок
к исследованию большого, но конечного множества U так
называемых неустранимых конфигураций. Им было по-
казано, что для любого максимального плоского графа G
найдется подграф G, изоморфный некоторой конфигура-
ции из U и такой, что если граф G является 4-раскра-
шиваемым, то 4-раскрашиваем и граф G. Позже число
таких неустранимых конфигураций было уменьшено до
1482. В 1976 году коллективу математиков и програм-
мистов, возглавляемому К. Аппелем и В. Хейкеном, уда-
лось правильно раскрасить все графы из множества U
263
четырьмя цветами, затратив на это около 2000 часов ра-
боты мощной ЭВМ, что позволило им заявить о доказа-
тельстве гипотезы четырех красок. Тем не менее трудно
согласиться с таким доказательством, поскольку и све-
дение общего случая к неустранимым конфигурациям,
и раскраску последних очень сложно повторить.
Понятия (плоской) карты и ее раскраски естественно
распространяются на другие поверхности.
Пусть S — некоторая поверхность, любая карта на
которой допускает раскраску % (5) цветами, и существует
карта на S, пе допускающая раскраски % (5)— 1 цвета-
ми. Тогда % (5) называется хроматическим числом по-
верхности S.
Теорема 59.3 (Г. Рипгель, Д. Янгс, 1968 г.). Если
Sp — сфера с р> 0 ручками, то
7 + ]/1 + 48р
2
х(5р) =
Подробно о раскраске карт, расположенных на про-
извольных поверхностях, см. в [26].
§ 60. Другие подходы к раскраске графов
В 1943 г. Г. Хадвигер выдвинул гипотезу, тесно свя-
занную с проблемой четырех красок.
Гипотеза Хадвигер а. Любой связный п-хрома-
тический граф стягиваем к Кп.
Для п С 4 гипотеза подтверждается. В самом деле,
при п = 1 утверждение тривиально. При п = 2 каждый
связный граф стягивается к ребру, а при п = 3 — содер-
жит цикл и потому стягивается к К?>. Следующая теоре-
ма доказывает гипотезу для п = 4.
Теорема 60.1. Каждый связный ^-хроматический
граф стягиваем к К±.
> Пусть G — связный 4-хроматический граф. Если в
G есть точки сочленения, то некоторый его блок дол-
жен быть 4-хроматическим, иначе из теоремы 53.3 сле-
довало бы, что %(G)< 4. Стянем G к этому блоку. По той
же причине блок останется 4-хроматическим после стя-
гивания ребер, инцидентных вершине степени 2. Таким
образом, не теряя общности, можно считать G блоком
со степенями вершин не менее трех. .
Пусть C = (V], V2, ..., vp, щ)—простой цикл макси-
мальной длины р в G. Очевидно, что р > 4. Простую
цепь, связывающую две несоседние вершины цикла С и
264
пе содержащую других вершин этого цикла, назовем
С-хордой. Покажем, что для любой вершины щ цикла С
существует С-хорда, которой принадлежит эта вершина.
Так как deg v\ 3, то имеется ребро е = ищ, не принад-
лежащее С. Если и е УС, то ребро е является С-хордой.
Пусть u&VC. Тогда по теореме 34.1 существует простой
цикл Ci=(vi, и, ..., V2, . •щ), содержащий ребро е и
а	й
Рис. 60.1
вершину v2. Цепь Л = (щ, и, ..., v2) должна иметь неко-
торую вершину отличную от и2 и принадлежащую
циклу С, иначе С не был бы простым циклом макси-
мальной длины. Часть цепи L от v\ до первой вершины,
принадлежащей циклу С, и будет искомой С-хордой.
Предположим, что существуют две С-хорды =
= (Vi, ..., Vj) и T2 = (vh, ..., vt) с общей вершиной t
вне С. Тогда часть графа, состоящая из С, Т\ и Т2, стя-
гивается к Х4. Один из вариантов стягивания изображен
па рис. 60.1, а.
Теперь рассмотрим случай, когда пе существует пе-
ресекающихся С-хорд. Любая С-хорда делит цикл С на
две простые цепи. Выберем такую С-хорду Т\, чтобы
одна из этих цепей С'=(pz, ..., Vj) была кратчайшей,
и возьмем вершину vk па этой цепи (такая вершина су-
ществует, поскольку С-хорда соединяет две несоседпие
вершины цикла). Рассмотрим некоторую С-хорду Т2 ==
= (^, ..., Vi}. Если при этом вершина vt будет располо-
жена на С', то цепь (vk, ..., vz), принадлежащая циклу
С, будет короче, чем С'. Следовательно, vt не лежит на
цепи С'. В этом случае часть графа, состоящая из С, Т\
и Т2, стягивается к К\. Один из вариантов стягивания
показан на рис. 60.1, б.
265
После того как будет получен граф Ki, оставшуюся
часть исходного графа стянем к К\. <
Известно, что утверждение гипотезы Хадвигера при
л = 5 эквивалентно гипотезе четырех красок. А именно,
верна следующая
Теорема 60.2. Следующие два утверждения экви-
валентны'.
1) гипотеза четырех красок верна*,
2) любой связный ^-хроматический граф стягива-
ем к К$.
В заключение этого параграфа рассмотрим один алге-
браический подход к проблеме раскраски плоских гра-
фов. Детально об этом см. [14].
Пусть G — плоский граф, и ip: VG -+• А (где А =
= {О, а, Ъ, а + Ъ} =(а) + (&) — прямая сумма двух цикли-
ческих групп второго порядка)—его раскраска. Тогда
условием правильности выбранной раскраски окажется
следующее условие: уу = 'ф(Рг) + 'ф(р;):^О для любого реб-
ра ViVj графа G. Поэтому для произвольного цикла С =»
= (pi, V2, ..., vn, vn+i), vn+i = vi, должны выполняться
условия
_  п
г/i.i+i^O, i = 1,п,	2ум+1 = 0,	(1)
i—1
Пусть теперь G — произвольный связный граф, каж-
дому ребру о#} которого поставлена в соответствие пере-
менная Уц. Получим систему уравнений S(G), записав
соотношения вида (1) для каждого цикла графа G, и си-
стему 8(G)—для каждого цикла из некоторого фикси-
рованного базиса циклов.
Лемма 60.3. Каждому решению системы S(G) при
фиксированной окраске 'ф(Ро) некоторой вершины Vq од-
нозначно соответствует правильная раскраска графа G
четырьмя цветами.
> Для заданной вершины va G VG рассмотрим про-
извольную цепь Ра = (ро, Pi, ..., ра) и примем
а-1
(^а) = 'Ф (*>о) + 2 УЛ.Л+11	(2)
fe==o
где уц составляют решение системы S(G].
В силу (1) значение 'ф(Ра) не зависит от выбора це-
пи Ра, поэтому оно определяет цвет вершины va. Так
как Угэ^О для ViV^EG, то любые смежные вершины
имеют различные цвета. Таким образом, раскраска, за-
даваемая формулой (2), правильная. <1
266
Так как граф может содержать большое число цик-
лов, то перейдем от системы уравнений 8(G) к систе-
ме 8(G).
Теорема 60.4. Каждому решению системы S(G}
при фиксированной окраске *ф(ь?о) некоторой вершины
Vq однозначно соответству-
ет правильная раскраска
графа G четырьмя цве-
тами.
> В силу леммы 60.3
достаточно показать, что
решение системы S(G)
является и решением си-
стемы 8(G). Для этого
вначале рассмотрим
простой цикл
произвольный
C = (vq, Vi, ..., Vi-i, vh Vi+i, ..., vp-i, vp, vP+i, ..., vn, y0J,
не принадлежащий базису циклов С графа G. Известно
(§ 21), что С можно представить в виде суммы по мо-
дулю 2 нескольких циклов из С. Пусть 67 = 671 ® б?2,
Сь С,
С1==(Ро, У1, Vh Pn + i, ..., Vn+h, Vp, Vp+i, ..., Vn, Vq},
C2 = (Vi, Vi+l, ..., Vp-\, Vp, Vn+k, Vn+l, Vt)
(рис. 60.2). Тогда
2 У1) ~ 2 Уг) 4“ 2 Уг) '
ij^EC ij^EC1 i)GEC2
— %(У1,п+1 + Уп+1,п+2 + . . . + Уп+hcp) = 0.
Аналогичные рассуждения можно привести и в том слу-
чае, когда цикл С является суммой не двух, а большего
числа циклов из базиса циклов С. Значит, соотношение
(1) выполняется для любого простого цикла. Если же
цикл С не простой, то необходимо представить его в ви-
де объединения нескольких простых циклов, для каждо-
го из которых выполняется (1). <
§ 61. Совершенные графы
Как отмечалось выше, хроматическое число и плот-
ность любого графа удовлетворяют очевидному неравен-
ству %(6?)>ф(6?). При этом, как свидетельствует теоре-
ма 54.5, разность %(£) — qp(GJ может быть как угодно
267
велика. В этом параграфе изучаются графы, обладающие
тем свойством, что хроматическое число и плотность не
только самого графа, но и каждого его порожденного
подграфа, равны.
Граф называется совершенным, если
Х(Я) = ф(Я)	(1)
для любого его порожденного подграфа Н.
Из этого определения непосредственно вытекает, что
всякий порожденный подграф любого совершенного гра-
фа является совершенным.
Очевидно, что все полные и пустые графы совершен-
ны. Примером совершенного графа может служить также
каждый двудольный граф, поскольку для любого его под-
графа Н либо %(Я) = ф(Я) = 2 (если Н непустой), либо
% (Я) = ф (Я) == 1 (при пустом Я).
Совершенные графы введены К. Бержем в 1960 году.
Интерес к этим графам связан прежде всего с двумя
обстоятельствами. Во-первых, многие трудно разрешимые
в общем случае задачи теории графов успешно решают-
ся для совершенных графов. Во-вторых, ряд широко из-
вестных классов графов содержится в классе совершен-
ных. Таковы, например, все двудольные, пороговые,
расщепляемые и триангулированные (см. § 62) графы.
Исследования, посвященные совершенным графам и,
в частности, связанной с ними гипотезе Бержа, речь
о которой пойдет ниже, во многом определяют лицо со-
временной теории графов.
Теорема 61.1. Граф, дополнительный к совершен-
ному графу, также является совершенным.
Эту теорему в виде гипотезы сформулировал К. Берж
в 1961 г. Позже ее независимо доказали Д. Р. Фалкер-
сон (1971 г.) и Л. Ловас (1972 г.). Ниже приводится
доказательство Л. Ловаса.
Лемма 61.2. Следующие два утверждения равно-
сильны*.
1) граф G является совершенным-,
2) в любом непустом порожденном подграфе G' гра-
фа G есть такое независимое множество вершин А, что
ф(С'-4)<ф((Г).	(2J
> Пусть G — совершенный граф, G' — его непустой
порожденный подграф. Тогда x(G') = ф(С'). Следова-
тельно, существует правильная ф(С')-раскраска графа G'.
Если А — какой-либо цветной класс при этой раскраске,
268
то множество А независимо и %(6Г —Л)^<р(С?')—1- Из
последнего неравенства вытекает (2), поскольку <р(Я)=^
=С%(Я) для любого графа Я.
Пусть теперь для некоторого графа G верно утверж-
дение 2). Нужно доказать, что для любого порожденно-
го подграфа G' графа G выполняется неравенство
x(G')<<p'(G')\	(ЗУ
Из неравенства (3) следует равенство плотности и хро-
матического числа, ибо противоположное неравенство
всегда верно. Воспользуемся индукцией по |G'I. Если
G' — пустой граф, то (3) тривиально. Пусть G' непуст,
IG'I = к> 1 и для каждого порожденного подграфа мень-
шего чем к порядка верно неравенство, аналогичное не-
равенству (3). Для независимого множества А вершин
графа G', удовлетворяющего неравенству (2), имеем по
индуктивному предположению:
X(G'-4) = <p(G'-4)<<p(G').
Но так как множество А независимо, то
Х(П<Х((?'-Л)+1<ф(С')+1, %(С')^ф(С'),
и равенство (3) доказано. <1
Пусть G и Я — произвольные графы. Будем считать
их множества вершин не пересекающимися и следующим
образом определим новый граф F. Отметим произвольную
вершину v графа G и положим VF =(Уб U VH)\v. Вер-
шины а и Ъ графа F будем считать смежными, если вы-
полняется одно из следующих трех условий:
1)	ab^EG,
2)	ab^EH,
3)	a^VG, b^VH, av^EG или b^VG, a^VH,
bv^EG.
Скажем, что граф F получается из графа G в резуль-
тате замены вершины v графом Н.
Лемма 61.3. Граф, полученный из совершенного
графа в результате замены вершин совершенными гра-
фами, также является совершенным.
> Очевидно, что достаточно рассмотреть лишь одну
замену вершины. Пусть G и Я — совершенные графы,
a F получается из G в результате замены вершины v гра-
фом И. Учитывая лемму 61.2, достаточно показать, что
в любом порожденном подграфе F' графа F есть незави-
симое множество вершин А, пересекающееся с каждой
269
наибольшей кликой графа F', Вначале пусть F' = F, За-
фиксируем какую-либо правильную <p(G)-раскраску гра-
фа G. Пусть В — цветной класс, содержащий вершину v.
Выберем в графе Н такое независимое множество вершин
С, что ф(Я — С)<ф(С). Теперь покажем, что множество
(5UC)\p = A удовлетворяет нужным условиям. В самом
деле, В независимо в С, С независимо в Н, Если же Ъ е
^В\р, с^С, то вершины Ь и v не смежны в G, а потому
Ъ и с не смежны в F, Итак, А — независимое множество
вершин графа F.
Остается показать, что А пересекается с каждой наи-
большей кликой графа F, Пусть К — одна из таких клик,
L = K(} VH, Если L=/=0, то L содержит какую-либо наи-
большую клику D графа Я, поскольку любая вершина
графа G — v либо смежна в F с каждой вершиной графа
Я, либо ни с одной из них. Так как D П С Ф 0, то КП
ПА¥=0. Если же £ = 0, то K^VG\v, ф(К)=|К|<
ф(С —	ф(С). Но очевидно, что ф(С)^ф(К). Сле-
довательно, |К| ==ф(бг), клика К пересекается с каждым
цветным классом любой правильной ф(С)-раскраски
графа G, КП(Я\р) =/= 0, значит, КПА =/= 0. Доказано,
что в графе F есть независимое множество вершин,
которое пересекается с каждой наибольшей кликой
этого графа.
Теперь заметим, что аналогичное свойство имеет лю-
бой порожденный подграф F' графа К, поскольку F' либо
получается из некоторого порожденного подграфа G' гра-
фа G в результате замены вершины v порожденным под-
графом Я' графа Я, либо является порожденным подгра-
фом графа G. <1
Лемма 61.4. В любом совершенном графе G есть
клика, пересекающая каждое наибольшее независимое
множество вершин графа G.
> Проведем доказательство от противного. Пусть G —
совершенный граф, для каждой клики В которого суще-
ствует такое наибольшее независимое множество вершин
А, что В П А = 0. Пусть, далее, Bi, ..., Вг — список всех
клик графа G, А, — наибольшее независимое множество
вершин, такое что А<ПВ1=/=0 (г = 1, г). Для произволь-
ной вершины v графа G обозначим через w(v) число всех
множеств Аъ содержащих эту вершину. Заменив в G
каждую вершину и полным графом Kw(c), получим граф
G', который по лемме 61.3 окажется совершенным. Оце-
ним число ф(б'). Очевидно, что всякая клика графа G'
есть объединение клик графов, заменивших в G вершины
270
какой-либо клики. Поэтому
ф (G') == max 2 w (*>)•
Поскольку каждое из множеств А5 вносит единицу в те
и только те из чисел w(v), для которых то
2 и>(у) =
Bi Л А-1.
Но очевидно, что
=	|Я4ЛЛД|<1.
Следовательно,
<p(G')<r-l.	(4)
7Т л ттрр
%(G')>lG'l/a0(G')	(5)
(теорема 54.7). Построим последовательность, выписав
поочередно все элементы множества Ai, все элементы
множества Л 2, ..все элементы множества Аг. Пусть I —
длина этой последовательности. Очевидно, что
I = S ГЛ1 =>ао(0-
<=1 '
С другой стороны, каждая вершина v графа G фигури-
рует в этой последовательности ровно w(y) раз, поэтому
z= 2 ш(р) = |С'|.
Наконец, очевидно, ao(G') = ao(G).
Неравенство (5) теперь принимает вид

Но <p(G') = %(G'), что противоречит совокупности нера-
венств (4) и (6). Полученное противоречие и доказыва-
ет лемму. <1
> Доказательство теоремы 61.1. Пусть G —
совершенный граф, Н --.непустой порожденный подграф
дополнительного графа G. Тогда Н — порожденный под-
граф графа G. Согласно лемме 61.4 в графе Н есть кли-
ка В, пересекающаяся с каждым наибольшим независи-
мым подмножеством вершин. В графе Н множество В не-
зависимо и пересекается с каждой наибольшей кликой.
Следовательно, в силу леммы 61.2 граф G является со-
вершенным. <
271
Напомним читателю, что c(G} означает число клико-
вого покрытия графа G. Очевидно, что ao(G) = ф(С),
c(G) = x(G), поэтому из теоремы 61.1 вытекает
Следствие 61.5. Граф является совершенным тог-
да и только тогда, когда ао(Я) = с(Н) для любого его по-
рожденного подграфа Н.
Приведем без доказательства теорему, характеризую-
щую совершенные графы в терминах многогранников.
С каждой бинарной матрицей А без нулевых столбцов
можно связать два многогранника: многогранник Р(А) =
= {х\ Ах^Л, х^О), введенный в § 28, и многогранник
РС(Л)—выпуклую оболочку множества целых точек мно-
гогранника Р(А). Очевидно, что ЯС(Л)^Р(Л).
Теорема 61.6. (В. Хватал, 1975 г.). Пусть А —
матрица клик графа G. Тогда для того, чтобы граф G
был совершенным, необходимо и достаточно выполнение
равенства Рс (А) = Р (А).
Легко видеть, что условием, необходимым для того,
чтобы граф был совершенным, является отсутствие в нем
порожденных простых циклов нечетной длины I > 5.
В самом деле, если С — такой цикл, то ср(С') = 2<
<Х(С) = 3. Из теоремы 61.1 вытекает, что таких циклов
не должен содержать и граф, дополнительный к совер-
шенному. В 1962 году К. Берж высказал предположение,
что эти два условия не только необходимы, но и доста-
точны для того, чтобы граф был совершенным.
Сильная гипотеза Бержа. Граф G является
совершенным тогда и только тогда, когда ни он, ни его
дополнение G не содержат порожденных подграфов вида
C2ft+i, fc > 2.
Эта гипотеза, не доказанная и не опровергнутая до
сего времени, инициировала исследование совершенных
графов и привела ко многим интересным результатам.
§ 62. Триангулированные графы
Граф G называется триангулированным (или хордаль-
ным}, если ни один из его порожденных подграфов не
является простым циклом длины I > 4. Это означает, что
в триангулированном графе для любого его простого цик-
ла длины I > 4 есть ребро, соединяющее две несоседние
вершины этого цикла. Такое ребро называется хордой.
На рис. 62.1 изображены два графа G и Я, из кото-
рых G является триангулированным, а Н не является.
272
Очевидно, что граф является триангулированным, если
все его компоненты — триангулированные графы. Следую-
щая характеризация связных триангулированных гра-
фов принадлежит Г. Дираку. В ней используется поня-
тие разделяющего множества вершин. Множество S вер-
шин графа G называется разделяющим множеством вер-
шин, если граф G — S
имеет больше компонент,
чем граф G.___Если при
этом Gi (Z = l, Z)—компо-
ненты графа G — S, то
порожденные подграфы
G(VGi U S) называются ча-
стями графа G относитель-
но S.	Рис. 62.1
Теорема 62.1. Связ-
ный граф является триангулированным тогда и только
тогда, когда любое его разделяющее множество вершин,
минимальное относительно включения, есть клика.
Е> Необходимость. Пусть G — триангулированный
связный граф, S — одно из его минимальных по включе-
нию разделяющих множеств вершин, G\, ..., Gp — компо-
ненты графа G — S, v — некоторая вершина, принадлежа-
щая множеству S. Тогда для любого индекса i= 1, р вер-
шина v смежна с некоторой вершиной графа Gi, иначе
множество S\v было бы также разделяющим.
Пусть щ и V2 — две произвольные вершины из S,
a	U\, Н2, . . ., Ui, У2),	=	Wt, к2) —
такие цепи минимальной длины, что (щ, u2, ..., ut)—
цепь графа G\, а (гщ, 102, ..., Wt) — цепь графа G2. По-
скольку граф G является триангулированным, то цикл
С = L\ U L2 имеет хорду. Так как длины цепей L\ и L2
минимальны, то эта хорда не может иметь ни один из
следующих видов:р^я, u5u52, wkwk2(i=i, 2, /1 =•
= 1, I, /2 = 1, Z, Ari = 1, t, Лт2 = 1, Z). А так как вершины
графов G\ и G2 друг с другом пе смежны, то она также
пе может иметь вид (7 = 1, Z, fc = l, Z). Таким обра-
зом, эта хорда совпадает с z?iz;2 и, следовательно, верши-
ны z?i и V2 смежны. Тем самым доказано, что множество
S является кликой.
Достаточность. Пусть в графе G любое мини-
мальное разделяющее множество вершин является кли-
кой. Рассмотрим произвольный простой цикл С графа G
18 в. А. Емеличев и др.
273
длины, большей трех:
С = (у\, Н, Р2,	Wft, щ),	& > 1.
Любой минимальный (щ, V2)-сепаратор S (см. § 35) дол-
жен содержать вершину и и хотя бы одну из вершин грг-.
Так как G(S) —полный граф, то для этой вершины
ребро uWi является хордой цикла С. <1
Теорема 62.2. Каждый триангулированный граф
является совершенным.
Доказательство теоремы основано на следующей
лемме.
Лемма 62.3. Пусть S — разделяющее множество вер-
шин графа G, являющееся кликой. Тогда если каждая
часть графа G относительно S — совершенный граф, то и
сам граф G — также совершенный.
> Пусть G' — произвольный порожденный подграф
графа G, ф(С') = ф, = VG'. Если S' = EG', то G'-
полный и потому совершенный граф. Если S' Ф VG' и
граф G' — S' связен, то G' — порожденный подграф не-
которой части графа G относительно множества S. По-
скольку всякая такая часть совершенна, то и G' — совер-
шенный граф. Остается случай, когда множество S' явля-
ется разделяющим для графа G'. Если G19 ,..,GP—
части графа G' относительно S', то любая из них является
порожденным подграфом некоторого совершенного гра-
фа — соответствующей части графа G относительно мно-
жества S. Поэтому она сама — совершенный граф. Сле-
довательно, % (G$) = ср (G|)^ ср. Вершины графа G', не
входящие в S' и принадлежащие различным частям G',
не смежны. Поэтому, раскрасив ср цветами вершины каж-
дого из графов Gi так, чтобы любая вершина из множе-
ства S' имела при всех этих раскрасках один и тот же
цвет, получим правильную ср-раскраску графа G'. Сле-
довательно, %(G') = ср = ср(G'). <
> Доказательство теоремы 62.2. Воспользу-
емся индукцией по числу вершин графа. Для графов по-
рядка п < 3 утверждение очевидно. Пусть G — триангу-
лированный граф, |G| =п>3, и пусть теорема верна для
графов с меньшим числом вершин.
Полный граф является совершенным. Если же граф G
не будет полным, то из теоремы 62.1 вытекает, что в G
существует разделяющее множество вершин S, являющее-
ся кликой. По индуктивному предположению все части
графа G относительно S — совершенные графы. Но тогда
274
по предыдущей лемме и сам граф G является совер-
шенным. <
Следующая теорема проливает свет на строение три-
ангулированных графов и окажется полезной в даль-
нейшем.
Вершина графа называется симплициальной, если ее
окружение — клика.
Теорема 62.4. Любой триангулированный граф
имеет симплициальную вершину. Более того, если этот
граф отличен от полного, то в нем есть по меньшей мере
две несмежные симплициалъные вершины.
> Утверждение теоремы очевидно для полных гра-
фов и легко проверяемо для графов, имеющих не более
трех вершин. Пусть G —- триангулированный граф поряд-
ка п > 3, отличный от полного, и пусть теорема верна
для графов, порядки которых меньше чем п. Пусть, да-
лее, и и v — две несмежные вершины графа G и S — ми-
нимальный (и, и)-сепаратор. Обозначим через Gu и Gv
части графа G относительно S, содержащие, соответствен-
но, вершины и и v. Покажем, что графы Gu и Gv имеют
симплициалъные вершины, не принадлежащие множест-
ву S. Если Gu — полный граф, то симплициальной явля-
ется любая его вершина. В противном случае ио индук-
тивному предположению граф Gu имеет две симплициаль-
ные вершины. Поскольку по теореме 62.1 граф G(S) —
полный, то хотя бы одна из них пе принадлежит S.
Аналогично показывается существование симплициальной
вершины, пе принадлежащей множеству S, в графе Gv.
Очевидно, что эти две симплициалъные вершины не
смежны. <
Легко показать, что триангулированным является вся-
кий расщепляемый граф. Связь между классами триан-
гулированных и расщепляемых графов устанавливается
следующей теоремой, полученной С. Фолдесом и П. Хам-
мером в 1977 году и содержащей характеризацию рас-
щепляемых графов в терминах запрещенных порожден-
ных подграфов.
Теорема 62.5. Для графа G следующие утвержде-
ния эквивалентны’:
1)	граф G расщепляем;
2)	оба графа G и G являются триангулированными;
3)	граф G не содержит порожденных подграфов вида
2К.2, С4 и С$.
>	1)=^2). Пусть G — расщепляемый граф. Тогда, по
определению, существует разбиение A U В = VG на клику
18’	273
А л независимое множество В. Пусть в G есть порожден-
ный простой цикл Ср длины р. По меньшей мере одна из
двух соседних вершин этого цикла должна быть в А. Но
в А любые две вершины смежны, поэтому р 3. Тем
самым доказано, что любой расщепляемый граф является
триангулированным. Поскольку дополнительный к рас-
щепляемому граф также расщепляем, то истинность им-
пликации 1)=>2) доказана.
Импликация 2)=>3) очевидна, поскольку порожден-
ный подграф триангулированного графа также должен
быть триангулированным, а графы 27^, С^ и С$ или их
дополнения не такие.
Остается доказать истинность импликации 3)=>1).
Пусть граф G не имеет порожденных подграфов вида 2К^
С4 и ССреди всех наибольших клик графа G выберем
такую клику А, чтобы граф G — А имел наименьшее чис-
ло ребер, и положим В = VG\A. Докажем, что либо В =
= 0 (и тогда граф G расщепляем, поскольку он полный),
либо В — независимое множество. Пусть, напротив, су-
ществует ребро ху, оба конца которого х и у принадлежат
множеству В. Каждая из вершин х и у не смежна хотя
бы с одной вершиной из клики А, поскольку последняя
максимальна. Если бы каждая вершина, входящая в А,
кроме некоторой вершины z, была смежна и с х, и с у, то
множество (4\z) U х U у было бы кликой, что противоречит
выбору клики А. Следовательно, в А существуют две не-
совпадающие вершины и и v такие, что хи Ф EG и
yv&EG.
Так как граф G не имеет порожденных подграфов
2К2 и G, то из двух возможных ребер хи и уи ровно
одно действительно есть в G. Пусть, например, xv Ф- EG,
yu^EG.
Если |Л| >2, то рассмотрим произвольную вершину
w?e/l\(nUp). Пусть вначале yw^EG. Тогда, если xw^
&EG, то 6? (я, у, v, w) = 2K2. Если же xw^EG, то
G(x, у, и, w) = C4. Следовательно, yw^EG и, таким об-
разом, у смежна с каждой вершиной из множества Л\р.
Поэтому множество А' = A\v U у является наибольшей
кликой. Если же вершины w не существует, т. е. |Л| =2,
то множество А' также является наибольшей кликой.
С другой стороны, \E(G — А') I > \E(G — Л) I, ху EG,
xv^EG. Поэтому в УС\Л существует такая вершина t,
что t^=y, tv^EG, ty^EG. Тогда в G должно быть ребро
xt, иначе G(t, х, у, v)=2K2. Аналогично tu&EG, иначе
G(t, х, у, и) = С\ (см. рис. 62.2, па котором отсутст-
276
вующие ребра обозначены пунктиром). Но тогда
G(£, х, у, и, р)==С5, что противоречит условию. Получен-
ное противоречие доказывает, что множество В независи-
мо и, следовательно, G — расщепляемый граф. <
Как показывают примеры, граф, дополнительный к
триангулированному, не обязательно сам является триан-
гулированным (например, граф 2/<2 = не является три-
ангулированным). Следовательно, класс всех расщепля-
емых графов уже класса триангулированных графов.
УПРАЖНЕНИЯ
1.	Определите хроматические числа и хроматические индексы
графов платоновых тел (рис. 1.7).
2.	Приведите пример двух графов с совпадающими степенны-
ми множествами (степенными последовательностями) и различны-
ми хроматическими числами.
3.	Покажите, что для множества вершин любого непустого гра-
фа G существует такое разбиение V\ U V2 = VG, что верно равен-
ство х(б7(ИО) +%(G(72)) = %(<?).
4.	Опишите графы, хроматический индекс которых равен 2.
5.	Граф называется критическим, если удаление любой из его
вершин приводит к графу с меньшим хроматическим числом. По-
кажите, что Кп является критическим графом при п >• 1, а Сп —
тогда и только тогда, когда п нечетно.
6.	Докажите, что всякий критический граф, являющийся ^-хро-
матическим:
а)	связен,
б)	не имеет точек сочленения,
в)	степень каждой его вершины не меньше чем к — 1.
7.	Докажите, что любая последовательная раскраска полного
А-дольпого графа есть А-раскраска.
8.	Приведите пример графа, последовательная раскраска вер-
шин которого не является минимальной.
9.	Докажите, что при последовательной раскраске графа ис-
пользуется пе более чем 1 -f- max 6 (7/)^ цветов.
277
10.	Покажите, что для раскраски карты, получающейся при
пересечении окружностей на плоскости, достаточно двух цветов.
11.	Докажите, что при любой правильной раскраске реберно-
го графа каждая вершина смежна не более чем с двумя вершина-
ми одного и того же цвета.
12.	Докажите, что для любого графа порядка п верны нера-
венства	_ ____________
2Vn^x(G) +X(G) < п + 1,
n^x(G)x(G) (п + 1)2/4.
Приведите примеры графов, для которых указанные границы
достижимы.
13.	Покажите, что для связного графа G порядка п верно не-
равенство
/(<?, t) ^t(t — l)n-1.
14.	Докажите теорему 55.6.
15.	Приведите пример полинома, удовлетворяющего условиям
теоремы 55.6, но не являющегося хроматическим.
16.	Докажите теорему 55.7.
17.	Предложите алгоритм для раскраски %'(Кп) цветами ребер
графа Кп.
18.	Используя упражнение 14 в главе IV, докажите, что для
любого двудольного графа G хроматический индекс x'(G) ра-
вен A(G).
19.	Докажите, что всякая карта, не содержащая вершин степе-
ни 2, имеет грань, граница которой содержит не более пяти ребер.
20.	Докажите, что реберный граф двудольного графа являет-
ся совершенным.
21.	Докажите, что теорема 56.3 о двудольных графах является
следствием теоремы 61.1.
22.	Не используя теоремы 62.5, докажите, что любой расщеп-
ляемый граф является совершенным.
23.	Докажите, что в любом триагулированном графе есть две
симплициальные вершины, расстояние между которыми равно
диаметру графа.
Глава X
Ориентированные графы
В приложениях часто приходится рассматривать гра-
фы с ориентированными ребрами, т. е. ребрами, для ко-
торых указаны начало и конец. Примерами таких графов
являются сети автомобильных дорог с односторонним дви-
жением или схемы программ для ЭВМ. Недостаточно
простых (неориентированных) графов и для описания
несимметричных отношений. Примерами подобных отно-
шений могут служить порядок выполнения комплекса ра-
бот, задаваемый с помощью сетевого графика, или тур-
нирная ситуация в спортивных соревнованиях.
В этой главе изучаются ориентированные графы.
§ 63. Основные определения
Пусть V — конечное непустое множество, V2 — его де-
картов квадрат. Ориентированный граф {орграф) — это па-
ра (7, Л), где A s V2. Элементы множества V называют-
ся вершинами орграфа G~(V, Л), а элементы множества
А — его дугами. Таким образом, дуга — это упорядочен-
ная пара вершин. Множества вершин и дуг орграфа G
обозначаются через VG и AG соответственно. Число IVGI
называется порядком орграфа G и обозначается через IGI.
Если я = (щ у)—дуга, то вершины и и и называются
ее концевыми вершинами, причем и называется началом
дуги х, a v — концом. Говорят, что дуга инцидентна каж-
дой из своих концевых вершин. Говорят также, что дуга
исходит из своего начала и заходит в свой конец. Дуга с
совпадающими началом и концом, т. е. дуга вида (у, у),
называется петлей. Можно определить ориентированные
графы с несколькими дугами, имеющими общее начало
и общий конец (мультиграфы). Такие дуги называются
параллельными.
На рисунке дуга изображается направленной линией,
идущей от начала дуги к концу. Направление линии
обозначается стрелкой. Например, для графа G, представ-
279
леавого аа рис. 63.1, VG = bi, v3,	v3}, AG =
Bi, %2, x3, X4, x$, xq, X/}, причем Xi и X2 — параллель-
ные дуги, a Xi — петля.
Вершины орграфа называются смежными, если они
являются концевыми для некоторой дуги. Дуги называ-
ются смежными, если они имеют общую концевую вер-
шину.	1
Пусть G некоторый орграф. Ориентированным марих -
рутом (или просто маршрутом) в графе G называете).;
х1	такая последовательность
----,	^ = (^0, ЗЦ, Щ, 372, . . Хп, Vn) (1)
/ X. т	его чередующихся вершин и
тз X?	дуг xh что Xi = (Vi-i,	(i =
=	n^' Такой маршрут назо-
7)	вем (y°’ vn)-маршрутом. Bep-
3	шины vo и vn назовем крайни-
„ л	ми, а остальные вершины
маршрута (1) — промежуточны-
ми (внутренними). Длиной маршрута называется число
входящих в него дуг. Маршрут называется цепью, если
все входящие в него дуги различны, и путем, если все
входящие в него вершины, кроме, возможно, крайних,
различны.
Если в орграфе G нет параллельных дуг, то маршрут
(1) может быть задан последовательностью входящих в
пего вершин: 5 = (i>o, v\, ..., vn). В любом случае марш-
рут можно задать последовательностью входящих в него
дуг: S = (x\, Х2, ..., хп).
Маршрут называется циклическим, если его первая и
последняя вершины совпадают. Циклический путь назы-
вается контуром. Очевидно, что любой (и, v)-маршрут при
u¥=v содержит (и, и)-путъ, а при u — v—контур.
Последовательность (1) чередующихся вершин и дуг
орграфа G, таких что Xi = (Vi_\, Vi) или Xi = (yi, Vi-\), на-
зывается полумаршрутом. Аналогично определяются по-
луцепь, полупуть и полуконтур.
Если в орграфе существует (и, v) -маршрут, то гово-
рят, что вершина v достижима из вершины и. Любая вер-
шина считается достижимой из себя самой.
Орграф называется сильным (или сильносвязным),
если любые две его вершины достижимы друг из друга.
Орграф называется односторонним (или односторонне-
связным), если для любой пары его вершин по меньшей
280
мере одна достижима из другой. Орграф называется сла-
бым (слабосвязным, связным), если любые две его вер-
шины соединены полупутем.
Поскольку любая вершина графа достижима из себя,
то одновершинный граф одновременно и сильный, и одно-
сторонний, и слабый.
Очевидно, что каждый сильный граф является одно-
сторонним, а каждый односторонний — слабым. Очевидно
Рис. 63.2
также, что любые две несовпадающие вершины сильного
орграфа принадлежат некоторому циклическому маршруту.
На рис. 63.2, а изображен сильный орграф, на
рис. 63.2, б — односторонний, а на рис. 63.2, в — слабый.
Маршрут, содержащий все вершины орграфа G, на-
зывается остовным.
Утверждение 63.1. Орграф является сильным
тогда и только тогда, когда в нем есть остовный цикличе-
ский маршрут.
> Необходимость. Пусть G— сильный орграф и
Т = (vq, xi, Vi, ..., хп, Vo)—его циклический маршрут,
проходящий через максимально возможное число вершин.
Если этот маршрут пе является остовным, то возьмем вне
его вершину v. Так как G — сильный орграф, то сущест-
вуют маршруты
Л = (Р0, Z/1, ..., v), T2 = (v, Z1, ..., Vo).
Но тогда циклический маршрут
T'=(vo, Xi, Vi, ..., Xn, Vq, yi, ..., V, Z\, . . ., Vq)
содержит большее, чем T, число вершин, что противоре-
чит выбору маршрута Т. Следовательно, Т — остовный
маршрут.
Достаточность. Пусть и и v — две произвольные
вершины орграфа G, а
Т = (уо, х, ..., v, у, ..., и, z, ..., vo)
— циклический маршрут. Тогда и достижима из v с по-
мощью маршрута (v, у, ..., и) —части маршрута Т,— а
v из и — с помощью маршрута (и, z, ..., vo, х, ..., v). <1
281
Аналогично доказывается
Утверждение 63.2. Орграф является односторон-
ним тогда и только тогда, когда в нем есть остовный
маршрут. Орграф является слабым тогда и только тогда,
когда в нем есть остовный полумаршрут.
Подграфы и порожденные подграфы ориентированного
графа определяются так же, как и для неориентиро-
ванного. Так же определяются и операции над оргра-
фами.
Введем важное понятие сильной компоненты орграфа.
Сильной (или сильно с в явной) компонентой ориентирован-
ного графа называется любой его максимальный относи*
тольно включения сильный подграф.
Очевидно, что отношение взаимной достижимости вер-*
шин ориентированного графа G рефлексивно, симметрич-
но и транзитивно. Следовательно, мы получим разбиение
множества VG на классы, объединив в один класс все
вершины, достижимые друг из друга. Подграфы, порож-
денные классами этого разбиения, и только они, служат
сильными компонентами орграфа G.
В орграфе могут быть дуги, не входящие ни в одну
из его сильных компонент.
Орграф G, изображенный на рис. 63.3, имеет четыре
сильные компоненты с множествами вершин {щ, i?2, ^3,^4),
{^5, Vq, vg}, {07} и {р9}.
Пусть {51, 52, ..., Sm} — множество всех сильных ком-
понент ориентированного графа G. Конденсацией орграфа
G называется орграф G*, вершины si, $2, ..., sm которого
соответствуют сильным компонентам орграфа G, и пара
(s^ Sj) является дугой в G* тогда и только тогда, когда в
G есть дуга, начало которой принадлежит компоненте 5г,
а конец — 5>.
На рис. 63.3 представлены орграф G и его конденса-
ция G*.
282
Утверждение 63.3. Конденсация G* любого оргра-
фа G не имеет контуров.
> Проведем доказательство от противного. Пусть Т =
= (so, #i, $i, ..$о)—контур в G*. Тогда каждая вер-
шина, входящая в компоненту 5{, достижима из любой
вершины, входящей в компоненту Sj. Но это противоре-
чит максимальности сильных компонент. <
Неориентированный мультиграф, получающийся в ре-
зультате снятия ориентации с дуг орграфа G, называется
основанием орграфа G и обозначается через Gb.
Очевидно, что орграф является слабым тогда и только
тогда, когда его основание — связный мультиграф.
Орграф называется несвязным, если его основание —
несвязный мультиграф.
Ориентированный граф называется турниром, если его
основание является полным графом. Этот класс графов
получил свое название в связи со спортивными турнира-
ми без ничьих, проводимыми по круговой системе. Резуль-
таты встреч можно описать ориентированным графом,
вершины которого соответствуют участникам соревнова-
ний, а дуга (и, v) есть в орграфе, если участник и побе-
дил участника и.
§ 64. Полустепени исхода и полустепени захода
Пусть G — ориентированный граф и v^VG. Множе-
ство концов всех дуг, исходящих из вершины и, обозна-
чается через Г(р), а множество начал всех дуг, заходя-
щих в v — через Г-1 (г).
Полустепенъю исхода d+(v) вершины и называется
число дуг, исходящих из и, т. е. d+(u)= |Г(у) I. Анало-
гично определяется полустепень захода d~(y) вершины и:
Степень deg v вершины v орграфа — это число инци-
дентных ей дуг:
deg v = d+ (р) + d~ (и).
Для произвольной бинарной m X n-матрицы А вектор
Ca==(ci, С2, ..ст), i-я координата с{ которого равна чис-
лу единиц в f-й строке этой матрицы, называется векто-
ром строчных сумм. Аналогично определяется вектор
столбцевых сумм dA = (di, d<z, ..., dn): координата di равна
числу единиц в i-м столбце. Очевидно, что
m	п
Я <4=% dj,	(1)
i«==l	j==l
283
поскольку каждая из этих сумм равна числу всех единиц
матрицы А.
Если А = A (G)— матрица смежности орграфа G, то
2лъ- = й+(о, 2^ = <г(/),
3=1	г=1
т. е. число единиц в Z-й строке матрицы -4(G) равно по-
лустепени исхода Z-й вершины, а число единиц в /-м
столбце равно полустепени захода у-й вершины. Таким
образом, для 4= .4(G) имеем
Са = (й+(1), d+(2),	d^n)),
dA = (d~(l), d~(2), ..., d-(n)).
Поэтому верно следующее утверждение, являющееся ана-
логом леммы о рукопожатиях.
Утверждение 644. Сумма полу степеней исхода
всех вершин орграфа равна сумме полустепеней захода и
равна числу его дуг:
2 d+(p)= 2 d~(v) = \AG\.
v^VG	veVG
Нетрудно убедиться в том, что равенство (1) не явля-
ется достаточным условием для существования бинарной
п X т-матрицы 4 с векторами строчных сумм сА и столб-
цевых сумм dA. Например, нет матрицы 4, для которой
сд = (3, 0),	= (2, 1).
Пара векторов с = (ci, с2, ..cm), cZ = (di, d^ ..dn)
с целыми неотрицательными координатами называется
графической, если существует бинарная пгХ ^-матрица 4,
для которой с а = с, dA = d. Если истолковывать эту мат-
рицу как приведенную матрицу смежности двудольного
графа, то вектор сА окажется списком степеней вершин
этого графа, принадлежащих одной доле, а вектор dA —
списком степеней вершин другой доли, так что условия
графичпости пары векторов являются условиями сущест-
вования соответствующего двудольного графа — реализа-
ции этой пары. Этим и объясняется термин «графическая
пара векторов».
При тп = п ту же матрицу 4 можно истолковывать как
матрицу смежности орграфа, и тогда условия графично-
сти пары векторов станут условиями существования ори-
ентированного графа с заданными списками полустепеней
исхода и полустепеней захода вершин.
284
Критерий графичности пары векторов устанавливается
следующей теоремой.
Теорема 64.2. Пара векторов
С == (щ, С2, . . Ст), Л (di, ^2, • • *ч dn) (2)
является графической тогда и только тогда, когда выпол-
няются следующие два условия:
1) последовательность
(ci + ш — 1, С2 + тп — 1, ..ст + тп — 1, d\, d2, ..., dn) (3)
графическая',
кп	п
2) 2 Ci = 2 di.
г=1	i=l
> Очевидно, что пара векторов (2) реализуется дву-
дольным графом тогда и только тогда, когда последова-
тельность (3) реализуется расщепляемым графом, для
которого (щ + тп— 1, C2 + m—i, ..., cm + m — 1) и
(di, d2, ..dn) — списки степеней вершин верхней и ниж-
пей долей соответственно. Поэтому доказываемое непо-
средственно вытекает из критерия расщепляемости гра-
фической последовательности (утверждение 49.3). <1
Коснемся вопроса о реконструируемости орграфов. Ги-
потезу Келли — Улама для ориентированных графов мож-
но попытаться сформулировать так же, как и для неори-
ентированных. По для орграфов эта гипотеза не верна.
Рис. 64.1
П. Стокмейер (1977, 1981 гг.) нашел несколько семейств
переконструируемых орграфов. Одно из них состоит из
сильных турниров специального вида. Два переконструи-
руемых турнира изображены на рис. 64.1. Ф. Харари и
Е. Палмер доказали (1967 г.), что любой турнир, не яв-
ляющийся сильным, реконструируем.
285
А. Рамачандран предложил новый вариант гипотезы
реконструируемости для орграфов. Пусть G — ориентиро-
ванный граф. Вместе с каждым подграфом Gv = G — р,
v^VG, будем рассматривать упорядоченную пару
(d+(v), d~(v)) полустепеней исхода и захода вершины о.
Орграф G назовем N-реконструируемым, если он опреде-
ляется с точностью до изоморфизма набором {(Gv, d+(v),
d~(v)): vze VG).
Гипотеза Рамачандрана (1981 г.). Любой
орграф N-реконструируем.
Эта гипотеза пока не доказана и не опровергнута.
§ 65.	Обходы
Определения эйлеровых и гамильтоновых ориентиро-
ванных графов сходны с аналогичными определениями
для неориентированных.
Цепь, содержащая каждую дугу орграфа, называется
эйлеровой. Связный орграф называется эйлеровым, если
в нем есть замкнутая эйлерова цепь.
Следующие две теоремы, характеризующие эйлеровы
орграфы, доказываются так же, как и в неориентирован-
ном случае.
Теорема G5.1. Для связного ориентированного гра-
фа G следующие утверждения равносильны:
1)	граф G эйлеров;
2)	для любой вершины и е VG верно равенство
d+(v) = d~(v)]
3)	граф) G является объединением контуров, попарно
не имеющих общих ребер.
Теорема 65.2. Связный орграф G содержит откры-
тую эйлерову цепь тогда и только тогда, когда в нем есть
две такие вершины v\ и i?2, что
й+(щ) = й-(щ)+1, d+(y2) = d-(i;2)~l
и d+(v)~d~(v) для любой вершины v, отличной от
V[ U V2.
Контур (путь) орграфа G называется гамильтоновым,
если он содержит все вершины G. Гамильтонов орграф —
это орграф, имеющий гамильтонов контур.
Вопросы, связанные с распознаванием гамильтоново-
сти орграфа и построением гамильтоновых контуров или
путей, являются столь же сложными, как и аналогичные
вопросы для неориентированных графов. Докажем одно
достаточное условие гамильтоновости орграфа.
286
Теорема 65.3 (М. Мейниел, 1973 г.). Пусть G —
сильный орграф порядка п > 1 без петель и параллель-
ных дуг. Если для любой пары и и v его несовпадающих
несмежных вершин справедливо неравенство degw +
+ deg v > 2п — 1, то в G есть гамильтонов контур.
Для доказательства этой теоремы проделаем некото-
рую предварительную работу.
Если v^VG, S^VG, то через E(v-+S) обозначим
множество дуг орграфа G с началом и и концом в 5,
Рис. 65.1
а через Е(щ 5) — множество дуг между и и S, т. е. дуг
вида (и, s) шт (5, р), где s^S.
Как и выше, множество вершин произвольного пути
Р будем обозначать через VP.
Лемма 65.4. Пусть P = (pi, Р2, ...» путь в ор-
графе G, v^VGWP, и пусть в G нет (рь ик}-пути, мно-
жество вершин которого совпадает с VP\iv. Тогда
\E(v, VP)\^k+l.
> Для любого i, 1 i к — 1, положим
А = \E(v<	{р}) I + |£(р	{р<+1}) I.
Очевидно, что
А < 1, i = 1, к — 1,
(1)
иначе в G существовал бы путь, запрещенный условием
леммы (рис. 65.1). Суммируя неравенства (1) по всем
i = 1, к — 1 и учитывая при этом возможность существо-
вания каждой из дуг (р, Pi) и (pft, р), получим
fe-i
\Е(у, КР)|<2 + 5 А<Л + 1. <
Пусть U VG. Путь Р в орграфе G назовем U-путем,
если он удовлетворяет следующим трем условиям:
1)	длина пути Р не меньше чем 2;
2)	начальная и конечная вершины пути Р принадле-
жат множеству 17;
3)	никакая из других вершин, входящих в Р, не при-
надлежит множеству U.
287
> Теперь перейдем к доказательству теоремы 65.3,
которое проведем от противного. Пусть орграф G удовлет-
воряет условиям теоремы и не является гамильтоновым
и пусть 5 = (щ, z?2, vk1 vi)—такой контур в G, мно-
жество вершин которого не является собственным под-
множеством множества вершин другого контура. Рассмот-
рим отдельно два случая.
1) В G нет 75-путей. Возьмем какие-либо две верши-
ны — одну в S, а другую — вне S. В сильном орграфе G
есть контур 5', содержащий эти две вершины и потому
отличающийся от 5. Эти два контура имеют ровно одну
общую вершину, скажем, ра, иначе в G был бы 75-путь.
Пусть теперь ya+i и v — вершины, непосредственно сле-
дующие за иа в контурах 5 и 5' соответственно (рис. 65.2).
Так как в орграфе G нет 75-путей, то вершина v не
смежна ни с одной из вершин, входящих в 5 и отличных
от Va- По той же причине для любой вершины и е
^7G\(75Uz;) верно неравенство \Е(щ {va+i, у}) 1^2.
Следовательно, для несмежных вершин v и ya+i имеем
deg v + deg pa+1 =	3	\E(u, {fa+i, v}) | +
ut VS \ va_|_ J
+	2	\E(U, {Va+l, l>})|<
u(=VG\(VS{Jv)
< (2 + 2 (A — 1)) + 2 (n — к — 1) = 2n — 2,
что противоречит условию теоремы (здесь первая сумма
учитывает дуги, соединяющие вершины z;a+i и v с вер-
шинами из 75, а вторая — дуги, соединяющие ya+i и v
с остальными вершинами графа).
2) В орграфе G есть 75-пути. Выберем среди них
путь
P=(Va, Ul, U2, .... иа, Ра+Т)
288
с минимальным у (см. рис. 65.3). Из максимальности
контура S следует, что у>1. Определим [3 как макси-
мальное среди таких чисел Z, что 1 < I у и в G есть
(Ра^т, Ра)-путь Р', для которого
VP' = VS\{va+il ..., pa+T-i)
(возможно, р = 1и тогда Р' = (ра+т, Ра+т+i, ..., Ра)). Та-
ким образом, I VP'\ = к — у + [3. Так как Р U Р' также яв-
ляется контуром, из максимальности контура S вытекает,
что (3 < у. Из выбора числа [3 следует, что в G нет
(ра+т, ра)-пути с множеством вершин VP' U {ра+Р}, так
что в силу леммы 65.4 вершина ра4_р соединена с Р' не
более чем к — у + [3 + 1 дугами.
Пусть Р" = (pa+T, pa + T+i, ..., Ра). Так как контур S
максимален, то в G нет (ра+т, ра)-пути с множеством вер-
шин VP" U и\. Из леммы 65.4 теперь следует, что верши-
на и\ соединена с Р" не более чем к — у + 2 дугами.
Из минимальности числа у вытекает, что ui не смеж-
на ни с какой вершиной pa+i, 1 i < у, и что для любой
вершины и = 7G\(F5U щ) выполняется неравенство
\Е(и, {ui, pa+P}) I 2.
Учитывая вышесказанное, получаем для несмежных
вершин и\ и pa+f3
deg + deg i>a+p =	2 I E (и, {i^, ya+p}) | +
+	2	| E(u, К Pa+₽})| =
ueVG\(vsu-ti1)
= | E (uv VP”) | + | E (ux, VS \VP") | + | E (pa+₽, VP’) | +
+ |£(ra+₽,VS\VP')| +	2	|£(u,{W1, Pa+₽})|.
tzeVG\(ysu^)
Учитывая полученные выше соотношения, а также то,
что
\VG\(VS и щ) 1 = п — к — 1, imEP'l —р-1
и в графе могут существовать дуги вида (ра+р, иа+г), (Ра-н,
ра+р), 1 < i < у, получаем
degщ + deg pa+P ^(k — 7 + 2) + 0 + (fc — 7 + [3 + 1) +
+ 2(7 - £ - 1)+ 2(n - к - 1)= 2n - 1 - [3,
что противоречит условию теоремы. <1
19 в. А. Емеличев и др.
289
Очевидно
Следствие 65.5. Сильный орграф порядка п без
петель и параллельных дуг, степень каждой вершины ко-
торого не менее п, имеет гамильтонов контур.
§ 66. Пути
Пусть
М = {Рь Р2, ..., Л)
(1>
— какое-либо множество путей орграфа G, попарно не
имеющих общих вершин. Если множества VPi вершин
этих путей составляют разбиение для VG, т. е.
VG = VPX U VP2 U ... U VPh
то множество путей М называется разбиением орграфа G
на пути. Минимальное число I путей, составляющих раз-
биение орграфа G, обозначим через 1(G).
Ниже фигурируют понятия числа независимости
ao(G) и хроматического числа %(G) орграфа G, которые
для ориентированных графов определяются так же, как
и для неориентированных, т. е. ao(G)== ao(G6), %(С)*=
= %(Gb).
Теорема 66.1 (Т. Галлаи и А. Милгрэм, 1960 г.).
Для любого орграфа G верно неравенство l(G)^ ao(G).
Фиксируем некоторое разбиение (1) орграфа G на пу-
ти. Пусть N(М)= Ui, а2, ..., ад, а^Рг,— множество на-
чальных вершин этих путей. Докажем более сильное ут-
верждение:
существует такое разбиение М' орграфа G на пути, что
N(M')^N(M), \М'\ ^ao(G).
> Доказательство последнего утверждения проведем
индукцией по п= IGI. Утверждение очевидно при п =
= 1, 2. Пусть п>2 и утверждение верно для орграфов,
порядки которых меньше п.
Вначале покажем, что, не ограничивая общности, мож-
но считать \М\ =^ao(G)+l. В самом деле, пусть \М\ >
>ao(G)+2. Рассмотрим орграф Gi = G — VP\. Очевид-
но, что ao(Gi)^ cto(G). По индуктивному предположе-
нию существует разбиение М\ орграфа G\ на пути с
N(M\)^N(M) и IJ/J С ao(Gi)^ ao(G). Но тогда М' =
= 71/1 U Pi — разбиение орграфа G с 7V(7J/')^ TV (71/) и
|7I/'|	a0(G)+1. Поэтому всегда можно считать, что
171/1 ^a0(G)+l.
290
Пусть теперь \М I = a0(G) +1. Тогда множество
N(M) = Ui, а,2, ..., а} не является независимым, т. е. в
нем есть хотя бы одна пара смежных вершин. Предполо-
жим, что (ai, a2)^AG. Если путь Pi состоит из единст-
венной вершины то объединив Р\ и Рг в путь (ai,
0,2, ..•), получим нужное разбиение.
Если же путь Pi=(ai, 61, ...) имеет более чем одну
вершину, то рассмотрим орграф Gi=G — аь По индук-
тивному предположению существует такое разбиение Mi
орграфа Gi на пути, что l#il ao(Gi) < ao(G) и
N(Mi)^ {&1? а2, аз, ..., at}. Если bi^N(Mi), то М' полу-
чим из 71/1, добавив вершину а\ к пути, начинающемуся
в Ъ\. Аналогично можно поступить и тогда, когда #2 е
^N(Mi). Если же bi^N(Mi) и а2& N(Mi), то М' =
= Mi U {(ai)}. <
Из теоремы 66.1 вытекают два важных следствия.
Орграф G называется транзитивным, если истинна
импликация
((х, y)^AG и (у, z)^ AG)=>(x, z)^ AG.
Следствие 66.2 (теорема Дилворта, 1950 г.). Если
орграф G транзитивен, то 1(G) = ao(G).
> Согласно предыдущей теореме Z(G)^ao(G). Но
две вершины транзитивного орграфа, принадлежащие од-
ной цепи, смежны, поэтому ao(G)^ 1(G). Итак, 1(G) =
= &о (G). <1
Следствие 66.3. В каждом турнире существует
гамильтонов путь.
> Поскольку любые две вершины произвольного тур-
нира Т смежны, то ао(Г)=1. Поэтому существует цепь
Р, содержащая все вершины турнира Т. <
Для сильных турниров верно следующее более общее
утверждение.
Теорема 66.4. Пусть Т — сильный турнир порядка
п. Тогда для любой его вершины и и для любого числа к,
3 к п, в Т есть контур длины к, содержащий вер-
шину и.
> Пусть S(u) и Р(и) — множество всех тех вершин
v и, соответственно, w турнира Т, для которых (и, v)&
АТ и (w, и)^АТ. Оба эти множества не являются пу-
стыми, поскольку орграф Т сильный. По той же причине
существует хотя бы одна дуга (v, w), идущая из S(u)
в Р(и) (рис. 66.1). Следовательно, вершина и лежит на
контуре длины 3.
19*
291
Далее воспользуемся индукцией по к. Пусть вершина
и входит в контуры всех длин от 3 до к, где к < п. По-
кажем, что она входит в контур длины к + 1.
Пусть С = (ро, v\, ..., vk)9 vq = vk = и,— контур дли-
ны к. Предположим, что для некоторой вершины ы, не
входящей в этот контур, су-
ществуют такие дуги (ip, х)
и (г/, w), что х s VC и г/
<= VC. Тогда в С есть такие две
смежные вершины Vi и vi+\,
что (р,, w) и (гг, 1Ч+1)—ду-
ги турнира Т (рис. 66.2). Сле-
довательно, вершина и вхо-
дит в контур
С' = (Pq,
Pi+1, . .	Щ), Vq = Vk = U,
длины к + 1.
Если же указанной выше вершины w нет, то множе-
ство вершин турнира Т, не входящих в контур С, можно
разбить на две части S(C) и Р(С) так, чтобы для любых
вершин а е S(С), b *= Р(С) и v С выполнялись усло-
вия (р, а)^ AG и (Ь, v) = AG. Так как орграф Т сильный,
то 5(C) и Р(С) не пусты и существует дуга, идущая из
некоторой вершины a^S(C) в некоторую вершину
^Р(С) (рис. 66.3). Таким образом, вершина и входит в
контур
С' = (Р0, л, Ъ, Р2, • •Рл), Щ = и,
длины к + 1. <1
Очевидно
Следствие 66.5. Сильный турнир гамильтонов.
Заметим, что предыдущее следствие вытекает также
из теоремы 66.3.
292
Теорема 66.6 (Т. Галлаи и Б. Руа, 1967 г.). Если
к—максимальная длина путей в орграфе G, то %(G)^
к + 1.
> Обозначим через В такое минимальное относительно
включения подмножество в AG, что орграф G\ = G — В
не имеет контуров. Для любой вершины и определим Цр)
как число вершин пути в орграфе G\ с началом в v, имею-
щем максимальную длину. Приписав каждой вершине v
цвет t(v), получим раскраску орграфа G не более чем
к + 1 цветами. Остается доказать, что эта раскраска пра-
вильная, т. е. что t(u)=£ t(y) для любых двух смежных
вершин и и V. Но если (u, v)^AG\, то t(u)> t(v). Если
же (и, v)^B, то Gi + (zz, и) имеет контур. Поэтому в Gi
существует (и, гг)-путь и, следовательно, t(y)> t(u).
Итак, доказано, что % (6?)=^ к + 1. <
§ 67. База и ядро
Пусть G — ориентированный граф, а В — такое под-
множество его вершин, что любая вершина из VG\B до-
стижима из какой-либо вершины, принадлежащей В.
Если, к тому же, множество В минимально относительно
включения среди всех подмножеств вершин с описанным
свойством, то оно называется базой орграфа С.
Очевидно, что в любом орграфе существует база и
что никакие две вершины базы не соединены маршрутом.
Поскольку вершины с нулевыми полуступенями за-
хода не достижимы ни из каких вершин, то все они при-
надлежат базе. В бесконтурном орграфе база состоит
только из таких вершин.
Для поиска базы в орграфе G, содержащем контуры,
рассмотрим его конденсацию G*, не имеющую контуров
согласно утверждению 63.3. Сильные компоненты оргра-
фа G, в которые не входят дуги из других сильных компо-
нент, соответствуют в орграфе G* вершинам с нулевыми
полустепенями захода. Назовем такие сильные компонен-
ты базовыми. Все вершины каждой сильной компоненты
взаимно достижимы и любая вершина небазовой компо-
ненты достижима из любой вершины некоторой базовой
компоненты. Таким образом, доказана
Теорема 67.1. Подмножество вершин В орграфа
является базой тогда и только тогда, когда В состоит из
вершин, принадлежащих базовым компонентам, причем
в каждую базовую компоненту входит ровно одна вер-
шина из В.
293
Понятие ядра для ориентированных графов вводится
так же, как и для неориентированных.
Множество S вершин орграфа G называется домини-
рующим^ если для любой вершины VG\S существует
такая вершина v е S, что (у, w)^AG. Напомним, что
множество S называется независимым, если никакие две

Рис. 67.2
Рис. 67.1
вершины из S не смежны. Множество вершин 5, являю-
щееся одновременно и независимым, и доминирующим,
называется ядром орграфа.
Орграф, изображенный на рис. 67.1, имеет два ядра:
51 — {pi, 52 = {^2, рД
Не в каждом орграфе есть ядро, в чем нетрудно убе-
диться, рассмотрев орграф, изображенный на рис. 67.2.
Рассмотрим одно достаточное условие существова-
ния ядра.
Теорема 67.2. Каждый орграф, не имеющий кон-
туров нечетной длины, обладает ядром.
> Пусть G — орграф, в котором нет контуров нечет-
ной длины. Для любого подмножества вершин W s VG
положим
Г(Ж)= и Г(ш)\ж.
Определим рекуррентно две системы подмножеств Во,
Bi, #2, ... и Vo, Vj, V2, ... множества VG. В качестве Во
возьмем любую из баз орграфа G и положим
Vo-0, Vi=B0Ur(B0).
Пусть уже определены Bi-i и V<. В качестве Bi возьмем
какую-либо базу подграфа Gi = G — V,, удовлетворяю-
щую условию
5^Г(Г(Вы)\^-1),
и положим
K+I = ViUBiUT(Bt).
294
Покажем, что нужная база действительно существует.
Пусть В — база в содержащая вершину и &
Г(Г(5г-1)\7г-1). Поскольку Вг-\ — база в СДи, то вер-
шина и достижима из какой-либо вершины w = Bi-i, и в
графе существует (w, р)-путь L (рис. 67.3). Этот
путь содержит по меньшей мере по одной вершине из
Г(5г-1) и из Г (Г (5<-1)\^-1). Пусть и — последняя вер-
шина пути В, принадлежащая можеству Г (Г (Вг-1) i).
Тогда все вершины, достижимые из вершины р, достижи-
мы и из и, т. е. В' = (B\z?)U и — также база. Будем про-
водить такие замены вершин до тех пор, пока не полу-
чим нужную базу Bi.
Поскольку
Ио <= V1 <= ... <= Vi <= 7г+1 <= . . .
и множество! VG конечно, то для некоторого индекса т
верно равенство Vm = VG. Положим
т—1
и Bi = s
i=0
и покажем, что S — ядро орграфа G. Из построения мно-
жества S вытекает, что оно доминирующее, ибо если v Ф
^5, то р = Г(ВЛ)\ИА для некоторого индекса к.
Осталось показать, что множество S независимо.
Пусть, напротив, в S есть две смежные вершины и и и,
и = Вр, v е Bq. Так как в базе смежных вершин нет, то
р q. Будем считать, что р < q. Из правила построения
множеств В5 следует, что (u,	(р, u) = AG. По
этой же причине существует путь
L = (#р, Ур, #р+1, Ур+1, • • •, #<?-1, Уд—\ч %q, и)
295
(рис. 67.4), где xq = v, х, = Bh у, e Г (Bj) \7j (7 = p, q — 1).
Из минимальности базы Bp следует равенство и = хр. Но
тогда путь L оказывается контуром нечетной длины, что
противоречит условию теоремы. Тем самым доказана не-
зависимость множества S.
Итак, множество S является независимым и домини-
рующим одновременно, т. е. S — ядро. <1
УПРАЖНЕНИЯ
1.	Докажите теоремы 65.1 и 65.2.
2.	Покажите, что в орграфе без контуров всегда есть вершина
с нулевой полустепенью захода и вершина с нулевой полусте-
пенью исхода.
3.	Докажите, что пара векторов (З2, 2) и( 3, 22, 1) является
графической, и постройте ее реализацию.
4.	Постройте ориентированный граф, для которого вектор
(З3, 22) является как списком полустепеней исхода вершин, так и
списком полустепеней захода вершин.
5.	Докажите, что следующие свойства орграфа G эквивалентны:
1)	G — бесконтурный граф;
2)	граф G и его конденсация G* изоморфны;
3)	каждый маршрут орграфа G является путем;
4)	вершины орграфа G можно упорядочить так, что его мат-
рица смежности будет верхней треугольной матрицей.
6.	Полустепень исхода вершины турнира называется количест-
вом очков вершины. Докажите, что в любом турнире расстояние
от вершины с максимальным количеством очков до любой другой
вершины равно 1 или 2.
7.	Докажите, что в транзитивном турнире существует ровно
один гамильтонов путь.
8.	Докажите, что ребра любого неориентированного графа мож-
но так ориентировать, что в полученном орграфе |d+(i?) — d~(v) |
1 для любой вершины v.
9.	Покажите, что любой турнир либо является сильным, либо
может быть превращен в сильный сменой ориентации только
одной дуги.
296
10.	Докажите, что неориентированный граф G является ос-
нованием некоторого сильного орграфа тогда и только тогда, ког-
да G связен и не имеет мостов.
И. Транзитивным замыканием орграфа G называется орграф
G, для которого VG = VG, a (u, v) <= AG тогда и только тогда, ког-
да в орграфе G вершина v достижима из и. Транзитивная редук-
ция орграфа G определяется как орграф с наименьшим числом дуг,
транзитивное замыкание которого совпадает с транзитивным замы-
канием орграфа G. Покажите, что если орграф не имеет конту-
ров, то его транзитивная редукция единственна.
12.	Пусть G — орграф без петель с п вершинами и m дугами.
Докажите, что если G является связным, но не сильным орграфом,
то п — 1 ш (п — I)2, а если G — сильный орграф, то п
ш п(п — 1).
13.	Докажите, что в орграфе порядка п, для любых двух не-
смежных вершин и и v которого верно неравенство d(u) + d(v)
2п — 3, существует гамильтонов путь.
14.	Орграф L(G), вершины которого соответствуют дугам ор-
графа G и (и, v) ^AL(G) тогда и только тогда, когда соответст-
вующие дуги порождают в G маршрут, называется реберным ор-
графом. Выразите число вершин и число дуг реберного орграфа
L(G) через аналогичные параметры орграфа G.
15.	Целочисленная функция g(v) 0, v е VG, называется
функцией Гранди орграфа G, если для любой вершины v значение
g(v) совпадает с минимальным из тех неотрицательных целых чи-
сел, которые не принадлежат множеству {g(u): и е Г(у)}. Покажи-
те, что если каждый подграф орграфа G обладает ядром, то сущест-
вует функция Гранди орграфа G.
Глава XI
Гаперграфы
Гиперграф — это такое обобщение простого графа, ко-
гда ребрами могут быть не только двухэлементные, но и
любые подмножества вершин. Подобные объекты в мате-
матике известны давно, однако введение термина «гипер-
граф» связано с успешным распространением на них ря-
да важных понятий и методов теории графов.
Отметим, что понятиями, близкими понятию «гипер-
граф», являются понятия сети (см. [32]) и блок-схемы
(см. [30]). Матроиды, которым посвящена гл. III, пред-
ставляют собой специальный класс гиперграфов.
§ 68. Основные определения и свойства
Пусть V — конечное непустое множество, <% — неко-
торое семейство непустых (необязательно различных)
подмножеств множества V. Пара (У, <F) называется аи-
перграфом с множеством вершин V и множеством ребер
. Заметим, что матроид естественно рассматривать как
гиперграф, ребрами которого служат циклы этого матрои-
да и только они. Свободный матроид превращается при
этом в пустой, т. е. не имеющий ребер гиперграф.
Тривиальный матроид оказывается гиперграфом, реб-
ра которого — все одноэлементные подмножества
вершин.
Равные подмножества в (S называются кратными реб-
рами гиперграфа. Множество вершин и семейство ребер
гиперграфа II обозначаются символами VH и (о II соответ-
ственно. Число |УЯ| вершин гиперграфа Н называется
его порядком и обозначается через \Н\. Если \H\t=n,
\ё>Н\~пг (с учетом кратности ребер), то Н называется
(и, тп)-гиперграфом.
Если вершина v V принадлежит ребру е , то
будем говорить, что они инцидентны. Каждой вершине
v^V гиперграфа Н сопоставим множество <?(р) всех ин-
268
цидентных ей ребер. Число №(v)l называется степенью
вершины р, а |е| — степенью ребра е. Поскольку ребра-
ми гиперграфа могут быть лишь непустые подмножества
вершин, то степень любого ребра не меньше единицы, т. е.
|е| > 1. Вершина гиперграфа, не инцидентная никакому
ребру, называется изолированной.
Две вершины и' и и" гиперграфа Н назовем смежными,
если существует ребро е которое содержит обе эти
вершины. Два ребра е и е" гиперграфа Н назовем смеж-
ными, если е Г) е” =# 0.
На рисунке ребро е удобно изображать сплошной ли-
нией, окружающей все вершины из е, если |е| >2 или
|е| =1. Если же |е| =2, то такое ребро е будем изо-
бражать линией, соединяющей две вершины этого ребра,
как и в случае обычных графов. На рис. 68.1 изображен
гиперграф с множеством вершин V = {z?i, z?2, ..и$} и
множеством ребер <S = {ei = {z?i, z?2, е2 = {”2,	^5,
?з = {р6, V7, v3}, е4={рз, УвЬ е5 = {уД, е6 = {у6}}.
Если в гиперграфе Н нет кратных ребер и степень лю-
бого ребра е равна h (I el = h), то гиперграф Н называет-
ся h-однородным (h-униформным). Ясно, что всякий про-
стой граф является 2-однородным гиперграфом. Тем са-
мым граф — частный случай гиперграфа.
Любому (п, тп)-гиперграфу Н =(V, без изолиро-
ванных вершин можно сопоставить (тп, п)-гиперграф
Я* =(У*, <^*), в котором V* = <F, а <F* — семейство всех
множеств &(v), v = V. Гиперграф Я* называется двой-
ственным к Я. На рис. 68.2 изображен гиперграф, двой-
ственный к гиперграфу рис. 68.1.
Очевидно, что (Я*)* = Я для любого гиперграфа Я,
не имеющего изолированных вершин.
299
Для любого Гиперграфа H = (V, определим граф
инциденций— двудольный граф К(Н) с множеством вер-
шин V U (S и множеством ребер {(у, в):(у, в)'=УХ<^,
v'= е}. Граф К(Н) называется кёниговым представлением
гиперграфа Н. На рис. 68.3 изображено кёнигово пред-
ставление К(Н) гиперграфа Н, приведенного на рис. 68.1.
Рис. 68.3
Очевидно, что К (Я*) получается из К(Н) лишь переме-
ной множеств V и (8 местами, причем все ребра сохра-
няются; таким образом, Я(Я*)=ЛДЯ).
В гиперграфе Я = (Е, <?Г) цепью длины Z>0 или
Vi+\)-цепью называется такая последовательность щ, ец
v2, е2, ..eh rz+i, что:
1)	все вершины z?i, v2, ..., vz+i, кроме, возможно, край-
них, различны;
2)	е2, ..., ei — различные ребра Я;
3)	Vi, vi+i ei для любого t *= 1, I.
Здесь и далее под различными ребрами гиперграфа Я
подразумеваются различные члены семейства (8Н (как
подмножества они могут совпадать; папример, на рис. 68.4
е\ и е2 — различные ребра).
Если Z>1 и vt+\ = щ, то цепь называется циклом.
Заметим, что для соответствующих понятий графа мы
добавили слово «простой» (простой цикл, простая цепь).
На рис. 68.4 v2, е$,	v?, е3, vs и щ, е^ v2, е2, v3 —
цепи, a v2, elf z?4, е3, Vi, е^ v$, v2 и щ, v2,	е±,
V7, e3l V4, е2, vi — циклы.
Очевидно, что существует биекция между цепями (цик-
лами) гиперграфа Я=(7, и простыми цепями (про-
стыми циклами) его кёнигова представления, концы ко-
торых принадлежат множеству V.
300
Пусть Я = (У, S)—гиперграф, 0 ¥= Vr V. Подгипер-
графом, порожденным множеством вершин V', называется
гиперграф H'=(V', S'), где S' = {в: в = е А V' =# 0,
e^S}.
Вершины и и v гиперграфа Н называются связанны-
ми, если и = v или в Н существует (и, р)-цепь. Легко
видеть, что отношение связанности есть отношение экви-
валентности на множестве вершин гиперграфа. Классы
этого отношения называются областями связности гипер-
графа Я, а порожденные областями связности подгипер-
графы называются компонентами (связными компонен-
тами) гиперграфа Я. Количество компонент гиперграфа
Я обозначается через к(Н). Если к(Н)=1, то гиперграф
Н называется связным. Очевидно, что к(Н) = к(К(Н)),
где к(К(Н))— число компонент графа К(Н).
Утверждение 68.1. (п, пг)-гиперграф Я не со-
держит циклов тогда и только тогда, когда
2 (|е|-1) = п-/г(Я).
> Очевидно, что гиперграф Я пе содержит циклов
тогда и только тогда, когда его кённгово представление
К(Н) является лесом. Но граф К (II) имеет k (II) компо-
нент, тп + п вершин и 2 | е I ребер. Поэтому на осно-
ef=&H
ванип следствия 13.4 имеем
2 | е\ = m + п — к(Н),
т. е.
2 (|е|-1) = п-*(Я). <
Утверждение 68.2. Гиперграф II не содержит
циклов тогда и только тогда, когда для любого непустого
301
подмножества 8' ^8Н выполняется неравенство
(1)
> Достаточность. Предположим, что Н содер-
жит ЦИКЛ Vl, ei, V2, С2, • • Vi, е(, Vl. Тогда, положив S’ =
= {ei, ег, ..ej, имеем
I и
I
е
и ег
1=1
I
и
1=1
(^iXj'i)
|eiVi| = 2 (|е41 — 1),
1=1	1 = 1
что противоречит неравенству (1).
Необходимость. Если гиперграф Н = (V, 8) не
содержит цикла, то для любого 8' — 8 гиперграф Н ~
= (У', 8') с множеством вершин V'= U е также не
содержит цикла. Поэтому на основании утверждения 68.1
имеем
2 (|e|-l) = l U е\-к(Н’)<\ U е|- <1
Поскольку всякому циклу гиперграфа соответствует
цикл в двойственном гиперграфе, то, применяя только
что доказанный критерий к двойственному гиперграфу
(разумеется, предварительно удалив изолированные вер-
шины из исходного гиперграфа), получаем
Утверждение 68.3. Гиперграф Н не содержит
циклов тогда и только тогда, когда для любого непустого
подмножества Vf <= V выполняется неравенство
I и ^И|> S
I v(=V' I r£V'	*
Приведем без доказательства (его можно найти в [20] )
еще один результат.
Теорема 68.4 (Л. Ловас, 1968). ТЕсли гиперграф Н
порядка п не имеет циклов длины Z>3, а Id > 2 и
1е А е'1 С 2 для любых различных е, е' = 8Н, то
2 (|е| —2)<n— к(Н).
302
Циклическим рангом v^) гиперграфа Н называется
циклический ранг его кёнигова представления К(Н):
v (Н) — v (К (Н)) = 2 \е\-(\Н\ + \%Н\) + к(К(Н)).
eG&H
Из этого определения в силу следствия 13.5 вытекает,
что гиперграф имеет единственный цикл тогда и только
тогда, когда у(Н)=1, т. е. когда S (|<?| —1) = лг —
ее^Н
— к(Н) + 1.
Кроме того, очевидно, что у(Я*) = v(#).
Паросочетанием в гиперграфе Н называется подмноже-
ство S' — для любых двух различных ребер е и е"
которого е' А е" = 0; таким образом, любые два ребра из
S' не смежны.
Паросочетание называется наибольшим, если число ре-
бер в нем максимально среди всех паросочетаний в Я.
Число ребер в наибольшем паросочетании гиперграфа Я
называется числом паросочетания и обозначается через
Пусть задано семейство Si, S2, ..., Sh непустых под-
множеств конечного множества S. Трансверсальным мно-
жеством этого семейства будем называть любое множе-
ство T^S, такое что 77П5г=#0 (f = l, к). Трансверсаль-
ным множеством гиперграфа Я будем называть трансвер-
сальное множество семейства его ребер. Таким образом,
множество Т s VH является трансверсальным множест-
вом гиперграфа Н, если для любого ребра е = £Н спра-
ведливо соотношение Г П е =/= 0.
Очевидно, что в случае, когда — наибольшее паро-
сочетание в Я, множество U в является трансверсальным
множеством гиперграфа Я.
Минимальное число вершин трансверсального множе-
ства называется числом трансверсальности гиперграфа Я
и обозначается т(Я).
Утверждение 68.5. Для любого гиперграфа Я
справедливо неравенство
а!(Я)^т(Я).
> Если Р — паросочетание в гиперграфе Я, а Т —
трансверсальное множество этого гиперграфа, то |Т| >
> |Р|. Отсюда имеем
т(Я) = min	max [ Z* | = с^,
308
где 2ГН — семейство всех трансверсальных множеств ги-
перграфа Н, SPH — множество всех паросочетаний в Я. <
Число г (Я) = max | е | называется рангом гипер-
графа Я.
Утверждение 68.6. Для любого гиперграфа Я
т(Я)^г(Я)а1(Я).
> Пусть Ро — ^Я — наибольшее паросочетание. Тог-
да |Ро1= а1(Я), a U £ — трансверсальное множество
гиперграфа Я. Поэтому
т(Я)<| II е|= 2 |в|Сг(Я)|Р0| = г(Я)а1(^)- <
I eGE7 0 I е£Р0
§ 69. Независимые множества
Множество^ вершин гиперграфа называется независи-
мым, если оно не содержит ребер. Пустое множество вер-
шин по определению независимо. Как и в случае графов,
наибольшее по мощности независимое множество вершин
гиперграфа Я называется наибольшим, а число вершин
в этом множестве называется числом независимости ги-
перграфа Я и обозначается через ао(Я). Через УН обо-
значается множество, элементами которого служат все
независимые множества вершин гиперграфа Я.
Очевидно, что изучая независимые множества вершин
в гиперграфе, естественно рассматривать гиперграфы без
кратных ребер. Опишем, как каждому такому гипергра-
фу поставить в соответствие монотонную булеву функцию.
Пусть Я — гиперграф, ГЯ = {1, 2, ..., п}, хи=(х\,
Х2, ..хп) — характеристический вектор произвольного
подмножества U VH. Определим булеву функцию /н,
положив /н(^) = 0 для п-мерного (0, 1)-вектора х = xv
тогда и только тогда, когда и^УН. Поскольку любое
подмножество независимого множества также независимо,
то функция fH монотонна и /н(0, 0, ..., 0) = 0.
Соответствие Я fu не является, вообще говоря, инъ-
ективным, поскольку ребра гиперграфа могут содержать-
ся одно в другом. Поэтому определенный интерес пред-
ставляют гиперграфы специального вида — антицепи. Ги-
перграф называется антицепью, если никакое из его ребер
не является подмножеством другого ребра. Очевидно, что
все /с-однородные гиперграфы и, в частности, все простые
графы — антицепи.
304
Пусть Н — произвольная антицепь с непустым мно-
жеством ребер, РЯ = {1, 2, ..п). Очевидно, что харак-
теристические векторы ребер гиперграфа Н попарно не-
сравнимы относительно порядка х = (#1, Х2, ..., хп)^
^У=(Уъ У2,	Уп)^=>(Хг^уг, 1 = 1, п). Поэтому суще-
ствует единственная монотонная булева функция п пере-
менных, множество нижних единиц которой совпадает с
множеством всех характеристических векторов ребер ги-
перграфа Н. Очевидно, что fH и есть такая функция. Для
антицепи, не имеющей ребер, fH = 0.
С другой стороны, пусть / — монотонная булева функ-
ция п переменных, /^ 1. Определим гиперграф Я/, поло-
жив VHf = {l, 2, ..., п} и объявив ребрами все подмно-
жества в VHf, характеристические векторы которых слу-
жат нижними единицами функции /. Поскольку эта функ-
ция монотонна, то гиперграф Hf окажется антицепью.
Очевидно, что = /.
Итак, соответствие /	— биекция между мно-
жеством монотонных булевых функций, отличных от тож-
дественно равной 1, и множеством антицепей.
Пусть теперь А — произвольная т X ^-матрица без ну-
левых столбцов, элементы которой — неотрицательные ве-
щественные числа. Рассмотрим систему линейных нера-
венств
АХ^В.	(1)
Здесь X — столбец неизвестных х\, Х2, ..хп, В — стол-
бец высоты т с неотрицательными элементами. Нас бу-
дут интересовать (0, 1)-решения этой системы. Определим
булеву функцию / п переменных, положив j(x\, я2, ...
..., ^п)=0 тогда и только тогда, когда (#i, #2, ..., хп)—
решение системы (1). Очевидно, что / — монотонная функ-
ция и /(0, 0, ..., 0) = 0. Скажем, что функция / задается
системой неравенств (1).
Легко понять, что любая монотонная булева функция,
отличная от тождественно равной 1, задается некоторой
системой линейных неравенств вида (1) с неотрицатель-
ными коэффициентами и правыми частями. В самом де-
ле, пусть / — такая функция, Hf — соответствующая ан-
тицепь, VHf — {1, 2, ..., n}, EHf = ki, е2, ...» kJ =
= Hi(i =1, т). Рассмотрим систему неравенств
+ • •	•	+	1,	1 = 1,т.	(2)
Очевидно, что вектор	x = xu=(xi,	#2,	...»	—решение
этой системы тогда	и только	тогда, когда	По-
20 в. А. Емеличев и др.	305
’Следнее означает, что /ну = 0- Но = /, следовательно,
функция f задается системой (2).
Если же антицепь Hf не имеет ребер, т. е. если /s О,
то в качестве системы неравенств (2) можно взять си-
стему Xi Cl (i = 1, п).
Очевидно, что система неравенств, задающая монотон-
ную булеву функцию, определяется неоднозначно.
Из всего сказанного выше очевидно вытекает сле-
дующее
Утверждение 69.1. Пусть f — монотонная булева
функция, отличная от тождественно равной 1, (1)—за-
дающая эту функцию система линейных неравенств, Hf —
соответствующая антицепь, VHf — {l, 2, ..., n), U^VHf,
ли — характеристический вектор подмножества U. Тогда
следующие высказывания эквивалентны:
1)	/(х₽) = 0;
2)	вектор Хи является решением системы (1);
3)	U^STHf.
Для того частного случая, когда все нижние единицы
«функции / имеют норму 2 (функция / графическая), ука-
занная связь между функциями, системами неравенств
и антицепями отмечалась ранее в § 28. В этой и только
в этой ситуации антицепь Hf является простым графом.
В точности так же, как и для графов, определяется
.пороговое число th (Я) произвольной антицепи Н. Но в
общем случае этот важный параметр изучался мало.
§	70. Раскраски
Так же, как для графов, вводится понятие вершинной
раскраски гиперграфов. Раскраска вершин гиперграфа Н
называется правильной, если любое ребро е &Н содер-
жит две вершины, окрашенные в различные цвета. Ясно,
что правильную раскраску могут допускать лишь гипер-
графы, каждое ребро которых имеет степень не меньше
чем 2. В этом параграфе рассматриваются только такие
гиперграфы. Кроме того, будем считать, что изолирован-
ных вершин гиперграф не содержит.
Гиперграф называется к-раскрашиваемым (k-цвет-
ным), если для него существует правильная раскраска в
к цветов.
Хроматическое число % (Я)— это наименьшее число
цветов, достаточное для правильной раскраски гипергра-
фа Я. Если % (Я) = к, то гиперграф Я называется к-хро-
матическим.
зов
Очевидно, что разбиению множества VH на независи-
мые множества Si, S2, ..., Sk соответствует правильная
раскраска вершин гиперграфа Н к цветами. Верно, ко-
нечно, и обратное утверждение.
Теорема 70.1. Для любого гиперграфа Н порядка
п справедливы неравенства
%(Н)ао(Н)>п,
2УпС%(Я) + а0(Я)<п+1,
где ао(Я)— число независимости гиперграфа Н.
> Рассмотрим разбиение множества VH на независи-
мые множества Si, S2, ..., SA, где /с = %(Я). Тогда будем
иметь
k
«= 2 |^|<Аа0(Я) = х(Я)а0(Я).
2=1
Отсюда сразу получаем %(Я) + ао(Я)> 2Vn.
Далее, пусть S — наибольшее независимое множество
вершин гиперграфа Н. Окрасим все вершины из S в один
цвет и используем п— ISI = п — ао(Я) других цветов
для окрашивания всех вершин из V\S в разные цвета..
В результате получаем %(Я) + ао(Я) п + 1. <
Важное место в теории графов занимают верхние оцен-
ки хроматического числа в терминах степеней вершин.
При естественном определении степени вершин сохраняет
силу теорема Брукса. При другом определении, которое
мы дадим ниже, получается более тонкая оценка хромати-
ческого числа, полученная И. Томеску.
Так же, как и для графов, через А (Я) будем обозна-
чать наибольшую из степеней вершин гиперграфа Я:
А (Я)-max |<Г(и)|.
Абсолютным гиперграфом будем называть гиперграф»
для любых двух вершин и и v которого существует ребро
е = uv. Оказывается, справедлива следующая теорема, яв-
ляющаяся обобщением теоремы Брукса (§ 54).
Теорема 70.2 (Л. Ловас, 1968 г.). Если Н — связ-
ный гиперграф, отличный от абсолютного, и Д(Я)> 3,т&
х(Н)^Л(Н).
Порядком dH(v) вершины v гиперграфа Я называется
мощность наибольшего подмножества S'	>2»
для любых двух различных ребер е' и е" которого е' П
20*	307
Clezz ={z?}. Если такого подмножества не существует, то
по определению dH(v)= 1.
Теорема 70.3 (И. Томеску, 1968 г.). Пусть
4S2, ..Sh — разбиение множества VH на независимые
множества. Тогда
%(Я)<; max min{i, d{ + 1},
где
d{ = max dH(v), i = 1, k.
Доказательства двух предыдущих теорем опускаем.
Если ISJ = 1 (j = 1, fc), то учитывая очевидное нера-
венство Д(Я)^ d(H), где d\H)= max получаем
reVH
Следствие 70.4. Для любого гиперграфа Н верно
неравенство
Х(Я)^(Я)+1.
Отсюда сразу имеем (ср. со следствием 54.2)
Следствие 70.5. Для любого гиперграфа Н верно
неравенство
Х(Я)^Д(Я)+1.
На первый взгляд кажется, что наличие ребер высокой
степени должно способствовать снижению хроматического
числа гиперграфа. Однако это не так, как показывает сле-
дующая
Теорема 70.6. Для любых целых чисел к > 1 и
h^2 существует такой гиперграф Я, что %(Я)> к и
k I h для любого ребра е s $Н.
> В качестве такого гиперграфа можно взять Л-одно-
родный гиперграф Я, построенный по следующему прави-
лу:	i?2, ...» где n^k(h — 1), §11— семей-
ство всевозможных подмножеств множества VH мощности
h. Поскольку ао(Я)^^—1, то на основании теоре-
мы 70.1 %(Я)> п!(h — 1), т. е. %(Я)^ к. <1
Более сильный результат приведем без доказательства.
Теорема 70.7 (П. Эрдёш, А. Хайнал, 1966 г.). Для
любых целых чисел h, к, Z > 2 существует h-однородный
к-хроматический гиперграф, который не содержит циклов
длины меньше I.
Известно, какую роль в теории графов играют бихрома-
тические графы, т. е. графы, хроматическое число которых
не превосходит 2. Простой, но очень важный критерий би-
308
хроматичности графа дал Д. Кёниг: граф не должен со-
держать циклов нечетной длины.
Гиперграф Н тоже будем называть дихроматическим,
«если % (Я)	2. Для гиперграфа пока не найдено крите-
рия бихроматичности в терминах его структуры.
Утверждение 70.8. Если гиперграф не содержит
циклов нечетной длины, то он является дихроматическим.
> Доказательство проводим по той же схеме, что и
доказательство теоремы 9.1, предполагая, что гиперграф
связен. А именно, сначала окрасим произвольную верши-
ну v гиперграфа Н в красный цвет, затем произвольную
вершину и, отличную от v, окрасим в красный цвет, если
расстояние d(u, v) — четное число, и в синий цвет, если
это расстояние нечетно. Если Н — не бихроматический
гиперграф, то найдутся две смежные вершины и и w, ок-
рашенные в один цвет, а тогда легко обнаруживается
цикл нечетной длины. <
Как показывает пример гиперграфа, изображенного на
рис. 70.1, условие утверждения 70.8 не являются необхо-
димыми.
Более широкий класс бихроматических графов нашли
Фурнье и Лас Верньяс. Этот результат приведем без до-
казательства.
Теорема 70.9 (Ж. Фурнье, М. Лас Верньяс, 1972).
Если в каждом цикле нечетной длины гиперграфа Н есть
три ребра, имеющие общую инцидентную вершину, то
гиперграф Н является дихроматическим.
Пример гиперграфа на рис. 70.1 показывает, что это
достаточное условие также не является необходимым.
Непосредственно из теоремы Кёнига следует
Утверждение 70.10. Если гиперграф является
дихроматическим, то он не содержит ни одного цикла
нечетной длины, состоящего лишь из ребер степени 2.
Пример гиперграфа, изображенного на рис. 70.2, пока-
зывает, что обратное утверждение неверно.
Доказательства теорем, опущенные в этом парагра-
фе, можно найти в [20].
309
§ 71.	Реализации гиперграфа
Пусть задан гиперграф Я=(У, &). Реализацией ги-
перграфа Н называется любой граф G, удовлетворяющий
следующим условиям:
1)	VG = VH;
2)	любое ребро графа G содержится в некотором реб-
ре гиперграфа Я;
3)	для любого ребра е порожденный подграф G(e)
является связным.
Реализацией ребра е е & гиперграфа Я является лю-
бой связный граф Ge, для которого VGe = е. Поэтому
Рис. 71.1
всякая реализация гиперграфа является объединением не-
которых реализаций всех его ребер.
На рис. 71.1 изображены гиперграф Я и две его реа-
лизации G' и G”.
Задачи построения реализации гиперграфов часто воз-
никают в электронике при проектировании и изготовлении
310
интегральных схем. Элементы такой схемы, как правило,
разбиты на группы. При изготовлении схемы элементы
каждой группы должны быть соединены проводниками.
Таким образом, можно считать, что спроектированная
схема задается с помощью гиперграфа, а изготовленная —
с помощью графа, являющегося реализацией заданного
гиперграфа. При этом соединять элементы можно произ-
вольным способом, лишь бы получающийся в результате
граф обладал заданными свойствами, например, был де-
ревом, планарным или гамильтоновым графом и т. д.
Следует отметить, что, как правило, задачи построения
подобных реализаций являются очень сложными для ал-
горитмического решения.
Сначала рассмотрим реализацию гиперграфа деревом.
Для этого введем определения.
Реберным графом гиперграфа Н = (У, называется
граф =	Я), множество вершин которого совпа-
дает с множеством ребер <S гиперграфа Я, при этом две
вершины графа Ь(Н) смежны тогда и только тогда, ког-
да смежны соответствующие им ребра гиперграфа Я. Та-
ким образом, L (Я)—граф пересечений ребер гипер-
графа Я.
Говорят, что множество {^i, ез, ..ек} попарно смеж-
ных ребер удовлетворяет условию Хелли, если
h
П е^0,
i=l
или, другими словами, если существует по крайней мере
одна общая вершина, инцидентная каждому ребру е^
Если любое множество попарно смежных ребер гипер-
трафа Я удовлетворяет условию Хелли, то говорят, что
гиперграф Я удовлетворяет условию Хелли.
Теорема 71.1. Реализация связного гиперграфа Я
деревом существует тогда и только тогда, когда Я удов-
летворяет условию Хелли, а реберный граф L(H) триан-
гулированный.
> Необходимость. Пусть для гиперграфа Я су-
ществует его реализация деревом Т. Сначала покажем,
что Я удовлетворяет условию Хелли. Доказательство про-
ведем индукцией по мощности множества попарно смеж-
ных ребер гиперграфа Я.
Два смежных ребра, конечно, удовлетворяют условию
Хелли. Преположим, что любое множество попарно смеж-
ных ребер в количестве к — 1 > 2 удовлетворяет условию
Хелли, и рассмотрим множество {ei, e%, . ек} попарно
311
смежных ребер гиперграфа Я. По индуктивному предпо-
ложению
k-i	k
^1 = П =7^	^2 = П ег	0 ч ^3 ~ е1 Г\ ek	0 •
г—1	г—2
Очевидно, что если хотя бы одно из пересечений
__________________	k
КП К(г=И= у, г, 7 = 1, 3) непусто, то непусто и А
г=1
а значит, любые к попарно смежных ребер удовлетворяют
условию Хелли. Поэтому остается рассмотреть случай,
когда существуют три различные вершины и = К, V2,
w^V%. Введем следующие обозначения: Pi—(щ у)-цепь,
Р2—(у, к?)-цепь, Рз-(Щ ш)-цепь в графе Т. Так как
Т — дерево, то VP\ П УР2 П ПРз ¥= 0 (иначе граф Т содер-
жал бы цикл). В то же время всякое ребро (t=l, к)
содержит не менее двух вершин из {щ v, w}, и реализа-
цией ej является дерево Ti. Поэтому всякое дерево K(Z =
= 1, к) содержит все вершины одной из цепей Рц Р2, Рз.
Отсюда имеем
А 2 А VP2 А ^Рз^ 0,
i=l
т. е. множество {вь е2, ..ek) удовлетворяет условию Хел-
ли. Следовательно, гиперграф удовлетворяет условию
Хелли.
Теперь методом от противного покажем, что реберный
граф L(H) = ((o, Е) является триангулированным. Пусть
в L(H) существует порожденный простой цикл C=(eir
е3	е2, ..., ер, щ),	Тогда этому
---циклу в Н соответствуют ребра
(у в2, . •ер, такие, что смежными сре-
е2(	/—। ди них являются лишь пары ребер
(	/	е\ и е2, е2 и вз, ..вр и е\ (рис. 71.2),
(	) а это значит, что при реализации
у	—Нх / ребер ei, е2, ..., ер появится цикл.
Однако это противоречит тому, что
---реализация Т гиперграфа Н являет-
р ся деревом.
Рис. 71.2	Достаточность. Рассмотрим
класс связных гиперграфов Я,
каждый из которых удовлетворяет условию Хелли,
а реберный граф L(H} является триангулированным. До-
кажем, что существует реализация любого гиперграфа
Я е Зё деревом.
312
Доказательство проведем индукцией по числу ребер
гиперграфа. Для гиперграфов с одним ребром утвержде-
ние очевидно. Пусть6 гиперграф Я = (У,	имеет
т > 2 ребер (|<§Г| = т) и реализация деревом любого ги-
перграфа из Ж с меньшим числом ребер существует. По-
скольку граф £(Я) = (^, £) триангулированный, то в нем
по теореме 62.4 существует симплициальная вершина во,
т. е. множество вершин ео U N(ео) является кликой в L(H).
Этой вершине в гиперграфе Н соответствует ребро во, все
смежные ребра которого обозначим через ei, в2, ..ek.
Так как они соответствуют вершинам 2V(eo) графа ЦН),
то для любых i = 1, /с, j = 1, к справедливо соотношение
П	&.
Поскольку гиперграф Н удовлетворяет условию Хел-
k
ли, то существует вершина vQ е П вг- Теперь рассмотрим
г=1
новый гиперграф H'=(V', &'), где V' — V\(eo\vo), S' =
= {e'i er = e\(eo\t?o),	e ¥= ео). Итак, I =	—
— 1 = m — 1. Поскольку ребра e3, e2, . . ., eh содержат
вершину vo, а остальные ребра гиперграфа H' остались
прежними (е' = е), то гиперграф Н' также удовлетворяет
условию Хелли. По той же причине граф L(H') изомор-
фен графу, полученному из L(H) путем удаления верши-
ны, соответствующей ребру ео, т. е. L(H')—триангулиро-
ванный граф. Следовательно, Н' Ж.
Поскольку |<?'| = т — 1, то по индуктивному предпо-
ложению существует реализация гиперграфа H'=(V',
&') деревом Т'. Очевидно, что реализация гиперграфа
Н деревом Т получается из дерева Т' путем добавле-
ния |eo\vol новых вершин и соединения их с верши-
ной Vo. <
Гиперграф Я, изображенный на рис. 71.1, удовлетворя-
ет условиям теоремы 71.1, поэтому существует его реали-
зация деревом; это дерево G' представлено на том же ри-
сунке.
Говорят, что гиперграф Я удовлетворяет ослабленному
условию Хелли, если для любого множества попарно смеж-
ных ребер {ei, в2, ..., ek} гиперграфа Я существуют две
такие вершины и, v е VH, что ег- Г) {и, v) Ф ® для каждого
i = 1, к.
Следующие две теоремы приведем без доказатель-
ства.
Теорема 71.2. Если гиперграф Я удовлетворяет
ослабленному условию Хелли и его реберный граф L(H)
313
триангулированный, то существует реализация Н планар-
ным графом.
Теорема 71.3. Если реберный граф гиперграфа Н
является планарным, то существует реализация Н планар-
ным графом.
В рассмотренных выше реализациях одно и то же реб-
ро реализующего графа может участвовать в реализации
нескольких ребер гиперграфа. Естественно возникают за-
дачи построения таких реализаций гиперграфа, в которых
это запрещено.
Пусть задан гиперграф
Я = (Р, <Г),	е2, ...» ej.
Строгой реализацией гиперграфа Н называется любой
граф G, удовлетворяющий следующим условиям:
1) VG = VH;
2) существует такое разбиение множества EG ребер
графа G на подмножества 2?i, Ег, ..., Ет, что граф, инду-
цированный множеством Eh является реализацией ребра
е{ гиперграфа Н.
Конечно, всякая строгая реализация гиперграфа яв-
ляется его реализацией.
На рис. 71.1 граф G" является строгой реализацией
гиперграфа Н, а граф G' не является такой реализацией
(почему?). Следующий пример показывает, что гиперграф
может не иметь строгой реализации.
Пример. Рассмотрим гиперграф Н = (V, ), где
V = {щ, у2, Уз, vAi, (S = {{щ, р2, УзХ (У1, У2, уЛ, {уц Уз, У4\
{у2, Уз, У4)}« Если бы существовала строгая реализация
этого гиперграфа, то она должна была бы иметь не менее
2-4 = 8 ребер, что невозможно для графа с четырьмя
вершинами.
Чтобы сформулировать критерий существования стро-
гой реализации гиперграфа Н =(V,= {ei, е2, ..., ет}?
воспользуемся одним фактом из теории матроидов.
Обозначим через Gi полный граф с множеством вер-
шин ei и положим Е = Е(Н)= U EGi. Рассмотрим
2=1
на множестве Е т таких матроидов М\,	..., Мт, что
Mi — циклический матроид графа Gi. Пусть рг- — ранговая
функция матроида Mi(i = i, т). Ясно, что р<(2?)= lej —
— 1. Очевидно, что существование строгой реализации ги-
перграфа Н =(У, <F) равносильно существованию попарно
непересекающихся баз Mi(i = 1, т). Последнее усло-
314
вне, в свою очередь, выполняется тогда и только тогда,
т
когда ранг матроида М = U Mi не меньше, чем
г==1
т	т
2 р«(^) = 2 (I ei I — !)• Теперь, применив теорему 24.1,
г=1	г=1
получим следующий критерий существования строгой реа-
лизации.
Теорема 71.4. Строгая реализация гиперграфа Н =
= (У, с т ребрами существует тогда и только тогда,
когда для любого 'множества А^Е выполняется нера-
венство
m	тп
141 > 2 ki I — m — 2 pi (Е\А)-
i=l	i=l
Отметим, что для построения строгой реализации ги-
перграфа существует эффективный алгоритм.
УПРАЖНЕНИЯ
1.	Покрытием гиперграфа Н называется такое множество вер-
шин U VH, что U П е 0 для любого ребра е Покрытие
называется наименьшим, если число вершин в нем наименьшее
«среди всех покрытий гиперграфа. Число вершин в наименьшем по-
крытии гиперграфа Н обозначается через ₽0(Я).
Покажите, что:
1)	для гиперграфа Н порядка п справедливо равенство
<х0(Я) +₽0(Я) = щ
2)	множество вершин U VH является покрытием гипергра-
фа Н тогда и только тогда, когда множество VH\U независимо;
3)	множество вершин U VH является наименьшим покрыти-
ем гиперграфа Н тогда и только тогда, когда множество VH\U яв-
ляется наибольшим независимым множеством в Н.
2.	Докажите, что реализация гиперграфа Н планарным графом
-существует, если кёнигово представление К(Н) этого гиперграфа
является планарным графом. Приведите пример, когда такая реа-
лизация гиперграфа существует, хотя его кёнигово представле-
ние — не планарный граф.
3.	Пусть Н— (У, <^)—гипеграф. Удалением ребра
типерграфа Н назовем операцию перехода к гиперграфу Н' —
= (V, &'), где <£' — <^\е0. Стягиванием ребра е0 гиперграфа
Н назовем операцию перехода к гиперграфу Н" — (У", где
V" — (У\е0) U ^о, Уо—новая вершина (ро^У),	~ <5\ U <^2,
= е' — (е\е0) U г>о, е^<§\е0, е П е0 0}, &2 — {е: еП
Л е0= 0, ее <^\е0}. Введением вершины i’oe У в ребро е0 гипергра-
фа И назовем операцию перехода от Я к гиперграфу Н' = (У7,
где У' == У U vq, — (ct’Vo) U е*, е* = е0 U *>о.
Пусть существует такая вершина vQ е У, что & (vQ) — е
|е01 > 1. Тогда удалением вершины v0 назовем переход от гипер-
графа Н к Н" = (У", <Г'), где У" = У\р0, %” = (#Vo) U е*, е* =
= eoVo.
315
Докажите следующие утверждения:
1)	если существует реализация гиперграфа Н планарным гра-
фом, то существует такая же реализация и гиперграфа Я, полу-
ченного из Я
— удалением любого ребра,
— стягиванием любого ребра,
— введением вершины в любое ребро,
— удалением вершины;
2)	если существует планарный граф, который является реа-
лизацией гиперграфа Я, полученного из Я стягиванием каждого
ребра некоторого подмножества ребер <§' cz <В*Я, то существует реа-
лизация планарным графом гиперграфа, полученного из Я стяги-
ванием любого подмножества ребер о %>"	&Н.
4.	В предыдущей задаче определены операции введения и уда-
ления вершины степени 1. Пусть — вершина гиперграфа Я =
— (7, S’) степени большей, чем 1, т. е. S> (р0) = {ei, е2, ..., еъ}?
к > 1, причем |ег-| > 1 (г = 1, к). Определим операцию удаления
такой вершины г0 из Я как переход от гиперграфа Я к гиперграфу
Н = (7,>), где V = V\v0, & = (^\<Г(ро)) U = U =
____	2 = 1
= ei\vo (Z = 1, к). Приведите пример гиперграфа Я, для которо-
го существует реализация плапарным графом, но не существует
такой реализации гиперграфа, полученного из Я удалением верши-
ны степени более чем 1.
5.	Покажите, что из существования реализации гиперграфа Я
планарным графом пе следует существование таких реализаций
всех его порожденных подгиперграфов.
6.	Докажите утверждение: для того чтобы гипеграф Я был
/^-раскрашиваемым, необходимо и достаточно, чтобы существовала
реализация гиперграфа Я, являющаяся /с-раскрашиваемым графом.
7.	Докажите утверждение: если существует строгая реализация
гиперграфа Н = (V, S’), то для всякого подмножества со вы-
полняется неравенство
у	+
где К(S’') — объединение полных графов, построенных на каждом
из множеств е е S".
Докажите, что обратное утверждение
1) неверно;
2) верно, если |е| ^3 для любого ребра е гиперграфа Я.
8. Докажите, что строгая реализация связного гиперграфа де-
ревом существует тогда и только тогда, когда гиперграф не содер-
жит циклов.
9. Найдите необходимое и достаточное условие существования
строгой реализации гиперграфа простым циклом.
Глава XII
Алгоритмы
В предыдущих главах упоминались задачи теории гра-
фов, имеющие важное практическое значение. Особый
интерес для приложений представляют алгоритмические
аспекты таких задач. На практике важно уметь с помощью
ЭВМ находить в графе наибольшее паросочетание и наи-
большее независимое множество, строить гамильтонов
цикл или гамильтонову цепь, выделять связные или дву-
связные компоненты и т. п. Иначе говоря, надо иметь
соответствующие алгоритмы, а в конечном счете и про-
граммы для ЭВМ.
Нетрудно (хотя порой и это требует некоторых уси-
лий) для каждой из упомянутых задач разработать алго-
ритм, реализующий перебор всех возможных вариантов.
Такой подход, однако, как правило, неприемлем из-за
чрезвычайно большого числа этих вариантов. Поэтому ну-
жен не просто алгоритм, а алгоритм, в некотором смысле
эффективный, причем эффективность алгоритма важно
уметь оценивать a priori. Этой цели служит анализ алго-
ритма.
Итак, под решением задачи «в алгоритмической поста-
новке» мы будем понимать разработку и анализ соответ-
ствующего алгоритма.
§ 72. Предварительные сведения
При анализе алгоритма решения какой-либо задачи
нас в первую очередь будет интересовать его трудоем-
кость, под которой мы понимаем время выполнения соот-
ветствующей программы на ЭВМ. Ясно, что этот показа-
тель существенно зависит от типа используемой ЭВМ.
Чтобы сделать наши выводы о трудоемкости алгорит-
мов в достаточной мере универсальными, будем считать,
что все вычисления производятся на некой абстрактной
вычислительной машине. Такая машина в состоянии вы-
полнять арифметические операции, сравнения, пересыл-
ки и операции условной и безусловной передачи управ-
317
ления. Эти операции считаются элементарными. Каждая
из элементарных операций выполняется за единицу вре-
мени и, следовательно, время работы алгоритма равно
числу выполненных им элементарных операций.
Память абстрактной вычислительной машины состо-
ит из неограниченного числа ячеек, имеющих адреса
1, 2, 3, ..., п, .. . Ко всем ячейкам есть прямой доступ.
Остановимся особо на представлении чисел в памяти
машины. При анализе алгоритмов наибольший интерес
представляет зависимость времени работы алгоритма от
числа вершин и (или) ребер графа. Выяснение этой за-
висимости удобнее проводить, если отвлечься от величи-
ны таких числовых параметров, как веса ребер взвешен-
ного графа. Поэтому будем считать, что любое число, не-
зависимо от его величины, можно разместить в одной
ячейке и каждая ячейка может содержать только одно
число. Сделанное допущение будет оставаться в силе на
протяжении этого и следующих пяти параграфов, в кото-
рых анализируется трудоемкость конкретных алгорит-
мов. В последнем параграфе этой главы мы несколько
изменим модель вычислительной машины, приняв, в част-
ности, иной способ представления чисел.
Алгоритмы можно описывать в терминах элементар-
ных операций. Однако такая запись была бы перегруже-
на непринципиальными деталями, заслоняющими основ-
ные идеи алгоритма.
Поэтому записывать алгоритмы будем в виде последо-
вательности пунктов. Каждый пункт содержит один или
несколько операторов (инструкций, правил), которые сле-
дует выполнить. Внутри пункта эти инструкции выпол-
няются последовательно в том порядке, как они записа-
ны. Если некоторый пункт не содержит указаний на
переход к другому пункту, то после выполнения всех его
инструкций следует перейти к следующему по порядку
пункту. Единственное требование, предъявляемое к ин-
струкциям, состоит в том, чтобы каждая из них легко
выражалась через элементарные операции.
В записи алгоритма некоторые его фрагменты будут
сопровождаться комментариями. Комментируемый фраг-
мент может быть отдельным оператором или пунктом, а
также группой последовательно расположенных операто-
ров либо пунктов. Комментарии будем писать в квадрат-
ных скобках и помещать в начале или в конце коммен-
тируемого фрагмента.
Хотя мы и условились при описании алгоритмов не
318
ограничивать себя каким-либо набором стандартных опе-
раторов, все же два таких оператора будут использовать-
ся постоянно. Во-первых — это оператор присваивания
а: =В. В результате его выполнения переменная а полу-
чает новое значение, равное В. Во-вторых — оператор
«конец», выполнение которого означает прекращение вы-
числений.
Рассмотрим теперь представление информации в па-
мяти машины. Всякую конечную последовательность эле-
ментов произвольной природы будем называть списком*
а число элементов списка — его длиной. Элементами мо-
гут быть числа, буквы алфавита, векторы, матрицы и
т. п. В той ситуации, когда каждый элемент списка S по-
мещается в одной ячейке (например, является числом)*
этот список будем размещать в п последовательных ячей-
ках памяти, где п — длина списка. Через 5(fc) будем
обозначать /с-й элемент списка S. Аналогично список S
длины п будем размещать в nd последовательных ячей-
ках, если для размещения каждого его элемента доста-
точно d ячеек. Такое представление списка обычно назы-
вается последовательным, и ниже используется только
это представление.
Пусть А = llAijH — матрица порядка пи А =*
= (Ац, А12, . . ., Ain, А21, А22, • • А^пч . • Ап\, Ап2ч •
. . ., Апп)—список ее элементов «по строкам». Принятый
нами принцип «одно число — одна ячейка» означает, что
матрица порядка п занимает п2 ячеек памяти.
Рассмотрим теперь представление графа G в памяти
машины. Пусть VG = {щ, i?2, •.Будем пользовать-
ся тремя способами представления.
Первый — задание графа матрицей смежности. Если
граф G взвешенный и ы(х, у) обозначает вес ребра ху, то
вместо матрицы смежности используется матрица весов
W(G}—W. У этой матрицы 1У^=ш(рй р;-), если гед е
е EG. Если же ViVj & EG, то полагаем Wi5 = 0 или Wa ~
= 00 в зависимости от задачи, которую предстоит решить.
Из сказанного выше о представлении матрицы в машине*
следует, что такой способ задания графа требует |G|2
ячеек памяти. В предыдущих главах веса предполагались
неотрицательными. Теперь снимем это ограничение и бу-
дем считать, что весами ребер могут быть любые вещест-
венные числа.
Второй способ — задание графа списком ребер Ё =*-
= (ei, 62, . .., е™), где m = |Z?G|, e^EG. Поскольку реб-
ро графа можно хранить, используя две ячейки (по од-
319
пой на каждую концевую вершину), то для хранения все-
го списка Ё достаточно 2т ячеек. Если граф взвешенный,
то под каждый элемент списка Ё можно отвести три
ячейки — две для ребра и одну для его веса, т. е. всего
потребуется Зт ячеек.
И, наконец, последний способ, который будет исполь-
зоваться,— представление графа списками смежности.
При таком способе каждой вершине кг ставится в соот-
ветствие список NVi вершин, смежных с кг. Под этот спи-
сок достаточно отвести deg кг- + 1 ячеек — по одной на
каждый элемент и одну ячейку для обозначения конца
списка. Кроме того, формируется список N =(2Vi,	...
..., Nn), где Ni — номер ячейки, в которой хранится пер-
вый элемент списка NVi. Следовательно, такой способ
представления графа требует 2 (deg к + 1) + п =
veVG
= 2т + 2п ячеек памяти. Если граф G взвешенный, то
для каждой вершины списка NVi отводится дополни-
тельно одна ячейка, содержащая число ш(кг, к,).
Хотя представление графа списком ребер является
наиболее экономным «по памяти», оно имеет существен-
ный недостаток. Чтобы определить, содержит ли граф
данное ребро, надо просматривать поочередно элементы
этого списка, а это может потребовать около 2т элемен-
тарных операций. Если же граф задан списками смежно-
сти, вычислительные затраты составят не более п + 1 та-
ких операций. Представление графа матрицей смежности,
требующее наибольших затрат памяти, обеспечивает, как
принято говорить, «прямой доступ» к ребрам графа. Уз-
нать, содержит ли граф ребро ViV$, можно, вычислив
ядрес k — in + j и сравнив М(к) с нулем, где М — мас-
сив, в котором построчно размещена матрица смежности
графа. Сказанное с очевидными изменениями переносит-
ся на случай взвешенных и ориентированных графов.
Выбор того или иного задания графа зависит от кон-
кретной задачи, которую предстоит решать.
Во всех рассматриваемых в этой главе задачах глав-
ной частью исходной информации служит граф. Кроме
этого, исходные данные могут включить номера одной
или нескольких выделенных вершин. Если, например, за-
дача состоит в отыскании цепи, соединяющей две задан-
ные вершины графа, то помимо графа необходимо задать
номера этих двух вершин.
После того как всем исходным данным задачи при-
320
своены конкретные значения и они размещены в памяти
ЭВМ, будем называть их входом задачи. Размером (или
длиною) входа считается число ячеек, занятых входом.
При анализе алгоритма решения любой задачи нас в
первую очередь будет интересовать зависимость времени
его работы от размера задачи, т. е. от размера входа. Од-
нако, как правило, это время зависит не только от раз-
мера входа, но и от других параметров задачи, т. е. вре-
мя работы алгоритма на входах одинаковой длины может
быть не одинаковым. Поясним сказанное па простейшем
примере. Пусть элементами списка 5r = (5i,	.., sm) яв-
ляются натуральные числа и требуется определить, со-
держит ли S число, кратное трем. Очевидный алгоритм
решения этой простой задачи состоит в следующем: про-
веряем поочередно делимость элементов списка 5 на 3
до тех пор, пока не встретится число sPl кратное трем,
или же не будут проверены все элементы S. Время вы-
полнения р таких проверок равно t = 2р (р делений и р
изменений адреса). Следовательно, при неизменной дли-
не входа тп время работы алгоритма будет изменяться в
пределах 2 t 2ш в зависимости от расположения под-
ходящего элемента sp в списке S. Наихудшим, очевидно,
будет случай, когда S не содержит чисел, кратных трем,
либо когда sm — единственное такое число. Один из ос-
новных подходов к определению понятия «трудоемкость
алгоритма» ориентируется именно на такого рода наи-
худший случай.
Определим трудоемкость (или сложность) алгоритма
решения данной задачи как функцию /, ставящую в соот-
ветствие каждому натуральному числу п время работы
/(п) алгоритма в худшем случае на входах длины п. Ина-
че говоря, f(n)—максимальное время работы алгоритма
по всем входам данной задачи длины п. Анализ эффек-
тивности каждого из представленных в последующих па-
раграфах алгоритмов заключается в выяснении вопроса:
как быстро растет функция /(п) с ростом п? При ответе
на этот вопрос обычно используют О-символику.
Будем говорить, что неотрицательная функция f(n)
не превосходит по порядку функцию g(n), если сущест-
вует такая константа с, что f(n)^cg(n) для всех тг>0;
при этом будем писать f(n) — O(g(n)). Часто встречаю-
щемуся далее выражению «трудоемкость (сложность)
алгоритма есть (равна, составляет) O(g(n))» придается
именно этот смысл. В частности, трудоемкость 0(1)
означает, что время работы соответствующего алгоритма
21 в. А. Емеличев и др.
321
не зависит от длины входа. Иногда вместо «трудоем-
кость алгоритма есть O(g(rc))» будем говорить «алгоритм
решает задачу за время O(g(n))».
Алгоритм с трудоемкостью О(п), где п — длина входа,
называют линейным. Линейный алгоритм ограниченное
(константой) число раз просматривает входную информа-
цию и для подавляющего большинства «естественных»
задач является пеулучшаемым (по порядку) в смысле
трудоемкости. Поэтому отыскание линейного алгоритма
для некоторой задачи часто является своего рода «послед-
ней точкой» в ее алгоритмическом решении.
Алгоритм, сложность которого равна О(пс), где с —
константа, называется полиномиальным. Особая роль
полиномиальных алгоритмов выяснится в § 78. Здесь заме-
тим, что все задачи, считающиеся трудными для алгорит-
мического решения, не имеют в настоящее время полино-
миальных алгоритмов. Более того, понятие «полиномиаль-
ный алгоритм» является сейчас наиболее распространен-
ной формализацией интуитивного представления об эф-
фективном алгоритме. Эта формализация, как и любая
другая, не свободна от недостатков. Так, например, едва
ли кто решится назвать эффективным алгоритм, время
работы которого на входе длины п составляет п100. Тем пе
менее отмеченный недостаток не столь серьезен, как это
может показаться на первый взгляд. На практике дело
обстоит таким образом, что появление полиномиального
алгоритма решения какой-либо задачи приводит в конце
концов к алгоритму, трудоемкость которого оценивается
сверху полиномом небольшой степени. В большинстве
случаев эта степень не превосходит трех и оценка, как
правило, имеет один из следующих видов: О(п3), О(п2),
О(пУп), O(nlogn), О(п).
Представленные в последующих параграфах алгорит-
мы используют две важные структуры данных. Это —
списки, в которых удаление элементов и включение но-
вых элементов производится специальным образом.
Список S назовем стеком, если удаление и добавление
элементов производится с одного конца. Выполнение этих
операций осуществляется с помощью переменной t —
адреса (указателя) первой ячейки, занятой последним
элементом списка S. Если каждый элемент занимает d
ячеек, то для удаления элемента из стека достаточно
«передвинуть указатель», т. е. выполнить одну элемен-
тарную операцию t:=t~d. Включение какого-либо эле-
мента а в стек S — это выполнение двух элементарных
322
операций: t := t + d, S(t):= а. Стек S пуст, если t < I,
где I — адрес первой ячейки S.
Пусть, например, каждый элемент стека £=(51, S2, S3,
S4, S5) занимает одну ячейку. Рассмотрим последователь-
ность операций (*, *, s7, s§, *, s9), где «*» означает уда-
ление элемента из S, a «s»» — добавление элемента sf к 5.
Тогда S изменяется следующим образом: (sb $2, S3, s4),
t = 4; ($i, s2, s3), Z = 3; (sb s2, s3, s7), t = 4; (sb s2, s3,
s7, s8), Z = 5; (si, 52, S3, S7), i = 4; (si, s2, s3, s7, s9), t = 5.
Список Q называется очередью, если все удаления
элементов из этого списка производятся с одного конца
Q, а добавления — с другого. Эти операции выполняются
с помощью двух указателей I и t. Переменная t имеет тот
же смысл, что и в предыдущем случае, а переменная I —
это адрес первой ячейки очереди Q. Удаление элемента
заключается в выполнении операции Z:=Z + cZ, а добав-
ление производится точно так же, как и в случае стека.
Пусть, например,	#2, #3, #4, #5) и последователь-
ность производимых над Q операций имеет вид (*, q§, *,
*, qi, *). Тогда результаты выполнения этих операций
выглядят так: (#2, <?з, q±, £5), Z = 2, i = 5; (</2, 7з, qi,
qs, £б), Z = 2, Д = 6; (#з, #4, 35, £б), Z = 3, Z = 6; (?4,?5Лб),
1=*^, *=6; (34, q^ Зб, 37), Z = 4, Z=7; (35, Зб, qi),
Описывая алгоритмы, мы, как правило, не указываем
в явном виде механизм изменения стека или очереди.
Вместо этого просто пишем «занести х в стек S (в оче-
редь 0» или «исключить х из стека S (из очереди 0».
Очевидно, что каждая из перечисленных операций вы-
полняется за время 0(1).
Будем считать, наконец, что вершины графа G, к ко-
торому применяется алгоритм, занумерованы числами
1, 2, ..., |G|. Это — имена вершин, и в процессе работы
алгоритма они не меняются, хотя при этом вершинам мо-
гут присваиваться и другие, дополнительные номера
(метки).
§ 73. Поиск в глубину
В этом параграфе рассматривается один из методов
обхода всех вершин и ребер графа. Этот метод, именуемый
поиском в глубину (сокращенно ПГ), послужил основой
для разработки ряда быстрых алгоритмов на графах.
Один из таких алгоритмов — алгоритм выделения дву-
связных компонент графа — приводится в § 74.
21*	323
Дадим вначале некоторые определения. Ориентирован-
ный граф	А) назовем ориентированным деревом
с корнем г е У, если каждая его вершина достижима из
г и основание графа D — граф Db — является деревом.
В тех случаях, когда недоразумение исключено, ориенти-
рованное дерево с корнем г будем называть просто
деревом.
Пусть G — неориентированный связный граф. В про-
цессе поиска в глубину вершинам графа G присваивают-
ся номера (ПГ-номера), а его ребра помечаются. В на-
чале ребра не помечены, вершины не имеют ПГ-номеров.
Начинаем с произвольной вершины vq. Присваиваем ей
ПГ-номер ПГ(^о)=1 и выбираем произвольное ребро
vqW. Ребро v$w помечается как «прямое», а вершина w
получает (из vq) ПГ-номер ПГ(ш)=2. После этого пере-
ходим в вершину w. Пусть в результате выполнения не-
скольких шагов этого процесса пришли в вершину х, и
пусть к — последний присвоенный ПГ-номер. Далее дей-
ствуем в зависимости от ситуации следующим образом.
1. Имеется непомеченное ребро ху. Если у вершины у
уже есть ПГ-номер, то ребро ху помечаем как «обратное»
и продолжаем поиск непомеченного ребра, инцидентного
вершине х. Если же вершина у ПГ-номера не имеет, то
полагаем ПГ(у) = А: + 1, ребро ху помечаем как «прямое»
и переходим в вершину у. Вершина у считается получив-
шей свой ПГ-номер из вершины х. На следующем шаге
будем просматривать ребра, инцидентные вершине у.
2. Все ребра, инцидентные вершине х, помечены.
В этом случае возвращаемся в вершину, из которой х по-
лучила свой ПГ-номер.
Процесс закончится, когда все ребра будут помечены
и произойдет возвращение в вершину р0.
Описанный процесс можно реализовать так, чтобы
время работы соответствующего алгоритма составляло
O(\EG\ + \G\).
Такой алгоритм (алгоритм мы сейчас рассмотрим.
Пусть граф G задан списками смежности, т. е. Nv — спи-
сок вершин, инцидентных вершине р, и vq — исходная
вершина, с которой начинается поиск. В процессе работы
алгоритма каждая вершина графа ровно один раз вклю-
чается в список Q и исключается из него. Вершина вклю-
чается в этот список сразу после получения ПГ-номера,
и исключается, как только произойдет возвращение из
этой вершины. Включение и исключение вершин произ-
водятся всегда с конца списка, т. е. Q — стек. Результат
324
работы алгоритма — четыре списка ПГ, F, Т ж В:
ПГ(г>)—ПГ-номер вершины у; F(y)~ имя вершины, из
которой вершина v получила свой ПГ-номер; Т и В —
соответственно списки ориентированных «прямых» и «об-
ратных» ребер графа G, Эти ребра получают ориентацию
в процессе работы алгоритма Именно, если ребро ху
помечается из вершины х как «прямое», то в Т заносит-
ся дуга (х, у), а если — как «обратное», то эта дуга за-
носится в В.
Алгоритм поиска в глубину в неориентированном
связном графе.
1.	ПГ(у0):=1, 2(1): = у0, F(vQ):=0, Т:=0, В =0,
к := 1, р:=1 [& — последний присвоенный ПГ-номер,
р — указатель конца стека Q, т. е. Q(p)—имя последней
вершины стека 2].
2.	v := Q(p) [у — исследуемая вершина].
3.	Просматривая список Nv, найти такую вершину ш,
что ребро vw не помечено, и перейти к п. 4. Если таких
вершин нет, то перейти к п. 5.
4.	Если вершина w имеет ПГ-номер, то пометить ребро
vw как «обратное» и занести дугу (у, w) в список В. Пе-
рейти к п. 3 и продолжить просмотр списка Nv. Иначе
Ат := Лт+ 1, ПГ(гр):= к, F(w)'.= v, ребро vw пометить как
«прямое» и дугу (у, w) занести в список Г, р := р + 1,
2(р):==^ [вершина w получила ПГ-номер и занесена в
стек 2] • Перейти к п. 2.
5.	р := р — 1 [вершина v вычеркнута из 2] • Если р =
= 0, то конец. Иначе перейти к п. 2.
Корректность алгоритма очевидна. Оценим его трудо-
емкость. Каждое включение и исключение вершины из
стека 2 выполняется за время 0(1). Поэтому для всей
работы, связанной с изменением стека 2? достаточно вре-
мени 0(|0|). Каждое выполнение п. 4 требует 0(1) вре-
мени, и для каждой вершины v^ VG этот пункт выпол-
няется deg v раз. Поэтому затраты на его выполнение в
целом составят О deg v ] = О (| EG\ ). Суммарное вре-
\reVG )
мя выполнения п. 3 также составит O(|JE'G|), если поза-
ботиться о том, чтобы каждая вершина списка Nv просма-
тривалась только один раз при всех выполнениях данно-
го пункта. Этого легко добиться, если, например, ввести
такую новую функцию (массив) t, что t(v)—помер пер-
вой непросмотренной вершины в списке Nv. Тогда сле-
дующий просмотр п. 3 следует начинать с вершины z —
325
Итак, трудоемкость алгоритма составляет O(\EG\ +
+ |G|). Ясно, что это время является наилучшим воз-
можным по порядку, так как каждая вершина и каждое
ребро графа G должны быть просмотрены хотя бы
один раз.
Легко видеть, что требуемый для реализации алго-
ритма объем памяти также составляет O(\EG\ + |GI).
На рис. 73.1 слева изображены граф G и списки смеж-
ности, которыми он задан. Справа представлены резуль-
таты применения к этому графу поиска в глубину из
(3,2,5)
= (4,1,5)
N3~ (1,5)
(2,5)
N5~ (2,1,3,4,7,6)
K6=(5,7)
N7~(5,6)
Рис. 73.1
вершины vo = 1- «Прямые» ребра проведены сплошными
линиями, а «обратные» пунктирными. Каждой вершине
приписан ее ПГ-номер.
Из способа построения множеств Т и В непосредствен-
но вытекают следующие утверждения.
Утверждение 73.1. Дуги множества Т образуют
ориентированное остовное дерево с корнем в вершине v$.
Это остовное дерево часто называют остовным глубин-
ным деревом (ОГД). Обозначать его будем также че-
рез Т.
Утверждение 73.2. Если ориентированное ребро
(х, у) принадлежит В1 то ПГ(гг)> ПГ(у), т. е. «обрат-
ные» ребра всегда ведут к ранее пройденным вершинам.
Поиск в глубину используется в качестве составной
части во многих алгоритмах. Отметим одну задачу, реше-
ние которой можно получить с помощью алгоритма <s^i
сразу, почти без дополнительных вычислительных за-
трат. Это — задача выделения связных компонент графа.
Чтобы решить ее за время О(\EG\ + |G|), достаточно
один раз просмотреть список вершин графа, выполняя
следующие действия. Если просматриваемая вершина vt
имеет ПГ-номер, то перейти к следующей. Иначе — поло-
жить	ПГ(г?о)=А: + 1, где к — последний при-
326
своенный ПГ-номер, и применить поиск в глубину. Пос-
ле его окончания (т. е. выделения компоненты, содержа-
щей Vi) продолжить просмотр списка, перейти к верши-
не Vi+i. Различать вершины разных компонент можно,
например, по их ПГ-номерам, если для каждой компонен-
ты запомнить последний ПГ-номер.
§ 74. Отыскание двусвязных компонент
В этом параграфе мы рассмотрим применение поиска
в глубину к выделению 2-связных компонент графа.
Здесь дело обстоит не так просто, как в предыдущей за-
даче. Конечно, можно было бы, удаляя поочередно вер-
шины графа и каждый раз выделяя связные компоненты,
найти его точки сочленения и блоки. Такой подход, од-
нако, приводит к алгоритму сложности по крайней мере
O(|G| • \EG\). Использование более глубоких свойств
ПГ позволяет получить линейный по сложности алгоритм
решения этой задачи.
В дальнейшем удобно использовать следующие терми-
ны. Пусть D= (F, А)—ориентированное дерево, х, у е
V. Назовем х отцом вершины у, а у — сыном верши-
ны х, если дуга (я, у) принадлежит А. Будем говорить,
что вершины х и у сравнимы, если одна из них достижи-
ма из другой. Если при этом у достижима из х, то х —
предок вершины у, а у — потомок вершины х. Подграф
графа D, порожденный множеством, состоящим из верши-
ны у и всех ее потомков, будем обозначать через Dy и
называть поддеревом с корнем у.
Пусть в графе G проделан поиск в глубину из верши-
ны vo и получены остовное глубинное дерево Т и множе-
ство обратных ребер В.
Следующие три утверждения дают теоретическую ос-
нову для разработки эффективного алгоритма выделения
двусвязных компонент.
Утверждение 74.1. Если дуга (х, у) принадле-
жит В, то х является потомком вершины у в Т.
> Надо доказать, что вершина х принадлежит подде-
реву Ту. Предположим противное. Согласно утверждению
73.2 вершина х получает свой ПГ-номер позже, чем у.
Поэтому присвоение вершине х ПГ-номера произойдет
не раньше, чем будут посещены все вершины дерева Ту и
произойдет возвращение в вершину s = F(y). Но возвра-
щение в s не может произойти прежде, чем все вершины
множества Nv получат ПГ-номера. Поскольку х Ny и
327
ПГ-номера к этому моменту не имеет, то получаем про-
тиворечие. <
Следующие два утверждения показывают, каким об-
разом поиск в глубину «реагирует» на точки сочленения
графа.
Утверждение 74.2. Вершина Vo является точкой
сочленения графа G тогда и только тогда, когда она име-
ет не менее двух сыновей.
> Пусть — точка сочленения графа G. Ясно, что
каждый блок графа, включающий вершину р0, содержит
по крайней мере одного из ее сыновей.
Пусть теперь $i, s%, .. ., sk—сыновья вершины v$.
Рассмотрим поддеревья TSi(i = 1, к). Ясно, что VG— vQ =
k
= U VTS,. Для доказательства несвязности графа G —
2 = 1
— vq достаточно показать, что в этом графе нет ребер,
связывающих вершины различных Тч. Но это сразу сле-
дует из утверждения 74.1. <
Будем говорить, что х — собственный предок (пото-
мок) вершины у, если х — предок (потомок) у и х =И= у.
Утверждение 74.3. Вершина и Vq является точ-
кой сочленения графа G тогда и только тогда, когда для
некоторого сына s этой вершины не существует дуги
(х, у)е В такой, что х—потомок (не обязательно соб-
ственный) вершины s, а у — собственный предок вер-
шины V.
> Пусть v — точка сочленения графа G и G\, G2, ...
..., Gm, m > 2,— блоки этого графа, содержащие верши-
ну и. Пусть, далее, v' = F(v), т. е. v' — отец вершины и.
Не теряя общности считаем, что вершина и' содержится
в блоке Gi. Каждый из остальных блоков Gi (i = 2, m)
должен, очевидно, содержать хотя бы одну вершину, яв-
ляющуюся сыном вершины v. Пусть, например, s — сын
вершины v и 5 е G2. Если теперь допустить существова-
ние «обратного» ребра ab (т. е. дуги (а, Ь)^В) такого,
что а — потомок 5, а Ъ — собственный предок вершины v,
то придем к существованию в графе G простого цикла,
содержащего вершины и' и s. Этот цикл образован про-
стой (а, Ь) -цепью, состоящей из «прямых» ребер и «об-
ратного» ребра ab. Это означает (согласно утвержде-
нию 36.3), что вершины 5 и v' принадлежат одному бло-
ку. Получили противоречие.
Докажем теперь вторую часть утверждения. Пусть
вершина s является сыном вершины v, для которого вы-
328
полняется условие, фигурирующее в формулировке ут-
верждения. Это условие вместе с утверждением 74.1 озна-
чает, что если аЪ—«обратное» ребро и а е Ts, то либо
Ъ е TS1 либо Ъ — и. Последнее означает, что все ребра
графа G, связывающие вершины множества VTS с верши-
нами VG\VTS, инцидентны вершине р, т. е. v — точка со-
членения графа G. <
Перейдем теперь непосредственно к разработке алго-
ритма выделения блоков графа. Чтобы уяснить схему
Рис. 74.1
применения ПГ к решению этой задачи, обратимся к при-
меру. На рис. 74.1 изображен граф «с точностью до бло-
ков». ПГ начинается в вершине vo. После нескольких ша-
гов придем в одну из точек сочленения графа, например,
в С2. Пусть, далее, выбирается и помечается как «прямое»
ребро С2Х блока В±. После этого дальнейшая работа ПГ
вплоть до возвращения в С2 происходит точно так, как
если бы было vo — С2 и блоков Z?i, В2, В3 в графе G не
было бы вовсе. Поэтому возвращение в С2 из х будет оз-
начать, что пройдены все ребра блоков В4, В5, Вб, Bq.
Таким образом, возвращение в С2 произойдет позже, чем
возвращения в Сз и С4 из висячих блоков В5, Вб, В7. Эти
рассмотрения приводят к следующему важному выводу.
Самое первое возвращение в точку сочленения произой-
дет сразу же после завершения обхода всех ребер некото-
рого висячего блока Bk. Это же справедливо и по отно-
шению к дальнейшему поведению ПГ в графе, получен-
ном из графа G удалением блока Bk.
Покажем, как использовать сказанное выше в пред-
положении, что у нас есть способ, позволяющий при
329
каждом возвращении из вершины v в F(v) определять,
является ли F(v) точкой сочленения. С этой целью заве-
дем стек 5, в который будем заносить всякое ребро гра-
фа G сразу после получения им пометки «прямое» или
«обратное». Таким образом, все ребра добавляются в ко-
нец списка 5. Пусть в пашем примере возвращение из
вершины у в с4 (см. рис. 74.1) является самым первым
возвращением в точку сочленения. Тогда к моменту воз-
вращения в с4 ребра блока Bq будут занимать все t по-
следних мест в стеке S, где t — число ребер этого блока.
Важно при этом, что ребро с4у занимает первое среди t
указанных мест. Это позволяет, просматривая стек
S справа налево, выделить (т. е., например, переместить
в отдельный список) все ребра блока Bq. Затем эти ребра
удаляются из S.
Итак, учитывая сказанное, необходимо уметь в про-
цессе ПГ быстро определять возвращение в вершину, яв-
ляющуюся точкой сочленения. Утверждения 74.2 и 74.3
дают соответствующие критерии, и нам надо их «алгорит-
мизировать». С этой целью для каждой вершины v е VG
определим множество Р(и). В это множество включим
вершину v и каждого ее предка ш, для которого сущест-
вует «обратное» ребро xw такое, что х — потомок верши-
ны v в остовном глубинном дереве Т. Иными словами,
множество Р(и) состоит из всех предков вершины v, ко-
торых можно достичь из г, проходя сначала несколько
(возможно, ни одной) дуг дерева Г, а затем одну дугу
множества В.
Введем теперь функцию l(v), v е VG, полагая l(v) =
= min ПГ(х). Например, в графе на рис. 73.1 Z(l)= 1,
xeP(v)
Z(2)= 1, Z(3)=l, Z(4)=3, Z(5)= 1, Z(6)= 3, Z(7)=3.
Используя функцию l(v), сформулируем утвержде-
ние 74.3 в следующем виде, более удобном для органи-
зации вычислений.
Утверждение 74.4. Вершина v^Vq является точ-
кой сочленения графа G тогда и только тогда, когда су-
ществует такой сын s этой вершины, что /(£)>ПГ(р).
Вычислить значение l(v) нетрудно, если известны зна-
чения функции I для всех сыновей вершины о. Именно,
если $i, S2, ..., sm — сыновья вершины v, то имеет место
формула
Z(i?) = min {{I($i), l(sz), ..., ПГ(р)} U
и{ПГ(1Р) I (p, w)^B}}.	(1)
330
Справедливость этого соотношения становится очевид-
ной, если заметить следующее. Множество предков вер-
шины р, достижимых из нее с использованием дуг дере-
ва Т и не более одной дуги из В, состоит из предков у,
достижимых таким же способом из вершин	sm, и
множества вершин, к которым ведут обратные ребра от
вершины р.
Используя соотношение (1), функцию I можно вычис-
лять попутно с выполнением обычных операций поиска
в глубину. При первом посещении вершины v вместе с
присвоением ПГ-номера полагаем ?(р) = ПГ(р). В даль-
нейшем это значение корректируется в соответствии с
формулой (1) следующим образом. Всякий раз, когда
происходит возвращение в вершину v из некоторого ее
сына s, полагаем Z(p):=min{Z(s), Z(p)}. Кроме того, ког-
да некоторое ребро vw помечается как «обратное», пола-
гаем Z(p):= min {Z(p), ПГ(и?)}. К моменту возвращения
из v в вершину х = F(v) будет вычислено истинное зна-
чение Z(p), которое в дальнейшем используется для кор-
ректировки Цх). Существенно, что каждая из этих кор-
ректировок требует только 0(1) дополнительного време-
ни. Поэтому ПГ вместе с вычислением функции I
по-прежнему будет выполняться за время O(\EG\ + |С|).
Еще одна добавка к «стандартному» поиску в глубину
связана с точками сочленения. Для обнаружения точки
сочленения достаточно после каждого возвращения в вер-
шину v из некоторого ее сына s сравнить величины Z(s)
и ПГ(р). Если окажется, что £($)^=ПГ(р), то все ребра
стека 5, начиная с последнего и кончая sv, удаляются из
этого списка. Удаленные ребра составляют один из бло-
ков графа G. Согласно утверждению 74.4 неравенство
Z(s)>nr(y) означает, что либо вершина v — точка со-
членения, либо и = Уо и v не является точкой сочленения.
Заметим, что второй случай не требует особого рассмот-
рения. В этом случае удаленные из стека S ребра соот-
ветствуют единственному блоку графа, содержащему vq.
И, наконец, последняя деталь. Выделение блока графа G
мы понимаем как удаление всех ребер этого блока из
стека S. Можно считать, что одновременно с удалением
из S каждое такое ребро заносится в некоторый другой
список, причем множество ребер разных блоков разделе-
ны в этом списке, например, символом 0. Процедура по-
строения этого нового списка очевидна, и чтобы не за-
громождать описания алгоритма, мы не приводим ее в
явном виде.
331
Сравнение l(s) с ПГ(р) производится |G| — 1 раз, и,
следовательно, суммарное время, затраченное на выпол-
нение сравнений, составляет О(I\GI). Каждое ребро гра-
фа один раз включается в стек S и один раз исключается
из него. Поэтому вся работа, связанная с изменением 5,
выполняется за время O(\EG\). Таким образом, поиск в
глубину вместе с выделением блоков будет выполняться
за время O(\EG\ + |G|).
Алгоритм поиска в глубину с выделением дву-
связных компонент.
1.	ПГ(р0):=1, Z(^o):=l, S:=0, F(po):=O, Т:=0,
p:=l, (?(!):= v0.
2.	v:=Q(p).
3.	Просматривая список Nv, найти такую вершину w,
что ребро vw не помечено, и перейти к п. 4. Если таких
вершин нет, то перейти к п. 5.
4.	Если вершина w имеет ПГ-номер, то поместить реб-
ро vw как «обратное», занести ребро vw в стек S, l(v): =
:=min{Z(p), ПГ(ш)} [выполнена корректировка Z(z?)].
Перейти к и. 3 и продолжить просмотр списка Nv. Иначе
ребро vw пометить как «прямое», к :== к + 1, ПГ(ш):= fc,
l(w): — к, F(w)~ v, р := р + 1, (?(р):= w. Перейти кп. 2.
5.	р : = р — 1. Если р = 0, то конец. Иначе перейти
к и. 6.
6.	Пусть x — F^v). Если /(р)>ПГ(гг), то перейти к
п. 7. Иначе 1(х) :== min U(x), l(v)} [выполнена корректи-
ровка Z(^)] и перейти к п. 2.
7.	Удалить из стека S все ребра вплоть до xv [уда-
ленные ребра составляют блок графа G]. Перейти к п. 2.
Пример. На рис. 74.2 изображен граф G и приве-
дены списки смежности его вершин. Этот граф имеет че-
тыре блока 51, В2, 5з, и две точки сочленения d и х.
Поиск в глубину начинается с вершины а, т. е. vo = а.
На рис. 74.3 отражена ситуация, сложившаяся непосред-
ственно перед выделением блока В±. К этому моменту
шесть ребер помечены как «прямые» и одно как «обрат-
ное». Прямые ребра проведены жирными линиями, а об-
ратное — пунктирной. Тем и другим придана соответ-
ствующая ориентация. Помеченные ребра расположены
в стеке S в том порядке, в котором они получали помет-
ки. Пара чисел (а, р), приписанная вершине у, имеет сле-
дующий смысл: а = ПГ(р), а р — значение Z(p), вычис-
ленное к рассматриваемому моменту.
После того, как ребро tx получило пометку «обратное»,
произошло возвращение в вершину z. При этом сравне-
332
ние величин ПГ(з)—6 и /(£) = 5 показало, что вершинам
не является точкой сочленения. Далее при возвращении
Рис. 74.2
из вершины z в х обнаруживается, что Z(z) = 5 = ПГ(я).
Следовательно, все ребра от tx до xz в стеке S составля-
ют блок графа G. Эти ребра — tx, tz, xz — удаляются из S,
и тем самым выделен блок Z?4.
После этого алгоритм работает так, как если бы бло-
ка В4 в графе G не было вообще. Ключевые моменты
дальнейшей работы алгоритма иллюстрируются на
рис. 74.4. Каждый из трех графов (вместе с их помет-
ками и стеком 5), изображенных на этом рисунке, отра-
жает ситуацию, создавшуюся непосредственно перед уда-
лением очередного блока. Выделение последнего блока,
333
т. е. удаление его ребер из стека 5, произойдет при воз-
вращении в вершину vq = а, для которой ПГ(а)=1 =
— 1(c). Таким образом, на вершину vq = а алгоритм
«реагирует» точно так же, как па точку сочленения.
Рис. 74.4
В заключение отметим, что поиск в глубину оказыва-
ется полезным и при отыскании 3-связных компонент
графа. Известен основанный на поиске в глубину алго-
ритм, решающий эту задачу за время О(\EGI + |G|).
§ 75. Минимальный остов
Задача о минимальном остове состоит в отыскании
остова минимального веса во взвешенном графе (G, w).
Она считается одной из самых «легких» оптимизацион-
ных задач па графах. Решение этой задачи можно полу-
чить с помощью «жадного» алгоритма, если указать про-
цедуру, которая по любому ациклическому множеству
ребер X <= EG и ребру е <= EG определяет, содержит ли
множество ребер X U е цикл графа G. В качестве такой
334
процедуры можно использовать, например, поиск в глу-
бину, поскольку выявление цикла в множестве X U е, где
е = ab, равнозначно отысканию (а, &)-цепи в порожден-
ном подграфе G(X). В процессе работы «жадного» алго-
ритма эта процедура выполняется не более \Е\ раз, и,
следовательно, затраты времени составят O(\EG\ • IGI).
Для упорядочения множества EG по неубыванию весов
известны алгоритмы сложности O(\EG\log I.E'Gl). Таким
образом, даже бесхитростная реализация «жадной» стра-
тегии поиска минимального остова приводит (независимо
от способа задания графа G) к алгоритму сложности
O(\EG\ • IGI), т. е. к полиномиальному алгоритму.
G этой точки зрения задача о минимальном остове дей-
ствительно является легкой.
Мы сейчас рассмотрим два алгоритма решения этой
задачи, имеющие лучшие оценки быстродействия.
Пусть Т = {(У1, Z0, (F2, Т2), (Fa, ^а)}-остов-
ный лес взвешенного графа G, Ff и Тг — множества вер-
шин и ребер Z-й компоненты леса 71, w(x, у)—вес ребра
ху графа G. Оба алгоритма построения минимального
остова опираются на следующую простую теорему.
Теорема 75.1. Пусть ребро аЪ имеет минимальный
вес среди всех ребер, у которых ровно один конец содер-
жится в VTi. Тогда среди остовов графа G, содержащих
Т U ab, найдется такой, вес которого не более веса любо-
го остова, содержащего Т.
> Пусть Т' — произвольный остов графа G, содержа-
щий Т и не содержащий ребра аЪ. Добавим это ребро к
Т'. Полученный граф будет содержать цикл S (теоре-
ма 13.1). Этот цикл включает ребро аЪ и по крайней ме-
ре еще одно ребро аЪ', у которого ровно один конец со-
держится в Fi. По условию ш(а, b)^w(a', Ъ'). Следо-
вательно,
w(Tf + аЪ — a'b'} = w(T')+ w(ab)— w(a'b')^ w(T').
С другой стороны, граф Т' + аЪ — а'Ъ' является остовом
графа G, содержащим Т U аЪ. <
Замечание. Легко показать, что каждый мини-
мальный остов должен содержать по крайней мере одно
из ребер минимального веса графа G. Следовательно, вся-
кий алгоритм построения минимального остова должен
хотя бы раз просмотреть всю входную информацию, будь
то матрица весов, список ребер или списки смежности
графа. В противном случае непросмотренное ребро
может оказаться единственным ребром минимального ве-
335
са графа, и это ребро не сможет войти в минималь-
ный остов.
Теорема сразу подсказывает следующую стратегию
построения минимального остова. На первом шаге рас-
смотрим остовный лес Z1 с лъ= |С?| компонентами. Каж-
дая его компонента состоит из одной вершины, т. е. V} =
= {z?J. Этот лес, очевидно, содержится в любом остове
графа G. Среди ребер, инцидентных щ, выберем ребро ми-
нимального веса и присоединим его к Т1. Согласно
теореме 75.1 существует минимальный остов, содержащий
лес Т2 = Т1 U [v±vk }, у которого компонента (7^, 7^)
содержит две вершины z?i и vk^ и ребро v±vk^ а осталь-
ные компоненты одновершинные. На следующем шаге
будет выбрано и добавлено к Т2 ребро минимального ве-
са среди ребер, соединяющих vk } с	z^J и т. д.
Итак, стратегия построения минимального остова со-
вершенно ясна: на каждом шаге присоединяется ребро,
минимальное по весу среди ребер, соединяющих уже по-
строенный фрагмент минимального остова с вершинами,
еще не включенными во фрагмент. Нам остается только
позаботиться об экономной реализации шагов этого про-
цесса. С этой целью свяжем с каждой вершиной х е VG
две метки а(х) и Р(^), смысл которых заключается в сле-
дующем. Пусть проделано к шагов и (71, Т$)-фраг-
мент минимального остова, построенный к этому момен-
ту, т. е. это компонента леса, к которой на предыдущих
шагах присоединялись ребра минимального веса. Тогда
а (х) == min w (rr, v) = w (x, z;*), |3 (x) = v*.
Таким образом, cc(rr)—вес минимального по весу реб-
ра, соединяющего вершину х с построенным фрагментом
минимального остова, а р(гг)—имя второй вершины это-
го ребра. Метки а(х) и р(гг) позволяют быстро находить
на каждом шаге ребро минимального веса. Кроме того,
после присоединения очередной вершины и к фрагменту
метки легко подкорректировать. Для этого достаточно
сравнить «старое» значение а(х) с х) и выбрать из
них меньшее в качестве «нового» значения а(х).
В приводимом ниже описании алгоритма построения
минимального остова помимо а(х) и использованы
следующие обозначения: FT1, ЕТ — множества вершин и
ребер строящегося фрагмента минимального остова; Nx —
336
окружение вершины х\ |G|=n. Граф G задан матри-
цей весов.
Алгоритм j/з построения минимального остова.
1.	Положить ЕТ : = 0, VT := {а}, где а — любая вер-
шина из VG. Каждой вершине х=^а приписать метки
а(х)= ш(х, а), если x^Na, и а(я)=оо, если х Ф Na,
£(#) = а.
2.	[отыскание вершины, «ближайшей» к фрагменту].
Выбрать вершину у* «= VGWT согласно условию
а(у*)= min а (у).
VEVGWT
3.	[увеличение фрагмента]. Пусть и' = $(и*). Изме-
нить VT и ЕТ, полагая VT := VT U {у*}, ЕТ : =
•=ЕТ U
4.	Если |FT| = п, то конец. Ребра, находящиеся в
множестве ЕТ, составляют минимальный остов.
5.	Для каждой вершины v е Nv* A (VG\VT) из-
менить метки следующим образом. Если a(v)> w(y*, и),
то a(v): = w(y*, v), P(p): = v*. Если же a(v)^ w(y*, v),
то метку вершины v не менять. Перейти к п. 2.
Утверждение 75.2. Алгоритм строит мини-
мальный остов за время О( |G|2).
> Так как всякий раз к ЕТ добавляется ребро, один
конец которого принадлежит VT, а другой нет, то граф
Т = (VT, ЕТ) на каждом шаге является деревом. После
завершения работы алгоритма это дерево будет остовным,
поскольку алгоритм прекращает работу только если
VT = VG.
Докажем минимальность остова Т. Для этого достаточ-
но доказать, что после А-го (к = 1, n—1) выполнения
п. 3 алгоритма граф Tk = (VTh, ЕТк) содержится в неко-
тором минимальном остове. Доказывать будем индукцией
по к. При к = 1 наше утверждение непосредственно сле-
дует из теоремы 75.1. Предположим, что оно справедливо
для некоторого к > 1, т. е. граф Тк, построенный в ре-
зультате к выполнений п. 3, содержится в некотором
минимальном остове. Учитывая правило выбора ребра е
для присоединения к Тк, применим теорему 75.1. Полу-
чим, что граф Тк+Х — Тк U е, построенный в результату
(& + 1)-го выполнения п. 3, также содержится в некото-
ром минимальном остове.
Выясним теперь быстродействие алгоритма. Однократ-
ное выполнение п. 2 требует времени не более O(|G|).
Столько же времени достаточно для обновления меток в
22 в. А. Емеличев и др.
337
п. 5, а п. 3 и п. 4 выполняются за время 0(1). Посколь-
ку каждый из пп. 2—5 выполняется п — 1 раз, то оценка
трудоемкости алгоритма — 0(Ю12). <1
Пример 1. На рис. 75.1 изображены граф G и по-
следовательность Тг (i = l, п— 1) фрагментов минималь-
ного остова, получающихся после каждой итерации алго-
ритма. Числа, приписанные ребрам графа О, означают
т3
Рис. 75.1

веса этих ребер. Каждой вершине х, еще не вошедшей
в Т\ приписана пара чисел [а(я), [}(#)], которыми она
помечена в результате i-ro выполнения п. 5 алгоритма.
Если граф G задан матрицей весов, то всякий алго-
ритм построения минимального остова в таком графе бу-
дет иметь сложность не менее чем O(|G|2), поскольку
он, согласно замечанию 1, должен просматривать все эле-
менты матрицы весов. Следовательно, в этой ситуа-
ции алгоритм имеет неуменыпаемую по порядку тру-
доемкость. Если же граф G задан списком ребер либо
списками смежности и \EG\ существенно меньше чем
IGI2, то быстродействие алгоритма далеко от опти-
мального. Другими словами, алгоритм J$3 недостаточно
эффективен в применении к «редким» графам, т. е. к гра-
фам, слабо насыщенным ребрами.
Рассмотрим еще один алгоритм построения минималь-
ного остова, ориентированный на работу именно с такими
графами. Этот алгоритм (алгоритм j/ч), как и предыду-
щий, опирается на теорему 75.1, однако более полно ис-
338
пользует предоставляемые ею возможности. Именно, ес-
ли в алгоритме ребро присоединяется всякий раз к
одной и той же компоненте леса, то в алгоритме реб-
ра присоединяются к каждой компоненте.
Пусть Т = {(Fi, Л), ..., (7Р, Тр)} — остовный лес
графа G. Назовем ребро аЪ минимальным по весу для
компоненты (Vz, 7\), 1 < I < р, если а е Vi, b&Vi и
ш(а, Ь)= min w(x, у). Будем говорить, что М =
x^Vi,y^Vi
= М(Т) — множество минимальных по весу ребер для ле-
са Т, если для каждого I = 1, р множество М содержит
хотя бы одно минимальное по весу ребро для компонен-
ты (Vh Ti) и, кроме того, М — минимальное по включе-
нию множество, обладающее этим свойством.
Утверждение 75.3. Если М — множество мини-
мальных по весу ребер для 7={(Vi, Т\), ..., (Vp, ТР)},
то граф Т' = Т + М не содержит циклов.
> Доказываем от противного. Предположим, что Т со-
держит цикл S, который не теряя общности будем счи-
тать простым. Пусть aibi, a2b2, ..., aibi — ребра множе-
ства S П М, выписанные в той последовательности, как
они расположены в цикле S. Этой последовательности
соответствует последовательность компонент (V^, ^),
(Vk2i Tk2), ...,(Vftz, Tkl) лесаT, такая, что^еУ^, 6xge
g= Vk2, а2 ge Vk2, b2 geV^, ..., at g= Vkl, Ъг ge Vk.. Выберем
среди ребер Uibi (f = l,Z) максимальное повесу. Пусть это
будет ребро а\Ь\. Ясно, что а\Ь\ является минимальным по
весу ребром по крайней мере для одной из компонент
Т^) или (У^2, Т\2). Не теряя общности считаем,
что ребро ди61 — минимальное по весу для (F& ,
Тогда w(a\, bi)=w(at, bi) и, следовательно, множество
M\aib\ содержит хотя бы одно минимальное по весу ребро
для каждой компоненты леса Т. Последнее противоречит
минимальности множества М. <
Перейдем теперь к изложению алгоритма ^4. Этот
алгоритм, так же, как и ^з, на первой итерации имеет
дело с остовным лесом графа G, состоящим из п = |G|
одновершинных компонент. Каждая итерация алгоритма
состоит в следующем. Вначале строится множество М
минимальных по весу ребер для леса Т, полученного в
результате предыдущих итераций. (Важно отметить, что
сделать это можно за один просмотр элементов множества
EG.) Затем с помощью поиска в глубину выделяются
22*	339
связные компоненты графа Т' = Т + М, который соглас-
но утверждению 75.2 является лесом. После этого начи-
нается следующая итерация с новым лесом Т', имеющим,
очевидно, меньше компонент, чем Т.
В приводимом ниже описании алгоритма <5^4 исполь-
зуются следующие обозначения. Ребра графа G содержат-
ся в списке Е, т. е. Е(1)—пара номеров концевых вер-
шин f-го ребра. Список W содержит веса ребер графа G,
т. е. W(i)—вес i-го ребра. Чтобы каждый раз строить
множество минимальных по весу ребер для текущего ле-
са за один просмотр списка Е, используются списки НМР,
BMP и КОМП:
НМР(/)—номер минимального по весу ребра для i-й
компоненты текущего леса;
ВМР(/)—вес этого ребра;
КОМП(/)—номер компоненты текущего леса, содер-
жащей вершину /.
Пусть, далее, ЕТ — множество ребер текущего леса
Т, а р — число его компонент; Е\ — множество мини-
мальных по весу ребер для текущего леса Т.
Алгоритм «52/4 построения минимального остова.
1.	ЕТ\=0, КОМП(/):=/, ВМР(/):=°о для i =
р:—тг. [Пн. 2—8 — построение множества Е\ минималь-
ных по весу ребер для леса Т].
2	:= J.
3.	’ Пусть’ Е(к) = ии; /:=КОМП(п), /:=КОМП(у)
[г и ; — номера компонент леса, содержащих вершины и
и v соответственно].
4.	Если i j, то перейти к п. 5, иначе перейти к п. 7.
5.	Если ip(u, р)= Ж(/с)< ВМР(/), то ВМР(/): =
у), НМР(/):=А:.
6.	Если w(u, v)= Ж(/с)< BMP(Z), то ВМР(/):==
р), HMP(Z):=fc.
7.	Если к = 1EGI, то перейти к п. 8. Иначе к : = к +1
и перейти к п. 3. [К моменту выполнения п. 8 первые р
элементов НМР содержат номера ребер, составляющих
множество минимальных по весу ребер для Т.]
8.	Просмотреть первые р элементов массива НМР и
сформировать множество Е\ минимальных по весу ребер
для леса Т.
9.	ЕТ := ЕТ U Е{ [ЕТ — множество ребер «нового»
леса Т'].
10.	Выделить с помощью алгоритма поиска в глуби-
ну связные компоненты графа Т' = Т + Е\ [обновлен
список КОМП, получено новое значение р].
340
11.	Если р = 1, то конец [ЕТ — множество ребер ми-
нимального остова]. Иначе перейти к п. 2.
Утверждение 75.4. Алгоритм зФь строит мини-
мальный остов за время O(\EG\ log |G|).
>	Нетрудно убедиться, что после каждого выполне-
ния п. 8 множество Е^ является множеством минималь-
ных по весу ребер для леса Т7, рассматриваемого в этот
момент. Поэтому согласно утверждению 75.2 граф Т' =
= Т + Е\ снова является остовным лесом. Это означает,
аз	аб
1-----------•	•----------Т
Рис. 75.3
что алгоритм строит некоторый остов графа G. Минималь-
ность этого остова доказывается с помощью теоремы 75.1
точно так же, как при обосновании предыдущего алгоритма.
341
Выясним теперь быстродействие алгоритма Для
однократного выполнения каждого из пн. 3—6 достаточ-
но времени 0(1) и, следовательно, построение Е\ осу-
ществляется за время O(|£’G|). Таких же затрат доста-
точно и для однократного выполнения пп. 8—11. Таким
образом, затраты на переход от Т к Т' = Т + Е\ (т. е. на
выполнение одной итерации) составляют ©(Ifi'Gl) опера-
ций. Оценим теперь число итераций алгоритма. Посколь-
ку одно ребро может быть минимальным по весу не бо-
лее чем для двух компонент леса Т, то на каждой итера-
ции |2?il > р(Т)/2. А так как Т + Е\ — лес, тор (Т + Е\)^
^р(Т)/2, т. е. на каждой итерации число компонент
уменьшается по крайней мере вдвое. Это означает, что
число итераций алгоритма не превосходит log |б?|, следо-
вательно, он строит минимальный остов за время
O(\EG\ log IGI). <1
Пример 2. Применим алгоритм ^4 к графу, изо-
браженному на рис. 75.2. На первой итерации будет най-
дено множество Ei = {ai<%2,	^4^7, Лба9, ми-
нимальных по весу ребер для леса, имеющего одновер-
шинные компоненты. Остовпые леса, полученные в ре-
зультате выполнения 1-й, 2-й и 3-й итераций, изображе-
ны на рис. 75.3. Последний из них является минимальным
остовом.
§ 76. Кратчайшие пути
Пусть G = (V, А) — ориентированный взвешенный
граф. Задача о кратчайшем пути состоит в отыскании пу-
ти минимального веса, соединяющего заданные началь-
ную и конечную вершины графа G при условии, что хо-
тя бы один такой путь существует. Начальную и конеч-
ную вершины обозначим соответственно через s и t;
(s, £)-путь минимального веса будем называть кратчай-
шим (5, t)-путем.
Вначале рассмотрим случай, когда веса всех дуг гра-
фа неотрицательны, т. е. w(e)^ 0 для каждой дуги е е А.
В этом случае решение задачи о кратчайшем пути явля-
ется существенно менее трудоемким, чем в общем случае.
Первый эффективный алгоритм построения кратчайшего
пути в графе с неотрицательными весами дуг предложил
Е. Дийкстра в 1959 г.
На каждой итерации этого алгоритма всякая вершина
v графа G имеет метку Z(y), которая может быть посто-
янной либо временной. В первом случае Г(у)— вес крат-
342
чайшего (s, и)-пути. Если же метка l(v) временная, то
l(v)—вес кратчайшего (s, р)-пути, проходящего только
через вершины с постоянными метками. Таким образом,
временная метка l(v) является оценкой сверху для веса
кратчайшего ($, р)-пути, и став на некоторой итерации
постоянной, опа остается такой до конца работы алгорит-
ма. Кроме Z(p), с каждой вершиной v графа G, за исклю-
чением s, связывается еще одна метка — 6(у). На каждой
итерации 0(р) является номером вершины, предшествую-
щей v в (s, р)-пути, имеющем минимальный вес среди
всех ($, р)-путей, проходящих через вершины, получив-
шие к данному моменту постоянные метки. После того
как вершина t получила постоянную метку, с помощью
меток 0(р) легко указать последовательность вершин, со-
ставляющих кратчайший ($, £)-путь.
Перед началом первой итерации алгоритма вершина s
имеет постоянную метку Z(s)=O, а метки I всех осталь-
ных вершин равны <*> и эти метки временные. Общая
итерация алгоритма состоит в следующем. Пусть р —
вершина, получившая постоянную метку Z(p) на преды-
дущей итерации. Просматриваем все вершины реГ(р),
имеющие временные метки, с целью уменьшения (если
это возможно) этих меток. Метка Z(p) вершины Г(р)
заменяется на Z(p)+iz;(p, р), если оказалось, что Z(p)>
>Z(p)+iz;(p, р). В этом случае говорим, что вершина v
получила свою метку Z из вершины р, и полагаем ©(р) —
= р. Если же Z(y)< Z(p) + iv(p, v), то метки 0 и Z вер-
шины v не изменяются на данной итерации. Алгоритм
заканчивает работу, когда метка Z(Z) становится постоян-
ной. Как уже говорилось выше, Z(Z)—вес кратчайшего
($, £)-пути, который будем обозначать через Р*. Этот
путь определяется с помощью меток 0 так:
Р*=($, ..., 03(Z), 02(Z), 0(Z), Z),
где Qk = 0 (0 (... 0 (р) ...)) для любой вершины v е VG.
k раз
Будем считать, что граф G задан матрицей весов ли-
бо списками смежности.
Алгоритм Дийкстры поиска кратчайшего пути. /
1.	Положить /($):= О и считать эту метку постоян-
ной. Положить Z(y):=oo для всех v^VG, v^s, и счи-
тать эти метки временными. Положить р := $.
2.	Для всех v е Г (р) с временными метками выпол-
нить: если l(v)> l(p)+ w(p, v), то l(p):= l(p)+ iv(p, v)
и 0(р):=р. Иначе l(v) и 0(р) не менять.
343
3.	Пусть V' — множество вершин с временными мет-
ками I. Найти вершину v*, такую что
Z(t>*) = min Z(z?)e
veV'
Считать метку Z(y*) постоянной меткой вершины и*.
4.	р := и*. Если p — t, то перейти к п. 5 [Z(Z)—вес
кратчайшего пути]. Иначе перейти к п. 2.
5.	Р*: = ($, ..., 03(Z), 02(Z), 0(£), t) [Р* — кратчай-
ший путь]. Конец.
Прежде чем перейти к обоснованию алгоритма, сде-
лаем три полезных замечания.
Замечание 1. Как легко видеть, алгоритм ^5
применим к смешанным и, в частности, к неориентиро-
ванным графам. Для этого достаточно каждое неориенти-
рованное ребро uv графа, имеющее вес ip (и, р), рассмат-
ривать как пару дуг (н, и) и (р, и) того же веса.
Замечание 2. Если п. 4 модифицировать так, что-
бы алгоритм заканчивал работу только после получения
всеми вершинами постоянных меток, то он будет строить
кратчайшие пути из s в каждую из остальных вершин.
Если к тому же вместе с превращением метки вершины
v* в постоянную (п. 3 алгоритма) заносить дугу (6(р*),
v*) в множество Л*, то после окончания работы алго-
ритма граф D=(7G, Л*) будет корневым ориентирован-
ным остовным деревом. Это дерево называют деревом
кратчайших путей из s графа G. Для любой вершины
v^VG единственный ($, р)-путь в дереве D является
кратчайшим (s, v) -путем в графе G.
Замечание 3. Алгоритм модифицированный
так, как указано в замечании 2, можно рассматривать
как алгоритм построения дерева D кратчайших путей из
вершины s графа G. С этой точки зрения алгоритм
аналогичен алгоритму построения минимального осто-
ва. Действительно, построение дерева D состоит в после-
довательном увеличении уже построенного фрагмента пу-
тем добавления некоторой дуги, «выходящей» из этого
фрагмента. При этом метки Z и 0 играют такую же роль,
как и метки а и £ в алгоритме ^з.
Утверждение 76.1. Алгоритм строит в графе
G кратчайший (s, 1)-путъ за время O(|G|2).
> Заметим вначале, что метка вершины v (Z(i?)=/= оо)'
равна весу (5, и)-пути, который построен алгоритмом к
этому моменту. Он определяется метками 0, имеющимися
на заданный момент. Поэтому для доказательства опти-
344
мальности ($, £)-пути, соответствующего постоянной мет-
ке l(t), достаточно доказать, что постоянная метка 1(у)
каждой вершины v равна весу кратчайшего ($, р)-пути.
Это утверждение будем доказывать по индукции. Пусть
вершина v получила свою постоянную метку на /с-й ите-
рации, т. е. после /с-то выполнения п. 3. При к = 1 спра-
ведливость утверждения очевидна. Предположим, что оно
верно для вершин, получивших свои постоянные метки
на итерациях 2, 3, . . ., к — 1. Обозначим через Р° ($, р)-
путь, построенный алгоритмом в результате к итераций,
а через Р* — кратчайший (5, р)-путь. По условию
w(PQ) = l(v). Пусть Vi и V2 — множества вершин, име-
ющих соответственно постоянные и временные метки пе-
ред началом к-й итерации. Рассмотрим две возможные
ситуации:
а)	Путь Р* содержит вершины из V2. Пусть v— пер-
вая (считая от $) такая вершина, принадлежащая Р*,
а вершина и' предшествует v на пути Р*, т. е. (z/, г?)^
«= АР*. Согласно выбору v имеем v' «= V\. Обозначим че-
рез Pi часть пути Р* от s до г?. По предположению ин-
дукции l(v')—вес кратчайшего ($, р,)~пУти- Поэтому
w(p*) = Z(p') + гр(р'р)>/(р).	(1)
Поскольку /(г?)—временная метка, а постоянная метка
Ци) вершины v выбирается на к-й итерации как наи-
меньшая из временных, то Z(z?)^Z(z;). Объединив это
неравенство с (1), получим
w (Р*) > w (Р*) > Z (у) = W (Р°),
т. е. Р°— кратчайший ($, р)-путь.
б)	Все вершины пути Р* входят в Vi. Пусть v' и
v"—такие вершины, что (z/, v)^AP* и (z/7, р)^ЛР°.
Обозначив через Р' часть пути Р* от 5 до и', согласно
предположению индукции имеем ш(Р7)	Z(z/). Поэтому,
если v' = v", то сразу получаем неравенство
zp(P*) = zp(P')+ w(y',	Z(z/)+	v)= w(PQ).
Допустим теперь, что v'¥= v". Поскольку v получает по-
стоянную метку Z(p) из и", а не из v', то
р(Р*)= Z(z/)+ ш(р', v)> Z(z/Z)+	р)= ш(Р°).
Таким образом, и в случае б) верно неравенство w?(P0)=^
zp(P*), т. е. Р° — кратчайший ($, р)-путь.
Оценим теперь трудоемкость алгоритма. Вычислитель-
ные затраты максимальны, когда вершина t получает по-
345
стоянную метку последней и граф G является полным.
В этом случае число итераций алгоритма равно I Gl — 1,
т. е. каждый из пп. 2—4 выполняется |G| — 1 раз. Оче-
видно, что п. 4 выполняется за время 0(1), а для вы-
полнения каждого из пп. 2, 3 достаточно времени O(|G|).
Рис. 76.1
Построение пути с помощью меток 0 можно осуществить,
затратив не более G(|G|) операций. Таким образом,
в целом время построения кратчайшего (5, £)-пути не
превосходят О(|G|2). <
346
Пример 1. На рис. 76.1 изображены пять копий Gk
(к = 1, 5) графа G, каждая из которых отражает ситуа-
цию, сложившуюся после очередной итерации алгоритма.
Около каждой дуги написан ее вес. Вершинам копии Gh
(к == 1, 5) приписаны метки, полученные ими в резуль^
тате выполнения первых к итераций. Некоторые дуги
обведены жирными линиями, т. е. отмечены. Добавление
такой дуги (а, Ь) при переходе от Gk к Gk+i означает,
что вершина b получила свою метку 1(b) из а и эта мет-
ка стала постоянной на (&+1)-й итерации. Вершина t
в нашем примере получает постоянную метку последней,
и отмеченные дуги Gs образуют дерево кратчайших пу-
тей из s.
При решении многих задач возникает необходимость
отыскания в невзвешенном графе (s, £)-пути с минималь-
ным количеством дуг. Такой путь, очевидно, можно най-
ти с помощью алгоритма Дийкстры. Для этого достаточ-
но присвоить всем дугам графа G веса, равные 1, и при-
менить алгоритм *2^5. Проследим работу алгоритма в этой
ситуации, обращая особое внимание на последователь-
ность, в которой вершины графа G получают постоянные
метки. Очевидно, что вначале постоянные метки 1 = 1
получат все вершины множества T(s). Затем метка 1 = 2
будет присвоена концам дуг, выходящих из Г($). Вооб-
ще, постоянную метку I = к получают еще не помечен-
ные вершины, являющиеся концами дуг, исходящих из
вершин с метками I = к — 1. Этот процесс обхода (и при-
своения меток) вершин графа называют поиском в ши-
рину в графе (на интуитивном уровне поиск в ширину
описан в § 9). По окончании поиска в ширину метка
1(х) вершины х равна минимальному числу дуг в (5, х}~
пути. Как и ранее, сам этот путь определяется метками
0. Осуществление поиска в ширину с помощью алгорит-
ма Дийкстры связано, как мы знаем, с вычислительными
затратами О( |G|2).
Рассмотрим алгоритм осуществляющий поиск в
ширину за время G(l£’Gl). В этом алгоритме метки I и
О играют ту же роль, что и в предыдущем, с той, одна-
ко, разницей, что метки I не делятся на временные и
постоянные. Как только вершина х получает метку
1(х)¥=<х>, эта метка сразу становится постоянной (т. е.
окончательной). За счет этого, в частности, достигается
экономия времени вычислений по сравнению с алгорит-
мом Дийкстры.
347
Особую роль в алгоритме «$$6 играет список Q. Каж-
дая вершина графа один раз заносится в этот список
и один раз из него вычеркивается. При этом вычеркива-
ется все время первая (на данный момент) вершина
этого списка, а только что добавленная вершина всегда
является последней в списке, т. е. Q — очередь. Вначале
в Q находится единственная вершина 5, Z(s)=O, а все
остальные вершины меток не имеют. Общая итерация
состоит в следующем. Выбирается первая вершина х в
списке Q, Каждой непомеченной вершине у Г (х) при-
сваиваются метки Z(p)=Z(^)+l и Q(y) — x, после чего
вершина у становится последней в списке Q, а вершина
х удаляется из Q, Алгоритм прекращает работу, как
только в Q не останется ни одной вершины. При этом
вершины, достижимые из s, будут иметь метки, а недо-
стижимые — нет. Для быстрого выполнения операций вы-
черкивания и включения элементов в Q используются
переменные указатели р и q — адреса первой и послед-
ней занятых ячеек списка Q соответственно.
Будем считать, что граф G задан списками смежно-
сти и Nv — список, содержащий концы всех дуг, исхо-
дящих из вершины v.
Алгоритм поиска в ширину.
1.	@(1):=^, р :== 1, q := 1, Z(s):= 0.
2.	х := <?(р), т : = IГ (а?) | [выбрана первая вершина х
очереди (?].
[Пп. 3—5 — присвоение меток непомеченным верши-
нам из Г (гг) ].
3.	к := 1.
4.	Если вершина z/ = 2Vx(A:) имеет метку, то перейти
к п. 5. Иначе l(y) := l(x) + 1, 0(у):=£, q:=q+l,
QYlY—y [вершина у помечена и включена в очередь <21
и перейти к п. 5.
5.	Если к~т, то перейти к п. 6, иначе к :== к + 1
и перейти к п. 4.
6.	р = р+ 1 [вершина х исключена из (2] •
7.	Если р > д, то конец [(2 = 0, т. е. все вершины,
достижимые из 5, получили метки], иначе перейти к п. 2.
Утверждение 76.2. Алгоритм присваивает
метки I и 0 всем вершинам графа, достижимым из вер-
шины s за время O(|2?G|). При этом (5, ..., 03(я), 02(я),
$(х), х) — (s, х)-путъ с минимальным числом дуг,
а 1(х)— число дуг в этом пути,
> Основные вычислительные затраты связаны с вы-
полнением п. 3 алгоритма. Суммарное время выполнения
348
этого пункта составляет О 2 I Nv |) = О (| EG |), по-
\veVG /
скольку каждый из списков Nv просматривается в точ-
ности один раз. Затраты на выполнение других пунктов,
очевидно, не превосходят этой величины.
Выше отмечалось, что результаты алгоритма ^6 (т. е.
метки I и 0) те же, что и в алгоритме Дийкстры, если
каждой дуге графа G приписать вес, равный 1. Поэтому
справедливость второго утверждения следует из утвер-
ждения 76.1. <
Замечание 4. Иногда требуется искать пути из
вершин множества X^VG во все остальные вершины.
Для решения этой задачи достаточно слегка модифици-
ровать алгоритм изменив в нем п. 1. Именно, в спи-
сок Q следует поместить все вершины множества X и
положить 1(х)=0 для каждой вершины х^Х. На мо-
дифицированный таким образом алгоритм будем ссы-
латься как на поиск в ширину из множества X.
Перейдем теперь к рассмотрению общей ситуации.
Будем считать, что в графе G допускаются дуги отрица-
тельного веса. Предлагаемый ниже алгоритм S&7 строит
в таком графе кратчайшие пути между всеми парами
вершин графа при условии, что в графе нет отрицатель-
ных контуров (контуров отрицательного веса). Если же
такой контур в графе имеется, то алгоритм сообщает об
этом и прекращает работу, оставляя задачу отыскания
кратчайшего пути нерешенной (см. ниже замечание 6).
Будем считать, что граф G, |Gl=n, задан матрицей
весов W = IlWijH, т. е. Wij = w(i, у), если (Z, j)<=AG,
и Wij = оо в противном случае. Кроме того, полагаем
Wa=0 для всех i=l, 2, ..., п. Алгоритм основан на
следующих соображениях. Пусть I, j, к — три любые вер-
шины графа G, и мы хотим получить (f, j)-путь, крат-
чайший среди (i, у)-путей, не содержащих внутренних
вершин, отличных от к. Очевидно, что для этого доста-
точно выбрать меньшую из двух величин и Wik +
+ Whj, которая и будет весом такого (i, у)-пути. Если
зафиксировать к и проделать эту операцию (назовем ее
t-операцией, примененной к индексу к) для всех пар /
(г, у), то получим матрицу W' == || W'a ||, у которой W'ij =
= min (Wij, Wik + Wkj}- Оказывается (это будет позднее
доказано), имея матрицу Ws весов кратчайших путей,
проходящих только через вершины множества S VG,
можно получить такую же матрицу для путей, проходя-
щих через множество S U {mi, S. Для этого доста-
349
точно применить f-операцию к индексу т и всем эле-
ментам матрицы Ws. Именно в этом и состоит итерация
алгоритма «5^7, который, начиная с W° = W, строит та-
кую последовательность матриц И70, И71, ..Wn, что Wm
получается из F1-1 применением ^-операции к индексу
т и матрице ТУ"1-1. Если в графе G нет отрицательных
контуров, то элемент ТУ^ матрицы Wm при каждом т
равен весу кратчайшего (Z, у)-пути, все внутренние вер-
шины которого принадлежат множеству {1, 2, ..., т}.
Таким образом, последняя из этих матриц, Wn, содержит
веса кратчайших путей между всеми парами вершин
графа. Для того чтобы после окончания работы алгорит-
ма иметь возможность быстро найти кратчайший путь
между любой парой вершин, будем на Л-й итерации вме-
сте с матрицей Wh строить матрицу Ph = || Рц ||. Вначале
полагаем Рц = Z(Z,y = 1, п). Далее, на /с-й итерации по-
лагаем Р^ = PiP1, если Wij = Wij~\ и Pij = Р^1, если
Wij = Wih1 +	Таким образом, Pij— номер верши-
ны, предшествующей вершине у в текущем (Z, у)-пути,
т. е. в кратчайшем (Z, у)-пути, все внутренние вершины
которого содержатся в множестве {1, 2, ..., к}, Матрица
Рп = || Р^ || играет ту же роль, что и метки 0 в пре-
дыдущих алгоритмах 3/5 и С помощью этой матри-
цы кратчайший (г, у)-путь j) определяется следу-
ющим образом: L(i, =	.., у’з, /2, Уь у), где у\ = Pij,
у2 = Pij , /з = Рь- , ...
Алгоритм S&7 отыскания кратчайших путей между
всеми парами вершин.
l.	W°:=W, к:=1, Р° ||, где Р°ц = г, если
Wij^oo, и Pij = 0 в противном случае.
2.	Выполнить для всех г,/=1,п: если
+ W&1, то №%: = Wfr1, P^j-.^Plr1- Иначе Wfj: = W^ljr
+ k
3.	Если для некоторого Z, 1 Z^n, W^<0, то конец
[в графе имеется отрицательный контур]. Иначе перейти
к п. 4.
4.	к :== к + 1. Если к = п + 1, то конец [Wn = || Wjj || —
матрица весов кратчайших путей, определяемых с по-
мощью матрицы Рп = || Pij ||].
Замечание 5. Алгоритм будет применим к сме-
шанным графам, если каждое неориентированное ребро
заменить на две дуги того же веса (см. замечание 2).
350
При этом следует учесть, что неориентированное ребро
отрицательного веса сразу приводит к отрицательному
контуру.
Замечание 6. Алгоритм «отказывается» строить
кратчайшие пути, когда в графе G имеются отрицатель-
ные контуры. В этом случае задача отыскания кратчай-
шего пути между двумя вершинами (или между всеми
парами вершин) остается корректной, но становится
очень трудной. Можно показать, что она не менее труд-
на, чем, например, задача о коммивояжере.
Перейдем теперь к обоснованию алгоритма S&7 и оцен-
ке его трудоемкости.
Утверждение 76.3. Пусть взвешенный ориенти-
рованный мультиграф L имеет эйлерову цепь, соединя-
ющую вершины а и Ъ. Если в L нет отрицательных кон-
туров, то в нем имеется такой {а, Ъ)-путь Р, что
w(L)> w(P).
> Будем считать, что мультиграф L не является пу-
тем (иначе утверждение тривиально). Поэтому он со-
держит некоторый контур S. Удалив из L все дуги этого
контура, получим мультиграф L'. Поскольку ш(5)>0,
то w(L)^w(L'). Кроме того, согласно теореме 65.2 по-
лустепени вершин мультиграфа L' удовлетворяют соот-
ношениям
d+(a) = d"(a)+ 1, d~(&)-d+(6)+ 1,
d+ (н) = d~ (v), v^a, b.
Поэтому вершины а и b принадлежат одной его сла-
бой компоненте L", и последняя содержит эйлерову
(а, Ь)-цепь. Продолжая подобным образом, получим тре-
буемый (а, &)-путь. <
Утверждение 76.4. Если в графе нет отрицатель-
ных контуров, то при всех k, i, j = 1,п Wij— вес крат-
чайшего (i, ])-пути, все внутренние вершины которого
содержатся в множестве {1, 2, . . ., к}.
> Доказываем индукцией по к. При к = 1 справедли-
вость утверждения очевидна. Предположим, что оно
справедливо для 2, 3, ..., к — 1, и рассмотрим Wij. Пусть
Р° — кратчайший (I, /)-путь, все внутренние вершины
которого принадлежат множеству {1, 2, ..., к}. Если Р°
не включает вершину к, то Wij = РЕ^и, согласно пред-
положению индукции, w(P°) = Wij-1 = Допустим
теперь, что Р° содержит вершину к. Обозначим через Р?
351
и 7^2 части пути PQ от i до к и от к до / соответственно.
Предположим, что один из этих путей, например Р?,
пе является кратчайшим, и пусть Р' — кратчайший (г,
к) -путь, все вершины которого содержатся в множестве
{1, 2, . . ., к~ 1}. Рассмотрим мультиграф L, получаю-
щийся из графа Р' U ^2 заменой каждой дуги, входя-
щей одновременно в Р' и двумя экземплярами этой
дуги. Очевидно, что L не содержит отрицательных кон-
туров. Поэтому, согласно утверждению 76.3, L содержит
такой (г, у)-путь Р, что w(L)^ w(P) и, следовательно,
w (Р°) = w (Pl) + w (Pl) > w (Р') + гр (Pl) =w(L)^w (Р).
Это неравенство противоречит минимальности Р°.
Таким образом, пути Р? и Р% являются кратчайши-
ми среди, соответственно, (г, к)- и (Л, /)-путей, все внут-
ренние вершины которых принадлежат множеству {1,
2, ..., А:—!}. Поэтому, воспользовавшись предположени-
ем индукции, получим
= wfr1 + wfr1 = w (Pl) + № (Pl) = W (P°). <j
Теорема 76.5. Время работы алгоритма не пре-
восходит G(|G|3). Если граф G не содержит отрицатель-
ных контуров, то Wij— вес кратчайшего (f, ])-пути в
графе G для всех I, 7 = 1, п, n=|G|. Если же такие
контуры в графе имеются, то существуют такие числа тп
и I, что WTi<Q.
> Справедливость первого утверждения теоремы оче-
видна, поскольку каждая из не более чем |G| итераций
выполняется за время O\G\2.
Второе утверждение теоремы непосредственно следует
из утверждения 76.4.
Допустим теперь, что граф G содержит отрицательные
контуры. Пусть тп — такой наименьший индекс, что для
некоторой вершины I в графе G имеется отрицательный
контур S, содержащий только I и некоторые вершины
множества {1, 2, . .., тп}. Ясно, что контур S включает
вершину тп. Тогда при любых i, j = 1, п число
равно весу кратчайшего (i, 7)-пути, все внутренние вер-
шины которого принадлежат множеству {1, 2, ..., тп~ 1}.
Доказательство этого факта дословно повторяет доказа-
тельство утверждения 76.4. Контуру S соответствуют
(I, тп)-путь Pi и {тп, /)-путь Р2, такие, что Pi U Р2 = S.
Поскольку внутренние вершины путей Pi и Р2 принад-
352
лежат множеству {1, 2, ..тп —1), то	Wmi *’
Следовательно, ЧС?1 + WT^w(P^ +
+w(P2)=in(S), т. e. Wz™ = min {0, W^+ W™.^} <0. <
Рис. 76.2
Пример 2. Ниже приведены результаты выполне-
ния каждой из четырех итераций алгоритма для графа,
изображенного на рис. 76.2:
(0 - 2 3 - 3\	/0 1 1 1\
оо	0	2	оо ।	pg	/ 2	0	2	2 ।
оо	ОО	О	— 3 I’	1	| 3	3	0	3 I
4	5	5	0/	' 4	4	4	0/
/0 — 2 3 -3\	/0 1 1 К
I оо 02 оо \	р1_|2022\
оо оо о -3 1’ г I з з о з Ь
\4	2 5	0/	\4 1 4 0/
(0	— 2	0	— 3\	/0121ч
оо	0	2	оо \ р2 _/ 2	0 2	2 \
оо	оо	о	— з ’	I 3	3 0	3
4	2	4	0/	\4	1 2	0 z
тг3 =
0 - 2 0 - 3\
оо 0 2 — 1 ।
оо оо 0 — 3 г
4	2	4	0/
/0 - 2 0 - 3\
3	0	2	— 1 \
1—10—31’
\4	2	4	0/
0 1 2 1\
2 0 2 3 ]
3 3 О 3 г
\4 1 2 0/
/0 1 2 Ь
4 0 2 3
4 1 0 3 Г
•4 1 2 0/
Найдем, папример, с помощью матрицы Р4 кратчайший
(2, 1)-путь: ^21 = 4, Р%4 = 3, Pg3 = 2. Следовательно, (2,
3, 4, 1)—кратчайший (2, 1)-путь.
23 в. А. Емеличев и др.	353
§ 77. Наибольшие паросочетания
и задача о назначениях
Задача построения наибольших паросочетании: в гра-
фе широко распространена, и для ее решения имеются
эффективные алгоритмы. Эти алгоритмы основаны на ме-
тоде чередующихся цепей, восходящем к Дж. Петерсену.
Пусть М — паросочетание в графе G. Цепь графа G,
ребра которой поочередно входят и не входят в М, на-
зывается чередующейся относительно М. Цепь длины 1
Рис. 77.1
по определению также чередующаяся. Ребра цепи назы-
ваются темными или светлыми, если они входят или,
соответственно, не входят в М, Вершины графа G, ин-
цидентные ребрам из М, называются насыщенными, все
другие вершины — ненасыщенными.
Рассмотрим, например, граф на рис. 77.1. Множество
ребер
М = U1, е7, ею)	(1) '
является в G паросочетанием;
р = (7, 8, 4, 1, 2, 5)	(2)
— чередующаяся относительно М цепь; ei = {1, 2}, ею =
= {4, 8}темные ребра Р; е3 = {1, 4}, е^ = {2, 5}, Щз «
= {7, 8} — светлые ребра Р; {1, 2, 3, 4, 6, 8} и {5, 7, 9,
10} — множества насыщенных и ненасыщенных вершин
соответственно.
Очевидно, что если в графе G существует чередую-
щаяся относительно паросочетания М цепь, соединяющая
две несовпадающие ненасыщенные вершины, то можно
построить в G паросочетание с большим числом ребер,
чем в М. В самом деле, в такой цепи число темных ре-
бер на единицу меньше числа светлых. Удалив из М
354
все темные ребра и присоединив все светлые, получим
новое паросочетание, в котором число ребер на единицу
больше. По этой причине чередующуюся относительно
паросочетания М цепь, соединяющую две различные не-
насыщенные вершины, будем называть увеличивающей
относительно М цепью в графе G.
Итак, отсутствие увеличивающих относительно М це-
пей необходимо, если паросочетание М наибольшее. Это
условие оказывается и достаточным. Именно, верна
Теорема 77.1. Паросочетание М в графе является
наибольшим тогда и только тогда, когда в этом графе
нет увеличивающих относительно М цепей.
> Необходимость условия теоремы, как выше отмеча-
лось, очевидна. Достаточность докажем от противного.
Пусть М\ также является паросочетанием в G и |AfJ >
> \М\. Рассмотрим граф Я, образованный ребрами, вхо-
дящими в сумму М и М\ по модулю 2, т. е. в (М UJfi)\
\(М О М\). Так как произвольная вершина v этого гра-
фа инцидентна не более чем одному ребру каждого из
паросочетаний М и М\, то ее степень не больше чем 2.
Если deg v = 2, то одно из инцидентных вершине v ребер
входит в М, другое — в М\. Поэтому любая связная ком-
понента графа Я является либо циклом, содержащим
одно и то же число ребер из М и из М\, либо чередую-
щейся относительно М цепью. Но |ЛЛ1 > |Л7|, следова-
тельно, среди этих компонент обязательно есть череду-
ющаяся относительно М цепь, крайние ребра которой
(первое и последнее) входят в М\. Тогда крайние вер-
шины этой цепи не насыщены паросочетанием М, что
противоречит условию теоремы. <
Для иллюстрации снова обратимся к графу G на
рис. 77.1. Чередующаяся относительно паросочетания (1)
цепь (2) соединяет ненасыщенные вершины 5 и 7. Сле-
довательно, можно построить паросочетание М' с боль-
шим числом ребер:
М' ~(М\{е\, вю})и{ез, е$, 613} = {вз, е$, eq, 613}.
Паросочетание М' также не является наибольшим:
(9, 10)—увеличивающая относительно М' цепь. Паро-
сочетание
М" = М' U {^15} = {ез, 65, eq, щз, 615}
— наибольшее, cci (G) == 5.
Таким образом, теорема 77.1 подсказывает следую-
щую стратегию поиска наибольшего паросочетания: на-
23*	355
чав с произвольного паросочетания М, строить последо-
вательность Mi ~ М, М2, Мз? ..в которой паросочета-
ние Mh+i получается из Mh с помощью только что рас-
смотренного изменения вдоль некоторой увеличивающей
цепи. Поскольку |Mfc+il = |MJ + 1, то для получения
наибольшего паросочетания потребуется не более IGI/2
итераций (т. е. переходов от Mk к Mft+i). В качестве М
можно взять, например, произвольное ребро графа или,
что лучше, некоторое максимальное паросочетание, так
m	_2» что исходное паросочетание
всегда имеется в нашем рас-
^\z/^ поражении. Поэтому разра-
Чл/\/	xwSc ботка эффективного алгорит-
ма’ основанного на указан-
ной стратегии, сводится к
построению процедуры, кото-
// Ч	// Ч рая быстро находит увели-
/	\	# ъ чивающую цепь в графе, ли-
_ бо выявляет ее отсутствие.
G	G Ограничимся случаем дву-
Рис. 77.2	дольного графа, хотя такая
процедура (а значит, и эф-
фективный алгоритм отыскания наибольшего паросочета-
пия) известна и в случае произвольного графа. Итак,
пусть G = (X, У, Е)— двудольный граф и М—паросо-
четание в этом графе. Поставим в соответствие графу G
и паросочетапию М вспомогательный ориентированный
двудольный граф G-(X, Y, Л), полагая
где А1 =« {(у, а*): х е X, y^Y, ху М}, А2 = {(z, у): х
еХ, ys У, ху <^EG\M}. Иными словами, чтобы получить
граф G, достаточно придать ориентацию «от У к X» всем
ребрам графа G, входящим в паросочетание М, и «от X
к У» всем остальным ребрам этого графа. На рис. 77.2
изображены граф G с паросочетанием М (выделено жир-
ными линиями) и граф G,
 Обозначим через Хм и YM множества ненасыщенных
вершин, входящих, соответственно, в X и У. Справедли-
вость следующего утверждения очевидна.
Утверждение 77.2. В графе G увеличивающая
относительно паросочетания М цепь существует тогда и
только тогда, когда в графе G существует (5, Г)~путъ,
у которого s се Хм, t е= УМф
356
Пусть Р — (s, /)-путь в графе G, se Хм, t о Ум, Р
соответствующая увеличивающая цепь в графе G и М\ —
паросочетание, полученное изменением М вдоль цепи Р.
Тогда вспомогательный граф Gi для графа G и паросо-
четания М\ можно получить из графа G заменой каждой
—>
дуги пути Р на обратную. Эта операция вместе с поиском
пути Р составляет итерацию приводимого алгоритма.
Предполагается, что граф G задан списками смежности.
Алгоритм построения наибольшего паросочетания
в двудольном графе.
1.	Построить какое-либо максимальное паросочетание
М в графе G.
2.	По графу G и паросочетанию М построить граф G.
3.	Пусть в графе G Х~ = {х: х е X, й“(д;)== 0), У+ ==
== {у: y^ Y, d+{y)=Q} [в графе G Х~ U У+— множе-
ство вершин, не насыщенных текущим паросочетанием].
Выполнить в графе G поиск в ширину (алгоритм s£q)
из множества Х~.
4.	Если в результате поиска в ширину ни одна из
вершин множества У+ не получила метки, то перейти к
п. 5. Иначе перейти к п. 6.
5.	Пусть Т = {(У1, Xi), (у2, х2), (ук, А)} —мно-
жество всех дуг, выходящих из множества У. Положить
М* == {yi^i, г/2-^2, ..., ул) [М* — наибольшее паросоче-
тание]. Конец.
—>	—>
6,	Пусть Р — (s, t)-nyrb в графе G такой, что s^X~,
—>
t е У+. Изменить граф G, заменив в нем каждую дугу
(а, Ь) пути Р на дугу (&, а). Перейти к п. 2.
Утверждение 77.3. Алгоритм s&s строит наиболь-
шее паросочетание в двудольном графе G=(X, У, EG)
за время G(|£'G| min {|Х|, |У|}).
> То, что алгоритм корректен и построенное им паро-
сочетание является наибольшим, следует из теоремы 77.1
и утверждения 77.2. Очевидно также, что число итера-
ций алгоритма (т. е. выполнений п. 2—5) не превосхо-
дит величины min{|X|, |У|}, поскольку на каждой ите-
рации, кроме последней, величины |X~i и |У+| умень-
шаются на единицу.
Согласно утверждению 76.2 п. 3 выполняется за вре-
мя G(|£'G|). Легко показать, что эта же оценка трудо-
357
емкости справедлива и для остальных шагов алгоритма.
Таким образом, время выполнения отдельной итерации
составляет O(\EG\), а алгоритма в целом —
O(\EG\min {|AJ, I УII). <
Вместе с наибольшим паросочетанием алгоритм
фактически находит и наименьшее вершинное покрытие
в графе G. В результате последнего выполнения п. 3 ал-
горитма будет установлено отсутствие пути из Х~ в У+
в графе G. Следовательно, только часть вершин этого
графа будет иметь метки после окончания поиска в ши-
рину из Х~. Обозначим через X' и У', соответственно,
множества непомеченных вершин доли X и помеченных
вершин доли Y. Положим Z = X' U У'. Будем считать,
что в графе G пет изолированных вершин.
Утверждение 77.4. Множество Z является наи-
меньшим вершинным покрытием графа G.
> Утверждение достаточно доказать для связных гра-
фов. Пусть (я, &)—произвольная дуга графа G. Если
а е У? Ъ е X, то эти вершины либо обе помечены, либо
пет. В обоих случаях дуга (я, Ь) инцидентна вершине
множества Z, Пусть а X, Ъ У. Тогда, если вершина а
не помечена, то а Z. Если же а помечена, то и вер-
шина Ъ помечена и, следовательно, Ъ Z. Итак, всякая
дуга графа G инцидентна некоторой вершине множества
Z, т. е. Z — покрытие графа G. Кроме того, легко видеть,
что \Z\ = |Т|, где Т — множество всех дуг графа G, ве-
дущих из множества У. Множеству Т в графе G соот-
ветствует наибольшее паросочетание. Поэтому из тео-
ремы 32.2 следует, что вершинное покрытие Z является
наименьшим. <
Использованный здесь метод чередующихся цепей иг-
рает важную роль и при решении более общих задач.
Одну из них мы сейчас рассмотрим.
Пусть G = (X, У, EG)—полный двудольный взвешен-
ный граф, 1X1 = |У| = п. Требуется найти в графе G
совершенное паросочетание, вес которого минимален.
Легко видеть, что это — упоминавшаяся ранее задача о
назначениях (см. гл. IV, § 30).
Совершенное паросочетание минимального веса назо-
вем для краткости оптимальным решением.
Задача о назначениях обладает двумя простыми свой-
ствами:
1. Поскольку для каждой вершины любое совершен-
ное паросочетание содержит в точности одно ребро, ин-
358
цидентное этой вершине, то множество оптимальных ре-
шений не изменится, если веса всех ребер, инцидентных
какой-либо вершине, увеличить (уменьшить) на одно и
то же число.
2. Если веса всех ребер графа неотрицательны и вес
некоторого совершенного паросочетания равен пулю, то
оно является оптимальным решением.
Пусть, как обычно, ш(х, у)— вес ребра ху. Будем
считать, что w(x, у)^0 для каждого ребра xy^EG.
Из первого свойства следует, что случай, когда имеются
ребра отрицательного веса, сводится к нашему. Кроме
того, это свойство позволяет, затратив О(тг2) операций,
перейти к взвешенному графу, у которого каждой вер-
шине инцидентно ребро нулевого веса и веса всех ребер
неотрицательны. Для этого достаточно изменить матрицу
весов графа G следующим образом: сначала вычесть из
всех элементов каждой строки минимальный элемент этой
строки, а затем то же самое проделать со столбцами.
Будем считать, что эта операция уже проделапа и граф
G обладает требуемыми свойствами.
Пусть Л <= X, В <= У и а — некоторое число. Будем
говорить, что к графу G применяется операция (А, В,
а), если сначала из веса каждого ребра, инцидентного
вершине из множества Л, вычитается а, а затем к весу
каждого ребра, инцидентного вершине из В, прибавля-
ется а. Согласно свойству 1 получившийся в результате
взвешенный граф имеет то же множество оптимальных
решений, что и граф G. Кроме того, ребра вида ab, где
а Л, Ъ В, в преобразованном графе будут иметь то же
веса, что и в исходном. Пусть 7Т = (Х, У, U)— двудоль-
ный граф и М — паросочетание в этом графе. Будем, как
и ранее, обозначать через Т = Т(Т, М) ориентированный
двудольный граф, полученный из графа Т путем ориен-
таций «от У к X» всех ребер паросочетания М и «от X
к У» остальных ребер этого графа.
Будем считать, что граф G задан матрицей весов.
Алгоритм построения совершенного паросочетания
минимального веса в двудольном взвешенном графе.
1.	Построить граф 7Т=(Х, У, Е7), U = {ху. w(x,
у)=0}.
2.	Найти в графе Т максимальное паросочетание М.
Пусть Хм и YM — множества вершин, не насыщенных
паросочетанием М и входящих, соответственно, в доли
Хи У.
359
3.	Если Хм = Ум = &, то конец [М — оптимальное
решение задачи]. Иначе построить граф Т =	М).
4.	Применить к графу Т поиск в ширину (алгоритм
<$^б) из множества Хм. Если найден (х, г/)-путь Р,
е Хм, у^ Ум, то перейти к п. 5. Иначе перейти к п. 7.
5.	Преобразовать граф Г, заменив в нем каждую ду-
гу пути Р па обратную. Пусть Хм = {х: х & X, d~(x) =
== 0), YM = {у: у е У, d+(y) = Q} [путем изменения И
вдоль увеличивающей цепи пайдено повое паросочетание
в графе Г = (Х, У, £7), ХМ^Х, Ум <= У — подмножества
вершин графа Т, не насыщенных новым паросочетанием].
6.	Если Хм = Ум = то конец [множество всех та-
ких ребер ху, что х X, у^У и {у, я)—дуга графа Т,
составляет совершенное паросочетание минимального ве-
са в исходном графе (?]. Иначе перейти к п. 4.
7.	Пусть Xf <= X и У7 <= У — подмножества вершин
графа Т, получивших пометки в результате поиска в
ширину (в п. 4). Среди ребер графа G, имеющих вид
ху, х е X', у е У - У', найти ребро минимального веса.
Пусть а — вес этого ребра.
8.	Модифицировать веса дуг графа G, применив к не-
му операцию (X', У', а).
—1ъ
9.	Модифицировать граф Т, добавив к нему все такие
дуги (х, у), что х^Х, у У — У', w(x, у)= 0, и удалив
все такие дуги (х, у), что х^Х — Х', у^У'. Перей-
ти к п. 4.
Займемся теперь обоснованием алгоритма Кор-
ректность пп. 1—3 не вызывает сомнений. Легко видеть
также, что каждый из этих пунктов можно выполнить
за время О(п2). Остальные пункты алгоритма рассмот-
рим более подробно.
Каждое выполнение п. 5 увеличивает на единицу
число вершин у е У, для которых d+(y) = 1. Следователь-
но, этот пункт выполняется пе более п раз. Наша бли-
жайшая цель — показать, что после выполнения пп. 4,
6—9 не более чем п раз подряд обязательно произойдет
переход к п. 5, т. е. очередное выполнение п. 4 закон-
чится отысканием пути Р. Рассмотрим подробнее
пп. 7—9. После окончания п. 4 и перехода к п. 7 каж-
дая дуга графа Т инцидентна по крайней мере одной
вершине множества (X-X')UY'. Это сразу следует из
утверждения 77.4. Таким образом, каждое ребро нулевого
360
веса в графе G инцидентно одной из вершин этого множе-
ства. С другой стороны, поскольку Хм=/=0, Ум=^^. то
X' =# X, Y' У. Поэтому из правила выбора величины а
в п. 7 следует, что а > 0. После модификации графа G в
п. 8 веса всех его ребер останутся неотрицательными (это
следует из правила выбора сс). В результате последующей
модификации графа Г (и. 9) его дуги по-прежнему будут
соответствовать ребрам нулевого веса в графе G, причем
дуги вида (у, х), х X, у е У, будут соответствовать па-
росочетанию нулевого веса в графе G. Модификация гра-
—>
фа Т в п. 9 обладает двумя важными свойствами. Во-пер-
вых, удаленные дуги этого графа направлены от
непомеченных вершин доли X. Поэтому все вершины,
достижимые из Хм в «старом» графе У, достижимы из
этого множества и в «новом» графе Т. Во-вторых, добав-
ленные дуги направлены от помеченных вершин доли X
к непомеченным вершинам доли У. Таким образом, при-
менение поиска в ширину к модифицированному графу
Т (п. 4) приведет к тому, что дополнительно будет по-
мечена по крайней мере одна вершина доли У. Посколь-
ку I У| = Z2, то после выполнения пп. 4, 7—9 не более
чем п раз подряд помеченной окажется некоторая вер-
шина множества Ум, т. е. будет найден путь Р, и затем
последует выполнение п. 5. Как уже было показано, п. 5
(а значит, и п. 6) выполняется не более п раз. Поэтому
каждый из пп. 4, 7—9 выполняется не более п2 раз.
Легко видеть, что трудоемкость каждого из пп. 1—9
не превосходит О(п2). Поэтому время работы алгоритма
в целом оценивается сверху величиной О(п4).
Как отмечалось выше, после выполнения п. 8 веса
всех ребер графа G остаются неотрицательными, и, сле-
довательно, множество оптимальных решений не меня-
ется. Условие окончания Хм = YM = & означает, что в
«последнем» графе Т имеется п дуг, направленных от X \
к У, которым соответствует совершенное паросочетание
нулевого веса в «последнем» графе G. Согласно свой-
ству 2 оно является оптимальным решением исходной
задачи.
Резюмируем все выше изложенное в виде теоремы.
Теорема 77.5. Алгоритм Л9 строит совершенное
паросочетание минимального веса в двудольном взве-
шенном графе 6?в(Х, У, EG), |Х| = |У| =тг, за вре-
мя О(п4).
361
Замечание. Известен алгоритм, решающий эту
задачу за время О(п3). В алгоритме «^9 оценка О (az4)
возникает, по существу, из-за того, что приходится О (az2)
раз выполнять операцию (Xх, Ух, а), которая сама тре-
бует времени О (az2). Снижение оценки до О (az3) дости-
гается за счет того, что результат этой операции удается
получить за время О (az).
Недавно опубликован алгоритм, оценка трудоемкости
которого во многих случаях предпочтительнее О (az3). Эта
оценка имеет вид <9(az2’5 log(AZjT)), где Т — наибольший из
весов ребер графа.
Пример. На рис. 77.3 представлена матрица весов
W = IIJ7J1 двудольного графа G=(X, У, EG), у которой
W{j = w(%i, Xj), Xi^X, y^Y. Там же изображен граф
Т, построенный по максимальному паросочетанию М =
= {^2У1, #1^2} нулевого веса в графе G. Соответствующие
этому паросочетанию дуги графа Т обведены жирными
линиями, а элементы матрицы W отмечены звездочками.
Перед первым выполнением п. 4 имеем Хм =
= {хз, #4, х$}, YM = {уз, У4, у5). Поиск в ширину из Хм
дает X' = {х2, хз, rr4, Х5}, Y' = {yj. Вершины множества
X' U Y' будем отмечать значком «+». Поскольку пути из
Хм в Ум нет, то переходим к пи. 7—9. Находим а =
= ТУ32 = 1 и выполняем операцию ({х2, хз, Х4, х$}, {yj, 1),
т. е. вычитаем 1 из всех элементов в строках 2, 3, 4, 5 и
прибавляем это число ко всем элементам первого столбца.
—►
В результате к графу Т добавится дуга (хз, у2). Моди-
фицированная матрица W (т. е. граф G) и граф Т пред-
ставлены на рис. 77.4.
Применение поиска в ширину к графу Т дает путь
Р =^(хз, у2, х\, уз) из Хм в Ум. Заменим (выполнение
п. 5) в графе Т дуги {хз, У2), ({/2, ^1), (^ь У$\ соответ-
362
ственпо на дуги (у2, #з), (#1, 1/2), (#5, #1). Новый граф Т
также изображен на рис. 77.4. В нем Хм = Ьц, я5}, YM —
=	1/4).
Снова выполнив поиск в ширину из Хм, получим
X' = {^2, ^4, £5}, Y' = {г/Л Среди элементов матрицы W,
лежащих на пересечении строк с номерами 2, 4, 5 и
столбцов с номерами 2, 3, 4, 5, находим минимальный.
Рис. 77.6
Получим а = Т4Л55==2. Результаты последующего приме-
нения к графу G операции (U2, ^4, х$},	2) и моди-
фицированный граф Т представлены на рис. 77.5. В этом
графе имеется путь Р==(х^ у$, х\, у4) из Хм в YM.
«Новый» граф Т\ полученный в результате выполнения
п. 5, также изображен на рис. 77.5. Поиск в ширину в
этом графе из множества Хм = {я4} дает X/ = {х2, х41,
Y' = {j/i). Находим а = РР45 = 1. Результаты последую-
щего выполнения пп. 8, 9 представлены на рис. 77.6.
Поиск в ширину из х4 дает X' = {х2, х4, х5), Y' = {z/b z/5}.
363
Находим а = W44 = 2. Получаем новые матрицу и граф
Т (рис. 77.7). В графе Т имеется (гс4, у3)-путь Р =
= (гг4? У4, лт, Z/з). Изменив этот граф в соответствии с п. 5,
получим новый (рис. 77.7), в котором Хм = YM = 0.
Пять его дуг, ведущих «от X к У», соответствуют ребрам
совершенного паросочетания минимального веса в исход-
ном графе G. Вес этого паросочетания равен 0 + 0+1 +
+ 6 + 3 = 10.
§ 78. Труднорешаемые задачи
Как уже говорилось выше, общепринятой является
точка зрения, согласно которой алгоритм считается эф-
фективным, если он имеет полиномиальную сложность.
Именно таковы все алгоритмы, рассмотренные в преды-
дущих параграфах. Заметим, однако, что за пределами
этих рассмотрений осталась большая часть важных за-
дач. Это, в частности, задачи отыскания в графе наиболь-
шего независимого множества, гамильтонова цикла,
ft-раскраски и ряд других. Все они характеризовались
нами как очень трудные еще до того, как мы приступили
к обсуждению алгоритмов. Дело в том, что, несмотря
на усилия многих специалистов, для решения подобных
задач до сих пор не найдено полиномиальных алгорит-
мов. Более того, имеются веские доводы, позволяющие
предположить, что таких алгоритмов не существует. Об-
суждению этих доводов и посвящен данный параграф.
Начнем с внесения изменений в вычислительную мо-
дель. Будем считать, что каждая ячейка абстрактной вы-
числительной машины может содержать только 0 или 1,
и целые числа рассматриваются в двоичной системе счис-
ления. В соответствии с этим всякое целое число а =# 0, 1
займет ]log led [ ячеек машинной памяти (]#[—-
наименьшее целое, не меньшее чем х). Рациональное
364
число, не являющееся целым, будем рассматривать в ви-
де несократимой дроби и представлять в машине как
упорядоченную пару целых чисел — числитель и знаме-
натель этой дроби. Время выполнения ьзж.кш элемен-
тарной операции примем равным сумме длин записей ее
операндов в двоичной системе счисления.
Далее будем рассматривать каждую задачу в так на-
зываемом распознавательном варианте, когда решение
задачи заключается в получении ответа «да» или «нет».
Всякий алгоритм решения такой задачи, будучи приме-
ненным к соответствующему входу, работает какое-то
время и затем, сообщив ответ «да» либо «нет», останав-
ливается. Для некоторых задач их «естественные» поста-
новки уже являются распознавательными. Таковы, на-
пример, задачи распознавания изоморфизма, изоморфной
вложимости, гамильтоновости, планарности, эйлеровости
графов. Однако чаще (а на практике — как правило) ис-
ходная постановка задачи является оптимизационной.
В оптимизационной задаче требуется выбрать из множе-
ства допустимых решений X такое решение х. вес (или
стоимость) которого w(x) минимален. В рассмотренных
нами оптимизационных задачах в качестве X фигуриро-
вали множества остовов, путей с заданной начальной
вершиной или паросочетаний данного графа. Каждой оп-
тимизационной задаче сопоставим ее распознавательный
вариант, который выглядит следующим образом. По за-
данным множеству X, весовой функции w и числу к тре-
буется определить, существует ли элемент х X такой,
что w(x)^k. Очевидно, что имея полиномиальный алго-
ритм решения оптимизационной задачи, легко получить
полиномиальный алгоритм решения соответствующей ей
распознавательной задачи. Можно показать, что при до-
вольно необременительных предположениях относительно
функции w верно и обратное. Мы пе будем на этом
останавливаться, поскольку для дальнейшего нам доста- у
точно только знать, что оптимизационная задача «не
проще» соответствующей распознавательной.
Итак, далее рассматриваются только распознаватель-
ные задачи. Определим Р как класс распознавательных
задач, каждая из которых может быть решена некоторым
алгоритмом за полиномиальное время. Мы уже знаем,
что в этот класс входят задачи о минимальных остовах,
кратчайших путях и наибольших паросочетаниях (име-
ются в виду распознавательные постановки этих задач,
как было условлено). В то же время было названо не-
365
сколько задач, принадлежность которых к классу Р не
установлена и считается сомнительной.
Теперь сделаем следующее важное наблюдение. Все
задачи, с которыми мы сталкивались до сих пор, неза-
висимо от того, установлена их принадлежность классу
Р или пет, обладают одним общим свойством: если вход
задачи таков, что имеет место ответ «да», то существует
полиномиальный алгоритм, доказывающий этот факт.
Поясним сказанное на примере. Пусть задача состоит
в выяснении, является ли граф гамильтоновым, и пусть
поступающий на вход граф G гамильтонов, т. е. в графе
G имеется гамильтонов цикл С. Тогда доказательство
гамильтоновости графа G заключалось бы в проверке
включения С ^G. Если, например, граф G задан матри-
цей смежности, то эту проверку можно выполнить с по-
мощью очевидного алгоритма, затратив О(тг) операций.
Подчеркнем, что речь идет лишь о существовании поли-
номиального доказательства — чтобы иметь это доказа-
тельство в своем распоряжении, надо знать цикл С.
Положение иное, если граф G не является гамильтоно-
вым. В этом случае нельзя утверждать даже, что полино-
миальное доказательство этого факта существует. Можно,
конечно, перебрать все (IGI — 1)! простых циклов длины
|б?| полного графа, проверяя каждый раз, содержится ли
цикл в графе G. Однако подобное доказательство требует
времени по крайней мере O((|G| —1)!), и, следователь-
но, не является полиномиальным.
Теперь мы хотим определить еще один класс распо-
знавательных задач, включив в него все задачи, облада-
ющие тем свойством, что если вход задачи имеет ответ
«да», то существует полиномиальный алгоритм, проверя-
ющий (доказывающий) этот факт. С этой целью допол-
ним множество обычных операторов, из которых мы со-
ставляли алгоритмы, одним особым. Пусть =
Л2, ..., Ат — последовательность, элементами KOTopoii
служат обычные операторы и один особый, запись ко-
торого имеет вид fe), h И, 2, ..., т}. Пусть,
далее, Q = q^ q% ..., qP — такой список, что гр = Zi либо
qt~ I2 (f=l, р). После того как 3$ и Q заданы, дей-
ствие особого оператора B(l^ Z2) определим так: в ре-
зультате /с-го (к С р) выполнения этого оператора уп-
равление передается оператору А^, если qk = l1, и Аг^
если qk = Z2, а при к > р вычисления прекращаются.
Итак, последовательности операторов и списку Q ста-
366
вится в соответствии обычный (детерминированный) ал-
горитм. Этот алгоритм будем обозначать через что-
бы подчеркнуть наличие двух компонент и Q. Список
Q будем при этом называть угадывающей последователь-
ностью, а последовательность — недетерминированным
алгоритмом. Подчеркнем особо, что недетерминирован-
ный алгоритм пе является алгоритмом, а представляет
собой чисто абстрактную конструкцию.
Будем говорить, что недетерминированный алгоритм
j/ решает распознавательную задачу за полиномиальное
время, если найдется такой полином р(п), что выпол-
няется следующее условие: каждый вход длины п этой
задачи имеет ответ «да» тогда и только тогда, когда для
него существует такая угадывающая последовательность
Q, что алгоритм s&q, будучи примененным к этому вхо-
ду, останавливается, сообщив ответ «да», и время его
работы не превосходит р(п). Заметим, что согласно это-
му определению каждому входу с ответом «да» должен
ставиться в соответствие свой алгоритм s&q. От этого ал-
горитма не требуется ничего иного, кроме правильной
реакции на свой вход. Поведение алгоритма на всех дру-
гих входах для нас безразлично.
Задача недетерминированно разрешима за полиноми-
альное время, если существует недетерминированный ал-
горитм, решающий ее за это время.
Определим теперь NP как класс всех распознаватель-
ных задач, недетерминированно разрешимых за полино-
миальное время.
Нетрудно видеть, что Р s NP. Действительно, полино-
миальный алгоритм решения всякой задачи из Р можно
превратить в полиномиальный алгоритм вида доба-
вив оператор B(l\, 12) так, чтобы он ни разу не сраба-
тывал. При этом в качестве Q можно взять произволь-
ную последовательность, например, состоящую из одного
элемента. Класс NP чрезвычайно широк. Например, боль-
шинству задач, встречающихся в предыдущих главам,
можно «естественным» образом сопоставить распознава-
тельные задачи. При этом окажется, что почти все они
принадлежат NP.
В качестве примера доказательства принадлежно-
сти задачи к NP рассмотрим задачу об изоморфном
подграфе, которую здесь сформулируем в следую-
щем виде.
Даны два графа G\ и 6?2, причем VG\ = VG2 = V.
Установить, существует ли такая подстановка s: V -> V,
367
для которой истинна импликация
(uv EG\)=> (s(u)s(p)^ EG%}.
Очевидно, что ограничение FGi = VG2, которого нет
в определении, приведенном в § 27, несущественно.
Удобно рассматривать эту задачу в матричной постанов-
ке. Пусть V = {1, 2, ..., тг}, А[ и А2— матрицы смеж-
ности графов Gi и G2 соответственно. Обозначим через S
матрицу подстановки s (см. § 6). Теперь задачу об изо-
морфном подграфе можно сформулировать так: опреде-
лить, существует ли такая матрица подстановки 5, что
все единицы матрицы	содержатся среди единиц
матрицы Л2, т. е. что матрица (А2 ~ SAyS~l) неотри-
цательна.
Недетерминированный алгоритм для решения этой
задачи выглядит следующим образом. ________
1.	Выполнить пп. 2—4 для всех Л==1,тг2 и перейти
к п. 5.
2.	5(3,4).
3.	th :== 0.
4.	__________________________
5.	Sij :== Для всех г, / = 1, п.
6.	A'
7.	Если матрица А2 — А' неотрицательна, то конец и
ответ «да». Иначе — конец.
Напомним, что — элемент матрицы 8, занимающий
позицию (ц /)•
Покажем теперь, как выбирать угадывающую после-
довательность Q. Рассмотрим произвольный вход задачи,
имеющий ответ «да». Это—пара симметрических (0,1)-
матриц А[ и Ла, для которой существует такая матрица
подстановки 8, что A2 — SAiS~l— неотрицательная мат-
рица. Заменим в матрице 50наЗи1на4ив качестве
Q возьмем последовательность элементов этой новой мат-
рицы, выписанных по строкам.
Работа алгоритма состоит из двух этапов. На пер-
вом этапе (пп. 1—5) с помощью Q строится матрица
подстановки, обеспечивающая изоморфное вложение. Со-
держанием второго этапа (пп. 6, 7) является проверка
того, что матрица 5 обладает нужным свойством. Поли-
номиальность алгоритма очевидна.
Напомним, что частными случаями задачи об изо-
морфном подграфе являются задачи об изоморфизме гра-
фов. о существовании в графе гамильтонова цикла или
клики заданного размера и ряд других. Таким образом,
368
попутно установлена принадлежность всех этих задач к
классу NP. Доказательство этого свойства для других
графовых задач проводится, как правило, столь же про-
сто. При этом работа алгоритма так же как и в
предыдущем случае, распадается на два этапа: 1) по-
строение некоторого варианта, 2) проверка того, что этот
вариант подходящий. Например, в задаче о й-раскраске
вершин графа такой алгоритм сначала припишет верши-
нам графа нужные цвета, а затем проверит, что любые
две вершины одного цвета не смежны.
Тот факт, что большинство «естественных» задач вхо-
дит в класс NP, свидетельствует о чрезвычайной важ-
ности вопроса: совпадают ли классы Р и NP? Эта не ре-
шенная до сих пор проблема считается важнейшей в
науке о вычислениях. Большинство исследователей скло-
няется к мнению, что P^NP. На первый взгляд ситуа-
ция P^NP не лишает нас возможности получить в бу-
дущем полиномиальный алгоритм решения какой-либо
из задач, названных нами «трудными». Однако это не
так. Как оказалось, из P=^NP следует, что ни одна из
этих «трудных» задач не имеет полиномиального алго-
ритма, а из существования такого алгоритма для одной
из них следует, что Р = NP.
Изложение соответствующих результатов опирается
на понятие сводимости одной задачи к другой. Предло-
жение «задача А сводится к задаче В» означает, в обще-
принятом смысле, что из решения задачи В можно по-
лучить решение задачи А. Нам необходимо уточнить это
понятие так, чтобы оно учитывало вычислительные за-
траты, связанные с получением решения одной задачи из
решения другой.
Пусть существует полиномиальный алгоритм F, кото-
рый, будучи примененным ко всякому входу I задачи Л,
строит некоторый вход F(I) задачи В. Если при этом
вход I имеет ответ «да» тогда и только тогда, когда от-
вет «да» имеет вход F(I), то говорят, что задача А по-
линомиально сводится к задаче В, и пишут А ос В. По-
скольку сводимостей, отличных от полиномиальной, мы
не рассматриваем, то слово «полиномиально» в дальней-
шем будем опускать и говорить просто «А сводится к В».
Нетрудно показать, что если задача А сводится к за-
даче В и В^Р, то и А^Р. Действительно, пусть st —
алгоритм решения задачи В и полиномы /?1(п),
таковы, что O(pi(n)) и О(р%(п)) — сложности алгорит-
мов F и st соответственно. Рассмотрим теперь алгоритм
24 в. А, Емеличев и др.	369
зФ' решения задачи А, состоящей из двух этанов.
На первом этапе вход I задачи А преобразуется алгорит-
мом F во вход F (I) задачи В. На втором этапе алгоритм
применяется ко входу F(I). Согласно определению F,
алгоритм сообщит ответ «да» тогда и только тогда,
когда вход I имеет ответ «да», т. е. алгоритм дей-
ствительно решает задачу А. Выясним теперь его слож-
ность. Если длина I равна п, то F(I) будет построен
за время O(pi(n)), и его длина —O(pi(n)). При этом
алгоритм будучи примененным ко входу F(J), затра-
тит время О(р2(Р1(я))). Таким образом, сложность алго-
ритма есть O(pi(n) + p2(pi(n))). Поскольку супер-
позиция и сумма полиномов также являются полинома-
ми, то — полиномиальный алгоритм.
Точно так же можно показать, что изЛ<*ВиВ°сС
следует А С.
Задачу А назовем NP-полной, если А е NP и любая
задача из NP сводится к А.
Из этого определения и предыдущих рассмотрений
сразу следует, что Р = NP, если хотя бы одна ЛФ-полная
задача входит в Р.
Говоря неформально, каждая ЛТ-полная задача «не
проще», чем любая задача из NP. Поэтому, доказав
ЛТ-полноту некоторой задачи, мы получаем веские осно-
вания считать ее трудной. Для доказательства ЛТ-пол-
ноты задачи достаточно установить ее принадлежность
к NP и показать, что к ней сводится некоторая ЛТ-пол-
ная задача. Чтобы воспользоваться этой схемой, надо
иметь в распоряжении хотя бы одну ЛТ-полную задачу.
Первой задачей, относительно которой было показано,
что она является ЛФ-полной, была задача о выполни-
мости. Пусть х\, х2, хз, ...— булевы переменные, прини-
мающие значения «истина» или «ложь», и ^1,^2, ^з,...—
их отрицания. Те и другие в совокупности называются
литералами. Пусть символы V и Д обозначают булевы
операции дизъюнкции и конъюнкции соответственно.
Формула щ V и2 V ... V ит называется элементарной дизъ-
юнкцией, если и\, и2, ..., Um — литералы. Пусть С\, С2, ...
..., Ср — элементарные дизъюнкции. Тогда выражение
вида Сг /\С2 Д ... Д Ср называется булевым выраже-
нием в конъюнктивной нормальной форме. Булево выра-
жение называется выполнимым, еесли входящим в него
переменным можно так присвоить значения «истина»
или «ложь», что значением выражения будет «истина».
Не все выражения являются выполнимыми. Например,
370
булево выражение V ^2) Л (^1 V ^з) Л (^2 V ^з)_ вы-
полнимо, а выражение V ^2) Л (xi V ^2) Л (xi V ^2) Л
Д (^ V а?2) не выполнимо. Задача о выполнимости
(ВЫПОЛНИМОСТЬ) состоит в определении, является
ли данное булево выражение в конъюнктивной нормаль-
ной форме выполнимым.
Следующая теорема, приводимая здесь без доказа-
тельства, лежит в основе теории УУР-полноты.
Теорема (С. Кук, 1971 г.). Задача ВЫПОЛНИ-
МОСТЬ является NP-полной.
В настоящее время известен значительный (и интен-
сивно пополняющийся) список УУР-по лных задач. В этом
списке находятся почти все задачи, получившие ранее
репутацию трудных для алгоритмического решения. Ни-
же приведены только те из них, с которыми мы сталки-
вались в предыдущих главах.
Некоторые УУР-полные задачи.
КЛИКА: Даны граф G и натуральное число к. Опре-
делить, содержит ли граф G клику мощности к.
НЕЗАВИСИМОСТЬ: Даны граф G и натуральное
число к. Определить, содержит ли граф G независимое
^-элементное множество вершин.
ИЗОМОРФНЫЙ ПОДГРАФ: Даны два графа G{ =
= (Р, ЕС) и 62 = (У, £2). Определить, существует ли под-
становка s: V У, для которой истинна импликация
(uv &Ei)^ (s(u)s(v)^ Т?2).
ВЕРШИННОЕ ПОКРЫТИЕ: Даны граф G и нату-
ральное число к. Определить, существует ли в графе G
вершинное покрытие мощности не более к.
ДОМИНИРУЮЩЕЕ МНОЖЕСТВО: Даны граф G и
натуральное число к. Определить, существует ли в гра-
фе G доминирующее множество мощности не менее к.
ГАМИЛЬТОНОВ ЦИКЛ: Дан граф G. Определить,
содержит ли граф G гамильтонов цикл.
ЯДРО: Дан ориентированный граф G. Определить,
содержит ли граф G ядро.
ВЕРШИННАЯ (РЕБЕРНАЯ) РАСКРАСКА: Даны
граф G и натуральное число к. Определить, существует
ли правильная fc-раскраска вершин (ребер) графа G.
Рассмотрим в качестве примера доказательство NP-
полноты задачи КЛИКА. Пусть Lh — граф, у которого
некоторые к вершин образуют клику, а остальные
п — к — изолированные вершины. Ранее мы установили,
что задача ИЗОМОРФНЫЙ ПОДГРАФ принадлежит
24*
371
NP. Если в этой задаче положить G2 = G, где G — граф,
фигурирующий в формулировке задачи КЛИКА, а в ка-
честве Gi выбрать граф Lk, то получим задачу КЛИКА.
Следовательно, задача КЛИКА принадлежит NP.
Покажем теперь, что ВЫПОЛНИМОСТЬ КЛИКА.
Пусть В = Ci V С2 V ... V Ст — произвольное булево вы-
ражение в конъюнктивной нормальной форме, {щ, пг, ...
..., ир} — множество входящих в него литералов. Будем
обозначать через С{ множество литералов, входящих в
элементарную дизъюнкцию Ci.
Поставим в соответствие выражению В граф G по
следующему правилу:
VG = {ру: ще С;},
EG =	и.{ =^= Uh) j
Таким образом, вершины графа G находятся во взаимно
однозначном соответствии с вхождениями литералов в
элементарные дизъюнкции. Две вершины смежны, если
соответствующие вхождения не противоречат друг другу,
т. е. элементарные дизъюнкции различны и оба литера-
ла могут одновременно принять значение «истина».
Пусть в графе G имеется клика размера к = т. Этой
клике соответствует набор таких т вхождений щ е
щ2^С21 .. .,Uim<=Cm, что	Поэтому после при-
своения всем Ui. (/=l,m) значения «истина» выраже-
ние В также примет это значение, т. е, В — выполнимое
выражение.
Наоборот, предположим, что В — выполнимое выра-
жение. Пусть переменным присвоены значения «истина»
или «ложь» так, что выражение В получило значение
«истина». Тогда каждая элементарная дизъюнкция G
должна содержать литерал имеющий значение «исти-
на». Ясно, что при этом u^^Uit. Следовательно, т вер-
шин и2г2, ..., vmim попарно смежны в графе G, т. е.
образуют клику размера т. Таким образом, выражение
В выполнимо тогда и только тогда, когда в графе G име-
ется клика размера к = т. Легко видеть, что построение
графа G по выражению В можно выполнить за время
О(р(п)), где р(п)—полином, а п — длина записи выра-
жения В (длина входа задачи ВЫПОЛНИМОСТЬ).
Имеется ряд задач, входящих в АР, для решения ко-
торых до сих пор не найдено полиномиальных алгорит-
372
мов и относительно которых неизвестно, являются ли они
TVP-полными. Наиболее заметной графовой задачей среди
них является задача об изоморфизме графов.
С другой стороны, большинство встречающихся на
практике задач не являются распознавательными и, сле-
довательно, не принадлежат классу NP. В то же время
ко многим из них удается свести некоторые АР-полные
задачи. В этой ситуации полезным оказывается следую-
щее определение. Задача называется NP-трудной, если к
ней сводится некоторая JVP-полная задача. Новый тер-
мин позволяет, например, избежать громоздких конструк-
ций типа «распознавательный аналог задачи Л является
TVP-полной задачей» и дает возможность говорить про-
сто, что «задача А АФ-трудна».
Теория Л^Р-полноты, помимо теоретического, представ-
ляет и чисто практический интерес. Доказав, что задача
Л^Р-трудна, разработчик алгоритмов получает достаточ-
ные основания, чтобы отказаться от поиска эффектив-
ного и точного алгоритма. Дальнейшие его усилия могут
быть направлены, например, на получение приближен-
ного решения, либо на получение решения в типичном
случае (в большинстве случаев).
УПРАЖНЕНИЯ
1.	Пусть («г, аз)—-любая пара следующих представлений
графа:
(<7i) — матрица смежности,
(а2)—список ребер,
(а3)—список смежности.
Покажите, что от аг- к а; можно перейти за время О(|сц| +
+ | б/j |), где ]	— длина представления аъ. (к = 1, 3).
2.	Покажите, как с помощью поиска в ширину распознать,
является ли граф двудольным.
3.	Связный граф, содержащий в точности один цикл, называ-
ется 1-деревом. Постройте эффективный алгоритм для отыскания
во взвешенном графе остовного 1-дерева минимального веса.
4.	Пусть граф G — дерево. Постройте алгоритмы сложности
O(|G|) для отыскания в графе G
а)	центра,
б)	диаметра.
5.	Выясните сложность алгоритма Флёри для построения эйле-
рова цикла (см. гл. VII, § 43).
6.	Разработайте алгоритм сложности	для построения
эйлерова цикла в эйлеровом графе G.
7.	Постройте алгоритм сложности О (| EG |) для отыскания про-
стого цикла в графе G.
8.	Пусть G — связный граф. Постройте полиномиальный алго-
ритм для отыскания гамильтонова цикла в графе G3.
373
9.	Пусть G — гамильтонов граф. Разработайте алгоритм слож-
ности OjjGl) для построения гамильтонова цикла в графе L(G),
при условии, что гамильтонов цикл графа G задан.
10.	Постройте алгоритм сложности ^(IGI) для раскраски вер-
шин планарного графа G в шесть цветов.
11.	Пусть взвешенный ориентированный граф G не содержит
контуров. Постройте алгоритм сложности O(|EG|) для поиска крат-
чайшего (s, £)-пути, при условии, что хотя бы один такой путь
в графе имеется.
12.	Разработайте алгоритм сложности	для отыскания
в графе G
а)	максимального паросочетания,
Ь)	максимального независимого множества,
с)	минимального доминирующего множества.
13.	Пусть tZi, d2, ..dn— графическая последовательность. Раз-
(п \
2	) Для построения реали-
i=i /
зации этой последовательности.
Список литературы
ОСНОВНАЯ
1.	Берж К. Теория графов и ее применения.-М.: ИЛ, 1962.—
319 с.
2.	Зыков А. А. Основы теории графов.— М.: Наука, 1987.—
381 с.
3.	О р е О. Теория графов.— М.: Наука, 1980.— 336 с.
4.	Свами М., Тхуласираман К. Графы, сети и алгорит-
мы.— М.: Мир, 1984.— 454 с.
5.	Татт У. Теория графов.— М.: Мир, 1988.
6.	Уилсон Р. Введение в теорию графов.— М.: Мир, 1977.—
207 с.
7.	X а р а р и Ф. Теория графов.— М.; Мир, 1973— 300 с.
ДОПОЛНИТЕЛЬНАЯ
8.	А й г н е р М. Комбинаторная теория.— М.: Мир, 1982.— 556 с.
9.	Ахо X., Хопкрофт Дж., Ульман Дж. Построение и
анализ вычислительных алгоритмов.— М.: Мир, 1979.— 536 с.
10.	Б ас а кер Р., С а ат и Т. Конечные графы и сети.— М.:
Наука, 1974.—368 с.
И. Белов В. В., Воробьев Е. М., Шаталов В. Е. Теория
графов.— М.: Высшая школа, 1976.— 392 с.
12.	Г а в р и л о в Г. П., С а п о ж е н к о А. А. Сборник задач по
дискретной математике.— М.: Наука, 1977.— 368 с.
13.	Г э р и М., Джонсон Д. Вычислительные машины и труд-
норешаемые задачи.— М.: Мир, 1982.— 416 с.
14.	Д о н е ц Г. А., Шор Н. 3. Алгебраический подход к пробле-
ме раскраски плоских графов.— Киев: Наукова думка, 1982.—
143 с.
15.	Е в с т и г н е е в В. А. Применение теории графов в програм-
мировании.— М.: Наука, 1985.— 352 с.
16.	Евстигнеев В. А., Мельников Л. С. Задачи и упраж-
нения по теории графов и комбинаторике.—Новосибирск, Изд-
во НГУ, 1981.— 88 с.
17.	Е м е л и ч е в В. А., К о в а л е в М. М., К р а в ц о в М. К. Мно-
гогранники, графы, оптимизация.— М.: Наука, 1981.— 341 с.
18.	3 е м л я ч е н к о В. Н., К о р н е е н к о Н. М., Тышкевич Р. И.
Проблема изоморфизма графов // Теория сложности вычисле-
ний, I. Записки научных семинаров ЛОМИ.— 1982.— Т. 118.—
С. 83-158.
19.	Зыков А. А. Теория конечных графов.— Новосибирск, Нау-
ка, 1969.— 543 с.
375
20.	Зыков А. А. Гиперграфы Ц УМН.— 1974.— Т, 29, вып. 6.—
С. 89—154.
21.	Коршунов А. Д. Основные свойства случайных графов с
большим числом вершин и ребер / УМН.— 1985.— Т. 40,
вып. 1.-С. 107—173.
22.	К р и с т о ф и д е с Н. Теория графов. Алгоритмический под-
ход.—М.: Мир, 1978.—432 с.
23.	Маркус К., Минк X. Обзор по теории матриц и матрич-
ных неравенств.—М.: Наука, 1972.— 232 с.
24.	П а п а д и м и т р и у X., Стайглпц К. Комбинаторная оп-
тимизация. Алгоритмы и сложность.—М.: 1985.—510 с.
25.	Р е й н г о л ь д Э., Н и в е р г е л ь т Ю., Д е о Н. Комбинатор-
ные алгоритмы. Теория и практика.— М.: Мир, 1980.— 476 с.
26.	Р и н г е л ь Г. Теорема о раскраске карт.—М.: Мир, 1977.—
256 с.
27.	С е р г и е и к о И. В. Математические модели и методы реше-
ния задач дискретной оптимизации.— Киев: Наукова думка,
1985.—381 с.
28.	Теория графов: Сборник переводов/Под ред. В. Б. Алексеева,
Г. II. Гаврилова, А. А. Сапоженко.— М.: Мир, 1974.— 223 с.
29.	X а р а р и Ф., Палмер Э. Перечисление графов.— М.: Мир,
1977.— 324 с.
30.	Холл М. Комбинаторика.—М.: Мир, 1970.—424 с.
31.	Ц в е т к о в и ч Д., Дуб М., 3 а х с X. Спектры графов. Тео-
рия и приложения.— Киев: Наукова думка, 1984,— 381 с.
32.	Яблонский С. В. Введение в дискретную математику.— М.:
Наука, 1986.— 384 с.
Предметный указатель
Автоморфизм графа 42
Аксиомы баз 64
—	независимости 66
—	ранга 67
—	циклов 67
Алгоритм детерминированный 367
—	Дийкстры 343
—	жадный 93
—	Краскала 60
—	линейный 322
—	недетерминированный 367
— отыскания кратчайших путей 350
— поиска в глубину 325, 332
-------ширину 348
— полиномиальный 322
—	построения минимального остова
337, 340
---наибольшего паросочетания
357
---совершенного паросочетания
359
—	Прима 61
—	укладки графа на плоскости 178
—	Флёри 195
База матроида 64
—	орграфа 293
Базис коциклов матроида 81
—	разрезов графа 84
—	циклов графа 84
---матроида 81
Валентность вершины 26
Вершина висячая 26
—	доминирующая 26
—	изолированная 26
—	концевая 26
—	периферийная 35
—	центральная 36
Вес подграфа 36
—	ребра 36
Вход задачи 321
Гиперграф 298
— абсолютный 307
— бихроматический 309
—	двойственный 299
—	Л-однородный 299
/i-униформный 299
Гиперграф ^-раскрашиваемый 306
<	— fe-хроматический 306
—	fe-цветной 306
—	связный 301
	—, удовлетворяющий условию Хел-
ли 311, 313
Гипотеза Бержа 272
—	Келли — Улама 18
—	Рамачандрана 286
—	- реконструируемости вершинной
18
*	реберной 18
—	Хадвигера 264
—	Харари 18
—	четырех красок 255
Грани карты смежные 255
Граница грани плоского графа 153
Грань плоского графа 153
-----внешняя 153
----- внутренняя 153
Граф 9
—	абстрактный 14
—	ациклический 53
—	бихроматический 237
—	взвешенный 36
—	внешнепланарный 189
-----максимальный 189
—	выпуклый прямолинейный 163
—	гамильтонов 196
.— гамильтоново связный 207
—	двойственный абстрактно 172
-----геометрически 169
—	двудольный 11
—	додекаэдра 11
—	дополнительный 15
—	икосаэдра И
—	клик 112
—	конечный 9
—	куба 11
—	кубический 33
—	неориентированный 9
—	непомеченный 14
—	обыкновенный 17
	— однородный 32
—	октаэдра 11
—	ориентированный 16
—	пересечений 38
—	Петерсена И
—	планарный 150
—	плоский 150
-----максимальный 158
—	полный 10
—	помеченный 14
-	— пороговый 224
<	— простой 17
я	— пустой 10
377
Граф раскрашиваемый реберно 248
—	расщепляемый 222
—	реберный 38, 311
—	регулярный 33
—	реконструируемый 18
—	решетки 207
—	самодополнительный 15
—	сбалансированный 15
—	связный 23
—	смешанный 16
—	совершенный 268
—	тетраэдра И
—	тороидальный 184
—	триангулированный 272
—	эйлеров 192
—	/t-дольный 11
—	^-раскрашиваемый 235
—	/1-СВЯЗНЫЙ 136
—	Zt-хроматический 236
Графы изоморфные 13
—	коспектральные 29
—	платоновых тел 11
Группа автоморфизмов графа 43
Дерево 53
— остовное 57
— с корнем ориентированное 324
— Штейнера 62
Дефицит двудольного графа 128
Диаметр 35
Длина входа задачи 321
—	маршрута 22
—	списка 319
Игра «Кругосветное путешествие»
196
Изоморфизм графов 13
— матроидов 73
Индекс хроматический 248
Искаженность графа 187
Каркас 55
Карта 255
— /t-раскрашиваемая 255
Класс цветной 238, 248
Клика 111
—	максимальная 111
—	наибольшая 111
Кобаза 68
Колесо 11
Колода графа 18
Компонента 24, 301
—	базовая 293
—	связная 24, 301
—	сильная 282
—	сильно связная 282
—	/t-связная 136
Конденсация 282
Контур гамильтонов 286
Коостов 72
Коцикл 69
Критерий Гавела — Хакими 211
—	Эрдёша — Галлаи 213
Куб п-мерный 20
Лемма о рукопожатиях 26
Лес 53
Лист 141
Емкость графа шенноновская 109
Задание графа списками смежно-
сти 320
---- списком ребер 319
Задача коммивояжера 206
— об остове минимального веса 60
— о восьми ферзях 102
----выполнимости 371
----гаремах 90
----кёнигсбергских мостах 191
----кратчайшем остове 60
------- пути 342
---- назначениях 124
----пересечении матроидов 100
---- пяти ферзях 109
---- свадьбах 87
----трех домах и трех колодцах
152
—	проектирования коробки скорос-
тей 237
—	размещения минимаксная 36
—	распознавательная 365
—	распределения оборудования 236
—	составления расписаний 236
—	Штейнера евклидова 62
		на графах 62
		прямоугольная 62
—	ЛГ-полная 370
—	IVP-трудная 373
Замыкание транзитивное 297
Звезда И
Знак Магомета 192
Маршрут 22
—	ориентированный 280
—	остовный 281
Матрица весов 319
—	инцидентности 31
—	Кирхгофа 30
—	клик 115
— смежности 27
--- приведенная 30
Матроид 64
—	бинарный 79
—	векторный 70, 74
—	графический 74
—	двойственный 69
—	дискретный 70
—	матричный 21
—	однородный 100
—	представимый 75
—	разбиения 92
—	разрезов графа 72
—	свободный 70
—	трансверсальный 92
—	тривиальный 70
—	циклов графа 72
Множество внутренне устойчивое
102
—	графа степенное 232
— доминирующее 109
---минимальное 109
---наименьшее 109
— независимое 102, 304
---максимальное 102
---наибольшее 102, 304
378
Множество ребер графа независимое
122
— трансверсальное гиперграфа 303
— элементов матроида зависимое
67
-------независимое 69
-------конезависимое 69
-------независимое 66
Мост 134
Мультиграф 15
— ориентированный 16
Набор независимых множеств мат-
роида 65
Неплотность графа 103
Область связности 24, 301
Обхват 22
Объединение графов 19
---дизъюнктное 19
—	матроидов 95
Окружение 10, 125
Оператор 318
—	«конец» 319
—	присваивания 319
Операция элементарная 318
Опора 111
Орграф 16
—	гамильтонов 286
—	односторонне связный 280
—	односторонний 280
—	реберный 297
—	сильно связный 280
— слабо связный 281
— транзитивный 291
— эйлеров 286
Ориентация графа 32
Основание графа 283
Остов 55
Отец вершины ордерева 327
Отождествление вершин графа 21
Очередь 323
Пара векторов графическая 284
Паросочетание 122, 303
— максимальное 122
— наибольшее 122, 303
— совершенное 123
Петля 16
Плотность 111
Подграф 17
—	индуцированный 17
—	остовный 17
— порожденный 17
Поддерево с корнем 327
Подразбиение ребра 160
Подцепь 22
Поиск в глубину 323
---ширину 37
Покрытие вершинное 111
---минимальное 111
---наименьшее ill
— реберное 122
---минимальное 122
---наименьшее 122
Полином графа характеристиче-
ский 29
---хроматический 247
Полуконтур 280
Полумаршрут 280
Полупуть 280
Полустепень захода вершины 283
—	исхода вершины 283
Полуцепь 280
Порядок гиперграфа 298
—	графа 9
—	матроида 65
Последовательность графа степен-
ная 26
—	графическая 209
—	правильная 209
—	производная 212
—	расщепляемая 223
—	угадывающая 367
—	униграфическая 211
Потомок вершины ордерева 327
Предок вершины ордерева 327
Представление гиперграфа кёнигово
300
—	матроида 75
—	списка последовательное 319
Проблема изоморфизма графов 115
—	изоморфного подграфа 115
—	изоморфной вложимости 115
—	Кёнига 47
—	клики 115
Произведение графов 20
---модульное 116
Пространство коциклов матроида
81
—	разрезов графа 84
— циклов графа 84
--- матроида 81
Псевдограф 16
Путь в орграфе 280
Радиус графа 35
Разложение матроидное 120
— множества вершин полярное 222
—	пороговое 228
Размер входа задачи 321
Ранг графа 28
—	коциклический 56
—	матроида 65
— подмножества элементов матрои-
да 67
—	циклический 56, 303
Раскраска вершинная 235, 306
—	минимальная 236
— последовательная 238
— правильная 235, 306
— реберная 248
Расстояние между вершинами 34
Расщепление вершины 22
Реализация гиперграфа 310
--- строгая 314
Реконструкция 18
Род графа 184
Сабли Магомета 192
Сепаратор 145
Система различных представителей
87
Слияние вершин 21
Сложность алгоритма 321
Спектр графа 29
Список 319
Стек 322
Степень вершины 26, 299
379
Степень графа 34
---- регулярного 32
---- сильная 108
— ребра 299
Структура данных 377
Стягивание ребра 21
Сын вершины ордерева 327
Цепь диаметральная 35
— простая 22
Цикл 22
—	гамильтонов 196
—	матроида 67
—	простой 22
—	эйлеров 192
Толщина графа 186
Точка сочленения 134
—	Штейнера 62
Трансверсаль 87
—	независимая 88
—	частичная 87
Триангуляция плоская 157
Трудоемкость алгоритма 321
Турнир 283
Тэта-граф 197
Часть графа 17
Число кликовое 111
— матроидное 120
— независимости 103, 304
— паросочетания 122, 303
—	покрытия вершинного 111
—	кликового 112
--- реберного 122
—	пороговое 228
—	связности 133, 134
—	скрещиваний 184
—	Хадвигера 21
Укладка графа 151
Упиграф 211
Эксцентриситет вершины 35
Фактор 17
Функция матроида коранговая 69 Ядро 294
---- ранговая 67
Центр графа 36
Цепь 22, 300
k-компопента 196
/-процедура 212
п-последовательность 209
Оглавление
Предисловие .	  °
Введение .............................................................................. ?
Глава 1. НАЧАЛЬНЫЕ ПОНЯТИЯ............................................................. 9
§ 1.	Определение графа .........
§	2.	Подграфы .	  17
§	3.	Операции над графами.........................ау
§	4.	Цепи, циклы, компоненты.................................22
§	5.	Степени вершин графа.....26
§	6.	Матрицы, ассоциированные с графом ....	27
§	7.	Регулярные графы.................................32
§	8.	Метрические характеристики графа ....	34
§	9.	Критерий двудольности графа.........................36
§	10.	Реберный граф....................................................38
§	11.	Группа автоморфизмов графа....42
§	12.	«Почти все» графы ..........................47
Упражнения........................................................................  31
Глава II.	ДЕРЕВЬЯ ................................33
§ 13.	Определение дерева.......................33
§ 14.	Матричная теорема Кирхгофа...............57
§ 15.	Остов минимального веса..................60
Упражнения.....................................63
Глава III. МАТРОИДЫ И ТРАНСВЕРСАЛИ................64
§ 16.	Азбука теории матроидов..................64
§ 17.	Двойственный матроид.....................68
§ 18.	Примеры матроидов........................70
§ 19.	Изоморфизм матроидов...................  73
§ 20.	Представление матроида .	  75
§ 21.	Бинарные матроиды .........	79
§ 22.	Трансверсали.............................87
§ 23.	Жадный алгоритм .........................92
§ 24.	Объединение и пересечение матроидов ...	95
Упражнения....................................  100
Глава IV. НЕЗАВИСИМОСТЬ И ПОКРЫТИЯ	....	102
§ 25.	Независимые множества и покрытия	....	102
§ 26.	Клика ...................................  Ш
§ 27.	Проблемы клики, изоморфной вложимости и изо-
морфного подграфа............................115
§ 28.	Интерпретации независимых множеств .	.	•	117
§ 29.	Паросочетания .	.	....................122
381
§ 30.	Паросочетания в двудольном графе
§ 31.	Двудольные графы и семейства подмножеств
§ 32.	Паросочетания и покрытия............
Упражнения................................
Глава V. СВЯЗНОСТЬ............................
§ 33.	Вершинная связность и реберная связность
§ 34.	Двусвязные графы....................
§ 35.	Теорема Менгера.....................
Упражнения................................
Глава VI. ПЛАНАРНОСТЬ.........................
§ 36.	Плоские и планарные графы .	.
§ 37.	Грани плоского графа. Формула Эйлера
§ 38.	Плоские триангуляции................
§ 39.	Критерии планарности................
§ 40.	Двойственность и планарность ....
§ 41.	Алгоритм укладки графа на плоскости
§ 42.	Характеристики непланарных графов
Упражнения .............................
Глава VII. ОБХОДЫ.............................
§ 43.	Эйлеровы графы ........
§ 44.	Гамильтоновы графы..................
Упражнения................................
Глава VIII. СТЕПЕННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ .	.
§ 45.	Графическая последовательность..............
§ 46.	Критерии графичности последовательности
§ 47.	Реализация графической последовательности с мак-
симальной связностью.............................
§ 48.	Гамильтонова реализация графической последова-
тельности .......................................
§ 49.	Расщепляемые графы..........................
§ 50.	Пороговые графы.............................
§ 51.	Пороговое разложение графа..................
§ 52.	Степенное множество графа...................
Упражнения........................................
Глава IX. РАСКРАСКИ
53.
54.
55.
56.
57.
Правильная раскраска ....
Оценки хроматического числа
Хроматический полином ....
Раскраска ребер ..................
Связь матроидных разложений графов с
§
ми...............................
§ 58.	Раскраска планарных графов
§ 59.	Проблема четырех красок
§ 60.	Другие подходы к раскраске графов
§ 61.	Совершенные графы...............
§ 62.	Триангулированные графы
Упражнения............................
раскраска-
Глава X. ОРИЕНТИРОВАННЫЕ ГРАФЫ .	.	.
§ 63.	Основные определения.............
§ 64.	Полустепени исхода и полустепепи захода
124
128
130
132
133
133
137
145
148
150
169
175
183
187
191
191
196
207
208
209
211
217
220
222
223
228
232
234
235
235
238
245
248
252
255
260
264
267
272
277
279
279
283
382
§ 65.	Обходы.................................
§ 66.	Пути...................................
§ 67.	База и ядро . .	.....................
Упражнения...................................
286
290
293
296
Глава XI. ГИПЕРГРАФЫ....................................................298
§	68.	Основные определения и свойства.298
§	69.	Независимые множества.304
§	70.	Раскраски.............................................306
§71.	Реализации гиперграфа..........................................310
Упражнения...........................................................315
Глава XII. АЛГОРИТМЫ................................317
§ 72.	Предварительные сведения...................317
§ 73.	Поиск в глубину............................323
§ 74.	Отыскание двусвязных компонент.............327
§ 75.	Минимальный остов..........................334
§ 76.	Кратчайшие пути............................342
§ 77.	Наибольшие паросочетания и	задача о назначениях 354
§ 78.	Труднорешаемые задачи......................364
Упражнения.......................................373
СПИСОК ЛИТЕРАТУРЫ.......................31Ь
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ....................	377
Учебное издание
ЕМЕЛИЧЕВ Владимир Алексеевич
МЕЛЬНИКОВ Олег Исидорович
САРВАНОВ Владимир Иванович
ТЫШКЕВИЧ Регина Иосифовна
Лекции по теории графов
Заведующий редакцией Е. ТО. Ходан
Редактор А. Д. Вайнштейн
Художественный редактор Т. Н. Колъченко
Технический редактор С. Я. Шкляр
Корректоры О. А. Бутусова, И. Я. Кришталъ
ИБ Кв 32506
Сдапо в набор 10.05.89, Подписано к печати 04.10.90.
Формат 84X108/32. Бумага тип. № 2. Гарнитура
обыкновенная. Печать высокая. Усл. печ. л. 20,16.
Усл. кр.-отт. 20,16. Уч-изд. л. 20,99. Тираж
22 000 экз. Заказ № 666. Цена 1 р.
Издательско-производственное и книготорговое
объединение «Наука»
Главная редакция физико-математической
литературы
117071 Москва В-71, Ленинский проспект, 15
Четвертая типография издательства «Наука»
630077 Новосибирск, 77, Станиславского, 25