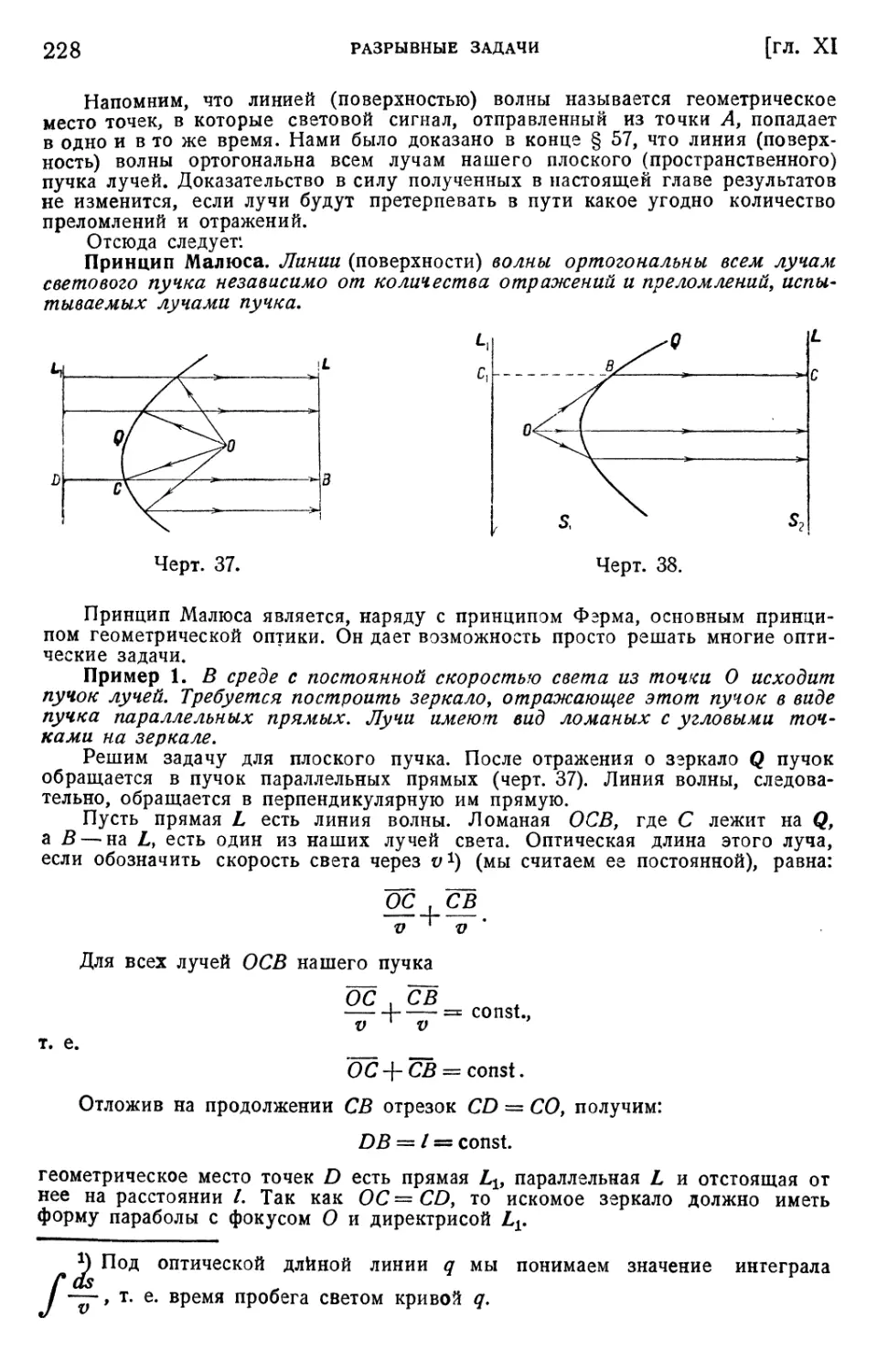
Текст
р с н о в ы
ВАРИАЦИОННОГО
ИСЧИСЛЕНИЯ
М. ЛАВРЕНТЬЕВ и Л. ЛЮСТЕРНИК
ОСНОВЫ
ВАРИАЦИОННОГО
ИСЧИСЛЕНИЯ
ТОМ ПЕРВЫЙ
ЧАСТЬ II
Утверждено Наркомпросом РСФСР
•в качестве учебника для университетов
ОБЪЕДИНЕННОЕ
НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО НК
ГЛАВНАЯ РЕДАКЦИЯ ОБЩЕТЕХНИ.ЧЕСКОЙ ЛИТЕРАТУРЫ И Н
МОСКВА 1955 ЛЕНИНГРАД
T 21-5-2
ТКК ЛЬ 89/93
Ko
Сдано
Редакция Г. А. Сухомлинова. Оформление В. Ф. Зазульской.
KopptKTypa A. X. Артюховой. Наблюдал за вылуск.м 1имофе:в.
-)дано в производство 30/1V i935 г. Под 1исано к печати 220A .935 г
Неч. лист. 25. Тираж 6( Ои. Формат 62х94Ум. Уч. авт. л. 3j,8.
Печ. зн. в 1 б^м. л. 108 8^0. Заказ № 669. Бум. л. 1272-Гл. ред.
общете.. дис .. № 41. У,:олн. Гл ачлита № В-1о-.Я9.
2-я Т1шогро4>ия ОНТИ им. Евг. Соколовой. Ленинград, пр. Красных Командиров, 29,
ПРЕДИСЛОВИЕ КО ВТОРОЙ "ЧАСЩ
Первая часть „Основ вариационных исчислений", посвященная функ-
функциям конечного числа переменных и их экстремумам, вышла отдельной
книжкой. Настоящая книга, II—IV части, содержит несколько расши-
расширенный университетский курс. Мы начинаем ее с „Основных понятий
и методов вариационного исчисления". На этой части (И) мы сознательно
остановились более подробно, так как, с одной стороны, эти понятия
имеют фундаментальное значение в анализе вообще; с другой стороны,
овладение основными понятиями и методами математической дисциплины
не менее важно, чем овладение ее рецептурой.
Начало II части естественно примыкает к I части: вариационные за-
задачи здесь рассматриваются как предельные задачи на экстремум функ-
функций конечного числа переменных. Сначала решаются отдельные частные
вариационные задачи, затем делается переход к решению общей задачи.
Подобные элементарные методы (конечно в другом изложении — инфи-
нитезимальном) были характерны для первого развития вариационного
исчисления. Но и после создания более общих формализированных ме-
методов элементарные приемы могут иметь преимущество при решении
отдельных задач.
Теорию функции конечного числа переменных мы начинали с #-мер-
ной геометрии, рассматривая функции многих переменных как функции
точки в л-мерных пространствах. Вариационное исчисление расширяет
понятие функции. Современная геометрия соответственным образом
обобщает основные геометрические понятия. В главе VI (и в начале
главы VII) мы приводим элементы абстрактной геометрии. Вариационное
исчисление с точки зрения современной математики есть диференциалыюе
исчисление для функций более общей природы, развертывающейся га
пространствах более общей природы.
Часть III изучает основные классические вариационные задачи с точки
зрения необходимых условий.
Глава XIII части IV содержит теорию второй вариации для простей-
простейшей и изопериметрической задачи. С нею связаны диференциальные
уравнения Штурма-Лиувклля. Наряду с теорией слабого экстремума
и сопряженных точек, в ней приводится экстремальная теория собствен-
собственных значений Куранта. В ней же иллюстрируется предельный переход
от функции конечного числа переменных к функционалам.
Глава XIV содержит излагаемую в геометрической форме теорию
поля и достаточные условия Вейерштрасса.
4 ПРЕДИСЛОВИЕ
Конец § 39, 44, 55, 61 и доказательство существования в § 80
можно при первом ознакомлении выпустить. Они содержат материал,
примыкающий к материалу второго тома.
В дополнениях мы приводим примеры экстремальных задач, решае-
решаемых специальными методами: несколько задач на экстремумы для вы-
выпуклых фигур и задачи, возникающие в теории аналитических функций.
Мы включаем с любезного разрешения автора неопубликованные реше-
решения проф. С. С. Ковнера одной интересной экстремальной задачи
(дополнение I, п. 4). Дополнение III написано И. М. Гельфандом и
Г. А. Сухомлиновым.
Второй том мы предполагаем посвятить: анализу общих задач вари-
вариационного исчисления теоретико-функциональными методами (вопросам
существования, апроксимативным методам) и топологическим методам.
Мы выражаем нашу благодарность редактору Главной редакции
общетехнической литературы ОНТИ т. Сухомлинову Г. А. за вниматель-
внимательное отношение к нашей книге.
Авторы.
ОГЛАВЛЕНИЕ
Предисловие ко второй части
ОСНОВНЫЕ ПОНЯТИЯ И МЕТОДЫ ВАРИАЦИОН-
ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
Глава V. Переход от экстремумов функций многих
переменных к вариационным задачам
27. Функционал 9
28. Элементарное решение некоторых вариационных задач 13
29. Принцип Мопертюи-Эйлера. Аналогия между оптикой и механикой . . 17
30. Элементарное решение некоторых изопериметрических задач .... 25
31. Простейшая задача вариационного исчисления. Уравнение Эйлера . . 29
32. Приложения 39
33. Метод счетного множества переменных 45
Глава VI. Обобщение основных понятий анализа
34. Дополнительные замечания об экстремумах функционалов 52
35. Абсолютный и относительный экстремум 54
36. Окрестности кривых. Сильный и слабый экстремум 56
37. Абстрактные пространства 59
38. Предельные соотношения в абстрактном пространстве 64
39. Функция точки абстрактного пространства 67
40. Линейные пространства . . . . ,. 69
41. Диференциал функции на линейном пространстве „ 74
42. Экстремум функции точки линейного пространства 76
Глава VII. Функционалы и вариация
43. Функциональные пространства 78
44. Компактность в функциональных пространствах 82
45. Линейные функционалы и вариации 91
46. Вариации для простейшего функционала 92
47. Основные леммы вариационного исчисления 95
48. Вариация в точке. Инвариантность уравнения Эйлера 98
49. Вторая вариация и условие Лежандра 104
ПРИМЕНЕНИЯ МЕТОДА ВАРИАЦИЙ
Глава VIII. Непосредственные обобщения простейшей задачи
вариационного исчисления
50. Пространственная задача 109
51. Вариация в точке в данном направлении. Принцип Гамильтона ... 112
52. Вторая вариация. Условия Лежандра 116
53. Свободные концы. Случай конца, перемещающегося по ординате . . 118
54. Условие трансверсальности 123
6 ОГЛАВЛЕНИЕ
55. Диференциал в нелинейном метрическом пространстве 197
56. Вариация интегралов от экстремалей 129
57. Случай свободных концов в пространственной задаче 132
58. Случай производных высшего порядка 136
59. Случай функций многих переменных . 143
Глава IX. Условный экстремум
60. Изопериметрическая задача 148
61. Правило множителей Эйлера-Лагранжа 160
62. Условие Лежандра 166
63. Условный экстремум 169
64. Трансверсальность 173
65. Применение к теории геодезических 175
66. Условный экстремум (неголономные связи) 180
Глава X. Вариационные задачи в параметрической форме
67. Параметрическая форма задания кривых 188
68. Условия однородности ! 189
69. Экстремумы функций от линии 193
70. Обобщения и приложения 200
71. Замкнутые экстремали. Метод нормальных вариаций 204
72. Приложения к теории геодезических 211
Глава XI. Разрывные задачи
73. Ломаные экстремали 215
74. Преломление экстремалей 219
75. Отражение экстремалей 223
76. Случай свободных концов 225
Глава XII. Односторонние вариации
77. Односторонние вариации для простейшей задачи 231
78. Задача Ньютона (поверхность вращения наименьшего сопроти-
сопротивления) 238
79. Пространственная задача 244
СЕМЕЙСТВА ЭКСТРЕМАЛЕЙ И ДОСТАТОЧНЫЕ
УСЛОВИЯ
Глава XIII. Вторая вариация и линейные вариационные задачи
80. Предварительные замечания 252
81. Существование минимума квадратических функционалов 254
82. Уравнение Штурма-Лиувилля 260
83. Условия положительности формы 264
84. Слабый экстремум 269
85. Уравнения в вариациях 270
86. Геометрическая теория сопряженных точек 272
87. Экстремальная теория собственных значений 275
88. Минимаксные экстремали 281
89? Теория Лежандра-Яксби квадратических функционалов 285
9О.'Квадратический функционал Jab как предел конечных квадратиче-
квадратических форм 286
91. Вторая вариация для изопериметрической задачи 290
92. Уравнение в вариациях и сопряженные точки для изопериметри-
изопериметрической задачи 304
ОГЛАВЛЕНИЕ 7
Глава XIV. Теория поля и достаточные условия сильного
экстремума
93. Геометрия экстремалей ?09
94. Поле экстремалей и трансверсали 311
95. Теория Кнезера 318
96. Услэзия Якоби 320
97. Геодезические эллипс и гипербола 324
98. Метод интегр ;рования Якоби • 327
99. Функция Вейерштрасса 332
100. Необходимые условия Вейерштрасса 337
101. Достаточные условия сильного экстремума 339
102. Теорема Осгуда . 345
Дополнение I. Экстремальные свойства выпуклых тел
1. Общие замечания . . 351
2. Выпуклое симметрическое тело в целочисленной сети . . ~ . . . . 353
3. Экстремальные свойства треугольника 357
4. Об экстремуме отношения объемов выпуклого тела и заключенного
в нем центральносимметрического тела 359
Дополнение II. О некоторых экстремальных задачах теории
конформных отображений
Примеры функционалов 367
Качественные принципы 369
Бесконечно малые вариации 370
Специальная вариация границы 372
Максимальное растяжение 374
Проблема коэфициентов 379
Дополнение III. Применение метода Ритца к доказательству
существования решений уравнения Штурма-
Лиувилля
Указатель 395
ОСНОВНЫЕ ПОНЯТИЯ И МЕТОДЫ ВАРИАЦИОННОГО*
ИСЧИСЛЕНИЯ
ГЛАВА V
ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ:
К ВАРИАЦИОННЫМ ЗАДАЧАМ
§ 27. Функционал
Общие понятия. Исследуем такую величину, как длина кривой.
Длина кривой есть переменная величина, она меняется вместе с кри-
кривой. Мы имеем здесь аналогию с функцией одного или нескольких
переменных. Длина есть также зависимая переменная величина, но она
зависит не от числовой переменной, а от кривой.
Пусть нам даны кривые, уравнения которых имеют вид:
У=У{х), (I)'
причем абсцисса х меняется в промежутке а <; х ^ Ь, а функция у (х)
обладает непрерывной производной у/ (х) при а ^ х ^ Ь. Тогда длина /
каждой такой кривой имеет вид:
ь
J=
С изменением функций у(х) меняется и кривая, изображающая эту
функцию, меняется и величина J—длина кривой A). J зависит от
вида функции у(х): различным функциям у(х) отвечают различные
значения J (различные длины). Мы будем писать:
J = J[y(x)).
Эта запись показывает, что J зависит от функции у(х).
ОПРЕДЕЛЕНИЕ. Пусть дан некоторый класс функций у(х). Мы ска-
скажем: J[y(x)] есть функционал от функции у{х) нашего класса, если
каждой функции у(х) отвечает некоторое значение J[y(x)].
Поскольку геометрически функции одного переменного изображаются
линиями, то функционал от них иногда называется функцией линии.
Пример 1. Рассмотрим совокупность всех непрерывных функций у(х),
заданных на отрезке ^^Ь
ь
= f y{x)dx
есть функционал от_у(лг); каждой функции у(х) отвечает определенное значе-
значение J[y(x)]. Этот функционал геометрически означает площадь, ограниченную
кривою у=у(х), осью Ох и ординатами х = а, х = Ь.
10 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [гл. V
Подставляя в равенство B) вместо у (х) конкретны? функции, мы будем
получать соответственные значения J[y(x)\. Положим для опрзделенности
а = О, Ъ = 1:
1
Если
1
у (х) = х, то J[y{x)] = J [х] = / х dx = -~- *
6
если у (х) =х\ то J [у {х)] = J [х*[ = I x^dx = -^-;
если
если
4 *
Пример 2. Другим примером функционала является длина кривой у =
Будем попрежнему считать д = 0, Ь=\\ рассмотрим совокупность всех непре-
непрерывных функций у (х), обладающих непрерывной первой производной. Под-
Подставляя в выражение
1
вместо у(х) определенные функции, получим определенные числовые значения
для J[y(x)].
Например, если у (х) = х, уг (х) = 1.
J[y(x)]=J[x] =
Если у (х) =
ех
(цепная линия,) то
V 2
— е~
2
е — е
.Можно было бы привести целый ряд других примеров функционалов.
§ 27] функционал
11
В настоящей главе, когда мы будем говорить о „всех кривых", мы
безоговорочно предполагаем, что мы ограничиваемся кривыми, анали-
аналитически выражаемыми уравнениями:
у=у(х)у
где х изменяется на некотором промежутке а^х^Ь, а у(х),
обладает непрерывной первой производной.
Экстремум функционалов. Уже с самого начала возникновения
анализа бесконечно малых наряду с задачами об экстремумах функций
п переменных появился целый ряд геометрических, механических и физи-
физических задач на отыскание экстремумов функционалов. Рассмотрим,
например, следующую задачу: среди всех плоских кривых, соединяющих
две заданных точки А (хо,уо) и В(хи ух), найти ту, для которой
длина принимает наименьшее значение.
Аналитически эта задача гласит: среди всех функций у=у(х), та-
таких, что
найти ту, для которой
v0
принимает наименьшее значение.
Мы знаем, что искомая кривая, дающая минимум длины, етгь пря-
прямолинейный отрезок, соединяющий точки А и В или, переводя на ана-
аналитический язык: J[y(x))= I V I -\-y'2 dx достигает минимального
значения, если функция у (х) есть у (х) —yo-\-k(x — л:0), где k=^—r' •
Задача о брахистохроне. Исторически первой задачей, возбудив-
возбудившей к себе общий интерес среди математиков, была задача о брахи-
стохоне, поставленная Иваном Бернулли: среди всех кривых, соединяю-
соединяющих две данные тонки А и В, найти ту, по которой тяжелая точка,
двигаясь из точки А, под влиянием силы тяжести попадет в крат-
кратчайший срок в точку В1).
Проведя вертикальную плоскость, проходящую через точки А и В,
ограничимся плоскими дугами, соединяющими эти точки. Примем за
ось Ох горизонтальную прямую, а ось Оу направим вертикально вниз.
Тогда точки А и В будут иметь соответственно координаты (а, 0)
и (by yx). Если тяжелая точка движется из А без начальной скорости,
то ее скорость v связана с ее ординатой у следующим соотношением:
где g — ускорение, силы тяжести, или
г) Мы здесь естественно предполагаем, что Л и В не лежат на одной вер-
вертикальной прямой. Если бы А\ В лежали на одной вертикальной прямой, то
решением задачи являлась бы эта прямая.
12 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
Пусть y=zy{x) есть уравнение кривой, по которой движется точка
из А в В. Скорость движения точки:
_ ds _ Vl -f У2 dx
v~ dt "" dt
где dt—элемент времени. Отсюда:
dt= Y
Интегрируя (З), получим время Г, потребное для покрытия пути из
точки А до точки В по кривой у=у(х):
J
x. C0
Очевидно, Т есть функционал, зависящий от функции у (х). Тре-
Требуется найти функцию у(х) [или, что то же самое, кривую у=у(х)]9
для которой Т принимает наименьшее значение. Решение этой задачи
мы дадим в следующем параграфе.
Принцип Ферма. Задача о брахистохроне'аналитически родственна
следующей физической задаче другой природы: в прозрачной среде
с переменной оптической плотностью даны две точки А и В, тре-
требуется определить траекторию луча света, идущего от точки А
к точке В. Эта задача сводится к задаче на разыскание экстремума
функционала на основании так называемого принципа Ферма: из всех
кривых, соединяющих точки А и В, траектория луча света есть ли-
линия, распространяясь вдоль которой свет придет из А в В в крат-
наитий'срок.
Остановимся на плоском случае. Примем за плоскость распростра-
распространения света плоскость хОу.
Пусть лг0, у0 и xvy1 суть координаты точек А и В, а у=у(х)>
хо^х-^>xi есть некоторая кривая, соединяющая эти точки. Повторяя
рассуждения, приведенные в предыдущем примере, получим: время Т
распространения света вдоль кривой у=у(х) из А в В выражается
интегралом:
~ J v\*>
dx; D>
этим самым задача определения траектории луча света сводится к опреде-
определению линии, для которой функционал принимает наименьшее значение.
Предмет вариационного исчисления. Решение отдельных задач на
отыскание минимума или максимума функционалов привело к созданию
новой математической дисциплины — вариационного исчисления.
В этой главе мы покажем, каким образом, отправляясь от задач на
разыскание экстремума функций многих переменных, можно предель-
предельным переходом подойти к решению задачи на разыскание экстремумов:
функционалов.
<§28]
ЭЛЕМЕНТАРНОЕ РЕШЕНИЕ НЕКОТОРЫХ ВАРИАЦИОННЫХ ЗАДАЧ
13
§ 28. Элементарное решение некоторых вариационных задач
Распространение света. Решим поставленную в предыдущем па-
параграфе задачу о траектории луча света, распространяющегося в плос-
плоскости хОу и идущего от точки А(хо,уо) к точке B(xvyl). Огра-
Ограничимся пока случаем, когда скорость v непрерывно зависит от у:
v — v(y). Будем обозначать через 5 нашу плоскую среду распро-
распространения света. Построим в плоскости хОу горизонтальную полосу
ширины уг—yo = h:
У1> E)
эта полоса ограничена'прямыми, параллельными оси Ох и проходя-
проходящими через точки А и В. Разобьем прямыми
=1.2, ..., п—
нашу полосу E) на п горизонтальных полосок (черт. 1):
h
^<У<Уо+-
^- (/ = 0, 1, ..., я—1). E0
Заменим мысленно -данную среду распространения света, с непрерыв-
непрерывным изменением скорости света, средой *Sn со скачкообразным изме-
изменением скорости све-
света, именно: в преде-
пределах i-й плоскости E'),
/ = 0,1..., п—1, ско-
скорость света vi будем
считать постоянной и
равной
С?+ЦЛ
JL
/
Черт. 1.
Задачу1? распростране-
распространения света в среде 5
мы будем рассматри-
рассматривать как предельную
задачу распростране-
ния света в среде Sn,
когда п неограниченно растет. Задача распространения света в среде Sn
есть задача на разыскание минимума функции (п—1)-го переменного;
эта задача была нами решена в § 15, пример 4.
В примере 4 § 15 мы уже определили путь луча света в среде,
в которой оптическая плотность; а следовательно и скорость, менялись
только скачками. В основу решения был как раз положен принцип
Ферма. Мы нашли, что в этом случае луч света представляет собою по-
полигон. Разобранная задача, однако, не исчерпывает задач, встречаю-
встречающихся в физике и астрономии на определение пути луча света.
Часто приходится иметь дело с средами с непрерывно меняющейся
плотностью. В этом случае путь луча будет кривая с непрерывно вра-
14 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [гл. V
щающейся касательной. Примером такой задачи может служить задача
определения пути, который проходит луч света от светящейся точки,
например звезды, до нашего глаза. Этот путь будет криволинеен, ибо
плотность атмосферы меняется непрерывно с высотой. Для большей
простоты примем, что поверхность земли есть плоскость (кривизна
земли мала по сравнению с толщиной атмосферы). Введем систему ко-
координат. За начало координат примем положение глаза. Светящаяся
точка пусть расположена в плоскости хОу, ось Оу направим верти»
кально вверх, ординату светящейся точки обозначим через h.
Пусть теперь v(x, у) есть скорость распространения света в точке
с координатами х, у. Эту скорость будем считать заданной функцией
от х и у, причем будем предполагать, что v (x, у) есть непрерывная
функция от х и у .
По принципу Ферма траектория луча света в Sn есть полигон, дви-
двигаясь по которому луч, исходящий из точки Л, достигнет в кратчай-
кратчайший срок точки В. Стороны полигона соединяют прямые у=уо-\
и у==уо-\- * —. Обозначим через х{ абсциссу i-й вершины этого
полигона (с ординатой уо-\ 1, получим для времени Тп движения
света по полигону выражение:
Условие минимума Тп (см. § 15):
c-^-l = k, G)
где ог — угол наклона i-й стороны полигона к оси Ox; k не зависит
от /. Условие G) определяет полигональную траекторию светового луча.
Перейдем теперь к пределу, когда я->оо. От скачкообразного рас-
распределения плотностей и скоростей света мы перейдем к непрерывному
их распределению; полигональные траектории перейдут в криволиней-
криволинейные, выражаемые уравнениями у=у (х); время Г движения света по
траектории выразится вместо суммы F) интегралом:
= ДУ1 + У dx,
J v (у)
(У)
Т есть предел соответственных ГЛ. Будем считать, что при этом пре-
предельном переходе полигональная траектория среды 5„, дающая мини-
минимум Тп9 переходит в криволинейную траекторию среды 5, дающую
минимум Т\ при этом направления сторон полигональной траектории
переходят в направления касательных к криволинейной траектории.
При этих гипотезах условие минимума G) для Тп перейдет в условие
минимума для Т:
v(y)
§ 28] ЭЛЕМЕНТАРНОЕ РЕШЕНИЕ НЕКОТОРЫХ ВАРИАЦИОННЫХ ЗАДАЧ 15
Если у=у(х) есть уравнение искомой траектории, то
1
cos 9
1
Уравнение G) перейдет в диференциальное уравнение:
—k= const. (8>
Полученное диференциальное уравнение с разделяющимися перемен-
переменными решается в квадратурах; его общий интеграл будет иметь вид:
где С—константа интеграции.
Отсюда заключаем, что в данной среде траектория луча света всегда
принадлежит двупараметрическому семейству кривых (8') (параметры:
С и k)\ из каждой точки M(xQ,y0) плоскости выходит пучок лучей:
У
vdy
Л —— Ал
:-xo-J-
— V*
Уравнение траектории этого луча зависит от одного параметра k, ко-
который можно найти, если известно или направление луча в рассматривае-
рассматриваемой точке или известна еще одна точка, через которую проходит луч.
Укажем на один частный случай, когда решение может быть пред-
представлено в конечном виде. Допустим, что скорость v распространения,
света пропорциональна высоте:
v = ау.
В этом случае уравнение семейства траекторий лучей примет вид:
J
или после интеграции и упрощений:
Таким образом в разбираемом случае траектории лучей суть дуг»
окружностей с центрами на оси Ох, Через каждые две точки прохо-
проходит единственная трактория.
Задача о брахистохроне. В качестве примера на применение полу-
полученного выше результата разберем задачу о брахистохроне — линии
наилучшего ската: среди всех линий, расположенных в вертикальной
плоскости и соединяющих точки Л и В, определить линию, скаты-
ваясь по которой тяжелая точка прибудет из А и В в кратчайшее
время (в начальный момент ската ее скорость принимается равной ртулю).
16 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
Проведем через точки Л и В вертикальную плоскость и снабдим ее
прямоугольной системой координат; за начало координат примем
точку А, а ось Оу направим вертикально вниз.
Пусть (а, Ь) суть координаты точки В, g — ускоренные силы тя-
тяжести. Время Г, необходимое точке, чтобы из А скатиться в В> будет
выражаться интегралом:
а
'"¦dx
J Vigy
[см. предыдущий параграф, формула C')]« Наша задача приводится
к разысканию кривой, вдоль которой интеграл Т принимает наимень-
наименьшее значение. В силу предыдущего искомая кривая должна удовлетво-
удовлетворять уравнению (8), причем v (у) — \^2gy) после чего уравнение при-
принимает вид:
или
У =
Для интегрирования полученного уравнения можно воспользоваться
-формулой (8'), но в данном случае этот путь приводит к громоздким
выкладкам, и оказывается целесообразнее разбираемое диференциальное
уравнение интегрировать непосредственно, вводя новое переменное <р
подстановкой:
Уравнение (9) после этого перейдет в следующее:
V = , , : -5— = #1 COS2 СЗ = —
. Диференцируя A0) по х, найдем:
у' = — kx sin 2ср -~ . A1)
Сопоставляя A1) и (9'), найдем соотношение между х и ср:
tg ср = — 2k{ cos cp sin cp -J-
или
dx
cos2 ср <ftp= —
Интегрируя полученное равенство, найдем общий интеграл уравне-
.«ия (9') в параметрической форме:
§ 29] АНАЛОГИЯ МЕЖДУ ОПТИКОЙ И МЕХАНИКОЙ 17
Для упрощения исследования полученного семейства кривых введем
новый параметр б, полагая 2ср == тс — 6. Уравнение семейства примет вид:
х = г(Ъ — sin
>
y = r(l— cos8), J
где г и С—произвольные постоянные. Кривая A2) есть циклоида,
образованная качением круга радиуса г по действительной оси. Точками
возврата будут точки действительной оси с абсциссами:
te нашем случае С=0, так как по условию задачи кривая проходит
через начало координат. Что касается г, то оно определится из усло-
условия прохождения кривой через точку ?.
Простейшая задача вариационного исчисления. Разобранные нами
задачи являются частными случаями следующей: среди всех кривых
у=у(х), соединяющих точки А(хо,уо) и B(xv j^), найти ту, для
которой интеграл
достигает минимума. Здесь F (х, у, У) есть заданная функция трех
аргументов лг, у, у'. J зависит от функции у(х) и есть, следовательно,
функционал от у(х). В задаче о брахистохроне мы имеем, например:
§ 29. Принцип Мопертюи-Эйлера. Аналогия между оптикой
и механикой. Аэронавтическая задача
Принцип Мопертюи-Эйлера. Пусть задано в плоскости поле сил
с заданной потенциальной функцией U(x, у). Скорость v точки при
движении в этом поле связана с U формулой:
где h — постоянная^™* скоренад^ направлены по нормалям к линиям
уровня:
U = const.
Пусть точка М е. иассой пС Движется в этом поле со скоростью
v = у 2U -f- h. Заменим движение точки М по ее криволинейной
траектории движением по ломаной траектории: на плоскости выделены
близкие друг другу линии уровня:
где Ut = UQ -— /Д(/, a At/—некоторая постоянная величина (черт. 2).
18 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
Будем считать, что в полоске между линиями U==Ui и U= U,. , 1 точка М
движется прямолинейно со скоростью
При переходе через линию уровня U=Ui_,1 точка получает импульс
•> •>
силы т (yi+i — ^), [направленный по нормали *) к линии уровня
->
U=Ui+v (Мы обозначаем здесь через vx вектор скорости в г'-й полосе.)
Точка опишет ломаную траек-
траекторию, пределом которой бу- *
дет криволинейная траектория
точки М. Так как импульс си-
силы направлен по нормали к
линии U=Uitv то составля-
составляющая по касательной к этой
линии не меняется в момент
перехода точки через нее, т. е.:
• v% cos a = vi+1 cos р, A3)
где аир — углы между напра-
направлением скорости точки М с
касательной к линии уровня
^—Ц-j-i Д° и после перехода
через нее.
Если бы мы имели в нашей плоскости движение совета со скоростью
в /-й полосе, равной —, то для его лучей условие A3) выражало бы
закон преломления.
Таким образом наши ломаные траектории точки М совпадают с пу-
путями луча света, скорость которого обратна скорости точки М. При
п -> оо ломаные траектории переходят в криволинейные, ломаные
лучи — в криволинейные лучи света, движущегося со скоростью
L 1
Черт. 2.
Траектория точки М при движении со скоростью t>==)^2?/+А сов-
падает с путей луча света, движущегося со скоростью
Так как луч света при скорости света vx
интеграла
= -^- реализует экстремум
i) Этот импульс силы'заменяет нормальное к линии уровня ускорение.
АНАЛОГИЯ МЕЖДУ ОПТИКОЙ И МЕХАНИКОЙ
19
§ 29]
то для траектории движущейся точки реализуется экстремум интеграла
fvds= I У211 4- h ds.
Интеграл / v ds, взятый вдоль траектории, называется действием.
Получаем вариационный принцип Мопертюи-Эйлера: из всех линий,
соединяющих заданные точки, экстремум действия, т. е. интеграла
I У 2U-\-h ds, достигается вдоль траектории точки М.
Аналогия между механикой и оптикой. Аналогия между принципами
Ферма и Мопертюи — была замечена давно. Гамильтон использовал ее
для построения своей теории уравнения механики, которой мы коснемся
дальше. В современной физике эта аналогия положила начало для
создания так называемой волновой динамики.
Пользуясь этой оптико-механической аналогией, мы можем, зная
траектории некоторого механического движения со cKOpocrbio"J^2?/-j-/z,
получить луч света, дви-
движущийся со скоростью
, и обратно.
Например: в поле сил
тяжести точка, имевшая в
начальный момент скорость
v0, движется по параболе
(черт. 3) со скоростью
v — V V — 2?У '
Черт. 3.
где g—ускорение силы тя-
тяжести, у — ордината точки
(горизонтальная прямая, проходящая через начальное ее положение,
взята за ось Ох). Из начальной точки А исходит пучок параболиче-
параболических траекторий, огибаемых также параболой (парабола безопасности).
Если скорость света в среде выражается формулой:
v== 1
~ y*-2gy >
то лучи, исходящие из начала координат, в силу механико-оптической
аналогии будут иметь форму парабол, огибаемых параболой безопасности.
Аэронавтическая задача Цермело. При наличии ветра по какой
траектории должен лететь самолет, чтобы из одной точки про-
пространства прилететь в другую в кратчайшее время.
Мы будем считать, что скорость ветра w (переменная величина, за-
зависящая от точки, но не зависящая от времени) в каждой точке про-
пространства горизонтальна, и в соответствии с этим ограничимся случаем
горизонтального полета. Сформулируем прежде всего поставленную
задачу как задачу вариационного исчисления. Возьмем систему коорди-
координат хОу в плоскости полета, и пусть А(хо,уо) и B(xvyx) (черт. 4) —
20
ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
начальная и4 конечная точки полета. Обозначим через w скорость ветра
и через w& w проекции этой скорости на координатные оси; wx, wy
суть заданные функции х и у. Пусть теперь самолет движется из А
в В по кривой
тогда, обозначая через с скорость движения самолета относительно воз-
духа (|с| — величина постоянная), через v = w-{-c — абсолютную ско-
Черт. 4.
Черт. 5.
рость его, через,сри ^ — углы, образованные векторами w и с с на-
правлениями полета, т. е. с вектором v, будем иметь:
\w\ sin 9 = | с\ sin^,
д- = Iv I = \w Icos ? + \c | cos cp = I w I cos cp -f-
где ^ есть элемент пути. Кроме того:
[a sin2
cos? = —«-
Wx_ dx
w\
Отсюда время Г, необходимое самолету для перелета из А в В по рас-
рассматриваемой трактории, выразится интегралом:
ds
-r i as
T= j ~ ^T=
J \w\ cos9 + у \c\2 — I
V \°\
§ 29 [ АНАЛОГИЯ МЕЖДУ ОПТИКОЙ И МЕХАНИКОЙ 21
Таким образом поставленная задача приводится к разысканию среди
всех кривых, соединяющих А и В, кривой, вдоль которой интеграл Т
принимает наименьшее значение.
Мы приведем сейчас элементарное решение этой задачи, данное
Мизесом 1).
Рассмотрим предварительно следующую простейшую задачу (черт. 5),
Вся плоскость хОу разбита прямой ААХ на две части Dx и D2. В каж-
каждой из полуплоскостей скорость ветра постоянна и определяется соот-
-» ->
ветственно векторами w1 и w2. Считая, что самолет в каждой из
полуплоскостей Ог и ?>2 движется по прямой, требуется определить
путь, двигаясь по которому самолет прилетит из точки О1 полуплос-
полуплоскости Dj в точку О2 полуплоскости D2 в кратчайшее время.
Искомый путь по условиям задачи будет ломаная с одной точкой
излома Р, расположенной на прямой AAV Таким образом наша задача
приводится к определению положения точки Р, или, по аналогии с за-
задачей на преломление света, к определению характера излома траектории
в точке Р.
Время Г, необходимое самолету, чтобы попасть, двигаясь по нашей
ломаной, из Ог в О2, есть функция точки Р, следовательно, искомое
условие мы получим, приравнивая нулю диференциал этой функции,
соответствующий бесконечной малой вариации точки Р.
-> -»
Сохраним обозначения: w скорость ветра, г> — скорость (абсолютная)
-»
полета, с — собственная скорость самолета. Имеем:
v = w -\- с.
Этому соотношению нам будет удобно придать ге#метрический вид: от
->
фиксированной точки О откладываем вектор w, от конца М построен-
->
ного вектора откладываем вектор с, конец которого обозначим через L;
—> -» -» -v
тогда OL = v. Когда собственная скорость с (норма с по условиям
задачи постоянна) блюдет иметь всевозможные направления, точка L
-»
опишет окружность с центром в точке М и радиуса \с\ = с.
Эта окружность называется окружностью скоростей, а плоскость,
в которой ведется построение, называется плоскостью скоростей.
Определим теперь изменение времени перелета из Ох в О2, когда
точка Р сдвигается на 8л: в точку Q. При этом изменении движения
треугольник скоростей О ML перейдет в новый треугольник OMLV
—>
Обозначим соответственно через <pi угол, образованный вектором ML
с нормалью к прямой AAV и через а угол MLO. Пусть при пе-
переходе к новому движению эти углы получат приращения 8© и 8а.
Пусть, кроме того, норма скорости v получит приращение Si;, а время
перелета в полуплоскостях Dx и D2 — соответственно Sj/ и 82?.
J) „Zeitschr. f. angew. Math. u. Mech.*, т. И, 1931.
22 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [гЛ. V
Построим теперь в плоскости движения четырехугольник С^Ж^Р,
подобный четырехугольнику OMLXL. Точка Рх будет, очевидно, точкой
пересечения прямой OXQ с окружностью радиуса МгР с центром в Mv
После описанных построений установим соотношения между введен-
введенными величинами. Прежде всего имеем:
OlP = vt=OL- t.
Отсюда:
Так как OL^ = v--\-ov и четырёхугольники OMLXL и С^Л^/^Р подобны, то
0^ = 0 + 0^.
Отсюда:
) (<+ 8ХО — (у -f to) * =
to-8^.
Проектируя вектор PXQ на М1Р1 и отбрасывая бесконечно малые выс-
высших порядков, получим:
—->
пр. PjQ = (у -f- St;) cos (а -|- 8а) 8^ = v cos a 8^.
С другой стороны,
пр. 7\Q = (Pj? -f PQ) = пр. PQ = sin <p Sep.
Отсюда, обозначая через мх проекцию скорости v на ось самолета
->
(на с), получим:
v cos a
Вполне аналогичные вычисления показывают, что, пренебрегая бес-
бесконечно малыми высших порядков, при переходе от пути Р02 к пути
QOX приращение 8^ времени перелета будет равно
где 9з есть Угол» образованный осью самолета (при полете в полу-
полуплоскости D2) с нормалью к прямой AAV а и2 есть проекция скорости
->-
v на ось самолета (тоже при полете в ZJ). Отсюда условие экстре-
экстремума примет вид:
или
Sincp1 _ sincp2
Соотношение A4) дает искомый закон „преломления" траектории
при переходе из среды с одной скоростью ветра в среду с другой ско*
§ 29] АНАЛОГИЯ МЕЖДУ ОПТИКОЙ И МЕХАНИКОЙ 23
ростью ветра. Это соотношение, легко видеть, определяет единствен-
-> ->
иым образом искомую траекторию. Если wx = w2, то ot = ср2, а зна-
-> ->
чит, vx = v2, т. е. троектория есть прямая.
Если плоскость полета разбита кривыми линиями (с непрерывно
вращающейся касательной) на ряд областей, в каждой из которых за-
задана своя постоянная скорость ветра, и если в каждой из областей
самолет летит по прямой, то троектория скорейшего перелета из одной
данной точки в другую будет ломаная (все точки излома лежат на дан-
данных кривых), причем в каждой точке излома будет иметь место A4),
где роль прямой AAt будут играть касательные к линиям раздела сред,
проведенные через точки излома траектории (то же, что в задаче
на рефракцию).
Пользуясь выведенным законом преломления, докажем прежде всего,
что если скорость ветра постоянная во всей плоскости, то линия ско-
скорейшего перелета (среди всех линий, соединяющих две данные точки)
-есть прямая. Для доказательства найдем сначала линию скорейшего
перелета среди я-звенных полигонов, соединяющих две данные точки.
С одной стороны, так как при удалении в бесконечность одной из точек
излома время перелета неограниченно растет, в силу теоремы Вейерштрасса,
искомый полигон существует. С другой стороны, если полигон реали-
реализует минимум перелета, то любые его два последовательные звена AiAi,l
и Ai, 1Ai, 2 дают минимальное время перелета из начала Ах одного
.звена в конец А{ другого звена. В 'таком случае в силу A4) эти
.звенья принадлежат одной прямой. Следовательно, искомый полигон
есть прямая.
Допустим теперь, что существует кривая, дающая меньшее время
перелета, чем прямая; тогда, вписывая в эту кривую полигон с доста-
достаточно большим числом звеньев, мы получим полигон, дающий также
время перелета меньше, чем прямая, что невозможно, ибо, как мы до-
доказали, среди полигонов минимум достигается на прямой *).
Таким образом в данном выше решении задачи о траектории ско-
скорейшего перелета в среде со скачкообразно меняющейся скоростью
ветра можно не оговаривать заранее, что в каждой области, где ско-
скорость ветра постоянна, самолет движется по прямой.
Пользуясь выведенным выше законом преломления, можно предель-
предельным переходом решать задачи на разыскание линии скорейшего пере-
перелета при непрерывно меняющемся (от точки к точке) ветре. Мы огра-
ограничимся здесь лишь простейшей задачей. Допустим, что плоскость по-
полета снабжена системой координат лгОу, и допустим, что в этой системе
->
координат скорость ветра w есть функция только лг. Иными словами,
мы допускаем, что обе компоненты wx и w вектора w суть заданные
функции х.
*) Этим мы доказали, что-" время полетало любой траектории не может быть
меньше, чем время полета по прямой. Предлагаем читателю попытаться дока-
доказать, что время криволинейного полета не может быть также равно времени
прямолинейного.
24 ПЕРЕХОД QT ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
Пусть, как раньше, Ох и О2 соответственно начало и конец пути
самолета. Проекцию отрезка ОХО2 на ось Ох разобьем на п частей и
через каждую точку деления проведем параллель к оси Ох. Этим сймым
плоскость полета будет разбита на п полосок. Будем считать прибли-
приближенно, что скорость ветра в каждой полоске постоянна и равна задан-
заданной скорости ветра в произвольной точке рассматриваемой полоски»
Для созданного разрывного
У
№
где 94 есть угол, образован-
образованный осью самолета при по-
полете в г-й полоске с осью
Ox, u{ есть проекции аб-
абсолютной скорости самолета
на его ось также в /-й по-
полоске, С — константа, не за-
зависящая от /.
Искомая траектория, оче-
очевидно, получится, когда ши-
ширина каждой полоски при
п -> оо будет стремиться к
нулю. Перейдем к пределу. В силу непрерывности поля ветра, в каж-
каждой точке Ж траектории будет выполнено условие:
поля скоростей ветра мьг
можем построить линию ско-
скорейшего перелета из Ох в.
О2—это будет полигон, в
/-й (в порядке возрастания;
абсцисс) вершине которого
будет выполнено условие:
= С, A5)
щ
Черт. 6.
sincp __
A6)
где ср есть угол оси самолета в точке М с осью Ох и и—проекция
скорости самолета на его ось в той же точке Ж.
Условию A6) можно придать вид диференциального уравнения.
Считая, что у=у(х) есть уравнение искомой кривой, можно выразить
ф и и через С, у' и через wx и wy — данные функции. Подставляя
эти выражения в A6), мы получим диференциальное уравнение первого
порядка для определения искомой траектории.
Получаемое при этом диференциальное уравнение имеет довольна
громоздкий вид, мы его здесь приводить не будем. Фактическое опре-
определение траектории по заданным С, wx, wy лучше определять непосред-
непосредственно из A6).
Приведем в заключение одну форму уравнения A6), которая имеет
интересную механическую интерпретацию.
§ 30} ЭЛЕМЕНТАРНОЕ РЕШЕНИЕ ИЗОПЕРИМЕТРИЧЕСКИХ ЗАДАЧ 25
Продиференцируем соотношени A6) по t; получим:
^ ^-=0. A7)
Обозначим через а направление оси самолета, а через b направление,.
->
перпендикулярное к а, и пусть wa и wh — проекции w на эти напра-
направления. Будем иметь:
Отсюда:
Ш~ dt = да mdt==U~da~ ''
Таким образом, если подставить в A7) найденное выражение для -у
и если через со = ~5- обозначить угловую скорость вращения caмoлefа,
то уравнение A7) примет вид:
dwn . ¦
О) COS CD = ^ Sin ф'
' па • '
но так как ~~^ = 0, то
dwa dwa
Отсюда:
§ 30. Элементарное решение некоторых изопериметрических
задач
Задача о тяжелой цепи. Покажем сейчас, что аналогичными пре-
предельными переходами могут быть весьма просто решены задачи, кото-
которые приводятся к так называемой изопериметрической задаче вариа-
вариационного исчисления. Как простейший пример разберем задачу на опре-
деленние форм равновесия тяжелой гибкой нерастяжимВй нити, закре-
закрепленной своими концами.
Задача определения формы равновесия такой нити сводится к опре-
определению такого ее положения, которое дает самое низкое положение
ее центра тяжести. Ограничимся нитями, расположенными в вертикаль-
вертикальной плоскости лгОу, причем за ось Ох принята горизонтальная прямая.
Мы приходим к следующей задаче: среди всех плоских линий (нитей)
данной длины, концы которых лежат в заданных точках Л(хо,уо)
и B(xlJyi), определить ту, у которой ордината центра тяжести
минимальная.
То обстоятельство, что мы ограничиваемся линиями данной длины,
есть следствие условия нерастяжимости нити.
—-~- есть производная wa в направлении а.
t26 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
Ордината У центра тяжести линии у —у (х) есть функционал, кото-
который выражается формулой:
A8)
* t/
где
A80
/
.Мы приходим к окончательной формулировке задачи. Среди всех линий
у=у(х), соединяющих точки А и В и удовлетворяющих условию A8'),
найти ту, для которой функционал Y достигает минимума.
Подобного рода задачи называются изопериметртескими (слово
„изопериметрическая* означает „равнодлинная").
Рассмотрим сначала приближенно гибкую нить как шарнирный по-
полигон с п звеньями. Обозначим через As длину отдельного звена много-
многоугольника. Пусть rcAs = /—длина нити. Сохраняя обозначения, принятые
при решении примера на равновесие шарнирного многоугольника, будем
иметь (см. § 16, задача 2):
Кроме того, обозначая через х% абциссу /-го шарнира, очевидно, будем
иметь:
Отсюда, деля почленно A9) и A9'), полупим:
V )
Заставим теперь As стремиться к нулю; тогда, обозначая через у {х)
уравнение искомой кривой, будем иметь:
хде о — угол между касательной и осью Олг, или
1
cos <р = -
V 1 +У2
Уравнение B0) в пределе перейдет в:
Полагая:
лолучим:
а' = а У 1 -fa2.
§ 30] ЭЛЕМЕНТАРНОЕ РЕШЕНИЕ ИЗОПЕРИМЕТРИЧЕСКИХ ЗАДАЧ 27
Решая последнее диференциальное уравнение, получим:
« = sha(AT-f Сх),
откуда
J а
Мы получим таким образом уравнение цепной линии (черт. 7), завися-
зависящее от трех параметров. Эти три параметра можно определить, поль-
пользуясь тремя начальными условиями задачи: 1) длина нити равна /,
2) и 3) кривая проходит через две заданные точки А и В.
Изопериметрическая задача в узком смысле. Среди замкнутых
линий данной длины определить линию, ограничивающую наибольшую
площадь.
Для решения будем считать приближенно замкнутую линию я-уголь-
ником. Как было показано в первой главе, в этом случае абсолютный
.экстремум достигается, когда я-угольник есть
правильный. Рассматривая поставленную задачу
как предельный случай (при я—^оо) решен- \ /&
ной, естественно считать, что искомая линия
будет предел правильных я-угольников с дан-
данным периметром, когда число звеньев неогра-
неограниченно растет, т. е. искомая линия есть ок- Черт. 7.
ружность.
Выше было отмечено, что приведенное рассуждение еще не дает
полного решения вопроса, предельный переход должен быть дополни-
дополнительно обоснован.
Дадим для данной задачи полное решение. Докажем, что окруж-
окружность действительно ограничивает наибольшую площадь. Допустим про-
противное, что существует кривая L той же длины /, ограничивающая
большую площадь. Пусть ог — площадь, ограниченная окружностью
длины /, и а2 — площадь, ограниченная кривой L. Пусть
o2-a1 = a>0. B\)
Строим два я-угольника длины /: один Рп — правильный и другой Qn
с равными звеньями, получаемый из вписанного в кривую L многоуголь-
многоугольника путем подобного растяжения. Выберем я настолько большим, чтобы
площадь о/ полигона Рп отличалась от at меньше, чем на -^-, и пло-
площадь а/ полигона Qn отличалась от о2 меньше, чем на -у :
°i— °i <Т ' I
a [ <22>
Отсюда, сопоставляя B1) и B2), получим:
а/ — а/>0,
что невозможно, ибо в силу решенной раньше задачи о1/Г > о2'.
28 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
Допустимые линии. Нам задан некоторый класс функций (или
линий), для которых задан функционал. Эти линии называются допусти-
допустимыми линиями. Мы ищем среди них ту, для которой функционал до-
достигает наибольшего или наименьшего значения.
.В задаче о брахистохроне допустимыми линиями были линии,
соединявшие точки А и В.
Возьмем другую, только что разобранную задачу. Среди всех за-
замкнутых линий данной длины найти ту, которая ограничивает наи-
наибольшую площадь. Здесь допустимыми линиями являются замкнутые
линии данной длины.
Овал постоянной ширины. Введем следующее понятие: шириной
в данном направлении данной выпуклой замкнутой кривой — овала — мы
назовем расстояние между касательными к
овалу, перпендикулярными данному напра-
направлению. Мы скажем, что данный овал имеет
постоянную ширину, если его ширина в лю-
любом направлении одна и та же (черт. 8).
Простейшим представителем овалов по-
постоянной ширины является окружность. Легко
I показать, что окружность далеко не един-
единственный овал, обладающий этим свойством;
существует целый класс овалов постоянной
ширины. Пользуясь данным определением,
поставим следующую задачу: среди овалов
Черт, g. данной постоянной ширины определить овал
наибольшей площади.
Эта задача дает нам новый пример из задач вариационного исчисления,
когда на класс допустимых линий накладывается некоторое специаль-
специальное ограничение. Эта задача, оказывается, редуцируется к разобранной
нами выше изопериметрической задаче (в узком смысле). Для этой цели
воспользуемся теоремой:
ТЕОРЕМА БАРБЬЕ (Barbier). Если овал имеет постоянную ши-
ширину Ь, то длина границы овала равна жд.
Итак, пусть Q есть данный овал постоянной ширины. Проведем
к этому овалу две параллельные касательные L и V. В силу постоян-
постоянства ширины овала, если мы овал Q будем катить (без скольжения)
по прямой L, то прямая Z/ будет все время оставаться касательной. Счи-
Считая некоторое положение овала начальным, обозначим через 6 угол
поворота овала при качении по L, и пусть ds— элемент дуги овала,
а <р — угол, образованный элементом ds с перпендикуляром к L в на-
начальном положении овала. Рассмотрим двойной интеграл
где / есть длина овала. С одной стороны, имеем:
§ 31] ПРОСТЕЙШАЯ ЗАДАЧА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 29
где | cos (ft -\-4)\ds есть, очевидно, проекция элемента ds на некоторое
фиксированное направление. Следовательно,
| cos F -|- о) | ds
есть удвоенная ширина овала в рассматриваемом направлении. Отсюда:
о
С другой стороны:
I 2г. I
./ ' J
0 0 О
Таким образом действительно:
Теорема Барбье позволяет нам заключить, что данный класс допу-
допустимых линий — овалы постоянной ширины b — принадлежит семейству
замкнутых линий постоянной длины ъЬ. Так как круг радиуса у
принадлежит к классу овалов постоянной ширины b и дает наибольшую
площадь среди всех замкнутых линий длины izb, то тем более он будет
давать наибольшую площадь среди овалов постоянной ширины Ь. (См.
И. Абельсон, Теорема Барбье, Метематич. просвещ. вып. 5).
§ 31. Простейшая задача вариационного исчисления.
Уравнение Эйлера
Постановка простейшей задачи вариационного исчисления. Мы
осуществили на частных примерах предельный переход от задач на
разыскание экстремумов функций многих переменных к вариационным
задачам. Этот предельный переход может быть без труда обобщен и
распространен на ряд других задач вариационного исчисления. Однако
осуществление его для каждой отдельной задачи требует довольно гро-
громоздких рассмотрений; по этой причине естественно возникает вопрос,
нельзя ли получить в общем случае признаки существования экстрему-
экстремумов интегралов так, чтобы этими признаками можно было пользоваться
непосредственно при решении конкретных задач. Нашей ближайшей
целью будет дать такие признаки для простейших задач вариационного
исчисления.
По аналогии с признаками существования экстремума функций
одного и многих переменных естественно намечаются три первоочеред-
первоочередные проблемы, которые нужно решить:
I. Найти такие необходимые условия, которым должны удовлетво-
удовлетворять искомые функции, чтобы, пользуясь ими, при наличии существова-
существования решения можно было искомую кривую фактически определять.
II. Найти достаточно общие признаки существования абсолютного
экстремума.
30 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [гЛ. V
III. Имея кривую, удовлетворяющую основному необходимому уело-
вию, установить критерии, по которым можно было бы судить, дает
ли эта кривая действительно экстремум и если дает, то будет ли это
максимум или минимум.
Заметим, что в задачах прикладного характера существование экстре-
экстремума очень часто косвенно устанавливается самой постановкой задачиг
по этой причине первостепенное значение приобретают проблемы
I группы. С этих проблем мы и начнем.
Пусть дана функция F(x,y,y'), непрерывная вместе с ее частными
производными по всем трем аргументам до второго порядка включи-
включительно. Пусть, кроме того, в плоскости хОу даны две точки А (а> Ь)
и B(avb1). Простейшая задача вариационного исчисления, как. было
указано в § 28, формулируется следующим образом: среда всех кривыхт
выражаемых уравнением:
у =у {х) (у (а) = Ь, у (ах) = Ьх)
(функция у (х) непрерывна вместе со своей производной в интервале
а^х^ах) и проходящих через заданные точки А и В, определить
ту, вдоль которой интеграл
J=fF(x,y,/)dx
а
принимает наибольшее или наименьшее значение.*
Уравнение Эйлера. Рассматривая поставленную задачу, Эйлер впер-
впервые доказал следующую теорему:
ТЕОРЕМА. Если кривая у=у{х) дает экстремум интегралу J,
то функция у = у (х), изображаемая этой кривой^ удовлетворяет
следующему диференциальному уравнению:
ру-4^ру—° <23>
Прежде чем переходить к выводу этой теоремы, укажем на ее прак-
практическое значение. Производя полное диференцирование по х второго
слагаемого левой части, получим:
-Г„? = 0' B4)
Отсюда видим, что если F , , не равно тождественно нулю, диферен-
циальное уравнение B3) — второго порядка, и следовательно, его общий
интеграл имеет вид:
у=/(х,а,$), B5)
где аир суть произвольные постоянные. Таким образом теорему
Эйлера можно формулировать так: если существует кривая у=у(х)ь
дающая экстремум, то она принадлежит семейству кривых B5), зави-
зависящих от двух параметров. Отсюда, если мы заранее уверены в суще-
существовании искомой кривой, то для ее фактического определения оста-
остается определить значение а и р. Но эти значения можно найти, поль-
пользуясь добавочным условием задачи: искомая кривая должна проходить
§ 31] ПРОСТЕЙШАЯ ЗАДАЧА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 31
через две данные точки Л (а, Ь) и В (av b^), т. е. неизвестные а и {?
должны удовлетворять условиям:
из которых аир можно определить.
Таким образом теорема Эйлера полностью для разбираемой про-
простейшей задачи, решает первую поставленную проблему. Это основное
необходимое условие является полным аналогом условия обращения
в нуль частных производных при разыскании экстремумов функций.
Ввиду основного значения теоремы для всей классической теории
и практики вариационного исчисления мы приведем два вывода этой
теоремы. Один вывод мы получим, обобщая приемы, употребленные
нами при решении частных задач: рассматривать вариационную задачу
как предельный случай задачи на разыскание экстремумов функций
многих переменных. Этот метод, исторически более ранний*), имеет
то большое преимущество, что непосредственно связывает задачу вариа-
вариационного исчисления с известной задачей на разыскание экстремумов
функций. К сожалению, при строгом проведении доказательств этим
методом уже в простейшей задаче приходится применять довольно
громоздкие и тонкие рассмотрения; выводы делаются еще более слож-
сложными, если перейти к задачам более общим. Этот вывод мы сейчас
дадим, причем сначала мы разберем случай, когда F зависит только
от х и у.
Другой метод — Лагранжа — использует специфичность задач вариа-
вариационного исчисления и непосредственно примыкает к дальнейшему раз-
развитию вариационного исчисления — к функциональному исчислению..
С этим выводом мы познакомимся ниже.
Случай, когда F не зависит от у. Мы дадим в настоящем пара-
параграфе первый вывод уравнения Эйлера. Разберем сначала простейший слу-
случай, когда подинтегральное выражение F не зависит от у: F = F(x,y')..
Функционал J принимает вид:
J= [ F{x,y')dx.
Рассмотрим семейство полигонов Пл с координатами вершин: xv y{
(/ = 0, 1,2,..., /г). При этом мы считаем абсциссы х% фиксированными.
(л:0 = а, Хп = ах); точно так же фиксированы две ординаты у0 = Ь,
yn = bv расстояние xi+1 — л^ = Длт постоянно. Полигоны Пп с увели-
увеличением п апроксимируют любую кривую у=у(х), проходящую через
точки Л (а, Ь)> В (av bx). Обозначим через у[ угловой коэфициент
/-го звена полигона Пп. Имеем:
3) Точнее, он является переводом на современный язык этих более ранних
методов.
32 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
На семействе полигонов Ип рассмотрим функцию полигона 2):
п — 1 п — 1
, т >— V Fix «"> — V */- у<+1"-'
w зависит только от j^, ^у2, ..., yn_v причем yi входит только в члены
Будем обозначать через F^(xiyy/) производную F(xvy/) по вто-
второму аргументу.
Пусть Jn достигает экстремума на полигоне IIW, его ординаты yv
уг ^.9уп_1 определятся из условий:
-^- = 0, B9)
где
= ^; (*¦_!» У,_1>—^ (*„ у/). C0)
Из B9) и C0) следует:
Fy^py:)-Fyixi_1,/i_x). C1)
Итак, в полигоне Пп, дающем экстремум Ул, величина Z7 f(xf, у!) при-
принимает одинаковые значения во всех вершинах:
^И-W/) == const- C2)
Перейдем теперь к задаче определения кривой, дающей экстремум У.
РАхматривая эту задачу как предельную для задачи нахождения экстре-
экстремума Jn, переходя к пределу в условии C2), получим для кривой П:
у=у(х), дающей экстремум У, уравнение:
/^ (*./)== const. C3)
Уравнение C3) для случая, когда F не зависит от у, есть интеграл
уравнения B3). В самом деле, диференцированием его по х получаем:
Наше доказательство нельзя считать окончательным. В самом деле,
обозначим через рп(х) функцию, изображающую полигон Пл, на котором
сумма B7) достигает минимума. Если задана совокупность рп, нет гаран-
гарантий, что она сходится и что предельная функция у {х) = lim pn (х)
те->оо
реализует экстремум интеграла J.
1) Под функцией J AIJ полигона \\п мы понимаем функцию J{у^
переменных уь yv ..., уп-\ ординат вершин этого полигона.
§ 31] ПРОСТЕЙШАЯ ЗАДАЧА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 33
К этому вопросу мы предполагаем вернуться во втором томе,
е главе об аппроксимативных методах вариационного исчисления. Пока
отметим более элементарный факт: если мы заранее знаем, что после-
последовательность рп(х) равномерно сходится, равно как и последова-
последовательность производных р/ (х), то предельная функция у (х) == lim pM (х)
ю->оо
удовлетворяет уравнению C3), Это обстоятельство вытекает из сле-
следующей леммы.
Лемма. I. Пусть последовательность полигонов:
определенных и однозначных при а <; х < ait равномерно сходится $ этом
интервале к функции f{x):
Vimpn(x)=f(x).
Пусть, кроме того, последовательность производных *)
также равномерно сходится в том же интервале к непрерывной функции
«Р (х). При этих условиях имеем:
Возьмем в интервале [а, ах] произвольную точку х и выберем число ч\
настолько малым, чтобы для любой пары точек хь х2 интервала [х — yj, *+*il
имело место неравенство:
К -|-.
Тогда при п достаточно большом [n^>N(e)] имеем:!
!/>/<*2>-P/(*i)
Отсюда при п достаточно большом, п^>Nb
C4)
С другой стороны, в силу равномерной сходимости, при достаточно большом
I/W-A.MK-J-.
следовательно:
/(X) —fix - V)) рп (х)—рп(Х —
< \ ¦ C5)
Сопоставляя C4) и C5), получим:
Так как t\ как угодно мало независимо от е, а е может быть сделано тоже
как угодно мплым, то отсюда заключаем, что f'(x) существует и равна у (х)
в каждой точке.
Рассуждениями, вполне подобными приведенным нами при выводе леммы I,
можно дополнить лемму I следующим предложением: сохраняя условия, при-
г) Значение р/(х) в угловой точке мы считаем равным угловому коэфи-
циенту звена, примыкающего слева к рассматриваемой точке.
34 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [гл. V
нятые в лемме I, обозначим через х^п) абсциссу /-й угловой точки я-га
полигона, и пусть рп" (х) есть ступенчатая кривая, равная:
р' \Х . , А — Р„г ( X. ) рп ( X.
^ rw У, ^-j-1/ rn \ г / rn \ г.
Рп \Х) == Щ\ Тп) "~
Добавляя теперь к условиям леммы I условия, что дг/п) = а + /Д*, где
дх -_ ?i ^~g ? и что последовательность
равномерно сходится к непрерывной функции <ИХ)> получим, что функция f (х}
обладает непрерывной второй производной, равной Ь(х) в каждой точке 1).
В силу доказанной выше леммы и сделанных предположений мы заклю-
заключаем, что последовательность р/ (х) равномерно сходится ку'(х). С другой
стороны, в силу C2) выражение -г—,F(xi} p/ (хг)) есть величина постоянная*,
не зависящая от ?:
jpFlXu Рн'{*<)] = С = const.
Следовательно, заставляя п стремиться к бесконечности, для искомой кривой
у=у(х) получим следующее диференциальное уравнение:
dyF(x>y') = const-
Случай, когда F не зависит от х. Разберем еще один частный
случай, допустим, что подинтегральная функция F(x,y,yf) не зависит
явно от х: найдем условие, которому должна удовлетворять кри-
кривая жу=жу(д:)) дающая минимальное значение интегралу:
= fF(y,/)dx.
Для решения поставленной задачи произведехМ замену переменных,
будем считать у за независимое переменное, а х как функцию у, под-
подлежащую определению. Наша задача при такой замене приведется
к разысканию минимизирующей кривой для интеграла:
= I F(yr-r\
J К dx)
" \ 7/
dy >
или, полагая
г) Укажем на один случай последовательности полигонов, когда эта тео-
теорема реализуется особенно просто. Допустим, что f(x) есть функция, обладаю-
обладающая непрерывными двумя первыми производных, и пусть рп (х) есть вписан-
вписанный полигон, тогда/>/(*)==-^^ или по формуле
Тейлора рп" (х) = f" (лг) -f e, где s стремится к нулю вместе с Aft.
§ 31] ПРОСТЕЙШАЯ ЗАДАЧА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 35
для интеграла J получим выражение:
Это есть случай, когда в подинтегральную функцию неизвестная функ-
функция явно не входит. Следовательно, искомая кривая должна удовле-
удовлетворять уравнению:
Ф ( у х'} = С
Перейдем к функции F:
ф*< = х'Fv -U +F = F(У'>У')-Уру О'>/) = с.
Это и есть искомое диференциальное уравнение для определения неиз-
неизвестной функции у(х). Уравнение Эйлера мы получим, продиференци-
ровав левую часть по лг.
Замечание. При этом выводе мы еще неявно воспользовались одним
допущением: в ранее разобранном случае мы получили уравнение Эйлера
в предположении, что искомая кривая есть однозначная функция лг, обладаю-
обладающая непрерывной производной. Таким образом, чтобы наш вывод уравнения
Эйлера для разбираемого случая был корректен, нужно еще допустить, что
разрешение нашей задачи дается функцией у (лг), обратная которой однозначна
или, то же самое, что у (лг) есть монотонная.
Покажем, что от этой гипотезы легко освободиться. В самом деле, в силу
доказанного каждый участок кривой у = у(х), где у' фО, должен удовлетьо-
рять уравнению Эйлера. Нам остается, следовательно, показать, что все эти
участки соответствуют одним и тем же значениям произвольных постоянных
интеграла. Но это последнее вытекает из того, что в точке, где один участок
переходит в другой, начальные данные совпадают.
Общий случай. Познакомимся теперь вкратце с аналогичным выво-
выводом уравнения Эйлера в общем случае. Мы остановимся лишь пэ
главной идее вывода и все детали отбросим.
Итак, пусть у=у(х) дает максимальное значение интегралу
<н
F(x9y,y')dx.
Рассмотрим, как и в предыдущем частном случае, семейства полиго-
полигонов ТТП с вершинами {xi1yi)(i = 0, 1, 2, ..., я), где абсциссы л^ вершин
и ординаты концов у0 и уп фиксированы, xt, ± — х. — А* = ——- •
На совокупности полигонов Пп определим функцию
где
36 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [гЛ. V
Как и в предыдущем случае, из членов суммы /п от yt зависят
только члены
= F
причем 1-й член содержит у{ как непосредственно, так и через третий
аргумент у/. Отсюда:
F(ху">к F &
где
AFPS (*еУе У/) = FVir К- yv У{) — Fy> (xi-v Л-х - Л-i)-
Для полигона Пп, дающего минимум /п, имеем:
1 = ° 0=1,2,...,«-!)
«ли:
'Vw,*')-^^ = o. C6)
В силу теоремы Лагранжа о конечных приращениях уравнение C6)
можно записать в виде:
^ **„ (х* Я Л'). C7)
где
—^-j. л=л-г -ье о< -л-i)' З7;=y'i~i
Задачу отыскания кривой ^=^(at), дающей экстрзмум интегралу/,
мы будем рассматривать как предельную для отыскания полигона, даю-
дающего экстремум сумме Jn при п->оо, Длг->0. Переходя к пределу
в уравнении C6), получим:
F -iff = 0
у dx у
Это уравнение Эйлера для кривой у—у(х), реализующей экстремум/.
Вариация. Мы видели, что основным методом в теории экстрему-
экстремумов функций п беременных было выделение диференциала функции,
т. е. главной линейной части приращения, и обращение этого дифе-
диференциала тождественно в нуль в точках экстремума. Функционал
§ 31] ПРОСТЕЙШАЯ ЗАДАЧА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 37
мы рассматривали как предел функции от полигона Пп:
В силу наших рассмотрений:
4 = 1
где Ьуг—бесконечно малые приращения ординат или [см. формула C7)
настоящего параграфа]:
**(*" >'«• ^ - ш F»; (*" у» к"*} *у* А*- C8)
Положим, что при п,у стремящемся к бесконечности, сумма Jn стре-
стремится к интегралу / и сумма в правой части C8)—к интегралу
Выражение C9) для функционала J есть аналог полного диференциала.
Оно называется вариацией функционала. Мы увидим ниже, что вариа-
вариация есть в некотором смысле главная линейная часть приращения функ-
функционала и что уравнение Эйлера есть условие ее тождественного обра-
обращения в нуль.
Метод Лагранжа заключался в создании алгорифма для определения
вариаций от функционалов, т. е. в создании диференциального исчис-
исчисления для функционалов. Конечно, в эпоху Лагранжа математика не
обладала достаточно широким и общим понятием функции, при кото-
котором метод Лагранжа мог бы быть воспринятым именно так. Поэтому
вплоть до новейшего времени понятие вариации определялось довольно
формально, и вариационное исчисление занимало несколько изолиро-
изолированное положение в анализе. Пересмотр основных понятий анализа,
более широкая точка зрения на понятие функции и основные орудия
анализа позволили преодолеть эту изолированность. С точки зрения
современного анализа вариационное исчисление есть диференциальное
исчисление функций более общей природы.
Более тонкое и глубокое исследование основных соотношений ана-
анализа позволило как раз также возродить в широкой степени методы
долагранжевского вариационного исчисления. Для нас эти методы суть
аппроксимативные методы. Мы аппроксимируем более сложные математи-
математические объекты более простыми; в данном случае функционалы функ-
функциями конечного числа переменных. Решая задачу для функций конеч-
конечного числа переменных и анализируя изменение ее решения в процессе
предельного перехода, мы получаем возможность подойти к предельной
задаче в тех случаях, когда непосредственное ее решение трудно и
даже практически невозможно. На протяжении этого тома мы подоб-
подобными аппроксимативными методами будем заниматься лишь эпизодически.
38 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [гл. V
Особый случай. Если F' , не равно тождественно нулю, то урав-
уравнение Эйлера есть уравнение второго порядка и его общий интеграл
содержит две произвольные постоянные, выбирая которые мы можем,
вообще! говоря, найти искомую экстремальную кривую. Рассмотрим
сейчас случай, когда
В этом случае подинтегральная функция F будет, очевидно, линейной
функцией от у':
F = M (x,y) +/N (х,у). D0)
Уравнение Эйлера примет вид:
"ду""* У "ду" ~dx
или после сокращений:
ду ~~ дх '
Если полученное соотношение Hie удовлетворяется тождественно, то оно
определит в плоскости хОу некоторую, вполне определенную кривую,
которая в общем случае через две фиксированные нами точки Л и В
проходить не будет — поставленная нами задача вариационного исчисле-
исчисления не разрешима.
В разбираемом случае уравнение D1) может дать решение задачи
на разыскание экстремума интеграла
ъ
J= Г (M-Ny')dx,
если за класс допустимых линий принять совокупность всех кривых
класса С^ у=у(х) (а < х < Ь). Например, для интеграла
J= f{? sin ~y — (x+,vJ ] dx
о
уравнение D1) дает:
2
Вдоль этой кривой интеграл J принимает значение —. Нетрудно по-
показать, что это будет максимальное значение интеграла. В самом деле,
1 2/A)
/ у' sin T.ydx= I sin7:ydy=—fcos,y@) —
0 @)
0 2/@)
Заметим, однако, что уже для интеграла
2
—
1
J= f {/ sin *У — (Х+У)'2 )dx (Iaf]< ?c)f
о
§ 32] приложения 39
уравнение D1) для которого имеет вид:
не даст ни максимума ни минимума. В самом деле, меняя кривую
у = — х в е близости от точки х = 1 на конечную величину, интеграл
1
— / (х-руJ dx изменится на величину порядка е, тогда как интеграл
о
о
1
f yr sin ay dx может при этом измениться на величину конечную.
о
Мы допустили, что соотношение D1) не выполняется тождественно;
допустим теперь, что D1) есть тождество. В таком случае подинте-
гральное выражение (M-\-Ny')dx — Mdx-\-Ndy есть полный дифгрен-
циал — значение интеграла зависит только от координат начала и конца
кривой у=у(х) и не зависит от пути интеграции — задача вариацион-
вариационного исчисления теряет смысл.
§ 32. Приложения
Задача о наименьшей поверхности вращения. Среди всех кривых:
\у(х) и У(х) непрерывны], имеющих концы в заданных точках
А(хо,уо) и В(хиу1) (черт. 9), требуется определить кривую, которая
при вращении ее около оси Ох образует поверхность минимальной
площади.
Эта задача является частным случаем общей задачи разыскания ми-
минимальной поверхности, проходящей через заданный контур или через
данную систему контуров. Физически эта задача приводит к определе-
определению формы жидкой пленки, натянутой на данный контур.
Обозначим через у=у(х) произволь-
произвольную кривую, удовлетворяющую отмечен-
отмеченным условиям. Как известно, площадь *S
поверхности, образованной вращением этой
линии около оси Ох, выражается инте-
интегралом:
Черт. 9.
Так как подинтегральная функция явно от х не зависит, то уравнение
Эйлера нашей задачи интегрируется в квадратурах. Первый интеграл
будет:
р-у' F/ -у /ГТ75 -/у jrff^T ~а>
где a — произвольная постоянная, или, после упрощений:
у^а]/ГТ/~-\ D2)
40 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [гл. V
Ради сокращения выкладок при интегрировании этого уравнения:
воспользуемся искусственным приемом: введем новую переменную <р-
Подставляя выражение у' в уравнение D2), получим:
у = а ]/ 1 -\- sh2 <р = а ch ср. D3)
Этим самым мы выразили у через ср. Попытаемся выразить также х
через ©• Для этой цели продиференцируем по х равенство D3):
' их
По условию У = sh cp, следовательно:
Отсюда
где C — новая произвольная постоянная. Таким образом общий интеграл
уравнения Эйлера в параметрической форме примет вид:
D4)
у = a ch ф
или
Уравнение D4) показывает, что семейства экстремалей есть семей-
семейства кривых, полученных из цепной линии
у = ch х
путем ее подобного преобразования с центром подобия в начале коор-
координат (а есть коэфициент подобия) и поступательного перемещения
в направлении оси Ох (|3 есть величина смещения).
Пользуясь отмеченным выше свойством подобия всех кривых, изо-
изображающих общий интеграл уравнения Эйлера, легко дать простой
геометрический прием для определения двух произвольных постоянных
из условия, что экстремаль должна проходить через две заданные
точки Л и В.
Займемся определением а. Пусть значение а, соответствующее иско-
искомой кривой, равно <х0. Обозначим через fo кривую
Of «0
и через Yi кривую
у — ch х.
Обозначим, кроме того, через Ах и Вх точки кривой f19 соответствую-
соответствующие (при подобном преобразовании) точкам А и В кривой ?о-
§ 32] приложения 41
Пусть теперь Со и Сг — точки пересечения прямых АВ и А1В1
с осью Ох. В силу подобия fo и Ti (центр подобия — в начале коор-
координат), с одной стороны:
АВ //1С-Ч
А1ВХ
с другой стороны, в силу того же подобия точка Сх получится как
пересечение с осью Ох геометрического места точек, делящих внешним*
образом в отношении .» отрезки прямых, параллельных АВ и заклю-
С В
ченных между точками кривой fi- Таким образом построив указанное
геометрическое место точек, мы найдем точку Q;" проведя через нее
параллель прямой АВ, мы найдем в пересечении с fi точки Ах и Bv
а отсюда по D5) — значение а0. Значение [3 определится сразу из условия
прохождения кривой через данную точку А (или В).
Пусть х0 < xv Проведем через А параллель оси Ох. Эта параллель
пересечет кривую y = <xoch -^— в двух точках: (?0, тH) и (?и т^). Считая
^с < $i> очевидно, получим:
Ро = хо — ^о»
где р0 есть значение C, соответствующее искомой кривой. Имея значе-
значение ог0, значение второй произвольной постоянной C можно всегда опре-
определить и притом единственным образом.
При определении а возможны три случая 2):
1. Через А и В возможно провести две кривые семейства; в этом
случае минимальную кривую можно определить, вычисляя интеграл
вдоль каждой из этих кривых, искомая кривая будет та, вдоль которой
интеграл будет иметь меньшее значение.
2. Через А и В можно провести одну, и только одну, кривую
семейства; здесь искомая кривая определяется единственным образом 2).
3. Не существует кривой семейства D5), проходящей через А и В~
в этом случае среди линий у=.у(х) нет кривой, дающей минимум
рассматриваемого интеграла: задача неразрешима.
Разберем подробно все эти случаи, предполагая, что точки А и В
расположены симметрично относительно оси Оу. Итак, допустим, что-
хг= — х0 и у±=у0; тогла |3 = О, и наша задача сводится к выясне-
выяснению, в каких случаях возможно определить константу а так, чтобы
кривая
y = ach-^ D6)
нроходила через точку А (х0, у0).
Для этой цели возьмем какую-нибудь кривую семейства D6), на-
например:
y = chx, D7)
г) Для дальнейшего будет существенно отметить, что построенное нами,
жыше геометрическое место точек есть кривая вогнутая.
2) Геометрическое место точек касается оси Ох.
42 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
и проведем к этой кривой касательные через начало координат: ОТ
и OTV как указано на прилагаемом чертеже 10:
ОТ:
ОТ,:
у = —
У
Пусть точка М (а, Ь) и М (— я, Ь) суть точки касания. Любая кривая
семейства D6) получается из кривой D7) путем ее подобного преобра-
преобразования с центром подобия в начале координат. Отсюда заключаем, что
каково бы ни было ос, кривая D6) целиком расположена внутри вер-
вертикального угла ТОТХ и касается прямых ОТ и О7\ в точках
Ма(аа, ab) и Ма (—па, ab).
Ког*да а меняется от нуля до оо, точка касания Mv скользит по
лучу ОТ от начала координат в оо, и семейство кривых D6) заполняет
весь угол ТОТХ так, что через каждую
точку, лежащую строго внутри угла, про-
проходят две кривые семейства, и через каж-
7 дую точку на луче ОТ—одна кривая.
Из этих геометрических построений
непосредственно следует, что если точка
Л, а следовательно и В, расположены
вне угла TOTV у0 < kx0, то задача ре-
решения не имеет. Если А находится на
ОТ 0^0 = ^0)» то можно провести кри-
кривую семейства D6) и притом только одну.
Наконец, если А находится внутри угла
TOTV то через точки А и В проходят
две кривые семейства D6); в этом случае
можно убедиться непосредственным под-
подсчетом, что интеграл будет иметь меньшее
Черт. 10.
значение, если взять ту из этих кривых, которая соответствует боль-
большему значению а, это можно обнаружить совсем просто, если х0 бес-
бесконечно мало, а у0 конечно. В самом деле, тогда кривая семейства D6),
соответствующая меньшему значению а, при вращении образует поверх-
поверхность площади 2ку029 а кривая, соответствующая большему значению,
при вращении образует поверхность площади 2тгл:0^0 (и в том и другом
случае пренебрегаем бесконечно малыми высших порядков); у0 — конечно,
х0 — бесконечно мало, следовательно, 2яу02 >2кх0у0.
В предыдущих примерах при любом расположении точек А и В
вариационные задачи имели вполне определенные решения, на данном
примере мы обнаруживаем впервые случай, когда эта задача не имеет
решения.
Дадкм вкратце объяснение этому явленно.
Итак, допустим, что точки А и В находятся вне угла ТОТУ (черт. 11).
Опустим из А и В перпендикуляры АА{ и ВВХ на ось Ох. Если
теперь вращать ломаную АА^^В около оси Ох, то мы получим по-
поверхность, состоящую из двух вертикальных кругов площади 2ту/02.
При гипотезе: ^о < kx0 можно доказать, что какова бы ни была линия L,
§ 32]
ПРИЛОЖЕНИЯ
43
соединяющая А с В и отличная от ломаной ААХВХВ, площадь поверх-
поверхности, образованной вращением L около оси Ох, будет всегда больше
2тиуо2 и> с другой стороны, как бы мало ни было число г>0, всегда
можно провести кривую, обладающую непрерывно вращающейся каса-
касательной так, что площадь соответствующей поверхности будет меньше
2тсуо24~8- Таким образом кривая, решающая разбираемую задачу, вы-
выражается в ломаную АА}В{В и не может содержаться в семействе
экстремалей, состоявшем из кривых с непрерывно вращающейся каса-
касательной, что вполне согласуется с приведенным выше критерием
возможности решения.
Планетное движение. Рассмотрим систему двух точек, взаимо-
взаимодействующих по закону ньютоновского тяготения. Считая одну точку
неподвижной, исследуем движение подвижной точки.
Переходя к полярным координатам (г, <р)> мы выразим потенциал
ньютоновского тяготения в виде —(у- — постоянная); обозначим че-
г - , а
рез v0 начальную скорость и че-
через г0 начальный радиус-вектор дви-
движущейся точки. Тогда:
Л.
г
Ji.
или
D8)
'о
Черт. 11.
В силу принципа Мопертюи-Эйлера орбита в исследуемом движении
«сть экстремаль интеграла
Так как подинтегральное выражение не зависит явно от <р, то уравне-
уравнение Эйлера принимает вид:
¦/¦-?¦+»
откуда
= C Г * , д
J rY2r + br*—C*
arccos
О- —
С, Сх — постоянные интефации. Окончательно приходим к уравнению
траектории:
'-1 + «с?,+ С» (е-УТ+Щ. D9)
Движение совершается по коническому сечению с эксцентриситетом
e~Y I ~\-hC2. В зависимости от начальной скорости v0 мы имеем
44 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
случай эллиптической, параболической или гиперболической орбиты;
При vo2<C—^- , h < 0, ?<1—случай эллиптической орбиты;
го
при т>02 — —?-, h = 0, е = 1 — случай параболической орбиты;
го
при т>02 > ——, h > 0, е > 1 — случай гиперболической орбиты.
В случае эллиптической орбиты мы найдем большую полуось а
эллипса из формулы:
а— С2 - 1 те 1 - 2 V»2 - h «ПЧ
а_т-__ —_, т.е. — _— — — — А. E0)
Полуось д полностью определяется начальным положением г0 и началь-
начальной скоростью vQj не завися от направления этой скорости. Направление
начальной скорости, как видно из предыдущих формул, не влияет на
то, будет ли наша орбита параболической, эллиптической или гипербо-
гиперболической.
Из D8) и E0) следует:
где г1 = 2а — г есть радиус-вектор точки эллиптической орбиты по
отношению к другому фокусу эллипса.
Поместим теперь притягивающую точку в другой фокус нашего»
эллипса и рассмотрим движение по той же эллиптической орбите. При
таком перемещении притягивающего центра роли радиусов-векторов г
и гх при этом переменятся, и в силу формулы E1) мы получим для
скорости vx нового движения:
Скорости движений по эллиптической орбите в случаях притяги-
притягивающей массы, помещенной в различных фокусах, обратно пропорцио-
пропорциональны.
Сравнивая выражения для времени Т и для действия U при движе-
движении по дуге траектории:
Г ds
U= f vds,
получим найденное И. Е. Жуковским свойство эллиптических орбит.
Время, в течение которого планета, притягиваемая солнцем, по-
помещенным в Фокусе F, пробегает дугу ЛВ эллиптической траектории»
равно постоянному множителю —, помноженному на действие npit
движении планеты по той же дуге, если бы солнце было располо-
расположено в другом фокусе (И. Е. Жуковский, Собрание сочинений, т. I,
стр. 355).
§ 33] МЕТОД СЧЕТНОГО МНОЖЕСТВА ПЕРЕМЕННЫХ 45
§ 33. Метод счетного множества переменных
Общий прием. К прямым методам вариационного исчисления отно-
относится также следующий метод. Допустим, что среди всех кривых, обра-
обращающихся в нуль в концах интервала [0, тг], мы желаем определить ту
кривую, вдоль которой интеграл
к
= fF(x,y,/)dx
принимает наименьшее значение. Для этой цели мы разложим искомую
функцию в тригонометрический ряд:
s\x\2x-\- ... -\-ansinnx-\- . ¦.
Это разложение мы могли предполагать не содержащим свободного
члена и косинусов, ибо в концах интервала у обращается в нуль, и
таким образом, не нарушая общности, мы можем считать -функ-
-функцию у нечетной: , ч , ч
Предполагая, что неизвестная функция обладает непрерывной произ-
производной, удовлетворяющей условию Липшица, получим:
у' = ai cosx-\-2a2 cos 2x-f-... -\-пап cos nx-\- ...
Подставив в выражение / вместо у и у' их разложения, мы получим /
как функцию счетного числа коэфициентов:
Наша задача приводится к определению тех значений ап> при кото-
которых J принимает наименьшее значение. Пользуясь условиями экстремума,
мы получим систему уравнений для определения ап:
-dir = 0 (« = 1,2,3,...)
В общем случае рассмотрение таких систем бесчисленного количе-
количества уравнений с бесчисленным множеством неизвестных вызывает
большие трудности, но в ряде частных задач этот путь дает легкое и
исчерпывающее решение задачи. Рассмотрим две задачи на применение
этого метода.
Кривая, охватывающая наибольшую площадь. Среди всех про-
простых замкнутых линий, имеющих данную длину, определить ту,
которая охватывает наибольшую площадь. Пусть
x = x(s), y=y(s) (O^s^/) E2)
есть уравнение простой замкнутой линии в параметрической форме, где
за параметр s принята длина дуги:
и где / есть данная длина кривой.
46 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
При этих обозначениях площадь 5 области, ограниченной кривой E2)„
выразится интегралом:
о
Наша задача приводится таким образом к следующей: среди функций
х = х (s), у =у (s), периодических с периодом / и удовлетворяющих
условию E3), определить те, для которых интеграл 5 принимает наи-
наибольшее значение.
Разложим х и у в ряды Фурье х):
1 , \ч / .__ 2пп , ,_ _, 2пп
cos s + d™
E4)
где ап, Ъп, сп, dn — неизвестные коэфициенты Фурье; отсюда:
dx yi / 2ъп . 2ъп , 2тс/г , 2тт \
ds ^V /~ ansn ] s ~\ / »cos i s) >
E5)
dy
Для дальнейших выкладок заметим две формулы из теории рядов
Фурье. Если ап (& = 0, 1, 2, . ..) и $h(k— 1, 2, ...) суть коэфициенты
Фурье интегрируемой в квадрате функции f(x) с периодом / и если ^А и
од — коэфициенты Фурье функции о (х) с тем же периодом /, то
г
4
-г //(*)? (*)rf*=-f а° то 4-
и
Выразим теперь через коэфициенты Фурье интеграл S. В силу E4)у
E5) и E7) получим:
5 = «2«(e,rf,-*,«,> E8)
Кроме того, в силу условия E3),
о
Отсюда, выражая интеграл E9) через коэфициенты Фурье, в силу E5)
и E6) получим:
х) Мы допускаем, что функции х (s) ну (х) обладают непрерывными про-
производными, удовлетворяющими условию Липшица. Эти гипотезы относительно
х (s)t У (s) нужны для того, чтобы иметь возможность разлагать их в ряды Фурье*
В конце мы покажем, что эти гипотезы не повлияют на общность решения.
§ 33] МЕТОД СЧЕТНОГО МНОЖЕСТВА ПЕРЕМЕННЫХ 47
Пользуясь полученными формулами E8) и F0), вычислим разность между
площадью круга, ограниченного окружностью длины /, и площадью S:
= 1-S {(««„-dj>-r (nba + cnf -f (л2_ i)(cn*+dn)*}>0.
Знак равенства достигается только при ах — d1== 0, Ъх -\- сх = 0, ап =¦
= ?Л = сЛ = ^„ = 0 (я = 2, 3, 4,...), т.е. когда
х = -х- а0 -\- ах cos s -j- bx sin 5,
1 . ,
у — -^ ^o — ^i cos s-\-a1 sin 5.
Следовательно, искомая кривая есть окружность:
9 '
Итак, среди всех замкнутых кривых данной длины /: x = x(s)9,
y—y(s)> удовлетворяющих отмеченным выше условиям непрерывности,
окружность ограничивает наибольшую площадь.
Покажем, что от введенных условий непрерывности функций xf (s)
и у (s) можно освободиться. В самом деле, допустим противное, что
среди всех линий данной длины / существует линия, ограничивающая
/2
площадь Sx > Z-. Тогда, очевидно, можно построить аналитическую
кривую длины / и ограничивающую площадь, как угодно близкую к Sv
т; е. площадь большую, чем -j—, но это противоречит доказанному
раньше, что всякая аналитическая кривая длины / ограничивает пло-
/2
щадь, меньшую ——.
Замечание. Можно решение разобранного примера строить несколько,
иначе: доказать сначала, что искомая кривая выпукла, и отсюда показать, что
для всех кривых, среди которых могут быть кривые, дающие максимум S,
законно писать разложение в ряды Фурье.
Крыло наименьшего индуктивного сопротивления. Допустим, что
в пространстве, наполненном идеальной несжимаемой жидкостью, посту-
поступательно двигается тело (крыло аэроплана конечного размаха), обла-
обладающее плоскостью симметрии, причем скорость движения v0 есть
величина постоянная, параллельная плоскости симметрии крыла. Выберем
ортогональную систему координат, неразрывно связанную с телом: пло-
плоскость yOz будем считать расположенной в плоскости симметрии,
ось Оу имеет направление v0. При этих условиях наше тело при дви-
движении будет испытывать со стороны жидкости определенное воздействие.
В силу симметрии мы можем считать, что равнодействующая всех сил
давления жидкости на крыло расположена в плоскости yOz. Обозначим
через Р слагающую этой силы по оси Oz и через Q — по оси Оу.
48 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
Компонента Р называется подъемной силой крыла, а компонента Q — ло-
лобовым сопротивлением.
Как показали исследования Жуковского, Чаплыгина, Прандтля и др.,
можно (считая жидкость идеальной и несжимаемой, следовательно, пре-
пренебрегая трением) дать теорию возникновения этих сил Р и Q, теорию,
достаточно хорошо согласующуюся с экспериментом. Мы сейчас дадим
нужные для дальнейшего две основные формулы этой теории.
Обозначим через Сх контур, полученный от пересечения границы
обтекаемого тела плоскостью, параллельной yOz и отстоящей от нее
на расстоянии х. Пусть теперь v — v (х> s) есть скорость жидкости
в точке, принадлежащей СТУ относительно крыла. Назовем циркуляцией Г
скорости v жидкости вдоль контура Сх следующий интеграл:
Г = Г v cos 0 ds = Г (х),
где ds есть элемент дуги контура Сх, а 6 есть угол, образованный ско-
->
ростью v с положительным направлением (в сторону возрастания s)
.кривой Сх *) в соответствующей точке. Имеем:
где /—размах крыла: разность между максимальными и минимальными
значениями х точек крыла.
При этих обозначениях подъемная сила Р (по теореме Жуковского)
будет равна:
т»
P = pv0 J T(x)dx, F1)
слагающая Q:
• /• s9 dr dc
^TS—7IIT' F2)
-i- -f'
где р — плотность жидкости. Выражение Q, вычисляемое по формуле F2),
носит название индуктивного сопротивления крыла (здесь не учиты-
учитывается трение).
После сделанных вводных замечаний поставим задачу: каким должно
быть распределение циркуляции Г(х) вдоль крыла, чтобы при дан-
данной подземной силе индуктивное сопротивление крыла было мини-
минимальным ?
х) Направление движения по Сх есть положительное, когда, двигаясь в этом
направлении, мы обходим Сх по часовой стрелке, если при этом на контур
смотреть с положительной стороны оси Ох.
§ 33] МЕТОД СЧЕТНОГО МНОЖЕСТВА ПЕРЕМЕННЫХ 49
Введем новое переменное 6:
Обозначим через Гх F) функцию, в которую при этом перейдет Г (х):
В силу отмеченных выше свойств функции Г имеем:
М*—в) = 1\@).
Полагая Г (— 6) = — Г (8), разложим функцию 1\ в ряд Фурье *):
1\ F) = At sin 6 -{- Л3 sin 36 -j- ...
Подставляя в F1), получим:
п
P=?Vq-L. j sin 6 (Ajsin 6 -[- Л3 sin 36 -f- ...) db = -|-/pxr0 Лх.
0
Отсюда:
л --^-
1 rJpv0
Таким образом можем считать коэфициент Фурье Л1 заданным, нам
нужно определить коэфициенты Л3, Л5,... так, чтобы Q было мини-
минимальным. Выразим Q через эти коэфициенты; для этой цели положим:
Будем иметь:
=~2~ /cos©.
Подставляя это выражение в F2) и пользуясь легко получаемой фор-
формулой:
У* cos ky дЕр -л Г flfcp - /'cos &cp — cos &8 -
COS cp — COS 6 J COS cp — COS 6 *J COS cp — COS 6 ^
0
получим:
Г d? d~ _ 2% {A .
I If. ' f / . Л 1^*1 SI
J ah x — $ / sin 0 l L
или
х) Пользуясь замечанием, сделанным при решении предыдущей задачи, мы
будем искать решение задачи, не нарушая его общности, среди функций Г (в)
таких, что как Г (9), так и Г7 F) разлагаются в сходящиеся ряды Фурье.
50 ПЕРЕХОД ОТ ЭКСТРЕМУМОВ ФУНКЦИЙ К ВАРИАЦИОННЫМ ЗАДАЧАМ [ГЛ. V
Таким образом:
Минимальное значение для Q получим, если положим А3 *=АЬ = ... =0;
в этом случае:
Г (а:) = —i?— sin 6 =
Таким образом наивыгоднейшая форма крыла соответствует эллипти-
эллиптическому распределению циркуляции. В этом заключается теорема Мунка.
Метод Рица. Описанный способ нахождения функций, реализующих
экстремум, приводит к задаче решения системы бесконечного множества
уравнений с бесконечным множеством неизвестных, задаче, вообще го-
говоря, чрезвычайно трудной. Метод Рица позволяет находить прибли-
приближенное решение задачи путем сведения ее к системе конечного числа
уравнений с конечным числом неизвестных.
Пусть требуется найти экстремум (для определенности — минимум)
функционала J (у), где у=у(х)— некоторый класс функций, пред-
представляемых в виде рядов:
оо
.у (*) =^2 ««?*(*);
а{ — некоторые вещественные коэфициенты, ф1? ф2, ..., <рп9 ... —неко-
—некоторая последовательность функций (обычно ортогональная).
Рассмотрим п — параметрическое семейство функций:
разлагаемых в конечные ряды по функциям ф, (а:). Для этих функций
J (у) вырождается в функцию конечного чиала переменных—именно
коэфициентов av a2, ..., ап:
Будем теперь искать среди функций у{п)(х) ту, которая обращает
J (y(n)) в минимум, т. е. будем искать последовательность из п коэфи-
коэфициентов: аг{п\ а2(п), ..., ап(п\ дающих минимум функции J(av а2, ..., яп)..
Числа afn\ а2(м), ...,яп(п) найдутся как решения системы п уравнений
с п неизвестными:
Им отвечает функция:
Пусть п неограниченно возрастает. Естественно ожидать, что функ-
функции Уп) (х) при этом стремятся к функции у (х), реализующей минимум
§ 33] МЕТОД СЧЕТНОГО МНОЖЕСТВА ПЕРЕМЕННЫХ 51
нашего функционала J(y). Во многих задачах это на самом деле имеет место.
Во всяком случае перед нами встают при этом следующие задачи:
a) исследовать сходимость последовательности функций Уп);
b) в случае сходимости Уп) (х) к некоторой функции у (х) доказать,
что предельная функция у (х) реализует минимум J (у);
c) если мы в качестве приближения к искомой предельной функции
у (х) принимаем одну из функций Уп) (х), то встает задача об оценке
ошибки, т. е. оценке разности
\у(х)-/п\(х)\.
Метод Рица нашел широкое применение как в теоретических иссле-
исследованиях (см., например, дополнение III), так и в задачах приближен-
приближенного нахождения экстремальной функции. Более подробно о нем —
во втором томе, в главе, посвященной аппроксимативным методам ва-
вариационного исчисления.
ГЛАВА VI
ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА
§ 34. Дополнительные замечания об экстремумах функционалов
Общее замечание. В предыдущей главе мы находили необходимые
условия того, чтобы данная линия давала экстремум некоторой функции
от линии. Методы, которыми мы решали подобные задачи, заключались
в аппроксимации наших функций от линии функциями от конечного числа
переменных, решении задачи об экстремуме для последних и переходе
к пределу. Мы не устанавливали законность перехода к пределу, мы
не рассматривали также вопроса, дает ли всегда предел экстремумов от
аппроксимирующих функций искомый экстремум функции от линии, ибо
это исследование выходило за пределы поставленной нами задачи. Такое
исследование, будучи проведенным, дало бы нам не только диферен-
циальное уравнение экстремали, но и аппроксимацию решения этого ди-
ференциального уравнения решением системы обыкновенных уравнений,
т. е. результат значительно больший; именно поэтому он связан с зна-
значительно более тонкими рассмотрениями, которыми мы займемся во вто-
втором томе. Для нашей более скромной задачи нахождения вида диферен-
циального уравнения искомой экстремальной кривой путь этот несколько
громоздок даже в простейшей задаче, если пожелать сделать его вполне
строгим. При переходе к более сложным задачам эти его недостатки
окажутся еще более заметными. При решении вариационной задачи мы
все время привязаны к функциям конечного числа переменных; у нас
нет пока алгорифма, специфического для функционалов и поэтому более
гибкого. Задача создания такого алгорифма была поставлена еще Эйле-
Эйлером и решена Лагранжем. Вместе с тем был найден шновый путь для
развития вариационного исчисления. Методы же Эйлера снова возроди-
возродились сравнительно недавно, когда всплыли вопросы об аппроксима-
аппроксимации решения вариационных задач.
Суть метода Лагранжа заключается в том, что на функции более
общей природы обобщаются те понятия, с помощью которых мы строили
теорию экстремума функций конечного числа переменных, именно поня-
понятия диференциала. Принцип, которым мы пользовались в этой теории:
в точке экстремума диференциал равен нулю, обобщается на функцио-
функционалы. Мы в дальнейшем избавимся от необходимости для каждой отдель-
отдельной вариационной задачи или для каждого цикла задач возвращаться
к апроксимирующим функциям.
Геометризация теории функций конечного числа переменных тоже
может быть перенесена в известной мере на теорию функционалов, как
§ 34] ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ ОБ ЭКСТРЕМУМАХ ФУНКЦИОНАЛОВ 53
мы это сделаем ниже. Мы построим „пространство", функция точки
которого и будет функционалом. В ближайших параграфах мы обобщим
некоторые основные понятия главы I.
Допустимые линии. Пока мы начнем с более тщательной и строгой
постановки задачи: найти линию, для которой некоторый функционал
достигает экстремума. Очевидно, нужно прежде всего дать характери-
характеристику того семейства линий, на котором наша функция определена,
среди которых ищется кривая, дающая экстремум. Такие линии назы-
называются допустимыми* линиями нашей вариационной задачи.
Задача наша будет формулирована следующим образом. Дан класс
С допустимых линий, на которых определена функция У(?) от линии f.
Найти необходимые условия того, чтобы для линии 7о нашего класса
функция J (i) достигала минимума (соответственно максимума), т. е.
чтобы i (т) ^-^ (То)> г^е К — любая другая линия этого класса [для мак-
максимума У(тО<./(То)]-
Определение класса допустимых линий меняется вместе с задачей.
В так называемой элементарной задаче вариационного исчисления допу-
допустимые линии были плоские кривые, соединяющие две заданные точки.
В изопериметрических задачах, рассмотренных в § 30, допустимые линии
должны были обладать определенной длиной. Эти ограничения непосред-
ственнно явствуют из условий задачи. Кроме того, на допустимые линии
мы налагаем еще ряд ограничений теоретико-функционального свойства,
зависящих также от характера задачи. Если мы рассматриваем функции
от линии, заданные интегралами / F (х, у, у') dx, то мы должны требо-
требовать, чтобы подинтегральное выражение и интеграл имели смысл. Напри-
Например, в класс допустимых линий подобной задачи, очевидно, не может
попасть линия, не имеющая нигде касательной.
Мы ограничимся пока для функций от линий, выражаемых интегра-
интегралами / F(x, у, y')dx, классом допустимых линий, состоящих из линий
у=у(х), где функция у(х) непрерывна вместе со своей первой произ-
производной. В дальнейшем мы перейдем к классу допустимых линий, имею-
имеющих точки перелома. В томе II мы перейдем к задаче в ее наиболее
общей трактовке.
Рассматривая линии, заданные уравнениями у=у(х), где у(х) —
однозначная функция, мы тем самым молча делаем еще одно ограниче-
ограничение на класс допустимых линий: последние пересекают прямые, парал-
параллельные оси Оу, только в одной точке. Чтобы избавиться от этого
ограничения, мы должны были бы перейти к параметрическому пред-
представлению уравнений кривой, что мы и сделаем ниже.
Таким образом класс допустимых линий мы ограничиваем в двух
направлениях: с одной стороны, ограничения теоретико-функциональ-
теоретико-функционального характера (например непрерывность функции, изображающей линию
и ее производных). От этих ограничений в связи с обобщением понятия
интеграла, длины кривой и т. п. можно частично отказаться и ставить
задачу в более общем виде. С другой стороны, мы делаем гипотезы,
меняющие по существу характер задачи (например равенство длин допу-
допустимых линий в рассмотренной изопериметрической задаче). Изменения
54 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ. VI
этих гипотез дают нам каждый раз новые задачи, требующие своих
методов решения.
Для сокращения письма в дальнейшем мы будем употреблять сле-
следующую терминологию.
Мы скажем, что кривая у —у (х) (а ^.х ^Ь) принадлежит классу Ci*
если функция у(х) непрерывна вместе со своей первой производной
при а^х^Ь. Мы скажем вообще, что кривая у =у(х) (а^.х^.д)
принадлежит классу Cw, если в закрытом интервале [а, Ь] функция у (л:)
непрерывна вместе со своими первыми п производными.
Вполне аналогично мы введем понятие класса Ci для кривых, задан-
заданных в параметрической форме: кривая принадлежит классу d, если она
обладает непрерывно вращающейся касательной.
За класс Di (Dw) мы примем непрерывные кривые, состоящие из
конечного числа кусков кривых класса Ci(Cn).
§ 35. Абсолютный и относительный экстремум
Абсолютный минимум. В теории экстремумов конечного числа пере-
переменных мы различали экстремум абсолютный и экстремум относитель-
относительный. Мы видели важность, такого расчленения задачи. Многие задачи
на абсолютный экстремум решались до конца применением теорем
Вейерштрасса и основного необходимого условия. Задачи на относи-
относительный экстремум удалось до конца решать рассмотрением второго
диференциала, причем исследование второго диференциала было специ-
специфическим методом для задач на относительный экстремум. Аналогичное
расчленение понятия экстремума мы произведем и для функций от* линий.
Мы скажем, что данная функция 7(j) от линии имеет в данном классе
допустимых линий абсолютный минимум, достигаемый на кривой То
нашего класса, если для любой кривэй *у нашего класса
Рассмотрим, например, длину кривой; за класс допустимых линий
примем совокупносгь кривых, соединяющих двэ данные точки А(х0, у0)
и*"В(х1У ух), выражаемых уравнениями:
где у(х) имеет непрерывную производную и
Длина выражается криволинейным интегралом
#1
J = f /
l
Абсолютный минимум длины достигается на ^прямолинейном отргзке,
определяемом уравнением:
§ 35]
АБСОЛЮТНЫЙ И ОТНОСИТЕЛЬНЫЙ ЭКСТРЕМУМ
55
Примечание. На этом примере видна искусственность ограничения
класса допустимых линий линиями с непрерывно вращающейся касательной.
Очевидно, прямолинейный отрезок будет давать абсолютный минимум длины,
если за класс допустимых линий принять совокупность линий, соединяющих
точки А, В и состоящих из конечного числа дуг с непрерывно вращающейся
касательной. Более того, для всякой линии т можно определить длину как пре-
предел длин вписанных в нее полигонов, стороны которых стремятся к нулю. Этот
предел, конечный или бесконечный, не зависящий от выбора последователь-
последовательности полигонов, существует для всякой кривой. Таким образом мы могли бы
для данной задачи принять за класс допустимых линий f совокупность всех,, не-
непрерывных кривых, соединяющих точки Л, В\ прямолинейный отрезок попреж-
нему давал бы минимум длины.
Кратчайшее расстояние на поверхности. Прежде чем определить
относительный экстремум, иллюстрируем это понятие простым примером.
Между двумя пунктами на поверхности земли находится высокая гора;
требуется соединить эти два
пункта дорогой кратчайшей дли-
длины. Нам выгодно, в смысле
уменьшения длины пути, объ-
объезжать гору при поездке из од-
одного пункта в другой; как
справа, так и слева найдется
кратчайший путь среди путей,
объезжающих гору. Если путь
справа меньше кратчайшего пу-
пути слева, то он и дает нам
абсолютный минимум длин ли-
линий на поверхности земли, сое-
соединяющих эти точки. Кратчай-
Кратчайший путь слева не будет да-
давать абсолютного минимума, но
он во всяком случае будет
короче других близких к нему путей, соединяющих эти точки
и объезжающих вместе с ним гору слева. Мы переведем этот пример
на аналитический язык.
На поверхности -к^ + у*)
z = Ne , A)
где N и К— положительные константы, даны дзе точки А ( — 1, А, z0)
и ВA, О, z^, A>0 (черг. 12). Требуется определить линию наи-
наименьшей длины среди лежащих на поверхности линий, соединяющих
эти точки.
*^ Мы рассматриваем только те кривые в пространстве, которые опре-
определяются двумя функциями: у =у (лг), z = z (лг). В данном случае из
условия, что линия принадлежит поверхности A), z (х) определена, если
определена у (х)\
*(*) = ,
Длина такой кривой есть функционал от у (х)\
Черт. 12.
56 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ. VI
Наша поверхность в точке х = О, у = О имеет апликату N и сколько
угодно малую апликату в другой точке при достаточно большом /С
Рассмотрим три вида линий, соединяющих точки А и В, определенных
уравнением у=у(х).
1. Линии, у которых у @) = 0, т. е. этинии проходящие через вер-
вершину возвышения, поднимающегося над началом координат. Так как
при К, стремящемся к бесконечности, наша поверхность стремится
к плоскости хОу с отрезком оси Oz длины Л/, то длина такого пути
при достаточно большом К близка к 2 -f- 2/С. При достаточно боль-
большом К эти линии по длине больше, чем К-\-\.
2. Линии, которые при движении от Л к В обходят точку (О, О, М),
со стороны положительных х, т. е. у которых j>@)>0.
3. Линии, у которых ^(ОХ 0, т. е. линии, обходящие вершину
(О, О, N) со стороны отрицательных х.
При h > 0 абсолютный минумум будет достигаться на некоторой
линии Го, очевидно, находящейся среди линий класса ?. Но при доста-
достаточно большом К среди линий класса 3 найдутся линии по длине
меньшие К-\- 1, т. е. меньшие любой линии класса 1. Наименьшая по»
длине из таких линий — обозначим ее через Г1—не дает, очевидно,,
абсолютного минимума, ибо /(Г^Х/^). Но эта кривая дает то, что
мы называем относительным минимумом, т. е. минимум среди кривых,,
„достаточно близкихи к Yt (принадлежащих вместе с Vt к классу 3).
Точное понятие относительного минимума требует предварительного'
определения понятия окрестности кривой, которым мы сейчас займемся.
В § 9, определяя понятие непрерывной функции точки я-мерного
пространства, мы видели, что это определение использует только свой-
свойство точек л-мерного пространства: обладать окрестностями. Определив
понятие окрестности кривой, мы сможем теорию непрерывных функций
распространить на случай функций от линии.
§ 36. Окрестности кривых. Сильный и слабый экстремум
Расстояние между кривыми. Пусть даны две кривые, определенные
уравнениями:
У=У (*) (х < х< х\
у=уЛх) (*о<*<«).
Близостью этих кривых, или расстоянием между этими кривыми, на-
назовем неотрицательное число г, равное максимуму I^O*)—у(х)\ на
отрезке х0 <^ х ^ xv Будем обозначать:
r=r[yt(x), y(x)].
Построим вокруг кривой у=у(х) полоску „шириной" 2/г (черт. 13)>
откладывая от каждой точки кривой по ординате в обе стороны отрезки
длины h. Близостью кривой у=у1(х) от кривой у=у (х) будет поло-
половина наименьшей „ширины"—такой полоски около у=у (х), заклю-
заключающей кривую у=уг(х). Пусть дана последовательность кривых:
. • • , У=Уп(х)> • • • > B^
§ 36]
ОКРЕСТНОСТИ КРИВЫХ. СИЛЬНЫЙ И СЛАБЫЙ ЭКСТРЕМУМ
57
близости которых от кривой у=у (х) стремятся к нулю. Это значит,
что последовательность B) равномерно сходится к у(х). Равенство
нулю близости двух кривых есть необходимое и достаточное условие
того, чтобы эти кривые совпадали. В функции от линии
подинтегральное выражение зависит не только от значения функции, на
и от ее производной. Поэтому iF (at, у, yr) dx для двух* линий,
близость которых очень мала, может сильно отличаться. Напри-
Например, криваяу= —sin nx
(О ^ х ^ тс) находится в
близости — от отрезка
оси Ох: у = 0. Между
тем
для
Черт. 13.
инт еграл / у'2 dx
6
этих линий равен
соответственно ~ и 0, и
эта разность остается не-
неизменной, когда п —> оо,
т. е. когда близости их
стремятся к нулю.
Таким образом при бесконечно малой близости двух кривых у и уг
значения функционалов J(y) и J(yt) могут отличаться на конечную
величину — функционал „разрывен". При выводе условий для экстре-
экстремума чрезвычайно, однако, важным всегда является свойство непрерыв-
непрерывности. По этой причине понятие близости, введенное выше, необхо-
необходимо существенно дополнить так, чтобы для двух „близких" кривых
изучаемые функционалы также отличались мало. Поэтому обобщают по-
понятие близости.
ОПРЕДЕЛЕНИЕ. Близостью п-го порядка кривых
у(х) и уг{х),
обладающих непрерывными производными до п-го порядка включи-
включительно, называется наибольший из максимумов выражений:
\У1{х)-у(х)\,
на отрезке х0 ^ х <; xv
Определенное выше понятие близости будет по нашему новому опре-
определению близостью нулевого порядка.
58 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ. VI
При рассмотрении функционалов
J
особую роль играет близость первого порядка. При непрерывности
функции F относительно у и у' достаточная малость близостей пер-
первого порядка двух кривых у =_у(лг) и у =yt (х) влечет за собой сколь
угодно малую абсолютную величину разности функционалов от этих
-функций. Поэтому в большинстве случаев под расстоянием между кри-
кривыми мы будем полагать их близость первого порядка.
Окрестность кривой. Мы называем г-окрестностью п-го порядка
кривой:
у=у(х) (xo<x<xi)
совокупность кривых:
^близость п-го порядка которых от кривой у=у(х) меньше е.
Таким образом е-окрестность нулевого порядка кривой у—у(х)
состоит из кривых, расположенных в полоске ширины 2з вокруг
кривой у(х).
Сильный и слабый экстремум. Мы скажэм, что функционал
со
J=fF(x,y,y)dx
зс0
достигает на кривой То сального относительного максимума, если для
всех допустимых линий 7» расположенных в некоторой е-окрестности
нулевого порядка кривой То» имеем:
Аналогично определяется относительный сильный минимум.
Мы скажем, что функционал J достигает на кривой То слабого мак-
<симума, если на всех допустимых линиях т> расположенных в некоторой
^-окрестности первого порядка кривой ^о> имеем:
Всякий абсолютный экстремум является в то же время и слабым и
сильным относительным экстрэмумом. Всякий сильный экстремум есть
в то же время и слабый, но не наоборот.
Пример U Пусть
Отрезок оси Ох дает слабый минимум /.
В самом деле, для у = 0, /=0, а для кривых, расположенных в е-близости
первого порядка этого отрезка, гдэ ? — любое положительное число, меньшее
единицы, |У|<1» подинтегральное выражение положительно при у 4= 0, и, сле-
следовательно, J положительно, обращаясь в нуль лишь при у = 0, т.е. для нашего
огрезка. Значит, на нем достигается слабый минимум.
37]
АБСТРАКТНЫЕ ПРОСТРАНСТВА
59
Сильный же минимум не достигается. Достаточно положить
1
v = —-= sin nx;
тогда
те
1 /*
J = — / sin2 nx A — п cos2 nx) dx =
п J
о
тс к
= — / sin2 nxdx — -^ I sin2 2/u: dx — ^-
П J 2 J In
0
4
и при л, достаточно большом для наших кривых, У<0. С другой стороны, все
эти кривые при п достаю iho большом лежат в сколь угодно малой окрест-
окрестности нулевого порядка кривой у = 0. Итак, сильный минимум не достигается
при у = 0.
Пример 2. Рассмотрим еще такой пример. Лодка с парусами идет вниз по
реке от точки А до точки В, (Реку будем себе представлять в виде канала
с параллельными берегами.) Ве-
Ветер направлен в сторону, про-
противоположную течению реки. ~ ———-
Кратчайший путь — путь по
шрямой ЛВ вниз по течению.
При этом нельзя пользоваться
парусом; движение будет совер-
совершаться течением воды. Если
двигаться по кривой, мало от-
отличающейся от отрезка ЛВ на-
направлением (черт. 14, близость
первого порядка), то мы не
сможем пока пользоваться па-
парусом и вследствие увеличения
пути удлиним его время. Но
при движении зигзагами (черт.
Черт. 14.
А
Черт. 15.
15), под значительным углом
к направлению АВ, мы сможем
уже использовать силу ветра,
и при достаточной его силе
настолько выгадать в скорости, что придем в точку В в более короткий срок
чем по прямой АВ. Отрезок АВ даст слабый минимум времени пути, не да-
давая сильного.
Для того чтобы не сужать развиваемых дальше методов специфич-
специфичностью *задач вариационного исчисления, как задач на разыскание экстре-
экстремумов интегралов, мы посвятим ближайший параграф рассмотрению
функционалов общего вида. Чтобы вести наши построения на языке
геометрии, мы предварительно познакомим читателя с теми геометриями,
в которых естественнее всего иллюстрировать функционалы.
§ 37. Абстрактные пространства
Расширение понятий геометрии. Теория функций п переменных
потребовала расширения геометрической тематики: создания геометрии п
измерений. Но и расширенная таким образом геометрия отставала от
анализа, поскольку понятие функции вышло за пределы функций п пере-
переменных, включив в себя функционалы или функции от линий. Разрыв
60 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ. VI
между геометрией и анализом был ликвидирован только после создания
Г. Кантором (Cantor) теории множеств.
Теория множеств рассматривает как единство любое множество про-
произвольных элементов. Если мы распространим на элементы некоторого
множества некоторые их взаимоотношения, являющиеся обобщением со-
соответствующих взаимоотношений между точками пространства, мы полу-
получим возможность распространить геометрические методы исследования
и на это множество. Таковы взаимоотношения близости двух элементов,
предельного элемента для последовательности, понятие окрестности
и т. п. Эти понятия свойственны не только точкам л-мерного простран-
пространства; как мы убедились в предыдущих параграфах, они легко перено-
переносятся, например, на совокупно-
совокупности функций. Можно поэтому сде-
сделать дальнейшее расширение те-
тематики геометрии: произвести
дальнейшее расширение понятия
пространства.
Французский математик Фреше
(Freche) ввел впервые в матема-
математику так называемые абстрактные
пространства, „точками" которых
могли быть элементы самой общей
природы. Для того чтобы сово-
Черт. 16. купности таких элементов имели
право именоваться пространствами,
естественно потребовать, чтобы между их элементами существовали неко-
некоторые соотношения, являющиеся обобщениями некоторых основных соот-
соотношений между точками л-мерного пространства. Мы убедились в глазе I,
что в определение целого ряда важнейших понятий анализа, например по-
понятия непрерывной функции, входили только самые общие свойства
я-мерного пространства, на котором эти понятия были определены.
Если при расширении понятия пространства сохраняются указанные
свойства, то на этих пространствах более общей природы можно опре-
определить и соответствующие понятия анализа. Обобщение геометрических
понятий связано таким образом с обобщением понятий анализа.
Аксиомы Хаусдорфа. Обобщение геометрических понятий можно
сделать различными методами. Мы остановимся на теории Хаусдорфа
(Hausdorff). Хаусдорф принимает за наиболее общее геометрическое
понятие окрестности.
Пусть нам дано множество М некоторых элементов т, которые
будем называть точками. Представим себе, что в множестве М можно
выделить систему частей (подмножеств), которые мы будем называть
окрестностями, удовлетворяющих следующим условиям:
1°. Каждому элементу т из М отвечает по крайней мере одна заклю-
заключающая его окрестность Um\ будем называть ее окрестностью точки т.
2°. Двум различным элементам т и тг можно отнести две их
окрестности U-m и f/Wl, не имеющие общих точек.
3°. Если точка /л2 принадлежит двум окрестностям {/ти ?/Wi,to существует
окрестность Um2 точки т2, содержащаяся целиком и в Um и в Umi (черт. 16).
§ 37] АБСТРАКТНЫЕ ПРОСТРАНСТВА 61
Свойства 1—3 называются аксиомами Хаусдорфа.
I Множество Ж, на котором нам удается ввести систему окрестностей,
называется абстрактным пространством (в смысле Хаусдорфа), а эле-
элементы т — его точками.
Примеры
1. Будем в качестве окрестности точки /z-мерного евклидова пространства
принимать любую сферу с центром в этой точке. Аксиома 1° удовлетворяется
сама собой. Аксиома 2° тоже: достаточно построить вокруг двух произвольных
точек по сфере, радиус которой не превосходит половины их взаимного расстоя-
расстояния. Наконец, если точка С принадлежит сферам ,S (A, rt) и S (В, г2), то доста-
достаточно провести вокруг точки С сферу S(C, r3) где г3>0 и меньше одновре-
одновременно обоих положительных чисел: г\—г (А, С) и г2 — г (В, С), чтобы сфера 5
(С, гг) целиком заключалась в сферах S(A, г±), S(B, г2) и, следовательно,
удовлетворялась аксиома 3°.
2. Рассмотрим совокупность С всех непрерывных функций:
у=у(х) (*o<*<*i)-
Окрестностью „точки* в С — функции у0 (х) может служить совокупность функ-
функций у^ (x), образующих е-окрестность нулевого порядка функции yQ (x). Легко
показать, что е-окрестности нулевого порядка удовлетворяют всем аксиомам по-
понятия окрестности. С может быть рассматриваемо как абстрактное пространство.
Метрическое пространство. Чрезвычайно важным понятием в гео-
геометрии является понятие расстояния. Мы постараемся ввести это поня-
понятие для абстрактных пространств. Расстоянием между точками А и В
называется некоторая функция г (Л, В) этих точек, удовлетворяющая
аксиомам, являющимся обобщением главных свойств понятия расстояния
в обычной геометрии. Эти свойства следующие:
1° г (Л, Л) = 0, г (Л, В) > 0, если Я^ф А.
2° г (Л, В) = г(В, Л).
3° г(А, В) + г(В, С)^г(Ау С).
Аксиома 1° утверждает, что расстояние между двумя точками по-
положительно и расстояние всякой точки от нее самой равно нулю; ак-
аксиома 2° называется аксиомой симметрии; аксиома 3° — аксиомой тре-
треугольника.
Понятие расстояния в евклидовом л-мерном пространстве удовле-
удовлетворяет этим аксиомам. Пространство, в котором введено понятие рас-
расстояния, называется метрическим.
Рассмотрим некоторые примеры метрических пространств.
Пространство 1(п). Мы раньше рассматривали л-мерное простран-
пространство с евклидовой метрикой. Можно ввести в л-мерном пространстве
другую метрику. Определить, например, расстояние между точками
Л (xv x2f.. .,*„) и В (yv y2,.. .,уп) следующим образом:
B
г=1
где /?1>1. Определенное таким образом понятие расстояния удовлетво-
удовлетворяет всем трем аксиомам метрики. В самом деле, очевидно:
1) гр (Л, Л) = 0, гр (Л, В) > 0 при Л ф В.
2) гр (Л, В) = гр(В, Л).
62 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ.
Наконец:
г, (Л, B) + rp(B9 Q>rp(A, С).
Последнее неравенство есть непосредственное следствие неравенства
Минковского, доказанного в конце главы III. Пространство с метрикой C)
обозначается 1^«
Пространство m(n). Можно также определить расстояние между точ-
точками А(хи #2,...,лгл) и В(у19 у2,..., уп) я-мерного пространства
как наибольшую из абсолютных величин разностей их координат:
г (А, ?) = тах{1*,+Л|} (/= 1,2,...,«). D)
л-мерное пространство с метрикой D) обозначается символом т^.
Убедиться в том, что введенное сейчас понятие расстояния удовле-
удовлетворяет всем аксиомам метрики, не представляет никаких затруднений*
Мы сейчас покажем, что х
max 1л-*,и112,...,п
т. е. метрика пространства m(n) может рассматриваться как предель-
предельная для метрик пространств 1^\
В самом деле, если левая часть равенства E) равна k> то, значит,
среди неотрицательных чисел \yt— х%\ есть, по крайней мере, одно
равное k. Имеем:
-xt\p)p<n*>k. F)
4=1
При р -> oo, np стремится к единице, следовательно, средняя часть
неравенства F) стремится к k; равенство E) доказано.
Гильбертово пространство. Непосредственным обобщением евкли-
евклидова пространства является гильбертово пространство. Точкой гиль-
гильбертова пространства называется счетная последовательность чисел:
сумма квадратов которых сходится. Расстояние между точками
A (*v хь- • •> ¦**••'•) и В (yv у2,..., хпУ...) определяется по формуле:
r(A,B)=V ZCVi-^)9. G)
4=1
Заметим прежде всего, что
(У. — ^iJ =У? — 2хМ — х? < 2 W +Л2)-
Таким образом из сходимости рядов 2*42,2Л2 следУет сходимость
ряда>?(^ — jc4J, и, следовательно, расстояние между точками гиль-
гильбертова пространства всегда можно определить по формуле G).
§ 37] АБСТРАКТНЫЕ ПРОСТРАНСТВА 63>
Пространство 1р. Точкой пространства.\р (р^ 1) называется после-
последовательность чисел:
Х\ч Х%, • • •> Хп> . . .,
для которых сходится ряд
сю
Расстояние между точками А (хи хъ ..., хп...) иВ(уиу2, ,уп, ...)
пространства \р определяется по формуле:
1
Заметим прежде всего, что из сходимости рялов
»i <i
следует сходимость ряда в правой части формулы (8). В самом деле,.
силу неравенства Минковского:
Т
Bл-*«1Т < B1*1 У +(S i^lT-
¦4=1 » = 1, 4=1
При п —> сх) правая часть стремится к конечному пределу, а потому
сходится и ряд неотрицательных чисел в левой части.
Пространство щ. Точкой пространства m является произвольна»,
ограниченная по абсолютной величине последовательность чисел:
Расстоянием г (Л, В) между точками A (xlf х29 ..., хпУ ...) и
В (ур ^2'--» **!»•••) пространства m называется [верхняя грань абсо»
лютных величин разностей^ — хг:
supjv, — хг\ (/=1, 2,..„л, ...)•
Для нас особенно важны следующие метрические пространства:
Пространство С- Совокупность С непрерывных функций у (х), оп-
определенных на отрезке хо<^х^х1У образует также метрическое про-
пространство. В качестве расстояния г (у, z) между функциями у (х) й
z (х) мы принимаем близость нулевого порядка этих функций:
/ (у, z) =
При таком определении расстояния, очевидно, [аксиомы 1—2 мет*
рики удовлетворяются. Далее, из неравенства:
при любых значениях х следует:
y(x) — z(x)\+ max |z(x) — а(х)\;
< <
()|
поэтому:
max \у[х) — и(х)\ < max |^(лг) — ^(jc)i+ max jj2T(at) — и
< < < < < <
64 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ. VI
Таким образом аксиома 3 тоже удовлетворяется; С может быть рас-
рассматриваемо как метрическое пространство.
Пространство Сп. Аналогично пространству С определяется про-
.странство Сп, элементами которого являются функции, определенные на
отрезке хо^х^хг и обладающие на нем своими п непрерывными
производными. Расстояние между функциями у (х) и z (x) простран-
пространства Сп определяется как их близости л-го порядка.
Сфера в абстрактном пространстве. Будем называть сферой ра-
радиуса г вокруг точки А абстрактного пространства М и обозначать
попрежнему через S (Л, г) совокупность точек А\ расстояние кото-
которых от А меньше г.
Совокупность сфер S (А, г) удовлетворяет всем аксиомам окрест-
окрестностей. Это следует из рассуждений, аналогичных тем, которые мы
применили выше к сферам ^-мерного евклидова пространства. Поэтому
за систему окрестностей метрического пространства будем принимать
систему его сфер.
Например, в л-мерном пространстве m(w) сферой радиуса г, описан-
описанной вокруг точки А, является л-мерный куб. с ребрами длины 2г, па-
параллельными осям координат, в центре которого находится точка Л.
В пространстве С сфера радиуса е, описанная вокруг у(х), есть е-ок-
рестность нулевого порядка функции, в пространстве Сп — е-окрест-
ность л-порядка.
§ 38. Предельные соотношения в абстрактном пространстве
Мы сейчас распространим некоторые понятия, определенные в § 8 для
/z-мерного пространства, на случай любого абстрактного пространства.
Предельный элемент. Пусть в абстрактном пространстве R задано
множество М. Точка А называется предельной для множества М> если
всякая окрестность UA точки А заключает по крайней мере одну точку В
множества Ж, отличную от А.
В частности для метрического пространства, где окрестностями
являются сферы, точка А является предельной для множества М, если
сфера 5 (Л, е) любого радиуса е, описанная вокруг А, содержит точку В
множества М, отличную от Л.
Эквивалентные системы окрестностей. Пусть мы ввели в абстрактном
пространстве R новую систему окрестностей. Так как понятие предельного эле-
элемента определяется через понятие окрестности, то с введением новой системы
окрестностей предельные соотношения могут нарушиться: точка Л, предельная
для множества М при прежней системе окрестностей, тможет перестать быть
предельной для этого множества при новой системе окрестностей.
Две системы окрестностей в пространстве R называются эквивалентными,
если при переходе от одной системы окрестностей к другой предельные соот-
соотношения сохраняются, т. е. если точка, предельная для некоторого множества
при прежней системе окрестностей, остается предельной и при новой системе,
и обратно.
Если в пространстве R мы вводим различным образом понятия расстояния
(вводим различные метрики), то тем самым мы вводим различные системы
окрестностей (сферы); окрестности в метрическом пространстве меняются с изме-
изменением метрики. Если системы сфер при двух различных метриках образуют
эквивалентные системы окрестностей, то метрики называются эквивалентными.
«§ 38] ПРЕДЕЛЬНЫЕ СООТНОШЕНИЯ В АБСТРАКТНОМ ПРОСТРАНСТВЕ 65
ТЕОРЕМА. Для того чтобы две системы окрестностей
я пространстве R были эквивалентны, достаточно, чтобы каждая окрест-
окрестность UA точки А пространства R первой системы заключала хотя бы одну
окрестность UAr той оке точки второй системы, и обратно,
В самом деле, пусть точка А является предельной для множества Af в пер-
первой системе. Это значит, что любая окрестность UA точки А первой системы
заключает точку В множества М9 отличную от А Пусть теперь UA есть про-
произвольные окрестности точки А второй системы. По предположению, [/А заклю-
заключает в себе некоторую окрестность UA первой системы окрестностей и, следова-
следовательно, содержит точку В множества М, отличную от А\ Итак, всякая окрест-
окрестность UA второй системы тоже содержит отличную от А точку множества Af,
т. е. А является предельной для М и при второй системе окрестностей. Теорема
доказана.
В частности, две метрики будут эквивалентны, если каждая сфера, описанная
вокруг точки при первой метрике, заключает в себе некоторую сферу, описан-
описанную вокруг этой же точки при второй метрике.
Например, мы ввели для я-мерного пространства ряд метрик: евклидову, ме-
метрику пространства 1р^ (р>Л), метрику пространства т^« Легко показать, что
все эти метрики эквивалентны.
В самом деле, каждая евклидова сфера, описанная вокруг точки (х{, хъ..., хп),
заключает внутои себя некоторый куб с центром в этой же точке и реб-
ребрами, параллельными осям координат, н обратно. Так как такой куб есть сфера
при метрике т^п\ то отсюда следует, что метрика евклидова и метрика про-
пространства т^ эквивалентны. Очень просто доказать также эквивалентность
этих метрик метрике пространства \JnK
Рассмотрим теперь гильбертово пространство 12; введем в нем новую ме-
метрику, именно метрику, аналогичную метрике пространства т: будем понимать
под расстоянием между точками
А (хь х2, ..., хп...) и В (уи у», ...,уп )
этого пространства г (Л, В) = sup | у{ — хг \ (I = 1, 2, 3,.. .п ). Легко показать,
что новая метрика не эквивалентна прежней.
Рассмотрим, например, последовательность точек:
где Г _1_ . ^.
{ О при 1 >л.
С точки зрения обычной метрики гильбертова пространства расстояние точки Ап
до нулевой точки О равно 1/ 2а« = 1; точка О не является предельной для
последовательности Ап] с точки зрения метрики пространства m расстояние
от Ап до О равно —=^\ точка О является предельной «цля последовательности А я.
У п
Естественно возникает вопрос, при каких условиях можно ввести в абстракт-
абстрактном пространстве R такую метрику, при которой система сфер была бы
эквивалентна системе окрестностей пространства R. Введение такой метрики
называется метризацией пространства R. Эта проблема была разрешена
Л. С. Александровым и П. С. Урысоном.
66 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА (ГЛ. VI
Область. Областью О абстрактного пространства R называется со-
совокупность его точек, обладающая тем свойством, что если точка А
принадлежит О, то существует окрестность UЛ этой точки, целиком
вводящей в •</. v
В качестве примера можно привести область я-мердаго простран-
пространства, определенную в § 8. Сфера (без границы) в любом метрическом
пространстве есть область. Общее, в силу аксиомы 3° окрестностей, вся-
к&я окрестность любой точки абстрактного пространства есть область.
Точка А ' абстрактного пространства R, не принадлежащая' области
(г и предельная для точек этой области, называется граничит точкой
области ?г. Совокупность всех граничных точек называется; границей б.
Область (? вместе с ее границей называется замкнутой* и обозна-
обозначается через О.
Замкнутое множество. Множество М точек абстрактной простран-
пространства R называется закнутым на R, если оно заключает все свой пре-
предельные точки. • , , :
ТЕОРЕМА. Область вместе со своей границей есть замкнутое
множбШвд. Доказательство этой теЬремыг данное в § 8 д#я случая
евклидова пространства, сохраняет силу и для любого абстрактного
пространства.
Сходимость. Мы скажем: последовательность. {Ан} точек пространства
R сходится к точке Л, если любая окрестность UA точки А содержит
почти все элементы последовательности Лн. Мы будем писать в этом
случае:
Нт Ап = А.
Элемент А называется пределом последовательдюстн Ан~
В метрическом пространстве, если
А = lim AH,
п->оо
ТО
lim г (А, АН) = Ъ.
В самом деле, окрестностями точки А в этом случае являются
сферы S(A> г); каково бы ни было положительное число г, почти все
Ап принадлежат сфере S (А, з), т. е. для почти всех п,
г (Л, Ап) < а,
Поэтому
lim r(A,.An) = 0.
Полнота. Последовательность [Ап] точек метрического пространства
R называется последовательностью Коши, если для любого положи-
положительного числа г можнь указать такое Nr что
^ -r(Ani 4w).<s,
когда' п > iV, т > М
Пространство R называется полным, если люба» последовательность
Коши его элементов сходится.
§ 39] ФУНКЦИЯ ТОЧКИ АБСТРАКТНОГО ПРОСТРАНСТВА 67
.Призером, полных пространств может служить евклидово я-мерное
пространство, а также л-мерные пространства 1^ и m(w).
Можно также доказать, что все пространства 1^, в том числе гиль-
гильбертово, а также пространство m — полные пространства.
Компактность. В теории непрерывных функций п переменных су-
существенную роль играло свойство компактности ограниченных замкну-
замкнутых множеств в я-мерном пространстве. Естественно распространить
это понятие для любых абстрактных пространств.
Множество Му заключенное в пространстве R, называется ком-
компактным в себе, если всякое бесконечное подмножество ЛГ множе-
множества М обладает хотя бы одним предельным элементом а, принадле-
принадлежащим М- Например, таковыми будут замкнутые ограниченные мно-
множества в я-мерных пространствах (см. § 8).
Можно говорить о компактности всего пространства. Пространство R
называется компактным, если всякое бесконечное множество его точек
обладает предельным элементом а из R.
Отрезок прямой, рассматриваемый как пространство, компактен. Не-
Неограниченная прямая некомпактна, так как последовательность ее точек
с целочисленными абсциссами 1, 2, 3,... не обладает предельным эле-
элементом, точно также все простанство R является некомпактным.
Компактное множество на R. Множество М называется компакт-
компактным на R, если всякое бесконечное его подмножество М' обладает
хоть одним предельным элементом а из R (в отличие от определения
компактности в себе а не обязательно должно принадлежать Ж).
Очевидно, всякое замкнутое компактное множество М компактно в
себе, ибо в случае замкнутости М предельные элементы подмножеств
множества М принадлежат Ж.
Примером компактных множеств может служить ограниченное беско-
бесконечное множество в «-мерном пространстве.
Компактность в малом. П. С. Александров ввел понятие пространства ком-
компактного » малом. Пространство R называется компактным в малом, если в
нем всякая точка а обладает хоть одной компактной окрестностью Ua.
я-мерные пространства Rn компактны в малом: достаточно в качестве
окрестности Ua точки а взять любую ограниченную окрестность, например
сферу с центром в а.
Если М — множество, компактное в пространстве R, а М% — бесконечное
подмножество множества М> то Mt тоже компактно в R. В самом деле, всякое
бесконечное подмножество множества Мх есть в то же время подмножество
множества Мг, а поэтому в силу компактности М обладает предельным
элементом на R. .
§ 39. Функция точки абстрактного пространства
Понятие непрерывной функции. Пусть каждой точке Л абстракт-
абстрактного пространства отвечает число /(Л). В этом случае f(A) называется
функцией точки абстрактного пространства.
/(А) называется функцией непрерывной в точке А, ш если каково бы
ни было положительное число г, найдется такая окрестность UA точки А>
что для любой точки А\ принадлежащей UА, будем иметь:
8.
68 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [гЛ. VI
Для метрических пространств это определение можно формулиро-
формулировать также в обычных терминах (также как непрерывность функции
точки евклидова я-мерного пространства): /(Л) непрерывна в точке Л,
-если для каждого положительного е можно определить такое положи-
положительное ЧИСЛО Т|, ЧТО .-,.,, ,/ЛЧ1 „
I/O*')—/И) |<. в,
коль скоро
г(Л',А0<т„
короче говоря, если |/(Л')—/(Л)| стремится к нулю вместе с г (А', А).
Функция, непрерывная в каждой точке пространства R, называется
непрерывной в R.
Например, интеграл / F(x, у, yr)dx непрерывен в пространстве
функций у—у(х), обладающих непрерывной производной, если функ-
функция F равномерно непрерывна относительно у и у' 1).
Непрерывные функции на компактных пространствах.
ТЕОРЕМА ВЕЙЕРШТРАССА 1. Непрерывная функция f (А) в ком-
компактном абстрактном пространстве R ограниченна сверху и снизу.
Пусть, например, непрерывная в R функция /(А) не ограниченна
сверху. Тогда найдется последовательность точек:
Av Л2, . . . , Лм, . . . (9)
такая, что f(An) неограниченно возрастает вместе с п. В силу компакт-
компактности последовательность (9) имеет хотя одну точку сгущения Ао.
Вследствие непрерывности /(А) можно построить окрестность UA точки
Aq, значения функции /(Л) в которой отличаются от /(Ло) меньше,
чем некоторое заданное положительное число в. Отсюда в точках А',
принадлежащих UAo, имеем:/(Л')</(Ло)-{--е» т- е- в UA функция/(Л)
ограниченна сверху. Но в окрестность U' попадет бесчисленное мно-
жество точек последовательности (9) со сколь угодно большими индек-
индексами, и по нашему предположению /(Аг) неограниченно растет вместе
с индексом. Наша гипотеза неограниченности /(А) приводит к проти-
противоречию.
ТЕОРЕМА ВЕЙЕРШТРАССА 2. Непрерывная функция /(Л) в ком-
компактном абстрактном пространстве R достигает в нем своего мини-
минимума и максимума.
Функция /(Л), как мы только что убедились, ограниченна. Пуеть
т — ее нижняя граница, построим последовательность точек
Av Л2, . . . , Лл, . . .
так, что
f(An)<m-\-en,
где еп — некоторая стремящаяся к нулю последовательность убывающих
*) За окрестность „точкиа у(х) здесь принимается окрестность первого
порядка.
§ 40] ЛИНЕЙНЫЕ ПРОСТРАНСТВА 69
положительных чисел. Последовательность А% имеет по крайней мере
одну точку сгущения Ао. Докажем, что f(A0) — т.
Допустим, что f(A0) ф т, следовательно,
Построим окрестность UA точки Ао, в которой значения функции отли-
отличаются от/(Л0) меньше, чем на~. Очевидно, если А' принадлежит ?/4 , та
Так как последовательность зм -> 0, то, начиная с некоторого индекса,
гп < ~ и точки Afi начиная с некоторого номера, должны лежать вне UАо
Но тогда точка Ао не могла бы быть точкой сгущения. Этим противо-
противоречием теорема доказана.
~ Мы видели, какую существенную роль играла теорема Вейерштрасса
в исследовании вопроса о существовании стационарных точек (§ 16).
Доказанное нами ее обобщение играет столь же важную роль в иссле-
исследовании экстремумов функций более общего вида, в частности функцио-
функционалов. Так как теорема доказана для компактных абстрактных про-
пространств, то естественно поэтому, что в вариационном исчислении боль-
большую роль будет играть изучение компактных семейств линий.
§ 40. Линейные пространства
Общие определения. Для того чтобы распространить на более обшир-
обширный класс функций аппарат анализа, мы прежде всего должны опреде-
определить понятие диференциала. В теории, функций п переменных диферен-
циал определялся как главная линейная часть приращения функции.
Но это определение требует определения понятия линейной функции.
Определение же линейной функции требует, чтобы над элементами на-
нашего пространства можно было производить операции сложения и умно-
умножения на постоянное число, причем в результате этих операций должны
получаться элементы нашего же пространства.
Операция сложения заключается в том, что двум элементам А и В
множества М относится третий элемент ?С этого же множества, обозна-
обозначаемый С=А-\-В. Эта л операция обладает следующими свойствами
(аксиомы сложения):
1°. Л + ? = ? + Л.
2°. Существует всегда единственный элемент, удовлетворяющий урав-
уравнению A -j-^ = B\ мы обозначаем его:
Х=В — А.
+4+
Относительно операции сложения линейное пространство образует комму-
коммутативную группу.
70 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ. VI
Операция умножения на вещественное число k должна удовлетво*
рять совместно с операцией сложения еще следующим условиями
4°. 1 -Л=Л.
5°.
6°
6°. (? + /)Л = ?Л-[-/Л.
7°. ?(Л4-?)==?Л + А>#.
Здесь А и В суть элементы множества М, k и /—вещественные числа.
8°. Пространство обладает еди«стйенным нулевым элементом в:
е = о.л = л—л,
где А — произвольный элемент.
Этим аксиомам удовлетворяли для векторов в /г-мерном простран-
пространстве ой?рации сложения и умножения на число. Этим же аксиомам
удовлетворяет обычное сложение непрерывных функций и умножение
их на постоянное число.
Пространство, для элементов которого установлены операции сло-
сложения и умножения на вещественное число, называется линейным про-
пространством. Простейшими линейными пространствами, а именно /1-мер-
ными линейными пространствами, мы занимались в главе I.
Линейные многообразия. Точки:
Ах, Л2, . . . , Аи
называются линейно независимыми, если они не удовлетворяют ника-
никакому равенству:
2 & Д = О
при любых kv не равных одновременно нулю.
Линейным п-мерным многообразием в абстрактном пространстве
называется совокупность точек Л, удовлетворяющих равенству:
где Аг — система линейно независимых элементов, tx — значения неко-
некоторых числовых параметров. Если одно из чисел t% приравнять единице,
остальные — нулю, то точка Л совпадет с соответственной точкой Л,;
точки At лежат на нашем многообразии. В частности одномерная прямая
определяется уравнением:
где Ао и В — заданные элементы М.
Если в линейному пространстве имеется не более чем k линейно не-
независимых элементов, то^все^остальные будут линейно выражаться через
эти элементы. Если мы фиксируем к линейно независимых элементов:
Av Л2, . . . , Аку
§ 40} ЛИНЕЙНЫЕ ПРОСТРАНСТВА 71
то всякий другой элемент А вместе с k элементами .Ai должен удовле-
удовлетворять линейному соотношению:
где не все числа 1{ и / равны одновременно нулю. Если /=0, то
2 1{Аг = 0, при не всех /* = 0, что невозможно, так как элементы Ai
линейно независимы, следовательно, /ф 0. Тогда
. к . к
Каждому элементу А можно отнести k чисел:
lv /2, . .. , /Л,
которые можно рассматривать как его координаты. Наше про-
пространство есть ^-мерное линейное пространство.
Прямая и вектор. Пусть дана прямая
A0)
и пусть
Назовем отрезком А А' совокупность точек прямой A0), отвечающих
значениям параметра t, удовлетворяющим неравенству to^.t^tv Отре-
Отрезок АА/ вместе с направлением на нем (от А к Аг или наоборот)
называется вектором. Мы обозначаем вектор символом ААГ. Вектор ААГ
есть отрезок ААГ с направлением от А к А\ Точка А называется
началом, А' — концом вектора.
Ничего не меняя в рассуждениях § 2, можно показать, что через
любые две точки можно провести единственную прямую. Таким образом
если даны две точки А и А'', то эти точки определяют единственный
—>
вектор ААГ. Отсюда, принимая некоторую точку О пространства за
нуль-точку, мы можем каждую точку А рассматривать как конец
вектора ОА с началом в нуль-точке. Линейное пространство можно,
следовательно, рассматривать как совокупность векторов.
Метрика. Мы будем в дальнейшем обозначать вектор ОА просто
буквой а. Наше пространство есть в одно и то же время совокупность
точек А и совокупность векторов а с началом в О и концами в этих же
точках.. Для дальнейших построений допустим, что наше линейное про-
пространство метрическое. Длиной вектора а назовем расстояние от О до
точки Л. Будем обозначать его символом |а||. Очевидно:
72 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ. VL
Будем называть метрику линейной, если
1°. г(а,*) = |а —ft||,
2°. ||ДаЦ=|*|-И>
где k — действительное число.
Этим условиям удовлетворяет, как легко видеть, метрика я-мернога
евклидова пространства, а также метрика пространств 1^ и m •
Гильбертово пространство, общее — пространство 1р, есть тоже линей-
линейное пространство с линейной метрикой. Достаточно рассматривать каж-
каждую точку А пространства \р как конец вектора а с началом в нулевой
точке и определить действия над векторами в пространствах по ана-
аналогии с действиями над векторами в я-мерных пространствах:
1°. Если
а = (аг, а2, . . . , апУ . . . ),
ft = (*1> *о» ' ' • > *и» ' • ')>
(kav
Линейная функция. Функция /(Л), определенная на линейном про-
пространстве, называется линейной, если она удовлетворяет следующие
условиям:
1°. /(Л + В)=/(Л)+/(Я).
2°. /(Л) — непрерывна.
Следствие. Если /04) есть линейная функция, то
ДАЛ) = А/04).
где А — произвольная константа. В самом деле, из свойства 1 ° следует::
f{2A)=f(A + А) =/(А) +/(Д) = 2/04)
и вообще
Далее:
ИЛИ
Наконец: в силу равенств A1) и A2) для любого рационального1 числа
Таким образом наше предложение доказано для рациональных значе*
ний k. ,B силу непрерывности функции /(Л) оно доказано для любого
значения к.
§ 40] ЛИНЕЙНЫЕ ПРОСГРАНСТВА 73
В частности, полагая &=0, получаем:
где В — нулевой элемент нашего пространства/
ТЕОРЕМА 1. Если f(A) есть линейная функция, то существует постояп-
ное положительное число К такое, что
I ЯЛ) к лги л ц. A3>
В самом деле, пусть это свойство не удовлетворяется; каково бы ни было-
число п, существует такой элемент А„ нашего линейного пространства, что
\f(Au)\>n{AJ. A4)
Обозначим через Вп элемент:
Имеем:
Поэтому последовательность элементов Вп сходится к нулевому элементу Ф„
В силу непрерывности f(A) мы должны иметь:
Но, с другой стороны, из A4) и A5) вытекает:
Приходим к противоречию.
ТЕОРЕМА 2 (обратная 1). Пусть функция f(A), заданная в линейном про*
странстве, удовлетворяет условиям:
V.f(A)+f(B)=f(A + B).
2°. |/(Л)|<;К\\А || * (К—некоторая константа).
В этом случае f(A) есть линейная функция от А.
В самом деле, при условиях теоремы имеем:
Поэтому для всех элементов Д лежащих в достаточно малой сфере вокруг А
разность f(B) — f(A) будет сколь угодно малой, т. е. функция f(A) непрерывна
в любой точке. Непрерывность вместе с условием 1° георемы и есть условие
линейности f(A). Таким образом теорема 2 доказана.
Пример. Координата аг точки А (аг, а^,..., аПУ...) гильбертова пространства)
есть линейная функция на гильбертовом пространстве: двум близким точкам'
соответствуют близкие 1-е координаты, сумме двух точек соответствует сумма;
/-х координат этих точек.
Билинейные функции. Рассмотрим функцию /(Л, В) от пары точек
Ау В линейного пространства R, линейную и относительно А и относи-
относительно В. Имеем:
/(Л,
Следовательно:
+ + ^fiA, B)+f(Au B) + f(A, B\)+f(Au В,). A6)
74 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [ГЛ. VI
Далее:
B). A7)
Функции /(Л, В), обладающие указанными свойствами, называются
билинейными. Если /(Л, Я)=/(#, Л), то билинейная функция назы-
называется симметрической.
Квадратические функции. Пусть F(А) = /(Л, Л), где /"—симметри-
/"—симметрическая билинейная функция. Функцию F(A), определенную таким обра-
образом, мы будем называть квадратической. Из A6) и A7) получаем:
Интеграл / [f(x)]*dx есть простейшая квадратическая функция в
функциональном пространстве Lr
§ 41. Диференциал функции на линейном пространстве
Первый диференциал. Пусть /(Л) — непрерывная функция в линей-
линейном пространстве R. Рассмотрим разность f(Ax)—/(Л), которую назо-
—>
вем приращением функции, а соответственный вектор AAt назовем при-
приращением переменного Л.
Если существует такая линейная функция L(A), что
где е стремится к нулю вместе с Ц^ — Л[|, то L(At*—Л) назовем
диференциалом функции /(Л), соответствующим приращению Л1 — Л,
и обозначим: df{A). Итак,
/(Л,) -/(Л) = df{A) -f s || Л, - А ||.
Иначе: обозначая Ах — Л через h:
Для того чтобы показать, что df(A) берется для приращения
«будем его обозначать иногда через df{A\ К). Очевидно:
d/(A; h + hl) = df(A; h) + df(A; h,\
df(A\ Щ = kdf{A\ A),
где k — действительное число.
Второй диференциал. Пусть функция /(Л) имеет в точке Л дифе-
диференциал df. Рассмотрим разность:
Эта разность есть величина высшего порядка малости сравнительно
с JAj. Если существует квадратическая функция приращения h> которую
мы обозначим через cPf(A\ h), такая, что
h) _/(Л) _ df(A; h) - d»f(A; h) =
х \
§ 41] ДИФЕРЕНЦИАЛ ФУНКЦИИ НА ЛИНЕЙНОМ ПРОСТРАНСТВЕ 75
тде et стремится к нулю вместе с ||А|), то сР/ называется вторым да-
ференциалом функции / в точке Л. Можно последовательно определить
3-й, 4-Й, . . . , я-Й диференциалы. Получим:
f(A + A) =f(A) + df(A; А) + d*f(A; *) + ...+ <Tf{A\ h) + s \hf,
где lim|e| = 0.
Функция, имеющая п последовательных диференциалов в точке Л,
называется п раз диференцируемой в точке А.
Функция, п раз диференцкруемая в каждой точке А пространства R,
называется п раз диференцируемой в пространстве R.
Замечание о диференциале. Пусть нам задана функция /(Л) в ли-
линейном пространстве R, обладающая в точке А диференциалом df(A\ К),
Рассмотрим произвольный элемент h из R и соединим его прямой:
Л + /А (— oo</<-fco)
с элементом Л. На проведенной прямой функция / обращается в функ-
цию параметра t.
Мы имеем в сил}г существования диференциала / в точке А:
где г стремится к нулю вместе с ||Й|), т. е. (поскольку h остается по-
постоянным) вместе с t Отсюда:
Итак, если существует диференциал d{A\ А), то для любого h суще-
существует производная ^ Г;—-\t=0* причем
Обратного утверждать нельзя. Из существования ¦- Т— \t=zQ не
следует еще существование диференциала ^//(Л; А) (см. примеры, рас-
рассмотренные в § 9) !).
Аналогично можно доказать, что если функция имеет 2-й, 3-й, ..., /1-й
диференциалы в-точке Л, то
4^г0, A8.2)
о, A8.3)
A8.
^ Некоторые авторы определяют диференциал функции/как Jp—J{
Очевидно, это определение общее определения дифереициала как главной линей-
линейной части приращения.
76 ОБОБЩЕНИЕ ОСНОВНЫХ ПОНЯТИЙ АНАЛИЗА [гД- VI
§ 42. Экстремум функций точки линейного пространства
Необходимое условие экстремума. Введенное нами понятие дифе-
ренциала позволяет обобщать на функции точки абстрактного линей-
линейного пространства основное необходимое условие существования экстре-
экстремума для этих функций.
ТЕОРЕМА 1. Для того чтобы функция / (Л) точки линейного
пространства, определенная в. некоторой области D нашего простран-
пространства (D может совпадать со всем пространством), в некоторой вну-
внутренней точке достигала экстремума, необходимо, чтобы ее дифе-
ренциал в этой точке тождественно равнялся нулю.
Пусть функция /(Л) в точке Ло достигает относительного минимума;
тогда
A9)
при всех Л, лежащих в сфере достаточно малого радиуса г с центром
вточкеЛ: М-4,К..
Допустим теперь, что диференциал функции отличен от нуля:
df{A0)^L(A — Л0)ф0;
тогда в любой сфере радиуса, меньшего г, существует бесчисленное
множество точек Л, как угодно^ близких к Ло и таких, что:
/.(Л — AQ)< — k || А-Ао ||,
где k — положительная константа, не зависящая от \\ А — Л^ || ; с дру-
другой стороны:
/ (Л) =/(Ло)+1 (Л - Ао) + 711] А - Ао || , B0)
где т) стремится к нулю вместе с || Л — Ло || . Отсюда существуют точки,,
как угодно близкие к Ло, такие, что:
А-Ао || .
Но при достаточно малом е слагаемое (— k ~j- т\) 1| Л — Ло || будет отри-
отрицательным, следовательно,
что противоречит неравенству A9).
Пользуясь замечанием о понятии диференциала в предыдущем пара-
параграфе, можно дать другое доказательство, редуцирующее нашу общую
задачу к^задаче экстремума функций одной действительной переменной*
В самом де:?е, функция параметра /:
при любом h должна при *=0 достигать своего относительного экстре-
экстремума, следовательно, при любом h имеем:
§ 42] ЭКСТРЕМУМ ФУНКЦИЙ ТОЧКИ ЛИНЕЙНОГО ПРОСТРАНСТВА 77
Отсюда в силу формул, связывающих производную по направлению и
диференциал, имеем:
Точки, в которых удовлетворяется равенство B1), будем называть
стационарными точками функции /.
Если первый диференциал функции / в точке Ло исчезает, то глав-
главной частью приращения функции / становится второй диференциал
d*f(A;h): f(A + h)f(A)^d*f(A;h). B2)
Поэтому вопрос о том, будем ли мы иметь случай максимума, мини-
минимума или случай более сложной стационарной точки для функций на
-общем линейном пространстве (также как и для разобранного в главе IV
•случая функций в л-мерном пространстве), решается исследованием
второго диференциала.
Из формулы B2) непосредственно явствует, что необходимым усло-
условием минимума функции / в точке Ао является требование, чтобы
второй диференциал был неотрицательной квадратической формой,
т. е. чтобы для любого h
. B3)
В силу элементарных условий минимума функций одного перемен-
переменного мы найдем необходимые условия минимума функции / в точке Ас
на прямой А = Ао -f- th :
Pf(Ah). B3)
Если точка Ао является точкой минимума / на линейном простран-
пространстве, то она является точкой минимума / на любой проходящей через Ао
прямой А0-\-Иг,. следовательно, неравенство B3) должно удовлетво-
удовлетворяться при любом h. Таким образом имеет место следующая теорема:
ТЕОРЕМА 2. Для того чтобы функция f достигала минимума
& стационарной точке Ао, необходимо, чтобы в этой точке
для любого h.
Читатель легко докажет следующую теорему.
ТЕОРЕМА 3. Для тою чтобы функция f достигала минимума
в стационарной точке Ао, достаточно^ чтобы для любого h в этой
точке удовлетворялось неравенство:
где С есть положительная константа.
ГЛАВА VII
ФУНКЦИОНАЛЫ И ВАРИАЦИЯ
§ 43. Функциональные пространства
Функциональными пространствами называются абстрактные про-
пространства, точками которых являются функции. Функции точки в функ-
функциональном пространстве называются функционалами. Как было отме-
отмечено выше, функциональные пространства суть пространства линейные.
Пространство С- Функциональным пространством является совокуп-
совокупность С всех непрерывных функций f(x), где а^х^Ь. Расстояние
между двумя точками пространства — функциями f{x) и о (х) опреде-
определяется как близость нулевого порядка, т. е. как тах|/(х)—<?(•*)!•
С этим пространством мы уже имели дело. Пространство это не-
некомпактно.
Сходимость в пространстве С означает равномерную сходимость
функций. В самом деле, пусть последовательностьmfx (д:), /2 (х), .. .
..., fn (дг), сходится (в смысле 1 сходимости в пространстве С)
к функции f(x). Имеем:
г (/> /«) -* ° ПРИ п -* °° •
Но
/-(/,/.)= max \f(x)—/n(x)\i
(каково бы ни было положительное число г, найдется такое число N,
что
max ;/(*)— /*(*)!<•
при я > N. Тем более для любого значения х, лежащего на отрезке
Аналогично, если непрерывные функции /п (а:) сходятся равномерно
к функции /(аг), то они сходятся к ней и в смысле метрики простран-
пространства С- Пространство С некомпактно в малом. Пусть, например, а — 0у
Ь=\. Функции
sin х, sin 2x, . . . , sin fix, .. .
имеют (в смысле метрики С) норму 1. В то же время из них нельзя
выбрать ни одной равномерно сходящейся подпоследовательности. На
пространство С обладает свойством полноты. Пусть
У л (*)> У-1 (*), • • • >У* (*), ...
§ 43] ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА 79*
есть последовательность Коши в смысле метрики пространства (}• Како-
Каково бы ни было число s > О, найдется такое число N, что
max \уя(х)—Ут(*)\<*> A>
если
п > Л, /д > Л/.
Фиксировав значение jc: а' = лг0, получим числовую последовательность:
Л (*о)> Л (*о)> • • • э -У* (*о)>
удовлетворяющую в силу неравенства A) критерию сходимости Коши.
Итак, последовательность
Ух (*)> Л (*)> •¦мЛD'"
для любого значения х (области определения функций этой последова-
последовательности) сходится к некоторому предельному значению у (х).
Мы сейчас докажем, что эта последовательность стремится к у (х)
равномерно. Тем самым будет доказано, что у (л:) есть элемент про-
пространства С и что уп (х) стремятся к у (х) в смысле метрики этого
пространства.
В самом деле, достаточно в неравенстве A) фиксировать п и стре-
стремить т к -\- оо , чтобы получить: для всякого з > О можно найти,
такое N, что
\У»(х)— .У (*).<*.
если п > N, т > Л. Равномерная сходимость j/n (л:) к у (х) доказана.
Вместе с тем доказано и свойство полноты С-
Пространство С играет большую роль в анализе.
Сепарабельность пространства С. Пространство R называется сепара-
бельным, если в нем существует счетное множество М точек М такое, что
любая точка пространства R есть предельная для М. Множество М называется
счетной всюду плотной сетью. Например, числовая прямая есть сепара-
сепарабельное пространство; всюду плотную сеть на ней образует совокупность, на-
например, рациональных чисел. Точно так же л-мерное пространство есть сепа-
сепарабельное пространство: счетную всюду плотную сеть на нем образует сово-
совокупность его точек с рациональными координатами.
Пространство С есть тоже сепарабельное пространство. В качестве счетной-
всюду плотной сети на С можно принять, например, совокупность всех по-
полиномов
... + апхп
любых степеней с рациональными коэфициентами aQf alt..., an. Совокупность
таких полиномов имеет счетную мощность. С другой стороны, какова бы ни
была функция/^), непрерывная на отрезке а^х^Ь, существует последо-
последовательность полиномов:
= ао
которая стремится равномерно к / (х) на отрезке а <;*<;?. Далее, можно*
подобрать рациональные числа
о * 1 > • • •» 8п
столь близкие к соответственным числам
Jn) Mi) An)
«О > «I > • ' • > «en >
80 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
чтобы полином
был сколь угодно близок в смысле метрики в С к Яг Выбрав фиксированное
.положительное Л, можно добиться в частности, чтобы
max |/>,W-VWKy.
Легко показать, что последовательность полиномов Яп* (л) с рациональ-
рациональными коэфициентами стремится равномерно вместе с Рп (х) к f (х). Так как
/(х) была выбрана произвольно из С, то отсюда следует, что совокупность
полиномов с рациональными коэфициентами образует всюду плотную сегь на С.
Два метрические пространства Rj и R2 называются изометричныма, если
*«ежду их точками можно установить взаимно-однозначное соответствие, сохра-
сохраняющее расстояние, т. е. расстояние между любой парой точек в пространстве
Rx равно расстоянию между их образами в пространстве R2, и обратно. Банах
доказал замечательное свойство пространства С: каково бы ни было метри-
метрическое сепарабельное пространство R, существует изоморфная ему часть О\
пространства С. Выражаясь образно: любое сепарабельное метрическое про-
пространство R можно вложить, сохраняя расстояния между его точками, в про-
пространство С.
Пространство Сп> Наряду с С нам придется иметь дело с про-
пространствами Сл.
Пространства Сп являются метрическими линейными функциональ-
функциональными пространствами, элементами которых являются функции у (х),
•определенные на отрезке а <^ х ^ b и обладающие на нем п непрерыв-
непрерывными производными. Если
то
т(у, z) = max {\у (*)-* (х)\, \У (*)-*' (*)i, ¦ • • ,\y(n\x)
?сли последовательность элементов
Vk(x) (A=l, 2,...)
пространства Сп сходится к^;(аг)зСм в смысле метрики этого про-
пространства, то, значит, функции ук (х) и их первые п производных схо-
сходятся равномерно соответственно к функции у (лг) и ее я первым про-
производным. Пространство Сп полное, но не компактное в малом.
Пусть функция у (х) есть элемент пространства Сп. Сфера радиуса г,
проведенная в Сп вокруг этого элемента, совпадает с е-окрестностыо
п-т порядка функции у (лг).
Пространство С/- Рассмотрим совокупность С/ всех функций у(х),
заданных на отрезке а^х^д, обладающих на нем непрерывной первой
производной. За расстоянием между функциями у (дг) и ух (х) из С,
принимается
г [у (*), ух (*)] = max | у (х) —уг (ж) |.
а < х < b
Итак, С/ состоит из тех же функций, что и С1У но в качестве
метрики в С^ принята метрика С- Пространство С/ фигурирует в ва-
вариационных задачах, связанных с нахождением сильного экстремума.
§ 43] ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА 81
Пространства Lp. Мы приведем сейчас пример линейных функциональных
пространств с метрикой, отличной от принятой в предыдущих примерах.
Рассмотрим совокупность Ц/ всех непрерывных на отрезке [я, Ь] функ-
функций f(x). Расстояние между функциями / (х) и f1(x)) входящими в L/, опре-
определим по формуле:
ъ 1
Очевидно, г (/, Л) — г (fu f), r(/,/i) = 0 только npnf = fl. Далее в силу не-
неравенства Минковского (см. § 16) имеем:
Таким образом все три аксиомы метрики удовлетворяются.
Так как г (/, Д) есть положительный однородный функционал первой сте-
степени относительно разности / — flf то наша метрика линейна. Ц/ можно рас-
рассматривать как линейное метрическое пространство, и под нормой элемента / (х)
надо понимать
Метрика функционального пространства С является предельной метрикой
пространства Ц/ при р, стремящемся к бесконечности. В самом деле, в про-
пространстве С расстояние между функциями / (х) и <р (х), входящими в С, равно
максимуму |/ — ср | на отрезке [а, Ь]. Обозначим этот максимум через с:
Если / не равно тождественно <р> то ?>0. Так как в некоторой точке flf се г
мента [а, Ь] функция |/—rf | равна с, то на некотором конечном интервале
длины /<[0 эта разность больше с — ?, где г — произвольное положительное
число, меньшее с* Имеем:
J \ JL JL
Последнее неравенство следует из того, что мы можем только увеличить инте-
интеграл, стоящий в средней части неравенства, если будем считать |/—ср | рав-
равным с на всем интервале [а, Ь]\ наоборот, мы уменьшим этот интеграл, если
заменим |/—<р| на выделенном интервале длины / через с — е, а на остальной
части интервала [а, Ь] разность |/ — ср | заменим нулем.
При р -> со, 1Р и (Ь — а) & стремятся к единице, поэтому:
ь 1
:-«< lira Г f\f—ffdx]p
р -+ оо L •' J
с — ?< lim | / |/ — ?Г ЛхГ <?.
'а
Так как г есть произвольное число, то
ь
г
lim
а
Пространства Lpr не являются полными. В самом деле, рассмотрим по-
последовательность функций:
Уп ix) (n = 1. 2, 3, ...),
im I" flf-yfdxY -с.
-> оо L J A
82 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
заданных на отрезке — 1 <; х •< h где
— 1 при —-1<!дг<; ,
пх при <С*< — *
п п
1 при :— < х < 1 .
Очевидно, функции уп (х) непрерывны. Далее
Уп (х) —Ут М ПРИ т > п
2 . . 1
всюду вне интервала <-*<—, на этом же интервале
Поэтому
Г \Уп (*) —Ут (¦*) \р dx= f \yn (*)—ут (х) \pdx<:~ •
-1 д
п
На пространстве Ц (/?>-1) функций, заданных на отрезке —1^*<1, после-
последовательность уп (х) есть последовательность Коши. Однако непрерывной фун-
функции, к которой стремились бы функции уп (х) (в смысле метрики L^), не
существует. Пространство L.' есть не полное пространство.
Пространство L.'. Рассмотрим теперь пространство функций у (х), измери-
измеримых в смысле Лебега, таких, что интеграл Лебега:
у (х) \Pdx (p > 1)
существует. Считая идентичными функции, отличающиеся друг от друга на мно-
множестве меры нуль, можно рассматривать такие функции у (х) как точки некото-
рого линейного метрического пространства Lpi причем за норму функции у(х)
примем
\\У\\ =
Можно доказать, что пространство L, является полным пространством»
§ 44. Компактность в функциональных пространствах
Пространство R. Совокупность R всех функций/(л:) @<;л;<;1K
удовлетворяющих неравенству:
где т — некоторая положительная константа, образует пространство.
Все функции, входящие в R, непрерывны. Метрика определяется,
как в пространстве С. Если функция f(x) есть предел последователь-
последовательности функций /п (л:), входящих в R, то f (х) тоже входит в R. В са-
самом деле, для любых х и л^, заключенных между 0 и 1,
1 l/.(*)-/.(*i)K»l*—*J. О)
Таким образом R есть полное пространство.
§ 44] КОМПАКТНОСТЬ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ 83
Построенное пространство R опять не компактно. В самом деле,
из последовательности точек-функций этого пространства:
тх -J- 1, тх -f- 2, ... , тх -j- #
нельзя выделить сходящейся подпоследовательности. Покажем, что R
компактно в малом.
Пространство R^. Пусть R^ есть пространство, состоящее из всех
точек пространства R таких, что:
ТЕОРЕМА ГИЛЬБЕРТА (Hilbert). Пространство RN компактно
(пространство R компактно в малом).
Переведя эту теорему на язык теории функций, получим: из всякой
последовательности функций:
/iD A (*),...,/•(*)>.... B)
удовлетворяющих условию l/A(X)|^Af и таких, что:
\f*{x)—fAXi)\<m\x — *i\ (a<x^b) C)
(т, Ny я, b суть константы, не зависящие от &), можно выделить равно-
равномерно сходящуюся подпоследовательность, причем пределом этой подпо-
подпоследовательности будет функция, удовлетворяющая условию C).
Заметив, прежде всего, что графики всех функций R^ принадле-
принадлежат прямоугольнику К с вершинами (я,—А/)/(я, АГ), (#, А/), (#,—А/);
перейдем к доказательству.
Разобьем сторону прямоугольника К, параллельную оси Ох, на п
частей, где п — любое целое число, а сторону, параллельную оси Оуу
на kn частей, где k есть наибольшее целое число, меньшее числа
•—тт г-. Проведем через точки деления прямые, параллельные соот-
соответственно оси Оу и Ох; тем самым разобьем прямоугольник К на
kn2 прямоугольников. Вертикальным столбцом прямоугольников назовем
совокупность прямоугольников деления, заключенных между двумя со-
соседними линиями деления, параллельными оси Оу. Каждая кривая, изо-
изображающая функцию из R^, задевает по крайней мере по одному пря-
прямоугольнику из каждого вертикального столбца. (Мы говорим, что
кривая задевает прямоугольник, если она имеет общие точки с ним или
его границей.)
Пусть/(л:) — функция класса R^, и пусть А (л:, у) и В(хиуг) —
две ее точки, лежащие в одном вертикальном столбце; следовательно:
Таким образом ординаты этих точек отличаются на число меньшее, чем
длины вертикальных сторон наших прямоугольников. Следовательно,
точки А и В могут принадлежать одновременно одному прямоугольнику
84 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
с границей или двум прилегающим друг другу прямоугольникам нашего
вертикального столбца. Итак, кривые у—/(х) задевают в каждом вер-
вертикальном столбце по одному или по два соседних прямоугольника.
Каждая кривая задевает некоторое количество (заключенное между п
и 2п) прямоугольников деления. Так как число комбинаций из них
конечно, a R^ есть множество бесконечное, то найдется бесконечное
множество R*J? функций f (х) из множества R^ таких, что все кривые
из R^ задевают одни и те же прямоугольники.
Проведя дополнительно прямые, параллельные осям Ох и Оу, де-
делящие пополам стороны прямоугольников деления, получим новое разде-
разделение прямоугольника /f, причем стороны прямоугольников деления
будут -тр- , 7>т- . Повторяя предыдущие рассуждения, мы констатируем
существование бесконечного множества R^ функций, входящих в R^ и
изображаемых кривыми, задевающими одни и те же прямоугольники но-
нового деления. Продолжая неограниченно процесс разделения на все более
и более мелкие прямоугольники, получаемые каждый раз разделением
пополам сторон прямоугольников предыдущего деления, докажем суще-
существование последовательности заключенных друг в друге множеств:
B) рC) р(р)
Здесь R(?) состоит из функций, изображаемых кривыми, задевающими
одни и те же прямоугольники р-го деления. Так как длина каждой сто-
2N
роны параллельной оси Оу прямоугольника р-го деления равна ———,
а в каждом вертикальном столбце все кривые из R^ задевают один или
два прилегающих прямоугольника, то для двух функций о (х) и ^ (л:)
из R<J? имеем:
Пусть теперь
— последовательность функций, где / (л:) принадлежит Rv . Так как
при />0, f ,г(х) принадлежит R^, то при любом положительном р
и / имеем:
Следовательно, последовательность /р (х) есть последовательность Коши,
поэтому она сходится, и притом равномерно, к некоторой предельной
функции f{x). Предельная функция для последовательности функций
из RN тоже принадлежит R^.
Выделение компактных функциональных пространств играет большую
роль в теории экстремумов функционалов, так как дает возможность
применять теорему Вейерштрасса.
§ 44] КОМПАКТНОСТЬ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ 85
Пространство R является частью пространства С. Вместе с тем R^.
есть компактная в себе часть пространства С- Всякое бесконечное под-
подмножество R^ компактно в R^, тем более, оно компактно в R и С-
Понятие равномерно непрерывной совокупности. Рассмотрим не-
некоторую функцию у (х) на отрезке а^х^Ь. Обозначим через еу (h)
функцию, равную fA
suplj/CXj)— y(x)\, D)
где х и хг принадлежат отрезку [а, Ь] и \х{—#|<^й. Функция гу (И)
для /z>-0 определяется функцией у (х); очевидно, гу @) = 0 , еу (h)
есть конечная невозрастающая функция h. Если у (х) непрерывна, то
еу (Ji) стремится к нулю вместе с /г; в этом заключается свойство равно-
равномерной непрерывности непрерывной функции у (х).
Рассмотрим теперь некоторую совокупность М непрерывных функ-
функций у (л:), заданных на отрезке а^х-^b. Обозначим через yjm (/г):
'1м (*) = SUP Ь (*i) — У (*) I >
где верхняя грань берется по всем функциям у (х), входящим в М, и
по всем отрезкам [л:, хх] длины не большей, чем /г, заключенным в [а, Ь].
Для всякой функции у (х) из М можно определить, как мы это де-
делали выше, функцию гу (к). Очевидно, для любого /г, riM (^) = sup гу (ti).
гу (Ji) есть верхняя грань разностей D) для одной функции у, т)м (/г)
есть верхняя грань этих разностей по всем функциям у (дг), входящим
в М. Попрежнему т]м (Ji) есть неубывающая функция от /г, sM @)=0.
Функция 7]м (h) может принимать и бесконечные значения. Например,
если М включает функции
sin х, 2 sin лт, 3 sin лг, . . . , п sin х, . . . ,
определенные на отрезке а ^ х ^ Ь, то ем (Ji) бесконечна при лю-
любом h > 0.
В самом деле, выбрав произвольные неравные числа хх и х такие,
что sin хх ф sin х и \х1 —х |< //, имеем :
ем (*) -^ SUP Л (s*n xi — sii>jc) = -|- оо .
Если все функции у (л:), входящие в М, удовлетворяют неравенству:
то
0 < sM (А) < 2Д/
для любого h-*Q [так как всегда в этом случае \у (л^)—j; (л:) | <С 2Л/].
ем(Л) есть \ невозрастающая функция от h, однако, вообще говоря,
она не стремится к нулю вместе с h.
Пусть, например, М состоит из функций
sin xy sin 2х, . . . , sin kx, . . . ,
определенных на отрезке 0<;л;<;1, h — любое положительное число.
Выберем достаточно большое целое число п > 2 такое, чтобы — < h .
86 функционалы и вариация [гл. VII
Если х = -?-9 ^=5-^-, то хх их заключены на отрезке
| х{ — х | <^ h и sin пх — sin nxl = 2. Итак,
зм(А)>2.
Но, с другой стороны, sM (/г) не превосходит 2, поскольку все функ-
функции sin ял; по абсолютной величине не превосходят 1.
Итак, гм (/г) = 2, если h > О,
ем (h) = 0, если h = 0.
Для 9 функций, входящих в пространство R sR(h) = nth. В этом случае
lira вр (А) = 0.
70 K
ОПРЕДЕЛЕНИЕ. Совокупность М функций у (х) (а<л:<?) назы-
называется равномерно непрерывной совокупностью, если, во-первых, суще-
существует постоянная Л/'^О, такая, что для всех у (х) из М
во-вторых,
lim
Примером равномерно непрерывной совокупности функций может слу-
служить пространство R^ предыдущего примера.
Все функции равномерно непрерывной совокупности являются функ-
функциями непрерывными.
Можно определить равномерно непрерывную совокупность функций
несколько иначе. Совокупность М функций у (х) (а <; х < Ь) называется
равномерно непрерывной совокупностью, если все функции удовлетво-
удовлетворяют неравенствам:
l°-J.y(*)l<W Для а<*<?, E)
2°- Ъ (Pi) —У (*) I < Ч (*)» если | ^ — j; !< h. F;
(Здесь Л/"—некоторая положительная константа, y\(h) — невозрастающая
функция, стремящаяся к нулю вместе с h.)
Оба определения эквивалентны. В самом деле, если совокупность
функций удовлетворяет первому определению, то достаточно положить
y) (h) — ем (Л), чтобы убедиться, что она удовлетворяет и второму.
Наоборот, если совокупность М функций удовлетворяет второму усло-
условию, то из неравенства
следует: ?М(А) стремится к нулю вместе с А, как только f\{h) стремится
к нулю вместе с /г.
Компактность в пространстве С. Рассмотрим теперь функциональ-
функциональное пространство R(^ ч)> состоящее из всех функций у (*), определенных
на отрезке 0 ^ х ^ 1 и удовлетворяющих условиям E) и F). Метрику
в R^ . примем совпадающей с метрикой в С.
§ 44] КОМПАКТНОСТЬ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ 87
ТЕОРЕМА АРЧЕЛА (Arzela). R{N } есть компактное пространство
или, рассматривая R(N ^ как часть С, R№ ч) есть компактная
в себе часть С.
Доказательство этой теоремы совершенно аналогично доказательству
теоремы на стр. 83, которая является частным случаем теоремы Арчела.
Обозначим: g1 = --^- {k — произвольное целое число), hx = -g-
(kx — целое число, большее 1); ht выберем настолько малым, чтобы:
-П (*i) < gi
(это всегда можно сделать, так как v\(h) стремится к нулю вместе с/г).
Построим последовательность чисел hv /г2,. .., hny.. . таких, что hn =
(kn — целое число) и ^(Ая) < Jf
Как и в предыдущем случае, построим прямоугольник с вершинами
{а,—Л/), (я,-j-N), ( — a%-\-N), (— а, — ЛГ); разобьем его на более
мелкие прямоугольники с основаниями h1 и высотами gv Каждая кри-
кривая у=у(х), где у(х) из R,N ,, расположена в большом прямоуголь-
прямоугольнике и пересекает некоторое количество прямоугольников подразделения.
Как и в предыдущем случае, такая кривая пересекает не более двух
прямоугольников, расположенных в одном вертикальном столбце. В самом
деле, если х и л1 — абсциссы двух точек нашей кривой, лежащих
в одном вертикальном столбце, то
\х — xi\<hv
а поэтому
\y(x)—y(x1)\<s(hl)<gv
(Разность ординат двух таких точек не превосходит высоты прямо-
прямоугольника подразделения.)
Аналогично, разбивая основной прямоугольник на все более и более
мелкие прямоугольники с высотами для п-го подразделения, равными
WL1 , и основаниями /гп, мы устанавливаем, что каждая кривая у=у {х),
где у (дг):из R(AT )9 пересекает не более двух прямоугольников п-го под-
подразделения. Как и в предыдущем случае, мы выделим подмножества
И3 R№,r
заключенные друг в друге и содержащие каждое бесчисленное множе-
множество элементов, причем все кривые у==у(х), где ^(a:)h3R^? , заде-
задевают одни и те же прямоугольники п-го подразделения. Если ср(лг)
и 6 (л:) принадлежат R^ у то \<?(х) — &(х)\ не превосходит удвоен-
удвоенной высоты я-го подразделения, т. е.
88 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
Выбрав из каждой совокупности *R^ } по одной функции^ (л;), получим:
Отсюда мы заключаем, что последовательность функций ур (х) схо-
сходится равномерно к предельной функции у(х), которая также принад-
принадлежит RW4)e
ТЕОРЕМА. Для того чтобы множество М функций у (х), при-
принадлежащих С, было компактно на С, необходимо и достаточно,
чтобы М было равномерно непрерывным и равномерно ограниченным
множеством функций.
Достаточность этого условия вытекает из теоремы Арчела. Всякое
равномерно непрерывное множество М функций есть часть компактного
в себе множества R^ Докажем необходимость этого условия.
Если М не равномерно непрерывно, то возможны два случая:
а) существует последовательность функций уп {х) из М и значения
хп на отрезке а < х < b такие, что
В этом случае очевидна некомпактность М, ибо ни последовательность
уп (х), ни любая ее подпоследовательность не может равномерно сходиться
ни к какой функции;
Ь) существует последовательность функций уп(х) из М и последо-
последовательность пар чисел х^п\ х±п\ удовлетворяющих условиям
n -*¦ со
(лг(?г) и х^ лежат на отрезке а ^х ^д) и таких, что
где г—положительная константа. Последовательность у^п\х) не может
равномерно стремиться ни к какой непрерывной функции у(х). Допу-
Допустим обратное: у{п)(х) равномерно стремится к некоторой непрерывной
функции у(х). Для у(х) можно указать такое положительное число /г,
что всегда
х\) У\х)\ ^ з ' I ^
коль скоро | лг1—л:|</г. Далее, в силу равномерной сходимости у^п) (л:)
к ^у (л:) существует такое число Л/, что для любого а
коль скоро п > N. Потребуем от я, кроме того, чтобы
IxW-^K* (9)
(что возможно, поскольку левая часть неравенства (9) стремится к нулю
при п -» оо). В CHwiy (8) и (9)
§ 44] КОМПАКТНОСТЬ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ 8&
с другой стороны,
IУ(п) {х™)-у(п)(*(я)) I< | Уй) (xln))-у (х^) \ + \у (* W)-у (*'">) j +
¦f \У (х(п))-у<п) (**») K-L. + S. + ^-^r,
что противоречит условию G).
Аналогично, никакая часть последовательности уп (дг) не может равно-
равномерно сходиться.
Пространства спрямляемых кривых. Рассмотрим теперь простран-
пространство, элементами которого являются плоские кривые ср, заданные в пара-
параметрической форме:
У = '**{?)•
Как известно, задание кривой в параметрической форме неоднозначно:
рассматривая t как монотонную функцию некоторого параметра т,
t=t(j), мы можем перейти к новому изображению той же кривой:
* = ?1 [<(*)]=*! СО,
,У = ?2[*(т)] = 42(т).
Пусть
Ао, Av Л2, ..., Ап A0)
точки кривой ср, отвечающие значениям параметра t:
Соединив последовательно точки A0) отрезками AiAi,x прямых, полу-
получим вписанный в кривую полигон рп. Если число п стремится к беско-
бесконечности так, чтобы максимум разности t/i,l — f. стремился к нулю,
то длина полигона рп будет стремиться к пределу (конечному или
бесконечному), называемому длиной кривой ср. Этот предел не зависит
ни от выбора последовательности полигонов, ни от выбора параметри-
параметрической формы задания кривой *). Кривые конечной длины называются
спрямляемыми.
Рассмотрим пространство R всех спрямляемых кривых <р> располо-
расположенных в ограниченной замкнутой плоской области Q, длины которых
не превосходят /. Пусть две кривые о и 6 пространства R заданы
в параметрической форме уравнениями:
г t
Обозначим через е максимум расстояний между точками кривых ср и ф,
отвечающих одному и тому же значению параметра, в зависит от пара-
параметрического задания кривых ср и ф. Определим теперь расстояние
от ср до ф:
r(?i ^) = inf з
1) Александров и Колмогоров, Введение в теорию функций дей-
действительного переменного, ГТТИ, 1935 г.
90 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
{как нижнюю границу чисел е при всевозможных видах параметрического
задания этих кривых). Определенная таким образом метрика в простран-
пространстве R, как нетрудно убедиться, удовлетворяет всем требованиям аксиом
метрики. В самом деле, сомнения могла бы вызвать только третья
аксиома: докажем, что и она удовлетворяется.
В самом деле, пусть
* = ?iW@. У = Ъ®Ю (/=1,2,3;
ррческие представления трех
Обозначим:
суть параметрические представления трех кривых <р , цР\ ^'
в1 = max у [?1B) @ - ?1A) (О]2 + [Ф2B) (О - ?2A) @12,
s2 = max У [9/3) (t) — 9^ (О]2 + [?iC) @ — ?2B) (О]2»
г3 = max j/" [9iA) (t) — 9XC) @]2+[?2A) @ — ^ @]2;
очевидно:
отсюда:
inf г3 ^ inf 3j -j- inf e0
или:
что и требовалось доказать.
Пусть о есть кривая из R длины 1Х ^ /. Примем на параметр ^
в точке А кривой ср значение —г- $, где 5 — длина дуги кривой с?, заклю-
заключенной между ее началом и точкой Л. Когда точка Л описывает кри-
кривую ф, параметр t изменяется от 0 до 1. Таким образом все кривые 9
из R изобразятся в виде уравнений:
3^ i ?2 V /' /
где 9i@ и ?з@ — ограниченные функции. В частности, если
х = 91@ = const,
то кривая вырождается в точку. Эти вырожденные в точки кривые мы
тоже отнесем к совокупности {9}.
Докажем, что пространство R компактно. С одной стороны, функции
У =
определяющие уравнение кривой 9 пространства R, удовлетворяют усло-
условию Липшица:
I ,z (+ \ и ^ a i ^ /I / /»
§ 45] ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ И ВАРИАЦИИ 91
В самом деле, из определения нашего параметра t длина дуги о между
точками [cpiC^), ?20i)] и [?i@> ?2@1 равна lx\tx —1\9 где /t — длина
кривой ср» так как разность между абсциссами и ординатами концов
дуги не превосходит длины этой дуги, то
причем lx^L С другой стороны, функции ©I (О И ?з @ равномерно
ограниченны.
Отсюда, применяя доказанную выше теорему, получим: из всякой
последовательности:
кривых пространства R, заданных нашими уравнениями х = ^i @>
у = cp2(i) (/) @ ^ t <! 1) можно выбрать подпоследовательность ?(Wl),
<?(Wl), . .. , <p(Wft)> ... , для которой 9i(Wi) @ и cp2(Wi) @ при 0 < t < 1 равно-
равномерно сходятся к предельным функциям <?i@ и ?%(?). Кривая с?,
изображаемая этими предельными функциями, имеет тоже, как легко
убедиться, длину, не превосходящую /. Следовательно, ср также при-
принадлежит R.
Таким образом нами доказана следующая теорема.
ТЕОРЕМА ГИЛЬБЕРТА. Совокупность всех спрямляемых кривых,
длины которых не превосходят данного числа I и расположенных
s закрытой ограниченной плоской области, компактна.
Заметим, что второе условие (принадлежать замкнутой ограниченной
области) можно заменить условием, чтобы один из концов всех кривых
находился в данной точке или принадлежал некоторому ограниченному
замкнутому множеству.
§ 45. Линейные функционалы и вариации
Общее определение. Линейные функции в функциональном про-
пространстве называются линейными функционалами. Линейные функцио-
функционалы L [у (х)] определяются следующими свойствами:
1°. L [у (х) +л (х)] =L\y (х)] + L [у, (х)],
2°. L [у (х)] есть непрерывный функционал.
В качестве примеров линейных функционалов в пространстве С
можно взять интегралы:
ъ
L[y\— y(x)dxy A1)
а
Ь
L[y] = fA(x)y(x)dx, AГ)
а
где Л (х) — произвольная функция от х.
92 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
Важный класс линейных функционалов в пространстве С предста-
представляют так называемые интегралы Стильтьеса (Stieltjes) 1), обозначаемые
так:
ь
*y(x)du(x), A2)
где и(х) — некоторая функция, с ограниченной вариацией; у(х) мы
считаем здесь непрерывной функцией 2).
Вариация как диференциал функционала. Мы, анализируя вопрос
об экстремуме диференцируемых функций, определенных на линейных
метрических пространствах, установили, что в точках экстремума первый
диференциал обращается в нуль. В применении к функционалам, т. е.
к функциям точки функционального пространства, мы должны были бы
получить как необходимое условие экстремума обращение в нуль первого
его диференциала. Нашей ближайшей задачей является определить пер-
первый диференциал функционала. Рассматривая в § 31 функционал как
предел функции от многоугольника, мы определили его диференциал
как предел диференциала этой функции. Сейчас мы определим его,
исходя из общих соображений.
Пусть J(y) есть функционал, зависящий от функции у(х). Дифе-
Диференциал функционала J(y), заданного в некотором функциональном
пространстве [при переходе от функции у(х) к новой функции ух (х)],
должен быть линейным функционалом L{y1—-у) от разности этих
функций такой, что:
есть величина, стремящаяся к нулю быстрее расстояния г (у, уг)у т. е.
J (Ух) = J(y) + L (Уг —У) + ?Г (Ух> У),
где г стремится к нулю вместе с г (уи у). Первый диференциал функ-
функционала J(у) называется его вариацией и обозначается символом 8/:
Итак, вариация функционала есть линейный функционал от приращения
функции, представляющей собою главную часть приращения этого
функционала.
§ 46. Вариация для простейшего функционала
Вывод вариации. Пусть нам дан функционал
ь
J = ff(x,y,/)dx,
а
где / обладает непрерывными производными второго порядка по всем
трем аргументам. Рассмотрим на функциональном пространстве Сх всех
х) Александров и Колмогоров, Введение в теорию функций дейст-
действительного переменного, ГТТИ, 1935.
2) Можно доказать, что всякий линейный функционал в С имеет вид A2)»
§ 46] ВАРИАЦИЯ ДЛЯ ПРОСТЕЙШЕГО ФУНКЦИОНАЛА 93
диференцируемых функций у (х), обладающих непрерывной производной,
причем за расстояния г (у, ух) между функциями у (х) и ух (х) примем
их близость первого порядка. Пусть у(х) и уг(х) — две функции, вхо-
входящие в Су Обозначим их разность символом 8у = 8у (лг) =yt (х) —у (х);
очевидно, Ьу обладает всюду непрерывной производной:
± оу=у\ (х)—У (х) = 8/ (х).
Имеем:
ъ
f(x, у ~г 8у» У "Ь ^У) —f(x, у у У)} dx =
а
Ъ Ъ
где черточка над вторыми производными fyy, fyy>, /у означает, что^они
берутся для аргументов дг, у-\-Ъхс>уу /-\-Ь^Ьуг (I6J-O, |62|<1).
Пусть е — г(у, у^)у т. е. s есть больший из максимумов \Ъу\ и | Ьуг J
на интервале [а, Ь\\ пусть N—наибольший из максимумов функций
Лу> fyv» fyy от тРех пеРеменных х, у, /, где
у' (х) — r(yv у)<у' < у\х) -\- г Су, У).
Очевидно,
Следовательно, этот интеграл стремится к нулю быстрее, чем г {у, у{).
Таким образом с точностью до величины порядка высшего, чем г (у, ух),
разность J{y±) — J(y) совпадает с интегралом:
Этот интеграл есть линейный функционал от оу(лг), следовательно:
ь
*J(y) = f ifyly+f,•*/)**.
a
Необходимое условие экстремума — обращение в нуль bJ(y) для
любой функции ?у(лг) — выражается теперь так:
ь
S/(V) = ((/, Зу +// ?) dx = 0.
94 ФУНКЦИОНАЛЫ И ВАРИАЦИИ [ГЛ. VII
Мы видели (§ 41), что диференциал df (A\ h) функции /, опреде-
определенной в линейном пространстве, при переходе от точки А к точке
A-{-h равен:
В частности вариация %J(y) должна равняться:
. A3)
В курсах вариационного исчисления часто определяют вариацию
непосредственно формулой A3).
Преобразования Лагранжа и Дю-Буа-Реймонда. Под знаком инте-
интеграла в выражении первой вариации стоит линейная функция от Зу
и оу\ Путем интеграции по частям можно преобразовать вариацию так,
чтобы под знаком интеграла стояла линейная функция только от Ьу
(так называемое преобразование Лагранжа) или о/ (преобразование
Дю-Буа-Реймонда^.
Интеграцией по частям получаем:
ъ ъ
а а
Если принять, что в точках а и b вариация равна нулю, то
Следовательно:
ъ ъ
У (у) = f(fv by +/.. 8/) dx = f (fy — ^ //) ЗУ dx.
a a
Это выражение мы получили также в § 31, рассматривая функцио-
функционал J(y) как предел функции от полигона и 87 (у) — как предел дифе-
ренциала этой функции.
Заметим, что мы считали функцию у(х) обладающей непрерывной
производной. Но У мы не считали диференцируемой. Поэтому преоб-
преобразование Лагранжа a priori незаконно.
Чтобы устранить добавочные гипотезы о существовании второй
производной У', Дю-Буа-Реймонд дал другое преобразование вариации.
Именно, обозначая
имеем:
§ 47] ОСНОВНЫЕ ЛЕММЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 95
Далее, интегрируя по частям:
ъ ъ
(*^hydx = [Nty]*— f№/dx.
J dx y L ^J« J y
a a
Полагая, как раньше, что Ьу в точках а и Ъ исчезает, получим:
ъ
Это преобразование не требует дополнительных гипотез о структуре
функции у(х).
§ 47. Основные леммы вариационного исчисления
Лемма Лагранжа. Пусть непрерывная функция М(х) обладает
тем свойством, что, какова бы ни была функция ч\ (х), имеющая
непрерывную производную и обращающаяся в нуль в точках а и Ь,
всегда:
При этих условиях М(х)еебО при всех х {а
В самом деле, пусть в некоторой точке с {а < с < Ъ) ф
например М(с) > 0. Отсюда в силу непрерывности М(х), при доста-
достаточно большом п, можно построить интервал лг0, хо-\-— , заклю-
заключенный внутри [а, Ь] и заключающий точку с, на котором М{х) больше
некоторого положительного числа т. Определим теперь функцию tj (л:)
следующим образом:
sin2 [п (х — лг0)] на интервале дг0, xQ-\~— L
ч(*)= L nJ
[ 0 вне интервала.
Функция ч\(х) непрерывна и обладает непрерывной производной,
т) (Ь) = т] (а) = 0. Следовательно, мы должны были бы иметь:
а
НО
ъ
f M{x)ri{x)dx =
а
=s / M(x)s\rPn{x — xo)dx> m I sin2n(x—лг0)dx = ^f > V-
Итак, гипотеза М(х) ф 0 где-либо на интервале [а, Ь] ведет к проти-
противоречию.
96 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
Из этой леммы из выражения для вариации:
b
и из требования, чтобы bj обращалось к нулю для произвольной функ-
функции Ъуу обладающей упомянутыми свойствами, Лагранж вывел уравне-
уравнение Эйлера: j,
ff0
Этому уравнению должна удовлетворять функция у=у(х), дающая
ь
J=ff(x,y,/)dx.
экстремум интегралу
ь
Кривые, удовлетворяющие уравнению Эйлера, называются экстремалями.
Вывод Лагранжа уравнения Эйлера содержал неточность, которую
мы отметили при определении преобразования Лагранжа.
ЛЕММА ДЮ-БУА-РЕЙМОНДА. Если для непрерывной функции М(х)
при любой непрерывной функции г\ (х), обладающей непрерывной про-
производной Tj (а) = т) (Ь) = 0, интеграл
ь
ГМ(х)г{(х) dx = О,
а
то М (х) постоянна во всем интервале [а; Ь).
Пусть М (х) не есть константа, тогда существуют на интервале [а, Ь]
по крайней мере две точки сг и с2, в которых функция М(х) прини-
принимает неравные значения, например: М(с^) > М(с2). Пусть dl и d.2 —
пара чисел, удовлетворяющих неравенству:
Можно построить при достаточно большом п пару интервалов дг0, х0 -j- — I
.\хи хх -|-~ , заключенных в интервале [а, Ь], не пересекающихся и
таких, что в интервале м:0, л:0-|-— имеет место неравенство:
M{x)>di9
а на другом из выбранных интервалов:
М (х) < dr
Определим функцию т{ {х) следующим образом:
s\n-n(x — л:0) на интервале дг0, х0 -f- — ,
— s'm2n(x — ATt) на интервале х,,;^--}-—,
О в остальных точках интервала [а> Ь].
§ 47] ОСНОВНЫЕ ЛЕММЫ ВАРИАЦИОННОГО ПРОСТРАНСТВА 97
X
Функция т|(х)= / if (x)dx непрерывна, обладает непрерывной про-
а
изводной if (x), и, кроме того, ?)(#) = О,
ь
/
= / sin2n(x— а*0) dx— / sin2n(x— xx)dx = 0.
xQ xx
По условию,
ь
f M(x) rf (x)dx= 0,
a
но, с другой стороны:
ъ o+ll
J ()( e) dx —
х0
Г M(x)rf{x)dx= J
— j M(x) sin*n (x — хх) dx > (dx — d2) J sin*nxdx> 0,
Xt 0
Итак, гипотеза приводит к противоречию.
Полный вывод уравнения Эйлера. Из леммы Дю-Буа-Реймонда легко
получить полный вывод уравнения Эйлера. Пусть дан класс допустимых
линий у=у(х)9 где у(х) есть функция, обладающая непрерывной про-
производной, причем все функции у(х) принимают при х=а и х = Ь
заданные значения у0 и yv На этом классе функций определен функ-
функционал
ъ
где/—непрерывная функция всех аргументов с непрерывными частными
производными первых двух порядков. Допустим, что функция у=у(х)
из класса допустимых линий дает относительный слабый экстремум функ-
функционала /. В этом случае
ъ
bJ= f { — N-\-fy.)h/dx = 0
а
при любой функции оу, обладающей непрерывной производной и равной
нулю в точках а и Ь. На основании леммы Дю-Буа-Реймонда:
X
/уГ — M=fyr— J fydx = C (С— константа).
а
Это есть так называемая интегральная форма уравнения Эйлера.
93 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
X
Функция N(x) = / fydx непрерывна и обладает непрерывной про-
а
изводной N'(x)=fy. Следовательно, обладает непрерывной производ-
производной по х также fy> — С+ЛГ(дг):
Итак, мы получили уравнение Эйлера, доказав при этом диференцируе-
МОСТЬ фуНКЦИИ fy:
Пусть теперь в некоторой точке (jc, у) кривой у —у {х) имеем:
Лу * о.
При переходе от точки с абсциссой х этой кривой к точке с абсцис-
абсциссой х-\-Ьх функции у(х) и yf (лг) получают приращения Ду и Ау',
которые вследствие непрерывности у{х) и у' (х) стремятся к нулю
вместе Алг. Имеем:
где вторые производные fxy*$ /уу>, fy'y* с чертами наверху означают зна-
значения этих функций при аргументах
При Ад: ~> 0 эти выражения стремятся к fxy> (лг, у, У), fyy> (лг, у, У),
y'y'i** У>У)> иу следовательно:
отсюда:
Итак, у" (х) существует во всякой точке кривой ^ = жу(д:), дающей
экстремум и в которой /уу ф 0.
Точки экстремали у =у (х), в которых /уу ф 0, называются регу-
регулярными.
Итак, мы не только вывели уравнение Эйлера, но и доказали (чего
мы заранее не предполагали) существование второй производной у" (х)
во всякой регулярной точке кривой, дающей экстремум.
§ 48. Вариация в точке. Инвариантность уравнения Эйлера
Определение функциональной производной. Вариация функционала
есть его диференциал. Попытаемся распространить на случай функ-
функционала другое основное понятие диференциального исчисления,
именно понятие частной производной. Пусть имеем функцию полигона
и У2>***> Уп) (см- § ^)» Мы знаем, что -j производная по орди-
§ 48] ВАРИАЦИЯ В ТОЧКЕ. ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ЭЙЛЕРА 99
нате yif есть предел отношения приращения функции F> когда орди-
ордината у% получает приращение Ьуг к площади, заключенной между поли-
полигоном (yv у2,..., уп) и измененным полигоном (yv у%у.. .,
В случае функции от линии мы не можем, не нарушая ее непре-
непрерывности, изменить одну ординату этой линии. По этой причине при
распространении понятия частной производной на функционалы мы
будем рассматривать приращения функционала, когда линия будет варьи-
варьироваться лишь в непосредственной близости от точки, в которой мы
желаем определить аналог частной производной.
Итак, пусть дан функционал:
J(?) = f F(x,y,/)dx
и кривая у=у(х)> на которой функционал J принимает определенное
значение. Мы будем предполагать во всем дальнейшем, что у=у(х)
обладает первой и второй непрерывными производными, a F—непре-
F—непрерывными частными производными до второго порядка включительно по
всем аргументам. Допустим, кроме того, что кривая у=у(х) не при-
принадлежит границе области, задания J, т. е, что для всех линий, доста-
достаточно близких к линии у=у(х), функционал / также определен.
Построим кривую
близкую к кривой у=у(х); пусть при этом yl(x) совпадает с у(х)
для всех значений лг, лежащих вне малого интервала [xv лг2], содержа-
содержащего некоторую избранную абсциссу с (хг < с < х2). Допустим, кроме
того, что в интервале [xv x2] вариация Ьу сохраняет знак. При этих
построениях кривые у (х) и yt (x) определяют некоторый бугорок,
возвышающийся над кривой у(х)\ площадь этого бугорка будет равна
>;= j bydX
Функциональной производной в точке с мы назовем предел отноше-
отношения приращения функционала J(y^) — J(y) к площади а, когда бугорок
стягивается в точку.
Легко видеть, что, не делая дополнительных гипотез относительно
закона стремления к нулю площади о, рассматриваемый нами предел
отношения в общем случае существовать не будет. Почтой причине,
принимая площадь а за бесконечно малую первого порядка, мы будем
считать, что (х2—л^) г2 (yv у) есть бесконечно малая высшего порядка
[где г (уи у) есть близость первого порядка кривых у(х) и уг(х)].
!) Если а будет отрицательна, то бугорок будет расположен под кривой
у = у (jc): by будет отрицательна.
100 функционалы и вариация [гл. VII
Условие будет выполнено, если, например, Ъу определить следующим
образом:
8 [ ±(л:2 —лг/бш^ДЗ^ при л:1<лг<д:2,
I 0 вне интервала \xv аг2],
и считать а > 2. Докажем, что при сделанных дополнительных гипо-
гипотезах функциональная производная существует в каждой точке интер-
интервала [а, Ь] и равна левой части уравнения Эйлера.
Имеем:
В силу гипотезы относительно непрерывности у (л:), у" (лг) и частных
производных функции F вдоль линии у=у(х) имеем:
где ео(х) есть непрерывная функция от лг, бесконечно малая вместе
с \х — с\. Кроме того, обозначая через Му N, Р соответственно зна-
значения Fyy, Fyy4 Fy>y', при х = с, у=у(с), / =/(с), получим для
< <
, у (х) + 68/) =
Fy'y' (х> У (х) + %, У (х) + ЬЬУ) = Р + е3,
где все ei стремятся к нулю вместе с r.(yv у) и (х2 — л^).
Обозначим через
при достаточно малом а, а, следовательно, достаточно малом е,
/ (Fiyty2 + 2Fyy'b 8У + Fy'yfPj/2) d
Так как множитель при 2R — величина порядка высшего по сравнению
с а (по предположению), то
Здесь функции Z7^^ Z7^^ Fy,y, взяты для значений аргументов
х9 у (х) + Qby (дг), у (дг) 4- боз/^ (х); 0 < б < 1.
§ 48] ВАРИАЦИЯ В ТОЧКЕ. ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ЭЙЛЕРА 101
где е4 бесконечно мало вместе с о, или
Таким образом уравнение Эйлера выражает тот факт, что в случае
экстремума J функциональная производная равна нулю в каждой точке.
Вариация в точке. В приложениях наряду с понятием функциональ-
функциональной производной оказывается очень плодотворным понятие вариации
в точке, являющейся аналогом понятия частного диференциала из тео-
теории функций п переменных.
Вариацией функционала / в точке х для кривой у=у(х) мы
назовем произведение функциональной производной функционала J
в точке х на площадь о бугорка, заключенного между кривыми у(х)
и ,{х) + Ьу(х):
Если кривая у=у(х) и вариация 8у удовлетворяют перечисленным
выше условиям, то вариация bxJ в точке есть главная часть приращения
функционала, когда мы варьируем кривую в непосредственной близости
от точки х.
Очевидно, что если мы проварьируем кривую у=у(х) в бесконечно
малых окрестностях точек: xv х2, ..., хк и обозначим через ои а2,..., ак
площади соответствующих бугорков 2), то главная часть приращения функ-
функционала будет равняться сумме вариаций функционала в точках:
Подобно тому как полный диференциал есть сумма частных диферен-
циалов, вариация функционала есть сумма его вариаций во всех точ-
точках. Равенство нулю вариации эквивалентно равенству нулю вариации
во всех точках.
Инвариантность уравнений Эйлера. Данное нами определение
функциональной производной в точке можно использовать для получе-
получения одного важного свойства экстремалей.
Сохраним обозначения предыдущего параграфа. Перейдем от системы
координат (лг, у) к криволинейной системе координат (я, v):
I ф 0.
Кривые 7* У=у(х) и ft* y=yi(x) B новых координатах будут выра-
выражаться соответственными уравнениями:
v = v (и), v = vx (и).
*) Стремление а к нулю надо понимать в смысле одновременного стремления
к нулю (х1—хг) и г(уи у).
2) Мы, конечно, здесь предполагаем, что вариации кривой в отдельных
точках удовлетворяют отмеченным выше условиям.
102 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
Бугорок, заключенный между обеими кривыми, имеет в новых коор-
координатах площадь о1# Отношение площадей этого бугорка в старых и
цовых координатах ~ стремится к функциональному определителю:
не равному по предположению нулю, когда бугорок стягивается в точку.
Функционал
a
переходит в функционал от функции v{u):
ьх
7(ву)=гУ1(^)= / /Н^р (й, *У)ГЛ(и> V)> ~
J L * * Чи
— / ^i(tt» ^ v')du.
Если г( . J( .
lim . = ()р
то в силу сделанных замечаний
lim Чу\)~
liA \J{y\)—J{y) m О_0
Функциональная производная от Jx{v) в каждой точке кривой f
обращается в нуль. Итак, если f является экстремалью для функцио-
функционала J(y\ то ^ является также экстремалью для Jl(v). Свойство кри-
кривой быть экстремалью инвариантно относительно преобразования
координат.
Аналитически это означает: если кривая у=у(х) являлась экстре-
экстремалью для интеграла J[y(x)], то всякий однозначный участок кривой
v=zv(u)9 определенный уравнением:
v)=y[o(u, v)]9 A4)
будет экстремалью для интеграла /j [*>(«)]; уравнение A4) будет инте-
интегралом уравнения Эйлера:
ЦЪ — АОй — о (\5Л
dv dvdv' — V' W
Таким образом: если общий интеграл уравнения Эйлера:
dF d dF _n
~ty~"fadx' — "'
для интеграла J[y(x)] будет:
у=у(х, а, р),
то общий интеграл уравнения Эйлера A5) для интеграла Jt[v(и)]
§ 48J ВАРИАЦИЯ В ТОЧКЕ, ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ЭЙЛЕРА 103
Уравнение Эйлера останется также инвариантным, если мы будем
задавать кривые f в параметрической форме; в геометрических задачах
эта форма задания линий особенно удобна потому, что позволяет нам
сразу освободиться от условия, что каждая кривая класса допустимых
линий пересекает параллель оси Оу в одной точке. Этому вопросу мы
дальше посвятим специальную главу.
Укажем сейчас на два приложения принципа [инвариантности урав-
уравнения Эйлера.
Пример 1. При исследовании и интегрировании уравнения Эйлера часто
используется замена переменных. Пользуясь принципом инвариантности, можно
это преобразование производить над подингегральным выражением и затем для
нового интеграла писать уравнение Эйлера — это и будет первоначальное урав-
уравнение, отнесенное к новым переменным.
В качестве примера рассмотрим интеграл:
= J
Семейство экстремалей определится уравнением:
г , d
Y~r
Заменой переменных
х = г cos 9, у = г sin <f
подинтегральное выражение перейдет в У1+У2 Же, следовательно, при той же
замене переменных уравнение A6) перейдет в
с общим интегралом:
Отсюда общий интеграл уравнения A6) будет:
г sin cp =s ar cos cp -f- p.j
Пример 2. Пусть дан функционал/(y), определенный для всех простых дуг y,
обладающих непрерывно вращающейся касательной, и пусть для линий Yt заданных
в прямоугольных координатах уравнением у=у(х) [функция у (х) и ее произ-
производная уг (х) однозначны и непрерывны], имеем:
о
= Г
Допустим теперь, что среди всех линий у (соединяющих две данные
точки А и В), на которых J (у) определен, существует линия то» дающая экстре-
экстремум /(y) и не изображаемая функцией у —у (х) класса С1 (существуют каса-
касательные То» параллельные оси Оу, некоторые параллели оси Оу пересекают кри-
кривую Yo по крайней мере в двух точках). В силу принципа инвариантности легко
видеть, что линия Yo будет интегральной кривой уравнения Эйлера
FFQ
В самом деле, мы всегда можем выбрать такую криволинейную систему
координат (ut v) так, чтобы в этой системе координат искомая кривая Yo изо-
изображалась функцией v = v(u) класса С}, но тогда Yo будет интегралом уравне-
уравнения Эйлера, написанного для J в системе координат (и, v), следовательно, в силу
104 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
принципа инвариантности уравнения Эйлера кривая ?о будет также интегралом
уравнения A7).
В качестве примера на приложение этого замечания можно указать на
задачу о линии наилучшего ската, когда начальная скорость равна нулю (§ 27).
В этой задаче экстремаль, удовлетворяющая начальным условиям, имеет в на-
начальной точке касательную, параллельную оси Оу, т. е. не принадлежит классу Сг.
В качестве второго примера отметим такую задачу: среди всех линий, соеди-
соединяющих две данные точки А к В, определить ту, которая при вращении около
оси Оу дает поверхность наименьшей площади. Мы видели, что если точки А я В
не слишком удалены одна от другой по сравнению с их расстоянием до оси Оу,
то искомая кривая есть цепная линия с осью симметрии, параллельной оси Ох,
линия, которая может пересекатьса параллелью оси Оу в двух точках и
тем самым может не принадлежать классу Ол Тем не менее эта кривая,
в силу принципа инвариантности будет удовлетворять уравнению Эйлера для
интеграла
А г
=2гс / лгу 1
выражающего площадь поверхности для кривых у =у (х) класса Сг.
§ 49. Вторая вариация и условия Лежандра
Билинейный и квадратический функционалы. Как мы видели
в теории функций п переменных, поведение функции в окрестности
стационарной точки определялось во многих случаях поведением квадра-
тической формы — именно второго диференциала функции (гл. IV). Эти
рассмотрения можно перенести на функции, заданные в линейном про-
пространстве (§ 41, 42), в частности — на изучаемые нами функционалы.
Прежде всего определим понятие билинейного и квадратического
функционала (ср. § 40). Мы называем функционал J(yyz) от двух функ-
функций у{х) и z{x) билинейным, если он есть линейный функционал
в отдельности относительно у(х) и относительно z(x).
Имеем:
J(ky, lz) = klJ(y, z).
Билинейный функционал J(y, z) называется симметрическим, если
для любой пары функций у{х) и z (x)
Квадратинеским функционалом У (^называется симметрический били-
билинейный функционал от двух совпавших функций:
J(y) = J(y,y)> 09)
где J(y, z) — билинейный симметрический функционал. Из A8) и A9)
следует: •
§ 49] ВТОРАЯ ВАРИАЦИЯ И УСЛОВИЯ ЛЕЖАНДРА 101>
Ъ
Tlpimepl.J(yfz)=/A(x)y(x)z(x)dx есть билинейный симметрический
а
функционал на С. ъ
есть соответственный квадратический функционал.
ь
Пример 2. J(у, г) = / [Ayz -f- В (yz' 4- zy') + Су'*/] dx есть билинейный
а
симметрический функционал в пространстве Cj всех функций, определенных
на отрезке а <; х <; ^.
6
= /'(Л^2 + ЧВуу' + Cyt) dx
а
есть квадратический функционал в том же пространстве.
Второй диференциал. Перейдем теперь к исследованию функциона-
функционалов вида: ъ
заданных на пространстве кривых класса Ci с фиксированными концами..
Разлагая в ряд Тейлора функцию / и вводя обозначение:
где Ьу (а) = Ьу (Ь) = 0, имеем:
^ dx, B2>
где
fyy =fyy [*. У W + 63^ (*)э У (х) -Г в«У (*)] ( I в | < I)-
и аналогично определяются/^, и /~у. При достаточно малом r(yv уУ
(расстояние понимается в смысле близости первого порядка):
где maxjej), maxje2|, max|e3| стремятся к нулю вместе с г (у,
Имеем:
где
о
• = /(•1 8^ + 2ч 8y*y + «e«/s
106 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ [ГЛ. VII
Так как
ТО
где ш1 и еб равномерно стремятся к нулю вместе с г(у9ух). Так как
\Sy\<rO>,yi), \?\<г(у,у1),
то
| в К (max | е41 + max | з61) гС^J.
Пренебрегая величинами порядка выше г(у,у$*, имеем из B2):
ягде 8J есть первая вариация функционала /:
Квадратический относительно Ьу функционал 82/ есть второй дифе-
ренциал функционала J< Мы будем его называть второй вариацией J.
Условие Лежандра. Рассмотрим однопараметрическое семейство
функций:
Рассматривая
iHa этом семействе как функцию t> получаем:
Ьу 3/ +/, у 8/а) dx B3)
Необходимое условие минимума J заключается в том, чтобы для
любой допустимой вариации оу
. B4)
или, что то же, вторая вариация 827 была неотрицательным квадрати-
ческим функционалом (§ 42).
§ 491 вторая вариация и условия лежандра 107
Так как 8у (л) =з 8у (*) = 0 и
ь ь ь
2 //„' Ь ? dx = f /„. d (8у») = - f± (/„.) by* dx,
a a
TO
ь
82/ = [ {Ply* 4- i?8/2) dx,
где
Установим сейчас одно необходимое условие неотрицательности формы:
ь
ТЕОРЕМА ЛЕЖАНДРА. Для того чтобы квадратический функционал
был неотрицательным, необходимо, чтобы на отрезке а
удовлетворялось неравенство:
Допустим, что для некоторого х0 (а <; х0 <; Ь)
В таком случае в силу непрерывности R(x) мы можем предполагать,
что на некотором сегменте [аг, Ьх] длины h > 0, заключающем точку
х0 и содержащемся в сегменте [a, ft], имеем:
/?(*)<— р
при аг <; х <; ftj (ftx = flij -\- А). Обозначим через Ж максимум |Р{дг)|
в интервале [д, ft] и построим функцию оу = 8у(лг):
sin2ir x~~.ai при «i<<ft1,
h ^ B5)
0 в остальных точках интервала.
Построенная функция 8у(дг) принадлежит классу Cv Имеем:
ь ъх
//-
J
a at
/ R—*
108 ФУНКЦИОНАЛЫ И ВАРИАЦИЯ (ГЛ. VII
При h достаточно малом Mh ^—становится отрицательным.Выбрав
соответственно h и подставив в B5), получим функцию 8у(лг), для
которой
ь
j(Р8у2 -J- #8/2) dX < 0.
а
Отсюда следует необходимое условие минимума:
УСЛОВИЕ ЛЕЖАНДРА, Для того чтобы экстремаль у =у (х) реали»
зовала минимум функционала
ъ
J=ff{x,y,y')dx,
а
необходимо, чтобы вдоль экстремали выполнялось неравенство:
Аналогично: для тою чтобы экстремаль у=у(х) реализовала
максимум функционала
необходимо, чтобы вдоль экстремали выполнялось неравенство
Для доказательства достаточно вспомнить, что необходимым усло-
условием минимума является неотрицательность второй вариации, и приме-
применить только что полученный результат.
ПРИМЕНЕНИЕ МЕТОДА ВАРИАЦИЙ
ГЛАВА VIII
НЕПОСРЕДСТВЕННОЕ ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ
ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
§ 50. Пространственная задача
Постановка задачи. До сих пор мы ограничивались рассмотрением
задач, когда функционал зависел от линий, расположенных в плоскости.
Многие из приведенных нами физических примеров при незначительном
обобщении приводят нас к задаче разыскания экстремумов функцио-
функционалов, зависящих от пространственных линий. Такова, например, за-
задача о рефракции.
Допустим, что скорость распространения света в неоднородной
среде есть заданная функция точки пространства (х, у, z):
требуется определить путь луча света, проходящего через две заданные
точки A(xo,yo,zo) и B(xvyvzi).
Применяя снова изложенный выше принцип Ферма, эта задача при-
приводится к определению линии, двигаясь вдоль которой луч из точки А
в точку В попадет в кратчайшее время. Если
У=У(*)>
есть уравнение произвольной кривой, соединяющей две заданные точки,
то время Г, необходимое свету, чтобы распространиться из А в В
(вдоль этой кривой), выразится интегралом:
v{x,y,z) пХ-
Этим самым наша задача приводится к определению линии в про-
пространстве, вдоль которой интеграл Т принимает наименьшее значение.
Мы займемся сейчас задачей отыскания экстремума от функционала,
зависящего от линии, расположенной в пространстве трех и более изме-
измерений. Эта задача может быть сформулирована так. Дана функция
р^лл • • • > .у»; л'.л'. >Уп)
2п -|~ 1 переменных:
Уп> Ух,У*', • • • » У*
110 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
F непрерывна вместе с ее частными производными по всем аргумен-
аргументам до второго порядка включительно. Среди всех кривых
[у/ (х) непрерывны] пространства п -f- 1 измерений, соединяющих две
данные точки А(а0, Ьг°, . . ., Ьп°) и B(aub^,bJ, . . ., bnl), опреде-
определить ту, вдоль которой интеграл
J= J F(&yv • • • > л; л'.л'*• > Уп)dx
«о
принимает экстремальное значение.
Близость пространственных кривых. При рассмотрении простей-
простейшей задачи мы уточнили постановку задачи, вводя понятие „е-близости"
двух кривых и расчленив общее понятие экстремума на экстремум
абсолютный, относительный сильный и относительный слабый. Все эти
понятия могут быть непосредственно распространены на поставленную
нами сейчас общую задачу.
Принимая, что расстояние между двумя точками пространства h -j-1
измерения выражается формулой:
мы скажем: две кривые находятся в е-близости, если расстояние точек
кривых, имеющих одинаковую координату ху меньше е при любом х\
две кривые имеют е-близость первого порядка, если не только расстоя-
расстояние между указанными точками, но также расстояние между производ-
производными кривыми:
Ух =У\ О)» Л ==V (*). • • • » Уп =Уп (*)
меньше в. Вводя таким образом понятие е-близости, мы ничего не
меняя в принятых выше определениях е-окрестности разного порядка>
определениях абсолютного, относительного и т. д. экстремумов, полу-
получим эти понятия для нашей общей задачи.
Совокупность определенных нами кривых в гё-f-l-мерном простран-
пространстве, где в качестве окрестности принята окрестность первого порядка,
рассматриваемая как функциональное пространство, совершенно анало-
аналогична пространству Ci-
Необходимые условия экстремума. В этой главе мы остановимся
лишь на выводе основных необходимых условий, которым должна удо-
удовлетворять всякая кривая класса допустимых линий, вдоль которой инте-
интеграл J принимает экстремальные значения.
ТЕОРЕМА. Если кривая
у1=у1(х\ ... , уп=уп(х)
принадлежит классу допустимых линий и дает экстремальное значе-
5QJ
ПРОСТРАНСТВЕННАЯ ЗАДАЧА
111
Hue интегралу J, то функции:yl=y1 (х), ... , уп =уп(х) удовлетво~
ряют системе диференциальных уравнений *):
p fLpy,n = o.
Роль этой теоремы в приложениях та же, что и ранее разобранных^
аналогичных необходимых условий в других задачах вариационного
исчисления.
Система A) есть система п диференциальных уравнений с п неиз-
неизвестными функциями: ух (дг), у2 (л:), . .. , уп (х). Каждое уравнение
в общем случае есть уравнение второго порядка. Таким образом общий
интеграл этой системы будет содержать 2п произвольных постоянных:
Каждая кривая семейства B) носит название экстремали для дан-
данной задачи вариационного исчисления. Таким образом в силу теоремы
каждая кривая, дающая экстремум интегралу J и принадлежащая классу
допустимых линий, есть экстремаль.
Задача фактического определения искомой кривой сводится таким1
образом к определению общего интеграла системы A) и произвольных
постоянных осг При данной выше постановке задачи эти постоянные
определяются из 2п условий прохождения искомой кривой череа
точки А и В.
Перейдем к доказательству теоремы. Чтобы возможно меньше изме-
изменить методы доказательств, выработанные раньше, будем интерпретиро-
интерпретировать систему неизвестных функций: у1=у1(х), .. . , Уп=уп(х) как
систему п кривых, расположенных в различных плоскостях хОуи
хОу2У ... , хОуп. При такой точке зрения данное нами понятие вариа-
вариации кривой у=у(х) в данной точке можно непосредственно применить
к данной задаче. Допустим теперь, что кривая
Л=Л(*) (/=1,2, ...,я)
дает минимум; в таком случае при всевозможных вариациях (доста-
(достаточно малых) функций yi=yi(x) интеграл J должен увеличиваться.
Следовательно, он должен увеличиваться, когда все функции у{ при
/ф? остаются без изменения, а кривая yk=yk(x) варьируется. В соот-
соответствии с этим будем считать, что все yi=yi(x) (/ ф k) фиксиро-
Какой именно экстремум—сильный, слабый, абсолютный — это безразлично.
112 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
ваны, тогда / есть функция линии ук=ук(х). В силу сделанного за-
замечания и основного необходимого условия такой простейшей задачи
вариация этого функционала должна равняться нулю в каждой точке.
Следовательно:
О существовании у/. При выводе уравнений A) мы сделали гипо-
гипотезу, что все функции уг{х) имеют непрерывные производные. Запи-
Записывая уравнения A) в форме Дю-Буа-Реймонда, можно показать, что
при некоторых условиях искомая кривая будет обладать также не-
непрерывной второй производной. Имеем:
Us
Fi 4х-ру>к = с* (Л=1,2,...,я), C)
где Ск есть константа. Вдоль экстремали выражение:
а?
а0
есть непрерывная функция, обладающая непрерывной производной. За-
Запишем систему C) в форме:
Допустим теперь, что функциональный определитель А =
вдоль некоторой экстремали ук=ук(х) отличен от нуля, и пусть Ск
в системе D) отвечают экстремалиук=ук(х)\ тогда, каково бы ни было
значение х (ао^х^.хх), существует решение системы D) относительно
ук, совпадающее с ук'(х) и диференцируемое вместе с Qk(x). Отсюда
заключаем, что если вдоль эсктремали А ф 0, то эта экстремаль при-
принадлежит классу С2-
51. Вариация в точке в данном направлении. Принцип
Гамильтона
Вариация в данном направлении. Для случая пространственных
задач определение вариации в точке непосредственно не обобщаемо
потому, что местные изменения кривой можно делать в любом напра-
направлении. Пусть дан функционал
ъ
а
определенный на линии y> заданной в (п-\- 1)-мерном пространстве
ix9 У)., • • • > Уп) уравнениями:
Кроме того, 7 есть кривая класса допустимых линий.
Пусть Yi — соседняя кривая этого класса, заданная уравнениями:
§ 51] ВАРИАЦИЯ В ТОЧКЕ В ДАННОМ НАПРАВЛЕНИИ 113
Положим, что функции Ъу. равны нулю всюду, кроме интервала
[х0 — е, х0 -f- е]э где х0 (а <; лг0 ^ Ь) — абсцисса некоторой точки ?.
Векторы с компонентами:
«х = 0, iyv .... 8ув,
соединяющие точки кривой f с точками (имеющими те же абсциссы х)
кривой -fi» будем считать параллельными на нашем интервале [дг0 — в,
хо-\-г]. Если обозначить через 8л длину соответственного вектора и
через рг его направляющий косинус по отношению к оси Oyv то
8yf = p48/z, причем pf постоянны для всех наших векторов. Имеем:
f
r0 - 9 i ¦-- l
П J7 4" e
/
i = l
При достаточно малом з имеем:
4
i l
где 8^V суть площадь цилиндрической поверхности, заключенной между
j и fj, образованной векторами Ъп. Итак,
Отсюда следует, что
w -^'^ГйЧ^- E)
онимается в том смысле что $п -т-
Стремление к нулю 8Л понимается в том смысле, что $
стремятся к нулю.
Выражение E) будем называть -вариацией функционала J в дан-
ной точке М(хо,уг) в данном направлении (pitp2y •••» Рл)-
Уравнение Эйлера означает, что вариация функционала J в любой
точке экстремали в любом направлении обращается в нуль. Наоборот,
если во всякой точке кривой сравнения вариация в ней по любому
направлению равна нулю, то кривая есть экстремаль, вариация функцио-
функционала равна нулю.
В § 48 мы доказали инвариантность уравнения Эйлера для случая
одной неизвестной функции. Совершенно аналогичные рассуждения по-
показывают, что система уравнений Эйлера
dyt dx ду/ v ' *¦
сохраняет свой вид, если мы перейдем от координат (xyyvy^ ..., уп)
к произвольным п -f-1 криволинейным координатам.
114 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Принцип Гамильтона. Пусть мы имеем механическую систему без связей,
состоящую из п точек, имеющих массы: }ть т2, ... , тп\ обозначая через.
(•** Ун zi) координаты /-й точки, имеем для кинетической энергии системы:
Пусть G Гесть потенциальная функция системы, зависящая otJ Sn координат
всех точек. Из ее определения следует, что силы, действующие* на i-ю точку,
имеют компоненты:
dG dG dG
дх, ' дуг ' dz% '
Силами инерции называются силы с компонентами:
приложенные к соответствующим точкам системы. Они, будучи приложенными
к точкам системы, уничтожили бы ее ускорение.
Пусть мы имеем некоторое движение системы, определяемое Зл функциями:
и пусть в некоторый момент I система занимает положение, определяемое 3/г
координатами ее точек. Пусть каждая из этих точек получает смещение oxh
Ьуь bzt. Принцип Даламбера для динамической системы без связей гласит:
Если к действующим на точки нашей системы силам добавить силы
инерции, то их совместная работа вдоль любого смещения равна нулю:
S[7 dG d**<
—1
Обозначив через
» = 1
получим;
Выражение
VI / dG , dG . dG
есть не что иное, как вариация в точке интеграла \G dt (напомним, что G зависит
только от координат), а выражение — ^ /я4 {r-^-Pi + ~jj?- Яг + -^gsr
есть вариация в точке от / Тdt\ обе вариации взяты в направлении pitqitrh
Следовательно, принцин Даламбера означает уничтожение вариаций по любому
направлению интеграла J (G + Т) dtt взятого по траектории хх == дг; (/), Уг
2* = zi(*)- А это означает (см. выше), что вдоль траектории:
§ 51] ВАРИАЦИЯ В ТОЧКЕ В ДАННОМ НАПРАВЛЕНИИ 115
(Зл-f- 1)-мерного пространства имеем:
O. F)
f
to
Равенство F) выражает принцип Гамильтона. Интеграл F) имеет размерность
см2
, т. е. размерность действия.
сек
Кривые сравнения:
*i = *« @ > У г = У1 @, ** = *i W
в (Зл + 1)-мерном пространстве (/, хь уь zt) соединяют те же точки [/0, a*, (t0),
Уг Со), *< (АЛ. №l» ** й)> ^ Й), *< й)]. что и кривая хг = х, (/), ^ = уг (t), z{ = *, (/).
Перейдем теперь от системы Ъп координат (хь yit z{), определяющих дви-
движение, к любой системе координат qb qb ... , qSn путем преобразования:
| = 1* 2, ..., л).
Кинетическая анергия обратится в некоторую квадратическую форму:
от производных новых координат по времени; afj зависят от координат
qx (*=1, 2, ..., п). Потенциал G перейдет в функцию от новых координат qt.
При переходе к новым координатам, очевидно, условие F) сохраняет свою силу.
Уравнения Эйлера для F) дадут нам:
io+il-Ai^o, G)
&4i dqt dt bq%
где через q% мы обозначаем --— #
Уравнения G) носят названия уравнения Лагранжа в механике.
Мы приняли за исходный пункт принцип Даламбера, вывели из него прин-
принцип Гамильтона и как следствие последнего — уравнение Лагранжа. Эти три
формы общих уравнений механики эквивалентны, и мы могли бы за исходную
точку принять любую из них. Принцип Гамильтона имеет ряд преимуществ
перед другими формами. Уравнение F) не зависит от системы координат, и
этим свойством инвариантности часто удобно пользоваться: мы уже восполь-
воспользовались им при выводе уравнений Лагранжа. Вариационная форма уравнений*
механики была использована Гамильтоном при построении его теории инте-
интегрирования этих уравнений (подробно эта теория будет изложена во втором
томе).
Так как Т есть квадратическая форма относительно ди то:
Выражение —г- называют обобщенным импульсом.
Пусть потенциальная энергия G и кинетическая Г не зависят в явной форме
от времени /. В этом случае имеем:
Вп
116 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Отсюда в силу (8):
H= — G+T=*Ct (9)
где С—постоянная величина. Выражение И есть не что иное, как полная энер-
энергия системы, и соотношение (9) выражает известный закон сохранения механи-
механической энергии.
С физической точки зрения принцип Гамильтона интересен тем, что в его
формулировке участвуют не координаты, а энергия потенциальная и кинети-
кинетическая. Поэтому этот принцип был распространен на физические процессы,
в которых кроме механической участвовали другие виды энергии (электриче-
(электрическая, тепловая и др.). Этот же принцип сохранился при переходе от классиче-
классической механики к механике релятивистической.
§ 52. Вторая вариация. Условия Лежандра
Вывод необходимых условий экстремума. Пусть в классе d
допустимых линий, расположенных в пространстве л-j-l измерений
(x,yv ...,yn) и заданных уравнениями уг=у%(х) (/=1, 2, ..., я),
выбраны две близкие кривые 7 и iv Пусть
I {ie lf 2, ..., л; v4(*) в
суть уравнения этих кривых. На классе Сг определен функционал
ь
( {? A0)
а
Имеем:
ь
,)-/(т) =
- /*Y(F8v
а
b
а
Ъ
где 8 есть величина высшего порядка сравнительно cr(y, fi)- Выражение
есть главная линейная часть приращения (вариация). Если Y есть экс-
экстремаль, то 8/== 0 и главной частью приращения становится квадрати-
ческий функционал (форма) от 8yif т. е. вторая вариация:
ь
Необходимое условие того, что f реализует минимум У, заключается
в силу общих соображений в, конце предыдущей главы в том, что
форма 8U неотрицательна.
§ 52]
ВТОРАЯ ВАРИАЦИЯ. УСЛОВИЯ ЛЕЖАНДРА
117
ТЕОРЕМА (условие Лежандра). Необходимым условием неотрица-
неотрицательности второй вариации является неотрицательность формы
во всякой точке М экстремали, или, что то же самое, выполнение
неравенств:
F F
F F
У,Ух У
>o
F
Г" УпУ'п 1
в каждой точке экстремали.
В самом деле, пусть в некоторой точке M(x,yvy2t ...>yn) экстре-
экстремали форма Ам принимает отрицательное значение. Приведем форму Лм
к каноническому виду линейным преобразованием
(/=1, 2, ...,л).
После приведения форма Лм (в точке М) примет вид:
при этом по крайней мере одно из собственных значений формы Ам>
например Х1Э будет отрицательным. После преобразований:
Ьуг = 2 <*<*4t 0# = 1, % •. ., Щ aik — постоянные)
и аналогичного преобразования производных:
ПодинтегральноеЛ выражение в 8V перейдет в
Ь22М*^;+2<ч
(i=lf
A2)
Здесь atj = а^, dtJ — bjv c{j = cj{ и являются некоторыми функциями
от х. В точке М
*« = *«. ^- = 0 при /фу.
Пусть Л — некоторое, достаточно малое положительное число, а от-
отрезок (х — Л, x-\-h) заключает абсциссу точки М. На куске экстре-
экстремали f, проектирующемся на этот отрезок, коэфициенты aiJt biJt c{j
совпадают с коэфициентами этих форм в точке М с точностью до ве-
величин, стремящихся к нулю вместе с к. Рассмотрим теперь следующую
вариацию экстремали у: вне отрезка [д:—A, x-\-h] вариация равна нулю:
^ = 0 (/=1, 2,..., л); на этом отрезке 82Г2 = 8-г3 ==...= 8^гЛ = 0,
что же касается bzv то он, равно как и его производная oz/, обра-
118 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
щается в нуль в конце отрезка, т. е. в точках х — hi x-\-h\ внутри
же этого отрезка он отличен от нуля. В этом случае выражение A2)
на отрезке [х — Л, x-{-h] сведется к
autej + UnbzxW + CnW2- A3)
Так как в точке М си==^1 < 0, то при достаточно малом h и на всем
отрезке [х — h, x-\-h]
сп < 0.
При этом вторая вариация примет вид:
. 8V= f (aniz\ + 2 V*M' + cnbzx'*)dx.
Знак этого выражения (см. § 49) при соответственном подборе функ-
функции oz1 совпадает со знаком clv который мы считали отрицательным.
Итак, если форма Ам в некоторой точке экстремали обладает хотя
одним отрицательным собственным значением, то вторая вариация 82/
может быть сделана отрицательной, отсюда и вытекает необходимость
условия Лежандра для минимума.
Пример. В принципе Гамильтона:
¦•/
О не содержит производных q{, а Т есть положительная определенная форма
ют этих производных:
Форма Ач для этого случая будет:
Ам =
Из положительности формы Т вытекает положительность формы Ам: усло-
условие Лежандра для минимума выполняется.
§ 53. Свободные концы. Случай конца, перемещающегося
по ординате
Постановка общей задачи. Во всех разобранных нами задачах за
класс допустимых линий мы принимали кривые, концы которых нахо-
находились в двух фиксированных точках. Сейчас мы перейдем к задачам
на определение экстремумов функционалов, принимая за класс допус-
допустимых линий более широкий класс.
Пусть дана функция F (дг, у, у'), удовлетворяющая обычным усло-
условиям непрерывности и диференцируемости; пусть, кроме того, в плос-
плоскости хОу даны две кривые © и ф:
У = ?(*)> У = Ъ(х)
класса Cv При этих обозначениях нашу задачу можно формулировать
следующим образом:
§ 53] СВОБОДНЫЕ КОНЦЫ. СЛУЧАЙ КОНЦА, ПЕРЕМЕЩАЮЩ. ПО ОРДИНАТЕ 119
Примем за класс допустимых линий совокупность линий у класса
d, имеющих концы соответственно на кривой с? и на кривой ф- Тре-
Требуется найти экстремум функционала:
где интеграл берется по линии у.
Заметим, что| пользуясь результатами гл. V или VII, мы можем не-
немедленно свести эту задачу к задаче на разыскание экстремума функ-
функции двух независимых переменных. В самом деле, если некоторая кривая
70 с концами в точках А и В решает поставленную задачу, т. е. если
70 дает экстремум интеграла среди всех линий класса допустимых ли-
линий, то эта линия Yo Дает экстремум J и среди всех линий класса Ci,
соединяющих точки А и В. Следовательно, в силу теоремы Эйлера
для простейшей задачи линия ^0 есть экстремаль. Отсюда, решая урав-
уравнение Эйлера: ,
мы получим двупараметрическое семейство кривых:
к которому будет принадлежать искомая кривая у0. Для определения fo
нам остается найти значение двух констант аир.
Пусть теперь х0 (а, Р), хг (а, C) суть соответственно абсциссы точек
пересечения линии / с кривыми ф и ф. Искомые значения а и р будут,
очевидно, давать экстремум следующего выражения:
j F { х, /«a, r?) f (х, а, ft } dx,
которое есть функция двух независимых переменных а и р.
Этот путь, принципиально возможный, практически очень громоздок,
по этой причине нашей ближайшей целью будет дать добавочные не-
необходимые условия, которым должна удовлетворять искомая кривая,
так чтобы из этих условий можно было непосредственно определять
произвольные постоянные а и ^.
Простейший случай. Начнем с рассмотрения простейшего случая,
когда кривые <р и ^ вырождаются в прямые, параллельные оси Оу:
х = а, х = д.
В этом случае наша задача ставится следующим образом:
Среди всех кривых класса Ci*. y—y(x) определить кривую, вдоль
которой интеграл: ,
J=fF(x,y,/)dx
принимает экстремальное значение.
Определяя, как обычно, вариацию функционала У как главную ли-
линейную часть приращения функционала при переходе от кривойy=zy(x)
120 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
к бесконечно близкой кривой уг = уг (х)~у(х) -f- ty (*), найдем
выражение этой вариации. Имеем:
ъ
(x> У» yi') — F{** У, У)] **'-=
dx -f гг (у, yt),
где г есть расстояние между кривыми — наибольшее из чисел max | Ьу
и max | by' |, a s стремится к нулю вместе с г. Итак, вариация нашего
функционала ZJ выражается так:
ь
j\ A4)
Согласно общей теории об экстремуме функционалов (гл. VII), если
кривая y=zy(x) дает экстремум функционалу У, то
при любой функции оу. Применив к выражению A4) преобразование
Лагранжа, получим:
ь
где Ъу0 есть значение оу при х — а — вариация у в левом конце, oyt
есть значение оу при х — Ь—вариация у в правом конце. В случае
экстремума вариация должна тождественно обратиться в нуль, следо-
следовательно, в, случае экстремума имеем:
Первое из полученных условий мы знали раньше, второе и третье
суть нужные нам условия на концах, те условия, из которых можно
определить произвольные постоянные а, ? в общем интеграле уравне-
уравнения Эйлера:
/>[*• П<*. ^ % Па, а, р)]=0, J
Полученные нами условия непосредственно применимы к задаче
разыскания экстремума интеграла
ь
F= f F(x, у. y)dx.
§ 53] СВОБОДНЫЕ КОНЦЫ. СЛУЧАЙ КОНЦА, ПЕРЕМЕЩАЮЩ. ПО ОРДИНАТЕ 121
когда за класс допустимых линий принимаются кривые класса Ci*
у=у(х), соединяющие данную точку А (с абсциссой а) и произволь-
произвольную точку прямой, параллельной оси Оу: х = Ь. В этом случае вариа-
вариация кривой в левом конце <>у0 должна равняться нулю, и из двух
условий на концах у нас останется одно:
Произвольные постоянные а и ;3 в общем интеграле уравнения Эйлера
мы можем определить, решая совместно второе уравнение из A7)
и уравнение /(я, а, $)=*у (а), где у (а) есть ордината данной точки А
Пример 1. Пусть дана точка А и вертикальная прямая L, не проходящая
через точку А. Но какой линии должна скатываться тяжелая точка, чтобы,
отправляясь с нулевой скоростью из А, достигнуть L
в кратчайшее время? А ^ ?
Предполагая, что искомая линия плоская, по- Lf
строим прямоугольную систему координат хОу: на-
начало координат поместим в точку А, ось Оу напра-
направим вертикально вниз, ось Ох пересекает прямую L
(черт. 17). При сделанной гипотезе искомая кривая
будет лежать в плоскости хОу.
Пусть х = а есть уравнение прямой Z,, в таком
случае наша задача на основании формулы C0 § 27
приводится к разысканию кривой, вдоль которой
интеграл
о,
J
УУ
Черт. 17.
принимает минимальное значение, причем за класс допустимых линий прини-
принимаются здесь линии класса Clf соединяющие начало координат с произволь-
произвольной точкой Z..
Согласно общей теории, если искомая кривая существует, то она есть эк-
экстремаль, т. е. в силу § 28 принадлежит семейству циклоид:
х = г F — sin 6) + С, у =5 г A — cos 6),
где г и С — произвольные постоянные. Из условия, что кривая проходит че-
через начало координат, и считая, что начальной точке соответствует 6 = 0,
получим, что С = 0. Остается определить г. Для этой цели воспользуемся
условием в конце.
В нашем случае:
F -
Следовательно, при х = 0 должны иметь у' = 0: в правом конце искомой
линии касательная к этой линии должна быть горизонтальна. Отсюда, прини-
принимая во внимание форму циклоиды, находим сразу кг —а.
Итак, окончательно искомая кривая есть:
а* = ~ @ — sin в), j/= — A —cos 9).
Пример 2. Балка со свободным концом. Балка АВ длины / закреплена
и конце А. Другой ее конец В свободен (черт. 18). На свободном конце В
к балке приложена нагрузка Р. Пренебрегая весом балки, определить форму
ее равновесия.
122 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Принимая за ось Ох горизонтальную проекцию балки, проходящую через
точку А, и обозначая через У ординату точки В, через а —угол наклонной
«асательной к балке в произвольной точке М, имеем:
i
Y— I dy~ I sin a ds.
J t/
АВ О
Потенциальная энергия сил тяжести (весом балки мы пренебрегаем) равна:
I
Потенциальная энергия упругих сил равна
г
i Pgsinads.
о
равна
Г J*'*ds,
о
da
•где а/г = -7—кривизна балки, /—модуль угругости. Отсюда общая потен-
потенциальная энергия:
U= f (Ja'* + Pg sin a) ds.
Конец А закреплен, в этом конце а задано: а = а0; в свободном конце В имеем
по только что доказанному /^, = 0, где F — подинтегральное выражение
/а'2 4-/>? sin а, т. е.
а' = 0.
В свободном конце кривизна балки равна нулю.
Уравнение Эйлера:
-с краевыми условиями: при $ = 0, a = d0, при s = l, a' = 0, определяет
yi профиль балки.
Черт. 19.
Пусть, например, ао = О. Если у~у(х) есть уравнение профиля балки, то,
считая, что профиль балки близок (в смысле близости первого порядка) к оси
Ох (черт. 19), имеем:
. dy dy
а = arctg -г- ~ -г-
s dx dx
Г мы пренебрегаем величинами второго порядка сравнительно су и -~-).
а
]> ds~dx*> ds*~ ds\dx*J ~dx*> J y
§ 54] УСЛОВИЕ ТРАНСВЕРСАЛЬНОСТИ 123
где а — абсцисса конца В). Уравнение балки примет вид:
= 0, /40 = 0.
Отсюда:
Условия на границах дают нам:
С> , /-* л с* __
и мы окончательно получаем:
При а0 = -^- вертикальная прямая а = -^- есть решение нашего уравнения
Эйлера, т. е. форма равновесия.
§ 54. Условие трансверсальности
Обобщение понятия расстояния между кривыми. Рассмотрим те-
теперь общий случай. Принимая за класс допустимых линий кривые у.
концы которых расположены на кри-
кривых (черт. 20):
•будем решать задачу на разыскание
экстремума интеграла 0
У = У F[(x, ^ /) rfx. Черт 20.
т
Новым в этой задаче, по сравнению с разобранным простейшим слу-
случаем, является то, что абсциссы концов двух различных кривых из
класса допустимых линий, вообще говоря, различны. Начнем с обобще-
обобщения понятия расстояния между кривыми. Итак, пусть ^:
У=У(х)
есть кривая класса Cv концы которой имеют абсциссы х0, xv и пусть ^:
другая кривая класса Cv концы которой имеют абсциссы хо-{-Ъхо,
х1-\-Ъх1. Рассмотрим совокупность М кривых класса С^. у=у(х),
заданных на отрезке [xQ, xt], концы которого не являются постоянными.
Будем обозначать такую кривую символом [у (лг); х0, хх]. Вне отрезка
[лг0, хх] функция у (х) не определена; мы можем ее распространить на
всю числовую прямую, полагая
\ У (*i) + (* — xi) У (*i) ПРИ x>xv
124 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [гЛ. VIII
Такое распространение будем называть распространением по касательным.
Определим расстояние в М:
{\xo-xQ\, \xi~~xQ\,y1(x)--y(x)\Xo.<x<Xot \yi(x)—y(x)\Xi<x<Xi.}.
Здесь х0' — меньшее из чисел х0, хо\ jc/— большее из чисел xvxv
Вывод вариации функционала. Назовем вариацией bj функционала
J при переходе от кривой f к кривой ^ главную линейную часть при-
приращения этого функционала, главную в том смысле, что:
^(Ti) —J(t) = ^(t) + v(Tp Т),
где е стремится к нулю вместе с г 1).
В случае экстремума должны иметь оУ===О. Займемся определением
U в общем случае. Имеем:
— f F{x, yv yi')dx+f
+/
, y, /)) dx a).
Обозначая ^ (л:)—y(x) — oy и пренебрегая величинами высшего по-
порядка сравнительно с г (^, ^j), т. е. отбрасывая бесконечно малые выс-
высшего порядка сравнительно с ол:0, Ъхх, Ьуу Ъу', имеем:
у F (х, yv yl')dx&bxl [F(x, у, /j]^.Ti,
хг
[F(x, yt,yx') — F (x, у, У)] dx « /(/=¦> + Fv, S/) rfx =
- -1 VJ'U,, - Ь t^8^x=,l+/ [^ - -ж-
а?о
x) Более детальное исследование понятия вариации с функциональной точки
зрения для этой задачи будет дано в следующем параграфе.
2) Для того чтобы иметь право писать это преобразование интегралов, оче-
очевидно, достаточно, чтобы функции у(х) и Ух(х) были определены для значений лг,
заключенных в интервале интеграции. Нами написанное соотношение имеет
место, если &лго>О и 5д:1>0. Если &*0<0, ^t<0, то первый интеграл надо
брать вдоль yt (х), а последний — в пределах от х0 до xv Наше преобразова-
преобразование надо также изменить для двух других случаев 1л:0>0, 5д:1<0 и «*0<0,
S>0. Какой из четырех случаев мы имеем— на дальнейшее не повлияет.
541
УСЛОВИЕ ТРАНСВЕРСАЛЬНОСТИ
125
После этого приращение функционала J примет вид:
Выразим значения Ьу в концах через 8л:0, &xv Начнем с 8у в правом
конце. Обозначая через В и С (черт. 21) точки пересечения ординаты,
соответствующей значению xv с кривой f и с кривой *\v а через К и
L — проекции С и Б на ординату, соответствующую значению хг -\-bxv
пренебрегая величинами высшего порядка сравнительно с bxv имеем:
КВ{« Ъхг [/ (хх)
СВ =
Отсюда:
С другой стороны;
следовательно:
Аналогично:
Подставив полученные выражения в A8), согласно определению 8У
получим:
Итак, пренебрегая членами порядка высшего сравнительно с г(^Лi)»
мы свели приращение J(^t)— J(t) к сумме линейного функцио-
нала
[F--
d
~~dx
FyA by dx от приращения by и линейных функций
от ЬхОу охх — смещений абсцисс концов. Это линейное выражение и
будет вариацией J.
Линейный функционал, входящий в выражение 8/, назовем вариацией J
в середине, а члены с 1х0, Ъхх — вариациями в концах: вариация в на-
начале равна:
вариация в конце равна:
126 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЛИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Вывод условий трансверсальности. Если вдоль кривой f интеграл J
достигает экстремума, то 87 = О, U должно равняться нулю при пере-
переходе ОТ f К ЛЮбоЙ блИЗКОЙ КрИВОЙ -)fl> в ЧаСТНОСТИ К КрИВОЙ fit
имеющей общие с f концы. Но в случае совпадения концов ^ и fr
од:о и bxt равны нулю, и 8у (х0) == Ьу (хг) = 0.
bJ-f[Fv-4rFy]bydx. A9)
«О
Выражение A9) должно быть равно нулю при произвольных 8у, обра-
обращающихся в нуль на концах интервала [х0, хг]. В силу результатов
предыдущей главы отсюда следует:
ty dx tV — U'
т. е. кривая у есть экстремаль.
Итак, в случае экстремума вариация интеграла J при переходе
к произвольной близкой кривой сводится только к вариации концов
(поскольку вариация в середине исчезает):
= - [F + («' -/) AVL-A + F+ W -У) ^
Следовательно, на концах кривой т должно иметь место:
W0, 1
так как ojc и охх — независимые переменные.
Условия B0) связывают угловые коэфициенты у' в концах кривой ^
с угловыми коэфициентами </ и ty кривых, по которым перемещаются
концы этой кривой. Условия B0) называются условиями трансверсаль-
трансверсальности. Полученный нами результат можно формулировать как теорему:
ТЕОРЕМА. Если кривая Г-
дает экстремум интегралу
т
среди всех кривых класса СР соединяющих две произвольные точки
двух данных кривых:
У У
то кривая у есть экстремаль, а в концах кривой f выполнены условия
трансверсальности B0).
Эта теорема дает решение поставленной нами задачи. В самом деле,
решив уравнение Эйлера, получим семейство экстремалей, зависящее от
двух параметров: 0 «
J У=/(х, а, рK
Абсциссы концов х0, хх кривой этого двупараметрического семейства
должны удовлетворять двум условиям трансверсальности и уравнениям:
f(xQ, а, Р) = ?(*о), f(xv <ц ft^
из этих четырех уравнений определяем лг0, xlr a,
§ 55] ДИФЕРЕНЦИАЛ В НЕЛИНЕЙНОМ МЕТРИЧЕСКОМ ПРОСТРАНСТВЕ 127
Если /7 = Л (х, y)Vl ~ЬУ2> т0 условие трансверсальности запишется
так:
или:
Если значение А в соответствующем конце отлично от нуля, та
равен нулю второй множитель, следовательно, направление касательных
к кривой ^ и к кривой, по которой скользит ее начало (или конец),
ортогональны.
Условие трансверсаль-
поста вырождается
/; условие ортогональ-
ортогональности.
Если один из кон- ?
цов кривой закреплен,
то условие трансвер-
трансверсальности должно со-
соблюдаться только для церт 22. Черт. 23.
свободного конца.
Пример. Найти кратчайшее расстояние от точки А до кривой Г (черт. 22).
Кратчайшее расстояние достигается по экстремали интеграла / Y\-\-yf(*dx,,
т. е. по прямой. Условие трансверсальности переходит в условие ортогональ-
ортогональности. Таким образом кратчайшее расстояние достигается по нормали к Г,
проходящей через точку А.
Аналогично кратчайшее расстояние между двумя кривыми (черт. 23) дости-
достигается по их общей нормали.
§ 55. Диференциал в нелинейном метрическом пространстве
Касательное пространство. В предыдущем параграфе мы опреде-
определяли диференциал — вариацию в функциональном пространстве, которое,
однако, нельзя считать линейным.
Совокупность кривых с расстоянием между ними, определенными
выше, концы которых лежат на кривых ф(лг) и й(дг):
образует метрическое пространство Т. Несмотря на то, что пространство Т
есть нелинейное прострартство, мы построим для определенного на нем
функционала
J= f F(x, у, /)dx
аналог понятию вариации функционалов, определенных на линейных-
метрических пространствах.
Итак, пусть дано метрическое пространство М (не предполагается
линейным) и функционал f(M) на нем. Пусть дано линейное про-
128 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
странство Ljf* которое можно было бы назвать „касательным к М
в точке Ма. LM удовлетворяет следующим условиям:
1°. Каждому элементу Мх из М, расположенному в некоторой сфере
5 (М, s) вокруг М, отвечает элемент Н из L^, который мы будем на-
называть образом Мх\ обратно, каждому Н из L^, расположенному на
некоторой сфере |Я|]<е, отвечает некоторый элемент Мг из М — его
образ. Связь между элементами М и LM взаимная 1). При этом М отве-
отвечает нулевой элемент в, и обратно.
2°. Существует такая положительная константа ту что
\\Щ<тг(М, Afx),
где Mi есть образ Н.
3°. Когда |Я|| стремится к нулю, то r(Mt Мх) -> 0; где Мх есть
образ Н.
Диференциал в точке. Мы назовем диференциалом / в точке М
линейный функционал l(H) — dfM(H), определенный на L^, такой, что
/{М,)~ f(M)=I(H)+s(H), B1)
где Н—образ Mv |e(/^)| есть величина высшего порядка малости
сравнительно с /(#).
ТЕОРЕМА. Если функция / (X) достигает экстремума в точке М.
в которой определены касательное пространство LM ti диференциал
dfM (H), то необходимо:
df
В самом деле, пусть для некоторого Н из LM
Рассмотрим элементы Ш (— оо < t < оо), образующие прямую. При
достаточно малом t каждому Ш отвечает его образ Mt из М; далее
ltH) U(H)
В силу B1) имеем:
f(Mt)—/{M) = te + *(H), B2)
где е(Н) есть величина высшего порядка малости сравнительно c§tH\\ —
= I * I' 11^1- При достаточно малом /, | г (Н)\ < —. Поэтому знак левой
части B2) при достаточно малом t совпадает со знаком члена tc. Но tc
меняет знак в зависимости от L Вместе с тем меняет знак и при-
приращение f(Mt)—f{M). Так как в силу условия 3° r{Mp M) при доста-
достаточно малом / может быть сделано сколь угодно малым, то в любой
сфере вокруг М найдутся точки Mv для которых f(A1t) > f (M)y равно
как и точки Mv для которых / (Mt) < / (М). В точке М не дости-
достигается экстремума.
Проанализируем с этой точки зрения разобранную в предыдущем
параграфе задачу. Пусть {у{х), х0, х{} из Т\ Для простоты положим,
1) Мы не требуем, вообще, оддозначноски.
§ 56} ВАРИАЦИЯ ИНТЕГРАЛОВ ОТ ЭКСТРЕМАЛЕЙ 129
что / (л:0) ф ?' (*о)>/ (*i) Ф ?(*i)- Каждому элементу [ух (х), То, х[}
из Т отвечает элемент оу(дг) из 1_„, где
ЧУ = Л (*) —.У С*) (лг0 < л: < хг).
(Если отрезок [дг0, х{] не покрывает отрезка [лг0, хг], то мы продолжим
функцию у(х) по касательной, так что она определится всюду на [лг0, хг].
Обратно, каждому йу(лг) из \_у при достаточно малом ||оу|| отвечает
| у1 (х\ лго> "*! } из Т.
Расширим у(х)-{-ьу(х) по касательным; при достаточно малом |]8у||
кривая у1(х)=у(х)-\-оу(х) пересечет кривые у и^. Абсциссы первых
точек их пересечения обозначим через (л:0, aTj); тогда { у1 (х)=у(х) -f-
+ ЧУ(*)» хо> -^i ] есть элемент пространства Т— образ Ьу (х) из Ly-
Легко убедиться, что
Далее, если ||8y|j—>0, то и соответственно
Таким образом касательное пространство \_ построено. Функционал
+ W + W -У) ^.„Л-1^+ (?' -У
ГДе гХо==/(^-У(^о) ' SXl = У(Л-УС^) еСТЬ линейный
нал на Ly. В то же время он есть главная часть приращения
J(yl{x), Xq, xx) — J(у (х), лг0, хх). Поэтому о/ есть диференциал (вариа-
(вариация) функционала J.
Вопрос о вариациях функционалов на нелинейных \ метрических
пространствах будет более подробно разобран во II томе.
§ 56. Вариация интегралов от экстремалей
Пусть дано семейство экстремалей ^ интеграла
7= f F(x, у, y')dx.
Так как для экстремали вариация интеграла / в середине равна нулю,
то при переходе от экстремали f нашего семейства к экстремали ^
вариация / сводится только к вариации в концах:
>j = _ {F-/F,\Jx9 - [/>]хДу0 -f [F-/FJ ^ + [Fu,]Xi 3Л. B3)
Если F = A Y 1 -гУ'* [А(х, у) есть функции х и у], то
F •— y'F , = ¦ , = A cos a F , = * = A sin %,
130 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
где а—угол наклона касательной к ?. Через а0, av Ло, Л, обозначены
значения а и Л в начале и конце •*.
Пусть
У *> охо = опо cos р0, оу0 = 3/!0 sin t30,
owj = "K^'2 -f 8ух2, Sxj = owj cos ^, oyx = S/i, sin ^ ,
тогда
oj = — Ло ояо cos (a0 — %) -f
х cos (a, —
B4)
Формулами B3) и B4) можно пользоваться для вычисления функцио-
функционала y(Ti) для экстремалей, близких к экстремали 7, если известно зна-
значение этого интеграла для экстремали ?.
Теорема Ламберта о планетных орбитах. В качестве применения этого
метода дадим доказательство Н. Е. Жуковского теоремы Ламберта в теория
планетных орбит.
Черт. 24.
Время, в течение которого планета описывает эллиптическую дугу ЛВ9
зависит только от длины 2с хорды АВ, большой оси 2а эллипса и суммы
радиусов-векторов по отношению к солнцу 2р.
Доказательство, которое мы сейчас приведем (по Н. Е. Жуковскому), осно-
основано на подсчете вариации интеграла, выражающего время движения.
Пусть F и Fi — фокусы эллиптической орбиты АВ, пусть при этом солнце
находится в F. Имеем:
FA
= 2a,
Отсюда:
= Aa-^ 2
2p.
Наряду с движением по дуге АВ, когда солнце находится в фокусе F, рассмо-
рассмотрим движение по той же дуге, когда солнце находится в F1 (черт. 24), Мы до-
доказали (конец § 32), что время при первом движении по АВ пропорционально
действию при втором движении. Следовательно, если мы докажем, что действие
при движении по лВ зависит только от 2а, 2с и 2р2 = 4а — 2р, то тем самым
докажем теорему Ламберта.
Рассмотрим совокупность дуг эллиптических орбит при движении вокруг
солнца, помещающегося в Fi9 с заданными 2а,2с,2рх. Повернув каждую орбиту
§ 56] ВАРИАЦИЯ ИНТЕГРАЛОВ ОТ ЭКСТРЕМАЛЕЙ 131
как твердое тело вокруг F, можно сделать хорды, стягивающие наши эллипти-
эллиптические дуги, параллельными. Допустим, кроме того, что все хорды между собой
равны. Итак, нам дано семейство дуг АВ эллипса с фокусом Fx (черт. 25),
стягиваемых равными и параллельными хордами АВ, причем F1A + FiB = 2p1.
Обозначив скорость при движении по такой дуге через v> выразим действие
интегралом
vds.
Каждая дуга нашего семейства есть экстремаль этого интеграла.
Докажем, что вариация интеграла I vds при переходе от любой дуги АВ
семейства к произвольной близкой дуге АхВг того же семейства равна нулю,
тем самым докажем постоянство действия на всех дугах и, следовательно, тео-
теорему Ламберта.
На основании формулы B4) получим:
о /
v ds = AAxvx cos 7± — ВВ^ cos ?2> i
где vt и v2 — скорости в точках А и Аь аг и а.2 —- углы, образуемые касатель-
касательными к АВ в точках А и В с векторами ААХ и BBV Так как отрезок Л?ра-
вен и параллелен Афъ то смещения AAV ВВХ равны и параллельны. Если мы
докажем, что vt cos at = v2 cos a2, то тем самым докажем, что о / v ds — 0. Пере-
Передвинем поступательно треугольник AXFXBX так, чтобы АХВХ совпало с ~АВ, вер-
вершина Ft этого треугольника переместится в положение Z7/, причем отрезок/-у7/
наралелен отрезкам ААХ и ВВХ. Отсюда углы аг и а2 можно рассматривать
как углы касательных к эллиптической дуге АВ в ее концах с направле-
направлением /у-/. Так как
то Fi и /у лежат на эллипсе G с фокусами А и В и большой осью, равной 2р.
При бесконечно малом смещении /уу направление этого смещения есть на-
направление касательной к эллипсу G в точке Ft. Нормаль к G в точке Ft есть
биссектриса угла AF^B. ^, ^
Пусть Н есть точка пересечения касательных в точках А и В к дуге АВ;
из свойств касательных к эллиптической дуге следует, что отрезок F^fi, сое-
соединяющий фокус Fx этой дуги с точкой пересечения Н касательных, есть бис-
биссектриса угла AF^B. Следовательно, F±H и есть нормаль к построенному нами
новому эллипсу G. Так как аг и а2 суть углы между направлениями АН и ВИ
и направлением /W касательной к G, то cos ах = sin F^HA, cos ak = sin FXHB,
и нам остается доказать, что v^sxnFXHA ^^v^sinF^HВ.
Пусть Кх и /С2— проекции Fx на продолжения касательных АНпВН. При-
Применяя теорему площадей к движению по дуге АВУ имеем:
B5)
но К\ = FtH sin /у^4, Кч = FxIi sin FxMBt и из равенства B5) следует:
1>! sinFtHA = v2 sin F^HB,
что и оставалось нам доказать.
Итак, теорема Ламберта доказана.
132 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Пользуясь ею, можно легко но данным 2а, 2с и 2/7 найти время t движе-
движения планеты по эллиптической дуге. И самом деле, прямолинейный отрезок FM
длины 2а есть предельный случай для эллиптических орбит с солнцем, распо-
расположенным в F. Отложив на нем две точки С и D такие, что FC = р— с,
FO = р-\-с, получим отрезок CD длины 2/7, сумма расстояний концов кото-
которого от F равна 2с. Этот отрезок CD есть предельный для эллиптических
дуг с заданными 2а, 2с и 2р. Обозначая через г расстояние точки отрезка
от F и зная, что скорость v при движении в поле тяготения с центром
в F равна
-" f^
имеем для времени t
р-г-с Л
/а /-./ г , а~ \ ( а — р — с . а — р — с\
t = 1 / — / Т/ dr= —-_--i { arccos sin arccos } —
r \x J V 2a — r \f ,, \\ a a J
p-c f <*
( a — p -f- с . a — p A- c\\ жслг%л
—-1 arccos - sin arccos —¦— j У, B6)
На основании теоремы Ламберта эта формула верна для всех эллиптических
дуг с заданным 2а, 2с, 2р.
Движение от А к F и обратно есть предельный случай полных обходов
эллипсов. с большей осью 2а. При этом движение по дуге, дополнительной
к АВ, дает в пределе следующее движение по отрезку FM: от С к F, от/7к М
и от М к D. Вычисляя время такого движения, получим по теореме Ламберта
время для движений по дугам, дополнительным к АВ. Результат будет отли-
отличаться от формулы B6) только знаком перед вторыми круглыми скобками
в фигурных скобках.
Формула B6) даст при а -> оо формулу Эйлера для параболического
движения:
з -л
t = —)= {{2p + 2cV + B/7 - 2с) Т].
Более подробным исследованием вариаций функционала на семействе
экстремалей мы займемся ниже, в гл. XII.
§ 57. Случай свободных концов в пространственной
задаче
Постановка задачи. Задача со свободными концами может быть
распространена на случай функционалов J:
{x, у1У у2,...,уя) у/у У2>---,Уп')<*х>
заданных на линиях я-мерного пространства.
Поставим более точно задачу: пусть в п-мерном пространстве дана
точка А и некоторое многообразие N k измерений {k < n); среди линий
класса Cv соединяющих точку А с произвольной точкой многообразия N,
требуется определить линию, вдоль которой J принимает экстре-
экстремальное значение.
§ 57] СЛУЧАЙ СВОБОДНЫХ КОНЦОВ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ 133
Случай трехмерного пространства. Мы ограничимся сейчас случаем,
когда п = 3 (случай пространства трех измерений).
ТЕОРЕМА. Если кривая у.
класса d дает экстремум интегралу J среди всех кривых класса С\>
соединяющих данную точку А с произвольной точкой кривой Г"
y=f(x), z = v(x), то в точке B(xl9 yu z{), принадлежащей у и Г,
имеем. [f (д.} __у^ ^ + w (х^ _ ^ ^ + F=Q^
Эта теорема, как легко видеть, дает нам уравнение, пользуясь ко-
которым можно определить все произвольные постоянные в общем инте-
интеграле уравнения Эйлера.
Для доказательства теоремы применим метод вариаций. Имеем:
г FM)dx т- Ия=а:;Ч = о •
Отсюда, интегрируя члены Fyfiy'> ^zfiz' по частям и обозначая через oyt
и bzx вариации оу и oz в свободном конце при х = х1У получим:
Л- Ж F
Так как в случае экстремума рассматриваемая кривая есть экстремаль,
то первые два члена пропадают и мы получим:
С другой стороны, повторяя рассуждения, сделанные нами при иссле-
исследовании плоской задачи, найдем:
/' (Хх) Ьхх =/ (Xj) 0Х{ + 0yiy V (ATj) 0^ = Z' (ATj) OArt 4- OZp
отсюда, подставляя в B7) выражения oyv oz{ через oxl9 получим искомое
соотношение.
Обобщения. Этот результат без труда обобщается на случай п не-
неизвестных функций, когда концы класса допустимых линий расположены
на кривой:
V =/ W
У » = /»(*)
пространства (п-\-\) измерений. В этом случае условие трансверсаль-
трансверсальности примет вид:
Обобщение условий трансверсальности. Найдем теперь условие
трансверсальности, когда свободный конец класса допустимых линий
134 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
принадлежит некоторому многообразию. Ограничимся опять случаем
пространства трех измерений, случаем, когда F есть функция от х, уу
2, У, z'. Будем считать, что многообразие (поверхность) задано ура-
уравнением:
г=/г(х,у). B8)
Допустим, что кривая -р
v=y(x), z = z(x) B9)
дает экстремум интегралу
J= />(*, у, z, у', z')dx
среди всех кривых, соединяющих точку А с произвольной точкой по-
поверхности B8). Пусть B(xv yv z^) есть конец кривой *\, принадлежащий
этой поверхности. Рассмотрим на поверхности B8) две кривые:
где /2 (х, z) есть уравнение B8), разрешенное относительно у. Кривая -у
тем более дает экстремальное значение интегралу J, если мы примем за
класс допустимых линий всевозможные кривые, соединяющие точку Л
с произвольной точкой кривой C0) или с произвольной точкой кривой C1).
Отсюда, применяя условие трансверсальности, выведенное нами раньше
для случая, когда концы допустимых линий принадлежат кривой, получим
следующие два соотношения:
U, -Ч
Это и есть искомые два добавочных условия, пользуясь которыми можно
определить постоянные интеграции.
Соотношениям C2) можно придать более симметричный вид, если
уравнение поверхности задать в общем виде:
f(x, у, z)^0
и найти выражения -=— и ~ . Имеем:
1 Ох Ох
К.
dz ox
1
1 ¦ C3)
1
ду __ дх
~ох ~" "~ дГ
§ 57] СЛУЧАЙ СВОБОДНЫХ КОНЦОВ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ 135
Отсюда, подставля
из C3), получим:
Отсюда, подставляя в C2) вместо Щ = — и Ц = ^ их выражения
Этот метод естественно распространяется на случай пространства
\п -f-1) измерений, когда концы допустимых линий должны принадле-
принадлежать некоторому многообразию k измерений.
Условие ортогональности. Разберем один важный для приложений
частный случай. Допустим, что подиитегральная функция F имеет вид:
Докажем, что в этом случае условие трансверсальности совпадает
с условием, что искомая кривая должна быть ортогональна к дан-
еой линии данной поверхности.
Очевидно, достаточно рассмотреть случай, когда концы допусти-
допустимых линий должны быть расположены на линии. Имеем:
F ' =¦= -у F ' = —
У *1 /* i Г'> I -/9 ' 2 -ш/
Отсюда условие трансверсальности примет вид:
Произведя сокращение и умножая на У1 4-У24-У2, получим:
/ 4- (?'—*0 ^-1т Уа ~г z'2 = о
или:
Это и есть условие ортогональности.
Легко получить обратное предложение: если условие трансверсаль-
трансверсальности совпадает при всех начальных данных с условием ортогональ-
ортогональности, то функция F имеет следующую структуру:
где V есть произвольная диференцируемая функция х, у, z.
В самом деле, по условию должны быть эквивалентны два соотно-
соотношения:
(от — у) FtJ- — (я — z') F, + F = 0, «у -}- я/ -f 1 = 0,
где m~f(x) и п = 'У(х) суть переменные, не зависящие от у' и z'•
Второмг соотношению лтожно придать вид:
у (т _у) 4- 2х (я — 2') -I- 1 4-У2 + 2'2 = 0.
136 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Отсюда, деля первое уравнение на F, второе на l-fy2-J-2/2 и поль-
пользуясь независимостью т и я, получим:
ру,
F
откуда ,
где К зависит только от ху у, z. Таким образом:
Задача. Пусть из точки Л дан световой сигнал. Определить луч АБ, по
которому сигнал впервые достигнет заданной поверхности М.
Задача сводится по принципу Ферма к нахождению экстремума интеграла:
ds
i
v (x,yt z)
где v(x,y,z)— скорость света и где кривая v соединяет точку А с В, Из пре-
предыдущего явствует, что луч АВ, по которому сигнал впервые достигнет поверх-
поверхности М, ортогонален к М,
Геометрическое место U точек, в которые световой сигнал, посланный из
точки А, попадет через равные промежутки времени, называется поверхностью
волны. Из только что разобранной задачи следует, что все лучи АС, соединяю-
соединяющие точку А с поверхностью волны, нормальны к последней. Это следует из
того, что каждый из этих лучей есть луч, по которому световой сигнал из Л
впервые достигает М,
Тем самым доказывается частный случай принципа Мал юса в геометриче-
геометрической оптике: поверхность волны для световою пучка ортогональна всем лучам
пучка. В гл. X мы убедимся, что принцип Малюса сохраняет силу, даже если
лучи претерпевают произвольное количество раз преломления и отражения.
§ 58. Случай производных высшего порядка
Постановка задачи. Развитый выше метод вариаций почти без видо-
видоизменений позволит решать также те задачи вариационного исчисления,
когда подинтегральная функция зависит не только от первой производ-
производной, но также от производных высших порядков.
Примерами задач такого рода могут служить задачи теории упру-
упругости: определить форму изогнутой оси балки при тех или других
условиях на концах. Как известно, эта задача приводится к разысканию
экстремума потенциальной энергии системы. С другой стороны, потен-
потенциальная энергия изогнутой балки зависит от кривизны. Таким образом
эта группа задач, вариационного исчисления имеет дело с разысканием
экстремальных кривых, когда подинтегральная функция зависит от произ-
производных первого и второго порядков неизвестной функции. Поставим
проблему в общем случае:
Среди всех кривых у—у(х), соединяющих две данные точки
А{хо,уо) и В [xv y2), определить ту, вдоль которой интеграл
(F — данная функция п-\-2 переменных: х, у, у\уп\... ,у) принимает
экстремальное значение.
§ 58] СЛУЧАЙ ПРОИЗВОДНЫХ ВЫСШЕГО ПОРЯДКА 137
Прежде всего сделаем более точные оговорки относительно функ-
функции F и класса допустимых линий. Функцию F будем, как обычно,
предполагать непрерывной вместе со всеми ее частными производными
первого и второго порядков по всем аргументам при хо^х^х1 и
при всех возможных значениях других аргументов. За класс допусти-
допустимых линий примем линии
у=у(х) {у{хо)=:уф у(хх) = \\),.
такие, что у\ у",. .., у{п) непрерывны при хо^х^Х{, класс допустимых
линий является частью функционального пространства С„-
Вывод уравнения Эйлера-Пуассона. Первый основной результат
в этой проблеме дается следующей теоремой.
ТЕОРЕМА. Если кривая "[: y=y(x)t принадлежащая классу допу-
допустимых линий, дает экстремум интегралу J, то она удовлетворяет
уравнению:
F* - ТВ? ^' + ?*F.' - • • • + •¦- Ч'Ъ- V) = °- (-34>
Выявим снова роль этого результата. Уравнение C4), как легко видеть,
в общем случае \-j-n Ру(п) ф 0 1 порядка 2п, следовательно, общий ин-
интеграл будет содержать 2п произвольных постоянных и будет иметь вид:
y=f(x,*v$v •-,**,'?»). C5)
Таким образом, если искомая кривая существует, то она содержится
в 2я-параметрическом семействе C5) кривых. Используя условия на
концах, мы можем исключить две произвольных постоянных и получим
семейство:
зависящее от 2/г — 2 произвольных постоянных. Обычно в задачах при-
прикладного характера и задачах геометрических к основным условиям разби-
разбираемой задачи добавляется еще ряд условий на концах. Если мы будем
иметь 2л — 2 таких добавочных условий, то этими условиями опреде-
определятся все произвольные постоянные, искомая кривая будет фактически
определена. Если добавочных условий нет или их число меньше 2д — 2.
то для определения произвольных постоянных необходимы дополнитель-
дополнительные исследования, которыми мы займемся несколько ниже.
Перейдем к доказательству сформулированной теоремы. Для разно-
разнообразия применим метод варьирования в точке. В соответствии с
тем, что под знаком интеграла фигурируют производные высших по-
порядков, сделаем некоторые добавочные ограничения на вариацию Ьгу
в точке х.
Положим:
j =И .V— а- ., \x—\a—,t при \х—а < ., |
Ку=\ L ~/] l K "/J , h" \ ^36)
О при \х'— а | > ?~,
138 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIH
Легко убедиться, что при х = а±——.
Можно общее принять
C6')
где т) (х) — непрерывная вместе с ее я первыми производными функ-
функция, равная нулю всюду кроме бесконечно малого интервала длины h,
содержащего точку а, а в этом И1ггервале у\ (х) ^= 0, и, наконец, при-
принимая, что а = / y](x)dx есть бесконечно малая первого порядка, мы
потребуем, чтобы
была, бесконечно малой высшего порядка. Легко подсчитать, что вве-
введенная нами вариация C6) удовлетворяет всем этим условиям.
Применяя рассуждения, проделанные при изучении простейшей задачи,
иметь:
+
= f
h
h
x—- -
F(x,y,y',...y(n))dx:
.+4-
+ 4-
Займемся первым интегралом. Разбивая его на сумму интегралов
« интегрируя по частям каждый из них столько раз, каков порядок произ-
производной от вариации 8^ = ^ фигурирует под знаком этого интеграла,
л. ол учим:
§ 58] СЛУЧАЙ ПРОИЗВОДНЫХ ВЫСШЕГО ПОРЯДКА 139
'
f F/ т," dx = [F,. гП ' - /<A F9
a-—2-
dx
a?4- Л-
Замечая, что все оиинтегрированные члены пропадают, в силу усло-
условия C6') получим:
где
0= f n(x)dX.
h
x --
Для указанной выше вариации C6) будем иметь:
h
t
где А — конечная величина, не зависящая от А. Таким образом, если
множитель при а не равен нулю, то вариация 8^./ есть бесконечно
малая порядка 4п -J- 1 относительно h. Оценим порядок второго инте-
интеграла. Главным членом этого интеграла будет последний член:
(п)у(п)т?пJ dx.
Для вариации C6) и при сохранении лишь низших степеней h при п
нечетном будем иметь:
А
'¦ = Ai'F&.
140 БОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Аналогично при п четном:
//>) +* Ъ^ dx = Ао* Fy{n)y{n) kAn + 2,
где Аг и* Л2—конечные константы, не зависящие от h.
Таким образом главной частью приращения интеграла является пер-
первая вариация. Следовательно, в случае экстремума эта вариация должна
равняться нулю в каждой точке:
Сокращая на о, получим искомре уравнение C4) Эйлера-Пуассона:
гу ~dx~ гу + dx* гу " * • "» V 1> ахп г№ — и*
Рассмотренное нами выражение приращения- интеграла J дает нам
также еще одно условие, необходимое для экстремума. При условии^
что первая вариация равна нулю, в каждой точке знак приращения
интеграла будет определяться главным членом второго интеграла, т. е-
членом:
2
Так как h положительно, то отсюда получаем следующий результат;
если кривая дает минимум (максимум), то вдоль кривой имеем:
F^n) у(п) > 0 . (Fy{n) у{п) ^ 0).
Это есть условие Лежандра для нашей задачи.
Замечай ие. Примененный нами метод страдает одним дефектом. Инте-
Интегрируя по частям, мы неявно сделали добавочное допущение относительно
существования у искомой кривой также производной порядка 2л. От этого
ограничения легко освободиться, если использовать прием Дю-Буа-Реймонда;
мы предлагаем это проделать читателю как упражнение. При этом методе
можно доказать, что если искомая кривая обладает п непрерывными произ-
производными (основная гипотеза) и если вдоль искомой кривой Fy(n) у(п) Ф 0, то>
искомая кривая обладает также непрерывными производными порядков:
(я + 1), (л + 2),...,2л.
Случаи понижения порядка уравнения Пуассона. В некоторых
случаях порядок уравнения Эйлера-Пуассона 2п может быть сразу снижен
на одну единицу.
1. Допустим, что подинтегральная функция не зависит явно от уТ
тогда уравнение Эйлера-Пуассона примет вид:
— F I ^ F JL( П(п) а'1 F П
или, интегрируя:
it' //V ij" " » * " * ~*~~ , n 1
if нл у dx
Это и есть искомый первый интеграл.
§ 58] СЛУЧАЙ ПРОИЗВОДНЫХ ВЫСШЕГО ПОРЯДКА 141
2. Допустим, что подинтегральная функция не зависит явно от неза-
независимого переменного х:
••I
= f
Произведем замену переменных. Будем считать за независимое перемен-
переменное у, а х примем за неизвестную функцию от у. Обозначая для крат-
, dx л ,f <№х ил dnx
кости через х производную — , вообще: х = —^, ... , лг ' = —п-,
получим:
, 1 „ х" „ Зх"ъ — Х'хт
Отсюда интеграл J в новых переменных примет вид:
f 1 х" гх"ъ — х'хггг
Этим' преобразованием мы сводим первоначальную задачу вариационного
«счисления к новой, причем в этой постановке в подинтегральное выра-
выражение неизвестная функция х — х(у) явно не входит. Следовательно,
диференциальное уравнение экстремалей, очевидно, одно и то же как
для интеграла J(y)> так и для интеграла J(x) и будет иметь первый
.интеграл. Полагая:
искомый первый интеграл будет иметь вид:
3. Укажем в заключение на один случай, когда можно сразу напи-
написать общий интеграл уравнения Эйлера-Пуассона. Пусть подинтеграль-
подинтегральная функция F зависит только от j/w\ В этом случае уравнение будет
иметь вид:
Hx^Fy^^°
или
Fyi») = Рн-1 С*),
где Рп_1(х) есть полином степени (п—1). Обозначая через /функцию,
обратную функции F („), получим:
Интегрируя:
у=
,,_i — произвольный полином степени п—1.
142 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Задача. На двух опорах А и В (черт. 26), расположенных в горизонталь"
ной плоскости, свободно лежит цилиндрическая упругая тяжелая балка.
Пренебрегая весом частей балкщ лежащих вне опор, требуется определить
форму изогнутой оси этой балки.
Все размеры, плотность и коэфициенты упругости балки считаются извест-
известными. Для решения воспользуемся принципом: если система $ устойчивом
равновесии, то при всех возможных перемещениях системы потенциальная:
энергия системы увеличивается.
Обозначим через 21 расстояние между опорами, через р — линейную плот-
плотность балки, ds — элемент дуги изогнутой оси балки. Введем систему коорди-
координат. Пусть Ох соединяет точки опоры, начало координат делит отрезок АВ
пополам и ось Оу направлена вертикально вверх. Вычислим теперь потенциаль-
потенциальную энергию балки, предполагая, что уравнение ее упругой оси есть у=у(х)*
Потенциальная энергия, созданная упругими силами при изгибе, будет равна
где L — длина части балки между опорами, ср есть угол, образованный касатель-
касательной с осью Ох и р. — постоянный коэфициент, зависящий от модуля упругости
и момента инерции поперечного сечения балки. Вычислим теперь потенциаль-
потенциальную энергию, созданную полем тяготения,
у Элемент балки ds будет иметь потенциаль-
потенциальную энергию, равную
ру ds.
Отсюда потенциальная энергия всех эле-
элементов балки равна
L
Черт. 26. ffydS-
U
Складывая найденные энергии, получим общую потенциальную энергию балки;
. ГдГф у"
Подставляя ds = у \1 + у' 2 dx и -—т- = •* » 3 (кривизна), получим;
A 4- у' 2) Т
l
В силу отмеченного выше принципа наша задача приводится к разысканию
максимума Е. Подинтегральное выражение от х явно не зависит, мы можем
таким образом воспользоваться изложенным выше приемом, чтобы сразу сни-
снизить порядок уравнения. Однако получаемое при ,этом уравнение четвертого
порядка имеет достаточно громоздкий вид и в общем случае элементарно не
интегрируется. По этой причине мы не будем заниматься его исследованием
в этом виде, а ограничимся обычным в этой задаче приближенным решением.
Считая, что изгиб балки невелик, будем пренебрегать вторыми степенями у'*
тогда выражение Е примет вид:
г
У
§ 59] СЛУЧАЙ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Напишем уравнение Эйлера:
Отсюда
yiv)e__?_.
общий его интеграл будет:
Четыре произвольные постоянные а, р, -у, & можно определить из начальных
условий. Из условий симметрии сразу имеем: а = f = о, кроме того, в концах
у" = о. Отсюда:
Наконец при х = /, у = 0:
Отсюда
°~~ 24JT 2~~рГ
Искомая ось есть парабола четвертого порядка.
§ 59. Случай функций многих переменных
Во всех предыдущих задачах мы имели дело с функционалами or
функций одного переменного. Мы теперь перейдем к задаче отыскания
экстремума функционала, зависящего от функции п переменных.
Постановка задачи. Зададим в n-мерном пространстве область Q>
которую для простоты будем считать ограниченной. Образуем класс Ci
функций ©(л^, лг2,. . ., лгя), заданных на области Q и ее границе, непре-
непрерывных на Q и на ее границе, обладающих непрерывными частными*
производными cpf = z>x. Назовем расстояние между функциями ф и 6*
класса Сг
г (ср, ф) ж тах{|<р (*!,..., хп) — 6 (хь..., хп) |, j 9* {xi9m.., дгя) — fy {хь.. .,хп)\}.
(i=\, 2,...,/i).
Совокупность тех функций ^, для которых г(<р,<}>) < з, образует s-окрест-
ность функций ср. Определим на Ci функционал
fF (х{9 ?, %) dxx dx2... dxn\ C7>
Q
здесь F — заданная непрерывная функция 2п-\-\ аргументов #,,<?*•
^ =<р4 (/=1, 2,...,/х), обладающая по всем аргументам частными
производными до третьего порядка включительно.
Обозначим через Ci совокупность тех функций ф класса Ср кото-
которые принимают на границе Q заданную систему значений. На границе Q
определена функция /04), и функция ср в каждой точке Л границы Q
равна:
?(Л)=/(Л). C8)
Среди всех функций класса d ищем ту, которая дает экстремум функ-
функционалу У(<р).
144 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗаДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
Пусть функция 9 w3Ci реализует экстремум /(?); функция Ь?
некоторая другая функция того же класса, расположенная в некоторой
s-окрестности функции ср. Очевидно, во всех точках границы
5?(Л)=0. C9)
Яопрежнему будем обозначать:
д <> л
дх{ J^ ix
Имеем:
= f f ...j\F (xv <? + 8?, ?, + &?,) — F (xv ъ <?,)] ^. . . dxn
* i
где т| есть величина высшего порядка сравнительно с r(«, »-)-8tp).
Выражение
¦есть главная линейная часть приращения У(в-}-8®) — i(»). Необходимое
условие того, что для о функционал /('¦?) достигает экстремума, есть:
.h + llf7**?i)dx1...dxn=O. D0)
Это тождество в Q должно иметь место для всех 8© класса Сх обра-
обращающихся в нуль на границе Q.
Преобразование Лагранжа. Можно, как мы это сделали в § 47,
привести путем интеграции по частям выражение U к более простому виду.
Проведем всевозможные прямые, параллельные оси Ох^ рассмотрим
интервал АВ, который принадлежит пересечению такой прямой с Q и
концы которого лежат на границе Q. Имеем:
в в в
f> ov.dx, = F Sep. !^— Г -?-(F )bvdx.= f
A A A
Здесь -^— (F ) есть полная производная функции
охг <?*
FVl[*v х2,..., хп> а(хи х.2,.. .,хн), ?,(*„хя,. .. ,хп),..., <?п{хи .v2,.. .,лг„)]D1)
по д:,:
§ 59] СЛУЧАЙ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ 145
Мы приходим на основании D1) и D0) к равенствам:
Q
ЛЕММА ЛАГРАНЖА. Если
Q
где М — непрерывная на Q функция, a yj — произвольная функция
класса d, обращающаяся в нуль на границе Q, то
Af = O
всюду в области Q.
В самом деле, пусть в точке Л области Q
примем для определенности с>0. Построим вокруг А прямоуголь-
прямоугольник /?:
целиком заключенный в Q и такой, что Л1 {А') > -^- > ^сли Л' из /? •
Определим функцию yj на Q следующим образом:
п
tj (х1э дг2, ..., хп) = JJ (х€ — а$* (*4 — *iJ,
если точка (xv х2, ..., дгя) находится в прямоугольнике J?;
если точка (xv дг2,..., лгп) лежит вне R.
Легко убедиться, что функция т) есть функция класса СР обращаю-
обращающаяся в нуль на границе Q, а поэтому мы должны рдоеть:
Г Г... /*
0.
146 ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. VIII
С другой стороны:
ff. . ./ Mfi dx,.. .dxn = ff. . .fM-ndx,.. .dxn >
Q
i = l
Приходим к противоречию.
Из леммы Лагранжа и равенства D2) получаем: если функционал J (?)
достигает экстремума для функции ср (дг^ дг2, ..., лгя), то функция
ф (дер лг2, ...,л:м) яа области Q должна удовлетворять уравнению
в частных производных:
2тйг/Ч=° D3>
(уравнению Эйлера-Лагранжа).
В развернутом виде уравнение D3) примет вид:
J t °- D4)
Кроме того, функция ? удовлетворяет условиям на границе C8).
Пример 1. Найти поверхность наименьшей площади, натянутую на дан-
данную линию
x = *(t), У=У(*)> z = z{f). D5)
Пусть уравнение поверхности будет
* = ? (*> У)-
Условие того, что поверхность натянута на линию D5), есть:
Площадь поверхности
J (?) = f f
Уравнение Эйлера примет вид:
-i-L '* }+±\ * 1-0. D6)
Условие D6) показывает, что искомая поверхность минимальной площади (так
называемая минимальная поверхность) обладает всюду средней кривизной,
равной нулю.
Пример 2. Интегралом Дирихле от функции ср, взятым по области Q
л-мерного пространства, называется интеграл:
%^-..^«. D7)
Определить условия, при которых функция у, принимающая заданные
значения на границе Q, дает мини чум интегралу Дирихле.
§ 59] СЛУЧАЙ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ 147
Уравнение Эйлера D4) примет вид:
п
В самом деле, в случае F' = ^42Xi\
{2 при / == /
О при /ф/.
Пользуясь оператором Лапласа, мы запишем уравнение D4) в виде:
Д? = 0.
Итак, уравнение Лапласа есть уравнение Эйлера для интеграла Дирихле.
Инвариантность уравнения Эйлера. Так же, как и для случая
функций одного переменного, мы можем убедиться, что уравнение
Эйлера D3) или D4) инвариантно 'относительно преобразования коор-
координат. Например, уравнение Лапласа, как уравнение Эйлера для инте-
интеграла Дирихле, инвариантно.
Рассмотрим плоский случай:
Перейдем от декартовых координат (лг, у) к полярным (р, 6). Имеем:
Отсюда:
D (?)=/
-7Г- = Sin t), -3— = COS 6.
р?р2 + у ?02] db d9. D8)
Составляя уравнение Эйлера для последнего интеграла в равенстве D8),
придем к уравнению Лапласа в полярных координатах:
• о
I p T 88
Аналогично можно построить для трехмерного случая уравнен>*е<Лапласа
в полярных координатах (или в какой-нибудь другой системе координат,
например в эллиптических координатах).
ГЛАВА IX
УСЛОВНЫЙ ЭКСТРЕМУМ
§ 60. Изопериметрическая задача
Примеры кзопериметрической задачи. Многие вопросы приложений
приводят к задаче разыскания кривой, дающей экстремум интегралу:
ъ
f(x,x,/) dx,
когда за класс допустимых линий принимаются кривые, соединяющие
две данные точки А и В и удовлетворяющие, кроме того, некоторым
добавочным условиям.
Начнем с рассмотрения конкретных примеров. В § 32 мы решали
задачу с минимальной поверхности вращения: среди всех однозначных
кривых класса Cv проходящих через А и В> найти такую, чтобы по-
поверхность, образованная вращением этой кривой около оси Ох7 имела
наименьшую площадь. Мы придем к существенно новым задачам, если
будем рассматривать только те поверхности, которые образованы вра-
вращением кривых, например, данной длины иди только тех кривых, ко-
которые при вращении около оси Ох образуют поверхность, ограничи-
ограничивающую вместе с плоскостями х — х0, х = хг тело данного объема.
Так как длина кривой выражается интегралом:
ь
а
то первую из поставленных задач можно формулировать так: среди всех
кривых у=у (х) класса d, вдоль которых интеграл К принимает
данное значение / и которые проходят через две заданные точки А и В,
определить ту, вдоль которой интеграл J принимает наименьшее или
наибольшее значение.
feo второй 'задаче ищется также минимум интеграла при условии, что
вдоль каждой кривой класса допустимых линий интеграл
ь
а
должен иметь заданное значение.
В качестве третьего примера укажем на разобранную нами в § 30
задачу о равновесии тяжелой цепи.
§ 60] ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА 149
Все эти примеры приводят нас к следующей общей проблеме:
Постановка задачи. Даны две функции F (л:, у> У) и G (дг, у, у).
Среди всех кривых у=±=у(х) класса Ci, вдоль которых интеграл
ъ
= J
принимает заданное значение, определить ту, вдоль которой интеграл
ь
J= f F{x,y,y')dx
а
принимает экстремальное значение.
Имея в виду общие установки и понятия, данные в предыдущей
главе, мы ставим здесь задачу найти основные необходимые условия,
которым должна удовлетворять искомая кривая, так, чтобы, зная за-
ранее, что кривая существует, можно было применением искомых усло-
условий ее фактически определить.
Прежде чем переходить к решению поставленной задачи, сделаем
несколько гипотез общего характера, необходимых при дальнейших выводах:
1°. Функции F и О мы будем предполагать обладающими непрерыв-
непрерывными частными производными первого и второго порядков при а ^х ^ Ъ
и при произвольных значениях переменных у> у'.
2°. Мы будем предполагать, что искомая кривая не является экстре-
экстремалью для интеграла К.
Скажем несколько слов в оправдание гипотезы 2°. Для того чтобы
задача имела смысл, мы должны потребовать, чтобы данное значение
интеграла К находилось между экстремальными значениями этого инте-
интеграла, т. е. не являлось экстремальным (в примере с тяжелой цепью и
в. первом из приведенных выше примеров мы должны были естественно
предполагать, что интеграл К—длина кривой — строго больше, чем
расстояние между данными точками). Таким образом там, где экстре-
экстремаль дает строгий экстремум, наше требование необходимо.
Случай, когда искомая кривая есть экстремаль интеграла К без того,
чтобы давать интегралу J экстремальное значение, мы назовем особым
и разберем его Отдельно. Этот случай вполне аналогичен соответствую-
соответствующему случаю в теории условного экстремума функций многих перемен-
переменных, когда в точке, где функция достигает условного экстремума,
частные производные от левых частей условий:
обращаются в нуль.
Решение задачи. Подход к решению, поставленной задачи дается
следующей теоремой.
ТЕОРЕМА ЭЙЛЕРА. Если кривая у = у{х) дает экстремум ин-
интегралу
ъ
= fF(x,y,y')dx
а
150
при условиях:
УСЛОВНЫЙ ЭКСТРЕМУМ
[гл. IX
и если у = у(х) не есть экстремаль интеграла /С, то существует
константа \ такая, что наша кривая у=у(х) есть экстремаль
интеграла
= fH(x,y,/)dx,
где H= +
Покажем сейчас же, что если заранее известно существование иско-
искомой кривой, то применением теоремы Эйлера эту кривую можно факти-
фактически определить. В самом деле, интегрируя уравнение Эйлера для
функции Ну получим общий
интеграл, зависящий от двух
произвольных постоянных ин-
интеграции а, р и от неизвест-
неизвестного параметра X:
У=У1х)
хг,
Черт. 27.
В силу теоремы Эйлера иско-
искомая кривая принадлежит этому
семейству. Остается определить
ос, (J, X. Для этой цели доста-
—*^х точно воспользоваться условием
/С=/ и условием, что кривая
проходит через две данные
точки А и В.
Перейдем к выводу теоремы Эйлера. Итак, допустим, что кривая
yz=zy(x) дает экстремум J и что эта кривая не есть экстремаль для
интеграла К. Для определенности примем, что этим экстремумом является
минимум интеграла J при условии K=L Возьмем в интервале [а, Ь]
две произвольные точки хх и х2 (черт. 27) и найдем приращение функ-
функционала J, когда у (х) проварьирована в окрестности точки лгА и точки х%.
В силу результатов § 46, 47, обозначая через А/ искомое прираще-
приращение У, получим:
где
о* =
it где ех и е2 стремятся к нулю вместе с at й а2.
§ 60] ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА 151
При произвольных вариациях i у и Ь^у кривая
у = Ух (х) ~у (х)
вообще говоря, не будет принадлежать классу допустимых линий. Для
того чтобы вариация была допустимой, необходимо и достаточно, чтобы
К (yj = К (у), т. е. чтобы:
A)
где гх' и е2' стремятся к нулю вместе с <зх и о2.
Выберем теперь точку х2 так, чтобы:
такая точка лг2 существует, ибо у=у(х) не есть экстремаль для /С.
.В таком случае условию A) можно придать вид:
B)
где е' стремится к нулю вместе с о{.
Полагая:
и заменяя в выражении А/ площадку о2 через ог из B), приращению
А/ можно придать вид:
где е стремится к нулю вместе с о1# Так как по условию кривая у=>у (х)
дает минимум /, то, следовательно, А/^0 при любой допустимой ва-
вариации, т. е. при любом значении ох, (достаточно малом). Следовательно,
при любом значении х вдоль кривой у=у(х) должны иметь:
Теорема Эйлера доказана.
Условная экстремаль. Уравнение C) дает 'полное решение также
следующей задачи: среди всех кривых, соединяющих две данные точки
и для которых интеграл К принимает заданное значение, определить
кривую, при вариации которой 87 = 0, коль скоро 8/^=0.
152 условный „экстремум [гл. IX
Назовем условной экстремалью всякую кривую, которая будет ре-
решать поставленную задачу (при произвольных фиксированных концевых
точках) и при произвольном фиксированном значении интеграла /С
ТЕОРЕМА. Уравнение C) есть условие, необходимое и достаточное
для того, чтобы кривая у=у(х) являлась условной экстремалью.
Докажем сначала, что условие C) достаточно. В самом деле,
если кривая удовлетворяет условию C), то 8 (J-\-\K) = O или
87 = — \ЪК,
а так как X—произвольно, то из условия 8/<Г= 0 следует 87=0, т. е.
кривая есть условная экстремаль.
При доказательстве, что условие C) необходимо, разберем от-
отдельно два случая:
1) на всяком интервале G—-т- G , Ф 0 и
У иХ У
2) существует интервал, который может совпасть со всем интерва-
интервалом [а, Ь]> на котором G —— G , = 0.
В первом случае необходимость условия C) получается дословным
повторением проведенного нами вывода формулы C), путем варьиро-
варьирования кривой в двух точках.
Во втором случае на тех участках интервала [а, Ь]> где G — --г- G , фО,
аналогично первому случаю, условие C) сохраняет силу, а на тех
участках, где G —-j--G. = 0, вариацию кривой можно считать про-
произвольной: равенство 8АГ= 0 выполняется тождественно, и, следовательно,
на этих участках должны иметь F —^— F. = О, т. е. условие C) ока-
оказывается также выполненным.
Принцип взаимности. Приведенные выше рассмотрения показывают,
что изопериметрическая задача вариационного исчисления приводится к
простейшей задаче для функции H==F-\-№. Заметив, что от умно-
умножения подинтегральной функции на константу семейство экртремалей
для интеграла останется тем же самым, мы можем функцию Н записать
в симметричной форме:
где Хх и Х2 суть константы. Такое представление функции Н нам пока-
показывает, что функции F и G в выражении Н фигурируют симметрична.
Если исключить случай \ = 0 и Х2 = 0, то семейство экстремалей будет
одно и то же, будем ли мы искать экстремум интеграла 7 при условии,
что интеграл К сохраняет постоянное значение, или будем искать
экстремум интеграла К при условии, что интеграл 7 сохраняет посто-
постоянное значение. В этом заключается принцип взаимности в его про-
простейшей форме.
Если Х2 = 0, то Н совпадает с точностью до постоянного множи-
множителя с F\ условная экстремаль интеграла 7 будет совпадать с безуслов-
безусловной экстремалью того же интеграла, и эта экстремаль в общем случае,
§ 60] ИЗОПБРИМЕТРИЧЕСКАЯ ЗАДАЧА 153
очевидно, не будет условной экстремалью для интеграла /С Аналогично,
если \г = 0, то И совпадает с G, условная экстремаль интеграла К
будет его безусловной экстремалью.
Обобщения. Разобранный выше метод решения простейшей изопе-
риметрической задачи можно легко распространить на случай, когда за
класс допустимых линий принимаются кривые класса Ci, соединяющие
две данные точки и удовлетворяющие k условиям:
ь
*4= f G{i) (x,y,/) dx = lt (/ = 1, 2, ...,*), D)
а
где функции G® удовлетворяют обычным теоретико-функциональным усло-
условиям, а 1{ суть константы.
ТЕОРЕМА. Если кривая у=у(х) дает экстремум интегралу
ь
J= fF(x,y,/)dx
а
среди всех кривых класса Cj, удовлетворяющих условию D), и еслиг
кроме того, определитель
^
(/,/=1,2,...,k) E)
не равен тождественно нулю9 то существует k констант Х{
(/ = 1, 2,..., ?) таких, что кривая у (х) удовлетворяет диференци-
альному уравнению:
где
Короче говоря: если у=у{х) есть условная экстремаль интеграла J и
ь
если Д Ф О, то она есть безусловная экстремаль интеграла / Них.
а
Примечание. Условие
Л (*1> *2>.--» *л)ФО
эквивалентно условию, что определитель Грамма для функций
i?i? (/=1,2,..., Л)
отличен от нуля, или, что то же самое, не существует постоянных сь е^...9 ек
B*<2>°) таких* что S С<Р< —° ПРИ а<х<ь (см- § 22)-
В самом деле, если существует система констант с% B с? > °)» Ддя *°-
юрых
2
то, очевидно, определитель
Ь(х1,х2,...,хк)~Ъ
для любых ^b лгз, ..., хк (д<^<^; /= 1, 2, ...,
154
УСЛОВНЫЙ ЭКСТРЕМУМ
[гл. IX
Пусть,» обратно: __
Обозначим через / наивысший ранг матриц Д (xlf х2, ..., xk) при всех системах
значений хг. В силу гипотезы ДееО имеем l<^k: Пусть:
@) @)
2 »•••!•**
есть система чисел такая, что матрица
(р,
имеет ранг /, и пусть
(Л 4= h 3» •••»
есть ее минбр /-го порядка, не равный нулю. Если
/ФА» Л* •••» Л»
то существуют постоянные: Xlf X2, ..., \г Qj V>^) такие, что
F)
G)
= 2 hpJ8(
s l
= Ь 2, ...,
Для любого х
имеем:
= 0. (9)-
Но так как его минор Аг ф 0 и элементы его последних столбцов связаны
соотношением (8), то элементы его первого столбца связаны тем же соотно-
соотношением:
Pj И = 2 18Р< W- <10>
8 Js
Вследствие произвольности jc соотношение A0) есть» соотношение тождествен-
тождественное; функции Pj, Pj, Pjj ..., Pj линейно зависимы, а тем более линейно
зависимы все k функций Ръ Ръ ..., Рг: их определитель Грамма равен нулю.
Доказательство теоремы. Итак, допустим, что кривая
у—у(х) удовлетворяет всем условиям теоремы. Проварьируем кривую
У—У(х) в бесконечно малой окрестности каждой из (A-J-1) точек:
хг, х29..., хк, х, причем точки xlt х2, ... , хк выберем так, чтобы для
этих значений определитель А был отличен от нуля. Обозначая через
^ixi*y) вариацию кривой в окрестности точки xiy положим
§ 60] ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА 155
В силу результатов предыдущей главы приращение функционала / при
переходе от кривой у— у (х) к кривой у=ух (х) будет равно:
где о4 есть площадь бугорка о (х1У у), возвышающегося над кривой
у=у (х) в окрестности точки хг:
Для того чтобы кривая у (х) давала экстремум, необходимо, чтобы
Д/>-0 при всех допустимых вариациях, т. е. при всех вариациях, для
которых интегралы Кг не меняются. Добавочные условия на вариацию
дают нам, как раньше, соотношения между о,:
где все числа в можно считать как угодно малыми. Отсюда в силу
условия ДфО мы можем всео4(/=1, 2,..., А) выразить через о;
AJ должен быть неотрицательным при любом о, если в выражении А/
считать о4 выраженными через о. Умножим /-е соотношение из A2) на
произвольное постоянное X, (/== 1, 2,..., k) и, прибавив левые части
всех полученных уравнений к правой части A1), получим:
где
Выберем теперь \ так, чтобы все множители при at (/= 1, 2,. . ., k)
обратились в нули (это возможно, ибо АфО и е как угодно малы),
но тогда в силу произвольности о для этих значений \t должны иметь:
d
при всех значениях дг. Здесь все \ и е4 зависят от дг, но поскольку
все е4 как угодно1 малы, то мы в окончательном соотношении можем их
все приравнять нулю. Мы получим для л, значения, не зависящие больше
от х\ и соотношение A3) перейдет в искомое уравнение:
Условная экстремаль для общей задачи. Как и в простейшей
задаче, уравнение A4) дает полное решение следующей задачи: среди
всех кривых, соединяющих две данные точки и для которых интегралы
Кг (i— 1, 2,..., k) принимают заданные значения, определить кривую,
при вариации которой §7 = 0, коль скоро 8/^ = 0 (/=1, 2,..., k).
156 условный экстремум [гл. IX
Если опять назвать условной экстремалью всякую кривую, которая
будет решать поставленную задачу (при произвольных фиксированных
концевых точках и при произвольных фиксированных значениях инте-
интегралов /Q, то мы будем иметь следующую теорему:
ТЕОРЕМА. Уравнение A4) есть условие необходимое и достаток**
для того, чтобы кривая у=у(х) являлась условной экстремалью.
Доказательство приводить не будем, ибо оно вполне аналогично при-
приведенному нами для простейшего случая.
Функцию Н можно представить в форме симметричной относительно
всех подинтегральных функций F и G®:
Н= X0F+ X,GA) + • • • + Ь*°(Л)-
Отсюда получаем для нашей общей задачи принцип взаимности: если
исключить случаи, когда \ обращаются в нуль, то совокупность от-
относительных экстремалей не зависит от того, будем ли мы искать
экстремум J при фиксированных Kt или будем искать экстремум Кг
при фиксированных J и Kj (J ф /).
Пример 1. Разберем первый из приведенных выше примеров (задача о тяже-
тяжелой цепи): найти минимум интеграла
x0
яри условии
/С= / Vl+y*dx = I.
XQ
Функция Н в этом случае примет вид:
Произведя замену переменного:
функция Н примет вид подинтегральной функции, отвечающей простейшей э*-
даче на определение минимальной поверхности.
Пользуясь добытыми результатами, получим семейство экстремалей задачис
у = a ch
а
Это есть общее уравнение цепной линии. Произвольные константы определя-
определяются из уравнений:
fyjZfytdx^ f ch—?л =
J J «
§ 30).
§ 60]
ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА
157
Пример 2. Среди всех кривых длины /, соединяющих две данные тонки
А и В1), определить кривую, ограничивающую вместе с отрезком АВ наи-
наибольшую площадь.
Примем за ось Ох прямую, проходящую через данные точки А и В (черт. 28);
тогда площадь, ограниченная кривой у=у(х), которую мы, очевидно, можем
всегда считать расположенной над осью Ох,
выразится интегралом: ц
ь
J =
где а, ? —абсциссы точек "А и В. Таким
образом наша задача приводится к разы-
разысканию максимума интеграла /при условии
ь
Черт28.
и при начальных условиях у (а) = у (Ь) = 0. Применяя правило Эйлера, нам надо
прежде всего определить семейство экстремалей для интеграла:
ъ
f
= fH(y,y')dXi
а
где
Первый интеграл уравнения Эйлера для интеграла / будет:
-JZ^
или:
Положим:
У'
тогда
у = а — X cos ср.
Диференцируя это соотношение по х, получим:
Отсюда:
Таким образом уравнение семейства экстремалей будет:
jc = X sin cp-f-р,
у = — X cos cp ¦+•а
или, исключая <р:
Следовательно, если искомая кривая существует, то эта кривая есть окруж-
окружность. Три параметра a, [J, X, определяющие положение и радиус окружности,
определятся, очевидно, единственным образом из условий прохождения окруж-
окружности через точки А и В и из условия, что длина искомой кривой равна./.
!) М,ы допускаем заранее, что
теряет смысл.
так как в противном случае задача
158 УСЛОВНЫЙ ЭКСТРЕМУМ (ГЛ. IX
Нетрудно показать, что решенная нами задача эквивалентна с изопериметри-
ческой задачей в узком смысле, разобранной нами в гл. V, § 30, 33.
Пример 3. Тяжелая жидкость, находящаяся в цилиндрическом стакане,
вращается с постоянной угловой скоростью около вертикальной оси, сов-
совпадающей с осью стакана. Определить форму свободной поверхности жид-
жидкости, считая, что движение установилось и что жидкость вращается как
твердое тело.
Введем цилиндрическую систему координат (г, ср; z\ причем за плоскость
(г, ср) примем дно стакана, а ось Oz будем считать проходящей через ось вра-
вращения. Ввведем следующие обозначения:/? — радиус стакана, h — высота уровня
жидкости над дном, когда жидкость находится в покое, ш — угловая скорость
вращения, fx — плотность жидкости. Пользуясь принципом Даламбера, постав-
поставленная динамическая задача может быть сведена к задаче статики, если к дей-
действующим силам добавить силы инерции.
Силы инерции — центробежная сила, действующая на элементарный объем
rdydrdz массы dm = pr dy drdz, будет равна
и направлена перпендикулярно к оси Oz и под углом ср к полярной оси. Отсюда
проекции X, Y на оси Ох и Оу силы инерции, приложенной в точке (г, ср» z) и
отнесенной к единице массы, будут равны:
X = оJг cos ср, Y = ш2г sin ср.
Эти силы допускают потенциал U1 = -7r- ш2/*2.
Таким образом наша задача приводится к определению равновесия жидкости
под действием: 1) сил инерции с потенциалом Ux = -д- <о2г2, 2) сил тяжести с по-
потенциалом ?/2= — gz, 3) сил давления. Силы трения отсутствуют, ибо жид-
жидкость считается идеальной.
Работа сил давления при всяком возможном перемещении системы равна
нулю. Таким обргйом потенциальная энергия W жидкости будет равна:
где интегрирование распространяется на все элементарные массы, С есть
постоянная. Пусть
z = z (г)
есть уравнение свободной поверхности (в силу симметрии поверхности z от f
не зависит); тогда, пользуясь выражением для элементарной массы, получим:
W
-<-///G~-<
R z(r) 2n
С - )>.? dr j \dzj (~ a>V2~
0 0 0
R
= С — т:р, / (u>V2* — grz) dr.
о
Кроме того:
R
I I I dm^Tty. I zrdr =
§ 60] ИЗОПЦРИМЕТРИЧЕСКАЯ ЗАДАЧА 159
Отсюда в силу принципа Дирихле х) наша задача приводится к определению
функции z — z(г), дающей минимум интегралу
R
(a)
о
о
при условии:
R
Г= f
R
rzdr = R*h. (b)
о
Для решения воспользуемся правилом Эйлера для изопериметрической
задачи, полагая:
Н = grz* —
Уравнение Эйлера примет вид:
Hz = 2grz — <D2r3 -f Xr = 0
или:
гд,е\ — постоянная, определяемая условием (Ь), откуда
Пример 4. Закон распределения Максвелла. Пусть в единице объема газа
заключено N молекул однородного газа. Обозначив через Т энергию (кинетиче-
(кинетическую и потенциальную) молекулы газа, через f(T) — функцию распределения
числа молекул в зависимости от энергии Т [т. е. f(T)dT означает число моле-
молекул, энергия которых заключена между Т и T + dT\, через Е—общую энергию
всех молекул газа, имеем:
Tf{T)dT=E.
ОО ,
Обозначим через Н функцню Больцмана Н= I f In fdT, пропорциональную
о
энтропии, функцию, которая может служить (с обратным знаком) мерилом ло-
логарифма вероятности данного распределения молекул по энергии, выражаемого
функцией распределения / (Т) 2).
*) Принцип Дирихле в статике сводит задачу об отыскании условий равно-
равновесия системы к задаче определения экстремума ее потенциальной энергии.
2) Если у нас имеется М предметов, распределенных но К группам (причем
вероятность предмета попасть в любую группу одинакова), то вероятность
того, что в первую группу попадет mlt во вторую /я2,..., в ?-ую mk предметов,
равна
М\ _1_
где 2/w*== М. Логарифм этой вероятности равен: In(М!) — 2In (т?)—М\пк
150 условный экстремум [гл. IX
Поставим теперь задачу о нахождении наиболее вероятного распределения
молекул по энергиям, т. е. задачу о нахождении минимума Н при условиях
<15) и A6). Эта изопериметрическая задача сводится к нахождению безуслов-
безусловного минимума от
Условие минимума:
дает нам:
ln/=-V-
или
где С = ?^~*"Ч Постоянные С и Ха найдем из условий A5) и A6):
§ 61. Правило множителей Эйлера-Лагранжа
Свойства линейных многообразий. Правило множителей Эйлера-
Лагранжа, выведенное для случая условного экстремума функций п пе-
переменных (§ 16) и изопериметрической задачи, может быть распростра-
распространено путем обобщения методов § 16 на случай условного экстремума
функций в общем линейном пространстве.
Будем в дальнейшем называть многообразием в линейном простран-
пространстве L совокупность точек а, определенную системой уравнений:
/.<«) = о.
Мы ограничимся случаем систем конечного числа уравнений. Если все
/tt (#) СУТЬ линейные функции, то многообразие называется линейным.
Линейное многообразие само есть линейное пространство.
В дальнейшем, определяя линейное многообразие V системой 'линей-
'линейных уравнений:
/4(а) = 0 (/=1, 2, ..., я), A7)
будем без оговорок полагать, что ни одно из уравнений A7) не есть
следствие остальных и, в частности, что ни одно из этих уравнений не
удовлетворяется тождественно для всех элементов а, принадлежащих
пространству Z,, в котором система A7) определена.
или приближенно I заменив по формуле Стирлинга In (.И!) через М In М — -у М I
равен:
М (In М — In k) — 2 miln Щ-
Следовательно, сумма 2 т^п mi c обратным знаком, с точностью до постоянного
числа Mln-^f изображает логарифм вероятности данного распределения. В нашем
случае? при переходе от дискретного распределения к непрерывному, роль этой
суммы перейдет к интегралу Н.
§ 61] ПРАВИЛО МНОЖИТЕЛЕЙ ЭЙЛЕРА-ЛАГРАНЖА 161
При этих оговорках мы отметим следующие свойства линейных
многообразий:
I. Если линейное многообразие V задано системой уравнений A7),
то всякий элемент Ь из L может быть представлен в виде:
где аи а2, ..., ап есть система фиксированных линейно независимых
элементов, лежащих вне Z/, элемент а принадлежит L'.
Докажем это свойство методом совершенной индукции. Пусть я=1:
многообразие V определяется единственным уравнением:
/(а) = 0. A70
В силу наших оговорок уравнение A7') не выполняется тождественно
на?; существует элемент а1 из L такой, что 1(ах) ф 0. Пусть Ь есть произ-
произвольный элемент L. Обозначим:
Очевидно,
/(а) = 0;
отсюда а принадлежит L' и b =±= а-{-tav гле t=~—^-.Теорема доказана.
Сделаем теперь гипотезу, что теорема верна для случая п—1 урав-
уравнений в системе A7), и докажем ее для случая п уравнений. Пусть V
есть линейное многообразие на ?,, определенное п уравнениями A7),
а Ln есть линейное многообразие, определенное одним уравнением
/л(а) = 0 из числа системы A7). В силу только что доказанного, для
произвольного Ь из L имеем:
A9)
где Ьх есть определенный элемент, который лежит вне Ln, а ап — в Ln.
Рассматривая Ln как линейное пространство, мы убедимся, что
многообразие V определяется на Ln системой (п—1) уравнений:
/i(a) = 0 (i = l, 2, ..., п— 1).
Так как по предложению теорема доказана для случая систем из (п—1)
уравнений, то на Ln существуют (п—1) линейно независимых элемен-
элементов av a2, ..., лп_1, лежащих вне Z/, таких, что для произвольного
элемента из Ln, а следовательно, для Ьх из Ln имеем:
А, B0)
где а принадлежит Z/. Обратив внимание, что ап лежит вне Ln> a,
при /<я —1 лежат на Ln и что av a2, ..., ап_х между собой
линейно независимы, получим, что все наши п элементов аг, а2У ..>,ап
линейно независимы. Сопоставив A9) и B0), получим нашу теорему.
162 УСЛОВНЫЙ ЭКСТРЕМУМ [ГЛ. IX
1L Если линейное многообразие L'\
lt(a) = O A=1, 2, ..., п) B1)
заключается в линейном многообразии Lo:
/0(а) = 0, B2)
то существует такая система постоянных Х1э Х2, ..., \п9 что
Л(а)вО. B3)
В самом деле, всякий элемент Ь из V по-предыдущему равен:
п
где а' из I/, и, следовательно, принадлежит V С ?0> а элементы
ах, о^, ..., ап линейно независимы и лежат вне L'. Поэтому в силу
B1) и B2):
<= 1
п
i= 1
Функции /у, рассматриваемые как линейные функции от tv t& ... , tnt
в силу наших условий линейно независимы, следовательно, определитель
| ij (щ) | ф 0 (/, у = 1, 2, ... , /г).
Рассматривая /0(&) как линейную функцию /г переменных tv t2, ..., /Л,
мы в силу результатов из теории линейных уравнений имеем:
что и требовалось доказать.
Обратная теорема о том, что из условия B3) следует заключаемость
Lf в L09 очевидна !).
ОПРЕДЕЛЕНИЯ. 1. Будем называть линейное многообразие La, ли-
линейным касательным многообразием к многообразию М:
/i(a) = 0 (/=1, 2, ... , п\
в точке а0, если совокупность точек ao-\-h из La удовлетворяет отно-
относительно А системе линейных уравнений
' dfi(a0;h) = 0 (i=l,2, .... л). B4)
2. Точка а0 из Af называется обыкновенной точкой, если ни одно из
уравнений системы B4) не есть следствие остальных.
1) Аналитически заключаемость многообразия V в многообразии Lq озна-
означает то, что уравнение B2) есть следствие уравнений B1).
§ 61] ПРАВИЛО МНОЖИТЕЛЕЙ ЭЙЛЕРА'ЛАГРАНЖА 163
Прямая а = ао-{-/А, где а0 принадлежит Ж, а a-f-A— касательному
многообразию L , называется касательной прямой к многообразию М
в точке а0.
В силу свойства I существует п линейно независимых элементов
А1э Л2, • • • » Лп из Z, таких, что
и что пространство Z, распадается на прямую сумму линейного много-
многообразия L^ и я-мерного линейного пространства с базисом А1,А2» ..., АЛ.
ТЕОРЕМА 1. Для любой касательной к М в точке а0 прямой
при любом достаточно малом по абсолютной величине t найдется
система чисел tv t2, ..., tn, зависящих от tn таких, что:
п
1) точка aQ-\-th-\- V /Д принадлежит М,
2) /| сутб величины малые высшего порядка сравнительно с L
Геометрически это означает, что достаточно близкие к а0 точки
касательной прямой удалены от многообразия М на величину высшего
порядка сравнительно с их расстоянием от точки касания а0.
Обратим внимание на то, что в силу определения диференциала
<§ 41):
fs (а0 + Ш + 2 *А) — ft («о) = *f} ( «о; * + 2 'А) + 8>. B5)
где е^ суть непрерывные функции переменных /, tv t2> ..., /п, прини-
принимающие значение высшего порядка малости сравнительно с th -f-
т. е. сравнительно с наибольшим по абсолютной величине из аргументов
Д так как
j O (/=1, 2, .... п),
то
^ ( а0; А + 2 'А) = S ^ rf/i («о; *i). B6)
<= 1
Так как а0 есть обыкновенная точка Ж, то
ИЛ(«о'э*|IФ° L(/. '=1. 2, ...,^ B7)
Требование, чтобы'.точка ао4-^А+2^А пРинаДлежала ^ вместе
с а0, в силу B5) и B6) приводится к условию:
2 W(«о''*«) = -•/ (/—1. 2, .•.,«). B8)
Вследствие неравенства нулю детерминанта B7) для определения tt сис-
систему уравнений можно заменить эквивалентной ей системой;
*, = Ч/, B9)
условный экстремум [гл. IX
где v\f суть линейные функции от в,. В силу свойств з^
Ч = 1ЦА*> fv ••• > О
ееть непрерывная функция от t, tl9 t%, ..., tn, причем значения r\j суть
величины высшего порядка малости сравнительно с наибольщим из чисел
|*|, Kl, \h\> .-о \tn\. Если все
то
При \t\$ меньшем некоторого фиксированного числа /0,
0 < 8i < " •
Итак, будем в дальнейшем полагать t ^ t0.
Фиксируем t A11 -^ \t01) и рассмотрим в n-мерном пространстве
(tv t» ..., О куб:
ККИ (i=h 2, ..., я).
Каждой точке T(tv t2, ..., tn) этого куба отвечает точка fa
где */== ¦»!,(*, ^, ..., *п), причем по Построению |^'|^ —1/|. Когда
точка Т пробегает весь куб, соответствующая точка Y пробегает неко*
торый континуум А, заключенный в меньшем кубе:
U«'l<-J-|*l («=1, 2, ..., я).
Преобразование, относящее каждой точке Т соответственную точку Y,
отображает непрерывным образом куб | tt |<; 11 \ на его замкнутую
часть А. В силу теоремы Брауера (Brauwer) при непрерывном отобра-
отображении выпуклого тела в я-мерном пространстве на его правильную
ч^сть обязательно существует неподвижная точка, т. е. точка, перехо-
переходящая в самое себя (см. часть I, дополнение III).
В применении к нашему случаю куб | /t.|<; 11\ должен содержать
точку T(tv t2, ..., tn), совпадающую с соответственной точкой
Y(t\\> ^2» •••» ^J» т- е- система уравнений B9) имеет решение и
притом удовлетворяющее неравенству:
|*,|<|/| (/=1, 2, ..., я).?C00
Равенство C1) показывает, что числа ^, получаемые при решении
этой системы, обладают высшим порядком малости сравнительно с /.
Так как уравнения B9) эквивалентны системе уравнений B8), то точка
принадлежит М. Теорема доказана.
Обобщение правила множителей Эйлера-Лагранжа. Докажем теперь
теорему, обосновывающую правила множителей Эйлера-Лагранжа.
§ 61] ПРАВИЛО МНОЖИТЕЛЕЙ ЭЙЛЕРА-ЛАГРАНЖА 165
ТЕОРЕМА 2. Если в обыкновенной точке а0 многообразия N:
?,(<*) = О (/=1, 2, ..., п)
достигается экстремум функции F на N, то существует система
констант Х1? Х2, ..., Хл таких, что
п
dF(a0', h) + ^ Х* фЪ (<> *) s °-
В этом заключается обобщение правила множителей Эйлера-Лагранжа.
Диференциалы предполагаются линейными функциями аргумента h.
Сначала докажем, что линейное касательное многообразие L^ к N
в точке а0 заключено в касательном (тоже в точке а0) многообразии:
dF(a0; *) = 0
к многообразию F(a) — F(a0) (см. свойство 2° линейных многообразий).
Пусть имеет место противное: существует элемент ao-\-h многообразия
L , для которого
) ^
Рассмотрим касательную прямую к N:
Из предыдущей теоремы следует, что для всякого достаточно ма-
малого по абсолютной величине \t\ можно подобрать п чисел ^ = ftj,
(/=1, 2, ..., п) таких, что limei = 0, а точка ло+^тУ^А пРи~
надлежит N. Имеем:
где s стремится к нулю вместе с t Далее
^ h) + ^\ttdF(а0; Л,) =
Отсюда:
где гг = s -f- N е4 rf/7 (а0; А^ стремится к нулю вместе с ? Так как
с ф 0, то знак разности F ( а0 -J-- tt -|- ^ ^Л — /^(ао) совпадает со
знаком cty и, следовательно, это приращение функции F будет прини-
принимать разные знаки в любой близости точки а0 в зависимости от знака L
Отсюда следует, что а0 не есть точка экстремума. Теорема доказана *.
Обоснование метода Эйлера для решения обобщенной изопери-
метрической задачи. Непосредственным следствием доказанной нами
теоремы является обоснование метода Эйлера для решения обобщенной
изопериметрической задачи.
1) См. Л. Л ю с т е р н и к, Об условном экстремуме функционалов, Мат.
сборник, т. 41, вып. 3.
166 УСЛОВНЫЙ ЭКСТРЕМУМ [ГЛ. IX
Пусть даны на линейном функциональном пространстве R функцио-
функционалы: J, 'Kif К2, ...» Кп* Не задаваясь аналитическим видом этих функ-
функционалов, положим, что они на нашем пространстве R обладают вариа-
вариацией. При этих условиях получим теорему, являющуюся обобщением
теоремы, доказанной в § 16.
ТЕОРЕМА 3. Пусть для функции у=:у(х) вариации:
Щ(у) (/=1, 2, ..., я)
линейно независимы. Для того чтобы функция у(х) реализовала
экстремум J(y) при условиях:
Kl(y) = tl = const (t = l, 2, ..., п),
необходимо, чтобы нашлись п постоянных чисел: \9 Ха, ..., \Л
таких, что
pS] C2)
Если, в частности, функционалы J и Kt заданы на Ci в виде:
ъ ъ
J = fF(x,y,y')dx, К=/о{(х9у,/)ах (*—1, 2, ..., я),
а а
то условие C2) примет вид:
где
В силу основных лемм вариационного исчисления в этом случае по-
получаем снова классическое правило Эйлера-Лагранжа для общего случая.
§ 62. Условие Лежандра
Необходимое условие Лежандра для простейшей задачи вариацион-
вариационного исчисления может быть без труда распространено на ' случай изо-
периметрической задачи.
Мы ищем минимум функционала
ь
J=fF(x,y,y')dx,
а
при условии
Ъ
а
и при начальных условиях:
'"\=yv
§ 62] УСЛОВИЕ ЛЕЖАНДРА 167
Пусть мы нашли функцию у = у(х), удовлетворяющую начальным
условиям и условию C3), и число X такое, что для этой функции
Пусть
(
другая функция, удовлетворяющая тем же начальным условиям и усло-
условию C3). В силу условия 8G = 0 имеем:
Необходимое условие того, что функция у — у(х) дает искомый
экстремум, заключается в том, чтобы при переходе к близкой функции
#у1=иу1(д:), удовлетворяющей упомянутым условиям, вторая вариация
была неотрицательна. Обозначив H — F-\-\Fv имеем:
ь
ЬЮ <= ± f (HJ? + 2Я„. W + Я,уЗ/») dx. C4)
а
Доказательство теоремы Лежандра. Мы докажем, что
необходимое условие (условие Лежандра) того, чтобы у=у(х) давала
минимум, заключается в том, чтобы вдоль кривой у—у(х): Н , ,^Q
В самом деле, пусть это условие не выполнено, т. е. для некоторого
значения х на интервале [a, b] #«ryr<0. Тогда вследствие непрерыв-
непрерывности Н^у, найдется интервал [av 6J, часть интервала [а, Ь], в каждой
точке которого
Отметим на этом интервале два заключенные в нем непересекающихся
интервала длины, равной достаточно малому положительному числу — :
[х09 хо-{-—у, \хх, -^i + — J,
х0 + ~ < хх < хх + -J- < bt < Ъ.
Пусть далее сг и г9 — два достаточно малых по абсолютной величине
числа, одно из которых во всяком случае отлично от нуля. Определим Ьу
следующим образом:
О вне обоих интервалов л:0, *0-{--?.l \xt, xt + ~\9
сх sin2 п (х — лг0) на интервале лг0, х0 4- — ,
га sin2 п (х — хг) на интервале \xv xt -}- — .
168 УСЛОВНЫЙ ЭКСТРЕМУМ [ГЛ. IX
Соответственным подбором отношения сг: с2 можно добиться того, чтобы
кривая
У
удовлетворяла условию C3).
Пусть, например, сх ф 0. Тогда, при достаточно большом /г, инте-
интеграл C4), взятый по интервалу лг0, ^о + "^~ при нашем подборе 8у(#)
отрицателен; если с2 тоже отлично от нуля, то тем же свойством обла-
обладает и интеграл по интервалу \xv jq-f-— . Во всяком случае, вторая
вариация ЬЮ стала отрицательной, тогда как для минимума она должна
быть неотрицательной. Итак, выполнение требования // , ,^0 необ-
необходимо для того, чтобы функция у(х) реализовала минимум; наоборот,
требование Ну, , <С 0 есть необходимое условие максимума. Формулируем
доказанную теорему:
ТЕОРЕМА ЛЕЖАНДРА. Если кривая у =у(х) дает условный мини-
минимум интегралу J: ъ
J=fF(x, у, y')dx
а
при условии
ъ
то вдоль кривой у = у(х) имеем:
где X — константа Эйлера изопериметрической задачи.
Обобщение на случай любого функционала. Вернемся к рассмо-
рассмотрению предыдущего параграфа. Мы ищем минимум функции /(а)
на многообразии N, заданном в линейном пространстве L системой
уравнений:
?|(«) = 0 ('=1, 2,...,п).
Пусть в точке а0 этого многообразия удовлетворяется условие:
Обозначим:
На многообразии N f совпадает с //, и вопрос о том, дает ли точка а0
минимум / на N, можно заменить вопросом, дает ли а0 минимум Н на N-
ТЕОРЕМА. Для того чтобы точка а0 была точкой минимума f
на N, необходимо, чтобы в этой точке форма
0; h)
была неотрицательной на линейном многообразии La> касательном
к N в точке а0.
§ 63] УСЛОВНЫЙ ЭКСТРЕМУМ 169
В самом деле, пусть найдется элемент aQ-\-h многообразия L >
для которого:
d*(aoi h) = — с*<0. C5)
На прямой ao-\-th имеем:
C50
При достаточно малом t каждому элементу прямой а0 -}- th отвечает
элемент b многообразия N такой, что:
ft = «o-H* + 2'A> C6)
i = l
где аг обозначают k фиксированных элементов, tK суть величины высшего
порядка сравнительно с ? Так как dH==0 в точке а0, то
t
= - №+2 «А
где | е | есть величина высшего порядка сравнительно с t\ kt есть зна-
значение билинейной формы, отвечающей второму диференциалу.
Из C7) видно, что главная часть разности /(/>)—f(a) есть — c2t2y
и при достаточно малом /
Теорема доказана.
§ 63. Условный экстремум
Постановка задачи на условный экстремум. В § 50 мы рассмо-
рассмотрели экстремумы функционалов, принимая за класс допустимых линий
совокупность пространственных кривых, соединяющих или две данные
точки или точки заданных линий. В приложениях к геометрии и меха-
механике имеют также большое значение задачи, когда за класс допустимых
линий принимаются кривые, расположенные на данной поверхности
или для случая многих неизвестных функций,,расположенные на некото-
некотором многообразии. Соответствующие вариационные задачи носят название
задач на условный экстремум. Методика и главные идеи этих рас-
рассмотрений полностью выявляются, если рассмотреть простейший случай
подобных задач.
Постановка задачи. Среди всех кривых:
у=у(х), z = z(x) ' C8)
класса Ci, соединяющих две данных точки А и В и расположенных
на данной поверхности
?(*, у, *) = 0 О, C9>
!) Поверхность мы будем предполагать без особых точек, в соответствие
с этим будем предполагать, что
170 условный экстремум [гл. IX
определить кривую, вдоль которой интеграл J:
у, *, У, z')dx D0)
¦/
Хо
принимает экстремальное значение.
Эта задача может быть без труда редуцирована к простейшей задаче
вариационного исчисления с одной неизвестной функцией. В самом деле,
решая уравнение C9) относительно z и вставляя полученные выраже-
выражения z и z' в функцию F, мы получим под знаком интеграла функцию,
зависящую только от х, у, у.
Такой путь, принципиально возможный, является во многих задачах
практически плохо реализуемым, ибо при его осуществлении приходится
диференцировать функцию, заданную неявно. По этой причине для ре-
решения этой задачи применяется прием, аналогичный соответствующим
приемам, которыми мы пользовались при рассмотрении задач на условный
экстремум функций многих переменных.
Метод Лагранжа. Для непосредственного решения поставленной выше
задачи Лагранжем был предложен метод, получивший название метода
неопределенных функциональных множителей. Этот метод состоит
в следующем.
Строим функцию:
Ф (х, у,< z, Уу z?) = F -f- X (х) 9i
где X (х) есть неопределенная функция от х. Ищем безусловный экстремум
интеграла
\= I Ф4х.
«•
Выписываем для этой задачи диференциальные уравнения Эйлера:
D1)
К системе D1) с тремя неизвестными функциями: у(х), z(x), Х(#) мы
добавляем данное соотношение:
?(*, У, г) = 0. D2)
Решение трех уравнений D1) и D2) будет содержать две произвольных
постоянных, которые определятся из начальных условий. Для того
чтобы оправдать это правило, установим два факта:
1. Если существует множитель X (х) такой, что кривая
дает безусловный экстремум Jt и принадлежит поверхности <р ==0, то
эта кривая дает условный экстремум интегралу У.
§ 63] условный экстремум 171
2. Если кривая
* У—У(х\ z = z(x)
дает условный экстремум интегралу /, то существует множитель Х(лг)
такой, что эта кривая есть экстремаль задачи на безусловный экстремум
интеграла Jv
Первый факт очевиден непосредственно. В самом деле, если кривая Г
дает безусловный экстремум интегралу Jv то, значит, она дает экстре-
экстремальное значение интегралу Jx среди всех кривых, соединяющих две
данные точки, в частности дает экстремальное значение среди кривых,
лежащих на поверхности <р —0, но для этих кривых прдинтегральные
выражения J и Jt совпадают при любых X (х).
Для доказательства второго факта воспользуемся методом вариаций !).
Допустим, что кривая Г: у=у(х), z = z(x) дает условный экстремум.
Тогда при всех допустимых 2) вариациях этой кривой вариация инте-
интеграла J должна равняться нулю. Произведем вариации 8у и bz в произ-
произвольной точке (at, у(х), z(x))\ тогда:
Найдем зависимость между ot и а2 из условия, что вариация догцг-
стимая. В каждой точке должны иметь:
ду
или, интегрируя по х в тех пределах, где 8у, 8г отличны от нуля, -ш
отбрасывая бесконечно малые высших порядков, получим:
Разберем сначала случай, когда вдоль кривой
^?.фО и -^-Ф0-
ду ~ dz ~
В этом случае, сравнивая D3) и D4), получим:
dy dz
1) Мы будем при этом вести вычисления, сохраняя лишь главные беско-
бесконечно малые. Сделать вывод вполне строгим можно следующим образом: во
всех формулах вместо отброшенных бесконечно малых поставить elf e^,...
В таком случае выражение D5) будет зависеть от этих е4. Предельный переход,
аналогичный § 60, 61, нам даст окончательное уравнение D5).
2) Допустимой мы называем ту вариацию, при которой кривая остается на
поверхности <р (х, у, z) = 0.
172 условный экстремум [гл. IX
Обозначая Это общее отношение через — X (лг), — вдоль кривой это отно-
отношение будет, очевидно, функцией только лг, — получим:
Построенная нами система уравнений есть система уравнений Эйлера,
определяющая экстремаль для безусловного экстремума интеграла
J {F+Щйх.
Особые случаи. Заметим прежде всего, что вдоль кривой не могут
одновременно обратиться в нуль -~- и •— . В самом деле, так как -~- ф О,
то в случае одновременного обращения в нуль производных -~- и —^-
касательная плоскость будет перпендикулярна оси Ох\ следовательно,
одна из производных у' (х) или 2? (х) обязательно обратится в беско-
бесконечность, чего быть не может в силу основных условий, наложенных на
класс допустимых линий.
Допустим теперь, что вдоль кривой
в этом случае вариация Ъу произвольна, а &гг = 0, и система уравнений
сведется к одному:
Кроме того, в силу D6) функция <р будет зависеть только от х и z:
ср(х, *) = 0. D7)
Таким образом в разбираемом случае дело сводится к решению
уравнений D5) и D7), которые получатся из правила Лагранжа, если
положить X (л:) == 0.
Геометрически это значит, что поверхность — носительница класса
допустимых линий, есть цилиндрическая поверхность с образующими,
параллельными оси Оу.
Случай -—• = 0 аналогичен разобранному, здесь все сводится к
решению уравнений:
§ 64] трансверсальность 173
§ 64. Трансверсальность
Обобщение условий трансверсальности. Дадим в заключение теории
условного экстремума интегралов решение задачи, когда за класс до-
допустимых линий принимаются кривые, принадлежащие данной поверхности
<р = 0 (многообразию) и соединяющие данную точку А с произвольной
точкой данной кривой Г:
.У =/(*), z
При этом мы предполагаем, что точка А и кривая Г принадлежат данной
поверхности.
Пользуясь методом Лагранжа, определяем прежде всего семейство
экстремалей задачи: найдем условный экстремум интеграла:
J=J*F(x, у, z, /, z')dx
при условии
?(*, У у z) = 0.
Искомое семейство экстремалей определится системой уравнений:
где положено: Ф =
В силу рассуждений § 54 искомая кривая будет принадлежать по-
построенному семейству, зависящему от двух произвольных постоянных.
Одно соотношение между постоянными мы получим из условия прохож-
прохождения искомой кривой через точку А. Найдем условие, которому должна
удовлетворять искомая экстремаль в свободном конце. Необходимое усло-
условие экстремума заключается в обращении в нуль первой вариации. Вместе
с тем для обращения в нуль первой вариации разбираемой задачи
достаточно, чтобы обратилась в нуль вариация интеграла:
J. = / ф dx
при переходе от искомой кривой к произвольной бесконечно близкой
кривой, соединяющей точку А с тонкой кривой Г. Отсюда, применяя
условия трансверсальности задачи на безусловный экстремум в свободном
конце, получим:
(/ (х) -У) Фу, + &' (*) - z') Ф,- -f Ф = 0.
Замечая, что
« что на поверхности ср = О Ф = F, получим в свободном конце условие:
(/ (х) -/) /у -f- (g' (x) - z') F.. + F = 0.
Мы показали, что это условие достаточно для обращения в нуль
первой вариации. Легко показать, что это условие будет также необ-
174 условный экстремум [гл. IX
ходимым; для этой цели достаточно пересмотреть данный нами выше
вывод условий трансверсальности в случае задачи на безусловный экстремум
и заметить, что там можно ограничиться таким варьированием, чтобы
после вариации кривая продолжала оставаться на поверхности.
Введение криволинейной системы координат. Мы дали выше общий
Метод для решения задач на условный экстремум, сведя эту задачу на
безусловный экстремум, увеличивая при этом число неизвестных функций.
Во многих вопросах, однако, бывает возможно притти к цели быстрее,
вводя на данной поверхности (на данном многообразии) криволинейную
систему координат.
Итак, пусть ищется экстремум интеграла
J=» jF(xy у, г, У, z')dx
при условии
(*> ) 0
Представляем уравнение поверхности в параметрической форме:
x=ft(u, v),
y=f2(u, v),
s=/8(ir, v)
и принимаем параметры и, v за криволинейные координаты на поверх-
поверхности. Произведем теперь под знаком интеграла J замену переменных,
вводя вместо лг, уу z координаты и и v. Имеем:
Положим:
где справа вместо лг, у, z, y'$ z' вставлены их выражения через a, v, 1/.
Интеграл / примет вид:
J = / Ф (к, v, vf) du.
щ
Наша задача привелась к простейшей задаче вариационного исчисления.
Условие ортогональности. В качестве примера на применение этого
метода решим такую задачу: каким условиям должна удовлетворять
функция Ф, чтобы условие трансверсальности свелось к условию орто-
ортогональности. Заметим, что эта задача не совпадает с решенной нами
выше, ибо в случае произвольных криволинейных координат условие
ортогональности будет отличаться от обычного vvx'— — 1. Для решения
поставленной задачи выберем сначала на поверхности специальную изо--
термич ескуюу систему координат S, т\.
§ 65] * ПРИМЕНЕНИЕ К ТЕОРИИ ГЕОДЕЗИЧЕСКИХ 175
Пусть в этих переменных подинтегральное выражение примет вид:
В этих координатах, как известно, условие ортогональности имеет вид:
где /(?) есть уравнение данной кривой. Следовательно, применяя добы-
добытый выше результат (частный случай, когда z = 0), получим:
Для того чтобы выяви^ структуру функции Ф в случае любой сие-
темы (и, v)y достаточно перейти от Е, Y) к переменным и> v. Заметим,
что диференциал дуги ds кривой на поверхности ср ===== 0 в случае изотер-
изотермической системы координат имеет вид:
(& =
отсюда
= v (е,
где Vj = -д-. Переходя к системе координат щ vy таким образои
получим:
Ф (и, *) dn = V2 (и, v) ds = V2 YE-\-2Fv' -\-Gv'Uuy
ф (tt, V) = V2 (и, v) V E + 2/V
где 1/2 получается из Vt подстановкой вместо ?, ч\ их выражений
через и, -у.
Как следствие приведенных выше рассмотрений получается, что
кратчайшая линия среди линий, расположенных на данной поверхности
и соединяющих данную точку с произвольной точкой данной кривой 1\
всегда ортогональна кривой Г.
§ 65. Применение к теории геодезических
Отыскание геодезических. Задача отыскания дуги у.
У=*У(х)> z = z(x)
наименьшей длины, так называемой геодезической дуги, соединяющей,
точки А (дг0, у0, z0) и В (xv yv z±) поверхности <р (лг, у, z) = 0, сво-
сводится к нахождению условного минимума интеграла
*1
у
х0
при условии
f(x9y
и условиях на границах:
У(*о)=Уоу
У (*!)=* УН
176 условный экстремум [гл. IX
По правилу множителей Лагранжа эта задача сводится к отысканию
«безусловных экстремалей интеграла
/ {V 1 +У2 + *'* — }
Составим уравнения Эйлера:
_ d yr
d
dx
Б силу формул Серре-Френе уравнения эти примут вид:
D8)
тде через cosap cosa2, cosa3 обозначены направляющие косинусы глав-
главной нормали к кривой ^ и где г есть радиус кривизны кривой f.
Отсюда:
сру : срг = cos a2 : cos a3*
Далее, из <р(х, у> z) — 0 следует, что вдоль кривой f. y=zy(x),
z = z(x) имеем:
+ У + = 0. E0)
Затем, так как главная нормаль к f ортогональна к касательной к той же
кривой и угловые коэфициенты касательной пропорциональны 1,У, z', то
cos ax -J- cos a2 у -[- cos a3 z' = 0.
Сопоставляя D8), D9) и E0), получим:
?» : ?у; ?• = cos ai: cos a2 = cos аз-
Но так как <рх, <pyJ yz в свою очередь пропорциональны направляющим
косинусам нормали к поверхности <р = 0, то отсюда получаем такой
результат: главные нормали к геодезической в каждой точке совпадают
с нормалью к поверхности.
Геодезическая окружность. Рассмотрим геометрическое место точек
поверхности
/(дг, у, z) = 0,
расстояние которых до данной точки А есть величина постоянная (черт. 29).
Такое геометрическое место точек называется геодезической окруж-
окружностью. Геодезическую окружность можно определить еще так: выпус-
выпускаем из точки А под всевозможными углами геодезические кривые и
§ 65]
ПРИМЕНЕНИЕ К ТЕОРИИ ГЕОДЕЗИЧЕСКИХ
177
вдоль каждой кривой от точки А откладываем дугу постоянной длины;
геодезическим кругом будет геометрическое место концов этих дуг.
Сами же дуги называются геодезическими радиусами.
Докажем, что геодезическая окружность ортогональна ко всем гео-
геодезическим, выходящим из точки А — центра геодезической окруж-
окружности. В самом деле, обозначим через Г геодезическую окружность.
Так как геодезическая, соединяющая А с произвольной точкой Г, есть
кратчайшее расстояние от А до Г, то, значит, эта геодезическая транс-
версальна к Г. Но для задач на минимальные, расстояния трансвер-
трансверсальность совпадает с ортогональностью, ибо расстояние определяется
интегралом / ds, который удовлетворяет
условиям доказанной выше теоремы г).
Геодезические линии и окружности как
инварианты при изгибании. Пусть мы под-
подвергаем поверхность изгибанию без растяже-
растяжения, т. е. изгибаниям, при которых длины
дуг не меняются. Так как длины линий не
меняются, то свойство линии давать мини-
минимум длин среди кривых, имеющих общие
с ней концы, сохраняется; иными словами,
свойство линии быть геодезической не ме-
меняется. Геодезические линии являются ин-
инвариантами изгибаний без растяжений.
Точно так же и геодезические окружности радиуса / переходят при
таких изгибаниях в геодезические же окружности радиуса /. Вычислив
длину такой окружности, мы получим величину, не меняющуюся при
изгибаниях. Имеет место следующая теорема:
ТЕОРЕМА. Длина геодезической окружности радиуса I равна
2тг/ + ~
где s стремится к нулю вместе с I; rv r2 — главные радиусы кри-
кривизны поверхности в центре А окружности.
Д оказательство. Примем за ось Az нормаль к поверхности в точке А,
за оси Ах, Ау — касательные к точке А к линиям кривизны поверхности /=0.
Перейдя в плоскости хАу от декартовых координат к полярным: р, f, мы полу-
получим в трехмерном пространстве цилиндрическую систему координат: р, <р, *>
в которой элемент дуги выразится по формуле:
ds2 = p2dfy2 -f- df- + dzK E1)
Выпустим из центра А геодезический радиус АВ длины / под углом а к оси хА.
Его кривизна — в точке А по теореме Эйлера выразится:
_L — cos2q I sin2 a
Черт. 29.
-г = 2 sin a cos а
D-
E2)
х) Мы предполагали геодезическую окружность настолько малой, чтобы
любые два геодезических радиуса, выходящие из А, не пересекались.
178 условный экстремум [гл. IX
Хочка В отклоняется на величину порядка Z3 от соприкасающейся плос-
плоскости к геодезическому радиусу в точке А, т. е. от, нормального сечения, обра-
образующего угол а с осью Ах. Координата <р точки В отличается, следовательно,
от а на величину порядка Z2:
«р + а + р/2, -d4 = (l+1*^H,1. " E3)
Очевидно, (J как функция а, имеет период 2ти. С точностью до малых высших
порядков сравнительно с / имеем:
/2 fi (d \ )
Формулы E4) вытекают из того, что с требуемой нами степенью точности для
определения z и р мы можем заменить геодезическую дугу длины / соприка-
соприкасающимся кругом радиуса г, причем для дуги этого круга длины / имеем:
(л /\ /2
= r 1 — COS — )Я^-р-
Ч г / 2r
р-^, p = rSin— »/—тт-r .
2r2 r r br*
Пренебрегая в выражении E1) для ds2 членами порядка выше ^dofi (а сле-
следовательно членом dp2), получим для диференциала дуги геодезической окруж-
окружности в силу формул E3) и E4) выражение:
Подставляя вместо — и их выражения из E2), получим:
i 3 COS2a Sin2a—-COS4a , 3COS2a sin2a—sm4a 1 . ол 1
-\ ^—r —~ \- Sin2 2a .
Интегрируя по частям, получаем:
2rc 2я 2л: 2ге
/ Sin4 a </a = / cos4a flfa = / COS3 aflf sin a = — 3 / COS2 a sin2 a da,
ooo о
Следовательно, при интеграции по а в пределах от 0 до 2тс члены, содержащие
в знаменателе rL2 и г22, пропадут; точно так же при интеграции по а в атих пре~
2л:
делах интеграл / -^-da = Oi так как р имеет период 2г..
о
Для определения, с точностью до величины порядка выше Z3, длины 5 гео-
геодезической окружности нужно проинтегрировать выражение E2) по а в преде-
пределах от 0 до 2тс. В силу только что сделанного замечания
Л, /з sin22a\
что и требовалось доказать.
§65] ПРИМЕНЕНИЕ К ТЕОРИИ ГЕОДЕЗИЧЕСКИХ 179
Отсюда получаем как следствие фундаментальную теорему Гаусса.
ТЕОРЕМА ГАУССА. Главная кривизна поверхности
не меняется при изгибании без растяжения. А
В самом деле, геодезическая окружность радиуса / переходит при таком
изгибании в геодезическую окружность такого же радиуса, причем длина
окружности
не меняется. Следовательно, значение Г + е не меняется при изгибании, но так
как при достаточно малом / может быть сделан сколь угодно малым, то Г не
меняется при нашей деформации.
Геометрия на поверхности. Геодезические линии на данной по-
поверхности
9 = 0.
образуют двупараметрическое семейство линий. Как мы увидим в гл. XIV,
если данная поверхность удовлетворяет некоторым общим теоретико-функ-
теоретико-функциональным условиям, то каждую точку поверхности ср = 0 можно
заключить в некоторую окрестность Z), обладающую следующими свой-
свойствами:
1°. Через любые две точки D можно провести одну и притом только
одну геодезическую.
2°. Дуга геодезической, соединяющей .две данные точки А и В окрест-
окрестности Z), дает минимум длин линий поверхности ср = 0, соединяющих А и В.
В соответствии с этим при изучении геометрии на поверхности есте-
естественно принять геодезические линии этой поверхности за „прямые" гео-
геометрии на поверхности.
Как мы увидим впоследствии, ряд предложений плоской геометрии рас-
распространяется на геометрию, на поверхности, если „прямую" понимать
в отмеченном выше смысле и если за „расстояние* между точками при-
принять длину отрезка „прямой", соединяющей эти точки.
Если поверхность ср = 0 задана в форме:
? (*, у, z) = 0,
то задача определения семейства геодезических сводится к определению
семейства „условных" экстремалей функционала
= Г V
/= Г V Т+/*+?*dx.
Если поверхность задавать в параметрической форме:
х — х(и, v), у=у(и, v), z = z(u, v),
то геодезические будут экстремали функционал!
Интеграл У, взятый вдоль отрезка „прямой", будет давать „расстояние"
&ежду концами этого отрезка.
180 условный экстремум [гл. IX
При геометрической интерпретации / можно, не прибегая к простран-
пространству, рассматривать J(-f) как „длину" линии у в геометрии Римана;
„прямые" поверхности превратятся в „прямые" римановой геометрии.
Целый ряд теорем такой геометрии мы докажем ниже, в гл. XIV.
§ 66. Условный экстремум (неголономные связи)
Заканчивая рассмотрение элементарных задач на применение метода
вариаций, остановимся еще на задаче, когда за класс допустимых линий
принимаются линии, удовлетворяющие некоторой системе диференциаль-
ных уравнений.
Общий случай. Пусть требуется найти экстремум интеграла
ъ
/= Jf (jc, у, z, /, z') dx , E5)
когда за класс допустимых линий принимаются пространственные кривые
класса Сц удовлетворяющие диференциальному соотношению:
?(*,.У,2>/,20 = 0 E6)
и удовлетворяющие на концах (при х = ау х = Ь) трем добавочным
условиям. К этой задаче может быть также применен изложенный нами
выше метод неопределенных множителей Лагранжа.
Пусть некоторая линия ч0:
у=у(х), г=*г(х)9
принадлежащая классу допустимых линий, дает искомый экстремум.
В таком случае при всякой допустимой вариации кривой ^о вариация
87 должна равняться нулю:
ь
U = f (Fy ly + F, 8* + /у 8/ -f /v 8У) dx = 0, E7)
a
причем в силу E6) вариации Ъу, bz должны удовлетворять соотношению:
8/ + ?.' ^ = °- E8)
Умножим левую часть E8) на множитель X dx, где X будем пока считать
произвольной функцией от дг, и прибавим полученное выражение к под-
интегральному выражению; получим:
ь
bJ= f { (Fy -f X?y) Sy-f (Fy, -f- X-V) 8/ }'dx +
a
b
+ f i (F* + 4) ** + C7.' + 40 M}dx=o.
a
Произведем теперь над каждым из интегралов или преобразование Ла-
Лагранжа или преобразование Дю-Буа-Реймонда. Остановимся, например,
на последнем (см. § 47).
§ 66] условный экстремум (неголономные связи) 181
После обозначений:
X X
Qi = f (Fv + *?J dx9 Q2 = f (F9 + Xcps) dx
J y 'v J
a a
и" применения преобразования Дю-Буа-Реймонда вариация примет вид:
ъ ъ
/Г
[Qi — (/%/ + ^?«0|] fy dx-\- I [Q2 — (F > -f- Хсрг')] 02: ^д: == 0.
J У J
Определим теперь X = X (x) из условия:
Предполагая, что X таким образом определить возможно, и замечая, что
У* ! Ъ
Сг by'dx = С 8у | = О,
для о/ получим:
о
3/ = J [Q3 — (F,- + Xe,.)] Зг' «/л = 0.
а
Так как между вариациями оу и о^г мы имеем лишь одно соотношение,
то отсюда вытекает, что вариацию oz мы можем считать произвольной
(подчиненной единственному условию быть равной нулю в концах интер-
интервала [а, Ь]). Следовательно, в силу леммы Дю-Буа-Реймонда
. Q2 — CV + *?*') = С* = const. F0)
Диференцируя по х соотношения E9) и F0) и полагая:
H
окончательно получим:
Итак, если возможно определить функцию X, удовлетворяющую
соотношению E9), то искомая кривая Чо будет удовлетворять сис-
системе FЦ.
Этим самым мы получили метод для определения искомой кривой -(о-
В самом деле, решая совместно уравнения E6) и F1), мы найдем не-
неизвестные функции:
X (лг, <х1У а2, а3, сс4, аб),
у(Х, «!, «2, 0С3, «4>аб)>
z (х, аг, а2, а3, а4, аб),
которые будут зависеть от пяти произвольных постоянных интеграции :
ai> а2> аз> а4» а5* Для определения этих постоянных мы должны исполь-
использовать условия на концах.
Таким образом все сводится к возможности определить функцию X,
которая давала бы для левой части E9) постоянное значение. Диферен-
182 . УСЛОВНЫЙ ЭКСТРЕМУМ [ГЛ. IX
цируя E9) по х, получим для определения X диференциальное урав-
уравнение первого порядка:
или:
Здесь, очевидно, значения <р и F берутся вдоль кривой у0, так что ко-
эфициенты при ~^~, X и свободный член уравнения будут вполне опре-
определенными функциями от х. Кроме того, для наших целей достаточно
найти хотя бы одно решение X (л:), удовлетворяющее E9) и правильное
в интервале [а, Ь].
Допустим дополнительно, что вдоль экстремали у0
. ?,'*°;
тогда, полагая:
^т— -Р. ^ -Q,
уравнение F2) примет вид:
dx v '
где Р и Q — непрерывные в интервале [а, Ь] функции от х\ отсюда
ъ ь ъ
]
]Pdx Г -fPdx
= е J е
X = е J е ах
а
есть искомое решение.
Вполне аналогично, если вдоль экстремали
то мы можем определить X из F0) и отсюда получить E9).
Особые случаи. Если вдоль экстремали пГо имеем:
то соотношение E8) дает зависимость только между вариациями Ьу
и &г; мы получаем случай задачи на условный экстремум, разобранный
нами в предыдущем параграфе.
Наиболее неприятным оказывается последний случай, когда вдоль
экстремали каждая из функций vyt и «pef He обращается тождественно
в нуль. Мы не будем подробно анализировать этот случай х), заметим
только, что если ^о Дает экстремум интегралу 7, то каждый кусок fo»
заключенный между точками с абсциссами ах, Ьх, будет давать экстремум
интегралу ъ
= f
1) Этот анализ мы дадим во втором томе для общей задачи Лагранжа.
§ 66] условный экстремум (неголономные связи) 183
при тех же условиях. Отсюда, выделяя из интервала [а, Ь] интервалы,
в каждом из которых или одна из <ру'> ?«' отлична от нуля или обе
одновременно тождественно равны нулю, мы можем заключить, что для
этих участков кривой f0, соответствующие X, можно определить, эти
участки 7о будут удовлетворять системе уравнений F1).
Постановка общей задачи Лагранжа. Приведенный выше метод
без всякого труда может быть распространен на задачи более общие.
Пусть, например, ищется экстремум интеграла
ь
I
при условии, что все линии класса допустимых линий удовлетворяют
системе k диференциальных соотношений:
?, (*. Л» Л. • • • > Уп\ УЛ У*> • • • > Уп) = ° 0"= 1. 2,. . . , А)
и некоторым условиям на концах в количестве 2n-\-k.
Подобно разобранному простейшему случаю можно доказать, что
если искомая кривая ^0 существует и если вдоль кривой один из глав-
главных определителей функциональной матрицы
дь \ // = 1, 2, ..., k\
ду{) \/=1, 2, ..., я/
dyt
все время отличен от нуля, то ?0 есть интегральная кривая еле-
дующей системы n-\-k диференциальных уравнений:
#„—-?-#, = 0 (/=1, 2,..., л),)
и ах * (б3)
?у=0 (у=1,2,..., *),]
где // = F-f- 2\? ?/ # г^? \/ О'7716 некоторые функции от х.
Эта теорема, как и в разобранных ранее простейших случаях, позво-
позволяет фактически определить искомую кривую, если предположить, что
искомая кривая существует. В самом деле, система F3) нам дает n-\-k
диференциальных уравнений, из которых k первого порядка и п второго
порядка. Следовательно, общий интеграл этой системы:
(' = 1,2 я)
будет содержать 2n-\-k произвольных постоянных. Согласно теореме
искомая кривая ^о принадлежит этому семейству, и для ее определения
остается найти значения постоянных ai. Для этой цели нам, очевидно,
достаточно воспользоваться условиями, в концах которых согласно до-
допущению имеется ровно 2n-\-k.
Если число условий на концах больше, чем 2n-\-k, то задача, во-
вообще говоря, неразрешима. Если число условий на концах меньше 2n-\-k>
то мы можем или подбирать остающиеся произвольные постоянные ai
так, чтобы для этих значений интеграл J, взятый вдоль f0, принимал
экстремальное значение, или, как это мы делаем в § 54, искать методом
вариаций дополнительных условий — обобщить понятие трансверсальности.
184 УСЛОВНЫЙ ЭКСТРЕМУМ [ГЛ. IX
Указанная задача носит название общей задачи Лагранжа. Этой
задачей мы подробнее займемся во втором томе.
Задача. По какой замкнутой кривой должен двигаться самолет, имею-
щий собственную скорость v0, чтобы в промежуток времени Т облететь
наибольшую площадь; предполагается при этом постоянное направление и
постоянная величина скорости ветра *).
Пусть ось Ох совпадает со скоростью ветра. Обозначим через а угол между
продольным направлением самолета и осью Ох, через x(t), y(t)—координаты,
изображающие положение самолета в момент t Скорость самолета v есть гео-
геометрическая сумма его собственной скорости v0 и скорости ветра а. Так как
компоненты v равны хг и _у', то:
xf = vQ cos ot + а, у' = v0 sin а, F4)
Площадь, ограниченная замкнутой траекторией самолета, выразится:
Т
-j f(yx'-xy')dx. F5)
о
Наша задача сводится к нахождению максимума F5) при двух условиях F4).
Для этого нам надо найти безусловный экстремум от интеграла
т
[ух' — xyf — \ (хг — v0 cos a — а) — \ (у' — v0 sin a)] dt\ F6)
о
здесь искомые функции: х (/), у (t\ <x = a (fy]
Составим для них уравнения Эйлера. Обозначив через F подинтегральное
выражение для F6), имеем:
Fx—§-Fx' = 0*™ _Г.-^.Су_Х1) = 0, F7)
Fa = 0 или — Хх sin a -f X2 cos а = 0. F8)
Из F7) и F70 следует:
2х + С2 = Хз, 2у + Ct = — Xj. F9)
Путем параллельного переноса начала координат можно добиться, чтобы
постоянные Q и С2 в выражениях F9) для хну стали равны нулю; тогда
*втр ^-iK G0)
Перейдем к полярным координатам. Обозначим через r= Yx2+y2 и у радиус-
вектор и аргумент точки (х, у), изображающей положение самолега в некото-
некоторый момент времени. Так как
У
то из G0) получаем:
~^-. G1)
х) Эта задача принадлежит академику С. А. Чаплыгину. См. Ветчинки н,
Динамика полетов.
§ 66] условный экстремум (нвголокомные связи)
Из FВ) следует:
Сравнение G1) и G2) дает нам:
185
G2>
G3
Направление самолета ортогонально радиусу-вектору. Подстановка G3) в F4>
приводит к следующей системе:
х' = — tf0 sin ? + а> У' = vo cos f•
Умножим первое уравнение на х, второе на у и, вспомнив, что х = г cos <р,
3/ =/• sin cp, получаем после почленного сложения:
/ +уУ = ax~ar cos y = ar sin. a
или:
Пользуясь формулой F4), имеем:
dr __ a dy
G5)
"О
Это есть уравнение конического сечения с
фокусом в начале координат. Так как — из Черт. оО.
vo
смысла задачи нужно считать меньшим единицы (скорость самолета должна
превышать скорость ветра), то уравнение G5) дает нам эллипс с эксцент-
эксцентриситетом — и большой осью, направленной по оси Оу (черт. 30).
Итак, кривая максимальной площади облета есть эллипс с большой осью,
перпендикулярной направлению ветра, с эксцентриситетом, равным отношению
скорости ветра к скорости самолета, причем направление самолета должно
быть перпендикулярно радиусу-вектору эллипса.
Связь между изопериметрической задачей и задачей Лагранжа.
Изопериметрическую задачу можно свести к задаче Лагранжа 1). Пусть
требуется найти экстремум от интеграла
G6)
при соответственных условиях на границе и дополнительных условиях
ь
Fi(x,y1,yl',...,y»yn',...)dx = ll (i=l, 2,..., т). G7)
Обозначив через
= Fsdx
,2,...,я|), G8)
Задача же Лагранжа к изопериметрической задаче не сводится.
186 условный экстремум [гл. IX
мы имеем:
«7 (?) = ^(*. л» л'. • • • - л. л'» • • •); <79>
причем
Wt(a) = О, ЧГ, (*) = /, (/=1,2,..., л). (80)
Итак, наша изопериметрическая задача эквивалентна задаче Ла-
Лагранжа: найти систему п-\-т функций: yv у2,..., ,yn; 4Tlf ЧГа,..., Ww,
связанных соотношениями G9), удовлетворяющих соответственным
условиям на границах для функций уг и условиями (80) для функций
?Г4, такую, чтобы она при заданных условиях реализовала экстремум
интеграла ь
f
Fdx.
Согласно методу Лагранжа наша задача сводится к отысканию без-
безусловного экстремума от
где ХДл:) — некоторые функции; Ft и F не зависят от Wt и их произ-
производных. Система п -f- m уравнений для нашей задачи Эйлера распадается
на систему п уравнений относительно функций у{\
и на систему т уравнений относительно функций ЧГ4, которые примут вид:
|-Xi==0 (*=1, 2,..., т),
т. е. множители Xi обращаются в постоянные числа.
Обратно, рассмотрим задачу: найти экстремум интеграла
ь
J в J F(<X'Уи У2'"'у Уп' У1'*у*' * *'J y*')dx (81)
а
при условиях
Ъ (х, у19..., уп\ ух', ..., у/) =0 (/ = 1, 2,..., т < л). (82)
Пусть нам задана на отрезке [а, Ь] замкнутая система ортогональных функций:
Каждое из условий (82) эквивалентно счетной сисгеме условий:
ъ
x^O (j = 1,2,...; / = 1,2,..., m).
Итак, задача Лагранжа эквивалентна изопериметрической задаче с счет-
счетным множеством условий. Если бы мы распространили метод Эйлера для ре-
§ 66] УСЛОВНЫЙ ЭКСТРЕМУМ (НЕГОЛОНОМНЫЕ СВЯЗИ) 187
шения изопериметрической задачи с конечным числом условий на случай счет-
счетного их числа, мы бы должны были свести нашу задачу к разысканию без-
безусловного экстремума от
ъ ,
Лт оо
здесь \j® — некоторые постоянные.
оо
Обозначим Х^ (л:) = 2 Kj®uj> предполагая сходимость ряда в правой части.
Вследствие произвольности коэфициентов \J^ функции Х^ произвольны, и мы
получаем правило множителей Лагранжа.
Наши рассуждения не являются, конечно, строгими.
ГЛАВА X
ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
§ 67. Параметрическая форма задания кривых
В плоских задачах мы рассматривали семейство допустимых линий,
представляемых уравнениями:
Поскольку f(x) предполагалась однозначной функцией от х, мы при-
принуждены были ограничиваться линиями, пересекающими прямые, парал-
параллельные оси Оуу только в одной точке. Это ограничение с точки зре-
зрения приложений к геометрии чрезвычайно суживало круг наших рас-
рассмотрений: сплошь и рядом экстремум должен был достигаться на линиях,
не удовлетворяющих этому условию.. Например, в изопериметрической
задаче (§ 60) о линии данной длины, ограничивающей вместе с задан-
заданным отрезком оси Ох наибольшую площадь, экстремум достигается на
дуге окружности, опирающейся на наш отрезок оси Ох как на хорду*
Если длина дуги превышала длину отрезка, умноженного на -^-, то соот-
соответственная дуга окружности уже не удовлетворяла поставленному выше
условию. Добавим, что при наших рассмотрениях координаты х, у не-
неравноправны и поэтому формулы, полученные нами, были несимметрич-
несимметричными относительно хну (например условие трансверсальности). В гео-
геометрических же задачах координаты, вообще говоря, равноправны.
Для того чтобы освободиться от этих неудобств и ограничений/мы
перейдем к параметрическому представлению уравнений кривых:
При преобразовании параметра (§ 10), определяемого уравнением:
t = yz9 мы получим:
* = ? [* W = ?! С0> у = ф Ы СО] = <W СО;
Требование, чтобы между параметрами t и z была установлена
взаимно-однозначная связь, т. е. чтобы и т была однозначной функ-
функцией 4 сводится к требованию, чтобы / (т) была монотонной функцией.
§ 68] условия однородности 189
Если мы потребуем сверх того, чтобы при возрастании обоих -парамет-
-параметров / и т мы имели обход дуги в одном и том же направлении, то
Х(т) должна быть возрастающей функцией. Кроме того, потребуем,
чтобы х(т) имела непрерывные производные первого порядка *)
—г- = х' (х)> которая, очевидно, не отрицательна. Если мы потребуем
также, чтобы существовала непрерывная производная обратной функции:
dz 1
то получим: у^ (т) > 0.
Пример. Уравнение окружности:
х = a cos t, )
у = a sin t ) '
посредством преобразования tg -у = и или t = 2 arctg и переходит в урав-
уравнение:
а A — Ф) _ 2аи
у/ Xfyfr VfXrf
Выражения -=-^- и —-^ ——~ не меняются при преобразовании параметра.
В этом можно убедиться как непосредственной проверкой, так и из геомет-
геометрического смысла этих выражений (угловой коэфициент касательной и кри-
кривизна кривой).
§ 68. Условия однородности
Вывод условий однородности. Рассмотрим кривую, определяемую
уравнением:
x = x(f), x=y(t),
и на ней дугу, определяемую значениями параметра t, удовлетворяю-
удовлетворяющими неравенству: tQ^tr^tv Рассмотрим теперь криволинейный
интеграл
/
to
взятый вдоль этой дуги. При преобразовании параметра интеграл
взятый вдоль этой дуги (т0 и tj — значения нового параметра, отвечаю-
отвечающие концами дуги), не равен, вообще говоря, интегралу 7. Требование
х) Точнее у (z) должно иметь непрерывные производные того же порядка,
какой должны иметь по условиям задачи функции x(t) и y(t).
190 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
независимости интеграла / Fdt, взятого вдоль дуги, от параметра
накладывает, очевидно, некоторые ограничения на F.
Пусть t = x (т); тогда
Равенство J—Jt дает нам:
/'f(x9 у, р?, У-Ш у/ (т) dz= Г F (х,у, х' (т),/ (т)) dz. A)
Если мы потребуем, чтобы независимость интеграла J от выбора пара-
параметра имела место для любой дуги, в частности для любой дуги нашей
кривой, то равенство A) имеет место для любых значений верхнего и
нижнего предела (лишь бы т0 < zx и функции л:(х), y(z) были для
соответственных значений т определены). Фиксировав нижний придел т0
будем рассматривать оба интеграла как функции верхнего предела. Сов-
Совпадение этих функций влечет за собой совпадение их производных, т. е.
F(x v *L J!L\y'-F(X v X' iA
Здесь %' (т) > 0, и при соответственном выборе функции х (")> у/ может
принять любое положительное значение k. Итак, при любом k > О
kF(x,y,-%-, ^A = F{x,y,x\yf)
\ К К /
или, обозначая — = kx:
F(x,y, k^x'y ky) = kxF (x,y, x',y'). B)
Таким образом функция F четырех переменных х, у, х\у' является
положительно однородной первой степени относительно л:', у' 1). В силу
теоремы Эйлера об однородных функциях
В дальнейшем мы будем без оговорок предполагать условие одно-
однородности выполненным. В этом случае интеграл
J=fF(x,y,x',y')dt,
г) Положительно однородной функцией р-ю порядка относительно пере-
переменных (x19x»...,xj называется функция f(xvx2,.. .,хт;хт+1,... ,хп)г
удовлетворяющая условию
f(kxv kx2,..., kxm; хт+1, .".. , хп) = kPf(xvx2) ... , х
при
§ 68] условия однородности 19 ?
взятый вдоль некоторой дуги, определяемой уравнением
* = *(<), У=У(*),
зависит только от этой дуги, но не зависит от параметрического ее:
представления.
Аналогично, для интеграла
J = j F (xv х29 . . . , хп9 хх'9 а:/,; . .., хп') dt,
взятого в я-мерном пространстве вдоль кривой:
Xi — Xi(f) (i=l,2, . . . ,л)»
условие независимости от выбора параметрического представления пос-
последней будет:
Г \Х±1 X%i . . . , Хп\ кХх , кХс? , . . . , &Хп ) =
= kF(xv x2i ...»хп] хх , х2 , ... , хп ).
Отсюда следует:
F(xv ... ,xn9xt', ... ,xn')dt = F(xv ... 9xn'9\dxv ... ,dxn)t
где dxi = x/ dt. Интегралу J можно таким образом придать вид:
J= J F (xv ... , xn9 dxv\dx2, . . . , dxn)\
F есть положительная однородная функция первой степени относительно
dxv dx2J ... , dxn.
Приведем ряд примеров функций линии 7= F dt, когда/7 удов-
удовлетворяет условиям однородности.
Пример 1. Площадь, ограниченная замкнутой кривой, выражается инте-
интегралом:
j xdy—ydx,
взятым вдоль этой кривой.
Пример 2. Длина дуги кривой в л-мерном евклидовом пространстве выра-
выражается интегралом:
(перед корнем всегда ставится знак плюс).
Пример 3. Длина дуги кривой в я-мерном римановом пространстве выра-
выражается интегралом
f Л1 2 aikdxidxb>
где aik — некоторые функции точки.
Во всех трех примерах подинтегральные выражения суть положительно
однородные функции первой степени относительно диференциалов.
Пример 4. При переходе к параметрическому представлению линий инте-
интересный вид принимает важный в механике интеграл действия
где U — потенциальная функция, Г—кинетическая энергия.
192 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
Имеем:
2r=Zi^>
дТ \л dqt T1 ~
•=--. импульсы, ^—пространственные координаты, ZJ>rjf —U = Е —
.полная энергия системы.
Введя параметр -с, через который выражается время t, а следовательно, и
пространственные координаты qit получаем:
Это выражение для действия , симметрично относительно пространственных
координат qi и временной координаты t\ при этом импульсам рг для простран-
пространственных координат отвечает полная энергия Е для временной, взятая с обрат-
обратным знаком.
Специальные параметрические представления. Интеграл
а
после введения параметра /, через который выражается дг, а значит и у,
примет вид:
Очевидно, что x'f(x,y, -~) есть однородная функция первой сте-
степени относительно У, у', так как, умножив xf и у' на k, мы получим:
(?)
Наоборот, пусть нам дан интеграл
взятый вдоль некоторой линии. Если можно за параметр t принять
абсциссу х, то:
Ч 1
1,/)=/(*,>,/), E)
и мы получим:
f F (х, у, х\ /) dt = у>(х, jf,./) dx.
Из C), D) и E) следует:
Fv' -/,', /V = -^Г (^ -/^') =/-у%- F)
Таким образом интегралы f F (х, у, х/, у') dt при специальном выборе
параметра t = х переходят в интегралы вида / / (х, у, у') dx, изучен-
изученные нами в гл. V и VII.
§ 69] ЭКСТРЕМУМЫ ФУНКЦИЙ ОТ ЛИНИИ 193
Во многих задачах в качестве параметра на кривой ? выбирают
длину 5 (дуга, отсчитываемая от начальной точки кривой до заданной
точки). В этом случае:
где 6 — угол, образуемый касательной к кривой ? с осью Ох.
Имеем:
jF (*, у, *',/) dt=j F (х, у, cos 6, sin 6) ds = //(*, У, 8) ds,
Y Y Y
где
f(^yfb) = F(xfy, cosG, sin6).
Следствия условий однородности. Так как F есть однородная функ-
функция первой степени относительно х/ и у', то из теоремы Эйлера об
однородных функциях следует:
Р=^Рх.Л-У'Ру G)
Диференцируя G) по xf и у', получаем после очевидных сокращений:
F=0 ' (8)
Из (8) следует:
F F F
ХХ ^JL === У У
/2
yn x'y' у
где Fx = Fx (x, y, x/', у') есть положительно однородная функция сте-
степени — 3 относительно xf, у\ В самом деле, при диференцировании
по х\ у' порядок однородности понижается каждый раз на t единицу;
поэтому Fx,y F , суть однородные функции нулевого порядка; Fx,x,, Fx, ,,
Fy, , — порядка однородности —1. Так как Ft получается из функций
порядка однородности — 1 делением их на однородные выражения по-
порядка 2, то Fx есть положительно однородная функция порядка — 3.
Диференцирование G) по х и у даст нам:
*' ! (ю)
§ 69. Экстремумы функций от линии
Близость кривых. Если F удовлетворяет условию однородности, то
I F dt есть функция от линии, так как зависит только от кривой инте-
интеграции, но не зависит от выбора ее параметрического представления.
194 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ, X
Естественно распространить развитую выше теорию экстремумов функций
от линий:
на наши новые функции от линии.
Определим прежде всего понятие близости двух кривых (с непре-
непрерывно вращающейся касательной).
Мы скажем, что кривая -^ находится в г-близости нулевого по-
порядка от кривой Т> если между всеми точками у и ^ можно установить
взаимно-однозначное и взаимно-непрерывное соответствие так, чтобы
расстояние между соответствующими точками не превосходило е. Мы
скажем (аналогично), что кривая ^ находится в е-близости первого
порядка кривой у если между всеми точками т и Ti можно установить
взаимно-однозначное и взаимно-непрерывное соответствие так, чтобы:
1) расстояние между соответствующими точками не превосходило
числа s,
2) угол между касательными (меньший ~j к f и 7i, проведенными
в соответствующих друг другу точках, не превосходил е.
.Примечание. Совокупность кривых ? с непрерывно вращающейся каса.
тельной образует метрическое пространство, если под расстоянием г(т, Yi) мы
назовем нижнюю грань чисел е таких* что Yi находится в е-близости первого
порядка к| (и обратно).
Вывод необходимых условий. Имея понятие г-близости, мы можем
автоматически распространить основные понятия вариационного исчисле-
исчисления: е-окрестность нулевого и первого порядка, абсолютный экстремум,
относительный экстремум, слабый и сильный экстремумы, на функции
линий:
рассматриваемые нами в этой главе.
Начнем, как обычно, с вывода основных необходимых условий,
которым должна удовлетворять кривая, реализующая экстремум. При
этом мы сразу примем за класс допустимых линий все кривые, обладаю-
обладающие непрерывно вращающимися касательными (класс Ci) и соединяющие
точки двух данных кривых.
Пусть задан класс {i} допустимых линий с непрерывно вращающи-
вращающимися касательными, концы которых лежат на заданных кривых Г^ и Г2,
определенных уравнениями
?(*>jO = 0. Ъ(х,у) = 9-
На кривых класса {у } определен функционал
J (?) = /F (*, У, *\ yjdt = fF О, у, dx, dy\ A1)
где F — непрерывная функция, имеющая непрерывные частные производ-
производные первых двух порядков по аргументам х, у, х\ у'\ кроме того, F
является положительно однородной первой степени относительно х/> yr m
§ 69] ЭКСТРЕМУМЫ ФУНКЦИЙ ОТ ЛИНИИ 195
ТЕОРЕМА. Если кривая f, заданная в параметрическом виде урав-
уравнениями
x = x{t\ y=y(f),
реализует экстремум функционала J (?), то:
1) х (t) и у (t) удовлетворяют уравнениям Эйлера:
A2)
2) на концах кривой^ удовлетворяются соотношения:
A3)
F , F ,
-~— = —— (на конце, лежащем на кривой
Ч 9
—Р^-- = —у— (на конце, лежащем на кривой Г2).
Vo? Чу
Если одна из кривых 1\ или Г2, или обе сводятся к точке (конец
фиксирован), соответственное условие A3) заменяется требованием,
чтобы 7 проходила через эту точку. Соотношения A3) называются усло-
условиями трансверсальности.
Кривая у:
х — х (f) v — v (f)
х—,xyi)> у—у yi),
где х (t) и у (t) удовлетворяют уравнению Эйлера, называется экстре-
экстремальной для 7G). Нашу теорему можно формулировать следующим
образом:
Для того чтобы кривая 7 давала экстремум интегралу J G), не-
необходимо, чтобы 7 была экстремалью и чтобы на свободных концах
удовлетворялись условия трансверсальности.
Формулированную теорему можно доказать двумя различными спо-
способами:
1. Рассматривать наш функционал как функцию пространственной
кривой:
* = *(*), У=У(*)
в пространстве (/, х, у) и использовать результаты гл. VIII.
2. Ввести для наших функционалов / Fdt понятие вариации как глав-
7
ной линейной части приращения функционала и искать необходимые
условия экстремума, приравнивая вариацию нулю.
Мы приведем оба доказательства, причем начнем с первого.
Пусть у:
x = x(t), y=y{t)
есть произвольная плоская кривая класса d плоскости хОу, соеди-
соединяющая точку кривой Fj с точкой кривой Г2. Обозначим через Q, Ф
и W цилиндрические поверхности, расположенные в пространстве (t, x, у)
с образующими, параллельными оси Ot, и пересекающие плоскость хОу
196 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
соответственно по кривым ?> 1\, Г2. Обозначим через ^ простран-
пространственную кривую [пространства (t, x, у)], заданную уравнением:
x = x(f), y=y(f).
Кривая Yi» очевидно, принадлежит поверхности Q и соединяет точки
поверхностей Ф и W; проекция ^ на плоскость (х, у) есть кривая ^.
Всевозможным параметрическим представлениям плоской кривой у
в пространстве (t, x, у) будут соответствовать всевозможные кривые fi,
расположенные на цилиндре Q и соединяющие точки цилиндров Ф и W.
Так как функционал /G) зависит только от вида линии у и не зависит
от ее параметрического изображения, то, следовательно, функционал
пространственной кривой:
/»
(х, у, х\ у') dt
будет зависеть только от вида цилиндра Q. Отсюда следует, что если
кривая 1 дает экстремум функционалу J (^) среди плоских линий (класса
Ci), соединяющих произвольную точку кривой Гх с произвольной точ-
точкой кривой Г2, то пространственная кривая будет реализовать экстремум
функционала ft ("h) среди всех пространственных кривых
x = x{t\ y=y(t)
класса d, соединяющих произвольную точку цилиндрической поверх-
поверхности Ф с произвольной точкой цилиндрической поверхности W.
На основании теории экстремумов для пространственных линий имеем
вдоль экстремальной линии:
F LF -о
а на концах условие трансверсальности:
где 8^, 8лг, Ьу суть приращения координат при допустимом сдвиге конца
линии fv
Из условий однородности [равенства A0)] получаем:
и условие A5) принимает вид:
Fx,bx-{- F , оу = 0. A6)
Для конца, лежащего на кривой Ти приращения 8а: и Ъу связаны соот-
соотношением:
vxlx-\-y оу = О. A7)
Из A6) и A7) следует:
-/¦ = 1Г- О8)
Та; Чу
§ 69] экстремумы функций от линии 197
Аналогично, для конца, лежащего на кривой Г2:
откуда
^ = -^-- A8')
Этим самым наша теорема полностью доказана.
Приведем теперь вкратце второй вывод теоремы, основанный на
рассмотрении вариации 87 (х) функционала 7 (?), т. е. главной линейной
части приращения 1). Пусть на классе {^} допустимых линий параметр t
в параметрическом представлении кривых меняется от 0 до 1, т. е.
1
= /> (х, у, х\ /) dt
Пусть уравнения близких кривых ^ и f имеют вид:
?: x = x(f)9 y=y(t);
f: *==лГ.@=*-|-8дг, y=y(t)=y-{-oy.
Отсюда
f
0
1
{ FJX+ руЬУ + FJS + ^-3/ } dt-
0
Выражение:
главная линейная часть приращения У(Т), называется вариацией y
Условие того, чтобы кривая т реализовала экстремум, заключается
в тождественном исчезновении вариации:
8/G) sO.
Преобразованием Лагранжа мы приводим вариацию S/ к виду:
"(if) = IF,**+ Г/у]м - [FJx+ F^y]_ +
г) Поскольку мы пространство не считаем линейным, вариация понимается
в смысле § 46.
198 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
Условие 8/== 0 требует обращения в тождества уравнений:
F ——'F =0
у at У
вдоль кривой y и для случая свободных концов условий трансверсальности:
для каждого конца.
Вейерштрассова форма уравнений Эйлера-Лагранжа. Легко видеть,
что уравнения A4) не независимы. В самом деле, если для простран-
пространственной кривой fx:
x = x(f), y=y(f)
имеем 8/х (fj) = 0, то для всякой.кривой iv
также имеем 871(^1)^0, где f(t) есть произвольная возрастающая
диференцируемая функция. Следовательно, если кривая
* = *(*), y=y(f)
есть интеграл системы A4), то
при произвольной функции /(/) будет также интегралом системы A4).
.Отсюда заключаем, что одну из функций x{t)y y(t) можно задать про-
произвольно, после чего другую можно найти, интегрируя любое из урав-
уравнений системы A4).
Аналитически это обстоятельство вытекает из того, что оба урав-
уравнения A4) являются следствиями одного^ уравнения.
Из формул (8), (9), A0) предыдущего параграфа следует:
=/ \.F**-F*y-pi (xy-x"y% A9)
Аналогично:
Так как обе производных д/, у' не могут одновременно обращаться
в нуль, то уравнения A4) эквивалентны одному уравнению:
^-^-^(^У—</) = «.• B0)
Это есть так. называемая вейерштрассова форма уравнения Эйлера-
Лагранжа.
§ 69] ЭКСТРЕМУМЫ ФУНКЦИЙ ОТ ЛИНИИ 199
Вейерштрассова форма уравнения Эйлера записывается иногда в сле-
следующем виде: - ___
ху? ух' /o/V\
Т = * Г> С20)
где г—радиус кривизны экстремали.
Инвариантность вейерштрассовой формы уравнения. Отметим
сейчас же одно важное свойство уравнения B0): вейерштрассова
форма уравнения Эйлера остается инвариантной по отношению
к преобразованию параметра.
В самом деле, кривизна — кривой не зависит от ее параметрического
вида. Функции ^ „ Z7 ж, и их разность есть функции положительно-
однородные нулевой степени относительно х\ у', а функция Fx — одно-
JL
родная степени —3 и (x/2-\-y/QJ—однородная степени ~}-3 относи-
относительно х', у\ Правая часть уравнения B0) есть, следовательно, функция
положительно однородная нулевой степени относительно л/, У, т. е. она
не изменяется от умножения аргументов х\ у' на положительное число.
Но переход от параметра / к т заключается в умножении х' и у'
dt
на -г-, которое мы считаем положительным.
Вторая вариация. Если первая вариация функционала
обращается в нуль, to главной частью приращения будет вторая вариация
SV, которую мы вычислим, как в § 52:
= J
*1
f (Fxytbxb/ + F^iyixT + F^bxW + F
to
Вспомним теперь результаты § 52. Необходимым условием миниму-
минимума J является неотрицательность второй вариации, это в свою очередь
требует неотрицательности квадратической формы:
А =
Из формулы (9) следует:
Условия А ^>0 сводятся к условию Ft ^> 0.
Отсюда следует теорема (аналог условию Лежандра): необходимое
условие минимума заключается в требовании Ft^>0.
200 ВАРИАЦИОННЫе ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
§ 70. Обобщения и приложения
Изопериметрическая задача. Используя результаты гл. IX, можно
легко получить основные необходимые условия для изопериметрической
задачи в 'параметрической форме. Пусть среди линий f•'
X = x(f), y=
класса Clf соединяющих две данные точки Л и В и удовлетворяющих
условию: „
K(i)= I Q(x,y, x',/)dt = l= const
ищется линия, вдоль которой функционал:
7
принимает экстремальное значение. Мы при этом, как раньше, предпо-
предполагаем, что функции F и G удовлетворяют условиям однородности и
диференцируемости.
ТЕОРЕМА. Если кривая ? дает искомый экстремум, то суще-
существует постоянное число X такое, что 7 есть экстремаль для
функционала:
Пример. Среди всех замкнутых линий, ограничивающих данную площадьш
найти ту, длина которой минимальна.
Замкнутую линию мы рассматриваем как линию, у которой начало совпа-
совпадает с концом. Итак, пусть уравнения:
есть уравнения произвольной замкнутой линии. Ищем экстремум интеграла
/ (х'2+у/2J dt
при условии
(Хуг —yx')dt = C.
Обозначая через
/¦
имеем:
F 3
F — F —) Fi — xyt — (х'2-4- v'2J~
1 ху* Гух' ~ д* Г1— хгуг — \л \У ) •
Для кривой, дающей экстремум, из условия B0) предыдущего параграфа
следует:
1-х.
Кривизна вдоль нашей замкнутой дуги постоянна. Значит, она есть окружность.
§ 70] ОБОБЩЕНИЯ И ПРИЛОЖЕНИЯ 201
Случай п независимых переменных. Рассмотрим интеграл
/ « O^i» -^2» • • • > *^п> *^1 > *^2 »• • •» ^п / »
взятый вдоль некоторой кривой:
*i = *i@ (*=1, 2,..., л).
F есть положительно-однородная функция первой степени относительна
всех дг/. При этих условиях наш интеграл зависит только от пути*
интеграции, но не зависит от его параметрического представления.
Применяя рассуждения,, аналогичные предыдущим, получим основные
необходимые условия для экстремума этого интеграла в форме:
^,-1^ = 0. B1>
В развернутом виде уравнение B1) принимает вид:
3 3
п уравнений системы B1) или B1') не независимы. Они связаны*
соотношением:
п
Это тождество есть следствие условий однородности. В самом деле,,
из теоремы Эйлера получим:
Диференцируя B3) Xj и х/, получаем:
F»;*j> B4)
/^//^ 'iF^/=°- B5)
Педстановка B4) и B5) в правую часть B2) доказывает нам это
тождество.
Геодезические линии. Пусть на я-мерном римановом многообразии*
длина дуги определяется интегралом
где
fds,
г, к
Линии, вдоль которых 8 / ds = 0, называются геодезическими.
х) Здесь ate суть непрерывные диференцируемые функции аргументов:
#i,..., хп. Кроме того, форма ds* предполагается положительно определенной.
202 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
Так как
fds— fi/S'a dXi dXk dt
J as~ J V 2Л* at dt ati
где t — параметр, то геодезические линии определяются из уравнения:
L ff«* ff< ^*1У^^ /26)
dxj dt dt dt *f у g dt
где для краткости обозначено
Sdxi dxk
a*k~dt ~dt '
Если параметр совпадает с длиной дуги s, то g = 1 и уравнение B6)
^перейдет в
daik dxt dxk d VI dx{
У ds
или
a^ dxf dxk yi dais dxf dxk
2
__ Y y у ^
2 ^ dxj~d? ~di ~-2jdxk~dF4F^2ji aV ds* '
Дадим более компактную форму уравнения B7), разрешенную отно-
d^Xf
сительно ^.
Так как при двойном суммировании по / и к
^L ^fl dXfc
Эхк ds ~ds~ ~~ —* dxt ds ds '
то отсюда мы можем записать уравнение B7) в следующем виде:
SdL^L-l\ (dav Ldakt_ da*k\dxjdxk
aV ds9- ~~ 2 ^ \dxk + dx{ dXj J ds ds *
Если аР суть элементы определителя, обратного |я^|, то
^xf _ 1у <у у /d«iy dajy daik \ dx{ dx^
~ds?-~TAa А\Жк + ~дх~1~~~Щ) ds ds •
Отсюда, обозначая:
л -"а*гл + э.ге а^.'
лолучим следующий окончательный вид уравнений геодезической динии:
Фхг __ ± у ij Tj dj^ dxje
ds2 "" 2^J « flfs ds e
Принцип Якоби. Принцип Гамильтона (§ 51) определяет движение
механической системы из уравнения
8/"(?/+Г) Л = 0. B8)
Подинтегральное выражение для консервативной системы в уравне-
уравнении B8) не содержит времени t в явном виде. Если система консервативна,
§ 70] ОБОБЩЕНИЯ И ПРИЛОЖЕНИЯ 203
то можно придать уравнению B8) форму, в которую t не входит также
под знаком диференциала. Условие консервативности имеет вид:
?/—r=/* = const., B9)
где
Отсюда
Из B8) и B9) следует, что для действительного движения
8 J'BU-±-h)dt=0
при условии B9), B9'). Но 8 / hdt = O. Следовательно:
S С (U-\-h)dt=0. C1)
Подставив C0) в формулу C1), получим:
= 0. C2)
Уравнение C2) выражает так называемый принцип Якоби.
Если рассмотреть пространство (д19 q2, ..., qn) с метрикой, опре-
определяемой квадратической формой:
то траектории определяются как геодезические линии в этом пространстве.
В случае одной материальной точки:
\2\(dzY
где ds — линейный элемент в евклидовом пространстве (х, у, z), и прин-
принцип Якоби обращается в принцип Мопертюи-Эйлера (§ 29):
= 0 или
Для случая движения n(j»'поверхности при отсутствии внешних сил
^ = const. Траектория определяется условием Ъ I ds=0; траектория
есть геодезическая линия на этой поверхности (принцип Герца).
Так как абсолютная величина скорости при таком движении по-
постоянна, то тангенциальное ускорение отсутствует. Налицо только нор-
нормальное ускорение, направленное по- главной нормали к траектории.
При отсутствии же внешних сил силы, действующие на движущуюся
точку, сводятся к силам реакции поверхности и направлены по нормали
к поверхности.
Итак, для геодезической линии нормаль к поверхности совпадает
с главной нормалью к кривой (ср. § 65).
204 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
§ 71. Замкнутые экстремали. Метод нормальных вариаций
Вывод уравнения Эйлера. Особый класс задач представляют те,
в которых в качестве допустимых линий фигурируют замкнутые кривые.
Рассмотрим класс {7} линий, заданных уравнениями:
= x(f), \
где x(f), y{f) — непрерывные и непрерывно-диференцируемые функции.
Наложим требования:
Эти требования дают нам не только замкнутость кривой, но и непре-
непрерывность направления касательной в точке замыкания, отвечающей
значениям параметра 0 и 1. Полагая для любого t:
) = x(t)9 y(t±n)=y(t).
где п — любое целое число, можно рассматривать x(t) и y(f) как пери
одические функции с периЪдом, равным единице. При изменении
от t0 до tQ-\-l мы получим кривую 7- Точкой замыкания:
может быть сделана любая точка кривой
Рассматривая вариацию функционала
получим:
О
Так как оба выражения в прямых скобках, отвечающие совпавшим кон-
концам f, равны, то отсюда выражение вариации примет вид:
j
о
Условие экстремума 87(j) = 0 дает нам уравнения Эйлера:
Замкнутая интегральная кривая уравнения Эйлера называется за-
замкнутой экстремалью.
Рассмотрим двупараметрическое семейство интегральных кривых уравне-
уравнений Эйлера 7 (а> Р)- Выбрав на каждой кривой по точке и обозначая через
7 Ф а» ?) ДУГУ кривой 7 (а. Р) длины s с началом в избранной на этой кривой
точке, получим трехпараметрическое семейство дуг 7 (s, a, §).
§ 71] ЗАМКНУТЫЕ ЭКСТРЕМАЛИ. МЕТОД НОРМАЛЬНЫХ ВАРИАЦИЙ 205
Требование совпадения абсциссы, ординат и направлений касательной
в конце и начале этой дуги дает нам три условия. Таким образом мы имеем
столько же условий для замкнутой экстремали, каково число параметров, опре-
определяющих дугу.
В некоторых задачах экстремали представляют собой кривые, уходящие
в бесконечность; в этом случае, конечно, замкнутых экстремалей нет (случаи,
когда мы имеем в качестве экстремалей прямые, цепные линии и т. д.).
В некоторых исключительных случаях все экстремали замкнутые (геодезические
на сфере).
Вопрос о существовании замкнутых экстремалей тесно связан с вопросом
о существовании периодических движений динамических систем, — вопрос,
которым мы детально займемся во втором томе. Здесь мы ограничимся про-
простейшей задачей о возможности периодического движения (по инерции) точек
на выпуклой замкнутой поверхности.
По принципу Герца (§ 70) эта задача сводится к задаче о существовании
замкнутой геодезической на выпуклой замкнутой поверхности. В § 72 мы дадим
решение задачи о существовании замкнутой геодезической на такой поверхно-
поверхности и ряда аналогичных задач. Для ее решения мы познакомимся предвари-
предварительно с некоторыми понятиями, представляющими и самостоятельный интерес.
Нормальные вариации. Пусть класс {^} допустимых линий состоит
или из замкнутых линий, или из линий, соединяющих две фиксированные
точки. На кривых класса {f} задан функ-
функционал
-7 Черт. 31.
Рассмотрим кривую f класса {^}, заданную уравнением:
и близкую к ней кривую fl из класса {f}, заданную уравнением:
@<*<1).
^Вектор с компонентами одг(^), by(t) соединяет точки кривых -у и Ti
;с одинаковыми значениями параметра t (черт. 31). Этот вектор будем
называть вектором смещения.
Задав параметрическое представление кривой -f> определим пара-
параметрическое представление кривой ^ так, чтобы все векторы смещения
выли нормальны к кривой -р
,;. Установим для кривой f положительное и отрицательное направление
Нормалей и обозначим через &n(t) функцию точки кривой -у, равную
клине вектора смещения, взятую со знаком плюс или минус, в зависи-
зависимости от того, направлен ли вектор смещения по положительному или
Отрицательному направлению нормали. Обозначив через а угол наклона
Касательной к кривой ^ (а есть функция t), мы имеем:
Sjc = — Ьп sin а, )
* . C3)
by = on cos а J ч '
206 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
(так как вектор смещения нормален к касательной). С другой стороны,
обозначив через ds элемент длины кривой' f и через dx, dy — его
компоненты, имеем:
xfdt = dx = ds cos ос, |
yfdt = dy =ds sin a. J
Определим теперь вариацию интеграла J яри переходе от кривой f
к кривой «Yi- Напомним еще равенства [см. равенства A9), A9'), § 69]:
d \ C5>
гу dtry' — X[r^ J
где
{ F} = - Fxy, + Fafy - Ft (x'y"—/x"). C6)
Преобразуем теперь вариацию й/(х), пользуясь формулами C3), C4), C5):
о
1 I
s, C7)
б б
где /—длина кривой -у. Приращение /Dt)— */(?) совпадает с вариацией
= J {F)
bnds
с точностью до величины второго порядка сравнительно с расстоянием
между кривыми fi и Т [с точностью до /"(?» TiJ]. В силу теоремы о
среднем
i i
{F}Do. (ЗГ)
Выражение Inds есть площадь бесконечно маленького прямоуголь-
прямоугольника с основанием ds и высотой Ьп (площадь эту мы считаем величиной
алгебраической, совпадающей по знаку со знаком высоты Ы).
Выражение 8J(x) называется нормальной вариацией функционала 7(т)-
Функциональная производная и вариация в точке. Сохранив
обозначения предыдущего параграфа, будем полагать, что hn(t) — O
всюду, за исключением некоторой малой дуги ССг кривой -у длины hy
заключающей точку А. Обозначим:
I Inds = bnds — o\
ее,
о означает площадь бугорка, заключенного между кривыми f и чг. Мы
будем полагать, что а есть величина низшего порядка малости сравни-
сравнительно с г (y, Тх).
§ 71] ЗАМКНУТЫЕ ЭКСТРЕМАЛИ. МЕТОД НОРМАЛЬНЫХ ВАРИАЦИЙ 207
Так как J (ух).— /(?) и ЗУ(х) отличаются друг от друга на величину
порядка г (у, TiJ»™ равенство
будет верным с точностью до величины порядка старшего, сравнительно*
с q. В силу равенства C7') имеем:
= f{F)bnds= {F}D
C\ C
где {F}^ есть значение функции {F} в некоторой внутренней точке D'
дуги ССГ В силу малости дуги ССг и непрерывности функции \F)
разность [F}D —\F)A будет величиной бесконечно малой вместе
с дугой CCV Следовательно.
C}Bs{/V).
Отсюда
^iHWsIF)^ C8)
Выражение {F}A о называется вариацией в точке А функционала J(f).
С точностью до величины порядка выше о вариация в точке совпадает
с приращением функционала J (у) (если, конечно, г (у, -fi)'2 будет вели-
величиной старшего порядка сравнительно с о).
Будем теперь стягивать наш бугорок к точке Л так, что дуга ССг
будет стягиваться в эту точку, а г (д, ?i) будет стремиться к нулю;.
при этом гG, Ti)* будет оставаться величиной высшего порядка малости
сравнительно с о, которое тоже стремится, конечно, к нулю. При этом:
llm Jib)~Jii) = {F}A. C9)
Это следует из того, что:
ПЪ) — ДТ) = {ПА о + ео, D0>
где е — величина, стремящаяся к нулю вместе с а.
Выражение {F}A называется нормальной функциональной произ-
производной от 7(/y) в точке Л.
Необходимое условие того, что кривая y реализует экстремум 7G),,
заключается в равенстве нулю нормальной функциональной производной
во всех точках кривой «Y-
; Нормальные вариации для случая пространственной задачи. Пусть.
в я-мерном пространстве (xv x2,...,xn) задан функционал:
J (?) = У F (х1У x2i..., хп) х/, х2',.. ., */) dt,
X
.Определенный на классе линий -у, заданных уравнением в параметрической
форме:
I !) Под знаком ^ в дальнейшем понимается равенство с точностью до вели-
1ин высшего порядка сравнительно с -.
208 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
Рассмотрим две близкие кривые -у и ^v уравнения которых имеют вид:
Параметр t на кривой Yi выбран так, что вектор смещения с компо-
компонентами 8л:Д?), соединяющий точки обеих кривых с общим значением
параметра, нормален к кривой ^- Векторы смещения образуют полоску
линейного двумерного многообразия между кривыми y и fr
Главная линейная часть приращения
1
— f F(xv.. .,*„,*/, <,..., *П')Л
т
называется нормальной вариацией J(y) и имеет
тде 8я = У?8лг2, cosp—__i СуТЬ угловые коэфициенты вектора
смещения.
Если за параметр принять длину дуги s; то
Х% =—
причем векторы смещения и элементы длины ортогональны друг другу:
^]cos a{ cos р4 == 0. D2)
г
При этом выражение для вариации примет вид:
V
Выражение о/г^5 есть площадь бесконечно маленького прямоуголь-
прямоугольника, опирающегося на вектор смещения и элемент дуги.
Пусть 8я = 0 всюду, кроме бесконечно малой дуги, окружающей
точку Л кривой «y; вместе с тем бесконечно мало и о= / ands. Мы
сбудем полагать, однако, что а есть величина порядка ниже второго
сравнительно с г(д, fi)-
Выражение V (Fx —7Г^х,\ cos $t есть функция точки кривой 7
i
м, кроме того, зависит от направления вектора смещения. Обозначим е,го:
xt-iF*;) cos'3j={F; A>cosM- D4)
§ 71] ЗАМКНУТЫЕ ЭКСТРЕМАЛИ. МЕТОД НОРМАЛЬНЫХ ВАРИАЦИЙ 209
Имеем по-предыдущему:
— ДТ)«*/(Т)«{'7; А> cos p4} f lads ={F- Л, cosp,} a. D5)
При наших предположениях: [F; Л, cosp,} о есть главная часть при-
приращения i(ti) — J(i)) она называется нормальной вариацией в точке А
в направлении (cosfij, cosp2, . ..,cospn). Самовыражение {F; Л, cos^}t
называется функциональной производной в точке А в данном напра-
направлении (cospf).
/ Если дуга вокруг точки Л, для которой Ьп ф 0, стягивается к точке Л
и одновременно г(т, Tfi)—>0, н0 так> что ° остается величиной низшего
порядка сравнительно с r(j, ?iJ, то
lim y(ri)^y(Y) = {F\ Л, cosp,}. D6)
Уравнения Эйлера означают обращение в нуль нормальной функцио-
функциональной производной от 7(«y) в любой точке по любому направлению.
Дадим сейчас новый вывод уравнений Эйлера, полезный для дальнейшего.
% Пусть в некоторой точке Л кривой т для некоторого направления
нормальная функциональная производная [F\ Л, cosf^} отлична от нуля.
^1одобрав соседнюю кривую Yi> Для которой главная часть приращения
}J(Ti) — J(X) B направлении (cosj^) вектора смещения сводится к вари-
вариации в точке Л: " ч rr . ,~ я * л
% J(b) — J(i)^{r> A cosp,} a,
|и изменив направление вектора смещения на обратное, получим новую
кривую f2, для которой:
{— Ъ A, cosftjo.
Фместе с нормальной вариацией, при достаточно малом о nr(f, -fi)*
Меняет знак и приращение функционала. Следовательно, ^ не дает нам
экстремума 7G). Итак, во всякой точке экстремальной кривой т для
Опобого нормального к ней направления имеем:
<47)
,^де cospi определяет любое направление, ортогональное кривой ?. В таком
]Случае вектор а с компонентами:
v у у v —Г7 d я
л\ 1 • л п. .... л, -_. где /v j " # —— _ — jr^
Должен быть направлен по касательной к кривой ^. С другой стороны,
$3 формулы однородности B2) § 70 следует:
Уде cosat — направляющие косинусы касательной к ^ в точке Л,
|. е. вектор а ортогонален к -f, отсюда a = 0 или
210 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ |>Л, X
Пример. В трехмерном пространстве рассмотрим функционал
у+у + ' dt,
) выражает, очевидно, длину кривой ?.
Обозначим через cos%4, cos б4 (/ = 1, 2, 3) направляющие косинусы каса-
сельной и главной нормали к кривой f в точке F. Полагая F = Yх'^т\"Уп"\'z™ >
получим:
/у = ¦ - _j= : = COS a3,
По формуле Серре-Френе:
F
Гх dsFx - R '
где /?—радиус кривизны кривой y в точке ^4. Аналогично:
Отсюда:
[F; A, cos pj = ~ 2j cos $i cos $i =
где «f есть угол между главной нормалью и нормальным направлением:
(cos plf cos Рз, cos pg).
Условный экстремум. Пусть мы рассматриваем в «-мерном про-
пространстве (xv х%, ..., хп) п — ^-мерное многообразие N, определенное
уравнениями:
На классе {^} допустимых линий, расположенных на N, задан функционал
Бесконечно малые векторы смещения Fд:(), соединяющие точку Л
кривой у из {^} с бесконечно близкой кривой того же класса *A9 рас-
расположены в п — ^-мерном линейном многообразии, касательном к N
в точке А. Допустимыми вариациями в точке являются, следовательно,
вариации, при которых вектор смещения расположен в линейном много-
многообразии, касательном к N. Условие экстремума (см. рассуждениие § 63)
заключается в том, чтобы при этих допустимых вариациях вариация J (^)
обращалась в нуль, или, что то же самое, нормальные функциональные
производные {F; A, cospj от функционала /(?) обращаются в нуль
в каждой точке А кривой -у для каждого направления (cosp,), нормаль-
нормального к 7 и расположенного в касательном к N в точке А линейном
многообразии.
? 72] ПРИЛОЖЕНИЯ К ТЕОРИИ ГЕОДЕЗИЧЕСКИХ 211
§ 72. Приложения к теории геодезических
Геодезические на поверхности. На поверхности <р (х, yf z) = О
ищем кратчайшую линию т, соединяющую две заданных точки этой
поверхности. Для функционала (см. пример в § 71)
У(?) = / yxf*+yr* + z'4Ldt D8)
нормальная функциональная производная \F\ A, cosj^} равна со* ,
где в — угол между направлением вектора смещения (cos8j, cos82, cos|38)
и главной нормалью. Если кривая т есть экстре-
экстремаль, то в каждой ее точке для всякого сме-
смещения ААг: (cospj, cosfJ, cosp8), расположен-
расположенного в плоскости Р, касательной в Л к по-
поверхности <р = 0, имеем:
eos e
R ~ "
——*
Так как направление ААХ нормально к кривой ^
(черт. 32), то плоскость, проходящая через
ШАА1 и через главную нормаль AM, является
нормальной плоскостью к кривой ? в точке А, и, следовательно, она
ортогональна к плоскости Р. Угол Ь между AM и ААХ есть угол
между AM и Р.
Условие —Q =0 дает нам: или 6 = -^-; направление главной нор-
нормали совпадает с нормалью к поверхности, или /? = оо; точка А есть
точка перегиба, направление главной нормали неопределенно.
: Получаем снова известный нам результат в несколько более уточнен-
уточненной форме.
Примечание. Выражение -— называется геодезической кривизной
г' ' *\-
Кривой у в точке А, Геодезическая линия есть кривая с равной нулю геоде-
геодезической кривизной. Нормальная функциональная производная (в данной точке)
рт длины кривой на поверхности есть ее геодезическая кривизна.
v Изопериметрическая задача на поверхности. Пусть нам дана не-
некоторая поверхность 5. Обозначим через {?} совокупность замкнутых
|фивых класса Ci» расположенных на поверхности 5. Пусть, кроме того,
Щ каждой точке А поверхности 5 задана функция точки:
F = F(A)
Обозначая через d& элемент поверхности S и через Q часть (одну
jp частей) поверхности 5, ограниченную замкнутой кривой -у, рассмо-
рассмотрим интеграл
будет функцией линии
212 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [ГЛ. X
Разберем следующую задачу: среди всех замкнутых линий класса {?},
для которых
J1(y) = t— const.,
определить линию наименьшей длины.
Для решения поставленной задачи отметим на линии т некоторую
фиксированную точку Р и точку Pv Проварьи^гем кривую *у в окрест-
окрестностях точек Р и Рх и обозначим через а и ах, как раньше, площадки,
ограниченные т и проварьированной кривой (а расположена в окрест-
окрестности точки Р, ох — в окрестности точки Рх), кроме того, о, а1 считаются
со знаком плюс, если расположены вне Q, и со знаком минус, если
расположены внутри Q. Очевидно, имеем:
A (Ti) — h (?) ~ F (р) * + F (pi) «i,
где fi — проварьированная кривая. Кроме того, обозначая через
длину линии -у, на основании предыдущего имеем:
где G(X) есть геодезическая кривизна линии ? в точке ЛГ.
Для того чтобы 7 решала поставленную задачу, необходимо, чтобы
для всякой допустимой вариации
и, кроме того:
О (Р) 0+0(^H! = О,
т. е. чтобы в каждой точке Pt дуги f выполнялось равенство:
О (PJ = ¦№№*), D9)
Решим теперь изопериметрическую задачу в узком смысле на по-
поверхности: среди всех замкнутых кривых, ограничивающих на поверх-
поверхности данную площадь, найти кратчайшую.
В данном случее
//, F-1.
и в силу предыдущего:
G = X = const
Итак, экстремальная кривая есть замкнутая кривая постоянной геодези-
геодезической кривизны. По принципу взаимности эта же кривая реализует
максимум площади ограниченной кривой при заданной длине.
*) Вполне строгим этот вывод правила множителей Эйлера может быть
сделан так же, как в § 60.
§ 72]
ПРИЛОЖЕНИЯ К ТЕОРИИ ГЕОДЕЗИЧЕСКИХ
213
Обратим внимание, что, вообще говоря, кривая постоянной геодези-
геодезической кривизны не совпадает с геодезической окружностью.
Замкнутые геодезические на выпуклых поверхностях. Восполь-
Воспользуемся предыдущими методами для исследования некоторых свойств
замкнутых выпуклых поверхностей (на выпуклых поверхностях мы имеем
постоянно положительную гауссову кривизну).
На всякой замкнутой выпуклой поверхности S имеется по край-
крайней мере одна замкнутая геодезическая х).
Пусть Q — некоторая область поверхности S, ограниченная кривой Т.
Назовем полной кривизной области Q интеграл:
Л G) =//Г Л.
Q
где Г есть гауссова кривизна поверхности. В силу теоремы Гаусса-
Бине:
где О есть геодезическая кривизна кривой f.
Полная кривизна выпуклой замкнутой поверхности 5 равна 4тг.
Кривая у называется делящей S по кривизне
пополам, если она делит S на две части оди-
одинаковой полной кривизны (черт. 33). Очевидно,
для такой кривой:
/»
Будем искать среди кривых ^ класса
пополам, кривую кратчайшей длины.
Положим:
Черт. 33.
, делящих 5 по кривизне
ds.
Мы ищем, таким образом, минимум 7(^) при условии У1(у) = 2тг.
Применяя метод, развитый нами ниже в § 80, можно доказать, что
искомый минимум достигается на Некоторой кривой из семейства {?}.
Докажем, что эта кривая есть геодезическая.
В самом деле, применяя формулу D9), для минимальной кривой
Ш получим:
О = ХГ. E0)
Это свойство выражает теорему Пуанкаре.
214 ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ [гл. X
Так как для нашей кривой
то
\frds~O, E1)
Но на поверхности S Г > 0, следовательно,
f Г ds > 0.
и равенства E0) и E1) дают нам:
Х = 0, G = 0:
искомая экстремальная кривая есть замкнутая геодезическая линия
(черт. 33).
ГЛАВА XI
РАЗРЫВНЫЕ ЗАДАЧИ
§ 73. Ломаные экстремали
Расширение класса допустимых линий* Рассмотрим функционал,
изучаемый в простейшей задаче вариационного исчисления:
J=fF(x,y,y')dx
или в параметрической форме:
/= />(*, у, *',/) dt,
q
где F суть функции непрерывные вместе со своими частными произ-
производными до третьего порядка, кроме того, функция F(x> у, х\ У)
удовлетворяет обычным условиям однородности. Принимая за класс до-
допустимых линий кривые класса С1Э соединяющие две данные точки Л
я Ву мы отмечали, что в силу некомпактности этого класса кривых может
случиться, что среди допустимых линий не существует кривой, вдоль
которой функционал принимает минимальное или максимальное значение.
Естественно в этих случаях искать экстремум среди кривых более общего
вида, чем кривые класса d- Первое расширение задачи вариационного
исчисления в этом направлении было дано Вейерштрассом, который стал
рассматривать в качестве допустимых линий линии с точками перелома.
Для краткости изложения введем одно определение. Мы скажем, что
кривая 7 принадлежит классу Dp если ? есть простая дута Жордана
« состоит из конечного числа дуг класса Сг (Если рассматривается
функционал У, то в определении Dt класс Ci понимается в смысле гл. VI,
при рассмотрении функционала / класс Сг понимается в смысле гл. X).
Общий конец двух кривых класса d, составляющих ^, мы будем назы-
называть точкой перелома кривой f.
Расширение задачи вариационного исчисления, данное Вейерштрассом,
Заключается в следующем: найти экстремум функционала J или I,
принимая за класс допустимых линий кривые класса Ov соединяющие
две данные тонки.
Мы ограничимся в этой задаче, как и раньше, выводом основных
необходимых условий, дающих возможность фактического определения
искомой кривой, реализующей экстремум. При этом мы проведем подробно
исследование для случая функционала / и будем попутно отмечать соот-
соответствующие результаты для функционала J.
216 РАЗРЫВНЫЕ ЗАДАЧИ [ГЛ. XI
Заметим прежде всего, что нижняя (верхняя) граница значений
функционала I на классе d совпадает с нижней (верхней) границей I
на классе Dp В самом деле, пусть ? есть кривая класса Dx с точками
излома Av Л2, ..., Ап. В е-окрестности каждой точки А% заменим
кусок кривой ?, попадающий в эту окрестность, дугой окружности,
касающейся в концах куска кривой ?, так, чтобы образовавшаяся кри-
А вая ?х принадлежала классу Ci
"^ (черт. 34).
' В силу непрерывности функ-
функции F (а:, у, х/', у') по всем
четырем аргументам: х, у, х\
у'9 очевидно, что разность
Черт. 34. K1J KW
стремится к нулю вместе с е.
Отсюда мы получим такой принципиально важный результат: если
минимум 1(?)достигается на классе С t вдоль кривой ?0, то, расширяя
класс допустимых линий линиями класса Dv минимум /(?) на классе 0г
будет достигаться вдоль той же кривой ?0 класса Сг
Это замечание может быть распространено на функционал /, а также
на функционалы более общего вида (случай п функций, изопериметри-
ческая задача, задача Лагранжа). Таким образом рассмотрение ломаных
линий имеет значение лишь тогда, когда экстремум не достигается на
линиях класса Ov
Вывод необходимых условий. Перейдем к выводу основного необ-
необходимого условия. Для этой цели выберем предваритедьно для каждой
кривой ? класса допустимых линий некоторое специальное параметри-
параметрическое представление. Итак, пусть ? — линия класса допустимых линий
имеет^ точек перелома^ Аи А2, . .., АкУ т. е. ^ состоит из k-\-l
дуг: AAV АхА<ь ..., АкВ класса Cv Установим вдоль? параметр t
меняющийся от 0 до на AAV от - _f до ^"j на
4 до 1 на
Кривыми, близкими (в смысле близости первого порядка) к кривой -у,
мы будем считать те кривые класса допустимых линий, которые могут
быть разбиты на k + 1 дуг, близких (близость первого порядка) к соот-
соответственным дугам кривой ?. За меру близости примем наибольшую из
мер близости отдельных соответственных k -j-1 дуг обеих кривых.
Пусть некоторая кривая ^ класса допустимых линий определяется
уравнениями: * = *(/), у = у®.
производные: х' (J), у' (f) существуют и непрерывны всюду, кроме зна-
значений t= . , . (i=l, 2, ..., k). Рассмотрим кривую у:
y) + y | \
класса допустимых линий, близкую к кривой ^ (близость первого порядка).
§ 73] ЛОМАНЫЕ ЭКСТРЕМАЛИ 217
Приращения ох(?), 8у(^) обладают непрерывными производными^
кроме конечного числа точек, соответствующих значениям: t=
1 1
— /G) = / F {*, У, х', /) dt — f F(х, у, х', у') dt
О
\
(/=1, 2, ..., k). При этих обозначениях приращение функционала /
при переходе от f к Т имеет вид:
1 1
(, у, , у) dt
О
и имеет следующую главную линейную часть (вариацию):
Ы = J (Fxbx + Fyly -f F/ox' + /у by') dt.
0
Преобразование Дю-Буа-Реймонда путем интегрирования по частям
интеграла
дает:
1
=У (Mix' + M/) dt, A)
о
где
t t
M = M(f) — F'— fFxdt] N=N(f) = F'—(F^dL
0 0'
Если кривая ? дает экстремум, то 8/== 0 при произвольных 8лг, оу,
удовлетворяющих вышеприведенным условиям. Условие тождественного»
обращения в нуль вариации 8/ дает нам:
Г Mbx'dt=0, Г №y'dt=O.
о о
На основании леммы Дю-Буа-Реймонда получаем:
М = const., N= const. B)
1 2 k f
При t не равном . , -пгтгг,. • *> TjTT' т* е* в точках> где х (О
, и у (?) непрерывны, равенства B) можно продиференцировать, и мы
получим:
Таким образом каждая из дуг ^, отвечающая изменению t между
и -jJ-t- (/ = 0, 1, ..., k — 1), есть экстремаль.
218 РАЗРЫВНЫЕ ЗАДАЧИ [ГЛ. XI
В точках перелома: Av Л2, ..., Ак функции xf (/), у' (t) имеют
разрыв; но так как в силу B)
t t
{ Fx. = const. — f Fx dt, /y = const. ~ Г Fydt
0
t
и так как интегралы / Fx dt, I Fy dt изменяются непрерывно при пере-
0 О
ходе через значения 1= kA-V Т0 ***' и Fv должны меняться непре-
непрерывно при переходе через эти значения, хотя х* (t), У @ делают ска-
скачок. Следовательно, в точках перелома tt = - - *-у имеем:
F \ =F I , F \ ==F I D^
&'' Ц 4- о & Ц — о' у' < ^ -f- о g/'i #г' — о' >¦ *
Условия D) называются условиями Seuepuimpacca-Эрдмана в точках
перелома.
Если за параметр t принять х, интеграл / F(x, у, х\ y')dt
обращается в интеграл:
fF(x, у, 1, У) dx = f f(x, у, У) dx.
Условия D) примут вид:
где ? есть абсцисса точки перелома.
Эти же результаты можно было бы получить следующим образом:
для того чтобы кривая т давала минимум интегралу /, необходимо,
чтобы каждая из?-{-1 дут: AAV AXA2, ..., АкВ минимизировала соот-
соответствующую часть интеграла /(т); а так как каждая из этих дуг есть
дуга с непрерывной вращающейся касательной, то она должна быть
экстремалью. Итак, кривая f должна состоять из k -f-1 дуг экстрема-
экстремалей. Варьируя точки излома Av получим, как раньше, условия Вейер-
штрасса-Эрдмана.
Кривая 7» заданная уравнением л: ==.*(?), yz=:y(f), называется лома-
ломаной экстремалью интеграла /(к), если она состоит из конечного числа
экстремальных дуг fv т2, ..., чк + 1 (во внутренних точках которых
удовлетворяется уравнение Эйлера) и если в точках стыка: Av A>, ..., Ак
удовлетворяется условие Вейерштрасса-Эрдмана:
Р \ р \ р \ р \
Гtf I t - 0 Гх'Ч4 + 0> Гу* » Ц - 0 — Гу' I ^ + О'
При этом определении полученные выше результаты можно формули-
формулировать следующим образом,
<§ 74] ПРЕЛОМЛЕНИЕ ЭКСТРЕМАЛЕЙ 219
ТЕОРЕМА. Если среди кривых класса Dp соединяющих точки А
и В, кривая т дает экстремум функционалу I или J, точ есть лома-
ломаная экстремаль.
Возможность фактического определения кривой. Покажем теперь,
что если кривая То» дающая экстремум функционалу /, существует, то,
пользуясь доказанной теоремой, эту кривую можно фактически опре-
определить. Для этой цели рассмотрим вопрос о числе произвольных
постоянных, входящих в определение кривой То- Кривая То состоит из
k-\-\ дуг экстремалей тг Семейство экстремалей есть двупараметриче-
ское семейство кривых. Следовательно, каждая дуга т; определяется
парой постоянных; всего нам надо определить 2k -f- 2 постоянных.
Далее: на дугах т* является произвольным положение концов Л,,
Aj, ..., ЛА. Выбор точки на дуге определяется одной постоянной.
Лтого в определение кривой то входит bk -j- 2 постоянных. Для их
определения имеются bk-\-2 условий: дуга Ti проходит через точку Л,
дуга То4-1 — чеРез точку В (два условия); конец Аг дуги т* совпадает
с началом дуги Т$4-1 (* условий); в каждой точке перелома Ai соблю-
соблюдаются два условия Вейерштрасса-Эрдмана Bk условий), итого Sk-\-2
условия, служащие для определения 3k + 2 постоянных.
Вопрос о числе постоянных особенно ясен, когда за параметр
принята абсцисса. В этом случае уравнение семейства экстремалей
имеет вид:
у=у(х, а, Р);
уравнение каждой из k -{-1 дуг Т/ имеет вид:
У=~У(х, a|f p#) (*=1, 2, 3, ...,
Абсциссы точек перелома обозначим через: ?1? Е9, ..., $кттт1* Для опре-
определения минимизирующей кривой то требуется определение 36-j-2
постоянных: a±t a2, ..., «k + 1, рг> ра, ..., Р> + 1. 6Х. S2» ••" ^' ^ля их
определения имеются условия в количестве
F \ — F
v' ад- о у
A=1, 2, ..., *),
/
где через Ео, т]0 и 5fc + 1, 7|fc + 1 обозначены координаты данных точек Л и В.
§ 74. Преломление экстремалей
Другой, значительно более важный, класс разрывных задач вариа-
вариационного исчисления составляют задачи, когда подинтегральная функция
^С*э У у х^^у') является разрывной вдоль некоторой линии <р(х, у) = 0.
К такой задаче мы придем, если будем определять луч света в среде,
220 разрывные задачи [гл. XI
плотность которой претерпевает разрыв вдоль некоторой линии (плоская
задача) или вдоль некоторой поверхности (пространственная задача).
Дадим прежде всего более точную постановку задачи.
Формулировка задачи. Пусть в плоскости хОу дана линия <р (хуу) = 0,
не имеющая особых точек и разбивающая плоскость на две дополни-
дополнительные области />! и Z>2. Пусть функция F(x, у, х', у') удовлетворяет
условиям однородности (см. § 68) и равномерно непрерывна вместе
со всеми своими частными производными до второго порядка включи-
включительно по всем четырем аргументам в любой конечной области, содер-
содержащейся или в Dt или в Z>2. Иными словами, мы предполагаем, что F
непрерывна во всей плоскости хОу, кроме линии <р = 0, вдоль которой
F и ее производные могут иметь разрыв первого рода. Пусть, наконец,
точка А принадлежит Dx и точка В принадлежит />2.
При этих обозначениях изучаемая в настоящем параграф* задача
формулируется следующим образом:
Требуется найти экстремум функционала
/= f F(x>y,x\/)dt,
принимая за класс допустимых линий линии у, обладающие следую-
следующими свойствами:
1°. Линии f соединияют точки А и В.
2°. Каждая линия ч есть линия класса Dt и состоит из дуги
класса d» принадлежащей области D19 и из дуги класса Сх, при-
принадлежащей области D2.
Вывод необходимых условий. Найдем основные необходимые усло-
условия для кривой, реализующей экстремум. Для этой цели, понимая
близость двух кривых класса допустимых линий так же, как в преды-
предыдущем параграфе, найдем главную линейную часть приращения (вариацию)
функционала /(у) при переходе от линии -у к линии ^, близкой (бли-
(близость первого порядка) к линии f. При вычислении искомой вариации
о/ будем считать, что при параметрическом задании линий ] и Т:
т: * = *,(*), у
параметр t в обоих случаях меняется в пределах 0, 1, причем значению
^ = 0 отвечает точка А, а значению t—l отвечает точка 1. Примем,
кроме того, что для обеих кривых значению t=7> отвечают точки
преломления f, «у; т. е. точки, в которых эти линии пересекают линию
9 = 0. При этих обозначениях функционал /(^) можно проставить
в виде суммы двух интегралов:
1
? 1
/СО = / Fix, у, х', /) Л+ у F(x, у, х', /)dt
§ 74] ПРЕЛОМЛЕНИЕ ЭКСТРЕМАЛЕЙ 221
Обозначим через С и Сг соответственно точки преломления линий
7 и Т. Пусть 8лг0, 5у0 суть компоненты вектора СС1; в таком случае
искомая вариация функционала /G) представится в виде суммы вариаций
интегралов в следующем виде:
1
f
Интегралы, стоящие в выражении вариации, будем называть вну-
внутренней вариацией /(?), а выражение
будем ^называть вариацией в точке перелома.
Допустим теперь, что среди кривых класса допустимых линий суще-
существует линия ^0, вдоль которой функционал /(ч) принимает экстремаль-
экстремальное значение. Для этой линии вычисленная выше вариация должна
тождественно равняться нулю. Следовательно, для кривой ^0 должна
тождественно равняться нулю как внутренняя вариация, так и вариация
в точке перелома. Из тождественного обращения в нуль внутренней
вариации заключаем, что обе дуги АС и СВ линии То суть экстремали.
Обращение в нуль вариации в точке перелома С нам дает:
Замечая, что 8л;0 и 8у0 суть компоненты вектора ССХ с концами на
кривой <р = 0, мы заключаем, что lxOi 8y0 должны удовлетворять
соотношению:
Таким образом для кривой То в точке С имеет место равенство E) при
любых 8лг0, 8у0, удовлетворяющих F).
Диференциальные соотношения E) и F) в точке преломления можно
заменить одним конечным соотношением. Для этой цели обозначим
222 разрывные задачи [гл. XI
через а угол, образованный касательной к кривой <р = 0 в точке С
с осью Ох. Пусть кроме этого:
При этих обозначениях имеем:
В этих формулах значения <рв и <ру берутся, очевидно, в точке С. Под-
Подставляя выражения 8jc0, byQ в E), окончательно получим:
, sin a) = (F , cos a -f F. sin oc) G)
y # = _-—о ^ t=—И
2 2
Так. как по условию Fx, и F , — однородные функции степени 0 отно-
относительно л/, у у то уравнение G) не зависит от параметрического пред-
представления кривой. Добытые результаты дают теорему:
ТЕОРЕМА. Если линия ?о принадлежит классу допустимых линий
и реализует экстремум функционала I, то 7о состоит из4 двух дуг
экстремалей, причем в точке перелома удовлетворяется соотношение G).
Так же, как в предыдущем параграфе, нетрудно убедиться, что
доказанная теорема при наличии кривой, реализующей экстремум /,
дает возможность эту кривую фактически определить.
Преломление экстремалей интеграла У. Приведенное выше решение
задачи на преломление экстремалей для функционала /можно перенести,
полагая /==дг, на функционал
ь
Доказанная выше теорема останется для ^функционалов J верной, <если
соотношение G) заменить соотношением:
[(F—yFy,) cos a + Fj sin аЦ_0 = [F—/Fy) cos а -f Fy, sin а]
где jc0 есть абсцисса точки преломления С.
Частный случай. Для приложений теории преломления экстремалей
особо важную роль играет случай, когда в выражении функционала /
подинтегральная функция имеет вид:
/,*',/) = Л {Ху у) Vl^l'
где Л (х, у) есть функция равномерно непрерывная вместе со своими
частными производными двух первых порядков в каждой конечной
области, принадлежащей Dx илнО2 (ср. конец § 54).
В разбираемом случае имеем:
у
== A cos 8, F , = А -- у' = A sin В,
где р = р(/) есть угол, образованный касательной к кривой x = x(t)9
y — y(f) с осью Ох. Отсюда условие F) примет в данном случае вид:
И соз (а — р)] = [A cos (я — р)] .
о +
§ 75] ОТРАЖЕНИЕ ЭКСТРЕМАЛЕЙ 223
Как мы видели в § 27 и 28, траектории светового луча суть
экстремали функционала:
Если принять, что --—--»- удовлетворяет условиям, наложенным нами
на Л (х, у\ то луч света при переходе через линию о = 0 будет испы-
испытывать преломление, причем в точке преломления будем иметь:
COS (а — Р) j __ COS (а — 8) j
\~\
Это соотношение обобщает применимость закона преломления, выведен-
выведенного нами для частного случая в § 15, задача 4.
§ 75. Отражение экстремалей
Третий вид разрывных задач получается из естественного рас-
распространения теории отражения световых лучей. Пусть в плоскости
хОу задана линия Г (черт. 35):
обладающая непрерывно вращающейся каса-
касательной и разбивающая плоскость на две
части R и №. Обозначим через {7} сово-
совокупность кривых, обладающих следующими
свойствами:
1°. Кривые 7 принадлежат /?.
2°. Каждая кривая ? соединяет две задан-
заданные точки Л и В.
3°. Кривая к состоит из двух дуг класса
d, ЛР и РВ, причем точка Р (точка от-
отражения) принадлежит линии Г (точка отражения Я, вообще говоря,
есть точка перелома для линий у).
Условия экстремума. Пусть теперь на семействе линий {f} задан
функционал
т
где F удовлетворяет обычным условиям непрерывности и условию
однородности. Для линий f определим, как раньше, параметр t так,
чтобы при изменении / от 0 до — мы получали часть АР дуги у»
j
а при изменении t от -г до 1 — часть РВ дуги ^. Пусть -f и Т—
близкие кривые (близость первого порядка) семейства {7) с точками*
отражения соответственно Р и Р'. Обозначим через:
уравнения кривых 7 H 7-
•224 разрывные задачи [гл. XI
Из предыдущего следует, что функции x(t), y(t), x(f), у (f) могут
«меть разрыв производной при t = -к •
Обозначим:
Очевидно, Зл^, byt суть компоненты вектора РР'.
Выделим теперь из приращения /(д) — /(х) главную линейную часть
8/(х), которую мы будем называть попрежнему вариацией V )
Обозначим через 1г и /2 части интеграла (8), взятые вдоль дуг АР и
кривой Y- Очевидно:
причем вариации Ыг и 8/2 определяются как вариации для задачи
со свободным концом:
Сумму интегралов в выражении (9) мы назовем внутренней вариа-
вариацией 1(у), а квадратную скобку — вариацией /(д) в точке отражения.
Повторяя рассуждения предыдущего параграфа, мы увидим, что
условие экстремума 8/(^) = 0 сведется к тождественному исчезновению
и внутренней вариации и вариации в точке отражения. Из первого
следует, что дуги АР и РВ каждая в отдельности суть экстремали.
Из второго условия следует соотношение:
С* к-о - >V Uo) ™ + С, к-о + /> k+о) Ь=0, A0)
где tx — параметр в точке отражения Р (ъ нашем случае ^=—-j. Это
условие аналогично условию в точке преломления предыдущей задачи.
Попрежнему обозначая через а угол наклона касательной кривой Г
в точке Р к оси Ох, из формулы A0) получим:
(^cosa + F^sina)|^0==(Fefcosa + ^sina)|^+o. A1)
Таким образом для того чтобы кривая -у класса допустимых линий
давала экстремум функционалу /, необходимо, чтобы:
1°. Кривая 7 состояла из двух дуг экстремалей функционала /G).
2°. В точке отражения Р удовлетворялось условие A1).
§ 76] СЛУЧАЙ СВОБОДНЫХ КОНЦОВ
Частный случай задачи. В частном случае, если
225
то
= А
FV = Л <*•
cos
sin ^
где р есть угол, образованный касательной к | с положительным на-
направлением оси Ох (касательная направлена в сторону возрастания f).
Условие A1) в точке отражения примет вид:
[Л cos (а — р)]х = [Л cos (а — р)] х .
2 2
Но так как А от производных не зависит и [А] — [А]л , то при
А ф 0 последнее равенство можно на А сократить, получим:
[cos (а — р)] ± = [cos (а — р)] ± . A2)
Следовательно, в точке отражения угол падения равен углу отражения.
§ 76. Случай свободных концов
Обобщение предыдущих задач. Разберем вкратце задачу, обобщаю-
обобщающую задачи, разобранные нами в двух предыдущих параграфах.
Пусть на плоскости задана ?-связ-
ная область /?, ограниченная линиями:
г19 г2, ..., гк (черт. 36), которые мы
будем называть в дальнейшем линиями
отражения* Внутри R проведены ли-
линии ср и ф, а также линии Si9 52, ..., Slt
которые мы назовем линиями прелом-
преломления. Рассмотрим семейство линий
{ 7 }»удовлетворяющих ниже следующим
условиям:
1°. Начало А линии f лежит на
линии <р, конец В этой линии лежит
«а линии ф.
\ 2°. Линии ^ лежат в области /?.
1 , 3°. Линии ^ пересекают по одному
|разу каждую из линий преломления st
Черт. 36.
ь
=1, 2, ...,
4°. Линии
а, ..., гк.
)
имеют по одной точке на каждой линии отражения ri9
226 разрывные задачи [гл. XI
Обозначим через Clf Ca, ..., Ск+1 точки, общие для кривой «у и
кривых^, 52, ...,«,; г1э г9, .. .,гл. Кривая ? распадается на *-}-/-+-1 ЩГг:
-"-
5°. Каждая из дуг: АС19 СХС2, ..., Сь+1В принадлежит классу Cv
На кривых {-у} определен функционатг
т
где Z7 — положительно-однородная функция первой степени относительно
х/', у. Мы считаем функцию F непрерывной относительно всех четырех
аргументов и обладающей непрерывными частными производными первых
двух порядков всюду, кроме линий преломления. При переходе через
линии преломления функция F и ее производные претерпевают разрыв
первого рода.
Вариация функционала. Рассмотрим две близких линии y и Т
из класса {^Ь заданных уравнениями:
X=x(f), , y=y(f);'
Параметр t выбран так, чтобы определенным значениям параметра
С» < *1 < *2 < • • • <
отвечали точки Clf С2, ..., Ск + 1 и С/, С/, ..., СЛ+г, в которых кри-
кривые f и Т достигают линий преломления и отражения. Далее обозначим
через А и А' начала кривых ^ и Т» лежащие на кривой ср, через В и
ZT — концы этих кривых, лежащие на кривой ф.
Выделим из приращения
1
/(?) — / (Т) = / [F Ос, У. ~х\ 7) - Z7 (*, ^. ^.
О
главную линейную часть — вариацию:
1
6
С помощью преобразования Лагранжа представим 8/(-у) в виде:
k+i
-4^) 4dt-
§ 76] СЛУЧАЙ СВОБОДНЫХ КОНЦОВ 227
Вариация 3/(f) распадается на пять частей:
1. Интеграл в выражении A3), который по-предыдущему мы называем
внутренней вариацией.
2—3. Сумма 2 [ ] в выражении A3), которая состоит из вариаций
i = l
в / точках преломления и вариаций в k точках отражения.
4. Член —(Fx$x-\~Fy$y)t^v который мы согласно терминологии
§ 54 будем называть вариацией начала.
5. Член (Fx$x-{- F ,by)t=zl — вариация конца.
Свобода перемещения кривых класса {-у } по линии <р и ф вызвала
появление двух добавочных членов 4) и 5) в выражении для вариации.
Вывод необходимых условий. Найдем необходимые условия, кото-
которым должна удовлетворять кривая ^ для того, чтобы на ней достигался
условный экстремум функционала /(х)- Это условие есть тождественное
исчезновение вариации 5/(Т):
8/(Ц) = 0. A4)
Из A4) вытекает:
ТЕОРЕМА. Для того чтобы кривая т класса {-у} реализовала
экстремум функционала 1(у), необходимо, чтобы:,
1. Кривая т состояла из k-\-l-\-l дуг экстремалей:
где А и В — начало и конец кривой у» Q —ее точки, лежащие на
кривых г{ и 5Г
2. В I точках Сг пересечения -у с линиями преломления должно
удовлетворяться условие G).
3. В k точках Cj кривой -f» лежащих на линиях отражения,
^должно удовлетворяться условие A1).
4—5. В точках А и В кривая f должна быть трансверсальна
соответственно кривым у и ty.
Требование 1 есть условие исчезновения внутренней вариации,
требования 2, 3 суть условия исчезновения вариаций в точках прелом-
преломления и отражения, требования 4—5 — условия исчезновения вариаций
в конце и начале.
В частности, если
F(х, у, х\/) = А{х^
то требование трансверсальности -у к линии о и ф обращается в требо-
требование ортогональности (§ 54), а условия в точках преломления и отра-
отражения принимают упрощенную форму A2).
Оптические применения. Доказанный нами в конце § 57 принцип Малюса
Может быть без труда обобщен сейчас на случай, когда лучи претерпевают про-
произвольное количество преломлений и отражений. Мы рассмотрим для простоты
Случай плоского светового пучка. Так как все рассмотрения § 74, 75 и настоя-
настоящего параграфа могут быть распространены на случай пространственной задачи
,(с заменой линий преломления и отражения соотвественно поверхностями пре-
йомления и отражения), то наш результат переносится и на случай простран-
пространственной задачи.
228
РАЗРЫВНЫЕ ЗАДАЧИ
[ГЛ. XI
Напомним, что линией (поверхностью) волны называется геометрическое
место точек, в которые световой сигнал, отправленный из точки А, попадает
в одно и в то же время. Нами было доказано в конце § 57, что линия (поверх-
(поверхность) волны ортогональна всем лучам нашего плоского (пространственного)
пучка лучей. Доказательство в силу полученных в настоящей главе результатов
не изменится, если лучи будут претерпевать в пути какое угодно количество
преломлений и отражений.
Отсюда следует1.
Принцип Мал юса. Ланий (поверхности) волны ортогональны всем лучам
светового пучка независимо от количества отражений и преломлений, испы-
испытываемых лучами пучка.
Черт. 38.
Принцип Малюса является, наряду с принципом Фэрма, основным принци-
принципом геометрической оптики. Он дает возможность просто решать многие опти-
оптические задачи.
Пример 1. В среде с постоянной скоростью света из точки О исходит
пучок лучей. Требуется построить зеркало, отражающее этот пучок в виде
пучка параллельных прямых. Лучи имеют вид ломаных с угловыми точ-
точками на зеркале.
Решим задачу для плоского пучка. После отражения о зеркало Q пучок
обращается в пучок параллельных прямых (черт. 37). Линия волны, следова-
следовательно, обращается в перпендикулярную им прямую.
Пусть прямая L есть линия волны. Ломаная ОСВ, где С лежит на Q,
а В — на L, есть один из наших лучей света. Оптическая длина этого луча,
если обозначить скорость света через v1) (мы считаем ее постоянной), равна:
~ОС СВ
v ' v
Для всех лучей ОСВ нашего пучка
V V '
const.,
т. е.
ОС + СВ = const.
Отложив на продолжении СВ отрезок CD = СО, получим:
DB = / = const.
геометрическое место точек D есть прямая 1^, параллельная L и отстоящая от
нее на расстоянии /. Так как OC=CD, то искомое зеркало должно иметь
форму параболы с фокусом О и директрисой Lx.
*) Под оптической длиной линии q мы понимаем значение интеграла
/ -^-, т. е. время пробега светом кривой q.
§ 76]
СЛУЧАЙ СВОБОДНЫХ КОНЦОВ
229
Вращая эту параболу вокруг ее главной оси, проходящей через О, полу-
получим параболоид вращения, который нам дает зеркало, отражающее простран-
пространственный пучок л}'чей, выходящих из фокуса О в виде пучка лучей, парал-
параллельных оси параболоида.
Пример 2. Плоскость разбита на две части St и S2, скорость света в S1
равна vlf в S2 равна и2. Какова должна быть линия раздела этих сред, чтобы
пучок лучей,"выходящих из точки О, принадлежащей Slf после преломления
о линию раздела пошел в S2 в виде пучка параллельных лучей?
Лучи будут состоять из ломаных с точками перелома на линии раздела
(черт. 38). Отложим на всех лучах, исходящих из О, отрезки равной оптической
длины; их концы дадут линию волны. Линия волны в S2 есть прямая, перпен-
Черт. 39.
Черт. 40.
дикулярная к параллельному пучку. Пусть L — такая линия волны. Если точка С
произвольного луча ОВС с точкой перелома В лежит на Z,, то:
ОВ , ВС . ,
. = const. = k,
v v
v2
Проведем прямую Lh параллельную L, так, чтобы В находилась между L и Lt
и чтобы расстояние между L и L± равнялось v2k = kx. Если С± есть пересечение
продолжения ВС с Lu то
ОВ=^- СВ.
v2
Линия раздела Q есть геометрическое место точек В, удовлетворяющих
уравнению:
Q есть коническое сечение с фокусом в О и директрисой ?1#
Если t/j <^ tjj, это коническое сечение обращается в гиперболу, причем так
как углы преломления меньше углов падения, то, очевидно, эта граница состоит
из ветви гиперболы, обращенной выпуклостью к О.
При v2y>Vi получаем эллипс с фокусом О и осью, имеющей направление
параллельного пучка (черт. 39), причем, так как углы падения меньше углов
отражения, точка О должка находиться в левом фокусе, если свет в параллель-
параллельном пучке движения справа налево.
Пусть пучок лучей исходит из О, преломляется или отражается вдоль Q
и собирается в фокусе F (черт. 40). Линии волны L вокруг F представляют
собой линии, стягивающиеся в фокус F. Оптические длины всех лучей пучка
одинаковы; это следует еще из того, что вариация оптической длины при пере-
переходе от одного луча OF к бесконечно близкому равна нулю, так как вариация
концов равна нулю.
230
РАЗРЫВНЫЕ ЗАДАЧИ
[ГЛ. XI
Пример 3. Построить форму зеркала, собирающего в точке F пучок лучей,
исходящий из точки О (скорость света постоянна).
Решим сначала задачу в плоскости. Луч имеет форму ломаной OCF,
где С — точка отражения (черт. 41). Оптическая длина постоянна для всех лучей
пучка. Вследствие постоянства скорости света
С оптическая длина пропорциональна обычной
~* "*" длине, которая тоже одинакова для всех лучей
пучка.
Геометрическое место точек отражения С
удовлетворяющих уравнению
ОС + 'CF= const,
и есть эллипс с фокусами в Q и F.
В пространстве решение задачи дается
эллипсоидом, получаемым вращением этого
эллипса вокруг большой оси.
Аналогично можно найти* такую линию
раздела сред S1 и S2 со скоростями v1 и v*>
что пучок лучей, исходящий ?из точки О
среды Slf собирается в точке F среды 52. Линия раздела есть геометрическое
место точек, расстояния которых р1 и р3 от точек О и F определяются
уравнением:
Ji_ + ^ = const.
v1 ^ v2
В декартовых координатах это уравнение дает кривую четвертого порядка.
Прием, использованный нами сейчас для исследования пучка лучей, будет
широко использован впоследствии в гл. XIV. Задачи геометрической оптики
привели впервые к исследованию семейства экстремалей. Из геометрической
олтики они были перенесены Гамильтоном на задачи более общего вида.
Черт. 41.
Опечатка
Стр. 230 сгрока 12, сверху напечатано Q следует читать О
ГЛАВА XII
ОДНОСТОРОННИЕ ВАРИАЦИИ
§ 77. Односторонние вариации для простейшей задачи
Ограничения на класс допустимых линий. До сих пор мы рас-
рассматривали задачи, когда на класс допустимых линий у—у(х\ кроме
общих условий теоретико-функционального характера, накладывались
условия: проходить через две данные точки: y(xx)—yv y(x^—y^
быть длиннее данной длины: /
вестных функций, например, — принадлежать данной поверхности
и т. д. Все задачи разобранного типа обладали одной специфической
особенностью: 'если вариация Ьу (х) была допустимой, то и вариация
— 8у(лг) также была допустимей. Эти задачи имеют полную аналогию
с задачами на разыскание экстремумов функций многих переменных,
когда область изменения переменных есть все пространство или есть
вся поверхность (условный экстремум). По аналогии с задачами функ-
функций конечного числа переменных, когда область изменения переменных
ограничена (ищется, например, минимум /(лг), где а^х^Ь)у могут
быть рассмотрены задачи вариационного исчисления, в которых класс
допустимых линий должен удовлетворять условиям, записываемым в форме
неравенств. Приведем ряд примеров.
Ищется кривая, минимизирующая интеграл
ь
J = f F{x,y,/)dx
а
среди всех кривых, проходящих через точки А, В и расположенных
вне некоторого круга. Последнее условие можно аналитически запи-
^Tb так: (х — а? + СУ — bf > г*, •
где а, Ь, г—заданные числа. Или общее: за класс допустимых линий
принимаются линии у=у(х) такие, что:
?(*, >0>О, A)
где о(х, у)—данная функция.
В задачах на определение экстремумов функционалов, зависящих от
линий в пространстве п -}-1 измерений, можно брать за класс допу-
допустимых линий кривые, лежащие в области:
- A')
232 односторонние вариации [гл. XII
Можно взять в качестве примера задачу, когда за класс допустимых
линий принимаются линии, вдоль которых интеграл К удовлетворяет
неравенству:
f B)
Наконец, во многих задачах за класс допустимых линий принимаются
выпуклые кривые у =у (лг). Условие выпуклости можно тоже написать
в виде неравенства: /(х)<0: C)
вдоль всей кривой вторая производная неположительна. Общее, если
линия может иметь точки перелома, то условием выпуклости будет: вто-
вторые разности вдоль всей кривой всюду неположительны:
А^<0. C0
Существенным отличием этих задач от ранее разобранных является
то, что если условия в форме A), или в форме B), или в форме C)
для кривой у=у (х) выполнены в смысле равенства и если при допу-
допустимой вариации 8у(лг) эти условия переходят в неравенства, то вари-
вариации— чу (л:) в общем случае уже не являются допустимыми.
Это обстоятельство является полным аналогом того, что мы имели
в задачах на экстремум функций многих переменных, когда экстремум
достигался на границе области задания функции.
Геометрическая интерпретация. При постановке простейшей
задачи вариационного исчисления мы выявили глубокую аналогию между
функциями, определенными в пространстве п измерений, и функциона-
функционалами, определенными в функциональном пространстве.. Вводя понятие
области в функциональном пространстве, мы сможем распространить эту
аналогию также на разбираемый круг вопросов.
Напомним, что некоторое множество точек функционального про-
пространства R образует область, если, какова бы ни была точка этого
пространства, некоторая окрестность этой точки также принадлежит
пространству. Например, если рассмотреть пространство С всех непре-
непрерывных функций /(л:), определенных на отрезке а^х^д, то мно-
множество непрерывных функций, удовлетворяющих условию /(л:) > 0,
будет областью рассматриваемого пространства.
Закрытой областью функционального пространства назовем область,,
к которой добавлены все предельные точки точек данной области.
Например, закрытой областью на R будет множество непрерывных
функций/(л:), удовлетворяющих неравенству /(х)!>0.
При этих определениях перечисленные нами задачи могут быть фор-
формулированы следующим образом: среди всех точек данной области
функционального пространства определить ту, в которой данный
функционал принимает экстремальное значение.
Простейшая задача. Начнем с рассмотрения простейшей задачи:
среди всех непрерывных кривых у— у (лг), производные которых непре-
непрерывны кроме, быть может, точек, лежащих на кривой <р (л:, у) = 0,
удовлетворяющих условию
(O>0 D)
§ 77]
ОДНОСТОРОННИЕ ВАРИАЦИИ ДЛЯ ПРОСТЕЙШЕЙ ЗАДАЧИ
233
и соединяющих заданные точки А и Б, найти ту, вдоль которой
интеграл J:
7 = f F(x, у, /)dx
E)
принимает экстремальное значение.
Ограничимся в этой главе выводом необходимых условий, пользуясь
которыми можно было бы искомую кривую фактически определять, если
она существует.
Неравенство 9 (ху У)^>® опре-
определит, как известно, в общем слу-
случае закрытую область с границей
9 (л:, у) = 0 (черт. 42). Мы будем
предполагать, что функция о(х, У)
однозначна и допускает непрерывные
производные первого порядка и что
система уравнений:
-*?.—О
dv
ду
= 0, © = !
Черт. 42.
имеет лишь конечное число реше-
решений; им отвечают точки, которые в диференциальной геометрии назы-
называются особыми точками. Прочие точки кривой <о(х, у) = 0 будем
называть обыкновенными.
Вывод условий экстремума. Таким образом условию D) можно
придать геометрический смысл: все кривые класса допустимых 'линий
должны принадлежать закрытой области, ограниченной кривой 9 = 0-
Допустим, что кривая ?,
дающая минимум в рассма-
рассматриваемом классе допусти-
допустимых линий, существует и
имеет уравнение:
у=у{х).
В общем случае искомая
кривая y может быть разбита
на последовательные куски ?!,
Та>• • • > Тй> -*-!> j-2>***> ¦*¦*—1»
где все куски *fi принадле-
принадлежат области ср (л:, y)^>0f
все куски Г, принадлежат
границе (черт. 43). Обозна-
Обозначим через Av Вх) Л2, В2; ... ; Ak_v Вк_г соответственно левые и
правые концы кривых 1\, Г2, ..., Гл_г Мы допускаем, что куски Г,
состоят из правильных точек кривой 9 = 0.
Нашей задачей будет выявить те условия, которым должны удовле-
удовлетворять: 1) кривые Yi при 9 > 0; 2) кривые Г4 и 3) кривые 7, в точках
соединения: At, Вг.
Черт. 43.
234 односторонние вариации [гл. XII
Условия для кривых «^ получаются сразу. В самом деле, так как
кривые Ti принадлежат области о > 0, то для этих кривых допустимы
двусторонние *) вариации и, следовательно, каждая кривая ^i должна
быть экстремалью для интеграла У, т. е. удовлетворять уравнению
Эйлера:
4
Займемся выводом условий для кривых Гг Для этих кривых воз-
возможны лишь односторонние вариации, причем очевидно, что если для
точек рассматриваемой кривой ~г*> 0, то допустимы лишь вариации
Zy ^ 0 (вдоль кривой <р — 0, следовательно, если -~- > 0, то при от-
отрицательном приращении оу о становится отрицательной и кривая
у=у{х)-\-Ъу(х) не будет принадлежать классу допустимых линий).
Аналогично, если ^-<0, то возможны лишь вариации Sy.^0. Зай-
Займемся первым случаем.
Так как наша кривая дает минимум, то при всех бесконечно малых
положительных вариациях Ьу вариация интеграла J должна быть неот-
неотрицательна. Применяя метод варьирования в точке, получим:
Отсюда вдоль каждой дуги Г„ для которой -~ > 0, имеем:
Аналогично для тех дуг Г.;, для которых -— < 0, имеем:
Объединяя оба случая для минимума, имеем:
для всех точек дуг 1\.
Рассмотрим последний вопрос — вопрос об условиях в точках Аг
Определим вариацию J при вариациях ючки Ах вдоль кривой Гг Эта
*) То-есть,если Ьу — допустимая вариация, то — оу является также допустимой.
2) Очевидно, что в силу однозначности у=у(х) вдоль дуги Fi функция
дер
-т- переменить знака не может.
§ 77] ОДНОСТОРОННИЕ ВАРИАЦИИ ДЛЯ ПРОСТЕЙШЕЙ ЗАДАЧИ 235
вариация будет состоять из двух частей: если мы через хг обозначим
абсциссу точки Aiy то
Ъ
F(x, у, /)dx+i f F(x9 у, y')dx.
Вариация первого интеграла была нами вычислена при решении
задач на „свободные концы":
• #
где k — угловой коэфициент касательной к кривой ср = 0 в точке Аг
Вариация второго интеграла сводится к уменьшению длины интервала
интеграции на Ьхг; отсюда
ъ
f F(x, У, f)dx = — F{xu у(х^к)Ьх.
Так как разбираемая вариация есть двусторонняя (с точностью до
малых высших порядков), то при экстремуме необходимо, чтобы сумма
двух вычисленных вариаций равнялась нулю. Получим:
F(x» y(xt)9 k) — F[xv у(хг), У(хг)] —
- (k -У (**)) F,. [xi9 у (хХ у (х,)} = О
или
t),-%)-F(x,, у(хг), У(х,
ду
.Полученное условие будет удовлетворяться, если
*=/(*), E0
т. е. если в точке А. касательная к ^ совпадает с касатальной к Гг
Если кривая ср = 0, а функция F , . ф 0 при любых у\ то реше-
решение EГ) есть единственное, таким образом в этом случае во всех точ-
точках, где минимизирующая кривая у=у(х) переходит из области <р>0
на границу области, касательная к кривой должна совпадать с каса-
касательной к границе. Иными словами, функция у=у(х), представляющая
уравнение минимизирующей кривой, обладает непрерывной производной.
Проведенный анализ задачи может быть оформлен в следующую
теорему.
236
ОДНОСТОРОННИЕ ВАРИАЦИИ
[гл. XII
ТЕОРЕМА, Если кривая у—у(х) среди всех кривых, соединяющих
две данных точки А и В и лежащих в области <р (л:, у) > 0 [/ не-
непрерывна кроме, быть может, точек границы <р(лг, у) = 0], дает мини-
мум интегралу У, то:
1. Во всех точках, лежащих внутри области, кривая у— у(х)
есть экстремаль: ,
2. Во всех точках кривой у—у(х), принадлежащих границе:
d
F —1
У dx
), если ^> О,
если
3. В точках перехода из области на границу области
( Hi.
- \ ду
Пример. В качестве первого примера на применение выведенных условий
разберем задачу на определение брахистохроны: среди всех кривых, лежащих
в вертикальной плоскости хОу выше пря-
прямой у = ах-\-Ь и соединяющих точки А
и В, найти ту, двигаясь по которой под
действием своего веса точка М придет
из А и В в кратчайшее время.
Сохраним обозначения, принятые в §72,
поместим начало координат в точку А и
обозначим через х\, У| координаты точки В
(черт. 44). Эта задача, как мы видели, сво-
сводится к разысканию минимума интеграла:
Черт. 44.
= г
У1
YJ
Семейство экстремалей будет состоять из циклоид:
*=rF — sin0) + C, y = r(l — cos
Для этой задачи имеем:
F)
Следовательно, экстремаль должна касаться границы области. Кроме того,
допустимые линии должны по условию принадлежать области:
дер
~ду~-~
Следовательно, для
должны иметь
кусков искомой кривой, принадлежащих границе,
§ 77]
ОДНОСТОРОННИЕ ВАРИАЦИИ ДЛЯ ПРОСТЕЙШЕЙ ЗАДАЧИ
237
Это условие для разбираемой задачи выполнено, ибо, с одной стороны,
F -A Ft== у"
и, с другой стороны, у" <С0, так как все экстремали — циклоиды, расположенные
под осью Ох, выпуклы.
В общем случае при решении имеется две возможности:
1. Через точки А и В можно провести экстремаль, принадлежащую данной
области ср>0; в этом случае эта экстремаль и будет давать искомую кривую.
2. Через точки А и В невозможно провесть экстремаль, целиком принадле-
принадлежащую области «р>0; в этом случае из точек А и В проводим циклоиды
семейства F), касательные к прямой у = ах + Ь. Пусть А± и В1 суть точки каса-
касания циклоид, соответственно выходящих из А и В (черт. 45). Искомая кривая
-будет состоять из циклоиды ААЬ отрезка А1В1 и циклоиды В±В.
Дадим в заключение один числовой .
I д \- ¦ *- х
пример. Пусть а = О, Ь = 1, хх = — B + Зтс),
В этом случае линия наилучшего ската
будет состоять из куска циклоиды:
х = ~- F - sin 6)
(О < е < тг),
\У
из горизонтального отрезка
: Ах (у»
Черт. 45.
7Г+ 1» 1) и куска циклоиды
X = -|_ F - Sin 6), у = — A - COS 6).
Случай параметрического задания кривой. Простейшую задачу,
разобранную нами выше, можно легко распространить на тот случай, когда
за класс допустимых линий принимаются кривые, задаваемые в параме-
параметрической форме: среди кривых х-
X = x(fi, y=y(t),
принадлежащих закрытой области:
и соединяющих точки Л и В этой области и обладающих непре-
непрерывно вращающейся касательной всюду, кроме, быть может, точек
границы 9 = 0, требуется определить кривую, вдоль которой интеграл:
у, *', /) Л
принимает экстремальное значение 2).
J) Кривую ср = 0 мы предполагаем замкнутой и обладающей непрерывно
вращающейся касательной.
2) Функция F предполагается удовлетворяющей обычным условиям одно-
однородности и непрерывности.
238 односторонние вариации [гл. XII
Используя добытый выше результат или оперируя непосредственно
с вариациями интеграла У, легко получить следующий результат: если
кривая ^ класса допустимых линий реализует искомый экстремум,
то -у состоит из дуг экстремалей интеграла J внутри области
<р > 0 и из кусков границы области о^О, причем в точках кривой у,
принадлежащих границе <р == 0, имеем:
дх ' ду ^
F(x, у, х\ /) — x'Fx,(x, у, х\ /)—/Fy,(x, у, х\ /) = 0,
где за х\ у/ и х\ у' можно принять направляющие косинусы каса-
касательных соответственно к кривой f и к кривой <р = 0.
Пользуясь условием однородности функции F и полагая для сокра-
сокращения письма:
нашим условиям можно придать более простой вид:
дх [ ду J '
или окончательно:
В частности, если область ?>-0 ограничена отрезком прямой, парал-
параллельной оси Оу, то наше условие примет вид:
F г — F г
у У
§ 78. Задача Ньютона (поверхность вращения наименьшего
сопротивления)
Подход к решению задачи. Будем рассматривать плоские кривые Г,
соединяющие начало координат О с точкой А (а, Ь). При вращении
вокруг оси Ох они дадут семейство поверхностей вращения с общей
осью Ох, вершиной О и опирающихся на общую окружность, получае-
получаемую вращением ординаты ААХ точки А (черт. 46). Вместе с кругом
эти поверхности ограничивают некоторые тела вращения. Задача заклю-
ЗАДАЧА НЬЮТОНА
239
чается в выборе среди этих . тел вращения тела, испытывающего при,
поступательном движении в сопротивляющейся среде (вода, воздух)
в направлении оси вращения со скоростью v наименьшее сопротивление.
Решение этой задачи зависит, конечно, от законов сопротивления,
Ньютон, исходя из очень грубых гипотез, дал
следующий закон сопротивления. Среда представля-
представлялась состоящей из неподвижных молекул. Каждый
элемент поверхности da> при поступательном дви-
движении встречает на своем пути эти молекулы, абсо-
абсолютно упругие удары их об элемент d<& опреде-
определяют его сопротивление. Пусть а — угол наклона
элемента к направлению движения оси Ох. Про-
Проекция элемента do* на плоскость, перпендикуляр-
перпендикулярную направлению движения, равна flfasina. Чи-
Число ударов элемента d<& о молекулы за единицу
времени пропорционально flfasina. Относительная
средняя скорость молекулы равна v. Разложив v
на скорость, нормальную к d®> равную v sin a и
направленную по flfo>, мы можем заменить удары нашей молекулы ударом
той же массы в нормальном направлении со скоростью v sin a; живая
сила ударов всех молекул на элемент d& за единицу времени пропор-
пропорциональна
v2 sin2 а я?о>.
Черт. 46.
На поверхности вращения кривой Г:
x = x(f), y
y(f)
при оси вращения, совпадающей с направлением движения, все точки
каждого бесконечно тонкого усеченного конуса, получаемого вращением
элемента длины, имеют общий наклон а к направлению движения-
Если оно совпадает с осью Ох, то
sin а =
У'
поверхность бесконечно тонкого усеченного конуса равна
ds = ъу У я'*
сопротивление его равно
где k — постоянный козфициент. Интегрируя по t вдоль кривой Г,,
получим сопротивление R поверхности вращения:
= kv* f
УУ'
¦dt.
Рассмотрим теперь всю поверхность в целом. Пусть в направлении,
обратном направлению движения, на поверхность падает пучок парал-
односторонние вариации [гл. XII
.лельных лучей. Часть поверхности будет освещена ими; назовем ее
„освещенной" частью. Часть поверхности будет находиться в тени,
отбрасываемой остальными частями. В столкновениях с молекулами будет
при нашей грубой схеме принимать участие только освещенная часть
поверхности, следовательно, общее сопротивление выразится интегралом
от сопротивления элемента поверхности, взятым по освещенной его части.
Если вся поверхность по нашей терминологии освещена, т. е. каждая
прямая, параллельная направлению движения, пересекает поверхность
только в одной точке, то интеграция берется по всей поверхности.
Естественно ограничиться при наших гипотезах поверхностями вра-
вращения, полностью освещенными, поскольку неосвещенные не участвуют
в сопротивлении.
Аналитическая постановка задачи. Итак, за класс допустимых
линий мы принимаем линии
х = х(у),
где х (у)— однозначная функция. Отправляясь от физического смысла
задачи, мы допустим еще дополнительно, что функции х{у) класса
.допустимых линий суть функции неубывающие. Несколько расширяя
класс допустимых линий, мы можем аналитически формулировать нашу
задачу следующим образом: среди кривых у класса D{> соединяющих
точки А и В и расположенных внутри прямоугольника:
определить кривую, вдоль которой интеграл:
г Г yy'*dt
J
J
принимает наименьшее значение.
Решение задачи. Составим прежде всего для нашей задачи уравне-
уравнение Эйлера. Подинтегральноё выражение F не содержит х. Следова-
Следовательно, экстремаль удовлетворяет уравнению:
/V = C= const.
Таким обрзом:
УУ**' с п\
Обратим внимание, что если хоть в одной точке экстремали х' или уг
равны нулю, то С = 0 и, следовательно, вдоль всей экстремали лг'=зО
или У = 0; экстремаль вырождается в прямую х = с или в прямую
у = с. Прямые у == с, параллельные оси Ох, нас не интересуют,
поскольку при вращении они дают неосвещенные поверхности.
Пусть теперь л/2 ф 0, У2 ф 0; тогда при наших предположениях
xf > 0, у > 0. Обозначим
хг
лолучим из условия G):
УЯ _п
§ 78] ЗАДАЧА НЬЮТОНА 241
Отсюда:
,= ™±?i. (8)
Приняв q за параметр, из (8) получим:
,/ __ *У __г -1 -4-2
dq v^
Итак, приняв q за параметр, получим уравнение экстремали в параме-
параметрическом виде:
При С=0, у = 0, т. е. экстремаль выродится в одну из прямолиней-
прямолинейных экстремалей, рассмотренных выше. Новые экстремальные кривые мы
получим при С ф 0. Для этих кривых ^у всегда отлично от нуля и имеет
один и тот же знак, т. е. эти экстремали не пересекают ось Ох. Но, оче-
очевидно, прямолинейные экстремали не соединяют начала координат
с точкой А, не лежащей на координатных осях, а криволинейные не
соединяют начало координат с А, поскольку они не пересекают оси Ох
и, следовательно, не проходят через начало. В нашей задаче минимум
не достигается на кривых с непрерывно вращающейся касательной, и
нам естественно его искать среди кривых с точками перелома.
Прежде чем к этому приступить, исследуем кривые семейства (9)
при q ф 0. Рассмотрим одну из этих кривых при С= 1, С1 =0; осталь-
остальные кривые при любых С и С{ получаются из нее подобным преобра-
преобразованием (с центром в начале координат и знаменателем преобразова-
преобразования С) и поступательным перемещением (параллельным оси Ох на рас-
расстоянии Q). Итак, ограничимся пока кривой:
A0)
Ири q—> оо, у-+оо и „v->oo. В самом деле, </24~~Тг4 растет быст-
быстрее, чем In q, и, следовательно, их разность стремится к -(- оо.
Итак, кривая A0) уходит двумя ветвями в бесконечность. При
q < 0 логарифм становится комплексным, следовательно, кривая A0)
определена только для положительных q. Так как — = —- есть угло-
угловой коэфициецт касательной, то, следовательно, в каждой из ветвей у
242 односторонние вариации [гл. XII
есть монотонно возрастающая функция от х. Очевидно, что х и у прн
каком-то конечном значении q достигают своего минимума.
Для значения q, дающего минимум х, имеем:
Для минимального значения у:
Так как миним}гмы х и у достигаются заведомо не для q = 0 и q = ос,
то — и —g- отличны от нуля и от бесконечности, на них можно сокра-
сократить, мы получаем для определения минимума х и у одно и то же
биквадратное уравнение:
3^ + 2^—1=0, .
у которого мы должны искать вещественный и притом положительный
корень. Решая это уравнение, мы обнаруживаем, что искомый корень —
единственный и равен:
д
Таким образом, когда q возрастает от —^ до оо, то х и у моно-
У 3
У
тонно возрастают; когда q убывает от -у= до нуля, х и у также
монотонно возрастают.
Заметим, что — есть угловой козфициент касательной к изучае-
изучаемой кривой, мы можем теперь достаточно точно охарактеризовать поведе-
поведение кривой. При q = —z= мы имеем точку возврата; ветвь кривой, со-
у 3
ответствующая q <—7=-, и ветвь крИЕой, соответствующая q > -^=, вог-
у з уз
нута. В точке Еозврата углевой козфкциент касательной равен
угол касательной с осью Ох равен 60°.
Условие Лежандра для минимума:
в силу того, что у > 0 и у > 0, нам дает:
у 2 _ Злг'2 =/2A — 3^>) > 0,
т. е.
<
Таким образом кривая, дающая минимум, может состоять только из
выпуклых кусков экстремали и из отрезков, параллельных координат-
координатным осям.
§ 78] ЗАДАЧА НЬЮТОНА 243
Покажем теперь, что точка излома может находиться только на
оси Оу (на границе прямоугольника). В самом деле, в точке излома
должны удовлетворяться условия Эрдмана:
которые для нашей задачи примут вид:
( '
В точке излома при у >> 0 возможны четыре случая:
1. Точку излома образуют отрезки параллелей оси Ох и оси Оу;
эти отрезки соответствуют значениям # = 0 и q = oo; условие A2) не
выполняется.
2. Точку излома образуют отрезок параллели оси Ох и дуга кривой
Ньютона.
3. Точку излома образуют отрезок параллели оси Оу и дуга кривой
"Ньютона; в этих двух случаях будет, очевидно, невыполнено усло-
условие A1).
4. Точку излома образуют две различные дуги кривой Ньютона.
Так как в силу условия Лежандра обе эти дуги соответствуют значе-
значениям ^^-г=, то легко видеть, что и в этом случае условие A1)
не выполняется ни при каких различных значениях qt и q2.
Нам остается показать, что точки излома не лежат также на оси Ох.
Так как кривая Ньютона при любых значениях произвольных постоян-
постоянных не пересекает оси Оху то наличие у экстремали точки излома на
этой оси (экстремаль в этом случае должна содержать кусок оси* Ох>
кусок параллели оси Оу) повлекло бы за собой наличие у кривой
точки излома при у > 0, что невозможно по доказанному выше. Отсюда
заключаем, что искомая кривая должна состоять из отрезка оси Оу
(кусок границы области) и из куска кривой Ньютона.
В точке излома на границе должно быть выполнено условие A2) *),
которое в нашем случае примет вид:
Отсюда в точке излома для кривой Ньютона получим:
т. е. в точке излома кривая Ньютона образует с осью Оу угол в 45°.
Итак, искомая кривая состоит из отрезка оси Оу и выпуклого
куска кривой Ньютона, выходящей из точки В и пересекающей ось Оу
под углом 45°. Нетрудно видеть геометрически, что этими условиями
искомая кривая определяется единственным образом.
*) См. конец предыдущего параграфа.
244
ОДНОСТОРОННИЕ4ВАРИАЦИИ
[гл. XII
§ 79. Пространственная задача
Постановка общей задачи. Рассмотрим теперь более общую за-
задачу: среда всех пространственных кривых:
Jy=y(x), z = z(x),
соединяющих две данные точки Л и В и принадлежащих закрытой
области <о (at, y> z) ^- 0, определить ту, вдоль которой интеграл
/= f F(x,y,z,/, zr)
dx
Черт. 47.
принимает экстремальное
значение.
В соответствии с* разо-
разобранной выше простейшей
задачей допустим, что иско-
искомая кривая т существует, и
пусть
У=У(х), z = z{x)
есть ее уравнение. По усло-
условию задачи эта кривая должна
состоять из кусков, принадлежащих области <р > 0, и из кусков гра-
границы о = 0 (черт. 47). Мы будем предполагать, что каждая точка
кривой у, принадлежащая границе, есть правильная точка поверхно-
поверхности о = 0. т. е. что в этой точке
" У>0. A3)
Свойства экстремальной кривой. По аналогии с простейшей зада-
задачей мы будем искать основные необходимые условия, которым должны
удовлетворять части кривой -f, расположенные внутри области, на гра-
границе области, и, наконец, найдем условия, которым должна удовлетво-
удовлетворять ^ в точках, где она переходит из области ср > 0 на границу ср == О
и с границы о = 0 в область z> > 0.
В области 9 > 0 каждый кусок ^, принадлежащий области о> О,
должен быть куском экстремали для интеграла /, ибо в противном
случае можно было бы заменить этот кусок новой кривой, так чтобы
полученная после этой замены кривая "^ давала по нашему желанию
меньшее или большее значение интегралу /.
Если кривая Y принадлежит поверхности 9== 0 и является куском
кривой у9 то эта кривая дает, очевидно,' экстремальное значение инте-
интегралу /, если за класс допустимых линий принять кривые, принадле-
принадлежащие поверхности ср == 0 и соединяющие концы кривой Y* Следова-
Следовательно, кривая ^ есть экстремаль задачи на условный экстремум
интеграла / (условие 9 = 0).
Для того чтобы выявить еще одно свойство кривой -у', обратимся
к методу вариаций и допустим для определенности, что кривая Y дает
минимум интегралу /. В таком случае при всех достаточно малых допу-
§ 79] ПРОСТРАНСТВЕННАЯ ЗАДАЧА 245
стимых вариациях кривой -{' вариация интеграла J должна быть неотри-
неотрицательной. Рассмотрим вариацию J в какой-нибудь точке кривой Y-
В силу условий задачи эта вариация не может быть произвольной, ибо
проварьированная кривая должна принадлежать области <?!>0. Так как
на кривой Y ? = 0, то, следовательно, при бесконечно малых прира-
приращениях функций у и z9 соответственно равных Ьуу oz, приращение ?
должно быть неотрицательным; отсюда для того чтобы вариации оуу oz
кривой *{ были допустимыми, необходимо и достаточно, чтобы:
ду > i ду ^ ^ ~ /л л\
/ 0у -4- --- О2Г > 0. A4)
При всех возможных вариациях кривой /, удовлетворяющих A4),
мы должны иметь оУ^О. Вычисляя оУ в произвольной точке, будем
иметь:
где
/ оу dxy з.2 = I bz dx.
Интегрируя A4) в бесконечно малых пределах, найдем, что для допу
стимой вариации должны удовлетворяться условия:
Отсюда заключим, что в случае минимума в каждой граничной точке
должны иметь;
ду dz
Аналогично в случаях максимума в каждой граничной точке должны
иметь:
Р ?./г г -р _-JLf/
У dx У z dx "
ах ах 0
ду ду
ду dz
Наконец, пусть А1 есть точка, в которой кривая Т из области
?>0 попадает на поверхность ср = О; ^i — конечный кусок кривой 7,
принадлежащий области <?>0 и имеющий конец в точке Аг\ Та — КУ"
сок кривой y» принадлежащий поверхности ф== 0 и имеющий начало
в точке Av Возьмем на дуге ^2 точку Л2, бесконечно близкую к точке
Аи и заменим дугу, состоящую из fi и А{А2, дугой Y> соединяющей
начало дуги -^ с точкой А2 (дуга Y находится в близости первого
порядка от кривой Yi)- Вычислим вариацию интеграла J при указанной
вариации дуги ^1# Если через 8дг обозначить проекцию отрезка ААХ
на ось Одг, то, используя формулы § 57 и замечая, что интеграл J,
246
ОДНОСТОРОННИЕ ВАРИАЦИИ
[гл. XII
взятый по бесконечно малой дуге АгА2, равен подинтегральному выра-
выражению, умноженному на 8л;, получим:
87 = /у (/- (?
где х, у, z суть координаты точки Лх; у\ z' суть значения, принимае-
принимаемые .функциями У {х), zr (x) в точке Аи если двигаться по у2, и /,
z? — значения тех же функций в точке Аи если к этой точке подхо-
подходить по кривой у,
F=F(x,y, г, У, ?).
Так как рассмотренная вариация двусторонняя, то при экстремуме
должны иметь: - -г ,ч , „ ,-, /ч ,Лс\
Г Г = Гу'(у y)~T*z\\Z Z )• A")
Это уравнение удовлетворяется, если положить у' =.у\ zf — z\ т. е.
когда кривая f есть кривая с непрерывно вращающейся касательной.
Указанное решение един-
единственно, если поверхность
Z = F(x,y, z, X, У) A7)
в' пространстве (X, У, Z)
имеет всюду положительную
(отрицательную) гауссову
кривизну. Для доказатель-
доказательства достаточно заметить,
что уравнение A6) выра-
выражает геометрическое пересе-
Черт. 48. чение поверхности A7) с ее
касательной плоскостью.
Особый случай. Как мы увидим в теории достаточных условий
экстремума, случай, когда в точке Ах касательная к чг совпадает с каса-
касательной к у2, является наиболее важным и имеет место в большинстве
задач прикладного характера. В соответствии с этим случай, когда
точки Аг суть угловые точки искомой кривой, мы будем называть
особым.
В особом случае, как мы увидим ниже, для определения всех про-
произвольных постоянных в уравнении экстремалей данной задачи нам
необходимо еще одно условие в тех точках Av где особый случай
рассматривается. Искомое условие мы получим, рассматривая добавоч-
добавочную вариацию кривой у. Проведем на поверхности о = 0 кривую q,
проходящую через Лi и ортогональную к Т{ в этой точке (черт. 48).
Возьмем на кривой q точку Л/, бесконечно близкую к точке Аг\ заме-
заменим теперь дугу ^ дугой ?/> имеющей конец в точке Л/ и общее
начало с ^ и бесконечно близкой к 7* (близость первого порядка),
а дугу 1\ — дугой Г/ поверхности 9 = °» имеющей начало в точке Л/
и общий конец с 1\ и соответственно бесконечно близкой к дуге
1\ (близость первого порядка). Такая вариация кривой ^ есть, оче-
очевидно, двусторонняя, следовательно, соответствующая вариация инте-
интеграла должна равняться нулю.
§ 79] ПРОСТРАНСТВЕННАЯ ЗАДАЧА 247
Обозначим через 8^ и 82У вариации интеграла J соответственно при
замене у, на у/ и 1\ на Г/Г В силу формул § 57 (задач на экстремали
со свободными концами) имеем:
где од: есть проекция отрезка АгАгг на ось Ох,
есть уравнение кривой смещения q, уг и z' суть значения у' (х), zr (д;)
в точке Аг для ^:
V=- {/V (/ —У)+К' & —Ъ +^\ *х>
гДгУ, zr суть значения у (х), zr {х) в точке Аг для Fi? F = F{x> у, z,y, z'\
Отсюда окончательная вариация интеграла J будет:
-Г F,./ - F,^' + Ft'P - Ft.z'.
Условие экстремума:
оУ=0
или, принимая во внимание A6):
-У
Кроме того, так как величины 1, /, z'\ 1, У, ~zr пропорциональны
соответственно направляющим косинусам касательных к кривым Г и q,
а эти кривые принадлежат поверхности <р = 0, то в точке Л, имеем:
дх ' ду ^ [ dz l
«тсюда
dz ду
Нашему условию можно, таким образом, придать окончательно такой вид:
ду dz
Условие A8) будет, очевидно, выполнено, если касательные к кри-
кривым ^ и Г, в точке Аг совпадают.
Условия A5), A6), A8) можно получить, рассматривая общую ва-
вариацию кривой Т- Обратно, легко показать, что при соблюдении усло-
условий A5), A6), A8) при произвольной бесконечно малой вариации кри-
кривой f вариация интеграла / будет неотрицательна.
248 односторонние вариации [гл. XII
Мы приходим таким образом к следующей теореме:
ТЕОРЕМА. Если кривая у:
дает минимум интегралу
(х, У, 2, у, z')dx
среди кривых у=у(х), z = z(x), принадлежащих замкнутой области
? (х, У, z)^>0 и соединяющих две данные точки А и В, и таких,,
что у' и z' непрерывны, кроме, быть может, точек, где у переходит
из области на границу области ср = 0, то:
1. Куски кривой у, принадлежащие области <р > 0, суть экстремали
для интеграла J.
2. Куски кривой у, принадлежащие границе области, суть экстре-
экстремали задачи на условный экстремум J при условии у = 0; вдоль каж-
каждой экстремали имеем:
р d_F p d_F
3. В точках, где у переходит из области на границу, имеют
место соотношения:
F-F-Fy, (У-У) -Fz. (? — /) = 0,
ду dz
Если исключить особый случай, то условие 3 можно заменить условием;
3'. Кривая у обладает непрерывно вращающейся касательной.
Фактическое определение кривой. Покажем, что найденных усло-
условий достаточно, чтобы при наличии искомой кривой ее можно было
фактически определить.
Итак, допустим, что искомая кривая у существует и содержит п
кусков 1\, принадлежащих поверхности о = 0. В таком случае у будет
содержать п-{~1 кусков у4, принадлежащих области о > 0. Пусть теперь
г = 6 (л:, а19 а2, а8, а4) j
есть уравнение семейства экстремалей для интеграла J и
г^ЫхГаЫ ) B0/
есть уравнение семейства экстремалей для задачи на условный экстре-
экстремум интеграла J при условии ср = 0. В силу положений 1 и 2 теоремы.
все у,, принадлежат семейству A9), и все Г4 принадлежат семейству B0).
Таким образом для определения кривой у нам нужно найти А{п-\-\)
констант:
«Д »Д *Л •/*> (*=1,2,\..,„ + !)
§ 79] ПРОСТРАНСТВЕННАЯ ЗАДАЧА 249t
для определения кусков т,- и 2я констант
я„ Ьк («=1, 2, ..., я)
для определения кусков Г.. Четыре соотношения между констан-
константами мы получим из условия, что кривая х* проходит через даннук>
точку Л, а кривая Г4 — через точку В. Кроме того, в каждой точке
АгA=\, 2, ..., 2п) мы имеем в силу теоремы два соотношения, таким
образом получим еще An уравнений. Остальные 2/г уравнений мы полу-
получим из условия, что конец «^ совпадает с началом Г..
Обобщение задачи. Развитая теория нам позволит решить следующую
задачу, которая является естественным обобщением предыдущего при-
примера: среда всех кривых пространства (лг, у, z), соединяющих две
данные точки А и В и расположенных выше плоскости
определить кривую, скатываясь по которой (начальная скорость равна
нулю) тяжелая точка М придет из А в В в кратчайшее время.
Если считать, что ось О к направлена вертикально и начало коор-
координат находится в точке Л, то наша задача приводится к разысканию
кривой, минимизирующей интеграл *
т=
о
среди кривых, принадлежащих области:
— z-\-px~qy-\-a^>0 B1)
и соединяющих две данные точки @, 0, 0) и (хи yl9 z{).
Для упрощения выкладок примем, что ось Ох паралельна плоскости.
— z-\-px-\- qy-\-a — 0; в таком случае /7 = 0, и условие B1) примет
вид:
Найдем теперь семейство экстремалей для Т в области — z-\~qy-\-
0. В силу результатов, полученных в примере § 28, экстремалями
будут служить циклоиды, расположенные в вертикальных плоскостях»
Уравнение семейства будет:
)
= rsina (в — sin в) + С2, [ B3)
= r{\—cosb),
где г, Cv C2, a — произвольные постоянные.
Найдем семейство экстремалей для Т при условии
это будут, очевидно, также циклоиды, расположенные в плоскости Рш
определенной уравнением — z -j- qy -L a = 0, получаемые качением
250 односторонние вариации [гл. Xll
окружности по прямой, параллельной оси Ох. Уравнение семейства
этих экстремалей, выходящих из точки лгОэ yQi z0 плоскости Pxi
будет:
* = /?(» —sin 0)-f С,
B4)
z={R(l — cos ft) — qy0— a} sinp,
где tg p = ^, а /? и С произвольные постоянные.
Возможны два случая:
1. Через данную точку В возможно провести циклоиду семейства B3),
.принадлежащую области B2), не имеющую между рассматриваемыми
точками точки возврата.
2. Циклоида семейства, проходящая через точку В, пересекает
плоскость Р.
В первом случае искомая кривая будет циклоида семейства B4),
выходящая из начала координат и проходящая через точку В. Так как
искомая кривая выходит из начала координат, то СХ = С^=^0. Две
другие произвольные постоянные г, а определятся из условия прохо-
прохождения кривой через точку В,
Во втором случае искомая кривая будет состоять из трех дуг,
каждая из которых будет определяться своим уравнением. Первой дугой
будет кусок кривой семейства:
х=агг cos ax (9 — sin 6), ]
y = rlsin7.l (H — sin6).
z = r± A — cos 6.
B5)
Второй дугой] будет кусок кривой семейства] B5), и третьей дугой
•будет кусок кривой семейства B4).
Таким образом для определения искомой кривой нам нужно найти
восемь произвольных постоянных: rv ax для определения первой дуги;
R, С для определения второй второй дуги и г, а, Си С2 для опре-
определения третьей дуги. Эти произвольные постоянные определятся из
следующих соотношений. Условие, что третья дуга проходит через
точку В, дает два соотношения; условие, что три дуги образуют не-
непрерывную кривую, даст нам еще два соотношения; остальные четыре
соотношения мы получим из выведенного нами в общей теореме условия,
которому должна удовлетворять кривая при переходе из области на
границу облгти. В нашей задаче это условие соответствует тому, что
при переходе от первой дуги ко второй и от второй к третьей каса-
касательная изменяется непрерывно.
Построению искомой кривой можно придать геометрический характер.
Для этой цели двупараметрического семейства B5) выделим однопара-
метрическое семейство кривых, касательных к плоскости z = qy-{-a,
и обозначим через Q геометрическое место точек касания, Q есть,
очевидно, некоторая кривая на нашей плоскости. Аналогично выделим
яз семейства B3) однопараметрическое семейство кривых, проходящих
§ 79] ПРОСТРАНСТВЕННАЯ ЗАДАЧА 251
через точку В и касательных той же плоскости —z-\-qy-\-a = 0.
Пусть кривая Qx есть геометрическое место точек касания. Построим
в каждой точке Q и Qt единичные векторы q и qv совпадающие с каса-
касательным вектором к соответствующей кривой семейства B5) или B3).
После этих предварительных построений проведем кривую семейства B4),
соединяющую некоторую точку М кривой Q с некоторой точкой Mi
кривой Q так, чтобы вектора q и qv соответствующие точкам М и Mv
•были касательными к проведенной кривой. При этих построениях кривая,
составленная из кусков кривых семейств B5), B4) и B3), будет искомая
кривая.
Пользуясь приведенной геометрической интерпретацией, сравнительно
нетрудно показать, что 8 отмеченных выше произвольных постоянных
определяются единственным образом.
СЕМЕЙСТВО ЭКСТРЕМАЛЕЙ И ДОСТАТОЧНЫЕ
УСЛОВИЯ
ГЛАВА XIII
ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ
До сих пор мы в основном имели дело с индивидуальной экстре-
экстремалью. Сейчас мы перейдем к изучению семейств экстремалей. Изу-
Изучение семейств экстремалей исторически началось в связи с задачами
геометрической оптики (см. § 57, 76) и затем было перенесено Гамиль-
Гамильтоном на вариационные задачи более общего вида (преимущественно
в связи с исследованием уравнений механики). Якоби, с одной стороны,
связал нахождение общего интеграла уравнений Эйлера (общего семей-
семейства экстремалей) с решением определенных уравнений в частных про-
производных первого порядка, с другой стороны, показал, что вопрос
о достаточных условиях слабого экстремума связан с поведе-
поведением экстремалей, соседних с заданной. Наконец, Вейерштрасс, изучая
теорию поля экстремалей, нашел достаточные условия для силь-
сильного экстремума. Таким образом полное решение вопроса о том,
дает ли данная экстремаль минимум или максимум, было дано только
на основе изучения семейств экстремалей, включающих данную.
Теория семейств экстремалей распадается на две части. Предмето\1
первой части является изучение бесконечно тонких пучков экстремалей
или семейств экстремалей, близких к данной. Эта теория возникла
в связи с теорией слабого экстремума. Теория слабого экстремума
более просто получается из рассмотрений, возникших в теории сильного
экстремума. Однако это не уменьшает математического значения этой
теории; она связана с изучением квадратических функционалов (второй
вариации), играющих фундаментальную роль в разных главах мате-
математики. Вторая часть занимается исследованием семейств экстремалей „im
grossen", т. е. не только в s-близости данной экстремали. Эти иссле-
исследования привели к созданию своеобразной геометрии, где роль прямых
играют экстремали. Помимо своего основного значения для вариационного
исчисления эта теория имеет и самостоятельный геометрический интерес.
В гл. XIII изучаются бесконечно тонкие пучки экстремалей и связан-
связанные с ними квадратические функционалы. Эта глава излагается теоре-
теоретико-функциональным методом. Гл. XIV в связи с ее геометризирован-
ным содержанием излагается геометрическими методами.
§ 80. Предварительные замечания.
Исследование поведения функции в окрестности стационарной точки
приводит к рассмотрению квадратических форм, именно второго дифе-
ренциала. Исследование поведения функционала в окрестности экстре-
экстремали приводит к исследованию второй вариации. Мы остановимся на
этом исследовании довольно подробно, так как вторая вариация есть
^ 80] ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 253
простейший вид квадратического фунционала, теория же квадратических
функционалов играет существеннейшую роль в самых различных главах
анализа.
Методы, выработанные при исследовании квадратических форм, пере-
переносятся в значительной степени на вариационное исчисление, а связан-
связанные с ними экстремальные задачи переходят в вариационные задачи.
Система линейных (вековых) уравнений § 25 превращается при этом
в линейное диференциальное уравнение, так называемое уравнение
Штурма-Лиувилля, играющее фундаментальную роль в математической
физике. Теория собственных значений квадратической формы перейдет
в теорию собственных значений квадратического функционала. Подобно
тому, как поведение функции в окрестности стационарной точки опре-
определялось знаками собственных значений второго диференциала, поведе-
поведение функционала в окрестности экстремали определяется знаками соб-
собственных значений второй вариации.
Мы в настоящей главе ограничиваемся почти исключительно анали-
аналитическими исследованиями, относя топологические проблемы во второй
том. Там же будет излагаться теория квадратических функционалов более
юбщего вида.
Непосредственный переход от квадратических форм конечного числа
•переменных ко второй вариации мы даем в § 80 при исследовании
существования абсолютного минимума квадратических функционалов,
а также в § 90, где квадратический функционал исследуемого нами
типа трактуется как предел квадратической формы.
Уже в § 52 мы видели, что поведение функционала
г (*> у, у') dx
зависит от характера второй вариации, т. е. от квадратического функцио-
функционала вида:
X,
где
у у'
Необходимым условием неотрицательности такого функционала было
выполнение условия Лежандра:
-Мы сейчас займемся более детально исследованием квадратических
функционалов вида:
<b№ = f {P*? + &l'*)dx9 A)
254 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. ХИГ
причем во всем дальнейшем будем полагать:
/?>0 при я<х<?, B)
т. е. будем считать, что выполняется усиленное условие Лежандра.
Кроме того, мы будем предполагать, что Р = Р{х) и /? = /?(х) суть
функции от х класса Cv
В гл. IV мы видели, что исследование квадратических форм тесно
переплетается с изучением некоторых линейных уравнений (связанных
с вековым определителем). Исследование функционала A) связано с ли-
линейными диференциальными уравнениями, так называемыми уравнениями
Штурма-Лиувилля, играющими фундаментальную роль в математиче-
математической физике.
Пространство R. Рассмотрим пространство R функций у (х), удовле-
удовлетворяющих следующим условиям:
1°. Функции у(х) определены на отрезке а^х^Ь и принадлежат
классу d *)•
2°. Для каждой функции у (х) пространства R имеем
Сфера S- Рассмотрим на R квадратическое многообразие S — сово-
совокупность функции, удовлетворяющих условию:
J'y*dx=l. C)
a
Это многообразие функций у=у(х) мы будем называть сферой.
Определим теперь квадратический функционал Jab формулой:
ь
dx, D)
где Р = Р(х)9 R = R(x) — функции класса С1?
/?(*)> О (я <*<?). E)
Из условий C) и E) легко получается, что на сфере S форма Jab
ограничена снизу. В самом деле, обозначая через т минимум Р при
а ^С х ^ Ь> получим:
Jab(y)>
§ 81. Существование минимума квадратических функционалов
Обозначим через с нижнюю границу значений Jab для функций
сферы S. Докажем, что существует функция у(х) на S, для которой
Jab(y) — c. Начнем с вывода трех предварительных лемм.
г) Наши дальнейшие рассуждения останутся верными, если мы расширим
пространство R, считая, что входящие в него функции у (х), принадлежат
классу Dx (т. е. допускают конечное число точек перелома).
§ 81] СУЩЕСТВОВАНИЕ МИНИМУМА КВАДРАТИЧЕСКИХ ФУНКЦИОНАЛОВ 255-
ЛЕММА I. Пусть нам даны лг —|— 1 чисел:
Уо> У и У» •> Уп
таких, что
где К-—положительное число; тогда
(/=1, 2,..., я
s — r
t — s
К
t—r
л). (8)
В самом деле, просуммируем неравенство G) сначала по / в пре-
пределах от /=/-[- 1 до l==s—1, очевидно, получим:
-Ы). (9)
Суммируя в свою очередь неравенство (9) по j от у = г до j = s—1,
получим:
м ^ is (s —r—l)(s —г)
или
<К
Вполне аналогично получается неравенство:
—
t —
— (V
)
A0)
A1)
Складывая неравенства A0) и A1), окончательно получим (8).
ЛЕММА 2. Если непрерывная в интервале [а, Ь) функция f(x) для
любой тройки чисел хи х2, х3 (а <; х1 < х2 < х3 <; Ь) удовлетворяет
неравенству:
Х2 — Х1
<К
A2)
где К есть константа, то ее производная f(x) существует и притом
непрерывна на сегменте а^х^Ь.
Допустим противное, что в некоторой точке х0 производная или
не существует или разрывна; в таком случае существует число р > 0
такое, что в любой окрестности точки х0: \х — л;0|</г можно найти
две пары точек хх<^х^ и х/ < х2г таких, что:
>?¦
Определим число хй из условия
— х
0
и выберем h настолько малым, чтобы при \х — хо|<Л имели:
I г Хл I о
A20
A3)
A4)
256 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ
и согласно условию леммы
/( /С*з)--Я*о)| ^ Р
х3 - хп | ^ 6 "
— х
[ГЛ. XIII
/15ч
Применим теперь неравенство A2) сначала к числам xv x2t х3, а затем
к числам дг/, х2', х/. Принимая во внимание A3), A4) и A5) получим:
j / (лг2) — f (х-^) f (x3) — / (Xq)
х0
Складывая эти неравенства, получим:
что невозможно в силу A2').
Существование минимума формы J. Проведем доказательство суще-
существования кривой, реализующей минимум формы /:
ъ
J
на сфере S:
:== 1
прямым методом.
Рассмотрим квадратическую форму п переменных:
п — 1
где
х{ = a -j- /Дат, &х =
— a
n)
Обозначим через J$n) абсолютный минимум этой формы на сфере S(n):
^2Дх= 1. «^егко видеть, что Jq71) будет совпадать с абсолютным
минимумом формы -уТ /п) при условии 2 У? = 1.
ЛЕММА 3. Обозначая через /0 абсолютный минимум Jah на S,
liminf/0(n)</0.
(n)
A6)
В самом деле, при произвольном е > 0 на S существует функция
() такая, что
Так как у (а) — у (д) = 0 и функция J'(jc) принадлежит к классу С2, то
при достаточно большом //можно ааппроксимировать (в смысле'близости
§ 81] СУЩЕСТВОВАНИЕ МИНИМУМА КВАДРАТИЧЕСКИХ ФУНКЦИОНАЛОВ 257
первого порядка) кривую у=у(х) таким полигоном с вершинами
If..., п — 1, уо=уп = О, Aat = —^-, что:
Л. ..- Vn_t)-3, A7)
Обозначая j;4 == .^ - ¦, получим:
п—1
2й2Д*=1. B0)
г = 1
Из B0) следует:
Сопоставляя A6), A7), A9) и B1), получим:
Л> Jab00 -«> J™CVp Л' • • •. Л-i) - 2г =
Я> Л- • • -. *„_,)- 2.] >т^ [/о(П)- 2.] .
При и -»• оо предыдущее неравенство переходит в неравенство:
m inf /0(n) — 2з] .
П->ОО J
Вследствие произвольной малости г и т) получаем:
/0>liminf/0(n).
п -> оо
Отсюда заключаем, что существует такая последовательность чисел
пи п21 ..., пк, ..., что lim inf Jo k существует и не больше Jo:
щ ->оо
lira inf У0(П*} < 70 i).
П^. -> ОО
Так как/о равно наименьшему собственному значению формы — /п^:
/W у (п)
Jo — Ло »
то для рассматриваемой подпоследовательности чисел п мы можем счи-
считать, что Х0(п)- ограничены снизу и сверху.
Условимся изображать совокупность чисел yv yv ..., уп__1 в виде
полигона Пп, /-я вершина которого имеет координаты (#-|-/Длг, уг).
х) В дальнейших рассмотрениях форм /п) мы будем считать, что п равно
одному из чисел яА(& = 1, 2, 3,...)-
258 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Форма /w) будет функцией полигона Ип. Применяя метод Эйлера, для
полигона Ип(х), реализующего минимум /п\ будем иметь:
Заменяя в фигурной скобке R(xt) по формуле Лагранжа:
/? (*,.) = R {xt _ х) + Д* R' (U) (х4 _ 1 < tt < xf),
полученному уравнению можно придать вид:
Пусть
я — тлях
О Шал
Из B17) получим:
, JL • ¦
max R' (х)
Лдг
с. B2)
Просуммировав B2) по / в пределах от i=j до i=*s, получим:
Ах
Длг
Дд:. B3)
Последнее неравенство можно преобразовать; во-первых, в силу нера-
неравенства Шварца имеем:
21л IД*
или, так как
-а. B4)
Далее, в силу леммы 3 при достаточно большом п имеем для минималь-
минимального полигона Ип:
B5)
откуда
где
Неравенство Шварца, примененное к B5), дает нам:
А
Ах
B6)
§ 81] СУЩЕСТВОВАНИЕ МИНИМУМА КВАДРАТИЧЕСКИХ ФУНКЦИОНАЛОВ
259
Из B3), B4) и B6) мы имеем для любых /, s:
S+TA
Ах
Ах
B7)
Но так как уо—уп = Оу то отношение s ""*".- принимает при
s = 1, 2, ..., п— 1 по крайней мере один раз отрицательное значение
и один раз положительное *); следовательно, получаем из B7):
Ах
S+TA
У'Ь — а
= сх = const.
B8)
Суммируя B8) по j от j = 0 до j =
получим:
12
<; п — 1 и замечая, что у0 = О,
Сг(Ь — а). . B9)
Подставляя B8) и B9) в B2), найдем:
\ (Ь — а) -\- ТСХ = С2 = const.
Ах2
Применяя к последнему неравенству лемму 1, получим:
у s—
Уг—У*
(s — г) Ах (t — s) Ax
<СЧ
Ах.
C0)
Таким образом для всякого минимального полигона выбранной последо-
последовательности мы имеем неравенства B8), B9), C0).
Из условий B8) и B9) заключаем, что последовательность:
П (х\ П (х) Л (х} C1Л
удовлетворяет условиям теоремы Гильберта о компактности семейства
функций (§ 45). Согласно этой теореме мы выделяем из последователь-
последовательности C1) равномерно сходящуюся подпоследовательность:
Пусть у=уо\х) есть предел этой подпоследовательности:
Построенная функция обращается в нуль в концах интервала (а, Ь\
непрерывна, и, кроме того, в силу C0) для любой тройки чисел
*i < Х2 < хз имеем:
Уо(Ч)—Уо(ч)
C2)
Все j/, нулями быть не могут, ибо ЪурАх = 1.
260 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ.'ХШ
т. е. в силу леммы 2 у0 (х) обладает непрерывной производной. Из
равномерной сходимости ПA), ПB), ..., П(п), ... следует также, что
Ь п
= lim
а
т. е. что построенная функция принадлежит сфере S- Нам остается
доказать, что
Для этой цели рассмотрим последовательность ступенчатых функций:
где
П{п)(хк . «) — n(nW
+^^ ^<^<JPfc + A* = ^+1. C3)
Пользуясь C0), нетрудно доказать, что последовательность C3) равно-
равномерно стремится к уо' (х). Отсюда:
ь
lim J (П(п)) = f (Py<? + tfy0'2) Лс =
П->оо в/
Так как в силу леммы 3 lim (/П(п)) = /0, то
Теорема полностью доказана.
§ 82. Уравнение Штурма-Лиувилля
Вывод уравнения Штурма-Лиувилля. Так как по доказанному абсо-
абсолютный минимум формы
ъ
а
при условии ь
достигается на кривой у =уо(х) класса Сх и так как все точки сферы S
ъ
правильны: 8 /y2dx =J= 0 для каждой функции у(х) сферы S, то кривую
а
У=Уо(х) можно определить методом Эйлера; для этой кривой имеем:
ь
где X — множитель Эйлера. Применяя уравнение Эйлера, получим:
*.y = 0. C4)
§ 82] УРАВНЕНИЕ ШТУРМА-ЛИУВИЛЛЯ 261
Для сокращения письма будем обозначать в дальнейшем через [у]
следующий оператор: .
Уравнение C4) называется уравнением Штурма-Лиувилля, При этом
обозначении уравнение C4) можно записать в виде:
Кроме того, что искомая функция у0 (х) должна удовлетворять урав-
уравнению C4), она должна удовлетворять условию:
ъ
fyo2(x)dx=l C5)
а
и условиям на концах:
У(Ь) = О. C6)
Собственные значения. Если отказаться от условия C5), то урав-
уравнение C4) при условиях C6) имеет при любом значении X, веществен-
вещественном или комплексном, решение: у==0. Это решение называется три-
тривиальным решением уравнения Штурма-Лиувилля.
При некоторых значениях X уравнение Штурма-Лиувилля может иметь
нетривиальные решения, удовлетворяющие начальным условиям C6).
Такие значения \ называются собственными значениями формы Jab.
Так как построенная выше функция Уо^хI) должна удовлетворять
при некотором значении к уравнению C4), то отсюда заключаем, что
у формы Jab при R > О собственное значение всегда существует.
Пример. Пусть ъ
а
где ?i>0 (с, С} — константы). Уравнение Штурма-Лиувилля примет вид:
~У = Ъ- C7)
Отсюда:
где
/n2 = -Azi?.. C8)
Условия на границах дают пару однородных уравнений относительно At и Л2:
Ахета + А2е~та = 0, АгетЬ + А2е~ тЬ = 0. C9)
Для того чтобы система C9) имела нетривиальное решение, необходимо
и достаточно, чтобы определитель ее равнялся нулю:
Следовательно: т(а — b) = nni, где i = У — 1, где п — произвольное целое
число. Из C8) получаем:
То-есть функция, реализующая абсолютный минимум Jab на S.
262 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Решение уравнения C7) при условии C6) можно задать в форме:
^=^-, D1)
где К— произвольное постоянное. При п целом, не равном нулю, получаем
нетривиальное решение.
Итак, собственные значения нашей формы будут все числа вида:
Собственные функции. Всякое нетривиальное решение уравнения
Штурма-Лиувилля . ,
при у (а) =у (Ь) = 0, отвечающее собственному значению X, называется
собственной функцией. Собственная функция у (х) называется нормиро-
нормированной, если ъ
/
a
у2 (x)dx— 1.
Для предыдущего примера функции D1) будут собственными функциями.
Основные свойства собственных значений и собственных функций.
Отправляясь о г того, что для уравнения Штурма-Лиувилля, при /? > О,
собственные значения и собственные функции существуют, установим
ряд важнейших свойств этих функций.
1°. Если у{х) собственная функция формы Jal9 то
В самом деле, так как уравнение Штурма-Лиувилля есть уравнение
второго порядка и коэфициент при у" отличен от нуля, то условиями
у (а) —0, у'(а) = 0 или y(b)=Qy у/ (Ь) = О интеграл определяется
единственным образом. Но этим же начальным условиям удовлетворяет
тривиальное решение у~0, следовательно, предполагая, что для соб-
собственной функции у=у(х), у(а) = 0 и у' (а) = 0, мы получаем, что
она — тождественный нуль, что противоречит определению.
2°. Если ух (х) и у>(х) суть собственные функции, отвечающие одному
и тому же собственному значению, то их линейная комбинация
где с1 и с2 — константы, есть или собственная функция или тривиальное
решение.
В самом деле, в силу свойств однородных линейных уравнений
у(х) есть интеграл уравнения C4), кроме того,
Итак, если у (х) Ф 0, то она есть собственная функция.
3°. Если у1(х) и у2(х) суть собственные функции формы Jab, отве-
отвечающие одному и тому же собственному значению, то ух и у2 линейно
зависимы, причем:
У (*) = У2 (х) / (fl) —Ух W/a (?) = 0.
§ 82] УРАВНЕНИЕ ШТУРМА-ЛИУВИЛЛЯ 263
В самом деле, в силу свойства 2° у(х) есть или собственная функ-
функция или тождественный нуль. Диференцируя у(х), получим у/ (я) = 0,
следовательно, в силу 1° у = 0.
Обратим внимание на следующие равенства:
ъ ъ
Jai = / (РУ2 + Я/2) dx = у [у] у dx. D2)
О
Это равенство получается интегрированием по частям выражения
ь
I Ry'2 dx и использованием условий: у(а)=у(Ь) — 0. Аналогично:
а Ь а Ъ
Кь 0% *) = / (Ру* + Я/*') dz = У' [jf] zdx = f[z]y dx. D3)
Теперь докажем следующее свойство:
4°. Если Хх и Х2 — два различных собственных значения формы Jah,
а у±{х) и у2(х) — соответствующие собственные функции, то функ-
функции ух (х) и у2 (х) ортогональны:
ь
J y1y2dx=0.
а
В самом деле, имеем:
Умножив обе части верхнего уравнения на у2 (лг), а нижнего на уг (х),
проинтегрировав в пределах от а до b и вычтя почленно полученные
результаты, мы в силу равенства D3) получим:
ъ
(Хх — Х2) / у1у2 dx = 0;
а
так как Хх ф Х2, то, следовательно,
ъ
г
а
5°. Все собственные значения формы Jab вещественны.
Пусть X есть комплексное собственное значение формы Jab,y(x) —
соответствующая собственная функция. Обозначая через к и у{х)
величины, им сопряженные, мы из уравнения
[у] = Ху
получим: г—, --
J [у] = Лу,
т. е. к есть тоже собственное значение формы Jabt а у — соответству-
соответствующая собственная функция. Но в силу свойства 4° при X ф X имеем:
ь ъ
yydx= J
264 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Последнее равенство возможно, только если \у\ тождественно равно
нулю, что противоречит нашим предположениям. Итак, Х = Х, т. е. X
есть число вещественное.
6°. Если X есть собственное значение формы Jab, а у(х)— соответ-
соответственная нормированная собственная функция, то
В самом деле,
Отсюда в силу формулы D2) имеем:
ъ
ъ
7°. Если у (х) есть собственная функция формы Jab, а у1 (х) — орто-
ортогональная к у (х) функция, то Jab (уу уг) = 0.
В самом деле, умножая обе части равенства D4) на^, после инте-
интеграции в силу равенства D3) получим:
ъ ъ
\У] Vtdx=
а а
8°. Если Хо [есть минимум формы JаЪ на S, то Хо есть наименьшее
из собственных значений формы Jab.
В самом деле, обозначим через уо(х) функцию, реализующую мини-
минимум Jab на S; имеем:
Jab CVo) = К
Эта функция удовлетворяет уравнению Штурма-Лиувилля. Пусть У —
соответственное собственное значение. В силу свойства 6° У = Хо. Пусть
теперь Хх — другое собственное значение с соответственной нормиро-
мнной функцией Ух(х). Имеем: Jab(yi)z=\v Но так как Хо реализует
минимум формы Jab, то Хо <^ Jab (ух) = Хх или, считая Хх ф Хо, Хх > Хо.
§ 83. Условия положительности формы
Если наименьшее собственное значение Хо формы Jab положительно,
то форма Jab существенно положительна; если Хо —0, то форма Jab
неотрицательна; при Хо < 0 форма может принимать и отрицательные
значения (см. § 82, 8°). Поэтому исследования положительности формы Jab
сводятся к изучению знака Хо. Пусть мы имеем две формы:
ъ
а
Ь
а
Если для любого х (a^x^b): R*^>RV P^PV то для любой
§ 83] УСЛОВИЯ ПОЛОЖИТЕЛЬНОСТИ ФОРМЫ 265'
функции у(х), Jai^-Jab* Следовательно, минимум Jab на S во всяком
случае не меньше, чем минимум Jab на той же сфере. Обозначив
через Хо и Хо' наименьшие собственные значения обеих форм, имеем:
^o^V- Отсюда следует свойство:
9°. Наименьшее собственное значение Хо формы
ь
Къ = / (Я/2 + РУ*) dx {R > 0)
а
удовлетворяет неравенству:
где положительное число сг есть минимум R(x) на отрезке (a, b), a
с — минимум Р(х) на этом же отрезке. Рассмотрим форму
ь
исследованную в примере § 81. |Пусть Хо' — наименьшее собственное
значение формы Уа&; в силу сделанного выше замечания *ко^ко' (так
как /?(лг)>^, Я(х)>с).
В силу D0) § 81 все собственные значения формы Jab имеют вид;
(я=1, 2, ...);
наименьшее из них (при п=1) равно:
Ао — {b
о {b^af
Отсюда, так как Хо ^> \0', окончательно получаем:
ъ
Будем теперь считать верхний предел b в интеграле Jab и I y2dx
а
переменным. Наименьшее собственное значение формы Jab станет функ-
функцией от Ь: Х0 = Х0(?). b мы считаем все время большим, чем а.
10°. При ЬХ>Ь, ХоF,)<Хо(*).
В самом деле, X0(^j) есть минимум
при условиях
Ь1) = 0, jy*dx=l, D5)
266 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
есть минимум ^
при условиях
Мы можем сказать: Хо(?) есть минимум Jabl при условиях D5) и до-
дополнительном условии: у = О при b <! х ^ bv
Таким образом Хо(?) определяется как минимум той же формы Jabl,
но при одном дополнительном условии, сравнительно с условиями, опре-
определяющими Хо (Ьг). Но при дополнительных ограничениях на класс функ-
функций сравнения минимум может только возрасти: Хо(&) ^-Хо(^1).
Покажем, что равенство Хо(?) —Хо(?]) невозможно. В самом деле,
пусть функция у0 (х) реализует минимум Jab при отмеченных выше усло-
условиях. Если бы мы имели равенство Хо(^) = Хо(^1), то функция уо(х), рав-
равная уо(х) на отрезке [а, Ь] и равная нулю на отрезке [b, ?J, реали-
реализовала бы минимум Jah при соответственных условиях, т. е. была бы
одной из собственных функций формы Jab\ что невозможно в силу
свойства 3°. Получаем теорему:
ТЕОРЕМА. Собственное значение Хо (Ь) есть монотонно убывающая
функция от Ь.
11°. При Ь, достаточно близком к а, Х0(?)>0.
В самом деле, обозначим через с(Ь) и сх(р) минимумы соответ-
соответственно функций R(x) и Р(х) на отрезке [а, Ь]. Так как /?(.*;)> О,
то с ^> 0. Если Ь, оставаясь больше а, убывает, минимумы с{р) и c1{U)
могут только возрасти. В силу свойства 9°:
С (Ь) п2
Положительный член __ ¦ при приближении b к а неограниченно
возрастает; сх (Ь) не убывает. Следовательно, Хо(?) неограниченно
возрастает, если Ь, убывая, стремится к a: iim ho(b) = -j-oo; во вся-
Ь •> а
ком случае при Ь, достаточно близком к а, Х0(?)>0.
С возрастанием Ь, Хо(?) убывает. При этом могут быть два случая:
1) Хо (Ь) все время остается положительным. В этом случае форма Jab
для любого b существенно положительна.
2) Хо(?) обращается в нуль при Ь= Ьо: Хо(^о) = 0. В этом случае
форма Jnb существенно положительна при а < b < b0. При b> b0 суще-
существует функция у(х), принадлежащая R, для которой Jab [у (лг)] < 0.
Отсюда вытекает следующее свойство.
12°. Для положительности Jab необходимо и достаточно, чтобы
на закрытом справа интервале [а, Ь] не заключалось решений урав-
уравнения Хо {х) = 0.
13°. Для неотрицательности формы Jai необходимо, чтобы на открытом
интервале (а, Ь) не заключалось корней уравнения Хо (д;) = 0.
§ 83] УСЛОВИЯ ПОЛОЖИТЕЛЬНОСТИ ФОРМЫ 267
14°. Если Jab есть положительно определенная форма, то длялюбой
функции у {х) из R удовлетворяются три неравенства:
ъ
^ь ОО > К (Р) f у* dx [Хо (Ь) > 0]; D5')
a
Ъ
ь (У) > Ц~ ff dx + 4- /У» dx. D7)
D6)
a
где d—некоторая абсолютная положительная константа;
ь ь
а а
Неравенство D7) есть следствие неравенств D5Г) и D6).
ъ
Докажем неравенство D5'). Если / y^dx=l, то неравенство
Ъ
очевидно, удовлетворяется. Если / y2dx = k? ^0, то
а
откуда также следует неравенство D5').
Докажем неравенство D6). Имеем:
ъ ъ
Jab (У) > с/ У2 dx -f с, f /* dx/ D8)
а а
где с и сг > 0 суть минимумы функций Р(х) и R (к) на отрезке (а, Ь).
Если с = 0, достаточно положить d = cv Пусть с =jfc 0. Рассмотрим два
возможных случая:
ъ ь
1. |с| / ^2^лг^-^- / У2^д;; тогда из D8) следует:
D9)
2- \с I / У2 dx > -f~ /У2 ^ TOr^a из D50 получаем:
а а
? Ь
Jab (У) > h (*) У'^2 ^ > -#fif / У2 ^ • E0)
Полагая d равным меньшему из чисел — и -^ , , , мы из D9)
м E0) получаем D6). 2 |??|
268 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Условие Якоби. Уравнение [у] = 0 есть частный случай уравнения
Штурма-Лиувилля [у] — \у при X = 0. Оно называется уравнением
Якоби.
Пусть, для некоторого Ъ > а, Хо (Ь) = 0. Обозначим через у0 (х)
функцию, реализующую минимум Jal при условиях:
уо(х) есть собственная функция формы Jab, отвечающая собственному
значению Хо (Ь) = 0, следовательно, у0 (х) есть нетривиальное решение
уравнения Якоби [у] = 0, пересекающее ось Ох в точках х = а, х= Ь.
15°. b есть первая после а точка пересечения интегральной кривой
уравнения [у] = 0 (у (а) = 0) с осью Ох.
В самом деле, если для некоторого b' {a < br < Ь) интегральная
кривая уравнения Якоби пересекает ось Ох в точке х = Ь', то форма
Jab' имеет в числе своих собственных значений значение нуль. ИоХ0(У)
есть наименьшее собственное значение Jabr. Следовательно, Хо (У) <; 0;
с другой стороны, так как Ь' < Ь, то Хо (У) > Хо (Ь) = 0. Наша гипо-
гипотеза ведет к противоречию.
Обратно, пусть у=у(х) есть интегральная кривая уравнения Якоби,
пересекающая в точке х = а ось Ох, и пусть b есть ближайшая к а
точка пересечения кривой у=у(х) с осью Ох; покажем, что при bx<^b
имеем Хо (Ьг) > 0.
В самом деле, допустим противное, что существует bt < b, для
которого Х0(^1)<^0; тогда в силу свойств 10°, 11° существует b2<ib,
при котором Х0(?2) = 0. Но в таком случае существует нетривиальный
интеграл у=у1 (х) уравнения Якоби, обращающийся в нуль при х = а
и х=Ь2. Функции у (л;) и уг(х) суть интегральные кривые уравнения
второго порядка, обращающиеся в нуль при х=а. В силу рассужде-
рассуждения предыдущего параграфа (свойства 1° и 2°) у(х) = су1(х); в част-
частности у (Ь2) = су1 (?2) = 0, что противоречит основному условию.
Сопряженные значения. Значения х, в которых нетривиальная инте-
интегральная кривая у = у(х) уравнения Якоби [У| = 0, у(а) = 0 пересе-
пересекает ось Ох, называются сопряженными с а. Очевидно, если а сопря-
сопряжено с Ь, то b тоже сопряжено с а.
Проведенный выше анализ нам дает:
16°. Корень уравнения Х0(?) = 0, ?> а, дает ближайшее к а
(справа) сопряженное к а значение.
В соответствии с этим свойства 12°, 13° можно формулировать сле-
следующим образом:
17°. Для того чтобы Jab была положительно-определенной формой,
необходимо и достаточно, чтобы в закрытом справа интервале {а, Ь)
не заключалось сопряженных с а значений.
18°. Для того чтобы Jab была неотрицательной формой, необходимо
и достаточно, чтобы в открытом интервале (а, Ь) не заключалось сопря-
сопряженных с а значений.
§ 84] СЛАБЫЙ ЭКСТРЕМУМ 269
§ 84. Слабый экстремум
Необходимые и достаточные условия слабого экстремума. Полу-
Полученные нами выше критерии положительности квадратической формы
позволяют нам сейчас дать весьма близкие между собой необходимые
и достаточные условия того, что данная экстремаль дает слабый мини-
минимум (условия Якоби).
ТЕОРЕМА 1. Если экстремаль y:
дает минимум интегралу:
J=J9F(x, у, /)dx
а
и если вдоль y
то открытый интервал (а, Ь) не содержит значений, сопряжен-
сопряженных с а.
В самом деле, мы видели (см. § 49), что необходимым условием
слабого минимума является неотрицательность второй вариации. Но если
интервал (а, Ь) содержит значение, сопряженное с а, вторая вариация
перестает быть неотрицательным квадратическим функционалом; необ-
необходимое условие минимума не выполняется. Теорема 1 доказана.
ТЕОРЕМА 2. Если экстремаль у.у=у(х) интеграла J соединяет
точки А {а, аг) и В (#, Ь^) и удовлетворяет условиям: 1) F , , > О
вдоль y, 2) закрытый справа интервал [а, Ь] не содержит значения,
сопряженного к а, то экстремаль y среди кривых, соединяющих
точки Л и В, дает интегралу J слабый минимум.
Для доказательства теоремы 2 воспользуемся свойством 14° квадра-
тических функционалов: если вторая вариация есть существенно поло-
положительная форма, то существуют две положительные константы d и dt
такие, что для любой допустимой вариации Ьу имеем:
ь ь
E1)
С другой стороны, обозначая через е наибольший из максимумов Ьу
и Ъу' на интервале (а, Ь), имеем из рассмотрений § 49:
ь
—J (У) = &J + /' (%2 + Лгё/*) **> E10
где L и М равномерно стремятся к нулю вместе с з.
Выбрав е настолько малым, чтобы L и М были на всем интер-
интервале {а, Ь) меньше -^- и -~- одновременно, мы для любой функции
из класса допустимых, лежащей в е-окрестности y, имеем:
Последнее неравенство есть следствие неравенства E1), E1') и на-
нашего выбора е. Функция у (х) реализует слабый минимум.
270 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Выполнение условий теоремы 2 гарантирует положительную опре-
определенность формы 62J и реализацию слабого минимума.
Теорема полностью доказана.
Как мы видели выше, при определении достаточных условий слабого
экстремума основную роль сыграло понятие сопряженной точки. Это же
понятие будет играть главную роль в теории поля экстремалей. Мы
сейчас покажем, что сопряженную точку можно определить, рассма-
рассматривая пучок экстремалей, выходящих из начальной точки; именно такое
определение сопряженной точки нам будет важно в теории поля.
Остановимся предварительно на некоторых вопросах теории дифе-
диференциальных уравнений.
§ 85. Уравнение в вариациях
Некоторые свойства диференциальных уравнений. Пусть нам дано
диференциальное уравнение л-го порядка
F(x, у,/,...,у™) = 0. E2)
Относительно функции' F мы будем предполагать, что она в области
ее задания обладает непрерывными частными производными по всем
аргументам х, у, у', ...,УП). Из общей теории диференциальных ура-
уравнений известно, что если точка (д:0, yQy y0/t ..., у0 ) принадлежит об-
области задания функции F, т. е. если F(x0, у0, уо\ ..., у0^) = 0 и если
в этой точке F лп) Ф ^> т0 ПРИ достаточно малом h > 0 существует
интегральная кривая т уравнения E2): у = у(х) (xQ <C x <^ xQ -f- h),
удовлетворяющая начальным условиям:
У(*о)=.Уо. /(*Ь)=Л'. ••..У-1)(*Ь) = Л("~1)- E3)
Если при этом вдоль кривой 7 имеем:
/у*> + о,
то всегда можно найти такое число р, что при чюбых^е, 8j/o,rJ>yor, ...
•••> ^Vo(W)> f(x)f удовлетворяющих неравенствам
1«1<Р. l^ol<«. 8yo'l<e, ...,|Wn)l<', 1№\<*>
где f(x) определена и непрерывна при xQ^x^xo-\-k, существует
инт егральная кривая f\' У = У 0*0 = У (х) 4~ ty (х) (аг0 <^ х -*С xq H~ К)
уравнения F=f(x)9 удовлетворяющая измененным начальным условиям:
у(х0) =.уо+ 8у0, / (дг0) =
ТЕОРЕМА ПУАНКАРЕ. Если в бесконечно мало, то кривая fi
находится в е/-близости /г-го порядка от кривой 7, где е' — беско-
бесконечно малая порядка е.
§ 85] УРАВНЕНИЕ В ВАРИАЦИЯ^ 271
Уравнения в вариациях. Принимая отмеченные свойства диферен-
циальных уравнений, поставим задачу определить с точностью до бес-
бесконечно малых высших порядков вариацию Ьу(х), предполагая основную
кривую у = у[х) известной. Имеем>
F(х, у + Ьу, / + 8/, ..., У™ + ЗУП)) =/(*). E4)
В силу теоремы Пуанкаре при е бесконечно малом все Ьу® суть
бесконечно малые порядка не ниже первого, отсюда, принимая во вни-
внимание, что F [х, у (х), .. ., у{п) (х)] = 0, получим:
/у\У + W/ + • • • + ^ (»)8УП) -Я*) + ч (л:), E4')
где т] (л;) есть остаточный член разложения F в ряд Тейлора, следова-
следовательно, на интервале х0 <С х ^ лг0 -J- Л максимум |т)(л:)| есть бесконечно
малая порядка выше первого [у\(х) зависит от Ьу®]. Значения частных
производных берутся здесь, очевидно, by®=O(i = o, 1, ..., п), так
что все коэфициенты при Ьу® суть определенные функции от х\ Ьу(х)
есть искомая вариация интеграла у(х), a 8yw^ = —^- Ьу.
Итак, неизвестная функция Ьу должна удовлетворять уравнению E4')
и начальным условиям:
Ьу = ЬуОУ 3/ = 8V, ..., 8у(л) = 8у0(Я) E3")
при аг = д:0. Рассмотрим теперь вместо уравнения E4') уравнение:
^ + V/ + • • • + Гу п)ЪУ{П) = fix). E5)
Так как правые части уравнений E4/) и E5) отличаются на беско-
бесконечно малую порядка выше первого, то в силу теоремы Пуанкаре инте-
интеграл <рС*О уравнения E5), удовлетворяющий начальным условиям E3')^
будет отличаться от искомой функции Ьу(х) на бесконечно малую
порядка выше первого. Кроме того, в силу той же теоремы все разности
\1пу Ъу<ю\х)\ (и = 1, 2, ...,«)
будут также бесконечно малые порядка выше первого.
Таким образом, решая уравнение E5) при условиях E3'), мы полу-
получим с точностью до малых высшего порядка искомую вариацию Ьу.
Уравнение E5) есть линейное уравнение, коэфициенты при неиз-
неизвестной функции Ьу и ее производных [при заданном основном реше-
решении v (х)] суть вполне определенные функции от х.
Наиболее важным в приложениях является тот случай, когда/(л:) = 0>
т. е. когда ищется главная часть изменения интеграла при варьировании
лишь начальных условий. В этом случае уравнение E5) примет вид:
Fjy+F**/+ • • ¦ +/>*Уя) = 0. E6)
Уравнение E6) носит название уравнения в вариациях] его интеграл
при бесконечно малых начальных условиях дает главную часть измене-
изменения интеграла уравнения E2) при соответствующих бесконечно малых
изменениях начальных условий.
'272 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Уравнение в вариациях для уравнения Эйлера. Найдем уравнение
в вариациях для уравнения Эйлера:
Получаем:
или, развернув и приведя подобные члены:
(F — F r) Sv — (F г ,5у') = 0.
V w Лс уу) у dx у уу у}
Вводя обозначения, аналогичные принятым нами в предыдущих пара-
параграфах: ,
р __ " р . р f , . р
УУ dx УУ ' У У *'
уравнение в вариациях примет вид:
Это есть уравнение Якоби, являющееся уравнением Эйлера для квадра-
тического функционала:
= J
§ 86. Геометрическая теория сопряженных точек
Сопряженная точка как точка пересечения двух бесконечно
близких кривых пучка экстремалей. Используя доказанный факт, что
уравнение Якоби есть уравнение в вариациях для уравнения Эйлера-
Лагранжа, можно дать новое определение сопряженных значений.
Пусть дано уравнение Эйлера-Лагранжа:
Обозначив через Yo экстремаль, уравнение которой
У=Уо(х)
выходящую из точки Л0(лг0, у0), допустим, что вдоль этой экстремали
Fyy ф 0. Построим теперь экстремаль 7а* у—у(х> а)> выходящую из
точки Ао\ при этом
Обозначим через Л/а), Л2(а), . .. точки пересечения экстремалей ^о
и Ya> расположенные в порядке возрастания их абсцисс. Точку Av к ко-
которой будет стремиться точка Л/а) при а, стремящемся к нулю, назо-
назовем i-й сопряженной точкой точки Ао.
Для того чтобы оправдать это определение, нам нужно прежде
гхего доказать, что предел Л/а) существует. Мы сразу докажем, что
§ 86] ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ СОПРЯЖЕННЫХ ТОЧЕК 273
абсцисса А/а) при а-^0 стремится к i-му сопряженному значению
для дг0. В самом деле, пусть
есть решение уравнения Якоби
LV]=O, E8)
построенного для экстремали ^о» и пусть хх < дг2 < дг3 < ... —решения
уравнения о(х) = 0 (х0 < дгх); дг^ есть, очевидно, г'-е сопряженное зна-
значение для х0. Так как уравнение E8) есть уравнение в вариациях для
уравнения E7), то в силу результатов предыдущего параграфа имеем:
у (л:, а) — у0 (х) = окр (дг) -J- аф (дг, а), E9)
где функция ф(лг, а) вместе с ее производной ф' (дг, а) равномерно стре-
стремится к нулю вместе с а на всяком конечном интервале лго<^дг<^#.
Абсциссы точек Ai (а) суть, очевидно, нули выражения E9). Покажем,
что, как бы мало ни было число в при достаточно малом а, /-й нуль
разности E9) отличается от х% меньше чем на е. Для этой цели построим
систему интервалов
(*oi хо + е)> (*i — s> хх -|-в), ..., (лгг. — s, дг, -f e). F0)
Для доказательства теоремы нам, очевидно, достаточно доказать, что
в каждом из интервалов системы F0) имеется при достаточно малом а
единственный нуль разности
у(х, а)—
Обозначим через т минимум функции [©(#)[, когда х принадлежит
закрытому интервалу [дг0, af-{-s] и не принадлежит ни одному из откры-
открытых интервалов системы F0). Очевидно, т > 0. Обозначим через р
минимум |<р'Ся)|, когда л: находится в любом из интервалов F0). В силу
свойств собственных функций о' (лг0) ф 0, следовательно, считая е доста-
достаточно малым, мы можем считать, что р > 0. Выберем теперь число т]
настолько малым, чтобы при всяком а ([ а [ < у\) имели место нера-
неравенства:
*)\<т, F1)
*,«)!</>¦ F2)
Покажем, что при [ а | < у\ и при хк — е < х < хк -f- e разность
у (х, а) —у0 (х) будет иметь единственный нуль. В самом деле, так как
на интервалах {xk_1-\mh> хк — Л) и (xk-\-h> xk+i — *)
\<р(х)\>т,
то в силу F0) и E9) на этих интервалах знак разности у0 (дг, а)—уо(х)
совпадает со знаком <?(х), но при переходе из одного интервала
в другой о(х) меняет знак, следовательно, в интервале (хк — A, xk-\-h)
разность у0 (л:, а)—уо(х) имеет по крайней мере один нуль. Если бы
нуль был не один, то нашлось бы число ? (| хк — 11 < К) такое, что
274 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. ХШ
тогда, диференцируя выражение E9), получим:
что невозможно, ибо по построению |<р'(с)|>Р> а 1Ф'(?> °01<Р«
Используя понятие сопряженной точки, мы можем дать новую фор-
формулировку критериев существования слабого минимума. Для того чтобы
дуга АВ экстремали ^0 давала слабый минимум, достаточно, чтобы
вдоль 7о было Fyy > 0 и чтобы закрытая дуга АВ не содержала
точек, сопряженных к А.
Аналогично в терминах сопряженной точки можно формулировать
необходимое условие Якоби.
Разберем несколько примеров на приложения развитой теории.
/•
Пример 1. Для интеграла I \\-\-yr<ldx экстремалями служат прямые. Пря-
Прямые, выходящие из одной точки, в дальнейшем не пересекаются; следова-
следовательно, в этом случае условия Якоби всегда реализуются.
Пример 2. Для интеграла / У A-{-2Byr + Суп dx, выражающего длину кри-
кривой у = у (х) на поверхности с элементом длины ds2 = A dx2 -\- 2В dx dy -\- С dy%
экстремалями служат геодезические. Если форма A dx* -f- 2B dx dy -f- С dy2 поло-
положительная, то условие Лежандра удовлетворяется в каждой точке геодезической.
Мы можем утверждать, пользуясь теоремой Якоби, что дуга геодезической АВ
дает слабый минимум длин кривых, соединяющих точки А и В, если она не
пересекается с бесконечно близкой геодезической дугой, выходящей из точки А.
В противном случае она перестает давать слабый минимум. Например, для;
случая сферической поверхности дуги больших кругов являются геодезическими.
Если дуга АВ большого круга содержит точку С, диаметрально противопо-
противоположную Л, т. е. дуга АВ больше половины большого круга, то АВ не, дает
минимума расстояний между А и В, так как в точке С дуга АВ пересекается
с бесконечно близкой дугой большого круга, соединяющего точки А к С. Если
дуга АВ меньше половины дуги большого круга, она наверное дает слабый
минимум длин кривых, соединяющих ее концы.
Пример 3. Задача о минимальной поверхности вращения (§ 32) сводится
к разысканию минимума интеграла:
ь
= f
Так как все экстремали задачи можно считать расположенными над осью Ох
0>>0), то условие Лежандра
выполнено для любой экстремали. Обратимся к условию Якоби. Как мы видели7
при произвольных точках А и В возможны три случая:
1. Через А и В экстремаль провести невозможно; задача неразрешима.
2. Через А и В можно провести единственную экстремаль; будет выполнено-
лишь необходимое условие Якоби.
3. Через А и В можно провести две экстремали: /верхнюю и нижнюю.
Данный нами раньше (§ 32) геометрический метод конструирования экстре-
экстремалей легко обнаруживает, что для верхней экстремали условие Якоби выпол-
выполнено, для нижней—не выполнено. Верхняя экстремаль дает во всяком случае
слабый минимум, а нижняя не дает ни максимума, ни минимума.
§ 87] ЭКСТРЕМАЛЬНАЯ ТЕОРИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 275
§ 87. Экстремальная теория собственных значений
Прямое определение собственных значений* В предшествующих
параграфах мы подробно изучили поведение наименьшего собственного
значения формы: ъ
J(У) = f {Py*+Ryrt) dx. F3)
а
Полученных результатов оказалось достаточно для решения вопроса
о слабом экстремуме. В более общей задаче, когда мы желаем изучить
поведение функционала вблизи экстремали, является существенным иссле-
исследовать все собственные значения и собственные функции формы. Заметим,
что это исследование представляет также большой самостоятельный
интерес, так как оно выявляет новые свойства линейных диференциаль-
ных уравнений.
Мы начнем с того, что дадим прямое определение собственных
значений.
В теории собственных значений квадратической формы п перемен-
переменных А = 2 ai)Pcix)i собственные значения и главные оси определялись
из экстремальных условий. Наименьшее собственное значение есть мини-
минимум А на сфере Е: 2^2 = 1. Пусть определены первые / собственных
значений и соответственных главных осей; (/-f-l)-e собственное значение
есть минимум А на пересечении сферы Е с (п—1)-мерным линей-
линейным многообразием, ортогональным первым / главным осям. Аналогично
можно определить собственные значения формы / в функциональном
пространстве.
ТЕОРЕМА. Пусть Xv Хо, .. ., \к_у—первые по величине {k— 1) соб-
собственные значения формы J(y); У1(х), у2(х), ..., ук_х(х) — соответ-
соответственные нормированные собственные функции; тогда k-e no величине
собственное значение равно минимуму J при условиях:
ъ ь
yidx = Q (/=1,2, ...,*— 1),
Л
X
F4)
а функция, реализующая условный минимум, есть k-я собственная
функция.
Прежде всего заметим, что методом § 82 можно доказать, что
минимум J (/? > 0) при условиях F4) достигается на некоторой кривой
класса Cj. Следовательно, на основании результатов § 60 функция у (х)>
реализующая условный минимум, должна давать безусловный минимум
функционалу
Ъ к-1
f {{Pf + Ry'*) - Ws - 2 2 W) dx, F5)
a i = 1
где \l и v. суть множители Лагранжа. Уравнение Эйлера-Лагранжа дает
л- F6)
276 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Умножим обе части уравнения F6) на у^ и, проинтегрировав в пре-
пределах от а до Ь, получим:
ь ь ъ ъ
x = V- f yyj dx -f Vjfyf dx -f ]? ъ/у& dx. F7)
В силу ортогональности собственных функций уг и у^ имеем:
ъ
fyiyjdx=O9
а
Далее ив D3) § 82:
ь ь ъ
f[y]yjdx = f[yj]y dx = Ijfyjy dx.
a a a
Принимая во внимание условие F4) и нормированность функций у^
из F7), получим:
v, = 0. F8)
Следовательно, наша функция у(х), реализующая условный минимум,
удовлетворяет уравнению Штурма-Лиувилля:
т. е. у(х) есть нормированная собственная функция формы /. Так как
У (^у) = |х (свойство 6^, то, значит, значение условного минимума есть
собственное значение.
Покажем, что [i есть непосредственное следующее по величине за Х1?
Х2, ..., \к собственное значение. В самом деле, допустим противное,
что [а есть собственное значение формы /, меньшее [i и отличное
от \и Х2, . . ., Хк; пусть у(х) есть соответственная собственная нормиро-
нормированная функция. Имеем:
ь ъ
fyt = 0 (f=l, 2, ..., k—l).
Следовательно, функция у(х) есть одна из допустимых функций
нашей изопериметрической задачи, при этом J(y) = \*< < \i = J(y)y что
противоречит определению у{х) как функции, реализующей наш услов-
условный минимум.
Единственность. Итак, существует кривая у—у(х) (собственная
функция), отвечающая собственному значению Хл, дающая условный
минимум форме J(y) и удовлетворяющая условиям F4). Кривая—у{х)
будет также удовлетворять всем условиям задачи, кроме того, очевидно,
J[y(x)]=J[—у{х)\- Следовательно, кривая у = —у(х) будет также
давать условный минимум для J. Докажем, что эта многозначность
в решении — единственно возможная.
§ 87] ЭКСТРЕМАЛЬНАЯ ТЕОРИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 277
ТЕОРЕМА. Для любой кривой у = у (л;), удовлетворяющей условиям:
ь
' \ F9)
fyiydx=0 (i=l, 2, ..., k— 1)
а '
и принадлежащей классу d или классу Dp имеет место неравенство:
J[y(x)]>J[yh(x)); G0)
знак равенства достигается только при у(х) = ук)
Неравенство G0) вытекает из определения ук(х)\ нам остается дока-
доказать, что для функций у(х)~~±ук(х) имеем:
Если у—у(х) принадлежит классу Ci, то неравенство G0) выте-
вытекает из единственности решения уравнения Штурма-Лиувилля при данном
собственном значении Хл.
л
Допустим теперь, что в некоторой точке с (а < с < Ь) у' (х) имеет
разрыв первого рода; если, кроме того, J(y) = J(yk)) то в угловой
точке [с, у (с)] должно выполняться условие Эрдмана (§ 73), которое
в нашем случае примет вид:
Так как по условию R ф 0, то
У(с — 0)=}
т. е. у (х) в точке с должна быть непрерывна. Теорема единственности
доказана.
Теория Куранта собственных значений формы У. Р. Курант в
ряде исследований использовал другое экстремальное определение соб-
собственных значений формы J(y).
Пусть рх (л:), р2С*г), ..., рк(х) — k функций класса Ct на (а, Ь).
Обозначим через Х(р1? р2, ..., рл) минимум формы J(у) на R при
условиях
ь
f
1,
а
Ъ
/Pi(x)y(x)dx-=0 (/=1, 2, ..., к).
а
ТЕОРЕМА J). Верхняя граница Х(ри р2, ..., рк) при произвольных
функциях pt равна Хл.
Ср. § 21.
278 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Другая формулировка: обозначим через Lfc_1 линейное пространство
в R, определенное (k — 1) линейными условиями
Верхняя граница минимумов J (у) на пересечение сферы I y2dx=l с Lk_1
а
при варьировании пространства Lk_t равна \к.
Для доказательства фиксируем сначала функции pv р9, ..., pfc_1.
Пусть у± (х\ у2 (х), . . ., ук_х (х) — собственные функции, соответствую-
соответствующие первым (k—1) собственным значениям \р Хо, ..., Xfc .
Рассмотрим ^-параметрическое семейство функций
к
имеем:
Подберем си с.„ ..., ск так, чтобы удовлетворялись условия:
ь к о к
J B ^*y^=S^=1'
Ь к — l к-1
f Pi (S СМ) dx== %cifpiyjdx = 0 (/=1^ 2' ..-,*—1). G2)
j 1 jl a
j =1 j=l a
к
В силу G1) и G2) функция N.^^принадлежит к классу функций, на ко-
торых минимум У равен Х(р1? р2, ..., р^.^. Следовательно,
так как \^С^к при j^.k, a 2 ?/=1. Таким образом верхний пре-
предел Х(рр р2, ..., pfc-1) не больше кк: именно \(yv у„ .. ., 3;ft-1)==4 •
В самом деле, в силу предыдущей теоремы \к есть минимум /(j>) при
условиях: ъ
/гах — О (/ — 1, 2, ..., А —1).
Следовательно, верхний предел для X (р1Э р2, . . ., рк_г) в точности
равен \к и достигается, когда pt=zyr
§ 87] ЭКСТРЕМАЛЬНАЯ ТЕОРИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ 27$
Из теоремы Куранта сразу следует оценка собственных значений Хп
при достаточно большом п. Оказывается, числа \п неограниченно растут
вместе с п, причем порядок \п равен порядку п2.
В самом деле, обозначим через X/ и \п" п-е по величине собствен-
собственные значения форм:
ъ ь
fief + с,/*) dx, f{Cy* + Ct/*) dx ,
a a
где с, c1 означают минимумы, а С и Сх — максимумы функций Р(х)
и R(x) на отрезке (а, Ь). Очевидно: С1^с1^>0. Покажем, что
Это неравенство непосредственно следует из теоремы Куранта. Мы можем
только уменьшить значение функционала Jab, если заменить Р(х) и R (х)
мх минимумами с и cv Поэтому при такой замене минимум Jab (при
каких-либо условиях) может только уменьшиться; число \п как верхняя
граница минимумов JаЬ (при некоторых условиях) поэтому не меньше Xf/.
Аналогично получим Хп ^\п".
Из равенства D0) § 81 следует, что п-е по величине собственное
значение X/ формы ь
a
\ r rwc\ I
Аналогично:
откуда
Зависимость собственных значений от верхнего предела. Будем
ь
считать верхний предел в выражении Jab— I (Py* -\-JRy'2) dx пере-
а
менным; 1-е собственное значение Х4 (д) (Ь > а) от Jab есть функция
ют Ь, причем для любого Ь, \ (Ь) > Х^. (?), если />у, в частности
<яри i>l Xi (*) > Xj (ft). Отсюда следует:
1°. При Ь, достаточно близком к а, все Xi (b) > 0. Это есть след-
следствие свойства 11° (§ 83). Далее имеем:
2°. Все функции ХД#) суть функции, монотонно убывающие при воз-
возрастании Ь~
В самом деле, пусть br^>b\ согласно теореме Куранта \(Ь') есть
верхняя грань минимумов Jab'(y) при фиксированных условиях: у(а) =
ь
= у (р') =0, I у* dx—l и при переменных /— 1 условиях:
J
а
= Q 0' = 1, 2, ..., /—1). ХД?) можно определить как верх-
280 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. ХШ
нюю грань минимумов Jab (у) при тех же условиях и дополнительном
условии на отрезке (ft, ft') у (х) = 0. Так как при дополнительных огра-
ограничениях на класс допустимых линий вариационной задачи минимум
может только повыситься, а следовательно, и верхняя граница подобных
минимумов может только повыситься, то ^i(ft/)<;^i(ft). Нам остается
доказать, что знак равенства невозможен.
Допустим противное, что \(ft') = \(ft). Обозначим через уг(х, ft)
/-ю собственную функцию формы J. Построим функцию
1/, (л:, ft) при а <; х ^ ft,
0 при ft < A:<ft'.
Функция у(х) принадлежит классу d- В силу сделанной гипотезы
Xi(ft)==Xi(ft/) получим:
что противоречит теореме единственности.
Итак, функции \ (ft) для значений ft, близких к а, положительны,
с возрастанием ft эти функции убывают и могут стать отрицательными;
в этом случае график функции Xt(ft) должен пересечь ось ft в точке ft.,
определяемой уравнением Xi(fti) = 0.
Числа ftp ft2, ..., fto ... расположены в возрастающем порядке.
В самом деле, если Xi(ftj) = 0, то \j (ftj < \ (Ь{) = 0 при у < г. Но так
как функция ^(ft) положительная для значений ft, близких к я, и отри-
отрицательна при ft = fto то она на интервале (a, ftj обращается в нуль
в точке bjy для которой ХД#у) = О; очевидно, fl<fty<ftr
ТЕОРЕМА. Корень bj уравнения \j (ft) = 0 рав^я у-лу сопряженному
значению для а.
Так как точки fty и значения, сопряженные к а, расположены в воз-
возрастающем порядке, то для доказательства теоремы достаточно показать>
что каждая точка bj есть сопряженное значение, и наоборот.
Итак, пусть b = bj. Обозначим через yj(x) у-ю собственную функ-
функцию Jab (у). Она удовлетворяет уравнению Штурма-Лиувилля:
при условиях
Так как XJ(fty) = O, то это уравнение Штурма-Лиувилля превращается
в уравнение Якоби:
Кривая y = yj(x) есть интегральная кривая уравнения Якоби, проходя-
проходящая через точку (а, 0). Эта же интегральная кривая проходит через точ-
КУ (bj> 0). Следовательно, bj есть одно из сопряженных к а значений.
Покажем, что и обратно: всякое сопряженное к а значение есть одно
из наших чисел.
§ 88] МИНИМАКСНЫЕ ЭКСТРЕМАЛИ 281
Пусть с есть сопряженное с а значение: в точке (с, 0) интегральная
кривая у = у(х) уравнения Якоби [у] = 0, проходящая через точку (а, 0)г
пересекает ось абсцисс. Интеграл уравнения Якоби у=у(х) есть инте-
интеграл уравнения Штурма-Лиувилля
при у(а)=у(с) = 0, для которого собственное значение Х = 0. Но X
должна равняться одному из значений \ (с). Следовательно, \ (с) = О,.
с = Ьг.
§ 88. Минимаксные экстремали
Теорема Морса. На основе добытого выше соответствия между
нулями собственных значений У{{р) и сопряженными значениями можно
доказать следующую теорему:
ТЕОРЕМА. Если форма
имеет k отрицательных собственных значений^ то открытый интер-
интервал (а, Ь) содержит k значений, сопряженных с а.
В самом деле, из условия теоремы следует, что:
(*) < К (»)< •. • < К (*) < 0, \+1 (*) > 0;
но так как при значениях с> близких к а, все Х<(с)>0, то в интер-
интервале (а, Ь) каждая из функций \ь(с) A=1, 2, 3, ..., k) имеет нуль7,
а все остальные \-(с) (j > k) нулей не имеют. Применяя теорему пре-
предыдущего параграфа, мы отсюда заключаем, что открытый интервал (ау by
содержит в точности k значений, сопряженных с а.
Классификация Морса экстремалей. Морс классифицирует экстре-
экстремали с закрепленными концами для интеграла
ь
K=f f(x, у, /)dx
а
по числу отрицательных собственных значений второй вариации
ъ
f
Экстремаль называется экстремалью 1-го порядка, если для нее
8/С== 0 и если вторая вариация имеет / отрицательных собственных
значений. Экстремаль первого порядка иногда называется минимаксной..
В силу только что полученных результатов условием того, что дан-
данная экстремаль есть экстремаль /-го порядка, является наличие i сопря-
сопряженных к а значений в открытом интервале (а, Ь). Или, что то же самое,,
экстремаль /-го порядка пересекает бесконечно близкие экстремали,,
имеющие с ней общее начало, в i точках, и притом не более чем
в / точках.
282 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. ХШ
Теорема Штурма. Мы до сих пор меняли верхний предел в интеграле
ъ
Jab = / (РУ2 + Я/2) dx (R > 0).
а
Если и нижний предел а считать переменным, то 1-е собственное
значение Xj формы Jab становится функцией двух переменных а и ft:
\г = \г(а, ft)- Относительно ft функции \(а, ft) суть функции убываю-
убывающие. Аналогично доказывается, что эти функции относительно пере-
переменного а суть функции монотонно возрастающие. Оба эти свойства
можно выразить следующей теоремой:
ТЕОРЕМА 1. Если отрезок (a', ft') заключен в отрезке {а, ft), не
-совпадая с ним, то а . , . , ,ч ^ , ,
\ \{а , ft ) > X(а, ft).
Расширим несколько понятие сопряженного значения. Мы назовем
число Ьг G=1, 2, ..., k) сопряженным значением к а справа, если
при ft,. > a, Xf (а> Ь() = 0 или, что то же, если интегральная кривая
уравнения Якоби, пересекающая ось Ох в точке х — а, имеет i-ю за
ней точку пересечения с осью Ох в точке x=bv
Назовем число ft/ i-м сопряженным значением к а слева, если ft/ < a
и если интегральная кривая f уравнения Якоби, пересекающая ось Ох
в точке х = а, пересекает эту же ось в точке х = Ь/, причем между
-ft/ и а находятся еще /—1 точек пересечения Т с осью Ох. Оче-
Очевидно, в этом случае а есть /-я сопряженная справа точка к ft/. Пусть
ft_., ft. (;=1, 2, ...)
.все левые и правые значения, сопряженные к а:
...<?_.<...< Ь_2 < *_, <a=*bo<bl<ba< ...<b.<...
ТЕОРЕМА 2. Если а' не совпадает ни с а, ни с одним из чисел Ь__.,
д., то каждый открытый интервал
(**-!'•**) (* = 0, -1, -2, ...)
содержит одно и только одно из значений, сопряженных к а'. Иначе
говоря: между каждой парой чисел ft., ft., г заключено по крайней
мере одно число Ь- , и обратно.
В самом деле, допустим противное, что, например, интервал^., fti,1)
содержит два значения bf и ft^+1» сопряженные к а'. Замечая, что Ь{,г
и ft'^.1 будут первыми сопряженными соответственно к bi и ft/, получим:
Но, с другой стороны, поскольку отрезок [bf, ^+1] целиком заключен
внутри [ft^, ft^ J, имеем в силу теоремы 1:
получаем противоречие.
§ 88] МИНИМАКСНЫЕ ЭКСТРЕМАЛИ 283
Так как при произвольных значениях /?(*)> О и Р(х) уравнение
Якоби [у] = 0 есть произвольное линейное однородное уравнение второго
порядка:
У+«/+.?-о1). (О
то доказанную теорему можно также формулировать следующим образом:
ТЕОРЕМА ШТУРМА. Если некоторая интегральная кривая урав-
уравнения A) пересекает ось Ох в точках а и Ь, то всякая другая инте-
интегральная кривая того же уравнения пересечет ось Ох по крайней
мере в одной из точек закрытого интервала [а, Ь], причем если одна
из точек пересечения есть точка а {или Ь), то точка b {или а) есть
также точка пересечения.
Укажем на одно простое следствие из доказанной выше теоремы:
Следствие. Если открытый интервал {а> b), a < Ь, содержит
единственное значение, сопряженное к а, пусть, например, аи то этот
интервал (а, Ь) содержит также единственную точку bv сопряженную
к Ь; при этом tft > bv
Понятие области в функциональных пространствах. Мы видели
в теории функций многих переменных (§ 25), что критические точки
различного типа можно характеризовать различной геометрической струк-
структурой области меньших значений. Эти геометрическо-топологические
исследования распространяются и на случаи функционалов.
Пусть дано функциональное пространство R непрерывных функций
у (я) {а <; х <; Ь) класса Ci, принимающих заданные значения: у [а) =у0,
у(Ь)—ух на концах интервала [at b). Расстояние между функциями мы
определяем в смысле их близости первого порядка. Пусть у —у {х) есть
функция, входящая в R. Окрестность у{х) на R есть ее г-окрестность
первого порядка.
Множество {^(дг)} функций, принадлежащих R, мы назовем областью,
если, какова бы ни была точка пространства R, т. е. функция у{х), при-
принадлежащая {у{х)}, существует ее е-окрестность, также принадлежащая
{у{х)\. Область D называется связной, если любые ее две точки уо{х)
и yt{x) можно соединить непрерывной кривой, принадлежащей целиком
области, иными словами, существует функция/(лг, ос) (O^a^l), не-
непрерывная относительно а и такая, что: f{x, 0)=^0(л;), f{x, 1)=^1(аг),
и при 0 < а < 1 функция /(*, а), рассматриваемая как функция только лг,
принадлежит области D-
Пусть на R определен функционал
ь
а
Выберем на R функцию уо{х). Совокупность функций у{х) из R, для
которых К{у) < К{у0), назовем областью меньших значений относи-
относительно Уо{х).
/и dx
(следовательно R' = uR) и умножая обе части на-
нашего уравнения на R, получим уравнение Якоби:
(
284 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Окрестность экстремальной кривой. Пусть уо(х) есть функция,
для которой &/С=0, т. е. кривая у—Уо(х) есть экстремаль. Кроме
того, пусть вдоль у = у0 (х) Fy'yr > 0. Рассмотрим пересечение Те неко-
некоторой е-окрестности функции у0 (х) с областью меньших значений для
Уо(х). Те есть, очевидно, область. Докажем теорему:
ТЕОРЕМА. Если дуга АВ экстремали yz=yo(x) (а <#<;?) со-
содержит только одну точку, сопряженную с А (отличную от В), то
при достаточно малом е область Tg не связна.
В силу условий теоремы отрезок (а, Ь) содержит одно значение \у
сопряженное с а справа, и одно значение ?', сопряженное с b слева. Со-
Согласно следствию из теоремы Штурма точка I' лежит между а и ?.
Возьмем на отрезке (?', ?) произвольную точку с. Отрезки (#, с) и (с, Ь}
не содержат точек, сопряженных одному из их концов. Обозначим:
с ь
Кг О) = JF (х, у, /) dx, К.2 (у) =Jf (х, у, /) dx.
а с
Среди всех функций у0 -(- Ъу, для которых оу (с) = оу (а) = by (b) == 0^
функция уо(х) реализует слабый минимум для Кх(у) и К2(у) (в силу
выполнения условия Якоби):
[коль скоро pCVo» Уо~{~^У) меньше некоторого sj. Примем е = гГ Для
всякой функции Уо-\-Ьу из Те 2>у(^)фО. В самом деле, если бы
ЧУ (с) = 0, то в силу сделанного выше замечания
АЧУо + 8;0 = *1<>о + 8Л + *2 0'о + ^^
Следовательно, Уо~\-Ъу не входит в Те-
Далее, так как наша экстремаль есть экстремаль первого рода, то
для нее вторая вариация
(by) = j (P by* -f R 8/8) rfx
может принимать и отрицательные значения. Пусть для функции 8у(лг)
Къ (8У) < 0- Имеем:
К(УО +1 by) — К {у о) = Р1аЬ (оу) + olf
К (у о —toy) — К(у0) = filab (by) + о2>
где Oj и о2 — величины порядка выше второго сравнительно с L При
достаточно малом t будем иметь:
К(Уо+*ЪУ) — К(Уо) < 0, К(уо — Пу) — К(уо) < 0,
и в то же время
Р(Уо. Уо±*оу)<г.
Таким образом обе функции Уо-\-гЪу, у0 — thy входят в Т8. Но
в таком случае, как мы видели, 8у(с)фО. Если, например, 8ву(^)>0, то
при t> 0
У о (с) + t оу (с) > у0 (с), у0 (с) — t оу (с) < у0 (с).
§ 89] ТЕОРИЯ ЛЕЖАНДРА-ЯКОБИ 285
Область Ts распадается, следовательно, на две непустых части: об-
область Т1Э состоящая из функций у(х), для которых у (с)—Уо(с)>®>
и' область Т2 функций уг(х), удовлетворяющих неравенству: уг(с) —
—.УоОО<0- Эти области разделены совокупностью Тз функций у2 (л:),
для которых у2(с)—Уо(с) = ®' Так как Т3 лежит вне Tg, то, следова-
следовательно, область Те не связна.
§ 89. Теория Лежандра-Якоби квадратических функционалов
Уравнение Якоби. Полученные нами выше критерии положитель-
положительности квадратического функционала:
dx G3)
исторически были получены, отправляясь от некоторого специального
преобразования квадратического функционала — преобразования Ле-
жандра.
Пусть w — w {х) есть произвольная функция от х класса С1э опре-
определенная в закрытом интервале [а, Ь]. Имеем:
ь ъ
f Boyb/w + 8у2^) dx = f d(wby*) = 0, G4).
а а
если 8у(а) = 8у(?) = О. Добавим к правой части G3) левую часть G4);
квадратический функционал примет вид:
,, ,,3/» } dx. G5)
Поставим теперь задачу подобрать функцию w так, чтобы подинте-
гральное выражение превратилось в полный квадрат. Для этого необ-
необходимо и достаточно, чтобы функция w удовлетворяла условию:
CW + «0-'Vr(/?» + e'/) = 0. G6)
т. е. функция 18) (х) должна удовлетворять диференциальному уравнению
первого порядка. Таким образом, если существует кривая класса d
в интервале [а, Ь], удовлетворяющая уравнению G6), то квадратическому
функционалу Jab можно придать вид:
*f I « yfyt )
G7)
Квадратический функционал Jab (by) не меняется от перемены знака у оу.
286 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
I Из полученного преобразования второй вариации немедленно сле-
следует: если в интервале [a, b]: a) Fy, , > 0 и Ь) существует интеграл
уравнения G6), то форма Jab положительна.
Лежандр, предполагая неявно, что интеграл уравнения G6) всегда
существует, считал, что для положительности формы достаточно, чтобы
F >Vf > 0- Пробел в теории Лежандра был обнаружен Якоби. Якоби
У У
свел задачу интегрирования уравнения G6) к задаче интегрирования не-
некоторого линейного уравнения второго порядка—„уравнения Якоби".
Положим:
•=-^-^г4' G8)
глеи = и(х)—новая неизвестная функция. Подставляя выражение для w
в уравнение G6), получим:
[u)=Pu—?{Ru') = O, G9)
где, как раньше, положено:
p = F d-F P = F
УУ dy УУ" У У
Уравнение G9) есть знакомое нам уравнение Якоби — линейное урав-
уравнение второго порядка. Замечая, что всякий интеграл уравнения G6)
выражается при помощи G8) через интеграл уравнения Якоби, мы за-
заключаем, что при F , , > 0 для существования интеграла уравнения G6)
(интеграл должен быть класса Ci в интервале [а, Ь]) необходимо и до-
достаточно, чтобы существовал интеграл уравнения G9), не имеющий
нулей в интервале [а, Ь], а это последнее сводится к тому, чтобы закры-
закрытый справа интервал (я, Ь\ не содержал точек, сопряженных к а.
Из преобразования Лежандра второй вариации также весьма просто-
получается необходимость условия F ,^^0 для положительности формы»
Подставляя в выражение G7) функционала JаЪ вместо w ее выра-
выражение через и из G8) (ифО при а^х^Ь), получим:
Jab J Г у у' и2 пХУ
а
это есть так называемое преобразование Якоби второй вариации.
§ 90. Квадратический функционал Jai как предел конечных
квадратических форм
Вывод уравнения Якоби предельным переходом. Развитая выше
теория квадратических функционалов JаЪ может быть получена предель-
предельным переходом из теории конечных квадратических форм, изложенной
нами в гл. IV. Не останавливаясь на деталях, укажем на основные
моменты этого предельного перехода (см. L. Lusternik, Ober einige
Anwendungen der direckten Method en. .., Мат. сборн., 1926).
§ 90] КВАДРАТИЧЕСКИЙ ФУНКЦИОНАЛ 287
Пусть дан квадратический функционал
ь
Jab (У) = f (РУ2 + Я/2) <**. (80>
заданный в пространстве R [ у (х)] — непрерывных функций; при этом
у(а)=у(Ь) = О и
R(x)>0 (а <*<?). (81)
Разобьем отрезок (а, Ь) на п равных частей и обозначим через yiy Pir
Rt значения функций у(х), Р(х), R(x) в /-й точке деления. Построим
теперь квадратическую форму п—1 переменных у±, у„ ..., уПятт1:
п—1
где
Л А Ь — а
Очевидно, имеем:
J [У О)! = lirn Jn -i (Л» Л' • • •» Л-1>5
знак предела понимается в том смысле, что при п -> оо,
и Vz.-^^W- Полагая:
au+i
а ==0, если j не равно г—1, i, i-{-l,
форма Jn_1 примет обычный вид:
В силу условия (81) при достаточно малом Ал:, очевидно, имеем:
>0 <0. (83>
Покажем теперь, как из условий положительности квадратических форм
получаются условия положительности функционала J[y(x)].
В силу теоремы Сильвестра для положительности формы Jn_t необ-
необходимо и достаточно, чтобы были положительны все члены последова-
последовательности:
До=1, Ах, Д2, ..., Vi> (84)
где ДЛ = |а^| (/,у = 1, 2, ..., Щ суть детерминанты. Общее число
отрицательных собственных значений формы Jn_1 равно числу перемен
знаков в последовательности (84).
288
ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Принимая во внимание специальную форму коэфициентов нашей
формы Jn_v придадим условиям Сильвестра несколько новый вид. Для
этой цели, считая уп_1 произвольным фиксированным числом, найдем
стационарную точку формы Jn_{, принимая во внимание, что а„ = 0
при Уф/— 1, /, / -{- 1, получим:
i = ° (*=1, 2, ..., л—1). (85)
Задавая в этой системе yv мы можем последовательно определить
у2 = ^И9 уг, ..., уп_1* Построим подигон Пп, г-я вершина которого
имеет координаты (/Ал:, у{); число точек пересечения полигона П„
с осью Ох совпадает с числом перемен знаков последовательности:
Покажем, что это число перемен знаков совпадает с числом перемен
знаков в последовательности (84). Для этой цели составим матрицу из
(Коэфициентов системы (85):
0
п
О 0 ... О а. __9а __л л « а ,
Обозначим через 8i детерминант, получаемый из этой матрицы вычерки-
вычеркиванием /-го столбца и умножением на (—1) г:
п — 1
Так как все члены а..+1 отрицательны, то
Отсюда, решая систему (85):
(87)
и подставляя значения для 8,, получим:
Уп
<88)
Так как все kt положительны, то из (88) непосредственно вытекает
нужный результат: число точек пересечения полигона Цп с осью Ох
совпадает с числом перемен знаков в последовательности (84). Следо-
Следовательно, принимая во внимание теорему Сильвестра, получаем, что
число отрицательных собственных значений формы Jn совпадает с числом
точек пересечения полигона Пп с осью Ох.
§ 90]
КВАДРАТИЧЕСКИЙ ФУНКЦИОНАЛ*?
289
Подставим теперь в систему (85), определяющую полигон Пм, вместо
их выражения (82); получим:
l (n
±) = 0 0 = 1,2, .... л —1).
Заставляя теперь п стремиться к бесконечности, последнее уравнение
перейдет в знакомое нам уравнение Якоби:
Полигон Лп перейдет в интегральную кривую ? уравнения Якоби, выхо-
выходящую из точки (а, 0). Число точек пересечения кривой Y (а <•?<#)
с осью Ох определит число отрицательных собственных значений ква-
дратического функционала Jal (теорема Морса). В частности, для поло-
положительности Jab достаточно, чтобы ^ не пересекала оси Ох в закрытом
справа интервале (я, Ь], и необходимо, чтобы не пересекала оси в откры-
открытом интервале (а, Ь).
Вывод условия Якоби треугольным преобразованием. Мы полу-
получили таким образом условия положительности функционала Jab, исполь-
используя теорему Сильвестра положительности конечной формы. К тому же
результату можно притти приведением формы Jn к нормальному виду
при помощи треугольного преобразования (§ 24). Как мы сейчас уви-
увидим, это преобразование в пределе дает преобразование Якоби второй
вариации.
Применим формулу C5) § 24 к форме Jn; получим:
где
ап а12 0
а21
(89)
о
о
о
о о
и где Д/^ получается из Д, заменой /-го столбца у-м. Имеем:
Кроме того, легко видеть, что в определителе Д^* + 1) все элементы
последнего столбца равны нулю, кроме элемента аи , ±9 стоящего на
пересечении последнего столбца с последней строкой. Следовательно:
Отсюда, подставляя в (89), получим:
290 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Обозначая теперь через ir)j, irJ, ..., г\п одно из нетривиальных реше-
решений системы (85), мы в силу формул (86), (87) и (88) (где у, заме-
заменены %) получим:
/ Пг « I
л-
(90)
Если теперь кривая у — интегральная кривая уравнения Якоби — не
пересекает на закрытом справа интервале (а, Ь) ось Ох, то то же самое
будет иметь место для полигонов Hn(y\v tj2, ..., т]Л). В этом случае
выражение справа в (90) имеет всегда смысл, причем при Ал;, стремя-
стремящемся к нулю, *— будет стремиться к единице, а вся правая часть (90)
будет стремиться к
у-
где r\ = ri(x) есть интеграл уравнения Якоби. Отсюда
Этот положительный (при R > 0) интеграл и есть искомая форма Якоби
для второй вариации.
В случае если отрезок [а, Ь] содержит k точек, сопряженных к а,
то предел формы Jn можно представить в виде суммы (я-[-1) положи-
положительных интегралов и п отрицательных членов. (См. Л. Люстерник
и И. Петровский, О приведении второй вариации к каноническому
виду треугольными преобразованиями, „Ученые записки МГУ", вып. II.)
§ 91. Вторая вариация для изопериметрической задачи
Изопериметрическая задача. При разыскании достаточных условий
слабого минимума в случае изопериметрической задачи основную роль
играет изучение квадратического функционала, когда на класс допусти-
допустимых функций наложен ряд условий. Мы дадим сейчас теорию квадра-
квадратического функционала, рассматриваемого на линейной части простран-
пространства R, а затем покажем, как из этой теории получаются достаточные
условия слабого минимума изопериметрической задачи и, общее, решение
вопроса о поведении функционала в близости первого порядка экстре-
§ 91] ВТОРАЯ ВАРИАЦИЯ ДЛЯ ИЗОПЕРИМЕТРИЧЕСКОЙ ЗАДАЧИ 291
мали. Заметим, что теория квадратического функционала представляет
большой самостоятельный интерес, поэтому мы разовьем эту теорию
несколько шире, чем это нужно для поставленной задачи вариационного
исчисления.
Пространство Rk. Квадратический функционал на Rft. Пусть нам даны
k непрерывных линейно независимых функций класса Ci переменной
^ ^ Pi(*)> Р2(*)> ••> РаО)-
Обозначим через Rk функциональное пространство, элементами которого
служат всевозможные непрерывные функции у=у(х) класса Ср удовле-
удовлетворяющие следующим условиям:
= 0, (91)
0. (92)
Пространство RA составляет, очевидно, часть пространства R, рассмо-
рассмотренного выше. Элементы пространства Rk суть все элементы простран-
пространства R, ортогональные функциям р4 (/=1, 2, ..., k).
Пусть теперь на пространстве Rk задан квадратический функционал
ь
где Р и R суть непрерывные с непрерывными производными функции
от х, причем R > 0 на отрезке [а, Ь]. Форму Jab мы назовем положи-
положительно-определенной на RA, если для всех функций R^ форма принимает
положительное значение: Jab (у) > 0. Форму Jab мы назовем неотрица-
неотрицательной на RA, если на RA всегда Jab (у) ^> 0.
Условия положительности формы Jab. Для приложений к изопери-
метрической задаче центральным является вопрос, при каких условиях
форма J'аЪ будет на Rk положительно-определенной (неотрицательной),
а также вопрос классификации этих форм по образцу § 88.
Так же как для формы, заданной в пространстве R, для изучения
формы Jab на Rk построим сферу единичного радиуса:
ь
= 1 (93)
и найдем критические значения JаЪ при условиях (91) и (93). Это есть,
очевидно, изопериметрическая задача. Покажем прежде всего, что изо-
периметрические условия (91), (92) и (93) удовлетворяют условию,
достаточному для применимости метода Эйлера-Лагранжа неопределенных
множителей. В самом деле, согласно § 60, если изопериметрические усло-
условия имеют вид: ,
I
Г (х, у, /) dx=l4 (/==1,2,..., &),
то для применимости метода Эйлера-Лагранжа достаточно, чтобы вдоль
292 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
экстремальной кривой функции G^ — ~- Gy,(i) (/=1, 2, ..., k) были
линейно независимы. В нашем случае О^ = р{у A=1, 2, ..., k),
Gk+1 —у2, и отмеченное условие линейной независимости приводится
к условию линейной независимости экстремальной функции ^>=^>(лг)от
данных k функций pv р2, ..., рк. Допустим противное, что у линейно
выражается через рг\
тогда, подставляя выражение для у в условия (92), получим:
к Ъ
f
отсюда заключаем, что для функций рг должен обратиться тождественно
в нуль определитель Грамма:
(Pi2) (P1P2) • • • (PiPft)
(Р2Р1) (Р22) • • • (Р2Ра)
= 0,
(P*Pi)
ь
где положено / piPjdx = (pipJ), что невозможно в силу линейной неза-
а
висимости функций pi#
Итак, все кривые класса Cv реализующие экстремум J при усло-
условиях (91), (92) и (93), можно получить, применяя метод Эйлера-Лагранжа.
Искомые кривые будут удовлетворять уравнению:
ъ
* f (
О
а
где jx и vw суть множители Лагранжа-Эйлера. Или, применяя уравнения
Эйлера:
Константы jx и v^ должны быть подобраны так, чтобы интеграл урав-
уравнения (94) удовлетворял условиям (91), (92) и (93).
Исследуем предварительно решение уравнения (94), заменяя усло-
условие (91) условием лишь в одном конце:
у(а) = 0. (9Г)
Построим вспомогательные уравнения:
[y]=W, (95)
(i==l, 2, .... А) (96)
х) Все сг равны нулю быть не могут, ибо в противном случае у ЕЕ 0, что
невозможно в силу условия (93).
§ 91] ВТОРАЯ ВАРИАЦИЯ ДЛЯ ИЗОПЕРИМЕТРИЧЕСКОЙ ЗАДАЧИ 293
и обозначим через у = уо(х) (Уо(/0 = 0) и уг=уг(х) (уг(а) = 0) какие-
нибудь решения соответственно уравнения (95) и уравнения (96) *).
При этих обозначениях общее решение уравнения (94) при условии (91')
бУдет:
С
где С — произвольная константа.
Определим теперь константы С и v® из условий (92) и (93). Гюд-
ставив выражение для у в условия (92), получим:
ъ . ъ
//
га а
или, используя сокращенную запись:
%=О- (97)
i
Таким образом для определения v^ и С мы получим систему k линейных
уравнений с k-\-l неизвестными, которая всегда имеет нетривиальное
решение.
Если ранг определителя системы (97) равен k, то общее решение
этой системы будет зависеть линейно от одного параметра t:
C=at, \
>«=«,*. } (98>
В этом случае решение уравнения (94) при условиях (91), (92) и (93)
будет единственным, ибо параметр t, остающийся произвольным, опре-
определится единственным образом из условия (93). Если ранг определителя
системы будет равен s < k, то С и v^ будут линейно зависеть от
k—5+1 произвольных параметров, решение уравнения (94) при усло-
условиях (91), (92) и (93) будет зависеть от k — 5 параметров. Таким
образом, каково бы ни было значение jx, существует решение уравне-
уравнения (94), удовлетворяющее условиям (91), (92) и (93), но это решение,
очевидно, в общем случае не будет обращаться в нуль при х=Ь,
т. е. не будет удовлетворять условию (91). Те значения ц, для которых
построенное нами решение уравнения (94) при х = b обратится в нуль,
мы назовем собственными значениями формы Jab на Rk.
Пусть [х есть одно из этих собственных значений. Ему отвечает по
крайней мере одна функция у(х), нетождественно равная нулю на от-
отрезке [а, Ь]9 и система констант v**\ при которых удовлетворяется урав-
уравнение (94) и условия (91), (92). Константы vw можно рассматривать как
компоненты некоторого вектора v в ^-мерном пространстве. Функция
у(х) называется собственной функцией Jab на Rk, отвечающей соб-
собственному значению [а, а вектор v назовем сопровождающим вектором.
Такие решения в силу условия /?>0, очевидно, существуют.
294 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
Основные свойства собственных функций. Установим по аналогии
с § 82—87 ряд важных свойств, которыми обладают собственные
функции.
• 1°. Если yv у2, ..., уп суть собственные функции формы /аЬ,
отвечающие собственному значению jx, то 2 с\Уг есть тоже собственная
функция Jab, щ отвечающая тому же значению [х, с сопровождающим
вектором, равным 2^ v^-
В самом деле, если v/*\ v2^, ..., у/г) суть компоненты сопровождаю-
сопровождающего вектора vW, то функция уг(х) удовлетворяет уравнению:
и условиям:
Уг (a) =yt (ft) = 0, (?jyt) = 0 (/ = 1, 2, ...,
Следовательно, функция Г=2с{Л1Уд0влетв0Ряет уравнению:
и условиям:
Отсюда следует, что совокупность всех собственных функций у(х),
отвечающих определенному собственному значению |а, образует линей-
линейное функциональное пространство L точно так же, как совокупность Е
всех сопровождающих векторов есть линейное многообразие k' ^ k
измерений. В дальнейшем отметим два случая:
а) Уравнение
при y(a)=y(b) = (pj,y) = O (/=1, 2, ..., k) имеет только тривиаль-
тривиальное решение у = 0.
Ь) Уравнение
[y]=W (99)
при у(а)=у(Ь) — 0 (/=1, 2, ..., ^) имеет нетривиальное решзние,
удовлетворяющее условиям:
(р.,^) = 0 0"=Ь 2, 3, ..., А) (990
(а является собственным значением фэрмы Jab на функциональном про-
пространстве R).
Так как уравнение (99) есть уравнение Штурма-Лиувилля, то, обо-
обозначив через У0(х) одно из его решений, мы получим все нетривиаль-
нетривиальные его решения в виде CYQ (л;), где С—произвольное постоянное.
§ 91] ВТОРАЯ ВАРИАЦИЯ ДЛЯ ИЗОПЕРИМЕТРИЧЕСКОЙ ЗАДАЧИ 295
2°. В случае „а" каждому сопровождающему вектору v из ? отве-
отвечает только одна собственная функция у (х).
В случае „btf каждому сопровождающему вектору v из ? отвечает
однопараметрическое семейство собственных функций у (х) из L, имею-
имеющих вид: y=yo-\~cYo, где уо(х) — одна из собственных функций с
сопровождающим вектором v и где Yo (x) есть решение уравнения Штурма-
Лиувилля (99).
В самом деле, если у1 (х) и уо(х) — две функции с сопровождающим
вектором v, отвечающие собственному значению [х, то yt —у0 есть функ-
функция с сопровождающим нулевым вектором. yt —у0 есть решение уравне-
уравнения Штурма-Лиувилля (99) при условиях (99'). В случае „а" ух—уо==О,
y1=y0-i в случае „Ь" У1—Уо~\-сУо* Итак, в первом случае у нас имеется
взаимно-однозначное соответствие между линейными пространствами L
и Е, во втором случае каждому элементу Е отвечает прямая в про-
пространстве L.
Отсюда следует:
3°. Каждому собственному значению ^ формы JаЪ на Rk отвечает
не более k -f- 1 линейно независимых собственных значений.
В самом деле, все сопровождающие векторы v являются линейными
комбинациями К векторов (k'^k): v1? v2, ..., v^, где k — kr-\-\ есть
ранг системы (97). В случае „а" каждому вектору уД/=1, 2, ..., k')
¦отвечает единственная собственная функция у„ в случае „Ъи каждому
вектору v{ отвечает семейство уг-\-сУ0 собственных функций. В слу-
случае „а" все собственные функции линейно выражаются через kr функций
JVi> Уъ • • •> ЛГ5 в случае „Ъи все они выражаются линейно через kf -\-1
функций у19 л> ..., Лг, Уо. -
Будем считать, что [а есть собственное значение кратности k'9 если
собственному значению [а отвечают К линейно независимых собственных
функций, т. е. что у нас имеется k' слившихся собственных значений.
В этом и заключается все основное отличие теории собственных зна-
значений формы Jab(y) на пространстве функций RA от разобранной выше
теории этой формы на пространстве функций R. В остальном теория
собственных значений формы Jab на RA почти дословно повторяет разо-
разобранную выше теорию собственных значений формы Jab на R.
Отметим наиболее существенные моменты этой теории:
4°. Собственные функции yt(x) и у2(х) формы JаЪ на Rft, отве-
отвечающие различным собственным значениям ри ^2, ортогональны.
В самом деле: *
к
г=1
296 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ.
Умножая первое из уравнений на у2, второе на у1 и проинтегрировав
в пределах от а до ft, в силу соотношений
ъ ъ
i
а а
Ъ Ъ
f Р<Л<** = JPiy2dx = 0 (i = l, 2, ...,
а а
получим путем почленного вычитания:
ъ
dx=0.
о
Так как \ьг ф у2, то / yty2 dx= 0.
а
Если мы имеем ^'-кратное собственное значение, которому отвечают
kf линейно независимых собственных функций, то можно эти kf линейно
независимых собственных функций выбрать взаимно ортогональными.
Нормировав собственные функции, отвечающие различным собственным
значениям, получим систему взаимно ортогональных собственных норми-
нормированных функций, причем каждому собственному значению отвечает
одна такая собственная функция (^'-кратное собственное значение
рассматривается как kr слившихся различных собственных значений).
5°. Значение формы Jab при нормированной собственной функции^
соответствующей собственному значению jx, равно [х.
В самом деле, пусть у(х) есть нормированная собственная функция,
отвечающая собственному значению jx, тогда для этой функции имеем;
ъ ъ
при / у? dx = 1, / рг у dx = 0; отсюда:
а а
Ъ Ь >Ъ
= f [y]ydX = y. J
Применяя Ъяетод § 80, можно показать, что абсолютный минимум
Jab (/? > 0), при условиях:
ъ ъ
O, (99">
достигается на некоторой кривой класса d; отсюда заключаем, что
этот абсолютный минимум равен значению Jab для одной из нормиро-
нормированных собственных функций формы Jab на Rk. Используя свойство 5°,
получим:
§ 91] ВТОРАЯ ВАРИАЦИЯ ДЛЯ ИЗОПЕРИМЕТРИЧЕСКОЙ ЗАДАЧИ 297
6°. Наименьшее собственное значение формы ]аЪ на Rh равно
абсолютному минимуму JаЪ при условиях (91), (92), (93).
Вполне аналогично получаем общий результат:
7°. /2-е по величине собственное значение формы JаЪ на Rk равно
верхней границе абсолютных минимумов Jab при фиксированных усло-
условиях (99") и (п—1) переменных условиях
ъ
J<?jydx=0 (j=l, 2, .••,/2—lV
а
Здесь, как и во всем дальнейшем, кратное собственное значение
считается столько раз, какова его кратность.
Из отмеченного выше существования кривой класса d, дающей
абсолютный условный минимум Jab, и из предложений 6° и 7° следует
также существование собственных значений и собственных функций,
формы Jab.
Будем- теперь считать верхний предел b в интегралах
ъ ъ
j 9jydx = O •
а а
переменным; тогда я-е собственное значение \ьп формы Jab на Rh будет
функцией от b: ji,n = jin(#). В силу рассуждений, приведенных в § 83
и 87, получим:
8°. Все функции \*>п(Ь) убывают с ростом Ь. При этом \>>п(Ь) ^ \*-т(Ь) *)>
если /2 > т. При ?, достаточно близком к а, все \ьп (Ь) положительны.
9°. Будем считать наименьшее собственное значение |ао(?) = |ао,
формы Jab положительным. Тогда имеют место для всякой функции у {х)
из Rk одновременно следующие неравенства:
а
Ъ
а
Здесь d—положительная константа, равная меньшему из чисел -~-
, где ct= min /?(#), *в= min P(x).
Сравнение собственных значений. В § 23 мы сравнивали собствен-
собственные значения квадратической формы на /2-мерном пространстве и на его
(п — &)-мерном многообразии. Мы можем аналогично сравнить собствен-
ные значения формы Jab на R (см. § 82—87) с изучаемыми нами
теперь собственными значениями формы Jab на RA.
*) Равенство рт (Ь) = \ьп (Ь) возможно лишь, если | п — т \ <; k\
298 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
10°. Обозначая через \п п-е (в порядке возрастания) собственное
значение Jab на R, а через un — п-е собственное значение Jab на Ru,
получаем:
Доказательство настоящего неравенства, основанное на теории
-Куранта собственных значений, совершенно аналогично второму из дока-
доказательств теоремы § 23.
Будем считать, что функции pt, р2, ..., рА, фигурирующие в усло-
условиях (92), определяющих пространство RA, суть переменные функции
{вместе с тем и пространство Rk является переменным). Собственные
значения рп обращаются в функционалы от р1э р2, ..., рА:
Н-п^МРпРг* ---эР*) (л=1>2, 3, ...).
Функции рг мы будем считать все время принадлежащими классу Ci>
далее будем полагать, что эти функции продолжают оставаться линейно
независимыми, т. е. что детерминант Грамма
\(PiPj)\ (/,;=1, 2, ...,?)
остается положительным. При этих условиях имеем:
11°. |ал суть непрерывные функционалы от р1э р2, ..., рА.
Докажем это свойство для наименьшего собственного значения jx0.
В основном это доказательство переносится и на случай любого рп.
Наряду с пространством RA, определенным равенствами:
ъ
y(a)=y(b) = 0, f?iydx = 0 (/=1,2,...,*), A01)
а
будем рассматривать пространство R/, определенное равенствами:
fydx = 0 (/=1,2,...,*), A02)
а
где
Обозначим через е наибольший из максимумов 8ру(у = 1, 2, ...,*)
на а^х^Ь. Докажем, что для всякой функции у(х) пространства RA,
лежащей на сфере S:
ъ
J><**=1,
а
можно построить функцию у(х) пространства R/, лежащую на S,
такую, что разность / (х)—у' (х) (а^Сх^Ь) может быть сделана
сколь угодно малой вместе с е.
§ 91] ВТОРАЯ ВАРИАЦИЯ ДЛЯ ИЗОПЕРИМЕТРИ^ЕСКОЙ ЗАДАЧИ 299
В самом деле, положим
имеем:
ъ
a j a a
Ь
= 2 CJ i(PiPj) + (*Р*Ру>} + fy^idx- A03>
j a
Так как функции p, линейно независимы, то определитель Грамма
\(PiPj)\>0 (/,; = 1,2,..., k).
При достаточно малом е и, следовательно, малых | Ьрг | имеем:
|(Р,Р/) + («Р|Ру)|>0 (/, У == 1, 2,...,*).
Поэтому система уравнений
(/=1,2,..., Л) A04)
разрешима относительно ^-. Так как в силу неравенства Шварца
то ?у — решения системы уравнений A04) — бесконечно малы вместе
с г. Функция у(х) принадлежит R/ [ср. A03) и A04)], причем
ъ
где т] бесконечно мало вместе с е#
Положим:
получим функцию пространства R/, лежащую на S, причем разности
У(х)—У(лг), у(х)—у(х) (а^х-^b) бесконечно малы вместе с е.
Поэтому: =
Jab (У) + Ъ< Jab (У) < Jab ОО + \, (Ю5)
где llm \ =±= 0, lim yj2 = 0. Отсюда заключаем, что при е достаточно
малом нижние границы JаЪ на RA и Jab на R/ отличаются одна от другой
как угодно мало. Но в силу экстремального определения собственных
значений отмеченные нижние границы JаЪ суть наименьшие собственные
300 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
значения ja0, \l0' формы Jab соответственно на RA и R/. Следовательно,
обозначив через 7]s наибольшую из абсолютных величин чисел тц, г\2:>
получаем:
К'
где lim т]3 = 0. Теорема доказана.
е-»0
Сопряженные значения. Значения bt, удовлетворяющие одному
из уравнений ^(^) = 0, будем называть значениями, сопряженными
с а. При i^jy очевидно, имеем bi^bJ. Так как для некоторых зна-
значений b значения функций \i(b) могут совпадать:
то здесь может также случиться, что l=j — i-\-\ таких функций одно-
одновременно обратятся в нуль (при этом / всегда меньше или равно &-J-1),
т. е. может иметь место равенство: bi=bi,1= ... = b.(j = i-\-l—1).
Такое сопряженное значение Ьг мы назовем сопряженным значением
кратности L
По аналогии с рассуждениями § 87 легко доказать следующую
теорему:
ТЕОРЕМА 1. Для того чтобы форма Jab на Rk имела р отрица-
отрицательных собственных значений, необходимо и достаточно, чтобы на
интервале а^,х < b заключалось р значений, сопряженных с а
(точнее: чтобы сумма кратностей этих значений равнялась р).
Отсюда как следствие:
ТЕОРЕМА 2. Для неотрицательности формы Jab на Rk необхо-
необходимо и достаточно, чтобы на интервале а<х<Ь не заключалось
ни одной сопряженной с а точки.
ТЕОРЕМА 3. Для положительной определенности формы Jab и Rk
необходимо и достаточно, чтобы на закрытом справа интервале
а < jc <; ? не заключалось сопряженных с а точек.
Условия Якоби существования слабого минимума. Применим
теперь развитую выше теорию к разысканию достаточных условий сла-
слабого экстремума изопериметрической задачи.
Пусть ищется слабый минимум интеграла
ь
J=*J'F(x,y,/)dx,
а
когда за класс допустимых линий принимаются кривые класса С1У
соединяющие две данные точки А (а, ах), B(b, b{) и удовлетворяющие
k условиям:
ъ
{i) = /i (/=1,2,..., Л), A06)
где /4 — константы. Функции F и G^ предполагаются непрерывными
вместе с их частными производными до третьего порядка включительно.
§ 91] ВТОРАЯ ВАРИАЦИЯ ДЛЯ ИЗОПЕРИМЕТРИЧЕСКОЙ ЗАДАЧИ
Пусть у:
( () () b
301
есть изопериметрическая экстремаль нашей задачи. Положим
р (г) d p (i)
В соответствии с § 60 мы в дальнейшем будем предполагать, что для
рассматриваемой экстремали функции р,(/ = 1, 2, ..., k) линейно незави-
независимы, т. е. что:
(Pi2) (P1P2)» ••• (PiPj
(Р2Р1) (Р22)> ••• (Р2РЛ)
I* 0.
A07)
При этих условиях изопериметрическая экстремаль будет обыкновенной
экстремалью для функционала:
= JH(x,y,
где /f = /7-f-2^^ \ СУТЬ множители Лагранжа-Эйлера. Таким обра-
образом экстремаль 7 будет удовлетворять уравнению:
87=0.
Отсюда, обозначая у(х)=у(х)-\-Ьу(х)} y(a) = av y(b) = bt" кривую,
удовлетворяющую условиям A06) и находящуюся в о-близости первого
порядка от экстремали 7» получим:
ъ
A08)
Ъ
+ J (Llf + Mb/ 2) dx,
где L и М равномерно стремятся к нулю вместе с е. Полагая, как выше,
IP = j \Нуу — -^ Нт,), R = y ИУУ'
соотношению A08) можно придать более простой вид:
ъ ь
J(y)—J(y) = f\Pty2 + Rty2)dx-{- J\lA/*-\-M*/*)dx. A09)
a a
Обозначим через R4 функциональное пространство, элементами кото-
которого являются всевозможные функции у(х) класса Cv удовлетворяющие
следующим условиям: ъ
= y(b) = 0, J Piydx = 0.
302 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
При этих обозначениях и условиях мы теперь можем формулировать
искомые признаки существования слабого экстремума.
ТЕОРЕМА. Для того чтобы экстремаль у. у=у(х), вдоль кото-
которой R > 0, давала слабый минимум интегралу J среди кривых
класса Clt соединяющих точки А и В и удовлетворяющих условиям
/^ = /Д/= 1, 2, ..., Л), необходимо, чтобы открытый интеграл (а, Ь)
не содержал значений, сопряженных с а для формы:
ъ
Kb = f (РУ2 + #/2) <**> A10>
а
на Rft; достаточно, чтобы закрытый справа интеграл (а, Ь] не содер-
содержал значений, сопряженных с а, для той же формы Jab на Rk.
Начнем с доказательства достаточности условий. Пусть у (х}
есть допустимая кривая нашей вариационной задачи, близкая к экстре-
экстремали у(х) (s — близость первого порядка):
Имеем:
ъ ъ
f+ f (/=1,2,...,A), A11)
где ч\=у—у и где Pv Rt суть значения Р{, Rt при средних значениях
аргументов:
,+*.q-y>. /+wj-,m I @<
у-УЯ I
Формуле A11) можно придать вид:
ъ
= O, A12)
где е4(/= 1, 2, .. ., К) стремятся к нулю вместе с г. В самом деле,
если с== max P(x), r— min /?(лг)>0, то
а а а,
Ъ Ъ
< (max Л 4"^r max ^) У Ti2rf* <Яг J Ч d*>
а а
где 9 = niaxPi +-^г max Ri при е-> 0 ограничено. Обозначим через
наименьшее собственное значение формы
ь
§ 91] ВТОРАЯ ВАРИАЦИЯ ДЛЯ ИЗОПЕРИМЕТРИЧЕСКОЙ ЗАДАЧИ 303
при условиях:
ъ
•Ч(а) = •»!(*) = О, J\ir[dx=0 (/ = 1, 2, ...,?)•
а
В силу условий теоремы jjl0 > 0. Ha основании свойства 11° § 91
(стр. 298) собственных значений наименьшее собственное значение |хол
формы Jab на пространстве, определяемом равенствами:
ъ
/(Pi + O^* = 0 (/=1,2, ...,?), A12)
а
при достаточно малых ei будет сколь угодно близким к |i0. Отсюда пргс
достаточно малом е будем иметь:
Ро'>-^. . (ИЗ)
Из свойства 9° следует, что существует также положительная кон-
константа dx такая, что:
ъ ъ ъ
a
Ъ
где Y] = Y] (л:), Y] (а) = т) (Ь) = 0 есть произвольная функция класса Сх
удовлетворяющая A12) А). Отсюда
Ъ Ъ
> f (-f+L),fdx+ f К + Ж) r{*dx,
где L и М равномерно стремятся к нулю вместе с е.
Таким образом при достаточно малом е будем иметь:
вторая часть теоремы полностью доказана.
Первая часть теоремы (необходимое условие) есть прямое следствие
рассмотрений § 62 и доказанных нами необходимых условий неотрица-
неотрицательности второй вариации.
!) При этом естественно предполагаем е настолько малым, чтобы ei = е,
(/= 1,2, ...,k) были непрерывны при a<<6
304 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
§ 92. Уравнение в вариациях и сопряженные точки для изопери-
метрической задачи
Геометрическая интерпретация условий Якоби. В § 86 мы дали
наглядную геометрическую интерпретацию условиям Якоби, связав задачу
разыскания сопряженных значений с задачей построения экстремали,
бесконечно близкой к данной. Эту теорию в известном смысле можно
распространить и на случай изопериметрической задачи, но получаемая
при этом картина оказывается здесь значительно менее четкой и более
сложной.
Мы здесь наметим эту картину лишь в самых общих чертах.
По аналогии с § 86 мы рассмотрим предварительно следующую
задачу. Пусть ^: у=у(х) есть изопериметрическая экстремаль
функционала^
JF(x,y,
когда за класс допустимых линий принимается совокупность кривых
класса d, соединяющих две данные точки А (а, ах) и В (Ь, Ьг) и
удовлетворяющих k условиям:
ь
Kt = f О® (дг, у, /)dx = /, (/ = 1, 2, ..., k);
а
требуется найти изопериметрическую экстремаль, бесконечно близкую
к данной экстремали ч х).
Для решения этой задачи обозначим через
уравнение искомой экстремали и будем считать, что Ьу и Ъу' бесконечно
малы. Так как у(х) и .У (•*:) +Sy (л:) суть изопериметрические экстремали,
то, следовательно, для этих кривых имеем:
f4 (х, y>/)—az г у (*. у. У)+
. / + ?) - -? Fy (х, у + by,
К11
где Xf. и X/ суть множители Лагранжа-Эйлера соответственно для одной
и для другой изоперимеарических экстремалей. Кроме того,
ъ ь
(\ = li A15)
Функции F и G® удовлетворяют тем же общим условиям, что и выше.
§ 92] УРАВНЕНИЕ В ВАРИАЦИЯХ 305
Вычитая постепенно левые части уравнений A14), уравнений A15),
отбрасывая бесконечно малые высших порядков и вводя принятые выше
обозначения, получим:
2)р' = 01)' (не)
=0 A = 1,2, ...,k). A17)
Уравнение A16) есть уравнение в вариациях для изопериметрической
задачи. Таким образом вариация изопериметрической экстремали Ьу удо-
удовлетворяет линейному уравнению второго порядка A16) и k условиям
ортогональности. Полагая \^г) = \/ — X., уравнение в вариациях примет
вид:
2^Р< = 0. A18)
Легко .видеть, что и обратно, если при некоторых значениях а(/)
мы получим решение уравнения A16), удовлетворяющее условию A17),
то с точностью до бесконечно малых высших порядков мы получим
уравнение изопериметрической экстремали, бесконечно близкой к данной.
Для этой цели достаточно заметить, что если 8y=/(jc) есть интеграл
ъ
A16) при а(г) = jjlow, f f(x)pi = 01 то oy = hf(x) будет интегралом
а
Ь
A16) при а(?) = h\io{t\ f Ъургс1х = 0 (/ = 1, 2, . . ., ri), где h — произволь-
а
ная константа.
Если написать уравнение Эйлера-Лагранжа изопериметрических экстре*
малей для квадратического функционала:
а
заданного в пространстве Rk:
ъ
a
то мы получим снова уравнение в вариациях A18). Этот факт имеет
простое объяснение на .основании первого добавления. В самом деле,
мы видим, что функционал
= fF(x,y,y')dx,
1) Напомним, что [8у] = — ШуГу.Ъу')— ( Нуу — —^ Нуу,} *у', где
_ р V ) г? о —G® — О ^
— r—2jKiui> ?i — uy (jx uyf *
306 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. XIII
рассматриваемый на линиях, удовлетворяющих условиям A15), вблизи
экстремали у: уо(х) (близость первого порядка) с точностью до беско-
бесконечно малых высших порядков совпадает с квадратическим функционалом;
ъ
J (Уо "Г Чу) - J Ы « Jai = f {РЪу* + Roy' s) dx,
а
заданным на пространстве Rk. Отмеченные выше совпадения уравнения
в вариациях с уравнением Эйлера-Лагранжа для квадратического функ-
функционала таким образом показывают, что изопериметрические экстремали
функционала У, близкие к f, совпадают, с точностью до бесконечно
малых высших порядков, с изопериметрическими экстремалями квадрати-
квадратического функционала
ь
Ji G) =
Сопряженная точка для изопериметрической задачи. Введем
теперь понятие сопряженной точки для изопериметрической экстремали.
Пусть ,;: вУ=.УС*г) есть попрежнему изопериметрическая экстремаль^
выходящая из точки А. Мы скажем, что точка С экстремали у есть
точка, сопряженная с А, если, как бы мало ни было число г, суще-
существует точка С (с7, с/), удаленная от С не больше чем на г и обла-
обладающая следующими свойствами:
1) С принадлежит т;
2) точки С и С можно соединить изопериметрической экстремалью
у=у(х), расположенной в г-близости от f и такой, что:
с' с
(х, у, /) dx = j G(i> (х, у, У) dx. A19)
а а
Точка С есть предельная точка точек пересечений С изопериметрической
экстремали у с бесконечно близкими изопериметрическими экстремалями,
удовлетворяющими условиям A19).
Как мы видели выше, с точностью до бесконечно малых высших
порядков всякую экстремаль, близкую к -f, можно представить в виде;
где Ьу удовлетворяет уравнению в вариациях:
условия A19) при этом примут вид:
с
J
A20)
Отсюда, пренебрегая попрежнему бесконечно малым высших порядков,
можно формулировать: для того чтобы точка С была сопряженной
с точкой Л, необходимо и достаточно, чтобы нашлось решение уравнения
в вариациях, З'довлетворяющее условиям ортогональности A20) и обра-
§ 92] уравнение в вариациях 307
щающееся в нуль в концах интервала (я, с), т. е. чтобы абсцисса
точки С была значением, сопряженным с а. Мы приходим к следующей
теореме: значение, сопряженное с а, равно абсциссе одной из точек
экстремали, сопряженных с А.
Приведенные выше рассуждения не дают, очевидно, строгого вывода
этой теоремы: этот вывод можно получить рассмотрением, аналогичным
§ 86—87.
Если абсцисса сопряженной точки есть сопряженное значение крат-
кратности ky мы говорим, что „сопряженная точка имеет кратность k".
Применим некоторые из добытых нами общих результатов к двум класси-
классическим изопериметрическим задачам.
1. Изопериметрическая задача в узком смысле. Эта задача сводится к на-
нахождению минимума
ь
при условии ь
К = j'y dx =
a
Как мы видели в § 60, экстремали суть всевозможные окружности:
Полагая:
а
будем иметь:
ь
r = JHdx,
Ъ-J = I j by'-jdx.
Так как вторая вариация выразилась квадратическим функционалом опре-
определенно положительным, то отсюда в силу теоремы 3 § 91 заключаем, что дуга
окружности осуществляет во всяком случае слабый минимум J при условии
K = s- Отсюда также следует, что любая дуга окружности, выходящая из
точки А (а, 0), не содержит точки, сопряженной с А. (В этом можно убедиться
легко из чисто геометрических соображений и отсюда, не рассматривая oV,
непосредственно убедиться также, что дуга окружности осуществляет искомый
минимум.)
Вполне аналогично можно обследовать изопернметрическую задачу в узком
смысле на поверхности.
2. Задача с тяжелой цепью. Эта задача приводится § 60 к разысканию
минимума
ь
при условии:
308 ВТОРАЯ ВАРИАЦИЯ И ЛИНЕЙНЫЕ ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. ХЩ
Семейство изопериметрических экстремалей будет определяться уравнением:
A21)
Полагая
7 = J нах,
а
будем иметь:
ь
— Ъур -\ г— 8у'3 I их.
JL. JL |
2 A+У2) 2 J
Так как вдоль экстремали A21) при а>0 (<х<0) имеем у -j-X> 0 и у" >о
(.У + ^ <С 0» У < 0), то отсюда заключаем, что для всякой вогнутой экстремали
имеем:
следовательно (теорема 3 § 91), всякая вогнутая экстремаль, удозлетворяющчя
условию К=1, реализует искомый минимум. Любая дуга цепной линии A21)
лишена сопряженных точек.
Теорема Морса для изолериметрической задачи. Назовем изо-
периметрическую экстремаль у экстремалью &-го порядка, если для нее
вторая вариация на соответственном функциональном пространстве Rh
имеет k отрицательных собственных значений.
Из рассмотрений настоящего параграфа мы, повторяя доказательство
теоремы Морса для простейшего случая, получим:
ТЕОРЕМА. Для того чтобы экстремаль Л В била экстремалью
k-го порядка, необходимо и достаточно, чтобы сумма кратностей
всех сопряженных к А точек, расположенных внутри АВ, равнялась k.
ГЛАВА XIV
ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО
ЭКСТРЕМУМА
§ 93. Геометрия экстремалей
Геометрический язык. В § 72 мы говорили о геометрии на поверх-
поверхности. Принимая в этой геометрии за „прямые" геодезические линии,
мы видели, что ряд теорем и понятий евклидовой геометрии распро-
распространяется на геометрию поверхностей. Если считать поверхность задан-
заданной параметрически, то семейство геодезических на этой поверхнссти
совпадает с семейством экстремалей функционала
J= fy Adu*-\-2Bdudv-\-Cdv*, (I)
где и и v — параметры, а А, В и С суть козфициенты первой дифе-
ренциальной формы поверхности:
ds* = Adu*-\- 2B dudv -f С dv*. B)
Функционал J дает длину линки «j; если 1 есть зкстремгль, то У (у)
есть „расстояние" между концами f. В соответствии с зтим одна из
центральных задач вариационного исчисления: дает ли данная экстре-
экстремаль 7 минимум или максимум функционалу J для случая функцио-
функционалов A), приводится к задаче: дает ли данная геодезическая Т минимум
длин кривых, принадлежащих поверхности и соединяющих концы ?.
Геометрическую интерпретацию функционала J G) и его экстремалей
можно сохранить, не прибегая к пространству. Экстремали функцио-
функционала J будут „прямые" в двумерной римановой геометрии (w, v) с эле-
элементом дуги B).
При изучении свойств семейств экстремалей функционала
J = f F(x, у, /)dx C)
или
/= f F{x, у, х\ y')dt v D)
оказывается весьма удобным распространить на этот функционал вторую
(из отмеченных двух) геометрическую интерпретацию функционалов
специального Еида A). Есякую экстремаль функционала C) условимся
называть J-прямой. Значение функционала i на к будем называть
310 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
J-длиной, /-длину экстремали, соединяющей точки А и В, условимся
считать J-расстоянием между точками А и В.
Введенные понятия позволяют говорить о неевклидовой геометрии
с диференциалом дуги:
ds — F (дг, уу /) dx.
Если F = "|/~1 +У2, то /-прямые превращаются в обычные пря-
прямые. Наша геометрия превращается в обычную евклидову геометрию.
При произвольной функции F1) и при любых координатах х, у вве-
введенная геометрия мало похожа на обычную геометрию: через две точки
не всегда возможно провести /-прямую, и может случиться, что через
две точки проходит несколько /-прямых, и, следовательно, /-расстояние
между двумя точками не есть однозначная функция координат этих
точек. Однако, как мы увидим ниже, при некоторых (достаточно
общих) дополнительных гипотезах относительно функции F в областях,
размеры которых зависят от вида функции F, наша геометрия будет
вполне естественным обобщением обычных геометрий. Во всяком случае
задача: дает ли данная экстремаль у минимум функционалу /, эквива-
эквивалентна в нашей геометрии задаче: дает ли /-прямая у „кратчайшую"
линию среди линий, соединяющих концы 7.
Форма Гамильтона уравнений Эйлера-Лагранжа для /. Для того,
чтобы не загромождать формулировок и доказательств большим коли-
количеством теоретико-функциональных оговорок и „особыми случаями", мы
в этом параграфе будем вести изложение в классическом духе: мы будем
предполагать все участвующие в рассмотрениях функции диференци-
руемыми столько раз, сколько потребуется; исключение переменных из
систем уравнений мы будем считать возможным; условия единственности
интегралов диференциальных уравнений будем предполагать выполнен-
выполненными и т. д.
/-расстояние между точками А и В есть функция четырех перемен-
переменных: координат х0, у0 точки А и координат лг, у точки В. Если коор-
координаты х0, у01 х, у получат приращения dxOi dyo> dx, dyy то /-длина
получает приращение dJ:
dj = [Н (х, у, /) dx -f р (х, v, /) dy] —
— [И(хф у0, у 0') dxo+p (дс0, у0, у о) dy, E)
где p = Fy>(x, у, у'), H=F—У/у, у0' ИУ СУТЬ угловые коэфи-
циенты соединяющей точки А и В экстремали в ее концах. Отсюда
следует:
= Я(Х, V, У), ~^=р(Х, у, у ),
у о* у*)* w^=
Ввиду основной роли, которую играют функции р и Н в теории
семейства экстремалей, естественно придать уравнению Эйлера-Лагранжа,
форму, в которой фигурировали бы явно функции р и Я. Для этой
1) Удовлетворяющей лишь обычным теоретико-функциональным условиям
непрерывности и диференцируемости по всем трем аргументам.
§ 94] ПОЛЕ ЭКСТРЕМАЛЕЙ И ТРАНСВЕРСДЛИ 311
цели мы наряду с переменными дг, у> у' будем рассматривать перемен-
переменные дг, у и р *= /у (ху у у У). Всякую функцию и (лг, у, У) трех аргу-
аргументов мы можем рассматривать, пользуясь соотношением р = /у, также
как функцию от дг, уУ р. Для сокращения письма мы условимся в даль-
дальнейшем обозначать через ихУ и?г иуг, как обычно, частные производные
функции и (Ху уу У), рассматривая ее как функцию от х, у, У, а
через {J[ у -.-- , -yj — соответствующие частные производные, рассма-
рассматривая и как функцию от дг, у и /?.
При этих обозначениях имеем в переменных х} уу уг\
= dF—У dp — p dy = /=; rfjc -f F/flfy -f-/? rf/ — /dp —pdyf =
С другой стороны — в переменных дг, уу р:
дН* , , дН , , dh ,
an. = - v ~ dx —.—ч— dy -L--.. - dp . F)
dx ' ду s i dp r v }
Следовательно:
dh__ A*L — f ^L — _ r
~dx~tx* ду ~ У dp ~ y '
Полученные соотношения позволяют нам уравнению Эйлера-
Лагранжа:
F*--dx-F—° G>
придать следующий вид:
дН __ dp \
ду ~~ cfx:' I
dh1==_<*У' f (8)
dp cfx i
Система уравнений (8) называется гамилътоновой формой уравне-
уравнений Эйлера или канонической формой. Она заменяет уравнение G)
второго порядка с одной неизвестной функцией двумя уравнениями пер-
первого порядка с неизвестными функциями у~у(х) и р=р(х).
Из F) и (8) следует, что вдоль экстремали
dx ~~~ дх *
В частности, если F*ne зависит явно от х, то:
--^— = 0, Н == const.
dx '
§ 94. Поле экстремалей и трансверсали
Понятие поля экстремалей. Введем ряд понятий, которые будут
играть основную роль в геометрии экстремалей.
Пусть имеем семейство { 7 } простых дуг f и односвязную область D,
обладающие следующими свойствами:
Г. Концы дуг семейства { ? } принадлежат границе D.
2°. Через каждую точку D проходит одна и только одна дуга
семейства.
312 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
При этих условиях мы скажем, что рассматриваемое семейство {т}
образует поле и что это поле покрывает область D* Если дуги ^
суть экстремали г) и образуют поле, то это поле мы назовем полем
экстремалей.
Собственное поле. В дальнейшем особую роль будут играть поля
экстремалей специального вида. Пусть мы имеем однопараметрическое се-
семейство {7} экстремалей функционала 7, уравнения которых имеют вид:
у = <р(х, а), (9)
и допустим, что при изменениях х и а в пределах
рассматриваемое семейство { ? } линий образует поле. В таком случае
очевидно, что при любом х (хг < х < х2) функция о (х, а) есть моно-
монотонная функция а, т. е. или -^-^0, или -ч-<^0 при любом
(у Л G0С
В дальнейшем мы будем безоговорочно предполагать, что:
1) -g->0 при а1<а<а2,
2) о непрерывна вместе со своими частными производными первого
порядка при всех значениях х и а, удовлетворяющих неравенствам A0).
3) Обозначая через а = /(лг, у) решение уравнения A) относи-
относительно а [при лг, у, принадлежащих области поля и при a^
мы будем предполагать, что у непрерывна вместе со своими частными
производными во всех точках области поля.
Всякое поле экстремалей, удовлетворяющее перечисленным выше
требованиям, мы будем называть собственным полем или просто полем.
Центральное поле. Другим специальным видом поля является так
называемое центральное поле. Допустим, что экстремали семейства { 7}
выходят из одной точки A (xv yx):
и допустим, что при л:1<л:<лг2, а!<а<;а2 это семейство экстре-
экстремалей образует поле. Такое поле мы будем называть центральным
полем, точку Л мы будем называть центром поля. В приложениях
этого понятия мы опять будем безоговорочно предполагать выполнен-
выполненными отмеченные выше условия — непрерывности © и у с их производ-
производными; кроме того, мы будем предполагать, что-р > Оприл^ <
Заметим, что если семейство линий
= ф(х, а)
\
Функционала J или /.
§ 94] ПОЛЕ ЭКСТРЕМАЛЕЙ И ТРАНСВЕРСАЛИ
образует центральное поле экстремалей, то семейство линий
х <лг/<л:<л:2,
образует собственное поле.
Поле для функционала /. В приложениях понятия поля к изучение
функционала / мы будем так же, как в случае функционала J, иметь
дело с полями, удовлетворяющими ряду теоретико-функциональных
Зтсловий. Остановимся на этих условиях. Пусть { -у} есть однопара-
метрическое семейство экстремалей функционала /:
* = ?(*> <*)>
Допустим, что при изменениях t и а в пределах
рассматриваемое семейство линий {7} образует поле. В приложениях
мы будем безоговорочно предполагать, что в замкнутом прямоуголь-
прямоугольнике A2) функции 9 и ^ непрерывны вместе со своими частными про-
производными ot, ©a, 4v ^а и что, кроме того, в том же прямоугольнике
ф]0. A3)
Обозначим через Q область, покрытую полем. Из принятых условий
относительно функций <р и ty следует разрешимость системы A1) отно-
относительно t и а: существуют функции
t=\{x, у),
а = Ь{х,у),
определенные и непрерывные вместе с их производными в области Q
и такие, что _
лг = ?[?(х, у), ф(лг, у)],
.У = <Н?(*> У)> <К*> У)]-
Если все линии 7> заданные системой A1), имеют концы в одной и
той же точке Л(лг, у) и если, какова бы ни была окрестность точки Л,
куски 7> расположенные внутри этой окрестности, образуют поле, то мы
скажем, что {7 j есть центральное поле экстремалей. Точка А назы-
называется центром поля.
В приложениях мы будем предполагать, что <р и ^ удовлетворяют,
как раньше, условиям непрерывности и что неравенство A3) имеет
место при t1<^t^t2, <x1^a^>a2. Заметим, что если линии 7> задан-
заданные системой A1), образуют центральное поле экстремалей, то при
любом положительном е линии у', определенные системой A1) и усло-
условиями U -f- е <С * ^ ?>» ai ^ а ^ а2» образуют поле, удовлетворяющее
всем отмеченным выше теоретикофункциональным условиям.
314 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Трансверсаль поля. Из результатов, установленных в гл. XIII, сле-
следует, что если ^уфО^фО) в точке A(xv у{) при некотором
значении у' (у' —у0'), то пучок экстремалей, выходящих из Л по
направлениям, близким к у0', в достаточно малой окрестности точки Л
образует центральное поле экстремалей *).
Пусть {-у}—поле экстремалей функционала J или /. Мы скажем,
что линия Г есть трансверсаль поля {-у), если всякая экстремаль у
1лоля, пересекающая Г, пересекает ее трансверсально.
Остановимся подробно на функционале J. Как известно, условие
трансверсальности в случае функционала J имеет вид:
F(x,y,,/)—/Fv
.У,
1 = 0,
A4)
Это условие связывает угловые коэфициеиты уг касательной к экстре-
экстремали с угловым коэфициентом-,1-трансверсального направления. Отсюда
заключаем, что если нам дано поле и если в каждой точке Иг -j- p2 ф О,
то в каждой точке поля нам известно направление трансверсали
поля, проходящей через эту точку. Все трансверсали поля получатся,
таким образом как решения диференциального уравнения первого
•порядка: hv
/у[х, <?(*, a), ?/(*,a)]g- =
где вместо параметра а, определяющего экстремали поля, следует под-
подставить выражение этого параметра через координаты точек поля.
Отсюда, принимая во внимание сделанные выше допущения относи-
относительно поля, мы получаем, что через каж-
дую точку поля проходит одна и притом
только одна трансверсаль. Таким образом при
условии #'2-|-/?2фО совокупность траисвер-
салей есть однопараметрическое семейство кри-
кривых, образующих поле. Такое поле мы бу-
будем в дальнейшем называть полем транс-
ее реале й.
Совокупность экстремалей и трансверсалей
образует сеть кривых, покрывающих область
(черт. 49). Для функционалов специального вида:
ЧеРт- 49. " -._ , , < л лГл , ,,
условие трансверсальности совпадает с условием ортогональности, и при
А ф 0 семейства экстремалей и трансверсалей образуют ортогональную
сетку кривых.
х) Добавочные условия, которым должно удовлетворять центральное
яоле, будут выполнены, если за параметр а мы примем значение j'or и будем
предполагать Ft обладающей непрерывными частными производными до
третьего порядка включительно.
§ 94] ПОЛЕ ЭКСТРЕМАЛЕЙ И ТРАНСВЕРСАЛИ 315
Построение поля экстремалей по трансверсали. Используя условие
трансверсальности, мы можем также решить задачу, обратную рассмот-
рассмотренной: дана трансверсаль Г поля; требуется построить само поле.
Условие трансверсальности нам дает в каждой точке трансверсали Г
направление экстремали поля. Таким образом задача построения поля
по заданной трансверсали сводится к построению семейства интегралов
уравнения Эйлера-Лаграижа, выходящих из точек Г по данным напра-
направлениям. Если для точек Г и для направлений трансверсальных к Г
f г , ф 0, то в этом случае рассматриваемая задача, как известно, ре-
решается единственным образом. Отсюда результат: траисверсаль поля
определяет само поле единственным образом г).
Раньше мы видели, что поле экстремалей определяет поле трансвер-
салей единственным образом; следовательно, каждая траисверсаль поля
экстремалей определяет единственным образом все поле трансверсалей.
Приведем несколько примеров полей экстремалей и трансверсалей.
Пример 1. Пучок параллельных прямых, экстремалей интеграла
J
образует поле, покрывающее всю плоскость. Трансверсалями поля будут слу-
служить прямые, ортогональные прямым пучка.
Пример 2. Пусть D — выпуклая область, не содержащая точки А. Семейство
отрезков, принадлежащих D и одновременчо пучку лучей, выходящих из А,
образует поле экстремалей,*покрывающее/>2). Если А не принадлежит границе /),
то поле собственное; если А принадлежит границе D, то поле центральное.
В обоих случаях трансверсалями поля будут служить дуги окружностей
с центром в точке А.
Пример 3. Пусть Г есть кривая класса С2. Проведем через каждую точку Г пря-
прямую 7, ортогональную к Г. В достаточно малой окрестности Г построенные прямые f
о
образуют поле экстремалей {*;} функционала Г У \ -\-уп dx\ сама линия Г
а
будет трансверсалью этого поля. Если вдоль каждой прямой поля, начиная от
точки, принадлежащей Г, отложить отрезок постоянной длины К то, как
известно, геометрическое место концов этих отрезков образует линию, ортого-
ортогональную всем прямым поля, т. е. построенное геометрическое место точек
есть трансверсаль поля. Давая h всевозможные значения, мы получим поле
трансверсалей. Указанный здесь метод построения поля трансверсалей, как мы
увидим ниже, распространяется на функционалы общего вида.
Пример 4. Семейство экстремалей интеграла (задача о брахистохроне,
см. § 28)
J= / У TJ dx
J Yy
l) Подчеркнем те условия, при которых мы получили этот результат: 1) чтобы
определить направление экстремали в точке трансверсали Г, нам надо опре-
определить у/ через х, у и -:- из A5), — мы предполагаем, что уг определяете»
единственным образом, 2) вдоль Г для у, определенных из A5), имеем:
2) За параметр я, определяющей прямую экстремаль поля, можно принять
угловой коэфициент этой прямой.
316 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
есть семейство циклоид с вершинами на оси Ох:
х = г (8 — sin 6) + С,
y = r{\ — cos 6).
Семейство этих экстремалей при С=0, Л1ОО2 образует поле экстремалей^
покрывающее область, ограниченную кривыми:
х = гх (В — sin 8), х = r2(8 — sin 8),
3/ = гх A — cos 8), у = /*2 A — cos 0)
и прямыми
л: = я, 0 < а < 27crlf jy = 2icr1#
5. Пусть точка Л есть обыкновенная точка поверхности ср. Проведем череа
точку А всевозможные геодезические этой поверхности. Рассмотрим кривые -у
этого семейства, попадающие в односвязную область D поверхности ср. Если
диаметр D будет достаточно мал и D будет расположена достаточно близко от
точки А, то кривые ? образуют поле экстремалей, покрывающее область D.
Теоремы о трансверсалях. Приведем ряд теорем основного значе-
значения, касающихся свойств поля экстремалей и поля трансверсалей. Все
эти теоремы имеют место как для случая
экстремалей функционала У, так и для случая
экстремалей функционала /. Доказательства
теорем в обоих случаях вполне аналогичны;
мы их приведем для случая функционала У.
Пусть { ^ } есть центральное поле экстре-
экстремалей с центром в А. Отложим на всех экстре-
экстремалях этого поля дуги равной У-длины, счи-
х тая, что начала всех этих дуг лежат в точке А.
Ч 50 Геометрическое место концов этих дуг есть
некоторая линия Г (черт. 50).
ТЕОРЕМА I. Линия Г есть трансверсаль нашего поля, т. е. (для
случая функционала J):
Fix, у, /)_(/_-fx)Fv,(x, у, /) = 0,
где у' и -~ —угловые коэфициенты касательной к экстремали -[ и
к кривой Г в точке их пересечения.
В самом деле, обозначив через J (В) У-расстояние от точки В кривой
Г до центра поля Л, имеем для всех точек кривой Г:
J(B) = const.,
где У (Я) есть интеграл / [F(x, у, y')dx, взятый вдоль дуги АВ экстре-
экстремали f. При переходе от точки В (х, у) к близкой точке В' (лг -\- dxy у ----- dy)
кривой Г имеем, следовательно:
8У=0.
Но вариация интеграла У сводится в данном случае к вариации У в
конце, т. е. из равенства 8У = 0 следует, что ^ и Г трансверсальны.
Имеет место также обратное предложение:
ТЕОРЕМА 2. Если кривая Г есть трансверсаль центрального поля
экстремалей с центром в А, то точки Г лежат на равном расстоя-
расстоянии от А.
§ 94] ПОЛЕ ЭКСТРЕМАЛЕЙ И ТРАНСВЕРСАЛИ 317
В самом деле, если В есть точка кривой Г, то J (В) есть /-расстоя-
/-расстояние от А до В. С другой стороны, приращение 87 при переходе от В
к близкой точке В\ расположенной на Г, равное Н dx-\-pdy, обращается
в нуль, так как линия Г трансверсальна к экстремали АВ.1 Итак:
J(A, 5)== const.
Пример 1. Если F— Vl+У'2, то экстремали у суть прямые, проходящие
через А, линия Г есть окружность; условие трансверсальности есть условие
ортогональности, и наша последняя теорема даст нам известный факт
ортогональности окружности к радиусам.
Пример 2. Если экстремали суть геодезические на поверхности, то транс-
версали центрального поля суть геодезические окружности; трансверсаль-
трансверсальность попрежнему означает ортогональность, и мы получаем ортогональность
геодезической окружности к геодезическим радиусам.
Пример 3. Для случая принципа Ферма центральное поле экстремалей
есть пучок световых лучей, исходящих от светящейся точки Л, линия Г есть
линия волны, т. е. геометрическое место точек, лежащих на равном оптическом
расстоянии от Л, т. е. геометрическое место точек, до которых одновременно
достигает световой сигнал, отправленный из точки А. Трансверсальность в
этом случае означает ортогональность. Наше предложение дает нам частный
случай принципа Малюса — линия волны ортогональна лучам.
Пример 4. Для случая принципа Мопертюи-Эйлера центральное поле
экстремалей есть пучок траекторий, исходящих из точки А при равных
начальных скоростях. Линия Г есть так называемая линия равного действия.
Она ортогональна всем,траекториям пучка, так как и в этом случае трансвер-
трансверсальность означает ортогональность.
ТЕОРЕМА 3. Если Т{ иТо — дзе транс-
версали поля {?}, то отрезки экстремалей
поля между Г\ и Г2 имеют одинаковую
J-длину.
Пусть АВ есть дуга экстремали f поля {^}
(черт. 51), заключенная между 1\ и Г2. При
переходе от дуги АВ к близкой дуге А'В\
заключенной между теми же трансверсалями,
длина J (А, В) получит приращение
U = (И, dxx -f л dyx) + (Hfdx%+p2 dx2),
Черт. 51.
где dxv dyv dx2, dy2 — приращения коорди-
координат концов дуги АВ. Вследствие условия трансверсальности в точках А
и В оба выражения в скобках равны нулю; следовательно,
Оказывается, что верно и обратное предложение.
ТЕОРЕМА 4. Пусть Г есть трансверсаль поля {^}. Если мы отло-
отложим на всех экстремалях у нашего поля в одном направлении дуги
одинаковой J-длины с началами на Г, то концы этих дуг образуют
тоже трансверсаль поля {^}-
Обозначим через 1\ геометрическое место точек В, одинаково уда-
удаленных от Г. Перейдем от дуги АВ экстремали ^ к близкой экстре-
экстремальной дуге А'В? той же длины, причем А и А' лежат на Г. Так как
приращение У-длины при переходе от АВ к А'ВГ равно нулю, то, обоз-
обозначая через dxv dyx и dx2, dy% приращения координат точек А и В,
имеем: 0=bJ= (Hi
318 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Первая скобка равна нулю вследствие трансверсальности ? и Г. Следо-
Следовательно, равно нулю и выражение во второй скобке, что дает нам транс-
трансверсальность f и Гг
Пример. Рассмотрим случай, когда j = \Vl-\-yn dx. Здесь поле экс-
экстремалей, трансверсальное кривой, есть пучок нормалей к кривой. Теорема 1
дает нам равенство отрезков нормалей между двумя кривыми с общими
нормалями. Если на всех нормалях к данной кривой отложить равные отрезки,
то согласно теореме 2 мы получим новую экстремаль, имеющую общие лор-
мали с первой экстремалью. Теорема 2 распространяется и на геодезические
нормали к кривым на поверхности (теорема Гаусса).
§ 95. Теория Кнезера
Пусть мы имеем кривую Г класса С2. Пусть (f} есть однопараме-
трическое семейство экстремалей функционала
= fF(x,y,/)dx
или
Функция F удовлетворяет обычным усло-
условиям непрерывности и диференцируемости.
Допустим, что экстремали f трансверсаль-
ны к Г и обладают огибающей 5 класса Ci
[семейство {^}, очевидно, не образует поля
Черт. 52. экстремалей У(?)]. Обозначим через z пара-
параметр, определяющий кривую нашего семей-
семейства, и пусть 7- есть кривая семейства, отвечающая значению {т. Обо-
Обозначим через А_ (черт. 52) точку пересечения ?т и Г и через В~ точку
пересечения х. и s. Введем положительные направления на линиях *{ и s.
На линии -[_ будем считать положительным направление от ^ к Л,.
Положительное направление на s определим так, чтобы в точках В .
положительные направления на ?т и 5 совпадали. Параметр т будем во
всем дальнейшем считать выбранным так, чтобы при его возрастании
точка Д_ двигалась в положительном направлении по s.
Обозначая через J. J-длину отрезка Д_Д_ экстремали 7-> будем
иметь:
где dxQ, dyQ, dx, dy суть приращения координат концов Д. и В_ экстре-
экстремали -у. при переходе от экстремали -^ к бесконечно близкой экстре-
экстремали -fT+dx. Вследствие трансверсальности ?т и Г первое выражение
в скобках исчезает. Далее:
Них +pdy = [F(х, у, у)]— (/ — у')р] dx,
§ 95] ТЕОРИЯ КНЕЗЕРА 3 1 S*
где у и/-—угловые коэфициенты кривых ?„ и 5 в точке Д.. Так как
в точке в обе кривые соприкасаются, от у'=у', и, следовательно:
Интегрируя это равенство в пределах от т0 до iv получим:
^, A6)
где интеграл в правой части взят по дуге Д. В„ кривой 5. По нашему
определению этот интеграл есть J-длина соответственной дуги Вш В^ .
Равенство A6) выражает собой теорему Кнезера:
ТЕОРЕМА 1 (Кнезера). Пусть имеем семейство экстремалей?
транс вер сальных к линии Г класса С2 и обладающих огибающей s
класса С]. Пусть А:Вг и AJ3% — две дуги нашего семейства с кон-
концами А1 и Лй на Г и концами Вг и В.2 на s. При этих обозначениях,
если точка Вх предшествует точке В%у то разность J-длин А2В2
и АхВг равна J-длине дуги огибающей, заключенной между точ-
точками Bt и В2.
Случай вырождения. Если линия Г вырождается в точку О, то
семейство экстремалей \^\ в теореме Кнезера превращается в пучок
экстремалей, выходящих из точки О; мы получаем следующий предель-
предельный случай теоремы Кнезера:
ТЕОРЕМА l''. Пусть имеем пучок экстремалей, выходящих из
точки О и обладающих огибающей s класса СР Пусть ОВ1 и ОВ2—
две экстремали нашего семейства с концами Вх и В2 на s. При
этих обозначениях, если точка Вг предшествует точке В.2, разность
J-длин QB2 и ОВг равна J-длине дуги ВХВ2 огибающей s.
Другой важный частный случай теоремы Кнезера мы получим, если
допустим, что огибающая 5 вырождается в точку Р, т. е. если все,
линии { ^} проходят через точку Р. В этом случае семейство {т} выро-
вырождается в пучок экстремалей, выходящих из Р и трансверсальных к IV
Если мы дополнительно допустим, что и линия Г выродилась в точку О,
то семейство {т J превратится в семейство кривых, проходящих через
точки О и Р. В этом случае по теореме Кнезера J-длины всех этих
линий будут между собой равны. Например, пучок больших кругов сферы,
выходящих из точки О, реализует последний случай.
Пример 1. Для случая, когда {?} есть семейство прямых (экстремалей для
Г у\ -j-y/ldx)y семейство {7} по теореме Кнезера есть семейство нормалей
к ; огибающая s есть эволюта кривой Г. Из теоремы Кнезера следует в этом
случае известное предложение о том, что дуги эволюты равны разности длин,
отрезков нормалей, касающихся эволюты в концах этой дуги.
Пример 2. Для случая геодезических на поверхности (экстремалей для
Г ds) семейство {7} обращается в семейство геодезических нормалей к кри-
кривой Г, их огибающая s — так называемая геодезическая эволюта кривой Г.
Теорема Кнезера обращается в теорему Гаусса:
Длина дуги геодезической эволюты к кривой Г равна разности длин
отрезков геодезических нормалей кривой Г, касающихся эволюты в концах
этой дуги.
320 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
§ 96. Условия Якоби
Необходимое условие Якоби. Мы видели в гл. XIII, что если экстре-
экстремаль 7» соединяющая точки А(хи уг), В(х2, у2) дает слабый минимум
функционалу / и если вдоль ^
У У ^ ^ 1 ^ ^ ^' V1' J
то дуга АВ не содержит точки, сопряженной с Л и отличной от В.
Приведенная выше теорема Кнезера об огибающей пучка экстремалей
позволяет установить это предложение геометрически независимо от
развитой в гл. XIII общей теории квадратического функционала. Это
геометрическое доказательство годится в одинаковой мере как при рас-
рассмотрении функционала У, так и функционала / (в случае функционала
/ надо естественно условие Fyy > 0 заменить условием Fx > 0). Отме-
Отметим, что нижеследующие рассмотрения приобретают особенно полную гео-
геометрическую наглядность, если потребовать дополнительно, что F > 0.
Черт. 53. ' Черт. 54.
Перейдем к доказательству необходимости условия Якоби. Допустим,
что при условии A7) дуга АВ содержит точку С, сопряженную с точ-
точкой А и отличную от В. Рассмотрим пучок экстремалей, выходящих из
точки А. Как известно, геометрическое место точек этих экстремалей,
сопряженных с точкой Л, образует огибающую 5 семейства. Условие
Якоби для слабого экстремума заключается в том, чтобы дуга АВ не
имела общих точек с s. Геометрически возможны четыре случая:
1) огибающая 5 не выродилась в точку и точка С касания экстре-
экстремали 7 с 5 есть правильная точка кривой !) (черт. 53);
2) огибающая не выродилась в точку, точка С есть точка возврата
для 5 (черт. 55), причем точки дуги АС экстремали 7, близкие к С, и
точки кривой 5, близкие к С, расположены по одну сторону от нор-
нормали к 5 в точке С;
3) огибающая s не выродилась в точку, точка С есть точка воз-
возврата для 5, причем точки дуги АС и s, близкие к С, расположены по
разные стороны от нормали к s в точке С (черт. 54);
4) огибающая s вырождается в точку (черт. 56).
Случаи 2, 3 и 4 можно считать „особыми" случаями. Мы остано
вимся лишь на случаях 1, 2 и 4, ибо в случае 3 геометрическое дока-
доказательство довольно громоздко.
!) В окрестности точки С кривые 5 есть кривые класса С^
§ 96]
УСЛОВИЯ ЯКОБИ
321
Первый случай. Из нашего допущения следует, что экстремаль у
касается огибающей 5 в точке С. Пусть АС есть экстремаль пучка,
касающаяся s в точке С. Из того, что точка С есть правильная
точка s, следует существование экстремали АС пучка, касающейся s
в точке С, предшествующей точке С. В силу теоремы Кнезера /-длина
АС плюс /-длина дуги СС огибающей s равна /-длине АС.
Покажем, что дуга СС огибающей 5 не есть экстремаль. В самом
деле, предполагая противное, мы получили бы, что через точку С про-
проходят две экстремали 5 и у, имеющие в точке С общую касательную.
Последнее невозможно, ибо в .точке С для направления / экстремали у
имеем Fy*y' > 0, и, следовательно, через точку С в направлении у'
можно провести единственную интегральную кривую уравнения Эйлера,
х. е. единственную экстремаль. Отсюда следует, что точки С и С
Черт. 55.
Черт. 56.
можно соединить дугой СС (отличной от дуги СС, огибающей s),
имеющей меньшую /-длину, чем дуга СС. Следовательно, кривая "(»
состоящая из дуг АС и С С, имеет меньшую /-длину, чем дуга АС
экстремали у, т. е. у не дает минимума /-длин дуг, соединяющих А
и С. Следовательно, тем более дуга АВ экстремали у не дает минимума
длин дуг, соединяющих А и В (речь, очевидно, идет о слабом мини-
минимуме, ибо кривые К и f находятся в близости первого порядка).
Приведенное рассуждение дает нам также следующий результат,
дополняющий формулированное выше условие Якоби, если дуга АВ
экстремали у дает слабый минимум функционалу J, если на АВ,
включая точку В, /^у > 0 и если точка С касания огибающей s
{пучка экстремалей, выходящих из А) с экстремалью ? есть правиль-
правильная точка кривой s, то С лежит строго вне АВ.
Четвертый случай. Рассмотрим теперь случай, когда огибающая 5
сводится к одной точке С, расположенной между А и В. Через точку С
в разбираемом случае проходит наряду с дугой АС экстремали у целое
семейство близких экстремальных дуг. Пусть АС есть одна из таких
дуг; /-длина АС совпадает с /-длиной АС\ „длина" ломаной АСВ, со-
состоящей из дуги АС и части СВ экстремали у, равна длине экстре-
экстремали АВ.
322 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Покажем, что в точке С излома линии АСЕ не удовлетворяется
необходимое условие Вейерштрасса-Эрдмана для ломаных экстремалей*
В самом деле, в силу условия Fy*y> > 0, при у', достаточно близких
к у'(У — направление f в точке С), в точке С имеем:
М*. л 7) Ф Jy (*,-у,/)•
Отсюда заключаем, что АСЕ не может давать относительно минимума
J-длин кривых, соединяющих точки А и В. Существует близкая к ЛСВ
(а следовательно к АВ) кривая, соединяющая те же точки 4 и В,
длина которой меньше J-длины АСЕ, следовательно и длины АВ.
Перейдем к рассмотрению особого случая 2.
Второй случай. В этом случае всякая экстремаль пучка, близкая
к экстремали 7, будет касаться 5 в точке С, предшествующей точке С.
Отсюда, как и в первом случае, заключаем, что 7 длина линии, соста-
составленной из дуг АС и С С, будет равна J-длине дуги АС. Так как дуга
С С не есть экстремаль (см. первый случай), то, следовательно, суще
ствует дуга АС, соединяющая А и С, находящаяся в близости первого
порядка от дуги АС и имеющая J-длину меньшую, чем дуга АС. Таким
образом дуга АС, а следовательно и дуг а АВ, не дает слабого минимума.
Условие Якоби для задачи со свободным концом. Приведенные
выше геометрические рассмотрения позволяют распространить необходи-
необходимое условие Якоби слабого минимума на случай задачи со свободным концом.
Пусть мы имеем семейство {к} экстремалей, трансверсальных к кри-
кривой Г. Пусть АВ — дуга одной из этих экстремалей, где А лежит на Г.
Если огибающая 5 семейства {f}, которая может состоять из одной
точки, пересекает АВ в точке С, лежащей между А и Вг то дуга
АВ не дает минимума J-расстояний между точкой В и кривой s. Дока-
Доказательство совершенно аналогично предыдущему, отличается от него
лишь тем, что теорема Кнезера применяется к семейству экстремалей^
трансверсальных к кривой Г, не вырождающейся в' точку, как в преды-
предыдущем случае. Отсюда получаем необходимое условие Якоби: для того
чтобы экстремаль АВ, трансверсальная в точке А к кривой Г, да-
давала минимум J-расстояний между точкой В и А кривой Г, необхо-
необходимо, чтобы АВ не пересекалась с бесконечно близкой транс вере аль-
ной к Г экстремалью.
Например, для того чтобы отрезок нормали к некоторой кривой х
давал минимум расстояния от точки Р до кривой ?, необходимо, чтобы
он не касался эволюты кривой.
Теорема Дарбу. Рассмотрим функционал J. Пусть АВ есть дуга
экстремали, реализующая абсолютный минимум J-длин кривых, соеди-
соединяющих точки А и В. Продолжим эту экстремальную дугу за точку В.
Пусть точка С есть сопряженная с А точка этой экстремали, т. е. С
есть точка, в которой наша экстремаль касается огибающей 5 семейства
§ 96] УСЛОВИЯ ЯКОБИ
323
экстремалей, выходящих из точки Л. Мы предполагаем, что огибающая 5
есть кривая класса Сх и не сводится к изолированной точке и что вдоль Л С
имеем Fx > 0. Мы видели, что существует в этом случае кривая АС,
J-длина которой меньше J-длины экстремальной дуги АС, — продолжения
дуги АВ. Пусть разность J-длин ЖГ и АС равна h > 0. На дуге АС
отметим точку С, разбивающую ЛС на две дуги: АС и С С, причем
пусть дуга СС по J-длине меньше ~. Так как дуга АС удовлетво-
удовлетворяет достаточному условию Якоби и вдоль этой дуги Fx > 0, то эта
дуга реализует относительный слабый минимум расстояний между точ-
точками А и С'. Покажем, что эта дуга не дает абсолютного минимума
J-расстояний между этими точками. В самом деле, ломаная АСС\ состоя-
состоящая из дуг ~АС и СС', имеет меньшую J-длину, чем АС (так как
разность J-длин дуг АС и АС больше, чем удвоенная J-длина дуги С С),
Заметим, что дуга АСС не лежит в окрестности первого порядка дуги
АС; таким образом мы не вступаем в противоречие с утверждением,
что АС реализует относительный слабый минимум J-длин.
Таким образом мы имеем на дуге АС точки двух классов: с одной
стороны, точки В первого класса — концы дуг АВ, дающих абсолютный
минимум J-расстояний между Л и В, и точки С' второго класса, для
которых дуги АС' не дают абсолютного минимума расстояний между
концами. При этом, если точка С принадлежит ко второму классу, то
к этому же классу принадлежит и всякая точка дуги АС, расположенная
ближе к Л. Сама точка С принадлежит, конечно, второму классу. Если
точка С принадлежит второму классу, то существует точка С' второго
класса на дуге АС (что доказывается совершенно аналогично тому, как
мы доказали существование точки С второго класса на дуге АС). Во
втором классе нет ближайшей к Л точки. Поэтому мы имеем в первом
классе последнюю точку D, реализующую дедекиндово сечение. Дуга
AD дает абсолютный минимум J-длин кривых, соединяющих ее концы,
но любая заключающая ее дуга AD' нашей экстремали уже этим свой-
свойством обладать не будет. Если мы будем двигаться по экстремали АС
от Л к С, то пройденная нами дуга будет реализовать абсолютный
минимум, пока мы не достигнем точки D. Пройдя же точку D, мы
будем иметь дугу, реализующую уже не абсолютный, а лишь относи-
относительный минимум, пока не достигнем точки С. Существование такой
точки D, отличной от сопряженной точки С, было доказано Дарбу.
Если огибающая 5 сводима к одной точке, наши рассуждения непри-
неприменимы. Возьмем, например, случай геодезических на шаре. Дуга боль-
большого круга дает абсолютный минимум длин, пока она меньше полу-
полукруга. Если же она больше полукруга, она перестает давать также и
относительный минимум J-длин.
324 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
§ 97. Геодезические эллипс и гипербола
7-эллипс. Под J-эллипсом мы подразумеваем геометрическое место
точек, сумма 7-расстояний которых от двух данных кривых 1\ и Г2 есть
величина постоянная (эти кривые могут выродиться в точки). Кри-вые 1\
и Г2 мы будем называть фокальными кривыми эллипса.
Пусть даны две кривые 1\ и Г2 класса d- Пусть А — точка, не
принадлежащая ни 1\, ни Г2. Проведем через точку А экстремали fi и
Т2, трансверсальные к Тг и к Г2; пусть Вх и В2— точки пересечения
(ближайшие к А) экстремалей ^1 и f2 соответственно с 1\ и Г2. Обо-
Обозначим через Jt {А) 7-расстояние от А до 1\, т. е. Ji (А) есть 7-длина
дуги ABV экстремали *[\\ обозначим аналогично через J2 (А) 7-расстояние
от А до Г2. При этих обозначениях уравнение семейства эллипсов
с фокальными кривыми 1\ и Г2 примет вид:
Перейдем от точки А (х,у) эллипса к близкой точке Ar (х -f- dx, у -j- dy)
того же эллипса. Будем иметь:
rf/iD)-f-tfJ3(A) = O. A8)
Но
dJx (А) = #! dx -\-рх dy, dJ2 (A) = H2dx-\-p2dy, A9)
где Hl и р1 суть значения функций H=F—У/у и p = F * в точке Л
при значении у\ равном угловому коэфициенту касательной к Ч\ в точке А\
Нъ и Р2 — значения тех же функций в той же точке Л, но при у\
соответствующем экстремали ^2. Из равенств A8) и A9) мы получаем
диференциальное уравнение семейства эллипсов с данными фокальными
кривыми:
4^+/>2) = 0) B0)
где -—-' есть угловой коэфициент касательной к У-эдлипсу в точке А.
Если F = V ! -\-У'*> т0
н= 1 У
, - +У2~ V i +yn '
экстремали ^ и ?2 СУТЬ прямые — нормали к 1\ и Г2. Обозначим
через рх и р2 углы прямых ^ и Т2 с осью Ох; уравнение B0) примет вид:
COS рт —Н Sin pi --— = — COS p .—Sin Pn —— . B1)
Обозначая через аг и а2 соответственно углы, образованные ^i и Т2
с касательной к эллипсу в точке А, уравнению B1) можно придать вид:
cos ах = — cos a2.
Последнее уравнение выражает следующее геометрическое свойство
У-эллипса: углы, образованные нормалью к эллипсу в любой точке А
с нормалями к фокальным кривым, опущенным из А, равны между
собой. Аналогично для поверхности: геометрическое место точек поверх-
поверхности, сумма расстояний которых (по поверхности) от двух данных
§ 97] ГЕОДЕЗИЧЕСКИЕ ЭЛЛИПС И ГИПЕРБОЛА 325
кривых Fj и Г2 есть величина постоянная, обладает тем свойством, что
геодезические нормали к кривым Tt и Г2, проведенные из произвольной
точки А нашего геометрического места, образуют в этой точке с его
геодезической касательной равные углы.
В частности, если рассмотреть на поверхности геодезический эллипс,
т. е. геометрическое место точек, сумма расстояний которых от двух
данных точек (фокусов) есть величина постоянная, то геодезические ради-
радиусы-векторы (геодезические дуги, соединяющие точки эллипса с фоку-
фокусами) образуют равные углы с касательной к геодезическому эллипсу.
7-гиперболы. Назовем J-гиперболой геометрическое место точек,
разность 7-расстояний которых от двух данных кривых Тх и Г2 есть
величина постоянная. Кривые 1\ и Г2 будем называть фокальными кри-
кривыми гиперболы.
Пусть А есть точка J-гиперболы, fi и ^2— ДУГИ экстремалей, про-
проведенные из точки А трансверсально к 1\ и Г2; Jx (А) и J2 (А) — их
J-длины. Имеем:
Jx (А) — J2 (А) = С = const.
и вдоль 7-гиперболы:
dJt(A) — dJ2(A) = 0,
откуда
Нх dx-\-pxdy — (Н2 dx-f-p.2dy) = О,
то-есть:
dx Pl~p2 '
где Ни Н2 и pv p2 — значения функций Я=/7 — y'Fy* и Р — ^у
в точке А для экстремалей ^ и т2, —у- — угловой коэфициент каса-
CLX
тельной к гиперболе в точке Л.
Мы можем рассматривать Н как функцию ху у, р. В этом случае
Нг=Н(х, у, /7j), Н2 = Н(х, у, р2), где х> у—координаты Л; уравне-
уравнение B2) примет вид:
dy Н(х, у, р2) — Н(х, у, pt)
dx Р2 — Р1
Пусть теперь s(I\, Г2) есть дуга гиперболы с фокальными кривыми
1\ и Г2, проходящая через точку Ао. Если Г2 будет неограниченно при-
приближаться к 1\ так, что, как бы мало ни было е, начиная с известного
момента, Г2 окажется в е-близости первого порядка от кривой 1\, то
в этом случае дуга гиперболы s(I\, Г2) будет неограниченно прибли-
приближаться к экстремали, проходящей через точку Ао и трансверсаль-
ной Тг. Иными словами: при слиянии фокальных кривых каждая дуга
гиперболы вырождается в дугу экстремали. Это свойство J-гиперболы есть
естественное обобщение случаев вырождения обыкновенной гиперболы.
Для доказательства обратим внимание, что если Г2 при своем изме-
изменении сливается с 1\, то f2 сливается с ^; следовательно, р2 стремится
к р19 и уравнение B3) перейдет в уравнение:
dA__dH_ B4)
dx dp'
326 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
В этом уравнении, в выражении р = /у (х, у, У), х, у суть коорди-
координаты точки Л, а у' есть угловой коэфициент касательной к fi
в точке Л. Уравнение B4) есть одно из уравнений канонической формы
уравнения Эйлера.
Для получения второго уравнения построим пучок экстремалей {f},
трансверсальных к 1\; линия тA будет, очевидно, принадлежать этому
пучку. Обозначим, как раньше, через 7(лг, у) 7-расстояние от точки
А(х, у) до 1\. В силу E) § 93 имеем:
здесь в выражениях Н=Н(х, у, р) и p = Fy>(x, у, у'), у' равен
угловому коэфициенту касательной к экстремали пучка {^} 2). Отсюда,
пользуясь условием полного диференциала, получаем:
дН дН др _ др
dy dp ду ~ дх '
Заменяя, согласно B4), -х— через — -—-, получим:
дН- дР i дР аУ /9еч
1у~"дх"*"ду ~dZ' ^0)
Если правую часть уравнения B5) заменить полной производной ~, то
оно вместе с B4) даст искомые уравнения Эйлера в канонической форме.
Приведенные рассуждения приводят нас к следующему результату:
ТЕОРЕМА 1. Если фокальная кривая Г2 сливается с фокальной
кривой 1\, то ветвь J-гиперболы, проходящая через точку А, превра-
превращается в экстремаль, проходящую через А и трансверсальную Т1 3).
Если линии 1\ и Г2 вырождаются в точки (фокусы), а экстремали
суть прямые, то доказанная теорема даст известный результат относи-
относительно вырождения обыкновенной гиперболы.
Если экстремали суть геодезические на поверхности, то теорема дает
естественное обобщение свойств обыкновенной гиперболы на 7-гипер-
болы геометрии на поверхности.
Из доказанной теоремы как следствие получаем такой результат:
ТЕОРЕМА 2. Если J(x,y, а) есть J-расстояние от точки А(х, у)
до линии Га: у = у(х, а), где а — параметр и если © непрерывна вместе
со своими частными производными, то
при произвольной постоянной C есть уравнение экстремали.
г) Второе слагаемое в E) § 93 пропадает в силу трансверсальности линий
7i к ri-
2) Берется экстремаль пучка, проходящая через Л, и касательная прово-
проводится в точке Л.
3) См. Л. Л ю стер ни к, Замечания к некоторым вариационным задачам,
„Ученые записки МГУ", вып. II.
§ 98] МЕТОД ИНТЕГРИРОВАНИЯ ЯКОБИ 327
В самом деле, уравнение:
J (х, у, of) — J (х, у, а) = const. B6)
определяет некоторую J-гиперболу. Постоянную величину в B6) выберем
равной |3(а'— а). Уравнение нашей J-гиперболы примет вид:
J(x,y,a')-J(x.y,a) = i { .
Если а'->а, т. е. кривая Га, стремится к Га, гипербола переходит
в экстремаль. Из уравнения B7) следует, что вдоль этой экстремали:
6J о
§ 98. Метод интегрирования Якоби
Из приведенных выше рассмотрений весьма просто может быть уста-
установлена связь между задачей интегрирования уравнений Эйлера (обыкно-
(обыкновенных уравнений) и некоторого уравнения с частными производными.
Докажем предварительно две теоремы.
ТЕОРЕМА 1. Если Г есть кривая класса Ct, то J-расстояние
точки А (х, у) от кривой Г удовлетворяет следующему уравнению
s частных ироизводных:
dJ г т f dJ\ /new
— = Н[х,у,^)> B8)
где Н есть функция от х, у, р, определенная в § 93.
В самом деле, /-расстояние есть 7-длина дуги экстремали т, соеди-
соединяющей А(х,у) с кривой Г и трансверсальной к Г. Пусть точка В есть
конец дуги f, лежащий на кривой Г. Перейдем от А к близкой точке
Ar {x -f- dx, y-\-dy). Обозначим через Y экстремаль А'В\ соединяющую
точку А' с кривой Г трансверсально последней. Пусть координаты конца В
экстремали ^, лежащего на Г, при переходе к дуге *[', получают при-
приращения dx0, dy0; приращение 7-расстояния при переходе от Л к Л' будет:
[см. E) § 93]. Но вторая скобка вследствие трансверсальности к к Г
пропадает. Следовательно, dJ= H dx-\-pdy. Отсюда:
и dJ dJ
Рассматривая Н как функцию х, у, /?, получим искомое уравнение:
dJ rrf dJ\
Ъ = Н (*>У>-ЗуГ
ТЕОРЕМА 2 (обратная). Если J {х, у)—функция переменных х, у,
непрерывная вместе со своими частными производными, удовлетворяет
уравнению B8), то найдется константа К такая, что J (х, у) — К х)
выражает J-расстояние точки А (х, у) от кривой J (х, у) = К>
х) К есть такая константа, что уравнение J(x, у) = К выражает действитель-
действительную кривую класса Clt
328 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
В самом деле, обозначим через Г кривую, выраженную уравнением
J(x> у) — К\ в силу теоремы 1 7-расстояние от точки А (х, у) до Г удовле-
удовлетворяет уравнению B8). Так как 7 в уравнение B8) явно не входит,
то, следовательно, 7* (х, у)-\-К есть тоже интеграл уравнения B8).
В силу геометрического смысла J*(x, у) и условий теоремы, вдоль Г имеем:
Отсюда в силу теоремы единственности интегралов диференциальнъге
уравнений вида B8) 7(л:, у) = 7* (л:, у); теорема доказана.
Эту теорему можно доказать, не прибегая к теории уравнений в частных
производных. Можно, например, непосредственно установить, что всякая
линия, пересекающая трансверсально все линии семейства 7 (х, у) = К?
есть экстремаль. Отсюда будет следовать, что семейство 7 (лг, jy) =/С есть
поле трансверсалей. Останется показать, что 7-расстояние между транс-
версалями J = KX и 7 = АГ2 в точности равно К2 — Kv
Уравнение B8), характеризующее 7-расстояние в нашей неевклидовой
геометрии, носит название уравнения Якоби-Гамилътона.
Якоби впервые показал, что задача интегрирования уравнения B8)
приводится к задаче интегрирования уравнения Эйлера и наоборот.
ТЕОРЕМА 3. Зная общий интеграл уравнения Якоби-Гамилътона
B8), можно найти общий интеграл уравнения Эйлера G) и (8) *),
и, обратно, зная общий интеграл уравнения Эйлера, можно найти
общий интеграл уравнения Якоби-Гамильтона.
Пусть, в самом деле, мы нашли общий интеграл уравнения Эйлера,,
зависящий от двух параметров:
у=у(х,а,$; B9)
из каждой точки х, у в любом направлении можно провести экстремаль
семейства B9). Пусть имеем произвольную кривую Г класса Cv В каждой
точке этой кривой можно отметить направление, трансверсальное к Г. По
этому направлению можно провести экстремаль семейства B9), трансвер-
сальную к Г, а значит, определить понятие 7-расстояния от произволь-
произвольной точки Аа(х, у) до Г. Это 7-расстояние удовлетворяет уравнению Якоби:.
дх \ ^ ду)
Так как в уравнение Якоби входит не сама функция 7, а лишь ее произ-
производные, то при произвольном постоянном К функция 7 (лг, у) -f- К будет
также решением уравнения Якоби.
Рассмотрим теперь однопараметрическое семейство Га плоских кривых,
не образующих поля трансверсалей ни в какой части плоскости. Обозна-
Обозначим через J(x,y, а) 7-расстояние точки А (х, у) от кривой Га. Умея
решать уравнение Эйлера, мы сможем, как мы только что видели, опре-
определить функцию 7 (л:, у, а). Добавив постоянную C, получим решение
J(x,y, ос) —}— р уравнения Якоби, зависящее от двух параметров (так назы-
называемый общий интеграл уравнения Якоби). Из условия, что Га не обра-
образуют поля трансверсалей, следует, что две произвольные постоянные а и ^
нельзя свести к одной.
*) § 93.
§ 98] метод интегрирования якоби 329
Пусть, наоборот, задан общий интеграл уравнения Якоби:
В силу теоремы 2 при заданном а функция У (дг, у, а) выражает /-рас-
/-расстояние точки Л (х, у) от кривой У (х, у, а) = К, где К— некоторая
константа. В силу теоремы 3, приравнивая -^- постоянному, получим
экстремаль: ^У
~fa~a' . C0)
Эта экстремаль зависит от двух параметров а и а'. Таким образом фор-
формула C0) дает нам общий интеграл уравнения Эйлера 1).
""" Добавление. Как известно, полным интегралом уравнения в частных
производных первого порядка называется интеграл уравнения, в выражении
которого содержится произвольная функция.
Рассмотрим У-расстояние точки А (л:, у) до произвольной линии Г класса С^
Функция У, будучи интегралом уравнения Якоби-Гамильтона, зависит от про-
произвольной линии Г, т. е. от произвольной функции. Следовательно, согласно
определению полного интеграла У (x, yt Г) есть полный интеграл уравнения
Якоби-Гамильтона.
Таким образом, зная общий интеграл уравнения Эйлера, мы можем по-
построить полный интеграл соответствующего уравнения Якоби-Гамильтона.
Пример 1. Пусть
в таком случае:
У2 '
У1+у2 ' Y'14-у2 '
Уравнение Якоби-Гамильтона будет иметь вид:
х J l \ду J
Возьмем в качестве линий Га прямые, проходящие через начало координат:
х cos a -f- у sin а = 0;
в таком случае У-расстояние У(лг, у, а) от точки А (х} у) до Га будет обычным
расстоянием от А до прямой:
J (х> У> °0 = х cos a -J- у sin а.
В силу теоремы 3 общий интеграл уравнения C1) будет иметь вид:
У = х COS a -}- У Sin а -j- f,
где аир — произвольные постоянные:
Пример 2. Пусть:
F — -1—-LJL— (принцип Ферма);
v(x,y)
в таком случае:
V' 1
Р=7 № + Р* =
[v(x, у)]2
!) Легко видеть, что в уравнении C0) произвольные постоянные а, а' нельзя
свести к одной произвольной постоянной; в противном случае данный интеграл^
уравнения Якоби имел бы вид: У (х, у) — у (а) -}- р, т.е. не был бы общим
интегралом.
330 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Уравнение Якоби-Гамильтона будет иметь вид:
J-расстояние от точки А (х, у) до произвольной кривой Г будет выражать
оптическое расстояние от А до Г.
Рассмотрим частный случай, когда v=y; в этом случае экстремали задачи
«суть окружности, ортогональные оси Ох. Примем за кривые Га снова прямые
х cos а-{-у sin а = 0;
тогда оптическое расстояние J(x, у, а) от точки А (х, у) до кривой Г^ примет
вид: (к N
где о и 9 суть полярные координаты точки А. Отсюда получаем следующий
-общий интеграл уравнения C2) при v=y:
где а1 и J — произвольные постоянные.
Случай разделения переменных. Мы докажем сейчас следующую
георему.
ТЕОРЕМА. Если уравнение Якобы можно привести к виду:
то уравнения Якоби и Эйлера можно решить в квадратурах.
В самом деле, полагаем:
*(*-ё)-. *(*&)--•¦
где а — произвольное постоянное. Решая каждое из этих уравнений
соответственно относительно -— и -т—, получаем:
Отсюда получаем сразу общий интеграл уравнения Якоби:
J = f Фх (х, a)dx + f Ф, (у, a) rfy.
Прихменяя теорему 3, получим общий интеграл соответствующего урав-
уравнения Эйлера:
да "" J да ах-Г J fa пУ'
Случай интегрирования Лиувилля уравнения геодезической. Пусть
элемент длины линии на поверхности имеет вид:
d& = [?1 (х) - ?2 (.у)] (dx*
Уравнение Якоби примет вид:
J есть длина геодезической.
§ 98] МЕТОД ИНТЕГРИРОВАНИЯ ЯКОБИ 331
Положим:
отсюда получаем общий интеграл уравнения Якоби:
J = fV<?A*)-«dxJc /V* — Ъ(У)<*У- C3)
Уравнение геодезических примет вид:
~~2 J
д? ] /» dx
J
Эти формулы найдены Лиувиллем.
Таким образом и уравнение геодезической C4), и выражение C3)
для ее длины находятся путем квадратуры.
К случаю Лиувилля приводится также интегрирование уравнения гео-
геодезических, если элемент длины имеет вид:
ds* = [?1 (х) + ?2 су)] [ф, (jc) «tea 4- б2 су) <*/].
В самом деле, полагая
«!»1(x)dbea = rf«», «fe (.y) dy* =
и выражая а: через и, у через *, получим:
Мы пришли к случаю Лиувилля. Длина геодезической выразится инте-
интегралом: ,
J = J V?i[x(u)]—adu-{-J Vo. — ^
Уравнение геодезической -г- = р примет вид:
?iW 2 р2 (_у)
Пример. Геодезические на эллипсоиде. Рассмотрим на эллипсоиде
— а2
эллиптическую систему координат (k2, &3) (см. § 11). В этих координатах элемент
дуги ds кривой на эллипсоиде выразится:
* = 1 Г (^-*1)(*»-*я)
4 L (А«-«i) (*» - «г) (*»- в
^ + (*з~%) (*з ~ «2) (*в-
Полагая
Vl ~ 4 (ftj-eOCfta-e^Cfts-ej) ' '2 4 (fti-
получим:
*2 ( + )fe^2 +
332 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
В силу предыдущего результата длина геодезической на эллипсоиде выразится
интегралом:
J \ л г j 2 .2 з
или:
to —etfto—
^ 2 J V to -
Уравнение геодезической имеет вид:
> ~ «2) (fa — аг)
AJ У (Аз —в
to —
= $ — const.
§ 99. Функция Вейерштрасса
Окружение экстремали полем. Развитая выше теория поля позво-
позволяет установить новые необходимые условия, а также условия, доста-
достаточные для того, чтобы данная экстремаль давала сильный экстремум.
Введем два новых понятия, существенных при дальнейшем изложении.
Мы скажем, что экстремаль ^о может быть окружена полем экстре-
экстремалей, если существует поле экстремалей {^\, обладающее следующими
свойствами:
1°. Экстремаль ^0 является одной из дуг поля {у}.
2°. Экстремаль ^о лежит строго внутри области, покрытой полем.
Эти определения годятся как для случая экстремалей функционала /
(обыкновенная форма), так и для случая экстремалей функционала /
(параметрическая форма).
В приложениях этого понятия мы будем предполагать, что поле {^},
окружающее ^о> есть собственное поле, т. е. поле экстремалей, удовле-
удовлетворяющее условиям, перечисленным в § 94.
Остановимся подробно на функционале У.
Существование поля. Пусть дана экстремаль ч0, соединяющая данные
точки A(xv yj и В(х2, у2) (черт. 57). Решим вопрос, при каких усло-
условиях экстремаль ^о можно окру-
окружить полем экстремалей. Рас-
Рассмотрим отдельно случаи функцио-
функционалов J и /. Начнем с функцио-
функционала J. Положим, что ни точка В, ня
какая другая внутренняя точка экс-
экстремали 7о не есть точка, сопряжен-
сопряженная с А, Пусть, кроме того, вдоль
> 0. В этом случае
Черт. 57.
имеем
у у
экстремали -уо и в ее концах А и В
существует точка А0(х0, у0), лежащая на продолжении экстремали
за точку А, такая, что экстремальная дуга А^В (включая ее концы Ло
и В) не содержит точек, сопряженных с Ао (см. § 86). Экстремальную
§ 99] ФУНКЦИЯ ВЕЙЕРШТРАССА 333
дугу А0В обозначим через -fi- Рассмотрим семейство экстремалей, про-
проходящих через точку Ло.
' = <?(л;, а) I
«! < а < а2,
Так как огибающая этого семейства (если она существует) не пере-
пересекает экстремали -fi> то достаточно узкая полоска Q, ограниченная
абсциссами х = лг2, х = х0' (х0 < х0' < л^) и кривыми у = <р (л:, а/),
^у = <р {л:, а2'), с^ < аг' < а/ < <х2, окружающая ^0» тоже не имеет общих
точек с этой огибающей. Дуги -f экстремалей нашего семейства, покры-
покрывающие область Q, образуют на ней поле экстремалей, заключающее
экстремаль -fo*
Примем за параметр ос, определяющий кривые пучка экстремалей,
выходящих из точки Ло, угловой коэфициент касательной к экстремали
пучка в точке Ло. Из принятых нами условий относительно функции
F{x, у, у') будет следовать, что построенное нами поле {-(}, окружающее
экстремаль -fo> будет собственное поле. Мы получаем таким образом
следующий результат.
ТЕОРЕМА. Для того чтобы экстремаль -fo можно било окружить
полем экстремалей, достаточно, чтобы:
1) вдоль экстремали -f0 {включая ее концы) имели Fy>y' > О,
2) дуга -(о вместе с одним из ее концов не содержала точки,
сопряженной другому концу.
Ничего не меняя в проведенных рассуждениях, мы для случая функцио-
функционала / получим следующее условие для существования поля, окружаю-
окружающего экстремаль -fo-
ТЕОРЕМА. Для того чтобы экстремаль ^0 функционала I можно
было окружить полем экстремалей, достаточно, чтобы:
1) вдоль -fo {включая ее концы) имели Fx > О,
2) дуга -fo вместе с одним из ее концов не содержала точки,
сопряженной другому концу.
Теорема Гильберта. Пусть нам дана экстремаль ^0 и пусть ^0 воз-
возможно окружить полем экстремалей \^}у покрывающим область Q. Тео-
Теорема Гильберта дает возможность вычислять значение функционала для -f0
при помощи криволинейного интеграла, взятого вдоль любой кривой,
¦соединяющей концы -fo и расположенной в любой достаточно малой
окрестности ^0.
Начнем с рассмотрения функционала J.
Пусть через точку Л(лг, у) области Q проходит экстремаль ^ поля {-f}",
обозначим через и{х, у) угловой коэфициент касательной к ?> прове-
проведенной в точке Л. Согласно условиям, которым удовлетворяет поле {^},
определенная нами функция и {х, у) есть функция определенная и непре-
непрерывная вместе со своими частными производными в области Q. Функция
и (лг, у) играет существенную роль в теории поля; она называется функ-
функцией наклона.поля {у}. Значение и{х, у) в точке Л(лг, у) будем назы-
называть наклоном поля в точке Л.
Проведем теперь через концы экстремали f0 трансверсали 1\ и Г2
поля {^} (черт. 57). /-расстояние J {А) произвольной точки А (х> у)
334 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
области Q до трансверсали 1\ есть однозначная функция х, у в области Q:
j(A) = J(x, у). В силу рассмотрений § 93 имеем:
dJ—Hdx-\-pdy,
где
Я = Щх, y) = F [х, у, и (лг, у)] — и (х, у) /у [*, у, и (х, у)],
р = р(х, y) = Fy> [x, у, и(х, у)].
Таким образом выражение Hdx-{-pdy есть полный диференциал. Сле-
Следовательно, криволинейный интеграл Hdx-\-pdy, взятый вдоль-
любой линии 7 класса Ov принадлежащей Q, есть однозначная
функция координат концов *(. В силу теорем о трансверсалях этот
интеграл равен /-расстоянию между трансверсалями поля, проведенными
через концы ^. Если линия у соединяет точки Л и В (является допу-
допустимой линией вариационной задачи), то интеграл Hdx-\-pdy выра-
Т
жает /-расстояние между трансверсалями Т1 и Г2, т. е. равен значению /
вдоль 7о: /» г
j =J F(x,y, /)dx.
Т y
Мы получили, таким образом, следующий результат:
ТЕОРЕМА ГИЛЬБЕРТА. Для любой линии ^ класса Ov принадле-
принадлежащей полю {•(} и имеющей концы в точках М(х0, у0) и N(x, y\
имеем: _ „
j — J(x0, у0),
где J(x, у) есть J-расстояние от точки (х, у) до трансверсали поля*
Если концы 7 принадлежат трансверсалям Тх и Г2, проходящим через
концы экстремали ^0, то J*(i) равен i(-fo)-
Распространим теорему Гильберта на случай функционала /. Итак,
пусть ^0 есть экстремаль функционала /. Сохраним геометрические по-
построения, проделанные при выводе теорем Гильберта для случая функцио-
функционала J. Пусть f есть экстремаль поля {^} (окружающего экстремаль -fo)>
проходящая через точку М (лг, у). Обозначим через и (х, у) и v (лг, у)
направляющие косинусы касательной к у, проведенной через точку М.
Обозначая, как раньше, через J(x, у) J-расстояние точки М(х, у) до
трансверсали поля 1\ (проходящей через конец -fo)> будем иметь:
dJ (х, у) = Fx* [х,у9и (х, у), v (дг, у)] dx -f Fy< [х, у, и (х, у), v (x, у)] dy =
— Н dx-\~ p dy.
Таким образом в разбираемом случае выражение Hdx-\-pdy будет
также полным диференциалом. Отсюда заключаем, что если в приведенной
выше формулировке теоремы Гильберта вместо Н и р подставить соот-
соответственно Fx> и Fy'y то теорема годится также для функционалов /.
§ 99] ФУНКЦИЯ ВЕЙЕРШТРАССА 335*
Функция Вейерштрасса. Введем следующие обозначения:
Е(х, у; и, u) = F(x, у, u) — F(x, у, u) — (u — u)Fu(x, у, и)
для случая функционала J и
Ег(х, у; и, V] и, v) = u [/у (ху у, и, v) — Fx> (лг, у, и, if)] +
+ v iFy' (х> У> и, V) — Fy' (*> У у и> *)]
для случая функционала /. Функции Е и Ех носят название функций
Вейерштрасса.
Используя теорему Гильберта, оказывается возможным весьма проста
найти выражение приращений функционалов J и / при помощи введенных
функций Вейерштрасса.
Начнем с функционалов J. Итак, пусть ^0 есть экстремаль, соеди-
соединяющая точки А и В. Пусть, кроме того, экстремаль *(о возможно окру-
окружить полем экстремалей {?}, покрывающим область Q. В таком случае
в силу теоремы Гильберта, какова бы ни была линия -f класса d, сое-
соединяющая точки Л и В и принадлежащая области Q, имеем:
Yo
Следовательно:
fF(x, у, /) dx = fHdx+pdy = f(H-\-p^L) dx.
(^ У, /)dx—fF(x, у, /) dx
т
(x. v. •/) dx —
Y Y Y
Заменяя Н и р их выражениями через F и вводя функцию ?", оконча-
окончательно получим:
M=fF (х, у, «(*, j/), ~)^. C5>
Y
Рассмотрим теперь функционал /. Сохраняя обозначения, принятые
выше, и применяя теорему Гильберта, получим:
У-» ll\Xi У)ч v \xi У)\ ах , гу [х> У-> 11\х> У)-» v \х, УI аУ •
Обозначая через cfs элемент дуги линии у и через а (х, у) и v (x, у}
направляющие косинусы касательной к-f в точке (л:, у): --- = и(х,у)>
—У- = у (х, у), будем иметь:
1 dt= j {Fx' [х, у, и (л:, у), v (х, у)] и4-
Y _
Л~ру' [*> У> п (х> У)> v ^» У)] v)ds-
«336 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Отсюда, принимая за параметр длину дуги, получим:
/(То)==
я, v) — v?yr{x, у, и, v)] ds.
t
Пользуясь условиями однородности, функцию F можно представить так:
F (лг, у, и, v) = uFx* (x, у, и, v) -}- vFy> (x, у, и, v).
Подставляя найденное выражение для F под знак интеграла и вводя
«функцию Вейерштрасса, окончательно получим:
Д/ = fE1(x9 y\ и, v, uy v) ds. C6)
Y
Формулы C5) и C6) носят название формул Вейерштрасса для
представления приращения функционала.
Из формул Вейерштрасса непосредственно вытекает следующий
результат: если экстремаль -fo можно окружить полем экстремалей,
то для того чтобы ^0 давала сильный экстремум, необходимо и доста-
точно, чтобы для любой линии -f класса Cv
соединяющей концы ^0, имели:
М
I Edx^O (обыкновенная форма),
/ Е1 dx ^> 0 (параметрическая форма).
Г,
Черт. 58.
f
Приведенный интегральный критерий сильного экстремума сам по себе,
в^силу своей громоздкости, практически мало удобен, но из этого критерия,
как мы увидим ниже, просто выводятся новые необходимые условия
сильного минимума, а также получаются практически ценные достаточные
условия. Прежде чем перейти к этим критериям, остановимся на геоме-
геометрической интерпретации функций Е. Мы ограничимся при этом случаем
функционала J.
Геометрический смысл функции Вейерштрасса. Пусть в области Q
дана точка М (х, у) и близкая точка М' {х -|- dx, y~\-dy) (черт. 58);
угловой коэфициент направления ММ! будет равен и=~. У-длина от-
отрезка ММ равна F (ху у, и) dx. С другой стороны, в области Q опре-
определена функция J точки, означающая расстояние точки до линии 1\. При
переходе от Ж к М\ J получает приращение:
F{x, у, u) — (u—u)Fy<(x, у, и),
где и — угловой коэфициент проходящей через М экстремали, dJ выра-
выражает расстояние между трансверсалями, проходящими через точки М и М\
.Разность F (х, у, и) dx — dJ дает, следовательно, избыток /-длины эле-
элемента ММ над /-расстоянием между трансверсалями, проходящими через
§ 100] НЕОБХОДИМОЕ УСЛОВИЕ ВЕЙЕРШТРАССА 337
точки М, Мг. Но F (х, у, u)dx— dJ=*=E (лг, у\ и, и) dx. Отсюда инте-
интеграл / Е (х, у; и, и) dx, взятый вдоль кривой f, равен избытку длины этой
кривой над расстоянием между трансверсалями, проходящими через концы -f.
Если оба конца у, А и В лежат на одной и той же экстремали ^
поля, то /-расстояние между проходящими через А и В трансверсалями
равно У-длине -f- Следовательно, здесь / Е (х, у\ и, и) dx означает избы-
__ т
ток У-длины f над У-длиной ? (Цермело).
§ 100. Необходимое условие Вейерштрасса
Необходимые условия сильного экстремума. Пусть экстремаль -fo
соединяет точки А, В. Опираясь на рассмотрения предыдущего параграфа,
установим следующее новое необходимое условие для того, чтобы -fo
реализовала сильный минимум.
ТЕОРЕМА. Для того чтобы экстремаль То реализовала сильный
минимум функционала У, соответственно /, необходимо, чтобы вдоль -fo
при любых значениях 6 удовлетворялось неравенство:
Е (х, У) У, tg6);>0 (обыкновенная форма) х),
?х (лг, у; х', У; cos 6, sin 6) >- 0 (параметрическая форма).
Доказательство этого предложения проводится совершенно одинаково
как для случая функционала У, так и для случая функционала /; по этой
причине мы ограничимся рассмотрением функционала У.
Предположим противное: в некоторой точке Мх (х, у) экстремали ^о
и для некоторого значения и имеет место обратное неравенство:
Е (х, у; у, а) < 0. C7)
Мы можем считать, что точка Mi отлична от концов А и В экстре-
экстремали ifo> в противном случае вследствие непрерывности функции Е можно
было бы заменить точку Мг близкой точкой экстремали, уже отлич-
отличной от концов 7о> Для которой
неравенство C7) по прежнему
удовлетворялось бы. Аналогич-
Аналогично мы можем считать, что на-
направление с угловым коэфициен-
том и не есть направление, ни
касательное, ни трансверсальное
нашей экстремали в точке Mv
Выберем на экстремали ^о точ~
ку М, лежащую между Мх и Л, такую, что дуга М[м не содержит пары
сопряженных точек (черт. 59). В таком случае мы можем построить поле
х) Это неравенство должны выполняться согласно условиям теоремы „вдоль* fo»
т. е. в любой точке М (х, у) кривой ?0» при значении у, равном угловому коэ-
фициенту касательной к fo» проведенной через точку NU Аналогичное пояснение
можно сделать ко второму неравенству: за х', у' можно принять здесь напра-
направляющие косинусы касательной к Yo в точке М.
338 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
экстремалей {^} с центром в точке Ж, охватывающее дугу ММХ экстре-
экстремали То- Проведем трансверсали ГиГ поля {^}, пересекающие То в Т04*
ках М2 и Mi9 где М^ расположена между М и М\. Далее из точки Мх
выпустим луч МгМ' с угловым коэфициентом и до пересечения с тран-
св?рсалью Г' в точке М\ Если точки Мг и М2 или, то же самое,,
линии Г и Г достаточно близки, то построение возможно и У-длина
отрезка М'МХ меньше У-расстояния между трансверсалями Г" и Г*
т. е. У-длина M'Mt меньше У-длины дуги М2Мг экстремали у0. Это сле-
следует из геометрического определения функции Е и условия Е < 0 (см. § 99).
Соединим теперь точку М' с точкой М экстремалью ММ' поля {^}.
У-длины дуги ММ' и ММ2 равны между собой (так как ММ' и ММ2 —
две экстремали центрального поля, концы М' и М2 которых лежат на
на одной трансверсали Г'). Отсюда следует: ломаная MM'MV состоящая
из дуг ММ' и отрезка MfMv обладает меньшей У-длиной сравнительна
с дугой ММХ экстремали ^0. Заменив в ^о ДУГУ ММХ ломаной ММ'М1У
мы получим кривую, соединяющую те же точки А и В, J-длина которой
меньше J-длины -fo- Мы приходим к противоречию с условием теоремы,
следовательно, неравенство C7) не может иметь место. Теорема доказана.
Условие Лежандра как следствие условия Вейерштрасса. Разлагая
функцию F (л:, у, и) в ряд по степеням {и — и), мы получим:
Е(х,у, и, u) = (u — u)*Fuu[x,y, « + »(«—«)], 0<0<1.
Если Е (х, у\ а, и)^0 при любом и, то, следовательно, и
^.Л*. У, « + »(и —«)]">0.
При к, стремящейся к и, это неравенство переходит в неравенство»
^™(*> У> «)>0,
представляющее собой необходимое условие Лежандра.
1 Вполне аналогично может быть установлена связь между условием
Вейерштрасса и условием Лежандра при разыскании экстремума функцио*
нала /. В самом деле, применяя к выражениям в квадратных скобках:
Е1=п [Fu (x, у, и, v) — Fu (x, у, и9
+^ № (х> У> и» ^) — Fv fa У» ">> v)]
(и = cos б, v = sin б, и = cos 6, v = sin 6),
формулу Лагранжа и используя соотношения
получим:
Е (х, у\ и, v\ ~п, v) = [1 — cos (?— 6)] F± (x, у, cos 6*, sin 6*),
где 6* заключено между 6 и 6 и где положено и = cos б, v = sin б,
и = cos О, 5 = sin в!
§ 101] ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА 339
Отсюда, если вдоль экстремали выполняется условие Вейерштрасса
^ Ег (х, у; х\ /; п, v) > 0
при любом значении Й, то вдоль этой экстремали имеем:
Ft (х, у, cos 6*, sin б*) > 0.
Условие Лежандра получается отсюда как предельный случай, когда 6
стремится к 6.
§ 101. Достаточные условия сильного экстремума
Перейдем к выводу достаточных условий сильного минимума, причем
рассмотрим отдельно условия минимума функционала J и функционала /.
Функционал J. Докажем следующую основную теорему:
ТЕОРЕМА. Для того чтобы экстремаль fo, соединяющая точки Л.
и В, давала сильный минимум J-длин кривых (класса С), соединяющих
точки А и В, достаточно, чтобы:
1) То можно было окружить полем экстремалей,
2) существовала окрестность экстремали ^0, в каждой точке (х, у)
которой при любом значении и имели:
Е (лг, у\ и (лг, у\ и) > 0,
где и (х, у) есть функция наклона поля.
В самом деле, при е достаточно малом всякая кривая у класса допу-
допустимых линий, принадлежащая е-окрестности нулевого порядка линии ^0,
будет принадлежать области, покрытой полем {-(}. Следовательно, в силу
формулы Вейерштрасса, для у будем иметь:
J (Т) - J (То) = /Е (х, у, и (х, у), п) dx.
т _
Но по второму условию теоремы при s достаточно малом вдоль ^
Е(х, у) и(х, у), и)>0.
Следовательно, существует з > 0 такое, что для любой кривой у класса до-
допустимых линий, принадлежащей е-окрестности экстремали ^0, будем иметь:
•/(T)--/(To)>0.
Теорема полностью доказана.
Сравнивая необходимые условия с достаточными условиями, мы видим,
что необходимые условия — условие Якоби и условие Вейерштрасса — на-
накладывают ограничения на F в точках изучаемой экстремали; среди достаточ-
достаточных условий первое — усиленное условие Якоби — также накладывает огра-
ограничения на F в точках самой экстремали, что же касается второго усло-
условия, то для его применения нам надо знать поведение F в некоторой
конечной окрестности изучаемой экстремали. Отсюда, естественно,
возникает вопрос, нельзя ли это второе условие заменить усиленным
необходимым условием Вейерштрасса:
Е (х, у\ и (ху у), и) > 0, E ф и)
вдоль экстремали.
340 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Приведем пример, который покажет, что отмеченного ослабления
в достаточных условиях сделать нельзя. Этот пример покажет также
недостаточность ослабленного услозия, если дополнительно допустить,
что вдоль экстремали /^у > 0 х).
Пример. Поставим задачу: найти минимум функционала
1
— \byy'* + 2bxyr*) dx {а > 0, Ь > 0),
о
принимая за класс допустимых линий линии класса С1? соединяющие точки,
А @, 0) и В A, 0).
Прямые, параллельные оси Ох, суть экстремали для /. Экстремаль fo»
соединяющая точки Л, В, есть отрезок [0, 1] действительной оси, и эта экстре-
экстремаль, очевидно, может быть окружена полем экстремалей. Кроме того, имеем:
Е (х, у\ у', и) = (и —УJ {а — Ыуу' + 6bxy'* — 4Ьи (у — xy
Вдоль 7о получим:
1
E = ut(a + 2ЬхФ) > 0 при и
Таким образом экстремаль Yo удовлетворяет первому из достаточных условий,
а также усиленному необходимому условию Веиерштрасса. Покажем, что тем
не менее Yo не дает сильного минимума. Для этой цели построим ломаную"?: АМВ.
Пусть /г>0 и k суть координаты точки М; имеем:
где е (h) стремится к нулю вместе с h. Отсюда видим> что при любом k можно
всегда подобрать h настолько малым, чтобы /(у)—/(ТоХ^ т- е- То не Дает
сильного минимума / среди линий класса Dlt а, следовательно, и среди линий
класса С1#
Сводка необходимых и достаточных условий минимума. Приведем
основные полученные выше необходимые и достаточные условия мини-
минимума функционала х%
г*
= fF(x,yy/)dx.
Для того чтобы линия т0: у=у(х) класса Ci> соединяющая точки А
и В среди кривых класса, соединяющих точки А и й, давала слабый
экстремум, необходимо, чтобы:
1) линия Yo была экстремалью, т. е.у =у (х) являлась интегралом урав-
уравнения Эйлера:
2) вдоль т0 выполнялось условие Лежандра
3) То Удовлетворяла условию Якоби: не содержать точек, сопряжен-
сопряженных своему концу, или, аналитически, интеграл уравнения Якоби
г) Это обстоятельство является отличительной чертой теории экстремума J
по сравнению с теорией сильного экстремума /.
§ 101] ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА 341
выходящий из точки (хи 0), на пересекал оси Ох в точках интервала
хх < х < х2.
Чтобы т0 Давала сильный минимум, необходимо дополнительно:
4) вдоль 7о выполняется условие Вейерштрасса: вдоль т0 при любых
значениях и имеем;, „ , . ч. л
* Е (х, у, /, «)> 0.
Для того чтобы линия То давала слабый минимум, достаточно чтобы:
1) То была экстремалью,
2) вдоль То (включая концы) выполнялось усиленное условие
Лежандра:
у у ^ '
3) То удовлетворяла усиленному условию Якоби: интеграл уравнения
Якоби, выходящий из точки (хи 0), не пересекал оси Ох в точках за-
закрытого справа интервала:
Х1 < Х
Для сильного минимума достаточно, чтобы дополнительно:
4) существовала окрестность т0, в каждой точке которой при любом
значении а: Е (х, у, и (х, у), п)> 0,
где и (х, у) есть наклон поля, окружающего То*
Строгий минимум. Мы скажем, что линия То Дает функционалу J
строгий сальный минимум, если существует е-окрестность нулевого
порядка линии То такая, что для любой кривой т класса допустимых,
принадлежащей этой окрестности и отличной от т0, имеем:
Из приведенного выше доказательства теоремы (стр. 339) непосред-
непосредственно следует, что если в условиях, достаточных для сильного мини-
минимума, мы условие Е ^> 0 заменим условием Е > 0 (при прежних значе-
значениях аргументов), то кривая будет давать строгий сильный минимум.
Упрощенное достаточное условие. Если данную экстремаль то
можно окружить полем экстремалей, то вопрос, будет ли данная экстре-
экстремаль давать минимум, сводится, таким образом, к определению знака
функции Вейерштрасса Е. Ввиду того, что функция Е имеет довольно
громоздкий вид, достаточное условие Вейерштрасса заменяют часто
условием более грубым, но более простым.
Изобразим функцию Вейерштрасса в виде:
Е{х> у\ и, l)=\(a — ufFjy,[x, у, а + в(«-а)] @ < 6 < 1) *).
Мы замечаем, что для положительности функции Е достаточно, чтобы
при любом значении t имело место неравенство:
1) Разлагая разность F(x, у, Ъ) — F (х, у, и) в ряд Тейлора по степеням
(м — и) со вторым остаточным членом.
342 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Отсюда мы получаем следующий упрощенный критерий существования
минимума. Для того, чтобы эстремалъ ?о> соединяющая точка А и В9
давала сильный минимум „длин" кривых, соединяющих А и В, доста-
достаточно, чтобы экстремаль ^о можно было окружить полем экстре-
экстремалей {у}, в каждой точке которого при любом t
Для того чтобы наглядно сравнить условия (стр. 340), дадим еще
одну геометрическую интерпретацию функции Вейерштрасса. Изобразим
в плоскости uOz график функции _
z = F{xy у, и),
где х, у, считаются фиксированными. В та-
таком случае уравнение
z=F(x, у, u)-\-(ii — u)Fy,(x, у, и)
изобразится в виде касательной Т к нашей
кривой L (черт. 60):
z = F{x, у, и),
Черт. 60. проведенной в точке (и, F(x> у, и)). Отсюда
функция Е в любой точке будет равна
разности ординат (при одной и той же абсциссе) точки кривой и
точки касательной. Условие положительности функции Е выразится
тем, что L должна располагаться над касательной 7*. Это условие
будет выполнено, если кривая L будет вогнутая, т. е. если F * »(х, у, и)
будет неотрицательна при любом и.
Пример 1. Задача о брахистохроне. Как мы видели, для этой задачи
при любом расположении точек
i, Уд, В (х2, у2) (*! < х2, ух < у2)
условия Лежандра и Якоби являются выполненными, следовательно, экстре-
экстремаль -/о» соединяющую Л и В, можно окружить полем экстремалей. Кроме того,
для этой задачи:
F л yi+y2 __ 1 __1__>0
у'у' дуп y~v Уу ~
A+У2J
при любом у и У; следовательно, экстремаль -/о Дает сильный минимум.
Пример 2. Задача о рефракции. Для этой задачи функция [F(x, у, yf)
имеет вид:
F= ,4
V (X, у)
Здесь условие Вейерштрасса выполняется для любой функции
Таким образом вопрос, будет ли экстремаль -/о давать минимум /-длин,
сводится всецело к вопросу, можно ли -/о окружить полем экстремалей. В част-
частности, когда скорость распространения обратно пропорциональна у, экстремали
§ 101] ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА 343
суть полуокружности, ортогональные оси Ох. В этом случае при любом рас-
расположении точек А и В можно построить экстремаль, соединяющую эти
точки, и можно также построить поле экстремалей, окружающее экстремаль -/о*
Дуга окружности дает сильный минимум.
Пример 3. Задача о геодезических. Функция F имеет вид:
F= Y Л + 2Ву' + Су7*,
где Л, В, С суть непрерывные функции х, у> и форма
положительна в любой точке (х, у), т. е. В2 — ЛС<0, Для этой задачи:
р АС-Б*
Гу'У — з~'
Следовательно, всякая геодезическая т0, которую можно окружить полем геоде-
геодезических, дает сильный минимум длин дуг, соединяющих А и В.
Пример 4. Наименьшая поверхность вращения. Так же как и в примере 2,
условия Вейерштрасса выполнены для любой экстремали; следовательно, среди
двух экстремалей, соединяющих точки А к В, верхняя экстремаль дает сильный
минимум площади поверхности вращения.
Функционал /. Для функционала / оказывается возможным дать
достаточные условия сильного минимума, ограничивающие поведение
поди«тегральной функции лишь в точках самой экстремали То-
ТЕОРЕМА. Для того чтобы экстремаль То, соединяющая точки
А и В9 давала сильный минимум функционалу
(х, у, х\ /)dt
среди линий класса Cv соединяющих точки А и В, достаточно, чтобы:
V) экстремаль т0 можно окружить полем экстремалей {•(},
2 ) вдоль экстремали ^0 было удовлетворено усиленное условие
Лежандра:
F1 (х, у, *', /) > О,
3') вдоль экстремали -fo nPu произвольном значении 6 удовлетво-
удовлетворялось усиленное условие Вейерштрасса:
Е (х, у; cos 6, sin 6; cos (F, sin b) > 0 при 6 ф 6,
где cos 6 и sin 6 суть направляющие косинусы экстремали f0 в точке
{*, у) (см. стр. 338).
Для доказательства введем вспомогательную функцию Е±1\ опре-
определяемую следующими условиями:
| ?*! (лг, у; cos б, sin 0, cos (Г, sin 6) —
Е^\х, у; cos 6, sin 6; cos ё", sin F) = | 1 — cos (G — 6)
I ^l (*> У у cos e» sin 6) при 1=6.
Согласно общим теоретико-функциональным условиям, наложенным на F,
построенная функция Е^ определена и непрерывна вдоль линий поля
|f} в некоторой окрестности кривой *@ при всех значениях G. Так как 9
344 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
фигурирует лишь под знаком периодических функций — косинуса и
синуса,—то отсюда заключаем, что при определении знака Е^ доста-
достаточно считать 6 меняющейся в пределах 0 <; 6~<; 2тг.
В силу условий 2' и 3', в некоторой замкнутой окрестности Qo кри-
кривой Yo вдоль линий поля {^} для всех значений 0 <^ 0 <^ 2тс имеем:
я « > о.
Отсюда заключаем, что в указанной окрестности Qo при 0 ^
Е^ достигает минимума, отличного от нуля:
Следовательно, в каждой точке Qo при всех значениях 6 имеем:
Ех > я [1 —cos E —6)].
Отсюда, какова бы ни была линия -у класса допустимых линий, при-
принадлежащая Qo, имеем:
— /(То)= f Exds> a f [l — cos(b —
7
Этим самым полностью доказано, что -fo дает сильный минимум.
: Строгий минимум. Так же как для случая функционала J, для функ-
функционала / можно ввести понятие строгого минимума. Мы скажем, что
линия 7о Дает строгий сильный минимум функционала /, если суще-
существует е-окрестность нулевого порядка линии ^о такая, что вдоль любой
линии f, отличной от -fa из этой окрестности., но имеющей с ней общие
концы, имеем: __
Нетрудно показать, что при условиях только что доказанной теоремы
мы имеем строгий сильный минимум. В самом деле, из формулы (А)
следует, что /(j) — /(jo) = O тогда и только тогда, когда
1— cos F — 6)ееО,
т. е. когда
6*"" л
= ь.
Используя условия, определяющие „собственное поле" (см. §94), и?
опираясь на теорему единственности интегралов диференциальных урав-
уравнений первого порядка, нетрудно показать, что из 6 = 6 следует совпа-
совпадение 7 и f0. Отсюда заключаем, что в условиях теоремы (стр. 333) при
Т, не совпадающей с fo> имеем:
т. е. 7о Дает строгий минимум.
§ 102] ТЕОРЕМА ОСГУДА 345
§ 102. Теорема Осгуда
Подход к оценке приращения функционала. Рассмотрим функцио*
налы J и /:
J= fF(x, Л /) dx, 1= fF(x, У, *, У) dsy
т т
которые мы изучали в двух последних параграфах. Было показано, что
если экстремаль ^о функционала J и / удовлетворяет соответственно
условиям 2), 3) и усиленному условию 4): Е > 0 (стр. 341) или условиям
теоремы (стр. 343), то эта экстремаль дает сильный экстремум соответ-
соответствующего функционала, т. е. при соблюдении этих условий существует
область Q, содержащая fo и такая, что
Л-г) > Л(то)> /(т)>/(то)
для любой линии f, содержащейся в Q и принадлежащей классу допу-
допустимых линий — линий класса Ci, имеющих общие концы с fo-
Эти результаты являются аналогами достаточных условий сильного
минимума функций одной и многих переменных. В теории экстремумов
функций точки (§ 17) было показано, что если точка Мо есть стацио-
стационарная точка для функции f(M) и если квадратический член разложения
/(Ж) в окрестности Мо есть положительно-определенная форма, то
в некоторой окрестности точки Мо имеем:
/(Ж)— f(M0)>k\MM0\*y
где k есть константа. Таким образом в теории экстремумов функций
точки достаточные условия давали возможность установить не только
знак разности f(M)—/(Жо), но позволяли оценить снизу эту разность
в зависимости от расстояния точки М до стационарной точки.
По аналогии с теорией экстремумов функций точки, естественно,
возникает вопрос о возможности для случая функционалов установить
не только знак разности J(f) — ^(То)> но также дать оценку этой раз-
разности в зависимости от расстояния линии f до экстремали fo*
Осгуд впервые показал, что при некоторых дополнительных условиях
относительно экстремали fo поставленный вопрос решается в положи-
положительном смысле. Теорема Осгуда и ее дальнейшие обобщения наряду
с большим самостоятельным значением, как мы увидим ниже, играет
основную роль при доказательстве сходимости некоторых приближенных
решений вариационных задач.
Разберем отдельно теорему Осгуда для функционалов J и /.
Функционал J. Сохраняя обозначения, принятые выше, докажем
следующую теорему:
ТЕОРЕМА 1. Пусть экстремаль т0: у—уо(х) функционала J соеди-
соединяет две данные точки А и В и удовлетворяет следующим условиям:
1) fo можно окружить полем экстремалей {if}.'
346 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Пусть, кроме того:
П ^ ^ ^Х ^ \ Х1 ^> X ^. Х<2
*х ~& *М |а|<«0 '
для ??&*: точек поля {f}> гдг ^ и [i2 ?у/яь константы.
2) Б области Q, покрытой полем, при любом значении уг имеем
F '*(х, у у у') > [а > 0, гд? |х — константа.
При этих условиях существует константа k такая, что
zde ^ — любая кривая класса Dj, соединяющая точки Л и В, принад*
лежащая Q и не принадлежащая в-окрестности fo-
В самом деле, согласно формуле Вейерштрасса (стр. 325) имеем:
/ — и {х, у)} Fy'yf (лт, уу f) dx,
Y
тде д (х, у) есть функция наклона поля и t—функция лг, заключенная
между и {х, у) и у\ Отсюда, принимая во внимание второе условие
теоремы, получим:
JW — J(То) >?/[/—и (х, У)Jdx.
Так как по условию дуга у: у = у(х) не принадлежит е-окрестности
дуги fo> т0 на ДУге Т существует точка С E, т)) такая, что:
h—.Уо(91>е- (В)
Обозначим через fi ДУГУ кривой f> соединяющую Л с С. Очевидно,
имеем:
J (Т) — ^(То) > Р У [/ — и (а:, ^)]2^. C8)
Ti
Обозначим через а = а(дг) параметр, определяющий линию поля {f},
лроходящую через точку [х,у(х)]. Функцию а = ос(лг) можно рассма-
рассматривать как уравнение линии у, если за координаты принять х и а.
Так как в силу условий теоремы каждая дуга поля среди линий класса D1?
соединяющих ее концы, реализует сильный экстремум функционала J, то
(если а = а (х) при а < х < Е не есть монотонная функция л;) в нера-
неравенстве C8) дугу -^ можно заменить дугой ^2: а = ах (л;), соединяющей
точки Л и С, для которой а==а1(д:) будет монотонной функцией х.
В соответствии с этим мы будем в дальнейшем считать функцию а = а (х),
определяющую fi> монотонной функцией х\ пусть для определенности —
возрастающей.
Для дальнейших оценок воспользуемся неравенством Шварца:
f?2(*)d*. f^2(x)dx^(^Ji<D(x)^\
§ 102] ТЕОРЕМА ОСГУДА 347
Полагая в этом неравенстве ср (х)=1 и ф (х)=у' (х)—и [х, у (#)], получим:
Tfi Ti
Принимая во внимание геометрический смысл и (д:, у), нетрудно ви-
видеть, что: ^ , .
{/(х) — и[х, y(x)]}dx= п? а) da (а = <*(*)).
Отсюда, принимая во внимание монотонность а = а (л;), получим:
Ti О
где а = О есть линия fo и а = ах есть линия поля, проходящая через
точку С. Так как по первому условию теоремы — > \ily то из (а)
и (Ь) получаем: ttl
Кроме того, в силу (В)
е
Отсюда окончательно:
<
Теорема полностью доказана.
Для оценки разности J(y) — /(fo) снизу в некоторых случаях ока-
оказывается более сильным метод, существенно отличный от метода,
использованного нами при доказательстве теоремы 1. Для иллюстрации
этого метода докажем следующую теорему:
ТЕОРЕМА 2. Пусть fo: У — Уо С*0 есть экстремаль функционала J,
соединяющая точки А и В и обладающая следующими свойствами:
1. fo можно окружить полем экстремалей {•(}: у = %(х, а),
<*2> Ial^ao> х(х> °)=ЛD Пусть, кроме того:
для всех точек поля {^}, где у>х и \i2—константы.
2. В каждой точке области Q, покрытой полем {f}, ^ри любых
значениях у' имеем: е ,
Пусть, кроме того, C(S, tj), atx < 6 < дг2, Jyj—Л(^)|>4 ^т6 точка
области Q.
При этих условиях существует константа k > 0, зависящая
только от вида функционала J и числа S, такая} что:
J(i)-J(fo)>^, C9)
где f — любая линия класса D1? соединяющая Л и В, принадлежа-
принадлежащая — Q и проходящая через С.
348 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
Заметим прежде всего, что нижняя граница разнести ) т)
есть возрастающая функция е (при фиксированном ?). В самом деле,
пусть Yi — кривая, соответствующая значению е==е1(<у1 проходит через
точку С(Е, т<), |т]— ^oG)|>si)- Пусть теперь Ct(i9 тг^) —точка обла-
области Q: |^i | < е2 < ei> расположенная относительно fo с той же ст0"
роны, что и точка С; т^ > 0. Проведем через Сг экстремаль т поля;
пусть Лх и В1— точки пересечения этой экстремали с кривой fi- Заме-
Заменим дугу А1В1 кривой "^ дугой экстремали -у; полученную дугу обозна-
обозначим через 72- В силу условий теоремы имеем А^) < ^(Yi)> т* е* для
всякого в2 < ег найдется кривая f2, соответствующая этому s2 и такая,
что J fa) — J (то) < i (Ti) — J (То)*> этим самым наше утверждение
доказано.
Из сделанного замечания следует, что при доказательстве теоремы
мы можем предполагать |y]| = s и е как угодно малым. Теми же рас-
рассуждениями нетрудно показать, что как бы мало ни было число т], при
доказательстве C9) можно ограничиться рассмотрением кривых f> Pac"
положенных в Tj-окрестности кривой -fo-
Проведем через точки Л и В пучки экстремалей функционала /.
Будем теперь число ?) считать настолько малым, чтобы:
1) через точку С (?, т^) проходила экстремаль каждого из построен-
построенных пучков,
2) каждая из двух экстремалей АС, СВ пучков могла быть окру-
окружена полем экстремалей {^}А {т}р>
3) область QA, покрытая {f }A, должна содержать дугу АС кривой
f, а область QB, покрытая {f}^ должна содержать дугу СВ кривой ^.
Так как по построению и условиям теоремы каждая из дуг АС и
СВ пучков экстремалей реализует сильный экстремум и так как дуги
АС и СВ кривой 7 принадлежат полям, окружающим дуги АС и СВ
пучков, то отсюда заключаем, что:
f
АО
J
f J Fdx,
АО СВ
где последние два интеграла берутся по соответствующим дугам пучков.
Пусть у = у1(х) есть уравнение дуги АС пучка экстремалей, выхо-
выходящих из А, и пусть и (х, у) есть функция наклона поля Q. При этих
обозначениях в силу формулы Вейерштрасса получаем:
I JG) — Hb) > f W (*)/- «(х, y)\\FyW (x, у, t) dx,
AC
причем t заключено между у/ (х) и u[x, yx]. Так как вдоль АС
функции ^/(лг)! и и(х, у) ограничены и так как /у^ > 0, то отсюда
заключаем, что вдоль AC Fyfy* (дг, у, t) имеет положительную нижнюю
границу [i3.
§ 102] ТЕОРЕМА ОСГУДА 349
Отсюда:
J(Т)- J(То)
АС
Рассуждая теперь, .как при доказательстве теоремы 1, получим оконча-
окончательный результат.
Комбинируя оба из приведенных выше методов, нетрудно установить
теорему, обобщающую каждую из доказанных выше теорем.
ТЕОРЕМА 3. Пусть -fo— экстремаль функционала J, соединяющая
две данные точки А и В и такая, что:
1. -fo можно окружить полем экстремалей {-у}, удовлетворяющим
тем же условиям, что и в теоремах I и 2.
2. Существует г\-окрестность кривой уо такая, что в каждой
точке (х, у) этой окрестности при любом значении у' имеем
3. Существуют окрестности точек А и В, в которых при любом
значении yry Fyy > [х > 0, где а — константа.
При этих условиях существует константа К такая, что
где f есть произвольная линия класса D1? соединяющая А и В, при-
надлежащая ^-окрестности и не принадлежащая е-окрестности
Кривой -ft).
Функционал /. Несущественным изменением методов, развитых выше,
предыдущие теоремы можно распространить на случай функционалов /.
Заметим сейчас же, что условия, при которых удается найти оценки
снизу для /(-у)— /(^о)? значительно меньше отличаются от условий для
сильного минимума /, чем это имегт место для функционалов J. При-
Приведем основную теорему, касающуюся оценки /(-() — /(to)*
ТЕОРЕМА 4. Пусть простая дуга 7о с концами А и В является
экстремалью функционала /. Пусть, кроме того, ^о удовлетворяет
условиям сильного минимума I (стр. 343), а в точках А и В пусть
дополнительно имеем:
Fi(xv y^Sos^ sin°6)>0,
F\ (X2> Уъ C0S.°> Sin 8)]>,0
при любых значениях б. При этих условиях существует ^-окрестность
дуги 7о и положительная функция /г(е)>0, 0 < г < yj такая, что:
7(т)-'(то)>л«,
где -у — любая дуга класса Dj, соединяющая А и В, принадлежащая
^-окрестности уо и нг принадлежащая ^-окрестности дуги ^0.
Обобщения. Без сущеегвенноги изменения тех же методов теорема Осгуда
может быть распространена на функционалы, зависящие от высших производ-
производных или от мяогих функций. Имеются также существенные результаты, обоб-
обобщающие теорему Осгуда для задач на условный экстремум.
Наряду с обобщением теоремы Осгуда на функционалы более общего вида
большой интерес представляет задача возможного уточнения теоремы Осгуда
350 ТЕОРИЯ ПОЛЯ И ДОСТАТОЧНЫЕ УСЛОВИЯ СИЛЬНОГО ЭКСТРЕМУМА [ГЛ. XIV
для простейшего случая: найти условия, возможно близкие к условиям, доста-
достаточным для сильного экстремума, при соблюдении которых имело бы место
заключение теоремы Осгуда.
Приложения. Последовательность кривых класса Dji
Ti» T2» • • •» Тя» • • • >
соединяющих точки А и В, мы назовем минимизирующей последовательностью^
для функционала J, если последовательность J (•/„), п = 1, 2, 3,..., при п -> оо
стремится к нижней границе значений У G), когда -у есть произвольная линия
класса допустимых линий.
Непосредственным применением теорем 2 и 3 мы получаем следующие
результаты:
Если экстремаль y0 удовлетворяет условиям теоремы 2, то всякая
минимизирующая последовательность кривых чп> принадлежащих области Q
и соединяющих тонки А и В, сходится к кривой -/о> причем каково бы ни:
было число е, эта сходимость является равномерной при х± + г < х < х2 — е.
Если ^экстремаль y0 удовлетворяет условиям теоремы 3, то-всякая ми-
минимизирующая последовательность кривых, принадлежащих Q и соединяющих:
А и В, равномерно сходится к кривой -/о-
ДОПОЛНЕНИЕ I
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ
1. Общие замечания
Особый класс вариационных задач представляют те, где за класс
допустимых линий {*f} принимаются замкнутые выпуклые линии *). Допу-
Допустимыми вариациями являются те, которые переводят выпуклую кривую
в выпуклую же.
Дадим вначале несколько определений. Из точки А выпуклой линии f
проведем всевозможные хорды АС, соединяющие точку А с другими
точками С кривой (черт. 61). Предельными для направлений хорд АС
будут два направления АВ и АВг, которые образуют два касательных
луча к кривой т в точке А. Эти направления существуют в каждой
Черт. 61. Черт. 62. Черт. 63.
точке кривой -у, поскольку направления хорд АС изменяются монотонно
при приближении С к Л. В силу выпуклости -у угол <р между напра-
направлениями АВ и АВг удовлетворяет неравенству:
О < ? < тт.
Если в некоторой точке Е ср = тс, то оба касательных луча EF
и EFV являющиеся продолжением один другого, образуют касательную
к кривой *у в точке Е.
Если А, С и С1 — три точки выпуклой кривой -у и лучи AD и ADX
суть продолжения хорд АС и ACV то в угле DXAD не заключаются
точки кривой f (черт. 62).
Пусть АВ (черт. 63) есть дуга выпуклой кривой -у, заключенная
между хордой АВ и касательными лучами АС и ВС к кривой -у, пересе-
пересекающимися в точке С. Допустимые вариации дуги АВ будут переводить
*) Здесь ;мы называем выпуклыми линиями линии, являющиеся границам»
выпуклых плоских тел (см. ч. I, стр. 137—141).
352
ДОПОЛНЕНИЕ I
€е в "дугу, заключенную в том же треугольнике АСВ, причем хорда А В
допускает только односторонние вариации — именно только те, которые
увеличивают площадь фигуры Q, ограниченной линией *у; наоборот,
ломаная ЛСВ допускает односторонние вариации — именно в сторону
уменьшения площади Q.
Рассмотрим теперь класс { ^} выпуклых кривых, заключенных в зам-
замкнутой области R. На кривых класса {f } определен функционал i(T)«
В силу общей теории экстремумов функций при односторонних вариа-
вариациях (гл. XII), экстремум J (j) достигается на выпуклой кривой ^> с0~
стоящей из дуг четырех родов:
.Черт. 64.
Черт. 65.
1)"дуг I\, вдоль которых вариация в точке от J (j) исчезает;
2) дуг Г2 — частей границы /?;
3) прямолинейных отрезков Г3, соединяющих концы дуг Г1 и Г2;
4)тломаных Г4, состоящих из пар касательных лучей к дугам 1\ и Г2.
Рассмотрим, например, задачу о максимуме площади выпуклой фигуры,
заключенной в замкнутой области #. Здесь J(*() означает площадь, огра-
ограниченную кривой 7- Так как для J (у) не существует экстремалей, то
граница у выпуклой фигуры в /?, имеющей максимальную площадь,
должна состоять только из дуг Г2, Г3, Г4 (черт. 64). При этом'хорда Л Л
из Г3, стягивающая концы двух дуг из Г2, должна обязательно^касаться
границы R в концах своих или посредине, в противном случае дуга АВ
допускает вариации, увеличивающие площадь, ограниченную Q (черт. 65).
Рассмотрим теперь следующую задачу: в области /?, ограниченной
кривой р, задана система точек Аг (/= 1, 2, . . . , п). Требуется по-
строить выпуклую фигуру Q наибольшей площади, заключенную
в JR, не содержащую внутри себя точек А{.
Наша задача есть частный случай предыдущей. Обозначим через /?х
многосвязную область, полученную выкидыванием на /? точек Аг. Гра-
Граница R1 состоит из кривой р и точек Аг По-предыдущему, граница ^
выпуклой фигуры Q, заключенной в R1 и обладающей максимальной
площадью, должна состоять из кусков границы /?х и прямолинейных
отрезков, касающихся границы /?1э но так как граница R1 состоит из
кривой р и точек Ар то прямолинейные отрезки — части у—должны
быть или касательными отрезками к р, или проходить через одну или
несколько точек Ах.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ 353
Рассмотрим случай, когда внутри отрезка FG, входящего в состав «у,
содержится только одна из наших точек АР причем FG не касается р.
Мы положим сначала, что концы F и G этого отрезка не лежат на р.
В таком случае точка Аг должна лежать на середине отрезка FG.
В самом деле, ,пусть, например, часть AXG
отрезка FG меньше части FA{. Пусть EF и
GH—прямолинейные отрезки части кри-
кривой *f> соседние к FG. Повернем (черт. 66)
отрезок FG вокруг точки Аг так, чтобы он
пересек отрезок GH в близкой к G точке G',
а продолжение отрезка EF—в близкой к F
точке F'. Так как отрезок FG не содержит
внутри себя кроме точки А} никаких дру-
других точек Ар я также точек границы р, то Черт. 66.
при достаточно малом угле поворота мы при
вращении FG не заденем этих точек Ау, переход от ломаной EFGH к
ломаной EF'G'H есть допустимая вариация соответственной части ли-
линии -у, притом увеличивающая площадь Q. В самом деле, при этой
вариации мы отнимаем от Q треугольник AfiG', но зато добавляем
к Q треугольник FF'A. большей площади. Следовательно, кривая y
не дает максимума площади ограниченной ею фигуры Q.
2. Выпуклое симметрическое тело в целочисленной сети
В теории чисел мы встречаемся со следующей задачей (Г. Минковский):
в п-мерном пространстве (хи х2, . .., хп) задана целочисленная сеть % х).
Найти выпуклое центрально-симметрическое тело с центром в одном
из узлов сети % наибольшего объема, не заключающее больше внутри
себя никаких узлов сети.
Не меняя общности задачи, можно считать, что центр этого тела
находится в начале координат О. Если подвергнуть пространство
(х1} дг2,...,лг„) линейному преобразованию
3
с целыми коэфициентами и детерминантом |#^. | = 1, то сеть Э1 перей-
перейдет в самое же себя, причем сохранятся объемы тел, их свойства выпук-
выпуклости, симметричности относительно О и свойство не содержать внутри
себя узлов сети 2(, кроме О; следовательно, каждое тело, реализующее
максимум для искомой задачи, может быть преобразовано в бесчислен-
бесчисленное множество других тел, тоже реализующих максимум площади.
Мы решим эту задачу сейчас для плоского случая, В силу общих
свойств решений подобных задач для экстремальной фигуры должны
быть допустимыми только односторонние вариации, уменьшающие ее
площадь. Эта фигура должна быть ©граничена прямолинейными отрез-
отрезками, заключающими узлы сети, причем, если внутри какого-либо гра-
граничного отрезка заключена только одна точка сети, то она должна
См. ч. 1, стр. 134—136.
354
ДОПОЛНЕНИЕ I
находиться посредине этого отрезка (см. конец предыдущего раздела).
Экстремальная фигура представляет собой центрально-симметрический
полигон Q, его периметр q содержит не менее двух пар симметрических
сторон, и, следовательно, q содержит не менее двух пар симметричных
относительно О узлов сети.
Пусть С и Cj—два соседних на полигоне Q узла сети (черт. 67).
Треугольник ОСС1 не содержит кроме точек С и Сх никаких узлов:
сети. В самом деле, вследствие выпуклости Q линии ОС и ОСг [лежат
внутри Q и не содержат по определению никаких узлов сети, кроме
концов; сторона CCt или проходит внутри полигона Q, тогда она тоже
не содержит узлов сети; или принадлежит границе Q, то, так как Сг
есть непосредственно соседняя к С узловая точка сети на Q, *на
отрезке СС1 других таких точек нет.
Итак, треугольник ОСС1 не содержит никаких узлов сети, кроме
своих вершин. Но тогда можно линейным преобразованием A) с целыми
Черт. 67.
Черт. 68.
коэфициентами а^ и детерминантом |afj.|=l преобразовать векторы ОС
и ОСХ в единичные векторы нашей системы координат, не меняя пло-
площадей фигур. Итак, нам достаточно ограничиться случаем, когда наш
полигон проходит через концы В и А единичных векторов и через
симметрические им точки Bu Av
В силу выпуклости полигона Q он не может иметь точек внутри,
углов, образованных продолжениями сторон квадрата АВА1В1. Наш
полигон может задевать только те узловые точки сети 31, которые
лежат в полоске между ККг и LL1 и между ММХ и NNX (черт. 68).
Пусть, например, он задевает какой-нибудь узел в первой из этих,
полос. Какой бы узел из этой полосы полигон Q ни задел, он во вся-
всяком случае при этом заденет точку С на нашем чертеже вместе с сим-
симметрической точкой Cv Рассмотрим возможные случаи:
1. Полигон Q задевает только три пары точек А и А19 В и В1У
С и Cjj тогда в силу предыдущего Q есть шестиугольник с центром
симметрии в О и, следовательно, с тремя парами равных и параллель-
параллельных сторон; точки А, В, С, Аг, Bv Cx лежат посредине этих сторон..
Площадь нашего шестиугольника, как это непосредственно видно из-
черт. 69, равна площади квадрата СОСгОх, т. е. равна 4.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ
355
la- Если две симметричных пары соседних сторон этого шести-
шестиугольника образуют продолжение одна другой, наш шестиугольник
обращается в параллелограм площади 4 (черт. 70).
2. Если кроме пар А и Av В и Ви С и Сг экстремальный поли-
полигон Q задевает еще узлы сети, то это могут быть: или пара Е, Ег
(черт- 70); полигон Q в этом случае есть тоже параллелограм пло-
площади 4; или пары D, D{, полигон Q совпадает с квадратом CDC1D1
площади 4 (черт. 70).
Итак, центрально-симметрическая выпуклая фигура с центром в узле
сети О, не содержащая внутри себя никаких других узлов этой сети и
обладающая максимально возможной площадью, есть или центрально-
симметрический шестиугольник или параллелограм площади 4. При этом
в случае шестиугольника посредине каждой его стороны лежит узел сети;
у параллелограма же или пара
сторон содержит по паре узлов
сети, другая же — по одному
узлу, лежащему посредине (слу-
(случай 1а), или же каждая сто-
сторона содержит по три узла
(случай 2).
Задача нахождения выпук-
выпуклого тела максимального объ-
объема с центром симметрии в узле
целочисленной сети при уело- с^\^и. О,
вии, что кроме центра тело не
содержит внутри себя ника-
никаких узлов сети, довольно про-
просто решаемая для плоского слу-
случая, значительно усложняется при переходе к пространствам высшего
числа измерений. Однако можно сразу доказать, что максимум объема
такого тела для случая n-мерного пространства равен 2П. (Для пло-
плоского случая, п = 2, как мы уже знаем, этот максимум равен 22 = 4).
ТЕОРЕМА МИНКОВСКОГО. Пусть в п-мерном пространстве
(xlf х2, . .., хп) задана целочисленная сеть % и выпуклое тело Q
с центром симметрии в одном из узлов сети 31, не заключающее
внутри себя никаких других узлов сети. Объем тела Q не превышает
в этом случае 2п.
Из точек целочисленной сети 91 выберем совокупность 23 всех узлов
с четными целочисленными координатами Bkv 2k2, . . . , 2kn). Точки
сети 23 назовем четными узлами. Обозначим через Q(B) тело с цен-
центром симметрии в четном узле В, образованное поступательным пере-
перемещением тела Q. Очевидно, Q(B) внутри себя, кроме точки В, не
заключает никаких узлов сети 2{. Рассмотрим совокупность всех
тел Q(B) с центрами симметрии во всех узлах В сети 23.
ЛЕММА. Если В и Вх—два узла сети 23, то соответственные
тела Q(B) и Q{B^) не имеют общих внутренних точек.
В самом деле, допустим противное: тела Q (В) и Q (В^ имеют
общую внутреннюю точку С. Построим параллелограм BCBXD, три вер-
вершины которого суть наши точки Б, С, Вх\ в силу симметрии тела Q(By)
Черт. 69.
Черт. 70.
356 ДОПОЛНЕНИЕ I
оно содержит внутри себя точку С{1 симметричную с С относительно Bv
Если перенести поступательно тело Q(B^) так, чтобы оно совпало
с Q(B), то вектор В1С1 совпадает с BD. Так как С{ лежит внутри (j
то D лежит внутри Q (В). Диагональ CD нашего параллелограма,
концы С и D которой лежат внутри выпуклого тела Q(#), целиком
лежит внутри Q(B). Следовательно, середина Е этой диагонали лежит
внутри Q(B). Но Е есть середина также второй диагонали BBV Обо-
Обозначим через 2k { и 21г 0=1, 2, . . . , п) координаты четных узлов В
и Bv Координаты точки D равны к{-\-1х (/= 1, 2, . .. , я), т. е. точка D
имеет целочисленные координаты или D есть узел сети 3(. Мы пришли
к противоречию с определением тел Q(B), которые не должны кроме
центра В содержать внутри себя узлы сети 3(. Итак, лемма доказана.
Обозначим теперь через R(B) куб:
2k{ — 1<х,<2*,-{- 1 A = 1, 2, ... , п) .
с центром в точке В. Объем R(B) равен 2". Тело Q(B) имеет общие
части с некоторыми из кубов R(B1) = R(B), /?(Ва), ... , R(Bk). Обо-
Обозначим эти части через аг, а2, ... , ак. Куб R(В) образован поступа-
тельным перемещением куба R^B^ на вектор ВгВ\ при перемещении на
вектор ВгВ часть а. тела Q(B), расположенная в R(B.), перейдет
в часть р/ тела Q(Bf), расположенную в кубе R(B), где #/ — точка,
симметричная с В{ относительно В. Таким образом частям av а2, .. . , ал,
на которые разбито тело Q(B), отвечают конгруэнтные им части
Pi> ?-2' • • • > Рл тел Я(В/)- Так как объем всех частей ^ не превосхо-
превосходит объема заключающего их куба R(B), т. е. rie превосходит 2Л, то,
следовательно, объем Q(B) не превосходит 2П. Теорема Минковского
доказана.
Если Pi-|-р2"~г • • •-f~P* совпадает с кубом R(B), то объем Q(B)
как раз равен 2'\ Следовательно, 2П есть максимум объема тел Q(B).
Возможны два случая:
1. Тела Q(B) не заполняют всего я-мерного пространства. Части |3.
этих сил, попавшие внутрь куба R (В), не заполняют всего этого куба.
В этом случае объем Q(B) меньше 2Н.
2. Тела Q(B) заполняют все /2-мерное пространство. Части р. этих
тел, попавшие внутрь R (В), заполняют этот куб. В этом случае
объем Q(B) достигает своей максимальной величины 2п.
Таким образом задача о нахождении тела Q (В) максимального объема
эквивалентна задаче разбиения «-мерного пространства на выпуклые
тела с центрами симметрии в узлах *}*.
Примечание. Линейным преобразованием можно перевести сеть 33 в
любую параллелепипедную сеть. Разбиение пространства на тела с центрами
симметрии в узлах параллелепипедной сети называется параллелепипед ним
разбиением.
Мы видели, например, что для плоского случая максимум объема Q(B)
достигается на параллелограмах и симметрических шестиугольниках. Соответ-
Соответственно этому возможно параллелепипедное разбиение плоскости лишь на па-
раллелограмы и симметрические шестиугольники.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ 357
3. Экстремальные свойства треугольника
В предыдущей задаче экстремум достигался на параллелограмах и
шестиугольниках. Ряд задач дают в качестве экстремальной фигуры
треугольник.
Задача 1. Из всех выпуклых фигур данной площади, опирающихся
на отрезок АВ оси Ох, найти тот, у которого центр тяжести
имеет наибольшую ординату.
Решение дается треугольником с основанием АВ Е _?
(черт. 71). В самом деле, пусть дана произвольная,
отличная от треугольника выпуклая фигура площади s,
опирающаяся на отрезок АВ, Пусть С — наиболее
удаленная от. оси Ох точка периферии этой фигуры.
Из двух дуг АС и АВ границы этой фигуры одна по
крайней мере отлична от прямой, например АС. ^ &
Пусть D есть точка дуги АС. Проведем хорду AD Черт. 71.
и продолжим ее до пересечения в точке Е с линией
абсцисс точки С. Заменим дугу АС ломаной АЕС. От нашей фигуры
в результате такой деформации будет отнят сегмент, заключенный
между дугой AD и хордой AD, и добавлен криволинейный треуголь-
треугольник, заключенный между DE, ЕС и дугой DC (частью АС). Варьируя
точку Е, можно добиться, чтобы присоединенная площадь равнялась
отнятой, т. е. чтобы в результате этой деформации площадь фигуры
не изменилась. Но тогда при указанной деформации центр тяжести
фигуры удалится от оси Ох, так как присоединенный треугольник DEC
расположен дальше от оси Ох, чем сегмент AD.
Такая деформация, увеличивающая ординату центра тяжести, пе-
перестает быть допустимой вариацией, коль скоро фигура обращается
в треугольник.
Задача 2. Выпуклая фигура S делится ^
прямой L, проходящей через центр тяжести,
на две части, Sx и S2. Найти минимум
выражения:
we <? ж\ площадь Sx
AiOi, On, L.) = =г •
v l 2 J площадь 52
Пусть прямая L пересекает границу ; фи-
фигуры 5 в точках А и В (черт. 72). Проведем
касательные в точках А и В к ; и обозна-
обозначим через С их точку пересечения. Пусть S{
принадлежит треугольнику ABC и отлична от
треугольника, в этом случае можно заменить 5г ЧертЛ72.
выпуклой фигурой R той же площади, но
с центром тяжести, более удаленным от L. Фигура S/ = S2-j-/?
выпукла, имеет ту же площадь, что и S — Sl-\-S2, и центр ее тя-
тяжести находится в 5Г Проведем через новый центр тяжести пря-
358 ДОПОЛНЕНИЕ I
мую /.j, параллельную L. Она разобьет S' на две части S/ и 5./э
причем
площадь S^ << площади R = площади S1?
площадь S/ > площади S2.
Следовательно,
Такая вариация границы S, уменьшающая отношение X, перестает
быть возможной, коль скоро S{ есть треугольник. Отсюда очевидно,
что в случае минимума X(St, S.2, /,) часть 5Х должна быть тре-
треугольником.
Итак, пусть S1 есть треугольник ABC. Часть S2 заключена в части
плоскости, ограниченной АВ и продолжениями AD и #? сторон тре-
треугольника Sj. Если можно заменить S2 выпуклой фигурой /?, заклю-
заключенной в этой же части плоскости, но с центром тяжести, более близ-
близким к L, то фигура SJL-J-S2 перейдет в фигуру R-^-Sx с центром
тяжести, смещенным в сторону St, следова-
следовательно, как мы убедились выше, этим мы мо-
можем уменьшить отношение X (Si, S2, L). Ми-
Минимум X будет достигаться, когда центр тяже-
тяжести S2 будет ближе всего к L. Но это прои-
произойдет в том случае, когда S2 есть трапеция
с основанием АВ и ему параллельным и боко-
боковыми сторонами AD и BE,
В самом деле, проведя из внутренней точки
Черт. 73. S2 прямую, параллельную АВ, получим трапецию
AMNB, получаемую из S2 (черт. 73) уда-
удалением сегмента, отсекаемого хордой MXNV и добавлением двух криво-
криволинейных треугольников АММХ и BNNV Передвигая эту прямую, можно
добиться положения, когда эта трапеция будет иметь площадь, равную
площади S2. Но ее центр тяжести сравнительно с центром тяжести S2
расположен ближе к L, так как отнятая часть от 52 расположена ближе
k4L, чем прибавленная.
"" Итак, минимум X(SV S2, L) достигается, когда S есть треугольник,
а прямая Ly проходящая через его центр тяжести, такова, что часть Sr —
треугольная, a S2 — трапецевидная часть.
В этом случае
4
X (S S L) = -
Переставив S.2 и SL, получим максимум для X(SV S2, L), рав-
равный — . Итак, всегда:
-L<X(SP 521 ?)< —.
Дальше мы приведем интересную экстремальную задачу, приводящую
к треугольникам, решенную С. С. Ковнером.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ
359
4. Об экстремуме отношения объемов выпуклого тела и заключен-
заключенного в нем центрально-симметрического тела
1. Пусть имеется выпуклое тело К\ если внутри него взять точку Р
•и Построить тело Ки центрально-симметрическое телу К, с центром
симметрии в точке Я, то общий объем тел К и Kv который мы обо-
обозначим через {К, Кх ) , будет обладать следующими свойствами:
1) это будет тело, вписанное в К,
2) выпуклое,
3) центрально-симметрическое с центром в Р,
4) максимальное по объему (и длине границы) из всех центрально-сим-
центрально-симметрических выпуклых тел, вписанных в/Си имеющих центр вР (черт. 74).
Последнее свойство вытекает из того, что вся-
всякое другое центрально-симметрическое относительно Р
тело, вписанное в /С, не может иметь точек, при-
принадлежащих К и лежащих вне { К, Кх } , так как
тогда оно обязательно имело бы точки и вне К-
2. Таким образом для всех
точек Р тела К единственным
образом определена функция —
объем максимального централь-
центрально-симметрического тела, имею-
имеющего центр в точке Р и впи-
вписанного в К.
Эта функция, следователь-
следовательно, достигает внутри тела мак-
максимума, и притом в одной или
нескольких точках.
Мы докажем, что именно
в одной.
Построим тела Kt и К/
около центров Р и Р', в каж-
каждом из которых, по предполо-
предположению, объем { /С, К\} соот-
соответственно {К, К/ } дости-
достигает максимума. Тела Кг и К/ расположены параллельно друг другу.
Проведем опорные прямые1), общие обоим телам Кх и К/ (черт. 75).
Взглянем теперь на это построение с несколько иной точки зрения:
представим себе цилиндр, имеющий основанием тело К и образую-
образующую, перпендикулярную плоскости черт. 75. Точно так же предста-
представим себе цилиндр с направляющею К± и наклонной образующею, проек-
проектирующеюся параллельно опорным прямым черт. 75. Тогда центрально-
симметрические тела {К, Кг} и {К, Кх' } представляют собою не что
иное, как сечения общего объема обоих цилиндров двумя плоскостями,
•параллельными плоскости чертежа. Но общий объем двух выпуклых
цилиндров есть выпуклое тело. Следовательно, тела { К, Кг} и {К, К/ }
суть два максимальных сечения этого выпуклого тела.
*) Опорными прямыми называются прямые, имеющие общие точки с гра-
границей выпуклого тела, не пересекающие его внутренние части.
Черт. 74.
Черт. 75.
360
ДОПОЛНЕНИЕ 1
Из теоремы Минковского-Бруннах) о соотношении объемов (или пло-
площадей) трех последовательных параллельных сечений выпуклого тела
следует: если два сечения равны по площади, то всякое промежуточ-
промежуточное может быть только больше или равно им по площади, в на-
нашем же случае, максимальных сечений, может быть, очевидно, только
равно. Из того же результата Минковского следует, что выпуклое телоу
три последовательных сечения которого равны
между собою, может быть только цилиндром*
у
Следовательно, тела {К,
К, Кх
')
Черт. 76.
как сечения цилиндра параллельными плоскостями,
не только равны по площади, но и конгруэнтны
и параллельно ориентированы. В то же время они.
вписаны в выпуклое тело К- Достаточно провести
к ним две параллельные опорные плоскости (черт-
76), чтобы получить вписанное в К центрально-
симметрическое тело, большее, чем {К, Кх) и.
( К, Ki }, что противоречит предположению.
3. Таким образом существует единственное максимальное выпуклое
центрально-симметрическое тело, вписанное в данное выпуклое. Обо-
Обозначая это максимальное центрально-симметрическое вписанное тело
через J и обозначая его объем через Vol/, ставим вопрос, в каких
пределах меняется Отношение объема тела J к объему тела К. Так как
тело К само может быть центрально-симметрическим,
то ясно, что верхний предел отношения
= 1.
Черт. 77.
Vol/C
Спрашивается, чему равен нижний предел этого
отношения и в каких телах он достигается. Эти тела
мы будем называть предельными.
4. Рассмотрим, как расчленяет тело J тело К, и
введем некоторые обозначения.
Граница тела J: QtJ в некоторых своих частях
совпадает с Gr /С, в некоторых лежит внутри тела К.
Соединяя радиусами-векторами концы кусков общей
границы J и К с центром J, мы получим конечное
число конических областей, которые назовем областями типа а. Обла-
Областями типа Ь назовем конические области, происшедшие от соединения
с центром J частей границы J, лежащих внутри К- Части же КУ лежа-
лежащие вне «/, назовем областями типа с или выступами (die Kappe по
терминологии Минковского) тела К (черт. 77).
Если бы против области b относительно центра симметрии лежала
также область типа Ь, то обе они могли бы быть увеличенными за счет
прилагающихся к ним выступов с без нарушения центральной симметрии
тела /. Но тогда J не было бы наибольшим центрально-симметрическим
!) Н. Minkowsky, Geometrie der Zahlen, стр. 209 и 243—248. См. также:
Blaschke, Kreis und Kugel, Leipzig 1916; Т. Bonnesen und W. Fenchel,
Teorie der konvexen Кбгрег, т. 3, Berlin 1934; Л. Люстерник,. Элементы теории
яыпуклых тел, ОНТИ, 1935.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ
361
Г
телом, вписанным в АГ. Следовательно, против области b относительно
центра всегда лежит область а. Против области а лежит или область Ь
или я. Области типа а, лежащие друг против
друга, мы будем обозначать а'. Установим теперь
основные количественные соотношения между
областями типа b и телом J.
5. Тело / получено пересечением тел К и КА.
Если Кх параллельно перенести в положение К/,
то {К, К{ } будет центрально-симметрическим
телом J' с центром в Р/'. Посмотрим, как изме-
изменился объем вписанного в К центрально-симме-
центрально-симметрического тела при этом переносе. Jr приобрело
часть /, заштрихованную (черт. 78), а потеряло
части У, обозначенные 2 и 3. Строя части 2/ и 3',
симметричные 2 и 3 относительно центра Р/',
подсчитываем соотношение объемов /, 2' и 3'.
Для этого на прямую, перпендикулярную напра-
направлению сдвига Кхг относительно К1 и лежащую
внизу черт. 78, проектируем границы верхней по-
половины тела J. Проекции границ областей типа b
назовем Рг Ь, типа а — соответственно Рг а и т. д.
Теперь поступаем следующим образом: рас-
расстояние каждой точки верхней относительно ли-
линии проектирования границы тела J вычитаем:
1) само из себя, 2) из расстояний до той же
линии соответствующих точек верхней границы
тела, 3) из соответствующих расстояний границ
областей 3', 1 и 2'.
Первое вычитание даст линию / черт. 78.
Второе даст изображенную пунктиром область II.
Третье вычитание даст ограниченную двойною
линией область ///.
Если через h обозначить длину сдвига К/
относительно Кг, то приобретенная Jr площадь
выразится так:
Мы пишем 2 »так как в общем случае частей
типа / будет не одна, а несколько; через d мы
обозначаем разность между цилиндрическим
объемом, опирающимся на границы ^-частей,
и коническими, вообще говоря, наростами /.
Потерянная телом J площадь выразится так:
Черт. 78.
Черт. 79.
где через / обозначены лежащие у краев области проектирования и не
принадлежащие ни У, ни Jf части фигуры.
362 ДОПОЛНЕНИЕ I
В итоге получится приращение площади, если
Дадим оценку правой части неравенства. Она достигнет минимума
при минимальном d, что соответствует случаю, когда граница выступа
служит продолжением границы У, и при максимальном /, что соответ-
соответствует случаю параллельности верхней грани части / и нижней части 2'
(черт. 79). В этом случае крайнее d=f. Вообще же говоря, крайняя
область d больше, а область / меньше, что показано пунктирными
линиями. Обозначая разность
2*--3-2/=**.
мы видим, что а^-0 и стремится к нулю вместе с /г. Следовательно,
если разность
то всегда можно подобрать такое малое h> что левая часть нера-
неравенства B) будет больше правой.
Если же V Рг? ^ Рг^^О, то это сделать нельзя. Геометриче-
Геометрический смысл этого результата следующий. Если для некоторого напра-
направления проектирования
4
то тело Кх можно перенести в этом направлении в положение К{ и
тело / увеличится по площади»
Этого нельзя сделать, если
У| Рг?<
Сопоставляя этот результат с уже упоминавшейся теоремой Минков-
ского-Брунна о пересечении выпуклых тел и с доказанной выше теоре-
теоремой о единственности максимального центрально-симметрического тела,
вписанного в данное выпуклое, получаем следующую теорему:
Необходимым и достаточным условием того, что данное цен-
центрально-симметрическое тело J, вписанное в выпуклое тело Ку есть
максимальное, служит неравенство:
2 Prft<4- РгУ
для любого направления проектирования.
6. Так как в процессе доказательства мы не пользовались никакими
геометрическими преобразованиями кроме параллельного переноса и
оценки объемов цилиндрических и конических областей, то ход дока-
доказательства остается неизменным в случае пространства любого числа
измерений.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ
363
7. Если стороны соответственно грани выступа с не являются продол-
продолжением соответствующих сторон прилегающих к ним границ я-частей,
то, продолжив эти границы я-частей, мы увеличиваем Vol/С, тело же /,
поскольку его границы, в том числе и границы ^-частей, не изменились,
остается максимальным центрально-симметрическим телом, вписанным
в увеличенное указанным построением тело К- Отношение v при
этом преобразовании уменьшилось. Следовательно, в предельном теле
стороны выступов с служат продолжениями прилегающих границ
а-частей.
8. В предельном теле границы ^-частей для плоского случая прямо-
прямолинейны.
В самом деле, если границы одной из ^-частей, назовем ее Ъп = bf -J- Д,
своею частью Д входят внутрь выступа с, то, срезав части Д, указанные
\
\
чЛ
I
1
v
i
i
i
Prfr
Черт. 80.
Черт. 81.
пунктиром на черт. 81, получим новое тело Кг со вписанным в него
центрально-симметрическим телом У.
Для направлений проектирования, в которых Pr J потерпела умень-
уменьшение, имеем:
Рг^^РгУ—2РгД.
В силу теоремы п. 5,
w—l
п—1
п — 1
откуда
Но левая часть есть сумма проекций всех ^-частей тела. Следовательно,
необходимые и достаточные условия экстремума имеют место, и тело Jr
есть максимальное из центрально-симметрических тел, вписанных в Кг.
В то же время
Vol .Г = Vol/- 2 Vol A Vol/
Vol К? Vol К — Vol A ^ Vol К '
и теорема доказана.
364 ДОПОЛНЕНИЕ I
Из того факта, что границы ^-частей прямолинейны, следует прямо-
прямолинейность границ и а-частей.
9. Мы назвали частями типа а' конические части тела У, границы
которых совпадают с границами К и против которых относительно
центра лежат такие же области.
п п п к
Vol #= 2 Vol л, + 2 Vol b. f 2 Vol ct + J] Vol <,
« n к
Vol /= ^ Vol я, + 2 Vol ^. + ^ Vol <;
так как каждая часть а{ центрально-симметрична части bj9 то
Vol ах = Vol Ъх
и
7i М к
Vol /С= 2 2J Vol *,+ 2 Vol ^ -f S Vo1 "Л
Vol У = 2 2Vol ^ 4- 2 Vol a/.
1 1
Оценим отношение
2 Vol в/
Отношение
не ограничено ничем и может меняться в пределах от нуля до беско-
бесконечности, второе же отношение
не превосходит определенного максимума.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ
365
Происходит это от того, что отношение выступа сь к прилежащей
к нему й,-части в силу теоремы п. 5 не может расти больше того зна-
чения, которое оно получит, если Рг^ = --Рг/, если высота кониче-
конического тела Ъх — минимальная из возможных и границею между с,х и Ьх
служит прямая линия.
Оценкой максимума этого отношения мы займемся дальше, здесь же,
обозначив п
2 Vole,
max-
заметим, что отношение
2-\-х
Vol AT 2 + x+y '
будучи положительным и меньшим единицы, достигает минимума только
тогда, когда
2 Vole, 2Vl<
2Vol6f
i
- = т и х=-
= 0.
Итак, в предельном теле отсутствуют а'-части.
10. Теперь рассмотрим, в какой связи нахо-
находится выступ сг с прилегающею к нему ^-частью.
В силу замечаний пп. 7 и 8 в предельном случае
выступ ограничен с наружной стороны продолже-
продолжением границ прилегающих а-частей, а с внутрен-
внутренней— прямолинейной границей ^-части. Через
центр О тела J проведем диаметр, параллельный
этой прямолинейной границе #гчасти (черт. 82).
Все тело К лежит между опорными прямыми к границам а-частей,
прилегающих к выступу с., т. е. в предельном теле, внутри или сли-
сливаясь с продолжением сторон выступа сг Отношение —г-^г- будет тем
больше, чем ближе лежит центр Отела У к общей границе Ь- и сг части.
Но в силу соотношения п. 5
г> , 1
Черт. 82.
и рассматриваемый диаметр не может лежать к границе выступа ближе
расстояния вершины выступа с до той же границы, и, следовательно,
max-
Vol
Vol bi
Такой выступ назовем максимальным.
= 1.
366
ДОПОЛНЕНИЕ I
11. В силу соображений п. 9
будут те, для которых
предельными телами на плоскости
max
= т
и все а -части равны нулю.
В силу п. 10 т^1, причем равенство будет достигаться, если
Vol я*
Vol Ь.г
= 1
для каждого значения /. В таком случае
. Vol J 2
min v5nf = T-
Зададимся одним максимальным выступом ct и, как в предыдущем
пункте, построим диаметр тела У, параллельный границе с^ и ^-частей*
Верхняя половина те-
тела К должна лежать вну-
внутри или сливаясь с про-
продолжением сторон высту-
выступа с, но так как выступ
сх максимальный, то
и, следовательно, границы
верхней половины К сли-
Черт. 83. ваются с продолжением
сторон выступа.
Таким образом построена верхняя половина тела У, и в силу era
центральной симметрии оно построено полностью. Так как в предельном
теле a'-части отсутствуют, то против а2 и аг лежат выступы с2 и с3,
образованные продолжением границ alf а2 и as (черт. 83).
Тем самым построено тело — треугольник, для которого отноше-
Vol bt л
v . = шах = 1 достигается для каждого выступа и у которого
в нем достигнуто, следова-
ние
отсутствуют а -части. Отношение f у =т
тельно, оно есть предельное.
Следовательно, и у всякого иного предельного тела для каждого
выступа достигается соотношение !) ° *== 1, т. е. все выступы являются
максимальными. Но так как мы построили все наше тело по од-
одному такому выступу, то тем самым доказана и единственность предель-
предельного тела.
Vol
х) В пространстве трех измерении, в предельном теле, отношение -^=—— не
достигает максимума ни в одном выступе.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ВЫПУКЛЫХ ТЕЛ 367
Отношение объема максимального центрально - симметрического
тела, вписанного в данное выпуклое тело К, заключено в грани-
2 _ Vol./ __ - ^ у
цах ~з^ \о\К причем нижняя граница достигается только
в треугольнике для максимального вписанного в него центрально-
симметрического шестиугольника.
Целый ряд экстремальных задач на теорию выпуклых тел можно
найти в книге: Bonnesen und F e n с h e 1, Theorie der konvexen Korper*.
[ДОПОЛНЕНИЕ II
О НЕКОТОРЫХ ЭКСТРЕМАЛЬНЫХ ЗАДАЧАХ В ТЕОРИИ
КОНФОРМНЫХ ОТОБРАЖЕНИЙ
В начале курса мы формулировали задачу вариационного исчисления»
как задачу разыскания экстремумов функционалов наиболее общего вида;
во всем дальнейшем, однако, мы ограничились изучением функционалов,
довольно специального вида, функционалов, задаваемых определенными*
интегралами. Легко видеть, что, оставаясь даже в сфере классических,
постановок, разобранные нами задачи далеко не исчерпывают вариацион-
вариационных задач, важных для анализа и его приложений.
В настоящем дополнении мы имеем в виду коснуться некоторых функ-
функционалов, с которыми часто приходится иметь дело в теории функций
комплексного переменного. Как мы ниже увидим, все эти функционалы
не имеют простого аналитического выражения через линию — аргумент;,
по этой причине исследование этих функционалов неизмеримо сложнее,
чем те исследования, которые мы имели раньше. Здесь мы имеем боль-
большое количество еще не разработанных вопросов.
Примеры функционалов. Пусть в плоскости комплексного пере-
переменного z = х -\- iy дан круг С: | z | < 1, радиуса единица и с центром
в начале координат. Пусть, кроме того, в плоскости комплексного пере-
переменного w — u-\-iv дана односвязная область D, ограниченная простой
замкнутой линией Г. Как известно из элементов теории функций ком-
комплексного переменного, какова бы ни была точка w0, принадлежащая />.,
и какова бы ни была точка w, принадлежащая Г, существует единствен-
единственная аналитическая функция
w=f(z),
реализующая конформное отображение круга С на область D *) и такая,,
что точке z = 0 отвечает точка w0 и точке z = 1 отвечает точка w.
Производная f (z), как известно, имеет простой геометрический смысл:
ее модуль |/'B)| характеризует „растяжение" при отображении в данной
точке z, ее аргумент argf(z) характеризует „поворот".
Рассмотрим |/'@)|. Каждому замкнутому контуру Г, охватывающему
точку w0, будет отвечать вполне определенное значение \f@)\; таким
образом |/'@)| есть функционал. Ряд задач теории аналитических функ-
!) Иными словами соотношение w =f(z) устанавливает взаимно-однозначное
и взаимно-непрерывное соответствие между точками круга и точками области D»
такое, что две произвольные линии в С, пересекающиеся под углом а, перехо-
переходят (в D) в две линии, пересекающиеся под тем же углом а; бесконечно малый,
круг, принадлежащий С, переходит в бесконечно малый круг, принадлежащий D.
,368 дополнение и
ций, как впервые показал Кобе, приводится к разысканию экстремума
этого функционала, когда на класс допустимых линий Г наложены неко-
некоторые добавочные ограничения. Об этих ограничениях мы будем говорить
подробнее ниже.
Для того чтобы дать второй пример функционала из теории кон-
конформных отображений, будем считать, что контур Г состоит из двух
простых дуг Г, и Г2, причем 1\ будем, считать фиксированной, а Г.2 —
переменной. При конформном отображении w = f(z) единичного круга
на область D (ограниченной кривой Г) дуге Гг будет отвечать на окруж-
окружности С вполне определенная дуга <хC. Обозначим через L длину этой
дуги. Каждой кривой Г2 будет отвечать вполне определенное значение L:
L есть функция линии. Считая, что контур Г1-]-Г|2 всегда охватывает
точку w0: wo=f@), можно ставить задачу найти максимум L.
Считая, что функция w=f(z), определенная раньше, разложена
в степенной ряд:
где, как известно,
мы можем рассматривать модуль я-го коэфициента \ап\ также как
функцию линии Г. Одной из трудных и интересных задач в теории кон-
конформных отображений является задача разыскания максимума —М.
а\
В качестве последнего примера формулируем одну задачу из теории
плоскопараллельного потока идеальной жидкости.
Пусть в плоскости комплексного переменного z дана простая дуга АВ.
Допустим, что дугу обтекает плоскопараллельный поток идеальной не-
несжимаемой жидкости при следующих условиях:
1) скорость жидкости в бесконечности равна V^y
2) точками разветвления и схода потока являются соответственно
точки А и В. Обозначим через Р равнодействующую сил давления по-
потока на дугу АВ. Как показали Н. Е. Жуковский и С. А. Чаплыгин,
вычисление Р сводится к задаче конформного отображения внешности
дуги АВ на внешность круга. Для вычисления отобразим конформно
внешность дуги АВ на внешность круга |<йу|=^1 при условии, чтобы
бесконечно удаленной точке плоскости z отвечала бесконечно удаленная
точка плоскости w. Пусть w=f(z) есть функция, реализующая это ото-
отображение. Обозначим через 20, 0 < 2Н < т:, дугу окружности \w\ = ly
концы которой отвечают в силу отображения концам дуги АВ. При этих
обозначениях имеем: А л/ о
4г. Ю cos 6
где [j — плотность жидкости. Таким образом „подъемная сила" Р дуги АВ
выражается через функционалы, отмеченные нами выше. Р есть функция
линии АВ, определяемая конформным отображением. Выбирая некоторые
специальные классы допустимых линий, можно ставить задачу, определить
среди разбираемого класса допустимых линий дугу с наибольшей подъем-
подъемной силой.
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 369
Отметим сейчас же трудности, которые мы встречаем при решении
поставленных задач. Приведенные выше примеры функционалов суть
функционалы, определяемые конформным отображением, а так как функ-
функции, дающие конформное отображение круга на область произвольного
вида, мы умеем определять лишь как суммы бесконечных рядов, то для
приведенных функционалов мы не имеем непосредственного аналитиче-
аналитического представления; результаты, добытые нами в задачах на разыскание
экстремумов интегралов, здесь оказываются неприложимыми.
Качественные принципы. Начнем с выяснения влияния вариации гра-
границы Г на два основных функционала [/'(О)! и L.
ПРИНЦИП ЛИНДЕЛОФА. Допустим, что единичный круг | z | < 1
конформно отображается на односвязные области D и Dv так что при
каждом отображении центр круга переходит в точку w0, принадлежащую
одновременно обеим областям. Обозначая соответственно через w = f(z)
и w=ft (z) функции, реализующие эти отображения, имеем в случае,
если область D содержится в области Dt:
Знак равенства достигается только тогда, когда области D и Dx
совпадают.
ПРИНЦИП МОНТЕЛЯ. Сохраняя принятые выше обозначения, допу-
допустим, что области D и Dt имеют общий кусок границы Г1# Обозначим
через L и L1 длины дуг окружности \z\ = 1, которые при отображениях
w=f(z) и w=fi(z) переходят соответственно в дугу Yv При этих
обозначениях, если D содержится в Dt, то:
знак равенства достигается, когда области D и Dt совпадают.
Для доказательства разберем сначала частный случай, когда*/^ есть
круг \w\ < 1 и^0 = 0. В этом случае область D получается выбрасыва-
выбрасыванием из круга | w | = 1 некоторой замкнутой области. Общая граница 1\
будет некоторой дугой f окружности |w| = l. Обозначим через Р(г9 <?)
(w = re%tp) гармоническую функцию, принимающую на границе D значе-
значения — In г, и через Q (г, <р) — гармоническую функцию, сопряженную
функции Р (г, <?):
1 3Q дР dQ дР
_ = —— f —- z=Z .
г ду дг дг ду '
Тогда в силу формулы Римана функция z = wep+iQ будет реализовать
конформное отображение области D на круг \z\ < 1, т. е. является функ-
функцией, обратной функции w=f(z).
Так как в разбираемом случае fx (z) ^ z, //@)=1, то для дока-
доказательства принципа Линделофа достаточно доказать, что: J/' '"' '
или что:
W—0
Так как граница D принадлежит кругу | w \ ^ 1, то отсюда следует,
что —In г всюду на границе D положительно или нуль, а значит, P(rt<f)
370 дополнение и
на границе области положительна или нуль; отсюда, в силу свойства
гармонических функций принимать свои экстремальные значения только
на границе, заключаем, что Р(г, <р) всюду больше или равна нулю.
Следовательно, гР@)>0, еР@)>1.
Из приведенных рассмотрений видно, что знак равенства может дости-
достигаться лишь в случае, когда на границе D — In r s= 0, т. е. когда область D
есть круг.
Для доказательства принципа Монтеля достаточно показать, что в точ-
точках т имеем:
или что в точках
Для доказательства этого заметим, что ' вдоль у. — In г = Р (г, «),
а внутри области D: Р(л ?)<>0> следовательно, вдоль ^
Перейдем к доказательству принципов для случая произвольной
области Dv Пусть:
w =/, (г)
есть функция, реализующая конформное отображение круга | z | < 1 на
область Dv ^@) = % Пусть />2 есть область круга \z\ < 1, перехо-
переходящая при этом отображении в область D. Обозначим через z = <p(C)>
<р @) = 0, функцию, реализующую конформное отображение круга | С | < 1
на область ZJ. При этих обозначениях очевидно, что функция
будет давать конформное отображение круга | z \ < 1 на область D,
/@) = w0. Кроме того, в силу доказанного частного случая принципа
Линделофа имеем | ср/ @) 1-^1; следовательно:
этим самым принцип Линделофа доказан полностью.
Докажем теперь полностью принцип Монтеля.
Пусть Lj и L суть длины дуг окружности | z | = 1, переходящих соот-
соответственно при отображениях w=f1(z)i w=f(z) в дугу Гг Воспользо-
Воспользовавшись введенной выше областью D2 и функцией <? (С), очевидно, что L
есть также длина дуги окружности |С|=1, которая при отображений
2 = ср(С) переходит в дуги Lv и, следовательно, в силу установленного-
частного случая принципа L ^ Lv
Бесконечно малые вариации. Отмеченные выше принципы дают знак,
приращения функционалов при весьма общих гипотезах относительно ва-
вариации границ. Добавим к этим принципам две количественные оценки
вариации тех же функционалов для случая, когда Dx есть круг, a D есть
область, бесконечно близкая к кругу. Из этих подсчетов мы в дальней-
дальнейшем извлечем наиболее важные приложения метода вариаций.
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 371
ТЕОРЕМА. Пусть в плоскости комплексного переменного z = reifp
дана односвязная область D, ограниченная простой замкнутой кривой
г=г (ср), г (ср -j- 2тг) = г (у), со следующими свойствами:
1) 11 —f(?)|< s> где е— любое положительное число, меньшее ¦!.
2) Функция г(ср) обладает непрерывной производной, удовлетво-
удовлетворяющей условию Липшица \ / (ср -\- Дер) — /"'(а) | < КЬу\ где К— кон-
константа.
При этих условиях, если мы через w=f(z), /@) = 0, обозначим
функцию, реализующую конформное отображение области D на круг9
| w | < 1, то будем иметь:
, . 1 /
где о2 есть площадь области, получаемой пересечением круга \ w | < 1
с внешностью D l), ot есть площадь области, получаемой пересечением
областей | w \ > 1 и D, о (е) есть величина, стремящаяся к нулю
вместе с е.
Для доказательства воспользуемся опять формулой Римана, в силу
которой имеем:
где Р (г, <р) есть гармоническая функция, принимающая на границе зна-
значения — In г (<р). Для подсчета Р @) построим вспомогательную гармони-
гармоническую функцию Рг (г, ср), правильную в круге г<1-|-е и принимающую
на окружности г = 1 -f- е значения — In г (ср) = р (<р).
В силу сделанных гипотез относительно функции г(<о) функция /?(<р)
удовлетворяет следующим условиям:
где /С2 — константа, зависящая только от константы К. При этих усло-
условиях, пользуясь интегралом Пуассона:
нетрудно показать, что
дг
s), где tj (е) стремится к нулю вместе
с е. Следовательно, на границе D имеем:
|^(r>?)—p(?)|<
Кроме того, на той же границе имеем:
г) Внешность D" есть область, получаемая выбрасыванием из плоскости
области D вместе с ее границей.
372 ДОПОЛНЕНИЕ II
Таким образом гармонические функции Р (г, ср) и Рх (г, ср) на границе D
отличаются меньше чем на 2е • т) (е); следовательно, модуль гармониче-
гармонической функции Р (г, ср) — Pj (г, ?) всюду внутри области D меньше 2г • tq (г),
в частности:
jP(O) — ^(OJKSh.^e). B)
Отсюда заключаем, что, пренебрегая бесконечно малыми высших порядков
по сравнению с г, мы можем Р @) заменить Pt @). Подсчитаем значе-
значение РДО). В силу A), полагая г=0, получим:
2тс 2*
6 О
где в силу условия |1—^(?)|<-9~ и г^е> следовательно, М($>) ограни-
ограничена константой, не зависящей от вида г (ср). Кроме того,
Г (^>) 2гс 2тс
10 0
2гс 2гс
0
ИЛИ
2к
1— '(?IW?=C2 — °l)+y
о
Отсюда
2*
и
-1}^?. C)
Сопоставляя B) и C), получим:
откуда окончательно:
Специальная вариация границы. Для дальнейших исследований нам
существенно понадобится одно специальное отображение, которым мы
сейчас займемся.
Обозначим через D (е, б) область, получаемую выбрасыванием из
круга | С [ < 1 прямолинейного отрезка длины в, выходящего из точки
С = ?г9 и принадлежащего радиусу нашего круга. Отобразим круг |г|<1
конформно на область D (е, 6) при условиях, чтобы начало координат
С = 0 переходило в начало координат z = 0 и чтобы при z = 0 произ-
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 373
водная -^- была действительным положительным числом. Такое отобра-
отображение, как известно, можно получить при помощи элементарных функций:
A + h) (У +1 е~Ъ) + 2* = &* + {- е-й, D)
где положено: А = -j -т——. При 6 = 0 получаем:
A+А)(г+1) + 2А = С + |. D')
Легко видеть, что в этом случае точке z = 1 будет отвечать свободный
конец выброшенного отрезка. Считая h бесконечно малым и пренебрегая
бесконечно малыми высших порядков, найдем для этого случая значения
первых трех производных при z = 0 и значение аргумента точки окруж-
окружности |С|=1, соответствующей точке 2 = в . Начнем с последнего
вопроса.
Пусть С = ? ? есть точка, соответствующая точке z = е , тогда,
подставляя в D'), найдем:
2 A 4- A) cos ф -f 2А = 2 cos ?. E)
Положим ф = ? 4" ^?* ^3 соотношения E) легко . видеть, что Аср и Л —
бесконечно малые одного и того же порядка; отсюда, подставляя в E)
ф = ср 4" А? и отбрасывая малые высших порядков, получим:
h cos cp — sin cp • Дф 4" А = 0
или ф
A? = Actgii). F)
Для того чтобы найти главные части -производных, упростим предва-
предварительно соотношение D7). Положим С = ?4-°) и подставим в DГ):
тогда, заметив, что ш — бесконечно малая порядка h, отбрасывая малые
высших порядков, соотношению D7) можно придать вид:
о) (г2 + 1) 4- hz (z2 4- 1) 4" 2А*2 =
Отсюда окончательно:
) { 2) G)
Из соотношения G) нетрудно получить главную часть функции, реализую-
реализующей конформное отображение круга на произвольную область D (е, 6);
для этой цели, очевидно, достаточно вместо z и С подставить соответ-
г'9 г г'9
ственно ze и (,? ; проделывая это, получим:
й ?*f^l = X(z, 6, А). '(8)
!) Эго соотношение дает, очевидно, главную часть Д<р при конечном
бесконечно малом h, при ср = 0 соотношение теряет смысл.
374
ДОПОЛНЕНИЕ II
Диференцируя соотношение (8) и полагая
значения производных в начале координат:
ХЧО, 6, А)=1— А,
/40, в, Л)= — 2-2АЛ
= 0, мы найдем нужные нам
(80
Максимальное растяжение. Применим теперь добытые выше вы-
выражения для вариаций функционалов к решению некоторых задач на
разыскание экстремумов этих функционалов. Начнем с задачи на разыскание
„максимального растяжения" при конформном отображении.
Дан класс функций w =f(z), /@) = 0, обладающих свойствами:
1) каждая функция правильна и однолистна в круге |z|<l,
2) каждая функция при | г|< 1, не принимает значение w=\.
Среди функций этого класса тре-
требуется найти функцию, для которой
производная \/ @) | была бы наибольшей.
Или, переходя на язык геометрии: сре-
среди всех односвязных областей плоскости w,
содержащих начало координат и не со-
содержащих точки w = l, требуется опре-
определить область такую, чтобы при кон-
конформном отображении круга | z | < 1 на
эту область (начало координат переходит
в начало координат) растяжение в начале
координат было максимальным.
Черт. 84.
Заметим прежде всего, что максимальное растяжение нужно искать
среди областей, получаемых выбрасыванием из плоскости линии ?, соеди-
соединяющей точку «» = 1 с бесконечностью (черт. 84). В самом деле, пусть
Dx есть произвольная односвязная область, содержащая начало, не
содержащая точки w = 1 и ограниченная простой замкнутой линией.
Построим линию ?, лежащую целиком вне области Dx и соединяющую
точку w = 1 с бесконечностью. Обозначим через D область, получаемую
выбрасыванием из плоскости w линии ?. Пусть w=/1(z) и w=f(z),
/@)=/х @) = 0, суть функции, реализующие соответственно конформ-
конформные отображения круга |г|< 1 на области Dx и D. Так как, очевидно,
область Dx содержится в области D, то в силу принципа Линделофа
получаем:
что доказывает высказанное утверждение.
Чтобы не усложнять дела теоретико-функциональными рассмотре-
рассмотрениями *), мы допустим, что линия ?, дающая максимум |/7(°)|» есть
простая аналитическая дуга. Пусть, как раньше, D — область с гра-
границей L и w—f(z), /@) = 0, функция, отображающая конформно круг
\z\ < 1 на эту область. Найдем вариацию \f @) | при вариации линии Z,.
Для большей ясности напомним читателю некоторые свойства конформ-
г) Этими вопросами мы будем заниматься специально во втором томе.
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ
375
ного отображения круга | z | < 1 на область Z), получаемую выбрасыва-
выбрасыванием из плоскости w аналитической линии. Пусть w0 есть произвольная
точка линии ? и пусть 1Х и /2 — две простые дуги, выходящие из
точки w0 и принадлежащие области D (черт. 85) (линии 1Х и 12 имеют
с ? общими только по одной концевой точке). Соединим свободные
концы линий 1Х и 1{ простой дугой /3 так, чтобы совокупность линий
1Р /3, U образовала простой замкнутый контур /, имеющий с ? общей
только точку w0. Мы скажем, что дуги 1Х и 1.2 приводимы, если область
ограниченная /, принадлежит Z), дуги 1Х и /2 не приводимы, если область,
ограниченная /, содержит точки ?. При таком определении все простые
дуги, принадлежащие D и имеющие один конец в точке wOf можно раз-
разбить на два класса Kt и К2: Две любые
линии класса Кг приводимы, две любые
линии класса К2 приводимы и две ли-
линии, одна из которых принадлежит Kv
а другая К2, неприводимы. При кон-
конформном отображении круга | z \ < 1 на
область D, если точка w области D
стремится к точке w0 по некоторой ли-
линии класса Кр то соответствующая
точка z будет стремится к определенной
точке Zq окружности |г| = 1, причем
предельная точка г0' для точки w0
будет одна и та же независимо от
того, по какому пути класса Kt
точка w будет приближаться к точке w0.
Аналогично, если w будет стремиться к w0
нии класса К2> то соответствующая точка
Черт. 85.
по какой-нибудь ли-
z будет стремиться
(к определенной точке z0" окружности |г|=з1, причем если w0 ф 1
w0 не есть конец линии ?), то z0" ф ^07. В соответствии с этим в за-
задачах на конформное отображение каждую точку w0 линии L рассма-
рассматривают как двойную точку — точка w0' и точка wo"\ к точке wof из
области можно подходить по линиям класса Ki, к точке w0" можно
подходить по линиям класса К2- В соответствии с этим всю линию L,
состоящую из двойных точек, рассматривают как двойную линию
L=?,~f-L_: линию L, образуют точки wo\ достижимые путями
класса К1? линию L_ образуют точки w0", достижимые путями класса К2.
Заметим, что, выбирая какую-нибудь точку w0 линии ?, мы разбиваем
выходящие из нее линии на классы Kj и К2 произвольно, разбиение на
классы путей для всех остальных точек мы ведем с таким расчетом,
чтобы у двух произвольных линий одного и того же класса, выходящих
мз двух бесконечно близких точек, нашлись точки, соединимые простой
дугой бесконечно малого диаметра, лежащей целиком в D. е-окрестность
линии ? можно разбить на две части: положительную и отрицательную;
положительную часть образуют точки, которые можно соединить с ?+
бесконечно малыми путями, а отрицательную — точки, соединимые бес-
бесконечно малыми путями с ?_. Вернемся к конформному отображе-
отображению w=f(z).
376 ДОПОЛНЕНИЕ II
Пусть z = F(w) есть функция, обратная функции f(z). Функция
z = F(w дает конформное отображение области D на круг | z | < 1.
Назовем значением функции F(w) в точке w0 предельное значение F (w)9
когда w стремится к w0. Пусть теперь при отображении z — F(w)
точкам w = 1, w = оо соответствуют точки zx и z^ окружности \z\ = Ь
Эти точки разбивают окружность | z \ = 1 на две дуги аир; когда
точка w описывает линию ?,, соответствующая точка z = F. (w) опи.
шет дугу ос, и когда w опишет дугу ?_, точка z = F_(w) опишет
дугу р. При условии, что кривая ?— аналитическая, каждая из функ-
функций F, (w) и F__ (w) также аналитична всюду вдоль ?, кроме конца
ЛИНИИ <ДО= 1.
Обозначая через Z7.' (w) и F^/ (w) значение производной Fr (w)
в точке w, принадлежащей ?, соответственно считая эту точку принад-
принадлежащей ?, или ?_ !), докажем, что если кривая ? дает максимальное
значение функционалу \/'@)\, то в каждой точке w0 линии ? мы
имеем:
или геометрически каждой дуге линии ? отвечают на окружности | z | = 1
две дуги одинаковой длины. Для доказательства (9) допустим против-
противное, что в некоторой точке (wQ) имеем:
тогда в силу непрерывности F/ (w) и
F _/ (w) существует дуга f, содержащая
w0, такая, что в каждой точке этой дуги
Черт. 86.
где k — некоторая константа, большая единицы. Построим дугу уг9
находящуюся в отрицательной части е-окрестности второго порядка дуги у
и совпадающую с т только в концах. Обозначим через 3 область огра-
ограниченную т и Y (черт. 86); кривую Y мы выбираем всегда так, чтобы
площадь 8 была порядка е. Пусть теперь Dx есть область, получаемая
выбрасыванием из D области 5 с ее границей. Функция z = F (w) даст,
очевидно, конформное отображение области Dx на круг, из которого
удалена часть 81? соответствующая области 8; пусть зх есть площадь
удаленной части. Так как дуга у аналитична, то при достаточно малом в
функцию z=F(w) можно аналитически продолжить за дугу ^ во всю
область 8. Обозначая через D2 область, получаемую из D заменой куска
границы т дугой Y* Функция z = F(w) будет давать конформное ото-
отображение проварьированной области Ъ2 на область А, которая получится
из круга | z | < 1 удалением Ьг и добавлением области 82, в которую
построенное аналитическое продолжение функции F(w) переводит
область 8. Пусть о2 есть площадь 82. В силу условия (9) одна из пло-
!) Иными словами F '(w0) есть предельное значение F(w)> когда w стре-
стремится к w9 по одной из линий класса Kle f
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 377
щадей а1 и а2 будет по крайней мере в № раз больше другой *);
пусть о2 > k*av Пусть теперь:
есть функция, отображающая 'конформно круг | С |< 1 на область Аг
ср @) = 0. В силу теоремы имеем:
С другой стороны, функция
дает конформное отображение круга | z | < 1 на проварьированную
область Z>2, /i@) = 0. Диференцируя A1) и принимая во внимание A0),.
получим:
Так как по условию k > 1 и так как, легко видеть, ох есть бесконечно
малая порядка е, то при достаточно малом е фигурные скобки больше
единицы; следовательно, при отображении круга | z | < 1 на область Z>2
\fif@)\>\f{0):
растяжение в начале 2 = 0 больше соответствующего растяжения при
отображении круга | z \ < 1 на первоначальную область D. Мы приходим
к противоречию с основным допущением. Итак, вдоль линии L имеем:
или геометрически: положительной и отрицательной сторонам дуги @, s)
отвечают на окружности две дуги, равные по длине. Таким свойством
будет обладать отображение, если мы за линию L примем луч, располо-
расположенный на действительной оси. Покажем, что это решение единственно-
Допустим, противное, что существуют две различные линии Lx и ?2,
удовлетворяющие найденному условию. Пусть D' и D" — области, полу-
получаемые выбрасыванием из плоскости соответственно линии Lx и Z,2*
Отобразим конформно:
*) Пусть 5 есть длина дуги, принадлежащей L и заключенной между точ-
точками w = 1 и w; пусть, кроме того, у\ = у\ (s) есть длина куска нормали к L
в точке s, заключенной между дугами f и -j', тогда, пренебрегая бесконечна
малыми высших порядков:
9
*1 =
«О
5= У |/?-/.(»)|-Ч(*)-|/'1(ю)|Л.
СТ2:
«о
Условие (9) показывает, что подынтегральное выражение для <т2 в Л2 раз>
больше, чем подинтегральное выражение для о1в
378 ДОПОЛНЕНИЕ II
область D' на область D" при условиях, чтобы начало координат пере-
переходило в начало координат и чтобы начало L{ (w = 1) переходило
в начало линии L2(W= 1): ^@) = 0, фA) = 1. При таком отображении
в силу свойств областей D' и D" функция ty(w) будет в каждой точке
•w линии Lt при подходе к этой точке с положительной и отрицательной
стороны L принимать одно и то же значение
Следовательно, функция ф (w), будучи правильна всюду вне линии ?,
будет непрерывна во всей плоскости, но в таком случае:
где а и ft — константы. Пользуясь условиями ф @) = 0, ф A) = 1, найдем,
что а=1 и ? = 0. Таким образом ф(до) = -а;, линия /^ совпадает
•с линией ?2.
Отсюда, отображая круг |г|<1 на „лучевую" область, мы получим
•единственную функцию, для которой (/'(О)! достигает своего, наиболь-
наибольшего значения:
.Диференцируя и полагая z = 0, мы найдем искомое максимальное зна-
значение функционала:
, Г4A-*)
w L
Используя приведенное выше решение, нетрудно решить задачу
«более общую: среди всех функций f(z) правильных и однолистных
s единичном круге,такиху что: 1) /@) = 0 и 2) f(z) =j= а при \z\ < 1,
требуется найти функцию, для которой \f(fi)\ принимает наиболь-
наибольшее значение.
Для решения этой задачи рассмотрим класс функций:
Этот класс функций удовлетворяет всем условиям решенной нами задачи,
следовательно:
щ\Г(°)\<*, ¦
Az
причем знак равенства достигается, когда F (z) = , . >2. Отсюда для
разбираемой задачи:
|/'@)|<4|а|; A3)
знак равенства достигается, если положить
Приведенные рассмотрения дают как следствие известную теорему
Кббе-Бибербаха.
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 379
ТЕОРЕМА. Если функция w=f(z)(f(Q) = 0, |/@)| = l) пра-
правильна и однолистна в единичном круге |z|<l, то множество ее
значений в плоскости w покрывает круг | w | < — .
. Для доказательства допустим противное, что существует функция
w==f(z), удовлетворяющая условиям теоремы и не принимающая при
] 2 | < 1 значения а, |я|<-т~; тогда в силу A3) получим:
что невозможно, ибо по условию/'@) | = 1.
Проблема коэфициентов. Одной из важных проблем в теории
конформных отображений является следующая задача: среди всех функ-
функций w =f(z) (/@) = 0, \f @) | = 1) правильных и однолистных в еди-
единичном круге | z | < 1 найти функцию, для которой | /(п) @) | прини-
принимает наибольшее значение.
Мы приведем решение этой задачи для случаев п == 2 (теорема Би-
бербаха) и п = 3 (теорема Ловнера).
Прежде чем приступить к решению, изменим несколько самую поста-
постановку задачи. Пусть F(z) (/7@) = 0) есть произвольная функция, пра-
правильная и однолистная в единичном круге; тогда функция
будет, очевидно, принадлежать к классу функций, определенному в усло-
условиях задачи, и
IF'@I '
Кроме того, если arg F^ @) = а и arg/7'(O) = p, то для функции:
3 — па а — Е
Ф(г) = еп~1 F{en~i z)
аргумент будет обладать следующими свойствами:
Следовательно:
ф{п)
Отсюда заключаем, что нашу задачу в общем случае можно формулиро-
формулировать также следующим образом: среди всех функций w = Ф (г), Ф@) = 0,
arg Ф' @) = 0, правильных и однолистных в единичном круге, найти
()
ф()@)
функцию, для которой Reel ф, (Q) принимает наибольшее значение.
Именно в этой постановке мы и будем решать задачу. Сделаем еще
одно небольшое упрощение задачи. Пусть L есть простая дуга, распо-
расположенная в плоскости w и обладающая следующими свойствами:
1) L не проходит через начало координат w = 0\
2) L соединяет точку а с бесконечно удаленной точкой;
380 ДОПОЛНЕНИЕ II
3) L обладает непрерывно вращающейся касательной и
4) при удалении в бесконечность L асимптотически приближается
к действительной оси.
Обозначим через DL область, получаемую удалением из плоскости w
линии L. Пусть w—fz(z), /х@) = 0 есть функция, отображающая
конформно круг на область D ъ. Из теории конформных отображений
известно, что, какова бы ни была функция Ф (z), Ф @) = 0, правильная
и однолистная в единичном круге, всегда можно построить последова-
последовательность линий:
*-1> *-2> ^3» • • •» **п,. . .,
обладающих перечисленными выше свойствами, и таких, что:
«К*)= lim/' (*),
причем сходимость, равномерная во всяком круге, (zj^Xl, внутрен-
внутреннем к кругу \z\ < 1. Отсюда:
Ф' @) = lim Д. ' @); Ф" @) = lim Д. " @); ...; Ф(ге) @) = lim Д. <п) @).
п п п
Следовательно, для разыскания абсолютного максимума функционалов
среди всех однолистных функций Ф (г), Ф @) = 0, нам достаточно найти
абсолютный максимум этих функционалов для функций fL {z).
Перейдем теперь к основной редукции задачи. Итак, пусть L есть
линия, определенная выше. Отметим на линии L точку P(s), где 5 есть
расстояние от а до Р (s), измеренное по линии ?. Обозначим через
D @) область, получаемую выбрасыванием из плоскости w всей линии Ly
и обозначим через D (s) область, которая получится, если к области
D @) добавить кусок линии L, заключенный между точками а и P(s). Пусть;
^ =/(/-, 5); /@, s) = 0, arg/ @, s) = 0 @ < 5 < сю)
есть функция, реализующая конформное отображение круга I z I < 1 на
область D(s). Найдем главные части приращений ,, ' гтЛ—-А"Ч
/ (U, 5 — /ЛГ) / [у, S)
ff/Г /Q ^ Д^\ у/// /Q А
и * у—г-—- д f / , Для этой цели, считая А^ бесконечно
/ \Уу S AS) J {V, S)
малым и пренебрегая бесконечно малым высших порядков, вычислим:
/@, 5 — As), /"@, 5 —As) и /"'(О, S —As).
При конформном отображении
w=f(z, s)
дуге [P(s), P(s — As)] линии L будет отвечать в круге |г|< 1 беско-
бесконечно малая дуга *у> выходящая из некоторой точки Q(s) окружности
J2r| = l, ортогонально к этой окружности. Пусть Ь есть область, полу-
получаемая удалением из круга | z \ < 1 дуги y, и пусть
— функция, отображающая конформно круг (С) < 1 на область 8.
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 381
При этих обозначениях, очевидно, имеем:
_. f(z, s — As)=/[<b (z), s].
Отсюда: J ч ' J LY v h J
y=^@, 5 — As)=//@, s)ij/(O),
f @, s — As) = /" @, s) Y2 @) +/ @, s) ?' @), A4)
f> (o, 5 — As) =/"' @, s)f з @) -f 3/40, 5)f @) +/ @, s)?"@).
Пренебрегая бесконечно малыми высших порядков, мы можем считать
отрезок 7 прямолинейным; тогда, обозначая через —• 6 аргумент точки Q,
мы можем положить:
где ^ есть функция, определенная в п. 4, и Д? есть новая бесконечно
малая, связанная с As и имеющая тот же порядок, что и 5,A dt =
= — р E) ds, |x (s) > 0. Используя формулы (8Г) и • снова отбрасывая
-бесконечно малые высших порядков, формулам A4) можно придать сле-
следующий вид:
/@, s —As)=/(O, *)A-Д0,
/' (о, s — As) =/' @, s) A — 2Д*) — 4/Д^/ @, .?),
/" (о, s _ As) =/" @, s) (I — ЗАО — \2^Mf @, s) — 12е2йД//@, 5).
Отсюда, полагая для сокращения письма:
Рч \s) —
о, S) »
получим:
^з = - B/>3
Полагая /72 = а2-}-^2' Рз^^^зЧ"'^ и деля на dt, получим:
dt ^
—¦ = — Bа3-{- 12a2cos6 — 12?2sin6-|- 12 cos 26),
% = — B&> -f 12aQ sin'6 + 12b* cos 6 -4- 12 sin 26).
at v з i 2 * i 2 i /
Сделаем несколько замечаний относительно полученной системы
уравнений. Действительные переменные а2, Ь2, а8, Ъъ и 6 суть функции
s@<;s<oo), a s можно рассматривать как монотонную функцию t>
причем так как отрицательному приращению As соответствует положи-
положительное приращение А^, мы можем считать, что при s, меняющемся от
оо до 0, t возрастает от некоторого Го>- — оо до конечного числа Г.
382 ДОПОЛНЕНИЕ II
Считая t независимым переменным и интегрируя полученную систему
диференциальных уравнений, мы получим выражения: я2, &2, аъ и Ь%
в зависимости- от функции 8:
t
е~*cos^Udt-\- сЛ,
в""'-sin 6 dt -f
— 4^* cos 6
4e* sin 8 y*«- Tsin 8 dx — 4e* C
Займемся определением произвольных постоянных Си С2, С3. Так:
как при 5, стремящемся в бесконечность, линия L асимптотически при-
приближается к действительной оси, то легко видеть, что фунция *,*'
будет стремиться к функции, реализующей конформное отображение
круга | z | < 1 на лучевую область (получаемую удалением из плоскости
луча, выходящего из точки w = — и расположенного на действитель-
действительной оси). Следовательно
f(z, s) _ z
Отсюда при s = oo или при t—T0 должны иметь:
Отсюда заключаем, что при / = То:
b = О
я3=18.
Разберем отдельно два случая: 1) То > — оо к 2) То = — оо»
В первом случае после подстановки получим:
С —е~То-
Г — 3
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 383
Полагая 8@ = 0 при t < Го и подставляя значения
t
я2 = — Ае"г JV cos 6 dt,
констант, найдем:
Ь<2 = — 4е~~* I ег sin 6dt,
— оо
а, = — 12е~~* [е2*^2Ь — Ае~* cos 6
— оо
t
-J- 4(?^sin 6 /'^Tsin 6 дГх} dt.
A5)
Если To = — оо, то при ty стремящемся к — оо, переменная б стре^
мится к нулю; отсюда легко убедиться, что t—> — оо, переменные а2г
Ь2 и ав> определенные формулами A5), стремятся соответственно
к —4, 0 и 18. Итак, представления а2у ?2, аъ по формулам A5) имеют
место в каждом из двух возможных случаев.
Таким образом, какова бы ни была область D, получаемая выбра-
выбрасыванием из плоскости линии L, удовлетворяющей перечисленным выше
условиям, функционалы Reel ф, ' и Reel *'•• могут быть пред-
пред, и Reel
ставлены первой и третьей из формул A5).
Рассматривая совокупность всех непрерывных функций 6 =
в силу предыдущего максимальные значения интегралов, стоящих справа
в A5), будут не меньше, чем максимальные значения изучаемых нами,
функционалов *).
Найдем максимум я2- ^ак как множители ег и e~t положительны
при всех значениях t и перед интегралом стоит знак минус, то максимум:
а2 получится, если cos 6 при всех значениях t будет принимать мини-
минимальное значение, т. е. равен —1, следовательно:
таХ
Но для функции w = —
Следовательно:
A —zy
га =4.
а) Можно показать, что не только каждому отображению w=fL(z) отве-
отвечает 8 (/), но и каждой непрерывной функции 6 = 6 (/) отвечает однолистная
функция. Принимая это. можно заключить, что максимумы интегралов равны
максимумам соответствующих функционалов.
384 ДОПОЛНЕНИЕ II
Перейдем к разысканию экстремума я3. Для этой цели произведем
предварительно некоторые преобразования правого интеграла
t
\2e~2t je2t cos 26 dt
— oo
t т
— oo — oo
t
— 48*T2' - j Jeb + 5) sin 8 (x) sin 6 (a) dz dz.
— oo — oo
В силу того, что выражения, стоящие под знаками двойных интегралов,
суть симметрические функции х и о, мы можем треугольные области
интеграции заменить прямоугольными; получим:
t
аг = — \2е~2г Jc2t cos 26 dt +
— oo
t t
— oo —oo
t t
— 24e~2' f /VT + 9) sin 8 (t) sin 6 (a) dz ds.
— oo —oo
Обозначая через J сумму первых двух членов в выражении а3 и пре-
преобразуя третий член, получим:
t
— со
Отсюда заключаем, что:
max 03-
Будем искать экстремум функционала J. Для этой цели найдем вариацию
J при варьировании 8 в некоторой точке t0. Найдем:
t
\J=24e~2t fe2t sin 2686 Л —
— oo
t t
— 24*Г2* у /VT +5) cos 6 (x) sin 6 (a) 86 (a) dz do —
— oo — oo
t t
— 24e~2t f /Vх+5) sin 6 (x) cos 6 (a) 86 (x) dz do.
— oo —oo
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 385
Полагая;
и приравнивая bf J нулю, получим:
t
e2to [sin 26 (to)] o — 2eta [sin 8 (to)] о Je" cos 8 (т) dz = 0. A50
— oo
После сокращения A5/) можно разбить на два уравнения:
sin 6 = 0, A6)
t
eto cos 8 (*0) = Jex cos 8 (x) dx. A б7)
— CO
Покажем, что второе уравнение может быть удовлетворено только при
cos 6 = 0. В самом деле, правая часть от t0 не зависит; обозначим ее
через С; получим:
cos 8 (х) = Се~~\
Подставляя найденное выражение для cos 8 под знак интеграла, получим:
t
— оо
что возможно только при С=0. Отсюда
cos 8 = 0. A7)
Подставляя выражение sin 8 = 0 в формулу для а3, найдем:
о» =18,
а при подстановке cos 0=1:
Отсюда, предполагая, что интеграл J достигает своего максимума при
некоторой непрерывной функции 6(/), мы получаем, что
тах/= 18.
Отсюда
Но так как для функции w = — : 74 =18, то, следо-
следовательно:
Добытые нами результаты можно формулировать следующей теоремой:
386 ДОПОЛНЕНИЕ III
ТЕОРЕМА. Если функция
w — z-{~ c2z2 -J- c%z3 -f- ...
правильна и однолистна в единичном круге |я|< 1, то
|г2|<^2 (теорема Бибербаха);
| св | <; 3 (теорема Ловнера).
Для доказательства достаточно заметить, что сп = —г I -r-g- , и
п. \^az J2--0
воспользоваться решением разобранной нами вариационной задачи.
Обзор современного состояния геометрических методов теории ана-
аналитических функций дан в докладе М. А. Лаврентьева (см. «Труды
II Всесоюзного математического съезда», т. I).
ДОПОЛНЕНИЕ III
ПРИМЕНЕНИЕ МЕТОДА РИТЦА К ДОКАЗАТЕЛЬСТВУ СУЩЕСТВО-
СУЩЕСТВОВАНИЯ РЕШЕНИЙ УРАВНЕНИЯ ШТУРМА-ЛИУВИЛЛЯ.
Гельфанд И. М. и Сухомлинов Г. А.
Доказательство существования первой собственной функции.
Согласно результатам, изложенным в главе XIII, § 80 вопрос о раз-
разрешимости проблемы Штурма-Лиувилля приводится к доказательству
существования функции, дающей минимум интеграла
f A)
О
при условии
f B)
Bа)
р, рг и q непрерывны, кроме того р > 0. Там же было приведено дока-
доказательство существования такой функции путем замены функционала J
конечной суммой и последующим переходом к пределу.
Здесь мы имеем в виду дать доказательство той же теоремы методом
Ритца.
Пусть функции <!>,(/= 1, 2, ...) линейно независимы, образуют пол-
полную систему на интервале [0, тг], диференцируемы и удовлетворяют
граничным условиям задачи, т. е. fy @) = tyf G1) = 0. В частности можно
положить ф4 = sin lx. Этот частный вид функций мы и положим в основу
ПРИМЕНЕНИЕ МЕТОДА РИТЦА 387
доказательства; доказательство при системе функций ty{ может быть про-
проверено совершенно так же. Положим
т
Л» =2 я* sin/x. C)
i=i
Решение поставленной задачи будет состоять в том, что мы заменим
в функционале J(y) функцию у через ут и получим, таким образом,
обычную задачу на максимум и минимум функции т переменных. Далее
докажем, что переход к пределу законен и предельная функция дает
решение вариационной задачи A). Подставляя ут в A) и B) [условия
Bа) выполнены автоматически вследствие соответствующего выбора функ-
функций sin ix], наша задача может быть формулирована следующим обра-
образом: Найти минимум функции
^ / s^ D>
при условии
Е„.
о
Уравнение E) есть уравнение /я-мерного эллипсоида, так как его
левая часть есть определенно положительная квадратичная форма отно-
относительно av a2, ...,ат. Ищется таким образом минимум непрерывной
функции на поверхности эллипсоида. По теореме Вейерштрасса этот
минимум достигается; обозначим его через J^. Так как точка, в кото-
которой этот минимум достигается, — внутренняя, то
2 aisinix) sin
— f {{р ( 2а»sin'ix) sifl/
(A =1,2, ..., m).
Умножив каждое равенство на произвольное Ah и просуммировав по А,
получим:
где
/{РУт\: + (Я - ХЙЛ.С,,} dx = 0, F)
Полагая в частности ?т=:ут9 получаем:
388 ДОПОЛНЕНИЕ III
или учитывая равенство E):
т. е. собственное значение квадратичной формы D) есть ее минимум
при условии E). Полагая т = 1,2, ..., k, ..., получим последователь-
последовательность минимумов:
Очевидно, что
г@) /(О) r@)
так как
и так как
i = min J (av UV • > *m'
7(^ = min У (fllf a2, ..., aj
J(av a2,..., am1 0) = J(alf a2) ..., am)
и таким образом в J{av a^ . .., ат, х) может меняться еще один аргумент,
что только уменьшает минимум. Кроме того последовательность G)
ограниченна, так как вследствие положительности р и условия B) при
любом т имеет место следующее неравенство:
к к
f (P/I + ЧУ г?) dx>f Wl dx > ?ппа ')•
О О
Следовательно последовательность G), как монотонная и ограниченная,
сходится. Таким образом существует
Из сходимости последовательности
следует
где М — константа. Отсюда
п
f
q/mdx
х) Через #min обозначен абсолютный минимум непрерывной функции
на замкнутом интервале @, г)
ПРИМЕНЕНИЕ МЕТОДА РИТЦА 389
А так как р > 0 и следовательно
'л "
/
О
то отсюда следует, что ут равностепенно непрерывны и равномерно
ограниченны *). В силу теоремы Арчела (§ 44) из нашей последователь-
последовательности yv у%, ..., ут, ... можно выделить равномерно сходящуюся под-
подпоследовательность
Уiv Уы* • • •» ^«1» • • • (8)
Пусть YLmyml=y. Докажем, что у удовлетворяет уравнению
Штурма-Лиувилля и дает минимум интегралу
Некоторая трудность будет здесь в том, что неизвестно, сходятся ли у'т.
Поэтому придется итти, следуя Ритцу, обходным путем.
Во-первых, предельная функция удовлетворяет условиям ^@) =
s=zy (тс) = 0 (так как им удовлетворяет каждая из функций ут). Дока-
Докажем, что эта функция имеет непрерывные первую и вторую производ-
производные. Для этого совершим предельный переход в равенстве F). Но прямо
его совершить нельзя, так как туда входят у'т. Для этого проинтегри-
г) Во-первых, семейство ут равномерно ограниченно. Действительно,
в силу равенства
И = У™ (*) = <>,
а
и, применяя неравенство Шварца, получим:
х х
\У»(*)Р = (TV-С*)dxJ<(*-«) J У'« dx<Мг(.Ь- а).
а а
Во-вторых, последовательность ут есть семейство равностепенно непрерывных
функций. В самом деле
\
/Ут dx
< dx* I yfldx4CM2\x2 — x11,
что и доказывает равностепенную непрерывность нашего семейства.
390
ДОПОЛНЕНИЕ III
руем его по частям. Интегрирование по частям первого слагаемого
нам дает:
J Py'Smdx = /PVmdym = - f ym
0 ' 0
0 0
= - f PVmy>*-hmf P'ymdx]+ f[f P'ymd
0 о ooo
K X К
= - /[РУш-fpymdx]Cmdx-^(*)f P'ymdx.
0 Q Q
Интегрируя второе слагаемое, имеем:
[
о
• о ооо
/С
0
[
0 0
Окончательно, соединяя оба слагаемые и воспользовавшись формулой F),
получаем:
я х «Та?
Ут~ f P/ndx-f f (9-^)y
О 0 0
я X
о о
~ ^^ dx ~ 1р'у™ dx]= °-
При интегрировании по частям у нас были две цели: во-первых,
избавиться от /т и, во-вторых, при основном интеграле получить общим
множителем Е^. Так как функции Cw являются совершенно произволь-
произвольными, мы можем потребовать, чтобы последовательность их вторых про-
производных См равномерно сходилась к какой-нибудь ^произвольно вы-
выбранной непрерывной функции. Это можно сделать, так как любую
непрерывную функцию можно апроксимировать тригонометрическими
полиномами (см., например, И. И. Привалов, Ряды Фурье). Тогда С^
и Сш также равномерно сходятся к непрерывным (и соответственное
число раз диференцируемым функциям) С и С. Заставляя теперь k про.
ПРИМЕНЕНИЕ МЕТОДА РИТЦА 391
бегать индексы последовательности (8) {ут> а следовательно и их интег-
интегралы сходятся равномерно), получим !):
к х х х
/VU- f P'ydx- f f (q-\U)ydx2]dx-
0 0 0 0
я x к
-C7(«) \f [(Я — Ь11))У<Ь?+ fp'y dx] = 0. (9a)
Ч о о J
Функцию Q можно выбрать так, чтобы ?' @) = С' (я) = 0. Тогда получаем:
1С X XX
Iс" [ру ~ Ip'y dx ~ //{ч ~
О О 0 0
Применяя лемму Дю-Буа-Реймона2), имеем:
ру
XX
~ iff (q-
0 0
if
0 0
Так как правая часть диференцируема, а выражение в квадратных
скобках в левой части тоже диференцируемо (как неопределенный
интеграл непрерывной функции), то диференцируемо и первое слагаемое
левой части, т. е. у имеет производную. Выполняя диференцирование,
имеем:
X **
(РУ)' —Р'У — /(Я- '^] )ydx = C2,
О
или, диференцируя еще раз, получаем:
т. е. у удовлетворяет уравнение Штурма-Лиувилля, которое можно
было бы получить как уравнение Эйлера данной задачи.
Докажем теперь, что функция у дает минимум интеграла A). Прямо
совершать предельный переход нельзя, так как ничего не известно
относительно сходимости ут.
!) Х^ тоже стремятся if некоторому пределу ХA), так как Х^ =
2) Пусть у=у(х) есть функция непрерывная в интервале а^.
и такая, что
для всех функций у=у(х) класса Сп> обращающихся в нуль на концах интер-
интервала вместе со своими производными до (п — 1)-го порядка включительно. При
этих условиях у есть полином не выше (я—1)-й степени. [Zermelo, Math.
Annalen, т. 58 A904).]
392
ДОПОЛНЕНИЕ III
Докажем сначала, что
Сделаем следующее очевидное замечание: если интегрировать (9) по
частям в обратном порядке, то получим, очевидно, исходное соотноше-
соотношение F). Следовательно, если интегрировать по частям таким же обра-
образом соотношение (9а), формально ничем кроме индексов от (9) не отли-
отличающееся, то получим следующее соотношение:
ГС
О
или, полагая C=j>, имеем:
О
Докажем теперь, что ХA) есть нижняя граница значений У [ср (х)]9 где
9 (лг) — любая допустимая функция. Допустим обратное. Тогда ХA) больше
нижней границы J[y(x)] (меньше нижней границы она быть не может),
так как J(y) = \^\ то существует функция <р(х), удовлетворяющая
условиям B) и Bа), и такая, что
J [? (*)] =/{р [?' (х)J + q [ср (*)]2j dx < XA) - ,.
О
Апроксимируем теперь <р' (х) некоторым полиномом
Рк(л:) = а04~агcosх-\- ... -\-акcoskx
так, что
Записав это соотношение в виде:
и проинтегрировав от 0 до х, получим:
Вводя обозначение:
аЛsinjc-j—^-sin2A:4-- ... + ^ S1
имеем:
Положив л: = ^ и учитывая условия Bа), получим:
ПРИМЕНЕНИЕ МЕТОДА РИТЦА 39&
т. е. | а01 < ех и следовательно:
Из этого следует, что функцию ср(лг) можно апроксимировать таким,,
состоящим из синусов, полиномом, что производная <р' С*) апроксими-
руется производной этого полинома. Следовательно, можно выбрать
номер к столь большим, что
\j[Qk(m-J[f^)}\<~
и следовательно:
(так как последовательность G) — монотонная невозрастающая). А
противоречит тому, что \^ есть минимум J(av a^ ...,яЛ).
Примечание. Мы не доказали сходимости последователь-
последовательности yv у2, ... к решению у, а только лишь сходимость неко-
некоторой подпоследовательности yiu y2v . .., закон образования кото-
которой не указан. Для практических же приложений важно знать
равномерную сходимость всей последовательности yv jy2, . . .
Теперь это нетрудно доказать. Действительно, мы доказали, что
каждая сходящаяся подпоследовательность сходится к решению
поставленной задачи. Если предположить, что вся последователь-
последовательность yv у2, .. . расходится, и, следовательно, существует другая
подпоследовательность, сходящаяся в некоторой другой функции
у^1' и она согласно вышесказанному тоже была бы решением
нашей постоянной задачи и соответствовала тому же собственному
значению. Это же невозможно, вследствие единственности реше-
решения. В силу компактности yv у.2) ..., упУ ... из сходимости этой
последовательности следует и равномерная сходимость.
Доказательство существования второй собственной функции.
Для того чтобы доказать существование функции у^\ дающей мини-
минимум интеграла A) при условиях B) и Bа) и дополнительном условии:
= 0, A0)
где У1* — первая собственная^функция, положим
2
Подставляя это выражение в A), снова получим квадратичную форму
коэфициентов. Выражение B) снова дает уравнение поверхности того же
эллипсоида. Полагая
т
i— 1
394 ДОПОЛНЕНИЕ III
где ар как и прежде, коэфициенты частных тригонометрических сумм,
равенство A0) дает:
2 bh I sin kx ( ^ ai sin ix )dx=0,
т. е. уравнение плоскости в m-мерном пространстве, проходящей через
начало координат. Эта плоскость пересекает указанный эллипсоид
и в сечении получается также эллипсоид, только меньшего числа изме-
измерений. Таким образом, мы снова можем применить теорему Вейерштрасса.
Соотношение F) в этом случае имеет вид:
f
с")
Если мы докажем, что |х = 0, то мы будем находиться в условиях, кото-
которые мы имели при доказательстве существования у^\ Следовательно,
see, что доказано относительно у^, автоматически будет перенесено наУ2).
Полагая в A1) Al = av получаем:
или, так как / y^
9
Q
С другой стороны, полагая в F) Ai = bif получим:
или
)^=о. A4)
Но левая часть равенства A4) есть в то же время правая часть равен-
равенства A3), а это и доказывает, что (а==0.
Таким же образом доказывается существование уР\ у и т. д.
УКАЗАТЕЛЬ
Абельсон 29
Абсолютный минимум 54
— экстремум 54
Александров П. С. 65, 67, 89, 92
Апроксимативные методы 37
Арчела теорема 87
Аэронавтическая задача Цермело 19
Балка со свободными концами 121
Балки изогнутой формы (задача)
141
Банах (Ban&ch) 80
Барбье теорема 28
Бибербаха-Кобе теорема 379—380
Билинейная симметрическая функ-
функция 74
— функция 73—74
Билинейный функционал 104
Блашке (Blaschke) 360
Близость кривых 56, 193
— — п-го порядка 57
— нулевого порящка 57
— пространственных кривых 110
Больцмана функция 159
Боннезен (Bonnesen) 360, 367
Брауера теорема 164
Брахистохрона 1, 15
Брахистохроны задача 236, 315, 342
Вариации бесконечно малые 371
— двусторонние 234
— односторонние 231
— нормальные 205
Вариационного исчисления простей-
простейшая задача 17
Вариация 35, 37, 197
— в концах 125
— внутренняя 221, 224, 227
— вторая 104—108, 106, 116—118, 199
для изопериметрической за-
задачи 290
— в точке 98—101, 207
— в точке «в данном направлении
112—114
—- в точке отражения 224
— в точке перелома 221
— границы специальная 373
— допустимая 171
Вариация интегралов от экстремалей
129
Вариация конца 227
— начала 227
— нормальная в точке в данном на-
направлении 209
для пространственной задачи
207
— функционала 92, 124, 226
«в середине 125
Вектор 71
— смещения 205
Вектор сопровождающий 293
Ветчинки н 184
Вейерштрасс 252
Вейерштрасса необходимые условия
337
— теоремы 68
— усиленное условие 343
— формула для представления щри-
ращения функционалов 336
— функции геометрический смысл
336
— функция 332—337
Вейерштрасса-Эрдмана условия 218,
322
Вейерштрассова форма уравнений
Эйлера-Лагранжа 198, 199
Вейерштрассовой формы уравнений
инвариантность 199
Взаимности принцип 152
Волновая динамика 19
Вторая вариация для изопериметри-
изопериметрической задачи 290
Выпуклое симметрическое тело 353
Выпуклые линии 351
Выступы 360
Гамильтон 19
Гамильтона принцип 114, 202
— форма уравнений Эйлера-Ла-
Эйлера-Лагранжа 310
Гамильтона-Якоби уравнение 327—
328
Гаусса теорема 179, 319
Гауссова кривизна 246
Геодезическая гипербола 325
— кривизна 211
— линия как инвариант изгибания
177
— окружность 176
Геодезические дуги 175 ;
396
УКАЗАТЕЛЬ
Геодезические (задача) 343
— (замкнутые) на выпуклых по-
поверхностях 213
— линии 201
— на поверхности 211
— на сфере 205
— на эллипсоиде 331
Геодезический радиус 177
— эллипс 324
Геодезической окружности центр
177
Геометрическая теория собствен-
собственных значений 272
Геометрический смысл функции
Вейерштрасса 336
Геометрия на поверхности 179
Герца принцип 203
Гильберта теорема 83, 91, 259, 333
Гильбертово пространство 72
Гипербола геодезическая 325
Грамма-оттределитель 153, 292
Граница области 66
Граничная точка 66
Группа коммутативная 70
Жордана простая дуга 215
Жуковский Н. Е. 44, 48, 130, 369
Изометричные (пространства 80
Изопериметрическая задача 29, 200
в узком смысле 307
на поверхности 211
Изопериметрической задачи кон-
константа 168
Изотермическая система координат
175
Импульс обобщенный 115
Инвариантность уравнений Эйлера
101, 147
Индуктивное сопротивление крыла
48
Инерции силы 114
J-гипербола 325
./-длина 309
«/-прямая 309
«/-расстояние 309
7-эллипс 325
Даламбера принцип 114
Дарбу теорема 322
Действие (интеграл) 19
Действия экстремум 19
Дирихле интеграл 146
— принцип 159
Диференциал ©тарой 74, 105
— в точке 128
— первый 74
— функции 74
Длина кривой 89
— линии в геометрии Римана 180,
191
Допустимая вариация 171, 351
Допустимые линии 28, 53, 215, 240
Допустимых линий класс 194, 231
Достаточное условие упрощенное
341
Достаточные условия минимума 77
Дю-Буа-Реймонда лемма 96
Задача изопериметрическая 26
— о брахистохроне И, 15, 342
— о геодезических 343
— о наименьшей поверхности вра-
вращения 39, 274
. рефракции 342
траектации луча света 12, 13
тяжелой цепи 25
— со свободными концами 132
— с производными высших поряд-
порядков 136
— Чаплыгина 184
Замкнутая область 66, 232
Замкнутое множество 66
Каноническая форма уравнений
Эйлера-Лагранжа 311
Касательное линейное многообразие
162
Качественные принципы 370
Квадратическая функция 74
Квадратический функционал 104,
253
Классификация Морса экстремалей
281
Кнезера теорема 319
— теория 318—319
Кобе 369
Кобе-Бибербаха теорема 379—380
Ковнер С. С. 358
Колмогоров Л. Н. 89, 92
Коммутативная группа 70
Компактное в себе множество 67
— пространство 67
Компактность в малом 67
пространстве 86
функциональных простран-
пространствах 82
Консервативности закон 203
Координат криволинейная система
174
Координаты элемента 71
Коши последовательность 66
Коэфициентов проблема 380
Кривая минимальной длины 200
— охватывающая наибольшую пло-
площадь 45
Кривизна геодезическая 211
— полная 213
Криволинейная система координат
174
УКАЗАТЕЛЬ
397
Кривые фокальные 324, 325
Кривых близость 193
Крыло наименьшего индуктивного
сопротивления 47
Куранта теорема 277—279
— теория собственных значений
277
Лагранжа задача {связь ее с изо-
иериметрической задачей) 185
— лемма 95, 145
— метод 31, 37, 52, 170
— общая задача 1831
— преобразование 94, 144, 180
—- уравнения 115
Лагранжа-Эйлера правило множи-
множителей (обобщение) 164
— уравнение 146
Ламберта теорема о планетных
орбитах 130
Лапласа оператор 147
Лежандра необходимое условие 338
— теорема 107
— усиленное условие 341, 343
— условие 106—108, 117, 140, 166—
168
как следствие условия Вейер-
штрасса 338
Лежандра-Якоби теория квадрати-
ческих функционалов 285—286
Леммы вариационного исчисления
96
Лемма Дю-Буа-Реймонда 96
— Лагранжа 95
Линейная метрика 72
—« функция 72
Линейно независимые точки 705
Линейное касательное многообра-
многообразие 162
Линейное многообразие 70, 160
Линейные пространства 69
— функционалы 91
Линейных многообразий свойства
161—162
Линии допустимые 28, 53, 240
Линии отражения 225
—• преломления 225
Линий допустимых «ласе 215
Линия волны 228
Лиувилля формулы интегрирования
геодезической 330
Лобовое сопротивление 48
Ловнера теорема 380, 386
Лучевая область 379
Люстерник Л. А. 290, 326, 360
Максвелла закон распределения 159
Максимальное растяжение 375
Малюса принцип 136, 227, 228
Метризация пространств 65
Метрика в абстрактных простран-
пространствах 71—72
— линейная 72
Минимаксная экстремаль 281
Минимаксной экстремали окрест-
окрестность 283
Минимизирующая последователь-
последовательность 350
Минимум абсолютный 54
— относительный 56
— строгий 341, 344
Минковский (Minkowsky) 360
Минковского задача 353
— неравенство 63
— теорема 355
Многообразие в линейном про-
пространстве 160
— линейное 70, 160
касательное 162
Многообразий линейных свойства
161—162
Множество замкнутое 66
— компактное ib себе 67
Монтеля принцип 370
Мопертюи-Эйлера принцип 17, 43,
203
Морса классификация' экстремалей
281
— теорема 289, 308
Мунка теорема -50
Наклона поля функция 333
Наклон поля 333
Неголономные связи 180
Необходимые условия экстремума
76—77, ПО
Неподвижная точка 164
Нормальная вариация 206, 208
в точке в данном направле-
направлении 209
— функциональная производная
207
— собственная функция 262
Ньютона задача 238
— кривая 245
Области типов а, Ь, с 360
Область 66
— в функциональных простран-
пространствах 232, 283
— закрытая 232
— лучевая 379
— меньших значений 284
— связная 283
Обыкновенная точка 162, 233
Овал постоянной ширины 28
Однородная функция 190
Однородности условия 189
Окрестностей системы эквивалент-
эквивалентные 64
398
УКАЗАТЕЛЬ
Окрестность кривой 56, 58
— минимаксной экстремали 283
— экстремальной кривой 284
Окружение экстремали полем 332
Окружности геодезической центр
177
Окружность геодезическая 176
— скоростей 21
Опорные прямые 359
Оптические применения 227
Ортогональности условие 127, 135,
174
Ортогональность собственных
функций 295
«Освещенная» часть 240
Осгуда теорема 345—349
Особые точки 233
Особый случай изопериметрической
задачи 149
Отражение экстремалей 223
Отражения линии 225
Парабола безопасности 19
Параллелепипедная сеть 356
Параллелепипедное разбиение 356
Параметрическая форма задания
кривой 188
Параметрические представления спе-
специальные 192
Перелома кривой точки 215
Периодические движения динами-
динамических семейств 205
Петровский И. Г. 290
Планетное движение 43
Плоскость скоростей 21
Поверхность волны 136
— вращения наименьшая 39, 343
наименьшего сопротивления
238
— наименьшей площади 146
Подъемная сила 48
Поле собственное 312, 332
— трансверсалей 314
— центральное 312, 313
— экстремалей 311—312
Полнота абстрактных пространств
66, 67
— пространства С 78
Положительно-определенная форма
291
Поля центр 312
Последовательность, Коши 66
Прандтль 48
Предел последовательности 66
Предельные тела 360
Предельный элемент 64
Преломление экстремалей инте-
интеграла 222
Преломления закон 223
Преломления линии 225
Преломления траекторий закон 23
Приращение функции 74
Проблема коэфициентов 380
Производная функциональная 99,,
206, 207
в точке в данном направле-
направлении 209
нормальная 207
Пространства изометричные 80
— линейные 69
Пространственная задача ПО
Пространство Гильберта 72
Пространство касательное 127
— компактное 67
— L 63
— ?р 82
— Ц/ 81
— m 63
— R 82, 254
— Rk 291
— Rtf 83
— С 63, 78
— С (сепарабельность) 79
— С/ 80
— С„ 64, 80
— спрямляемых кривых 89
— функциональное 78
Прямая касательная 163
«Прямые» геометрии на поверх-
поверхности 179
Пуанкаре теорема 213, 270
Пуассона интеграл 372
Пуассона-Эйлера уравнения 137—
140
Равномерно непрерывная совокуп-
совокупность 85—86i
Радиус геодезический 177
Разбиение параллелепипедное 356
Расстояние между кривыми 56, 123
— (кратчайшее) от точки до кри-
кривой 127
Растяжение максимальное 375
Регулярные точки экстремали 98
Рефракция {задача) 342
Римана геометрия (длина линии)
180
Рица метод 50
Света распространение (задача) 12„
13
Свободные концы 118
Сельвестр 287
Серре-Френе 176, 210
Сеть параллелепипедная 356
— счетная всюду плотная 79
Сила подъемная 48
Силы инерции 114
Сильного экстремума достаточные
условия 339
необходимые условия 337 \
Симметрическая билинейная функ-
функция 74
УКАЗАТЕЛЬ
39&
Симметрический билинейный функ-
функционал 114
Системы окрестностей эквивалент-
эквивалентные 64
Скоростей окружность 21
Скоростей плоскость 21
Смещение вектора 205
Собственная функция нормирования
Собственное поле 312, 332
262
Собственные значения 261, 293
— функции 262, 293
Собственных значений геометриче-
геометрическая теория 272
— значений зависимость от верх-
верхнего предела 279
и собственных функций
основные свойства 262—264
¦ сравнение 297
экстремальная теория 275—
281
— функций' основные свойства 294
теорема единственности 276—
277
Совокупность равномерно непре-
непрерывная 85—86
Сопровождающий вектор 293
Сопряженная точка «ратная 307
Сопряженные значения 268, 300
кратные 300 \
¦ слева 282
справа 282
— точки 272
для изопериметрической за-
задачи 306
Стационарные точки 77
Ступенчатые функции 260
Сфера в функциональном про-
пространстве 254
Сходимость в абстрактном про-
пространстве 66
Счетная всюду плотная сеть 7Ь
Точка неподвижная 164
— перелома кривой 215
Точки линейно независимые 70
— обыкновенные 233
— особые 233
Трансверсалей поле 314
Трансверсали 311, 316
Трансверсаль поля 314
Трансверсальности условие 123, 126,
195
— условий обобщение 133
Трансверсальность 172—175
Треугольное преобразование 289
Тривиальное решение уравнения
Штурма-Лиувилля 261
Тяжелая цепь (задача) 25, 156, 307
Узлы четные 355
Уравнение в вариациях 270—272
для изопериметрической
задачи 305
— для уравнения Эйлера 272
— Эйлера-Лагранжа 272
Урысон П. С. 65
Условия положительности формы
291
Условная экстремаль 152, 155, 15$
Условный экстремум 169, 180, 210
Фенхель (Penchel) 360, 367
Ферма принцип 12, 329
Фокальные кривые 324, 325
Форма неотрицательная 291
— положительно определенная 291
— свободной поверхности жидко-
жидкости 158
Функционал 9, 78
Функционала вариация 37, 92, 226
— нормальная вариация 206
Функционал билинейный 104
— квадратический 104, 253
— линейный 91
Функционалов экстремум 11
Функциональная производная 206^
207
в точке 99
в данном направлении 209
нормальная 207
Функциональное пространство 78
Функция линии 9
— наклона поля 333
— непрерывная в пространстве 68
в точке 68
— точки абстрактного простран-
пространства 67
Фурье ряды 46
Центральное поле 312, 313
Центр геодезической окружности
177
— поля 312
Цепная линия 27
Цермело аэронавтическая задача 19-
Циклоида 17, 237
Циркуляция 48
Чаплыгин С. А. 48, 369
Чаплыгина С. А. задача 184
Четные узлы 355
Шварца неравенство 258
Штурма-Лиувилля уравнение 253,
254, 260—262
Штурма теорема 282
Экстремалей геометрия 309—811
— отражение 223
— поле 311—312
Экстрамалей преломление 219—220,
222
400
УКАЗАТЕЛЬ
Экстремали" 96, 111
— ломаные 215
— окружение полем 332
— регулярные точки 98
Экстремаль 195
— 2-го порядка 281
— минимаксная 281
Экстремальная теория собственных
значений 275—281
Экстремальной кривой окрестность
284
Экстремаль условная 152, 155, 156
Экстремум абсолютный 54
Экстремума необходимые условия
76—77
— сильного достаточные условия
339
Экстремума сильного необходимые
условия 337
Экстремум действия 19
— относительный 54, 58
— сильный и слабый 56, 58
— слабый 269
— условный 169, 180, 210
— функций от линий 193
Элемент предельный 64
Эллипс геодезический 324
Эллиптических орбит свойство 44
Эрдмана-Вейерштрасса условия 218,
322
Эрдмана условия 245
Эйлера константа изопериметриче-
ской задачи 168
Эйлера-Лагранжа травило множи-
множителей 160—166
Эйлера-Лагранжа правило множи-
множителей (обобщение) 164
уравнений каноническая
форма 311
— форма Гамильтона 310
— метод решения обобщенной изо-
периметрической задачи 165
Эйлера-Мопертюи принцип 17, 43,
203
Эйлера-Пуассона уравнения 137—
140
Эйлера теорема 149
—¦ формула для параболического
движения 132
— уравнение 30, 34, 35, 96, 97, 146,
204, 209, 234
(интегральная форма) 97
(особый случай) 38
— уравнений инвариантность 101,147
Якоби-Гамильтона уравнение 327—
328
Якоби-Лежандра теория квадрати-
ческих функционалов 285—-286
Якоби метод интегрирования 327—
332
—¦ преобразование второй вариа-
вариации 286
— принцип 202, 203
— усиленное условие 339
— условия 269, 289^ 320—323
существования слабого мини-
минимума 300
— уравнение 268, 285—286, 289