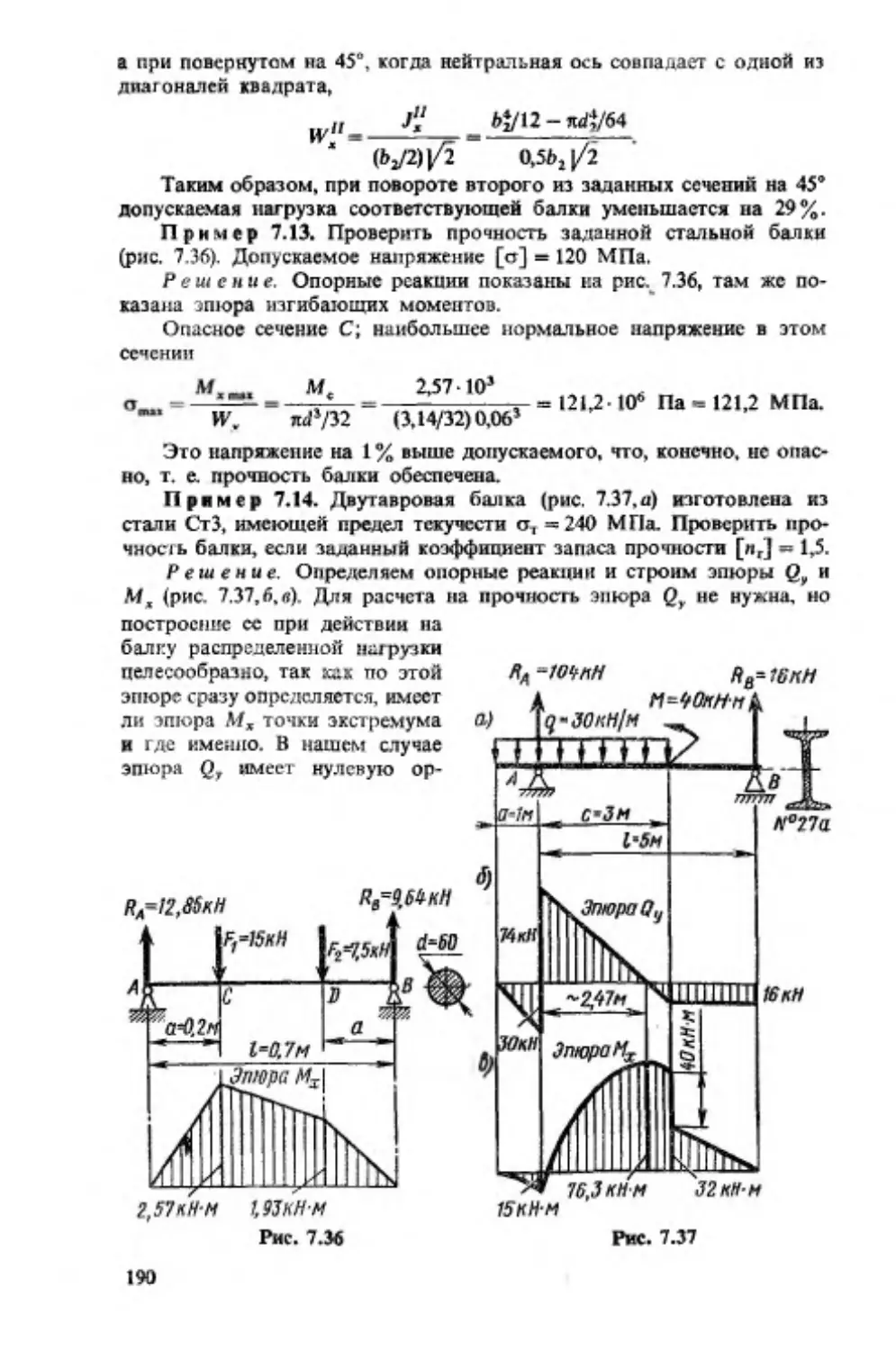
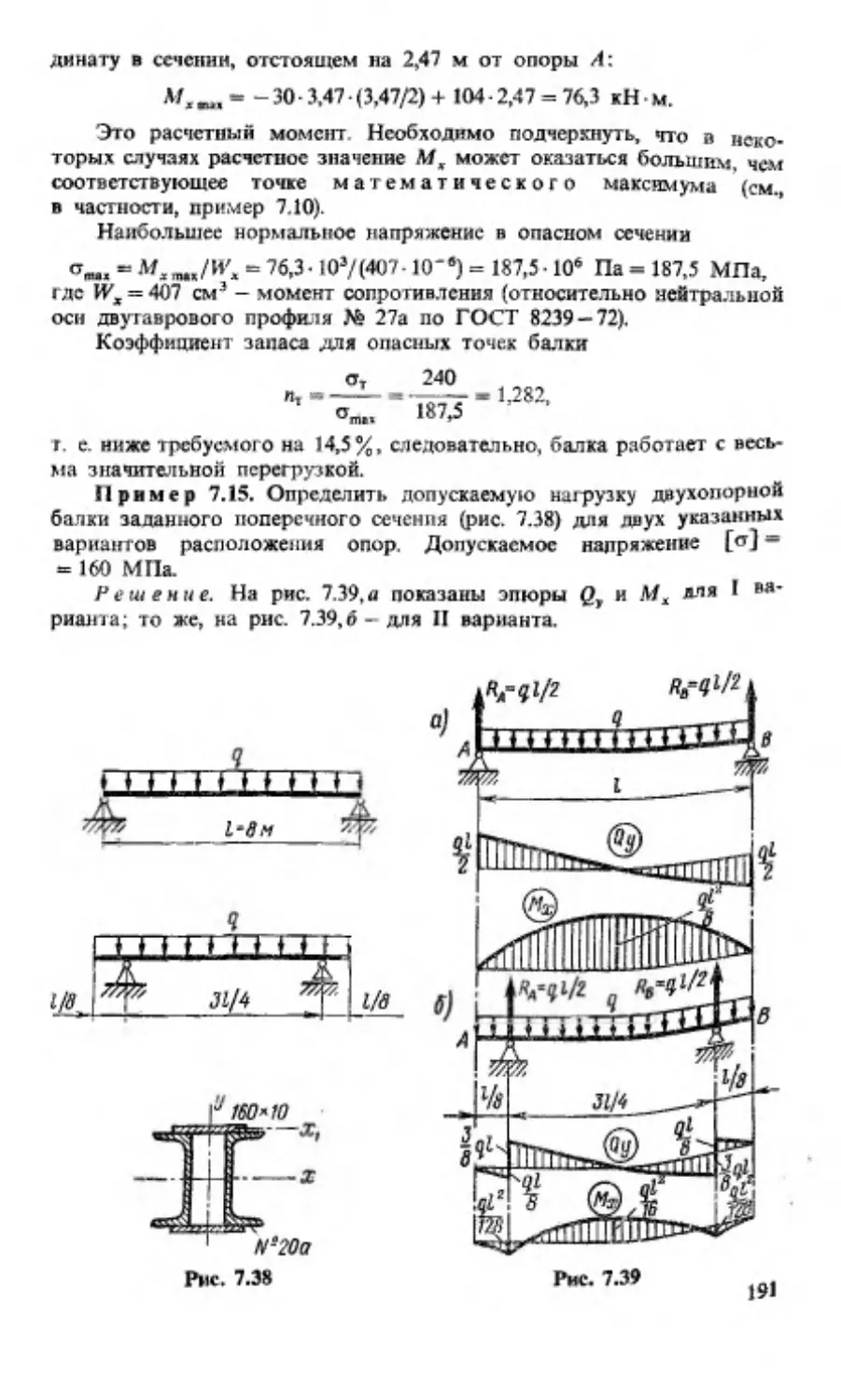
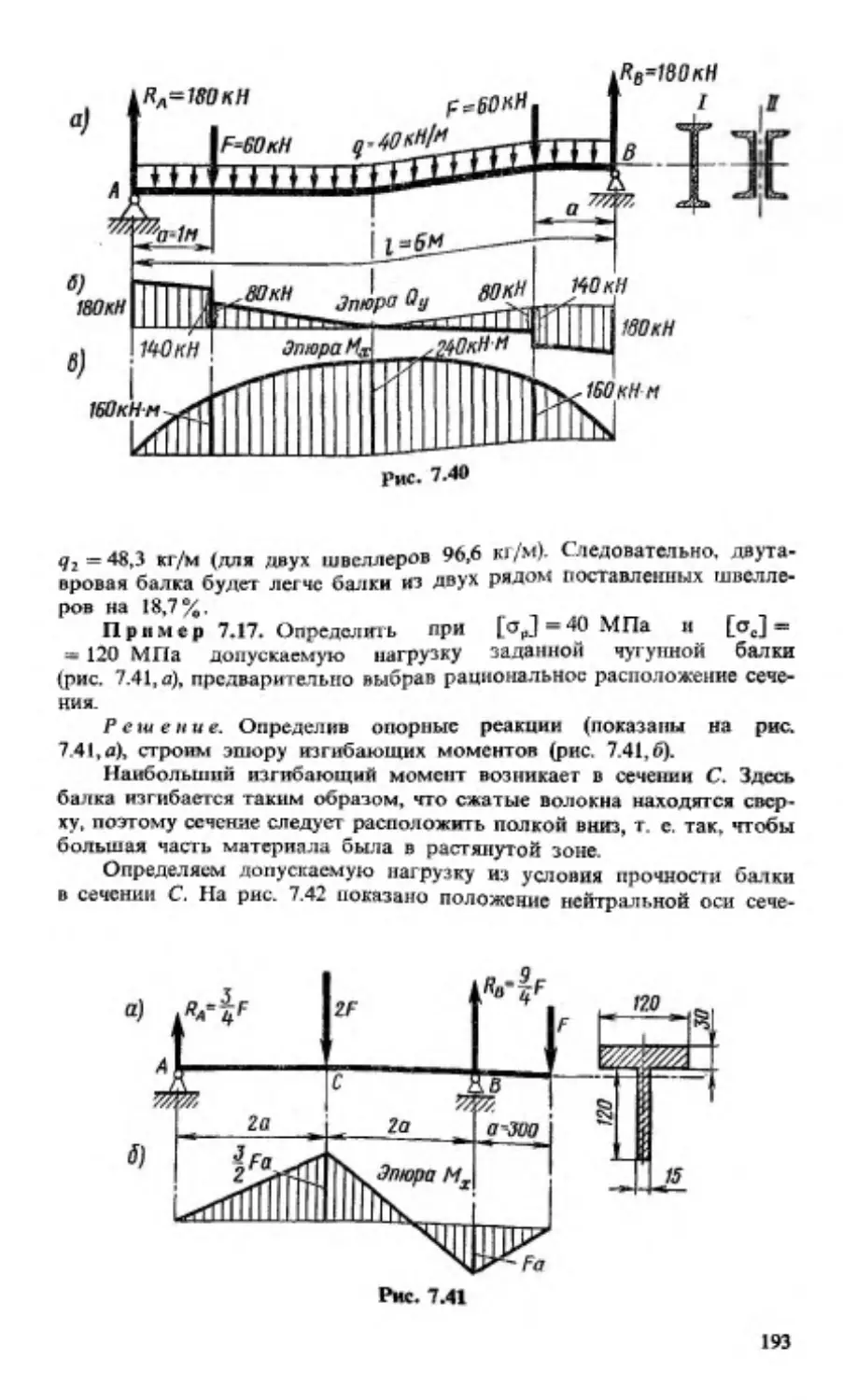
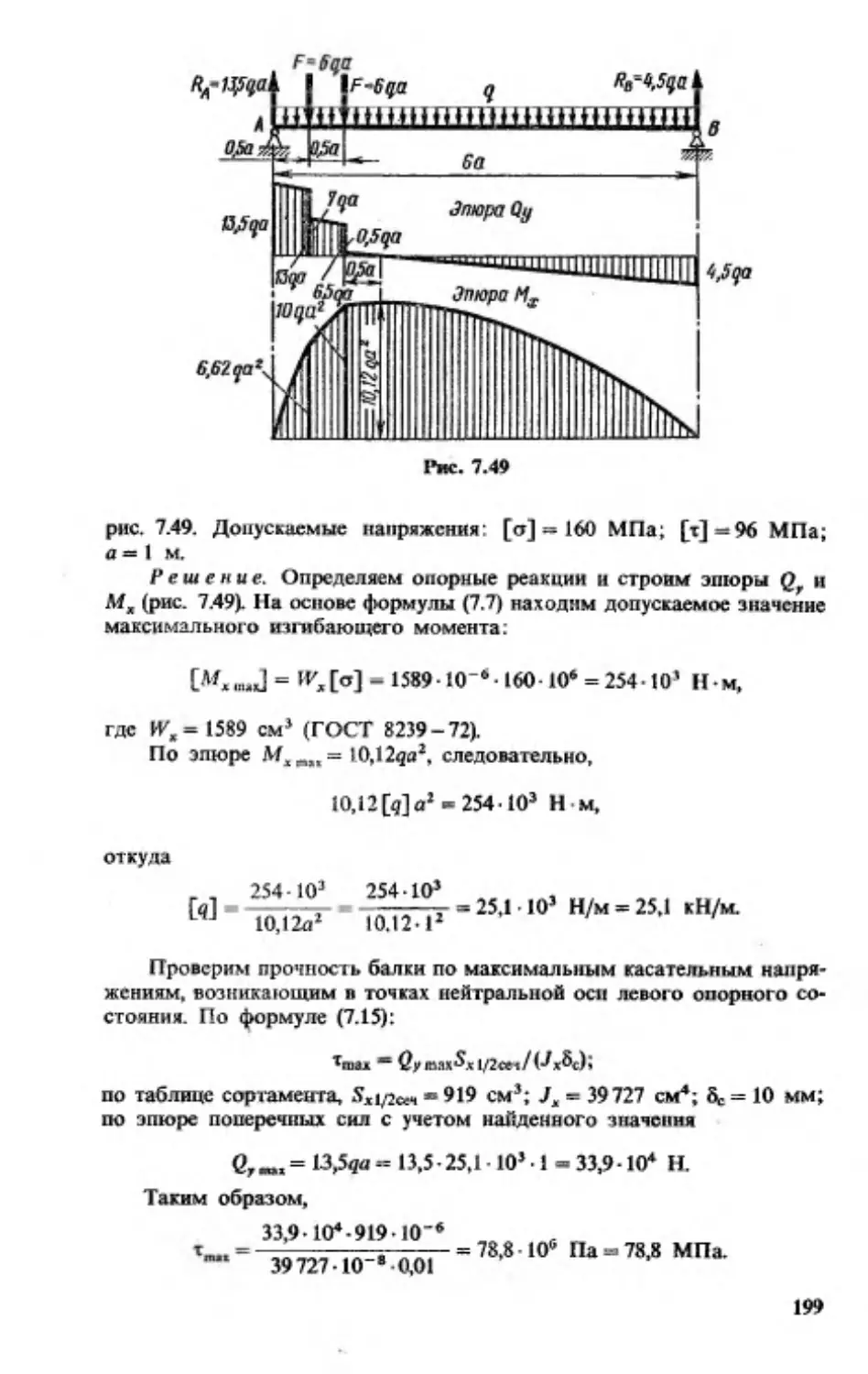
Текст
‘о
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
Г. М. Ицкович
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
Издание седьмое,
исправленное
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебника
для учащихся машиностроительных
техникумов
Москва «Высшая школа» 1986
Б Б К 30.21
И 96
У Д К 539.3/8(075)
И 96
Ицкович Г . М .
С опротивление м атери ал ов: У ч еб, для учащ ихся
маш ин о стр о и т. техникум ов. — 7 -е и зд ., испр. — М .:
Вы сш . ш к., 1 9 8 6 .— 352 с.: ил.
В учебнике наряду с теоретическим материалом имеется более
ста подробно разобранных примеров решения задач. Таким образом,
учебник одновременно является руководством к решению задач и дает
возможность самостоятельного изучения предмета по учебнику без по
мощи преподавателя.
3 настоящее издание (б-е —в 1982 г.) внесены новые стандарты
ЕСКД, единицы СИ и размерности величин.
, , 2105010000- 225
И ------------------------113—86
001(01)—86
©
БК 30.21
605
© Издательство «Высшая школа», 1976
Издательство «Высшая школа», 1986, с изменениями
П РЕДИ СЛ О ВИ Е
Настоящее издание является стереотипным.
В учебник внесены в основном изменения, касающиеся
новых стандартов ЕСКД, обозначений, единиц СИ и размер
ности величин.
Как и в предыдущем издании, дополнительный материал
для удобства читателей отмечен крупными звездочками. По
скольку теоретический материал сопровождается большим
количеством подробно разработанных примеров, решения
задач по всем темам и разделам, учебник может быть особенно
полезен учащимся заочной формы обучения при самостоя
тельном изучении курса.
Глава X написана Е. В. Лавровой.
Все замечания и пожелания по данному изданию учебника
издательство просит направлять в адрес издательства: 101430,
Москва, ГСП-4, Неглинная ул., 29/14.
Глава
I
ОСНОВНЫ Е П О ЛО Ж ЕН И Я
§ 1.1. Задачи сопротивления материалов
Сопротивление материалов представляет собой одно из на
правлений механики деформируемого твердого тела, которое
под действием приложенных к нему сил изменяет свою форму
и размеры —деформируется.
На основе методов сопротивления материалов и смежных
областей механики деформируемого тела (математической
и прикладной теории упругости, математической и прикладной
теории пластичности, статики и динамики сооружений) выпол
няют расчеты машин, аппаратов, приборов, конструкций про
мышленных и гражданских сооружений. Эти расчеты служат
для обеспечения надежности и долговечности проектируемых
конструкций при минимальной затрате материалов для их
изготовления.
Для балки, показанной на рис. 1.1, методами статики абсо
лютно твердого тела может быть решена задача об определе
нии реакции шарнирно-неподвижной опоры А и реакции тяги
ВС, возникающих под действием приложенной к балке нагруз
ки (в нашем случае силы F). Эти реакции показаны на чертеже,
реакция тяги ВС условно несколько смещена от оси тяги. На
помним, что тело называют абсолютно твердым (или абсолют
но жестким), если независимо от приложенных к нему сил рас
стояние между любыми двумя точками тела остается неиз
менным. Реальные твердые тела под действием приложенных
к ним сил деформируются; в рассматриваемом случае тяга
удлинится, а балка изогнется примерно так, как показано
штриховыми линиями на рис. 1.1.
Допустим теперь, что балка разгружена: сила F удалена.
При этом в зависимости от силы F (силу тяжести конструкции
не учитываем), материалов, размеров балки и тяги могут воз
никнуть два случая (конечно, полагаем, что при действии силы
F ни один из элементов конструкции не разрушается).
4
1. Балка и тяга полностью
восстанавливают те формы и
размеры, которые они имели
до нагружения; в этом случае
говорят, что в системе (конст
рукции) при заданной нагрузке
возникают лишь упругие дефор
мации.
2. Деформации балки и тяги
уменьшаются, но система все
же остается в деформирован
ном состоянии; такое положе
ние означает, что в системе при
заданной нагрузке возникают
наряду с упругими также и пластические (остаточные) деформа
ции.
Как правило, возникновение пластических деформаций свя
зано с нарушением нормальной работы конструкции и потому
считается недопустимым.
Пусть, например, тяга, изготовленная из стального прутка,
имеет круглое поперечное сечение, а балка (также стальная) —
двутавровый профиль. При заданной силе F следует выбрать
диаметр сечения тяги и номер двутаврового профиля балки,
чтобы ни один из элементов конструкции не разрушился и
в нем не возникли пластические деформации. При соблюдении
указанных условий балка и тяга имеют достаточную прочность.
Легко понять, что возможна и обратная постановка задачи:
размеры и материалы балки и тяги известны и требуется опре
делить то наибольшее значение силы F, при котором про
чность конструкции обеспечена.
Из рассмотренного примера вытекает, что первая задача со
противления материалов —расчет элементов конструкций на
прочность. При этом подчеркиваем еще раз, что в сопротивле
нии материалов под нарушением прочности понимают не толь
ко разрушение в буквальном смысле слова- —разрыв, излом,
но и возникновение пластических (остаточных) деформаций.
Говоря о достаточной прочности конструкции, полагают,
что прочность обеспечена не только при заданном значении на
грузок, но и при некотором их увеличении, т. е. конструкция
имеет определенный запас прочности.
В конструкциях одноразового применения допустимо воз
никновение пластических деформаций. Для некоторых машин
и аппаратов химических производств, а также в некоторых дру
гих случаях допускают возникновение небольших местных пла
стических деформаций, которые не являются признаком нару5
шения прочности. В кратком курсе
сопротивления материалов расчеты,
где учитывается развитие пластиче
ских деформаций, нс рассматрива
ются.
Возникновение упругих деформа
ций в нагруженной конструкции
неизбежно, также неизбежны и обус
ловленные этими деформациями пе
ремещения отдельных точек конст
Рис. 1.2
рукции. Так, в частности, в рассмат
риваемом примере конец балки по
лучает некоторое вертикальное перемещение / (рис. 1.1). Мо
жет оказаться, что значение / больше допустимого по усло
виям нормальной работы конструкции, хотя ее прочность
вполне достаточна. В этом случае говорят, что конструкция
имеет недостаточную жесткость.
Вообще жесткостью называют способность материала или
элемента конструкции сопротивляться упругим деформациям.
Можно также сказать, что жесткостью конструкции называют
ее способность воспринимать нагрузку без существенного из
менения геометрических размеров. На рис. 1.2 показан пример,
иллюстрирующий последствия недостаточной жесткости кон
струкции: значительные прогибы валов зубчатой передачи при
водят к неравномерному распределению нагрузки по длине
зубьев, что связано с повышенным износом и даже опасностью
поломки зубьев.
Вторая задача сопротивления материалов —расчет элементов
конструкций на жесткость.
Соответствующий расчет при проектировании конструкции
должен обеспечить выбор таких ее размеров, при которых
упругие перемещения, вызванные рабочими нагрузками, будут
лежать в допустимых пределах.
Обратимся еще к одному примеру (рис. 1.3, а), отличающе
муся от первого лишь тем, что здесь стержень ВС, поддержи
вающий балку, испытывает не растяжение, а сжатие. Если стер
жень ВС сравнительно длинный и тонкий, то при некоторой
силе F он может внезапно изогнуться (выпучиться), как показа
но штриховыми линиями на рис. 1.3,6, или, как говорят, поте
рять устойчивость. В этом случае стержень В С помимо сжатия
будет испытывать так называемый продольный изгиб. Иными
словами, при достижении нагрузкой критического значения пер
воначальная прямолинейная форма равновесия стержня стано
вится неустойчивой и возникает новая устойчивая форма равно
весия —криволинейная. При этом качественном изменении
б
F
характера деформации конструкция практически выходит из
строя: она или разрушается, или в ней возникают недопустимо
большие перемещения (прогибы). Поэтому расчет конструкции
должен обеспечить такое соотношение нагрузок, размеров
и свойств материалов, при котором гарантирована (с опреде
ленным запасом) устойчивость заданной (прямолинейной)
формы равновесия.
Итак, третья задача сопротивления материалов —расчет эле
ментов конструкций на устойчивость.
Подводя итог всему сказанному выше, заключаем, что со
противление материалов дает основы расчета элементов кон
струкций на прочность, жесткость и устойчивость.
Сопротивление материалов —расчетно-теоретическая дис
циплина, основные положения которой проверяются и допол
няются экспериментальными исследованиями. Опытная про
верка теоретических расчетов и формул необходима потому,
что они основаны на ряде упрощающих предпосылок и допу
щений. Эти предпосылки и допущения связаны как со свойства
ми материалов, так и с характером деформаций элементов кон
струкций. В ряде случаев приходится специально изготовлять
модель проектируемой конструкции (или отдельных ее элемен
тов) и подвергать ее испытаниям, чтобы получить данные о ха
рактере и величине деформаций, так как чисто теоретическим
путем создание методов расчета оказывается вообще невоз
можным. Наконец, необходимо учесть, что все расчеты, выпол
няемые методом сопротивления материалов, базируются на
знании физико-химических свойств конструкционных материа
лов. Эти свойства определяют путем лабораторных испытаний
специально изготовленных образцов.
При решении задач сопротивления материалов широко при
меняют уравнения равновесия различных систем сил, полу
ченные в статике абсолютно твердого тела. Вместе с тем не все
7
.
6L
кI -f
k -f
I
А
.//тЛм/мг
приемы и методы статики могут быть ис
пользованы в сопротивлении материалов. За
мена одной системы сил другой, статически
эквивалентной, в частности перенос силы по
линии ее действия и замена ряда сил их рав
нодействующей, резко изменяет характер де
формации детали и поэтому недопустима. По
ясним это положение некоторыми приме
рами.
На рис. 1.4, а, б показан брус, нагружен
ный растягивающей силой F; в первом слу
чае сила приложена к концу бруса, во вто
ром она перенесена по линии действия в не
F
которую точку В. В результате этого перено
Рис. 1.4
са деформироваться будет не весь брус, а
только часть АВ.
Перенос сил по линиям их действия может привести к еще
более резкому изменению характера деформации, чем в рас
смотренном случае. Например, в результате переноса сил, при
ложенных к торцам бруса (рис. 1.5, в), можно получить нагру
жение, показанное на рис. 1.5, б, т. е. брус будет испытывать не
растяжение, а сжатие.
На рис. 1.6, а изображена балка, нагруженная парой сил на
левой опоре. Штриховой линией показан характер ее деформа
ции. При переносе этой пары сил в положение, показанное на
рис. 1.6, б, характер деформации резко изменяется. При втором
положении нагрузки допускаемое по условию прочности значе
ние момента пары вдвое больше, чем в первом. Реакции опор
балки в том и другом случаях, конечно, одинаковы.
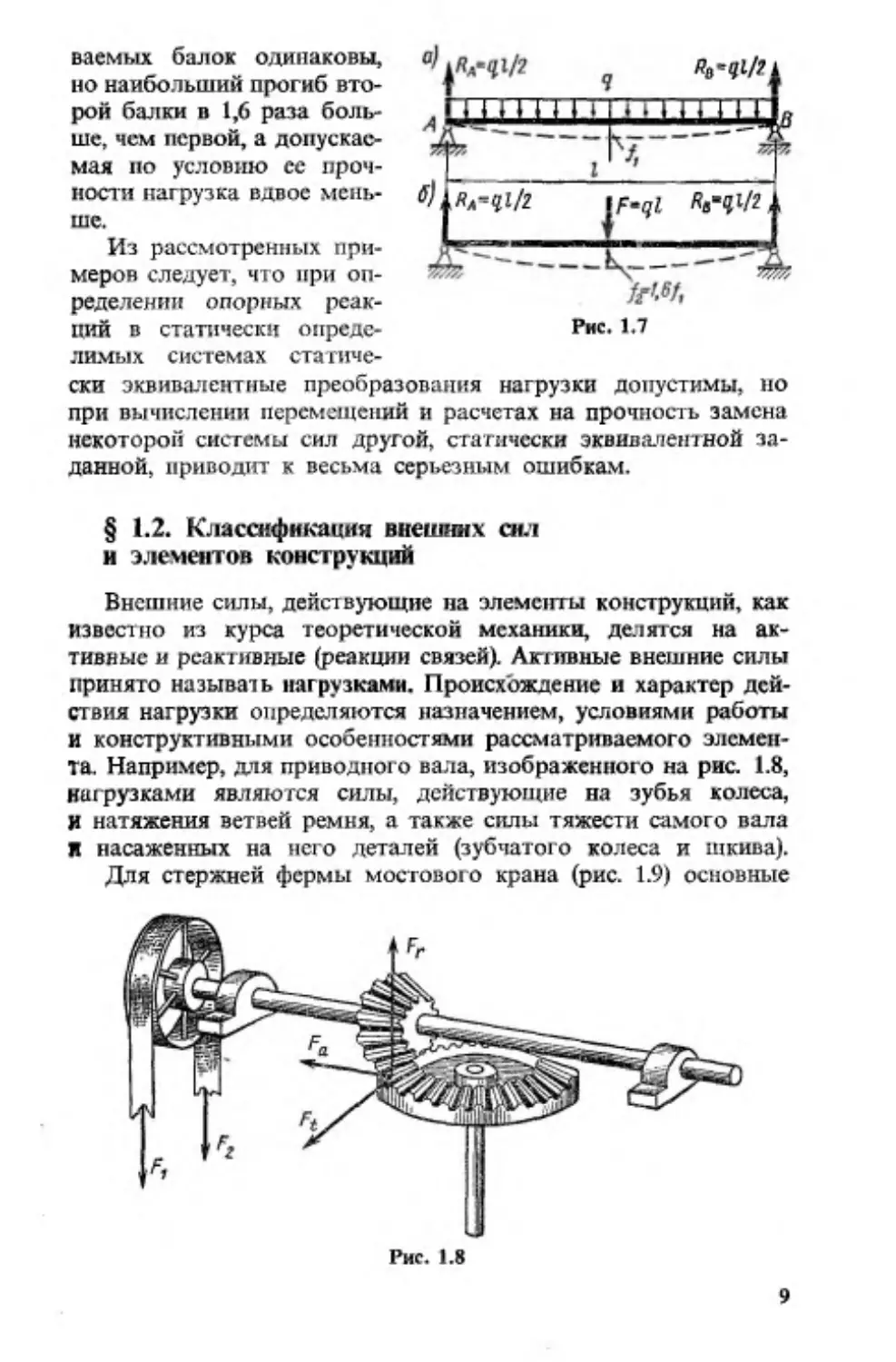
На рис. 1.7, а, б показаны две одинаковые балки, первая на
гружена равномерно распределенной нагрузкой интенсив
ностью q, а вторая —силой F = ql (т. е. силой, равной равно
действующей этой нагрузки). Опорные реакции рассматри-
8
ваемых балок одинаковы,
RB=q.l/Zk
но наибольший прогиб вто
рой балки в 1,6 раза боль
з ш
ж
ш
ш
т
ше, чем первой, а допускае
мая по условию ее проч
ности нагрузка вдвое мень б) п ^ ч М г
I F=ql Ла=?*/2М
ше.
Из рассмотренных при
—
тт
меров следует, что при оп
ределении опорных реак
Рис. 1.7
ций в статически опреде
лимых системах статиче
ски эквивалентные преобразования нагрузки допустимы, но
при вычислении перемещений и расчетах на прочность замена
некоторой системы сил другой, статически эквивалентной за
данной, приводит к весьма серьезным ошибкам.
§ 1.2. Классификации внешних сил
и элем ентов конструкций
Внешние силы, действующие на элементы конструкций, как
известно из курса теоретической механики, делятся на ак
тивные и реактивные (реакции связей). Активные внешние силы
принято называть нагрузками. Происхождение и характер дей
ствия нагрузки определяются назначением, условиями работы
и конструктивными особенностями рассматриваемого элемен
та. Например, для приводного вала, изображенного на рис. 1.8,
нагрузками являются силы, действующие на зубья колеса,
И натяжения ветвей ремня, а также силы тяжести самого вала
Я насаженных на него деталей (зубчатого колеса и шкива).
Для стержней фермы мостового крана (рис. 1.9) основные
Рис. 1.8
9
Рис. 1.9
нагрузки —силы тяжести поднимаемого груза и тележки; мень
шее значение имеют силы тяжести фермы.
Основная нагрузка барабана парового котла —давление на
ходящегося в нем пара.
В случае если рассматриваемый элемент конструкции дви
жется с ускорением, то к числу действующих на него нагрузок
относятся также силы инерции.
Силы тяжести данной части конструкции и силы инерции,
возникающие при ее ускоренном движении, являются объемны
ми силами, т. е. они действуют на каждый бесконечно малый
элемент объема. Нагрузки, передающиеся от одних элементов
конструкции к другим, относятся к числу поверхностных сил.
Поверхностные силы делятся на сосредоточенные и распреде
ленные. При этом следует помнить, что сосредоточенных сил,
конечно, не существует —это абстракция, вводимая для удоб
ства технических расчетов. Сила рассматривается как сосредо
точенная, если она передается на деталь по площадке, размеры
которой пренебрежимо малы в сравнении с размерами самого
элемента конструкции. Например, силу давления колеса вагона
на рельс можно рассматривать как сосредоточенную, так как
хотя колесо и рельс в месте соприкосновения «деформируются,
но размеры площадки, получающейся в результате этой дефор
мации, ничтожно малы по сравнению с размерами как рельса,
так и колеса.
Нагрузки, распределенные по некоторой поверхности, ха
рактеризуются давлением, т. е. отношением силы, действующей
на элемент поверхности нормально к ней, к площади данного
элемента, и, следовательно, выражаются в паскалях (1 Па =
= 1 Н/м2), МПа и т. д.
Во многих случаях приходится встречаться с нагрузками,
распределенными по длине элемента конструкции, например
можно говорить о силе тяжести единицы длины балки, при
10
этом если сечение балки непостоянно, то и сила тяжести еди
ницы ее длины будет переменной.
Распределенная по длине нагрузка характеризуется интеншвностьго, обозначаемой обычно q и выражаемой в единицах
силы, отнесенных к единицам длины: Н/м, кН/м и т. п.
По характеру изменения во времени различают:
статические нагрузки, нарастающие медленно и плавно от
нуля до своего конечного значения; достигнув его, в дальней
шем не изменяются. Примером могут служить центробежные
силы в период разгона и при последующем равномерном вра
щении какого-либо ротора;
повторные нагрузки, многократно изменяющиеся во времени
по тому или иному закону. Примером такой нагрузки служат
силы, действующие на зубья зубчатых колес;
нагрузки малой продолжительности, прикладываемые к кон
струкции сразу или даже с начальной скоростью в момент кон
такта (эти нагрузки часто называют динамическими или
ударными). Примером ударной является, например, нагрузка,
воспринимаемая деталями парового молота во время ковки.
Вопрос о связях и их реакциях достаточно подробно рас
смотрен в курсе теоретической механики. Здесь ограничимся
лишь напоминанием о наиболее распространенных тинах
связей.
Шарнирно-подвижная опора (односвязная опора) схематиче
ски изображается, как показано на рис. 1.10, а. Реакция такой
опоры всегда перпендикулярна опорной поверхности.
Шарнирно-неподвижная шора (двухсвязная опора) схематиче
ски изображена на рис. 1.10,6. Реакция шарнирно-неподвижной
Опоры проходит через центр шарнира, а ее направление зави
сит от действующих активных сил. Вместо отыскания числово
го значения и направления этой реакции удобнее искать от
дельно две ее составляющие.
В жесткой заделке (трехсвязная опора) возникают реактив
ная пара сил (момент) и реактивная сила; последнюю удобнее
представлять в виде двух ее составляющих (рис. 1.11).
Если связью служит стержень с шарнирами по концам
(рис. 1.12), то реакция направлена вдоль его оси, т. е. сам стер
жень работает на растяжение или сжатие.
Рис. 1.10
Рис. 1.11
И
Формы элементов конструкций чрезвычайно разнообразны,
но с большей или меньшей степенью точности каждый из них
можно при расчетах рассматривать либо как брус, либо как
оболочку или пластину, либо как массив.
В сопротивлении материалов в основном изучают методы
расчетов на прочность, жесткость и устойчивость бруса, т. е.
тела, два измерения которого невелики по сравнению с треть
им (длиной). Представим себе плоскую фигуру, перемещаю
щуюся вдоль некоторой линии таким образом, что центр тяже
сти фигуры находится на этой линии, а плоскость фигуры ей
перпендикулярна. Полученное в результате такого движения
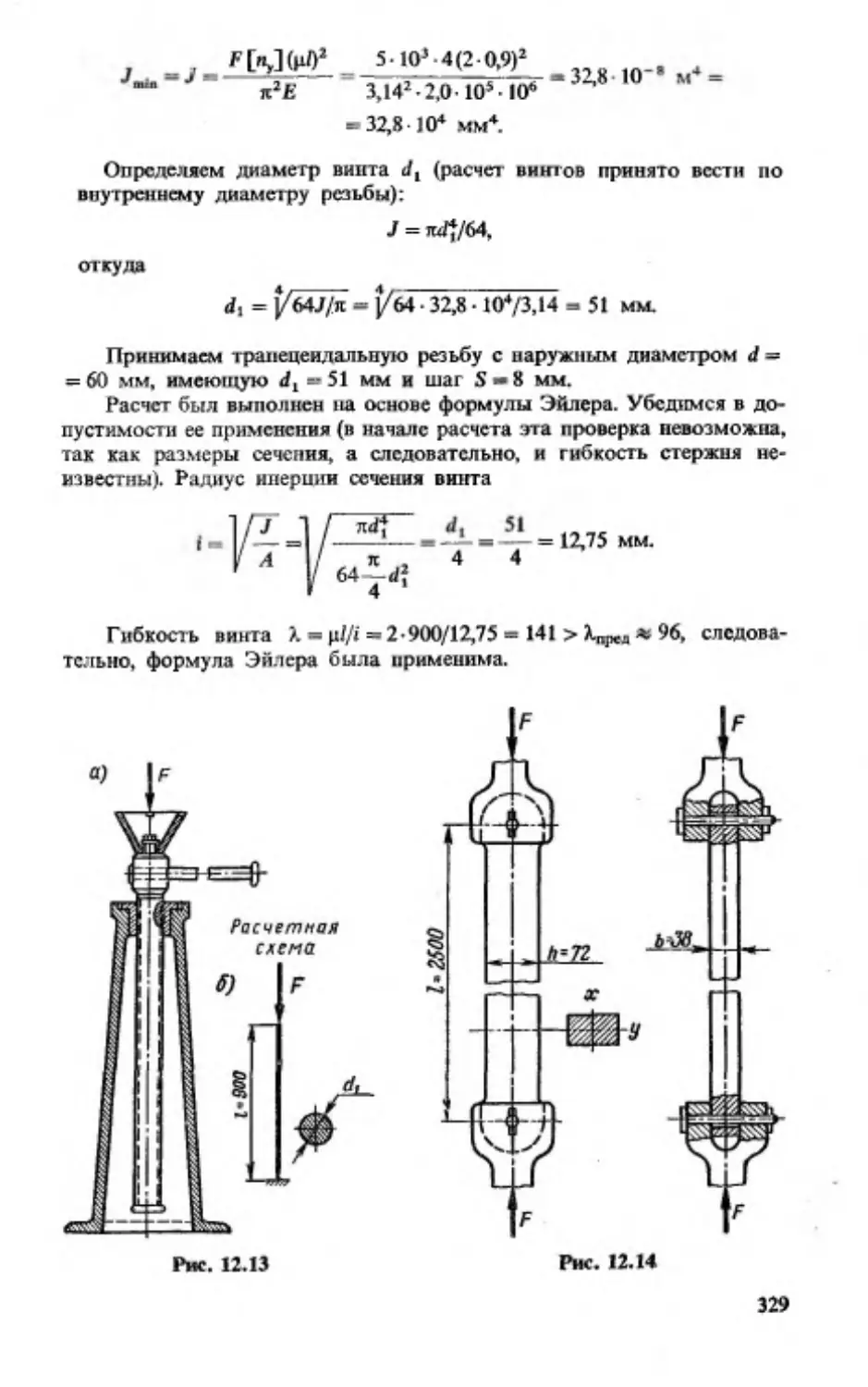
тело и есть брус (рис. 1.13).
Плоская фигура, движением которой брус образован,
является его поперечным сечением, а линия, вдоль которой
перемещался ее центр тяжести, —осью бруса.
Ось бруса —это геометрическое место центров тяжести его
поперечных сечений. В зависимости от формы оси бруса и того,
как изменяется (или остается постоянным) его поперечное сече
ние, различают прямые и кривые брусья с постоянным, не
прерывно или ступенчато изменяющимся поперечным сечением
(рис. 1.14). В качестве некоторых примеров деталей, рассчиты
ваемых как прямые брусья, можно указать приводной вал
(см. рис. 1.8), любой из стержней фермы мостового крана (см.
рис. 1.9); крюк этого крана рассчитывают как кривой брус.
■ш
Рис. 1.14
12
Рис. 1.15
Пластина и оболочка (рис. 1.15) характеризуются тем, что их
толщина невелика по сравнению с остальными размерами.
Пластину можно рассматривать как частный случай оболочки,
так сказать, «распрямленную» оболочку. Примерами деталей,
рассматриваемых как оболочки и пластины, являются раз
личные резервуары для жидкостей и газов, элементы обшив
ки корпусов кораблей, подводных лодок, фюзеляжей само
летов.
Массивом называют тело, все три измерения которого —ве
личины одного порядка, например фундамент под машину, ша
рик или ролик подшипника качения.
§ 1.3. Допущ ения относительно свойств материалов
и характера деформаций
Наука о сопротивлении материалов, отказываясь от приня
того в теоретической механике допущения об абсолютной
жесткости тел, все же не может при построении теории расче
тов на прочность и жесткость отразить все многообразие
свойств реальных материалов. Поэтому в сопротивление мате
риалов приходится вводить ряд допущений относительно
свойств материалов, позволяющих построить достаточно про
стую и удобную для инженерной практики теорию расчетов
элементов конструкций. Конечно, эти допущения таковы, что
полученные на их основе выводы достаточно точно совпадают
с результатами соответствующих экспериментальных исследо
ваний.
Рассмотрим эти допущения.
1. Материал однороден, т. е. свойства любых сколь угодно
малых его частиц совершенно тождественны. Это допущение
достаточно обосновано для металлокристаллических материа
лов, например для стали, и менее обосновано для материалов
типа чугуна.
2. Материал полностью заполняет весь объем тела без ка
ких-либо пустот, т. е. тело рассматривается как сплошная среда.
Допущение о сплошности тела можно рассматривать как след
ствие допущения однородности материала. Представление
о теле как о сплошной среде дает возможность применять при
исследованиях, выполняемых в сопротивлении материалов, ме
тоды анализа бесконечно малых величин (дифференциальное
и интегральное исчисления).
3. Материал изотропен, т. е. физико-механические свойства
его по всем направлениям одинаковы. Материалы, не обладаю
щие указанным свойством, называют анизотропными.
4. В известных пределах нагружения материал обладает
13
идеальной (совершенной) упругостью, т. е. после снятия нагруз
ки деформации полностью исчезают.
Перейдем к рассмотрению допущений, связанных с характе
ром деформаций элементов конструкций.
При нагружении упругого тела оно деформируется и от
дельные его точки перемещаются относительно своих первона
чальных положений, соответствующих недеформированному
состоянию тела.
Первое основное допущение, используемое во всех разделах
этого курса, состоит в том, что
перемещения точек тела (конструкции), обусловленные его
упругими деформациями, весьма малы по сравнению с размерами
самого тела.
Из этого допущения следует, что изменения в расположении
сил, происходящие при деформации конструкции, не следует
учитывать при составлении уравнений равновесия (при определе
нии реакций связей), а также и при определении внутренних сил
(см. § 1.4).
Это положение иногда называют принципом начальных
размеров.
Для того чтобы лучше понять значение рассмотренного до
пущения, обратимся еще раз к схеме конструкции, изображен
ной на рис. 1.1. Предположим, что требуется найти реакцию
тяги ВС (силу R c); для этого надо составить уравнение равно
весия в виде суммы моментов всех сил относительно центра
шарнира А. Если учитывать деформации балки и тяга, то
получим
Z M A = F(a1 + сх) —(/?c sinp1)fl1 = 0.
Размеры а,, с1 и угол pt неизвестны (их определение весьма
сложно); принцип начальных размеров позволяет принять аг =
= a; Cj — с; pt = р, т. е. вести расчет, исходя из недеформированной схемы конструкции.
Еще одной иллюстрацией при
менения принципа начальных раз
меров служит рис. 1.16. При со
ставлении уравнений равновесия
для узла А не учитывают измене
ния угла между стержнями, т. е.
вместо F = 2Ri cos oti принимают
F — 2Ri cos а.
Второе важнейшее допущение:
перемещения точек упругого те
ла в известных пределах нагруже
ния прямо пропорциональны силам,
вызывающим эти перемещения.
Сущность этого допущения
пояснена примером, представлен
ным на рис. 1.17. Конструкции (или,
Рис. 1.18
как часто говорят, системы), для
которых справедлива указанная
прямая пропорциональность между силами и соответствую
щими перемещениями, называют линенно-деформнруемыми.
Для линейно-деформируемых систем справедлив принцип не
зависимости действия сил, который можно сформулировать сле
дующим образом: результат действия группы сил не зависит от
последовательности нагружения ими конструкции и равен сумме
результатов действия каждой из сил в отдельности.
Сформулированное положение называют также принципом
сложения действия сил или принципом суперпозиции.
Под результатом действия сил в зависимости от конкрет
ной задачи могут пониматься перемещение той или иной точки
тела, значение внутренней силы упругости и т. п. Подчерки
ваем, что, говоря о действии какой-либо силы, всегда имеют
в виду эту силу вместе с соответствующими ей реакциями свя
зей. Один из примеров применения принципа независимости
действия сил иллюстрирует рис. 1.18, не требующий дополни
тельных пояснений.
§ 1.4. М етод! еечеш ш , Внутренние силы
в поперечных сечениях бруса
Прочность твердого тела обусловлена силами сцепления
между отдельными его частицами. При деформации тела, вы
званной действием приложенных к нему внешних сил, внутрен
ние силы изменяются. В дальнейшем под внутренними силами
будем подразумевать не их абсолютные значения, а только те
приращения, которые вызваны действующими на тело нагруз15
Рис. 1.19
Рис. 1.20
ками. При возрастании внешних сил увеличиваются и внутрен
ние силы, но лишь до определенного предела, при превышении
которого наступает разрушение. Это предельное значение вну
тренних сил зависит от физико-механических свойств материа
ла данного тела.
Для расчета на прочность необходимо иметь возможность
определять внутренние силы по заданным внешним силам. Ос
нову для решения этой задачи дает метод сечений. Познако
мимся с этим методом.
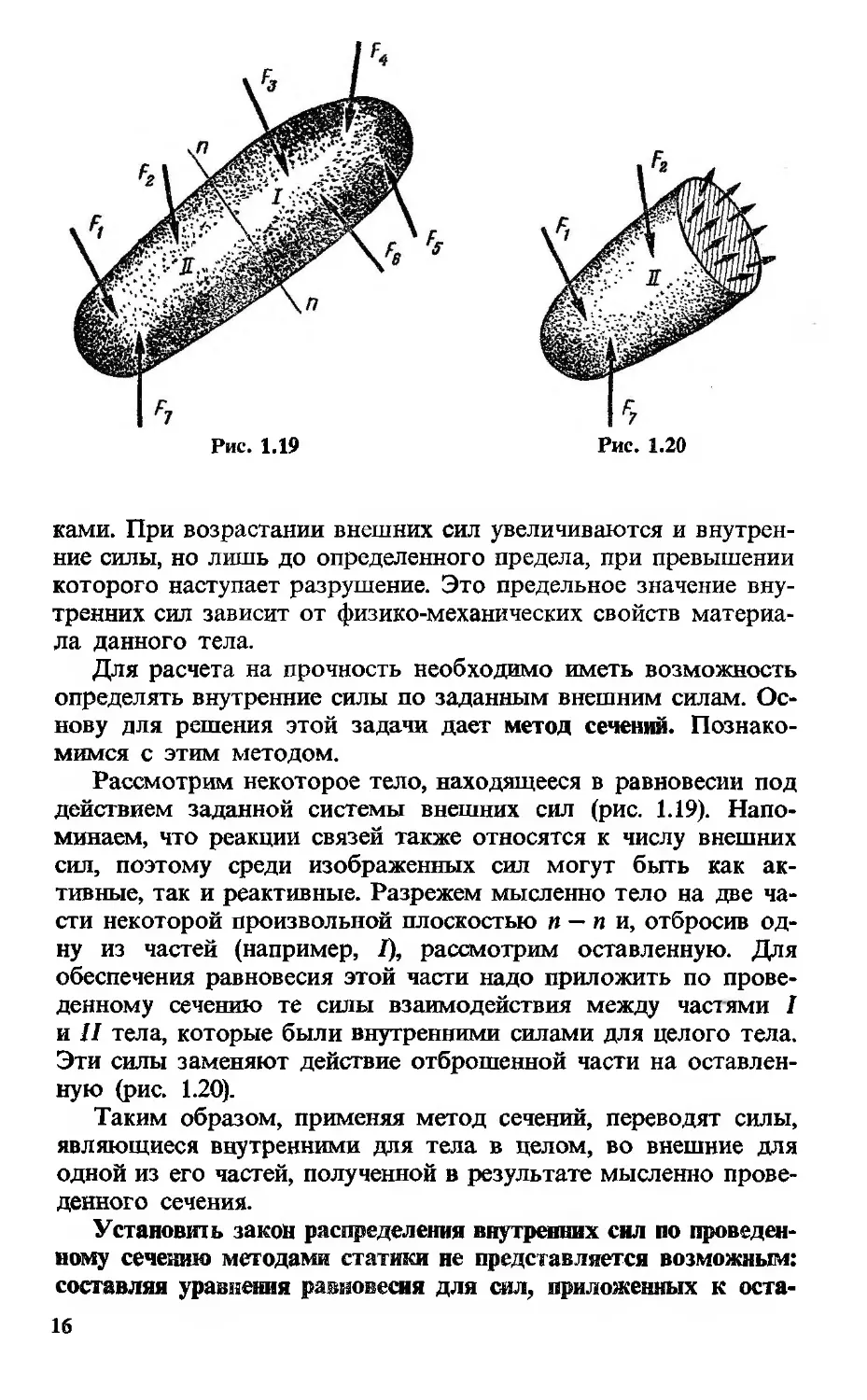
Рассмотрим некоторое тело, находящееся в равновесии под
действием заданной системы внешних сил (рис. 1.19). Напо
минаем, что реакции связей также относятся к числу внешних
сил, поэтому среди изображенных сил могут быть как ак
тивные, так и реактивные. Разрежем мысленно тело на две ча
сти некоторой произвольной плоскостью и —и и, отбросив од
ну из частей (например, I), рассмотрим оставленную. Для
обеспечения равновесия этой части надо приложить по прове
денному сечению те силы взаимодействия между частями I
а II тела которые были внутренними силами для целого тела.
Эти силы заменяют действие отброшенной части на оставлен
ную (рис. 1.20).
Таким образом, применяя метод сечений, переводят силы,
являющиеся внутренними для тела в целом, во внешние для
одной из его частей, полученной в результате мысленно прове
денного сечения.
Установить закон распределения внутренних сил по проведен
ному сечешпо методами статики не представляется возможным:
составляя уравнения равновесия для сил, приложенных к оста16
влениой части тела, можно лишь найти статический эквивалент
внутренних сил (главный вектор и главный момент), возникаю
щих в рассматриваемом сечении.
Принципиально совершенно безразлично, какую из частей
тела (I или II) отбросить, так как из третьего закона Ньютона
следует, что силы, действующие от части II на часть I, равны
по модулю и противоположны по направлению силам дей
ствия части I на II. Практически удобнее оставлять ту часть,
к которой приложено меньше внешних сил, так как уравнения
равновесия для нее будут иметь более простой вид.
Выше было обращено внимание на недопустимость замены
одной системы внешних сил другой, статически эквивалентной.
Это указание относилось к телу в целом. При рассмотрении
равновесия оставленной части допустимы любые статически эк
вивалентные преобразования приложенных к ней внешних сил
(замена их равнодействующей и т. д.).
В дальнейшем наиболее часто метод сечений будет приме
няться для определения статических эквивалентов внутренних
сил, возникающих в поперечных сечениях прямого бруса, по
этому специально остановимся на этом вопросе.
Рассмотрим прямой брус, находящийся в равновесии под
действием произвольной системы внешних (активных и реак
тивных) сил (рис. 1.21). Рассечем его на две части (/ и II) неко
торой произвольной плоскостью, перпендикулярной его про
дольной оси, и отбросим одну из частей (например, I). Выше
уже говорилось о том, что внутренние силы по сечению распре
делены сплошь, но как именно они распределены, с помощью
уравнений равновесия установить нельзя. Вместе с тем из тео
ретической механики известно, что любая система сил может
быть приведена к ее главному вектору и главному моменту, ко
торые статически эквивалент
ны заданной системе сил. Далее
известно, что главный вектор си
стемы может быть представлен
в виде трех составляющих по
осям выбранной системы коор
динат. Аналогично, главный
момент может'быть также раз
ложен на составляющие по
осям координат, т. е. заменен
тремя моментами, каждый из
которых стремится повернуть
тело вокруг одной из коорди
натных осей. Эту систему выби
раем следующим образом:
17
начало координат О помещ аем в центре тяжести рассматри
ваемого поперечного сечения (рис. 1.22), ось Oz направляем по
внешней нормали к сечению, т. е. вдоль оси бруса, оси Ох и Оу
располагаем в плоскости сечения, ось Оу —по оси симмет
рии поперечного сечения и ось Ох — ей перпендикулярно*.
Составляющие главного вектора и главного момента вну
тренних сил, возникающих в поперечном сечении бруса, носят
название внутренних силовых факторов в этом сечении.
Н а рис. 1.23 показаны шесть внутренних силовых факторов,
возникающих в поперечном сечении бруса в общем случае его
нагружения.
Составляющие главного момента по осям принятой си
стемы координат, как известно, векторы, но для большей на
глядности они показаны в виде дугообразных линий со стрел
ками на концах.
Указанные шесть внутренних силовых факторов имеют сле
дующие наименования: N z —продольная (или нормальная сила);
Qx, Qy —поперечные силы; М . — крутящий момент; М х,
Му —изгибающие моменты.
Каждый из них связан с определенным видом деформации
бруса. Так, например, если не равна нулю только продольная
сила N z, брус работает на растяжение или на сжатие. Если не
равна нулю поперечная сила Qx (или Qy, или обе одновремен
но), брус работает на срез (сдвиг).
* В том случае, когда поперечное сечение бруса не имеет ни одной
оси симметрии, оси Ох и Оу совпадают с так называемыми главными
центральными осями сечения. Это понятие разъяснено в гл. VI.
18
При наличии в поперечных сечениях бруса только крутяще
го момента М г имеет место деформация кручения. В случае ес
ли не равен нулю изгибающий момент Мх или Мг брус рабо
тает на чистый изгиб либо в плоскости yOz (при Мх ф 0), либо
в плоскости xOz (при Му Ф 0).
Таким образом , разложение главного вектора и главного
момента внутренних сил на составляющие имеет не фор
мальный, а ясно выраженный физический смысл.
Для определения каждого из внутренних силовых факторов
надо составить соответствующ ее уравнение равновесия для
всех сил, действующих на оставленную часть бруса (рис. 1.23).
Как известно, для пространственной системы произвольно рас
положенных сил таких уравнений может быть составлено
шесть и в каждое из них войдет лишь один внутренний сило
вой фактор, который и будет определен из этого уравнения.
Например, для определения продольной силы Nz проецируем
силы, приложенные к оставленной части бруса, на ось z:
I
О СТ,
части
Z = NX+ £
Fiz = 0.
(1.1)
О СТ.
части
Аналогично составляются и остальные уравнения равнове
сия.
На основе уравнения (1.1) и других подобных уравнений
можно сформулировать правила для определения внутренних
силовых факторов. Например,
продольная сила в произвольном поперечном сечении бруса
19
численно равна алгебраической сумме проекций на продольную
ось Oz бруса всех внешних сил, приложенных к его оставленной
части.
Продольная сила, возникающая в проведенном сечении,
принадлежащем оставленной части, равна по модулю и проти
воположна по направлению силе, возникающей в том же сече
нии, но принадлежащем отброшенной части. То же относится,
конечно, и ко всем остальным внутренним силовым факторам
(рис. 1.24).
Поэтому можно сформулировать правило для отыскания
N z и несколько иначе:
продольная сила в произвольном поперечном сечении бруса
численно равна алгебраической сумме проекций на продольную
ось Oz бруса всех внешних сил, приложенных по одну сторону от
рассматриваемого сечения.
Аналогично формулируются правила
остальных внутренних силовых факторов.
для
отыскания
§ 1.5. Напряжении
Внутренние силы, как уже указывалось, распределены по се
чению тела (в частности, бруса) сплошь, при этом в общем слу
чае их значение и направление в отдельных точках сечения раз
личны. Для суждения об интенсивности внутренних сил
в определенной точке данного сечения введено понятие
о напряжении.
Выделим в окрестности интересующей нас точки сечения
малую площадку, площадью ДА; допустим, что на этой пло
щадке возникает внутренняя сила AR (рис. 1.25). Отношение
этой внутренней силы к площади выделенной площадки назы
вается средним напряжением рср в окрестности рассматривае
мой точки по проведенному сечению (на площадке АА):
Pcp = AR/AA.
(1.2)
Чем точнее нужно знать интенсивность внутренних сил
в данной точке сечения, тем меньше должна быть выделенная
площадка.
В пределе при стремлении АА к нулю получим истинное на
пряжение в данной точке рассматриваемого сечения:
р = lim AR/AA.
аЛ-»о
(1.3)
Заметим, что при уменьшении площадки АА («стягивании»
ее в точку) AR также стремится к нулю, но из физических со20
Рис. 1.25
Рис. 1.26
ображений очевидно, что рассматриваемое отношение будет
величиной конечной.
Напряжение в данной точке по рассматриваемому сечению
есть величина векторная (вектор AR делим на скаляр АЛ); на
правление этого вектора совпадает с предельным направлением
вектора АЛ, которое он имеет при уменьшении АА до нуля*.
В Международной системе единиц (СИ) в качестве единицы
напряжения принят паскаль (Па).
Паскаль —это напряжение, при котором на площадке в
1 м 2 возникает внутренняя сила, равная 1 Н, но эта единица
очень мала, поэтому используется кратная ей единица —мега
паскаль, 1 МПа = 106 Па.
Через данную точку тела можно провести бесчисленное
множество сечений, различно ориентированных в пространстве,
и, конечно, в общем случае возникающие на них напряжения
будут различны. Поэтому
нельзя говорить о напряжении в данной точке, ие указывая
площадки (сечения), на которой это напряжение возникает.
Разложим вектор напряжения р на две составляющие: од
ну —направленную по нормали к сечению, вторую —лежащую
в плоскости сечения (рис. 1.26). Составляющую напряжения, на
правленную по нормали к площадке ее действия, назовем нор
мальным напряжением и обозначим а (сигма), а составляющую,
лежащую в плоскости сечения, —касательным напряжением
и обозначим.! (тау). Между напряжениями р, л и т существует
следующая очевидная зависимость:
(1.4)
* При уменьшении площадки ЛА изменяется как числовое значе
ние, так и направление вектора элементарной внутренней силы AR. На
правление вектора напряжения р совпадает с предельным направле
нием вектора АД.
21
Такое разложение полного напряжения имеет определенный
физический смысл. Действительно, нормальное напряжение
возникает тогда, когда частицы материала, соприкасающиеся
по рассматриваемой площадке, под действием приложенных
к телу нагрузок стремятся отдалиться друг от друга или сбли
зиться в направлении нормали к этой площадке, т. е. при рас
тяжении или сжатии. Касательные напряжения связаны со
сдвигом частиц материала по плоскости рассматриваемого
сечения.
В ряде случаев оказывается удобным разложить вектор р не
на две, а на три составляющие, направленные параллельно
координатным осям. На рис. 1.27 показано это разложение
применительно к точке, взятой в поперечном сечении бруса.
Для этих составляющих принято следующее правило индексов:
первый индекс указывает, какой оси параллельна нормаль
к площадке действия рассматриваемого напряжения, второй
индекс показывает, какой оси параллельно данное напряжение.
Согласно этому правилу, нормальное напряжение должно бы
ло бы иметь два одинаковых индекса (в нашем случае ст„), но
принято писать лишь один из них. В тех случаях, когда нужно
указать, что речь идет о касательном напряжении, возникаю
щем в поперечном сечении бруса, а направление напряжения не
играет роли, его можно обозначать хг, опуская второй индекс.
Часто применяют также обозначение х (без индексов).
Зависимость между полным напряжением и тремя его со
ставляющими выражается формулой
(1.5)
Установим связь между напряжениями и внутренними си
ловыми факторами в поперечном сечении бруса.
Умножая напряжения a z, xzx и xzy на площадь dA площадки
Рис. 1.27
22
Рис. 1.28
их действия,
(рис. 1.28):
получаем
элементарные
внутренние
силы
dNz = az dA; dQx = rzx dA; dQy = xzy dA.
Суммируя эти элементарные силы по всей площади сечения,
получаем выражения составляющих главного вектора внутрен
них сил:
IV =
f
А
(УгйА;
( 1 .6 )
Qx
1 ^2* ^-<4:
А
( 1 .7 )
Qy = \ x zyAA.
( 1 .8 )
А
Умножая каждую из элементарных сил на расстояние до со
ответствующей оси, получаем элементарные моменты внутрен
них сил:
dMz = (xzx dА) у - (тгуdA) х ; dМ х = (<szdA)y;
dМ у = (ст2dA) х.
Суммируя элементарные моменты по всей площади сече
ния, получаем выражения для составляющих главного момента
внутренних сил:
M z = J (тzxy - Tzyx)dА;
(1.9)
А
Mx= J °ХУАА’
(1-Ю)
MJ,= J a zxcL4.
(1.11)
А
А
Обращаем внимание, что выражения (1.6)—(1.11) не служат
для вычисления внутренних силовых факторов; значения по
следних определяют с помощью метода сечений, как указано
в § 1.4. Эти выражения можно рассматривать как записанные
с помощью математических символов определения, выражаю
щие физическую сущность внутренних силовых факторов.
В дальнейшем эти выражения будут использованы при опре
делении напряжений по известным внутренним силовым факто
рам.
Итак, от внешних сил с помощью метода сечений к вну
тренним силовым факторам, от них на основе интегральных
зависимостей и дополнительных гипотез к напряжениям —та
ков в общих чертах план решения основной задачи сопротивле
ния материалов об определении напряжений, возникающих
в поперечных сечениях бруса при различных видах его нагруже
ния.
23
Глава
II
РА С ТЯ Ж ЕН И Е И СЖ АТИЕ
§ 2 .1 . Силы в поперечны х сечениях бруса
При растяжении (сжатии) прямого бруса в его поперечных се
чениях возникает только один внутренний силовой фактор — про
дольная сила, обозначаемая Nz или N.
Прямые брусья, работающие на растяжение или сжатие,
часто называют стержнями.
Простейшие случаи растяжения и сжатия представлены на
рис. 2.1, а и 2.2, а: в центрах тяжести торцовых поперечных се
чений бруса приложены две равные и противоположно напра
вленные силы, линии действия которых совпадают с осью
бруса.
Продольные силы, соответствующие деформации растяже
ния, условимся считать положительными, а сжатия —отрица
тельными. При растяжении продольная сила направлена от се
чения (рис. 2.2,6), а при сжатии —к сечению (рис. 2.1,6).
При сжатии сравнительно длинного и тонкого бруса прямолиней
ная форма его равновесия может оказаться неустойчивой (см. рис. 1.3).
В этой главе будем во всех случаях полагать, что опасность потери
устойчивости исключена. Расчеты на устойчивость рассмотрены
в гл. XII.
Более общие случаи работы бруса на растяжение (сжатие)
показаны на рис. 2.3, 2.4.
Из рассмотренных примеров следует, что, для того чтобы
Рис. 2.1
Рис. 2.2
Рис. 2.3
24
N- 2FC0S J 0 '
брус работал на растяжение (сжатие), равнодействующая внеш
них сил, приложенных по одну сторону от любого поперечного
сечения бруса, должна быть направлена вдоль его оси. Только
при этом условии все внутренние силовые факторы, кроме про
дольной силы, будут равны нулю.
Модуль и направление (знак) продольной силы определяют
ся из уравнения равновесия, составленного для отсеченной
(оставленной после проведения сечения) части бруса:
I
ОСТ.
части
Z=0;
N+ £
Fi2 = 0,
ост.
часг и
откуда
N=~ I
Fiz,
ОСТ.
части
т. е. продольная сила в произвольном поперечном сечении бруса
численно равна алгебраической сумме проекций на его продоль
ную ось Oz всех внешних сил, приложенных к оставленной
части.
Направление N противоположно направлению проекции (на
ось Oz) равнодействующей внешних сил, приложенных к оста
вленной части.
Приведенная формулировка не может рассматриваться как
определение понятия «продольная сила», она указывает лишь
метод для нахождения ее значения и направления.
Продольной силой в поперечном сечении бруса называется
равнодействующая внутренних нормальных сил, возникающих
в этом сечении.
Допустимо и такое определение: продольной силой в поперечном
сечении бруса называется направленная вдоль его оси составляющая
главного вектора внутренних сил, возникающих в этом сечении.
25
Элементарная нормальная сила, возникающая на бесконеч
но малой площадке поперечного сечения, равна произведению
нормального напряжения a z на площадь йА указанной пло
щадки, т. е, dN = ст2йА. Сумма (равнодействующая) этих эле
ментарных сил представляет собой определенный интеграл
N = J <згйА.
А
Это математическое выражение эквивалентно приведенному
словесному определению понятия «продольная сила».
В тех случаях, когда продольные силы в различных попе
речных сечениях бруса неодинаковы, закон их изменения по
длине бруса удобно представить в виде графика, называемого
эпюрой продольных сил. Аргументом при построении этого гра
фика является координата поперечного сечения бруса (z),
а функцией —продольная сила (JV).
Таким образом, эшора продольных сил —это график функ
ции N = f(z). Далеко не всегда можно составить выражение
указанной функции, справедливое при всех значениях коор
динаты z (для всего бруса). Приходится разбивать брус на
участки, для каждого из которых будет свое выражение функ
ции N = / (z).
Эпюру продольных сил строят в первую очередь для того,
чтобы использовать ее при расчете бруса на прочность; она
дает возможность найти наибольшие значения продольных сил
и положение сечений, в которых они возникают.
Пр име р 2.1. Построить эпюру продольных сил для бруса,
изображенного на рис. 2.5, а.
Р е ш е н и е . Разбиваем брус на участки, начиная от свободного
конца. Границами участков являются сечения, в которых приложены
внешние силы.
Применяя метод сечений,
оставляем правую и отбрасыва
ем левую часть бруса: это по
зволяет не определять реакцию
заделки. Проводя произволь
ное сечение а — а на участке I и
составляя для части бруса, по
казанной отдельно на рис. 2.5, б,
уравнения равновесия £ Z =
ОСТ.
части
Рис. 2.5
26
= 0, получаем F - iV/ = 0, отку
да JV/ = F.
Легко видеть, что во всех
поперечных сечениях данного
участка продольная сила оди
накова. То же относится и ко
всем остальным участкам, поэтому совершенно безразлично,
где проводить сечение в пределах того или иного рассматриваемого
участка.
Проводя сечение b — b на. участке II и рассматривая правую оста
вленную часть бруса (рис. 2.5, в), получаем
2 Z = F1- F 2 - N ll = F - 2 F - N II = 0,
ОСТ.
части
откуда Ын = - F .
Знак минус указывает, что фактическое направление силы JVjj про
тивоположно показанному на рис. 2.5, в, т. е. сила Nu направлена к се
чению и, следовательно, участок II испытывает сжатие.
Аналогично определяем продольную силу в произвольном сечении
с —с участка III (рис. 2.5,г): Nui = 3F.
Конечно, для определения продольных сил нет необходимости
изображать каждый раз отдельно отсеченную часть бруса, можно про
сто найти алгебраическую сумму проекций на ось бруса внешних сил,
приложенных по одну сторону от рассматриваемого сечения.
Применяя метод сечений, можно было бы каждый раз оставлять
левую и отбрасывать правую часть бруса, но тогда решение следовало
бы начинать с определения реакции заделки (рис. 2.5, а), так как эта ре
акция относится к числу внешних сил, приложенных к оставленной (ле
вой) части бруса.
Для построения эпюры N проводим ось абсцисс графика (ось или
базу эпюры) параллельно оси бруса (рис. 2.5, й). В пределах каждого из
участков продольная сила постоянна, т. е. эпюра параллельна оси абс
цисс. Значения продольных сил откладываем в выбранном масштабе
от оси эпюры; при этом положительные значения N (растяжение) от
кладываем вверх, а отрицательные —вниз от оси. Условимся ось
эпюры проводить тонкой, а саму эпюру —толстой линиями.
В местах приложения сосредоточенных сил на эпюре получаются
скачкообразные изменения ординат —«скачки». Размер «скачка» равен
приложенной в соответствующем месте бруса внешней сосредоточен
ной силе. При нагружении бруса сосредоточенными силами эпюра
N всегда имеет такой характер, как в рассмотренном примере.
Скачкообразные изменения ординат эпюры N носят условный ха
рактер, так как условно и само понятие «сосредоточенная сила». Фак
тически внешняя сила распределена по некоторой небольшой части
длины бруса; в пределах этой части значение N изменяется (например,
в зоне приложения силы F2 от значения + F до —F) по некоторому
закону, установить, который не представляется возможным. Не
известный криволинейный переходный участок эпюры заменяют ус
ловным «скачком».
Эпюру принято штриховать; при этом штриховка перпендикулярна
оси эпюры —каждая линия штриховки (ордината графика) дает в при
нятом масштабе значение продольной силы в противолежащем попе
речном сечении бруса.
Пр ■ м е р 2.2. Для бруса, изображенного на рис. 2.6,а, построить
эпюру продольных сил, возникающих от действия сосредоточенной
27
силы F и силы тяжести бруса.
Удельная сила тяжести (удельный
вес) материала бруса у, площадь
поперечного сечения А.
Р е ш е н и е . В данном случае
брус нагружен помимо сосредото
ченной силами, равномерно распре
деленными по его длине, поэтому
продольная сила при переходе от
сечения к сечению изменяется не
прерывно, а не скачкообразно, как
это имеет место при действии ряда
сосредоточенных сил (см. пример
2. 1).
Проведем поперечное сечение,
отстоящее на расстоянии z от сво
бодного конца бруса, и рассмотрим равновесие нижней оставленной
части, изображенной отдельно на рис. 2.6,6.
Внешними силами, действующими на эту часть, являются сила F
и сила тяжести этой части G2 = уAz. Проецируя на ось г все силы, дей
ствующие на оставленную часть, получаем
JV=F + G2 = f + у Az.
Таким образом, N изменяется по длине бруса по линейному зако
ну. Для построения эпюры находим значения N в крайних сечениях:
при z = 0 Nz=0 —F и при z = l 1V2=, = F + yAI = F + G, где G =
= уAl —сила тяжести всего бруса.
Построенная по этим данным эпюра показана на рис. 2.6, в. Поло
жительные значения N отложены вправо от оси эпюры.
§ 2.2. Напряжения в поперечных сечениях бруса
При растяжении (сжатии) бруса в его поперечных сечениях
возникают только нормальные напряжения. Равнодействующая
соответствующих элементарных сил ст2dA —продольная сила
N —может быть найдена с помощью метода сечений. Для того
чтобы иметь возможность определить нормальные напряжения
при известном значении продольной силы, необходимо устано
вить закон их распределения по поперечному сечению бруса.
Эта задача решается на основе гипотезы плоских сечений
(гипотезы Я. Бернулли), которая гласит:
сечения бруса, плоские и нормальные к его оси до деформа
ции, остаются плоскими и нормальными к оси и при деформации.
При растяжении бруса (изготовленного, например, для
большей наглядности опыта из резины), на поверхности ко
торого нанесена система продольных и поперечных рисок
(рис. 2.7, а), можно убедиться, что риски остаются прямоли
нейными и взаимно перпендикулярными, изменяются лишь
28
а)
S)
'{
Рис. 2.7
расстояния: между поперечными рисками несколько увеличи
ваются, а между продольными —уменьшаются (рис. 2.7, б).
Описанный опыт можно рассматривать как подтверждение
гипотезы плоских сечений; при этом предполагают, что внутри
бруса деформации имеют тот же характер, что и на его
поверхности.
Представим себе, что брус состоит из бесконечно большого
числа продольных элементов, имеющих бесконечно малые
(«точечные») поперечные сечения. Эти элементы здесь и в даль
нейшем будем условно называть волокнами.
Из гипотезы Бернулли следует, что все волокна в рассма
триваемом случае деформируются одинаково. При однород
ном материале равным деформациям соответствуют одина
ковые напряжения. Таким образом, приходим к заключению,
что
при растяжении (сжатии) бруса нормальные напряжения рас
пределены но его поперечному сечению равномерно.
На рис. 2.8 представлена так называемая пространственная
эпюра нормальных напряжений, возникающих в поперечном
сечении бруса. Подчеркнем, что распределение напряжений не
зависит от формы поперечного сечения.
Для определения нормальных напряжений используем вы
ражение N = J a zcL4. Вынося стг (постоянная величина!) за знак
интеграла, получаем
N = oz J dA = uzA,
А
где А —площадв поперечного сечения бруса.
Опуская индекс г, окончательно получаем
а = N/A.
(2.1)
Для нормальных напряжений принимают то же
правило знаков, что и для продольных сил, т. е.
при растяжении считают напряжения положи
тельными.
F
Рис. 2.8
29
Щ
*: '"
растяжении
Ь/2
**
F
F
Л /4
Эпю ра б
В сеч.I
В сечЖ
1 1
Всеч.Ш
Рис. 2.9
Фактически распределение напряжений в сечениях бруса,
примыкающих к месту приложения внешних сил, зависит от
способа приложения нагрузки и может быть неравномерным.
Экспериментальные и теоретические исследования показывают,
что это нарушение равномерности распределения напряжений
носит местный характер. В сечениях бруса, отстоящих от ме
ста нагружения на расстоянии, примерно равном наибольшему
из поперечных размеров бруса, распределение напряжений
можно считать практически равномерным (рис. 2.9).
Рассмотренное положение является частным случаем прин
ципа Сен-Венана, который можно сформулировать следующим
образом:
распределение напряжений существенно зависит от способа
приложения внешних сил лишь вблизи места нагружения.
В частях, достаточно удаленных от места приложения сил,
распределение напряжений практически зависит только от стати
ческого эквивалента этих сил, а не от способа их приложения.
Таким образом, применяя принцип Сен-Венана и отвлекаясь
от вопроса о местных напряжениях, имеем возможность (как
в этой, так и в последующих главах курса) не интересоваться
конкретными способами приложения внешних сил.
В местах резкого изменения формы и размеров поперечного
сечения бруса также возникают местные напряжения. Это явле
ние называют коинеитрацией напряжений, которую в этой главе
учитывать не будем.
В тех случаях, когда нормальные напряжения в различных
поперечных сечениях бруса неодинаковы, целесообразно по
казывать закон их изменения по длине бруса в виде графи
ка —эпюры нормальных напряжений.
30
а)
¥ /
А3=10смг
т /
__ л = т кн
Аг-8см г
ж
л
IZ
Aj-S cm2
—
F^80KH
I-
I
Эпюра N
6)
120 кН
70кН
JELL
Ж
80 КН
Эпюра б
в)
120 МПа
70 МПа
Ж
150МПа
И
160МПа
100МПа
Рис. 2.10
П р и м е р 2.3. Для бруса со ступенчато-переменным поперечным
сечением (рис. 2.10, а) построить эпюры продольных сил и нормальных
напряжений.
Р е ш е н и е . Разбиваем брус на участки, начиная от свободного
конца. Границами участков являются места приложения внешних сил
и изменения размеров поперечного сечения, т. е. брус имеет пять
участков. При построении только эпюры N следовало бы разбить брус
лишь на три участка.
Применяя метод сечений, определяем продольные силы в попе
речных сечениях бруса и строим соответствующую эпюру (рис. 2.10,6).
Построение эпюры N принципиально ничем не отличается от рассмо
тренного в примере 2.1, поэтому подробности этого построения
опускаем.
Нормальные напряжения вычислим по формуле (2.1), подставляя
значения оил в ньютонах, а площадей —в квадратных метрах.
Для участка /
cr/ = N/ M 1 =80 103/(5 1 0 '4)= 160-106 Па = 160 МПа;
для участка II
а и = N h /A2 = 80-103/ (8 -10" 4) = 100-106 Па = 100 МПа;
для участка III
ст7// = N n , / A 2 = 120-107(8- Ю '4) = 150-106 Па = 150 МПа.
Аналогично вычисляем
С7к=120МПа
и сги=-70М П а.
В пределах каждого из участков напряжения постоянны, т. е. эпю
ра на данном участке —прямая, параллельная оси абсцисс (рис. 2.10, в).
Для расчетов на прочность интерес представляют в первую оче
редь те сечения, в которых возникают наибольшие напряжения. Суще31
ственно, что в рассмотренном случае они не совпадают с теми
сечениями, где продольные силы максимальны.
В тех случаях, когда сечение бруса по всей длине постоянно, эпю
ра о подобна эпюре N и отличается от нее только масштабом, поэто
му, естественно, имеет смысл построение лишь одной из указанных
эпюр.
§ 2.3. Деформации и перемещения
Рассмотренный в предыдущем параграфе вопрос об опреде
лении нормальных напряжений теснейшим образом связан
с расчетами бруса и шарнирно-стержневых систем (например,
ферм) на прочность. Умение вычислять деформации и переме
щения необходимо для расчетов на жесткость, а также для
определения сил в статически неопределимых системах.
Выделим из бруса, изображенного на рис. 2.11, я, бесконеч
но малый элемент длиной dz. Этот элемент отдельно изобра
жен (в двух проекциях) на рис. 2.11,6; штриховыми линиями он
показан в деформированном состоянии —длина элемента уве
личилась, а размеры поперечного сечения уменьшились. Прира
щение длины элемента обозначим A(dz). Отношение прираще
ния (изменения) длины элемента к его первоначальной длине
называется относительным удлинением или продольной деформа
цией:
е = A (dz) /dz.
(2.2)
Очевидно, продольная деформация —безразмерная вели
чина. В некоторых случаях ее выражают в процентах. При рас
тяжении продольную деформацию считают положительной,
а при сжатии —отрицательной.
Отношение изменения Аа размера поперечного сечения
к его первоначальному значению называют относительным по
перечным сужением (расширением) или поперечной деформацией;
е' = Аа/а.
а)
Р и с. 2.11
32
(2.3)
При растяжении поперечные раз
меры бруса уменьшаются и г' по
принятому правилу знаков —величи
на отрицательная.
Продольную и поперечную де
формации называют также линей
ными деформациями (общее наиме
нование).
Для подавляющего большинства
конструкционных материалов с до
статочной для практики точностью
можно считать, что
в известных пределах нагружения
между продольной деформацией и
соответствующим (действующим в ее
направлении) нормальным напряже
нием существует прямо пропорциональная (линейная) зависимость.
Это положение носит название закона Гука и записывается
в виде
о = Е&.
(2.4)
Коэффициент пропорциональности Е называют модулем
продольной упругости (другие названия: модуль нормальной
упругости; модуль упругости; модуль упругости 1-го рода; мо
дуль Юнга). Очевидно, Е имеет ту же размерность, что и на
пряжение, т. е. выражается в Па или МПа.
Модуль продольной упругости —физическая постоянная
данного материала, характеризующая его ж е с т к о с т ь . Чем
жестче материал, тем меньше он деформируется при данном
напряжении. На рис. 2.12 дано графическое представление зако
на Гука для двух материалов, имеющих различные модули
Продольной упругости.
Пусть по оси ординат графика принят масштаб та (Па/мм),
а по оси абсцисс —тв (1/мм).
Значение модуля продольной упругости найдем из выраже
ния (2.4):
Е = ст/е
или по графику:
Е = (та/тс) tg a ,
г. е. модуль упругости Е прямо пропорционален тангенсу угла
наклона к оси абсцисс прямой, т. е. графика, изображающего
закон Гука.
33
Т аблица2. 1. Значения модуля продольной упругое™ Е и коэффициента
Пуассона р для некоторых материалов
Материал
Е,
МПа
Сталь .......................................................... (1,9...2,15)-105
Чугун серый (СЧ12 —28, СЧ15—32 и др.) (0,8...),5)- 105
Чугун серый (СЧ12 —28, СЧ15 —32 и др.)
(СЧ28-48, СЧ32-52, СЧ35-56,
СЧ38 —60)................................................ (1,2... 1,55)-105
Медь техническая....................................... (1,1.4,3)-105
Бронза оловянная
(Бр ОЦС6-6-3, Бр ОФЮ-1 и др.) . . . (0,8...!,2)-105
Алюминиевые сплавы............................. (0,69...0,71)-105
Дерево вдоль волокон............................. (8,8...15,7)-103
Текстолит.....................................................
(6,0... 10)-103
Каучук..........................................................
7,85
й
0,26...0,33
0,23...0,27
0,24...0,28
0,31...0,33
0,32...0,35
0,33...0,36
—
0,47
Для каждого материала модуль продольной упругости ко
леблется в узких пределах (табл. 2.1). Например, для стали Е =
= (1,9...2,15) • 105 МПа. При этом весьма важно иметь в виду,
что значение Е для стали практически не зависит от ее химиче
ского состава и термической обработки.
Опытным путем установлено, что при простом растяжении
или сжатии отношение поперечной деформации к продоль
ной —величина постоянная для данного материала. Это отно
шение, взятое по абсолютному значению, называется коэффи
циентом поперечной деформация или коэффициентом Пуассона:
И- = Iе'/е |.
(2.5)
Значения коэффициента Пуассона для различных материа
лов находятся в пределах от 0 до 0,5 (табл. 2.1).
Минимальное значение коэффициент Пуассона имеет для
пробки (ц = 0); максимальное —для каучука (р « 0,5). Для боль
шинства металлов и сплавов значение коэффициента Пуассона
колеблется в сравнительно узких пределах: от 0,23 до 0,35 (в
среднем примерно 0,3).
Перейдем к вопросу об определении изменения длины (уд
линения или укорочения) бруса. Из выражения (2.2) имеем
A (dz) = g dz - изменение длины бесконечно малого элемента,
а из выражения (2.4) —закон Гука
£ = и /Е
и
A (dz) = е dz = (ст/Е) dz.
34
Нормальное напряжение, возникающее в поперечном сече
нии бруса, выразим через продольную силу и площадь сечения:
а = N/A.
Подставляя значение от в выражение для A(dz), получаем
A (dz) = N dz/ (ЕА).
(2.6)
Для определения изменения длины А/ всего бруса (или
участка бруса) следует просуммировать значения A(dz) по всей
длине, т. е. взять интеграл
/
В наиболее общем случае, когда законы изменения N и
А (или одной из этих величин) различны для отдельных участ
ков бруса, при определении АI интегрирование ведут в пре
делах каждого из участков, а затем результаты алгебраически
суммируют:
к
(2 .8)
/=1?1
В частном случае (см. рис. 2.11, л), когда поперечное сечение
бруса или отдельного его участка постоянно и продольная си
ла во всех сечениях одинакова, из (2.7) получаем
М = Ш/(ЕА).
(2.9)
Выражение (2.9) часто называют формулой Гука, а произве
дение ЕА условно называют жесткостью сечения бруса при
растяжении (сжатии).
При практических расчетах иногда удобно ввести понятие
жесткости бруса (участка бруса):
С = EA/L
(2.10)
Жесткость бруса численно равна силе, вызывающей удлине
ние (или укорочение) бруса, равное единице длины: 1 м или
1 см и т. п.
При расчетах в единицах СИ коэффициент жесткости выра
жают в ньютонах на метр (Н/м).
Величину, обратную коэффициенту жесткости, называют
коэффициентом податлшостн:
Р = 1/С = 1/(ЕА).
( 2. 11)
35
Ф г 'Ъ л Л Ь , (F,+Ft)h ,
ж~ e a +~Ea ~ + — Та
Рис. 2.13
Коэффициент податливости численно равен удлинению
(укорочению) бруса, вызванному силой, равной единице силы:
1 И, или 1 кН.
Пользуясь понятием коэффициента жесткости или коэффи
циента податливости, взамен формулы (2.9) получаем
Al = N/C
(2.12)
или
Л/ = рЛГ.
(2.13)
Дополнительно остановимся на случаях, когда формула
(2.9), а также, как следствие, и формулы (2.12), (2.13) применимы
лишь к отдельному участку бруса. Такие случаи иллюстрирует
рис. 2.13: а —ступенчатое изменение поперечного сечения;
б —скачкообразное изменение продольной силы; в —ступенча
то-переменное сечение и скачкообразное изменение продольной
силы, т. е. комбинация случаев а и б. Изменение длины бруса
(удлинение или укорочение) равно алгебраической сумме удли
нений (укорочений) отдельных участков:
к
i=l
В случаях когда поперечное сечение бруса или продольная
сила или обе эти величины изменяются по его длине непрерыв
но (рис. 2.14), удлинение (укорочение) бруса следует вычислять
по формуле (2.7).
36
При растяжении (сжатии) бруса его поперечные сечения
перемещаются в направлении оси. Перемещения являются
следствием деформаций, но эти понятия необходимо строго
разграничивать. Например, в случае, представленном на
рис. 2.15, деформируется лишь левая часть бруса (участок АВ),
а участок ВС перемещается как абсолютно твердое тело. Пере
мещения всех сечений этого участка одинаковы и равны удли
нению части АВ бруса:
XB = Xc = ^ A B = Fa/(EA).
Перемещение произвольного сечения бруса равно изменению
длины участка, заключенного между этим сечением и заделкой.
Например, для сечения, отстоящего на расстоянии z от за
делки (рис. 2.15),
К = А1г = Fz/(EA),
где z < а.
Г рафик Xz = / (z), показывающий перемещения поперечных
сечений в функции их расстояния z от неподвижного конца бру
са (или сечения, условно принятого за неподвижное), называет
ся эпюрой перемещений (рис. 2.15); стрелкой на эпюре показано
направление перемещений.
Взаимное
перемещение
двух сечений равно измене
нию длины .части бруса,
заключенной между этими
сечениями (рис. 2.16).
* Остановимся на опре
делении перемещений узлов
(шарниров) стержневых си
стем.
Эти перемещения опре-
Рис. 2.16
37
деляют по известным удлинениям и укорочениям стержней,
сходящихся в рассматриваемом узле.
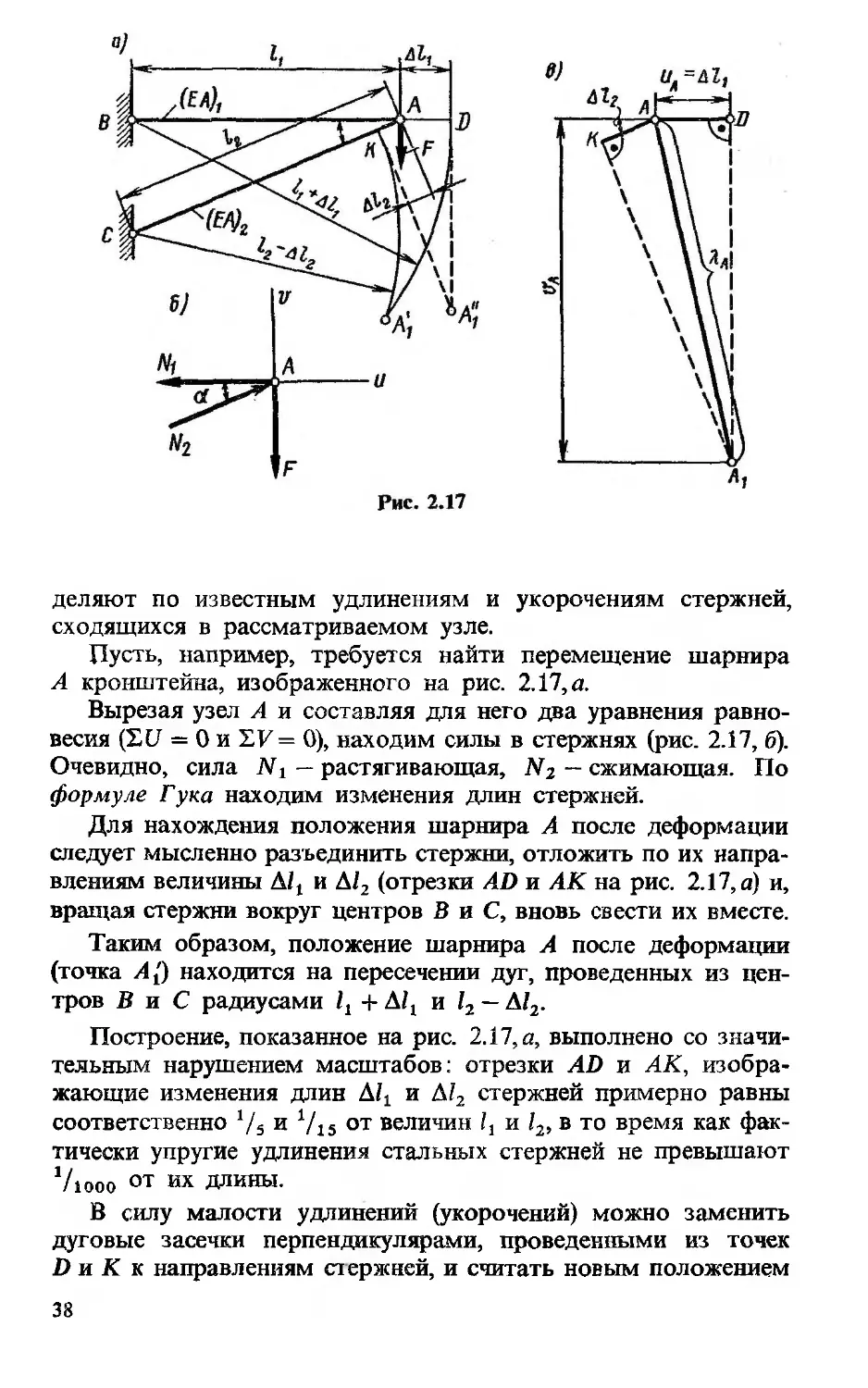
Пусть, например, требуется найти перемещение шарнира
А кронштейна, изображенного на рис. 2.17, а.
Вырезая узел А и составляя для него два уравнения равно
весия (ЕС/ = 0 и YV = 0), находим силы в стержнях (рис. 2.17, б).
Очевидно, сила N x —растягивающая, N 2 —сжимающая. По
формуле Гука находим изменения длин стержней.
Для нахождения положения шарнира А после деформации
следует мысленно разъединить стержни, отложить по их напра
влениям величины Д/j и Д/2 (отрезки AD и АК на рис. 2.17, я) и,
вращая стержни вокруг центров В и С, вновь свести их вместе.
Таким образом, положение шарнира А после деформации
(точка А 0 находится на пересечении дуг, проведенных из цен
тров В и С радиусами lx + A lt и 12 —Д/2.
Построение, показанное на рис. 2.17, я, выполнено со значи
тельным нарушением масштабов: отрезки AD и АК, изобра
жающие изменения длин Alt и Д/2 стержней примерно равны
соответственно Vs и Vis от величин /, и /2, в то время как фак
тически упругие удлинения стальных стержней не превышают
Vюоо от их длины.
В силу малости удлинений (укорочений) можно заменить
дуговые засечки перпендикулярами, проведенными из точек
D и К к направлениям стержней, и считать новым положением
38
W/SSS*
шарнира точку А'[. Если бы удалось выпол
нить рассмотренные построения без иска
жения масштабов (для этого потребовался
бы лист бумаги весьма больших разме
ров —порядка 2 х 1 м), можно было бы убе
ЙЕ'
диться, что дуговые засечки и перпендику
а 1
ляры практически сливаются.
Достоинством указанного построения,
называемого диаграммой перемещений,
является его простота и возможность
выполнения в произвольном масштабе, не
связанном с масштабом чертежа самой
ЫОкН
стержневой системы.
Диаграмма перемещений может быть
Ри с. 2.18
построена отдельно, как показано на
рис. 2.17, в; при этом, если построение выполнено в доста
точно крупном масштабе, можно не устанавливать аналити
ческой зависимости между Д/i, Д/2 и перемещением узла
А, а, замерив отрезок диаграммы AAi и умножив его на
масштаб, получить искомое перемещение. На этом же чертеже
показаны горизонтальная иА и вертикальная vA составляющие
полного перемещения. *
П р и м е р 2.4. Определить размеры поперечного сечения сталь
ной (Е = 2,1 • 105 МПа) штанги (рис. 2.18) при условии, чтобы ее удли
нение равнялось [Д!] = 2 мм (здесь и в дальнейшем квадратные скобки
употребляются для обозначения допускаемого значения той или иной
величины —удлинения, напряжения и т. д.). Чему при этом будут
равны напряжения в поперечном сечении штанги?
Р е ш е н и е . По формуле Гука, учитывая, что продольная сила во
всех поперечных сечениях штанги одинакова (N = F), имеем
Д/ = N1/ (ЕА) = Fl/(EA),
откуда требуемая площадь сечения при ДI = [Д/]
А -а 2
FI
Е [Д/]
«МО3-2,5
2,1-105'106•2 • 10“ 3
3,57• 10~4 м2 = 357 мм2;
а = |/357 = 18,9 мм, округляя, принимаем а = 19 мм. Напряжение в по
перечном сечении штанги
сг = ff/A = F/a2 = 60-103/0,192 = 166-106 Па = 166 МПа.
Определим, чему равно относительное изменение площади попе
речного сечения, если коэффициент Пуассона ц = 0,28.
Продольная деформация
е = а/Е = 166/(2,1 ■10б) = 79,0-10“ 3.
39
Поперечная деформация
е ' = —Цб= -0,28- 79,0- 10~s = - 2 2 , 1 -Ю^5.
Площадь сечения деформированной штанги
А' = (а + е’а)2 = а2 + 2г'а2 + (s')2 = а2 [1 + 2s’ + (s')2].
Пренебрегая величиной (е')2 как малой высшего порядка малости,
получаем
А' =а(1 + 2е').
Относительное изменение площади сечения
А ~ А- 100 % = й (1+2sl ~ a ЮО% = 2s' • 100 % =
= 2 ( —22,1 • 10“ 5) 100% = -0,0442%.
Полученный результат носит общий характер в том смысле, что
в стадии упругих деформаций изменение площади поперечного сечения
бруса ничтожно мало и поэтому при определении напряжений и пере
мещений всегда оперируют первоначальной площадью сечения. >
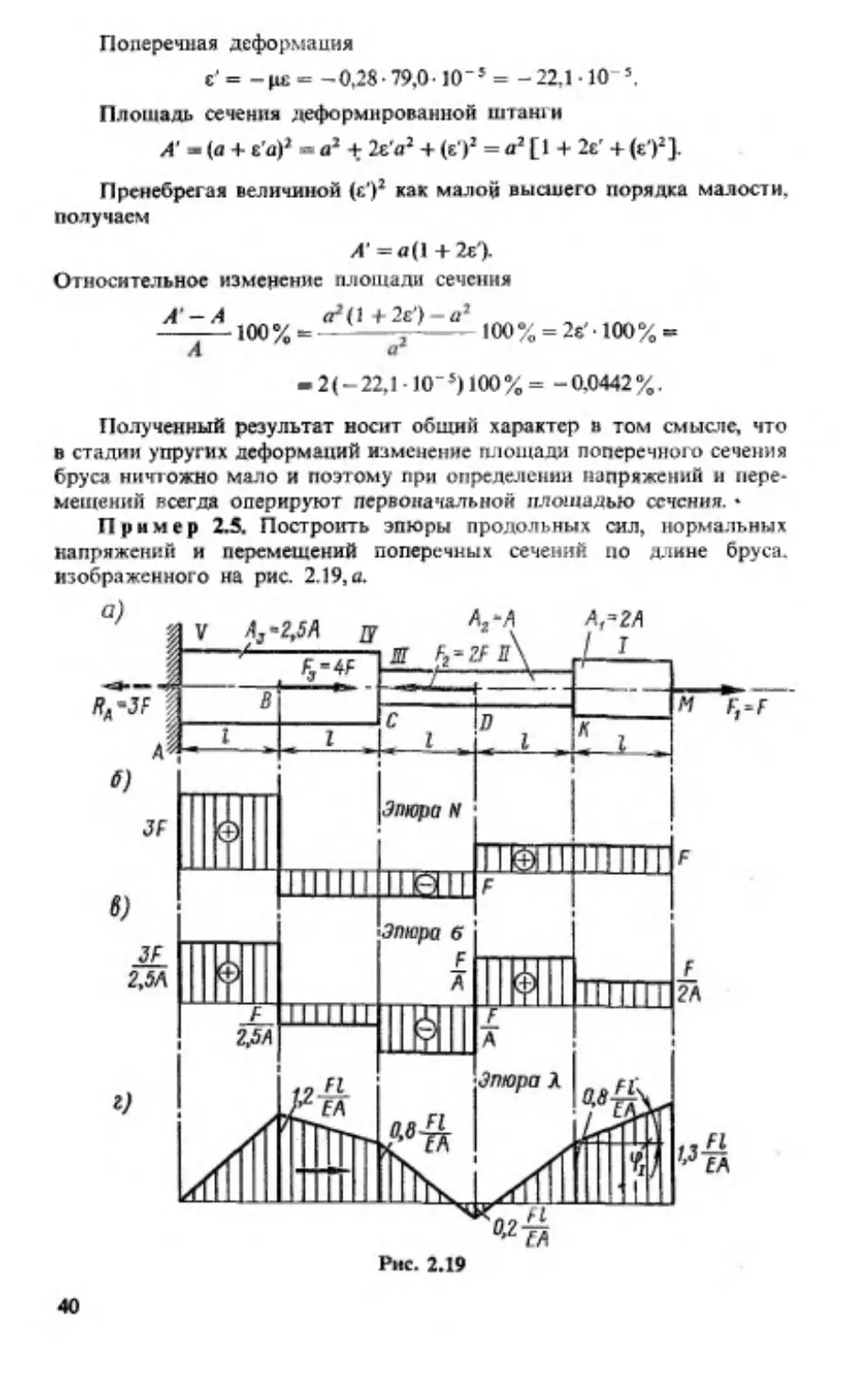
П р и м е р 2.5. Построить эпюры продольных сил, нормальных
напряжений и перемещений поперечных сечений по длине бруса,
изображенного на рис. 2.19, а.
40
Р е ш е н ы е. Разбиваем брус на участки, начиная от свободного
конца. Границы участков проходят через точки приложения внешних
сил и места изменения размеров поперечного сечения. Строим эпюры
продольных сил (рис. 2.19,6) и нормальных напряжений (рис. 2.19, в),
как изложено выше в примерах 2.1 и 2.3.
Для построения эпюры перемещений достаточно определить пере
мещения сечений, совпадающих с границами участков, так как между
указанными сечениями эпюра линейна.
Сечение А неподвижно, т. е. Хл = 0 (построение эпюры перемеще
ний следует всегда начинать от неподвижного или условно принятого
неподвижным сечения).
Перемещение сечения В равно изменению длины (в данном случае
удлинению) участка АВ (участка V) бруса:
3FI
FI
= 1,2
ЕЛ '
¥ • 2,5А
Сечение В перемещается вправо; соответствующую ординату ус
ловно будем считать положительной и отложим (в выбранном масш
табе) вверх по оси эпюры (рис. 2.19, г).
Перемещение сечения С равно алгебраической сумме изменений
длин участков V и IV бруса:
Хц = А1у —
Nyl
Y -z м
Хс = А1у + A ljy ~
3F!
£•2,5.4
Nyl i N,yl
Y Y J a + Е ■2,5/1
FI
Е ■2,5А
FI
ЕА
--------------------- =0,8----- .
То же самое можно записать несколько компактнее:
FI
Ya
£-2,5/4
Сечение С также перемещается вправо.
Аналогично,
Хс — Xg + Aliy = 1,2
FI
=
0,8
FI
EA
FI
FI
------ = - 0, 2 - —
ЕА
ЕА
ЕА
Знак минус указывает, что сечение D перемещается влево (так как
ранее было принято считать перемещения вправо положительными).
Значения Хц и Ху указаны на эпюре (рис. 2.19, г); читателю реко
мендуется самостоятельно проверить определение соответствующих
ординат.
Тангенс угла наклона эпюры к оси абсцисс пропорционален нор
мальным напряжениям, возникающим в поперечных сечениях данного
участка бруса. Например (рис. 2,19, г),
Xg —Хс ■+■Al/ц = Хс "Ь
tg<Pi
N,„1
Хм ~ Хк
-
Ali
о
F
= — = е/ = ^ = Е . 2 А -
П р и м ер 2.6. По данным предыдущего примера построить
эпюры перемещений от действия каждой из сил в отдельности.
41
Р е ш е н и е . При действии силы F, = F (рис. 2.20, а) деформирует
ся (растягивается) весь брус. Границами участка служат сечения С, К,
М —места изменения размеров поперечного сечения; перемещения
этих сечений:
F-21
FI
Ясг, : --------- = 0,8------:
£•2,5,4
ЕЛ
FI
F-21 „ FI
F-21
- + ------= 2,8-— ;
^KF, = ^CF, + EA =0,8—
EA EA
EA
FI
FI
F/
Fl
+ 0,5------ =3,3^-AfF, —^-KF1+ -E-2A =2,8----EA
EA
Ha
Соответствующая эпюра дана на рис. 2.20,6.
При действии силы F2 (рис. 2.20, в) сжимаются участки АС и CD
бруса; эпюра перемещений дана на рис. 2.20, г. Участки DK и КМ не
деформируются, и все поперечные сечения этих участков перемещают
ся влево вместе с сечением D.
Сила £ 3 растягивает участок АВ бруса (рис. 2.20,6); эпюра переме
щений дана на рис. 2.20, е.
На всех эпюрах стрелки указывают направления перемещений.
Если просуммировать все три эпюры перемещений, получим, как
это следует из принципа независимости действия сил, эпюру Я от
совместного действия всех заданных сил (эпюру, представленную на
рис. 2.19, г).
Пр и м е р 2.7. Определить удлинение бруса постоянного попереч42
ного сечения, нагруженного равномер
но распределенной нагрузкой интен
сивностью q (рис. 2.21).
Р е ш е н и е . Определим продоль
ную силу, возникающую в произволь
ном поперечном сечении бруса. При
меняя метод сечений и рассматривая
условие равновесия нижней остав
ленной части длиной г (рис. 2.21),
получим
JV = qz,
где qz —равнодействующая распреде
ленной нагрузки, действующей на ос
тавленную часть.
Так как продольная сила переменна —изменяется по длине бруса
по линейному закону (см. эпюру N на рис. 2.21), то удлинение опреде
ляем по формуле (2.7):
I
о
i
N dz
Г qz
ql2
~ Ш ~ ~ J £ j d Z - 2ЕА '
о
Учитывая, что ql = G - равнодействующей всей нагрузки, дей
ствующей на брус, выражение для АI можно записать так:
Итак, удлинение бруса постоянного сечения от действия равномер
но распределенной по его длине нагрузки вдвое меньше, чем удлине
ние от сосредоточенной силы, равной равнодействующей этой нагруз
ки и приложенной к свободному концу бруса.
Примером равномерно распределенной осевой нагрузки может
служить собственная сила тяжести бруса, при этом q = yA и G =
= уА1 —сила тяжести (вес) всего бруса.
Перемещение произвольного поперечного сечения бруса, отстоя
щего на расстоянии и от свободного конца, равно удлинению части
бруса, заключенного между заделкой и этим сечением:
"
Jf #е а
qz~
dz = 2ЕА
2ЕА
т. е. перемещения изменяются по квадратичному закону; эпюра %—
парабола (рис. 2.21).
П р и м е р 2.8. Определить перемещения сечений 1 —1 и II — II
бруса, изображенного на рис. 2.22. Учесть влияние силы тяжести бруса
(удельная сила тяжести равна у)Р е ш ение. Перемещение сечения I — I равно удлинению верхней
части бруса длиной а. Для этой части сила F и сила тяжести нижеле
жащих частей бруса являются сосредоточенными нагрузками, а соб
ственная сила тяжести —равномерно распределенной нагрузкой. По43
Эпюра N Эпюра б
льзуясь результатом, полученным в предыдущем примере, и применяя
принцип независимости действия сил, имеем
Х ,- Д /. = — + - ^ + ^ - +
1
“ ЕА2
ЕА2
ЕА2 2ЕАг
где GH= у A tl{ —сила тяжести нижней части; GB1 = уА2(12 —а) —сила
тяжести участка верхней части, расположенного ниже сечения I —/;
GB2 = уА2а —сила тяжести участка, расположенного выше сечения
/ - /.
Перемещение сечения I I - I I равно удлинению всего бруса, т. е.
А,// —Д/в + А/в.
Удлинение нижней части складывается из удлинений от силы
F (сосредоточенной!) и силы тяжести этой части (распределенной!):
дI
G J,
Fly
(у1 ^ ) 1 ,
н
Е А 1 2ЕА1
ЕА1
2ЕА1
Удлинение верхней части складывается из удлинений от сосредо
точенной силы, равной F + G„, и равномерно распределенной нагруз
ки —силы тяжести GB этой части:
д/
l ! b ~"
(^ +
FI
)<2
G J i ^ (F + y l i A J l j
g h
ЕА2
+
2ЕА2
ЕАг
(у1гА 2)12
2Е А 2
На рис. 2.22 показаны эпюры N, а и А, построенные при l2 = 12 *= /;
А2 = ЗАи F = 4yAtl.
При решении этого примера определение удлинений было выпол
нено без интегрирования (в явном виде), хотя продольная сила по дли
не бруса переменна. Это объясняется использованием формулы для
определения удлинения от действия собственной силы тяжести бруса,
полученной при решении примера 2.7.
П р и м е р 2.9. Определить (не учитывая влияния силы тяжести)
изменение высоты бруса, имеющего форму усеченного конуса
(рис. 2.23).
Р е ш е н и е . Площадь поперечного сечения бруса изменяется по
его высоте непрерывно, и хотя продольная сила постоянна (N = —F),
для определения укорочения бруса надо применить формулу (2.7). Про44
длим образующие конуса до их пересечения в точке О и примем эту
точку за начало координат. Такой выбор начала отсчета упрощает
дальнейшие выкладки. Из подобия треугольников ОАВ и OCD легко
установить, что расстояние точки О от верхнего основания конуса ?0 =
= /. Площадь произвольного поперечного сечения, находящегося на
расстоянии z от начала координат:
А=
Из чертежа (рис. 2.23) имеем dz/z = d/l0; d2 = zd/l и, следовательно,
л .
4
I2
Применив формулу (2.7) и подставив абсолютное значение силы
N, получим укорочение бруса:
А/ =
f Ndz
J EA
1
Fdz
n
d2
z2-—1 E—
4
;2
*
4FI2
End2
i 21
,
4FI2 /
End2 \
Z
4FI2 Г dz
End2 z2
2/
//’
2FI
End2
Интегрирование проведено в пределах от / до 21, что соответствует из
менению z в пределах действительной высоты бруса.
П р и м е р 2.10. Определить перемещение шарнира А симметрич
ной стержневой системы, изображенной на рис. 2.24, а. Материал
стержней - дюраль; Е = 7 ,0 '104 МПа.
Р е ш е н и е . Вырезая узел А, определяем силы в стержнях
(рис. 2.24,6):
А1-
1(7=0;
- N 1 sin а + N 2 sin а = 0;
N x = JV2;
ZV= 0;
N i cos а + N 2 cos а —F = 0;
N j = TV2 = F/(2 cos a).
Находим удлинения стержней:
A/j = Al
N tl
F
2 cos a
TX
h
cos a
ЁА
=
Fh
2EA cos2 a
45
Строим диаграмму перемещений (рис. 2.24,а): на продолжении
стержней АС и AD откладываем в произвольном масштабе отрезки*
изображающие
и А12; из полученных точек В и B i проводим пер
пендикуляры к направлениям стержней. Очевидно, что эти перпендику
ляры пересекаются на оси симметрии системы. Перемещение (Х.^) шар
нира А изображается отрезком AAV который определяется из
прямоугольного треугольника АВА1 (или ABLA l):
ХА = A/j/cosa.
Подставляя значение А1Ы получаем
\ А = Fh/(2EA cos3а).
Подстановка числовых значений дает
12•10-2
3 14
1•7,0 • 104 ■106 ———(0,0222 —0,0182)cos3 25°
0,00183 м.
§ 2 .4 . Энергия деформации при растяжении
При нагружении упругого тела внешние силы совершают
работу на перемещениях, которые получают точки их приложе
ния в результате деформации тела (конструкции). Вследствие
этой работы накапливается потенциальная энергия V деформи
рованного тела.
Следовательно, деформированное упругое тело является как
бы аккумулятором энергии.
Заводя, например, пружину патефона, расходуют определен
ную работу, которая переходит в энергию деформации пру
жины. Последняя используется для вращения диска с пластин
кой, т. е. переходит в кинетическую энергию их движения.
Предположим, что процесс нагружения совершается мед
ленно (статически). При этом можно не учитывать кинетиче
ской энергии частиц деформируемого тела. Если, кроме того,
пренебречь незначительными тепловыми потерями и рассея
нием энергии, то, следовательно, работа внешних сил W цели
ком перейдет в потенциальную энергию деформации V:
W —V.
(2.15)
В дальнейшем будет показано, что это соотношение может
быть использовано для определения перемещений в упругих
системах.
Определим работу внешних сил при статическом нагружении
упругой системы, предполагая, что система линейно-деформируемая, т. е. между силами и соответствующими перемещения
ми существует линейная зависимость.
46
Пусть к шарниру В сим
метричной стержневой си
стемы (рис. 2.25, а) приклады
вается сила F, весьма мед
ленно возрастающая от ну
ля до своего конечного зна
чения. В данном случае мы
встречаемся с необходимо
стью определения работы
переменной силы.
Для решения поставлен
ной задачи проще всего ис
пользовать график зависи
мости между силой и пере
мещением (рис. 2.25, б). При
бесконечно малом приращении dX перемещения можно считать
силу постоянной и соответствующая элементарная работа
d W = F d k.
На графике (рис. 2.25,6) эта работа выражается площадью
элементарной трапеции (густо заштрихована), которую по
малости размера dX можно рассматривать как прямоугольник.
Полная работа силы F, совершенная ею в процессе возраста
ния перемещения от 0 до Хк, равна сумме элементарных работ
и выражается площадью треугольника, заштрихованного на
рис. 2.25,6:
W = 0,5FKXK.
Этот результат можно сформулировать следующим обра
зом:
работа силы, статически приложенной к лвнейио-деформируемой системе, равна половине произведения конечного значения
силы на конечное значение соответствующего перемещения.
Сформулированное положение обычно называют теоремой
Клапейрона.
В случае если направление перемещения не совпадает с ли
нией действия силы, под соответствующим перемещением сле
дует понимать проекцию полного перемещения на направление
силы.
В дальнейшем, опуская индексы при F и X, будем записы
вать теорему Клапейрона в виде
W = 0,5FX.
(2.16)
Результат, полученный для линейно-деформнруемой системы,
верен не только при растяжении (сжатии), но и при любом дру
гом виде деформации.
47
Выведем формулу для определения потенциальной энергии
деформации системы по известным продольным силам, возни
кающим в поперечных сечениях стержней. Выделим из стержня
бесконечно малый элемент (длиной dz), как показано на
рис. 2.25, а. Энергия деформации, накапливаемая в этом эле
менте при его удлинении, равна работе продольных сил N (по
отношению к выделенному элементу эти силы являются внеш
ними) на взаимном перемещении торцов элемента. Указанное
перемещение равно удлинению элемента A(dz), и на основании
теоремы Клапейрона имеем
dV = 0,5Л1A(dz).
Выражая Adz по формуле Гука, получаем
d V = N 2 dz/(2EA).
Суммируя полученные значения по всей длине стержня,
определяем
(2.17)
i
Для всей системы
к
Для стержня (участка стержня) постоянного поперечного се
чения при условии, что продольная сила по длине стержня не
изменяется, на основании формулы (2.17) имеем
V = N 2l/(2EA).
(2.19)
Вообще при выборе формулы для вычисления энергии де
формации следует ориентироваться на указания, сделанные
в отношении определения изменения длины бруса (см. § 2.3).
Для оценки целесообразности применения того или иного
материала в различного рода амортизирующих устройствах
используется понятие удельной энергии деформации, т. е. энер
гии, накопленной в единице объема упругого тела. Это же по
нятие играет важную роль при исследовании некоторых вопро
сов, связанных с условиями перехода материалов в пластиче
ское состояние.
Удельная энергия деформации и равна отношению полной
энергии dV к объему dr элемента стержня:
и = dV/dv = N 2 dz/(2EA dr).
48
Учитывая* что dv = A dz, получаем
и = N 2 dz/ (2ЕАА dz) = N2/ (2ЕА2), но N/A = а,
поэтому окончательно
и = о 2/(2Е).
(2.20)
Единицей энергии в СИ является джоуль (Дж), а объема —
кубический метр, поэтому единицей удельной энергии деформа
ции будет джоуль на кубический метр (Дж/м3).
Пр и мер 2.11. Определить опускание шарнира А симметричной
стержневой системы (см. рис. 2.24).
Р е ш е н и е . В § 2.3 (см. пример 2.10) эта задача была решена
с помощью построения диаграммы перемещений. Решим ее исходя из
равенства работы внешних сил и потенциальной энергии деформации:
(а)
W=V.
По формуле (2.16) W —0,5FXA. Энергия деформации каждого из
стержней
= N 2l/(2EA). Энергия деформации системы К= 2 К,. Си
лы в стержнях (см. пример 2.10) Ni = N 2 = F/(2cosa). Длины стержней
I, = l2 —к/cos ос. Энергия Деформации
V = 2(\ t2 cos
~—
ос J) 2“cos~a / (2£/4)Подставляя значения W и V в выражение (а), получаем
0,5FXa = l ( ——— —^ ^—/( 2 ЕА),
\ 2 cos a / cos a
откуда XA =Fh/(2EA cos3 ос), т. e. тот же результат, который был полу
чен в примере 2.10 другим путем.
П р и м е р 2.12. Сравнить удельную энергию деформации для ре
зины при напряжении ст/ = 4,0 МПа и для стали при напряжении оц =
= 160 МПа. Принять £ рез = 0,008 • 103 МПа; £ ст = 2,1-105 МПа.
Р е ш е н и е . На основе формулы (2.20) имеем:
с}
'рсз “ 2£рез
Uct —
(4 • 106)2
2-0,008 ЮМО6
(160-106)2
2Ест
2-2,1 •103•106
1,0-106 Дж/м3;
= 0,061-106 Дж/м3.
Энергия деформации в единице объема стальной детали примерно
в 16 раз меньше, чем в резиновой, хотя напряжения в первой в 40 раз
выше, чем во второй. Эту способность резины к накоплению большой
энергии деформации при невысоких напряжениях (безопасных для ее
прочности) используют, применяя резину в различных амортизирую
щих (смягчающих толчки, удары и колебания) устройствах.
49
§ 2.5. Напряженное состояние при растяжении
(сжатии)
В начале курса при первом знакомстве с понятием «напряжение» было подчеркнуто, что нельзя говорить о напряжении
в данной точке тела, не указывая положения площадки, на ко
торой оно возникает. Действительно, через точку можно прове
сти бесчисленное множество различно ориентированных пло
щадок, и, конечно, в общем случае нет никаких оснований
предполагать, что возникающие на них напряжения одинаковы.
Совокупность нормальных и касательных напряжений, воз
никающих на всем бесчисленном множестве площадок, ко
торые можно провести через данную точку, характеризует на
пряженное состояние в этой точке.
Исследовать напряженное состояние в данной точке —это
значит получить зависимости, позволяющие определить напря
жения, возникающие в любой проведенной через нее площадке.
Для решения этой задачи надо знать напряжения по любым
трем взаимно перпендикулярным площадкам, проведенным че
рез исследуемую точку (доказательства этого положения не
приводим). Эти площадки и возникающие на них напряжения
(они, повторяем, должны быть известны) называют исходными.
При исследовании напряженного состояния в различных
точках прямого бруса в любом случае его нагружения ис
ходными являются напряжения, возникающие на площадках,
соответствующих поперечному и двум продольным сечениям,
проходящим через рассматриваемую точку. При растяжении
(сжатии) прямого бруса в поперечных сечениях возникают
только нормальные напряжения, определяемые по формуле
az = N/A.
Индекс z показывает, что это напряжение возникает на пло
щадке, нормаль к которой параллельна оси z (см. правило ин
дексов для напряжений, изложенное в § 1.5). В продольных се
чениях нет ни нормальных, ни касательных напряжений.
Отсутствие нормальных напряжений в продольных сечениях
является следствием того, что при растяжении (сжатии) нет взаимного
надавливания волокон бруса. В отсутствии касательных напряжений
легко убедиться, рассекая брус продольной плоскостью и рассматри
вая условие равновесия одной из его отсеченных частей.
Для исследования напряженного состояния мысленно выре
жем вокруг произвольной точки бруса бесконечно малый па
раллелепипед (рис. 2.26, а). В дальнейшем такие элементарные
параллелепипеды будем называть элементами или частицами.
50
а)
, / г " ___ '_У
Ч
<4 If
/
-*Jjz
G)
А
_
Г
I
У-
Рис. 2.26
В рассматриваемом случае совершенно безразлично, где имен
но вырезать эту частицу, так как напряженное состояние всех
точек бруса одинаково - однородное напряженное состояние.
Для того чтобы выделенный элемент находился в равнове
сии, следует приложить к его граням внутренние силы, заме
няющие действие отброшенных частей тела (бруса) на оста
вленную. Обращаем внимание, что здесь мы поступаем
в полном соответствии с требованиями метода сечений, но ес
ли ранее при определении продольных сил было достаточно
рассечь брус плоскостью, совпадающей с интересующим нас
поперечным сечением, то новая задача —исследование напря
женного состояния —потребовала иного применения этого ме
тода: элемент вырезан шестью сечениями.
Выделенный элемент (модель напряженной точки) изобра
жен отдельно на рис. 2.26,6. На его гранях, совпадающих
с плоскостями поперечного сечения бруса, возникают нор
мальные напряжения, остальные четыре грани от напряжений
свободны.
Мысленно разрежем выделенный из бруса элемент пло
скостью, нормаль к которой составляет произвольный угол а
с осью г. Это наклонное сечение показано на рис. 2.27, а. На
рис. 2.27,6 отдельно изображена бесконечно малая трехгранная
призма, отсеченная от элементарного параллелепипеда.
На ее наклонной грани возникают напряжения ст, и хв, под
лежащие определению.
Рис. 2.27
51
Составим уравнения равнове
сия элементарной призмы. При
этом для разделения неизвестных
выберем оси проекций, как пока
зано на рис. 2.28. Обращаем внима
ние, что уравнения равновесия со
ставляются, конечно, для сил, а не
для напряжений, т. е. каждое из
напряжений следует умножить на
площадь грани, на которой оно
возникает.
Пусть площадь наклонной грани dA, тогда возникающие на
ней силы равны a,, dA и та dA.
Напряжение о. возникает на грани, имеющей площадь
d/l cos я; соответствующая сила равна о , dA cos а.
Составляем уравнения равновесия;
Хпрт = 0 ; —ст2dA cos a cos а + tr, dA О,
откуда
ста т a, cos а;
Епрг = 0;
( 2 .21)
—а . dA cos а sin а + та dA —0,
откуда
т„ = ст2cos a s i n
ос,
или
= 0,5a2sin2a.
(2.22)
Сделаем некоторые выводы из полученных результатов.
Наибольшее нормальное напряжение возникает в поперечном
сечении бруса:
^шах
^я=0°
^х
N/A..
Наибольшее касательное напряжение возникает на площадке,
наклоненной под углом 45° к оси бруса, и равно половине нор
мального напряжения, возникающего в соответствующей точке
поперечного сечения:
•Стах=1:а=45" = ^ /2-
(2-23)
Из формулы (2.22) вытекает равенство (по абсолютному
значению) касательных напряжений, возникающих на взаимно
перпендикулярных площадках:
К 1 = К + 9 о4
52
Это равенство носит назва
ние закона парности касатель
ных напряжений. Более общая
его формулировка и доказа
тельство будут даны в § 3.3.
Рис. 2.29
Касательные
напряжения,
возникающие на взаимно пер
пендикулярных площадках, направлены всегда оба к ребру или
ог ребра пересечения этих площадок (рис. 2.29).
П р и м е р 2.13. Н а й т и требуемый диаметр поперечного сечения
с т е р ж н я (рис. 2.30) и з у с л о в и я , чтобы возникающие в нем наибольшие
к а с а т е л ь н ы е н а п р я ж е н и я н е превышали 80 МПа.
Р е ш е н и е .
И з ф о р м у л ы (2.23) следует, что напряжение в попе
р е ч н о м сеч ен и и
ст2 =
2ттах
=2-80 = 160 МПа,
но стг = N/A. В данном случае N = F (в любом поперечном сечении).
Следовательно, А ^ N/ст2; nd1/4 = А 5* F/а, или
4-90-103
d>
3,14 160 106
= 26,8- 10-
м = 26,8 мм.
Пр и м ер 2.14. В сжатом стержне (рис. 2.31) напряжения по
одной из площадок: а , = -6 0 МПа; т, = 24МПа. Вычислить на
ибольшие нормальные и касательные напряжения, возникающие в дан
ном стержне.
Р е ш е н и е . Напряжения в наклонном сечении [формулы (2.21),
(2.22)]:
<т„ = <Tzcos2a;
(1)
тя = 0,5<TjSin2oc.
(2)
d
F=90kH
Рис. 2.30
53
Из этой системы уравнений найдем напряжение a z в поперечном
сечении стержня, которое и является наибольшим нормальным напря
жением.
Разделив (2) на (1), получим
т„
0,5 sin 2ot
sin а cos а
— = ------ j---- = —— 2------= tett
er,
cos-1а
cos-‘ а
Подставив числовые значения, найдем
tg а = 24/—60 - —0,4.
По известной формуле тригонометрии,
1
1
1 + tg2 а
1 + 0,42
= 0,862.
Из формулы (1)
аг = ст,/cos2 а = —60/0,862 = —69,6 МПа.
По формуле (2.23) находим максимальное касательное напряжение
Iтюм I = I а жI/2 = 69,6/2 = 34,8 МПа.
§ 2.6. Общие сведения о механических
испытаниях материалов
Конструктор, выбирая материал для проектируемой детали,
а затем рассчитывая ее на прочность (жесткость, устойчивость),
должен располагать данными о механических свойствах мате
риала, т. е. его прочности, пластичнрсти и т. п., а также знать
значения упругих постоянных —модуля продольной упругости
Е и коэффициента Пуассона р.
Основные механические характеристики, определяемые при
испытаниях материалов:
1. Прочность —способность материала, не разрушаясь, вос
принимать внешние механические воздействия.
2. Пластичность —способность материала давать значи
тельные остаточные деформации, не разрушаясь.
3. Упругость —способность материала восстанавливать
после снятия нагрузок свои первоначальные формы и размеры.
4. Твердость —способность материала сопротивляться про
никновению в него другого тела, практически не получающего
остаточных деформаций.
Характер нагружения (статическое, динамическое, повторно
переменное) и условия работы деталей машин и инженерных
сооружений весьма разнообразны. Располагая сведениями
о свойствах материала при определенном виде деформации
(например, растяжении) и характере нагружения (например, ста
тическом), судить о его свойствах при других условиях можно
54
лишь весьма приближенно, что в ряде случаев недопустимо.
Поэтому механические испытания материалов отличаются
большим разнообразием.
По характеру нагружения различают испытания статические,
динамические и испытания на усталость (при переменных
напряжениях).
По виду деформации различают испытания на растяжение,
сжатие, срез, кручение, изгиб. Реже проводят испытания при
сложном нагружении, например на совместное действие изгиба
и кручения.
Большинство испытаний проводится при нормальной (ком
натной) температуре, но для деталей паровых котлов, турбин,
реактивных двигателей и т. п. необходимо знать их свойства
при высоких температурах.
В некоторых случаях возникает необходимость в испыта
ниях конструкционных материалов при низких температурах.
Механические испытания проводят на образцах, формы
и размеры которых установлены ГОСТами или техническими
условиями.
За последние годы широкое распространение получили натурные
испытания отдельных деталей и узлов машин. В зависимости от целей
испытания деталь (узел) либо доводится до разрушения, либо иссле
дуется напряженное состояние в отдельных ее точках при заданных на
грузках. В этом случае для измерения деформаций широко применяет
ся электротензометрия.
В сл у ч ая х , к о г д а т е о р е т и ч е с к о е о п р е д е л е н и е напряжений недоста
т о ч н о н а д е ж н о и л и в о о б щ е н е в о з м о ж н о , и з г о т о в л я ю т модель рас
с ч и т ы в а е м о г о о б ъ е к т а и з с п е ц и а л ь н о г о о п т и ч е с к и активного материа
л а , н а г р у ж а ю т ее и о с в е щ а ю т п о л я р и з о в а н н ы м светом. Изображение
м о д е л и с п о м о щ ь ю с п е ц и а л ь н о й о п т и ч е с к о й у с т а н о в к и проецируется
н а э к р а н . Э т о и з о б р а ж е н и е о к а з ы в а е т с я п о к р ы т ы м системой полос,
а н а л и з и р у я р а с п о л о ж е н и е и о к р а с к у к о т о р ы х м о ж н о о п р е д е л и т ь на
пряж ен ия в м одели.
Механические испытания имеют большое значение не толь
ко для расчета на прочность, но и для контроля качества мате
риала или выпускаемых изделий. При этом испытаниям могут
подвергаться как специально изготовленные образцы, так и са
ми изделия (детали или узлы).
Широко применяют механические испытания и в процессе
создания новых конструкционных материалов, которые дол
жны обладать определенными механическими свойствами.
Помимо испытаний, при которых определяют механические
характеристики, важное значение имеют различные технологи
ческие испытания (пробы), выявляющие соответствие свойств
металла тому или иному технологическому процессу, например
55
испытание листовой латуни на выдавливание с целью опреде
ления ее пригодности для изготовления деталей холодной
штамповкой.
§ 2.7. Статические испытания на растяжение
Наиболее распространенным является испытание на растя
жение статической нагрузкой. Его достоинства —однородность
напряженного состояния образца в области, достаточно уда
ленной от головок (формы и размеры стандартных цилиндри
ческих образцов показаны на рис. 2.32,а,б,в*; образец в пока
зан в более крупном масштабе), сравнительная простота
оборудования и методики эксперимента по сравнению с боль
шинством других испытаний. Однородность (т. е. тождествен
ность для всех точек тела) напряженного состояния позволяет
легче обнаружить начало общей пластической деформации
образца, что очень важно для определения соответствующих
механических характеристик.
Испытания проводят на разрывных или универсальных
машинах с механическим или гидравлическим силообразованием. На рис. 2.33 показан общий вид одной из машин с меха
ническим нагружением, дающей максимальную силу 5000 кгс
(50 кН).
Перемещение винта 1, жестко связанного с нижним захва
т о м 2 машины, осуществляется через систему передач вручную
и л и о т электродвигателя. Сила от верхнего захвата 3 через си
ст е м у рычагов передается маятнику 4. Отклонение маятника
а)
____________
200
.83"
Г 1 1
W 25
220
310
f
П ----г— „.it-_______ f_I T L —
'
д) _ п
' L
120 ^
240
' '
е»
26 22 112
'1
-П Cvj '
к
.30 <о
г 36 1 7
Рис. 2.32
* Плоские образцы применяют сравнительно редко, в основном
для определения свойств листовых материалов.
56
Рис. 2.33
вызывает поворот ст р е л к и силоизмерительного устройства 5,
что позволяет д л я л ю б о г о момента испытания установить зна
чение силы, р а с т я г и в а ю щ е й образец.
Нагружение о б р а з ц а осуществляется вследствие взаимного
перемещения з а х в а т о в , которое происходит настолько медлен
но, что ускорениями частиц материала в процессе деформиро
вания можно пренебречь (как известно, это и является характе
ристикой статического нагружения).
Машина снабжена диаграммным аппаратом 6, который
в процессе испытания вычерчивает график зависимости между
силой F, растягивающей образец, и соответствующим удлине
нием А/. Поворот барабана пропорционален перемещению
нижнего захвата машины (т. е. А/), а перемещение карандаша
вдоль образующей барабана пропорционально отклонению
маятника (т. е. F).
На рис. 2.34 показан примерный вид диаграммы растяже- .
ния, полученной при испытании образца из малоуглеродистой
стали. В начальной стадии испытания (до точки А с ординатой
57
Fпц) зависимость между
силой и удлинением ли
нейна, т. е. справедлив
Рис. 2.35
закон Гука. При растяги
вающей силе Fy (точка
В), почти не отличающейся от Гпц, в образце возникают
первые остаточные деформации. При некотором значении рас
тягивающей силы FT наблюдается рост удлинения без увеличе
ния нагрузки. Это явление называется текучестью металла. Со
ответствующий участок диаграммы (почти горизонтальная
линия) называется площадкой текучести.
В этой стадии деформации полированная поверхность
образца становится матовой и на ней можно обнаружить сетку
линий, наклоненных к оси образца под углом примерно 45°
(рис. 2.35). Это так называемые линии Людерса — Чернова,
представляющие собой следы сдвигов частиц материала. На
правление указанных линий соответствует площадкам, на ко
торых при растяжении образца возникают наибольшие каса
тельные напряжения.
По окончании стадии текучести материал вновь начинает
сопротивляться деформации, здесь связь между силой и удли
нением нелинейна: удлинение растет быстрее нагрузки. Этот
участок диаграммы называют зоной упрочнения. При силе, при
мерно равной Fm, на образце появляется местное утонынение —шейка, в результате сопротивление образца падает и его
разрыв происходит при силе, меньшей Fm.
Ясно, что сила и удлинения, соответствующие указанным
характерным точкам диаграммы, зависят не только от свойств
материала, но и от абсолютных размеров образца. Для получе
ния механических характеристик материала (т. е. для того,
чтобы исключить влияние абсолютных размеров образца) эту
диаграмму перестраивают: все ординаты делят на начальную
площадь поперечного сечения А0, а все абсциссы —на началь
ную расчетную длину 10. В результате получают так называе
мую условную диаграмму растяжения в координатах: относи
тельное удлинение е, нор
мальное напряжение а. Эта
диаграмма (рис. 2.36) по
добна исходной (отличается
от нее только масштабом).
Условной эта диаграмма на
зывается потому, что напря
жения и деформации отне
сены к начальным площади
и длине образца.
58
На условной диаграмме растяжения (рис. 2.36) отмечены
точки (и их ординаты), соответствующие механическим харак
теристикам, которые могут быть получены при статических ис
пытаниях на растяжение.
°пц = ^пцМо —предел пропорциональности —наибольшее напря
жение, до достижения которого справедлив закон
Гука;
а у = Fy /А0 —предел упругости —наибольшее напряжение, до
достижения которого в образце не возникает
остаточных деформаций;
а , = F.r/A0 —предел текучести - напряжение, при котором про
исходит рост пластических деформаций образца
при практически постоянной нагрузке*;
о пч = Fm/A 0 —предел прочности (или временное сопротивле
ние) —условное напряжение, соответствующее
наибольшей нагрузке, выдерживаемой образцом
до разрушения.
Можно пользоваться и таким определением: предел прочности —
это отношение максимальной силы, которую способен выдержать
образец, к начальной площади его поперечного сечения.
Отметим, что в определениях пределов пропорционально
сти, упругости и текучести не подчеркнуто, что это условные
напряжения, т. е. отнесенные к первоначальной площади сече
ния образца. Это связано с тем, что до начала образования
шейки площадь сечения образца почти не отличается от перво
начальной. При максимальной нагрузке Fm это различие весь
ма существенно, что и отражено в определении понятия «предел
прочности».
В момент разрыва образца истинное, т. е. отнесенное к дей
ствительной, а не к начальной площади сечения образца, сред
нее напряжение в наиболее тонком месте шейки существенно
выше предела прочности.
Строго говоря, понятия «предел прочности» и «временное сопро
тивление» не совсем тождественны. Первое из них относится к случаю,
когда образец разрушается без образования шейки, что характерно
для хрупких материалов. Второе относится к пластическим материа
лам, на образцах из которых перед разрушением появляется шейка.
Временное сопротивление часто обозначают щ или ст„. В нашем курсе
эти понятия разграничивать не будем и примем указанное выше обо
значение а лч (в учебной и специальной литературе встречаются также
обозначения аь> ств, овр, общие для пластичных и хрупких материалов).
* Это напряжение называют также физическим пределом текуче
сти в отличие от условного, определение которого будет дано ниже
(см. с. 63).
59
Определение предела пропорциональности непосредственно
по диаграмме, автоматически записанной в процессе испытания
(см. рис. 2.34), может быть выполнено лишь грубо приближен
но. В случае необходимости получения наиболее точных значе
ний испытание проводят, увеличивая нагрузку образца ступеня
ми и замеряя с помощью тензометров соответствующие
удлинения. Строя по этим данным график (или составляя та
блицу), определяют ту нагрузку, при которой отклонение
от закона пропорциональности равно обусловленному тех
ническими условиями испытаний. Например, берут нагрузку,
соответствующую той точке графика, для которой тангенс угла
наклона касательной к оси абсцисс на 20% меньше тангенса
угла наклона его первоначального прямолинейного участка.
Разделив эту нагрузку на площадь сечения образца, получают
так называемый условный предел пропорциональности (подроб
нее см. [9]).
Для определения предела упругости также приходится вести
нагружение образца ступенями. После каждой ступени нагруз
ки образец п о л н о с т ь ю р а з г р у ж а ю т и тщательно заме
ряют его длину. В результате определяют условный предел
упругости —напряжение, при котором в образце впервые по
являются остаточные деформации, имеющие заданную малую
величину (например, 0,001, 0,003, 0,005 %). Размер допуска оста
точной деформации, принятый при определении условного
предела упругости, указывают в виде индекса, например
«Чехи - условный предел упругости, соответствующий оста
точной деформации 0,001%.
Как уже говорилось, числовые значения пределов пропор
циональности и упругости для большинства материалов почти
совпадают, но физический смысл этих характеристик, конечно,
различен.
Из изложенного следует, что определение пределов пропор
циональности и упругости связано с необходимостью проведе
ния весьма точных и трудоемких экспериментов. Поэтому при
промышленных испытаниях в подавляющем большинстве слу
чаев ограничиваются определением пределов текучести и про
чности.
Пластичность материала оценивают значением относитель
ного остаточного удлинения при разрыве, определяемого по
соотношению
5 = [(/к-/о )//о ]-Ю О % ,
где /к, /0 —длины расчетной части образца, соответственно ко
нечная (после разрыва) и начальная.
60
На диаграмме растяжения
(см. рис. 2.36) 5 выражается от
резком OL.
Рис. 2.37
Для одного и того же мате
риала значение 5 различно в за
висимости от отношения ра
счетной длины 10 к диаметру
d образца, при испытании кото
рого она получена. Стандарт
ные цилиндрические образцы
имеют отношение lo/d = 10 или
lo/d = 5 (см. рис. 2.32). Первые
называют десятикратными или
условно «длинными», а вто
рые —пятикратными или ус
ловно «короткими» образцами. Полученное при испытании
«длинных» образцов значение относительного остаточного уд
линения при разрыве обозначают 510, а в случае
«коротких» —85, при этом для данного материала всегда 85 >
> 8)0.
После разрыва образца замеряют его диаметр в наиболее
тонком месте шейки (рис. 2.37), вычисляют соответствующую
площадь сечения Ак и определяют относительное остаточное
уменьшение площади начального сечения образца при разрыве:
^ = [(A0~ A J / A o]-100%.
C r x i:!Z i
Эта механическая характеристика, так же как и 8, служит
для оценки пластичности материала.
Остановимся дополнительно еще на некоторых вопросах,
связанных со статическими испытаниями малоуглеродистой
стали (и других пластичных материалов) на растяжение.
Опытным путем установлено, что при разгрузке образца,
растянутого так, что в нем возникают напряжения выше пре
дела упругости и даже выше предела текучести (например, от
точки N диаграммы на рис. 2.38), линия разгрузки оказывается
прямой, параллельной начальному участку ОА диаграммы.
Следовательно, полная деформация образца состоит из двух
частей —упругой, исчезающей после снятия нагрузки, и оста
точной (пластической).
Полное удлинение, соответствующее нагрузке F u выражает
ся отрезком ОЬи упругое —отрезком ML, и пластическое —
отрезком ОМ оси абсцисс диаграммы (рис. 2.38).
Упругая деформация и при напряжениях, больших предела
пропорциональности, может быть определена по закону Гука,
это следует из того, что линия разгрузки —прямая. Параллель
61
ность этой линии начальному участку диаграммы указывает,
что модуль упругости Е при разгрузке имеет то же значение,
что и при нагружении в пределах справедливости закона Гука.
Если подвергнуть повторному нагружению образец, ко
торый был предварительно растянут до возникновения в нем
напряжений, больших предела текучести, то оказывается, что
линия нагрузки практически совпадает с линией разгрузки,
а часть диаграммы, лежащая левее точки, от которой произво
дилась разгрузка, не повторяется. Таким образом, в результате
предварительной вытяжки материала за предел текучести его
свойства изменяются: повышается предел пропорциональности
и уменьшается пластичность. Это явление называют наклепом.
В определенном смысле можно говорить, что в результате на
клепа материал упрочняется (подробнее это будет разъяснено
несколько ниже).
Уменьшение пластичности материала при наклепе подтвер
ждается следующим. Пластичность материала характеризуется
значением относительного остаточного удлинения при разрыве
8. При отсутствии наклепа значение 5 пропорционально отрез
ку OL оси абсцисс диаграммы (рис. 2.38), а при наклепе оно
пропорционально меньшему отрезку ML, так как часть диа
граммы, лежащая левее точки N, не повторяется. На рис. 2.39
представлена диаграмма растяжения, на которой показан про
цесс разгрузки и повторного нагружения, проведенный несколь
ко раз.
Наклеп может быть также следствием холодной обработки
металла. Например, при изготовлении клепаных конструкций
отверстия для заклепок зачастую продавливают (пробивают)
на специальных прессах. В результате материал у краев отвер
стия оказывается наклепанным, обладает повышенной хруп
костью и при действии переменных напряжений в этой зоне
возможно появление трещин. Поэтому целесообразно проби
вать отверстия меньшего диаметра, чем требуется, а затем рас
сверливать их до заданного размера. При этом наклепанная
часть материала будет удалена.
62
б, МПа
В других случаях наклеп полезен и его создают специально.
Например, провода, тросы, стержни для арматуры железобе
тонных конструкций зачастую подвергают предварительной
вытяжке за предел текучести.
Подробно рассмотренная выше диаграмма растяжения,
имеющая ясно выраженную площадку текучести, характерна
лишь для малоуглеродистой стали и некоторых сплавов
цветных металлов.
Диаграммы растяжения некоторых пластичных металлов
и сплавов (например, среднеуглеродистой стали, меди, дюралюмина) не имеют площадки текучести. Для них вводится по
нятие условного предела текучести, представляющего собой на
пряжение, при котором относительное удлинение образца
равно 0,2 % (рис. 2.40). Условный предел текучести обозначают
СТ0,2В технической литературе и в таблицах ГОСТа обычно не разгра
ничивают обозначения физического и условного пределов текучести,
применяя единое обозначение а т.
Условный предел текучести определяют также для легиро
ванной стали и ковкого чугуна. С повышением содержания
углерода прочность стали повышается, а ее пластичность па
дает. Это хорошо видно из представленных на рис. 2.41 диа
грамм растяжения, для качественной конструкционной углеро
дистой стали нескольких марок.
Хрупкие материалы, например чугун, характерны тем, что их
разрушение происходит при очень малых остаточных деформа
циях. На рис. 2.42 приведена диаграмма растяжения чугуна, из
которой видно, что даже в начальной стадии растяжения обна
руживается отклонение от закона Гука. При расчетах это от
клонение не учитывают.
63
При испытании на растяжение образцов серого чугуна опре
деляют предел прочности, обозначаемый сгп.,.Р или а„.р. Для об
разцов из ковкого чугуна, кроме того, определяют относи
тельное остаточное удлинение при разрыве б.
§ 2.8. Статические испытания на сжатие
Строительные материалы, такие, как бетон, цемент, раз
личные естественные камни, испытывают в основном на сжа
тие.
Дерево испытывают на сжатие как вдоль, так и поперек
волокон.
Сталь испытывают на сжатие значительно реже, чем на
растяжение.
Образцы для испытания на сжатие стали и чугуна имеют
форму цилиндра с отношением высоты к диаметру h/d = 1/3.
Длинные образцы применять нельзя, так как даже при незначи
тельной внецентренности приложения сжимающей нагрузки
они изгибаются и результаты опыта сильно искажаются. На
результаты испытания влияет трение между плитами пресса
и торцами образца, а также соотношение его размеров.
На рис. 2.43 показан вид образца из малоуглеродистой ста
ли до и после испытания. При больших сжимающих нагрузках
образец пластически деформируется (расплющивается), но не
разрушается. Таким образом, для пластичных материалов по
нятия «предел прочности при сжатии» не существует. Бочко
образная форма деформированного образца объясняется тем,
что силы трения, возникающие между плитами пресса и торца
ми образца, препятствуют свободному расширению прилежа
щих к торцам частей материала.
Условная диаграмма сжатия малоуглеродистой стали
(рис. 2.44) до предела текучести подобна диаграмме растяже
ния, но площадка текучести выявлена слабо.
При пластической деформации образца его сечение увеличи
вается и нагрузка, требуемая для дальнейшего сжатия, возра
стает, что и объясняет характер диа
граммы за пределом текучести.
Рис. 2.43
64
Значения пределов пропорциональности
и текучести для пластичных материалов
при растяжении и сжатии практически оди
наковы.
Для большинства пластичных материа
лов в результате испытаний на сжатие определяют условный предел текучести аод.
В тех случаях, когда пределы текучести при растяжении
и сжатии различны, их обозначают соответственно с 0 2р и ст0 2с
(или стхр и сттс). К материалам, для которых сг0 2с>ст0 2р, отно
сятся некоторые легированные стали, подвергнутые закалке.
Например, для стали ЗОХГС ст0 2р « 0,88сто 2с. Такие материалы
называют хрушсопласгичными.
На рис. 2.45 показан характер разрушения образца из серо
го чугуна (трещины, появляющиеся на образце в начале разру
шения, направлены под углом примерно 45° к его оси). На
рис. 2.46 показана соответствующая диаграмма сжатия. При
возникновении первых трещин нагрузка начинает падать и ис
пытание прекращается. Единственная характеристика, получаев, МПа
в
Рис. 2.46
Р и с. 2.47
65
Т а б л и ц а 2.2. Механические характеристики некоторых
машиностроительных материалов
Материал
Стали:
С т З ........................
С т 5 ........................
3 0 ........................
4 5 .........................
40Х ........................
Чугупы:
С Ч 12-28. . . .
С Ч 21-40. . . .
ВЧ50—1,5 . . .
К Ч 37-12 . . .
Дюралюмин Д16 . .
Текстолит .................
МПа
°пч.с>
МПа
°т (ст0,2)>
МПа
8, % Ф.%
-
220...240
260...280
300
360'
800
27... 15 —
21...19 —
21
50
40
16
10
45
388...470
500...620
500
610
1000
—
—
-
120
210
500
370
450... 540
60...ПО
500
950
1600
—
130... 150
-
—
—
380
290...440
—
—
—
1,5
12
14...8
—
—
—
мая в результате этого испытания, —предел прочности при
сжатии стпч с.
Чугун значительно лучше сопротивляется сжатию, чем рас
тяжению. Предел прочности при сжатии в 3—4,5 раза выше,
чем при растяжении [о пч с « (3 -г- 4,5)стп,1р].
Наглядное представление о сравнительных свойствах низ
коуглеродистой стали и серого чугуна при растяжении и сжа
тии дают диаграммы, показанные на рис. 2.47: а —растяжение
иизкоуглеродистой стали; б —то же, серого чугуна; в — сжатие
низкоуглеродистой стали; г —то же, серого чугуна.
Для подавляющего большинства конструкционных мате
риалов модуль упругости при растяжении и сжатии одинаков.
Сведения о механических характеристиках некоторых материа
лов даны в табл. 2.2.
§ 2.9. Коэффздиешы запаса прочности.
Допускаемые напряжения
Конструкционные материалы можно разделить на три ос
новные группы: пластичные, хрупкопластичные и хрупкие.
Эта классификация относится к свойствам материалов при
одноосном растяжении (сжатии) в нормальных условиях (малая
скорость нагружения, комнатная температура и т. п.). Измене
ние характера нагружения и условий работы существенно
влияет на свойства материалов: в частности, материал, пла
стичный при нормальной температуре, становится хрупким при
66
низкой температуре. Таким образом, правильнее говорить не
о пластичном и хрупком материале, а о пластичном и хрупком
состояниях материала. Но тем не менее обычно пользуются
приведенной классификацией, помня, при каких ограничениях
она справедлива. Механические испытания материалов позво
ляют определить те напряжения, при которых образец из дан
ного материала разрушается или в нем возникают заметные
пластические деформации. Эти напряжения называют пре
дельными (или опасными).
В качестве предельных напряжений для указанных трех
групп материалов при статическом нагружении принимают
следующие механические характеристики:
для пластичных материалов (разрушению их предшествует
возникновение больших пластических деформаций) —физиче
ский стт или условный а 02 предел текучести, практически
одинаковый при растяжении и сжатии;
для хрупкопластичных материалов (разрушение их происхо
дит при сравнительно небольших пластических деформациях) —
условный предел текучести, значение которого при растяжении
и сжатии различно: сго,2р < оо,2с;
для хрупких материалов (разрушение их происходит при
очень малых пластических деформациях) —предел прочности,
значение которого при растяжении и сжатии различно: стпч р <
^ ^"пч.с*
Возвращаясь к вопросу об изменениях механических
свойств стали при наклепе, уточним, в каком смысле следует
понимать, что наклеп приводит к упрочнению материала, хотя
предел прочности практически остается неизменным. Если диа
грамма растяжения данной стали имеет (до наклепа) площадку
текучести, то диаграмма растяжения этой же стали, но подверг
нутой наклепу, площадки текучести иметь не будет. Следова
тельно, до наклепа роль предельного напряжения играл физи
ческий предел текучести с х, а после наклепа —условный предел
текучести ст0 2; при этом ст02 > стт, т. е. наклеп привел к повы
шению предельного напряжения —упрочнению. Если диаграм
ма растяжения вообще не имеет площадки текучести, то влия
ние наклепа скажется в повышении условного предела текуче
сти. Это хорошо видно на рис. 2.39.
Для обеспечения прочности элементов конструкций необхо
димо так выбрать их размеры и материал, чтобы возникающие
в них при эксплуатационных нагрузках напряжения были мень
ше предельных. Конечно, если наибольшие рабочие напряже
ния в детали близки к предельным (хотя и меньше их), проч
ность детали гарантировать нельзя, так как действующие
нагрузки, а следовательно, и напряжения практически никогда
67
не могут быть установлены совершенно точно; в ряде случаев
расчетные напряжения вообще могут быть определены лишь
приближенно, наконец, возможны отклонения действительных
механических характеристик применяемого материала от при
нятых при расчете.
Отношение предельного напряжения опред к наибольшему
расчетному напряжению сг, возникающему в элементе кон
струкции при эксплуатационной нагрузке, обозначают буквой
п и называют коэффициентом запаса прочности (или, как иногда
говорят, коэффициент запаса):
И= <*„ред/ст-
(2.24)
Из сказанного выше следует, что значение п должно быть
больше единицы (и > 1), иначе прочность конструкции будет на
рушена. Естественно возникает вопрос: на сколько больше еди
ницы должно быть значение и, чтобы прочность рассчитывае
мого элемента конструкции можно было считать обеспечен
ной? Ясно, что чем больше и, тем прочнее конструкция, тем
большим запасом прочности она обладает. В то же время со
вершенно очевидно, что очень большие запасы приводят
к перерасходу материала, делают конструкцию тяжелой, неэко
номичной. В зависимости от назначения конструкции и целого
ряда других обстоятельств (несколько подробнее об этом будет
сказано ниже) устанавливают значение минимально необходи
мого коэффициента запаса прочности. Этот коэффициент обо
значают [и] и называют требуемым (или нормативным) коэф
фициентом запаса прочности.
Прочность элемента конструкции считают обеспеченной, если
его расчетный коэффициент запаса прочности не ниже требуемо
го, т. е.
п ^ [и]:
Это неравенство называют условием прочности.
Используя выражение (2.24), перепишем условие прочности
в виде
" = °пред/СТ> И Отсюда можно
прочности:
получить и такую формузаписиусловия
ст<стпрсд/[п].
Правую часть последнего неравенстваназывают
скаемым напряжением и обозначают
[о] = Опред/И 68
(2.25)
(2.26)
допу
(2.27)
В случае если предельные, а. следовательно, и допускаемые
напряжения при растяжении и сжатии различны, их обозна
чают соответственно [ а р] и [стс].
Пользуясь понятием «допускаемое напряжение», можно ска
зать, что прочность конструкции обеспечена, если возникающее
в ней наибольшее напряжение не превышает допускаемого, т. е.
ст < [а].
(2.28)
Это неравенство [так же как и неравенства (2.25) и (2.26)] назы
вают условием прочности.
В некоторых случаях целесообразно разграничивать поня
тия и обозначения расчетного и требуемого коэффициентов за
паса по отношению к пределу текучести и по отношению
к пределу прочности. Первые обозначают соответственно лт
и [лт], вторые —лпч и [лпч]. Эти обозначения использованы
в табл. 2.3, где приведена расшифровка формулы (2.27) приме
нительно к указанным в начале параграфа трем группам мате
риалов. Там же даны ориентировочные значения величин [лт]
и [п,1ч].
2.3. Допускаемые напряжения и коэффициенты запаса
прочности при статических нагрузках
Х рупкопластичны й
Х рупкий
[<т| = [стр] = |<тс] = СТт/[/1т]
или [а] = [Ср] = [ а J = а оа/[пт]
[<rp] = CJ0i2p/[«T];
[стс] = а 0>2с/[лг]
[^р] — стпч.рЛЛпч];
[°сЗ = ^пч.сД^ичЗ
Орнен 1 ировочное
значение требуемого
коэффициента запаса
прочности
i4*
о
П ласти ч н ы й
Зависимость для выбора
допускаемого напряжения
при растяжении и сжатии
II
Материал
V
Таблица
[rtr] = 1,6...2,5
К „ ] = 2,5...5,0
Даже при минимальных значениях [л] обеспечена работа
материала в пределах упругости, т. е. [а] < а у (или о т).
Значение принимаемого при расчете допускаемого напряже
ния в значительной степени определяет надежность и эконо
мичность конструкции. Чем ниже допускаемое напряжение,
т. е. чем выше заданный коэффициент запаса, тем, следователь
но, осторожнее произведен расчет, тем выше надежность кон
струкции, но расход материала велик и конструкция неэконо
мична. Повышение допускаемого напряжения позволяет со
здать более легкую и экономичную конструкцию, но если это
повышение произведено недостаточно обоснованно, то кон
струкция будет ненадежной.
69
В тех случаях, когда значение коэффициента запаса прочно
сти (допускаемого напряжения) не обусловлено обязательными
нормами, конструктор (расчетчик), выбирая значения [и], дол
жен учитывать целый ряд факторов, связанных как с приме
няемыми методами расчета, так и с материалом рассчитывае
мой детали и условиями ее эксплуатации. Основные факторы,
влияющие на выбор требуемого коэффициента запаса прочно
сти, следующие:
а) точность определения действующих нагрузок и приме
няемых методов расчета;
б) степень однородности применяемого материала, его
чувствительность к недостаткам механической обработки и из
ученность свойств;
в) ответственность детали.
В настоящее время принято представлять коэффициент запаса
в виде произведения нескольких частных коэффициентов запаса,
каждых! из которых отражает влияние на надежность расчета какоголибо определенного фактора или группы факторов. Такое разделение
общего коэффициента запаса позволяет более точно учесть многообра
зие свойств материалов и конкретных условий работы конструкций
и проектировать их более экономичными без снижения надежности.
Указанные выше три группы факторов отражены тремя частными
коэффициентами запаса: [п] = [и,] [и2] [я3].
Представление о значениях допускаемых напряжений, при
нимаемых при расчетах элементов машиностроительных кон
струкций на действие статических нагрузок, дает табл. 2.4.
Т а б л и ц а 2.4. Ориентировочные значения допускаемых напряжений
для некоторых машиностроительных материалов при статических
нагрузках
Материал
Допускаемые
напряжения, М П а
[СТр]
Чугун:
СЧ12-28 . . .
СЧ15-32 . . .
СЧ21-40 . . .
ВЧ50—1,5 . . .
Сталь:
СтЗ и Ст4 . . .
С т 5 ...................
4 5 ........................
Дюралюмин . . .
Текстолит . . . .
70
20...30
25...40
35...55
80...120
Примечания
[ос]
70...110)
90... 150 >
160...2003
305...410
140. .170-,
175...210)
180...210 J '
70. .150
30...40
50...90
О тливки из серого
ч у гу н а
В ы с о к о п р о ч н ы й чугун
Для м е т а л л о к о н с т рукций к р а н о в ы х
сооруж ений
В заключение настоящего параграфа подчеркнем, что на
протяжении всего курса сопротивления материалов будут
встречаться три упоминавшиеся уже категории напряжений.
1. Предельные (или опасные) напряжения, при достижении
которых появляются признаки непосредственного разрушения
или возникают пластические деформации.
Эти напряжения зависят от свойств материалов и вида дефор
мации, например для серого чугуна предельное напряжение
(предел текучести) при сжатии <тпч с примерно в четыре раза вы
ше предельного напряжения при растяжении стпчр.
2. Допускаемые напряжения —наибольшие напряжения, ко
торые можно допустить в рассчитываемой конструкции из ус
ловий ее безопасной, надежной и долговечной работы.
Эти напряжения зависят от свойств материала, вида деформа
ции и требуемого (принятого или заданного) коэффициента запаса
прочности.
3. Расчетные напряжения, которые возникают в элементе
конструкции под действием приложенных к нему нагрузох.
Эти напряжения зависят от действующих на элемент кон
струкции нагрузок и его размеров.
§ 2.10. Расчеты на прочность при растяжении (сжатии)
Условие прочности
а ^ [а ]
или п — g "-pej > [«]
ст
должно соблюдаться для всех точек рассчитываемого элемента
конструкции, поэтому под ст следует понимать наибольшее рас
четное напряжение.
Здесь необходимо сделать оговорку: незначительное превы
шение наибольших расчетных напряжений над допускаемыми,
конечно, не опасно, так как допускаемое напряжение составляет
лишь некоторую часть от предельного. Обычно считают, что
это превышение может составлять до 3 % от допускаемого на
пряжения. Иными словами, в отдельных случаях считают воз
можным иметь коэффициент запаса несколько меньший, чем
требуемый (заданный). Если расчетное напряжение значительно
ниже допускаемого, это является свидетельством нерациональ
ности конструкции, перерасхода материала.
В зависимости от цели расчета (постановки задачи) разли
чают три вида расчетов на прочность: 1) проверочный, 2) про
ектный и 3) определение допускаемой нагрузки.
Эта классификация видов расчета относится ко всем разде
лам курса, а не только к растяжению (сжатию). При расчетах
71
на жесткость и устойчивость также возможны все три ука
занных варианта постановки задачи.
Рассмотрим несколько подробнее каждый из трех ука
занных видов расчета.
При проверочном расчете нагрузка бруса, его материал (а
следовательно, допускаемое или предельное напряжение) и раз
меры известны. Определению подлежит наибольшее расчетное
напряжение, которое сравнивают с допускаемым. С прове
рочными расчетами встречаются, в частности, при экспертизе
выполненных проектов.
Расчетная формула (условие прочности при растяжении или
сжатии) имеет вид
сг = N/A ^ [ст],
(2.29)
где а —напряжение, возникающее в опасном поперечном сече
нии бруса (опасным называют сечение, для которого коэффи
циент запаса прочности имеет наименьшее значение); N —про
дольная сила в указанном сечении; А —площадь опасного
поперечного сечения; [о] —допускаемое напряжение ([<тр] при
растяжении и [<тс] при сжатии).
В ряде случаев при проверочном расчете удобнее сопо
ставлять не расчетное напряжение с допускаемым, а сравнивать
расчетный коэффициент запаса прочности для опасного сечения
с требуемым, т. е. проверять, соблюдается ли неравенство
И= °пред/а > [«]•
При проектном расчете нагрузки и материал (допускаемые
напряжения) известны * и из формулы (2.29) определяют тре
буемую площадь сечения бруса А.
В некоторых случаях проверочный расчет удобнее вести
в форме определения допускаемой нагрузки. В частности, это це
лесообразно при изменении режимов тех или иных технологи
ческих процессов, когда возникает необходимость в повышении
нагрузок существующего оборудования и, следовательно, надо
знать их предельно допускаемое по условию прочности значе
ние.
При этом расчете размеры бруса и его материал (допускае
мое напряжение) известны, определению подлежит нагрузка,
которую можно допустить по условию его прочности. На осно
ве формулы (2.29) определяют допускаемое значение продоль
* Зачастую проектировщик (конструктор) сам определяет рабочие
нагрузки, выбирает материал и допускаемое напряжение, но в задачах
сопротивления материалов они для рассматриваемой категории расче
та полагаются известными.
72
ной силы [IV]. По этому значению с помощью метода сечений
определяют допускаемое значение внешних сил —нагрузок (см.
ниже пример 2.18).
Указанные три категории расчетов иллюстрируются чис
ловыми примерами.
П р и м е р 2.15. Проверить прочность тяги ВС (рис. 2.48,о). Мате
риал —сталь СтЗ, допускаемое напряжение [а] = 160 МПа.
Р е ш е н ы е. Продольную силу N, возникающую в произвольном
поперечном сечении тяги, определяем, применяя метод сечения и рас
сматривая равновесие балки AD (рис. 2.48,6):
Z M A = 0;
FI —(IVsin а)а =0,
откуда N = Fl/a sin а; подставляя числовые значения, получаем
N = 40 •2,5/ (2,0 •sin 30°) = 100 кН.
Напряжения в поперечном сечении тяги
N
100-103
о = — = ---------------- = 162-106 Па = 162 МПа,
А
2-3,08 • 10-4
где площадь поперечного сечения одного равнобокого уголка 40 х
х 40 х 4 A t =3,08 см2 (по табл. ГОСТ 8509 —72). Площадь сечения
тяги A —2AV
Напряжение выше допускаемого всего на 1,25%, следовательно,
прочность тяги обеспечена.
П р и м е р 2.16. Проверить прочность ступенчатого чугунного
бруса (рис. 2.49, а), если требуемый коэффициент запаса прочности
[и] = 4. Предел прочности материала бруса на растяжение 0 ПЧр =
= 150 МПа и на сжатие а пч с = 580 МПа.
TV
73
Р е ш е н ы е. Строим эпюры продольных сил (рис. 2.49,6) и нор
мальных напряжений (рис. 2.49, в), как это изложено в примерах
2.1, 2.3.
Наибольшие по абсолютному значению напряжения возникают
в поперечных сечениях участка I, работающего на сжатие.
Коэффициент запаса прочности для этого участка
П[ = стпч. с/ст/ = 580/127 = 4,57.
Расчет нельзя считать законченным, так как в поперечных сече
ниях участка III возникают напряжения растяжения, которые хотя
и значительно меньше (по абсолютному значению) напряжений сжатия
в сечениях участка I, но могут оказаться более опасными, так как чу
гун значительно хуже работает на растяжение, чем на сжатие. Для
участка III коэффициент запаса прочности
Щп = Опч.р/о-/// = 150/35,3 = 4,25.
Прочность бруса достаточна, так как пщ > [и].
В литературе встречается определение опасного сечения как тако
го сечения, в котором возникают наибольшие напряжения. Рассмо
тренный пример показывает, что такое определение для брусьев из ма
териалов, различно сопротивляющихся растяжению и сжатию, не
всегда справедливо.
Пример 2.17. Определить из расчета на прочность требуемые
диаметры стержней ВС, CD и СК в конструкции, изображенной на
рис. 2.50, а. Принять сг = 150 МПа.
Решение. Применяя метод сечений (рис. 2.50, б), определяем
продольные силы, возникающие в поперечных сечениях стержней от
действия равномерно распределенной нагрузки, приложенной на участ
ке BL балки AL. Составляя уравнение равновесия для сил, прило
женных к балке AL, получаем
1,МА—0; —К,а + qa- 1,5а = 0,
откуда
= l,5ga.
На основании закона равенства действия и противодействия реак-
74
ция R 2, приложенная к балке, равна по модулю и противоположна по
направлению силе N„ действующей на стержень ВС.
Составляя уравнения равновесия для сил, приложенных к узлу
С (проецируя все силы на горизонтальную и вертикальную оси),
получаем
JV, cos 45° —N 3 cos 45° = О,
откуда N 2 = ЛГ3; 2N 2 cos 45° —N t = 0.
Подставляя значение IV,, имеем
N 2 = N 3 = l,Sqa/(2 cos 45°).
На основе формулы (2.29) требуемая площадь поперечного сечения
стержня ВС
N i _ \,Sqa _ 1,5-50-103 • 1,2
[а ]
[<т]
150-106
=
0 ,6 - 10-
Диаметр этого стержня
d, = ]/4A ,/я = у'4 ■600/3,14 = 27,5 мм.
С некоторым округлешзем принимаем d1 = 28 мм.
Для стержней CD и СК имеем:
ЛГ2
2_3
=
И
2-150-10е cos 45°
1,5qa
2 [о] cos 45°
—0,424■ 10" 3 м 2 = 424 мм2;
d2 = d 3 = ]/4Ajit = j/4^424/3,14 = 23,2 мм.
Приняв d2 = d3 = 23 мм, получим, что напряжения в соответ
ствующих стержнях с?! = а 2 ~ 157 МПа, т. е. на 4,66% выше допу
скаемых. Если принять d2 = d 3 ~ 24 мм, то tj, = сг2 = 141 МПа, т. е. на
6 % ниже допускаемых. Следует принять d2 = d 3 = 24 мм, так как пре
вышение расчетных напряжений над допускаемыми не должно быть
более 3 %.
П р и м е р 2.18. Определить допускаемую нагрузку для системы,
изображенной на рис. 2.51, а. Стержни изготовлены из дюралевых труб
одинакового поперечного сечения. Допускаемое напряжение [о] =
= 75 МПа.
Р е ш е н и е . Вырезаем узел А (рис. 2.51,6) и определяем реакции,
выражая их через неизвестную пока силу F:
2 26 = 0; Fsin [3 —R, sin а = 0;
sm
sin 45°
R t =F
=F ————= 1,67F;
sm a
sin 25°
2У = 0; R, cos а + R2 —F cos (3=0;
R2 = F cos p —-R, cos a,
75
/У2
—l,67Fcos25° = —0,806F. Знак минус указывает, что предварительно
выбранное направление реакции Rz ошибочно. На основании закона
равенства действия и противодействия реакции R 1 и R2, действующие
на шарнир А, по модулю равны силам N u N 2, возникающим в стерж
нях (рис. 2.51, в). Таким образом, N t = 1,67F, N 2 = —0,806F.
Сильнее нагружен стержень 1; из условия прочности этого стерж
ня определяем допускаемую нагрузку конструкции:
[lV j = l,6 7 [ F ] = ^ [ a ] ,
откуда
3,14
[F] =
Л[>]
(302 - 242)1(Г6-75-106
1,67
1,67
= 11,4-103 Н = 11,4 кН.
При нагрузке, равной допускаемой, стержень АС будет недогру
жен, в его поперечных сечениях возникают напряжения
Iоде I =-
|JV2|
0.806F
0,806-11,4.103
■= 36,1-106 Па =
3,14
(ЗО2 - 242) - 10"
= 36,1 МПа,
т. е. на 52% ниже допускаемых. Полученный результат указывает на
нерациональность конструкции. Следует всегда стремиться к тому,
чтобы все элементы конструкции были полностью нагружены, т. е.
чтобы напряжения в них были близки к допускаемым.
§ 2.11. Статически неопределимые системы
В предыдущих параграфах был рассмотрен ряд примеров
определения перемещений и расчетов на прочность.
76
Во всех этих примерах применение метода сечений позволя
ло установить зависимость между продольными силами, воз
никающими в поперечных сечениях стержней, и действующими
на систему (конструкцию) внешними силами. Иными словами,
внутренние силы определялись только на основе условий рав
новесия отсеченной части системы (или отдельного бруса). Си
стемы, подобные рассмотренным, называют статически опреде
лимыми.
Системы, в которых внутренние силовые факторы, в частно
сти продольные силы, не могут быть определены с помощью
только метода сечений, называют статически неопределимыми
системами. Соответственно задачи, связанные с расчетом ука
занных систем, также принято называть статически неопреде
лимыми.
Некоторые примеры статически неопределимых систем при
ведены на рис. 2.52.
Брус, изображенный на рис. 2,52, а, жестко заделан обоими
концами; в заделках возникают реакции, направленные вдоль
оси бруса. Таким образом, на брус действует система сил, на
правленных по одной прямой; статика в этом случае дает одно
уравнение равновесия, неизвестных же сил две.
Для балки, подвешенной на трех параллельных стержнях
(рис. 2.52,6), можно составить два уравнения равновесия, ко
торых, конечно, недостаточно для определения сил в стерж
нях. Эти две конструкции относятся к категории один раз ста
тически неопределимых систем —число неизвестных на едини
цу больше числа уравнений статики. Вообще степенью статаческой неопределимости называется разность между общим
77
числом неизвестных и количеством независимых уравнений
равновесия, которые можно составить для данной системы.
Один раз статически неопределима также система, пред
ставленная на рис. 2.52, е; вырезая узел А, можно составить для
него два уравнения равновесия (плоская система сходящихся
сил), а неизвестных сил в стержнях три.
Примеры дважды статически неопределимых систем даны
на рис. 2,52, г, д.
Для решения статически неопределимой задачи надо соста
вить помимо уравнений статики так называемые уравнения
перемещений, основанные на рассмотрении деформации си
стемы (иногда говорят, что это геометрическая сторона задачи)
и применении закона Гука. Поясним это указание простейшим
примером.
Пусть требуется определить силы в стержнях, на которых
подвешена невесомая весьма жесткая балка, нагруженная силой
F, как показано на рис. 2.53. Стержни изготовлены из одинако
вого материала и имеют одинаковые сечения. Система один
раз статически неопределима: для плоской системы парал
лельных сил статика дает два независимых уравнения равнове
сия, а неизвестных сил три. Обозначим реакции, так же как
и силы, действующие на стержни, через N u N 2, N 3.
Составляем уравнения равновесия приложенных к балке сил
(рис. 2.54):
£ У = 0;
N t + N 2 + N 3 - F = 0;
ЕМ Д= 0; N ta —N 3a =0.
(1)
(2)
В результате деформации стержней балка займет положе
ние, показанное на рис. 2.54 штриховыми линиями. Действи
тельно, предположение о высокой жесткости балки позволяет
пренебречь ее изгибом, а симметрия самой системы и нагрузки
приводит к заключению, что все стержни удлиняются одинако-
-X
/ &h
А
-пгб-
г
' F
Рис. 2.53
78
Рис. 2.54
во. Таким образом, геометрическая сторона задачи может быть
выражена уравнением
Лh = М2 = А/3.
Выражая удлинения стержней по формуле Гука, получим
N J ! (ЕА) = N 2l/ (ЕА) = N 3l/(ЕА), откуда
N 3 = N 2 = N 3.
Решая совместно уравнения (1) и (3), находим
в стержнях:
(3)
силы
Nx —N 2 —N 3 = F/3.
Силы, возникающие во всех трех стержнях, оказались
одинаковыми, но было бы ошибкой считать, что этот резуль
тат —следствие лишь симметрии системы; то, что силы одина
ковы, обусловлено не только симметрией, но и равенством
жесткостей стержней. Пусть, например, площадь сечения каж
дого из боковых стержней вдвое больше, чем среднего (А2 = А;
Ах = А3 —2А). В этом случае из условия равенства удлинений
стержней получаем
N t/ 2 = N 2 = N 3/2.
(3')
Решив совместно уравнения (1), (2) и (3'), найдем
Nx = JV3 = ОДР; 1V2 = ОДР.
Увеличение жесткости боковых стержней привело к увеличе
нию возникающих в них сил и уменьшению сил —в среднем
стержне. Полученный результат отражает общее свойство ста
тически неопределимых систем: при прочих равных услови
ях в более жестких элементах системы возникают большие
силы.
Конечно, в других статически неопределимых задачах урав
нения перемещений иные, чем в рассмотренном примере,
и практически невозможно дать общие исчерпывающие указа
ния, пригодные для всего многообразия задач этой категории.
Только рассмотрение ряда конкретных примеров позволяет по
лучить достаточно полное представление о методике решения
статически неопределимых задач.
П р и м е р 2.19. Для бруса, жестко заделанного обоими концами
и нагруженного вдоль оси силами Ег и F2, приложенными в его про
межуточных сечениях (рис. 2.55, а), требуется построить эторы про
дольных сил, нормальных напряжений и перемещений поперечных се
чений. Проверить прочность бруса, если материал —сталь Ст4 (стх =
= 260 МПа); требуемый коэффициент запаса [ит] = 1,6.
79
О)
ЗА
/
____ V = = z =
«4
4S
2а
а
2а
j
р
А~ЗСМг
Ft=2F
2F
/* '
F =6 0 k H
2А
-
' ---------
£1
_а_
/
^
"я
За
F
' 7 п
у х
в
Рис. 2.55
Р е ш е н и е . В з а д е л к а х б р у с а возникают реакции, н а п р а в л е н н ы е
вдоль его оси . И м е е м с и с т е м у си л , направленных по о д н о й прямой,
для которой с т а т и к а д а е т о д н о уравнение равновесия:
£ Z = 0;
- R A + Fl + F2 - R B = 0.
(1)
сил две, следовательно, система один раз
Н е и зв е с т н ы х р е а к т и в н ы х
статически н е о п р е д е л и м а .
Для составления уравнения перемещений отбросим одну из заде
лок, например п р а в у ю , и з а м е н и м ее действие на брус соответствую
щей реактивной силой RB (рис. 2.55,6). Получим статически опреде
лимый бр у с, нагруженный кроме заданных сил F, и f 2 неизвестной
реактивной силой R B = X. Этот статически определимый брус нагру
жен так же, как заданный статически неопределимый, т. е. эквивален
тен ему. Эквивалентность этих двух брусьев позволяет утверждать, что
второй брус деформируется так же, как первый, т. е. перемещение Хв
сечения В равно нулю, так как фактически (в заданном брусе) оно
жестко заделано:
Хв = 0.
Применив принцип независимости действия сил, перепишем это
уравнение в виде
Хв = XBFl + ХВВг + Хвх = 0,
(2)
т. е. перемещение от совместного действия всех сил равно алгебраиче
ской сумме перемещений от действия каждой силы в отдельности.
В обозначениях перемещений первая буква индекса указывает
о перемещении какого сечения идет речь; вторая —причину, вызываю
щую это перемещение (сила F, и т д.).
На рис. 2.56 показаны схемы нагружения бруса каждой из сил
в отдельности, там же показаны соответствующие реакции левой
заделки.
Пользуясь этими схемами, определим перемещения: 2F-2a
XBF = --------- равно удлинению участка АС;
Е •ЗА
F -4а
Fa
X B f 2 = ----------------- 1
------------ равно сумме удлинений участков AD и DE.
Е *3^ ЕА.
80
( Х- Аа
Х-2а
Х-3 а \
--------- 1----------- 1----------I равно сумме укорочений участV Е- зА ЕА
Е-2А )
ков AD, DK, КВ.
Подставляя значения
и Хвх в уравнение (2), имеем
v= -
2F■2а
FAa
Fa
( Х- Аа
Х-2а
XIа\
Е-ЪА
Е-ЪА
ЕА
\ Е- ЪА
ЕА
E-2AJ
откуда X = 22F/29.
Статическая неопределимость раскрыта —имеем статически опре
делимый брус, заделанный одним концом, нагруженный и з в е с т н ы
ми силами F„ F2 и X = 22F/29 (рис. 2.57, а). Эпюры продольных сил
--------- 1---------- (-------- ( --------- 1----------1-------- J = О,
Рис. 2.57
81
и нормальных напряжений строят обычным путем, как для любого
статически определимого бруса. Эти эпюры даны на рис. 2.57,6, в.
Наибольшие по абсолютному значению напряжения возникают
в поперечных сечениях участка Е К —это опасные сечения.
Проверка прочности:
щ = о х/сттах = 260/151,6 = 1,72 > [пТ].
Построение эпюры перемещений ничем не отличается от изложен
ного в примере 2.5. Эта эпюра дана на рис. 2.57,г; для сокращения за
писей введено обозначение |3 = а/ (ЕА). Построение эпюры начинаем от
левого защемленного конца бруса:
Ха = 0;
Хс = А1ас
=
(65/29) F ■2а
£-3,4
7
----F ■2а
130
29
144
к!) —!..(■~ А.1со —----- В£ 4-------------- =
—В£.
87
Е М
87 F
О п р е д е л е н и е остальных характерных ординат эпюры X предла
г а е м в ы п о л н и т ь читателю самостоятельно. Н а правом конце бруса,
в сеч ен и и В , о р д и н а т а эпюры X р а в н а нулю, т а к как в заданном брусе
э т о сеч ен и е ж е с т к о закреплено, именно из этого условия определено
зн ач ен и е X .
*
*
♦
Кратко остановимся на решении одной из задач, аналогичных рас
смотренной. Предположим, что до нагружения бруса между его
правым торцом и заделкой имеется малый'зазор 8 (рис. 2.58, я). Масш
таб, в котором на чертеже дана величина зазора, во много раз больше,
чем масштаб отрезков а, 2а и т. д. Если при нагружении бруса зазор
не закрывается, то система статически определима. Если удлинение
бруса (в предположении, что он может деформироваться свободно,
т. е. правая заделка вообще отсутствует) больше зазора, то между
правым торцом бруса и заделкой возникает сила взаимодействия,
определить которую с помощью одних лишь уравнений статики нель
зя —задача будет статически неопределимой. Отличие ее от предыду
щей состоит в том, что суммарное (от заданных сил и правой опорной
реакции) перемещение правого торца бруса следует приравнять не ну
лю, а зазору: Хв = Ь.
Примем для определенности, что 8 = 2Fa/ (ЕА) = 2р/\ Перемеще
ние сечения В от действия сил £, и F2 (в предположении, что правая
заделка отсутствует), как было найдено выше,
11 Fa
11
= - x - {Ms
1
2 3 ЕА
з
e. Xbf > 8 и, следовательно, система статически неопределима. СоXb f = X b f , + X b f 2 — —
t.
82
а)
ЗА
F .-2 F
р
/
/*
■ /-
А\
.
б)
в)
2а
_
-4 -
.
2а
_
2А
/
/
а
а
ь
За
.л .
X-%F
llf
w
Эпюра N
29
10,
29'
77£
87 А_
г)
19 F
WF
87 А
23 А I бторо ff
5_£
иш ш
о)
Г "
' 8'« а
\Ш£_
ШоС
Эпюра A 191piг 87Г L
29А 219„с
Миши*
iii
29А
2jiF
■
Рис. 2.58
с та в и м и реш и м уравн ен ие перем ещ ений, р а сс м ат р и в ая брус, и зо б р а
ж е н н ы й н а ри„с. 2 .5 8 ,6 :
~Хв = 1-b f 1 + 1~b f 1 + к в х — 5
или
11
29
___р/г__^_рХ = 2рF
(о п р е д е л е н и е Х в х с м - в ы ш е), о т с ю д а X = 10F /29.
П о с т р о е н и е э п ю р N, а, X в ы п о л н я е т с я т а к же, к а к и в случае
с у т с т в и я з а з о р а , у к а з а н н ы е эпюры даны на рис. 2.58,в,г,д.
от
Очевидно, на правом конце бруса ордината эпюры X равна на
чальному зазору 5.
П р н м е р 2.20. Весьма жесткая балка подвешена на трех
стальных стержнях одинакового сечения А = 4 см2 и нагружена силой
F, как показано на схеме (рис. 2.59, а). Определить допускаемое значе
ние силы F, если для материала стержней [а ] = 160 МПа.
Р е ш е н и е . Система один раз статически неопределима, так как .
неизвестных сил три, а статика дает два уравнения равновесия (пло
ская система параллельных сил). Рассекаем стержни и составляем
83
уравнения равновесия сил, дей
ствующих на балку (рис. 2.59, б):
1У= 0;
N x + N 2 + N 3 - F = 0;
0)
гмА= 0;
— N 2a + F3a — N 34a = 0
(#
JV2 + 4 N 3 = 3F.
(2)
или
М ы предположили, что все
стержни растянуты. Если в ре
зультате решения получим от
вет для силы в каком-либо
стержне со знаком минус, это
укажет, что предположение бы
ло неверно и фактически этот
стержень сжат.
В силу жесткости балки изгибом ее можно пренебречь. В результа
те деформации стержней балка несколько опустится и наклонится,
оставаясь прямолинейной. Примерное положение балки после дефор
мации стержней показано на рис. 2.59,6 ш триховыми линиями (конеч
но, удлинения стержней показаны сильно преувеличенными).
Очевидно, А А 1 = Д /,; В В 1 = Д/2; D D t = Д/3.
Проведя вспомогательную прямую А 1К, параллельную первона
чальному положению балки, из рассмотрения подобных треугольников
А 1Е В 1 и A 1K D 1 получим
B 1E / { D i K) = а/(4а) = 1/4
или
(Д/2 - Д / 1)/(Д /3 - Л / 1) = 1 /4 .
Выражая удлинения стержней по формуле Гука, получаем уравне
ние перемещений в виде
N 2- 3 l / ( E A ) - N r 2l/(EA)
1
N 3- 4 l / ( E A ) - N r 2l/(EA) ~ Т ’
откуда
6JV2 - 3N, = 2JV3.
(3)
Реш ая совместно уравнения (1), (2) и (3), выражаем силы в стерж
нях через искомую силу F :
N 2 = 2/35 F; N 2 = 9/35 F; N 3 = 24/35 F.
Наибольш ая продольная сила, а следовательно, и напряжение воз
никают в стержне 3. Составляя для него условие прочности, опреде
ляем допускаемое значение силы F:
N 3/ A = (24/35) (F/A) < [гг],
84
откуда
[F] = (35/24) А [о ] = (35/24)- 4 -1 0 '4 • 160-106 = 93,3 ■ 103 Н =93,3 кН.
При этом стержни 1 и 2 будут недогружены:
_ IV, _ (2/35)• 93,3 103
° А~ ~ Т
4-1(Г~
JV,
(9/35) •93,3 ■103
сгд = -
4 ' КГ
13,3-106 Па = 13,3 МПа;
: 60-10* П а = 60 МПа.
Пр и мер 2.21. Система из трех ш арнирно соединенных стальных
стержней нагружена, как показано на схеме (рис. 2.60, я). Определить
из расчета на прочность требуемые площ ади сечений стержней, если
А г = А 2 = А; А 3 — 2 А и [ст] = 140 МПа.
Р е ш е н и е . Система один раз статически неопределима: статика
дает для плоской системы сходящихся сил два уравнения равновесия,
а неизвестных сил в стержнях три.
Вырезаем узел А (рис. 2.60,6) и составляем уравнения равновесия
действующих на него сил. Предполагаем, что стержни 1 и 2 растянуты
(силы JV1 и N 2 направлены от узла), а стержень 3 сжат (сила N 3 на
правлена к узлу):
£Г==0;
-JV , sin cp + N 2 sincp = 0
(1)
JV, cos<p —F 4- N 2 costp + N 3 = 0
(2)
и
S 1 = 0;
или, учитывая (1),
2JV, cos<p + JV3 = F.
(2')
Зависимость между изменениями длин стержней получаем из диа
граммы перемещений, показанной на рис. 2.60, я: на продолжении
стержня 1 откладываем произвольный отрезок, соответствующий Д/,
и опускаем из его конца перпендикуляр на направление стержня 3. По
лучаем точку А,, дающую положение шарнира А после деформации
(подробнее о построении диа
грамм перемещений см. в § 2.3).
Очевидно, перемещение шарни
ра А (Л,д) равно укорочению
стержня 3 (Д13). Из прямоуголь
ного треугольника ABA i имеем
Д/3 = -
А/,
COS ф
Уз
ЕА,
NJJ(EA)
СОЗф
N3h
JVjft/costp
Е ■2 А
Е А cos <р
85
откуда
2 N
cos2 tp '
Решая совместно (2) и (3), получаем
JVj = JV2 = F
cos2 9
/ [ 2 ( 1 + cos3 ф)];
1V3 = F j ( \ + cos3 ф).
Напряжения в стержнях:
а 1 = а 2 ~ N J A = F cos2 ф /[2 A (1 + cos3 ф)];
o 3 = N J { 2 A ) = F / [2A (1 + cos3 <p)].
Очевидно, напряжения в стержне 3 больше, чем в стержнях 1 и 2,
поэтому требуемую площ адь сечения определяем из условия прочно
сти стержня 3:
о 3 = F / [2А (1 + cos3 ф)] < [ а ] ,
откуда
А>
100-103
F
2 [ о ] (1 + cos2 ф)
2 ■140 • 106 (1 + cos3 30°)
= 2,16- 1(Г4 м 2 =
= 216 м м 2;
А : = А 2 = А = 216 м м 2;
А 3 = 2 А = 432 м м 2.
Стержни 1 и 2 недогружены:
F cos2 ф
3
2
10 0 -103 cos2 30'
2.4(1 + cos3 ф) ~ 2 -2 1 6 -1 0 "6 (1 + cos3 30°)
105-106 П а =
= 105 М Па.
Однако отсю да нельзя делать вывод о возможности уменьшения
их сечений, так как силы в стержнях найдены при вполне определен
ном соотношении их жесткостей, указанном в условиях задачи. Если
уменьшить сечения боковых стержней, то и силы в них уменьшатся,
а в среднем стержне сила возрастет. В рассмотренном примере отра
жена существенная особенность проектного расчета статически не
определимых систем — необходимость соблюдения заранее заданного
(или выбранного) соотношения жесткостей элементов. К ак известно,
в статически определимых системах можно выбирать сечение каждого
стержня совершенно независимо от сечений остальных стержней си
стемы (см. пример 2.16).
П р и м е р 2.22. Определить силы, возникающие в поперечных се
чениях стержней 1, 2, 3, 4, 5 заданной системы (рис. 2.61, а). М атериал
и площ ади поперечных сечений всех стержней одинаковы.
Р е ш е н и е . Неизвестных сил пять. Применив м етод сечений
(рис. 2.61,6) и рассмотрев условия равновесия узлов (шарниров) Л и В,
получим, что для каждого из них м ож но составить два уравнения ста
тики, т. е. всего четыре уравнения, и, следовательно, число не-
86
б)
известных на единицу превышает
число независимых уравнений ста
тики — система один раз статически
неопределима.
Уравнения равновесия даю т:
N 1 = Nf,
(1)
2 N i cos <р = N 3;
(2)
N3
N 3 = N S;
(3)
•Л1 С
N 3 + 2 N 4 cos ф = F.
(4)
Д ля составления уравнения пе
ремещений будем рассуждать сле
дую щ им образом : если бы средний
стержень бы л абсолю тно жестким,
то перемещения узлов А и В были
бы одинаковыми. Стержень 3 растя
гивается и, следовательно, фактически узел В опустится ниже, чем узел
А, за счет удлинения этого стержня:
^■в —"б-а + А!,.
П остроив диаграм м у перемещений для узлов А и В (аналогично
предыдущему примеру), установим связь между перемещением узлов
и удлинениями стержней (рис. 2.61,а):
ХА = Д/j/cos ф ;
Xg = Д ^ с о в ф .
Выразив удлинения через силы и коэффициенты податливости,
получим:
ХА ==: Pj
/cos ф ; ?./; = Р4 N J cos \|/; Д1г = Рэ N 3
или окончательно уравнение перемещений дает
P4JV4/cos ф = P ,y ,/c o s ф + Р3ЛГ3.
(5)
Введя дополнительное обозначение р = а/ ( ЕА ) и учитывая, что
Pi = р/совф; рз = зр ; р4 = 4 р /со вф , в результате совместного решения
уравнений (2), (4) и (5) получим:
2 F cos3 ф
1
2
4cos3 ф + cos3 vj/ + 6 cos3ф cos3 ф ’
4 F cos3 ш
ДГ = ________________ ___________ ;
3
4cos3 ф
cos3 ф Н- 6 COS3 ф cos3 ф
F (2cos3 ф + cos3 ф + 6 cos3 ф cos3 ф)
4
5
2 (4 cos3 ф
cos3 ф Н- 6 cos3 ф cos3 ф) cos ф
§ 2.12. Температурные и начальные напряжения
в статически неопределимых системах
Из курса физики известно, что при повышении температуры
линейные размеры тела увеличиваются, а при охлаждении —
87
уменьшаются. Абсолютное значение удлинения (укорочения)
стержня, вызванного изменением его температуры на At град,
определяется по формуле
А/, = otI At,
где а —коэффициент линейного расширения материала стерж
ня, а I —его длина.
В случае если при нагреве (охлаждении) стержня ничто не
препятствует изменению его длины, в нем не возникает ника
ких напряжений. Например, при нагревании стержня ВС, под
держивающего шарнирно закрепленную одним концом балку
(рис. 2.62), он удлиняется, вызывая поворот балки вокруг шар
нира А.
Иное положение в статически неопределимых системах. Ес
ли нагреть стержень ВС статически неопределимой системы,
изображенной на рис. 2.63, то его свободному удлинению,
а вместе с тем и повороту балки (считаем ее абсолютно жест
кой) препятствует стержень DK. В результате в стержне ВС
возникает сжатие и опускание точки В (кв) будет меньше, чем
свободное температурное удлинение (Д},) стержня. При этом
стержень DK испытывает растяжение.
В задачах на температурные напряжения особенно важно
четко разграничивать понятия «растяжение» и «удлинение»,
«сжатие» и «укорочение». Так, в рассмотренном примере стер
жень ВС хотя и удлиняется, но испытывает при этом сжатие.
При нагревании бруса, жестко защемленного обоими конца
ми (рис. 2.64, а), опоры (заделки) препятствуют его свободному
Р и с. 2.64
удлинению. В заделках возникают реактивные силы, вызываю
щие сжатие бруса. При охлаждении такого бруса он, не имея
возможности свободно укорачиваться, будет испытывать рас
тяжение (рис. 2.64,6).
Таким образом, изменение температуры статически неопреде
лимой системы (или отдельных ее частей) вызывает напряжения
в ее элементах (температурные напряжения).
Существует еще один вид напряжений, которые характерны
только для статически неопределимых систем. Это так назы
ваемые начальные или монтажные напряжения.
Причиной их возникновения может, в частности, явиться не
точность изготовления отдельных элементов конструкции.
Пусть, например, стержень ВС в статически неопределимой
системе (рис. 2.65) был изготовлен короче проектного размера
на малую величину 5. При сборке системы придется растянуть
этот стержень и прикрепить его к балке. Сокращаясь (в силу
своей упругости), стержень несколько приподнимет конец бал
ки, что вызовет сжатие стержня DK. После сборки балка зай
мет положение, показанное на рис. 2.65 штриховыми линиями.
Стержень ВС будет при этом растянут на величину А!вс,
меньшую 5.
В статически определимой системе неточность изготовления
ее элементов напряжений не вызовет. Действительно, если стер
жень ВС, поддерживающий балку (рис. 2.66), изготовлен не
сколько короче, чем требовалось, то для сборки конструкции
достаточно повернуть балку вокруг шарнира А и прикрепить
к ней стержень. Так как этому повороту ничто не препятствует,
то и напряжений в стержне ВС не возникает.
Конечно, речь шла о весьма малых ошибках изготовления
стержней (порядка 1/2000—1/1000 от их длины), при которых ,
сборка системы (статически неопределимой) вызывает малые
упругие деформации и перемещения.
89
В качестве второго примера
возникновения монтажных на
пряжений укажем прочноплот
ные болтовые соединения. Для
обеспечения герметичности со
единения частей трубопровода
болты должны быть достаточно
сильно затянуты, при этом
фланцы труб будут испытывать
сжатие, а сами болты - растя
жение.
Начальными соответствую
щие напряжения называют по
тому, что они возникают в кон
струкции до приложений к ней
рабочих нагрузок.
П р и м е р 2.23. С тальной брус,
жестко защ емленный обоим и кон
цами в неподвижных опорах (рис. 2.67, а), нагревается на At = 30 °С
по сравнению с температурой сборки. П остроить эпюры продольных
сил, нормальных напряжений и перемещений поперечных сечений.
Р е ш е н ы е. При нагреве бруса в его заделках возникаю т реакции
R a и « в , для определения которых статика дает л и ш ь одно уравнение:
£ Z = 0;
RA - R B = О
или
R a = R b = R.
(I)
Следовательно, система статически неопределима.
Дальнейший ход решения аналогичен примеру 2.19: отбрасываем
правую заделку и заменяем ее действие на брус искомой реактивной
силой R B ==X. Полученный таким образом брус (рис. 2.67,6) эквива
лентен заданному, а полное перемещение сечения В (вызванное
нагревом — X Bt и силой X — Хвх) равно нулю:
Хв = 0
или
XBt + ХВх = О,
(2)
где XBt = Alt = ct(/, + /2 + У At - температурное удлинение бруса, осво
божденного от правой заделки, т. е. имею щ его возможность свободно
' л,
/ XI t
Xi 2
Х13 \
удлиняться: ХВх = Л<х = —! ---------1---------- 1---------! — изменение длины
\ EAt
ЕА2
ЕА3)
(укорочение) бруса (рис. 2.67,6) о т действия только силы X . Знак минус
указывает, что направление перемещения Хв х противополож но темпе-
90
ратурному. Подставляя значения Xst и Хвх в уравнение (2), имеем
a(/j
lj -Ьl^)Al —
XJi
EA,
xit
Xl3 \
EA2 + EA3J
=
0.
( 2')
Приняв для стали а = 1,25-10 б, £ = 2,0■ 105 МПа, после подста
новки числовых значений в уравнение (2') получим
12,5 ■1 0 “ 6(1,0 + 1,2 + 1,5) 3 0 ~
2 fl
1
/ X I,0
X • 1,2
X -1,5 \
То5• 106 ^ 1 0 1 0 - 4 + 5 -10~4 + 7-10- 4 / ~ ’
откуда X = 5 0 ,1 • 1 0 3 Н = 50,1 кН.
Продольная сила во всех поперечных сечениях бруса одинакова
(рис. 2.67, в):
N = X = 50,1 ■103 Н = 50,1 кН.
Нормальные напряжения, возникающие в поперечных сечениях
бруса (ст = N /Л), показаны на эпюре (рис. 2.67, г).
При построении эпюры X изменение длины каждого из участков
бруса определяем как алгебраическую сумму свободного температур
ного удлинения и укорочения от действия силы X:
Хс = M a c = М,М - XI,/{EA,);
}. т,—/./■ --- AICD —X(j 4- ctl2&t —Xl2/(EA2).
Перемещения, полученные после подстановки числовых данных,
указаны на эпюре X (рис. 2.67,0).
П р и м е р 2.24. В представленной на рис. 2.68, а системе, состоя
щей из трех стальных стержней одинакового поперечного сечения,
средний стержень был изготовлен короче, чем требуется, на малую ве
личину 8. Определить напряжения, возникшие в стержнях после сборки
системы.
Р е ш е н ы е. Очевидно, что после сборки средний стержень будет
О)
С
D
Е
растянут, а крайние —сжаты. Вырежем узел А (рис. 2.68, б) и составим
для него два уравнения равновесия:
2 А '= 0 ;
/V, sin<p —JV3sin<p = 0; N t = N};
(1)
2 Y = 0; —N l cos <p + iV2 - N 3 cos cp = 0
или. учитывая (1),
ЛГ2 = 2iVj costp.
(2)
Для составления уравнения перемещений изобразим в крупном
масштабе схему деформаций (рис. 2.68, в). После сборки шарнир зай
мет некоторое положение А,, промежуточное между А и А0. При этом
средний стержень окажется растянутым на А/2, а крайние —сжатыми
соответственно на A/t и А/3. Узел А поднимается на ХА. Уравнение
перемещений в данном случае имеет вид
ХА + Д/2 = 5.
(3)
Связь между ХА и А/, (или Д/3) устанавливаем по диаграмме
перемещений:
ХА = AI J cosip;
A/3/cos cp + Д/2 = 5 или NJ/(EA cos2 <p) + N 2l/(EA) —8.
(3')
Решая совместно уравнение статики (2) и уравнение перемещений
(3'), найдем
6£/4cos2 <р
28ЕА cos3 <р
Л Ч = У 3 =-т^— ;---- N.
/ ( 1+2 cos3 <р)
/(1 + 2cos3 (р)
Напряжения в стержнях:
28£cos3<p
5Е cos2 (р
/ (1 + 2 cos3 cp)
A
/ ( l + 2 c o s 3(p)
П р и м е р 2.25. Стальной болт и дюралевая трубка помещены
между двумя весьма жесткими шайбами (рис. 2.69, а).
Определить, на сколько оборотов можно затянуть гайку, если шаг
резьбы S = 2 мм, допускаемое напряжение для болта [ c r ] CT = 80 МПа,
для трубки И д = 60 МПа. Принять £ ст = 2 1 0 5 МПа, Еа =
= 0,7 • 105 МПа.
Р е ш е н и е . При затягивании гайки трубка будет сжиматься,
а болт —растягиваться. Применяя метод сечений и составляя уравне
ние равновесия для сил, действующих
на оставленную часть (рис. 2.69, б),
получим
Ч ”■а,
" =
_ АА
У б = У тр.
Таким образом, задача статиче
ски неопределима, так как неизвестных
сил две, а статика для системы сил,
направленных по одной прямой, дает
лишь одно уравнение.
Для составления уравнения пере92
мещений будем рассуждать следующим образом: при завертывании
гайки на i оборотов она переместится на Х = iS. Так как вначале
торец гайки касался шайбы, то это перемещение могло быть осу
ществлено за счет деформаций болта и трубки. Предположим, что
трубка абсолютно жесткая, тогда перемещение гайки равно удлине
нию болта. Если допустить, что трубка податливая, а болт абсолют
но жесткий, то перемещение гайки равно сжатию (укорочению) трубки.
Фактически обе детали податливы и при затягивании гайки дефор
мируются. Следовательно, перемещение гайки равно сумме абсолют
ных значений удлинения болта и укорочения трубки:
А = iS = М 6 + | Д/хр |, или X = i S = р6^ б + РтрЛ^трВычислим допускаемые силы для болта и трубки (для болта не
учитываем влияние резьбы):
[Л ]б=|>]с
nd2
80 106-3,14 0,022
=25,1 103 Н = 25,1 кН;
3 14
[N]Tp = И д —U>2 ■<Ф = 60 106——-(0,032 0,0222) = 19,6-103 Н
= 19,6 кН.
В качестве допускаемой должна быть принята меньшая сила
[JV]Tp = 19,6 кН.
Вычисляем коэффициенты податливости болта и трубки:
Рб
_______ 0,1_______
6
2 - 105- 10б(3,14/4)0,022
1,59 10“ 9 м/Н;
0,1
Ртр —
£ дЛтр
0,7 • 105 • 106 (3,14/4) (0,032 - 0,0222)
=4,38■ 10~9 м/Н.
Определяем допускаемое по условию прочности число оборотов
гайки:
[JV]Tp(p6 + Ртр)
19,6-103(1,59 + 4,38) 10= 0,0585 об,
S
2-10 3
т. е. допускаемый угол поворота гайки [<р] = 21°06'.
м
=
Глава
Ш
Н А П РЯ Ж Е Н Н О Е И Д Е Ф О РМ И РО В А Н Н О Е
С О СТО ЯН И Я
§ 3.1. Общие сведения о напряженном состоянии
в точке тела
В § 2.5 были даны первичные понятия о напряженном со
стоянии в точке деформируемого тела и проведено исследова
ние напряженного состояния для точек растянутого (сжатого)
бруса. Здесь, не приводя пока никаких доказательств, рассмо
трим основные положения общей теории напряженного состоя
ния.
Напомним, что
напряженное состояние в данной точке тела характеризуется
совокупностью нормальных и касательных напряжений, возни
кающих на бесчисленном множестве различно ориентированных
в пространстве площадок, которые можно провести через эту
точку.
Предположим, что в окрестности исследуемой точки выде
лен бесконечно малый элемент, имеющий форму прямоуголь
ного параллелепипеда, и напряжения, возникающие на его гра
нях, известны. Каждое из этих напряжений может быть
разложено на три составляющих, параллельных координатным
осям. Таким образом, в общем случае на трех исходных пло
щадках возникают девять составляющих напряжений, пока
занных на рис. 3.1, а (напряжения на невидимых гранях элемен
та не изображаем). Правило индексов для напряжений было
дано на с. 22. Указанные девять величин называют компонен
тами напряженного состояния в данной точке.
94
Из условия равновесия выделенного элемента следует, что
составляющие касательных напряжений, возникающих на
любых двух взаимно перпендикулярных площадках, перпендику
лярные общему ребру этих Площадок, равны по абсолютному
значению, т. е.
Т
*ху
'— Т
‘
ку х 9
7vyz
Т
УУ
Т
vz x
'— Т
'‘x z
*
Это положение называют законом парности касательных напря
жений. Следовательно, из девяти компонентов напряженного
состояния независимы лишь шесть.
В некоторых случаях оказывается более удобным выделить
элемент в виде бесконечно малой четырехгранной пирамиды
(тетраэдра), как показано на рис. 3.1,6. Три грани пирамиды,
совпадающие с координатными плоскостями, —это исходные
площадки, а четвертую грань (площадку) проводят произволь
но и возникающие на ней напряжения определяют из трех
уравнений равновесия, составленных для сил, действующих на
тетраэдр.
Итак, первое положение теории напряженного состояния
может быть сформулировано следующим образом:
напряженное состояние в точке тела задано, если известны на
пряжения на любых трех проходящих через нее взаимно перпен
дикулярных площадках.
Имея зависимости, позволяющие найти напряжения по лю
бой площадке, далее исследуют вопрос о наибольших нор
мальных и наибольших касательных напряжениях для рассма
триваемой точки.
Среди бесчисленного множества площадок, которые можно
провести через исследуемую точку, имеются три взаимно пер
пендикулярные площадки, касательные напряжения на которых
отсутствуют. Эти площадки и возникающие на них нормальные
напряжения называют главными.
Главные напряжения обозначают
с 2, ст3; при этом ин
дексы расставляют лишь после того, как эти напряжения вы
числены, так чтобы выполнялись алгебраические неравенства
CFj 5s ст2 ^ ст3.
Для данной точки тела а, - наибольшее (в алгебраическом
смысле), а ст3 —наименьшее напряжение. Напряжения растяже
ния считают положительными. О напряжении а 2 говорят, что
это промежуточное главное напряжение.
В частных случаях, когда два (или все три) главных напря
жения равны между собой, число главных площадок бесконеч- ■
но велико. Итак, в общем случае главных площадок три,
в частных случаях их бесконечно много.
Если главные напряжения в данной точке известны (заданы
95
или определены), то наиболее удобно принять их за исходные.
Классификацию видов напряженного состояния ведут по
главным напряжениям.
Если все три главных напряжения отличны от нуля, напря
женное состояние называют объемным, пространственным или
трехосным. В случае если одно из главных напряжений равно
нулю, напряженное состояние называют плоским или двух
осным, и, наконец, если лишь одно из главных напряжений от
лично от нуля, напряженное состояние линейное, или одноосное.
Элементы, выделенные главными площадками, для различных
частных случаев напряженного состояния показаны на рис. 3.2:
а —трехосное растяжение; б —трехосное сжатие; в —трехосное
смешанное напряженное состояние; г —двухосное растяжение;
д —двухосное сжатие; е —частный случай двухосного смешан
ного напряженного состояния —чистый сдвиг; ж —одноосное
растяжение; з — одноосное сжатие. Площадки, свободные от
напряжений, так называемые нулевые главные площадки, по
крыты точками.
Максимальное для данной точки тела касательное напряже
ние ттах возникает на площадке, параллельной вектору ст2 и де
лящей пополам прямой угол между площадками действия а , и
стзЭто напряжение равно полуразности максимального и мини
мального главных напряжений.
*та. = (СТ1 —ОГ3)/2.
(3.1)
Площадка, на которой воз
никает напряжение ттах, отме
чена на рис. 3.3 штриховкой.
На площадке, перпендикуляр
ной отмеченной (для того что
бы не усложнять чертеж, эта
вторая площадка не показана),
возникает такое же по значению
касательное напряжение.
Рис. 3.2
96
Рис. 3.3
§ 3.2. Исследование напряженного состояния
при известных главных напряжениях
В предыдущем параграфе было указано, что для исследова
ния напряженного состояния должны быть известны напряже
ния на любых трех взаимно перпендикулярных площадках,
проходящих через данную точку. Математическая сторона та
кого исследования наиболее проста, когда исходные напряже
ния, т. е. напряжения, известные в начале исследования,—
главные. Один из таких случаев рассмотрен в § 2.5 —исследо
вание напряженного состояния в точках растянутого (сжатого)
бруса было проведено по известным главным напряжениям.
Это обстоятельство ранее не подчеркивалось лишь потому, что
понятие о главных напряжениях введено позднее, а при изуче
нии материала гл. II в нем не было необходимости.
Для любой точки растянутого (сжатого) бруса одна из
главных площадок совпадает с его поперечным сечением, а ну
левые главные площадки (их бесчисленное множество) совпа
дают с продольными сечениями. Напряжение, возникающее
в поперечном сечении бруса при его растяжении, —это главное
напряжение cTj; при сжатии —главное напряжение ст3.
Предположим, что в окрестности некоторой точки тела вы
делен элемент, грани которого совпадают с главными площад
ками (рис. 3.4, а); напряжения ст1; ст2, ст3 на этих гранях из
вестны. Ограничимся определением нормальных и касательных
напряжений для серии площадок, параллельных одному из
главных напряжений.
Серией или семейством площадок называют совокупность
бесчисленного множества площадок, параллельных одной и той
же оси или, что то же самое, перпендикулярных одной и той же
плоскости.
Рассечем элемент произвольной плоскостью, параллельной
вектору сг3 (рис. 3.4, а), и из уравнений равновесия, состав
ленных для сил, действующих на отсеченную трехгранную
Рис. 3.4
97
призму (рис. 3.4, б), определим напряжения, возникающие на на
клонной площадке. Обозначив дА площадь указанной площад
ки и спроецировав все силы, действующие на выделенную при
зму, на оси v и t (см. § 2.5), получим:
£„рv = 0; а асЫ —(<?! dA cos a) cos а —(а2 АА sin а) sin а = 0,
откуда
сгя = Oj cos2 а + a 2sin2a;
(3-2)
r npt = 0; i ttdA —(о, cMcosa) sina + (o2dA sina)cosa = 0,
откуда
та = (<Tj —o 2)sin acosa,
или
t a = 0,5 (a, —a 2) sin 2a.
(3.3)
Проанализируем полученные результаты. В первую очередь
отметим, что
напряжения, возникающие па площадках рассматриваемой се
рии, не зависят от главного напряжения, параллельного этим пло
щадкам (в рассматриваемом случае от а 3).
Этот результат вполне понятен и очевиден —ведь вектор
напряжения перпендикулярен плоскости, в которой лежат оси
проекций, и, следовательно, проецируется на каждую из них
в точку, т. е. не входит в уравнения равновесия.
Воспользовавшись известными формулами тригонометрии
cos2 a = 0,5(1 + cos 2a); sin2 a = 0,5(1 —cos 2a),
взамен формулы (3.2) получим
a x = 0,5 (c^ + (т2) + 0,5 (otj —a 2)cos 2a.
Очевидно, наибольшее значение ста будет при a = 0°
max ст0= CTj и минимальное —при а = 90° min = ст2.
Следовательно, наибольшее и наименьшее нормальные на
пряжения для рассматриваемой серии площадок —это главные
напряжения.
Пользуясь формулой (3.3), легко получить подтверждение
закона парности касательных напряжений для исследуемого
частного случая. Действительно,
sin 2а = —sin 2 (а + 90°)
и, следовательно,
К 1 = |та + 90°|.
98
Из этой же формулы следует, что наибольшее для данной
серин площадок касательное напряжение возникает на площад
ке, нормаль к которой составляет угол 45° (или 135°) с на
правлением
т. е. т а х т , = т12 = 0,5 (а 3 —о 2).
Формулы (3.2), (3.3), конечно, справедливы (при соответ
ствующей замене индексов) для любой из трех серий площа
док, каждая из которых параллельна одному из главных на
пряжений. Для каждой из этих серий площадок есть свое
наибольшее касательное напряжение:
С1 ~ а 2
т12 = ---- ----- (для площадок, параллельных сг3);
(У 2
<7
3
т 2 з “ ----- х----- (Для площадок, параллельных c rj;
Т 13
(для площадок, параллельных ст2).
Вспоминая правило индексов, согласно которому <jt ^ а 2 ^
> а 3, заключаем, что из трех, так сказать, частных максиму
мов т наибольшим, т. е. действительно максимальным для
данной точки тела, оказывается т13.
Сделаем еще один вывод из формулы (3.3): в частном слу
чае при а 1 = ст2 ни на одной площадке исследуемой серии не
возникает касательных напряжений, т. е. все площадки этой се
рии главные. Если все три главных напряжения равны между
собой: 0 ! = ст2 = ст3, то для данной точки тела любая проходя
щая через нее площадка главная.
§ 3.3. Чистый сдвиг
Рассмотрим частный случай п л о с к о г о напряженного со
стояния, для которого отличные от нуля главные напряжения
равны по модулю и противоположны по знаку (рис. 3.5, а).
41
99
Такое напряженное состояние носит название чистого сдвига
(происхождение этого названия разъяснено несколько ниже).
Максимальное главное напряжение следует обозначить <т1; ми
нимальное а 3; по условию, ст, = —а 3; промежуточное главное
напряжение а 2 = 0.
На рис. 3.5,6 показана проекция элемента на плоскость, со
впадающую с нулевой главной площадкой (отмечена на
рис. 3.5, а точками). Для серии площадок, перпендикулярных
плоскости чертежа, на основании формул (3.2), (3.3) и условия
Oj = —а 3 имеем:
о а= Oj cos2 а + сг3 sin2 а = Oj cos2 а —о 1sin2 а,
или
(3.4)
а „ = а , cos 2а;
Xа
sin 2а =
sin 2а,
2
или
x„ = a 1sin2a.
(3.5)
Максимальное для исследуемой серии площадок касатель
ное напряжение определим, положив в формуле (3.5) a = 45°,
тахта= <
у1. Это напряжение максимально для данной точки те
ла, а не только для исследуемой серии площадок, так как эти
площадки параллельны вектору сг2 (см. с. 98 и 99).
Итак, при чистом сдвиге
Х 13
= Хтах =
СТ1 —
— °
3-
(3-6)
Подставив в формулу (3.4) a = 45° (или a =135°), обнару
жим, что ст„=45° —о а=135' = 0, т. е. на площадках действия мак
симальных касательных напряжений нормальные напряжения
отсутствуют; эти площадки показаны на рис. 3.5,6.
Чистый сдвиг —единственный случай плоского напряженно
го состояния, когда через точку можно провести две взаимно
перпендикулярные площадки, на которых касательные напря
жения максимальны, а нормальные напряжения отсутствуют.
Итак, наряду с определением
чистый сдвиг — это частный случай плоского напряженного
состояния, при котором не равные нулю главные напряжения
равны по значению и противоположны по знаку,—
возможно и другое определение, вытекающее из проведен
ного исследования:
чистым сдвигом называют такое плоское напряженное состоя
100
ние, при котором в окрест
ности данной точки можно
выделить элемент таким
образом, чтобы на четы
рех его гранях были толь
ко равные между собой
касательные напряжения.
Это последнее опре
деление можно рассмат
ривать как объяснение
названия, принятого для
данного напряженного со
стояния.
В качестве примера,
иллюстрирующего
воз
никновение чистого сдви
га, рассмотрим кручение тонкостенной трубы (рис. 3.6, а).
Из условия равновесия отсеченной части трубы, изобра
женной отдельно на рис. 3.6, б, следует, что в поперечном
сечении (любом) возникает лишь один внутренний силовой
фактор - крутящий момент М„ численно равный внешнему
моменту М. В поперечном сечении трубы возникают каса
тельные напряжения, так как только касательные силы дают
момент относительно продольной оси z бруса. Без большой
погрешности, учитывая тонкостенность трубы, можно принять,
что по толщине стенки напряжения распределены равномерно.
Совершенно очевидно, что все точки трубы, расположенные на
любой прямой, параллельной оси z, находятся в одинаковых
условиях. Таким образом, во всех точках трубы напряженное
состояние одинаково —однородное напряженное состояние.
Это обстоятельство повышает надежность и точность экспери
ментального исследования, поэтому опытное изучение чистого
сдвига проводят путем испытания на кручение тонкостенных
трубчатых образцов.
Убедимся, что напряженное состояние в любой точке
трубы —действительно чистый сдвиг.
Двумя поперечными сечениями, отстоящими друг от друга
на расстоянии dz, и двумя радиальными сечениями, угол между
которыми d\|/, вырежем из стенки трубы бесконечно малый эле
мент (рис. 3.6, а). Он изображен отдельно на рис. 3.7, а. В силу
бесконечной малости элемента можно рассматривать его как
прямоугольный параллелепипед с ребрами, равными dz, 8
и (D/2)dv|i. На площадках, соответствующих поперечным сече
ниям, как было установлено, возникают касательные напряже
ния т. Соответствующие им внутренние силы образуют пару.
101
б)
а)
Вид К
К
чз
Euless
Рис. 3.7
Если предположить, что возникают только эти напряжения,
равновесие элемента не будет обеспечено, следовательно, на
гранях параллелепипеда, совпадающих с продольными (ра
диальными) сечениями трубы, также должны возникнуть вну
тренние касательные силы (напряжения т'). Они образуют пару,
момент которой уравновешивает момент сил, возникших по
площадкам поперечных сечений (рис. 3.7,6). Остальные две гра
ни элемента от напряжений свободны, так как они принадле
жат наружной и внутренней поверхностям трубы, к которым
никаких сил не приложено. Итак, на четырех гранях выделенно
го элемента есть только касательные напряжения, а две грани
от напряжений свободны, что соответствует второму определе
нию понятия «чистый сдвиг».
Составим уравнение равновесия сил, действующих на выде
ленный элемент, учитывая, что напряжения г действуют на
площади 5 •0,5.0 •d\|/, а напряжения х' — на площади 5 •dz и пле
чи соответствующих пар сил равны dz и 0,50 d\|/:
(x5 0,5£>dil/) dz = (т'5 dz 0,5D) d\|f,
откуда
Этот результат не содержит ничего нового: составив и ре
шив уравнение равновесия, мы просто иначе, чем ранее, доказа
ли закон парности касательных напряжений. Достоинство это
го доказательства состоит в том, что при рассмотрении
условия равновесия элемента становится особенно ясным, что
парные касательные напряжения направлены оба одновремен
но либо к ребру, либо от ребра пересечения площадок, на ко
торых они возникают.
Рассмотрим теперь вопрос о деформации сдвига. Изобра
зим элемент, выделенный площадками, на которых возникают
только касательные напряжения, в проекции На плоскость, па
102
раллельную свободной от напря
as
г
h"|
жений грани (рис. 3.8). Учитывая,
i
щ
что нас интересуют деформации
h
I 1
элемента, а не его перемещения
{ К
! /'
J
как твердого тела, будем счи
Z4
тать одну из граней неподвиж
ной. В результате деформации
т Ъ di
элемент примет форму, показан
ную на рис. 3.8 штриховыми ли
Рис. 3.8
ниями. Мерой деформации сдви
га служит изменение первоначального прямого угла между
гранями элемента, называемое углом сдвига и обозначаемое у.
Угол сдвига выражается в радианах.
В известных пределах, зависящих от свойств материала, ме
жду углом сдвига и соответствующим касательным напряже
нием существует прямая пропорциональность —закон Гука при
сдвиге. Математическая запись этого закона имеет вид
х = Gy.
(3.7)
Здесь G —упругая постоянная материала, характеризующая его
жесткость при деформации сдвига и называемая модулем сдви
га или модулем упругости 2-го рода. Очевидно, размерность
модуля сдвига та же, что и напряжения.
Можно доказать, что для изотропного тела между тремя
упругими постоянными —модулем продольной упругости Е,
коэффициентом Пуассона р и модулем сдвига G —существует
следующая зависимость:
G = E/[2(l + p)].
(3.8)
Как известно, значение коэффициента Пуассона лежит
в пределах 0 < р < 0,5 (см. с. 34). Следовательно, модуль сдвига
составляет 0,33...0,5 от модуля продольной упругости. Для
многих металлов и сплавов, в частности для стали, G « 0,4Е;
в среднем для стали G = 8,0 • 104 МПа.
Удельная энергия деформации при чистом сдвиге опреде
ляется по формуле
m= t2/(2G),
(3.9)
аналогичной выражению (2.20), определяющему удельную энер
гию деформации при одноосном (линейном) напряженном
состоянии.
Г л а в а IV
П Р А К Т И Ч Е С К И Е РА СЧЕТЫ НА СРЕЗ И СМ ЯТИЕ
§ 4.1. Основные понятия. Расчетны е формулы
Детали, служащие для соединения отдельных элементов ма
шин или строительных конструкций, - заклепки, штифты,
болты и т. п. —во многих случаях воспринимают нагрузки,
перпендикулярные их продольной оси.
Поперечная нагрузка в указанных деталях возникает, в част
ности, при растяжении (сжатии) соединяемых элементов. Со
ответствующие примеры приведены на рис. 4.1: а —штифт,
б —заклепка, в —болт, поставленный без зазора, г —шпонка.
Такой же характер нагружения соединительных деталей имеет
место и при передаче вращающего момента, например в пока
занном на рис. 4.2 соединении шестерни с валом с помощью
штифта. Последний при передаче момента от шестерни к валу
(или наоборот) несет нагрузку, перпендикулярную его оси.
Действительные условия работы рассматриваемых деталей
сложны и во многом зависят от технологии изготовления от
дельных элементов конструкции и ее сборки.
Практические расчеты этих деталей носят весьма условный
характер и базируются на следующих основных допущениях:
1. В поперечном сечении в о з н и к а е т т о л ь к о од ин в н у тр е н н и й си
л о в о й ф а к т о р —поперечная си л а Q ;
2. К а с а т е л ь н ы е н а п р я ж е н и я , в о зн и к а ю щ и е в попер ечном се че
н и и , р а сп р е д е л е н ы п о е го п л о щ а д и р авн о м е р н о ;
3. В случае если соединение осуществлено несколькими
одинаковыми деталями (болтами и т. п.), принимается, что все
они нагружены одинаково.
104
Разрушение соединительных элементов (в случае недоста
точной прочности) происходит в результате их перерезывания
по плоскости, совпадающей с поверхностью соприкосновения
соединяемых деталей (рис. 4.3). Поэтому говорят, что эти эле
менты работают на срез, и возникающие в их поперечном сече
нии касательные напряжения также называют напряжениями
среза и обозначают тср.
На основе сформулированных выше допущений получаем
следующее условие прочности:
top = бМср < K p ],
(4Л)
где тср —расчетное напряжение среза, возникающее в попереч
ном сечении рассчитываемой детали; Q —поперечная сила; при
нескольких одинаковых соединительных деталях Q = F/i
(F —общая нагрузка соединения, i —число болтов, заклепок
и т. п.); А ср- площадь среза одного болта, заклепки и т. п.;
[твр] —допускаемое напряжение на срез, зависящее от материа
ла соединительных элементов и условий работы конструкции.
В машиностроении при расчете штифтов, болтов, шпонок
и т. д. принимают [тер] = (0,25...0,35)стт, где сгт —предел теку
чести материала штифта, болта и др.
Меньшие значения принимают при невысокой точности опре
деления действующих нагрузок и возможности не строго ста
тического нагружения.
Формула (4.1) является зависимостью для проверочного рас
чета соединения. В зависимости от постановки задачи она мо
жет быть преобразована для определения допускаемой нагруз
ки или требуемой площади сечения (проектный расчет).
Расчет на срез обеспечивает прочность соединительных эле
ментов, но не гарантирует надежности конструкции (узла) в це
лом. Если толщина соединяемых элементов недостаточна, то
давления, возникающие между стенками их отверстий и соеди
нительными деталями, получаются недопустимо большими.
В результате стенки отверстий обминаются и соединение ста
105
новится ненадежным. В случае если
изменение формы отверстия зна
чительно (при больших давлениях), а
расстояние от его центра до края
элемента невелико, часть элемента
может срезаться (выколоться), как
схематически показано на рис. 4.4.
Давления, возникающие между
Рис. 4.4
поверхностями отверстий и соедини
тельных деталей, принято называть
напряжениями смятия и обозначать их стсм. Соответственно
расчет, обеспечивающий выбор таких размеров деталей, при ко
торых не будет значительных деформаций стенок отверстий, на
зывают расчетом на смятие. Распределение напряжений смятия на
поверхности контакта деталей весьма неопределенно и в значи
тельной степени зависит от зазора (в ненагруженном состоя
нии) между стенками отверстия и болтом (заклепкой и др.).
Расчет на смятие носит условный характер и ведется в пред
положении, что силы взаимодействия между деталями равномер
но распределены по поверхности контакта н во всех точках нор
мальны к этой поверхности.
Соответствующая расчетная формула имеет вид
<*см—** 1 0"‘4 см) ^
Ы
-
(4.2)
Здесь F/i —нагрузка на одну соединительную деталь; Асм —
расчетная площадь смятия; [сгсм] —допускаемое напряжение на
смятие.
В машиностроении для болтовых, штифтовых и шпоночных
соединений принимают: для деталей из малоуглеродистой ста
ли [<7см] = 100...120 МПа; для деталей из среднеуглеродистой
стали [стсм] = 140... 170 МПа; для деталей из чугунного литья
[стсм] = 60...80 МПа. Зачастую контактирующие детали изго
товлены из различных материалов; в этих случаях при выборе
допускаемого напряжения ориентируются на материал той де
тали, прочность которого меньше.
За расчетную площадь смятия при контакте по плоскости
(см. рис. 4.1, г) принимают действительную площадь соприкос
новения Асм = tl, где I —размер шпонки в направлении, перпен
дикулярном плоскости чертежа; при контакте по цилиндриче
ской поверхности (см. рис. 4.1, а, б, в) принимают площадь
проекции поверхности контакта на диаметральную плоскость,
т. е. Аш —dS. При различной толщине соединяемых деталей
в расчетную формулу следует подставлять <rmin.
В некоторых конструкциях соединительные детали (штифты,
106
шпонки) работают на срез по продольным сечениям (см.
рис. 4.1,г и пример 4.3); Предпосылки расчета и его методика
остаются такими же, как и при срезе по поперечным сечениям.
Помимо расчетов на срез и смятие необходима проверка
прочности соединяемых элементов на растяжение по ослаблен
ному сечению, т. е. проходящему через центр отверстия, и рас
чет на срез (выкалывание) части элемента от центра отверстия
до его края. Все указанные виды расчетов рассмотрены в сле
дующем примере.
П р им ер
4.1.
Тяги 1 и 2 соединены между собой с помощ ью
ш т ы р я 3 , вставленного в их проушины, и нагружены, как показано на
рис, 4 .5 . Определить допускаемое значение сил F, растягиваю щ их тяги,
при следующих значениях допускаемых напряжений: на растяжение
[о-p] = 120 М П а; на срез [тср] —80 М П а; на смятие [стсм] = 210 М Па.
Р е ш е н и е . Допускаемая нагрузка соединения определяется из
расчета тяг на растяжение, ш ты ря на срез, стенок отверстий в тягах на
смятие и краев проушины на срез (выкалывание).
В результате каждого из указанных расчетов в общ ем случае по
лучаю тся различные значения допускаемой нагрузки.
Решением задачи является такая нагрузка, при которой обеспечена
прочность всех элементов конструкций, т. е. наименьш ая из полу
ченных по результатам отдельных расчетов.
1. Определение допускаемой нагрузки из расчета тяги 1 на
растяжение:
а) по сечению I ~ I (неослабленное сечение)
[FP]i = K ] 4 ^ = 120- io6
3,14-0,0242
= 54,2 • 103 Н ;
б) по сечению I I — I I (это сечение показано отдельно на рис. 4.5)
[ F p lii
= [>„] • 2 (bt - d j
= 120 • 106 ■2 (0,44 - 0,02) •0,008 = 46,1 • 103 H.
10
Поверхности
смятия проу
шины тяги 1
q
АНТ тяги 2 по
сечению Л-Л
2
Плоскость
среза
Поверхность смятия
проушины тяги 2
Плоскость
среза
Рис. 4.6
2. Определение допускаемой нагрузки из расчета тяги 2 на
растяжение:
а) по сечению III —III (неослабленное сечение)
[Р р ]”ш = [ о р ] Ь 2Ъг = 120-106-0,03-0,012 = 43,2.10э Н;
б) по сечению II - II (рис. 4.5)
[Fp}u = |> Р] (D - <*ш) 52 = 120 • 106 (0,04 - 0,02) • 0,012 = 28,8 • 103 Н.
3. Определение допускаемой нагрузки из расчета штыря на срез.
Штырь 3 имеет две плоскости среза (рис. 4.6):
[F c p ]
= l>cp]-2
ltd
.
ЗД4 0.022
= 80-106 -2 —------1-----= 50,2 • 103 Н.
4.
Определение допускаемой нагрузки из расчета стенок отверстий
в проушинах на смятие.
Для тяги 1 расчетная площадь смятия, через которую передается
сила F:
,4£м = 28 [£1ш = 2 -8 • 20 = 320 мм2.
То же, для тяги 2:
Л’см = b2dul = 12 • 20 = 240 мм2.
Таким образом, достаточно произвести расчет для более нагру
женной, т. е. имеющей меньшую площадь смятия, проушины тяги 2:
[Тем]'' = Осм]Мш = 210 -106 •240-10" 6 = 50,4 103 Н.
5.
Определение допускаемой нагрузки из расчета краев проушин
на выкалывание:
а) для проушины тяги 1 *
* Заметим, что, хотя обычно выкалывание происходит по липни,
наклоненной к направлению силы (см. рис. 4.4), практически расчет ве
дется на выкалывание по линиям ab и cd для проушины тяги / и по
линии ак и cl для проушины тяги 2 (см. рис. 4.5).
108
[FB1IK]' = [tcp] ■ 2е ■ 25t = 80 ■ 106 • 2 • 0,023 ■ 2 • 0,008 = 589• 103 H;
б) для проушины тяги 2
|/вьпс]" = [tcp] •2е282 = 80 • 106•2 •0,02 •0,012 = 38,4 • 103 Н.
Здесь не учитываем незначительную разницу между размером е2
и длиной линий ак и cl.
Таким образом, допускаемая нагрузка соединения [F] = [Тр]/; =
= 28,8 • 103 Н = 28,8 кН ограничивается прочностью тяги 2 на растя
жение по сечению, проходящему через центр отверстий для штыря.
Следует заметить, что значительное различие в значениях допу
скаемых нагрузок, определенных из условий прочности отдельных эле
ментов конструкций, указывает на ее нерациональность. Всегда сле
дует стремиться к тому, чтобы все элементы конструкции обладали
равной прочностью —это обеспечит наиболее полное использование ее
материала.
В рассматриваемом примере целесообразно несколько изменить
размеры Ь1, Ь2 и D, с тем чтобы допускаемая нагрузка была равна при
мерно 50 кН, т. е. определялась условием прочности штыря на срез.
Рекомендуем читателю выполнить соответствующий расчет и опреде
лить новые размеры bv Ъ2 и D.
П р и м е р 4.2. Определить диаметр D и высоту h головки стерж
ня, нагруженного растягивающей силой F (рис. 4.7), Расчет выполнить
исходя из условия равнопрочности стержня на растяжение, головки на
срез и ее опорной поверхности на смятие. Допускаемые напряжения:
[ар] = 140 МПа;
[тф] = 100 МПа;
Решение. 1. Определяем
допускаемую нагрузку из условия
прочности стержня на растяжение:
[fp] =
bP]^f
=
ц
ci
= 140-106 3>14-0>0322 _ 112,6- 103Н.
4
2. Определяем диаметр опорной поверхности головки из усло
вия ее прочности на смятие:
[стсм] = 250 МПа.
п
Ъж
,
•е?
33
Г*
рис, 4,7
«см = F/Асм ^ |о См |Принимая F = [F p], получаем
LFpi
'^ М
откуда
7ZM
' я[<тш]
+
+ 0,0342 = 0,0417 м = 41,7 мм.
= / ^
< 3,14-250-10е
Принимаем D = 42 мм.
109
3. Определяем высоту головки из условия прочности на срез:
Тср —F[Аср ^ [тср].
Площадь среза равна боковой поверхности цилиндра высотой h
и диаметром d0 (место возможного среза условно показано на рис. 4.7
волнистыми линиями).
Принимая F = [Fp], получаем
тсР = [ f р]/(.Kd0h) ^ [тср]>
откуда
[ f P3 _
П2,б .103
= 0(01055 м = 10,55 мм.
"rtrf0 [xcp]
ЗД4-34-10“ 3 • 100 106
Принимаем й = 11 мм.
П р и м е р 4.3. Проверить проч
ность штифтового соединения виль
чатого кривошипа с валом (рис. 4.8),
если [тср] = 65 МПа и [осм] =
= 90 МПа, F = 2,8 кН.
Решение. Окружная сила,
передаваемая штифтом, связана с
силой F, приложенной к кривошипу,
соотношением
Ft = Fh/(0,5 4) = 2,8-180/(0,5 ■ 40) =
• = 25,2 кН.
Напряжения среза, возникаю
щие в продольном сечении штифта:
Тср = Ft/ (dl) = 25,2 -103/ (0,012 -0,05) = 42 • 10® Па = 42 МПа = 0,645 [т^].
При проверке соединения на смятие учтем, что поверхность кон
такта, через которую передается сила F,, представляет собой четвер
тую часть поверхности цилиндра размерами d и /. Для поверхности
полуцилиндра расчетная площадь смятия равна dl, следовательно,
в данном случае 4 СМ=0,5Л;
crCM=Ff/(0,5<й) = 25,2-103/(0,5-0,012-0,05) = 84-106 Па = 84 МПа =
—0,932 [сУсьЛ§ 4.2. Р асчет заклепочных соединений
Неразъемные соединения деталей машин и строительных
конструкций имеют две основные разновидности: заклепочные
и сварные.
Неразъемными эти соединения называют потому, что для их
разборки необходимо разрушить соединительные элементы заклепки, сварные швы.
Рассмотрим некоторые вопросы расчета заклепочных соеди110
нений для случаев, когда
соединяемые
элементы
работают на растяжение
или сжатие.
На рис. 4.9, а представ
лено соединение двух по
лос внахлестку, а на
рис. 4.9, б —встык с одной
накладкой. В том и другом
случае при разрушении
заклепок срез каждой из
них происходит по од
ному поперечному сече
нию (отмечено волнистой
линией), поэтому эти со
единения называют одно
срезными. На рис. 4.10, а
показано
соединение
встык с двумя накладками,
а на рис. 4.10, б —прикреп
ление к фасонному листу
узла фермы стержня, состоящего из двух равнобоких прокатных
уголков. В том и другом случае срез каждой заклепки при раз
рушении происходит по двум поперечным сечениям и соединение
называют двухсрезным.
Расчет заклепочных соединений ведется на срез и смятие на
основе допущений, указанных в предыдущем параграфе. Между
склепываемыми элементами развиваются значительные силы
трения, и работа заклепок на срез начинается лишь после того,
как внешние силы станут больше сил трения и начнется сдвиг
склепанных полос. При расчетах это обстоятельство не учиты
вают.
Склепываемые элементы (полосы, уголки и т. п.) рассчиты
вают на растяжение (сжатие) с учетом ослабления их попе
речных сечений отверстиями для заклепок.
Расстояние е от центра первой заклепки до края полосы
(см. рис. 4.9, а) принимают обычно равным удвоенному диаме
тру заклепки. При таком расстоянии прочность края полосы
на срез (выкалывание) обеспечена и специальный расчет не
нужен.
Диаметр отверстия в склепываемых элементах на 0,5... 1 мм
больше диаметра непоставленной заклепки. В расчетные фор
мулы входит диаметр d отверстия, так как в выполненном со
единении заклепка практически полностью заполняет отвер
стие.
Ill
Зависимости
вид:
а) на срез
д л я п роверочны х расчетов и м ею т следую щ и й
т ср =
F/
<
[ хср ].
( 4 .3 )
гд е i — о б щ ее чи сл о закл еп о к , п ер ед аю щ и х за д а н н у ю н агр у зк у
F; в к о н с т р у к ц и я х , п р е д с т а в л е н н ы х н а р и с . 4.9; а и 4.10,6,—э т о
о б щ е е ч и с л о з а к л е п о к , а в с о е д и н е н и я х в с т ы к (см. рис. 4.9,6
и 4.10, я) —э т о ч и с л о з а к л е п о к п о о д н у с т о р о н у стыка; к — чис
л о п лоскостей ср еза одн ой закл еп ки : д л я конструкций, при ве
д е н н ы х н а р и с . 4.9, к — 1, а н а р и с . 4.10 к = 2;
б ) н а смятие
о См = Fl(idb) «С[о см].
(4.4)
При о д н о с р е з н ы х с о е д и н е н и я х (см . рис. 4.9) вместо 5 надо
подставлять в ф о р м у л у з н а ч е н и я м е н ь ш е й из толщин склепы
в а е м ы х элементов, а при д в у х с р е з н ы х —меньшей из вели
чин б или 28н (рис. 4.10, а). Для соединения, показанного
на рис. 4.10, б, под 5„ надо понимать толщину полки
уголка.
При п р о е к т н о м расчете заклепочного соединения диаме
тром заклепок задаются, принимая его примерно равным
(1,5...2,5) б. При различной толщине склепываемых элементов
под 8 понимают меньшую из них. Затем определяют допускае
мую силу на одну заклепку:
а) из условия прочности на срез
JT//2
(4.5)
б) из условия прочности на смятие
Кем] = [ < ^ 5 .
(4.6)
По меньшей из допускаемых сил определяют требуемое
число заклепок:
i > F/Qmia.
(4.7)
Для заклепочных соединений стальных конструкций промы
шленных и гражданских сооружений, а также подъемных кра
нов допускаемые напряжения на срез и смятие принимают по
следующим данным, сведенным в таблицу:
112
Допускаемые напряжения, МПа
при продавленных
отверстиях
Материал
конструкции
С таль Ст2 .
С таль СтЗ .
.
.
.
.
при сверленых или
рассверленных
(после продавливания)
отверстиях
м
[^см]
fccpl
[<Уш)
100
100
240
280
140
140
280
320
П р и м е р 4.4. Проверить прочность заклепочного соединения,
изображенного на рис. 4.11. Допускаемые напряжения:
[стр] = 160 М Па; [тср] = 140 МПа; [о см] = 320 МПа.
Р е ш е н и е .
1. Проверяем полосу на растяжение. На рис. 4.11 по
казана эпюра продольных сил для полосы, построенная на основе до
пущения, что каждая заклепка передает силу F / i . Расчет следует вы
полнить для сечения I — I , в котором возникает наибольшая
продольная сила N j = F , и для сечения I I —I I , сила в котором меньше,
чем N x ( N 2 = 4/5 F) , но и расчетная площадь также меньше.
Для сечения
Nj
<Т' ~
Лт1
I -
I
F
~ S (b-d)
~
280-103
0,012(0,18 - 0,023)
‘
а
= 149 М Па < [стр].
Здесь Ант/ —так называемая площадь н е т т о сечения I — /, т. е. рас
четная площадь —полная площадь за вычетом площади отверстий для
заклепок.
Для сечения I I —I I
N,,
А тИ
4/5 F
4/5-280-103
= 8 (Ь -2 4 ) = 0,012(0,18 - 2-0,023)
еА5Ш Ш
139-106 Па.
ж-ж
Ml
113
2. Проверяем заклепки на срез:
тср
F
280-103
= 135-10® Па = 135 МПа.
3,14-0,0232
—
4
3. Проверяем соединение на смятие, учитывая, что 5 < ок:
F
280-Ю3
= 203 -10® Па = 203 МПа.
5-0,023-0,012
Расчет показывает, что прочность соединения обеспечена. Возмож
но даже небольшое уменьшение толщины полосы, так как расчеты на
растяжение и смятие обнаруживают некоторые резервы прочности.
П р им ер 4.5. Стержень фермы, состоящий из двух швеллеров
№ 18а, соединен с фасонным листом (косынкой) узла фермы заклепка
ми расчетным диаметром d = 17 мм (рис. 4.12). Определить требуемое
число заклепок при допускаемых напряжениях:
Осм
т
[о р] = 160 МПа; [а см] = 320 МПа; [тср] = 140 МПа.
Проверить прочность стержня.
Р е ш е н и е. Допускаемая сила на одну заклепку из условия про
чности на срез
[Оср] —[Тср] к
nd2
140-10®-2
3,14 • 0,0172
= 63,5 ■103 Н.
Здесь принято к = 2, т. е. заклепки двухсрезные.
Допускаемая сила на одну заклепку из условия прочности на
смятие
[Сем] = [<тсм]
= 320-10® ■0,017 -0,009 = 49,0-103 Н.
Толщина косынки меньше удвоенной толщины стенки швеллера,
поэтому она и принята в качестве расчетной.
Требуемое число заклепок определяем из условия прочности на
смятие, так как [б ш] < [Сер]:
i > 77 [Сем] = (580- Ю3) / (49 • 103) « 11,8.
Принимаем i — 12.
114
Напряжение в опасном сечении
{I
-
1)
стержня
F
F
580-103
= 148.10* Па < [аР].
А^Г ~ 2A - 6dd
2-22,2-10~^ —6 0,017-0,005
Здесь А = 22,2 см2 —площадь сечения одного швеллера № 18а (по
ГОСТ 8240-72).
Глава V
КРУЧЕНИЕ
§ 5.1. Основные понятия.
Эпюры крутящих моментов
Кручение —это такой вид деформации бруса, при котором
в его поперечных сечениях возникает единственный внутренний
силовой фактор —крутящий момент, обозначаемый М г или М х.
Деформация кручения возникает при нагружении бруса па
рами сил, плоскости действия которых перпендикулярны его
продольной оси. Моменты этих пар будем называть скручи
вающими моментами и обозначать М.
На рис. 5.1, а изображен брус, работающий на кручение под
действием приложенных к нему скручивающих моментов. Это
условное изображение моментов применено взамен показанно
го на рис. 5.1,6, где дано нагружение этого же бруса парами
сил.
Во всех случаях будем считать, что алгебраическая сумма
скручивающих моментов равна нулю, т. е. брус находится
в равновесии.
На рис. 5.2, а, б изобра
жен тот же брус в ортого
нальной проекции. При этом
на рис. 5.2, а дан еще один
Ф
г)
Рис. 5.1
Рис. 5.2
115
способ условного изображения внешних моментов, часто при
меняемый в технической литературе; момент представлен в
виде двух кружков. Кружок с точкой обозначает силу, направлен
ную на наблюдателя, а кружок с крестом - силу, направленную
от наблюдателя.
Применяя метод сечений и рассматривая равновесие остав
ленной части (рис. 5.2, в, г), приходим к выводу, что внутренние
силы, возникающие в поперечном сечении бруса, должны дать
момент (крутящий момент), уравновешивающий внешние мо
менты, приложенные к оставленной части.
Итак, крутящий момент, возникающий в произвольном попе
речном сечении бруса, численно равен алгебраической сумме
скручивающих моментов, приложенных к оставленной части.
В более общем случае нагружения бруса, когда в его попе
речных сечениях возникает несколько внутренних силовых фак
торов, крутящий момент вычисляется как алгебраическая сум
ма моментов относительно продольной оси бруса всех
внешних сил, приложенных к его оставленной части.
При кручении бруса в его поперечных сечениях возникают
только касательные напряжения. Действительно, момент отно
сительно продольной оси бруса дают только внутренние каса
тельные силы (нормальные силы параллельны этой оси). Кроме
того, наличие внутренних нормальных сил, приводящих к силе
или паре сил, противоречит условию равновесия отсеченной ча
сти бруса. Наличие самоуравновешенной системы внутренних
нормальных сил, естественно, не противоречит условию равно
весия, но такие случаи не рассматриваются.
Следовательно,
крутящим моментом называется результирующий момент от
носительно продольной оси бруса внутренних касательных сил,
возникающих в его поперечном сечении.
Для расчета на прочность, так же как и при растяжении
(сжатии) бруса, надо найти его о п а с н о е с е ч е н и е . В слу
чае если размеры поперечного сечения по длине бруса по
стоянны, опасными будут сечения, в которых крутящий момент
максимален. График, показывающий закон изменения крутя
щих моментов по длине бруса, называется эпюрой крутящих
моментов. Построение этих эпюр принципиально ничем не от
личается от построения эпюр про
дольных сил и производится на
основе сформулированного выше
правила вычисления крутящих
моментов. Для бруса, изображен
ного на рис. 5.2, а, б, эпюра Мг
представлена на рис. 5.2, д.
116
Рис. S.4
Знак крутящего момента не имеет физического смысла, но
для определенности при построении эпюр условимся о следую
щем правиле знаков. Будем считать крутящий момент положи
тельным, если для наблюдателя, смотрящего на проведенное
сечение, он представляется направленным по часовой стрелке
(рис. 5.3). Соответствующий внешний момент направлен про
тив часовой стрелки.
Характер деформации при кручении существенно зависит от
формы поперечного сечения бруса. Методами сопротивления
материалов задача о напряжениях и перемещениях при круче
нии может быть решена только для бруса круглого сплошного
или кольцевого поперечного сечения.
При некоторых дополнительных допущениях можно решить
задачу о кручении брусьев тонкостенного замкнутого профиля.
Теория кручения бруса круглого поперечного сечения на
иболее часто используется при расчете различных валов. В ка
честве примера на рис. 5.4 показан так называемый трансмис
сионный вал с насаженными на него шкивами ременных
передач.
Легко видеть, что под действием натяжений ремней вал по
мимо кручения испытывает и изгиб. Если пренебречь влиянием
изгиба (так поступают при предварительном, ориентировочном
расчете валов), расчетная схема вала будет иметь вид, пред
ставленный на рис. 5.5. Там же
показана эпюра крутящих мо ш И,Г 1
Их ш
К
'Ь
ментов.
га
чJ
4 ) **
Мг Ч>
При равномерном вращении
вала алгебраическая сумма при
ложенных к нему вращающих
моментов равна нулю.
Вращающие моменты, дей
ствующие на каждый из шкивов,
ЭпюраMi
к
Рис. 5.5
117
могут быть выражены через соответствующую мощность
и угловую скорость по формуле, известной из курса теоретиче
ской механики:
М = Р/ю,
(5.1)
где М - момент, Н м ; Р - мощность, Вт; со - угловая ско
рость, рад/с.
Вращающий момент может быть выражен также и через
силы натяжения ветвей ремня. Например, для шкива I (рис. 5.4)
М , = 0,5D,F[ - 0 , 5 = 0,5Dt (F; - F2'),
(5.2)
где Dj —диаметр шкива.
§ 5.2. Напряжения и перемещения при кручении
бруса круглого поперечного сечения
Теория кручения бруса круглого сплошного или кольцевого
поперечного сечения основана на следующих допущениях.
1. Поперечные сечения бруса, плоские и нормальные к его
оси до деформации, остаются плоскими и нормальными к оси
и при деформации (гипотеза Бернулли).
2. Радиусы поперечных сечений при деформации бруса не
искривляются.
3. Материал бруса при деформации следует закону Гука
(это допущение является общим для всех видов деформаций,
изучаемых в нашем курсе).
Так как в поперечных сечениях бруса при кручении не воз
никают продольные силы, то расстояния между сечениями не
изменяются.
Представление о характере деформации можно получить,
подвергая скручиванию резиновую модель бруса с нанесенной
на его поверхности сеткой продольных и поперечных рисок
(рис. 5.6, я). Поперечные риски не искривляются, а расстояние
между ними не изменяется, что подтверждает справедливость
гипотезы плоских сечений. Продольные риски обращаются
в винтовые линии (рис. 5.6,6).
Справедливость принятых допущений подтверждается, кро6)
a
м
Рис. 5.6
118
ме того, и тем, что полученные на основе их формулы совпа
дают с формулами, полученными в теории упругости без этих
допущений, и хорошо согласуются с экспериментальными
данными.
Рассмотрим брус, жестко защемленный одним концом и на
груженный на свободном конце скручивающим моментом
М (рис. 5.7). При деформации бруса его поперечные сечения
повернутся на некоторые углы по отношению к своему перво
начальному положению или, что то же, по отношению к непо
движному сечению (заделке). Угол поворота будет тем больше,
чем дальше отстоит данное сечение от заделки. Так, для про
извольного сечения I, отстоящего от заделки на расстоянии 2,
он равен срг, для сечения II — срг + dtp. Здесь dtp - угол поворо
та сечения II относительно I, или угол закручивания элемента
бруса длиной dz.
Вообще угол поворота произвольного сечения равен углу
закручивания части бруса, заключенной между этим сечением
и заделкой. Таким образом, угол поворота tp торцового сече
ния представляет собой полный угол закручивания рассматри
ваемого бруса.
Применяя метод сечений, легко убедиться, что крутящий
момент во всех поперечных сечениях бруса одинаков: Mz —M.
Выразим его через касательные напряжения, возникающие
в поперечном сечении. При этом учтем, что в любой точке по
перечного сечения касательное напряжение направлено перпен
дикулярно радиусу, проведенному в эту точку (рис. 5.8). Такое
направление напряжений следует из характера деформации:
119
Рис. 5.8
Рис. 5.9
при повороте произвольного поперечного сечения (см. рис. 5.7)
каждая его точка (кроме лежащей на оси бруса) перемещается
по дуге окружности, концентричной контуру сечения. Иными
словами, направление этого перемещения, а значит и возни
кающего в этой точке касательного напряжения, перпендику
лярно соответствующему радиусу (рис. 5.9). Элементарная ка
сательная сила, приходящаяся на площадку dА, равна т d.4, а ее
момент относительно оси z (точки О)
dMz = (т йА) р.
(5.3)
Суммируя эти элементарные моменты, получим следующее
выражение для крутящего момента:
М .= j xpd.4.
(5.4)
Хотя крутящий момент может рассматриваться как извест
ная величина (он определяется с помощью метода сечений че
рез заданные внешние моменты), использовать выражение (5.4)
для вычисления касательных напряжений невозможно, так как
закон их распределения по поперечному сечению пока неизве
стен. Для выяснения этого закона рассмотрим более подробно
вопрос о деформациях.
Выделим часть бруса двумя бесконечно близкими попе
речными сечениями I п II (см. рис. 5.7). Будем считать выде
ленную часть бруса защемленной в сечении I (рис. 5.9), что
вполне допустимо, так как нас интересуют ее деформации, а не
перемещения в пространстве как твердого тела. Точка В, взятая
на контуре сечения II, в результате его поворота на угол d<p
перейдет в положение В1. Деформация сдвига соответствующе
го элемента бруса (торец этого элемента, лежащий в сечении
120
11, зачернен) характеризуется углом сдвига утах. Из прямо
угольного треугольника АВВи учитывая, что BBt = г d(p, и в си
лу малости деформаций t g y « y , получаем
Ушах ~ r d < p /d 2 .
Выделяя мысленно из рассматриваемой части бруса ци
линдр произвольного радиуса р (рис. 5.9) и повторяя те же рас
суждения, имеем
у = pdcp/dz.
(а)
Применяя закон Гука для сдвига (т = Gy), получим следую
щее выражение для касательного напряжения:
x = Gpd<p/dz.
(б)
Подставляя (б) в (5.4), получаем
М .= |G p 4 %
■J
dz
При интегрировании по площади поперечного сечения ве
личина dcp/dz постоянна и, так же как и G, может быть вынесе
на за знак интеграла:
M : = G - ~ - j V dA.
(в)
Интеграл, входящий в выражение (в), представляет собой
величину геометрического характера, называемую полярным
моментом инерции сечения и обозначаемую J p:
Jp = f Р2 dA
(5.5)
А
Полярный момент инерции представляет собой взятую по всей
площади сечения сумму произведений площадей элементарных
площадок на квадраты их расстояний до начала координат (цен
тра тяжести сечения).
Очевидно, он имеет размерность L4. На его вычислении
остановимся несколько ниже. Возвращаясь к выражению (в),
перепишем его теперь в виде
dtp
М: = GJp
dz ’
откуда
d<p/dz = M J(G J p).
(г)
121
Подставляя
значение
dcp/dz в (б), имеем
т = GpMz/(GJp),
или окончательно
Т = M:P/Jp.
(5.6)
Формула (5.6) позволяет
определить значение касательного напряжения в любой точке
поперечного сечения. Из этой формулы следует; что касательные
напряжения распределены вдоль любого радиуса сечения по
линейному закону.
Эпюры касательных напряжений для круглого сплошного
и кольцевого поперечных сечений показаны на рис. 5.10.
В точках, равноудаленных от центра сечения, напряжения
одинаковы.
Наибольшего значения касательные напряжения достигают
в точках контура поперечного сечения.
Они могут быть определены путем подстановки в (5.6) вме
сто р его наибольшего значения, т. е. г:
Tm ax =
M zr/Jp.
Введя обозначение Wp = I p/r, получим следующее выражение
для максимального касательного напряжения:
Тшах = M .JW p.
(5.7)
Величину Wp, равную отношению полярного момента инер
ции сечения к его радиусу, называют полярным моментом со
противления сечения. Его размерность —L3. Очевидно, по
лярный момент сопротивления является геометрической характе
ристикой прочности бруса круглого поперечного сечения при
кручешш.
Формулу для определения углов закручивания получим из
выражения (г). Угол закручивания элемента бруса длиной dz
равен
dq> = М , dz/(GJp).
Суммируя элементарные углы закручивания, найдем пол
ный угол закручивания бруса (или отдельного его участка):
122
В самом общем случае, когда для отдельных участков бруса
законы изменения крутящих моментов или полярных момен
тов инерции (или тех и других величин одновременно) раз
личны, следует пользоваться формулой
(5.9)
В частном случае, если диаметр бруса постоянен и крутя
щий момент имеет во всех сечениях одинаковое значение,
Ф = M.J/(GJP).
(5.10)
В случае постоянства крутящего момента лишь в пределах
отдельных участков бруса или ступенчатого изменения его по
перечного сечения формулу (5.10) можно применять только по
участкам.
Все приведенные формулы дают значение угла ф в радиа
нах. При их применении следует учитывать указания по ис
пользованию аналогичных формул для определения изменения
длины бруса при растяжении (см. с. 35).
Произведение GJP условно называют жесткостью сечения
круглого бруса при кручении.
Модуль сдвига характеризует жесткость материала, а по
лярный момент инерции является геометрической характеристи
кой жесткости бруса.
Обратимся к выводу формул для вычисления полярного
момента инерции и полярного момента сопротивления. Выве
дем эти формулы для кольцевого сечения внутренним диаме
тром d0 и наружным d (рис. 5.11). Разобьем сечение на бесчис
ленное множество бесконечно тонких колец. В выражении
• / „ = J p 2d>l
А
за элемент площади dА примем пло
щадь одного из указанных колец:
dA = 2rcpdp.
Площадь весьма тонкого кольца
можно вычислить как площадь пря
моугольника со сторонами 2жр и dp,
в который обратится кольцо, если
его мысленно разрезать и распря
мить. Подставляя значение dA в
выражение для Jp и интегрируя, по123
лучаем
dll
dj2
-J'
=
p22rcpdp = 2я-
dof 2
- dt).
A>/2
Вводя обозначение с = d jd и вынося за скобки d*, оконча
тельно получим
ndA
(5.11)
( 1 - с 4)* 0 ,Ы 4( 1 - с 4)..
Jp
32
Для круга d0 = 0, а следовательно, с = 0, поэтому
(5.12)
J = Jtd4/32 « 0,W4.
Выражения для
получим, разделив / р на наружный ра
диус сечения d/2.
Таким образом, для кольца
Wp = М 3/16)(1 - с4) « 0,2d3(1 - с4)
(5.13)
и для круга
Wp = та*3/16 « 0,2d3.
(5.14)
§ 5.3. Расчеты на прочность и жесткость при кручении
Прочность бруса, работающего на кручение, считают обес
печенной, если наибольшие касательные напряжения, возни
кающие в его опасном поперечном сечении, не превышают
допускаемых:
тшах *£ 1>к].
Конечно, незначительное (до 5...6%) превышение расчетного
напряжения над допускаемым не опасно.
Как известно из предыдущего, эти наибольшие напряжения
возникают в точках контура поперечного сечения и вычисляют
ся по формуле (5.7). Таким образом, получим следующее усло
вие прочности:
(5.15)
Эта формула служит для проверочного расчета на про
чность.
При проектном расчете и при определении допускаемой на
грузки (момента) из формулы (5.15) соответственно находят Wp
или [А/.].
Крутящий момент А/,, который входит в приведенные рас
124
четные формулы, с помощью метода сечений должен быть вы
ражен через в н е ш н и е (скручивающие) моменты.
Расчет ведется для опасного поперечного сечения. Для бру
са постоянного диаметра опасным является сечение, в котором
возникает наибольший крутящий момент. Если диаметр бруса
не постоянен, может оказаться, что наибольшие напряжения
возникают не там, где крутящий момент максимален, следова
тельно, в этом случае вопрос об опасном сечении должен быть
исследован дополнительно (см. ниже пример 5.1).
Допускаемое напряжение [тк] для пластичных материалов
назначают в зависимости от их предела текучести при круче
нии (при сдвиге) тт, т. е.
[тк] = Тт/[ит],
(5.16)
а для хрупких —в зависимости от предела прочности
[тк] = тпч/ [ипч].
(5.17)
Для пластичного материала диаграмма зависимости между
касательным напряжением и углом сдвига (характеристика ма
териала при сдвиге), полученная путем соответствующей обра
ботки результатов испытаний на кручение, показана на
рис. 5.12. Площадка текучести на этой диаграмме отсутствует.
В качестве предела текучести тт условно принимают напряже
ние, при котором остаточный угол сдвига равен 0,003 рад.
Учитывая, что, по экспериментальным данным, предел теку
чести при кручении связан с пределом текучести при растяже
нии зависимостью тт «(0,55...0,60)а т, принимают для стали
[тк] »(0,55...0,60) [стр]; для чугуна [тк] » (1,0...1,2)[стр].
Указанные значения допускаемых напряжений можно при
нимать лишь в случае чистого кручения. Практически на круче
ние обычно рассчитывают валы, которые помимо деформации
кручения испытывают также изгиб. Не учитывая при ориенти
ровочном расчете валов влияние изгиба, делают ошибку, при
водящую к уменьшению фактическо
го коэффициента запаса прочности.
Для компенсации этой ошибки и
обеспечения прочности вала допус
каемое напряжение на кручение
принимают пониженным; для кон
струкционной углеродистой стали
обычно [тк] = 20...35 М Па
Во многих случаях вал должен
быть рассчитан не только на проч
ность, но и на жесткость при круче
нии. В качестве примера можно ука
125
зать на ходовые винты токарных станков, при деформации
которых шаг их резьбы изменяется, а следовательно, и шаг
резьбы, нарезанной на этом станке, получается с некото
рой погрешностью. Задавая определенный допуск на точность
изготовляемой резьбы, тем самым ставят требование ограниче
ния угла закручивания ходового винта. Чем выше должна быть
точность нарезанной резьбы, тем меньшую деформацию ходо
вого винта можно допустить.
За меру жесткости при кручении принимают относительный
угол закручивания (угол закручивания на единицу длины) вала,
обозначаемый <р0 (встречается обозначение 0).
Из приведенного примера должно быть ясно, что в отличие
от допускаемого напряжения, зависящего в первую очередь от
материала вала, допускаемый угол закручивания зависит от на
значения вала.
Значения допускаемых углов закручивания, встречающих
ся в различных отраслях машиностроения, весьма разно
образны;
наиболее
распространены
значения
[<р0] =
= (4,38... 17,5)-10_3 рад/м = 0,25... 1,0 град/м.
Условие жесткости при кручении имеет вид
Фо = Мг/(С /рК [ ф 0].
(5.18)
При проектном расчете отсюда определяют требуемое зна
чение Jр, а затем по формуле (5.11) или (5.12) вычисляют диа
метр вала. Из двух значений диаметра вала, определенных из
расчетов на прочность и жесткость, в качестве окончательного
(исполнительного размера) должен быть, конечно, принят боль
ший.
В заключение настоящего параграфа остановимся на срав
нительной оценке валов круглого и кольцевого поперечных се
чений. Из эпюр касательных напряжений, приведенных на
рис. 5.10, видно, что, удаляя материал вблизи оси вала, его
прочность снижают весьма незначительно, так как эта часть
материала для вала сплошного сечения малонагружена. При
равных площадях поперечного сечения, а следовательно, при
одинаковой массе валов кольцевое сечение обладает большими
полярными моментами инерции и сопротивления, чем сплош
ное, т. е. вал кольцевого сечения оказывается жестче и прочнее.
Наконец, при равной прочности или равной жесткости, т. е.
при одинаковых значениях Wp или Jр, полый вал получается
легче сплошного. Пусть d и d0 —соответственно наружный
и внутренний диаметры кольцевого сечения и dK—диаметр
сплошного круглого сечения. При равной прочности валов,
приравнивая полярные моменты сопротивления их сечений,
получаем (к^3/16) (1 —с4) = nd3K/l6, где по-прежнему с = d0/d.
126
Выражая d через йю име
ем
d = dxfl/T ^c*.
(5.19)
Отношение масс валов
(при одинаковом материале
и длине) равно отношению
площадей их поперечных се
чений :
А/Ак =
= [ 7 4 л2 ( 1 - с2Ш 7 4 ^ ) =
= d2( l - c 2)/d l
или, используя зависимость (5.19), окончательно
Л /Л = ( 1 - с 2) } /( 1 - с Л)2.
(5-2°)
При равной жесткости валов, приравнивая полярные мо
менты инерции их сечений, аналогично получаем
А/Ах = |/ (1
с2)/(1 + с2).
(5.21)
Графики, построенные по зависимости (5.20) и (5.21), пред
ставлены на рис. 5.13: кривая 1 соответствует равной прочно
сти, а 2 —равной жесткости.
П р им ер 5.1. Ступенчатый стальной брус круглого поперечного
сечения жестко заделан одним концом и нагружен, как показано на
рис. 5.14, а. Построить эпюры крутящих моментов, максимальных ка
сательных напряжений и углов поворота поперечных сечений. Прове
рить прочность бруса при [тк] = 60 МПа.
Р е ш е н и е . Эпюру крутящих моментов строим, начиная от сво
бодного (левого) конца, что позволяет не определять реактивный мо
мент в заделке. Проведя произвольное сечение а —а на участке АВ
и составляя для оставленной части (рис. 5.14,6) уравнение равновесия
2 М 0, = 0, получаем М{ — М.
Согласно принятому правилу знаков, считаем момент Ml отрица
тельным. Крутящий момент сохраняет постоянное значение ( —М) во
всех сечениях участка АВ и ВС. Для остальных участков находим кру
тящие моменты как алгебраические суммы внешних моментов, прило
женных по одну сторону (в нашем случае —по левую) от сечения. От
сеченные части отдельно не изображаем. Эпюра М г дана на
рис. 5.14, в. Вообще следует заметить, что построение эпюры крутящих
моментов совершенно аналогично построению эпюры продольных
сил.
127
Для нахождения опасного сечения строим эпюру максимальных
касательных напряжений, пользуясь формулой
Tma* = M J W P, где Wp = nd3/ 16.
Для участка АВ
м[
1,0-10М б
- rife - y i W
- а ‘ ■№ Ш - 2М МП1
Аналогично определяем ттах в поперечных сечениях остальных
участков бруса.
Ординаты эпюры ттах (рис. 5.14, г) откладываем в ту же сторону,
что и соответствующие ординаты эпюры М г. Знак касательного напря
жения при расчете на прочность никакой роли не играет, и принятое
направление ординат эпюры условно.
Опасными оказались поперечные сечения участков ВС и CD. Таким
образом, опасными оказались не те сечения, в которых крутящий мо
мент максимален. Условие прочности ттах < [тк] выполняется. Очевид
но, что материал бруса использован нерационально; даже в опасном
сечении максимальное напряжение на 32% ниже допускаемого.
Эпюру углов поворота строим, начиная от защемленного конца.
Ординаты этой эпюры в выбранном масштабе дают значения углов
поворота соответствующих поперечных сечений бруса. Эпюра строит
ся совершенно аналогично эпюре линейных перемещений (см. § 2.3).
128
В пределах каждого из участков бруса эпюра линейна, поэтому доста
точно вычислить углы поворота только для граничных сечений участ
ков: угол поворота сечения К, равный углу закручивания участка K L :
3 • 103 • 0,4 •32
GJvp 8 ■104 • 106 • 3,14 • 0,08“
М У«
-3 ,7 3 -1 0 '3 рад,
где принято для стали G = 8-104 МПа.
Угол поворота сечения D относительно К, равный углу закручива
ния участка DK:
M‘va
~GjJ
1,0 ■103 •0,4 • 32
8-10М 06-3,14-0,084
1,24-10'3 рад.
Абсолютный угол поворота сечения D (относительно заделки) ра
вен алгебраической сумме углов закручивания участков KL и DK. Та
ким образом, ордината эпюры <р в сечении D равна
Фкь + Фск = ( —3,73 + 1,24)-10"3 = -2,49-10~3 рад.
Аналогично вычисляют углы поворота остальных граничных сече
ний. Эпюра <р представлена на рис. 5.14, д. Рекомендуем читателю вы
полнить остальные вычисления, необходимые для построения этой
эпюры.
П р и м е р 5.2. Вал диаметром d = 60 мм имеет частоту вращения
п —600 об/мин. Определить из расчетов на прочность и жесткость до
пускаемую мощность, которую может передавать вал, если [тк] =
= 35 МПа, [ф0] = 0 ,4 град/м.
Р е ш е н и е . Допускаемый по условию прочности крутящий мо
мент, равный в данном случае передаваемому валом вращающему мо
менту, определим на основании формулы (5.15):
ltd3
[X T = [ M J = Wp [тJ = —
[Тк] ^
3,14 0,Об3
16
•35-106 = 1485 Н м.
Для определения допускаемого момента из расчета на жесткость
воспользуемся формулой (5.18):
[Л/]" = [MJ" = G J , [ф0] = 8,0- 101О-^ ~ (6 0 - К Г 3)4^ — 0,4 = 710 Н м.
Здесь принято для стали G = 8,0’ 1010 Па. Множитель ic/180 = 3,14/180
служит для перевода ф0 из град/м в рад/м. Диаметр вала для согласо
вания единиц подставлен в метрах.
Окончательно принимаем меньшее из двух значений: [М] =
= 710 Н м. Соответствующую мощность найдем, воспользовавшись
формулой (5.1):
[Р] = [М] ш = [ М ] - ^ - = 710 3,1 з0600 = 44,6 • 103 Вт = 44,6 кВт.
129
П р и п р и н я т о м зн а ч е н и и д о п у с к а е м о г о м о м е н т а м а к с и м а л ь н ы е к а
с а т е л ь н ы е н а п р я ж е н и я в п о п е р е ч н о м сеч ен и и в а л а р а в н ы
М2
710
= 16,7 ■106 Па = 16,7 МПа,
тmax
~WS ~ (3,14/16)-0,Об3
т.
на 52,3% ниже допускаемых.
П р и м е р 5.3. Определить из расчетов на прочность и жесткость
требуемые размеры поперечного сечения вала (рис. 5.15) в двух ва
риантах: а) сечение —круг, б) сечение —кольцо с отношением вну
треннего диаметра к наружному с = 0,7.
Сечение вала считать по всей длине постоянным. Принять [тк] =
= 25 МПа и [ф0] = 5,3 10_3 рад/м. Вал вращается с угловой ско
ростью со = 23 рад/с.
Выбрать наиболее рациональную последовательность расположе
ния шкивов на валу.
Решение. Приняв расположение шкивов, указанное на рис. 5.15,
получим схему вала и эпюру крутящих моментов, показанные на
рис. 5.16.
Вращающие моменты, передаваемые каждым из шкивов (значения
скручивающих моментов), вычислены по формуле (5.1).
Поменяв местами шкивы 1 и 2, получим расчетную схему и эпюру
Мг, показанные на рис. 5.17. Очевидно, второй вариант целесообраз
нее, так как в этом случае расчетный крутящий момент M zmax =
= 1132 Н м значительно меньше, чем в первом варианте, где Mzmax =
= 2087 Н ■м. Нетрудно убедиться, что при иных вариантах расположе
ния шкивов расчетный крутящий момент не уменьшится. Из рас
смотренного можно сделать общий вывод: приемный шкив
надо расположить между шкивами, передающими мощности рабо
чим машинам таким образом, чтобы моменты, передаваемые
участками вала слева и справа от него, были по возможности оди
наковы.
е.
130
О п ределяем треб уем ы й полярны й м о м ен т сопроти вления
в а л а из расчета н а п р о ч н о с т ь :
1132
-гПб = 45,3
’ • 10“
25•106
Диаметр вала круглого сечения
w > Мгпих
р" Ы
dK=
=45,3’ 103
сечения
м м 3.
16 •45,3 • 103
= 61,5 мм.
3,14
16W.
п
Наружный диаметр вала кольцевого сечения
3 _______
d=
3
16 W„
It (1 — с4)
' 16 -45,3-103
= 67,2 мм.
3,14(1 - 0 , 74)
Требуемый полярный момент инерции сечения вала из расчета на
жесткость fl>0] подставляем в рад/м)
J”
Д и ам етр
М ._
1132
=267-10“
G [ср0]
8 • 104 ■10б • 5,3 • 10~ 3
вала круглого сечения
dK-
'32-267-104
=72,5 мм.
ЗД4
' 327.
Наружный диаметр кольцевого сечения
d■
4 _____ _
1/ ш
ТС(1 —с4)
4
32■267•104
=77,5
3,14(1 - 0 , 74)
мм.
Требуемые размеры сечения получились из расчета на жесткость
больше, чем из расчета на прочность, поэтому их и принимаем в каче
стве окончательных с небольшим округлением: = 72 мм, d = 78 мм.
131
"й----
По кривой
2
(см.
рис. 5.13) устанавливаем, что
при с = 0,7 вал кольцевого
L
—
сечения будет легче сплошно
d„rt0 'в! (Ч?
го вала примерно на 42%.
П р и м е р 5.4. Два оди
наковых вала соединены
муфтой
со
штифтами
Рис. 5.18
(рис. 5.18). Выяснить, что ог
раничиваетпередаваемый
момент; прочность валов, муфты или штифтов. Принять для валов
[тк]' = 40 МПа, для муфты [тJ " = 20 МПа, для штифтов [тср] = 100 МПа.
При расчете валов и муфт ослабление их отверстиями для штиф
тов не учитывать.
Р е ш е н и е . 1. Допускаемый момент из условия прочности валов
[М ] в = [МJ B = [ x j Wpb = 40 • 106 • 3,14 • 0,043/16 = 502 H ■ m .
I
Ъш----------
т яг л
2. Допускаемый момент из условия прочности муфты
3,14-0,0683
[М ]м = [М г]м = [т J ' W pM = 2 0 -106
16
п
т
= 1090 Н-м.
3. Допускаемый момент находим из условия прочности штифтов.
Штифт работает на срез. Учитывая наличие двух плоскостей среза,
получаем следующее расчетное уравнение:
=
р
ы
сила, действующая на штифт, связана с передаваемым моментом
зависимостью
F
= M /(0,5d).
Подставляя значение F в условие прочности, получаем
= м ш / ^2 -0 , 5 «
[тср],
откуда
[М]ш = ^
[Тср3 = о,04 3’1--'° ’01 100-106 = 314 Н-м.
4
4
Таким образом, наименее прочными элементами конструкции
являются штифты. Для увеличения допускаемого момента можно по
ставить на каждой половине муфты два штифта, одновременно не
сколько уменьшив их диаметр. Толщину втулки (муфты) можно не
сколько уменьшить, так как муфта значительно прочнее вала.
§ 5 А Энергия деформации при кручении
При кручении, так же как и при других видах деформации
бруса, работа внешних сил (скручивающих моментов) расхо
132
дуется на создание в деформиМ
руемом теле определенного за
паса энергии (потенциальной
энергии деформации). Выведем
формулу для определения этой
энергии, рассматривая брус, S?
жестко заделанный одним кон
цом и нагруженный на свобод
ном конце скручивающим мо
ментом М (рис. 5.7). Как и ра
нее (см. § 2.4), будем считать,
что нагружение осуществляется
статически в пределах действия
Рис. 5.19
закона Гука. Таким образом,
зависимость между скручивающим моментом и углом закру
чивания линейная. График этой зависимости представлен на
рис. 5.19,
Из курса теоретической механики известно, что работа мо
мента (пары сил) равна произведению момента на угол поворо
та. При приращении угла поворота на величину dtp соответ
ствующая элементарная работа
dW —М d t p .
Эта работа выражается на графике (рис. 5.19) площадью гу
сто заштрихованной трапеции, которую по малости dtp можно
рассматривать как прямоугольник.
Вся работа, очевидно, выразится площадью треугольника,
заштрихованного на рис. 5.19, т. е.
(5.22)
W = 0,5MKtpK,
где Мк и <рк —соответственно конечные значения скручивающе
го момента и угла закручивания.
Таким образом, получено выражение теоремы Клапейрона
(см. § 2.4) для случая кручения.
Учитывая, что работа внешних сил (моментов) равна энер
гии деформации и в рассматриваемом случае крутящий мо
мент во всех сечениях одинаков: М,К= МК, имеем
W = V = 0,5Мгкфк.
(5.23)
Опуская индекс «к» и выражая угол закручивания по формуле
(5.10), окончательно получаем следующее выражение для энер
гии деформации при кручении участка бруса, в пределах кото
рого М 2 —const и Jp = const:
V = M\lj (2GJp).
(5.24)
133
При ступенчатом изменении сечения или крутящего момен
та
(5.25)
V=
В случае если Л/г и Jp (или обе эти величины) изменяются
по длине отдельных участков непрерывно, следует пользовать
ся формулой (см. также с. 48)
(5.26)
и
§ 5.5. Расчет цилиндрических винтовых пружин
Винтовые пружины широко применяют в различных обла
стях машиностроения и приборостроения: в качестве элементов
амортизирующих (смягчающих толчки и удары) устройств (на
пример, рессоры некоторых типов трамвайных вагонов), а так
же для возврата движущихся деталей в исходное положение
(например, клапанные пружины двигателей), для силоизмерения
(в динамометрах); в качестве устройств, аккумулирующих энер
гию (боевые пружины огнестрельного оружия), и элементов ре
гистрирующих и записывающих приборов.
По форме винтовые пружины делят на цилиндрические, ко
нические и фасонные. Здесь рассмотрим только расчет цилин
дрических винтовых пружин растяжения (рис. 5.20, а) и сжатия
(рис. 5.20,6), изготовленных из проволоки круглого поперечно
го сечения.
г
534
Расчет пружин растяжения и сжатия на прочность и жесткость
одинаков, но для пружин сжатия при H / D 5= 2,6 (Я —высота пружины
в свободном состоянии; D —ее средний диаметр) возникает опасность
потери устойчивости (выпучивания). Такие сравнительно высокие пру
жины монтируют в гильзах или на оправках, препятствующих выпучи
ванию пружин.
Угол наклона а витков пружины будем считать небольшим
(а < 15°); только при этом условии излагаемая ниже прибли
женная теория дает удовлетворительные результаты.
Рассечем виток пружины (рис. 5.20,6) плоскостью, проходя
щей через ее ось. Учитывая введенное ограничение, можем счи
тать, что это сечение является для витка поперечным, т. е.
принимаем а = 0 и рассматриваем пружину как бы состоящей
из колец, расположенных в плоскостях, перпендикулярных ее
продольной оси. Рассматривая условие равновесия отсеченной
части пружины, изображенной отдельно на рис. 5.20, в, заклю
чаем, что в поперечном сечении витка возникают два внутрен
них силовых фактора *: поперечная сила Q, —F и крутящий мо
мент M z = F ■0,5D.
Таким образом, в поперечном сечении витка возникают
только касательные напряжения. Для их определения введем
два допущения.
1. Касательные напряжения, связанные с наличием крутяще
го момента, определяются так же, как при кручении прямого
бруса круглого поперечного сечения. Эпюра этих напряжений
для точек горизонтального диаметра дана на рис. 5.21, а.
2. Касательные напряжения, связанные с наличием попереч
ной силы, распределены по сечению равномерно. Эпюра этих
напряжений дана на рис. 5.21,6.
Рис. 5.21
* Если учитывать угол наклона витка, получим четыре внутренних
силовых фактора:
N z = Fsiact;
Qs - F
cosa;
M = F 0 ,5 D sin a ;
M„ =
F
•0,5D cos a.
135
Суммируя касательные напряжения, возникающие в точках
горизонтального диаметра сечения витка, получаем результи
рующую эпюру, показанную на рис. 5.21, в.
Опасной, очевидно, оказывается точка А, ближайшая к оси
пружины.
Для этой точки имеем
^Л =
^m ax
^ A fz max 4 “ ^Qy
или, учитывая, что
= M J W p = 16F-0,50/(nd3) = %FD/ (nd3)
и
*Qy = Qy/A = 4F/(nd2),
получаем
ттах = 8FD/(nd3) + 4F/(nd2) = [HFD/(nd3)] [1 + d/(2D)l
(a)
Отношение среднего диаметра пружины D к диаметру про
волоки d обозначим
сп = D/d,
тогда взамен выражения (а) имеем
Тт ах = [ 8 ^ / М 3)][1 + 1/2сп].
(б)
Отношение сп называют индексом пружины; обычно сп =
= 5...12.
При указанных значениях сп второе слагаемое в скобках со
ставляет не более 0,1 от первого. Если пренебречь вторым сла
гаемым, т. е. учитывать лишь напряжения от кручения, прене
брегая напряжениями, соответствующими поперечной силе,
получится следующая приближенная формула:
ттахa 8F D /M 3).
(в)
Эта формула дает значение напряжения, меньшее действи
тельного, т. е. погрешность формулы идет не в запас прочно
сти расчета. Формула (в) приближенна не только из-за прене
брежения влиянием поперечной силы: более существенная
погрешность получается из-за того, что при ее выводе не учте
на кривизна витков. Действительно, распределение натяжений
от кручения принято без должных оснований таким же, как для
прямого бруса круглого сечения, а ось витков пружины пред
ставляет собой пространственную кривую —винтовую линию.
Исследования напряжений в пружинах, выполненные мето
дами теории упругости, позволяют уточнить значение ттах пу
136
тем введения в формулу (в) поправочного коэффициент!
зависящего от индекса пружины и угла подъема ее витков.
С учетом указанного коэффициента условие прочности пр>
жины можно записать в виде
SfD
(5Т ‘
Значения поправочного коэффициента к принимают по еле
дующим данным (без учета влияния угла а):
сп ..............................
к ..............................
2
1,37
5
1,29
6
1,24
8
1,17
10
1,14
12
1,11
Несколько менее точное, но вполне приемлемое для практи
ческих расчетов значение к получается по формуле
/с = (4сп + 1)/(4с„-4).
(5.28;
Пружины изготовляют из высококачественной стали, поэто
му допускаемые напряжения, принимаемые при их расчете
имеют весьма высокие значения: [т] = 200..Л000 МПа.
Выведем формулу для определения изменения высоты пру
жины под нагрузкой (для пружин сжатия эту величину назы
вают осадкой). Работа внешней статически приложенной силы
определяется по теореме Клапейрона
W = 0,5FX,
(I)
где F и X —конечные значения растягивающей (сжимающей)
силы и перемещения точки ее приложения (осадки пружины).
Эта работа равна энергии деформации пружины, которая
может быть вычислена по формуле (5.24):
V = М\1/ (2GJр).
(II)
Энергией, связанной с наличием поперечных сил, пренебре
гаем. В выражении (II) под I следует понимать полную длину
проволоки пружины I fa nDn, где п —число витков.
D
л dA
Учитывая, что М г —F — и Jp =
-, и приравнивая правые
32
части выражений (I) и (II), получаем
0,5FX = [(0,5-FD)2tlDm] /(2Gnd4/32)
или окончательно
Х = 8 F D 3n / ( G d %
(5-29)
137
Пользуясь понятием о коэффициенте жесткости, можно
представить формулу (5.29) в виде
X = F/C,
(5.29а)
где С = Gd4/ (8В ъп) —коэффициент жесткости пружины, численно
равный силе, вызывающей осадку, равную единице длины.
Если вместо коэффициента жесткости ввести величину, ему
обратную, —коэффициент податливости, то получим
X = рЕ,
■
(5.296)
где Р = 8D3n/(Grf4) —коэффициент податливости пружины, чис
ленно равный изменению ее высоты, вызываемому силой, рав
ной единице силы.
П р и м е р 5.5. Спроектировать цилиндрическую пружину сжатия
из проволоки круглого сечения, имеющую заданную рабочую характе
ристику (рис. 5.22, а).
При наибольшей нагрузке FK0H расчетное напряжение в пружине
не должно превышать допускаемого [т]= 4 3 0 МПа; принять с„ = 6.
Р е ш е н и е . Характеристикой пружины называют зависимость
между нагрузкой пружины и изменением ее высоты, задаваемую обыч
но в виде графика.
На рис. 5.22, б показана пружина в свободном состоянии (X = 0).
При установке в механизм пружина получает предварительную осадку
Хнач, соответствующую силе Fm4 = 200 Н. Предварительно сжатая
пружина показана на рис. 5.22, в. При работе механизма пружина до
полнительно сжимается на
Хр = 35 мм (Хр —рабочий
ход пружины). Пружина,
сжатая наибольшей рабочей
нагрузкой FKOH= 800 Н, пока
зана на рис. 5.22, г. При этой
нагрузке между витками
пружины имеются неболь
шие зазоры. Если увеличить
нагрузку до значения Епред,
то витки сомкнутся («сядут»
друг на друга) и при даль
нейшем увеличении нагрузки
пружина будет работать как
брус. Поскольку укорочение
такого бруса весьма мало
по сравнению с осадкой
пружины, можно считать,
что после посадки витков
дальнейшее возрастание на
грузки не вызовет увеличе
ния осадки, т. е. характери
стика при F > Faрад представ
ав
ляет собой прямую, параллельную оси ординат. Конечно, приведенны
рассуждения носят несколько отвлеченный характер, так как нагрузк
выше FКОд не должна допускаться.
Спроектировать пружину - это значит определить D, d и п. Тре
буемый диаметр проволоки определим из условия прочности пру
жины:
, =
fc-
BFKO„D
nd3 < м .
где fc = 1,24 (при с„ = 6 см с. 137).
Учитывая, что D/d = с„, получаем
, 8Тконсп г
■к----^—■<[!],
ltd2
откуда
I k8FK,
'1,24-8-800-6
=5,93-10" 3 м = 5,93 мм.
3,14-430- 10б
Принимаем d = 6 мм, тогда D = cnd = 6-6 = 36 мм.
Определяем число витков, учитывая, что приращению нагрузки
ДF = FK0H—Flm4 = 800 —200 = 600 Н соответствует возрастание осадки
на Хр = 35 мм:
Хр = 8AFD3n/(Gd4),
d>
"И
откуда
Gd4Xp
8 •104-106 •0,0064 •0,035
П~ 8AFD3 =
8 •600 •0,0363
= 16,2,
где принято G — 8 • 104 МПа.
Полное число витков пружины сжатия должно быть на
1,5—2 витка больше числа рабочих витков (полученного по расчету),
так как крайние витки, соприкасающиеся с опорными тарелками, прак
тически не участвуют в деформации пружины. В нашем случае можно
принять Иполн = 18. Учитывая, что высота спроектированной пружины
в свободном состоянии примерно в четыре раза больше ее среднего
диаметра, следует смонтировать пружину в гильзе или на оправке,
чтобы исключить опасность ее выпучивания (потери устойчивости).
Г л а в а VI
ГЕО М Е ТРИ Ч ЕС К И Е Х А РА К ТЕ РИ С ТИ К И
П Л О СК И Х СЕЧЕНИЙ
§ 6 .1 . С татические моменты плоских сечений
Рассмотренные в предыдущих главах расчеты на растяже
ние (сжатие) и кручение позволяют сделать вывод, что площадь
поперечного сечения бруса является геометрической характери
стикой его прочности и жесткости лишь при равномерном рас
139
пределении напряжений по поперечному сечению. При неравно
мерном распределении напряжений, имеющем место при
работе бруса на кручение, его прочность и жесткость зависят
от новой, более сложной геометрической характеристики —по
лярного момента инерции (для бруса круглого сечения).
Нетрудно убедиться, что в случае изгиба бруса площадь се
чения не может служить характеристикой его жесткости. Дей
ствительно, из двух брусьев (рис. 6.1) с равновеликими площа
дями поперечных сечений первый при данной нагрузке
деформируется значительно с и л ь н е е второго (например, при
h/b = 2 п р о г и б ы п е р в о г о б р у с а в четыре раза больше, чем
в т о р о го ).
Э т а гл а в а курса п освящ ен а о зн ако м л ен и ю со св о й ств ам и
и м ето д ам и вы числения сп ец и альн ы х геом етрических х ар ак те
р и с т и к п л о ск и х сечений, и с п о л ь зу е м ы х п р и р а с ч е т а х н а и зги б ,
н а и зги б с р ас тя ж ен и е м и в р я д е д р у ги х случаев.
В ы ч и с л е н и е э т и х х а р а к т е р и с т и к с в я з а н о с необходимостью
оп р ед ел ен и я к о о р д и н а т ц ен тр а тяж ести сечен и я; п р и эт о м
в расчетн ы е зави си м о сти вх о д ят геом етрически е х ар ак тер и сти
к и , н а з ы в а е м ы е статическими моментами се ч е н и я.
Статическим моментом плоского сечения (рис. 6.2) относи
тельно оси Ои называется взятая по всей площади сечения сумма
произведений площадей элементарных площадок на их расстоя
ние до этой оси, т. е.
S„ = f v d А.
А
А н алогично, статический
момент
сечен и я о т н о с и т е л ь н о оси
Ov
S„ = f и dA.
А
Статический момент имеет размерность L3.
В зависимости от положения оси, относительно которой вы
140
числяется статический момент, он может быть положительным,
отрицательным или равным нулю. При известных статических
моментах и цлощади сечения координаты его центра тяжести
определяются по формулам
uc = S J A ;
1
vc = S J A .
J
( 6. 1)
В случае известных координат центра тяжести статические
моменты определяют из выражений
Из формул (6.2) вытекает весьма важное для дальнейшего
следствие:
статический момент сечения относительно любой центральной
(проходящей через центр тяжести) оси равен нулю.
В тех случаях, когда сечение может быть разбито на про
стейшие составные части, площади и координаты центров тя
жести которых известны, положение центра тяжести всего сече
ния определяют по формулам
А 1и1 + А 2и2 +
A t + A 2+
+ А„ип _
...
+ А,
A ,vt + A 2 v 2 + ... +A„vn
А | + А2 + ... + Ал
’
(6.3)
где Л,, Л2, ..., Л„ —площади отдельных частей сечения, а ы,,
и2, ..., н„ и »|, v2, ..., «„ —координаты их центров тяжести.
Каждое из слагаемых, стоящих в числителе выражений (6.3),
141
представляет собой статиче
ский момент данной части
сечения относительно соот
ветствующей оси. На рис. 6.3
приведен пример разбив
ки сечения на простейшие
составные части.
Для сечений, составлен
ных из профилей стандарт
ного проката (например, для
сечения, изображенного на
рис. 6.4), площадь каждого
профиля и остальные необхо
димые для расчетов размеры
принимают по таблицам
ГОСТов
на
прокатную
сталь.
П Р нм ер 6.1. Определить
координаты центра тяжести
сечения, имеющего форму по
лукруга радиуса г (рис. 6.5).
Р е ш е н и е . Центр тяжести
находится на оси симметрии
O v , следовательно, надо найти
лишь одну координату v c .
Определим статический мо
мент сечения:
5„ = J v
dA.
А
Разобьем сечение на бес
конечно тонкие полоски шири
ной 2и и толщиной dp, кото
рые можно рассматривать как
элементарные прямоугольники, Toi
dA —
Выразим координаты и и р через радиус г и угол <р:
и = rcos<|>;
р = /-sirup;
dp найдем, взяв дифференциал правой части выражения для р:
dp = d(rsinq>) = rcoscpdrp.
После подстановки р и d A в выражение для
получаем
л/2
я/2
S„
и интегрирования
2
S„= | 2г cos sp(г cos (р) г sin (pdcp = 2/-3 J cos2 ф sin срdtp ==— г3,
о
о
3
142
Координату vc найдем по формуле (6.1):
»с =
~А~
2/3г3
4
я г 2/ 2
Зя
0,424т.
Этот результат полезно запомнить.
§ 6.2. Осевые и центробежные моменты инерции
плоских сечений
Осевым моментом инерции плоского сечения относительн
данной оси называется взятая по всей площади сечения сумм;
произведений площадей элементарных площадок на квадраты и:
расстояний до этой оси (рис. 6.6).
Из этого определения следует, что момент инерции относи
тельно оси Ох представляет собой определенный интеграл
Jx = j y 2dA.
А
Аналогично, момент инерции относительно оси Оу
J = j х 2 dА.
У к
Осевой (его иногда называют экваториальным) момент
инерции является величиной с у щ е с т в е н н о п о л о ж и
т е л ь н о й , так как независимо от знака координаты про
извольной площадки соответствующее слагаемое положитель
но, ибо в него входит квадрат этой координаты. Размерность
осевого момента инерции —L4.
Пользуясь рис. 6.6, установим связь между полярным
и осевыми моментами инерции сечения. По определению, Jp =
= J р2 dА, но р2 —у2 + х2, следовательно,
Jp = J р2 dA = J {у2 + x2)d А = J у2 &А + J х2 dА.
Окончательно
JP = Jx + Jr
(6.4)
Сумма осевых моментов
инерции относительно двух вза
имно перпендикулярных осей
равна полярному моменту инер
ции относительно точки пере
сечения этих осей (начала коор
динат).
143
При определении осевых моментов нерции в некоторых
случаях приходится встречаться с еще одой новой геометриче
ской характеристикой —центробежным мментом инерции.
Эта геометрическая характеристика приставляет собой взя
тую по всей площади сечения сумму произедений площадей эле
ментарных площадок на произведение к расстояний до двух
данных взаимно перпендикулярных осей:
J xy=SAXydA.
Центробежный момент инерции имет размерность L*.
В зависимости от расположения осей он южет быть как поло
жительным, так и отрицательным и в частных случаях равным
нулю.
§ 6.3. Главные оси и главные момгнты инерции
Оси, относительно которых центробеяный момент инерции
равен нулю, называют главными осями иногда их называют
главными осями инерции). Через любую точку, взятую в пло
скости сечения, можно провести в общем случае пару главных
осей (в некоторых частных случаях их м*жет быть бесчислен
ное множество). Для того чтобы убедиться в справедливости
этого утверждения, рассмотрим, как изменяется центробежный
момент инерции при повороте осей на 9*° (рис. 6.7). Для про
извольной площадки dA, взятой в первой квадранте системы
осей хОу, обе координаты, а следователыо, и их произведение
положительны. В новой системе координат х 1Оу1, повернутой
относительно первоначальной на 90°, произведение координат
рассматриваемой площадки отрицательно. Абсолютное значе
ние этого произведения не изменяется, г е. х у = —х1у1. Оче
видно, то же самое имеет место и для любой другой элемен
тарной площадки. Значит, и знак су'ммь: dAxy, представляю
щий собой центробежный момент инерции сечения, при
повороте осей на 90° меняется на противоположный, т. е. Jxy =
* ~ Jw
В процессе поворота осей центробежный момент инерции
изменяется непрерывно, следовательно, при некотором положе
нии осей он становится равным нулю. Эти оси и являются
главными.
Хотя мы и установили, что главные ося можно провести че
рез любую точку сечения, но практический интерес предста
вляют только те из них, которые проходят через центр тяжести
сечения — главные центральные оси. В дальнейшем, как прави144
У
х
Рис. 6.7
Рис. 6.8
ло, для краткости будем называть их просто главными осями,
опуская слово «центральные».
В общем случае сечения произвольной формы для определе
ния положения главных осей необходимо провести специальное
исследование. Здесь ограничимся рассмотрением частных слу
чаев сечений, имеющих по меньшей мере одну ось симметрии
(рис. 6.8).
Проведем через центр тяжести сечения ось Ох, перпендику
лярную оси симметрии Оу, и определим центробежный момент
инерции J xy. Воспользуемся известным из курса математики
свойством определенного интеграла (интеграл суммы равен
сумме интегралов) и представим Jxy в виде двух слагаемых:
J ху
J х у dA = f xydA + | xydA,
i,
A2
A
где A t и А2 — части сечения, расположенные соответственно
справа и слева от оси симметрии. Очевидно,
J xydA = — f xydA.
At
A2
так как для любой элементарной площадки, расположенной
справа от оси симметрии, есть соответствующая слева, для ко
торой произведение координат отличается лишь знаком.
Таким образом, центробежный момент инерции относитель
но осей Ох и Оу оказался равным нулю, т. е. это главные оси.
Итак, для нахождения главных осей симметричного сечении
достаточно найти положение его центра тяжести. О дной. из
главных центральных осей является ось симметрии, вторая ось
ей перпендикулярна.
145
Рис. 6.9
Конечно, приведенное доказательство остается в силе, если
ось, перпендикулярная оси симметрии, проходит и не через
центр тяжести сечения, т. е.
ось симметрии и любая, ей перпендикулярная, образуют
систему главных осей.
Нецентральные главные оси, как уже указывалось, интереса
не представляют.
Осевые моменты инерции относительно главных цен
тральных осей называют главными центральными (или сокра
щенно главными) моментами инерции. Относительно одной из
главных осей момент инерции м а к с и м а л е н , относительно
другой —м и н и м а л е н . Например, для сечения, изображен
ного на рис. 6.8, максимальным является момент инерции Jx
(относительно оси Ох). Конечно, говоря об экстремальности
главных моментов инерции, имеют в виду лишь их сравнение
с другими моментами инерции, вычисленными относительно
осей, проходящих через ту же точку сечения.
Таким образом, то обстоятельство, что один из главных моментов
инерции максимален, а другой —минимален, можно рассматривать
как объяснение того, что они (и соответствующие оси) называются
главными. Равенство же нулю центробежного момента инерции отно
сительно главных осей —удобный признак для их нахождения.
Некоторые типы сечений, например круг, квадрат, пра
вильный шестиугольник и др. (рис. 6.9), имеют бесчисленное
множество главных центральных осей. Для этих сечений любая
центральная ось является главной.
Не приводя доказательства, укажем, что,
в случае если два главных центральных момента инерции се
чения равны между собой, у этого сечення любая центральная
ось главная и все главные центральные моменты инерции
одинаковы.
§ 6.4. Зависимость между моментами инерции
относительно параллельных осей
Установим зависимость между осевыми моментами инер
ции относительно двух параллельных осей, из которых одна
центральная (рис. 6.10).
146
Пусть момент инерции JXo
относительно центральной оси,
площадь сечения А и расстоя
ние а между осями х0 и
известны.
Определим момент инерции
JXi. Расстояние от произволь
ной площадки dА до оси х 0
обозначим у0, а до оси х х обо
значим y t. По определению,
J Xl = I
у\ л а
.
А
По чертежу (рис. 6.10)
= у0 + а.
Подставляя значение у х в выражение доя J Xi, получим
Jх = j (у0 + a)2 dA = f yl 6.А + 2а f у0 dA + a2 i dA
А
А
Л
А
Учитывая, что, по определению, jy2 dA = J Xa и J у0 dA = SXo,
А
А
можем записать Jx = JXo + 2aSXo + а2А.
Ось х0, по условию, ц е н т р а л ь н а я , следовательно,
SХа
0.
Окончательно получим следующую формулу изменения мо
мента инерции при переходе от центральной оси к параллель
ной ей нецентральной:
JXi = J Xo + а2А.
(6.5)
Аналогично,
Jyi = Jyo + с2А.
(6.6)
Подчеркиваем, что
относительно любой нецентральной оси момент инерции боль
ше, чем относительно параллельной ей центральной.
§ 6.5. Моменты шерции некоторых
простейших сечений
1.
Круг и кольцо (рис. 6.11). Воспользуемся зависимостью
между полярным и осевыми моментами инерции
Jp^Jx + Jy
В данном случае в силу симметрии Jx —Jy, следовательно,
Jp = 2Jx = 2Jy
147
шш
J x ~ J y — J p /2-
Как известно, для круга Jp = jirf4/32 и для кольца Jp =
= (ltd4/32) (l - с4), где с = djd.
Таким образом, главные моменты инерции в рассматривае
мом случае могут определяться по следующим формулам:
для круга
Jx = J V= Kd4/64 « 0,05с/4;
(6.7)
для кольца
Jx = Jy = (тсс/4/64) (1 - с4) « 0,05с?4 (1 - с4).
(6.8)
2. Полукруг (рис. 6.12). Главными центральными осями
являются ось симметрии у и перпендикулярная ей ось х. Со
вершенно очевидно, что момент инерции полукруга Jy вдвое
меньше, чем момент инерции круга относительно той же оси:
J y = 0,5 (nd4/64) = тм'4/128 = л»-4/8.
(6.9)
То же значение имеет момент инерции относительно оси х ,:
J xt = J y = к г 4/ 8.
Воспользовавшись зависимостью (6.5) и найденным в при
мере 6.1 значением ординаты центра тяжести полукруга
ус « 0,424г, получим
J x = J Xl -
У2с А = ~
- 0,424V - ^
1 ,
или окончательно
Jx х 0,Пг4 да 0,00686d4.
(6.10)
3. Прямоугольник (рис. 6.13). Определим сначала момент
инерции J Xi относительно оси хх, совпадающей с основанием.
148
По определению,
JXl =$У21 dA.
А
Разобьем сечение на элементарные прямоугольники (по
лоски) шириной b и толщиной (высотой) dу и тогда dA = bdyt.
Подставляя значение dA в выражение для JXi и интегрируя,
получаем
h
rXi = J*y{b dyt
b У1 ; JXl=bh3/ 3.
( 6. 11)
Главный центральный момент инерции Jx найдем, приме
нив формулу (6.5):
Jх, —Jх А- и2А,
откуда
Jx = JX] - а2А.
В данном случае расстояние между осями а = й/2 и A = bh,
следовательно, Jx — Ыi3/3 —(к/2)2 bh, или окончательно
Jx = bh3/ 12.
Аналогично, момент инерции относительно оси у
= hb3/12.
(6-12)
(6.12а)
Вообще следует запомнить, что в выражение для момента
инерции прямоугольника размер стороны, перпендикулярной
рассматриваемой оси, входит в третьей степени. Для квадрата
со стороной Ь на основании формулы (6.12) имеем
Jx = Jy = b4/ 12.
(6.13)
4.
Треугольник (рис. 6.14). Вычислим сначала момент инер
ции JXi относительно оси хь совпадающей с основанием. Раз-
149
бивая сечение на элементарные полоски, как показано на
рис. 6.14, имеем dA = Ъх
и
JXl = f bxyl dj>t .
О
Из подобия треугольников АВС и А 1ВС1 получаем
K / { h - y 1) = b/h или Ьх = (b/h)(h - у х)а
Подставляя значение Ьх в выражение для J X
*1i и интегрируя,
находим
h
н
Л
-ф - y j y l d y ^ b
-
4
A il
h 4
у\ dyj - — yf d.yt
bh3
3
b h4
ft 4 ’
или окончательно
= bh3/12.
(6.14)
Момент инерции относительно центральной оси х найдем,
применив формулу (6.5):
Jx = JXt~ a 2A.
В данном случае а = 6/3 и А = (1/2)bh;
Jx = bh3/12 —(ft/3)2 (1/2) bh,
или
Jx = bh3/36.
(6.15)
Обращаем внимание, что для
произвольного треугольника ось х
не является главной.
Для равнобедренного треуголь
ника (рис. 6.15) оси х и у главные,
так как ось у является осью сим
метрии. Главный момент инерции
Jx вычисляется по формуле (6.15).
Момент инерции Jy найдем, приме
няя формулу (6.14) и рассматривая
сечение как сумму двух прямоуголь
ных треугольников с катетами h
и Ь/2, причем катет Ъ/2 перпендику
150
лярен рассматриваемой оси. Подчеркиваем, что для каждого
из этих треугольников ось у совпадает с основанием и тогда
J„ —2h (b/2)3/12,
или
Jy = hb3/ 4 8 .
(6.16)
§ 6.6. Вычисление моментов инерции составных
сечений, имеющих ось симметрии
Главные центральные моменты инерции простейших сече
ний вычисляют по готовым формулам, наиболее распростра
ненные из которых приведены в предыдущем параграфе. Раз
меры и геометрические характеристики профилей стандартного
проката приведены в таблицах ГОСТа.
Для вычисления главных моментов инерции сложных (со
ставных) сечений их разбивают на простейшие части, моменты
инерции которых определяют по готовым формулам или та
блицам. Дальнейший расчет ведут в следующем порядке (попрежнему ограничиваемся сечениями, имеющими не менее
одной оси симметрии).
1. Определяют положение центра тяжести сечения, а следо
вательно, и главных центральных осей.
2. Вычисляют (или берут из таблиц) значения моментов
инерции отдельных частей сечения относительно собственных
центральных осей, параллельных главным центральным осям
в с е г о сечения.
3. Вычисляют моменты инерции частей, составляющих сече
ние, относительно его главных центральных осей. При этом ис
пользуют зависимость между моментами инерции относитель
но параллельных осей [см. формулу (6.5)].
4. Определяют главные центральные моменты инерции все
го сечения путем суммирования для каждой из главных осей
величин, вычисленных в п. 3.
Таким образом, при вычислении моментов инерции со
ставных сечений руководствуются следующим правилом:
момент инерции сечения относительно данной оси равен сумме
моментов инерции составляющих это сечение частей относитель
но той же оси.
Это правило вытекает из известного свойства определенно
го интеграла: интеграл суммы нескольких слагаемых равен
сумме интегралов этих слагаемых.
В ответственных случаях во избежание ошибок при вычис
лении главных моментов инерции составных сечений следует
151
определять их дважды, разбивая сечение на составные части
различными способами. Совпадение результатов расчетов, вы
полненных при различных разбивках сечения, является гаран
тией правильности решения.
П р и м е р 6.2. Определить главные центральные моменты инер
ции таврового сечения, изображенного на рис. 6.16.
Р е ш е н и е . 1. Определяем положение центра тяжести сечения,
разбивая его на два прямоугольника:
A xvx + A2v2
1,5-12-6+ 3-12-13',5
= 11 см.
А 1 + А2
1,5-12 + 3-12
Оси х и у —главные центральные оси сечения.
2. Вычисляем моменты инерции каждого из прямоугольников от
носительно с о б с т в е н н ы х центральных осей:
= ЬхкЦ12 = 1,5 • 12э/12 = 216 см4;
M i/1 2 = 12 • 1,53/12 = 3,38 см4;
= М1/12 = 12 ■3712 = 27 см4;
J) =
Л 1 = Ъ2ЬЦП = 3 • 12712 = 432 см4.
3.
Вычислим моменты инерции каждого из прямоугольников от
носительно главной оси х:
для прямоугольника 1
где ах = vc —vx = 11 —6 = 5 см —расстояние между осями х и хх;
J l = 216 + 52• 12-1,5 = 666 см4;
для прямоугольника II
lll = j l + aU 2,
где а2 = v2 —vc = 13,5 —11 = 2,5 см —расстояние между осями х и х2;
J “ = 27 + 2,52 • 12 • 3 = 252 см4.
4. Вычисляем главные моменты инерции сечения:
Jx = j\ +
j “ = 666 + 252 = 918 см4;
Jy = J] + j “ = 3,38 + 432 = 435 см4.
Главная ось у совпадает с центральными осями составляющих
прямоугольников, поэтому при вычислении Jy не понадобилось ис
пользовать зависимость между моментами инерции относительно па
раллельных осей.
П р и м е р 6.3. Определить максимальный главный центральный
момент инерции заданного сечения (рис. 6.17).
Р е ш е н и е . Сечение имеет две оси симметрии, которые и являют
ся главными центральными осями. Очевидно, максимален момент
инерции относительно оси х. Сечение рассматриваем как состоящее из
152
v
у
Ь2~-/20
.
tT
§
S? II
^
II
'2
Рис. 6.16
вертикальной полосы 1, двух горизонтальных полос II и четырех не
равнобоких уголков III.
1. Определяем моменты инерции частей сечения относительно
собственных центральных осей, параллельных главной оси х :
для полосы I
j'Xi = 1,0- 40712 = 5330 см4;
для полосы II
J " = 18 ■1,6712 = 6,14 см4;
для угонка III по таблице ГОСТ 8510 —72
7™ = 47,1 см4.
Заметим, что в таблице ГОСТа этот момент инерции обозначен
./у Вообще при пользовании таблицами ГОСТа необходимо весьма
внимательно следить за правильностью выбора требуемых характери
стик, ни в коем случае не основываясь на формальном совпадении
индексов.
2. Определяем моменты инерции частей сечения относительно оси
.х;
j'x ~ J lx2 — 5330 см4 (оси х и X] совпадают);
J* =
+ “2Л 2 = 6,14 + 20,82 • 1,6 = 12 460 см4.
Моментом инерции горизонтальной полосы относительно оси
(собственной центральной оси), конечно, пренебрегаем, так как он весь
ма мал по сравнению со слагаемым а\Аг \
j l ” = J » 1 + а]А3 = 47,1 + 18,422 • 15,5 = 5310 см4.
Площадь сечения и положение центра тяжести (см. размер
15,8 мм на рис. 6.17) взяты по табл, ГОСТ 8510—72.
153
3.
Определяем момент
инерции Jx:
Jx = J rx + 2J’1 + 4 j'“ =
= 5330 + 2- 12 460 + 4-5310 =
= 51 490 см4.
Для проверки можно ре
шить задачу, разбивая каж
дый прокатный уголок на
два прямоугольника. Рас
хождение (за счет пренебре
жения закруглениями полок)
в результате первого и вто
рого решений не свыше 5 %
укажет на правильность то
го и другого решений.
П р и м е р 6.4. Определить главные центральные моменты инер
ции заданного сечения (рис. 6.18). Выбрать расстояние с из условия,
чтобы все центральные оси сечения были главными.
Р е ш е н и е . Равенство главных моментов инерции относительно
осей х и у является условием, при котором все центральные оси будут
главными (см. с. 146). Момент инерции относительно оси х не зависит
от расстояния с. Определим его значение:
Jx = 2Jl + 2JlJ ,
где j[ = 304 см4 —момент инерции швеллера (по ГОСТ 8240—72) и
j'J — момент инерции полосы;
Jx = 2-304 + 2(16-1,03/12) + 6,52- 16-1,0 = 1962 см4.
Момент инерции относительно оси у
Jy = 2Ji + 2JI' = 2 (J'n + а2А,) + 2./'' =
= 2 (31,2 + а2 • 13,3) + 2 (1,0 - 163/12) = 745 + 26,6а2.
Здесь Jy[ = 31,2 см4 —момент инерции швеллера относительно соб
ственной центральной оси yt ; AL= 13,3 см2 —площадь швеллера.
Приравнивая значения Jх и Jy, получаем
1962 = 745 + 26,6а2,
откуда
а = (/(1962 - 745)/26,6 = 6,89 см.
По чертежу имеем
с/2 = a - z0
с = 2а - 2z0 = 2 •6,89 - 2 • 1,54 = 10,7 см.
154
Г л а в а VII
П Р Я М О Й И ЗГИ Б
§ 7.1. Основные понятия и определения
И з г и б —это такой вид деформации бруса, при котором
в его поперечных сечениях возникают изгибающие моменты.
В большинстве случаев одновременно с изгибающими момен
тами возникают и поперечные силы; такой изгиб называют по
перечным; если поперечные силы не возникают, изгиб назы
вают чистым.
С геометрической точки зрения изгиб характеризуется тем,
что ось бруса, прямолинейная до деформации, при изгибе ста
новится кривой линией (условно говорят —изогнутая ось бру
са). Для кривого бруса изгиб связан с изменением кривизны его
оси.
Деформация изгиба возникает при нагружении бруса сила
ми, действующими в плоскостях, проходящих через его про
дольную ось, и перпендикулярными этой оси, и парами сил,
действующими в тех же плоскостях. В случае если все нагрузки,
а следовательно, и реакции связей действуют в о д н о й пло
скости, изгиб называют плоским.
Ограничимся рассмотрением брусьев, поперечные сечения
155
которых имеют по меньшей мере одну ось симметрии. Как из
вестно, ось симметрии и перпендикулярная ей центральная ось
являются главными центральными осями сечения. Плоскость,
проходящая через продольную ось бруса и одну из главных
центральных осей его поперечного сечения, называют главной
плоскостью бруса.
В случае, если силовая плоскость, т. е. плоскость действия
нагрузок, совпадает с одной из главных плоскостей (рис. 7.1),
имеет место прямой изгиб бруса. Линию пересечения силовой
плоскости с плоскостью поперечного сечения бруса называют
силовой линией; из сказанного следует, что при прямом изгибе
она совпадает с одной из главных центральных осей попереч
ного сечения.
При прямом изгибе деформация происходит в силовой плоско
сти, т. е. в этой плоскости располагается ось изогнутого бруса.
Если силовая плоскость не совпадает ни с одной из главных
плоскостей бруса (рис. 7.2) или, что то же самое, силовая линия
не совпадает ни с одной из главных центральных осей его по
перечного сечения, изгиб называют косым. Такое название
объясняется тем, что при этом виде изгиба ось изогнутого бру
са не лежит в силовой плоскости. Брус изгибается «косо» в том
смысле, что направления нагрузок и прогибов не совпадают.
156
убеждаемся, что в общем случае прямого изгиба в поперечных
сечениях бруса возникают два внутренних силовых фактора:
поперечная сила Qy и изгибающий момент Мх.
Действительно, внешние силы лежат в плоскости zOy и при
этом перпендикулярны оси Oz, следовательно, их проекции на
оси Ох и Oz, так же как моменты относительно осей Оу и Oz,
равны нулю (см. выше § 1.4). Конечно, в частном случае может
оказаться, что внешние силы, приложенные по одну сторону от
рассматриваемого сечения, приводятся к паре сил, т. е. попе
речная сила Qy равна нулю, и в поперечном сечении возникает
только изгибающий момент М х. Как указано выше, такой из
гиб называют чистым; в рассматриваемом случае —чистым
прямым изгибом. Общий случай прямого изгиба, при котором
и изгибающий момент, и поперечная сила не равны нулю, бу
дем называть поперечным прямым изгибом.
Достаточно очевидно и подтверждается опытом, что брус
при изгибе деформируется таким образом, что часть его воло
кон испытывает растяжение, а часть —сжатие. Волокна, распо
ложенные в выпуклой части изогнутого бруса, растягиваются,
а в вогнутой —сжимаются (рис. 7.4). Границей между областя
ми растяжения и сжатия является слой волокон, который лишь
искривляется, не испытывая
при этом ни растяжения,
ни сжатия. Это так называе
мый нейтральный слой. Ли
ния пересечения нейтрально
го слоя с плоскостью по
перечного сечения бруса на
зывается нейтральной осью
или нулевой линией (см.
рис. 7.1 и 7.4).
Рис. 7.4
157
а)
в)
Консоль
ч
Рис. 7.5
Брусья, работающие на прямой изгиб, принято называть
балками. Схемы основных типов статически определимых ба
лок показаны на рис, 7.5: а — простая консоль; б —двухопор
ная балка без консолей; в —двухопорная балка с одной кон
солью; г —двухопорная балка с двумя консолями. Расстояние
между опорами балки называют пролетом, а длину балки, за
щемленной одним концом (рис. 7.5, а), иногда называют выле
том. Консолью называют часть балки, расположенную по одну
сторону от опор (рис. 7.5,е, г).
§ 7.2. Поперечные силы и изгибающие моменты
В предыдущем параграфе было установлено, что при пря
мом поперечном изгибе в поперечных сечениях бруса (балки)
возникают два внутренних силовых фактора: поперечная
сила Qy и изгибающий момент М х. Зависимости между этими
внутренними силовыми факторами и напряжениями в попереч
ном сечении бруса (см. § 1.5) таковы:
Q*= K-yd/l; M x = l a zyAA.
Следовательно, в поперечных сечениях бруса в рассматри
ваемом случае изгиба возникают как касательные, так и нор
мальные напряжения.
Приведенные зависимости позволяют дать следующие
определения поперечной силы и изгибающего момента:
Поперечной силой Qy называется равнодействующая внутрен
них касательных сил, возникающих в поперечном сечении бру
са*.
Изгибающим моментом Мх называется результирующий мо
мент внутренних нормальных сил, возникающих в поперечном се
чении бруса, взятый относительно нейтральной оси этого сечения.
* В более общем случае нагружения бруса, например при попереч
ном косом изгибе, равнодействующая внутренних касательных сил
упругости дает две составляющие: Qy и Qx.
158
Конечно, приведенные зависимости между Qy и Мх и напря
жениями не могут быть использованы для вычисления попе
речных сил и изгибающих моментов. Их определяют с по
мощью метода сечений через действующие на брус внешние
силы.
Так же как при изучении растяжения (сжатия) и кручения,
для наиболее наглядного представления о характере изменения
внутренних силовых факторов (Qy и Мх) по длине бруса и для
нахождения его предположительно опасных сечений строят со
ответствующие графики —эпюры поперечных сил и изгибающих
моментов.
Учитывая, что при прямом поперечном изгибе все внешние
силы расположены в одной плоскости, при определении вну
тренних силовых факторов нет надобности прибегать к аксоно
метрическим изображениям, применявшимся в предыдущем
параграфе.
Брус (балку) изображают одной линией, к которой прило
жены заданные нагрузки. Эта линия представляет собой про
дольную ось бруса.
Рассмотрим двухопорную балку, изображенную на
рис. 7.6, а. Будем считать, что опорные реакции известны —они
определяются из двух уравнений равновесия, составленных для
балки в целом. Применим метод сечений и рассмотрим усло
вие равновесия левой отсеченной части балки, показанной от
дельно на рис. 7.6, б. В проведенном поперечном сечении возни
кают два внутренних силовых фактора (Qy и M J, заменяющих
действие отброшенной части балки на оставленную. Конечно,
в том же сечении, но принадлежащем отброшенной части
(рис. 7.6, в), возникают такие же по значению, но противопоа)
тттгггпшш
b
1
а
6)
ШУ
М-г
ш
ж
зягэ*
в)
м*
1
р’qzл1. ) ( ( т
'1
a-z
Рис. 7.6
159
ложно направленные поперечная сила и изгибающий момент
(см. также рис. 1.24).
Внешние и внутренние силы, приложенные к оставленной
части бруса, образуют плоскую систему параллельных сил, для
которой, как известно, статика дает два уравнения равновесия.
Составим эти уравнения. Возьмем сумму проекций на ось,
параллельную силам, й сумму моментов относительно той точ
ки продольной оси, через которую проходит проведенное
сечение:
£ У = 0; R .A —qz —Qy = О,
откуда
Qy = RA- q z ;
£ М к = 0; R a z —qz (z/2) - М х = О,
откуда
Мх =
R az
-
qz2j l .
Здесь при определении проекции сил на ось Qy и момента
относительно точки К той части распределенной нагрузки, ко
торая действует на оставленную часть бруса, были применены
известные теоремы статики о проекции и моменте равнодей
ствующей.
Обобщая полученные результаты на все случаи прямого по
перечного изгиба, приходим к следующим правилам для вычис
ления поперечных сил и изгибающих моментов.
Поперечная сила Qy в произвольном поперечном сечении бруса
численно равна алгебраической сумме внешних сил, приложенных
к его отсеченной части.
Изгибающий момент М х в произвольном поперечном сечении
бруса численно равен алгебраической сумме моментов всех внеш
них сил, приложенных к отсеченной части, относительно той точ
ки продольной оси бруса, через которую проходит рассматривае
мое сечение.
Эти правила вычисления Q y и М х относятся к рассматриваемому
в настоящей главе случаю прямого поперечного изгиба; в более об
щем случае нагружения бруса для их определения надо составлять со
ответствующие уравнения равновесия. Так, в частности, при вычисле
нии Q y в общем случае берется не сумма сил, приложенных
к отсеченной части, а сумма их проекций на ось О у .
Таким образом, мы сначала дали определения поперечной
силы и изгибающего момента, раскрывающие физическую сущ
ность этих понятий, а затем установили практические правила
для их вычисления по заданным внешним силам.
160
6)
Рис. 7.7
Для определенности при построении эпюр поперечных сил
и изгибающих моментов установим для них правила знаков.
На рис. 7.7, а показаны бесконечно малый элемент, выре
занный из балки, и возможные направления поперечных сил
в его торцовых (поперечных) сечениях. Поперечные силы счи
таются положительными, если они стремятся повернуть элемент
по часовой стрелке.
Знак изгибающего момента связан с характером деформа
ции бруса:
изгибающий момент считается положительным, если элемент
бруса изгибается выпуклостью вниз (рис. 7.7,6), т. е. таким
образом, что его сжатые волокна находятся з верхней части.
Положительные ординаты эпюры изгибающих моментов
будем откладывать вверх от оси абсцисс, т. е. в сторону
сжатых волокон балки, поэтому указанное правило знаков для
Мх часто называют правилом сжатого волокна.
Практически при построении эпюр удобнее устанавливать
знаки Qy и Мх по внешним силам; при этом результат должен
быть одинаков с получаемым при определении знаков непос
редственно по внутренним силам.
Совпадение результатов получится при применении следую
щих правил.
Внешняя сила, стремящаяся повернуть отсеченную часть бал
ки по часовой стрелке вокруг той точки оси, которая соответ
ствует проведенному сечению, вызывает положительную попереч
ную силу.
Применяя, например, это правило к балке (рис. 7.6) и рас
сматривая левую отсеченную часть (см. рис. 7.6,6), заключаем,
что R a дает положительную, а сила qz (равнодействующая той
части распределенной нагрузки, которая приложена к оставлен
ной части) —отрицательную поперечную силу в сечении К. Ес
ли рассматривать правую отсеченную часть (см. рис. 7.6, в), сле
дует считать, что сила Кв дает отрицательную, а силы F и
q(a —z) —положительные поперечные силы. Конечно, значение
Qy получится по абсолютному значению и по знаку тем же
самым, что и при рассмотрении левой отсеченной части.
6 Г. М. Ицкович
161
Для определения знака изгибающего момента следует во
образить отсеченную часть балки защемленной в проведенном
сечении.
Внешняя сила (момент), изгибающая эту часть выпуклостью
вниз, т. е. таким образом, что сжатые волокна находятся сверху,
дает положительный изгибающий момент.
Поясним это правило на примере той же балки (см.
рис. 7.6). Рассматривая левую отсеченную часть и представляя
ее защемленной в сечении К, заключаем, что сила R a дает по
ложительный изгибающий момент, так как изгибает рассма
триваемую часть балки выпуклостью вниз (рис. 7.8, а). Распре
деленная нагрузка изгибает эту часть выпуклостью вверх
(рис. 7.8,6), т. е. дает отрицательный изгибающий момент.
Подчеркнем, что, рассматривая отсеченную часть балки за
щемленной в том сечении, где определяется изгибающий мо
мент, мы освобождаем ее от всех фактически существующих
опорных закреплений.
Таким образом, подставляя в алгебраические суммы, даю
щие значения Qy и М„ каждое из слагаемых со своим знаком,
устанавливаем не только абсолютные значения, но и знаки ис
комых внутренних силовых факторов.
Следует иметь в виду, что при принятом правиле знаков
внешние силы, направленные вверх, всегда, т. е. независимо от
того, приложены ли они к левой или к правой отсеченной части
балки, дают положительный изгибающий момент.
Рассмотрим ряд простейших примеров построения эпюр
поперечных сил и изгибающих моментов.
Пр и м е р 7.1. Построить эпюры Q} и М х для балки, защемлен
ной одним концом и нагруженной на свободном конце парой сил с мо
ментом М (рис. 7.9, а).
Р е ш е н и е . Проведем произвольное поперечное сечение на рас
стоянии г от свободного конца балки и рассмотрим условие равнове
сия левой отсеченной части, изображенной отдельно на рис. 7.9,6. Оче
видно, поперечная сила Qy равна нулю, так как нагрузка (внешние
силы), приложенная к оставленной части, представляет собой пару сил,
которая, как известно, ни на одну ось проекции не дает. Следователь
но, балка работает на ч и с т ы й и з г и б .
162
мл = п
a) F
5)
*
If
г
\р
* i
мх
Эпюре Qy
Т
Ь)
;
F
Эпюр а Мх
щщЬ
Рис. 7.9
Рис. 7.10
Изгибающий момент Мх равен по абсолютному значению внеш
нему моменту:
МХ= М.
От координаты z значение Мх не зависит, т. е. Мх одинаков во
всех поперечных сечениях балки. Балка изгибается выпуклостью вниз,
следовательно, Мх > 0.
При применении метода сечений была оставлена часть балки, при
мыкающая к свободному концу; если оставить правую часть балки, то
предварительно (до применения метода сечений) следует определить
реакции заделки. В этом нет необходимости. Поэтому для балок, за
щемленных одним концом, проводя сечение, целесообразно отбрасы
вать ту часть, которая примыкает к заделке. При этом значения реак
ций получатся, так сказать, «автоматически», так как очевидно, что Qf
и М х в сечении заделки равны соответственно реактивной силе и реак
тивному моменту; в нашем случае МА = М (рис. 7.9, а). Эпюры Qy и
Мх даны на рис. 7.9, в.
П р и м е р 7.2. Построить эпюры Qy и Мх для балки, изображен
ной на рис. 7.10, а.
Р е ш е н и е , Проводим сечение на расстоянии z от свободного
конца балки и рассматриваем левую отсеченную часть (рис. 7.10,6).
К этой части приложена только одна внешняя сила F, стремящаяся по
вернуть ее вокруг точки К против часовой стрелки, следовательно,
Qy = —F, т. е. поперечная сила во всех сечениях одинакова (не зависит
от координаты z).
Мысленно защемляя оставленную часть балки в сечении К, за
ключаем, что сила F изгибает ее выпуклостью вверх, т. е. изгибающий
момент отрицателен. Он численно равен моменту силы F относитель
но точки К:
Mx = - F z .
163
Следовательно, изгибающий момент изменяется вдоль балки по
линейному закону (координата z входит в выражение Мх в первой
степени) от нулевого значения на свободном конце до наибольшего
значения М хтах— —FI в заделке. Эгаоры Qy и Мх даны на рис. 7.10, в.
П р и м е р 7.3. Построить эпюры Qy и Мх для балки, изображен
ной на рис. 7.11, а .
Р е ш е н и е . Поперечная сила в произвольном поперечном сече
нии, отстоящем на расстоянии z от свободного конца (рис. 7.11,6), чис
ленно равна сумме внешних сил, приложенных к оставленной части,
т. е. их равнодействующей qz. Изгибающий момент в том же сечении
равен сумме моментов внешних сил относительно точки К, т. е. (по
теореме Вариньона) равен моменту их равнодействующей qz, линия
действия которой проходит по середине отрезка г; поперечная сила
и изгибающий момент в рассматриваемом случае отрицательны:
Qy = ~ q z ; Mx = - q z 2/ 2.
Таким образом, поперечная сила изменяется вдоль балки по ли
нейному закону, а изгибающий момент —по квадратичному, т. е. эпю
ра М х —парабола с вершиной на левом конце балки. Для построения
эпюры Qy достаточно найти ее ординаты в двух сечениях при г = 0
и при z = 1: при z = 0 Q — 0, при г = / Оу= - q l .
Для построения эпюры Мх следует определить три-четыре ее
ординаты.
При z = 0 Мх = 0, при z = 1/2 М х = —q ( l / 2 f / 2 = - q l 2/K: при z = /
М х = - ql2/2.
Эпюры Qy и Мх п о к а з а н ы на рис. 7.11, в.
П р и м е р 7.4. Построить эпюры Qy и Мх для балки, изображен
ной на рис. 7.12, а.
164
Решение.
О п р е д е л я е м р е ак ц и и . В с и л у с и м м е т р и и
R
a
= R
b
= F/2.
Б у д е м н а з ы в а т ь у ч а с т к о м б а л к и ее ч а с т ь , в п р е д е л а х к о т о р о й з а
к о н ы и з м е н е н и я к ак п о п е р е ч н о й с и л ы , т а к и и з г и б а ю щ е г о м о м е н т а
о с т а ю т с я п о с т о я н н ы м и . Г р а н и ц а м и у ч а с т к о в я в л я ю т с я сеч ен и я, в к о
т о р ы х п р и л о ж е н ы в н е ш н и е (а к т и в н ы е и л и р е а к т и в н ы е ) с о с р е д о т о
ч е н н ы е с и л ы и л и м о м е н т ы , а т а к ж е сеч ен и я, г д е н а ч и н а е т с я и л и к о н
чается р асп р едел ен н ая н агр у зка. Р а с см а тр и в а ем а я б ал к а и м еет два
у частка: д л я пер во го у частка 0 < z ; g 0 ,5 / , д л я в то р о го 0
П р о в о д я сеч ен и е н а п е р в о м у ч а с тк е и р а с с м а т р и в а я л е в у ю о т с е
ч е н н у ю ч а с т ь (рис. 7 .12,6), п о л у ч а е м :
Q yl
=
R
a
= F /2 ;
M xl = R
az
= (F /2 ) z.
Д л я в то р о го участка балки, л евая отсеченная часть к о то р о й п о к а
з а н а н а ри с. 7.12, в, и м е е м
Q y ll = R
M xU
=
R
az
a
~ F = F /2
— F ( z — 1/2)
=
- F = -F /2 ;
F z /2
-
F
(z -
1/2).
Т а к и м о б р а з о м , п о п е р е ч н а я сила в п р е д е л а х к а ж д о г о из у ч а с т к о в
п о с т о я н н а , а и з г и б а ю щ и й момент и з м е н я е т с я п о л и н е й н о м у за к о н у
(рис. 7 Л 2 , г , д ) .
Н а и б о л ь ш и й и з г и б а ю щ и й момент п о л у ч а е т с я в среднем сечении
п р и z = 0 ,5 1.
Обращаем внимание, ч т о под сосредоточенной силой (сечение С )
на эпюре Qy п о л у ч а е т с я скачок, равный этой силе. В сечении, взятом
бесконечно близко слева от С , Q y c = + F/2, а бесконечно близко спра
ва от С,
= —F/2. Конечно, этот скачок носит условный характер,
так как само понятие сосредоточенной силы является условным, вве
денным лишь для удобства расчетов. Фактически сила F распределена
по некоторой небольшой части балки, в пределах которой поперечная
сила изменяется от значения +F/2 до —F/2, т. е. эпюра Qy на весьма
малом участке в окрестности точки С проходит через нулевое значение
(рис. 7.13). При этом не представляется возможным установить закон
изменения поперечной силы на этом малом участке, и условно совме
щая сечения / —/ и I I —I I , получают на эпюре скачок.
Разумеется, все сказанное в полной мере относится к встречав
шимся ранее скачкам на эпюрах продольных сил и крутящих мо
ментов.
П р и м е р 7 .5 . Построить эпюры Qy и М х для двухопорной балки,
изображенной на рис. 7.14, а.
Р е ш е н и е . Определяем опорные реакции. В данном случае это
можно сделать, не составляя уравнений равновесия. Действительно,к балке приложена пара сил, следовательно, и реакции должны образо
вать пару сил с тем же по значению, но противоположно напра
вленным моментом, т. е.
R a = R b = M/1.
165
0K R . M
М“а~ 1
I
м г ■> я
1
с
Ъ
в
' К
г
ш
1 * 2 .
1
^
51
Эпн \ра Иц
................. М
г
Эпюра мх
м
v?|
^ттШТПТ
т
Рис. 7.14
Балка имеет два участка. В произвольном сечении первого участ
ка*, т. е. при O ^ z ^ l / 2 :
Qyl — R a = M /l;
M xi
= R Az = M z/l.
Следовательно, поперечная сила постоянна, а изгибающий момент
меняется по линейному закону от нуля до М /2 . Для произвольного се
чения на втором участке, выражая Qyц и М хц через внешние силы, при
ложенные слева от сечения, получим:
Q yн = йд
= M /l;
M xU
=R a z
- M
=
M z/l
-
М.
При z = 1/2
М "£
= Ml/21 - М = - М/2,
а при z = /
М хВ =
Ml/l - М = 0.
Обращаем внимание на то, что там, где к балке приложен внеш
ний сосредоточенный момент, на эпюре М х получается скачок, эквива
лентный этому моменту (рис. 7.14,6), а на эпюре Qs это не отражается.
В предыдущем примере достаточно подробно был разъяснен во
прос об условности скачков, получающихся на эпюре поперечных сил.
Приведенные там рассуждения в полной мере применимы и к настоя
щему случаю, так как понятие сосредоточенного момента также услов
но, как и понятие сосредоточенной силы.
* Начиная с этого примера, как правило, отсеченную часть от
дельно показывать не будем; тем не менее рекомендуем учащемуся
при самостоятельном решении задач, пока не будут приобретены до
статочные навыки построения эпюр Qy и М х, обязательно изображать
отсеченную часть отдельно.
166
§ 7.3. Дифференциальные зависимости между
интенсивностью распределенной нагрузки,
поперечной силой и изгибающим моментом
Построение эпюр поперечных сил и изгибающих моментов
существенно упрощается при использовании дифференци
альных зависимостей между интенсивностью распределенной
нагрузки q, поперечной силой Qy и изгибающим моментом Мх.
Для вывода этих зависимостей выделим из балки (рис.
7.15, а) двумя поперечными сечениями, расстояние между ко
торыми равно dz, бесконечно малый элемент. Этот элемент
в крупном масштабе показан отдельно на рис. 7.15,6. Действие
левой и правой отброшенных частей балки на выделенный эле
мент заменяем поперечными силами и изгибающими момента
ми, возникающими в соответствующих сечениях. Так как выде
ленный элемент бесконечно мал и в его п р е д е л а х к балке не
п р и л о ж е н о в н е ш н и х со ср е д о то ч е н н ы х сил в м о м е н то в , значения
поперечных сил и изгибающих моментов в сечениях I — I
и II — II могут различаться лишь на б е ск о н е ч н о малые вели
чины.
Пусть в сечении I — I поперечная сила и изгибающий мо
мент равны соответственно Qy и Мх, а в сечении II —II —Qy +
+ dQy и Мх + dМх. Составим уравнения равновесия для выде
ленного элемента.
Проецируя все силы на вертикальную ось, получаем Qy +
+ q d z - ( Q y + dQy) = 0, откуда
d S y / d z = q.
(7.1)
Это и есть первая из дифференциальных зависимостей. Та
ким образом,
167
производная от поперечной силы по длине балки равна интен
сивности распределенной нагрузки.
Составляя сумму моментов относительно точки К, полу
чаем
Мх + Qydz + (q dz) (dz/2) - (Mx + dM J = 0.
Пренебрегая q(dz)2/2 как бесконечно малой высшего поряд
ка, имеем
d M J d z = Qy
(7.2)
Итак, получена вторая дифференциальная зависимость:
производная от изгибающего момента по длине балки равна
поперечной силе.
Из зависимостей (7.1) и (7.2) следует, что
интенсивность распределенной нагрузки равна второй про
изводной от изгибающего момента по длине балки:
d 2M Jd z 2 = q.
(7.3)
§ 7 .4 . Общ ие указания к построению эпюр
поперечных сил и изгибаю щ их моментов
Поперечные силы и изгибающие моменты являются функ
циями абсцисс поперечных сечений балки. В § 7.2, применяя ме
тод сечений, мы сначала составляли аналитические выражения
этих функций, а затем по полученным уравнениям строили со
ответствующие графики, т. е. эпюры поперечных сил и изги
бающих моментов. Для простейших примеров такой путь при
водил к цели достаточно быстро. В более сложных случаях
значительно целесообразнее строить эпюры, вычисляя значения
е Уи мх только для сечений, совпадающих с границами участ
ков, и лишь в отдельных случаях определяя некоторые проме
жуточные значения.
Ниже приводится ряд правил, используемых при таком спо
собе построения эпюр (по характерным точкам). Одни из них
являются следствиями из дифференциальных зависимостей ме
жду Чу Qy и ^ ху Другие вытекают непосредственно из метода
сечений.
1.
Если на некотором участке балки отсутствует распреде
ленная нагрузка, то эпюра Qy — прямая, параллельная оси абс
цисс, т. е. Qy = const. Действительно, q —dQyjdz, а в рассматри
ваемом случае производная q = 0, следовательно, функция (Qy)
сохраняет постоянное значение.
Эпюра моментов на этом участке —наклонная прямая, что
следует из зависимости Qy = dMx/dz. В данном случае про
168
изводная Qy постоянна, следовательно, сама функция (Мх)
линейна.
2. Если на некотором участке балки имеется равномерно
распределенная нагрузка, то эпюра Qy —наклонная прямая,
а эпюра Мх —парабола (кривая второго порядка). Рассуждаем
аналогично случаю 1: если производная (q) постоянна, функция
(Qy) линейна. Используя зависимость между Qy и Мх, заклю
чаем, что если производная (Qy) изменяется по линейному зако
ну, то функция, дающая закон изменения Мх, квадратичная,
т. е. имеет порядок на единицу выше.
3. Если на некотором участке:
а) Qy > 0, то изгибающий момент возрастает (слева напра
во);
б) <2У<0, то изгибающий момент убывает;
в) Q y = 0, то изгибающий момент постоянен (чистый изгиб).
4. Если поперечная сила, изменяясь непрерывно, например
по линейному закону, проходит через нулевое значение, то
в соответствующем сечении изгибающий момент имеет экстре
мальное (максимальное или минимальное) значение (равенство
нулю первой производной является признаком экстремума
функции). Касательная к эпюре Мх параллельна оси балки.
5. Под сосредоточенной силой на эпюре Qy происходит
скачкообразное изменение ординат —скачок, равный прило
женной внешней силе, а на эпюре Мх —резкое изменение угла
наклона (излом) смежных участков эпюры.
6. В точках, соответствующих началу и концу участка,
в пределах которого к балке приложена распределенная нагруз
ка, параболическая и прямолинейная части эпюры Мх сопря
гаются плавно, если на границах указанного участка не прило
жено сосредоточенных сил.
7. Если распределенная нагрузка направлена вниз, то пара
бола, представляющая собой эпюру Мх, обращена выпу
клостью вверх, г. е. «навстречу» нагрузке.
8. В сечении на свободном или шарнирно опертом конце
балки изгибающий момент равен нулю, если там не приложена
сосредоточенная пара сил, а если она приложена —равен мо
менту этой пары. Поперечная сила в этом сечении равна внеш
ней сосредоточенной силе (активной или реактивной).
9. Там, где к балке приложена сосредоточенная пара сил, на
эпюре Мх получается скачкообразное изменение ординат —
скачок, равный моменту этой пары. На эпюре Qy это не
отражается.
10. В сечении, совпадающем с заделкой, Qy и Мх численно
равны опорной реакции и реактивному моменту.
169
Построение эпюр по характерным точкам с использованием
изложенных правил рассмотрим на раде примеров.
П р и м е р 7.6. Построить эпюры Qy и Мх для балки, изображен
ной на рис. 7.16.
Р е ш е н и е . Определяем опорные реакции исходя из того, что
они образуют пару сил с моментом, численно равным М, но противо
положно направленным (рис. 7.16,а):
Ra =Rb = мц
.
В сечении на левой опоре QyA - М/1, где M/I —приложенная внеш
няя сила. Распределенная нагрузка отсутствует, следовательно, эпюра
Qy —прямая, параллельная оси абсцисс (рис. 7.16,6). В сечении А изги
бающий момент равен нулю. В сечении В он равен приложенному там
внешнему моменту.
Для определения знака Мх следует вообразить правую отсеченную
часть защемленной весьма близко от точки В (чтобы не учитывать мо
мента от реакции RB). Легко видеть, что момент М изгибает эту часть
балки так, что сжатые волокна находятся сверху, т. е. Мх положите
лен. По двум найденным значениям строим эпюру (рис. 7.16,6), учиты
вая при этом, что она линейна, так как Qy постоянна.
П р и м е р 7.7. Построить эпюры Qy и Мх для балки, изображен
ной на рис. 7.17, а.
Р е ш е н и е . Определяем опорные реакции:
2МЛ= 0;
F- 5а —М —Rg-4a = 0
или
Rb •4а = F ■5а —Fa/2,
откуда
RB = 9/8 F;
2Мв = 0; - R a -4o +Fa —F-a/2 = 0,
170
откуда
Ra = 1/8 F.
Для проверки правильности определения реакций составляем сум
му проекций на ось, параллельную силам:
—Ял + &в —F — —1/SF + 9/8F —F = 0.
Таким образом, реакции определены верно.
В сечении на левой опоре Qyx = —'/а
Это значение сохраняется
на всем протяжении участка I. В сечении на правом конце балки Qyc =
= F. На участке I I поперечная сила также постоянна. Построив эпюру
Qy (рис. 7.17,6) для участков I и II, убеждаемся, что в месте приложе
ния к балке сосредоточенной силы Rg = 9/ аF на эпюре Qy получился
скачок, равный этой силе.
Для построения эпюры Мх (рис. 7.17, в) достаточно определить
его значение в трех сечениях А, В и С и соединить полученные точки
прямыми линиями (распределенной нагрузки нет). В сечении А изги
бающий момент равен нулю (здесь нет внешней пары сил). Изгибаю
щий момент в сечении В отрицателен (в этом легко убедиться, проводя
произвольное сечение на участке I и рассматривая левую отсеченную
часть, мысленно защемленную в проведенном сечении и нагруженную
силой R a ', она изгибает ее выпуклостью вверх):
МхВ= - Кд - 4 а= - 1/ s F-4a= - 1/2Fa.
В сечении С Мхс = */а Fa — приложенному здесь внешнему момен
ту, который изгибает консоль выпуклостью вниз.
П р им ер 7.8. Построить эпюру Qy и Мх для балки, изображен
ной на рис. 7.18, а.
Р е ш е н и е . В силу симметрии R a —R b = qV2. В сечении А попе
речная сила равна + ql/2, а в сечении В - равна - ql/2. Между ука
занными значениями Qy изменяется по линейному закону (рис. 7.18,6).
Эпюра Мх —парабола, направленная выпуклостью навстречу на
грузке. В опорных сечениях М ха = Мхв = 0. В сечении по середине
пролета, где Qy = 0, изгибающий момент имеет максимальное значе-
171
ние. Найдем его, беря сумму моментов всех сил, приложенных слева
от этого сечения, относительно точки С:
м
„ I
ql I _ q l I
qi2 = ql2
ma,
Л2
2 '4
2 '2
8
8
Эпюра М х изображена на рис. 7.18, в.
П р и м е р 7.9. Построить эпюры Qy и Мх для простой консоли,
изображенной на рис. 7.19, а.
Р е ш е н и е . Строим эпюры, начиная от свободного конца балки,
что позволяет не определять опорные реакции. Начинаем с эпюры Q,.
На свободном конце QyA = 0, так как здесь к балке не приложено
сосредоточенной силы. На участке I Qy меняется по линейному закону.
Для построения этой части эпюры надо знать два значения Qy; одно
из них известно. Определяем Qy в сечении В как сумму сил, прило
женных к балке слева от этого сечения:
QyB= —2qa.
На участках I I и III распределенная нагрузка отсутствует, следо
вательно, сохраняется то же значение поперечной силы:
Qyii = Qyш = QyB•
Наличие сосредоточенной пары сил на эпюре Qy не отражается.
В сечении D на эпюре Qy —скачок вверх, равный приложенной си
ле, и правее этого сечения Qviv = —qa. Нетрудно убедиться, что опор
ная реакция равна qa.
Строим эпюру изгибающих моментов.
На свободном конце М хА = 0, так как сосредоточенной пары сил
в сечении А нет. На участке / момент изменяется по квадратичному
закону, при этом касательная к эпюре в сечении А горизонтальна, так
как QyA - 0. Эпюра обращена выпуклостью вверх, т. е. навстречу на
грузке. Определим М х в сечении В:
МхВ — - qlaa = - 2qa2.
На участке II Мх изменяется по линейному закону (Qyи = const).
Находим момент в сечении, бесконечно близком (слева) к точке С:
М^с* = -2qa-2a = - 4 qa2.
В сечении В прямолинейный и криволинейный участки эпюры Мх
сопрягаются плавно, так как сосредоточенной силы в этом сечении не
приложено. В сечении С на эпюре М х скачок вверх соответствует мо
менту приложенной пары, так как при рассмотрении равновесия левой
отсеченной части этот момент изгибает оставленную часть балки вы
пуклостью вниз. Следовательно, бесконечно близко справа от сечения
С изгибающий момент равен алгебраической сумме момента от рас
пределенной нагрузки и момента М пары сил:
—(&а ■2а + qa2 — —'iqa1.
На участке I I I М , изменяется по линейному закону. В сечении
D имеем
,,
. ,
,
, ,
М хо = —q2a ■за + qa = —5qa .
172
Аналогично, на участке IV эпюра Мх линейна и в сечении Е
М хе = —q2a ■4а + да2 + qa-а — —6да2.
Конечно, под сосредоточенной силой на эпюре Мх должен быть
излом. Реактивный момент в заделке равен изгибающему моменту
в сечении Е, т. е. 6qa2. Эпюры Qy и Мх даны на рис. 7.19, б, в.
П р и м е р 7.10. Построить эпюры Qy и Мх для двухопорной бал
ки (рис. 7.20, я).
Р е ш е н и е . Определяем опорные реакции:
'EMа = 0; q-4a-2a + 2qa-4a + 2qa2 —R b -5o + qa-6a = 0;
Rb ~ 4,8qa ;
E M g = 0; R a ■5a —q •4a ■3a —2qaa + 2qa2 + qaa = 0;
R 4 = 2,2qa.
Для проверки правильности определения реакций составляем сум
му проекций всех сил на вертикальную ось:
R a —М а — Ft + R b —F2 —2,2qa —4qa —2qa + 4,8qa —qa = 0.
Строим эпюру поперечных сил.
В сечении на левой опоре поперечная сила равна соответствующей
опорной реакции. На участке I Qy изменяется по линейному закону.
Для построения эпюры на этом участке надо найти еще одно значение
Qy Определяем Qy в сечении, взятом бесконечно близко слева от
точки С:
„
„
QyC = 2,2qa —4qa = —1,8qa.
В этом месте на эпюре Qy получается скачок на 2qa, а далее правее
этого сечения Qy сохраняет постоянное значение до опоры В:
Q y S = Q l l = - 1,8 q a - 2 q a --
А * 2-Ча
а)
Л
шш
<
3
су
C
SJ
m nw
Эпюра Qy
1,8qa
Ща
Эпюра мх
»)
RfWqa.
F,=2qa M=2oa;
Ш
i Е
a V7.V а .
4а
б) —
- 3,8 q a .
2,42qa2
0,8qaf
I
О зИ
I
-qa2
Рис. 7.20
173
В сеч ен и и В —с к а ч о к в в ер х
ная сила остается п о с т о я н н о й :
на
Кв = 4,8qa, и на у ч а с т к е Ш
поп ереч
Qyin — - 3,8ga + 4,8qa = qa.
Для проверки можно построить эпюру, начиная с правого конца
балки. Например, в произвольном сечении, взятом в пределах участка
III, Qyiu = F2 = qa (равно сумме сил, приложенных к правой оставлен
ной части).
Строим эпюру изгибающих моментов. В сечении А
МхА = 0.
На участке I изгибающий момент изменяется по квадратичному
закону, при этом в сечении, где эпюра Qy проходит через нуль, эпюра
Мх (парабола) имеет максимум. Определим значение Мх шм. Для этого
предварительно найдем абсциссу z0 сечения, в котором Qt = 0. Проще
всего определить значение г0, разделив отрезок АС = 4а в отношении
(11/5): (9/5) = 11:9; получим:
z0 = (4я/20) 11= 2,2а;
Мх max ~ B aZq qz0 *z0/2 " 2,2qa •1,'Io.a
q •2,2a *2,2n/2 " 2,42qa2.
Определяем изгибающий момент в сечении С:
МхС = R a ' 4а —q •4а ■ 2а = 2,2<jo ■4а —q ■4а •2а = 0,8qa2.
По трем найденным значениям Мх на участке I приближенно
строим параболу. Для более точного построения эпюры можно допол
нительно вычислить е щ е н е с к о л ь к о значений Мх.
Оставшуюся часть эпюры удобнее строить, начиная с правого
конца балки.
В сечении на правом свободном конце M xd = 0.
На участке III М х изменяется по линейному закону. Изгибающий
момент в сечении, расположенном бесконечно близко справа от опоры
В, М
= —qa2. Момент на участке III отрицателен, так как балка из
гибается выпуклостью вверх.
В сечении В на эпюре Мх получается скачок на М —Iqa2, причем,
если эпюра строится начиная справа, скачок получается вниз, так как
момент М изгибает правую оставленную часть выпуклостью вверх.
В сечении, бесконечно близком к В и лежащем слева от него, JVfJjf =
= —3qa2. Остается соединить прямой точки эпюры на границах участ
ка II. Эпюры Qy и М х изображены на рис. 7.20, б, в. Параболический
и прямолинейный участки эпюры М х на границе участков II и III не
имеют плавного сопряжения.
П р и м е р 7.11. Для балки, жестко защемленной одним концом,
задана эпюра поперечных сил (рис. 7.21). Определить действующую на
балку нагрузку и построить эпюру изгибающих моментов. Принять,
что сосредоточенных пар сил (активных) к балке не приложено.
Р е ш е н и е . Указание об отсутствии внешних сосредоточенных
пар необходимо потому, что на эпюре Qy наличие этого вида нагрузки
не отражается и без этого указания условия были бы неопределен
ными.
]рав
174
Ч гЧ
ЧтгЧИ
Ж жжжжжжжж и
И
2а Ш F=2q,a
Зпмра
Qy
1^-ггтпТГГПТ|?Д
аа
2ца
Эпюра М-
I
2qa2
> ■
Рис. 7.22
Очевидно, балка имеет три участка нагружения, границами ко
торых являются изломы или скачки на эпюре Qy На левом конце бал
ки Qy —0, следовательно, сосредоточенной силы здесь не приложено.
На первом участке поперечная сила изменяется по линейному за
кону, т. е. здесь к балке приложена равномерно распределенная
нагрузка, направленная, очевидно, вниз (стремящаяся повернуть левую
часть балки против часовой стрелки). Интенсивность этой нагрузки
qi = 2qa/a = 2q.
На втором участке Qyu = const, следовательно, распределенная на
грузка отсутствует. На границе участков I и II скачка на эпюре Qy нет,
это указывает, что здесь к балке не приложено сосредоточенной силы.
На границе участков II и III на эпюре Qy скачок составляет 2qa,
следовательно, здесь к балке приложена сила F = 2qa. Эта сила стре
мится повернуть левую часть балки по часовой стрелке, т. е. направле
на вверх.
На участке III имеется равномерно распределенная нагрузка, на
правленная вверх. В этом случае эпюра Qy линейна и положительна.
Значение интенсивности этой нагрузки определяем по известному зна
чению поперечной силы в сечении А (рис. 7.22):
—q{a + F + qn -2 а — qa
или
- 2 qa + 2qa + q{1 ■2a = qa,
откуда
Чп = ЗА
На рис. 7.22 показана эпюра Mx. На участке III эпюра М х обра
щена выпуклостью вниз и касательная к ней в крайней левой точке
участка горизонтальна. На границе участков II и III имеется излом.
Параболический и прямолинейный участки эпюры на границе участков
I я II сопрягаются плавно.
175
Учащемуся рекомендуется объяснить все отмеченные особенности
эпюры исходя из дифференциальных зависимостей между Qy и Мх
и проверить определение характерных ординат эпюры Мх.
§ 7 .5 . Н ормальны е напряжения при изгибе
Выше было установлено, что при поперечном прямом изги
бе в поперечных сечениях балки возникают нормальные и каса
тельные напряжения. В частном случае, когда поперечная сила
равна нулю, имеет место чистый изгиб и в поперечных сечениях
балки касательные напряжения отсутствуют. Этот случай рас
смотрим в первую очередь. Для выяснения закона распределе
ния нормальных напряжений по поперечному сечению балки
и вывода формулы, определяющей напряжение в произвольной
точке поперечного сечения, будем исходить из следующих
допущений.
1. При чистом прямом изгибе справедлива гипотеза Бер
нулли, т. е.
поперечные сечения бруса, плоские и нормальные к его оси до
деформации, остаются плоскими и нормальными к оси и после
деформации.
2. Волокна бруса при его деформации не надавливают друг на
друга.
Рассматривая деформацию резиновой модели бруса с нане
сенной на его поверхности сеткой продольных и поперечных
рисок, обнаруживаем, что поперечные риски, оставаясь прямо
линейными, поворачиваются на некоторые углы и их парал
лельность нарушается (рис. 7.23).
Эта картина деформации, наблюдаемая на поверхности бру
са, в известной степени подтверждает справедливость гипотезы
Бернулли. Кроме того, формула, получаемая на основе ука
занных допущений, совпадает с выведенной с помощью точных
методов теории упругости без использования этих допущений.
Рис. 7.23
176
Рис. 7.24
Для вывода формулы, определяющей нормальные напряже
ния, возникающие в поперечном сечении балки, рассмотрим
балку, изображенную на рис. 7.24, а. Определив опорные реак
ции (в силу симметрии RA = RB = F) и построив эпюры попе
речных сил и изгибающих моментов (рис. 7.24, б, в), заключаем,
что средняя часть балки (участок CD) находится в условиях чи
стого изгиба: поперечная сила во всех сечениях этого участка
равна нулю. Двумя бесконечно близкими поперечными сече
ниями выделим из этого участка элемент длиной dz. Отдельно
(в крупном масштабе) этот элемент в деформированном со
стоянии изображен на рис. 7.25. Длина волокон, лежащих
в нейтральном слое, при изгибе не изменяется. Обозначим след
нейтрального слоя на плоскости чертежа и —и, а его радиус
кривизны — р (рис. 7.25). Определим линейную деформацию
произвольного волокна, отстоящего на расстоянии у от ней
трального слоя. Длина этого волокна после деформации (длина
дуги т —т) равна (р + y)d0. Учитывая, что до деформации все
волокна имели одинаковую длину dz, получаем, что абсолют
ное удлинение рассматриваемого волокна
A(dz) = (р + y)d0 —dz;
следовательно, его деформация, равная отношению абсолютно
го удлинения к первоначальной длине,
е = A (dz)/dz = [(р + у) d0 —dz]/dz.
Очевидно, dz = р d0, так как длина волокна, лежащего
в нейтральном слое, при деформации не изменилась. Следова
тельно,
e = [(P + y )d 0 -p d 0 ]/(p d 0 ),
откуда
е = у/р.
(а)
Рис. 7.25
177
Для перехода от деформаций х напряжениям применим за
кон Гука (как и ранее, полагаем, что возникающие напряжения
не превышают предела пропорциональности)
<тг = Ее.
(б)
Подставляя сюда е = у/р, получаем
= Еу/ р.
(в)
Возможность применения закона Гука в форме зависимости
(б) обусловлена принятым допущением о ненадавливании воло
кон балки друг на друга, т. е. предположением, что каждое из
них находится в состоянии одноосного растяжения или сжатия.
Выражение (в) показывает, что нормальное напряжение
в произвольной точке поперечного сечения прямо пропорцио
нально ее расстоянию у от нейтральной оси, т. е. по высоте се
чения нормальные напряжения изменяются по линейному зако
ну. По ширине сечения они распределены равномерно (не
зависят от координаты х).
Нормальные напряжения в торцовых поперечных сечениях
выделенного элемента показаны на рис. 7.25. Там же показано
его поперечное сечение, совмещенное с плоскостью чертежа,
чи дана эпюра нормальных напряжений. Как обычно, напряже
ния растяжения считаем положительными (знак плюс на эпю
ре), а сжатия —отрицательными.
Условность этой и ей подобных эпюр, которые будут неод
нократно встречаться в дальнейшем, заключается в том, что ее
ординаты, выражающие нормальные напряжения в соответ
ствующих точках поперечного сечения, лежат в плоскости сече
ния, в то время как сами напряжения перпендикулярны этой
плоскости. Большей наглядностью обладают простран
ственные эпюры; для бруса прямоугольного сечения такая про
странственная эпюра показана на рис. 7.26.
Возвращаясь к рис. 7.25, заметим,
что нейтральная ось (она принята за
координатную ось Ох) делит поперечное
сечение бруса на две части, в одной
из которых (в нашем случае в нижней)
возникают растягивающие, а в другой —
сжимающие напряжения. В точках, ле
жащих на самой нейтральной оси,
нормальные напряжения равны нулю.
Таким образом, наряду с определени
ем нейтральной оси как линии пересе
чения нейтрального слоя с плоскостью
поперечного сечения можно дать и дру178
гое: нейтральней осью или нулевой линией называется гео*
метрическое место точек поперечного сечения бруса, в которых
нормальные напряжения равны нулю.
Положение нейтральной оси пока не известно; также не из
вестен радиус кривизны нейтрального слоя, поэтому выраже
ние (в) нельзя применять для определения нормальных напря
жений.
Положение нейтральной оси определим из условия, что про
дольная сила в поперечном сечении равна нулю. Зависимость ме
жду продольной силой и нормальными напряжениями записы
вается так:
N ,= S o zdA.
А
Подставляя вместо а , его значение по выражению (в) и при
равнивая продольную силу нулю, получаем
уАА = 0.
Отношение Е/р —величина постоянная и может быть выне
сена за знак интеграла:
<14 = 0.
Очевидно, Е/р ^ О (рассматриваем деформированный брус,
т. е. радиус кривизны не равен бесконечности), следовательно,
J у&4 = 0.
А
Но, как известно, этот интеграл представляет собой стати
ческий момент сечения относительно оси Ох (нейтральной
оси); он равен нулю лишь в случае, если эта ось цент
ральная.
Силовая линия (ось Оу) совпадает с осью симметрии сече
ния, т. е. является одной из главных центральных осей. Ней
тральная ось ей перпендикулярна и проходит, как мы установи
ли, через центр тяжести сечения, т. е. это вторая главная
центральная ось.
В рассматриваемом случае изгиба перпендикулярность силовой
и нулевой линий следует из того, что точки сечения, лежащие на об
щем перпендикуляре к силовой линии слева и справа от нее, находятся
в одинаковых условиях, так как силовая линия совпадает с осью сим
метрии поперечного сечения.
179
Для определения радиуса кривизны нейтрального слоя ис
пользуем зависимость между изгибающим моментом и нор
мальными напряжениями. Элементарная нормальная сила рав
на сг, dA, ее момент относительно нейтральной оси dМ х —
= (агйА)у, суммируя эти элементарные моменты по всей
площади сечения, имеем
Mx = $ a zydA.
А
Подставляя сюда значение а, по выражению (в), получаем
МX j o zydA
Учитывая, что J у2 dA = Jx —момент инерции относительно
оси Ох, можно записать
M, = EJx/p
или
1/р = Мх / (EJJ,.
(7.4)
Кривизна нейтрального слоя (изогнутой оси бруса) прямо про
порциональна изгибающему моменту и обратно пропорциональна
произведению модуля продольной упругости материала бруса на
момент инерции его поперечного сечения относительно нейтраль
ной оси.
Произведение EJх условно называют жесткостью сечения
бруса при изгибе. Модуль Е характеризует жесткость материа
ла, а момент инерции Jx является геометрической характери
стикой жесткости бруса при изгибе.
Подставляя найденное значение кривизны в выражение (в),
получаем
<тг = Еу/р = EyMJ(EJx) = (Mx/Jx)y.
Опуская индекс z (нормальные напряжения в поперечном се
чении бруса принято обозначать просто с без индекса, указы
вающего их направление), окончательно имеем
o = (Mx/Jx)y.
(7.5)
Формула (7.5) дает возможность вычислить нормальное на
пряжение в произвольной точке поперечного сечения. Значения
изгибающего момента Мх и расстояния рассматриваемой точ
ки от нейтральной оси (координаты у) следует подставлять по
абсолютному значению. Будет ли напряжение в данной точке
180
растягивающим или сжимающим, легко установить по харак
теру деформации балки или, что то же самое, по эпюре изги
бающих моментов, ординаты которой откладывают в сторону
сжатых волокон балки.
Формула (7.5) выведена для случая чистого прямого изгиба
бруса. При поперечном прямом изгибе предпосылки, поло
женные в основу ее вывода, нарушаются: поперечные сечения
бруса вследствие возникновения в них касательных напряжений
искривляются (гипотеза Бернулли несправедлива); кроме того,
в этом случае имеет место, хотя и весьма незначительное,
взаимное надавливание волокон. Тем не менее, как показывают
экспериментальные и точные теоретические исследования, эта
формула дает значения нормальных напряжений и для случая
поперечного изгиба с точностью, вполне достаточной для прак
тических расчетов.
В предыдущем изложении мы ограничились рассмотрением слу
чая, когда поперечное сечение бруса имеет по меньшей мере одну ось
симметрии, с которой совпадает силовая линия. При этом взаимная
перпендикулярность силовой и нулевой линий является вполне оче
видным следствием симметрии нагружения бруса. В общем случае,
когда поперечное сечение не имеет ни одной оси симметрии, силовая
и нейтральная линии будут взаимно перпендикулярны и, как следствие,
будет справедлива формула (7.5) для нормальных напряжений лишь
при условии, что силовая линия совпадает с одной из главных цен
тральных осей поперечного сечения изгибаемого бруса. Справедли
вость этого утверждения может быть доказана следующим образом.
Пусть действующие на брус нагрузки расположены в главной пло
скости zOy, т. е. силовая линия совпадает с главной осью. Внешние
силы момента относительно оси Оу не дают, следовательно, и момент
М у внутренних сил относительно этой оси равен нулю. Зависимость
между моментом М у и нормальными напряжениями такова (см.
с. 23):
М у = J аде d/4.
А
Подставляя сюда csz —Ey/ р и приравнивая Му нулю, получим
Е
\xydA = О,
Р
но — # 0 , следовательно, J ху dA = 0.
Р
л
Этот интеграл представляет собой центробежный момент инерции
сечения Jxy. Он равен нулю лишь относительно главных осей, которые;
как известно, взаимно перпендикулярны. Таким образом, доказано по
ложение о взаимной перпендикулярности силовой и нулевой линий
при нагружении бруса в главной плоскости.
181
Значит, формулой (7.5) можно пользоваться во всех случаях прямо
го изгиба, понимая под Jx момент инерции относительно главной цен
тральной оси поперечного сечения, перпендикулярной плоскости дей
ствия нагрузки.
§ 7.6. Расчеты на прочность при изгибе
Балки рассчитывают на прочность по наибольшим нор
мальным напряжениям, возникающим в их поперечных сече
ниях. При поперечном изгибе балок наряду с нормальными, как
известно, возникают и касательные напряжения, но они в по
давляющем большинстве случаев невелики и при расчетах на
прочность не учитываются. О некоторых особых случаях, в ко
торых влиянием касательных напряжений пренебречь нельзя,
сказано в следующем параграфе.
Расчет балок из пластичных материалов
Прочность балки из пластичного материала обеспечена, если
наибольшие по абсолютному значению нормальные напряже
ния, возникающие в опасном поперечном сечении, не превы
шают допускаемых. Для балки, поперечные размеры которой
по всей длине постоянны (пока только такими балками и огра
ничимся), опасное сечение то, в котором возникает наибольший
по модулю изгибающий момент.
Наибольшие нормальные напряжения возникают в точках
опасного поперечного сечения, максимально удаленных от
нейтральной оси. Будем называть эти точки опасными.
Величину максимального напряжения найдем по формуле
(7.5), подставляя в нее вместо текущей координаты у значение
Утих — расстояние от опасной точки до нейтральной оси. Тогда
получим условие прочности в виде
М.х шах
(7.6)
max
Ушах < М
Здесь [а] —допускаемое напряжение, принимаемое при ста
тическом нагружении таким же, как и в случае растяжения
(сжатия) бруса из того же материала.
В случае если поперечное сечение балки симметрично отно
сительно нейтральной оси, оказывается возможным привести
формулу (7.6) к более удобному виду. Для указанных сечений
Ушах = Л/2, где h —высота сечения (размер в направлении, пер
пендикулярном нейтральной оси), следовательно,
о,max
182
Разделим числитель и знаменатель этого выражения на /г/2:
введем обозначение
и получим окончательное условие прочности в следующем
виде:
Мхг
= —гп— < [ст].
(7.7)
Wr
—
m ax
- г
Т
Таким образом, введена новая геометрическая характери
стика поперечного сечения Wx, представляющая собой отноше
ние момента инерции относительно данной оси к половине вы
соты сечения. Эту геометрическую характеристику называют
осевым, моментом сопротивлении или моментом сопротивления
при изгибе. Ее часто называют просто моментом сонротивленш
в отличие от подобной геометрической характеристики, встре
чавшейся при рассмотрении кручения бруса круглого попереч
ного сечения и называемой таямрньм моментом еоярэ'итлеяга.
Момент сопротивления тгеет размерность I A
Из формулы (7.7) следует, что момент сопротшлешя —это
геометрическая характеристика прочности бруса, работающего
иа прямой изгиб. Действительно, чем больше момент сопро
тивления, тем меньше напряжения, возникающие в поперечном
сечении балки при данной нагрузке (изгибающем моменте),
и тем большую нагрузку может безопасно выдержать балка
при данном значении допускаемого напряжения (при данном
материале).
Формула (7.7) представляет собой зависимость для прове
рочного расчета. В случае необходимости из нее можно опреде
лить требуемый момент сопротивления или допускаемый по
условию прочности изгибающий момент.
Связь между допускаемыми значениями максимального из
гибающего момента и действующей на балку нагрузки уста
навливается по эпюре М х.
Значения моментов сопротивления прокатных профилей
(двутавров и швеллеров) приведены в таблицах соответствую
щих ГОСТов.
Моменты сопротивления круга, кольца и прямоугольника
найдем, воспользовавшись формулами для главных цен
тральных моментов инерции этих сечений (см. § 6.5):
183
а) круг
W
*
J,
KclA'/64
rf/2
<//2 ’
= - - - = ------—
или
^ = ^ - * 0 , W 3;
(7.8)
б) кольцо
*
J , (nd*/64) (l —c4)
d/2
df2
или
Ж* = M 3/32)(l - с4) « 0,Ы3(1 - C4);
(7.9)
в) прямоугольник
bh3/12
W = —i^ = --- '
х
й/2
ft/2 ’
или
Wx
= bh2/6.
(7.10)
Во избежание ошибок еще раз подчеркиваем, что в формуле
(7.10) h — сторона прямоугольника, перпендикулярная оси, от
носительно которой вычисляется момент сопротивления.
При применении для балок из пластичных материалов сече
ний, симметричных относительно нейтральной оси, обеспечи
вается равенство наибольших растягивающих и сжимающих
напряжений (рис. 7.27). Для указанных материалов это, конеч
но, целесообразно, так как допускаемые напряжения на растя
жение и сжатие для них одинаковы.
Нетрудно понять, что не все симметричные сечения одина
ково рациональны. Действительно, распределение нормальных
напряжений таково, что та часть материала, которая располо
жена вблизи нейтральной оси, почти не используется. Это
указывает, в частности, на нерациональность круглого сече
ния —при его применении
большая часть материала
бруса оказывается в малонагруженной области. Не
многим выгоднее квадратное
сечение. Наилучшее решение
вопроса о рациональном ис
пользовании материала дает
184
применение двутаврового сечения. В двутавровой балке основ
ная часть материала сосредоточена в полках, т. е. в зоне
наилучшего его использования (в зоне наибольших напряже
ний). Роль стенки балки, воспринимающей сравнительно не
большую часть изгибающего момента, состоит в обеспечении
монолитной работы сечения как единого целого.
Поскольку момент сопротивления является геометрической
характеристикой прочности изгибаемого бруса, очевидно, сле
дует стремиться к тому, чтобы при данной затрате материала
он был максимален. При заданной длине балки затрата мате
риала (масса балки) прямо пропорциональна площади попереч
ного сечения. Следовательно, чем больше Wx и меньше А, тем
рациональнее форма сечения балки. Для количественной оцен
ки рациональности сечения удобна безразмерная характеристика
гwX =
W J]/ A \
которую называют удельным осевым моментом сопротивления.
Например, для круга wx —0,141; для кольца (при с = 0,7) wx =
= 0,294; для двутавра № 10 (по ГОСТ 8239 —72) wx = 0,955; для
№ 20 w* = 1,33.
Необходимо иметь в виду, что при изменении положения
сечения по отношению к действующей нагрузке прочность бал
ки существенно изменяется, хотя площадь сечения и остается
неизменной. Например, для бруса прямоугольного сечения
с отношением сторон h:b = 3, расположенного, как показано
на рис. 7.28, а, допускаемая нагрузка в три раза больше, чем
для того же бруса, но повернутого на 90° (рис. 7.28,6). Анало
гично для двутавра № 20а, показанного на рис. 7.29, а, допу
скается нагрузка больше, чем для показанного на рис. 7.29,6,
в 7,2 раза.
Из приведенных примеров следует, что сечение надо распо
лагать таким образом, чтобы силовая линия совпадала с той
из главных осей, относи
тельно которой момент
инерции минимален, или,
что то же самое, так, что
бы ось, относительно ко
торой момент инерций
максимален, была нейт
ральной осью сечения.
Более кратко это указа
ние можно сформулиро
вать так:
следует стремиться к
185
Рис. 7i29
тому, чтобы изгиб бруса происходил в плоскости его наиболь
шей жесткости.
В большинстве случаев с увеличением момента инерции се
чения возрастает и его момент сопротивления, но возможны
и исключения, когда нерациональное увеличение момента инер
ции приводит к уменьшению момента сопротивления, т. е.
к снижению прочности бруса. Один из подобных примеров
приведен на рис. 7.30: приварка полос к двутавру приводит
к уменьшению ¥/х, так как высота сечения возрастает ощути
мее, чем его момент инерции.
Интересно отметить, что если у круглого сечения срезать
сегменты, как показано на рис. 7.31, то момент сопротивления
возрастает, достигая максимального значения, когда стрелка
срезаемого сегмента равна ОДЫ. При большей стрелке сегмен
та момент сопротивления становится меньшим, чем у круглого
сечения. Не следует забывать, что уменьшение момента инер
ции сечения не всегда допустимо, так как оно приводит к сни
жению жесткости балки.
Рис. 7.30
186
Рис. 7.31
Расчет балок из хрупких материалов
Хрупкие материалы применяют Для изготовления неко
торых работающих на изгиб элементов машиностроительных
конструкций. В частности, из серого чугуна отливают различ
ного рода рамы, станины, подшипниковые подвески и т. п.
Как известно, серьга чугун работает на сжатие значительно
лучше, чем на растяжение; отношение соответствующих допу
скаемых напряжений
!> J /I> p ] = 3-4,5.
Очевидно, применение сечений, симметричных относительно
нейтральной оси, в рассматриваемом случае нерационально —
материал в сжатой зоне бруса будет значительно недогружен,
что приведет к его излишней затрате, а значит, к увеличению
массы конструкции.
Для балок из хрупких материалов, различно сопротивляю
щихся растяжению и сжатию, целесообразно применять сечения,
не симметричные относительно нейтральной оси, например тавро
вое, несимметричное двутавровое, П-образное (рис. 7.32). При
этом целесообразно располагать сечение таким образом, чтобы
большая часть балки находилась в растянутой зоне (см. эпюру
нормальных напряжений на рис. 7.32), при этом растянутые во
локна оказываются приближенными к центру тяжести сечения.
Рациональное и нерациональное расположение сечения
чугунной тавровой балки показаны на рис. 7.33. При указанных
на чертеже расстояниях от нейтральной оси до крайних точек
сечения допускаемая нагрузка в случае, показанном на
рис. 7.33, а, в 2,22 раза больше, чем в случае, показанном на
рис. 7.33,6.
Очевидно, следует стремиться к тому, чтобы максимальные
растягивающие и максимальные сжимающие напряжения
в опасном поперечном сечении балки были одновременно равны
187
Рис. 7.33
Рис...7.34
соответствующим допускаемым напряжениям, т. е.
max
Е^рЗ ’
- с max
C ^ cJ*
При этом материал балки используется наиболее рацио
нально. Но
сш
ах ^ х тл х У ь !^ х У
*Тр max
'!^ x m a х У к /^ х ®
max
где уц и yL —расстояния от нейтральной оси соответственно до
наиболее удаленных точек растянутой и сжатой зон сечения
(см, рис. 7.32 и 7.33). Следовательно, для обеспечения указанно
го условия наиболее рационального использования материала
сечение должно иметь такую конфигурацию, при которой
Ук/Уь=[а р]/[<тс].
(7.11)
Соотношение (7.11) выполняется далеко не всегда, поэтому
условие прочности чугунной балки выражается двумя неравен
ствами :
(7.12)
Если Ук./У1 > [стР] / [ стс]> опасными являются точки растяну
той зоны, максимально удаленные от нейтральной оси, и для
расчета на прочность достаточно использовать только первую
из формул (7.12). Аналогично, при Ук/Уь< [CTp ]/[CTd достаточ
но выполнить расчет по второй из формул (7.12).
Все сказанное о расчете чугунной балки относилось в основ
ном к случаю, когда эпюра изгибающих моментов на всем ее
протяжении однозначна. В случае если эпюра Мх имеет участки
разных знаков (например, в случае схемы нагружения, предста
вленной на рис. 7.34), следует расположить сечение таким обра
зом, чтобы там, где изгибающий момент по абсолютному зна
чению максимален (сечение 1 —1 на рис. 7.34), большая часть
материала (например, полка таврового сечения) находилась
в растянутой зоне. При этом помимо расчета на прочность, вы
188
полненного по одной из формул (7.12) для указанного сечения,
необходимо произвести расчет по максимальным растягиваю
щим напряжениям для сечения с наибольшим моментом про
тивоположного знака (сечение 2 - 2 на рис. 7.34). Здесь хотя из
гибающий момент и меньше, но большая часть материала
находится в сжатой зоне и может оказаться, что именно это се
чение является опасным (см. пример 7.17).
Рассмотрим ряд примеров расчета на прочность при изгибе.
П р им ер 7.12. Две балки с поперечными сечениями, показанны
ми на рис. 7.35, а, б, нагружены вертикально направленной изгибающей
нагрузкой. Выяснить, как изменится допускаемая нагрузка для каждой
из балок при повороте их вокруг продольных осей на 45°.
Р е ш е н и е . Из формулы (7.7) следует, что допускаемое значение
максимального изгибающего момента определяется по зависимости
т. е. при заданном значении допускаемого напряжения допускаемый
изгибающий момент зависит только от момента сопротивления попе
речного сечения балки. Для обоих заданных сечений любая централь
ная ось - главная, поэтому при повороте балки (сечения) момент инер
ции относительно нейтральной оси остается постоянным.
Для сечения, показанного на рис. 7.35, а:
,,
к_
х
64
12'
Для этого сечения постоянным остается и момент сопротивления
4
< / 6 4 - ЬУ12
* 4,/2
0,54,
так как расстояние от нейтральной оси до максимально удаленных от
нее точек сечения не изменяется (равно 4,/2).
Для срчения, показанного на рис. 7.35,6:
,11_ bj _ ПС^2
х ~ 12
64 '
Для этого сечения при расположении, показанном на чертеже:
w ,i
х
J’J
bJ2
b y n -n d j/6 4
0,5b2
189
а при повернутом на 45°, когда нейтральная ось совпадает с одной из
диагоналей квадрата,
WU
j'J
= Ь\/12 —ndt/64
*
{b J 2)]/2
0,5Ьг ]/2
Таким образом, при повороте второго из заданных сечений на 45°
допускаемая нагрузка соответствующей балки уменьшается на 29%.
П р и м е р 7.13. Проверить прочность заданной стальной балки
(рис. 7.36). Допускаемое напряжение [о] = 120 МПа.
Р е ш е н ы е. Опорные реакции показаны на рис. 7.36, там же по
казана эпюра изгибающих моментов.
Опасное сечение С; наибольшее нормальное напряжение в этом
сечении
Мс
2,57-10*
= 121,2-10* Па = 121,2 МПа.
тс43/32 “ (3,14/32)0,06*
Это напряжение на 1 % выше допускаемого, что, конечно, не опас
но, т. е. прочность балки обеспечена.
П р и м е р 7.14. Двутавровая балка (рис. 7.37,а) изготовлена из
стали СтЗ, имеющей предел текучести а т = 240 МГ1а. Проверить про
чность балки, если заданный коэффициент запаса прочности [ит] = 1,5.
Р е ш е н и е . Определяем опорные реакции и строим эпюры Qy и
М х (рис. 7.37, б, в). Для расчета на прочность эпюра Qy не нужна, но
построение ее при действии на
балку распределенной нагрузки
целесообразно, так как по этой
эпюре сразу определяется, имеет
ли эпюра Мх точки экстремума
и где именно. В нашем случае
эпюра Qy имеет нулевую ор-
wr
Рис. 7.37
190
динату в сечении, отстоящем на 2,47 м от опоры А:
Мх шах - - 30 •3,47 •(3,47/2) + 104 •2,47 = 76,3 кН •м.
Это расчетный момент. Необходимо подчеркнуть, что в неко
торых случаях расчетное значение М х может оказаться большим, чем
соответствующее точке м а т е м а т и ч е с к о г о максимума (см.,
в частности, пример 7.10).
Наибольшее нормальное напряжение в опасном сечении
сгтах = М ц ш / ^ i = 76,3 • Ю3/ (407• 10“ б) = 187,5 • 106 Па = 187,5 МПа,
где Wx = 407 см3 —момент сопротивления (относительно нейтральной
оси двутаврового профиля № 27а по ГОСТ 8239 —72).
Коэффициент запаса для опасных точек балки
240
1,282,
187J
т. е. ниже требуемого на 14,5 %, следовательно, балка работает с весь
ма значительной перегрузкой.
П р и м е р 7.15. Определить допускаемую нагрузку двухопорной
балки заданного поперечного сечения (рис. 7.38) для двух указанных
вариантов расположения опор. Допускаемое напряжение [<т]=
= 160 МПа.
Р е ш е н и е . На рис. 7.39, а показаны эпюры Qy и М х лпя I ва
рианта; то же, на рис. 7.39,6 —для II варианта.
пт
1Х Ш Х Ш Х
?
.Ш
1/8х 4
1*8м
2
L U X E C G
Я/4
^
1/8
160*10
№20а
Рис. 7.38
Рис. 7.39
191
Определяем момент инерции и момент сопротивления поперечно
го сечения балки:
Jх —2 {Jх шв + J х пол) —2 {Jхшв + .1х. пол 4 й Лпол)'
Jx шв = 1660 см* — момент т е р ц и и швеллера относительно оси
х; JXi „од = I3• 16/12 см* — момент инерции полосы относительно
Здесь
собственной центральной оси, параллельной главной центральной оси
всего сечения. Э тим слагаемым ввиду его малости в сравнении
с остальными пренебрегаем; а = 10,5 см —расстояние между осями
х и х ,; Л1ЮЛ= 16 см 2 — площ адь сечения полосы;
Jx = 2 (1660 + 10,52 16) = 6840
W =-
6840
h/2
11
см4; '
= 621 см3.
Допускаемое значение максимального изгибающего момента
определяем по формуле (7.7):
МЛ Шла = Wx
[о]-I = 62ЫО~ 6 • 160-10* = 994-102 Н •м,
А Iоткуда для I варианта
Ы ,(2/8 = [МХП^
или
м , = 8 [ М х mJ
/I2
= 8■ 994-102/82 - 124,2• 102 Н/м.
Аналогично для II варианта
М н*1/ 16 = [A#xmJ
или
Ы // = 16[MxmaJ / / 2 = 16-994-102/82 =248,4-102 Н/м.
Таким образом, при наличии консолей допускаемая нагрузка воз
росла в нашем случае вдвое. Рекомендуем читателю определить длины
консолей (в долях /) из условия, чтобы изгибающие моменты
в опорных сечениях и посередине пролета балки были одинаковы,
и вычислить для этого случая [<;],
П р и м е р 7.16. Определить требуемые размеры поперечного се
чения балки в двух вариантах, указанных на рис. 7.40, а. Допускаемое
напряжение [о] = 160 МПа.
Р е ш е н и е . Определяем опорные реакции и строим эпюры Qy и
М х (рис. 7.40, б, в). Из формулы (7.7) следует, что требуемый момент
сопротивления поперечного сечения балки определяется из выражения
Wx > Мхтах/[ст] = 240-107(160-106) = 1,5- К Г 3 м3 = 1500 см3.
По ГОСТ 8239 —72 выбираем двутавр № 50, имеющий Wx =
= 1589 см3.
Требуемый момент сопротивления о д н о г о швеллера
Wx ш„ = W J 2 = 1500/2 = 750 см3.
По ГОСТ 8240 —72 выбираем швеллер № 40, имеющий Wx шв =
= 761 см3. Масса 1 м двутавра № 50 qt = 78,5 кг/м, а швеллера № 40
192
q2 = 48,3 кг/м (для двух швеллеров 96,6 кг/м). Следовательно, двута
вровая балка будет легче балки из двух рядом поставленных швелле
ров на 18,7%.
П р и м е р 7.17. Определить при [<?,,] =40 МПа и [<зс] =
= 120 МПа допускаемую нагрузку заданной чугунной балки
(рис. 7.41, а), предварительно выбрав рациональное расположение сече
ния.
Р е ш е н и е . Определив опорные реакции (показаны на рис.
7.41, а), строим эпюру изгибающих моментов (рис. 7.41,6).
Наибольший изгибающий момент возникает в сечении С. Здесь
балка изгибается таким образом, что сжатые волокна находятся свер
ху, поэтому сечение следует расположить полкой вниз, т. е. так, чтобы
большая часть материала была в растянутой зоне.
Определяем допускаемую нагрузку из условия прочности балки
в сечении С. На рис. 7.42 показано положение нейтральной оси сече-
193
Эпюра 6 Эпюраб
в сея. С
в сея.В
ния (положение центра тяжести
сечения было определено в
примере 6.2). Расчет ведем по
наибольшим
растягивающим
напряжениям, так как
У к / У п — 4/11 > [ а р] / [ о с].
Условие прочности
Ортах = (УК = iMc/Jx) ук < [Стр].
Подставляя М хС = (3/2) Fa,
получаем
(3/2) Fa
~~j 7 ~
Ук
[ о р] ,
откуда
2-918-10_ 8■40■106
2 J x [O p ]
Ъаук
~
3 "1 Д 0 4
_
= 2,04 • 104 Н.
Значение момента инерции относительно нейтральной оси (Jx =
= 918-10-8 м4) взято из примера 6.2.
Расчет нельзя считать законченным —может оказаться, что сече
ние В опаснее рассмотренного, так как хотя Мхв < Мхс, но сечение
расположено таким образом, что полка находится в сжатой зоне, т. е.
нерационально.
Условие прочности для сечения В
°р т а х
или, подставляя
М хц
=
=
Fa,
а ь
=
(М в/ J J y t <
[>р]
имеем
Crpmax=(f "A/j H . sS |> J ,
откуда
т =
ayL
918-10_8-40-106
0,3-0,11
11,13 -103 Н.
Окончательно принимаем меньшее из двух найденных значений
допускаемой нагрузки, т. е. 11,13 кН. Итак, опасным сказалось сечение
В, хотя изгибающий момент в нем не максимален.
На рис. 7.42 показаны эпюры нормальных напряжений для сече
ний В и С, построенные при нагрузке, равной допускаемой. Напряже
ния равны допускаемым лишь в крайних верхних точках сечения В;
в остальных точках как этого, так и всех остальных сечений напряже
ния ниже допускаемых.
Предлагаем читателю произвести расчет для случая расположения
сечения полкой вверх и убедиться, что такое расположение нерацио
нально —допускаемая нагрузка окажется меньше, чем при рассмотрен
ном положении сечения.
194
§ 7,7. Касательные напряжения
при прямом поперечном изгибе
В поперечных сечениях балок, как было установлено выше,
при чистом изгибе возникают только нормальные, а при попе
речном изгибе —как нормальные, так и касательные напря
жения.
Из закона парности касательных напряжений следует, что
в продольных сечениях балки, параллельных нейтральному
слою, также возникают каса
тельные напряжения (рис. 7.43).
Для данной точки балки каса
тельное напряжение т:гу, возни
кающее на площадке попереч
ного сечения, равно касатель
ному напряжению ту2, возни
кающему на площадке про
Рис. 7.43
дольного сечения, проведенного
через ту же точку.
Наличие касательных напряжений в продольных сечениях
балок подтверждается также и результатами следующего про
стого опыта. Представим себе две одинаково нагруженные
двухопорные балки (рис. 7.44), одна из которых состоит из ря
да отдельных положенных друг на друга и ничем не скре
пленных брусьев. Каждый из этих брусьев деформируется неза
висимо от других (влияние сил трения между брусьями не
учитываем), имея собственный нейтральный слой. В результате
деформации отдельные брусья, составляющие балку, взаимно
сдвинутся. В целой балке взаимного сдвига ее продольных
слоев не происходит; это и указывает на наличие в продольных
плоскостях касательных напряжений, препятствующих этим
сдвигам. Попутно заметим, что прогибы целой балки будут
значительно меньше, чем балки, состоящей из отдельных
брусьев.
195
Касательное напряжение в произвольной точке поперечного
сечения бруса (т = xzy) при прямом поперечном изгибе опреде
ляется по формуле
т = тzy = xyz = QySxJ { J xb).
(7.13)
Здесь Qy —поперечная сила, возникающая в рассматривае
мом поперечном сечении бруса; Sxl0 —статический момент от
носительно нейтральной оси поперечного сечения его части,
расположенной по одну сторону от прямой, проведенной через
исследуемую точку параллельно нейтральной оси. Эта часть се
чения заштрихована на рис. 7.45; Jx —момент инерции всего
поперечного сечения относительно его нейтральной оси;
b —ширина поперечного сечения —размер в направлении, па
раллельном нейтральной оси (при переменной ширине сечения
значение Ъ надо брать на уровне исследуемой точки).
Эту зависимость называют формулой Журавского.
Из закона парности касательных напряжений следует, что
формула (7.13) дает также значение касательного напряжения
Ту,, возникающего в продольном сечении балки.
В основу вывода формулы Журавского положено допуще
ние о равномерном распределении касательных напряжений по
ширине сечения (рис. 7.45). Это допущение обеспечивает доста
точную точность формулы при ширине сечения, меньшей его
высоты. Так, при отношении b/h = 1 отклонение от равномер
ного распределения составляет 12,6 %, а при b/h =
= 0,5 —лишь 3,3 %.
Для сечений, контур которых не параллелен силовой линии (на
пример, треугольник, круг), полное касательное напряжение не парал
лельно силовой линии. В точках контура оно параллельно касательной
к контуру (рис. 7.46). Формула Журавского для указанных сечений
дает приближенное значение составляющих т, параллельных силовой
линии, распределение этих составляющих х,у по ширине сечения при
нимают равномерным. В формулу (7.13) следует подставлять b = Ьх.
IУ
ш
ш
шшт
к
-
J
]
ь
Рис. 7.45
196
,
Применим формулу Журав
ского для исследования закона
распределения касательных на
пряжений по высоте прямо
угольного поперечного сечения
балки.
Составим выражение для
статического
момента
S^,
(рис. 7.47). Как известно, ста
тический момент равен произ
ведению площади на коорди
нату ее центра тяжести:
«Ус,
u
ft W 2)
где ю = [(Л/2) - I'll b и yc = — ------- ;
A + Zl .
4
2 ’
= [(ft/2) - yt] ft [(ft/4) + (У./2)] = (bh2/ 8) [1 • (2yi/ft)2].
Принципиально безразлично, брать ли статический момент
заштрихованной или всей остальной части сечения, так как по
абсолютному значению они равны: их сумма дает статический
момент всего сечения относительно оси х, который равен нулю
(ось х —центральная).
Подставляя в формулу (7.13) значение SX(a, получим
z = Qy(bh2/S ) [ l- ( 2 y J h ) 2/\/(Jxb)
или, учитывая, что Jx = bh3/ 12,
(Щ2J]
f 2M 1
l ft ) J
126, bh2
3 Qy
11bh3 8ft
2 bh
{h )
Переменная у: входит в полученное выражение в квадрате,
т. е. т изменяется по высоте сечения по параболическому зако
ну, достигая максимума в точках нейтральной оси (рис. 7.47).
В крайних точках сечения при yt = + h/2 касательные напряже
ния равны нулю. Принимая у1 = 0, найдем
xmax = 3Qy/(2bh) = 3Qy/(2A).
(7.14)
Таким образом, максимальное касательное напряжение
в рассматриваемом случае оказалось в полтора раза больше
среднего, вычисляемого как частное от деления поперечной
силы на площадь сечения.
В балке прямоугольного сечения максимальные касатель
ные напряжения возникают в тех точках, где нормальные на
197
пряжения равны нулю (на нейтраль
ной оси), и, наоборот, в крайних
точках сечения, где нормальные на
пряжения максимальны, касательные
напряжения равны нулю. Сказанное
справедливо также для балок круг
лого сечения.
Результат, полученный для балки
прямоугольного сечения, можно ис
пользовать для вычисления Касатель
ных напряжений в стенке двутавро
вой балки. Не останавливаясь на до
казательствах, укажем, что в полках
двутавровых балок возникают гори
зонтально направленные касательные
напряжения xzx, а вертикальные т2„
близки к нулю, при этом для вычисления последних формула
Журавского неприменима. На рис. 7.48 показано направление
касательных напряжений в полке и стенках двутаврового
профиля и дана эпюра т в стенке.
Напряжения в верхней (нижней) точке стенки найдем, под
ставляя в формулу (7.13) статический момент площади полки
S xп относительно нейтральной оси и принимая ширину сечения
равной толщине стенки:
ТК = Q y S x n / V M
Максимальное касательное напряжение (возникает в точках
нейтральной оси) найдем из выражения
Т'.ф.ах “ О
12ссч / (7х^с),
(7.15)
где Sxi/2ce4 —статический момент полусечения относительно
нейтральной оси (в таблице ГОСТа на прокатные двутавры эта
величина обозначена Sx).
В прокатной или сварной двутавровой балке, имеющей
сравнительно большую высоту, касательные напряжения могут
быть значительны при условии, что балка нагружена больши
ми сосредоточенными силами и длина ее невелика или эти
силы приложены близко к опорам. В этом случае помимо ос
новного расчета на прочность по нормальным напряжениям
следует проверить максимальные касательные напряжения
в том сечении, где поперечная сила имеет наибольшее значение.
Обычно принимают (для стальных балок) [т] = 0,6 [<т].
П р им е р 7.18. Определить из расчета на прочность допускае
мую нагрузку двутавровой балки № 50, нагруженной, как указано на
198
Rfl= m a k
I
\F -6 q a
q
Яв= Щ а к
рис. 7.49. Допускаемые напряжения: [о] = 160 МПа; [х] = 96 МПа;
а = 1 м.
Решение. Определяем опорные реакции и строим эпюры Qf и
М х (рис. 7.49). На основе формулы (7.7) находим допускаемое значение
максимального изгибающего момента:
I м * шJ
где
=
Wx
[сг] = 1589 • НГ« • 160 • 106 = 254-103 Н •м,
W x — 1589 см3 (ГОСТ 8239-72).
По эпюре М х m;ij = 10,12qa2, следовательно,
10,12 [q] а2 = 254-103 Н м ,
откуда
254-103
и = 10,12а2
254-103
10,12-12
= 25,1 • 103 Н/м = 25,1 кН/м.
Проверим прочность балки по максимальным касательным напря
жениям, возникающим в точках нейтральной оси левого опорного со
стояния. По формуле (7.15):
тпшх — 6 у т а х ^ х 1 /2 с е ч / (*lx^c) >
по таблице сортамента, 5*1/2сеч = 919 см3; J x = 39727 см4; 8С= 10 мм;
по эпюре поперечных сил с учетом найденного значения
Qy та* = 13,5qa ---- 13,5 •25,1 • 10s -1 = 33,9 ■104 H.
Таким образом,
33,9-104-919- 10~®
- = 78,8 • 10® Па = 78,8 МПа.
39 727-10- 8 0,01
199
§ 7.8. Перемещения при изгибе.
Основные понятия
В ряде случаев работающие на изгиб элементы машино
строительных и строительных конструкций должны быть рас
считаны не только на прочность, но и на жесткость. К деталям,
рассчитываемым на жесткость, относятся, в частности, валы
зубчатых и червячных передач и многие части металлорежущих
станков.
Как известно из предыдущего, расчет на жесткость элемен
та конструкции, имеющего форму бруса, заключается в опреде
лении наибольших перемещений его поперечных сечений и со
поставлении их с допускаемыми, зависящими от назначения
и условий эксплуатации данного элемента. Например, рас
считывая вал на жесткость при кручении, ограничивают углы
поворота поперечных сечений вокруг его продольной оси. На
помним также, что решение статически неопределимых задач
на растяжение (сжатие) связано с составлением уравнений пере
мещений, т. е., по существу, с определением линейных переме
щений поперечных сечений рассчитываемых брусьев.
Расчет на жесткость при изгибе, очевидно, требует предва
рительного изучения вопроса о перемещениях поперечных сече
ний балок.
Рассмотрим простую консоль, нагруженную на свободном
конце силой F, линия действия которой совпадает с одной из
главных осей поперечного сечения балки (рис. 7.50).
При деформации балки центры тяжести ее поперечных сече
ний получают линейные перемещения, а сами сечения повора
чиваются вокруг своих нейтральных осей. Допущение о мало
сти перемещений позволяет считать, что направления линейных
перемещений перпендикулярны продольной оси недеформированиого бруса. Эти перемещения принято называть прогибами.
Прогиб произвольного сечения обозначим v, а наибольший
прогиб —стрелу прогиба —/ . Геометрическое место центров
тяжести поперечных сечений деформированного бруса, т. е. ось
изогнутого бруса, условно называют изогнутой осью или чаще
упругой линией. Эта линия —плоская кривая, лежащая в сило
вой плоскости. Совпадение плоскости деформации с пло-
Рис. 7.50
200
скостью действия нагрузки является характерной особенностью
прямого изгиба. Более того, можно сказать, что именно по
этой причине рассматриваемый случай изгиба называют
прямым.
При повороте поперечные сечения остаются перпендику
лярными изогнутой оси бруса, что следует из справедливости
гипотезы Бернулли.
Следовательно, угол (0) поворота поперечного сечения равен
углу между касательной к упругой линии в данной точке и осью
недеформированкого бруса.
Таким образом, ордината упругой линии и угол наклона ка
сательной, проведенной к ней в данной точке, полностью опре
деляют линейное и угловое перемещения соответствующего
поперечного сечения балки; следовательно, отыскание этих
перемещений сводится к исследованию формы упругой линии.
§ 7.9. Дифференциальное уравнение упругой линии
и его интегрирование
Упругую линию балки можно рассматривать как график не
которой функции, определяемой характером нагружения балки,
ее размерами и материалом. Сама функция представляет собой
текущую ординату упругой линии, а ее аргументом является
абсцисса центра тяжести произвольного поперечного сечения
балки, т. е.
v = Ф (2 ).
(а)
Для определения этой функции воспользуемся зависи
мостью междукривизной оси бруса (кривизнойнейтрального
слоя) и изгибающим моментом
1/р= MX/(EJX).
(б)
Из курса математики известно следующее выражение кри
визны некоторой кривой:
1/р =
V"/
[1 + (в')2] 3/2.
(в)
Первая производная (»') от функции дает значение тангенса
угла наклона касательной к графику этой функции. В пределах
упругих деформаций балки эти углы весьма малы —порядка
тысячных долей радиана. Если даже принять, что угол наклона
касательной равен 0,01 рад, то и в этом случае квадрат первой
производной ничтожно мал по сравнению с единицей. Действи
тельно, при малых углах, как известно, можно считать, что тан
генсы равны соответствующим углам, следовательно, при 0 =
= 0,01 рад tg 8 = v' = 0,01 и (г/)2 = (0,01)2 = 10~4.
201
Таким образом, вместо точного выражения кривизны мож
но принять приближенное
1/р * v" = d2o/dz2,
обеспечивающее определение перемещений с точностью, впол
не достаточной для практических расчетов.
Подставляя значение кривизны в соотношение (б), получаем
v" = d 2y/dz2 = М х / (EJJ.
(7.16)
Выражение (7.16) называется приближенным дифферен
циальным уравнением упругой линии. Для балок постоянного се
чения его обычно записывают в виде
EJxv" = М х.
(7.17)
Правая часть зависимости (7.17) представляет собой уравне
ние изгибающих моментов, т. е. аналитическое выражение зако
на изменения изгибающего момента по длине балки
M x = Y ( z ) [где ф = EJX<S>(z)],
которое легко составить для любой статически определимой
балки.
Знаки левой и правой частей выражений (7.16) и (7.17) совпа
дают при условии, что ось у направлена вверх (рис. 7.50), т. е.
для линейных перемещений v направление вверх принято за
положительное.
Итак, выражение второй производной исследуемой функции
можно считать известным. Для нахождения первой производ
ной, т. е. углов наклона, касательных к упругой линии балки
(углов поворота поперечных сечений), следует проинтегриро
вать левую и правую части выражения (7.17). В результате
получим
EJxv' = EJXtg 0 « EJXB = J Mx dz + C.
(7.18)
Интегрируя затем зависимость (7.18), получаем
EJxv = Я (Мх dz) dz + Cz + D.
(7.19)
Подставив сюда уравнение изгибающего момента, выпол
нив интегрирование и найдя постоянные интегрирования С и D,
получим в развернутом виде выражение функции (а), а следова
тельно, получим возможность определить прогиб любого попе
речного сечения балки. Аналогично из уравнения (7.18) можем
определить угол поворота произвольного поперечного сечения.
Постоянные интегрирования определяют из так назы
ваемых граничных условий, зависящих от способов закрепле202
ния (вида и расположения опор) балки, как показано ниже на
конкретных примерах.
П р и м е р 7.19. Определить угол поворота и прогиб сечения на
свободном конце балки, изображенной на рис. 7.51.
Р е ш е н и е . В заделке возникают реактивная сила R a = ql и реак
тивный момент М а —д/2/2.
Изгибающий момент в произвольном поперечном сечении балки,
проведенном на расстоянии г от заделки, найдем, беря сумму момен
тов относительно точки К всех внешних сил, расположенных слева от
нее:
Мх = —ql2/2 + qlz —gz2/2.
Приближенное дифференциальное уравнение упругой линии имеет
вид
EJX(dV dz2) = EJxv" = ф" (z) = М х
или
EJxv" = —ql2/2 + qlz - gz2/2.
(a)
Интегрируя обе части этого уравнения, получаем
EJxv' = EJfi = - ql2z/2 + qlz2/2 - qz3/6 + C.
(6)
Интегрируя выражение (б), найдем
EJxv = - ql2z2/4 + qlz316 —qz*/24 + Cz + D.
(в)
Для определения постоянных интегрирования С и D учтем, что
левый конец балки жестко закреплен, т. е. его угол поворота и прогиб
равны нулю. Итак, первое граничное условие получаем в виде 0Х=0 =
= 1>.'=0 = 0, второе —а1=,0 = 0. Подставляя в (б) vx=0 = 0 и z = 0, полу
чаем С —0.
Аналогично из (в), принимая »г_0 = 0, находим D = 0.
Получаем следующие окончательные уравнения углов поворота
поперечных сечений (углов наклона касательных к упругой линии)
и упругой линии:
EJxv' = - ql2z/2 + qlz2/2 —qz3/6
(r)
EJxv = —ql2z2/4 + qlz3/6 —qz*/24.
(д)
203
Угол поворота крайнего правого сечения найдем, подставляя в (г)
z = l:
EJxv'z=l = EJXQB = —ql2l/2 + qll2/2 - ql3/6 = - q l 3/6
или
0B= - q l 3/(6EJx).
Знак минус указывает, что сечение поворачивается по часовой
стрелке (здесь для углов применяется то же правило знаков, что и
в курсе тригонометрии).
Прогиб свободного конца получим, подставив в (д) z = I:
EJxvz=l = EJxvB = - q l 2l2/4 + qll3/6 - ql*/24 = - q l */8
или
VB= -ql*/(XEJx).
Положительное направление оси у принято, если она направлена
вверх, знак минус указывает, что прогиб vB направлен вниз.
П р и м е р 7.20. Определить максимальный прогиб заданной бал
ки (рис, 7.52) и сравнить его с прогибом по середине пролета.
Р е ш е н и е . Опорные реакции показаны на рис. 7.52. Изгибаю
щий момент в произвольном поперечном сечении равен
М х = R
Приближенное
az
ди ф ф еренц иальное
E J x v" =
П осле первого
= M z /i.
уравнение упругой линии
Mz/l.
(а)
интегрирования
EJxv' = EJxe = Mz2/ (/ •2) + С,
(б)
EJxv = Mz3/ ((• 6) + Cz + D.
(в)
а после второго —
В сеч ен и ях А и В балка имеет
зд е с ь равны н у л ю . Следовательно,
шарнирные опоры, т. е. прогибы
имеем такие граничные условия:
1) i>.^0 = 0; 2) 1>г=1 = 0.
Используя первое граничное условие, из (в) получаем
EJxt)2=o = 0 = D.
204
Второе граничное условие дает
EJxvs=l = 0 = Ml3/(l-6)+CI,
откуда
С = - M i l 6.
Окончательно получаем следующие уравнения углов поворота
и упругой линии:
EJxv’ = EJJd = Mz2/(l ■2) - Ml/6;
(г)
EJxv = Mz3/ (Z•6) - M/z/6.
(д)
Прогиб по середине пролета найдем, подставляя в (д) z = Z/2:
М (Z/2)2 Ml (1/2)
MZ2
Л=,/2_ / ~ б
б-
"Тб”
ИЛИ
v^ II2 = - M 1 2/(16EJx).
В сечении, где прогиб максимален, касательная к упругой линии
параллельна оси балки, т. е. iiz=,0 = 0 (известное из курса математики
условие экстремума функции). Подставляя в (г) z = z0 (значение абс
циссы сечения с максимальным прогибом) и приравнивая полученное
выражение нулю, имеем
О= M z l/(l ■2) —Ml/6,
откуда
г0 = //|/з » 0,577/.
Подставляя в (д) z = r 0, найдем максимальный прогиб:
£Jxi>raax = Mz 2/ (I- б) - Mlz0/6 = MZ3/(6Z•3|/3) - МП/(6 j/з);
о.™ - -M /2/(9 [/3 £ ^ )« -MZ2/(15,57£JJ.
Характерно, что, несмотря на явно несимметричное нагружение
балки, максимальный прогиб получился близко к середине пролета
(смещен в сторону приложенного момента всего на 0,0771) и превы
шает прогиб при z = 1/2 лишь на 2,34%. Этим обстоятельством часто
пользуются при практических расчетах, принимая для двухопорных ба
лок без консолей при нагрузке, направленной в одну сторону, в каче
стве максимального прогиб по середине пролета. Ошибка получается
весьма незначительной, а расчет существенно упрощается.
§ 7.1 0 . Энергия деформации при изгибе
Наиболее общий метод определения перемещений в упругих,
системах —энергетический. В основу этого метода положено
условие равенства работы внешних сил, приложенных к линейно-деформируемой упругой системе, и энергии деформации
системы.
205
Работа статически приложенной внешней силы, как извест
но, равна половине произведения конечного значения силы на
конечное значение соответствующего перемещения (теорема
Клапейрона).
Работа произвольной системы внешних сил (рис. 7.53) равна
полусумме произведений конечного значения каждой из сил f (
на конечное значение соответствующего перемещения Л;:
=
(7.20)
В дальнейшем будем всегда считать, не оговаривая этого
специально, что речь идет именно о конечных значениях стати
чески приложенных сил и соответствующих перемещений. При
применении энергетического метода как линейные, так
и угловые перемещения обозначают А с тем или иным
индексом.
Формула (7.20) представляет собой общее выражение тео
ремы Клапейрона для произвольной системы сил. Было бы
ошибочным считать эту зависимость составленной на основе
принципа независимости действия сил —здесь каждая из сил
умножается на перемещение, которое зависит от всех прило
женных сил.
Для определения работы внутренних сил, численно равной
потенциальной энергии деформации, выделим из балки
(рис. 7.53) в пределах участка, находящегося в условиях чистого
изгиба, бесконечно малый элемент dz. Этот элемент в дефор
мированном виде в крупном масштабе показан на рис. 7.54.
Из курса теоретической механики известно, что работа мо
мента (пары сил) равна его произведению на соответствующий
угол поворота. Здесь, учитывая статический характер приложе
ния нагрузки согласно теореме Клапейрона, надо взять полови
ну указанного произведения:
dV = dW = Mxd&/2.
206
(а)
Длина волокна п —п, лежащего в нейтральном слое, равна
первоначальному размеру элемента dz, следовательно,
dz = р d0
или
d0 = (l/p)dz.
По формуле (7.4),
1/р = M J ( E J X) и d0 = М х dz/{EJx).
Подставляя это значение d0 в выражение (а), получаем
dV = M 2x dz/(2EJx).
(б)
Выражение (б) представляет потенциальную энергию дефор
мации изгиба бесконечно малого элемента балки. Оно получе
но для элемента, находящегося в условиях чистого изгиба. При
поперечном изгибе помимо изгибающих моментов возникают
поперечные силы, но при определении энергии деформации
ими в подавляющем большинстве случаев можно пренебречь
и считать зависимость (б) применимой во всех случаях прямого
изгиба. Для вычисления энергии деформации балки в целом
следует просуммировать значения dV по всей ее длине. При
этом следует учесть, что закон изменения изгибающих момен
тов для отдельных участков балки различен, поэтому вычисле
ние определенных интегралов надо вести отдельно для каждо
го участка длиной
а затем результаты суммировать.
Окончательно формула для определения энергии деформа
ции изгиба имеет вид
(7.21)
С учетом поперечных сил формула для вычисления энергии де
формации при прямом поперечном изгибе
У=
(7.22)
h
h
Здесь к —коэффициент, зависящий от формы поперечного сечения бал
ки. Например, для прямоугольного сечения к = 1,2. Остальные обозна
чения известны из предыдущего.
Можно показать, что, как правило, второе слагаемое не превы
шает 2 —3% от всей энергии деформации, а во многих случаях имеет
еще меньшее значение.
207
П р и м е р 7.21. Определить
энергию деформации изгиба
______ _______ 1 балки (рис. 7.5®, не учитывая
влияния поперечных сил.
Т
Р е ш е н и е . Балка имеет
1
два участка нагружения. При
Ри с. 7.55
нимая начало координат на ле
вом конце балки, получаем сле
дующие выражения для изги
I
а
я
бающих моментов:
П .Н Н 1
1
Z,
М,J = - q z 2/2 при 0 ^ z < а ;
а
а
F
М " = - q a [ z - ( a / 2)]
Р и с. 7.56
при а ^ z
2а.
По формуле (7.21) имеем
(M')2dz
2EJr
’ M l dz
2EJr
_ h-qz*/2fdz
2EJX
J
J
C(m 'J)2dz
J 2EJX
f [ —qa (z —a/2)]2 dz
2EJr
17
-q2a5.
30EJ.
П р и м е р 7.22. Определить прогиб конца консоли (рис. 7-5<§Г
Р е ш е н и е . Для определения прогиба воспользуемся условием
равенства работы внешних сил и энергии деформации W = V.
Работа силы F при статическом нагружении балки равна W =
= Ff/2. Энергию деформации найдем по формуле (7.21):
I
f M2dz
V= —- .
J 2E J X
о
Изгибающий момент в произвольном поперечном сечении балки
М х = - F z в данном случае имеем один участок нагружения
V=
C(-Fz)2 dz
F 2/3
-------'----- = -------- .
J 2EJX
6EJX
о
После подстановки в исходное равенство значений W и V полу
чаем F f /2 = F2l3/(6EJX), откуда / = FP/(3EJJ.
Этот прием определения перемещений применим лишь в тех про
стейших случаях, когда балка нагружена одной силой и требуется
найти прогиб в точке ее приложения. Но даже и в этих случаях значи
тельно удобнее пользоваться общим энергетическим методом, ко
торый изложен в § 7.11.
§ 7 .1 1 . И нтеграл М ора
Рассмотрим вывод общей формулы для определения пере
мещений при изгибе.
Пусть требуется определить прогиб в точке К двухопорной
балки, изображенной на рис. 7.57, а. Для упрощения вывода по
казываем только одну силу, но формула, которая будет получе
на, справедлива при любых на
грузках.
Приложим к ненагруженной
балке в точке К некоторую силу
Т (рис. 7.57, б). Состояние балки
при ее нагружении силой Т назы
вают вспомогательным или фик
тивным, так как в действитель
ности его не существует и оно
нужно лишь для вывода формулы
перемещений. Определим работу
внешних сил и энергию деформа
ции для вспомогательного состоя
ния балки.
Работа силы Т на перемещении Акт (здесь первый индекс
указывает точку, в которой определяется перемещение, а вто
рой —причину, вызвавшую это перемещение) определяется по
теореме Клапейрона :
WT = 7г ТАкт.
(а)
Соответствующая энергия деформации определяется по
формулам (7.21):
I,
где М хТ — изгибающий момент в произвольном сечении балки,
возникающий от действия силы Т. Конечно, WT — VT, т. е.
/■
Приложим к балке, нагруженной силой Т, заданную силу F
(рис. 1.51, в).
Точка К получит дополнительное перемещение АКР>.
а сила Т совершит дополнительную работу:
WTF=
t a k f.
(г)
209
В этом выражений нет множителя 1/ 2, так как в процессе
нагружения балки силой F сила Г была уже приложена и ее
значение не изменилось. Сила F совершит работу на перемеще
нии AFF точки ее приложения:
Wf = 1/ 2FAf f .
(д )
Энергия деформации, соответствующая нагружению балки
силой F (рис. 7.57, а), равна
VF =
(е)
При этом WF = VF или
(ж)
Итак, полная работа внешних сил представится как сумма
трех слагаемых:
W = W
t
+ W
f
+ W
tf
=
= 1/2 ТАкт+ 1/2FAf f + TAk f .
(з )
Энергию деформации при совместном действии сил Т и
F найдем по формуле (7.21), принимая Мх = М хТ + М хР (к вы
числению изгибающих моментов применим принцип независи
мости действия сил):
Раскрывая скобки,
к
к
к
и приравнивая правые части выражений (з) и (и), получим
= Y f _ M*Tdz •
Чг ТАКТ + 1/ 2FAf p + TAkf, ■
U J 2Eh
V ГM 2xFdz
Y ГM xFM xTdz
'Li 2EJ* Li EJ*
210
‘
Учитывая, что первое и второе слагаемые левой части
равны соответственно первой и второй суммам интегралов
правой части [см. выражения (в) и (ж)], получаем
ТА K F
V Г M xFM xTdz
"Li ej*
'
Для определения искомого перемещения АКР разделим обе
части полученного выражения на Г, тогда
M xf (Mxt /T) d z
A kf —
EJX
Величина M xT/T, имеющая размерность длины, предста
вляет собой изгибающий момент в произвольном сечении бал
ки, вызванный действием силы, равной единице (безразмерной!)
и приложенной в той точке, перемещение которой определяет
ся. Обозначим этот момент М х и назовем его единичным
моментом.
Окончательно получаем следующую формулу для опреде
ления перемещений, называемую формулой или интегралом
Мора:
M xFM l dz
(7.23)
&KF
ЁГХ
Из вывода следует, что интеграл Мора, позволяющий опре
делить перемещение произвольного сечения балки, имеет сле
дующий физический смысл: э т о р а б о та ед и н и чн о й с и л ы н а пере
м ещ ени и ее т о ч к и п р и л о ж е н и я о т за д а н н о й н а гр у з к и . Отсюда
следует, что, если при вычислении интеграла Мора результат
получается со знаком плюс, направление приложенной единич
ной силы совпадает с направлением искомого перемещения
(при совпадении направлений силы и перемещения точки ее
приложения работа положительна). Знак минус укажет, что эти
направления прямо противоположны.
Влияние поперечных сил на перемещения в балках весьма незначи
тельно. Лишь в случае очень коротких балок, нагруженных большими
сосредоточенными силами, может оказаться, что это влияние суще
ственно.
Если учитывать как изгибающие моменты, так и поперечные силы,
то интеграл Мора имеет вид
ГMxFM1dz V"1 ГkQyFQi dz
(7.24)
4 C F '■
"Li
EJX ~~
+Li
GA
’
211
где Q~f и Q1 —соответственно выражения поперечных сил от заданной
нагрузки и от единичной силы для произвольного поперечного сечения
балки. Остальные обозначения известны из предыдущего. О коэффи
циенте к см. с. 207.
Для вычисления перемещения с помощью интеграла Мора
нужно выполнить следующие операции:
1) составить уравнение изгибающих моментов M xF от за
данной нагрузки;
2) освободив систему (балку) от заданной нагрузки, прило
жить к ней силу, равную единице в той точке, где определяется
перемещение, и по направлению этого перемещения;
3) составить уравнение изгибающих моментов М у от этой
единичной силы;
4) вычислить сумму интегралов (7.23) от произведения обо
их моментов, деленного на жесткость сечения.
Если определению подлежит не прогиб, а угол поворота ка
кого-либо поперечного сечения, то к разгруженной балке сле
дует приложить в этом сечении не силу, а пару сил с моментом,
равным безразмерной единице (сокращенно —единичный мо
мент). В остальном техника определения перемещений не
изменяется.
Так же как при определении прогибов, направления поворо
та сечения и приложенного единичного момента совпадают, ес
ли результат вычисления интеграла Мора получается со зна
ком плюс.
В случае если жесткость сечения балки постоянна на всем ее
протяжении или в пределах отдельных участков, то взамен
формулы (7.23) получим
Р е ш е н и е . Для определения
перемещения по методу Мора со
ставляем выражения изгибающих
моментов для участков 1 и II бал
ки, при этом для участка I начало
координат принимаем на левом
конце балки, а для II —на правом:
M' f = (Т/2)21
Рис. 7.58
212
Ml'F = (F/2)z2
(O ^z^l/2);
(0 « г2«//2).
Прикладываем к ненагруженной балке по середине пролета силу,
равную единице (рис. 7.58,6), и составляем выражения единичных мо
ментов, выбирая начало координат так же, как и при составлении вы
ражений M xF:
М1 —(1/2) Z\
(0<Zl<//2);
М l ‘=(l/2)z2
(0 ^ z2 < 1/2).
Очевидно, что подынтегральные выражения для участков I я II
совершенно одинаковы; поэтому достаточно определить интеграл
лишь для одного участка и результат удвоить. Применив формулу
(7.25), получим
vk f
M xFM l
= &KF =
1/2
dz =
И2
2
\ F z
EJX } 2 1 2 1 1
F
2
z3
или Акт =
з
О
о
Я3
48ЁГХ'
Положительный результат указывает, что прогиб направлен так
же, как единичная сила, т. е. вниз.
Для определения угла поворота левого опорного сечения при
кладываем в этом сечении пару сил с моментом, равным единице
(рис. 7.58, в). Уравнения единичного момента составим отдельно для
участков I и II, по-прежнему принимая начало координат в первом
случае на левом, а во втором —на правом конце балки. Можно было
бы составить и одно уравнение единичного момента для всей балки,
но все равно интегрирование пришлось бы вести по участкам, так как
уравнение M xF для участков I и II различно:
(O ^z^l/2);
M l' =( l /l ) z2
(0 s: z2 < 1/2).
По формуле (7.25) имеем
1/2
= Ляг -
j y
я ( l - - f j d z , + | ~ z 2\ z 2 dza]
О
1 (F I2
0
FI2
= ---------------------------- 1--------- , или A .F = 16ЁГ
EJX V 2 8
2 24
2 24 /
F l1
F l1 \
Знак плюс указывает, что сечение поворачивается в направлении
единичного момента, т. е. по часовой стрелке.
Обычно при определении перемещений в балках интеграл Мора
вычисляют графо-аналитическим способом (см. § 7.12), кот орый значи
тельно удобнее, чем рассмотренный в этом примере аналитический
метод.
213
§ 7 .1 2 . П равило Верещ агина
Вычисление интеграла Мора, представленного в виде фор
мулы (7.25)
M xFM 1dz,
Акг
I,
целесообразно выполнять графо-аналитическим способом, на
зываемым правилом Верещагина. Выведем это правило.
Каждое из слагаемых, входящих в формулу (7.25), имеет вид
л
- - JjWxrMidz,
С
где e n d — пределы интегрирования, т. е. абсциссы сечений,
являющихся границами рассматриваемого участка.
С математической точки зрения задача сводится к вычисле
нию определенного интеграла от произведения двух функций:
M xF = f 1(z) и М j = / 2(z). Здесь уместно напомнить, что в под
ынтегральное выражение формулы (7.25) входят не какие-либо
частные значения изгибающих моментов, а аналитические зави
симости, дающие закон изменения этих моментов по длине
данного участка балки. Графики указанных функций предста
вляют собой эпюры изгибающих моментов M xF и M t.
Предположим, что функция f t (z) произвольна, a / 2(z) ли
нейна, т. е. может быть записана в виде / 2 (z) = kz + b (извест
ное из курса математики уравнение прямой линии, где к —
угловой коэффициент прямой, b —отрезок, отсекаемый ею на
оси ординат). Пусть графики этих функций имеют вид предста
вленный на рис. 7.59. Для вычисления интеграла
J / i ( z ) / 2(z)dz
С
подставим в подынтегральное выражение вместо / 2 (z) ее
значение.
Получим
| f t (z) f г (*) dz = J / t (z)(kz + b) dz = A:J / j (z) z dz + b J / , (z) dz.
c
c
c
c
Величина f l {z)dz представляет собой площадь элементар
ной криволинейной трапеции, заштрихованной на рис. 7.59.
Следовательно, второй из интегралов дает площадь, ограни
214
ченную графиком функции
(z), осью абсцисс и двумя
прямыми г , — с и z2 = d. В
дальнейшем сокращенно бу
дем
говорить —площадь
графика нелинейной функ
ции или площадь нелиней
ной эпюры. Обозначим эту
площадь со.
Первое подынтегральное
выражение f x (z) z dz дает
статический момент элемен
тарной площади относитель
Рис, 7.59
но оси ординат; следова
тельно, первый интеграл
представляет собой статический момент всей площади со
относительно этой оси:
/1
Sy» = J / i (z)zdz.
Вспомним, что статический момент площади равен ее
произведению на координату центра тяжести (см. с. 141),
получаем
Sya = mzc.
Таким образом приходим к выражению
i
J / , (z) f 2(z) dz = k<azc + bm = со(kzc 4- b).
Величина, стоящая в скобках, представляет собой ординату
графика линейной функции, соответствующую абсциссе zt, т. е.
это ордината, расположенная под центром тяжести графика не
линейной функции. Обозначая эту ординату т)с, окончательно
имеем
л
J / i ( z ) / 2(z)dz = coric,
т. е. определенный интеграл от произведения двух функций, из
которых одна линейна, а вторая произвольна, равен произведе
нию площади графика произвольной функции на взятую под ее
центром тяжести ординату графика линейной функции.
Возвращаясь к исходной зависимости (7.25), можем теперь
215
записать ее в следующем виде:
M xFM l dz =
(7.26)
Формула (7.26) представляет собой математическое выраже
ние правила Верещагина.
Для отдельного участка балки это правило формулируется
следующим образом:
каждое из слагаемых, входящих в интеграл Мора, равно про
изведению площади ю нелинейной эпюры изгибающих моментов
на ординату г\с линейной эпюры под центром тяжести нелинейной,
деленному на жесткость сечения (£•/,.) данного участка балки.
Для определения линейного или углового перемещения,
т. е. вычисления интеграла Мора в целом, следует просумми
ровать указанные слагаемые для всех участков балки.
Ниже на ряде конкретных примеров показано, что всегда
есть возможность разбить балку на такие участки, в пределах
каждого из которых по крайней мере одна из эпюр (чаще эпю
ра единичных моментов) будет линейна.
Вычисление интеграла Мора по правилу Верещагина часто
называют способом перемножения эпюр. При этом эпюру М хР
обычно называют грузовой, а эпюру М, —единичной.
Есть случаи, когда вычисление интеграла Мора не может
быть выполнено по правилу Верещагина. Это относится, вопервых, к брусьям с криволинейной осью —для них обе эпюры
изгибающих моментов M xF и М , нелинейны; во-вторых, к бал
кам с непрерывно переменным сечением (такие балки рассма
триваются в § 7.14), для которых величина EJX не может быть
вынесена за знак интеграла [см. формулу (7.23)] и, следователь
но, неприменимы преобразования, выполнявшиеся при выводе
правила Верещагина.
Приведем некоторые практические указания по применению
правила Верещагина.
1. Произведение площади нелинейной эпюры на ординату
линейной считается положительным, если площадь и ордината
расположены по одну сторону от оси балки (осей эпюр).
2. Если в пределах данного участка обе эпюры линейны, то
принципиально безразлично, площадь какой эпюры брать и на
какой эпюре —ординату.
3. В зависимости от разбивки балки на участки одна и та
же эпюра будет либо линейной, либо нелинейной, и поэтому
вопрос о том, где брать площадь, где —ординату, решается
различно. Поясним сказанное примером. Пусть требуется най
ти прогиб посередине консоли (в точке К), нагруженной на
216
свободном конце силой F
(рис. 7.60, а). Строим эпюру мо
ментов M xF (рис. 7.60, б). При
ложив к разгруженной балке
(рис. 7.60, в) в точке К силу,
равную единице, строим эпюру
М j (рис. 7.60, г).
Попутно заметим, что эпю
ры, построенные специально для
применения правила Верещаги
на, обычно не штрихуют.
Если принять в качестве уча
стка интегрирования всю длину
балки А В, то эпюра М, оказы
вается ломаной (толстая линия
на рис. 7.60, г), т. е. при приме
нении правила Верещагина она
должна рассматриваться как нелинейная. В тех же пределах
эпюра М хГ линейна. Следовательно, надо умножить площадь
единичной эпюры ю — 1/ 812 на ординату грузовой эпюры г|с =
= 5/6 FI, соответствующую центру тяжести единичной.
Если считать, что имеется два участка интегрирова
ния —АК и КВ, то в пределах каждого из них обе эпюры ли
нейны и безразлично, где брать площадь, а где —ординату. За
метим, что при такой разбивке на участки для второго из них
(КВ) произведение площади на соответствующую ординату
равно нулю, так как эпюра М г —нулевая (т. е. отсутствует) на
всем его протяжении. Конечно, более удобен первый из ука
занных способов определения участков интегрирования.
4.
Если одна из эпюр криволинейна, а вторая —ломаная,
следует разбить эту вторую эпюру на отдельные участки,
в пределах которых она линейна (рис. 7.61, в). Если обе эпюры
ломаные и границы участков у них совпадают, то надо разбить
обе эти эпюры на линейные участки, как показано, например,
Рис. 7.61
на рис. 7.61,6. При этом может оказаться, что на одном из
участков удобнее брать площадь эпюры M xF, а на другом сле
дует брать площадь эпюры М\ (рис. 7.61,6). Всегда надо брать
площадь той эпюры, которая в пределах данного участка
однозначна.
5.
Во многих случаях оказывается удобным строить грузо
вую эпюру в так называемом «расслоенном» виде. Сущность
этого расслоения состоит в следующем: уравнение изгибающе
го момента M xF представляет собой многочлен; например, для
участка III балки, изображенной на рис. 7.62, это уравнение
имеет вид
М
= - F z + M - q ( z ~ b)72.
xF
Вместо того чтобы строить график этого многочлена, как
это делалось ранее, для применения правила Верещагина целе
сообразно строить отдельные графики (эпюры), каждый из ко
торых соответствует одному из слагаемых. При этом во мно
гих случаях удобно строить эпюры, подходя с двух сторон
к месту излома единичной эпюры (см., в частности, пример
7.25).
6.
Если балка имеет консоли (одну или две), а определению
подлежит линейное или угловое перемещение какого-либо сече
ния, расположенного между опорами, следует, мысленно отре
зав консоли, заменить их действие на оставленную часть балки
соответствующими поперечной силой и изгибающим момен
том (рис. 7.63).
В табл. 7.1 приведены значения площадей эпюр и коорди
нат их центров тяжести, которыми и надлежит пользоваться
при определении перемещений.
218
Т а б л и ц а 7.1. Площади эпюр и расстояния до их центров тяж ести
П р и м е ч а н и е . Данные для параболических эпюр справедливы
лишь при условии, что эпюры имеют вершину в точке А, т. е.
касательная’к эпюре в этой точке параллельна оси балки.
219
П р и м ер 7.24. Определить про
гиб по середине пролета и угол по
ворота левого опорного сечения за
данной балки (рис. 7.64, а).
Р е ш е н и е . Определив опорные
реакции, строим эпюру изгибающих
моментов от заданной
нагрузки
(рис. 7.64, б). Прикладываем по середи
не пролета единичную силу (рис. 7.64, в)
и строим соответствующую эпюру из
гибающих моментов (рис. 7.64, г).
Единичная эпюра состоит из двух
одинаковых линейных участков. Эпю
ру M xF разбиваем на две одинаковые
части. Площадь и положение центра
тяжести каждой из этих частей даны
в табл. 7.1.
В данном случае достаточно вы
полнить «перемножение» эпюр для
одного участка и результат удвоить.
Ординату г|с единичной эпюры можно определить либо из подо
бия треугольников CEN и CDL (рис. 7.64, г), либо как произведение
R a z c, т. е. по общему способу вычисления изгибающего момента в за
данном сечении:
«Л
„ (2/3) (<j/2/8) (1/2) (5/32) I
vKF-= &KF = 2
EJv
EJ r
ДK F
5
=
ql*
W ~Ё7Г
Для определения угла поворота сечения А прикладываем еди
ничный момент (рис. 7.64,6) и строим соответствующую эпюру изги
бающих моментов (рис. 7.64, е). Эта эпюра линейна на всем протяже
нии балки. Площадь всей эпюры М хр (по табл. 7.1)
ю = (2/3) (ql2/8) I = (1/12) q l 3,
ее центр тяжести находится на середине пролета, и соответствующая
ордината эпюры M l
в; = i/2.
Искомый угол поворота
соц;
® "
=
АAF= U T
(1/2) q l 3 (1/12)
ЁГХ
ql3
-
24177-
П р и м е р 7.25. Определить прогиб свободного конца заданной
балки (рис. 7.65, а).
Р е ш е н и е . Эпюра M xf показана на рис. 7.65,б. Это параболиче
ская эпюра, но не того типа, для которого в табл. 7.1 приведены зна
чения и и г,; касательная к этой эпюре в точке К не горизонтальна.
Для получения эпюр, удобных для перемножения, строим отдель220
но эпюры от сосредоточенной силы F и от распределенной нагрузки
q (рис. 7,65,в,г). По табл. 7.1 находим:
а>, = (1/2) ql2l = (1/2) ql3; l - zlc = (2/3) 1;
w2 = (1/3) (qP/2) 1 = (1/6) gl3; / - z2C = (3/4) 1.
Соответствующие ординаты единичной эпюры (рис. 7.65, д):
Лк: =(2/3)1;
Пгс = (3/4) 1.
Искомое перемещение
'-{ L
Акт = -=7" (<airlic + о>2 Л2 с): EJ
J, ' 2
>
11 ql4
A K F
=
14
П р и м е р 7.26. Определить прогиб но середине пролета заданной
балки (рис. 7-66, а).
221
Решение.
Грузовая
(рис. 7.66, б) и е д и н и ч н а я (рис. 7.66, г)
эпюры —ломаные и при этом места
излома у них не совпадают. Поэтому
построим грузовую эпюру в расслоен
ном виде, подходя с двух сторон к
месту излома единичной эпюры
(рис. 7.66, в).
На рис. 7.66, в отмечены площади
отдельных частей расслоенной эпюры,
а на рис. 7.66, д указаны значения со
ответствующих ординат единичной
эпюры. Перемножая эпюры (множи
тели, произведение которых дает
площадь эпюры, условно взяты в
квадратные скобки), получаем
&k f
1
Ж
т
= ' . K m c + “ гЛгс + ®зЛзс) =*
н
н
н
— (I + а) +
о
1 Fa Г 1 1 1
2~2~Y ]Jy
После алгебраических преобразований получаем
Fa
(З/2 - 4а2).
48EJX
П р и м е р 7.27. Определить прогиб по середине пролета заданной
балки (рис. 7.67, а).
Р е ш е н и е . В пределах межопорной части балки грузовая эпю
ра - линейная (рис. 7.67, б), а единичная (рис. 7.67, в) —ломаная. Следо
вательно, надо взять площадь единичной эпюры, а ординату —грузо
вой. Для консоли перемножение эпюр дает нуль, так как единичная
эпюра на этом участке отсутствует.
Перемножая эпюры, получаем
F13
64EJX
Знак минус указывает, что направление перемещения точки К про
тивоположно направлению единичной силы.
§ 7.13. Расчеты иа жесткость при изгибе
Работающие на изгиб элементы строительных и машино
строительных конструкций во многих случаях должны быть
рассчитаны не только на прочность, но и на жесткость. При
этом зачастую оказывается, что требуемые размеры поперечно
го сечения бруса (балки), определенные из расчета на жест
222
кость, получаются большими, чем требуемые по условию
прочности.
В большинстве случаев условие жесткости выражается нера
венством
/< [/],
(7.27)
т. е. максимальный прогиб (стрела прогиба / ) не должен пре
вышать допускаемого [ /] . Значение допускаемого прогиба за
висит от назначения и условий работы рассчитываемой кон
струкции и колеблется в широких пределах. Обычно допускае
мую стрелу прогиба указывают в долях пролета (межопорного
расстояния 0 балки. Например, для ручных грузоподъемных
кранов [ /] = 1/400, то же, электрических [ / ] = //700; для валов
и шпинделей металлорежущих станков [ / ] = 0,0005...0,0010 I.
Для обеспечения нормальной работы подшипников сколь
жения и роликовых подшипников качения иногда ставится до
полнительное условие жесткости —ограничение угла поворота
опорных сечений:
(7.27а)
При этом допускаемый угол поворота составляет в среднем
0,001 рад.
В тех случаях, когда конструктивные и технологические тре
бования не накладывают особых ограничений на форму попе
речных сечений проектируемого элемента конструкции, следует
применять такие сечения, которые обеспечивали бы возможно
большую жесткость при наименьшем расходе материала.
Жесткость балки прямо пропорциональна моменту инерции Jx
ее поперечного сечения относительно нейтральной оси, а рас
ход материала (масса балки) прямо пропорционален площа
ди сечения А. Для оценки рациональности формы попереч
ного сечения балки, размеры которой определяются из
расчета на жесткость, удобна безразмерная характеристика
i.= J /A 2.
Например, для двутавра № 20 (при изгибе в плоскости на
ибольшей жесткости) j = 2,56; для того же двутавра при изгибе
в плоскости наименьшей жесткости j = 0,161; для круга j =
= 0,0795; для квадрата j = 0,0834; для кольца (при с = 0,7) j =
= 0,232.
Для ускорения и упрощения расчетов на жесткость
в табл. 7.2 приведены значения прогибов и углов поворота се
чений для некоторых часто встречающихся случаев нагружения
балок.
223
Т а б л и ц а 7.2. Значения прогибов и углов поворота поперечных сечений для некоторых случаев нагружения балок
Продолжение табл. 7.2
П р и м е ч а н и е . Везде указаны абсолютные значения прогибов и углов поворота.
П р и м е р 7.28. Проверить прочность и жесткость стальной балки
(рис. 7.68), если [о] = 160 МПа и [ / ] = 1/600.
Поперечное сечение балки —двутавр № 50; 7* = 39 727 см4; Wх =
= 1589 см3.
Р е ш е н и е . Наибольший изгибающий момент возникает в сече
нии по середине пролета. В силу симметрии нагружения балки макси
мальным будет прогиб также по середине пролета. Обращаем внима
ние на то, что сечения с максимальным изгибающим моментом
и имеющее максимальный прогиб совпадают отнюдь не всегда.
Максимальный изгибающий момент
Мхтхх —R^-Aa —q -За (3/2) а = 75 -4 —20-3(3/2) =210 к Н м .
Максимальные нормальные напряжения в опасном сечении
Мг
W,
210-10э
= 132 • 10б Па = 132 МПа.
1589-10_6
Максимальные напряжения ниже допускаемых на 17,5%.
Для определения максимального прогиба прикладываем к разгру
женной балке по середине пролета единичную силу, строим эпюру М,
и расслоенную эпюру Мхр. Перемножая эшоры M XF и М 1 для одной
половины балки и удваивая результат, найдем стрелу прогиба:
f = *KF=TTx { [ \ Ra
•4й•4й]{ - [
j
W
•За]1 г}:
J - 75 • Ю3 - 4 -1 - 4 -1 I 1 -![А. 9 20 10* 1- 3 1 13'8 1
64 J
L2
J в !!_з 2
226
2 - 103
•(800—146) = 16,5-10 3 м=16,5 мм.
2 • 10s • 10е ■39 727 ■10-8
Допускаемый прогиб
[ / ] = //600 = 8000/600 = 13,3 мм.
Следовательно, максимальный прогиб превышает допускаемый на
24,0%, т. е. жесткость балки совершенно недостаточна.
П р и м е р 7.29. Проверить прочность и жесткость балки
(рис. 7.69, а), если [о] = 120 МПа; [ / ] = 0,001/; Е = 2,0-105 МПа.
Решение. Определив опорные реакции, строим эпюру изгибаю
щих моментов (рис. 7.69,6). Проверяем балку на прочность:
“- - л Г
мш<м
Проверку на жесткость производим приближенно, принимая, что
максимальным будет прогиб по середине пролета. Ранее (см. с. 205)
было указано, в каких случаях прогиб по середине пролета мало отли
чается от максимального. Этот прогиб определим, используя данные
табл. 7.2 и применяя принцип независимости действия сил:
VKF = vK F l + vK F l = ~ j ~ ( 3 l 2 - 4a?) +
- 4 a 2>-
Учитывая, что
Jx = nd*/64 = 3,14 •604/64 = 63,6• 104 мм4 = 63,6 • 1 0 '8
m4,
и подставляя числовые данные, получаем
6 -103 0,35
/ = «к = 48 •2 • 105 • 10б •63,6 • 10 г~Г8 (3-1,12 -4 -0 ,3 5 2) +
9 - 1 0 3 '0 ,2 5
48 •2 • 105 • 106 •63,6 • 10" 8
(3 • 1,12 - 4 •0,252) = 2,325 • 10' 3 м =
= 2,325 мм.
Допускаемый прогиб
ГЯ =
/
1100
1000
1000
- 1,1 мм.
Таким образом, максимальный прогиб превышает допускаемый
более чем вдвое, т. е. жесткость балки совершенно недостаточна. В то
же время прочность ее обеспечена —максимальные напряжения ниже
допускаемых на 12,9%. Для обеспечения достаточной жесткости балки
надо увеличить момент инерции ее поперечного сечения в 2,12 раза,
что равносильно увеличению диаметра в |/2Д 2 = 1,21 раза.
П р и м е р 7.30. Определить из расчетов на прочность и жесткость
при [о] = 160 МПа и [ / ] = //800 требуемый номер двутаврового про
филя для заданной балки (рис. 7.70, а), Е ~ 2,0- 105 МПа.
227
Р е ш е н и е . Построив эпюру М х (рис. 7.70,б), из условия прочно
сти определяем требуемый момент сопротивления поперечного сече
ния балки:
W x ^ M xm al \ d \
= 54-103/(160-106) = 338-10_6 м 3 = 338 см3.
По ГОСТ 8239 —72 подходит двутавр № 27 с 1 ^ = 371 см3.
Для расчета на жесткость используем данные табл. 7.2. В силу
симметрии нагружения балки максимальный прогиб получается по се
редине пролета.
Стрела прогиба от силы 2F , приложенной по середине пролета,
равна
„
2F13
f 2Г —---- ---,
2
48EJX
то же, от силы F
Fa
/ г - 24E J , -(З/2 —4a2).
Суммарный прогиб от всех заданных сил
f
— f lF
+
f F
2F l$
48E J X
+ -r~ rr~ (3 f2 —4а2).
'
24ЕЛ
Подставляя в это выражение / = 8а, получаем
, 64Fa3 41Fa3
/ = - -3E- J. X +~ 6 E J r
\15Fa3
6E J ,
Условие жесткости
6 E JX U J
отсюда требуемый момент инерции
J =
175
18 - 103 ■0,62
~6
0,01-2-105-106
800
=0,01a,
По ГОСТ 8239 —72 подходит двутавр № 33 с J x = 9840 см4.
Из двух номеров профилей (полученных из расчетов на прочность
и жесткость) окончательно принимаем больший,
228
§ 7.14. Балки переменного сечения
Д л я б ал о к п о стоян н ого поперечного сечения расчет н а
прочн ость вы п олн яется по сечению, в к о то р о м возн и кает н а
и бо л ьш и й и зги баю щ и й м ом ент. Э то опасное сечение; по усло
ви ю прочности н о р м ал ьн ы е напряж ения в опасных точках сече
ния (т. е. н аи б ол ьш и е напряж ения) не д ол ж н ы п ревы ш ать
допускаем ы х. В о всех остальны х точках это го сечения, а те м
более во всех остал ьн ы х сечениях балки, м ате р и ал исп ользует
ся не п ол н остью — р аб о та ет при напряж ениях более низких,
чем допускаем ы е. К ак бы ло сказано вы ш е, д л я более п олн ого
и сп ользования м атер и ал о в следует п рим енять рац и о н ал ьн ы е
ф о р м ы поперечны х сечений, н априм ер д л я стальны х б ал о к —
двутавровое.
С ледую щ ий ш аг н а пути создания более легких конструк
ций — это прим енение б ал ок переменного сечения. П р и э т о м по
во зм о ж н о сти следует стрем иться к том у, чтобы н аи б ольш и е
н о р м ал ьн ы е напряж ения во всех сечениях бы л и одинаковы ,
т. е. что бы все сечения бруса бы ли р а в н о о п а с н ы .
Брус, удовл етворяю щ и й это м у условию , н азы ва ю т брусом
равного сопротивления изгибу. Т еоретически он наиболее вы го
ден (обеспечивает наим еньш ую за тр ат у м атериала).
И сследуем д л я некоторы х частны х случаев вопрос о ф о р м ах
(законах изм енения р азм е р о в поперечного сечения) брусьев р а в
н о го сопротивления изгибу.
Р асс м о т р и м простую консоль п рям о у го л ьн о го поперечного
сечения, нагруж енную силой на св о б о д н о м конце (рис. 7.71).
Вы ясним, как д о л ж н а м еняться ш и рина сечения при п о сто ян
ной его вы соте, если наиб ол ьш и е н о р м ал ьн ы е напряж ени я во
всех поперечны х сечениях одинаковы .
Д л я балки постоян н ого сечения опасное сечение в зад елк е;
условие прочности им еет вид
М.
Wx
FI
■<[а].
b h 2/ 6
Д л я п рои звол ьн ого сечения, отстоящ его на расстоян и и z от
сво бо д н ого
конца,
условие
п рочн ости тако в о :
Fz
(^max)z
..
h^/6 ^
где bz — ш ирина р ассм атр и вае
м о го сечения.
П о условию равнопрочности,
(^ m a x )z
^m ax
или
- <ш
- ,1
ку д а
Таким образом, в рассматриваемом случае ширина сечения
должна меняться по линейному з а к о н у , как показано на
рис. 7.71.
Практически на свободном конце балки следует сделать не
которое уширение (показано на рис. 7.71) штриховыми линия
м и ), так как в противном случае к а с а те л ь н ы е н а п р я ж е н и я в се
чениях, близких к месту приложения силы, будут чрезвычайно
велики (теоретически в сечении под силой будут равны беско
нечности).
В качестве второго примера рассмотрим также консоль пря
моугольного сечения, но теперь будем исходить из условия
равнопрочности (равноопасности) всех сечений при постоянной
их ширине и перем енной высоте. Аналогично предыдущему, для
сечения в заделке имеем
FI
Ыг/6
[а].
Для произвольного сечения
(CW)z
hh\ /6 ^
Принимая (сгтах)г = а тах, получаем
Fz
FI
ThT]6 _ bh2/6 ’
откуда hi = h2(z/l) или h, = h]/7[l
В этом случае в ы с о т а сечения должна изменяться по п а р а б о
л и че ск о м у ' з а к о н у . Брус равного сопротивления изгибу, имею
щий прямоугольное сечение переменной высоты, показан на
рис. 7.72.
Оси и валы различных машин, как правило, имеют круглое
поперечное сечение, диаметр которого по их длине не остается
постоянным. При этом большей частью сечение является сту
пенчато-переменным, т. е. ось
(вал) состоит из отдельных ци
линдрических частей разного
диаметра (рис. 7.73, а); реже от
дельные участки оси (вала)
имеют
коническую
форму
(рис. 7.73, 6). В обоих указан230
ных случаях целесообразно принять за основу для выбо
ра продольного профиля оси форму бруса равного сопро
тивления изгибу. При этом теоретический (обеспечивающий
равиоопасность всех сечений и наивыгодиейший в смысле
затраты материала) профиль должен располагаться в пре
делах действительного (быть вписанным в него), как пока
зано штриховыми линиями на рис. 7.73, а, б. Если бы тео
ретический профиль выходил за пределы действительного,
прочность оси была бы недостаточна, Нетрудно доказать, что
для осей по рис. 7.73, а, б теоретический продольный профиль
каждого из участков представляет собой кубическую параболу.
Отступления от теоретического профиля связаны как с техно
логическими трудностями изготовления оси подобной формы,
так и с необходимостью создания такой конструкции, при ко
торой обеспечивается удобство посадки и крепления насажи
ваемых на ось (вал) деталей —колес, подшипников и т. п.
При расчетах на прочность брусьев, имеющих ступенчато
переменное поперечное сечение, во многих случаях трудно
сразу установить, какое сечение опасно, и расчет приходится
выполнять для нескольких сечений.
Опасным является сечение, в котором возникают наибольшие
нормальные напряжения; оно может и не совпадать с сечением,
в котором изгибающий момент имеет наибольшее значение.
*При определении линейных и угловых перемещений в бал
ках переменного сечения правило Верещагина можно приме
нять лишь при условии ступенчатого изменения сечения, разби
вая брус на участки, в пределах которых Jx = const. При не
прерывно-переменном сечении следует вычислять интеграл Мо
ра непосредственно. В случаях, аналогичных представленному
на рис. 7.73,6, слагаемые интеграла Мора, соответствующие
цилиндрическим участкам, могут быть вычислены по правилу
231
Верещагина, а для конических —путем непосредственного инте
грирования.
Пр и м е р 7.31. П роверить прочность оси (бруса ступенчато-пере
менного сечения), изображенной на рис. 7.74, а. М атериал оси — сталь
с пределом текучести сг0 2 = 320 М П а; [ит] = 3,0.
Р е ш е н и е . Н а рис. 7.74, б, в изображены расчетная схема оси
и эпю ра изгибающих моментов. В рассматриваемом случае затрудни
тельно сразу указать, какое сечение является опасным, так как диам етр
оси непостоянен. Определим максимальные нормальные напряжения
в сечениях 1 — 1, 2 — 2 , 3 — 3 , 4 — 4 , 5 — 5 . Соответствующие значения из
гибающих моментов указаны на эпюре:
М ; _,
800
п®тц2-2
^тахЗ-3
^ т а х 4 —4
^ та х5~5
М2-2
W2-2
6900
0,1 •0,0853
Мз-з
8000
W3 - 3
0 J 0.0953
М4_4
W4.4
МЗ-5
W5_5
5800
0,1 ■0,093
1600
0,1 • 0,073
” Mn,i
= 11 2 -106 П а = 112 М П а;
= 93,1 - 106 П а = 93,1 М П а;
= 79,4-106 П а = 79,4 М П а;
= 46,7 • 106 П а = 46,7 М Па.
Сравнение полученных результатов позволяет установить, что
опасным является сечение 2 —2. Коэффициент запаса прочности для
опасного сечения
«Т = СТо,2/Чтх2-2 = 320/112 = 2,86,
что ниже требуемого всего на 4,67% , и, следовательно, проверка
прочности дала удовлетворительные результаты.
232
Г л а в а Vin
КОСОЙ ИЗГИБ, РАСТЯЖЕНИЕ (СЖАТИЕ)
С ИЗГИБОМ
§ 8.1. Косой изгиб
Изгиб называют косым, если плоскость действия изгибаю
щего момента, возникающего в поперечном сечении бруса, не
совпадает ни с одной из его главных плоскостей.
Различают плоский косой изгиб и пространственный косой
изгиб.
При плоском косом изгибе (см. рис. 7.2) все нагрузки распо
ложены в одной плоскости, т. е. существует общая для всего
бруса силовая плоскость. Следовательно, углы, составляемые
силовыми линиями с главными центральными осями, во всех
поперечных сечениях бруса одинаковы. В рассматриваемом
случае упругая линия бруса —плоская кривая, но, как уже гово
рилось (см. с. 156), в отличие от прямого изгиба плоскость,
в которой она расположена, не совпадает с силовой пло
скостью. Именно эта особенность характера деформации обус
ловливает наименование косой изгиб.
При пространственном косом изгибе нагрузки, вызывающие
изгиб, расположены в разных продольных плоскостях бруса.
Соответственно углы между главными центральными осями
поперечных сечений и силовыми линиями не постоянны по
длине бруса.
Упругая линия бруса в этом случае —п р о с т р а н с т в е н н а я
кривая.
Силы, перпендикулярные продольной оси бруса, но не со
впадающие по направлению ни с одной из главных цен
тральных осей его поперечного сечения, всегда могут быть раз
ложены на составляющие по этим осям. Точно так же
и моменты, действующие в про
извольных продольных плоско
стях, могут быть разложены
на составляющие относительно
главных центральных осей. Та
ким образом, схему нагружения
бруса всегда можно привести
к такому виду, как показано
на рис. 8.1.
При поперечном косом изгибе
(как плоском, так и простран
ственном) в поперечных сечени
233
ях бруса возникают четыре внутренних силовых фактора:
поперечные силы Qx и Qy и изгибающие моменты Мх и Мг
При чистом косом изгибе поперечные силы отсутствуют. Для
расчетов на прочность и жесткость практически безразлично,
будет ли изгиб чистым или поперечным, так как влияние
поперечных сил, как правило, не учитывают.
Эпюры внутренних силовых факторов целесообразно
строить, располагая их в главных плоскостях бруса, т. е. при
меняя перспективное изображение. Эпюры Qк и Му следует
располагать в плоскости zOx, т. е. откладывать их ординаты
параллельно оси Ох, а эпюры Qy и Мх —в плоскости zOy, от
кладывая ординаты параллельно оси Оу. Пример такого по
строения эпюр приведен на рис. 8.2.
При плоском косом изгибе можно строить результирующие
эпюры Q и М, не раскладывая предварительно силы по
главным центральным осям.
Рассмотрим вопрос об определении напряжений и переме
щений при косом изгибе. Без ущерба для общности рассужде
ний и получаемых результатов ограничимся случаем нагруже
ния бруса (простой консоли) одной силой, приложенной
в плоскости его торцового поперечного сечения таким обра
зом, что ее линия действия составляет угол р с главной цен-
234
тральной осью Оу (рис. 8.3, а). Разложим эту силу на соста
вляющие Fx и Fy по главным осям поперечного сечения.
Каждая из этих составляющих вызывает прямой изгиб бруса
в одной из главных плоскостей: сила F —в плоскости zOy и си
ла Fx —в плоскости zOx. Следовательно,
косой изгиб можно рассматривать как совокупность двух
прямых изгибов во взаимно перпендикулярных плоскостях.
На рис. 8.3, б показаны внутренние силовые факторы, возни
кающие в поперечном сечении бруса. В рассматриваемом част
ном случае имеем:
Qx = Fx = Fsin$;
Qy = Fy = Fcos P;
Mx = FyZ = Fz cos P;
My = Fxz —Fz sin (3.
В опасной точке (точках) поперечного сечения бруса каса
тельное напряжение, за очень редким исключением, либо равно
нулю, либо весьма мало по сравнению с нормальным напряже
нием, поэтому
расчет на прочность при косом изгибе будем вести только по
нормальным напряжениям.
Нормальное напряжение в произвольной точке поперечного
сечения бруса определяется на основе принципа независимости
действия сил как алгебраическая сумма нормальных напряже
ний оМх и оМу, каждое из которых обусловлено одним из
прямых изгибов:
сг = с Мх + а му-
(8-1)
В эту формулу каждое из напряжений должно быть подста
влено со своим знаком, определяемым из рассмотрения харак
тера деформации бруса. Например, для точки К (рис. 8.3,6) на
пряжение <зМх положительно —напряжение растяжения, так как
сила Fy вызывает изгиб бруса выпуклостью вверх, а напряже
ние ам отрицательно —напряжение сжатия, так как сила Fx
изгибает брус выпуклостью вправо (если смотреть от свобод
ного конца в сторону заделки). Аналогично могут быть опреде
лены знаки напряжений и для любой другой точки поперечного
сечения.
Напряжения иМх и а Му определяем, применяя формулу (7.5)
для нормальных напряжений при прямом изгибе:
<Jmx = (Mx/Jy)y; GMy = (My/Jy)x;
c = ( M J J x)y + (M,/Jy)x.
(8.2)
Так же как и в формулу (8.1), каждое из слагаемых должно
быть подставлено в выражение (8.2) со своим знаком. При этом
значения изгибающих моментов Мх и Му, а также координаты
235
исследуемой точки х и у
берут по абсолютному зна
чению, а знак приписывают
всему слагаемому в делом,
ориентируясь, как
было
разъяснено, на характер де
формации бруса.
Наглядное представление
о распределении напряжений
стмх и аму по поперечному
сечению бруса дают соот
ветствующие эпюры, изобра
женные на рис. 8.4. Как и в
случае прямого изгиба, эти
эпюры условно совмещены
с плоскостью поперечного
сечения. Для построения
эпюры суммарных напряже
ний надо предварительно найти положение нулевой (нейтраль
ной) линии.
Нулевой или нейтральной линией называется геометрическое
место точек поперечного сечения, в которых нормальные напря
жения равны нулю. Исходя из этого определения и приравнивая
нулю правую часть выражения (8.2), получаем
(Mx/Jx)y + (My/Jy)x = О
или
Му Jx
у — ------ ------X.
(8.3)
Мх Л
Эта формула показывает, что нулевая линия —прямая, про
ходящая через начало координат и имеющая угловой коэффи
циент, определяемый из выражения
I * I = Itg ср | =
Му Jx
М х Jy
В рассматриваемом частном случае, подставляя
Мх = Fz cos Р и Му = Fz sin Р,
получаем
Fz sin Р Jx
1* | = | tg ф | =
— tg|3
Fz cos P Jy
Jy
(8.4)
(8.5)
Анализируя это выражение, приходим к выводу, что в отли
чие от прямого изгиба нулевая и силовая линии не будут
236
взаимно
перпендикулярны
(tg ф ф —tg Р) *. Лишь в част
ном случае, когда Jx = Jy, угол
между нулевой и силовой ли
ниями будет прямым (tg ф =
= —tg Р), но это значит, что
любая центральная ось сече
ния —главная ось (см. с. 145),
а значит, вообще изгиб будет
прямым.
Для сечений типа круга,
квадрата и т. п., у которых все
центральные оси —главные, ко
сой изгиб невозможен.
Совершенно очевидно, что
нулевая линия проходит всегда
Нулевая
через те квадранты сечения, в
линия
которых знаки напряжений ам
Рис. 8.5
и а м противоположны.
Надо иметь в виду также,
что нулевая и силовая линии проходят через разные квадран
ты сечения: так, например, если силовая линия проходит через
I и III квадранты, то нулевая —через II и IV.
Для построения результирующей эпюры нормальных на
пряжений проводим через центр тяжести сечения под углом ф
к оси Ох нулевую линию и параллельно ей две касательные
к сечению (рис. 8.4). Ось эпюры ст проводится перпендикулярно
нулевой линии.
Так как эпюра а линейна, что следует из формулы (8.2), то
для ее построения кроме уже известной нулевой точки доста
точно вычислить какую-либо одну ординату, например точку
А или В. Эта ордината получается путем суммирования значе
ний амх и ому для соответствующей точки (суммируемые
ординаты эпюр стМх и а Му отмечены на рис. 8.4).
Большей наглядностью обладают пространственные эпюры
нормальных напряжений (рис. 8.5), но все же обычно строят
плоские эпюры, так как это требует меньшей затраты времени.
Прогибы при косом изгибе определяют на основе принципа
независимости действия сил путем геометрического суммиро
вания прогибов, получающихся в направлениях главных осей.
* Следует учесть, что угол р отсчитывается от оси Оу, а угол
<р—от оси Ох, поэтому взамен известного из аналитической геоме
трии условия перпендикулярности прямых кук2 = —1 или кг = —\/к2
здесь было бы tg ср = —tgp.
237
Для бруса, жестко защемленного одним концом и нагру
женного силой на свободном конце, используя данные
табл. 7.2, получаем следующие выражения для прогибов тор
цового сечения:
F /
FI3cosp
Fxl3
FI3 sin Р
Ъ.EJX ~ 3EJX ’
3EJX
3EJr '
Полный прогиб свободного конца
f-Vfl+fr
Определим направление полного прогиба:
f У f Р cos Р/ (3EJX)
fx
FI3sin Р/ (3EJy)
(8 .6)
где ф —угол между направлением полного прогиба и осью Ох
(см. рис. 8.4). Сопоставляя формулы (8.5) и (8.6), заключаем, что
при плоском косом изгибе направление полного прогиба пер
пендикулярно нулевой линии, а значит, действительно не совпа
дает с силовой линией.
Угол поворота поперечного сечения бруса приближенно ра
вен геометрической сумме его углов поворота вокруг осей Ох
и Оу :
9 * 1 /е * + е*
Для расчета на прочность надо найти опасное поперечное
сечение и опасную точку в этом сечении. Для бруса постоянно
го поперечного сечения при плоском косом изгибе, как прави
ло, опасно то сечение, в котором изгибающие моменты
максимальны.
Исключением может быть брус из материала, различно сопроти
вляющегося растяжению и сжатию; при некоторых формах поперечно
го сечения может оказаться, что есть два предположительно опасных
сечения, для каждого из которых надо произвести расчет.
При простейших схемах нагружения, например подобных
показанным на рис. 8.3 и 8.5, положение опасного сечения оче
видно (в заделке) и без построения эпюр изгибающих момен
тов.
При пространственном изгибе отыскание опасного сечения
может быть несколько осложнено из-за того, что при неко
торых схемах нагружения изгибающие моменты Мх и Му до
стигают своих наибольших значений в разных сечениях. В ука
занных случаях приходится выполнять расчет для двух (редко
для большего числа) предположительно опасных сечений (см.
пример 8.4).
238
У
в точтг СИМальнь1е напряжения растяжения и сжатия возникают
Для й ■’ наи^0Лее удаленных от нулевой линии (рис. 8.4 и 8.5).
женшо °а И3 МатеРиала> Различно сопротивляющегося растяи сжатию, должны быть составлены для условия про
чности (рис. 8.6);
а pmax =
М
м.
—j— s'*
Ув +• ~ г~ Хв < | > р] ;
J х
J v
м„
- ~ У а + —г ~ха « [ < ] •
Jx
Jy
(8.7)
Для брусьев из материалов с К ] = [< 1 (пластичные мате
риалы) используется лишь то из условий (8.7), которое соответ
ствует большему по абсолютному значению напряжению.
При [сгр] < [ а с] (хрупкие и хрупкопластичные материалы)
первое из условий (8.7) достаточно, если стргаа! ^ |стсшах|.
В формулы (8.7) каждое из слагаемых надо подставлять со
своим знаком, устанавливаемым по эпюрам омх и Ому. В боль
шинстве случаев для опасной точки знаки обоих слагаемых
одинаковы.
Формулы (8.7) представляют собой зависимости для прове
рочного расчета. При известных размерах поперечного сечения
бруса из них нетрудно определить допускаемое значение на
грузки. Сложнее выполнить проектный расчет, так как в фор
мулу входят две геометрические характеристики сечения Jx
Hj в общем случае приходится задаваться размерами сече
ния., проверять их расчетом на прочность, при неудовлетвори
тельных результатах расчета корректировать размеры и вновь
239
производить проверку. Для сече
ний простой формы, например для
прямоугольника, расчет упрощает
ся, особенно в случае заданного
отношения его сторон (см. при
мер 8.3).
Если поперечное сечение бруса
имеет две оси симметрии и точ
ки, одновременно максимально уда
ленные от обеих указанных осей
(например, прямоугольник или
двутавр), то для отыскания
опасной точки нет надобности
в определении положения нуле
вой линии. Действительно, по
эпюрам омх и Ому (рис. 8.7)
совершенно очевидно, что опас
ными (для бруса из пластичного материала) будут те из угло
вых точек сечения, в которых знаки стмх и аму совпадают.
В случае хрупкого материала опасной окажется точка А,
в которой возникают напряжения растяжения. Для рассматри
ваемых сечений условие прочности можно представить в более
простой и удобной форме. Учитывая, что
х А = Ь/ 2 ;
у А = к/ 2 ;
J y/ 0 , 5 b = W y ;
J J 0 ,5 h = Wx,
получаем
v max = M x/ W x + M y/ W f ^ l a l
(
8. 8)
Конечно, использование этой формулы для сечений, от
личных от указанных, ошибочно, так как она имеет смысл
лишь в случае, если
о п а сн а я т о ч к а м а к си м а л ь н о у д а л е н а од новр ем ен но о т о б е и х
гл а в н ы х осей О х и О у .
Пр нм ер 8 .1 . Проверить при [сг] = 160 МПа прочность двута
врового бруса, изображенного на рис. 8.8. Определить значение и на
правление полного прогиба свободного конца бруса. Выяснить, как из
менятся наибольшие нормальные напряжения и прогиб, если сила
F будет приложена вертикально.
Решение. Брус работает на плоский косой изгиб. Раскладывая
силу F на составляющие по главным центральным осям (рис. 8.8), при
водим косой изгиб к сочетанию двух прямых изгибов.
Изгибающие моменты в опасном сечении (в заделке) равны:
М Х та*= 7 7
(Рcos (3)1= (11 103cos 20°) 1,2 12,4 103 Н м;
Мум = Fxl = (F sin Э) / = (11 • 103 sin 2 0 °) 1,2 = 4,51 •103 Н -м.
=
240
-
=
•
•
Эпюры нормальных напряжений, возникающих в опасном сече
нии, показаны на рис. 8.9. Знаки на эпюрах поставлены в соответствии
с характером деформации бруса: сила Fy (вызывающая момент М х) из
гибает балку выпуклостью вверх; сила Fx (вызывающая момент
Му) —выпуклостью вправо (если смотреть от свободного конца).
Очевидно, опасные точки —А и В. Так как материал балки рабо
тает на растяжение и сжатие одинаково, эти точки равноопасны.
По ГОСТ 8239 —72 для двутавра № 24а имеем:
J x
— 3800 см4;
W
х = 317 см3; Jy = 260 см4; Wy = 41,6 см3.
Наибольшее напряжение (в точке А)
.
А
Мддц
Wx
М утах
Wy
12,4 -103
317-1(Г6
4,51 • 103
41,6-1(Г6
147,4-106 Па =
= 147,4 МПа.
Наибольший прогиб от каждой из сил в отдельности определяем,
используя данные табл. 7.2. В вертикальной плоскости (от силы Fy)
Fyl3
1 М 0 3 cos 20° ■l,23
f y— - =
= 0,782• 10" 3 m = 0,782 мм.
3EJX 3-2,0* 105 -106-3800-10“ 8
В горизонтальной плоскости (от силы Fx)
FJ3
11 • 103 sin 20° • 1,23
3 •2,0 • 105 • 106 •260 -10
Полный прогиб
Д - 3EJy
4,17-10-3 м = 4,17 мм.
/ = V f l + f y = )/4,172 + 0,7822 = 4,24 мм.
241
4
1 ? 4
9
Рис. 8.10
Угол между направлением полного прогиба и осью у (рис. 8.10):
tg \|/ = / х/ / , = 4,17/0,782 = 5,33; ф = 79°23'.
Направление полного прогиба значительно отклоняется от линии
действия силы в сторону плоскости наименьшей жесткости.
В случае нагружения балки вертикальной силой
Mv
Wr
FI3
T>EJ
11 • 103-1,2
FI
= 41,6-106 Па = 41,6 МПа;
W.
317-10-6
11 •103.1,23
3-2,0-105-106-3800-10'
г = 0,833-10-3 м = 0,833 мм.
Таким образом, убеждаемся, что отклонение линии действия силы
©т плоскости наибольшей жесткости приводит к резкому возрастанию
напряжений и прогибов. В рассмотренном примере при косом изгибе
напряжения в 3,54 раза, а прогиб в 5,1 раза больше, чем при прямом
изгибе в плоскости наибольшей жесткости.
П р и м е р 8.2. Определить допускаемую нагрузку для чугунного
бруса, изображенного на рис. 8.11,а. Принять [ а р] = 35 МПа; [стс] =
= 140 МПа.
Рис. 8.11
242
Р е ш е н и е . Брус работает на плоский косой изгиб. Изгибающие
моменты в опасном сечении (в заделке):
M*ma,, = (fcosPH;
Mymar - ( F sinp)/.
Характер эпюр нормальных напряжений, связанных с каждым из
изгибающих моментов, показан на рис. 8.11,6. Очевидно, что опасная
точка находится на контуре сечения в первом квадранте, но в отличие
от предыдущего примера на основе эпюр омх и аму точно установить
ее положение нельзя. Для того чтобы ее найти, определим сначала по
ложение нулевой линии. Угловой коэффициент нулевой линии опреде
лим по формуле (8.4):
|fc| = |tgq>| =
Ы4
Мх J,
tg Р = b/h = 60/90 = 2/3; р = 33°40';
3,14-1204
60•903
= 653•104 мм4 = 653-10"8
64
12
Ьк3
12
,
653
|fe| = |tg(p| = —
о•F*
II
СО
t/l
603•90
Ь3к
3,14-1204
мм4 = 855-10-8
12
64
12
Подставляя значения tgP, Jх и Jy в выражение для к, найдем
2
-— = 0,509; Ф*27°.
Угол ф надо отложить от оси х так, чтобы нулевая и силовая ли
нии проходили через разные квадранты сечения. Нулевая линия и эпю
ра результирующих нормальных напряжений показаны на рис. 8.11,6.
Наиболее удалены от нулевой линии точки А а В. Из них опаснее
точка А, так как в ней возникают напряжения растяжения, а [ а р] <
< К ].
Условие прочности:
-УЛ+-
FI cosP
ал =
-* л $ [а р];
FI sin Р
-- --- Уа + -- --- * а < [ffj-
Значения хА и уА найдем, учитывая, что отрезок ОА перпендикуля
рен нулевой линии:
ха = (d/2)sin ф = (120/2)sin 27° = 27,3 мм;
у а = (d/2) cos ф = (120/2) cos 27° = 53,4 мм.
Подставляя числовые значения, представим условие прочности
в виде
F ■0,8 sin 33°40'
F ■0,8 cos 33°40'
0,0534 +
0,0273 < 3 5 -10е
855 • 1 0 ~
653-10~8
243
откуда
35 • 106
= 5,1 • 103 H = 5,1 kH.
cos33°40'
sin 33°40'
— •0,0534 + ------- — •0,0273
),8 (
653-10"
855-10"
П р о м е р 8.3. Определить при [a ] = 160 МПа допускаемую на
грузку для заданного бруса (рис. 8.12,
Р е ш е н и е . Определив опорные реакции (показаны на рис.
8.12, а), строим эпюры Мх и Му (рис. 8.12, б, в). Опасное сечение —либо
С, либо D. Какое из них непосредственно по эпюрам, изгибающих мо
ментов установить нельзя, так как хотя результирующий момент боль
ше в сечении С, но в сечении D больше момент Му, связанный с изги
бом в плоскости наименьшей жесткости бруса.
Выполним расчет для того и другого предположительно опасного
сечения. Наибольшие напряжения растяжения (во всех поперечных се
чениях) возникают в точке К (рис. 8.12, а); такие же по модулю напря
жения сжатия возникают в точке L.
Для сечения С имеем
[F] =
шах = M * c / W x + M yc / W y < [с г ].
По ГОСТ 8239-72 Ж, = 1231 см3, Wy = 101 см3. Подставив чис
ловые значения в условие прочности, получим
(25/7) Fa _ (2/7) Fa
< О ] = 1б0-ю6,
шах
1231-КГ6 + 101-10“ 6
откуда
160-106
F' = = 27,9 ■103 Н.
25
7-1231-10"
7-101-10
Рис. 8.12
244
Аналогично для сечения D
= Мх/>/^>: + MyD/Wy < [а],
_ т
pmax
^
+ т * .
1231-10'
„
101- 1 0 '6
откуда
160-Ю6
= 19,44-10’ Н.
10
,1•1231■10"6 7-101•10~6 /
Следовательно, опасным оказалось сечение D; окончательно при
нимаем меньшее из двух найденных значений:
[F] = F" = 19,44 кН.
F" ■
§ 8 .2 . Пространственны м изгиб бруса круглого
поперечного сечения
Определение напряжений (расчет на прочность) при про
странственном изгибе бруса круглого (сплошного или кольце
вого) поперечного сечения имеет некоторые особенности. Ко
нечно, и в этом случае примени
мы общие формулы (8.1) —(8.4),
(8.7) [неприменима формула
(8.8) ], но целесообразнее вести
расчет, не используя этих фор
мул.
Пусть брус круглого по
перечного сечения нагружен, как
показано на рис. 8.13, а; соот
ветствующие эпюры Мх и Му
даны на рис. 8.13, 6, в (поясне
ния к рис. 8.13, г даны ниже).
245
Рассмотрим вопрос об определении напряжений в про
извольном поперечном сечении бруса, например в сечении 1 — 1.
Как известно, составляющая главного момента системы сил по
некоторой оси представляет собой вектор, направленный вдоль
этой оси. Воспользуемся этим векторным изображением для
изгибающих моментов. В рассматриваемом сечении отложим
в выбранном масштабе вектор момента Мх вдоль оси Ох,
а вектор момента Му — вдоль оси Оу (рис. 8.14). Значения мо
ментов берем по эпюрам Мх и Му, соответствующие ординаты
отмечены на этих эпюрах (см. рис. 8.13), но для общности рассуждений и упрощения обозначений индексы 1 —1 опускаем.
Условимся направлять эти векторы вдоль соответствующих
осей таким образом, чтобы для наблюдателя, смотрящего
с конца вектора, момент представлялся стремящимся повер
нуть сечение вокруг данной оси по ходу часовой стрелки.
Складывая геометрически векторы Мх и Му, получаем век
тор результирующего изгибающего момента:
М к = J/ М 2Х + М 2у.
(8.9)
Вновь обращаясь к курсу теоретической механики, вспом
ним, что вектор момента перпендикулярен плоскости действия
соответствующей пары сил; следовательно, силовая линия
(след плоскости действия нагрузки на плоскости поперечного
сечения) перпендикулярна вектору М„.
В круглом сечении все центральные оси —главные, поэтому
нормальные напряжения можно определить непосредственно
по результирующему (суммарному) изгибающему моменту Ми,
как при обычном прямом изгибе. Нулевая линия при прямом
изгибе перпендикулярна силовой, т. е. расположена вдоль век
тора М„. Эпюра нормальных напряжений показана на
рис. 8.14. Опасны, очевидно, точки А и В пересечения контура
сечения с силовой линией. Для пластичного материала эти точ
ки равноопасны, для хрупкого опаснее точка А. Расчет на про
чность производим по формуле
<*гаа* = M„/WK= ]/Мх + М у /Wn < [а],
(8.10)
где Wu —момент сопротивления при изгибе.
Нахождение опасного сечения в данном случае не предста
вляет затруднений —опасно то сечение, в котором результи
рующий изгибающий момент имеет наибольшее значение.
В некоторых случаях для отыскания опасного сечения строят
эшору моментов Ми, определяя в каждом сечении его значение
по формуле (8.9); при этом эпюру условно располагают в пло
скости zOyt как показано на рис. 8.13, г. Условность такого
246
изображения связана с тем, что фактически направление векто
ра Ми в разных поперечных сечениях неодинаково. Заметим,
что эпюра Ми линейна только на первом участке.
П р и м е р 8.4. Определить при [с ] = 120 МПа допускаемую на
грузку для бруса круглого поперечного сечения (d = 80 мм), нагружен
ного, как показано на рис. 8.12, а.
Р е ш е н и е . Определим результирующие изгибающие моменты
в сечениях С и Л, использовав построенные на рис. 8.12, б, в эпюры М х
и Му:
Мкс = ]/МхС + Мус = f f ~ - F a J + { j F a J = 3,58Fa;
M„D = ] / m J d + Myo =
+ ' y j F a j = 1,6Fa.
Опасное сечение —С. Нетрудно убедиться, что ни в одном из сече
ний участка CD (а тем более участков АС и BD) результирующий мо
мент не превышает значения МисУсловие прочности
= Мя mJ W a = МкС/(яб3/32)« [о],
откуда
[МвС] = 3,58 [F] а = (Kd3/ 32) [а]
или
nd3 [а]
3,14-0,83-120-106
1,69 -103 Н.
32-3,58а
32-3,58-1
Интересно отметить, что при той же схеме нагружения, но иной
форме поперечного сечения бруса (см. пример 8.3) опасным оказывает
ся другое поперечное сечение —не то, где результирующий изгибаю
щий момент максимален.
т =
§ 8.3. Изгиб с растяжением (сжатием) бруса
большой жесткости
Рассмотрим сочетание пространственного изгиба и растяже
ния (или сжатия) прямого бруса (рис. 8.15, й). Если в числе дей
ствующих на брус нагрузок есть силы, направления которых
не совпадают ни с одной из главных центральных осей, их сле
дует разложить на составляющие по этим осям, т. е. привести
схему нагружения к аналогичной схеме, представленной на
рис. 8.15, а.
В произвольном поперечном сечении бруса возникают пять
внутренних силовых факторов (рис. 8,15,6): продольная сила
NZ(N); поперечные силы Qx и Qy; изгибающие моменты Мх и
247
Му. В частных случаях неко
торые из указанных величин
могут быть равны нулю.
Например, если равны нулю
поперечная сила Qx и изги
бающий момент М р будет
сочетание прямого изгиба в
главной плоскости zOy с рас
тяжением или сжатием. Влия
ние поперечных сил учиты
вать не будем.
Для определения положе
ния опасного поперечного
сечения следует построить
эпюры Nz, Мх и Му\ при
этом может оказаться, что
эти внутренние силовые фак
торы достигают своих наи
больших значений не в од
ном и том же сечении. Сле
довательно, и расчет на
прочность приходится вы
полнять для двух, а иногда
и большего числа предполо
жительно опасных сечений.
Линейные перемещения
определяют путем геометри
ческого суммирования пере
мещений в трех взаимно пер
пендикулярных направлени
ях —вдоль осей х, у, г.
Применение принципа независимости сил при определении
перемещений (а также внутренних силовых факторов и, следо
вательно, напряжений) допустимо лишь при условии, что рас
считываемый брус обладает достаточно большой жесткостью.
Для бруса малой жесткости, например изображенного на
рис. 8.16, было бы ошибочным определять прогибы только от
нагрузки q, не учитывая влияния сжимающей силы F. Точно
так же, определяя изгибающий момент в каком-либо сечении,
например в заделке, следует учесть, что в результате деформа
ции бруса сила F кроме сжатия вызывает и изгиб —дает в за
делке изгибающий момент, равный Ff, который суммируется
с моментом от нагрузки q.
Будем считать, что рассчитываемый брус всегда имеет на
столько большую жесткость, что можно не учитывать измене
248
ний, происходящих в расположении сил при его деформации
(так называемый принцип начальных размеров), и вести расчет
на основе принципа независимости действия сил.
При нагружении бруса внецентренно приложенной силой, па
раллельной его продольной оси (рис. 8.17, а), также получается
сочетание изгиба с растяжением или сжатием (в зависимости
от направления силы). Применив метод сечений, легко устано
вить, что в любом поперечном сечении бруса возникают три
внутренних силовых фактора (рис. 8.17,6):
N Z= F; Mx = FyF; M y = FxF,
где y>F и xf — координаты полюса (точки приложения силы)
в системе главных центральных осей.
Таким образом, в общем случае внецентренного растяжения
(сжатия) получается сочетание чистого косого изгиба с цен
тральным растяжением или сжатием.
Чистый косой изгиб, в свою очередь, сводится к двум
чистым прямым изгибам во взаимно перпендикулярных плоско
стях.
Конечно, определение каждого из изгибающих моментов
как произведения силы на соответствующую координату полю
са допустимо лишь при условии достаточно большой жестко
сти бруса, позволяющей пренебрегать изменениями расстояний
от силы до главных осей какого-либо сечения, вызванными де
формацией бруса.
В отличие от схемы нагружения на рис. 8.15, а при внецентренном растяжении (сжатии) значения внутренних силовых
г
Рис. 8.17
рис. 8.18
249
факторов не зависят от положения поперечного сечения по
длине бруса. Они одинаковы во всех поперечных сечениях (силу
тяжести бруса не учитываем). Это обстоятельство упрощает
расчет на прочность, так как вопрос об определении опасного
сечения отпадает —здесь все сечения равпоопасиы *.
В частных случаях, когда полюс находится на одной из
главных центральных осей сечения (рис. 8.18, а, б), получается
сочетание чистого прямого изгиба с растяжением или сжатием.
По схеме, данной на рис. 8.18,й,—чистый изгиб относительно
оси х и растяжение, а на рис. 8.18,6 —чистый изгиб относи
тельно оси у и также растяжение.
Изгиб бруса будет прямым (независимо от положения по
люса) также в случаях, когда форма поперечного сечения та
кова, что все его центральные оси —главные (круг, кольцо
и т. п.).
Нормальные напряжения, возникающие в поперечном сече
нии бруса, нагруженного, как показано на рис. 8.15 или 8.17,
можно на основе принципа независимости действия сил рас
сматривать как результат наложения трех систем напряжений:
определяемых его растяжением или сжатием (aWz), напряжений
от прямого изгиба в главной плоскости zOy (стМг), то же, пря
мого изгиба в главной плоскости zOx (ом})Эпюры нормальных напряжений crv_, иМх, аМу изображены
на рис. 8.19. Напряжения a Nz распределены по сечению равно
мерно, и соответствующая эпюра может быть расположена
произвольно, но удобнее, когда ось этой эпюры параллельна
одной из главных центральных осей сечения, как показано на
рисунке. Знаки на эпюрах поставлены в соответствии с напра
влениями внутренних силовых факторов, показанных на
рис. 8.15,6 и 8.17,6.
Нормальное напряжение в произвольной точке поперечного
сечения определяется как алгебраическая сумма трех указанных
напряжений:
( 8. 11)
сг = СТдгг.+ Омх + ОМу*
или на основании формул (2.1) и (7.5)
Nz Мх
Му
(8.12)
а —------1------ у Ч-------х.
А
Л
Jv
Каждое из слагаемых должно быть подставлено в эту фор
мулу со своим знаком, определяемым по соответствующим
* Рассматриваются брусья постоянного поперечного сечения, при
этом все силы (внецентренно растягивающие или сжимающие брус)
приложены только в одном сечении.
250
эпюрам нормальных напряжений или, что то же самое, по ха
рактеру деформации бруса.
Иногда строят пространственные эпюры нормальных на
пряжений. Такие эпюры для бруса прямоугольного поперечно
го сечения при сжимающей продольной силе даны на рис. 8.20.
Результирующая эпюра а получена путем суммирования эпюр
Стд,7, сгмх, аму- Практически суммирование производится только
для угловых точек сечения и концы полученных векторов сум
марных напряжений а соединяют прямыми линиями.
*Для нахождения опасной точки поперечного сечения в об
щем случае приходится сначала определить положение нулевой
линии. Приравняв нулю правую часть выражения (8.12), полу
чим уравнение нулевой линии
х = 0.
Разделив это уравнение почленно на N./A, приведем его
к виду
(8.13)
А Му
+ _
А Мх
Это известное из курса аналитической геометрии уравнение
прямой линии в отрезках, которое в сокращенной записи имеет
вид
х/ах + у/ау = 1.
251
Здесь ах и ау —отрезки, отсекаемые нулевой линией на осях
координат (главных центральных осях сечения) и определяемые
из выражений
«U =
А М /
\ а у \
А Мх
(8.14)
Итак, при сочетании изгиба с растяжением (сжатием) нуле
вая (нейтральная) линия —прямая, не проходящая через начало
координат (центр тяжести сечения). В частных случаях, когда
Мх (или Му) равен нулю, т. е. при растяжении (сжатии) и пря
мом изгибе, нулевая линия параллельна одной из главных осей.
Например, при Мх = 0 из (8.14) получаем ау = со, следователь
но, нулевая линия параллельна оси Оу.
Отрезки ах, ау надо отложить от начала координат так,
чтобы нулевая линия не проходила через тот квадрант сечения,
для которого знаки aNz, аМх, &му совпадают. Для случаев внецентренного растяжения (сжатия) знаки всех этих трех напряже
ний одинаковы в том квадранте, где находится полюс, следова
тельно,
нулевая линия не может пересекать тот квадрант сечения,
в котором расположен след линии действия силы (полюс).
После определения положения нулевой линии строится ре
зультирующая (суммарная) эпюра нормальных напряжений
(см. рис. 8.19). Ее построение аналогично изложенному на
с. 237 для случая косого изгиба.
Для бруса из пластичного материала опасной будет точка,
наиболее удаленная от нейтральной линии (точка А на
рис. 8.19), и условие прочности запишется в виде
N, Мх
М„
а тах = —г + -Г-Ул + ~ х л ^[&].
(8.15)
A Jx
Jy
Знаки каждого из слагаемых устанавливают по построенным
эпюрам CTW2, аМг, &му- В большинстве случаев для опасной точ
ки знаки всех слагаемых совпадают.
Для брусьев из хрупкого или хрупкопластичного материала
в случаях |crcmax| > |<тртах| приходится вести расчет для двух
точек. Эпюры напряжений для такого случая показаны на
рис. 8.21; условия прочности:
1<*сmax1 I&А |
N,
М.
М..
J - + ~]^Ув + ~ х в < [Ор];
У
N.
Мх
Му
/Л
1—1
0
шах
~ - л —
252
уА’ Х
ХА
Для бруса прямоугольно
го или двутаврового попе
речного сечения (как и вооб
ще для бруса с сечением,
имеющим точки, наиболее
удаленные одновременно от
обеих главных осей) расчет
упрощается, так как для на
хождения опасной точки не
нужно определять положения
нулевой линии. Действитель
но, рассматривая эпюры a N,
показанные на
рис. 8.20, без построения
суммарной эпюры а устанавливаем, что наибольшие
напряжения растяжения и сжатия возникают соответственно
в точках В и А.
Для бруса из материала, различно сопротивляющегося рас
тяжению и сжатию, условия прочности записываются в виде
мх
м„
+ — - + - / - <[«
L=
= ~
WX w y
А
(8.17)
м у
Мх
К
I = I см I =
А
W
Wx
ГГу
При растягивающей продольной силе опасна точка, в кото
рой возникает наибольшее растягивающее напряжение. В фор
мулах (8.17) слагаемое N z/A положительно и расчет ведется
лишь по первой из этих формул. Для бруса из пластичного ма
териала всегда используется лишь одно из условий (8.17),
а именно то, которое соответствует наибольшему по абсолют
ному значению напряжению.
В заключение остановимся на расчете бруса круглого
(сплошного или кольцевого) поперечного сечения.
К нормальным напряжениям от изгиба, определяемым по
суммарному изгибающему моменту (см. с. 246 и рис. 8.14), до
бавляются равномерно распределенные по сечению нор
мальные напряжения от растяжения или сжатия. Используя
рис. 8.14, на котором дана эпюра напряжений Оми от изгиба,
дополним его эпюрой напряжений a Nz от растяжения (сжатия).
Ось этой второй эпюры расположим параллельно оси эпюры
стми (рис. 8.22, а). Суммируя значения Стми и стnz для крайних то
чек, получаем результирующую эпюру нормальных напряже
ний ст, показанную на том же рисунке. Эта эпюра построена
253
в предположении, что сХмиюах > Iа ыг I. в противном случае эпю
ра с не пересечет своей оси, т, е. напряжения во всех точках се
чения будут иметь одинаковые знаки. Такой случай показан на
рис. 8.22,6.
Для бруса из пластичного материала опасной будет та из
точек пересечения контура сечения с силовой линией, в которой
знаки о>;2 и <7м„ совпадают (точка А на рис. 8.22, а). Условие
прочности
<7mal = NJ A + M J W и < [а],
(8.18)
где по-прежнему
М к = ]/м 1 + м ) .
Для бруса из хрупкого материала при сжимающей продоль
ной силе и эпюре о с участками разных знаков (такой случай
показан на рис. 8.23) следует составить два условия прочности:
max ~ ~
254
АД Ми
~А~ ~ W u
ь1
1—
V/
|СТста*! = 1<Ы =
АД М„
Т + н Г ^ 1ар|:
(8.19)
В эти формулы должны быть подставлены абсолютные значе
ния JV, и МиП р и м е р 8.5. Проверить при [ст] = 160 МПа прочность стально
го бруса, нагруженного, как показано на рис. 8.24, а.
Р е ш е н и е . Сила Ft вызывает растяжение бруса, а сила
F2 —прямой поперечный изгиб в вертикальной плоскости.
На рис. 8.24, б показана расчетная схема бруса. На том же рисунке
показаны эпюры продольных сил N. и изгибающих моментов М х. Так
как N z во всех сечениях одинакова, а изгибающий момент достигает
наибольшего значения в сечении заделки, то, очевидно, оно и будет
опасным.
На рис. 8.25 показаны эпюры нормальных напряжений в опасном
поперечном сечении от растяжения on. и от изгиба чмх- Знаки на эпюре аМх поставлены в соответствии
с характером деформации —сила
F2 изгибает брус выпуклостью
вверх.
Напряжения от растяжения
<%2 = N J A = F JA =
= 80- 103/(0,06 - 0,12) =
= 11,1- 10е. Па = 11,1 МПа.
Наибольшее напряжение от изгиба
■>му
М,
Wx
Fil
bh2/6
16-103 • 0,8
= 88,9 • 106 Па =
0,06 • 0,122/6
= 88,9 МПа.
255
Эпюра бт
Эпюра в^х
Эпюра s
Опасными оказываются верхние точки поперечного сечения здесь наибольшие напряжения от изгиба суммируются с напряжениями от растяжения. Определяем напряжения в опасных точках:
<т
v m ax
—ом
4Wг
i r l x max
= 11,1
+ 88,9
= 100 МПа.
7
7
Брус работает со значительной недогрузкой —максимальные напряже
ния ниже допускаемых на 37,5%.
Складывая (алгебраически) ординаты эпюр crw.. и амх для крайних
точек сечения, получаем результирующую эпюру напряжений. Точка
пересечения этой эпюры с ее осью определяет положение нулевой ли
нии (н.л.). Заметим, что для расчета на прочность ни построение
эпюры результирующих напряжений, ни определение положения нуле
вой линии в этой задаче не нужно.
П р и м е р 8.6. У края растянутой полосы образовалась трещина.
Для того чтобы предотвратить ее дальнейшее распространение, это
место высверлили, как показано на рис. 8.26, а. Определить, насколько
повысились наибольшие растягивающие напряжения в результате это
го высверливания. Выяснить, не будет ли более целесообразно высвер
лить полосу симметрично с двух сторон (второе сверление показано
штриховой линией).
Р е ш е н и е . В неослабленном сечении, например 1 —1 (или, что то
же самое, в любом сечении до высверливания полосы), нормальные на-
256
пряжения распределены равномерно —ц е н т р а л ь н о е р а с т я ж е
ние
N. F
80-103
<5/_/ = — = — = ------------- = 100-106 Па = 100 МПа.
'
А
ЪЬ 0,08-0,01
Разрез полосы по ослабленному месту (при одностороннем свер
лении) показан на рис. 8.26,6. Полюс F (след линии действия силы на
плоскости поперечного сечения) расположен на главной оси О У, но
смещен относительно центра тяжести (оси х) сечения на некоторое
расстояние е = ур (расстояние е называют эксцентриситетом). Здесь по
лоса испытывает растяжение и чистый прямой изгиб относительно оси
Ох. Внутренние силовые факторы в сечении 11 —11:
NX= F; Mx = Fe.
Эксцентриситет е определяется как разность расстояний от нижне
го края полосы до центров тяжести неослабленного и ослабленного
сечений:
е = {Ь/2) —(Ь —г)/2 = г/2 = 10/2 = 5 мм.
На рис. 8.26,6 показаны эпюры напряжений с г; Смх и ау/_/; (ре
зультирующая эпюра):
Nz
F
80-103
114,3 • 10б Па =
Лнехт0 " (Ь - г ) 8 ~ (0,08 -0 ,0 1 )-0 ,0 1
= 114,3 МПа;
Мх
Fe
80-103-0,005
„„„
- „
= ------- -----= -------- ------ = ---------------- ---------- = 49,0 • 106 Па =
(И',)„етто
(6 - г ) 2 8/6
(0,08 - 0,01)2 •0,01/6
= 49,0 МПа.
Здесь /1нетто и (И/^нетто —соответственно площадь и момент со
противления ослабленного сечения.
Наибольшие суммарные напряжения возникают в точках, лежа
щих на стороне А —А сечения:
(ум
*“
° Л -//
= 114,3 + 49,0 = 163,3 МПа.
Одностороннее высверливание привело к возрастанию напряже
ний на
ст// // —сг/_/
163,3 —100
Ла% = Л 1-"™ *---- — -*100% = --------------100% = 63,3%.
100
При двустороннем высверливании полосы было бы центральное
раст яжение и
N,
F
80-103
<Уц-ц = ---- — = ------------ = ------------------------- - = 133,3 -106 Па =
Л„'етто
(Ь —2г)8
(0,08 - 2 -0,01) -0,01
= 133,3 МПа,
т. е. возрастание напряжений (по сравнению с неослабленной полосой)
равнялось бы 33,3 %. Следовательно, хотя во втором случае уменьше
ние площади сечения и значительнее, чем в первом, но благодаря от
257
сутствию изгиба напряжения возрастают не так резко, как при одно
стороннем сверлении.
П р и м е р 8.7. Стальной брус, сваренный из двух швеллеров
№ 12, жестко защемлен одним концом и нагружен, как показано на
рис. 8.27, а. Определить допускаемое значение нагрузки, если [ст] =
= 160 МПа.
Р е ш е н ц е . Равномерно распределенная нагрузка q вызывает из
гиб бруса в вертикальной плоскости, сила Ft - изгиб в горизонталь
ной плоскости, сила F2 —растяжение. Расчетная схема бруса и эпюры
внутренних силовых факторов (продольной силы N . и изгибающих мо
ментов Мх и Му) даны на рис. 8.27,6. Эпюры поперечных сил не
строим.
Продольная сила во всех поперечных сечениях одинакова: изги
бающие моменты имеют наибольшие значения в сечении заделки, сле
довательно, это сечение оказывается опасным.
Для определения опасной точки строим эпюры нормальных на
пряжений отдельно от растяжения о>;2 и изгиба в каждой из главных
плоскостей. Так как действующие силы пока не известны, эпюры
строим без числовых данных (похазываем характер этих эпюр на
рис. 8.28). Знаки на эпюрах омх и ад^ ставим, ориентируясь на
рис. 8.27; нагрузка q изгибает брус выпуклостью вверх, а сила
F j —выпуклостью влево (если смотреть от свободного конца бруса
в сторону заделки). Опасная точка —А; в ней напряжения от изгиба
У
258
в обеих главных плоскостях максимальны и совпадают по знаку с на
пряжениями от осевой силы (растяжения).
Условие прочности записывается так:
<*та« =
<Умх„ + о м > = N J A + M J W X+ My/Wy ^ [Of].
Определяем геометрические характеристики сечения:
Jz = 2JX= 2 • 304 = 608 см4 = 608 • 10 8 м4,
где
= 304 см4 - момент инерции одного швеллера; ул = Ч2 =
= 60 мм —половина высоты сечения;
Wx = Jx/yA —608■ 10~8/0,06 = 101,3• 10 6 м3;
J , = 2 ( J y[ + z 20 A t ) = 2 ( 3 1 ,2 . 1 0 - 8 + 0,0154* -13,3 • 1 0 "'4) = 125,4 - 1 0 " 8 м 4,
где Jyt = 31,2 см4 —момент инерции одного швеллера относительно
главной центральной оси; z0 —расстояние между осями у1 и у; х А =
« Ь — 52 мм - ширина полки швеллера;
W y = J y/х А =
125,4 • 10 ~8/0,052 = 24,1 • 10 “ 6 м 3;
А = 2 А Х = 2 -1 3 ,3
= 26,6 с м 2 = 26,6-10“ 4 м 2.
Подставляя в условия проч
ности значения внутренних си
ловых факторов и геометри
ческих характеристик и учиты
вая, что I = 0,8 м, получим
&д •0,8
" 26,6- 10“ 4
д ■0,82/2 4.
101,3- 10“6
-|----- 3--!— !----- -
, <?■0 ,8 2
0 2
« 160- 106,
24,1- 10“6
откуда [<j] = 14,7 • 103 Н/м =
= 14,7 кН/м.
Опасная точка найдена без
определения положения нуле
вой линии; все же рекомендуем
учащемуся в порядке упражне
ния найти ее положение (отрез
ки ах и ау) и вычислить край
ние ординаты суммарной эпю
ры напряжений (показана на
рис. 8.28).
П р и м е р 8.8. Определить
коэффициент запаса прочности
для опасной точки бруса, изо
браженного на рис. 8.29, а. Пре
дел текучести материала бруса
<зх = 240 МПа.
+
259
Р е ш е н и е . Силы, действующие на брус, вызывают простран
ственный изгиб и растяжение. На рис. 8.29,6 показана расчетная схема
бруса и построены эпюры внутренних силовых факторов N z, М х и М у
Опасное поперечное сечение —в заделке, так как моменты Мх и
М у имеют там наибольшие значения, а N . во всех сечениях одинакова.
Положение опасной точки может быть найдено, как изложено на
с. 246, но в этом нет надобности, так как независимо от ее положения
соответствующее нормальное напряжение определяется по формуле
= N J A + M „ / W H.
Подставляя
N , = 6.F = б • 2 ,5 • 1 0 3 = 15■ 1 0 3 Н ;
Ми = У M l + M j = ]/2,552 + 0,752 *= 2,66 кН-м,
получаем
2,66 ПО3
15 -103
130,6 - 10б Па = 130,6 МПа.
тах 3,14-0,0674
3,14 0,063/32
Коэффициент запаса по отношению к пределу текучести
пт= стт/стта« = 240/130,6 = 1,84.
Глава
IX
Г И П О Т Е ЗЫ П Р О Ч Н О С Т И И И Х П Р И М Е Н Е Н И Е
§ 9.1. Основные понятия о гипотезах прочности
В случае о д н о о сн о го н а п р я ж е н н о го состояния оценка прочно
сти в данной точке конструкции производится путем непосред
ственного сопоставления возникающего в ней рабочего напря
жения либо с предельным, либо с допускаемым напряжением.
Коэффициент запаса прочности равен отношению предельного
напряжения к рабочему (расчетному): п = сгпред/<у.
Подчеркнем еще раз, что возникновение текучести или признаков
хрупкого разрушения хотя бы в одной точке конструкции (бруса) рас
сматривают как нарушение прочности конструкции в целом. Расчет на
прочность, основанный на таком представлении об опасном состоянии
конструкции, называют расчетом по опасной точке или расчетом по до
пускаемым напряжениям. В современной расчетной практике приме
няют также и другие методы расчета (по предельным нагрузкам или
несущей способности, по расчетным предельным состояниям), осно
ванные на иных представлениях об опасных (предельных) состояниях
конструкций; здесь эти методы не рассматриваются (см. [2, 4, 9, 11,
]).
Предельное напряжение определяют при механических ис
пытаниях данного материала на одноосное растяжение и сжа
12
260
тие. Для пластичных материалов за предельное напряжение
принимают предел текучести стт (или ст0 2 для материалов, диа
грамма растяжения которых не имеет явно выраженной пло
щадки текучести); для хрупкопластичных материалов сг02р или
сто , 2с ~ условный предел текучести при растяжении или сжатии;
для хрупких материалов сгпч с —предел прочности соответ
ственно при растяжении или сжатии. В случае кручения (при
чистом сдвиге) для многих материалов возможно также непо
средственное определение коэффициента запаса прочности, так
как имеются установленные экспериментально значения тпред.
Возникает вопрос, как подойти к оценке прочности в общем
случае сложного (объемного или плоского) напряженного со
стояния.
Пусть в исследуемой точке возникает напряженное со
стояние, характеризуемое определенными из расчета главными
напряжениями о 1^ а 2 '^ ст3. Как известно из предыдущего (см.
гл. III), три главных напряжения полностью определяют напря
женное состояние в данной точке тела. Допустим далее, что
в лабораторных условиях для данного материала осуществлено
напряженное состояние, подобное заданному в опасной точке
рассчитываемой детали. Подобным» называют напряженные
состояния, для которых отношения главных напряжений одина
ковы, т. е.
мм
(Т^.О^'^З “
. су2 а 3 *
При некотором значении главных напряжений (ст1пр, ст2пр,
а 3пр) напряженное состояние в некоторой точке (точках) образ
ца становится предельным, т. е. либо наступает текучесть, либо
появляются признаки хрупкого разрушения. Величина, показы
вающая, во сколько раз нужно увеличить возникающие в ис
следуемой точке главные напряжения, для того чтобы напря
женное состояние стало предельным, представляет собой
коэффициент запаса прочности
п — СТ! п р /СТ1 =
СТ2 л р / ° 2 = < Н „ р Л н .
Подчеркиваем, что написанное выражение имеет смысл
лишь в случае, если предельное напряженное состояние подобно
заданному.
Практически изложенный подход к расчету на прочность
при сложном напряженном состоянии возможен лишь в редких
случаях. Действительно, разнообразие напряженных состояний
безгранично, чрезвычайно велика также номенклатура приме
няемых материалов, и создать каждое из могущих встретиться
на практике напряженных состояний, да к тому же для всех ма
261
териалов в лабораторных условиях невозможно как по техни
ческим, так и по экономическим причинам.
Следовательно, располагая ограниченными эксперимен
тальными данными о свойствах определенного материала —
значениями предельных напряжений при одноосном растяже
нии и сжатии, необходимо иметь возможность оценить его
прочность в условиях любого сложного напряженного состоя
ния. Это становится возможным при применении так назы
ваемых гипотез прочности (теорий предельных напряженных
состояний).
Будем называть два напряженных состояния равноопаснымн
или эквивалентными, если они переходят в предельные при уве
личении соответствующих им главных напряжений в одно и то
же число (п) раз. Это означает, что коэффициенты запаса
прочности для эквивалентных напряженных состояний одина
ковы.
Остается решить вопрос, что же является критерием (при
знаком) равноопасности различных по характеру (неподобных)
напряженных состояний. Допустим, что решение этого вопроса
существует (его дают гипотезы прочности). Тогда для расчета
на прочность в случае сложного напряженного состояния сле
дует заменить его равноопасным (эквивалентным) ему одно
осным растяжением и сравнить соответствующее напряжение
с предельным (или с допускаемым) для данного материала.
Этот подход к оценке прочности при объемном (или плоском)
напряженном состоянии иллюстрируется условной схемой, по
казанной на рис. 9.1.
Напряжение при одноосном растяжении, равноопасное за
данному сложному напряженному состоянию, называют экви
валентным напряжением сгЭ!Ш
. Из приведенных рассуждений сле
дует, что эквивалентное напряжение —это лишь некоторая
условная расчетная величина, а не какое-либо реально возни
кающее напряжение. Значение эквивалентного напряжения за
висит не только от заданного напряженного состояния ( т . е. со
ответствующих ему главных напряжений), но и от принятого
для расчета признака равноопасности напряженных состояний.
Заменяем
%
262
"пред
Гипотезы, указывающие признаки равноопасности (критерии
эквивалентности) различных напряженных состояний, называют
гипотезами прочности. Другие наименования: теория пре
дельных напряженных состояний (гипотезы возникновения те
кучести и гипотезы прочности); гипотезы пластичности и хруп
кого разрушения; теории прочности.
Как следует из изложенного, применение гипотез прочности
избавляет от необходимости проведения громадного количе
ства экспериментов. Эти эксперименты были бы неизбежны
для установления предельных напряженных состояний, соответ
ствующих различным комбинациям, возникающим в исследуе
мой точке детали главных напряжений. Вместе с тем сами ги
потезы прочности нуждаются в экспериментальной проверке.
Тот или иной критерий эквивалентности может быть основой
для практических расчетов лишь при условии, что для ряда
частных случаев он проверен опытным путем и результаты экс
перимента оказались достаточно близки к результатам теоре
тического расчета.
Независимо от принятой гипотезы прочности после опреде
ления эквивалентного напряжения условие прочности можно
представить в виде одного из следующих неравенств;
п = ^предМиш > И
(9.1)
<
( 9 .2 )
или
| > р ].
§ 9.2. Определение эквивалентных напряжений
по различным гипотезам прочности
Рассмотрим критерии эквивалентности по трем гипотезам
прочности, наиболее широко применяемым в современной рас
четной практике, и приведем зависимости для вычисления экви
валентных напряжений.
Гипотеза наибольших касательных напряжений. Согласно
этой гипотезе, два напряженных состояния равноопаспы, если
максимальные касательные напряжения для них одинаковы.
Сформулированное условие, в частности, означает, что мак
симальные касательные напряжения для заданного напряжен
ного состояния и эквивалентного ему одноосного растяжения
одинаковы, т. е.
^тах ^эквДля заданного напряженного состояния по формуле (3.1)
*т а х = (< *1 “
СТ3) / 2 ;
263
i,г2'= Ш
М П а
ZL
б " =120 МПа
б/=110 МПа
/
/
ба =20 МПа
6^ = 20 МПа
Рис. 9.2
для эквивалентного одноосного растяжения на основе форму
лы (2.23)
^ЭКВ ^ЭКВ/—
Учитывая, что рассматриваемую гипотезу часто называют
третьей теорией прочности, будем обозначать эквивалентное
напряжение стэШ, с тем чтобы по этому обозначению без до
полнительных пояснений было ясно, по какой гипотезе опреде
ляется эквивалентное напряжение. Так называемые первая
и вторая теории прочности в настоящее время почти не
применяются.
Приравнивая ттах и хэкв, получаем
СТэш=
~ а з-
(9.3)
Очевидным недостатком этой гипотезы, обнаруживаемым
даже по виду расчетной формулы, является пренебрежение
влиянием промежуточного главного напряжения а 2. Напри
мер, два напряженных состояния, показанных на рис. 9.2, по
рассматриваемой гипотезе равноопасны, хотя для первого из
них ст2 близко к CTj, а для второго ст2 = 0 .
Тщательно поставленные опыты показали, что для пла
стичных материалов эта гипотеза дает удовлетворительное
совпадение экспериментальных данных с теоретическими.
Ошибка от пренебрежения влиянием сг2 не превышает
Ю -15% .
Качественным подтверждением рассматриваемой гипотезы
могут служить опыты, в которых кубики из различных мате
риалов подвергались трехосному равномерному сжатию (так
называемое гидростатическое сжатие). Даже при чрезвычайно
высоких давлениях (значение р достигала в некоторых опытах
десятков тысяч паскалей) не удавалось достичь предельного на
пряженного состояния. Так как при указанном виде нагружения
ст1 = сг2 = ст3 = —р и, следовательно, тшах = 0 , то по гипотезе
наибольших касательных напряжений переход в предельное со
стояние невозможен.
264
Гипотеза М ора. С огласн о этой гипотезе, два напряженных
состояния равноопасны, если д л я соответствую щ их главны х на
пряжений (cr'i, ст'з и су/, о'з) соблю дается соотношение
су/
— усу/ =
су/
— усу/.
О тс ю д а вы текает следую щ ая ф о р м у л а д л я эквивалентного
напряж ения:
<*3iv = cry -
vct3.
(9.4)
И н декс IV связан с тем , что эту гипотезу иногда н азы ваю т
четвертой теорией прочности. К оэф ф ициент v пред ставл яет со
бой отн ош ение предельны х напряж ений при одноосны х р а с т я
жении и сж атии, т. е. д л я хрупких м атер и ал о в
V
= ст
v
/ст
!
^ п ч , р / '- 'п ч , с »
д л я хрупкопластичны х м атери ал ов
V= СТ0 ,2р/СТ0 ,2сЕ сли принять, что коэф ф ициенты зап аса прочности по о тн о
ш ен и ю к п ред ел ьн ы м напряж ениям растяж ения и сж ати я
одинаковы , т о у м о ж н о определить из вы раж ения
V = [ сур] / [ сус].
Д л я пластичны х м атер и ал о в у = 1 и ф орм ул а (9.4) о к азы
вается в это м случае тож дественной ф орм ул е (9.3), т. е. суэШ =
= а э1У
Г и п о теза М о р а не учиты вает влияния п ром еж уточн ого
гл ав н о го напряж ения а 2 — это несом ненны й ее н едостаток.
О п ы ты п ок азы ваю т, что достаточн о точны е резу л ьтаты ги п о
т е за М о р а дает л и ш ь д л я напряж енны х состояний см еш ан н о го
типа, т. е. дл я тех случаев, к огд а а , и <т3 разн о зн ач н ы (в
частны х случаях ст, или ст3 м о ж ет б ы ть равн о нулю).
П р и оценке прочн ости стэ1У следует со п оставл ять с п р е
д ел ьн ы м или доп ускаем ы м напряж ением д л я одноосного р астя
жения.
Гипотеза удельной потенциальной энергии изменения формы.
С о гл асн о этой гипотезе, два напряженны х состояния равно
опасны, если удельная потенциальная энергия изменения ф орм ы
д л я них одинакова.
П ер вон ачал ьн о б ы л а предлож ена ги п о теза полн ой п о тен
ц и ал ьн о й энергии деф орм ации, согласно к о то р о й д в а н ап р я
ж енных состояния равноопасны , если удельная п отен ц и альн ая,
эн ерги я д л я них одинакова. Э ксперим енты не п одтверд и ли это й
ги п отезы . Д остаточ н о о б р ати ться к уже упом и н авш и м ся о п ы
265
там с гидростатическим сжатием, чтобы убедиться в расхожде
нии теоретических соображений и результатов эксперимента.
Действительно, при гидростатическом сжатии происходит на
копление энергии деформации, а значит, при каком-то ее значе
нии должен был бы наступить переход материала в предельное
состояние, однако этого не происходит, как бы велико ни было
действующее давление (возникающие напряжения).
При деформации элемента (бесконечно малой частицы тела)
в общем случае изменяются и его объем, и его форма. При ги
дростатическом сжатии, очевидно, изменения формы не проис
ходит. Это дало основание предположить, что в качестве кри
терия эквивалентности надо принимать не всю удельную
потенциальную энергию, а только ту ее часть, которая связана
с изменением формы элемента.
Формулу для определения эквивалентного напряжения по
рассматриваемой гипотезе, которую иногда называют пятой
теорией прочности*, приводим здесь без вывода:
/
2
[ ( о -i -
о 2 ) 2 + (с т 2 -
а 3) 2 + ( а 3 -
а Д 2] .
(9 .5 )
Эта гипотеза хорошо согласуется с опытными данными для
пластичных материалов. Для них она точнее, чем гипотеза на
ибольших касательных напряжений. Подчеркнем, что согласно
энергетической гипотезе условие эквивалентности определяется
значениями всех трех главных напряжений [см. формулу (9.5)].
§ 9.3. И сследование упрощенного плоского
напряженного состояния
При расчете бруса в случаях, требующих применения гипо
тез прочности, т. е. в тех случаях, когда в опасной точке напря
женное состояние не одноосное, оказывается удобным опреде
лять стэкв не через главные напряжения, а через напряжения,
возникающие в поперечном сечении бруса. Для того чтобы
иметь такую возможность, исследуем напряженное состояние
в точках бруса в общем случае его нагружения.
При работе прямого бруса на совместное действие изгиба
и кручения, или кручения и растяжения (сжатия), или изгиба,
кручения и растяжения (сжатия) в большинстве его точек воз
никает плоское напряженное состояние. В частности, для бруса
круглого сечения исключение составляют лишь точки, лежащие
на его продольной оси.
* В некоторых учебных пособиях (см., например, [2]) она назы
вается четвертой теорией прочности.
266
0)
Рис. 9.3
Выделим бесконечно малый элемент у контура поперечного
сечения бруса, работающего на совместное действие кручения
и растяжения (рис. 9.3, а). Отдельно этот элемент показан на
рис. 9.3,6; в силу его бесконечной малости он может быть
изображен в виде прямоугольного параллелепипеда.
Исходные площадки совпадают с поперечным и про
дольным (радиальным) сечением бруса, а также с площадкой,
касательной к его наружной поверхности. На площадке попе
речного сечения возникают нормальное напряжение (ctz = NJA)
и касательное напряжение (ггу = M z/W p). На площадке про
дольного сечения возникает только касательное напряжение xyz
(из-за отсутствия взаимного надавливания волокон бруса); при
этом Tyz = Т2у.
Площадка, касательная к наружной поверхности, от напря
жений свободна —нулевая главная площадка.
Равенство нулю одного из главных напряжений указывает,
что рассматриваемое напряженное состояние, действительно,
плоское (более строго утверждение, что напряженное состояние
не объемное). В общем случае плоского напряженного состоя267
ния на обеих ненулевых исходных площадках возникают и нор
мальные, и касательные напряжения. Здесь нормальное напря
жение по одной из них (продольной) равно нулю, т. е. имеет
место не общий, а частный случай плоского напряженного со
стояния, который принято условно называть упрощенным пло
ским напряженным состоянием.
Если выделить элемент в любой другой точке (не на конту
ре), изменится лишь значение исходных касательных напряже
ний. Если брус испытывает, кроме того, изгиб, то изменится ве
личина ст2; например, для одной из точек пересечения контура
с силовой линией
v z = N z/A + M B/W a.
Таким образом, рассматриваемый случай напряженного со
стояния оказывается для бруса наиболее общим. Действитель
но, чистый сдвиг и одноосное напряженное состояние (простое
растяжение или сжатие) можно рассматривать как частные слу
чаи этого напряженного состояния; первый из них имеет место,
если в данной точке о 2 = 0 , второй —при т2 = О (здесь и в даль
нейшем для упрощения обозначений второй индекс у т опу
скаем).
Ограничимся исследованием напряжений для серии площа
док, перпендикулярных нулевой главной площадке. Одна из та
ких площадок показана на рис. 9.3, в. На рис. 9.3, г показана
элементарная призма, одной из граней которой является эта
наклонная площадка. Пусть площадь наклонной грани равна
( L 4 , тогда dA cos а —площадь вертикальной грани, а сЫ sin а —
горизонтальной. Система элементарных сил, действующих на
выделенную призму, показана на рис. 9.3, д и в ортогональной
проекции —на рис. 9.3, е.
Для определения напряжений ау и тх на наклонной грани
составим уравнения равновесия действующих на призму сил:
£ npv =
dA +
(т 2
0 ;
dA cos a ) sin а —(ст2 dA c o s
+
(т2 dA sin а )
c o s а
=
а )
cos а +
0,
откуда
<т2 = ст2 cos2 а —т2 sin 2 а;
т„ dA
=
Snpt = 0 ;
(т2 d A c o s а) cos а - (а 2 dA
c o s а ) s in
+ (т2 dA sin а) sin а = 0,
268
(9.6)
а
+
или
т„ = 0,5crz sin 2а + тг cos 2а.
(9.7)
Найдем положение площадок, на которых касательные на
пряжения равны нулю, т. е. главных площадок.
Приравнивая правую часть выражения (9.7) нулю, получим
0,5стг sin 2 а 0 + т2 cos 2 а 0 = О,
откуда
tg2a 0 = —2tz/ ctz.
(9.8)
Здесь а 0 —угол между осью z и нормалью к главной
площадке.
Как известно из курса тригонометрии, данному значению
тангенса соответствуют два угла, отличающихся на 180° (2 а([ =
= 2 ао + 180°); следовательно, для угла а 0 имеем из выражения
(9.8) два значения, отличающихся на 90°. Таким образом, среди
исследуемой серии площадок есть д в е взаимно перпендику
лярные главные площадки, а значит, напряженное состояние
действительно плоское. Третья главная площадка (одна из
исходных) —нулевая.
Определим, как расположены площадки, на которых нор
мальные напряжения достигают экстремальных значений. Для
этого возьмем производную правой части выражения (9.6)
и приравняем полученный результат нулю. Угол, определяю
щий положение искомых площадок, обозначим <х1:
da„
d
,
—-— = ——(a. cos a —т, sin 2 a) = —2 <t. cos a sm a —
da
da z
—2 tzcos 2 a или a z sin 2 a t —2 xz cos 2 aj = 0 ,
откуда
tg 2at = -
/ ст2.
2 tz
(9.8a)
Сопоставляя формулы (9.8) и (9.8a), убеждаемся, что а 0 = а А,
т. е. экстремальные нормальные напряжения возникают на
тех площадках, на которых касательные напряжения равны
нулю.
Для определения главных напряжений надо подставить
в (9.6) значения а 0 (или, что то же самое, a t) из (9.8). Учитывая,
что все тригонометрические функции данного угла могут быть
выражены через одну из них, можно получить зависимость, не
269
содержащую этих функций. Производя соответствующие за
мены, получим
= -у- ± 4 | / оГ + 4 т|.
(9.9)
min
&
^
Эта формула дает значения двух главных напряжений. Одно
из главных напряжений в рассматриваемом случае равно нулю.
Очевидно, что оно является промежуточным между опреде
ляемыми из (9.9), так как здесь второе слагаемое по абсолют
ному значению больше первого, т. е. a min < 0. Значит, равное
нулю главное напряжение должно быть обозначено ст2.
Итак, при напряженном состоянии, условно названном
упрощенным плоским, имеем следующие значения главных
напряжений:
н = ' Т + у | / <т* + 4т‘ ;
0;
(9.10)
Для определения положения площадок, на которых возни
кают экстремальные касательные напряжения, возьмем первую
производную от выражения (9.7) и приравняем ее нулю:
dx„
<1 / 1
—-— = —— ~-CT,sin2 a + т, cos 2 a = a , cos 2 a —2 x.sin 2 a
da
da \ 2
/
z
или az cos 2 a 2 —2xz sin 2 a 2 = 0 , откуда
tg2a 2 =<jz/(2 tz).
(9.11)
Здесь a 2 —угол между нормалью к площадке, на которой каса
тельные напряжения экстремальны, и осью z.
Рассуждая, как и ранее, заключаем, что таких площадок две
и они взаимно перпендикулярны. Сопоставляя выражения (9.8)
и (9.11), получим, что углы 2а 0 и 2а 2 отличаются на 90° [про
изведение тангенсов этих углов равно (—1)]. Следовательно,
углы а 0 и а 2 отличаются на 45°.
Таким образом, площадки действия экстремальных каса
тельных напряжений являются бессекторнымн по отношению
к главным (делят углы между ними пополам).
Для определения максимального касательного напряжения
следует подставить в (9.7) вместо а значение а2, опре
270
деляемое из (9.11). В результа
те соответствующих преобразо
ваний получаем
*тм = - J l/<*z +
(9-12)
Сравнивая формулы (9.10) и
(9.12), нетрудно заметить, что
= (<?i - ст3)/2.
(9.13)
На рис. 9.4 для некоторого
упрощенного плоского напря
женного состояния показано
взаимное расположение исходных, главных и площадок дей
ствия максимальных касательных напряжений (на этих пло
щадках для упрощения чертежа нормальные напряжения не
показаны). Не следует забывать, что это изображение услов
но —фактически все указанные площадки проходят через одну
и ту же точку.
Эквивалентные напряжения при упрощенном плоском напря
женном состоянии. Подставляя значения главных напряжений
по формулам (9.10) в выражения (9.3), (9.4), (9.5) для эквива
лентных напряжений, получим:
CT3iv=
О т = 1/ о г,+ 4л*\
(9.14)
2
(9.15)
<V+
2
V az + 4Ч ’
CT3V= 1/<з\ -!- Зт?.
(9.16)
В дальнейшем при расчетах бруса будем пользоваться по
следними формулами, не определяя главных напряжений.
Еще раз указываем, что и ,и г, - напряжения на площадке поперечиого сеченет бруса, проходящего через исследуемую (опасную или
предположительно опасную) точку.
При применении формулы (9.15) ст2 должно быть подставлено со
своим знаком.
П р и м е р 9.1. Сравнить опасность двух напряженных состояний
(рис. 9.5). Механические характеристики материалов имеют следующие
значения: для первого элемента a j 4 p = 120 МПа, о1ч.с —360 МПа;
для второго элемента oJ(, p = 180 МПа, С т п , . с = 420 МПа.
Р е ш е н и е . В данном случае механические характеристики мате
риалов сравниваемых элементов различны, поэтому сопоставление
значений эквивалентных напряжений лишено смысла. Сравнивать надо
коэффициенты запаса прочности, конечно, применяя в том и другом
случае одну и ту же гипотезу прочности. Так как в том и другом слу271
помпа
Г
7
А Я-
у
1 Г‘"
1 7 51=гомпа
1
\
/
вомпа
7 б^иомпа
Ь
0 / г
Z
в?=тмпа
Рис. 9.5
чае материал хрупкий (это следует из заданных значений механических
характеристик), то расчет выполним по гипотезе Мора.
Для первого элемента (точки) главные напряжения имеют следую
щие значения:
<у\ =Су = 40 МПа; а \ ^ а ] = 2 0 МПа;
а ’ = ст’ = —100 М П а
Эквивалентное напряжение
120
а'у = а/ —vcr' = а}---- = 40 ——— (—100) = 73,3 МПа.
360
Коэффициент запаса прочности
I
_,'пч р
120
obv
73,3
Для второго элемента (точки)
= 1,64.
а “ = о " = 6 0 МПа; o f = сг“ =40 МПа; а ” = а ” = ■140 МПа.
Эквивалентное напряжение
180
->пч.р II
1П стз = 60 - 420 (-140) = 120 МПа.
Коэффициент запаса прочности
CT3lV = <з1 -
с7уп
чс
ПЧ.
с
«пч =
p/o'iv = 180/120 1,5.
Таким образом, и^ч < и|1Ч, следовательно, второе из заданных на
пряженных состояний опаснее.
§ 9.4. Расчет бруса круглого поперечного сечения
на изгиб с кручением
Валы различных машин представляют собой в большинстве
случаев прямые брусья круглого сплошного или реже кольце
вого сечения, работающие на совместное действие изгиба
и кручения. При ориентировочном расчете валов, рассмотрен
ном в гл. V, влияние изгиба не учитывалось, но допускаемые
напряжения на кручение принимались весьма невысокими, что
272
должно было в известной мере компенсировать ошибку,
являющуюся следствием пренебрежения изгибом.
Применение гипотез прочности позволяет рассчитывать
валы, учитывая совместное действие изгиба и кручения.
При расчете валов, а также других элементов конструкций,
испытывающих одновременное действие изгиба и кручения,
влиянием поперечных сил, как правило, пренебрегают, так как
соответствующие им касательные напряжения в опасных точ
ках бруса невелики по сравнению с касательными напряжения
ми от кручения и нормальными напряжениями от изгиба.
На рис. 9.6, а показан вал, на который насажены зубчатое
колесо диаметром d1 и шкив ременной передачи диаметром d2.
На зубчатое колесо действуют окружная F, и радиальная Fr
силы, на шкив —силы F x и F2 натяжения ветвей ремня. Для со
ставления расчетной схемы вала (рис. 9.6,6) все силы должны
быть приведены к его оси. При переносе силы Ft к оси вала
добавляется скручивающая пара с моментом M 1 = F ,(d 1/2)
(рис. 9.6, в); аналогично, при приведении сил Fj и F 2 получается
скручивающая пара с моментом М 2 = F t (djl) —F 2 (d2/2) =
= (^i ~ F 2)(dJ2) (рис. 9.6,г).
При равномерном вращении вала (только такой случай
и рассматривается) М 1 = М 2, что следует из основного уравне
ния динамики для вращательного движения (см. также с. 116,
117).
Подшипники, на которые опирается вал, рассматриваются
при его расчете как пространственные шарнирные опоры, т. е.
связи, препятствующие линейным перемещениям, но не ме
шающие повороту закрепленных сечений вала.
На основе расчетной схемы определяют опорные реакции
и строят эпюры М г, М х и М у, по которым определяют опасное
сечение вала. Как известно из предыдущего, расчет на изгиб
бруса круглого поперечного сечения ведется по результирую
щему изгибающему моменту М я = у М х + М у, следовательно,
для вала, диаметр которого по всей длине постоянен, опасным
будет сечение, в котором одновременно возникают наибольшие
крутящий Мг и изгибающий М я моменты (несколько ниже
определение опасного сечения будет уточнено). В рассматривае
мом случае опасным будет сечение С под серединой шкива.
Проанализируем вопрос об опасных точках поперечного се
чения. На рис. 9.7, а показаны моменты в сечении, проведенном
бесконечно близко слева от С. Применяя векторное изображе
ние изгибающих моментов, найдем положение силовой и нуле
вой линий и построим эпюру нормальных напряжений а Ми
(рис. 9.7,6). Касательные напряжения от кручения распределены
вдоль любого радиуса по линейному закону и достигают мак
симального значения в точках контура сечения. Очевидно,
опасными являются точки пересечения контура с силовой ли
нией, в которых одновременно и нормальные напряжения от изги-
а
274
ба, и касательные напряжения от кручения имеют наибольшие
значения.
Для пластичного материала точки А и В равноопасны, для
хрупкого или хрупкопластичного опаснее точка А, в которой от
изгиба возникают нормальные напряжения растяжения.
На рис. 9.7, в показан элемент, выделенный у опасной точки
А, и возникающие на его гранях напряжения
=
= M./W и> Xz
XMzmax
М zj А [Г
В опасной точке возникает упрощенное плоское напряженное
состояние.
Валы, как правило, изготовляют из среднеуглеродистой
конструкционной или реже легированной стали. Их расчет вы
полняют на основе третьей и пятой гипотез прочности.
Составим расчетную зависимость по третьей гипотезе про
чности.
По формуле (9.14)
<*эш = l / a z + 4 t z ;
подставляя в нее значения стг и т2, получаем
=1
Учитывая, что для круглого (сплошного или кольцевого) се
чения Wp = 2 WK, имеем
Озш = ] /{ M J W t f + M M J 2 W tf = - М^ — ■
Внешне эта формула аналогична расчетной зависимости для
определения максимальных нормальных напряжений при изги
бе, поэтому величину, стоящую в числителе, называют эквива
лентным (или приведенным) моментом, при этом условие про
чности имеет вид
°эк= = М эиЛ < [ а ] .
(9.17)
Таким образом, расчет бруса круглого поперечного сечения
на изгиб с кручением ведется аналогично расчету на изгиб, но
вместо изгибающего момента в расчетную формулу входит так
называемый эквивалентный момент, который зависит от изги
бающих и крутящего моментов, а также от принятой гипотезы
прочности. По гипотезе наибольших касательных напряжений,
М зШ= /М 2 + М? = I/М 2х + М 2у + М 1
(9.18)
Независимо от применяемой гипотезы прочности расчет*
ную формулу можно привести к виду (9.17).
275
Если выполнять расчет по пятой теории прочности, то, во
спользовавшись формулой (9.16), после преобразований, анало
гичных рассмотренным, получим
/Щ+ 0,75м ? = ]/ М 2Х + М 2у + 0,75М\.
М эУ = 1
(9.19)
При проектном расчете определяют требуемое значение мо
мента сопротивления поперечного сечения:
(9.20)
Учитывая, что для сплошного круглого сечения W„ =
—nd3/32 к 0,Id3, получаем следующую формулу для определе
ния требуемого диаметра вала:
d>
(9.21)
Понятие «эквивалентный момент» не имеет смысла при изги
бе с кручением бруса некруглого поперечного сечения. Неприме
нимо оно и в случае, если помимо изгиба и кручения брус кругло
го сечения испытывает растяжение или сжатие.
Для бруса с постоянным диаметром опасная точка находит
ся в сечении, для которого эквивалентный момент имеет на
ибольшее значение. Это сечение также называют опасным. Для
отыскания опасного сечения иногда помимо эпюр М х, М у, М 2
строят эпюру Ми, а затем эпюру М экв. Практически в этом нет
необходимости; в случае если по эпюрам Мх, Му, М г положе
ние опасного сечения нельзя определить, проще вычислить М жв
для нескольких сечений, чем строить эпюры Ми и Мэкв.
П р и м е р 9.2. Вал зубчатой передачи (редуктора) изготовлен из
стали 35 (ох = 310 МПа). К левому концу вала (рис. 9.8, а) подводится
от электродвигателя мощность Р = 28 кВт. Частота вращения вала
п = 630 об/мин. Проверить прочность вала в сечении под серединой
зубчатого колеса, не учитывая влияния шпоночной канавки. Принять
[пт] = 4,0. Расчет выполнить по пятой гипотезе прочности.
Р е ш е н и е . Момент, передаваемый валом:
М = Р/со = 28 • 103/66 =425 Н • м,
где
со = ген/30 = 3,14 •630/30 = 66 рад/с.
Выражая этот момент через окружную силу М = F(d/2), найдем
F = 2M/d = 2 •425 • 10790 = 9470 Н = 9,47 кН.
276
Fr =0,3B4Ft
N
я/
м
-Й -
i
В
-й
I • ПО
г/Л/7 II Ж
Ft = 9,47кН
6)
_М ХЛ=$/35КН'\ У
глл• >,72«У\ 1гг
_____ \ U,
9 -
A '7ГРГ-
Mz
* ь ,п т \
£=I ™к"
Sn
1М $*85 * У
425Н-М
ПбН-м
i^ rT T T rT T rm |? llW i^
Рис. 9.8
Радиальная сила (по соотношению, указанному на рис. 9.8, а)
F, = 0.364F, = 0,364-9,47 = 3,44 кН.
Составляем расчетную схему вала (рис. 9.8,6), строим эпюру кру
тящих моментов (очевидно, кручение испытывает лишь левая часть ва
ла условно до середины зубчатого колеса) и, определив опорные реак
ции, строим эпюры изгибающих моментов Мх и Му.
Эквивалентный момент для сечения под серединой колеса
Мэу = ]/M l + M y2 + 0,75M l = |/l4 6 2 + 4032 + 0,75• 4252 = 565 Н-м.
Эквивалентное напряжение для опасной точки рассчитываемого
сечения
565-103
= 61,9 • 10б Па = 61,9 МПа.
o3v
0Д-0,0453
Коэффициент запаса
пт= от ст,у = 310/61,9 = 5,01 > [пт].
П р и м ер 9.3. На рис. 9.9, о дан чертеж вала зубчатого редукто
ра; там же условно тонкими линиями показаны зубчатые колеса, наса
женные на этот вал, и подшипники, на которые он опирается. Вал
передает мощность Р = 14 кВт при угловой скорости ш = 32 рад/с. На
рис. 9.9, б вал с зубчатыми колесами показан схематично и даны силы,
действующие на зубья колес. Принимая [гг] = 45 МПа, определить
требуемые диаметры dB\ и d,,2 вала под серединами зубчатых колес.
Расчет выполнить по гипотезе наибольших касательных напряжений.
277
Р е ш е н и е .
С оставляем
р а с ч е т н у ю сх ем у в а л а , п р и в о
д я в с е д е й с т в у ю щ и е н а н е го
с и л ы к т о ч к а м , л е ж а щ и м н а о си
в а л а . П р и п е р е н о с е си л F t i и
F ,2 до б авл яю тся пары
си л с
м ом ен там и
M Ki = 0 , 5 F t i d \
и
А /к2 — 0,5 F t2d 2, с к р у ч и в а ю щ и м и
в а л . П р и п е р е н о с е с и л ы F al
д о б а в л я е т с я п а р а си л с м о
м е н т о м М х = 0,5 F a l d u в ы з ы в а ю
щ и м и з ги б в п л о с к о с т и z O y .
Р а с ч е т н а я схема в а л а и з о б р а
ж е н а н а р и с . 9.10, а (с и л а Fal
д л я я с н о ст и ч е р т е ж а н е с к о л ь к о
см ещ ена
от
оси
в ал а).
На
ри с. 9.10, б, в , г д а н ы э п ю р ы к р у
тящ и х и и зги б аю щ и х м о м ен
тов. П ри за д а н н о й конструкци и
(см . ри с. 9.9, а ) с и л а F a п е р е
д ается н епосредственн о на п р а
вы й п од ш ип ник, не в ы зы в а я р а с
тяж ения или сж ати я вала. И з
у с л о в и я р а в н о в е с и я в а л а (его
278
равномерного вращения) следует, что Мкi = М к2. При атом
М т = М к2 = Р/о) = 14 • 103/32 = 437,5 Н • м.
Применяя формулу (9.18), вычисляем эквивалентные моменты для
сечений К и С:
(МэШ)к = V M x2K + М уК + М :к = [,/54,62 + 4222 + 437,52 = 610 Н-м;
(МэШ)с = 1/М*с + Щс + Мгс = \ f 149,82 + 5522 + 437,5г = 720 Н • м.
Применяя формулу (9.21), находим требуемые значения dBi и </в2:
з
з
dB\ ^
32(Мэщ)к
132•610-103
яГст]
3,14 •45.10*
3
= 51,3 10“
3
32-720-103
- = 54,7-10"
3,14-45-106
С некоторым округлением принимаем
= 52 мм и 4)2 = 55 мм.
dB2 >
/ 32 (М эШ)с
л [о ]
§ 9.5. Р асчет бруса круглого поперечного сечения
в общ ем случае его нагружения
В наиболее общем случае нагружения бруса в его попе
речных сечениях возникают все шесть внутренних силовых фак
торов. В подавляющем большинстве практических расчетов
влияние поперечных сил не учитывают и, следовательно, расчет
на прочность ведут по четырем внутренним силовым факто
рам: Nz, М х, М у, M z, т. е. на сочетание растяжения (сжатия),
пространственного изгиба и кручения.
При рассмотрении расчета бруса круглого поперечного се
чения на совместное действие изгиба и растяжения (сжатия) бы
ло установлено (см. с. 253), что опасна та из точек пересечения
контура сечения с силовой линией, в которой знаки напряжений
от изгиба и осевого нагружения совпадают. Касательные на
пряжения от кручения максимальны во всех точках контура.
Следовательно, указанная точка оказывается опасной и при на
личии кручения, В этой точке имеет место упрощенное плоское
напряженное состояние и в зависимости от принятой для рас
чета гипотезы прочности эквивалентное напряжение вычисляет
ся по одной из формул (9.14), (9.15), (9.16). При этом исходные
напряжения стг и t z для опасной точки определяют из зависи
мостей
= N JA + M JW a.
_ M JW p
Для хрупкого материала при применении гипотезы Мора a z .
следует подставлять в формулу (9.15) со своим знаком. Заме
тим также, что в этом случае при сжимающей продольной силе
279
расчет следует выполнить для обе
их точек пересечения контура с
силовой линией.
При работе бруса на совмест
ное действие кручения и растяже
ния или сжатия нормальные напря
жения от осевой нагрузки распре
делены по поперечному сечению
равномерно; касательные макси
мальны в точках контура сечения,
следовательно, эти точки и будут
опасными. Напряженное состояние
по-прежнему упрощенное плоское.
При вычислении эквивалентного
напряжения а г и тг определяются
по формулам
az = NJA; i z = M JW r
П р и м е р 9.4. Проверить проч
ность винта домкрата (рис. 9.11) гру
зоподъемностью 100 кН, учитывая,
что в поперечных сечениях нарезанной
части винта помимо продольной си
лы возникает крутящий момент
М г = 540 Н • м. Внутренний диаметр резьбы d, = 48 мм. Расчет
выполнить по третьей гипотезе прочности. Принять [а] = 80 МПа.
Р е ш е н и е . Нормальные напряжения в поперечном сечении винта
(по абсолютной величине)
100- 103
N.
~А
nd\/4 (3,14/4) •0,0482
Касательные напряжения в т о ч к а х
fz = iMz
М,
W.
М,
nd3J16
=55,3-106 Па = 55,3 МПа.
контура
поперечного сечения
540 • 103
■= 24,9• 106 Па:
(3,14/16) -0,0483
= 24,9 МПа.
опасной точки по гипотезе наи
Э к в и в а л е н т н о е напряжение для
больших к а с а т е л ь н ы х напряжений
сын = ]/v l + 4т-- = j/55,32 + 4'24,92 = 74,4 МПа,
что ниже д оп ускаем ого на 7 % .
П р и м е р 9.5. П р о в е р и т ь прочность б р у с а кольцевого поперечно
го сеч ен и я, н а г р у ж е н н о г о , к а к указано на ри с. 9.12, а. Р а с ч е т вести по
пятой гипотезе прочности, принимая [ст] = 100 МПа.
Р е ш е н и е . На рис. 9.12,6 показаны эпюры внутренних силовых
факторов (кроме Qy, влияние которой при расчете не учитывается).
Определяем геометрические характеристики поперечного сечения
бруса:
280
М.г1200 Н-м
900 Нм
Рис. 9.12
3,14-ВО2
4
А
= 1180 мм2 =
= 1180-1(Г6 м 2;
3,14- 803
16
= 41,6-103 м м 3 =
= 41,6-1(Г6 м 3;
Жи = — ^ „ = — -41,6-103 = 20,8-103 мм3 =20,8-К Г 6 м3.
2
р
2
Вычисляем исходные напряжения в опасной точке опасного (в за
делке) поперечного сечения:
а ' = сгЛ, = N ./A = 18-103/1180-10"6 = 15,25-106 Па = 15,25, МПа;
o'' =
= Mx/W„ = 1200-107(20,8 • 10“ 6) = 57,7 • 106 Па = 57,7 МПа;
а 2 = ст! + а" = 15,25 + 57,7 « 73 МПа;
тг = тМгта = M J W p = 900-107(41,6-10-6) = 21,6-106 Па =21,6 МПа.
Эквивалентное напряжение по пятой гипотезе прочности
<bv = V ° z +
= |/732 + 3-21,62 « 82 МПа.
Брус недогружен на 18%.
§ 9.6. Расчет тонкостенных цилиндрических
и сферических резервуаров
Резервуары для газов и жидкостей обычно представляют
собой тонкостенные оболочки, срединная поверхность которых
(т. е. поверхность, делящая пополам толщину оболочки)
281
является поверхностью вра
щения. Наиболее распрост
ранены резервуары, состоя
щие из
цилиндрических,
сферических и конических
оболочек.
Ограничимся рассмотре
нием расчета на прочность
только цилиндрических и
сферических оболочек при
действии постоянного по
всей их внутренней поверх
ности газового давления.
Сведения о расчетах резер
вуаров при действии давле
ния жидкости, переменного
.по высоте резервуара см.,
например, в [2, 4, 9, 12].
При действии на резерву
ар наружного давления определение напряжений и расчет на
прочность выполняются так же, как и при внутреннем давлении,
но помимо этого расчета необходим расчет на устойчивость
(см, [9]).
Цилиндрические и сферические резервуары можно рассма
тривать как тонкостенные и, следовательно, пользоваться при
веденными ниже формулами (за исключением расчетов, тре
бующих повышенной точности) при условии, что pmjn: 5 > 10,
где pmin —минимальный радиус кривизны срединной поверхно
сти, 5 —толщина стенки резервуара.
Определим напряжения, возникающие в продольном (мери
диональном) и поперечном сечениях цилиндрического резервуа
ра (рис. 9.13, в), находящегося под действием внутреннего да
вления (р) газа.
Двумя поперечными сечениями, расстояние между которы
ми равно а, и продольным сечением, проходящим через ось ре
зервуара, выделим его часть, изображенную отдельно на
рис. 9.13,6, и рассмотрим условие ее равновесия. В меридио
нальном сечении возникают только нормальные напряжения ста
(окружные или кольцевые напряжения), которые в тонкостен
ном резервуаре можно считать равномерно распределенными
по толщине стенки. Отсутствие касательных напряжений в рас
сматриваемом сечении следует из симметрии нагружения ре
зервуара.
На элементарную полоску внутренней поверхности выде
ленной части резервуара действует внешняя сила d F =
282
ствующей всех сил давления, надо взять интеграл по всей вну
тренней поверхности выделенной части резервуара.
Сила, действующая на каждой из площадок продольного
сечения, равна ств5а.
Проецируя все силы на ось у, получаем уравнение равнове
сия
о
откуда
(9.22)
oe =pD/(25).
Рассекаем резервуар плоскостью, перпендикулярной его
продольной оси, и рассматриваем условие равновесия оста
вленной части (рис. 9.14). В поперечном сечении цилиндриче
ского резервуара возникают только нормальные напряжения
ат (меридиональные напряжения), равномерно распределенные
по площади сечения. Соответствующая сила уравновешивает
силу давления газа на днище резервуара. Проецируя все силы
на ось z, получаем уравнение равновесия
omnDb + pnD2/4 = О,
откуда
(9.23)
om= pD/{45).
Следовательно, окружное напряжение вдвое больше мери-
Рис. 9.14
Рис. 9.15
283
дионалыюго (ств =.2 crm); поэтому вполне естественно, что разру
шение цилиндрических резервуаров (скажем, в результате ава
рийного повышения давления) имеет характер продольной тре
щины.
В точках стенки резервуара возникает плоское напряженное
состояние —двухосное растяжение; при этом сте и а т —главные
напряжения. Учитывая правило индексов для главных напряже
ний и соотношение между величинами ст0 и а т, получим: а , =
= а в, ст2 = а т, ст3 = 0 .
Строго говоря, для точек стенки у внутренней поверхности резер
вуара напряженное состояние объемное: третье главное напряжение не
равно нулю —это напряжение сжатия, численно равное давлению в ре
зервуаре (ст3 = —р). В тонкостенных резервуарах р значительно мень
шее (в несколько десятков раз), чем Ое, сгт, поэтому принимают, что во
всех точках <т3 Р 0, т. е. считают напряженное состояние стенок резер
вуара плоским и однородным.
Условия прочности по гипотезе наибольших касательных
напряжений и по гипотезе Мора совпадают, так как ст3 = 0 [см.
формулы (9.3) и (9.4)]:
О э ш = CT3 iv = CTi = cr0 = p D / ( 2 5 ) < [ с т р] .
( 9 .2 4 )
По гипотезе энергии формоизменения, подставив в формулу
(9.5) (У3 = сте, а 2 = стш и а 3 —0, получим
<?эу =
]/ai + ai~ а»ат-
Воспользовавшись формулами (9.22) и (9.23), окончательно
получим следующее условие прочности:
стэУ= 1/3 pD/ (45) % 0,433 (pD/5) < [а].
(9.25)
В тонкостенном сферическом резервуаре (рис. 9.15) для лю
бой точки стенки все площадки, совпадающие с сечениями,
проходящими через центр сферы, главные. Возникающие на
этих площадках напряжения растяжения равны между собой:
Cj = ст2 (рис. 9.15). Эти напряжения можно определить, рассе
кая резервуар произвольной меридиональной плоскостью
и рассматривая условие равновесия оставленной полусфериче
ской части. Не приводя вывода, аналогичного проделанному
для цилиндрического резервуара, дадим окончательный резуль
тат:
< П = о 2 =рВ/(Щ.
(9.26)
Условия прочности по третьей, четвертой и пятой гипоте
284
зам прочности в данном случае (при o-j =ст2 и а 3 = 0 ) совпа
дают:
стэШ= a ,IV =CT,V=ст, = pD/(45) < [стр].
(9.27)
П р им е р 9.6. Определить по пятой гипотезе прочности при
[о] = 100 МПа требуемую толщину стенок цилиндрического резервуа
ра и его полусферических днищ (рис. 9.1 3 , а), если D = 2,5 м и р —
= 1,4 МПа.
Р е ш е н ы е. Условие прочности для цилиндрической части
ct3v ~
0,433рВ/8ц < [о],
откуда
8ц > 0,433
pD
И
= 0,433
1,4 -2,5
100
15,2 -К Г 3 м = 15,2 мм.
Обычно полученную из расчета на прочность толщину стенки уве
личивают на 1,5 —3 мм с учетом ее возможного ослабления в резуль
тате коррозии, поэтому примем 8Ц= 17 мм.
Для сферической части, применив формулу (9.27), получим
<тэу = р О / ( 4 8 сф) Й |[с г],
откуда
pD
Т М =
1,4-2,5
=
8,75' 10
м = 8,75 мм'
Принимаем а сф = 11 мм.
Глава X
СО П РО ТИ ВЛЕН И Е УСТАЛОСТИ
§ ЮЛ. Основные понятия об усталости м еталлов.
П редел выносливости
В предыдущих разделах учебника были рассмотрены во
просы прочности деталей, работающих в условиях статическо
го нагружения. Как известно, возникающие при этом напряже
ния чрезвычайно медленно увеличиваются от нулевого до
некоторого конечного значения и затем в течение длительного
времени остаются постоянными. Однако преобладающая часть
деталей машин и различных механизмов в процессе эксплуата
ции работает в условиях переменных напряжений. Многочис
ленные опыты и анализ поломок различных деталей машин
и сооружений позволили установить, что при переменных на
пряжениях разрушение деталей происходит при напряжениях,
значительно меньших предела прочности, а в ряде случаев
и предела текучести материала, причем срок службы детали до
285
момента ее разрушения зависит от возникающих в ней макси
мальных напряжений. Так, чугунные балки, способные в тече
ние ряда лет выдерживать без разрушения статическую нагруз
ку, близкую к ее предельному значению, при переменной
нагрузке, составляющей лишь половину от предельной статиче
ской, разрушаются менее чем через 1 0 0 0 циклов нагружений,
в то время как значительная часть деталей машин за время
их эксплуатации испытывает миллионы циклов нагружений.
Например, по данным, систематизированным Н. Н. Давиденковым, железнодорожный мост за время его эксплуатации
в среднем выдерживает 2 • 10 б циклов нагружений, коленчатый
вал авиационного двигателя —1 ,8 • 1 0 7, ось подвижного состава
железных дорог —2 - 1 0 8, вал паровой турбины — 1 ,6 • 1 0 го, ло
патки паровых турбин — 1 0 11 циклов нагружений.
Разрушения деталей вследствие возникновения переменных
напряжений носят название усталостных. Такое название
объясняется тем, что долгое время существовало мнение, будто
под влиянием переменных напряжений металл «устает» и вме
сто пластичного становится хрупким. На такую мысль наводил
внешний вид излома деталей: даже пластичный материал в ме
сте излома имеет две зоны —зону 1, имеющую тонковолокни
стое строение, гладкую с отшлифованной, блестящей поверх
ностью, и зону 2 , имеющую крупнозернистый вид, шерохова
тую, матовую, характерную для хрупкого излома (рис. 10 . 1).
Техника микрофотографирования позволила проследить за
процессом разрушения при переменных напряжениях.
Процесс разрушения начинается с появления микротре
щины, которая с течением времени увеличивается. Под влия
нием переменных напряжений края образующейся трещины то
расходятся, то сходятся, нажимая друг на друга, благодаря че
му происходит обмятие краев трещины, сглаживание, шлифо
вание поверхности. С увеличением трещины уменьшается раз
мер неразрушенной части детали, воспринимающей всю
нагрузку. Когда же сечение вследствие роста микротрещины
ослабнет настолько, что возникающие в
нем напряжения значительно возрастут и
материал не сможет их выдержать, про
исходит внезапный излом.
Часть усталостного излома, возникаю
щего в завершающей стадии разрушения,
из-за недостатка прочности сечения по тре
щине называется доломом. В этой зоне
видны относительно крупные зерна, сохра
нившие острые края, сама поверхность
излома матовая.
Рис. 10.1
286
Таким образом, под усталостью понимается процесс посте
пенного накопления повреждений материала под действием пере
менных напряжений, приводящий к изменению свойств, образова
нию трещин, их развитию и разрушению.
Рассмотрим возникновение переменных напряжений на при
мере работы вращающейся оси, нагруженной постоянными си
лами F (рис. 10.2, а).
Ось работает на изгиб. На участке CD ось испытывает
чистый изгиб. Проследим за изменением напряжения в точке
К контура поперечного сечения. Напряжения при изгибе в лю
бой точке поперечного сечения находим по формуле
а —(Мх/ Jx) у.
При повороте оси расстояние у точки К до нейтральной ли
нии сечения будет изменяться от нуля, когда точка К лежит на
нейтральной линии сечения, до уКтах = ^/2, когда точка К зани
мает верхнее или нижнее положение. Для любого положения
точки К ее расстояние от нейтральной линии может быть по
лучено из формулы
У —‘Уг 8*п ФПри равномерном вращении <р= <at, где о —угловая ско
рость вращения оси. Тогда у = d/ 2 sintoi. Следовательно, <зк —
= (Мх /Jx) d/ 2 sin т.
Но (Mx/Jx)(d/2) = amxx, тогда подставив это выражение
в предыдущую формулу, получим
ОК =
sin®f-
(101)
287
Из формулы видно, что
напряжения меняются по си
ш
^
нусоидальному закону. Гра
фик изменения напряжения
представлен на рис. 10.2,6.
За один полный оборот
оси точка попеременно по
падает из зоны растяжения
в зону сжатия. В положении
в точке возникают мак
симальные напряжения рас
тяжения, в положении Кг
напряжения равны нулю, так
как точка оказывается на ну
левой линии, в положении
К ъ точка К испытывает мак
симальное напряжение сжатия, в положении К4 ее напряжение
снова равно нулю. При каждом новом обороте оси изменение
напряжения в любой ее точке повторяется.
Если к той же оси помимо сил F, вызывающих ее изгиб,
приложить силы Fj (рис. 10.3, а), то ось будет испытывать так
же деформацию растяжения. Тогда в любой момент времени
напряжение в точке К сечения равно алгебраической сумме на
пряжений растяжения и изгиба и может быть найдено по
формуле
а к —F JA + a max sin tot.
(10.2)
б Ж \
IШШ.
б
В этом случае график изменения напряжений останется си
нусоидальным, но сама синусоида сместится вверх относитель
но оси абсцисс (рис. 10.3,6).
Совокупность последовательных значений напряжений за
один период их изменения при регулярном нагружении назы
вается ц и к л о м напряжения. Каждый цикл характеризуется сле
дующими параметрами: максимальным напряжением сттах, ми
нимальным напряжением a min, средним напряжением стт
и амплитудой напряжений цикла ста.
Наибольшее по алгебраическому значению напряжение
цикла называется максимальным напряжением цикла. М и н и
мальное напряжение цикла —это наименьшее по алгебраическо
му значению напряжение цикла.
Циклы могут быть знакопостоянными или знакопеременны
ми. Цикл напряжений, изменяющихся только по абсолютному
значению, называется знакопостоянным, а цикл напряжений,
изменяющихся по значению и по знаку, принято называть
знакопеременным.
288
Средним напряжением цикла называется постоянная (поло
жительная или отрицательная) составляющая цикла напряже
ния, равная алгебраической полусумме максимального и мини
мального напряжений цикла:
<*т= (<?max + <*min)/2 ИЛИ Тт = (Ттах + Tmin)/2.
(10.3)
Наибольшее числовое положительное значение переменной
составляющей цикла напряжений называется амплитудой на
пряжений цикла. Амплитуда напряжений цикла численно равна
алгебраической полуразности максимального и минимального
напряжений цикла:
= (^max
^min)/2 ИЛИ Та
(^max
^min)/2,
(10.4)
Цикл, у которого максимальные и минимальные напряже
ния равны по абсолютному значению, но противоположны по
знаку, называется симметричным (см. рис. 10.2,6). Для симме
тричного цикла ат= 0, ста = сттах.
Знакопостоянный цикл напряжений, изменяющихся от нуля
до максимума (crmin = 0) (рис. 10.4, а) или от нуля до минимума
(а шах = 0) (рис. Ю.4, б), называется отнулевым. Для такого ци
кла
^а
'"max(min)/2 ДЛИ ^а
“max (min)/2*
Цикл изменения напряжений, изображенный на рис. 10.3,6,
относится к так называемому асимметричному циклу.
Отношение минимального напряжения цикла к максималь
ному называется коэффициентом а си м м е тр и и ц и к л а напряжений
и обозначается R a или R x:
Я* = ^ min A W ; R r = t min Атах*
Для симметричного цикла коэффициент асимметрии
= CTmin/CTmax= ~ 1, Для отнулевого R a = 0, если а т > 0, и
= —оо, если ат < 0.
( 10*5)
Rn =
R„ =
289
Циклы, имеющие одинаковые коэффициенты асимметрии,
называются подобными.
Как показывают эксперименты, закон изменения напряже
ний во времени практически не оказывает влияния на про
чность детали, существенны лишь значения сттах и a min.
Кроме того, установлено, что эффект усталостного разру
шения материалов имеет место только в том случае, если на
пряжения превысят определенный уровень, причем в зависимо
сти от того, насколько будет превышен этот уровень, число
циклов до разрушения будет различным. При больших напря
жениях для разрушения достаточно небольшого количества ци
клов нагружения и, наоборот, при малых напряжениях деталь
может проработать практически бесконечно долгое время.
Для того чтобы оценить способность какой-либо детали
противостоять усталостному разрушению, необходимо в пер
вую очередь знать, как материал сопротивляется усталости,
т. е. иметь такую механическую характеристику, которая могла
бы количественно охарактеризовать способность материала со
противляться усталостному разрушению. С этой целью прово
дятся испытания на усталость. Испытанию подвергаются лабо
раторные образцы, имеющие в пределах рабочей части строго
цилиндрическую форму. Их диаметр обычно составляет
5... 10 мм, шероховатость поверхности образцов не грубее R a =
= 0,32.
Наиболее распространены испытания на изгиб при симме
тричном цикле изменения напряжений. Для проведения испыта
ния изготовляют большую партию совершенно одинаковых
образцов. Первый образец нагружают таким образом, что воз
никающие в нем максимальные напряжения заведомо ниже
предела прочности материала, но выше предела выносливости
(максимальные напряжения составляют приблизительно
0,6...0,7 от предела прочности материала образцов). В следую
щих образцах максимальные напряжения цикла уменьшают
и всякий раз с помощью имеющегося на машине счетчика обо
ротов фиксируют число циклов нагружений, которое выдержал
каждый образец до разрушения. По результатам испытания
строят кривую зависимости числа циклов нагружений до раз
рушения от максимального напряжения, создаваемого в образ
це (рис. 10.5). Эта кривая но
сит название кривой усталости.
По мере уменьшения созда
ваемого в образце напряжения
число циклов до разрушения на
чинает расти очень быстро, по
Рис. 10.5
этому кривая усталости имеет
290
значительную протяженность вдоль оси абсцисс. Для многих
материалов эта кривая асимптотически приближается к не
которому значению, т. е. начиная с какого-то напряжения,
несмотря на длительность испытаний, образцы не прояв
ляют никаких признаков разрушения, поэтому при каком-то
числе циклов испытание следует прекратить.
Практика проведения испытаний показала, что образцы, вы
державшие при заданном напряжении 10 • 106 циклов нагруже
ний, могут при данном напряжении проработать неограничен
но долгое время. Поэтому продолжительность испытаний
оговаривается.
Предварительно задаваемая наибольшая продолжитель
ность испытаний на усталость называется базой испытаний.
Однако следует заметить, что не для всех материалов можно
установить напряжение и соответствующее ему число циклов
нагружений, выдержав которое образец не разрушился бы
в дальнейшем. Так, для цветных металлов и для закаленных до
высокой твердости сталей кривая усталости не имеет асимпто
тического участка и, следовательно, при каждом значении на
пряжения можно было бы довести образец до разрушения, но
для этого потребовалось бы проводить испытания в течение
длительного времени.
Если кривую усталости перестроить в логарифмических
координатах, т. е. по оси абсцисс откладывать lgN, а по оси
ординат —lg сттах, то кривая усталости будет иметь более ком
пактный вид и будет изображаться двумя прямыми (наклонной
и горизонтальной), имеющими точку пересечения при некото
ром числе циклов N G (рис. 10.6). Число циклов, соответствую
щее точке перелома кривой усталости, представляемой двумя
прямыми линиями, называется абсциссой точки перелома кривой
усталости.
Максимальное по абсолютному значению напряжение ци
кла, при котором еще не происходит усталостного разрушения
до базы испытания, называется пределом выносливости и обо
значается aR, где индекс R соответствует коэффициенту асим
метрии цикла. По кривой уста
лости, перестроенной в лога
рифмических
координатах,
можно найти значение предела
выносливости — механической
характеристики, позволяющей
количественно оценить сопро
тивление усталости образца.
Напряжение, соответствующее
горизонтальному участку кри
291
вой усталости, построенной в логарифмических координатах,
соответствует пределу выносливости образца, который при
симметричном цикле будет обозначаться ст ,, при отнулевом —а 0.
В ряде случаев, в частности для расчета деталей, не
предназначенных для длительной эксплуатации, возникает не
обходимость в определении наибольшего значения напряжения,
которое может выдержать образец при заданном числе циклов
нагружений N < N G. В таком случае на кривой усталости по за
данному числу циклов N определяют соответствующее напря
жение aRN (рис. 10.6), называемое пределом ограниченной вынос
ливости, под которым понимают максимальное по абсолютно
му значению напряжение цикла, соответствующее задаваемой
циклической долговечности.
Многочисленные испытания показали, что предел выносли
вости существенно зависит от вида деформации образца или
детали. В связи с тем, что испытания на выносливость при рас
тяжении и сжатии, а также при кручении требуют более слож
ного оборудования, чем испытания на выносливость при изги
бе, они проводятся значительно реже. Поэтому при отсутствии
опытных данных соответствующие пределы выносливости
определяют по известному пределу выносливости при симме
тричном цикле изгиба на основе следующих эмпирических со
отношений [7]:
<т_1р« 0,75сх_,;
(10.6)
т_ 1«0,6сг_1.
(10.7)
Следует заметить, что между пределами выносливости при
изгибе и кручении зависимость примерно та же, что и между
пределами текучести при кручении и растяжении. В случаях,
когда нет опытных данных о значениях предела выносливости
даже и для симметричного цикла изгиба, приходится вычис
лять их по известным значениям пределов прочности по сле
дующим приближенным эмпирическим соотношениям [12]:
для сталей
ст_ j « (0.4...0,5) а пч,
(10.8)
причем для углеродистых сталей берут значения ближе к ниж
ней границе, для легированных —к верхней;
для цветных металлов предел выносливости изменяется
в более широком диапазоне
ст_! = (0,25...0,5) стпч;
292
(10.9)
для серого чугуна
ст_! « 0,45стпч.р,
(10.10)
где а пч р —предел прочности при растяжении.
§ 10,2, Ф акторы, влияющие на снижение
предела выносливости материалов
При оценке прочности деталей, работающих в условиях ста
тического нагружения, свойства материала детали отождест
влялись со свойствами материала образца, при этом не учиты
валась разница ни в форме, ни в размерах детали и образца, на
котором были получены предельные напряжения, т. е. предпо
лагалось, что при равных номинальных напряжениях опасность
разрушения образца и детали, выполненной из такого же мате
риала, как и образец, одинакова. Многочисленные экспери
менты показали, что при переменных напряжениях в расчетах
на сопротивление усталости необходимо учитывать ряд факто
ров, которые существенным образом влияют на сопротивление
усталости детали в то время, как на статическую прочность
они оказывают незначительное влияние. К наиболее суще
ственным факторам относятся концентрация напряжений, абсо
лютные размеры поперечных сечений детали, состояние по
верхности —ее шероховатость, наличие коррозии, окалины
и др. Рассмотрим более подробно влияние этих факторов на
сопротивление усталости.
Концентрация напряжений. Теоретические и эксперимен
тальные исследования позволили установить, что в тех местах
детали, где имеются разного рода отверстия, выточки, пере
ходы от одних размеров и форм сечений к другим, какие-либо
внутренние или внешние пороки в материале, а также в зоне
контакта деталей наблюдается значительное возрастание дей
ствительных напряжений по сравнению с номинальными, вы
численными по обычным формулам сопротивления материа
лов. Явление повышения напряжений по сравнению с номи
нальными называется концентрацией напряжений, а причина,
вызвавшая их возникновение, —концентратором напряжений.
К концентраторам напряжений относятся всякого рода выточ
ки, надрезы, отверстия, шпоночные пазы, места резкого измене
ния размеров сечений детали и др. Зона распространения по
вышенных напряжений носит чисто местный характер, т. е.
ограничивается небольшой областью, непосредственно приле
гающей к очагу концентрации, и поэтому эти напряжения часто
еще называют местными.
Для того чтобы понять, в чем заключается явление концен
293
трации напряжений, рассмотрим при
мер: пусть полоса шириной b и тол
щиной 8 (рис. 10.7) растягивается си
лами F и имеет небольшое сквозное
отверстие диаметром d. Заметим, что
длина полосы много больше шири
ны Ь, а та, в свою очередь, много
больше толщины полосы и диаметра
отверстия (Ь > 5d). В любом попе
речном сечении полосы продольная
сила N z = F и номинальные напря
жения, т. е. напряжения без учета кон
центрации, будут найдены по формуле
а = N J A = F / А . Опасным будет сече
ние, ослабленное отверстием, пло
щадь которого А = bb—bd = ЦЬ —d).
Если же нарисовать истинную кар
Рис. 10.7
тину распределения напряжений, то
окажется, что в непосредственной
близости к отверстию напряжения резко возрастают —пик
напряжений —и на небольшом удалении выравниваются. На
пример, при Ъ ^ 5d максимальные напряжения у края от
верстия приблизительно в три раза больше номинальных; в
точках, находящихся от оси отверстия на расстоянии I — 1,5 d,
превышение напряжений порядка 7%.
Основным показателем повышения напряжения в непосред
ственной близости к концентраторам напряжений служит тео
ретический коэффициент концентрации напряжений. Отноше
ние максимального нормального напряжения в зоне концентра
ции к номинальному называется т е о р е т и ч е с к и м к о э ф ф и ц и е н т о м
к о н ц е н т р а ц и и и обозначается ас:
^m ax Л-^ном'
Аналогично,
= ^тахЛ-иомЕстественно поставить вопрос: имеет ли место концентра
ция напряжений при статическом нагружении? Да, имеет. Но
на прочность деталей, выполненных из пластичных материа
лов, площадка текучести которых имеет достаточную протя
женность, она влияния не окажет, а потому в расчетах учиты
ваться не будет. Это объясняется тем, что максимальные
напряжения в местах концентрации, достигая предела текуче
сти, перестают увеличиваться и текучесть материала распро
294
страняется на остальную часть сечения. Дальнейшее увеличение
нагрузки приводит к распространению текучести в глубь сече
ния, т. е. происходит выравнивание напряжений в ослабленном
сечении. Для хрупких материалов концентрация напряжений
должна учитываться и при статическом нагружении. В этом
случае при достижении в ослабленном месте максимальным
напряжением значения, равного пределу прочности материала,
появляется трещина, которая быстро увеличивается и приводит
к разрушению детали.
При напряжениях, переменных во времени, наличие концен
тратора напряжения на образце приводит к снижению предела
выносливости независимо от того, из какого материала он вы
полнен. Это объясняется тем, что многократное изменение на
пряжений в зоне очага концентрации приводит к образованию
и дальнейшему развитию трещины с последующим уста
лостным разрушением образца. Однако различные материалы
по-разному реагируют на наличие одного и того же концентра
тора, т. е. обладают различной чувствительностью к концен
трации напряжений. Для того чтобы оценить влияние концен
трации напряжений на снижение сопротивления усталости
образца с учетом чувствительности материала к концентрации
напряжений, вводят понятие эф ф ективного коэф ф ициента кон
центрации, который представляет собой отношение предела вы
носливости образцов без концентрации напряжений к пределу
выносливости образцов с концентрацией напряжений, имею
щих такие же абсолютные размеры сечения, как и гладкие
образцы:
К а —ст_i/ст_ 11С или К х = т_ 1/т_ 1к,
(10.11)
где ст_(, т_ 1 —пределы выносливости образцов без концентра
ции напряжений при симметричном цикле; <т_1к, т_ 1к —
пределы выносливости образцов с концентрацией напряжений.
Теоретический и эффективный коэффициенты концентрации
связаны определенной зависимостью
Ча = (Ка - 1)/(оса - 1) или qx = (Кх - 1)/(ост - 1), (10.12)
где qa или qx —коэффициент чувствительности к концентрации
напряжений.
Различные материалы обладают различной чувствитель
ностью к концентрации напряжений. Более хрупкие высоко
прочные стали чувствительнее к эффекту концентрации напря
жений, которая сильнее сказывается на снижении предела
выносливости, а чугун, наоборот, малочувствителен к концен
трации напряжений. В расчетах К а и Кх следует брать из та295
Рис. 10.8
Рис. 10.9
блиц и графиков, приведенных в справочниках и другой
литературе.
На рис. 10.8 (см. [7]) представлены значения эффективных
коэффициентов концентрации, обусловленных наличием шпо
ночной канавки. На рис. 10.9 (см. [12]) приведены графики, ха
рактеризующие эффективные коэффициенты концентрации при
растяжении и сжатии в местах резкого изменения поперечного
сечения. Кривая 1 относится к материалам, имеющим сгГ1Ч=
= 400 МПа, а кривая 2 —стпч = 800 МПа.
Для уменьшения концентрации напряжений используются
различные конструктивные методы: внешние обводы деталей
делают по возможности более плавными, радиусы закругления
в местах резкого изменения размеров по возможности увеличи
вают и, наконец, если это возможно, вводят разгрузочные
канавки.
Шероховатость поверхности. Шероховатость поверхности
оказывает существенное влияние на снижение предела выносли
вости материала. Это связано с тем, что более грубая поверх
ность детали создает дополнительные места концентрации на
пряжений и, следовательно, возникают условия для появления
микротрещин. На поверхности всегда имеют место дефекты,
связанные с качеством ее механической обработки. Поэтому
усталостные трещины в большинстве случаев начинаются
с поверхности.
Отношение предела выносливости образцов с данной шеро
ховатостью поверхности а _ 1л к п р е д е л у выносливости образ
цов с поверхностью н е грубее R „ = 0,32 (по ГОСТ 2789-73)
а_ j называется к о эф ф и ц и е н то м в л и я н и я ш е р о х о в а то с ти п о в е р х
н о с ти :
K F = <у_ 1П/сг_j
296
или
К Р = т _ 1а/ т _ 1.
(10.13)
Для повышения сопротивления усталости широко исполь
зуют различного вида упрочнения поверхности: наклеп, поверх
ностную закалку токами высокой частоты, химико-термиче
скую обработку. Влияние этих факторов учитывается введе
нием так называемого коэффициента влияния поверхностного
упрочнения
K v = a _ ly/u _ u
(10.14)
где ст_1у —предел выносливости упрочненных образцов;
ст_ j —предел выносливости неупрочненных образцов.
Значения коэффициентов K F и K v в расчетах берут из таб
лиц и графиков справочников.
На рис. 10.10 (см. [12]) даны значения коэффициента K F
в зависимости от шероховатости и состояния поверхности де
тали: 1 — полированная поверхность; 2 —шлифованная поверх
ность; 3 — тонко обточенная поверхность; 4 — поверхность
с грубой обточкой; 5 —поверхность с наличием окалины.
Влияние абсолютных р а зм е р о в п о п е р е ч н о го се че н и я . Опыт
ным путем установлено, что с увеличением размеров попе
речных сечений образцов предел выносливости падает. Испыта
ния на гладких образцах показали, что эффект влияния
абсолютных размеров поперечного сечения существенно про
является при изгибе и кручении и практически отсутствует при
растяжении. В большей степени изменение размеров сказывает
ся у алюминиевых и магниевых сплавов и в значительно мень
шей степени у углеродистых и легированных сталей. Однако
если провести испытание на образцах с концентрацией напря
жений, то влияние абсолютных размеров скажется более замет
но, причем не только при изгибе и кручении, но и при
растяжении.
Влияние абсолютных размеров на снижение усталостной
прочности учитывают в расчетах введением так называемого
к о э ф ф и ц и е н та влияния абсолютных размеров п о п е р е чн о го сече
ния. Этот коэффициент равен отношению предела выносливо-
297
сти a _ ld гладких образцов диаметром d к пределу выносливо
сти ст_! гладких образцов по ГОСТ 2860-76:
к л = ° - и М - 1 или K d = t - u h - i .
(10.15)
На рис. 10.11 (см. [7]) представлены кривые зависимости
коэффициента K d для стали от диаметра детали: 1 —для валов
из легированных сталей; 2 —для валов из углеродистых сталей.
Для стали можно принимать K d при изгибе, растяжении и кру
чении приблизительно равными.
§ 10.3. Расчет на усталость
Расчет на усталость в большинстве случаев выполняют как
проверочный. Как и при расчете на статическую прочность,
цель проверочного расчета заключается в определении коэффи
циента запаса прочности в опасной точке рассчитываемой дета
ли и сравнении его с нормативным. Прочность детали считает
ся обеспеченной, если ее коэффициент запаса прочности не
меньше требуемого (нормативного). При вычислении коэффи
циента запаса прочности деталей, находящихся под воздей
ствием статических нагрузок, механические свойства материала
детали отождествлялись с механическими свойствами материа
ла образца, т. е. считалось, что поведение материала образца
и материала детали будет одинаковым, если в них возникнут
равные номинальные напряжения независимо от различия
в форме и размеров образца и детали. Поскольку, как ранее
было выяснено, при переменных напряжениях на предел вынос
ливости материала существенное влияние оказывают и форма,
и размеры поперечных сечений образцов, и шероховатость их
поверхности, то, естественно, рассчитывая на сопротивление
усталости конкретные, реальные детали, размеры и форма ко
торых отличаются от стандартных образцов, необходимо
учесть все факторы, снижающие сопротивление усталости.
Совместное влияние всех трех факторов учитывают введе
нием в расчет так называемого коэффициента снижения предела
выносливости
K = (K J K d+ l / K , . - l ) / K v '
(10.16)
или
K = (Kt (Kd + \IK F- l ) / K v.
Опытным путем установлено, что на значении предела вы
носливости сказываются не только вышеперечисленные фак
торы, но и немаловажную роль играет влияние асимметрии
298
цикла. В расчетах влияние асимметрии цикла учитывается
коэффициентом фп или фх, называемым коэффициентом чув
ствительности к асимметрии цикла напряжений. Для асиммет
ричного цикла коэффициент запаса может быть найден по
формуле
«о = СТ- l/(X <*a + Фа°т) ИЛИ Ит = Т_ J (Кх, + фтТJ ,
(10.17)
где К вычислен по формулам (10.16); сга, с т, ха, тга вычислены
по формулам (10.3) и (10.4).
Коэффициенты ф„ и ф, можно определить по формулам
Фа =
- (У0)/а 0; ф, = (2т_ t - т0)/т0,
(10.18)
где сг0, х0 —пределы выносливое! и, определенные по результа
там испытаний на усталость при отнулевом цикле напряжений.
При отсутствии значений сг0 и т0 их можно вычислить по
приближенным формулам (см. [7])
при изгибе:
ст0 « 1,6ст_ j ;
(10.19)
при сдвиге:
т0 ж 1,9т_!.
Если среднее напряжение цикла —напряжение сжатия (ат<
< 0 или тт <0), то ф„ или фТ следует взять равным нулю.
Для симметричного цикла crm= 0 (хт= 0), поэтому формулы
(10.17) упрощаются:
”a = cr- l / ( ^ a ) ИЛИ Щ=
/(Кха).
(10.20)
В случае возникновения в опасной точке детали упро
щенного плоского напряженного состояния, например при со
вместном действии изгиба и кручения, общий коэффициент за
паса прочности можно вычислить по приведенной (без вывода)
формуле
1У = 1К + 1/«?,
( 10.21)
где п —общий коэффициент запаса прочности детали;
иа —коэффициент запаса прочности по нормальным напряже
ниям; пт —коэффициент запаса прочности по напряжениям т.
П р и м е р 10.1. Н айти коэффициент запаса прочности детали, из
ображенный на рис. 10.12. Деталь выполнена из легированной стали
(стпч = 800 М Па, ст_ 1р - 3 0 0 М Па) и нагружена силами F, значения ко
299
торы х изменяю тся по симметричному
циклу, причем Fmm = 80 кН. Поверх
ность детали шлифованная. П ринять
D = 100 м м , d = 50 мм.
Р е ш е н и е . Вычислим максималь
Рис. 10.12
ные номинальные напряжения. П о
скольку деталь работает на растяже
ние и сжатие, то напряжение можно найти по формуле
= F m ax /M 2/4) = 80- 103/ (3,14• 0,052/4) = 40 106 П а =
= 40 М П а.
Коэффициент запаса прочности найдем по формуле (10.20), используя
(10.16):
„ = ________ ^
'
_________.
[(K „/K J + l/K F - l ) / K j a a
Д ля симметричного цикла ста = а та1 = 40 М Па. Значения К а возь
мем по рис. 10.9 (кривая 2); К „ = 1,6, так как г/ d = 0,2.
Значение коэффициента Ка найдем по рис. 10.11 (кривая 1). Д ля
d = 50 м м Kd= 0,71. Коэффициент KF = 0,92 для ш лифованной поверх
ности при стпч = 800 М П а (см. рис. 10.10); Kv = 1, так как поверхность
неупрочненная. П одставив найденные значения, получим
п —п „=
300
------------------------------------= 3,2.
(1,6/0,71+ 1 /0 ,9 2 -1 )-4 0
П р и м е р 10.2. Оценить прочность вала (рис. 10.13,а,б), выпол
ненного из углеродистой стали <упч = 500 М П а, если [и] = 2 . Поверх
ность неупрочненная. Считать, что нормальны е напряжения изгиба из
меняю тся по симметричному циклу, касательные напряжения круче
ния — по отнулевому. Ослабление сечений вала шпоночными канавка
ми не учитывать. Значения коэффициентов К„, K t, Kd, KF принять по
рис. 10.8; 10.10; 10.11. Поверхность вала полированная.
Р е ш е н и е . Д ля отыскания предположительно опасных сечений
необходимо построить эпю ры крутящего и изгибающих моментов,
предварительно определив реакции опор. В силу симметрии нагруже
ния
Х А
= Х в = F J2 = 3000/2 = 1500 Н ;
YA = YB = F J2 = 1100/2 = 550 Н.
Сила Fr изгибает вал в вертикальной плоскости, а сила F, — в го
ризонтальной плоскости и создает деформацию кручения. Вычислим
изгибающие моменты.
В вертикальной плоскости
М хЛ = 0; М хС = YAa = 550 • 0,07 = 38,5 Н - м ; М хВ = 0.
В горизонтальной плоскости
М уА = 0; М ус = Х Аа = 1500-0,07 = 105 Н м ; М уВ = 0.
Очевидно, кручение испытывает лиш ь левая часть вала условно до
300
середины шестерни, причем крутящий момент М г равен внешнему при
ложенному моменту М.
Эпюры М„ M s, M z изображены на рис. 10.13, в, г,д.
К предположительно опасным надо отнести два сечения: сечение
под серединой шестерни (максимальный изгибающий момент) и сече
ние выходного конца вала (минимальные размеры).
Найдам коэффициент запаса прочности сечения вала под середи
ной шестерни. Из эпюр видно, что в этом сечении возникает крутящий
момент М г = М = 108 Н •м и изгибающие моменты равны М хс =
= 38,5 Н •м и М ус =105 Н •м. Найдем результирующий изгибающий
момент:
МяС = ] / М2хС + Щ с = /3 8 ,52 + 1052 = 112 Н м .
Напряжения изгиба изменяются по симметричному циклу, значит,
0 ,
СГа
'Т щ а х '
По условию имеем право не учитывать ослабление сечения шпо
ночным пазом, поэтому напряжение найдем как для круга сплошного
сечения:
ст1ш,х = МиС/0,1 4 = 112/(0,1-0,033) = 42• 106 Па = 42 МПа.
301
Найдем коэффициент запаса прочности по напряжениям изгиба.
Для симметричного цикла имеем
"" [ ( KJ Kd+ l / K , - l ) / K J a3Вычислим предел выносливости о _ 1. Для стали можно воспользо
ваться соотношением (10.8):
сг_ j « 0,4сгпч = 0,4 ■500 = 200 МПа.
По рис. 10.11 (кривая 2) найдем Kd —0,87, а по ррс. 10.8 опреде
лим Ка = 1,64. Для полированной поверхности Кр = 1 (см. рис. 10.10,
прямая 1). Подставляя числовые значения, получим
200
п„ = ------------------ = 2,5.
° (1,64/0,87)-42
Касательные напряжения меняются по отнулевому циклу, поэтому
Вычислим максимальные касательные напряжения:
ттах = M J W p = MJ(0,2d32) = Ю8/ (0,2- 0,032) = 20- 10б Па = 20 МПа.
Тогда
То —Тт ~ Ттах /2 = 20/2 = 10 МПа.
Определим коэффициент запаса прочности по касательным напря
жениям, Для отнулевого цикла при KF = 1, K v = 1 имеем
т
т-1
К,/КЛ + Ьтт-
Вычислим т_ 1; пользуясь приближенной зависимостью (10.7):
х-
1
* 0,6а_ 1 = 0,6 • 200 = 120 МПа.
Найдем значения Kt = 1,4 и К ё = 0,87 по рис. 10.8 и 10.11. Опреде
лим коэффициент фт, Согласно формуле (10.18), ф, = (2 t_ t —т0)Д 0; со
гласно формуле (10.19), т0 «1,9т_1. Подставляя числовые значения,
получим:
т0 « 1,9 ■120 = 228 МПа; ф, = (2 -120 - 228)/228 = 0,052.
Подставляя числовые значения найденных величин, получим
120
П,~ (1,4/0,87)-10 + 0,052.10 =7,5'
Общий коэффициент запаса прочности по формуле (10.21) равен
1/п2 = 1/п2 + 1/п2.
Откуда
п = % n j/n l + п2 = 2,5 •7,5/(/2,52 + 7,52 = 2,4.
Аналогично вычисляется коэффициент запаса прочности выходно
302
го конца вала. Из эпюр (рис. 10.13, в, г, д) видно, что этот участок вала
работает только на кручение, поэтому
= _____ J-i____
"
(KJK,)т .
+
ф ,С
Как и раньше, \ —тга = ттм /2. Но
ттах = Мг/(0,2<ф = 108/(0,2■ 0,0223) = 51 • 106 Па = 51 МПа,
тогда та = тт = 51/2 = 25,5 МПа.
Вычислим коэффициент запаса прочности:
120
* (1,4/0,91) •25,5 + 0,052 ■25,5
Из расчета видим, что для обоих сечений коэффициент запаса про
чности оказался не ниже нормативного, значит, прочность вала
достаточна.
п = и = ------------------------------- = 3,0.
Г л а в а XI
КОНТАКТНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ
§ 11.1. Основные понятия
В зубчатых и червячных передачах, в шариковых и роли
ковых подшипниках, в кулачковых и во многих других механиз
мах и узлах машин передача сил от одной детали к другой
осуществляется путем непосредственного контакта этих дета
лей. При этом в контактирующих деталях возникают местные
деформации и напряжения, называемые контактными. Несмо
тря на то что в большинстве случаев контактные напряжения,
возникающие в деталях машин, весьма высоки (зачастую зна
чительно выше предела текучести материала деталей), они не
влияют на о б щ у ю прочность деталей. Это объясняется тем,
что контактные напряжения и деформации имеют резко выра
женный местный характер, быстро уменьшаясь по мере удале
ния от зоны контакта.
Надежность большинства указанных деталей определяется,
как правило, не общей их прочностью (например, применитель
но к зубчатым колесам —не прочностью зубьев на изгиб),
а прочностью работах поверхностей деталей, или, как принято
говорить, контактной прочностью.
Контактные напряжения могут быть постоянными или
мало изменяющимися во времени, как, например, в упорных
подшипниках крюков для подъема грузов или в опорных роли
ках поворотных кранов. Под малой изменчивостью напряже
ний во времени понимают как сравнительно небольшие ампли
303
туда циклов, так и общее небольшое число циклов нагружения
за весь срок службы детали. В этих случаях расчет ведут на
статическую контактную прочность. Нарушением статической
контактной прочности считают возникновение трещин (для
хрупких материалов) или появление пластических деформаций
в зоне контакта.
В некоторых случаях возникновение небольших местных пластиче
ских деформаций считают неопасным и полагают, что прочность до
статочна, если указанные деформации не превышают устанавливаемых
экспериментально допускаемых значений.
Значительно чаще контактные напряжения многократно ци
клически изменяются во времени, как это имеет место, в част
ности, на рабочих поверхностях зубьев зубчатых колес. В этих
случаях при недостаточной контактной прочности происходит
усталостное разрушение рабочих поверхностей деталей. Харак
тер усталостного выкрашивания поверхности зуба колеса зуб
чатой передачи условно показан на рис. 11.1.
Расчеты как на статическую контактную прочность, так
и на контактную усталость, очевидно, связаны с необходи
мостью выяснения зависимостей между нагрузками, действую
щими на контактирующие тела, характеристиками материала
тел, геометрией их поверхностей и возникающими напряже
ниями.
Решение задачи об определении контактных напряжений
и деформаций не может быть дано методами сопротивления
материалов; результаты, полученные методами теории упруго
сти, для некоторых частных случаев контакта приведены в сле
дующем параграфе. Здесь остановимся на самой постановке за
дачи и допущениях, положенных в основу ее решения.
При теоретическом решении этой задачи рассматриваются
два тела, ограниченных криволинейными поверхностями и на
груженных силами, прижимающими эти тела друг к другу
(рис. 11.2). При отсутствии нагруз
ки соприкосновение тел происходит в
одной точке (начальный точечный кон
такт, рис. 11.2) или по линии (на
чальный линейный контакт, см. ниже
Рис. 11.1
304
Рис. 11.2
рис. 11.7). Нагрузка, нормальная к поверхностям контакта, вы
зывает местные деформации контактирующих тел, в результате
которых начальный точечный или линейный контакт переходит
в контакт по некоторой малой площадке, имеющей в общем
случае форму эллипса. В некоторых частных случаях начально
го точечного контакта (см. следующий параграф) контактная
площадка имеет форму круга; при начальном линейном кон
такте, например при контакте цилиндров с параллельными
образующими, —форму прямоугольной полоски. Давление,
передаваемое от одной детали к другой, распределено по кон
тактной площадке неравномерно.
Отметим, что в тех случаях контакта, когда соприкоснове
ние ненагруженных деталей происходит по некоторой площад
ке конечных размеров, а не в точке и не по одной линии (на
пример, контакт шпонки и шпоночного паза ступицы, насажен
ной на вал детали), принято говорить не о контактных
давлениях и напряжениях, а о напряжениях смятия и применять
условный метод расчета, изложенный в гл. IV.
В результате решения контактной задачи определяют фор
му и размеры контактной площадки, закон распределения кон
тактных давлений и величину сближения контактирующих тел.
При этом решение базируется на следующих предпосылках.
1. Материалы контактирующих тел однородны и изо
тропны.
2. Силы, приложенные к соприкасающимся телам, таковы,
что процесс деформации протекает в пределах справедливости
закона Гука.
3. Поверхность контакта весьма мала по сравнению с об
щей поверхностью каждого из соприкасающихся тел.
4. Поверхности соприкасающихся тел совершенно гладкие,
и, следовательно, силы давления, передаваемые через поверх
ность контакта от одного тела к другому, нормальны к этой
поверхности.
Наибольшие по абсолютному значению нормальные напря
жения для точек, принадлежащих поверхности контакта, могут
рассматриваться как известные, так как эти напряжения числен
но равны контактным давлениям в соответствующих точках.
Однако, как известно из предыдущего, для оценки прочности
при сложном —плоском или объемном —напряженном состоя
нии недостаточно определить лишь наибольшее напряженке,
надо знать все три главных напряжения.
В том, что в точках зоны контакта возникает объемное на
пряженное состояние, легко убедиться из простейших физиче
ских соображений, рассмотрев какой-либо частный случай кон
такта деталей, скажем, контакт колеса с рельсом. Мысленно
305
выделив бесконечно малый параллелепипед в окрестности не
которой точки головки рельса (рис. 11.3), заключаем, что да
вление, действующее на верхнюю грань параллелепипеда, дол
жно вызвать деформации не только в направлении оси г, но
и в направлении осей х и у. Этим деформациям препятствует
материал рельса, окружающий мысленно выделенный паралле
лепипед, и, следовательно, на его гранях, перпендикулярных
осям х и у, возникают напряжения сжатия. Конечно, приве
денные рассуждения позволяют получить лишь качественное
представление о характере напряженного состояния; обстоя
тельное исследование, дающее количественные результаты зна
чения главных напряжений, выполняют методами теории упру
гости.
§ 11.2. Контакт тел, ограниченных сферическими
и цилиндрическими поверхностями
При контакте двух тел, ограниченных сферическими поверх
ностями произвольных радиусов, площадка контакта имеет
форму круга —круговая площадка контакта. Такую же форму
имеет эта площадка при контакте двух цилиндров с взаимно
перпендикулярными осями и равными радиусами. Здесь огра
ничимся рассмотрением лишь первого из указанных случаев,
разновидностями которого являются: а) контакт двух вы
пуклых сферических поверхностей (рис. 11.4, а); б) контакт тела,
ограниченного выпуклой сферической поверхностью, со сфери
ческой впадиной (рис. 11.4,6); в) контакт тела, ограниченного
сферической поверхностью, с плоскостью (рис. 11.4, в).
Закон распределения контактных давлений по площадке
контакта дан на рис. 11.5, я в виде пространственной эпюры, на
которой р обозначено давление в произвольной точке площад306
ки контакта, а р0 —максимальное давление, возникающее в ее
центре. В сечении любой плоскостью, проходящей через ось z,
например плоскостью zOy, плоская эпюра, показывающая рас
пределение давлений вдоль любого диаметра контактной пло
щадки, ограничена полуокружностью радиуса р0 (рис. 11.5,6).
Радиус а контактной площадки, максимальное давление р0
и сближение 5 контактирующих тел определяют по следующим
формулам:
а = 0,9086 l/riFpn,,;
р0 = 0,5784
( 11. 1)
(
11. 2)
Ч 2Р 2
пР ’
8 = 0,8255 f/(nF)2/Pnp-
(11.3)
В этих формулах т| —комбинированная упругая постоянная
материалов контактирующих тел, связанная с их модулями
упругости Et и Е2 коэффициентами Пуассона щ и ц2 зависи
мостью
B = ( l - B ? ) / F i + (1-B 2 )/F2-
(11-4)
Приведенный радиус кривизны в месте контакта рпр опреде
ляют из формулы
l/ p „ P = l / * i ± l / * 2 -
(11-5)
Знак минус перед вторым слагаемым принимают при кон
такте сферы со сферической впадиной (см. рис. 11.4,6); при кон
такте сферы с плоскостью (см. рис. 11.4, в) К2 — со.
Для большинства металлов и сплавов без большой погреш
ности можно принять р 1= р 2 =0,30; тогда взамен формул
307
(11.1) —(11.3) получим:
а = 1,109 y^Fрпр/Еар;
Ро = 0,3880
3
(
11. 6)
(11.7)
(11.8)
Здесь дополнительно введено обозначение
Епр = '2.Е1Е2/{Е1 + Е2).
(11.9)
Величину Е„р иногда называют приведенным модулем упру
гости контактирующих тел.
Несмотря на то что для материалов соприкасающихся тел
справедлив закон Гука, все рассмотренные величины зависят от
нагрузки (силы F) нелинейно. Отсюда следует, что к кон
тактным задачам припциц независимости действия сил неприме
ним. Пусть, например, при действии силы F2 максимальное
контактное давление равно р01. Предположим далее, что кон
тактирующие тела дополнительно нагружаются силой F2 =
= 2F и т. е. нагрузка возрастает в три раза. При этом макси
мальное контактное давление, как следует из формулы (11.2)
или (11.7), р01 2 =Poi |/3, т. е. р0 возрастает не в три, а лишь
в 1/3 *1,44 раза.
Познакомимся с основными результатами исследования на
пряженного состояния в точках зоны контакта. Ограничимся
случаями, когда р, = р2 = 0,30.
Рис. 11.6
308
Для точки в центре контактной площадки (рис. 11.6) макси
мальное по абсолютному значению главное напряжение а 3 =
= —р0 возникает на грани элемента, касательной к поверхно
сти контакта. Остальные два главных напряжения для этой
точки также сжимающие и равны между собой: a t - а2 —
— —0,8р0. Во всех других точках максимальное по модулю на
пряжение меньше р0.
Наибольшее напряжение растяжения возникает в любой
точке контура контактной площадки (рис. 11.6): CTj = О,133р0;
при этом
= —а 3 и ст2 =0, т. е. здесь в отличие от централь
ной точки не объемное, а плоское напряженное состояние; точ
нее, его частный случай —чистый сдвиг (см. § 3.3).
Если оценивать контактную прочность, применяя метод
расчета по опасной точке, то надо выбрать ту или иную гипо
тезу прочности и потребовать, чтобы для опасной точки вы
полнялось неравенство —условие прочности:
<5-шя« [о].
При этом возникает вопрос, какая именно точка зоны кон
такта опасная. Или, иными словами, для какой точки по вы
бранной гипотезе прочности эквивалентное напряжение макси
мально.
Исследование этого вопроса для случая круговой площадки
контакта показывает, что точка, для которой сгэШ максимально,
лежит на нормали к центру контактной площадки на глубине
0,48а под поверхностью. Значения главных напряжений для
этой точки даны на рис. 11.6: <у1 = а 2 = 0,18ро; <т3 = —0,80р0 и,
следовательно (см. с. 264),
сгэШ= с?! - о 3 = —0,18р0 - (-0,80р0) = 0,62р0.
Подчеркнем, что, как следует из известной формулы
? .„ а х
=
(< П
-
с тз ) / 2 ,
для указанной точки максимальное касательное напряжение
имеет наибольшее значение:
т Еаи6 = [ —0,18р0 - (—0,80ро)]/2 = 0,31р0.
шах
При круговой площадке контакта наибольшее значение эк
вивалентного напряжения по гипотезе энергии формоизмене
ния оказывается таким же, как по гипотезе наибольших каса
тельных напряжений:
<тэу = 0,62ро.
309
. Для случая контакта ци
линдров с параллельными
образующими (рис. 11.7,а) —
начальный линейный кон
такт —при решении контакт
ной задачи принято дополни
тельное допущение: цилинд
ры имеют бесконечно боль
шую длину. Контактная пло
щадка ограничена двумя па
раллельными
прямыми —
контактная полоска; по ее
ширине давление распреде
лено по эллиптическому закону. Максимальные давления дей
ствуют в точках средней линии контактной полоски. Прост
ранственная эпюра контактных давлений, ограниченная по
верхностью эллиптического цилиндра, показана на рис. 11.7,6.
Сечение этой эпюры плоскостью, перпендикулярной линии
начального контакта, т. е. эпюра распределения давлений
по ширине полоски контакта, дано на рис. 11.7, в.
Полуширина Ъ контактной площадки и максимальное кон
тактное давление р0 при равномерно распределенной по длине
цилиндров нагрузке интенсивностью q (рис. 11.7, а) опреде
ляются по формулам*, обычно называемым формулами Гер
ца:
Ь = 1,128 |ЛиР„Р;
Ро =
0.5642 lA / p n p p .
(11.10)
(11.11)
Значения г| и рпр определяют по формулам (11.4), (11.5).
В учебной и справочной литературе по деталям машин ча
ще приводят следующие формулы для величин b и р0, полу
ченные при pj = р2 = 0,30:
Ъ=
1,522 j/gpIip/Enp;
Ро = 0,4180 ]/qEnp/ Pnp,
(11.12)
(11.13)
где Епр определяется по формуле (11.9).
Приведенные формулы показывают, что и в случае началь
ного линейного контакта характерный размер контактной пло
* Сравнительно громоздкую и имеющую ограниченное примене
ние формулу для определения 8 не приводим; соответствующая фор
мула дана, например, в монографии [9].
310
щадки и максимальное дав
ление зависят от нагрузки
нелинейно.
В точках средней линии
контактной площадки на
пряженное состояние —трех
осное Сжатие (рис. 11.8), ха
рактеризуемое главными на
пряжениями
<Ti = —0,6р0;
ст2 = сг, = —р 0. Значение
соответствует (Х; =
= 0,30.
При оценке прочности по
гипотезе наибольших каса
тельных напряжений опасна
точка, лежащая на нормали к средней линии контакт
ной площадки на расстоянии 0,786 от поверхности
контакта (рис. 11.8). Для этой точки
= —О,180ро; с 2 =
= —0,288р„; сг3 = —0,780ро и, следовательно,
т
наиб
m ax
—
—0,18ро —( —0,78ро)
0,ЗЦРо>
L
<тэШ= —0,18ро —( —0,78ро) = 0,60ро.
При применении гипотезы энергии формоизменения опас
ной оказывается точка, лежащая на той же нормали, но не
сколько ближе к поверхности - на расстоянии 0,706; эквива
лентное напряжение
стэУ- 0,557р0.
Итак, при контактной площадке в виде прямоугольной по
лоски, так же как и в случае круговой площадки контакта, эк
вивалентное напряжение оказывается равным максимальному
контактному давлению р0, умноженному на некоторый число
вой коэффициент. Обозначив его с, получим условие прочности
в виде
ст:ж„ = ср0 < [а] или р0 < [о]/с.
Таким образом, есть возможность вести расчет на про
чность без вычисления а экв непосредственно по величине р0:
Ро <
[РоЗ-
Допускаемое контактное давление устанавливают на основе
экспериментальных исследований контактной прочности и опы
та эксплуатации машин и сооружений. Практически в болынин311
стве случаев при записи условия прочности приняты иные обо
значения, чем приведенные. Учитывая, что р0 численно равно
наибольшему по модулю главному напряжению для той точки
контактной площадки, на которую передается это давление,
т. е. р0 = | <т31, пользуются термином «контактное напряжение»
и вводят соответствующее обозначение а к = р0, | ст31= стк. При
этом условие прочности записывают в виде
стк<[сгк].
(1114)
Допускаемое контактное напряжение [стк] зависит в основ
ном от свойств поверхностных слоев материала деталей и от
характера изменения контактных напряжений во времени. Зна
чения [а к] существенно выше, чем допускаемые напряжения,
принимаемые при оценке общей (на растяжение, изгиб и т. п.)
прочности деталей. Из приведенных выше рассуждений полу
чается, что [ o j больше обычных допускаемых напряжений
в 1/с раз, т. е. ориентировочно в 1,6... 1,7 раза. Практически
[а к] превышает допускаемые напряжения, применяемые при
расчетах на общую (или, как иногда говорят, объемную) про
чность, в 3...5 раз. Некоторые соображения о причинах такого
различия в величинах допускаемых напряжений приведены
в специальной литературе (см., например, [9]).
Для иллюстрации сказанного о значениях [стJ приведем не
которые числовые данные. При расчетах стальных зубчатых
колес (напряжения изменяются по циклу, близкому к отнулевому) принимают [стк] х 400...700 МПа, а в случаях, когда по
верхности зубьев подвергнуты специальной термической или
термохимической обработке, обеспечивающей их высокую
твердость, [ a j может быть в 2—2,5 раза выше, чем указано.
При определении статической грузоподъемности шариковых
и роликовых подшипников принимают [стк] х 2000...3000 МПа
и выше.
П р и м е р 11.1. Для опоры на шпиле (рис. 11.9) счетно-решающе
го устройства определить допускаемую нагрузку F . При найденном
значении [£] определить радиус контактной площадки. Материал кер
на —сталь У10А (£ст = 2,0-105 МПа; цст = 0,30); материал подуш
ки —агат (£а = 1,0-105 МПа; ра = 0,30*). Допускаемое контактное на
пряжение [стк] = 5000 МПа. Радиус керна гкер = 0,10 мм; радиус
опорной поверхности подушки гп = 0,80 мм.
* В технической литературе нет экспериментальных данных о зна
чении р для агата; расчетные формулы, применяемые при проектиро
вании узлов приборов, основаны на указанном значении и.
312
Р е ш е н и е . На основе формулы (11.7) и указаний о расчете на
прочность, приведенных выше, имеем
Стк = р0 = 0,3880 {/f'f^p/Pnp ^ К ] .
Отсюда
Ы 3р2ир
т - 0,38803Ejp’
где [см. формулы (11.5) и (11.9)] 1/рпр = 1/гкер - 1/г„ = 1/0,10 - 1/0,80 =
= 8,75 1/мм; рпр = 1/8,75 = 0,1142 мм;
2 £ ст£ а
£ пр
2 - 2 , 0 - 1 0 5 ■1 , 0 - 1 0 5
£ ст + £ а ~
МПа.
2 , 0 - 10 5 + 1 , 0 - 1 0 5
Подставив в выражение для [F] числовые данные, получим
(5 0 0 0 ^ ^ 4 2 ^ ^
LJ
н
0,38803(1,33 • 105• 106)2
По формуле (11.6) определяем радиус контактной площадки:
а = 1,109 [/£ р пр/£ пр = 1,109 f/l,58- 0,1142/(1,33 • 105) =
= 12,3-10“ 3 мм = 12,3 мкм.
П р и м ер 11.2. Проверить контактную прочность рабочей поверх
ности ходового колеса (рис. 11.10) тележки мостового крана при рас
четной нагрузке на колесо F = 40 кН. Материал колеса —стальное
литье 55Л; [стк] = 650 МПа. Тележка работает на рельсе с плоской
головкой. Определить полуширину контактной полоски. Для колеса и
рельса £ = 2,0-105 МПа.
313
Р е ш е н и е . Максимальное контактное давление определим по
формуле (11.13), подставив в нее
q
=
F/B =
4 0 • 1 0 3/ 0 , 0 7 = 5 7 1 • 1 0 3 Н / м ;
Е пр =
1/Рпр = 1/Ркол +
£ = 2 , 0 '1 0 5 М П а ;
1 /Р р = 1 /1 2 5
1 / м м = (1 • 1 0 3) / 1 2 5
1 /м ,
где радиус кривизны поверхности колеса ркол = D/2 = 125 мм и радиус
кривизны поверхности рельса с плоской головкой рр = оо;
Ро = 0,418
= 0 ,4 1 8
Рпр
= 4 0 5 • 106 П а
/571 -103-2-105•106■103
125
= 405 МПа.
Условие прочности Ро = о к < [стк] выполняется. Полуширина контакт
ной полоски [см. формулу (11.12)]
Ь
1 ,5 2 2
571-10М25
2-10М0М 01
912-10“6 м = 912 мкм.
Г л а в а XII
У С Т О Й Ч И В О С Т Ь СЖАТЫХ СТЕРЖНЕЙ
§ 12.1. Устойчивость упругого равновесия.
Критическая сила
К числу задач курса сопротивления материалов помимо
рассмотренных в предыдущих главах расчетов на прочность
и жесткость относятся также расчеты на устойчивость, предва
рительное понятие о которых было дано в гл. I. Расчет на
устойчивость имеет первостепенное значение для тех элементов
конструкций, которые представляют собой сравнительно
длинные и тонкие стержни, тонкие пластинки и оболочки. Здесь
будут рассмотрены лишь простейшие случаи расчета на устой
чивость сжатых стержней.
Напомним основные понятия о видах равновесия, известные
из курса теоретической механики.
Равновесие называют усто йч и вы м , если при любом малом
отклонении от положения равновесия тело возвращается в ис
ходное положение по устранении причины, вызвавшей это от
клонение. Примером может служить шарик, который положен
на сферическую поверхность, как показано на рис. 12.1, а. Рав
новесие называют неустойчивы м , если при любом малом от
клонении от положения равновесия тело не возвращается в ис
ходное положение, а все дальше отклоняется от него.
В состоянии неустойчивого равновесия находится шарик, поме
314
Р и с . 1 2 .1
щенный в верхней точке сферической поверхности (рис. 12.1,6).
При безразличном равновесии тело, будучи отклонено, остается
в равновесии и в новом положении (рис. 12.1, в).
Для задач механики абсолютно твердого тела характерно,
что вид равновесия не зависит от значений действующих на те
ло сил, в частности в рассматриваемом примере не зависит от
веса шарика. В сопротивлении материалов, т. е. в механике де
формируемого тела, основным является установление зависи
мости вида равновесия от сил, действующих на элемент
конструкции.
Рассмотрим сравнительно длинный и тонкий прямоли
нейный стержень, нагруженный центрально приложенной сжи
мающей силой (рис. 12.2 а). Если приложить к стержню попе
речную нагрузку, т. е. слегка изогнуть его, то при малых
значениях сжимающей силы после снятия поперечной нагрузки
стержень вернется в прямолинейное состояние. Это значит, что
прямолинейная форма равновесия оси стержня устойчива. При
большем значении сжимающей силы слегка изогнутый попе
речной нагрузкой стержень после ее устранения медленнее, как
бы «неохотнее» возвращается в прямолинейное состояние. Но
все же прямолинейная форма равновесия еще устойчива. Нако
нец, при некотором значении сжимающей силы прямолинейная
форма равновесия оси стержня становится неустойчивой и воз
никает новая устойчивая форма равновесия —криволинейная.
Происходит выпучивание стержня (рис.
12.2,6). Существенно, что при достижении
сжимающей силой того значения {крити
ческого), при котором прямолинейная фор
ма равновесия оси стержня становится не
устойчивой, для перехода к криволинейной
форме нет надобности прикладывать к
стержню поперечную нагрузку и изгиб
стержня происходит без видимых внешних
причин.
Изгиб стержня, связанный с потерей ус
тойчивости прямолинейной формы его равно
весия, называют продольным изгибом.
315
Рис. 12.3
Н а основе изложенного можно дать следующее определе
ние:
то наибольшее значение центрально приложенной сжимающей
силы, до которого прямолинейная форма равновесия стержня
устойчива, называется критическим.
Итак, при сжимающей силе, меньшей критической, стержень
работает на сжатие; при силе, большей критической, стержень
работает на совместное действие сжатия и изгиба. Даже при
небольшом превышении сжимающей нагрузкой критического
значения прогибы стержня и возникающие в нем напряжения,
как правило, недопустимо велики.
Характер нарастания прогибов стержня при превышении си
лой критического значения иллюстрирует рис. 12.3. Если при
силе, незначительно большей критической, стержень не разру
шается в буквальном смысле слова, то конструкция все же вы
ходит из строя в результате возникновения больших перемеще
ний. П оэтому с точки зрения практических расчетов критическая
сила должна рассматриваться как разрушающая нагрузка.
Потеря устойчивости первоначальной формы упругого рав
новесия при достижении нагрузкой критического значения ха
рактерна не только для сжатых стержней, но и для других эле-
Рис. 12.4
316
Рис. 12.5
ментов конструкций. Например, при сжатии кольца или тонкой
оболочки радиально направленными силами (рис. 12.4, а) при
некотором их значении (критическом) круговая форма оси
кольца становится неустойчивой и оно приобретает форму, по
казанную на рис. 12.4,6. Характер деформации кольца суще
ственно изменяется: при нагрузке, меньшей критической, коль
цо работало на сжатие, а после потери устойчивости —на
сжатие и изгиб.
Консоль вытянутого прямоугольного сечения, работающая
на прямой изгиб в плоскости наибольшей жесткости (рис.
12.5, а), при критическом значении изгибающей силы закручи
вается (рис. 12.5,6) и вместо изгиба испытывает совместный из
гиб и кручение. Этот случай называют потерей устойчивости
плоской формы изгиба.
Таким образом, все задачи расчета на устойчивость харак
терны тем, что при достижении нагрузкой критического значе
ния происходит резкое качественное изменение характера де
формации элемента конструкции. При этом новый вид
упругого равновесия, соответствующий нагрузкам, большим
критических, связан, с недопустимо большими перемещения
ми —с выходом конструкции из строя. Следовательно, расчет
на устойчивость должен обеспечить работу элемента конструкции
при первоначальной форме его упругого равновесия, т. е. при на
грузках, меньших критических.
Применительно к расчету сжатых стержней из сказанного
следует, что должны быть обеспечены такие соотношения ме
жду размерами стержня, характеристиками его материала
и действующей на него нагрузкой, при которых гарантируется
его работа на сжатие без опасности продольного изгиба. Это
значит, что фактически действующая или допускаемая сжимаю
щая сила должна быть в некоторое число раз меньше критиче
ской. Это условие устойчивости прямолинейной формы равно
весия стержня может быть представлено так:
[ F ] = f Kp/[n y],
(12.1)
где [F] —допускаемое значение силы, сжимающей стержень;
FKP—критическое значение сжимающей силы для рассчитывае
мого стержня; [иу] —заданный (требуемый) коэффициент запа
са устойчивости,
Отсюда следует, что для расчета на устойчивость не
обходимо иметь зависимости для определения критической
силы.
317
§ 12.2. Ф ормула Эйлера
Рассмотрим вопрос о критической силе сжатого стержня,
оба конца которого закреплены шарнирно* (рис. 12.6,а). Пусть
стержень находится в несколько изогнутом состоянии
(рис. 12.6,6). Допустим, что потеря устойчивости происходит
при напряжениях, не превышающих предела пропорционально
сти. а пц материала стержня. При этом условии справедливо
дифференциальное уравнение упругой линии [см. формулу
(7.4)]
1/р « d2u/dz 2 = M/(EJ).
В рассматриваемом случае абсолютное значение изгибаю
щего момента в произвольном поперечном сечении стержня
определяется из выражения М —Fv и дифференциальное урав
нение изогнутой оси стержня имеет вид
d2v
Fv
Hz2 = ~ ~ЁТ
Знак минус поставлен потому, что независимо от выбора поло
жительного направления оси Оу знаки кривизны 1/р и орди
наты прогиба v будут противоположны.
В результате решения этого дифференциального уравнения
и использования граничных условий, определяемых способами
закрепления концов стержня, получается следующее выражение
для критической силы, называемое формулой Эйлера:
FKp = n2EJmiJ l 2.
(12.2)
Очевидно, что при потере устойчивости изгиб стержня проис
ходит в плоскости наименьшей жесткости, т. е. каждое из его
поперечных сечений поворачивается вокруг той из главных
осей, относительно которой момент инерции минимален, по
этому в формулу Эйлера входит величина Jmin.
Заметим, что для стальных стержней, рассчитываемых на
устойчивость по формуле Эйлера, применение высококаче
ственной легированной стали не имеет смысла, так как модуль
упругости для стали всех марок практически одинаков. Следо
вательно, при данных размерах стержня замена обычной стали
легированной не дает увеличения его грузоподъемности.
* Здесь и в дальнейшем применяются такие же обозначения шар
нирных опор, как и в предыдущих главах курса, но при этом подразу
мевается, что эти опоры являются пространственными, т. е. характер
закрепления конца стержня во всех направлениях одинаков. В частно
сти, шарнирно-неподвижная опора препятствует линейным перемеще
ниям как в плоскости, так и вне плоскости чертежа.
318
* Покажем ход преобразо
ваний. приводящих к получе
нию формулы Эйлера.
Предварительно несколько
. уточним саму постановку зада
чи о нахождении критической
силы*. По Эйлеру, признаком
неустойчивости формы равнове
сия
служит
существование
смежной (т. е. сколь угодно
близкой к исходной) отклонен
ной формы равновесия при не
изменной нагрузке. Возникно
вение такой возможности зави
сит от уровня нагрузки. Если
сжимающая сила достигает кри
тического значения, то происходит разветвление (бифур
кация) форм равновесия и при F > F устойчивой стано
вится отклоненная форма. Таким образом,
определению подлежит то минимальное значение сжимающей
силы, при котором наряду с прямолинейной формой равновесия
становится возможной слегка искривленная форма.
Введем обозначение
k ^ F / ( E J min),
(а)
тогда взамен исходного дифференциального уравнения полу
чим
v" + к.4 = 0.
(б)
Это так называемое однородное дифференциальное уравнение
второго порядка. Его решение имеет вид
v = A sin kz + В cos kz,
где А и В —постоянные интегрирования.
В справедливости приведенного решения можно легко
диться путем его подстановки в выражение (б).
Значения А и В определяются из граничных условий.
z = 0 v = 0. Подставим эти значения в (б), получаем 5 = 0.
довательно, уравнение упругой линии таково:
v = Asm kz,
убе
При
Сле
(в)
т. е. ось изогнутого стержня имеет форму синусоиды.
* См.: Пановко Я. Г,, Губанова
упругих систем. М., 1967.
И.
И. Устойчивость и колебания
319
Второе граничное условие вытекает из равенства нулю про
гиба нижнего конца стержня, т. е. при z = I v = 0. Подставляя
эти значения в (в), получаем
0 = A sin kl.
Решение А = 0 соответствует прямолинейной форме равно
весия сжатого стержня (» = 0 ) и поэтому не представляет
интереса.
Следовательно,
sin Ы = 0 .
(г)
Наименьший корень (обозначим его ккр), удовлетворяющий
(г): kspl — ж, позволяет определить значение критической силы
(корень /с = 0 соответствует F = 0, т. е. не имеет смысла):
ккр = п / 1 и к2р = ж1/1 г .
Учитывая соотношения (а), получаем:
я 2//2 = FKp/(EJmJ ; FKP= п2EJmjn/I2 *
Рассмотренный пример шарнирного закрепления обоих кон
цов стержня, когда его изогнутая ось при потере устойчивости
представляет собой одну полуволну синусоиды, принято назы
вать основным случаем продольного изгиба.
При других способах закрепления концов
стержня формулу для определения критиче
ской силы можно, так же как и для основ
ного случая, получить путем составления и ре
шения соответствующего дифференциального
уравнения. Для некоторых простейших случаев
можно прийти к формуле для критической
4-7С2Е1т1П
F« rr
F SI
Ы \
W 77,
Рис. 12.8
320
•ш
МО
F
F
F
г)
I
М-2,0 {i-0,S
Рис. 12.9
S]
F
н*
ТШ
М,о
силы путем сопоставления формулы изогнутой оси с той,
которая получается у стержня с шарнирно закрепленными
концами. Например, стержень с жестко защемленным нижним
и свободным верхним концом при потере устойчивости изо
гнется, как показано на рис. 12.7. Он будет находиться в таких
же условиях, как половина стержня на рис. 1 2 .6 , б, его изо
гнутая ось представляет собой четверть волны синусоиды.
Следовательно, критическую силу можно определить по фор
муле Эйлера для основного случая, подставив в нее удвоен
ную длину стержня вместо фактической:
^кр
= n2EJmia/ ( 2 0 2 .
Для стержня с жестко закрепленными концами форма изог
нутой оси показана на рис. 12.8. Здесь одна полуволна сину
соиды занимает половину длины стержня и в формулу ( 1 2 .2 )
надо подставить вместо фактической длины ее половину.
Итак, при любом способе закрепления концов стержня фор
мулу для критической силы можно представить в виде, анало
гичном (12 .2 ), но вместо фактической длины стержня надо вве
сти так называемую приведенную длину /прив:
FKp = n2EJmJP npm.
(12.3)
Приведенную длину стержня удобно выразить через факти
ческую длину и некоторый коэффициент р, зависящий от спосо
бов закрепления концов стержня:
^прив
1 ^ '
Коэффициент р называют коэффициентом приведения длины;
его значения для наиболее часто встречающихся случаев закре
пления концов стержня приведены на рис. 12.9: а —оба конца
стержня закреплены шарнирно (могут сближаться); 6 —нижний
конец жестко защемлен, верхний —свободен; в —оба конца
жестко защемлены (могут сближаться); г —нижний конец за
креплен жестко, верхний —шарнирно (могут сближаться);
д —нижний конец закреплен жестко, верхний имеет «плаваю
щую» заделку (не может поворачиваться, но может смещаться
перпендикулярно оси стержня).
Из рассмотренных примеров (см. рис. 12.7, 12.8) следует, что
коэффициент ц представляет собой величину, обратную числу
г| полуволн синусоиды упругой линии стержня, потерявшего
устойчивость:
р = 1/тр
321
Таким образом, в общем случае будем записывать формулу
Эйлера в виде
FKp = n 2£ J min/(p О2(12.4)
Если выводить формулу Эйлера, пользуясь точным выражением
кривизны (см. с. 201), то значение критической силы совпадает со зна
чением, определяемым формулой (12.2), но одновременно может быть
получена формула для определения прогибов.
Максимальный прогиб для стержня с шарнирно закрепленными
концами определяется по формуле
v ^ ^ ^ iy V F ^ /F -F ^ /F .
(12.5)
На основе этой формулы нетрудно получить подтверждение при
веденных в предыдущем параграфе данных о чрезвычайно быстром
нарастании прогибов при превышении сжимающей силой критическо
го значения. Например, при F = 1,01/'кр из (12.5) получим гтах = 0,0895/,
т. е. стрела прогиба составляет ~ 9 % от длины стержня.
§ 12.3. Критическое напряжение.
Пределы применимости формулы Эйлера
Нормальное напряжение в поперечном сечении сжатого стерж
ня, соответствующее критическому значению сжимающей силы,
также называют критическим.
Определим критические напряжения еткр, исходя из фор
мулы Эйлера. По определению,
G kp =
F kp/ A .
(
12. 6)
Подставляя вместо F Kp ее значение из формулы (12.4), получаем
csrp = n 2E J miJ [ i i i l ) 2 A l
Геометрическую характеристику сечения
ix = f f j A ,
имеющую размерность L, называют радиусом инерции сечения
относительно данной оси (например, оси х). Следовательно, от
ношение JmiajA в формуле для сткр представляет собой квадрат
минимального главного центрального радиуса инерции попе
речного сечения стержня г21п. Таким образом,
СТкр=Л 2Й 2;п/(р92.
Разделив числитель и знаменатель на (2lin, получим
сткр = п2£/(pZ/imin)2.
322
Отношение приведенной длины стержня к минимальному
радиусу инерции его поперечного сечения по предложению
проф. Ф. С. Ясинского называют гибкостью стержня (или стой
ки). Это весьма удобная безразмерная геометрическая характе
ристика сжатого стержня, показывающая его сопротивляе
мость потере устойчивости; она одновременно отражает
и длину стержня и жесткость его поперечного сечения:
Используя понятие гибкости X стержня, получаем следую
щую окончательную формулу для критического напряжения:
сткр = п2Е/Х2.
(12.7)
При выводе формулы Эйлера была использована зависи
мость между изгибающим моментом и кривизной оси стержня,
полученная на основе закона Гука (см. § 7.5). Отсюда следует,
что, как уже указывалось в предыдущем параграфе,
формула Эйлера справедлива лишь в пределах применимости
закона Гука, т. е. при условии, что критическое напряжение не
превышает предела пропорциональности материала стержня:
° к р "Ч <Т,щ.
Подставляя значение сткр по (12.7), получаем
о кр = к2Е/Х2 < стгщ,
отсюда
Х ^п\/Е /(У па.
Величину, стоящую в правой части этого неравенства, обо
значим Хпред и назовем предельной гибкостью (иногда гово
рят —граничная гибкость):
^ пр ед = Я 1 / £ / СГпц-
( 1 2 .8 )
В отличие от гибкости стержня, представляющей собой его
геометрическую характеристику, предельная гибкость зависит
только от физико-механических свойств материала стержня и не
зависит от его размеров. Предельная гибкость — величина по
стоянная для данного материала.
Пользуясь понятием предельной гибкости, удобно предста
вить условие применимости формулы Эйлера в виде
X > А.„ред,
(12.9)
т. е. формула Эйлера применима лишь в тех случаях, когда гиб
кость рассчитываемого стержня больше иля равна предельной
гибкости для материала, из которого он изготовлен.
323
В качестве примера вычислим значение Япред для угле
родистой стали 45, имеющей модуль продольной упругости
£ « 2 ,0 -1 0 5 МПа
и
предел
пропорциональности
стпц« 270 МПа:
^пред = ^ 1 ^ Ё /^ = 3,141/2,0 -107270 » 85.
В случае неприменимости формулы Эйлера критические на
пряжения определяются по эмпирическим формулам, соста
вленным Ф. С. Ясинским на основе опытов, проведенных рядом
исследователей. Для некоторых конструкционных материалов
формула Ф. С. Ясинского (ее иногда называют формулой Тетмайера—Ясинского) имеет вид
сткр = а - ЬЯ,
(12.10)
т. е. зависимость критического напряжения от гибкости линей
на. В формуле (12.10) а и b —определяемые опытным путем
коэффициенты, постоянные дня данного материала. Коэффи
циенты а и b имеют размерность напряжения.
При некотором значении гибкости (обозначим ее Я0) <ткр,
вычисленное по формуле (12.10), становится равным предельно
му напряжению при сжатии, т. е. пределу текучести (а, или
ст0,2с) для пластичных материалов или пределу прочности (апч с)
для хрупких. При гибкости, меньшей Я0, принимают, что кри
тическое напряжение совпадает с предельным, в частности для
пластичных материалов сткр = стт. Таким образом, в зависимо
сти от гибкости сжатые стержни условно делят на три
категории.
1. Стержни большой гибкости (Я > Япрсд), для которых рас
чет на устойчивость ведется по формуле Эйлера и зависимость
сткр от Я —гиперболическая: сткр = к2£/Я2 (так называемая ги
пербола Эйлера).
2. Стержни средней гибкости (Я0 ^ Я < Япред), рассчиты
ваемые на устойчивость по эмпирической формуле Ф. С. Ясин
ского. Для них зависимость а кр от гибкости линейна: а кр = а —
-
ЬЯ.
3. Стержни малой гибкости (Я <Я0), рассчитываемые не на
устойчивость, а на прочность. Для них критическое напряжение
считается постоянным: окр = с т, или сткр = ст02с, или а кр = <тпч с.
Для стали СтЗ характер зависимости критического напряже
ния от гибкости представлен на рис. 12.10. На этом графике
штриховой линией показано продолжение гиперболы Эйлера
в область ее неприменимости ( Я < Я п р е д ) ; она проходит выше
линии критических напряжений^ установленных опытным пу
тем. Это значит, что при неправильном применении формула
324
Эйлера дает п р е у в е л и ч е н н о е значение критического напряжения
(критической силы), следовательно, и допускаемое значение
сжимающей силы получается преувеличенным, что может по
влечь за собой аварию конструкции.
Приведем для некоторых материалов значения коэффициен
тов а и Ь, а также значения гибкости, при которых применима
формула (12.10).
Материал
С т ал ь :
Ст2 . . • ......................
С т З .................................
20, С т 4 ......................
4 5 ......................................
Д ю ралю мин Д16Т . . .
Сосна, ель . . . . . .
а,
.
.
.
.
МПа
406
29,3
Ъ, МПа
Xq
^пред
0,70
1,14
1,15
1,67
1,83
0,194
60
60
60
52
30
—
105
100
96
85
53
70
Для стержней из чугунного литья (при X < Хпрея т 80) поль
зуются параболической зависимостью
сгкр = 776 - 12Х + 0,053Х2 МПа.
(12.11)
Формула применима при сгкр<стпч с. Например, для чугун
ного литья СЧ15-32 стпч с« 650 МПа и ),0 = 10.
В зависимости от постановки задачи (цели расчета) разли
чают следующие виды расчетов на устойчивость.
Проверочный расчет, при котором определяется фактический
325
коэффициент запаса устойчивости пу и сравнивается с тре
буемым или нормативным его значением [иу]:
ny= F Kp/F>[_ny],
(
12. 12)
где F —фактическое значение сжимающей нагрузки.
Определение допускаемой нагрузки:
т = ^ к р / [ « у] .
(1 2 .1 3 )
Проектный расчет —определение требуемых размеров попе
речного сечения стержня.
При использовании формулы Эйлера в результате проект
ного расчета определяется требуемое значение минимального
момента инерции поперечного сечения стержня:
J ^F ln ^W ltfE ).
(12.14).
После определения J min, А и imin следует проверить гибкость
стержня и сравнить ее с предельной, т. е. установить, правиль
но ли была применена формула Эйлера. Если окажется, что
при принятых размерах X < А.пред, необходимо произвести
пересчет. При выполнении проектного расчета по формуле
Ф. С. Ясинского приходится вести его путем ряда попыток, так
как сткр зависит от гибкости, а она до определения размеров се
чения неизвестна.
Значение требуемого коэффициента запаса устойчивости за
висит в основном от назначения рассчитываемого стержня
и его материала. Так, для стальных стержней принимают:
в строительных конструкциях [иу] = 1,7 ч- 2,0, для элементов
машиностроительных конструкций, например для ходовых вин
тов металлорежущих станков, [пу] = 3,5 ч- 5,0. Для чугунных
стержней в среднем [пу] = 5,0; для деревянных в среднем [иу] =
= 3,0.
Из формулы Эйлера, а также из формулы Ф. С. Ясинского
следует, что критическая сила возрастает с увеличением мини
мального момента инерции поперечного сечения стержня. Так
как устойчивость стержня определяется значением минималь
ного момента инерции его поперечного сечения, то, очевидно,
нет смысла применять такие формы сечений, у которых мини
мальный и максимальный моменты инерции значительно отли
чаются друг от друга (например, прямоугольное, двутавровое).
Рациональны сечения, у которых любая центральная ось
является главной, следовательно, все главные моменты равны
между собой. Стойка, имеющая такое сечение, обладает равноусгойчивостью во всех направлениях. Из течений указанного
типа следует выбирать такие, которые обладают наибольшим
326
моментом инерции при наименьшей пло
щади (затрате материала). Указанным тре
бованиям удовлетворяет кольцевое сечение.
Часто применяют также сечения, составлен
ные из прокатных профилей, расположен
ных таким образом, что все главные мо
менты инерции полученного составного се
чения одинаковы (см. ниже пример 12.5).
Для обеспечения совместной работы состав
ного стержня отдельные его ветви должны
быть связаны надежной соединительной ре
шеткой.
П р и м е р 12.1. Проверить на устойчивость
сжатую стойку трубчатого' сечения (рис. 12,11)
из хромомолибденовой стали (стпц = 540 МПа,
Е = 2,15 • 105 МПа), если требуемый коэффици
ент запаса устойчивости [пу] = 3,5.
Р е ш е н и е . Определяем предельную гибкость для материала
стойки:
=к \/Е /а т = 3,141/2,15 • 10s ■106/(540-106) = 63.
Х,п
Для определения гибкости стойки вычисляем момент инерции ее
поперечного сечения (в данном случае любая центральная ось главная
и все центральные моменты инерции равны между собой)
Jtd4
.
3,14-764 Г
64
[
мм —
= 81,4-10“
затем площадь сечения
И
3,14 -762 Г
ltd 2
,
= - — (1 —с2) =
4
4
I
и радиус его инерции
А
64
Y 1 - 1319 мм 2
76/
J
‘min = i = l^m inM = (/81,4.1071319 = 24,8 мм.
Коэффициент приведения длины р « 0,7 (см. рис 12.9).
Гибкость стойки
X= р1Д*п= 0,7 - 2,5 • 103/24,8 = 70,7.
Так как гибкость стойки больше предельной (X > К,релХ то крити
ческую силу определяем по формуле Эйлера
K2E J ml„
^кр —‘
т 1
3,142 • 2,15-105- 106 • 81,4-10“
- = 564-103 Н = 564 кН.
(0,7 - 2,5)2
Определяем коэффициент запаса устойчивости и
с заданным:
Пу = F y p /F
сравниваем
= 564/150 = 3,76 > [пу].
327
П р и м е р 12.2. Д л я з а д а н н о й с т о й к и д в у
т а в р о в о г о п о п е р е ч н о г о с еч ен и я (р и с . 12.12) о п
р е д е л и т ь д о п у с к а е м о е зн а ч е н и е с ж и м а ю щ е й с и
л ы . М ат ер и а л стой ки — с та л ь С тЗ, коэф ф ициент
з а п а с а у с т о й ч и в о с т и [ пу] = 2 ,0 . В ы я с н и т ь , как
и зм ен и тся д о п у ск аем ая н агрузка, если длину
стойки у м ен ьш и ть вдвое.
Р е ш е н и е .
О п р ед ел яем ги б к о сть стойки
X = u IJi ■ .
К о э ф ф и ц и е н т п р и в е д е н и я д л и н ы р = 0,5 (см .
р и с . 12.9); imin = iy = 2,63 с м (п о Г О С Т 8 2 3 9 - 7 2 ) ;
X 3 ^ 0 ,5 • 7,2 • 103/26,3
>>7»7
Р и с . 12.12
3,142 - 2,0- 10s - 10б - 2 6 0 - 10- 8
n 2E J „
[F]=
[« у ]
137.
Д л я с т а л и С т З Хпред = 1 0 0 (с м . с. 325), с л е д о
в а т е л ь н о , X > Хпред и ф о р м у л а Э й л е р а п р и м е
ним а.
О п р ед ел яем доп у скаем о е зн ачени е сж и м аю
щ ей си л ы :
■198 • 103 Н =
2 (0,5- 7,2)2
[ и у] ( Ц / ) 2
= 198 к Н ,
г д е п р и н я т о £ = 2 , 0 - 1 0 5 М П а ; /m in = J y = 2 6 0 с м 4.
П ри ум еньш ении дли н ы стойки вдвое критическая си ла в о зр астет
не в ч еты р е р а за, к ак м о ж н о б ы л о б ы о ж и д а ть исходя и з ф о р м у л ы Э й
л е р а , а м ен ь ш е.
Г и б к о с т ь у к о р о ч е н н о й с т о й к и X, = 6 8 ,5 , т . е. м е н ь ш е п р е д е л ь н о й ,
и ф о р м у л а Э й л ер а н еп ри м ен и м а. Д о п у скаем у ю н агрузку о п р едел яем ,
п о л ь з у я с ь э м п и р и ч е с к о й ф о р м у л о й (12.10) и д а н н ы м и , п р и в е д е н н ы м и
н а с. 3 25:
сткрА
lF'] = Т ы Г Г
( а — Ь Х г) А
( 3 1 0 - 1,14-68,5) 106 >3 7 ,5 - 10~ 4
Ы
2
= 4 5 3 - 103 Н = 453 к Н .
Т а к и м о б р а з о м , к р и т и ч е с к а я с и л а в о з р о с л а л и ш ь в 2,29 р а з а . Э т о т
прим ер подтверж дает, что использовани е ф орм улы Э й лера в области
ее н е п р и м е н и м о с т и п р и в о д и т к з а в ы ш е н н о м у зн а ч е н и ю к р и т и ч е с к о й ,
а з н а ч и т , и д о п у с к а е м о й н а гр у зк и .
П р и м е р 12.3. О п р е д е л и т ь и з р а с ч е т а н а у с т о й ч и в о с т ь т р е
б у е м ы й д и а м е т р в и н т а д о м к р а т а (рис. 12.13,а) г р у з о п о д ъ е м н о с т ь ю
F = 5 0 кН .
М а к с и м а л ь н а я в ы с о т а п о д ъ е м а г р у з а I = 900 м м ; т р е б у е м ы й к о э ф
ф и ц и е н т з а п а с а у с т о й ч и в о с т и [н у] = 4,0. М а т е р и а л в и н т а — с т а л ь С т4.
Р е ш е н и е .
Т р еб у ем ы й м о м ен т ин ерци и п оп еречн ого
сеч е
н и я винта определяем исходя из ф орм улы Э йлера п о соотнош ен ию
(12.14).
Р а с с м а т р и в а е м в и н т к а к с т о й к у с н и ж н и м ж ес тк о з а щ е м л е н н ы м
и в е р х н и м с в о б о д н ы м к о н ц о м (см . р а с ч е т н у ю сх ем у н а р и с . 12.13,6),
т. е. р = 2; £ = 2 ,0 - 1 0 5 М П а :
328
,
f W M 2
к 2Е
5 -10». 4(2-0,9)2
3,142 • 2,0-105 ■I06
32,8 10
= 32,8-104 мм4.
Определяем диаметр винта dl (расчет винтов принято вести по
внутреннему диаметру резьбы):
J = Ы\! 64,
откуда
ck = У (АЗ1%= У64 ■32,8 • 104/3,14 = 51 мм.
Принимаем трапецеидальную резьбу с наружным диаметром d =
= 60 мм, имеющую dl =51 мм и шаг S —8 мм.
Расчет был выполнен на основе формулы Эйлера. Убедимся в до
пустимости ее применения (в начале расчета эта проверка невозможна,
так как размеры сечения, а следовательно, и гибкость стержня не
известны). Радиус инерции сечения винта
— =
= 12,75 мм.
4
4
Гибкость винта X = p//i = 2 •900/12,75 = 141 > 7.пред ~ 96, следова
тельно, формула Эйлера была применима.
329
Пример 12.4. Стержень прямоугольного сечения закреплен та
ким образом, что в плоскости наибольшей жесткости концы его могут
свободно поворачиваться, а в плоскости наименьшей жесткости пово
рот концевых сечений исключен (рис. 12.14).
Определить допускаемое значение центрально приложенной сжи
мающей силы, если ГпЛ=4,0. Материал стержня —сталь 45, Е =
= 2,0 • 105 МПа.
Р е ш е н и е . В рассматриваемом случае закрепление концов
стержня в главных плоскостях инерции различно, поэтому расчет сле
дует вести исходя из опасности потери устойчивости вокруг той из
главных осей, относительно которой гибкость стержня м а к с и
мальна.
Определяем радиусы инерции сечения:
V
ЫР
12bh~ ]/l2
w
=20’8 мм:
b
38
= 11 мм.
Ubh
3j46
|/l2
■У
Определяем значение гибкости относительно главных осей Хх =
= |VA*: Pi = 1,0 (концы стержня могут поворачиваться):
Хх = 1 ■2500/20,8 = 120;
Xt = р2l/iy; р2 = 0,5 (концы стержня не могут поворачиваться):
2., = 0,5-2500/11 = 114.
Таким образом, опаснее потеря устойчивости в плоскости наи
большей жесткости, т. е. (FKp)x < (Ткр)у.
Определяем допускаемое значение сжимающей силы. Расчет ведем
по формуле Эйлера, так как Хх > Харед « 85:
(Ркр)х
и =
К]
n2EJr
3,142-2,0-105-106
ККМ 2
0,038-0,0723
12
4(1 •2,5)2
= 93 • 103 Н =93 кН.
§ 12.4. Растет сжатых стержней на устойчивость
по коэффициентам продольного изгиба
Расчет сжатых стержней на устойчивость можно по форме
привести к расчету на простое сжатие, принимая в качестве до
пускаемого некоторую часть от критического напряжения:
о = F/A < [сту],
где [ o j = ст. /[иу] —допускаемое напряжение на сжатие с уче330
том опасности продольного изгиба, или, короче, доп уск аем ое
напряжение при р асчете на устойчивость.
Обычно [<3у] выражают через основное допускаемое напря
жение на сжатие для данного материала:
[а у]=ср[стс].
Здесь ф < 1,0 —коэффициент понижения основного доп уск ае
м ого напряжения на сж ати е или коэф ф ициент продольного изги
ба; [<тс] —основное допускаемое напряжение на сжатие, т. е.
установлено без учета продольного изгиба:
1>с]
^п ред/ И
'
Связь между коэффициентом ф, критическим напряжением
а ,р, предельным напряжением стпргд и коэффициентами запаса
прочности [и] и устойчивости [«у] легко установить следую
щим образом:
[ ° у ] = Ф Ь с ] = Ф ^ п р е д / [и ] = а кр/ [ п у] ,
откуда
Ф:
м
КУ
(12.15)
Значение коэффициента ф зависит от материала стержня
и от его гибкости. Для строительных конструкций значения
этих коэффициентов включены в строительные нормы и прави
ла проектирования (СНиП). Некоторые значения ф по СНиПу
приведены в табл. 12.1.
При выполнении расчетов на устойчивость по коэффициен
там ф расчетная зависимость имеет следующий вид:
ст = F/Л ф [стJ .
(12.16)
Этот метод расчета универсален в том смысле, что он не
связан с пределами применимости формулы Эйлера и может
быть использован при всех значениях гибкости, для которых
имеются табличные значения коэффициента ф.
Коэффициент запаса устойчивости в этом расчете в явном
виде не фигурирует, он включен в величину ф.
Расчет сжатого стержня по формуле (12.16) внешне совер
шенно подобен расчету на простое сжатие, но фактически это
расчет на устойчивость, гарантирующий работу стержня
с коэффициентом запаса устойчивости, предусмотренным при
составлении таблиц ф.
Для элементов машиностроительных конструкций в боль
шинстве случаев приняты более высокие коэффициенты запаса
331
Т а б л и ц а 12.1. Значения коэффициента продольного изгиба
Ф
Гибкость
стали СтЗ,
Ст4
стали Ст5
0
20
40
60
70
80
90
100
110
120
140
160
180
200
220
1,00
0,97
0,92
0,86
0,81
0,75
0,69
0,60
0,52
0,45
0,36
0,29
0,23
0,19
0,16
1,00
0,96
0,90
0,80
0,74
0,67
0,59
0,50
0,43
0,37
0,28
0,23
0,19
0,15
0,13
ДЛЯ
чугуна
СЧ12-28,
СЧ15-32,
СЧ18-36,
СЧ21-40
дерева
(сосна, ель)
1,00
0,91
0,69
0,44
0,34
0,26
0,20
0,16
—
—
—
—
—
—
1,00
0,97
0,87
0,71
0,61
0,49
0,38
0,31
0,25
0,22
0,16
0,12
0,10
0,08
-
и, кроме того, нет строгой регламентации значений допу
скаемых напряжений, поэтому не рекомендуется выполнять их
расчет по коэффициентам ф. Исключением являются элементы
стальных конструкций подъемно-транспортных сооружений
(ферм мостовых кранов и т. п.), для которых расчет по коэф
фициентам ф предписан соответствующими нормами.
Пр и м е р 12.5. Определить допускаемую
нагрузку для стойки из стали СтЗ (рис. 12.15),
[стс] = 160 МПа. Принять, что швеллеры, из ко
торых состоит стойка, надежно связаны между
собой и сечение работает как монолитное. Рас
стояние с между швеллерами выбрать из ус
ловия равноустойчивости стойки во всех направ
лениях.
С каким коэффициентом запаса устойчивос
ти работает стойка при нагрузке, равной до
пускаемой?
Р е ш е н и е . Равноустойчивость стойки во
всех направлениях будет обеспечена при равен
стве моментов инерции относительно осей
х и у (см. с. 326). Момент инерции сечения
относительно оси х не зависит от расстояния
с и определяется непосредственно на основе таб
личных данных:
^ = 2 ^ = 2-304 = 608 см4,
332
где j \ —304 см4 —момент инерции одного швеллера по ГОСТ
8240 - 72. Момент инерции относительно оси у
Jy = 2(^1+cjA1X
где J lyi = 31,2 см4 —момент инерции швеллера относительно собствен
ной главной центральной оси yt ; A t = 13,3 см2 —площадь сечения
одного швеллера.
Условие равноустойчивости
подставляя числовые значения, получаем
608 = 2 (31,2+ c f - 13,3),
откуда С! =4,5Г см;
с = 2 (с, - z0) = 2 (45,1 - 15,4) = 59,4 мм.
Определяем допускаемую нагрузку:
[F] = Ф[стс] А.
Гибкость стойки
X = pl/imin = 0,5 •700/4,78 = 73,2,
imin = ix = i = 4,78 см
(по
ГОСТ
8240—72);
<р = 0,81 —
0,81 —0,75
---------—------ 3,2 « 0,79 (интерполируя данные табл. 12.1).
где
А = 2А1 =2-13,3 = 26,6 см2;
[Г] = 0,79 • 160-10® ■26 •610“4 = 337 ■103 Н = 337 кН.
Определяем коэффициент запаса устойчивости, который соответ
ствует таблице <р для данных материала и гибкости:
[ " y ] = f KP / M -
Так как гибкость стойки меньше предельной (для стали СтЗ
7.иред = 100), то Гкр определяем по эмпирическому соотношению
FKp = А (а —ЬХ) = 26,6-10“ 4 (310 —1,14- 73,2)-106 = 603-103 Н=603 кН;
[ О = ^ кр/ И = 603/337 = 1,79.
Глава
ХШ
ЗА Д А Ч И Д И Н А М И К И В С О П Р О Т И В Л Е Н И И
М А ТЕРИ АЛ О В
§ 13.1. Расчет элементов конструкций
при заданных ускорениях
В предыдущих главах учебника были рассмотрены расчеты
элементов конструкций при действии статической нагрузки,
а также при возникновении в них переменных во времени на
пряжений. В этой, последней, главе курса даются краткие сведе
ния о некоторых динамических задачах сопротивления мате
риалов. К задачам динамики в сопротивлении материалов
относятся:
1) расчеты движущихся деталей при заданных ускорениях;
2) расчеты на действие ударной нагрузки;
3) расчеты йа прочность и жесткость при колебаниях.
Здесь будут рассмотрены лишь решения некоторых простей
ших задач, относящихся к первым двум категориям задач
динамики.
Определение напряжений и перемещений при заданных
ускорениях основано на приведении задач динамики к задачам
статики с помощью известного из курса теоретической механи
ки принципа Даламбера (метода кинетостатики). Напомним,
что этот принцип состоит в следующем: если в любой момент
времени к каждой материальной точке данной системы прило
жить силу инерции этой точки, то эти силы инерции будут урав
новешиваться заданными силами, действующими на систему,
и реакциями связей, т. е. система может рассматриваться как
находящаяся в состоянии покоя (или равномерного прямоли
нейного движения).
Сила инерции равна произведению масал материальной точки
на ее ускорение и направлена в сторону, противоположную
ускорению.
Применение этого метода к задачам сопротивления мате
риалов показано на ряде примеров.
Пример 13.1. Определить при [а] =70 МПа требуемый диа
метр троса, на котором подвешен груз массой тг = 3000 кг (рис.
13.1, а), поднимаемый с постоянным ускорением а = 4 м/с2. Массу тро
са не учитывать.
Реш ение. Применяя принцип Даламбера, прикладываем к под
нимаемому грузу силу инерции
РИ= ща,
направленную противоположно ускорению (рис. 13.1,6).
334
Применяя метод сечений (рис. 13.1, в), определяем продольною си
лу, возникающую в поперечном сечении троса:
Z Z = J V - G - F „ = 0,
где G = тгд —сила тяжести груза (д = 9,81 м/с2 —ускорение свободно
го падения);
N = G + F„ = тТд + mTa = mr(g + а).
Так как массу троса не учитываем, то продольная сила во всех его по
перечных сечениях одинакова.
При mr в кг, д и а в м/с2 получаем силу тяжести G в Н.
Условие прочности
N
т т(д + а )
=
4“ < [ '
откуда требуемый диаметр троса
d > |/[4 т г(з + а)] / (я [<т]).
Подставляя числовые данные, получаем
/ 4- 3000(9,81 +4)
'
3,14-70-106
з
м = 27,4 мм;
принимаем d = 28 мм.
П р и м е р 13.2. Определить напряжения в поперечном сечении
тонкостенного кольца, равномерно вращающегося в своей плоскости
с угловой скоростью со (рис. 13.2, а). Найти наибольшее допускаемое
значение окружной скорости точек кольца, если оно изготовлено из чу
гуна с удельным весом у = 7,5 • 104 Н/м3 и [стр] = 25 МПа.
Р и с. 13.1
335
Р е ш е н и е . При равномерном вращении касательное ускорение
любой точки кольца равно нулю, а нормальное определяется по
формуле
ап = v2/R = a 2R.
где v —окружная скорость; R —расстояние рассматриваемой точки от
оси вращения.
В рассматриваемом случае, учитывая малую (по сравнению с его
диаметром) толщину кольца, можно считать расстояния всех точек
кольца до оси вращения одинаковыми и равными D/2, где D —средний
диаметр кольца.
Приложим к каждому элементу кольца центробежную силу инер
ции, что позволит применить уравнения равновесия. Силы инерции
равномерно распределены по окружности кольца и направлены по ра
диусам от центра. Интенсивность центробежных сил инерции, т. е. их
значение, приходящееся на единицу длины окружности кольца;
4и = щап‘,
здесь т1 = уА/д —масса единицы длины кольца (где А —площадь его
поперечного сечения, д —ускорение свободного падения).
Подставляя в выражение для дИ значения а„ и ш,, получаем
—
Чя _
г2
д D/2
у А ы 2Р
2у
Для определения внутренних сил, возникающих в поперечных се
чениях кольца, рассечем его по горизонтальному диаметру и рассмо
трим условие равновесия оставленной части (рис. 13.2,6).
Учитывая малую толщину стенок кольца, можно принять, что
нормальные напряжения распределены по его поперечному сечению
равномерно, т. е. кольцо работает на растяжение (наличие изгибаю
щих моментов связано с неравномерным распределением напряжений,
следовательно, согласно принятому допущению, они отсутствуют).
Продольные силы N, возникающие в поперечных сечениях кольца,
определим, проецируя все силы; действующие на полукольцо, на ось z
(рис. 13.2,6). Сила инерции, приходящаяся на элемент кольца, соответ
ствующий центральному углу diр, определяется из выражения
D .
уЛш2Р2
yAv2 ,
dF„ = q„ — dip =
-----dip = ------ dip.
2
4g
g
Ее проекцию на ось z найдем, умножая dFu на cos<p. Так как
каждая из этих элементарных сил инерции различно наклонена к оси z,
то уравнение равновесия приходится составлять в интегральной фор
ме; оно имеет вид
«/2
EZ = -2 N + 2
J
О
336
^ - c o s <рd(p = О,
или
jt/2
уЛи2
0
yAv2
sin <p
N=
в
о
Заметим, что интегрирование выполнено в пределах одной четверти кольца и результат удвоен. Нормальное напряжение в поперечном
сечении кольца
yAv2
о = N/A =
дА ’
или окончательно
а = уv2/g.
Характерно, что напряжения во вращающемся кольце не зависят
от площади его сечения и пропорциональны квадрату окружной
скорости.
Условие прочности равномерно вращающегося кольца
ст = уv2/g < [стр].
Отсюда найдем наибольшую допускаемую окружную скорость
М = 1/[<ур] 0/У■
Подставив числовые данные, получим
м =
^25Л 0^8Г
т/По*
= 57,2 м/с.
Практически для чугунных шкивов ременных передач допускают
более низкую окружную скорость, чем полученная в рассмотренном
примере, а именно не свыше 30...35 м/с. Это связано с двумя обстоя
тельствами. Во-первых, последствия разрыва обода шкива настолько
опасны, что приходится принимать значительно более высокие коэф
фициенты запаса прочности, чем обычно (т. е. более низкие допу
скаемые напряжения, чем были приняты здесь). Во-вторых, из-за нали
чия спиц обод испытывает не только растяжение, но и изгиб
и фактические напряжения в нем выше определяемых по формуле, по
лученной для тонкостенного кольца. Следовательно, пренебрегая при
расчете изгибом обода, надо опять-таки снизить допускаемые напря
жения.
§ 13.2. Приближенны й м етод расчета на удар
Работа машин во многих случаях сопряжена с ударными
нагрузками, которые либо обусловлены назначением этих ма
шин (например, ковочное оборудование), либо являются неже
лательным следствием различных конструктивных факторов
(например, зазоров в местах сопряжения деталей).
Расчет деталей машин на прочность при ударной нагрузке
связан, с одной стороны, с определением возникающих при
337
ударе напряжений, с другой —с установлением свойств мате
риалов при ударном нагружении. Решение первой из этих задач
относится к области сопротивления материалов, второй —в ос
новном к области материаловедения.
Определение напряжений и деформаций при ударе —одна
из наиболее сложных задач сопротивления материалов
и смежных наук —теории упругости и теории пластичности, ко
торая еще далека от своего окончательного решения. Здесь бу
дет рассмотрен лишь наиболее простой и весьма прибли
женный метод расчета на удар, базирующийся на следующих
основных допущениях.
1. Материал упругой системы (рассчитываемого элемента
конструкции) при деформациях, вызванных ударной нагрузкой,
следует закону Гука и система является линейно-деформируе
мой, при этом модуль упругости имеет то же значение, что
и при статическом нагружении*.
2. Работа силы тяжести падающего (ударяющего) груза
полностью переходит в потенциальную энергию деформации
элемента конструкции, испытывающего действие удара (таким
образом, не учитывается затрата энергии на местные деформа
ции в зоне контакта соударяющихся тел).
3. Масса упругой системы (элемента конструкции), воспри
нимающей действие ударной нагрузки, мала по сравнению
с массой ударяющего груза, т. е. система рассматривается как
невесомая.
4. Удар считается неупругим, т. е. после соприкосновения
ударяющего груза с упругой системой он не отскакивает и при
ее деформации движется с ней совместно.
Рассмотрим удар груза силой тяжести Q, падающего с вы
соты h на некоторую упругую систему, например цилиндриче
скую винтовую пружину (рис. 13.3).
Работа силы тяжести определяется из
выражения
W = Q (h + \ a),
(а)
где X — перемещение той точки (сечения)
упругой системы, по которой ударяет падаю
щий груз (индекс «д» указывает, что пере
мещение вызвано динамической нагрузкой).
Составим выражение для потенциальной
* Экспериментальные данные подтверждают, что модуль упруго
сти для данного материала практически не зависит от скорости
деформации.
338
энергии деформации упругой системы. Учитывая первое из
принятых допущений, воспользуемся теоремой Клапейрона,
тогда потенциальную энергию деформации можно определить
как половину произведения некоторой динамически действую
щей силы F на соответствующее перемещение:
Va = FaXJ2.
(б)
Для линейно-деформируемой системы
K = F JC ,
(в)
где С —коэффициент жесткости упругой системы, численно
равный силе, вызывающей перемещение в 1 см (1 мм и т. д.).
Из (в) имеем
А = ск
Подставляя значение Fa в выражение (б), получаем
уд= 0.2 А
(г)
На основании второго из принятых допущений приравни
ваем работу силы тяжести падающего груза потенциальной
энергии деформации упругой системы:
W = V a.
Приравнивая правые части выражений (а) и (г), получаем
Q(h + XJ = CXfl/2,
откуда
(2Q/C)h + (2Q/C)Xa = X l
Но Q/C = Х„, где Х„ - перемещение, вызванное силой, равной
весу Q падающего груза, при ее статическом действии. Таким
образом, имеем
2X„h + 2Х„ХЛ= Ц или XI - 2ХСТХД- 2X„h = 0.
Определим из этого квадратного уравнения значение Хд:
Xд =
+ 1 / + 2XCTh.
(13.1)
Второй кореш, квадратного уравнения, соответствующий
знаку минус перед радикалом, дает отрицательное значение Ха
и поэтому не нужен.
Выражение (13.1) можно представить в виде
Xa = XCT{ l + y i + 2h/XCT).
(13.2)
339
Величину, стоящую в скобках, обычно называют динамиче
ским коэффициентом /с , или коэффициентом удара; он равен
ka = l
+ ] / l + 2йДст.
(13.3)
Таким образом, перемещение, вызванное действием ударной
нагрузки, равно перемещению от статически приложенной силы,
равной весу падающего груза, умноженному на динамический
коэффициент:
Хд = кДК„.
(13.4)
Линейная связь между силами и перемещениями позволяет
сделать вывод, что напряжения в упругой системе от действия
ударной нагрузки во столько же раз больше возникающих при
статическом приложении такой же по значению нагрузки, во
сколько раз динамические перемещения больше статических,
т. е.
Од = /сда ст.
(13.5)
Следовательно, определение перемещений и напряжений
при ударе сводится к определению перемещений и напряжений,
вызванных статически приложенной силой, равной весу падаю
щего груза, и вычислению динамического коэффициента.
Полученные формулы верны как в случае растягивающего
и сжимающего, т, е. продольного, удара по стержню или пру
жине, так и в случае изгибающего, т. е. поперечного, удара по
балке. Различие состоит лишь в зависимостях, используемых
для вычисления статических напряжений и перемещений. Это
указание подробнее разъясняется в приведенных ниже приме
рах.
В частном случае мгновенного безударного приложения на
грузки, которое может рассматриваться как действие груза, па
дающего с высоты h = 0, из формулы (13.3) получим
/сд = 2.
Следовательно, перемещения и напряжения, вызванные дей
ствием мгновенно приложенной силы, вдвое больше, чем при
статическом действии такой же по значению силы.
В случае если высота падения груза велика по сравнению
с X. , можно пользоваться упрощенной формулой для
вычисления динамического коэффициента:
кя = j/2/гДдр.
(13.6)
Эта формула получается из выражения (13.3) в результате
пренебрежения единицей как по сравнению с отношением
2йДот, так и по сравнению с ]/2h/X„.
340
В заключение отметим, что, как следует
из полученных формул, динамический коэффи
циент снижается при уменьшении жесткости
упругой системы (т. е. увеличении Хст). Поэто
му для смягчения ударов широко применяют
различного типа пружины и рессоры, обладаю
щие значительной податливостью (небольшой
жесткостью).
П р и м е р 13.3. Груз массой т = 60 кг падает
//4 У/Ml___
1
1х\
а =20
на диск, укрепленный на конце стержня (рис. 13.4).
Определить наибольшую допускаемую высоту h
падения груза при условии, что напряжения, воз
■
никающие в поперечных сечениях стержня, не
превышают предела пропорциональности а пц =
9
С
1
= 210 МПа.
Диск считать недеформирующимся: Е — 2,0 х
вш|ijза
х 105 МПа. Применить упрощенную формулу для
динамического коэффициента.
Рис. 13.4
Р е ш е н и е . Приравнивая напряжения, возни
кающие в поперечном сечении стержня при ударе,
пределу пропорциональности, получаем
о*д = ХцОст “ ^пц»
(а)
где 1сд = ]/2йД0Т.
Перемещение нижнего конца стержня при статическом приложе
нии силы Q=mg
>.ст = Q/C,
где С = ЕА/1 —жесткость (коэффициент жесткости) стержня.
Напряжения, вызванные статическим действием силы:
<тет = QIA.
(б)
(в)
Подставляя в выражение (а) значение кд и учитывая (б) и (в),
имеем
\/2hCIQ-QA = ana,
откуда наибольшая допускаемая высота падения груза
ВД = < Л 2/(26С).
Подставив значение С, а затем числовые данные, получим
г ,
*■ J
ст2цЛ2
2Q(EA/[)
а 2пц1А
2 mgE
(210-106)2- 1,5[(3,14/4)-0,022]
2-60-9,81-2-10s • 106
= 88,2-10"3 м = 88,2 мм.
П р и м е р 13.4. На стальную балку двутаврового поперечного се
чения по середине пролета падает груз массой т = 100 кг (рис. 13.5).
Сопоставить наибольшие статические и динамические напряжения
в поперечном сечении балки и прогибы под грузом для случаев изгиба
балки в плоскости наибольшей и наименьшей жесткости.
341
Рис. 13.5
Р е ш е н и е . Рассмотрим сначала случай изгиба балки в плоско
сти наибольшей жесткости. Наибольшие нормальные напряжения
в поперечном сечении балки при статическом нагружении
100-9,81-3
QI
= 2,32 ■106 Па = 2,32 МПа,
Wx
4WX 4-317-10‘
где Q = тд — сила тяжести груза; fVx = 317 см3 принято по таблице
ГОСТ 8239-72.
Динамический коэффициент
—
ka = l + \ / t + 2h/f„,
где f „ = Ql3/(48EJJ (см. табл. 7.2) —прогиб по середине пролета при
статическом нагружении.
Для случая изгибающего удара статическое перемещение обозна
чено / ст взамен Хст при продольном ударе. Принимая Е =
= 2,0- 10s МПа и по таблице ГОСТ 8239 —72 Jx = 3800 см4, получаем
100- 9,81 -З3
^
48•2•105•106•3800•10"8
= 7,27-10-
м = 0,0727 мм.
Динамический коэффициент
2-10
17,7.
7,27-10“ 2
Динамический прогиб и наибольшие динамические напряжения
[см. формулы (13.4), (13.5)]:
/д = &д/ст = 17,7• 7,27-К Г 2 = 1,29 мм;
<тл = клаС1 = 17,7 •2,32 = 41,1 МПа.
кя= 1 +
При изгибе балки в плоскости наименьшей жесткости {Jy —
= 260 см4; Wy = 41,6 см3) аналогично получаем:
О/
4Wy
/ci
100-9,81-3
з Г = 17,7-106 Па =17,7 МПа;
4-41,6-10
100-9,81-З3
— = 1,06 -10 3 м = 1,06 мм;
48-2-105-106•260-10"8
Ql3
48EJy
,
f
д
r
2h
11
+ T ^ =1 + r
TW
+W
==5’46:
/д = кдfct = 5,46 • 1,06 = 5,78 мм;
Од =/СдСгст = 5,46 • 17,7 = 96,8 МПа.
342
При статическом действии нагрузки напряжения во втором случае
больше, чем в первом, в 7,63 раза, а при ее ударном действии —лишь
в 2,36 раза. Это различие объясняется тем, что во втором случае жест
кость балки значительно (в 14,6 раза) меньше, чем в первом, что при
водит к существенному уменьшению динамического коэффициента.
П р и м е р 13.5. Определить из условия прочности стальной дву
тавровой балки (рис. 13.6, а) наибольшую допускаемую высоту паде
ния груза массой т = 200 кг, если [а ] = 160 МПа и груз падает по
середине пролета. Как изменится допускаемая высота падения груза,
если жесткие шарнирные опоры балки заменить цилиндрическими вин
товыми пружинами (рис. 13,6,6), имеющими и = 10 витков; D =
= 100 мм; d = 20 мм?
Для материала балки £ = 2,0 105 МПа, для материала пружин
G = 8,0-104 МПа.
Применить упрощенную формулу для динамического коэффи
циента.
Р е ш е н и е . Условие прочности балки
(Уд = /СдОГсг ^ [о].
Наибольшее нормальное напряжение при статическом действии
рилы
_ М хпих
Wx
mgl
4WX
200-9,81-3
= 13,5 - 106 Па = 13,5 МПа,
4 -1 0 9 -1 0 '6
где по таблице сортамента для двутавра № 16 принято Wx = 109 см3.
Для обеспечения условия прочности балки динамический коэффи
циент не должен превышать следующего значения:
[кд] ={ст]/ост = 160/13,5 = 11,85.
По формуле (13.6)
кд-1/2
где /ст =
m gl3
4аЁГХ
200 9,81 -З3
= 0,633-10" 3 м = 0,633 мм.
48-2-105•106 - 873 - 10-8
а)
ЛИЛ®
1/2
~К %
г=зм
№16
Рис. 13.6
343
Приравнивая значение /сд допускаемому, получаем
/сд = |/2Щ бЗЗ =
[/Сд]
= 11,85,
откуда [ft] = 44,4 мм.
При установке балки на пружины полное статическое перемеще
ние по середине пролета балки будет равно сумме ее статического про
гиба и осадки пружины, соответствующей действию силы Q/2 (нагруз
ка, действующая на пружину при статическом приложении к балке
силы Q):
/ст =
mgl1
48ЕЛ,
8
2
Gd*
200-9,81
8---- ------ ОД3-10
200-9,81-З3
-+ 48 ■2 • 105 ■106 •873 • 10" 8 ' 8 • 104 • 106 •0,024
=0,633-10~3 + 6,13• 10“ 3 =6,76-IQ- 3 м = 6,76 мм.
Составляя выражение для динамического коэффициента и прирав
нивая его найденному выше допускаемому значению, получаем
кд = ]/2 h /f„ = l/2ft/6,76 = [fcj = 11,85,
откуда [ft] =475 мм.
Таким образом, уменьшение жесткости упругой системы позво
ляет значительно увеличить допускаемую ударную нагрузку (в данном
случае увеличить допускаемую высоту падения груза).
ЗА К Л Ю Ч Е Н И Е
Итак, закончив рассмотрение м етодов расчета элемен
тов конструкций на прочность, жесткость и устой
чивость, читатель — учащийся техникума — может считать
себя подготовленным к изучению инженерно-конструк
торской дисциплины о назначении, устройстве, принци
пах работы и проектировании деталей машин и меха
низмов — следую щ его раздела технической механики.
В книге главным объектом изучения фигурировал
брус (стержень, балка), изготовленный из одного ма
териала, как правило, из стали. А для ее получения в
количестве, необходим ом для нуж д народного хозяйства
страны, приходится добывать огромные массы руды,
природные же рессурсы последней неумолимо умень
шаются. К ром е того, перед проектировщиками и кон
структорами машин и оборудования все чаще возникают
на первый взгляд вообщ е неразрешимые задачи. На
пример, требуется совместить высокую прочность с вы
сокой пластичностью или — небольш ую плотность мате
риала совместить с высокой прочностью изделия. П о
следняя проблема, в частности, возникает постоянно
перед создателями авиационной и космической техники.
Эти и другие подобны е проблемы пытаются разрешить
сейчас с помощ ью новых композиционных материалов,
в которых металлы играют не единоличную роль, а
подчас и далеко не главную.
К числу композиционных материалов относится из
вестный всем ж елезобетон, появившийся еще во второй
половине X IX века, и до сих пор это один из ос
новных материалов строительных конструкций. Как из
вестно, стальная арматура железобетона воспринимает в
основном растягивающие нагрузки, а бетон — сжи
мающие.
В настоящее время все большее и большее распро
странение приобретаю т различные стеклопластики, в
которых упрочнителем служит стеклянное волокно. П о
345
мимо стали и стекла в качестве армирующих ма
териалов используется, например, бор, графит и др.
Пластмасса, содержащая волокна бора в качестве
упрочнителя (боропластик), отличается очень высокой ме
ханической прочностью (ств = 1400 М П а), применяется
в авиационной и ракетной технике.
Бороалюминий имеет еще более высокий предел
прочности (1600 М Па).
Пластмассы с упрочнителем из углеродных (гра
фитовых) волокон (в виде жгутов, матов или руб
ленных волокон) называются углепластиками. Они об
ладают высокой прочностью (ств = 1400 М П а), жест
костью, это термически и химически устойчивые электрои теплопроводные материалы с небольшой плотностью
и низким коэффициентом линейного расширения; идут
на изготовление деталей летательных аппаратов, судов,
автомобилей, спортинвентаря и др.
К началу следующ его тысячелетия при изучении
сопротивления материалов, учащиеся безусловно все чаще
и чаще станут встречаться и с другими компози
ционными материалами. К этом у времени значительно
усовершенствуются методы расчета на прочность, жест
кость и устойчивость, а благодаря широкому повсе
местному внедрению вычислительной техники учащиеся
смогут решать более сложные задачи, чем те которые
были изложены в этой книге.
СПИСОК ЛИТЕРАТУРЫ
1. Батурин А. Т., Ицкович Г. М., Панич Б. Б., Чернин И. М.
Детали машин. М., 1971.
2. Дарков А. В., Шпиро Г . С. Сопротивление материалов. М.,
1975.
3. Ицкович Г. М., Винокуров А. И. Сопротивление материалов
(руководство для учащихся механико-машиностроительных специаль
ностей заочных техникумов). М., 1962.
4. Ицкович Г. М., Винокуров А. И., Минин Л. С. Руководство
к решению задач по сопротивлению материалов. М., 1970.
5. Ицкович Г . М., Винокуров А. И., Барановский И. В. Сборник
задач по сопротивлению материалов. Л., 1972.
6. Кинасошвили Р. С. Сопротивление материалов. М., 1975.
7. Кудрявцев В. И. Детали машин. Л., 1980.
8. Куприянов Д. Ф., Метальников Г. Ф. Техническая механика.
М., 1975.
9. Пономарев С. Д., Бидерман В. Л., Лихарев К. К., Макушин В. М.,
Малинин И. И., Феодосьев В. И. Расчеты на прочность в машинострое
нии. М., т. I, 1956; т. 2, 1958; т. 3, 1959.
10. Рубашкин А. Г., Чернилевский Д. В. Лабораторно-практические
работы по технической механике. М., 1975.
11. Сопротивление материалов/Под ред. А. Ф. Смирнова. М.,
1975.
12. Феодосьев В. И. Сопротивление материалов. М., 1979.
13. Чернавский С. А. [и др.] Курсовое проектирование деталей
машин. М., 1979.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Амплитуда цикла напряжений
289
Анизотропность 13
Балка 157, 229
Брус 12, 229
Гибкость стержня 323
— — предельная 323
Гипотеза Мора 265
— наибольших касательных на
пряжений 263
— плоских сечений 28, 117, 175
— энергетическая 265
Деформация 4, 32
— пластическая
(остаточная)
5
— поперечная 32
— продольная 32
— упругая 5
Жесткость 6, 7, 33
— бруса 35
— сечения бруса 35, 122, 180
Закон Гука 33, 102
— парности касательных напря
жений 53, 94
Изгиб косой 155, 233
— поперечный 154
— прямой 155, 235
— чистый 19, 154, 156, 175
Изотропность 13
Индекс пружины 13
Интеграл Мора 211
348
Концентрация напряжений 30,
293
Коэффициент динамический 340
— жесткости 137
— запаса прочности 68
— податливости 35, 137
— приведения длины 322
— продольного изгиба 331
— Пуассона 34, 102
— снижения предела выносли
вости 298
Кручение 19
Массив 13
Метод сечений 16
Модуль продольной упругости
33
— — — приведенный 308
— сдвига 102
Момент изгибающий 18, 107,
156, 159
— — правило знаков 160, 161
— инерции главный 145
— — осевой 142, 150
— — полярный 120, 142
— — центробежный 143
— крутящий 18, 114, 115
— —, правило знаков 116
— скручивающий 114
— сечения статический 139
— сопротивления сечения осе
вой 183
— — — полярный 121
-- эквивалентный 275, 276
Нагрузка 9
— динамическая 11
— повторная 11
— статическая 11
Наклеп 62
Напряжения 20
— главные 94, 261
— допускаемые 68, 71, 330
— касательные
21,
100,
101,
103, 115, 121, 195
— контактные 303
— критические 322
— начальные (монтажные) 39,
90
— нормальные 21, 28, 52, 175
— предельные 67, 71
— температурные 89
— цикла максимальные 288
— — минимальные 288
— эквивалентные 262, 264, 266,
271
Оболочка 13
Однородность 13
Осадка пружины 136
Пластина 13
Пластичность 54
Правило Верещагина 214, 215
Предел выносливости 291, 292
— пропорциональности 59, 60,
64
— прочности 59
— упругости 59, 60
— текучести 59, 60, 64
Принцип начальных размеров 14
— Сен-Венана 30
— суперпозиции 45
Прогиб 200
Прочность 5, 7, 54, 69
— контактная 303
Пружина цилиндрическая 133
Растяжение 18, 24
Сдвиг 18
— чистый 99
Сжатие 18, 24
Сила внешняя 9
— внутренняя 15
— критическая 317
— поперечная 18, 103, 156, 157,
159
— продольная 18, 19, 20, 25
Силовой фактор 18
Смятие 105, 111
Состояние напряженное в точке
50, 93, 94
— — об'ьемнос 96
— — однородное 51
— — плоское 96
— — подобное 261
Срез 18, 111
Статически неопределимые сис
темы 77
Степень статической неопреде
лимости 77
Т в е р д о с т ь 54
Т е о р е м а К л а п е й р о н а 47, 338
У г о л з а к р у ч и в а н и я 118, 121
— — д о п у с к а е м ы й 125
— — о т н о с и т е л ь н ы й 125
— с д в и г а 120
У п р у г а я л и н и я б а л к и 200, 202
У п р у г о с т ь 14, 54
У с л о в и е ж е с т к о с т и п р и кр у ч е н и и
125
— — — изгибе 223
— п р о ч н о с т и п р и и з г и б е 183, 188
— — — к р у ч е н и и 123
— — — р а с т я ж е н и и (с ж а т и и ) 71
— — — с м я т и и 105
— — — с р е з е 104
У с т а л о с т н о е р а з р у ш е н и е 285,
304
У с т о й ч и в о с т ь 7, 314
Формула Герца 310
— Журавского 196
— Эйлера 318
— Ясинского 324
Хрупкость 63
Цикл напряжений 288
— — симметричный 289
— — отнулевой 289
— — симметричный 289
Энергия деформации при изгибе
207
— — — кручении 132
— — — растяжении 49
Эпюра грузовая 216
— единичного момента 220
— единичной силы 216
— изгибающих моментов 158
— касательных напряжений кру
чения 121
— крутящих моментов 115
— нормальных напряжений из
гиба 178
— поперечных сил 58
— продольных сил 26
349
ОГЛАВЛЕНИЕ
П редисловие................................................................... ' . . . .
3
Г л а в а I. Основные положения..........................................................
4
§ 1.1. Задачи сопротивления м атериалов.............................
4
§ 1.2. Классификация внешних сил и элементов конструкций
9
§ 1.3. Допущения относительно свойств материалов и харак
тера деформаций...............................................................
13
§ 1.4. Метод сечений. Внутренние силы в поперечных сече
ниях б р у са ............................................................................
15
§ 1.5. Н а п р я ж е н и я .............................................................
20
Г л а в а II. Растяжение и сж а ти е ....................................................
§2.1. Силы в поперечных сечениях бруса................................
§ 2.2. Напряжения в поперечных сечениях бруса. . . .
§ 2.3. Деформации и перем ещ ен ия...............................
32
§ 2.4. Энергия деформации при растяжении ............. .........
§ 2.5. Напряженное состояние при растяжении (сжатии). .
§ 2.6. Общие сведения о механических испытаниях материа
лов ..................................................................................
§ 2.7. Статические испытания на растяжение............
56
§ 2.8. Статические испытания на сж атие.....................
64
§ 2.9. Коэффициенты запаса прочности. Допускаемые на
пряжения ................................................
§ 2.10. Расчеты на прочность при растяжении (сжатии) . .
§ 2.11. Статически неопределимые систем ы ........................
§ 2.12. Температурные и начальные напряжения в стати
чески неопределимых системах..................................
Г л а в а III. Напряженное и деформированноесостояния . . . .
§ 3.1. Общие сведения о напряженном состоянии в точке
т е л а ..................................................................................
§ 3.2. Исследование напряженного состояния при известных
главных напряжениях....................................................
§ 3.3. Чистый сдвиг...................................................................
24
24
28
46
50
54
66
71
76
87
94
94
97
99
Г л а в а IV. Практические расчеты на срез и смятие................... 104
§ 4.1. Основные понятия. Расчетные формулы.......................... 104
§ 4.2. Расчет заклепочных соединений......................................
110
Г л а в а V. Кручение , . .................................................................... 115
§ 5.1. Основные понятия. Эпюры крутящих моментов . . . 115
§ 5.2. Напряжения и перемещения при кручении бруса круг
лого поперечного сечения......................................................118
§ 5.3. Расчеты на прочность и жесткость при кручении . . . 124
350
§ 5.4. Энергия деформации прикручении.................................... 132
§ 5.5. Расчет цилиндрических винтовых пружин . . . .
134
Г л а в а VI. Геометрические характеристики плоских сечений. . . 139
§ 6.1. Статические моментыплоскихсечений................................139
§ 6.2. Осевые и центробежные моменты инерции плоских
се ч е н и й ....................... ................................................. 143
§ 6.3. Главные оси и главные моменты инерции................... 144
§ 6.4. Зависимость между моментами инерции относительно
параллельных о с е й ............................................................... 146
§ 6.5. Моменты инерции некоторых простейших сечений . . 147
§ 6.6. Вычисление моментов инерции составных сечений,
имеющих ось сим м етрии ................................................. 151
Г л а в а VII. Прямой и з г и б ................................................................155
§ 7.1. Основные понятия и определения................................... 155
§ 7.2. Поперечные силы и изгибающие моменты . . . .
158
§ 7.3. Дифференциальные зависимости между интенсивно
стью распределенной нагрузки, поперечной силой и
изгибающим м о м е н т о м ............................................
167
§ 7.4. Общие указания к построению эпюр поперечных
сил и изгибающих м о м ен то в ........................ .... .
168
§ 7.5. Нормальные напряжения при изгибе........................
176
§ 7.6. Расчеты на прочность при изгибе.............................
182
Расчет балок из пластичных материалов . . . .
182
Расчет балок из хрупких материалов........................
187
§ 7.7. Касательные напряжения при прямом поперечном
и з г и б е .............................................................................
195
§ 7.8. Перемещения при изгибе. Основные понятия . . . 200
§ 7.9. Дифференциальное уравнение упругой линии и его
интегрирование..................................................................... 201
§ 7.10. Энергия деформации при изгибе........................................ 205
§ 7.11. Интеграл М о р а .....................................................................209
§ 7.12. Правило Верещагина........................................................... 214
§ 7.13. Расчеты на жесткость при изги бе................................... 222
§ 7.14. Балки переменного сечения..................................................229
Г л а в а VIII. Косой изгиб, растяжение (сжатие) с изгибом . . . 233
§ 8.1. Косой и з г и б ..........................................................................233
§ 8.2. Пространственный изгиб бруса круглого поперечного
сечения . . . ; ................................................................ 245
§ 8.3. Изгиб с растяжением (сжатием) бруса большой
ж е с тк о с ти .............................................................................. 247
Г л а в а IX. Гипотезы прочности и их применение................... »
260
§ 9.1. Основные понятия о гипотезах прочности........................ 260
§ 9.2. Определение эквивалентных напряжений по различным
гипотезам прочности...........................................................263
§ 9.3. Исследование упрощенного плоского напряженного
с о с т о я н и я .............................................................................. 266
§ 9.4. Рисчет бруса круглого поперечного сечения на изгиб
Скручением.............................................................................. 272
§ 9.5. Расчет бруса круглого поперечного сечения в общем
случае cm ищ рутения...........................................................279
§ 9.6. Расчет ншкосленных цилиндрических и сферических
резервуаров ..........................................................................281
351
Г л а в а Х . Сопротивление усталости ...................................................... 285
§ 10.1. Основные понятия об усталости металлов. Предел
в ы н о сл и в о сти .................................................................... 285
§ 10.2. Факторы, влияющие на снижение предела вынос
ливости м атериалов.......................................................... 293
§ 10.3. Расчет на усталость...............................................................298
Г л а в а XI. Контактные напряжения н деформации..............................303
§ 11.1. Основные понятия...............................................................303
§ 11.2. Контакт тел, ограниченных сферическими и цилин
дрическими поверхностями.................................................306
Глава
XII. Устойчивость сж а ты х стерж ней .
. . .
314
§ 12.1. Устойчивость упругого равновесия. Критическая
с и л а .................................
314
§ 12.2. Формула Э й л е р а ...............................................................318
§ 12.3. Критическое напряжение. Пределы применимости
формулы Э й л е р а ................................................................322
§ 12.4. Расчет сжатых стержней на устойчивость по коэф
фициентам продольного изгиба. . . . . . . .
330
Г л а в а XIII. Задачи динамики в сопротивлении материалов . . . 334
§ 13.1. Расчет элементов конструкций при заданных ускоре
ниях ....................................................................................... 334
§ 13.2. Приближенный метод расчетана уд ар...............................337
Заключение.................................................................................................345
Список л и те р ату р ы ............................................................................................. 347
Предметный ук азател ь ........................................................................................348
Учебное издание
Георгий Меерович Ицкович
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Научный редактор А. И. Аркуша
Зав. редакцией К. И. Аношина. Редактор Л. Н. Чупеева. Младший
редактор Н. В. Траханова. Художественный редактор Т. А. Дурасова.
Технический редактор Р. С. Родичева. Корректор Р. К. Косинова
ИБ № 5859
Изд. № ОТ-594. Сдано в набор 27.09.85. Поди, в печать 14.03.86.
Формат 84 х 108/32. Бум. тип. № 1. Гарнитура тайме. Печать высокая.
Объем 18,48 уел. печ. л. 18,48 уел. кр.-отт. 18,99 уч.-изд. л. Тираж
220 000 экз. Зак. № 95. Цена 75 коп.
Издательство «Высшая школа», 101430, Москва, ГСП-4, Неглинная
ул., д. 29/14.
Ордена Октябрьской Революции, ордена Трудового Красного Знамени
Ленинградское производственно-техническое объединение «Печатный
Двор» имени А. М. Горького Союзполиграфпрома при Государствен
ном комитете СССР по делам издательств, полиграфии и книжной тор
говли. 197136, Ленинград, П-136, Чкаловский проси., 15.