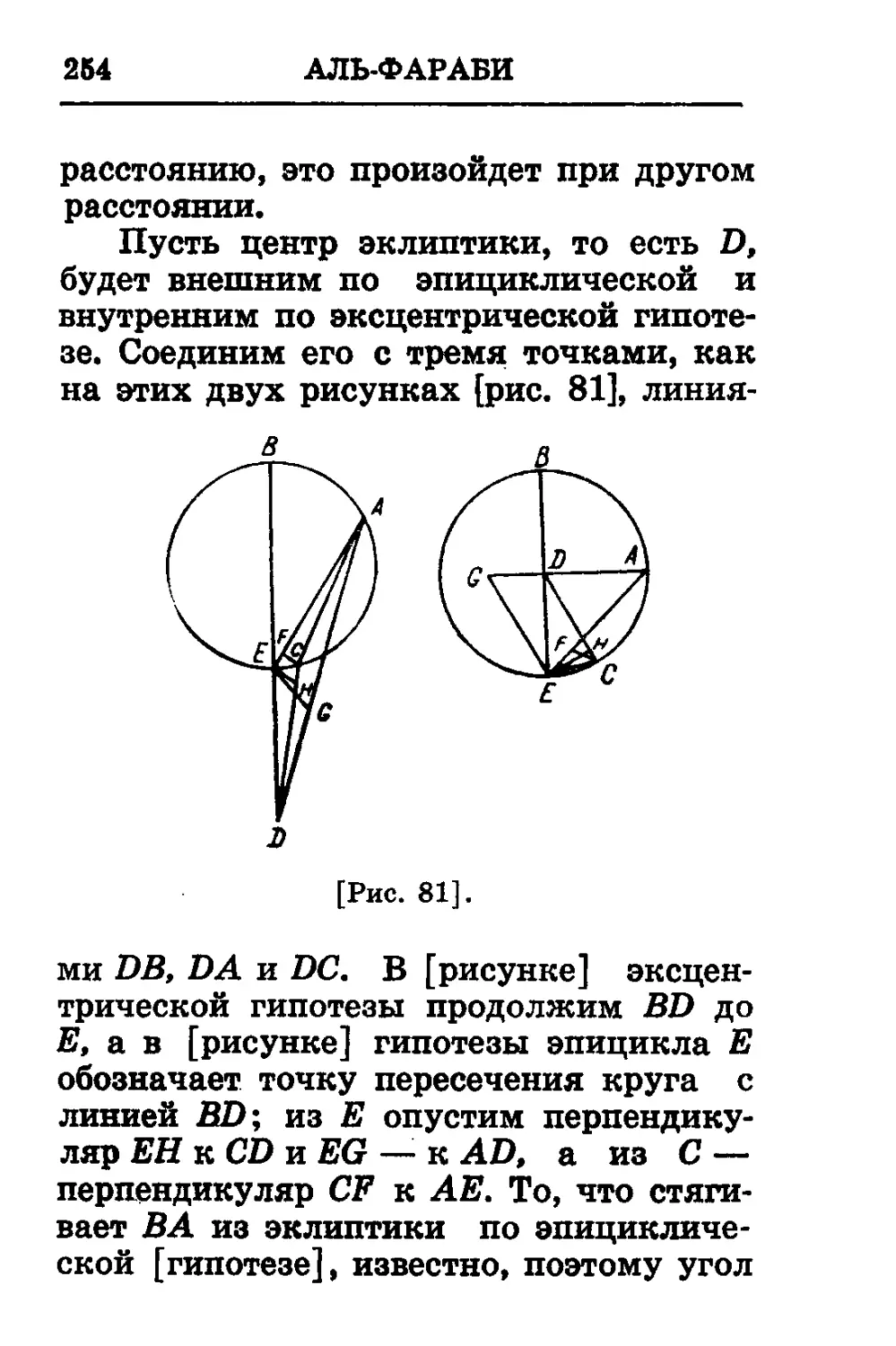
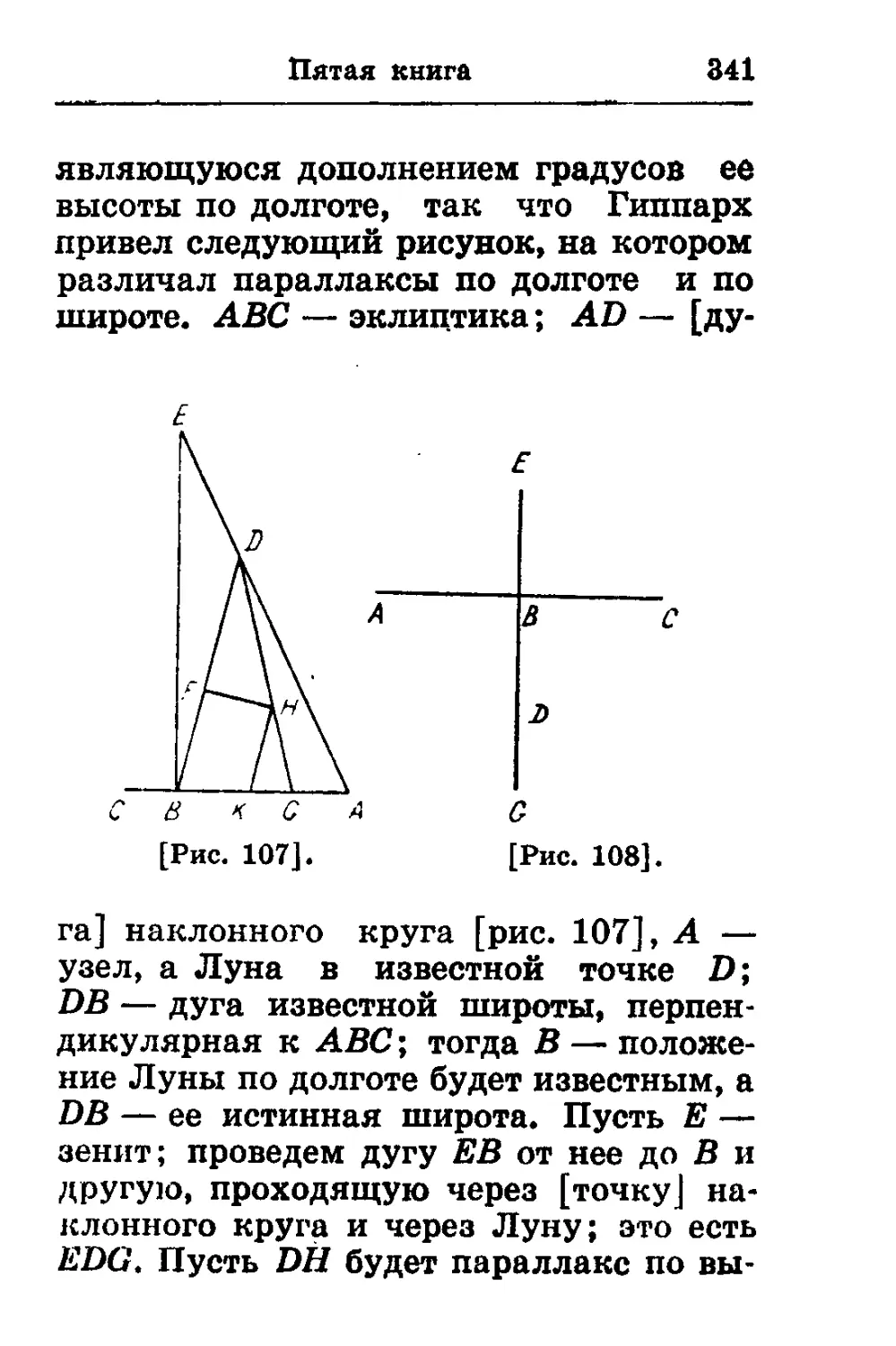
Текст
1100-летию со дня рождения
Абу Насра Мухаммада ибн Мухаммада
ибн Тархана ибн Узлаг аль-Фараби ат-Турни
ПОСВЯЩАЕТСЯ
Tyulemissov Madi yj
tmadi1@gmail.com
АКАДЕМИЯ НАУК КАЗАХСКОЙ ССР
ИНСТИТУТ ФИЛОСОФИИ И ПРАВА
Аль-Фараби
КОММЕНТАРИИ
К „АЛЬМАГЕСТУ"
ПТОЛЕМЕЯ
Часть первая
Перевод с арабского
А. КУБЕСОВА и Дж. аль-ДАББАХА
Вступительная статья А. КУБЕСОВА,
Примечания А. КУБЕСОВА
и В. А. РОЗЕНФЕЛЬДА
Издательство «НАУКА» Казахской ССР
А Л М А-А Т А — 1 9 7 б
001
Ф—240
Большое значение в развитии астрономии и
тесно связанной с ней тригонометрии в странах
средневекового Ближнего и Среднего Востока
имел «Альмагест» Птолемея — своеобразный
свод астрономических знаний, древних греков.
Аль-Фараби был одним из первых комментато-
ров «Альмагеста» Птолемея. Он написал по
этой тематике два трактата: „Комментарии к
«Альмагесту»” и «Книга приложений». Аль-Фа-
раби чрезвычайно точно передает мысли Птоле-
мея с обширными выкладками и толкованием
его текста. „Комментарии к «Альмагесту»*1
являются продолжением уже опубликованных
естественно-математических трудов аль-Фараби
(«Математические трактаты»). Эта книга содер-
жит первых пять частей из тринадцати частей
„Комментариев к «Альмагесту» “.
Перевод этого сочинения с арабского на рус-
ский язык выполнен по рукописи Британского
музея.
Книга рассчитана на широкий круг читате-
лей, интересующихся вопросами истории науки.
РЕДАКЦИОННАЯ КОЛЛЕГИЯ:
А. М. Кунаев (ответственный редактор),
О. А. Ж а у т ы к о в, А. Ж. М а ш а н о в,
Б. А. Розенфельд (редактор по переводу).
20201—091
407(07)—76
98—75
© Издательство «Наука» Казахской ССР,
1975 г.
АЛЬ-ФАРАБИ
И ЕГО ОБРАБОТКИ «АЛЬМАГЕСТА»
Абу Наср аль-Фараби, 1100-летие ко-
торого отмечается в 1975 г. во всем ми-
ре, был не только великим философом-
мыслителем, но и одним из крупнейших
ученых-энциклопедистов своего вре-
мени.
Исследование научного наследия
аль-Фараби имеет многовековую исто-
рию, однако его научные труды изу-
чены далеко но полностью. В особен-
ности это относится к его трудам астро-
номического содержания. Последние ис-
следования, проведенные в АН КазССР
по выяснению заслуг аль-Фараби в раз-
витии науки, показывают, что он был
выдающимся астрономом.
В своей классификации нйук аль-Фа-
раби по сложившейся традиции считает
астрономию математической наукой. В
«Перечислении наук», определяя пред-
8 Аль-Фараби и его обработки «Альмагеста»
мет астрономии, он относит астрологи-
ческие предсказания к ремеслам и
считает истинной наукой только наблю-
дательную и математическую астроно-
мию [1, стр. 26—27].
В знаменитом трактате «Что пра-
вильно и что неправильно в приговорах
звезд» на основе законов логики и дости-
жений естествознания аль-Фараби изла-
гает свою концепцию на предмет науки
о небесных светилах. Он одним из пер-
вых на Востоке подвергает уничтожаю-
щей критике юдициарную астрологию,
согласно которой земные дела и собы-
тия управляются различными располо-
жениями небесных светил, ремесло ас-
трологов квалифицирует как занятие,
лишенное всяких научных основ,
опирающееся преимущественно на субъ-
ективно-психологические моменты вос-
приятия отдельных людей. В противопо-
ложность астрологии отдает предпочте-
ние истинно научному способу познания
Вселенной, т. е. астрономии, и пред-
лагает изучать астрономические явле-
ния с широким привлечением математи-
ческих методов [2, стр. 214—217]. Кри-
тика астрологических предсказаний,
начатая в этом трактате, впоследствии
развивалась такими крупнейшими уче-
ными, как аль-Бируни (973—1050), Ибн
Аль-Фарабй и его обработки «Альмагеста» 9
Сина (980—1037), Роджер Бэкон (1214—
1294).
В астрономическом наследии аль-
Фараби большое место занимают его
обработки «Альмагеста» Птолемея
(Пв.).
Как известно, исходным моментом
для развития астрономии в странах
Ближнего и Среднего Востока был «Аль-
магест» Птолемея, переведенный с гре-
ческого на арабский язык в начале IX в.
В дальнейшем эта работа комментирова-
лась и перерабатывалась (836—901) аль-
Баттани (850—929), аль-Фараби (ок.
870—950), Абу-Вафой (940—998), аль-
Бируии, Насир ад-Дином ат-Туси (1202—
1274) и др.
«Альмагест» Птолемея — энцикло-
педическое сочинение по астрономии —
состоит из 13 книг ’. Первые две книги
трактуют об общих принципах птоле-
меевской астрономии, о суточном дви-
жении небесной сферы, о главных дви-
жениях Солнца, Луны и планет, а так-
же о некоторых явлениях, связанных с
небесной сферой и ее движением (про-
должительность дня и время восхода и
1 Этот труд Птолемея еще не издан на рус-
ском языке. Мы в дальнейшем ссылаемся на не-
мецкий перевод [3].
10 Аль-Фараби и его обработки «Альмагеста»
заката светил в различных широтах
земного шара); здесь же приводятся
тригонометрические сведения, необхо-
димые в астрономических вычислениях,
а также таблицы хорд (или равных
удвоенным линиям синусов) через каж-
дые 1/2° до 180°.
Третья книга «Альмагеста» посвя-
щена продолжительности года и теории
Солнца, четвертая — продолжительно-
сти месяца и теории движения Луны. В
пятой книге приводится подробное рас-
суждение о лунном параллаксе и о рас-
стояниях Солнца и Луны. В шестой кни-
ге говорится о затмениях Солнца и Лу-
ны. В седьмой и восьмой книгах содер-
жится звездный каталог, заключающий
в себе 1028 звезд и описание прецессии.
Последние пять книг содержат тео-
рию движения пяти планет (Меркурий,
Венера, Марс, Сатурн, Юпитер).
Большой интерес для истории науки
представляет научный метод, по кото-
рому был построен «Альмагест». В из-
вестной мере нам кажется справедли-
вым тезис о том, что Птолемей, который
специально не занимался методологиче-
скими вопросами естественных наук,
оставил методологию «Альмагеста». На
всем протяжении этого сочинения после-
довательно проводится весьма плодо-
Аль-Фараби я его обработки «Альмагеста» 11
творная для естественных наук идея,
согласно которой сначала изобретаются
временные гипотезы, из них выводятся
математические следствия, последние
сравниваются с результатами наблюде-
ний. Методологию Гиппарха и Птоле-
мея, на наш взгляд, полностью освоил и
развил дальше аль-Фараби, что оказало
решающее влияние на открытое провоз-
глашение им экспериментально-теорети-
ческого метод а исследования природы и
поотроекия научных теорий [2, стр.
169—174].
В «Альмагесте» содержится богатый
математический материал, относящий-
ся преимущественно к тригонометриче-
ским и алгебраическим методам, из ко-
торого впоследствии исходили многие
математики Востока, в том числе аль-
Фараби [4, стр. 200—204]. Птолемею
принадлежит еще ряд трактатов: «Гео-
графия», «Гармоника», «Оптика», «Тет-
рабиблиос» и др. Аль-Фараби был хоро-
шо знаком почти со всеми сочинениями
Птолемея, некоторые из них он под-
верг тщательной обработке. Детальное
изучение научной преемственности меж-
ду этими корифеями науки античности
и средневековья является одной из важ-
нейших задач историков науки и фило-
софии.
12 Аль-Фараби и его обработки «Альмагеста»
Аль-Фараби был одним из первых
комментаторов «Альмагеста» на средне-
вековом Востоке. Его „Комментарии к
«Альмагесту»” (Шарх ал-Маджисти), к
которым примыкает «Книга приложе-
ний» (Китаб ал-Лавахик), сохранились
в единственной рукописи, хранящейся в
Британском музее (Лондон, № 7368).
Оба эти трактата до сих пор не издава-
лись ни на одном языке и почти не ис-
следовались.
„Комментарии к «Альмагесту»” аль-
Фараби составил на основе сокращения
и переработки текста Птолемея. Поэто-
му автор иногда называет их «Сокра-
щенным Альмагестом» (Мухтасар аль-
Маджисти), свои добавления и примеча-
ния он особо оговаривает.
В предисловии „Комментариев к
«Альмагесту»” аль-Фараби о своих пла-
нах работы над «Альмагестом» пишет:
«Мы теперь в состоянии изложить все
части созданной великим Птолемеем
книги «Альмагест» об астрономической
науке. При этом мы будем следовать
его словам, за исключением редких слу-
чаев, где мы излагаем некоторые мето-
ды, предложенные нашими современни-
ками. Наши [собственные] исследова-
ния приведены в «Книге приложений».
Аль-Фараби и его обработки «Альмагеста» 13
Мы старались сделать это сочинение
по возможности более понятным. С этой
целью мы опустили вычисления и разъ-
ясняем только доказательства. Желаю-
щий может проверить эти вычисления.
Мы не будем упоминать даты каждого
наблюдения, а ограничимся указанием
[промежутков времени] между каждыми
двумя наблюдениями. Что касается таб-
лиц, то кто хочет поместить их в нашей
книге, пусть так и сделает, а если захо-
чет, пусть сократит их. Мы решили не
повторять многократно предложения,
общие для нескольких светил, так как
между этими светилами много общего
как в математическом, так и астрономи-
ческом отношении. В «Альмагесте» они
повторяются, так как их вычисления
различны» [стр. 47—48].
Из этого вытекает, что „Коммента-
рии к «Альмагесту»” написаны аль-
Фараби прежде всего как учебно-педа-
гогй^еское сочинение, построенное на
основе, существенно отличающейся от
установки Птолемея при составлении
«Альмагеста».
Птолемей в своем «Альмагесте» в
каждом случае стремится дать числен-
ные характеристики исследуемых астро-
номических явлений на основе приме-
нения теоретических математических
14 Аль-Фараби и его обработки «Альмагеста»
методов к числовым данным, получен-
ным эмпирическим путем, т. е. путем
наблюдений. Он начинает с опреде-
ленной геометрической предпосылки, из
которой затем выводит арифметические
следствия. Тем самым Птолемей делает
принципиальный шаг вперед по пути
теоретизации (геометризации) по срав-
нению со своими восточными предшест-
венниками и современниками, приме-
нявшими в астрономии исключительно
арифметические методы без каких-либо
геометрических моделей.
Аль-Фараби в этом направлении по-
шел еще дальше, оперируя исключи-
тельно геометрическими моделями и
предпосылками в исследовании астро-
номических соотношений. У него число-
вые данные либо совсем отсутствуют,
либо встречаются как редкий рудимент,
пережиток метода изложения «Альма-
геста». Его интересует в основном, из-
вестна или не известна искомая величи-
на; при этом аль-Фараби доводит до
рацга терминов слова «известная»
(ма'лум) и «неизвестная» (маджхул);
метод изложения у него алгебраиче-
ский, что достигается с помощью широ-
кого введения тригонометрических
функций (линий) и расширения поня-
тия числа до положительного действи-
Аль-Фараби и его обработки «Альмагеста» 16
тельного числа. Благодаря этому теоре-
тико-методическому приему не только
значительно сокращается объем ком-
ментируемого сочинения, но, что осо-
бенно важно, сам излагаемый материал
становится намного понятнее читате-
лям.
В работе аль-Фараби много добавле-
ний и усовершенствований методическо-
го характера. Например, в отличие от
Птолемея движения планет он по воз-
можности изучает совместно, так как,
по его мнению, «у светил много обще-
го как в астрономическом, так и в ма-
тематическом отношении». «Коммента-
рии» аль-Фараби являются выдающим-
ся образцом методического мастерства
средневековья и заслуживают специ-
ального рассмотрения в этом плане. Сле-
дуя своему принципу изложения, аль-
Фараби в «Комментариях» объясняет
принципы составления многочисленных
астрономических таблиц по Птолемею,
встречающихся в «Альмагесте», но са-
мих таблиц не приводит. Хотя он не за-
дается целью сделать какие-либо суще-
ственные отклонения от содержания
«Альмагеста» Птолемея, тем не менее
мы здесь встречаем ряд новых добавле-
ний и примечаний астрономического и
математического характера, отражаю-
16 Аль-Фараби и его обработки «Альмагеста»
хцих результаты его собственных иссле-
дований, а также достижений арабских
предшественников и современников, на-
пример ученых Академии аль-Мамуна.
Чтобы ясно представить структуру и
особенности изложения комментариев,
необходимо вкратце остановиться на со-
держании этого сочинения аль-Фараби.
Первая книга „Комментариев” по-
священа изложению содержания пер-
вой книги «Альмагеста» Птолемея. Она
начинается с подробного изложения об-
щих положений Птолемея, предпослан-
ных указанному сочинению, а именно:
о том, что небо имеет сферическую фор-
му и сферическое движение; что Земля
имеет вид сферы и что она расположена
в центре всего неба; что величина Земли
по сравнению с небом неощутимо ма-
ла; что Земля не имеет никакого дви-
жения; что в небе существуют два раз-
личных вида первых движений.
Относительно положения Птолемея
о том, что Земля не совершает никакого
вращательного движения, аль-Фараби
замечает, что он в своей «Физике» дал
другое доказательство невозможности
движения Земли.
Какова суть этого доказательства —
не известно, однако в «Каноне Мас'уда»
аль-Бируни имеется одно доказательст-
Аль-Фараби и его обработки «Альмагеста» 17
во невозможности вращения Земли во-
круг своей оси, основанное на физиче-
аргументах. [5, 272—273]. Может
быть, это и есть доказательство аль-Фа-
раби? Категорически ответить на этот
вопрос, по крайней мере сейчас, пред-
ставляется невозможным.
Кстати заметить, что и в «Перечис-
лении наук» аль-Фараби утверждает,
«что 'Земля в целом не движется ни со
своего места, ни на своем месте» [1,
стр.27]. Таким образом, он придержи-
вается общепринятых в то время догм
геоцентрической системы Птолемея, со-
гласно которой Земля считалась непо-
движно покоящейся в центре мира, а
все небесные светила движущимися во-
круг нее.
Однако аль-Фараби в других тракта-
тах то в явной, то в неявной форме вы-
сказывает мнение об относительности
знаний о Вселенной, сомневается в пра-
вильности отдельных тезисов, утвержде-
ний, укоренившихся в астрономии того
времени. Например, в указанном выше
астрологическом трактате он открыто
признается, что ему небесная гармония
известна не в такой степени, как музы-
кальная. Система мелодий и система
созвездий «условны, а не даны приро-
дой, где совершенно нет изменения и
2-89
18 Аль-Фараби и его обработки «Альмагеста»
естественного противоречия» [1, стр.
297].
Здесь, по-видимому, аль-Фараби
критикует Птолемея, который в своем
«Учении о гармонии», вслед за пифаго-
рейцами утверждал взаимосвязь между
музыкальной и небесной гармонией. За-
тем он подробно излагает способ опре-
деления хорд в круге. При этом, следуя
своему принципу, в отличие от Птоле-
мея не приводит числовых данных, чис-
ловых вычислений и таблиц хорд Птоле-
мея, однако объясняет способ построе-
ния этих таблиц. Здесь аль-Фараби
несколько совершенствует тригономе-
трический аппарат Птолемея для облег-
чения понимания трудных математиче-
ских выкладок, имеющихся в этом тру-
де. Прежде всего он везде заменяет хор-
ды синусами: «Синус есть половина
удвоенной хорды». Это- одно из первых
известных нам введений синуса при
комментировании «Альмагеста».
Аль-Фараби далее высказывает лем-
му, равносильную плоской теореме си-
нусов для произвольного вписанного
треугольника, и доказывает ее для впи-
санного прямоугольного треугольника.
Следуя Менелаю и Птолемею, он приво-
дит предпосылки об определении двух
дуг по сумме или разности и отношению
Аль-Фараби и его обработки «Альмагеста* 19
удвоенных полухорд этих дуг. При до-
казательетве предпосылки об определе-
нии дуг по их разности он приводит
случай, когда хорда разности двух дуг
параллельна диаметру. Этот случай,
когда диаметр сферы параллелен одной
и* хорд сторон фигуры секущих, лежа-
щих в плоскости диаметра, отсутствует
у Менелая. Далее аль-Фараби дает ряд
разъяснений сущности составления от-
иошеяий. Рассмотрение составных отно-
шений в дальнейшем получает большое
развитие в сочинениях последующих
математиков. Сферическую теорему о
секущих аль-Фараби доказывает как
Менелай, рассматривая три случая, а не
как Птолемей, который ограничился
только одним. При доказательстве ее
он, следуя Птолемею, останавливается
на измерении дуги, заключенной между
тропиками, с помощью особых инстру-
ментов — кольца на шесте и стенного
квадранта, затем дает сведения из сфе-
рической тригонометрии. При этом за-
мечает, что это продолжение и дополне-
ние геометрических сведений, приведен-
ных выше в связи с составлением
таблиц хорд.
Следует особо отметить, что аль-Фа-
раби, проводя арифметические опера-
ции над составными отношениями, вы-
20 Аль-Фараби и его обработки «Альмагеста»
ражающими теорему Менелая, факти-
чески рассматривает каждое отношение
тригонометрических линий как число.
Обобщая метод Птолемея по вычитанию
одного числового отношения из другого,
он пишет: «Для легкого способа отбра-
сывания отношения от отношения мы
требуем два числа, которые были бы не
больше и не меньше его, тогда отноше-
ние одного к другому — как одно из
двух отношений, остающихся [при от-
брасывании] из Hgro, и находится тре-
тье число: затем рассматриваем отно-
шение этого третьего числа ко второму
из двух первых чисел, которые не боль-
ше и не меньше его. Если нет отноше-
ния, то [имеем отношение] к другому;
это отношение двух неизвестных» [см.
стр. 98].
Здесь, по-видимому, аль-Фараби для
каждого из трех отношений тригономе-
трических линий старается найти опре-
деленное число и произвести арифмети-
ческие действия над этими числами. В
его обработках часто встречаем выраже-
ния «число линий», «количество вели-
чины». При этом он систематически
использует арифметические термины.
Так, в «Книге приложений», решая про-
стейшие тригонометрические и алгебра-
ические уравнения, аль-Фараби свобод-
Аль-Фараби и его обработки «Альмагеста» 21
но умножает и делит число на тригоно-
метрические линии. В связи с этим, на
наш взгляд, большой интерес представ-
ляет одна тригонометрическая теорема,
использованная им при определении
«уравнения дня», которая гласит:
«Произведение каждого числа на тан-
генс дуги равно делению этого числа на
кртангенс той же дуги» ,[6, стр. 194].
Доказательство этой теоремы требу-
ет введения единичного тригонометриче-
ского круга и рассмотрения каждой
тригонометрической линии как числа.
Идея расширения понятия числа до
положительного действительного числа
имелась потенциально в «Альмагесте»
Птолемея. По утверждению И. Г. Баш-
маковой [7], в «Альмагесте» и в грече-
ских комментариях к нему достаточно
явно выступает идея пополнения обла-
сти чисел так, чтобы каждое отношение
величин могло быть выражено числом.
Первым осуществлением этого было рас-
ширение числа до положительных ве-
щественных чисел. Птолемей применил
и вполне адекватный аналитический
аппарат для выражения этих чисел —
шестидесятеричные дроби. Аль-Фараби
в своих обработках «Альмагеста» и в
других трудах развивает это начинание
до более высокой ступени, что является
22 Аль-Фараби и его обработки «Альмагеста»
большой заслугой ученого в истории ма-
тематики и ее приложений [2, стр.
157—164]. Эти его попытки расширить
понятие числа в дальнейшем были ус-
пешно развиты аль-Бируни, Омаром
Хайямом (1048—1123) и др.
Таким образом, улучшив несколько
математический аппарат «Альмаге-
ста», аль-Фараби объясняет способы оп-
ределения дуги между равноденствен-
ным кругом и эклиптикой и восхожде-
ний на прямой сфере. Во втором случае
он значительно дополняет объяснения
Птолемея и обобщает его рассуждения
относительно восхождения в прямой
сфере на случай восхождения в наклон-
ной сфере.
Вторая книга «Комментариев» аль-
Фараби начинается так же, как у Пто-
лемея, с изложения обитаемой части
Земли вообще. Затем он, следуя Птоле-
мею, приводит способы определения по
заданной величине наибольшего дня
дуги горизонта, отсекаемой небесным
экватором и наклонным кругом, и вы-
соты полюса; далее на основании изло-
женного определяются отношения гно-
монов к полуденным теням во времена
равноденствия и солнцестояний. В по-
следнем случае в изложении аль-Фара-
би имеются некоторые улучшения в ме-
Аль-Фараби и его обработки «Альмагеста» 23
тодическом плане. В отличие от Птоле-
мея, он доказывает независимость этих
отношений от длины и положения гно-
мона. Мы полагаем, что именно это об-
стоятельство позволило ему в «Книге
приложений» определить линии танген-
сов, то есть обращенной тени гномона,
котангенса, или плоской тени гномона,
как отрезки касательных к кругу с ра-
диусом, равным гномону, т. е. 60 частям
[1, стр. 73—74].
Представлениями гномоники в даль-
нейшем успешно пользовался аль-Виру-
ни, который не только тангенс и котан-
генс, но и секанс и косеканс рассма-
тривал . в гномонике как стороны
прямоугольного треугольника; под ду-
гой круга он понимает также высоту
Солнца [8, стр. 59—60].
Далее аль-Фараби весьма бегло пе-
речисляет характерные особенности, па-
раллели, приведенные Птолемеем, и на
свой манер, лаконично излагает метод
Птолемея по определению восхождения
в наклонной сфере, включая сюда част-
ные вопросы, связанные с восходами,
способы нахождения углов, образуемых
наклонным кругом и горизонтом. Он в
ряде мест предполагает о возможном
существовании населенной части Зем-
ли и за пределами «обитаемой четвер-
24 Аль-Фараби и его обработки «Альмагеста*
ти», указанной Птолемеем: «Что каса-
ется того, какие страны и какие местно-
сти там, то, когда Птолемей писал
«Альмагест», он не знал об этом и ска-
зал: то, что говорят об этом, является
предположением. Позднее он узнал о
некоторых и включил их в [свою] «Гео-
графию» [см. стр. 114].
По-видимому, аль-Фараби сам много
размышлял над этим вопросом, что
видно из следующих его высказываний:
«Относительно широты мы не нашли
никаких обитаемых местностей, для ко-
торых при двух равноденствиях тени
гномона в середине дня были бы направ-
лены к югу. Возможно, кто-нибудь дру-
гой после нас найдет то, чего мы не
смогли найти», или в «в частности мы
говорили много по этому поводу; это
можно найти в моих книгах по естество-
знанию» [см. стр. 102,103, 114].
Следует заметить, что в своих есте-
ственнонаучных сочинениях Аристотель
также высказывал предположения о су-
ществовании на юге экватора земель,
близких по своим климатическим усло-
виям к землям северного полушария.
Таким образом, мы видим, что аль-
Фараби стоял на передовой позиции в
распределении стран по географическим
климатам. Как известно, почти все сред-
Аль-Фараби и его обработки «Альмагеста» 25
невековые ученые до него не в состоя-
нии были отойти от традиции античной
географии и считали населенной только
«Обитаемую четверть». Они предполага-
ли, в частности, что жить южнее первой
параллели, т. е. экватора, невозможно.
Позднее, как бы подтверждая предполо-
жение аль-Фараби, аль-Бируни научно
доказывает обитаемость островов у бе-
регов Африки, расположенных южнее
экватора [8, стр. 193—194].
Во второй книге аль-Фараби неодно-
кратно ссылается на «Географию» Пто-
• лемея, что подтверждает близкое его
знакомство с этим крупным географиче-
ским сочинением античности.
В комментариях к третьей книге
«Альмагеста», аль-Фараби подробно
объясняет рассуждения Птолемея о го-
довом промежутке времени. Однако он
при этом делает существенное дополне-
ние. Логически обобщая рассуждения
Птолемея по определению среднего дви-
жения Солнца, он дает универсальное
определение среднего движения планет
и приводит общий метод его нахожде-
ния. «Среднее движение — это такое
действительное или предполагаемое дви-
жение, при котором [светило] за равное
время [проходит] одинаковые [дуги].
Это движение светила по предположе-
26 Аль-Фараби и его обработки «Альмагеста»
нию происходит в соответствующей ему
небесной сфере, охватывающей Землю.
Оно свойственно или самому светилу,
или сферическому телу, несущему све-
тило и передвигающему его вдоль эк-
липтики благодаря своему движению.
За равные времена оно проходит, равные
дуги, а центральные углы при центре,
[стягиваемые] этими дугами, равны. Это
называется равномерным движением...
Среднее движение — промежуточное
между наименьшим и наибольшим [дви-
жениями] ...
Истинное движение — это такое-
движение, которое [фактически] нахо-
дится по отношению к эклиптике» [см.
стр. 156—157].
Останавливаясь далее, подробно на
методе определения среднего движения
светил, он в конце пишет: «Первое, что
требуется для определения среднего дви-
жения,— это возвращение к одной и той
же неподвижной точке или к точкам,
между которыми имеются равные дуги.
Если оно найдено, то для определения
среднего движения ограничимся этим.
В противном случае потребуем другой
род, затем третий, как будет показано
в надлежащем месте». После установле-
ния временной величины года он оста-
навливается на гипотезах Птолемея от-
Аль-Фараби и его обработки «Альмагеста» 27
носительио равномерного и кругового
движения Солнца, Луны и планет —
на гипотезе эксцентритета и гипотезе
эпицикла и доказывает три условия, при
выполнении которых наблюдаемые яв-
ления будут одинаковыми при каждой
ИЗ НИХ.
Далее аль-Фараби весьма подробно
объясняет теорию неравенств Солнца,
приведенную Птолемеем. При этом он
ш>даъц)Ждде!Гъа^кнее открытие, сделан-
ное арабскими предшественниками
(астрономами мамуновской обсервато-
рии), об изменении долготы апогея
Солнца, что является его важной заслу-
гой в теории Солнца. Он пишет: «Птоле-
мей утверждал, что апогей Солнца не-
подвижен и не перемещается. Что каса-
ется позднейших [ученых], то наблю-
дения, проведенные во времена Мамуна
тем же методом, показали, что апогей
Солнца отклоняется от места, указан-
ного Гиппархом, по отношению к дви-
жению неподвижных звезд. Это же ус-
тановили и мы по своим наблюдениям,
произведенном после [начала] сочине-
ния этой книги» [см. стр. 194].
Последнее свидетельство аль-Фараби
показывает, что он был и превосходным
практиком-наблюдателем.
Как известно, в данном вопросе Пто-
28 Аль-Фараби и его обработки «Альмагеста»
лемей допустил ошибку: он принял не-
изменной долготу апогея Солнца. На
самом деле она постепенно увеличивает-
ся, что впервые было установлено сред-
неазиатским астрономом Халидом аль-
Мервурриди, участвовавшим в истори-
ческом измерении величины Земли в дни
Халифа аль-Мамуна (IX в.). Правиль-
ность такого предположения, на наш
взгляд, подтверждается данными аль-
Бируни в «Каноне Мас’уда», где он при-
водит результаты Халида аль-Мервур-
риди и других измерений долготы
апогея Солнца [8, стр. 107—108] и при-
веденным свидетельством аль-Фараби.
Следует отметить, до сих пор в ли-
тературе это открытие приписывалось
аль-Баттани (850—929), что не совсем
точно.
После изложения принципа состав-
ления таблиц неравенства Солнца на от-
дельных участках эклиптики аль-Фара-
би комментирует рассуждения Птоле-
мея об эпохе среднего движения
Солнца, о неравенстве суток.
В комментариях к четвертой книге
«Альмагеста» аль-Фараби излагает со-
держание глав о том, на каких наблю-
дениях следует строить теорию движе-
ния Луны, о периодах лунных движе-
ний, о частных значениях средних
Аль-Фараби и его обработки «Альмагеста» 29
движений Луны. Затем, следуя за Пто-
лемеем, он доказывает положение о том,
что при простой гипотезе о движении
Луны, будь она гипотезой эксцентритета
или эпицикла, видимые явления будут
одинаковыми. Перед определением пер-
вого и простого лунного неравенства аль-
Фараби вносит важное дополнение к
Птолемею. Прежде чем предложить спо-
соб определения первого и простого не-
равенства Луны, он приводит предпо-
сылки, которые служат теоретико-мето-
дической базой в нахождении положе-
ния Луны и ее аномалии через наблюде-
ние в двух группах по три затмения,
приведенные в дальнейшем Птолемеем.
Аль-Фараби указывает на третье не-
равенство Луны, которое возникает за
счет движения Луны не по эклиптике,
а по собственной орбите. Он правильно
полагает, что Птолемей не учитывал его
из-за малой широты Луны.
После этого аль-Фараби, следуя Пто-
лемею, подробно объясняет способ опре-
деления первого и простого лунного не-
равенства и вкратце излагает содержа-
ние глав, посвященных исправлению
движений Луны по долготе и аномалии
и их’ эпохе, исправлению движений Лу-
ны по широте и их эпохе; затем оста-
навливается на том, что разница в при-
80 Аль-Фараби и его обработки «Альмагеста»
f ЛА-ЭД taif й<.«* «я»4Ъ
f
«WissSiM? • < <^;:; : ; Ж< ‘
Страницы 11—12 рукописи „Ком
Аль-Фараби и его обработки «Альмагеста» 31
ментарии к «Альмагесту»".
32 Аль-Фараби и его обработки «Альмагеста»
нятой Гиппархом величине лунного не-
равенства получается не от различия
сделанных предположений, а вследствие
вычисления.
Комментарии к пятой книге аль-Фа-
раби, как и Птолемей, начинает с описа-
ния устройства армиллярной сферы, за-
тем излагает гипотезу для объяснения
двойного неравенства Луны. После это-
го он переходит к определению величи-
ны Луны, зависящей от положения от-
носительно Солнца, и величины отноше-
ния для эксцентритета лунного круга.
Более подробно он комментирует гла-
вы, посвященные наклонности эпицикла
Луны. Затем он объясняет принцип сос-
тавления таблиц для полных нера-
венств Луны, не приводя самих таблиц
(по своей установке) и способ вычисле-
ния движения Луны в целом.
После доказательства положения
Птолемея о том, что эксцентрический
круг не производит никакой заметной
разницы в сизигиях, аль-Фараби объяс-
няет параллаксы Луны и переходит к
определению расстояний Луны и вели-
чин видимых диаметров Солнца, Луны
и земной тени в сизигиях. При опреде-
лении расстояния Солнца он доказыва-
ет предпосылку о том, что длина сред-
ней линии трапеции равна полусумме
Аль-Фараби и его обработки «Альмагеста» 33
длин ее мяований, которая отсутствует
;-в «Ая»Магеств»> но на эту теорему Пто-
ЛеявейЬ ссылается, считая ее известной;
в «Началах» Евклида этого предложе-
ния нет.
После объяснения содержания гла-
вы о частных значениях параллаксов
Солнца и Луны аль-Фараби останавли-
вается на составлении таблиц параллак-
сов и определении величины параллак-
тического смещения Луны для любого
ее положения. Здесь он делает Птолемею
существенное дополнение, методического
характера.
В этой книге на основе метода Пто-
лемея вычисления числовых значений
параллаксов он делает, на наш взгляд,
важное обобщение: открыто вводит по-
нятие «число линии» в единицах вы-
бранного отрезка линии. Это является
важным шагом в развитии понятия дей-
ствительного числа.
В комментариях к шестой книге
[6, стр. 97—116] аль-Фараби сначала
останавливается на описании таблиц
средних сизигий и определении перио-
дических и истинных сизигий, после
чего излагает содержание глав, посвя-
щенных затмениям Солнца и Луны, про-
межуткам между ними, а также состав-
лению таблиц затмений. Он дает разъ-
3-89
84 Аль-Фараби и его обработки «Альмагеста»
яснение методам вычисления лунных и
солнечных затмений, вносит добавле-
ние Птолемея, рассматривая случай,
когда Луна расположена на экваторе
[6,стр. 113].
В комментариях к седьмой книге
«Альмагеста» [6, стр. 116—118] аль-
Фараби в очень сжатой форме излагает
сведения Птолемея о том, что неподвиж-
ные звезды всегда сохраняют одно и то
же положение по отношению друг к
ДРУГУ» говорит о движении сферы не-
подвижных звезд и его направлении, а
также о способе составления каталога
неподвижных звезд.
В девятой книге „Комментариев”
[6, стр. 122—152] аль-Фараби в отли-
чие от Птолемея, рассмотревшего в от-
дельности теорию движения каждой из
пяти планет — Меркурия, Венеры, Мар-
са, Юпитера и Сатурна,— излагает их
аналогичные свойства по возможности
параллельно (суммарно). Таким обра-
зом, в этой книге отражено содержание
девятой, десятой и одиннадцатой книг
«Альмагеста» Птолемея.
В связи с этим следует заметить, что
и в знаменитом трактате Н. Коперника
«О вращениях небесных сфер» теория
движения планет рассматривается в
основном только в пятой книге, тогда
Аль-Фараби и его обработки «Альмагеста» 36
как каждой из теорий движения Солн-
ца и Луны посвящена самостоятельная
книга [0}«
АЛЬ-Фараби сначала излагает по-
следовательность расположения сфер
Солнца, Луны и пяти планет, периоди-
ческого возвращения этих планет. За-
тем он останавливается на основных по-
ложениях гипотез о пяти планетах и на
характере их различия. После этого
приводит способы определения апогеев
Меркурия, Венеры и их перемещения.
Здесь же изложены методы нахождения
отношения эксцентритетов и эпициклов
Меркурия и Венеры, а затем разъясня-
ется рассуждение Птолемея о том, что
планета Меркурий в течение одного обо-
рота дважды становится в ближайшем к
Земле положении. Аль-Фараби здесь же
излагает методы исправлений периоди-
ческих движений Меркурия и Бенеры и
переходит кг рассмотрению теории дви-
жений остальных трех планет на осно-
ве эксцентрической гипотезы. Он дает
метод определения трех верхних пла-
нет — Марса, Юпитера и Сатурна, а
также определяет величины их эпицик-
лов, после чего переходит к изложению
способа исправлений периодических
движений указанных планет. Далее он
останавливается на том, каким образом
36 Аль-Фараби и его обработки «Альмагеста»
по периодическим движениям определя-
ются геометрически истинные положе-
ния планет, а также на принципе состав-
ления таблиц их аномалий. Книга
заканчивается кратким изложением спо-
соба вычисления долготы пяти планет.
В комментариях к двенадцатой кни-
ге «Альмагеста» [6, стр. 152—166] аль-
Фараби сначала рассматривает предва-
рительные положения, касающиеся пря-
мых и попятных движений каждой из
пяти планет — Сатурна, Юпитера, Мар-
са, Венеры и Меркурия, затем вкратце
останавливается на построении таблиц
противостояний планет и приводит ме-
тод определения наибольших отклоне-
ний Венеры и Меркурия от Солнца.
В комментариях к последней, три-
надцатой книге «Альмагеста» [6, стр.
203—214] аль-Фараби рассматривает
следующие вопросы: гипотезы относи-
тельно движения пяти планет по широ-
те; характер изменений и величина ин-
клинаций и обликваций для каждой
планеты; составление таблицы для от-
дельных движений по широте пяти пла-
нет; о том, что особенности восходов
Венеры и Меркурия согласуются с при-
нятыми гипотезами; метод определения
расстояний планет от Солнца.
В приложении к «Комментариям»
АЛь-ФАраби й его обработки «Альмагеста» 37
[6, стр. 214—218] для облегчения не-
которых задач математической астроно-
мии приведено доказательство предло-
жения, заменяющего «Теорему о секу-
щих», которое эквивалентно теореме
синусов для сферического прямоуголь-
ного треугольника.
Забегая несколько вперед, скажем,
что аль-Фараби в «Книге приложений»
одним из первых в истории математики
доказывает как самостоятельное пред-
ложение и теорему тангенсов для прямо-
угольного сферического треугольника.
Открытия часто приписывались Абу-л-
Вафе. Правда, частные случаи этих тео-
рем рассматривались и в «Альмагесте».
Например, сферическая теорема сину-
сов в виде приема решения конкретной
задачи использовалась в 14 главе I кни-
ги «Альмагеста», а сферическая теорема
тангенсов — аналогично в 16 главе [10,
стр. 552—553].
Птолемей не рассматривает их как
математические теоремы и поэтому,
естественно, не дает их непосредствен-
ного доказательства.
Эти открытия аль-Фараби и других
ученых Востока сыграли чрезвычайно
важную роль в формировании тригоно-
метрии как отдельной отрасли матема-
тики.
38 Аль-Фараби и его обработки «Альмагеста»
В самом конце «Комментариев» име-
ется отметка, из которой видно, что она
переписана в 628 г. хиджры, в послед-
ней десятидневке месяца Рамазана, в
г. Дамаске. Эта дата по современному
летоисчислению соответствует послед-
ней декаде июля 1231 г.
Комментарии аль-Фараби к «Альма-
гесту» сыграли важную роль в освоении
восточными учеными наследия Птоле-
мея. Свидетельством этого является тот
факт, что Ибн Сина целиком включил
их в астрономический раздел своей эн-
циклопедии «Книга исцелений». Следу-
ет отметить, что аль-Фараби был авто-
ром не дошедшего до нас большого
энциклопедического труда «Второе уче-
ние» (от-Та'-лим ас-сани), состоявшего
из двадцати частей. Структура этого со-
чинения, по-видимому, близка к струк-
туре указанного энциклопедического
труда Ибн Сины, который средневеко-
вые историки науки рассматривали как
сокращение «Второго учения». Большая
близость между „Комментариями к
«Альмагесту»” аль-Фараби и астрономи-
ческой частью «Книги исцеления» поз-
воляет предположить, что эти «Коммен-
тарии» наряду с «Большой книгой му-
зыки» и сводом логических сочинений
представляют собой сохранившиеся ча-
Аль-Фараби и ei*o обработки «Альмагеста» 39
сти (обрывки) этого грандиозного энци-
клопедического произведения аль-Фа-
раби [2, стр. 16].
Другой трактат аль-Фараби, связан-
ный с «Альмагестом», как мы уже вы-
ше отмечали, носит название «Книга
приложений». Это подлинный арсенал
формул тригонометрии и математиче-
ской астрономии. В нем автор еще более
математизирует содержание «Альмаге-
ста», все задачи решаются чисто геоме-
тро-алгебраическими средствами. Имен-
но здесь (26 глава) он одним из первых
выделяет и доказывает как особые
предложения сферические теоремы си-
нусов и тангенсов для прямоугольного
треугольника. При этом аль-Фараби по-
стоянно прибегает к своеобразной со-
кращенной записи данных и хода ма-
тематических рассуждений.
«Книга приложений» состоит из
глав, каждая из которых, как правило,
освещает один конкретный вопрос, по-
священный решению в общем виде той
или иной задачи астрономии и геогра-
фии. Главы оформлены в виде геометри-
ческих предложений наподобие «На-
чал» Евклида.
В сохранившихся главах «Книги
приложений» (она обрывается на 59
главе, в рукописи отсутствуют некото-
40 Аль-Фараби и его обработки «Альмагеста»
рые главы), кроме чисто тригонометри-
ческих вопросов (первые 14 глав), рас-
сматривается ряд основных проблем
математической астрономии и матема-
тической географии, такие, как опреде-
ление уравнения Солнца, первого и вто-
рого уравнения Луны; изучение изме-
нения видимого радиуса эпицикла
Луны и планет; вычисление пропорцио-
нальных минут для таблиц небесных
светил; нахождение первого уравнения
Меркурия; определение первых уравне-
ний других планет, широты Луны, пер-
вого склонения, прямого восхождения,
второго склонения, широты местности,
расстояния (азимута) восхода, высоты
светил по данному азимуту и азимута
по высоте, уравнения дня, восхождения
в данной местности, предела высоты
Солнца и других светил, половины дуги
дня Солнца, затмений Луны и Солнца,
определение расстояния Луны от Земли
и параллакса Луны и др.
Аль-Фараби в этом труде свои мате-
матические достижения применяет для
решения конкретных задач астрономии
в основном через решение различных
плоских и сферических треугольников.
Если Птолемей ограничивался рассмо-
трением частного случая решения за-
дач, то аль-Фараби его как бы обобщает.
Аль-Фараби и его обработки «Альмагеста» 41
Новизна применяемых при этом ма-
тематических методов аль-Фараби со-
стоит как в широком применении триго-
нометрических функций на основе'рас-
ширения понятия числа, так и в общем
подходе к решению поставленных задач.
Он, по существу, решает ряд простейших
алгебраических и тригонометрических
уравнений, полученных с помощью гео-
метрических и тригонометрических от-
ношений между линиями и углами в
круге, при этом в изобилии оперирует
различными сложными функциями сфе-
рической астрономии, которые выража-
ются в виде комбинаций основных три-
гонометрических функций.
Некоторые сведения о содержании
этого труда можно получить в работе
[2]. Приведем лишь один пример, кото-
рый демонстрирует творческое отноше-
ние ученого к астрономо-математическо-
му наследию Птолемея.
На основе установленных функцио-
нальных зависимостей между вторыми
уравнениями Луны и планет, с одной
стороны, и углами, взятыми в качестве
аргументов,— с другой, аль-Фараби по-
строил свою теорию интерполяции таб-
лиц движения светил. В этой теории
важное значение имеет метод определе-
ния так называемых пропорциональных
42 Аль-Фараби и его обработки «Альмагестй»
минут, для нахождения которых он
предлагает ряд правил. Показывая на
конкретных примерах практику вычис-
лений этих коэффициентов, он пишет:
«Вот это мы получили на основании то-
го, что было в «Альмагесте», и того, что
мы сами приводили на основании дока-
зательств и вычислений. Что касается
таблиц, то в них получаются некоторые
расхождения между данными вычисле-
ний о величине разности при макси-
мальном и минимальном расстояниях и
[наблюденными] положениями светил в
этих граничных местах. Это расхожде-
ние заметнее и больше для Марса, а
для пяти планет меньше. Я не знаю при-
чину этого» [6, стр. 170].
Здесь аль-Фараби, по-видимому, сом-
невается в правильности принципов, на
которых были построены указанные
таблицы. Тем самым он как бы ставит
вопрос об истинных причинах кажуще-
гося положения явлений, связанных с
движениями небесных светил. Нельзя
не отметить также обнаруженный им
факт более резкого расхождения дан-
ных теории и наблюдений относительно
описания движения Марса, так как
именно эти предельные уклонения в
долготах и радиусах-векторах Марса бы-
ли одним из тех самых источников, из
Аль-Фараби и его обработки «Альмагеста» 43
которых выросла (спустя 700 лет после
аль-Фараби) благодаря знаменитым ис-
следованиям Кеплера теория истинного
эллиптического движения планет. Это
открытие аль-Фараби вполне согласует-
ся с постулатом об условности и относи-
тельности знания о Вселенной и показы-
вает правильность и плодотворность его
методологической установки об экспе-
риментально-математическом изуче-
нии природы.
Как было отмечено, „Комментарии
к «Альмагесту»” и «Книга приложений»
аль-Фараби изучаются впервые. Однако
уже предварительное сравнение их со-
держания с «Альмагестом» Абу-л-Вафы
позволяет определенно высказать пред-
положение о преемственной связи в
этих трудах и влиянии аль-Фараби на
астрономическое творчество великого
хорасанского ученого. Наши исследова-
ния позволяют высказать гипотезу о
том, что многие формулы «Книги при-
ложений» служили основой, математи-
ческим аппаратом знаменитых таблиц
астрономической школы Улугбека [11,
стр. 156—274].
Несомненно, что обработки аль-Фа-
раби «Альмагеста» еще не раз будут
предметом изучения у историков средне-
вековой науки. Наши исследования мы
44 Аль-Фараби и ei'o обработки «Альмагеста*
считаем первым шагом в освоении
довольно богатого астрономического на-
следия мыслителя. Однако уже приве-
денный обзор трактатов астрономиче-
ского содержания аль-Фараби показыва-
ет, что он был не только крупным тео-
ретиком астрономии своей эпохи, но и
превосходным практиком-наблюдате-
лем, сыгравшим большую роль в разви-
тии астрономии средневекового Востока.
Наш перевод осуществлен по ука-
занному выше единственному списку
„Комментариев к «Альмагесту»”. В дан-
ном издании включены первые пять
книг «Комментариев». В примечаниях
широко привлечены выдержки из само-
го «Альмагеста», в частности, приведе-
ны все математические и астрономиче-
ские таблицы. При этом мы воспользо-
вались неопубликованным переводом
«Альмагеста» с греческого на русский
язык профессора И. Н. Веселовского.
Из-за отсутствия русского издания это-
го классического сочинения естествозна-
ния древности считаем, что такой мате-
риал будет для читателей небесполез-
ным.
Весьма возможны неточности и раз-
ночтения при переводе, допущенные
из-за плохого состояния рукописи, а так-
Аль-Фараби и его обработки «Альмагеста» 45
же из-за недостаточной квалификации
переводчиков.
В переводе арабских буквенных обо-
значений в тексте и при чертежах мы
придерживались общепринятой в Совет-
ском Союзе транскрипции арабского ал-
фавита. В случае пропусков в тексте или
при необходимости добавления слов для
лучшего понимания эти слова помеща-
ются в квадратных скобках, а таблицы
из «Альмагеста» выделены мелким
шрифтом. На полях перевода отмечены
страницы упомянутой рукописи из фон-
да Британского музея.
КОММЕНТАРИИ К «АЛЬМАГЕСТУ» 1
[Введение]
1 /Во имя Аллаха милостивого и ми-
лосердного! Слава Аллаху — господину
всех миров; да благословит он своего
пророка Мухаммеда и весь его род!
Мы теперь в состоянии изложить все
части созданной великим Птолемеем 2
книги «Альмагест»3 об астрономиче-
ской науке. При этом мы будем следо-
вать его словам, его методу, за исключе-
нием редких случаев, где излагаются
некоторые способы, предложенные на-
шими современниками. Паши [собствен-
ные исследования] приведены в «Книге
приложений» 4. Мы старались сделать
содержание этого сочинения по воз-
можности более понятнымб, поэтому
опустили в его предложениях вычисле-
ния и разъясняем только доказательст-
ва предложений. Желающий может
АЛЬ-ФАРАБИ
47
проверить эти вычисления. Мы не будем
упоминать даты каждого наблюдения, а
ограничимся указанием [промежутков
времени] между каждыми двумя на-
блюдениями. Что касается таблиц, то
кто хочет поместить их в нашей книге,
пусть так и сделает, а если захочет,
пусть сократит их. Мы решили не повто-
рять многократно предложения, одина-
ковые для нескольких светил, так как
между ними много общего как в мате-
матическом, так и астрономическом от-
ношении. В «Альмагесте» они повторя-
ются, потому что их вычисления
различны. Пусть Аллах даст успех и
поддержку!
Я прошу людей науки простить
[мои] неточности и заполнить пробелы.
Аллах исправляет лучше всех, слава
ему во всех случаях, да благославит он
наиблагого пророка и приветствует сво-
их избранных рабов.
48
Введение
Титульный лист „Комментариев
к «Альмагесту»
ПЕРВАЯ КНИГА6
Посвящена 7 нескольким положениям 8
О том, что небо имеет сферическую
форму и сферическое движение
Подтверждением сферичности этого
движения является восход и заход не-
подвижных звезд. Они действительно
восходят на востоке, затем поднимают-
ся вверх над нами до тех пор, пока не
достигнут зенита9, затем начинают
опускаться в сторону запада до тех пор,
пока не достигнут горизонта, и исчеза-
ют. Затем они возвращаются точно к тем
местам, где восходили. При этом мо-
менты восхода и захода в общем одни
и те же.
Далее, если мы направимся в сторо-
ну севера и юга, то окажется, что то,
что было скрыто от нас, теперь совер-
шенно не скрывается, а то, что не было
скрыто, скрывается постоянно или на
время. Если мы пойдем дальше, то уви-
дим больше того, что было скрыто, а с
другой стороны будет наоборот. Чем
4—89
БО
АЛЬ-ФАРАБИ
медленнее заходит какая-нибудь из этих
звезд, тем больше ее дуга дня и тем бы-
стрее зайдет [звезда], противоположная
этой звезде, и тем меньше ее дуга дня.
Каждый раз, когда появляется что-то
из того, что было скрыто, исчезает про-
тивоположное ему из того, что было
видно, и становится невидимым. Если
мы приблизимся к полюсу, к которому
мы направлялись, и [будем наблюдать]
все, что имеется там, то мы дойдем до
места, где [звезды] или всегда видны,
или всегда скрыты. Мы увидим, что те
[звезды], которые не скрываются, вра-
щаются около полюса. Чем ближе [звез-
да] к [полюсу], тем уже ее орбита и
медленнее ее вращение в соответствии с
узостью ее орбиты. Все звезды проходят
свои круги за один и тот же [промежу-
ток времени], эти круги параллельны.
Все это наблюдается при круговом дви-
жении. Полюсы этого [движения] — в
стороне нахождения вечно видимых
звезд. Если бы это движение не было
таким, то все расстояния между звезда-
ми и их величины не было бы одинако-
выми по видимости во всех частях
Земли.
/Причиной увеличения этих величин,
которое мы наблюдаем при восходе и
заходе, является влажный водяной пар,
Первая книга
51
окружающий Землю и находящийся
между [нашими] глазами и этими звез-
дами. Все, находящееся за этой средой,
кажется большим. По этой же причине
предметы в воде кажутся большими,
причем чем глубже, тем они больше.
Подтверждением правильности ука-
занного положения служит несостоя-
тельность других мнений: например
тех, кто считает, что звезды движутся
по прямой до бесконечности. Интересно
знать, как они вернутся снова по пря-
мой со стороны востока. Если же они
возвращаются с той [стороны], куда
уходят, почему же этого не видно? По-
чему же их размеры и расстояние меж-
ду ними не уменьшаются, когда их рас-
стояние от нас увеличивается, а остают-
ся неизменными и кажутся больше при
заходе? Мнение, состоящее в том, что
[звезды] загораются и гаснут и что они
загораются в одних местах, а гаснут в
других, нелепо, так как оно приписыва-
ет благородным [небесным] телам не-
свойственные им качества и к тому же
предполагает, что одна и та же вещь то
загорается, то гаснет в зависимости от
места нахождения, поскольку звезды,
видимые некоторым народам, скрыты от
других. На это указывают и наблюде-
ния над Затмениями Луны,
52
АЛЬ-ФАРАБИ
Наблюдением над затмением Луны
установлено, что в некоторых странах
это [затмение] произошло после ее вос-
хода, в других — что она взошла затем-
ненной, а в третьих, что [затмение
произошло] до восхода [Луны] и она
взошла уже ясной. Аналогичное наблю-
дение было произведено при заходе [Лу-
ны]. Почему же она должна загораться
в одних местах и гаснуть в других? По-
чему звезды, которые постоянно видны
у некоторых народов, всегда загораются
у них, а у других гаснут?
Правильность нашего мнения под-
тверждает совпадение трех наблюдений,
говорящих об одном центре. Эти [на-
блюдения] согласуются с формой, то
есть с тем, что небосвод сферичен. Оче-
видно, что эта форма наиболее подходя-
щая для быстрого кругового движения.
Она охватывает максимальный [объем]
и наиболее удобна для самого большого
тела. Поскольку небосвод — это простое
тело с подобными частями, одна и та же
природа не может сделать в нем угол
или в одной его части создать кривизну,
а в другой нет. Все его части должны
быть подобны по своей природе. Это мо-
жет быть только на сфере. Только сфера
может иметь сечения, подобные между
собой.
Первая книга
63
Светила [также] заставляют наблю-
дателя убедиться в том, что сущность
[небосвода] такова: светила сферичны,
так как если бы они были плоскими или
имели бы поверхности формы, отличной
[от сферы], то они выглядели бы разны-
ми по форме на различном расстоянии
от наблюдателей. Поэтому окружающий
их небосвод имеет их форму.
Он сказал : среднее из этих доказа-
тельсгв-— самое надежное.
О том, что Земля сферична по виду
На сферичность Земли нам указыва-
ет опережение и запаздывание восхода
восходящих и захода заходящих
[звезд] у жителей стран, расположен-
ных по долготе, а также видимость веч-
но видимых и невидимость вечно неви-
димых звезд у жителей стран, протяжен-
ных по широте. Все это происходит
из-за сферичности [Земли]. Положение
с долготой выясняется по лунным зат-
мениям, а положение с широтой — по
звездам двух полюсов.
3 /Если бы Земля была вогнутой, то
звезды сначала восходили бы на западе
и запаздывали на востоке, а это не
так. Установлено, что затмения Луны
[происходили] на востоке в более позд-
54
АЛЬ-ФАРАБИ
ние часы ночи, а на западе — в более
ранние. Эта разница [во времени] полу-
чается благодаря сферичности Земли.
Если бы она была плоской, то восход
и заход происходили бы одновременно
[для всех местностей], с некоторым от-
клонением в горных и- возвышенных
районах.
Если бы Земля была граненой с плос-
кими гранями, не позволяющими ей
быть сферичной в целом по виду, то
восход и заход происходили бы для од-
ной грани в один и тот же час и значи-
тельно отличались бы для различных
граней. Если же грани не очень влияют
на сферичность в целом, то наблюдается
запаздывание времени затмений и их
опережение в местностях различной
долготы с Востока на Запад благодаря
сферичности Земли. Точно так же об-
стоит дело с восходами и заходами
звезд; они не согласуются ни с [положе-
нием] одной плоскости, ни с [положе-
нием] многих плоскостей.
Земля не может иметь цилиндриче-
ской формы, при которой ее поверх-
ность выпукла по долготе с востока на
запад и имеет две плоские поверхности
у полюсов. В этом случае восход и за-
ход неподвижных звезд одновременно
наблюдали бы все люди, живущие у
Первая книга
65
одного полюса, скрытые или видимые
[звезды] были бы одними и теми же
для них, и население круглой поверхно-
сти не могло бы видеть ничего из вечно
видимых звезд.
Положение с запада на восток будет
таким же, как с севера на юг, так что
рассуждения должны быть одними и
теми же для всех направлений.
Поверхность воды в море также
сфернчкк' Так, если мы будем плыть
по морю, а на каком-то расстоянии от
нас будет находиться гора, то первое,
что будет видно с нее — это вершина,
затем начнет появляться то, что ниже
ее вершины и было скрыто до этого.
Только горб воды мог скрывать его.
О том, что Земля находится неподвижно
в центре [мира]
Он сказал: если Земля не находи-
лась бы неподвижно в самой середине
[мира], то она была бы расположена на
равных расстояниях от обоих полюсов
вне оси; или же она должна была бы
находиться на оси и отклонена к одно-
му из полюсов, или же она должна
была бы находиться вне оси и отклоне-
на к одному из полюсов. Если бы имело
место первое, у жителей экватора день
56
АЛЬ-ФАР АВИ
и ночь никогда не были бы равны, так
как плоскость горизонта в этом случае
никогда не делила бы небесный свод
пополам. Что касается другого климата,
то этого равенства не будет, когда Солн-
це находится в поясе первого движения,
то есть на небесном экваторе 10, так как
различные горизонты и эклиптики не
делят [друг друга] пополам и равенство
не будет иметь место в двух точках пе-
ресечения эклиптики 11 и небесного эк-
ватора, которые мы упомянем ниже; это
произойдет на другом круге, параллель-
ном небесному экватору к северу или к
югу от него. Поэтому верхняя дуга
каждого из параллельных кругов не
будет равна нижней дуге противопо-
ложного ему [круга], имеющего такое
же расстояние от небесного экватора.
Поэтому день одной из этих дуг не
будет равен ночи другой. Действитель-
ность противоречит этому. [В этом слу-
чае] в местностях, отклоненных к вос-
току или к западу [друг от друга], вре-
мя между восходом и приходом в зенит
не будет равно времени между прихо-
дом в зенит и заходом, и размеры и рас-
стояния* [светил] нельзя видеть одина-
4 ковыми во всех местах/.
Что касается второго случая, то, ес-
ли бы он был, следовало бы, что гори-
Первая книга
S7
зонт делит [небесную] сферу пополам
только при прямой сфере, а в местно-
стях, отклоненных к одному из двух
полюсов, дуги будут различны: дуга,
примыкающая к этому полюсу, мень-
ше, а примыкающая к противоположно-
му [полюсу] — больше. Чем ближе мы
подходим к полюсу, тем малая дуга
меньше, а большая дуга больше. Если
же мы окажемся около полюса, то верх-
няя дуга, отсекаемая горизонтом, будет
наименьшей из всех дуг [круга], а ниж-
няя — наибольшей. Однако дело об-
стоит не так: во всех странах и во всех
местностях небесный свод делится по-
полам и всегда видно шесть знаков
Зодиака. Горизонт будет пересекать
эклиптику, делясь ею пополам, и эк-
липтика будет делиться им [также по-
полам] , и если соединить эти две части,
то получится целый [круг].
Если бы Земля не находилась под
небесным экватором, являющимся по-
ясом Вселенной, делящим ее пополам
параллельными [горизонту кругами],
то тени гномонов на востоке и на запа-
де во время равноденствий не были бы
на одной и той же линии на плоскостях,
параллельных горизонту. Поэтому, если
бы Земля была отклонена от центра, уве-
личение и уменьшение дней [и ночей]
58
АЛЬ-ФАРАБИ
были бы не такими, каковы они в дей-
ствительности, а Луна никогда не за-
тмевалась бы всякий раз, когда она диа-
метрально противоположна Солнцу.
О размерах Земли относительно
[небесной] сферы
Если бы размеры Земли не были бы
неощутимыми по сравнению с небом так
же, как [размеры] центра [круга] по
сравнению с его окружностью, и если
бы она имела ощутимые [размеры], то
расстояния между звездами и их вели-
чины не ощущались бы одними и теми
же, когда они [находятся] в середине
неба или у горизонта, потому что их
приближение, т. е. нахождение в середи-
не неба, приводило бы к их увеличе-
нию, а удаление — к уменьшению; но
дело обстоит не так, поскольку в таком
случае применение инструментов для
наблюдений на поверхности Земли, а
не в самом центре привело бы к ощути-
мым расхождениям, и положения, осно-
ванные на этих наблюдениях, не были
бы правильными; и скрытая [часть]
небесной сферы была бы больше ви-
димой в соответствии с величиной ра-
диуса Земли, так как истинная середи-
на [Вселенной] — это плоскость, разде-
Первая книга
69
ляющая Землю пополам, а не плоскость,
проведенная через глаз. Если же разме-
ры Земли относительно [небесной] сфе-
ры малы, то эти [две части] как бы
совпадут друг с другом и будут видны
приблизительно шесть знаков Зодиака.
О том, что Земля не имеет
поступательного движения
Поступательное движение опровер-
гается тем же [рассуждением], которым
мы опровергли отклонение от центра.
Если бы она обладала прямым движени-
ем вверх, вниз или вбок, то ее частицы
никогда не могли бы примыкать к ней
с противоположной стороны. Стран-
ность, состоящая в том, как может тя-
желое [тело] удерживаться на одном
месте и не падать, отпадает, так как мы
знаем, что верх — это всегда сторона
неба, а низ — всегда сторона центра
[Земли]. Вселенная не имеет ни верх-
ней, ни нижней стороны, поскольку все
[части] сферы одинаковы. Центр Все-
ленной — предел движения тяжелого
[тела], а ее горизонт и сторона неба —
это предел движения легкого [тела].
Все частицы Земли стремятся к центру
по направлениям, перпендикулярным к
60
АЛЬ-ФАРАБИ
* ‘ ' *.х*
?
Ц*ч
< v- г •’W*’* 'wr^'- ^Г^тИТ^^у^т^1’’ •"‘•’W’ ^^МГ’УМЧН'
f' :
Страницы 1—2 рукописи
Первая книга
61
„Комментарии к «Альмагесту»”.
62
АЛЬ-ФАРАБИ
поверхности Земли; они таковы по сво-
ей природе.
Что же касается кругового движе-
ния Земли вокруг себя, то некоторые
люди утверждали, что небесный свод
неподвижен, а Земля движется в сторо-
ну востока и поэтому кажется, что не-
бесная сфера движется, а светила восхо-
дят. Некоторые считают, что оба эти
тела движутся, но в противоположных
направлениях.
Рассмотрев эти суждения, Птолемей
выразил удивление по поводу того, что
предельно тяжелым вещам / приписыва-
ется быстрое движение; он говорит: ес-
ли бы Земля имела подобное движение
в [сторону] востока в отличие от [дру-
гих] физических тел, то было бы необ-
ходимо, чтобы никакая вещь, которая
летит или которую толкнули или броси-
ли, не могла опередить ее; поэтому все
вещи отставали бы [от нее] и среди них
не было бы видно ничего, движущегося
на восток.
Если скажут, что воздух также дви-
жется вместе с Землей и имеет подобное
движение, то это невозможно. Если бы
это было верно, то было бы необходимо,
чтобы все находящиеся в воздухе тела,
стремящиеся вниз, двигались бы мед-
леннее Земли и воздуха. Тогда не было
Первая книга
63
бы видно ничего из вещей, движущихся
в воздухе на восток, напротив, они по-
стоянно отставали бы в направлении за-
пада. Вещи в воздухе не прилипают к
нему, не сцепляются с ним и не движут-
ся вместе с ним, иначе они в воздухе не
двигались бы ни вперед, ни назад и не
колебались.
Если бы Земля обладала подобным
движением, то тяжелые вещи падали
бы не вертикально, а с отставанием. Все
это то, что он сказал. Мы уже доказали
невозможность такого движения для
Земли в «Физике» ,2.
Речь о том, что Вселенная имеет
одно общее движение
Он сказал: так как мы видели, что
светила, особенно неподвижные звезды,
восходят на востоке и заходят на запа-
де и затем возвращаются через каждые
сутки, причем расстояния между ними
остаются неизменными, а круги, описы-
ваемые их движением, параллельны, то
нам ясно, что все они имеют одно общее
движение, являющееся движением Все-
ленной ,3. Пояс этого единого движе-
ния — небесный экватор, а остальные
круги параллельны ему. Небесный эква-
тор называемся равноденственным [кру-
64
АЛЬ-ФАРАБИ
гом], потому что если Солнце окажется
в какой-либо точке этого круга, то день
и ночь для всех местностей равны.
Что касается других светил, таких
как Солнце, Луна и планеты, то они не
сохраняют своих расстояний до непо-
движных звезд, а всегда запаздывают
на востоке и движутся не по параллель-
ным, а по различным [кругам], пересе-
кающим параллельные с севера и юга
стороны в определенных соотношениях
и порядке14. Если рассмотреть непо-
движные [звезды], то, как выясняется
позже, они также кажутся запаздываю-
щими на востоке по линиям, параллель-
ным эклиптике, [по которой движется]
Солнце 15.
Далее мы должны различать первое
движение с запада от движения с вос-
тока, противоположного ему. Из того,
что мы сказали, необходимо, чтобы оно
проходило по наклонным кругам, пере-
секающим пояс первого движения. Сле-
довательно, имеются два пояса: наклон-
ных кругов и небесного экватора. Пояс
наклонных [кругов] — сфера неподвиж-
ных [звезд] и круг эклиптики Солнца,
как мы выясним позже 1в. Первая из
двух точек пересечения эклиптики Солн-
ца с небесным экватором называется
весенней. Если Солйце пройдет через
Первая книга вб
нее, то начинается весна. Вторая из
этих двух точек осенняя, так как в ней
[происходит] осеннее равноденствие.
Если через два полюса эклиптики и
пояс первого движения провести круг,
пересекающий их, то этот круг рассечет-
ся на две дуги — северную и южную,
определяющие расстояние наклонения;
на эклиптике определяются две точ-
ки — северная и южная. Северная —
это точка летнего солнцестояния, так
как, когда Солнце достигает ее, начи-
нается лето для всей обитаемой [части
Земли], которая нам известна. Южная
6 точка — точка зимнего солнцестояния/.
Планеты, Солнце и Луна видны вос-
ходящими и заходящими вместе с не-
подвижными [звездами], поэтому ясно,
что первое движение охватывает и вто-
рое движение и применяется к [телам]
второго движения вместе с [телами]
собственного движения.
Неподвижные звезды движутся не
только на запад. Должно существовать
другое движение, охватывающее всю
Вселенную и применимое ко всем те-
лам, а не только к светилам.
Что же касается того, что это дви-
жение не является собственным [дви-
жением] неподвижных звезд, а также
планет, то это потому, что они очень
6-89
66
АЛЬ-ФАРАБИ
медленно движутся на восток; это при-
суще всем светилам. Но все светила дви-
жутся быстро, что обнаруживается срав-
нением с четырьмя упомянутыми выше
воображаемыми точками 17, о которых
мы еще будем говорить. Поэтому оно
было заметно и требует тонкого [наблю-
дения] .
Что касается сферы, не содержащей
светил, то, если бы [на ней] было свети-
ло, оно [неизбежно] было бы видно, так
как все небесные светила видны и не
скрывают свой свет от зрения.
Об определении хорд частей круга
Основная задача состоит в определе-
нии отношений хорд и нахождении их
дуг и углов, расположенных на поверх-
ности шара. Начнем с определения
хорд; в первую очередь следует устано-
вить [способ нахождения] хорды любой
данной дуги и дуги любой данной хор-
ды, считая, что круг разделен на 360, а
диаметр — на 120 частей 18.
В этом месте совершенно не рассма-
тривается отношение частей диаметра к
частям окружности 19. Хорда одной ше-
стой [круга] равна полудиаметру, кото-
рый известен 20. Хорда четверти [круга]
также известна по книге Евклида21 —
Первая книга
67
это корень удвоенного квадрата хорды
одной шестой [круга] 22. Хорда трети
[круга] также известна — это корень
утроенного квадрата полудиаметра23,
т. е. хорды одной щестой [круга], так
как квадрат этой стороны есть то, что
остается [при вычитании] из квадрата
диаметра квадрата первой хорды 24.
Сторона восьмиугольника определя-
ется через стороны квадрата тем же
приемом.
Если мы хотим определить хорды од-
ной десятой и одной пятой круга, то на
диаметре АС построим полукруг [рис. 1],
из его центра восставим перпендикуляр
DB; разделим CD пополам в Е и соеди-
ним Е и В. Отложим EG, равную ЕВ, и
соединим G и В. Мы утверждаем, что
DG равна стороне десятиугольника и
что она известна, a BG — сторона пяти-
угольника, которая также известна.
Доказательство этого. Поскольку CD
разделена пополам в Е и к ней прибав-
лена DG, то CG на GD и ED на себя
вместе равно EG на себя25, т. е. ЕВ на
себя, а это есть ED на себя и DB на себя.
Отбросим общую ED, тогда остается
CG на GD, равная DB на себя, то есть СД
на себя. Следовательно, CG разделена в
точке D в среднем и крайнем отноше-
нии 26, где длинная сторона CD — сто-
68
АЛЬ-ФАРАБИ
рона шестиугольника. Поэтому неиз-
бежно короткая сторона, т. е. DG,—
сторона десятиугольника, как было от-
мечено. Поскольку они квадрируют
BG, то BG — сторона пятиугольника.
Поскольку СЕ известна, то известна ЕВ,
[Рис. 1]. [Рис. 2].
т. е. EG; их сумма CG известна и CD, по-
7 этому DG, BG/также известны. Сторона
десятиугольника равна 37; 4,55, а сто-
рона пятиугольника — 70, 32,3.
Теперь предпосылаем предложение,
необходимое в дальнейшем. Мы его не-
сколько упростим: в каждом четырех-
угольнике, вписанном в круг, произведе-
ние одной диагонали на другую равно
сумме произведений противоположных
сторон27. Если четырехугольник равно-
сторонний, то доказательство очень про-
стое.
Первая книга
69
Пусть четырехугольник с различны-
ми сторонами, например ABCD, вписан
в круг [рис. 2], проведем диагонали.
Пусть угол ABD больше угла DBC, так
что дуга AD, стягиваемая первым уг-
лом, больше в данном четырехугольни-
ке. Построим угол АВЕ, равный углу
DBC. Поскольку углы ВА.Е и BDC нахо-
дятся на одной дуге, то они равны. По-
этому треугольники [АВЕ и DBC] по-
добные и произведение АВ на CD равно
DB на АЕ. Поскольку угол ABD равен
углу ЕВС и углы ВСЕ, ADB равны меж-
ду собой, то треугольники [СВЕ и ABD]
подобные. Следовательно, произведение
ВС на AD равно [произведению] DB на
СЕ. Сумма ВС на DA и АВ на CD равна
сумме BD на СЕ и BD на АЕ, то есть
[произведению] BD на СА. Это и есть
то, что мы хотели доказать.
Теперь докажем, что хорда избытка
полукруга над двумя дугами с извест-
ными хордами известна.
Для того, чтобы облегчить нахожде-
ние хорды дуги, являющейся избытком
полукруга над двумя дугами, мы прило-
жим эти дуги и их хорды [начиная] из
концов диаметра [круга]. [Избытком]
будет дуга, находящаяся между этими
двумя [дугами]. Эта дуга и ее хорда
равны [соответственно] избытку и его
70
АЛЬФАРАБИ
хорде, находящимся у одного конца
диаметра; при этом дуги с известными
хордами находятся друг за другом у
другого конца.
Пусть искомая хорда СВ; требуется
ее определить через хорды DC и АВ,
выходящие из концов диаметра AD
[рис. 3]; соединим DB и С А, они изве-
стны, так как являются хордами — до-
полнениями данных дуг до полукруга;
хорда и диаметр известны; угол, [опи-
рающийся] на диаметр,— прямой. Сле-
[Рис. 3].
[Рис. 4].
довательно, произведение одной [диаго-
нали] на другую известно; DB и СА
известны и поэтому известно [произве-
дение] СВ на AD; разделив это на из-
вестную AD, получим СВ.
Отсюда выясняется, что остаток от
полукруга после [отбрасывания] двух
дуг с известными хордами имеет извест-
ную хорду. Этот [остаток] равен тому,
Первая книга
71
что здесь находится в середине. Если это
известно, то известна и хорда разности
между двумя дугами с известными хор-
дами, как [например] хорда разности
дуг одной шестой и одной пятой части
[круга] 28.
Так же можно определить хорду по-
ловины дуги, хорда которой известна.
Соединим точки В и С [рис. 4];
ВС — известна, разделим ее дуги попо-
лам в D. Проведем хорды BD и CD. Мы
утверждаем, что эти хорды известны.
Соединим А и В, А и D, отложим АЕ,
равную АВ, соединим D и Е. Поскольку
ЕА и AD соответственно равны АВ и
AD, а углы А находятся на равных ду-
гах, то треугольники [EAD и BAD] рав-
ные. Следовательно, их основания BD
и DE равны и поэтому ED равна DC. В
треугольнике EDC [из угла D] опустим
8 перпендикуляр DG. Поскольку АВ/, то
есть АЕ, известна и АС известна, то ос-
таток ЕС я его половина EG известны;
AG — известна, GC — известна. Пря-
моугольный треугольник ADC подобен
прямоугольному треугольнику DGC
Следовательно, АС относится к DC как
DC к CG; DC — средняя и поэтому из-
вестна 29. Мы нашли способ определения
по данной хорде дугй" двенадцати граду-
сов, хорды шести градусов, хорды [трех
72
АЛЬ-ФАРАБИ
градусов], хорды полутора градусов
и хорды трех четвертей градуса.
Мы утверждаем, что если даны две
маленькие дуги, хорды которых извест-
ны, то можно определить хорды суммы
этих дуг. Например, пусть хорды АВ и
ВС известны. Мы утверждаем, что хор-
да суммы этих дуг известна. Положим,
что эта сумма меньше половины круга.
Пусть искомая хорда АС [рис. 5]. Про-
ведем диаметр AD, соединим С и D. По-
скольку АВ, ВС известны, то оставшая-
ся DC также известна. Следовательно,
будет известной и оставшаяся хорда до
полукруга АС. Доказательство этого в
«Альмагесте».
Проведем диаметр BGE [рис. 6];
соединим CD, DE, СЕ и DB', ВС извест-
на и поэтому СЕ также известна; подоб-
Первая книга
73
но этому известна BD, так как АВ изве-
стна. Через диагонали СЕ и BD будут
известными ED и CD, являющиеся сто-
ронами четырехугольника. Отсюда бу-
дет известной [искомая] АС30.
Если из данной дуги отсечь дугу с
наименьшей хордой и постепенно скла-
дывать эту дугу с другими частичными
дугами с известными хордами, то хорды
их сумм будут известными. Точно так
же будет, если мы возьмем кратные
наименьшей дуги.
Птолемей принимает, что [самая
подходящая] наименьшая хорда есть
хорда полуградуса; если известна [хор-
да] полуградуса, то можно вычислить
хорду одной четверти и одной восьмой
части градуса. Однако способ деления
пополам, примененный им, не приводит
его к [хорде] полуградуса, что облегчи-
ло бы нахождение остальных [хорд].
При вычислении хорд мы дошли до
хорды разности одной шестой части и
одной пятой части [круга]. Это сорок
восемь [градусов]. Деление пополам
приводит нас к хорде двадцати четырех
[градусов], затем двенадцати, шести,
трех, полутора; половины и одной чет-
верти. Оно не ведет к определению хор-
ды одного [градуса] и хорды полугра-
ДУса.
74
АЛЬ-ФАР АВИ
Точно так же деление пополам од-
ной шестой части [круга] приводит к
хорде тридцати, пятнадцати, семи с по-
ловиной [градусов]. Оно не приводит к
одному [градусу] или к полуградусу.
Если начинать деление . пополам дуги
одной десятой части [круга], то можно
дойти до четырех с половиной и до двух
с четвертью [градуса].
Если можно было бы определить хор-
ду третьей части известной дуги с по-
мощью линий, то можно найти это че-
рез хорды полутора градусов.
Он сказал: если это невозможно, то
нужно прибегать к способу приближе-
ний, который опирается на следующее
положение. Отношение длинной хорды
к короткой в одном и том же круге
9 меньше отношения/болыпой дуги к
меньшей31. Пусть хорда СВ длиннее
хорды АВ. Я утверждаю, что отноше-
ние длинной хорды ВС к короткой хор-
де АВ меньше отношения дуги СВ к
дуге АВ. Соединим А и С [рис. 7]. Раз-
делим угол В пополам прямой линией
BD, которая пересечет СА в Е. Прове-
дем CD и DA; они равны как хорды
равных дуг, потому что углы при В
равны. Опустим из D перпендикуляр
DG; он расположится внутри треуголь-
ника ECD, потому что разделит попо-
Первая книга
75
лам основание равнобедренного тре-
угольника. СЕ длиннее ЕА, так как СВ
длиннее ВА в силу деления угла В по-
полам. Поскольку угол G прямой, то он
больше угла DAC, но неизбежно мень-
ше внешнего угла DEA, который боль-
ше оставшегося угла DEG. Поэтому
сторона AD длиннее DE, a DE длиннее
DG. Если примем точку D за центр и
на расстоянии DE опишем сектор, рас-
положенный внутри треугольника DEA,
который пересекает DA в Н, то он рас-
положится вне треугольника DEG.
Продолжим перпендикуляр до пересе-
чения с ним в точке F. Тогда отношение
сектора DEF к сектору DEH, то есть от-
ношение угла GDE к углу ADE, больше
отношения треугольника EDG к тре-
76
альФаравй
угольнику ADE, то есть отношения ос-
нования СЕ к основанию ЕА этих тре-
угольников, имеющих одинаковую вы-
соту. Присоединяя отношение, получим,
что отношение GA к АЕ меньше отно-
шения суммы всего угла GDA к углу
EDA; удвоением получим, что отноше-
ние всего СА к АЕ меньше отношения
всего угла CDA к углу ADE, выделяя 32
отношение угла CDB к углу BDA, полу-
чим, что отношение СЕ к ЕА, то есть
СВ к В А, меньше отношения дуги СВ
к дуге ВА.
Пусть теперь в этом круге AD —
хорда градуса и половины (рис. 8]. Это
по вычислению будет одна часть —
тридцать четыре минуты пятнадцать се-
кунд; хорда АС — хорда одного граду-
са, которая неизвестна. АВ — хорда по-
ловины с четвертью градуса; это состав-
ляет сорок семь минут восемь секунд.
Поскольку отношение дуги AD к дуге
АС [есть] отношение равного с полови-
ной к равному, то отношение хорды
AD к АС меньше отношения равного с
половиной к равному. Следовательно,
АС больше двух третей AD; поэтому
АС больше одной части двух минут пя-
тидесяти секунд, это и есть [значение]
двух третей AD. По такому же вычис-
лению АС меньше АВ с третью, то есть
Первая книга
77
одной части двух минут пятидесяти се-
кунд.
Таким образом, одна и та же вещь в
двух вычислениях получается большей
меньше одного и того же [числа]. По-
этому АС приблизительно равна одной
части — двум минутам пятидесяти се-
кундам 33. Это есть то, что мы хотели
найти.
[Путем деления пополам дуги одно-
го градуса можно найти и хорду полу-
градуса] .
Далее способом сложения двух дуг,
хорды которых известны, получаются
величины хорд других дуг, возрастаю-
щих через полуградус.
Птолемей составил для них таблицу,
начиная от полуградуса и увеличивая
через каждый полуградус до ста вось-
10 мидесяти /градусов34.
Сначала он в таблицу расположил
числовые значения дуг и [хорд], а за-
тем значения, соответствующие хорде
одной минуты дуги, с тем, чтобы найти
хорду искомой дуги, которая больше
или меньше того, что имеется [в табли-
це], на несколько минут. Для этого
умножим соответствующее значение
[хорды] одной минуты на число минут
в разности и прибавим или вычтем. Это
приближение неощутимо [отличаете#
78
АЛЬ-ФАРАБИ
от истинного]. Что касается истинного,
то дуги не относятся [друг к другу] как
их хорды. Это первая цель.
Об определении склонения
Что касается второй цели, то она
состоит в определении дуги между солн-
цестояниями для того, чтобы, разделив
ее пополам, найти наибольшее склоне-
ние 35, а также в установлении основ
(принципов, предпосылок) нахождения
[других] неизвестных дуг кругов, на-
черченных на поверхности сферы. Среди
них [дуги] склонений градусов эк-
липтики м, т. е. дуги, находящиеся меж-
ду точками градусов эклиптики и точ-
ками сечения небесного экватора и яв-
ляющиеся частями круга, проходящего
через полюсы небесного экватора и это-
го градуса. Среди них также другие ду-
ги, которые мы подробно разъясним
позже.
Способ наблюдения склонения та-
ков: возьмем медный круг, окружен-
ный четырьмя [попарно] параллельны-
ми плоскостями. Разделим его, насколь-
ко это возможно, на градусы и минуты.
[Возьмем] другой круг, который будет
вращаться по первому кругу, но не бу-
дет заслонять сделанные на нем деле-
Первая книга
79
ния, и установим оба эти круга с
предельной точностью. Сделаем на диа-
метре внутреннего [круга] два [неболь-
ших, противоположно расположенных]
указателя, как это делается в астроля-
бии. Поставим [указанные круги] на
устойчивом столбе, пересекающем плос-
кость горизонта под прямым углом.
Плоскости этих двух кругов будут рас-
положены в круге меридиана.
Что касается того, что их плоскости
должны пересечь плоскость горизонта
под прямым углом, то это осуществляет-
ся с помощью отвеса. Для того, чтобы
они были в плоскости меридиана, нуж-
но провести полуденную линию, для
чего нужно найти предельно ровное ме-
сто на земле так, что если налить на не-
го воду, то она не стекает в [одну] сто-
рону. Поставим на этом месте прямой
столб из меди, дерева или другого [ма-
териала] . Сделав его основание центром,
опишем наибольший из тех кругов,
на окружности которых конец тени
[столба] в течение некоторого времени
падает четко и не рассеянно. Далее бу-
дем следить за концом тени, когда она
падает на [окружность] этого [круга]
до полудня, а также, когда она падает
на нее второй раз после полудня. Отме-
тим эти две точки и разделим дугу меж-
80
АЛЬ-ФАРАБИ
ду ними пополам и отметим эту середи-
ну. Линия, проведенная от нее через
центр, и есть меридиан.
Теперь установим [инструмент] 37
по этой [линии] и с его помощью
будем находить высоту Солнца все вре-
мя, начиная с южной [точки] равноден-
ствия, пока не определим предела его
понижения. Отметим тот градус, до ко-
торого доходит гибкий указатель. Точ-
но так же поступим, когда Солнце на
севере, пока не определим предел его
высоты. Отметим градус, до которого
доходит указатель как в астролябии м.
То, что находится между двумя отме-
ченными точками,— удвоенное [наи-
большее] склонение, половина этого и
есть наибольшее склонение. Линия, сое-
диняющая середину [полученной дуги]
с центром, находится на плоскости не*
бесного экватора.
Склонение можно найти и более лег-
ким способом, если взять призму, имею-
щую точные квадратные и прямоуголь-
ные грани.
Пусть, например, одна из ее гра-
ней— квадрат ABCD [рис. 9]. Из цен-
тра В радиусом АВ опишем четверть
круга АС. Разделим ее на девяносто
градусов и, по возможности, на минуты.
Установим ее пр полуденной линии так,
Первая книга
81
И
чтобы ее плоскость пересекла плоскость
горизонта под прямым углом, и поста-
вим угол В на южной стороне. Поста-
вим в точке В с помощью отвеса пер-
пендикулярный шест так, чтобы его
тень доходила до дуги/AC. [Поставим]
в точке С такой же шест так, чтобы тень
шеста, поставленного в В, падала на де-
ления [дуги] ежедневно. Чем больше
будет высота [Солнца], тем ниже будет
его [тень], чем больше будет пониже-
ние, тем выше тень. Если мы дойдем до
двух пределов — высоты и понижения,
то мы узнаем то, что между ними. По-
зади дуги с северной стороны мы долж-
ны подложить что-то, что не позволи-
ло бы тени рассеиваться 39.
Птолемей говорит, что, опираясь на
наблюдения, главным образом на [из-
6-89
82
АЛЬ-ФАРАБИ
мерение] относительно точки зенита и
расстояние от нее, мы нашли дугу меж-
ду солнцестояниями, [равную] сорока
семи градусам и больше двух третей, но
меньше половины и одной четверти гра-
дуса, а это близко к тому, что сказал
Эратосфен40, и совпадает с [тем, что
привел] Гиппарх41.
С помощью этого инструмента мож-
но найти широту местности; для этого
определим градус небесного экватора и
возьмем расстояние зенита от него, ко-
торое равно дополнению широты до де-
вяноста [градусов]. На инструменте это
то расстояние, что между С и равноден-
ственным кругом. Оно само и является
высотой полюса.
Имеются и другие приемы для этого
наблюдения; о них мы расскажем в
«[Книге] приложений».
Для дополнения первой цели приво-
дим одну геометрическую предпосылку:
если на линиях АВ и АС, образую-
щих между собой угол, взять две точки
D и Е и соединить их концами, то отно-
шение АС и АЕ составлено из отноше-
ний CD к DG и BG к BE 42 [рис. 10].
Доказательство этого. Проведем ЕН
параллельно CD, тогда АС относится к
АЕ как CD к ЕН. Пусть CD — промежу-
точная [величина]. Тогда отношение
Первая книга
83
CD к ЕН составлено из отношений CD
к GD и GD к ЕН.
CD имеет отношение к GD, и GD
имеет отношение к ЕН. Можно вставить
любую величину между двумя величи-
нами и составить с ними два отноше-
ния, для которых она будет средней, и
тогда отношение одной из двух величин
к другой будет иметь определенное от-
ношение, составленное из этих двух от-
ношений, если средняя величина та же,
но не другая.
Если же изменить ее, то [упомяну-
тое отношение будет составлено] из дру-
гих двух отношений. Но АС- относится к
АЕ как CD к НЕ. Поэтому он взял вели-
чину, отношение АС к которой [состав-
лено] из отношения CD к GD и [отноше-
ния] GD к НЕ (по книге «Начала»
Евклида). Тогда [отношение, составлен-
ное] из отношения АС к этой величине,
и отношение этой величины к АЕ тако-
во же, как [отношение, составленное]
из отношения CD и DG и [отношения]
DG к ЕН.
Мы здесь долго [обсуждали] это с
тем, чтобы ты понял [сущность] состав-
ления отношений.
Но GD относится к ЕН как GB к
BE. Итак, возьми отношение CD к DG,
а затем [отношение] GD к ЕН или [от-
84
АЛЬ-ФАРАВИ
12 ношение] GB/к. BE. Следовательно, от-
ношение СА к ЕА составлено из двух
отношений: CD к DG и BG к BE. Также
выделением получится, что отношение
СЕ к ЕА составлено из отношения CG к
GD и из отношения
BD к ВА. Прове-
н<^/ \ дем АН параллель-
но ЕВ [рис. 11]; ес-
ли продолжить CD,
в то она обязательно
[Рис. 11]. пересекается с АН.
Это потому, что угол
GEC, то есть НАС, и угол АСН вместе
меньше двух прямых. Пусть они пере-
секаются в точке Н. Отношение СЕ к
ЕА равно отношению CG к GH, то есть
составлено из двух отношений: CG к
GD и GD к GH. Поскольку два тре-
угольника [ADH и BDG], в силу [равен-
ства] вертикальных углов и параллель-
ности противоположных сторон, подоб-
ные, то, присоединяя стороны, получим,
что отношение GD к GH равно отноше-
нию BD к ВА. Следовательно, отноше-
ние СА к ЕА составлено из указанных
нами отношений 43.
Первая книга
85
Об определении синусов
Пусть АВС круг с центром D и на
круге даны произвольные три точки С,
ВтиА так, что каждая из СВ и ВА мень-
ше полукруга [рис. 12]. Тогда синус
АВ относится к синусу ВС как АЕ к
ЕС, сумма которых будет хорда, разде-
[Рис. 12].
ляющая полудиаметр, проведенный к
точке В. Под синусом понимается поло-
вина хорды удвоенной дуги. Поэтому
отношение одного синуса к другому —
это отношение хорд. Проведем [линии]
синусов СН и AG, которые неизбежно
будут перпендикулярными к диаметру.
Поскольку треугольники подобные, то
AG относится к СН как АЕ к ЕС. Это и
есть искомое44.
Предпосылка, необходимая в этом.
Если известны углы, то определяется и
отношение их сторон. Если утлы впи-
86
АЛЬ-ФАРАБИ
саны в круг и нам известна дуга каж-
дого угла, то это — отношение соответст-
вующей хорды к диаметру такого кру-
га; причем если угол прямой, то его
хорда — диаметр. Поэтому если извест-
ны один из углов или другая сторона и
ее отношение к хорде прямого угла, то
этого достаточно, чтобы определить ду-
гу, на которую опирается угол; после
этого находится оставшаяся дуга, до-
полняющая данную до пулукруга, и ее
хорда, которая будет третьей стороной.
Поэтому если узнаем отношение углов
и их величины, то определим и их соот-
ветствующие дуги. Отсюда следует, что
если известны дуга СА и отношение
двух синусов дуг СВ и В А, то будут из-
вестными каждая из этих дуг45.
Проведем из центра D перпендику-
ляр DG [рис. 13]. Поскольку AD, то есть
половина диаметра, известна, то полови-
на хорды и дуга известны. Поэтому от-
ношение АЕ к СЕ известно; отношение
всей хорды к СЕ известно. Тогда СЕ и
ЕА будут известными; разность EG из-
вестна и DG известна, потому что в тре-
угольнике AGD угол G — прямой и
AD, AG известны, и поэтому треуголь-
ник известен. Точно так же в треуголь-
нике DEG EG известна, это разность
между известными; определяются и
Первая книга
87
каждый из углов этих треугольников.
13 /Тогда весь угол D будет известным.
Следовательно, дуга АВ и оставшаяся
дуга СВ будут известными.
Пусть будет круг АВС с центром D
и пусть DA и СВ встретятся в Е [рис.
14], тогда синус СА относится к синусу
АВ как СЕ к BE. Опустим перпендику-
ляры СН и BG на АН, которые парал-
лельны и являются синусами дуг АС
и АВ, они относятся как СЕ к BE.
Если дается одна дуга СВ и отноше-
ние синусов известно, то АВ известна.
Продолжим ВС до встречи с DA в Е
[рис. 15], опустим на ВС перпендикуляр
DG. Поскольку угол BDG, стягиваемый
половиной дуги, известен и прямой угол
известен, то известна сторона DB. Тре-
угольник DGB с прямым углом изве-
стен, то есть известны его стороны и уг-
лы. Поскольку отношение синусов, то
88
АЛЬ-ФАРАБИ
есть отношение СА к АВ, известно и
СВ известна, то известно и отношение
СЕ к BE. Избыток BE будет известным.
Поэтому СЕ и BE известны.
Треугольник EGD и угол GDE изве-
стны; угол BDG известен, поэтому ос-
ставшийся угол EDB известен, следова-
тельно, дуга АВ из-
вестна. Если эти
линии встретятся
с другой стороны
[рис. 16], то СН оп-
ределяется таким
образом, как мы
определили дугу АВ
в первом предложении. Будет известна
вся ВН. Но полукруг HDA известен и
поэтому оставшаяся дуга ВА известна.
Когда эти линии параллельны, то
есть не встретятся, то пусть BE будет
синусом АВ [рис. 17], она неизбежно
Первая книга
89
перпендикулярна диаметру АН; CG —
синус АС, которая также перпендику-
лярна АН’, следовательно, углы В, С
между параллель-
ными — прямые; ---q
фигура СЕ — пря- / \
моугольник. Тогда /_______\
BE и CG равны; но tf 5 (Я
CG является также \ J
синусом СН, дуга
СВ известна, поло- |-рис 17].
вина ее дополнения
до полукруга будет известна, это есть
[дуга] ВА 46.
Эта предпосылка служит для пони-
мания предложения о секущих. Вот это
предложение. Даны четыре дуги боль-
ших кругов, описанных на поверхности
сферы, каждая из этих дуг меньше по-
лукруга; пусть дуги С А и В А встретят-
14 ся в А‘, из С/ и В проведены две дуги,
пересекающиеся в G; пусть они пересе-
кают СА и ВА вЯиЕ.
Мы утверждаем, что отношение си-
нуса дуги СЕ к синусу дуги ЕА состав-
лено из отношения синуса дуги CG к
синусу дуги GD и отношения синуса
дуги DB к синусу дуги ВА 47. Для об-
легчения доказательства этого предло-
жения положим, что диаметр каждого
90
АЛЬ-ФАРАБИ
круга и каждая его хорда расположены
в одной плоскости. Возьмем центр [сфе-
ры], и пусть он будет Н; соединим его
с точками пересечений кругов линиями
ЕН, НВ и НС [рис. 18]. Хорды AD и ВН
обязательно должны быть расположены
в одной плоскости; ВН параллельна
AD или не параллельна. Если не парал-
лельна, то они встретятся в одном из
двух направлений; пусть AD встретит-
ся с НВ в сторону D в [точке] F. Прове-
дем хорду АС, которая необходимо пе-
ресекает полудиаметр его круга в L.
Точно так же хорда CD пересекает GH
в К. Поскольку линии НЕ, HG и НЕ
встретятся с дугой EGB, то все они на-
ходятся в одной плоскости; это есть
упомянутая плоскость. Продолжим AD
в прямом направлении до этой плоско-
сти ; FA также находится в этой плоско-
сти. Точки L, К и F [одновременно] на-
Первая книга
91
ходится на двух плоскостях: одна из
них — плоскость дуги EGB, другая —
плоскость треугольника ACD, если их
соединим, то получится прямая LKF,
как это доказано в книге Евклида. По-
скольку между двумя встречающимися
прямыми АС и AF проведены линии
CD и FL, пересекающиеся в точке К, то
отношение CL к AL составлено из от-
ношения СК к KD и отношения FD к
FA. Но CL относится к LA как синус
дуги СЕ к синусу ЕА; точно так же СК
относится к KD как синус дуги CG к
синусу дуги GD; FD относится к FA как
синус дуги BD к синусу дуги ВА. Следо-
вательно, отношение синуса дуги СЕ к
синусу дуги ЕА составлено из отноше-
ния синуса дуги CG к синусу дуги GD и
отношения синуса дуги BD к синусу ду-
ги В А. Это и есть требуемое [доказа-
тельство] .
Теперь рассмотрим случай, когда
эти линии встретятся в стороне А. Это
отсутствует в книге [Птолемея].
Для этого приводим одну предпо-
сылку. Мы утверждаем, что если отно-
шение [величины] А первой к В второй
составлено из отношения С третьей к D
четвертой и отношения Е пятой к G
шестой, то отношение С третьей к D чет-
вертой составлено из отношения А пер-
92
АЛЬ-ФАРАБИ
этого. Возьмем С,
В А
G j Е В । С
J F н
[Рис. 19].
15
вой к В второй и отношения G шес-
той к Е пятой [рис. 19]. Доказательство
D, Е, G и Н, F, J,
отношение Н к J та-
кое же, как /А к В.
Пусть J сделаем
средйей между Н и
F, тогда отношение
Н к F, то есть отно-
шение С к О, кото-
рые соответствуют
третьей и четвер-
той, составлено из
отношения Н к J.
то есть отношения А к В, которые
соответствуют первой и второй, и [отно-
шения] J к F, то есть шестой к пятой.
Это и есть то, что мы хотели предпо-
слать.
Сделаем так, что AD и ВС встрети-
лись в стороне А в [точке] F [рис. 20];
дополним половины кругов BDAK и
BGEK, они. встречаются на диаметре в
точке, отличной от F, потому что FA
расположится вне сегмента круга BDA.
Однако, как уже было доказано в пре-
дыдущем предложении, отношение [си-
нуса] CG первой к синусу GD второй
составлено из отношения синуса СЕ тре-
тьей к синусу ЕА четвертой и отноше-
ния [синуса] КА пятой, то есть синуса
Первая книга
93
[Рис. 20].
[Рис. 21].
АВ [так как КАВ — полукруг] к сину-
су KD шестой, то есть синусу DB (так
как KDB — полукруг). Поэтому отно-
шение синуса СЕ третьей к синусу ЕА
четвертой будет составлено из отноше-
ния синуса CG первой к синусу GD вто-
рой и отношения синуса BD шестой к
синусу ВА пятой. Это и есть то, что мы
хотели доказать.
Что касается случая, когда [линия
AD] параллельна ВН, то для доказа-
тельства предложения приводим сле-
дующую предпосылку. Если А к В от-
носится как С к D и отношение Е к G
единичное 48, то отношение А к В со-
ставлено из отношения С к D и отноше-
ния Е к G [рис. 21]. Пусть Н равно В,
тогда отношения А к Н и С к D одина-
ковые; отношение Н кВ есть отношение
Е к G. Поскольку отношение А к В со-
ставлено из отношений А к Н и Н к В,
94
АЛЬ-ФАР АВИ
то оно составлено из отношений С к D
и Е к G. Тем самым доказано, что от-
ношение А к В составлено из отноше-
ния [А к В] и единичного отношения.
Каждое отношение составлено из отно-
шения, равного себе, и единичного отно-
шения.
[Рис. 22].
[Рис. 23].
После доказательства этого мы ут-
верждаем, что хорда AD парал-
лельна ВН [рис. 22], дополним полукруг
BDA до конца диаметра, это точка F.
Проведем хорды АС и DC; опустим из
центра D перпендикуляр DX, находим
центр, это — Н; соединим [линией] Е
и Н, которая пересекает хорду АС в L;
HG пересекает хорду CD в К; соединим
К и L. Поскольку диаметр BF, рута
EGB, линия НЕ, точка L лежат в одной
плоскости, то можно провести в плоско-
сти EGBH через точку L линию, парал-
лельную диаметру, т. е. AD. Следова-
Первая книга
95
тельно, несомненно, можно провести
также через точку L на плоскости ADC
линию, параллельную линии AD. Я
утверждаю, что это линия LK. Пусть
параллельная [линия], выходящая из
L, будет другой; что касается плоскости
EGBH, то, возможно, будет параллель-
ная линия LM; относительно плоско-
сти ADC, возможно, будет параллель-
ная линия LQ. А каждая из этих ли-
ний — LM и LQ параллельна линии
DA; следовательно, они параллельны
между собой; но они встречаются в L.
Таким образом, они параллельны и не
параллельны, это нелепо. Поэтому
16 DA/ параллельна только LK. Таким об-
разом, из боковых сторон треугольника
ADC проведена линия, параллельная ос-
нованию. Следовательно, отношение CL
к LA равно отношению СК к KD и по-
этому отношение синуса СЕ к синусу
ЕА равно отношению синуса CG к сину-
су GD. Пусть составим [первое] из это-
го отношения и единичного отношения;
единичное — отношение синуса BD к
синусу ВА, каждый из которых есть
DX; синус BD равен синусу АВ, потому
что AD параллельна НВ, отсюда [дуга]
ЕА равна [дуге] BD и [дуга] DF равна
дуге АВ, так как синусы DF и ВА есть
DX, Поэтому отношение синуса BD к
96
АЛЬ-ФАРАБИ
синусу В А — единичное отношение; от-
ношение синуса CG к синусу GD — от-
ношение синуса СЕ к синусу ЕА. Тогда
отношение синуса СЕ к синусу ЕА со-
ставлено из отношения синуса CG к си-
нусу GD и отношения BD к синусу ВА.
Это и есть то, что мы хотели доказать.
Мы утверждаем также, что, присое-
диняя и выделяя отношения, получим:
отношения синусов СА к ЕА составле-
но из отношения синусов BG к BE. До-
полним полукруги СА и CD. Пусть они
встретятся в F [рис. 23]. Но было дока-
зано, что отношение синуса дуги FA,
то есть СА первой, к синусу дуги ЕА
составлено из отношения синуса FD
третьей к синусу FD четвертой и отно-
шения синуса BG к синусу BE; синусы
[дуг] FA, АС и FD, DC одинаковы. От-
сюда получается требуемое. Это и есть
то, что мы хотели доказать 49.
Примем это за основу по выяснению
вопросов, касающихся [измерения] дуг.
Определим способ вычисления склоне-
ния 50 через каждый градус. Это есть
величина дуги, ограниченной градусом
эклиптики и небесным экватором и взя-
той по кругу, проходящему через оба
полюса небесного экватора и через гра-
дус [эклиптики].
Пусть ABCD — круг, проходящий
Первай ййиМ 97
через четыре полюса51 [рис. 24], а
АЕС — полукруг небесного акватора,
BED — полукруг эклиптики; Е — их
точка [пересечения], то есть точка ве-
сеннего [равноденствия],
так что В и D будут со- А.-------.В
ответственно [точками] f \ / \
зимнего и летнего солн- I rVTfj у*
цестояний. Пусть ЕН I Ед I
— известная [дуга] эк- \ / \С/
липтики, например, она \^/
равна 30 градусам, G —
полюс небесного эквато- [Рис 24].
ра; проведем дугу GHF
[большого круга]. Тогда НЕ будет
склонением НЕ, величину которого тре-
буется определить. Поскольку между
дугами ABG и AFE проведены две ду-
17 ги —IGHF и. ЕНВ, пересекающиеся в
Н, то отношение синуса GA к синусу
ВА составлено из отношения синуса GF
к синусу FH и отношения синуса ЕН к
синусу ЕВ; но синус AG известен, он —
синус девяноста [градусов]; синус ВА
известен — он синус полного склонения.
Из оставшихся двух отношений — отно-
шение синуса ЕН к синусу ЕВ — отноше-
ние известных величин, то есть отноше-
ние тридцати градусов к синусу четверти
круга. После вычитания остается отно-
шение синуса GF к синусу FH, которое
7-89
98
АЛЬ-ФАРАБИ
[также] будет известно. Поскольку каж-
дое из отношений и синус GF известны,
то известен и синус FH. Итак, FH изве-
стна 62. Для легкого способа отбрасыва-
ния отношения из отношения мы требу-
ем два числа отношения, которые были
бы не больше и не меньше его, тогда
отношение одного к другому — одно из
двух отношений, остающихся [при от-
брасывании] из него, и находится третье
число; затем рассматриваем отношение
этого третьего числа ко второму из двух
первых чисел, которое не больше и не
меньше его. Если нет отношения,, то
[имеем отношение] к другому, это —
отношение двух данных неизвестных 53.
Вычисляя, получим для HF 11; 39,
39, а для двух знаков Зодиака 54, [то
есть для 60 градусов],— 20; 30, 9.
Птолемей по этому способу вычис-
лил значения [склонений] через каж-
дый градус квадранта [и поместил] в
двух рядах, каждый из этих рядов, в
свою очередь, состоит из четырех рядов
по столбцу: один ряд —.для числа гра-
дусов [эклиптики]; другие — для гра-
дусов, минут и секунд [склонения] 55.
Первая книга
99
О восхождении в прямой сфере
После изложения того, что касается
градусов склонения, Птолемей перехо-
дит к определению восхождения в пря-
мой сфере. В прямой сфере56 полюсы эк-
ватора находятся на горизонте, а пояс
[движения] проходит через зенит без
отклонения, поэтому небесная сфера
движется перпендикулярно к полуден-
ной линии на Земле, а полюсы экватора
находятся на горизонте. Таким образом,
восхождение — это часть небесного эк-
ватора, восходящая вместе с частью эк-
липтики 56 а.
Если небесная сфера прямая, то гра-
дусы восхождения и градусы меридиана
равны и между ними нет разницы, так
как движение происходит вокруг полю-
сов земного экватора. Если два полюса
на горизонте, то небесный экватор и ме-
ридиан пересекаются в зените. Если же
сфера наклонная 57, то дело обстоит ина-
че, так как движение происходит не
вокруг двух полюсов зенита, а вокруг по-
люсов небесного экватора, поэтому дви-
жение частей в течение равных [про-
межутков] времени одинаковое, так что
разные движения следует устанавли-
вать по их времени.
Установлено, что один оборот — это
160
АЛЬ-ФАРАБИ
18
один день и одна ночь. Если определен
градус, в котором восходит светило, а
он определяется по экватору и по эк*
липтике, то можно определить, с каким
градусом небесного экватора восходит
каждый градус и все градусы эклипти-
ки. Градус небесного экватора измеряет-
ся частями дня и ночи.
Пусть дан рисунок склонения. Яс-
но, что нужно взять те градусы небес-
ного экватора и те градусы эклиптики,
то есть отрезок круга, проведенного в
этом климате из полюса небесного эква-
тора и проходящего через градус восхож-
дения до небесного экватора. Тогда то,
что между [горизонтом и эклиптикой],—
место восхожденияss.
Если представить себе, что сфера
движения небесного экватора неподвиж-
на, а по ней движется круг горизонта
до тех пор, пока [светило] не достигнет
меридиана и не вернется опять к кругу
горизонта /, и если наблюдать за его
движением между его положениями на
востоке и положением его восхода, то
величина, которую мы представили се-
бе, что она движется, обязательно будет
дугой, проведенной из полюса небесно-
го экватора и доходящей до небесного
экватора. То же самое получится, если
меридиан будет двигаться. Все другие
Первая книга
101
линии, начерченные этим воображае-
мым движением, будут одинаковыми
до экватора и разными после негоВ9.
Если нужно опреде-
лить нам его [прямое д .
восхождение] по тому
же рисунку, то это и / —Xg
есть линия EF [рис. 25]. [ Vн |
Поскольку отношение \ Д. /
синуса GB к синусу ВА \ I \У
составлено из отноше- _________
ния синуса GH к синусу в
HF (которые известны, грис 25-.
так как HF уже узнали, 1
a GF — четверть [круга]
и GH будет известна, поэтому их сину-
сы известны) и отношение синуса EF к
синусу ЕА; последний известен и по-
этому синус EF известен. Следователь-
но, EF известна. По вычислению она
равна 27; 50, для двух знаков Зодиа-
ка — 57; 44, для третьей части четвер-
ти Зодиака — 32; 16 градусам ®°.
В таблице поместим его значение
для каждого из десяти градусов [эклип-
тики] начиная от Овна последователь-
но ”.
ВТОРАЯ КНИГА62
«СОКРАЩЕНИЯ АЛЬМАГЕСТА» 63
Об обитаемых частях Земли
и упоминание о целях книги
Он сказал64: Земля делится земным
экватором, параллельным небесному эк-
ватору, и одной из линий, проходящей
через два полюса небесного экватора,
на четыре части: две южные, две север-
ные четверти; обитаемая часть — при-
близительно одна северная четверть.
Расстояние от линии зимнего экватора
до полюса называется широтой, а то,
что от востока до запада — долготой.
Обоснование нашего утверждения о
том, что обитаемая часть есть северная
четверть, заключается в следующем.
Относительно широты мы не нашли ни-
каких обитаемых местностей, для кото-
рых при двух равноденствиях тени гно-
мона в середине дня были бы направле-
ны к югу. Я говорю, возможно, кто-ни-
будь другой после нас найдет то, чего
Вторая книга
103
мы не смогли найти65. Относительно
долготы мы обнаружили, что лунные
затмения опережают или запаздывают
для всей обитаемой части Земли самое
большее на двенадцать часов.
Это общее рассмотрение; в частно-
сти, [в этой книге] будет рассматривать-
ся каждая местность в соответствии с
ее широтой и нахождением под парал-
лельным небесному экватору кругом,
для которого известна высота полюса.
Высота полюса определяется с помощью
наблюдения предела высоты одной из
вечновидимых звезд и предела ее пони-
жения : разделим пополам разности
между ними и прибавим ее на предел
понижения 66, или она находится опре-
делением градуса небесного экватора с
помощью упомянутого инструмента.
Она определяется как разность между
числом 90 и величиной этого градуса,
которая равна высоте полюса 67.
Кроме того, нужно знать обстоятель-
ства Солнца, то есть когда оно бывает в
зените; если бывает, то сколько раз:
один или два; отношение [величин] по-
луденных теней к гномонам в дни солн-
цестояний и равноденствий; отношение
самого короткого дня к равноденствен-
ному; состояние видов их разницы;
[сюда же относятся] определение вое-
104
АЛЬ-ФАРАБИ
ходов [градусов эклиптики], а также
определение величины углов, располо-
женных между дугами больших кругов,
и их отношения, которые служат осно-
вой в определении возможного наиболь-
шего дня в наклонных климатах по
19 сравнению / с экватором. На линии
земного экватора дни и ночи не отлича-
ются [по длине] друг от друга, там день
и ночь всегда равны.
Теперь определим величину дуги го-
ризонта, расположенной между небес-
ным экватором и косым кругом. Эта
дуга называется азимутом восхода®8.
Об определении азимута восхода
Начертим рисунок, соответствую-
щий [параллели, проходящей] через
остров Родос, где высота полюса 36 гра-
дусов, а наибольший день содержит 14
с половиной [равноденственных] часов.
Пусть ABCD — полуденный круг [рис.
26]; половина горизонта — BED, поло-
вина небесного экватора — АЕС; юж-
ный полюс — G, а Н — [точка] зимнего
солнцестояния в квадранте FH, выходя-
щем из полюса G. [Пусть сначала дана
величина наибольшего дня] и требуется
определить ЕН, которая является ази-
мутом восхода.
Вторая кнжга
106
Поскольку вращение совершается
вокруг полюса небесного экватора G, то
F и Н обязательно попадут на полуден-
ный круг АВ в одно и то ясе время, ко-
торое определяется [дугой] FA небес-
ного экватора. Если начинать от середи-
ны [неба] под Землей до восхода, то это
время определяется обязательно дугой,
равной FC. Поэтому продолжительность
дня определяется удвоенным временем
FA, а продолжительность ночи — удво-
енным временем FC, потому что полу-
денный круг пересекает пополам каж-
дую высокую и низкую дугу. Дуга EF
есть половина разности между наиболь-
шим или наименьшим днем и [равно-
денственным]. Это для данной [парал-
лели] равно одному часу с четвертью.
106
АЛЬ-ФАР АВИ
Поскольку 24 часа соответствуют 360
градусам, то каждый час равняется 15
градусам; следовательно, указанное
время будет равно восемнадцати вре-
менным градусам и 45 минутам, отсю-
да полуденное время FA известно.
Следовательно, отношение синуса
ЕА к синусу FA составлено из отноше-
ния синуса ЕВ к синусу НВ и отноше-
ния синуса GH к синусу GF. Отсюда бу-
дут известны ВН и НЕ69.
Покажем, как по данным величинам
дня и дуги горизонта найти высоту по-
люса, по которой расстояние от горизон-
та будет известным. Пусть требуется
найти BG на том же рисунке, что меж-
ду полюсом и горизонтом. Поскольку от-
ношение синуса EF к синусу FA состав-
лено из отношения синуса ЕН к синусу
НВ и отношения синуса GB к синусу
GA и все эти синусы известны, то остав-
шийся синус GB известен; следователь-
но, известна дуга GB 70.
Теперь мы хотим определить разно-
сти между наибольшим и наименьшим
днем, то есть удвоенную разницу по от-
ношению к равноденственной. Это и
есть удвоенная дута EF, которую следу-
ет определить. Поскольку отношение си-
нуса дуги GB к синусу дуги ВА состав-
лено из отношения синуса GH к синусу
Вторая книга
107
HF и из отношения синуса FE к синусу
ЕА, то будет известной удвоенная EF
на основании того, что мы знаем 71.
Дугу ЕН также можно определить
исходя из дуги расстояния полюса, ес-
ли те остальные будут известными, по-
скольку отношение синуса GA к синусу
АВ составлено из отношения синуса GF,
то есть девяносто градусов, к синусу FH,
то есть склонения, и из отношения сину-
са ЕН к синусу ЕВ, которое известно 72.
20 Независимо от того, будет ли / изве-
стное склонение южным или северным,
является ли оно полным склонением или
склонением градуса, все обстоятельства
сохраняются.
Он сказал: отсюда следует, что
равные части отрезков [круга эклипти-
ки], т. е. одинаково отстоящие от той
же точки солнцеворота, имеют одно и
то же склонение, одну и ту же дугу го-
ризонта, одинаковый день и тот же вос-
ход. [Вместе с тем доказано], что ча-
сти, расположенные на одном и том же
расстоянии от той же точки равноденст-
вия, имеют с обеих сторон [небесного
экватора] одинаковые положения, [то
есть образуют равные между собой дуги
горизонта и накрест равные друг другу
части суток разного наименования].
Это значит, насколько уменьшается
108
АЛЬ-ФАР АВИ
продолжительность дня и ночи в одной
стороне, настолько увеличивается в дру-
гой стороне и наоборот.
Пусть на том же рисунке точка К
описывает круг, параллельный небесно-
му экватору [рис. 27]. Пусть КМ — от-
резок этого круга, a HL — отрезок, на-
крест расположенный к нему. Очевидно,
они равны между собой. Предположим,
что точка N — северный полюс; прове-
дем через К и N дугу NK, пересекаю-
щую небесный экватор в X; тогда СХ
будет равна FA, потому что СХ подоб-
на КМ, так как они расположены меж-
ду двумя дугами, выходящими из полю-
са небесного экватора. Таким же обра-
зом FA подобна HL; следовательно,
Ёторая кайга 100
КМ и HL равны. Так как две подобные
дуги, расположенные в одном и том же
круге, будут равными, точно так же ос-
тавшиеся ЕХ и EF равны. Таким же
образом две стороны ХЕ и ХК тре-
угольника ХЕК соответственно равны
сторонам FE и FH другого треугольни-
ка, углы F и X прямые, следовательно,
основание КЕ равно основанию ЕН.
Отсюда ясно, что если провести хорды
дуг в указанных двух треугольниках,
то соответственно будут равными вос-
хождения, азимут восхода, склонения в
двух сторонах.
Об определении отношения гномонов
к [полуденным] теням во времена
равноденствий и солнцестояний 73
Около Е опишем меридиан АВС,
АЕС — его диаметр, А — зенит [рис.
28], из С проведем линию, параллель-
ную горизонту. Пусть CG будет [прямой],
на которую падает тень, СЕ — гномон 74.
Поскольку Земля мала по сравнению с
небесной сферой, то безразлично, будет
ли гномон на поверхности Земли или
же в самом ее центре. Пусть точка В —
точка равноденствия на полуденном
круге, тогда ВЕК будет [равноденствен-
ным] лучом, a CN — его тенью, пусть
lid
АЛЬ-ФАРАБИ
21
H — точка летнего солнцестояния, а
НЕЕ — его луч, a CD — тень этого лу-
ча; L — точка зимнего солнцестояния,
LEM — его луч, CG — тень этого луча.
Расстояние зенита от небесного эквато-
ра равно высоте полюса, угол АЕВ из-
вестен; поскольку наибольшее склоне-
ние и в северной и в южной сторонах
известны, то дуги НВ и BL известны;
поэтому будут известными дуга АН и
ее угол. Следовательно, дуга АН и ее
угол будут известными. Если определе-
ны эти дуги /, то будут известны их
центральные углы, их вертикальные уг-
лы будут углами треугольников при
центре, угол С — прямой, СЕ — 60 час-
тей, поэтому все треугольники известны,
потому что треугольник вполне решает-
ся по двум углам и стороне, то есть по
этим данным находятся остальные. Если
Вторая книга
111
точки С и Е расположить в центре близ-
ко друг к другу и принять любую из них
центром круга, а другую — концом гно-
мона, то это не повлияет на круг и до-
казательство будет одно и то же 75.
Пусть О будет основой гномона, а
Е — его концом; проведем из О перпен-
дикуляр ОХ так, чтобы тень падала на
нее; она будет параллельна линии CN;
то и другое отношение — одно и то же.
Точно так же, если точку Е сделаем
основой гномона, Q — концом в этом
направлении, ЕХ — перпендикуляром,
X, Z, Р — концами теней, когда нет
различия между углами, которые обра-
зуются при Е и при Q, близкой от нее.
По проведенному уже вычислению ли-
ния CD, являющаяся тенью при летнем
солнцестоянии, будет равна 12,55; ли-
ния CN, являющаяся равноденственной
тенью,—48,36, а линия CG — тень при
зимнем солнцестоянии — 103,20. Тем
самым уже доказано, что если известны
высота полюса и склонение, то можно
легко определить отношение теней и гно-
мона.
Отсюда легко узнать высоту [полю-
са] и склонение по данному отношению
теней и гномона, так как можно опре-
делить эти дуги по углам указанного
треугольника. Однако надежным путем
112
АЛЬ-ФАРАВЙ
определения наибольшего склонения и
высоты полюса является [приведенный
выше] первый способ, потому что полу-
денная тень неизвестна ввиду непрерыв-
ности перехода теней от убывания к
увеличению и от увеличения к убыва-
нию и поэтому трудно наглядно отме-
чать время равноденствия, а также те-
ни во время зимнего солнцестояния
трудно различимы.
Об особенностях кругов,
параллельных небесному экватору76
Птолемей нарисовал круги, парал-
лельные небесному экватору и проходя-
щие через зенит местности, находящей-
ся под ними. Он взял расстояния меж-
ду этими [параллелями] через каждую
четверть часа. На земном экваторе ночь
и день всегда равны. Если направимся
в сторону полюса, наблюдается раз-
ность [между ними]. Чем ближе к по-
люсу, тем больше эта разность. Он вы-
брал [параллели], о которых будет идти
речь, через каждую четверть часа.
Он сказал: что касается земного эк
ватора, то он служит границей [между]
нашей обитаемой и необитаемой пустой
южной частью. Поскольку сфера [у эк-
ватора] прямая, то горизонт делит по-
Вторая книга
113
полам все круги, параллельные небес
ному экватору, поэтому там день и ночь
всегда равны. Что касается других мест,
то один только небесный экватор делит-
ся пополам кругом горизонта, а осталь-
ные круги делятся на неравные части.
Для каждого круга, который ближе
к полюсу, примыкающему к обитаемой
местности, верхние отрезки параллели
больше нижних, поэтому день длиннее
ночи. Кругу земного экватора свойст-
венно, что тень направляется иногда к
югу, когда Солнце проходит на север от
него, а иногда — к северу, когда Солнце
проходит к югу от него. Предел длины
и роста тени у [экватора] бывает в пол-
день во время солнцестояния. Это будут
двадцать шесть с половиной частей гно-
мона из шестидесяти частей. Для его
жителей все звезды будут восходящими
и заходящими, среди них не будет ни
вечно невидимых, ни вечно видимых.
Он сказал: что касается того, есть
ли жители там или нет, то по этому по-
22 году говорят, что, / возможно, есть, так
как в том месте [все времена года]
должны быть предельно умеренны. Там
Солнце не задерживается долго в зени-
те, а быстро смещается, поэтому лето
бывает умеренным. Оно не удаляется
сильно от зейита йри солнцестоянии, по-
8-89
114
АЛЬ-ФАРАБИ
этому зима будет умеренной. В частно-
сти, мы говорили много по этому пово-
ду; это можно найти в моих книгах по
физике.
Что касается того, какие страны и
какие местности там, то, когда Птоле-
мей писал «Альмагест», он не знал об
этом и сказал: то, что говорят об этом,
является предположением. Позднее он
узнал о некоторых и включил их 77 в
[свою] книгу «География» 78.
Что касается других параллелей, где
есть обитаемые местности и высота по-
люса в каждой из них равна широте
[данной параллели], то для них имеют-
ся вечно видимые звезды, они описыва-
ют круги, среди которых наибольший
с полудиаметром, равным широте [с
центром в этом полюсе], касается гори-
зонта, но эти звезды — вечно невиди-
мые с другого полюса.
После линии земного экватора есть
второй круг, параллельный линии эква-
тора. Для него наибольший день — 12 с
четвертью часов; его широта 4; 15 гра-
дуса. Эта параллель проходит через
остров Тапробани. Поскольку широта
меньше [наибольшего] склонения, то
она будет иметь двусторонние тени, так
как Солнце два раза находится в зени-
те ; тогда не бывает тени. Когда его рае-
Вторая книга
115
стояние от точки летнего солнцестоя-
ния в обеих сторонах будет равно 79; 30
градусам, равноденственная тень будет
иметь 4;25 частей из шестидесяти; лет-
няя тень 21 ;20, а зимняя — 32.
У следующей параллели наибольший
день равняется 12; 30 [часам], широ-
та—8;25, градусам; он проходит че-
рез Авалийский залив; имеет двусторон-
ние тени; Солнце здесь два раза будет
в зените, когда оно отстоит от точки
[летнего] солнцестояния в обеих сторо-
нах на расстоянйи 69 градусов; равно-
денственная тень будет иметь 8; 50 ча-
стей, летняя тень — 16; 35, зимняя —
37; 54 частей.
Четвертая [параллель] имеет наи-
больший день — 12 и три четверти [ча-
сов], широту— 12; 30 градусов и про-
ходит через Адуллийский залив, она
имеет двусторонние тени, так как Солн-
це дважды бывает в зените; равноденст-
венная тень будет иметь 18; 20 частей,
летняя — 12, а зимняя 44; 40.
Наибольший день пятой [паралле-
ли] — 13 часов, широта— 16; 27 гра-
дусов. Проходит она через остров Ме-
роэ; имеет двусторонние тени, так как
Солнце дважды бывает в зените, [когда
оно отстоит от точки летнего солнце-
стоянйя] на расстояний 45 градусов;
116
АЛЬ-ФАР АВИ
равноденственная тень равна 17; 45 час-
тям, летняя — 7; 45, а зимняя — 51.
У шестой [параллели] наибольший
день 13 с четвертью часов, широта 20;
14 градусов. Она проходит череа Напа-
ту, имеет двусторонние тени, так как
Солнце дважды бывает в зените, [когда
отстоит от точки летнего солнцестоя-
ния] на расстоянии 31 градус, равно-
денственная тень равна 22; 10 частям,
летняя — 3;45, а зимняя — 38; 10.
Седьмая [параллель] имеет наи-
больший день 13 с половиной часов,
широту — 23; 51 градус и проходит че-
рез Сиену, у которой широта равна
[наибольшему] склонению, поэтому она
имеет только северные тени, так как
Солнце только один раз бывает в зени-
те при точке солнцестояний; равноден-
ственная тень равна 26; 30 частям, зим-
няя — 65; 50, а летняя будет без тени,
и на тех параллелях, которые севернее
этой, будет иметь только одну тень;
Солнце никогда не бывает в зените.
На восьмой [параллели] наибольший
день 13 и три четверти часа, широта
27; 12 градусов. Она проходит через
Птоламиду; равноденственная тень рав-
на 36; 50 частям, зимняя — 74; 10, лет-
няя — 3; 30.
У девятой [параллели] наибольший
Вторая книга
117
день 14 часов, широта 30; 22 градуса.
Проходит через страны Нижнего Егип-
та; летняя тень равна 6;50 частям;
равноденственная — 35; 05, зимняя —
83; 05.
Наибольший день десятой [паралле-
ли] 14 с четвертью часов, широта 33,
18 градусов. Проходит через середину
23 / Сирии, летняя тень равна 10 частям,
равноденственная тень — 39; 30, а зим-
няя — 93; 05.
Одиннадцатая [параллель] имеет
наибольший день 14,30 часов, широ-
ту — 36 градусов и проходит через Ро-
дос, летняя тень равна 12,55 частям,
равноденственная 47; 50, зимняя —
103; 20.
У двенадцатой [параллели] наиболь-
ший день 14,45 часов, широта 38; 35 гра-
дусов. Она проходит через Смирну; лет-
няя тень равна 15; 40 частям, равноден-
ственная — 48; 36, а зимняя — 114; 55.
Наибольший день тринадцатой [па-
раллели] 15 часов, широта — 40; 56
градусов. Она проходит через страну
Сехитуос (Геллеспант), летняя тень рав-
на 18; 30 частям, равноденственная —
52; 10, а зимняя — 127; 50.
Четырнадцатая [параллель] имеет
наибольший день 15,15 часов, широ-
ту — 43; 15 и проходит через Массилию,
118
АЛЬ-ФАРАБИ
летняя тень равна 20; 50 частям, равно-
денственная — 55; 55, а зимняя — 144.
У пятнадцатой [параллели] наиболь-
ший день 15,30 часов, широта — 45; 10
градусов. Она проходит через середину
Понта; летняя тень равна. 23; 15 час-
тям, равноденственная — 60 и соответст-
вует частям гномона, а зимняя — 155.
Наибольший день шестнадцатой [па-
раллели] 15,45 часов, широта — 46; 51
градусов и проходит через реку Истру;
летняя тень равна 25; 30 частям, равно-
денственная — 63; 55, а зимняя — 171;
30.
Семнадцатая [параллель] имеет наи-
больший день 16 часов, широту —
48; 32 и проходит через устье реки Бо-
рисфени; летняя тень равна 27; 30 час-
тям, равноденственная — 67; 60, а зим-
няя — 188; 35.
У восемнадцатой [параллели] наи-
больший день 16,15 часов, широта 50; 15
градусов. Параллель проходит через
середину Меотидского озера (моря); лет-
няя тень равна 29;55 частям, равно-
денственная — 71; 40, а зимняя — 208;
20.
Наибольший день девятнадцатой
[параллели] 16,30 часов, широта —
51; 40 градусов, проходит она по югу
Британии; летняя тень равна 31;25 ча-
Вторая книга
119
стям, равноденственная — 75; 25, а зим-
няя — 229; 30.
Двадцатая [параллель] имеет наи-
больший день 16,45 часов, .широту —
52; 50 градусов и проходит через устье
Рейна; летняя тень равна 33;20 час-
тям, равноденственная — 79; 05, а зим-
няя — 253; 10.
У двадцать первой [параллели] наи-
больший день 17 часов, широта — 54; 30
градусов. Проходит она через устье
Ганайс; летняя тень равна 34;55 час-
тям, равноденственная — 82; 35, а зим-
няя — 278; 45.
Наибольший день двадцать второй
параллели — 17,15 часов, широта —
55 градусов. Она проходит через [юг]
страны Великой Британии; летняя
тень равна 36; 15 частям, равноденст-
венная — 85,40, а зимняя — 304; 30.
Двадцать третья [параллель] имеет
наибольший день 17,30 часов, широту
56 градусов и проходит через середину
страны Великой Британии; летняя тень
равна 37; 40 частям, равноденствен-
ная — 88; 50, а зимняя — 335; 15.
У двадцать четвертой [параллели]
наибольший день 17, 45 часов, широ-
та — 57 градусов. Проходит через мест-
ность, называемую Катурактонией, в
стране Британии; летняя тень равна
120
АЛЬ-ФАРАБИ
39; 20 частям, равноденственная —
92; 25, а зимняя — 372; 05.
Наибольший день двадцать пятой
[параллели] 18 часов, широта — 58
градусов. Она проходит через юг Малой
Британии, летняя тень равна 40; 40
частям, равноденственная — 96, а зим-
няя — 449; 50.
Двадцать шестая [параллель] имеет
наибольший день 18,30 часов, широту —
59; 30 градусов и проходит через сере-
дину Малой Британии.
Он сказал: теперь уже мы не поль-
зуемся приращением в одну четверть
часа, потому что дальние круги близко
прилегают друг к другу по расстоянию.
Мы говорим: параллель, для которой
наибольший день будет 19 часов, а ши-
рота — 61 градус, проходит через край-
ний север Британии, а параллель, для
которой наибольший день 19, 30 часов,
а широта 62 градуса, проходит через
Эбудские острова; [параллель], для ко-
торой наибольший день 20 часов, а ши-
рота 63 градуса, проходит через остров
Фулу; [параллель], для которой наи-
больший день 21 час, а широта 64; 30
градусов, проходит через неизвестные
24 племена [славян79]. На параллели /, где
наибольший день 22 часа, широта 65;
30 градусов; [на параллели], где наи-
Вторая книга
121
больший день 23 часа, широта 66 гра-
дусов; [параллель], для которой наи-
больший день 24 часа, а широта 66; 30
градусов является круготеневой, так
как Солнце там не заходит только в
день летнего солнцестояния и тени гно-
монов вращаются по кругу. Здесь круг
летнего солнцестояния будет вечно ви-
димым, а круг зимнего солнцестоя-
ния — вечно невидимым, так как они
будут накрест противоположно касаться
круга [горизонта] земли, потому что
параллель описанной вершиной Рака ка-
сается горизонта.
Если полюс эклиптики будет вра-
щаться вокруг полюса небесного эква-
тора, то полюс эклиптики будет к югу
от полюса экватора. Когда широта яв-
ляется полным склонением, то полюс
эклиптики должен быть в зените и сов-
падает с полюсом горизонта; поэтому
круг эклиптики совпадает с кругом [го-
ризонта] Земли. Тогда [тропик] Рака
будет спускаться вниз до тех пор, пока
он не коснется горизонта с севера, а
[тропик] Козерога будет подниматься
вверх до тех пор, пока он не коснется
горизонта с противоположной южной
[стороны]. Если восходит точка весен-
него [равноденствия], то круг эклипти-
ки является горизонтом, так как в это
122
АЛЬ-ФАР АВИ
время полюс эклиптики находится в зе-
ните, а полюс небесного экватора будет
к северу от него. Поэтому Рак неизбеж-
но будет на горизонте и на меридиа-
не, а Овен — на Востоке. Если кто-ни-
будь захочет добавить [что-либо] к
этому, он сможет сделать это из предпо-
сланных принципов 80.
Отсюда ясно, что там, где высота
полюса приблизительно равна 67 граду-
сам, [Солнце] совсем не заходит на про-
тяжении половины знака Зодиака с
обеих сторон Рака, т. е. от точки [летне-
го] солнцестояния; здесь наибольший
день будет продолжаться приблизитель-
но целый месяц; там, где высота полю-
са будет 69; 30 градусов, [Солнце] не
заходит на протяжении одного знака
Зодиака, и наибольший день будет про-
должаться приблизительно два месяца;
там, где высота полюса 73; 20 градусов,
[Солнце] не заходит на протяжении по-
лутора знаков Зодиака, расположенных
между двумя созвездиями — Тельцем и
Львом, и наибольший день будет про-
должаться приблизительно три месяца.
Там, где высота полюса 78;20 градусов,
[Солнце] не заходит на протяжении
двух знаков Зодиака в каждую из двух
сторон, и наибольший день будет про-
должаться приблизительно четыре ме-
Вторая книга
123
сяца; там, где высота полюса 84 граду-
са, оно не заходит на протяжении двух
с половиной знаков Зодиака в каждую
из двух сторон, и наибольший день бу-
дет продолжаться пять месяцев. Там,
где высота полюса 90 градусов, [Солн-
це] не заходит на протяжении трех
знаков Зодиака в каждую сторону, и
наибольший день будет продолжаться
шесть месяцев. При этом южная поло-
вина шесть месяцев не восходит, а се-
верная половина шесть месяцев не захо-
дит. Таким образом, шесть месяцев бу-
дет день, а шесть месяцев — ночь. Здесь
круг небесного экватора есть круг гори-
зонта, являющегося большим кругом
обеих частей небосвода: вечно видимой
и вечно невидимой и общей границей
между ними.
О восхождениях относительно широт 81
Мы уже говорили о восхождениях в
прямой сфере. Теперь будем говорить о
восхождениях в наклонной сфере.
Мы утверждаем, что дуги [эклипти-
ки], равноотстоящие от южной и север-
ной точек равноденствия в отношении
широт, имеют одинаковые восхождения.
Пусть ABCD — меридиан [рис. 29],
BED — круг горизонта, АЕС — небес-
124
АЛЬ-ФАРАБИ
ный экватор, G — точка весеннего рав-
ноденствия, GH — дуга северного на-
клонного круга; пусть F — та же самая
точка, ее соединим с другой и получим
25
дугу южного наклонного круга KF, рав-
ную GH, их восхождения FE и EG. Мы
утверждаем, что они равны. Предста-
вим полюс, соответствующий точке G,
находящийся в L; с другой стороны
пусть это будет точка М. Проведем че-
рез эти полюсы отрезок круга LEM и
дуги FL, LK, GM и МН больших [кру-
гов]. Дуга GH по данному / равна дуге
KF, дуга LK равна дуге МН, потому что
два треугольника равны. Поэтому дуги
ЕК и ЕН, являющиеся азимутами вос-
хода, равны, дуги ME и EL равны как
расстояние от полюса до точки [небес-
Вторая книга
129
ного экватора]. Следовательно, стороны
треугольника ЕНМ такие же, как соот-
ветственные стороны треугольника ELK.
Следовательно, угол ELK равен углу
ЕМН, но угол KLF равен углу HMG, так
как они стягиваются равными дугами.
Две стороны равны соответствующим
сторонам другого, углы FLE и EMG
равны. Тогда основание ЕЕ равно осно-
ванию EG.
Мы утверждаем, что если восхожде-
ния каждой из двух равных дуг на-
клонного [круга] находятся на двух
сторонах одной точки солнцестояния,
тогда то, что между одной из них и точ-
кой солнцестояния, равно тому, что
между другой и той же точкой солнце-
стояния. Например, [восхождения] двух
знаков Зодиака — Овна и Девы. Если
сложить их, они будут равны сумме вос-
хождений соответствующих двух дуг на
линии экватора.
Пусть ABCD — меридиан [рис. 30],
BDE — половина горизонта и АСЕ —
половина небесного экватора; GH —
южная дуга, расстояние которой от зим-
него солнцестояния равно расстоянию
дуги FH, G — осенняя, а Е — весенняя
точка, Н будет общей точкой круга го-
ризонта и этих двух дуг, потому что эти
дуги лежат внутри одного и того же
126
АЛЬ-ФАРАБИ
круга, параллельного небесному эква-
тору.
Проведем через Н и полюс небесно-
го экватора четверть большого круга,
которая будет в прямой сфере равно-
значна горизонту. Это — KHL. По-
скольку FE — восхождение FH, EG —
восхождение HG, то сумма FG есть вос-
хождение двух дуг в этом [климате].
Но FL — восхождение FH на прямой
сфере и GL — восхождение HG на пря-
мой сфере; их сумма равна FG, это
сумма восхождений не в прямой сфе-
ре 82. Отсюда мы выяснили, если опреде-
лим восхождения только для одной чет-
верти, то этого достаточно для опреде-
ления его и для других [четвертей].
вычислим это для острова Родос, о
Вторая книга
127
котором мы выше упомянули. И пусть
ABCD—меридиан [рис. 31], BED —
круг горизонта, ЛЕС — половина круга
небесного экватора, GHF — половина
круга эклиптики, Н — точка весеннего
равноденствия; DK — высота полюса,
К — точка полюса; через нее проведем
четверть круга, проходящего также че-
рез пересечение наклонного круга и го-
ризонта, то есть через точку L до точки
М. Пусть, например, LH будет один
знак Зодиака, соответствующий Овну.
Требуется найти величину ЕН.
Доказано, что отношение синуса KD
к синусу DC составлено из отношения
синуса KL к синусу LM и из отноше-
ния [синуса] ЕМ к [синусу] ЕС; но
26 DK — это высота полюса /, DC — оста-
128
АЛЬ-ФАРАБИ
ток после отнятия известной дуги KD от
известной дуги КС; KL известна, так
как она расстояние начала Тельца от
полюса небесного экватора, которое есть
дополнение его склонения; ЕС известна,
будет известна и ME; НМ — восхожде-
ние Н в прямой сфере, которое извест-
но; отсюда НЕ известна. По вычисле-
нию восхождение Овна, которое соответ-
ствует острову Родоса, будет равно
19; 12 градусам. Отсюда следует, что и
Рыба имеет такое же восхождение; Ве-
сы дополняют восхождение Рыбы в пря-
мой сфере, а Дева — восхождение Овна.
Если линия HL содержит сумму
[двух знаков Зодиака], соответствую-
щих Овну и Тельцу, то, поскольку мы
знаем восхождение одного Овна, будем
знать восхождение другого. Для восхож-
дения Тельца остается 22; 46 градусов.
Точно так же определяется [восхожде-
ние] Водолея через [восхождение] Ры-
бы, Льва — через Девы, Скорпиона —
через Весы.
Поскольку для данной широты, то
есть для острова Родос, известны наи-
больший и наименьший дни, то ясно,
что одна часть от Рака до Стрельца соот-
ветствует 217; 30 временным [граду-
сам] , другая — 142; 30. Таким образом,
две четверти, прилегающие к точке ве-
Вторая книга
129
сеннего равноденствия, будут с извест-
ными восхождениями. Каждая из них
восходит вместе с 71; 15 [временными
градусами]. Из этого видно, сколько ос-
тается для каждого из Тельца и Козеро-
га. Оно будет составлять 29; 17 граду-
сов, а каждое из созвездий Рака и Тель-
ца — 36;15 градусов. Это правило дает
возможность определить восхождения и
для более мелких делений, чем полного
знака Зодиака. Птолемей упомянул, что
для этого есть другой более легкий и
удобный способ.
Он сказал: пусть ABCD — меридиан
[рис. 32], АЕС — половина круга небес-
ного экватора, GH — половина эклип-
тики, пусть Е совпадает с точкой весен-
него равноденствия на пересечении го-
ризонта BED. Проведем известную дугу
9-89
130
АЛЬ-ФАРАБИ
EF и построим дугу FK, пересекающую
горизонт и параллельную небесному эк-
ватору. Пусть южный полюс небесного
экватора — точка L; построим четвер-
ти кругов LFM и LKN', известно, что
ЕМ — восхождение EF на экваторе, по-
скольку в потенции горизонт для тех же
самых есть линия FM. В этой местности
восхождения равны дуге MN из-за того,
что FK параллельна MN и подобна ей,
так как их отсекли две подобные дуги,
[проведенные] из полюса. А подобные
же дуги восходят вместе. Но FK — это
та [дуга], на которой вращался парал-
лельный круг с того времени, когда F
до Е была на горизонте. Тогда EN — из-
быток восхождений экватора над вос-
хождением этой широты. На этом ри-
сунке можно ошибиться и думать, что
когда точка F находится на горизонте,
точка М также находится на горизонте,
и они восходят вместе, то есть EF и ЕМ
[равны], а это не так. Это бывает на
горизонте экватора. Здесь же на гори-
зонте BED вместе с F имеется другая
точка, расстояние которой до Е [равно]
расстоянию от М до N.
Мы сделаем рисунок более простой,
чем этот.
27 Пусть АВС — меридиан / для места,
широта которого известна [рис. 33],
Вторая кяига
131
АЕС из круга небесного экватора,
BED — половина горизонта, G — юж-
ный полюс, Н — общая точка [горизон-
та] и [параллели] зимнего солнцестоя-
ния, проведем GH до Е, т. е. до четвер-
ти круга, К — общая точка [горизонта]
и [параллели] градуса [эклиптики];
проведем GKL. Тогда отношение синуса
дуги ЕН к синусу HG составлено из от-
ношения синуса ЕЕ к синусу EL и из
отношения синуса LK к синусу KG. Что
касается синуса ЕН, то он известен, так
как он — синус полного склонения, и
поэтому синус HG известен; синус LK
известен как склонение градуса эклип-
тики; синус KG известен как дополне-
ние склонения; синус ЕЕ известен как
половина разности между наибольшим
и наименьшим днями; они известны нам
для данной широты, равной высоте по-
132
АЛЬ-ФАР АВИ
люса. Мы доказали, что это можно
узнать, если определить высоту полюса.
Тогда оставшийся синус LE известен;
LE — разность между восхождением по
широте и восхождением в прямой [сфе-
ре]. А восхождение в прямой [сфере]
известно 83.
Птолемей далее составил 84 таблицу,
поместив в первый столбец знаки Зодиа-
ка, во второй — десятки градусов, так
как различие меньше этого не сущест-
венно ; в третий — временные градусы
и минуты; в четвертый — сложенные
[времена], начиная от Овна как начала
квадранта 85.
Из всего изложенного выше ясно, что
если ты вычислишь [восхождение] для
одного квадранта, то этого достаточно
[для остальных].
О частных вещах, связанных
с определением восхождений86
Из того, что можно определить че-
рез восхождение, в первую очередь сле-
дует отметить нахождение величины
дня и ночи по данному градусу Солнца.
Что касается дня, то посчитаем време-
на дуги дня в отношении местностей от
градуса [эклиптики], занимаемого
Солнцем, до противоположного ему гра-
Вторая квита
133
дуса; что касается ночи, то поступаем
в обратном порядке. Тогда пятнадцатая
часть этого будет число равноденствен-
ных часов. Если эту сумму разделим на
двенадцать, то получим время косого
часа 87.
Другой, более легкий способ. Возь-
мем шестую часть разности сложенных
времен в таблице восхождений градуса
[эклиптики], занимаемого Солнцем
для дня, или градуса противоположно-
го этому для ночи, прибавим ее к пят-
надцати временным северным граду-
сам 88 и отнимем ее из южных [граду-
сов], т. е. вычтем сложенные времена
для круга, параллельного небесному
кругу, от сложенных времен для круга,
параллельного данному климату, пото-
му что эта разность соответствует чет-
верти круга, которая приходится на
долю шести часов; отсюда будет изве-
стен косой час.
Далее, умножив [количество] косых
часов на [число] временных градусов
этого дня или ночи после деления на
пятнадцать, получим [количество] рав-
ных часов 89. Можно превратить ровные
[часы] в косые.
Если будет известен косой час, то
отсюда вычислим восхождение. Для
этого умножим его на [число] часов,
134
АЛЬ-ФАРАБИ
прошедших от восхода или захода Солн-
ца, и затем это число отсчитаем от гра-
дуса, [занимаемого] Солнцем (днем),
или противоположного градуса (ночи),
в соответствии с восхождением широты
[местности] в последовательности [зна-
ков] Зодиака и получим восхождение.
Если мы хотим [определить] градус
середины неба, то умножим [число] ко-
сых часов от полудня прошедшего дня
на соответствующее одному часу число
временных [градусов]; затем получен-
ное число отсчитаем от градуса в после-
довательности знаков Зодиака по вос-
хождениям в прямой сфере. Тот градус,
на который достигло это число, и есть
середина неба над Землей.
28 Если известно / восхождение и нуж-
но найти середину неба над землей, то
возьмем сумму чисел из составленной
[таблицы], соответствующую восхожде-
нию, и из нее вычтем девяносто времен-
ных [градусов] и получим то, что соот-
ветствует временному [градусу] в [таб-
лице] для прямой сферы. Следователь-
но, будет известна середина неба. [На-
оборот], если прибавим к тому, что
[соответствует градусу середины неба в
таблице], девяносто часовых [граду-
сов], то получим соответствующее вос-
хождение страны.
Вторая книга
136
Ясно, что для живущих под одним и
тем же меридианом Солнце будет от-
стоять от полудня или полуночи на оди-
наковое [число] равных часов, для тех
же, кто живет на разных меридианах,
оно будет различно, при этом опережа-
ет или отстает на [разность, выражен-
ную во временных градусах] небесного
экватора, которая по величине равна
[разности] градусов между этими мери-
дианами.
Об определении угла,
образуемого пересечением эклиптики
и меридиана
Изложим обстоятельства, относя-
щиеся к углу, расположенному между
эклиптикой и меридианом.
Он сказал, что прямой угол на сфе-
ре есть угол, стягиваемый четвертью
большого круга, полюсом которого слу-
жит [вершина] указанного угла. Отно-
шение этого угла к четырем [прямым]
углам, образуемым пересечением дуг
больших кругов, есть отношение этой ду-
ги к кругу, который представляет собой
четырежды взятую указанную дугу.
Эта дуга стягивает девяносто градусов,
а искомый угол получается как часть
этого.
186
АЛЬ-ФАР АВИ
Здесь мы хотим определить величи-
ны углов, образуемых пересечениями
косого круга и меридиана, косого круга
и горизонта и косого круга и круга, про-
ходящего через зенит к данной части
(точки). Определение этих углов очень
полезно, особенно необходимо для на-
хождения параллакса 90 Луны.
Он сказал: пусть мы будем говорить
о восточно-северном угле из четырех об-
разуемых углов. Для простоты начнем
прежде всего с угла, образуемого косым
кругом и меридианом. Сначала дока-
жем, что каждые две данные [точки],
одинаково отстоящие от точки равноден-
ствия, образуют два равных упомяну-
тых угла. Пусть АВС — [дуга круга]
небесного экватора [рис. 34], DBE — из
косого круга, G — полюс небесного эк-
ватора, В — точка равноденствия, и
пусть ВН и BF равны, дуги КН и FL —
из меридиана. Поскольку треугольники
КНВ и BFL имеют [попарно] равные
стороны, то на основании того, что мы
знаем, они подобные. Следовательно,
угол Н равен соответствующему углу
BFL, то есть углу GFE, в силу их вер-
тикальности.
Пусть АВС — из эклиптики, В —
точка солнцестояния [рис. 35]. Мы
утверждаем, что ‘если две дуги, равно-
Вторая книга
187
29
[Рис. 34].
[Рис. 35].
отстоящие от этой точки, например BE,
ED, и образуют с меридианом два угла,
расположенных в одну и ту же сторону,
например восточную, то эти углы рав-
ны двум прямым. Эти углы — GDB и
GEC.
Действительно, угол GEC вместе с
углом GEB равен двум прямым, углы
GEB и GDB равны, как стягиваемые
равными дугами GD и GE. / Это пото-
му, что [расстояния] от полюса до двух
точек [эклиптики],- равноотстоящих от
точки солнцестояния, одинаковы, то
есть склонения одинаковы.
А также докажем, что два угла
солнцестояний между меридианом и
[эклиптикой] прямые.
Пусть ABCD — [рис. 36],
АЕС — половина косого круга, А —
точка зимнего солнцестояния. Сделаем
А полюсом и из него на расстоянии,
138
АЛЬ-ФАРАБИ
равном стороне квадрата, [вписанного в
большой круг], опишем круг DEB91.
Дуга DE будет равна четверти круга,
так как меридиан ABCD проходит через
полюс DEB и полюс эклиптики. Следо-
вательно, [угол] DAE прямой. Точно
так ясе определим угол у [точки] лет-
него [солнцестояния].
Пусть подобно этому ABCD будет
меридианом [рис. 37], АЕС — половина
круга небесного экватора, AGC — поло-
вина эклиптики, А — точка осеннего
равноденствия. Через [точку А] как из
полюса опишем полукруг BGED. По-
скольку круг ABCD проходит через по-
люсы круга АЕС, каждая из AG и ED
составляет четверть круга, таким обра-
Вторая книга
139
зом, G будет точкой зимнего солнце-
стояния, a GE — известна; следователь-
но, вся GD будет известна; стягивае-
мые ею угол GAD и оставшийся GCD
будут известны.
Пусть на этом рисунке BGD — полу-
круг эклиптики
[рис. 38], BG— [дуга,
соответствующая]
Деве, G
осеннего
ствия и
полукруг
экватора.
к са В опишем поло-
вину большего кру-
га KEFH. Каждая
из дуг ВН, BF и ЕН
обязательно ока-
жется равной чет-
Тогда отношение синуса
— точка
равноден-
AGEC —
небесного
Из полю-
верти круга.
ВА к синусу АН, которое известно, со-
ставлено из отношения синуса BG к си-
нусу GF и из отношения синуса EF к
синусу ЕН. BG — [дуга, сответствую-
щая] Деве, известна, GF как дополне-
ние ВС известна, ЕН — четверть кру-
га — известна; итак, искомая EF из-
вестна. Поскольку ЕК известна, то вся
KEF известна; следовательно, искомый
угол KBF известен. Поэтому угол Скор-
пиона будет известным, а каждый из
140
АЛЬ-ФАР АВИ
углов, остающийся от двух прямых, —
тоже известен.
Если GB принимает другое значение,
то мы определим угол, а также проти-
воположный ему угол с другой стороны
этой точки и со стороны точки солнце-
стояния. Так определяются все углы.
Об определении угла,
образуемого эклиптикой
и горизонтом
Что касается угла, образуемого ко-
сым кругом и горизонтом в прямой сфе-
ре, то можно показать, что он равен уг-
лу, образованному наклонным кругом и
меридианом. А что касается того, что
на наклонной сфере, то мы утверждаем,
что угол, образуемый горизонтом и ду-
гой из наклонного круга, измеряемой от
точки равноденствия, и [угол], образуе-
мый горизонтом и дугой, восхождение
которой равно восхождению этой дуги
и находящейся на том же расстоянии от
той же точки, равны. Эта дуга находит-
ся под землей.
30 Пусть ABCD / — меридиан [рис. 39],
АЕС — небесный экватор, BED — гори-
зонт, MLK — наклонная дуга над зем-
лей, НЕ — другая, равная ей дуга под
землей, G — точка осеннего равноден-
Вторая книга
141
ствйя (восходящая), а К — та же самая
точка под землей. Мы утверждаем, что
углы EHG и ELK равны, потому что по
[Рис. 39].
доказанному треугольники ELK и
EGH — с равными сторонами и углами.
Дуги ЕК и EG равны по построению.
Следовательно, эти углы будут рав-
ными.
Два [диаметрально] противополож-
ных [угла], образуемые наклонным
кругом и горизонтом, то есть восточный
и западный углы, вместе равны двум
прямым.
Пусть ABCD — круг горизонта,
АЕС — наклонный круг, они пересе-
каются в А и С [рис. 40]. Поскольку
углы EAD и DAG, взятые вместе, равны
двум прямым и угол GCD равен углу
14i
АЛЬ-ФАРАВЙ
GAD, то углы DAE и DCG [вместе] рав-
ны двум прямым.
Так как два угла при точках, равно-
отстоящих от точки равноденствия и
горизонта, одинаковые, то их восхожде-
ния и захождения одни и те же. Поэто-
му восточные и западные углы при двух
точках, равноотстоящих от одной и той
же точки солнцестояния, вместе равны
двум прямым. Эти углы — восточно-се-
верный со стороны востока и западно-се-
верный со стороны запада. Если опре-
делим восточный, то [тем самым] опре-
делим и западный [угол], так как это
остаток от двух прямых. Чтобы пока-
зать, как это делается, мы обратимся к
первому рисунку [34]. Если точки Н и
L находятся на одном и том же рас-
стоянии от точки солнцестояния, то
угол GHEравен углу ELK’, следователь-
Вторая книга
143
но, западный угол DBK вместе с СВЕ ра-
вен двум прямым, так как он вместе с
ELK равен двум прямым.
Нарисуем параллель, где высота по-
люса 36 градусов, ABCD — меридиан
[Рис. 41]. [Рис. 42].
[рис. 41], AED — восточный полукруг
горизонта, EG — четверть небесного эк-
ватора, ЕВ — четверть наклонного кру-
га, Е — точка осеннего равноденствия,
а ЕС — четверть наклонного круга, у
которой Е — точка весеннего равноден-
ствия, С — точка зимнего, а В — летне-
го солнцестояния. Дуга DG — известна,
так как она представляет собой величи-
ну, которая остается после вычитания
[от прямого угла] высоты полюса; CG
и BG известны как наибольшие склоне-
ния; СВ и BG известны; Е — полюс
144
АЛЬ-ФАРАБИ
полуденного круга. Таким образом,
каждый из углов, образуемых при Е,
будет известен; будут известны углы у
начала Весов и Овна.
Предположим, что требуется опреде-
лить, например, восходящий угол Тель-
ца. Пусть ABCD — меридиан [рис. 42],
a BED — восточная половина горизон-
та, АЕС — половина эклиптики, Е
31 начало Тельца /.
Мы уже показали, что для этого кли-
мата восходу начала Тельца соответст-
вует земной столб 92 — 17; 41 градусов
Рака; тогда дуга ЕС будет меньше чет-
верти окружности. Из полюса Е на рас-
стоянии, равном стороне квадрата, то
есть EG, построим дугу [круга] FHG и
дополним четверти круга ЕСН и [£DF].
Тогда дуги DCG и FHG будут равнять-
ся двум четвертям [круга], так как го-
ризонт BEF проходит через полюсы
GCD, GHF. Это потому, что Е — полюс
GHF, затем круг горизонта проходит
через полюс меридиана, как и меридиан
обязательно проходит через полюс го-
ризонта. Следовательно, полюс GCD на-
ходится на горизонте BED.
Расстояние С от небесного экватора
известно; расстояние небесного эквато-
ра от точки G, то есть от нижнего зени-
та, известно, тогда их сумма, то есть
Вторая книга
145
CG, известна; оставшаяся дуга, то есть
CD, известна. Точка Н, находящаяся
от Е на [расстоянии] девяносто граду-
сов, известна, и ее расстояние от небес-
ного экватора известно; расстояние не-
бесного экватора от G известно, так как
высота полюса известна. G — полюс го-
ризонта с нижней стороны. Дуги GH и
HF известны.
Отношение синуса ED к синусу DF
составлено из отношения синуса ЕС к
синусу СН и из отношения синуса GH к
синусу GF. Но дуга ED — то, что оста-
ется от четверти круга после вычитания
азимута восхода, это — дуга горизонта
до начала Тельца для данной местности,
DF — дополнение до девяноста граду-
сов ; ЕС, СН и GF — известны. Отсюда
становятся известны GH и HF. Следо-
вательно, будет известен угол CED.
Об определении угла,
образуемого пересечением эклиптики
и круга, проходящего
через полюсы горизонта
Из величины этих углов будут опре-
делены и величины соответствующих
дуг, заключенных между [эклиптикой
и] кругом, проходящим через полюсы
горизонта, то есть то, что между зеци-
10-89
146
АЛЬ-ФАР АВИ
том и сечением этого круга с наклон-
ным кругом. Мы утверждаем, что каж-
дая из дуг, отстоящая от одной и той же
точки солнцестояния, отсекает [по обе-
им сторонам меридиана} одинаковые
временные [углы], и два угла, взятые с
ними в одной стороне, равные двум
[Рис. 43]. [Рис. 44].
прямым, и две дуги, проходящие через
зенит и [концы] этих дуг, будут рав-
ными.
Пусть АВС — дуга меридиана
[рис. 43], В — точка зенита, С — полюс
небесного экватора; проведем ADE и
AGH из одной и той же точки А солнце-
стояния так, чтобы G и D находились
на равных расстояниях от нее. Из по-
люса С к временным [точкам], то есть
к концам одинаковых AG и AD, прове-
дем дуги CG и CD, а также дуги BD и
BG от зенита В. Поскольку AG и AD
. Вторая книга
147
равны и углы при С равны, стороны GC
и ВС равны сторонам DC и СВ, основа-
ния DB и BG равны между собой, соот-
ветствующие углы тоже равны. По уже
доказанному, углы CDE и CGA [вме-
сте] равны двум прямым. Но BDC ра-
вен CGB и, следовательно, BGC и BDE
[вместе] равны двум прямым. Это то,
что мы хотели доказать.
У каждой из точек эклиптики, от-
32 стоящей к востоку / и западу от мери-
диана на одинаковые временные [углы],
будут равны дуги больших кругов, про-
веденных через зенит и эти точки, а
сумма углов восточной и западной дуг
равна удвоенному углу, образуемому
при точке на меридиане, если обе полу-
ченные точки будут находиться или се-
вернее, или южнее зенита. Допустим,
что [эти точки] расположены южнее.
Пусть ABCD — дуга меридиана
[рис. 44], С — зенит, D — полюс небес-
ного экватора, АЕ, ВНЕ — дуги наклон-
ного круга, расположенные так, что
точкиЕпН — одна и та же точка (вос-
точная и западная). Проведем через них
и зенит, [а также] полюс дуги СЕ, СН,
DH. Как и раньше, доказывается, что
треугольники DHC и DEC имеют рав-
ные стороны и углы, поэтому равны уг-
лы при D, равны между собой DE и DH;
148
АЛЬ-ФАРАБИ
следовательно, равны их основания —
дуги, [проходящие] через зенит, то есть
СЕ и СН.
Я утверждаю, что углы CEG и СНВ
[вместе] равны удвоенному DE, взято-
му при меридиане. Поскольку углы
DEG и DHB, которые получаются от пе-
[Рис. 45].
[Рис. 46].
ресечения эклиптики с меридианом в од-
ной и той же точке, равны, а угол DEC
равен углу DHC, то, следовательно, уг-
лы DEC и СНВ [вместе] равны углу
DEG', таким образом, если прибавить
их к углу DEG, то CEG и СНВ [вместе]
будут равны удвоенному DEG.
Пусть эти две точки А и В располо-
жатся севернее точки С [рис. 45]. По-
скольку DEG есть DHB, a DEK — DHL,
то углы DEC и DHC равны как соответ-
ственные, поэтому угол DEK равен DHL,
Вторая книга
149
я, следовательно, весь [угол] LHB равен
сумме [углов] DEG и DEK; если приба-
вить LHB к KEG, остающегося от DEG
[при взятии DEK], то эта сумма будет
равна удвоенному углу DEG.
В подобном же рисунке положим,
что одна из точек, то есть восточная от
середины неба точка А, расположена к
югу от зенита, а точка В — севернее от
него. Я' утверждаю, что вместе взятые
углы CEG и LHB будут на два прямых
больше удвоенного угла DEG [рис. 46].
Поскольку угол DEC равен углу
DHC, в силу равенства сторон двух тре-
угольников, то угол DEC вместе с DHL
равен двум прямым. Но угол DEG есть
DHB, потому что эти углы, как мы уже
упомянули, образованы пересечением
дуг, проходящих через полюс и данную
точку эклиптики в обеих сторонах; тог-
да, если сложить [сумму] DEG и DEC
[с суммой] DHB и DHL, получится удво-
енный DEG, то есть DEG и DHB [вме-
сте], и сумма DEC и DHL, которая рав-
на двум прямым. Таким образом, эта
сумма равна удвоенному DEC и двум
прямым. Следовательно, CEG и LHB
33 [вместе] будут больше удвоенного /
DEG, т. е. DEG и DHB [вместе], на двух
прямых, то есть на DEC и LHD [вме-
сте].
150
АЛЬ-ФАРАБИ
Если предположим, что точка А се-
верней, а В — южней от зенита [рис.
47], то углы KEG и СНВ вместе меньше
удвоенного DEG, который равен DEG и
DHB вместе. Избыток удвоенного DEG
над KEG и СНВ вместе есть CHD и DEK
[вместе], которые, как мы знаем, рав-
ны двум прямым.
Существует более легкий, чем этот,
способ определения угла, образуемого
наклонным кругом и [большим кру-
гом], проходящим через зенит, и дуг,
взятых в этом круге, когда известны [ве-
личины] углов и дуг в меридиане или
в круге горизонта. Пусть сначала требу-
ется определить угол, расположенный
Вторая книга
161
между ними, то есть между [кругом],
проходящим через зенит, и косым [кру-
гом] в отношении горизонта.
Пример этого. Пусть ABCD — мери-
диан [рис. 48], BED — горизонт, А —
зенит, [то есть] полюс горизонта,
GEH — данная дуга наклонного [кру-
га] ; высота полюса 36 градусов. Если
G — точка в середине неба, то круг
АВС будет тем же кругом зенита, про-
ходящим через G. Поскольку точка G,
дана, то угол G известен; AG известна.
Пусть проведем круг АЕС через вос-
ходящую точку Е и полюс [горизонта]
А, тогда дуга АЕ будет равна четверти
круга. Поэтому угол AED будет пря-
мым, а угол, образуемый пересечением
косого [круга] и горизонта, то есть
DEH, известен, следовательно, весь угол
АЕН известен; поэтому дуги, стягиваю-
щие эти углы, известны.
Точно так же если будет известно
расстояние между точкой и меридиа-
ном, то [прямые] часы, то есть дуга па-
раллельных кругов, будут известны.
Пусть точка G на меридиане заменяет
точку Н, которая представляет начало
Рака [рис. 49], и пусть оно отстоит к
востоку от меридиана по дуге паралле-
ли на один прямой час. Точка будет из-
вестной по сказанному выше. Точка вое-
162
АЛЬ-ФАРАБИ
хождения известна. Проведем через А
и Н круг зенита до Е и С; дуга FHG из-
вестна, HF известна; AG по сказанному
выше известна; дуга DG — остаток от
четверти [круга] известна; тогда дуга
[Рис. 49]. [Рис. 50].
BG известна. Отношение синуса извест-
ной GB к синусу известной АВ составле-
но из отношения синуса известной АЕ к
синусу неизвестной ЕН и синуса извест-
ной FH к синусу известной FG. Отсюда
определим ЕА и АН и, следовательно,
дугу зенита.
Если хотим определить угол AHF,
34 то пусть вокруг полюса Н / на расстоя-
нии, равном стороне [вписанного] квад-
рата, опишем отрезок KLM большего
круга [рис. 50]. Поскольку дуга АЕС
Вторая книга
163
проходит через полюсы кругов EFM и
KLM, то каждая из ЕМ а КМ равна чет-
верти круга. Отношение синуса извест-
ной ЕН к синусу известной ЕК (так как
ЕК остаток от четверти [круга]) состав-
лено из отношения синуса известной HF
к синусу известной FL и из отношения
синуса неизвестной ML к синусу изве-
стной КМ, становится известной ML и,
следовательно, оставшаяся LK будет
известной. Поэтому известны углы KHL
nAHF.
Точно так же вычисляются [места]
точек одно за другим.
Затем он составил таблицу по этому
же способу и для каждого климата 93.
Она начинается с параллели, проходя-
щей через остров Мероэ, где наибольший
день равняется тринадцати прямым ча-
сам и продолжается с приращением по
полчаса до [параллели], где наиболь-
ший день равняется шести. Он взял
[для дуг эклиптики приращения] по
одному знаку, для широты — по полча-
са, для положения [кругов к западу и
востоку] от середины неба — по одному
[прямому] часу. В первом столбце по-
местил числа, [выраженные] в прямых
часах расстояний от меридиана, когда
эклиптика наклонна к меридиану; во
втором столбце — величины дуг между
154 АЛЬ-ФАРАБИ
наклонным кругом и зенитом; в тре-
тьем столбце — величины углов у [каж-
дого рассматриваемого] сечения [для
положений] к востоку, а в четвертом —
западных [углов]. При этом он отмеча-
ет, что в первом случае берутся углы к
северу от сечения и прямой угол содер-
жит девяносто градусов.
Что касается стран, их широт и дол-
гот, то он обещал создать отдельную
книгу и [позднее] написал свое сочине-
ние «География» ®4. Помощь от Аллаха!
ТРЕТЬЯ КНИГА 95
О временной величине года 96
Среднее движение — это такое дей-
ствительное или предполагаемое движе-
ние, при котором [светило] за равное
время [проходит] одинаковые [дуги].
Это движение светила по предположе-
нию происходит в соответствующей ему
небесной сфере, охватывающей Землю.
Оно характерно или самому светилу,
или сферическому телу, несущему све-
тило и передвигающему его вдоль эк-
липтики благодаря своему движению.
За равное время оно проходит равные
дуги, а центральные углы при центре,
[стягиваемые] этими дугами, равны.
Это движение называется равномер-
ным 97.
Если бы светила или несущие их [те-
ла] обладали одинаковыми движения-
ми за равное время по отношению к эк-
166
АЛЬ-ФАРАВЙ
липтике и проходили бы равные дуги на
ней за одно и то же время, то среднее
равномерное движение было бы доста-
точным для [установления] эфемерид 98.
Если измерить [дуги] эклиптики, то
нельзя обнаружить, что при движении
планет они за равное время проходят
равные дуги, на самом деле они различ-
ны: иногда меньше, иногда больше.
Среднее [движение — промежуточное]
между наименьшим и наибольшим. По-
этому оно и называется средним. Ано-
малия встречается во многих вещах, ко-
торые упомянем [ниже].
Каждая планета имеет свою сферу, в
которой ее равномерное движение опи-
сывает за равные времена равные дуги,
действительные или предполагаемые.
Истинное движение — это такое дви-
жение, которое [фактически] находится
по отношению к эклиптике. В движени-
ях планет может быть более одной ано-
малии, но у Солнца имеется только од-
на аномалия, которую мы и упомянем
[ниже].
35 I Известный способ нахождения
среднего [движения] таков: требуется
найти промежуток времени, за который
планета всегда возвращается к одному
и тому же положению, то есть к одной
и той же точке или к разным точкам,
Третья книга
167
прошедшим равные дуги сверх полных
кругов, безразлично в одном обороте
или в следующих друг за другом оборо-
тах. Последовательные возвращения
планеты могут быть различными, но
эта аномалия имеет предел. Затем дви-
жение возвращается к своему началу и
начинается в том месте, где еще не бы-
ло аномалии, и аномалии повторяются
в тех же положениях и последователь-
ности до последней из них. Поэтому ме-
сто одного возвращения определяется
многими возвращениями, все вместе они
являются возвращением аномалии. Если
имеется такой [промежуток] времени,
за который планета всегда возвращает-
ся к одной и той же точке или к точкам,
между которыми имеются равные дуги,
или же аномалии всегда возвращаются,
как мы упомянули, то этот промежуток
времени переводится в сутки или часы.
Затем одно полное и разделенное на
равные дуги возвращение, в том числе
и возвращение подобных аномалий,
разделятся на этот [промежуток време-
ни]. Полученное в частном является
долей этого дня или часа. Затем по ней
находится доля месяца, года и [перио-
дов из нескольких] лет для среднего
движения. Поскольку можно определить
среднее [движение] этим методом, мы
168
АЛЬ-ФАРАБИ
не отказываемся от него и не [стремим-
ся] к его определению другими метода-
ми. Первое, что требуется для опреде-
ления среднего движения,— это возвра-
щение к одной и той же неподвижной
точке или к точкам, между которыми
имеются равные дуги. Если найдены
возвращения такого рода, то есть за
равные промежутки времени, то для оп-
ределения среднего движения ограни-
чимся этим. В противном случае потре-
буем другой род, затем третий, как бу-
дет показано в надлежащем месте.
Рассмотрение положения Солнца
предшествует рассмотрению всех пла-
нет, так как определение их обстоя-
тельств возможно только после опреде-
ления движения и положения Солнца,
как мы покажем 99 [ниже].
Птолемей начинает с уточнения сред-
него движения Солнца. Исследуя наблю-
дение за ним, он нашел, что различие в
возвращении Солнца к одной и той же
неподвижной точке эклиптики, по кото-
рой вычисляются эфемериды, несуще-
ственно. Когда эти [возвращения] ока-
зывались различными, он находил, что
причиной этого была неправильность
или в делениях, или в их установке,
или же упущение исследователя при
пользовании этими [инструментами] и
Третья книга
159
наблюдение в неправильном направле-
нии. Истинное наблюдение Солнца со-
стоит в рассмотрении промежутка вре-
мени возвращения [Солнца] к одной и
той же неподвижной точке эклиптики;
предпочитаются точки равноденствий
и солнцестояний, особенно, если [тело],
несущее светило, не имеет другого дви-
жения по причине движения его апогея.
Мы смотрим, являются ли эти проме-
жутки времени равными. Если они рав-
ны, то среднее движение определяется
так, как было сказано.
Наблюдая за Солнцем, Птолемей на-
шел эти промежутки времени равными
и определил [величины] этих промежут-
ков времени, которые мы упомянем ни-
же. Это наблюдение производилось с
помощью кольца 10°, сделанного из ме-
ди или другого металла и ограниченного
четырьмя плоскими гранями, каждая
противоположная пара из которых па-
раллельна; его прочно устанавливали
на неподвижной основе в плоскости не-
бесного экватора, то есть посередине
между солнцестояниями, как мы об
этом уже сказали, что определено на-
блюдением; или же в плоскости круга,
параллельного небесному экватору и
проходящему через одну из точек солн-
цестояний; или же на каком-нибудь
160
АЛЬ-ФАРАБИ
желательном для наблюдателя круге из
параллельных кругов, описанных точ-
ками, отмеченными на эклиптике.
Установка в плоскости [круга] оз-
36 начает / описание круга в плоскости
данного круга так, чтобы, продолжая
диаметр этого внутреннего круга в обе
стороны, можно было бы получить диа-
метр или хорду другого. Далее известно,
что если кольцо такого рода установле-
но именно так на плоскости небесного
экватора или в плоскости одного из па-
раллельных кругов, проходящих через
точки солнцестояния или через другие
[точки] эклиптики, и если Солнце на-
ходится в точке равноденствия или в
точке солнцестояния [или в другой точ-
ке эклиптики], то тень со стороны, при-
мыкающей к Солнцу, полностью совпа-
дает с противоположной стороной и ни-
когда не упадет на грани, находящиеся
с южной и с северной стороны, и [Солн-
це] полностью осветит эти две грани. В
таком случае мы узнаем, что Солнце до-
стигло этой точки.
Точно так же на кольце [можно]
установить алидаду с двумя диоптра-
ми 101, чтобы алидада была симметрич-
ной и вращалась бы вместе с Солнцем.
Это наблюдение трудно провести, если
совпадение центра сверила с рассматри-
Третья книга
1в1
ваемой точкой происходит ночью. По-
этому [в таком случае] необходимо при-
бегнуть к другому наблюдению, которое
мы упомянули в главе, посвященной оп-
ределению склонения.
Известно, что если разделить попо-
лам [расстояние] между пределом вы-
соты, когда Солнце достигает предела
склонения, и пределом понижения, ког-
да Солнце достигает предела южного
склонения, получится место, до которо-
го поднимается Солнце, когда оно в точ-
ности находится на небесном экваторе.
Если это происходит ночью, то мы рас-
смотрим разность между высотами пре-
дыдущего и последующего полудня [и
разность между высотой последующего
полудня] и высотой, соответствующей
небесному экватору, тогда [вторая] раз-
ность относится к первой приблизитель-
но так же, как [промежутки] времени с
того момента, когда Солнце находится
в данной точке [до последующего полу-
дня] к [промежутку] времени между
двумя полуднями.
Наблюдение с помощью солнцестоя-
ния трудно в обоих случаях, так как
предел высоты и предел понижения от-
личаются в течение короткого [проме-
жутка] времени и при этом различие
незаметно, поскольку разность склоне-
11-89
162
АЛЬ-ФАРАБИ
ний по обе стороны от солнцестояния
мала.
Рассматривалось возвращение Солн-
ца к четырем точкам, при этом найде-
но, что эти возвращения [происходят] в
равные [промежутки] времени. Точно
такими же нашел их Гиппарх, за исклю-
чением осенних возвращений, когда на-
блюдается различие в четверть суток.
Птолемей обосновал причину этого
в одном из упомянутых обстоятельств
погрешностью в делениях инструмента
или его [неправильной] установкой, так
что если допускается погрешность в
шесть минут, то есть в одну десятую
градуса, то это [приведет] к указанно-
му различию. Поэтому [погрешность] в
одну минуту, принятая им в книге, мо-
жет привести к отклонению от истины
на половину дня, так как если Солнце
отходит от точки равноденствия на чет-
верть градуса, то это приведет к такой
же [погрешности], как и шесть минут.
Он упоминает, что, возможно, [люди]
вначале установили инструменты точно,
а затем оставили их, и эта [точность]
нарушилась, а они не исправляли эти
[инструменты] перед каждым наблюде-
нием. Он упоминает также, что на коль-
це, установленном в Александрии, име-
лось неравенство между ее освещенной
Третья книга
163
и затемненной [частями] в день равно*
действия. Эти [отклонения] отмечались
в двух случаях — некоторые в одно вре-
мя, а другие — в другое время, в одно и
37 то же время они не наблюдаются. / Од-
нако Птолемей отметил, что его много-
численные наблюдения и изученные им
работы Гиппарха, которых еще больше,
согласуются в том, что промежуток вре-
мени возвращения — один и тот же, и
он равен тремстам шестидесяти пяти
суткам и приблизительно четверти су-
ток. О нем мы еще упомянем, его нельзя
обнаружить на близких расстояниях, а
можно определить только при более да-
леких наблюдениях, в которых накап-
ливается значительная разница. При
древних наблюдениях эта разница была
подобна неравенству, [происходящему
по причине неточной] установки инстру-
ментов и неизбежной ошибке. При этом
он приблизительно указал величину это-
го недостатка, рассмотрев наблюдения
Гиппарха и сопоставив их со своими. Он
опирался на Гиппарха больше, чем на
кого-либо другого. Наблюдения в [день]
равноденствия — наиболее точные; те
же, которые [производятся] в [дни]
солнцестояний, трудно проверить. Пто-
лемей приблизительно за триста лет до
него установил, что если возвращение
164
АЛЬ-ФАРАБИ
[совершается] за триста шестьдесят
пять с четвертью суток, имеется недо-
статок по величине одних суток. Поэто-
му для каждого года разница составляет
одну трехсотую одних суток и, следова-
тельно, [промежуток] времени возвра-
щения — триста шестьдесят пять суток
четырнадцать минут и сорок восемь се-
кунд ,02. Затем он вычислил это по на-
блюдениям древних [астрономов] — Ме-
тона 103 и Евктемона ,м, а затем Ари-
старха 105 и нашел, что получается то
же самое и что Гиппарх согласен с этим
во многих своих сочинениях.
Таков путь вычисления среднего про-
хождения [Солнца] по отношению к че-
тырем точкам. Что касается возвраще-
ний Солнца по отношению к неподвиж-
ным звездам, то их можно найти двумя
способами: путем наблюдения Солнца
при восходе и заходе, если при этом
видна одна из ярких неподвижных
звезд, а также нахождением расстояния
между Солнцем и этой звездой с по-
мощью инструмента, который мы упо-
мянем позже; путем наблюдения Луны
в середине ее затмения, то есть, когда
она диаметрально противоположна ис-
тинному Солнцу. [Затем] определяется
ее положение на эклиптике в результате
ее движения. Если при этом она не име-
Третья книга
166
ет параллакса, то легко установить ее
градус путем определения высоты ее
азимута и широты местности. Отсюда
находится ее истинное положение на
эклиптике с помощью принципов, при-
водящих [к этому] в случае, когда в се-
редине затмения центр Луны не имеет
широты. Отсюда можно определить гра-
дус Солнца, поскольку оно не имеет
параллакса. Если же центр Луны имеет
широту, то путь к этому более длинный
и при этом легче ошибиться. Таким
образом, промежуток времени возвраще-
ния [Солнца] оказывается больше упо-
мянутого. Вот почему Гиппарх догады-
вался, что неподвижные звезды движут*
ся около полюса эклиптики. Поэтому
Птолемей пренебрег наблюдениями,
проведенными относительно этих звезд.
Нет разницы, считать ли солнечный год
по возвращениям к неподвижным звез-
дам, движущимся около точки, где
Солнце и Луна [начинают] расходиться,
или считать его по отношению к плане-
те Сатурн; в обоих случаях годы полу-
чаются различными. Хотя это неравен-
ство мало для близких оборотов, оно
увеличивается для более далеких оборо-
тов. Иногда это неравенство невозмож-
но обнаружить. Наиболее грубыми яв-
ляются наблюдения при затмениях, в
166
АЛЬ-ФАР АВИ
которых требуется найти [положение]
центра Луны относительно неподвиж-
ных звезд, когда Солнце на самом деле
находится в диаметрально противопо-
ложной ей точке.
Далее Птолемей рассмотрел различ-
ные наблюдения, чтобы при их помощи
найти возвращения Солнца и опреде-
лить, совершаются ли они за равные
промежутки времени, а с их помощью
проверить [результаты], полученные
другими методами. Гиппарх упомянул,
что когда он провел вычисления для
двух наблюдений лунного затмения, он
при одном из этих наблюдений затме-
ния расстояния Луны и Симака Безо-
ружного 108 обнаружил, что положение
Симака опережало точку осеннего [рав-
ноденствия] на шесть с половиной гра-
дусов, а через одиннадцать лет с не-
многим, когда провел вычисления для
второго наблюдения, Симак Безоруж-
38 ный опережал точку / осеннего [равно-
денствия] на пять с четвертью граду-
сов; к этому приводят измерения.
Однако нельзя сказать, что Симак Безо-
ружный за этот промежуток времени
переместился на такую величину; по-
этому он пришел к выводу, но без уве-
ренного утверждения, что, возможно, у
Солнца имеется еще одно неравенство,
Третья Книга
167
Ьтличное от того, о котором мы будем
говорить. Оно получается вследствие то-
го, что его возвращения за равные про-
межутки времени не одинаковы.
Птолемей же отказался от этого ме-
тода, так как его наблюдения возвраще-
ний Солнца за тот же самый промежу-
ток времени соответствовали указан-
ным измерениям. Разница, полученная
при наблюдении, когда для уточнения
положения Луны было необходимо
уточнить положение Солнца, не должна
была вызывать сомнения в самом прин-
ципе, а происходит от второстепенных
вопросов, поэтому в случае необходимо-
сти приходится сомневаться [только] в
этих второстепенных вопросах. Кроме
того, Луна может иметь параллакс, а
инструменты, с помощью которых на-
блюдаются расстояния, могут обладать
погрешностью. Возможно, причиной это-
го явилось то, что одно из этих двух на-
блюдений проводилось в исследованных
обстоятельствах, а другое — в неиссле-
дованных, или же то, что исследование
движения Солнца от точки весеннего
[равноденствия] до середины времени
затмения в его среднем продвижении не
проводилось. Сам Гиппарх тоже знал
это и поэтому не придавал своему
168
АЛЬ-ФАРАБИ
[предположению большого] значения,
он не утверждал, что Солнце обладает
еще одним неравенством и не отвергал
утверждения о том, что солнечный год
является упомянутым промежутком
времени. Поэтому неравенства, получен-
ные при других наблюдениях, в кото-
рых имеется погрешность, не рассма-
тривались. [Птолемей] указывал, что
его цель состояла в рассмотрении всех
встречающихся ему вещей до одной.
Точно так же, когда Гиппарх наблюдал
другие затмения, предварительно опре-
деляя истинное положение Солнца в
середине затмения и рассматривая сере-
дины этих затмений относительно про-
тивоположного им центра Солнца; с их
помощью он нашел положения непо-
движных звезд, расстояния которых от
Луны известны, а также доказал, что
возвращения Солнца не отличаются су-
щественно от тех, которые получаются
при других наблюдениях. [Птолемей]
сказал: когда я проверил [наблюдения
при] затмениях с целью выяснения [это-
го вопроса], я обнаружил, что они не
отличаются существенно от того, что
должно быть. Я говорю, что нужно рас-
смотреть также состояние Солнца [и
установить], имеет ли оно параллакс, с
помощью наблюдений в весьма отдален-
ФретьМ mfa
169
иых друг от друга городах на севере и
на юге, больше ли разница в его высо-
те в меридиане, которая вызвана разли-
чием широт [этих городов], а также
наблюдать его там, где оно находится в
зените и городах, недалеких от этих по-
ложений, и выяснить соответствует ли
эта разница по высоте [разнице] широт.
Если же окажется, что Солнце обладает
параллаксом, то определяется его вели-
чина в соответствии с этим. Выясняется,
что истинные высоты и тени предме-
тов отличаются от наблюдаемых и вы-
численных. Подтверждение существова-
ния параллакса [Солнца] приносит вред
при уточнении места Солнца и времени,
в которое оно приходит в данную точку;
однако оно безвредно при определении
солнечного года и промежутка времени
возвращения Солнца к известной точке,
так как, если возвращение по видимости
таково же, как раньше, и город [один и
тот же], возвращение по градусам эк-
липтики произойдет к одной и той же
точке, однако отличной от той, которая
определяется наблюдением.
эд / Возвращение Солнца происходит
на эклиптике в одной и той же точке,
которая [может] быть отлична от той
точки, которую дает наблюдение. Вооб-
ще если оно не возвратится в одну и ту
170
АЛЬ-ФАРАВЙ
же точку, то оно не возвратится и к од-
ному и тому же параллаксу на высоте
[точек] солнцестояний и равноденст-
вий.
После того, как среднее движение
[Солнца] получено этим способом, он
захотел составить таблицы107, избав-
ляющие от вычисления каждого проме-
жутка времени. Он поместил в них то,
что пройдено Солнцем за один час, за
24 часа, за месяц, за год, за восемнад-
цать лет и за [промежутки времени],
кратные восемнадцати годам. Если тре-
буется найти то, что пройдено в сред-
нем за данный промежуток времени, то
найдем в таблице эти годы, сложенные
или отдельные, и другие промежутки
времени. Если в таблице имеется [про-
межуток] , то возьмем градусы, минуты,
секунды и все остальное, находящееся
против этого. Если же имеется избыток,
то посмотрим, какова его величина, и
найдем в таблице то, что находится про-
тив него, и, прибавив к найденному, по-
лучим точное [среднее положение Солн-
ца] в данный промежуток времени.
Третья книга
171
О гипотезах, предполагаемых
для равномерного движения,
происходящего по кругу
Если уже мы получили среднее дви-
жение Солнца, то для нахождения эфе-
мерид Солнца этого недостаточно, так
как за равные промежутки времени
Солнце проходит неодинаковые дуги
эклиптики. Оно проходит то меньше, то
больше, как мы упомянем [ниже]. На-
блюдением было найдено, что промежу-
ток времени, за который оно проходит
от весеннего равноденствия до летнего
солнцестояния, отличается от того, за
который оно проходит от последнего до
осеннего равноденствия. Также было
найдено, что [время], за которое оно
проходит от осеннего до весеннего рав-
ноденствия, меньше времени, за которое
оно проходит от весеннего до осеннего
равноденствия. То же самое относится к
частичным дугам. Но мы не можем ска-
зать, что оно движется то медленнее, то
быстрее, так как по закону небесных
движений они равномерны и не имеют
различий по отношению к самим себе.
Если же они представляются и кажутся
[неравномерными], то это [только]
по отношению к нам 108.
Эта неравномерность происходит
iti
АЛЬ-ФАРАЙЙ
только по одной из двух причин. Первая
причина: если Солнце движется по экс-
центричному кругу, то та часть [круга],
которая находится со стороны одной по-
ловины эклиптики, например северной,
больше другой его части, если наиболь-
шее удаление — с северной стороны.
Солнце или любая планета движется
или по своему [эксцентричному] кругу
в своей сфере, тогда [оно проходит]
больше его половины, или же по [са-
мой] эклиптике, тогда [оно проходит]
ее половину, а с другой [южной] сторо-
ны будет наоборот. Таким образом, оно
пройдет обе половины эклиптики за раз-
ные [промежутки] времени 109.
Вторая причина: если [Солнце] дви-
жется не по кругу, концентричному с
эклиптикой, и не по эксцентричному
кругу, то его тело находится на круге,
не охватывающем Землю, а не на кру-
гах светил, охватывающих Землю. Оно
движется по этому кругу, называемому
эпициклом. Центр этого круга может
двигаться по кругу, концентричному с
эклиптикой 11 °.
Далее ясно, что если движение пла-
неты совершается по эпициклу в том же
направлении, что и центр эпицикла, то
нам кажется, что Солнце движется бы-
стрее среднего, когда находится в апогее
Третья книга
173
своего эпицикла, и медленнее среднего,
когда находится в перигее, так как пла-
нета неизбежно изменяет свое положе-
ние, в котором находилось бы Солн-
це, если бы не двигалось [по эпициклу].
Если движение центра эпицикла со-
вершается по концентричному деферен-
40 ту / равномерно, то это — среднее дви-
жение [планеты], безразлично дви-
жется ли она, следуя движению своего
эпицикла, или же совсем не движется.
Движение планеты обладает избытком
или недостатком [по отношению к сред-
нему движению] потому, что она дви-
жется по своему эпициклу. Если плане-
та находится на нижней стороне эпи-
цикла, то кажется, что она движется
назад. Центр эпицикла может также
двигаться по эксцентричному деференту
эксцентра, тогда его движение по дефе-
ренту неравномерно. Из этого вытекает
много аномалий.
Однако движение Солнца не может
обладать аномалиями, обусловленными
одной из этих .двух гипотез — эксцен-
трической гипотезой при равномерных
движениях и экциклической гипотезой
при движении Солнца по эпициклу про-
тивоположно его равномерному движе-
нию по концентрическому кругу в сто-
рону востока. 'J
174
АЛЬ-ФАРАБИ
Птолемей выбрал первую гипотезу,
так как ее легче предположить, а не из-
за явной необходимости в ней. Он вы-
брал наиболее легкое из этих двух дви-
жений, потому что убедился в том, что
при предположениях о некоторых усло-
виях и предпосылках обе гипотезы оди-
наково соответствуют всему тому, что
происходит на самом деле.
При каждой из двух гипотез необхо-
димо иметь наименьшее и наибольшее
расстояние. При эксцентрической гипо-
тезе наибольшее расстояние находится
в конце диаметра, проведенного через
центры Земли и эксцентрического круга
со стороны центра эксцентрического
круга, а наименьшее расстояние — с
другой стороны. При эпициклической
гипотезе ясно, что [наибольшее расстоя-
ние находится в апогее эпицикла, а наи-
меньшее — в его перигее]. Если планета
находится в середине между этими дву-
мя различными расстояниями и не сме-
щается ощутимо к одному из них, то
видимое движение будет равно движе-
нию центра эпицикла и являться сред-
ним движением.
Именно на наибольшем и наимень-
шем расстояниях имеет место предел
аномалии; пределом аномалии считает-
ся наибольшая разность между средним
Третья книга
176
и видимым [движениями]. Аналогич-
ное наблюдается при эксцентрической
гипотезе ,н.
Мы утверждаем, что если имеются
две равные дуги, одна из которых отло-
жена от наибольшего расстояния, а
другая — от наименьшего, то большим
[Рис. 51].
[Рис. 52].
из двух углов, образуемых диаметром и
линиями, проведенными из центра эк-
липтики к концам этих двух дуг, будет
тот, который при наименьшем расстоя-
нии.
Что касается случая эксцентриче-
ской гипотезы, то пусть ABCD — эксцен-
трический круг [рис. 51], имеющий
176
АЛЬ-ФАР АВИ
центр эклиптики Е, DGEA — диаметр,
проходящий через оба центра, и А —
апогей, D — перигей; дуги АВ и CD —
равные. Проведем ЕВ, ЕС, GB, GC. По-
скольку углы AEB, DEC равные и угол
АЕВ как внешний угол треугольника
EGB больше угла EGB, то есть AGB, и
поэтому угол DEC больше AGB. Следо-
вательно, угол DGC как внешний угол
треугольника CEG намного больше это-
го угла.
Что касается случая эпицикличе-
ской гипотезы, то пусть АВС — концен-
трический [с эклиптикой круг], имею-
щий центр Е и [полу]диаметр АЕ
[рис. 52]; вокруг точки А опишем эпи-
цикл, имеющий [полу] диаметр FA,
пусть эпицикл движется от А, а свети-
ло — от G в сторону В. Если светило на-
ходится в G или F, то оно не имеет дви-
жения, отличного от движения точки А,
41 и если место светила / отлично от них, и
оно проходит [дугу] GH, то опередит
равномерное [движение] на дугу АН, а
если проходит [дугу] GK, то отстает от
равномерного движения на дугу АК, то
есть на АН; GH больше FK, так как ес-
ли через точку А проведем перпендику-
ляр к АЕ, то получится диаметр, кото-
рый будет касательной к концентриче-
скому [кругу] и отсекает в сторону G
Третья книга
177
[дугу] меньше, чем отсекает концентри-
ческий [круг]; время, за которое оно
проходит [дугу] АН, больше того, за
которое оно проходит [дугу] АК. Если
оно движется противоположно этому
движению, то все будет наоборот. Следо-
вательно, его движения в равные [вре-
менные] дуги будут не равными, а раз-
личными. В первом положении при апо-
гее движение медленнее, а в перигее —
быстрее, а во втором положении, когда
движение происходит по концентриче-
скому [кругу], будет наоборот.
Таким образом, по эксцентрической
гипотезе движение, которое кажется за-
медленным и меньшим, [происходит]
при апогее, а то, [которое кажется] бы-
стрым и большим,— при перигее. Что
касается эпициклической гипотезы, то
возможно и то и другое в соответствии
с направлением движений светила в
апогее: если они совпадают, то быстрее
будет при апогее, а если противополож-
ны, то быстрее — в перигее 112.
Докажем предположение о том, что
все явления одинаково можно объяс-
нить при случаях обеих гипотез, если
выполняются следующие три условия:
во-первых, чтобы линия, соединяющая
оба центра, относилась к полудиаметру
эксцентра как полудиаметр эпицикла к
12-89
178
АЛЬ-ФАРАБИ
полудиаметру концентрического дефе-
рента ; во-вторых, чтобы дуга деферента,
пройденная центром эпицикла, была по-
добной [дуге] эпицикла, пройденной
светилом за то же время; в-третьих, ес-
ли направления двух движений при эпи-
циклической гипотезе противополож-
ны 113 в квадранте, видимом от апогея.
Сначала мы докажем 114, что при
каждой из двух гипотез предел разно-
сти, вызванной неравенством, достига-
ется, когда видимое [расстояние] от апо-
гея составляет четверть [круга].
Пусть ABCD — эксцентрический
круг вокруг центра Е, имеющий диа-
метр АЕС [рис. 53], центр Земли нахо-
дится в G, проведен через него перпенди-
куляр BGD на диаметр, который разде-
лит пополам эклиптику и вместе с
общим диаметром составляет две четвер-
ти [круга]. Проведем ЕВ; АВ стягива-
ет угол АЕВ истинного [движения], а
угол AGB — видимого [движения]. От-
ношение АВ из эклиптики к АВ из экс-
центра — отношение этих углов, раз-
ность между этими углами и есть нера-
венство. Поскольку угол АЕВ внешний,
который больше внутреннего угла G на
угол В, то угол В — предел разности
между средним и уравненным [движе-
ниями], являющийся избытком нера-
Третья книга
179
венства. Точно так же угол, ограничи-
вающий разности между внешним и
внутренним из различных центров,—
это угол уравнения 115. Мы утверждаем,
что нельзя построить из внутренних ли-
ний в сторону В угол, не меньший, чем
42 угол В. / Пусть построим угол F к апо-
гею или угол К к перигею, проведем
также линии ED, EF, DF, GF и GK;
углы D и В в равнобедренном треуголь-
нике DEB равны; точно так же углы
D и F из треугольника EDF равны; DG,
то есть GB, короче, GF, как было дока-
зано в [„Началах”] Евклида, так как
GF стягивает угол FDG, который боль-
ше GFD, то угол EFG меньше угла GDE,
то есть GBE. Поскольку хорда GD, то
есть GB, длиннее GK, то угол GKD
180
АЛЬ-ФАРАБИ
больше угла GDK", но весь К равен все-
му D, значит, EDG, то есть EBG, боль-
ше EKG. Следовательно, угол В больше
всех углов, находящихся на противопо-
ложных точках окружности П6.
Тем самым доказано, что дуга АВ,
соответствующая времени [перехода]
от наименьшего движения к среднему
движению, больше дуги ВС, соответст-
вующей времени [перехода] от средне-
го к наибольшему движению при пери-
гее; разность этих дуг есть дуга нера-
венства, соответствующая углу В,
потому что угол АЕВ больше прямого
на угол EBG, а ВЕС меньше прямого на
тот же угол.
Докажем аналогичное в случае эпи-
циклической гипотезы. Прежде чем
приступить к этому, я утверждаю, что
мы должны сначала знать, что как в
истинном, так и в видимом [движениях]
расстояние светила от апогея эпицикла
не [равно] четверти круга. По-ви-
димому, оно заключает в себе наиболь-
шее неравенство, когда линия, выходя-
щая из глаза до светила, касается эпи-
цикла. Если же она пересекает его, то
при этом расстоянии [светило] не име-
ет наибольшее неравенство, так как для
каждой пересекающей [линии] можно
найти такую точку [эпицикла] вне этой
Третья книга
181
линии, при которой прямая линия, сое-
диняющая ее с глазом, дала бы боль-
шее, чем то, расстояние от центра эк-
липтики. Таким образом, линия, прохо-
дящая через наиболее отдаленную точ-
ку от центра эклиптики, должна быть
касательной. Но касательная через [точ-
ку] истинной четверти [с любой] из
двух сторон параллельна диаметру эпи-
цикла и поэтому не может дойти до гла-
за по прямой, так как глаз находится на
диаметре. Поэтому касательная линия,
проведенная из глаза, будет иметь дру-
гую точку касания. Если же соединить
глаз с точкой той линии, что касается в
[точке] четверти, то эта [линия] пересе-
чет эпицикл, и поэтому может произой-
ти пересечение до нее. Точка касания
линии, проведенной из глаза, тоже
должна доходить до [точки] пересече-
ния эпицикла с концентрическим [кру-
гом], так как если бы она была [точ-
кой] этого пересечения и мы провели
бы линию из центра эпицикла до нее, то
угол, образованный у нее, был бы равен
углу, образованному у центра диамет-
ром, проходящим через оба центра, и
линией, проведенной из центра эпицик-
ла, поскольку обе стороны треугольни-
ка равны. Тогда [касательная] не была
бы перпендикулярна [к диаметру], ина-
182
АЛЬ-ФАРАБИ
че в одном треугольнике имелись бы два
прямых угла. Эта [точка] касания тоже
не может быть дальше точки пересече-
ния, так как если бы она была там, то
угол, образованный [касательной] и по-
лудиаметром эпицикла, был бы больше
угла, который у центра, поскольку пер-
вый [угол] прямой. Тогда линия, сое-
диняющая оба центра, была бы длиннее
касательной, это нелепо, так как она
равна ее части.
Далее угол, образованный касатель-
ной и диаметром эпицикла, прямой, и
он больше того, который соответствует
ему в случае пересечения. Также цен-
тральный угол в случае касания больше
центрального угла в случае пересечения,
так как этот [угол] при пересечении яв-
ляется частью того, [что при касании].
Поэтому третий [угол при касании]
43 меньше, чем соответствующий ему / в
первом случае. Таким образом, разность
неравенства, к которой приводит этот
угол в случае касательной, меньше дру-
гой разности неравенства. Это нелепо,
так как это — угол предела неравенства.
Итак, выясняется, что место [точки ка-
сания] — до пересечения эпицикла с
концентрическим [кругом]. Отсюда
доказывается, что дуга предела нера-
венства больше дуги, ограниченной
Третья книга
183
центром эпицикла и [точкой] пересече-
ния концентрического [круга с эпицик-
лом].
Пусть АВС — концентрический круг
с центром D [рис. 54], EGH — эпицикл
с центром A, BDGEA — диаметр, прохо-
дящий через эти центры, пусть точкой
видимой четверти [круга] будет Н; до-
пустим, что движение по концентриче-
скому кругу разделит деферент на ча-
сти, подобные частям, на которые раз-
делится эпицикл движением светила.
Угол ADC есть неравенство между сред-
ним движением при Е и видимым дви-
жением при Н; по предположению, Н
кажется находящейся на четверти [кру-
га] . Угол D — предел разности неравен-
ства и уравнения. Если DH — касатель-
ная, то АН обязательно пересекает ее
перпендикулярно; восстановим из точ-
ки А перпендикуляр AF на диаметр.
Избыток истинной четверти [круга] над
К будет угол К АН, равный углу D;
продолжим АК до встречи с DH\ они
пересекутся, так как сумма двух углов
D и FAD меньше двух прямых, по-
скольку угол F — общий и угол А тре-
угольника FAD равен углу Н треуголь-
ника HFA. Отсюда следует, что угол
РАН равен углу D. Это разность нера-
венства.
184
АЛЬ-ФАРАБИ
Из всего этого следует, что дуга ЕН,
которая определяет время [перехода]
из наименьшего движения к среднему,
будет больше дуги Н, которая опреде-
ляет [время перехода] от среднего к
наибольшему движению; разность меж-
ду ними — удвоенная дуга КН, то есть
[удвоенная] дуга АС, так как эти дуги
подобны между собой.
Разность есть удвоение этого, так
как одна из них меньше истинной чет-
верти на эту [величину], а другая боль-
ше ее на эту [величину].
Из этого также доказывается, что
при обеих гипотезах движение подобно
среднему [движению] и совпадает с
ним, когда достигается предел разности
неравенства. Однако обе гипотезы сов-
падают не только в [рассмотрении] пре-
дела неравенства, а также частных не-
равенств для частных дуг. Поэтому ес-
ли соблюдать [условия] предпосылки,
то уравнение будет одним и тем же за
равные [промежутки] времени, под
уравнением имеется в виду разность не-
равенства. Это имеет место независимо
от того, будет ли [указанное] отноше-
ние одним и тем же при обеих [гипоте-
зах] , которое произойдет, если полудиа-
метр эпицикла равен линии, соединяю-
щей оба центра, или же это отношение
Третья книга
185
подобно, то [есть] полудиаметр эпицик-
ла относится к линии, соединяющей
[оба центра], как полудиаметр концен-
трического [круга] к полудиаметру
эксцентра.
Сначала положим, что отношение
одинаковое. Пусть АВС — концентри-
ческий круг [рис. 55], имеющий центр в
D; GK — эпицикл с центром В. EGH —
эксцентр с центром F; общий диаметр
•концентрического круга и эксцентра
[Рис. 55].
[Рис. 56].
EDC-. когда центр эпицикла отсекает
АВ, то светило отсекает KG, подобную
44 АВ. Соединим FG, DG / и BG. Посколь-
ку FD и GB по предположению равны,
то FG и DB также равны, так как полу-
чается параллелограмм, угол FGD, ко-
торый является разностью неравенства
по эксцентрической гипотезе, равен на-
186
АЛЬ-ФАРАБИ
крест лежащему GDK, который пред-
ставляет собой разность неравенств по
эпициклической гипотезе. Внутренний
угол ADB равен внешнему односторон-
нему с ним AFG; GBK также внешний
угол, поэтому дуги треугольника подоб-
ные. Следовательно, место светила в
них одно и то же; разность неравенства
в них одна и та же при одинаковом вре-
мени. Ясно, то же самое получится для
любых дуг.
Что касается доказательства при
случае, когда это отношение подобное,
то пусть АВС — [круг] деферента, име-
ющий центр D [рис. 56], a EG — эпи-
цикл, имеющий центр В, пусть эпи-
цикл отсекает АВ, а светило отсекает
EG, подобную АВ; проведем круг экс-
центра больший, чем деферента, это
круг НЕ с центром К, а также меньший
его, это М с центром N. По условию по-
лудиаметр эпицикла относится к линии,
соединяющей центры, как полудиаметр
деферента к полудиаметру эксцентриче-
ского [круга]. Проведем BG, а также
продолжим GD, проходящую через М
дуги LM до F — из дуги ЕН; продол-
жим DB до Е, то есть до апогея.
Мы утверждаем, что все эти дуги по-
добные. Поскольку GE подобна АВ, то
угол GBE равен углу ADB; BG и DA
Третья книга
187
параллельны; угол BGD треугольника
GDB равен накрест лежащему, угол
D — общий для треугольников MDN и
FKD, их стороны, содержащие этот
угол, пропорциональны, так как сторо-
ны DG и BD пропорциональны их сто-
ронам. Поскольку отдельные углы рав-
ны и содержащие их стороны пропор-
циональны, то BG относится к DG как
DK к KF; по предположению отноше-
ние BG и DK равно отношению DA к
FK и отношению DG к DF; таким обра-
зом, соответственные углы в треугольни-
ках равны, то есть углы GDB, DFK и
DMN равны; линии BD, MN и FK парал-
лельны, следовательно, углы ADB, НКР
и LNM равны, поэтому их дуги будут
подобными. Итак, светило будет усма-
триваться по одной и той же прямой
DMGF, при этом оно будет казаться на-
ходящимся соответственно в точках F,
MnG.
Мы утверждаем также, что когда в
видимом движении [светило] пройдет
равные дуги от наибольшего и от наи-
меньшего расстояния, то в обоих поло-
жениях происходящее от неравномерно-
сти видимое неравенство будет одинако-
вым, потому что, когда [светило] нахо-
дится в стороне апогея, уравнение
уменьшается, а когда в стороне пери-
188
АЛЬ-ФАР АВИ
гея — возрастает. Такое же наблюдает-
45 ся/при обеих гипотезах. Докажем это по
эксцентрической гипотезе. Проведем из
центра Земли G какую-нибудь [рис. 57]
[линию], пересе-
кающую диаметр,
перпендикулярно,
пусть это DGB, ко-
торая неизбежно
отсекает равные ви-
димые дуги DC и
А.В, потому что
[стягиваемые ими]
углы как верти-
кальные равны; соединим D и Е, Е и
В; ясно, что углы D и В равны в силу
равнобедренности [треугольника], но
угол DEG меньше внешнего BGC, кото-
рый соответствует неравномерному дви-
жению при перигее и [меньше] угла
DGC на угол D, а угол AGB при апо-
гее, который равен DGC при перигее,
[меньше АЕВ] на угол D. Это есть
разность между видимым и средним
[движением], каждый из равных углов
В и D есть разность между видимым и
средним [движением].
Согласно этому среднее [движение]
иногда больше видимого исправленного,
а иногда меньше его. Однако они рав-
ны. Следовательно, прибавляемое и вы-
Третья книга
180
читаемое в них одинаковы. Что касается
случая эпициклической гипотезы, то
пусть этими двумя дугами в эпицикле
будут произвольно взятые дуги EG и
HF, которые отсекаются одной и той же
линией, выходящей из D и являющейся
центром концентрического [круга]. Из-
вестно, что по видимости они равны, то
есть вызывают одно и то же неравенст-
во, потому что разность неравенства, то
есть угол D, для них обоих один и тот
же. Но эти дуги различные. Соединим
А и Н, А и G, тогда угол EAG больше
AGD на угол ADG, AHG больше вну-
треннего DAH на угол D; но, как было
доказано, угол G — это угол видимого
движения в апогее, потому что он—раз-
ность между ним и внешним углом,
EAG есть то, что соответствует средне-
му, то есть углу D. Таким образом, угол
G меньше угла EAG, соответствующего
среднему [движению], на угол D.
Что касается перигея, то угол види-
мого движения при нем — угол AHG,
равный углу AGH, больше среднего уг-
ла, соответствующего FAH, также на
угол D, а в действительности меньше
ЕАС также на угол D. Следовательно,
среднее движение в наибольшем рас-
стоянии будет больше видимого на та-
кой угол, на который меньше оно в
190
АЛЬ-ФАРАБИ
наименьшем расстоянии от видимого,
если указанное отклонение будет точно
таким же.
О видимом неравенстве движения
Солнца
Птолемей исследует неравенства
[движения] Солнца. Он говорит: хотя
возвращения Солнца происходят за
[равные] промежутки времени, однако
обнаруживается, что оно не проходит
четверти [эклиптики] за равные време-
на; поэтому оно не переходит дуги,
меньшей четверти, за равные [проме-
жутки] времени. Следовательно, види-
мое движение Солнца неравномерное.
Однако его неравенство наблюдается в
одних и тех же местах. Для его [объяс-
нения] предпочтительно привлечь экс-
центрическую гипотезу. Поэтому необ-
ходимо найти правило [нахождения]
его уравнения по этой гипотезе.
Сначала определим величину соеди-
няющей линии и место наибольшего рас-
стояния в эклиптике. Гиппарх на основе
наблюдений нашел, что время [движе-
ния] от весеннего равноденствия до лет-
него солнцестояния — девяносто четыре
46 и половина / дня, а от этого солнцестоя-
ния до осеннего равноденствия — девя-
Третья книга
191
носто два с половиной дня 117. Используя
эти данные, он вычислил, что сое-
диняющая линия (эксцентритет) состав-
ляет двадцать четвертую часть полудиа-
метра эксцентра; [точка] наибольшего
расстояния предшествует [точке] летне-
го солнцестояния примерно на 24; 30
градуса, отсюда вытекает, что в этой
четверти движение несколько замедлен-
ное.
Птолемей, исходя из метода Гиппар-
ха, по-своему доказывает указанное
явление в соответствии со своими на-
блюдениями. Он нашел по наблюдению,
что время от осеннего до весеннего рав-
ноденствия равно 178 и одной четверти
дня, а от весеннего до летнего солнце-
стояния 94 с половиной дням. Из этого
следует, что апогей и отношение линий
соответствуют тому, что было приведено
Гиппархом.
Пусть ABCD — круг Зодиака с цен-
тром Е [рис. 58], FKLM — эксцентриче-
ский круг с центром G, А — [точка] ве-
сеннего равноденствия, а В — летнего
солнцестояния; из точки G проведем
линию NGO, параллельную АС, которая'.
пересекает BD в X; линия PG, парал-
лельная BD, пересекает АС в Q. По-
скольку GN выходит из центра, a QF —
из другой точки диаметра BG, то GN
192
АЛЬ-ФАРАБИ
длиннее ее; проводим перпендикуляр
FX на GN, который будет параллель-
ным DB и пересекает [GW] внутри кру-
га и отсекает GX, равную QF; его про-
должим до Т, в X [линия] FT разделит-
ся пополам.
Точно так же проведем КС, которая
в С разделится пополам; тогда точки
F, К, L и М являются точками четверти
в эксцентрическом [круге], [точка] F,
которая видна по направлению А, соот-
ветствует [точке] весеннего равноденст-
вия, а К, соответствующая точке В,—
[точка] летнего солнцестояния. Анало-
гичное наблюдается и с остальными
точками.
На основе наблюдений Птолемей оп-
Третья книга
193
ределяет период прохождения [Солн-
цем] дуги KLM, следовательно, нахо-
дит части среднего движения, что КМ
меньше полукруга и равна удвоенной
дуге ОК, что КО — ее половина, опреде-
ляет, насколько она меньше четверти
[круга], и находит ее меньшей на дугу
КР, но КР — известна; по наблюдению
Птолемей находит KF и поэтому КР из-
вестна, определяет FN — избыток над
четвертью.
Продолжим линию, соединяющую
центры до эклиптики, это EGH', по-
скольку движение замедленное в север-
ной половине, из двух квадрантов на
KF окажется апогей, который находит-
ся в точке Н; поскольку дуга FN извест-
на, то ее половина FT и ее хорда FXT из-
вестны, ее половина FX известна: точно
так же КС известна, следовательно, па-
раллельные с ними QG и GX известны;
таким образом, четыре стороны ЕХ бу-
дут известными и поэтому диагональ
(хорда прямого угла) известна, то есть
соединяющая линия известна; цен-
тральные углы известны из треугольни-
ка; это угол АЕН, то есть дуга АН из-
вестна. Таким образом, определено от-
ношение соединяющей линии к полу-
диаметру деферента; определяется рас-
стояние апогея от [точки] весеннего,
13-49
194
АЛЬ-ФАРАБИ
равноденствия и, следовательно, ква-
дранты эксцентрического круга будут
известными.
Таким образом, найдены место
апогея и отношение соединяющей ли-
нии согласно тому, что было у Гиппар-
ха 118.
Птолемей утверждал, что апогей
Солнца неподвижен и не перемещается.
Что касается позднейших [ученых], то
наблюдения, проведенные во времена
Мамуна 119 тем же методом, показали,
что апогей Солнца отклоняется от места,
47 указанного Гиппархом / по отношению
к движению неподвижных звезд. Это же
установили и мы по своим наблюдени-
ям, [произведенным] после сочинения
этой книги 12°.
Далее он показывает, что предел не-
равенства достигается при девяносто
двух градусах и двадцати трех минутах
от апогея эксцентрического круга или
эпицикла. Сначала это докажем при
эксцентрической гипотезе. Он сказал:
пусть из центра эклиптики Е восстано-
вим перпендикуляр на диаметре и [про-
должим его] до точки В [рис. 59]. Сое-
диним В и D. По доказанному этот угол
DBE соответствует пределу разности,
обусловленной неравномерностью [дви-
жения], стороны треугольника BED из-
Третья книга
195
вестны, потому что известно отношение
BD к DE по предыдущему предложе-
нию ; угол Е — прямой, остальные уг-
лы известны, то есть угол В известен
по вычислению. [Предел неравенства]
[Рис. 59].
[Рис. 60].
составит два градуса двадцать три ми-
нуты 121, каких в четырех прямых со-
держится 360 градусов; ADB как внеш-
ний угол известен и поэтому дуга АВ
известна по вычислению вышеуказан-
ным [способом], она больше прямого
[угла] на предел неравенства.
Что касается случая эпицикличе-
ской гипотезы, то пусть АВС — концен-
трический круг, BEG — эпицикл с цент-
ром А [рис. 60], DG — касательная, про-
веденная из центра, тогда А обязательно
перпендикулярна к ней; отношение
AG и АВ известно по треугольнику,
196
АЛЬ-ФАР АВИ
стороны и углы по указанному нами
способу будут [также] известными; по-
этому угол D известен, то есть дуга раз-
ности известна, внешний угол EAG че-
рез два угла треугольника известен;
следовательно, дуга EBG, то есть рас-
стояние от апогея, известна. Результаты
вычисления соответствуют указанным
выше.
Об определении частных
[значений] неравенств
Что касается того, как можно опре-
делить эфемериды [движений] Солнца,
то мы утверждаем, что когда опре-
делим расстояния среднего движения
от апогея, то мы определим и то, что
приходится на долю неравенства, и уз-
наем местонахождение [Солнца] в
эклиптике.
Сначала докажем это в случае экс-
центрической гипотезы; пусть АВС —
концентрический круг [рис. 61] с цент-
ром D; EGH — эксцентрический [круг]
с центром F; пусть дуга EG известна;
соединим F и G, D и G; [дуга] АВ из
эклиптики и есть искомая [величина],
она видна из [центра эксцентра] по ду-
ге GE.
Продолжим GF до К, то есть до ос-
нования перпендикуляра DK, проведен-
Третья книга
197
ного из центра; таким образом, угол К
и угол KFD как вертикальный с извест-
ным углом EFG будут известными; FD
как диаметр описанного около [прямо
угольного] треугольника [F.KD] изве-
стен; тогда стороны и углы этого тре-
угольника по тому, что было сказано,
[Рис. 61].
[Рис. 62].
будут известны 122, следовательно, FD
как одна из сторон известна, таким об-
разом, KF и FG известны по отношению
и поэтому KG известна и KD / извест-
ив на; К — прямой угол, отсюда DG из-
вестна и угол разности [неравенства],
то есть угол G, известен; углы FDG и
KDF известны; следовательно, угол
ADG известен и [искомая дуга] АВ из-
вестна ; если положить EG равной трид-
1д8
АЛЬ-ФАРАБИ
цати градусам, то АВ будет равна 28,51
градуса.
Мы утверждаем также, что если счи-
тать известным угол дуги эклиптики
или угол разности, то и другие из ука-
занных углов будут известны. Предпо-
ложим, что угол D известен; опустим
перпендикуляр FL на DG [рис. 62]. По-
скольку углы D и L прямоугольного тре-
угольника FDL известны, то DF извест-
на по отношению к FLf в треугольнике
стороны и углы треугольника известны
по тому же отношению; отношения DF
к FG и FD к FL известны, угол L —
прямой и LG известна из известного тре-
угольника FLG, все углы известны, угол
G, равный разности неравенства, изве-
стен, внешний угол EFG и [дуга] EG
известны.
И пусть на этом же рисунке угол G
известен, гипотенуза FG также извест-
на. В треугольнике FGL известны сторо-
ны и углы, отсюда треугольник FLD
будет известным по двум сторонам и
прямому углу; следовательно, угол D,
внешний угол F и дуга EG известны.
Что касается доказательства этого в
случае эпициклической гипотезы, ког-
да известна дуга от апогея, то пусть
АВС — концентрический круг с цен-
тром D [рис. 63], a EGHF — эпицикл с
Третья книга
199
центром A; D соединим с точкой апо-
гея А, допустим EG — известна и пусть
она составляет тридцать градусов; сое-
диним G и A, D и G; опустим перпенди-
куляр GK на DE; углы GAK и GKA из-
[Рис. 63].
вестны, GA известна; все стороны и
углы треугольника будут известными;
тогда AD будет известна в отношении
к AG. Таким же образом находится и
АК, отсюда KD будет известна, а угол
К — прямой и поэтому KG известна,
так как из треугольника GKD будет из-
вестен угол D. Получается тот же ре-
зультат, что и в случае эксцентриче-
ской гипотезы.
Теперь докажем в случае эпицикли-
ческой гипотезы и обратное. Пусть из-
200
АЛЬ-ФАРАБИ
вестей угол G, который соответствует
дуге от [точки] весеннего равноденст-
вия по эклиптике, которое известно;
опустим перпендикуляр AL на DG
[рис. 64], угол L прямой, линия AG и
угол G известны; линия AL известна
из треугольника; в треугольнике ALD
углы будут известными, так как угол
D — данный, следовательно, угол GAE
и дуга EG будут данными. Пусть угол
D известен, тогда, по аналогичному рас-
суждению, треугольник DAL будет из-
вестным, и поэтому AL и AG известны,
угол ALG — прямой; поскольку сторо-
на и два угла известны, то и угол G из-
вестен; отсюда также угол GAE и по-
этому дуга EG будут известны; вычис-
ление вполне согласуется с тем, что
было выше. Это все, что касается дуг в
49 сторону апогея. /
Затем рассмотрим дуги в сторону
перигея, для которой берем квадрант из
другого рисунка [рис. 65]. Пусть Н —
известная дуга, отложенная от перигея,
которую мы примем равной тридцати
градусам; соединим F и G, D и G, про-
должим F до В, опустим из D на FG пер-
пендикуляр DK, который известен;
аналогично тому, как мы уже доказали,
треугольник FDK будет известным, угол
К — прямой; в треугольнике DKB так-
Третья книга
201
же известны углы и стороны, и поэтому
в треугольнике FDB будет известен угол
BDC, то есть дуга ВС известна.
С другой стороны, если дается угол,
то будем считать угол D известным, опу-
стим перпендикуляр из F до встречи с
[продолжением] GD [рис. 66] в точке
L; тогда по доказанному выше стороны
и углы треугольника FLD будут извест-
ными; точно так же и в треугольнике
FLG, FDB и оставшийся угол GFH изве-
стны; угол G положим данным, то есть
разность неравенства известна, угол
L — прямой, тогда линия GF и тре-
угольник известны по отношению, а
также FL и FD известны, угол L — пря-
мой, поэтому стороны и углы треуголь-
ника FLD известны; отсюда угол FDL,
то есть угол BDC и дуга ВС известны, и
угол GFH, то есть дуга GH, известны.
Пусть теперь это же самое докажем
202
АЛЬ-Ф АРАВИ
[Рис. 67].
[Рис. 68].
в случае эпициклической гипотезы;
пусть сначала будет известна [дуга] HF
со стороны перигея [рис. 67], опустим
перпендикуляр НК на ПА. Поскольку
НА и угол А дуги HF известны и угол
К прямой, то известны углы и стороны
треугольника АНК‘, по доказанному
прежде углы и стороны треугольника
KHD известны; угол D и дуга АВ из-
вестны.
Что касается того, когда дается угол,
то пусть сначала положим видимый
угол в эклиптике известным; опустим
перпендикуляр AL на DB [рис. 68],
АНВ — видимый угол в эклиптике, по-
тому что он соответствует среднему
Третья книга
203
[движению] и по предположению урав-
нение известно; тогда два треугольни-
ке ка /, то есть треугольник ALH по из-
вестной стороне АН и углам L и Н и
треугольник ALD по известным двум
сторонам AL и AD, известны, следова-
тельно, угол D известен.
А теперь пусть угол D будет извест-
ным ; тогда углы и стороны треугольни-
ка ALD будут известными по известной
стороне и известным углам D и L, ко-
торый прямой; также стороны и углы
треугольника ALH будут известными
по двум сторонам — AL и LH и пря-
мому углу L, и, следовательно, искомый
угол HAF известен.
Далее, после того, как был указан
способ нахождения неравенств, чтобы
иметь их готовые значения, Птолемей
составил таблицу неравенств для част-
ных дуг 123. При этом поскольку он до-
казал, что разность неравенства в дру-
гой половине равна соответствующему в
этой половине и прибавляемые величи-
ны в одной из них будут вычитаемы в
другой, он ограничился неравенством,
имеющим место [только] в одной поло-
вине между двумя указанными расстоя-
ниями.
Так как для дуг, примыкающих к
наибольшему расстоянию, неравенство
204
АЛЬ-ФАРАБИ
меньше, то он разделил прилегающий к
этому квадрант на пятнадцать частей,
каждая из которых соответствует шести
[градусам], и поместил их неравенства.
Поскольку для квадранта, прилегающе-
го к наименьшему расстоянию, неравен-
ство больше, то его разделил на трид-
цать частей, каждая из них соответст-
вует трем [градусам]; поэтому он при-
нял эти числа через каждые три [гра-
дуса].
В первом столбце содержится число,
соответствующее движению от апогея,
во втором — число, соответствующее
движению от перигея. В третьем — це-
лые числа градусов и минут прибавляе-
мого и вычитаемого неравенства; они
прибавляются, если среднее берется из
второго [столбца], и вычитаются, если—
из первого [столбца].
Далее он требует [установить] эпоху
среднего движения Солнца, которая на-
чинается с середины первого дня царст-
вования Набонассара, и эпоху Солнца в
тот день истории. Он показал среднее
положение Солнца в двух осенних рав-
ноденствиях, наблюденных из наиболь-
шего расстояния, как на этом рисунке
[рис. 69].
Он сказал: пусть G — точка осенне-
го [равноденствия] в эксцентрическом
Третья книга
206
[круге], Н — его перигей; опустим пер-
пендикуляр FK к GD, дуга СВ круга
эклиптики известна,
расстояние [точки]
осеннего [равноден-
ствия] от перигея;
тогда угол избыт-
ка, то есть [угол]
G, известен. Отсю-
да следует, угол
[H]FG также будет
известным. С по-
мощью вычисления
получается, что ду-
га HG равна 63;
20.
потому что она —
[Рис. 69].
51
После определения среднего [движе-
ния] Солнца он нашел промежуток
времени между настоящим наблюдени-
ем и началом эпохи, / установил число
полных оборотов за это время, отбросив
их, нашел прибавляемую дугу и ее на-
чало на эксцентрическом круге; это
есть среднее положение Солнца в нача-
ле эпохи. Уточнив это, он узнал, как
находятся эфемериды Солнца.
Он сказал: среднее [движение]
Солнца находится с помощью определе-
ния промежутка времени с начала эпо-
хи ; к этому прибавляется эпоха и отни-
маются полные обороты до градуса апо-
206
АЛЬ-ФАРАБИ
гея; остаток берется в столбце среднего
[движения], затем находится соответст-
вующее ему уравнение, которое прибав-
ляется или отнимается по тому [прави-
лу] , о котором мы уже сказали.
Из всего этого выясняется, что поло-
жение Солнца может быть получено с
помощью геометрических доказа-
тельств; причем это не зависит от того,
предполагается ли, что эклиптика равна
эксцентрическому кругу или же больше
него, ибо рассматриваются углы у цент-
ра эклиптики и треугольники, имеющие
углы, общие для обоих кругов — равно-
го эксцентрическому или больше него;
если они у центра круга, [не] равного
[эксцентрическому], то дуги подобны.
О неравенствах суток
Далее, когда Птолемей разъяснил
обстоятельства Солнца, он закончил эту
книгу разъяснением [вопроса] о сут-
ках.
Он сказал: судя по тому, что видно,
можно думать, что сутки — это поворот
[небесного экватора] на триста шестьде-
сят градусов, и это двадцать четыре ча-
са. Это период возвращения точки не-
бесного экватора, восходившей вместе с
Солнцем в перый день или бывшей вме-
сте с ним в полдень, к линии горизонта
Третья книга
207
или к линии меридиана. При этом пред-
почитается меридиан, так как периоды
возвращений к нему равны во всех кли-
матах. Именно так думают вообще об
этом вопросе. Но истинные сутки — это
время возвращения Солнца к кругу го-
ризонта или небесного меридиана, а
Солнце проходит за сутки средним дви-
жением приблизительно 59 минут. Сле-
довательно, период возвращения Солнца
превышает период возвращения той точ-
ки, которая была [вместе с ним], так
как оно отстает от нее. Поэтому средняя
[продолжительность] суток 360 времен-
ных градусов и 59 минут, а это — двад-
цать четыре часа и пятьдесят девять
девятисотых часа. Однако, как было
сказано выше, движение Солнца нерав-
номерно, приращение движения Солнца
по эклиптике не одно и то же и равные
приращения по эклиптике имеют не од-
ни и те же временные градусы восхож-
дения и прохождения небесного мери-
диана. Следовательно, существуют два
вида неравенств суток. Хотя это нера-
венство не имеет [существенной] вели-
чины при малом числе суток, оно обла-
дает ощутимой величиной, когда число
суток увеличивается.
Поскольку предел разности, возни-
кающей из-за аномалии [движения]
208
АЛЬФАРАБИ
Солнца, наблюдается там [между поло-
жениями], в которых движение равно-
мерно, [в них] разность незаметна.
Промежуток времени между каждым из
двух противоположных расстояний и
этой точкой [равномерного движения]
приводит к наибольшему уравнению, а
наибольшая разность имеет место с дру-
гой стороны, в противоположном на-
правлении. Поэтому промежуток време-
ни со стороны апогея избыточен и урав-
нение вычитается, а [промежуток вре-
мени] со стороны перигея недостаточен,
уравнение прибавляется и достигает
двух градусов двадцати трех минут.
Удвоение этого дает разность между
равномерным и неравномерным движе-
нием приблизительно в четыре и три
четверти градуса. Одна половина эклип-
тики отличается от другой на удвоение
этого удвоения, то есть на девять с по-
ловиной градусов. Поэтому количество
суток при движении от середины до се-
редины будет отличаться от [количест-
ва] средних суток на четыре и три чет-
верти градуса. На такую же величину
вместе все избыточные и все недостаточ-
ные сутки отличаются от средних су-
ток. Поэтому длинные сутки отличают-
ся от коротких на удвоенную [величи-
52 ну],, то есть / на девять с. половиной.
Третья книга
209
градусов. Это наибольшая разность по
причине Солнца.
Что же касается наибольшей разно-
сти по причине восхождений, то ее надо
рассматривать или по отношению к го-
ризонту, или по отношению к середине
неба. Если рассматривать ее по отно-
шению к восходам и заходам на го-
ризонте, то в большинстве стран наи-
большая разность отличается в двух по-
ловинах [эклиптики], разделенных
двумя солнцестояниями. Каждая поло-
вина эклиптики отличается от средней
величины на разность между наиболь-
шим и средним днями, то есть вдвое
больше нужной. Это соответствует -раз-
ности между наибольшим и наимень-
шим днем в зависимости от климата.
[Если же рассмотреть] ее по отноше-
нию к прохождению середины неба, то
имеется только одно неравенство наи-
большей разности, к которому приводят
восхождения. Неравенство разности
восхождений не изменяется в [различ-
ных] климатах. Предел его уменьшения
имеет место между серединой Водолея и
началом Скорпиона, а предел увеличе-
ния.— между началом Скорпиона и се-
рединой Водолея. Разность неравенства
вместе с уравнением составляет четыре
с половиной градуса. В этом же самом
14-89
210
АЛЬ-ФАРАБИ
месте доля наибольшей разности изме-
нения движения Солнца составляет при-
близительно три и две трети градуса.
Складывая их, получим восемь и одну
треть градуса. Это сумма двух нера-
венств вместе с уравнением. [Разность
же] между наибольшим и наименьшим
числами вдвое больше. Это не изменя-
ется в различных климатах.
За начало эпохи принимается не на-
чало дня, а полдень, так как разность
в нем одна и та же, где бы это ни было,
а по отношению к горизонту она изме-
няется в зависимости от знака Зодиака,
даты во всех странах не совпадают.
Разность, полученная при соедине-
нии этих двух [разностей] — разности
от движения Солнца и от неравенства
его прохождения через середину неба,
то есть того, что следует прибавить или
вычесть, вместе составляет восемь и од-
ну треть временных градусов или поло-
вину и одну восемнадцатую часа. Это
потому, что прибавление происходит от
Скорпиона до середины Водолея, а вы-
читание — от Водолея до Весов. Следо-
вательно, наибольшая разность, опреде-
ляемая неравенством [движения] Солн-
ца,— три и две трети градуса, а [наи-
большая разность, определяемая]
прохождением [Солнца] через середину
Третья книга
211
неба,— приблизительно четыре и две
трети временного градуса. Это получает-
ся, если восхождения и уравнение Солн-
ца сложить, так чтобы получилась наи-
большая [величина]. Если это так, то
сутки превысили бы друг друга на поло-
вину этой наибольшей разности и полу-
чилось бы шестнадцать и две три вре-
менного градуса, или один и одна девя-
тая часа. Эта величина не приводит к
большим изменениям Солнце и другие
[планеты]. Но для Луны получается
ощутимая разность, близкая к трем пя-
тым градуса.
Далее он сказал о сутках и их уста-
новлении: сутки начинаются с полудня
или с полуночи; находим положение
Солнца в начале их и берем истинное и
среднее [значения положения Солнца].
[Затем] находим восхождение в прямой
сфере между двумя истинными [значе-
ниями] и выражаем разность в часах.
Если восхождение превышает средние
солнечные сутки, то прибавляем эти
часы; если же они меньше, то вычита-
ем их; то, что получится,— есть истин-
ные сутки. Таким же способом поступа-
ем в случае сложенных средних равно-
мерных движений.
53 /С помощью этого метода мы мо-
212 АЛЬ-ФАРАБИ
жем перейти и обратно от временных
суток к средним равномерным.
Затем он упорядочил положение
Солнца относительно начала его эпохи.
Оказалось, что при среднем движении
оно на 0; 45 градусе Рыб, а в истинном
[движении] —на 3;08 [градусах].
ЧЕТВЕРТАЯ КНИГА 124
О наблюдениях,
которые следует использовать
для познания движения Луны
После изложения вопроса о Солнце
Птолемей в первую очередь рассмотрел
вопрос о Луне. Наблюдать за Солнцем
легче, чем за Луной, так как тело Зем-
ли не имеет ощутимой величины относи-
тельно орбиты Солнца и наблюдение,
произведенное с поверхности Земли, не
отличается значительно от «истинного
наблюдения» из центра Земли, если бы
можно было его произвести. Это разли-
чие называется параллаксом, который
представляет собой дугу эклиптики, ог-
раниченной концами двух линий, одна
из них проведена из глаза, а другая —
из центра Земли, причем они встреча-
ются в центре светила, а затем расхо-
дятся после него и идут до эклиптики.
Так как Луна ближе к Земле, она имеет
параллакс ощутимой величины. Только
214
АЛЬ-ФАРАБИ
в зените эти две линии, проведенные из
глаза и из центра Земли, совпадают.
Следовательно, с самого начала при на-
хождении истинного положения Луны и
выяснении общих вопросов следует по-
лагаться не на инструменты наблюде-
ния, а на лунные затмения: лунные
затмения отличаются от солнечных,
происходящих в зависимости от положе-
ния наблюдателей и изменяющихся с
изменением [места] наблюдения, так
как затмения [Солнца происходят],
когда Луна находится между глазом и
Солнцем; лунные же затмения пред-
ставляют собой исчезновение света
Солнца с тела Луны из-за преграждения
его Землей. Это происходит с самой Лу-
ной и не зависит от наблюдателя |25.
[Истина] Солнца может быть уста-
новлена в любое время, которое мы по-
желаем. Но когда Луна находится в се-
редине затмения, она диаметрально
противоположна Солнцу. Поэтому мы
можем определить истинное положение
Луны в середине затмения. Таков путь
полного наблюдения за Луной. Что ка-
сается частных вопросов, то можно ис-
пользовать для них каждое из наблю-
дений, как мы покажем ниже.
Четвертая книга
215
Об определении
времени оборотов Луны 126
При наблюдении Луны нашли, что
она не похожа на Солнце и не соверша-
ет одинаковых оборотов относительно
одной из неподвижных звезд или одной
неподвижной точки за равные проме-
жутки времени. Так же найдено, что
Луна обладает неравенством, ускорени-
ем, замедлением и средним [движени-
ем] ; имеется неравенство и по ее ши-
роте в каждом градусе эклиптики. Пер-
вое упомянутое неравенство не может
быть объяснено эксцентричным кругом,
не имеющим собственного движения,
так как в этом случае были бы определе-
ны положения максимального, мини-
мального и среднего движения, это не-
равенство вызывается эксцентричным
кругом, перемещающимся на равные ду-
ги и переносящим [Луну] вперед и на-
зад. Определили, что такое [изменение
происходит] по причине эпицикла. В
частности, было установлено, что наи-
большее неравенство наблюдается в те
сутки, когда Солнце диаметрально про-
тивоположно [Луне] и во время затме-
ний, и неравенство меньше наибольшего
неравенства в квадратуре Солнца. Это
может быть только на эпицикле, а эпи-
216
АЛЬ-ФАРАБИ
цикл должен быть на эксцентричном
круге. Иногда эпицикл бывает ближе, и
в этом случае его радиус [при движе-
нии] по эклиптике больше, а иногда
54 [эпицикл] / дальше, что приводит к
меньшему [радиусу его].
Из этого вытекает, что эпицикл [Лу-
ны] движется по эксцентричному дефе-
ренту, к которому эпицикл относится
как Солнце к его эксцентричному кру-
гу, движение [Луны] по эпициклу не
подобно движению эпицикла по дефе-
ренту. Иначе промежутки времени ее
возвращения были бы равны, как было
сказано. [Движение Луны] также не
быстрее [движения эпицикла], иначе ее
возвращение по эпициклу, являющееся
возвращением ее неравенства, казалось
бы возвращением по долготе, то есть воз-
вращением движения к среднему. Было
найдено, что движение [по эпициклу]
отстает, так что если [Луна] возвра-
щается к этому неравенству и имеет та-
кого рода неравенство, то возвращение
произойдет при большей долготе.
Далее нашли, что отклонение Луны
к северу или к югу от эклиптики не по-
стоянно в одном и том же положении;
если бы это было не так, то ее видимое
возвращение было бы [одновременным]
и по долготе, и по широте, то есть при
Четвертая кйига
217
ее возвращении в одной точке долготы
она возвращается к той же широте, ко-
торую она имела в этой точке. Опреде-
лили, что наклонный круг движется на
запад в соответствии с ее движением,
что эклиптика и наклонный круг не пе-
ресекаются постоянно в одной и той же
точке, а [точка их пересечения] дви-
жется на запад в соответствии с движе-
нием наклонного [круга]. Если разде-
лить величину разности между этими
движениями за один оборот на сутки и
часы, то получатся их доли. Из этого
следует, что если бы пересечение имело
место в неподвижной [точке], то затме-
ния не могли бы происходить в любых
местах и не было бы разности между
широтами в любом месте, а отношение
Луны к неподвижным звездам, кото-
рые приближаются и удаляются от нее
по широте, оставалось бы ' одним и
тем же.
Поскольку дело обстоит так, что
среднее движение Луны можно найти
не первым способом, упомянутым в гла-
ве о Солнце, а вторым: берется проме-
жуток времени, содержащий полные
лунные месяцы и несколько полных
оборотов по дойготе вместе с избыточной
дугой, которая^ повторяется, по той
причине, что она обязательно должна
218
АЛЬ-ФАРАБИ
быть в каждом таком промежутке вре-
мени с такими оборотами по долготе,
число которых такое же [как число
дуг]. Если имеется избыток, то число
возвращений неравенств будет таким
же. Если бы не было возвращения нера-
венств, то обороты по долготе не были
бы подобными. Астрономы старались,
чтобы возвращения по широте за те же
промежутки времени были подобны;
это осуществляется, если концы этих
[возвращений] имеют подобные состоя-
ния при затмениях Луны. Если положе-
ние с широтой отличается [от этого], то
они проводят для нее специальное на-
блюдение. При полных лунных оборотах
месяцы не должны быть полными, так
как за один месяц Солнце [также] про-
ходит некоторое расстояние и Луна не
догонит Солнце. Поэтому в этом случае
необходимо прибавить к возвращениям
по долготе дугу до полного месяца, каж-
дый раз прибавление всегда равно этой
дуге.
Этим способом древние смогли опре-
делить промежутки времени между
месяцами. Это проводится с помощью
нахождения [времени] каждого возвра-
щения к противостоянию или к соедине-
нию 127. Легче [использовать] противо-
стояние, [чем соединение], из-за
Четвертая книга
219
[свойств] затмения. Когда затмения по-
вторяются, то месяцы становятся изве-
стными. Что касается того, что нужно
сделать, чтобы возвращения неравенст-
55 ва были полными, то мы / покажем это
вскоре.
Это можно сделать, когда затмения,
ограниченные концами месяцев, проис-
ходят в одной и той же точке, северной
или южной, что узнается при равенстве
величины затмения и постоянстве рас-
стояния от Земли, а также при подобии
времени между началом и соединением.
Если [Луна] возвращается ко всем сво-
им неравенствам во всех случаях, то
древние при наблюдении этих времен от-
носительно неподвижных звезд нашли
во всех случаях промежуток времени в
шесть тысяч пятьсот восемьдесят пять и
одна треть суток, за которые совершает-
ся двести сорок одно возвращение по
долготе. Солнце [за этот промежуток]
сверх оборотов проходит десять и две
трети градуса. [За этот промежуток со-
вершается] двести тридцать девять воз-
вращений аномалий, двести сорок два
возвращения по широте и двести двад-
цать три месяца. Они называют это вре-
мя «периодическим временем», так как
за это время обстоятельства повторяют-
ся еще раз. Стремясь [избавиться от]
220
АЛЬ-ФАРАБЙ
дробей суток, они увеличивают это в три
раза; вместе с ним увеличивается И
[число] возвращений; они называют
полученное время «вычисленным из-
влеченным временем».
Когда Гиппарх рассмотрел свои на-
блюдения и наблюдения древних вави-
лонян и халдеев, которые жили в Хал-
дее128, он написал, что полученные ими
результаты ошибочны и что промежу-
ток времени, охватывающий это, состав-
ляет сто двадцать шесть тысяч семь су-
ток и один прямой час. Он нашел, что
это составляет приблизительно четыре
тысячи двести шестьдесят семь месяцев,
четыре тысячи пятьсот семьдесят три
возвращения аномалии и четыре тыся-
чи шестьсот двенадцать оборотов по
долготе по эклиптике без семи с поло-
виной градусов, которых недостает
Солнцу. Это [вычисление] производи-
лось по отношению к неподвижным
звездам. Средний месяц равнялся у него'
двадцати девяти суткам тридцати од-
ной минуте пятидесяти секундам вось-
ми терциям и двадцати квартам 129. Он
определил месяцы с помощью затмений.
Если бы он вычислил их с помощью сое-
динений и противостояний, то получен-
ные им числа были бы меньше. Этот
способ [состоит] в том, что находится
Четвертая книга
221
общее число, которое делит число меся-
цев, т. е. четыре тысячи двести шестьде-
сят семь и число оборотов аномалий, то
есть 4573; эти два числа делятся на
[общий делитель] и получается двести
пятьдесят один месяц и двести шестьде-
сят девять возвращений аномалий.
Что касается числа возвращений по
широте, то он не нашел его при этих
затмениях по указанному условию, так
как стороны величин не одни и те же.
Если он хочет найти возвращения по
широте, он должен рассмотреть проме-
жуток времени больше пяти тысяч че-
тырехсот пятидесяти восьми месяцев и
пяти тысяч девятисот двадцати трех
оборотов по широте. Если принять ре-
зультаты Гиппарха, разделить этот про-
бе межуток на / число месяцев, то ясно,
что получится [число] суток в месяце.
Если же разделить возвращения после
их перевода в градусы на [число] всех
суток, то получится продвижение за од-
ни сутки как по долготе, так и по ши-
роте или по аномалии.
Градусы среднего [движения] по
долготе могут быть вычислены более
легким способом. Средний месяц явля-
ется полным оборотом вместе с дугой
прохождения Солнца за известное время
среднего месяца. Полный оборот вместе
222
АЛЬ-ФАРАБИ
с дугой Солнца известен, поэтому сред-
ний месяц Луны известен.
Птолемей пожелал рассмотреть то,
что установил Гиппарх, и проверить его.
Он изобрел способ более легкий, чем
способ Гиппарха, добавил его к первона-
чальному, объяснил трудность приме-
нения этого способа, связанную с,нера-
венством, имеющим место при движе-
нии Луны, так как если промежутки
времени возвращений по долготе равны,
то обороты не обязательно должны быть
подобными из-за неравенства, имеюще-
го место и для Солнца и для Луны. Что
касается Солнца, то нужно обеспечить,
чтобы дуги, которые оно проходит пос-
ле оборотов, были равными, а это не
всегда наблюдается из-за неравенств;
бывает так, что промежутки времени
между месяцами совпадают [друг с
другом], а избытки Солнца и Луны не
равны. Например, в случае Солнца, ес-
ли промежуток времени — половина го-
да, и в первом [промежутке] оно дви-
жется по дуге, начинающейся от [точ-
ки] среднего движения в Рыбах, то, как
мы знаем, за половину года оно прохо-
дит половину эксцентричного круга и
меньше половины эклиптики на 4; 45
[градусов]. Если во втором [промежут-
ке] оно движется после возвращения от
Четвертая книга
223
[точки] среднего движения в Деве, то за
половину года оно проходит половину
эксцентричного круга и больше полови-
ны эклиптики на 4;45 [градусов]. По-
этому оно проходит равные [части] экс-
центричного круга, но не равные [граду-
сы] эклиптики. Однако нужно добиться
того, чтобы при прохождении Солнца
совсем не было бы неравенства или было
бы одно и то же неравенство. Для этого
нужно, чтобы имелись полные обороты
Солнца на орбите Луны, а дробные их
[части], представляющие собой две ду-
ги, прибавлялись бы к первоначальным
[оборотам] на половине, начинающейся
от апогея и до перигея в первом проме-
жутке времени и на половине от пери-
гея до апогея — во втором, для того,
чтобы не было неравенства или чтобы
начало и конец обоих [промежутков]
времени было бы в одной и той же точке
неравенства, а это не бывает в последо-
вательных [промежутках] времени, или
чтобы начало обоих [промежутков] вре-
мени было бы на равных отрезках от
концов двух разных расстояний. Напри-
мер, Солнце начинает [движение] в на-
чале затмения первого [промежутка]
времени на некотором расстоянии от
апогея и перигея в одной стороне, а в
Конце втброго [промежутка] оно Пахо-
224
АЛЬ-ФАРАБИ
дится на таком же расстоянии [от них]
с другой стороны. Или, например, Солн-
це начинает движение из точки на ка-
ком-то расстоянии от апогея, завершает
обороты у апогея и к этому прибавляет-
ся дуга, чтобы быть на таком же рас-
стоянии от апогея, как расстояние пер-
вой точки, где оно начало [движение].
То же самое наблюдается и в отношении
перигея при условии, чтобы оно имело
бы одно и то же неравенство и чтобы
дуги, прибавляемые к полным оборотам
по эклиптике, были бы равны.
То же самое должно быть и для Лу-
ны. Может случиться, что возвращения
Луны в эклиптике за равные промежут-
57 ки времени / равны, но [из этого] не сле-
дует, что она возвращается к той же
аномалии, что и при начале [движе-
ния], или к той же широте. Что касает-
ся аномалии, то аналогично тому, что
мы сказали о Солнце, если Луна дви-
жется после оборотов, начиная от нача-
ла первого [промежутка] времени, [из-
меняя] свою скорость от быстрой к мед-
ленной, а во втором [промежутке] — от
медленной к быстрой, то мы увидим, что
за два равных [промежутка] времени
она проходит равные дуги эклиптики по
долготе, хотя за каждый из этих [про-
межутков] времени она не заканчиваем
Четвертая книга
225
оборота неравенства и не возвращается
к первому неравенству. Это служит при-
мером того, что она не имеет никакого
избытка неравенства в одном из двух
[промежутков] времени. Точно так же
будет, если она в каждом из двух про-
межутков времени [начинает] двигать-
ся из одного и того же положения отно-
сительно избытка или недостатка и
вернется к тому же положению, но раз-
ность неравенства будет одна и та же
и окажется, что она прошла равные ду-
ги эклиптики, хотя и не вернулась к то-
му же неравенству. Этого нельзя избе-
жать.
Если два начала движения на дугах
находятся на равных расстояниях от
апогея или перигея с обеих его сторон,
то, как мы сказали о Солнце, окажется,
что Луна начала [движение] из некото-
рой точки, закончила оборот в ней, за-
тем оказалась в апогее или в перигее,
затем закончила обороты у апогея или
у перигея, а затем добавила дугу, рав-
ную той, которую она добавила в первой
сфере. Поэтому мы видим, что она про-
шла равные дуги эклиптики, но не вер-
нулась к своему неравенству.
Что касается широты, то о ней было
сказано раньше. Необходимо выбрать
для неравенства и для широты то, что
15-89
226
АЛЬ-ФАРАБИ
обеспечивает этуразницу. Для неравен-
ства необходимо, чтобы начала имели
бы большое неравенство по величине в
действительности или потенциально.
Это более предпочтительно и правильно,
хотя можно обойтись и без этого,г и
имеет место в действительности, если
начало расстояний — с большим нера-
венством и если Луна начинает движе-
ние в одном промежутке времени с за-
медлением и сохраняет это движение
так, чтобы она не окончила его ни с
ускорением, ни о замедлением. В таком
случае неравенство увеличивается осо-
бенно в конце первой четверти или трех
четвертей круга, когда предел разности
удваивается, при этом [Луна] не воз-
вращается к двум упомянутым [нача-
лам] и нельзя видеть, чтобы за равные
промежутки времени она прошла рав-
ные дуги по долготе или чтобы она за-
кончила возвращение. Это имеет место
потенциально, если в одном промежут-
ке времени Луна начинает движение со
среднего движения и приближается к
быстрому, а в другом промежутке — на-
чинает со среднего и приближается к
медленному. Если при этом движении
она будет в {конце] первой четверти
или трех четвертей, то предел разности
удвоится, а если же она будет в середи-
Четвертая квита
227
не, то увеличивается в четыре раза. По-
тенциальное неравенство может быть
больше этого, и ошибки не должно про-
изойти. Поэтому Луна проходит равные
дуги эклиптики, когда она еще не за-
кончила возвращения неравенства.
Гиппарх исправлял неравенства
Солнца, заставляя его начинать в одном
промежутке времени с большим ускоре-
нием и не кончать с замедлением, а в
другом — наоборот. Что же касается
широты, то упомянутое выше служит
для предосторожности при нахождении
узла.
Ясно, что этот способ не легкий, хо-
58 тя он / дает возможность наблюдать за
искомым; если учитывать все, что ска-
зано о нем.
Однако месяцы и обороты по долго-
те, найденные Птолемеем тем способом,
он добавил к древним. Они совпадают с
тем, что нашел Гиппарх; а [найденные
им] неравенство и широта расходятся:
он нашел более длинный промежуток
времени для неравенства и более корот-
кий для широты.
228
АЛЬ-ФАРАБИ
О частных
и равномерных движениях Луны
Прежде чем начать исследования
этого добавления, Птолемей построил
таблицу движения Луны по долготе,
неравенству и широте с помощью того,
что он получил. Он установил движение
Луны по долготе делением градусов од-
ного оборота и дуги среднего прохожде-
ния Солнца за один месяц на [число су-
ток] в месяце, что дает приблизительно
13; 10, 34, 58, 33, 30, 30 [градусов] для
одних суток. Затем он разделил это на
часы и их части, умножил число оборо-
тов неравенства на 360, чтобы сделать
их градусы, разделил полученное на
[число] суток в том промежутке време-
ни, который был у Гиппарха, и получил,
что равномерное движение среднего не-
равенства за сутки [равно] 13; 3, 53,
56, 29, 38, 39 [градусам]. Однако, когда
он проверил это своим методом, он на-
шел его меньше; он нашел, что в сут-
ках 13; 3, 53, 56, 17, 51, 59 [градусов].
Затем он разделил это на часы. Точно
так же он действовал для оборотов по
широте и получил, согласно принципу
Гиппарха, за одни сутки 13; 13, 45, 39,
40, 17, 19 [градусов], а согласно его ис-
Четвертая книга
229
следованию, получилось больше, а имен-
но 13; 13, 45, 39, 48, 56, 37, 45.
Мы покажем, что средняя элонга-
ция 130 представляет собой движение на
эксцентричном [круге]. Элонгация —
это удаление Солнца от Луны и поэто-
му есть разность между их средними
движениями, равная 12; 11, 25, 41, 20,
17, 59 [градусам] в сутки. Разделив это
на часы и их части и умножив на [чис-
ло] суток полных месяцев, а именно
тридцать, а затем на [число] суток
египетского года 131, а именно триста
шестьдесят [пять], и отбросив из всего
этого полные обороты, Птолемей нашел
то, что остается. Затем он умножает на
восемнадцать для того, чтобы построить
таблицу 132, состоящую из трех соеди-
ненных таблиц, одна из которых для ко-
личеств лет, последовательно превышаю-
щих [друг друга] на восемнадцать лет;
вторая — для каждого отдельного года
до восемнадцати лет, за которыми ча-
сы, а третья — для месяцев, за которы-
ми дни. Каждая таблица содержит один
столбец для движений по долготе; дру-
гой — для движения по неравенству;
третий — для движений по широте; чет-
вертый — для движения по элонгации.
Каждый столбец разделен по широте на
шесть разрядов,
280
АЛЬ-ФАР АВИ
О том, что Луна имеет одно
и то же неравенство как относительно
эксцентрического круга,
так и относительно эпицикла
Птолемей начал с объяснения спосо-
ба, который он дал специально для оп-
ределения движения по аномалии.
Сначала он сказал: хотя у Луны
имеются второе и третье неравенства,
отличные от тех, которые мы покажем и
которые были упущены большинством
наших предшественников, мы не будем
говорить о них здесь, так как лунные
затмения будут рассматриваться только
в противостояниях, а второе и третье не-
равенства, оказывается, не имеют зна-
чительной величины в противостояниях.
Второе неравенство является наиболь-
шим в квадратурах, а третье — в двух
гексагональных аспектах133. Первое
неравенство считается первым, так как
оно может иметь место без других нера-
венств, тогда как последние имеют ме-
сто только вместе с ним. Поэтому ему
отдается предпочтение и речь вначале
должна идти о нем 134.
Несмотря на то, что обстоятельства
этого неравенства, то что происходит с
ним и что следует из него, одни и те
59 же / при эпициклической гипотезе и при
Четвертая Ьнига
231
эксцентрической гипотезе, предпочти'
тельно основывать это неравенство при
обоих гипотезах так, чтобы эксцентри-
ческий круг был бы деферентом эпицик-
ла; это продолжение того, о чем мы го-
ворили раньше. Что касается того, как
из обеих гипотез по этому вопросу мо-
жет вытекать одно и то же, в то время
как движение по аномалии не подобно
движению по долготе, и не похоже на
движение Солнца, где* они подобны друг
другу, и в то время, как отношение ду-
ги, описанной по эпициклу ко [всему]
кругу [эпицикла], меньше отношения
дуги, описанной по эксцентрическому
кругу ко [всему], то это доказывается
тем, что мы утверждаем: деферент яв-
ляется концентричным, поскольку мы
еще не рассматривали эксцентрического
круга и не заменяем еще концентриче-
ский деферент эксцентричным, что необ-
ходимо приводит к первому неравенству.
Что касается условия, которое нуж-
но предположить для обеспечения по-
стоянного наличия этого неравенства,
когда Луна находится на эпицикле, на-
ходящемся на деференте, или на эксцен-
тричном круге, а не на эпицикле, оно
таково: движение эпицикла по деферен-
ту описало бы дугу, большую, чем дуга
Луны, по эпициклу, и чтобы дуга экс-
232
АЛЬ-ФАРАБИ
центрического круга, которую описывает
Луна, когда она находится на нем, была
бы подобна дуге эпицикла, но чтобы экс-
центрический круг двигался по направ-
лению, противоположному движению
Луны, и описывал дугу подобной избыт-
ку дуги референта над дугой эпицикла и
чтобы движение Луны происходило в
сторону востока, было бы противопо-
ложно движению Вселенной. Рассужде-
ние будет одним и тем же при обеих ги-
потезах, были ли отношения равны или
подобны между собой. Допустим снача-
ла, что они равны, и пусть АВС — кон-
центрический [с эклиптикой] круг с
центром D, имеющий полудиаметр AD
и эпицикл EG вокруг центра С [рис. 70].
Пусть при движении [эпицикла] из А
до С светило проходит из Е до С?; про-
ведем CG и DCE. Тогда дуга АС будет
Четвертая книга
233
больше дуги этого круга, подобной EG.
Пусть дуга ВС относится к кругу АВС
как EG к своему кругу; проводим DB.
Ясно, что угол ADB есть угол разности
между средним движением и движением
аномалии, а это есть предполагаемая
нами величина движения эксцентра,
когда Луна находится на нем, за равное
время и по этой же гипотезе.
Возьмем DH, равную CG, и проведем
HG; поскольку дуга ВС подобна дуге
EG, то ясно, что угол BDC равен соот-
ветствующему ему углу GCE. Отсюда
очевидно, что CGDH — параллелограмм.
Если из точки Н на расстоянии HG опи-
шем дугу FG, то она будет иметь тре-
буемое отношение к эксцентру. Пусть
линия HBF пересекает эту дугу в точке
F, тогда внешний угол FHG эксцентра
равен внутреннему соответствующему
углу HDC, то есть внешнему углу GCE,
поэтому дуга GF будет подобной EG.
Следовательно, если светило опишет ду-
гу FG, а линия FD — дугу АВ или же
дугу EG, а его центр — дугу АС, то оно
будет видно по одной и той же прямой
и опишет одну и ту же дугу и, наоборот,
оно не будет видно по другой прямой.
Он сказал: теперь докажем это, если
60 указанные отношения / будут подобны-
ми по наблюдению.
234
АЛЬ-ФАР АВИ
Пусть HFK — эксцентрический круг
с центром L, М — центр эклиптики,
FK — дуга, описанная движением кру-
га [эксцентра] так, чтобы они из эклип-
тики отсекли [дуги] в указанном отно-
шении. Тогда угол HMF соответствует
этим градусам эклиптики; соединим
точки F, L и М на диаметре, проведем
LK, МН и МК [рис. 71].
[Рис. 71].
Пусть АВС — концентрический круг,
имеющий центр D; и пусть центр его
эпицикла прошел по нему дугу АС, а
светило — по эпициклу дугу EG, подоб-
ную FK; возьмем АВ, подобную HF;
проведем полудиаметр AD и [линии]
BD, DG, CG и ОСЕ. Поскольку DC к CG
из треугольника DCG относится как LK
к LM из треугольника KLM и углы L
и С равны, так как они дополняются до
двух прямых после прибавления двух
равных углов GCE и FLK, то эти два
Четвертая книга
236
треугольника подобны. Поэтому угол М
равен углу G. Но ВС подобна FK, то
есть EG; следовательно, углы BDC и
GCE равны и BD, GC параллельны меж-
ду собой; угол BDG равен углу DGC, то
есть LMK. Однако было доказано, что
угол ADB как разность [этих движе-
ний] равен углу HMF, таким образом,
весь угол М равен ADG. Это то, что мы
хотели доказать.
Об определении первого
и простого неравенства Луны
После выяснения этого обстоятель-
ства Птолемей перешел к выбору эпи-
цикла для этого неравенства. Он счита-
ет, что Луна не имеет широты и как бы
находится на плоскости эклиптики. Это
облегчает выяснение того, что он рас-
сматривает и позволяет обходить за-
труднения, связанные с вычислением
широты, которая, как мы покажем поз-
же, не вызовет существенного расхож-
дения, если ее отбросить.
Однако сначала нужно представить
себе, что на сфере несущей Луны име-
ются круг в плоскости эклиптики, кон-
центричный с ней, и другой круг, на-
клоненный к ней на величину широты,
центр которого совпадает с ее центром,
236
АЛЬ-ФАР АВИ
и [круг, центр которого] равномерно
движется [по этому кругу] вокруг цент-
ра эклиптики на величину избытка дви-
жения по широте над движением по дол-
готе, так что его апогей перемещается, а
в его плоскости находится эпицикл, дви-
жущийся по нему в сторону востока.
Луна же движется в сторону Запада.
Хотя это так, деферент считается нахо-
дящимся на плоскости эклиптики.
Что касается выяснения величины
неравенства, то прежде всего мы приве-
дем предпосылки, полезные для этого
предложения и для определения значе-
ний уравнения.
Мы утверждаем: если средняя дуга
меньше полукруга, когда оба уравнения
прибавляются или оба вычитаются, то
уравнение между истинной и средней
дугами за время прохождения средней
дуги есть разность между двумя исход-
ными уравнениями, которые определя-
ются градусами [точек], ограничиваю-
щими этот промежуток времени135.
Докажем это сначала для случая экс-
центрической гипотезы. Пусть круг
ABCD — эксцентрический круг с цент-
ром Е [рис. 72] и АЕВ — его диаметр,
проходящий через оба центра, G —
61 центр/эклиптики; пусть светило нахо-
дится в D, тогда его уравнением, соот-
Четвертая книга
237
[Рис. 72].
ветствующим градусу D, будет угол
EDG. Если оно переходит в С, то его
среднее движение за это время опишет
дугу CD, а его урав-
нением, соответст-
вующим градусу С,
будет [угол] ECG;
соединим D и С.
Предположим, что
оба эти уравнения
различны. Пусть
EDG больше ECG.
Мы утвержда-
ем: очевидно, что
углы ECD и EDC обязательно равны. Ес-
ли мы отнимем из угла С угол GCE и
прибавим к углу D угол EDC, то полу-
чатся углы GCD и GDC, являющиеся
углами треугольника CGD. Поскольку
угол EDG больше угла GCE, то прибав-
ляемое больше отнимаемого. Поэтому
углы GCD и GDC [вместе] больше углов
ECD и EDC. Следовательно, угол CED
треугольника EDC, соответствующий
среднему [движению], больше угла
CGD, соответствующего истинному [дви-
жению]. Поэтому избыток угла EDG
над углом ECG будет уравнением между
двумя дугами: видимой, то есть углом
G, и средней, то есть углом Е. Это и
есть разность уравнений, соответствую-
238
АЛЬ-ФАРАБИ
щих двум градусам. Следовательно, ес-
ли угол уравнения С будет больше угла
[уравнения] D, то угол G будет больше
угла-Е и разность уравнений будет по
величине той же самой.
Докажем это для случая эпицикли-
ческой гипотезы. Пусть CGD — концен-
трический круг с центром Е; С и D —
точки центров эпицикла, причем он пе-
ремещается из С в сторону D [рис. 73].
Когда центр эпицикла находится в С,
то светило находится в А и уравнение,
соответствующее градусу С, — угол
СЕ А; когда же эпицикл переходит в
D, то светило переходит в В, уравнение,
соответствующее градусу О,— угол DEB
видимого круга эпицикла. Истинной ду-
гой является дуга, противолежащая уг-
лу АЕВ, где А — точка эпицикла, нахо-
Четвертая книга
239
дящаяся в С, а В — точка эпицикла, на-
ходящаяся в D. Средней дугой является
дуга, противолежащая углу CED; угол
CED превосходит упомянутый угол АЕВ
на угол BED, из которого вычтем угол
АЕС. Разность между ними есть раз-
ность между углами двух дуг. Но угол
BED больше угла DEA на угол АЕВ.
Это и есть избыток уравнения градуса.
Точно так же, если мы предполо-
жим, что светило вначале находилось в
В, затем перешло в перигей, потом — в
апогей, затем — в А. Тогда видимый
угол будет ВЕА, где В — [точка] эпи-
цикла, когда он находится в С; А —
[точка] эпицикла, когда он находится
в D. Этот угол превосходит средний,
то есть угол DEC, на угол ВЕС, а сред-
62 ний / превышает этот на угол AED. Раз-
ность между этими избытками есть
угол АЕВ, который и есть уравнение.
Он же сам не что иное, как раз-
ность между двумя уравнениями гра-
дусов.
Если одно уравнение является при-
бавляемым, а другое — вычитаемым, то
разность между двумя дугами, то есть
уравнение между этими дугами, есть
сумма этих двух уравнений. Докажем
это сначала по эксцентрической гипоте-
зе на том же круге, что был выше.
240
АЛЬ-Ф АРАВИ
Пусть С — точка между перигеем и
апогеем, a D — между апогеем и пери-
геем [рис. 74]. Указанная дуга есть ду-
га CAD; угол С — прибавляемое урав-
нение, а угол D — вычитаемое уравне-
ние. Но угол видимости и истинная ду-
га есть сумма внутренних углов СЕА и
AED, а средний угол есть сумма внеш-
них углов СЕА и AED. Они превосходят
сумму С и О, а их сумма есть разность
уравнений.
Докажем это также для случая эпи-
циклической гипотезы. Пусть уравне-
ние АЕС — вычитаемое [рис. 75], а
BED — уравнение прибавляемое. Тогда
угол CED образует истинную дугу, а
угол АЕВ — среднюю дугу, которая
меньше видимой на сумму двух уравне-
ний. Точно так же будет, если рассмо-
Четвертая книга
241
сделать.
В
[Рис. 76].
трим обе гипотезы совместно. Пусть
угол С — вычитаемый, а угол D — при-
бавляемый [рис. 76]. Расположим ли-
нии углов в противоположных направле-
ниях, что легко можно
Мы утвержда-
ем : из всего, что
мы привели, выте- .
кает, что если неко- /
торая дуга образует I
прибавляемое урав- I
некие, то дуга, до- \
полняющая ее до
круга, образует точ-
но такое же, но вы-
читаемое уравне-
ние. Если же эти уравнения одного и
того же рода, то мы сделаем рисунок
случая эксцентрической гипотезы.
Мы утверждаем: если светило про-
ходит CABD и возвращается к D, то
видимая линия образует угол CGA, два
прямых и угол BGD, а средняя дуга об-
разует угол DEA, два прямых [угла] и
угол BED, то есть угол CGA с прибавле-
нием угла С, два прямых [угла] и угол
BGD с вычитанием угла D. Таким обра-
зом, из предыдущего [угла] вычитается
угол С и к нему прибавляется угол G.
Вычтем угол С из D, получим, что вы-
16—80
242
АЛЬ-ФАР АВИ
читаемый [угол] есть избыток D над С.
На такой же [угол] средняя дуга пре-
вышает дугу DC.
Что касается случая эпицикличе-
ской гипотезы, когда оба уравнения од-
[Рис. 77].
нородные, то если эпицикл движется от
D до С в сторону G, а светило — от А
до В [рис. 77], то видимый угол и угол
HFK известны и средний угол и угол
63 LMN известны; поэтому средний/пре-
восходит на угол СЕВ и меньше на угол
AED; разность между ними угол ВЕА.
Из рисунка, где оба уравнения были
неоднородными, известно, что их сумма
также есть уравнение, но прибавляемое.
Что касается случая эпициклической
гипотезы, когда уравнения противопо-
ложные, то, что имеется в углах DEC
после определения LMN, меньше того,
что имеется в углах АЕВ после опреде-
Четвертая книга
248
ления HFK, на два
угла — DEB и АЕС,
вместе взятых.
Точно так же и в
случае эксцентриче-
ской гипотезы: два
угла G со стороны А
меньше двух углов Е
со стороны А на два [РиС1 ?8].
угла — С и D вместе
[рис. 78].
После установления этих вещей вы-
ясним положение двух уравнений в
каждом из трех древних и современных
[Рис. 79].
затмений. Пусть эксцентрический круг
EGH описан около D и пусть центр эпи-
цикла в Е [рис. 79]; когда центр в Е,
244
АЛЬ-ФАР АВИ
то светило на 24;30 градусах Девы; за-
тем оно заканчивает обороты, и центр
проходит через Н до G. Светило движет-
ся из А в перигей, затем в В, что на
53; 45 градусах Девы. Тогда уравнение
прибавляется, и ADB будет известен.
Далее центр перемещается из G в Е, в
Н, тогда светило перемещается из В в
А пока не дойдет до С, что на 3; 15 гра-
дусах Рыб. Центр перемещается на из-
быток углов GDH над двумя прямыми.
Истинный перемещается на избыток уг-
лов BDC над двумя прямыми. Избыток
среднего есть угол CDH. Если вычесть
угол HDB, от GDB остается избыток
среднего, то есть вычитаемое уравне-
64 ние — угол BDH.I
Так как дуга АСВ имеет прибавляе-
мое уравнение, которое достигает рас-
сматриваемой разности CKD между
средним и истинным, то ее остаток,
то есть дуга АВ, будет иметь вычитае-
мое уравнение такой величины из-за
того, что мы показали. Вычитаемое
уравнение дуги ВАС на 5; 37 [градусов]
меньше уравнения дуги В А, то есть
прибавляемого уравнения дуги АСВ,
что [равняется] 3;24 [градусам]. По-
этому дуга АС должна иметь прибав-
ляемое уравнение на величину избытка
прибавляемого уравнения над вычитае-
Четвертая кййга
&45
мым уравнением, то есть на BEG, так
как если светило находится в А, а центр
эпицикла в любой желаемой точке, на-
пример в G, как он есть на самом деле,
то здесь нет разности; истинное прой-
дет остальные углы из ADC, когда
[центр] эпицикла в G, а средний прой-
дет остальные углы из ADH. Превыше-
ние истинного будет на угол ADC. Это
избыток уравнения АСВ над уравнени-
ем ВАС. На этот [угол] истинное пре-
вышает среднее.
Теперь покажем соответствующие
обстоятельства в случае других трех
затмений. Пусть Е — место эпицикла
246
АЛЬ-ФАРАБИ
при первом затмении [рис. 80], и Луна
находится в А на 43; 15 градусах Скор-
пиона. Пусть центр перемещается в G
не через Н; когда центр достигнет G,
светило будет в В на 25; 10 градусах
Овна; тогда среднее образует оставший-
ся угол EDG, а истинное — оставшийся
угол ADB, который меньше среднего на
сумму углов GDB и ADE. Далее центр
перемещается из G в Н, тогда светило
будет в С на 24; 05 градусах Девы.
Тогда получится, что [среднее] пере-
мещается на весь угол GDH, истин-
ное — на сумму двух углов — BDA и
ADH, что превышает средний на угол
BDG и меньше на угол CDH, являю-
щийся частью угла BDH, то есть BDG.
Поэтому разность между ними, то есть
угол BDC, и есть прибавляемое уравне-
ние. Первое уравнение состояло из сум-
мы двух углов — ADE и GDB, то есть
ADG и GDB. Поэтому разность между
этим и первым [уравнением] есть угол
CD А, что тоже является прибавляемым
уравнением, так как если мы предста-
вим себе, что оба центра и светило дви-
жутся и светило находится в А, когда
центр находится, например, в точке F,
то F должна быть там, где отношение
угла дуги ADG у центра D к углу дуги
ADB, пройденной [центром] эпицикла и
Четвертая книга
247
светилом за один и тот же промежуток
времени, будет таким же, как отноше-
ние двух движений у центра за один
оборот или как [отношение] любых
двух дуг, которые они проходят за один
и тот же промежуток времени.
Допустим, [центр] пройдет дуги не
больше полукруга и пусть F будет там,
где G; тогда цен^р пройдет угол HDG,
а видимый угол CDA превышает сред-
ний на два угла — CDH и GDA. Если
он пройдет дуги больше полукруга и
дойдет, например, до Е, то среднее бу-
дет суммой двух углов — HDG и GDE,
а видимое превышает их на столько же,
на сколько он превышал там. Из этого
вытекает, что если часть любой дуги
прибавляемого уравнения превышает
это уравнение на некоторую величину,
то остальная часть превышает остаток
уравнения. Было также доказано, что
если часть любой дуги прибавляемого
уравнения меньше этого уравнения на
65 некоторую величину, то / остальная
часть превышает [остаток] уравнения
на величину избытка прибавляемого
уравнения над вычитаемым.
Теперь мы утверждаем: апогей мо-
жет находиться только на дуге АВ. Ес-
ли дуга ВСА с прибавляемым уравнени-
ем, то дуга АВ — с вычитаемым урав-
248
АЛЬ-ФАРАБИ
Страницы 45—46 рукописи
Четвертая кнйга
249
/<СжЛ>*и**Ч^***«ЛИВ*'' **'34
-' ч
-44^й^л4(Л5«4»^ , ;
^*)рЧ/ИМ»^»М»ММДЛ<<. .^а;..-'’’
^ИйЯ^ЛеЛНвЬ-г*
й^*м»<ЙЦ^
i
&
^ИййеЙИ
йАЩнЫ^
„Комментарии к «Альмагесту»**.
260
АЛЬ-ФАР АВИ
нением, причем на столько же, на
сколько то превышает. Это легко уста-
новить из сказанного выше.
Теперь вернемся к книге. Мы гово-
рим, что Птолемей использовал три
древних и три современных затмения и
вычислил на их основе геометрическим
путем неравенства движения Луны. Что
касается древних, то Солнце в середи-
не промежутка первого из них по ис-
тинному времени в Александрии соглас-
но началу эпохи было на 24;30 граду-
сах Рыб. Это можно установить по
историческим записям, по которым изве-
стны год, месяц, день и час, когда в Ва-
вилоне произошло это затмение. [Раз-
ность] долгот между Вавилоном и Алек-
сандрией известна, поэтому известен
час этого затмения в Александрии. Он
получил среднее [движение] Солнца от-
носительно Александрии, поскольку там
[проводилось] его измерение, и затем
исправил его.
Что касается второго затмения в се-
редине второго затмения, то, согласно
тем же измерениям, Солнце было на
тридцати с половиной и четвертью гра-
дусах Рыб; поэтому Солнце и Луна пос-
ле отбрасывания полных оборотов про-
шли триста сорок девять градусов пят-
надцать минут, а время между этими
Четвёртая кнйга
затмениями, согласно историческим за-
писям,— триста пятьдесят четыре суток
и два с половиной абсолютных часа,
или, если учесть поправки неравенств
суток, два часа тридцать четыре ми-
нуты.
В середине третьего затмения Солнце
было приблизительно на трех с четвер-
тью градусах Девы; поэтому разница
[от второго до третьего] — сто шестьде-
сят девять градусов тридцать минут, а
прошло 176 суток и двадцать с полови-
ной абсолютных часов, или с поправкой
двадцать и одна пятая часа.
Поэтому, по мнению Гиппарха, в
первое время Луна пройдет [за вычетом
полных кругов] триста шесть градусов
и двадцать пять минут по аномалии, а
по долготе — триста сорок пять граду-
сов и пятьдесят одну минуту.
Если уже известны величина дуги
исправленного прибавления и величина
средней дуги, то разность между уста-
новленными по наблюдениям дугами
будет уравнением, которое дают величи-
ны дуг; она равна разности между
уравнениями двух дуг или сумме этих
уравнений, как мы доказали выше в
случаях обеих гипотез. Если сравнить
положение, установленное по наблюде-
нию, со средним за этот промежуток
ш
АЛЬ-ФАРАБЙ
времени, то получится дуга уравнения
по эклиптике 3;24 прибавляемых [гра-
дусов] , а за второй промежуток времени
избыток по аномалии будет 150; 26
[градусов], а по долготе 170;07 [граду-
сов] , а уравнение — 37 вычитаемых
минут.
Птолемей привел рисунок, в котором
показал всю дугу, отсеченную линией,
выходящей из центра эклиптики до точ-
ки Луны на эпицикле или до точки Лу-
ны на эксцентре, самой отдаленной от
точек трех затмений. На дуге, проходя-
щей через три точки [затмений], он от-
секает дугу и доказывает, что по эпици-
клической гипотезе центр эпицикла не
может находиться на хорде этой отсе-
ченной дуги. Это привело его к вычис-
лению отношения [между] диаметрами
концентрического [круга] и эпицикла.
После того, как он на этом же рисунке
gg определил линию, выходящую / из гла-
за до Луны, которая полностью пересе-
кает эпицикл, и ее часть является хор-
дой эпицикла.
Пусть имеется концентрический
круг и на нем в одном из двух рисунков
находится эпицикл, а во втором — экс-
центрический круг. Пусть А — место
Луны в середине первого затмения и она
движется из А в сторону С, заканчива-
Четвертая книга
258
ет обороты и [доходит] до В; затем дви-
жется из В, заканчивает обороты
и достигает точки С третьего зат-
мения. АСВ и ВАС известны по ме-
тоду Гиппарха, в котором небольшое
изменение, вызванное перемещением
этих [дуг], не оказывает влияния на
само время. Если дуга АСВ будет с
прибавляемым уравнением на 3;24 гра-
дуса и АВ, [дополняющая] до полно-
го оборота, будет с вычитаемым уравне-
нием на ту же величину, а дуга ВАС
будет с вычитаемым уравнением на 37
минут, то дуга АС будет с прибавляе-
мым уравнением на величину, незначи-
тельно отличающуюся от величины вы-
читаемого уравнения дуги ВА; то есть
от 3;24 [градусов], а именно на 37 ми-
нут, и поэтому равна трем градусам
двадцати четырем минутам без тридца-
ти семи минут. Зная величину этого из
рисунка, представляющего указанное
соотношение, можно с помощью вычис-
ления найти, что прибавляемое уравне-
ние АС есть два градуса и сорок семь
минут. Если прибавить к этому трид-
цать семь минут, то получится 3;24
[градуса].
Далее ясно, что перигей не находит-
ся на дуге ВАС, так как она меньше по
254
АЛЬ-Ф АРАБИ
расстоянию, это произойдет при другом
расстоянии.
Пусть центр эклиптики, то есть D,
будет внешним по эпициклической и
внутренним по эксцентрической гипоте-
зе. Соединим его с тремя точками, как
на этих двух рисунках [рис. 81], линия-
[Рис. 81].
ми DB, DA и. DC. В [рисунке] эксцен-
трической гипотезы продолжим BD до
Е, а в [рисунке] гипотезы эпицикла Е
обозначает точку пересечения круга с
линией BD; из Е опустим перпендику-
ляр ЕН к CD и EG — к AD, а из С —
перпендикуляр CF к АЕ. То, что стяги-
вает ВА из эклиптики по эпицикличе-
ской [гипотезе], известно, поэтому угол
Четвертая книга
256
BDA известен. Также по эксцентриче-
ской гипотезе [-ВА] стягивает из эклип-
тики то, что между местами двух зат-
мений, которое известно; поэтому угол
BDA известен. Угол D прямой, поэтому
соотношение углов [и сторон] треуголь-
ника GDE известно, известны также его
стороны. Угол ВЕА известен из дуги
АВ, поэтому остальной угол AED изве-
стен. Угол G прямой, поэтому углы и
стороны треугольника AEG известны.
Так как дуга ВАС известна, то угол
BDC, стягиваемый дугой уравнения по
эпициклической гипотезе, известен.
Соответствующий ему [угол] по эксцен-
трической гипотезе со стороны двух
восстановленных расстояний известен.
Оставшийся угол EDH известен. Также
Н — прямой, поэтому углы и стороны
67 треугольника DEH / известны. Если от-
нять два известных по дуге угла ВЕА и
АЕС, то оставшийся угол СЕН известен.
Но угол СНЕ прямой, поэтому углы и
стороны прямоугольника EHD извест-
ны по обеим гипотезам.
Мы легко найдем также соотноше-
ние углов и сторон двух треугольни-
ков — ЕСЕ и АСЕ. Отношение линии
АС ко всем известным линиям будут
известны. Но ее отношение к диаметру
известно, поэтому отношение линии СЕ
256
АЛЬ-ФАРАБИ
к диаметру также будет известно и ду-
га СЕ будет известна. Тогда вся дуга
ВАС будет известна и хорда BE будет
известна и будет иметь известные отно-
шения ко всем ли-
ниям. Линия BE
будет равняться 117
частям 37 минутам
и 32 секундам диа-
метра. Поэтому она
меньше диаметра,
ВАСЕ меньше по-
лукруга, и центр
эпицикла не нахо-
дится на ВАСЕ.
Пусть центр эпи-
цикла — точка К
[рис. 82]; продол-
жим DMK до L,
L — апогей, М —
[Рис. 82].
L — апогей, М — перигей. Если при-
бавить к [произведению] DL на DM
[произведение] известной КМ на себя,
что можно найти, то получится [произ-
ведение] KD на себя. Таким образом,
KD известна и DL будет также извест-
на. По вычислению получается, что КМ
относится к KD как 5; 13 к 60.
Опустим из К перпендикуляр KN к
BE и [продолжим] его до X. Он разде-
лит пополам дугу BE и хорду BE. Пай-
Четвертая книга
257
дя величину KD и ND и доказав, что
угол N прямой, можно быстро опреде-
лить углы треугольника KND. Также,
найдя NK и КВ и доказав, что угол N
прямой, ты определишь углы треуголь-
ника KBN. Тогда ты определишь два
угла при К, то есть весь угол DKB и ос-
тавшийся угол BKL. Поэтому ты опре-
делишь дугу BL, а затем дугу МВ, до-
полняющую ее до полукруга. По вычис-
лению получается, что дуга BL, то есть
расстояние Луны до перигея в середине
второго затмения. Гравна] 12; 24 [гра-
дусам] , а угол KDB — 59 минутам; это
величина дуги LB, которая стягивает
из эклиптики. Поэтому получается, что
середина [второго затмения] была на
14; 44 [градусах] Девы, а исправлен-
ное, как мы сказали, было на 13; 45
[градусах] Девы.
Рассматривая три современных зат-
мения, он показал, что положение
Солнпа в первом из них на 13; 15 [гра-
дусах] Тельца, а Луна, противополож-
ная ему, в Овне, в третьем — на 14; 30
[градусах] Рыб, а Луна, противополож-
ная ему,— в Деве. Между первым и вто-
рым затмениями прошел один египет-
ский год, сто шестьдесят шесть суток и
двадцать три с половиной с одной, вось-
мой частью прямых абсолютных часов,
89
258
АЛЬ-ФАР АВИ
68
или двадцать три с половиной с одной
четвертью часов, а дуга, отсеченная се-
рединами [этих затмений], составляла
16;55 [градусов].
Между вторым и третьим [затме-
ниями] прошел один египетский год,
сто тридцать семь суток и пять с поло-
виной прямых / абсолютных часов, а от-
сеченная дуга составляла 137; 55 [гра-
дусов]. Во втором затмении имеется вы-
читаемое уравнение ня 7; 42 [граду-
сов], так как среднее [движение] Лу-
ны за этот промежуток времени равно
169; 37 [градусам] после отбрасывания
[полных] оборотов, что превышает ис-
правленное на эту величину. Олнако из-
быток дуги по аномалии после [полных]
оборотов равен 110;21 [градусам]; эта
величина стягивает величину уравнения
из эклиптики. Третье затмение имеет
прибавляемое уравнение на 1;21 [гра-
дус], так как среднее [движение Луны]
равно 137:32 [градусам] после отбра-
сывания [полных] оборотов, а это пре-
вышает исправленное, которое прибав-
ляет ту же величину, так как дуга, ос-
тавшаяся после [полных] оборотов при
движении по аномалии, за этот проме-
жуток времени составляет 81 ;36 [граду-
сов]. Эта величина стягивает [упомяну-
тую] величину уравнения.
Четвертая книга
259
[Рис. 83].
Если мы сделаем для этих трех зат-
мений такой же рисунок, как для пер-
вых трех, то выяснится, что дуга АВСЕ
больше полукруга и что центр эпицик-
ла находится на ней; легко определя-
ются соотношения линий и углов [рис.
83]. [Сначала] находятся величины дуг
СЕ, ВС и BE, из чего выясняется, что
апогей находится на дуге ВА, так как
дуга АВ меньше на 7; 42 [градусов] и
[равна] 110;21 [градусам]. Дуга ВС
превышает уравнение на 1; 21 [градус]
и она [равна] 81;36 [градусам]. Поэто-
му дуга СЕА должна превышать на ос-
тавшиеся градусы, то есть на 7; 21 [гра-
дусов] . Таким образом, каждая из двух
260
АЛЬ-ФАРАБИ
[Рис. 84].
дуг — ВС и СЕА имеет прибавляемую
дугу и поэтому апогей не находится на
них, а остается на АВ. По вычислению
линия АЕ получилась 88; 40; 17.
Если это уже
выяснилось, то так
же, на таком же
рисунке, приведен-
ном для трех пер-
вых затмений, тем
же способом опре-
делить величину ли-
нии КМ относитель-
но KD; по вычис-
лению это оказа-
лось 5; 14 к 60.
На таком же ри-
сунке [рис. 84] и
тем же способом
может быть определена величина ду-
ги AL; по вычислению она оказалась
5;43 [градусов]. Оставшаяся дуга LB,
то есть расстояние Луны во втором за-
тмении, будет составлять 64; 38 [гра-
дуса], если дуга АВ содержит 110; 21
[градусов]. Угол LDB, который вычи-
тается из среднего движения, равен
3; 20 [градусам]. Поэтому среднее [по-
ложение] Луны будет находиться при
этом на двадцати девяти градусах й
тридцати минутах Овна 136.
Четвертая кйига
261
Об исправлении равномерных
движений Луны по долготе
и аномалии
Если это уже выяснено, то [теперь
переходим] к исправлению среднего
движения Луны и ее аномалии. Это лег-
ко сделать, если найти промежуток вре-
мени между древними и современными
затмениями, например, между вторым
затмением из древних и вторым затме-
нием из современных. Этот промежуток
69 времени равен восьмистам / пятидесяти
четырем египетским годам, семидесяти
трем суткам и двадцати трем с одной
третью [часам]. За этот промежуток к
[полным] оборотам по долготе прибав-
ляется 224;46 [градуса], а по анома-
лии — 52; 31 [градуса]. Это сходится с
тем, что следует из предыдущих прин-
ципов относительно долготы, но расхо-
дится с ним относительно аномалии, ко-
торая больше на семнадцать минут.
Если разделить это на [число] дней
упомянутого промежутка времени, то
получится доля одного дня, которую
следует вычесть от [среднего дневного
движения]; это одиннадцать кварт, со-
рок шесть квинт и тридцать девять
секст. Исправленное дневное [движение
аномалии] будет 13; 3, 53, 56,17, 51, 59.
262
аЛЬ-Фарабй
Об эпохе равномерных движений
Луны по долготе и аномалии
Далее он получил эпоху [среднего
движения по Эре] Набонассара 137 с по-
мощью определения времени между ней
и вторым из древних затмений таким
же образом, как он сделал в случае
Солнца.
Об исправлении движений Луны
по широте и об их эпохе
Птолемей, переходя к выяснению об-
стоятельства широты, сказал: в этом
мы последовали Гиппарху, у нас по-
лучилась ошибка относительно широты
Луны; по мнению Гиппарха, Луна укла-
дывается в своей орбите приблизитель-
но шестьсот пятьдесят раз, а в круге
[земной] тени, примыкающем к средне-
му расстоянию в двух соединениях,—
два с половиной раза. Предположив это
и найдя величину широты, мы смогли
судить о величинах частных затмений и
определить границы, после чего насту-
пит затмение Луны. Из этого мы уста-
новили средние движения по широте че-
рез определение величины затемненной
части в середине времени [затмения] и
определение ее широты в середине вре-
Четвертая книга
263
мени этого затмения у определенного
узла 138. Затем мы находим движение
по широте, для чего возьмем промежу-
ток времени между затмениями с оди-
наковыми величинами затмений и с из-
вестными широтами, так как известны
продолжительность затмения и долгота.
С помощью упомянутого метода по на-
блюдаемому среднему движению мы на-
ходим избыточное уравнение исправ-
ленного движения. С помощью среднего
[движения] мы находим эпохи [движе-
ния] по широте и избыточную дугу
после [полных] оборотов. Он сказал: в
настоящее время мы пользуемся более
современными методами, избавляющи-
ми от применения тех принципов. Когда
нам удалось уточнить среднее [движе-
ние] по широте, действуя обратно, мы
заново исправили движение по широте,
а затем исправили те самые принципы,
установили их негодность.
Что касается того метода, которому
мы следовали, то [его суть такова]: бе-
рем промежуток времени между затме-
ниями, равными по величине тьмы, по
времени [прохождения] середины зат-
мения и по стороне. Если удается, то
мы берем эти затмения у одного и того
же узла, то так и сделаем, а если не
удается, то допустим, что они у двух уз-
264
АЛЬ-ФАРАБИ
лов. Мы знаем, что когда затмение об-
ладает указанным свойством, то Луна
точно возвращается к своей широте,
так как два затмения могут быть подоб-
ными только при одинаковой величине
захода. Если же при одном затмении
Луна находится во Вселенной ближе к
Земле, то круг тени при этом будет ши-
ре, а при другом затмении — наоборот.
70 Когда она находится / ближе, она за-
темняется на какой-то промежуток вре-
мени и имеет некоторую широту, то есть
расстояние до эклиптики, a bq втором
случае она [начинает] затемняться
только тогда, когда ее широта меньше
той широты. Однако если [все-таки] это
случится, то не будут равны ни время
середины затмения, ни [промежутки]
времени между началом и появлением.
Если же эти времена равны при подобии
величины затемнения, то определяется,
что оба затмения произошли примерно
в одном и том же отрезке 139.
Он сказал: при одном из рассматри-
ваемых нами наблюдений имелись два
подобных затемнения у одного и того
же узла и в одной и той же стороне
[эклиптики]; узел был нисходящий 14°,
сторона южная, а величина — шестая
часть диаметра, то есть в два пальца *41.
Первое из этих затмений наблюдалось в
Четвертая книга
265
Вавилоне, а второе — в Александрии.
Между ними шестьсот пятнадцать еги-
петских лет, сто тридцать трое суток,
двадцать один с половиной с одной тре-
тью равноденственного часа. Что каса-
ется расстояния, то оно было близко к
[полученному] в середине.
Из даты и эпохи было найдено, что
при первом из них расстояние Луны от
апогея эпицикла было 100; 19 [граду-
сов] , а при втором — ее расстоянии от
апогея с другой стороны было 251; 53
[градус]. Ее исправленное место при
первом] было меньше среднего на пять
градусов, а при втором — больше на че-
тыре градуса пятьдесят три минуты. Она
[по исправленному движению] верну-
лась к своей широте, а по среднему от-
ставала от полного оборота на сумму
двух поправок, то есть на девять граду-
сов и пятьдесят три минуты. По прин-
ципам Гиппарха, оба уравнения, [вме-
сте взятые], за этот промежуток време-
ни'должны быть больше этой величины
на девять минут, так что их сумма рав-
нялась приблизительно десяти градусам
и двум минутам. Поэтому движение по
широте, по его принципам, меньше то-
го, что нашел Птолемей. Птолемей раз
делил эти девять минут на промежуток
времени и прибавил долю одних суток
266
АЛЬ-ФАР АВИ
к суточному среднему движению по ши-
роте, записанному Гиппархом. Величи-
на этого прибавления 0; 0,0, 0, 8, 39,18.
Птолемей привел еще два затме-
ния142, совпадающих по всем показате-
лям, кроме узла: первое — это одно из
[Рис. 85].
диаметра, то есть
трех вавилонских
затмений, которое
произошло у восхо-
дящего узла, а дру-
гое — у нисходя-
щего узла; оба они
южные, то есть Лу-
на затмилась с юж-
ной стороны на ве-
личину четверти
на три пальца. Для
определения этого он нарисовал рису-
нок [рис. 85]. Он построил наклонный
круг АВС с диаметром АС, где А —
восходящий узел, С — нисходящий
узел, а В — северный конец.
При первом затмении Луна находи-
лась в D, так как, когда затмение. со
стороны юга, центр Луны оказывается
к северу от эклиптики. При втором [зат-
мении] она находилась в Е. AD и СЕ
должны быть равны между собой.
Если мы еще этого не знаем, то мож-
но вычислить дату по эпохе и найти
среднее движение Луны по долготе и
Четвертая книга
267
аномалии; из ее движения по аномалии
следует, что расстояние Луны до апогея
эпицикла при первом [затмении] соста-
вит 12;24 [градусов]. Затем, определив
величину ее поправки, можно найти,
что ее исправленная величина будет
меньше среднего на пятьдесят девять
минут. Это и есть ее поправка.
Расстояние Луны от апогея [эпицик-
ла] будет равно 2;45 [градуса], а вы-
читаемая поправка — тринадцать ми-
нут. Пусть середина Луны при первом
[затмении] будет в G, так что DG явля-
72 ется вычитаемой / поправкой, а при вто-
ром— в Я, так что ЕН является вычи-
таемой поправкой; их величины извест-
ны. Так как промежуток времени между
затмениями известен,— он [равен] двум-
стам восемнадцати египетским годам,
тремстам девяти суткам и двадцати трем
и одной двенадцатой равноденственного
часа,— то избыточная дуга над [пол-
ными] оборотами при среднем периоди-
ческом движении Луны по долготе изве-
стна. По вычислению она составляет сто
шестьдесят градусов и четыре минуты.
К ней прибавляется поправка первого
затмения и из нее вычитается поправка
второго затмения. Полученная дуга DE
будет в середине полукруга, тогда ос-
тальная часть разделится на две поло-
268
АЛЬ-ФАРАБИ
вины. Если расстояние до двух узлов од-
но и то же, то одна половина оставшей-
ся дуги есть AD, а вторая — дуга СЕ.
По вычислению [каждая из них] равна
9; 35 [градусам].
Определяются [также] дуги AD и
СН среднего движения в обоих [затме-
ниях], находятся их расстояния до се-
верного конца и до средней точки. Из
этого он определяет эпоху Луны по ее
широте для даты Набонассара.
Далее Птолемей приводит таблицу
для первой поправки 143, в которой
[сначала] приведены градусы по анома-
лии через каждые шесть градусов и че-
рез три градуса; это сделано в двух
столбцах, как в случае Солнца. В тре-
тьем столбце он дает прибавляемые и
вычитаемые поправки, где показано,
сколько градусов поправки соответству-
ет [для градусов аномалии, взятых] че-
рез каждые шесть [или три] градуса, а
вопрос о том, когда следует ее приба-
вить или вычитать,— ясный 144.
О том, что принятая Гиппархом разница
величины [лунного] неравенства
получается не из-за принципов,
по которым он действовал,
а вследствие вычисления
Далее Птолемей перешел к выясне-
нию причины допущенной Гиппархом
Четвертая книга
269
ошибки в величине движения по анома-
лии и в величине отношения полудиаме-
тра эпицикла к полудиаметру деферен-
та. По гипотезе эксцентра оно должно
быть равным отношению шести и одной
четверти к шестидесяти, а по гипотезе
эпицикла — отношению четырех граду-
сов и сорока шести минут к шестидеся-
ти. Поэтому для них величина макси-
мальной поправки будет разной, так
как в первом случае она достигает 5; 49
[градусов], а во втором — 4;34.
По исследованию Птолемея уста-
новлено, что в обоих случаях это отно-
шение равно отношению 5; 15 к 60 и
что максимальная разность составляет
пять градусов. Он упомянул, что это
произошло у [Гиппарха] не по причине
ошибочных принципов, а по причине
ошибочного вычисления. Затем пока-
зал, как это [случилось], и сказал:
здесь подействовало не одно, а разные
обстоятельства: допущена ошибка или
в наблюдении, или в вычислениях про-
межутков времени эпохи и даты. Он
сказал: Гиппарх рассматривал три зат-
мения, наблюдаемых в Вавилоне, и
одинаково поступил с ними; для перво-
го он нашел дату, промежуток времени
между ним и началом эпохи и время, на
которое отличаются времена Вавилонии
270
АЛЬ-ФАРАБИ
и Александрии, и определил, в каком
часу середина [затмения] наступила в
Александрии. Исходя из этого он опре-
делил среднее и исправленное положе-
ния Луны. Таким же образом он посту-
пил со вторым затмением и [нашел]
промежуток времени между ними. Так
72 же он поступил и с третьим./
Птолемей обнаружил, что у Гиппар-
ха допущена ошибка в [вычислении ко-
личества] часов промежутка времени
между первым и вторым затмениями,
так как при проверке оно оказалось
превышающим полные дни [и часы] на
три пятых часа, тогда как Гиппарх счи-
тал, что оно превышает на половину и
одну четверть часа. При проверке ок-
залось, что избыточная дуга при движе-
нии составляет 173;28 [градуса], а у
Гиппарха — 172; 52,30. Точно так же
произошла ошибка у [Гиппарха] в [вы-
числении количества] часов промежут-
ка времени между вторым и третьим
[затмениями]; при проверке оно оказа-
лось превышающим на два часа. Это
превышение у Гиппарха составляло
один и две третьих часа. Избыточная
дуга при проверке [составляла] 175; 44
[градусов], а у Гиппарха — 175;7,30.
Вслед за этим Гиппарх таким же об-
разом рассматривает другие три затме-
Четвертая книга
271
ния и говорит, что они наблюдались в
Александрии. При первой проверке Пто-
лемей нашел, что промежуток времени
между первым и вторым [затмениями]
есть сто семьдесят восемь суток и шесть
с половиной и одной третью равноденст-
венного часа, градусы движения Солнца
180; 11. У Гиппарха промежуток време-
ни есть сто семьдесят восемь суток и
шесть равноденственных часов, градусы
[Солнца] 180; 21. При проверке Птоле-
мей нашел, что промежуток времени
между вторым и третьим [затмениями]
есть сто семьдесят шесть суток и две
третьих часа, градусы избыточной дуги
18; 55. У Гиппарха промежуток време-
ни есть сто семьдесят шесть суток и
один с одной третью равноденственного
часа, градусы 168; 33. Вот это причина
той ошибки, которая допущена [Гиппар-
хом].
ПЯТАЯ КНИГА 115
Об уточнении положений Луны
[Птолемей] сказал: то, что необхо-
димо для уточнения положений Луны в
ее совпадающих и противостоящих сое-
динениях [с Солнцем], и [для определе-
ния] времени затмений,— это первое
уравнение, и знания его достаточно для
этого. Что же касается [всех] прочих
отдельных положений при движении
[Луны], то его недостаточно. Оказыва-
ется, что для этого существует второе
неравенство.
Прежде всего нам нужно знать спо-
соб изготовления инструмента, который
необходим для наблюдения [небесного]
тела.
Об изготовлении инструмента,
при помощи которого измеряются
[положёнйя] светил
Изготовим два одинаковых кольца,
ограниченных четырьмя поверхностям
Пятая книга
273
ми, очень ровно [обточенными], и сое-
диним их по диаметру [перпендикуляр-
но друг другу]. Одно из них установим
в положении круга эклиптики, а дру-
гое — в положении меридиана. Найдем
на меридиане полюс круга эклипти-
ки,— это нетрудно, потому что [для
этого] мы определяем при помощи кру-
га эклиптики на кольце по четверти ме-
ридиана. Укрепляем здесь стержень,
проходящий через обе стороны [коль-
ца], изготавливаем [еще] два кольца
упомянутого вида [и помещаем их] так,
чтобы одно из них располагалось сим-
метрично обоим [первым] кольцам сна-
ружи и могло вращаться относительно
них, а второе — так, чтобы эти два пер-
вых -кольца были симметричными от-
носительно него, заключая его в себе, и
чтобы вращение этого кольца происхо-
дило внутри двух [первых] в тесном со-
прикосновении с ними. После этого
укрепим их на стержнях — одно свер-
ху, а другое снизу [то есть снаружи и
внутри]. Изготовим [еще одно] кольцо
[и установим его] таким образом, что-
бы его заключало в себе внутреннее
кольцо и чтобы [это последнее кольцо]
перемещалось в нем по направлению к
обоим полюсам; делаем на нем две от-
метки, подобные отметкам на астроля-
18-89
274
АЛЬ-ФАРАБИ
бии. Таким образом, два кольца, укреп-
ленные на стержнях, будут перемещать-
ся относительно двух первых колец по
долготе, а внутреннее [кольцо] будет
перемещаться по широте. Потом нахо-
дим на кольце меридиана наибольшее
склонение, а из этого находим оба по-
73 люса небесного экватора. Помещаем / в
эти точки два стержня, устанавливая на
них снаружи кольцо, охватывающее
все остальные; таким образом, распре-
делены [все кольца]: и то, что для эк-
липтики, и то, что для меридиана, и
[внешнее], заключающее в себе все ос-
тальные, и другие кольца. Если устано-
вить это [последнее] кольцо в плоскости
горизонта перпендикулярно линии ме-
ридиана в соответствии с широтой мест-
ности и высотой полюса, наблюдаемой в
ней, то вращение колец на стержнях бу-
дет подобным вращению Вселенной ,46.
Птолемей сказал: мы устанавливали
это кольцо в соответствии с широтой
местности, и если Солнце и Луна вместе
находятся над землей, мы передвигаем
верхнее кольцо, проходящее через оба
полюса круга эклиптики, пока оно не
дойдет до того градуса круга эклиптики,
в котором находится Солнце в тот час.
Мы продолжаем передвигать кольцо
меридиана, проходящее через полюса,
Пятая книга
275
пока оно действительно не достигнет пе-
ресечения с плоскостью, примыкающей
к Солнцу. Тогда верхнее [кольцо] и
кольцо эклиптики затеняют друг друга,
особенно если использовать [два отвер-
стия], подобные отверстиям на астроля-
бии. Если через них будет видно свети-
ло, не имеющее широты, то переместим-
ся [относительно инструмента] так,
чтобы это светило было видно [как бы]
на плоскости кольца, особенно если мы
использовали [отверстия], подобные
отверстиям на астролябии. Потом мы
вращаем другое кольцо, находящееся
внутри, а в нем поворачиваем то, что
внутри него по направлению к обоим по-
люсам, пока не увидим в отверстиях
[другое] светило или Луну, и при этом
видим первое на соответствующем ему
градусе. Прикрепив к [внутреннему
кольцу] внешнее кольцо, мы получим
дугу от пересечения первого кольца с
кольцом эклиптики и от пересечения
другого кольца [с ним же] — это дуга
долготы — и другую дугу между отвер-
стием в кольце, вращаемом через по-
люсы, и кольцом эклиптики — это дуга
широты как на юге, так и на севере 147.
Можно укрепить еще одно внешнее
кольцо [с делениями] соответственно
градусу светила, которое совершало бы
276
АЛЬ-ФАРАБИ
относительно него вращение, имитирую-
щее вращение небосвода, и при помощи
него измерять [положение] других све-
тил.
О принципе, который мы применяем
в вопросе двойного неравенства Луны
Птолемей сказал: когда мы изгото-
вили этот инструмент и произвели [при
его помощи] многочисленные наблюде-
ния, то обнаружили в положениях Луны
такие соединения, которые соответству-
ют тому, что вытекает из предполагае-
мых принципов. [Эти соединения] не
имеют каких-либо ощутимых отклоне-
ний, кроме тех, которые неизбежны для
параллакса. Если в обеих квадратурах
Луны [по отношению] к Солнцу Луна
находится в апогее или перигее эпицик-
ла, то дело обстоит именно так. Если же
[Луна] находится в квадратуре в других
положениях, кроме апогея и перигея, то
мы находим это уравнение несоответст-
вующим изложенным выше принци-
пам, а именно: прибавляемое оказыва-
ется большим, а вычитаемое — мень-
шим. Если же случается, что Луна
находится там, где имеет место предель-
ное уравнение, то мы находим его значи-
тельно превышающим пять градусов,
Пятая книга
i'll
74
которые мы допустили как предел раз-
ности уравнения в вычитании или сло-
жении.
Поэтому мы предполагаем, что
центр эпицикла движется не по концен-
трическому кругу; иначе не изменялось
бы его предельное уравнение, а по экс-
центру в обеих квадратурах [Луна] на-
ходится на наименьшем расстоянии и
поэтому видна [больше], создавая боль-
ший видимый угол, стягивающий боль-
шую дугу эклиптики.
Если в двух квадратурах [Луна] на-
ходится в перигее эксцентра, то при
обоих соединениях она будет в апогее.
Если же Луна попадает в перигей дваж-
ды в месяц в течение одного оборота, то
это или невозможно, или же эксцентр
движется / против движения центра
эпицикла так, что он бывает в перигее
и в апогее дважды в месяц. Из этого
вытекает, что эксцентр движется к вос-
току в том же направлении, что и на-
клонный круг, [находящийся] в его
плоскости. Поэтому на его плоскости,
то есть на плоскости наклонного круга,
имеется движение, перемещающее эпи-
цикл к востоку, и другое движение, пе-
ремещающее его на удвоенную элонга-
цию, когда центр эксцентра переносится
к западу. Если бы движение эксцентри-
278
АЛЬ-ФАРАБИ
ческого круга было бы вокруг его цен-
тра, то не изменялись бы положения
апогея и перигея. Но поскольку они из-
меняются, то весь [эксцентрический
круг] движется так, что его центр пере-
мещается по другому кругу, изменяя и
его апогей. Рассматривая истинные по-
ложения, [проходимые] за равные [про-
межутки] времени, и необходимое урав-
нение, он показал, что за равные [про-
межутки] времени центр эпицикла опи-
сывает равные дуги наклонного круга.
Если же уравнения относительно эпи-
цикла нет, то это имеет место на [наи-
большем и наименьшем] расстояниях
вблизи них. Он показал, что за равные
[промежутки] времени [центр эпицик-
ла] проходит неравные дуги эксцентри-
ческого круга, это не может быть для
двух эксцентрических кругов. Поэтому
мы показываем, что движение центра
эпицикла равномерно вокруг центра на-
клонного круга, а не вокруг центра экс-
центра. Так как за один средний месяц,
начинающийся от соединения, Луна со-
вершает полный оборот и дугу, прохо-
димую Солнцем в его среднем движе-
нии, то, если [в начале месяца] средняя
Луна находится в апогее эксцентра,
эксцентр за [один] месяц совершит
[один] оборот без дуги, [пройденной]
Пятая книга
279
Солнцем в его среднем движении. Это
потому, что в начале среднего месяца
Луна находится в апогее и, совершая
оборот по долготе, описывает избыточ-
ную дугу, и апогей, встречая Луну со
стороны, противоположной ее движе-
нию, достигает ее и доводит до конца
этой дуги. Ей остается пройти в точно-
сти такую дугу, чтобы дойти до исход-
ного положения, где они разошлись.
Поэтому Луна проходит [один] оборот и
дугу, а деферент при своем движении в
сторону запада [совершает один] обо-
рот без этой дуги. Избыток движения
средней Луны над движением деферен-
та, вызванным движением наклонного
круга, [равен] удвоению этой дуги, по-
скольку первое превышает [полный
оборот] на эту [дугу], а второе недоста-
ет до него на ту же самую [дугу]. Он
показал, что движение эксцентра, выз-
ванное движением наклонного круга,
вместе с этой дугой, а не с ее удвоени-
ем, равно избытку [движения] средней
Луны по долготе над [движением] сред-
него Солнца за один оборот [Луны].
Если удвоить это, то есть разность меж-
ду средним движением Луны и Солнца,
то получится сумма продвижения апо-
гея и наклонного круга с востока и сред-
него движения Луны в последовательно-
280
АЛЬ-Ф АРАВИ
сти знаков Зодиака, если Солнце, точка
апогея, центр эпицикла и точка наклон-
ного круга расходятся одновременно.
Это и есть два оборота: движение апо-
гея и наклонного круга вместе со сред-
ним [движением] Солнца — первый
[оборот, а движение центра эпицикла
без среднего движения Солнца — вто-
рой]. Поэтому истинная величина, про-
ходимая эпициклом по эксцентру,— два
оборота.
Я утверждаю: если Солнце, центр
эпицикла Луны и апогей расходятся
[одновременно], то апогей проходит не-
которую дугу, а центр [эпицикла] про-
ходит в другую сторону такую же дугу
и удвоенное продвижение Солнца.
Солнце проходит свою известную дугу в
направлении движения центра. Поэтому
получается, что расстояние между цент-
ром и апогеем равно удвоению этой ду-
ги [вместе] с удвоенным продвижением
Солнца, а расстояние между центром и
Солнцем равно этой дуге [вместе] с ду-
75 гой продвижения Солнца. / Поэтому
расстояние между двумя светилами рав-
но половине расстояния между апогеем
и центром. Так как избыток этого [рас-
стояния] над продвижением Луны по
долготе есть движение эксцентра, опре-
. деляемого [движением] наклонного кру-
Пятая книга
281
га, то, если вычесть ив этой удвоенной
разности не продвижение [Луны] по
долготе, а [ее] среднее движение по
широте, движение наклонного круга
прибавится к движению по долготе и
остается движение эксцентра, [опреде-
ляемое] движением апогея. Следова-
тельно, движение эксцентра равно остат-
ку от вычитания продвижения [Луны]
по широте из удвоенной разности между
средним Солнцем и средней Луной. По-
этому движение самого апогея равно ос-
татку от вычитания среднего продвиже-
ния [Луны] по широте из удвоенного
избытка средней Луны над средним
Солнцем. Птолемей называет этот избы-
ток элонгацией, а всю дугу, содержа-
щую все движения,— двойной элонгаци-
ей. При вычислении получилось, что
продвижение апогея за одни сутки со-
ставляет 11; 9 градусов. Птолемей дал
чертеж для объяснения этого поня-
тия 148. Он говорил: пусть АВС — на-
клонный круг, описанный из Е [рис. 86],
Е — также центр эклиптики. Пусть
АЕС — диаметр наклонного круга, про-
ходящий через оба центра, а С? — центр
эксцентра DH [в некоторое время].
Пусть [вначале] точка А одновре-
менно — северная граница [Луны],
точка апогея, точка [начала] Овна,
282
АЛЬ-ФАРАБИ
центр эпицикла Луны и среднее Солн-
це. Вся плоская фигура АВС вместе с
[кругом] DH продвигается за одни сут-
ки от А в направлении D и пройдет ду-
гу AF, величина которой три минуты,
так что северная граница окажется в
точке F, это конец Рыб. Плоская фигу-
ра эксцентра вместе с линией ED вра-
щается в том же направлении и [описы-
вает] дугу, большую, чем AF, это дуга
AD. Центр эпицикла вращается от А в
направлении В, и линия ЕА переходит
в линию ЕВ так, что этот [центр] ока-
жется, например, в точке Н и пройдет
[дугу] АВ относительно наклонного
круга, если бы он был неподвижным.
Пятая книга
283
Однако в действительности северная гра-
ница движется, и между центром эпи-
цикла и северной границей будет дуга
FB, равная 13; 14 [градусам]. Поэтому
[центр эпицикла] в действительности
опишет эту дугу, эпицикл пройдет от
апогея дугу DH и между эпициклом и
северной [границей] составит 13; 14
[градусов], а между северной границей
и положением апогея — 11; 9 [граду-
сов] . Их сумма — 24; 23 [градуса] —
удвоенное продвижение средней элонга-
ции за одни сутки, то есть удвоенный
избыток средней Луны над средним
Солнцем, это приблизительно двенад-
цать градусов и одиннадцать с полови-
ной минут. Так как Солнце и Луна в те-
чение месяца один раз диаметрально
противоположны и один раз соединяют-
ся, причем и то и другое происходит в
апогее, то ясно, что в течение месяца
они дважды бывают в средних квадрату-
рах, когда эпицикл находится в перигее.
Чем ближе эпицикл к середине [между
апогеем и перигеем], тем видимая раз-
ность неравенства больше, так как угол
при глазе [наблюдателя], образованный
одной и той же вещью, изменяется и
становится то больше, то меньше в за-
висимости от близости и дальности —
284
АЛЬ-ФАР АВИ
чем вещь дальше, тем угол меньше, а
чем вещь ближе, тем угол больше.
Если [рассматривать] движение
эпицикла по эксцентру не относительно
центра эксцентра, а относительно цент-
ра наклонного круга, то оно не будет
иметь другого уравнения, кроме величи-
ны той же разности на эпицикле, и
эксцентр будет влиять на это только
благодаря близости и дальности. Напри-
мер, из точки А, диаметрально проти-
76 воположной [точке] С [рис. 87], и/из
С опишем два круга эпицикла, один из
которых MN, а другой — FX. Так как
точка Е не находится в центре эксцен-
тра, поскольку мы предположили, что
Е — центр эклиптики, и через нее и че-
рез центр эксцентра проходит прямая
линия, то наибольшей будет линия, про-
веденная из Е к эксцентру ЕА, а наи-
меньшей — ЕС. Следовательно, види-
мый предел разности будет не меньше
того, что при А, и не больше того, что
при С, то есть при затмениях, соедине-
ниях и противостояниях и, [следователь-
но, он имеет место] в квадратурах 149.
Пятая книга
285
Об определении [величины]
неравенства Луны в зависимости
от ее расстояния от Солнца
Затем он находит предел этого
неравенства, определяя положение Лу-
ны по отношению к положению Солн-
ца и исходя из расстояния между ними
с помощью упомянутого выше инстру-
мента. Если оно близко к квадратуре,
когда Луна близка к середине неба, то
параллакса не будет. При вычислении
он нашел, что Луна находится на своем
эпицикле в точке, где линия, проведен-
ная из глаза, касается его. [Он полу-
чил] это не из одного наблюдения, а из
[нескольких] последовательных на-
блюдений Гиппарха. Установив по-
ложение Луны, он нашел, что оно
отличается от среднего на [величи-
ну], большую предела уравнения, кото-
рый он нашел в начале. Тогда этот пре-
дел составлял пять градусов, а те-
перь — семь и две трети [градуса]. По
наблюдению, проведенному Птолемеем,
вычитаемое уравнение было такой же
величиной, как и прибавляемое уравне-
ние, рассчитанное Гиппархом.. Это под-
тверждает его предыдущее интуитивное
[предположение].
Он потребовал найти из этого [вели-
286
АЛЬ-ФАРАБИ
движется по
сказал:
FG — эпи-
чину] отношения для линии, соединяю-
щей два центра, при этом он исходит из
того, что центр эпицикла
эксцентрическому кругу.
Он
пусть
цикл [с центром] в
С, являющейся пе-
ригеем эксцентра
АВС [с центром] в
D [рис. 88]. Если
при этом не будет
параллакса, пусть
Е — центр эклип-
тики, то есть точ-
ка глаза [наблюда-
теля] . Проведем
EFB — касательную к эпициклу в точ-
ке F, которая перпендикулярна к CF.
Угол СЕВ, соответствующий пределу не-
равенства, известен; прямой угол F из-
вестен; поэтому в треугольнике [СЕР]
отношение СЕ к CF известно. Но отно-
шение для DC известно, поэтому отно-
шение ДЕ к DC известно. [При вычис-
лении] оно получилось [равным] отно-
шению 10;19 к 39;22.
Я утверждаю, что при этом в дейст-
вительности будет известным то, что
между плоскостью горизонта и центром
эпицикла, а не то, что между центром
Пятая книга
287
Земли и [центром эпицикла], и что угол
при центре Земли меньше. Но отноше-
ние для полудиаметра Земли можно оп-
ределить и прибавить к той величине.
Об определении стороны,
к которой склоняется эпицикл Луны
Когда Птолемей продолжал наблю-
дение, он нашел, что в тригональном 150
и гексагональном аспектах появляется
третье неравенство. Отсюда он заключа-
ет, что диаметр эпицикла, соединяю-
щий его апогей с перигеем, проходил не
через центр эклиптики и не через центр
77 эксцентра, /а через точку, расстояние ко-
торой от центра эклиптики в сторону
перигея эксцентра близко к расстоянию
между двумя центрами. Проходить
здесь означает, что когда центр эпицик-
ла находится в апогее или в перигее
эксцентра, то его диаметр совпадает с
диаметром эксцентра, проходящим че-
рез них, и оба образуют одну прямую
линию. Если центр [эпицикла] смещает-
ся от этой точки деферента, то эти ли-
нии расходятся и становятся не парал-
лельными друг другу, так что обязатель-
но соблюдается их пересечение внутри
деферента, если продолжить диаметр
эпицикла в его направлении. Это пере-
288
АЛЬ-ФАРАБИ
сечение происходит не в точках цент-
ров, а в другой точке. Пересечение при-
водит опять к совпадению, и конец диа-
метра эпицикла всегда сохраняет
примыкание к этой точке.
Что касается способа нахождения
этого неравенства 181, то это Птолемей
осуществил с помощью наблюдений, в
том числе двух наблюдений, проведен-
ных Гиппархом; одно из них осущест-
влено упомянутым инструментом; при
этом видимое Солнце находилось на
7;45 [градусах] Тельца; видимое место
Луны — на 21; 40 [градусах] Рыб, ис-
тинное— на 21;27,30 [градусах] Рыб;
действительное расстояние между [по-
ложениями] Луны и Солнца составляло
313;42 [градусов]; среднее расстояние
между ними — 314; 28 [градусов]. Ме-
сто Луны в среднем движении [по дол-
готе] было на 22; 13 [градусах] Рыб, а
ее расстояние от средней наиболее отда-
ленной точки эпицикла равнялось
185;30 [градусам]. Исследуя положе-
ние Солнца и среднее [положение] Лу-
ны, ее неравенство и уравнение, он на-
шел, что это среднее [положение] опе-
режало по отношению к эклиптике свое
место, исследуемое по наблюдению, так
что уравнение стало вычитаемым, центр
эпицикла — приблизительно в середине
Пятая книга
289
между апогеем и перигеем эксцентра, а
прохождение по аномалии должно быть
больше половины круга от апогея, а
это приводит к тому, что уравнение
должно быть прибавляемым. Но оно
получилось вычитаемым и не имеет
места прохождения на половину круга
от апогея эпицикла. Поэтому должен
быть неподвижный апогей, расстояние
которого от этого [апогея] не достигает
половины круга и который нам не ви-
ден. Поэтому мы покажем [все относи-
тельно] видимого апогея; Луна была
расположена к западу от видимого пе-
ригея и к востоку от среднего перигея,
относительно которого вычисляется
среднее [положение]. Поэтому средний
перигей отстает по эклиптике от види-
мого перигея на расстояние от Луны до
видимого перигея. Если бы [перигей
эпицикла] считался примыкающим к
точке, являющейся центром эклиптики,
то этого бы не произошло.
Затем он показал положение этой
точки с помощью рисунка и сказал:
пусть АВС круг эксцентра около D, его
диаметр, проходящий через центр эк-
липтики Е, — линия АВС [рис. 89]. А —
апогей, С — перигей. GHF — эпицикл
около В движется, например, от В к А;
Луна движется из G к Н, затем к F;
19-89
290
АЛЬ-ФАР АВИ
соединим DB, а также ЕВ; [DB] пересе-
кает эпицикл в F, это видимый перигей.
Но расстояние среднего [положения]
78
[Рис. 89].
Луны от среднего [положения] Солнца
известно, поэтому его удвоение извест-
но. Это расстояние апогея от центра эпи-
цикла по эклиптике, которое составля-
ет триста пятнадцать градусов с лиш-
ним, его удвоение больше, чем круг, и
остаток после вычитания целого оборо-
та от этого удвоения известен. Однако
его среднее [значение] известно не от-
носительно круга деферента, а относи-
тельно концентрического с наклонным
круга. Тогда угол АЕВ будет известен,
так как он находится у центра наклон-
ного [круга]. Поскольку угол /АЕВ
стягивает [дугу] меньше четверти [кру-
Пятая книга
291
га], то есть острый, то если опустить из
D перпендикуляр на ЕВ, он расположит-
ся внутри треугольника; пусть им бу-
дет DK. Отношения в треугольнике
DEK известны, так как угол DEK из-
вестен ; угол К — прямой. Поэтому DK
известен [по отношению] к DB, КВ, яв-
ляющаяся одной из сторон прямого
[угла], будет известной. Следовательно,
ЕВ известна. Пусть Луна [находится]
в Н, соединим ЕН. Из В восстановим
перпендикуляр BL к ЕН. Поскольку
угол В прямой, то он известен; угол
BEL, являющийся [углом] уравнения,
определяется из наблюденного истинно-
го положения. Поскольку среднее [поло-
жение] находится по вычислению и
разность между обоими положениями
известна, то отношения в треугольнике
BEL известны. Проведем BE', посколь-
ку ВН и BL из треугольника BHL изве-
стны, а [угол] L прямой, то угол BHL
известен; поэтому оставшийся угол
FBH будет известен. Следовательно, ду-
га ЕН, то есть расстояние между Луной
и видимым перигеем, будет известна.
Однако расстояние Луны в аномалиях
от среднего перигея известно.
Пусть по вычислению средний пери-
гей, опережающий Н по эклиптике, бу-
дет в точке М; соединим ВМ и продол-
292
АЛЬ-ФАР АВИ
жим ее по прямой. Как мы знаем, она
обязательно пересечет линию АС; пусть
она [пересечет ее] в N. Из Е опустим
перпендикуляр ЕХ [к B2V]; он распо-
ложится внутри треугольника, так как
угол АЕВ острый и внутренний угол
ENX острый. Поскольку дуга ЕН изве-
стна, дуга НМ, то есть то, что между
средним перигеем и местом светила, из-
вестно из прохождения по средней ано-
малии, то дуга ЕМ известна. Поэтому
угол ЕВХ известен. Но [угол] X прямой
и линия ЕВ известна, поэтому ЕХ извест-
на. Поскольку угол АЕВ известен и угол
ЕВ известен, то оставшийся угол ENB
известен; поэтому отношения в тре-
угольнике XEN известны. По вычисле-
нию получается, что если DE — 10; 19,
то Е — 10; 18. Пересечение двух линий
АС и BN будет внутри эксцентра. Таким
образом, выясняется истинность примы-
кания со стороны перигея при этом на-
блюдении.
Он говорил: мы докажем аналогич-
ное со стороны апогея. Он рассмотрел
наблюдение Гиппарха на острове Родос
и нашел указанным методом, что сред-
нее [положение] Луны отлично от ее
истинного положения; при вычислении
выходит, что она [находится] на 27; 20
Пятая книга
293
[градусах] Льва, а по видимости она
на 29 [градусах] Льва. При этом она
была близка к середине неба и не имела
параллакса по долготе. Ее расстояние от
79
видимого апогея меньше того, что опре-
деляется по вычислению на основе ука-
занных выше истинных принципов.
Аналогичным методом он доказал те
же вопросы, которые он доказал по пер-
вому рисунку; они не отличаются за
исключением того, что точка Н в апо-
гее, перпендикуляр BL n&pfi&s, не дохо-
дя до [точки] Н, и перпендикуляр DK
на другой стороне [рис. 90]. Он определил
угол DEK и [линии] DK, / КЕ и ЕВ и
[затем] — ЕВ. Но оставшийся угол
ВЕН уже найден, a L — [прямой], по-
этому он вычислил отношения сторон и
294
АЛЬ-ФАРАБИ
углов треугольника EBL. Но стороны
BL и ВН известны и угол L прямой, по-
этому он определил угол BHL и весь
[угол] ЕВН-, остаток от двух прямых
НВ известен, он находит дугу HG. Ду-
га НМ определена по вычислению. Это
расстояние от среднего апогея. Отсюда
он определил дугу GM и угол GBM, то
есть EBN. Затем он находил и все ос-
тальные углы и дуги по этому образцу.
Получилось, что если DE — 10; 19, то
EN—10; 20, так что они [очень] близ-
кие. Если мы прибавим примерно то,
что вычиталось, то получится такое же
отношение. Таким образом, он опреде-
лил, что это прохождение сохраняется и
не изменяется.
Как с помощью линий
определить истинное движение Луны
по его равномерным движениям
Птолемей показывает, как геометри-
ческим путем определяется расстояние
Луны по средним отдельным движени-
ям, чтобы найти ее истинное положе-
ние.
Он сказал: мы можем определить
это из приведенного нами рисунка, если
мы проведем рассуждение в обратном
порядке. Предположим, что углы АЕВ
Пятая книга
295
и МВН известны. Вместо перпендикуля-
ра ЕХ мы опустим перпендикуляр NX
к ЕВ; а вместо BL — перпендикуляр
HL к ЕВ (рис. 91]. Мы находим отноше-
ния в треугольнике DKE из прямого
[угла] и из угла КЕА. Затем находим
отношения в треугольнике KDB через
определения DB и KD и прямого угла.
Тогда ЕВ будет известна; треугольник
XEN равен и подобен треугольнику
KDE; NX равна DK. Находим остаток
ХВ, треугольник BXN и угол EBN,
то есть MBG. Следовательно, дуга MG
известна, но дуга МН известна, поэто-
му дуга GH и угол GBH известны. Угол
HLB — прямой, поэтому [половина]
хорды BL известна; тогда вся EL из-
вестна. [Сторона] LH треугольника
296
АЛЬ-ФАР АВИ
BLH известна, поэтому ЕН и угол LEH,
то есть разность уравнения, известны.
Об определении [метода]
составления таблиц для полного
неравенства Луны152
Когда он определил способ установ-
ления этого уравнения с помощью ли-
ний, он составил таблицы для полного
неравенства Луны. В [таблице] пер-
вый столбец содержит [числа аргумен-
тов] от единицы до ста восьмидесяти
[градусов] в порядке возрастания, а в
другом — наоборот. В третьем столбце
дано уравнение апогея эпицикла в отно-
шении места центра эпицикла от апо-
гея, деферента и для каждого места
[содержится] значение угла уравнения
апогея. В четвертом столбце [дается]
80 уравнение первого неравенства, / имею-
щее место, когда центр эпицикла Луны
находится в апогее эксцентра, а Луна
движется [по эпициклу] противопо-
ложно [последовательности знаков
Зодиака]. Он привел уравнение для каж-
дой величины движения [Луны] по ано-
малии, которое соответствует ее уравне-
нию в противостояниях и в затмениях.
В пятом столбце он поместил избытки
уравнений, получающиеся при нахож-
Пятая книга
297
дении центра эпицикла в перигее и дви-
жения Луны по аномалии. Он привел
[здесь] соответствующий этому ее дви-
жению избыток уравнения неравенства,
записанного в четвертом столбце. Это
уравнение получается в квадратурах.
Так как центр эпицикла может нахо-
диться не только в одном из двух про-
тивоположных расстояниях, то есть в
апогее или перигее, а между ними, то
он привел соответствующий избыток
уравнения и в этом случае. Для этого
он сначала сделал рисунок, подобный
предыдущему.
Птолемей сказал: пусть градусы
элонгации будут известными, например,
шестьдесят [градусов], угол АЕВ —
удвоенная элонгация [рис. 92]. Прове-
дем линию EMN, касающуюся [эпи-
цикла] в точке М. Отношения в прямо-
угольном треугольнике EDL известны.
Поскольку ВМ известна, то, как мы ви-
дели, ЕВ станет известной. ВМ, то есть
перпендикуляр к касательной, изве-
стен; поэтому угол ВЕМ известен, это
есть угол предела разности уравнения
при [значении] элонгации сто двадцать
[градусов], что больше простого урав-
нения на один градус пятьдесят три ми-
нуты; избыток этого уравнения при пе-
ригее составляет два градуса тридцать
298
АЛЬ-ФАРАБИ
девять минут. Это [приблизительно] два
и две трети градуса; [если принять их]
за шестьдесят [минут], то [1;53 граду-
са соответствует] 42 минутам и 38 се-
кундам. Он поместил это против ста
двадцати. Так же он вычислил и для
всех других [градусов], составил ше-
стой столбец и поместил в каждую ячей-
ку то, что соответствует числу, записан-
ному против него в первых двух столб-
цах, представляющему значение элонга-
ции. Во втором столбце дается избыток
наибольшего уравнения для этих граду-
сов над наибольшим уравнением в апо-
гее. Это не берется в отношении значе-
ний уравнения, а полученное представ-
ляет [число] шестидесятичных долей от
Пятая книга
299
двух третей градуса, которое пред-
ставляет наибольшее уравнение в
перигее. Поскольку невозможно рассмо-
треть одновременно оба перемещения,
одно из которых — перемещение центра
эпицикла, а другое — перемещение
Луны, то он удовлетворился переме-
щением центра эпицикла и. неподвиж-
ностью Луны в отношении точки ка-
сания.
После этого он заполнил последний
столбец, где поместил предельное рас-
стояние Луны от северной границы, ко-
торая является дугой ее широты, огра-
ниченной наклонным кругом и эклипти-
кой на большом круге, проходящем че-
рез полюсы эклиптики и стоящем к ней
под прямыми углами. Значения этих
дуг вычисляются тем же методом, что и
склонения градусов эклиптики при из-
вестном наибольшем склонении. Таким
же образом легко вычисляются широты
наклонного [круга] при известной наи-
большей широте, равной приблизитель-
но пяти градусам.
81 Если мы хотим найти эфемериды /
Луны, то берем средние движения по
долготе, широте и аномалии от среднего
апогея и движение элонгации: удвоим
расстояние между средними [положе-
ниями] Солнца и Луны относительно
300
АЛЬ-ФАРАБИ
данной местности и данной эпохи. Отни-
мем от нее полные обороты с тем, чтобы
осталась [дуга], которая меньше круга.
Затем находим удвоенную элонгацию в
двух столбцах; берем его уравнение из
третьего столбца и [пропорциональные]
минуты153 из шестого столбца. Если
число из первого столбца, то прибавим
уравнение к неравенству, которое мы
запоминаем; если из второго столбца, то
его вычтем; тогда выравнивается нера-
венство Луны, если она не находится в
апогее и перигее. Затем находим из
столбца число и берем то, что соответст-
вует ему в четвертом и пятом столбцах;
запоминаем то, что в четвертом столбце,
и умножим то, что в пятом столбце, на
минуты, взятые из шестого столбца, и
делим на шестьдесят. То, что получает-
ся,— это разность, которую следует при-
бавить [к тому, что] в четвертом [столб-
це]. Если исправленное движение Луны
по кругу эпицикла меньше ста восьми-
десяти [градусов], то отнимаем его от
[градусов] среднего [положения] Луны
по долготе и широте; если же больше,
то прибавляем его. То, что получено по
долготе, мы отсчитываем от [числа]
градусов, полученных для Луны, тогда
оставшееся число покажет ее истинное
положение. Соответствующее число для
Пятая книга
301
широты, [отсчитываемой] от северной
границы, мы берем из столбца широты.
Ты знаешь, что широта бывает южной
или северной в зависимости от расстоя-
ния от северной границы 154.
О том, что неравенство
по причине эксцентрического круга
'не имеет ощутимой величины
во время соединений и противостояний
Когда Птолемей закончил это пред-
ложение, кто-то ему сказал: при на-
блюдении за затмениями ты предпола-
гал, что центр эпицикла находится в
апогее деферента, что это обязательно
при противостояниях и соединениях;
затем ты основываешь уравнение на
этом; однако дело обстоит не так при
истинных соединениях и противостоя-
ниях, при которых происходят затме-
ния; это обстоит действительно так при
средних соединениях и противостояни-
ях, при истинных же соединениях и про-
тивостояниях у Солнца может быть
уравнение, центр эпицикла также мо-
жет отклоняться от апогея, пока не про-
изойдет истинная встреча, что приводит
к уравнению из-за приближения Луны
к Земле, снижения Луны и наибольше-
го приближения ее к Земле. Он сказал,
302
АЛЬ-ФАРАБИ
что это отклонение не вызывает сущест-
венной разницы в уравнении, так как
это отклонение приводит к уравнению
по одной из двух причин: оно либо ис-
ходит по причине приближения центра
эпицикла к Земле, либо изменения наи-
большего приближения. Там, где одна
из этих [причин] приводит к пределу
соответствующего уравнения, другая не
вызывает при этом существенной разни-
цы, так как предел избытка уравнения,
к которому приводит изменение апогея,
бывает тогда, когда [Луна] находится
в апогее или в перигее эпицикла, при
двух же средних расстояниях это не
имеет существенного значения. Предел
избытка уравнения, к которому приво-
дит различие [в расстоянии], наблюда-
ется в том случае, когда она находится
около касательной линии, а там примы-
кание не вызывает существенной разни-
цы уравнения.
Он сказал: пусть будут эксцентриче-
ский круг и эпицикл, как приводилось
неоднократно на рисунке, и пусть эпи-
82 цикл смещен на дугу /АВ [рис. 93].
Истинное Солнце или диаметрально
противоположно Луне, или отклонено в
сторону запада. Тогда наибольшая ве-
личина разности между двумя средни-
ми есть сумма двух уравнений: одна из
Пятая кйига
303
них прибавляется, а другая вычитается.
Пусть наибольшее прибавляемое урав-
нение Солнца — два градуса двадцать
три минуты, а наибольшее вычитаемое
уравнение Луны, которое получается
при касательной линии,— десять [гра-
дусов шесть минут]. Это предел средних
расстояний или предельное расстояние
между средним [положением] одного и
средним [положением] другого, диаме-
трально противоположного ему, это рас-
стояние известно во всех случаях; удво-
енное расстояние между ними будет
известно, так что угол АЕВ, соответст-
вующий удвоенной элонгации, будет из-
вестен. Проведем касательную ЕЕ и DM,
перпендикулярную к BE, и перпендику-
ляр BF. Определим два треугольника —.
304
АЛЬ-ФАР АВИ
DEM и DMB, как это было сделано, на-
ходим линию ЕВ\ BF известна. Опреде-
лим прямоугольный треугольник ВЕЕ,
в котором известно отношение ЕВ к BF,
поэтому угол ВЕЕ становится извест-
ным; по вычислению он равен 5;3 [гра-
дусам] , что больше на две минуты того,
что в апогее. Отсюда последует ошибка
меньше одного градуса, так как она
равна одной шестнадцатой часа.
Такая разница может получиться в
самом наблюдении и не поддается ис-
правлению. Она происходит по причине
приближения центра эпицикла на экс-
центре [к Земле].
Что касается разницы, получающей-
ся из-за наклонности к апогею, то он
также показал с помощью другого ри-
сунка, что она не оказывает заметного
влияния.
Птолемей сказал: пусть Луна [на-
ходится] в L, то есть в среднем перигее
[рис. 94]; тогда угол АЕВ содержит при-
близительно удвоенное [значение] сол-
нечного неравенства. Это потому, что
Луна в этом месте не имеет заметной
разности первого неравенства. Поэтому
если [разность] неизбежна, то она от-
носится к Солнцу и равна расстоянию
между средними. Угол АЕВ стягивает
удвоение этого. Проведем EL и опустим
Пятая книга
805
из D перпендикуляр DM к ЕВ, а из G —
перпендикуляр — GX к ЕВ, из L — пер-
пендикуляр LN. Определим ЕВ и В<? пу-
тем последовательного [вычисления]. В
треугольнике GXB отношение известной
GB к GX и к ХВ равно отношению изве-
стной В соответственно к LN и NB; от-
сюда определим LN и NB. В треуголь-
нике LEB находим угол BEL. По вычис-
лению он равен четырем минутам;
происходящая при этом ошибка не до-
стигает одной восьмой часа, следова-
тельно, и эта ошибка [происходит] в са-
мом наблюдении.
20-89
306
АЛ Ь-Ф АРАВИ
О параллаксах Луны
83 Ты уже знаешь / смысл параллакса
Луны. Теперь необходимо провести ис-
следование и определить, каким обра-
зом мы можем различить ее истинное
место от видимого и наоборот. Это зави-
сит от ее расстояний от Земли, а опре-
деление расстояний — от параллакса,
из которого мы находим расстояния и
затем все остальные неравенства.
Птолемей сказал: Гиппарх начал
исследование, исходя из [наблюдений]
Солнца. Из [разных] явлений, происхо-
дящих для двух светил, тебе будет по-
казано, что ты можешь рассчитать рас-
стояние до [одного] из них через опре-
деление расстояния другого. Гиппарх
рассмотрел сначала обстоятельства рас-
стояния Солнца, а из этого — расстоя-
ния Луны. Он добился нахождения рас-
стояния Луны, исходя из предположе-
ния, что Солнце имеет ощутимый парал-
лакс, хотя и очень маленький. В этом он
противоречит себе. При рассмотрении
некоторых солнечных затмений он ут-
верждал, что Солнце совсем не имеет
параллакса, а здесь утверждает, что оно
имеет достаточно большой параллакс. У
него есть подобная путаница в утверж-
дении не только о самом параллаксе, но
Пятая книга
307
также и о вычислениях расстояния Лу-
ны.
Далее Птолемей начинает с построе-
ния инструмента, годного для наблюде-
ния расстояний, и называет его [инстру-
ментом] с двумя ответвлениями 155. Его
устройство таково: берутся две медные
линейки, ограниченные четырьмя пло-
скими поверхностями, причем каждые
две [противоположные плоскости] —
параллельные и равные, их ширина при-
близительно втрое больше толщины, а
толщина — приблизительно равна тол-
щине мизинца. Закрепим одну линейку
на конце другой с помощью оси и шар-
нира так, чтобы одну можно было за-
крепить неподвижно, а другую вращать.
Построим на той, которую мы решили
закрепить, два отвесных кирпичика, а
на одной грани другой [линейки] — два
противоположных и равных друг другу
по длине и ширине диоптра, как два
диоптра астролябии; поставим их как
можно дальше друг от друга и в диоп-
тре, обращенном к свободному [концу],
сделаем очень маленькое отверстие, а в
том, который обращен к оси,— более
широкое так, чтобы через него можно
было видеть всю Луну через другой
диоптр. Начертим в каждой из двух
более широких плоскостей линию, раз-
308
АЛЬ-ФАРАБИ
деляющую плоскость пополам, разде-
лим ее на шестьдесят частей и каждую
часть — на ее минуты. Закрепим в сво-
бодном конце плоскую линейку, кото-
рая может вращаться так, чтобы она
могла соединить [концы] первых двух
линеек, когда они расположены друг к
другу под прямым углом. Поставим ли-
нейку, не имеющую диоптров, перпен-
дикулярно к плоскости горизонта; это
осуществляется с помощью подвешива-
ния отвеса.
После этого мы закрепим ее, чтобы
она не отклонилась [от этого положе-
ния] . Мы сделаем так, чтобы другая ли-
нейка вращалась вокруг нее в плоско-
сти меридиана. Для этого мы предвари-
тельно найдем меридиан и направим к
небу тот конец [первой линейки], на
котором находится ось, а другой ее ко-
нец направим к земле.
Если мы хотим наблюдать широту
Луны в круге меридиана и ее расстоя-
ние от Солнца, то смотрим на нее через
диоптр движущейся линейки в оба от-
верстия. Отметим величину угла, обра-
зованного между двумя линейками, по-
ставив линию с делениями, начерчен-
ную на третьей линейке, на концы двух
линий, проведенных на двух [первых]
линейках. Обе эти линии равны. То, что
Пятая книга
S09
отсечется между этими концами от тре-
тьей линейки, и будет хордой дуги [ме-
84 ридиана] между зенитом и/положени-
ем Луны на круге меридиана, то есть
круга, проходящего через полюсы небес-
ного экватора. Может случиться, что
этот [круг] проходит и через полюсы
эклиптики, если Луна находится в солн-
цестояниях. Для наблюдения широты
[Луны] из двух солнцестояний предпо-
читается летнее, а из двух границ —
северная, поскольку, когда Луна нахо-
дится в них, она не имеет такого парал-
лакса, как в противоположном конце.
Он сказал: для определения широты
мы наблюдали Луну в Александрии в
[точке] летнего солнцестояния в север-
ной границе. Благодаря "Этому сущест-
венной разницы между видимым и ис-
тинным ее положениями не отмечалось;
ее расстояние от зенита в это время рав-
нялось приблизительно двум и одной
восьмой градуса.
Следовательно, наблюдаемые широ-
ты в разные времена должны быть по-
добными по ощущению и равны пяти
градусам.
Для наблюдения параллакса предпо-
читаются зимнее солнцестояние и юж-
ная граница, так как параллакс увели-
чивается при увеличении расстояния от
310
АЛЬ-ФАРАБИ
зенита и предел параллакса достигает-
ся при пределе расстояния. Одно из
наблюдений, ведущих к нахождению об-
стоятельства параллакса, было произве-
дено, когда Солнце заходило, а расстоя-
ние от зенита до Луны в круге мери-
диана было пятьдесят, половина, треть
и одна двенадцатая градуса и дата,
[принятая] для [начала] эпохи, и эфе-
мерид приводили к тому, что истинное
положение Солнца было на 5; 28 [гра-
дусах] Весов; истинное [положение]
Луны — на 3; 10 [градусах] Козерога;
[аргумент] широты — на 354; 40 [гра-
дусах] от северной границы; ее широта
на 4; 59 [градусах] к северу [от круга,
проходящего через полюсы эклиптики [,
склонение точки эклиптики, в которой
находилась [Луна], 23;49 [градусов],
расстояние меридиана от зенита, то есть
широта местности — Александрии, в
которой производилось наблюдение,
30;58 [градусов]; истинное расстояние
Луны от зенита равно сумме широты
местности и склонения градуса [эклип-
тики] с вычетом широты Луны; это 49
градусов и 48 минут; ее видимое рас-
стояние равнялось 50;55 [градусам].
Следовательно, получается параллакс в
один градус и семь минут; весь этот
[параллакс] по широте, и ничего суще-
Пятая книга
311
ственного не происходит по долготе, так
что точка находилась в начале [граду-
сов] Козерога, а Луна наблюдалась,
когда она была близка к меридиану.
Об определении расстояния Луны
Пусть круг АВ представляет Землю,
CD — круг, проходящий через центр Лу-
ны и места наблюдения, центр этого
круга есть центр Луны [рис. 95].
[Рис. 95].
EG — круг, по отношению к кото-
рому Земля не имеет параллакса.
Пусть Луна находится в точке D, К —
центр Земли и центр каждого из [этих]
кругов; продолжим KD до Н из круга
EG± пусть точка А — место наблюде-
512
АЛЬ-ФАРАЙЙ
ния и линия ADF — линия наблюде-
ния; тогда FH будет [дугой] параллак-
са. F — видимое место Луны, а Н — ее
истинное место. Проведем КАСЕ до зе-
нита и линию AG, параллельную линии
КН. Тогда поскольку диаметр Земли не
имеет ощутимого значения по отноше-
85 нию к кругу EG /, то GF будет больше
HF на неощутимую [величину]. Угол
ЕКН известен, так как его стягивает
известное истинное расстояние; тогда
угол EAG известен. Угол EAF известен,
потому что его стягивает видимое рас-
стояние, поэтому остается угол GAF из-
вестным по наблюдению. Это равно уг-
лу ADK. Из точки А опустим перпен-
дикуляр AL на КН. Тогда отношения в
треугольнике AKL будут известны, [от-
сюда] вычисляем АК, то есть полудиа-
метр Земли. Также треугольник ADL
имеет два известных угла: прямой, угол
ADL и известную сторону AL; DAL —
оставшийся угол, [поэтому] можно счи-
тать, что все три угла известны. Две
стороны [угла] DAL известны, поэтому
отношение всей KD к КА известно. Та-
ким образом, отношение расстояния Лу-
ны от центра Земли к полудиаметру
Земли в этом наблюдении известно.
По вычислению находим, что если
АК [равна] единице, то KD — 39; 45.
Йятай йнигй
313
Таким образом, с помощью этого рисун-
ка найдено расстояние'Луны во время
наблюдения. Из этого можно опреде-
лить отношение ее расстояний в сизиги-
ях и квадратурах и отношение диаметра
ее эпицикла к диаметру Земли. Начер-
тим эксцентр и эпицикл, и пусть Луна
будет в [точке] L эпицикла, проведем
соединительные линии аналогично то-
му, что было раньше [pjic. 96]; прове-
дем перпендикуляры DM и GN.. Поло-
жение Луны по аномалии известно из
указанного наблюдения. Расстояние Лу-
ны от среднего апогея 262; 20 [граду-
са], следовательно, от среднего перигея
К она отстоит на оставшиеся градусы
после [вычета] полукруга, то есть на
82;20 [градуса]. Но FK, то есть урав-
нение между перигеями, по вычислению
314
АЛЬ-ФАРАВЙ
равняется дополнению 82; 20 до девяно-
ста градусов, то есть семи градусам и
двум третям [градуса], вся дуга LKF —
девяносто градусов, значит, угол
LBF — прямой.
Поскольку угол АЕВ, стягиваемый
удвоенной элонгацией, известен, то тре-
угольник DME равен и подобен тре-
угольнику EGN; отношения в них из-
вестны. Точно так же будет известен
треугольник DGB по двум сторонам и
прямому углу, тогда отношения DE, BE
и других линий будут известными. По-
скольку угол EBL прямой и его сторо-
ны ЕВ и LB известны, то будет извест-
на EL по отношению к BL. Из преды-
дущего рисунка известно его отношение
к полудиаметру В эпицикла; полудиа-
метр эксцентра DB, среднее расстояние
в сизигиях ЕА, среднее расстояние в
квадратурах ЕС и две соединяющие
[линии] известны по отношению к по-
лудиаметру Земли. Итак, линия ЕА —
59, ЕС — 38;43, BL — 5;10, EL —
39;45.
Он сказал: из определения этих рас-
стояний и углов, образованных при гла-
зе, можно определить расстояние Солн-
ца и его величину. Если будем наблю-
дать середины затмений и их высоты
относительно неподвижных звезд, имею-
Пятая книга
S15
щих постоянные долготы и широты, и
относительно Солнца, то мы можем най-
ти средние времена затмений и отсю-
да — долготу и широту. Что касается
инструментов, которыми определяют
время (с помощью водяных измерите-
86 лей) или времен восхождений, j [выра-
женных] в прямых [часах], то они не
приводят к нахождению этого.
Об определении величин диаметров
Солнца, Луны и [земной] тени,
видимой в сизигиях
Что касается способа определения
расстояния Солнца, то сначала он при-
водит предпосылку: [Гиппарх] наблю-
дал величину диаметра Солнца с помо-
щью [инструмента] с двумя ответвле-
ниями, просматривая через оба его
отверстия и отмечая угол между [линей-
ками] ; величина этого угла не изменя-
ется во всех расстояниях Солнца. Что
касается Луны, то ее диаметр изменяет-
ся по видимости в зависимости от рас-
стояния; она видна под таким же [уг-
лом], что и Солнце, когда она находит-
ся в наибольшем расстоянии [от Зем-
ли], а в других местах Луна видна под
большим [углом, чем Солнце]. Утверж-
дение ученых о том, что она видна под
316
АЛЬ-ФАРЛЕЙ
таким ясе [углом], что и Солнце в сред-
нем расстоянии, ошибочно; они ошиба-
лись такясе при измерении угла, под
которым видно Солн-
це.
Он сказал: мы на-
шли этот [угол] мень-
ше упомянутого ими.
Вообще нет необходи-
мости в этих измерени-
ях при уточнении рас-
стояния Солнца и его
величины. Птолемей
при определении ве-
[Рис. 98].
А
СК В
[Рис. 97].
личины диаметра Солнца не произвел
измерения угла указанной линейкой,
потому что ее трудно установить и уточ-
нить, а пользовался некоторыми лунны-
ми затмениями, как мы покаясем поз-
Пятая книга
317
же. Наблюдение с помощью этой линей-
ки помогло установить, что если угол
наблюдения Солнца и угол наблюдения
Луны равны, когда они видны под од-
ним и тем же углом, то утверждение о
равенстве их расстояний не будет оши-
бочным. Что касается измерения этого
угла при помощи указанного инстру-
мента, то здесь можно допустить боль-
шую ошибку. Поэтому он при измере-
нии обоих диаметров не исходит из [ве-
личины] этого угла, а пользуется им
только при вычислении их видимого ра-
венства.
При рассмотрении полных солнеч-
ных затмений было установлено, что
иногда у них есть продолжительность,
а иногда нет. Когда у них есть продол-
жительность, то ясно, что [поскольку
при этом] диаметр Луны по видимости
неизбежно больше диаметра Солнца и
так как она движется под ним и расхо-
дится с ним, то она является [причи-
ной] его покрытия. Если же у них нет
продолжительности, то оба диаметра
равны по видимости, так как если бы
диаметр Луны был меньше, то Солнце
не затмевалось бы полностью, а если бы
диаметр Солнца был меньше, то полное
затмение имело бы продолжительность.
Не бывает такого солнечного затмения,
318
АЛЬ-ФАРАБИ
имеющего продолжительность, когда
Луна находится на наибольшем рас-
стоянии. Полные затмения Солнца при
средних и близких расстояниях Луны
от Земли обладают продолжительно-
стью. Отсюда доказывается, что диа-
метр Луны при наибольшем расстоянии
равен диаметру Солнца.
Что касается величин диаметров, то
Птолемей показал способ их нахожде-
ния, [исходя] из двух затмений, при од-
ном из них затмевалась четверть его
диаметра с южной стороны. Вычисление
эфемеридов Солнца и Луны показало,
что Луна находится на расстоянии 9; 20
[градусов] от узла и ближе к апогею
эпицикла; расстояние между ними при-
близительно двадцать градусов без се-
ми минут. Но центр эпицикла не может
быть близким к апогею деферента; по-
этому это расстояние от узла входит в
данной части конуса [тени], то есть
когда Луна находится вблизи апогея
эпицикла, который сам близок к апогею
деферента, то это приводит к тому, что
такая часть диаметра Луны попадает в
тьму.
При втором — северном затмении
затмевалась половина диаметра Луны, а
эфемериды Солнца и Луны приводили к
тому, что расстояние [Луны] от узла
Пятая книга
319
равнялось 7;48 [градусам], а [ее] рас-
стояние от апогея эпицикла было близ-
§7 ко к первому расстоянию / и равнялось
двадцати восьми градусам и пяти мину-
там. Такая разница не оказывает на
расстояние от Земли какого-либо зна-
чительного влияния. Это расстояние от
узла приводит к тому, что затемнение
доходит до центра круга тела Луны.
Ширина Луны в первом положении бы-
ла равна 0; 48; 30, ширина Луны во
втором положении — 0; 7; 50; следова-
тельно, четверть диаметра Луны состав-
ляет 0; 7; 50. Вся Луна в этом положе-
нии стягивает по большому кругу —
0; 31; 20. Половина диаметра конуса [те-
ни] в этом месте стягивает указанную
во втором наблюдении ширину, так как
затмение доходит до центра круга Лу-
ны, а центр конуса [тени] всегда нахо-
дится на эклиптике. Это меньше удвоен-
ного радиуса тела Луны и три пятых
его половины на незначительную [вели-
чину]. Он проверил этот результат и
подтвердил его с помощью других мно-
гочисленных наблюдений.
320
АЛЬ-Ф АРАВИ
Об определении расстояния Солнца
и о том, что выясняется из этого
Он сказал: после вычисления этого
переходим к изложению метода опреде-
ления расстояния Солнца и его величи-
ны, который основывается на рассмотре-
нии лунного затмения. Для этого при-
водим одну предпосылку. Пусть в
треугольнике АВС проведена ВН парал-
лельно его основанию [рис. 97] и пусть
DE равна BD. Из точки Е проведена
другая параллельная линия — EG. Тог-
да GE и СВ вместе вдвое больше DH.
[Доказательство]. Проведем GK парал-
лельно BE. Тогда ясно, GE и ВК вместе
вдвое больше DF. Поскольку СК отно-
сится к ЕН как KG к FG, то есть как
BE к DE, а BE вдвое больше DE, то С7Г
вдвое больше FH. Следовательно, GE
и ВКС вместе вдвое больше DFH 156.
Пусть KLM — круг Земли, HGE —
круг Луны в наибольшем ее расстоянии,
АВС — круг Солнца во время его зат-
мения Луной [рис. 98]; их тела каса-
ются конусом зрения, пусть эти круги
[лежат] на одной и той же плоскости.
Пусть эта плоскость отсекает плоскость
АХС от конуса, по которому проходят
[лучи] Солнца, образуя тени Земли, а
от гонуса зрения, охватывающего Солн-
Пятая книга
321
це и Луну,— плоскость ANC. Соединим
точки касания кругов с сечениями двух
конусов линиями АС, ЕН и КМ; про-
должим ЕН до I; пусть OQ — диаметр
круга тени, когда Луна находится в наи-
большем расстоянии; пусть линия
DX — стрела большого конуса, прохо-
дящая через все центры, то есть через
D,F и N. Она пересекает OQ в Р; ты
знаешь, что всякие две линии, прове-
денные из одной и той же точки и ка-
сающиеся одного и того же круга, рав-
ны между собой; поэтому каждые две
из линий XN и AN; МН и NE, а также
ХС и ХА, ХО и XQ равные и образуют
равнобедренные треугольники, и основа-
ние каждого треугольника отсекает рав-
ные его стороны; поэтому АС и ЕН,
АС и КМ, АС и OQ будут параллельны-
ми; все они [лежат] на одной и той же
плоскости, параллельны между собой и
являются в чувстве диаметрами, хотя
это не так в действительности, а отлича-
ются друг от друга на незначительную
[величину]. Угол ANC и его половина
FNH известны; угол NFH — прямой,
потому что он равен углу NFE; линия
FN, представляющая наибольшее рас-
стояние,— известна, поэтому отношения
углов и сторон треугольника FNH из-
88 вестны; отношение HFI к FN, которое
21-89
322
АЛЬ-ФАРАБИ
имеет известное отношение к полудиа-
метру Земли MN,— известно; отноше-
ние FH к PQ известно, поэтому PQ из-
вестна. QP и FI [вместе] — есть удвоен-
ная MN, поэтому их сумма известна;
PQ и FH известны, оставшаяся HI изве-
стна; NM относится к HI как NC к СН,
то есть как ND к DF. Выделяя, полу-
чим, что избыток MN над HI относится
к HI как известная NF к известной FD;
FD известна, следовательно, ND извест-
на. FH относится к DC как NF к ND, по-
этому CD известна. ND, то есть расстоя-
ние Солнца от Земли, получилось при
этом наблюдении равным 1210, а линия
CD, то есть полудиаметр Солнца,— при-
близительно равен 5; 30 [земным полу-
диаметрам] . Можно определить EN, CN,
NP, NX; таким образом, получается,
что линия NX — 268; если предполо-
жить диаметр Луны единицей, то диа-
метр Земли будет равен 3;24, диаметр
Солнца — 18; 48. Но отношение сфер
друг к другу — это тройное отношение
их диаметров. Тогда объем Земли в
39,15 раза больше объема Луны, а объ-
ем Солнца в сто семьдесят раз больше
объема Земли. Итак, он показал то, что
хотел.
Пятая книга
323
О частных [значениях] параллаксов
Солнца и Земли
Птолемей переходит к выяснению
обстоятельства параллакса Луны через
определение ее расстояний. Если Луна
находится в некотором известном рас-
стоянии, то как определить ее парал-
лакс? Он начертил рисунок [рис. 99]
для параллакса, аналогичный предыду-
щему рисунку; так что истинное поло-
жение Луны будет в Н, а видимое — в
F. Ее параллаксом будет HF, которая в
чувстве равна GF.
Птолемей сказал: пусть расстояние
Луны от Зенита [содержит] известное
[число] градусов, тогда угол К изве-
стен, L — прямой. Поэтому отношения в
треугольнике AKL известны; точно
так же в треугольнике ALD угол ALD
и, следовательно, угол GAF будут изве-
стны. Так как между ним и тем, кото-
рый у центра, нет различия по отноше-
нию к кругу EF, дуга GF, то есть та, ко-
торая не отличается в чувстве от HF,
будет известной; это и есть параллакс
для известного расстояния. Таким же
образом он вычислял для [расстояний]
через каждые шесть градусов вплоть до
девяноста. Затем он взял разницу, соот-
ветствующую каждым шести градусам,
324
АЛЬ-ФАРАБИ
и разделил ее на три. При этом он при-
менял сокращение и приближение и
приложил полученное к таблице с ин-
А
[Рис. 99]. [Рис. 100].
тервалом через каждые два [градуса].
Он составил таблицу для параллак-
сов 157, в первый ее столбец поместил
градусы квадранта, увеличивающиеся
через каждые два градуса вплоть до де-
вяноста. Это градусы расстояния от зе-
нита. Во второй столбец — параллакс
Солнца; в третий столбец — параллакс
Пятая книга
326
Луны в первом случае; в четвертый
столбец — избыток параллаксов [Лу-
89 ны] / во втором случае над [тем, что] в
первом случае, в пятый столбец — па-
раллакс [Луны] в третьем случае. Так
как упомянутые выше расстояния Луны
определились, когда [эпицикл находит-
ся] в двух апогеях или в двух перигеях
согласно способам деления, которые мы
знаем, то, если центр Луны или центр
эпицикла отклоняется, для нахожде-
ния параллакса нам нужно определить
его расстояние.
Пусть ABCD — эпицикл и G центр
Земли [рис. 100]; проведем GDA, где
D — видимый перигей, А — видимый
апогей, В — точка смещения от видимо-
го апогея, в котором первоначально на-
ходилась Луна, [дуга смещения] равна
тридцати градусам. Проведем СВ, опу-
стим из точки В на диаметр перпенди-
куляр ВН, который известен; поэтому
ЕН известна; поэтому GH и ВН извест-
ны, следовательно, их гипотенуза GB
известна.
Пусть Луна на этом рисунке нахо-
дится в С; [ее расстояние] от перигея
известно; опустим перпендикуляр СЕ,
определим ЕЕ, следовательно, линия GE
известна. Поэтому GC известна незави-
симо от того, где был центр эпицик-
326
АЛЬ-ФАР АВИ
ла — в апогее или в перигее. Если же
он находится между ними, то пусть
АВС — эксцентр с центром Е [рис. 101],
G — центр Земли, А — апогей, С — пе-
ригей [эксцент-
ра] ; центр эпицик-
ла находится в точ-
ке В; продолжим
GB до D и [опу-
стим к ней] перпен-
дикуляр ЕН; про-
ведем ЕВ и ED;
пусть [каждый из]
углов AGB и DGC
шестьдесят граду-
[Рис. 101]. сов, когда круг со-
держит четыре
прямых. Если центр Луны в В, то рас-
стояние между двумя светилами трид-
цать градусов, потому что оно рав-
но половине расстояния от апогея; ес-
ли же он в D, то расстояние — сто двад-
цать градусов. Поскольку соединяющая
сторона EG и угол AGB известны, Н —
прямой, то НЕ известна; также Е, ЕВ
[известны]; угол Н — прямой, поэтому
НВ и, следовательно, вся GB известна.
Поскольку прямой угол Н известен, сто-
роны ЕН и ED известны; через GH из-
вестна GD. Поскольку одно из двух рас-
стояний эпицикла GC и второе из дан-
Пятая книга
327
ных расстояний GA, а также BG и BD
[известны], то на первом и на этом ри-
сунке определяется то расстояние, ког-
да она отклонена от первых упомянутых
расстояний. Таким образом, он находит
все расстояния Луны в любом положе-
нии.
Он составил шестой столбец, где по-
местил полученные избытки первого
расстояния над последовательными рас-
стояниями, получающимися при смеще-
нии Луны от апогея эпицикла, при
[нахождении] эпицикла в апогее дефе-
рента; они взяты по отношению к наи-
большему избытку, то есть к диаметру
эпицикла и к избытку наибольшего рас-
стояния при наибольшем смещении, [и
выясняются] отношения этого избытка
к диаметру эпицикла, принятого за
шестьдесят. При этом он вычислял,
что диаметр эпицикла — 10; 30; полу-
диаметр эксцентра—49;41 и среднее
расстояние — 60.
Седьмой столбец для [пропорцио-
нальных] минут, на которые он поправ-
90 ляет то, что в четвертом столбце, / и
прибавляет его к третьему [столбцу].
Затем, применяя тот же способ, он со-
ставил восьмой столбец для этих же
[значений], когда центр эпицикла [на-
ходится] в перигее. Числа аргумента
328
АЛЬ-ФАР АВИ
представляют градусы смещения отно-
сительно [перигея] по аномалии. Так
как их сто восемьдесят градусов, то они
не могут быть исчерпаны [числом] де-
вяносто или сорок пять, то есть числом
строк для градусов. Поэтому он взял
два градуса вместо каждого градуса, и
ставил все, что вычислял, против поло-
вины градусов, для которых он вычис-
лял. Например, он [нашел], что диа-
метр эпицикла 16, а расстояние центра
эпицикла от центра эклиптики шесть-
десят. Этот восьмой столбец содержит
[пропорциональные] минуты, на кото-
рые он поправляет то, что в шестом
столбце, и прибавляет его к пятому
[столбцу]. Если он получает избыток
первого расстояния над расстоянием,
найденным при смещении на шестьде-
сят градусов, то он записывает его про-.
тив тридцати. Он составил девятый
столбец, в который поместил величину
избытка первого расстояния над рас-
стояниями, которые получаются при
смещении центра эпицикла. Он
взял эти избытки и их отношения
к наибольшему избытку, являю-
щемуся разностью между тем, [что
получается], когда центр [эпицикла]
находится в апогее, и тем, [что получа-
ется] , когда он находится в перигее; ве-
Пятая книга
320
личина этой разности 20; 38, а расстоя-
ние центра эпицикла от центра Земли
шестьдесят. Этот девятый столбец со-
держит [пропорциональные] минуты,
которыми поправляют разность между
тем, что в третьем столбце, и тем, что в
пятом столбце, и которые прибавляются
также к третьему. Так как это смещение
образует угол у центра Земли, являю-
щийся удвоенным расстоянием между
двумя светилами, то отношение чисел в
строках [аргумента] к этим избыткам
есть отношение для удвоенного расстоя-
ния между двумя светилами. Если
удвоенное расстояние превышает гра-
дусы [целого] оборота, то он удваи-
вает остаток. Так как его изложение
здесь подобно его изложению для пер-
вого смещения и каждый градус он при-
нимает за два градуса, то принятое ме-
сто удвоенного расстояния будет поме-
щено не против удвоенного расстояния.
Птолемей показал, что если смещение
Луны или центра эпицикла приводит к
известным расстояниям, то оставшееся
расстояние после отбрасывания того,
что остается до полного оборота до апо-
гея, также будет известно и равно пер-
вому [смещению].
330
АЛЬ-ФАР АВИ
Об уравнении параллакса
и подробностях этого
Он сказал: если мы хотим опреде-
лить величины параллакса, мы должны
рассмотреть [прямые] часы между ме-
ридианом и [положением] светила. Это
дуга из параллельных кругов между
ними, которая была определена. Потре-
буем угол этой дуги из таблицы углов
для заданного климата и [двенадцатой
части] Зодиака согласно тому, что при-
ведено в предыдущих книгах.
Мы находим соответствующую дугу
этого угла из [второго] столбца. Это бу-
дет дуга между зенитом и светилом, то
есть дополнение его высоты. Вносим это
в строки аргумента, и если это [светило]
будет [не] Солнце, то мы возьмем то,
что против этого в столбцах, [соответст-
вующих] четырем случаям, каждого в
отдельности. Затем по той же указан-
ной причине мы разделим пополам
[число] градусов по исправленной ано-
малии от истинного апогея; если они
меньше 180, то мы их используем [не-
посредственно], а если больше, то возь-
мем половину избытка трехсот шести-
десяти над этим числом. Если это уже
сделано, то мы возьмем значение, что
против этого, в восьмом и в седьмом
Пятая «нита
331
столбцах; [число] в седьмом для урав-
нения того, что в третьем, берем [от
разности], найденной нами в.четвертом
столбце, прибавляя это к [числу] в тре-
тьем столбце. [Число] в восьмом для
уравнения [того, что] в пятом, берем
[от разности] в [шестом] и прибавляем
это к [числу] в пятом [столбце]. Затем
мы вносим меньшее [число] градусов
из расстояний между двумя светилами
91 или между Луной и / установленной
[точкой], [диаметрально] противопо-
ложной Солнцу, в строки аргумента. Да-
лее мы посмотрим на это расстояние;
если оно меньше 90, то возьмем само
это число или избыток 180 над ним.
Если же оно больше 180 и меньше 270,
то возьмем его избыток над 180. Возь-
мем также то, что против него в девя-
том столбце; находим разность между
параллаксами в третьем и пятом столб-
цах, исправленными теми, что в седь-
мом и восьмом столбцах; умножим ее
на то, что получилось в девятом, и раз-
делим на 60; прибавим полученное к
меньшему из этих исправленных [парал-
лаксов]. То, что получится, и будет
[окончательно] исправленный парал-
лакс по кругу высоты.
Однако при этом Луна [считалась]
находящейся на самой эклиптике и не
332
АЛЬ-ФАРАВИ
имеющей широты; поэтому данные
[здесь] углы вместе с их [прямыми] ча-
сами и дугами соответствуют градусам
эклиптики. Если принять, что Луна [не]
имеет широту, то это только условно,
поскольку мы хотим показать [ее] па-
раллакс как по долготе, так и по широ-
те. Что касается способа его осуществле-
ния, то я покажу его с помощью рисун-
ка, чтобы легко было его представить.
Пусть ABCD — круг горизонта,
AJN — дуга меридиана, точка I — се-
верный зенит [рис. 102], дуга CGE —
половина эклиптики, G — градус Луны
северной эклиптики, М — полюс эклип-
тики. Из точки М проведем дугу до G
и далее до F, которая представляет ис-
тинное место Луны в своей широте. Ду-
Пятая книга
333
га ЕКВ — дуга высоты. Известно, что
она проходит через истинное и видимое
места Луны. Поскольку через центр Лу-
ны проходят линии из центра эклипти-
ки, а также [из] зенита, то их пересе-
чение есть центр Луны. [Центр Луны]
и центр эпицикла примыкают к одной
и той же точке по долготе и широте; по-
этому линия [из] зенита проходит че-
рез оба положения [Луны].
Пусть точка К — ее видимое место;
тогда дуга FK будет ее полным склоне-
нием ; оно южнее, так как F ближе к
зениту, чем К, а К находится к югу.
Проведем из полюса эклиптики к [точ-
ке] К, являющейся ее видимым местом,
дугу МНК, которая пересекает эклип-
тику в Н. Н ближе к востоку, чем G, и
она была бы ее местом в эклиптике, ес-
ли бы Луна действительно находилась
в К. Но это — видимость. Поэтому Н —
видимое место Луны в эклиптике, а
GH — параллакс Луны, по долготе, к
востоку, по направлению последова-
тельности знаков Зодиака, так как К
дальше от горизонта, чем место пересе-
чения, то есть дальше, чем G. Посколь-
ку точка N — место пересечения между
зенитной и эклиптической [линиями],
то НК длиннее FG; поэтому видимая
широта больше [истинной]. Возьмем
334
АЛЬ-ФАРАБИ
HL, равную GF, тогда LK будет разни-
цей между истинной и видимой широ-
тами, которая является параллаксом по
широте. Поскольку дуги МН и MG рав-
92 ны, то MF и ML равны / ; а также FL
в действительности короче GH. Однако
иногда можно считать эти дуги прямы-
ми линиями, так как в этом месте они
маленькие. Если сделать их прямыми
линиями, а углы G и Н — прямые, то
FL условно параллельна и равна GH 158.
Поскольку здесь нет большой по-
грешности, то FL будет приблизительно
равной параллаксу по долготе, то есть
GH. Тогда все три стороны треугольни-
ка FKL являются параллаксами; FK —
полный параллакс, FL — долготный и
KL — широтный. Так как угол FGN
прямой, угол FNG — острый и угол
INC — тупой, который раскрывается в
направлении по последовательности зна-
ков Зодиака, поэтому северный зенит-
ный угол тупой.
Мы можем рассуждать в обратном
порядке и говорить: если северный зе-
нитный угол тупой, то прямой угол и
его смещение восточные. Если Н рас-
положится ближе к N, чем G [рис. 103],
тогда [смещение] западное; К рас-
положится между N та F, поэтому сме-
щение при северном зените будет к се-
Пятая книга
335
веру. Это невозможно, потому что сме-
щение должно быть удалением, а не
приближением.
Представим это на другом рисунке
[рис. 104], где зенит северный, а Луна
имеет юго-западную широту. Определим
смещения, соответствующие этому [по-
ложению]. Представим себе, что полное
[смещение] к югу, как было раньше, а
долготное — к западу. Найдем, что се-
веро-восточный угол острый, поскольку
соответствующий ему после прямого уг-
ла [тоже] острый. Их соседний север-
ный [угол], который в стороне горизон-
та,— тупой, как это было на первом ри-
сунке. Если ты сделаешь зенит, то есть
336
АЛЬ-ФАРАВИ
1, южной точкой, то смещение окажется
северным и все обстоятельство с углами
будет наоборот. Из этого выясняется,
что видимая долгота может быть на сто-
роне истинной долготы, тогда первая
больше второй; или она может быть не
на ее стороне, тогда меньше не достает
ее. Точно так же и относительно широ-
ты. Если эклиптика находится между
зенитом и светилом, то видимая широта
будет на противоположной стороне и
больше истинной широты. Если же эк-
липтика не находится на стороне зени-
та [от светила], то параллакс по широте
может быть вычитаемым.
Пример этого. Пусть ABCD — круг
горизонта, AGK — меридиан, CGE —
Пятая книга
837
эклиптика, СНЕ — наклонный круг,
I — зенит, F — истинное положение Лу-
ны, BEI — круг высоты, I — видимое
положение Луны KFMX и KIL — дуги
из [круга] широты. Ты знаешь, что
F1 — полный параллакс, X — градус
93
[места] светила, XF — его истинная
широта, NI — его широта по видимости,
MF — вычитаемый параллакс по широ-
те, / изображение которого может быть
такое маленькое, что [кажется], что
здесь вообще отсутствует параллакс по
широте. Это бывает тогда, когда и зе-
нит, и Луна находятся на круге эклип-
тики.
Пример этого. [Пусть] ABCD — го-
ризонт [рис. 105], АЕС — меридиан,
Е — зенит, I — истинное место Луны,
32-89
338
АЛЬ-ФАРАБИ
G — ее видимое место, дуга IG — ее пол-
ное смещение, это и есть сам [парал-
лакс] по долготе; она не отходит от
эклиптики и, следовательно, не имеет
видимого, истинного [параллакса] по
широте.
Изображение этого смещения может
быть очень маленькое и [кажется [, что
совсем отсутствует параллакс как по
долготе, так и по широте. Это бывает,
если Луна находится в девяноста [гра-
дусах] от горизонта. Ты знаешь, что она
не всегда находится в девяноста [гра-
дусах] на меридиане; она может быть
смещена. Она бывает на меридиане тог-
да, когда круг через четыре полюса сов-
падает с меридианом.
Птолемей допускал многочисленные
положения; он рассмотрел состояние
Луны, когда она на меридиане, и нашел,
что она не имеет существенного парал-
лакса по долготе. Действительно, дело
обстоит так, как он говорил, если Луна
в упомянутом положении. Приведем
рисунок для случая смещения.
Пусть ABCD — горизонт [рис. 106],
CLE — эклиптика, IL — меридиан, L —
середина неба на [градусах] эклиптики
от начала Козерога и до конца Близне-
цов; дуга между точкой L и точкой
восхода С больше девяноста [граду-
Пятая книга
339
сов]; точка М, то есть полюс круга
эклиптики, находится на стороне запа-
да, F — градус светила, когда оно нахо-
дится [непосредственно] в этой точке
или в К. Пусть I — зенит, BFI — высо-
та, IF или IK — дополнение видимой
высоты. BF разделит дугу СЕ пополам.
FK или КМ — смещение, поскольку
рассуждение для обоих одно и то же.
Если [Луна] опишет [круг] через полю-
са круга ABCD и [полюса] эклиптики,
то эти два круга будут разделены на
квадранты, описанный круг пройдет че-
рез F, совпадет с кругом высоты и при-
ведет к параллаксу по широте на [вели-
чину] дуги KF или КМ. Это одновре-
менно параллакс по высоте и по широте.
Дуга IF называется широтой климата
видимости. В этом положении види-
мость по зениту вертикальна. Таков спо-
соб определения обстоятельства парал-
лакса.
Если полное смещение уже опреде-
лено, а его угол, который оно стягивает,
прямой, то легко рассчитать смещения
[по долготе и по широте], так как эти
линии прямые и образуют прямоуголь-
ник с известными углами и сторонами.
Поэтому если это смещение известно и
угол при одном его конце известен и
оно стягивает прямой [угол], то все уг-
340
АЛЬ-ФАРАБИ
лы и отношения их сторон также [из-
вестны].
Из рисунков ясно, что если зенит се-
верный, то параллакс южный, а если он
94 / южный, то параллакс северный. Если
наклонный круг находится между зени-
том и эклиптикой, то смещение по ши-
роте недостаточно относительно ис-
тинного [положения]; если же эклипти-
ка находится на середине, то смещение
по широте избыточно. Что касается дол-
готы, то если зенитный северо-восточ-
ный угол тупой, то смещение по долго-
те к востоку; если же он острый, то — к
западу. Смещение со стороны юга про-
исходит в направлении, противополож-
ном знакам Зодиака: если со стороны
севера, то наоборот. Если угол прямой,
то смещения по долготе не наблюдается.
Когда Птолемей показал все это, он
отметил, что рассуждения его предше-
ственников о параллаксах по высоте не
точные, а приближенные, но это и то,
что он не принимает во внимание па-
раллакса Солнпа, не мешает в [нахож-
дении! промежутков времени затме-
ний ,89.
Их рассуждения приближенные, а не
точные потому, что вместо дуги высоты
Луны, когда она на круге [горизонта]
Земли, они исйользовали другую ДУ^У,
Пятая книга
341
являющуюся дополнением градусов ее
высоты по долготе, так что Гиппарх
привел следующий рисунок, на котором
различал параллаксы по долготе и по
широте. АВС — эклиптика; AD — [ду-
[Рис. 107].
Е
В С
Ъ
G
[Рис. 108].
га] наклонного круга [рис. 107], А —
узел, а Луна в известной точке D;
DB — дуга известной широты, перпен-
дикулярная к АВС; тогда В — положе-
ние Луны по долготе будет известным, а
DB — ее истинная широта. Пусть Е —
зенит; проведем дугу ЕВ от нее до В и
другую, проходящую через [точку] на-
клонного круга и через Луну; это есть
EDG. Пусть DH будет параллакс по вы-
342
АЛЬ-ФАРАБИ
соте, DF — [параллакс] по широте и
HF, то есть КВ,— [параллакс] по дол-
готе. Если дуга EDG, то есть истинное
расстояние, известна, то дуга DH, то
есть ее смещение, будет известно. Как
было упомянуто выше, известной будет
дуга от зенита до известной точки на
эклиптике, а не на наклонном круге и не
на чем-нибудь другом. Если угол EGC с
эклиптикой известен, то будет достигну-
то определение искомых смещений по
долготе и по широте из определения DH,
если ее можно определить, и определе-
ния угла FHD, равного углу EGC, по-
скольку FH параллельна АС, и из оп-
ределения угла DFH, поскольку он ра-
вен прямому углу DBA. Отсюда отноше-
ния треугольника FH известны. Однако
известны ЕВ, а не GDE, и угол ЕВС, а не
угол EGC. Гиппарх принимает дугу ED
за данную; он делает так, чтобы дуга
EG была данной и угол EDH был извест-
ным и ED была данной; отсюда ED да-
на. Доказательство Птолемея огра-
ничено для одного расстояния, напри-
мер, для расстояния AD. Он сказал: од-
нако мы утверждаем, что если центр
Луны находится на меридиане к северу
или к югу, то смещение по высоте поч-
ти совпадает с меридианом. Тогда, как
тебе уже известно, смещение по высоте и
Пятая книга
343
по широте будет одно и то же, как было
отмечено раньше.
Пример этого. АВС — [дуга] эклип-
тики [рис. 108], а линия DBE перпенди-
кулярна к ней; В — зенит. Пусть Луна
находится в D или в Е; тогда его широ-
та относительно эклиптики будет DB
95 или BE, и / дуги и углы в заданной точ-
ке В будут известными, а искомыми
будут дуги и углы при заданной и изве-
стной точке D или Е. Если мы сделаем
точку D, отличную от точки В, зенитом
и эклиптику перпендикулярной к гори-
зонту, то дуга от G до В совпадет с
градусами Луны, которые идут от В до
D или до Е; на этом рисунке они пред-
ставляют восточное и западное смеще-
ния; это тоже известно. Тогда не будет
параллактического смещения ни по ши-
роте, ни по долготе, ни избыточного, ни
недостаточного. Разность в этом будет
разностью между ЕВ и GD или между
GB и GE-, это и есть параллактическое
смещение; углы между этими линиями
будут только прямыми, и определение
здесь легкое.
Если же зенит находится на эклип-
тике, а Луна вне ее имеет широту, как
на этом рисунке [рис. 109], где зенит,
например, в А и D или Е — положение
светила, В — его градус, тогда дуги
344
АЛЬ-ФАРАБИ
АВ и AD будут отличаться, как и дуги
АВ и АЕ и при D и Е образуются углы,
отличные от углов при В, и AD, я АЕ
будут известными, если они будут за-
[Рис. 109].
менять их хорды, поскольку различие
между ними небольшое. Они будут из-
вестными, потому что АВ и BD или АВ
и BE известны, и угол [В] прямой, от-
сюда AD, то есть истинное расстояние
от зенита, известно. Из этих известных
[величин] определяется его смещение.
Что касается того, если оба зенита и
положение Луны смещены от эклипти-
ки, то это можно определить, если сна-
чала провести дугу южной или северной
ЙМтая Кнйгй
345
высоты, а затем найти параллактиче-
ское смещение.
Пусть ABF— эклиптика [рис. 110],
Е — место Луны на северном наклон-
ном круге, a D — на южном; они изве-
стны ; ЕВ и BD — дуги широты, стоя-
щие под прямыми углами к АВЕ при
В; G — зенит, GEF — дуга высоты, пе-
ресекающаяся с эклиптикой в F, DG —
дуга высоты, пересекающаяся с эклип-
тикой в Н. Мы хотим определить GE и
GD. Проведем дугу высоты GBK. Изве-
стно, что она образует при В известный
угол; опустим перпендикуляры EL и
DK на GB. Поскольку угол GBA изве-
стен, то остаток от прямого угла LBE
известен; точно так же DBK известен;
углы L и К прямые; ЕВ и BD известны.
Поэтому треугольники BEL и BKD из-
вестны, так как их стороны и углы по
отношению к равным между собой
[сторонам] ЕВ и ВА, отсюда оставшаяся
GL известна. L — прямой угол, поэтому
гипотенуза GE известна. Точно так же
96 угол В известен; угол К — прямой, /
BD известна, поэтому ВК и KD извест-
ны; вся GBK и KD известны; К — пря-
мой, поэтому GD известна; также два
угла при G известны, отсюда северо-вос-
точные углы F и Н треугольников GEL
и GKD известны. Поскольку угол F
346
АЛЬ-ФАРАБИ
меньше известного зенитного угла В на
известный угол FGB, то угол Н больше
того же угла В на известный угол DGB.
Мы уже определили GE и GD, отсюда
определяем их смещение по высоте; мы
определили и углы Н и F, образованные
эклиптикой и дугами высоты, и нам не
нужно определять другие углы вместо
них, а достаточно для нас найти углы
треугольника смещений.
Он сказал: таким образом, выясни-
лось, что наибольшая разность в этих
углах, разности между которыми мы
уже определили, имеет место, когда В
является зенитом; тогда при В не об-
разуется тот угол, который был образо-
ван с дугой от зенита, и дуги между
G и D или Е образуют прямые углы при
В, так как [дуги], соединяющие Е с В
W.D с В, находятся на эксцентре и тогда
разность будет прямым углом; это та-
кого же рода разность, как разность
между существованием и исчезнове-
нием.
Точно так же наибольшая разность
между этими дугами в этом случае ни-
когда не дает дугу высоты, если Луна
находится в В. Если же он в Е или D,
то дуга от зенита до Луны приблизи-
тельно равна широте, то есть равна ей с
небольшим параллактическим смещени-
Пятая Книга
34?
ем, получающимся вследствие, этого рас-
стояния от зенита, поскольку оно одно
и то же с обеих сторон, как было опреде-
лено. Если положение эклиптики тако-
во, что круг через зенит перпендикуля-
рен к эклиптике, тогда
дугой AD или АЕ и
дугой АВ будет дугой
смещения по широте;
если же зенит и Луна
находятся на эклип-
тике, как изображено
на этом рисунке [рис.
111], тогда дуга от зе-
нита, то есть AD или
АЕ, больше АВ, но
меньше DB и ЕВ, так
разница между
как сумма двух сто- [рис. щ].
рон [треугольника]
больше третьей и угол В больше,
чем угол D или угол Е на угол А,
так как углы А и Е [вместе] равны
прямому [углу] и поэтому разность
меньше прямого [угла]. Если предпола-
гается смещение зенита и Луны [от эк-
липтики], как было показано на рисун-
ке, где G была зенитом и где требовались
всякие другие вещи, то GB длин-
нее GE, но меньше широты ЕВ, так как
угол FBE прямой и поэтому угол ВЕР
острый, а угол GEB тупой; отсюда GB
548
АЛЬ-ФАР АВИ
длиннее [GE], но меньше ЕВ, так как
сумма двух сторон меньше третьей. Что
касается дуги, то она длиннее GB, так
как GBD больше прямого угла, посколь-
ку он является внешним углом тре-
угольника с прямым углом в К. [Поэто-
му] GD длиннее [GB], но меньше BD.
Что касается углов, то, как было най-
дено, два угла в В больше двух углов —
F и Н на два угла D [и Е соответствен-
но] и каждый из последних меньше
прямого угла.
Птолемей показывает способ вычис-
ления на основе этого правильного мето-
да нахождения параллакса, по которо-
му берет дополнение дуги высоты ис-
тинного градуса, например BG / на этом
рисунке и величину угла ABG, который
равен углу LEB, так как внешний угол
DBG равен [сумме] двух углов — L и
Е, а их сумма составляет два прямых
[угла]; чтобы получить центральный
угол, удваиваем его, находим соот-
ветствующую этому углу дуговую ве-
личину. Таким образом, получается ду-
га. Далее берем хорду этой дуги, это
LB, затем берем хорду — дополнение
этой дуги до полукруга — EL; опреде-
лим отношение одной [хорды] к дру-
гой и к ЕВ, взятой за диаметр, .равный
ста двадцати частям; умножим [каж-
Пятая книга
349
дое из этих чисел] на число гипотенузы
ЕВ, являющейся широтой, то есть на
[число] широты ЕВ, а не на число диа-
метра ЕВ, например, на пять градусов,
а не на сто двадцать; число широты ЕВ
известно. Разделим полученное на сто
двадцать, тогда определится, сколько в
каждой из этих двух дуг таких единиц,
какие в числе широты ЕВ.
Точно так же определим стороны
треугольника BKD, которые равны
[соответствующим] сторонам треуголь-
ника BLE', не тоебуется новых вычис-
лений, так как BE равна BD, BL равна
ВК, две остальные стороны тоже равны.
Если Луна находится в Е, отйими чис-
ло LB от [числа] GB, а если Луна на-
ходится в D, то прибавь. Таким обпазом,
будут известны в первом [случае] луга
GL, во втором — дуга GK, если отнял,
то возьми [сумму] квадратов GL и EL,
[измеряемых] такими единицами, ка-
кие в числе широты ЕВ160; возьми ко-
рень этого [числа] и получится Е. Перед
этим ты должен умножцть GL на [чис-
ло] широты и разделить полученное на
сто двадцать. Итак получается GE. Точ-
но так же, если Луна находится в D, то
умножим число DK на себя, то есть EL
на себя, [измеряемую] частями широты,
й умножим KG на себя, [измеряемую]
350
АЛЬ-ФАРАБИ
теми же частями; найдем корень из их
[суммы] и получим GD.
Из всего этого вытекает, что ты уд-
ваиваешь маленький угол, находишь
его дугу; берешь ее хорду и хорду до-
полняющей [дуги] до ста двадцати [гра-
дусов] и запоминаешь, что получается.
Если зенит и широта [Луны] находят-
ся на одной стороне [от эклиптики], то
отнимешь то, что получается для перво-
го угла, от дуги дополнения высоты гра-
дуса долготы; если же они противопо-
ложные, то прибавляешь. Берешь квад-
рат суммы или разности вместе с квад-
ратом хорды запоминаемого другого
угла и находишь корень из этого, полу-
чается [дуга] дополнения высоты Луны.
Пятая книга окончена, слава Аллаху
и [помощь] от него.
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
«КОММЕНТАРИЕВ К «АЛЬМАГЕСТУ»
АЛЬ-ФАРАБИ
1. В титульном листе рукописи на-
писано: „Комментарии к «[Альмаге-
сту»”. Книга, известная под неарабским
названием Маджисти, [касающаяся]
геометрической и связанной с ней
астрономической науки, являющаяся
одной из величайших книг древности,—
это сочинение Птолемея.
Здесь же книга комментариев Абу
Насра аль-Фараби, ценная по существу,
нужная [ученикам], завершающим
[изучение] геометрии и астрономии.
Аллах более сведущ [в них].
Великая книга — сочинение по ас-
трономии с чертежами и таблицами...
Сочинение „Комментарии к Маджи-
сти” принадлежит выдающемуся учено-
му Абу Насру аль-Фарабй. „Маджисти”
— греческое слово Мачисте. Значение
362
Примечания
его по-арабски — „Великое [постро-
ение] ”, так что название книги по-араб-
ски будет: «Книга великого построения
астрономии геометрическим методом».
2. Автор „Альмагеста” (см. прим. 3)
Клавдий Птолемей (Klaudios Ptolemais),
у 'аль-Фараби Битлимиус, знаменитый
греческий астроном, работал в Алексан-
дрии во П в. н. э.
3. „Альмагест” (аль-Маджисти) —
общепринятая в Европе и на средневеко-
вом Востоке форма названия основного
астрономического сочинения Птолемея
(см. прим. 2) «Математическая система»
(Syntaxis mathematike). Название «Аль-
магест» — один из вариантов названия
Megiste syntaxis («Величайшая систе-
ма»). «Альмагест» — книга, известная в
настоящее время под этим названием,
происходит от средневековой латинской
тианскрипции Almagest арабского аль-
Маджисти. В дальнейшем мы будем
ссылаться на немецкий перевод «Аль-
магеста» [3].
♦Альмагест» является сводом астро-
номических знаний греческих астроно-
мов древности.
Во введении «Альмагеста» о своих
целях при составлении этого сочинения
и последовательности изложения Пто-
лемей пишет: «Так вот и мы пытаемся
Примечания
353
усилить любовь к науке о вечном и
неизменном, преподав то из этой науки,
что уже было передано предшествующи-
ми нам выдающимися исследователями,
со своей стороны внеся добавления, ко-
торые были получены за время, про-
шедшее от них до нашей эпохи. Поэто-
му мы попытаемся все то, что в настоя-
щее время считаем нужным, выпустить
в свет, изложить с возможно большей
краткостью и так, чтобы несколько про-
двинувшиеся в этой науке могли следо-
вать далее. Чтобы это сочинение было
вполне законченным, все нужное для
науки о небе мы изложим в свойствен-
ном ей порядке, а чтобы не делать это
сочинение очень длинным, все то, что
было достаточно разъяснено древними,
мы только приведем, а то, что совсем
не было понято, мы постараемся в ме-
ру наших сил разработать подробнее...
Предлагаемое нами сочинение начи-
нается с рассмотрения общего положе-
ния Земли по отношению ко всему не-
бу; при переходе к последовательному
изложению отдельных частей нам сле-
дует повести речь о положении нового
круга, а также отдельных мест обитае-
мой памп Вселенной, затем о получаю-
щихся для каждого места различий го-
ризонта вследствие наклонностей сферы.
23-8»
354
Примечания
Предварительное рассмотрение всего
этого облегчит нам изучение остального.
На втором месте нам следует рассмо-
треть движение Солнца и Луны и все
соответствующие им явления; без их
предварительного усвоения невозможно
исчерпывающим образом рассмотреть
все, относящееся к светилам. Наконец,
говоря согласно намеченному плану о
светилах, нам, конечно, следует начать
с рассмотрения сферы так называемых
неподвижных звезд, а после этого пе-
рейти к пяти блуждающим звездам или
планетам. Каждый из этих предметов
мы попытаемся разъяснить, пользуясь в
качестве начал и оснований при их ис-
следовании очевидными и не вызываю-
щими сомнений наблюдениями древних
астрономов и нашими собственными, а
затем выводя из них следствия при по-
мощи доказательств на геометрических
чертежах» [3, стр. 4—6].
4. Книга приложений (Китаб ал-Ла-
вохик) — одно из сочинений аль-Фара-
би, посвященное также обработке «Аль-
магеста» Птолемея [6, стр. 160—200].
5. Из этого вытекает, что „Коммента-
рии к «Альмагесту»” написаны аль-Фа-
раби прежде всего как учебно-педагоги-
ческое сочинение, рассчитанное для
учащихся. На самом деле, в древности и
Примечания
355
средние века «Альмагест» входил в чис-
ло основных книг, подлежащих изу-
чению.
6. Словом «книга» мы в соответствии
с установившейся традицией переводим
арабское «макалат», обозначающее со-
ставную часть «Альмагеста». Встречаю-
щееся в дальнейшем слово «китаб», оз-
начающее книгу «Альмагест», мы пе-
реводим как «сочинение».
7. Первая книга «Альмагеста» Пто-
лемея состоит из следующих глав:
Введение
О последовательности изложения.
О том, что небо имеет сферическое
движение.
О том, что Земля в целом имеет вид
сферы.
О том, что Земля находится в сере-
дине неба.
О том, что по сравнению с небом
Земля является точкой.
О том, что Земля не совершает ника-
кого поступательного движения.
О том, что в небе существуют два
различных вида первых движений.
О специальных понятиях.
О величине прямых в круге.
Таблица прямых (хорд) в круге.
О дуге, заключающейся между тро-
пиками,
356
Примечания
Предварительные теоремы для до-
казательств сферики.
О дугах между равноденственным
кругом (небесным экватором) и эклип-
тикой.
Таблица склонений.
О восхождениях на прямой сфере.
8. Положения или принципы, поло-
женные в основу «Альмагеста», следую-
щие: 1) небо имеет сферическую форму
и движется сферически; 2) Земля —
сферична по своей форме; 3) Земля
расположена в центре всего неба;
4) величина Земли по отношению к небу
неощутима; 5) Земля не имеет никако-
го движения; 6) в небе существуют два
различных вида первых движений. Этим
принципам посвящены соответственно
III—VIII главы I книги «Альмагеста»
[3, стр. 6—24].
9. Зенит — точка небесной сферы,
находящаяся прямо над головой на-
блюдателя. Слово «зенит» произошло от
первого слова арабского выражения
«самт ар-ра’с», которое средневековые
латинские переводчики транскрибирова-
ли сначала zemth, а затем из-за описки
переписчика, заменившего m па ni, ста-
ли писать zenith.
Под зенитной параллелью здесь по-
нимается небесный меридиан — фалак
Примечания
357
нисф ан-нахар, дословно «орбита полу-
дня» — большой круг небесной сферы,
проведенный в направлении с севера на
юг и являющийся общим перпендикуля-
ром эклиптики и небесного экватора
(см. примечания 10 и 16). Он проходит
через зенит и южную точку горизонта;
латинское слово meridianus — перевод
слова «полуденный». Большой круг
земной поверхности, проведенный в
том же направлении, т. е. высекаемый
из земной поверхности плоскостью не-
бесного меридиана — земной меридиан,
проходящий через точку, в которой на-
ходится наблюдатель.
Горизонт — круг небесной сферы,
высекаемый из нее плоскостью, перпен-
дикулярной прямой, ооединяющей точ-
ку земной поверхности, в которой нахо-
дится наблюдатель, с центром Земли, и
проходящей через центр Земли (истин-
ный горизонт) или через точку, в кото-
рой находится наблюдатель (видимый
горизонт). На рисунке 112 большой
круг SWNO — истинный горизонт, точ-
ки S, W,N,O — соответственно его юж-
ная, западная, северная и восточная точ-
ки, большой круг ZSZ'N — небесный ме-
ридиан, точка Z — зенит, точка Z'-на-
дир — точка, диаметрально противопо-
ложная зениту (от арабского назир —
358
Примечания
«соответствующий», диаметрально про-
тивоположный). В настоящее время ме-
ридианом называют любой большой
Г
[Рис. 112].
круг небесной сферы, перпендикуляр-
ный к экватору.
10. Небесный экватор — му'аддил
ан-нахар, дословно — «уравнивающий
день»; латинское слово aequator — пе-
ревод слова му'аддил — «уравниваю-
щий».
11. Эклиптика — см. прим. 16.
12. Здесь речь идет о доказательстве
положения геоцентрической системы
Птолемея о неподвижности Земли. Аль-
Фараби в «Перечислении наук», поддер-
живая этот тезис, писал: «Земля в це-
лом не движется ни со своего места, ни
на своем месте» [1, стр. 27].
Примечания
359
В данном случае он имеет в виду
физическое доказательство невозможно-
сти движения Земли, приведенное им в
«Физике». Какова суть этого доказа-
тельства — нам неясно. Но нам извест-
но доказательство аль-Бируни в «Кано-
не Мас'уда» о невозможности вращения
Земли вокруг своей оси, основанное на
физических аргументах. Признавая
как математик правомерность допуще-
ния такого движения Земли, аль-Биру-
ни как физик сильно сомневался в воз-
можности этого, на что в своих иссле-
дованиях указали К. Наллино, П. Г.
Булгаков [5, стр. 271]. В частности, аль-
Бируни пишет: «... Мы же знаем, что
если отделившееся от Земли тело нахо-
дится в зенитном положении, то при
наличии какого-то движения вместе с
Землей, когда она подвергнется воздей-
ствию добавочной силы, [т. е. силы, дви-
гающей в ту или иную сторону тело],
последняя заставит его отклониться от
воображаемого покоя [в зените], и в
процессе этого выявятся разные влия-
ния этой силы, обусловленные различ-
ными ее направлениями. А именно: си-
ла, заставляющая [тело двигаться] в
сторону востока, сложится с естествен-
ным [предполагаемым] восточным дви-
жением Земли], а сила, заставляю-
360
Примечания
щая [тело двигаться] в сторону за-
пада, будет противиться движению
[Земли], сталкиваться с ним. При
этом были бы различны и прыжки
прыгуна, и полеты стрел, пущенных в
этих направлениях, и полеты птиц. Все
это так же различалось бы и [при дви-
жении тел] в направлении на север и
на юг вследствие расширения [диамет-
ров параллелей Земли] в одном из этих
направлений и сужения в другом. Но
ничего этого в действительности нет, и,
следовательно, нет у Земли, [находя-
щейся] на своем месте, вращательного
движения вокруг ее центра» [10,
стр. 85].
Мы предполагаем наличие преемст-
венной взаимосвязи между упомянутым
физическим доказательством аль-Фара-
би и этим доказательством аль-Бируни.
13. Первое, западное движение не-
бесной сферы — суточное, оно происхо-
дит за счет вращения Земли вокруг ее
оси.
14. Это восточное движение Солнца,
Луны и планет, направленное навстре-
чу суточному движению. Оно происхо-
дит за счет обращения планет вокруг
Солнца.
К планетам аль-Фараби, вслед за
греками, относит Солнце (Афтаб и
Примечания
361
Шаме), Луну (Камар), Меркурий (Ута-
рид), Венеру (Зухра), Марс (Маррих),
Юпитер (Муштари) и Сатурн (Зу-
хад).
Солнце и Луну аль-Фараби иногда
называет общим словом «наййиран» —
«два (главных) светила». Наши назва-
ния пяти последних планет — имена
римских богов, соответствующих богам,
именами которых являются греческие
названия планет. Греческие названия
были введены в V веке до н. э. под
влиянием вавилонских астрономов, дав-
ших планетам имена вавилонских богов
(Набу, Иштар, Шамаш, Мардук, Нер-
гал).
15. Основным видимым движением
небесных светил аль-Фараби считает и
«движение неподвижных звезд», проис-
ходящее за счет прецессии (предваре-
ния равноденствия), т. е. движения зем-
ной оси в пространстве, при котором она
описывает конус с периодом 26 000 лет.
При прецессии долготы неподвижных
звезд изменяются на 50' 26" за год.
16. Наклонный пояс (круг) или круг
знаков Зодиака, так называемая эклип-
тика (фалак ал-бурудж), является боль-
шой окружностью на видимой небесной
сфере, по которой совершается видимое
движение Солнца; вдоль этой же линии.
362
Примечания
но с некоторыми отклонениями от нее
движутся Луна и планеты. Эклиптика
разделена на 12 равных участков, каж-
дый из которых Солнце проходит за ме-
сяц. Эти участки, называемые знаками
Зодиака (бурудж), соответствуют одно-
именным созвездиям Зодиака: Овен
(Хамал — «ягненок»), Телец (Саур —
«бык»), Близнецы (Джуза), Рак (Сара-
тан), Лев (Асад), Дева (Сунбула — «ко-
лос»), Весы (Мизан), Скорпион (Акраб),
Стрелец (Каус — «лук»), Козерог (Джа-
ди — «козленок»), Водолей (Далв —
«ведро»), Рыбы — (Хут — «рыба»).
Арабские названия созвездий Зодиа-
ка — частью переводы греческих, ча-
стью — древневавилонских названий.
Современные названия этих созвез-
дий — переводы с греческого, за исклю-
чением Весов, являющихся переводом с
арабского.
17. Четыре воображаемые точки эк-
липтики — это две точки пересечения
небесного экватора с эклиптикой, кото-
рые называются точками равноденствия
(весеннего или осеннего), и две точ-
ки эклиптики, в которых Солнце нахо-
дится в моменты солнцестояний, поэто-
му их называют точками солнцестояний
(летнего и зимнего); они лежат на пол-
пути между точками равноденствия. На
Примечания
363
рисунке 113 А, С — соответственно точ-
ки весеннего и осеннего равноденствия,
а В и D — точки летнего и зимнего
солнцестояний.
18. Аль-Фараби, следуя за Птолеме-
ем, в этом положении приводит сведе-
ние из тригонометрии хорд греков. Как
известно, в «Альмагесте» Птолемей за-
имствовал у вавилонян деление круга
на 360 градусов и шестидесятичные
дроби. Роль наших синусов у него игра-
ли хорды (см. прим. 44). Птолемей при-
нимает радиус круга за 60 частей
(диаметр соответственно за 120).
19. Отношение длины окружности к
диаметру или «отношение частей диаме-
тра к частям окружности», называемое
в настоящее время «числом л», являет-
364
Примечаний
ся иррациональным отношением. Истин*
ная природа этого числа ко времени
аль-Фараби была еще не выясненной;
по-видимому, именно поэтому он не счи-
тает уместным затрагивать этот вопрос
в своих „Комментариях к «Альмаге-
сту»”.
Весьма возможно, что к нему он воз-
вратился в других сочинениях; впрочем,
именно аль-Фараби одним из первых на
Востоке теоретически обосновал идею
расширения понятия числа, фактиче-
ски рассматривая любое отношение гео-
метрических величин как число (рацио-
нальное и иррациональное).
Развивая идею аль-Фараби и других
математиков, аль-Бируни в «Каноне
Мас'уда» специально рассматривает
приближенное значение числа л и вы-
сказывает принципиально новое сообра-
жение по поводу иррациональности это-
го числа: «У окружйости круга к его
диаметру имеется некое отношение, по-
этому у числа окружности к числу диа-
метра также есть отношение, хотя оно
и иррациональное» [10, стр. 271].
Таким образом, если «число диаме-
тра» — натуральное число (по аль-Биру-
ни равно 2), то «число окружности» —
число в новом обобщенном смысле, т. е.
Примечания
366
то, что мы называем положительным
иррациональным числом.
20. То есть вб=Я.
21. Евклид, у аль-Фараби Уклидис,
знаменитый александрийский матема-
тик, жил в IV—III вв. до н. э. «Книга
Евклида», называемая аль-Фараби,—
это основное произведение Евклида.
«Начала» — свод почти всей древнегре-
ческой математики представляет собой
обработку сочинений греческих матема-
тиков IV в. до н. э. Гиппократа Хиос-
ского (I—IV и XI книги), Архита Та-
рентского (VII—IX книги), Евдокса
Книдского (V, VI и XII книги) и Теэтета
Афинского (X и Х1П -книги).
Равенство a^=R доказано Евклидом
в 15 предложении IV книги «Начал»
[12, стр. 140].
22. Здесь доказывается, что квадрат
а4 равен удвоенному квадрату радиуса,
т. е. сц—ИУ2.
23. Здесь доказывается, что квадрат
аэ равен утроенному квадрату радиуса,
т. е. а3=2?УЗ.
24. Следует отметить, что здесь и
везде в дальнейшем аль-Фараби систе-
матически применяет к геометрическим
величинам арифметические термины
«рычитание», «умножение», «деление»,
366
Примечания
«извлечение корня». Такое словоупот-
ребление было новшеством, введенным
математиками IX в. Греческие матема-
тики, например, вместо произведения
отрезков всегда говорили о «прямо-
угольнике, построенном на этих отрез-
ках». Многие математики средневеково-
го Востока употребляли в этом смысле
выражение «плоскость из А на В».
Аль-Фараби в своих трудах, творче-
ски развивая это перспективное для
физико-математических наук начина-
ние багдадских ученых, открыто отож-
дествляет числа и геометрические ве-
личины. Оно сыграло большую роль в
расширении понятия числа до положи-
тельного действительного числа [2,
стр. 157—169].
25. Это 6 предложение II книги «На-
чал» [12, т. 1, стр. 67], которое перево-
дится на алгебраическое тождество:
(a + b)b+
26. Прямолинейный отрезок называ-
ется разделенным в крайнем и среднем
отношении, если он относится к больше-
му из отрезков, на которые он разделен,
как больший к меньшему. Это построе-
ние проводится Евклидом в 11 предло-
Примечания
367
жении II книги «Начал» [12, стр. 75].
Это сечение часто называют «золотым
сечением». Меньшая часть DG, равная
а ю, является решением задачи о деле-
нии в среднем и крайнем отношении,
т. е. решением уравнения
Д + х = _д
X X *
равносильного квадратному уравнению
x2+Rx—R2=0, решение которого есть
x=4(V5-1).
27. Это знаменитая теорема Птоле-
мея, которая в современном обозначе-
нии пишется так:
ACBD=ADBC+ABDC.
28. Здесь показывается, как опреде-
лить хорду разности двух данных дуг.
Птолемей доказывает это несколько
иначе. Он пишет: «Изложив это, возь-
мем полукруг ABCD на диаметре АС,
из точки А проведем две прямые — АВ,
АС и пусть величина каждой из них
будет дана в частях, каких в заданном
диаметре содержится 120; затем прове-
дем соединяющую ВС; я утверждаю,
что последняя тоже будет данной.
Действительно, проведем соединяю’
368
Примечания
щие ВС и DC, тогда, очевидно, и они бу-
дут данными, вследствие того, что каж-
дая из них дополняет до полуокружно-
сти. Теперь поскольку в круге имеется
четырехугольник ABCD, то, следова-
тельно, произведение АВ-CD вместе с
произведением ADBC равно произве-
дению АС • BD.
AB CD+AD BC=AC BD.
Но произведение ЛС-BD дано; также
дано и произведение АВ-CD; следова-
тельно, будет данным и произведение
AD-ВС; но AD — диаметр, поэтому бу-
дет данной и прямая ВС.
Таким образом, нам стало ясно, что
если даны две дуги и стягивающие их
прямые, то будет данной и прямая, стя-
гивающая дугу, равную разности двух
заданных дуг. Известно, что при помо-
щи этой теоремы мы сможем записать
выражения для немалого числа других
прямых при помощи разностей задан-
ных основных дуг; таким образом, имея
величины прямых, стягивающих 60 и
72 градуса, мы найдем прямую, стяги-
вающую дугу в 12 градусов» [3, стр. 29].
Это доказанное правило равносиль-
но нашей формуле: sin(a—P)=sina-
• posp—sinp cosa (см, прим. 44).
Примечания
369
29. Здесь показывается, как опреде-
лить хорду половины данной дуги. До-
казанное правило равносильно нашей
формуле: 2sin2-2~ =1—сова.
30. Здесь объясняется, как найти хор-
ду суммы двух данных дуг. Доказанное
правило равносильно нашей формуле
sin(a+P)=sina cosp+sinp cosa.
30а. Имеется в виду невозможность
трисекции угла (деление угла на три
равные части) с помощью циркуля и
линейки.
31. Доказываемое здесь неравенство
sin a . a
равносильно неравенству < у «ес-
ли а>р.
32. В конце доказательства исполь-
зуются вышедшие в настоящее время из
употребления обозначения действий над
пропорциями. Современная запись бу-
дет выглядеть так:
l GDE GE
LADE '> АЕ-
После этого применяется операция
присоединения:
L GDE+ L ADE _ L GDA GE+EA _ GA
lADE lADE> АЕ АЕ’
24-89
370
Примечания
г, lCDA . С А
Затем к неравенству , > -т-ег,
J LADE АЕ’
полученному с предыдущего с помощью
действия удвоения, применяется опера-
ция выделения:
L CD A— L ADE = L CDE ’ СА—АЕ ^СЕ,
LADE LADE АЕ АЕ
33. Здесь воспроизведено приближен-
ное вычисление Птолемея хорды 1°, ко-
торая оказывается больше и меньше
]р2'50", откуда делается вывод о том,
что хорда 1° равна 1р2'50//.
В «Альмагесте» все вычисления, а
также результаты записываются в ше-
стидесятеричных вавилонских дробях.
Например, chdl°« 1р2'50"= 1 4- — +
.60
“Г 602‘
Деление градусов, применявшееся
астрономами и математиками средневе-
кового Востока: минута — дакика, бук-
вально «уменьшенная», так же, как и
латинская minuta — 60-я доля градуса
или часа, секунда — санийа — «вторая»
(первоначально «вторая уменьшенная»),
так же, как латинское secunda — 60-я
доля минуты, терция — салиса — «тре-
тья», так же, как латинское tertia —
60-я доля секунды, кварта — раби'а —
Примечания
371
«четвертая», так же, как латинское
quarta — 60-я доля терции.
Шестидесятеричные дроби широко
применялись средневековыми астроно-
мами стран ислама и Западной Европы,
называвшими арифметику этих дробей
«исчислением астрономов».
34. Таблица хорд Птолемея приведе-
на нами в приложениях (таблица 1) к
этой работе.
В первом столбце указана дуга, во
втором — значение хорды, соответст-
вующей этой дуге. В третьем столбце —
«пропорциональные минуты», разность
между величинами хорды для данного и
предыдущего значения, умноженная на
1/30. Если считать, что между двумя
соседними значениями дуги функция за-
висимости хорды от дуги является ли-
нейной, то «пропорциональные минуты»
равны приращению хорды за 1'.
35. «Наибольшим склонением» аль-
Фараби считает угол, равный макси-
мальному склонению точки эклиптики,
которое достигается в точках солнце-
стояния. Склонение 6 точки отсчитыва-
ется от небесного экватора по большому
кругу, проходящему через эту точку и
полюсы мира. Наклон эклиптики е по-
лучается как полуразность полуденных
372
Примечания
высот Солнца во времена летнего и зим-
него солнцестояния.
36. Градусы Зодиака — дараджат
ал-бурудж, буквально — «ступень» —
окружности, в данном случае
эк-
липтики, латинское слово градус — пе-
ревод этого слова. Эклиптика делится
на 12 «знаков Зодиака» или «зодиакаль-
ных созвездий», каждое из которых со-
держит 30 градусов. Слово бурудж —
множественное число от бурдж — «за-
мок».
37. Здесь описываемый инстру-
мент — кольцо на шесте, с помощью
которого Птолемей измеряет разности
высот солнцестояний, необходимые для
определения наклонения эклиптики.
Это градуированный круг на подставке,
внутри которого вращается малый круг
с указателем так, что при помощи тени
и указателя можно снимать отсчеты по-
луденной высоты Солнца. . Кольцо —
составная часть большинства угломер-
ных инструментов. От латинского назва-
ния кольца armilla происходит назва-
ние древнейшего угломерного инстру-
мента — армиллярной сферы. Кольца
или их части, называемые лимбами, яв-
ляются важнейшими составными частя-
Примечания
373
г-гшлгь
ми астролябий, квадрантов и секстан*
тов.
38. Астролябия — устурлаб — угло*
мерный инструмент для наблюдения за
светилами.
39. Описанный инструмент — гра*
дуированный стенной квадрант, уста*
новленный в плоскости небесного мери-
диана. Центром его является шест, ук-
репленный в его верхнем южном углу.
40. Эратосфен Киренский (275—
135 г. до н. э.) — александрийский уче-
ный-энциклопедист, впервые измерив-
ший радиус земного шара и поло-
живший начало математической геогра-
фии и хронологии.
41. Гиппарх, у аль-Фараби Ибарх'ус
— величайший астроном древности. Ро-
дился около 190 г. до н. э. в Никее в
Битинии, большинство своих наблюде-
ний проводил на острове Родосе.
Автор первого звездного каталога
(1028 звезд); при сравнении с наблюде-
ниями звезд, сделанными за 150 лет до
него александрийскими астрономами,
установил, что долготы звезд не остают-
ся постоянными; таким образом, была
открыта прецессия. Гиппарх также оп*
ределил элементы солнечной орбиты (на
основании данных наблюдений вави*
лонских астрономов) и ввел в астроно-
374
Примечаний
мию эксцентрический круг. Работы Гип-
парха до нас почти не дошли, но
«Альмагест» Птолемея в основном пред-
ставляет собой обработку его астроно-
мических сочинений.
42. Это знаменитая теорема Менелая
о трансверсалях или теорема о полном
[Рис. 114].
четырехстороннике. Плоский полный
четырехсторонник можно получить из
произвольного четырехугольника про-
должением каждой пары его противо-
положных сторон до пересечения
[рис. 114]. Восточные математики, в том
числе аль-Фараби, называют ее предло-
жением о «фигуре секущих» (шакл ал-
кита'). Плоская теорема Менелая в сов-
ременных обозначениях имеет вид:
АЕ CD GB 1 АЕ CG DB
СА * DG * = 1 И СЕ ‘ DG ' АВ
Примечания
an
Математики Ближнего и Среднего Вос-
тока формулировали эти соотношения с
помощью составных отношений:
АС _ СР СВ СЕ CG DB
АЕ ~ DG BE И АЕ — PG АВ’
Менелай — геометр и астроном I в.
н. э., работавший в Риме около 100 г.
н. э. До нас дошла в арабском переводе
«Сферика» Менелая, в которой установ-
лена указанная теорема о трансверса-
лях, являющаяся основой всей тригоно-
метрии Птолемея.
43. Приведенное здесь доказательст-
во плоской теоремы о секущих у аль-
Фараби по существу совпадает с доказа-
тельством, приведенным Птолемеем.
Составное отношение впервые встре-
чается у Евклида, который применил
его в 23 предложении VI книги «Начал»,
утверждающем что «равноугольные па-
раллелограммы имеют друг к другу со-
ставное отношение их сторон» [12,
стр. 203].
Составное отношение по современной
терминологии представляет собой про-
изведение двух отношений: там, где
мы сказали бы, что отношение -g явля-
С Е
ется произведением отношении -р- и ^г>
578
Примечаний
греческие и средневековые математики
А
говорили, что отношение «составлен
Л
„ С Е
но» из отношении -уг- и -=г.
U Jf
44. Аль-Фараби несколько совершен-
ствует тригонометрический аппарат Пто-
лемея для облегчения понимания труд-
ных математических выкладок, имею-
щихся в этом труде. Прежде всего он
заменяет хорды синусами: «Синус есть
половина хорды удвоенной дуги». Слово
джиб-синус является арабской транс-
крипцией индийского слова jiva — «те-
тива, хорда», сокращением выражения
ard-jiva — «полухорда». Наш термин
«синус» происходит от латинского сло-
ва sinus — «впадина, пазуха», являю-
щегося буквальным переводом арабско-
го слова джайб; был введен средневеко-
Примечаний
37?
выми латинскими переводчиками
арабских астрономических трактатов.
Если BD — хорда дуги BD=2а
[рис. 115], то ВС — линия синуса дуги
АВ=а, т. е. sina=-|-chd2a. Это одно из
первых известных нам введений синуса
при комментировании Птолемея. Далее
при изложении «Альмагеста» аль-Фара-
би всюду заменяет хорду дуги 2a сину-
сом дуги а, в частности, он переформу-
лирует упомянутую выше теорему Мене-
лая о секущих, которая служила у Пто-
лемея основным средством для решения
сферических треугольников-Хотя такая
замена сама по себе кажется не столь
существенной, однако переход от хорды
к полухорде благоприятствовал широко-
му введению в астрономии различных
функций, связанных со сторонами и
углами прямоугольного треугольника.
В «Книге приложений» аль-Фараби
одним из первых все основные тригоно-
метрические линии рассматривает еди-
нообразно в тригонометрическом круге
[1, стр. 73—74].
45. Эта лемма равносильна плоской
теореме синусов для произвольного тре-
угольника, вписанного в круг. Аль-Фа-
раби одним из первых доказывает ее
для прямоугольного треугольника. Пер-
№
Примечаний
вое общее доказательство этой теоремы
принадлежит Ибн Ираку, учителю аль-
Бируни.
46. Здесь аль-Фараби, следуя Мене-
лаю и Птолемею, приводит доказатель-
ства предпосылки об определении двух
дуг по их сумме или разности и отноше-
нию полухорд этих удвоенных дуг. В
последнем случае, т. е. при доказатель-
стве предпосылки об определении дуг по
их разности, аль-Фараби приводит слу-
чай, когда хорда разности двух дуг па-
раллельна диаметру, который отсутству-
ет у Менелая и Птолемея. Это необходи-
мо для доказательства сферической
теоремы Менелая, когда диаметр сферы
параллелен одной из хорд сторон фигу-
ры секущих, лежащих в плоскости диа-
метра.
47. Эта сферическая теорема Мене-
лая для «фигуры секущих», полученная
на сфере аналогично плоской «фигуре
секущих» [рис. 116]:
sin СЕ sin CG sin DB
sin EA sin GD sin BA
48. Единичное отношение (нисба ва-
хида) — отношение двух равных вели-
А
чин, то есть -г-.
А
49. Сферическую теорему о секущих
Примечания
аль-Фараби доказывает как Менелай,
рассматривая три случая, а не как Пто-
лемей, который ограничился только од-
ним случаем.
Заметим, что при доказательстве
этой теоремы аль-Фараби добавляет так-
же к тексту две предпосылки для разъ-
яснения сущности действия составления
отношений.
50. Склонение (майл) — одна из эк-
ваториальных координат точки на не-
бесной сфере, отсчитываемое по большо-
му кругу, проходящему через полюсы
мира. Здесь под склонением имеется в
виду угол между эклиптикой и небес-
ным экватором, равный максимальному
склонению точек эклиптики. В настоя-
щее время этот угол называется накло-
нением экватора к эклиптике и обозна-
чается буквой Е, а термин «склонение»
применяется ко всем точкам небесной
сферы, а не только к точкам эклип-
тики.
51. Круг, проходящий через четыре
полюса, большой круг небесной сферы,
являющийся общим перпендикуляром
небесного экватора и эклиптики. Этот
круг проходит через точки солнцестоя-
ния, вследствие чего его называют ко-
люром солнцестояния.
52. Из теоремы Менелая
880
Примечайий
sin GA sin GF . sin EH
sin BA sin FH sin EB ’
когда GF=AG=EB=90°, получится
соотношение •:
sin FH sin. EH
sin BA sin 90° ’ ' '
являющееся частным случаем теоремы
синусов для прямоугольного треуголь-
ника. Птолемей не дает непосредствен-
ного доказательства, которое приведено
аль-Фараби в конце „Комментариев к
«Альмагесту»” и в «Книге приложе-
ний» (26 глава).
Учитывая, что наклон эклиптики
АВ — е, эклиптическая долгота ЕН—к
и склонение градуса эклиптики HF—б,
из соотношения (1) получим формулу:
sin6=sinX-sine.
53. Аль-Фараби, по-видимому, обоб-
щая операции, примененные Птолемеем
над составными отношениями, каждое
отношение тригонометрических линий
рассматривает как число. Он считает,
что каждое из трех отношений, участ-
вующих в составном отношении, имеет
определенное числовое значение, и пред-
лагает произвести арифметические дей-
ствия над этими числами.
Примечания
381
Первые шаги в этом направлении
были сделаны еще в позднеэллинскую
эпоху одним из комментаторов Евклида
(по-видимому, Теоном), добавившим к
«Началам» и так называемое пятое оп-
ределение VI книги — определение «со-
ставного отношения»: «Говорится, что
отношение составляется из отношений,
когда количества этих отношений, пере-
множаемые между собой, образуют не-
что» [12, стр. 174].
Смысл этого определения стал поня-
тен математикам только после работ
аль-Фараби и особенно аль-Бируни.
В «Науке звезд», определяя состав-
ное отношение, в частности, он пишет:
«Иногда вместо составления говорят о
перемножении ».
Во II главе V книги «Канона
Мас’уда», рассматривая составные от-
ношения, выражающие эту же теорему
Менелая, аль-Бируни писал об одном из
отношений, входящих в эту теорему:
«Если разделить синус FC на синус СВ,
получится то, что относится к единице,
как синус FC к синусу СВ» [10, стр 477],
и, вводя аналогичные величины для
двух других из этих отношений, гово-
рил, что «одна из этих величин являет-
ся произведением двух других». Эти ве-
личины, по существу, совпадают с «ко-
382
Примечания
личествами отношений», о которых идет
речь в упомянутом определении состав-
ного отношения в «Началах» Евклида и
«числом отношения» аль-Фараби.
Теория составных отношений и при-
вела впоследствии Омара Хайяма
(1048—1131) к явному расширению по-
нятия числа до положительного дейст-
вительного числа. Он обобщает способ
определения числовой величины отно-
шения тригонометрических линий на от-
ношение любых однородных непрерыв-
ных величин.
54. Чтобы показать различия стилей
изложений Птолемея и аль-Фараби, при-
водим это место из «Альмагеста», так
как это характерно для всех доказа-
тельств предложений «Альмагеста»: «О
дугах, заключенных между равноденст-
венными и наклонными крупами: до-
казав изложенную выше теорему, сна-
чала вычислим упомянутые дуги таким
образом. Пусть ABCD — большой круг,
проведенный через полюсы кругов —
равноденственного, [т. е. небесного эк-
ватора], через середины зодиакальных
созвездий, [т. е. эклиптики], АЕС — по-
луокружность равноденственного круга,
a BED — половина круга, проходящего
через середины зодиакальных созвез-
дий; пусть точка Е представляет их
Примечания
383
пересечение, соответствующее весенне-
му равноденствию, так что В будет точ-
кой зимнего, a D — летнего солнцеворо-
тов. На окружности АВС возьмем
полюс равноденственного круга АЕС, до-
пустим, что он будет в точке G. На кру-
ге, проходящем через середины зодиа-
кальных созвездий, возьмем дугу ЕН,
равную 30 таким частям, каких во всем
круге 360; через точки GnH прове-
дем дугу GHF большого круга и поста-
вим задачу определить величину НЕ.
При этом здесь и вообще во всех подоб-
ных вычислениях во избежание повто-
рений будем в каждом отдельном слу-
чае предполагать, что говорится о чис-
ленной величине дуг или прямых,
выраженных в градусах, или частях;
относительно дуг будет говориться о та-
ких частях, которых в окружности боль-
шого круга содержится 360, а относи-
тельно прямых — о частях, каких в диа-
метре круга 120.
Так как на чертеже в две дуги AG
и АЕ больших кругов вписаны две дру-
гие — GF и ЕВ, пересекающие друг
друга в точке Н, то отношение прямой
под удвоенной дугой GA и прямой АВ
складывается из отношения прямой под
удвоенной FG к прямой под удвоенной
FH и отношения прямой под удвоенной
384
Примечания
НЕ к прямой под удвоенной ЕВ. Но
удвоенная дуга GA равна 180 градусам,
а стоящая под ней прямая — 120 час-
тям, удвоенная же дуга АВ в соответ-
ствии с принятым нами отношением 83
к 11 равна 47; 42,40 градусам, а стоя-
щая под ней прямая — 48; 31,55 час-
тям. И далее удвоенная дуга НЕ равна
60 градусам, а стоящая под ней пря-
мая — 60 частям, удвоенная же дуга
ЕВ равна 180 градусам, а прямая под
ней — 120 частям; следовательно, если
из отношения 120 к 48,31,55 мы выде-
лим отношение 60 к 120, то останется
отношение прямой под удвоенной дугой
GF к прямой под удвоенной ЕН, а
именно — 120 к 24,15,57. Удвоенная
дуга GF равна 180 градусам, а стоящая
под ней прямая — 120 частям; следо-
вательно, прямая под удвоенной дугой
ЕН равна 24; 15,57 таким же частям;
таким образом, удвоенная дуга ЕН рав-
на 23; 19,59 градусам и сама ЕН —
приблизительно 11; 40 таким же граду-
сам.
Теперь предположим, что дуга ЕН
равна 60 градусам, а все остальное ос-
тается таким же; тогда удвоенная дуга
ЕН становится равной 120 градусам, а
прямая под ней — 103; 55,23 частям.
Следовательно, если мы опять из отно-
Примечания
385
шения 120 к 48; 31,55 выделим отноше-
ние 103; 55,23 к 120, то останется отно-
шение прямой под удвоенной GF к пря-
мой под удвоенной FH, то есть отноше-
ние 120 к 42; 1,48. Но прямая под
удвоенной FH составляет 120 частей;
тогда прямая под удвоенной FH будет
равна 42; 1,48 частям, следовательно,
удвоенная дуга FH равна 41; 0,18 граду-
сам, FH равна 20; 30,9 таким же граду-
сам, что и требовалось показать [3,
стр. 51—53].
55. Таблица склонения Птолемея
приведена нами в приложениях (таб-
лица 2).
56. Прямая сфера (по латыни
sphaera recta) — положение небесной
сферы на земном экваторе. В этом слу-
чае оба полюса неба (точки Р и Р') на-
ходятся на горизонте, а небесный эква-
тор проходит через зенит и надир (Z и
Z]). Термин «прямая сфера» объясняет-
ся тем, что в этом случае все суточные
параллели перпендикулярны к гори-
зонту.
56а. Восхождение градуса эклипти-
ки — градус («Заман») небесного эква-
тора, восходящий вместе с этим граду-
сом эклиптики. Сокращением выраже-
ния «восхождение в прямой сфере»
(т. е. на земном экваторе) является сов-
25-89
386
Примечания
ременный термин «прямое восхожде-
ние», означающее одну из экваториаль-
ных координат, отсчитываемых по не-
бесному экваториальному кругу от
точки весеннего равноденствия.
57. Наклонная сфера (по латыни
sphaera oblique) — положение небесной
сферы, наблюдаемое на промежуточной
широте (между экватором и полюсом).
В этом случае полюс неба Р находится
на высоте <р, равной широте местности.
Термин «наклонная сфера» объясняется
тем, что в этом случае все суточные
параллели наклонены к горизонту. На
земном полюсе неба Р совпадает с зе-
нитом Z и все неподвижные звезды
движутся по кругам, параллельным
горизонту, поэтому в этом случае не-
бесная сфера называется «параллель-
ной сферой» (sphaera parallela).
58. Здесь рассуждения аль-Фараби
более обширны, чем у Птолемея, кото-
рый ограничился весьма сжатым объяс-
нением цели трактуемой темы. Для
сравнения приводим его: «После этого
следует определить числовые величины
дуг равноденственного круга, получаю-
щихся в пересечении его с кругами,
проведенными через его полюсы и за-
данные конечные точки отрезков на ко-
сом кругу; таким образом, мы будем
Примечания
387
иметь выраженные в равноденственных
часах времена прохождения через ме-
ридиан отдельных частей круга, прохо-
дящего через середины зодиакальных
созвездий, одинаковые для всех местно-
стей, а также через горизонт на прямой
сфере вследствие того, что только в этом
случае он проходит чепез полюсы равно-
денственного круга» [3, стр. 53]. Как
видно, Птолемей в отличие от аль-Фара-
би в этой главе совершенно не затраги-
вает случая наклонной сферы.
59. Из-за трудночитаемости рукопи-
си перевод последнего абзаца следует
считать приблизительным.
60. В этом предложении приведен ме-
тод определения прямых восхождений
точек эклиптики, для чего из теоремы
Менелая
sin GB sin GH sin EF
sin BA sin'/ZF sinEA ’
когда GH=90°—FH, GB=^°—AB и
EA = 90°, получается соотношение
tgFH __ ein EF
tg AB ~~ sin 90е’
оно является теоремой тангенсов для
прямоугольного сферического треуголь-
388
Примечания
ника. Птолемей не дает его непосредст-
венного доказательства, которое одним
из первых дал аль-Фараби в «Книге при-
ложений» (26 глава). Учитывая, что на-
клон эклиптики АВ—е, склонение гра-
дуса эклиптики FH—6 и прямое восхож-
дение точки эклиптики ЕН — а, из
соотношения (2) получим формулу:
61. Приводим эту таблицу из «Аль-
магеста». «Таким же образом, следуя
указанному методу для каждого деся-
тиградусного отрезка косого круга, мы
вычислим имеющее с ним одинаковое
время прохождения дуги равноденствен-
ного круга; мы"сделали это по той при-
чине, что для дуг с меньшим числом
градусов мы не будем иметь существен-
ных отличий от равномерного возраста-
ния разностей. Мы укажем и эти дуги,
чтобы иметь под рукой времена, в ка-
кие каждая из них проходит через ме-
ридиан, как мы сказали, для всех мест-
ностей и через горизонт на прямой сфе-
ре, взяв начало десятиградусных отрез-
ков в точке весеннего равноденствия.
Итак, первый отрезок 9; 10 времен-
ных градусов, второй 9; 15, третий 9;25,
Примечания
389
таким образом, для первой двенадцатой
части получается вместе 27; 50 времен-
ных градусов. Четвертый отрезок содер-
жит 9; 40, пятый 9; 58, шестой 10; 16
временных градусов; таким образом,
вторая двенадцатая часть имеет 29; 54
временных градусов. Седьмой отрезок
содержит 10; 34 временных градусов,
восьмой 10; 47, девятый 10; 55, так что
опять у третьей двенадцатой части при
точках солнцеворота получается 32; 16
временных градусов, а для всего ква-
дранта — соответственно девяносто.
Сразу же становится ясным, что для
остальных квадрантов весь порядок
оказывается таким же, ибо для каждо-
го из них все происходит одинаково, по-
скольку мы предполагаем сферу пря-
мой, то есть равноденственный круг, не
имеющий никакого наклона к горизон-
ту» [3, стр. 57].
62. Вторая книга «Альмагеста» Пто-
лемея состоит из следующих глав:
О положении обитаемой нами Земли
вообще.
О том, как по заданной величине
наибольшего дня определяются дуги го-
ризонта, отсекаемые равноденственным
и косым кругом.
О том, как при тех же предположе-
ниях определяется высота полюса.
390
Примечания
О том, как вычисляется, где, когда и
сколько раз Солнце бывает прямо над
головой.
О том, как на основании изложенно-
го определяются отношения гномонов к
полуденным теням во времена равно-
денствий и солнцеворотов.
Перечень характерных особенностей
для отдельных параллелей.
Об одновременных выхождениях на
наклонной сфере частей кругов —
проходящего через середины зодиа-
кальных созвездий и равноденствен-
ного.
Таблица восхождений по дугам в
десять градусов.
О частных вопросах, связанных с
восходами.
Об углах, образуемых проходящим
через середины зодиакальных созвездий
и полученным кругами.
Об углах, образуемых тем же косым
кругом с горизонтом.
Об углах и дугах, образуемых тем
же кругом с проведенным через полюс
горизонтом.
Значения упомянутых углов и дуг
для различных параллелей.
63. Аль-Фараби иногда „Коммента-
рии к «Альмагесту»” называет „Сокра-
щением «Альмагеста»”.
Примечания
391
64. В начале второй книги «Альма-
геста» Птолемей пишет: «После того,
как в первой книге этого сочинения мы
изложили вкратце необходимые сведе-
ния относительно положения Вселенной,
а также все относящееся к прямой сфе-
ре и считаемое полезным для теоретиче-
ского рассмотрения предложенного, мы
попытаемся в дальнейшем изложить
все, что происходит на наклонной сфере,
опять излагая наиболее существенное и
насколько возможно понятное». [3,
стр. 58].
65. Аль-Фараби, по-видимому, не-
сколько отходя от Птолемея, предпола-
гает, что обитаемы те места, где во вре-
мя равноденствий тени направлены не
только к югу, но и к северу.
66. Аль-Фараби рассматривает спо-
собы определения широты (<р) обитае-
мых частей Земли, которая измеряется
высотой полюса над горизонтом, что
отсутствует в «Альмагесте».
Если Атах И Amin— СООТВвТСТВвННО
наибольшая и наименьшая высоты не-*
заходящих звезд, то, по аль-Фараби,
Атах Amin । , Атах ~|~Ат1 п
2 Г — 2 *
67. Это правило аль-Фараби, которо-*
392
Примечания
го также нет в «Альмагесте», соответст-
вует формуле:
<? = 90-^±Ч
а
где Л1 и Лг — высоты Солнца в истин-
ный полдень в дни летнего и зимнего
солнцестояний.
68. Азимут восхода (са'ат аль-маш-
рик), этот термин отсутствует в «Альма-
гесте». Восточные математики под этим
понимали дугу горизонта от точки Солн-
ца в данный день до точки востока.
69. Здесь фактически установлено
следующее соотношение:
cosEH=cosEF cose.
70. Здесь фактически установлено
следующее соотношение:
tg EF
SUU₽ = ЦЁН‘
71. Здесь фактически установлено
следующее соотношение:
sinFE=tg<p-tge.
Полученное выражение дуги FE в
градусах при переводе в часы делится
на 15.
72. Доказано другое соотношение
Примечания
393
для определения азимута восхода ЕН:
sinEH=
sin е
cos <р
73. Аль-Фараби пропустил главу
«Альмагеста» о том, как вычисляется,
где, когда и сколько раз Солнце бывает
прямо над головой, где говорится:
«При помощи вышеприведенных дан-
ных легко вычислять, где, когда и
сколько раз Солнце бывает прямо над
головой. Действительно, непосредствен-
но очевидно, что для точек, находящих-
ся на параллелях, отстоящих от равно-
денственного круга далее, чем все рас-
стояние точки летнего солнцеворота,
т. е. приблизительно 23; 51,20 градусов,
Солнце никогда не будет прямо над го-
ловой, для точек, находящихся как раз
на таком расстоянии, оно будет только
один раз во время самого летнего солн-
цеворота, а для точек, лежащих на рас-
стоянии, меньшем указанного числа
градусов, Солнце два раза окажется
прямо над головой; соответствующее
время легко получается по приведен-
ной выше таблице склонений. Действи-
тельно, взяв во втором столбце таблицы
число градусов, на которое рассматри-
ваемая параллель отстоит от равноден-
ственного круга (конечно, внутри летне-
394
Примечания
го тропика), мы получим в соответст-
вующем месте первого столбца число
градусов первого квадранта, показываю-
щее, на сколько Солнце отстоит от каж-
дой из равноденственных точек по на-
правлению к точке летнего солнцеворо-
та, когда оно становится прямо над
головой для точек, лежащих на указан-
ной параллели» [3, стр. 65—66]. Но
этот материал аль-Фараби вкратце изла-
гает в главе «Об особенностях кругов,
параллельных небесному экватору».
74. Гномон (микийас), шест, разде-
ленный на определенное количество
(здесь на 60) частей, по тени которого
определялись время, высота и азимут
Солнца и ряд других данных. Греческое
слово gnomon означает «указатель».
Гномоны чаще всего устанавливались
вертикально на горизонтальной плоско-
сти и горизонтально на вертикальной
стене.
75 Аль-Фараби вносит существенное
дополнение к рассуждениям и рисунку
Птолемея.
76. В этой главе аль-Фараби, следуя
Птолемею, кратко резюмирует мате-
риал, касающийся разделения земной
поверхности на «климаты» в зависимо-
сти от продолжительности наибольшего
Дня.
Примечания
396
Климаты (арабское — «иклим») —
широтно-климатические зоны по астро-
номо-географическому принципу, при-
нятому в античности, по которому оби-
таемые части земной поверхности
делились в соответствии с продолжи-
тельностью дня летнего солнцестояния
или величиной склонения Солнца.
Впервые деление ойкумены на семь
«климатов» по широтному принципу
встречается у аль-Хорезми. Позднее аль-
Бируни в своих сочинениях руководст-
вуется этим и другими принципами.
77. По-видимому, здесь аль-Фараби
считает возможной обитаемость этой
параллели, что обсуждалось в упоми-
наемом им сочинении «Естествозна-
ние». Отметим, что в своих естественно-
научных сочинениях Аристотель также
предполагал о существовании на юге
экватора земель, близких по своим кли-
матическим условиям к землям северно-
го полушария. Впоследствии аль-Бируни
также полагал, что «обитаемые [земли]
не оканчиваются сразу же за пределами
седьмого климата или перед началом
первого, но они сокращаются и идут от-
дельными обособленными пятнами» [9,
стр. 193].
78. «География» (Джаграфиус)—со-
чинение Птолемея в восьми книгах, ос-
396
Примечания
нову которого составляют таблицы гео-
графических координат населенных
пунктов и карты Земли. Судя по неодно-
кратным ссылкам, содержание этого
трактата было хорошо известно аль-Фа-
раби.
79. В «Альмагесте» — «неизвестные
скифские племена».
80. Теоретические соображения, при-
веденные в этом абзаце, отсутствуют в
«Альмагесте» и служат для понимания
дальнейших рассуждений Птолемея от-
носительно явлений, наблюдаемых в
более высоких широтах.
81. Эта глава в «Альмагесте» начи-
нается так: «После изложения того, что
вообще наблюдается на различных кли-
матах, нам следовало бы показать, как
для каждого климата определяются од-
новременно восходящие часовые граду-
сы равноденственного круга и соответ-
ствующие дуги зодиакального; отсюда
нами будут последовательно выведены и
все остальные подробности.
Мы будем пользоваться названиями
знаков Зодиака и для обозначения соот-
ветствующих им двенадцати равноден-
ственных и солнцеворотных точек; пер-
вую двенадцатую часть, начинающуюся
от точки весеннего равноденствия и
идущую в направлении мирового движе-
Примечания
397
ния, мы будем называть Овном, вто-
рую — Тельцом и так далее, согласно
установленной последовательности 12
зодиакальных созвездий.
Покажем сначала, что равные дуги
зодиакального круга, начинающиеся от
одной и той же равноденственной точ-
ки, будут всегда одновременно восхо-
дить с равными же кругами равноденст-
венного круга» [3, стр. 21].
82. Доказанное правило для нахож-
дения значений местного восхождения
а? градуса точек эклиптики сводится к
формуле
а? = а—Да, вшДа= tg6 • tgcp,
где а — прямое восхождение градусов
эклиптики, Да — «уравнение дня».
Уравнение дня — дуга небесного эк-
ватора от пересечения его большим кру-
гом, проходящим из полюса мира через
точку восхода светила до точки восто-
ка (дуга ЕМ), или же дуга суточной па-
раллели от пересечения последней боль-
шим кругом, проходящим из полюса
через точку, до точки восхода светила.
Этот термин отсутствует в «Альмаге-
сте».
83. Здесь доказывается правило, рав-
носильное соотношению:
398
Примечания
sin(a—a<p)== sint^f tg8,
где FE — выражение в градусах поло-
вины разности между наибольшим и
наименьшим днями;
с другой стороны, по доказанному
выше
FE=tg<p-tge.
Из этих соотношений получается та же
формула для нахождения восхождений
градуса эклиптики:
sin(a—a<p )=sinAa=tg6tgcp.
84. Птолемей, производя подробные
вычисления значений одновременных
восхождений градусов эклиптики (через
10 градусов) для параллели, проходящей
через остров Родос (широта, т. е. высота
полюса 36 градусов, наибольший день
14,5 часа), далее пишет: «Итак, вычис-
лив таким же образом восхождения для
каждых десяти градусов и на остальных
параллелях, чтобы быть готовыми ко
всякого рода практическим приложени-
ям, мы приведем их в таблицах для ис-
пользования в дальнейшем, начиная с
самого равноденственного круга и до па-
раллели с наибольшим днем в 17 часов,
давая приращения по полчаса, так как в
Примечания
899
пределах получаса разности несущест-
венно отличаются от получающихся при
равномерном изменении. Поставив 36
десятиградусных делений круга, для
каждого дадим ниже и временные гра-
дусы восхождений для соответствующе-
го климата и величины, получаемые
при их сложении» [3, стр. 93].
85. Аль-Фараби не приводит утоми-
тельные для читателей вычислительные
выкладки для нахождений числовых
значений восхождений точек эклипти-
ки и сразу указывает на готовые табли-
цы восхождений по дугам в десять гра-
дусов.
Эта таблица приведена нами в при-
ложениях (таблица 3).
86. Начало этой главы в «Альмаге-
сте» выглядит так: «После того, как мы
приведенным выше образом показали
времена восхождений, то все остальное,
относящееся к этому предмету, делает-
ся легко понятным и нам не понадобят-
ся ни геометрические доказательства
каждого из этих сведений, ни составле-
ние излишних таблиц, но общий ход
рассуждения будет вполне ясным при
помощи только приведенных выше таб-
лиц» [3, стр. 93].
87. Сезонный или косой час — 1/12
продолжительности соответствующего
400
Примечания
дня или ночи. Ввиду неравенства этих
дуг (кроме дней равноденствия) сезон-
ный час ночи не равен сезонному часу
дня.
88. Градусы времени, или временные
градусы,— градусы небесного экватора.
89. Равноденственные (равновели-
кие), или прямые часы,— часы в на-
шем употреблении, т. е. 1/24 средних
суток.
90. Параллакс — ихтилаф манзар —
«различие видения» — угол между пря-
мыми линиями, соединяющими светило
с наблюдателями, находящимися в диа-
метрально противоположных точках
земного шара (суточный параллакс) или
в диаметрально противоположных точ-
[Рис. 117].
ках земной орбиты (годичный парал-
лакс). Особое значение для практиче-
ской астрономии имеет параллакс Луны.
Если М означает Луну [рис. 117], С —
центр Земли, А — точку на земной по-
Примечаний
461
верхности, где Луна стоит над головой
наблюдателя, а. В — другую точку зем-
ной поверхности, то наблюдатели, нахо-
дящиеся в А или В, одновременно ви-
дят Луну вдоль линий СМ и ВМ, разни-
ца направлений между которыми
измеряется углом ВМС, носящим назва-
ние параллакса и зависящим от рас-
тояния Луны и положения наблюда-
теля.
91. Сторона квадрата, вписанного в
большой круг сферы,— раствор цирку-
ля, которым описываются на поверхно-
сти сферы ее большие круги. Такой
большой круг, описанный из точки пе-
ресечения двух больших кругов, явля-
ется их общим перпендикуляром. Угол
между двумя пересекающимися боль-
шими кругами сферы равен расстоянию
между ними по этому большому кругу.
92. Колышек Земли (ватад) — место
пересечения эклиптики с полуночным
кругом, соответствующим полуденному
кругу. В Европе «Колышки» назывались
cardines или puncta cardinalis — «кар-
динальные точки» — точки пересечения
эклиптики с меридианом и горизонтом.
Верхний из них называется «колышком
середины неба» («середина неба» — не-
бесный меридиан), нижний — «колыш-
ком Земли».
26-89
402
Примечаний
93. Эта таблица приведена в прило-
жениях нашей работы (таблица 4).
94. В «Альмагесте» почти не приво-
дятся сведения, касающиеся географии
стран света, в том числе координатов
местностей; эти материалы даны в «Гео-
графии» Птолемея.
95. Третья книга «Альмагеста» со-
стоит из следующих глав:
О продолжительности годового про-
межутка времени.
Таблица средних движений Солнца.
О предположениях, касающихся рав-
номерного кругового движения.
О видимом неравенстве Солнца.
О составлении таблиц неравенства
на отдельных участках.
Таблицы солнечной аномалии.
Об эпохе среднего движения Солнца.
О вычислении положения Солнца.
О неравенстве суток.
96. О целях этой книги «Альмаге-
ста» Птолемей пишет: «Изложив в пре-
дыдущем сочинении совершенно необхо-
димые математические сведения о небе
и земле, о наклонности проведенного
через середины зодиакальных созвездий
солнечного круга, о связанных с нею
частных явлениях на прямой сфере, о
наклонной для каждого климата, мы
полагаем, что после этого следует изло-
Примечания
403
жить теории, касающиеся Солнца и Лу-
ны, а именно исследовать все, происхо-
дящее при их движениях, так как без
предварительного исследования, изло-
женного выше, никакое явление, относя-
щееся к светилам, не может быть изуче-
но. В дальнейшем мы должны прежде
всего получить теорию солнечного дви-
жения, без которой, в свою очередь, не-
возможно полностью охватить все, ка-
сающееся Луны» [3].
97. Птолемей в «Альмагесте» не дает
общего определения среднего движения
для всех светил, то есть Солнца, Луны и
пяти планет.
98. Эфемериды — таквим (букваль-
но — «исправление», этот же термин
означает и календарь). Наш термин
«эфемерида» происходит от греческого
слова, означающего «дневник, запись
на каждый день».
99. Аль-Фараби дает общий для
Солнца, Луны и планет способ нахожде-
ния периода среднего движения и тем
самым существенно дополняет содержа-
ние соответствующей главы «Альмаге-
ста», которая сразу же начинается с оп-
ределения продолжительности годового
промежутка времени.
100. Аль-Фараби здесь считает нуж-
ным более подробно описать этот ин-
404
Примечания
струмент (зат аль-халык), тогда как в
соответствующем месте «Альмагеста»
мы читаем о нем всего несколько фраз,
якобы принадлежащих Гиппарху:
«Вообще же неравенства годовых проме-
жутков могут быть точно установлены
при помощи наблюдений На установлен-
ном медном кругу в так называемом
квадратном портике; на этом кругу
равноденствие, видимо, отличается тем,
что его вогнутая поверхность начинает
освещаться с обеих сторон».
101. Алидада — идада — буквально
«сторона линейки» — подвижная ли-
нейка в астролябии и других угломер-
ных инструментах (слово «алидада» —
транскрипция слова аль-идада).
Диоптры — два приспособления с
отверстиями, прикрепленные к алидаде,
с помощью которых она направляется
на данный объект.
102. Таким образом, время оборота
Земли вокруг Солнца — тропический
год, т. е. промежуток времени между
двумя весенними равноденствиями, ра-
вен
А=3654- “Йодня-
103. Метон — греческий астроном,
Примечания
405
работал в Афинах. Открыл 19-летний
цикл в 432 г. до н. э.
104. Евктомен —- греческий астро-
ном, сотрудник Метона, занимался на-
блюдением солнцестояний.
105. Аристарх Самосский (около
300 г. до н. э.) — великий астроном и
математик древности, впервые выдви-
нувший гипотезу о вращении Земли
и движении ее и планет вокруг
Солнца.
106. Симак Безоружный — звезда
Спика, т. е. а созвездия Девы.
107. Эту таблицу мы привели в при-
ложениях к данной работе (табли-
ца 5).
108. Кажущаяся аномалия Солнца и
других светил — неравномерность види-
мого движения этих светил по эклипти-
ке. Древнегреческие астрономы вслед
за Аристотелем исходили из предполо-
жения о том, что Солнце и все светила
равномерно обращаются вокруг Земли,
исключение составлял только Аристарх
Самосский. Неравномерность движения
Солнца объясняется одной из двух экви-
валентных гипотез: эксцентрической
или эпициклической (см. прим. 109,
110). Движение Луны и планет объясня-
ется с помощью комбинации этих гипо-
тез.
406
Примечания
109. Согласно эксцентрический гипо-
тезе, неравномерность видимого движе-
ния Солнца но небесной сфере объясня-
ть ется тем, что оно дви-
жется равномерно по
некоторому кругу, рас-
положенному в пло-
скости эклиптики
(плоскости видимого
движения Солнца), но
эксцентрично к ней.
На рисунке 118 АВС—
эксцентрический круг,
Е — его центр, F —
центр мира (центр Земли), А — апогей
(аудж) Солнца, т. е. его наибольшее рас-
стояние от наблюдателя, D — его пери-
гей (хадид), т. е. наименьшее расстоя-
ние, В — одно из положений Солнца.
Угол EBF=G — называется «уравнени-
ем» Солнца или его «поправкой».
110. Согласно эпициклической гипо-
тезе, Солнце вращается по небольшому
кругу — эпициклу, центр которого обра-
щается вокруг Земли по большому кру-
гу — деференту, а его центр совпадает с
центром Земли. Эпицикл — фалак тад-
вир, буквально «орбита приведения во
вращение», деферент — фалак аль-ха-
мил, дословно «несущая орбита».
Примечания
407
111. Комментарии аль-Фараби сущ-
ности двух гипотез более общи и по-
дробны, чем объяснения в тексте «Аль-
магеста», в котором читаем следующее:
«Причины же кажущейся неравномер-
ности можно объяснить главным обра-
зом двумя первоначальными и просты-
ми гипотезами. Действительно, если их
движение усматривается происходящим
по имеющей один центр с миром окруж-
ности, находящейся в одной плоскости
с кругом, проходящим через середины
зодиакальных созвездий, и наш глаз
без большой погрешности можно счи-
тать находящимся в центре мира, то
для объяснения неравномерности следу-
ет допустить, или что они совершают
равномерные движения не вокруг цент-
ра, или же хотя и вокруг этого центра,
но не просто по этим окружностям, а
по перемещаемым ими другим окружно-
стям, называемым эпициклами. Какую
бы из этих гипотез мы ни приняли, ока-
жется,что для наших глаз в одинаковые
промежутки времени они будут прохо-
дить неодинаковые дуги по окружности,
проходящей через середины зодиакаль-
ных созвездий и имеющей один центр с
миром» [3, стр. 152].
408
Примечания
112. Последнее доказательство отсут-
ствует в «Альмагесте», по-видимому,
оно добавлено аль-Фараби.
[Рис. 119].
113. Это не что иное, как теорема ки-
нематики о паре вращений, принадле-
жащая Аполлонию Пергскому (около
200 г. до н. э.), которая в переводе на
язык древней астрономии означает, что
система эпицикла и деферента, при ус-
ловии равных и противоположно на-
правленных вращений, эквивалентна
неподвижному эксцентру [13, стр. 87—
90].
Поясним совпадение видимого дви-
жения Солнца при эксцентрической и
эпициклической гипотезах [рис. 119, а,
Примечания
409
б]. На рисунке 1, б за деферент принята
концентричная орбита с центром в цент-
ре мира. Пусть F — центр мира, Е —
центр эксцентра, А и П — соответствен-
но апогей и перигей эксцентрической ор-
биты, S — Солнце, X — средняя долгота
Солнца (средний аргумент), X — его ис-
тинная. долгота (уравненный аргумент),
0 — уравнение Солнца, а — аномалия
Солнца. Чертежи 10,а, б наглядно пока-
зывают совпадение X, X и 9 при обеих
гипотезах.
114. Дальше в «Альмагесте» даются
следующие разъяснения, которые аль-
Фараби не приводит здесь, так как он во
введении к этой главе предпослал об-
щие объяснения движениям светил (в
том числе Солнца): «... и что время дви-
жения от апогея до упомянутого средне-
го положения будет дольше времени
движения от этого среднего положения
до перигея. Отсюда получается, что при
гипотезе эксцентров всегда, а при гипо-
тезе эпициклов тогда, когда перемеще-
ния светил от апогея идут в направле-
нии против последовательности знаков,
время перехода от места с наименьшим
движением к среднему будет больше
времени движения от места со средним
движением к месту с наибольшим дви-
жением, так как при каждой из этих
410
Примечания
гипотез наименьшее движение получа-
ется в апогее; при гипотезе же эпицик-
лов, когда движения светил по эпицик-
лам производятся от апогея в направле-
нии последовательности знаков, наобо-
рот, время движения от места с
наибольшим движением к среднему бу-
дет больше времени движения от места
со средним к месту с наименьшим дви-
жением, так как в этом случае апогею
будет соответствовать наибольшее пере-
мещение».
115. Уравнение (тадил) или поправ-
ка — важное понятие в теории движе-
ния светил. Угловые расстояния, отсчи-
тываемые в эклиптике при центре (Пто-
лемей называет эту точку «глаз наблю-
дателя или центр круга, концентричного
с эклиптикой») от некоторой определен-
ной его точки [рис. 120] — точки весен-
него равноденствия, получили название
долгот. vEA, равная чЕА, есть долгота
апогея; обозначим ее через л; угол
vFP есть видимая долгота светила, ко-
торую обозначим X, от нее отличают
среднюю долготу, определяемую направ-
лением на центр эпицикла.
Долготы считаются в эклиптике в
направлении видимого годичного дви-
жения Солнца, от запада к востоку (это
направление и считается прямым), каж-
Примечания
411
дые 30° долготы соответствуют одному
«знаку Зодиака». Вступления Солнца в
знаки Овна, Рака, Весов, Козерога, т. е.
моменты, когда его долгота равна 0, 90,
180, 270°, означают начала времен года.
Таким образом, у=л+Л, где угол
X равен углу AFP, которым (поскольку
л сохраняет постоянное значение) изме-
ряется неравномерное движение свети-
ла, воспринимаемое наблюдателем: най-
ти закон изменения его с течением вре-
мени — основная задача теории светил;
для этого требуется связать угол X с ка-
ким-либо равномерно возрастающим уг-
лом. В этой схеме эта связь осуществля-
ется следующим образом. Продолжим
радиус деферента FK до пересечения с
412
Примечания
эпициклом в точке Ар Эта точка и про-
тиволежащая ей В\ — так называемые
истинный апогей и истинный перигей.
Угловое расстояние светила от истин-
ного апогея, т. е. угол А\КР, равный
углу РЕА, есть, по Птолемею, аномалия
планеты, мы будем обозначать ее че-
рез %.
Таким образом, задача заключается
в том, чтобы найти выражение X через
X, но имеем: —х, обозначая через
х угол ЕРЕ=РЕК, то есть тот угол, под
которым наблюдатель усматривает ра-
диус эпицикла или под которым из Р
усматривается эксцентриситет эксцен-
тра ЕЕ. Углы, отсчитываемые при цен-
тре деферента F, назывались в средние
века центрами: угол AFK, равномерно
возрастающий, есть средний центр
(centrum medium); угол х — периодиче-
ское неравенство или уравнение этого
центра (aequatia centri), поэтому /. есть
центр, отягченный его неравенством
[13, стр. 92—93].
116. Здесь геометрически доказано
утверждение о том, что наибольшее зна-
чение уравнения центра соответствует
значению Х=90°.
В нашей записи из соотношения
sinx=esinX, которое легко можно полу-
Примечания
413
чить из треугольника PEF при Л=90°,
мы имеем sinxmax —е, где е — эксцен-
триситет эксцентра.
117. Одним из кардинальных фак-
тов в теории Солнца древних является
установление того, что внутри года
наблюдаемое движение Солнца не оста-
ется равномерным: равные углы по ви-
димой долготе Солнце проходит в неоди-
наковые интервалы времени. Так, астро-
номическая весна (промежуток, когда
видимая долгота Солнца возрастает от
0 до 90°) длится 94,5 дня; астрономиче-
ское лето (промежуток времени, когда
видимая долгота увеличивается от 90
до 180°), составляет 92,5 дня.
На трех данных — на величине сред-
него суточного движения р и на длине
весны и лета — Гиппарх, а за ним и
Птолемей строят теорию Солнца, кото-
рую и излагает по-своему аль-Фараби.
118. Гиппарх получал
П=65°30/; е=^.
119. Аль-Мамун — багдадский ха-
лиф, правивший в 813—833 г., покрови-
тель наук в арабском Халифате. При
дворе аль-Мамуна работали аль-Хорез-
ми, аль-Мервази, аль-Джаухари, аль-
Фергани, уроженцы Хорезма, Мерва,
Фараба и Ферганы.
414
Примечаний
120. В связи с определением долго-
ты апогея Солнца аль-Фараби здесь за-
трагивает очень важный вопрос теории
Солнца — о движении апогея Солнца.
Как известно, Птолемей здесь допу-
стил существенную ошибку: он принял
как незыблемый факт, что долгота апо-
гея М Солнца навсегда сохраняет одно
и то же значение, то самое, которое на-
шел Гиппарх, а именно: л=65°30'.
Из текста видно, что аль-Фараби
своими наблюдениями подтверждает
важное открытие, сделанное арабскими
предшественниками об изменении апо-
гея Солнца, что является его большой
заслугой в теории Солнца и показывает,
что он был не только крупным теоре-
тиком астрономии, но и превосходным
практиком-наблюдателем.
При этом аль-Фараби считает, что
это открытие принадлежит астрономам
мамуновской обсерватории. Есть боль-
шие основания полагать одним из его
авторов среднеазиатского ученого Ха-
лида аль-Мервурриди, участвовавшего в
историческом измерении величины Зем-
ли в дни халифа аль-Мамун (начало
IX в.) и, по свидетельству аль-Бируни,
проводившего исследования по измере-
нию долготы апогея. Аль-Бируни, срав-
нивает наблюдения точек равноденст-
Йримечания
415
вий и солнцестояния Птолемея, Бану
Мусы, аль-Мервурриди, аль-Баттани,
Абу-л-Вафы и свои наблюдения. Дела-
ет тот же вывод и аль-Фараби: «Из все-
го, что изложено, ясно, что апогей
Солнца перемещается, это противоречит
тому, что считал Птолемей» [8, стр.
107—108].
В литературе распространено мне-
ние, по которому факт перемещения
апогея Солнца был впервые установлен
аль-Баттани (850—929), что не совсем
точно.
121. Здесь находится числовая вели-
чина наибольшего значения уравнения
центра:
sin Xmax=e;
Xja^:=CtT'C sin 2 23 •
122. Имеется в виду доказанная в
первой книге теорема синусов для впи-
санного прямоугольного треугольника.
123. Эта таблица приведена в прило-
жениях к настоящей работе (таблица 6).
124. Четвертая книга «Альмагеста»
Птолемея состоит из следующих глав:
На каких наблюдениях следует
строить теорию Луны.
О периодах лунных движений.
416
Примечания
О частных значениях средних дви-
жений Луны.
Таблица средних движений Луны.
О том, что при простой гипотезе о
движении Луны, будет ли она гипотезой
эксцентра или эпицикла, видимые явле-
ния будут одними и теми же.
Определение первого и простого не-
равенства движения Луны.
Об исправлении значений долготы и
аномалии Луны.
Об эпохе равномерных движений
Луны по долготе и аномалии.
Об исправлении средних движений
Луны по широте и об их эпохе.
Таблица первого или простого нера-
венства Луны.
О том, что разница в принятой Гип-
пархом величине лунного неравенства
получается не от различия сделанных
предположений, а вследствие вычисле-
ния.
125. Лунные затмения происходят во
время прохождения Луны через земную
тень, иначе говоря, в то время, когда
Земля становится между Луной и
Солнцем, а солнечные — во время про-
хождения Луны по диску Солнца. За-
тмение Луны происходит следующим
образом: пусть S — Солнце, Т — зем-
ля, L — Луна [рис. 121]. Поскольку за-
Примечания
417
тмение происходит при попадании Лу-
ны в конус земной тени, то лунное за-
тмение видно совершенно одинаково на
всем земном полушарии, обращенном к
Луне, и для всех точек Земли начина-
ется в один и тот же момент. По мест-
ным часам каждой точки Земли этот
момент будет находиться в разное вре-
мя суток в зависимости от долготы мест-
ности, что и лежит в основе определе-
ния разности долгот с помощью наблю-
дения лунных затмений. Лунное зат-
мение наступит при условии, если Луна
находится в точке эклиптики, диаме-
трально противоположной положению
Солнца. Этим и объясняется то, что дан-
ные о положении Солнца и Луны, полу-
чаемые в момент лунного затмения, бо-
лее точны, чем результаты измерений с
помощью инструментов, дающих менее
27-89
418
Примечания
точный результат вследствие параллак-
тического смещения Луны.
126. В этом параграфе рассуждение
аль-Фараби как по содержанию, так и
по объему значительно отличается от
соответствующей главы «О периодах
лунных движений» «Альмагеста». Для
сравнения считаем необходимым приве-
сти полный текст этой главы.
«Этого краткого изложения вполне
достаточно для того, чтобы мы видели,
по каким наблюдениям следует вообще
определять все необходимое для теории
движения Луны. Попробуем теперь из-
ложить, каким методом древние пользо-
вались, чтобы представить движение
Луны, а также какой метод и мы сами
считаем полезным для установления ги-
потез, наиболее соответствующих на-
блюдениям.
Так как нам кажется, что Луна не-
равномерно как по широте, так и по
долготе, и не всегда в одинаковое время
проходит круг через середины зодиа-
кальных созвездий и совершает возвра-
щение к той же широте, то без опреде-
ления времени, необходимого для вос-
становления ее неравенств, было бы
невозможно найти и другие ее периоды.
Согласно произведенным подробным на-
блюдениям она имеет наибольшие, наи-
Примечания
419
меньшие и средние движения безраз-
лично во всех частях Зодиака. Точно
так же во всех частях Зодиака она бы-
вает и самой северной, и самой южной,
и находящейся на самом круге, прохо-
дящем через середины зодиакальных
созвездий; поэтому, естественно, что
древние математики старались найти
некоторый промежуток времени, в тече-
ние которого Луна всегда совершала бы
одинаковое движение по долготе, так
как только по истечении этого проме-
жутка могло бы произойти восстановле-
ние неравенства. По изложенным выше
причинам, сопоставляя наблюдения
лунных затмений, они смотрели, за ка-
кое количество месяцев пройденное по
долготе расстояние будет всегда равным
таким же расстояниям за одинаковое
количество месяцев и будет содержать
равные количества целых оборотов или
с добавлением каких-нибудь равных дуг.
Более древние вообще считали, что этот
промежуток времени содержит 6585
дней с одной третью. В течение этого
промежутка времени они видели, что
примерно совершается 223 месячных
обращения, 239 возвращений аномалии,
242 возвращения к той же широте, 241
оборот по долготе и что, кроме того,
Солнце в течение этого промежутка к
420
Примечания
своим 18 круговым обращениям добав-
ляет еще 10 градусов и две трети, если
относить все возвращения к неподвиж-
ным звездам. Это время они назвали
«периодическим», как первым возвра-
щающим в исходное состояние почти все
движения. Для получения целого числа
дней они утроили эти 6585 1/3 Дней и
получили число дней, равное 19 756, ко-
торое они назвали экселигмом. Утраи-
вая и остальные числа, они получили
669 месяцев, 717 восстановлений анома-
лии, 726 возвращений к той же широте,
723 оборота по долготе и, кроме того,
32 градуса, которые Солнце добавляет к
54 своим полным обращениям.
Однако Гиппарх на основании хал-
дейских и собственных наблюдений по-
казал, что все это не совсем точно. Дей-
ствительно, на основании изложенных
им наблюдений он показывает, что пер-
вое число дней, по истечении которых
время затмений делает полный цикл в
одинаковое число месяцев и в одинако-
вых движениях, равно 126 007 дням с
одним равноденственным часом; в тече-
ние этого времени он находит 4267 ме-
сяцев, 4573 полных возвращений анома-
лии, 4612 обращений по Зодиаку без
7,5 градуса, которых недостает Солнцу
для совершения 345 полных оборотов
Примечания
421
по отношению к неподвижным звездам.
Он нашел, что средняя продолжитель-
ность месяца, получаемая делением при-
веденного числа на 4267 месяцев, будет
приблизительно содержать 29; 31, 50,
8, 20 дней. В течение этого промежутка
от одного лунного затмения до другого
соответствующего будут пройдены оди-
наковые расстояния; таким образом,
становится ясно, что неравенство тоже
восстанавливается, так как этот проме-
жуток времени всегда содержит такое
же число месяцев, и что к одинаковым
4611 обращениям по долготе прибавля-
ются равные дуги в 352; 5 градуса,
как требуют времена соединений с
солнцем.
Если искать не число месяцев меж-
ду соответствующими лунными затме-
ниями, а только от одного полнолуния
или новолуния до такого же соединения,
то время возвращения неравенства ока-
залось бы меньшим, и если взять только
их общий делитель — семнадцатую
часть, получился бы 251 месяц и 269
восстановлений аномалии. Однако ука-
занное время не может дать целое чис-
ло возвращений к той же широте; дей-
ствительно, возвращение затмений, по-
видимому, сохраняет только равенство
периодов по времени и по долготе, но не
422
Примечания
по величине и одинаковости затмений,
по которым определяется широта.
Найдя предварительно время возвра-
щения неравенства, Гиппарх опять стал
сравнивать, промежутки времени между
месяцами, имеющими крайние затме-
ния совершенно одинаковые как по ве-
личине, так и по продолжительности,
для которых не имеется никакого разли-
чия в аномалии, так что вследствие это-
го получалось и возвращение к той же
широте; он показал, что такой период
содержит 5458 месяцев и 5923 возвра-
щения к широте.
Таким методом пользовались наши
предшественники для подобных иссле-
дований. То, что он не был ни простым,
ни удобным, но требовал большого вни-
мания, мы можем видеть из следующе-
го. Если допустить, что продолжитель-
ности двух периодов равны друг другу,
то это не даст нам ничего полезного, ес-
ли в каждом из этих периодов не будет
никакой связи или будет всегда одина-
ковая разница в аномалии Солнца. Если
же этого не случится, то и само оно, а
также Луна не сделают одинаковых об-
ращений в равные промежутки време-
ни. Действительно, если, например, каж-
дый из сравниваемых промежутков
кроме целых и равных друг другу го-
Примечания
423
дов будет содержать половину продол-
жительности года, то Солнце, двигаясь
в течение этого времени в первом про-
межутке от среднего положения в Ры-
бах, а во втором — от среднего положе-
ния в Деве, пройдет в первом промежут-
ке расстояние приблизительно на 4 и
три четверти градуса меньше полуок-
ружности, а во втором на столько же
больше полуокружности, таким обра-
зом, и Луна в равные времена пройдет
в первом промежутке кроме целых кру-
гов еще 175 с четвертью, а во втором —
184 с четвертью градусов. Поэтому, во-
первых, следует сказать, что промежут-
ки по отношению к Солнцу должны со-
держать целое число полных его обра-
щений, нужно чтобы в одном из проме-
жутков прибавлялась полуокружность
от апогея, а в другом — от перигея, или
чтобы в каждом из промежутков начало
было в одном и том же месте, или чтобы
для первого затмения в одном проме-
жутке и второго в другом получались с
обеих сторон одинаковые расстояния от
перигея и апогея. Только при таких ус-
ловиях в каждом промежутке или сов-
сем не получится разницы в аномалии,
или разница будет совершенно одинако-
вой, так что добавляемые дуги окажут-
ся равными или между собой или меж-
424
Примечания
ду собой и дугами равномерного дви-
жения.
Мы полагаем, что подобным же об-
разом следует отнестись к движениям
Луны. Действительно, если на это не
обратить внимания, то окажется, что
Луна часто может проходить равные ду-
ги по долготе и в одинаковые времена
без полного восстановления ее неравен-
ства. Получится движение с одинаково
увеличивающейся или уменьшающейся
скоростью, но движение не будет закан-
чиваться с той же скоростью при усло-
вии : если в одном промежутке Луна нач-
нет движение с наибольшей скоростью и
закончит с наименьшей, а в другом нач-
нет с наименьшей и закончит с наиболь-
шей, если в обоих промежутках места с
первой скоростью одного и последней
скоростью другого были равноотстоящи-
ми от одного и того же места с наимень-
шей или наибольшей скоростью. В каж-
дом из этих случаев или не будет никакой
разницы в неравенстве, или же разница
будет одной и той же, и вследствие это-
го получатся по долготе одинаковые ду-
ги, но неравенство никогда не будет вос-
становленным. Следовательно, в выби-
раемых промежутках не должно иметь
места ни одно из этих явлений, если
нужно, чтобы они содержали период
Примечания
425
восстановления неравенства. Наоборот,
нам нужно выбирать промежутки, кото-
рые возможно лучше могут показать
неравенство, если они не содержат це-
лых периодов восстановления неравенст-
ва и начинают движение от мест с
различными скоростями по величине
или по потенции. По величине, если в
одном промежутке движение начнется с
наименьшей Скоростью и не закончится
наибольшей, а в другом когда начнется
с наибольшей и не закончится на наи-
меньшей скорости. Таким образом, по-
лучится наибольшая разница в дугах,
пройденных по долготе, если будут опи-
саны не полные круги аномалии, но с
добавлением лучше всего одной или трех
четвертей кругов аномалии, так как про-
межутки будут отличаться на удвоен-
ную разность в неравенстве.
По потенции же, если в обоих проме-
жутках движение начнется со средней
скоростью, но не с той же самой, а имен-
но в одном промежутке возрастающей,
а в другом — убывающей, приращения
долгот будут больше всего разли-
чаться между собой, если до восста-
новления неравенства опять будет недо-
ставать одной или трех четвертей круга
аномалии, так что получается двойная
разница в неравенстве, а для полукру-
426
Примечания
га — четверная. Мы видим, что вследст-
вие этого и Гиппарх, проявляя величай-
шую осторожность при выборе проме-
жутков в таком исследовании, для Луны
пользовался двумя промежутками, из
которых в одном движение начиналось
с точки с наибольшей скоростью и не
заканчивалось в точке с наименьшей, а
в другом движение начиналось с точки
с наименьшей скоростью, но не заканчи-
валось в точке с наибольшей; он также
исправлял разницу, получающуюся от
солнечного неравенства, хотя она была
и наибольшей и составляла приблизи-
тельно двенадцатой части Зодиака,
причем в обоих промежутках она не
была ни той же самой, ни производящей
ту же разницу в неравенстве или в до-
бавлении к числу описанных Солнцем
полных кругов.
Мы говорим это не для того, чтобы
оспаривать предложенный метод полу-
чения периодических восстановлений,
но чтобы настоятельно подчеркнуть,
что при настоящем внимании и соответ-
ствующем вычислении можно испра-
вить предложенный способ; если же
опустить какую-нибудь из изложенных
характерных особенностей, то можно
очень сильно ошибиться в искомом опре-
делении; я хочу показать также, на-
Примечания
427
сколько трудно получить точное нали-
чие всех этих необходимых условий,
даже если очень умно сделать выбор
соответствующих наблюдений.
Таким образом, для указанных пе-
риодических возвращений при вычис-
лении согласно методу, предложенному
Гиппархом, оказалось, что для месяцев
при наиболее точном вычислении не
получалось никакой заметной разницы
с истиной, но для аномалии и широты
наблюдалась очень заметная ошибка,
что мы и выяснили при помощи наибо-
лее простых и удобных методов, упо-
требляющихся для подобного исследова-
ния, как мы сейчас покажем при опре-
делении величины лунного неравенства.
Сначала, что будет очень полезно для
дальнейшего, мы дадим отдельные сред-
ние движения по долготе, широте и
аномалии, в соответствии с указанными
выше временами периодических возвра-
щений, а также добавим поправки, по-
лучающиеся после исправления тем ме-
тодом, который мы изложим в дальней-
шем» [3, стр. 194—203].
127. Противостояние (мукабала) —
случай, когда долготы двух светил
отличаются на 180°, соединение (идж-
тима) — совпадение долгот двух све-
тил.
428
Примечания
128. Халдеи — семитические племе-
на в Южной Месопотамии, образовав-
шие в конце 7 в. до н. э. Ново-Вавилон-
ское государство.
129. Это так называемый синодиче-
ский месяц, в течение которого Луна
возвращается в прежнее положение от-
носительно Солнца.
130. Если Ль — средняя долгота Лу-
ны, Ag — средняя долгота солнца, то раз-
ность Аь —As называют средней суточ-
ной величиной элонгации Луны (от
латинского слова elangotio — «удале-
ние»),
131. Египетский год содержит ровно
365 суток и поэтому называется равным
(равновеликим) в отличие от римского,
в котором бывает 365 и 366 суток.
132. Эта таблица приведена в прило-
жениях (таблица 7).
133. Здесь квадратура (тарби') и гек-
сагональный аспект (тасдис), тригио-
нальный аспект (таслис) — расположе-
ние светил в знаках Зодиака, имеющих
расстояния соответственно 90, 60 и 120°.
134. Первое неравенство в движении
Луны объясняется с помощью эпици-
клической гипотезы [рис. 122]. Центр
эпицикла А по концентрическому кру-
гу и Луна М по эпициклу двигались в
Примечания
429
противоположные стороны (центр А —
против часовой стрелки, а Луна — по
часовой стрелке) и совершали в абсолют-
ном движении полный оборот относи-
тельно прямой АЕС, все время проходя-
щей через Солнце в течение одного си-
нодического месяца (29,5 дня); тогда
движение Луны казалось наиболее
медленным в точке М эпицикла и наи-
более быстрым в точке N. От сложения
двух вращений в противоположные сто-
роны получилось движение Луны во-
круг Земли по эксцентрическому кругу,
центр F которого все время находится
на прямой, соединяющей центр Е Земли
с Солнцем [9, стр. 599].
430
Примечания
135. Эта предпосылка и ее следствие
отсутствуют в «Альмагесте» и являются
собственным добавлением аль-Фараби.
Они служат теоретико-методической ба-
зой в определении положения Луны и
ее аномалии через наблюдение в двух
группах по три затмения, приведенной в
дальнейшем Птолемеем.
136. По мнению О. Нейгебауера,
здесь мы имеем оригинальный пример
применения тригонометрии к решению
астрономической задачи, где описан ма-
тематический метод определения длины
радиуса эпицикла Луны и положения
апогея. Эта задача представляет собой
простейший случай более общей задачи
определения параметров орбиты на ос-
новании ряда наблюденных положений.
Она тесно связана также с важной гео-
дезической задачей — определением по-
ложения наблюдателя по отношению к
трем данным точкам [4, стр. 201—204].
Эта задача в данном случае такова:
по известным скоростям изменений ано-
малии у и средней долготы X центра
эпицикла определить г и момент, когда
Луна имеет минимальную скорость, т. е.
находится в апогее эпицикла.
В тех единицах, в которых радиус
деферента равен 60, радиус эпицикла
был найден равным 5; 15.
Примечания
431
137. Набонассар (у аль-Фараби Бух-
тунассар) — вавилонский царь, царство-
вал в 747—733 гг. до н. э. Начало эры
Набонассара, упоминавшейся в «Альма-
гесте»,— 26 февраля 747 г. до н. э., день
вступления Набонассара на престол.
138. Узел — «'укда» — точка пересе-
чения эклиптики с орбитой Луны.
139. Здесь аль-Фараби указывает,
что при определении движения Луны по
широте по ее затмениям надо учиты-
вать, что при одной и той же величине
широты величина тени Луны может
быть различной. Она зависит от расстоя-
ния Луны от апогея эпицикла (если при-
держиваться эпициклической гипоте-
зы), то есть от расстояния Луны от Зем-
ли. Тень наибольшая при положении
Луны в высшей точке эпицикла (когда
Луна ближе всего к Земле) и уменьша-
ется по мере движения Луны по эпицик-
лу к его высшей точке (причем учитыва-
ется перемещение узла лунной орбиты).
Таким образом, для того чтобы судить
об истинном возвращении по широте,
необходимо, чтобы для двух затмений
величина затмений была одной и той же
и расстояния Луны от апогея эпицикла
были бы одинаковыми.
140. Названия восходящего и нисхо-
дящего узлов Луны — «голова» (рас) и
432
Примечания
«хвост» (занаб) связаны с древним суе-
верием о голове и хвосте Дракона, жи-
вущего в узлах лунной орбиты и пожи-
рающего Солнце во время затмений, ко-
торые могут произойти лишь в узлах.
141. Палец (исба') — ок. 2 см.
142. Аль-Фараби объясняет метод
Птолемея вычисления движения Луны
по широте. Если известны данные на-
блюдений двух затмений, разделенных
большим промежутком времени, и были
равны величины затмения для равных
расстояний Луны от высших точек их
эпициклов, то их широты также равны;
следовательно, по средним фазам зат-
мений можно получить эпоху периоди-
ческих изменений широты, т. е. за про-
межуток времени между указанными
затмениями движение Луны содержит
целое число оборотов по широте. Если
же Луна в обоих затмениях находится
на различном расстоянии от высшей
точки эпицикла, это дает возможность
определить среднее движение Луны по
широте за указанный промежуток вре-
мени, а следовательно, и среднее годо-
вое, месячное и суточное движение Лу-
ны по долготе.
143. Положение Луны в произволь-
ный момент времени определяется его
средней долготой X («средним движени-
Примечания
433
ем»), истинной долготой % («истинным
движением»), уравнением 9= [Л—X] и
аномалией а [рис. 123].
[Рис. 123].
144. Эта таблица приведена в прило-
жениях (таблица 8).
145. Пятая книга «Альмагеста» со-
держит следующие главы:
Об устройстве астролябии.
О гипотезе для объяснения двойного
неравенства Луны.
О величине неравенства Луны, зави-
сящего от положения относительно
Солнца.
О величине отношения для эксцен-
тритета лунной орбиты.
О наклонности лунного эпицикла.
О том, как геометрически по перио-
дическим движениям определяется ис-
тинное положение Луны.
28-89
434
Примечания
Составление таблицы для полного
неравенства Луны.
Таблица полного лунного неравен-
ства.
О вычислении полного движения Лу-
ны в целом.
О том, что эксцентрический круг Лу-
ны не производит в сизигиях никакой
существенной разницы.
О параллаксах Луны.
Об устройстве параллактического ин-
струмента.
Определение расстояния Луны.
О величинах видимых диаметров
Солнца, Луны и земной тени в сизигиях.
О расстоянии Солнца и о том, что оп-
ределяется вместе с ним.
О величинах Солнца, Луны и Земли.
О частных значениях параллаксов
Солнца и Луны.
Таблица параллаксов.
Об определении параллаксов.
146. Описанный здесь инструмент —
«Армиллярная сфера», арабские астро-
номы его называли «зат альхалак», до-
словно «обладающее кольцами» (по ла-
тыни armilia — «кольцо»).
147. Таким образом, для определе-
ния двух сферических координат свети-
ла достаточно измерить одну из них, а
вторая координата определится поворо-
Примечания
436
том армиллярной сферы, необходимым
для совмещения светила с его символом
на круге, изображающем эклиптику,
или кругом широты, проходящим через
светило.
148. Эти объяснения аль-Фараби бо-
лее подробны, чем соответствующие рас-
суждения Птолемея, поэтому для срав-
нения необходимо привести это место из
«Альмагеста»: «Так как теперь при по-
мощи этого прибора указанные наблю-
дения становятся простыми, то оказа-
лось, что расстояние Луны от Солнца
как по записям Гиппарха, так и по на-
шим собственным наблюдениям иногда
были одинаково вычисленными по изло-
женной выше гипотезе, иногда же не-
одинаковыми и отличались то меньше,
то больше. Когда же мы больше стали
размышлять о характере этого неравен-
ства, то заметили, что во время новолу-
ний или полнолуний оно или очень мало
или совершенно не дает никакой замет-
ной погрешности, отличной от той, кото-
рую могли бы произвести лунные парал-
лаксы, в обоих же положениях Луны,
разделенной пополам, разница бывает
наименьшей или даже совершенно от-
сутствует, если Луна оказывается в
апогее или в перигее эпицикла, и наи-
большей, если она бывает в промежуточ-
436
Примечания
ных положениях, тогда получается са-
мая большая разница по сравнению с
первым неравенством. Если первое нера-
венство приходится вычитать, то в каж-
дой из четвертей положение Луны опре-
деляется числом, меньшим того, которое
получается после вычитания перво-
го неравенства, если же его надо при-
бавлять, то большим, возрастая пропор-
ционально величине первого простафе-
реза. Таким образом, указанные особен-
ности позволили нам заключить, что
лунный эпицикл следует предположить
движущимся по эксцентрическому кру-
гу, причем он становится более удален-
ным от Земли в новолуниях и полнолу-
ниях и более близким в обоих положени-
ях Луны, разделенной пополам; все
будет происходить, если мы добавим к
первой гипотезе такое исправление.
Вообразим в плоскости лунной орби-
ты круг, концентрический с проходя-
щим через середины знаков вследствие
отсутствия широты, как мы упомянули
выше, и движущийся против последова-
тельности вокруг полюсов круга через
середины знаков, перемещаясь на столь-
ко, на сколько движение по широте опе-
режает движение по долготе, а Луна об-
ращается по так называемому эпицик-
лу, двигаясь против последовательности
Примечания
437
знаков на дуге, прилежащей к апогею
эпицикла соответственно восстановле-
нию первой аномалии. В этой наклонной
плоскости мы предполагаем два равно-
мерных движения по направлению про-
тивоположных друг другу, совершаю-
щихся оба вокруг центра круга через
середины знаков, причем одно из них
увлекает центр эпицикла в направлении
последовательности знаков Зодиака в
соответствии с движением по широте, а
другое перемещает центр и апогей на-
ходящегося в той же плоскости эксцен-
тра, на котором всегда находится центр
эпицикла. Это движение совершается
против последовательностц знаков, при-
чем величина его будет равна разности,
которая получится, если мы вычтем ши-
роту из удвоенной элонгации, т. е. раз-
ности среднего лунного положения по
долготе по сравнению с солнечным. На-
пример, если в один день центр эпицик-
ла в своем движении пройдет приблизи-
тельно 13; 14 градусов в направлении
знаков, то на круге через середины зна-
ков он покажется передвинувшимся на
13; 11 градусов долготы вследствие того,
что весь косой круг отступит против
последовательности знаков на величину
разности в три шестидесятых; но апо-
гей эксцентра, в свою очередь, отступит
438
Примечания
против последовательности знаков на
11; 9 градусов, на которые удвоенные
градусы элонгации, а именно 24; 23,
превышают 13; 14 градусов аргумента
широты. Таким образом, вследствие
противоположности обоих этих движе-
ний, совершающихся, как мы сказали,
вокруг центра круга через середины зна-
ков, движение центра эпицикла будет
отличаться от движения центра эксцент-
ра на дугу, получающуюся после сложе-
ния 13; 14 и 11; 9 градусов, что прибли-
зительно в два раза больше 12; 11,30
градусов элонгации. Вследствие этого в
течение среднего месяца эпицикл два
раза обернется по эксцентру, причем
возвращение к апогею эксцентра пред-
полагается совершающимся в средних
теоретических новолуниях и полнолу-
ниях.
Чтобы сделать это предположение
более наглядным, вообразим опять в на-
клонной плоскости лунной орбиты круг,
концентрический с проходящим через
середины знаков; пусть его центр бу-
дет Е...»
149. Таким образом, в этой главе
аль-Фараби, следуя за Птолемеем, пред-
полагает, что получившийся эксцентри-
ческий круг не остается неподвижным,
а совершает в течение месяца один обо-
Примечания
439
рот по часовой стрелке вокруг Земли по
отношению к линии, соединяющей центр
Земли с Солнцем; следовательно, пря-
мая СЕА всегда будет биссектрисой уг-
ла между линиями, направленными к
центрам эксцентрического круга и эпи-
цикла.
В изображенном на нашем рисун-
ке (прим. 134) положении Луна, на-
ходящаяся в неподвижной точке М
на эпицикле, будет в новолунии и
в апогее эксцентрического круга. Если
центр F последнего сделает четверть
оборота и окажется на линии Е справа
от Е, то центр эпицикла А будет на той
же линии слева от Е, а Луна, находя-
щаяся в точке М эпицикла, совершаю-
щего поступательное круговое движе-
ние, будет в квадратуре и в перигее экс-
центра. Еще через четверть оборота
точка F и центр эпицикла А окажутся
на прямой ЕС, обе ниже точки Е; центр
эпицикла А будет опять в наибольшем
расстоянии, а Луна, находящаяся на
линии ЕС, будет в апогее и в полнолу-
нии. Таким образом, описанный меха-
низм приводит к тому, что полнолуние
и новолуние совершаются в апогее экс-
центра, а квадратуры — в его перигее
[9, стр. 559, 600].
440
Примечания
[Рис. 124].
150. Тригональный аспект — см.
прим. 133.
151. Способ нахождения этого так
называемого первого неравенства обос-
новывается с помощью следующей гипо-
тезы Птолемея. Пусть Е — центр мира,
АС — эклиптика [рис. 124]. Вокруг Е
по кругу ZZ'Z"Z"' движется центр дефе-
Примечания
441
рента лунного эпицикла (таким обра-
зом, непрерывно изменяющий свое
положение). По окружности этого дефе-
рента (не показанной на чертеже) дви-
жется центр эпицикла Луны, а по эпи-
циклу — сама Луна в направлении,
противоположном движению центра
эпицикла. Все три вращения происходят
в плоскости орбиты Луны, наклоненной
к эклиптике на 5°. При соединениях и
противостояниях Солнца и Луны центр
эпицикла Луны совпадает с апогеем
Солнца (точки А и С), а Луна лежит в
апогее своего эпицикла, причем центр
деферента для Луны находится в точ-
ках Z и Z". Когда центр эпицик-
ла попадает в точки В и D, центр
деферента находится, соответственно, в
442
Примечания
точках Z' и Z"'. Точки В и D соответст-
вуют четверти оборота Луны за время
одного оборота (синодический месяц,
равный 29,5 суткам), центр эпицикла
Луны дважды будет в апогее (в точках
А и С) и дважды в перигее (в точках В
и D). Каждой точке Z, W, Z' круга, по
которому движется центр деферента,
соответствует симметричная ей точка
Z", W, 7,"', от положения которой зави-
сит на соответствующем эпицикле поло-
жение его среднего апогея (точки М,
М', М"). Истинные апогеи эпициклов —
точки М, N, М" — на продолжении пря-
мых, соединяющих центр мира с центра-
ми эпициклов. Средний и истинный апо-
геи совпадают в точках апогея и пери-
гея центра эпицикла. В остальных точ-
ках деферента они отстоят друг от друга
на некоторую дугу NM, называемую
первым уравнением или неравенством.
Поэтому ясно, что апогей Луны совер-
шает один оборот по зодиакальной орби-
те в месяц, если из этого движения
вычесть движение Солнца, так как
они движутся в противоположные сто-
роны.
Первое неравенство — дуга разности
или угловое расстояние между средним
и истинным апогеями на эпицикле.
Пусть ABCD — эксцентричная орби-
Примечания
443
та Луны с центром Е в некоторый мо-
мент времени [рис. 125], G — центр ми-
ра, С — центр лунного эпицикла, Н —
положение Луны на эпицикле, F — точ-
ка, симметричная для центра эксцен-
тричной орбиты Луны, ВС — среднее
расстояние между Солнцем и Луной
(пусть ВС=АВ). _ Тогда /LEBG=
= /LAEB—Z-AGB=k^ -—As =0 (уравне-
ние Солнца), Z-AGC=2(Kl —As)— двой-
ная элонгация Луны, К — истинный
апогей Луны в эпицикле, М — средний
апогей, лежащий на линии FM, дуга
МОН — средняя аномалия Луны (МР+
+РН), дуга КОН=КО+ОН — истин-
ная аномалия, где PH и. ОН, соответст-
венно,— избытки средней и истинной
аномалии над половиной оборота:
РН=МРН—180°, ОН=КОН—180°. Ду-
га КМ, равная углу GCF,— первое нера-
венство Луны, КМ—РН=РО. При этом
эксцентриситет EG орбиты, т. е. рас-
стояние между центрами, равен GF.
152. Здесь аль-Фараби, следуя Птоле-
мею, приводит правило вычисления эфе-
мериды Луны по таблицам.
153. Пропорциональные минуты —
см. прим. 34.
154. Эта таблица приведена нами в
приложениях (таблица 9).
155. Инструмент с двумя ответвле-
444
Примечания
ниями — буквально «Зат ашшуба-
тайн» — триквет, параллактический ин-
струмент, состоящий из трех линеек.
156. Здесь аль-Фараби доказывает
теорему о том, что длина средней линии
трапеции равна полусумме длин ее ос-
нований, на которую Птолемей ссыла-
ется, считая ее известной; в «Началах»
Евклида эта теорема отсутствует.
157. Эта таблица приведена нами в
приложениях (таблица 10).
158. Птолемей при вычислении па-
раллакса Луны по долготе и широте от-
носительно эклиптики принимает их
как отношение хорд, стягивающих эти
хорды, так как, по его мнению, эти ду-
ги «не очень отличаются от прямых».
Развивая эту ценную идею, аль-Фа-
раби считает целесообразным при надоб-
ности заменить малые дуги с прямыми
линиями. Далее он рассматривает па-
раллактический треугольник с малыми
сторонами. Такой способ замены впо-
следствии был положен в основу диффе-
ренциального и интегрального исчисле-
ния.
159. Считая рассуждения Птолемея
в этом месте не очень обстоятельными,
аль-Фараби дает им подробные объяс-
нения с помощью рисунков, отсутствую-
щих у Птолемея. Для сравнения
Примечания
446
приводим начало этой главы из «Аль-
магеста», которая называется «Об опре-
делении параллаксов»:
«Теперь, если мы хотим определить
величину параллактического смещения
Луны для любого ее положения и преж-
де всего того, которое получается на
большом круге, проведенном через нее
и полюс горизонта, мы должны рассмо-
треть, на сколько равноденственных ча-
сов в заданном климате она отстоит от
полуденного круга; найденную величи-
ну мы вносим в таблицу углов для соот-
ветствующих климата и двенадцатой
части Зодиака; во втором столбце таб-
лицы мы найдем соответствующее это-
му часу число градусов, или полное, или
же с добавкой, приходящейся на часть
часа; это число, представляющее рас-
стояние Луны от полюса горизонта по
тому же проведенному через нее боль-
шому кругу, мы вносим в таблицу па-
раллаксов и смотрим, в какую строчку
первого столбца оно попадает, а также
пишем соответствующие этому числу
величины, находящиеся в следующих
за солнечным параллаксом четырьмя
столбцами, то есть в третьем, четвертом,
пятом и шестом, каждую отдельно. Пос-
ле этого, определив для этого часа ве-
личину аномалии по отношению к ис-
446
Примечания
тинному апогею или непосредственно,
или, если она превышает 180 градусов,
ее дополнение до 360 градусов, и взяв
всегда только половину определенных
таким образом градусов для внесения в
числа первого столбца, смотрим, сколь-
ко шестидесятых в отдельности соответ-
ствует этому числу в 7-ом и 8-ом столб-
цах; стоящее в 7-ом столбце число ше-
стидесятых долей берем от разности,
стоящей в четвертом столбце, и всегда
прибавляем к значению параллаксов в
третьем столбце; сколько же шестиде-
сятых стоит в 8-ом столбце, столько мы
берем от разности в шестом столбце и
все это опять всегда прибавляем к па-
раллаксу из 5-го столбца; для получен-
ных таким образом двух параллаксов
мы образуем разность; затем берем рас-
стояние Луны в среднем движении или
от Солнца, или от диаметрально ему
противоположной точки, выбирая всег-
да меньшее из обоих этих расстояний, и
вносим его в числа первого столбца;
опять сколько шестидесятых соответст-
вует ему в 9-ом и последнем столбце,
столько мы берем от найденной разности
параллаксов и полученную величину
всегда прибавляем к меньшей, то есть
к определенной из третьего и четвертого
столбцов; полученная сумма покажет
Примечания
447
нам параллактическое смещение Луны
по тому ясе большому кругу, проведен-
ному через нее и полюс горизонта; сол-
нечный параллакс в подобном положе-
нии для солнечных затмений берется
просто из соответствующих градусов
второго столбца для величины дуги от
полюса горизонта.
Чтобы определить параллакс Луны по
отношению к кругу, проходящему через
середины зодиакальных созвездий как
по долготе, так и по широте, мы вносим
в ту ясе самую часть таблицы углов
число равноденственных часов, на кото-
рое Луна отстоит от полуденного круга,
и смотрим соответствующие этому чис-
лу часов градусы; если Луна еще не
дошла до полуденного круга, мы смот-
рим их в третьем столбце, если уясе
прошла, то в четвертом; если найденное
число градусов будет менее 90, то мы
пишем его, если же оно больше 90, то
пишем его дополнение до 180°; такова
будет величина наименьшего из углов
при рассматриваемом сечении, выра-
женная в градусах, каких один прямой
угол содержит 90. Удвоив записанное
число градусов, вносим его в таблицу
прямых в круге вместе с его дополнени-
ем до 180°; отношение прямой, стяги-
вающей дугу с этим удвоенным числом
448
Примечания
градусов, к прямой, стягивающей дугу,
представляющую дополнение до полу-
окружности, дает нам отношение парал-
лакса по широте к параллаксу по дол-
готе, так как соответствующие дуги
этих кругов не очень отличаются от
прямых. Помножив теперь числа, полу-
ченные для этих прямых, на найденную
величину параллакса для большого кру-
га, проходящего через полюс горизонта,
и разделив полученные величины на
120, мы получим соответствующие па-
раллаксы, равные найденным после де-
ления числам.
Относительно параллаксов по широ-
те мы можем вообще сказать, что если
полюс горизонта на полуденном круге
стоит севернее делящей небо пополам
точки зодиакального круга, то парал-
лакс будет смещать к югу; если же по-
люс горизонта будет ниже той, которая
делит небо пополам, то параллакс по
широте будет к северу; что же касается
параллаксов по долготе, то, поскольку
величины данных в таблице углов дают
северный угол из тех двух, которые об-
разует дуга Зодиака, идущая в направ-
лении последовательности знаков, при
параллаксе по широте к северу парал-
лакс по долготе будет иметь направле-
ние против последовательности знаков,
Примечания
449
если рассматриваемый угол будет боль-
ше прямого и в направлении последова-
тельности, если он меньше прямого; ес-
ли же параллакс по широте будет к
югу, то наоборот; при рассматриваемом
угле, большем прямого, параллакс по
долготе будет в направлении последова-
тельности знаков, если же он меньше
прямого, то против последовательности.
Во всем изложенном выше мы счита-
ли, что Солнце не имеет никакого за-
метного параллакса, зная, впрочем, что
учитываемый в дальнейшем его парал-
лакс производит некоторую разницу.
Однако мы считаем, что получаемая
вследствие этого неточность в наблю-
даемых явлениях не является настоль-
ко существенной, чтобы изменять что-
нибудь в произведенных без ее учета
вычислениях, которые мы вкратце изло-
жили выше ; подобно этому при опреде-
лении параллаксов Луны мы довольст-
вуемся углами и дугами, образованными
у круга через середины знаков пе-
ресечения с большим кругом, проведен-
ным через полюсы горизонта, тогда как
следовало бы взять углы, получаемые у
косого круга Луны. Мы делали так, по-
скольку получающаяся вследствие этого
разница в сизигиях для затмений не-
ощутима, а если изложить и это, то до-
29-89
460
Примечания
казательства стали бы очень сложны-
ми, а вычисления трудными, ибо зти
углы нельзя было бы определить для
каждого положения Луны на Зодиаке
или расстояния от узлов; они будут
очень сильно изменяться как по вели-
чине, так и по положению» [3, стр.
324—326].
160. Из последних двух абзацев вид-
но, что аль-Фараби на основе метода
вычисления числовых значений парал-
лаксов здесь также делает важное обоб-
щение: он открыто вводит понятие
«число линии в единицах» выбранного
отрезка линии (в данном случае в еди-
ницах числа ЕВ). Применение к непре-
рывным величинам термина «единица»
является дальнейшим развитием аль-
Фараби арифметической терминологии,
о которой* мы говорили в примеча-
нии 24.
ЛИТЕРАТУРА
1. Аль-Фараби. Математические трак-
таты. Алма-Ата, 1972.
2. К у б е с о в А. Математическое наследие
аль-Фараби. Алма-Ата, 1974.
3. Ptolemaus. Handbuch der Astronomic,
Bd. 1, Ubers. K. Manitius, Vorwort und Berichti-
gung von O. Neigebaner. Leipzig, 1963.
4. Нейгебауэр О. Точные науки в
древности. М., 1968.
5. Булгаков П. Г. Жизнь и труды Биру-
ни. Ташкент, 1972.
6. Аль-Фараби. Шарх аль-Маджисти.
Арабская рукопись. Британский музей, 7368.
7. Башмакова Н. Г. О понятии числа
в математике первых веков нашей эры. В сб.:
«История и методология естественных наук».
Вып. 14, М., 1973, 49—59.
8. Розенфельд Б. А., Рожанская
М. М., Соколовская 3. К. Абу-р-Райхан
ал-Бируни. М., 1973.'
9. Коперник Николай. О вращениях
небесных сфер, перевод проф. И. Н. Веселовско-
го; статья и общая редакция члена-корреспон-
дента АН СССР А. А. Михайлова, М., 1964.
462
10. Абу Ра й х а н Бирун и. Избранные
произведения, т. V, часть первая, Ташкент, 1973.
11. Кары Ниязов Т.Н. Астрономиче-
ская школа Улугбека. М., 1950.
12. Евклид. Начала. Пер. и комментарии
Д. Д. Мордухай-Болтовского, при ред. участии
М. Я. Выгодского и И. Н. Веселовского, т. I,
кн. I—VI. М.—Л., 1948.
13. Николай Коперник. М.—Л., 1947.
Приложения
454
Приложений
Таблица 1
Таблица прямых хорд в круге
Дуги Прямые Шестидесятые
(градусы) (хорды) доли
1 2 1. з
0; 31,25 0’,1, 2,50
1 1; 2,50 0;1, 2,50
1 V* 1:34,15 0;1, 2,50
2 2; 5,40 0;1, 2,50
2 1/2 2;37, 4 0;1, 2,48
о 3; 8,28 0;1, 2,48
3 >/а 3; 39,52 0;1, 2,48
4 4 ‘/а 4;11,16 4;42,40 0;1, 2,47 0;1, 2,47
5 5; 14, 4 0;1, 2,46
6*/i 5;45,27 0;1, 2,45
С в */а 6; 16,49 6;48,11 0;1, 2,44 0;1, 2,43
7 7 */» 7; 19,33 7;50,54 0;1, 2,42 0;1, 2,41
8 8;22,15 0;1, 2,40
8 ’/• 8;53,35 0;1, 2,39
9 9; 24,54 0;1, 2,38
9 10 9; 56,13 10;27,32 0;1, 2,37 0;1, 2,35
10 »/а 10;58,49 0;1, 2,33
11 11;30, 5 0;1, 2,32
Il 4i 12; 1,21 0; 1, 2,30
12 12; 32,36 0;1, 2,28
12 */а 13; 3,50 0;1, 2,27
13 13; 35, 4 0;1, 2,25
13 1/. 14; 6,16 0;1, 2,23
14 14; 37,27 0;1, 2,21
14 V, 15; 8,38 0;1, 2,19
15 15; 39,47 0;1, 2,17
15 */а 16;10,56 0;1, 2,15
Приложений
465
1 2 8
16 16; 32. 3 0;1, 2,13
16 V. 17; 13, 9 0;1, 2,10
17 17; 44,14 0;1, 2, 7
17 i/, 18; 15,17 0;1, 2, 5
18 18;46,19 0;1, 2, 2
18 !/• 19; 17,21 0;1, 2, 0
19 * 19;48,21 0;1, 1,57
19 V, 20 20; 19,19 0;1, 1,54
20; 50,16 0;1, 1,51
20 i/4 21 21;21,11 21; 52, 6 0;1, 1,48 0;1, 1,45
21 1/ 22; 22,58 0;1, 1,42
22 22; 53,48 0;1, 1,39
22 1/ 23; 24,39 0;1, 1,36
/8 2Я 23; 55,27 0;1, 1,33
92 1 / 24; 26,13 0;1, 1,30
л» /з 24; 56,58 0;1, 1,26
24 V, 25 25; 27,41 0;1, 1,22
25; 58,22 0;1, 1,19
26; 29, 1 0;1, 1,15
25 V» 26 26; 59,58 0;1, 1,11
27;30,14 0;1, 1, 8
26 ’/2 28; 0,48 0;1, 1, 4
27 28; 31,20 0;1, 1, 0
27 1/, 28 28 i/2 9Q 29; 1,50 0;1, 0,56
29;32,18 0;1, 0,52
30; 2,44 0;1, 0,48
29 >/2 30 30; 33, 8 0;1, 0,44
31; 3,30 0;1, 0,40
30 >/2 31; 33,50 0;1, 0,35
31 32; 4, 8 0;1, 0,31
31 '/» 32; 34,22 0;1, 0,27
32 33; 4,35 0;1, 0,22
32 «/. 33; 34,46 0;1, 0,17
33 34; 4,55 0;1, 0,12
33 «/. 34; 35, 1 0;1, 0, 8
456
Приложемжя
1 2 3
34 35; 5, 5 0;1, 0, 3
34 я/. 35; 35, 6 0; 0,59,57
35 36; 5, 5 0; 0,59,52
35 1/, 36; 35, 1 0; 0,59,48
Зв 37; 4,55 0; 0,59,43
36 1/, 37; 34,47 0; 0,59,38
37 38; 4,36 0; 0,59,34
37 1/, 38; 34,22 0; 0,59,24
38 39; 4, 5 0; 0,59,22
38 */2 39; 33,46 0; 0,59,16
39 40; 3,25 0;0,59,11
39 1/, 40; 33, 0 0;0,59, 5
40 41; 2,33 0;0,59, 0
40 >/2 41; 32, 3 0; 0,58,54
41 42; 1,30 0; 0,58,48
41 i/2 42; 30,54 0; 0,58,42
42 43; 0,15 0; 0,58,36
42 1/, 43; 29,33 0;0,58,31
43 43; 58,49 0; 0,58,25
43 >/, 44; 28, 1 0; 0,58,18
44 44; 57,10 0;0,58,12
44 i/2 45; 26,16 0;0,58, 6
45 45; 55,19 0;0,58, 4
45 i/2 46; 24,19 0; 0,57,54
46 46; 53,16 0; 0,57,47
46 */2 47; 22, 9 0; 0,57,41
47 47;51, 0 0; 0,57,34
47 Чг 48; 19,47 0; 0,57,27
48 48; 48,30 0; 0,57,21
48 */2 49; 17,11 0; 0,57,14
49 49; 45,48 0;0,57, 7
49 «/. 50; 14,21 0;0,57, 8
50 50; 42,21 0; 0,56,53
50 >/2 51; 11,18 0; 0,56,46
01 51; 39,41 0; 0,56,39
01 41 52, 8, 0 0; 0,56,32
Приложений
46?
1 1 2 | 8
62 52; 36,16 0; 0,56,25
62 V. 53; 4,29 0; 0,56,18
53 53; 32,38 0; 0,56,10
53 V» 54; 0,43 0;0,56, 3
54 54; 28,44 0; 0,55,55
54 Vi 54; 56,42 0; 0,55,48
55 55; 24,36 0; 0,55,40
55 Vi 55; 52,26 0; 0,55,33
56 56; 20,12 0; 0,55,25
56 Va 56; 47,54 0; 0,55,17
57 57; 10,33 0;0,55, 9
57 Vi 57; 43, 7 0;0,55, 1
58 58; 10,38 0; 0,54,53
58 V2 58; 38, 5 0; 0,54,45
59 59; 5,27 0; 0,54,37
59 Vi 59; 32,45 0,0,54,29
60 60; 0, 0 0; 0,54,21
60 Vi 60; 27,11 0; 0,54,12
61 60; 54,17 0;0,54, 4
61 Vi 61; 21,19 0; 0,53,56
62 61; 48,17 0; 0,53,47
62 Vi 62; 15,10 0; 0,58,39
63 62; 42, 0 0; 0,53,30
63 v« 63; 8,45 0; 0,53,22
64 * 63; 35,25 0; 0,53,13
64 Vi 64; 2, 2 0;0,53, 4
65 64; 28,34 0; 0,52,55
65 Vi 64; 55, 1 0; 0,52,46
66 " 65; 21,24 0; 0,52,37
66 Vi 65; 47,43 0; 0,52,28
67 Z 66; 13,57 0; 0,52,19
67 Vi 66; 40, 7 0; 0,52,10
68 67; 6,12 0;0,52, 1
68 Vs 67; 58, 8 0;0,51,52
69 ’ 67; 58, 8 0; 0,51,43
69 V, 68; 23,59 0;0,51,33
4&8
Приложений
1 1 2 3
70 68; 49,56 0; 0,51,23
70 »/, 69; 15,27 0; 0,51,14
71 69;41, 4 0;0,51, 4
71 Чз 70; 6,36 0; 0,50,55
72 70; 32, 4 0; 0,50,45
72 1/. 70; 57,27 0; 0,50,35
73 71; 22,44 0; 0,50,26
73 Va 71; 47,56 0; 0,50,16
74 72; 13, 4 0;0,50, 6
74 Чз 74; 38, 7 0;0,49,56
75 73; 3, 5 0; 0,49,46
75 Чз 73; 27,58 0; 0,49,36
76 73; 52,46 0; 0,49,26
76 Чз 77 74; 17,29 74; 52, 7 0; 0,49,16 0;0,49, 6
77 Чз 75; 6,39 0; 0,49,55
78 75;31, 7 0; 0,48,45
78 Чз 75; 55,29 0:0,48,34
79 76; 19,46 0; 0,48,24
79 V2 80 76; 42,58 0; 0,48,13
77; 8, 5 0;0,48, 3
80 Vi 81 77; 32, 6 0;0,47,52
77; 56, 2 0; 0,47,41
81 V2 82 78; 19,52 0; 0,47,31
78; 48,38 0;0,47,20
82 Чз fio 79; 7,18 0;0,47, 9
79; 30,52 0; 0,46,53
83 Чз 84 79; 54,21 0;0,46,47
80; 17,45 0; 0,46,36
84 Чз 80; 41, 3 0; 0,46,25
85 87; 4,15 0; 0,46,14
85 Чз 81; 27,22 0;0,46, 3
86 81; 50,24 0; 0,45,52
86 Чз 82; 18,19 0; 0,45,40
87 82; 36, 9 0; 0,45,29
87 Чз 82; 58,54 0; 0,45,18
SVjSei «эЯ***! ^lo^coei ^44°®°!
«5 з З 2* ®2 S2 £2 ®2 S3 £3 £! 2 S Л d d d
Ирилойсёййй
00 ю
ш1О
Ю СО 03 1-4
SSSJS^iSiSiSSSS^rfrZ^OOOOOO^^^OOOrHrHr-KNtNOJCQCOCQ^^^io^
аоооооооооаоаоаоаоаоаоаоаоаоооаоаоооаоа)а)а>о0>фа>с>с>е*ос*а)0>ое>а>
460
Приложений
1 2 8
106 95; 50,11 0; 0,37,42
106 ч- 96; 9, 2 0; 0,87,29
107 96; 27,47 0; 0,37,16
107 1/, 96; 46,24 0;0,87, 3
108 а 97; 4,56 0; 0,86,50
108 1/, 97; 23,20 0; 0,36,36
109 97; 41,38 0; 0,36,23
109 1/, 97; 59,49 0;0,36, 9
110 98; 17,54 0; 0,35,56
110 1/. 98; 35,52 0; 0,35,42
111 * 98; 53,43 0; 0,35,29
Ш V2 99; 11,27 0; 0,35,15
112 99; 29, 5 0;0,35, 1
И2 >/а 99,46,35 0; 0,34,48
113 100; 3,59 0; 0,34,34
ИЗ 1/. 100;21,16 0; 0,34,20
114 100; 38,26 0;0,34, 6
114 1/, 100; 55,28 0; 0,33,52
115 * 101; 12,25 0; 0,33,39
115 1/, 101; 29,15 0; 0,33,25
116 '8 101; 45,57 0;0,33,11
116 11. 102; 2,33 0; 0,32,57
117 102; 19, 1 0; 0,32,43
117 1/„ 102; 35,22 0; 0,32,29
118 102; 51,37 0; 0,32,15
118 Ч. 103; 7,41 0;0,32, 0
119 * 103; 23,44 0; 0,33,46
119 1/. 103; 39,37 0; 0,31,32
120 '* 103; 55,23 0; 0,31,18
120 1/, 104; 11, 2 0;0,31, 4
121 ’ 104; 26,34 0; 0,30,49
121 */. 104;41,59 0; 0,30,35
122 104; 57,16 0; 0,30,21
122 V» 105; 12,26 0;0,80, 7
123 105; 27,30 0; 0,29,52
123 1/» 105; 42,26 0; 0,29,37
Приложения
461
1 1 2 1 3
124 105; 57,14 0; 0,29,23
124 1, 106; 11,55 0;0,29, 8
125 '2 106; 26,29 0; 0,28,54
125 1Z 106; 40,56 0; 0,28,39
126 '* 106; 55,15 0; 0,28,24
126 107; 9,27 0; 0,28,10
127 '* 107; 23,32 0; 0,27,56
127 ,, 107; 37,30 0; 0,27,40
128 107; 51,20 0; 0,27,25
128 108; 5, 2 0; 0,27,10
129 '* 108;18,37 0; 0,26,56
129 108;32 5 0; 0,26,41
130 '2 108; 45,25 0; 0,26,26
130 108; 58,38 0; 0,26,11
131 '» 109; 11,44 0; 0,25,56
131 109; 24,42 0; 0,25,41
132 '« 109; 37,32 0; 0,25,26
132 109; 50,15 0; 0,25,11
133 '» 110; 2,50 0; 0,24,56
133 ,, 110;15,18 0; 0,24,41
134 '* 110; 27,39 0; 0,24,26
134 ,, 110; 39,52 0; 0,24,10
135 '» 110;51,57 0; 0,23,55
135 111; 3,54 0;0,23,40
136 '2 111; 15,44 0; 0,23,25
136 1, 111; 27,26 0;0,23, 9
137 '* 111; 39, 1 0:0,22,54
137 1/ 111; 50,28 0; 0,22,39
138 '2 112; 1,47 0; 0,22,24
138 1/, 112; 12,59 0;0,22, 8
139 112;24, 3 0; 0,21,63
139 1/. 112;35, 0 0;0,21,37
140 112; 45,58 0; 0,21,22
140 112; 56,29 0;0,21, 7
141 113; 7, 2 0; 0,20,51
141 V, 113; 17,25 0; 0,20,36
462
Приложения
1 1 2 1 3
142 113;27,44 0;0,20,20
142 7g 113:37,54 0;0,20, 4
148 113;47,26 0;0,19,49
143 7g 113;57,50 O;O,19,33
144 114; 7,37 0;0,19,17
144 7g 114:17,15 0;0,19, 2
145 114;26,46 0; 0,18,46
145 7g 114;36, 9 0;0,18,30
146 114:45,24 0; 0,18,14
146 7g 114:54,31 0;0,17,59
147 115; 3,30 0;0,17,43
147 7g 115:12,22 0; 0,17,27
148 115:21, 6 0;0,17,ll
148 7. 115:29,41 0:0,16,55
149 115:38, 9 0;0,16,40
149 7, 115:46,29 0;0,16,24
150 115:54,40 0;0,16, 8
150 7g 116; 2,44 0;0,15,52
151 116; 10,40 0;0,15,36
151 7g 116; 18,28 0;0,15,20
152 116;26, 8 0;0,15, 4
152 7. 116:33,40 0;0,14,48
153 116:41, 4 0;0,14,32
153 7g 116:48,20 0;0,14,16
154 116:55,28 0;0,14, 0
154 7g 117; 2,28 0;0,13,44
155 117; 9,20 0:0,13,28
155 7g 117;16, 4 0;0,13,12
156 117; 22,40 0:0,12,56
156 7g 117; 29, 8 0:0,12,40
157 117; 35,28 0;0,12,24
157 7g 117;41,40 0;0,12, 7
158 117; 47,43 0:0,11,51
158 7g 117; 53,39 0:0,11,85
159 117; 59,27 0:0,11,19
159 7g 118; 5, 7 0:0,11, 8
Приложения
463
1 1 2 | 3
160 118:10,37 0:0,10,47
160 ’/2 118;16, 1 0;0,ю,31
161 118:21,16 0;0,ю,14
1611/2 118;26,23 0;0, 9,58
162 118:31,22 0;0, 9,42
162 ‘/а 118:36,13 0;0, 9,25
163 118;40,55 0;0, 9, 9
168 i/2 118:45,30 0;0, 8,53
164 118;49,56 0;0, 8,37
164 >/, 118:54,15 0;0, 8,22
166 118:58,25 0;0, 8, 4
166 i/2 119; 2,26 0;0, 7,48
166 119; 6,20 0;0, 7,31
166 i/8 119; 9, 6 0; 0, 7,15
167 119:13,44 0;0, 6,59
167 i/2 119;17,13 0;0, 6,42
168 119;20,34 0;0, 6,26
168 1/. 119:23,47 0;0, 6,10
169 119:26,52 0;0, 5,54
169 i/2 119:29,49 0;0, 5,37
170 119:32,37 0;0, 5,20
170 >/i 119;35,17 0; 0, 5, 4
171 119;37,49 0; 0, 4,48
171 Va 119:40,13 0;0, 4,31
172 119:42,48 0;0, 4,14
172 i/2 119:44,36 0;0, 3,58
173 119;46,35 0;0, 3,42
173 1/а 119;48,26 0:0, 3,26
174 119;50, 8 0:0, 3, 9
174 Vi 119:51,43 0:0, 2,53
175 119:63,10 0:0, 2,36
175 >/, 119:54,27 0;0, 2,20
176 119:55,38 0;0, 2, 3
176 1/. 119:56,39 0;0, 1,47
177 119:57,32 0:0, 1,30
177 >/, 119:58,18 0;0, 1,14
464
Приложения
1 1 2 1 3
178 119;58,55 0;0, 0,57
178 1/, 119; 59,24 0;0, 0,41
170 119; 59,44 0;0, 0,25
179 119; 59,56 0;0, 0, 9
180 120; 0, 0 0;0, 0, 0
Таблица 2
Таблица склонений
Дуги Дугй
эклип- тики небесного эква- тора ЭКЛИП- ТИКИ небесного эква- тора
1 1 2 3 4
1 0; 24,16 20 7;57, 3
2 0; 48,31 21 8;20, 0
3 1; 12,46 22 8; 42,50
4 1;37, 0 23 9; 5,32
5 2; 1,12 24 9;28, 5
6 2; 25,22 25 9; 50,29
7 2; 49,30 26 10; 12,46
8 3; 13,35 27 10; 34,57
9 3; 37,37 28 10; 56,44
10 4; 1,38 29 11; 18,25
11 4; 25,32 30 11; 39,59
12 4; 49,24 31 12; 1,20
13 5; 13,11 32 12; 22,30
14 5; 36,53 33 12; 43,28
15 6; 0,31 34 13; 4,14
16 6;24, 1 35 13; 24,47
17 6; 47,26 36 13; 45, 6
18 7; 10,45 37 14; 5,11
19 7; 33,57 38 14; 25, 2
Приложения
466
11 2 1 з 4
39 14; 44,39 65 21; 30,11
40 15; 4, 4 66 21; 41, 0
41 15; 23,10 67 21; 51,25
42 15; 42, 2 68 22; 1,25
43 16; 0,38 69 22;11,11
44 16; 18,58 70 22; 20,11
45 16; 37,20 71 22; 28,57
46 16; 54,47 72 22; 37,17
47 17; 12,16 73 22; 45,11
48 17; 29,27 74 22;52,89
49 17; 46,20 75 22; 59,41
50 18; 2,53 76 23; 6,17
51 18; 19,15 77 23;12,27
52 18; 35, 5 78 23; 18,11
53 18; 50,41 79 23; 23,28
54 19; 5,57 80 23; 28,16
55 19; 20,56 81 23;32,30
56 19; 35,28 82 23; 36,35
57 19; 49,42 83 23;40, 2
58 20; 3,31 84 23; 43, 2
59 20; 17, 4 85 23; 45,34
60 20; 30, 9 86 23; 47,39
61 20; 42,58 87 23; 49,16
62 20; 55,24 88 23; 50,25
63 21; 7,21 89 23; 51, 6
64 21; 18,58 90 23; 51,20
30—89
466
Приложения
Таблица 3
Таблицы восхождений по дугам
в десять градусов
Прямая сфера
Наибольший день 12 ч Высота полюса
0;0 градусов
Знак Зодиа- ка Десятки гра- дусов Град.- МИН Сложен- ные време- на
1 2 3 4
Овен 10 9; 10 9; 10
20 9;15 18; 25
30 9;25 27; 50
Телец 10 9;10 37; 30
20 9;53 47; 28
30 10; 16 57; 44
Близнецы 10 10; 34 68; 18
20 10;47 79; 5
30 10; 55 90; 0
Рак 10 10; 55 100;55
20 10;47 111;42
30 10;34 122;16
Лев 10 10; 16 132;32
20 9;58 142;30
30 9;40 152;10
Дева 10 9;25 161;35
20 9; 15 170;50
30 9;10 180; 0
Весы 10 9; 10 189;10
20 9;15 198;25
30 9;25 207;50
Приложения
467
1 | 2 | 8 | 4
Скорпион 10 9;40 217:30
20 9; 58 227;28
30 10;16 237;44
Стрелец 10 10; 34 248;18
20 10; 47 259; 5
30 10;5б 270; 0
Козерог 10 10; 55 280;55
20 10;47 291;42
30 10; 34 302;16
Водолей 10 10;16 312;32
20 9;58 322;30
30 9;40 332;10
Рыба 10 9;25 341;35
20 9;15 350;50
30 9; 10 360 ; 0
Знак Зодиака Десятки градусов АвалИтский за- лив. Наиболь- ший день 12 Члч. Высота полюса 8; 25 град. Мероэ. Наиболь- ший день 13 ч. Высота полюса 8; 16, 27 град.
град.— мин. сложен- ные вре- мена град. — мин. Сложен- ные вре- мена
1 2 | 3 1 * 1 5 6
Овей 10 8;35 8;35 7; 58 7;58
20 8;39 17;14 8; 5 • 16; 3
30 8;52 26; 6 8;17 24:20
468
Приложения
1 |2 1 8 1 * 1 « 1 в
Телец 10 9; 8 35; 14 8; 36 32; 45
20 9; 29 44; 43 9; 1 41; 57
30 9;51 54; 34 9;27 51; 24
Близнецы 10 10; 16 64; 49 9; 56 61; 20
20 10; 35 75; 24 10;23 71; 43
30 10; 61 86;1Б 10;47 82; 30
Рак 10 10; 69 97; 14 11; 3 93; 33
20 10; 69 108;13 11;11 104;44
30 10; 53 119; 6 11; 12 115;56
Лев 10 10;41 129;47 11; б 127; 1
20 10; 27 140;14 10; 55 137;56
30 10;12 150;26 10; 44 148;40
Дева 10 9; 58 160;24 10; 33 159;13
20 9;51 170;15 10; 25 169;38
30 9;45 180; 0 10; 22 180; 0
Весы 10 9;45 189;45 10122 190;22
20 9;51 199;36 10; 25 2ОО;47
30 9; 58 209;34 10; 33 211;20
Скорпион 10 10; 12 219;46 10; 44 222; 4
20 10;27 230;13 10;55 232;59
30 10;41 240;54 11; 5 244; 4
Стрелец 10 10; 53 251;47 11;12 255;16
20 10; 59 262;46 11; 11 266;27
30 10; 59 273;45 11; 3 277;30
Козерог 10 10; 51 284;36 10; 47 288;17
20 10135 295;11 10; 23 298;40
*30 10-15 305;26 9;56 308;36
Приложений
469
1 I2 1 8 1 * « 6
Водолей 10 9;б1 315;17 9127 818; 3
20 9; 29 324;46 91 1 327; 4
30 9; 8 333;64 8;36 335;40
Рыбы 10 8j52 342;46 8;17 343;57
20 8189 351;25 81 5 342; 2
30 8;35 360; 0 7; 58 360; 0
Знак Зодиака Десятки градусов Сиена. Наиболь- ший день 18 V, ч. Высота полю- са 23; 51 град. Нижний Египет. Наибольший день 14 ч, Высо- та полюса 80;22 град.
град. —мин. сложен- ные вре- мена град,— мин. сложен- ные вре- мена
1 I 2 'з 4 5 6
Овен 10 7;23 7; 23 6;48 6;48
20 7129 14; 52 6; 55 13; 43
30 7; 45 22; 37 7;10 20; 53
Телец 10 8; 4 30; 41 7;33 28; 26
20 8;31 39; 12 8; 2 36; 28
30 9; 3 48; 15 8; 37 45; 5
Близнецы 10 9;36 57; 51 9; 17 54; 22
20 10;11 68; 2 10;0 64; 22
ВО 10148 78;45 10;88 75; 0
470
Приложений
1 | 2 | 3 | 4 | 5 | 6
Рак 10 11; 7 20 11;23 30 11;32 89; 52 101; 15 112;47 11;12 11 ;34 11; 51 86; 12 97; 46 109;37
Лев 10 11; 29 124;16 11; 55 121;32
20 11126 136;41 11;54 133;26
30 11;16 146;57 11 ;47 145;13
Дева 10 И; 5 158; 2 11;40 156;53
20 11; I 1691 3 11;35 168;28
30 10;67 180; 0 11; 32 180; 0
Весы 10 Ю; 57 190;57 11; 32 191;22
20 11; 1 201;58 11 ;35 203; 7
зо 11; б 213; 3 11;40 214;47
Скорпион 10 11;16 224;19 11;47 226;34
20 11;25 235;44 11; 54 238;28
30 11;29 247;13 11; 55 250;23
Стрелец 10 11;32 258;45 11;51 262;14
20 11;23 270; -8 11; 34 273;48
30 11; 7 281;15 11;12 285; 0
Козерог 10 10;43 291;58 10; 38 295;38
20 10;11 302; 9 10; 0 305;38
30 9; 36 311;45 9; 17 314;55
Водолей 10 9; 3 320;48 8; 37 323;32
20 8;81 329;19 8; 2 331-;34
30 8 ; 4 337;23 7;33 339; 7
Рыбы 10 7;45 345; 8 7; 10 346;17
20 7;29 357;37 6;55 353;12
30 7;23 360; 0 6;48 360; 0
Приложений
471
Знак Зодиака Десятки градусов Родос. Наибольший день 14 Чяч. Высота полюса 36; 0 град. Геллеспонт. Наибольший день 15ч. Высота полюса 40; 56 град.
град.— мин. сложен- ные вре- мена град,— мин. сложен- ные вре- мена
1 2 3 4 5 1 6
Овен 10 6;14 6;14 5; 40 5;40
20 6; 21 12; 35 5;47 11 ;27
30 6;37 19; 12 6; 5 17; 32
Телец 10 7; 1 27; 13 6;29 24; 1
20 7;33 33; 46 7; 4 31; 5
30 8;12 41; 58 7;46 38; 51
Близнец ы 10 8;56 50; 54 8;38 47; 29
20 9;47 60; 41 9;82 57; 1
30 10; 34 71; 15 10; 29 67; 30
Рак 10 11 ; 16 82; 31 11;21 78; 51
20 11 ; 47 94; 18 12; 2 90; 53
30 12; 12 106;30 12; 30 103;23
Лев 10 12;2О 118;50 12;46 116; 9
20 12;23 131;13 12; 52 129; 1
30 12; 79 143;32 12;51 141;52
Дева 10 12;13 155;45 12; 45 154;37
20 12; 9 167;54 12; 43 167;20
30 12; 6 180 ;0 12; 40 180; 0
472
Приложения
1 | 2 | 3 | 4 | 6 | 6
Весы 10 12; 6 20 12; 9 30 12;13 192; 6 12;40 204;15 12; 43 216;28 12; 45 192;40 205123 218; 8
Скорпион 10 12; 19 228;47 12; 51 230; 59
20 12;23 241;10 12; 52 243151
30 12;20 253;30 12; 46 256;37
Стрелец 10 12;12 265;42 12;30 269; 7
20 11;47 277;29 12; 2 281; 9
30 И; 16 288;45 11121 292;30
Козерог 10 10;34 299;19 10; 29 302; 59
20 9;47 309; 6 9;32 312;31
30 8;56 318; 2 8;38 321; 9
Водолей 10 8;12 326;14 7;46 328;55
20 7;33 333;47 7; 4 335;59
30 7; 1 340;48 6; 29 342;28
Рыбы 10 6;37 347;25 6; 5 348;33
20 6;21 353;46 5147 354;20
30 6;14 360;0 5; 40 360 ;0
Приложений
4t3
Знак Зодиака Десятки градусов Средний Понт. Наибольший день 15 ‘/а ч. Высота полюса 45;1 град. Устье Борисфена* Наибольший день 16 ч. Высо- та полюса 48 град.
град.— мин. сложен- ные вре- мена град.— мин. сложен- ные вре- мена
1 2 3 4 5 6
Овен 10 5; 8 5; 8 4;36 4;36
20 5;14 10;22 4;43 9;19
30 5;33 15; 55 5; 1 14; 20
Телец 10 5;58 21153 5;26 19; 46
20 6134 28; 27 6; 5 25; 51
30 7;2О 35; 47 6; 52 32;43
Близнецы 10 8;15 44; 2 7; 53 40; 36
20 9; 19 53; 21 9; 5 49; 41
30 1О;24 63; 45 10;19 60; 0
Рак 10 11; 26 75;11 11; 31 71;31
20 12115 87; 26 12; 29 84; 0
30 12; 53 100;19 13;15 97; 15
Лев 10 13; 12 113131 13; 40 110;55
20 13122 126;53 13;51 124;46
80 13;22 140;15 13; 54 138;40
Дева 10 13; 17 153;32 13; 49 152;29
20 13; 16 166;48 13; 47 166;16
80 13;12 80; 0 13; 44 80; 0
«4
Приложений
1 2 3 * 1 5 | 6
Весы 10 13; 12 193;12 13;44 193;44
20 13; 16 206;28 13; 47 207; 31
30 13; 17 219;45 13;49 221;20
Скорпион 10 13;22 233; 7 13; 54 235:14
20 13; 22 246;29 13; 51 249; 5
30 13;12 259;41 13; 40 262;45
Стрелец 10 12; 53 272;34 13;15 276; 0
20 12; 15 284;49 12;29 288;29
зо 11 ;26 296;15 11;31 300; 0
Козерог 10 10; 24 306;39 10;19 310;19
20 9;19 315;58 9; 5 319;24
30 8;15 324;13 7;53 327;17
Водолей 10 7; 20 331;33 6; 52 334; 9
20 6;34 338; 7 6; 5 340;44
30 5;58 344; 5 б;26 345;40
Рыбы 10 5;33 349;38 5; 1 350;41
20, 5;14 354;52 4143 355124
30 б; 8 360; 0 4; 36 360; 0
Приложений
475
Знак Зодиака Десятки градусов Юг Британии. Наибольший день 16 Высота полюса б1;30 град. Устье Танаиса. Наибольший день 17 ч. Высо- та полюса 54; 1 град.
град.— мин. сложен- ные вре- мена град.— мин. сложен- ные времена
1 2 2 3 4 5
Овен 10 4; 5 4; 5 3;36 3; 36
20 4;12 8;17 3;43 7;19
30 4;31 12; 48 4; 0 11; 19
Телец 10 4J.56 17; 44 4;26 15; 45
20 5134 23; 18 5; 4 20; 49
30 6;25 29; 43 5; 56 26; 45
Близнецы 10 7;29 37; 12 7; 5 33; 50
20 8;49 46; 1 8;33 42; 23
30 10;14 56; 15 10; 7 52; 30
Рак 10 11; 36 67; 51 11; 43 64; 13
20 12; 45 80; 36 13; 1 77; 14
30 13; 39 94; 15 14; 3 91; 17
Лев 10 14; 7 108;22 14136 105;53
20 14; 24 122;44 14; 52 120;45
30 14; 24 137; 8 14; 54 135;39
Дева 10 14;19 151;27 14; 50 150;29
20 14;18 165;45 14; 47 165; 6
30 14; 15 180; 0 14; 44 180; 0
4t6
ПриложёниЙ
1 1 2 1 8 1 < 1 5 1 «
Весы 10 14;15 194;15 14р14 194;44
20 14;18 206;33 14; 47 209;31
80 14; 19 222;52 14;5О 224;21
Скорпион 10 14;24 237;16 14; 54 239;15
20 14; 22 251;38 14; 52 254; 7
80 14; 7 265;45 14; 36 268;43
Стрелец 10 13;39 279;24 14; 3 282;46
20 12; 45 292; 9 13; 1 295;47
30 11; 36 303;45 11 ;43 307;30
Козерог 10 10;14 313;59 10; 7 317;37
20 8;49 322;48 8;33 326;10
30 7; 29 330;17 7; 5 333;15
Водолей 10 6;25 336;42 5l56 339;11
20 5; 34 342;16 5; 4 344;15
30 4; 56 347;12 4;26 348;41
Рыбы 10 4;31 351;43 4; 0 352;41
20 4; 12 355;55 3;43 356;24
30 4; 5 360; 0 3;36 360; 0
Приложения
477
Таблица 4
Таблица значении углов и дуг,
образуемых пересечением эклиптики и круга,
проходящего через полюсы горизонта
0 7;24 90 ;0 - 0 4;47 111;0 -
1 15; 55 25;26 154;44 1 15;20 0;1 42 ;0
2 29; 3 9;15 170;45 2 29;28 8;0 34;0
3 54; 42 1;38 178;22 3 43; 40 9;15 32;45
4 56; 25 175; 7 5;53 4 58; 13 8;39 33;21
б 70; 2 170;18 9;42 5 72;36 6;53 37; 7
6 83;27 264;41 15;19 6 86;41 5;37 36;23
6;30 90;0 160;57 18; 3 6;14 90;0 4;9 37;51
Лев Весы
0 4; 3 102;30 - 0 16;27 113;51 -
1 14; 20 26; 3 174;57 1 22;8 154;53 72;49
2 28;42 15; 28 9; 32 2 33;50 173;17 54;25
3 42; 43 10; 5 14;55 3 47;20 1;23 46;19
4 56; 49 6; 19 18;41 4 61;22 5; 8 42;34
5 70; 38 2;33 22;27 5 75;39 7; 9 40;33
в 84; 17 177; 0 28; 0 0 90;0 7;24 40;18
6; 26 90;0 174; 51 30; 9
478
Приложения
1 I 2 | 8 | 4 |5 | 6 | 7 8
Скорпион Козерог
0 28;71 111; 0-0 40;18 90;0 -
1 31;46 139; 0 53; 01 42;54 111;24 68;36
2 40;52 157;59 64; 12 49;58 128;51 51; 9
3 52;30 169;23 52;378 59;35 141;39 38;11
4 65;40 176;41 45; 19 4 71;4 151;25 28;35
5 79;18 1;41 40;195 83;31 153;48 21;12
5,46 90:0 4; 8 37;515;30 90;0 161;57 18; 3 Стрелец Водолей
0 36;57 102;30 - 0 36;57 77;30 -
1 39;46 125; 12 79;481 39; 46 100;12 54;48
2 47; 15 143; 5 61;552 47;15 118; 5 36;55
3 57;33 156; 3 48;57 3 57;33 131; 3 23;57
4 69;30 164;48 40;124 69;30 139;48 15;12
5 82;18 171;43 33;17 5 82;18 146;43 8;14
5; 35 90; 0 174; 51 30; 9 5; 35 Рыбы 90г,0 149; 51 5; 9 Телец
0 28; 4 69;0 - 0 4;47 69;0 -
1 31;46 97;0 41; 01 15;20 138;0 180;0
2 40;52 115;59 22; 12 29;28 146 ;0 172;0
3 52; 30 127; 23 10;373 43;40 147;15 170;45
4 65;40 134;41 3;194 58; 3 146;39 171;21
5 79;18 139; 21 178;19 5 72;36 144;53 173; 7
5;4690;0 142;9 175;516;14 Овен 90;0 142; 9 17б;51 Близнецы
0 16;27 66;9 - 0 41;3 77;30 -
1 22; 8 107; 11 25; 71 14;20 1;3 153;57
2 33; 50 125; 35 6;432 28;42 170;28 164;32
8 47; 20 133;41 178;378 42;43 165;5 1б9;55
4 61;22 137;26 174;524 56; 49 161;19 173;41
5 75;39 139; 27 172;515 70;38 157;33 177;27
6 90; 0 139; 42 172;366 84;17 152;0 3; 0
6;25 90;0 149;51 5; 9
Приложения
479
П. Параллель через Сиеиу.
Наименьший день 13 */г ч.,
высота полюса 23; 51 градуса
3 о л 66 я >> и Углы восточн. Углы запади. 3 ей g >> Углы восточн. Углы запади.
11 2 I 8 4 |5 6 7 8
Рак
О 0;0 90;О
1 13;43 176;15
2 27;23 173;51
3 41;20 168;15
4 54;27 166;51
5 67;42 162;42
6 80;36 157;59
6;47 90; 1 153;46
Лев
О 3;21 102;30
1 14;18 176; 4
2 27;56 180; О
3 41;44 179; 3
4 55;14 177;18
5 68;43 173;40
9 81;52 168;56
9;38 90;0 166;53
Скорпион
О 35;31 111;0
1 38;25 133;15
2 46; 2 150;18
3 56;80 161;41
4 68;31 169; 5
5 81; 22 174; 30
5,39 90;0 176«,41
Дева
- О 12;11 111;0 -
3;45 1 18;42 158;40 63;20
6; 9 2 30;57 173;44 48;16
11;45 3 44;22 178; 3 44;57
13; 9 4 58; 1 180; 0 42;0
17;18 5 71;43 179;15 42;45
22; 1 6 85;20 177;39 44;21
26;14 6;21 90; 0 176;41 45;19
Весы
- О 23;51 113;51 -
28; 56 1 27;56 144;10 83;32
25; 0 2 37;36 162;13 65;29
25;57 3 49;42 171;45 55;57
27;42 4 62;47 176;59 50;43
31;20 5 76;20 179; 3 48;39
36; 4 6 90;0 180;0 47;42
38; 4
Козерог
- О 47;42 90; 0 —
88;45 1 49;52 108; 3 71;58
71;42 2 55;52 123;31 56;29
60;19 3 64;37 135;37 44;23
52;55 4 75;12 144;57 35; 3
47;30 5 86;54 152;0 28; О
45;19 5;15 90;0 153;46 26;14
480
Приложения
1 1 2 1 8 1 4 |б | 1 6 1 7 1 8
Стрелец Водолей
0 44;21 1О2;ЗО - 0 44:21 77;80 -
1 46;40 121:30 88;80 1 46:40 96:80 58:30
2 58; 4 137:16 67;44 2 53; 4 112116 22;44
3 62;18 149:26 55;8б 8 62;18 124;25 80;35
4 73;20 157;58 47; 2 4 78;20 132;58 22; 3
б 85; 22 164;46 40;14 6 85;23 189;46 15;14
5;22 I 90;0 166:53 38; 7 5:22 90;0 141;53 13; 7
Рыбы Телец
0 86;21 69;0 - 0 12:11 69:0 -
1 38;26 91;1б 46; 45 1 18;42 116:40 21:20
2 46; 2 108:18 29;42 2 30;57 131;44 6;16
3 56;30 119;41 18:19 3 44;22 136; 3 1;57
4 68;31 127; 5 10:65 4 58; 1 138; 0 0;0
б 81;22 132:30 6:30 Б 71;43 187:15 0;45
5; 39 90:0 134;41 3;19 в 85:20 135:39 2;21
6;21 90;0 134;41 3;19
Овен Близнецы
0 23;61 66; 9 - 0 3;21 77;80 -
1 27:66 96:28 35;50 1 14;18 151; 4 3;56
2 37:36 114;31 17:47 2 27;56 155; 0 0;0
3 49:42 124; 3 8;1б з 41:44 154; 3 0t57
4 62;47 129:17 3; 1 4 55;14 152;18 2;42
б 76;20 131:21 0;57 Б 68;43 148:40 6; 20
6 90;0 182;18 0;0 6 81;52 143;56 11; 4
6;38 90;0 141;58 18; 7
Прилой^ёййй
481
1П. Параллель через Нижний Египет.
Наибольший день 14 ч., высота полюса
__________30; 22 градусов_______
Часы Дуги Углы восточн. 1 | Углы ; западн. Часы Дуги Углы i восточн. Углы западн.
1 2 3 4 сл 6 7 8
Рак Дева
0 6;31 90;0 - 0 18;42 111;0 -
1 14;66 150;0 30 ;0 1 23;18 145;18 76;42
2 27; 23 159;33 20;22 2 33;30 162;25 59;35
3 40;19 160;50 19;30 3 45;36 169;31 52;26
4 53;14 158;51 21; 9 4 58;21 172;10 49;50
5 65;55 156;0 24; 0 5 71;15 172;28 49;32
6 78;15 151;49 28;11 6 84; 7 171; 5 50;55
7 90;0 146;28 Лев 33;32 6;28 90; 0 169;55 52; 5 Весы
0 9; 52 102; 30 - 0 30;22 113;51 - 33;35 137;32 90;10
1 16;45 153;13 51;47 1
2 28;44 166;22 38;38 2 41;39 154;19 73;23
3 41;31 169;26 35; 34 3 52;25 164;10 63;32
4 54;27 169; 8 35;52 4 64;28 169;47 57;55
5 67;17 167; 1 37;59 5 77; 6 172;21 55;21
6 79;48 163;46 41; 14 6 90; 0 173;29 54;13
6;51 90;0 159;49 Скорпион 45; 11 Козерог
0 42;2 111;0 - 0 54;13 90;0 -
1 44;26 129;32 92; 28 1 56; 6 105;34 74;26
2 50;48 144;38 77; 22 2 61;22 119;23 60;37
3 60;19 155;38 66; 27 3 69;17 130;46 49;14
4 71;20 162;56 59; 4 4 78;59 139;30 40;30
5 83;19 167;54 54; 6 5 90;0 146;28 33;32
5; 32 90;0 169;55 52; 5
31-89
482
Приложения
1 1 2 1 3 1 4 | 5| 6 | 7 | 8
Стрелец Водолей
0 50;52 102;30 - 0 50;52 77;30 -
1 52;53 118;39 86;21 1 52;53 93;39 61;21
2 58;27 132;51 72; 9 2 58;27 107;51 47; 9
3 66;44 144;1 60; 59 3 66; 44 119; 1 35;59
4 76;51 152;37 52;23 4 76;51 127;37 27;23
5 88; 9 158;43 46;17 5 88; 9 133;43 21;17
5;9 90; 0 159;49 45;11 5;9 S0; 0 134;49 20;11
Рыбы Телец
0 42;2 69;О - 0 18;42 69;0 -
1 44;26 87;32 50;28 1 23;18 103;18 34;42
2 50;58 103;38 35;22 2 33;30 120;25 17;35
3 60;19 113;33 24;27 3 45;36 127;34 10;26
4 71;20 120;56 17; 4 4 58;21 130;10 7;50
5 83;19 125;54 12; 6 5 71;15 130;28 7;32
5;32 90;0 127;55 10; 5 6 84; 7 129; 5 8;55
6; 28 90; 0 127;55 10;5
Овен Близнецы
0 30;22 66;9 - 0 9;52 77;30 -
1 33; 35 89;50 42;28 1 16;45 128;13 26;47
2 41;3d 106;37 25;41 2 28;44 141;22 13;38
3 52; 25 116; 28 15;Ю 3 41;31 144;26 10;34
4 64;28 122;5 10;13 4 54;27 144; 8 10;52
5 77;6 124;39 7;39 5 67;17 142; 1 12;59
6 90;0 125;47 6;31 6 79;48 138;46 16;14
6; 51 90;0 134;49 20;11
Приложений
483
IV. Параллель через Родос. Наибольший день 14 */г ч., высота полюса 36 ;0 градусов
Часы Дуги Углы восточн. 1 Утлы запади. Часы Дуги Углы восточн. Углы запади.
Рак Дева 0 12;9 90;0 - 0 24;20 111 ;0 - 1 17;47 133;14 46;46 1 27;51 137;38 84;22 2 28; 22 147;46 32;15 2 36;24 1бЗ;б9 68; 1 3 40;27 151;46 28;14 3 47;14 162;10 59;50 4 52;36 151;52 28; 8 4 59 ; 0 166:40 56;20 5 64;36 149;54 30; 6 5 71; 5 166;34 55; 26 6 76;16 146;25 33;35 6 83; 9 165;30 56;30 7 87;23 141;30 38;30 6;35 90; 0 164; 7 57;53 7;15 90;0 140; 1 39;59 Лев Весы 0 15;30 102;30 - 0 36;0 113;51 - 1 20;20 139;32 65;28 1 38;37 133;23 94;19 2 30;28 155;19 49;41 2 45;31 148;23 79;19 3 42; 6 160;37 44;23 3 55; 6 158; 9 69;33 4 54;12 162;11 42;49 4 66; 9 163;58 63;44 5 66; 17 161; 5 43;55 5 77;56 166;36 61; 6 6 78; 7 158;10 46;50 6 90;0 167;51 59;51 7 89;27 153;39 51;21 7;4 90;0 153;36 51;24 Скорпион Козерог 0 47;40 111;0 - 0 59;51 90;0 - 1 49;42 126;50 95;10 1 61;30 103;45 76;15 2 55;26 140;20 81;40 2 66;12 116;10 63;50 3 63;48 150;34 71;26 3 73;22 126;36 53;24 4 73; 55 157;51 64; 9 4 82;24 134;56 45; 4 5 85; 5 162;23 59;32 5;45 90;0 140; 1 39;59 5;25 90; 0 164; 7 57;53
484
ПриЛбйсейия
1
2 | 3 | 4 | 5 | 6 | 7 | 8
Стрелец
0 56; 30 102; 30
1 58; 14116;39
2 63;13 129;23
3 70;41 189; 47
4 80; 2 147;47
4;86 90; 0 153;36
- 0
88;21 1
75;37 2
65;18 3
57;13 4
51; 24 4;
Водолей
56;30 77;30 -
58; 14 91; 39 63;21
63;18 104;23 50;37
70;41 114;47 40;13
80; 2 122;47 32;13
56 90; 0 128;36 26;24
Рыбы
0 47;40 69;0
1 40;42 84;50
2 55;26 98;20
3 63;48 108;34
4 73;55 115;51
5 85; 5 120;28
5;26 90; 0 122; 7
Телец
24;20 69;0 -
27; 51 95;38 42;22
36;24 111;59 26;1
47;14 120;10 17;50
59; 0 123; 4 14;20
71; 5 124;34 13;26
83; 9 123;30 14;30
35 90; 0 122; 7 15;53
- 0
53;10 1
39;40 2
29; 26 3
22; 0 4
17;32 5
15; 58 6
6;
Овен
0 36;0 66; 9 -
1 38;37 85; 41 46;37
2 45; 31 100;47 31;31
3 55; 6 110;27 21;51
4 66; 9 116:16 16; 2
5 77:56 118;54 13;24
6 90;0 120; 9 12; 9
Близнецы
0 15;30 77;30 -
1 20; 20 114;32 40;28
2 30; 28 130;19 24; 41
3 42; 6 135;37 19;23
4 54;12 137;11 17;49
5 66;17 136; 5 18;55
6 78; 7 133;10 21;50
7 89;27 123;39 26;21
7;4 90; 0 128;36 26;24
Приложения
486
V. Параллель через Геллеспонт.
Наибольший день 15 ч.,
высота полюса 40; 56 градусов
Часы Дуги Углы восточн. Углы западн. Часы Дуги Углы восточн. Углы западн.
1 ьэ 3 1 б в 7 00
Рак Дева
0 17:15 90:0 - 0 29;1в 111:0 -
1 21:18 122;32 57:28 1 32; 5 132;80 89:30
2 30:17 138;29 41;31 2 39:22 147:30 74:80
3 41;37 144;18 35;42 3 49; 3 156; 0 6в;0
4 52;25 145;38 34;22 4 59;50 160; 8 61;53
5 63:47 144;28 35;32 5 71; 5 161:24 60;36
6 74;48 141:30 38;30 6 82;22 160:40 61;20
7 85;9 137; 5 42;55 6:42 90;0 158;59 63; 1
7;30 90;0 134; 16 Лев 0 20; 26 102;30 45;44 - 0 Весы 40:56 113;51 -
1 24; 5 131; 6 73; 54 1 43; 8 129; 57 97;45
2 32;37 147; 0 58; 0 2 49; 7 143:38 84; 4
3 43; 8 153:50 51;10 3 57:42 153; 8 74;31
4 54;19 156; 5 48;55 4 67;50 158;47 68;55
5 65;36 155; 8 49;52 5 78;45 161;59 65;43
в 76:46 153:24 51;8в 6 90;0 162;55 64;47
7 87;24 148; в 7;16 90;0 148; в Скорпион 0 52;3в 111:0 55; 54 56:54 - 0 Козерог 64;47 90;0 -
1 54:23 124;4в 97:14 1 6в;15 102;27 77:83
2 59;25 136;55 85; 5 2 70:30 113;35 66;25
3 66;58 146:24 75;36 3 77; 4 122;55 57; 5
4 76;15 153;10 68; 50 4 85;18 130;58 49; 2
486
Приложения
1 1 2 | 3 4 | 5 \ 6 | 7 | 8
5 86;38 167:45 5;18 90;0 158;59 64:15 4:30 90:0 134;16 45;44 63;1
Стрелец Водолей
0 61;26 102:30 1 63;0 115; 5 2 67:24 126:29 з 74:13 136:10 4 82;48 143;45 4;44 90:0 148; 6 - о 61:26 77:30 - 89;55 1 63:0 90; 5 64;55 78;31 2 67;24 101:29 53;31 68;50 3 74;13 111:10 43;50 61:15 4 82;48 118;45 36:15 56:54 4;44 90;0 126; 6 31;54
Рыбы Телец
0 52;36 69:0 - 0 29:16 69;О -
1 54;23 82;46 55;14 1 32; 5 90:30 47;30
2 59:25 94;55 43; 5 2 39:22 105;30 32;80
3 66;58 104;24 33;36 3 49; 3 114; 0 24;0
4 76:15 Ш;Ю 26;50 4 59;50 118; 7 19;53
5 86;38 115;45 22;15 5 71; 5 119;24 18;36
5;18 90;0 116:59 21; 1 6 82;22 118;40 19:20
6;42 90;0 116;59 21; 1
Овен Близнецы
0 40:56 66; 9 - 0 20;26 77;30 -
1 43; 8 82;15 50; 3 1 24; 5 106; 6 48;54
2 49; 7 95;56 36;22 2 32;37 122; 0 33;0
3 57;42 105;26 26;52 3 43; 8 128;50 26;10
4 67;50 111; 5 21;13 4 54;19 131; 5 23,; 55
5 78;50 114;17 18; 1 5 65;36 130; 8 24;52
6 90:0 115;13 17; 5 6 76;46 128;24 26;36
7 87;24 124; 6 30;54
7;16 90;0 123; 6 31;54
Приложения
487
VI. Параллель через Средний Понт.
Наибольший день 15 ’/з ч.,
высота полюса 45 ;1 градусов
3 о cd Ст1 к Углы восточн. Углы запади. а о cd tr s >> Углы восточн. Углы запади.
11 2 3 5 6 8
Рак Дева
0 21;10 90; 0 - 0 33;21 111;0 -
1 24;32 116; 5 63;55 1 35; 43 129;15 92;45
2 32;12 131;30 48;30 2 42; 4 142;50 79;10
3 42; 1 130;17 41;43 3 50;46 151; 9 70;51
4 52;59 140;31 39;29 4 60;44 155;31 66;29
5 63; 4 140; 2 39;58 5 71;12 157; 3 64;57
в 73;24 137;32 42;28 6 81; 46 156;81 65;29
7 83;17 133;26 46;34 6;48 90:0 154;43 67;17
7;45 90;0 129;21 Лев 50; 39 Весы
0 24;31 102;30 - 0 45; 1 113;51 -
1 27;29 124;49 80;11 1 46;55 128;19 99;23
2 34;48 140;47 64;13 2 52;17 140;26 87;16
3 44;20 148; 5 56;55 3 60; 1 149; 4 78;38
4 54;37 151; 5 58;55 4 69;19 154;48 72;54
5 65;15 151; 7 53453 5 79;28 157;55 69;47
6 75;39 149;20 55;40 6 90;0 158;50 68;52
7 85;39 145;39 59; 21
7;28 90;0 143;25 Скорпион 61; 35 Козерог
0 56;41 111;0 - 0 68;52 90;0 -
1 58;19 123;31 98;29 1 70;14 101;11 78;49
2 62;49 134;16 87;44 2 74; 5 111;30 68;30
3 69;42 143;12 78; 48 3 80; 6 120;29 59;31
4 78; 16 149;31 72;29 4 87;42 128;13 51;47
5 87;56 154; 6 67;54 4:15 90:0 129;21 50;39
6; 12 90 ;0 154;43 67; 17
488
Приложения
1 1 2 | 3 | 4 | 5| 1 в | 7 | 8
0 Стрелец 65;81 102;30 - 0 Водолей 65;31 77;30 -
1 66;55 113:50 91;10 1 66;55 88;50 66;10
2 70;58 124;21 80; 39 2 70;58 99;21 5Б;39
3 77;14 183;19 71;41 3 77;14 108;19 46;41
4 85;10 140:20 64; 40 4 85;10 115;20 39;40
4;32 90;0 143;25 61;35 4;32 90;0 118;25 36;35
0 Рыбы 56;41 69;0 - 0 Телец 33;21 69;0 -
1 58; 19 81; 31 56;29 1 35;43 87;15 50;45
2 62;49 92;16 45;44 2 42; 4 100;50 37;10
3 69;42 101;12 36;48 3 50;46 109; 9 28;51
4 78;16 107;31 30;29 4 60; 44 113:31 24;29
5 87;56 112; 6 25;54 5 71;18 115; 3 22;57
5; 12 90;0 112;43 26;17 6 81;46 114:31 23;29
6;48 90;0 112;43 25;17
Овен Близнецы
0 45;1 66; 9 - 0 24;31 77;30 -
1 46; 55 80; 87 51;41 1 27;29 99;49 55;11
2 52; 17 92;44 39;34 2 34;48 115;47 39;13
3 60; 1 101;22 30;56 3 44;20 123; 5 31;55
4 69; 19 107; 6 25;12 4 54;37 126; 5 28;55
5 79; 28 110;13 22; 5 5 65;15 126; 7 28;53
6 90;0 111, 8 21;10 6 75;39 124;20 80;40 7 85;39 120;89 34;21 7;28 90;0 118;25 36;35
Приложения
489
g
ев
О
1
2
3
4
б
6
7
8
УП. Параллель через Ворисфен.
Наибольший день 16 ч.,
высота полюса 48; 32 градусов
1 I 2 | 3 | 4 I 6 | 6 | 7 | 8
Рак
Дева
24;41 90;0 -
27;30 111;44 68;16
34; 9 126; 7 53;53
43; 2 133;18 46;42
52;44 136; 6 43;54
62;40 136; 4 43;54
72;24 134; 0 46; О
81;88 130;16 49;44
90;0 124;58 35; 2
О 36;52 111;0
1 38;56 126;45
2 44;31 139; 7
3 52;25 147; 9
4 61; 35 151;36
5 71;22 153;23
6 81;17 152;58
6;54 90;0 151;22
95; 15
82;53
74; 51
70;24
68; 37
69; 2
70; 38
Лев
Весы
О 28; 2 102;80 - О
1 30;32 122; 9 82;51 1
2 36;55 135;54 69; 6 2
3 45;30 143$28 61;32 3
4 55; 8 146;50 58;10 4
5 64;59 147;19 57;41 5
6 74; 47 145;46 59;14 6
7 84;10 142;27 67;33
7;40 90;0 189:20 65;40
48; 32
50; 21
54; 59
62; 5
70:41
80; 8
90; О
113;51
126;30
187;40
145; 46
151;18
154;23
155;19
101;12
90; 2
81; 56
76;24
78; 19
72;28
Скорпион . Козерог
О 60;12 111; 0-0 72;23 90;0 -
1 61; 38 122; 5 99;55 1 73;38 100;15 79;45
2 65;36 132;10 89;50 2 77;10 169;47 70;13
3 72; 5 140;26 87;34 3 82;44 118; 3 61;57
490
Приложения
11 2 1 3 1 4 1 | 5 1 6 | 7 1 8
4 80;3 146;28 75;32 4 90;0 124;58 55; 2
б 89;3 161; 2 70;58
5;6 90;0 151;22 70;38
Стрелец Водолей
0 69; 2 102;30 - 0 69; 2 77;30 —
1 70;20 112;49 42;11 1 70;20 87;49 67; 11
2 74; 2 122;31 82;29 2 74; 2 97;31 57;29
3 79;48 130;49 74;11 3 79;48 105;49 49; 11
4 87;14 737;25 67;35 4 87;14 112;25 42; 33
4;20 90;0 139;20 65;40 4;20 90;0 114;20 40; 40
Рыбы Телец
0 60; 12 69; 0 - 0 36;52 65;0 —
1 61; 38 80; 5 57; 55 1 38;56 84;45 53; 15
2 65;36 90;16 47;44 2 44;31 97; 7 40; 53
3 72; 5 98;26 39;34 3 52;25 105; 9 32; 51
4 30; 3 104;28 33;32 4 61;35 109;36 28; 24
5 89; 3 109; 2 28;58 5 71;22 111;23 26;37
5;6 90; 0 109;22 28;38 6 81;17 110;53 27; 2
6; 54 90;0 109;22 28; 38
Овен Близнецы
0 48;32 66; 9 - 0 28; 2 77;30 —
1 50;21 78;48 53;30 1 30;32 97; 9 57; 51
2 54;59 89;58 42;20 2 36; 55 1Ю;54 44; 6
3 62; 5 98; 4 34; 14 3 45; 30 118;28 36; 32
4 70;41 103;36 28;42 4 55; 3 121;50 33; 10
5 80; 8 106;41 25;37 5 64;59 122;19 32;41
в 90; 0 107;37 24;41 6 74;47 120;46 34; 14
7 84; 10 117; 27 37; 33
7;40 90; 0 114;20 40;40
Приложения
491
Таблица 5
Таблицы равномерного движения Солнца
Расстояние от апогея 265; 15 градусов.
Среднее начальное положение О;45 градусов
Рыб для 1 числа месяца Тот 1-го года
Набонассара
Восемнадцати* летки Градусы
1 2
18 355;37,25,36,20,34,30
36 351; 14,51,12,41,9,0
54 346:52,16,49,1,43,30
72 342; 29,42,25,22,18,0
90 338:7,8,1,42,52,30
108 333:33,38,3,27,0
126 329:21,59,14,24,1,30
144 324:59,24,50,44,36,0
162 320:36,50,27,5,10,30
180 316:14,16,3,25,45,0
198 311:51,41,39,46,19,30
216 307:29,7,16,6,54,0
234 303:6,32,52,27,28,30
252 298:43,58,28,48,3,0
270 294:21,24,5,8,37,30
288 289:58,49,41,29,12,0
306 285:36,15,17,49,46,30
324 281; 13,40,54,10,21,0
342 276:51,6,30,51,55,30
360 272:28,32,6,12,30,0
378 268:5,57,43,30,4,30
396 273:43,23,19,32,39,0
414 259:20,48,55,53,13,30
432 254:58,14,32,13,48,0
450 250:35,40,8,34,22,30
468 246:13,5,44,54,57,0
492
Приложения
1 1 2
486 504 522 540 558 576 594 612 630 648 666 684 702 720 738 756 774 792 810 241; 50,31,21,15,31,30 237; 27,56,57,36,6,0 233-,5,22,33,56,40,30 228:42,48,10,17,15,0 224:20,13,46,37,49,30 219:57,39,22,58,24,0 215:35,49,59,18,58,30 211; 12,30,35,39,33,0 . 206; 49,56,12,0,7,30 202:27,21,48,20,42,0 198:4,47,24,41,16,30 193:42,13,1,1,51,0 189; 19,38,37,22,25,30 184:57,4,13,43,0,0 180:34,29,50,3,34,30 176:11,55,26,24,9,0 171:49,21,2,44,43,30 167:26,46,39,5,18,0 163; 4,12,15,25,52,30
Прибавление расстояния от апогея Солнца
5; 30 градусов Близнецов до среднего
начального положения в 1-й год Набонассара
на 0; 45 градусах Рыб 265; 15 градусов
Простые годы Градусы
1 2
1 2 3 4 5 359; 45,24,45,21,8,35 359:80,49,80,42,17,10 359:16,14,16,3,25,45 359; 1,89,1,24,34,20 358:47,3,46,45,42,55
Приложений
49§
1 1 2
6 7 8 9 10 11 12 13 14 15 16 17 18 358; 32,28.32,6,51,30 358; 17,53,17,28,0,5 358:3,18,2,49,8,40 357; 48,42,48,10,17,15 357; 34,7,33,31,25,50 357:19,32,18,52,34,25 357:4,57,4,13,43,0 356:50,21,49,34,51,35 356; 35,46,34,56,0,10 356:21,11,20,17,8,45 356; 6,36,5,38,17,20 355:52,0,50,59,25,55 355:37,25,36,20,34,30
Часы Градусы
1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0:2,27,50,43,3,1 0;4,55,41,46,6,2 О;7,23,32,9,9,3 0:9,11,22,52,12,5 0:12,19,13,35,15,6 0:14,47,4,18,18,7 0:17,14,55,1,21,9 0:19,42,45,44,24,10 0:22,10,36,27,27,11 0:24,38,27,10,30,12 0:27,66,17,59,33,14 0:29,34,8,36,36,15 0:32,1,59,19,39,16 0:34,29,50,2,42,18 0:36,57,40,45,45,19 0:39,25,31,28,48,20
ш
Приложения
1 1 2
17 18 19 20 21 22 23 24 0; 41,53,22,11,51,21 0:44,21,12,54,54,23 0:46,49,3,37,57,24 0:49,16,54,21,0,25 0:51,44,45,4,3,27 0:54,12,35,47,6,28 0:45,40,26,30,9,29 0^59,8,17,13,12,31
Египетские месяцы Градусы
30 60 90 120 150 180 210 240 270 300 330 360 29:34,8,36,36,15,30 58:8,17,13,12,31,0 88:42,25,49,48,46,30 118:16,34,26,25,2,0 147:50,43,3,1,17,30 177:24,51,39,37,33,0 206:59,0,16,13,48,30 236:33,8,52,50,4,0 266:7,17,29,26,19,30 295:41,26,6,2,35,0 325:15,34,42,36,50,30 354:49,43,19,15,6,0
Дни Градусы
1 2
1 2 3 0:59,8,17,13,12,31 1:58,16,34,26,25,2 2:57,24,51,39,37,33
Приложений
49$
1
2
4
б
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
3:56,33,8,52,50,4
4:55,41,26,6,2,35
5:54,49,43,19,15,6
6:53,58,0,32,27,37
7:53,6,17,45,40,8
8:52,14,34,58,52,39
9:51,22,52,12,5,10
10:50,31,9,25,17,41
11;49,39,26,38,30,12
12:48,47,43,51,42,43
13:47,56,1,4,55,14
14;47;4,18,18,7,45
15:46,12,35,31,20,16
16:45,20,52,44,32,47
17:44,29,9,57,45,18
18:43,37,27,10,57,49
19:42,45,44,24,10,20
20:41,54,1,37,22,51
21:41,2,18,50,35,22
22:40,10,35,3,47,53
23:39,18,53,17,0,24
24:38,27,10,30,12,55
25:37,35,27,43,25,26
26:36,43,44,56,37,57
27:35,52,2,9,50,28
28:35,0,19,23,2,59
29:34,8,36,26,15,30
496
Приложения
Таблица 6
Таблица солнечного неравенства
Градусы равно- мерных движе- ний Общие числа Простаферезы (уравнения)
1 2 3
Квадранты 6 354 0; 14
у апогея 12 348 0;28
18 342 0;42
24 336 0;56
30 330 1; 9
36 324 1;21
42 318 1;32
48 312 1;43
54 306 1;53
60 300 2; 1
66 294 2; 8
72 288 2; 14
78 282 2;18
84 276 2;21
90 270 2;23
Квадранты 93 267 2;23
у перигея 96 264 2;23
99 261 2;22
102 258 2; 21
105 255 2;20
108 252 2;18
111 249 2;16
114 246 2; 13
117 243 2; 10
120 240 2; 6
123 237 2; 2
126 234 1; 58
129 231 1;54
132 228 1;49
Приложения
497
1 2 8
Квадранты 136 226 1;44
у перигея 138 222 1; 39
141 219 1; 33
144 214 1;27
147 213 1;21
150 210 1;14
153 207 1; 7
156 204 1; 0
159 201 0;53
162 198 0;46
165 195 0;39
168 192 0;32
171 189 0;24
174 186 0; 16
177 183 0; 8
180 180 0; 0
Таблица 7
Таблица средних движений Луны
Прибавление долготы, 12; 22 градусов
Тельца
Восемнадцати- летки Градусы
1 2
18 36 54 72 90 108 126 144 168; 49,52,9,9,45,0 337:39,44,18,19,30,0 146:29,36,27,29,15,0 315:19,28,36,39,0,0 124:9,20,45,48,45,0 292:59,12,54,58,30,0 101:49,5,4,8,15,0 270:38,57,13,18,0,0
32—89
498
Приложения
> 1 2
162 180 198 216 234 252 270 288 306 324 342 360 378 396 414 432 450 468 486 504 522 540 558 576 594 612 630 648 666 684 702 720 738 756 ' 774 792 810 79;28.49,22,27.45,0 248:18,41,31,37,30,0 57:8,33,40,47,15,0 225:58,25,49,57,0,0 34:48,17,59,6,45,0 203:38,10,8,16,30,0 12:28,2,17,26,15,0 181:17,54,26,36,0,0 350:7,46,35,45,45,0 158:57,38,44.55,30,0 327:47,30,54,5,15,0 136:37,23,3,15,0,0 305:27,15,12,24,45,0 114:17,7,21,34,30,0 283:6,59,30,44,15,0 91:56,51,39,54,0,0 260:46,43,49,3,45,0 69;36:35,58,13,30,0 238:25,7,23,15,0 47:16,20,16,33,0,0 216:6,12,25,42,45,0 24:56,4,34,52,30,0 193:45,56,44,2,15,0 2:35,48,53,12,0,0 171:25,41,2,21,45,0 340:15,33,11,31,30,0 149:5,25,20,41,15,0 317:55,17,29,51,0,0 126:45,9,39,0,45,0 295:35,1,48,10,30,0 104:24,53,57,20,15,0 275:14,46,6,30,0,0 82:4,38,15,39,45,0 250:54,30,24,49,30,0 59:44,22,33,59,15,0 228:34,14,43,9,0,0 37:24,6,52,18,45,0
Приложения
499
Прибавление аномалии 268; 49 градусов
Восемнадцати* летки Градусы
1 2
18 38 54 72 90 108 126 144 182 180 198 216 234 252 270 288 306 324 342 360 378 396 414 432 450 468 486 504 522 540 558 576 156,56,14,36,22,10,30 313;52,29,12,44,21,0 110; 48,43,49,6,81,30 267; 44,58,25,28,42,0 64; 41,13,1,50,52,30 221;37,27,38,13,3,0 18:33,42,14,35,13,30 175; 29,56,50,57,24,0 332; 26,11,27,19,34,30 129:22,26,3,41,45,0 286; 18,40,40,3,55,30 83:14,55,16,26,6,0 240:11,9,52,48,16,30 37:7,24,29,10,27,0 194:3,39,5,32,37,30 350; 59,53,41,54,48,0 147:56,8,18,16,58,30 304; 52,22,54,39,9,0 101;48,37,31,1,19,30 258; 44,52,7,23,30,0 55:41,6,43,45,40,30 212:37,21,20,7,51,0 9; 83,85,56,30,1,30 116:29,50,32,52,12,0 323;26,5,9,14,22,30 120; 22,19,45,36,33,0 277; 18,34,21,58,43,30 74; 14,48,56,20,54,0 231; 11,31,34,43,4,30 28; 7,18,11,5,15,0 185; 3,32,47,27,25,80 341:59,47,23,49,36,0
500
Приложения
1 1 2
594 612 630 648 666 684 702 720 738 756 774 792 810 138; 56,2,0,11,46,30 295;52,16,36,33,57,0 92:48,31,12,56,7,30 249; 44,45,49,18,18,0 46:41,0,25,40,28,30 203:37,15,2,2,39,0 0:33,29,38,24,49,30 157:29,44,14,47,0,0 314:25,58,51,9,10,30 111:22,13,27,31,21,0 268:18,28,3,53,31,30 65:14,42,40,15,42,0 222:10,57,16,37,52,30
Прибавление широты 354; 15 градусов
Восемнадцати- летки Градусы
1 1 2
18 36 54 72 90 108 126 144 162 180 198 216 234 252 156:50,9,49,19,31,30 313:49,19,38,39,3,0 110 ;'ЗО,29,27,58,34,30 267:20,39,17,18,6,0 64:10,49,6,37,37,30 221:0,58,55,57,9,0 17:51,8,45,16,40,30 174:41,18,4,36,12,0 331:31,28,23,55,43,30 128:21,38,13,15,15,0 285:11,48,2,34,46,30 82:1,57,51,54,18,0 238:52,7,41,13,49,30 35:42,17,30,33,21,0
Приложения
501
1
270
288
306
324
342
360
378
396
414
432
450
468
486
504
522
540
558
576
594
612
630
648
666
684
702
720
738
756
774
792
810
2
192; 32,27,19,52,52.30
349; 22,37,9,12,4,0
146; 12,47,58,31,55,30
303; 2,56,47,51,27,0
99:53,6,37,10,58,30
256:43,16,26,30,30,0
53;33,26,15,5O,l,3O
210; 23,36,5,9,33,0
7; 13,45,54,29,4,30
164; 3,55,43,48.36,0
320; 54,5,33,8,7,30
117; 44,15,22,27,39,0
274; 34,25,11,47,10,30
71; 24,35,1,6,42,0
128; 14,44,50,26,13,30
25; 4,54,39,45,45,0
181; 55,4,29,5,16,30
338:45,14,18,24,48,0
135;35,24,7,44,19,3O
292; 25,33,57,3.51,0
89;15,4Э,46,23,22,30
246; 5,53,35,42,54,0
42:56,3,25,2,25,30
199:46,13,14,21,57,0
356:36,23,3,41,28,30
153:26,32,53,1,0,0
310:16,42,42,20,31,30
107:6,52,31,40,3,0
263:57,2,20,59,34,30
60:47,12,10,19,6,0
217:37,21,59,38,37,30
502
Приложения
Прибавление элонгации: 70;37 градусов
Восемнадцати* летки Градусы
1 2
18 36 54 72 90 108 126 144 162 180 198 216 234 252 270 288 306 324 342 360 378 396 414 432 450 468 486 504 522 540 558 576 173;12,26,32,49,10,30 346:24,53,5,38,21,0 159:37,19,38,27,31,30 332:49,46,11,16,42,0 146:2,12,44,5,52,30 319:14,39,16,55,3,0 132:27,5,49,44,13,30 305:39,32,22,33,24,0 118:51,58,55,22,84,30 295:4,25,28,11,45,0 105:16,52,1,0,55,30 278:29,18,33,50,6,0 91:41,45,6,39,16,30 264:54,11,39,28,27,0 78:6,38,12,17,37,30 251:19,4,45,6,48,0 64:31,31,17,55,58,30 237:43,67,50,45,9,0 50:56,24,23,34,19,30 224:8,50,56,23,30,0 37:21,17,29,12,40,30 210:33,44,2,1,51,0 23:46,10,34,51,1,30 196:58,37,7,40,12,0 10:11,3,40,29,22,30 183:23,13,18,33,0 356:35,56,43,7,43,30 169:48,23,18,56,54,0 343:0,49,51,46,4,30 156:13,16,24,35,15,0 329:25,42,57,24,25,30 142:38,9,30,13,86,0
Приложения
503
1 1 2
594 612 630 648 666 684 702 720 738 756 774 792 810 315; 50,36,3,2,46,30 129; 3,2,35,51,57,0 302; 15,29,8,41,7,30 115; 27,55,41,30,18,0 288;40,22,14,19,28,30 101;52,48,47,8,39,0 275:5,15,19,57,49,30 88; 17,41,52,47,0,0 261:30,8,25,36,10,30 74:42,34,58,25,21,0 247; 55,1,31,14,31,30 61:7,28,4,3,42,0 234;19,54,36,52,52,30
Прибавление долготы
Простые годы Градусы
1 1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 129:22,46,13,50,32,30 258:45,32,27,41,5,0 28:8,18,41,31,37,30 157:31,4,55,22,10,0 286:53,51,9,12,42,30 56:16,37,23,3,15,0 185:39,23,36,53,47,30 315:2,9,50,44,20,0 84:24,56,4,34,52,30 213:47,42,18,25,25,0 343:10,28,32,15,57,30 112:33,14,46,6,30,0 241:56,0,59,57,2,30 11:18,47,13,47,35,0
504
Приложения
1 1 2
15 16 17 18 140; 41,33,27,38,7,30 270;4,19,41,28,40,0 39:27,5,55,19,12,30 168:49,52,9,9,45,0 Прибавление долготй
Часы Градусы
1 1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0:32,56,27,26,23,46 1:5,52,54,52,47,32 1:38,49,22,19,11,18 2:11,45,49,45,35,5 2:44,42,17,11,58,51 3:17,38,44,38,22,37 3:50,35,12,4,46,23 4:23,31,39,31,10,10 4:56,28,6,57,3,56 5:29,24,34,23,57,42 6:2,21,1,50,21,28 6:35,17,29,16,45,15 7:8,13,56,43,9,1 7:41,10,24,9,32,47 8:14,6,51,35,56,33 8:47,3,19,2,20,20 9:19,59,46,28,44,6 9:52,56,13,55,7,52 10:25,52,41,21,31,38 10:58,49,8,47,55,25 11:31,45,37,14,19,11 12:4,42,3,40,42,57 12:37,38,31,7,6,43 13:10,34,58,33,30,30
Приложения
505
Прибавление аномалии
Простые годы Градусы
1 2
1 88:43,7,28,41,13,55
2 177:26,14,57,22,27,50
3 266:9,22,26,3,41,45
4 354152,29,54,44,55,40
5 83:35,37,23,26,9,35
6 117:18,44,52,7,23,30
7 261:1,52,20,48,37,25
8 349:44,59,49,29,51,20
9 78; 28,7,18,11,5,15
10 167:11,14,46,52,19,10
11 255:54,22,15,33,33,5
12 344:37,29,44,14,47,0
13 73:20,37,12,56,0,55
14 162:3,44,41,37,14,50
15 250146,52,10,18,28,45
16 339:29,59,38,59,47,40
17 68:13,7,7,40,56,35
18 156:56,14,26,22,10,30
Прибавление аномалии
Часы Градусы
1 | 2
1 2 3 4 5 0:32,39,44,50,44,40 1:5,19,29,41,29,20 1:37,59,14,32,14,0 2:10,38,59,22,58,40 2:43,18,44,13,48,20
506
Приложения
1 1 2
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 3;15,58,29,4,28,0 3:48,38,13,55,12,40 4:21,17,58,45,57,20 4:53,57,43,36,42,0 5:26,37,28,27,26,40 5:59,17,13,18,11,20 6x31,56,58,8,56,0 7;4,56,58,8,56,0 7:37,16,27,50,25,19 8:9,56,12,41,9,59 8:42,35,57,21,54,39 9:15,42,22,39,19 9:47,55,27,13,23,59 10:20,35,12,4,8,39 10:53,14,56,54,53,19 11:25,54,41,45,37,59 11:58,34,26,36,22,39 12:31,14,11,27,7,19 13:3,53,56,17,51,59
Прибавление широты
Простые годы Градусы
1 2
1 2 3 4 5 6 7 8 148:42,47,12,44,25,5 297; 25,34,25,28,50,10 86:8,21,38,13,15,15 234:51,8,50,57,40,20 23:33,56,3,42,5,25 172:16,43,16,26,30,30 820:59,30,29,10,55,35 109:42,17,41,55,20,40
Приложения
607
1 2
9 268; 25,4.64,39.45,46
10 47; 7,62,7,24,10,50
11 196; 50,89,20,8,36,65
12 344; 88,26,82,63,1,0
13 133; 16,13,45,87,26,5
14 281; 59,0,68,21,51,10
15 70;41,48,11,6,16,15
16 219:24,35,23,50,41,20
17 8:7,22,36,35,6,25
18 156; 60,9,49,19,31,30
Прибавление широты
Часы Градусы
1 2
1 0:38,4,24,9,32,22
2 1;6,8,48,19,4,48
3 1; 39,13,12,28,37,5
4 2; 12,17,36,38,9,26
5 2; 45,22,0,47,41,48
6 3:18,26,24,57,14,9
7 3:61,80,49,6,46,81
8 4:24,35,18,16,18,52
9 4; 57,39,37,25,51,14
10 5:30,44,1,35,23,35
11 6; 3,48,25,44,55,57
12 6:36,52,49,54,28,19
13 7:9,57,14,4,0,40
14 7; 43,1,38,1,38,1
15 8:16,6,2,23,5,23
16 8:49,10,26,32,37,45
17 9:22,14,50,42,10,6
18 9:55,19,14,51,42,28
508
Приложения
1 1 2
19 20 21 22 23 24 10; 28,23,89,1,14,49 11; 1,28,3,10,47,11 11 ;34,32,27,20,19,32 12; 7,36,51,29,51,54 12; 40,41,15,39,24,15 13; 13,45,39,48,56,37
Прибавление элонгации
Простые годы Градусы
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 129;37,21,28,29,23,55 259;14,42,56,58,47,50 28; 52,4,25,28,11,45 158; 29,25,53,57,35,40 288; 6,47,22,26,59,35 57:44,8,50,56,23,30 187; 21,30,19,25,47,25 316:58,51,47,55,11,20 86:36,13,16,24,35,15 216; 13,34,44,53,59,10 345:50,56,13,23,28,5 115; 28,17,41,52,47,0 245; 5,39,10,22,10,55 14; 43,0,38,51,34,50 144; 20,22,7,20,58,45 273; 57,43,34,50,22,40 43; 35,5,4,19,46,35 173:12,26,32,49,10,30
Приложения
609
Прибавление элонгации
Часы Градусы
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 16 17 18 19 20 21 22 23 24 0;30,28,36,43,20,45 1:0,57,13,26,41,30 1:31,26,60,10,2,15 2:1,64,26,53,23,0 2:32,23,3,36,43,45 3:2,51,40,20,4,30 3:33,20,17,3,25,15 4:3,48,53,46,46,0 4:34,17,30,30,6,45 5:4,46,7,13,27,30 5;35,14,43,56,48,15 6:5,43,20,40,9,0 6:36,11,57,23,29,44 7:6,40,34,6,50,29 7:37,9,10,50,11,14 8:7,37,47,33,31,59 8; 38,6,24,16,52,44 9:8,35,1,0,13,29 9:39,3,37,43,34,14 10:9,32,14,26,54,59 10:40,0,61,10,15,44 11:10,29,27,53,36,29 11:40,58,4,36,57,14 12:11,26,41,20,17,59
510
Приложения
Прибавление долготы
Месяцы Градусы
30 60 90 120 150 180 210 240 270 300 330 360 35 *,17,29.16,46,15,0 70; 34,58,83,30,30,0 105; 52,27,50,15,45,0 141; 9,57,7,1,0,0 176; 27,26,23,46,15,0 211:44,55,40,41,30,0 247; 2,24,57,16,45,0 282;19,54,15,2,0,О 317; 37,23,30,47,15,0 352:54,52,47,32,30,0 28:12,22,4,17,45,0 63;29,51,21,3,0,0
Дни Градусы
1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 13:10,34,58,33,30,30 26; 21,9,57,7,1,0 39; 31,44,55,40,31,30 52:42,19,54,14,2,0 62,52,54,52,47,32,30 79:3,29,51,21,3,0 92:14,4,49,54,33,30 105; 24,39,48,28,4,0 118:35,14,47,1,34,30 131:45,49,45,35,5,0 144:56,24,44,8,35,30 158:6,59,42,42,6,0 171:17,34,41,15,86,30 184:28,9,39,49,7,0
Приложения
611
1 1 2
16 197; 38,44,38,22,37,30
16 210; 49,19,36,56,8,0
17 223 *,59,54,35,29,38,30
18 237;10,29,34,3,9,0
19 250;21,4,32,36,39,30
20 263;31,39,31,10,10,0
21 276:42,14,29,43,40,30
22 289:52,49,28,17,11,0
23 308:3,24,26,50,41,30
24 316:13,59,25,24,12,0
25 329:24,34,23,57,42,30
26 342:35,9,22,31,13,0
27 355:45,44,21,4,43,30
28 8:56,19,19,38,14,0
29 22:6,54,18,11,44,30
30 , 25:17,29,16,45,15,0
Прибавление аномалии
Месяцы Градусы
1 2
30 31:56,58,8,55,59,30
60 63:53,56,17,51,59,0
90 95:50,54,26,47,58,30
120 127:47,52,35,43,58,0
150 159:44,50,44,39,57,30
180 191:41,48,53,35,57,0
210 223:38,47,2,31,56,30
240 255:35,45,11,27,56,0
270 287:32,43,20,28,55,30
300 319:29,41,29,19,55,0
330 351:26,39,38,15,54,30
360 23; 28,37,47,11,54,0
512
Приложения
Прибавление аномалии
Дни Градусы
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
13;3,53,56,17,51,59
26:7,47,52,85,43,58
39:11,41,48,53,35,57
52:15,35,45,11,27,56
65:19,29,41,29,19,55
78:23,23,37,47,11,54
91:27,17,34,5,3,53
104:31,11,30,22,55,52
117:35,5,26,40,47,51
130:38,59,22,58,39,50
143:42,53,19,16,31,49
156:46,47,15,34,23,48
169:50,41,11,52,15,47
182:54,35,8,10,7,46
195:58,29,4,27,59,45
209:2,23,0,45,51,44
222:6,16,57,3,43,43
235:10,10,53,21,35,42
248:14,4,49,39,27,41
261:17,58,45,57,19,40
274:21,52,42,15,11,39
287:25,46,38,33,8,38
300:29,40,34,50,55,37
313:33,34,31,8,47,36
326:37,28,27,26,39,35
339:41,22,23,44,31,34
352:45,16,20,2,23,33
5:49,10,16,20,15,32
18:53,4,12,38,7,31
81:56,58,8,55,59,30
Приложения
613
Прибавление широты
Месяцы Градусы
30 60 90 120 160 180 210 240 270 300 330 360 36; 52,49,54,28,18,30 73;45,39,48,56,37,0 110;38,29,43,24,55,30 147:31,19,37,58,14,0 184:24,9,32,21,32,30 221:16,59,26,49,51,0 258:9,49,21,18,9,30 295:2,39,15,46,28,0 331:55,29,10,14,46,30 8:48,19,4,43,5,0 45:41,8,59,11,23,30 82:33,58,53,39,42,0
Дни Градусы
1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 13:13,45,39,48,56,37 26:27,31,19,37,53,14 39:41,16,59,26,49,51 52; 55,2,3945,46,28 66:8,48,19,4,43,5 79:22,33,58,53,39,42 92:36,19,38,42,36,19 105:50,5,18,31,32,56 119:3,50,58,20,29,33 132:17,36,38,9,26,10 145:31,22,17,58,22,47 158:7,57,47,19,24 171:58,53,37,36,16,1 185:12,89,17,25,12,38 198:26,24,57,14,9,15
33-89
514
Приложения
1
2
16 211:40,10,37,3,5,52
17 224:53,56,16,42,2,29
18 238:7,41,56,40,59,6
19 251:21,27,36,29,55,43
20 264,35,13,16,18,52,20
21 277:48,58,56,7,48,57
22 291:2,45,35,56,45,34
23 304:16,30,15,45,42,11
24 317:30,15,55,34,38,48
25 330:44,1,35,23,35,25
26 343:57,47,15,12,52,2
27 357:11,32,35,1,28,39
28 10:25,18,34,50,25,16
29 23:39,4,14,39,21,53
30 36:52,49,54,28,18,30
Прибавление элонгации
Месяцы
Градусы
30 5:43,20,40,8,59,30
60 11:26,41,20,17,59,0
90 17:10,2,0,26,58,30
120 22:53,22,40,35,58,0
150 28:36,43,20,44,57,30
180 34:20,4,0,58,57,0
210 40:3,24,41,2,56,30
240 45:46,45,21,11,56,0
270 51:30,6,1,20,55,20
300 57:13,26,41,29,55,0
330 62:56,47,21,38,54,30
360 68:40,8,1,47,54,0
Приложения
515
Дни Градусы
1
2
3
4
б
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
12; 11,26,41,20,17,59
24; 22,56,22,40,35,58
36; 34,20,4,0,53,57
48; 45,46,45,21,11,56
60; 57,13,26,41,29,55
72:8,40,8,1,47,54
85; 20,6,49,22,5,53
97; 31,33,30,42,23,52
109:43,0,12,2,41,51
121:54,26,53,22,59,50
134:5,53,34,43,17,49
146:17,20,16,3,35,48
158; 28,46,57,23,53,47
170;40,13,38,44,11,46
182:51,40,20,4,29,45
195; 3,7,1,24,47,44
207:14,33,42,45,5,43
219:26,0,24,5,23,42
231:37,27,5,25,41,41
243:48,53,46,45,59,40
256:0,20,28,6,17,39
268:11,47,9,26,35,38
280:23,13,50,46,53,37
292:34,40,32,7,11,36
304:46,7,13,27,29,35
316:57,33,54,47,47,34
329:9,0,86,8,5,33
341:20,27,17,28,23,32
353:31,58,58,48,41,31
5:48,20,40,8,59,30
616
Приложения
Таблица 8
Таблица первого или простого
неравенства Луны
Общие числа Простаферезы (уравнение)
1 2
6 354 0;29
12 348 0;57
18 342 1 ;25
24 336 1;53
30 330 2; 19
36 324 2;44
42 318 3; 8
48 312 3;31
54 306 3;51
60 300 4; 8
66 294 4;24
72 288 4;38
78 282 4;49
84 276 4; 56
90 270 4;59
93 267 5; 0
96 264 5; 1
99 261 5; 0
102 258 4;59
105 255 4;57
108 252 4;53
111 249 4;49
114 246 4;44
117 243 4;38
120 240 4;31
123 237 4;24
126 234 4; 16
129 231 4; 7
182 228 3;57
Приложений 617
1 1 2
135 225 3;46
138 222 3;35
141 219 3;23
144 216 3;10
147 213 2;57
150 210 2;43
153 207 2;28
156 204 2; 13
159 201 1;57
162 198 1;41
165 195 1;25
168 192 1; 9
171 189 0;52
174 186 0;35
177 183 0;18
180 180 0; 0
Sid
Приложения
Таблица 9
Таблица полного лунного неравенства
Общие числа] Простаферезы апогея эксцентра Простаферезы эпицикла по дол- готе н ширрте (1-е неравенство) Избыток эпицик- ла (2-е неравен- ство) Избыток в шести- десятых долях 1 Широта
1 2 3 4 б 6
Северный предел
6 364 0;53 0;29 0;14 0;12 4;б8
12 348 1;46 0;57 0;28 0;24 4;54
18 342 2; 39 1;25 0;42 1;20 4; 45
24 336 3;31 1; 53 0; 56 2;16 4; 34
30 330 4;23 2;19 1;10 3;24 4; 20
36 324 5;15 2;44 1;23 4;32 4; 3
42 318 6; 7 3; 8 1;35 6;25 3;43
48 312 6;58 3;31 1;45 8; 18 3;90
54 306 7;48 3;51 1;54 10; 22 2;56
60 300 8; 36 4; 8 2; 3 12; 26 2; 30
66 294 9;22 9;24 2;11 15; 5 2; 2
72 288 10; 6 4; 38 2;18 17; 44 1;33
78 282 10; 48 4;49 2;25 20; 34 1; 3
84 276 11; 27 4; 56 2;31 23; 24 0;32
90 270 12; 0 4;59 2;35 26; 36 0; 0
93 267 12; 15 5; 0 2;37 28; 12 0; 16
96 264 12; 28 5; 1 2; 38 29; 49 0;32
99 261 12;39 6; 0 2;39 31; 25 0;48
102 258 12; 48 4; 59 2; 39 33; 1 1; з
103 255 12; 56 4;57 2;39 34; 37 1; 17
108 252 13; 3 4; 53 2; 38 36; 14 1;33
111 249 13; 6 4;49 2; 38 37; 50 1;48
Приложения
519
1 1 2 1 3 1 4 1 б 1 6
114 246 13; 9 4;44 2;37 39; 26 2; 2
117 243 13; 7 4;38 2;35 41; 2 2;16
120 240 13; 4 4;32 2;32 42; 38 2; 30
123 237 12; 59 4;25 2;28 44; 3 2;43
126 234 12; 50 4; 16 2;24 45; 28 2;56
129 231 12; 36 4; 7 2;20 46; 53 3; 8
132 228 12;16 3;57 2; 16 48; 18 3;2О
135 225 11; 54 3;46 2;11 49; 32 3; 32
138 222 11 ;29 3;35 2; 5 50; 45 3;43
141 219 11; 2 3;23 1;58 51; 59 3;53
144 216 10; 33 3;10 1 ;51 53;12 4; 3
147 213 10; 0 2;57 1;43 54; 3 4; 11
150 210 9;22 2;43 1;35 54; 54 4; 20
153 207 8;33 2;28 1;27 55; 45 4;27
156 204 7;48 2; 13 1;19 56;36 4;34
159 201 6;56 1; 57 1;11 57; 15 4; 40
162 198 6; 3 1;41 1; 2 57; 55 4;45
165 195 5; 8 1 ;25 0;52 58; 35 4;50
168 192 4; 11 1; 9 0;42 59; 4 4;54
171 189 3; 12 0;52 0;31 59; 26 4;56
174 186 2;11 0 ;35 0; 21 59; 37 4; 58
177 183 1; 7 0; 18 0; 10 59; 49 4;59
180 180 0; 0 0; 0 0; 0 60; 0 5; 0
Южный предел
620
Приложения
Таблицы
Параллаксы Луны
ла лаксы Солнца 1-й случай разн. для 2-го третий случай
1 2 3 4 5
градусы
2 0;0, 7 0; 1,54 0;0,23 0; 3, 0
4 0;0,13 0; 3,48 0;0,45 0; 6, 0
6 0;0,19 0; 5,41 0;1, 7 0; 9, 0
8 0;0,25 0; 7,34 0;1,29 0; 11,40
10 0;0,31 0;9,27 0;1,51 0; 14,20
12 0;0,37 0;11,19 0;2,12 0;17, 0
14 0;0,42 0; 13,10 0;2,33 0; 19,40
16 0;0,48 0;15, 0 0;2,54 0; 22,20
18 0;0,53 0; 16,49 0;3,15 0;25, 0
20 0;0,58 0; 18,36 0;3,36 0; 27,40
22 0;1, 4 0; 20,22 0;3,57 0; 30,20
24 0;1, 9 0;22, 6 0;4,18 0;33, 0
26 0;1,14 0; 23,49 0;4,39 0; 35,20
28 0;1,20 0; 25,30 0;4,59 0; 37,40
30 0;1,25 0;27, 9 0;5,18 0;40, 0
32 0;1,30 0; 28,46 0;5,37 0; 42,20
34 0;1,35 0; 30,21 0;5,55 0; 44,40
36 0;1,40 0; 31,54 0:6,13 0;47, 0
38 0;1,44 0; 33,24 0:6,30 0;49, 0
40 0;1,49 0; 34,51 0:6,47 0;51, 0
42 0;1,54 0; 36,14 0;74 0;53, 0
44 0;1,58 0:37,37 0;7,20 0;55, 0
46 0;2, 3 0; 38,57 0;7,35 0:57, 0
48 0;2, 8 0; 40,14 0;7,49 0;59, 0
50 0;2,12 0;41,28 0;8, з 1; 0,40
52 0; 2,16 0; 42,39 0;8,16 1; 2,20
54 0;2,20 0;43,45 0;8,29 1; 4, 0
Приложения
Б21
Таблица 10
параллаксов
Шестидесятые доли
разн. для 4-го для апогея для перигея для экс- центра
6 7 8 8
минуты
0; 0,50 0;14 0;11 0;15
0; 1,40 0;28 0;22 0; 30
0; 2,30 0;42 0;33 0;45
0; 3,20 1;22 1; 7 1; 33
0; 4,10 2; 2 1;41 2;21
0; 5, 0 2;42 2;15 3; 9
0; 5,50 3;35 3;13 4;22
0; 6,40 4;28 4;11 5;35
0; 7,30 5;21 5; 9 6; 48
0; 8,20 6; 39 6; 25 8; 25
0; 9,10 7;57 7; 41 10; 2
0; 10,0 9;15 8;57 11; 59
0; 10,50 10; 50 10; 29 13; 32
0; 11,40 12;25 12; 1 15; 25
0; 12,30 14; 0 13; 33 17;18
0; 13,20 15; 52 15; 22 19; 23
0; 14,10 17; 44 17;11 21; 28
0;15, 0 19; 36 19; 0 23;33
0; 15,40 21; 36 20; 59 25; 40
0; 16,20 23; 36 22; 58 27;47
0;17, 0 25; 36 24; 57 29; 54
0; 17,40 27; 40 27, 1 32; 0
0; 18,20 29; 44 29, 5 34; 6
0;19, 0 31; 48 31; 9 36; 12
0; 19,40 33; 52 33; 14 38; 9
0; 20,20 35; 56 35;19 40; 6
0;21, 0 38; 0 37;24 . 42; 3
OOOOooQogO-q«q-q-4-ao5oajaa>gJO’
oooi^toOoooi^tJoaiaiiitooMoi
<D
О
00©0©0000©0©©©©00©
to to to jo to tO JO to jo jo to to tO IO tO JO JO JO
СЛ СЛ СЛ O'Ok *> rfk co co co COtO to to
H‘t-‘©o<oOo-o0s1t>.tooooo»rf4>o<oa>co
0©000©0©000©00000©
с,С"о’слслСлслслслспсл>&.>^>б-^|(‘-А>£.
СоИ w CJCOtOtO to t-HO© ©OOS® O'*
co co to’to" ст сон* lii.'S-* co сл м tol». o>. f; £
lixCo'Oi->cocoltkto>h.i-‘ai-4oiooaoo<>o
O©OOO©OOOOOOOOOOOO
hHHhhHhh"''" ” ' ” 00 00
о ©ООО О О ©Ф© ©JO ©JO Ф© ox
н'Н-1 м * ох сл rfk co co tot-»* co to
-qO©a>itk.l-‘«>tk©COO©l-‘tOCoeo
Приложения
их H* >-* |_i Hl !- J-U |-> l-i |-> )-> 010
© 00 С» oo J<| jO-3 ® СЛ СЛ Jk. CO to JO JO 00 7^. to
0k № to* to 0k* - - - ©ф
©©©ФОФОООООООООО
Приложений
623
6 | 7
8
0; 21,20 40; 0 39; 24 43; 49
0; 21,40 42; 0 41; 24 45; 35
0;22, 0 44; 0 43; 24 47; 21
0; 22,20 45; 50 25; 13 48;49
0; 22,40 47; 40 47; 20 50; 17
0;23, 0 49; 30 48; 51 51; 45
0; 23,10 50; 56 50;24 52; 57
0; 23,20 52; 22 51; 57 54; 9
0; 23,30 53; 48 53; 30 55; 41
0; 23,40 54; 57 54; 41 56; 12
0; 23,50 56; 6 55; 52 57; 3
0;24, 0 57; 15 57; 3 57; 54
0; 24,10 57; 57 57; 47 58; 26
0; 24,20 58; 39 58; 31 58;58
0; 24,30 59; 21 59; 25 59; 30
0; 24,40 59; 34 59; 30 59; 40
0; 24,50 59; 47 59; 45 59; 50
0;25, 0 60; 0 60; 0 60; 0
СОДЕРЖАНИЕ
Аль-Фараби и его обработки «Альмагеста» 7
Введение ................................46
Первая книга.............................49
О том, что небо имеет сферическую фор-
му и сферическое движение . . 49
О том, что Земля сферична по виду . . 63
О том, что Земля находится неподвижно
в центре [мира] .... 55
О размерах Земли относительно [небес-
ной] сферы...........................58
О том, что Земля не имеет поступательно-
го движения ..... 59
Речь о том, что Вселенная имеет одно об-
щее движение ..... 63
Об определении хорд частей круга . . 66
Об определении склонения ... 78
Об определении синусов ... 85
О восхождении в прямой сфере . 99
Вторая книга............................102
Об обитаемых частях Земли и упомина-
ние о целях книги .... 102
Об определении азимута восхода . . 104
Об определении отношения гномонов к
[полуденным] теням во времена рав-
ноденствий и солнцестояний . . 109
Об особенностях кругов, параллельных
небесному экватору .... Ц2
О восхождениях относительно широт . 123
О частных вещах, связанных с определе-
нием восхождений .... 182
Об определении угла, образуемого пересе-
чением ЭКЛИПТИКИ И меридиана . 186
Об определении угла, образуемого эклип-
тикой и горизонтом . 140
Об определении угла, образуемого пересе-
чением эклиптики и круга, проходя-
щего через полюсы горизонта . . 146
Третья книга 165
О временной величине года . . . 155
О гипотезах, предполагаемых для равно-
мерного движения, происходящего
по кругу............................171
О видимом неравенстве движения Солнца. 190
Об определении частных [значений] не-
равенств ..... 190
О неравенствах суток .... 206
Четвертая книга ..... 218
О наблюдениях, которые следует исполь-
зовать для познания движения Луны. 218
Об определении времени оборотов Луны. 215
О частных и равномерных движениях
Луны ...... 228
О том, что Луна имеет одно и то же не-
равенство как относительно эксцент-
рического круга, так и относительно
эпицикла ..... 230
Об определении первого и простого нера-
венства Луны........................285
Об исправлении равномерных движений
Луны по долготе и аномалии 261
Об эпохе равномерных движений Луны по
долготе и аномалии . . . 262
Об исправлении движений Луны по ши-
роте и об их эпохе..................262
О том, что принятая Гиппархом разница
величины [лунного] неравенства по-
лучается не из-за принципов, по ко-
торым он действовал, а вследствие
вычисления ..... 268
Пятая книга............................272
Об уточнении положений Луны . . 272
Об изготовлении инструмента, при помощи
которого измеряется [йоложение]
светил ...... 272
О принципе, который мы применяем в воп-
росе двойного неравенства Луны . 276
Об определении [величины] неравенства
Луны в зависимости от ее расстояния
от Солнца ..... 283
Об определении стороны, к которой скло-
няется эпицикл Луны . . . 287
Как с помощью линий определить истин-
ное движение Луны по его равномер-
ным движениям .... 294
Об определении [метода] составления таб-
лиц для полного неравенства Луны . 296
О том, что неравенство по причине экс-
центрического круга не имеет ощути-
мой величины во время соединений
и противостояний .... 301
О параллаксах Луны .... 306
Об определении расстояния Луны . 311
Об определении величин диаметров Солн-
ца, Луны и [земной] тени, видимой
в сизигиях ..... 316
Об определении расстояния Солнца и о
том, что выясняется из этого . . 320
О частных [значениях] параллаксов Солн-
ца и Земли..............................323
Об уравнении параллакса и подробностях
этого ..................................330
Примечания к переводу „Комментариев к
«Альмагесту»” аль-Фараби 861
Литература.............................451
Приложения............................ 463
Аль-Фараби
Комментарии к «Альмагесту» Птолемея.
Пер. с араб. А. Кубесова и Дж. аль-Даббаха.
Ч. I— Алма-Ата, «Наука», 1976.
т. [АН КазССР. Ин-т философии и
права].
Ч. I. Вступ. статья А. Кубесова, примеч.
А. Кубесова и В. А. Розенфельда. 1975. 527с.
2 р. 41 к.
001(584)(09)+52(09)
Необходимые исправления:
На стр. 138 рисунки 36 и 37 поменять местами.
Подписи без изменения.
Абу Наср Мухаммад
Аль-Фараби
КОММЕНТАРИИ
К «АЛЬМАГЕСТУ» ПТОЛЕМЕЯ
Утверждено к печати Ученым советом
Института философии и права
Академии наук Казахской ССР
Редактор Л. Н. Василкова
Худож. редактор И. Д. Сущих
Техн, редактор 3. И. Ророкина
Корректор Р. И. Орешкина
* * ♦
Сдано в набор 26/V 1975 г. Подписано к печати
17/VH 1975 г. Формат 70Х90'/32. Бумага № 1.
Усл. печ. л. 19,1. Уч.-изд. л. 22.
Тираж 6000. УГ05122. Зак. 89. Цена 2 р. 41 к.
* * *
Издательство «Наука» КазССР.
Типография издательства «Наука». Адрес изда-
тельства и типографии: г. Алма-Ата, ул. Шев-
ченко, 28.