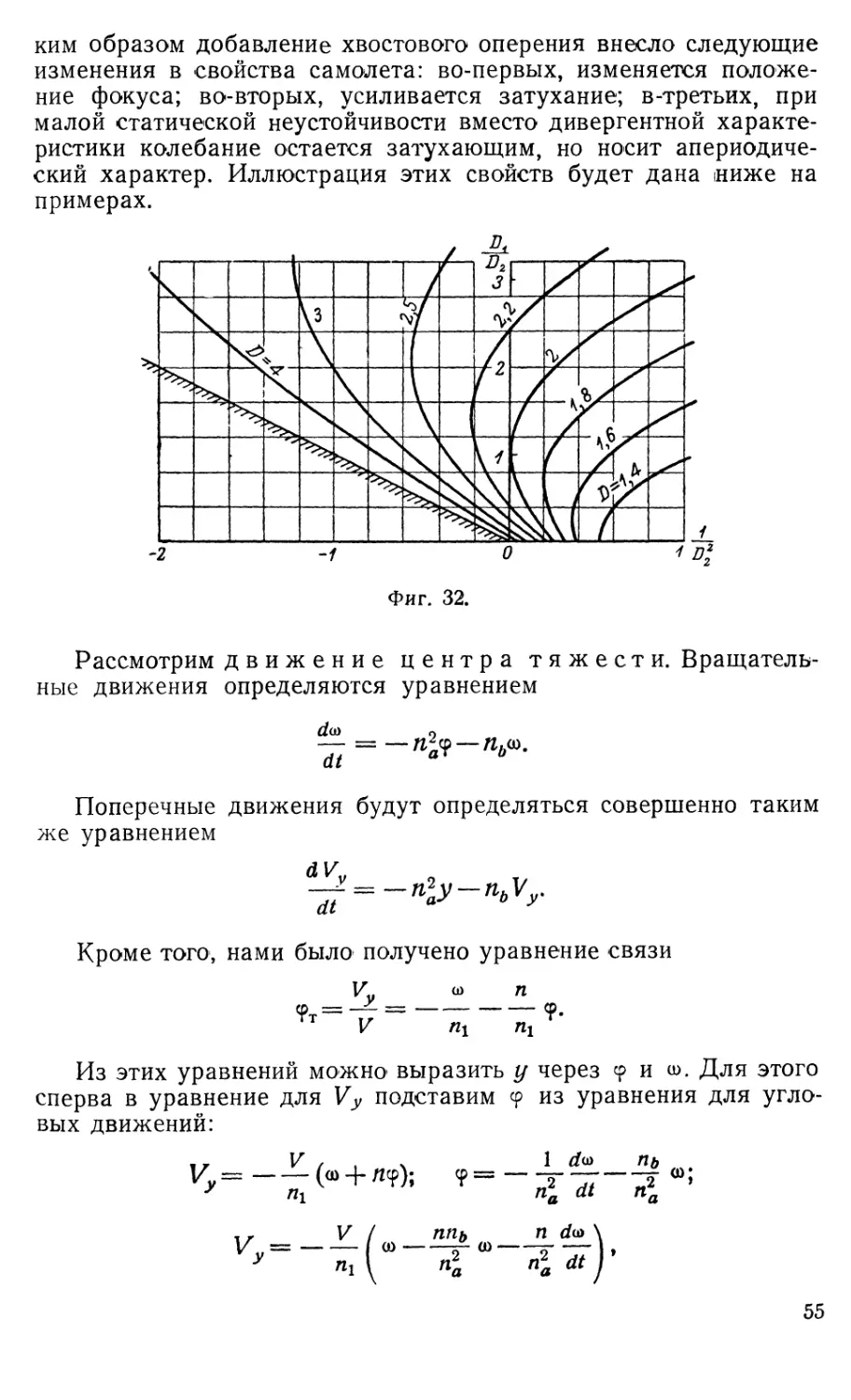
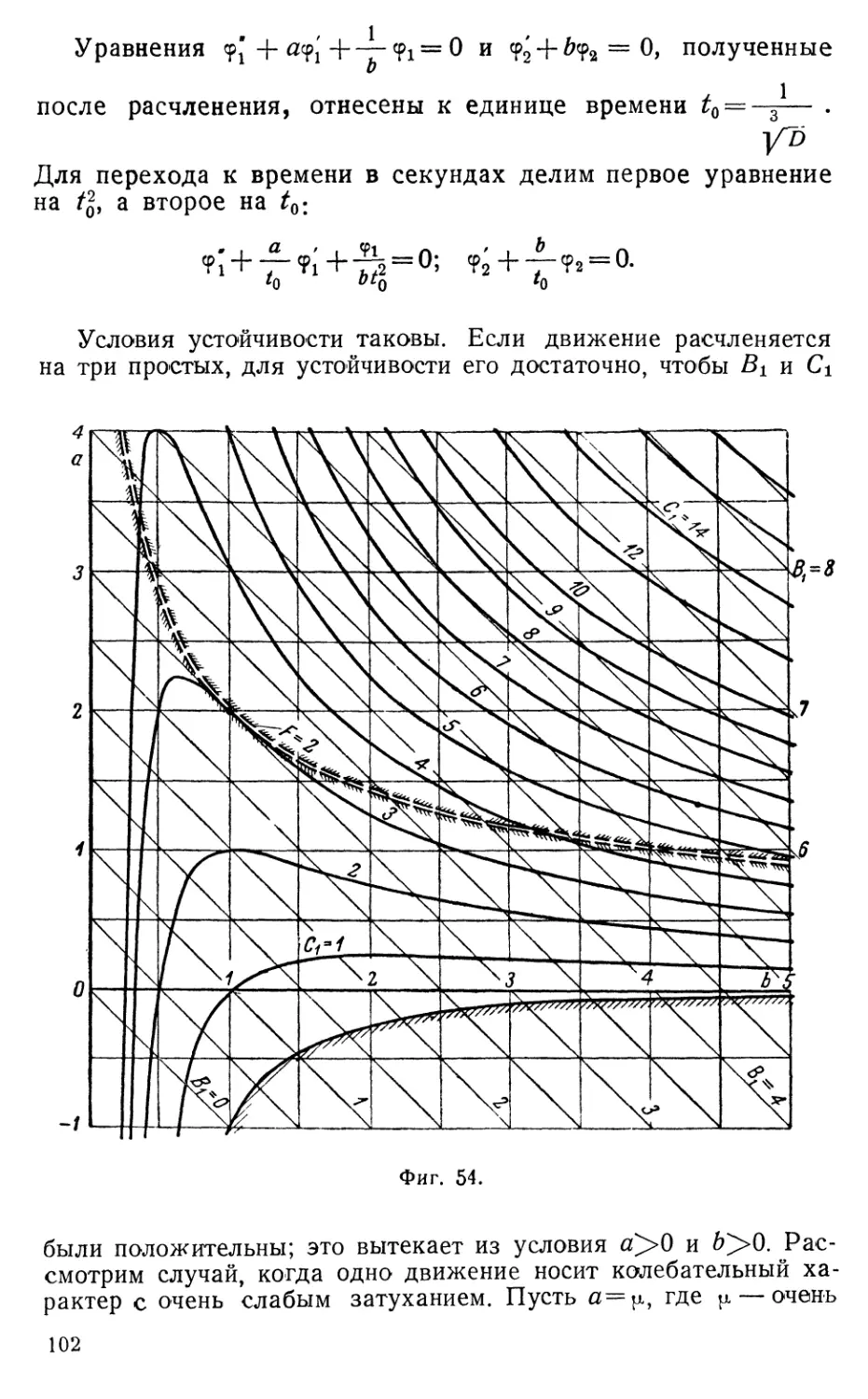
Текст
ДИНАМИЧЕСКИЕ
Заслуженный деятель науки и техники
В. С. пышнов
ДИНАМИЧЕСКИЕ
СВОЙСТВА САМОЛЕТА
ДЕЙСТВИЕ МАЛЫХ ВОЗМУЩЕНИЙ
ГОСУДАРСТВЕННОЕ
ИЗДАТЕЛЬСТВО ОБОРОННОЙ ПРОМЫШЛЕННОСТИ
Москва 1951
ПРЕДИСЛОВИЕ
Термином «самолет» можно называть все летательные маши-
ны, летающие на динамическом принципе. Однако исторически
термин «самолет» был присвоен летательным машинам, которые
первоначально назывались аэропланами. Особенностью этих ма-
шин является неподвижное крыло, а наиболее характерным свой-
ством —необходимость достаточной скорости, а следовательно, и
определенного минимума кинетической энергии для осуществле-
ния полета.
Кинетическая и потенциальная энергии сообщаются самолету
действием тяги двигателя, причем направление силы тяги почти
совпадает с направлением полета. Двигательные группы бывают
различные — винтовые, воздушно-реактивные и ракетные. Источ-
ником движения может быть и сила тяжести — тогда полет на-
зывается планированием. Применяется также буксировка дру-
гим самолетом или иными средствами.
Разносторонние свойства самолета можно группировать по
различным признакам. Наиболее часто/свойства самолета груп-
пируются по таким разделам, как маневренность, управляемость
и устойчивость.
Часто пытаются дать краткие определения маневренности,
управляемости или устойчивости самолета, однако в нескольких
словах охарактеризовать эти понятия нельзя.
Маневренность, управляемость и устойчивость самолета явля-
ются качественными категориями, каждая из которых определяет-
ся рядом свойств и числовых показателей. Комплекс этих показа-
телей меняется в зависимости от условий применения самолетов,
а также в процессе развития конструкции самолета и расширения
наших знаний в области динамики полета и условий работы эки-
пажа.
Под маневренностью понимается совокупность всех
возможных движений данного самолета. Однако такое определе-
ние совершенно неконкретно. Маневренность можно определять
граничными условиями. Так существует минимум и максимум
скорости, минимум радиуса кривизны, максимум вертикальной
скорости и пр. Одни ограничения определяются энерговооружен-
з
ностью самолета, другие — прочностью его конструкции, третьи—
предельными аэродинамическими силами, четвертые—управляе-
мостью и т. д. В задачу данной рйботы не входит систематизация
этих ограничений. Маневренность самолета может характеризо-
ваться также некоторыми сложными движениями, представляю-
щими интерес при использовании самолета для тех или иных це-
лей. Целесообразные или выгодные маневры могут быть весьма
разнообразны.
Управляемость самолета может ограничивать манев-
ренность; поэтому первое требование к управляемости заключает-
ся в том, чтобы она не вносила существенных ограничений ма-
невренности. Обычно бывает желательно, чтобы ограничения,
вызываемые управляемостью, были близки или даже несколько
перекрывали ограничения, вносимые другими условиями.. Напри-
мер, если некоторые режимы полета ограничиваются наступле-
нием срыва обтекания, хорошо, когда управляемость мешает пе-
реводу самолета на опасные режимы. Другой пример — маневрен-
ность ограничивается предельно допустимой перегрузкой; тогда
желательно, чтобы условия управляемости затрудняли получение
чрезмерных перегрузок.
Маневренность самолета определяется силами, действующими
на самолет и сообщающими ему линейные и угловые ускорения.
Управление самолетом заключается в управлении величиной и
направлением сил и моментов для выполнения маневров или при-
дания самолету определенного положения в пространстве.
Проблема управляемости имеет ряд сторон. Основные из них:
1) аэродинамическая — определяет предельные значения
углов атаки, углов скольжения и скорости накренения в прямо-
линейном и криволинейном движении;
2) динамическая — определяет характер движения самолета
при переходе с одного режима на другой под действием органов
управления;?
3) психо-физическая — связана с действиями летчика при пе-
ремене режима полета или при противодействии внешним возму-
щениям, нарушающим режим полета или сообщающим нежела-
тельное ускорение. К этой стороне проблемы управляемости от-
носится большое число вопросов, правильное разрешение которых
связано с изучением условий работы человеческого организма:
усилия, необходимые для управления самолетом, перемещения
рычагов управления, скорости и ускорения этих перемещений,
восприятие показаний, на основе которых летчик должен дей-
ствовать органами управления, и пр.
Устойчивость относится к свойствам самолета, предо-
ставленного самому себе или предварительно подвергнутого дей-
ствию возмущения. В более сложных случаях эти возмущения
действуют непрерывно по некоторому закону или действия управ-
ления следуют одно за другим, как реакция летчика или специ-
ального автопилота на движения самолета.
4
Цель изучения вопросов устойчивости заключается в разра-
ботке мероприятий, которые: 1) сделали бы самолет более управ-
ляемым, а следовательно, и более маневренным и 2) сделали
бы самолет менее подверженным внешним возмущениям как для
разгрузки летчика и упрощения работы автопилота, так и для
ослабления эффекта «болтанки». К самолету может быть предъ-
явлено требование, чтобы он сохранял режим полета или выпол1
нял заданную программу полета без участия летчика. В этом
случае отклонения от желаемого движения при действии опре-
деленных возмущений не должны превышать заданной величины.
Методически вопросы динамики полета можно сгруппировать
и иначе: полагая, что желаемые углы атаки, скольжения и крена
устанавливаются весьма быстро, можно изучать полет под дей-
ствием уже известных сил. Этот раздел был мною назван динами-
кой управляемых движений и он относится целиком к маневрен-
ности самолета. К этому разделу могут быть присоединены и
некоторые вопросы управляемости, относящиеся к балансировке
самолета на определенных режимах.
Затем можно выделить круг вопросов, относящихся к поведе-
нию самолета под действием слабых возмущений (внешних или
вызванных действием управления). Допущение о слабости воз-
мущений и, следовательно, малости изменения элементов движе-
ния позволяет внести методические упрощения. Этот круг вопро-
сов и рассматривается в данной работе.
Наконец можно рассматривать поведение самолета под дей-
ствием сильных возмущений, которые коренным образом меняют
характер полета. Одну из задач этого круга вопросов разрешил
Н. JE. Жуковский еще в 1891 г. в работе «О парении птиц» — при
сильном возмущении исходного прямолинейного полета им были
получены петлеобразные траектории. В дальнейшем этот раздел
динамики полета получил слабое развитие из-за большой его
сложности.
ВВЕДЕНИЕ
Вопросы управляемости и устойчивости самолета стояли в
центре внимания конструкторов первых самолетов и ученых —
основоположников теории полета. При отсутствии достаточных
знаний о силах, действующих на самолет, вопросы управляе-
мости и устойчивости нельзя было успешно разрешать даже при
наличии общей теории устойчивости. Последующую историю во-
проса можно подразделить на развитие общей теории устойчи-
вости и приобретение конкретных знаний о силах и моментах.
Важно также, что обе эти стороны вопроса воздействовали друг
на друга. Первоначально в аэродинамических трубах изучались
аэродинамические силы, действующие на отдельные части само-
летов, и была разработана некоторая методика расчета самолета.
Когда стали испытывать полные модели самолетов, методы рас-
чета подверглись значительным изменениям. Наконец, когда по-
лучили развитие испытания самолета в полете, теория вновь под-
верглась большим изменениям.
Недостаток знаний в области управляемости и устойчивости
явился источником многих трудностей в истории развития авиа-
ции. Были случаи, когда самолеты оказывались неуправляемыми;
можно привести немало примеров, когда в эксплоатации находи-
лись самолеты явно неустойчивые, полет на которых был утоми-
телен, а «слепой» полет—опасен. Неудачи в разрешении вопро-
сов устойчивости приводили даже к появлению ошибочных тео-
рий о ненужности и даже вреде устойчивости.
Задачи, стоящие перед теорией управляемости и устойчивости,
менялись или вернее развивались — менялась схема самолета и
свойства его двигательной группы. Первоначально решалась
скромная задача о получении равновесного состояния при нор-
мальных режимах полета и наличии тенденции к сохранению рав-
новесия. Рост скорости полета и увеличение полетного веса заста-
вили обратить особое внимание на усилия, которые необходимо
прилагать к рычагам управления. Развитие техники слепого по-
лета, применение автопилотов привели к необходимости изменять
требования к характеристикам устойчивости. При переходе к об-
ласти звуковых и сверхзвуковых скоростей произошло коренное
6
изменение характеристик аэродинамических сил. Если общие тре-
бования к устойчивости и управляемости остались прежними, то
способы разрешения этих требований изменились.
Предметом настоящей работы являются методические вопро-
сы. Об этом уже было сказано в предисловии. Исторически сло-
жились две теории устойчивости — статическая и динамическая.
Статическая теория была явно не полной, но она имела ясное
физическое содержание, ее выводы были просты и связь с прак-
тическими результатами была достаточно убедительной для кон-
структоров.
Динамическая теория была основана на абстрактных матема-
тических операциях, параметры самолетов группировались в
сложные коэффициенты и сама необходимость выполнения тре-
бований, вытекающих из динамической теории, не была убеди-
тельной для конструкторов самолетов.
Н. Е. Жуковский в своих лекциях по «Основам воздухоплава-
ния» основное внимание уделял изложению статической теории
устойчивости и, в частности, разъяснил важность соблюдения
основного принципа — продольного V. Сущность этого принципа
состоит в том, что плоскости нулевой подъемной силы крыла и
стабилизатора должны составлять тупой угол, открытый вверх;
тогда, если крыло стоит под таким углом, при котором подъемная
сила отсутствует, то подъемная сила стабилизатора дает момент,
стремящийся увеличить угол атаки. Положение центра тяжести
самолета должно быть выбрано так, чтобы при выбранном про-
дольном V равновесие моментов достигалось на желаемом угле
атаки. Однако как в этих лекциях, так и в курсе «Динамика аэро^
планов в элементарном изложении» Жуковский указывал, что
главная задача устойчивости состоит в получении колебаний с
достаточно' сильным затуханием или лучше — апериодического
движения. Наиболее полно теория продольной устойчивости была
исследована Жуковским применительно к дирижаблю (58-я лек-
ция по основам воздухоплавания). Уравнения, написанные при-
менительно к дирижаблю, в сущности ничем не отличаются от
уравнений для самолета. В этой работе Жуковский показывает
весьма важную роль не только затухания, но и поперечных дви-
жений, вызываемых изменением подъемной силы. Это> обстоятель-
ство будет подробно разъяснено в данной работе.
Крупным вкладом в теорию устойчивости является открытие
С. А. Чаплыгиным фокуса крыла и системы крыльев. В работах
«К общей теории крыла моноплана» и «Схематическая теория
разрезного крыла» Чаплыгин показывает, что перемещение цент-
ра давления характеризуется некоторой «параболой устойчи-
вости», параметры которой могут быть найдены теоретически. Да-
лее Чаплыгин показывает, что момент подъемной силы относи-
тельно фокуса параболы является постоянной величиной, не
зависящей от угла атаки. Следовательно, фокус параболы устой-
7
чивости является аэродинамическим фокусом крыла. Понятие фо-
куса оказалось весьма плодотворным при изучении устойчивости
самолета.
Автор долгое время занимался усовершенствованием статиче-
ских теорий управляемости и устойчивости. Следует заметить, что
в процессе этого усовершенствования в статические теории стали
вводиться динамические элементы — это начало сближать их с
динамическими теориями. Вместе с тем другие авторы старались
динамическим теориям придать возможную наглядность. Раздель-
ное существование статической и динамической теорий не может
быть оправдано. На две эти теории можно смотреть как на два
исторически сложившихся пути.
В механике при рассмотрении задач пользуются аналитиче-
ским и геометрическим методами. Существуют различные мнения,
какой из этих методов лучше. Аналитический метод более после-
довательный и общий — он строится на некоторой общей теории,
частным случаем применения которой является решаемая задача.
Однако смысл решения бывает заслонен формальными операция-
ми, которые в сущности имеют вполне конкретный смысл. Гео-
метрическое решение требует индивидуального подхода к данной
задаче. Но когда решение найдено, задача становится наглядной,
особенно для людей, привыкших мыслить образами и обладающих
развитой зрительной памятью.
Противопоставлять аналитический и геометрический методы
решения было бы неправильно. Широкое и общее решение более
логично выполняется аналитическими методами. Если решение
имеет прикладные цели, следует предпочесть геометрические ме-
тоды. Практик, особенно инженер, привыкший к чертежам и диак
граммам, легче поймет геометрическое решение. Некоторые счи-
тают, что в современных технических расчетах применяются та-
кие математические операции, которые не могут быть изложены
понятно для практиков. С этим нельзя согласиться. М. В. Ломоно-
сов очень резко выступал против тех, кто пишет неясно. Практика
самолетостроения показала, что неясный для конструктора метод
расчета не получит должною распространения и во всяком слу-
чае не принесет той пользы, которую он мог бы принести, будучи
изложен ясно и доступно.
Поборником ясного и доступного изложения был Н. Е. Жу-
ковский. В 1894 г. им была произнесена речь на IX съезде рус-
ских естествоиспытателей и врачей «О значении геометрического
истолкования в теоретической механике». В этом интереснейшем
докладе Н. Е. Жуковский ясно показывает преимущества гео-
метрических толкований. В конце доклада он указывает на целе-
сообразность применения специальных моделей, иллюстрирую-
щих теорию.
Вопросы, рассмотренные автором в данной работе, может
быть, не новы, но они излагаются с применением геометрического
8
толкования и иллюстрируются возможно более простыми механи-
ческими моделями. Основная задача автора состояла в том, что-
бы сделать динамическую теорию достоянием более широкого
круга специалистов и ликвидировать разрыв между статической
и динамической теориями.
Из данной работы видно, что изменение метода исследования
позволило более четко выявить ряд важных свойств самолета.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Продольные движения
G — вес самолета;
т — масса самолета;
g — ускорение силы тяжести;
х, у, z — координатные оси, связанные с самолетом, а в некоторых слу-
чаях — полусвязанные; ось х направлена вперед, у — вверх,
z — вправо;
Уа — приращение силы по оси у при изменении угла атаки а;
Л4а—приращение момента вокруг оси z, вызванное изменением угла
атаки а;
лга=— — расстояние от центра
а
тяжести самолета до его фокуса. Фокусом
самолета называется точка приложения приращения аэродина-
мических сил, вызванного изменением угла атаки а;
— поперечное ускорение, т. е. ускорение в направлении, перпенди-
кулярном направлению движения;
<Р — продольный наклон самолета, отсчитываемый от начального или
конечного положения;
?т — угол поворота вектора скорости, т. е. изменение угла наклона
касательной к траектории;
,Да=<р—<рт— изменение угла атаки;
(«>=?'—угловая скорость вращения самолета вокруг оси z;
хп — смещение фокуса, вызванное действием перегрузки;
хш—смещение фокуса, вызванное действием аэродинамического тор-
можения при вращении;
Рр — сила, лрилагаемая к ручке управления;
Мр—момент, действующий на самолет, в результате приложения уси-
лия к ручке управления;
г Мр
Ер——^ —длина приведенного рычага руля высоты;
Yv — приращение подъемной силы, вызванное изменением скорости;
V — скорость полета;
Mv — приращение продольного момента, вызванное изменением ско-
рости;
xv — расстояние от центра тяжести до точки приложения приращения
подъемной силы, вызванного изменением скорости;
Г/ — радиус инерции самолета относительно оси z;
I — момент инерции самолета относительно оси z\
Li — расстояние от центра тяжести до центра ускорения;
10
п—характеристика затухания, равная производной углового (линей-
ного) ускорения по угловой (линейной) скорости;
«о — характеристика частоты колебаний, т. е. производная ускорения
по смещению;
1
А)=— — фактор периода;
п0
D — фактор затухания;
т — период колебания;
п2 — характеристика изменения кривизны траектории, равная произ-
водной угловой скорости вращения вектора скорости по изме-
нению угла атаки,
по.
п2
п
——фактор затухания, определяемый действием оперения;
Ло
п2
Х>2=——фактор затухания, определяемый действием крыла;
По
п? — характеристика частоты колебаний в сложном движении;
п. — характеристика затухания в сложном движении;
— характеристика воздействия изменения скорости полета на угло-
вое ускорение;
— характеристика воздействия изменения скорости на поперечное
ускорение;
— характеристика продольного ускорения, возникающего от изме-
' нения угла атаки,
Щ — характеристика продольного ускорения, возникающего от изме-
нения скорости;
л7 — характеристика воздействия перегрузки на угловое ускорение;
Р — тяга двигателя;
aV2 2G
и==-----=--------—характеристика относительной плотности самолета;
да
—характеристика роли оперения в затухании,
^2
х0 — характеристика продольной статической устойчивости,
— характеристика углового ускорения, создаваемого автопилотом;
Т7! и —факторы затухания составляющих движений.
Боковые движения
Q — сила, умножение которой на угол атаки или угол скольжения
дает соответственно подъемную или боковую силы,
Оф — то же для фюзеляжа при скольжении;
Ов. о — то же для вертикального оперения;
Ок — то же для крыла,
Ор —то же для самолета в целом;
Z — боковая сила (с соответствующими индексами, указывающими,
к чему эта сила приложена),
р = фт—угол скольжения,
ф — путевой угол самолета,
11
фт — поворот вектора скорости центра тяжести;
7 — угол крена;
£ф — отношение градиента боковой силы фюзеляжа по углу скольже-
ния к градиенту подъемной силы крыла по углу атаки;
^в.о — то же для вертикального оперения;
Лф» З'ф — координаты фокуса фюзеляжа;
Лв.о’-Ув.о—координаты фокуса вертикального оперения;
Ук — вертикальная координата бокового фокуса крыла;
х$> — координаты бокового фокуса самолета (фокуса скольжения);
фк — поперечный угол крыла;
фк.э—эффективный поперечный угол крыла;
Zi — боковая координата точки приращения* подъемной силы одного*
полукрыла при Изменении угла атаки;
z% — боковая координата точки приращения подъемной силы одного
полукрыла при вращении вокруг осей х и у;
— угловая скорость вращения вокруг оси х;
ш —то же вокруг оси у;
0 — продольный угол наклона траектории;
I — момент инерции самолета относительно оси х;
I —то же относительно оси у;
У
гх — радиус инерции относительно оси х;
г —то же относительно оси у\
Л4Э — момент от элеронов;
9
По — производная углового ускорения вокруг оси у по углу сколь-
жения;
п — то же по угловой скорости^;
л3 — то же по угловой скорости ;
л2 — производная угловой скорости вращения вектора скорости па
углу скольжения;
— производная углового ускорения вокруг оси х по углу сколь-
жения;
л6 — то же по <0^;
л7 — то же по
СТАТИЧЕСКАЯ ТЕОРИЯ ПРОДОЛЬНОЙ УПРАВЛЯЕМОСТИ
И УСТОЙЧИВОСТИ
Статическая теория устойчивости очень примитивна по своему
смыслу. На протяжении значительного периода развития самоле-
тостроения требования к устойчивости, определяемые этой тео-
рией, сводились к тому, что у самолета должна быть тенденция к
удержанию определенного угла атаки. Эту тенденцию опреде-
ляли по соотношению между коэффициентом момента и измене-
нием угла атаки. Вопрос рассматривался в двух вариантах: 1) изг
менение угла атаки происходит очень быстро и потому скорость
полета сохраняется неизменной; 2) изменения угла атаки и ско-
рости согласованы таким образом, что величина подъемной силы
остается неизменной. Первый вариант назывался устойчивостью
угла атаки, второй — устойчивостью режима полета.
В практике самолетостроения на соблюдение этих условий
обращалось основное внимание. С точки зрения общей теории
устойчивости условия статической теории не могут рассматри-
ваться как достаточные. Однако самолету присущи свойства, при
которых соблюдение условий статической теории оказывается
обычно достаточным для обеспечения устойчивости в ее широком
понимании4
Статическая теория продольной управляемости рассматривает
только условия равновесия моментов в горизонтальном полете
в диапазоне углов атаки от посадочного до соответствующего от-
весному пикированию, а иногда — и полету на спине. Эти усло\-
вия просты, но выполнение их необходимо. В качестве меры ста-
тической управляемости использовалось соотношение между ве-
личиной изменения угла атаки и величиной изменения положения
руля высоты. Для определенной аэродинамической схемы само-
лета можно было найти такое геометрическое место положений
центра тяжести, пр^ котором одновременно соблюдались условия
статической устойчивости и управляемости.
По мере роста полетного веса самолетов и диапазона скоростей
полета в вопросах управляемости все большее внимание стали
привлекать задачи уменьшения усилий, прилагаемых к рычагам
управления, и уравновешивания самолета при отсутствии усилий
со стороны летчика. Статическая теория была распространена
13
на криволинейный полет, и это потребовало включения в эту теон
рию некоторых динамических элементов. Устойчивость угла атаки
и режима полета сменялась устойчивостью по перегрузке и по
скорости. При рассмотрении статической устойчивости и управляе-
мости первоначально исходили из законов перемещения центра
давления крыла и всего самолета. Затем сочли более удобным
рассматривать только моменты крыла и других частей самолета
относительно центра тяжести. Эти моменты изучались на основе
экспериментов в аэродинамических трубах и был собран и об-
работан материал, необходимый для практйческих расчетов.
Повышение интереса к моментам повлекло за собою некоторую
недооценку роли сил, которые эти моменты вызывает. На npol-
дольные движения самолета стали смотреть как на простое вра-
щение вокруг оси zf проходящей через центр тяжести.
Мы уже указали, что С. А. Чаплыгиным было сделано. важное
открытие в области аэродинамики хорошо обтекаемых тел. Он
показал, что система аэродинамических сил, действующих на
тело, может быть сведена к равнодействующей, приложенной
в некоторой точке — фокусе параболы устойчивости, и паре сил,
момент которой не зависит от угла атаки. При рассмотрении
устойчивости или управляемости мы исходим из некоторого рав-
новесного состояния, когда все силы и моменты находятся в рав-
новесии. Если затем по некоторым причинам произошло нару-
шение равновесия или нужно изменить режим полета путем1
изменения угла атаки, то нас будут интересовать только' измене-
ния сил, приложенных в фокусах частей самолета, так вдк пары
сил относительно^ фокусов останутся без изменения. Таким об-
разом фокус можно' рассматривать как точку^ в которой прила-
гается приращение аэродинамических сил, вызванное изменением
угла атаки. Это приращение можно, разбить на две составляющие
по принятым осям; проведя направление действия приращения,
можно получить плечо относительно центра тяжести и найти
приращение момента. Для простоты мы будем рассматривать
только момент от составляющей приращения, направленной по
нормали к хорде крыла, и принимать эту составляющую равной
приращению подъемной силы. Если полет происходит на боль-
ших углах атаки и превышение фокуса над центром тяжести
значительно', нужно учесть и момент от тангенциального прира-
щения. Соотношение между нормальным и тангенциальным при-
ращениями аэродинамических сил крыла может быть получено
из поляры крыла второго рода, т. е. в связанных осях; прибли-
жённо можно принять, что тангенциальная составляющая равна
нормальной, умноженной на удвоенный истинный угол атаки, и
направлена вперед (при увеличении угла атаки). Истинным
углом атаки мы называем угол атаки, необходимый для получе-
ния данного су при бесконечно большом удлинении крыла.
Перейдем к изложению понятий устойчивости по перегрузке
и по скорости.
14
Пусть самолет летит прямолинейно и равномерно. В этом
случае все силы находятся в равновесии, и при этом безразлично,
какие именно силы и моменты действуют на самолет. Теперь
пусть по некоторой причине изменился угол атаки и одновременно
изменились некоторые из действующих сил. Наиболее значи-
тельно будет изменение подъемной силы Уа; эта сила будет
приложена в фокусе самолета на расстоянии ха от центра тя-
жести. От силы Ya мы получим момент 7Иа, ускорение по вер-
тикали изменение перегрузки Дп = —. Тенденция возвра-
щения к первоначальному углу атаки будет иметь место при
условии, что фокус находится позади центра тяжести, как пока-
зано на фиг. 1. Если под действием перегрузки возникают допол-
нительные моменты, например, от деформации самолета, силу Уа
нужно приложить не в аэродинамическом фокусе самолета, а на
расстоянии х от центра тяжести, определяемом из условия
\[дМ дУ\ . /дМдп дУ\]
х = — [ — * — I *7- (----; — I ,
[\ да да / \ дп да да / J
дМ к
где —Дп —момент, вызванный изменением перегрузки.
дп
Для оценки степени устойчивости величину х делят на сред-
нюю аэродинамическую хорду крыла, хотя лучше делить на ра-
диус инерции, соответствующий вращению вокруг оси г. Измене-
ние угла атаки при постоянной скорости вызвало перегрузку,
и потому, если самолет имеет тенденцию противодействовать
изменению перегрузки, он обладает статической устойчивостью
По перегрузке.
Предположим, что мы желаем удержать самолет в состоянии
измененной перегрузки (фиг. 2). В этом случае траектория по-
лета будет криволинейной, а вектор скорости и вместе с ним
самолет будут вращаться с угловой скоростью ш=
Момент М, прилагаемый к самолету для удержания его в
криволинейном движении, должен быть равен моменту, с кото»-
1S
рым самолет сопротивляется изменению перегрузки, плюс аэро-
динамический момент от сопротивления самолета вращению:
М=Уа\{д-^
I \ да
да] \дп да да] \дш да
ЭГ\1
da /]
При отклонении руля высоты мы приложим к самолету мо-
мент Л1р, а к ручке управления летчик доджен будет приложить
силу ДРР. Между Мр и ДРр существует простое соотношение,
получаемое из предположения, что сила ДРР действует непо-
средственно на самолет при помощи рычага длиной Lp= —.
ДРр
Тогда мы получим характеристику управляемости по перегрузке,
которую обычно называют градиентом усилия по перегрузке:
dPD G , . . х
- — —- (хл + хп + лш).
иП
Отсюда видно, что условие устойчивости по перегрузке пра-
вильнее было бы определять условием (xa +xn+%w) >0, однако
более важно, чтобы у самолета была начальная тенденция к
устранению перегрузки, и потому момент от вращения не следует
принимать во внимание при оценке устойчивости. При расчете
усилий нужно пользоваться фокусом самолета с освобожденным
рулем высоты. Если система управления не уравновешена, к ука-
дРр
занному значению
нужно прибавить весовое усилие на
ручке.
Перейдем к вопросу об устойчивости и управляемости по ско-
рости. Предположим, что в результате изменения силы тяги или
наклона траектории изменилась скорость полета. Изменение
скорости вызовет изменение подъемной силы Y у. Если при этом
угол атаки не изменится, приращение подъемной силы составит
Гг = —ДУ2« — Д1Л.
у дУ* У2
16
Наличие силы Уг приведет к появлению ускорения Jy, под
действием которого траектория будет возвращаться к исход-
ному направлению. Степень устойчивости можно охарактери-
зовать величиной или Такиц образом, если угол
атаки не меняется, режим полета устойчив.
Теперь допустим, что при изменении скорости равновесие
моментов нарушается и появляется момент Mv. Тогда силу
Уу нужно приложить на расстоянии хг ——— от центра тя-
жести (фиг. З)1. Под действием Мг самолет будет менять
угол атаки, но тогда в фокусе появится сила Уа, которая даст
момент ЛЪ—УаХа. Равновесие наступит при условии Л4г-|-
+ Ма = 0 или Угхг + К«х« = 0, а полное приращение подъемной
силы составит
Ar=rr+ra=yJl-^.
\ Ла /
Теперь характеристикой устойчивости режима будет величина
тДР xj'
Тенденция к выправлению наклона траектории будет опре-
деляться условием
ла—> 0 при ха > 0.
Если мы желаем удержать самолет в равновесии при изменен-
ном наклоне траектории или при измененной скорости, нужно
иметь равновесие моментов при условии ¥а +Уу=0. Если на
начальном режиме давление на ручку отсутствовало, то теперь
к ней нужно приложить усилие
о М Yv , ч
Рр — - — (Ха Ху).
i На фиг. 3 xv отложено влево от центра тяжести, т. е. в данном примере
оно отрицательно.
17
Тогда в качестве критерия управляемости по скорости может
служить величина
У2^Р=_О
дУ‘ Lp 4 77
Схема, иллюстрирующая равновесие моментов при изменив-
шейся скорости, показана на фиг. 4.
Если при изменении скорости полета величины всех сил,
действующих на самолет, изменяются в одинаковой степени,
то Л4у = 0 и лу=0. Причинами появления момента Му могут
быть: 1) эффект тяги двигательной группы; 2) действие де-
формации самолета; 3) действие специальных устройств.
Фиг. 4.
Зависимость силы тяги от скорости может быть различна;
при винтовых установках рост скорости сопровождается падением
тяги. Однако момент Му возникает не только от непосредствен-
ного действия тяги, направление которой не проходит через центр
тяжести самолета. Образование силы тяги обычно вызывает из-
менение обтекания самолета, что ведет к изменению моментов
крыла и особенно оперения. Этот вторичный эффект тяги обычно
превосходит прямой ее эффект. Если под действием управ-
ления двигателем или вследствие изменения скорости полета
произошло изменение силы тяги на величину ДР и одновременно
действующий на самолет момент изменился на величину ДМ,
то равноценный эффект можно получить, приложив силу кР на
некотором расстоянии у от центра тяжести. Эту точку можно
назвать фокусом тяги. Фокус тяги может быть сильно сдвинут
по отношению к оси винта.
Изменение силы тяги требует изменения усилия, прилагае-
мого к ручке управления, что дает еще одну характеристику ста-
тической управляемости
дРу кМ __ у
дР ДРДр Lp ’
Предположим, что под действием аэродинамических сил кон-
струкция самолета несколько деформируется; с ростом скорости
эта деформация будет увеличиваться примерно пропорционально
18
квадрату скорости. Наличие деформации приводит к появлению
дополнительного момента, пропорционального величине дефорь
мации и квадрату скорости. В итоге момент от деформации будет
пропорционален четвертой степени скорости. Предположим, что
на исходном режиме момент от деформации был уравновешен
равным по величине аэродинамическим моментом, т. е. на исход-
ном режиме М = аУ*—bV% =0. При изменении скорости полу-
чим
^aV^aVl,
т. е. на самолет стал действовать дополнительный момент
= V2.
Если этот момент действует в неблагоприятном направлении,
нужно или принять меры к уменьшению деформаций или ком-
пенсировать эффект от деформации. Схемы подобных устройств
(для компенсации) несложны, но они должны быть проверены
на вибрацию.
Применяются устройства, момент которых не зависит от ста-
рости полета. Принцип их действия основан на следующем.
Пусть на самолет действует некоторый момент Л1о, величина ко-
торого не зависит от скорости полета. Этот момент уравновешен
моментом, пропорциональным квадрату скорости, Л1о—aV^ =0.
Тогда при изменении скорости получим
M = M0 — aV2 и
° dV‘ V20
Подбирая Af0, можно получить желаемое х v для обеспечения
статической устойчивости самолета на заданном режиме. Устрой-
ство, которое сообщает самолету постоянный момент, выполнено
так. На руль высоты действует длинная пружина; при отклонении
руля растяжение пружины незначительно и момент можно счи-
тать постоянным. Пружина отклоняет руль вниз, пока момент
аэродинамических сил не уравновесит момент пружины. При
изменении скорости руль будет поворачиваться так, чтобы дей-
ствующая на него нагрузка оставалась неизменной, и поэтому
момент отклонения руля вокруг центра тяжести самолета также
будет постоянен. Уравновешивающий момент создается отклоне-
нием триммера. Момент пропорционален квадрату скорости; если
нагрузка на руль уравновешивается моментом триммера, поло-
жение руля при изменении скорости меняться не будет, но подъ-
емная сила оперения будет пропорциональна квадрату скорости.
В качестве характеристик статической управляемости служат
усилия, необходимые для уравновешивания моментов, вызывае-
мых выпуском шасси, открытием щитков или закрылков и пр.
19
Пусть самолет был сбалансирован на некотором режиме, когда
давление на ручку отсутствовало. Пусть затем летчик выпустил
посадочные щитки, предоставляя ручке управления свободу, т. е.
не оказывая на нее давления. При опускании щитков произойдет
приращение подъемной силы крыла Ущ и появится некоторый
момент Мш. Такой же эффект мы получим, приложив силу Ущ
в некоторой точке на расстоянии хщ = —^-(фиг. 5). У изолиро-
Тщ
ванного крыла сила Ущ приложена примерно на расстоянии 45(0/о
хорды от передней кромки. Однако, если принять во внимание
действие измененной подъемной силы крыла на оперение, поло-
жение Ущ окажется сдвинутым еще дальше вперед и может ока-
Фиг. 5.
заться даже впереди центра тяжести. Под действием момента
от силы Ущ самолет будет менять угол атаки и вместе с этим
в фокусе появится сила Уа, которая уравновесит момент силы Ущ.
Суммарное поиращение подъемной силы составит
ДУ=Ущ+Уа.
Так как
Гщхщ+ УаХа = 0; ,
Ха
то
Повидимому, выгодно, когда Ущ оказывается между центром
тяжести и фокусом самолета. Тогда при выпуске щитка подъем-
ная сила увеличится, но самолет получит импульс на опускание
носа. Этот импульс желателен и обычно он производится летчи-
ком, так как с выпущенными щитками наклон траектории планиг
рования увеличивается Желаемое положение силы Ущ требует
соответствующего подбора оперения самолета и определенной
его центровки.
20
ПРОСТЕЙШИЕ ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПРОДОЛЬНЫХ ДВИЖЕНИЙ САМОЛЕТА
Предположим, что самолет летит прямолинейно и равномерно;
это значит, что' все силы и моменты находятся в равновесии. За-
тем пусть равновесие нарушилось и появились некоторые неурав-
новешенные сила и момент. Такое же действие можно получить
от одной силы, приложенной в некоторой точке, которую для
самолета мы назвали фокусом. Пусть произошло изменение
подъемной силы Л У (фиг. 6). Под действием силы ДУ мы полу-
. ДК
чцм поступательное ускорение ]=--, под действием момента —
угловое ускорение =
.Угловое ускорение вызовет окруж-
ные ускорения /1= тогда можно* найти точку, в которой ли-
нейное ускорение будет равно нулю. Это будет так называемый
центр ускорения. Его положение найдем из условия
\ т
Ввиду того что до начала действия возмущения в относи-
тельном движении было состояние покоя, центр ускорения явится
и центром вращения. Таким образом в случае внезапного изме-
нения угла атаки начальное движение самолета состоит в уско-
ренном вращении вокруг центра ускорения, который у статически
устойчивого самолета лежит на расстоянии Li впереди самолета.
Если самолет неустойчив, центр вращения будет расположен
сзади. Подобным образом удобно объяснять зависимость устой-
чивости от взаимного расположения центра тяжести и фокуса.
На фиг 7 приведена схема модели для демонстрации указан-
ного свойства самолета. Модель самолета надета на ось, проходя-
щую через центр тяжести модели; ось прикреплена к рычагу, кото-
рый вращается на опоре, и вся система уравновешена балансиром.
Недалеко от центра тяжести модели имеются штифты, к которым
могут быть приложены возмущающие силы. На модели нанесена
ось, указывающая положение модели, а рядом на специальной
21
подставке протянута нить, показывающая начальное положение
модели Модель и рычаг должны быть тщательно уравновешены,
а трение в шарнирах — мало. Устанавливаем модель так, чтобы
направление нити совпадало с осью самолета, и затем сообщаем
модели возмущение, ударяя по штифту ТогДа точка пересечения
нити с осью самолета укажет центр вращения Подобная схема
может быть использована для экспериментального определения
момента инерции тела.
Предположим, самолет пролетает зону мелких восходящих и
нисходящих потоков. Тогда толчки разного направления будут
быстро чередоваться и качание самолета будет происходить во-
круг центра ускорения Такое поведение самолета можно наблю-
дать при полете в тихий, но жаркий летний день
Укажем некоторые практические выводы, вытекающие из
подобного рассмотрения поведения самолета. Если экипаж мо-
жет быть размещен довольно тесно, имеет смысл разместить его
в носовой части фюзеляжа, а степень статической устойчивости
увеличить для приближения центра ускорения к носу фюзеляжа
Если пассажирская кабина очень длинна, центр ускорения нужно
удалить вперед, чтобы ускорения в передней и задней частях
кабины различались не слишком сильно. Это потребует уменьше-
ния запаса статической устойчивости.
Подобным образом можно рассматривать положение центра
ускорения в момент сбрасывания груза, при стрельбе из пушек
и пр. Интересно рассмотрение положения центра ускорения в
случае посадки при толчке шасси о землю.
Простейшей динамической характеристикой управляемости
может служить угловое ускорение при отклонении руля или
приложении к рычагу управления некоторой силы При выпол-
нении самолета по схеме «летающее крыло» отклонение руля
высоты также приводит к появлению существенного линейного
ускорения и тогда тоже удобно рассматривать положение центра
ускорения.
22
Обозначим угловое ускорение самолета через 9", перемеще-
ние конца ручки — хр и усилие, прилагаемое к ручке,— Рр. Тогда
получим следующие характеристики:
д<?" . дРр . дРр
ду ’ дхр 9 дРр ’ ду ’ дхр дхр ’ дРр
Раскрывая их, будем иметь
<¥' дСуГ>0 Wr.o^o
ду да I а I дхр дхр dSp / ’
дРр __/\2 дтт с А • дРр ____________д/Ищ с А • dyzz ____________-^р
дхр \дхр/ д&р Г‘ ° Р р’ ду дхр дар г’ ° р р’ дРр I
полнении фигур высшего пилотажа. Градиенты —L-
дР^
г дГ
Градиент
Рассмотрение вопроса с точки зрения динамики полета может
дать указание на необходимые значения углового ускорения,
исходя из маневров, выполняемых в обычном полете и при вы:-
ду" *
и будут
дХр
диктоваться физиологическими условиями. Желательные значе-
ния градиентов могут быть выявлены путем анализа свойств до-
статочно большого числа самолетов или путем постановки экспе-
риментов на специальном стенде.
почти не зависит от скорости полета; однако
при малой скорости для приложения некоторого' усилия будет
требоваться более значительное перемещение ручки. У маневрен-
ных машин должно быть достаточно велико, примерно
р
0,3—0,6, у мало маневренных 0,05—0,1, у тяжелых машин —
0,005—0,01.
Для того чтобы получить представление о реакции самолета
на перемещения ручки управления и на прилагаемые к ней уси-
лия, нужно' сделать модель, в которой воспроизводились бы ука-
занные характеристики. На фиг. 8 показана такая простая схема.
Вообще говоря, нужно было бы воспроизвести и демпфирование,
но это выполнить сложнее и при рассмотрении быстрых и не-
глубоких отклонений не имеет серьезного значения.
Стержень, обладающий определенной упругостью на круче-
ние, одним концом защемлен на опоре; на другом конце сделана
шарнирная опора и присоединен балансир с некоторым момен-
том инерции I, изображающий самолет. К стержню прикреплена
ручка управления, которая делит упругий стержень на две части:
первую 1 — от балансира до ручки и вторую 2 — от ручки до
защемленной опоры. Если ручка закреплена, при повороте ба-
лансира вокруг оси стержня будет возникать момент М± = —Л 91,
23
который определит частоту колебаний балансира, и мы получим
характеристику колебаний
При освобожденной ручке поворот балансира будет вызывать
закручивание обоих участков стержня и частота колебаний ба-
лансира понизится, что как бы соответствует уменьшению сте-
пени статической устойчивости с освобожденной ручкой. Крутя-
щий момент действует на оба участка, и полный угол закручива-
ния сложится из углов закручивания каждого из участков. Тогда
характеристика колебаний балансира определится условием
. М М „ М АВ
Т.-т; Т.=7; 4=^ = —^^
_ АВ
/2 (А+В)1
Быстро отклоняя ручку, мы вызовем закручивание обоих уча-
стков стержня на равные углы и создадим крутящие мо-
менты и М2=В^2', момент будет передан балансиру,
который придет в движение и после ряда колебаний успокоится
в отклоненном положении.
Определим угловое ускорение при смещении конца ручки:
х „Ах д(о" А
Ф = ; ф* =--------; -?- = .
Т L r 1 L дх IL
24
дР
Найдем жесткость ручки, определяемую производной — :
г> М1Ч-ЛТ2 ' _ ____ х р х (А+В) 9 дР А + В
L . <Р1 — ?2— L , £г , дх Lt •
Мы получили четыре уравнения с четырьмя неизвестными;
решая их, получим выражения для параметров модели через
заданные динамические характеристики:
^3 - -а •
I ч I I ^*0 2
df Л \ й /2
АВ А „
7(Д + В) 2 IL 3
. О? «l«2fl4
Д + В=а4-4; В = -Ц^
«з аз
дР
— О'3’ j —
ох 1
л / \ г А
д= (а1_а2); 1=—•
йз ах
А + В ~ .
г — Дл,
L* *’
L = —
Если нужно воспроизвести неустойчивый самолет с освобож-
денным или зажатым управлением, схему модели нужно услож-
нить, присоединив к балансиру груз, лежащий выше оси враще-
ния, или применить дестабилизирующую пружину. Можно раз-
работать схему, параметры которой могут быстро изменяться.
К балансиру следует прикрепить длинную стрелку или неболь-
шой проекционный фонарик, изображение которого на экране
будет создавать иллюзию вращения. Еще лучше применить схему,
в которой сам экспериментатор поворачивается вместе с моделью
кабины самолета.
Динамические характеристики имеют примерно' такое зна-
чение:
ду” 40 х„
=-------h ri = 0,12^4- 0,15£ф.
дч суг1
Здесь л*—запас статической устойчивости, составляющий
обычно 5— 1О°/0 средней хорды крыла; при освобожденном
управлении ха уменьшается на 3 —5°/0 средней хорды крыла.
Величина £ф—длина фюзеляжа.
Значение можно приближенно выразить так:
д'?’ = 70
дхр CyLT о
где 1Г. 0 — расстояние от центра тяжести до фокуса оперения.
о д'?" л дРр d-i’ ду’
Значения —— уже были указаны, а —Е- = -2— : —г-.
дРр J } дхр дхр дРр
25
ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЙ, ПРИВОДИМЫХ
К ПРОСТОМУ ЗАТУХАЮЩЕМУ КОЛЕБАНИЮ
Простое затухающее колебание является наиболее типичным
случаем движения тела в сопротивляющейся среде. Под терми-
ном простое затухающее колебание мы подразумеваем движение,
определяемое линейным дифференциальным уравнением второго
порядка, когда на тело действуют силы или моменты, линейно
связанные с перемещением и величиной скорости. К рассматри-
ваемым движениям, кроме собственно затухающих колебаний,
будет относиться и апериодическое движение.
Для того чтобы движение самолета определялось уравнением
второго порядка, необходимо сделать некоторые допущения, а
для этого нужны соответствующие основания. Возможны такие
характеристики самолета, когда желательные допущения не мо-
гут быть сделаны. Однако в большинстве случаев можно ввести
ряд упрощений и тогда сложное движение расчленяется на со-
ставляющие — простые затухающие колебания. Нужно заметить,
что такое расчленение можно произвести всегда с достаточной
точностью и это будет показано в данной работе.
Рассмотрение частных упрощенных случаев, которым посвя-
щена эта глава, позволит раскрыть важные динамические свой-
ства самолетов и послужит ступенью для перехода к рассмотре-
нию более сложных видов движения.
Общие сведения по теории затухающих колебаний
Теория затухающих колебаний применяется во многих зада-
чах техники и ее изложение можно найти в учебниках матема-
тики, механики и специальных работах. Обычно всякое тело
совершает колебательное движение, если при отклонении от по-
ложения равновесия возникают силы или моменты, стремящиеся
вернуть тело в положение равновесия. Если силы пропорцио-
нальны первой степени удаления, мы получим гармоническое
колебание, т. е. синусоидальный закон изменения перемещений,
скоростей и ускорений по времени. Если, кроме того, действуют
силы, прямо пропорциональные скорости движения и стремя-
щиеся остановить тело, мы получим простое затухающее коле-
бание. При колебаниях самолета с малыми амплитудами можно
выделить силы и моменты, пропорциональные отклонению и
первой степени скорости.
На фиг. 9 и 10 показаны системы тел, совершающих простое
затухающее колебание (поступательное или вращательное).
Основное колебание создается силами упругости пружины; при-
чина затухания символически изображена в виде сетки, связан-
ной с телом и взаимодействующей с окружающей средой. Так
как между поступательным и вращательным движениями нет
принципиальной разницы, мы пока будем говорить О' поступа-
тельном движении.
26
Простое затухающее колебание определяется массой тела
дР
т, производной силы по смещению — и производной силы
др
по скорости перемещения —. Введем обозначения:
дх'
дх" 1 дР . дх" 1 дР
— =-------=—nf- — —------------= —п.
дх т дх дх' т дх’
Тогда получим дифференциальное уравнение
„ дР , , дР „ . . , , п
тх ——х 4-------х или х +nx' + nix = Q.
дх1 дх
Решить дифференциальное уравнение — значит, найти функ-
цию, которая удовлетворяет условию, записанному в виде урав-
нения. Данное уравнение говорит, что сумма значений перемен-
Фиг. 9.
Фиг. 10.
ного, его первой и второй производных, умноженных на некото/-
рые постоянные, равна нулю. Это условие может быть соблюдено
в том случае, если дифференцирование соответствует умножению
на некоторый множитель X. Тогда получим
х' = Хх; х" = Х2х; — = Хх; х=Сеи.
’ dt
Подставив выражения для х' и х" в уравнение и сократив
на еи, получим так называемое характеристическое уравне-
ние, решая которое найдем X:
X2 + „k + ra2 = 0;
Квадратное уравнение имеет два корня, следовательно, наше
дифференциальное уравнение удовлетворяется двумя функци-
ями и соответствует двум движениям x1 = CjeXi/ и х2~С2е'^.
В общем случае оба движения могут иметь место одновре-
менно и тогда общее решение записывается в виде
Х = Х1 + х2.
27
Функция является наиболее типичной для описания различ-
ных явлений. Она изображает рост или уменьшение, когда интен-
сивность изменения прямо пропорциональна значению функции.
Из сложения двух таких движений мы можем получить два ха-
рактерных вида апериодического движения.
Если n2Q > корни характеристического уравнения будут
комплексными, и для этого случая нужно искать другое решение
дифференциального уравнения. Функция еи обладает тем свой-
ством, что при дифференцировании она не меняется — происхо-
дит только умножение на постоянную величину X. Тригонометри-
ческие функции sin а и cos а обладают тем свойством, что при их
дифференцировании происходит последовательная смена синуса
„ d'l
на косинус и т. д. и умножение на постоянный множитель ш =.
dt
Поэтому попробуем представить искомое решение в таком виде:
x = x1 + xI; хх = xi.oe-’i'cos pf; х2 = Хаде-’1* sin pt
Подставим любое из частных решений в дифференциальное
уравнение:
x = x0£~’i/cospf; х'= — x07j<?~Vcos!if—Xoptf-’i*sinpf;
x" = x^e-^ cos pf 4- 2х0т]ре-ч/ sin pf—xop2e_,iz cos pt
xoe~’1/ fa2 cos + 2?ip sin pf—p2 cos pf—пч\ cos pf—
—np sin pf+cos pf] = 0.
Отсюда
(т]2—p2—nq + n2) cos pf + (2tqp — np) sin pf=0.
Это равенство удовлетворяется при любом t, если каждая из ско-
бок равна нулю. Тогда
П П* 2 Л2 9 Л
V) = — ;----------------р/-------------h п2 = 0;
I 2 4 1 2 0
9 9 И2
г=п20~—
Принятые выше решения удовлетворяют исходному уравне-
нию, и, следовательно, искомая функция состоит из двух колеба-
тельных движений с затухающей амплитудой. Одно движение
следует закону косинуса, второе—закону синуса:
п п.
““9" ~ o’
•*1 = Xi,o£ cos pY; х2 = *2,о£ sin yt.
Значения Xi.o и х2,о могут быть найдены по начальным зна-
чениям х и х'. Если при f = 0 х = х0 и х' = 0, то х^о — х0 и
Хо,0 — 0.
28
Период колебания
Величину £0 = — назовем фактором периода, а величину
D=~—фактором затухания; т0 — период колебания при от-
ло
сутствии затухания. Если D > 2, период т становится мнимым,
а движение —апериодическим.
Изменение х по закону затухающего колебания можно пред-
ставить как изменение проекции радиуса-вектора г, который вра-
щается с угловой скоростью pi и непрерывно укорачивается по
закону
r = rof 2 ; x = rcosp.£.
Для определения характеристики затухания рассматривают
изменение амплитуд за период или полупериод, или время, в те-
чение которого радиус-вектор уменьшается в два раза:
— = 2; 1g—=0,3 = —*! = — .
г г 4,6 п
Если интересоваться изменением амплитуд, т. е. отношением двух
смежных максимальных удалений от положения равновесия, нуж)-
яо подставить время, равное полупериоду:
1 гп 1 х„ тс 1
lg—~ = —R------------7=- •
гл + 1 хп+1 4’6 "1/ 1 _ 1
|/ Г>2 4
Как видим, изменение амплитуд зависит только от фактора
затухания D = —. Для справочных целей приводим таблицу
"о
значений — и -
т0 ХП
D 0,25 0,50 0,75 1,0 1,25 1,50 1,75 2,0
1,008 1,031 1,078 1,152 1,28 1,51 2,06 со
хп 0,67 0,445 0,28 0,162 0,081 0,031 0,0035 0
29
При рассмотрении затухающих колебаний часто ограничива-
ются определением периода колебания и затухания по времени
или амплитудам. Решение различных задач по приведенным фор-
мулам представляет большое неудобство. Для инженерного рас-
чета можно заготовить графики колебаний для разных факторов
затухания D. Тогда единственным вычислением останется пере-
счет масштаба для времени и амплитуд. Для составления графи-
ков преобразуем дифференциальное уравнение, придав ему «ка-
чественную» форму. Введем единицу времени
Тогда уравнение можно привести к виду
t%x" + Dt^x' + х = О,
Обозначив —=f, найдем производные:
А)
, 1-7 //1
X =---Х И Х =-^-Х ,
*0 <0
где черта над х’ или х" означает дифференцирование по Л
Подставляя в уравнение, получаем
х" + Dx + х = 0.
Если обозначить x=xt0=V, то х" — V1, и тогда будем
иметь
Решения этого уравнения при Z? > 2:
х = 4- С2е^,
при D < 2
пользуясь ими, можно построить графики колебания и апериоди-
ческого движения для различных значений D. Подобный график
приведен на фиг. 11. По оси ординат отложено смешение —, по
А'о
оси абсцисс — время —. Начальное отклонение в момент оста-
30
новки движения принято равным единице, а за единицу времени
у 1 т-
принято tQ =—. Если затухания нет, диаграмма представляет
л0
собой просто синусоиду. По мере роста значения фактора зати-
хания полуволна удлиняется и последующая амплитуда умень-
шается. При Z>>2 движение становится апериодическим и кривая
больше не пересекает ось абсцисс. Данный график легко может
быть перестроен для нужного значения начальной амплитуды и
в функции действительного времени t. Величины, отложенные по
оси ординат, на данном графике являются отношениями величины
отклонения х к исходной амплитуде х0. За начало отсчета вре-
мени принят момент наибольшего отклонения. Левее этой точки
отложены значения времени с отрицательным знаком, т. е. рас-
сматриваются отклонения для моментов времени, предшествую!-
щих моменту остановки движения. По данному на фиг. 11 не-
большому участку колебательного движения можно последова-
тельным перестроением построить желаемое число полуволн за-
тухающего колебания.
Для исследования затухающего колебания удобно построить
график в координатах V и х. Тогда в зависимости от значения
фактора затухания D получается характерная форма диаграммы.
Подобная диаграмма называется диаграммой на фазовом поле.
Для сокращения будем называть ее фазовой диаграммой.
Построение фазовой диаграммы можно произвести, пользуясь
уравнениями
_£т"
2тг -Г 2 t
x = rcos—1\ r = ;
т
гу V / D ~г . 2тс . 2тг
V =---= —Г —COS -----t-\---sm----t .
По \ 2 т т т /
Уравнение фазовой диаграммы обладает интересными геометри-
ческими свойствами, позволяющими сравнительно просто по-
строить эту диаграмму. Остановимся на этих свойствах. Составим
уравнение
V' = V~ =— VD—x; — =—^~ — D.
dx dx V
На поле V, х (фиг. 12) берем некоторую точку и соединяем ее
с началом координат. Построение элемента фазовой диаграммы
ясно из чертежа. Как видим, элемент ds можно получить, про-
ведя дугу из точки g, отстоящей от начала координат на рас-
стоянии Og=VD. Таким образом дифференциальное уравнение
определяет кривые, которые могут быть построены при помощи
специального приспособления. Действительно, пусть мы имеем
циркуль, одна ножка которого чертит кривую, а другая находит-
ся на оси х и смещена от начала координат на расстояние %i= VD.
Тогда, чтобы пишущая ножка двигалась только по касательной,
32
она должна быть снабжена роликом подобно планиметру. Более
грубо диаграмма может быть построена из отрезков дуг.
Если иметь начальную_точку для V и разбить скорость (ось
ординат) на интервалы Д V, то будут известны средние значения
скорости, а по ним легко найдем центры, из которых нужно про-
водить дуги. Пример построения показан на фиг. 13.
Фиг. 12.
Фиг. 13
или разметку значений —.При помощи этой разметки мы свя-
жем фазовую диаграмму с диаграммой колебаний. На фиг. 14
приведена диаграмма с разметкой — для значений D от 0 до 2.
На фиг. 15 приведены фазовые диаграммы для апериодического
движения. Для каждого значения D поле диаграммы разделяет-
ся на две зоны двумя прямыми, углы наклона которых и
определяются условием
ctg<p= — tg<p—D; tg<pi,2=------^±1/^ — 1.
Мы уже указывали, что апериодическое движение склады-
вается из двух движений = и л2 = С2е^. При разных
знаках х± и х2 получаем ветвь I кривой, при одинаковых —
ветвь //. Прямые соответствуют только одному из движений.
Если оба движения имеют одинаковый знак, мы попадаем
в зону острого угла между прямыми, где затухание идет
более быстро. Если знаки слагаемых движений различны, мы
попадаем в зону тупого угла между прямыми. Попадание
. К
в ту или иную зону зависит от начальных значений — или
хо
зз
co
~. Удобство пользования фазовой диаграммой заключается
в том, что по начальным значениям или — легко по-
л0 dx
лучить начальное состояние движения —, а затем, пере-
*0
ходя на диаграмму колебаний, можно также легко построить
все движение.
При D — 2
1 п 1 п 1 Г1 « - г'
2 =----н---I / 1----=------• © = ф е 2
2 — 2 V 4 2 Т
tt = Dn0 = 2п0.
Однако это не единственное решение; уравнению удовлетво-
ряет также решение — . Подставим его в уравнение:
——t ——t
п . п . _ п л
п П п f I , П“ ~ Z
? =—2 + ;
2 2 4
Чье
п , , п* , пг , . п2 Л п
И Ьл И— г = 0,
2----------------------4-2-4/
т. е. получим тождество.
Таким образом решение; нужно написать так:
? = ?</? +<tbte
Пусть, например, в начальный момент <р = ?о и ?о~^-
Тогда найдем <рв и <рй:
?о = ?а; ?'= — Тв + ъ=0; ?«=?<,=То-
Если га0 = 1, п = 2 и <р0=1» получим = -М);
этому случаю соответствует диаграмма на фиг. 16.
Забежим немного вперед и подумаем, хорошо ли иметь силь-
ное затухание, т. е. большое D. Быстрое уменьшение отклонения
очень желательно, однако при D= 1,5 мы имеем уже практически
апериодическое движение. Если D больше двух и тело* получило
начальный толчок, фаза удаления от положения равновесия бу-
дет короткой, но фаза приближения к положению равновесия
очень затянется и теоретически будет бесконечно велика. Полу-
чив возмущение, тело все время будет иметь одностороннее сме-
щение, что может быть весьма нежелательно.
35
На фиг. 16 приведены основные характеристики затуха-
ющих колебаний в функции величины D. В верхней части
фигуры даны значения отношения смежных амплитуд Х"—,
•%п
характеризующие затухание за полупериод колебания; рядом
с этой кривой нанесена приближенная зависимость Х" — »
хп
» 0,125(2 —D)3, которая оказалась очень близкой к точной
зависимости. Как видно, с ростом фактора затухания D зату-
хание резко усиливается и при D, большем 1,5, колебание
практически апериодично. Так, если взять начальную ампли-
туду за 100%, то при 0 = 1,5 через полупериод амплитуда
составит только 3%, а через период —около 0,1%.
Вторая кривая в верхней части фиг. 16 дает значения .
Эту величину нужно понимать так. Пусть мы имеем момент оста-
новки движения, когда амплитуда равна х0; затем начнется дви-
жение в обратную сторону, скорость которого будет расти и до-
стигнет некоторого максимума Vmax; разделив Ктах на /0, получим
VmaX. Следует заметить, что при последовательных колебатель-
ных движениях значения Утах уменьшаются в той же степени, что
и амплитуды.
В нижней части фиг. 16 кривая указывает на рост периода
затухающего колебания по сравнению с незатухающим гармони-
ческим колебанием при увеличении D. Одно полное гармониче-
ское колебание можно разделить на четыре фазы — удаление от
положения равновесия (дважды) и приближение к нему (тоже
дважды).
Каждая фаза занимает время
= -у- /о- При затухающем
колебании будем иметь время удаления и время приближе-
ния /2; на фигуре показаны изменения
2 '1 и JLA.
тс
Как видим, при апериодическом движении время удаления ста-
новится небольшим, но время приближения бесконечно велико.
Возрастающие колебания получаются при п<Х) и, следова-
тельно, при отрицательном D. Фазовая диаграмма V по х остает-
ся в сущности та же, но ее нужно или обернуть вокруг оси у,
или просто читать против часовой стрелки.
36
Фиг. 16.
37
Дивергентное движение
Апериодически неустойчивое или дивергентное движение по>-
лучается в том случае, если действующая сила линейно связана
с отклонением от положения равновесия и при этом стремится
удалить тело от положения равновесия. С неустойчивыми харак-
теристиками равновесия необходимо бороться, но свойства не-
устойчивого движения полезно знать.
Простым примером неустойчивого равновесия может служить
схема, показанная на фиг. 17. Эту схему нужно рассматривать
в горизонтальной плоскости, когда вес груза не дает
момента относительно оси вращения. Составим уравнение дви-
жения
<р’ = — +
где
, 1 дМ 1 дМ
0 I д'? I д'?'
Составляем характеристическое уравнение, решаем его и на-
ходим искомую функцию
X1.2=-T±1Z
х = Сге^ + С2е^.
Один корень X отрицателен, другой — положителен. Следова-
тельно, движение разлагается на'два, из которых одно — устой-
чивое, другое — неустойчивое. На фиг. 18 показаны два варианта
сложения этих движений (кривые 1 + 2 и 1+2'). Естественно, что
итоговое движение в обоих случаях будет неустойчиво, так как
по мере затухания одного движения второе развивается.
На фиг. 19 показано построение фазовой диаграммы дивер-
гентного движения в координатах V., х, а на фиг. 20 даны при-
меры фазовых диаграмм для различных D.
При D = 0 получаем гиперболы, и при любом возмущении
тело энергично удаляется от положения- равновесия. Иначе об-
стоит дело при наличии торможения. При большом D и наличии
начального смещения тело тоже уходит от положения равнове-
сия, но темп прироста скорости значительно меньше. Если в ис-
ходном положении смещения нет, но тело получило некоторую
начальную скорость, то вначале скорость убывает, как и в случае
затухающего колебания, и после прохождения некоторого мини-
мума вновь начинает расти. При D = 4 начальная скорость убы-
вает почти в десять раз.
38
Каждая из асимптот, показанных на фиг. 20, соответствует
одному из составляющих движений. Наклоны асимптот легко по-
лучить следующим образом:
, dx' 1 ~
tgT=—= ------D\
dx tg?
tg2 <p 4. D tg <p — 1 = 0;
tg?i,2= ±]/ ^+1-^-;
tg'Pa^
1
tg<Pi
Прямая с положительным наклоном соответствует неустойчивому
движению, с отрицательным — устойчивому. Действительно, при
Фиг. 17.
положительном наклоне скорость направлена в сторону откло-
нения и, следовательно, отклонение растет; при отрицательном
наклоне скорость направлена против отклонения и движение
стремится к положению равновесия.
Если D >5, можно приближенно принять tg^
tg ?2= — D.
Пусть движение идет по неустойчивой прямой. Найдем
время удвоения отклонения:
dt_^ dx . 2,3 . х2 0,69
X tg <pn0 ’ 1 tg <pn0 * XV nQ tg cpx
При D^>5 приближенно получим /1 = 0,69 . Величина слу-
no
жит основной характеристикой дивергентного движения.
39
Фиг. 19.
D = 0
Фиг. 20.
40
Если нужно управлять неустойчивой системой, например, ле-
теть на неустойчивом самолете, необходимо периодически оста-
навливать возникающее движение и приводить систему в поло-
жение равновесия.
Чем меньше тем быстрее нужно реагировать на нарушения
равновесия. Человек, стоящий на одной точке, находится в со-
стоянии неустойчивого равновесия, однако при достаточном на-
пряжении ему удастся балансировать. Значение в этом случае
равно примерно х/4 сек. Если составляет десятки секунд, не-
устойчивость весьма мало заметна. Вопрос о том, с какой не-
устойчивостью справиться легко, с какой трудно, можно обсле-
довать на модели, аналогичной показанной на фиг. 8, сделав
балансир в виде одного груза, поднятого выше точки опоры.
Физическая природа простых затухающих колебаний
и механические модели движения
Колебательное движение — один из самых распространенных
видов движения. Однако природа колебаний бывает весьма раз-
личной. Весьма обычны колебания тел под действием сил упру-
гости и силы тяжести. Если тело, кроме колебания, не участвует
в другом движении, затухание вызывается или силами трения или
силами, пропорциональными квадрату скорости колебательного
движения. Затухание, пропорциональное первой степени ско-
рости колебательного движения, возникает обычно в том случае,
если тело участвует в некотором постоянном (неколебательном}
движении по1 отношению к среде, с которой оно взаимодействует.
Самолет и его части взаимодействуют с движущейся воздушной
средой, и отсюда возникают условия, создающие колебания с не-
которым затуханием. Интересно, что весьма сходное явление
возникает при взаимодействии колеса с грунтом.
В теории колебаний обычно рассматривают два вида энер-
гии — кинетическую энергию движения тела и потенциальную
энергию, в качестве которой может быть принята энергия упру-
гой деформации или энергия перемещения в поле земного тяго(-
тения и т. п. В случае колебания, вызванного взаимодействием
тела и движущейся среды, понятие потенциальной энергии
приобретает иной смысл. Возьмем для примера крыло, находя-
щееся в потоке и имеющее возможность вращаться относительно
точки, расположенной впереди крыла (фиг. 21). Действие воз-
душного потока будет определять как само колебание, так и
затухание. Пусть тело наибольшим образом удалилось от поло-
жения равновесия. В этом положении никакой кинетической
энергии у него нет, и поток будет стремиться вернуть тело в по-
ложение равновесия.
Таким образом энергия для каждого размаха колебания чер-
пается из общей энергии встречного потока. Отсюда нетрудно
41
сделать вывод, что в процессе колебания сопротивление тела
движению будет увеличено. В результате будет уменьшаться ско-
рость потока или скорость движения тела. Однако расход энергии
на колебание обычно очень незначителен по сравнению с обшей
кинетической энергией потока или кинетической энергией тела
при его движении относительно среды.
Предположим, что крыло имеет весьма большой момент инер-
ции при вращении около указанного центра. В этом случае коле-
бание будет медленным и затухание очень слабым. Тогда можно
найти среднее сопротивление в процессе колебания. Величина
этого сопротивления зависит от амплитуды. Предположим те-
перь, что мы принудительно будем сокращать период гармони-
ческого колебания, не меняя его амплитуды. Если в этом случае
среднее сопротивление понизится, то можно утверждать, что ко-
лебание стремится к затуханию, так как снижение сопротивления
указывает на уменьшение энергии, передаваемой средой телу
для колебательного движения.
Уменьшение сопротивления в процессе колебания особенно
четко выявляется при рассмотрении момента перехода через по-
ложение равновесия с .некоторой скоростью (фиг. 22). В этом
случае для крыла возможно появление даже отрицательного
сопротивления, т. е. тяги. Приведенная на фиг. 21 схема коле-
блющегося крыла может быть использована для демонстрации
затухающего колебания или дивергентного движения, которое
получится, если поместить центр вращения позади крыла. Однако
можно предложить более простую установку.
Предположим, что у нас имеется рычаг, вращающийся вокруг
некоторой точки и имеющий на конце штифт, который скользит
по подвижной поверхности, например, барабану. Для получения
желаемого момента инерции к рычагу приделаны грузы (фиг. 23).
Если окружная скорость вращения барабана, будет превосхо-
дить возможную поперечную скорость штифта при колебаниях
настолько, что линия, прочерчиваемая штифтом на барабане, не
будет отклоняться более чем на 15° от горизонтали, то сила тре-
ния штифта будет давать моменты, пропорциональные первой
степени угла отклонения и первой степени угловой скорости. Углы
отклонения рычага должны лежать в пределах, при которых
можно принять изменение синуса этих углов линейным.
42
Сила трения штифта Q будет направлена по касательной к
траектории, записываемой на барабане, и, следовательно, наклон
силы трения будет пропорционален угловой скорости движения
рычага. Тогда уравнения и характеристики движения будут иметь
вид
= м = — q/A? + ; ?" = —п<р';
Л° / ’
D== —
VI nQ
Пользуясь этими соотношениями, можно рассчитать размеры
модели, соответствующей любым значениям факторов периода и
затухания. Если штифт сделать из карандаша, то на ленте можно
получить запись колебаний. Вводя в данную схему упругий эле-
мент, можно' более легко изменять период колебания.
Дивергентное движение можно легко получить изменением
направления вращения барабана по отношению к рычагу. Слож-
нее выполнить установку для демонстрации возрастающих коле-
баний. Дело в том, что силы, вызванные скоростью колебания,
почти всегда препятствуют движению. Можно использовать не-
которые аэродинамические эффекты, связанные с развитием
срыва обтекания. Однако в этом случае трудно получить линей-
ную зависимость силы от скорости движения.
Для получения возрастающих колебаний можно воспользо-
ваться и такими соображениями. Проинтегрируем уравнение дви-
жения
cp' + ncp + n^ j ср dt = 0.
Этому уравнению будет удовлетворять система с весьма малым
моментом инерции, на которую действуют моменты, зависящие
от угловой скорости ср', угла ср и значения J ®dt. Для получения
43
возрастающих колебаний нужно, чтобы п<0; величина j ®dt
может быть представлена в виде некоторого нового угла или
линейного перемещения, получаемого1 путем интегрирования угла
поворота.
Наиболее просто возрастающие колебания можно получить
следующим образом. Напишем уравнение движения, проинтегри-
руем его и затем исключим члены, содержащие <?':
ср" + пу + п^ср = 0; ср' + nep + п?0 j ср dt = 0;
<р" + (по—п1)ч—ппо J ?<# = 0.
Полученное уравнение является, строго говоря, дифферен-
циальным уравнением третьего порядка. Можно подобрать его
коэффициенты таким образом, чтобы результирующее движение
состояло из устойчивого апериодического движения, которое бу-
дет мало заметно, и возрастающих колебаний. Из последнего
условия следует, что коэффициент J ydt должен быть положи-
телен, так как п<0.
На фиг. 24 показана конструктивная схема модели для де-
монстрации возрастающих колебаний. Модель состоит из букси-
руемой тележки, движущейся с некоторым трением Q и скоро-
стью V. Прилагая к передней части тележки буксирующую силу,
равную силе трения, получим момент М. Составим уравнение
движения тележки
М = — Qa (ср + ф) == — Qa f(p + ?
-+^ ;
ь ь
’' + v(1 + t)t + 7?^ = 0'
Заметим, что
y = V
Тогда получим
„ . Qa /1 . а \ . QaV Г п
/ \ о / lb J
Qa /- , а \ о 9 Qa „ о
— 1 Н =п2—-п2; = — пп*
I \ Ь ) 0 'lb 0
44
Следует заметить, что когда амплитуда колебаний становится
достаточно большой, возрастание ее прекращается и колебание
продолжается с постоянной амплитудой. Подобные колебания
буксируемых тележек и саней часто наблюдаются на практике.
На фиг. 25 показана несколько видоизмененная схема модели,
которая также может служить для демонстрации возрастающих
колебаний.
СЛУЧАИ ПРОДОЛЬНЫХ ДВИЖЕНИЙ, ПРИВОДИМЫХ
К ПРОСТОМУ ЗАТУХАЮЩЕМУ КОЛЕБАНИЮ
При рассмотрении продольных движений самолета получаем
три дифференциальных уравнения. Объединение их приводит к
одному уравнению высокого порядка, определяющему некоторое
сложное движение. Сложное движение можно разложить на сум-
му простых движений, определяемых уравнениями первого и
второго порядков. Как производить это разложение, будет расска-
зано ниже. Однако во многих случаях продольного движения са-
молета можно с некоторым приближением прямо найти простое
движение. Так, если произошло изменение угла атаки, то в ре-
зультате возникшего движения будет происходить такое слабое
изменение скорости полета, что его можно совсем не принимать
во внимание. Движения в условиях постоянства скорости назы-
вают малыми или короткопериодическими.
В случае изменения скорости полета происходит движение,
в процессе которого угол атаки тоже меняется. Однако- часто
удается связать изменение угла атаки с изменением скорости
простым образом. Такие движения называются большими
или длиннопериодическими. Начнем с рассмотрения
малых колебаний.
Малые движения узкого крыла без оперения
Предположим, что самолет состоит из очень узкого крыла и
вращение вокруг оси z дает весьма малые моменты, являющиеся
функцией угловой скорости. Крыло снабжено балансирами, рас-
положенными так, что при вращении вокруг центра тяжести мо-
45
дель статически устойчива и имеется достаточно большой мо-
мент инерции Эта схема соответствует самолету типа «летающее
крыло» с очень большим удлинением
Будем рассматривать движение с малыми возмущениями,
когда углы поворота крыла и траектории малы, а величина ско-
рости остается неизменной. Возможное движение крыла состоит
из изменения продольного угла ср и поперечных движений вдоль
оси у Источником нарушения равновесия сил и моментов в дан-
ном примере может быть только изменение угла атаки, связанное
с углом поворота крыла и поперечным движением Для простоты
будем вести отсчет углов от состояния равновесия*
А vy
Да = <р —срт; ?т=-£,
где ср* — изменение угла наклона траектории, или угол поворота
вектора скорости центра тяжести.
При рассмотрении вопроса можно было бы поступить обычным
образом, составив два уравнения движения соответственно' двум
возможным движениям. Однако в данном случае можно сразу
упростить задачу. Дело в том, что при обоих возможных движе-
ниях возникает некоторая сила Y, приложенная в аэродинамиче-
ском фокусе крыла, расположенном на расстоянии xQ позади
центра тяжести. Следовательно, центр ускорения будет всегда
находиться в одном месте на расстоянии Li впереди самолета
(фиг. 26). Так как исходное движение было прямолинейным и
поперечная скорость была равна нулю, центр ускорения будет
одновременно центром вращения. В итоге мы получим тело, кото-
рое вращается вокруг центра ускорения и имеет момент инерции
1=1о+тЬ\. На это тело действует момент, зависящий от угла
о Vу
отклонения ср и угловой скорости со = —.
Д*+*о
Составим уравнение колебания относительно центра уско-
рения
ztZ<o дМ , дМ
' — = — ср -|-----со;
dt ду да>
dm »
---= —П~Ъ— Г№.
dt-°Т
46
Характеристики колебательного движения могут быть пред-
ставлены следующим образом:
дМ дУ
— Xq —
д'? ___да _ G ХО __ g х0
4 а 4 а г/ ’
±^(L,X]2.
V да ^ + Х<>> ’
п° I
дМ_ _
д<&
дМ
__ dm 1 дУ fj . чл
п =---------=-------(L. + х0)2 ==
I /К да ‘ 07
Фактор затухания можно представить в виде
Су дсу
а да ’
дсУ №SL ri Г*
У да 2G L xQ
Мы привели два различных по форме выражения для D. Пер-
вое из них равно отношению времени, за которое самолет проле-
тает расстояние, равное радиусу инерции, к периоду колебания
маятника длиной деленному на 2?г. Из этого выражения
видно, что увеличение скорости полета, степени статической
устойчивости и угла атаки ухудшает затухание. Увеличение мо-
мента инерции сказывается благоприятно. Во втором выражении
исключена скорость полета, и тогда оказалось, что характеристи-
ка затухания определяется производной —зависящей от удли-
да
нения крыла и обычно мало меняющейся; величиной ——, на-
зываемой относительной плотностью самолета (L — полная дли-
на самолета), отношением радиуса инерции к полной длине са-
молета -------величиной сравнительно постоянной; отноше-
нием —,которое можно принять за относительную характеристи-
к-
47
ку статической устойчивости; наконец, фактор затухания зависит
от плотности воздуха.
Из этого анализа можно сделать такие важные выводы, зату-
хание малых колебаний и даже апериодическая характеристика
могут быть получены и при полном отсутствии демпфирующих
моментов при вращении вокруг центра тяжести. Для получения
желаемой характеристики затухания нужно ограничивать сте-
пень статической устойчивости, характеризуемую величиной х0-
Если скорость и высота полета велики, то величина — должна
г«
быть столь мала, что ее практическое осуществление будет весь-
ма затруднительно. Вообще заданное Хо может быть обеспечено
только с некоторым приближением.
Хотя вопрос в сущности уже рассмотрен, однако мы подойдем
к нему еще раз несколько иначе, так как это облегчит переход
к более сложному случаю.
Составим уравнения для вращательного и поперечного дви-
жений
7d(o дМ А dVy dY л
/ — = —Да: т—-= — Да.
dt да dt да
Заметим, что
дМ дУ
— =-------*о;
да да
. Vy 1 dVy d^
Да = ср — ср ; ср = ; а) =---—= --LF.
Т Тт» Тт у т v dt dt
Тогда уравнения движения примут вид
/^-== — ^Х0(<р —<рт); /пУа>т=у^(<р — <рт)
dt да да
ИЛИ
-«о('р-'Рт); =«ое?—?т)-
Здесь
х0 . _mVxn .
, lift — ,
0 да I ’ 1 / ’
отношение
дУ
48
“>=—»i?t5 — ?т = -^
В результате преобразований получим уже известное нам вы-
ражение для фактора затухания
— = — П10>т;
at
dw
П0 2
(о== —nfrf— п2со;
8r‘
£>= — = —
л, V
Напишем уравнения движения в таком виде:
= ?т); /иКх0(от=^х0(<р—срт).
at да да
Эти уравнения можно рассматривать как уравнения колеба-
ния двух тел, упруго связанных между собой. В самом деле,
дУ / х
---*о(9— 9т) является моментом, пропорциональным углу по-
да
ворота одного тела относительно другого. Второе тело имеет очень
малый (нулевой) момент инерции, но* на него действует тормозя-
щий момент тУхо^т- Соответствующая механическая схема по-
казана на фиг. 27. Эта система тел будет
совершать простое затухающее колебание
аналогично системе, показанной на фиг. 10.
Однако данная система имеет ту особен-
ность, что ее положение равновесия не
фиксировано и, следовательно', внешнее
возмущение не только создаст колебания,
но и изменит положение равновесия.
Изменение положения равновесия можно
найти исходя из таких соображений. Одно
тело обладает кинетической энергией, а вто-
рое расходует энергию при взаимодействии
с окружающей средой. Зная начальные зна-
чения о)0 и (ср—cp>r)Oj можно найти равно-
весное положение по отношению к началь-
ному. По начальному значению угловой скорости тела найдем
его момент количества движения /а>0. Этот момент количества
движения будет передан среде через сопротивление второго тела.
Напишем выражение для момента количества движения, пере-
данного среде,
J Мdt = J mVx^dt—mVxQ J dcpT = /nVxocpTO.
Оказалось, что он равен производной момента по угловой ско-
рости, умноженной на смещение второго тела. Отсюда получим
/га'/ло?то + ^во = 0; ®т0=-<“о=——•
т Vxq Hi
49
Таким образом смещение равновесного положения не зависит
от начального смещения (<р — а только от начальной угловой
скорости. Например, если в начальный момент имеется некоторое
(ф— <р-г)о, т е тела смещены одно относительно другого, но* ^о = О,
то второе тело будет находиться в положении равновесия, т. е.
<Р^го = О. Можно* было бы найти положение равновесия исходя из
фазы колебания. Это мы будем делать применительно к более
сложным случаям.
Движение крыла с оперением в упрощенном виде
Мы сейчас не будем разъяснять, какие именно упрощения
здесь будут сделаны, поскольку вслед за данным примером бу-
дет рассмотрен и более сложный.
Пусть мы имеем два крыла, из которых переднее большое —
собственно крыло, а заднее малое — оперение. Эта система обла-
дает некоторым аэродинамическим фокусом, т. е. при изменении
угла атаки приращение подъемной силы Y находится в некото-
рой точке независимо от исходного угла атаки. Центр тяжести
находится впереди аэродинамического фокуса на расстоянии х0,
и тогда при изменении угла атаки будет возникать момент М =
= ^-а=У%о- При наличии угловой скорости to будет также воз-
da
никать момент, который пока напишем в форме М=-<d.
da>
Составим уравнения движения системы:
jdm dY , ч дМ т г dY , ч
7—=——х0(? —?т)/пУ<от= —(<р —<рт)
at ool d<o da
Мы получили два уравнения второго и первого порядков с
неполным числом членов. Благодаря этому данная система может
быть сведена к одному уравнению второго порядка. В результате
одно из движений, например, вращательное, можно рассматри-
вать как свободное, а второе движение будет следящим с неко-
торым сдвигом фаз. Преобразуем уравнения:
«о(? —
at
Тт)-
Здесь
дУ
дУ х0 1 ЭМ тУхй пЗ, да
п‘ =------; п=-----------: пх=--------; «» = — =-------.
0 да I ’ I да, I 2 т mV
50
Очевидно,
dm
— = — flay — ZliOX-.
dt T
Проинтегрируем последнее уравнение, полагая, что значе-
ния <р и <рт отсчитываются от равновесного положения:
ш — — И<р—«1®т.
Найдем отсюда <рт и подставим в выражение для —
dt
dw п% nfa
— = — -------ш-------? = — п^ — пьох
(л* Tlj
Здесь
«2=^ + пп2; яд = п-|-л,; D="—.
па
Прежде чем заняться анализом фактора затухания, остановимся
на механической модели этого движения. Составленные уравне-
ния соответствуют случаю движения двух упруго связанных тел,
каждое из которых оказывает сопротивление движению, завися-
щее от скорости движения. Кроме того, второе тело обладает весь-
ма малой массой. Подобная схема для вра-
щательного движения показана на фиг. 28
Эта система обладает также тем свойством,
что под действием возмущения меняется по-
ложение равновесия. Сдвиг фаз движений
обоих тел может быть найден из выражения
<рт=-----(со + Пер).
П1
Как видно, сдвиг фаз зависит от и, т. е. от
фактора торможения вращательных движений
тела.
Модель, показанная на фиг. 29, иллюстри-
рует относительное движение самолета, пока- фиг-
зывая вращение самолета и вращение отно-
сительного потока Получается такая картина, как если бы само-
лет был связан с вектором скорости при помощи некоторой пру-
жины. Кроме того, самолет и вектор скорости имеют некоторые
сопротивления вращению. При изменении степени статической
устойчивости нужно' соответственно менять упругость пружины
или ее плечо и, кроме того, сопротивление вращению вектора
скорости. Случай статической неустойчивости не может быть
воспроизведен на такой модели.
Для демонстрации видимого со стороны движения самолета
можно предложить иную модель. Как мы уже показали, самолет
51
без оперения колеблется вокруг центра ускорения. При наличии
оперения тоже происходит колебание вокруг этого центра, но,
кроме того, сам центр совершает некоторое колебательное движе-
ние. Это можно показать с помощью следующих преобразований:
==Г?Т; V —— <р——
J «1 «1 J
— = У— — £/p+z; г= —V— fcpdf.
п1 Л1 J
Для демонстрации движения можно предложить такую модель
(фиг. 30). Плоская модель самолета, имеющая массу т, при-
креплена к легкому стержню а, вращающемуся относительно точ-
ки О. Это вращение соответствует движению самолета относи-
тельно центра ускорения. Точка О вместе со стержнем b может
Фиг. 30.
перемещаться по. вертикали вдоль оси О'—О'. К стержню b
прикреплены ролики d, которые касаются движущейся ленты и
52
могут поворачиваться на угол ф относительно направления дви-
жения ленты. Этот поворот кинематически связан с поворотом
et Ф 1
стержня а, так что направления их обратны а отношение— =—k.
?
Такая кинематическая схема дает поперечное смещение точки О
со скоростью, пропорциональной углу поворота модели само-
лета ср.
На модели самолета имеется штифт, который касается движу-
щейся ленты, вследствие чего к нему приложена некоторая сила
трения Q; эта сила и приводит модель в действие. Сила Q на-
правлена по касательной к линии, которую стержень а будет
Vv
прочерчивать на ленте; угол будет равен —,где Vy — верти-
кальная скорость модели и V — скорость движения ленты. Мо-
мент силы Q будет вызывать поворот стержня а вокруг оси О, а
поворот стержня а на угол с? будет вызывать поворот роликов
на угол ф и движение стержня b по вертикали со скоростью К=
= Уф. Меняя массу т, силу трения Q, длину стержня а, соотно-
шение углов — и скорость движения ленты можно получить
различные примеры движения. Если модель будет расположена
в вертикальной плоскости, потребуются дополнительные баланси-
ры для устранения силы тяжести.
Перейдем к рассмотрению фактора затухания D, который мы
получили в виде
D = —
па
п+п2
|/~ п^пп2
Если бы движение происходило только вокруг центра тяжести
самолета, мы получили бы фактор затухания
Если бы п=0, но остались две степени свободы, мы получили
бы фактор затухания
Поэтому
jj ~ + _______^2 . J_____
~ y i+zW / 1 A ’ ° "о ‘КТ+ад
]/
Таким образом фактор затухания рассматриваемого движения
определяется выражением, в которое входит фактор затухания
определяемый торможением вращательных движений, и фак-
тор Z>2, определяемый действием поперечных движений самолета.
53
Однако из написанного выше выражения непосредственно не ви-
ден характер этой зависимости. Для иллюстрации приведены две
диаграммы (фиг. 31 и 32). На фиг. 31 по осям координат отложе-
ны D± и D2t а параметром нанесенных кривых служит величина D.
Пока Di и D2 малы, D равно примерно их сумме, однако по мере
их роста D становится меньше этой суммы Если D2^>2, добав-
ление Di 1начинает даже снижать фактор затухания. В результа-
те движение может стать периодическим. Это свойство движения
нужно признать весьма благоприятным, так как при значениях D
от 1,4 до 2,0 Отношение смежных амплитуд практически равно
нулю, но равновесное состояние восстанавливается достаточно
быстро. На недостаток апериодического движения при D, значи-
тельно большем 2, мы уже указывали.
Если *о<О, т. е. если нет статической устойчивости, и0 будет
мнимым, а вместе с ним будут мнимыми и D2. Однако вели-
чина D может остаться действительной и при этом она будет
больше 2, т. е. движение будет апериодическим (см. фиг. 32). Та-
1 Влияние поперечных движений на частоту и затухание малых про-
дольных колебаний самолета было показано в работе В. П. Ветчинкина
«Продольные колебания и продольная динамическая устойчивость самолета».
(Труды 3-й Всесоюзной конференции по аэродинамике 1933 г., изд. ЦАГИ
1935 г.).
54
ким образом добавление хвостового оперения внесло следующие
изменения в свойства самолета: во-первых, изменяется положе-
ние фокуса; во-вторых, усиливается затухание; в-третьих, при
малой статической неустойчивости вместо дивергентной характе-
ристики колебание остается затухающим, но носит апериодиче-
ский характер. Иллюстрация этих свойств будет дана ниже на
примерах.
Рассмотрим движение центра тяжести. Вращатель-
ные движения определяются уравнением
— = — n^cp — nh&.
dt аГ *
Поперечные движения будут определяться совершенно таким
же уравнением
Кроме того, нами было получено уравнение связи
К а) п
Срт= — =-------------ср.
V ni nt
Из этих уравнений можно' выразить у через ср и Для этого
сперва в уравнение для Vy подставим ср из уравнения для угло-
вых движений:
У =----------(<> + «?);
7?!
1 du пь
па dt п2а
ппь
— ш
п dio \
"a dt / ’
? = —
55
а потом проинтегрируем его:
У = —L. <? 1
nnh \ п
—I-----—<0
2 I 2
па / па
па\ ? у
Здесь
— = А.; D = ; <о = —.
Па па
Пусть нам известна фазовая диаграмма для вращательного
движения (фиг. 33). Тогда мы можем найти, в какой точке этой
диаграммы Vy=0:
--= -~П\ tg Ф =----=-------=-----
9 9 па у 1 + Di£>2
где а> = <о£0-—угловая скорость, отнесенная к единице вре-
1
меня Л = — .
Для расчета поперечных движений можно составить различ-
ные выражения. Наиболее прост и удобен такой порядок расчета.
Имеем уравнения для вращательного и поступательного колеба-
ний и уравнение связи.
у" =—nby'— nty у' = —-(?'4-л<р).
«1
56
Интегрируем уравнение вращательного движения и урав-
нение связи:
?' = — — nl J ydt-, y=-^-[^ + n^dty,
вводим условие У = 0 при <р'= — п<р:
и* J vdt— —(nb—ri)<f= —n2<p;
К / - пп2 \ V L;
у = — <? I 1--Л1= — ср----= — ср-----1---
«1 п2а п+П1 (1 + П1Л2)
Это уравнение дает связь между ср и у в момент остановки
поступательного движения, т. е. при максимальном значении
=Уо. Расчет ведем таким образом. По известным начальным усло-
виям вращательного движения, пользуясь фазовой диаграммой
и диаграммой колебаний (см. фиг. 11 и 14), строим диаграмму
вращательного движения. По условию— =——на фазовой диа-
? "а
ср ф
грамме находим —, а по этому значению — на диаграмме коле-
но ?о
баний получаем сдвиг по времени амплитуд вращательного и
поступательного движений. Теперь остается только найти амплиь
туду поступательного движения, что позволяет нам сделать полу-
ченное выше уравнение. Затем простым перестроением диаграм-
мы колебаний получим диаграмму поступательного движения
(см. фиг. 33).
Приведем пример такого расчета. Имеем следующие ис-
ходные данные: D—\\ — = 2; Рг = 0,75; Z)2 = 0,375. Когда
вращательное движение будет проходить через максимальное
положительное отклонение, поступательное движение будет
приближаться к своему максимальному отклонению. Оно на-
ступит при условии — =--------Р-. - .. = —0,614. По диаграмме
<р У 1
на фиг. 14 для D—1 получим — = 0,75, а по диаграмме на
<?0
фиг. 11 получим сдвиг максимальных отклонений по времени
— = 0,78. Если ср0 = О,1 и А; = 50 ж, получим ср = 0,075 и
zo
0,075
140,75.0,375
j/=—50
= —2,9 М.
Усложненный случай движения крыла с оперением
Выше мы рассматривали случай, когда на самолет действова-
ла только сила, вызываемая изменением угла атаки в результате
вращения самолета и вектора скорости, и момент, вызываемый
57
угловой скоростью вращения самолета. На самолете обычно ска-
зывается запаздывание скоса потока. Дело в том, что по мере
изменения угла атаки меняется скос потока за крылом, который
меняет воздействие крыла на оперение. Однако вследствие нали-
чия расстояния между крылом и оперением изменение скоса при-
ходит с некоторым запаздыванием; это запаздывание пропорцио-
нально скорости изменения угла атаки. Так как угол атаки а =
= ©—сргг, то скорость его изменения а'= ср'—<?'т; поэтому в общем
случае в уравнения нужно ввести силу и момент, зависящие от ср'
и ср'т. Как видно, в уравнении моментов эффект запаздывания
скоса сложится с эффектом торможения оперения.
Угловая скорость вращения самолета, вообще говоря, дает не
только тормозящий момент, но и силу, и потому в уравнение пси-
перечного поступательного движения нужно ввести силу, завися-
щую от <?'. При полете с освобожденным управлением положение
руля высоты под действием ускорений в системе управления мо-
жет быстро меняться, и тогда возникают силы и моменты, опре-
деляемые угловым ускорением вращения самолета ср" и nonei-
речным ускорением у", которое соответствует вращению вектора
скорости ?'т— —. Напишем выражения для углового ускорения
и скорости вращения вектора скорости, т. е. уравнения движения;
коэффициенты уравнений обозначим просто буквами:
<р" = + b<f' + 4- d<f't 4-/<Рт>
Аср'+а?+
Теперь нужно исключить одно из неизвестных, например с?т;
это удобнее сделать, пользуясь определителем. Подставим реше-
ния
ср = Л£х/; срт==5ех/
в уравнения движения
Л [(1 — а)Р — bl — — =
-A(gk2 + Ak + A?) + 5[(l-/)k^m] = 0.
Составляем определитель этой системы, приравниваем его
нулю и решаем его:
(1 - а) V-Ь\ — с =()в
— (gX2 + Ak + A) Х(1— 1) — т ~ ’
(1 — л)(1 — Z) X3 —(1 — Z) X2 —с(1—Z)X —m(l~a)k2 +
+ bml 4- тс — gd№—gfl2 — dhl2—hfl — kd\—kf= 0.
Получили кубичное уравнение, соответствующее дифференци-
альному уравнению третьего порядка. Однако необходимо ввести
58
условие т=—k\ f=—с, определяемое равноценностью поворотов
самолета и вектора скорости в отношении изменения угла атаки.
Тогда свободные члены уравнения сократятся, а затем можно
произвести сокращение и на X; уравнение станет квадратным. Ха-
рактеристики движения выразятся так:
п *0 - я) - - dh
о ch — bk — c (1 — I) — kd
11 „ = ------------------.
a — a} (\ — — gd
Таким образом, несмотря на усложнение, мы опять получили
простое затухающее колебание, но его характеристики выража»-
ются более сложно.
БОЛЬШИЕ ПРОДОЛЬНЫЕ ДВИЖЕНИЯ
Движение самолета, сохраняющего постоянный продольный
наклон
До сих пор мы рассматривали примеры движений, в которых
можно' было принять допущение о постоянстве скорости. Теперь
мы перейдем к примерам, в которых скорость переменна, однако
внесены еще некоторые условия, благодаря которым характер
движения остается достаточно простым.
Колебания, характер которых определяется изменением подъ-
емной силы в результате изменения скорости, называются длинно-
периодическими или фугоидальными. Впервые они были иссле-
дованы Н. Е. Жуковским в его работе «О парении птиц».
В. П. Ветчинкин специально исследовал колебания с большими
амплитудами («Динамика самолета», ОНТИ, 1933). Длиннопе-
риодические колебания рассматриваются также в обычных тео-
риях динамической устойчивости. Мы остановимся здесь на трех
случаях длиннопериодических колебаний. Эти случаи интересны
тем, что они дают важные практические выводы, на которые ра-
нее не было обращено должного внимания; эти случаи иллю-
стрируют также использование теории простых затухающих ко-
лебаний.
Простейший случай фугоидальных колебаний имеет место при
условии, что угол атаки постоянен и сила тяги все время уравно-
вешивает силу сопротивления. Из последнего условия следует, что
сумма потенциальной и кинетической энергии остается постоян-
ной, и мы получаем такой закон зависимости квадрата скорости
от ВЫСОТЫ;
V2 + 2gh — const; = — 2g.
dh
59
При постоянном угле атаки подъемная сила пропорциональ-
на квадрату скорости, и мы получаем уравнение колебания
dF= Fo dV» _2 G .
dh Vl dh * V20 ’
dVy 2^2 2
(\r \2
Л’,
dVy dY л A
tn —- — — bh\
dt dh
Здесь
y = bh
, 2g*
и ло=4-
ко
Получили гармоническое колебание с периодом
т = — = Vo = O,453V'o-
Ло g
Этот период равен периоду колебания маятника длиной
V02
/= -^-или периоду колебания тела, подвешенного на пружине,
деформация которой под действием веса тела равна I. Заметим
также, что при полете с большой скоростью период фугоидаль-
ного колебания очень велик.
Можно было бы дальше вносить последовательные усложне-
ния, однако мы считаем возможным сразу усложнить вопрос в
пределах, позволяющих получить простые затухающие коле-
бания.
Полет с постоянным углом наклона самолета имеет большую
практическую важность. Самым элементарным видом пилотиро-
вания самолета является сохранение продольного наклона по
отношению к горизонту постоянным. Автопилот тоже удерживает
определенный наклон самолета. Кратковременные нерегулярные
нарушения продольного наклона не могут заметно изменить ха-
рактер движения, поскольку период колебания обычно достаточ-
но велик. Забегая вперед, можно указать, что полет с постоянным
углом наклона дает весьма благоприятную характеристику по-
ведения самолета, за исключением некоторых особых случаев.
Составим уравнения движения для случая полета с постоян-
ным углом наклона самолета. Заметим, что в этом случае самолет,
стремится к некоторому прямолинейному равномерному движе-
нию, характеристика которого может быть получена из обычногр
аэродинамического расчета. Это, конечно, не относится к самоле-
там, не имеющим установившегося режима полета. Ось х распо-
ложим вдоль направления установившегося движения, а ось у—
перпендикулярно к нему. Возмущенное движение будем рассмат-
ривать по отношению к равномерному установившемуся движе-
нию; тогда Vx будет скоростью вдоль оси х в относительном
60
движении. Обозначим через X приращение силы по оси х при
возмущении. Эта сила составится из изменений сил тяги и ло-
бового сопротивления при нарушении скорости и угла атаки и
из проекции подъемной силы на ось х при нарушении наклона
траектории; проекция силы тяжести меняться не будет. Вдоль
оси у при возмущении будет действовать сила Y, которая явится
приращением подъемной силы при изменении угла атаки и ско-
рости полета. Изменением проекций других сил будем пренебре-
гать вследствие малости рассматриваемых возмущений.
Уравнения движения напишем так:
dVx дХ.г , дХ
т—- =—vx-i-------К
dt дУ дУ у
И
При постоянном угле наклона самолета наличие верти-
кальной скорости приведет к изменению угла атаки Да =
Уу дх
— Тогда производные и можно представить
в виде
дХ __д_Х_ да дХ д?т . _да 1_ .
дУу "“да дУу дУу ’ да “ да ’ дУу ~ У ’
дх __ y q. дсрт ___ 1 .
д<рт “ ’ dVy У ’
дХ 1 dQ G / дХ dQ
-----=-----------; —= —- , так как при изменении угла
д Уу V да V \ да да Г
атаки меняется только сила сопротивления):
дУ дУ да 1 дУ 1 G
дУу да дУу У да У а
Заметим, что угол атаки а
соответствующего су = 0.
Производная будет
нужно отсчитывать от положения,
состоять из двух частей: из про-
изводной от тяги винта — и из производной от силы сопро-
тивления Q, пропорциональной квадрату скорости:
дЛ^дР __ дО_ = дР___ 20_ . ^==2—^2 —
дУ дУ дУ дУ У ' дУ У У *
61
Напишем уравнения движения в виде
dVv dVx i g\
—-= — nyv + niVx\ —=—n6Vx+( n5 IV ;
at 2 y x dt 6 x \ 6 v ) y
i dY g 1 dY ' 2g
2 mV da Va ’ m dV V
n — 1 _ g J?_ = g dcx .
s mV da GV dcy a Va dcy ’
n =____1_ ^X= ^g_£x_ё_дЛ.= i^S_ Cx_.
6 m dV V Cy G dV V cy ’
У cy dP
l~ ~ 2G dV '
Проинтегрируем уравнения движения:
Vy= -пгу + п4х-, Vx=/n5 — -^-}y-n6x.
Теперь путем подстановки можно исключить члены, относящиеся
к горизонтальному или вертикальному движению; тогда получим
уравнение движения по одной из осей
Уу= —+ у — П^у — (n2 + «6) — П'"аУ~ nbVy’
где
п1 = п2п6 + п4/-^- — п6\; пь = (п2 + пеУ, D=—.
\ V /
Обычно п6— бывает отрицательным, и колебание очень
энергично затухает. Если п6—положительно, т. е. эффект
торможения от изменения угла атаки больше, чем эффект
действия силы тяжести при наклонении траектории, то частота
растет и при некотором п5 — движение может стать дивер-
гентно неустойчивым. Однако предварительные исследования
показывают, что такой случай не встречается на практике.
Для движения по оси х получим аналогичное выражение
V'x=-^-^Vx.
Уравнения связи движений имеют вид
x = -^Vy + ^-y; у =------------?--
щ у п< g
V
«в
g
п* “V "6-F
62
Для построения траектории движения удобно воспользовать-
ся диаграммами на фиг. 11, 14, 15. Пример построения будет по-
казан ниже.
Остановимся на вопросе о механической модели движения.
Очень проста модель, иллюстрирующая изменение скоростей для
случая, когда = — -^-положительно, но мало по абсолютной
величине. Преобразуем уравнения движения:
Vy = -п2Уу + п^х; V’x= n^y—n^V^
Разделим их на скорость полета V и введем обозначения:
vy
<рт = ~ — изменение наклона траектории;
Vx
срс —относительное изменение скорости.
Тогда получим
= — Мт + «4?с; <Рс = Мт — «6?с-
Теперь умножим второе уравнение на -^4 , а затем к пер-
л5
вому уравнению прибавим и вычтем п4срт, а ко второму при-
бавим и вычтем п4срс:
?Т= —Мт + Мс + Мт —Мт = —(«! —<)?т + Л4 (?с —?т);
?С = - <Рс + ВДт + Мс — «А = - «4 № - 1 ) ?с +
«5 л5 \ «5 /
+ П4(?т — ?с)-
Эти уравнения определяют движение механической системы,
состоящей из двух тел с крайне малой массой, но взаимодействуй^
щих с окружающей средой так, что силы взаимодействия тормо-
зят движение пропорционально первой степени скорости; каждое
тело упруго связано с неподвижной точкой, и, кроме того, оба
тела упруго связаны между собой. Такая схема показана на
фиг. 34. Совершенно очевидно, что эта система устойчива и зату-
63
хание колебаний происходит весьма энергично. Однако, если и'5
велико, связь второго тела с неподвижной точкой становится ди-
вергентной, т. е. сила отталкивает тело от неподвижной точки, и,
кроме того, торможение второго тела становится малым, так как
я'5 входит в знаменатель характеристики торможения. Механиче-
ская схема, иллюстрирующая изменение координат, показана на
фиг. 35; как видим, она лишена сил упругости.
Если п'5 отрицательно, что обычно имеет место, механическая
модель явления будет более сложной. Закон изменения скоростей
движения представляется уравнениями
?; = — ?2 = — С?т —/?с-
Эти уравнения показывают, что скорости движения зависят от
координат. Для получения этой связи можно воспользоваться
свойством ролика, катящегося по барабану. На фиг. 36 показана
64
схема модели, удовлетворяющей системе уравнений. Вилки, удер-
живающие ролики, качаются около точек О' и О". Эти точки в
свою очередь смещаются в зависимости от смещения роликов. Бы-
строта смещения ролика по барабану зависит от угла наклона
вилки.
Пусть левый ролик сместился вверх на величину <рт, тогда
точка О" опустится и второй ролик пойдет вниз, опуская точку О'.
Таким образом каждый ролик стремится к положению равнове-
сия, но, кроме того, ролики содействуют друг другу в этом стремг
лении.
Проанализируем кратко затухание колебаний. Раскроем вы-
ражения для Пь и п2а:
(с \
1 + 2м — .
СУ /
Cv
Поскольку а мало, а — велико, можно принять пь = п2-
сх
Далее
= л?/2м -2а-^ + 2а2
л2 / \ су дсу
Тогда
Если угол атаки мал, член 2а2 относительно мал. Раскроем
с*. дс~
выражения для — и —:
Су дСу
СУ
СХ--- ^ХО 4“ г
кА
сх схо Су, дсх о Су
— ‘ , j О' ’
су су dcy ™
сг дсх cxq Су
Су дсу Су пк ’
Теперь фактор затухания
где
да
65
Подставляя примерное значение <\0 — 0,02, получим
Г> = 10.
Затухание оказалось весьма большим.
„ , • сх дс,.
При некотором довольно большом угле атаки =
Су dCy
Тогда фактор затухания D выразится очень просто:
О=—Ь .
а]/2
Напомним, что угол атаки а нужно отсчитывать от положения,
соответствующего cy—Q. Если же кривая су по а; не является
строго прямолинейной, нужно в точке, соответствующей режиму
полета, провести касательную и отсчитывать угол атаки от по-
ложения, соответствующего точке пересечения касательной с
осью абсцисс (фиг. 37).
1
Из выражения £) =
—7= видно, что затухание достаточно ве-
ау 2
лико и движение имеет апериодический характер. Движение приг
обретает периодический характер при
L..-^<^2, т. е.при а>0,35
или при а большем 20°. Это возможно при полете с разрезными
крыльями вблизи Сушах. Однако этот случай необходимо анали-
зировать, применяя полное выражение для D.
Посмотрим, в каком случае колебание может стать дивергент-
ным; с этой целью подставим выражение для
— и —-
СУ дСУ
66
в формулу для п2а:
BQ« 2к.
где
Последнее неравенство может иметь место, когда I отрицательно
и достаточно велико по абсолютной величине; это значит, что
при увеличении скорости тяга должна расти.
Остановимся еще на случае, когда снижение самолета с по-
стоянным углом наклона сопровождается не ростом, а падением
скорости. В этом случае прирост сопротивления от изменения угла
атаки должен быть больше прироста составляющей силы тяжести;
это сводится к условию и5--— >0. Раскрывая его, получим
1/а дсу
2СУ> СУ ,|Л Л -
-ГСХ Bq Itk
1
тсХ
1 .
Во ’
к
Во
ТС
Таким образом для обеспечения нормальной зависимости меж-
ду изменением высоты и изменением скорости удлинение крыла
должно быть большим 2.
Движение, при котором изменение угла атаки связано
с движением центра тяжести
Рассмотрим следующий случай больших продольных движе-
ний самолета. Пусть самолет имеет достаточно большой запас
продольной статической устойчивости и малые колебания носят
периодический характер с малым периодом, но сильным затуха-
нием. Это весьма типичный случай для самолета. Большие коле-
бания, сопровождаемые изменением скорости и высоты полета,
протекают медленно; тогда можно сделать допущение, что ма-
лые колебания отсутствуют, или если по некоторой причине они
и возникли, то успевают полностью затухнуть за время, состав-
ляющее незначительную долю периода больших колебаний.
Однако отсюда не следует, что угол атаки остается постоянным.
На самолет действуют моменты, связанные с изменением скорости
и наличием поперечного ускорения или кривизны траектории. По-
этому в процессе больших колебаний будет происходить изме-
нение угла атаки соответственно фазе больших колебаний. В про<
цессе больших колебаний продольный наклон самолета будет изн
меняться, а следовательно, будут иметь место и угловые ускоре-
ния; однако эти ускорения очень незначительны и момент, создаю-
щий угловое ускорение, весьма мал. Тогда можно считать, что
продольные моменты находятся в равновесии. Напишем теперь
три уравнения движения: первое из них определяет равновесие
моментов, второе — поперечное ускорение и третье — продоль-
ное ускорение. Оси координат выберем, как и для случая, рас-
смотренного выше, т. е. ось х направим по направлению устано-
вившегося движения. Тогда
г „ дМ А дМ , дМ . дМ . п
---ф + — КН-----/v = 0;
г да dV х djyJy
dY А , dY
mJy==~T^a+^V^
Л да dv
дХ Vv дХ
Используем обозначения:
vy iy
9 1 дМ п2 = ; 0 / да 1 дМ 2 V дМ п — "г '; До — I ду’ 3 I dV
„ V дМ I 31 у 1 dY 1 dY а mV да 4 т dV
1 дХ . п________\_д!С
mV да ’ 6 т dV*
Тогда уравнения движения принимают вид
«оДа+п<р' — п|<рс + п7?;=0;
—пад«—=°;
?с + гаБДа+-р-?т+П6?с = 0.
В рассмотрение вопроса внесем еще одно упрощение — будем
считать, что изменение угла атаки -мало по сравнению с измене-
нием наклона траектории и потому угловая скорость вращения
самолета равна угловой скорости вращения траектории ср'= <р'т.
Теперь из первого и второго уравнений, исключив можно най-
ти изменение угла атаки:
Д ««о + (П + П1) ( ДаП2 + Л4<Рс) — «зТс =* °;
- ntli - nirti
да = <р----г-----------.
П0 + ПП2 + П2П7
68
Оказалось, что величина угла атаки зависит только от ско-
рости полета. Для краткости обозначим а = а<рс. Теперь уравне-
ния движения преобразовываются к виду
?; = ?с (а»2 + «<);?'=— <рс (вгаБ + п6) — ?т.
Дифференцируя и подставив <р', получим
+ (и6 + ап^ («4 + ап2) <рс = О
ИЛИ
?с + ЗДс + Па?с = °-
Мы получили уравнение колебаний с характеристиками:
пь = пй + апь- п2а=^-(п4 + ап,); D = ~.
и па
Если угол атаки постоянен, характеристиками движений будут
Коэффициенты пв и являются частными производными го-
ризонтального и вертикального ускорений по скорости полета:
djx djy 1g
п —------- • п = —4 = — .
dV dV V
Для случая постоянной тяги или пологого планирования
получим
nft = n6 =
2£
V
сх
СУ
“ и- п.
Как видим, фактор затухания зависит от аэродинамического
качества, т. е. затухание вызывается изменением лобового» сопро-
тивления.
Если планирование крутое, в составляющую силы тяжести в
уравнении для продольного ускорения нужно ввести косинус
среднего угла наклона траектории.
Для того чтобы движение не имело дивергентной характери-
стики, необходимо выполнение условия
аи2 + п4 >0; а>—— ; а>—2а.
л2
Как видим, при увеличении скорости может происходить
уменьшение угла атаки, но на величину, не превышающую 2а.
69
Условие отсутствия дивергентного- движения можно написать и
в таком виде:
П3 — Л4 (« + «?) «4
а — —s------------>-------;
По + Л2(« + я7) «2
”1 xvV __”о = Х<У .
п\ r2i па г?
Ха —Ху > 0.
Величина ха представляет собой расстояние между аэродина-
мическим фокусом самолета и центром тяжести; величина ху
является расстоянием между точкой приложения приращения
подъемной силы при изменении скорости самолета и центром тя-
Ха. —Ху
жести. Величина --------является хорошо известной характери-
стикой статической устойчивости при переменной скорости.
Посмотрим, в каком случае колебания окажутся возрастаю-
щими. Для этого, с одной стороны, должно быть n6 + czn5>0, но,
с другой стороны, движение не должно быть дивергентным; тогда
получим
1 > ( — а^\
\ п4/ п5 щ ’
Раскроем величину — — :
лб л4
2gi сх g дсх
6 V Су 6 Va дсу
— = 2а;
«2
«6 л2 _ . сх дсу
«в «4 су дсх '
Теперь неравенство принимает вид:
\ П4/ Су сх
где
\dV dV)
Множитель I определяет влияние изменения силы тяги. Так
как изменение силы тяги обычно усиливает градиент изменения
продольного ускорения при изменении скорости (отрицательный
по знаку), то величина />1. Из полученного условия следует, что
сх дсу „
------— должно быть меньше единицы, что может иметь место
су дсх
70
только при полете с углом атаки, большим наивыгоднейшего, так
° Су- dCf
как при (наивыгоднеишем угле атаки —.
су дсу
Мы показали, что затухание, вызываемое силой сопротивле-
ния, при большом аэродинамическом качестве довольно слабое.
Поэтому на затухании сильно- будут сказываться второстепенные
силовые факторы, которые обычно даже не принимаются во вни-
мание. Одним из таких факторов является трение в управлении
рулем высоты. Проверку затухания больших колебаний произво-
дят обычно с освобожденным управлением. В этом случае, в про-
цессе колебаний, руль несколько поворачивается. Силы трения в
системе управления или гидравлическое сопротивление при на-
фиг. 38.
личии рулевой машинки автопилота вызывают запаздывание по-
ворота руля. Это запаздывание может повести к энергичному
раскачиванию самолета, хотя в случае простого- трения амплиту-
да колебаний стремится к некоторому пределу. Предположим,
колебания близки к гармоническим, и в нижней части волны руль
высоты приподнят (фиг. 38). При переходе через положение рав-
новесия руль должен бы стоять нейтрально, но он запоздает и
останется еще несколько приподнятым. Это поведет к увеличе-
нию угла атаки, а следовательно, к увеличению подъемной силы,
которая и будет усиливать поперечные колебания. Поднятие руля
в нижней части волны будет иметь место особенно- у длиннохво-
стого самолета. Можно- так подобрать характеристики аэродина-
мической и весовой компенсации руля, что в нижней части волны
он будет опускаться. Это- усилит затухание, но при излишне силь-
ном повороте руля движение станет дивергентным.
Движение, при котором угол атаки зависит от скорости
по траектории и вертикальной скорости
Когда летчик управляет самолетом в условиях хорошей види-
мости, он контролирует в основном продольный наклон самолета.
Как было показано, это дает очень устойчивый режим полета.
71
Когда была поставлена задача о полете при отсутствии видимости
земли и линии горизонта, то первоначально пытались управлять
самолетом в продольном отношении, ориентируясь по указателю
скорости. Такой полет оказался неустойчивым, так как летчик
обычно раскачивал йашйну, часто доводил ее до критического
угла атаки и сваливался в штопор. Однако некоторые, более вни-
мательные летчики действовали рулем высоты, сообразуясь не
только, с величиной скорости, но и быстротой ее изменения. Тогда
полет становился более устойчивым.
Судить о быстроте изменения скорости по обычному указате^
лю скорости довольно трудно, и возникла необходимость в до-
полнительном приборе, обеспечивающем устойчивый слепой по-
лет. Таким прибором явился вариометр, или указатель верти-
кальной скорости.
Предположим, летчик отклоняет руль высоты и этим меняет
угол атаки, сообразуясь с величинами отклонений скорости и верй-
тикальной скорости от значений, соответствующих исходному
установившемуся режиму полета. Пусть, кроме того, указатель
скорости имеет некоторое запаздывание, пропорциональное вели-
чине изменения скорости. Тогда летчик невольно будет менять
угол атаки и соответственно этому запаздыванию, т. е. соответ-
ственно' величине производной скорости по времени. Аналогич-
ным образом будет работать автопилот, реагирующий на изме-
нения скорости полета и вертикальной скорости.
Изменение угла атаки представим следующим образом:
да=—I/
dV
v + V'
дУ y'dVx x
J' л
Затем составим выражения для ускорений вдоль осей
у и х:
т/' 1 дУ * । 1 dY iz
=------ДаН---—- V‘
у т да тдУ
,,, 1 дх . 1 дХ Vv
V’ =------ДаН---------g-£ .
х т да т дУ 6 V
у V
Введем переменные ?с = — и обозначим
м Vo
V
да л
О --- =“
0 дУ
Знаки мы выбрали так, чтобы при увеличении скорости угол
атаки увеличивался, но тогда запаздывание даст обратный
эффект, т. е. продольное ускорение Vrx будет приводить к умень-
шению угла атаки; ускорение по вертикали должно уменьшать
угол атаки. В выражения для ускорений вводим коэффициенты
72
n-2, tu, п5 и ne, которые мы уже применяли. В итоге получаем три
дифференциальных уравнения:
д а — а?с + = 0;
п2Да—п4<Рс = 0;
+п5 д«+w«?c + — ?т=°-
Подставляя для каждого переменного решения
<рт=Лех/, <рс = Веи, Да=Сех*,
получим систему характеристических уравнений:
А X—Вп4—Сп2 = 0,
А + В (К + п6) 4- Спъ = О,
A b -I- В (ch—ci) 4“ С= 0»
Составляем определитель системы и приравниваем его нулю:
к —ГЦ ^2
g V X 4- = 0;
ь сХ — а 1
отсюда
X2 (1 — сп6) 4- X ( апъ 4- nt 4- bn2—n2cj 4-
4- ап2 4- bn2ns 4” «4 — Ьп±п5) = 0.
Отсюда легко получить характеристики затухающего, колеба-
ния. Причиной неустойчивости могут явиться отрицательные зна-
ки коэффициентов при X2 и X; первое мало вероятно, но если 6 = 0,
то коэффициент при X может стать отрицательным и это поведет
к появлению возрастающих колебаний. Подбирая значения а и b
и стараясь снизить значение с, т. е. эффект запаздывания, можно
получить желаемую характеристику колебания с сильным зату-
ханием.
Влияние изменения плотности воздуха
При очень большой скорости полета период медленных коле-
баний весьма велик, и в процессе колебаний происходит значи-
тельное изменение высоты полета. Перемена плотности воздуха
в этом случае может заметно повлиять на характер изменения
73
подъемной силы и тяги двигательной группы. В выражение для
лг2
частоты медленных колебаний входила величина 2 простей-
те
шем случае, когда угол атаки постоянен и продольные силы на-
ходятся в равновесии, период
Величина 2-^ являлась производной вертикального уско-
рения по высоте:
= О g*
ду G dh V20'
Если принять во внимание изменение плотности воздуха,
„ dY
получим такое выражение для производной —:
dh
LLVdL. dY — dY dV*
\ VQ) pi ’ dh dV2 dh
dh s’
dY = G ,
dV2 K2 ’
Здесь Vo-скорость полета для исходного невозмущенного
Pl
режима, — — относительная плотность для исходного невоз-
Ро
мущенного режима; значение —~ можно принять рав-
dh
ным
для тропосферы а = 0,0001, для стратосферы а = 0,00012.
Произведя подстановку, получим
74
коле-
Значения ускорений, вызываемых поперечными движениями,
оказались увеличенными, и это поведет к некоторому уменьше-
нию периода колебаний. Для простейшего случая больших
баний получим
т = ———1/0&; 6 =
g
1
Поправка на изменение периода при а = 0,0001
= 0,85 составит
и
Т
Го
VQ м/сек 100 200 300 400
b 0,97 0,91 0,82 0,73
С ростом скорости т стремится к пределу:
2~
V '
П'ри а = 0,00012 и — = 0,75 период т= 170 сек.
Го
Можно было бы показать, что изменение тяги в зависимости
от высоты приведет к раскачиванию колебаний. Однако одновре-
менное изменение силы сопротивления будет компенсировать
эффект изменения тяги.
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ РАССМОТРЕННЫХ
СЛУЧАЕВ ДВИЖЕНИЯ, ПРИВОДИМЫХ К ПРОСТОМУ
ЗАТУХАЮЩЕМУ КОЛЕБАНИЮ
Размеры горизонтального оперения самолета
Горизонтальное оперение самолета выполняет следующие функ-
ции. Во-первых, оно служит для управления самолетом, причем
момент оперения пропорционален его площади и длине плеча.
Затем оперение усиливает статическую устойчивость самолета,
вызывая смещение аэродинамического фокуса назад. Эффект
оперения в этом отношении также пропорционален его площади,
плечу и зависит от удлинения оперения, поскольку с увеличе-
нием удлинения растет градиент изменения подъемной силы по
углу атаки. Наконец оперение является основным источником со-
здания демпфирующего момента, и эффект его в этом случае
пропорционален площади, квадрату плеча и также зависит от
удлинения оперения.
75
Управление самолетом можно было бы обеспечить сравни-
тельно небольшим оперением, причем его можно располагать как
спереди, так и сзади самолета. Нужно заметить, что момент для
управления может быть создан и иными средствами, например»,
смещением центра тяжести, поворотом крыла, использованием
реактивных средств или тяги винтов. Эффект оперения в отноше-
нии статической устойчивости не имеет особого значения, по-
скольку нужный запас статической устойчивости может быть по-
лучен путем соответствующего расположения центра тяжести са-
молета даже при полном отсутствии оперения. Остается разо-
брать вопрос О' демпфирующем действии оперения.
Мы уже указали, что демпфирование продольных колебаний
самолета имеет место даже в случае полного отсутствия демп-
фирующего момента при вращении самолета вокруг центра тя-
жести. Фактор затухания малых продольных колебаний самолета
мы представляли в виде
Раскроем выражения для Z)j и Р2‘
Л — п . Л — — л2 . „2_ 1 дм_ gx^G — g - „
U! — , и2-----— , По — — — — —2~ ~ *0>
Ло Пх nQ 1 да Gr-a ria
D\ _пп\ _ да) / L \2а ~~_. дМ___&ст о £2
1>2 ~ «о """ су \ П / ’ °>—V’ S V’
V
Таким образом фактор затухания D определяется тремя параь
метрами: Хо, ?] и р. Параметр р характеризует некоторую услов-
ную относительную плотность самолета; параметр х0 — степень
статической устойчивости; параметр т] —демпфирующее действие
при вращении вокруг центра тяжести. Все эти параметры без-
размерны и независимы друг от друга. Фактор частоты имеет вид
га«=77==5~; я>«о(1+ад)=(-У-^——•
rt р. \ r{ J н
76
Заметим, что величина Хо составляет от 0,02 до 0,1 и в более
редких случаях достигает 0,15—0,2. Величина т) у среднего само-
лета — около 2,0—2,5. Величина р. в зависимости от типа само-
лета и высоты меняется в очень широких пределах. Пример-
ные значения р. для различных самолетов приведены в таблице.
Самолет Р Самолет
Планер-паритель 5 Средний бомбардиров- щик 100
Учебный самолет 10 Истребитель на сред- них высотах 150
Транспортный самолет 17 Истребитель на боль- ших высотах 200- 300
дс
Значение —= для среднего самолета составляет около 0,7;
do)
дс L
тогда при —= 4 и —=3,5—4 получим tq = 1,7—2,8. Для изоли-
да г,
рованного крыла при отнесении коэффициента момента к хорде
дс»» ____________ Л Q
производная =0,8; тогда для самолета типа «летающее кры-
ди>
ло» значение т] будет зависеть от отношения радиуса инерции к
средней хорде. При достаточно малом радиусе инерции величи-
на т) может быть получена не меньшей, чем у самолета с хвостом.
У самолета схемы тандем при отнесении коэффициента к общей
площади крыльев и расстоянию между фокусами крыльев про-
дет 1 г
изводная —=- составляет около 1,5; однако радиус инерции са-
молета получится более значительным.
Рассмотрим зависимость фактора затухания от ц, и co-
г.- 1
отношения тогда получим
п
п=- 1+1
у
Если т) мало, фактор
£>=----L=~.
У
Отсюда следует, что хорошее затухание при заданном ха мож-
но получить только для самолета с малым значением р.. Для на-
глядности на фиг. 39 даны зависимости р. от ха при разных D для
значений т) = 0; 1,5 и 3,0. Например, при т] = 0, ха=0,1 и D=1
77
78
и должно быть не более 10. Практически это возможно для плане-
ра или очень тихоходного самолета. При 7]= 1,5 хорошее затуха-
ние может быть получено при значительно больших р,; так, при
= 0,1 и D=1 р, может доходить до 45. Для самолетов с очень
большим р потребуется более эффективное оперение.
Увеличение D может быть получено путем снижения ха, одна-
ко это связано с уменьшением частоты колебаний и потому не-
желательно'.
Если затухание, создаваемое неподвижным оперением, ока-
жется недостаточным, нужно поставить автопилот, который дает
отклонения руля высоты, пропорциональные угловой скорости
вращения самолета. Этот вопрос будет рассмотрен в главе «Ма-
лые колебания с автопилотом».
Характер малых колебаний
Малые колебания состоят из вращательного движения вокруг
центра тяжести и поступательного- движения самолета. Оба коле-
бания имеют одинаковые характеристики, но фазы их сдвинуты.
Устройство модели для демонстрации малых колебаний уже бы-
ло описано; приведем примеры малых колебаний.
Выберем произвольно условия движения. Пусть движение
стремится к горизонтальному полету; в начальный момент само-
лет отклонен на угол фо=0,25, а угловая скорость равна нулю.
Характеристики самолета таковы:
и=150; = 2; ха = 0,05; V = 200; г, = 1,2.
Тогда получим следующие характеристики затухающего ко*
лебания:
п2 = __2ОО^_/2_ + оо5\ и £ _1_ = 0)3; £>=1.
а 150-1,22 \150 ) па
Имея фо=0,25 и зная, что это соответствует моменту останов-
ки углового движения самолета, пользуясь диаграммой на фиг. 11
для D= 1 и ^о=О,3, строим диаграмму угловых движений само-
лета (фиг. 40). Несколько сложнее построение возмущенного
движения центра тяжести. Как мы уже выяснили, момент оста-
новки поперечного движения соответствует фазе угловых движе-
ний, определяемых условием — = —— =—0,67. На диаграмме
_ <р па
в координатах ср, о>, которая дана в левой части фиг. 40, находим
точку, соответствующую — =—0,67, и для этой точки находим
9
— =0,74 и ф =0,185, что' соответствует времени /=О,8/о-
<Ро
Теперь находим */0, соответствующее остановке поперечного
движения в момент времени /=0,8 и по этой найденной точке,
79
пользуясь диаграммой колебаний на фиг. 11, строим диаграмму
поперечных движений:
л=-’£'<Д7“-3’75; £''Х=25’5-
Поперечную координату можно искать еще по формуле
Диаграмма изменения координаты у дана на фиг. 40; слева
— V
на фиг. 40 дана диаграмма 14= — по у и показана начальная
Па
точка #№ч, соответствующая выбранному начальному условию
движения. Как видим, моменту остановки углового движения при
крайнем положительном отклонении соответствует движение
центра тяжести к крайнему нижнему положению. На фиг. 41 по-
80
казана схема полученного колебания; размеры самолета и вели-
чины вертикальных перемещений показаны в одинаковом масшта-
бе; перемещения по горизонтали даны в уменьшенном масштабе.
На фиг. 42 показан результат расчета возмущенного движе-
ния самолета с теми же начальными условиями, что* и в первом
примере, но с иными характеристиками движения. Здесь взят
самолет, у которого нет статической устойчивости, но у которого
вследствие действия оперения движение носит апериодический ха-
Ч
w
~w
Фиг. 42.
рактер с характеристикой D = 4. Координаты самолета и его раз-
меры показаны в одинаковом масштабе. Как видим, в этом при^-
мере перемещения по вертикали оказались значительными.
Поведение самолета при действии возмущения
Всякое возмущение, вообще говоря, должно являться источ-
ником возникновения как малых, так и больших движений, при-
чем вначале будут происходить малые колебания и, когда они
практически затухнут, можно будет обнаружить большие коле-
бания. Однако такой анализ был бы пригоден для одиночного
возмущения или во всяком случае для возмущений, период повто-
рения которых меньше, чем несколько- периодов больших коле-
баний. Если возмущения быстро следуют одно за другим, можно,
обнаружить только1 малые колебания и, наконец, при весьма боль-
шой частоте возмущений и малые колебания будут затушеваны
возмущениями.
Возмущения, вызываемые вертикальными течениями, при сред-
них скоростях полета чередуются с интервалами, за время кото-
рых можно наблюдать проявление малых колебаний вплоть до
их практического затухания. Поэтому возмущение, вызываемое
вертикальным течением, мы рассмотрим только применительно
к малым колебаниям. Обычно считают что самолет так быстро
влетает в восходящий или нисходящий поток, что в первый мо-
мент наблюдается только изменение угла атаки в результате
сложения скоростей. Это- и определяет начальную фазу возник-
ших колебаний. К сожалению, мы еще очень мало знаем о струк-
81
туре возмущений и начальном воздействии их на самолет. Если
в начальный момент самолету будет сообщен некоторый враща-
тельный импульс, начальная фаза будет иной, и это скажется на
итоговом возмущении. По указанной причине рассмотрение дей-
ствия возмущения будет носить условный характер, и мы в своем
исследовании будем исходить из той точки зрения, что в первый
момент происходит только изменение угла атаки на величину
д w
&а= — , гдя w — скорость восходящего потока.
Внезапное увеличение угла атаки вызовет приращение подъ-
емной силы ДУ и ускорение в вертикальном направлении у"^.
Одновременно появится пикирующий момент и угловое ускорение:
aV дУ к дУ w
ДГ =— Да =-------
да да К
„ 1 дУ „ 1 дм А 9А
После ряда колебаний установится некоторый новый наклон са-
молета, отличный от начального, на величину <ра; на такую же
величину изменится наклон траектории <рт:
это будет наклон траектории по отношению к движущейся воз-
душной среде. Сама среда продолжает подниматься, и, следова-
тельно, истинный новый наклон траектории составит ?а+Аа.
В процессе перехода к новому направлению прямолинейного дви-
жения будут происходить колебания по отношению к новому дви-
жению. Тогда для угловых движений можно написать
<Р = ?а+Ф; ?' = Ф'; <р' = Ф";
здесь угол ф представляет составляющую колебания, которая
в начальный момент равна фнач=—а затем стремится к нулю.
Аналогично поперечное движение представится так:
y=yd+ty r aVt+z+wt;
здесь уа — начальный сдвиг новой прямолинейной траектории по
отношению к начальному положению; ^raVt—подъем при дви^
жении по новой траектории; z— поперечное колебательное дви-
жение центра тяжести; wt — переносное движение вместе с воз-
душной средой.
Очевидно, что в начальный момент
У ~,Уа4_^нач— 0; £нач= У а»
82
Для начальных поперечных скорости и ускорения получим
Лач = ?т а V+ W + 2’ = 0; у" = Хач = <ач’
В итоге рассмотрение вопроса свелось к следующему. Про-
дольный наклон мгновенно изменился на величину <ра и одно-
временно возникло колебательное движение, начальный угол ко-
торого ^4=—?«, начальная угловая скорость которого отсут-
ствует, но имеется начальное угловое ускорение ф"наЧ=—
Отсюда ясно, что начальная фаза колебательного движения есть
крайнее отклонение в момент остановки движения.
Для поперечного движения центра тяжести получим: наклон
траектории мгновенно изменился на величину началь-
ная точка новой прямолинейной траектории сместилась на вели-
чину уа и одновременно появилось колебательное движение с
начальной координатой гнач——уа', начальная скорость по отно-
шению к воздушной среде г'нач=—а начальное ускорение
£"нач= n2W.
Зная начальную фазу колебательного движения, можем найти
начальную фазу поперечного движения, определив сдвиг фаз ко-
лебаний по' времени из условия, что при z'=0 отношение — =— — .
Ф Па
Пример такого расчета уже был показан. Таким образом нам
остается только найти значения сра и у а, построить колебания по
известным начальным фазам, начальным координатам и харак-
теристикам колебания D и /0. Складывая все составляющие угло-
вых и поперечных движений, получим схему возмущенного дви-
жения.
Чтобы определить <?а, напишем два уравнения для угловых
движений, которые вполне равноценны:
ty" + пь¥ + == 0; ф* + лф' + = 0.
Подставив начальные значения
= — п2Да; ф' = 0; ф = —
получим
„2
А П°
<?а=-Да-Т.
па
Отсюда следует, что если самолет статически устойчив, после
попадания в восходящий поток наклон его уменьшится и относи-
тельная траектория станет нисходящей. В частности, при
Угол сра=—Да, т. е. самолет повернется как флюгер навстречу
относительному потоку; в относительном движении траектория
будет нисходящей, а в абсолютном — наклон не изменится.
83
Значение уа найдем по уравнению, связывающему поперечное
движение с угловым:
У а ^нач ^Фнач 4~ D
па 1\ т / нач
„2
Л п°
нач ?а А а 2 ;
м2 (
Л(\ /
1
па \
/ П \2
ППЬ I л Г \ ^0 /
^)=4’£1Т^Г
На фиг. 43 и 44 показаны примеры расчета возмущенного
движения при попадании самолета в восходящий поток.
Самолет 1 на фиг. 44 — это обычный статически устойчивый
самолет; после возмущения он несколько опустил нос, но> в аб-
солютном движении поток его быстро поднимает. У самолета 2
т] = 0, т. е. нет демпфирующего момента при вращении вокруг
центра тяжести; восходящий поток дал некоторый бросок вверх,
но наклон траектории в абсолютном движении не изменился.
Третий пример (кривая 3) относится к статически неустойчивому
самолету, но у которого и движение носит затухающий
апериодический характер. Как видно, возмущение оказалось
очень сильным.
Естественно возникает вопрос, какая характеристика возму-
щенного движения была бы желательна, если не прибегать к осо-
бым конструктивным мероприятиям вроде упругой подвески
крыльев. Для ответа на этот вопрос нужно было бы исследовать
движение отдельных частей самолета. Если экипаж может быть
расположен тесно, его целесообразно размещать в носовой части,
усиливать запас статической устойчивости и подбирать оперение
из условия получения фактора затухания около £>=1,5. Для длин-
84
кого пассажирского самолета наиболее неприятны угловые уско-
рения в начальный момент, и потому целесообразно снижать х0.
В 1910—20 гг. и даже позже значительная часть самолетов
была статически неустойчива; центровка некоторых самолетов
доходила до 50 и даже 60'% хорды. Тем не менее эти самолеты
не имели дивергентной характеристики вследствие относительно
большого т] и малого Однако полет в неспокойной атмосфере
был крайне неприятен. Причина этого ясна из данного исследо-
вания. Таким образом отсутствие статической устойчивости даже
не только по условиям управляемости (обратные усилия и откло!'
нения рулей), но и по условиям поведения в неспокойном воз-
духе.
Характерным примером возбуждения больших колебаний мо-
жет служить попадание самолета в среду с иной горизонтальной
скоростью, или проще — изменение скорости ветра. Предполо-
жим, что самолет вошел в среду, которая движется навстречу со
^скоростью и; тогда в начальный момент будем иметь продольное
возмущение У*нач=^; 1Л/Нач=0. Зная характеристику больших
колебаний, найдем начальные условия по отношению к новым
условиям полета и затем можем построить траекторию возму-
щенного движения.
Рассмотрим пример, когда продольный наклон самолета
остается постоянным. При входе во встречный поток у самолета
будет избыток кинетической энергии по отношению к воздушной
среде. Постоянство наклона самолета приведет к тому, что после
затухания возмущения полет будет происходить с тем же накло-
ном траектории и с той же скоростью, что и перед возмущением,
85
но избыток кинетической энергии реализуется в подъем траекто-
рии на высоту уа. В начальный момент входа в поток поперечное
ускорение
V' 1 &Y
Уу=^ыи = п*и
и продольное ускорение
1 дх
V —-----— not.
х т dV 5
Рассматривая начальное состояние по отношению к новому
установившемуся, будем иметь начальную координату —уа,
начальное ускорение V'y = tuu, но не будем иметь начальной по-
перечной скорости; для продольного движения имеем некоторую
начальную координату, начальную скорость Vx— и и начальное
ускорение V* =—п5и. Подставив начальные условия в уравнение
для поперечных движений, получим унач:
у у = п, Vx = - п2а у -nbVy=- rfy иач;
v —_____у — 211 о
Лнач“ о х 2
па па
Начальная фаза поперечных движений определяется условием
-^-=0. Напомним формулы для коэффициентов и составим вы-
У
ражёние для у^я.
п1 = п2п6 + п^—п5у, Пь = П2 + Пь, Пг = -^-, =
g ’дсх _ 2g сх g дР .
6 а У дсу ь V су G dV
__________________1__________
Унач— g (сх дсх\ V дР
дсу) Q dV
Пользуясь диаграммой на фиг. 11, строим зависимость у от t
(фиг. 45). Таким образом в результате действия встречного по-
тока траектория оказалась поднятой на величину у^ч. Продоль-
ные движения получим по формуле
па Vy п2
п4 у
Для начального момента будем иметь
•^нач З'нач
«4
По
па
86
Значения х в относительном движении подсчитываем по
указанной формуле, причем Vy/y берем по диаграмме на фиг. 15
в зависимости от у/уй. Теперь можно построить траекторию
Фиг. 45.
относительного движения. Пример, приведенный на фиг. 46,
построен для таких исходных условий:
У = 80; « = 10; а-0,18; -^=13,5; -^=11;
сх дсх
gdp
GdV
-0,009.
«. = 0,7; «. = 0,25; «5 = 0,063; л6 = 0,027; «2 = 0,036;
па = Ь,\Ы\ £0 = 5,35; «„=1,023; D = 4; уна,= — 72,5;
хнач=—200.
87
Действие управления
Действие управления можно рассматривать следующим обра-
зом. В начальный момент при отклонении руля высоты возникает
сила, сообщающая самолету угловое и поперечное ускорение. Это
состояние можно рассматривать как возмущенное по отношению
к некоторому вращению с постоянной угловой скоростью и дви-
жению по дуге окружности. На это движение будут наложены
малые колебания. Полученное криволинейное движение можно
рассматривать как возмущенное состояние по отношению к не-
которой новой прямолинейной траектории с измененным углом
Фиг. 47.
1~большие колебания; 2-малые колебания; 3—новый режим.
наклона и скоростью». Переход от криволинейной траектории к
прямолинейной будет происходить в виде медленных колебаний.
Схема такого движения показана на фиг. 47.
Периоды больших и малых колебаний настолько различны,
что оба движения можно рассматривать раздельно. Начнем с ма-
лых колебаний и вначале примем, что руль высоты дает пару
с моментом Л40. Начальное угловое ускорение Когда
движение установится, угловое ускорение будет отсутствовать,
самолет и вектор скорости будут вращаться с угловой скоростью
но угол атаки окажется измененным на величину а». Найдем
значения ®'аи аа:
, ?о ^0 П2 У а „2 In2 п0 1 па л 4-— П2 4>'а ? ;0; ?; = и2аа=?а; ; + = 0 ^0
88
Движение самолета разложим на относительное и перенос-
ное. Для вращательного движения переносным движением
Y = + будет вращение с угловой скоростью <$а при на-
чальном положении 70; относительное движение будет состо-
ять из вращательных затухающих колебаний с углами ф. Для
поперечного движения центра тяжести переносное движение
состоит из движения с постоянным ускорением и", причем
, «о
вектор скорости вращается с угловой скоростью сра = —;
обозначим начальную координату через и0, начальную попе-
речную скорость Uq и начальный наклон траектории ут0 =
ыо
=—. Тогда можно написать такие соотношения:
v
?=т+Ф=то + (р?+Ф; ?'=?Л+Ф'. ?" = Ф";
J/ = U + Z = Uo + «oi+«;Y+Z; И" = (Ра1/; Уу = ио + Ча*У + г'»
?т = -^ = Тто + ?/ + Фп bo = V’ = <?т = '?а + Фг
В начальных условиях действует только угловое ускоре-
ние; тогда из выражений для ср, срт и у получим
То—Фо; ?о=?«+%=°; ?о=io+Фо=0; ф0=—ъ;
«о=—z0; «о=—20; Тто=— Фт0; 5<0=—<?а-
Когда движение установится, относительное движение за-
тухнет и движение будет соответствовать переносному дви-
жению:
?’=%>; сРт=='Ра; Ф=°; Фт=0; Ф'=°; 'К=о-
Из условия ср—?т = аа следует
То —Тт0 = аа-
Напишем теперь уравнения движения через относительное
и переносное движения:
?'= — Ло(<Р-<Рт)—л'р' + сРо== — «о(То + ?^ + Ф — Тто — Ю +
+ П<?а + ~ Ча = “ П0 (Ф - Фт) — «Ф':
л2
?т = «2 (а. + Ф — Фт); ?т — пг*а = Фт = п2 (ф ~ Фт)-
Уравнения движения для относительного движения оказались
обычными затухающими колебаниями с характеристиками малых
80
колебаний. Для построения относительного движения и опреде-
ления начальных условий переносного движения рассмотрим
начальную фазу колебаний. В начальный момент нам известны
для относительного движения угловое ускорение Фо= ¥о и Угла"
вая скорость <Ро=—отсюда мы можем найти начальную
координату относительного движения
?0 = — Л’Фо + Фо«а = ?о р? —1);
, ?0 / Г» "2 Л ' D
па \ па i па
Аналогично для движения центра тяжести получим: угло-
вая Скорость вращения вектора скорости относительного
движения отсюда поперечное ускорение
= —(f>aV; из уравнения для вращения вектора скорости най-
дем наклон траектории и поперечную скорость Vг:
Фто= — t?a=M4,o—Фто)=л2“в; Ъ== v='^+a«==tf^;
к па
наконец, по уравнению поперечных движений найдем попе-
речную координату z:
У Л = — vi0; — V<?a>
ф'у
2o=^-(l-Da).
па
Начальные условия для переносного движения будут обратны
условиям относительного движения:
«0=—Zo; м0=—у-го; Ут0= — ^т0= — .
па
Теперь можно построить абсолютное движение. Для этого
строим относительное движение по уравнениям
“=«0+«^+ио-?- = —1+
z па 2
и на него накладываем колебательное движение, начальные
условия кото-рого нам известны, а метод построения описан
выше.
Переходим к случаю, когда нужное принять во внимание силу,
действующую на самолет при отклонении руля. Это необходимо
при руле высоты, расположенном относительно близко от центра
тяжести, и особенно если рулем (высоты служит продолжение
крыла, как это делается у «летающих крыльев» (фиг. 48).
В этом случае, как показывают эксперименты, возникающая при
ЗО
отклонении руля сила лежит даже не в пределах площади руля,
а значительно впереди него. Фокус руля в этом случае находится
примерно на расстоянии 45% хорды крыла от передней кромки,
а центр тяжести — на расстоянии 5—10% хорды; при этом соот-
ношение расстояний хв и х0 доходит до 4 и даже 2. Пусть в ре-
зультате отклонения руля возникла сила Уо, которая в начальный
момент сообщит самолету угловое ускорение ср" , поперечное
ускорение VyQ или приведет к вращению вектора скорости
Уохв . Го
?о=—; ?то=-^«
Когда вращение установится, величины ?а и ао можно
найти по формулам:
— п&а~ «'4 = °; с?а=П2аа + ,?'т6>
'Po+'M’rt ?о (, Ло\ То Л . п Х<Л
=---------=------ 1------I; — 11 J-------------1.
л4-Н1 хв/ па \ П1 хв/
Оказалось, что эффект действия руля высоты снизился и, кро-
ме того, начальная фаза колебательного движения стала иной.
Напишем уравнения движения в таком виде:
г ff д/VI / х । dAf f । дж
= —(? —<рт) + — <р +Afo;
da d<p
Mo = KoxB; Af1 = r0^o;
da d<px
dM
Вспоминая механическую модель движения (см. фиг. 29) для
случая действия руля, приходим к выводу, что к модели самолета
нужно приложить момент Af0, а к вектору скорости — момент
—xomV.
Фиг. 49.
В
о
!
(фиг. 49). Поскольку стрелка, изображающая вектор скорости,
не имеет момента инерции, она сразу начнет вращаться вниз,
вызывая опускание самолета, и только позже, когда самолет
начнет поворачиваться под действием момента Af0, вектор ско-
рости последует за ним.
91
Движение самолета опять расчленяем на переносное и отно-
сительное, но только теперь начальные условия изменятся по
сравнению с теми, что мы имели ранее. Координаты абсолютного
движения будут следующие:
? = То+'р?++; ?' = ?а + Т; ?’ = Ф";
y = u^uot + u" -^- + z; Vy = u0 + u,'t + z'; u" = <?'aV;
?т = Тто + ?^ + Фт; Тто = -у; Ф* = Т7’ ^^'Ь + Фт-
Для начального момента будем иметь
Фо = ?о'’ Фо=—Фо=—ъ;
ФтО = ?тО —V» ФтО=—Тто’, г0=— «О-
Когда движение установится,
<р" = 0; ф = 0; фт = 0; ф' = 0; =
<f' = Y = <fa\ ? —<рт=То —Тто = ав.
Теперь найдем начальные условия для относительного
и переносного движений:
• 9 » ’ , ' / 1,1 *0 \
'Ро=-«2аФо-«в'Ра; Фо = ?а — + — —° ;
\ "-а ^2 ^2 -^в /
Фо _ _/ __па । па \
Фо \ п2 хв /
Для поперечного движения
ФтО = ?т0 “ Фо - ФтО = — «а-
По фф, и <рт0 найдем начальное ускорение V'^ и начальную
скорость Vz0 относительного движения центра тяжести, а затем
по уравнению колебания найдем начальную координату гл:
va= Т^=ф;э0У; Vz0 = ^lfiV.
Координаты переносного движения:
и = н0 + «^+«"-^; ^ = ^4-^;
и0=—г0; и0=—Уг0; W = ^aV.
На фиг. 50—51 приведены диаграммы движений, возникающих
под действием руля высоты, причем было принято — = 3, что
соответствует летающему крылу. На фиг. 50 показано относи-
92
тельное движение, а на фиг. 51 —переносице и абсолютное, при-
чем по вертикальной оси масштаб взят более крупным. Как ви-
дим, в начальный момент траектория несколько опустилась, а за-
тем уже стала интенсивно подниматься.
Большие колебания при действии управления можно рассчи-
тать следующим образом. По уравнению больших колебаний,
принимая ускорение равным нулю, находим новое движение по
прямой с новым углом наклона и новой скоростью. Начальное
состояние будет характеризоваться поперечным и продольным
ускорениями, вызванными изменением угла атаки на величину
Па, и начальными продольной и поперечной скоростями по отно-
шению к новому установившемуся движению. Тогда можно найти
начальные координаты относительного движения, начальную
фазу движения и затем, пользуясь диаграммами колебания для
нужного фактора затухания, построить относительное движение.
При изменении режима полета летчик проявляет особое вни-
мание к поведению самолета. По этой причине движение самолета
нельзя рассматривать как вполне свободное и пользоваться ха-
рактеристиками больших колебаний. Однако один вид больших
колебаний имеет большое практическое значение — полет с по-
93
стоянным углом наклона, удерживаемым летчиком или автопи^
лотом. Когда летчику нужно изменить режим полета, например,
перейти с горизонтального полета на режим быстрого подъема,
он рулем высоты ставит самолет под другим углом и меняет ре-
жим работы двигателя. Если при перемене режима изменение
наклона самолета должно быть значительным, летчик во избе-
жание большой перегрузки меняет положение самолета посте-
пенно или ступенями. Примером таких действий может служить
выравнивание при посадке. Поскольку сложное действие можно-
расчленить на ряд простых, рассмотрим поведение самолета при
быстром изменении продольного наклона. Пусть до изменения наЬ
клона самолет имел скорость V, угол наклона =0 и угол на-
клона траектории ^=0. Это не значит, что самолет летел гори-
зонтально с нулевым углом атаки; просто мы приняли начальное
положение за нулевое. После поворота самолета на угол
установился новый режим полета, характеризуемый скоростью
Va, изменением наклона траектории и поперечной скоростью
по отношению к начальному движению
V& а— V<рт а.
Если мы будем новое движение рассматривать как основное,
то исходное состояние после поворота самолета на угол будет
характеризоваться величинами:
^РтО VyO ^уа'
Уравнения движения для случая = const будут иметь вид
dV dV / я \
—£ = _цу ±пух) —- = —л6V + ( /I/,
dt 2 У 4 х dt ь х \ & у / У
где
сх ё др
V су G dV
или после преобразований
п2а = п2п6 + п4-^-—п4пъ, пь = п2 + пе.
Пользуясь этими уравнениями и исходными данными, можем
найти начальные фазы продольного и поперечного колебаний, на-
чальные координаты в относительном движении и затем построить
траекторию относительного движения. Проделаем это на примере.
Пусть самолет летел горизонтально со скоростью 50 м/сек, с углом
94
атаки а = 0,16; будем считать, что угол атаки близок к наивы-
годнейшему, когда — =—- =12. Далее примем, что градиент
^х ОСХ
изменения тяги по скорости в два раза меньше градиента изме-
нения сопротивления по скорости, т. е. ’ эт0 УСЛ0“
вие вытекает из допущения о постоянстве коэффициента полез-
ного действия винта. Коэффициенты в уравнениях движения
будут иметь следующую величину:
п2—1,22; и4 = 0,39; п5 =0,1; и6 = 0,05;
иь=1,27; п2а =0,098; na=0,313; D=4,05.
Как видим, движение имеет апериодическую характеристику.
Найдем новое движение после изменения продольного наклона
самолета на величину сра=0,05. Новый режим установившегося
полета можно найти обычными методами аэродинамического рас-
чета, но* можно воспользоваться и уравнениями движения. Пово-
рот самолета на угол сра=0,05 даст увеличение угла атаки на ту
же величину и вызовет продольное и поперечное ускорения:
V;o=-«5VTa=-O,25,
^ = «№ = 3,05.
Подставив эти значения ускорений в уравнения движения,
найдем начальные значения скоростей по отношению к новому
движению, а затем по преобразованным уравнениям колебания —
начальные координаты:
140=6,1; Vyo=—0,55; 14=50—6,1=43,9 м1сек;
Хо=—70,8 м; уо=—24 м.
Получим, что в процессе возмущенного движения самолет
приближается к точке, которая в начальный момент лежит впе-
реди и выше. По начальным координатам и скорости находим
начальные фазы и затем, перестраивая диаграммы колебаний,—
траекторию движения. Результат построения для данного примера
приведен на фиг. 52.
Пока скорости полета невелики, самолет после изменения
наклона (в процессе апериодического движения) практически
довольно быстро> подходит к новому режиму. Однако' при боль^-
шой скорости полета приближение к новому режиму происходит
медленно, и может встать вопрос о применении иного способа
изменения режима полета. Выскажем некоторые соображения
по оценке действия руля высоты, рассмотрев ряд практических
вопросов. Значительное по силе и длительное по времени откло-
нение руля высоты применяется при выполнении маневров и фи-
гур высшего пилотажа, например, виража, петли. Изложение
9S
метода расчета фигур высшего пилотажа не входит в задачу
данной работы. Нужно только заметить, что, выполняя криво-
линейный полет, летчик стремится выдерживать постоянную угло-
вую скорость вращения самолета. Это относится не только к ви-
ражу, но к петле и другим фигурам. С точки зрения управляе-
мости выполнение фигур характеризуется некоторым законом
изменения угла отклонения руля и усилия, прилагаемого летчи-
ком к органам управления. Эти усилия могут быть разделены
на усилия, определяемые скоростью полета и режимом работы
двигателя, и на усилия, определяемые наличием перегрузки.
Первые усилия могут быть найдены путем рассмотрения равно-
весия в прямолинейном полете. Грубо говоря, эти усилия пропор-
циональны скоростному напору, однако особенности двигатель-
ной группы приводят к существенному отклонению от этого за^
кона.
Усилия, определяемые наличием перегрузки, могут быть опре-
делены с помощью приведенных выше соотношений между мо-
ментом от действия управления и режимом установившегося
криволинейного движения:
М Мп
ср =------- =-------,
а I(n+nx) Z /_ 7) \
х0+ —
\ р- /
Момент, создаваемый рулем, может быть выражен через
прирост усилия:
М= ДР£В,
ф' = Sn — — ДР —------— ,
у 1 /- Ч \
I Ло +
\ р- /
причем, как уже указывалось, длину LB можно считать не зави-
сящей от скорости полета, пока в характере аэродинамических
нагрузок сохраняется закон пропорциональности скоростному наг
96
пору и не возникает резких изменений в спектре обтекания.
Тогда получим выражение для связи приростов усилия и пере-
грузки
dP
dn
Grj
Сравнительно небольшие изменения режима полета могут
быть рассмотрены описанным методом, однако здесь есть неко-
торые трудности. Изменение режима прямолинейного полета мо-
жет состоять из изменения скорости и наклона траектории. Если
изменение скорости легко определяется по прибору, то измене-
ние наклона траектории определяется по косвенным признакам —
изменению высоты полета и вертикальной скорости. При анализе
изменения наклона траектории можно ограничиться рассмотре-
нием одного переносного движения, поскольку относительное
движение в процессе затухания быстро исчезает. В начальный
момент действия руля высоты в сторону увеличения наклона
траектории в переносном движении появляется отрицательная
вертикальная скорость YtoV; затем траектория начинает вра-
щаться с угловой скоростью и, когда нужно будет прекратить
вращение траектории, произойдет второй скачок переносной ско-
рости.
Отсюда видно, что скачки вертикальной скорости не повлияют
на время поворота траектории, но зато выравнивание траектории
нужно произвести с некоторым упреждением. Величину упрежде-
ния по времени и по углу поворота можно выразить следующим
образом:
А ' D
дТт= —iTO=tPa —;
па
D
Па
П (1 +у))
\ И /
<?а
При малом запасе статической устойчивости Д/ может стать
значительным, порядка 1—2 сек.
В процессе управления самолетом чаще всего применяются
небольшие довороты с целью сохранения продольного наклона
самолета. Если самолет неустойчив, летчик должен довольно
часто поправлять положение самолета. Если самолет статически
устойчив, но выдерживает режим нетвердо, т. е. при небольшим
нарушении равновесия сильно меняет режим полета, то летчику
приходится временами поправлять машину. Если же самолет
статически очень устойчив и твердо выдерживает режим полета,
то все же в случае сильного возмущения, при возникновении
больших колебаний с большой амплитудой, возникает необходи-
мость во временном удержании самолета в одном положении
Для ускорения затухания больших колебаний. Наконец, если ма-
шина управляется автопилотом, действие руля будет'пропорцио-
нально отклонению самолета от исходного положения.
97
Если интересоваться только продольным наклоном самолета,
то мы будем наблюдать колебания с характеристиками не п2 и п,
как при чистом вращении вокруг центра тяжести, а п2 = п2-\~пп2
и пъ = п + п2 вследствие влияния движения центра тяжести. Ха-
рактеристика затухания D также будет иной. Поскольку поло-
жение самолета, вообще говоря, не будет соответствовать уста-
новившемуся режиму полета, отличие будет состоять в величина*
скоростей по траектории и в величине вертикальной скорости. Это
вызовет появление моментов, сравнительно медленно изменяю-
щихся по величине, соответственно приближению режима полета
с данным наклоном к установившемуся. Таким образом управле-
ние наклоном самолета аналогично управлению телом, на кото-
рое действуют силы, зависящие не только от отклонения, но и от
скорости отклонения, а также силы, относительно медленно ме-
няющиеся по времени вследствие изменения режима полета.
Рассмотрим действие управления за малые промежутки вре-
мени, когда эффектом больших колебаний можно пренебречь.
Первый случай — рулем высоты был сообщен момент, необ-
ходимый для желаемого изменения положения на угол с?а. На-
чальное состояние можно, рассматривать как возмущенное по
отношению к новому положению. Тогда начальное ускорение
?0= -»а?0 = «2Л-
Это состояние на фазовой диаграмме изобразится, как пока-
зано' на фиг. 53,а; в этом случае самолет будет совершать зату-
хающее колебание относительно нового положения. Такой стиль
управления пригоден при значениях фактора затухания D =
= 1,2—2.
Второй случай — может быть использован при слабом зату-
хании, т. е. при малых значениях D. Сообщим самолету угловое
ускорение, характеризуемое величиной (фиг. 53,6). Когда
самолет в процессе колебания перейдет через положение равно-
весия и окажется в крайнем удалении, имея отрицатель-
ное ускорение, передвинем руль вторично* в том же направлении,
что и в первый раз — этим уничтожится ускорение, и самолет
окажется остановленным в новом положении. Время, потребное
для изменения положения, будет равно полупериоду малых ко-
лебаний, а начальное действие руля определится условием
?а='Ро + 'Р1 = 'Ро(1 +-^±L)-
V <fn >
Такой стиль управления требует выработки у летчика неко-
торого ритма в работе. Время изменения положения вполне
определенно, однако нет оснований бояться, что оно будет ве-
лико — слабое затухание имеет место при большом запасе ста-
тической устойчивости, когда период колебаний мал.
98
Третий случай — относится к апериодическому движению,
когда D^>2. Управление одним движением в этом случае может
дать нехорошую характеристику, так как подход к положению
равновесия окажется затянутым. Применяя два движения рулем,
причем первое — более сильное, чем это необходимо для нового
положения равновесия, а второе — соответственно новому поло-
жению, можно сократить начальную стадию движения, хотя тео-
ретически время перехода останется бесконечно большим. При-
Фиг. 53.
меняя три движения, можно сделать время конечным: вначале
создаем повышенное ускорение с таким расчетом, чтобы самолет
стремился пройти желаемое положение равновесия со значитель-
ной скоростью (фиг. 53,в); когда самолет будет близок к желае-
мому положению равновесия, рулю дается обратное отклонение
(для торможения); в момент остановки руль ставится в положе-
ние, определяемое условием равновесия.
Четвертый случай — относится к дивергентной характеристике
самолета. Здесь необходимо не менее двух движений рулем.
Первым движением сообщают самолету ускорение в желаемом
направлении, причем начало координат фазовой диаграммы бу-
дет смещено влево (фиг. 53,г). Когда самолет будет приближать^
<я к новому положению, рулем высоты меняют знак ускорения,
99
передвигая начало координат фазовой диаграммы вправо так,
чтобы данное положение самолета попало на асимптоту, а само
начало координат совпало с новым положением равновесия. Рас-
чет этого движения легко выполнить графически на фазовой
диаграмме; однако практически не удается сразу попасть в поло-
жение равновесия и потребуется дополнительное движение ру-
лем. Если летчик неопытен, то, отыскивая положение равновесия,
он может раскачать самолет. Таким образом мы приходим к
своеобразному выводу — если самолет имеет собственную коле-
бательную характеристику, движения рулями просты; если же
характеристика самолета апериодична или дивергентна, действия
рулями носят колебательный характер.
ДВИЖЕНИЕ, ОПРЕДЕЛЯЕМОЕ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЕМ ТРЕТЬЕГО ПОРЯДКА
В некоторых случаях в результате преобразования уравнений
движения получается одно уравнение третьего порядка
ср'" + Вер" + Сер' + Оср = 0.
Решение этого уравнения может быть получено в виде
<Р = ?1 + ?2 + ЧУ» = <р2 = Сех»'; <?3 = С3е^,
т. е. сложное движение расчленяется на три простых.
Решение уравнения можно также представить в виде
? = ?i = ?i,oev; ?2 = sin (yt + у0),
где сложное движение расчленено на два, из которых одно коле-
бательное. Займемся вопросом о расчленении движений. Разде-
лим исходное уравнение на D и введем единицу времени tQ=
1
ср'" + Bxcp" + С\ср' + ср = 0; Вг = В£о; = Ct%.
Как видим, характер движения определяется только двумя
параметрами В± и Сх; коэффициенты при первом и последнем
членах равны единице. Из двух составляющих движений одно
определяется уравнением второго порядка, другое — уравнением
первого порядка. Представим их в виде
+М1=о; 'р;+м2=о-
Из этих уравнений нужно исключить <р, и <р2. В уравнение
для подставим <р1==<р—<р2 и затем продифференцируем его:
+ а?' + М—(?2 + atP2 + = 0;
?"' + «?" + ' + а?; + М2) = о.
100
Пользуясь уравнением для <р2, получим
?2=— Ms! = ?2”=—
Подставим эти выражения в написанные выше уравнения и
исключим ср2-
ср'" + (а + &2) ср" + (Z\ 4- <р' + = 0.
Тот же результат можно получить простым перемножением
характеристических уравнений для двух исходных уравнений:
X2 4-^4-^ = 0; Х + &2 = 0;
X3 4- (я 4~ Ь%) X2 4" (bL 4~ ^^2) X 4- ^1^2 0.
Так мы и будем делать в дальнейшем для объединения урав-
нений, изображающих составляющие движения.
У исходного уравнения третьего порядка коэффициент при
последнем члене равен единице. Мы удовлетворим этому усло-
вию, если примем Ь2=Ь; Ь±=— . Тогда
X3 4- X2 4- ^*1Х 4-1 = 0,
где
BL = a + b\ C1==ab + —; В = а]Л/>.
ъ
Величина F является фактором затухания для уравнения
второго порядка, т. е. для составляющего движения срь
По известным Bi и С± нужно найти а и Ь. Это легко сделать
с помощью графика, построенного в координатах а, &. Уравне-
ние Ci = ab+— дает серию кривых с параметром Cf, уравнение
ь
Bi=a + b — серию наклонных прямых с параметром Bi, который
соответствует значению Ь при <z=0 (фиг. 54). Искомым реше-
нием будет точка пересечения кривой и наклонной прямой с нуж-
ными параметрами и С\. На графике можно нанести линии
F=co-nst, ПО' которым путем интерполяции можно найти соответ-
ствующее значение F и сделать вывод о характере первого со-
ставляющего движения. Заметим, что если В^>2, то движение
апериодично и мы получаем три пары значений для а и Ь. Можно
взять любую из них, так как в этом случае сложное движение
может быть расчленено на три простых, а комбинируя их, можно
получить три сочетания по два движения. Наконец, можно взять
три значения b соответственно трем точкам пересечения и полу}-
чить три составляющих движения:
?i = ; ?2 = ; <р3 = ?3,o^“v.
101
Уравнения «pj + a<pj + = 0 и + = О, полученные
после расчленения, отнесены к единице времени ^0 = ~г— •
]Л>
Для перехода к времени в секундах делим первое уравнение
на Ц, а второе на /о:
?1 + ~?1+“2 = 0; ?2 + 7" = °-
Jq DIq Iq
Условия устойчивости таковы. Если движение расчленяется
на три простых, для устойчивости его достаточно, чтобы Вг и С±
были положительны; это вытекает из условия а^>0 и &^>0. Рас-
смотрим случай, когда одно движение носит колебательный ха-
рактер с очень слабым затуханием. Пусть где у. — очень
102
малая, но положительная величина. Тогда из исходных уравне-
ний получим
Ь = В1 у; = В& ~ В^ + —-- ;
£>1— {Л В\ — [1
ад-с^-в^-^0; >0.
^1+^1
По условию отсутствия апериодической неустойчивости
Cj>0 и Вх > 0. Условием затухания колебаний будет
ед-1>0; ^>1; С1 = -^~;
Dr
Если это условие не выполнено', но В± и С± положительны,
одно из составляющих движений будет давать колебания с воз-
растающей амплитудой. Для уравнения третьего порядка можно
построить фазовую диаграмму, но в этом нет нужды, так как дви-
жения разлагаются на более простые. Начальные условия для
каждого составляющего движения можно получить по начальным
условиям решаемой задачи.
Малые колебания с автопилотом
Идея применения автопилота для повышения устойчивости
самолета возникла давно. Вначале предлагались сравнительно
простые устройства, связывающие руль высоты с маятником или
флюгером, или пластинкой, воспринимающей давление встреч!-
ного потока. Указанные устройства давали полезный эффект,
так как моменты, вызываемые флюгером или маятником, увели-
чивали степень статической устойчивости самолета. Действие
пластинки, воспринимающей давление встречного потока, прида-
вало самолету устойчивость по скорости. Однако эти устройства
не приводили к коренному изменению свойств самолета и не
обеспечивали проведения длительного полета без участия лет-
чика.
Тогда внимание изобретателей было привлечено к использо-
ванию свойств гироскопа. Н. Е. Жуковский весьма интересовался
автопилотами и разрабатывал оригинальные схемы. В 42—43-й
лекциях по основам воздухоплавания Жуковский впервые дает
обстоятельный обзор действия различных автопилотов, в том
числе гироскопических. Весьма интересная схема автопилота с
электрической рулевой машинкой для дирижабля была предло-
жена К. Э. Циолковским еще в 1898 г.
юз
Из рассмотренных примеров продольных движений самолета
видно, что высокая частота малых колебаний при весьма высо-
ком затухании обеспечивается относительно просто определен-
ным запасом статической устойчивости и тормозящим действием
оперения. Значительно хуже обстоит дело с обеспечением зату-
хания больших колебаний. Как было показано', большие коле-
бания становятся апериодическими, если самолет удерживает
постоянный наклон. Средством для удержания постоянного на-
клона самолета явился автопилот, основой которого послужил
свободный гироскоп, достаточно надежно удерживающий свое
положение при помощи остроумных корректирующих устройств.
Автопилот, стремящийся сохранить постоянный наклон самолета,
обеспечивает устойчивую характеристику малых колебаний само!-
лета даже в том случае, когда нет естественной статической
устойчивости. Однако отсюда не следует, что при наличии авто-
пилота нет надобности заниматься анализом малых колебаний
самолета, так как, во-первых, каждому автопилоту свойственно
некоторое запаздывание действия; во-вторых, в некоторых слу-
чаях тормозящее действие оперения оказывается недостаточным
для обеспечения энергичного затухания колебаний, и тогда на
автопилот может быть возложена дополнительная функция —
усиление затухания. Если характеристики автопилота подобраны
неправильно, у самолета возникают автоколебания.
Рассмотрим малые продольные движения самолета, полагая,
что имеется автопилот, вызывающий моменты, пропорциональные
углу отклонения самолета о и угловой скорости вращения само-
лета ср'. Моменты, создаваемые автопилотом, представим в виде
МА = ~ а'^ + ~Ь^-
dtp ду
Величина а<?7 характеризует запаздывание реакции автопило-
та на изменение продольного угла; это запаздывание принимаем
пропорциональным скорости изменения наклона, т. е. скорости
вращения самолета. Аналогично для реакции автопилота на ско-
рость вращения запаздывание составляет 6?", т. е. пропорцио-
нально угловому ускорению. Составим теперь уравнения движе-
ния:
г „ дМ , ч . дМ , , дМк z , дМ^ , , •
/ <р'= (? —ср) + — ср + ——(ср —аср) 4- ——— (ср — Ь<? ),
да ду дер дф
' дУ, \
w^cp = (ср—ср).
да
Введем обозначения:
„2_ 1 дм. п- 1 дМ. П2-_________________1
° Iz I2 dtp' 12 dtp
1 дМ А 1 дУ
---------— ; =------------.
lz ду' mV да
104
Тогда уравнения движения примут вид
?" + — ?т) + л?' + п2 (<р — аср') + л9 (<?' - *<р") = О,
—?Т)=О, или после простых преобразований
ер" (1 — Л9&) + (п + п9 — ап§ <?' + (п2 + л|) ср — и2<рт = О,
Л2? — Л2ерт = 0.
Подставим в уравнения движения решения ср = Дех/, <рт =
= Веи:
Д [к« (1 — 6п9) + к (п + щ—ап$ + (п2 + п2)] — Вп2 = О,
Ап2—В(к + п2) = 0.
Составим определитель системы
к2 (1 — йп9) + X (п + п9 — ап2) + (л2 + л2) - п2
п2
—(X + п2)
= 0
и раскроем его:
X3 (1 — bn9) + X2 (л + п2 + п9 — ап2 — п2Ьп9) +
+ X (л2 + л2 + пп2 + л2л9 — ап2п2) + л2л2 = 0.
Полученное уравнение можно кратко записать в виде
aw+b\2 + c\+d=o.
Апериодическая неустойчивость проявится, если один из коэфг
фициентов окажется отрицательным; однако это может иметь
место при исключительно сильном запаздывании действия авто-
пилота. Условием отсутствия возрастающего колебания для урав-
нения третьего порядка является неравенство
ВС—А£>>0.
Если это выражение раскрыть, получим относительно1 слож-
ную комбинацию из динамических характеристик самолета, одна-
ко анализ условий, при которых отсутствуют возрастающие ко-
лебания, не представит затруднений.
Качественный анализ поведения самолета с автопилотом от-
носительно прост. Предположим, самолет имеет большой запас
статической устойчивости, т. е. обладает энергичным стремлением
к сохранению угла атаки; тогда малые колебания будут иметь
высокую частоту. В этом случае задачей автопилота будет являть-
ся только относительно медленное исправление нарушений про-
дольного наклона. Если же статическая устойчивость мала, авто-
пилот должен реагировать значительно быстрее, создавая же(-
105
лаемую частоту малых колебаний. Однако чрезмерно высокая ча-
стота приведет к ухудшению затухания и росту запаздывания.
Автопилот, реагирующий на угловую скорость, необходим в
том случае, если естественное затухание явно недостаточно из-за
слабости тормозящего действия оперения или чрезмерно большого
момента инерции. Недостаточность естественного затухания мо1-
жет иметь место у обычного самолета относительно малых раз-
меров, летящего на очень большой высоте. Однако> без особой
необходимости не следует увеличивать реакцию автопилота на
угловую скорость.
Совершенно по-иному нужно подходить к выбору автопилота
для беспилотных машин. В этом случае на автопилот ложится
необходимость компенсации недостатков предварительной регу-
лировки; кроме того, собственные характеристики машины часто
не бывают известны с достаточной точностью.
ОБЩИЙ СЛУЧАЙ ПРОДОЛЬНОГО ДВИЖЕНИЯ САМОЛЕТА
ПОД ДЕЙСТВИЕМ МАЛОГО ВОЗМУЩЕНИЯ
Общий случай продольного движения самолета под действием
малого возмущения уже хорошо изучен и изложен в большом ког
личестве работ по теории динамической устойчивости.
Автор решил изложить этот вопрос в несколько измененном
виде, полагая, что в новом изложении он окажется более доход-
чивым и найдет более широкое применение при расчетах самог
летов.
В рассмотренных выше вопросах хотя движение и обладало
двумя и даже тремя степенями свободы, но- произвольное пере-
менное было только одно — угол атаки или скорость. Теперь,
когда мы хотим ввести оба переменных одновременно, в иссле!-
дование необходимо' внести такое упрощение, при котором оба
переменных не входили бы в один член уравнения, иными сло-
вами, чтобы каждое переменное было самостоятельно. Такое
разделение возможно только в случае, если имеются в виду от-
носительно небольшие изменения переменных.
Многие силы и моменты, действующие на самолет, зависят от
произведения угла атаки на квадрат скорости. Угол атаки а
является разностью между наклоном некоторой оси, связанной с
самолетом, и наклоном вектора скорости, т. е. а = <?— ф*г. Пусть
с?о, ?то и У2о — начальные значения указанных величин. Давая
им приращения, получим
? = ?о + дТ> V2= ДУа;
<Pv2 = (?o+ д'р)(1/о+ Д 1/2) = '?о^ + ?оД^+ 1/2Дср + Д?Д V2.
Малость приращений позволяет пренебрегать значением чле-
нов, в которые входят произведения приращений, т. е.
?V2 = ?0V02 + ?oAV2+ у02дг
106
Не нужно думать, что речь идет о весьма малых изменениях.
Допустимые приращения грубо можно найти так. Представим
выражение для «V2 в виде
<РУ2 = Т<У® 1
ДИ* Ду Дер ДУ2'
?о + 9о V®.
О ДУ2 Дф
Если даже значения —г и — принять равными 0,15, вели-
ко 'Ро
чина — будет равна 0,0225, что составляет 2,25% от 1
<Fo Vo
и 7,4% от суммы ^С + — . В технических расчетах такая точ«
^0 ?о
ность может быть допустимой.
При устойчивом движении начальные возмущения уменьша,-
ются и справедливость сделанных допущений оправдывается.
Если же движение неустойчиво, возмущения растут и сделанные
допущения станут незаконными. Отсюда следует, что, если исход-
ное движение оказалось неустойчивым, дальнейшая судьба его
будет нам неизвестна. Исследование движений самолета имеет
целью не просто констатацию свойств машины, но и изыскание
мер, при помощи которых движение может быть сделано устой-
чивым.
Уравнения продольных движений
Продольное движение самолета определяется координатами х
и у и углом наклона самолета о. Координаты х и у удобно брать
в относительном движении, т. е. полагая, что начало координат
движется прямолинейно и равномерно* со скоростью установив-
шегося движения. Угол у также будем отсчитывать от исходного
установившегося движения. Таким Образом, если движение еще
не возмущено или колебания уже успокоились, координаты будут
равны нулю.
Особенностью свободного полета самолета является независи-
мость действующих сил и моментов от координат х и у\ правда,
изменение высоты сказывается на величине сил, но это будет от-
носиться к особым задачам полета. В общем случае уравнения
движения нужно было бы написать в виде трех многочленов, в koi-
торые входят переменные и их первые и вторые производные.
Смысл каждого уравнения заключается в том, что итоговое
ускорение по соответствующей координате равно сумме ускоре-
ний, вызываемых различными факторами; например, для вра-
щательного движения можно написать
„ д<?" н . Эф" „ . Эф* z , Эф" t , Эф" z .
f = -£~У +гт,х + + +
ду дх" дуг ох
, д'?" , Эф" , Эф"
Эср ду дх
107
Частные производные мы рассматриваем как некоторые ко-
эффициенты, причем, как правило, они отрицательны. Тогда, пе-
ренеся все члены в левую часть, получим
?' + М’ + cix" + ^1?' + ?1У' +fix' + £1? + hi v + kix = 0;
а2?" + У’ + с2х" + d2<?' + е2у’ +f2x’ + gw + h2y + k2x = 0;
«з?" + ьзУ" + x" + 4)?' + e3y' +f3x' + g3<p + h3y + ksx = 0.
Теперь займемся упрощениями. Прежде всего исключим
члены, содержащие х и у; затем будем считать, что продольное
ускорение х” не дает моментов и не воздействует на подъемную
силу, а поперечное ускорение у" не воздействует на продольную
силу, хотя это вообще возможно. Далее будем считать, что угло-
вое ускорение и угловая скорость не воздействуют на силы. На-
конец, произведем замену переменных:
?т=^-> сРт=^'» <Рс = ~> Vy- после чего уравнения
примут вид
?'+< <р;++<?т + Л'?с=о;
?:+^2<р+е2'рт+/2'?с=0;
?с + ^3? + *3<?т +/з?с = 0.
Подставляем коэффициенты, с которыми уже имели дело
ранее:
?" + п/ + «2<р + п^т—«2<рт—п2<рс = 0;
+п«?т ~ Мс=0;
?С + + (у — «5 ) ?Т + «6<Рс = °-
Заметим, что эффект запаздывания скоса потока, определяе-
мый производной угла атаки, должен быть включен в коэффи-
циенты п и п7; в коэффициент п7 включен также эффект пере-
грузки.
Решение системы уравнений
Имеем три дифференциальных уравнения — одно второго под-
ряд к а и два уравнения первого порядка. Эти уравнения могут
быть объединены в одно уравнение, порядок которого будет ра-
вен сумме порядков уравнений, т. е. четвертого порядка. Под-
108
ставляя 9 =czexz, c?T = feexz, cpc = cexz, получим характеристические
уравнения:
а(12 + пХ + п2) + Ь (п7Х — ^) —=
— ап2 + b (X + я2) — сп± = О;
апь + b \ + с (Л + лб)= о*
Для исключения величин а, b и с составим определитель
X2 + «X + «2 П,Х-П2 -пз
-«2 X +л2 — = 0.
«Б _g__ „ v Пъ X + л6
Вычеркивая в этом определителе третью строку и третий
столбец, получим случаи уже рассмотренных продольных дви-
жений с постоянной скоростью. Вычеркнув первую строку и перг
вый столбец, получим движение с постоянным углом наклона.
Если же в первом члене первой строки выбросить X2 и /гХ, полу-
чим случай, когда угол атаки простым образом связан со ско>-
ростью движения.
Раскрывая определитель, получим характеристическое урав-
нение четвертой степени
Х4 + ВХ3 + СХа + £)Х + £’ = 0,
где
В = п + + п6, С = п2 + пп2 + nnQ + n2n6 +
+ п4п5 + п2пъ
D = п2п6 + nn2n6—— ««Лб + y + №№ + п|п6,
и соответствующее ему уравнение четвертого порядка
ср/г + В<%'" + Сер" + £2 ср' + £*ср = 0.
В зависимости от значения коэффициентов этого уравнения
движение можно расчленить на два-четыре составных движе-
ния. Каждый действительный корень характеристического урав-
нения даст составляющее движение вида ? = а каждая
пара сопряженных комплексных корней — составляющее движе-
ние вида
? = ?о^ cos pl.
109
Для того чтобы движение было устойчиво, все составляющие
движения должны быть устойчивы, а, значит, все действитель-
ные корни X и действительные части комплексных корней — от-
рицательны.
Для уравнения четвертого порядка в зависимости от значения
коэффициентов можно получить три вида решений. Первое ре-
шение, для случая когда все корни отрицательны, представляет-
ся в виде
? = ?1 + ь + ?з+?4;
?i = ?i,oeXi/; ?2 = ?2,o^v; ?з = ?з,о£Хз/; ?4 = ?4,оех<
Значения и знаки <pi,o» <р2.о, ?з,о и ср4.о будут зависеть от на-
чальных значений ср0, ср0, ср*, ср0", у™. В зависимости от знаков
начальных координат составляющих движений получим четы-
ре варианта движений, представленные на фиг. 55.
Если получаются две пары комплексно сопряженных кор-
ней, решение представится в виде
cos (т]^ + Ti); <f>a = <p2,oev cos (V + Ya),
т. e. получили два периодических затухающих колебания, нави-
тые одно на другое (фиг. 56). Наконец, если два корня действи-
тельны, а два — комплексно сопряженные, получим периодиче-
ское затухающее колебание, навитое на апериодическое движе-
ние (фиг. 57).
Дальнейшая наша задача будет состоять в расчленении дви-
жения. Кроме того, интересно найти признак устойчивости еще
до расчленения движений. Предварительно произведем такое
преобразование. Разделим уравнение на £ и введем единицу
, 1
времени —, тогда получим уравнение
]/£
<pIV + + Cfp" + Dtf' + ср = О,
где
C^Ct^ D^Dt*.
Таким образом уравнение характеризуется тремя безразмер-
ными коэффициентами С± и Di.
Найдем условия устойчивости для составляющих движений,
независимо от того, апериодические они или колебательные. По-
требуем, чтобы характеристическое уравнение имело действи-
тельные отрицательные корни, т. е. Х = — р., где ц>0. При этом
условии характеристическое уравнение, левую часть - которого
обозначим через г, примет вид
Z = + Е = 0.
110
ш
Для нахождения корней уравнения можно построить функцию z
по переменному р, и графически получить действительные корни.
Подобная функция показана на фиг. 58. Можно утверждать, что
необходимое (но не достаточное) условие получения четырех
действительных корней заключается в том, что все коэффициен-
ты перед р и свободный член должны иметь одинаковый знак.
Если это условие не соблюдено, возможное число пересечений в
области положительных р становится меньше четырех.
Однако, несмотря на одинаковые знаки коэффициентов и на
соответствующие выгибы кривой, могут получиться два пересече-
ния (кривая 2) или вовсе не получиться (кривая 5) и тогда два
или четыре корня станут комплексными, указывая на колеба-
тельный характер одного или обоих составляющих движений.
Перейдем к рассмотрению вопроса об устойчивости, исходя
из других соображений. Движение, определяемое уравнением
четвертого порядка, можно представить как простое сложение
двух движений, определяемых уравнениями второго порядка: о =
==c?i+c?2. Если какое-либо составляющее движение апериодич/-
но, его можно в свою очередь разложить на два, но к этому прак-
тически не приходится прибегать.
Напишем уравнения второго порядка для составляющих дви-
жений:
= О,
/?2 + ^'Р2 + А'Р2 = О-
112
Составим для них характеристические уравнения и перемно-
жим их; тогда найдем коэффициенты уравнения четвертого по-
рядка:
ак2 + Ьк + с = 0; fk2 + gk -f- h = 0;
А V + Вк* + Ск2 + Dk + Е= 0;
A = af\ B = ag-\-bf-, C = cf+ah + bg\
D = cg+bh\ E = ch.
Для устойчивости составляющих движений требуется, чтобы
значения a, b, с, f, g и h были положительны; отсюда следует,
что значения А, В, С, D и Е тоже будут положительны как для
апериодического, так и для периодического затухающего* движе-
ний. Решая уравнения, связывающие коэффициенты уравнений
второго порядка и коэффициенты уравнения четвертого* поряд-
ка, по известным A, Bf С, D и Е можно найти характеристики
составляющих движений. Этим вопросом мы займемся несколь-
ко дальше. Рассматривая указанные уравнения, можно сделать
следующие выводы. Если отрицательно а или Д движение будет
апериодически неустойчиво и величина А также станет отрица-
тельной. Если отрицательно с или h, движение тоже будет апе-
риодически неустойчиво и величина Е будет отрицательна. Но
если будет отрицательно b или g, движение окажется неустой-
чивым, хотя значения А, В, С, D и Е могут оставаться положи-
тельными.
Таким образом необходимо найти еще дополнительное усло-
вие устойчивости. Предположим, величина где р, — весьма
малая, но положительная величина, и движение устойчиво*. Под-
ставим у, в уравнения для коэффициентов:
Д=а/; В = а£+н/; С = cf+ ah + y-g;
D = cg + ^h\ E=ch.
Так как члены, содержащие у,, малы, то* в двух уравнениях,
например, для В и D, пренебрежем ими; тогда получим такие
соотношения:
B = ag- D = cg- — = —;
D С
cf——af= A — ; ah = —ch — — E\
J а В c D
подставив их в уравнение для С, найдем искомый критерий устой-
чивости:
с=л4+^4+^=0’ ^>0;
£> L)
С-А—-Е—>0-, R = BCD—AD2 — EB*>Q.
в D
из
Таким образом, кроме положительности А, В, С, D и Е, необг
ходимо, чтобы дискриминант R, называемый обычно дискрими-
нантом Рауса, также был положителен. Для преобразованного
дифференциального уравнения четвертого порядка критерий
устойчивости принимает вид
Разделим дифференциальное уравнение
Л <pIV + Вер'" + С?" + Dy + Еу = О
на О, проинтегрируем его и введем единицу времени ^0 =
= 1/ — ; тогда уравнение примет вид
+ C2<pz + ср + Е2 j ср^ = О.
Условием устойчивости будет
С2 — А2— Е2 0.
Нужно указать, что применительно к самолету выполнение
условия устойчивости не имеет большого практического1 значе-
ния. Величина R=BCD—AD2—ЕВ2 в количественном отношении
ни о чем не говорит; выражение = —В\—D\ , где все
величины безразмерны, позволяет уже судить о некоторых свой-
ствах движения, как будет показано далее. Простая констатация
устойчивости не может удовлетворить при исследовании свойств
самолета. Так, например, даже если один коэффициент уравне-
ния отрицателен, одно из движений будет апериодически неустой-
чиво, но эта неустойчивость может оказаться практически неза-
метной. С другой стороны, если условие устойчивости соблюде-
но, но затухание амплитуд при малом периоде слабое, характе-
ристика самолета должна быть признана неудовлетворительной.
Поэтому необходимо, получив уравнение четвертого порядка,
разложить его на составляющие уравнения второго порядка, по
которым можно составить полное представление о свойствах
движения. Это-разложение будем производить пользуясь пре-
образованным уравнением, в котором за единицу времени была
выбрана величина ,—
/£
?iv + ву" _|_ С1?" + ру + ? = 0
Характеристическое уравнение будет иметь вид
X4 + В^3 + Qk2 + + 1 = 0.
Это уравнение можно рассматривать как произведение двух
уравнений второй степени, каждое из которых соответствует не-
которому дифференциальному уравнению второго порядка.
114
Напишем эти уравнения:
+trfyi=0; ?2+°2?2+=0;
факторы затухания и периода в этих уравнениях
р ____________ а1 . р _ а2 . / 1 . л
Г1~ Г2~ "У” , Ч —“Г" , Г2= —
И ^2 &2
Отнесем оба уравнения к единице времени tQ:
(АуТ1==о;
*1 \ ч /
?2 + ^«‘7"?2+ (‘7") ?2 = о.
h \ *1 /
Напишем соответствующие им характеристические урав-
нения
X2 + FiAx + pLy = 0; k2 + F2-^k + (Ay = o
и перемножим их:
Чтобы последний член был равен единице, нужно положить
— = k, — = — ; тогда уравнение примет вид
<i *г k
х4+(т- + F^\ хз + №++ (4 + F*kV+1=°-
\ Л / \ kz / \ £ /
Отсюда получаем
B1 = F1k + -^- C^^ + ^ + F^- D^-^ + F.k.
k k2 k
Пользуясь этими выражениями для известных Ви и Dlf
можем найти факторы затухания F\ и Л2 и характеристики
частот составляющих движений bx = kjt^ b2=\{ktQ.
Если нам заданы Л, F2 и kf найти Bi, Ci и D± очень просто. Ре-
шение обратной задачи представляет большие неудобства. Мож-
но предложить различные способы решения задачи. Так, можно
заготовить таблицы значений Fi, F2 и k для различных Bi, Ci и D±
и, пользуясь ими, прибегать к интерполяции. Можно предложить
также разнообразные виды графических решении. Мы опишем
графическое решение, при применении которого серия сложных
кривых может быть заготовлена заранее, а каждое частное реше-
на
ние потребует нанесения только одной прямой по двум точкам,
причем рассчитывать нужно положение только для одной точки.
Разложим движение на два составляющих; условимся первым
считать движение с большей характеристикой частоты, вторым—
с меньшей. Значение k будем принимать всегда большим едини-
цы. Введем такие обозначения: если
В.>Ои
то
Bi ’ 1 В,
если Вх < Dit примем £=^-<1,
= Н2 = ^-
1 Dj 2 Dj
Условие £<1 принято потому, что оно делает более удоб-
ным графическое решение. Произведем такие преобразования:
^1±£L = ± FXF2 + (Г? + Л), = aF^ + (Fl + Fl),
где
а=&+—',
исключим отсюда и определим
п Bl+Dl ( 4 \ „
B1D1------1 L = Ь---------1 .
а \ а /
аВ^ - Bl -Dl
2 — - ~
a2 — 4
Мы имеем также
FrF4 = Сг — а.
Вводя принятые обозначения, получим два уравнения:
Н^1г = а- ~/г ~Х НгН2-С'~а
а2-4 ’ В?
Первое уравнение дает сравнительно сложную зависимость //1//2
от а, но имеет только один параметр L. Пользуясь этим уравне-
нием, строим серию кривых с параметром L. Для удобства поль-
зования этими кривыми графики следует построить для различ-
ных диапазонов значений НХН2 и а в разных масштабах, как
показано на фиг. 59—62. Второе уравнение дает прямую, прохо-
дящую через точку a = Ci; вторая точка должна быть подсчитана
по уравнению, задаваясь произвольным Н^Н2 или а.
Нанося прямую на график, по пересечению ее с кривой, соот-
ветствующей определенному L, получим HJh и а (фиг. 59), при
116
х
S. \
1
1 1
1 1
1 1
1 > А 1 ! IZ ? 8
РТ !
и. *1
р
Ь1
?\ 9 1. 2Х f 4 а
1
1 *1
Фиг. 59.
1П
118
этом, вообще говоря, приходится прибегать к интерполяции по
значению L. Для получения k при известном а удобно пользо-
ваться специальным графиком.
Имея Н±Н2 и по уравнениям
kF1+-^-Fa = Blf
k
J-F. + kF^D,
k
легко найти F± и F%.
В некоторых случаях кривая и прямая имеют три точки пе-
ресечения (пунктирная прямая на фиг. 59). Это означает, что оба
составляющих движения апериодические.
Как уже было указано, апериодическое движение может быть
разложено на два более простых, и, следовательно, мы можем
разложить движение на четыре составляющих. Из четырех дви-
жений можно составить три пары комбинаций по два. Это и
дает три точки пересечения. Можно выбрать любое из этих реше-
ний, они вполне равноценны. Заметим также, что' три решения
возможны при достаточно больших значениях а.
Описанный выше способ разложения движений достаточно
прост, если заготовлены графики //1Z/2 по а. В некоторых слу-
чаях разложение может быть выполнено упрощенно. Таких слу-
чаев несколько.
Первый случай — и Сх относительно' велики, a D± мало.
Рассматривая уравнения
kF1 + — F2 = ; — F± + kF 2 = Dlf
приходим к выводу, что причиной малости может быть
77 F? г? В]
только малость г2; тогда — очень мало и г1 = —- ; произве-
k k
дение FtFa будет мало и отсюда получим
/С, *
Это и есть известное разложение Берстоу; подставив зна-
чения Сг и Dif получим
Ус . p__D____bVe
У~Ё ' 1 VC ’ 2 УСЕ J. •
Вполне аналогичен случай, когда
л о. Тогда
^ = С,; Л
Ct и велики, а ма-
/с' сг
р ___ В]
1 2 — т Г г
119
Найдем признаки, указывающие на возможность прибли-
женного разложения движения. Условие а — Сх справедливо
только при малом значении . Допустим, что величиной
Q
< 0,02 можно пренебречь.
Q
Тогда
BiQDt -B*-D* = R
Ci Cf-4Ci C?-4C1 ’ ’
0 < R < C?-4C!.
Теперь можем найти Ft и F2:
Почти всегда можно принять 1-----у = 1; если же и -
Cj BjCj
мало, например, менее 0,02, то
F __
Тогда для Fa получим
р __ D1 ___Bi
' cf
При B1<D1 и —^—<0,02
£>iCi
р ___ B>i . р _ Bi ____D,
* ГсГ’ Г1 Vc[ *•
Возможен случай, когда значения Bt и Dt близки друг
к другу и малы, а велико; если будет удовлетворено усло-
вие 0 <5 R < Cf — 4С, и —Рг -- < 0,02 или Вх— < 0,02, тогда
1 1 BA AG
упрощенным разложением будет
Л = или F2 = -^ ; k^Ct.
у G1 г
В случае продольных движений обычно можно воспользо-
ваться разложением, вытекающим из малости £>i, и тогда полу-
чим уравнения движения в виде
?; + £?! += 0; ?'2 + (-^ — -f-?2 = 0.
\ с с» / с.
120
Сравним результаты этого упрощенного разложения с полу>
ченными ранее малыми колебаниями с постоянной скоростью и
большими колебаниями, выведенными из условия, что величина
угла атаки связана только со скоростью. Начнем с малых коле-
баний; развернем коэффициенты:
В = л + л2 + п6==п!71 + 7]+^-'); г; = 2;
\ «А /
— ^0,05; В=п + п2 = пй;
С = ng + пп2 4- ппе 4- п2л6 4- -у—п^ъ = ng 4-
+ «2h + r2(1+O + 2al!— Т"] ~«о + ЛЛ2 = /га-
L «А *1 J
Отсюда видно, что, если пренебречь малыми членами, мы
получим полное совпадение со случаем колебаний при постоян-
ной скорости.
Теперь перейдем к большим колебаниям. По разложению
характеристика частоты
£ _ g (”2^3-1-яоп4) .
С V (пд+пгч+п2п7)
она же по приближенному выводу
, g , . х g («2«| + я0Л4)
п? = — (п. 4- an,) =--------з-----------
К V («о+ ПЛ2+П2Л7)
выражения оказались тождественными. Однако коэффициенты
1 / г» ВЕ\
затухания несколько различны: —ID------;
пь = п6 4- ап2 = (D — пп4 .
Как уже указывалось, затухание больших колебаний в силь-
ной степени зависит от побочных факторов. Для получения
эффективного затухания больших колебаний необходимы специ-
альные меры — лучше всего использовать автопилот, реагирую-
щий на продольный наклон.
В заключение остановимся на определении исходных условий
для составляющих движений. Как уже было получено, движение,
определяемое уравнением четвертого порядка, может быть рас-
членено на два движения, каждое из которых определяется урав-
нением второго порядка. Составляющие движения носят колеба-
тельный или апериодический характер и могут быть легко по-
строены с помощью диаграмм колебаний. Однако предваритель-
121
но нужно найти начальную фазу и начальную амплитуду для каж-
дого движения.
Прежде всего нужно знать начальные значения для элемен-
тов движения. Пусть известны начальный угол наклона, началь-
ная угловая скорость, начальное угловое ускорение, начальные
значения составляющих скорости центра тяжести и его ускоре-
ния. Тогда находим для соответствующих условий установившее-
ся движение. По разности этих значений найдем начальные усло-
вия по отношению к конечным. Расчет этих условий будет зави-
сеть от характера рассматриваемой задачи и будет производиться
по формулам
?' = — «О? — М + «оТт + П1Чс; = п2? — «2?т + «4?с;
/ g \ V V х
+ —адс; ?т=у; =
Дифференцируя выражение для ср", получим ср"', подставив
значения <р' и ср^. Теперь будем иметь исходные значения
для ср, ср', ср* и ср'". При определении <р" и ср'" использованы
начальные значения срт, срс, ср^ и ср^.
Угловое движение было расчленено на составляющие:
^ + М; + ^1 = 0; (а)
Фг+М2+ ^2 = 0; (Ь)
? = Ф1 + Фа; = +
Дифференцируя их, получим
К'+м;+эд=°; (с)
К'+М2+^’К=о; (d)
?" = ф; + Ф2';
ср"'=4,;" + ф"'.
Теперь мы имеем восемь уравнений с восемью неизве-
стными; найти нужно значения фп ф', ф2 и ф2. Исключим сна-
чала ф'" и ф'", сложив уравнения (с) и (d):
ср'" + ахф' + а2ф' + ед; + Ь^2 = 0.
Подставляя сюда ф', ф' и ф2, получим
- al) ср' + ед2ср = (ц2 - bl - al + bl) ф; +
-НМ?—МРФь (е)
122
Затем складываем уравнения (а) и (Ь):
?" + + «2^2 Н“ + ^2 “
подставляя
Ф2=<?'—ф; и Ф2=?—фп
придем к уравнению
?" + + - а2) ф; - (bl - 6|) фр (f)
Остались два уравнения с неизвестными фТ и фг, дальней-
шее решение их ясно. Определение ф2 и составляющих движений
центра тяжести производится вполне аналогично.
БОКОВЫЕ ДВИЖЕНИЯ САМОЛЕТА
Силы и моменты при боковом движении самолета
Боковые или несимметричные движения самолета сопровож-
даются вращениями самолета вокруг осей х и у и смещениями
центра тяжести вдоль оси г. Эти оси можно рассматривать как
поточные или скоростные или как связанные с самолетом. Будем
пользоваться разными осями в зависимости от типа решаемой
задачи, но в большинстве случаев малость отклонения самолета
от исходного прямолинейного движения позволит нам не делать
различия между системами осей.
Как и при рассмотрении продольного движения, будем поль-
зоваться непосредственно силами, моментами и их градиентами
по соответствующим переменным, а не коэффициентами сил и
моментов, как это часто делается.
Для понимания свойств самолета в боковом движении нуж-
но ясно представлять себе характер действия сил и моментов.
С этой целью придадим им возможную наглядность. Силы и
моменты, которые нас интересуют при изучении бокового движе-
ния, слагаются из действия подъемных сил отдельных элемен-
тов самолета.
Пусть мы имеем некоторый крылообразный элемент самоле-
та. При наличии угла атаки он обладает некоторой подъемной си-
лой, пропорциональной углу а (фиг. 63). Образование подъемной
силы можно себе представить как результат сложения двух сил;
одна из них направлена вперед и связана с телом, а вторая ори-
ентирована по набегающему потоку. Такая схема в сущности
изображает закон Эйлера, по которому сила, действующая на
струю, равна равнодействующей двух сил, одна из которых со-
ответствует секундному количеству движения подходящего по-
тока, а другая —секундному количеству движения уходящего
отклоненного потока, взятому с обратным знаком.
Таким образом возникновение силы в фокусе и ее рост в за-
висимости от увеличения угла атаки можно представить просто
123
как эффект поворота одной из двух равных сил, приложенных
в фокусе. Сила сопротивления или тангенциальная составляющая
могут быть получены как проекции полного приращения аэро-
динамической силы на соответствующую ось. Однако, если на-
чальное состояние соответствует отсутствию поперечных сил, что
типично для бокового движения, приращения силы сопротивления
или тангенциальной силы будут
у зависеть от квадрата изменения
угла и потому будут малы. Что
касается сил сопротивления
—Ч---—или тангенциальных сил, не
V связанных с образованием по-
перечных сил, то природа их
возникновения связана с поте-
Фиг. 63. рей количества движения ухо-
дящего* потока.
Если нас интересует нормальная сила в связанных осях, то-
нужно оставить только силу Q, ориентированную по потоку, и
спроектировать ее на ось у; величина этой силы будет
K=^a=Qa;
да Х ’ да
Подобным образом можно рассматривать боковые силы, дей-
ствующие на фюзеляж 2ф и вертикальное оперение Z& 0, прилог
Фиг. 64.
жив две исходные силы Q# и QB. о в фокусах фюзеляжа и опе-
рения (фиг. 64); поворачивая эти силы по направлению потока
при скольжении, получим моменты, равные моментам боковых
сил:
ф ^ф-^ф = <?ф?Хф; ТИу В.О = ZB. qXв. о~ Qb. оР«^В о*
124
Эффект отклонения руля направления можно представить
как поворот силы, связанной с оперением и направленной
dcv dcv
вперед, на угол nHSH, где пн=тг , • Исходными силами для
00 да
фюзеляжа и оперения являются:
_^Ф_, G ь _( дс2ф дсу\5Ф
Уф- -ЛФ а > д? да) s >
~ ^в.о . ° . / ^сгв. о dc\Sa o 9в.о
Ув. о = ~^в.о ; ka.0 — I — • •
ор а \ д£ да) S q
При наличии угла скольжения р получим градиенты мо-
ментов:
Qb. о-^в. о»
Qb. о_Ув. о»
дМу ф дМу в. 0
йА* = _<зЛ1 2^,
^ф>ф’ 00
При наличии угловой скорости вращения вокруг оси у силу
О) X
QB.o нужно дополнительно повернуть на угол т. е-
по направлению местного потока с учетом вра-
получим производные моментов по угловой ско-
в. о
направить ее
щения; тогда
роста оу.
<WyB.o
до>
у
— О — •
^В-0 у ’
дМ
ЛВ.О ха
в. о
Момент фюзеляжа от вращения нельзя получить простым по-
воротом силы по направлению местного потока, так как при вра-
щении разные части фюзеляжа будут иметь разные составляюг
щие скорости по оси z. Обычно моментом фюзеляжа от вращения
пренебрегают. С помощью специального испытания модели фю-
зеляжа в аэродинамической трубе можно получить градиент его
момента по Нужно* заметить, что Хф обычно отрицательно.
Более сложную схему мы получим для крыла. Во1-первых,
при скольжении происходит изменение нормальных и тангенци-
альных составляющих сил, действующих на каждое полукрыло.
Эффект скольжения довольно сложен. На нем сказывается по-
перечный угол крыльев, который при скольжении приводит к по-
явлению разности углов атаки; большое значение имеет влияние
фюзеляжа и моторных гондол, подвесных баков и других над|-
строек. На поперечный момент крыла, вызываемый скольжением,
большое влияние оказывает аэродинамический эффект скользя-
щего потока; он особенно велик на больших углах атаки и при
125
стреловидности. Влияние скользящего потока, фюзеляжа и дру-
гих частей будем условно приводить к некоторому эквивалент-
ному поперечному углу крыльев фк.э, т. е. к фиктивному измене»-
нию углов атаки при скольжении. Тогда при скольжении получим
изменения подъемных сил каждого полукрыла
ду=^Фк.эр.
2а
Силы ДУ приложим в некоторых точках, на расстоянии zY от
оси фюзеляжа и назовем эти
Фиг. 65.
точки боковыми фокусами крыла
(фиг. 65). Сложив силы ДУ,
получим равнодействующую ZK
на расстоянии ук= —над кор-
Фк
нем крыла. В этой точке прило-
жим силу QK= — фк фк. э.; тогда
а
поворот ее под действием сколь-
жения будет давать нужную бо-
ковую силу и момент. При на-
личии стреловидности это ска-
жется на значении фк.э, кото-
рое будет сильно меняться в за-
висимости от су. При стреловид-
ных крыльях угол фк обычно
делают отрицательным; однако,
если фк.э положительно, по-
строение у& нужно производить,
как если бы угол фк был поло-
жителен, т. е. откладывая у&
вверх; ук откладывается вниз
только при отрицательном фюэ,
что почти не встречается на
практике. Можно было бы
предложить схему сил, которая
отражает свойства стреловид-
ных крыДьев, но мы не будем
прибегать к сложным схемам.
Перейдем к моментам крыла, вызванным вращением. Момент
вокруг оси х, вызванный вращением вокруг этой оси, можно вы-
разить в виде
/И = — qb —— dz = q ~ —bz2dz=----- — z2.
J да4 V 7 V J да V а 2
Точка приложения равнодействующей сил, вызванных вра-
щением, для каждого полукрыла находится на расстоянии z2 от
плоскости симметрии; эту точку можно назвать фокусом при вра-
126
щении. Следует заметить, что z2>Zi *. Пусть в фокусах вращения
G
крыла приложены силы —, которые располагаются по относи-
2а
тельному потоку в плоскости, параллельной плоскости ху. При
вращении эти силы поворачиваются на угол = в разные
стороны соответственно относительному потоку и создают мо-
мент, тормозящий вращение вокруг оси х (фиг. 66).
Вращение вокруг оси х вызывает также момент вокруг оси у.
Его выражение будет получено, если подъемные силы в отдель-
ных сечениях повернуть в соответствии с местным изменением
угла атаки, вызванным вращением вокруг оси х. Тогда
ДР^+ДР,)^;
где Рх и Ру — погонные нагрузки на крыло по соответствующим
осям, и
L L
2 2
= j bJ\zdz = [ Pyz*dz +
2 L h
2 2
I
2
CD 2 C CD G
— Pvz^dz = —Yz^2 — ^
V2a J y V 2 2
__Z_
2
<0^2
V ’
* Расстояние Zi близко к расстоянию до центра тяжести площади полу-
крыла; расстояние z2 близко к радиусу инерции площади крыла при вра-
щении вокруг оси х.
127
Схема получения этого момента достаточно проста; для этого
нужно в фокусах вращения приложить подъемные силы полу-
крыльев, связав их под прямым углом с силами действую-
щими назад (фиг. 66); тогда при вращении вокруг оси х эти
силы будут поворачиваться вместе с силами— .
Необходимо указать, что нужный момент вокруг осиг/отвра-
G
щения вокруг оси х получается, если взять проекции сил -—,при-
2а
ложенных к крыльям на расстояниях Z2, которые давали момент
вокруг оси х. Если есть начальный угол атаки а и затем от вра-
щения вокруг оси х происходит дополнительное изменение угла
атаки Да = ф , то изменение составляющих сил вдоль оси х
самолета:
G
ДХ1,2 = — [cos (а + Да) —cos а].
2а
Ввиду малости а, Да и а + Да
COS (а 4: Да) — 1-- (а± Да)2; cosa» 1-- а2;
ДА’1.2= Ч-—Да=Ч-—
~ 2 — 2 V
Тогда производная момента по угловой скорости
дМ г 4
э&х v
т . G
Таким образом, если принимать во внимание наклон сил —
к оси х, никаких дополнительных сил вводить не нужно. Если
принять более наглядную схему, показанную на фиг. 66, учить;-
G
вать проекции сил -на ось х не нужно.
2a
При вращении вокруг оси у мы уже получили тормозящий
момент от вертикального оперения. Это вращение даст момент
крыла вокруг оси х в результате изменения подъемных сил из-за
разности скоростей в различных сечениях крыла. Приращение
скорости ДУ в некотором сечении на расстоянии z будет равно
Д V—^yZ. Тогда момент Мх можно выразить следующим образом:
i
Я,= Г‘£1»; — = 2—;
1 J аи dv v
“2
Y х2 _
Мх= — 2 — V2~ — ’ x2 = z2 V 2.
128
Момент Мх можно1 представить как результат смещения подъ>-
емной силы в сторону на величину —— . Это смещение можно
получить, если в точке А на расстоянии х2 расположить стрелку,
которая ориентирована по относительному потоку, полученному
сложением скорости полета и окружной
скорости в точке Л;
тогда пересечение направления стрелки с осью z даст величину
смещения подъемной силы (фиг. 67).
Смещение подъемной силы может быть получено также с
помощью геометрической схемы, показанной на фиг. 68. Это сле-
дует из условия:
а у 2’
V
Ъ rz *
129
Балансировка в несимметричном полете
Перед тем как перейти к сложным случаям бокового движе-
ния, начнем с более простых. Прежде всего рассмотрим равно-
весие сил и моментов в прямолинейном полете. В случае полной
симметрии обтекания балансировка получается просто в силу
симметрии. Однако полная симметрия встречается редко. Основ'-
:юй причиной несимметрии является одностороннее вращение
винтов.
Эта простая причина приводит к довольно сложной картине
несимметричной нагрузки самолета. Прежде всего имеет места
реактивный момент вокруг оси х, величина которого определяется
достаточно просто по известным мощности и числу оборотов вин-
та. Уравновешивание реактивного момента может быть достиг-
нуто различными средствами, но при этом обычно* появляется
момент вокруг оси у, который также нужно уравновесить.
Воздушный поток набегает на ось винта с некоторым углом
атаки. Это приводит к тому, что сила тяги лопасти меняется в за-
висимости от ее положения и в результате общая сила тяги винта
оказывается смещенной в сторону лопастей, движущихся вниз.
Смещение тяги вызывает момент вокруг оси у, который может
быть вычислен, причем в расчете необходимо принимать во вни-
мание нестационарность течения, поскольку в процессе вращения
угол атаки лопасти быстро меняется.
Струя за винтом закручена, а в результате прохождения око-
ло крыла и фюзеляжа она приобретает еще боковое отклонение.
Давление такой струи на вертикальное оперение и стенки фюзе>-
ляжа приводит к образованию боковой силы и момента вокруг
оси у. Моменты вокруг осей х и у могут быть уравновешены
элеронами и рулем направления с последующим снятием шар-
нирных моментов триммерами или другими устройствами. Боко)-
вая сила, будучи неуравновещена, вызвала бы криволинейный
полет. Уравновесить ее можно проекцией силы тяжести, для чего
необходим некоторый крен, или приданием самолету некоторого
скольжения, что дополнительно потребует уравновешивания мо-
ментов от скольжения. Отсюда следует, что при одностороннем
вращении винтов самолет будет лететь по прямой с некоторым
креном или скольжением. Однако практически эти явления почти
незаметны.
Рассмотрим прямолинейный полет со скольжением. Если на-
правление воздушного потока составляет некоторый угол 3 с
плоскостью симметрии, на самолет начинают действовать момен-
ты вокруг осей х и у и боковая сила. Моменты при отклонении
элеронов и руля направления можно представить как произведе-
ния усилий, прилагаемых к ручке управления и педалям, и не-
которых плеч рычагов, подобно тому, как мы это делали для руля
высоты:
Д4 =РэАэ; =
А 3 9 9' У П НН
130
Отсюда легко найти усилия, которые нужно приложить к
органам управления для удержания самолета в состоянии сколь-
жения. Для сохранения прямолинейности полета боковую си-
лу Z нужно уравновесить проекцией силы тяжести, или, вернее,
проекцией подъемной силы при угле крена у:
Z=y tg y = G sin у.
Если плечо руля направления относительно мало, нужно при-
нимать во внимание боковую силу руля направления. В некото-
рых случаях принимают во внимание и момент от тангенциальных
сил, вызванных элеронами. Тогда условия равновесия будут вы-
ражены тремя уравнениями, совместное решение которых позво-
лит решить задачу.
Аналогично рассматривается случай полета с остановленным
боковым двигателем. Из рассмотренной схемы нужно удалить
момент от тяги двигателя, поскольку он остановлен, и добавить
момент от сопротивления неработающей двигательной устаной-
ки. В случае простого скольжения можно построить зависимость
угла крена, усилий и отклонений органов управления от угла
скольжения (фиг. 69). При наличии начального момента вокруг
оси у и отсутствии скольжения уже потребуется отклонение руля
направления. Нагрузка на вертикальное оперение дает боковую
силу, которую нужно уравновесить приданием самолету крена,
и момент вокруг оси х, который нужно уравновешивать элерона-
ми. Следовательно, и при отсутствии скольжения потребуется
отклонение рулей и крен. Если добавить скольжение, отклонение
рулей и крен изменятся, как и в случае простого скольжения
(фиг. 70). Из графиков на фиг. 70 видны условия полета с оста-
новленным боковым двигателем. Можно лететь без скольжения,
но с креном; можно лететь без крена, но со скольжением на
остановленный двигатель и с очень сильным отклонением руля
направления; можно лететь с неотклоненным рулем направления,
131
но тогда будет скольжение на работающий двигатель и значи-
тельный угол крена.
В качестве примера боковой балансировки в прямолинейном
полете рассмотрим еще полет в несимметричном восходящем по-
токе. При полете параллельно облачному фронту или горному
склону самолет длительное время может находиться в восходя-
щем потоке с переменной по размаху скоростью. Пусть правое
крыло находится в более сильном восходящем потоке, тогда дей-
ствие этого потока сходно с эффектом, получаемым при вращении
самолета вокруг оси х вправо. Поворачивая соответствующим
образом силы, приложенные в фокусе вращения, получим момент
вокруг оси х, действующий влево, и момент вокруг оси у, тоже
заворачивающий влево. Если момент Мх уравновесить отклоне-
нием элеронов, то момент вокруг оси у останется, и его нужно
будет уравновешивать рулем направления. Расчет заворачиваю-
щего момента очень прост. Для этого нужно подъемные силы,
приложенные в фокусе вращения, повернуть в разные стороны
на углы расстояние г2 равно примерно радиусу инерции
площади крыла относительно оси х. Чем больше скорость полета,
тем слабее заворачивающий момент.
Балансировку в криволинейном полете рассмотрим для уста-
новившегося виража и пологой спирали. Угловую скорость во-
круг оси виража раскладываем на угловые скорости вокруг
осей у и Z. Вопрос о продольной балансировке мы уже рассматри-
вали. Вращение вокруг оси у вызывает момент вокруг оси у, пре-
пятствующий вращению, и момент вокруг оси х, стремящийся
усилить крен. Очевидно, что для равновесия потребуется откло-,
нить руль направления в сторону виража, а элероны*—против
виража. В случае виража со скольжением к полученным откло-
нениям рулей нужно добавить отклонения по условиям скольже-
ния. Например, при скольжении на опущенное крыло элероны
должны быть отклонены дополнительно в сторону скольжения,
а руль направления — против скольжения, в результате чего он
может оказаться отклоненным против виража. Кроме того, при
скольжении угол крена должен быть изменен для компенсации
действия боковой силы. При скольжении на опущенное крыло бо-
ковая сила будет действовать против виража, и крен нужно уве-
личить. Расчет равновесия при вираже не представляет принци-
пиальных затруднений, и мы его не приводим. При вираже
вращение самолета происходит относительно оси, не совпадаюг
щей с главными осями самолета. По этой причине имеет место
инерционный момент, стремящийся выровнять крен. Однако этот
момент так мал, что его не принимают во внимание.
При выполнении пологой спирали к движению, которое было
при вираже, добавляется движение опускания. Это приводит к
изменению распределения углов атаки по размаху крыла, как
при вращении вокруг оси х. Угловую скорость получим, если
132
угловую скорость виража <в спроектируем на направление век-
тора скорости центра тяжести:
&>х= — cd sin
Изменение распределения углов атаки поведет к образованию
момента, который будет стремиться выровнять крен; при некото-
рых условиях он превысит накреняющий момент, вызываемый
различием в скоростях разных точек по размаху крыла. Угловая
скорость вызовет также момент вокруг оси у, действующий
против виража.
Пусть угол крена относительно невелик и наклон спирали 0
также невелик. Найдем, при каком условии моменты от угловых
скоростей фу и окажутся уравновешенными:
Л/Г G zi z3)
^=TV“'-2CV^=0’
sin 0- 0
2 cos у 2 cos y
a —-------
2a>
У
Отсюда следует, что если наклон спирали 0 больше угла ата-
ки, умноженного на удвоенный косинус угла крена, у самолета
появится стремление к выравниванию крена. Это возможно при
достаточно малом су. При восходящей спирали эффект будет
обратным — у самолета усилится тенденция к увеличению угла
крена.
Поперечная балансировка в случае необычного управления
Кроме обычной двойной системы бокового управления, со-
стоящей из руля направления и элеронов, встречаются системы
только с одним из этих органов, или системы, в которых оба
органа связаны кинематически.
Наиболее значительный момент от бокового управления не-
обходим для вращения вокруг оси х, т. е. накренения или вырав-
нивания крена. Если элероны отсутствуют, для движения крена
используют скольжение и различие в скоростях крыльев. Такое
различие в скоростях достаточно эффективно только при сочета-
нии большого размаха крыльев с малой скоростью полета, как,
например, у; планеров. Для усиления эффекта скольжения
крыльям нужно придавать большой поперечный угол, а это при-
водит к неприятному поведению самолета при боковых порывах
ветра.
Если самолет управляется одними элеронами, он должен
иметь мощные кили или специальные аэродинамические тормоза
на концах крыльев для уравновешивания момента вокруг оси у,
вызываемого вращением вокруг оси х.
Птицы не имеют вертикального оперения. В машущем полете
момент вокруг оси у легко создается более энергичным взмахом
одного из крыльев. При парении птицы испытывают трудности в
управлении вокруг оси у; они обычно распускают хвост, меняют
133
положение центра тяжести так, чтобы хвост оказался нагружен-
ным и затем поворачивают хвост около оси х. Используют они,
невидимому, и сопротивление концов крыльев.
Нужно заметить, что у велосипеда руль выполняет две функ-
ции — управления поворотом и управления креном. Это объеди-
нение функций усложняет действие рулем и известным образом
ограничивает управляемость.
Наиболее целесообразной системой управления одним орга-
ном является система элеронов, связанных с рулем направления.
Обычно эта связь выполняется кинематически и приводится в
действие ручкой или штурвалом. Подобная система была испы-
тана в 1935 г. на самолете По-2; применяется она и теперь на
некоторых спортивных самолетах.
Связь органов управления выполняется так, что элероны и
руль направления одновременно отклоняются в одну сторону.
Момент вокруг оси у, вызываемый вращением вокруг оси х,
равен моменту элеронов, умноженному на угол атаки. Исходя из
этого можно подобрать уравновешивающий момент руля направ-
ления. Однако эта связь будет соответствовать только одному
режиму полета, а на других режимах действие элеронами будет
сопровождаться скольжением в ту или другую стороны. При тат-
кой системе управления полет с умышленным скольжением ста-
нет невозможен.
Моментные характеристики подобных самолетов следует сни-
мать после тщательного исследования условий балансировки на
разных режимах. В частности, желательно, чтобы при устано-
вившемся вираже руль направления и элероны оставались от-
клоненными в сторону виража, а при нейтральном положении
управления — самолет самостоятельно приходил в прямолиней-
ный полет без крена.
Изолированное движение крена
При отклонении элеронов движение самолета, вообще говоря,
будет довольно сложным. Под действием момента Мх начнется
вращение вокруг оси х; от этого вращения возникнет момент
вокруг оси у; сами элероны также дают некоторый момент вокруг
оси у\ наконец под влиянием крена траектория станет криво-
линейной, причем плоскость кривизны траектории также будет
меняться.
Изолированное движение крена можно представить себе при
известных ограничениях: во-первых, угол крена не должен пре-
восходить некоторого значения; во-вторых, примем, что угол ата!-
ки мал и потому момент Му от вращения вокруг оси х мал. Если
рассматривать малые промежутки времени, то нарушение прямо-
линейности траектории будет незначительным. Несмотря на из-
вестную условность, рассмотрение изолированного движения кро-
на представляет практический интерес и позволит выяснить не-
которые особенности движения крена.
134
Пусть на самолет стал действовать момент Мэ вокруг оси х.
Вначале момент даст угловое ускорение у"о = -^~; по мере раз-
вития вращения будет расти противодействующий аэродинамиче-
ский момент и в конце концов установится равномерная ско-
рость вращения (оа. Действующий момент Мэ можно выразить
через угол отклонения элеронов $э или через усилие, прилагае-
мое к ручке управления: M3 — P3L3. Заметим, что при отсутствии
аэродинамической компенсации элеронов Ьэ составляет около
100 м\ при наличии компенсации или бустерного управления L3
может быть сделано весьма значительным: 500—1000 м и более.
Эффективность элеронов удобно определять по формуле
(DVZ (Ьк гч
—— = —. Это отношение для различных самолетов меняется
21/5^ дВэ
в пределах ОД —0,4. Тогда по моменту торможения вращения
мы можем найти начальный момент элеронов. В самом деле,
. дМ* ~
когда установится вращение, Мэ-]---<&а = 0; в этом случае
действующий момент элеронов уравновешен тормозящим мо-
ментом крыла и, следовательно, начальный момент равен тор-
мозящему при установившемся вращении:
G 9 дак 21/
Мэ —---ЙО) ; 0) =----- -0 ;
э aV 2 а а д&э I 9
2G zl дак
М =------- --- 8э; M3 = P3L3.
9 / Э 3d
а I (?оэ
Таким образом мы имеем два выражения для начального мо-
мента — через угол отклонения элеронов и через усилие в управ-
лении. Соответственно будем иметь два выражения для устано-
вившейся скорости вращения:
2V дак .
I дЪ3
Перейдем к рассмотрению вопроса о характере вращения во-
круг оси х при действии элеронами как в сторону вращения, так
и против нее. Уравнение вращения напишется в виде
н Мэ , 1 дМх , 9
1 =-/ + ——=То-«Х
*Х &ШХ
аУЬэ Рэ
О) —------2. _Л
?2 G
где
г G о 1 g / z2 \2
/,= — г2- п==----------- = — — •
g 1Х aV \ГХ1
Отношение радиуса инерции площади крыла к радиусу
инерции массовому — обычно несколько больше единицы.
135
Уравнение движения ч"=ч"о—пх^ довольно простое и инте-
грирование его не представляет затруднений. Постараемся при-
дать решению более наглядную форму. Начнем с зависимости
угловой скорости крена от времени (фиг. 71). Если элероны от-
клонены в сторону вращения, темп роста угловой скорости за-
медляется, и установившееся вращение достигается через беско-
нечно большое время. Если при некоторой угловой скорости эле-
роны поставлены нейтрально, торможение также теоретически
займет бесконечно большое время. Для получения конечного
1—элероны отклонены в сторону враще-
ния; 2— элероны нейтральны; 3—элероны
отклонены против вращения.
времени торможения требуется обратное отклонение элеронов с
последующей установкой их в нейтральное положение в момент
остановки вращения.
Для исследования зависимости скорости накренения от угла
крена уравнение вращения представим в виде
„ ,dl' . , dY lo
7=7-"^
Та
7о
— 1):
По этому уравнению строим график, показанный на фиг. 72.
Из него видно, что, если по достижении некоторой угловой ско<-
рости элероны поставить нейтрально, путь торможения будет
вполне определенным и его можно вычислить:
136
где 7' —угловая скорость в момент установки элеронов в ней-
тральное положение. Путь разгона 7р также может быть
найден:
/ь Л
-- ^Х I--1 I 9
<*7 \7' /
вводим переменные
z=l—Л-; dz =-------X~rd\\
la la
тогда
nx \nx /
интегрируем:
где величина А есть функция отношения угловых скоростей
71
— в момент начала торможения;
— = y0 является некоторой безразмерной величиной, харак-
пх
теризующей режим вращения, и равна пути торможения, если
начальная угловая скорость равна установившейся —у'а.
В приводимой ниже таблице даны значения А в зависи-
мости от -Ч-.
fa
7' Ь 0,10 0,20 0,40 0,60 0,80 0,90 0,95 0,99 0,999
А 0,0058 0,022 0,11 0,314 0,8 1,4 2,04 3,61 5,9
7т 7р 17,2 9,1 3,6 1,9 1,0 0,64 0,46 0,27 0.17
Путь торможения при нейтральных элеронах выражается
формулой
7' 7т 71' 7р .
тт= — ; — = —; — = А.
пх 70 fa 7о
137
Тогда отношение пути торможения к пути разгона
Тр
значения — также приведены в таблице. Соотношение между
7р
путями разгона и торможения иллюстрируется графиком на
фиг. 73. Если элероны были резко отклонены, а затем быстро
поставлены нейтрально, путь торможения больше пути разгона
и это неприятно для пилотирования. При слабом действии эле-
ронами быстро установится почти равномерное вращение, хотя и
с малой угловой скоростью. Путь торможения будет мал, но
общее время накренения значительно.
На фиг. 74 дана зависимость угловой скорости от угла
крена при одинаковых значениях угла крена ?а = тр + тт и раз-
личных начальных моментах УИЭ. По оси абсцисс отложено
7 7' , Идг
— , по оси ординат — , где ?.=—. На кривых указаны зна-
la lb 1а
чения Л- для момента установки элеронов в нейтральное по-
1а
г г f
ложение. Значения /Иэ пропорциональны значениям =
lb 71 1ь
эти значения помечены на кривых разгона
1 Ь =
Л ^л;7р 1хПх1? ’
Как видно из диаграммы на фиг. 74, увеличение среднего зна-
чения угловой скорости сопряжено со значительным ростом на-
138
чального момента. Диаграмма на фиг. 74 пригодна для любых
самолетов.
Если поставить условие, чтобы ход торможения составлял не
более 20% всего угла накренения, нужно взять Л>4.
Примем А = 4. Тогда
по ь л То
*[Р = 0,8-(а = —А;
пх пх 1хп.
Подставляя А = 4, найдем Л/э:
Жэ = РД = 0,2-га/Х-
Раскрывая значения 1Х и пх.
!х = — г2-, nx= — /—i
Х g х Х “V krj
Су
где а = —— , получим
дсу
да
= ^|-p2№V2.
э GL3 \ да I Г2Х г
Отсюда следует, что усилие, прилагаемое к управлению, долж-
но быть пропорционально желаемому углу крена, квадрату ско-
рости полета и квадрату плотности воздуха, или иначе пропор-
ционально скоростному напору и плотности воздуха. Если под-
ставить момент Мэ, выраженный через угол отклонения элеро-
нов, получим
2G z2 дак 5Э g (дс daK\(z2\* р SZ
м -----------о_; —=— —- : — —----------------
а / д?)э 160 \ да дЪэ/\Гх/ Ро @
или приближенно
а9 р SI
1а Ро G ’
Отсюда следует что угол отклонения элеронов должен быть
пропорционален желаемому углу крена, плотности воздуха и об-
G
ратно пропорционален величине— .
Простейшие случаи боковых движений
Подобно тому как мы делали при рассмотрении продольных
движений, к простейшим боковым движениям отнесем началь-
ные движения при действии возмущения. Пусть самолет подверг-
ся действию бокового течения, которое, 'складываясь с основ-
ным движением встречного потока, даст быстрое образование
139
скольжения с углом £ (фиг. 75). На крыло, фюзеляж, оперение
и другие части самолета будут действовать боковые силы. Сло-
жив их, получим боковой фокус самолета — точку прило-
жения равнодействующей боковых сил; координаты этой точки
обозначим через хр и%
На схеме, показанной на фиг. 76, кроме строительных осей,,
самолета нанесем главные оси инерции Xi и z/i. Пусть координа-
ты бокового фокуса в осях Xi, z/i будут а и Ь, масса самолета — т
и моменты инерции относительно
главных осей —
4 = тг/, 1у = тгу.
Предположим, сила Z имеет по-
ложительное направление. Составим
выражение для линейного ускоре-
ния произвольной точки, лежащей
в плоскости ху. Это ускорение сло-
жится из поступательного ускорения
самолета z 0=— и произведения
угловых ускорений на соответствую-
щие координаты:
Приравнивая ускорение нулю, получим уравнение для оси
ускорения, т. е. линии, на которой ускорение в направлении
оси z отсутствует. Так как вначале движения не было, то эта
ось явится также осью вращения. Найдем точки пересечения
этой оси .с главными осями:
.. . а Ъ \ ~
14—2 У—=°;
г I
Гу )
если
если
^ = 0, то =
*1 = 0, то уа= — —;
положительные знаки для а и b соответствуют фиг. 76.
Перейдем к оценке положения оси вращения. Чем дальше
ось от центра тяжести, тем меньше начальное угловое ускоре-
ние, тем слабее влияние порывов ветра в полете. Для оценки
наклонения оси ускорения нужно поставить условие, чтобы в ре-
зультате вращения появлялись факторы, противодействующие
возникшему вращению. В одной из старых теорий поперечной
устойчивости самолета, разработанной Дюшеном в 1911—12 гг.,
140
делалось предположение, что при боковом импульсе вращение
происходит вокруг продольной главной оси инерции, и затем де-
лался вывод, что при положительном поперечном угле крыльев
главную продольную ось целесообразно делать приподнятой.
Рассматривая этот вопрос, видим, что без специального на-
клонения оси инерции вращение происходит вокруг «приподня-
той» оси. При вращении вокруг приподнятой оси быстрее исче-
зает скольжение и связанные с ним моменты. Ранее высказыва-
лась мысль, что' при сильно опущенной оси устойчивость дости-
гается обратным поперечным углом крыльев, и подтверждалось
это опытами с простейшими летающими моделями.
В качестве второго примера простейших боковых движений
рассмотрим поведение самолета в восходящем потоке с перемен-
ной по размаху крыла скоростью. Нас интересует только разли-
чие восходящих потоков в различных частях крыла, и потому мы
схему действия потока представим, как показано на фиг. 77. Та-
кой поток даст изменение углов атаки в сечениях крыла и мо,-
менты вокруг осей х и у. Эти моменты равноценны моментам,
возникающим при вращении вокруг оси х. Найдем отношение
этих моментов (напомним, что момент вокруг оси х возникает
141
от изменения нормальных составляющих аэродинамических сил,
а вокруг оси у — от тангенциальных составляющих):
G г2 ^2
М = — (О - M=G —
х а V у V
Му
Мх
Соотношение между моментами очень простое — результи-
рующий вектор момента направлен просто по линии полета. Если
накреняющий момент кренит самолет вправо, то момент вокруг
оси у заворачивает его тоже вправо.
Фиг. 78.
Результирующая ось вращения может быть найдена методом,
описанным выше. Есть еще один способ определения положения
оси ускорения. Пусть момент представлен на схеме в виде век-
тора М, и, кроме того, на схеме нанесен также эллипсоид инер-
ции, или, вернее, -его проекция на плоскость ху. Полуоси полуг
1 1
ченного эллипса равны и —=..
V lx Viy
Через направление вектора момента проводим касательную
к эллипсу плоскость, перпендикулярную вектору момента. Тогда
ось вращения 00 пройдет через начало координат и точку каса-
ния (фиг. 78).
Поведение самолета будет зависеть от того, как расположит-
ся ось 00 по отношению к направлению встречного потока. Пусть
момент М дает положительное вращение, т. е. вправо, и пусть
большая полуось эллипса инерции совпадает с линией нулевой
подъемной силы крыла. Тогда ось 00 окажется приподнятой па
142
отношению к оси потока, и по отношению к потоку поворот будет
происходить вправо, создавая скольжение на правое крыло, и
это будет давать полезный эффект, противодействующий основ-
ному моменту М.
Поднятие оси инерции х2 будет усиливать этот эффект. При
опущенной оси х2 вращение будет происходить в обратную сто-
рону, создавая скольжение на левое крыло и усиливая вредный
накреняющий момент. В этом случае отрицательный поперечный
угол крыльев дал бы благоприятный эффект.
Рассмотрение данного случая осложняется тем, что в нерав-
номерном восходящем потоке, подвергнутом воздействию крыла,
могут иметь место боковые скосы потока, которые, действуя на
вертикальное оперение, дадут дополнительный момент вокруг
оси у.
Аналогичным образом можно было бы рассмотреть начальные
боковые движения, вызываемые быстрым отклонением руля на-
правления, элеронов и остановкой бокового двигателя.
Малые боковые движения самолета
Малые боковые движения самолета имеют известное сход-
ство с малыми, продольными колебаниями. Основным фактором
последних являлись моменты, вызываемые изменением угла ата-
ки и угловой скоростью относительно оси z. Соответственно
основным фактором, определяющим малые боковые колебания^
являются моменты вокруг оси у, вызываемые скольжением и
угловой скоростью вращения относительно оси у.
На характер малых продольных колебаний большое влияние
оказывали движения центра тяжести самолета, вызываемые из-
менением подъемной силы. При путевых колебаниях самолета
будут возникать боковые аэродинамические силы, которые вы'-
зовут боковые движения центра тяжести. Кроме того, путевые
колебания самолета будут сопровождаться колебаниями крена.
Крен также сообщает самолету боковые ускорения. Анализ пока-
зываем, что действия крена и скольжения сдвинуты по фазе почти
на 90° и что при больших скоростях полета действие крена зна-
чительно меньше, чем скольжения.
Градиент боковой силы по скольжению почти в 10 раз слабее,
чем градиент подъемной силы по углу атаки. По этой причине
боковые движения центра тяжести малы, и это позволяет сде-
лать допущение, что малые боковые колебания состоят только
из качаний вокруг центра тяжести. Правильность этого допуще-
ния может быть в каждо-м случае легко проверена.
Хотя малые боковые движения состоят в основном из путе-
вых качаний, однако сопутствующие качания крена окажут су-
щественное влияние на характеристики колебаний.
При вращении вокруг оси х сильное действие оказывает тор-
можение вращению; это позволяет не считаться с моментом, иду-
143
щим на создание углового ускорения, и полагать, что аэродина-
мические моменты, действующие вокруг оси х, находятся в равно-
весии. Составим уравнения движения, смысл которых заключает-
ся в следующем. Угловое ускорение вокруг оси у определяется
моментом от скольжения, моментом торможения вертикального
оперения и побочным моментом, вызванным вращением вокруг
оси х. Вокруг оси х действуют момент от скольжения, тормо-
зящий момент крыльев и момент, вызываемый вращением вокруг
оси у. Угол скольжения [3 равен углу поворота самолета ф, по-
скольку поворот вектора скорости мы во внимание не принимаем.
Таким образом
дМ дМ дМ
^ШХ т дшу
Введем обозначения:
2 1 <>М По= ; п = 1 dMv 1 dMv , = * ;
/у до>у /у до>х
2 1 дМг 1 дМх 1 дМх
tie — • ц - •
, /1/0 1х 1х ^^у 1х
Ф' + пф' + »о Ф—М' = °; М' + п1 Ф 4- = 0.
Производя подстановку ф = аех/, \=bekt, получаем характе-
ристические уравнения:
а (X2 + т. + п2) — &л3Х = 0;
а (и6Х + га2) 4- Ьп^ = 0.
Составляем определитель системы, приравниваем его нулю:
К2 4-пХ 4-д2 —га3Х
гавХ4-га2 д,Х
и раскрываем его:
2
>М"+—’4+^+—=0;
\ «7 / «7
характеристики колебания будут:
nb = n + n6-^; nt = n* + nl-^.
144
Величину — можно рассматривать как множитель, транс-
ит
формирующий момент вокруг оси х в момент вокруг оси у.
Момент крыла вокруг оси х, вызываемый вращением вокруг
оси у, трансформируется в тормозящий момент вокруг оси у.
Момент крыла вокруг оси х, вызванный скольжением, трансфор-
мируется в момент вокруг оси у, повышающий частоту боковых
колебаний. С ростом скорости полета и соответственным умень-
шением угла атаки трансформирующий множитель уменьшается.
Трансформирующий множитель выражается следующим образом:
л3 1Х /дМ дМД 1Х
— — — —- : — = а —.
л7 1у / 1у
При полете на большом угле атаки эффект от вращения во-
круг оси х становится доминирующим. Нужно заметить, что,
если летающая модель самолета выполняется с крылом в виде
плоской пластинки, величина Пз становится равной нулю и вра-
щение вокруг оси х не дает заворачивающего момента.
С целью иллюстрации расчета малых колебаний рассмотрим
пример для транспортного самолета с такими исходными данны-
ми: полетный вес 0=18 000 кг\ размах крыльев Z=28 м; удельная
нагрузка -^-=225 кг/м^ угол атаки а = 0,2; ^=0,8; скоростной
напор 7=280 кг/м^ скорость полета V=75 м/сек\ 1У—
= 20000 кг/сек^м-, /«.= 10000 кг/сек2м\ Zi = 6 м\ г2 = 7 ж; — =
а
= 90 000. Пусть боковая сила фюзеляжа 7ф = 4000^3 приложена
на расстоянии 3,5 м впереди центра тяжести самолета; боковая
сила вертикального оперения ZB.O=3500 В приложена на расстоя-
нии 2 м выше и 10 м позади центра тяжести самолета. Боковая
сила крыла ZK=9OO|3 приложена на расстоянии 60 м выше цент-
ра тяжести. Сложив боковые силы, получим результирующую си-
лу Zp =8400^ с координатами у з = 7,3 м, х₽ = 2,5 м. Теперь полу-
чим коэффициенты: п2о=1,О; и=0,25; и2=0,07; и3 = 0,65; п25=6,0;
п6 = 2,5; п7 = 6,3; — =0,1; nb^0,5; n2a=l,6; ца=1,26; /)=0,4; т =
и7
= 5,2 сек.
Рассмотрим теперь движение крена. Движение крена может
быть получено после исключения ф из исходных уравнений и по-
следующего интегрирования уравнения
( по \
, Ф \ Л5 /
т=ф- - .
Лз + —=- «7
"I
145
Фаза для максимального угла крена может быть получена
из уравнения для движения крена при условии у' = 0:
, л2
«1Ф + М' = 0; ^- =-----
Ф «в
Используя данные рассмотренного выше примера, получим
— 0,1 .
I
По условию для максимального крена будем иметь
Г = _6д0=_2,4; 9.
ф 2,5 ф
Пользуясь фазовой диаграммой для D = 0,4, при "^" = —1,9
— = 0,4; тогда отношение максимального крена к предшест-
Фо
вующему максимальному углу путевого отклонения
7о = - 0,4 ф0 (0,59 • 2,4 + 0,1) = - 0,61 ф0.
В данном примере угол крена составляет около половины
угла поворота и почти совпадает по> фазе с максимальной угло^
вой скоростью поворота.
Расчет моментов относительно осей х и у от скольжения пред-
ставляет большие трудности и связан с возможностью получения
значительной ошибки. Причины это-
го следующие. Вертикальное опере-
ние находится в потоке, заторможен-
ном и деформированном действием
крыла и фюзеляжа. Нагрузка на го-
ризонтальное оперение также силь-
но сказывается на нагрузке верти-
кального оперения. Учет этих фак-
торов возможен только при помощи
специального испытания или нали-
чии достаточно большого количества
статистических
скольжения на крыло сильно зави-
сит от формы крыла и особенно —
его концевой части. Подвеска кон-
цевых баков не только сильно ме-
самолета, но и градиент момента крыла
данных. Действие
няет моменты инерции
по углу скольжения.
На практике иногда наблюдается, что в области малых углов
скольжения вертикальное оперение сильно затенено фюзеляжем
и находящимися на нем надстройками (фиг. 79). Получающаяся
при этом зависимость момента оперения от угла скольжения па-
146
казана на фиг. 80. Если добавить дестабилизирующее действие
фюзеляжа, можно получить местную неустойчивость.
В этом случае устойчивое равновесие будет в крайних точках
при наличии некоторого скольжения; полет окажется криволи-
нейным с некоторым креном. Однако, если точки устойчивого рав-
новесия близки, слабые импульсы будут перебрасывать самолет
1—момент оперения; 2—момент оперения и фюзеляжа.
из стороны в сторону и в итоге могут иметь место колебания с
некоторой незатухающей амплитудой. Подобного рода колебания
могут быть исследованы экспериментально.
Большие боковые движения самолета
Большие боковые движения характеризуются в основном сме-
щениями вдоль оси z, т. е. нарушением прямолинейности траек-
тории центра тяжести. Начнем рассмотрение вопроса с упрощен-
ных случаев. Предположим, что самолет обладает свойством
весьма быстро устранять возникающие скольжения. Полагая, что
скольжение отсутствует, можно не рассматривать движения во-
круг оси у. Боковая аэродинамическая сила также будет отсут-
ствовать, и для движения по оси z получим только эффект крег
на. При положительном накренении, т. е. вправо, будем иметь
проекцию силы тяжести на ось z и отсюда — положительное уско-
рение:
/и = О sin От.
dt 4 ‘
При положительном вектор скорости полета будет
вращаться вправо, т. е. вращение будет отрицательным по
знаку с угловой скоростью
^=4/=- _Ld±£ = _JL,
dt т V dt V 1
147
где
При отсутствии скольжения скорость вращения самолета вокруг
оси у должна быть равна скорости вращения траектории или ф'=
= ф'т. В результате крен вызывает поворот, а поворот будет спо-
собствовать накренению вследствие изменения скорости вдоль
размаха. Пренебрегая моментом, идущим на сообщение углового
ускорения вокруг оси х, получим уравнение равновесия моментов
вокруг оси х, вызванных угловыми скоростями вращения вокруг
осей х и у:
дМ,
д<лх
Подставим
и У
ф' =------— г,
тогда
Л7Т'—«в у 7 = °-
Полученное уравнение характеризует движение, апериоди-
чески неустойчивое. Для оценки степени неустойчивости рассмот-
рим время удвоения угла крена:
dt V п7 g п6
Приняв —= 2, получим
Т1
if=0,69 — —; — = — ;
g пв п6 2а
t
Р
Значения t
дсУ л
для 7 = 4.
да
дСу
= 0,1421 _2_Ро.
2^ а ’ з_ S
G Ро
в зависимости от----— и
S р
су даны в таблице
G Ро у 7 10 50 100 500 1000
^сек* 1,8 4,0 5,6 12,5 18 су=1,0
^сек* 55 126 180 | 400 | 560 су=0,1
148
При больших значениях t неустойчивость для летчика неощу-
тима, особенно если самолет подвергается возмущениям разноь
го знака. Заметная неустойчивость проявляется при /<Ч0. Таким
образом неустойчивость при полете без скольжения может иметь
значение только в случае очень малых — при больших су.
о
В качестве второго примера рассмотрим поведение самолета,
сохраняющего курсовой угол. Это может иметь место как при
действии автопилота, так и при соответствующем действии лет-
чика. Моменты вокруг оси у, как и выше, рассматривать не нуж-
но. Долей момента вокруг оси х, идущей на создание углового
ускорения, также будем пренебрегать. Тогда уравнения движе-
ния запишутся в виде
aV2 п . dZVz дМ
at 1 ар v д^х
г V
дМхУг _Q.
d₽ V
или
Z№ — =—П1
z'
4 V’
«5
1 dZ
;
2 mV аз
Интегрируя второе уравнение и подставляя найденное значе-
ние у в первое уравнение, получим
т= z" + nzz' + ^-«4z=0;
Пь = п^ п2а = -^п^
Для этого колебания факторы периода и затухания будут вы-
ражаться формулами:
= О = _К_.
Па V gn4 Па У gn4
Проведем анализ полученных характеристик:
nb
aV*
n2
a 6 V
aV = l/ с^^-,
У Ь 9
I
2 ’ 2 4
z2
Z. —
149
Нужно заметить, что величина -у- зависит от cv (особенно
у стреловидных крыльев) и меняется от 0,1 до 0,3. Тогда получим
= — = 2,5/Т н-5,0/Т-
«а
Для размаха крыльев 7=10—40 м получим т0 = 8—32 сек.
Значения фактора затухания приведены в таблице.
О Ро * SI Р 1 5 25 100
D 0,8 0,35 0,16 0,08 -^=0,1
D 0,46 0,20 0,09 0,045 -/-=0,3
Если не брать планеры или самолеты с очень малым то
движение получается периодическим с относительно слабым за-
туханием. При полете с малым су, когда -у- тоже мало, движе-
ние может оказаться апериодическим.
Таким образом, если курсовой угол фюзеляжа удерживается
постоянным, самолет будет совершать качания с крыла на крыло
со слабым затуханием. Отсюда следует, что изолированная кур-
совая стабилизация не может дать удовлетворительного резуль-
тата.
Наблюдая за накренением самолета, летчик может действо-
вать элеронами или рулем направления. Устранение крена будет
приводить к энергичному затуханию колебаний.
Рассмотрим теперь большие колебания самолета, не внося
специальных ограничений, но* прибегая к ряду упрощений. Боко-
вые линейные ускорения вызываются действиями крена и сколь-
жения; тогда уравнение для боковых движений будет иметь вид
/nz' = G-r + ^-(']i — Фт) или 4>;=-Д- =7 + и2(ф-фт),
где
_ 1 dZ q . .
150
Напоминаем, что положительный поворот самолета Ф и по-
V2
ворот вектора скорости --------происходят влево, а положи-
тельное, скольжение (+ф) происходит на правое крыло, т. е.
поворот самолета больше, чем поворот вектора скорости.
В отношении вращательных движений вокруг осей х и у де-
лаем допущение, что действующие аэродинамические моменты
от скольжения и угловых скоростей непрерывно находятся в рав-
новесии:
дМ}
дМ
дМ,
дМ.
"у
дМх , , , дМх , л
=0.
00) „
да)
Используя принятые обозначения
9 1 dMv 1 dMv 1 dMv
0 ly 1у дШу ’ 3 1у дых
1 дМх 1 дМх,, „ _ 1 дмх
5 1Х ’ 1Х дШу 1Х до>х
получим
М—'К—Мт—77=°;
лФ ’+ng Ф—ng 4>т—М=0;
М' + П} Ф - «5 Фт + М' = 0-
Производя подстановку ф = аеи, фт = йех/, f = будем
иметь
ап2 — b (X + п2) — = 0;
а (лХ 4- «2) _ Ьп% — сп3Х — 0;
a (n6X + nl) — Ьп\ + сп^ = 0.
Составляем определитель системы и приравниваем его нулю:
п2 nX + «2 (^ + ni) ~П1 V — «8х = 0.
П6Х4-Л2 ~П1 л7Х
151
Раскрывая определитель, приходим к уравнению
К8 + п^ + ^ = 0,
где
ЛгПзП6+Пзл|4-ЛоП7+ЛЛгП7
ЛП7 + Л3Лб
9 g {nnj - п20 Л6)
а У(лл7+л3л6)
В выражения для коэффициентов входят моменты инерции,
однако они могут быть сокращены. Условие отсутствия дивер-
гентной неустойчивости может быть написано в виде
дМ дМ дМх дМ
пп2 > пм2- ---- : —>-------- : —.
5 °’ д? д<»у до>у
Подставляя значения градиентов моментов по скольжению и
угловой скорости, получим
2 / ?2\2
— ----I----I ос
•*₽ ^в.о\ L /
Значения kB.o
лежат в пределах 0,06—0,03; значения у—
в пределах 0,5—0,8; тогда — больше 8а — 25а.
Рассмотренный случай больших боковых колебаний исполь-
зуется обычно для пояснения сущности боковой устойчивости.
Если указанное условие не соблюдено, у самолета наблюдается
спиральная неустойчивость. Это значит, что если самолет накре-
нился и стал двигаться по кривой, противодействие вертикальног
го оперения вызовет некоторое скольжение. Однако момент во-
круг оси х от вращения вокруг оси у окажется больше, чем об-
ратный момент от скольжения, и у самолета появится тенденция
увеличивать возникший крен.
Во избежание спиральной неустойчивости необходимо опре-
деленным образом подобрать соотношение между моментами
вокруг осей х и у от скольжения, или, что то же самое, соотно!-
шение между координатами фокуса скольжения. Количественное
исследование показывает, что наличие спиральной неустойчи-
вости не является большой помехой для пилотирования самоле-
та, если время удвоения отклонения достаточно велико.
Как видим, спиральная неустойчивость может иметь место
при полете на большом угле атаки. Для ее устранения в этом
. ЭМХ
случае может потребоваться такое значение —которое может
152
повести к неприятным броскам на крыло при полете в порывистом
ветре.
Посмотрим, в каком случае колебания могут оказаться воз-
растающими. Если п2о<О, значение па возрастает, и, следователь-
но, увеличивается частота колебаний, но одновременно умень-
шается Пъ и, следовательно, снижается затухание. При некото-
ром достаточно^ большом, но отрицательном п20, т. е. при значи-
тельной флюгерной неустойчивости, колебания станут возрастаю-
щими. При D<Z—2 движение станет апериодически неустойчивым.
Может вызвать удивление, что при слабой флюгерной не-
устойчивости большие колебания могут удовлетворительно за-
тухать. Объяснить это можно' так. Пусть возникло небольшое
скольжение; под его действием появятся моменты, усиливающие
скольжение и накреняющие самолет. Скольжение и крен будут
вызывать поворот траектории, и вращение вектора скорости мо-
жет перегнать поворот самолета. Тогда скольжение изменит свой
знак и появится момент, устраняющий крен.
Для иллюстрации приведем два примера. Пусть самолет летит
на сравнительно большом угле атаки а = 0,2; соотношение межь
ду ^и Хр равно трем, но тормозящий эффект вертикального опе-
рения относительно невелик. Тогда получим такие коэффициенты
и характеристики движения: п = 0,25; м20=1; п2=0,07; п3=0,65;
м25=6,0; и6 = 2,5; п7 = 6,3; У=70 м/сек\ Пь = 3,25; пЧ——0,044;
£>=15,5.
Движение оказалось спирально неустойчивым. Найдем время
удвоения отклонения
^ = 0,69-^-=51 сек.;
~г1а
время удвоения отклонения оказалось таким значительным, что
неустойчивость будет практически незаметна.
Условия второго примера отличаются от первого тем, что
угол атаки уменьшен до а = 0,1, скорость полета увеличилась до
100 м/сек; кроме того, тормозящее действие вертикального опе-
рения увеличено на 50’%. Теперь будем иметь такие коэффициен-
ты и характеристики движения: м20 = 2; и=0,53; п2=0,1; п3=0,32;
п25= 12; и6= 1,8; п7=М),0; пь=6,0; ма=0,27; £> = 22.
Фактор затухания оказался очень большим, движение—апе-
риодическим с очень вялым возвращением к положению равног
весия (время уменьшения отклонения в два раза составляет око-
ло одной минуты).
Анализ малых и больших боковых движений достаточно груб,
но он помогает разобраться в природе боковых движений. Раз-
ложение на малые и большие боковые движения должно быть
произведено исходя из общих уравнений. Этому вопросу посвя-
щается дальнейшее изложение.
153
Общий случай бокового движения самолета под действием
малого возмущения
Составим уравнения бокового движения. Боковое ускорение
определяется боковой силой от скольжения с углом р = <|>—фт и
проекцией подъемной силы при крене с углом у:
—=—ф: = — у—«а (ф—фл
у dt т V VT т ’
Угловые ускорения при вращении вокруг осей х и у опреде-
ляются скольжением и аэродинамическим эффектом вращения
вокруг этих осей:
<WV .
М =-77 О—ФтН
др
дМ.
дМ,
ди>.
дМх
Ф'
д&.
д<л
Вводя принятые обозначения
2 1 дМу 1
0 /уд?' /„ д«>„
1 дМУ 1
п,=------s п? =
’ 1у д^х 5
дМу.
—у
1 дМх
fx д? ’
n7=__L^; ^ = 2а,
д&х m
1 dZ
п2—-------;
2 mV
1 дМх
п& =------;
/г ’
приведем уравнения бокового движения к виду
м-(ф;+Мт)-y ч=0;
(ф" + пф' + га2ф) — «2 фт—п3/ = О;
(М' + Ф)~ «5 Фт + (l" + «7Т') = °-
Производя подстановку ^ = аеи, <^т = Ьеи, y = cekl и сокра-
щая на еи, получим систему уравнений. Составляем опреде-
литель этой системы и приравниваем
— (^ + ^2)
“«о
“«5
его нулю:
___£
V
— ns\
к2 + п,к
= 0.
дМх ,
I •
к2 + пк + П2
«6к + «5
154
Раскрывая определитель, получим характеристическое урав-
нение четвертой степени
^ + B^ + C^ + D\ + E = 0,
где
В — п 4- п2 + п7; С = nl + пп2 + ппч + гаал7 -|- п3л6;
D = ng п7+nanl + п2п3п6 + -J- пI + nn2w7; Е=-£ ( пп}—п^л,).
Способ разложения уравнения четвертого порядка на два
уравнения второго порядка был уже описан выше. Для этого
вводим единицу времени г0 = и находим коэффициенты-
/Е
уравнения:
B^Bfa Dt = D^;
L- — или L =—, но £ < 1.
Di Bi
Затем на графике фиг. 60 — 62 наносим прямую по уравне-
нию Hfli — -—0 или НХН2=^^- и по пересечению с ли-
В? £)2
нией, соответствующей нужному значению L, находим Н^Нъ и а.
Далёе по уравнениям
kF1 + F2 = Ba, + kFi — ^ = A2 + — ;
л=4‘>
к
находим
/*1, F^ и
Условие отсутствия колебательной неустойчивости опреде-
ляется выражением BCD—D2—ЕВ2^>0\ оно очень неудобно для
анализа. Обычно, исходя из этого условия, и варьируя некото-
рые параметры, например, и строят граничные линии, раз-
деляющие устойчивую и неустойчивую области. Практически бо-
лее интересно найти условия, при которых обеспечивается неко-
торый минимум факторов затухания. Условия, при которых мож-
но получить желаемые характеристики устойчивости, удобнее
искать обратным путем. В этом случае можно воспользоваться
значительным упрощением. Например, поставим условие, что ха-
рактеристики частот отличаются достаточно сильно, /f>3, и, сле-
довательно,
a^2>9; Ct>9.
155
Найдем теперь условия затухания быстрых колебаний. О сла-
бости затухания быстрых колебаний будет свидетельствовать ма-
лость величины Bi. Это легко усмотреть из уравнений
лн^4=в*: ^4+^=0,.
к. А
Малость отношения позволяет упростить условие
устойчивости и представить его в виде
в?
^1>0; BC-D>0.
jDi
Принимая В=п, и подставляя значения коэффициентов-
С и D, будем иметь
ВС—D = ra2(ra + n2) + nMn6(n7—л2)—л3 + 4) > °-
Если подставить средние характеристики самолета и поде-
лить уравнение на п%, получим
25 + 500аа—0,05а — А. /_£_№ > 0.
SI р \гх } I
Возрастающие колебания могут появиться при большом
большом 4 и относительно малом радиусе инерции гх.
Например, пусть —= 300; — = 30; (—=100; ^=0,2.
S SI \ гх / *
Тогда
25 + 500а2 — 30а ^ = М
Р
Найдем минимум величины /V:
— = 1000 а — 30 — =0; а = 0,03—.
da р р
Подставляя найденное значение а, получим
/7 = 25—0,45 (—7.
\ Р /
Значения N для данного примера на разных высотах полета
указаны в таблице; приведенные величины а соответствуют
минимуму N, но* не превышают 0,2.
156
Н км 0 5 10 15 20
а 0,03 0,05 0,09 0,19 0,20
N 24,5 23,8 21 7 -38
Как видно, выше 16 км самолет стал колебательно неустойчив.
Рассмотренный упрощенный случай соответствует приближен-
ному разложению, вытекающему из малости В19 когда
„ R D . „ D
nbi = а--Пь2= — .
с* о
Слабое затухание больших колебаний будет иметь место при
условии, что Di мало, и тогда приближенное условие устойчи-
вости будет иметь вид
CD—В£>0.
Малое D при большом Е может быть только при п20<0; этот
случай уже был нами рассмотрен.
Сравнивая боковые и продольные движения, можно отметить
следующие различия: 1) малые продольные движения обладали
большим фактором затухания, а большие продольные движе-
ния— малым; при боковых движениях мы получили малый фак-
тор затухания для малых движений и большой — для больших;
2) малые продольные движения можно было рассматривать ynpol-
щенно исходя из допущения о постоянстве скорости; малые боб-
ковые движения не могли быть рассмотрены упрощенно.
Характер боковых движений зависит от многих параметров.
Обычно исследуют влияние координат бокового фокуса при
скольжении на устойчивость боковых движений. Для характери-
стики устойчивости на диаграмме, в которой по осям отложены
координаты фокуса или производные по углу скольжения от ко-
эффициентов моментов относительно осей х и у, наносятся
пограничные линии: одна — по условию £=0, чем отделит-
ся область спиральной неустойчивости, вторая — по условию
157
BCD—D2—EB2 = 0, чем отделится область колебательной не-
устойчивости.
Более интересно было бы нанести на диаграмме линии зна-
чений факторов затухания для обоих колебаний. Как мы уже
указывали, небольшая спиральная неустойчивость не имеет
практического значения; с другой стороны, важно позаботиться
о достаточной частоте и высоком факторе затухания малых бо-
ковых колебаний.
Если полет происходит на значительном угле атаки, можно*
принять во внимание, что изменение угла крена будет приводить
к изменению угла скольжения. Для угла скольжения имеем вы-
ражение sin {3 = Проекцию вектора скорости на ось z полу-
чим следующим образом. В исходном положении проекции ско-
рости на оси самолета
Vr= V cos a; = — V si па.
л у
После поворота вектора скорости на угол фт в плоскости
полета
= V cos фт cos a; Vy= — Vcos>pTsina; IZz= —Vsin<pT.
После поворота самолета на угол ф вокруг оси у
VX=V cos 4Tcos a cos ф4* Vsin фтзт ф;
V = — V cos фт sin a;
V 2 = — V sin фт cos ф 4- V cos a cos фт sin ф.
После поворота вокруг оси х самолета на угол крена х
V2 = V (—sin фт cos ф cos х + cos a cos фт sin ф cos 7 4-
4- cos фт sin a sin 7).
Полагая ф, фт и у малыми, получим
₽ = у = —фт4-фсоза4-781па=»ф —фт4-7«.
В остальном выражения для моментов остаются без изме-
нения.
Если главные оси инерции составляют значительный угол с
осями, в которых ось х направлена по плоскости нулевой подъ-
емной силы, анализ колебаний можно вести двояко. Один из спо-
собов заключается в том, что уравнения вращения составляются
относительно главных осей инерции. Тогда выражения для мо-
ментов от скольжения окажутся измененными вследствие изме-
нения координат фокусов скольжения крыла, фюзеляжа и вер-
тикального оперения. Соответственно изменятся моменты тормо-
жения оперения при вращении вокруг осей х и у. Изменится и
158
выражение для угла скольжения, в которое войдут угол пово-
рота траектории и составляющие от углов поворота вокруг осей
х и у. При вращении вокруг осей х и у получим моменты, в ко>-
торых будут учтены эффекты изменения скорости и угла атаки.
Можно составить уравнения вращения относительно «хордо-
вых» осей самолета. Выражения для моментов упростятся, но
зато число членов увеличится, так как угловое ускорение отно-
сительно принятых осей получится путем сложения составляющих
от вращения относительно главных осей.
Остановимся на автопилоте для боковых движений. Причи-
нами изменения направления полета могут служить действие кре-
на и действие скольжения. Если самолет имеет достаточно боль-
шую килевую поверхность и хорошо отрегулирован, скольжение
легко самоустраняется. Возникший крен если и имеет стремление
к уничтожению, то это обычно происходит медленно, и, пока вы-
ровняется крен, самолет успевает значительно' изменить курс под-
лета. Следовательно, для обеспечения прямолинейности полета
нужно прежде всего применить автопилот, быстро устраняющий
крен, работающий от свободного гироскопа. Если применить авто-
пилот только устраняющий крен, самолет будет в общем лететь
прямо, но останутся малые курсовые колебания, которые часто
плохо затухают; кроме того, самолет сможет медленно менять
направление полета в силу недостатков регулировки и отсутствия
какой-либо тенденции итти по желаемому курсу. Поэтому на
автопилот, кроме устранения крена, должна быть возложена за-
дача приведения самолета к заданному курсу, для чего исполь-
зуется обычно руль направления; в случае плохого затухания кур-
совых колебаний автопилот должен реагировать на угловую ско-
рость поворота и обеспечивать быстрое затухание.
ВЗАИМОДЕЙСТВИЕ ПРОДОЛЬНЫХ И БОКОВЫХ
ДВИЖЕНИИ
Существует ряд факторов, связывающих продольные и боко-
вые движения. Такими факторами являются некоторые моменты,
например, гироскопические, когда вращение вокруг оси z вызы-
вает момент вокруг оси у и обратно. Хвостовое оперение часто
находится в струе винта или в сфере ее влияния. Эта струя за-
кручена, и поэтому смещение оперения влево — вправо вызывает
изменение нагрузки на горизонтальное оперение, а смещение
вверх — вниз вызывает изменение нагрузки на вертикальное опе-
рение. Неравномерность скоса потока за крылом при скольжении
и вращении вокруг осей у и х вызывает дополнительные моменты
вокруг оси z.
Другими связывающими факторами являются действия изме-
ненной траектории полета. Так, при накренении появляется уско-
рение вдоль связанной оси у, направленное вверх. При крене саг
молет движется по кривой, причем траектория будет искривлена
159
и в плоскости ху. Это вызовет изменение угла атаки и даст уско-
рение вдоль оси у. Колебания центра тяжести в вертикальной
плоскости в сочетании с креном приводят к дополнительному
скольжению.
Рассмотрим взаимодействие малых продольных и боковых
колебаний. Предположим, что малые колебания состоят из вра-
щения вокруг оси у, вокруг оси z и малых смещений вдоль оси у.
Далее будем считать, что путевой угол ф и угловая скорость фЛ
дают моменты вокруг оси г; соответственно изменение угла атаки
и угловая скорость относительно оси z дают моменты вокруг
оси у. Тогда можно написать следующие три уравнения дви|^
жения:
г дМ.2 . х , dMz t । dMz . , dMz , z
</р Оыу Oo)g оа
. dY , .
тУ?т<рт).
да
Перепишем их схематично в виде
<р*++ М—й1?т+=0;
ф" 4- ааф' 4- £2ф 4- саср' 4- rf2<p — <Z2?T = 0;
<Рт—аз?4-«з?т=0-
Подставим решения: <р = Доех<; ф = Боеи; <рт = СоеЧ
Получим
0-г + 4* &1) 4- Вй (схХ 4- f/J—Со&! = 0;
+ Во (^2 4* 4“ ^г) — C0d2 = 0;
—Ааз + (X 4- а2) = 0.
Составляем определитель системы, и раскрываем его: приравниваем его нулю
I2 + + Ь± -j- d^
^3 = 0;
-az 0 ^ + <*3
4- В)? + Ck* + D\+E=0,
где
В = Л14"ОаН_в8> C—bt 4-Ьг4-4~я2Лз—
~~ I ^1^а I ^з^а ”1” а1аааз d^c2 j
Е—4~ Oia3&a ~~ d^c ““ did^.
160
Если бы движения рассматривались раздельно, т. е. при
отсутствии связи, мы получили бы движения с характеристи-
ками
ср" + ту = 0; w = + р^Ь^а^
ф" + пф' + ?ф = О; п = а^ q = b2.
Перемножая характеристические уравнения для этих диф-
ференциальных уравнений, будем иметь
к4 + к8 (т + п) + к2 (р + q + mri) + к (mq + tip) ^pq = Q
или
к4 + В'кз + С'к2 + D'k + £' = 0.
Тогда для связанных движений получим
к4 + к8 (т + п) + к2 (р + q-^mn — c1c2) + к (mq + пр — —
— — (\d2) +pq — dtc2a3 — dtd2 = 0.
Как видно, коэффициент В остался без изменения. Если
взаимодействие происходит только через угловые скорости, то
В=В'* С = С' —с1с2\ D — D'—с^а^, Е~Е'.
Анализ начнем с самого простого случая, когда я3=0, т. е.
движением по* оси у пренебрежем; тогда в результате взаимо-
действия, изменится только коэффициент С. Постоянство значе-
ний В и Е будет вытекать из условий
Подставив эти значения в выражения для С и D, можно про-
анализировать изменение характеристик движений, однако этот
анализ очень неудобен. Перейдем к коэффициентам В1у С± и Dlf
введя единицу времени /0 = ’
/£
В1 = В/О; C^Ctl- D^Dtl; L=%-.
Тогда /о и L будут постоянны, а взаимодействие будет менять
только значение С\, уменьшая его.
При графическом решении будем иметь кривую с параметром L
и наклонную прямую, построенную по уравнению Я1Я2=("1 2Д •
Bi
При условии взаимодействия и, следовательно; уменьшении G
прямая будет сдвигаться влево (фиг. 81), величина а=& + —
будет уменьшаться, а "следовательно, будет уменьшаться и k, ха-
рактеризующее отношение частот. Что касается факторов, зату-
161
ханий, то вначале FjF2 будет расти, пока не Достигнет максиму-
ма, а затем упадет и даже станет отрицательным, указывая на
неустойчивые колебания.
Если принимать во внимание движение по вертикали, то ве-
личина L будет уменьшаться, так же, как и Тогда при усиле-
нии взаимодействия вместе со смещением прямой нужно перехо-
дить на уменьшенные значения L. При этом также будет проис-
ходить сближение частот. Напомним, что Л <4 свидетельствует о'
том, что колебания с более высокой частотой затухают сильнее.
Если А>1, сильнее затухают колебания с меньшей частотой.
Фиг. 81.
Рассмотрение взаимодействия больших колебаний представ-
ляет большие трудности. Вообще говоря, этот вопрос требует ино-
го' метода решения, так как задача ПО' существу не линейная. Да-
же если отбросить нелинейные зависимости, мы получаем систему
из шести уравнений и затем определитель шестого порядка, ре-
шение которого довольно громоздко. Частоты больших продоль-
ных и боковых колебаний различаются обычно довольно, сильно,
и потому эффект взаимодействия колебаний сведется в сущности
к простому наложению «отзвука» колебаний. Например, к боль-
шим продольным колебаниям добавятся слабо выраженные про-
дольные колебания с характеристиками боковых колебаний и
обратно.
Вынужденные колебания самолета
Предположим, что' на тело действует сила или момент, кото-
рые меняются по некоторому периодическому закону. Тогда тело
также будет совершать некоторое колебательное движение. Будем
исходить из условия, что возбуждающее колебание следует гар-
моническому закону. В этом случае уравнение движения будет
иметь вид
ср" + пу' + ср — a sin bt.
162
Величина а представляет собой максимальное ускорение, вы-
зываемое периодическим моментом, а b определяет частоту воз-
буждающего колебания. При отсутствии возбуждающего момен-
та движение определялось бы дифференциальным уравнением
второго порядка; само возбуждение также определяется уравне-
нием второго порядка — гармоническое колебание. В итоге мы
должны получить движение, определяемое уравнением четверто-
го порядка. Это уравнение получим, дифференцируя дважды
исходное уравнение и исключая a sin bt:
ср" + ср = a sin bt; ср'" + лер" + п* ср' = ab cos bt;
<fv + nv"' + n%<?',== — ab2 sinbt— — &2(cp" + ncp' + /z2 cp);
cp/y + nep"' + (n2 + &2) cp" + nby + П2 &2cp = 0.
Это уравнение определяет движение, которое можно разло-
жить на несколько составляющих движений. Если составить дис-
криминант Рауса, то окажется, что он равен нулю. Действитель-
но, имеем
ср/г + Ву + Сер" + Dcp' + £ср = о,
где
В = п; С=п2 + 62; D = nb2; Е=п2Ь*;
дискриминант
R^BCD-D2 — EB2 = n2b2(n2 +&2) - л*&2л2 = 0.
Отсюда следует, что по крайней мере одно из составляющих
движений не затухает и, следовательно, является простым гармо-
ническим колебанием.
Найдем характеристики составляющих движений. Введем
,11 Д.Ж
единицу времени tQ = -. — = --- и коэффициенты
Bi==Bta==ih]
(«о*)
Дифференциальное уравнение преобразуется к виду
tp/y++£>1?' + <р=о.
Составляющие движения, как это было получено ранее
определяются уравнениями
+ = ^-F1 + kFz==D1-, kt + ^ + F1F2^C1,
k k kz
где F, и F2—факторы затухания составляющих движений, а
и —^ — характеристики их периода. Так как R = 0, то
k
FiF2 = 0; отсюда следует С1==Л2+ — = — — ; & — — .
& ь п0 л0
Теперь легко получаем характеристики составляющих дви-
жений:
п
пЪ2
(п0&)2
м Z-
«0^1 + — F2 = П;
О
F2 = 0; F1 = ^-; Ъ = \ 4 = 4-
л0 л0 b
Получили очень интересный результат — одно движение имеет
частоту и затухание соответственно собственным затухающим
колебаниям; второе колебание имеет частоту вынуждающего ко-
лебания и лишено затухания. Отсюда можно было бы решить,
что оба колебания совершенно самостоятельны и не связаны.
Однако это не так. Действие затухания определяет амплитуду не-
затухающих колебаний и создает сдвиг фаз между возбуждением
и незатухающими колебаниями.
Предположим, что с момента возникновения возбуждения
прошло достаточно много времени и одно составляющее движе-
ние затухло. Найдем амплитуду незатухающего колебания и срав-
ним фазы этого» колебания и возбуждающего момента. Сдвиг фаз
можно представить как результат сложения двух движений; по-
этому оставшееся незатухающее колебание представим в виде
? = ?i + ?2 = ?i.o sin bt + ср2,о cos bt.
Это решение должно удовлетворить исходному уравнению
движения
ср* + пу + п2 ср = a sin b t.
Найдем ср' и ср":
ср' = b (cpi,о cos bt — ср2,о sin bt),
ср* = — b2 (ср^о sin bt + cp2,o cos bt),
подставим найденные величины в уравнение движения:
— b* (cpi.o sin bt + ср2,о cos bt) + nb (cpi.o cos bt—cp2j0 sin bt) +
+ ло (тьо sin bt + cp2,o cos bt) = a sin bt
164
и сгруппируем члены с sin Ы и cos bt:
sin bt (n2Q — &2?i,o—nb'&w—a) +
+ cos &/(«2cp2,o—&2<f>2,o + «&cpi,o) = O.
Эта сумма может быть равна нулю в том случае, если оба вы-
ражения в скобках равны нулю. Тогда мы получим два уравне-
ния, из которых можно найти <pi,o и ¥2,0:
?1,о(«о — &2) —?2,0«& = а; <р2,о(«о — + ?1,о = о.
Умножив второе уравнение на ——— и, сложив с пер-
«0 —
вым, будем иметь
al . nb
Т1»о = — 7-------2----х ; ?2.0 = — <Р1,0—2 — •
b / И* "о А «о-*
“9--- + -- — 1
Ьг !
Определив <?i,0 и 920, можем найти амплитуду и сдвиг фаз
колебаний. Проще всего найти эти величины, построив график
колебания по уравнению ? = <?i,o sin a+ ®2,о cos а, где a.—bt, и
сравнив его с графиком sin а. Однако это можно сделать и ана-
литически. Поставив условие 7=0, получим два выражения:
cpi.osin a-f-<p2,oCOS a = 0; <р = <р0 sin (a-f-ро) = 0; а4-Р0=1:-
Из первого выражения получим а:
зная а, найдем ро = тг —а.
Амплитуду ср0 найдем, положив
= —₽0;
То = ?1,о Sin (у — Poj + <р2,0 cos (у — М = cpi,o cos Йо + Ф2,о sin
Из полученных выражений для ?1>0 и <р2,о видно', что сдвиг
фаз колебаний определяется действием затухания. Если п=0,
получим
<11
?2,о = 0; Т1,о = —у—2-
Ь I — - 1
165
Если частота собственных колебаний весьма мала, амплитуда
вынужденных колебаний
При По, совпадающем с Ь, амплитуда окажется бесконечно
большой — известное явление резонанса.
Построение сложного движения состоит из простого сложе-
ния вынужденного и собственного движений. Для лучшего усвое-
ния вопроса начнем с колебаний без затухания. Пусть возбуж-
дающее ускорение следует закону a sin bt.
Результирующее движение сложится из собственного ?с и
вынужденного
<Р = ?с + <Рв-
Каждое из этих движений, происходящих по гармоническому
закону, но со сдвинутыми фазами, разобьем на составляющие:
?с = ?а,о sin nJ 4- cpft)0 cos nJ.
?в = sin bt + cfrf.o cos bt.
Найдем первые и вторые производные:
О cos nJ — n0<?b 0 sin nJ + 0 cos bt—byd 0 sin bt,
?" = — «0 0 sin nJ—«2 <pd 0 cos nJ—b^c о sin bt—b^d 0 cos bt.
Чтобы построить движения, нужно найти четыре величины
?ао. ?4<|> ?ео и ?do’, для этого нужно знать или выбрать на-
чальные условия. Пусть при £ = 0 выполняются равенства
<р = 0, <р' = 0 и <р’ = 0.
Тогда
?fto + tPdo = O> «о?ао + ^о = 0, n^0 + ^4io = 0,
откуда
Ъо = О; ?ао = О; <рс0= — ?ао V-
о
Как видим, оба составляющих движения — собственное и вы-
нужденное — следуют закону синуса, а амплитуды их обратно
пропорциональны частотам или прямо пропорциональны перио-
дам. Теперь будем иметь
? = ?а0 (sin nJ— sin bt} ф" = — <f>a0(«2sin nJ—bn0 sin bt).
Подставим найденные значения ср и <р" в уравнение движе-
ния 4- ri~v = a sin bt-.
n3
— «2 sin nJ 4- Ьпй sin bt4- n? sin nJ--- sin bt = — sin bt-,
Ь <PaO
166
отсюда
„з
а 1 по а
— = Ьпй—- <?aQ=——------—;
ФаО " о / *_ по I
М «о ь )
° по
Таким образом найдены амплитуды вынужденного и соб-
ственного колебаний.
Построив синусоиды для обоих колебаний и сложив ордина-
ты, получим сложное движение (фиг. 82). Характерной особен-
Фиг. 82.
ностью этих колебаний в случае близких частот, является наличие
биений, т. е. периодического изменения амплитуды результирую-
щего колебания. Частота биений равна разности частот слагае-
мых колебаний.
При сближении частот период и амплитуда биения будут
расти, а в случае резонанса — станут бесконечно велики. По-
строить колебание для случая резонанса изложенным выше ме-
167
тодом невозможно, так как составляющие гармонические колеба-
ния имеют бесконечно большую амплитуду. Случай резонанса
имеет свое особое решение; найдем его.
Очевидно; что в случае резонанса после возникновения воз-
буждения колебание будет возрастающим. Однако это не будет
возрастающее колебание, рассмотренное нами ранее. В этом лег-
ко убедиться, попробовав подставить решение в виде <? = Сеи.
Фиг. 83.
Поэтому, полагая, что возбуждение действует по закону a cos bt,
а амплитуда растет прямо пропорционально времени, будем
искать решение в виде sin bt:
+ = а cos bt\ ft sin bt\ cp'=/sin bt+fbtcosbf
cp* = 2fb cos bt—ftb2 sin bt= —fb4 sin bt-\- a cos bt\
2/6 cos bt—ftb2 s\nbt+ftb*sm bt= a cos bt\
W = a-
2b
t. e. © = — / sin bt.
T 2b
Это движение показано на фиг. 83. Если возбуждение дей-
ствует по закону a sin bt, решение оказывается несколько более
сложным: =ft cos bt+g sin bt, однако существенное различие
наблюдается только на первых волнах.
Перейдем теперь к случаю, когда собственные колебания за-
тухают. Построение движения в этом случае достаточно просто-.
Если возбуждение действует по закону a sin bt, вынужденное не-
затухающее колебание <?в независимо от начальных условий мож-
но построить, пользуясь выражениями
?B = ?i,osin&r+cp2ocos&r; Фю=-----------------;
Тв ’ Т ’ Т ’ Ьг 1)« ’
168
Для построения собственных колебаний нужно знать началь-
ные условия, т. е. для некоторого момента времени знать любые
две из трех величин: 9о, 9'о или "о- Результирующее движение с?
слагается из вынужденного незатухающего 9В и собственного за-
тухающего 9с движений, т. е. 9= 9в!+?с. Начальные значения
для вынужденного колебания можно легко найти по известному
времени. Имея начальные условия итогового движения и вынуж-
денного, легко получаем начальные условия затухающего движе-
ния 9с о и 9'со. По этим данным нетрудно построить и само за-
тухающее колебание. Сложив колебания, найдем итоговое движе-
ние. Пусть в начальный момент t=Q нет ни смещения, ни скорости,
ни ускорения: 9о = О; 9zo=O; 9"о = О. Для вынужденного незату-
хающего движения получим
?в = ?i,o sin bt + ?2,о cos bt\
'Рв0 = ?2, о; <Р;0 = СР1.0^; ?в"о = — ?2,0&2.
Тогда начальные условия затухающего колебания будут
?со=—?2,о; ?'0=—
Имея -^-5, по фазовой диаграмме получим — и затем пе-
?с0 ?са
рестроением диаграммы колебания для нужного значения
D построим движение. Пусть а—\\ & = 1; пй = 1,22; п = 0,61;
0 = 0,5; 6 = 1,22; £»= 1,5-
Для незатухающего колебания получим
<Р1.о=1,25; <р2,о=—1,51; тв = —=6,28 сек.
ъ
Строим это колебание (фиг. 84); начальные условия его:
?во=—1,51; ?;0=1>25-
Тогда начальные условия для затухающего колебания:
<рс0 = 1,51; <^0 = —1,25; — = -^~ = -0,68.
?с о ?С 0 п0
По фазовой диаграмме для =0,68 получаем -^ = 0,76, а
?с 0 ?с О
по диаграмме колебаний —= 0,71. Отсюда начальная ампли-
туда затухающего колебания 9Са=2,22; расположится она на
^1=0,57 сек. левее начальной точки; период незатухающего коле-
бания тв=6,28; период затухающего колебания для м0=1,22 и
Z> = 0,5 тс=5,3. На фиг. 84 построены составляющие и резуль-
тирующее колебания.
169
В случае nQ = b, если фактор затухания не очень мал, нет ясно
выраженного явления резонанса. Незатухающее колебание в этом
случае будет следовать закону
?1,о = О; ?2,о=—?в=—7 COSbt.
Тогда начальные условия для затухающего колебания бу-
дут иметь вид
а , Л
Результирующее движение строится просто, как показано на
фиг. 84, для jD = 0,5. Через две волны после начала действия воз-
170
буждения практически осталось только незатухающее колебание
с относительно небольшой амплитудой.
При £>>1 собственное затухающее колебание исчезает весьма
быстро, и характеристика собственных затухающих колебаний
будет сказываться только на амплитуде незатухающих колеба-
ний и на сдвиге его фаз по< отношению к возбуждению.
Рассмотрим продольные вынужденные колебания самолета.
Источником этих вынужденных колебаний могут служить умыш-
ленные периодические движения рулем высоты или колебания
руля высоты, производимые автопилотом, который попал на ре-
жим автоколебаний.
Предположим, что возбудитель сообщает самолету продоль-
ные угловые ускорения по закону <?"о=а sin bt. Предположим так-
же, что частота вынужденных колебаний относительно велика, и
.потому можно рассматривать колебания при условии постоянства
скорости полета. Уравнения движения будут иметь вид
ср" = — л2 (ср—срт) — лер' 4- a sin bt\
?т=«2(?—?т); 'Рт=г4,; ?т=
ф
Подставим из второго уравнения <р— <рт = — в первое урав-
Л2
некие, проинтегрируем его, найдем сртл2 и найденное значение
сртл2 подставим в первое уравнение:
по
ср" =----ср' — nep' + a sin bt\
л2
„2
ср =-----срт —лер----COS Ы\
л2 Ь
Л2 Срт = — П2 ср' — ПП2<? “ Л 2 ~ COS bt\
v" + fy/p'4-л2ср—- <2 sin bt+~-n2 cos bt = O,
где
пь = п + л2; л2=л2 + пл2.
Как видим, угловые колебания будут происходить так, как
если бы возбуждение действовало по закону sin (bt+\^). Най-
дем характеристики незатухающих колебаний, представив их в
форме
? = sin bt 4- ср6 cos bt.
171
Определим отсюда у' и ср" и подставим найденные значе-
ния <р' и ср" в полученное выше уравнение:
ср' = сра& cos bt—yb b sin bt\
= — d2 (cpa sin bt-\- c₽& cos bt);
sin bt (a—<?ab2 + ?an2a— <fbnbb) +
+ COS bt[ + ?»"« + Wifi ) = °-
Приравнивая нулю каждую из скобок, получим два урав-
нения, из которых найдем сро и ъь:
чАп2а-Ь2) — уьпьЬ = а-,
4№а ~ + Wbb =-----
_ (»g ~ Ьг) — пф _ _ _ пъь___________ап2
^^(п^-ЬЧ+ф*’ Ь(п2а — Ьг)
При па = Ь
ап? а
Cp6==“”h7’
Ь2пь опь
Зная характеристики возбудителя и получив испытанием
в полете <рЛ и <р6, можно подсчитать п2а и пь, а затем и и п.
Аналогично можно^ рассмотреть путевые движения и движе-
ния крена. Нужно только заметить, что ускорение, создаваемое
колебанием рулей, должно быть известно достаточно точно.
Использование вынужденных колебаний позволяет практически
определить динамические характеристики самолета.
Если возмущение не следует гармоническому закону, можно
искать решение в форме, соответствующей закону возбуждения,
или применить разложение возмущения на ряд гармонических
колебаний. В частности, можно* рассмотреть действие восходяще-
го потока воздуха, скорость которого растет или по линейному
закону или по гармоническому. При перемене характера дей-
ствия возмущения следует искать новое начальное состояние соб-
ственных движений и затем продолжать построение новой стадии
движения.
ЗАКЛЮЧЕНИЕ
В данной работе рассмотрен ряд примеров движения самоле-
та— продольных и боковых. Анализ этих движений позволяет
установить свойства самолета в тех случаях, когда внешние воз-
действия или действия органов управления относительно слабы,
172
•а самолет имеет устойчивую собственную характеристику движе-
ний. Если собственная характеристика неустойчива, анализ дви-
жения тоже можно производить, но только в области, где отно-
сительное изменение параметров движения можно считать малым.
Рассмотренные примеры не исчерпывают всех случаев, кото-
рые могли бы быть рассмотрены по принятой методике, но мы по-
лагаем, что читатель на основе данной работы сможет самостоя-
тельно исследовать интересующие его вопросы.
Автор надеется что настоящая работа будет содействовать бо-
лее широкому применению методов динамического исследования
полета самолета.
содержание
Стр.
Предисловие........................................................ 3
Введение .......................................................... 6
Основные обозначения.............................................. 10
Статическая теория продольной управляемости и устойчивости ... 13
Простейшие динамические характеристики продольных движений
самолета....................................................... 21
Частные случаи движений, приводимых к простому затухающему
колебанию...................................................... 26
Общие сведения по теории затухающих колебаний................ 26
Дивергентное движение.......................................... 38
Физическая природа простых затухающих колебаний и механи-
ческие модели движения..................................... 41
Случаи продольных движений, приводимых к простому затухающему
колебанию...................................................... 45
Малые движения узкого крыла без оперения....................... 45
Движение крыла с оперением в упрощенном виде............... 50
Усложненный случай движения крыла с оперением................ 57
Большие продольные движения....................................... 50
Движение самолета, сохраняющего постоянный продольный на-
клон ...................................................... 59
Движение, при котором изменение угла атаки связано с движе-
нием центра тяжести........................................ 67
Движение, при котором угол атаки зависит от скорости по траек-
тории и вертикальной скорости ............................. 71
Влияние изменения плотности воздуха............................ 73
Примеры использования рассмотренных случаев движения, приводи-
мых к простому затухающему колебанию....................... 75
Размеры горизонтального оперения самолета................. . . 75
Характер малых колебаний....................................... 79
Поведение самолета при действии возмущения..................... 81
Действие управления ........................................... 88
Движение, определяемое дифференциальным уравнением третьего по-
рядка ........................................................ 109
Малые колебания с автопилотом............................... ЮЗ
Общий случай продольного движения самолета под действием малого
возмущения..................................................... Ю6
Уравнения продольных движений................................. 107
Решение системы уравнений.................................. 108
174
Стр.
Боковые движения самолета...................................... 123
Силы и моменты при боковом движении самолета............... 123
Балансировка в несимметричном полете....................... 130
Поперечная балансировка в случае необычного управления ... 133
Изолированное) движение крена . •.......................... 134
Простейшие случаи боковых движений......................... 139
Малые боковые движения самолета............................ 143
Большие боковые движения самолета.......................... 147
Общий случай бокового движения самолета под действием малого
возмущения . /........................................... 154
Взаимодействие продольных и боковых движений................... 159
Вынужденные колебания самолета............................. 162
Заключение..................................................... 172
Редактор Я М Котляр Техн редактор Н Н, Пискарева
Г-71012 Поди в печ. 16/Х 1951 г. Уч.-изд л 8,73. Форм бум. 60x92i/i«
51/2 б л. —11 печ. л Тираж 3000 экз. Цена 6 руб. Заказ 417/1337
Типография Оборонгиза
Замеченные опечатки
Стр. Строка Напечатано Должно быть
39 3 снцзу h=
49 10 сверху дУ да dY да
80 3 » (м«+«)
80 3 V Ь=^-25,5 L,=^-=25,5
82 8 V W t w ~V
82 13 V -Унач -Унач
101 15 V ВХ2
109 8
119 1 снизу 3 с2 3 С?
121 15 сверху (П2+ «з + 'г0Л4) (я2п|+п^п4)
155 1 снизу G,>9 Ct>9
в с. П ы ш н о в, Динамические свойства самолета