6 февраля 2001 года в возрасте 59 лет перестало биться сердце автора этой книги, профессора, доктора технических наук, директора Института интеллектуальных систем и технологий, академика Российской Академии Естественных наук, академика и вице-президента Академии инженерных наук РФ (АИН РФ), президента Северо-Западного Отделения АИН РФ (СЗО АИН РФ), заслуженного изобретателя РФ Анатолия Александровича ЕРОФЕЕВА.
Научный вклад характеризуется разработкой фундаментальной теории интеллектуальных систем на базе континуальных управляемых функциональных сред; теории процессов управления, возбуждения и стабилизации высокочастотных акустических волн и микровибраций в твердотельных пьезоэлектронных системах с использованием нелинейных явлений (на уровне открытия). Ерофеев А. А. развил теорию управления сложными многомерными, многосвязными резонансными объектами со смешанными видами модуляции полезного сигнала; разработал новые методы и способы управления пьезоэлектронных систем как нелинейных многосвязных систем с модуляцией и нелинейной оптимизацией процессов. Им разработан принципиально новый класс акусто-, опто- и пьезоэлектронных устройств и систем, а именно пьезотрансформаторы и источники электропитания на их основе; пьезодвигатели, пьезомикроманипуляторы, пьезоприводы с системами управления; сегнетопьезоэлектрические запоминающие устройства (ЗУ) вычислительной техники; измерительные пьезопреобразователи параметров движения и другие устройства и системы автоматики, вычислительной техники и радиоэлектроники.
Оригинальность основных идей, их научная новизна и значимость подтверждены полученными 110 патентами и авторскими свидетельствами на изобретения. Всего опубликовано 400 научных работ, из которых 24 — научные монографии.
УЧЕБНИК ДЛЯ ВУЗОВ
ТЕОРИЯ АВТОМАТИЧЕСКОГО
УПРАВАЕНИЯ
2-е издание, дополненное и переработанное
Рекомендовано Государственным комитетом Российской Федерации по высшему образованию в качестве учебника для студентов высших учебных заведений, обучающихся по направлениям “Автоматизация и управление ”, “Системный анализ и управление "
Санкт-Петербург 2003
ПОЛИТЕХНИКА
ИЗДАТЕЛЬСТВО
УДК 519.71(075.9); 681.5
ББК 32.965.4; 32.81я73
Е60
Федеральная программа книгоиздания России
Рецензенты: доктор технических наук профессор В. Б. Яковлев, доктор технических наук профессор Р. А. Нелепин
| библиотека
Ерофеев А. А.
Е60 Теория автоматического управления: Учебник для вузов. — 2-е изд., перераб. и доп. — СПб.: Политехника, 2003. — 302 с.: ил.
ISBN 5-7325-0529-6
Учебник соответствует программе курса лекций по теории автоматического управления для бакалавров. Содержит основные идеи и представления о классической и современной теории управления. Отражен образовательный стандарт курса в рамках концепции «модели—анализ—синтез». Изложение доведено до алгоритмических процедур и охватывает в едином плане теорию управления с ориентацией на многомерность—теорию всех типов систем (непрерывных, дискретных, в том числе и особых).
Учебник предназначен для студентов вузов, а также может быть полезен для инженеров и аспирантов.
УДК 519.71(075.9) 681.5
ББК 32.965.4; 32.81я73
ISBN 5-7325-0529-6
© Издательство «Политехника», 2002
ОТ АВТОРА
В данном учебнике представлена программа дисциплины «Теория автоматического управления» (ТАУ), разработанная для подготовки бакалавров по направлениям «Системный анализ и управление» и «Автоматизация и управление». Учебник построен на материале курсов лекций, читаемых автором на кафедре «Интеллектуальные системы управления» Санкт-Петербургского государственного технического университета (СПбГТУ).
В книге кратко изложены основные положения обобщенной теории управления, использующие в основном операторно-частотные методы, понятия передаточной функции одномерных и многомерных систем и соответствующие временные и частотные характеристики. Цель изложения — получить базовые представления о теории управления. Особенностью изложения является ориентация на многомерность. Книга имеет самостоятельное значение при обучении ТАУ по непрофильным направлениям и специальностям и является базовой вводной по отношению в целом к курсу ТАУ.
В данной книге не отражены в полном объеме разделы ТАУ по нелинейной теории, теории оптимальных, адаптивных, самонастраивающихся, игровых и интеллектуальных систем управления, так как эти разделы предполагается рассмотреть в отдельной книге.
В целом курс ТАУ содержит методы решения информационных проблем систем управления от простейших (одномерных, одноконтурных) до сложных иерархических систем с информационными технологиями управления (интеллектуальных систем управления).
Дисциплина «Теория автоматического управления» (или «Теория управления») является общепрофессиональной дисциплиной, входящей в состав федерального компонента стандарта по указанным выше направлениям. При реализации образовательного стандарта по данной дисциплине концепция ТАУ в основном отображена в виде «модели — анализ — синтез».
Книга базируется на научно-педагогическом опыте автора, а также является, как, впрочем, и большинство учебников, в известной мере компилятивной. В ее основе многочисленные учебники по ТАУ [1—12]. В изложении материала соблюдены традиции, разработанные такими представительными учеными СПбГТУ, авторами учебников по ТАУ, как акад. А. А. Воронов. проф. А. А. Первозванский, проф. Е. И. Юревич. Безусловно, данный учебник, как и любой другой, не может охватить всю информацию по ТАУ. Поэтому желающим более глубоко изучить современную теорию управления предлагается обращаться к специальной литературе, которая здесь частично представлена.
Основное предназначение учебника вытекает из первородного определения понятия высшая «школа» (SCHOLA): «Sapienter Cogitare Honeste, Operare Logui Argute» — «Мудро мыслить, благородно действовать, лаконично говорить» [Ян Амос Коменский (Komensky), 1592—1670 гг.]. Сегодня студент ВУЗа, завтра — специалист, профессионал должен помнить и претворять в жизнь Это, «...сеять разумное, доброе, вечное ...».
Автор глубоко благодарен всем сотрудникам (особенно Л. Н. Сергеевой) и студентам СПбГТУ, непосредственно помогавшим в работе над рукописью. В частности, большую практическую помощь при редактировании оказали С. А. Ерофеев и Е. П. Клинова.
Автор будет признателен всем читателям, приславшим свои замечания по книге в адрес СПбГТУ: 195251, г. Санкт-Петербург, ул. Политехническая, 29, СПбГТУ.
5
отзыв
на первое издание учебника А. А. Ерофеева «Теория автоматического управления» (Изд-во «Политехника», 1998 г.; 295 с.)
Современная цивилизация стремится к созданию информационного общества, а приоритетной и конечной целью использования информации является управление. В общем плане управление можно трактовать как организацию целенаправленного взаимодействия информации, энергии и вещества. Универсальность принципов управления позволяет применять их к объектам любой природы: техническим, технологическим, производственным, экономическим, экологическим и социальным. Автоматическое управление — это такая «чудотворная» технология, которая использует обратную связь для улучшения функционирования огромного числа объектов от паровых машин и космических станций до систем стабилизации кровяного давления и частоты работы сердца.
Дисциплина «Теория управления», читаемая в большинстве технических вузов, является одной из главных составляющих кибернетики. Она имеет явно выраженный интегративный характер и формирует у будущих специалистов системное мышление и целостное видение явлений мира техники, природы и общества, рассматривая их в постоянном взаимодействии, как различные стороны единого непрерывно изменяющегося во времени процесса. Предмет синтезирует знания студентов по естественным и общепрофессиональным наукам и дает примеры их конструктивного применения при изучении специальных дисциплин.
В свое время в нашей стране по теории автоматического управления был издан целый ряд замечательных монографий, учебных пособий и учебников. Однако написаны они были относительно давно, сохранившихся экземпляров в библиотеках стало недостаточно для обеспечения нормального учебного процесса. Необходимость в новых учебниках и учебных пособиях по теории автоматического управления назрела давно. Это, прежде всего, связано с тем, что дисциплина «Теория управления» входит в состав федеральной компоненты Государственных образовательных стандартов (ГОС) многих специальностей и направлений высшего профессионального образования.
Традиционое изложение теории управления требует большого объема книги. В большинстве учебников по «классической» теории управления значительное место уделяется материалам по математическим основам, а также способам, приемам и графоаналитическим методам упрощения вычислений, которые потеряли свою актуальность в связи с революционными достижениями и в области вычислительной техники и информатики. По этой же причине практика проектирования и реализация алгоритмов управления претерпела значительные изменения. Ряд книг по так называемой современной теории управления, как правило базируется на абстрактном, преимущественно формально-алгебраическом подходе, трудном для студентов технических вузов и затрудняющем изучение фундаментальных свойств и «механизмов» управления.
6
В настоящее время в связи с переходом к многоуровневой системе подготовки специалистов особую актуальность приобретает подготовка учебника по теории управления, имеющего сравнительно небольшой объем. Этот учебник необходим, прежде всего, для подготовки бакалавров и по существу содержит некоторые основы теории автоматического управления. Вполне очевидно, что основная трудность связана с отбором материала из того необходимого, относящегося как к «классической», так и «современной» теории управления. Здесь нет пока единой точки зрения и должны быть представлены самые различные отечественные и зарубежные школы.
Особенностью и достоинством рецензируемого учебника является его небольшой объем. Подобный учебник был написан академиком Е. П. Поповым в 1989 году и превратился в реликтовое издание. Необходимость издания таких кратких учебников назрела давно. В этом заинтересованы не только студенты, но и преподаватели этой дисциплины, а также широкий круг специалистов, осваивающих впервые теорию автоматического управления.
Автор излагает основные положения теории управления на базе линейных конечномерных стационарных моделей, использующих операторно-частотные методы, понятие передаточной функции и временные характеристики. Достоинством такого изложения является доступное студентам освоение информационно-алгоритмического подхода принятого в теории управления, отражающего причинно-следственный характер взаимодействия элементов и подсистем в сложных системах управления. В дальнейшем это существенно облегчает структурный анализ и синтез при проектировании автоматических и автоматизированных систем с элементами искусственного интеллекта, а также позволяет выбирать варианты действий при отказах и авариях в процессе эксплуатации.
К положительным особенностям рецензируемого учебника следует также отнести четкое разделение материалов, посвященных математическим моделям (главы 1, 2, 3) , анализу (главы 4, 6, 7) и синтезу (главы 8, 9, 10) систем управления. Автор стремился к сбалансированному изложению «классической» и «современной» теории управления, рассмотрев такие фундаментальные свойства систем, как устойчивость, чувствительность, инвариантность, управляемость, наблюдаемость. Главы 5 и 11 посвящены соответственно динамике систем автоматического управления при стационарных случайных воздействиях и особым системам управления.
Президент Международной ассоциации по управлению, автоматизации и информатике, председатель научно-методического совета Министерства образования РФ по направлению «А втоматизация и управление», заслуженный деятель науки и техники РФ, д. т. н., профессор В. Б. Яковлев.
ПРЕДИСЛОВИЕ
Теория автоматического управления (ТАУ) является базовой основой кибернетики или науки об управлении — одной из относительно молодых областей науки. Теория управления, хотя и прошла яркий путь своего развития, но в настоящее время продолжает интенсивно развиваться в сторону создания теории интеллектуальных систем управления — предельной формации парадигмы теории управления.
Примерно до шестидесятых годов XX века ТАУ имела сильную инженерную направленность и базировалась в своей основе преимущественно на рассмотрении процессов в системе «регулятор—объект управления» (ОУ). Как системная наука, ТАУ впитала в себя многие методы инженерных направлений (из области электро-, радиотехники, энергетики, связи и др.) и придала им существенное развитие. Создав собственные методы анализа и синтеза, прикладная ТАУ сыграла выдающуюся роль на этапе становления многих современных инженерных дисциплин. Прикладную или инженерную ТАУ сегодня именуют «классической», подчеркивая этим определенную завершенность форм ее развития как науки об управлении. Классическая ТАУ, преследуя цель «оптимизации в малом», решает задачи оптимизации и адаптации при малых отклонениях относительно заданного режима работы системы управления.
Основы «современной» ТАУ идеологически заложены в «классической» ТАУ и составляют с ней неразрывную связь. Современная ТАУ, преследуя цель «оптимизации в целом», применительно, в основном, к системно-сложным ОУ, превращается в совокупность методов и средств, осуществляющих интеллектуальное управление и составляющих основу теории интеллектуальных систем управления. Характерной обобщающей чертой последних является максимально эффективное использование всех ресурсов системы при многокритериальной оптимизации процессов в целом в условиях, как правило, частичной неопределенности информации о свойствах ОУ и среде его функционирования.
В ТАУ наиболее важным является понятие модели — определенной математической абстракции, характеризующей процессы любой природы — физической, биологической, экономической и др. Модель — это процесс, выраженный через связи между переменными входа, выхода и переменными состояния; переменные состояния аналогичны обобщенным координатам, а их пространство является фазовым. Обычно применяют векторно-матричное описание ОУ в пространстве состояний, что позволяет использовать единый математический аппарат для исследования различных непрерывных и дискретных систем. Именно такой обобщенный подход положен в основу данной книги, основное назначение которой — служить учебником по курсу ТАУ для технических университетов.
Президент СПбГТУ, академик РАН Ю. С. Васильев
8
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ АВТОМАТИЧЕСКИХ СИСТЕМ
Теория автоматического управления (ТАУ) относится к классу важнейших общеспециальных дисциплин, входящих во все типовые программы инженерного образования. ТАУ изучает процессы управления, методы исследования и основы проектирования систем автоматического управления (САУ). ТАУ изучает принципы построения САУ, закономерности протекающих в них процессов в целях построения работоспособных и точных САУ; методами ТАУ осуществляются анализ и синтез САУ.
История развития ТАУ непосредственно связана с историей создания различных высокоточных механизмов, из которых наиболее известными являются следующие: хронометры, часы, секундомеры; поплавковые регуляторы водяных часов; маятниковый регулятор хода часов (X. Гюйгенс, 1675 г.); поплавковый регулятор питания котла паровой машины (И. И. Ползунов, 1765 г.); центральный регулятор скорости паровой машины (Дж. Уатт, 1784 г.); первое программное устройство управления ткацким станком от перфокарты (узор на ковре) (Ж. Жаккар, 1808 г.); регуляторы (братьев С. и Ж. Понселе, 1830 г.) и др.
В настоящее время ТАУ представляет собой единую научную базу для решения задач управления объектами различной природы (физической, химической, биологической и т. п.), имеющую развитые методы исследования САУ— их анализа и синтеза (расчета и проектирования).
§ 1.1. ОСНОВНЫЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
Автоматика — отрасль науки и техники, охватывающая совокупность методов и технических средств, освобождающих человека от непосредственного выполнения операций по контролю и управлению производственными процессами и техническими устройствами. Автоматика — это древнегреческое слово, обозначающее самоусиление, са-модействие, от слов «ауто» — сам и «матос» — усиление.
Кибернетика — наука об общих закономерностях процессов управления в различных системах (в технике, химии, биологии и т. д.).
Техническая кибернетика — наука об общих закономерностях процессов управления в различных технических системах.
Автоматизация — замена умственной деятельности человека работой автоматических устройств.
Механизация — замена мускульной физической силы человека работой технических устройств.
Технические устройства — совокупность производственных машин и механизмов, выполняющих определенные функции по преобразованию энергии и совершению полезной работы, а также позволяю
9
щих в нужном направлении изменять технологический процесс, влияя
на его параметры и регулируя их в нужном направлении.
Управление — процесс, обеспечивающий необходимое по целевому назначению протекание процессов преобразования энергии, вещества и информации, поддержание работоспособности и безаварийности функционирования объекта путем сбора и обработки информации о состоянии объекта и внешней среды, выработки решений о воздействии на объект и их исполнение. Здесь цель является причиной управления и задающие воздействия определяются на основе знания цели.
Регулирование — частный случай управления, цель которого заключается в обеспечении близости текущих значений одной или нескольких координат объекта управления к их заданным значениям.
Объект управления (регулирования) — определенное техническое устройство (самолет, станок, паровая турбина и т. д.), для достижения результатов функционирования которого необходимы и допустимы специально организованные воздействия. Объект управления, на который подаются управляющие воздействия, можно назвать управляемым объектом. Объектами управления (ОУ) могут быть как отдельные объекты, выделенные по определенным признакам (например, конструктивным, функциональным), так и совокупности объектов — комплексы. В зависимости от свойств или назначения объектов могут быть выделены технические, технологические, экономические, организационные, социальные и другие объекты управления и комплексы.
Цель управления в технических системах — определенные значения или соотношения значений координат процессов в объекте управления или их изменение во времени, при которых обеспечивается достижение желаемых результатов функционирования объекта.
Управляющее воздействие — воздействие на объект управления,
предназначенное для достижения цели управления.
Система автоматического управления — система, состоящая из объекта управления и устройства управления, в которой автоматически выполняется заданный процесс.
Устройство управления (УУ) или регулятор — совокупность устройств, с помощью которых осуществляется управление главным технологическим параметром (физической величиной).
Регулятор или УУ в САУ воздействует на объект управления и обозначается в функциональных схемах в виде, представленном
ю
на рис. 1.1.
Регулятор вырабатывает управляющие (регулирующие) воздействия, которые, воздействуя на ОУ, поддерживают на заданном уровне или изменяют по определенному закону регулируемую величину.
Внешние воздействия — задающие воздействия g, определяющие требуемый закон (алгоритм) регулирования выходной величины ОУ, и возмущающие воздействия f, нарушающие требуемую функциональную связь между выходной величиной ОУ и задающим воздействием.
Выходной величиной (координатой) ОУ y(t) или регулируемой (управляемой) величиной является обычно главный технологический параметр (скорость, мощность, напряжение и т. д.).
Возмущение — внешнее воздействие на любое звено (элемент, подсистему) САУ, затрудняющее, как правило, достижение цели управления. Обычно выделяют основные возмущения, существенно влияющие на регулируемую величину, и помехи.
Задающее воздействие g(t) — воздействие на устройство управления, предназначенное для достижения цели управления.
Помехи — возмущения, вызывающие искажение сигналов в САУ, обычно незначительно влияющие на регулируемую величину и труднодоступные для измерения n(t).
СА У разомкнутые и замкнутые. Разомкнутые САУ — это системы, в которых заданное значение выходной величины ОУ достигается при помощи регулирующего (исполнительного) органа, устанавливаемого в определенное положение; при этом значение выходной величины ОУ может существенно отклоняться от его заданного значения в силу влияния внешних параметров окружающей среды, а также изменения внутренних свойств ОУ, параметров САУ. Вследствие этого возникает необходимость автоматического поддержания выходной величины на заданном уровне; эта задача решается с помощью замкнутой САУ. В случаях, когда не требуется высокая точность поддержания заданного значения выходной величины САУ y(t), замкнутая система может применяться с использованием человека-оператора.
В замкнутой САУ так же, как и в разомкнутой системе, производится измерение текущего значения y(t). Однако здесь заданное значение сравнивается с текущим значением y(t), поступающим через элемент обратной связи (ЭОС) на специальный элемент сравнения (ЭС), который вырабатывает сигнал ошибки САУ; последний обычно усиливается в САУ до значения, достаточного для управления исполнительным механизмом (ИМ), приводящим в движение регулирующий орган ОУ. Следовательно, замкнутая САУ — это система с обратной связью.
Обратная связь в САУ — зависимость y(t) от текущих воздействий на ОУ и от его состояния, обусловленного предшествующими воздействиями на объект. Обратная связь может быть естественной (присущей объекту) или искусственно организуемой. При этом различают отрицательную обратную связь (ООС) и положительную обратную связь (ПОС) как обратные связи, действующие в первом случае в сторону уменьшения, а во втором — в сторону увеличения отклонений текущих значений координат объекта от их предшествующих значений. Следовательно, ООС позволяет строить наиболее точные САУ, так как несет в себе информацию обо всех изменениях регулируемой
11
величины; ПОС служит для изменения внутренних свойств отдельных звеньев САУ.
Сигнал ошибки (рассогласования) в замкнутой САУ определяется как разность между заданным g(t) и текущим y(t) значениями регулируемой величины e(Z) = ± (g(Z) - у(/)]; может принимать три значения: е (0 = 0 (состояние покоя САУ) и e(Z)$ 0 (переходной режим САУ).
§1.2. ТИПОВАЯ ФУНКЦИОНАЛЬНАЯ СХЕМА САУ
Функциональная схема САУ представляет собой совокупность соединенных определенным образом элементов (звеньев, блоков) системы по выполняемым ими функциям, независимо от их физической природы.
Типовые функциональные схемы САУ представлены на рис. 1.2, где приняты следующие обозначения (см. рис. 1.2, а):
33 — задающий элемент; служит для задания определенного закона (алгоритма) управления выходной величины; обычно это потенциометры, кулачки, магнитные ленты, проволока, нивелир, луч света и т. п.;
ЭГОС — элемент главной обратной связи (чувствительный элемент, первичный преобразователь — датчик); служит для измерения текущего значения регулируемой величины y(t) и преобразования ее в другого рода yoc(z), удобную для технической реализации схемы;
ЭС — элемент сравнения (выявляющий элемент); служит для выявления разницы между заданным и текущим значениями регулируемой величины и формирует полезный сигнал (сигнал ошибки, сигнал рассогласования);
ППЭ — последовательный преобразующий элемент; служит для преобразования сигнала, поступающего с элемента сравнения, в такой сигнал, который позволяет УУ (регулятору) придать системе желаемые динамические свойства;
УЗ — усилительный элемент; служит для усиления поступающего сигнала до значения, достаточного для приведения в действие исполнительного элемента — ИЗ (механизма);
ИЗ — исполнительный элемент; служит для перемещения регулирующего органа ОУ в направлении компенсации сигнала рассогласования, преобразованного УУ (регулятором);
РО — рабочий (регулирующий) орган;
ОУ— объект управления — техническое устройство, преобразующее один вид энергии в другой и совершающее полезную работу;
ПЗВ — преобразовательный элемент возмущения; служит для преобразования основного возмущения в сигнал, воздействующий на УУ;
ЭМОС — элемент местной обратной связи; служит для придания системе требуемых динамических свойств;
ЧЭ — чувствительный элемент; служит для измерения основного возмущения.
12
г)
Рис. 1.2
СА У условно состоит из двух каналов: канал I — канал прямой связи, содержит все элементы, преобразующие сигнал в одном (прямом) направлении (от ЗЭ к ОУ); канал II — канал обратной связи, несет информацию о регулируемых параметрах для сравнения их на входе системы (от ОУ к ЭС).
Типичными элементами САУ, относящимися к информационной и энергетической части, являются: измерители различных физических величин, называемые чувствительными элементами или датчиками, вводящие в систему управления информацию о задачах управления
13
и результатах управления; функциональные преобразователи или вычислительные устройства (блоки хранения и преобразования информации), осуществляющие определение параметров управления и заданное их преобразование и вырабатывающие сигналы управления; исполнительные элементы (устройства), непосредственно осуществляющие управление.
Совокупность элементов функциональной схемы образует замкнутый контур, охватывающий объект управления. Поэтому САУ является замкнутой или системой управления с обратной связью. На рис. 1.2, б—г приведены упрощенные варианты обозначения функциональных схем САУ.
§ 1.3.	ПРИНЦИПЫ УПРАВЛЕНИЯ И КЛАССИФИКАЦИЯ САУ
В рассматриваемой САУ (см. рис. 1.2) в качестве основного применяется принцип управления по отклонению, т. е. с помощью чувствительного элемента измеряется текущее значение регулируемого параметра ОУ и определяется в элементе сравнения (ЭС) значение отклонения регулируемого параметра от заданного е(?) = g(z) - уос(0-В САУ, кроме того, применяется также принцип управления по возмущению и комбинированный принцип (объединяющий оба принципа) (см. рис. 1.2, а).
Если в САУ отдельно (автономно) применяется только принцип управления по возмущению, то САУ при этом считается разомкнутой (по цепи ЭГОС). Эти САУ называются инвариантными по возмущению или просто инвариантными САУ (рис. 1.3, а, б). Здесь на
Рис. 1.3
14
рис. 1.3, а представлен развернутый, а на рис. 1.3, б — упрощенный вариант обозначения схемы САУ.
САУ, работающие по принципу управления по отклонению, имеют преимущества перед САУ, работающими по принципу управления по возмущению, так как в них ведется учет всех возмущений, прикладываемых к САУ в любой ее точке, т. е. на любом из элементов САУ, и, кроме того, достигается высокая точность поддержания заданного значения регулируемой величины, а при управлении по принципу возмущения такая точность принципиально не может быть получена.
Комбинированный принцип управления объединяет оба принципа: управление по отклонению и по возмущению; этот принцип называют также компаундированным по возмущению.
Исторически сначала были разработаны первые САУ, работающие по отклонению, а затем вторые. Впервые САУ, работающая по отклонению, была внедрена И. Ползуновым в 1765 г. для регулирования объема воды в котлах (поплавковый регулятор). Принцип управления по возмущению был впервые применен Понселе в 1830 г. для регулирования скорости паровой машины (в центральном регуляторе скорости Уатта) и был впоследствии назван принципом Понселе—Чиколева (1874 г.). Русский ученый Чиколев впервые применил этот принцип для регулирования тока в осветительной нагрузке от генератора постоянного тока с независимым возбуждением.
Классификационные признаки САУ, характеризующие понятия, относящиеся к принципам управления, можно выделить на основе анализа факторов, определяющих алгоритм или закон управления в САУ, т. е. выработку и реализацию управляющих воздействий. Так, по степени использования информации о состояниях ОУ при управлении САУ подразделяют на САУ с обратной связью и без обратной связи; по степени использования при управлении информации о возмущениях — САУ с управлением по возмущению или объединеннокомбинированные САУ. По степени использования при управлении информации о параметрах и структуре ОУ САУ подразделяют на адаптивные САУ: беспоисковые, поисковые, с идентификацией; САУ с переменной структурой; неадаптивные САУ. По степени определенности (заданности) преобразования координат в системе управления — САУ детерминированные или стохастические САУ. Вид математической модели преобразований координат в САУ определяет САУ как линейные и нелинейные (релейные, логические и др.); вид управляющих воздействий — САУ аналоговые (непрерывные) и дискретные (прерывистые, импульсные, цифровые); по степени участия человека-оператора в управлении — САУ ручные, автоматические и автоматизированные (человек-оператор в контуре управления).
Необходимо отметить, что многие системы управления создаются на основе комплексирования нескольких принципов управления, поэтому допустимы составные определения, например, как цифровое управление с идентификацией и др.
15
Рассмотрим более детально принципы управления, связанные с тем или иным признаком классификации САУ.
Классификация систем автоматического управления осуществляется по следующим признакам.
1.	По виду задающего сигнала различают:
системы автоматической стабилизации, задающий сигнал в которых g(t) = const (/), а выходной параметр САУ поддерживается на уровне заданного значения (у(0 = const (/));
системы программного управления, задающий сигнал в которых зависит от задающей программы; например, g(t) = F(t) и соответствует программе задания угла наклона оси ракеты при запуске с переходом от перпендикулярного к горизонтальному движению ракеты;
следящие системы, изменение задающего сигнала в которых происходит по случайному закону, заданному тем или иным способом [например, угол поворота выходного вала следящей системы должен соответствовать задающему углу поворота a (t), здесь ошибка е (г) = а (/) - р (г)]. Это различные системы наведения с РЛС, системы телеуправления и самонаведения, автопилоты, целеуказатели курса летательных аппаратов (ЛА) с РЛС и другие САУ движением летательных аппаратов. Например, автопилот, когда и311д = отек, где V — угол тангажа, характеризующий отклонение горизонтальной оси ЛА в вертикальной плоскости; реально в автопилоте учитываются обычно три взаимодействия ЛА: по тангажу о, по курсу 1|/ (управление движением в горизонтальной плоскости) и по крену 9 (управление поворотом ЛА вокруг собственной оси), здесь главный ЧЭ — гироскоп, сохраняющий неизменное направление в пространстве.
2.	По виду (топологии) функциональной схемы (по степени связности процессов в объекте и степени сложности структуры объекта управления) различают:
одноконтурные САУ — с одной регулируемой величиной (системы включают в себя один канал обратной связи); многоконтурные САУ — с одной регулируемой величиной (включают в себя один канал главной обратной связи и несколько каналов местной обратной связи) и многоконтурные САУ с несколькими регулируемыми величинами (содержат несколько каналов главных обратных связей и также могут быть местные обратные связи) — многомерные САУ; последний класс САУ подразделяют на (рис. 1.4, а):
многоконтурные несвязанные системы — это такие системы, в которых УУ (регуляторы) не связаны между собой вне объекта управления;
многоконтурные зависимые системы — это системы, в которых изменение одной величины приводит к изменению других регулируемых величин;
многоконтурные независимые системы — это такие системы, в которых изменение одной регулируемой величины не приводит к изменению других регулируемых величин;
многоконтурные связанные системы — это такие системы, в которых УУ (регуляторы) связаны между собой вне объекта управления (рис. 1.4, б);
16
mi югоконтурные автономные связанные системы—это системы, в которых изменение одной регулируемой величины не приводит к изменению других регулируемых величин (обычно за счет ис-кхситвенных компенсирующих связей);
многоконтурные неавтономные связанные системы — ио системы, в которых изменение одной регулируемой величины ведетк изменению других] югулируемых величин (рис. 1.4. в).
3.	По воздействию чув-с пштельного (измерительного) элемента на регулирующий орган (РО) различают:
система прямого управления (например, с регулятором И. Ползунова), когда непо-сре. югвенно (прямо) происходи 1 передача воздействия чув-спштельного элемента (поплавка) на РО (задвижку). 11елостатки таких систем: необходимо наличие достаточно большого количества энергии для передачи воздействия ЧЭ на РО; такой энергии часто не имеется. Кроме того, реакция РО на ЧЭ снижает его чувствительность и значительно уменьшает точность работы системы. Поэтому в системах, где необходима повышенная точность к управлению и нет достаточной энергии для прямого регулирования, применяют косвенное управление.
4.	По виду зависимости регулируемой величины от внешнего воздействия различают:
Рис. 1.4
2 А. А. Ерофеев
17
статические САУ — это системы, в которых при возмущающем воздействии регулируемая величина у (t) по окончании переходного процесса принимает значения, пропорциональные возмущающему воздействию. Следовательно, статические САУ характеризуются зависимостью выходной величины от внешнего возмущающего воздействия; статическую характеристику САУ оценивают коэффициентом неравномерности, или статизмом, который вычисляется по формуле
§ = -^п1ах ~ -Утш _ Л'тах _ ।
J^min J’min
Достаточными признаками для отнесения систем к классу статических являются следующие: определенному значению внешнего воздействия соответствует одно определенное значение регулируемой величины; регулирующий орган занимает строго соответствующее положение по отношению к регулируемой величине; между чувствительным элементом и ОУ в САУ включаются статические звенья. Статическое звено САУ — это звено, между выходной и входной величинами которого существует строго определенная функциональная связь; графически эта связь является статической характеристикой звена у = F(x);
астатические САУ — это системы, в которых при внешнем воздействии f и окончании переходного процесса значение регулируемой величины устанавливается равным заданному, т. е. в установившемся режиме разность между заданным и текущим значениями регулируемой величины равна нулю (е = 0). Достаточными признаками астатических систем являются следующие положения: значение регулируемой величины равно заданному независимо от внешнего воздействия; определенному значению регулируемой величины соответствует несколько положений регулирующего органа; между чувствительным элементом и ОУ находится одно или несколько астатических звеньев. Под астатическим звеном понимают звено, в котором выходная величина в установившемся режиме находится в неустойчивом (безразличном) положении равновесия; при внешнем воздействии выходная величина астатического звена выходит из неустойчивого (неопределенного) рановесия и изменяется по строго определенному функциональному закону; характеристика астатического звена имеет статизм 5 = 0.
5.	По виду воздействия регулирующего органа (или ИЭ, УУ) на объект управления различают:
системы непрерывного управления (аналоговые), в которых между выходной и входной величинами существует определенная непрерывная функциональная связь у = F(x), где функция является аналитической непрерывной функцией, и системы прерывистого управления (дискретные), в которых функция F(g) является дискретной. Последние подразделяются на системы релейного действия, импульсные и цифровые системы.
В системах релейного действия в структуре САУ имеются один или несколько релейных элементов — РЭ (элементов порогового действия, типа 0,1). У этих элементов при входном сигнале, меньшем
18
Ucp (Ucp — напряжение срабатывания), РЭ отключен и его контакты в цепи, например ИЭ, разомкнуты. При входном сигнале, большем [/ср, РЭ срабатывает и замыкает свой контакт; при этом ИЭ развивает некоторый полезный момент М для перемещения РО ОУ. При уменьшении входного сигнала ниже напряжения отпускания Uorn контакт РЭ в цепи ИЭ размыкается и его момент М = 0.
Импульсные САУ характеризуются наличием импульсного элемента в схеме, выходная величина которого представляет собой последовательность импульсов. Амплитуда, длительность и частота следования импульсов являются функцией входной величины. Существует много модификаций импульсных САУ, различающихся по принципу осуществления модуляции входного сигнала: времяимпульсные, широтно-импульсные, амплитудно-импульсные и САУ с комбинацией этих модуляций.
Цифровые САУ — это САУ, в контуре управления которых для реализации алгоритмов управления встроены ЭВМ или цифровые вычислительные устройства.
Системы комбинированного типа: аналого-дискретные, дискретно-аналоговые или цифроаналоговые, аналого-цифровые — представляют собой смешанную реализацию рассмотренных выше структур.
6.	По характеру звеньев, включаемых в САУ, системы делятся на линейные и нелинейные.
Линейные системы включают в себя линейные звенья, характеристики которых имеют следующий вид: у = а+кх (УаеЯ), где к =(y-d)/x = tgq> —статический коэффициент передачи звена.
В линейных системах между выходной y(t) и входной x(t), g(t) величинами существует линейная функциональная зависимость (в статическом и динамическом режимах работы). Процессы, происходящие в этих системах, описываются линейными дифференциальными уравнениями.
В зависимости от вида дифференциального уравнения линейные системы подразделяются на следующие типы:
1) обыкновенные САУ, описываемые обыкновенными линейными дифференциальными уравнениями (уравнениями типа «вход-выход»):
2 d2у dy ,	, dx ,
do —у + О] — + у = к}х + к2 -- + k3f(t); dt dt	dt
(a^p2 +alp+\)y = (ki + k2p)x + k3f(t)
или в переменных состояния:
х = Ах + Ви;
у = Сх + Du,
где А, В, С, D — матрицы; и — вектор управления;
2) САУ с распределенными параметрами, описываемые дифференциальными уравнениями в частных производных, например:
19
2*
ди _^di di
dx dt’ dx dt’
где x — пространственная координата;
3)	системы с запаздыванием, описываемые линейными дифференциальными уравнениями с запаздыванием:
dy , ,	.
«о +У = к1х(1-т), at
где т —- время чистого запаздывания;
4)	системы с переменными параметрами; коэффициенты и матрицы коэффициентов в уравнениях являются зависимыми от времени — это нестационарные системы; такие системы описываются, например, следующими уравнениями:
х = A(t)x+B(t)w,
у = C(t)x + D(t)u или
dnv	dmf
a^t) ; +... + «„(Оу = WJ + - + b'^ dt	dt
все системы с постоянными параметрами [ а, = const (/) ] называются стационарными; при а, = a,(f) — САУ называются нестационарными;
5)	импульсные (и цифровые) системы, описываемые линейными разностными уравнениями (уравнениями в конечных разностях). Здесь используют прямые разности: А у>[и Л = у[(« + 1) Г] - у[пТ]; обратные: Уу[пТ} = у[пТ\-у[(п-\)Т\ —первого и более высоких порядков: а2Я«г] ... \ку[пТ]-, ч2у\пТ]... vAy[n?l; vAy[«T] = AAy[(«-^)]-
Уравнения САУ имеют вид:
«оА^[н7]+«1Аму[лЛ+ - +^y[«n=V[«n 2(А)Я«Л= а^ку[ПТ\+а^кАу[пТ\+ ... +aky[nT\ = bQf[nT\- QW){nT\ = ДУ) ДиТ\ или (уравнения в переменных состояния):
х[(и + 1)Т] = Ах[пТ\ + Ви[пТ}-, y[nT] = Cx{nT\+Du[nT\.
Нелинейные С А У включают в себя одно или несколько звеньев с нелинейными характеристиками: y = F](x); / = F2(x,x); y = F„(x, х, ..., у) и т. д., где F— нелинейная функция (рис. 1.5).
Нелинейные системы — это также любые системы, в которых нарушается линейность уравнений динамики.
Все реальные САУ обычно являются нелинейными, но САУ с несущественной нелинейностью характеристик -— линеаризуют. Несущественно нелинейные характеристики показаны на рис. 1.5, а (1, 2); они
20
не содержат разрывов непрерывности. Существенно нелинейные характеристики содержат изломы, разрывы непрерывности первого рода и т. д. [показаны на рис. 1.5, а (3), б, в, г].
Теория линейных систем в настоящее время полностью разработана, поэтому целесообразно сводить там, где это возможно, нелинейные САУ к линейным, используя методы линеаризации.
Однако нелинейные САУ богаче по своим возможностям, в том числе и в смысле улучшения качества процессов.
7. По степени самонастройки, адаптации, оптимизации и интеллектуализации различают:
Экстремальные системы (системы с самонастройкой программы) — это САУ, в которых значение регулируемой величины автоматически поддерживается на экстремальном значении (максимуме, минимуме) при различных значениях возмущающих воздействий f(t), заранее неизвестных (рис. 1.6). Здесь программа изменения y(t) определяется автоматически в процессе работы САУ. В САУ добавлено специальное устройство автоматического поиска экстремума (УАПЭ), которое на основе анализа определенных характеристик ОУ выдает на вход САУ воздействие g(t) = g3. В результате УУ (регулятор)
21
Рис. 1.6
вырабатывает управляющее воздействие р(?) или u(t) определяющее оптимальное поведение САУ при изменении y(t), например работу САУ на экстремальном значении у=уп1ах (рис. 1.7). Здесь на рис. 1.7 представлены различные типы экстремальных характеристик ОУ вида У = Ф (/) (рис. 1.7, а) или у = <р (х) (рис. 1.7, б, в), где/, х — соответственно возмущающее и управляющее воздействия; gradF = 0 нэ уЭКС1р.
Обычно при проектировании САУ всегда преследуют экстремальную цель управления. Экстремальные системы по существу являются системами автоматической стабилизации выходной величины уэклр = const (0 или экстремума некоторого функционала J = F(y, х, у, х, ..., /). В последнем случае САУ решают не только задачу экстремального управления, но и задачу оптимизации, т. е. являются оптимальными САУ.
Системы с самонастройкой параметров (собственно самонастраивающиеся системы) — это системы, в которых автоматически в зависимости от переменных заранее неизвестных внешних условий (по / g) устанавливаются оптимальные значения параметров системы. Следовательно, УУ работает таким образом, чтобы регулируемая величина на выходе САУ изменялась по наивыгоднейшему (оптимальному) закону в соответствии с априори заданным критерием качества — функционалом J. Под функционалом J могут рассматриваться сложные функции полезности, максимума прибыли, минимума потерь или минимума расхода энергии при работе САУ и т. п.
22
Рис. 1.8
В роли J могут быть использованы и простые оценки качества процессов, например: минимум длительности переходного процесса /пп =min или минимум среднеквадратичной ошибки управления е 2 =min и т. п. Здесь в схему САУ входит устройство самонастройки (УСН) — анализатор качества или оптимизатор, который определяет отклонение характеристик замкнутой САУ от желаемых (эталонных) и в зависимости от состояния системы — некоторой функции F(e, g, z, у) — воздействует на УУ. Следовательно, такие системы — это системы с самооптимизацией или иначе, адаптивные САУ со стабилизацией и с оптимизацией качества (оптимальные по быстродействию, по точности, по технико-экономическим показателям и т. п.). Упрощенная функциональная схема такой САУ приведена на рис. 1.8.
Системы с самонастройкой структуры — это собственно самоорганизующиеся или самоалгоритмизирующиеся системы, в которых в зависимости от переменных, заранее не определенных, внешних условий производится оптимальная настройка структуры системы таким образом, чтобы регулируемая величина на выходе изменялась по наивыгоднейшему (оптимальному) закону в соответствии с заданным критерием качестваДв простейшем случае, например, минимумом ошибки управления е2 =min). Автоматический поиск наивыгоднейшей (оптимальной) структуры САУ дает возможность решать более сложные задачи при управлении сложными ОУ — комплексами (рис. 1.9).
На рис. 1.9 идентификатор производит сбор и обработку информации о работе ОУ; САУ строится как система принятия решений об управлении сложным ОУ.
Рис. 1.9
23
Системы комбинированного типа с самонастройкой структуры и параметров, объединяющие в своем составе определенные идейные фрагменты рассмотренных структур. Все эти САУ являются также и оптимальными САУ.
Интеллектуальные системы управления (ИСУ). Необходимо отметить, что в классическом понимании САУ, включающие разнообразные ОУ, воспринимались как системы, процессы в которых принципиально прогнозируемы и управляемы. Ошибки в управлении и подчас неработоспособность систем рассматривали часто как недостаток знаний (обычно об ОУ). Наращивание объема знаний в процессе эксплуатации САУ (принцип обучения и самообучения) было отражено как раз в создании обучающихся адаптивных САУ с гибкими алгоритмами управления и идентификации ОУ и процедурами принятия решений. Обучающиеся адаптивные САУ — это системы с накоплением, запоминанием и анализом информации о поведении сложного ОУ, среды функционирования и САУ в целом и изменении алгоритмов управления в зависимости от опыта и условий работы. Область применения ИСУ — управление сложными объектами с плохо изученной динамикой, свойства, условия работы которых априорно недостаточно известны, существенно непостоянны (с дрейфом параметров, характеристик ОУ и среды функционирования). Это, в частности, и открытые неравновесные системы, в которых постоянно идут процессы организации и самоорганизации, когда после некоторых периодов количественного изменения своих параметров они могут качественно (скачкообразно, «катастрофично») изменять свои характеристики.
ИСУ первого поколения — это адаптивные или самоприспосаб-ливающиеся системы, обладающие способностью приспосабливаться к изменению внешних условий, а также улучшать свою работу по мере накопления опыта (свойство самообучения). В этих условиях обыкновенные, неадаптивные САУ неработоспособны либо работают неудовлетворительно, требуя постоянного квалифицированного наблюдения.
ИСУ нового поколения строятся как самообучающиеся, самонастраивающиеся системы с гибкими процедурами принятия решений об управлении (нечеткое управление), как системы, основанные на знаниях и формирующие новые знания в процессе управления и функционирования. Разновидности ИСУ строятся и как экспертные системы (ЭС), встроенные в контур управления, работающие, в частности, в интерактивном режиме с лицом, принимающим решение (ЭС, как интеллектуальная ОС). Экспертные ИСУ представляют собой развитые структуры: от интеллектуальных датчиков до программных систем с выработкой лингвистических управляющих воздействий. В задачи ИСУ входят: экспертная оценка ситуации управления (на уровне машинного планирования эксперимента); синтез УУ; оценка информационной чувствительности и ранжирование каналов управления; синтез управляющих воздействий, в том числе и в виде функ
24
ций принадлежности с лингвистическими переменными L (типа >, <, «норма» и т. д.)1; анализ среды функционирования; планирование траекторий; использование логико-лингвистических систем и т. п.
В ИСУ фрагментарно и комплексно используются современные достижения систем искусственного интеллекта, продукционные способности во многих направлениях, автоматическое и адаптационное программирование, алгоритмизация и т. д. В целом интеллектуальные системы управления можно оценивать на современном этапе как «разумные» системы, оптимизирующие процессы управления, эффективно работающие при решении задач управления сложными объектами в условиях неопределенной информации о свойствах ОУ, среды функционирования и т. п. Возникновение ИСУ предопределило развитие нового направления в теории управления, а именно разработки прикладных методов искусственного интеллекта (ИИ) и создания на их основе методологии построения САУ, ориентированных на разработку и использование знаний и развитие теории нечетких моделей динамических управляемых систем, теории нечетких алгоритмов и регуляторов.
Особенно эффективными для целей управления оказались открытые системы, способные с течением времени совершенствовать свое поведение. Прогресс в области разработки экспертных систем (ЭС) привел к созданию включенных в систему управления активных ЭС. С развитием ИСУ развивались и аппаратные средства поддержки процессов, протекающих в них: специальные процессоры поддержки языков высокого уровня (ЛИСП, ПРОЛОГ); специальные процессоры для интеллектуальных баз данных и баз знаний (в том числе и для логического вывода, основанного на знаниях); специальные процессоры для интеллектуального интерфейса (обработка изображений, текста, речи); аппаратно реализованные средства обработки нечеткой и лингвистической информации (нечеткие процессоры, «Fuzzy Processors»}, нечеткие компьютеры («Fuzzy Computers») [15-18].
Общесистемный подход к решению таких задач привел к необходимости формирования теории ИСУ на стыке искусственного интеллекта, исследования операций и ТАУ. Основной предмет исследования теории ИСУ — разработка конкретных структур САУ в рамках общей концепции архитектуры ИСУ, претендующей на интеллектуальное поведение при решении различных задач. Структура ИСУ, в частности, может соответствовать уровням, упорядоченным в соответствии с базовым принципом IPDI (Increase of Precision with Decrease of Intelligence): точность управления тем выше, чем меньше интеллектуальность системы, и наоборот, точность управления тем ниже, чем выше
'Например, L= {NB,NM,NO, РО, PS, PM, РВ},где N н> «-»;Р н> «+»;В н» «>»; М ь» «норма»; S «<»; Он «~ О »; функции принадлежности: S-; Z- типа, треугольные, трапецеидальные, колоколообразные и т. д. Перевод «четких» знаний (#) в L (—> ) соответствует операции «фазификации», a L — в «четкие» знания — «дефазификации»; (t-> —знак соответствия).
25
интеллектуальность данного уровня иерархии системы. Класс ИСУ соответствует следующим пяти принципам:
—	наличие взаимодействия управляющей системы с реальным внешним миром с использованием информационных каналов связи (данный принцип подчеркивает непосредственную связь интеллектуальных систем с внешним миром); ИСУ получают из него знания и влияют на него. Выполнение этого принципа позволяет организовывать канал связи для извлечения знаний и организации целесообразного поведения;
—	принципиальная открытость системы с целью повышения интеллектуальности и совершенствования собственного поведения (открытость системы обеспечивается наличием самонастройки, самоорганизации и самообучения). Система знаний ИСУ состоит из двух частей: поступающие знания и проверенные знания. Этот принцип позволяет организовывать пополнение и приобретение знаний;
—	наличие механизмов прогноза изменений среды функционирования и собственного поведения системы в динамически меняющемся внешнем мире. В соответствии с этим принципом ИСУ не полностью интеллектуальна, если она не обладает возможностью прогноза изменений внешнего мира и собственного поведения (система без прогноза может попасть в критическую ситуацию);
— наличие у системы структуры построения, соответствующей принципу IPDI, что намечает пути построения сложных ИСУ в случае, когда неточность знаний о модели ОУ или о его поведении может быть скомпенсирована за счет повышения интеллектуальности создаваемой системы или соответствующих алгоритмов управления;
— сохранение функционирования (возможно, с некоторой потерей качества) при разрыве связей или потере управляющих воздействий от вышестоящих уровней иерархии ИСУ. Этот принцип определяет лишь потерю интеллектуальности, но не прекращая функционирования при отказах в работе высших уровней иерархии системы. Сохранение автономного функционирования в рамках более простого поведения системы очень важно для автономно функционирующих систем в реальном внешнем мире.
Исходя из изложенного, для ИСУ вводят понятия интеллектуальности «в малом» и интеллектуальности «в большом». ИСУ, организованная в соответствии со всеми пятью принципами, называется интеллектуальной «в большом». Такие системы должны иметь иерархическую структуру с несколькими рангами: обучения, самоорганизации (настройка), прогноза событий, работы с базой знаний и базой событий, формирования решений, планирования операций по реализации решения, адаптации, исполнительного уровня. Самый нижний уровень таких систем занимают традиционные САУ; ИСУ, структурно не организованные в соответствии с перечисленными пятью принципами, но использующие при функционировании знания для преодоления неопределенности входной информации, модели управляемого
26
объекта или его поведения, есть системы, интеллектуальные «в малом». Примером таких систем могут служить САУ с нечеткими регуляторами (контроллерами). САУ с нечетким регулятором называют иерархически двухуровневую систему управления, «интеллектуальную в малом», на нижнем уровне которой находится, например, традиционный ПИД-регулятор, а на верхнем — база знаний (БЗ) и устройства перевода в лингвистические и четкие знания (с помощью лингвистических правил-знаний).
В зависимости от типа используемого регулятора и способов формирования базы знаний (и особенностей механизма вывода) нечеткий регулятор может быть адаптивным, самообучающимся и нечетким регулятором с активной экспертной системой. Если в структуре нечеткого регулятора на нижнем уровне иерархии используются адаптивные, самоорганизующие ПИД-регуляторы, то улучшаются функционирование и динамические характеристики исполнительного уровня, но не затрагиваются вопросы интеллектуализации его поведения. Изменение способов формирования базы знаний дает возможность повысить интеллектуальный уровень системы вплоть до «интеллектуальности в большом».
Интеллектуальные или нечеткие алгоритмы управления (НАУ) представляются набором нечетких правил, результат которых на выходе нечеткого регулятора (HP) не определенное значение (число), а нечеткое множество, описываемые посредством некоторых функций принадлежности логической переменной. НАУ являются принципиально нелинейными, базирующимися на эмпирических знаниях в виде некоторой совокупности правил (таблиц решений). Для вывода правил используются различные методы, в частности метод «максимума-минимума». Машина вывода (МВ) формирует НАУ по цепи БЗ-МВ. В соответствии с нечеткими алгоритмами на выходе HP формируются нечеткие указания (термы), содержащие рекомендации, основанные на логическом подходе к моделированию процессов, происходящих в сложном ОУ с учетом воздействий на него среды функционирования. Логические модели работы ОУ содержат основные понятия — ее атрибуты: часть из них составляют входные воздействия (х), часть — функции, определяющие состояния ОУ (у), между которыми непосредственно (или через промежуточные переменные) устанавливается функциональная взаимосвязь в виде логических функций L с учетом действия внешних возмущений (/). Логические функции, относящиеся к определенному блоку свойств ОУ, обычно формируют в виде таблиц, отображающих функциональные зависимости — табличные функции, например y = max(xb х2). Сборка модели функционирования сложного ОУ (композиция) производится из блоков посредством создания цельной иерархической функциональной сети (схемы) ОУ [15-18].
ИСУ обеспечивают эффективное управление в широком диапазоне начальных условий, с качеством не хуже или на уровне линейных САУ, и HP не надо подстраивать в процессе работы (робастное уп
27
равление). Таким образом, в ИСУ реализуются принципиально новые и более эффективные алгоритмы с применением нечеткой логики управления и искусственных нейронных сетей (ИНС). ИНС обладают таким полезным свойством, как способность к обучению, что делает универсальным их применение в различных сложных условиях функционирования ОУ. Обычно используют ИНС прямого распространения (персептроны) и сети Хопфилда; они входят в HP, служат фактически БЗ, содержащей информацию о желаемом поведении системы. Например, ИНС прямого распространения с сигмоидальной функцией нелинейности нейрона. В совокупности работа ИСУ с НАУ позволяет достаточно точно имитировать действия эксперта (человека-оператора) в процессе принятия решений при управлении сложными ОУ.
Функционирование ИСУ, например в автоматическом режиме для целей автономной навигации космических ЛА1, характеризуется выработкой и коррекцией как целей и алгоритмов управления («внутри» ИСУ), так и «оптимальным» построением структуры самой ИСУ с наивыгоднейшим процессом управления и поведения в целом с учетом текущего определения свойств (моделей) сложного ОУ и параметров среды функционирования («внешнего мира»). Применение в ИСУ интеллектуальных технологий управления с комплексным использованием достижений ТАУ, ИИ, нейрофизиологии определяет разработку новых методов и средств управления, например параллельных нечетных алгоритмов управления, динамических ЭС-адаптивных регуляторов; нейросетевых, транспьютерных, сигнальных нечетких регуляторов и т. д.
Теория ИСУ в ТАУ является, по-видимому, предельной формацией парадигмы теории управления. С точки зрения ТАУ, ИСУ — это многомерные, многосвязные системы со многими х, f, й, у, сильными возмущениями, нелинейностями, с неточностью математического описания, возможностью использования нечетких знаний типа «knowhow», лингвистического описания процессов, с обработкой большого объема информации в реальном времени. Теория уделяет значительное внимание интеллектуальным технологиям в ИСУ: анализу и синтезу описательно заданных объектов (ситуаций), выделению базового ядра, описанию информационных потоков и т. п. Теория ориентирована на широкий круг проблем, имеющих описательное и лингвистическое представление. Понятие интеллекта здесь воспринимается как атрибут системы определенного уровня сложности.
Важнейшей особенностью ИСУ является ориентация на системно открытые объекты с автоматической выработкой решения внутри управляющей системы на основе сформированного и накопленного в ней знания [13-18].
1 Примером ИСУ ЛА является известная система управления полетом и силовой установкой гиперзвукового самолета нового поколения X-29 (USA, 1992 г.)
28
§ 1.4. ЗАДАЧИ ТАУ И ХАРАКТЕРИСТИКА ПРОЦЕССОВ УПРАВЛЕНИЯ
Процессы, происходящие в САУ, как у всякой динамической системы, делятся на установившиеся и переходные. Установившийся процесс в САУ характеризуется постоянством внешних воздействий и других условий работы ОУ и системы в целом. Изменение этих условий вызывает переходные процессы в САУ и требует управления системой. Основной причиной возникновения переходных процессов в САУ обычно является изменение условий работы ОУ и непостоянство внешних возмущений. Инерционность, присущая всем без исключения техническим устройствам, вызывает замедление процессов во времени.
Основные проблемы ТАУ связаны с кибернетическими проблемами и сводятся к определению и теории общих закономерностей управления в информационном аспекте (сбору и обработке информации), к проблеме устойчивости, качества, оптимизации.
При рассмотрении процессов в САУ наиболее важное значение имеют проблемы устойчивости системы, качества и оптимизации процессов управления.
Устойчивость — это свойство процессов в САУ и самой САУ приходить в установившееся состояние, так как замкнутые САУ весьма склонны к потере устойчивости при действии возмущений. Неустойчивость системы выражается, например, в возникновении колебаний со все возрастающей амплитудой — расходящихся колебаний. Переходные процессы, соответствующие устойчивой системе, должны сопровождаться уменьшением отклонения выходной координаты САУ у(г) со временем, т. е. отклонения должны не возрастать, а уменьшаться — затухать.
Устойчивость — необходимое условие работоспособности САУ.
Качество процессов управления характеризуется комплексом показателей и интегрально оценивается тем, насколько процесс управления в реальной САУ близок к заданному (желаемому). Количественно комплекс показателей определяется критериями качества J (скалярные, векторные, интегральные критерии), которые выбираются в соответствии с целью управления и структурой САУ. Качество процессов управления может оцениваться и такими простыми параметрами, как величиной максимального отклонения y(f), вызванной скачком возмущения; колебательностью переходного процесса, его длительностью (критерии точности и быстродействия) и весьма сложными, соответствующими комплексным технико-экономическим показателям работы сложного ОУ и САУ в целом.
Критерии точности управления характеризуют погрешность САУ в установившихся режимах. Для обыкновенных САУ обычно точность определяется величиной установившегося отклонения y(t) от заданного значения (после окончания переходного процесса).
Оптимизация, адаптация и интеллектуализация САУ — это процесс создания САУ в соответствии с принципами, изложенными выше.
29
Проблемы устойчивости, качества, оптимизации и интеллектуализации составляют основной информационный аспект ТАУ. Энергетический аспект, связанный с расчетом и выбором элементов и САУ в целом, в ТАУ не рассматривается; эти вопросы рассматриваются в специальных курсах.
Глава 2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
§2.1	. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ УПРАВЛЕНИЯ И МЕТОДЫ ИХ ИДЕНТИФИКАЦИИ
Одной из первоочередных задач, которую необходимо решить при проектировании САУ, является получение математической модели объекта управления. Главным в ТАУ является именно составление математического описания функционирования ОУ, его свойств и соотношений между ними, позволяющее оценивать (прогнозировать) информацию об изменении состояния объекта при приложении к нему внешних воздействий. В общем случае в ТАУ объект управления представляет собой абстрактный (математический) объект, связанный с множеством свойств Vh которые обычно характеризуются числами или наборами чисел; при этом сам объект описывается отношениями между этими свойствами. Следовательно, абстрактный объект или просто ОУ характеризуется множеством переменных вместе с отношениями между ними.
Объекты управления в зависимости от степени сложности делятся по числу выходных координат на одномерные (с одной выходной координатой) и многомерные (с несколькими выходными координатами). Если выходные координаты связаны между собой, то ОУ — многосвязный (рис. 2.1, а). Соответственно УУ (регуляторы) являются одноканальными или многоканальными (многосвязными); выбор типа УУ (регулятора) и закона управления в САУ в значительной степени определяется статическими и динамическими свойствами ОУ.
Реальные ОУ, как правило, относятся к сложным объектам с дрейфом характеристик, значительной инерционностью То и временным запаздыванием т, большим уровнем помех и т. д.
Если и = (иь ..., ит)г —m-мерный вектор входных переменных (управляющих и возмущающих); х = (х,, ...,	— «-мерный вектор
переменных состояния, полностью характеризующих поведение ОУ; y = (yif ..., у/)т — /-мерный вектор наблюдаемых или выходных координат, то в нормальной форме уравнения состояния сложного ОУ будут иметь вид (рис. 2.1, б):
30
x(z) = A(t)x(t) + B(t)u(t);
y(t) = C(f)x(t)+D(t)u(t),
где A, B,C,D — матрицы (обычно D=0). Матричная передаточная функция ОУ: W0(p) = С(рЕ - A)~l B+D (Е — единичная матрица).
Модели объектов управления, отражающие в значительной мере реальные процессы, можно представить на основе их физического и математического описания. Описать ОУ можно с помощью математического описания физических явлений или экспериментально. Определение характеристик ОУ по данным экспериментальных исследований называется идентификацией.
В общем виде такая идентификация состоит в отыскании по входным и выходным сигналам ОУ (звена, системы) эквивалентной ему системы из некоторого заданного класса.
Идентификация базируется на использовании как априорной информации об ОУ при определении структуры модели (структурная идентификация), так и на обработке данных измерения для получения необходимой апостериорной информации (параметрическая идентификация). Обычно структуру модели ОУ на первоначальном этапе идентификации стремятся выбирать на основе широко используемого в инженерной практике линейного метода анализа и синтеза реальных систем (класс линейных или линеаризованных уравнений).
Различают математические модели трех типов: детерминированные, статистические (стохастические), адаптивные. Детерминированные модели ОУ рассматривают обычно в виде передаточных функций J¥0(p) -= А(р)/В(р). Статистические моде
Рис. 2.1
31
ли ОУ характеризуются набором статистических параметров и функций распределения. При этом используют методы математической статистики, корреляционный, дисперсионный и регрессионный анализы. Адаптивные модели ОУ используют для ОУ с недостаточной априорной информацией о его свойствах. Применяют и комбинированные модели ОУ — детерминированно-стохастические, детерминированно-адаптивные и др.
Очевидно, что чем точнее модель ОУ, тем выше точность результатов проектирования САУ. Однако при сложных моделях ОУ резко возрастает и трудоемкость синтеза УУ и проектирования САУ в целом. Поэтому обычно используют два типа моделей ОУ: точные — на этапе анализа и отладки УУ и САУ; приближенные — на этапе синтеза УУ. Это оправдано основным свойством САУ с обратной связью — их малой чувствительностью («грубостью») к внешним воздействиям.
Детерминированные модели в виде передаточных функций типовых ОУ имеют вид:
W0(p) = —^~e
ТоР
iv0(p)= к(>
0 тоР+1
Щ,(р) = “------------’
0	(т;р+1)(г2р+1)
где приближенно е =1-рт при разложении в ряд Тейлора и е~рт ~ (1-т/?)/(1 + тр) при разложении в ряд Пада. Если ОУ имеет W0(p) = ^0/(Т;р+1)(Т2р+1)Л', где N определяет число апериодических звеньев с постоянной времени Т2, то ОУ с такой передаточной функцией можно считать без запаздывания. Однако, в общем случае сомножитель вида ]J(T2p+l)N лучше учитывать через е-рт при У = 8-Н0-
Статистические (и адаптивные) модели получают с применением активных и пассивных методов идентификации и соответственно планирования эксперимента; активный эксперимент с генерацией на входе ОУ детерминированных и (или) случайных воздействий с последующей обработкой результатов, пассивный — в режиме нормального функционирования ОУ (итерационные и неитерационные методы). Идентификация ОУ (линейная, нелинейная) проводится на определенном уровне качества идентификации, определяемом критериями идентификации или адекватности модели и ОУ (например, минимизацией интегральной оценки)
32
т
/[Звых. эксп.
О
(0-Увыхмод.(0]2<*.
Теории идентификации и планирования эксперимента достаточно хорошо разработаны и включают в себя комплекс методов корреляционного и регрессионного анализа, методы малого параметра и стохастической аппроксимации, эвристические методы, методы эстимации ОУ и др.
Безусловно, реальный ОУ отличается от построенной математической модели, поэтому важно сравнивать некоторые главные особенности физического ОУ и соответствующей математической модели (гарантировать их точное совпадение невозможно). В связи с этим приемлемость модели следует понимать в плане ее «полезности».
Объекты, имеющие характеристику, показанную на рис. 2.2, а, называют объектами с самовыравниванием, здесь /с0 = [у„ (0 —> —»оо] — конечно. Распространены также характеристики ОУ, аналогичные приведенным на рис. 2.2, б. Объекты с такой характеристикой называют объектами без самовыравнивания, или астатическими объектами . Передаточная функция таких ОУ имеет вид W0 = e~px/Тор.
Идентификация ОУ осуществляется в двух направлениях: определение структуры (вида) WQ(p) (структурная идентификация) и определение параметров W0(p) (параметрическая идентификация).
Различают два способа получения детерминированной модели ОУ.
1.	Передаточную функцию W0(p) определяют по временным характеристикам ОУ: w(t) — весовой и (или) переходной функциям (рис. 2.3, 2.4). Если известна (экспериментально получена) переходная функция h(t), то различными методами по ней можно определить w(f) (см. рис. 2.3), а также передаточную функцию ОУ [2,10]. При «грубой» идентификации передаточная функция Ио(р) (например, к
=) определяется непосредственно по h(t) (см. рис. 2.2). Тор+1
Рис. 2.2
3 А. А. Ерофеев
33
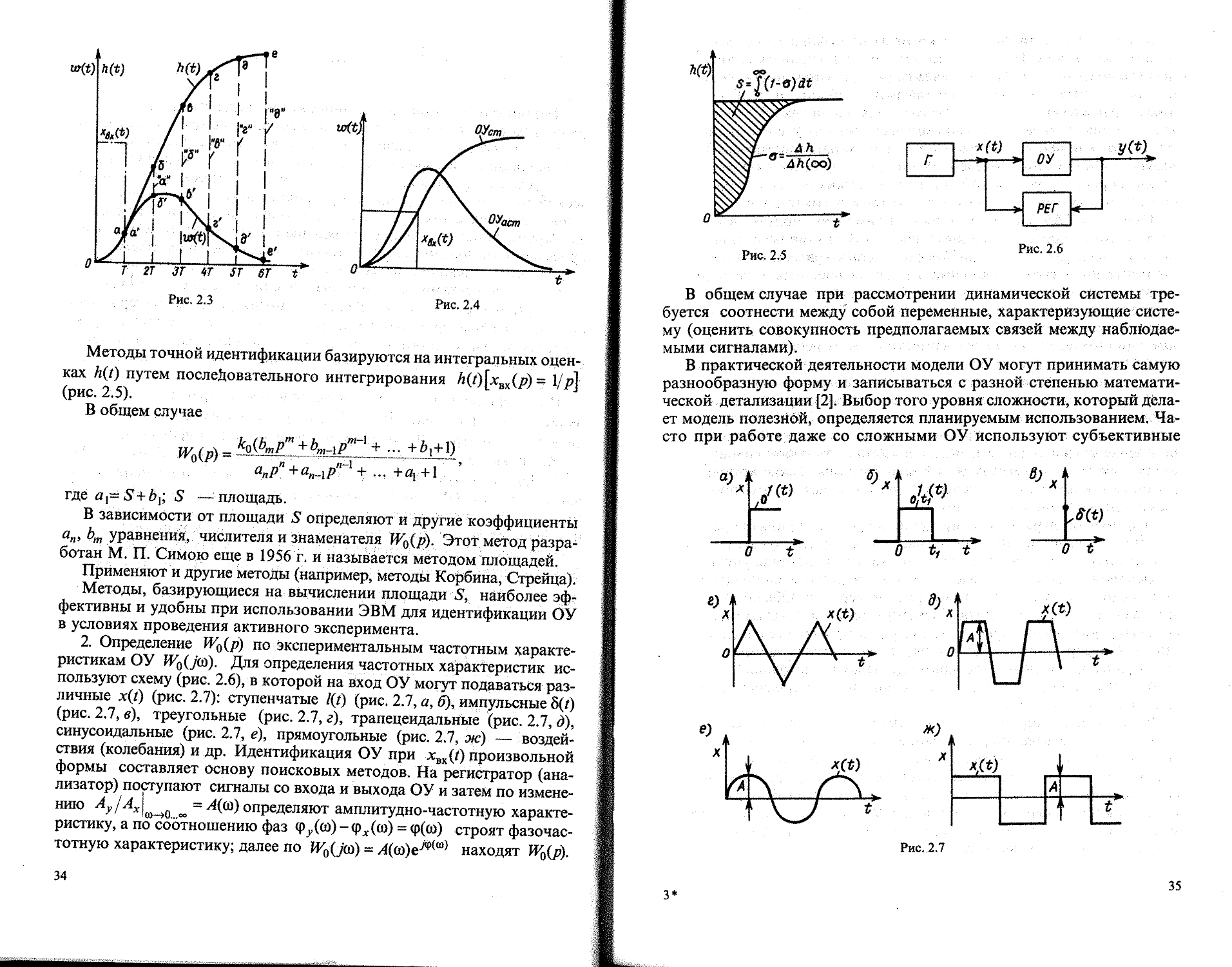
Методы точной идентификации базируются на интегральных оценках h(t) путем последовательного интегрирования	= 1/р]
(рис. 2.5).
В общем случае
= к0^тРт	'+	+^1+1)
° а„рп+ап^рп~1 + ... +Ц]+1
где aftS+b^, S —площадь.
В зависимости от площади S определяют и другие коэффициенты а„, уравнения, числителя и знаменателя WQ(p). Этот метод разработан М. П. Симою еще в 1956 г. и называется методом площадей.
Применяют и другие методы (например, методы Корбина, Стрейца).
Методы, базирующиеся на вычислении площади S, наиболее эффективны и удобны при использовании ЭВМ для идентификации ОУ в условиях проведения активного эксперимента.
2.	Определение Ж0(р) по экспериментальным частотным характеристикам ОУ Во(усо). Для определения частотных характеристик используют схему (рис. 2.6), в которой на вход ОУ могут подаваться различные х(0 (рис. 2.7): ступенчатые /(/) (рис. 2.7, а, 6), импульсные 8(?) (рис. 2.7, в), треугольные (рис. 2.7, г), трапецеидальные (рис. 2.7, д'), синусоидальные (рис. 2.7, е), прямоугольные (рис. 2.7, ж) — воздействия (колебания) и др. Идентификация ОУ при хвх(/) произвольной формы составляет основу поисковых методов. На регистратор (анализатор) поступают сигналы со входа и выхода ОУ и затем по изменению Ау/Ах\ °° = Л(со) определяют амплитудно-частотную характеристику, а по соотношению фаз Ф?(ю) - фх((о) = ф(со) строят фазочастотную характеристику; далее по Ид (уса) = А((о)еМш) находят Ио(р).
34
Рис. 2.6
В общем случае при рассмотрении динамической системы требуется соотнести между собой переменные, характеризующие систему (оценить совокупность предполагаемых связей между наблюдаемыми сигналами).
В практической деятельности модели ОУ могут принимать самую разнообразную форму и записываться с разной степенью математической детализации [2]. Выбор того уровня сложности, который делает модель полезной, определяется планируемым использованием. Часто при работе даже со сложными ОУ используют субъективные
35
з*
(вербальные) модели, описание которых производится без математических выражений. Примером может служить управление автомобилем или видеомагнитофоном, телевизором. Для описания свойств ряда промышленных ОУ используют числовые таблицы и (или) графики. Такие графические модели, например, для линейных ОУ (систем) могут быть представлены своими импульсными характеристиками (реализациями), переходными или частотными характеристиками. Графическое представление моделей ОУ широко используется в различных задачах проектирования САУ; язык графических моделей хорошо приспособлен к решению многих задач анализа и синтеза САУ.
Однако в ТАУ наиболее широко применяют модели, в которых соотношения, описывающие связи между системными переменными, задаются в виде разностных, дифференциальных уравнений. Такие модели называются математическими или аналитическими моделями. Математические модели могут быть снабжены набором поясняющих прилагательных (непрерывные и дискретные по времени, линейные или нелинейные, сосредоточенные и распределенные, детерминированные или стохастические) в зависимости от типа используемых уравнений. Математическое моделирование реальных процессов, по существу, является составной частью всех технических научных дисциплин.
В процессе машинного моделирования (проектирования) моделью системы являются специальные программы для ЭВМ или программные системы, так как программа, с помощью которой описывается поведение сложных систем, может представлять собой совокупность взаимодействующих между собой подпрограмм. Такие компьютеризованные представления сложных ОУ (и систем) называются программными или машинными моделями.
Эти модели играют большую роль в процессе принятия решений, в системах искусственного интеллекта и, в общем случае, системах, основанных на знаниях, т. е. интеллектуальных системах управления.
Основой построения моделей являются данные наблюдений, использование результатов некоторых измерений. Обычно при формировании модели выполняют декомпозицию системы на такие подсистемы, свойства которых можно определить из ранее накопленного опыта и информации (из использования физических законов, результатов ранее проводимых экспериментальных исследований).
Формальное математическое объединение этих подсистем создает модель системы в целом.
Решение задач идентификации требует, как правило, экспериментальных данных ведения регистрации входных и выходных сигналов системы и формирования модели в результате обработки соответствующих данных. Эта задача не имеет эффективного решения, и чаще всего ее целесообразно рассматривать в более простой форме: на основе априорных сведений о природе ОУ задана его математическая модель; в модель входит набор параметров, значения которых заранее неизвестны и подлежат оценке.
36
§2.2	. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ САУ
Целью исследования САУ является решение задачи анализа или задачи синтеза системы. Если система задана, включая структуру и значение параметров, то требуется определить только ее свойства, т. е. провести анализ. Во втором случае (синтеза), наоборот, задаются требования к САУ, т. е. свойства, которыми должна обладать система; в результате синтеза необходимо создать систему, удовлетворяющую этим требованиям. Ясно, что задача синтеза неоднозначна в своем решении и намного сложнее задачи анализа САУ.
В общем виде задача исследования САУ базируется на математическом описании системы, исследовании ее устойчивости и качества установившихся и переходных режимов.
Создание математического описания—построение модели САУ — обычно сопровождается разбиением ее на звенья, т. е. осуществляется декомпозиция САУ, и описанием этих звеньев (аналитически в виде уравнений, связывающих входные и выходные координаты звена, либо графически, в виде характеристик, описывающих ту же связь). Совокупность уравнений (или характеристик) отдельных звеньев определяют уравнения или характеристики системы в целом.
Любая САУ осуществляет преобразование информации, т. е. каждой функции на выходе ставится в соответствие определенная функция на входе, поэтому каждой детерминированной САУ соответствует вполне определенный оператор системы А. Это соответствие между входной функцией x(t) и выходной функцией y(t) можно записать в виде
y(t) = Ax(t).
Следовательно, через оператор системы А обозначена вся совокупность математических действий, которые нужно произвести, чтобы данной входной функции x(t) сопоставить соответствующую выходную функцию системы y(t) или, наоборот, y(t) сопоставить x(t). Здесь оператор системы А является полной, исчерпывающей ее характеристикой, объединяющей любые математические действия: алгебраические, дифференцирование, интегрирование, сдвиг по времени, любые функциональные зависимости, а также любые логические действия. Оператор САУ полностью определяется системой уравнений, описывающих работу всех элементов, из которых состоит данная система. Следовательно, при решении задачи анализа САУ оператор А задан структурой САУ и составом ее звеньев, т. е. всей совокупностью описывающих САУ уравнений, что предопределяет закон, по которому для любого входного воздействия можно найти выходную величину системы и, таким образом, определить оператор системы управления. При решении задачи синтеза необходимо задать оператор системы, что означает задать совокупность действий (определенный алгоритм), которые необходимо осуществить над входной функцией, чтобы получить выходную.
37
В случае описания поведения САУ конечным числом дифференциальных уравнений, связывающих входную и выходную функции, для полного и однозначного определения выходной функции необходимо задать начальные условия, которые могут быть учтены, например, путем добавления к входной функции x(t) некоторых слагаемых.
Наиболее рациональным является использование метода пространства состояний. При этом состояние системы определяется так, чтобы задание входной функции и начального состояния однозначно определяло выходную функцию и текущее состояние системы в любой момент времени. Для линейных САУ оператор А является линейным, а множество состояний S является конечномерным линейным векторным пространством. При этом, если множество состояний X есть континиум, САУ представляет собой объект с непрерывным пространством состояний. Если J счетное множество, то САУ — объект с дискретным пространством состояний.
При изучении принципа действия САУ обычно рассматривается ее функциональная схема, в которой система разбита на звенья, исходя Из их назначения, т. е. выполняемых ими функций. При математическом описании САУ разбивают на звенья по принципу удобства получения этого описания, т. е. систему разбивают на возможно более простые мелкие звенья направленного действия, передающие воздействия только в одном направлении — со входа на выход. При этом целесообразно, чтобы каждое звено в динамике описывалось дифференциальным уравнением не выше второго порядка и изменение состояния такого звена не влияло на состояние предшествующего звена (работающего на его вход).
Уравнения звеньев обычно записываются через переменные состояния x(t) в нормальной форме, в виде системы дифференциальных уравнений 1-порядка, разрешенных относительно первых производных (форма Коши):
x(t) = Ax(t) + Bu(t)
или
dx,	,	,
~~^ = a‘1xl+	+
где (%],..., х„)т —вектор состояниях; %i, ...,х„ —фазовые координаты; (ц,	ит)т —вектор управления и .
Переменные состояния аналогичны координатам, а пространство их изменения является фазовым. Декомпозиция САУ на звенья направленного действия позволяет составить математическое описание каждого такого звена без учета его связей с другими звеньями. Следовательно, математическое описание в целом САУ представляет
38
Рис. 2.8
совокупность независимо составленных уравнений (или характеристик) отдельных звеньев, образующих систему и дополненных уравнениями связи между звеньями.
Математическое независимое описание звеньев позволяет легко составить структурную схему системы из прямоугольников, изображающих звенья схемы, и стрелок, соединяющих входы и выходы звеньев (рис. 2.8, а). Стрелками показывают не только связи между звеньями, но также и внешние воздействия, приложенные к отдельным звеньям системы. Уравнение (или характеристика) звена структурной схемы обычно записывается прямо внутри прямоугольника в виде передаточной функции (рис. 2.8, б) или в виде некоторой обобщенной функции F(x) (рис. 2.8, в).
Структурная схема определяет основу математического описания САУ.
§	2.3. ЛИНЕАРИЗАЦИЯ ЗВЕНЬЕВ И СИСТЕМ
На практике все разнообразные по физическим свойствам системы в большинстве случаев являются нелинейными, т. е. практически в системе присутствует одна или несколько нелинейностей. К ним относят люфт, упор, насыщение, ограничение и т. д. Анализ нелинейных систем более сложен и, по существу, всегда является приближенным. Однако существует большой класс нелинейных систем, которые при определенных допущениях можно линеаризовать, т. е. систему сделать линейной в математическом смысле. При математическом описании САУ обычно разбивают на ряд элементарных звеньев, имеющих линейные статические характеристики, и на ряд звеньев с нелинейными статическими характеристиками. Линеаризация такой системы сводится к линеаризации уравнений, описывающих нелинейные звенья.
Методика составления линеаризованных дифференциальных уравнений (по первому аналитическому способу линеаризации) сводится к следующему.
1.	На основании изучения физических свойств реальной системы определяется число степеней свободы (число независимых переменных), производится ее декомпозиция и составляются исходные дифференциальные уравнения по звеньям.
39
2.	Определяется рабочая точка установившегося режима работы звена (системы), в которой необходимо определить поведение звена (системы) при малых отклонениях от установившегося значения координат состояния (х°, у0).
3.	Если в структуре САУ есть нелинейное звено, описываемое нелинейной функцией
F(x, х, у, у, y,...,f, /,/,...) = О,	(2.1)
которая представляет собой несущественную нелинейность (аналитическая нелинейная функция в области малых приращений), то ее можно разложить в ряд Тейлора в окрестности рабочей точки (0) при, например, внешнем возмущении /= 0.
4.	В процессе управления в САУ в переходном и установившемся режимах х, у мало отклоняются от их программных значений х°,у°, исходя из принципа работы замкнутой САУ. Следовательно, для уравнения (2.1) можно записать, что х=х°+Дх(г), х = Дх; у = уй + &y(t); у = Ду; у - &у, где знак Д характеризует малые отклонения (вариации).
5.	Уравнение нелинейного звена в установившемся состоянии:
Г(х°,0,у°,0,0)° =0.	(2.2)
6.	Разлагая нелинейную функцию — уравнение (2.1) в ряд Тейлора, получим
.0 ГЭГ?. (ЭГ?Д.
Г(х, у) + — Дх+ Ч Дх + I дх J	{дх )
dF}\ Гэг?.. Гэг?.. _ . ^у) W {Ъ)	(23)
или
Г(х,у)°+(-/>1)Дх+(-й0)Дх+а2Ду+а1Ду+а0Ду+Г„ =0,
где Rn определяет члены порядка малости; п > 2 (произведения и степени малых отклонений с коэффициентами) — остаточный член, который стремится к нулю при
(Дх—»0;
[Ду—>0.
7.	Из уравнения (2.3) вычитают уравнение (2.2) и, опуская знак Д, рассматривают х, у уже в отклонениях, заменяя на нуль все последующие члены разложения как малые величины высшего порядка
40
(R„ = 0). В результате получают линеаризованное дифференциальное уравнение динамики звена в малых отклонениях:
d2y dy , dx , a0-1-+al--+a2y=^--+bix
dt dt	at
или в операторной форме
(йод2 + ахр+а2)у = (bap+bjx.
(2.4)
(2.5)
Следует заметить, что положение о малых отклонениях для возму-щенияДг) обычно неприменимо, так как они могут иметь значительную величину.
Отличие линеаризованного уравнения (2.4) от уравнения звена с нелинейной функцией (2.1) заключается в следующем: линеаризованное уравнение является приближенным, так как в нем отсутствуют члены высшего порядка малости; уравнение (2.4) записано только в отклонениях, т. е. неизвестными функциями времени являются не прежние полные величины (х, у), а их отклонения (Дх, Ду), которые характеризуют состояние звена в неустановившемся режиме (при отклонении от установившегося состояния с х°, у0); уравнение (2.4) является линейным относительно отклонений.
Частные производные здесь являются постоянными коэффициентами при отклонениях (или переменными коэффициентами, если F содержит t в чистом виде). Этот способ линеаризации справедлив для нелинейных функций, для которых возможно разложение в ряд Тейлора, т. е. когда функция F является аналитической в рабочей области (малые приращения).
Таким образом, уравнение (2.4) дает результат решения задачи линеаризации исходного уравнения (2.1), и его называют дифференциальным уравнением звена (или САУ) в отклонениях или «в вариациях».
Обычно практически линеаризацию производят сразу по аналогии с уравнением (2.4), но не проводя предварительных выкладок (второй способ). При этом используют графический смысл проведенной линеаризации.
Если статическая характеристика звена нелинейна, то ее часто называют характеристикой с переменным по входной величине коэффициентом передачи.
Известно, что решение дифференциального уравнения с определенными начальными условиями дает интегральную кривую. Предположим, что уравнению (2.1) с начальными условиями уравнения (2.2) соответствует интегральная кривая, где точка 0 соответствует начальным условиям уравнения (2.2) (рис. 2.9, а). Если к этой интегральной
41
кривой F(x) в точке 0 провести касательную, то угол, составленный
( dF}0
этой касательной и осью абсцисс, будет равен а = arctg — = arctg к;
\ dx ) к - tg а (рис. 2.9, а).
Суть линеаризации состоит в замене кривой искомого решения нелинейного уравнения (2.1) прямой, касательной к искомой кривой в точке, соответствующей начальным условиям. Такая замена будет, очевидно, справедливой только для тех отклонений А х, при которых кривая незначительно отличается от касательной. Следовательно, допустимая область отклонений и определяет возможности линеаризации исходной системы. При этом вместо частных производных находят частные разности Ду, Ах.
Для уравнения (2.4), когда выражения записаны в отклонениях, графически это будет означать перенос начала координат в точку О (рис. 2.9, б). Для реальных систем возможности такой линеаризации часто справедливы для достаточно больших значений отклонений; чем больше эти значения отклонений, тем больше к данным системам применим термин «линейные системы».
Основываясь на графической интерпретации способа линеаризации, примененяют способ графической линеаризации. Согласно ему, нелинейные статические характеристики линеаризуются графически, т. е. проводят касательную к кривой, соответствующей реальным условиям (рис. 2.9, кривая /) и заменяют ее линеаризованной характеристикой (прямая 2). Тогда для малых отклонений система является линейной. При этом для упрощения знак «А» перед переменными опускают, предполагая, что эти переменные — малые отклонения от установившегося состояния и линеаризация уже проделана. Следует заметить, что рассмотренная линеаризация уравнений совершенно недопустима при скачкообразных нелинейных функциях F (типа «релейных» характеристик). Такие функции и характеристики являются существенно нелинейными и изучаются в теории нелинейных САУ (см. п. 3.3).
42
Третий способ линеаризации объединяет вьпперассмотренные условия и порядок линеаризации, т. е. сразу записывают уравнения звена (системы) в отклонениях, например, в векторно-матричной форме [2].
Четвертый способ линеаризации основан на определении коэффициентов дифференциального уравнения по методу наименьших квад-ратов(МНК) [2].
§	2.4. ФОРМЫ ЗАПИСИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ САУ
Обычно дифференциальные уравнения системы записывают в таком виде, где значения регулируемой величины и ее производных располагаются в левой части уравнения. Значения входных воздействий (управляющих и возмущающих) и их производных располагаются в правой части. При этом уравнение САУ примет вид
d^y	, dmf , dm~Xf
On----------p+ ... +a„j> = Zh~-f-6---r- + ... + bmf
dtn * dtn~i n dtm 4 dtm~'
или
(a^pn+aYpn~} + - +an)y = (bapm'+bipm~l + ... +bm)f,
где a0, at, ..., a„ — постоянные коэффициенты левой части уравнения; Ьо, Ь\, ..., Ьт — коэффициенты правой части уравнения.
Значение выходной величины САУ, кроме того, обычно приводится к форме с единичным коэффициентом, т. е. коэффициенты уравнения делят на а„, Ьт.
Обозначим через «р» символ дифференцирования р в d/dt, иначе называемый алгебраизированным оператором дифференцирования (d'/dt' тождественно равно р1). Эта алгебраическая величина условно представляет собой функцию времени; р не обладает свойством коммутативности и является сомножителем только как ру (pf), но не УР Up)- Если пользоваться преобразованием Лапласа (или Карсона— Хевисайда), с помощью которого рассмотрение процессов из временной области переносится в комплексную, то уравнение (2.5) будет также справедливо. При этом р будет являться комплексным числом р = с±]оз (иногда вместо р пишут л = с±усо).
Функцию, например, у (Z) заменяют функцией у(р) = J y(t) e~p,dt = о оо
=	(/)}; функцию f (t) заменяют функцией ф(р) = | /(Г) eTp,dt =
о
= £{/(/)} или y(t) = y(p), а /(Z) = ф(р), где L{y(0}> L{f(t)} — преобразование Лапласа (ПЛ); у (р), ф (р) — изображения; у (/), f (0 — оригиналы функций.
43
Если F(p) = pjf(t)e p!dt, то это преобразование Карсона А'{/(/)}.	?
о
Следовательно, через оператор р имеет место связь преобразований. 1 При этом, если пределы у интеграла «- <*>, <~», то это двустороннее ‘ преобразование Лапласа. Обратное двустороннее преобразование | Лапласа создает возможности перехода от изображений к оригиналам:
1	с+>
=	y(t) = L~l{y(p)}.
J с-/о)
К разностным переменным х [пТ], у[пТ] и уравнениям применяют прямое дискретное преобразование Лапласа, например для у [л Т]:
^(р) = £Я«Ле'₽пГ,	!
л=0
где у (р) — изображение; у [и Г] — оригинал. Здесь преобразование Лапласа одностороннее; двустороннее, если пределы у суммы « -°°». Переход от изображений к оригиналам осуществляется с по- | мощью обратного (двустороннего) преобразования Лапласа:
c+J<o0/2	|
у\пТ\ = -— [ у(р)е”₽пГф.
^С0° с-;<о0/2
Преобразование Лапласа применимо, если /(г) = О при t < 0 и существует абсцисса абсолютной сходимости — «с»; тогда существует интеграл Лапласа.
Основное достоинство преобразования Лапласа (и других родственных преобразований) — замена операций дифференцирования и интегрирования оригиналов алгебраическими действиями над изображениями.
В курсе высшей математики доказываются специальные теоремы и представлена теория преобразования Лапласа; составлены таблицы оригиналов и изображений наиболее распространенных функций, которые широко используются и в ТАУ. Напомним также, что при р = JG) получаем для функции, например /(/), прямое преобразование Фурье (ПФ):
Д» = J /(0е->'; Д» = Г{/(0}
и обратное преобразование
44
/(/) = —/F^e^to; f^ = F 1 {Л»}-2л —oo oo	00
При J|/(r)|2<&<°° (ограничение энергии у функции) и I|/(f)p?<
<00 — условия Дирихле, с = 0 и путь интегрирования совпадает с мнимой осью j на комплексной плоскости р. Аналогично при р = j(a можно записать дискретное преобразование Фурье:
* 00
F(>)= £е->лГ/[пГ]
Л=-оо
и дискретное обратное ПФ:
1
f[nT] = - Г F(j(o)e>',rd(o.
“° -i/2
Таким образом, от ПФ легко перейдем к ПЛ (и наоборот), если f(t) = 0 при t < 0; ПФ и ПЛ — линейные аналитические преобразования.
Первая стандартная символическая форма записи линейного дифференциального уравнения (2.5) имеет вид:
(Т2р2+ Tlp+T)y = к(Тр+1)х,	(2.6)
где
а,
°2
т2 _ «о. -г -	размерностьЬх
«2 q а2 размерность аг
Здесь Т — постоянные времени звена, измеряющиеся в секундах, характеризуют инерционность звена; к — передаточный коэффициент звена.
Эта форма отражает операторно-структурное описание — на языке операторов звеньев и структуры связей.
Вторая стандартная форма записи дифференциального уравнения — через передаточную функцию звена:
W(p) = у{р} =	= к____7>+1	,	(2.7)
х(р) а$р2 +а]р+а2	Г22р2 + Т1р+1’
где W (р) характеризует отношение изображений (по Лапласу) выходной величины звена к входной при нулевых начальных условиях и равенстве нулю всех внешних возмущений. Нулевые начальные условия дают возможность однозначного определения W(p), ибо
45
начальные условия могут быть разнообразны [если рассматривать W(p) просто как отношение изображений у к х]; нулевые начальные условия рассматривают относительно у, т. е. при t < 0, у = О d""ly п
и все производные --~~	=0 — система находится в покое.
dtn 1
/so
В общем случае система автоматического управления описывается либо в форме дифференциального уравнения
dny dn~'y	L dmx L dm~'x
a.---+ a,----( + ... + a„y = Ch-+ o,---r+ ... + bmx
dtn r1 "	45 dtm 1 dtmA
или
ay ay	, d x , d x ,
a------+ an_,--T+ ... +алу-Ьт-----+ bm_,-, + ... +br,x,
dtn dt"-'	dtm dtm~{
либо в его свернутом виде (уравнения типа вход-выход):
(W+т^Рп~'+...+i)y=аду"+т^р"1-' + - +i)x
или
0(р)у = Я(р)х.
В случае работы САУ при нескольких входных воздействиях х,
Q(p)y(p) = ^Ri(p)Xi(p), ы
или иначе:
п
y(p) = ^^i(p)Xi(p), /=1
где Q(p) — собственный оператор; R^p)—операторы воздействия (входные операторы). Здесь х,- — входные воздействия на САУ (i = 1,2, ..., и); Q(p) и R,(p) — полиномы (символические) относительно р: Wt(p) = - R'kPl — передаточная функция САУ для /-го входного воздействия.
Q(p)
Эту форму записи оператора W (р) называют еще полиномиальной.
Уравнение статики звена получают из (2.6), (2.7) при р = 0; у = кх.
Третья стандартная форма записи дифференциального уравнения применяется относительно переменных состояния, когда САУ описывается векторно-матричным дифференциальным уравнением:
46
x(r) = Л(г)х(О+5(0«(0;
y(t) = C(f)x(f) + D(t)u(t),
где A — квадратная матрица коэффициентов
41
Ai
рица управления
Am	Gi	Qn
: ; С — матрица	выхода	:	:
Ат	Сц	Аи
D — матрица обхода системы
А1 " Ami
:	: ; и = ит)т —
А " Ат
т-мерный вектор входных переменных (управляющих и возмущающих); х = (хь..., хп)т—«-мерный вектор переменных состояния координат, полностью характеризующих состояние системы; у = (у[, yt)r — /-мерный вектор наблюдаемых или выходных переменных.
Если САУ описана в виде уравнений типа вход-выход:
(аор”+а1рп 1 +...+a„)y = (bopm+blpm ’+ ... +bm)u,
то возможен переход к уравнениям состояния и наоборот; разработаны различные способы перехода от одних уравнений к другим.
Часто для САУ D = 0, тогда:
x(Z) = Ax(t) + Ви(г);
y(t) = Cx(t).
При нулевых начальных условиях х(0) = 0 получим матричные передаточные функции САУ (ОУ):
х(р) г 1-1
WX(P) = ^Р) = А В =
И^(р) =	= с[рЕ-а]~} B + D = СФ(Р)В + О-,
у(р) ^) = Z7G=:C’ у х(р)
47
где Ф(р) = [рВ- Л]-! — характеристический многочлен матрицы А — резольвента матрицы А. Характеристическое уравнение Ф(р) = = \рЕ~ А]1 = 0. Корни характеристического многочлена Ф(р) — соб-ственные числа матрицы А. Здесь ВТ1 [ф (/>)] = Ф(0 = еЛ/ = У,—— —
п=0 п-матричный экспоненциал или матрица перехода.
В передаточной функции
А	Ь\Р+1*
W(p) =-----------------
ОоР +агр- +а2р+а3
или

корни числителя R(p) называются нулями, а корни знаменателя Q(p) — полюсами. Аналогично уравнения состояния можно записать и для линейных дискретных САУ
x(k+1) = Ax(k) + Bu(k) + Ff(k)-. y(k) = Cx(k) + Du(k) + F'f(k),
если для непрерывных САУ уравнения состояния имеют вид
x(i) = Ax(t) + Bu(t) + Fflfy, y(f) = Cx(t)+Du(t)+F'f(f).
Пх пи
ПУ nf
Управляемость, возмущаемость, достижимость, наблюдаемость, устойчивость, стабилизируемость САУ целиком и полностью определяются матрицами А, В, С, D, F. Здесь матрица параметров
А В F
Р= с Q р,‘> матрица «размерности» N = ны матрицы с f(t) пропадают.
Пример. Описание процессов в последовательном колебательном контуре RLC (рис. 2.10). Здесь, если напряжение U (вход х), а ток I (выход у), то
. При «у = 0 чле-
О-й
О-
/?
L
Z=.v
Рис. 2.10

1 , и Ldlldt [dt + RI
С
или в операторной форме, после преобразований, получим:
i/(p) = (W2 + t2p+D^) />С ’
48
где 7]=L/7?; T2 = RC. Тогда
=	=	, k=llR.
U(p) T^ + ^p+l
От операторно-структурного описания процессов к эквивалентному описанию процессов в нормальной форме можно перейти, используя стандартную процедуру (если W(р) звена является правильной дробью]. Следует заметить, что нормальная форма является обычно естественной при первичном описании реальных ОУ,
Описание процессов в нормальной форме (в пространстве состояний). Если выбрать переменные состояния л-] = С/с, a x2 = LI, тогда:
dx, 1
---L ------х
dt	ТХТ2
т 1
У = / = ~£Х2
или в форме
х = Ах + Ви; у = Сх,
получим
X; О 1/(7]72) X]
1 -1/7]]|х2
U; у = |0 1 L
X;
u = U.


Если процессы в контуре описать уравнением:
7’2^ + 2^T^ + y = W, л2 Л
тогда
0Л(р) = Ж= *-----------------.
V(.P) Т2р2 + 2Ъ,Тр+}
_	dy dx.
Если принять у = х,;	-f- = —- = х2,	то
dt dt
dxt „.	dx2 1 2E x	kU(t)
	L = X2 dt		£=	x	-X2 + dt T2 T	T2
Таким образом, здесь
	0	1	I	r	° i
A =	1	_2^	; x = R B =	к u = U.
	. 			1 Y"-!		 - I
	T2	T	Ix2|	r2|
В общем случае, если процессы в звене (САУ) описываются уравнением
(аорп+а1рп~1 + ... +a„)y = kU,
то, если принять
(п-1)
х}=у = х; х2=х;	х3=х; ...; хп= х ,
49
4 А. А. Ерофеев
тогда получим
dxx _ dx2 dt ~X2’ dt
= x3;
^xn _ an -	_	Д-
dt Oq
fli
—x„ + k—
Ц) во
или x = Ax + Bu; y = Cx+Du, где
0	10-0	v х	0 -^1	dx 0	0	1-0	Y x	о •^2	dt а- о о о - 1 ;*= :;в = ; _ал a»-i ап-2 ...	dn~xx	к «0	«0	«0	"	^п-1	Oq
w = [7; C = (1, 0, ..., 0);/) = 0.
Наличие в правой части многочлена (1%рт + ... + Ьт) не изменяет матрицы Л, Я и/); изменяется лишь С-(Ьт, Ьт_х, ...,	0, ..., 0).
Если Ц) = 1> £ = 1. то
А =	0	1	0	...	0 00	1	... 0 0	0	0	...	1 —— ап_х	— а„-2		~ai	to и	0 0 1
Эта форма уравнений называется канонической формой фазовой переменной.
Управляемость САУ— САУ управляема (полностью управляема), если она может быть переведена из любого начального состояния х(г0) в любое другое x(tx) в произвольный момент времени t = t0 путем приложения кусочно-непрерывного воздействия u(t), t е (Zo, tx) за конечный интервал времени - г0.
Наблюдаемость С А У (дуальное понятие управляемости) — САУ наблюдаема (полностью наблюдаема), если все ее переменные состояния можно непосредственно или косвенно определить по выходному (измеряемому) вектору системы. При наличии какой-либо переменной состояния, изменение которой не влияет на выходной вектор САУ, система ненаблюдаема.
Для оценки управляемости и наблюдаемости линейных стационарных САУ применяют критерий Гилберта (основан на использовании канонического уравнения состояния) и критерий Калмана {осно
50
ван на рассмотрении матрицы управляемости М = [в, АВ, А2В,
Л"-1 В] размерности п х (пт) или матрицы наблюдаемости А = [сг, АТСТ, (Ат)2Ст, (ЛГ)И-1СГ] размерности и х (п 7)}; например, если матрицы М и L имеют ранг п то САУ полностью управляема и наблюдаема.
Принцип дуальности (двойственности) дает возможность оценивать по условиям наблюдаемости одной САУ управляемость другой (сопряженной) или по условиям управляемости—наблюдаемость другой сопряженной системы.
Метод пространства состояний широко используется при решении задач наблюдаемости, управляемости, оптимизации, адаптируемости САУ. При этом уравнения САУ могут иметь вид х = f(x,u,t) или х = A(f)x + B(f)u, х еХ, и 6 Си др.
При исследовании условий полной наблюдаемости часто используют линейный оператор Ляпунова (оператор дифференцирования):
дх ди dt
гдеР—функции-столбцы.
Понятие управляемости в ТАУ рассматривается при различных условиях, накладываемых на управление. Число видов управляемости — множество управлений we С (порядка 30), например, управляемость в «малом», полная и неполная управляемость с учетом различных ограничений и условий. Необходимый и достаточный аналитический и структурный критерии управляемости в настоящее время обоснованно существуют лишь для линейных САУ.
В ТАУ широко применяется операторно-структурный анализ САУ (с использованием скалярных или векторных структурных схем), т. е. анализ на языке операторов звеньев и структуры связей. При этом классы операторов (собственные, воздействий, входные и т. п.) чрезвычайно разнообразны; не меньшим разнообразием характеризуются и структуры связей.
Для САУ, когда в прямом канале управления ОУ включен адаптируемый регулятор (АР)1, свойство полной адаптируемости определяет существование и единственность вектора «идеальных» настроек АР по отношению к произвольно допустимому вектору параметров ОУ (свойство гарантирует абсолютную параметрическую инвариантность САУ). По аналогии существуют: критерии адаптируемости САУ (полной, слабой, частичной адаптируемости), а также связь между управляемостью ОУ и адаптируемостью САУ к данному ОУ.
Так, если ОУ описывается системой уравнений вида
1 Возможно включение АР в прямом канале и в канале обратной связи.
51
4*
х = A (Z)x(z) + y(t) = C(t)x(t) + D(t)u(t),
то при D = 0 и когда АР является пропорциональным интегро-диф-ференцирующим (ПИД) регулятором, в случае квадратных матриц В и С, достаточным условием полной адаптируемости САУ (при выполнении определенных условий) может быть вырождение матриц В и С, а необходимым условием det С  В # 0.
Следует напомнить, что в адаптивных САУ недостаток априорной информации компенсируется за счет более полного использования оперативной (текущей) информации об ОУ и среде его функционирования. Априорную и апостериорную информацию, используемую для управления в САУ, называют информационным обеспечением управления (информационным множеством). Обычно предполагают оптимальное адаптивное управление, хотя возможно неоптимальное управление с высокоразвитой адаптацией. В адаптивных оптимальных САУ используют «полные модели управляемых процессов»; САУ содержит системы оптимального (субоптимального) оценивания и идентификации. Понятие идентифицируемости (параметрической) можно считать и как частный случай наблюдаемости. Идентификацию следует рассматривать как результат определения параметров управляемого процесса модели САУ по измерениям определенных наблюдаемых величин.
Формирование оптимального управления на основе «полной модели» осуществляется в соответствии с заданным критерием оптимизации (целевой функцией). В адаптивных САУ могут также использоваться модели управляемого процесса различного вида: упрощенные, феноменологические, прогнозирующие. Структуры САУ строятся с использованием, например, поисковых и беспоисковых режимов, с информацией о частотных, временных, модельных (эталонных)1 характеристиках ОУ и САУ в целом. Методы синтеза адаптивных САУ развиты для определенных систем, например, для беспоисковых на основе принципа инвариантности, на основе функций Ляпунова. Адаптивное управление в САУ допускает возможность использования не-индентифицированных алгоритмов, например, основанных на методе рекуррентных целевых неравенств.
§2.5. ВРЕМЕННЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
Динамические свойства линейных звеньев и САУ в целом могут быть описаны дифференциальными уравнениями и представлены графическими характеристиками. Применяют два типа таких характе
1 Эталонная модель может быть явной или неявной.
52
ристик — временные (переходные) и частотные. Характеристики могут быть сняты экспериментально или построены по уравнению звена (можно и по экспериментальным характеристикам составить уравнение звена). С помощью этих характеристик можно определить реакцию звена (САУ) на возмущение произвольного вида.
Переходные и частотные характеристики однозначно связаны с уравнением звена (САУ) и наряду с ним являются исчерпывающим описанием динамических свойств звена (САУ).
ВРЕМЕННЫЕ (ПЕРЕХОДНЫЕ) ХАРАКТЕРИСТИКИ
Переходная характеристика звена h (t) представляет собой переходный процесс изменения во времени выходной величины звена, вызванного подачей на его вход единичного ступенчатого воздействия 1(0- Единичное ступенчатое воздействие — это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным (рис. 2.11, а).
Аналитическое выражение единичного ступенчатого воздействия — единичная ступенчатая функция — обозначается 1(0 и мо-
[О при / < 0;
жетбыть описана следующим равенством: 1(0 = С	или
о1(О — единичная функция типа «после»; если 1(0 =
при t < 0; при ?>0,
1о(О— единичная функция типа «до» (рис. 2.11, г).
Если ступенчатая функция равна 1 между двумя моментами времени и t2, то это единичная функция типа «между»: Z|l/2(0 (рис. 2.11, д). Функция с запаздыванием приведена на рис. 2.11, е.
Таким образом, переходная функция h (0 — это выражение для у (/) при х (Z) = 1(0- Предполагается, что 1(0 имеет ту же размерность, что и физическая величина на входе звена. При t —> <» h(t) = й(°°) =
= /гус/;/) = Л(0)/е(0) = 1Г(0);/г„еР(О = /г(О-й(°°) = АЧ	.
Если х(0 не единичная ступенчатая функция x = A-l(z), то y = Nh(t).
Ступенчатое воздействие— это мгновенный скачок нагрузки на вал двигателя, мгновенный поворот вала входной оси следящей системы, скачок температуры и т. д. — наиболее неблагоприятное воздействие для САУ. Связь между й (?) и W (р) устанавливается через обратное преобразование Лапласа
h(t) = L~l [W(p)x(p)] = L~l
53
а)
д)	е)
Рис. 2.11
так как х(р) = L[l(z)] = \/р, а Ь[Л(О] =	. На рис. 2.11, б, в, пред-
ставлены также спектры амплитуды и фазы единичного ступенчатого сигнала X(w) = 0,58(<b)- j/at.
Наряду с h (Z) применяется импульсная переходная характеристика, представляющая собой реакцию звена на единичный импульс.
Единичный импульс — это математическая идеализация предельно короткого импульсного сигнала (рис. 2.12). Реально — это кратковременный удар нагрузки на вал двигателя, ток короткого замыкания, отключение с АПВ и т. п. При этом, так как длительность импульса весьма мала по сравнению с длительностью переходного процесса Znn, то с большой степенью точности реальный импульс можно представить в виде единичного импульса с некоторым масштабным коэффициентом. Единичный импульс 8 (Z) — импульс, площадь которого равна единице при длительности равной нулю и высоте рав-
54
Рис. 2.12
ной бесконечности: J8(0<ft = l (на рис. 2.12, а он условно показан в виде утолщения на оси ординат). На рис. 2.12, б, в показаны также соответственно спектры амплитуды и фазы единичного импульсного сигнала.
Ступенчатая функция и дельта-функция относятся к классу обобщенных функций, первые производные которых представляют собой дельта-функции.
Аналитическое выражение для импульсной переходной характеристики — импульсная переходная функция звена или весовая функция звена (функция веса), обозначается w (0. Как уже упоминалось, выражение для единичного импульса соответственно называется единичной импульсной функцией или дельта-функцией 8 (0.
f°°, t = 0;
Таким образом, w (0 — это .у (г) при х(0 = 8(0 = -1
Если х (?) — неединичная импульсная функция, т. е. х (0 = к 8 (0, то y(t) = kw(t).
Далее воспользуемся известным соотношением: дельта-функция связана с единичной ступенчатой функцией
8(0=1'(0 = ^. at
Откуда следует аналогичная связь между переходной и весовой функциями линейных звеньев
dh(t) w(t) = h(t) = ~~~j~~, at
и наоборот
h(t) = J w(t)dt.
о
Учитывая эти соотношения между переходной и весовой функциями, будем применять главным образом h (0, имея в виду, что w (0 при необходимости можно всегда получить. Связь между и>(0 и W(p) получается аналогично: Л[8(0] = 1, т. е. 8(р) = 1 и
55
w(t) = L~l [W)8(P)] = L~x[W{p)},
c+>
LA[W(p)] = ^ jwWdp.
C~j®
Зная переходную h(t) или весовую w(t) функцию, можно определить реакцию звена у на произвольное входное воздействие х при нулевых начальных условиях с помощью интеграла Дюамеля—Карсона (интеграл свертки). Интеграл Дюамеля позволяет представить произвольный сигнал совокупностью единичных регулярных сигналов (скачков)
t
x(t) = x -01(0+J (tZx(T) / dx) -01(/ - x)dt
о
или совокупностью единичных импульсов
t
x(t) = j х(т)-08(/ - r)dx.
о
Тогда
Х0 = h(t)x(G)+1 h(t - x)x(x)dx, о
где х (?) — значение x^(t) при t = 0.
t
Или y(t) = h (O)x(r) + J w(t - x)x(x)dx.
о
Здесь т — вспомогательное время интегрирования, изменяющееся в пределах от нуля до рассматриваемого текущего значения времени t.
На рис. 2.13 дана геометрическая интерпретация этих выражений [4]. Реакция звена на произвольное воздействие x(t) может быть определена как предел суммы реакций на ступенчатые воз-„	„ . dx ,	..
действия высотой Дх = — Дт, на которые можно разложить х (?) при dt
Дт—>0 (см. рис. 2.13, а), или на х(/) = lim х(0, где х(0 — после-
Дт->0
довательность прямоугольных импульсов (см. рис. 2.13, б). Выражение для у (г) через весовую функцию и» (г) геометрически интерпретируется на рис. 2.13, б как предел суммы реакций на импульсы шириной Дт при Дт -»0. Его можно представить и в таком виде
t
y(t) - h(0)x(t)+^w(x)x(t-r)di.
о
56
Выражения для y(t) через h(t) и w(Z) легко получить друг из друга, так как они являются вариантами интеграла Дюамеля или интеграла свертки (свертка функций).
Заметим, что первое слагаемое h (0)х (/) в выражениях для у (t) у реальных инерционных звеньев (обычно второго и более высокого порядка) равно нулю, так как реакция на их выходе всегда отстает от входного воздействия, т. е. Л(0) = 0. Поэтому в дальнейшем выражения для Х0 приводятся без первого слагаемого:
y(t) = J и’(т)х(/ - т)Л о
или
y(i) = | x(x)w(t - t)dz.
о
В выражениях для y(f) в качестве верхнего предела интеграла вместо t может стоять °°, так как при t < т, т. е. при отрицательных значениях аргумента функции h(t - т) и w(t - т) равны нулю.
Между h(f), w(t) и W(p) существуют взаимосвязи, определяемые преобразованием Лапласа для и>(0 и Карсона для h(t)
W(p) = ^w(t)e~pldt-, о
Ж(р) = J h(t)e~ptdt. о
57
Эти взаимосвязи являются чрезвычайно важными, так как позволяют по W(p) найти h(t), w(t), и наоборот.
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
Широкий класс функций времени может быть представлен бесконечной суммой гармонических колебаний различных частот (спектральное разложение — ряд Фурье).
Частотные характеристики описывают отношения установившихся вынужденных колебаний на входе и выходе звена, вызванных гармоническим воздействием на входе.
Пусть на вход звена (рис. 2.14, а) подано моногармоническое воздействие
X = хм COS to0Z,
где хм — амплитуда; со0 — угловая частота воздействия. Спектр этого сигнала приведен на рис. 2.14, б и представляет собой дискретную функцию (в0 =const(/); ф((0) имеет скачкообразный характер (см. рис. 2.14, в).
На выходе звена будут (по окончании переходного процесса) гармонические колебания с такой же частотой <оо, как и входные, но отличающиеся по амплитуде и фазе. В установившемся режиме выходной сигнал звена
y=yMcos((00Z + 9),
где уы — амплитуда установившихся колебаний выхода; ф — фазовый сдвиг между входными и выходными колебаниями.
Рис. 2.14
58
При хм = const (г) амплитуда ум и фаза ф установившихся колебаний на выходе звена зависят от частоты колебаний. Увеличивая от нуля до (о —> оо частоту колебаний и определяя установившиеся значения амплитуды и фазы выходных колебаний (для разных частот), можно получить зависимость от частоты отношения амплитуд Л (со) = = ум(<о)/хм((о) и сдвига фаз выходных и входных установившихся колебаний <р((о). Эти зависимости называются соответственно Л (и) — амплитудной частотной характеристикой (АЧХ) и ф(со) — фазовой частотной характеристикой (ФЧХ). Аналитические выражения Л (со) и ф(оо) называются соответственно амплитудной и фазовой частотными функциями.
Используем символическую форму записи гармонических функций, т. е. представим установившиеся колебания на выходе и входе звена в виде
х = ^“Ге>'+е-^1 = х' + х";
.21	•*
У = 2k р'«0'+ч>) + е-л«о'+ч» ] = у + у"
или (в символической форме) х = хме>';
Символичность заключается в отбрасывании членов уравнений с сомножителями , так как по формуле Эйлера
е^+е ««и	1
cos см =---------: smart- — leJ -eJ I,
2	2j \	/
cos at+j sin at = e7M; cos at - j sin at = e~jtor.
Поскольку в линейных САУ на основании принципа суперпозиции можно рассматривать только х' и соответственно у', то при подстановке в уравнение звена в общем случае Q(p)y = R(p)x, учтем следующие очевидные выражения для к-й производной от х и у:
/(хме>г) = (/(0)Лхме>';
/(^ey(te,+<p)) = (»fcyMe«.
В результате подстановки (и преобразования) получим
59
QU®)yMeJ{t0‘+® =	
I
I
Откуда = 2^?1еЛ>(“). так Как б(У“) ^м(ю)
a
Им(м) Х.м(«)
= А(а>), то
Я(» е(»
= W{p)\p=jisj=W(j^,
Следовательно, аналитические выражения для частотных характеристик могут быть получены по передаточной функции W(p) подстановкой р = j(o; комплексная величина FT(jco) представляет собой функцию со и называется амплитудно-фазовой частотной функцией. Подстановка p=j(a справедлива и основывается на формальной аналогии двустороннего (|) преобразования Лапласа и частотного двустороннего преобразования Фурье.
Пример 1. Если « = Lpi, а 7 = 7ме-*“ = 1(f), то и =	или й = jtstLI.
dt
1 I	j	d
Пример 2. Если и = — fidt>->~~то й = ~—. Следовательно, —н» уо>, С о рС ja>C	dt
Г	1	1	dr
\dt — I-» — при нулевых начальных условиях, т. е. — (временная область) соот-J	р ]ш	dt
ветствует ja> (частотная область). Здесь и — напряжение на индуктивности L (пример 1) и емкости С (пример 2);«	» — знак соответствия.
Модуль mod Wfjco) представляет собой выражение для АЧХ А (со), а аргумент arg W(J(o) — выражение для ФЧХ <р (о).
В полярных координатах АФХ имеет вид (на комплексной плоскости)
Ж(уй) = Дй)ел’(“).
При построении АФХ значения со(- от 0 до °° наносятся вдоль характеристики через определенные интервалы (рис. 2.15). АФХ для —to = -ооч-О зеркальна относительно вещественной оси (показана пунктирной линией). Смысл знаков «-» и «+» при (о заключается в том, что они соответствуют отрицательным и положительным скоростям вращения векторов на комплексной плоскости. Кроме того, при использовании диапазона -<» ч- +<х> многие формулы получают более удобный и симметричный вид. Очевидно, если имеется амплитудно-фазовая частотная характеристика W(j(o), то можно по этим точкам построить характеристики Я(<о) и <р(со). АФХ можно
60
построить и в прямоугольной системе координат (на комплексной плоскости). При этом координатами будут проекции U(di) и Ци) вектора Л (со) на соответствующей оси; зависимости <7(со) и И(со) называются соответственно действительной (вещественной) и мнимой частотными характеристиками (ВЧХ и МЧХ).
Тогда в алгебраической форме:
4z(7W) = ReBz(» +
+ jTm^(» = t/(co) + jV((o).
Напомним, что j = 4-1; +J — означает поворот в комплексной плоскости на угол л/2 против часовой стрелки; -j—поворот на л/2 по часовой стрелке; j2 — поворот на угол п.
Связь между частотными функциями следующая:
1Г(У(о) = Л(со)еЛ'(“) = Л(со)[со8 (р ((й) + у sin ф ((D)] = t/(w) + jK(co).
Здесь А (со) = у1и2((й) + К2(со) —четная функция; ф(со) = arctg—— — £7(со) нечетная функция, где Щ-со) = С((о) = Л (со) cos ф(со) — четная функция; Г (-со) = -У(со) = А (со) sin ф(со) —нечетная функция.
Иногда для различия у замкнутой САУ применяют другие символы, например, Ф(7’со) = //(to)e7V(“) = Р(со) + jQ((ai), которые аналогично связаны между собой. Здесь также Ф(7’со) — отношение изображения Фурье выходных и входных величин при нулевых начальных условиях.
Если, в общем случае,
1П/(О)_^»-^«О)Н-УЪ«О) 2(» Се((о) + 7Те(со)’
где индексами R и Q отмечены части соответствующих комплексных величин в числителе и знаменателе дроби, то после освобождения от мнимой части в знаменателе получим
61
где
и((д} = ^(^6(м) + Иг(<о)Ид(ш) U^ + V^’
K(M) Vr^Uq^-Ur^Wq^} t/2(co) + re2((o)
Построение АФХ no U (со) и V (со) обычно трудоемкая работа, так как умножение частотной передаточной функции на комплексносопряженную величину в знаменателе повышает в два раза степень. Проще строить АФХ в полярных координатах, вычисляя непосредственно
mod Я(усо)
А (со) = —ТТ7.7ГТ1 J mod \Q( усо)|
Ф (cd) = arg	- arg g(yco) = arctg Я(усо) - arctg g(yco);
при необходимости легко получить и U (со), V(со).
ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
Логарифмируя выражение для IK(yco) = A (coje^^, получим
In W(joi) = In А (со) + уф (со).
На практике удобнее пользоваться десятичными логарифмами
(loga N = к ак = N\. 1ёЖ(» = 1gА (со) + уф(со)/2,3
и строить отдельно ЛАХ и ЛФХ. ЛАХ строится в виде зависимости
L (со) = 201g А (со),
т. е. 201g |Ж(усо)| = /(1g со); ЛФХ строится в виде зависимости ф (со) от 1g со. Главным достоинством ЛАХ является возможность построения их во многих случаях практически без вычислительной работы, например, суммированием или в виде асимптотических ЛАХ (совокупности отрезков прямых линий с наклонами, кратными 20 дБ/дек). Кроме того, уменьшается кривизна характеристик в логарифмических
62
координатах. При со->°о |Ж(усо)|-эО; Г(со)-»-«>; частоте со = О соответствует бесконечно удаленная точка:
1g со —> —при со —> 0 (1g О = —со)/
В качестве единицы измерения величины 201g А (со) используют децибел: 1 дБ = 0,1 Б. 1Б соответствует усилению мощности сигнала в 10 раз, 2 Б — в 100 раз, ЗБ — в 1000 раз и т. д. Так как мощность сигнала Р пропорциональна квадрату амплитуды, a lg А2 = 21g А, то усиления в белах, выраженное через отношение амплитуд А, равно 21g А (соответственно в децибелах оно равно 201g Л). При этом значения Л (со) и L(co) связаны между собой следующими соотношениями [знак «+» у L(co) соответствует усилению и Л (со) > 1, L(co) >0, знак «-» у L(co) соответствует ослаблению и Л(со)< 1, L(co) <0]:
Я(ш) .... 0,001 0,01 0,1 0,316 0,89 1,0 1,12 = 2$0 3,16 10 100 1000
L, дБ .... -60 - 40 - 20 -10 -1 0	1	10 20 40 60
С применением ЛАХ диапазон изменения коэффициента усиления значительно сужается.
ЛФХ строится в полулогарифмических координатах, т. е. в виде зависимости ср от 1g со; использование логарифмического масштаба на оси ординат не имеет смысла, так как фазовый сдвиг цепочки звеньев (перемножаемых) получается в виде суммы фазовых сдвигов отдельных звеньев.
На оси абсцисс часто указываются значения частоты со (рад/с). Единицей приращения 1g со является декада, соответствующая изменению частоты в 10 раз или октава, соответствующая изменению частоты в два раза (1 октава равна 0,303 декады, так как 1g 2 = 0,303). Наклон ЛАХ соответствует 20 дБ/дек s 6 дБ/окт (точнее 6,06 дБ/окт). Кроме ЛАХ и ЛФХ можно построить также ЛАФХ.
При использовании логарифмического масштаба точка, соответствующая со = 0, находится слева в минус бесконечности (1g 0 = ) и ЛАХ строятся не от нулевой частоты, а от достаточно малого, но конечного значения со, которое и откладывается в точке пересечения кооординатных осей. Очевидно, что логарифмирование возможно только, если величина ИИ(усо) безразмерная (размерность х и у одинакова). Условно можно логарифмировать величины и с размерностями, например, со [1/с], как 1g со]/со2; аналогично
Л] [размерность Д]
lg Л^змерно/гьЛ]’ еСЛИ РазмеРности У 4 и А одинаковые.
Обычно для наклона ЛАХ применяют символические обозначения, соответствующие 1 = 20 дБ/дек [со знаком «-», если Л (со) = 1/Тсо, или «+», если А (со) = Гео]; 2=40 дБ/дек [со знаком «-», если Л (со) = 1/Т2со2, или «+», если Л(со) = Г2со2]; 3 = 60 дБ/дек [со знаком «-» , если Л (со) = 1/Г3со3, или «+», если Л (со) = Г3со3 ].
63
В общем случае исчерпывающее описание звена с помощью частотных функций требует знания амплитудно-фазовой частотной функции либо любой пары функций: А (со) и <р (со) или (/(со) и Г(ш).
Для минимально-фазовых звеньев существует однозначная связь между образующими эти пары функциями и для полного описания таких звеньев достаточно иметь только одну из них.
Для минимально-фазовых звеньев:
. .	1 f 41n^(v)]f t
cp((0) = — I	—y^lnctg
n _J tZ(lnv/co)
In v/(0 ~2~
<7 In (v/co);
... . If K(v)dv .... If t/(v) , C7((o) = -~	; И(о>) =	—
n J v —co	n J V-0)
—-OO	— ОС
где v — переменная интегрирования.
Анализ (и синтез) минимально-фазовых САУ можно производить, используя, например, только ВЧХ U (со) или АЧХ К (со). Обычно для минимально-фазовых звеньев строят АЧХ. Принципиальная связь между АЧХ и ФЧХ такова, что ср растет с увеличением наклона АЧХ; при этом для ЛАХ можно приближенно считать, что участку ЛАХ с наклоном ± 20 дБ/дек соответствует ф = ± п/2, а участку ЛАХ с наклоном ±40 дБ/дек нф(ы) = ±п.
Пример. Устойчивое минимально-фазовое звено с Wl(p) = kl(Tlp+X), где д = -1/7[; неустойчивое неминимально-фазовое звено с W2(p) = kl(T2p-\), где й=+1/7^. Здесь Ф2(ш) = -arctg соТ2 - л > ф|(о>) = -arctg со7] при As(со) = Л2(<о).
Частотные характеристики звеньев (и САУ) могут быть сняты экспериментально с помощью инфранизкочастотной аппаратуры. Экспериментальное исследование имеет смысл, если САУ линейна или близка к линейной. Сигналы сложной формы используются для получения спектра частот, например, прямоугольный синус:
4а Г •	1 . ,	1 . с 1
х = — smwz+sm3aH+sm5(iH+... .
п L	3	5
Глава 3. ДИНАМИЧЕСКИЕ СВОЙСТВА ЗВЕНЬЕВ САУ И ИХ ХАРАКТЕРИСТИКИ
§ 3.1. КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ САУ
Передаточные функции САУ (и сложных ОУ) представляют собой обычно полиномиальные сомножители вида:
64
R( D) ^iPm *" • • • + fyn W{p) = ^ = ^~n-----------
QtP) OqP + ... +an
±2^kTkp±D
i=l j=l k=\
prX[(TlP±\)[[{T^ ±2^mTmp±\)
Ы	m=l
Типовые динамические звенья (ТДЗ) САУ подразделяются на обыкновенные и особые (табл. 3.1).
1. Обыкновенные ТДЗ описываются дифференциальными уравнениями первого или второго порядка или передаточной функцией W(a) =	, являющейся математической моделью элемента САУ.
Q(.P)
Эти ТДЗ все минимально-фазовые (нули и полюсы W((?) имеют отрицательные или равные нулю вещественные части).
2. Особые ТДЗ — неминимально-фазовые, неустойчивые звенья, звенья с распределенными параметрами [иррациональные — W(p) с подкоренными выражениями, трансцендентные с е“рт —трансцендент-
Таблица 3.1. Классификация типовых динамических звеньев
1. Обыкновенные ТДЗ		
1.1. Статические (позиционные)	1.2. Интегрирующие (астатические)	1.3. Дифференцирующие (форсирующие)
1.1.1.	Идеальное 1.1.2.	Первого порядка 1.1.3.	Второго порядка 1.1.4.	Второго порядка колебательное 1.1.5.	Второго порядка консервативное	1.2.1.	Идеальное 1.2.2.	Идеальное и-го порядка 1.2.3.	Инерционное первого порядка 1.2.4.	ПИ- звено (изодром-ное) первого порядка 1.2.5.	ПИИ-звено (изодром-ное) второго порядка	1.3.1.	Идеальное 1.3.2.	Идеальное п -го порядка 1.3.3.	Инерционное первого порядка 1.3.4.	ПД-звено (форсирующее) первого порядка 1.3.5.	ПД-звено инерционное 1.3.6.	ПДД-звено (форсирующее ) второго порядка 1.3.7.	Форсирующее звено второго порядка
2. Особые ТДЗ		
2.1.	Устойчивые неминимально-фазовые 2.2.	Неустойчивые неминимально-фазовые 2.3.	Трансцендентные, с запаздыванием	2.4.	Иррациональные 2.5.	Дискретные 2.6.	Звенья с модулированным сигналом	2.7. Нелинейные 2.8. Смешанные
5 А. А. Ерофеев
65
ные W(p)], дискретные звенья, звенья с модулированным сигналом и др. (см. табл. 3.1). Они составляют основу особых САУ: САУ с переменными параметрами, САУ с запаздыванием и распределенными параметрами, импульсные САУ или дискретные САУ, нелинейные САУ и др. (Неминимально-фазовые ТДЗ, если полюс передаточной функции или хотя бы один нуль имеет положительную вещественную часть). Напомним, что корни уравнения R (р) = 0 — нули передаточной функции, а корни уравнения Q (р) = 0 — полюса передаточной функции. У неминимально-фазовых ТДЗ дфнтф > дФтф при одинаковых АЧХ.
Сложные звенья (ОУ) описываются посредством передаточных матриц:
W(p) = {Wy (р)} = Q-' (p)R(p) = С[рЕ-А}~{ B + D.
Как было указано выше, для расчета различные САУ обычно разбивают на динамические звенья. Сложные САУ разбивают на простые методом декомпозиции. Динамическое звено — устройство любого физического вида и конструктивного оформления, описываемое определенным дифференциальным уравнением. Классификация динамических звеньев поэтому и производится по виду дифференциального уравнения или, что то же, по W{p), так как одним и тем же дифференциальным уравнением могут быть описаны разнообразные устройства (механические, гидравлические, пневматические, электрические). В ТАУ это будет одно звено, независимо от физической природы. Если хвх = х, хвых = у, а возмущение f (z), то статическая характеристика любого звена может быть изображена прямой линией (рассматривается линейная, точнее, линеаризованная САУ).
ОбыкновенныеТДЗ подразделяют в основном натри группы (рис. 3.1):
1)	звенья статического или позиционного типа, где у = кхх, в установившемся режиме (кх — коэффициент передачи звена) (рис. 3.1, а);
2)	звенья интегрирующего типа, где у = к2х, в установившемся режиме или при y = k2^xdt; у(р) = (к2/ р)х(р) — откуда и его название (рис. 3.1,6); здесь размерность fc2=c-1 при х и у одной размерности;
dx
3)	звенья дифференцирующего типа, где у = к2—; у(р) = к3рх(р} dt
в установившемся режиме, откуда и название звена (см. рис. 3.1, в). Здесь к3 измеряется в секундах; дифференцирующие звенья еще иначе называют форсирующими, фазоопережающими звеньями.
Упрощенная классификация обыкновенных динамических звеньев по виду W(p) включает обычно 17 разновидностей, так называемых типовых динамических звеньев (ТДЗ), описываемых дифференциальным уравнением не выше второго порядка (см. табл. 3.1). Из них: пять позиционных, в том числе с инерционными свойствами; пять интегрирующих; семь дифференцирующих, в том числе с инерционными свойствами. Существуют расширенные таблицы ТДЗ из 19 звеньев: где
66
Рис. 3.1
7 — позиционных, в том числе с инерционными свойствами; 5 — интегрирующих; 7 — дифференцирующих; таблицы из 24 и более звеньев [1-9].
§3.2. ОБЫКНОВЕННЫЕ ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ САУ
Рассмотрим уравнения, переходные и частотные характеристики наиболее часто встречающихся типовых звеньев (табл. 3.2.-3.8).
Здесь и ниже информация, относящаяся к тому или иному звену, кодируется номером, согласно табл. 3.1
Статические звенья. Все статические звенья (код 1.1) в установившемся статическом режиме описываются одинаковым уравнением Уст = кхст-
Статическое идеальное звено (пропорцианальное, масштабное, усилительное, безъемкостное, безынерционное) (код 1.1.1). Его уравнение в статике и в динамике у = кх, т. е. процесс передачи информации проходит без искажений, усиливаясь в к раз. Его АФХ — точка, <р((в) = 0.
К такому звену сводятся все статические звенья первого порядка, если можно пренебречь инерционностью, т. е. принять Т= 0. Это звено — идеализация реальных звеньев, так как в действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до а имеет определенную полосу пропускания Д<вп =сов-(ои.
Таблица 3.2. Обыкновенные типовые динамические звенья
Тип звена * г|	1 Уг	Передаточная функция W(p)	Операторное уравнение
1.1. Статические (позиционные)		
1.1.1. Идеальное (усилительное, безынерционное)	к	у = кх
1.1.2. Первого порядка (апериодическое, инерционное)	к ~Tp+i	(Тр+Т)у = кх; Д=—
67
5*
Продолжение табл. 3.2
Тип звена х »|	1 Уг	Передаточная функция W(p)	Операторное уравнение
1.1.3. Второго порядка колебательное	к Т2р2+2с,Тр+1	(Т2р2+2£,Тр+1)у = кх; 0<5<1
1.1.4. Второго порядка (апериодическое, инерционное)	к	_	к T?p2 + TiP+\ (Т3р+1)(Т4р+1)' T3.4 = ^li±^-4TAT32:T4	(7f/ + 7ip+l)y = fo; Г, >2Т2;^1
1.1.5. Второго порядка консервативное	к Т2р2+1	(Т2р2+1)у = кх;^ = 0
1.2. Интегрирующие (астатические)		
1.2.1. Идеальное	к. JL. т =1 р’ ТИр' “ к	ру = кх
1.2.2. Идеальное и-го порядка	« = U-р	рпу = кх
1.2.3. Инерционное первого порядка		t	 р(7р+1)	р(Тр+\)у = кх
1.2.4. ПИ-звено (изод-ромное) первого порядка	W=V-; kl=kT р	р	ру = к(Тр+\)х
1.2.5. ПИИ-звено (изод-ромное) второго порядка	к(Т2р2+2^Tp+l)_, к к 2	+ т" о » Р	РР кг = кТ2\ кх=к2^Т	р2у-к(Т2р2+2^Тр + ])х; 0<£<1
1.3. Дифференцирующие (форсирующие)		
1.3.1. Идеальное	кр	у = крх
1.3.2. Идеальное л-го порядка	кр", л = 1,2,...	у = крпх
1.3.3. Инерционное первого порядка	кр Тр+\	(Тр+Т)у = крх
1.3.4. ПД-звено (форсирующее) первого порядка	£(7р + 1)	у = к(Тр+\)х
1.3.5. ПД- звено инерционное	fc(W) TJp+1	(Т1Р+Г)у = к(Тр+1)х
1.3.6. ПДД-звено (форсирующее) второго порядка	fc(7V+2<7p+l)	у = к(Т2р2 +2£,Тр+Г)х; 5<1
1.3.7. Форсирующее второго порядка	кр(Тр+Ху, к(Т2р2+Г)	у = кр(Тр+\)х-, у = к(Т2р2+\)х-, 5 = 0
68
Таблица 3.3. Временное характеристики статических звеньев
h
h = k-oKO
„	0),	в
0 = arctg —— = arctg—; o>(£ a
are
, ft , Gi COT c,=ke ₽;ln—= — °2 p
69
Продолжение табл. 3.3
Например, реальные электронные усилители обычно обладают некоторой инерционностью и их характеристики /г(г),Л(со), <р(со) в действительности имеют вид, представленный на рис. 3.2.
Примеры: механический редуктор (без учета скручивания и люфта); безынерционный (широкополосный) усилитель, делитель напряжения; рычажное соединение; первичные пребразователи (датчики) — потенциометрические, индуктивные, вращающиеся трансформаторы, тахогенераторы (х = <о; у = ия тг) и т. д.
Статическое звено первого порядка (апериодическое, инерционное, одноемкостное, релаксационное) (код 1.1.2).
Уравнение, передаточная функция, временные и частотные характеристики звена представлены в табл. 3.2-3.4, под кодом 1.1.2.
Если временные (или частотные) характеристики звена получены экспериментально, по ним можно определить значения Т як как показано, например, для h(f) и получить таким образом уравнение звена.
70
Таблица 3.4. Частотные характеристики статических звеньев
71
Продолжение табл. 3.4
АФЧХ W (усо) амплитудная А (со), фазовая ф(ш), вещественная С/(со) и мнимая V ((d) частотные характеристики
Амплитудно-фазовая частотная характеристика
АЧХ, логарифмические характеристики: асимптотическая амплитудно-частотная /.(со) и фазочастотная <р (<о)
1.1.3. Статическое втрого порядка:
W(Jw) =----------------,
(1-ш2Т2) + ja2^T
А= . ..................  ,
71 + <о22Г2(252-1) + ш4Т4
. «25Т I
Ф! =-arctg--5-т шт«ь
1-сгГ2
fc(l-co2T2)
U 1+<о22Т2(252-1)+со4Т4'
-к<х>2£,Т
у =-----------.---------
1 + ш22Т2(252 -1)+й)4Г*
1 при со0=-
U = 0; v = ~
25
Цш) = 201g к - 201g [(1 - Я2)2 + + 452П2]1/2
Продолжение табл. 3.4
АФЧХ амплитудная А (со), фазовая ф (со), вещественная U (со) и мнимая V (со) частотные характеристики
Амплитудно-фазовая частотная характеристика
АЧХ, логарифмические характеристики: асимптотическая амплитудно-частотная £(о>) и фазочастотная ф (со)
1.1.4. Статическое второго порядка колебательное:
i"
(Г(уш) =----------------;
(1-ш2^2) + >7;
__________к___________.
71+<о2(7|2-2^)+<о472Г
шТ?
Ф = -arctg ----е-у,
l-<o2?f
к(1-а2Т?) l+o)2(7J2-2^2)+to47^’
TZZ \ к'Т'‘У	I
Г(ш2) = -Л; ш2 = —
Ч	*2
1
А = ф + <o27f)(l + ш2Т?)р;
к
к

к
 а = ^; ф = -90°;
________-faoTj_________ 1 + 0)2(Т;2-2722) + ф4^*
Ф = -arctg со Ту - arctg <а 7J;
1
<04=v ‘4
Продолжение табл. 3.4
74
Рис. 3.2
Чем больше величина постоянной времени Т, тем длиннее переходной процесс tn в звене. Теоретически zn — время нарастания экспоненты й(/)— равно бесконечности; практически за длительность переходного процесса tn принимают время от начала процесса до момента, когда выходная величина достигла 95 % установившегося значения. В случае экспоненты это время равно ЗТ; иногда принимают Гп = (4+5)Т{4Т 1-э 98,2%у(°о), 5 Т н» 99,3%у («=)).
Амплитудно-фазовая частотная функция представляет собой полуокружность с радиусом кН и центром в точке {кН, 0) на действительной оси. Здесь (и далее) в уравнения частотных функций входит 2л Т _
член 0)7’ =—Т = 2л—— = £2 = со — это относительная безразмерная частота.
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) звена приближенно представляется ломаной линией, которая называется асимптотической ЛАЧХ. Эта характеристика составлена из двух асимптот — прямых, к которым стремится ЛАЧХ: при со —> 0, соТ«1 и 71 + Т2со2 «1, т. е. L (to)« 201g к-, присо-»«> и 71 + Т2со2 «соТ, т. е. L (со) = 201g к-201g to Т.
Во втором случае характеристика представляет собой прямую, имеющую наклон dL {(Hildas = - 20дБ/дек (при увеличении to на декаду (в 10 раз) L (to) = 201g к - 201g 10 to Т= 201g к - 201g to Т-201g 10). Следовательно, L (to) уменьшается на 201g 10, т. е. на 20 дБ. Таким образом, прямая, параллельная оси абсцисс на уровне 201g к, — первая асимптота; вторая асимптота, к которой стремится ЛАЧХ при
75
co —> оо, прямая с наклоном в - 20 дБ/дек. Обе асимптоты пересекаются в точке, соответствующей частоте сос=1/Т (сопрягающая частота). При сос = 1/ Т L (со) = 201g к - 201g 72 = 201g к - 3,03 дБ. Следовательно, максимальное расхождение между истинной и асимптоматической ЛАЧХ ровно 3,03 дБ и в обе стороны от сос уменьшается. Поэтому практически в качестве ЛАЧХ статических звеньев первого порядка используют асимптотическую ЛАЧХ.
Фазовая частотная характеристика при изменении со от 0 до °° изменяется как кососимметричная кривая от 0 до - п /2 (при со = 1/77, ср = - п /4).
Значение полосы пропускания звеном частот, соответствующее ширине частотной характеристики, определяет быстродействие звена: чем больше шп, со звена, тем меньше /п и инерционность — постоянная времени Т звена.
Выражения для частотных функций, записанных через Q имеют более простой вид. Например, А (£2) = fc(l + Q)1^2 и т. д.
Для дискретного звена W(z) = к z / T(z - е~т,,1т), где ТК—период (такт) квантования; z = ерТ*.
Примером статических звеньев первого порядка являются :
1)	генератор постоянного тока (х = С/возб, у = U* г);
2)	двигатель любого типа (электрический, гидравлический, пневматический и т. д.), механические характеристики которого — прямые линии, для различных х (Ux в электродвигателе, расход Q жидкости в гидродвигателе и т. д.);
3)	резервуар с газом, жидкостью (х = Д перед впускным отверстием, у = Р2 в резервуаре);
4)	нагревательная печь (х = Q — количество поступающей в единицу времени теплоты, у = f);
5)	термопара (х = Е, у = t°);
6)	тиристорные, электромагнитные усилители, гидро-, пневмоусилители и т. д.
Статическое колебательное звено второго порядка (код 1.1.3).
Уравнение звена имеет вид:
2 d2y dy
Т2 7I + T]7t+y = kx, dr dt
гр
в котором Т\ и Т2 связаны условием £ = —— <1, т. е. 2Т2 >ТХ. 27j
Обычно уравнение этого звена записывают в виде (Т2 = Г, 7] - 2£Т): (Т2р2 +2^Тр+\)у = кх, или
' р2 2с,р у = кх, {я Я J
76
или
d2y	dy	2	,
~~-+2§со0£+(о^ = А:1х, at	dt
где Aj =£(0q; <7 = 1/T = (00 —угловая частота свободных колебаний (при отсутствии затухания) или собственная частота незатухающих (резонансных) колебаний; § — параметр затухания (коэффициент относительного затухания), показатель демпфирования (0 < Е, <1).
Условие 0 < § < 1 означает, что корни характеристического уравнения 7^2/?2+ 7Jp+l = 0 являются комплексными, равными
д2=-а±/Р =
-т;±а/712-4г22
2Т22	Т
= -§(00±/(00Jl-§2 =
= -§(001/(0! =-а ±/(0!-
Здесь вещественная часть корня равна а = §/Г = §д = §о>0 и определяет коэффициент затухания или декремент затухания переходного процесса; мнимая часть £ = q^l - §2 = (ооз/1-§2 = о»! характеризует собственную (фактическую) частоту затухающих колебаний. Значение а2 + р2 = q2 = (0q или д/а2 + р2 = ®0 и определяет частоту свободных колебаний; отношение р/а = [(1/§2) -1]!^2 = СО] /§со0. При § -> 0 а -» 0, а р->в)0; при §	1 а —> (й0, а р -> 0.
Уравнение установившегося (статического) режима звена имеет аналогичный вид, что и у статического звена первого порядка Зет
Характеристики звена представлены в табл. 3.3 и 3.4 под кодом 1.1.3.
Колебательность переходного процесса звена с ростом § уменьшается, исчезая совсем при § > 1.
По экспериментальной характеристике h(t) можно определить пара-Т2 1 метры колебательного звена: к = усг при хст = 1; Т2 = Т% = —г = —2 ;
2Е	2л	0)0
Т, = — = 27А, где То = — — период колебаний, определяемый по (00	Р
переходной характеристике р = 2л/Г0. Величину а , характеризующую степень затухания колебаний, можно определить из выражения Ст]/ст2 = е“7“/2, или о3/о! = е“г°, где Oj, а2 и ст3 — превышения амплитуды колебания относительно установившегося значения, отстоящие на время, равное л / Р — полупериоду колебаний То. Отсюда, на-
пример, а = ™1п	= —231g —;
То °) *о СТ1
3 ЗТ tp а £ ’
а_е-ла/р _е-ла/о>| _ е-5я/(Н2)1П.
77
Выражения для амплитудно-фазовой и других частотных функций при введении £2 = а>Т сильно упрощаются. При £ = 1/ 72 = 0,707 = £оп выражение дляЛ (со) примет вид Л(Й) = к/(1 + О.2)^2; при этом rp -»zpmin (о = 5%). Для 0,38 < £ < 0,707 Ам = к/(2^1 - £2) при Й = ^1 -2£2.
Асимптотическая ЛАЧХ колебательного звена при к > 1 представляет собой ломаную линию, состоящую из двух асимптот: при со —> 0 асимптота идет параллельно оси абсцисс на расстоянии 201g к', при (о —> о° асимптота имеет наклон - 40 дБ/дек. Точка пересечения асимптот соответствует <ос = 1/Т. Уравнение первой асимптоты получается при (оТ « 1: L (со) = 201g к', уравнение второй асимптоты получается при Й » 1 ий2 »2£й: Цй) ==201g Аг — 201g й2 =201g к--401g Й. Ошибка Д£(и4) = -201g [(1-ю2 /со2) + (2^со/и2)]1/2|о<т<й)с и ДТ((о4) = - 201g [(1 - со2 /со2) + (2£/о2 /о)2)р|0<(а<„; Д<р(Й, Q =
8 (1-й2)2+4йЧ|0<Ю<“’
При увеличении частоты на декаду L (со) имеет наклон второй асимптоты в - 40 дБ/дек.
Расхождение между асимптотической и истинной ЛАЧХ при 0,38 < § < 0,707 не превышает 3 дБ (как и для статического звена первого порядка). Поэтому для звеньев при таких значениях £ можно пользоваться асимптотическими ЛАЧХ. При значениях 0,707 < £ < 0,38 асимптотическую ЛАЧХ необходимо вычислять; иногда ЛАЧХ корректируют с помощью формул ошибки Д L, Д <р или графиков поправок, дающих разность между истинной и асимптотической ЛАЧХ. Например, при £ = 1 ошибка уже равна 6 дБ.
Связь между параметрами колебательного звена и частотными характеристиками позволяет по экспериментальным частотным характеристикам определить параметры и получить уравнение звена.
Колебательные звенья — это системы, способные накапливать два вида энергии — кинетическую 1УК и потенциальную Wn (двухемкост-ные системы). Процесс колебания сопровождается переходом одной энергии в другую и наоборот, причем время 7] характеризует способность системы демпфировать (тормозить) колебания, а время Т2 — способность раскачивать САУ.
Примеры колебательного звена: электрический резонансный RLC контур; электрический двигатель при достаточно большой постоянной времени цепи якоря (4ТЯ >ТМ); механический демпфер (катаракт); упругие механические передачи; гироскопические элементы и т. д.
Статическое звено второго порядка (апериодическое, инерционное звено второго порядка) (код 1.1.4) описывается аналогичным уравнением, как и колебательное звено второго порядка, только здесь £> 1.
При^=1 (7]=2Т>)
78
к	к	к Л
W(p) =------, =----------т—т- =  -- ———.
(1 + рТ)	1 + 2рТ+р2Т2 1 + рТ1 + рТ
При § - Т{/2Т2 > 1 корни уравнения становятся вещественными:
_-7]±7т;2-4г22
л,2	„ 2	т ’
так как значение (yjt2 -1) положительно. Для дискретного звена
W(z) = kzTKeTJTlT2^z-eTJT^.
Характеристическое уравнение, соответствующее данному звену, имеет уже не комплексные, а отрицательные действительные корни (pl = -eq, р2 = -а2). Поэтому такое звено не является колебательным, а представляет собой последовательное соединение двух статистических звеньев первого порядка с постоянными времени ВД(Д=-1/Т3; А = -17Т4).
По экспериментальной кривой h (/) можно легко определить пара метры звена, а именно значения Т3 и Т4 [см. h(f) в табл. 3.3]. Выражения для h (/) можно иначе записать:
Л(0 = л{1-[а2/(а2 - ocj )]е-а'г +[а,/(а2 -«1)]е”“2'}’оМа,^2 или
Л(0 = *[1-(1-с«)е-<и}о1(0|а=а1=в2.
Следовательно, неколебательное статическое звено второго порядка может быть заменено в структурной схеме САУ двумя звеньями первого порядка, т. е., строго говоря, его нельзя считать элементарным звеном.
Для дискретного звена
Це-Ш_е-тк/т4) (Г3 - Т4) (z - е~г‘/Гз )(z - e~TjTi)'
У статических звеньев в силу их инерционности Л (со) по мере увеличения частоты падает до нуля; при этом, чем менее инерционно звено, тем больше его полоса пропускания. Теоретически, АЧХ продолжается до бесконечности, но практически полоса пропускания оценивается значением частоты, при котором Я (со) становится мень
79
ше определенного (достаточно малого) значения. Это значение обычно берут равным 0,05 (на этой частоте амплитуда ум падает до 5 % амплитуды хм ).
Частным случаем статического звена второго порядка является так называемое консервативное звено (код 1.1.5) при £ = 0 (у этого звена 7] = 0). Консервативное звено отражает идеальный случай, когда можно пренебречь рассеиванием энергии в звене (например, считать 7? = 0 в контуре RLC). Консервативное звено получается также при охвате двух последовательно соединенных интегрирующих звеньев жесткой отрицательной обратной связью (ООС).
Переходные характеристики такого звена представляют собой незатухающие колебания с частотой 0)0 =1/7. На этой частоте скачком претерпевают изменения ф отО до 180°. Характеристики звена приведены в табл. 3.3, 3.4 под кодом 1.1.5.
Идеальное интегрирующее звено (И) (астатическое, нейтральное) (код 1.2.1, табл. 3.5, 3.6) описывается уравнением в интегральной форме
/ у = k^ x(x)dx + у$.
о
Выходная величина звена пропорциональна интегралу от входной величины, коэффициент передачи И-звена имеет размерность 1/с. Характеристики звена приведены в табл. 3.5 и 3.6, код 1.2.1.
ЛАЧХ звена имеет вид L (о) = 201g (Ш) = 201gк-201g(о и представляет собой прямую, имеющую наклон к оси абсцисс: - 20 дБ/дек. При ® = 1 ее ордината равна 201g к. Для дискретного звена W (z) = kzl(z - 1).
Идеальные интегрирующие звенья л-го порядка (код 1.2.2) с W(p) -^КрТп)п> п=1,2,..., имеют подобные характеристики с той лишь разницей, что наклон ЛАЧХ пропорционален л—порядку звена, а именно: при и = 1 — наклон - 20 дБ/дек; при л = 2 — наклон - 40 дБ/дек и т. д. Каждое И-звено вносит фазовый сдвиг в -90°  Следовательно, И-звено л-го порядка создает фазовый сдвиг: - пп /2.
Реальные интегрирующие звенья (инерционное И-звено, интегрирующее звено с замедлением) (код 1.2.3) обычно обладают определенной инерционностью. Поэтому их выходная величина не равна точно интегралу от входной величины. Реальное инерционное интегриру-к ющее звено с передаточной функцией Ж(р) =---------- можно пред-
р(Тр+1)
ставить как последовательное соединение двух звеньев; интегрирующего звена и статического звена первого порядка. Следовательно, реальное интегрирующее звено уже не является элементарным типовым звеном, а представляет собой последовательное соединение двух известных типовых звеньев. Характеристики реального И-звена приведены в табл. 3.5 и 3.6 под кодом 1.2.3. Для дискретного звена
W(z) = kz(l-e~T‘IT)/ ((z-l)(z-e~r‘/r)).
80
Таблица 3.5. Временные характеристики интегрирующих звеньев
1.2.1
Л = А*01(/); а = arctg к
A = fcp-7’(l-e~'/r)J0l(Z); а = arctg к
й = (й1+й/)-01(г); а = arctg к
1.2.5
й = (кг + к\1 + Хсг2 j-ol(z)
И" = W (/)
W
w = k&(t)
и- = й18(/) + А:.о1(О
и> = [ fc23 (t) + fc| +2ta]3(t); а = arctg 2k
Й = Й(О
Примеры интегрирующих звеньев: операционный усилитель в режиме интегрирования (х = иь 7 = 1/2); гидравлический демпфер (х = = F; у = е); интегрирующий привод (а = A: j" udt); гироскоп; гидравлический двигатель, выходом которого является перемещение
6 А. А. Ерофеев
81
to
Таблица З.б. Частотные характеристики интегрирующих звеньев
АФЧХ W ( jta) амплитудная А (со), фазовая ф (со), вещественная V (со) и мнимая И (со) частотные характеристики	Амплитудно-фазовая частотная характеристика			АЧХ, логарифмические характеристики: асимптотическая амплитудно-частотная L (со) и фазочастотная ф (ю)				
1.2.1. Идеальные:								
		(0=0® +.		А	।	L			
= — = ~j— jto	(0	(0 k	к Л = ~; ф==-90°; tf = 0; V~~ (!)	(0	-•t	о t			\	201дк			
							1	-90	Ш'
								
						ш °	1	а>^ ш	
1.2.3. Инерционное: W(Jv>) =—Л	; -co T+Jw l Л = —ф = -90° - arctg coT; covl+co2/’2 U =		• v =	—	 l+co2T2’	<o(l + co2T2)			с	Z.' 0 0 -90 -135 -180 f^pad		-гобб/дек		
	14 Й -i.					-408Б/д«. 1^\	>	<1>о = '		
						Шв \ tt>tp ttt	” Т		
	€7(0) = -кТ при <оТ = 1; кТ А = ^-, ф = -135°; V2 (/=jz=_AI 2					се II 8- 3 8	| 2 	!11-		
Продолжение табл. 3.6
АФЧХ W (Jto) амплитудная А (со), фазовая <р (со), вещественная U (со) и мнимая V (со) частотные характеристики
Амплитудно-фазовая частотная характеристика
АЧХ, логарифмические характеристики: асимптотическая амплитудно-частотная L (со) и фазочастотная ф (со)
1.2.4. ПИ-звено (изодромное):
л = -71+ш2Т2;
<0
Ф =-90° + arctg соТ;
U = kT;
v=--
_______ (О
1.2.5. ПИИ-звено (изодромное) второго порядка:
-СО
А = к, v'l + u>22T2(2c2-l) + w47'4;
со2
ш2^Т
Ф = arctg---=-т--180 ;
1-со2Г
U(0) = U(°°) = kT;
при <о7' = 1 А = JikT', ф = 45°;
U = kT; V = -кТ
(/ = -А(1-ш2Т2); со2
к — — -------(О
шс=1; 4/(0) = fcT2;
при О)Т = 1 А = 2кТ% Ф = -90°; <7 = 0;
V = ~2^кТ2
поршня /, а входом — давление жидкости, подаваемой в цилиндр; электродвигатель (х = и, у = ф = ja>dx + ф0); емкость (х = i, у = U =
' ° 1 '
= 1/с|zJx + f70);индуктивность (х = и, у=Ф=~ ^иск+Ф0).
о	"о
При этом реальные инерционные интегрирующие звенья соответствуют перечисленным устройствам, если более точно рассмотрены их уравнения.
Изодромное звено первого порядка (код 1.2.4) с передаточной функцией
, к к(\ + Тр) W(p) = £,+- = ------
Р Р
где Т = ~~, а кх = к Т, представляет собой параллельное соединение двух известных типовых звеньев: идеального интегрирующего звена к !р и безынерционного звена/q. Передаточную функцию ПИ-звена часто представляют в виде:
т.р
где ТК — постоянная интегрирования.
ППИ-звено (изодромное звено второго порядка) (код 1.2.5). Это звено с передаточной функцией W(p) = k2 + kxlр+к/р2 представляет собой параллельное соединение трех известных типовых звеньев: П-звена (к2), И-звена (Zq/p) и звена (/с/р2). Характеристики ПИ-и ППИ-звеньев представлены в табл. 3.5, 3.6 соответственно под кодами 1.2.4 и 1.2.5. Здесь
W(p) =	+ Тр) /р ь-> W(z) = fc(l + T)[z + T/(l- 7)] /(z-1).
Эти звенья выделены здесь по той причине, что реальные устройства САУ часто описываются такими передаточными функциями (как единое целое).
Дифференцирующие звенья (код 1.3).
В идеальном дифференцирующем звене (Д) (код 1.3.1, табл. 3.7, 3.8) выходная величина пропорциональна производной от входной величины; коэффициент передачи звена к измеряется в секундах.
Передаточная функция и характеристики дифференцирующего звена обратны передаточной функции и характеристикам интегрирующего звена.
Идеальные дифференцирующие звенья n-го порядка (код 1.3.2, табл. 3.7, 3.8) имеют передаточную функцию W(р) = крп = ТЛрп, п - 1, 2,.... При этом наклон их ЛАЧХ пропорционален п и равен « 20 дБ/дек, а фазовый сдвиг равен п • it 12.
84
Реальные дифференцирующие звенья (код 1.3.3, табл. 3.7,3.8) представляют собой дифференцирующие звенья, обладающие конечной инерционностью; осуществляемое ими дифференцирование не является точным. Передаточная функция реального дифференцирующего звена (без статизма) имеет вид:
Ж(р) =
Ар = кйтДР. Тр+\ Тр+\'
при Т—> 0 реальное звено стремится к идеальному (А=А^).
Реальное инерционное дифференцирующее звено уже не является
типовым; его можно заменить последовательным соединением иде-
ального дифференцирующего звена и статического звена первого
порядка с Wl(p) = k-p и
Ж2(р) =
1
7р+Г
Реальное инерционное дифференцирующее звено со статизмом или
ПД-звено (код 1.3.5, табл. 3.7, 3.8) с передаточной функцией вида
Т2р+1	Т2р+1
при 7] > Т2, ТЛ>Т2 представляет собой последовательное соединение двух звеньев с Wl(p) = l/(T2p+l) и W2(p) = к^р+1) = ка(1 + Тар).
Форсирующее идеальное ПД-звено первого порядка (код 1.3.4, табл. 3.7, 3.8) с W(p) = к(Тр+\) здесь входит как составная часть этого звена (7J = Т). Характеристики идеального ПД-звена первого порядка зер-
Таблица 3.7. Временные характеристики дифференцирующих звеньев
h = h (0	
1.3.1	
Л 	W
и	t	° 	Г
h = k8(t)	w = kp8(t) = k8(t)
1.3.2	
II	и' = |з(0-Ае'г.о1(0
Л*	
А/7|	
*7	г	0 	-g,		 .	 t к/Тг'
85
Таблица 3.8. Частотные характеристики дифференцирующих звеньев
АФЧХ W (/со) амплитудная A (со), фазовая ф (со), вещественная U (со) и мнимая V (со) частотные характеристики	Амплитудно-фазовая частотная характеристика		
1.3.1. Идеальное: = Jkar, А = fco); Ф = +90’; U=b, V = ko>			w-*oo
	-J		ш»0 *
1.3.3. Инерционное первого порядка: W(m) = —		; 1 + jaT A = —f=^=-, ф = 90° -arctgcoT; 4\+<o2t2 U _ кТы2 v _ k<o 1+со2Г2’	l + co27’2	k_ - &	/\k5’\o)’Oo +	
	-J, A <1 U(o\	и	°e	<?	os	§ 2S	7	II	Q e «	'	ч|- 2-	S	<k-	••	-ч!* II - -° toll N>|	
АЧХ, логарифмические характеристики: асимптотическая амплитудно-частотная £(со) и фазочастотная ф(со)
L
О
'Оср 1 ш
Цсо) = 201g £+201g со
90
0 а>
шср = |; ZX=)=201g|
Продолжение табл. 3.8
АФЧХ W (yco) амплитудная A (co), фазовая Ф(со), вещественная U (co) и мнимая V (co) частотные характеристики	Амплитудно-фазовая частотная характеристика	АЧХ, логарифмические характеристики: асимптотическая амплитудно-частотная L (со) и фазочастотная Ф (со)	
1.3.4. ПД-звено:			
»r(» = lt(l + усоТ);	J	la^oo	А	ж	fMpoel
Я = *с/1 + со2Г2;	-f J 	X	/		,	-У	95	/ 	~ И; .	 7\
Ф = arctg со Т; U = k\			•О и	и	ас	Ш
V = ka>T	l/(0)=(/(o°) = fc		шс=1 IT-, I(0) = 201g к
1.3.6. ПДД-звено:			
W(Ja) = A[(l - со2Г2) + >2£Г];	<50^. +j '		L tWOB/Oen .
А = kjl + co22Z'2(2^2 -1) + со4?"4;	_J v UlcO			 : /(w \\i^z
			0	<»е at
	U(f3) = k-t		
<Р arctg ’ ; 1-<о2Т2	1	... . co Аг2§		р,град
			180-2	
t/ = fc(l-co2T2);	T	T		90	^aQjg
	ф(шс)=90°; Л(сос) = 2^		п 		
V = kw2^T			а>с to
Продолжение табл. 3.8
88
кально обратны апериодическому звену первого порядка. Для этого „ ч , ll + ftoT,)2
звена А (со) = к I	> <р(со)= arct§ ® 7] - arctg со Т2; при
со = (7JТ2)-1/2 ф(и) = Фт(®) = arcsin [(/} -Т2)/(7J + Г2)]. Временные характеристики звена имеют вид:
h(t) = л[1-(1-т)е''/Г2]-01(г); Н0 = -^-(1-т)е '/Г2-о1(/) + Ь:5(О;
где т = 7J / Т2 > 1.
Кроме рассмотренных различают еще дифференцирующие (форсирующие) звенья второго порядка или ПДД-звенья (код 1.3.6, табл. 3.7, 3.8) с передаточной функцией ИДр) = к(Т2р2+2^Тр+1), при < 1 имеющие характеристики соответственно зеркально обратные колебательному звену или при £ > 1 статическому неколебательному звену второго порядка. Во втором случае это звено представляет собой последовательное соединение двух форсирующих звеньев первого порядка с Wi(p) = к(1 +рТг) и W2(p) = \ + рТ2, где
Обратные АФХ дифференцирующих звеньев 1 и 2 порядка совпадают по форме с АФХ соответствующих статических звеньев, т. е.
—?— = Wo(ja).
Дифференцирующие (форсирующие) звенья второго порядка могут иметь и несколько другой тип передаточных функций (код 1.3.7, табл. 3.7, 3.8).
Кроме того, эти звенья, уже как реальные, имеют инерционность, когда в знаменателе стоит член (7]р+1). Характеристики дифференцирующих звеньев приведены в табл. 3.2, 3.7 и 3.8 под соответствующими кодами 1.3.1-1.3.7.
Примеры дифференцирующих звеньев: тахогенератор постоянного тока (х = а, у = иТГ при RH -> °°); операционный усилитель в режиме дифференцирования (х = щ, у = и2; W(p) = Тар, Тл= RC); ем-z	-du.	.	.	_ di
кость (х = и, y = ic = c—); индуктивность (x = i,y = u2=L —) и т. д.
dt	at
§3.3. ОСОБЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ САУ
Особые динамические звенья САУ — это устойчивые неминимально-фазовые звенья (содержат нули в правой полуплоскости), неустойчивые звенья (содержат полюсы в правой полуплоскости), звенья
89
с распределенными параметрами: иррациональные и трансцендентные (количество нулей и полюсов стремится к бесконечности) и др. (см. табл. 3.1)..
Звенья с распределенными параметрами описываются уравнениями в частных производных, отражающими связь процессов во времени и пространстве, т. е. зависящих от t и I, уже не являющихся обыкновенными дифференциальными уравнениями.
Устойчивые неминимально-фазовые звенья (код 2.1, табл. 3.1). Передаточные функции этих звеньев имеют, например, вид:
^ = 4^4#	(д=+1/7[, й=-1/Т2);
=	(й=1/7], й=1/т2, й=-1/Т3),
1 + /?7з
т. е. содержат в числителе передаточной функции члены, определяющие наличие положительных корней — нулей ТТ(р). Следовательно, устойчивые неминимально-фазовые звенья (НМФЗ) имеют нули передаточной функции в правой полуплоскости, в то время как их полюсы — отрицательные вещественные числа.
Для примера рассмотрим звено первого порядка с передаточной ,	.. ч к(\-рТ})	,
функцией W(p)=„------Такого вида передаточными функциями
(l + pT^)
обычно описываются дифференциальные или мостовые измерительные RC схемы, широко применяемые на практике (рис. 3.3, а—в). Для мостовой схемы, приведенной, например, на рис. 3.3, в, при Rq = 1:
ц(р) 2(7р+1)
где
T = RiCi=R2C2.
Временные характеристики звена с W (р) имеют вид :
й(0 = А:[1-(1+т)е"//Г2]-01(0;
w(/) = -А:т8(?) + ке
У2
где т = Т]/Т2^1 [при т = 1 W(p) н> W^p)].
Амплитудно-частотная функция звена определяется выражением
90
которое совпадает с выражением для Л (со) минимально-фазового 1 4- п 7*
звена, когда W(p) = к——соответственно аналогичны иЦю) (код 1 + рТг
1.3.5, табл. 3.7 и 3.8). Для минимально-фазового звена <рт(со) = = arctg coTJ - arctg соГ2 < ФнДш) = -arctg (i)7J -arctg &T2; фнда(<о) при изменении (0 изменяется от 0 до - л. Для сравнения напомним выражение для h(t) минимально-фазового звена: ДД/) = &[1-(1-т)е-''/Г2|01(г).
На рис. 3.4 приведены временные (рис. 3.4, а, в) и частотные (рис. 3.4, д, е) характеристики звена, а также для сравнения представлены характеристики hm(t) (рис. 3.4, б) и wm(t) (рис. 3.4, г) минимально-фазового дифференцирующего (форсирующего) звена при т>1.
Аналогом минимально-фазового звена с W(р) = к (Тр + 1) является звено с W (р) = к (Тр - I) и при одинаковых А (со) их <р (со) существенно различаются. Указанные примеры легко можно продолжить.
Неустойчивые звенья являются неминимально-фазовыми (код 2.2, табл. 3.1). Все вышерассмотренные звенья были устойчивые; полюсы их передаточных функций имели отрицательные действительные части. Неустойчивые неминимально-фазовые звенья имеют полюсы и нули с положительной действительной частью.
91
Неустойчивыми, по определению, являются звенья, передаточные функции которых отличаются от передаточных функций рассмотренных выше звеньев изменением знака перед любым из членов знаменателя на отрицательный. Например, к неустойчивым звеньям относятся звенья со следующими передаточными функциями:
к	к	к
--- -------- (3.1); __i------- (3.2);   --------- (3.3);
-^Y+TiP+i	т2У-т]р+1	Tjy+Tjp-i
----(3.4);	(3.5); -Д—т (3.6);
1-2^Тр+Т2р2	Т2р2-1	р(Тр-1)
92
к	к
(3.7);	(3.8).
1-7р	Тр-\
Здесь, например, выражению (3.4) соответствует квазиколебателыюе звено с отрицательным затуханием; (3.5) — квазиконсервативное звено.
Переходные характеристики всех неустойчивых звеньев неограниченно растут со временем.
Рассмотрим, для примера, звено с передаточной функцией к
W(p) =------, Это неустойчивое звено первого порядка (звено с от-
7р-1
рицательным статизмом), так как его полюс р = +1/Т, а нулей вообще нет. Передаточная функция здесь отличается от передаточной функции статического звена первого порядка отрицательным знаком перед единицей. Его переходная и весовая функции описываются следующими уравнениями:
h(f) = k[e~llT -1) о1(О;
w(t) = ^T8(t).
Амплитудно-фазовая частотная функция имеет вид
. &(1+/соГ) к . козТ
W(ja) = ——vv- =---------+j---------x-v •
1 + Т2со2 1 + Т20)2	1 + Т2со2
Его АЧХ совпадает с т4т(со) — АЧХ статического звена первого порядка, т. е.
Л(о>) =..I к—~,
71 + 7%)2
а ФЧХ не совпадает:
ср(со) = arctg соТ - л = -[-фт(со)+л] = фт(со) - л.
—> —; это звено создает
При со-» О, ф(со)->-л, при со-» со ф(со)
л
больший (неминимальный) фазовый сдвиг
. Временные
и частотные характеристики звена приведены на рис. 3.5.
Звено с постоянным запаздыванием {трансцендентное звено)
(код 2.3, табл. 3.1) воспроизводит без искажения на выходе вход-
ную величину. При этом выходная величина запаздывает относительно входной на постоянное время т. Уравнение звена имеет вид
93
y = kx(t-x) или в операторной форме у = ке рхх, так как в соответствии с теоремой запаздывания
L{x(t - т)} = е~хрх(р),
где еГхрх(р) — изображение Лапласа.
Разложение правой части уравнения в ряд Тейлора в операторном виде также дает:
м>-г)=Д+—+—
1!	2!	3!	«! J
Так как у = 0 при t < т, то время запаздывания т называют также временем «чистого» запаздывания.
Соответственно передаточная функция звена имеет вид :
W(p) = ке"1”.
Амплитудно-фазовая частотная функция звена
W (Joi) = кеГ^ = A: (cos (от - ,/sin сот).
Здесь
А((й) = к; (р((о) = -(от;
С/((о) = fecoscox; K((o) = -A:sin(OT.
Временные характеристики звена описываются уравнениями:
94
й(г) = k-ol(t - т); w(t) = kS(t-т).
Если входной сигнал — гармоническая функция х(?) = xMsin со t или x(jco) = xMe>', то Xz) = ^Msin (о(^-т)лили ХУЮ) = Ьсме>('~т).
На рис. 3.6 представлены временные (рис. 3.6, а, 6) и частотные (рис. 3.6, в — д) характеристики звена. Как следует из рис. 3.6, г, АФХ звена представляет собой окружность с радиусом R = k и с центром в начале координат.
Звенья с запаздыванием являются неминимально-фазовыми устойчивыми звеньями. Они имеют бесчисленное множество полюсов (в левой полуплоскости) и нулей (в правой полуплоскости) с модулем, стремящимся к Это соответствует решению уравнения е~рт = 0.
Реальные звенья с запаздыванием обычно обладают инерционностью и их передаточные функции имеют вид: Ж(р) = Ле-/п/(1 + 7)>) или W(p) = ке~^ /(7}р+1)(^р+1).
95
Следовательно, в общем виде, уравнение любого звена с запаздыванием можно записать в виде Q(p)у = R(p)e~pTx, которому соответствует передаточная функция W(p) = ^^-e~pt = W0(p)e~px, где Wo(p)— Q(p) линейная часть звена без запаздывания.
Передаточные функции реальных трансцендентных звеньев различного типа (звеньев с распределенными параметрами) часто содержат составляющие типа гиперболических функций. Например, передаточная функция гидротурбины с трубопроводом длиной I имеет следующий вид:
И/( } J-2pOthpr 1 l + poth/>T 7р+Г
где т = 21/с — время постоянного запаздывания; с — скорость распространения гидравлического удара; р0, Т — параметры.
Передаточная функция гидравлического трубопровода длиной I
W(p) = -k\hpx, или
W{p) = е'1", где т = bfk ; к — параметр.
Длинная электрическая линия без потерь (длиной /п) имеет
W(p) =—-— или 1Г(р) = е“т'", сЬу/п
где у = pJbC', L, С—параметры линии на единицу длины (см. п. 11.2).
Существуют и другие различные выражения для W(p) трансцендентных звеньев подобного вида:
th (Гр)- th (Тр) • 2kthVP) Р l + th(Tp)’ l + Hh(Tp)
и т. д.
Примеры трансцендентных звеньев с запаздыванием: транспортеры, ленты магнитной записи, акустические линии связи, трубопроводы (т = //v), крупные нагревательные объекты (ОУ), линии электропередачи и т. п.
Иррациональные звенья (код 2.4, табл. 3.1) — их передаточные функции имеют, например, следующий вид:
W (р) = к/-jp’,
(3.9)
к/{\ + 4рТ)-,	(3-Ю)
96
кЦ(\+рту,	(3.11)
к^-	(3.12)
к р4р’	(3.13)
к/рЦ^^ту,	(3.14)
k<r^h>.	(3.15)
Эти звенья еще иначе можно назвать: полуинтегрирующее (3.9); полуинерционное первого рода (3.10); полуинерционное второго рода (3.11); звено затухания (полузапаздывания) (3.12) и т.п. Здесь везде в формулы для W(p) входит у[р — иррациональное выражение. К числу таких звеньев обычно относятся звенья с распределенными параметрами, которые описываются уравнениями в частных производных, зависящих от пространственных координат / и времени t.
АФХ звеньев W(усо) выражается также иррациональной функцией.
Например, для полуинтегрирующего звена с W = к/у[р :
h(t) = 2k^-0l(t);
w(t) = к!-Jnt;
А^ = к/4&’, <р(со) = -£(w) = 201g£-101gw
(имеет наклон в -10 дБ/дек).
Для полуинерционного звена первого рода:
W (» = к/ (1 +	А (со) = к [1 + (2й Г)1/2 + ш г] ;
Ф(ю) = -arctg |((0T)vyp2 + (со Г)‘/2]}
7С
и изменяется от 0 до -45°, т. е. стремится к - — при (о —> . Здесь L(o>) = 201gA:(npH(ar<l) и £ (ю) = 201g £ - 101g со Т (при (йТ > 1); при а>Т> 1 имеет наклон в -10 дБ/дек. На частоте оос =1/Т Д£((о)=-5,3 дБ.
Для звена затухания (полузапаздывания) — трансцендентного иррационального звена:
7 А, А. Ерофеев
97
W(ja) = e~^; А(ш) = е-'1^; ф(<й) =-7wT/2; L(co)= -8,77<oT/2•
Это звено также не является минимально-фазовым, так как имеет нули в правой полуплоскости.
Временные характеристики звеньев (3.10) и (3.12) имеют соответственно следующий для звена (3.10)
вид:
А: w(x,t) = -
для звена (3.12)
h(x,t) = F'(x, 0-оФ); и>(х, 0 = 0,5е’П4'^т/(л?3), где
£'(*,') = erfc fi/t /2
— выражение в квадратных скобках, соответствующее erfc (х), представляет собой табулированный интеграл вероятности н» н> erfc |(1/г /2 .
На рис. 3.7 — 3.9 приведены временные (а, б) и частотные (в—0) характеристики иррациональных звеньев: соответственно для звена (3.9) —на рис. 3.7, для звена (3.10) — на рис. 3.8, для звена (3.12) — на рис. 3.9. Для сравнения здесь же пунктиром представлены переходные характеристики h(t) в И-звене (на рис. 3.7) и /^(0 в статическом звене первого порядка (при том же значении рис. 3.8).
Дискретные (импульсные) звенья (код 2.5, табл. 3.1) — звенья с дискретизацией процесса по времени и по уровню в зависимости от типа квантования сигнала. Эти звенья составляют основу или главную особенность цифровых и импульсных систем. Дискретное звено может быть цифровым (квантование по времени и по уровню), импульсным (квантование по времени) и релейным (квантование по уровню). Дискретное звено с квантованием по времени содержит импульсный элемент (ИЭ), преобразующий входной дискретный сигнал х [ пТ ] в выходной у [ пТ ], параметры которого (амплитуда, частота, фаза и др.) функционально зависят от х [ пТ], где Т = Тк — период кван-
98
тования сигнала; п = 0, 1, 2, ... . Дискретному звену с произвольной формой сигнала импульса эквивалентно последовательное соединение простейшего (идеального) ИЭ (модулятор 8-функций) с некоторым формирующим звеном (элементом, цепью). Например, для импульсов прямоугольной формы (у = 1; у = Тп/Т) формирующее звено имеет:
1 _ р-PT	7 — 11	_
W(p) = k~—----~кТ, W(z) = k -, z = epT;
P	z P
, Isin (coT/2)|
y(0) = fcl_J_^2le co/2
для импульсов треугольной формы:
W(p) = k----т
Р
W(z) = k^-^-^ Tzz pl
z ч -(<оТ	'
„„ • ч 4к . 2 ДТ™
W(j(a) = —7sm— е v
Тео2 I 2 )
99
7*
100
Формирующие звенья обычно относят к непрерывной части (НЧ) системы, состоящей т. о. из ИЭ (одного или нескольких) и НЧ. В ИЭ применяют три основных вида квантования АИМ, ШИМ и ФИМ (ам-плитудно-, широтно- и фазо-импульсную модуляцию входного сигнала) при Т = Тк = const (t), частотно-импульсную модуляцию (ЧИМ) при Тк = var (0 и смешанные виды (ЧШИМ, АФИМ и др.) При АИМ: Ти = уТ = cons(0(O<y< 1), а единичный импульс y\(f) = 1(0-1 (t-уТ), тогда у = ^x{nT}yx(t~nT) при у[пТ] = кхх[пТ], где кх—коэффи-л-0
циент АИМ. При ШИМ Тп = уТ = var(t) (0 < у <1) при фиксированной амплитуде импульсов Ая = const (0, Уи = кгх [пТ\ при у„Т<Т, тогда оо
У =	«7) sign х[пТ], где /с2 —коэффициент ШИМ, yt = 1(0-
п=0
-l(t-ynT). При ФИМ Ти = const (0, А.л = const (г), но внутри каждого периода Т имеет место сдвиг импульса по времени на величину
е„ = &3х[иТ] при упТ<Т. Тогда у = А^у^-пТ-епТ)sign х[пТ].
п=0
При ЧИМ обычно Ти= const (0, Аи = const (0, но TK=var(0, т. е.
/к = А- = var (0; /к = Л, где к4 — коэффициент ЧИМ.
В дискретном цифровом звене обычно величина одной дискреты сигнала по уровню а = const (0, тогда у [пТ\ = ка sign х [пТ\, где к — целое число дискрет: а(к - 0,5) < \х [п 7] | < а(к + 0,5). Здесь у = 1 {ТК = 7) и имеет место кодо-импульсная модуляция, т. е. х (0 переводится в цифровую величину у [п 7]; значение а соответствует единице числа, к—число. При этом чем больше количество разрядов (меньше а) и частота /к (меньше Тк), тем точнееДп7] воспроизводит* (0. Квантование по уровню является нелинейной операцией и, следовательно, цифровые звенья являются НЗ. Однако при числе разрядов «>8-5-16 j[n7] s х[п7] и кодо-импульсную модуляцию можно заменить линейной АИМ.
Дискретные звенья с ШИМ, ФИМ, ЧИМ, а также звенья со смешанными видами модуляции являются нелинейными. Кроме того, в них могут содержаться типовые нелинейности. Нелинейное звено всегда стремятся представить в виде совокупности линейного ТДЗ и типового НЗ. Импульсы на выходе дискретных звеньев обычно заменяют эквивалентными прямоугольными (экстраполяция нулевого порядка), трапецеидальными (экстраполяция 1-го порядка) и параболами (экстраполяция 2-го порядка) и передаточные функции звеньев по форме записи зависят от принятого вида эквивалентирования.
Для импульсных элементов (и систем), как уже отмечалось, характерна замена:
1) р = ~-’, z = = ерТ; p = lnz/T; z = (w+l)/(w-l) или w = 1	1 z + 1
(модифицированное ^-преобразование);
101
2) q = j<£>T = уа>(-л < О) < л); z = e-^, или озТ= Я , q =jSl, z = eja, w-=^2Jtg^/2)/T= J^k=jK; p = 2th^/T или p =2(z-l)/(z + l)T; X — абсолютная псевдочастота (Л «(о при co T< 2).
Связь между переменными р и р не является взаимооднозначной из-за периодичности функции (2л/7). Здесь 7z/(z-l)2 c^nT^t = = —z-; z(z-l)	1[иТ]н> ol(r) =' -; 1 8[пТ]н> 3(C) =’1; обычно обозна-
’ Р2	' Р х
чают Т = Тк (такт квантования)1.
Типовые дискретные звенья обычно являются аналогами соответствующих ТДЗ, хотя существуют и специфические дискретные звенья.
Звенья с модулированным сигналом (код 2.6, табл. 3.1). Это звенья, сиг- ' налы в которых (передающие воздействия) являются огибающими несущих колебаний переменного напряжения (тока) с относительно высокой несущей частотой соо (радиосигналы, сигналы управления в системах переменного тока). Изменение знака сигнала в таких звеньях соответствует изменению фазы несущей частоты на 180°.
Здесь входной сигнал х(/) = хм(?)е^0' или x = xM(Z)cos(o0(Z) = = (хМо sin Q.t) cos (O0t = (xM(i 2)[sin (o)0 + &)t - sin (o)0 — Я)г],	где Я «
(0 + (00z x	’	'	'
=------(a-io0) = a-(o0—угловая частота изменения огибающей
2со
сигнала — аналоговой функции xM(f) (при (о ~ (00); Я «со0.
Для описания этих звеньев применяют эквивалентные частотные передаточные функции по огибающей Жэ(уЯ).
Например, для статического звена первого порядка с W(p) = = 1/(Тр+1) эквивалентная передаточная функция
ВД = ГГ^-’ 1 + 7>
где*э= 1	; Тэ = Т/(1 + (02Т2).
1 + (OqTz
Примерные характеристики «симметричного» звена: переходная h (/) и АЧХ (для фиксированной фазы <р=0) приведены на рис. ЗЛО, а, б.
Постоянную времени звена Т здесь можно определить как Т = 2/ Дсоп, где Дшп = 2/ Т — значение полосы пропускания на уровне А = к/& .
Переход к обычной форме частотной передаточной функции производится заменой p = jQ., т. е. W3(p) ~ Ж(у(00 + р) .
1 Другие соответствия: T2z(z + 1)/(2(Z-1)3 4-[nTf/2i-H2/2=’l/p3; z/fz-e417)^
<4е““г" н>е_“г='1/(/>+«); z/(z+l)^sin^nTi-*sin (l-e‘<J)z/(z^l)z-e~<IJ)«-l-e~ar^
=1/р(р+а); zsin(DT/(z2-2zcoscoT+l)<—sincoTziiAsinwT^-- -—-	и т.д.
/г+(1Г
102
Рис. 3.10
Эквивалентную частотную передаточную функцию по огибающей И^эС/О) можно представить в виде
= JF3[j((o-(flo)]= Ж[у(о)0 +й)].
Эти формулы, строго говоря, справедливы только для симметричной относительно соо частотной передаточной функции, когда
^э(Р)»^(Р+>о) = ^(Р->о).
Для несимметричной функции
= 0,5{Ж[7(£2+®о)]+ W [y(Q-®0)]}.
Обычно частотные передаточные функции реальных звеньев не являются симметричными. Поэтому к использованию этих формул следует относиться с осторожностью.
Звено с модулированным сигналом при <оо = 0 можно рассматривать как частный случай звена с немодулированным сигналом.
Пример. Если в колебательном контуре (см. рис. 2.10) у = £/2 — напряжение на сопротивлении R (выход), то передаточная функция fV(p) =	= --Д?---( где
T2 = RC; T\=L!R.	Т\Т2Р +T2p+l
Еслишо=О,а Л((в)|ш=0 =l(Zr = l), то для данного контура 4(а>)н> Д„(<о) — АЧХ апериодического звена. Для симметричной относительно резонансной частоты »о значения боковых частот (см. рис. 3.10), где о)12=Та+Р, а = 1/27;; р=[(1/47^)+(1/т;т2)] , а ш0 = р = (о, + а>2)/2. Эти условия выполняются, если T2<4Tt или R <2-JlTc . При этом контур представляет собой апериодическое звено первого порядка по огибающей модулированного сигнала с W3(p) = 1/(1 + Тр), где 7' = 2/Д<вп =2L/R = 2Ti; Дшп =ш2-о>1 = 1/7J -RIL-, и = ш0.
103
Типовые нелинейные звенья (код 2.7, табл. 3.1) имеют нелинейные статические характеристики у = F(x) (см. рис. 1.5), предельными случаями которых являются характеристики типа пороговых (релейных). В последнем случае, когда входная величина x(t) звена переходит некоторое пороговое значение хпор(0 [ *ср(0 или хот(0 ], то выходная величина y(t) звена изменяется скачком от yj(r) до y2(f) [или наоборот от y2(t) до Ji(0] (см. рис. 1.5, б). Наличие одного или нескольких нелинейных звеньев (НЗ) делают САУ нелинейной. Каждому типу нелинейной характеристики соответствует вполне определенное НЗ. Так как нелинейных характеристик существует довольно много, то велико и количество НЗ (см. Приложение). Однако обычно выделяют две группы НЗ с однозначными и неоднозначными характеристиками (что очень важно при исследовании динамики нелинейных САУ). Однозначные характеристики для примера представлены на рис. 1.5: с зоной нечувствительности и ограничением [рис. 1.5, в (7)], с ограничением (насыщением) [рис. 1.5, в (2)], пороговые [рис. 1.5, б (/)]. Неоднозначные характеристики представлены на рис. 1.5,а(3), 1.5,6(2), 1.5г и представляют собой координатное запаздывание (или опережение). Неоднозначные нелинейности—двухзначные (или многозначные) подразделяются на пассивные и активные: пассивные — когда за период Т входного сигнала нелинейность обходится против часовой стрелки [см. рис. 1.5, б (2), 1.5 г] и в выходном сигнале наблюдается фазовое запаздывание; активные — когда обход происходит по часовой стрелке и ву(0 наблюдается фазовое опережение1.
Уравнение «вход-выход» НЗ: y(t) = Ft[x(t)], где Ft[%(?)] —нелинейная функция или характеристика НЗ. Для однозначных характеристик НЗу = F(x), то есть нет временной зависимости Ft(x(t)), которая имеет место для неоднозначных характеристик, когда y(t) зависит как от значений x(t), так и от значений времени t. В последнем случае уравнение НЗ представляет собой строго говоря не функцию, а функционал. Обычно НЗ рассматриваются как безынерционные со статическими нелинейностями и их уравнения являются нелинейными алгебраическими уравнениями. Если САУ содержит ряд НЗ, то есть имеет место их параллельное, последовательное или встречно-параллельное соединение, то НЗ стремятся заменить одним эквивалентным НЗ с результирующей нелинейной статической характеристикой.
Анализ САУ с НЗ обычно ведут с применением методов линеаризации, когда характеристику НЗ заменяют на линеаризованную (у = к () х). Здесь аргумент к (•) зависит от вида линеаризации (их различают четыре: статическая, дифференциальная, гармоническая, стохастическая). Например, эквивалентная передаточная функция НЗ гармонически линеаризованного (с инерционностью первого порядка) имеет вид: Wp = &(/(1 + 7] р), где ки 7J—эквивалентные переменные па-
1 Пассивные иначе называют с положительным гистерезисом, активные — с отрицательным.
104
раметры НЗ как функции коэффициентов гармонической линеаризации qi(A) и (Л) (в общем случае функции амплитуды Л и частоты колебаний ш). Здесь, с учетом свойств фильтра линейной части нелинейной САУ переменная x(t) на входе НЗ всегда близка к синусоиде x(l)~A- sinсог, т.е. САУ хорошо пропускает только первую гармонику нелинейных колебаний ХО и ослабляет высшые гармоники; тогда y(t)= = F(A sin см)- Линеаризованное уравнение НЗ для первой гармоники ХО
имеет вид: у = Г(х) =
q2 q^P
х = ^(Л, р)х = кгх,
то есть кг пред-
ставляет собой комплексную функцию. Для неоднозначных характеристик НЗ коэффициент q2 * 0, причем для петлевых (с гистерезисом) характеристик qx >0,q2< 0. Для однозначных характеристик НЗ q2 =0 и коэффициент кг вещественный. Здесь WH3(A,p) = У\(р)/х(р) передаточная функция звена [^(р)—соответствует первой гармоники Х0]- Коэффициент кт определяют, в общем случае, как комплексный коэффициент усиления или как эквивалентную амплитудно-фазовую характеристику НЗ:
Жнз(Л,(0) = qi(A, со) + jq2(A, со) = Лнз(Л,(в)еЛ’(Лю),
где
АЮ(А, со) = |[<7! (А, со)]2+[q2 (А, со)]2 } , фю(Д со)=arctg [^(Л, со)/^(А, со)] — соответственно эквивалентные амплитудная и фазовая характеристики НЗ. Удобством для анализа нелинейных САУ является тот факт, что коэффициенты qt и q2 заранее вычислены для всех видов типовых нелинейных характеристик (НЗ) и представлены в виде таблиц, графиков [1,2,5]. Как уже отмечалось, в общем случае, эти коэффициенты зависят от значений Л и со, хотя для многих НЗ они являются только функциями амплитуды Л или иногда только функциями частоты со (у так называемых псевдолинейных корректирующих звеньев).
Если линейная часть САУ является недостаточно хорошим фильтром, то эквивалентная ЖНЗ(Л, р) будет зависеть от высших гармоник п
х(г) = Д sin (s)t + Л( sin (fart + ф,), где Л;, <р; — соответственно амплиту-
/=л
да и фаза i-й гармоники. Это учитывают, когда требуется оценить влияние высших гармоник на появление автоколебаний в нелинейной САУ. На практике обычно ограничиваются влиянием лишь 3-й гармоники.
Коэффициент статической линеаризации НЗ кс(х) = у/х = [f(x)/x]. Коэффициент дифференциальной линеаризации кл(х) = dy / dx = = [JF(x) / dx}. Если на входе НЗ х (/) стационарный случайный процесс, плотность распределения которого р (х), то коэффициент сгохас-тической линеаризации к„ = к„(в2х) = kCT(Dx) = — jF(x)xp(x)dx, где
-со
ах, Dx — соответственно среднеквадратическое отклонение и дис
105
Персия. Коэффициенты стохастической линеаризации определяются для НЗ с однозначной нечетной характеристикой также как А:ст0 = Му/ Мх, =+(Dy/Dx)l/2; здесь к„л == ka(Dx). Для некоторых частных случаев s кт, например, когда х (?) = A sin (cot + <р), где ср — случайная фаза [9].
Линеаризация создает приближенную адекватность выхбдных характеристик НЗ и линеаризованного и широко используется при анализе нелинейных САУ. Возможны варианты совместных видов линеаризации НЗ, например стохастическая и гармоническая и др. Следует заметить, что ранее рассмотренные методы линеаризации (см. п. 2.3) применяют для так называемых «несущественных» нелинейностей; здесь же рассматриваются только существенные нелинейности: ступенчатые, кусочно-линейные, многозначные функции с разрывами непрерывности 1-го рода, степенные и трансцендентные функции.
Обычно на практике на входе НЗ действуют либо гармонический либо случайный сигнал (или их комбинация), поэтому наибольшее распространение получили методы гармонической и стохастической линеаризации (или их комбинация). В результате линеаризации, например гармонической, нелинейность заменяют прямой с наклоном равным q(A) и фазовым углом (р (А). При стохастической линеаризации также заменяют НЗ эквивалентным линейным, которое адекватно с НЗ преобразует математическое ожидание Мх и дисперсию Dx (или среднеквадратическое отклонение ), т. е. Му = Муэ, Dy ~ Dy3 или А/[(у- уэ)2]—> rain. При стохастической линеаризации обычно считают, что на вход НЗ поступает случайный сигнал близкий к нормальному закону распределения, который получается за счет эффекта «нормализации», создаваемого инерционной линейной частью САУ (см. гл. 5). Эффект «нормализации» тем сильнее, чем уже полоса пропускания САУ по сравнению со спектром x(t).
Необходимо отметить, что в общем случае, при прохождении через НЗ случайного сигнала x(t) с неизвестным заранее законом распределения р(х), происходит искажение р(х). Однако, допущение о том, что x(t) на входе НЗ имеет нормальное распределение и неучет реальных искажений р(х), обосновывается двумя факторами: инерционность приближает процесс прохождения случайных сигналов в САУ к нормальному закону, что справедливо даже тогда, когда реальный закон р(х) далек от нормального; при изменении законар(х) даже в широких пределах на входе НЗ на его выходе значения коэффициентов стохастической линеаризации изменяются незначительно.
Для типовых НЗ в случае нормального закона распределения имеются готовые выражения коэффициентов стохастической линеаризации, которые однозначно определяются через Мх и Dx (oY) [2, 4].
Кроме типовых НЗ со статическими нелинейностями различают НЗ с динамическими нелинейностями, когда нелинейные свойства проявляются в динамике НЗ (например, в связи с наличием нелинейного трения).
106
Примерами также могут служить любые нелинейные дифференциальные, разностные и интегральные уравнения НЗ. Другие примеры: так если уравнение НЗ имеетвид:у = [&}(х)/(1 + 7}(х)р)]х, то параметры Л], 7J зависят от координатах (или ее производных), или если кх(х, t) и/или7](х,/) зависят от координатах и времени t для НЗ с динамическими нелинейностями видаДх,рх),то характеристика зависит от Л и со. Линеаризованные модели НЗ учитывают влияние нелинейности на свойства САУ, т. к. коэффициенты модели изменяются в зависимости от уровня внешних воздействий и начальных условий.
Следует отметить, что нелинейные характеристики обычно естественно присущи реальным САУ (типа люфт, гистерезис, трение, насыщение, зона чувствительности и др.) и их влияние (зачастую вредное) стремятся уменьшить, т. к. они существенно ухудшают характеристики САУ. Однако для придания некоторым нелинейным, оптимальным и самонастраивающимся САУ желаемых динамических свойств разработаны специально искусственно вводимые НЗ, например, в виде корректирующих нелинейных звеньев [2]. Это также например пороговые (релейные) НЗ, псевдолинейные корректирующие звенья, логические НЗ, НЗ с переменной структурой и НЗ, формирующие разнообразные законы управления (см. гл. 9, п. 9.6). Для НЗ разработаны классификации по различным признакам, например, однозначные — неоднозначные, четные — нечетные, симметричные — несимметричные, непрерывные (гладкие) — разрывные и т. д. [1, 2, 5]. Составлены таблицы типовых и особых НЗ с нормированными характеристиками; число НЗ в них составляет примерно от 8 до 30. В таблицах приводятся также необходимые данные по коэффициентам гармонической, стохастической (и совместной) линеаризации, амплитудных, фазовых и др. характеристик НЗ [1, 2].
При синтезе нелинейных САУ применяют корректирующие НЗ, псевдолинейные, а также обычные линейные корректирующие звенья (см. гл. 8, п. 10.4). Корректирующие НЗ позволяют создать большее разнообразие форм частотных характеристик, в том числе зависимых от амплитуды А, т. е. придают САУ некоторые свойства самонастройки по величине ошибки е. Кроме того, они позволяют ослабить вредное влияние естественных НЗ в САУ. Псевдолинейные звенья позволяют осуществлять коррекцию в САУ фазовых характеристик независимо от амплитудных (и наоборот).
Дискретные НЗ — это, во-первых, (по своей природе) НЗ с широтно-импульсной и фазо-импульсной модуляцией, а также НЗ с цифровым кодированием. Во-вторых, это дискретные НЗ с определенным видом нелинейности характеристик, например, с нелинейной амплитудно-импульсной модуляцией и т. п.
Все разнообразие нелинейных звеньев (и САУ) подразделяют на два больших класса. Первый, когда в нелинейную функцию звена входит только одна переменная х [F(x) или F(x, р) — с производными и т. п.],
107
так называемые одномерные нелинейности. Второй, когда функция НЗ содержит две и более переменных (х(), т. е. эквивалентное НЗ имеет две и более нелинейности, так называемые многомерные нелинейности F(xi). Примером последних служат, в частности, показатели оптимальности или экстремума функции J; Jo =F(x, f) (см. рис. 1.7). Заметим, что многомерные нелинейности обычно стремятся свести к соединению одномерных, используя последовательные, параллельные (согласное, встречное) соединения одномерных НЗ. Также как и для линейных в нелинейных САУ применяют эквивалентные преобразования (см. п. 4.3).
Кроме рассмотренных типовых НЗ, существует класс так называемых особых НЗ, например множительное звено, когда у = х,х2 при зависимых сигналах и х2, в частности это НЗ с параболической четной у = х2 или нечетной y = x2signx = x|x| характеристикой. Особые НЗ широко применяют при построении оптимальных, экстремальных, адаптивных и самонастраивающихся САУ, при формировании нелинейных алгоритмов (см. п. 9.6).
Смешанные особые звенья (код 2.8, табл. 3.1) отражают наличие ряда смешанных особых признаков, например, трансцендентное иррациональное звено (код 2.3,2.4, табл. 3.1) и т. п. В основном это реальные звенья с распределенными параметрами (ОУ), состояние которых описывается с помощью функций распределения, дифференциальных уравнений в частных производных (гиперболические, параболические, эллиптические), интегральных уравнений и более сложных функциональных уравнений. Вид передаточных функций этих звеньев содержит дробно-рациональные функции от аргумента р, иррациональные и другие выражения.
К смешанным особым звеньям обычно относят реальные ОУ, процессы в которых носят зависимый пространственно-временной характер; часто носителем информации в них выступает многомерный сигнал. Это различные пространственно-протяженные ОУ, например летательные аппараты (ЛА), нагревательные, диффузионные и тепловые ОУ, устройства функциональной электроники (пьезоэлектроники) и др. Как правило, это тела с пространственно-сложной формой (часто с изменяющимися параметрами), например, летательный аппарат — сложное тело с изменяющейся массой1. Такие ОУ описываются различными типами передаточных функций (по различным каналам передачи воздействий).
I. Примеры описания сложных ОУ.
Летательные аппараты по различным каналам управления имеют следующий вид передаточных функций W(p): 1/рТ; 1+рТ; кр; к/(Тр+\у, к/7p(l + 7Jp) и т. д., например:
1 Например, ракета «Энергия» (с ЛА «Буран») имела стартовую массу 20 000 т, к концу взлета 200 т (изменение массы в 100 раз).
108
самолет
Wc(P) =
v(p) = к
M(p) T2p2+2^Tp+\
или
Wc(p)~
v(p)____&TlP+l)
8B(P)~ p(T2p2+2^Tp+l)'
где v — угол тангажа; 8B — угол отклонения рулей высоты; М — управляющий момент рулей;
баллистическая ракета
W (р) = V(p) «_____k(T2p+2^T2p+\)_______
Р 5в(р) (7;У+2^7]р+1)(Т3р-1)(Т4р-1)’
представляет собой неустойчивое неминимально-фазовое звено, требующее сложного управления; здесь 8В — угол поворота камер двигателя;
космический летательный аппарат (КЛА) с одним подвижным двигателем
Uy(p) p2Jz	иу{р) р1 Jy
гдеу —угол тангажа; ср — угол поворота сопла; —коэффициент передачи УУ поворотом сопла; иу — управление углом поворота сопла двигателя; J Jz — главные моменты инерции КЛА соответственно относительно оси Оу и оси Oz.
II. Примеры ОУ-звеньев с распределенными параметрами.
1.	Исходное уравнение (/ — расстояние)
... д2х ... д2х Э2х , Эх , /1чЭх ....	.. .
О АТ+Зга7++А(0 37+^(0 37 + ^(0* = М(А 0•
Э/ oldt dt vi dt
Если A = ata3-(a2/2)2 <0, то это гиперболическое уравнение (волновое уравнение ):	= 0 (простейший случай).
dr dt2
Если Д = 0, то это параболическое уравнение (уравнение тепло-d2x dx проводности или диффузии):----------= 0 (простейший случай).
dl2 dt
Если Д > 0, то это эллиптическое уравнение (уравнение потенциа-Э2х Э2х
лов): —-------- = 0 (простейший случай).
dr di
109
2.	Исходное уравнение
ду а ду дх . л -----~—h ки = О,
дх b2 dt dt
где у, и — переменные; а,Ь,к — параметры ОУ. Здесь
W(p) = ~— у]р(к + p) th (xJp(k+p) lb), ap
где x = llb (y = 0,x = l).
3.	Исходное уравнение
йЭ22_Э2 = О(о<%</, t>0). дх dt
Здесь №-(P)=sln-,^l±'-1.
smj^p/al
III. Примеры звеньев смешанного типа с НЗ: дискретное нелинейное, нелинейное звено с запаздыванием, НЗ с переменной структурой, НЗ логического типа и т. д.
Здесь звенья смешанного типа включают в себя различные комбинации особых и обыкновенных типовых звеньев, в том числе и разные комбинации НЗ, а также обыкновенных и НЗ. Например, соединение двух НЗ с линейным звеном последовательно, параллельно или встречно-параллельно (как, например, у нелинейных корректирующих звеньев) и т. п.
Это также НЗ, реализующие различные нелинейные алгоритмы управления, содержащие функциональные, логические, оптимизирующие и параметрические составляющие (см, п. 9.6).
Г л а в а 4. АНАЛИЗ ОДНОМЕРНЫХ САУ. АЛГОРИТМИЧЕСКИЕ СХЕМЫ САУ
В результате декомпозиции САУ на звенья направленного действия и получения описания звеньев в виде передаточных функций, переходных или частотных характеристик составляется алгоритмическая структурная схема, по которой затем можно получить передаточную функцию или характеристики системы в целом.
Алгоритмическая структурная схема САУ, как и функциональная (информационная) схема, отражает процесс передачи информации со входа системы на выход, причем функциональная схема разбивает по
ет САУ по блокам в соответствии с выполняемыми ими функциями, а алгоритмическая (структурная) — по динамическим свойствам. Алгоритмическая схема САУ представляет собой динамическую модель САУ в виде графического изображения системы уравнений динамики (алгоритмов), записанных обычно в виде W(p).
§4.1. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИЙ ЗВЕНЬЕВ [АЛГЕБРА W(/01
Если известны уравнения всех звеньев САУ, то ее описанием является система этих уравнений. Исключая промежуточные переменные, можно получить дифференциальное уравнение высокого порядка, связывающее выходную величину САУ с входной величиной [возмущением и (или) задающим воздействием]. Однако проще можно получить описание САУ, если оперировать передаточными функциями звеньев, типовыми структурами их соединений и построением эквивалентных (свернутых) структур.
Последовательное соединение звеньев направленного действия представлено на рис. 4.1, а. В этом случае имеем систему уравнений:
y\ = Wx{p)x-,
У2 - w2(p)yi;
уп = W„(p)y^.
Исключая промежуточные переменные, получим у„ = [Wl(p)W2(p)...
п
... Wn(p)]x= W3(p)x, где W3(p) = ЦW^p); h^t) = L~x\W3{p)jp} w3(t) =
= 2Г1[Илэ(р)]. При этом минимально-фазовые звенья дают минимальнофазовые W3(p).
Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций звеньев. Это значит, что их можно заменить одним эквивалентным звеном с передаточной функцией W3(p).
Пример. Рассмотренное ранее реальное интегрирующее звено, например с передаточной функцией W (р) = kip (Тр + 1), эквивалентно последовательному соединению
1
звеньев с передаточными функциями к/p и
Параллельное соединение звеньев направленного действия представ-
лено на рис. 4.1, б. Здесь
У = У\ + Уз + + Уп =1^1(Р) + W2(p) +... + Wn(p')]x = W3{p)x,
где у = 1Уэ(р) = ^£и<(р); /г(г) = ^/г1.(1); w(0 = £w/(0-
1 = 1	1=1	1=1	1=1
111
s uu
Wf w2...
Передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев. В структурной схеме их можно заменить одним эквивалентным звеном с передаточной функцией W3(p).
Пример. Если Vfi(p) = k^p, a W2(p) = it,TO W3(p) = k(T3p + l), где Т3=кД/к. Если = а W2(p) = k/(Tp + l), то W3(p) = ^^V где T3=T + (k/k„).
р(.Тр + 1)
Встречно-параллельное соединение. Звено, охваченное обратной связью, представлено на рис. 4.1, в; здесь обратная связь может быть положительной или отрицательной. Схема такого звена описывается уравнениями:
У = W„(p)(x± уос) = Wn(p)E ;
Уос = Вду.
Исключив отсюда уос, получим
где Ж3(р) =
Wa{p) . 1ТЖр(р)’
____Wn(p)_____
l + Wn(p)W0C(p)
х = W3(p)x,
Wp(p) = Wn(p)Woc(p). Здесь h,(t) = Г’[Ж3(р)/р];
У —
112
w3(f) = L7x[W3{p)\, знак «-» соответствует положительной обратной связи, а знак «+» — отрицательной. Обратная связь, осуществляемая через статическое звено, называется жесткой (пропорциональной) обратной связью; FFoc(0)^0. Если И/ос(0) = 0, в статике сигнал обратной связи равен нулю; обратная связь действует только в динамике. При Woc(p) = коср = рТд —обратная связь называется гибкой дифференцирующей обратной связью, или гибкой обратной связью по скорости. Если Woc(p) = ^7?, такая обратная связь называется гибкой обратной связью по ускорению. При Woc(p) = рпТ” (или другое дифференцирующее звено) — обратная связь называется гибкой дифференци-к 1
рующей обратной связью. При ИС =	=---- (или другое интег-
р РК
рирующее звено) обратная связь называется гибкой интегрирующей. к {Т 1и
Если №ж(р) = ——-------— ПИ-звено, то обратная связь называ-
ется изодромной.
Функция W3(p) называется передаточной функцией замкнутой системы, a Wp(p) —передаточной функцией разомкнутой системы, т. е. цепочки из всех звеньев системы, получающейся после разрыва обратной связи (знак «~» на рис. 4.1, в).
Пример 1-Если Wn(p) = *->«,, a Woc(p) = «oc(p)/Qoc(p), то
W,(p)=pj----5----:
T + W'oJP) к
1 Qoc(P)
Иос(Р) Лос(р)'
При Woc(p) = pTll или И(1С(р) = —-- здесь соответственно W3(p) = -~ — или W3(p) = „	рТ« *	- рТя - .
= рТи, т. е. получаем эквивалентное звено, обратное первичной передаточной функции.
Пример!. Рассмотрим интегрирующее звено с передаточной функцией Wn(p) = = k-J р, охваченное ООС через идеальное статическое звено с передаточной функцией fPoc(P) “ ^ОС’
к.
w (р) = £— =------,
1+*оД р
, 1 _ 1 где *з=т-“; г>=,,	-
"•ОС	*1*ос
Таким образом, интегрирующее звено, охваченное жесткой обратной связью, стало эквивалентно статическому звену первого порядка, т. е. не является интегрирующим.
ПримерЗ. Если W = Woc(p) = koc, то |Р3(р) = -А-, где кэ = ТТТТ"' 7р ч-1	1 + /ЭР	1 т к «ос
Тэ=~—	при к^-1/к Тэ-Т/2 или Тэ=о% а £э = £/2 или кэ=<*>.
1 х л ко с
Охват апериодического звена жесткой обратной связью не изменяет структуру % (р), но изменяет величины Т3 и к3; положительная обратная связь (ПОС) увеличивает величины к3 и Т3, отрицательная обратная связь (ООС) уменьшает их.
8 А. А. Ерофеев
ИЗ
Свойство ООС уменьшать инерционность звена, а именно постоянную времени Т— замечательное свойство, так как увеличения к можно легко достигнуть большим включением безынерционных усилителей.
ПОС действует обратным образом и часто дает неустойчивое звено.
Лос
При И'ос(р) =------ (инерционная жесткая обратная связь) W3(p) описывается
ТосР + 1
уравнением:
... , ч т
W~(p) « ........:...-.., Тпс < Г.
эКК Тэр + 1 ос
Следовательно, инерционность ООС приводит к дополнительному форсирующему воздействию (по производной, как у ПД-звена), т. е. повышает быстродействие за счет замедления роста сигнала уОс-
Гибкие дифференцирующие или интегрирующие ОС позволяют также радикально изменять свойства соединений звеньев и в целом САУ.
Пример. Так, если %c(P) = ^осР- a Wn(p) = k/p, то
к =
’ 1±*ЛОс’
%1(р)-~> где Р
где Т3-Т±кко(..
к	к
Если W„(p) =----, то W31(p) =-
Тр+Г 2 Тэр+Г
Инерционная гибкая обратная связь по скорости вида
, ^осР
Wnc(p) = ~-------
ОС 'Г ' гг> . 1
ТЖР +1
повышает быстродействие (ООС), а при ПОС — снижает его. При IFOC = VTKp соответственно
^+i к
w32(p) = —----------
22и£_+2и£+1
к к
, ч £и(Хр+1)
При Woc(p) = и и----- соответственно
Р
Гэ1р2+Тэ2р + 1
114
где к3 = ^~; Тэ1 = ТИТ + ~; Тз2 = Т+Ти, а Жэ2.(р) =	где
*и	кки	Т3р + 1
к = к  т=^кЛ~
3 (1 + А^н)’ 3 (1+ккн)‘
Таким образом, различные соединения звеньев преобразуют исходные структуры звеньев и их параметры в другие; при этом возможно преобразование неустойчивых звеньев в устойчивые (и наоборот).
§4.2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗАМКНУТОЙ САУ
Простейшие одноконтурные САУ. Простейшие одноконтурные одномерные САУ, приведенные на рис. 4.2, содержат всегда ООС, создающую замкнутый контур системы. Это определяется основным принципом действия САУ, управляющее устройство в которых осуществляет управление объектом по функции отклонения величины у от его значения, определяемого заданием величины х. При этом все изменения выходной величины объекта, вызванные какими-либо возмущениями, будут компенсироваться в результате действия управляющего устройства. Следует заметить, что одномерные САУ любой сложности, состоящие из последовательных, согласно- и встречно-параллельных соединений звеньев (звеньев с ОС) (рис. 4.3), всегда путем преобразований можно привести к виду, показанному на рис. 4.2.
Обычно для целей анализа определяют следующие три основные передаточные функции замкнутой САУ: W3f(p), W3x(p), WM(p).
В общем случае одноконтурной САУ (см. рис. 4.2) при х = 0:
115
8*
Рис. 4.3
Индексы f и у показывают, какие точки системы связывает передаточная функция (возмущающее воздействие f — выход у).
Рассмотрим порядок определения величины W3j(p): прих = 0 структурную схему (см. рис. 4.2, а) условно располагают таким образом, чтобы f было на месте х. Далее производится обычное преобразование структурной схемы, где W/?(p)=W£(p), a WJ>(p) = Wi(p)W2(p)W0C(p).
у(р)
Передаточная функция W3 f (р) =----= ——----- называется пе-
f(p) 1 + %(р)
редаточной функцией замкнутой СА У по возмущению.
Передаточная функция, связывающая величину у с задающим воздействием х (при/=0):
W3X(p) =
у(,р) _ Wxy(P)
Х(р) 1 + Wp(p)
называется передаточной функцией замкнутой СА У по управляющему воздействию, где Wxy(p) = Wl(p)W2(p).
В следящих системах, задачей которых является обеспечение слежения у завеличинойх обычно передаточная функция Wxy(p) = W,(p), а lV0C(p) = 1 (см. рис. 4.2, б).
W„(p)	WAz)
Тогда W (р) = —Р-----или WUz) = — --------.
1 + %(р)	зИ l + %(z)
При использовании в качестве выходной величины в САУ кроме у еще и ошибки (рис. 4.4) е = х - уос, учитывая, что
%(Р)
Уос 1 + Wp(p)
х,
будем иметь
w (р) =	= —?— = i _ ш (р).
3Et х(р) 1 + %(р)
не
Рис. 4.5
Рис. 4.4
Эта передаточная функция называется передаточной функцией замкнутой САУ для ошибки по задающему воздействию. Передаточная функция, определяемая по этой формуле, широко используется при исследовании точности работы следящих систем и других САУ в режиме изменения задающего воздействия.
Передаточная функция замкнутой СА У для ошибки по возмущающему воздействию
так как при х = О е = - у (единичная обратная связь).
Когда на систему в общем случае, действует одновременно несколько возмущений, то на основе принципа суперпозиции (реакция линейной САУ равна сумме реакций на fi) получим
у - <1------f .
1+%(р) '
При одновременном действии на САУ, например,/и х (см. рис. 4.2):
= ^о(р)/+И^(р)х
у .	....	1 + ^(^
или в общем случае:
п	т	I
2Х/Ж + ^Wx.y(p)xj + ^WXky(p)xk +...
v= ..............................~_____
1+%(р)
117
Знаменатель Ж3(р) представляет собой характеристическое уравнение системы £>(р) = 1 + Wp(p) = 0, которое характеризует внутренние свойства системы, ее свободное движение и поэтому одинаково для всех видов передаточных функций замкнутых САУ, т. е. не зависит от внешних воздействий (определяется только параметрами системы).
Внешние воздействия могут подаваться на суммирующие элементы не только непосредственно (см. рис. 4.2, а), а и через звенья с передаточными функциями W(p), например, через W3(p)— воздействие/, а через ЗУДр) — воздействие х (см. рис. 4.2, в). В этом случае, так как эти новые звенья не входят в замкнутый контур САУ, а включены с ним последовательно, их наличие не изменяет передаточной функции разомкнутой системы Жр(р) и, следовательно, знаменателя передаточных функций замкнутой системы. Передаточные функции новых звеньев входят в числители этих функций.
Многомерные САУ. В общем случае матричные передаточные функции многомерных САУ определяются аналогично таковым для одномерных САУ:
[W3/ (р)] = [Е + W^p)T\Wfy{p^
[WM(p)] = [Е + Жр(р)Г’[И;/р)];
[W3e(p)] = [E + Wp(p)F1,
где Е — единичная матрица; [Е + Wp(p)]~i — обратная матрица.
Для простейших многомерных, многосвязных САУ (рис. 4.5) [y] = [W3X(p)][x] + [iy3y(p)][/]. Здесь [И^у(р)] и [W/y(p)] — матричные передаточные функции размерностью п х п и тх п соответственно. Например, для двумерной САУ :
Л =W11(p)x1 +W12(p)x2 +Wfjyi(p)fl +И>2Л(р)/2;
У2 = W2l(p)xf + W22(p)x2 +	(p)/j + Why2 (p)f2
или
[у] = [ИЛ[Х]+ [%][/].
§ 4.3. ПРАВИЛА ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ
Для многоконтурных одномерных (и многосвязных, многомерных) САУ, содержащих произвольное число связанных друг с другом контуров, как уже отмечалось, осуществляется преобразование схем в эквивалентную одноконтурную. При проведении преобразований руководствуются рядом правил. В их число входят уже рассмотренные правила пре
118
образования последовательно и параллельносоединенных звеньев. Кроме того, применяются и другие правила, которые достаточно очевидны и вытекают из условий сохранения неизменными сигналов на выходе схемы при выполнении соответствующих преобразований. Например, при переносе сумматора вперед (В), т. е. по стрелке основного контура, в ветвь добавляется звено с передаточной функцией W2 — обойденного звена основного контура. При переносе сумматора назад (Н) добавляется звено с обратной передаточной функцией В обоих случаях сигнал на выходе части основного контура сохраняется неизменным.
Перенос точки разветвления диктует обратное правило преобразования: при переносе точки вперед в ветвь добавляется звено с I/W2 = УИ2~1> а при переносе назад — звено с передаточной функцией Щ.
Правила преобразования структурных схем сведены в табл. 4.1
Таблица 4.1. Правила структурных преобразований
Исходная схема
Эквивалентная схема
1. Перенос сумматора
Вперед
2. Перенос точки разветвления
Вперед
Назад
119
Продолжение табл. 4.1
120
Рис. 4.6
Задача преобразования многоконтурной структурной схемы САУ обычно сводится к приведению ее к схеме с неперекрещивающи-мися контурами, после чего каждый из этих контуров может быть заменен эквивалентным звеном с W3(p).
Пример 1. Схема с прямыми перекрещивающимися связями (рис. 4.6, а).
Пример 2. Схема с обратными перекрещивающимися связями (рис. 4.6, б).
Пример 3. Схема с перекрещивающимися прямыми и обратными связями (рис. 4.6, в).
§4.4. МАТРИЧНО-ТОПОЛОГИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ
Передаточные функции сложных САУ можно определить по структурной схеме и без приведения ее к одноконтурной путем применения диаграмм прохождения сигналов (из теории графов). Графы прохождения сигналов подобны структурным схемам и также используются для наглядного изображения математических зависимостей в САУ (см. рис. 4.1). Направленный сигнальный (ориентированный) граф (указано направление сигнала) — более компактная форма записи структурных схем. Правила преобразования графов подобны правилам преобразования структурных схем (табл. 4.2).
121
Таблица 4.2. Алгебра W (р). Соответствие структурных схем графам
Структурная схема		Граф	
Исходная	Приведенная	Исходный	Приведенный
Звено САУ			
х 	 У 	» W —		 ..		—
Последовательное соединение звеньев			
	X	и -—» W, И/, у »	Wt	Wf У	W1WZ	
			л vZ	        У
Параллельное соединение звеньев			
г-Н W, |	г x	tA. у	х	У -—»		xQ		 feOv
—>.			
	 L*] wt |	1			
Встречно-параллельное соединение			
——»| Wn I	 	* r Wn Уг		«Ул
т —	H-WhWtc		xO"	
1	1 И/дс Р—J х ,/Оу	и/	У,	х	W '	Л w	w
	*	1 + W	xOr .	
			xO	*oy
Основные понятия топологических методов анализа: граф, совпадающий со структурной схемой; сигнальные графы и обобщенные сигнальные графы. Сигнальный граф—условное графическое изображение системы уравнений; сигнальный граф Мэзона требует приведения системы уравнений к причинно-следственной форме (типа вход-выход).
Граф представляет собой совокупность вершин (узлов), начала, конца и ребер. Ребро (ветвь, дуга) тождественно равно оператору W (р). Вершины графа — переменные (сигналы): у, и, х и т. д. В общем случае ребра — коэффициенты a, b, с, 7], kt и т. д. в уравнениях САУ; дуга направленна и характеризуется символом к (W) (весом дуги).
Структурную схему САУ рассматривают как один из видов графа прохождения сигналов. Направленный (сигнальный) граф САУ строится по уравнениям, записанным, как и структурная схема САУ, в принятой условно-разрешенной форме.
Для упрощения графа и вычисления (получения) выражения для передаточной функции сложной многоконтурной САУ применяют следующую топологическую формулу Мэзона (приводится без доказательства):
s^pH^rid+^xp)
Г	“1*
П(1+^,(р))
1=1
гДе (/О — различные прямые передаточные функции от узла т к узлу и; Wnpk (р) — передаточные функции разомкнутого контура (со знаком «+» для ООС); Ц — произведение включает все /-замкнутые /=1
контуры САУ; знак «*» — означает исключение из скобки всех членов, содержащих произведения W (р) одних и тех же звеньев [включая звенья с передаточной функцией W (р) = 1].
Форма — сигнальный граф Мэзона имеет также следующий вид:
1 т	1 т
ТО=’VMC/’)=
где Wnpi(p) = Wj — передаточные функции отдельных z-x простых путей от входа к выходу схемы; т — число простых путей; А (р) = Д — определитель сигнального графа:
Д(р) = 1 - Е ТО + S Е V}(p) - £ £ £ Vm?) +....
/=1	/=1 >1	i=l >14=1
124
Рис. 4.7
Здесь второй член равен сумме передаточных функций всех контуров; третий и четвертый члены и т. д.— суммы произведений двух, трехи т.д. передаточных функций контуров, не пересекающихся друг с другом (не имеющих общих вершин); п}, п2, п3— общее число таких сочетаний. Определитель А,(р) = А,-— это А (р) после изъятия из схемы г-го прямого пути, дополнение г'-го пути; если i-й путь проходит через все вершины, то А; (р) = 1. Знаки «+» и «-» у передаточных функций зависят от знака сигналов на выходе соответствующих звеньев.
Пример. Рассмотрим схему, изображенную на рис. 4.7, где имеются три контура, обозначенных I, II, III [4]. Для этой схемы передаточные функции контуров (внимание на знаки):
W} = -И'3И,10; Wn=-W6W9- Wm=-W2W3W4W9.
Передаточные функции прямых путей:
Wnp, =	%Р2 =-W7W8Wl0: 1Рпрз = W)W2IV3IV4W5;
w„P4	%р5 =«;
Определитель графа:
Д(р) = 1 - - Wn - Ufo + WtWn = 1 + И'зй'ю + W(,W9 +	•
Соответственно дополнения: Д((р) = 1-И) = 1 + W3W10 — с изъятым первым прямым путем не соприкасается только контур I, поэтому его передаточная функция остается; Д2(р) = 1-И)] = 1 +WgW, — со вторым прямым путем не соприкасается только контур II; Д3(р) = Д4(р) = Д5(р) = Д6(р) = 1 — с соответствующими прямыми путями соприкасаются все три контура схемы.
Передаточную функцию САУ получим подстановкой приведенных выше выражений в формулу для й'з(р).
§4.5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТОЙ САУ (ОПРЕДЕЛЕНИЕ И ПОСТРОЕНИЕ)
Частотные функции САУ и составляющих ее звеньев определяются выражениями для соответствующих передаточных функций при подстановке в них р - j(o. Следовательно, амплитудно-фазовая частотная функция последовательно соединенных звеньев
125
ИД» = П = Я(<в)е7ф(ш) = Пд((0)еш = 1=1	1=1
= 4(ю)е^(ш)Л2(а))ел(ш)... 4((в)ел(“) = 4Я2...Де7(Ф1+ф2+ +ф'), п	п
где А((з)) = J"j4(co); ф(и) = У, Ф;(®) — амплитудная и фазовая функ-i=i	i=i
ции соединения звеньев; Д((й) и Ф;(со) — функции f-го звена.
Выражение для ЛАХ цепочки звеньев: п	п
ад = £ Д» = £ 20 lg |И}(у<й)| 1=1	1=1	’
где — ЛАХ отдельного звена.
Таким образом, частотные характеристики последовательного соединения звеньев в виде ЛАХ и ЛФХ получаются путем суммирования ординат характеристик отдельных звеньев.
Асимптотические ЛАХ соединения звеньев строятся сразу без построения ЛАХ отдельных звеньев. Вначале определяют сопрягающие частоты <d; = 1/7} и значение 201g к. Ордината ЛАХ при со = 1 равна 201g к, где к — общий коэффициент передачи, равный произведению коэффициентов передачи звеньев. Через точку со = 1, 201g к проводится асимптота с наклоном (т - г) 20 дБ/дек = 20 v дБ/дек, где т — число дифференцирующих (Д), г — число интегрирующих (И) звеньев. На оси абсцисс (обычно указывают наряду с 1g со непосредственно и значения со) откладываются значения сопрягающих частот со, =1/7}, где 7} — постоянные времени звеньев. Первая асимптота проводится от оси ординат до наименьшей сопрягающей частоты, далее производится ее излом с изменением наклона в соответствии с типом звена, которому принадлежит данная сопрягающая частота; аналогично характеристика продолжается в сторону увеличения частоты, претерпевая изломы последовательно на каждой сопрягающей частоте. При необходимости ЛАХ уточняется путем учета поправок для колебательных звеньев.
Для получения ЛФХ ординаты звеньев суммируются:
Л
ф((0) = arg [ИД»] = arg [И<(»].
i=i
Предельное значение ф» звеньев (при и—> °°) будет равно (и-- т)л/2, где п — порядок дифференциального уравнения, а т —число идеальных дифференцирующих звеньев.
126
127
В качестве примера на рис. 4.8 приведены ЛАХ и ЛФХ последовательно соединенных одного интегрирующего кх/р и двух статических jt, ^3
звеньев первого порядка —-- и------ (k = ktk2k3; Т2>Т3,к>к ).
T2P + I Т3р + 1
Построение эквивалентной АФХ звеньев осуществляется непосредственно по АФХ отдельных звеньев путем перемножения модулей А; векторов Wj(j№i) при одинаковых значениях частоты (фазы <р( складываются). На рис. 4.9, а приведен пример построения двух АФХ kt к2 последовательно соединенных статических звеньев: —1— и —-—.
Tjp + 1 Т2р + 1 АФХ группы параллельно соединенных звеньев п	п	п	п
= YWiti®) = Х4ИеМ(Ш) = 1=1	/=1	/=1	1=1
АФХ строится путем геометрического суммирования векторов
W<(j(O) = t7((o)) + jVi((p) при одинаковых частотах (рис. 4.9, б).
АФХ звена с обратной связью строится согласно выражению
и;(» =
1+^PO)
— путем построения векторов Wn(у®) и 1Ур(усо)
при одинаковых значениях ю.
Разработаны специальные номограммы, позволяющие находить любые виды частотных характеристик замкнутой системы (звена с ООС) для случая И^(усо) = И^(у(0)/[1 + И^(уи)], по любым частотным характеристикам разомкнутой системы W (усо) (контура) [2]. Если
^(» = - -Ж l+WJOtolH^O) l+H'tyto)
т. е. И^с (р) 1 (000), то это выражение надо предварительно привести к виду:
W3(j(P) =
Jp(7W) 1+Wp(jco)
VHn(jto), где Wp(Joi) =
____£_____
и£(>5<(>)’
По номограммам могут быть найдены и логарифмические характеристики для выражения, стоящего в квадратных скобках; при этом искомые характеристики звена с ООС определяются для случая последовательно соединенных звеньев. Алгоритмические схемы САУ, таким образом, содержат информацию о составе элементов, топологии причинно-следственных связей между ними, структуре и параметрах операторов И<(р). Формы отображения схем САУ могут быть различными—символьными (уравнения), алгебраическими (матрицы) или теоретико-множественными в форме диаграмм графов.
128
Глава 5. СТАЦИОНАРНЫЕ ДИНАМИЧЕСКИЕ РЕЖИМЫ САУ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
§ 5.1. СЛУЧАЙНЫЕ ПРОЦЕССЫ
Задание воздействий в виде детерминированных функций времени далеко не всегда возможно в связи с самой природой воздействий. В этих случаях воздействия на систему рассматривают как случайные функции времени. Например, принципиально случайными по своей природе являются: возмущающее воздействие в виде шума в электронном усилителе регулятора; для автопилота воздействие ветра на самолет; колебания тяги ракетных двигателей; для следящей системы радиолокационной станции — сопровождение цели и т. д.
Выходная величина САУ при наличии случайных воздействий будет также изменяться случайным образом. Поведение САУ, находящихся в условиях случайных воздействий, исследуется методами теории вероятности.
Отметим, что случайный (стохастический или вероятностный) процесс —- это изменение случайной величины как параметра в функции времени, или — это функция времени, значение которой в каждый момент времени является случайной величиной. Случайные процессы подразделяются на стационарные и нестационарные.
Стационарный случайный процесс — это установившийся случайный процесс в статистическом смысле, когда все вероятностные характеристики его неизменны во времени [const (0]; стационарный случайный процесс — аналог стационарного детерминированного процесса. Нестационарный случайный процесс имеет вероятностные характеристики (хотя бы одну), зависящие от времени [var (/)]. Нестационарные процессы различают по характеру и скорости проявления нестационарности и чем меньше скорость, тем они легче поддаются ста-ционаризации. Очевидно, что стационарные процессы можно считать частным видом нестационарных. Нестационарные (Н) процессы всегда стремятся свести к стационарным (С), например, если существует эквивалентный оператор	хс(0, т. е. процессы в САУ обычно
рассматривают приближенно как стационарные.
Количественная оценка случайных величин и функций определяется посредством:
вероятности р(х,) = lim -= 0-s-1 дискретной случайной величины п	N—><~ N
закона (функции) распределения вероятностей случайной величины (в табличной, аналитической или графической форме): F (х) = р(х < х,) =
х(-<х
9 А. А. Ерофеев
129
плотности вероятности р(х-) для описания распределения непрерывной случайной величины-
закона (функции) распределения плотности вероятности р(х,): ,,	„ ,	, ч dp(xi < х < х, + Аг)
в дифференциальной форме р (xt) =	!-----1----- или в интег-
х-	dx
ральной форме F (xt ) = p{x <xi)= J р(х) dx.
Типовыми законами распределения реальных случайных величин являются: распределение Гаусса или нормальное распределение; равномерное и экспоненциальное распределение; распределение Пуассона р(х) = Хже-х/х!; распределение Релея, Коши, Лапласа и др. (здесь Л представляет собой среднее значение данной дискретной величины, полученной по результатам большого количества опытов). Реальные законы распределения сводятся к типовым с некоторой аналогией в том, как реальные детерминированные воздействия сводят к типовым воздействиям (ступенчатым, гармоническим, линейно возрастающим и т. п.). Для стационарного случайного процесса закон распределения не меняется во времени: р(х, t)=р(х).
Практически доказано, что всякая непрерывная случайная величина, представляющая собой результат действия достаточно большого числа независимых случайных причин, имеет нормальное распределение (см. п. 3.3 — НЗ). Поэтому основное использование в САУ имеет одномерное нормальное распределение, определяемое функцией Гаусса (рис. 5.1, а):
(х-тх)2
р(х) = Д е 2а*
л/2ло.
_dF(x) dx
; F(x) =
-mt)2
2°x dx
1
роятности р(х, у) = р(х)р(у) = -— -ехр •
2лога„
(- о® < х < о°), где р (х), F (х) — соответственно плотность вероятности и функция распределения вероятностей. Для нормального закона вероятность нахождения случайной величины составляет: в интервале ±o v-0,682, ±2o v-0,954, ± Зо г-0,997; обычно ограничиваются рассмотрением интервала ± 2ох («правило 2сг»).
В общем случае можно определить «-мерные законы распределения для случайных переменных функций разных размерностей (и). Так, нормальный двумерный закон определяет следующая функция плотности ве-(х-тх)2 , (у-ту)2} 2ст2
2а2у j ’ если имеет место нормальные и взаимно-независимые одномерные (1-р2 )-1/2 распределения пох ну. Для зависимых процессов р(х, у) = —:——----х
2лстгст„
130
x exp
Д x-mr I ---* + ax )
' У-Шу^ (x-mx)(y-m )
I ay J	axay
где
1
2(1 ^р;,.)
pXJ, = Л/[(х-тл.)(^-шр] = ^(т)/оха>, (см. ниже). Двумерная плотность распределения вероятности отражает свойства двух случайных переменных (х, у): р(х, у) = d2F(x, у) / дхду, в отличие от одномерной р(х) = ЭГ(х) /Эх. Плотность вероятности р(х,у) здесь представляет поверхность, а объем, ограниченный этой поверхностью, | j р(х, у) dxdy = 1,
—ОО —ОО	ОО
также как и площадь под одномерной кривой и осью абсцисс J р(х) dx = ОО	—ОО
= F(x) \ = 1(F(°°) = 1, F{-°°) = 0). Обычно в САУ ограничиваются рас
смотрением одномерного (и иногда двумерного) закона распределения, преимущественно нормального (см. п. 3.3).
Кроме закона распределения р(х) необходимо знать еще его временные (частотные) свойства.
Законы распределения (одномерные, двумерные и, в общем случае, и-мерные) исчерпывающе определяют случайную величину, но на практике широко применяют количественные характеристики случайных величин:
а)
ОО	оо
J/?xdx-F(x)|=/
-Оо	-оо

131
9*
среднее значение (математическое ожидание) тх = М [л] = ©О	ОО
= ^xp(x)dx; тх = ^х{рр,
дисперсия Dx - М[(х-/ил.)2] = ^(х-тх)2 p(x)dx и среднеквадра-
тическое отклонение ах - Для двумерных случайных величин ©О ОО
(х,у) кроме дисперсии Dx = | §(х-тх)2р(х, y)dxdy и Dy =
ОО ео	-®о “ОО
= J ^(.У~1Пу)2р(х, y)dxdy возникает новая характеристика — взаимная —оо —оо	ео оо
дисперсия (или ковариация) Dxy = а2ху = J |(х - тх)(у- ту)р(х, у) dxdy.
Для реального стационарного случайного процесса в САУ [тх = = mx(f) = const (г), ох = стх(г) = const (г)] практически всегда справедлива гипотеза об его эргодичности, заключающаяся в том, что среднее по множеству x(t) равно среднему по времени х(г):
1 Т
х= lim— \x(t)dt, т. е. x(t) = x(t) = тх = M[x(t)]. г-*» 2Т J
-т
Среднее по множеству х(?) для случайной функции х (?) определяется для каждого момента времени /, посредством усреднения повеем реализациям процесса.
Свойство эргодичности значительно упрощает определение вероятностных характеристик стационарных случайных процессов посредством статистической обработки одной реализации случайного процесса. При тх = 0 случайная функция (или величина) х°(/) называется центрированной. Таким образом, случайное воздействие можно в общем случае представить: x(t) = mx(f) + x°(f) и y(t) = my(f) + y°(t). Для линейных САУ, исходя из принципа аддитивности (суперпозиции), каждая из составляющих может быть определена отдельно: my(t) как реакция на mx(t) n.y°(f) как реакция на x°(t). Если х°(г) рас-сматриватся как помеха, a mx(t) — полезный сигал, то х°(/) называют иногда аддитивной помехой.
Корреляционные функции служат для количественной оценки случайного процесса, оценивая быстроту изменения случайного процесса во времени. Из них корреляционная (или автокорреляционная) функция 7?(т) представляет собой среднее значение произведения двух значений функции, сдвинутых на определенный промежуток времени т:
Rx (т) = М [х (г)х (г + т)] или т
RM = lim(V2T) fx(t)x(t + x)dt
Т-и» *
-т
132
и
/?/т)=М[у(0у(г + т)]
или
т
Ry (т) = ?lim (1/2Т) J у (t)y (t + т) dt.
-т
Взаимокорреляционная функция Rxy (т) = М [х(f)y (t + т)]; Ryx (?) =
i т
= М [у (t)x(t + ?)] или Rxy(x) = lim — [ x(t)y(t+ x)dx [аналогичнодля т—>°° 2Т *L
М*)]-
На рис. 5.1, б, в приведены типичная корреляционная функция и ей
соответствующий процесс x(t); Rx(x) с ростом х убывает, что отражает ослабление влияния (корреляции) на текущее значение случай-
ной функции ее предыдущего значения при увеличении.
Рис. 5.1, г, д отражает один из предельных случаев, когда Rx(t)— косинусоида с частотой о»!, не зависящая от сдвига фаз ср. Время (или интервал) корреляции случайного процесса обозначают через xR, при котором \Rx(xr)\<^(~5%).
Основные свойства корреляционной функции Rx(x).
1.	Максимальное значение корреляционная функция имеет при х = 0: RX(O) = mx + Dx или 7?х(0) = М Jx2(o] = x2(f) = x2, т. е. равно среднему значению квадрата x(t).
2.	Rx (т) — четная функция: Rx(x) = 7?л(-т).
3.	Для случайного процесса с ростом х корреляционная функция Rx(x) < Rx(0) всегда убывает тем быстрее, чем быстрее изменяется во времени случайный процесс x(t) [связь между значениями x(z) и х (z + т) ослабляется].
4.	Предельное значение корреляционной функции при т —> равно квадрату среднего значения [х (z)]J2 или Rx (°°) = mx = [*0)] > так как при t -> оо значения случайной функции независимы и соответствуют постоянной составляющей в виде среднего значения тх.
5.	Для центрированного случайного процесса тх = 0 и /?^о(О) = Dx, a R 0(оо) = 0. Здесь нормированная корреляционная функция рх(т) = = R*0(x)/Dx<> =1 при т = 0, рх(0) = 1. В общем случае Рд(т) = = Rx(x)/Dx<L
6.	Для суммы случайных процессов x(t) = xl(t) + x2(t): Rx('c) = = R (т) + R (т) + Rx x (т) + Rxx (t); o2 = o2 + 2o2 v + o2 .
7.	Для независимых Xj(z) и x2(z): если x(/) = Xj(Z)x2(0, то Av(t) = = RXt(x)RX2(x), а если x(p = х^О + ХгО), то Rx(x) = RXf(x) + RX2(x); Dx = DXi + DX2 = o2_ + a22; о2|Хз = 0, см. 6.
133
8.
п
Для х(0 = ц, + sin (cozZ + <pz) Rx(x) = а%
i=i
+
cos со;т.
Таким образом, при известной Rx(x) легко определяются х = х = = тх = jRx(°°y, М[х2] = J2 = ЯДО); Dx = Rx(0)-Rx(°°y ох = =Jd~x. Взаимная корреляционная функция Rxy(x) обладает примерно теми же свойствами, что и автокорреляционная функция: Яху(0) = = м [*(0Яо]; Rxy{°°} = т2т2; Rxy(x) = Ryx(-x) [но Rxy(x) * ЯЛ/(-т)]; Т?2/т) <[Ях(0) + Я/0)]; \Rxy(x)\<[ЛХ(О)7?ХО)]1/2; |7?х/т)| <0,5[Дх(0) +
+Я/0)]; рх/т) = Rx.M/fi\D~y = Rxy(x)Iахсу < 1; Я2/т) < Rx(0)Ry(0).
Если процессы x(t) ny(t) статистически независимы и хотя бы один из них центрирован, то Rxy(x) = 0. Нецентрированную корреляционную функцию называют еще ковариационной. Для оценки меры линейной статистической связи двух случайных величин х, у применяют коэффициент корреляции г^(т) = ох?(т) / ох(0)ст_),(0), rxy < 1; для независимых (или некоррелированных) величин rYJ,=0. Коэффициент корреляции, как видно, тесно связан с корреляционной функцией Яг>,(т). Для оценки меры изменчивости процесса используют иногда коэффициент вариации 0 = a[x(t)]l М [x(z)].
Спектральная плотность 5х(ш) случайного процесса х(1) — это частотная функция, характеризующая спектральный (частотный) состав процесса, представляющая собой частотную функцию для средних значений квадратов амплитуд гармоник, на которые может быть разложен случайный процесс. Поскольку мощность гармонического сигнала пропорциональна квадрату его амплитуды, спектральная
плотность определяет распределение среднего значения мощности процесса по спектру (по гармоникам). Поэтому ее называют спектральной плотностью мощности, так как S' (со) определяет среднюю 1 °°
мощность процесса: Яс_ =— Sx(a>)d(a; dP^Jdas = SA.(to) /я. ло
Для стационарного случайного процесса x(t) спектральная плотность представляет собой изображение Фурье корреляционной функции: оо	со
SY(&)) = |ях(т)е“70Пс/т или SY(a)) = 2jKY(T)cosa)TA.
—оо	О
Корреляционную функцию можно выразить с помощью обратного преобразования Фурье через спектральную плотность:
2Д J
или в тригонометрической форме, учитывая, что ^.(и) = Sx (—оэ) — четная функция:
134
i
7?х(т) = — I \(0))COS (ОТ <7(0.
Я0
I 00	J 00
Откуда Rx(0') = |Sx(to)<7co и Dx = — | S 0(w)<Z(o. Ширина энергети-
ка	ль л'
ческого спектра случайного поцесса Д(о = 7?х(0)/ SAG) = Dx / SX(G), где оо
Sx (0) = 2J Rx (т) dt; для узкополосных процессов Дсо = Rx (0) / Sx (со0) = о
= Dx/Sx(a>0), (o0 — центральная или несущая частота (см. рис. 3.10, б). Интервал корреляции тЛ = 1 /2Дсо = тк; максимум тКм - 0,5 ||рх(т)рт.
На рис. 5.2, а, б приведены зависимости Д((о) и соответствующие им корреляционные функции 7?(т) для центрированных стационарных случайных процессов.
Здесь наблюдается аналогичная связь, как между обычной частотной и переходной характеристиками: чем шире график корреляционной функции, тем уже график спектральной плотности (и наоборот). В предельном случае, когда х (t)=a=const (z), корреляционная функция постоянна (прямая 5) и равна Rx(x) = а2; спектральная плотность Sv((o) = 2ла28((о) / 0 только при to = 0 (дельта-функция). В другом идеальном предельном случае Rx = а8(т) (прямая 7), a Sx(to) = а = const (z), когда х (Z) — чистый случайный стационарный процесс (белый шум); здесь rR = 0 и 7?Л.(т) — дельта-функция. Для синусоиды%(Z) (см. рис. 5.1,3) (две дельта-функции при +(0] и —со1).
fyAT),Svx(aD
Рис. 5.2
135
Случайный процесс в виде белого шума, когда Лх(т) = 0 при т S О, физически не реализуем, так как ему соответствует бесконечный спектр и соответственно бесконечная мощность. Реальные случайные процессы имеют конечные мощности и спектры (см. кривые 2, 3, 4 на рис. 5.2, а, б). Однако часто их можно приближенно представить в виде белого шума, если ширина спектра процесса значительно больше полосы пропускания системы. Здесь аналогично рх(т) вводят нормированную^ спектральную плотность, имеющую размерность времени (со) = |рх(т)е"7ИТг/т	(и)/7)х. Максимумы 5х(ш)
показывают на каких частотах сосредоточена основная мощность процесса; ох = JSx((d)d(j) — площади под кривой Sx(со) и осью абсцисс, о
Подобно Rxy(x) применяется взаимная спектральная плотность, представляющая изображение Фурье взаимной корреляционной функции:
Sx,(®)= /Ях?(т)е-^,
где
2л J
аналогично
5^(0)) = J= Ж,х(»Sx(<o) и Ryx(x).= Syx(G>).
—оо
Так как W3X(jd)) = Syx(fi))/Sx(со) и если Ух(со) = 1 (белый шум), то Syx(oi) =	a Ryx(x) н» и-'(т), где w (т) — импульсная переход-
ная характеристика САУ. Размерность Sx((a)-x2c, х — размерность случайного процесса.
Следует отметить, что Rxy(r)* Ryx(r); Rxy(x) = Ryx(-x), a 5х/®) = 5*х(®) = 5?х(-и). Здесь Sxy(J(d) = Syx(-J(ii) = = Sxy((o)-jSxy((ii). Если x(t) = X](0+x2(z), to 5Л.(со) = 5'Л|(а)) + 5Л.2(<а) + +5Х2(со) + 5'Х1Х2(и) + 5Х2Х|((О).
При Rxy(x) = Ryx(x) = 0 и SyjX®) = Зух((й) = 0 сигналы не корре-лированы. Функции R (т) и S(co) не содержат сведений о фазе, а дают информацию только об амплитудах процессов. Передаточную функцию, например замкнутой САУ, можно представить в виде
= P((o)+7e((o) = [5';x(£o)/5x(o))]-j[s;v((o)/Sx(co)].
136
Комплексная спектральная плотность (комплексная функция рас-пре-деления амплитуд спектра) Sx „(уса) = S,x.J,(a>)e-/v(“), где (со) определяет амплитудный спектр; у (со) определяет фазовый спектр (функция распределения начальных фазовых углов спектра).
§ 5.2. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ В САУ
Стационарным случайным внешним воздействием х(г) соответствуют стационарные случайные изменения выходной величины y(t) САУ (если САУ стационарна). Связь между характеристиками процессовх(с) иу(0 на входе и выходе САУ через средние значения Mx(t) и My(t) (неслучайные величины) имеет вид (см. рис. 5.2, в):
My = W3(p)Mx или
М = А Мх + ВМ Mv = СМХ + DMU.
Для стационарного случайного процесса, когда Мх = const (г) и Му = const (г), связь между ними определяется по уравнению статики М y = W3(tyMx.
Связи между корреляционными функциями и спектральными плотностями процессов на выходе и входе САУ в дифференциальной форме через передаточную функцию САУ имеют вид:
я/т) = |едж3(-р)вд и
5/ш) =^3(»|2Sx(co) = Л2(со)5Дсо),
где |FK3(»|2= W3(» Ж3(->) = (Р(со) + уе(со))(Р(<о) - Д2(со)) = (Р2(со) + + е2(«)) = Л2(«).
Если к системе одновременно приложены в разных точках два стационарных случайных сигнала x(f) и Дс), то на основе принципа суперпозиции имеем:
S/w) = Азх (со) Sx (со) + 4y(w) S/co)
и
SE(a>) =
1
1 + R»
2
Sx(®) +
I+ИЧ»
2
Sz((0).
Приведенные соотношения позволяют находить корреляционные функции или спектральные плотности выходной величины САУ по известным корреляционным функциям или спектральным плотностям
137
входных воздействий. Эти соотношения являются важными для решения задачи анализа (оценка точности САУ) и задач синтеза САУ на заданную точность при статистически заданных внешних воздействиях.
Все вышеизложенное аналогично и для линейных импульсных
1 я
САУ, а именно, например, ЛхГо1 = х2[п] = - Г 5*(со)<йб; 5*((о) = по
= |»£(./®)| -V(co); 5*(ш) =	5*у(й) = |^(Jc5)|(ш) ит.д.
т—-ПО-
ТОЧНОСТЬ САУ при стационарных случайных воздействиях можно оценить через дисперсию процесса, характеризующую стационарную погрешность системы:
1	1	1
Dy = — Г У О (со)4*о =	Г |и;(»12у о(<оМо) = - [ 5 „ (со)е*о
2п J у	2it J	Л	л j у
—оо	-оо	О
Закон распределения случайного сигнала при прохождении через линейную САУ в общем случае может изменяться, кроме случая его нормального распределения, когда он сохраняется неизменным, но с другими значениями Му и Dy.
Здесь обычно представляют

GQ)
A(j(0)	A(J(o)A(-Jo))>
где G(jco) = А>(»2(" 1) + ^(»2(п~2) +... +^_„	Л(» = Оо(»" +
+ а1(усо)" ’ + ... + а„.
Вычисление Dy производят через стандартный (табулированный) интеграл Jn, значения которого для конкретных п<10 заранее вычислены и сведены в таблицы [2, 7]:
2п-~|Л(»| 2ао д«
где Д„=аяД„_] — матрица Гурвича (см. п. 6.2), а М„ =
А)	А	-	A.-1I
ciq	...	О j
= 0	at	а3	...	О |.
О	О	0	...	ап
Здесь для устойчивой САУ все нули А (усо) левые и расположены в верхней полуплоскости; G (/со) содержит только четные степени.
138
Для п = 1	для п = 2 J2 =-----------— ; для « = 3
2ао«!	W?,
т =______________^з_
3	2^(00^-Д]Д2)	И Т- «•
А»-1
Иногда [2] табличный интеграл Jn записывают в форме:
п
1 Г
^<КрМ-р)
или
1 7
2л До dU^d(-jti))
где c(p) = cn_1p"4 + ... + q/>+c0, d(jp) = dnpn + d„_lpn~l +... +dlp+d0,
,	_c^+<^</2
тогда Jx =^T, J2 =	ит.д.
2^^ 2d^dxd2
На границе колебательной устойчивости САУ An4 = 0, дисперсия D —>оо.
у	1 °°
Обычно кроме Dy определяют дисперсию ошибки РЕ = — J УЕ((о)б?й),
2тс
2	—о©.
где в общем случае Se (со) =| ЖЗЕ (jco)j Sx (со) + ИДе (”Л>)	/ (У®) Sxf (Л>) +
	'	г	г	ги
;	+и^(>)и;/(->)У/х(>)+|и;/(7(в)!у/(о)); wxu^ = [^wpu^\ ;
W3f(ja) = ^(jo))[l + ft/»]’1.
Если сигналы на входе САУ x(f) и помехи (возмущения) /(Z) не коррелированы, то выражение для 5Е(и) упрощается. Таким образом, соответственно De=D*+ D*d + D{x + D[ или Z>E = Dx + Р/.
Среднее значение квадрата ошибки САУ
I	<
Е2(0 = Ше(0 +
где щЕ (/) = тх (0 + т[(Z).
Среднеквадратичное значение ошибки САУ £ск(0 = 1/е (О, а при znE(Z) = 0 еск(0 ~	Если х (/) = 0, a f{t) — случайный стационар-
ный процесс с 5/(и), то спектральная плотность ошибки будет SE(co) =
Ре=ЗД = -[5е((»)(/(0, Л'
139
II2	।	,2
= |ИЛ3/((О)|	(co). Аналогично, если/(/) = О, то 5E(®) = |Wz3e(co)| 5х(<о),
где ИС (ко) =--------.
36 l + W^jco)
Дисперсия выходной величины САУ при взаимной независимости x(Z) и fit)
Dy=Dx+Df.
Синтез САУ по условию обеспечения требуемой точности в стационарном случайном режиме сводится к определению передаточной функции САУ, для которой выполняется неравенство
(и)<Ло, %
где Dynon — предельно допустимое заданное значение дисперсии выходной величины.
Таким образом, для оценки динамической точности САУ определяют два первых вероятностных момента случайных процессов Му и Dy, что эквивалентно определению Sy(ai) или Ry(x).
По заданной Dyд0П определяется У,, (со), далее находится амплитудно-частотная характеристика САУ, при которой выполняется неравенство, а по ней, при необходимости, определяется №3(р).
Случайные величины, аргументами которых являются^екторы, образуют пространственные или пространственно-временные случайные поля (в состав аргументов поля входят координаты пространства х, у, z и, во-втором случае, еще и время t). Случайные поля бывают скалярными, например плотность воздуха и его температура \f(x, у, z, /)], и векторными, например турбулентность атмосферы w(x, у, z, t), т. к. скорость ветра — это вектор с тремя составляющими wx,wy,wz.
Если на ОУ (или САУ) воздействует одновременно ряд внешних воздействий x,(z), fk(t), то вектор g(t) = [x,(z), fk(t)]T образует векторный случайный процесс. Его математическое ожидание М [g (/)] также является вектором , a Rg, Dg, Sg — есть соответственно корреляционная матрица, матрица дисперсий и матрица спектральных плотностей, например У?(со) = JR^tT^th. Случайные поля и векторы имеют важное значение при рассмотрении статистической динамики и оптимизации систем управления ЛА.
Нахождение оптимальной передаточной функции является полным решением задачи синтеза САУ. Теоретически оптимальная передаточная функция обычно не может быть реализована в силу своей сложности. Поэтому результаты синтеза следует рассматривать как теорети
140
ческий предел, к которому нужно стремится, позволяющий оценить степень совершенства практической САУ.
Пример 1. Типичные R (т) и 5 (ш):
7?](т) =	^(w) = Dx2al(a2 +<о2), a=const;
Я2(т) = Охеа^' cos W|T ; S2(<а) = Рхсс|[а2 + (co -Ш02] + |a2 +	+ <d)2]
Я3(т) = Dxe’a^(cos Ш]Т + у sin
S3(a>) = 2PxJ(a+Y(oI)((o2 +a2)2 +(a-у(О1)ш2у^2(а2 -<n2)(o2 +(a2 +w2)4 + <o4 j.
Пример 2. Связь эквивалентных прямоугольников Л,(т) и5э(ш):
Гл(О),|т1<т1 [ЭД.НСШ! 5(0)	лЛ(0) я
ед = | 0,|т|>т1 ; 5’(“) = | 0,|ш|>ш1 ; Т1 = W); “1= 5(0)’ W = 2=COnSt'
Так, для /?](т) и St(a>) (см. пример 1):
Я|(0) =	, 5[(0) = 2Dv/a и Т! =1/а, СО] = ла/2.
Пример 3. Сигналы:
х(0 = A sin ((!>[/ + <р)	5х(о>) = --[8 (и - Ш|)+8(<о +<0|)];
"	(	" Л2	1
*(0=4> + У, Aj sin ((О,/ + (₽, )>-> 5х(<о) = 2л ( Ло8(ш) + —[8 (со - со,) + 8(ш+a>i)] к
i=i	I	(=1 4	J
к
Пример 4. Пусть JFp(p) = y-^, Sx(w) = l, тогда
Dx =^SA.(<o)= к^- Sy(w) = k2Sx(<o)l(l + T2w2) = -~^^. х IT х 2Т у	l + TW
Пример 5. Пусть W3t(p) = 1 (y = g), 1У30ПТ(» = 5g(<o)/[Sg(co) + S’/(co)}
Пример 6. Пусть (^(p) = p а Ял.(т) = а28(т); Ry(x) = ^е-^, а Яху(т) =
= ^е'т/Г; при 5^) = ^: 5/ш) = —4-т, а 5	.
1	1+(О2Т2	1 + J&T
Пример 7. Статистическое дифференцирование и интегрирование:
»'(/’) = ?. 5/ш) = (й25х(а>);
141
W(p) = ^, SJ,(<o) = <o4Sx(<o) ит.д.: 4n) =<o2"Sx(w); 
W(p) = \l?, 5/ш) = 5х(ш)/<о4 ит.д.: £<,">= 5х(<о)/ш2п.
Глава 6. УСТОЙЧИВОСТЬ САУ
§ 6.1.	ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ ЛИНЕАРИЗОВАННЫХ САУ.
ТЕОРЕМЫ ЛЯПУНОВА
Рассмотрим понятие об устойчивости на основе представлений механики. Если подразумевать под системой некоторый шар, то можно сформулировать по отношению к нему понятие об устойчивости.
1.	Если шар находится на вогнутой поверхности, то при наличии силы F эквивалентной внешнему воздействию, шар можно вывести из состояния покоя (рис. 6.1, а). Предположим, что сила такова, что шар дошел до точки х. Если теперь исчезает воздействие F, то, очевидно, шар под воздействием силы тяжести после совершения нескольких колебаний около точки равновесия А придет в установившееся состояние (или состояние покоя), соответствующее точке А. Это пример устойчивого равновесия (система является устойчивой).
2.	Если шар находится на выпуклой поверхности и к нему приложена некоторая сила F, то под воздействием этой силы шар, будучи отклоненным в точку х, после прекращения воздействия силы не придет в установившееся положение (в точку А). Такое состояние системы является неустойчивым (рис. 6.1, б).
3.	Если шар находится на шероховатой ровной поверхности и к нему приложена сила Г, то шар выйдет из состояния равновесия и после снятия воздействия придет в новое состояние равновесия. В зависимости от величины и знака силы F шар может иметь бесчисленное множество точек равновесия. Такое состояние носит название нейтрально-устойчивого, т. е. система является нейтрально-устойчивой (рис. 6.1, в).
Устойчивость — это свойство САУ возвращаться в заданный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.
А
Рис. 6.1
142
Типичные кривые переходных процессов показаны на рис. 6.2 в неустойчивой (рис. 6.2, а) и устойчивой (рис. 6.2, б) САУ. Исследование устойчивости САУ имеет огромное значение, так как САУ в замкнутом виде обычно склонны к неустойчивой работе.
Основной задачей САУ является выработка таких управляющих воздействий, которые приводили бы после возмущения САУ к устойчивому состоянию. Для линейных САУ: устойчивая (неустойчивая) САУ устойчива (неустойчива) при любом по величине внешнем воздействии, т. е. всегда либо устойчива, либо неустойчива. Для нелинейных САУ этот вопрос значительно сложнее (см. п. 9.6); устойчивость может быть в «малом», в «большом» и в «целом» — устойчивость при любых начальных условиях (САУ абсолютно устойчива). Если САУ неустойчива, то достаточно любого воздействия, чтобы в ней начался расходящийся процесс — апериодический (кривая 1 на рис. 6.2, а) или колебательный (кривая 2 на рис. 6.2, а). В случае устойчивой системы переходной процесс, вызванный воздействием, затухает и система возвращается в установившееся состояние.
Таким образом, устойчивую САУ можно определить как систему, переходные процессы в которой являются затухающими и ее выходная величина остается ограниченной при действии на систему ограниченных по величине воздействий.
Впервые свойства устойчивости были исследованы русским ученым А. М. Ляпуновым в 1892 г. в работе «Общая задача об устойчивости движения». Он ввел понятия возмущенного и невозмущенного движений, асимптотически устойчивого движения. Теоремы А. М. Ляпунова позволяют судить об устойчивости нелинейных реальных САУ по их линеаризованным уравнениям (уравнениям первого приближения).
Линейные САУ описываются неоднородными линейными уравнениями с постоянными коэффициентами:
dny dn~xy	,dmf , .
----h Q\---у Л-d. y — h\	4-... + bmf\ dtn dtnA	dtm
(a^pn + axpn~x + ...+an)y = (l*pm + ...+bm)f
143
или в общем виде
y=W3{p)f = [M(p)lD{p)]f,
где
Wfy{p^Wp(p)
W (р) =	;
Р Q(P)
Wfy{p)-
Rfy(P)
Qfy(p) ’
Ж3(р) =
v — знак «или».
Здесь, если степень Q (р) равна п, a R (р) — т, то из физических соображений гаси; в противном случае из W(p) можно выделить слагаемое с р порядка га-и, соответствующее дифференцирующим звеньям, которые естественным образом практически не реализуются.
Решение этого неоднородного уравнения в общем виде состоит из двух слагаемых:
У(1) УустО) + Л (О ^частСО + Уобщ(0 Лын(0 + Усв(0-
Здесь ууст(0 = Ласт(0 = Лын(0 — частное решение неоднородного уравнения с правой частью, описывающее вынужденный режим системы, устанавливающийся по окончании переходного процесса [при Ласт = const (7) — это будет установившееся движение]; уп - уобщ = усв— переходная (свободная) составляющая, находится как общее решение однородного уравнения
^(/’)Лв(Р) = 0; усв(0 = Я0“ Лын(0.
описывающее переходной процесс в системе, вызванный данным возмущением.
САУ будет устойчива, если переходные процессы уп(г), вызванные любыми возмущениями, будут затухающими, т. е. если с течением времени уп(0 будет стремится к нулю(усв—>0 ).
Решение уп(0 однородного дифференциального уравнения имеет вид:
Л(0 = Хс'ейг = с!еД! + с2еЙ/ + • • + cnG-P"‘ • Здесь с, —постоянные интег-м
рирования, определяющиеся начальными условиями и возмущением; pt —корни характеристического уравнения D (р) = а$рп + ахрп~х +... + ап = 0.
Многочлен D(p) является знаменателем передаточной функции W3(p) системы. Следовательно, D(p) = 1 + Wp(p) = [/?(р)+б(р)]/б(р) = = £>'(Р)/6(Р); D'(p) = R(p) + Q(p), где R (р) и Q (р) — числитель и знаменатель передаточной функции Wp(p).
Характеристика переходного процесса уп(0 в САУ представляет собой сумму составляющих, количество которых определяется числом корней характеристического уравнения D(p).
144
В общем случае корни р, являются комплексными: phpM = = ±а, ± уР,-, где щ может быть положительной или отрицательной величиной (рис. 6.3).
Каждая пара комплексносопряженных корней дает сос-ставляющую переходного процесса, равную
С.е(“-+А)/ +с.+1е<“/-А)/ =
= е“''(с,.е^ +С/+1е-А') =
= ci-ea,'sin(P1z + (pi) = = Леа,г sin (Ру + ср;),
Область устойчивости
4Г-
Рис. 6.3
,	/	/ 2 , 2	С; + С: , 1
где с- и ф;- определяются через с, и с/+1: с,- = ^ct +с,+1; tg <р, = -—
Cj - С,_1
Эта составляющая представляет собой синусоиду с амплитудой, изменяющейся во времени по экспоненте: если а,•<0, то составляющая будет затухать; при а, > 0 получатся расходящиеся колебания (рис. 6.4, б, в). Если а,- = 0, что соответствует паре мнимых корней, то будут незатухающие синусоидальные колебания (рис. 6.4, г). Условием затухания данной составляющей является отрицательность действительной части соответствующей пары сопряженных корней.
Будем говорить об асимптотической устойчивости, если при t —> °° свободная составляющая стремится к нулю, т. е. усв(Г) -> 0 (затухает).
Рис. 6.4
10 А. А. Ерофеев
145
В случае, когда Р, = 0, имеем действительный корень р,- = а,-, которому соответствует составляющая переходного процесса c(e“,z экспонента (рис. 6.4, а) . Здесь 1нэ р, =-ар, 2н> р,- = а;; 3i—>р(=0 ит. д. (см. рис. 6.3),
Следовательно, переходной процесс в САУ состоит из колебательных и апериодических составляющих: колебательная составляющая соответствует паре комплексно-сопряженных корней, а апериодическая — действительному корню. Общим условием затухания всех составляющих и всего переходного процесса в САУ является отрицательность действительных частей всех корней характеристического уравнения системы (полюсов-нулей знаменателя передаточной функции системы). Корень с положительной действительной частью всегда дает расходящуюся составляющую переходного процесса; пара сопряженных чисто мнимых корней ±дает незатухающую гармоническую составляющую переходного процесса (с частотой ± /Р,). САУ при этом находится на границе устойчивости.
Физические реальные САУ строятся всегда таким образом, чтобы они были устойчивыми, т. е. после окончания внешнего воздействия они переходят в состояние нового установившегося равновесия. Если система по каким-либо причинам окажется неустойчивой, то принимаются меры по приданию системе нужных свойств устойчивости. Все реальные системы являются нелинейными и линеаризация их производится путем отбрасывания членов, содержащих различные нелинейности. Поэтому закономерно ставится вопрос, будет ли реальная система устойчива, если устойчива линеаризованная система. Русским ученым А. М. Ляпуновым (1892 г.) были доказаны следующие теоремы (сформулированы в работе «Общая задача устойчивости движения»).
Теорема 1. Если корни дифференциального уравнения линеаризованной системы содержат только отрицательные вещественные части, то линеаризованная система является устойчивой (невозмущенное движение асимптотически устойчиво) и никакие добавки в виде членов с различными нелинейностями не могут сделать систему неустойчивой. Вывод: определяя устойчивость линеаризованной системы, можно говорить и о свойствах устойчивости реальной системы.
Теорема 2. Если корни или хотя бы один корень дифференциального уравнения линейной системы содержат положительную вещественную часть, то линейная система является неустойчивой и никакие добавки в виде членов с различными нелинейностями (члены высшего порядка малости) не могут сделать систему устойчивой. Вывод: если линеаризованная система неустойчива, то неустойчива будет и реальная система.
Теорема 3. Если корни дифференциального уравнения линейной системы или хотя бы один из них будут равны нулю или чисто мнимы, то свойство устойчивости линейной системы будет неопределенным (критическим). Система находится на границе устойчивости.
146
При этом добавки в виде нелинейностей могут различным образом влиять на поведение системы и по линеаризованным уравнениям, строго говоря, нельзя судить о том, что происходит на границе устойчивости системы. Вывод: поведение реальной САУ не всегда даже качественно определяется ее линеаризованным уравнением, так как малые члены могут сделать САУ устойчивой или неустойчивой;
Решение уравнения системы представляет некоторую траекторию х (0 в пространстве переменных состояния (хь..., хп) = [х]г. Устойчивость зависит от свойств функции переменных Й[х]т = Vn и п
dV/dt = ^(ЭК/Эх,)х,-. Обычно используют квадратичные формы V = 1=1
=	=МГ[ЛИ —функции Ляпунова. Для устойчи-
'=1 М
вости линейной системы функции V должны быть определенно положительными всюду за исключением положения равновесия (например, начала координат).
Для исследования устойчивости нелинейных САУ имеются другие теоремы А. М. Ляпунова, которые используются, например, для прямого второго метода Ляпунова и др.
Следовательно, общее условие устойчивости линейной системы можно сформулировать так: условием устойчивости системы является расположение всех корней характеристического уравнения (полюсов передаточной функции системы) в левой комплексной полуплоскости. Наличие корня на мнимой оси означает, что система находится на границе устойчивости.
Общее решение однородного разностного уравнения [см. п. 1.3 (6)], аналогично рассмотренному выше, при некратных корнях характеристического уравнения имеет вид (в сокращенной записи):
X«] = C1Z1n+C2z£ + ...+Qz£,
где zz(z = 1,2,...,£) — корни характеристического уравнения (a$zk + + axzk~x +... + ак = 0); cz — произвольные постоянные. Здесь условие устойчивости |z(-i<l.
Вопрос о корнях D(p) может быть решен путем непосредственного решения дифференциальных уравнений и нахождения корней. Однако прямое исследование корней возможно лишь для системы 1, 2, 3, 4-го порядка (есть их аналитические выражения), причем с повышением порядка (3, 4) трудности их нахождения существенно возрастают (их выражения малоудобны). Для суждения об устойчивости САУ практически не требуется находить корни ее характеристического уравнения, так как существуют косвенные признаки, по которым можно судить о знаках действительных частей этих корней и тем самым об устойчивости системы, не решая самого характеристического уравне-
ю*
147
ния. Эти косвенные признаки называются критериями устойчивости (КУ). Различают аналитические (алгебраические) КУ и графо-аналитические (частотные) КУ.
§6.2. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
Существует ряд критериев устойчивости (КУ) в аналитической форме — Рауса (1877 г.), Гурвица (1895 г.), Льенара—Шипара (1914 г.), Шур—Кона, Джури—Бланшара. По существу их различает лишь форма, поэтому, например, первые два часто называют критерием Рауса—Г урвица.
Алгебраические критерии не требуют выполнения вычислительной процедуры определения корней; условия устойчивости сводятся к выполнению ряда алгебраических неравенств, связывающих коэффициенты уравнения системы. Посредством алгебраических критериев определяются условия асимптотической устойчивости автономных замкнутых САУ обычно при п<15.
Критерий Рауса—Гурвица. Этот критерий в алгоритмической форме (как оказалось, удобной для ЭВМ) был предложен английским математиком Раусом (1877 г.), а затем, в определительной форме, математиком Гурвицем (1895 г.). Критерии Рауса и Гурвица связаны между собой простыми соотношениями. Приведем без доказательства эти критерии в форме Рауса и Гурвица; заметим лишь, что критерий Гурвица можно достаточно просто получить из критерия Рауса.
Отметим также, что критерий Рауса формулируется в табличной форме.
Таблица Рауса состоит из Су -коэффициентов, связанных с коэффициентами Oq ... а„ полинома D(p), где i — номер столбца, j—номер строки (их число равно п +1):
с/+1,;-2
rj-3 I	_ cl,y-2
, I д>з - cm, j-2 - O-3C/+1,;-1; rj-3 - ~ 1	Cl .• 1
Здесь строка 1 содержит а, с четными индексами, строка 2 — с нечетными коэффициентами. Коэффициенты строк 3 ...(»+ 1) подлежат определению (с,-7):
си -ц»;	c2i - д2;	С31	•••'>
П2=«ь	с22 = а3;	с32 =а5 >'>
_а1а2-а0д3. с13 -	> «1	_ ага4 -а^а5. с23 -	> а\	с33 - «1
148
„ _a3cl3~alc23	.	. _	a5cl3 ~ aic33 .	„ _a1c\3	alc43 .
c14 -	,	c24 -	,	<-34 ~	»
c13	C13	c13
„	c14c23 ~c13c23 .	„ _ c14c33 ~c13c34 .	„ _ c14c43 c13c44 .
c15 =----------------’	C25 “	>	c35 -	~	>
c14	44
И T. Д.
Критерий устойчивости Рауса. САУ устойчива, если коэффициенты первого столбца таблицы при Яд > О положительны: сп = > О, С12=«1>0, С]з > 0,	, С] п+1 > 0.
Критерий Рауса был предан забвению его современниками (как раз из-за его «неудобной» алгоритмической формы).
В 1895 г. Гурвиц предложил свой КУ, выраженный в замкнутой форме. Возьмем многочлен:
D(P) = а^Р" + а\РпЛ + •   + ап-\Р+
где полагаем > 0. Это всегда можно обеспечить умножением многочлена на -1. Составим из коэффициентов этого многочлена определитель (матрица Гурвица)

fl I а3 I а5 I а3 I
«9
0 Я| Й3 .	1
_0_	f2_ f4 ! «6
0 0 Я] а3 а5
0
0
0
0
0
0
«7
0 0 0 0 0
Этот определитель называется определителем Гурвица, он имеет п строк и п столбцов. Первая строка содержит все нечетные коэффициенты, начиная с а,, до последнего; после чего строка заполняется до числа п элементов нулями. Вниз от 1 строки столбцы определителя заполняются коэффициентами с индексами, убывающими каждый раз на единицу; ниже ciq пишутся нули.
В результате в главной диагонали определителя записываются последовательно все коэффициенты я,-, кроме Яо, начиная с я,.
Критерий устойчивости Гурвица. Для устойчивости замкнутой САУ необходимо и достаточно, чтобы (условие устойчивости) определитель Гурвица и все его диагональные миноры были положительны при Oq > 0. Эти миноры показаны в определителе Дп пунктирными линиями.
149
Пример. Для и = 4 D(p) = aopi + а{р3 + а2Д2 + а3р + а4:
q aj О
Д„ = Д4 =
«о О
«2 «I
«4
“3
О «о а2
О
О
О
О,
Условия устойчивости: >0; Д| = at >0;
Д3 — й3Д2 ~
«1
«1 «о
О
«4
= а3Д2 - а2а4 >0; Д4 = а4Д3 >0 (Д„ = а„Д„_| > 0).
Таким образом, условия устойчивости САУ сводятся к требованию положительнос-
ти всех коэффициентов а, и предпоследнего минора Д3; условие Д2 > 0 при этом вытекает из неравенства Д3>0(а4>0).
Д2 = 0(^2 - Ogfij > 0;
Следует отметить, что критерий Гурвица можно также доказать непосредственно на основе теоремы Ляпунова, используя функцию K = [xf[P][x] [2,8].
Итак, для устойчивости САУ «л» порядка определитель Гурвица Д„ = аяДп_] > 0. Очевидно, САУ будет находиться на границе устойчивости, если Дл = 0. Это обычно возможно, если Д,1Ч =0 — граница колебательной устойчивости. Можно показать в общем случае системы и-го порядка, что в условия устойчивости в качестве одного из них входит требование положительности всех коэффициентов уравнения.
Недостатки КУ Рауса—Гурвица.
1. Условия устойчивости, получаемые из критерия Рауса—Гурвица, усложняются с ростом порядка системы.
2. Для системы достаточно высокого порядка оказывается затруднительным выяснить влияние на устойчивость системы значений отдельных параметров звеньев, входящих в состав коэффициентов уравнения. Это связано с тем, что, как правило, одни и те же параметры одновременно входят в несколько коэффициентов уравнения системы. Поэтому критерий Рауса—Гурвица применяют только для систем относительно невысокого порядка и прежде всего для анализа устойчивости, когда надо определить, устойчива ли система при известных значениях всех ее параметров. При решении задачи синтеза системы, когда требуется выбрать значения отдельных параметров системы, критерий Рауса—Гурвица становится неудобным уже для систем выше четвертого порядка.
Критерий Льенара—Шипара. При и > 5 удобнее применять одну из модификаций критерия Гурвица, называемую критерием устойчивости Льенара—Шипара (1914 г.), который более прост и требует раскрытия меньшего числа определителей, чем критерий Гурвица. Число условий устойчивости при его применении снижается примерно вдвое. Здесь САУ устойчива, если при а, >0 только Д^ >0 или Ai+I >0, где k = 1, 3, 5, 7,... . Например, при л = 4, а(>0 САУ устойчива, если Д3 > 0 (обычно Oq = 1).
150
Для линейных импульсных систем используют критерий Шур— Кона, Джури—Бланшара на основе характеристического уравнения в форме z-преобразования: D (z) = zn + qz"4 + aQzn~2 + ... + an = 0. Здесь определитель Шур—Кона Аа для устойчивости замкнутой САУ должен быть At < 0 (нечетные к) или Afc+1 > 0 — четные индексы (к + 1), где к= 1, 3, 5, 7,....
В настоящее время вычислительные процедуры для всех критериев существуют в алгоритмической форме и оформлены в виде пакетов прикладных программ (ППП) на языках ПЛ-1, Паскаль, Фортран, АПЛ и др. [2]. Алгоритм Гурвица состоит из составления и вычисления определителей, анализа их условий положительности. В качестве примеров можно назвать ППП LCAP2, CLADP и др.
Программы предназначены для вычисления коэффициентов Рауса, определителей Гурвица или Шур—Кона по характеристическому уравнению аналоговой, дискретной или аналого-дискретной САУ и выдачи результатов в форме: САУ устойчива (1) или неустойчива (0). Для многомерных, многосвязных САУ исследование устойчивости производится по фундаментальным матрицам с использованием специальных алгоритмических процедур (например, матричный критерий устойчивости Зубова и др.) [2].
§ 6.3. ЧАСТОТНЫЕ (ГРАФОАНАЛИТИЧЕСКИЕ) КРИТЕРИИ УСТОЙЧИВОСТИ
Устойчивость САУ по виду частотных характеристик определяется с помощью частотных критериев, основанных на использовании принципа аргумента (из теории функций комплексного переменного). Это критерии Михайлова, Найквиста и D-разбиения. Важным преимуществом частотных критериев является возможность их применения для нелинейных САУ.
Критерий устойчивости Михайлова (предложен в 1938 г. русским ученым А. В. Михайловым) основан на рассмотрении многочлена D (р)— характеристического полинома W3(p) : О(р) = а$рп + + ахрп~х + ... +а„. В соответствии с теоремой Безу D(p) = а$(р ~Р\)(р~ -Рг) (Р_Ря) = 0> гДе Рп —корни Dip). Подставим в этот многочлен вместо р мнимую переменную jto. В результате получим комплексную функцию
D(» = £/(co) + ;r(o)) = a0(j(o)"+a1(»"-1+ ... + ап =
= ОоО-й)0~А) 0®-р„).
Приведем принцип приращения аргумента аксиоматически (без доказательства): изменение аргумента (фазы) D(j(o) при изменении со от - оо до + оо равно произведению (/ - т)п = (п- 2т)п, где т — число
151
корней с «+» вещественной частью; 1=п-т — число корней с «-» вещественной частью; п — порядок характеристического уравнения, т. е. Д arg D(/со) = (и - 2т)п. Если т = 0, то при - оо < и < - оо AargDQw) = пл —устойчивая
САУ; при 0<со<°о AargZ)(yto) =
71 тт
= п— . На плоскости р каждый корень изображается вектором,
т. е. р-р, —вектор.Вращение вектора против часовой стрелки
принимается за положительное направление (рис. 6.5).
В jD(j(o) Цсо) — действительная часть, полученная из членов Dtp), содержащих четные степени р: С(со) = ап -ай_20)2 + а„_4(04 ..., а По
мнимая часть, полученная из членов D(p) с нечетными степенями р:
а„ч(0-а„_3(03+а„_5(05 ... (так как j = J-i ; у2 = -1; у3=-/ч=-у)-Задаваясь (0 = 0 •*-«>, изобразим £>(/со)в виде годографа на комплекс-ной плоскости (рис. 6.6, а); годограф называется частотным годографом Михайлова. Здесь (см., например, кривую 1) каждому значению соответствуют определенные значения Е7(со), И(<в) и определенная
точка на плоскости.
При со = 0 Z7(co) = a„, И((о) = О, функция Z>(j(o) = a„, а ап=к+1 — в большинстве случаев, т. е. годограф начинается на действительной оси. При со —> оо функция D (усо) неограниченно возрастает.
Критерий Михайлова: замкнутая система устойчива, если годограф /)(у(о) начинаясь присо = О на действительной положительной полуоси, огибает с ростом от 0 до °° против часовой стрелки начало координат, проходя последовательно в положительном направлении
152
п квадрантов, где л — порядок системы. При этом изменение аргумента AargD(jo)) равно п\ В общем случае AargZ)(j<o) = (n-2ra)-,
но в устойчивой САУ т = 0.
На рис. 6.6, а годограф 1 относится к устойчивой САУ, годографы 3, 4, 5,6,7 — к неустойчивым системам.
Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова через начало координат (кривая 2 на рис. 6.6, а). В этом случае существует значение со, при котором D(jo3) характеристическое уравнение системы имеет пару сопряженных мнимых корней р = ± у(3.
Следствие КУ Михайлова. Система устойчива, если годограф Михайлова последовательно пересекает вещественные и мнимые оси, начинаясь на вещественной оси. Следовательно, необходимо и достаточно, чтобы точки пересечения годографа Михайлова положительной оси и мнимой перемежались между собой (критерий перемежаемости корней).
Изменение параметров САУ перемещает годограф D(Jaa) (см. рис. 6.6, а) либо влево от начала координат (САУ устойчива), либо вправо (САУ неустойчива). Вычислительный алгоритм, реализующий КУ Михайлова, прост и состоит в вычислении значений С (со) и К (со) для со = 0, Дсо, 2Асо, ... (Асо — шаг квантования) и в последующей проверке выполнения условия A arg D (усо) = /иг/2.
На рис. 6.6, б приведены годографы устойчивых систем разных порядков до и = 6. Построение годографа Михайлова осуществляется обычно непосредственно по Z>( jco) с помощью численных расчетов на ЭВМ.
Недостатки критерия Михайлова: с увеличением порядка САУ (л > 4-i-5 ) объем вычислений резко возрастает. Поэтому целесообразно использовать эффективные, высокопроизводительные алгоритмы и программы расчета (ППП).
Критерий устойчивости Найквиста. Этот критерий называется точечным критерием (предложен в 1932 г. американским ученым Г. Найквистом). Он позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутой системы )Ур(уа)). В ТАУ этот критерий был по-новому обоснован, обобщен и применен Михайловым в 1938 г., поэтому его также называют КУ Найквиста—Михайлова. АФХ разомкнутой САУ можно получить как аналитически, так и экспериментально, что выгодно отличает критерий от алгебраических КУ. КУ Найквиста имеет ясный физический смысл: связь стационарных частотных свойств разомкнутой САУ с нестационарными свойствами замкнутой САУ.
Доказательство этого критерия осуществляется также на основе принципа приращения аргумента. При этом за основу берется характеристический полином разомкнутой САУ g(j(o) соответствующий Bzp(jco) = 7?(j(o)/2(j(o). Так как QQto) и ^(усо) для анализа проще, чем D{ую) и W3{jc5), то и критерий проще.
153
Рассмотрим два случая состояния разомкнутой САУ.
Первый случай КУ. Если разомкнутая САУ устойчива, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы функция H'pQco) не охватывала критическую точку (-1,0) при изменении и от 0 до
На рис. 6.7, а характеристики 1 и 4 соответствуют устойчивым системам, характеристика 3 — неустойчивой, а характеристика 2 — нахождению системы на границе устойчивости. Например, для САУ с АФХ 2 необходимо уменьшить коэффициент передачи, АФХ сожмется к началу координат, в результате чего САУ станет устойчивой. При увеличении коэффициента передачи кр АФХ устойчивой системы при кр = ^ркр охватит точку (-1, 0), и система потеряет устойчивость.
154
Критическая точка (-1,0) соответствует случаю Ир(7'о)) = -1 или А (й))е^ф(ш) = -1, что имеет место при <р (щ) = -180° и А (а>) = 1 (е~71 800 =
=cos 180° -j sin 180° = -l). Физически это означает, что амплитуда
Я„((0)
Ах = А„, т. е. А (со) =	— = 1
у	Л(<й)
торая при со=0 равна 0, дает
(амплитуды совпадают), а фаза, ко-Ф (со) = - л. При - л происходит
запаздывание фазы выходного сигнала на -180° по отношению к
входному сигналу.
В электронных системах САУ при нечетном числе каскадов ф(со) = -180° (000) или ф (со) = 0 при четном числе каскадов (ПОС).
АФХ, или частотные годографы W (jai), показанные на рис. 6.7, а, принадлежат статическим системам.
На рис. 6.7, б приведены АФХ астатических систем с разным порядком астатизма; кривые 7, 2 и 3 относятся к системам соответственно с астатизмом 1, 2 и 3-го порядков. АФХ астатических систем при (0 = 0 уходят в бесконечность, так как у амплитудно-фазовой функции 1Кр(у(о) имеется множитель 1/(/®)г, где г — порядок астатизма. При г = 1 характеристика 1Кр(у(о) при (0 = 0 уходит в бесконечность вдоль отрицательной мнимой полуоси; при г = 2 — вдоль отрицательной действительной полуоси; при г = 3 — вдоль положительной мнимой полуоси. Если мысленно соединить находящееся в бесконечности начало АФХ астатической САУ с положительной дей-
ствительной полуосью дугой бесконечного радиуса (рис. 6.7, б, штрих-пунктирные линии), то в случае устойчивой системы точка (-1, 0) не должна охватываться АФХ (кривые 7, 2, 3). Кривые 1а, 2а и За (36) соответствуют неустойчивым системам с астатизмом 1, 2 и 3-го порядков. Если САУ содержит статические и астатические звенья, то САУ с г > 1 носит название структурно-неустойчивой, так как АФХ имеет тенденцию к охвату критической точки (-1, 0) (рис. 6.7, г).
Второй случай КУ. Для систем неустойчивых в разомкнутом состоянии, когда при 0<(0<°° Aarg<2(j(o) = (п - 2т') Aarg [Z)(jco)/<2(y(o)] = = Aarg[l + lEpO’d))] = ~(2m'-2m) = (m'-фн - 2л = т'л (ш = 0), 2	2
критерий Найквиста имеет такую формулировку: если разомкнутая
САУ неустойчива, то для устойчивости системы в замкнутом состоянии необходимо и Достаточно, чтобы АФХ разомкнутой системы
FEp(j(o) охватывала критическую точку (-1, 0) при изменении (о от О т'
до оо — раз в положительном направлении против часовой стрелки (при т = 0).
Оба случая могут быть объединены следующей формулировкой КУ: замкнутая САУ устойчива, если число пересечений функции Wp(J(£i) отрицательной полуоси левее точки (-1,0) сверху вниз «+» больше на т'/2 раз числа пересечений в обратном направлении «-». Здесь т' — число полюсов передаточной функции разомкнутой системы
155
с положительной действительной частью (т' — число правых корней уравнения Q (р) = 0 разомкнутой САУ; т — число корней с положительной вещественной частью уравнения D (р) = 0 замкнутой САУ).
Таким образом, приращение аргумента Aarg2(yco) = («-2w/)n/2 при 0 < со < °°, а для устойчивой замкнутой САУ (т = 0) Aarg£)(j(o) =
71	Г	1	/и'
= и—; тогда A arg [1 + Wp (jco) ] = A arg D(jai) - A arg Q( jco) = — 2л, т. e. замкнутая САУ устойчива, если годограф FFp(jco) охватывает т'/2 раз точку (-1, 0) в положительном направлении (против часовой стрелки).
На рис. 6.7, в в качестве примера показаны две АФХ неустойчивой в разомкнутом состоянии САУ вследствие наличия правых корней, но устойчивой в замкнутом состоянии. Характеристика 1 соответствует т' = 1 (ли'/2 = 0,5; «0,5 пересечения»), а характеристика 2 — значению т' = 2 (т’/2 = 1). При т' = 0 (разомкнутая САУ устойчива или нейтрально-устойчива) для устойчивости замкнутой САУ разность пересечений сверху вниз «+» и снизу вверх «-» должна быть равна 0 (Aarg [1 + jyp(jco)] = т'п = 0).
Следовательно, при применении критерия Найквиста необходимо предварительно определять число правых полюсов Wp(p).
Для одноконтурной САУ, когда знаменатель Wp(p) представляет собой произведение знаменателей передаточных функций отдельных звеньев, число т' находится легко, поскольку полюсами Wp(p) являются полюсы передаточных функций отдельных звеньев. Например,
т' = 1; pf = 1/7]
У WJp) =----------L2-2---------.
У	(Т]р-1)(Т2р+1)(Т3р+1)
Для сложных многоконтурных систем, особенно с перекрестными связями, задача определения числа т' значительно усложняется (в этих случаях иногда целесообразно отказаться от применения критерия Найквиста).
В вычислительном аспекте алгоритм оценки устойчивости по КУ Найквиста аналогичен алгоритму по КУ Михайлова, хотя здесь и существует некоторая трудность в формализации события не охвата критической точки (-1,0).
Логарифмический критерий устойчивости Найквиста. Об устойчивости САУ, в соответствии с критерием Найквиста, можно судить совместно по АФХ и ФЧХ разомкнутой системы. При этом обычно используют логарифмические характеристики, что представляет большое удобство в силу простоты их построения.
Неохват АФХ устойчивой разомкнутой САУ Wp(j(£) критической точки (-1,0) имеет место, если на частоте, где I Я(со)| = 1, L (со) = 0, фаза ф (<в) > - п, т. е. абсолютное значение фазы меньше п, так как в точке (-1,0) |Я((о)| = 1, а ф(со) = -л.
156
Первый случай КУ. Критерий устойчивости Найквиста для САУ, устойчивых в разомкнутом состоянии, сводится к тому, что ЛАХ должна пересечь ось абсцисс раньше, чем ФЧХ пересечет значение-л, т. е. на частоте (0с значение фазы должно быть меньше - л . Точкам пересечения ИИр(уо)) с полуотрезком (-°°,-1] соответствуют точки, для которых L (со) > 0 и <р (со) = - л, -Зл, -5 л, полу отрезку (—1,0] соответствует L (со) < 0.
На рис. 6.8 приведены ЛАХ L (со) и пять вариантов ЛФХ ср (со). Для ЛФХ 1 и 4 замкнутая САУ устойчива (характеристика 4 соответствует АФХ 4 на рис. 6.7, а); случай ЛФХ 2 соответствует нахождению замкнутой САУ на границе устойчивости, а ЛФХ 3,5—неустойчивой замкнутой системе.
Второй случай КУ. Для замкнутых САУ, неустойчивых в разомкнутом состоянии, условия устойчивости следующие: при положительной ЛАХ число пересечений ЛФХ уровня -л снизу вверх «+» должно быть на т'/2 раз больше числа пересечений в обратном направлении «-» (при m'-Q разность пересечений должна быть равна 0).
Запасы устойчивости в САУ. Факта наличия устойчивости САУ при оценке устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, т. е. степени удаленности САУ от границ устойчивости. Система, которая находится близко к границе устойчивости, практически при ее реализации может оказаться неустойчивой (причины — неточность математического описания, погрешности линеаризации, неточность определения параметров САУ и их изменение во времени и др.).
При применении критерия Рауса—Гурвица запасы устойчивости определяются «сильностью» выполнения входящих в этот критерий неравенств. При использовании критериев Михайлова и Найквиста запасы устойчивости определяются степенью удаленности по рас-
157
стояниям соответствующих характеристик от границы устойчивости. Для критерия Михайлова это будет удаление годографа D(yco) от начала координат, а для критерия Найквиста — удаление характеристики Wp(yto) от точки (-1; 0). При этом алгебраические КУ и КУ Михайлова дают лишь качественное представление о запасах устойчивости (по «сильное™» неравенств и степени удаленности).
Основное распространение в качестве количественной меры запасов устойчивости получили две величины — запас устойчивости по фазе у = Дф = л-Лф(й)с) и запас устойчивости по амплитуде (по усилению, по модулю) Д£ = h, вытекающие из критерия Найквиста (см. рис. 6.7, а).
Запас устойчивости по фазе определяется величиной у (или у
у% = —-100%), на которую должно возрасти запаздывание по фазе в системе на частоте среза (ос, чтобы система оказалась на границе устойчивости (при юс |илр(у(Ос)| = 1; на границе устойчивости <ос =	).
Запас устойчивости по амплитуде (по усилению) определяется величиной Д£ допустимого подъема ЛАХ, когда САУ выходит на границу устойчивости. Запас устойчивости по амплитуде представляет собой запас по коэффициенту передачи кр разомкнутой системы по отношению к его значению, критическому по устойчивости кр кр.
При проектировании в зависимости от класса САУ рекомендуется выбирать у >30°-60°, ДА >6-20 дБ (примерно двойной запас коэффициента передачи по устойчивости) или через h > 0,2-0,4.Иног-давместой берут величину а = 1/|илр(у(0я)| =/:р<кр/£ и Д£ = 201ga = =-201g |FKp(j(O„)| =-£(©„); Д£ = 201g £р. кр -201g к.
Для устойчивых САУ запас устойчивости в форме а больше 1 (Д£ > 0), для неустойчивых — меньше 1 (АД < 0). Для гарантированности выполнения требований по запасам устойчивости САУ около точки (-1; 0) иногда вычерчивают запретную область, куда АФХ не должна входить.
Инверсный критерий устойчивости Найквиста. В расчетной практике иногда пользуются инверсным критерием устойчивости, основанным на построении инверсного частотного годографа:
1 S(y'co) G(yw) =---------=	.
BZp(>) A(yo)
В этом случае все вычисления, особенно для сложных систем, значительно упрощены, так как степень Q (усо) обычно больше степени 7? (усо) Следовательно, геометрическая интерпретация инверсного критерия обратна предыдущей, т. е. точкам, лежащим внутри (вне) окружности единичного радиуса на плоскости lFp(y'(o), соответствуют точки, лежащие вне (внутри) окружности единичного радиуса на плоскости
158
Рис. 6.9
G(jO3). Поэтому критерий устойчивости Найквиста, основанный на использовании инверсной характеристики G (усо), формулируется следующим образом.
Первый случай КУ. САУ устойчива, если охватывает точку (-1; 0) для случая устойчивой разомкнутой САУ (рис. 6.9, а).
Второй случай КУ. САУ устойчива, если число пересечений G (усо) интервала (-1; 0) действительной оси снизу вверх больше на т'/2 числа пересечений в обратном направлении, где т' — число правых корней разомкнутой САУ (рис. 6.9, 6). Здесь цифры 1-6 на рис. 6.9 наглядно отражают прохождение годографов й^(усо) и G(yco) относительно критической точки (-1; 0).
§6.4. УСТОЙЧИВОСТЬ СИСТЕМ С ТРАНСЦЕНДЕНТНЫМИ И ИРРАЦИОНАЛЬНЫМИ ЗВЕНЬЯМИ
Для систем, содержащих один или несколько трансцендентных звеньев, например звеньев с запаздыванием,
^) = g|e^=^np(p)e^,
где И/пр(у>) = №(р) — передаточная функция предельной САУ при т = 0. При p=j® FF(yco) = FFnt,(yco)e“7tOT	Так как при
20)
больших со модуль W (усо) мал, то годограф САУ с запаздыванием закручивается вокруг нуля. Алгебраические критерии устойчивости в обычной форме здесь непригодны, но есть их аналоги. Поэтому удобнее всего КУ Найквиста: САУ с запаздыванием устойчива, если годограф (T(y'co) не охватывает критическую точку (-1; 0) (первый случай). Наличие запаздывания в САУ при больших т может привести САУ к потере устойчивости. Критическое время запаздывания
159
Рис. 6.10
ткр =У/Юя,фт((0) = ф((0)-- (от. При сложной форме АФХ ткр может быть несколько (рис. 6.10).
Системы с иррацио-
нальными звеньями имеют
%(/>) =
rUp) : R(q)
Q(Jp) Q(4) ’
где q = Jp . При p=jvi
Алгеб-
%(» =
Qty/fa)
раические критерии здесь также непригодны. Частотные КУ применимы аналогично вышерассмотренным случаям, так как
принцип аргумента здесь
справедлив (р = q2). Практически также более удобен КУ Найквиста.
Сравнение критериев устойчивости
1.	Независимо от выбранного критерия результат по анализу устойчивости САУ должен быть один и тот же.
2.	Прямое использование алгебраических критериев (в частности, Рауса—Гурвица) целесообразно, если характеристическое уравнение САУ имеет порядок п < 4.
3.	Критерий Рауса—Гурвица и особенно критерий Льенара— Шипара в алгоритмической форме целесообразны до п < 15 при использовании ППП и ЭВМ.
4.	Критерий Михайлова целесообразен при исследовании сложных многоконтурных САУ, когда необходимо выяснить влияние изменения структуры САУ и средств стабилизации на ее устойчивость.
5.	Критерий Найквиста (обычная или инверсная форма) целесообразно применять при исследовании сложных САУ. Этот критерий единственно применим, когда часть (или все) характеристик отдельных элементов САУ заданы экспериментально. Он применим при анализе САУ, описываемой аналитически передаточными функциями, отличными от дробно-рациональных функций: иррациональных, показательных, трансцендентных — с запаздыванием и др.
6.	КУ Михайлова и Найквиста графически наглядны и позволяют оценивать запасы устойчивости; особенно здесь целесообразен КУ Найквиста, так как круг вопросов, исследуемых этим КУ по устойчивости, шире.
160
§ 6.5. ОБЛАСТИ УСТОЙЧИВОСТИ САУ
Критерии устойчивости дают возможность при заданных параметрах САУ судить только о том, устойчива САУ или нет. Они позволяют также проследить влияние некоторых параметров при их изменении на устойчивость САУ и, в частности, определить предельные параметры Агкр, ткр.
Для исследования влияния различных параметров САУ на ее устойчивость разработаны специальные методы, основанные на анализе перемещения корней характеристического уравнения в комплексной плоскости и построения корневых годографов или областей устойчивости САУ в пространстве параметров САУ (коэффициентов характеристического уравнения).
Метод корневого годографа. Корневым годографом называется геометрическое место корней характеристического уравнения при изменении одного из параметров САУ (обычно кр) от нуля до °°.
Характеристическое уравнение замкнутых САУ представляется в виде D(p) = R(p) + vQ (р)= 0, где v — переменный параметр САУ (к или Т). Далее, изменяя 0 < v < <», необходимо найти перемещение всех и-корней характеристического уравнения. Другие параметры звеньев САУ заданы и определяются из физических и конструктивных соображений конкретной реализации САУ.
Если при изменении v от 0 до °° при определенном v корень характеристического уравнения попадает на мнимую ось, САУ будет на границе устойчивости; при тех V, когда часть корней переходит слева направо мнимую ось, САУ будет неустойчива. Предложен ряд правил, которыми пользуются при исследовании влияния параметров САУ на ее устойчивость методом корневого годографа.
Метод корневого годографа в силу некоторой сложности и меньшей наглядности получил меньшее распространение (практически им пользуются редко). Более широкое распространение получил метод D-разбиения.
Определение и построение областей устойчивости САУ. В общем случае рассматривается задача о разбиении пространства параметров (коэффициентов) на области устойчивости САУ. Знание областей устойчивости в пространстве параметров дает возможность рационального их выбора в процессе проектирования САУ.
Наиболее ценным практическим результатом является построение областей устойчивости в плоскости каких-либо двух параметров, влияние которых на устойчивость САУ исследуется.
Впервые область устойчивости системы прямого действия в плоскости двух коэффициентов уравнения была построена русским ученым И. А. Вышнеградским (1876 г.). Иногда ее называют критерием Вышнеградского для характеристического уравнения 3-го порядка:
=0
11 А. А. Ерофеев
161
где z = р^ад/ч = —
или в его нормированном виде (форме Вышнеградского):	Л
z3 + Az2 + Bz+ 1 = 0,	i
— новая переменная; Qo = ^а3/ад — средне-. а, Йп «I о _ °2 Й0 _ а2
геометрический корень; А =----=	—; ° -	- „ / - — па-
аз	аз
раметры Вышнеградского.
Согласно критерию Гурвица, при А > 0 и В > 0 условие устойчивости АВ > 1 определяется из определителя
А
1 о
д3 _
В О
А 1
1
- Д2.
Вышнеградский вывел его за 20 лет до Гурвица и раньше появления КУ Рауса. На плоскости параметров А и В (рис. 6.11) наносится граница устойчивости АВ = 1 — это есть равнобокая гипербола Вышнеградского с осями координат в качестве асимптот; гипербола — изображение мнимой оси в плоскости Л и В. Область устойчиости САУ лежит выше этой кривой. Вышнеградский построил и другие кривые для определения вида (характера) переходного процесса: I— область, соответствующая апериодическому затухающему процессу; II — монотонный затухающий процесс колебательного характера; III — периодический затухающий процесс; IV — неустойчивый переходной процесс.
Впоследствии диаграмма Вышнеградского была дополнена другими линиями: степени затухания, интенсивности процессов и т. д.
Недостаток критерия Вышнеградского — параметры САУ (к или 7) в неявном виде входят в выражения коэффициентов Л и В, следовательно, чтобы определить поведение САУ при изменении одного или двух
параметров, требуется довольно трудоемкая работа. Кроме того, ограниченность в рассмотрении САУ — уравнения САУ должны быть не выше 3-го порядка. Напомним, что для уравнения 2-го порядка
p2+aip+a2=0 (д2=~0>5а1±чМ—«г) в плоскости аъ аг область устойчивости — первый квадрант (^ > 0, а2 > 0).
Метод D-разбиений. Обычно пользуются методом D-разбиений, который дает непосредственно общее решение вопросов
162
о влияни и изменения данных параметров на устойчивость САУ и обеспечивает возможность определения ряда качественных показателей. При этом используется характеристическое уравнение замкнутой САУ в форме: D(p) = рп + ахрп~х +... + ап = 0; а$ -1. При р = j(0: D(/(o) = = (»" +а1(»пЧ +... +а„ = Х(ы, vb v2) + jY(a, vb v2), где vb v2 — исследуемые параметры.
Построение области устойчивости в плоскости одного комплексного параметра. Требуется выяснить влияние параметра v (к или 7), например параметра регулятора, на устойчивость САУ. Характеристическое уравнение САУ записывается в виде:
D(p) = R(p) + vQ(p)=0,
куда V входит линейно. При p=j<a:
D (» = R (jco) + v Q(j<a) = 0, откуда v = -	= X (co) + jY(co).
Изменяя co от О до “° и находя X, Y, построим границу D-разбиения (рис. 6.12). Практически интересуются D-разбиением не на всей плоскости, а лишь на ее действительной оси, отвечающей действительным значениям v {к или Т). Граница D-разбиения — геометрическое расположение мнимой оси в плоскости одного параметра. Переход через границу D-разбиения означает переход через мнимую ось. Так как v вещественное число, то нас интересует отрезок устойчивости на вещественной оси; хотя V = X (со) + jY(со) и может рассматриваться во всей области комплексного параметра. Это используется в нелинейных САУ.
Кривая D-разбиения делит плоскость на ряд областей, например на пять: I-V (см. рис. 6.12, б).
Штриховка кривой D-разбиения производится слева при изменении со от -оо до -к», что соответствует положению мнимой оси в координатной системе и расположению левых устойчивых корней. Отсюда очевидно, что претендент на область устойчивости — область I, окруженная штриховкой. Отрезок устойчивости [а, Ь] — область изменения v для устойчивой САУ (рис. 6.12, а, б). Для проверки области устойчивости / берется любое значение v в этой области и, пользуясь одним из критериев, осуществляется проверка устойчивости САУ. Если при данном v САУ устойчива, то область I — область устойчивости. Здесь (см. рис. 6.12) D(p) = (1 + р7])(1 + рТ2)(1 + рТ3) + к = 0; ккр =
= (7J + Г2 + Т3) ~ + — + — -1 = X (сов). Область IV (рис. 6.12, б) так ^7] Т2 Т3)
же является областью устойчивости (отрезок устойчивости [с, d\).
Обычно задачу D-разбиения решают с помощью вычислительных алгоритмов на ЭВМ, применяя ППП.
163
11*
Построение области устойчивости в плоскости двух параметров. При проектировании САУ часто требуется выявить влияние на устойчивость не одного, а двух параметров, например т и v (к и 7). Предположим, что эти параметры входят также линейно в характеристическое уравнение замкнутой САУ.
Порядок построения кривой D-разбиения следующий.
Выделяют составляющие характеристического уравнения САУ D(p)- R(р) + Q(p) = 0, зависящие от двух параметров:
тЛ(р) + Уб(р) + Р(/>) = 0.
При p-j(i>
rR(J(0) + vgO) + Р(» = t/(w) + уК(<в) = О,
где Л(» = 7?1(ю) + у7?2((0); б(» = 0(0)) +j62(co); P(Ja) = 7^(co) +
Здесь 77(co) = x7?,((o) + vQx(a>) + ^(co) = 0; K((o) = t7?2(co) + v£2(co) + +P2(co) = 0 — соответственно вещественная и мнимая части. В результате получают два параметрических уравнения с двумя неизвестными т и V. Решая эти уравнения относительно т и V, получим т = Д| / Д; v = Д2 / Д, где Д — главный определитель;
W) /?2(<в)
ад 22(®)
- R\Qz~ RzQ.6
164
По этим уравнениям для каждого со определяют т и v; исключая промежуточный параметр (о, строят границу D-разбиения в плоскости двух параметров т и v как функцию т = /(v) (рис. 6.13). Здесь Д, Дь Д2 — нечетные непрерывные функции со, так как вещественные части R, Q, Р — четные функции, а мнимые R,Q,P — нечетные. Отсюда следует, что т и v —четные функции<в,т.е. можно ограничиться рассмотрением положительных значений частот 0 <(0<°°.
Особые случаи. Особые прямые (О П). Если при некоторых со Д = 0, a и Д2*0, то точка границы D-разбиения в плоскости т и v уходит в оо. Знак у Д может измениться только при со = О и со = оо Если при некоторых сои D = О (например, при со = 0 всегда D = 0) и Д]=Д2=0 (если Д1=0, то и Д2=0), тот hv будут неопределенными. Параметрические уравнения становятся эквивалентными и определяют собой прямую в плоскости т, V, т. е. для этого значения сои (исключительная частота) в плоскости т hv получим не точку, а прямую, называемую особой прямой. При этом уравнения линейно зависят друг от друга и одно уравнение вытекает из другого: x = -[ve1(co) + ^(co)]//?1(co) = -[ve2(co) + P2(co)]/2?2(co). Особые прямые (так называемые концевые) обычно отвечают значениям со = 0 и со = ±°°. В этом случае Oq и а„ зависят от т hv, т. е. а0=а0(т, v) и а„=ап(х, V) и для получения уравнений особых прямых необходимо Oq и а„ приравнять нулю (а„=0—дает особую прямую при со = 0, аоо=0—для со = °о).
Правила штриховки границы D-разбиения. Граница D-разбиения в плоскостит и v штрихуется слева при со—>°°, если Д>0, неправа, если Д < 0. Так как граница D-разбиения для + <» и - <» совпадает (т и v четные функции со, а Д — нечетная функция), то она штрихуется дважды с одной и той же стороны (рис. 6.13, а).
Штриховка концевых особых прямых одинарная и производится так, чтобы вблизи точки сопряжения прямой и кривой заштрихованные и незаштрихованные стороны были направлены друг к другу (рис. 6.13, а, б, в). Особые прямые служат дополнительной границей определения области устойчивости.
Концевые ОП соответствуют апериодической границе устойчивости. Кроме концевых существуют промежуточные ОП (при со *0 и со Ф оо), когда пара комплексных корней попадает на границу устойчивости (обычно для САУ с п > 4). Эти ОП, таким образом, соответствуют колебательной границе устойчивости и имеют двойную штриховку. Так, если при со * 0 Д] = 0, а Д переходит через 0 и меняет знак (весьма редкий случай), то появляется особая прямая, штрихуемая по вышеизложенному правилу, но двойной штриховкой (рис. 6.13, г).
Если при со * 0 Д| = 0, а Д пройдя через 0, не меняет знак, то особая прямая не штрихуется и выбрасывается из рассмотрения, т. е. особая прямая не является дополнительной границей устойчивости и вычерчиванию не подлежит (рис. 6.13, д'). Здесь на рис. 6.13, д ориентация штриховки ОП показана условно исходя из общих положений о штриховке ОП.
165
166
При рассмотрении границы D-разбиения по двум параметрам следует правильно ориентировать оси. Для приведенной выше формы записи уравнений, когда т стоит на первом месте, a v на втором (1 — вещественное уравнение, 2—мнимое уравнение) т откладывается на оси абсцисс, a v — по оси ординат. В случае перемены местами осейт hv соответственно меняется ориентация штриховки относительно правой и левой сторон на противоположную.
Аналогично, как и при D-разбиении в плоскости одного комплексного параметра, найденные претенденты на область устойчивости должны проверяться (область I: vb ть рис. 6.13, а). Для этого в каждой из претендентов на область устойчивости берется значение параметра и одним из известных КУ проверяется САУ на устойчивость. Если при выбранном параметре САУ устойчива, то, следовательно, эта область будет областью устойчивости.
Метод D-разбиения требует строгого соблюдения формальных процедур метода, иначе его применение может привести к грубым ошибкам.
§ 6.6. ОБОБЩЕННЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
Метод D-разбиения считается обобщенным критерием устойчивости САУ, так как все рассмотренные ранее критерии устойчивости могут быть доказаны исходя из представления о границе D-разбиения. Годограф Михайлова и АФХ разомкнутой САУ (в рамках КУ Найквиста) можно рассматривать как границы D-разбиения по специально подобранным параметрам: D(jo) = X и 7?(j(o)/6(jco) = X'.
Таким образом, метод D-разбиения оценивается как общий метод исследования устойчивости САУ, позволяющий установить связь между различными критериями: Рауса—Гурвица, Михайлова, Найквиста и др.
Так, по критерию Гурвица при Д„ = апЬ.п_\ = 0 в САУ определяются границы устойчивости:
Д„-1 = 0pt = ±у’Р(; ап = 0 i-э р, = 0; = 0 рк = «>.
Эти уравнения охватывают три случая попадания САУ на границу устойчивости, возможные пути перехода корня из левой полуплоскости (с-а,) в правую (с+а,). Первый случай соответствует Ди_1(т, v) = 0и превращению пары комплексных корней в чисто мнимые ±уР( (колебательная граница устойчивости — в САУ незатухающие колебания); второй — соответствует превращению одного из действительных корней в нулевой (переход его в начало координат); третий — превращению этого корня в бесконечный корень (переход его из левой полуплоскости в бесконечность). Два последних случая соответствуют переходу корня из левой полуплоскости в правую без
167
превращения в мнимый корень (через начало координат или бесконечность). При переходе через колебательную границу устойчивости знак у определителя Дя_[ меняется на противоположный. Здесь варьируемые параметры т и v входят в выражения для v), а„(т, v) и Оо(т!v)- При этом границам апериодической устойчивости соответствуют уравнения ^(т, v) = 0 и п„(т, v) = 0; корни на этих границах равны ± оо и 0. Здесь неустойчивость САУ обусловливается экспоненциальными членами, изменяющимися апериодически. Критерий Рауса—Гурвица, как уже отмечалось, хорошо программируется, так как он сводится к простым арифметическим операциям (хотя и многочисленным).
По критерию Михайлова система находится на границе устойчивости, если годограф	- £7(<о) + J И(со) проходит через начало ко-
ординат. Уравнения границы устойчивости в пространстве варьируемых параметров т и v имеют вид:
U(x, V, <й) = 0; К(т, V, ю) = 0.
Эти уравнения также включают три названных выше случая попадания САУ на границу устойчивости (нулевой корень соответствует со = 0; бесконечный — со = °°). Исключая из этих уравнений параметр со, получают уравнение границы устойчивости, связывающее входящие в выражения 17(т, V, со) и K(x,v, со) варьируемые параметры т и V.
По критерию Найквиста уравнения, определяющие границу устойчивости, имеют вид:
[/(т, v, со) = -1; Г(т, v, со) = 0,
где U и V—действительная и мнимая части РКр(/со). Эти уравнения соответствуют прохождению АФХ ^Гр(7®) через критическую точку (-1; 0) и приводят к таким же параметрическим уравнениям, что и уравнения, получаемые из критерия Михайлова.
Следует отметить, что в принципе при D-разбиении может не оказаться области устойчивости. Это означает, что ни при каких т САУ не может быть устойчива, т. е. по отношению к ним (т, v) САУ структурно неустойчива. Структурно неустойчивая система не может быть сделана устойчивой путем изменения значений ее параметров. Для получения устойчивости в этом случае необходимо изменить структурную схему САУ.
Решение уравнений относительно т и v в общем виде возможно, если т и v входят в уравнения линейно. В остальных случаях метод решения зависит от типа нелинейности уравнений.
При трех варьируемых параметрах область устойчивости получается трехмерной и представляет собой объем устойчивости САУ, как показано на рис. 6.14, где т, v и у — варьируемые параметры. Граница устойчивости при этом представляет собой трехмерную поверхность; при т, v или у = const (г) — плоскость двух параметров. В общем случае п варьируемых
168
параметров (коэффициентов) области устойчивости представляют собой многомерный объем (или гиперповерхность) в многомерном «-мерном пространстве. Совокупность коэффициентов а, ~(а^,ап) геометрически отражает точку «-мерного пространства с осями координат а0,<2|,ап \ каждой такой точке соответствуют определенные значения корней д, рп. Необходимым условием устойчивости для всех критериев является положительность всех коэффициентов а, характеристического уравнения.
Для САУ высокого порядка расчет
целесообразно проводить с использованием ЭВМ; разработаны специальные новые методы в теории управления, алгоритмы и ППП,
рассчитанные на ЭВМ. Вычислительные процедуры численного анализа устойчивости САУ в области возможных значений параметров
организуются с помощью специальных алгоритмов и построения аппроксимирующей сетки. Области устойчивости САУ получают объединением в одно множество точек, в которых САУ устойчива, при заданных диапазонах изменения параметров кт < к < км и Тт < Т < Тм . При этом алгоритмы могут базироваться на различных КУ, в том числе и на обобщенном КУ D-разбиения.
Глава 7. КАЧЕСТВО ПРОЦЕССОВ УПРАВЛЕНИЯ
§ 7.1. СТАЦИОНАРНЫЕ РЕЖИМЫ САУ
Устойчивость САУ является необходимым, но не достаточным условием эффективной реализации САУ. Не менее важное значение имеет качество переходных процессов, т. е. характер их протекания, в частности, длительность, колебательность, перерегулирование и др.
К процессам управления в САУ обычно предъявляют три основных требования: по устойчивости, по точности в установившихся статических и динамических режимах и по качеству переходных процессов. Точность как оценка качества в установившихся режимах определяется при рассмотрении стационарных режимов САУ.
САУ как динамическая система может находиться в одном из двух режимов — стационарном (установившемся) и переходном. Существуют два вида стационарных режимов САУ — статический и динамический.
169
Стационарный статический режим (статика) — это режим, при котором система находится в состоянии покоя; все внешние воздействия и параметры самой системы не меняются во времени.
Стационарный динамический режим — когда внешние воздействия изменяются по какому-либо установившемуся закону; система приходит в режим установившегося вынужденного движения. При этом стационарный динамический детерминированный режим — это режим, при котором на систему действует детерминированное (регулярное) стационарное воздействие (например, установившийся моногар-монический режим). Стационарный динамический случайный режим является установившимся в статистическом смысле; приложенные к системе воздействия представляют собой стационарные случайные функции (см. гл. 5).
Стационарный статический режим (статика) САУ. Уравнение статики замкнутой САУ определяется из уравнения динамики САУ при р = 0:
У =w f(O)f = f
Лет. 3 rr 3f WJct	1 + JK (0) /cT’
где yCT — приращение выходной величины САУ, вызванное приращением внешнего воздействия /ст (рис. 7.1).
В случае статической системы
W(0) = k=bni или кр = ~~, Wfy(ty = kfy р р а„
И Jct.3 ^з \ + к -^ст>
где kyyfcr = уст. р = Др — отклонение в разомкнутой САУ (рис. 7.1, а, б, в, где 1 — статическая САУ, 2—астатическая). Тогда требуемое значение кр, по условиям заданного отклонения Д 3 — точности замкнутой САУ, равно:
Лет. 3	413
В замкнутой САУ статическое отклонение у от воздействия f уменьшается в (l + fcp) раз. Например, при кр =99 — в 100 раз (если Др = 30%, то Д3 = 0,3% при изменении возмущения f на 100%).
Отношение
является мерой статической точности САУ и называется статизмом.
170
Для следящих систем статическая ошибка слежения за х:
1	' -	1	-^ст
£eT=i^XcT=uVCTXv>1'
Для случая нескольких внешних воздействий суммарное статическое отклонение
т
СТ/У/СТ’
S -
— статизм системы по возмущению /.
§ 7.2. СПОСОБЫ ПОВЫШЕНИЯ ТОЧНОСТИ САУ
Статическая зависимость выходной величины от внешних воздействий обычно является нежелательной, поскольку создает погрешность управления. Поэтому статизм САУ необходимо уменьшать.
171
Статическое отклонение, как было отмечено, уменьшается при увеличении коэффициента передачи САУ. Однако для полного устранения статического отклонения требуется увеличивать коэффициент передачи до бесконечности (кр -» °°).
Другие пути полного устранения статического отклонения в САУ при конечном значении коэффициента передачи сводятся к следующему.
Статическое отклонение устз будет в САУ отсутствовать при наличии /ст, если ПРИР = 0 выражение у(р) также обратится в нуль. Принципиально это возможно, если ^(0) = °° или Wry(0) = 0.
Равенство ^(0) = °° реализуется введением в САУ вне Wfy(p) интегрирующего звена, т. е. переходом к астатической САУ; Иу-ДО) = 0 реализуется введением компенсирующего воздействия по возмущению (инвариантного управления).
При введении в статическую САУ интегрирующего звена вне участка системы от места приложения f до у, статическое отклонение устз=0 из-за наличия в знаменателе Wp(p) множителя р от функции к/р интегрирующего звена, a Wp(p)\^=^.
САУ может приобрести астатические свойства благодаря наличию астатического управляющего устройства, содержащего интегрирующее звено, или астатического объекта управления.
Второй путь устранения статического отклонения САУ сводится к получению ИД ДО) = 0 применением управления по возмущению — компенсация возмущений (методы теории инвариантности). При этом на основе измерения внешнего возмущения f управляющее устройство осуществляет такое воздействие на объект управления, чтобы компенсировать влияние данного возмущения на выходную величину.
Схема САУ с системой компенсации возмущения приведена на рис. 7.2, а.
Условие компенсации влияния на Уст
к-
Уст = (kf у +^/и^о)Лт =0 при Ауи = —7^-
/с0
Выражение для к^и определяет коэффициент передачи управляющего устройства в зависимости от параметров объекта управления.
В целом для замкнутой САУ с системой компенсации возмущения (рис. 7.2, б)
У =^f Лт'3 1 + ИД(О) /ст’
где Wfу($) = к/у+к/ккй. При kfii = -к^/к^ Wfy(ty = Q и замкнутая САУ инвариантна по отношению к влиянию возмущения /. Следует отметить, что компенсация ведется относительно определенного (измеренного) Д и не делает систему астатической, так как существу-
172
Рис. 7.2
ют другие нескомпенсированные возмущения, создающие некоторое статическое отклонение Уст.з- Хотя суммарное статическое отклоне-
ние уст = -------- резко уменьшается (примерно на порядок), так
1 + /ср
как осуществляют компенсацию наиболее сильно влияющего (основного) возмущения. В целом установившееся статическое отклонение САУ (статическая ошибка) определяется по формуле:
i+wAp)\p^x"+ > + W
/	/г	ХУ	i=i JiX г
У <™+У ст-3~1 + £рХст+l +
Первое слагаемое здесь дает составляющую ошибки, определяемую управляющим воздействием.
Составляющую у'тз всегда можно свести к нулю либо путем использования неединичной обратной связи, либо путем масштабирования управляющего воздействия (или регулирующей величины). В астатических САУ при р—>0 — W(p)->°° и у'стз—>0. Неединичная
173
обратная связь обычно применяется для уменьшения ошибки, вызванной х в замкнутых САУ.
Если y=W3x((f)x--------------х, то у = х при JV3X(^) =
Н^пЖосСО)
= ——— = 1; тогда необходимо, чтобы кое = {кп-У)1кп-
1 + какое
Действие неединичной обратной связи наиболее эффективно в статической системе, так как простым изменением кос можно получить Уст. з = т- е- «астатизм» системы относительно управляющего воздействия. При этом значению задающего воздействия х точно соответствует регулируемая величина на выходе системы у. Таким образом, элементарным приемом — уменьшением кос на незначительную величину по сравнению с единицей (при кп = 100 кос = 0,99) можно в САУ получить астатизм первого порядка относительно х, что означает отсутствие статической ошибки и равенство нулю первого коэффициента ошибки с0 = 0.
Условие И/Зх(р) = 1 теоретически дает возможность построения САУ полностью инвариантной по отношению к управляющему воздействию с дополнительным введением обратной связи по производным от регулируемой величины, т. е.
Жос(р) =	= а0-{Т\Р+ т\рг + Т& + ...)
WAP)
—разложение в ряд по степеням. Однако реализация полной инвариантности по этому условию практически невозможна, так как невозможно точно ввести высшие производные, входящие в и даже при выполнении этого условия САУ будет находиться на границе устойчивости. Таким образом, неединичная обратная связь в статиче-ской системе дает ус'т з = 0, и поэтому их используют лишь как средство повышения точности замкнутой САУ.
Случай W3X(p) = 1, когда у =* х является предельным по жесткости требований. Такую САУ нельзя физически реализовать, так как в ней должны действовать системы неограниченно большой мощности; САУ также не осуществляет фильтрацию помех. Поэтому реально W3x(p) должна стремиться к некоторой оптимальной W3 опт (р), определяемой в соответствии с тем или иным критерием.
Рис. 7.3
174
wec(.p) —
Рис. 7.4
Аналогичные результаты дает в статической системе масштабирование по х или у (рис. 7.3). При включении масштабирующего устрой-
Лр+1	к 1 + Ар
ства т = ——, тогда у = — -------—^х, т.е. аналогично х = .и.
fcp	1 + кр кр
Такое масштабирование делается практически во всех статитичес-ких САУ, что позволяет рассматривать их по отношению к управляющему воздействию как «астатические». Следует отметить, что при этом кр должно быть const (t); если кр нестабилен, то в САУ
имеет место статическая ошибка у„ = --ухс3, где Лк/А —относи-к
тельное изменение кр по сравнению с расчетным (коэффициент ошибки с0 = ЛА:/А2 ^0).
Формально при исследованиях САУ всегда можно перейти от неединичной обратной связи к единичной и наоборот.
Схемы (рис.7.4) должны быть эквивалентны, поэтому: FP3i(p) =
=---------------= -JEaifL = jjz (р) откуда
1+РГп(р)ИИос(Р) 1 + Жэ(р)
1Р3(р) =--F-------------•
Следует отметить, что проблема получения в САУ высокой точно-сти является единой в смысле получения в САУ требуемых качественных показателей—запасов устойчивости, быстродействия. Следовательно, эту проблему нельзя решать отдельно в отрыве от других. Поэтому другие способы повышения точности САУ будут рассмотрены позднее, после изучения вопросов качества процессов в САУ.
Отметим также, что реально _р"т никогда не обращается в нуль, даже при использовании САУ с высоким порядком астатизма.
Использование принципа управления по возмущению также обращает в нуль часть слагаемых, находящихся под знаком суммы в выражении для усг з.
175
§ 7.3. СТАЦИОНАРНЫЕ ДИНАМИЧЕСКИЕ ДЕТЕРМИНИРОВАННЫЕ РЕЖИМЫ САУ
Стационарные (установившиеся) динамические режимы, как уже отмечалось, возникают при приложении к САУ внешних воздействий, изменяющихся во времени по определенному установившемуся закону, например моногармонического воздействия и воздействий, изменяющихся с постоянной производной — скоростью или ускорением. Мерой динамической точности САУ служит вынужденная составляющая ошибки Зв(г) — ее максимальное 8ВМ или среднеквадратичное значения:
Зек = Um
7'—>оо
т	“1V2
|/[Зв(0]2Л
1 о
1. Стационарный режим САУ при входном гармоническом воздействии: /(z) = /mcoscOa.7 или g(t) = gM sin (akt приводит к тому, что выходная величина системы у совершает вынужденные колебания:
у = yMcos(w^ + <p), где а,(со) = |^0)^(0)); <p = argPK3/(».
Амплитуда и фаза колебаний у при этом определяются частотными характеристиками замкнутой системы, т. е. в общем случае W3X{j(f>), W3Z{j(£>). Соответственно динамическая ошибка САУ, например, от задающего воздействия:
ед(0 = Ем (w)sin [(0/ + фе (со)],
где
EM(w) = |^3e(»|gM(®);
Фе((0) = arg^3e(j(0);
WM = ЖР(»/[1 + JFpO)].
Среднеквадратическая ошибка еск = 0,707 ем (со). Малые значения ед(0 имеют место при	>1, когда |Игр(7Ю)| »1, т. е.
ЕмС®) “gM(“)/l^p(»|. Динамическая ошибка от f(t) определяется аналогично с заменой ЖЗЕ(/0)) на Жз/СЛ0).
176
2. Стационарный динамический режим САУ при воздействии f или
g, изменяющихся с постоянной к-й производной:
f -£f-nkf fycr dfk P
например, с постоянной скоростью v=pf (когда f= v t), с постоянным ускорением a = p2 f (когда f = at2/2) и т. д. Тогда
Уусг /[1 + Жр(р)]’
при р—>0 Уусг-*00, когда W/y(0) = kfy, Wp(0) = kp*0, т.е. у непрерывно возрастает.
Устранение установившегося отклонения Ууст при непрерывно изменяющемся воздействии совпадает с условиями устранения установившегося отклонения' в стационарном статическом режиме САУ. Первый путь также связан с выбором Wp(p), т. е. введением в САУ интегрирующих звеньев, а второй — с выбором Wfy(p), т. е. с компенсацией влияния возмущений. При этом отклонение Ууст = когда порядок астатизма САУ г > к, где к — порядок воздействия, если Wjy(p) не содержит интегрирующих звеньев (ууст =	при
г = к). Порядок астатизма САУ должен быть г+1, т.е. увеличен на/, если ИД (р) содержит / интегрирующих звеньев.
Компенсация влияния возмущений, изменяющихся с постоянной производной, достигается также путем применения управляющего воздействия по возмущению и его производным. При этом в статической САУ при возмущении /, изменяющемся с постоянной скоростью, ууст = 0 обеспечивается использованием компенсирующих воздействий по этому возмущению и его первой производной: при возмущении, изменяющемся с постоянным ускорением, необходимо добавить воздействие по второй производной и т. д.
В астатической САУ порядок производных от возмущения, которые должны компенсироваться управляющим устройством, увеличивается в зависимости от порядка астатизма и количества интегрирующих звеньев в передаточной функции Wfy(p).
§ 7.4. КОЭФФИЦИЕНТЫ ОШИБОК В САУ
Для оценки точности САУ используется величина ошибки е в различных типовых режимах установившегося движения от действия различных управляющих или вомущающих воздействий, например:
х(0 = [х0 +%!? +... + х///!]-01(г) или
177 12 А. А. Ерофеев
x(p) =Xq!p+ xjp2 +... + xt IpM.
Здесь x(t) = g(t) или x(t) = f(f).
' 1
Изображение ошибки e(p) = W(p) X хк—^-, где W (p) — переда-,	_	fc=o P
точная функция ошибки от соответствующего воздействия; W (р) = = И<ЗЕ(р)либо W3f{p).
В общем случае связь между ошибкой и воздействием, например g (f) может быть определена через интеграл Дюамеля
ео
Бд(0 = g(t)	T)wA(T)tft,
О
где и>д(т) — импульсная переходная функция.
Вынужденная составляющая ошибки. Существует метод — метод коэффициентов ошибок, по которому можно определить коэффициенты ошибок с0,...,с„ при типовых движениях САУ, в предположении ед,..., сп = const (t), что справедливо при сравнительно медленно меняющихся g(t) или f(t).
Разлагая в степенной ряд, например, выражение
^^P) = W3!,(p)g(p) = T-^77-g{p)
1	+ »р(р)
по комплексному параметру р получим:
Ед(р)= c0+qp+^p2 + ^p3 + - + ^ckpk g(p).
Разложение ошибки в ряд по производным от воздействия дает возможность определить вынужденную составляющую ошибки (оригинал изображения):
eA(O = cog(t) + c1g(z) + —+ + l4t) + kr =
= Cogo(‘) + YC^g(k)(t') + kr, k~\ K‘
oo	OQ
где сд,сх,...,сг_х —коэффициенты: c0 =1-|^д(т)А; q=Jwa(T)(ft; о	о
oo	co
c2 = (-1)|т2и»д(т)Л ; ...; cf-i = (-l)r~2Jтг-1 wA(t)rft; kT —остаточный о	о
член порядка n > г.
178
Если внешние воздействия изменяются медленно, то в этом выражении число членов можно ограничить значением к « 3 + 5. Так как L[w(i)] = W(p)— связана с передаточной функцией САУ, то можно записать разложение в ряд для W (р) при р->0:
W(p) = сь + <лР+ “ ЪР2 + • • • + у; СкРк> 2	к'.
где с0 = W(p)\p=Q; q = dW(j>)!d^; c2 = d2W(p)ldp2\p=0;
dkW(p)
Ск~ dpk
’ £ = 0,1,2, ....
/т=0
Тогда, например, если
Wv(p)
Wk) =	= 1 - W3(p) = 1 -	=
= 1 - j (r)e ’"dt = J д (т)е-ртЛ, о	о
d^p) ,к
то co = limW/3£(p) = [H'3£(O)] или в общем случае ск = р->0
к = 0,1,2, ..., где ск — коэффициенты ошибок, полностью определяющие зависимость вынужденной составляющей ошибки от структуры САУ и ее параметров.
Аналогично можно записать и для возмущающего воздействия fit) (если /(г) 6	— плавная функция времени):
е/0 = V(0 + q /(0 +... +	/(М)(0 + К
~ dW3f(p)~\ dp
ит. д.
и определить Cq = [ W3j (/>)] j	q =
Таким образом, оригинал для установившейся ошибки дает основную формулу метода коэффициентов ошибок:
..	,. dg(t) с2 d2g(f) ск dkg(f)
ев(0=cog(0+сг^+ “ -V2 + • • • + м яа dt 2! dr к\ dr
179
12*
где с^, q, c2, .•,ck — коэффициенты ошибок. Здесь q> = ——» — — i + fcp Arp коэффициент ошибки по положению в установившемся режиме: с0 * О только в статических САУ и в том случае, если не приняты меры по ее устранению (например, посредством масштабирования или использованием неединичной обратной связи). В САУ с г = 1 с0 = О,
a q =77 (kv = Qv —добротность САУ по скорости); в САУ с г = 2 ”	2
q> = q = 0, а с2 = —- (ка = Qa — добротность САУ по ускорению) *^а
и т. д. Здесь q — характеризует ошибку движения с постоянной скоростью, с2 — с постоянным ускорением. При исследовании ошибки САУ от f принципиально можно получить все коэффициенты ошибок равными нулю при г любого порядка. Астатизму по g (г) может соответствовать ев по/(см. формулу для £/(0 и наоборот).
Проблема повышения точности САУ связана с проблемой изыскания способов, позволяющих установить значение коэффициентов ошибок и сделать часть из них равными нулю (или все, в зависимости от цели функционирования САУ).
Значения коэффициентов ошибок определяются разложением в ряд Тейлора соответствующих выражений от передаточной функции
замкнутой САУ по ошибке: ск =
dkW(p) dpk
Так,если
W (р) =----J---=brnR-+--+^
"	1 + Жр(р) a„/ + ...+flb
1	2
= q)+qp+-c2p +
1 j	х-, 1 к
+ ... + ^р i.^X ,fckp ,
то
—(^-а^о);
«о
2
с2 = ~“(Р2 -«2с0 “«Л);
Ц)
при к > т;
САУ
Ц) = 1 + ^Р
аг = 0 при г > п.
11
и
(кр »1). Косвенной оценкой точности САУ является
= к\ «о
Для статической _ kfy к/у
1 + *р кр
у nf добротность САУ: по скорости Qv = kv =---------= —
.Ууст Тск
где
Лк — дополнительная скоростная (кинетическая) ошибка в режиме
САУ с v=const (?)
«ь к
q =
С к =
Ък^
с0/ “
кр ГГ
180
по ускорению
где Лк — допол-
Туст Туск у Lc _
нительная ошибка в режиме САУ с а = const (t). Используя kv, ка, , ,	_	, и!
можно определить коэффициенты ошибок, например, с ка: сп = --,
к(„-2}
2	6	24	Г 2/(01	П «	/ах/
тогда с2 = —;	с3 = —	с4=—-	а = -=~ .	Добротность	САУ
ка	ks V г )
пропорциональна кр (см. формулы для Qv и Qa ). Обычно коэффициенты ошибок не определяют более с4, так как ск > с4 практически не оказывает влияния на точность САУ и их не учитывают.
Пример. Пусть Wv(p) = -^-, тогда W3Z(j>) = — pQ(p)	i+W'pCp) R(p} + pQ(p) D(p)
Если R(p) = kp, a Q(p) = a2pl+0^+1, to D(p) = kp+pQ(p) = a2p3+aip2+p+kp.
_1]
кр ) ’
gW “ к кр
если gW = go + vo(O +
Следовательно, <?o=O (Z>0=0) ; Cj= -—(&]=!,a0=kp)', c2 = --~-(ах-c2=~(a2-k-v>	fCD Лр	Лр
-2 — + —); Здесь e
Лр Лр
Л	Я
+at2l2 (g(t) = v0 + at; g = a). Так как обычно a,, ь> 7J илито ck тем мень-
i=l	ы
ше, чем меньше и больше кр (при Лр—ск&~—>0 ). Так, если Q(p) = (l + *р
+7]р)(1 + Т2р), то а2=Т]Т2, a a^Ti + T^ . Здесь размерность у q —[с], у с2—[с2].
§ 7.5.	КАЧЕСТВО ПЕРЕХОДНЫХ ПРОЦЕССОВ В САУ
Качественные показатели (качество) переходных процессов в САУ обычно рассматриваются на основе анализа переходных процессов, вызванных внешним воздействием.
В случае произвольного внешнего воздействия переходной процесс у (t) в САУ представляет собой решение уравнения
D{p}y{f) = M(p)flj) и имеет вид
У(1) = Ууст(0 + Уп(0 = Ууст(0 +	.
i=i
Качество переходного процесса в целом зависит как от собственных свойств системы, так и от внешнего воздействия (величины, места его приложения, характера изменения в о времени). Последнее оп-
181
ределяет правую часть уравнения. Качество переходного процесса зависит также от начальных условий, определяющих состояние системы	
в момент приложения воздействия (изменение постоянных интегрирования Cj). Следовательно, переходной процесс при одном и том же Ж воздействии может в широких пределах изменять свои показатели при ж вариации начальных условий (например, при нулевых начальных условиях — быть монотонным; при других — существенно колебательным).
Поэтому при оценке качественных показателей переходных процессов в САУ необходимо всегда оговаривать воздействие и начальные условия.
Обычно качество переходных процессов оценивают для ступенчатого воздействия (при нулевых начальных условиях) в виде единичного скачка ol(z) или импульса 5 (?) (рис. 7.5, а, б). Здесь характеристики у (?) соответствуют внешнему воздействию в виде изменения задающего воздействия (а) и в виде изменения возмущения (б); на рис. 7.5, в — соответствуют изменению динамической ошибки 8д(г) = y(t}~ ууст = у(0~у(°°). Кривые 1,2,3 отражают варианты протекания переходного процесса: 1 — колебательный; 2 — апериодический; 3 — монотонный. Выходная величина у (?) САУ по окончании переходного процесса управления (рис. 7.5, а) получает некоторое приращение Усг-
Переходные процессы (ПП) численно характеризуются следующими прямыми показателями качества, определяемыми непосредственно по кривым h(f) или w(/), полученным экспериментально или расчетным путем, где w(t') — импульсная переходная характеристика (функция веса); h (f)—переходная характеристика.
1.	Время переходного процесса /п п или время регулирования zp. Оно характеризует быстродействие системы и определяется как время от начала переходного процесса до момента, когда отклонение выходной величины становится близким к установившемуся значению с заданной точностью 5, т.е. |y(z)-y(°°)] <8 при t>tp. Обычно в качестве 8 берут 5%-ное отклонение от у(°°) = ууст = = lim h(t) = lim р W3(p)/p = Ж3(0).
/—»оо	р—>0
2.	Перерегулирование о % или максимальное отклонение у (г) в переходной период. У переходных процессов, вызванных изменением задающего воздействия g(/)=ol(z) (рис.7.5, а), максимальное отклонение определяется относительно нового установившегося значения
о =	100% =	j оо% =	100%.
Joo	JyCT	^уСТ
Перерегулирование характеризует склонность САУ к колебаниям, а следовательно, и запас устойчивости САУ. Обычно считают, что запас устойчивости САУ является достаточным, если о <10+30%;
182
183
иногда требуется, чтобы переходной процесс был монотонным (о=0). В реальных устойчивых САУ может достигать 50+70%.
У переходных процессов, вызванных возмущением (рис. 7.5, б), максимальное отклонение определяется величиной утах = ум, приходящейся на единицу /(/) = 1(0; иногда здесь определяют Oo/0 = 2«±ioo%.
№1
3.	Колебательность переходного процесса К, определяемая обычно числом колебаний (с частотой (В,- = 2л/т,- ), равным числу минимумов кривой переходного процесса в интервале времени от 0 до /п п = Zp (рис. 7.5, а) или числом перерегулирований за этот же интервал. Иногда колебательность оценивают отношением амплитуд соседних максимумов К =	= е'“,Т/ и выражают в процентах; например,
УМ1
незатухающим колебаниям соответствует колебательность в 100% (а,- = 0). Колебательность при уменьшении до нуля второго максимума переходной характеристики (ум2 —> 0) стремится к нулю (неколебательный процесс). Обычно допускается не более одной-двух волн колебаний в САУ; иногда и они недопустимы. В ряде случаев допускается три-четыре волны колебаний. Колебательность, как оценка, задается обычно дополнительно к о.
4.	Степень затухания ПП v = ——— = 1 - — 2 = 1 - е~а'Т/, где 7м1	З’м1
т,-=2л/Р; = 2л/со/ —период колебаний; Р,=о), —частота колебаний; а,-, Р,- —действительная и мнимая части/-го корня (р, = -а,- ± ур( ). Так как т,-= 2л/Р,-, то \|/= 1 - е-2гах'^'; здесь |а,/Р,| . Значения ц/ изменяются от 1 до 0; обычно оптимальное значение \|/опт =0,75-5-0,982.
Отношение |Р/а| = ц = -2л/1п(1-у) называется степенью колебательности (цопт =4,52-5-1,57); иногда вводят ш = 1/ц = |а/Р| (wonT = = 0,221-5-0,636). Тогда у = 1 - e-2”^ = 1 - е-2гол. Отношение гр/т; — также дает оценку величины колебательности.
5.	Декремент затухания: d = -^1—= -^1 = —1----равен отно-
Тм2-Т- Ду м2
шению двух смежных перерегулирований; d' = — - = ea'T'. Логариф-
Ум2 j
мический декремент затухания d" = In = а,т,- или d" = —In |ум1 /yml I.
Ум2	П
Для САУ 2-го порядка 147 нэ £; d', d" характеризуют быстроту затухания ПП.,
6.	Временные дополнительные оценки качества:
1)	переходное время запаздывания 7ЗП: от z = 0 до гн>0,5_уте;
2)	гч.з = т — время чистого запаздывания;
184
3)	время нарастания ta от t4 3 до tc н> у„;
4)	/м — время первого максимума у (г);
5)	tc — время первого согласования, когда у (t) = =у (°°);
На рис. 7.6 показана область допустимых отклонений регулируемой величины y(t)/у,„ в переходном процессе. ,
Комплекс временных ка-
чественных показателей ПП характеризует быстродействие САУ.
7.Максимальная скорбеть отработки (dy/df)^ = dh(fydt = [w(r)]M и равна максимальному значению импульсной переходной характеристики (рис. 7.5, б).
8. Динамическая точность САУ 5Д(?) н> к, - y(t) (рис. 7.5, б) оценивается максимальной ошибкой 8М =|8в(/)| и среднеквадратичной
ошибкой 8СК =
ПП в САУ
V 1 о
при скачкообразных воздействиях подразделяют на
монотонные, у которых dy(t)!dt не меняет знак; апериодические —
dy(t)!dt меняет знак не более одного раза и колебательные— dy(t)ldt изменяется периодически (рис. 7.5). В качестве оптимального (желаемого) ПП обычно выбирают апериодические Л(г) или h(t) слабоколебательного типа (щ ~ 0,982; ц. = л/2 ~ 1,57; т = 0,636).
Следовательно, переходные процессы в САУ характеризуют в ос
новном ;ра комплекса показателей качества: первый, оценивающий временные показатели (1,6), определяющий быстродействие САУ; второй, оценивающий колебательность процессов (2, 3, 4, 5, 7, 8), опреде-
ляющий интенсивность процессов.
ПП в САУ должен заканчиваться как можно быстрее; чем меньше 1р, тем качественнее САУ. Существуют определения оптимальной по быстродействию и предельной по быстродействию САУ. Теоретически ?пп °°- Однако реально считают, что в разомкнутой САУ гп ц ®(3-*-4)7^, где Ты —наибольшая (максимальная) постоянная времени звена или ОУ. Это связано с наличием в реальной САУ зазоров, люфтов и т. д., которые ограничивают ПП до (3 -5-4)7^,.
Выполнение требований при выборе структурной схемы и значений параметров САУ в отношении перечисленных показателей качества переходного процесса требует компромисса в связи с противоречивостью этих требований (рис. 7.7).
185
Так, если в статической САУ установить малый коэффициент передачи кр, то переходная характеристика будет неколебательной, плавномонотонной (е С(“)). При увеличении к р будет увеличиваться быстродействие САУ (уменьшаться tm), но одновременно с этим будет нарастать колебательность К (см. рис. 7.7, а, б). Если кр = копт, то ?р = /опт, при этом К < 2. Оптимальному времени регулировки
186
соответствует колебательность К <2, это означает, что за время переходного процесса выходной сигнал должен совершать не более 2-х колебаний. При дальнейшем увеличении кр вплоть до его критического значения £ркр, соответствующего границе устойчивости, колебательность возрастает до 100%. Длительность переходного процесса ?ц.П’ которая с ростом кр вначале уменьшалась, начиная с/опт, будет нарастать (рис. 7.7, а). Перерегулирование ст растет незначительно с ростом /опт,: ст < 30% при кр £ копт (см. рис. 7.7, в). Однако по мере роста амплитуды колебаний перерегулирование ст увеличивается до 100% (при &ркр). Граничному значению кр = кргр соответствуют предельные параметры ПП: гр, огр (= 70%) и К{ см. рис.7.7, а—в).
§ 7.6. КРИТЕРИИ КАЧЕСТВА ПЕРЕХОДНЫХ ПРОЦЕССОВ.
ЧАСТОТНЫЕ КРИТЕРИИ
Оценка качественных показателей по h (z) составляет, как уже отмечалось, группу прямых методов исследования качества САУ. Однако существует возможность судить об основных показателях качества переходных процессов в САУ без построения ПП по каким-либо косвенным оценкам, которые определяются более просто, чем h (?). Такие косвенные оценки называются критериями качества переходных процессов. Они позволяют связать также показатели качества непосредственно со значениями параметров САУ. При исследовании качества переходных процессов эти критерии играют роль, аналогичную критериям устойчивости.
Существуют три группы критериев (оценок) качества — частотные, корневые и интегральные.
ЧАСТОТНЫЕ КРИТЕРИИ КАЧЕСТВА
Оценка качества ПП может производиться по различным частотным характеристикам замкнутой системы
ВД = Л(®)еЛ(ю) = Р3«о) + Шсо) =
= Л3(<о)со8<рз((1)) + /Л3(и)5тф3(®).
Для минимально фазовых систем качество переходных процессов обычно оценивается по амплитудно частотной характеристике (АЧХ) и вещественной частотной характеристике (ВЧХ) замкнутой системы Л3(со) и Р3(и) (рис. 7.8, а, б). Напомним, что у таких систем АЧХ и ФЧХ однозначно связаны и, следовательно, например, по АЧХ можно определить свойства САУ, в том числе и качество пере-
187
ходных процессов. В ТАУ в основном оценивают колебательность и длительность переходной характеристики/г (?) по АЧХ и ВЧХ замкнутой САУ.
ОЦЕНКИ КАЧЕСТВА ПП ПО АЧХ ЗАМКНУТОЙ САУ
Колебательность определяется по величине относительного максимума АЧХ, называемого показателем колебательности М, который является косвенным показателем колебательности САУ:
Ам(со) _ А(<ор) _ ^р(» 4(0) " 4(0) " 1 + Жр(»
188
Например, для колебательной САУ 2-го порядка (кривая Г):
п_?2ч-1/2
М =	, £<0,707; шр=ш0(1Ч2)1/2.
В общем случае при М < 1 переходная характеристика системы не колебательна; при возрастании Mi чем больше М, тем больше колебательность. При Л3(сор) -»°° М °° и колебательность возрастает до получения незатухающих с частотой сор колебаний, соответствующих границе устойчивости САУ (пара сопряженных мнимых полюсов ±J0)p).
Если ^(уш) = (7(со) + у'К(со), то
и2 + У2
или Мм =	.	.
_(\ + U)2 + V2_
1/2
; я3(0) = 1
Жр(» ---------- при лз(0) = 1
м
1 + Жр(»
для астатических САУ с г = 1.
Мм
следует, что в диапазоне час-
и'рС»
Из соотношения W3(jy>) = pto)
тот, где Лр(<о) = |1Ур(у(о)| >1 Л3(со) ft 1, а <р3(й)н>0; при Яр((о)<1 Л3(со) ft Лр(со), а Ф3((в) ft фр(со). При co = (onpft(oc Лр(о>) = = [2cos Дф(сопр)] «[2cos Аф(сос)]-1= [2cos Дф]-1, юпр “ 2сос cos Дф, Дф = у = л — фр(сос); максимум рр(со)] «1/cos у, а М = 1/sin у.
Обычно считается оптимальным М = 1,1 + 1,5. При этом переходная характеристика имеет слабую колебательность с частотой, близкой к частоте сор резонансного пика АЧХ, с ст» 0,1+0,3, ус»30+50° — запас САУ по фазе на частоте среза ис. Допустимо в САУ и значение М: 1,5 < М < 1,7 и вплоть до 2,0 — 2,5; для следящих САУ обычно М< 1,1—1,3.
Длительность /р = /п п переходной характеристики определяется шириной Л3(<в): чем шире АЧХ САУ, тем короче h (?), т. е. мень-ше ^п.п-
Длительность h (t) может быть оценена в первом приближении по значению <ор, так как частота колебаний переходной характеристики примерно равна <ор. Учитывая, что время tM близко к половине периода колебаний этой частоты, можно определить:
л	0,5	л	0,5
~ — = ---, а г_« — = <ор	/р	®с /с
Если h (?) САУ в течение /р имеет 1—2 волны колебания, то /р »(1+2)— «(2+4) — так как <йса<вР> то /_«^-^. Для р (ор шр	р шс
189
оценки быстродействия САУ могут быть использованы также: частота среза (ос, полоса пропускания САУ о)пр, эквивалентная полоса оо	оо
пропускания САУ (оапр = J|W3(jw)|2dm = | Л32(о))й?со. о	о
ОЦЕНКИ КАЧЕСТВА ПП ПО ЛАХ РАЗОМКНУТОЙ САУ
Колебательность и длительность переходной характеристики замкнутой САУ в первом приближении могут быть оценены непосредственно по параметрам ЛАХ разомкнутой САУ: частоте среза и величинам запасов устойчивости по фазе и амплитуде. В случае колебательной h (г) резонансная частота <ор АЧХ замкнутой САУ близка к частоте среза сос ЛАХ разомкнутой системы. Поэтому значения tu и tp могут быть определены аналогично при подстановке Wp =0)с, например, в случае неколебательной h (0, tp ~ л/о)с.
Колебательность считается допустимой, если ЛАХ на частоте среза (0с имеет наклон -20 дБ/дек; чем шире участок с таким наклоном, тем меньше колебательность. При ширине этого участка около одной декады и нахождении <ос ближе к его концу перерегулирование в САУ не будет превышать 20—30%. Если запас по фазе у > 30°, запас по амплитуде 6 дБ (что соответствует 2 в линейном масштабе), то h(t) имеет слабую колебательность.
ОЦЕНКИ КАЧЕСТВА ПП ПО ВЧХ ЗАМКНУТОЙ САУ
Колебательность и д л и дельность переходной характеристики могут быть определены по вещественной (действительной) частотной характеристике Р3((о) замкнутой САУ. Колебательность и длительность ПП здесь зависят также от относительного максимума N = Рзы/Р3 (0) а 7^/ДО) и ширины (соп) частотной характеристики. Связь h(t) и Р(а>) определяется, например, следующим выра-, / ч 2 7	. sin (0? ,
жением: я(0 = —J Доз)——— <ко, справедливым для устойчивой замкну-
той САУ, когда W3(p) не содержит правых и мнимых корней.
На рис. 7.8, б приведены различные формы характеристики Р3(т) = Дсо). Для вогнутой характеристики 7, когда Дсо) > 0, dPjdm<Q, d2P) dm2 >0, h(t) — монотонная функция и перерегулирование о = 0. Для кривой 2 в области низких частот относительный максимум N = 1, Дсо) > 0, dP (со) 1dm < 0, величина перерегулирования о < 18%. Кривым 3, 4 [с пиком, Т’(со) > Р (0)] соответствуют колебательные h(f), причем величина о [%] растет с увеличением N: о = [1,18Д - Д0)]/Д0). При А-»оо амплитуды колебаний возрастают:
190
САУ выходит на границу колебательной устойчивости. ПриА= 1,2 величина о <50%; при N= 1,5 величина а <80%. Наличие минимума у ВЧХ (кривая 4) также увеличивает колебательность h (/).
Длительность h (Z) в первом приближении оценивают шириной Р(щ), определяемой значением частоты положительности соп, при котором положительная часть Р(о>) < ДвР(0): zp > — . Для кривой
ВЧХ 1 z_ >47C/ €Dn; для кривой «трапецеидальной» ВЧХ 2 t =(1+4)— =
, Л	(0п
= к—.
®п
Для кривых ВЧХ 3 и 4 *р связано с соп аналогичной обратно пропорциональной зависимостью. Значение коэффициента пропорциональности к зависит от величины У, увеличиваясь вместе с N, т. е.	, где 4 < к < 10.
Значению Р (0) соответствует Луст = /г(°°), а значению Р(«>) !-> /г(0). Конечную часть Р (со) (диапазон высоких частот) определяет полоса частот (0п < и < й)сщ (о)сщ — интервал существенных частот), которая практически не оказывает влияния на показатели качества ПП. Она определяет характер ПП при t >, 0, т. е. его начальную часть и, следовательно, может оцениваться более грубо; Дв = ±(0,1+0,2)Р(0). Диапазону низких частот (0 < (о < сон) соответствует ±ДнР(0), что определяет конец ПП. Средняя часть Р (о) в основном определяет все качественные показатели ПП.
Детальные и более точные зависимости, связывающие показатели качества системы с характеристиками А3 (со), P3(w), а также и с другими, например с <23(со), содержатся в работе [2].
На основе вышесказанного можно сделать следующие выводы.
1.	Близкие по форме АЧХ и ВЧХ САУ имеют близкие по качеству ПП.
2.	Частота сос определяет быстродействие САУ; чем больше сос, тем меньше t?- Но при значительных сос вместе с полезным сигналом проходят и помехи, поэтому не следует стремиться делать <вс чрезмерно большой.
3.	Наличие пика в АЧХ (М > 1) и ВЧХ (N < 1) говорит о колебательности САУ.
4.	Если в АЧХ или ВЧХ САУ имеется разрыв на определенной частоте (0 = (1)р, то в САУ на этой частоте возникают незатухающие колебания (САУ находится на колебательной границе устойчивости).
5.	Если АЧХ или ВЧХ имеет разрыв при со = 0, то в САУ имеет место апериодическая граница устойчивости.
6.	Острый пик АЧХ или ВЧХ при ир. говорит о сильной колебательности с частотой, близкой к щр( и'значительном о [%].
7.	С увеличением М и N возрастают tp, К, (0с, (йм=сор, о и уменьшается ус; следовательно, увеличение М и N ведет к ухудшению качества САУ.
191
8.	Из соотношения Р (со) = А (со) cos ф (со) следует, что Рм(ю)> >4,(со).
9.	Характеристики Р (со) позволяют более точно оценивать качество переходного процесса, но требуют большей трудоемкости, чем, например, при применении ЛАХ.
10.	Оценки качества ПП в общем случае могут быть определены по соответствующим характеристикам разомкнутой САУ, благодаря связи АЧХ и ФЧХ замкнутой и разомкнутой САУ.
Приведенные оценки качества ПП относятся к минимально-фазовым системам; однако в первом приближении они могут быть применены и к неминимально-фазовым системам. При этом погрешность тем больше, чем больше различаются ФЧХ САУ.
Оценки качества переходных процессов, вызванных произвольным воздействием х (/) (неединичным ступенчатым), можно получить аналогично при предварительном преобразовании произвольного воздействия в эквивалентное воздействие в виде единичной ступеньки. Для характеристик это отражается в виде перехода к обобщенным час-
2 °°
тотным характеристикам, когда y(z) = — jRe[lF3(jo))x(ja))]cos(OZz/a) [при x(t) =0 1(0, х= 1/р, y(t) = h(t) =—1 Р((о)^^б/(о ].
Оценка качества ПП может быть произведена и по кривой D-разбиения, так как последняя по определению связана с частотными свойствами замкнутой САУ.
§ 7.7. КОРНЕВЫЕ КРИТЕРИИ КАЧЕСТВА
Оценка качества переходных процессов по корневым критериям производится по значениям полюсов (корней знаменателя) и нулей (корней числителя) передаточной функции замкнутой САУ
№3(р) =
М(р) D(p)
j=i п
/=1
определяющей и соответственно h(t) = U\W3{p) / р]. Здесь Pi,Pj — полюсы и нули, которые с точностью до постоянного коэффициента Zb/до определяют передаточную функцию системы. Эту форму записи W3(p) иногда называют факторизованной.
При исследовании точности САУ важным было расположение в комплексной плоскости полюсов передаточной функции. При оценке качества ПП необходимо учитывать и расположение нулей. В част-
192
ном случае, когда Pj отсутствуют, качество ПП определяется только полюсами передаточной функции. При этом напомним, что у„(0 = ^(0 = Хс'еД/ > гДе Pi =ai - J$i — корни характеристического i=i
уравнения, в которых а; определяет затухание ПП (декремент затухания); Р,- — частоту затухающих колебаний. Переходной процесс в устойчивой САУ представляет собой совокупность затухающих апериодических и колебательных составляющих (определяются парами комплексно-сопряженных корней).
Следовательно, длительность ПП определяется по оценкам сверху самой длительной составляющей, а колебательность — самой колебательной составляющей.
Степень быстродействия САУ оценивают с помощью критерия длительности (степени устойчивости Т|), определяемого ближайшим расстоянием от мнимой оси до корня рл. Время затухания составляющей переходного процесса, определяемой величиной сле~’1' или 1 1 ст,е-*’'sinPf, считают приближенно длительностью ПП:/„^1пе.
3	В °
Если 5 = 0,05сл, то tp = - « 37}м, так как т] = 1/7]м, где 7}м =	—
наибольшая постоянная времени звена или САУ; \а,\т - Л — степень устойчивости.
Степень устойчивости Г| служит мерой удаления САУ от границы устойчивости — мнимой оси (рис. 7.9, а).
Колебательность САУ оценивается с помощью критерия колебательности — степени колебательности ц = [(3,-/az| = tgум (см. рис. 7.9, б). Чем больше ц, тем больше колебательность всего переходного процесса К = е”2п//ц ; следовательно, ц является оценкой сверху колебательности. Степень колебательности ц = -2л/1п(1 -\|/) = 1/т, где m = = |оС;/Р(-| = tgф; если у = 0,9, то ц = 2,72, т = 0,367; у = 0,15 соответствует т = 0,221.
13 А. А. Ерофеев
193
Значения т] и ц можно определить через параметры САУ с помощью критериев устойчивости, использующих многочлен
О(р) = «о/ +Я1Р"’1 +... +an_ip+a„ = OoYfip-pi) = 0. 1=1
Обобщенной количественной оценкой коэффициентов уравнения и его корней рп, а также относительной мерой быстродействия служит среднегеометрический корень Qo = д/[«„/«о| = д/|аР2	, который чем боль-
ше, тем меньше /р; й0 s кр, так как, например, в статических САУ ап = кр +1, а в астатических а„ = кр (для САУ 2-го порядка Йо - соо, поэтому Qo иногда называют собственной частотой колебаний по аналогии как для систем второго порядка). Среднегеометрический корень Qo в комплексной плоскости определяет геометрический центр всех корней D (р) — точку на вещественной оси (расстояние всей группы корней от мнимой оси).
Диаграмма Вышнеградского (см. рис. 6.11), в частности, является примером применения корневых критериев качества (здесь £20 = ^a3/aQ, см. п. 6.5), на которой можно построить поле линий равных значений ц (О < т] < 1) и ц (О < ц< «>). По заданным ц и ц по диаграмме можно найти значения коэффициентов А и В и определить, тем самым, требуемые параметры САУ. В общем случае, если произвести подстановку z = p/Q0, то можно записать уравнение D (р) в нормированной форме Вышнеградского (см. п. 6.5) zn+Alzn~,+... + Akzn~k + ... + A„_!z+l = O, где Ак = ак /ц,; zk = рк/Щ. Тогда исходное уравнение D (р) = 0 можно также записать в виде: рп + 4Qop"4 +... + Ак^крп~к +... + Qg = 0. При решении этого уравнения используют относительное время т = Q.ot. Время t ~ где — время ПП САУ с нормированным уравнением D (р) = 0. Так как ц и у (степень затухания, см. п. 7.5) взаимосвязаны ц = - 2л / In (1 - ц/), то поле линий равных значений ц отражает и поле линий равных значений ц/.
Если произвести подстановку в D (р) р = q - Т|, т. е. ввести новую переменную q = р + т|, то этот переход соответствует в комплексной плоскости параллельному смещению мнимой оси влево на т]. Тогда можно определить критическое значение Л = [ос,-\т как варьируемого параметра, при котором многочлен Dq окажется на границе устойчивости.
РАСЧЕТ САУ НА ЗАДАННЫЕ п ИЛИ ц (т)
Если величина т]3 задана, то подстановкой р = -т]+уо) в W(р) разомкнутой САУ можно получить так называемые расширенные АФХ разомкнутой системы. В этом случае расчет САУ ведут на заданную степень устойчивости 1%. Тогда, если в САУ т]с > ц3, то соответствующие расширенные АФХ разомкнутой системы не должны охватывать критическую точку (-1; 0).
194
Аналогично изложенному для т| можно произвести следующую замену переменной p = ±jqe~\ где у = arctg ц. Эта подстановка соответствует повороту мнимой оси против часовой стрелки на угол (л/2- у) (рис. 7.9, б).
Критическое значение ц определяется значением параметра у, при котором многочлен D (q) окажется на границе устойчивости (один из корней попадает на мнимую ось в результате ее поворота).
Если ц3 или т3 заданы, то подстановкой р = - тел ± усо (ц = тел) в W (р) разомкнутой системы можно произвести расчет САУ на заданную степень колебательности. В этом случае также расширенные АФХ не должны охватывать точку с координатами (~1;0), если тс>т3.
Расширенные АФХ широко используются при определении параметров оптимальных настроек регуляторов промышленных САУ [10].
Оценка длительности и колебательности переходных процессов в САУ по значениям Г] и ц является оценкой сверху, т. е. действительный ПП может иметь лучшее качество.
Корневые оценки качества ПП пригодны только для систем, передаточные функции которых не имеют нулей (при нулевых начальных условиях).
Для САУ выше второго порядка этими подстановками пользоваться можно, если есть уверенность, что ПП в САУ близок по форме к ПП САУ второго порядка, иначе может быть получена существенная погрешность результатов. Для других видов передаточных функций оценка качества только по полюсам может дать большую ошибку, причем действительный переходной процесс может быть как лучше, так и хуже, чем в САУ второго порядка. Однако и здесь качество переходного процесса будет тем лучше, чем большет] и меньшец; причем чем большец, тем выше быстродействие, и чем меньше ц, тем меньше ст и К.
По значениям т] и ц можно построить предельные кривые переходных процессов (верхняя называется мажорантой vM, нижняя — минорантой vm). Реальный переходной процесс должен располагаться между ними, т. е. vm(0<vp(z) <vM(?) при TVm<xp <Tv>j, x = x\t (рис. 7.10, а, б — различные варианты).
Рис. 7.10
195
13*
Из характеристического уравнения D (р) = 0 для случая вещественных корней и нулевых начальных условий можно получить уравнения мажоранты:
^м(0 = е-
т2
1 + Т + — 2!
+ ... ч-------
(л-1)!
и миноранты Om(z) = е-т (здесь ст [%] = 0). Для САУ, имеющих среди корней одну пару комплексно-сопряженных, при прочих равных условиях миноранта б т (?) = -в м (?), а стм [%] <	• 100%.
§ 7.8. ИНТЕГРАЛЬНЫЕ КРИТЕРИИ КАЧЕСТВА
Интегральные критерии качества позволяют характеризовать кривую переходного процесса определенным числом, которое комплексно оценивает параметры переходного процесса (о, ?р) в целом на заданном интервале 0 < t < Т (обычно Т -ь °°).
Нахождение показателя, который качественно характеризует переходной процесс в целом, задача весьма актуальная. Такие оценки обычно являются функционалами и выражаются в виде интегралов
т	т
J = jF[/0)pz=/F(x1,x2, ...,x„)dt, о	о
где f (?) — функция, характеризующая процесс в системе, например /(?) = yn(t) = h(°°) -h(t) = &y(fy, F— заданная функция. Минимальное значение данного функционала обеспечивает оптимальное протекание переходного процеса в САУ.
Задача минимизации функционалов решается вариационными методами или методами динамического программирования. Изучение этих методов относится в большей степени к классу оптимальных и самонастраивающихся систем, в которых САУ сама осуществляет поиск в пределах варьируемой структуры (или параметров) оптимума протекания переходного процесса.
Оценки качества переходного процесса могут быть произведены с помощью следующих функционалов:
линейных (моменты m-го порядка):
“	«. m
Лин = J F(t)^y(t)dt = J У, ск (t)ky(t)dt, 0	0<:=0
где ck(t) = cktm или ck(f) = ск1тъ~ш, т = 0, 1, 2,...;
196
квадратичных:
оо	со л	п
J2n = J Vndt = J ^CyXiXjdt = ХсуЛ’ 0	oi/=l	I,J=1
где V„ — квадратичная форма переменных САУ; Су — заданные коэффициенты квадратичной формы; Jy = J XjXjdt — также интеграль-о
ные квадратичные оценки. Следует заметить, что интегральная оценка определенно положительной квадратичной формы координат устойчивой САУ равна функции Ляпунова от начальных значений координат.
Линейные интегральные оценки являются интегралами вида
"	оо
jlm=jAy(om
о
или
J}m = J Ay(i)e~altmdt, т = 0, 1, 2,... . о
Обобщенные квадратичные оценки имеют вид:
d2txy dt2
+ ... + Т2"
/=1
где
В частности применяют следующие квадратичные интегральные
оценки:
со
J22 -
dt и т. д.
О
197
Здесь Д у (t) = у (оо) - у (t) = = Д h (Z) — отклонение выходной величины САУ от нового установившегося значения у (°°) (рис. 7.11).
Целесообразность и удобство в применении интегральных оценок заключается в том, что существуют готовые формулы и таблицы расчета [2], вы-
ражающие различные оценки через коэффициенты Ъ^, ..., Ь„ и а„
„ ,	, Л/(р) b^pm +blpm~l + ...+bm_ip+bm 1
передаточной функции W3(p) = —— = —-----------------------
О(р) а^рп +а1рп 1 +... +a„_lp+ari р
Простейшая линейная интегральная оценка JI0 = J Aj'(z)t/z геометрически представляет собой площадь под кривой Ду (Г) (рис. 7.12, а); чем меньше эта площадь, тем выше быстродействие САУ и предпочтительнее переходной процесс. Интегральные критерии качества обычно эффективно используются для определения оптимальных значений варьируемых параметров. Для этого, используя выражение для J10 через коэффициенты передаточной функции системы, можно найти оптимальные значения варьируемых параметров (т, v) из уравнений J10 = /(v) и 9J|0/3v = 0, соответствующие минимуму J10. Вычисление оценки J10 производится при входном ступенчатом еди-
198
к____L.
то при р = О Ж3(0) = к; тогда JiQ = lim-Тр+У = lim .= кТ.
р->о p p-iO p(Tp+l)
Следовательно, качество переходного процесса в апериодическом звене определяется произведением А: Г; чем больше 710 тем больше и хуже качество переходного процесса. Для улучшения качества переходного процесса необходимо уменьшить Т (и изменить соответственно к) до оптимального значения (см. рис. 7.7).
Интегральная оценка 710 применима только к системам, у которых переходные процессы монотонны, что резко ограничивает применимость данного критерия. Если переходной процесс колебательный (рис. 7.12, б, кривая 7), то значение 710 не может служить мерой его качества, так как площади разного знака под кривой переходного процесса будут вычитаться друг из друга. Например, ухудшение качества переходного процесса при переходе к незатухающим колебаниям сопровождается уменьшением 710 до нуля (рис. 7.12, б—кривая 2). со
Следующая линейная оценка 7и=|Ду(0^ равна моменту площа-о
ди относительно начала координат. Оценки более высоких порядков
определяют моменты т-го порядка функции Ду (z): Jlm = j &y(t)t dt. о
Линейные интегральные оценки приемлемы только для САУ с монотонными переходными процессами. Интересно отметить, что710 = = с0,	=(-l)q,	=(-l)mcm, где с0,сх,...,ст —коэффициенты
ошибок, т. е. Jlm =(-i)m[dmW3e(p)/dpm]\^0 или ст =(-l)mJlm/rn!
Для САУ с колебательным переходным процессом (рис. 7.12, в) применяют квадратичные интегральные оценки J2n  Простейшая квадратичная оценка /20 = j" [Ду(г)]2<^, что соответствует площади под кривой Ду (Z): о
1 т	l 1	к
Ло = ;ТА £в^к -	Вк = ь1-к +
2ап^ к=о ап	,=1
к = 0,т; т<п; т = п-\.
Здесь A — старший определитель Гурвица; Д^ — определители, получаемые из Д заменой (тп - к + 1)-го столбца столбцом [ап_х ,ап,0,... •.., Of; Bm = b2m- Bm_i = b2m_x - 2bmbm_2; Bo = . Иа границе устойчивости Д = 0 и 720 = °°. Оценка 720 является относительной мерой быстродействия САУ: меньшей J20 соответствует более быстродействующий переходной процесс (см. рис. 7.12, в — кривые 1, 2).
199
В общем случае Ду(р) = 1К3(0)- —FK3(p) и при p=ja> J20 = Р
| оо	1 °°	I	2
= - Г|ДХ»|2^со = - f Уд/соЖ где = |Ду(»| — спектраль-
71 о	п 0
ная плотность.
Следует заметить, что в общем случае вычисление J2n сводят к определению в частотной области интеграла J2n =	+
Т2п °г	2
+ " Г Ду(п)(у<в)| dto, которому ставится в соответствие интеграл 2п J1	!
.	1 г	,
J ~ 2 J /)( )£)(—• j определяемый с помощью рекуррентных соотношений; табулированное значение интеграла Jn = = J f 37Т7/~4^где c(p) = cQ + ...+cn_lpn~x; d(p) = dQ + ... +d„pn [2]. 2лу
Г- A \ boPm + +bm	, 7 A)
Если ДХ/2) =------„---------> то при и = 1 J20 = — —; при п = 2
а^р + ...+ап
r Ь^+$а2
J го ~	------- и т. д. Формулы для вычисления J20 составлены до
TjO^fl2 п~ 10 [2].
При минимизации J20 и выборе варьируемых параметров обычно получают колебательный переходной процесс с высоким о [%] идо-вольно большой колебательностью. Например, на рис. 7.13 приведены две кривые, удовлетворяющие одному значению <720; кривая 1 дает некачественный переходной процесс, кривая 2—переходной процесс, близкий к оптимальному.
Предельным переходным процессом, очевидно, будет процесс, при котором интегральная оценка J20 стремится к нулю, т.е выходная величина САУ должна соответствовать заданной величине (Ду=0). Однако такой переходной процесс в линейных САУ не может быть физически реализован из-за инерционности звеньев САУ, а также возникающих в системе весьма значительных перегрузок. Когда такой процесс неприемлем, переходят к улучшенной интегральной квадратичной оценке.
,2f 4/Д^У ' I dt )
dt =
о
20 J 0
2 dt.
200
Интегральная оценка J21 состоит из суммы двух частей: первой, соответствующей J20, и второй, позволяющей учесть скорость изменения Ду(0 с весом 7] [ограничение на скорость изменения Ду(0] (см. рис. 7.12, в — кривая 2).
Минимум оценки J21 по сравнению с J20 будет при менее колебательном переходном процессе. При этом плавность протекания переходного процесса определяется выбором величины весового коэффициента 7J2. Оптимальным переходным процессом при минимизации J21 является экстремаль — кривая первого порядка — экспонента АУопт(0 = Ду(0)е“'/7! (рис. 7.14, а) или ХО = (1-е-'/7‘)уоо (рис. 7.14 , б), где Ду(0) 1-> ут (см. рис. 7.11).
Более сложные интегральные критерии качества J2ll, содержащие вторую производную с весовым коэффициентом Т? (рис. 7.14,6) и следующие производные от Ду(0> применяют, когда целесообразно приблизить переходной процесс соответственно к экстремали — кривой второго [ а2у + а{у + у = у°у, 0^ = Т2; ц = (7J2 - 27^)1/2 ] и следующих порядков. При этом увеличение 7J, Т2, приводит к перерегулированию а [%] = 0, но увеличивает /р; при малых же Тп уменьшение колебательности будет незначительным. Выбор Тп осуществляется в соответствии с постоянной времени экстремали, к которой стремится переходной процесс.
Интегральные критерии применяются при исследовании качества переходных процессов, вызванных основными внешними воздействиями, для определения оптимальных значений von варьируемых , a/)m(v) п dj2n(v) ..
параметров (из ——-....- = 0 или —= 0); численную оценку са-
3v	ov
мих показателей качества переходного процесса они не дают.
Интегральные оценки в качестве критерия оптимальности широко используются при синтезе оптимальных САУ. При этом von соответствует Jim min или J2n mjn, если соответствующая 32J(von)/dv2n >0; v\-^kj,Tj. Например, для двух параметров: dJ(k, Т)/дк = 0, dJ(k,T)/dT = Q, если J = J(k,T).
201
Пример 1. Определить для Wv(p) = kl[p{\ + 7»] оптимальное значение fcon, соответ-,	о	А , '	\ + рТ ,	1 + кТ	,	\ + кТ 7?к Л
ствующее J2I min. Здесь Ьу(р) = --.—-;	/21 = —— +-г~. Опреде-
[гТ+р+к 2к	2к 2
ление коп из выражения ЭУ21 >дк = 0 дает
/ \1/2
к = _L =_L г 2+TiT, Оп Г2	Т ’ а ^21min “
V21 J	'1	2/7]
Пример 2. Пусть Ду(р)= ^^ =——-------------1. Тогда j20 = -J— х
У\р) аор +aifT+а2р+а3 р	2а А
х(В tA|+2?oAo)—М-’ °з
где Д=а3(а1а2-воа3); До = a2(aia2-aoa3)+afo3; Д( = а|а,;
Bi=bl; B0=bl. Если М(р) = Ь0, ТО Рг<> = (1>112а1л.)Л.о.
1	1+4S2
Пример 3. Пусть ЙИ,(р) = —----. Тогда /20 =....
{Г+2£р + \	4£
, _ с	,	.	.	4£2+2	Эл,
£ = 0,5 при 720=720min; ^=-5-— и из ~|J =0
hl = Almm-
и из = ® получим
получим £ = 0,707 при
§ 7.9. МЕТОДЫ РАСЧЕТА (ПОСТРОЕНИЯ) ПЕРЕХОДНЫХ ПРОЦЕССОВ
Определение переходных процессов в САУ и построение// (/) осуществляется аналитическими и графоаналитическими методами на основе передаточных функций и частотных характеристик замкнутой САУ. Если отдельные звенья в САУ описаны экспериментально полученными характеристиками, то от них следует переходить к передаточным функциям.
Переходные характеристики САУ являются наиболее наглядным описанием динамических свойств системы.
Аналитические методы основаны на непосредственном решении дифференциального уравнения системы D (р)у = М {p)f. Классический метод решения дифференциального уравнения дает искомое решение, состоящее из установившейся (вынужденной) и переходной составляющих переходного процесса:
/(0 = ^уст(0 + л(0,
п где Уп(0 = ^jciePlt-/=1
Основные трудности нахождения этого решения сводятся к определению постоянных интегрирования с( и корней характеристического уравнения р(. Известно, что корни уравнения могут быть в радикалах найдены достаточно просто только для уравнений с п < 3. При порядке п > 3 используются приближенные итерационные методы нахождения корней (методы последовательного приближения).
202
Классический метод решения дифференциального уравнения наиболее тесно связан с физикой процессов в реальных САУ, а поэтому понятен и общедоступен. К его недостаткам относятся:
необходимость выполнения достаточно сложных математических операций дифференцирования и интегрирования; с возрастанием порядка дифференциального уравнения сложность метода возрастает;
достаточно трудоемкий процесс учета начальных условий и определение связанных с ними постоянных интегрирования;
затруднен процесс определения частного решения дифференциального неоднородного уравнения, определяемого его правой частью.
Операционный метод расчета переходных процессов использует для решения дифференциального уравнения САУ преобразование Лапласа. Метод более прост, так как в этом случае постоянные интегрирования находятся по известным формулам.
Математические операции здесь существенно упрощаются, так как дифференциальное уравнение заменяется алгебраическим. Легко учитываются начальные условия, что позволяет избежать сложных выкладок по определению постоянных интегрирования. Достаточно просто решаются в целом неоднородные дифференциальные уравнения САУ. К недостатку метода относится трудность в переходе от изображений к оригиналу и наоборот.
Графоаналитические методы {частотные) построения переходных процессов в САУ основаны на аналитической связи временных и частотных характеристик САУ, что вытекает из родственности преобразований Лапласа и Фурье. Частотный метод является частотным аналогом операционного метода.
Достоинства здесь те же, что и у операционного метода, но этот метод нагляднее и проще. Шире комплекс решаемых задач: определение устойчивости, качественных показателей, запасов устойчивости в САУ. Этот метод дает возможность проводить анализ и синтез САУ. Здесь возможно непосредственное использование экспериментальных характеристик САУ. Поэтому частотные методы получили среди инженерных методов большое распространение.
Частотный метод построения ПП в САУ впервые разработан В. В. Солодовниковым в 1948 г.
Связь между временными w(r) и h{t) и частотными характеристиками САУ вытекает из обратного преобразования Фурье:
w(Z) = 2 J	d(o а — | P(®)cos (orJco;
—оо	0
2 °°
w(t) = — | Q(cd) sin o)Z(Z(o;
203
,/Л 2 f Л®) • .j 2 г n, , sin coz , h(f) = — —— sm mtdm = — P(m)--------------dm;
Я' (0	nJ0 co
oo , , 4	2 f , COS (0Z ,
h(t) = - 6(co)-------dm + P(0),
я* co
— подынтегральное выражение интегрального синуса
'-с?со. Напомним, что h(t) - L-11 [И^(/>)]— L а — = 01(?) = I Pi Р
Г sin со/ , л ---------^й) =
j со 2
sm coz где-------—
со г sin coz Si coz =-----
I ®
1 1 7 sin coz , = „+	-----dm,
2 л J co
С помощью этих выражений можно построить w(z) или A(z) путем графического нахождения входящих в них интегралов по заданной Р(со). Обычно широко применяется построение h(t)— кривой переходного процесса поР(со).
Разработаны методы построения переходных характеристик по Р((о). В частности, метод Добровольского основан на разбиении кривой Р (со) на прямолинейные участки. Для каждого участка 0—1, 1—2, 2—3 и т. д. путем вычислений интеграла определяют ПП, так как в этом случае h(t) легко берется (интеграл линейный, Р(со) выражается уравнением прямой линии). Общая кривая ПП строится путем суммирования частичных кривых ПП. Однако этот метод трудоемок и ведет к достаточно громоздким вычислениям.
В случаях, когда Р(со) задана экспериментально (графиком или таблицей), а аналитическое вычисление интеграла вызывает определенные трудности, площадь под кривой Р(со) разбивают на типовые трапеции (В. В. Солодовников) или треугольники (А. А. Воронов).
Наибольшее распространение получил метод типовых (нормированных) трапеций.
Типовая единичная трапеция, приведенная на рис. 7.15, характеризуется параметрами: Р (0) = 1; corf— полоса равномерного пропускания частот; со0 = 1 — полоса полного пропускания частот (или иногда сос); X = corf/(oo —коэффициент наклона (0 < Л < 1);
, 1  I-co/cOq , . , , , 2 1 (	cost-cosXt')
A“)=olmt(+ ——-— mrflmo, Лх(т) =	- I Sit-XSiXt +
1“/.	Я 1 — Л
1 .	т .
f Sin (ОТ ,	rsmx	,
Si т =-------dm = -----dx.
I	{ x
т
204
При X = 0 типовая трапеция вырождается в треугольник; переходной процесс при этом носит монотонный апериодический характер
2 (рис. 7.16,а): ср =4л/соо, й(т) = — Si(r)-
Л
1-COST т
и(т) = 2(1 - cos т)/пт2
При Л = 1 (<о0 = (ad) типовая трапеция вырождается в прямоуголь-2
ник; ПП носит колебательный характер (рис. 7.16, б): й(т)= -Si(x),
t = 4л/(о0- Время регулирования при трапецеидальной частотной ха-р	л 4л
рактеристике изменяется в пределах — < tp < — (при 8 = 0,05); соо ®о
при X = 0,2 + 0,25 (о = 5%, £ = 0,7). Величина перерегулирования о [%] при изменении X от 0 до 1 не превышает 18% (рис. 7.16, в):
г	2.2
( sin х/x)dx = 1,85; при X = 1 —Si т = —1,85 = 1,1777. В табулирован-о	л л
ных таблицах [1, 2] приводятся значения й(т) (заранее вычислены все значения) при изменении коэффициента X с шагом 0,05 от 0 до 1, где т = со0/ = 0-5-50 — относительное время; таблица составлена по фор-, ,. 2 7	. sin со? .
муле h(t) = — J Р(со) ——— dti).
Порядок расчета кривой переходной функции h (/) при этом следующий:
1) разбивают характеристику Р (со), полученную тем или иным способом, на типовые трапеции, т. е. представляют ВЧХ суммой Р(со) = £/>(“) (рис. 7. 17, а, б);
<=1
2) для каждой типовой трапеции определяется значение Р (0) при со = 0 и определяется коэффициент наклона X = Wj/coo;
Рис. 7.16
205
3)	по полученному коэффициенту наклона X и по /г-функциям для соответствующего коэффициента X определяются значения й-функций /гх(т), где r = 030t;
4)	переход к реальному времени производится при помощи выражения t - т/соо; значения Л (г) получают умножением h(t) = P(O)hK(t);
5)	в масштабе реального времени строят кривые 4(0 в соответствии со знаком «+» или «-» ВЧХ и далее в соответствии со свойством п
линейности, суммируя их, определяют h3(t) = ^lhi(t), где п— ко-
1=1
личество трапецеидальных вещественных характеристик (рис. 7.17, в). При этом Р(0) н» /г(°°), а Р(°°) 1-> /г(0).
Пример. Пусть характеристика Р(<о) (рис. 7.18, а) имеет следующие параметры:
Р(0) = 5, юо = 1ОО1/с, <orf = 50 1/c, коэффициент наклона Л = — = 0,5. По Х = 0,5
<оо
и таблицам Л-функций выписываем значения Л^(т); / = т/<о0 = т/100[с]. Тогда Л(г) = Р(О). /^(/) = 5Лх(0 и переходная функция h (z) имеет вид, приведенный на рис. 7.18, б.
ВЧХ Р (со) можно получить аналитически, а также графически, накладывая АФХ разомкнутой системы на вещественные круговые диаграммы (номограммы) [2].
Если АФХ разомкнутой САУ задана в виде логарифмических характеристик, то пользуются логарифмическими номограммами для построения вещественных частотных характеристик [2].
206
Вместо графоаналитического построения ПП по Р (со) можно расчет ПП в САУ выполнить аналитически, т. е. воспользоваться методами численного интегрирования с помощью ППП на ЭВМ. В этом случае для решения дифференциальных уравнений САУ применяют различные ППП [2].
§ 7.10. ЧУВСТВИТЕЛЬНОСТЬ САУ
Параметры САУ практически всегда отличаются от идеализированных расчетных, что может привести к заметным отклонениям статических и динамических свойств САУ от реальных. Чувствительность САУ определяет степень влияния изменения отдельных параметров на характеристики САУ. В качестве оценки используются частные производные по варьируемому параметру уу {к или 7) — функции
Эл
Эу,-
или
и,=
Э/„
\°
, где у, —выход-
чувствительности Uy =
ная координата САУ;' Jn '— заданный критерий качества. При этом индекс «0» отмечает номинальный расчетный режим САУ при v7 = v0. Применяют также функцию чувствительности (ФЧ) передо
даточной функции Sj(p)=
ЭЖ3(Луу)
Эуу сительную) функцию чувствительности
> логарифмическую (отно-
LVj(p) =
' din И,3(р,Уу)У
Э1пу7 J
^3(AVy)


Если в САУ варьируется ряд параметров Av j, то определяют измене-т
ние оценки качества AJ = Jvar - Jn = ^Uу Av j.
207
Функции чувствительности определяют также иногда как
U{p) = [dW3(p)/dWvf
или как полулогарифмическую: [— Э1п W3(p)где Wv = Wv(p) — передаточная функция варьируемого элемента САУ.
В общем случае логарифмическая функция чувствительности (первого порядка):
( din /V
din VJ
где I — исследуемая характеристика; 5v — вариация (отклонение) параметра v (к или 7).
Если
ед
х{р) D(p)
то
LVJ(P) = ~
ЭП(р) dv, W dv
d\p)
-о
М(р) х(р)
_/э^(р)У 9V;
х(р);
MVj(p)D(p')-M(p)Dv.(p)
.. dM(p) D = дП(Р)
где Mv. =	
Если подставить р = усо, то можно получить функции чувствительности частотных характеристик САУ, например <pv(co) =
Применяют также временные функции чувствительности переходных характеристик; чувствительности корней; дисперсии выходной переменной по значению и др.
САУ, которые при всех возможных вариациях параметров vy относительно их расчетных значений сохраняют необходимый запас устойчивости, называют робастными (или параметрически грубыми, нечувствительными). Они сохраняют устойчивость САУ при достаточно сильных возмущениях.
Таким образом, в общем случае при исследовании чувствительности САУ используют ФЧ: абсолютные ($}; =dF/dVj)°, относительные (логарифмические) Sj = (din F/dln vy)°, полуотносительные (полулогариф-
208
мические) Sj = (Э1п F/dvy)° или Sj = (dF/dln vz)°. Здесь vy =v0— вектор расчетных (номинальных) значений параметров САУ; j = 1, 2, ..., т. При этом также широко применяют операторные, частотные, временные, корневые, критериальные (по критерию качества, например, Jlm, J2n) и другие выражения ФЧ (в виде скаляров, матриц, таблиц, уравнений).
В конкретных исследованиях обычно стремятся использовать ту формулу представления ФЧ, которая оказывается наиболее удобной при решении поставленных задач (например, регулировки и настройки САУ); стремятся также по возможности от ФЧ высокого и-го порядка переходить к ФЧ первого порядка, осредненных по величинам вариаций параметров.
Оценка чувствительности САУ посредством ФЧ имеет определенные недостатки, например, временные ФЧ отражают зависимость от входных величин, что не позволяет рассматривать их как характеристики только данной САУ. Применение ФЧ обычно допустимо при вариации параметров не более 25-30 % от их номинальных значений.
Чем меньше чувствительность или ФЧ, тем меньше влияние, например, изменения параметра vy- или в целом (р) на свойства САУ (по модулю), т. е. тем более высококачественной будет САУ. Теоретически идеальным пределом являются САУ с нулевой чувствительностью, когда осуществляется полная компенсация изменений v; [схемная, увеличением кос, к? —> °° и т. п.], т. е. реализуется переход к инвариантным САУ. Следует отметить, что обычно звеном САУ с варьируемыми параметрами является либо ОУ (учитывается неста-ционарность его параметров), либо УУ (регулятор) с варьируемыми параметрами настройки (кр, Тя, TR).
Для обычных САУ чувствительность по отношению к ОУ равна Щ)е(7’) = 1_И/з(/’)=У0 + ^р(/7))’ т- е- этим САУ с нулевой чувствительностью соответствуют САУ с нулевой ошибкой. В САУ с компенсацией с 1Ук(р) требуется, чтобы WK(p) = 1/ЙИоу(р) или ИЛк(р) = = \/Wyy(p) (условия нулевой чувствительности). Однако реализовать эти условия практически невозможно по физическим соображениям. Поэтому САУ с нулевой чувствительностью представляют собой тот идеал, к которому желательно стремиться с учетом реальных условий.
Глава 8. КОРРЕКЦИЯ СВОЙСТВ САУ
§ 8.1.	ВИДЫ КОРРЕКЦИИ
Для выполнения требований по устойчивости, точности и качеству переходных процессов применяют коррекцию динамических свойств САУ. Коррекция используется для обеспечения устойчивости неус-
14 А. А. Ерофеев
209
тойчивой САУ, расширения запасов и области устойчивости, повышения качественных показателей переходных процессов. Коррекция осуществляется с помощью введения в систему корректирующих звеньев (КЗ) с определенной, заранее подобранной, передаточной функцией типа W (р) динамических звеньев.
Корректирующие звенья могут включаться последовательно (рис. 8.1, а) или параллельно (рис. 8.1,6, в) с основными звеньями САУ. Соответственно они делятся на последовательные и параллельные КЗ и представляют собой звенья, вводимые в САУ для изменения ее динамических и статических свойств. Проблема получения в САУ требуемых точности в типовых режимах, запасов устойчивости и быстродействия — является единой.
Для линейных САУ все виды соединений корректирующих звеньев эквивалентны, т. е. каждое из них дает полностью подобные в динамическом отношении САУ. Эквивалентность корректирующих звеньев может быть получена из условий равенства W (р):
^э1=^э2 = ^эЗ -ИЛИ ^Ki^0 = W0 + WK2 = W0/(l±W0^K3).
Тогда можно получить шесть формул перехода от корректирующих звеньев одного типа к корректирующим звеньям другого типа
WKi(p)
1	:Л« + ^2.
1±ИЬ^з	’
\±wawK
и/кз(/’) = и;с(р) = ±и/^1 ИпРК.,
^к2
Ж02 + Ж01ГК2
Линейные корректирующие звенья, устройства (пассивные, активные) подразделяются на пять групп: с запаздыванием по фазе и изменением ЛАХ на - 20 дБ/дек; с запаздыванием по фазе и изме
Рис. 8.1
210
нением ЛАХ на - 40 дБ/дек; с опережением по фазе и изменением ЛАХ на + 20 дБ/дек; с опережением по фазе и изменением ЛАХ на + 40 дБ/дек; с опережением или запаздыванием по фазе и изменением ЛАХ на ± 20 дБ/дек или ± 40 дБ/дек (корректирующие звенья комбинированного типа).
§ 8.2.	КОРРЕКТИРУЮЩИЕ ЗВЕНЬЯ ПОСЛЕДОВАТЕЛЬНОГО ТИПА
Корректирующие звенья последовательного типа применяются в САУ с электрическим сигналом в виде напряжения постоянного тока U, который функционально связан с ошибкой е, т. е. U = f (е), например, U = ке. Корректирующее звено реализуется на пассивных или активных jRLC-элементах (чаще на элементах RC).
Если сигнал — модулированное напряжение переменного тока, то применение пассивных ЯС-элементов, хотя принципиально и возможно, но практически затруднительно из-за их сложности.
Для модулирующего сигнала в настоящее время применяют обычно только последовательные корректирующие звенья, например, дифференцирующие звенья с симметричными характеристиками относительно несущей частоты. Звено должно подавлять несущую частоту, т. е. выделять полезную огибающую сигнала.
Корректирующие звенья в большинстве случаев представляют собой типовые динамические звенья, основное назначение которых изменять свойства САУ в нужном направлении, например, изменить качество ПП.
Корректирующие звенья могут быть выполнены из различных по физической природе элементов: электрических, механических, гидравлических и т. д. Наиболее простой реализацией являются корректирующие звенья из RС и RL активных и пассивных элементов.
Широкое применение получили следующие последовательные корректирующие звенья: пропорционально-дифференцирующие (ПД), пропорционально-интегрирующие (ПИ), пропорционально-интегро-дифференцирующие (ПИД). Пассивные корректирующие звенья могут быть представлены в виде обобщенной схемы (рис. 8.2, а); передаточная функция такого корректирующего звена:
211
14*
им г1(р)+г2(Р)-
где Z](/>), z2(p) — сопротивления в операторной форме.
Передаточная функция активного корректирующего звена №а(р)» « ~z2(p)/zi(p) и может быть представлена в виде обобщенной схемы на рис. 8.2, б. Отсюда могут быть получены любые КЗ с W(p) из 7?ЛС-элементов: г}(р); z2(p)=l/pC; R; рЦ 1/рС||Л; 1/рСлЯ; R/\\/pC/\pL и другие комбинации (л —знак «И», || —знак «параллельно»).
Пропорционально-дифференцирующее звено. Идеальное ПД-звено имеет следующую передаточную функцию (рис. 8.2):
( k \ ^пд (р) = кп ± клр = £п 1 ± р = ка (1 ± тлр),
где Гд — кл I ка.
Например, если
Zi(/’)=^i/(l + ^iCi/’)! z2(p) = T?2,
то Wa(p) = -кп(\ + Тар)-, при этом kn=R2/Rv, TJl=RlCv
Выходная величина звена содержит две составляющие — пропорциональную входной величине с коэффициентом кп и пропорциональную с коэффициентом + ка ее первой производной.
Пропорционально-дифференцирующие (ПД) звенья, создающие на выходе, кроме того, составляющую, пропорциональную второй производной, являются ПДД или ПД2 -звеньями. Это соответствует последовательному включению двух ПД-звеньев:
^(/’) = ^1М1+^1р)(1+^д2р) = ^пГд7д2/’2+(га1+гд2)/’+1Ь где ка — кп^кп^.
Введение воздействия по производной с помощью ПД-звена изменяет значение коэффициента при р в первой степени в многочлене D (р) замкнутой САУ. Применение ПД2 -звена (со второй производной) или двух ПД-звеньев приводит к изменению коэффициента при р2 и т. д. Это изменяет условия устойчивости и качество переходных процессов в САУ. Например, применение ПД-звеньев позволяет сделать структурно неустойчивые САУ структурно устойчивыми, т. е. обеспечивает устойчивость САУ с астатизмом выше первого порядка. Следовательно, САУ с астатизмом порядка г > 1 может быть сделана структурно устойчивой при введении положительных воздействий по производным от первого до ( г - 1)-го порядка.
212
Можно аналогично показать, что с помощью ПД-воздействий можно сделать устойчивой САУ, структурно неустойчивую из-за наличия в ней неустойчивых звеньев [в D (р) есть члены с отрицательными коэффициентами]. Применение дополнительных воздействий по производным соответствующего порядка позволяет изменить в£>(р) знак этих коэффициентов.
Если ПД-звено соединить со статическим звеном первого порядка, то получим
(к„ ± к,.р)к{}	,	1 ± Т„р
ВД = WQ(p)W^p) = п .............°- = кокп
Тор + 1	1 + Тор
h(t) = kMt)±kaho(t')>
где /%(г) — переходная функция статического звена.
Переходные характеристики приведены на рис. 8.3. Здесь характеристике 1 соответствует отрицательное воздействие по производной (кл < 0), 2 — такое же, но положительное воздействие (ка > 0). Положительное ПД-воздействие повышает быстродействие в САУ. При Тл = То (характеристика 4 на рис. 8.3) получается идеальное безынерционное звено, когда W3l(p) = как0; при Та > То — характеристика 5.
Влияние ПД-воздействий на переходную характеристику инерционного звена любого порядка аналогично выше рассмотренному случаю, но чем выше порядок WQ(p), тем выше порядок производной, требуемый для полной компенсации инерционности [требуются дополнительные воздействия до соответствующей порядку W0(p) производной]. Практическое применение нашли дополнительные воздействия по производным первого и второго порядков; более вы
сокие производные используются редко.
Положительное ПД-воздействие форсирует течение переходного про
цесса (убыстряет его); отрицательное ПД-воздействие замедляет течение переходного процесса.
На рис. 8.4 приведены ЛАХ и ФЧХ ПД-звена, обратные частотным характеристикам статического звена первого порядка. ПД-звено является фильтром верхних частот, так как ЛАХ растет с увеличением частоты, расширяет полосу пропускания САУ, т. е. повышает ее быстродействие. ФЧХ ПД-звена положительна, звено уменьшает суммарное запаздывание по фазе в САУ (до 90° при и -э °°).
213
Реальное ПД-звено обычно обладает инерционностью, его передаточная функция
W (D) = k-^P = k т - Кп , гр

ь
где Та=^ ТВД«ТД; кп =kjTa -коэффициент передачи звена.
Инерционное ПД-звено представляет собой последовательное соединение идеального ПД-звена и статического звена первого порядка. Это звено влияет слабее на быстродействие и соот-
ветственно на область устойчивости САУ; при Та = Тпд влияние уменьшается до нуля (рис. 8.5, а).
Форсирующее действие звена происходит за счет начального всплеска характеристики h(t) = + (1 - ка )е~^Г"д j-ol(0 над уровнем ступеньки (рис. 8.5, б); здесь (рис. 8.5, в)
тв. ~
При Тлд = 0 звено становится идеальным ПД-звеном.
Частотные характеристики ПД-инерционного звена представляют собой сумму характеристик идеального звена и инерционного звена первого порядка; ПД-звено (рис. 8.6).
НО = 5(0-
•oKO-
подавляет нижние частоты
214
Пропорционально-интегрирующее звено (ПИ-звено). Идеальное ПИ-звено имеет передаточную функцию
^пи(р) = ± кп = кп	=А(1 ± Тир);
р Кр р
реальное ПИ-звено —
^-±к
w (V)^P	" 1 кч±кпР 1±КР _к*1±КР
' ттР+1 рт^р+i "ада+тад pi+ад’
где К=кп/ки.
Таким образом, ПИ-звено эквивалентно последовательному соединению интегрирующего звена и ПД-звена. Например, если
z,(p) = 7?1; z2(p) = R2 + ~^-,
рс2
то
Wa(p) = -= -к
7]р р Кр ’
где К=^С2, Tl = RlC2; kp = R2/Rx.
ПИ-звено обычно применяют для повышения порядка астатиз-ма при сохранении устойчивости и необходимого качества переходных процессов. При этом знак для воздействия по интегралу должен быть положительным; знак воздействия по производной может быть любым.
Частотные свойства ПИ-звена, как фильтра нижних частот, «обратны» таковым у ПД-звена (рис. 8.7). Здесь пунктиром показано изменение ЛАХ при наличии инерционности звена.
Пропорциональное интегродифференцирующее звено. Идеальное ПИД-звено имеет передаточную функцию
k	к ( к к
^пид(^) = “±*п±*д/’ = — 1±7t/’±TiP	=
р	р ка ки )
к„(1±Тир±ТаТдр2) Кр
реальное ПИД-звено —
— ±к„+к„р	( г гг, Л ,, „	_ о.
р -к« ±тв.Кр ±Кр+1 к„ (^Кр^ККр ) адр+i р t адр+i J Кр (ТпидР+1)
где К=кп/к»> К = ка/кп-
215
ПИД-звено эквивалентно последовательному соединению либо интегрирующего звена и ПД-звена с воздействиями по двум производным, либо ПИ-звена и ПД-звена с одной производной. ПИД-звено повышает порядок астатизма (как и ПИ-звено); дает более сильную коррекцию динамических свойств САУ.
Выбирая параметры Тк, Тя, Ттл, можно получить временные характеристики звена, позволяющие отнести его к звеньям форсирующего типа. При этом ПИД-звено в области средних частот подавляет сигнал.
На частотах ю -э 0, со —> звено не вносит фазовых искажений, вносит отрицательный фазовый сдвиг в нижней части области средних частот, положительный фазовый сдвиг — в верхней части области средних частот (рис. 8.8).
В общем случае у реального ПИД-звена (рис. 8.8)
w(р) =	+ ^Р+1 _ (Т{р+1)(Т2р+Т)
a^+cw+l (Т3р+1)(Т4р+1)’
21^ где Th Т2, Ту, Т4 определяются по формулам: Тщ =----.-----rpf ’
/7	V**
а1±(«1 “Н)
ЛАХ звена имеют на средних частотах «корытообразную» форму; обычно справедливы соотношения Ту > 7] > Т2 > Т4. Здесь 7}, Т2 — постоянные времени числителя, Ту, Т4 — знаменателя. Звено пропускает нижние и высокие частоты и подавляет средние частоты.
Для коррекции динамических свойств САУ используют также ПИДД- или ПИД2-звенья с воздействием по первой и второй производной.
216
При алгоритмическом синтезе дискретных САУ в качестве передаточных функций последовательного корректирующего звена обычно используют функции вида: W^z) = а^ + а^"1; W2(z) =	W3(z) =
l + ijz 1
az z-1	.	. ao + aiz-1+a2z-2	4
_----+----,а<1 или H/3(z) =------i-n--Здесь Wdz) соответ-
z-lz	1 + qz+Z^z
ствует дифференцирующему звену [аналог W}(p) = 1 + Тар], JF2(z) —-I I 'J'' p
аналогу пассивного ПД- или ПИ- звена W2(p) = Go-— [ Go = Tw /Та;
+ Ткр
при Та > Тп — ПД-звено, при ТЛ<ТК— ПИ-звено], FF3(z) — аналогу ПИД-звена (w3(p) = (ТдТир2 + Тир+1)/Тир).
§ 8.3.	ПАРАЛЛЕЛЬНЫЕ КОРРЕКТИРУЮЩИЕ ЗВЕНЬЯ
Согласно-параллельные корректирующие звенья. Обычно эти звенья применяют при формировании алгоритмов управления, например ПИ-, ПИД- и др. [10], в тех случаях, когда необходимо осуществить сложный закон управления с введением de Idt, ^edt и других функций от е, например в виде ПИ-устройств (изодромных).
Введение интегралов от ошибки управления J edt соответствует поднятию нижних частот и преследует цель уменьшить значение установившейся ошибки управления (или сделать ее равной 0).
Введение производных ( ё, ё и т. д.) соответствует поднятию верхних частот и преследует цель увеличить запас устойчивости системы (рис. 8.9). При этом для разных вариантов включения дифференцирующих звеньев в схему (см. рис. 8.9, а, б) получим соответственно разные формулы:
= (1 + ад(1 + Т2р) = Т,Т2р2 +(7J + Т2)р+1;
W32(P) = (1 + T2p)TlP+1 = Т^р2 + TiP+L
Здесь дифференцирующие звенья изображены идеальными с ^(р) = 7]р.
Рис. 8.9
217
Встречно-параллельные корректирующие звенья — обратные связи. Корректирующие обратные связи могут быть отрицательными, положительными, а также жесткими и гибкими.
Корректирующие устройства-звенья в виде обратной связи (ОС) находят наиболее широкое распространение вследствии удобства технической реализации и обладают следующими достоинствами:
простота — вследствии того, что на вход элемента ОС поступает обычно сигнал высокого уровня с выхода САУ, что не только не требует усилителей, но, напротив, требует ослабления сигнала для его согласования с входным сигналом;
в реальной САУ, как правило, всегда имеют место нелинейности (силы трения, люфт, зазор, зона нечувствительности и т. д.), которые при охвате САУ ООС существенно ослабляют свое влияние на процессы управления. Поэтому использование ООС с йИкз(р) = Woc(p) по сравнению с WKl и дает возможность улучшить переходный процесс в САУ;
ООС дает лучший эффект, когда в САУ вследствии действия внешних факторов (t°, t и т. д.) изменяются параметры — коэффициенты усиления, постоянные времени и др., т. е. ООС стабилизирует параметры САУ или участка САУ, охваченного ООС.
Благодаря перечисленным достоинствам ООС нашла широкое распространение в технике САУ.
В целом влияние различных корректирующих звеньев сводится к созданию в САУ управляющих воздействий по производным и интегралам, дополнительных воздействий в контуре САУ в виде корректирующих обратных связей вокруг отдельных частей системы и корректирующих воздействий в функции внешних возмущений f и их производных рк f.
Корректирующие обратные связи применяются (в основном как отрицательные) для уменьшения влияния инерционности и нелинейности звена, нестабильности его параметров во времени; влияние ПОС противоположно влиянию ООС на вышеуказанные свойства.
Обратные связи в динамическом отношении могут оказывать самое различное действие; аналогично последовательным корректирующим звеньям их можно разделить на три основных вида: подавляющие высокие частоты (аналоги — интегрирующие звенья); подавляющие нижние частоты (аналоги — дифференцирующие звенья); подавляющие средние частоты (аналоги — ПИД-звенья).
Аналогию обратным связям с видом последовательного корректирующего звена можно установить при помощи формул перехода. Расчетным путем при синтезе САУ наиболее просто определяются параметры последовательных корректирующих звеньев. Поэтому обычно важно иметь возможность перехода от последовательного корректирующего звена с передаточной функцией PPK1(p) к эквивалентной обратной связи, когда
218
woc{p) = ±
WQ(p)WKX{p)
В качестве примеров можно привести случаи перехода от последовательного корректирующего звена, включенного на выходе усилителя с коэффициентом ку, к обратной связи (обратная связь электрическая или неэлектрическая):
при WKi(p) = кп-> Woc(p) =
при W^p) = ~^(Tx>T2) ПИ-звено ^woc{p) = k^^ (ПД-1+ цр	1+17р
звено);
при WAp) = ^^>l^ ПД-звено Жос(р) = kl(l + TlP) -7](1 + Т2р)
апериодическое звено и т. д.
Жесткая ООС (£ос) [если Ид(/>) —колебательное звено второго порядка], снижая инерционность, одновременно увеличивает его колебательность, что нежелательно, так как может способствовать росту колебательности в целом САУ.
Если И’о(р) = £q/р, то применение ООС (с к^) снижает порядок астатизма системы и соответственно ведет к улучшению ее устойчивости и качества переходных процессов. Например, обычно жесткой ООС охватывают электрические и гидравлические двигатели, используемые в качестве исполнительных для перемещения органов управления объектами (двигатели — интегрирующие звенья, если их выходная величина — перемещение или угол поворота вала).
Инерционность ООС приводит к увеличению быстродействия САУ за счет замедления роста сигнала обратной связи на ее входе, что эквивалентно введению форсирующего воздействия по производной (как при применении ПД-звена). Инерционность ПОС, наоборот, затягивает переходной процесс.
Гибкая обратная связь, например JT0C(p) = коср, не влияя на коэффициент передачи охватывающего звена, изменяет коэффициент при р в знаменателе передаточной функции W0(p). Если
W0(p) = k0/(T0p+T), то W3(p) =
(Г0±Л0кОс)/’ + 1
Здесь ООС увеличивает постоянную времени, а положительная — уменьшает. Следовательно, применение положительной гибкой обратной связи повышает быстродействие (форсирует входной сигнал) без уменьшения коэффициента передачи; отрицательная гибкая обратная связь, наоборот, затягивает переходной процесс. В случае звена вто
219
рого порядка гибкая ООС увеличивает Т2 и, соответственно, £ = 7^/27j, т.е. является эффективным средством уменьшения колебательности.
Гибкая обратная связь по второй производной (по ускорению), когда ИЛос(р) = коср2, дает
Q(p) + k0kocp2’
т. е. изменяет коэффициент при р2 (применяется в САУ второго и более высокого порядка).
Инерционность гибкой ООС повышает быстродействие, инерционность ПОС —снижает его. Например, широкое распространение получила инерционная гибкая обратная связь с 1У0С(р) = = ^осР/(КсР+^) ВОКРУГ интегрирующего звена (изодромная обратная связь).
§ 8.4. СПОСОБЫ УВЕЛИЧЕНИЯ ЗАПАСОВ УСТОЙЧИВОСТИ САУ
Увеличение запасов устойчивости, стабилизация и демпфирование САУ связаны с рациональным изменением коэффициентов а„, Ьп дифференциального уравнения САУ (или полюсов и нулей) таким образом, чтобы САУ имела наибольшие запасы устойчивости. Заметим, что так как W3(p) САУ тесно связана с Wp(p), то это приводит к изменению коэффициентов дифференциального уравнения и разомкнутой САУ.
Если САУ в разомкнутом состоянии устойчива (не имеет полюсов в правой полуплоскости), то по виду ее АФХ, в соответствии с критерием Найквиста, можно судить об устойчивости САУ. Демпфирование САУ связано с деформацией АФХ таким образом, чтобы кривая не охватывала критическую точку и была удалена от нее на требуемые запасы устойчивости (/г, у). Удаление АФХ от критической
точки определяют на основании какого-нибудь критерия качества, наиболее просто с помощью показателя колебательности М (например, ум = arcsin 1/Л/3 для САУ с г = 1). АФХ не должна заходить
внутрь окружности, соответствующей заданному значению М3 = const
-=='Х-	— )
Л/2-Г
Деформация АФХ (демпфирование САУ) осуществляется тремя основными способами с помощью корректирующих звеньев различного
вида, например последовательных корректирующих звеньев.
1.	Деформация АФХ с подавлением высоких частот. Идея способа заключается в том, чтобы так деформировать АФХ разомкнутой САУ ЙГр(усо) в области высоких частот со > со в, чтобы она имела же-
220
Рис. 8.10
лаемый вид по М3 (рис. 8.10, а). Подавление усиления на высоких частотах всегда сопровождается появлением отрицательных фазовых сдвигов (-Дер (со)). Этот способ наиболее просто реализуется у статических САУ посредством введения в прямой канал управления САУ
апериодического звена первого порядка с W0(p) =	с боль-
1 + 7о/?
шой постоянной времени То и к0 = 1. Если к0 *1, то должно выдерживаться соотношение к$/Тй =<вс =const так, чтобы Wp(p) = = к/(Тор+1). Наглядно это можно продемонстрировать с помощью логарифмических характеристик (рис. 8.11), где исходная САУ (7—1) неустойчива; скорректированная САУ (2—2) имеет необходимые запасы (у, ДЕ). Следовательно, включение апериодического звена с большой постоянной времени То делает остальные постоянные времени Т/ САУ малыми параметрами.
Кроме этого, демпфирование САУ может быть осуществлено и более сложными КЗ, например, путем введения ПИ-звена (или его аналогов) с W(p) =	1/Т^Д (Та>Т) и др. Этот способ
Тяр	ТиР+*
221
Рис. 8.11

увеличения запасов устойчивости получил еще название демпфирование с введением отрицательных фазовых сдвигов (запаздывание по фазе), которое вызывает «закручивание» — поворот АФХ по часовой стрелке (см. рис. 8.10, б).
Достоинством способа демпфирования САУ с подавлением высоких частот является высокая помехозащищенность системы, так как вводимые КЗ представляют собой фильтры низких частот. Недостатком спо
соба является уменьшение быстродействия в системе. Поэтому способ применяется тогда, когда к системам по быстродействию не предъявляется высоких требований.
В астатической САУ первого порядка, состоящей из минимально-фазовых звеньев, желаемый запас устойчивости может быть всегда получен при введении последовательного ПИ-звена. В САУ с г = 2 запас устойчивости может быть получен подавлением высоких со только в некоторых случаях.
2.	Деформация АФХ с поднятием высоких частот. Идея способа заключается в том, чтобы развернуть высокочастотную часть АФХ в положительном направлении, т. е. против часовой стрелки. Тогда система за счет деформации АФХ приобрела бы требуемые запасы устойчивости (см. рис. 8.10, в). Положительный сдвиг АФХ САУ производится с помощью дифференцирующих звеньев, которые дают фазовые упреждения (опережения) или положительный сдвиг по фазе + Д<р (со). Таким образом, включая в прямой канал САУ звенья D-или ПД-типа, например, lVK(p) = 1 + ТДр, будем получать дополнительный положительный фазовый сдвиг: +фк(со) = arctg со Тд. При >сов—>оо фк(со)—>90°, что и вызывает «закручивание» конца АФХ относительно начала координат в высокочастотной области.
Однако наряду с внесением положительного фазового сдвига одновременно с возрастанием со возрастает и модуль КЗ Лк(со) = = д/1 + со2Тд ; возрастает коэффициент передачи и, следовательно, через систему будут проходить высокочастотные помехи.
Если сдвиг по фазе от одного звена оказался недостаточным, необходимо включение двух дифференциальных звеньев:
^к(Р) = (1 + ГД1/>)(1 + ТД2р).
222
Тогда Фк(со) = arctg О)ТД| +arctg а>Тд2. Однако при этом будет увеличиваться модуль, так как Лк (со) = ф + (О2?^2	+ со2Тд22.
Тот же эффект можно получить, включая в прямой канал САУ пассивные дифференцирующие звенья с замедлением 1Кк(р) =
_ _А—"----, где Кд<1, /д »/ф. Эти звенья подавляют нижние
7фР+1
частоты, а для высоких частот имеют модуль Лк((о)==1, т. е. положительный фазовый сдвиг вносится не за счет поднятия <ов, а за счет подавления низких частот. Так как здесь кл < 1, а уменьшение коэффициента усиления кр допускать нельзя по условиям заданной точности, то требуется соответствующее увеличение коэффициента кр в 1/'ка раз.
Недостатком этого способа демпфирования является свободное прохождение повышенного уровня высокочастотных помех САУ. Последнее может нарушить ее работу. Достоинство способа — увеличение быстродействия САУ.
Способ повышения запасов устойчивости посредством введения дифференцирующих звеньев (или их аналогов в виде ОС) позволяет для всех систем (в том числе неминимально-фазовых) получить требуемые запасы устойчивости и повысить быстродействие САУ. Иногда для ограничения уровня помех применяют специальные узко- и широкополосные фильтры, что, правда, усложняет САУ.
3.	Деформация АФХ 1 (см. рис. 8.10, г) с подавлением средних частот. Идея способа заключается в том, что основные показатели качества системы, в том числе и запасы устойчивости, определяют средние частоты. Таким образом, если подобрать КЗ, которое подавляет диапазон средних частот -со2 (см. рис. 8.10, г), то можно получить желаемый вид АФХ (2) с требуемыми запасами устойчивости при практическом сохранении быстродействия САУ (ее полосы пропускания). Технически этот способ осуществляется включением в прямую цепь управления интегродифференцирующих (ИД), ПИД-зве-ньев (или их аналогов в виде ОС). Этот способ является более универсальным и наиболее распространенным.
К этому способу примыкает по своим свойствам вариант демпфирования САУ с введением отрицательных фазовых сдвигов за счет использования неминимально-фазовых звеньев, например, с WK(p) = \-Тр
=----г и с фк(сй) =-2arctg® Г. Обычно его применяют в случае,
1 + Тр
когда разомкнутая САУ неустойчива (содержит консервативные звенья, колебательные звенья с малым затуханием и т. п.). В результате обеспечивается устойчивость и сохраняется быстродействие САУ, т. е. ее полоса пропускания, так как Лк(<а) = 1. Использование других способов здесь затруднительно.
В практике проектирования САУ могут использоваться комбинации этих способов, например, третьего и второго.
223
Глава 9. АЛГОРИТМЫ И ПРОГРАММЫ УПРАВЛЕНИЯ В САУ
§ 9.1. АНАЛОГОВЫЕ (НЕПРЕРЫВНЫЕ) АЛГОРИТМЫ
Устойчивость и качество процессов управления в САУ в значительной мере определяются законом (алгоритмом) управления, реализуемым в САУ. Формирование алгоритма в САУ зависит от цели управления, структуры и состава ее звеньев. В промышленных САУ управляющие устройства (УУ) (регуляторы) обычно проектируют как некие самостоятельные устройства, реализующие тот или иной алгоритм, так как структура таких САУ состоит, как правило, из УУ и ОУ. Хотя и здесь в формирование алгоритма входит учет W (р) таких звеньев, как исполнительный механизм (ИМ), УЭ, ЗЭ, ЭОС, корректирующих звеньев и др.
В соответствии с известным законом необходимого разнообразия (У. Р. Эшби) сложным ОУ должны соответствовать УУ с разнообразием управляющих воздействий. Следовательно, диапазон изменения структуры алгоритмов управления чрезвычайно широк и простирается от простых (типовых) алгоритмов для простых (типовых) ОУ до интеллектуальных алгоритмов управления для сложных или системно-сложных ОУ. В состав простых алгоритмов обычно включают типовые линейные и нелинейные (аналоговые и дискретные) алгоритмы управления, которые здесь рассматриваются ниже. Структуры сложных алгоритмов также чрезвычайно разнообразны и включают как сложные комбинации простых алгоритмов, например, многомерные (многосвязные) алгоритмы (см. п. 9.5), так и специфические (специальные) алгоритмы типа нечетких (или лингвистических) алгоритмов, алгоритмов с четкими и нечеткими данными с использованием баз данных, баз правил (БП), баз знаний (БЗ), способных к обучению и самообучению (на основе, например, искусственных нейронных сетей), генетических алгоритмов, и в общем случае, интеллектуальных алгоритмов (см. п. 1.3 (7)) [15]. В сложных ИСУ используют, в частности, базы алгоритмов [14,15].
Алгоритмы управления могут быть реализованы аппаратно, программно-аппаратно или программно. В общем случае передаточная функция УУ (рис. 9.1):
w ( ) =	= Ьтрт +ЬтАрт-} + ... + bQ
Р	е (р)	а„рп + ап_1рп~х +... + ^
Дифференциальное уравнение линейного УУ имеет вид:
(Г„рй + ... + Т22р+7]р+1)Кр)-Е(р) ^д(„-1)Р(" 1) + --- + Рд1Р+^до+ ^1 + /(Р) [&/0 + kf\P + •   + /(m-l)P”’ * ]>
224
где далее обозначим клХ = ка; ка0 s skx, кд_х=к0; п = 0, 1, 2, ... ;
т = 1, 2, • • • •
Здесь левая часть отражает инер-
УУ

ционные свойства УУ, а правая —	Рис 9 j
алгоритм (закон) управления (вторая
квадратная скобка относится только к комбинированным УУ).
У идеального комбинированного УУ (регулятора) при /=0 (7}=а i = l,n): ИЛри(р) = 44 = ^д(л-1)/’"’1 +   + кар+кх + к(>-. Здесь £\PJ	Р
к}=кр = !/?>, где 3 характеризует статизм. Вынесем кх из Wpn(p),
получим
^p.h(p)=[^+i+^+W+...+t^_1)p''-1U,
к *яР	J
где
Т = —1 • Т	Т - ^Д;  Т -
и к0’ л <’ Д2 V’ д("-1) ~	’
Иначе выражение для передаточной функции УУ можно записать так:
к
WpM(p) = -~(1 + ТКр+ тцтлр2 + ...), Тир
где правая часть описывает, в частности, ПИД-регулятор, или регулятор с пропорционально-интегрально-дифференциальным законом управления (без учета + ...).
У реального аппаратного УУ Wp(p) = ^риРРб(р), где W6(p) =
=----------2---------» — передаточная функция инерционного
1 + Тхр+Т2Р + ... + Тпр балластного звена.
Рассмотрим типовые (унифицированные) идеальные линейные алгоритмы (законы) управления.
1.	Пропорциональный алгоритм управления. Временные характеристики УУ приведены на рис. 9.2, а. Здесь е (г) — входной сигнал (сигнал ошибки системы), е (?) = х3(?) - yQC (?); ц (г) — регулирующее воздействие на выходе УУ. Алгоритм управления характеризует функциональную связь между ц (?) и е (?). Для идеального П-регулятора (рис. 9.2, б):
ц(?) = ЛрЕ(?).
Реальная характеристика УУ имеет нелинейный характер и содержит «зону насыщения» с уровнями Ц] и ц2 (рис. 9.2, б).
15 А. А. Ерофеев
225
Передаточная функция для такого регулятора имеет вид Wp(p) = = ц(р)/е(р) = кр. Фактически передаточная функция аппаратного регулятора имеет вид W(p) = Wpif(p')lV5(p'), где обычно W5(p) = = 1/(Т6р +1). Здесь 8 = 1 / кр =lim Wp (р) определяет статизм регулятора (при к0 = 0) или остаточную неравномерность регулирования. Параметр настройки — кр.
Частотные характеристики определяются коэффициентом кр , так как Wp(Ja>) = kp; L((o) = 201g&p.
Для увеличения запасов устойчивости, уменьшения статической ошибки в САУ применяют модификацию П-алгоритма следующего вида:
Н(0 = *ре(0 + Мз(0,
где к3 — коэффициент усиления по цепи формирования задания x3(t).
Введение члена k3x3(t) в алгоритмы управления широко практикуется, особенно для промышленных систем со скачкообразным изменением задания x3(t) (систем программного управления и т. п.).
2.	Интегральный алгоритм правления. Характеристики И-регулято-ра приведены на рис. 9.3. Алгоритм управления здесь имеет вид
И(0-_ |е(т)</т (рИС. 9.3, fl); и о
или
dp(t)ldt = kHE(t) (рис. 9.3, б).
В операторной форме
Н(р) =	£(р)>
ТИР
226
где Тк —постоянная интегрирования; кн = 1/Ти —коэффициент пе-реда-чи. Передаточная функция идеального И-регулятора Wp(p) =
= ц(р)/е(р) = 1/Тир. Реально УУ содержит также W6(p) = —~—
Гбр+1
На рис. 9.3, а приведены характеристики ц (?) для различных значений Тъ\ здесь аналогично имеет место и «зона насыщения». Как видно из рис. 9.3, а, чем больше значение Т§, тем сильнее алгоритм управления отличается от идеального (Тб = 0).
При ступенчатом воздействии входного сигнала выходная координата регулятора возрастает до бесконечности (реально до насыщения; например, усилителя регулятора). И-управление применяется для ОУ, обладающего существенным самовыравниванием. Если самовы-равнивание невелико, то системы с И-регулятором могут быть склонны к неустойчивости. И-управление делает установившуюся ошибку стремящейся к нулю (астатическое управление).
Для всех типов УУ существуют настроечные параметры, которые перестраиваются в зависимости от характеристик ОУ: W0(p), h (г), /(/). Они различны для различных ОУ. Для И-регулятора настроечный параметр Тп. Частотные характеристики И-регулятора:
ИС(» = —
Р >ТИ шТи
где 1//= е”-'(я/2).
Фазовый сдвиг И-регулятора — фиксированная величина: Ф = = -л/2 = const (t). Передаточная функция И-регулятора может быть записана так: W(p)=kp/р, где кр=\/Тя. Тогда Ци) = 201g|/cp|--201g со. При Тя —> оо И-регулятор становится П-регулятором; при Ти—>0 кр->оо, но крТя = const и тогда имеем И-регулятор.
Для тех же целей (как было отмечено в п. 1) формируется модифицированный И-алгоритм управления вида
Ц(0 = “- |е(т)А + /с3х3(г).
** о
3.	Пропорционально-интегральный алгоритм управления. Характеристики ПИ-регулятора (изодромного регулятора) приведены на рис. 9.4. ПИ-регуляторы обеспечивают хорошую устойчивость с одновременным устранением установившейся (статической) ошибки. При Ти —> °о получаем П-регулятор. При Тя —>0 кр -э оо, Но крТя = const и тогда — И-регулятор.
Алгоритм управления имеет вид:
Ц(0 = *р e(t) + -Me(T)dT
I о
227
15*
или
d\k(t)/dt = kp[dE(t)/dt + kvy(t)].
Передаточная функция ПИ-регулятора:
FFp(p) = Jl+-?-
I Кр.
W+Kp) Кр
где Тк —время интегрирования, называемое также временем изодрома, временем «удвоения» [ когда ц(Ти) 2крг(0), т. е. удваивается по сравнению с &пе(0) = ц(0)]. Здесь также у реального УУ обычно 1 р
= —7, причем аналогично, чем больше значение Т6, тем Кр+>
существеннее отличается процесс в УУ от идеального (см. рис. 9.4).
Параметры настройки ПИ-регулятора: Ти и кр. Частотные характеристики:
nz (/т) =	+ тГ )e~y(7t/2) = к 1+(—1	.
j®TK в>тя{1+](а1к)е \(оги;е
L(co) = 201g |k„| +201g Jl + I —— I ; (р(со) =-arctg 1 1 V (“М
1 соТи
Модификация И-алгоритма также, как и для П- и И-алгоритмов, содержит дополнительный член k3x3(f).
Для ОУ-инерционных звеньев первого порядка с т (или без т) ПИ-регулятор является квазиоптимальным, минимизирующим интегральный критерий качества процессов, например, интегральную квадратичную оценку качества Ко = J[Д£(012^-
4.	Пропорционально-дифференциальный алгоритм управления. Характеристики ПД-регулятора приведены на рис. 9.5. Алгоритм управления имеет вид:
Ц(0 = ^р[е(0 + Kd^ldt ]•
Передаточная функция идеального ПД-регулятора Wp(p) = ц (р)/Е (р)= = кр(1 + ТДр).
Параметры настройки: кр и Тл (Тя — постоянная дифференцирования — упреждения). Для ПД-регулятора:
Жр(» = &р(1 + >ТД) = кр/+(Тат)2^-,
Жр(7(0) = fcp(l + усоТд) = kJl+iT^)2^- Ф(<о) = arctg шТд.
228
Если в ПД-алгоритме присутствует только Д-составляющая, то Wp(p) = крТлр, а W(j(O) = JwkpTa; Wp(ja) = крТаш Ф = ^ = = const.
Модификации ПД-алгоритма имеют следующий вид:
p(t) = kp[e(t) + Tady(t) / dt];
КО = Лр[е(0+T^ty'dt ]+k3x3(t);
КО = fcp[e(0 +Tady(t)/dt]+k3x3(t),
где y(t) = yac(t) —текущее значение регулируемой координаты (параметра) ОУ.
5.	Пропорционально-интегрально-дифференциальный алгоритм управления. Характеристики ПИД-регулятора приведены на рис. 9.6. П-, И-, ПИ-, ПД-регуляторы могут быть получены из ПИД-регулятора соотвествующей настройкой параметров.
Алгоритм идеального ПИД-управления
(рис. 9.6, характеристика 7),
а передаточная функция идеального ПИД-регулятора
(	1	\ к (тиТдр2 + Гир+1)
Wp(p) = Кр)/£(р)=d 1+z?-+тяр =--------------------
\ -*hP )	*мР
Параметров настройки у ПИД-регулятора три: кр, ТК, Та. ПИД-алгоритм часто формируют, заменяя Та =Тнк или ТК=ТД/'к, где О < л < Лтах. В этом случае передаточная функция ПИД-регулятора
229
w^p) = kv^^^-
У аппаратных ПИД-регуляторов обычно передаточная функция балластного звена имеет вид 1Тб(р) = 1/(Тб2р2 + Т61р+1) = 1/(7^2/ + +2£67^р+1), где ^б = Зб1/27^2. Если £б<1, то балластное звено является колебательным, при £б > 1 — апериодическим второго порядка. Параметр для случая < 1 стремятся иметь в пределах 0,4 < £б < 0,7. Причем здесь чем меньше значение (меньше Т61, Т^2), тем ближе процесс на выходе УУ к идеальному (рис. 9.6, характеристика/). При W6(p)^l УУ становится идеальным. Значению Ц = 2кре(0) аналогично соответствует значение Ти (рис. 9.6).
Частотные характеристики ПИД-регулятора (рис. 9.7):
Jz	\ 7 Г 1 'I
( 1	Y -Jarctg —-~<оГд
1+ —----соТ е
I соТ,
L(co) — 201g Ikpl + 201g Jl+1-<o7L
1 1 V 1®ТИ
(p((0) = -arctg -4- -соТ, ^(oT„
Регуляторы с ПИД-алгоритмом управления получили наибольшее распространение и относятся к числу регуляторов, формирующих квазиопти-мальный алгоритм управления. Так, для ОУ с передаточными функциями
230
Wx(p}=koe^/(Txp+\)(T2p+\) и ^2(р) = Лое-рт/(1+^+7’2У) квазиоптимальные значения параметров настройки равны:
^(WM; ти1 = т\ + т2, тах=тхт2/(тх+т2) и к?2 =
= кпТ1/кох; Тд2=Т2/тх; Ти=7],
где ^П=1/А:им (или «0,5+1,0). Наличие частотно-зависимых И- и Д-составляющих в ПИД-алгоритме обеспечивает устойчивость и минимизирует статическую и динамическую погрешности САУ. При этом каждая из составляющих ПИД-регулятора будет вносить основное воздействие в закон управления в соответствующей области спектра входного сигнала: И — в низкочастотной, Д — в высокочастотной. Системы с ПИД-регуляторами обладают свойством «грубости» при дрейфе параметров ОУ и регулятора и эффективны даже при от-сутствии полной априорной информации о свойствах ОУ.
Модифицированный ПИД-алгоритм имеет вид
ц(0 = kv е(?) + ~ J е(т)(/т + Тд о	at
Здесь так же, как и в модификациях ПД-алгоритма, введение в ц (Г) сигнала производной от регулируемого параметра ОУ Та =dy(f)/dt вместо Ta=dz(t)/dt улучшает в ряде случаев качественные показатели работы САУ при скачкообразных изменениях задания x3(f), что обычно характерно для пусковых режимов САУ и для систем программного управления.
ЭФФЕКТИВНОСТЬ ЛИНЕЙНЫХ АЛГОРИТМОВ УПРАВЛЕНИЯ
Если объект управления с самовыравниванием, то для него при скачкообразном возмущении переходный процесс имеет форму кривой 1, при этом статизм объекта определяется значением 80 (рис. 9.8). При
Рис. 9.8
Рис. 9.9
231
включении УУ(Р) (рис. 9.9) процесс в автоматической системе для И-регулятора имеет форму кривой И и не имеет статической ошибки при t —> оо . Если включен П-регулятор, то переходный процесс в автоматической системе имеет форму кривой П и статическая ошибка равна 8П = 80/(l + fco£p). Если объект управления без самовыравни-вания, то 8п=80/^оА:р. Следовательно, чем больше значение кр, тем меньше 8П(8П « 80). Призаданной Зп кр = = (кб/к0) ~(1/к0), где к5 =80/8п. Для объектов управления без самовырав-нивания кр = к^1ко. При включении ПИ-регулятора существенно улуч-
шаются динамические свойства автоматической системы и ее переходной процесс. САУ с ПИД-регулятором имеет лучшие качественные показатели: меньшие величину перерегулирования о (примерно на 15—20%) и время регулирования (на 25—30% от tpK). Наличие интегральной составляющей в ПИД- и ПИ-алгоритмах делает статическую ошибку системы стремящейся к нулю. Д-составляющая на участке ?0-Z] форсирует переходный процесс, увеличивая регулирующее воздействие ц (?) на ОУ, и имеет максимальное значение при t0 (рис. 9.10). На участке t\-t2 Д-составляющая препятствует большому отклонению выходной величины ОУ в другую сторону.
§ 9.2. РЕАЛИЗАЦИЯ АНАЛОГОВЫХ АЛГОРИТМОВ УПРАВЛЕНИЯ
Особенности реализации аналоговых алгоритмов управления в промышленных УУ (Р) аппаратного типа на уровне обобщенных функциональных и структурных схем подробно в форме Wp(p) = ~ ^ри(Р)^б(Р) рассмотрены в работе [10].
Звенья, формирующие алгоритмы управления, обычно являются, как и КЗ, пассивными или активными четырехполюсниками. В частности, пассивные КЗ описываются, например, следующими выражениями:
ц = Ай2 + В12; = Сй2 + DI2
или
- Л1 [Ц - 42Zj; i2 - -А21щ + А22/},
где ЛИ=П/|Л|; А12 = В/^; Л21=С/|Л|; Л22 = Я/|Л1; |Л| = ЛП-ВС; А, В, С, D — обобщенные параметры четырехполюсника.
232
Рис. 9.11
Рис. 9.12
Для схемы, приведенной на рис. 9.11,
ц zHA + B . й, zTD+B Ц zHC + D	IH zrC + A
Передаточная функция четырехполюсника, выраженная через обобщенные параметры, имеет вид:
^(Р) = ^4 = № - А)/(Ф1 - Л/>) = 4! - 4г .	; •
ц(р)	А22Ц + 12
Схему на рис. 9.11 можно представить иначе, как показано на рис. 9.12, в виде простейшей схемы пассивного четырехполюсника. Тогда
W(p) = z2zh/(z2 +zh)
Zj + Zr + [z2ZH/(z2 + ZH)]
Z3 _ ZBMX 2\ + 2r + Z3 ZBX + ZBbIX
где zr + Z] = zBX, a z2zH /(z2 + zH) = zBBIX = z3.
Если zr —> 0, a zH —> оо, to W(p) = ———.
zl+z2
Электронные регуляторы (как и активные КЗ) формируют алгоритмы управления в САУ наиболее близкие к идеальным.
Основным элементом электронного регулятора в аппаратном исполнении обычно является усилитель [например, операционный (рис. 9.13)].
Здесь приведены: принципиальная схема (рис. 9.13, а), модель (рис. 9.13, б) и характеристики выход-вход (рис. 9.13, в) усилителя;
— коэффициенты передачи по напряжению усилителя соответственно по инвертирующему и неинвертирующему входам.
Передаточная функция электронного регулятора (рис. 9.14) имеет вид:
233
w (p} = н(р) = -»вь,х(р) =	=_____wBX(P)
P xjj>) UM l + W'ytP^acG’)	+
При
wp(p)^wBX(p)/wac(p)^/Zo,
где
wm(P) =
<Ap) s z, Mbx(P) ^o+Z!
"вых=О’ гвых~*О
Рис. 9.13
w0^=^p}^-z^--
-«вых(Р) ^+Zt
«вх=°
Ии=к|-
Схемы, передаточные функции, характеристики и параметры УУ на основе операционного усилителя приведены в табл. 9.1.
Следует заметить, что в реальных регуляторах с Д-составляю-щей значение мВЬ1Х возрастает в момент скачка ивх (?) (рис. 9.15, а) не до бесконечности, как показано на рис. 9.15, б, в, а до некоторого конечного значения (рис. 9.15, г), так что площадь, ограниченная кривой мвых(0> примерно равна 5Д = ивхТдкп, где ка = 1 для Д-регулятора и ка =зд/(^, + 2г)2 для ПД-регулятора. Следовательно, эти регуляторы правильно формируют законы управления только для малых скачков ивх или при медленных изменениях ивх, пока ивых не достигает насыщения. Паразитная постоянная времени тд = Тдкс, где кс ~zr/R\ для Д-регулятора и кс = zr /( Rq + zr) для ПД-регуля-
234
Рис. 9.14
тора (обычно кс «1). Наличие тд ухудшает качество управления. Кроме того, так как здесь коэффициент усиления самого усилителя высок (к„ -» оо), то даже малые скачки ивх приводят к насыщению регулятора (регулятор стоит на электрическом «упоре»). Все это обусловливает тот факт, что регуляторы типов Д и ПД применяются самостоятельно сравнительно редко.
Недостатком приведенных схем ПИД-регуляторов является взаимозависимость параметров настройки к?, ТК, Та. Это приводит к тому, что при изменении одного параметра изменяются другие.
У большинства регуляторов Тл/Та <0,25. Здесь, как и уПД-регу-ляторов, Тд = Тд£с(тд « Тд), а 5Д «	(рис. 9.15, г).
Для развязки параметров настройки в ПИД-регуляторах применяют активную обратную связь. Однако достичь полной развязки параметров настройки в схемах ПИД-регуляторов на одном усилителе
235
Таблица 9.1. Электронные регуляторы
Алгоритм	Схема	Передаточная функция	Характеристики
Пропорциональный	у-СТЗ - г- Z] = Яр Zq = Яд	оГ|о? и н	Л = Яр; w = fcp5(/); Т(ц>) = 201g Яр; <р(ю) = 0
Интегральный	я Г4^ ±1	X 1 21 ~ ~г'’ z(> ~ ^0 РЧ	и, р Ткр где Т„ = RgCi	й = Яр/; w = kp; Л(со) = 201g кр- 201g ш; Ф(со) = -я/2
Дифференциальный	-I, н, «—1 ь-Д-frU* Z!=^; Zo = -L-РЧ>	Wp = Top, где Tfl=^C0	Л = Яр5(/); h,=v2('); £(ш) =201ga>7^; <p(w) = jt/2

Продолжение табл. 9.1
	Алгоритм	Схема		Передаточная функция	Характеристики
	Пропорциональноинтегральный			=4 г* Ч. Ь< гЕ +1 ь-	.Л о д1	С	аНа? II	и	§	051 “> -	к*	п	11 Iй-	Л 4" К-	о Ь?	« II	Z
		1ТЪ				
		-м «мХмв	Mtaav	«мяв» 2О = Яо; Z1=^+ ™ Р<\			Л	1	.	.
					v	Г"/^	ш Л	Уп,'1- *	р,с ~2 ^рЛУ Г	"Р ZX(o) = 201g*p+201g 1+—Ц ; L Ю] ф(“)=~arctg (штн) л=Ц1+£|
ю u>	Пропорциональнодифференциальный	.X, 1 J/дкЗ ± [fa , - . - '° 1 + ЯдСор’	—и !=«!	Wp = ka(.\ + Tap), где	к„= —; «0 7}, =ЯоСо	Л = Яр[1 + Тд8(/)]; /	5 ?\|/2 Ц(0) = 201g Яр +201gll + 7^<o2j ; <р(о)) = arctg а)Тд
Продолжение табл. 9.1
238
с активной обратной связью не удается. Поэтому при построении ПИД-регуляторов с относительно полной развязкой параметров настройки строят схемы с использованием двух, трех и более операционных усилителей, используя модульный принцип построения [10]. Для управления объектами с различными к0, т, То настройки параметров делают взаимно независимыми, а диапазоны изменения Тд, Ти, ка — достаточно большими.
Всем типам реальных УУ(Р) присущи элементы нелинейности (например, типа «насыщения»); они имеют ограниченные область линейных режимов (ОЛР) и область нормальной работы (ОНР), которые близки друг другу. Обычно	усо) и зависит,
особенно вне ОЛР, от амплитуды и частоты входного сигнала.
§ 9.3. ДИСКРЕТНЫЕ АЛГОРИТМЫ
Дискретные алгоритмы управления подобны аналоговым, но принцип формирования составляющих дискретных алгоритмов несколько иной. К дискретным относятся регуляторы, вычислительные операции в которых осуществляются в дискретные моменты времени Т. Передаточную функцию линейного дискретного регулятора в общем виде можно представить как отношение двух полиномов и записать следующим образом:
* <,) =
или с учетом z = ед получим
w*(z} = a>»z "'+a>n-iz (m 0 + ---W *+«о. bnz~n + b^z^”^ +... + t\z~l + b^
tn In то=• i=0	/ ;=0
Эти выражения соответствуют также передаточной функции рекурсивного цифрового фильтра (фильтра с бесконечной памятью). Здесь W*(q), W (z) определены в смысле дискретного преобразования Лапласа q = рТ; z = eg; Т — период квантования.
Дискретные регуляторы обладают большим быстродействием, высокой точностью при управлении процессами и значительными пределами изменения параметров настройки Т„,Тд,к,Т.
Здесь также широко используют типовые идеальные дискретные алгоритмы управления (унифицированные алгоритмы): П, С (суммарный), ПС (пропорционально-суммарный), ПР (пропорциональноразностный) и ПСР (пропорционально-суммарно-разностный) — аналоги П, И, ПИ, ПД и ПИД.
239
Например, уравнение идеального пропорционально-суммарно-разностного (ПСР) регулятора имеет вид (рис. 9.16):
Н = *1е[иЛ+*2Хе[гТ]+^Е[«Л при nT>t>(n-l)T
/=1
ИЛИ

др П	?
^Ее[/Л+^[Е£«71-Е[(«-1)Л]
1=1	1
где кх s fcp; Ги = кхТ/к2; Тд = к3Т/кх. На рис. 9.16 цд (/) соответствует дискретному процессу, ца(г)—аналоговому.
При численном интегрировании по методу прямоугольников, когда
И'фэ = илэ(/’) = (1~е-/’7’)/р, Ж(2)=(1-гч)/р=(г-1)/гр.
(для ИИЭ W3 — 1), передаточная функция и частотные характеристики ПСР-ре-гулятора записываются следующим образом:
W(q) = [А} (1 - е~9) +	+ Лз (1 - e-’)2]A;
*	e9	e9 — 1
W (q) = k,+k2----+ кЛ—
1	2e9-l	3 e9
W(z) = kt+k2 + к3 -z-1 Z
W( jQ) = fc Sin	e~J^ri2 + k2_ -JM 4, sin2Q772
J 1 OT/2	QT 3 Q7
где Q — частота входного сигнала.
При интегрировании по методу трапеций
^(Z) = кj + ^г+1) +	.
1	2(z-l) Tz
Из этих формул можно легко получить выражение для W (z) и характеристики для П, ПС, ПР-регуляторов.
240
Например, уравнение дискретного суммарного — С(И)-регулятора имеет вид
ц =	при пТ<t <(и+1)Т,
/=1
т. е. здесь операция интегрирования е (<) заменена операцией суммирования значений е, определяемых в дискретные моменты времени iT (рис. 9.17). Передаточ-
ная функция и частотные характеристики С(И)-регулятора имеют вид:
аппроксимация по методу прямоугольников
, е?
W(q) = k2/<p W (.q) = k2-——; еч -1
Z
W(z) = k2~~-, z-1
= (k2/£lT)eJnl2: аппроксимация по методу трапеций
2 4-1
W(z) = k2T--------
2 2(z-l)
При T—>0 пТя = Т/к2 дискретный регулятор идентичен аналоговому И-регулятору. Квантованием по уровню в цифровом С (И)-регу-ляторе можно также пренебречь, если выбрать значения Де и Ац достаточно малыми, а значение к2 в 1,5-2 раза меньшим критического, соответствующего границе устойчивости.
Составляющая П или дискретный П-регулятор в отличии от аналогового вносит запаздывание (Q772) и имеет отличный (незначительно) от к^ fcj коэффициент усиления по первой гармонике .
П-регулятор тождественен без учета коэффициента кх фиксатору или экстраполятору нулевого порядка: W*(z, p) = (z-1)/(гр).
Шум квантования по уровню как однородно распределенный «белый шум» имеет среднеквадратическое значение (дисперсию) #2/12, где q — уровень квантования (цена младшего разряда). В дискретных (цифровых) регуляторах на основе микропроцессоров N > 8 -ь 16, что позволяет в расчетах пренебречь квантованием по уровню.
Уравнение ПС-регулятора имеет вид (рис. 9.18):
п
p = klE[nT}+k2^E[iT],
/=1
16 А. А. Ерофеев
241
й_____к.
к,Т/кг
•и g(t)
е^-4
j /Ч--1
X.(«N
Рис. 9.18
пТ<t <(л+1)Т	1
или (аппроксимация методом прямо- Ц угольников)	|
ix(nT) = M«D+VLE£[!'rl	I
ГИ м	i
я пТ <t <(и+1)7’,	Я
где к2 = Тка/Тн; кх = кп.	]
Передаточная функция и частотные Я характеристики ПС-регулятора имеют вид:	;

t
^) = №(1-е’9) + ^Ш W* (д) — к\ + к2—~^—', W(z) = кх+к2~~— е? -1	z — 1
, sinQr/2[, к?
’п'п)’‘'-аг7П1+*?+
____h2______'
41с2 sin2 Q772
\ 1/2
x
хе4°та^,.8аг,^.г>,,]
При Т = 0, кр = кх и Ти= кхТ/к2 дискретный ПС-регулятор подобен аналоговому ПИ-регулятору. При этом характеристики дискретного ПС-регулятора близки к характеристикам аналогового ПИ-регу-лятора, если £2 74 0,2, а Т < 0,1 ТК (£27^ <3). Параметры настройки ПС-регулятора: кх, к2 и Т.
Программирование ПС-алгоритма в приведенном виде приводит в процессе настройки к тому, что любое изменение значений кп и Ти вызывает резкие изменения значений ц, что недопустимо. Поэтому обычно используют другое выражение ПС-алгоритма:
ц[иЛ = РМ[нЛ+6[(и-1)7’+рПп/Ти]е[ИГ],
где Р = ±1 — коэффициент. Здесь Тка)Т„ < 1, иначе САУ будет неустойчива. Второе слагаемое в приведенном выражении соответствует b [пТ\.
Параметры ПСР- и ПИД-регулятора связаны при Г —> 0 следующими соотношениями: = кх, Тп = кхТ/к2; Тя = Тк3/кх. При этом характеристики ПСР- и ПИД-регуляторов близки друг к другу, если О.Т< 0,1. Параметры настройки ПСР-регулятора: кх, к2, к3 и Т.
Алгоритм ц в представленном виде для ПСР-регулятора, называемый позиционным, также неудобен для реализации в ЭВМ, так как для получения ц необходимо кроме текущего значения е [пТ] помнить все предыдущие значения от е (0) до е [(и - 1)7]. Это значит, что
242
через некоторое время работы САУ для вычисления этого выражения не хватит памяти (из-за необходимости хранения всех промежуточных значений). Так как при переходе от (i - 1)-го к !-му такту в алгоритме добавляется лишь один новый член, то позиционный алгоритм можно модернизировать, сделав его рекуррентным. Для этого записывают алгоритм для ц[(п-1)7] (для предыдущего такта), вычитают его из р. [и7] и получают:
п 7] = ц[(п -1) Л+кр{(1 + Тд / Т)е(пТ) + (-1 + TIТК - (2Та/Т))х
хе[(п-1)Л+(Гд/Ле[(п-2)Л}>
или
ц[и Л = р[(и -1) Л+kfi [и л - к2е[(п -1) Л + к3е[(п - 2)7],
или
Ш	+ fc3e„_2,
где *1 = ^р((1 + 7/27и) + 7д/7]; ^ = ^р(1-7/27и+27д/Л; к3 =кр(Тя/Т).
Для вычисления ц [и7] необходимо запомнить лишь ц (и -1)7 и значения е на интервалах квантования п, л-1, и-2.
Обычно, чаще используют ПСР-алгоритм в виде (с учетом того, что Е = *з-УаС; 7=^ас)
и[лЛ = Ц[(и-1)Л+^{[е[«Л-е[(»-1)Л]+(Г/Ти)е[(л-1)Л+
+ (Тд/Т)[-у[пТ]+2у[(п-1)Т}-у[(п~2)Т]]}.
Используются и другие оригинальные алгоритмы (быстрого умножения, параллельных вычислений), позволяющие увеличить скорость обработки информации.
Кроме аналоговых и дискретных регуляторов существуют комбинированные аналого-цифровые регуляторы; например, при формировании ПСР-закона в ц (г) П-составляющая соответствует аналоговому регулятору, т. е. равна kpE(t).
В зависимости от периода 7 и шага квантования q дискретные регуляторы можно приближенно рассматривать как импульсные (q -э О, характеристика квантователя близка к линейной с WK(p) ~кг) или как аналоговые (при выполнении соответствующих условий эквивалентности при q —> 0, 7 -э 0).
Передаточную функцию дискретного регулятора с экстраполято-ром (фиксатором) нулевого порядка приближенно можно получить сразу по И^ри(Р) заменой р на А £11 (аппроксимация по способу 7z+l
243
16*
трапеций Боксера—Тамера) с последующим умножением результата на2/(г+1). Другие значения FFp(z) получаются при использовании известных способов приближенного численного интегрирования, например, способа прямоугольников: 1/рь-э 7z/(z + l), способа Симп-сона: 1//>нэ1 у l(z2+4z + l)/(z2-l) идр.
Так, для ПСР-алгоритма при аппроксимации по способу прямоугольников

V (-п
Т )
1 + 2— U-1
Т
т
-1----2
-2
т
, ( Т 2 тл Z-1
= к„\ 1 +-----+-4------
Ти 2-1 Т 2
I—> kS 1 + ----ь Т.р j.
Р1 тКр
В случае, когда значения q и Т таковы, что условия эквивалентности не выполняются, характеристики дискретных УУ будут зависеть от q и Т и могут существенно отличаться от характеристик аналоговых регуляторов (обычно в худшую сторону), как за счет W6(p,z), так и из-за ошибок, обусловленных квантованием сигналов. Заметим, что САУ с дискретным регулятором принципиально свойственно запаздывание, в среднем равное т ~ Т/2, так как сигнал ошибки е [и 7] формируется только в дискретные моменты времени, между которыми САУ разомкнута.
§ 9.4.	РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ АЛГОРИТМОВ
Особенности аппаратной реализации дискретных алгоритмов управления на уровне обобщенных функциональных и структурных схем УУ подробно представлены в работе [10]. Основные функции формирования требуемого алгоритма управления ц [и 7] в них выполняет цифровое вычислительное устройство (процессор). К числу дискретных УУ аппаратного типа относят также дискретные импульсные регуляторы (ИР), иногда их называют импульсными аналоговыми регуляторами, которые позволяют уплотнить каналы передачи информации и обеспечить многоканальное обегающее управление ряда координат ОУ. Импульсные регуляторы содержат импульсный элемент (модулятор), осуществляющий амплитудно-импульсную, широтно-импульсную или время-импульсную модуляции (АИМ, ШИМ, ВИМ) входного сигнала е (I). В ИР частота квантования wK задается принудительно, обычно сок == 6сос; ИР также реализуют рассмотренные выше дискретные алгоритмы управления.
244
При определенных условиях [выбором значения сок; соответствующий И^асС7)] импульсный регулятор в динамическом отношении можно привести к эквивалентному непрерывному регулятору. Так, выбором частоты квантования сок >2(йс, (йЕ <(шк-<вс) у ИР с АИМ и юк > Зсос, сое < (сок -2и)с у ИР с ШИМ и ВИМ их можно привести к аналоговому обыкновенному регулятору. ИР с АИМ являются линейными и обычно включают в себя импульсный модулятор (дельта-импульсный модулятор) и формирующий элемент с W^3(p), охваченный обратной связью с JFQC(p).
ИР с ШИМ и ВИМ (ФИМ) являются нелинейными регуляторами, однако при у < 0,3 (у = ги / 7) и Е] < 0,3 (Е( = т3 / Т, т3 — длительность задержки импульса относительно начала периода квантования Г) они могут рассматриваться как линейные ИР с АИМ. В ИР соответствующим выбором обратной СВЯЗИ С ^ас(Р) можно сформировать любой алгоритм управления стандартного типа.
Из трех принципов реализации дискретных УУ (аппаратного, программного и аппаратно-программного) аппаратно-программный (комбинированный) базируется, как правило, на основе микропроцессоров или программно-управляемых вычислительных устройств. В настоящее время микропроцессоры получили широкое распространение в регуляторах различного назначения. Такие регуляторы называют программируемыми контроллерами или программно-управляемыми устройствами (ПУУ). ПУУ эмулируют, т. е. выполняют функции логических систем управления, следящих систем, регуляторов соотношения переменных, регуляторов адаптивного, каскадного, многосвязного управления, регуляторов комбинированного управления (по возмущению) с упреждением и запаздыванием, с подстройкой обратной связи, с компенсацией чистого запаздывания, цифровой фильтрации и т. п. В локальных САУ ПУУ выводят объект управления на заданный режим, производят автоматическую идентификацию ОУ в режиме его работы и решают задачи аналитического синтеза оптимального алгоритма управления (захват процессов управления). ПУУ функционируют в соответствии с заложенными в них алгоритмами, программами (фильтрации, идентификации, управления), которые могут быть достаточно разнообразными и определяются целями управления.
Изменение функциональных возможностей ПУУ обеспечивается программными средствами, что создает свойство гибкости по алгоритмам.
Сравнение дискретных (цифровых) и аналоговых регуляторов позволяет отметить следующие особенности. Аппаратные аналоговые регуляторы обладают «жесткой» структурой и формируют строго определенные (наперед заданные) алгоритмы управления. Смена алгоритмов или расширение диапазонов настройки параметров за обусловленные пределы практически недопустимы. Регуляторы сложны в настройке и перенастройке; параметры настройки, как правило, не соответствуют оптимальному ведению процессов управления; скорость и точность обработки информации в аналоговой форме мала; низкой является
245
помехоустойчивость. Недостатками аналоговых регуляторов является также дрейф параметров из-за старения элементов, температурный дрейф параметров. При решении сложных задач управления увеличивается аппаратное обеспечение и усложняется структура регуляторов. Поэтому аналоговые регуляторы целесообразно применять при решении простейших задач одноканального управления простыми стационарными ОУ.
Дискретные (цифровые) регуляторы (особенно при реализации на основе микропроцессоров) обладают гибкостью и сопрягаемостыо, легкостью изменения параметров и характеристик благодаря их программируемости; возможностью реализации нетривиальных и эффективных сложных алгоритмов с идентификацией ОУ и адаптацией параметров, многофункциональностью в применении и многоканально-стью в управлении несколькими ОУ или сложными ОУ. Их отличают высокая помехоустойчивость, практическое отсутствие влияния разброса параметров, старения и температурного дрейфа элементов, отсутствие элементов настройки, низкие массогабаритные показатели, более высокое быстродействие, низкая стоимость и повышенная надежность. В процессе управления можно изменять параметры настройки по программе, возможны параметрическая адаптация, легкая модификация, усложнение или смена алгоритмов управления за счет изменения (смены) программ. При этом усложнение алгоритмов не усложняет аппаратного обеспечения и практически не влияет на надежность контура управления. Эффективность и скорость программирования могут быть достаточно высокими за счет использования программных модулей, а также высокого уровня проблемно-ориентированных языков программирования. Точность реализации алгоритмов управления определяется числом разрядов (длиной информационного слова). Так, при N= 8 максимальная погрешность составляет 0,8%, при N = 12 — 0,05%, при N = 16 — 0,003%. Быстродействие цифровых регуляторов качественно определяется временем цикла и тактовой частотой fr.
Следовательно, цифровые регуляторы и ПУУ на базе микропроцессоров целесообразно применять при решении сложных задач многоканального управления сложными нестационарными одним или несколькими ОУ. При этом для нестационарных объектов (близких к линейным) наиболее эффективно использовать ПИД-алгоритмы, так как более сложные алгоритмы не создают больших преимуществ, к тому же не имеют отработанных методик расчета оптимальных настроек регуляторов. Такие системы управления, базирующиеся на распределенной сети микропроцессоров, могут объединяться для реализации алгоритмов более высокого уровня и быть непосредственно связанными с ЭВМ АСУ. При этом измерительные, вычислительные и управляющие устройства максимально приближены к ОУ и составляют локальные микропроцессорные САУ, объединенные в единую сеть с мощной ЭВМ АСУ.
246
§ 9.5.	МНОГОСВЯЗНЫЕ (МНОГОМЕРНЫЕ) РЕГУЛЯТОРЫ
Многосвязные регуляторы (МР) используются для управления многосвязными (многомерными) ОУ. На входы МР поступает вектор ey(z) или е7[«Л; на выходе МР формируется вектор управляющих воздействий Ц» (0 и™ МЛП; где J, i — число воздействий на входе и выходе МР соответственно (обычно i = j). Передаточная матрица (оператор) W МР определяется из следующего векторно-матричного уравнения:
где 1ц| и ]е| — векторы-столбцы, обозначаемые двойными стрелками (рис. 9.19). Формирование |е| осуществляется в многомерных сумматорах. Как следует из записанного уравнения, МР содержит i сепаратных регуляторов и j перекрестных регуляторов (z % j). МР подразделяются на автономные, применяемые для управления в автономных САУ, и неавтономные—для неавтономных САУ. САУ с МР автономна, если выполняются условия инвариантности каждой регулируемой величи
ны у,- по отношению к заданиям на остальные у{_{ переменные.
В качестве сепаратных регуляторов обычно используют линейные
или нелинейные «стандартные» ляторы. Перекрестные регуляторы в автономных САУ предназначены для компенсации взаимного влияния между переменными и поэтому их иначе называют компенсаторами. В неавтономных САУ перекрестные регуляторы обеспечивают
аналоговые или дискретные регу-
Рис. 9.19
координацию работы сепаратных
каналов и их называют координаторами. Если в Wy(p) все передаточные функции, кроме диагональных, равны нулю, такой МР назы
вают диагональным регулятором; его передаточная матрица имеет вид:
^и(Р)
W(p) =
О
Wdp)
О
247
Рис. 9.20
В САУ с МР (рис. 9.20) показатели качества подразделяют на сепаратные, групповые и общие. МР характеризуются степенью связи между каналами управления, например, для двух каналов:
W^P)W22(P)
Структура и параметры МР определяются на основе заданных требований к САУ конкретного ОУ. В связи с этим МР являются специальными; их синтез и проектирование производятся индивидуально.
§ 9.6.	НЕЛИНЕЙНЫЕ АЛГОРИТМЫ УПРАВЛЕНИЯ (БАЗОВЫЕ ПРЕДСТАВЛЕНИЯ)
Выбор алгоритма управления должен соответствовать требованиям, предъявляемым к точности и качеству процессов управления в САУ. Чем выше эти требования, тем сложнее алгоритм управления и УУ (регулятор). При управлении нестационарными ОУ с широким диапазоном отношений x/TQ =0,1-НО, при значительном дрейфе их характеристик и параметров линейные регуляторы с жесткой (постоянной) структурой не обеспечивают оптимальности процессов управления. Для таких объектов целесообразно применять нелинейные алгоритмы управления, реализуемые с помощью нелинейных УУ (регуляторов). У таких регуляторов алгоритмы управления, параметры или структура изменяются скачкообразно (или по другой программе) в соответствии с логическими алгоритмами в зависимости от переменных состояния ОУ и е ((), Ц (0 и т. д.
Применение нелинейных УУ позволяет стабилизировать ОУ при больших (сильных) возмущениях (недопустимых для линейных регуляторов), повышает устойчивость САУ, создает возможность стабилизировать структурно-неустойчивые ОУ.
Часто при реализации нелинейных алгоритмов управления применяют типовые линейные алгоритмы в сочетании с логическими алгоритмами, формируемыми с помощью функций переключения. Для нелинейных
248
регуляторов часто нет необходимости выполнять условия высокой стабильности и точности настроек параметров регуляторов для данного ОУ.
В сравнении с линейными применение нелинейных регуляторов увеличивает точность регулирования, снижает перерегулирование о на 30-50%, уменьшает время регулирования в два-три раза, значительно расширяет области устойчивости, уменьшает фазовый сдвиг (инерционность) систем и значение интегрального квадратичного критерия качества J2o = JE2(r)rft. Следовательно, с помощью нелиней-о
ных регуляторов как регуляторов с гибкой (переменной) структурой достигается квазиоптимальное управление ОУ в условиях, когда применение линейных регуляторов не обеспечивает даже их достаточной устойчивости и требуемого качества. Это связано с тем, что нелинейные регуляторы изменяют в нужном направлении сразу несколько свойств САУ, делают их инвариантными к изменению параметров и внешних возмущений, оптимизируют системы по определенным критериям. Нелинейные регуляторы используют также как формирователи дополнительных корректирующих воздействий (в дополнение к основным, которые формируются линейными регуляторами). В последнем случае p(z) = |Лр(/) + цк(0 > где Цр(0 — основное регулирующее воздействие (например, ПИД-регулятора); pK(Z)— сигнал коррекции нелинейного регулятора.
В общем случае нелинейные алгоритмы представляют собой нелинейные функции, например, типа .F](|J., d\i/dt, ...); F2(e, dz/dt, fat, ..., p, f, g) и др.
В нелинейных алгоритмах можно выделить составляющие логического, функционального, оптимизирующего и параметрического типов. Логические составляющие представляют совокупность логических операций управления, определяемых функциями переключения F(t). Функциональные составляющие определяются нелинейными функциями Fb F2, причем подразумевается содержание в них как статических, так и динамических нелинейностей. Оптимизирующие составляющие предопределяют оптимизацию процессов управления в смысле экстремума (минимума, максимума) какой-нибудь величины или функционала с учетом реальных ограничений. Параметрические составляющие формируются обычно в виде нелинейной функции текущих координат.
Формирование логических составляющих алгоритмов управления производится на основе анализа знаков z,dz!dt и их комбинаций в виде сумм, произведений и т.п.: (E + tfe/dz); е (е + dz!dt), т. е F’ (t) = sign е; F" (t) = sign dz/df, F'" (z) = sign (e + dz/dt) и т. п.; модуля функции |е|, d\z\/dt и их аналогичных комбинаций |е|<7е/Л и др. [10].
При формировании функций переключения следует учитывать, что
£ = jelsign е; dz/dt = (J|E|/t/z)sign е; sign zdz/dt = sign (d|E|/zZz)|e|;
249
sign e[^e + k2(dtldt)] = sign (Jtje] + fc2rfei Idt).
При этом модульные функции переключения имеют преимущества по сравнению с функциями переключения других типов [например, типа линейных комбинаций в vtdzldf. Fx(t) = EdE/dt; F2(t) = e(^e +k2dE,/df)]. Эти преимущества упрощают реализацию УУ (исключается операция умножения), создают предпосылки создания более устойчивых структур САУ (устраняются автоколебания вблизи положения равновесия — при малых Е и dE/dt, которые могли возникнуть из-за необходимости переключения структуры САУ).
Функции переключения формируются иногда без применения операций дифференцирования е (?) в так называемом косвенном виде [10]. Эти функции переключения эффективны для применения в условиях действия помех (нет дифференциаторов) и используются для создания регуляторов с переменной структурой.
Функции переключения иногда формируют с использованием только пропорциональных составляющих (их называют пропорциональны-t
ми) или в виде интегралов, например, F(t) = J е(т)с/т спереключае-о
мым пределом интегрирования (их называют интегральными).
В ряде случаев функции переключения образуются только путем перемножения е(t)F(t), где F(t)[f t или Ft'*) — дискретная функция, отражающая тот факт, что на интервале процесса (гь t2) E(t) умножается на F(t). Обычно при этом F(t) равна 0 или-1 (инвертирование) или к (уменьшение или увеличение сигнала в (?) в к раз). Временной интервал kt = t2 - t{ может определяться в виде фазового интервала с учетом, что период Т = 2п /со, т. е. в виде фазовых углов <р2> Ф1 •
Логические составляющие многообразны и иногда имеют сложные функции переключения, например
Fi(t) = sign (е + £ё|е[); F2(t) = sign e^Je] + ^2|ё|)+ sign ё(/с3|е| + к4|ё|).
В общем случае функцию переключения F (t) можно записать в виде:
. dE , । ф| dE F(0 = wU, е—у, е, -Li, е+—, dt dt dt
J)ep dt
du
, Ц, —, ••• dt
и т. д. Функции переключения удобно записывать через обобщенные функции, используя единичные функции типа «до» (f), «после» ,о1(О и «между» /о16.
В практике САУ нашли применение следующие алгоритмы с использованием различных функций переключения [10].
1.	Нелинейный П-регулятор с переменным коэффициентом передачи регулятора кр; его алгоритм управления ц(г) = y(fcp)E(z), где V(^P) = ^P1 •1/1(0 + ^р27|1(0 — нелинейный коэффициент, характери
250
зующий изменение кр во времени. Момент переключения определяется, например, в функции знака изменения линейной комбинации произведения F(f) - е (deJdt) ё 0; в момент выходная координата достигает h (<»). Однако в силу инерционности происходит перерегулирование, которое желательно уменьшить. В момент можно выбрать кр2 таким, чтобы перерегулирование значительно уменьшилось; при этом уменьшается время регулирования 1р. Применение данного алгоритма управления эффективно для ОУ с запаздыванием.
2.	Нелинейный И-регулятор с переменной постоянной интегрирования Ти. Алгоритм управления имеет вид
И(0 = V “ J е(т)Л, \l«Jo
I 1 I
где W — нелинейный коэффициент, управляемый посредством V и J
функции переключенияF(t), например, Д(1) = kte + k2de / dt; ks и k2 — весовые коэффициенты.
Регуляторы с переменной постоянной интегрирования (Ти = var) обычно применяют для объектов без самовыравнивания, т. е. для структурно-неустойчивых объектов, придавая САУ достаточные запасы устойчивости при хорошем качестве протекаемых процессов.
3.	Нелинейные ПИ-регуляторы. Существуют три варианта нелинейных ПИ-алгоритмов управления с переменным коэффициентом передачи
УИ О
с переменной постоянной интегрирования
p(O = fcpE(Z) + v
с переменными коэффициентом передачи кр и постоянной интегрирования Тп
где — нелинейные коэффициенты, изменяющиеся каждый в соответствии со своей функцией переключения /J(z) и F2(t), например
У1=*Р|-Ч(0+Лр2-Г11(0;
251
V2 =T„t \(f) + THi-h 1(0; /г1(0 = Е kfl + k2 ~+k3\i(t) ;
F2(t) = EdE/dt^Q.
Моменты переключения в общем случае tx * t2 и определяются функцией переключения.
4.	Полупропорциональное управление — ПП-регулятор. Его алгоритм управления имеет вид:
М(0 =
&ре(0 при F(0>O,
Мпих — при F(t)<0,
где F(f) = EdE/dt, или иначе
Ц(0 = ЛрЕ(0 ’ 1/, (0 + ^рЕ-тах 01)'t, Ь, (0-
Полупропорциональное управление в эквивалентном отношении аналогично ПИ-управлению, но при этом свободно от недостатков, которые свойственны реализации И-составляющей. Следовательно, в системах с ПП-регулятором достигается свойство астатичности, т. е. принципиально можно сделать статическую ошибку равной нулю. Особенно эффективно ПП-управление по сравнению с обычным П-управ-лением для объектов, где отношение и/Т0 >2-5-10. Однако в САУ с ПП-регулятором необходимо более точно определять параметры ОУ, и эти САУ более чувствительны к нестабильности параметров ОУ, чем САУ с ПИ-регуляторами.
5.	Пропорционально-полуинтегральное управление — ППИ-регу-лятор. Алгоритм управления имеет вид
ц(0 = кр
1 — при d&\/dt >0;
где V =	' . ,
0— при df\J dt <0.
Здесь до момента переключения t{ управление ведется по ПИ-алго-ритму, когда е (<Уе /dt) > 0, а при е (ds /dt)<0 осуществляется пропорциональное управление. При этом действие И-составляющей стабилизируется на уровне, достигнутом при е (dE /dt) = 0. В динамическом отношении ППИ-управление эквивалентно ПИ-управлению (при значительно большей области устойчивости) при определенной настройке параметров кр и Ти.
252
6.	Нелинейные ПИД-регуляторы. Алгоритмы управления имеют несколько модификаций* В зависимости от значения е (?) производят включение или выключение И-составляющей: при |е| < 5 — ПИД-уп-равление; при |е| > 8 — ПД-управление, где 8 — уровень переключения или зона введения И-составляющей. Существуют и некоторые другие модификации нелинейных ПИД-алгоритмов, в частности ПИД-алгоритмы как комбинация Д-составЛяющей и вышерассмотренных нелинейных ПИ-алгоритмов управления.
7.	Полупропорциональное управление со сбросом регулирующего воздействия — ППС-регулятор. Алгоритм управления ППС-регуля-тора имеет вид:
ц(0 = *рЕ(О-1г1(О+(^р	+
или
Ц(/) = £сУ(Е(7)) +
кр-кс кр
I
о
где
1 —при d\E\/dt > 0;
0—при</|е|/Л <0;
ze[0, л/со].
Следовательно, здесь при F (/) = Е (Je /dt) > 0 ППС-регулятор работает как П-регулятор; при t - tx происходит сброс регулирующего воздействия на величину Дц(/) = (&р-&с)Етах(0 и его фиксация на этом уровне в интервале от tx до t2. При t > t2 ППС-регулятор опять работает как П-регулятор.
В динамическом отношении ППС-регулятор в первом приближении эквивалентен ПИД-регулятору при определенной настройке его параметров. Следовательно, ППС-регулятор придает системам свойства астатического управления, расширяет область устойчивой работы и в целом улучшает качество процессов в САУ.
8.	Пропорциональное управление со сбросом и запоминанием регулируемого воздействия — ПЗС-регулятор. Алгоритм управления аналогичен ППС-регулятору, где F(t) = кх |е| + £2^1е| /dt — модульная функция переключения. До ?1э покаК(/)>0 управление ведется по П-зако-ну; в момент tx, когда функция переключения F(t) = 0, происходит сброс регулирующего воздействия на величину, определяемую ке, и его запоминание до момента t2, пока F (?) < 0. В моменты t > t2 осуществляется опять пропорциональное управление, пока F (t) = 0 и т. д. Здесь, как и у ППС-регулятора, кс = 0,4+0,6. Настройка на t2 ведется подбором значений кх, к2. ПЗС-регулятор, создавая опережение по фазе, придает САУ свойство астатичности (8СТ —э 0) и эти САУ характеризуются большей точностью и меньшей длительностью
253
переходных процессов. Необходимо отметить, что ПЗС-регулятор при = 0, к2 = 1 превращается в ППС-регулятор.
9.	Пропорциональное управление со сбросом и запоминанием регулирующего воздействия и введением интегральной составляющей — ПЗСИ-регулятор. В алгоритм управления (как у ПЗС-регуля-t
тора) добавляется И-составляющая M?(M^)J Vi[£(T)]cfr, где о
_|1—при Т](?)<0;	_[1—при F(t)>0;
V1 0—при /;(/)> 0, а V (0—при F(t)<0.
Модульные функции переключения:
F(t) = Tdp\Jdt-£|е|; F^t) = T^/dt\-b,
где 5 — зона введения И-составляющей. Время регулирования здесь сокращается в два-три раза, уменьшается также перерегулирование. При этом значительно расширяется область устойчивости, умень-
I
шается значение J20 = |е2(т)</г. Таким образом, ПЗСИ-управление о
в определенном смысле эквивалентно ПИД-управлению. Системы с ПЗСИ-регуляторами обладают свойствами астатичности и имеют в целом улучшенные качественные показатели. ПЗСИ-управление целесообразно использовать для объектов управления с отношением т/То =0,1+10.
10.	Полупропорционально-дифференциальное управление—ППД-регулятор. Алгоритм управления имеет вид:
ФСО dt

fcp|dE(?)/?/? + Tfld2e(?)/d?2] = fcp/E(?)- приТ(?)>0, 0 — при F(t) < 0,
где F(t) = E(?)«fe(?) / dt.
Следовательно, при F (?) > 0 [i(t) = kp[s(t) + Ta(dE(t) / dt)] ППД-ре-гулятор работает как ПД-регулятор; при F (?) < 0 регулирующее воздействие ц (?) сохраняется на уровне, достигнутом при етах(?). Иначе алгоритм управления можно записать так:
Н(О = М
о
dE г V —+ ТД dr
d2£ dr2 ,
dr,
где V = •
1 — при ф| /' dt > 0; 0—при ф)/ dt <0.
254
ППД-регуляторы по динамическим свойствам эквивалентны ПИД-регуляторам при определенных настройках параметров. ППД-регуляторы расширяют области устойчивости, придают САУ астатические свойства. Однако эти САУ являются чувствительными к точности определения и стабильности параметров ОУ.
11.	Функциональные, логические, оптимизирующие и параметрические составляющие алгоритмов управления. Нелинейные алгоритмы могут содержать комбинации составляющих функционального, логического, оптимизирующего и параметрического типов.
Рассмотренные выше алгоритмы не исчерпывают класса нелинейных алгоритмов. Их число достаточно велико. Так, можно отметить распространенные нелинейные функциональные алгоритмы (составляющие) вида:
|Л1 (0 = кхг + к2г + куё. + &4ё|ё|;
Ц2(0 = Е±&1|ф + &2е3;
ц3(г) = кхг + Assign Е|е|1/и - &3 |е|ё;
ц4(/) = е±Лё|ё|;
p5(/) = e+(fc1+fc2|ei)sign ё;
ц6(0 = ё + /с[Ё!е;
p7(z) = e2sign е;
ц8(г) = e+e|£jE+Л2ё|.
Алгоритм щ(0, например, используют для расширения параметрической устойчивости в контурах стабилизации летательных аппаратов; ц2(0— для повышения быстродействия САУ; ц3(/), ц4(0 — для повышения качества и точности управления в установившихся режимах (е (/) <1); ц5(г) — для улучшения амплитудно-фазовых характеристик и повышения запасов устойчивости САУ. Здесь, в общем случае, везде ц(0— нелинейная функция от е(г): е, е2, ..., е*; ё, ё, е; sign е, ..., обеспечивающая воздействия по статическим и динамическим нелинейностям, создающим форсировку переходного процесса, повышенную точность и т. д., т. е. улучшенные показатели качества САУ. Для регуляторов, реализующих эти алгоритмы, можно определить эквивалентные амплитудно- и фазочастотные характеристики по передаточной функции и коэффициентам гармонической линеаризации:
FF(4,p) = ?1(4) + -^p
со
255
или 1F(4,» = й(4, (0) + М4, ®) = Л(4, С£>)еЛ>(л”“).
Здесь запись FF(4>P) по форме соответствует линейному звену с введением производной (см. п. 3.3).
Нелинейные логические алгоритмы (составляющие) также чрезвычайно разнообразны и определяются различными логическими функциями переключения (sign), например, типа
р.л1(г) = sign (е + /сё1е|); p.l2(r) = sign е(4 |е| + Лг2|ё|) + sign ё(А:3|е|+А?4|ё[); Илз(0 = 1 ПРИ F(e4)>0; 0 — при F(y., ё) = 0; -1 при—F(e4)<0 и т. д. Для цл1(/), например, Д(4,(о) = l/2fao24.
Разработаны алгоритмы с выполнением операций мажорирования и сложных логических функций от п переменных. Использование логических составляющих в нелинейных алгоритмах приближает процессы в САУ к оптимальным. Заметим попутно, что если е и dzldt имеют одинаковый знак, то е растет, и наоборот.
Нелинейные оптимизирующие алгоритмы (составляющие) базируются, как правило, на использовании функций переключения с одного значения +хтах на -хтах. Моменты переключения определяются комбинациями п значений координат, где п — суммарный порядок уравнения САУ с регулятором. Эти алгоритмы обычно содержат комбинации составляющих функционального и (или) логического типов, например:
ц01(0 = sign [кг + ё|ё|]; цОг(О = je|sign (Л2ё|ё| + е);
ИозО) = е + Assign у; РоДО = £ + ё + sign yln(l - ё / sign у);
1105(1) = к{г+(к2-к3^г + г и др.
Оптимальные алгоритмы обеспечивают минимум ошибки, максимум быстродействия, поддерживают на экстремальном уровне определенные параметры САУ или комбинацию (функционал) параметров САУ в условиях действия ограничений на управляющие функции и фазовые координаты ОУ.
Нелинейные параметрические алгоритмы (составляющие) базируются на управлении по отклонениям от заданной программы (закона), определяемой через текущие значения скорости и координат ОУ. Эти алгоритмы представляют собой достаточно сложные функции: ц(/) = Ф(е, |ei, ё, |ё|, ..., ц, у, х, ...), т. е. зависят от е, ц, у, х, их модулей и комбинаций сумм, произведений и т. п.
12.	Регуляторы с переменной структурой. Структура регулятора изменяется, и регулятор может быть в определенные моменты времени ПИ-, ПИД-, ПД-, ПЗС-регулятором и т. п. Изменение структуры производится в соответствии с выбранной функцией переключения F (!)
256
посредством различных приемов [10]. В регуляторах с переменной структурой могут вводиться различные составляющие ц (/); линейные — Д, ПД, ПИД с варьируемыми параметрами кр, Та, Ти ; нелинейные (х2, х112, хк и др.) для оптимального управления ОУ с т, ОУ с экстремальными характеристиками; осуществляться мажорирование сигналов, адаптивная фильтрация и т. д. В регуляторы может вводиться блок самонастройки, который обеспечивает автоматическую подстройку структуры и параметров регулятора (кр, Та, Т„) в функции от изменения динамических параметров объекта управления и действующих на объект возмущений. Следовательно, такие регуляторы примыкают к классу адаптивных регуляторов с переменной структурой (переменными алгоритмами) управляемыми (подстраиваемыми) параметрами.
Нелинейные дискретные алгоритмы. В большинстве случаев нелинейные дискретные алгоритмы управления представляют собой дискретные аналоги непрерывных алгоритмов. Их реализация определяет класс нелинейных дискретных регуляторов. В качестве примера рассмотрим нелинейный дискретный алгоритм полупропорционального управления:
VW/„r)=:fA:iVe[”7’]npi1 FW>0;
' [0 при F(t)<0,
где F(Z) = e[«T]Ve[«T]; Vp[«T] = ц[лТ]-ц[(и-1)Г]; Ve[«T] = е[иТ]--е[(л-1)Л.
Характеристики ПП-регулятора, качество процессов управления САУ с дискретным ПП-регулятором аналогичны САУ с аналоговым ПП-регулятором, если Т <(0,1^-0,2)т [т — время запаздывания ОУ; W0(p) = кое~рх/(Тор+1) ]. Автоколебания в САУ с цифровым ПП-ре-гулятором, вызываемые квантованием по уровню, обычно не превосходят значения, соответствующего одному кванту и при Де / Детахх х (Дц/цтах) < 10~2 -ИО-3 практически не влияют на качество процессов.
Алгоритм функционирования дискретного ППД-регулятора имеет вид
Ац[«Л = 
A?] £ve [п 7"] + A:3V3e [п Г]} при F(t)>0; 0{ц[лТ] = М[(«-1)Л} при F(t)<0,
где F(t) = е[«Т]Уе[и7"]—функция переключения; \72е[пТ]= ^е[пТ]--Уе[(и-1)Л — обратная разность второго порядка. Дискретный ППД-регулятор имеет три параметра настройки: к{, к3, Т. При Т 0 связь параметров аналогового и дискретного нелинейных ППД-регуляторов следующая: кр = кь к3Т = ТЛ. САУ с дискретными и аналоговыми ППД-регуляторами примерно равноценны при Т < 0,1 т (т — время
17 А. А. Ерофеев
257
запаздывания ОУ); их применение эффективно для ОУ при т0/7^>2+10. Однако свойство «грубости» (робастности) САУ с ППД-регуляторами выражено значительно слабее, чем в САУ с ПИ- иПИД-регуляторами, т. е. они более чувствительны к точности определения и стабильности параметров ОУ.
Аналогично рассмотренным дискретным ПП- и ППД- алгоритмам управления можно записать и другие дискретные аналоги непрерывных нелинейных алгоритмов.
Реализация нелинейных алгоритмов. Особенности аппаратной реализации нелинейных алгоритмов управления на уровне обобщенных функциональных и структурных схем УУ (Р) приведены в работе [10]. При реализации нелинейных алгоритмов в УУ обычно используются блоки логических и нелинейных операций (БЛО и БНО). Законы переключения, определяемые F(t) формируются БЛО; количество БНО может быть различным. БНО непосредственно формируют нелинейную характеристику управления под действием сигналов с БЛО [10]. БЛО может включать в себя элементы дифференцирования, интегрирования, суммирования и т. д., выполняющие различные элементарные операции по формированию соответствующих функций переключения из анализа и сравнения знаков е (0, dt Idt, iej, d\t\!dt и их комбинаций в виде сумм, произведений и т. п. В качестве формирующих сигналов, как уже отмечалось, могут использоваться /(0, yQC(0, у(0, р(0 и т. д. БНО непосредственно формируют регулирующее воздействие и в своем составе содержат ключевые логические элементы формирования нелинейных статических параметрических характеристик управляющего (компенсирующего) типа и др. Звено (звенья) с компенсирующими нелинейностями FK(xK) может включаться по отношению к звену (звеньям) с основной нелинейностью САУ F0(x0) последовательно, параллельно или последовательно и параллельно. При этом получаемое эквивалентное звено, например F3(x3) = FK(xK)F0(x0) = К или F3(x3)= = F0(x0) = к3, имеет при точной компенсации линейную результирующую характеристику. Однако точная компенсация из-за влияния инерционности, запаздывания т, дестабилизирующих факторов, изменяющих параметры F0(x0), практически невозможна. Поэтому возможны режимы недокомпенсации или перекомпенсации, причем режим переком-пенсации часто более предпочтителен. При желании обеспечить более точную компенсацию нелинейности F^x^) в условиях переменности ее параметров иногда вводят схемы компенсации адаптивного типа, когда параметры FK(xK) адаптивны к изменению параметров Г0(х0). Эти структуры являются достаточно сложными и не всегда приемлемы.
Вводимые нелинейности управляющего типа FK(xK) могут также изменять форму эквивалентной нелинейности F3(x3) таким образом, чтобы в САУ исключались нежелательные режимы (например, автоколебательные). В качестве FK(xK) используют нелинейные характеристики различного типа: с насыщением, с зоной нечувствительности, релейные с дифференцированием и др. [10] (см. п. 3.3).
258
Кроме них могут использоваться различные кусочно-нелинейные и нелинейные характеристики. При реализации нелинейных характеристик применяют операции возведения в квадрат, извлечение корня, умножение и деление, логарифмирование, антилогарифмирование, определение модуля вектора, вычисление степенных и тригонометрических функций и др. Общий принцип формирования нелинейностей в схемах связан с включением специального НЗ — нелинейного эле-
мента (НЭ), обозначаемого как F
+ «2
-»1
= F(h)i->F(x).
Необходимо отметить, что разнообразные активные нелинейные корректирующие устройства (НКУ), используемые для коррекции нелинейных систем, часто можно условно рассматривать также как определенный класс нелинейных регуляторов.
Так, с помощью НКУ могут формироваться сложные нелинейные функции (алгоритмы) управления, например, вида
Л(*э) = И1к(х1к)И1(Ж1 +
F3(x3) =	+ [F2k(x2 к)Ж2(р) - F3 к(х3 к)^3(р)]Г4к(х4 к)Ж4(р)
и др. Обычно НКУ вводят сильно форсирующие воздействия, устраняя (уменьшая) в конечном итоге влияние основных нелинейностей на свойства САУ. В САУ с НКУ используют линейные корректирующие устройства (ЛКУ) И<(р) в сочетании с FK(xK), причем ЛКУ выбирают по требуемым показателям работы САУ, а нелинейные компенсирующие звенья FK(xK) — по соображениям компенсации или деформации основных нелинейностей F0(x0).
Нелинейные алгоритмы управления, формируемые нелинейными УУ можно определять в ряде случаев как оптимизирующие (оптимальные) законы.
Схемы нелинейных регуляторов с переменной структурой и параметрами, реализующие нелинейные законы управления логико-аналитического типа, приближаются по своим свойствам к регуляторам адаптивного типа, если изменение параметров и структуры регулятора является функцией задающих, возмущающих воздействий и переменных параметров (характеристик) ОУ.
Для реализации нелинейных (дискретных) алгоритмов используют табличное задание нелинейных функций, различные методы их аппроксимации (кусочно-ступенчатые, кусочно-линейные и др.), разложение в степенной или иной ряд (по функциям Хаара, Уолша и т. п.). В качестве элементарных операций также применяют возведение в квадрат, извлечение квадратного корня и др.
Основу нелинейных УУ составляют функциональные преобразователи различного принципа действия. При этом алгоритмы преобразований реализуются как аппаратными (структурными), так и про
259
17*
граммными или программно-структурными методами. Эффективным является реализация неоднозначных (многомерных) нелинейных функ- ций с помощью многомерных нейронных сетей [см. п. 1.3 (7)], а также элементов нечеткой логики [15-18].
Свойства дискретных и аналоговых САУ с нелинейными алгоритмами при соответствующем выборе параметров настроек и периоде квантования Т эквивалентны друг другу (в определенных ограниченных пределах). Следует отметить, что нелинейным СА У, в отличие от линейных, присущи целыйдяЭ особенностей, а именно (главные из них):
1.	САУ может иметь несколько устойчивых положений равновесия [устойчивость «в малом», «в большом», «в целом»], в то время как линейная САУ может быть устойчивой в целом (или неустойчивой). Равновесные состояния нелинейных САУ «в малом» обычно соответствуют особым точкам типа «устойчивый фокус» (д, =-а( ± у'Р,-, см. п. 6.1), «устойчивый узел» (р,- = -а;); неустойчивые состояния — особым точкам типа «неустойчивый фокус» (pt - + af ± ур, ), «неустойчивый узел» (pi = + a,), «седло» (р, = ±а,-). Особая точка типа «центр» соответствует р, =± у'Р(. Отметим, что фазовые траектории (портреты) нелинейных САУ dy/dx = R(x, y)!Q(x, у) - F(x, у) в окрестностях особых точек близки к фазовым портретам линейных САУ (особые точки соответствуют поведению линейных САУ второго порядка), но вдали от них они могут иметь качественные отличия, в частности содержать: замкнутые особые траектории типа предельных циклов, ряд особых точек (или не иметь их, как в САУ с гистерезисом), отрезки равновесия (бесконечное число точек равновесия), сепаратисы, бифуркации и т. п. [2, 5, 7]. В линейной САУ может быть только одна особая точка (для конкретных р,); вблизи особой точки обычно нелинейная САУ исследуется методами линейной теории. В нелинейных САУ принято определять устойчивость конкретного движения (возмущенного, невозмущенного и т. д.), а не ее устойчивость в целом.
2.	Автоколебания (АК) или периодические процессы соответствуют устойчивым предельным циклам; обусловлены в основном внутренними свойствами САУ. У линейных это соответствует нахождению САУ на колебательной границе устойчивости (наличие пары чисто мнимых корней ±у'Р,, см. п. 6.1). Параметры и характер АК (симметричных, несимметричных) зависят от типа НЗ, начальных условий и др. факторов. Например, для САУ с нечетным НЗ параметры симметричных АК (со, Л) можно определить на основе гармонического баланса амплитуд и фаз |йИн(Л)РКл(усо)1 = 1 или Лн(Л)Лл(со) = 1, Фн(Л) + Фл(<0) = -7С.
3.	Конечная длительность переходных процессов (из-за наличия НЗ), в то время как у линейных САУ процессы затухают в бесконечности.
4.	Финитный (конечный) уровень выходных координат; у неустойчивых линейных САУ значения выходных переменных растут неограниченно, хотя реально они ограничены конечными ресурсами САУ.
260
5.	Невыполнение принципа суперпозиции—при сложении воздействий реакция САУ не равна сумме реакций на отдельные воздействия, т. е. характер процессов в нелинейных САУ зависит от начальных условий, уровней воздействий, их частотных спектров и др. факторов.
В заключение необходимо заметить, что наряду с рядом отмеченных преимуществ нелинейных алгоритмов их реализация значительно сложнее, чем линейных алгоритмов; они менее универсальны (часто индивидуальны) и их трудно унифицировать. Обычно САУ с нелинейными регуляторами более чувствительны к определению и стабильности параметров ОУ, т. е. обладают менее выраженными свойствами «грубости» систем. Следует также отметить, что одним из основных алгоритмов управления в САУ является ПИД-алгоритм и его различные нелинейные модификации. Синтез нелинейных алгоритмов ведется применительно к ТЗ на САУ с учетом свойств и особенностей конкретного ОУ и среды его функционирования.
Более развитые модификации нелинейных алгоритмов применяют в ИСУ (см. п. 7 гл. 1) в виде так называемых интеллектуальных алгоритмов или алгоритмов с нечеткой логикой управления. Это также сложные алгоритмы с иерархической многоуровневой структурой с координацией по уровням управления для достижения глобальной цели функционирования ИСУ [13—18].
Выбор периода Т =ТК или частоты квантования сок имеет важное значение в системах с дискретными (цифровыми) регуляторами, алгоритмы функционирования которых были рассмотрены выше. Выбор значения Тк зависит от свойств сигнала, метода его восстановления и назначения системы управления. Внутри периода Тк управляющее воздействие, как правило, постоянно, и характер процессов в САУ определяется лишь свойствами ОУ и действующих возмущений fk (/). При больших значениях Тк могут проявляться недемпфируе-мые колебательные составляющие собственного движения ОУ и высокочастотные возмущающие воздействия. Поэтому с этой точки зрения целесообразно уменьшать значение Тк. Но чем оно меньше, тем большее быстродействие необходимо от микроЭВМ (и тем выше, как правило, их стоимость). Поэтому выбор значений Тк должен быть оптимальным [10].
Если считать, что значения х3 и со3, fk и W/к известны, то УУ должно обеспечивать отслеживание й3 и подавление (йд. Тогда Тк <min(n/(o3, л/(Од,л/а>0,гр/л), где соо —собственная частота; t — длительность регулирования (гр > пТк, п — порядок САУ). Р В САУ с полосой пропускания (0п сок >(6-И0)о>п или Тк<(0,3-*--Н),5)1р (То » Тк). Для колебательных САУ Np = tvlTK — число периодов квантования за время переходного процесса; нижний предел дает теорема Котельникова—Шеннона. При выборе значений Т = Тк на нижнем пределе сок > 2ютах((Отах ~ 3(0с), т. е. ®к>6(ос, где сос \WH (j<a)| < 0,1. Это приводит к завышению быстродействия микроЭВМ (условие минимальных искажений частотного спектра непре
261
рывного сигнала при прохождении его через импульсную цепь, что не вполне естественно для замкнутых САУ).
Если <вк£(1)с+(ое, а cdc~cd£, т.е. юк£2о)с, соотношение T<n/ti>c определяет условие отсутствия пульсации квантования в сигнале ошибки е ((0с — частота среза системы; со8— максимальная частота в спектре сигнала ошибки). Эти условия соответствуют условиям эквивалентирования систем с дискретными регуляторами системам с аналоговыми регуляторами, определяют идентичность обеих систем по значению среднеквадратической ошибки управления, запасам устойчивости. Выбор Т по условиям обеспечения заданного времени переходного процесса zp САУ определяется соотношением Tct^n, где п — минимально возможное число интервалов дискретности, равное порядку системы п. Для следящих систем рекомендуется Т < (88 / Ё)1/2, где 8 — заданная ошибка слежения, Ё — максимальное ускорение входного воздействия е (/). При настройке параметров регулятора посредством изменения времени цикла Гнеобходимо учитывать это, так как значение Т можно изменять или принимать его постоянным. Для ОУ с запаздыванием т Т< (0,1 +0,3)т; если использовать оценку /с — время первого согласования (см. п. 7.5), то Т<(0,07+0,15)/с.
Значение Т следует оценивать также с учетом допустимого ухудшения запаса устойчивости
Т< (0,1+0,5) /й)р<л/сос.
При расчете САУ приближенное условие эквивалентности обычно принимают на уровне нижней границы, т. е. Т <2 /<ос; используют также и условие вида Т<(2/шс)М/(М+1), где М — показатель колебательности. Выбор периода Т по условиям требуемой точности САУ является наиболее жестким [10].
Глава 10. СИНТЕЗ И ПРОЕКТИРОВАНИЕ САУ
§ 10.1. ЗАДАЧИ И МЕТОДЫ СИНТЕЗА
Задача синтеза — разработка САУ с наилучшими показателями качества, т. е. задача оптимального синтеза структуры и параметров САУ.
Требуемые показатели качества или критерии оптимальности (целевые функции) можно достичь путем интерактивного анализа САУ. При этом, на основе исходной структуры САУ, рассчитываются основные характеристики, определяются показатели качества спроектированной САУ и сравниваются с требуемыми показателями. Анализ позволяет определить эвристическим путем вид и место включения
262
КЗ; далее для скорректированной САУ производится снова анализ показателей качества. Если они удовлетворяют требуемым, то на этом анализ заканчивается; если удовлетворяют не в полной мере, то производится уточнение структуры КЗ и места их включения.
Задача синтеза сводится к определению структуры, параметров и места включения КЗ сразу, исходя из требуемых показателей качества. При этом основные функциональные узлы САУ (ОУ, УЭ, ИЭ и др.) считаются заданными в соответствии с техническим заданием и представляют неизменную часть ч (р) САУ.
Задача синтеза промышленных САУ, в связи с их четким определением fKH4 (р), включающей ОУ и УУ (регулятор), ведется в направлении выбора структуры и параметров УУ, обеспечивающих оптимальный ПП и экстремальное значение заданных показателей качества. При известном ОУ и выбранном УУ (Р) осуществляется расчет оптимальных параметров настройки УУ (Р). При этом используются типовые УУ (регуляторы), в состав которых уже входят корректирующие устройства. Поэтому синтез для этих САУ сводится к выбору типового УУ (регулятора), обеспечивающего требуемый алгоритм управления, и оптимальной настройке его параметров в соответствии с динамическими характеристиками ОУ.
Показатели качества САУ при синтезе обычно оцениваются интегрально:
fk
J = j F[y(f), x(t), f(t)}dt, h
Ч.
например, при минимуме /р: J = ^l dt = tk -tQ = грт;п — САУопти-Ч гк	°°
мальна по быстродействию; J = j[е(/)]2<7/ н» J = j[e(0]2<7? —САУ /о	О
оптимальна по точности в динамике.
Критерий J в общем случае представляет собой следующие функции: полезности, минимума потерь, максимума прибыли, обобщенной работы и т. д.
Разработан ряд методов синтеза САУ. Очевидно, лучшим методом был бы метод, который обеспечивал бы требуемые показатели качества, оптимальный переходной процесс и необходимые запасы устойчивости САУ.
Первая группа. Графоаналитические методы инженерного динамического синтеза САУ: корневые, корневого годографа, стандартных переходных характеристик, частотные.
Вторая группа. Аналитические методы, обеспечивающие синтез оптимальных САУ (с жесткой настройкой, адаптивных). Это синтез САУ по интегральным критериям качества ПП, по критерию среднеквадратичной ошибки. Здесь используются вариационные методы, дина
263
мического линейного и нелинейного математического программирования, принцип максимума, метод Винера—Хопфа, метод модального управления, метод аналитического конструирования оптимальных регуляторов (АКОР) и др.
Третья группа. Методы прямого синтеза посредством ППП, аналоговое и цифровое моделирование САУ, синтез с использованием ЭВМ. При этом реализуется наиболее полное исследование и синтез САУ с учетом нелинейностей, зависимости параметров САУ от времени и т. д. Однако синтез САУ (моделирование) на ЭВМ базируется на использовании расчетных методов. Аналитические и графоаналитические методы синтеза позволяют часто исследовать САУ в более общем виде и найти оптимальное среди многих решений.
Методы инженерного динамического синтеза (в основном, графоаналитические) предполагают выбор структуры и параметров корректирующих устройств и рационального места их включения для получения САУ с требуемыми (желаемыми) показателями качества.
Кратко приведем оценки методов инженерного динамического синтеза САУ.
1.	Корневой метод заключается в том, что по заданной структурной схеме САУ с уже включенными КЗ определяют характеристическое уравнение. Затем варьируются параметры КЗ таким образом, чтобы получить требуемые значения коэффициентов характеристического уравнения. Этим обеспечивают желаемый вид ПП с заданными косвенными показателями качества — т] и ц; обычно процессы в САУ стремятся сделать квази-или оптимальными с о [%] = 5%. Напомним (см. п.7.7), что между коэффициентами Oq ... а„ и корнями характеристического уравнения D (р) = 0: д ... рп существует жесткая связь, т. е. если задать д (г], ц), то можно получить желаемые af уравнения Z)(p) = 0. Связь между коэффициентами характеристического уравнения и показателями качества р, ц определена лишь для систем до 3-го порядка. Для систем с более высоким порядком эти связи становятся сложными и делают невозможным синтез САУ, что является недостатком корневого метода. Другим недостатком является затруднительная необходимость определения структуры, параметров и места включения КЗ. Поэтому эффект решения зависит от опыта проектанта; метод не получил широкого распространения.
2.	Метод корневого годографа является более универсальным. Синтез сводится к определению наиболее рационального расположения корней характеристического уравнения D (р) = 0 замкнутой САУ при вариации одного или двух параметров (v, т). Значение параметра, определяющее наиболее рациональное расположение корней, является решением задачи синтеза. Метод требует знания ряда правил; широкого распространения не получил.
3.	Метод стандартных переходных характеристик сводится к тому, что для статических САУ любого порядка, а также систем с астатизмом г первого, второго порядка и отрицательными вещественными
264
корнями можно определить вид типовых передаточных функций и соответствующий им вид стандартных характеристик h (t) (рис. 10.1, кривые 1-5). По выбранной (желаемой) переходной характеристике /гж(г) определяется вид типовой передаточной функции, сравнение которой с исходной передаточной функцией дает ответ на то, каким образом следует изменить структуру исходной системы с помощью корректирующих звеньев.
Недостаток метода — построение типовых характеристик воз-
можно только при отрицательных вещественных корнях, поэтому можно синтезировать лишь узкий класс линейных систем.
§ 10.2. ЧАСТОТНЫЕ (ГРАФОАНАЛИТИЧЕСКИЕ) МЕТОДЫ СИНТЕЗА
Метод логарифмических амплитудных характеристик (ЛАХ). Наиболее распространенным является частотный метод синтеза САУ, так как построение асимптотических ЛАХ практически возможно без вычислительной работы. Синтез САУ производится в следующем порядке.
1.	По виду передаточной функции Wp(p) строится ЛАХ Lp(w) исходной САУ (САУ должна быть минимально-фазовой).
2.	На основе требований, предъявляемых к САУ, строится желаемая ЛАХ: £ж(со).
3.	Производится синтез УУ (Р) или КЗ последовательного типа:
Wx(p) = Woy(p)l¥yy(p),
ИЛИ
ВД = WM = wv(p) wK3(p).
Тогда
Wyy(p) = Wx{p)!Woy{p) или И/ з(Р) = ^ж(Р)/
4.	Путем вычисления из ординат ЛАХ исходной системы ординат ЛАХ желаемой САУ получим ЛАХ КЗ: LK3(ffl) = £.ж(со)-£р((1)). Так как ЛАХ однозначно определяет вид ср (со) у минимально-фазовой САУ и весь характер ПП, то для рассмотрения достаточно одних ЛАХ.
5.	По виду ЛАХ КЗ определяется структура, схема и параметры корректирующего звена. При необходимости осуществляют переход на эквивалентные параллельные КЗ или ООС.
6.	Производится поверочный расчет ПП с учетом реальной структуры и места включения корректирующего звена, оценка запасов устойчивости и показателей качества скорректированной САУ. Если скорректированная САУ удовлетворяет заданным показателям качества, то синтез на этом заканчивается. В противном случае уточняет-
265
ся структура, параметры КЗ и место его включения; далее производится поверочный расчет.
Важное значение по методу ЛАХ имеет правильное построение желаемой ЛАХ.
Построение желаемой ЛАХ производится в следующем порядке.
1. Разбивают желаемую ЛАХ на три части (рис. 10.2) и осуществляют построение низкочастотной (0<со<оэн), среднечастотной (сон < со < сов) частей ЛАХ, их сопряжение и построение высокочастотной части ЛАХ (со > сов).
Низкочастотная часть ЛАХ определяется требуемыми точностными показателями (характеризует ошибку САУ) и ее наклон зависит от порядка астатизма г (числа интегрирующих звеньев): £ж(со) =
266
= 201g fcp-r201g co. При r=l наклон ЛАХ составляет -20дБ/дек; при г = 2: -40дБ/дек, т. е. наклон ЛАХ равен -г-20дБ/дек, г = 0, 1, 2... . Пересечение этой асимптотой оси абсцисс (показано на рис. 10.2 пунктирной линией) определяет значение добротности САУ по скорости kv =QV = Ucl. На частоте со = 1 Z.(co) =201g кр, где кр— коэффициент усиления разомкнутой САУ [&р = 8р/83-1 = (1/с0)-1]. На частоте юн =шР/(ов = (0,2+0,6)(0с Цсон)> 201g Лр(сон)= 201g 1/8 > > 26 дБ при 8 = 0,05. Первая сопрягающая частота со!с = при
однократном изломе определяется как отношение: со1с =
2q

_Qa .
Qv’
при двукратном изломе coIc = 4q /с2 = 2g, /Qv = 2ка / kv, где ка = Qa = = 2fc2 — добротность САУ по ускорению; сь с2 — коэффициенты ошибок САУ.
Среднечастотная часть ЛАХ характеризуется частотой среза: сос =(0,6+0,9)<пп, где соп — частота положительности Р (со) (см. рис. 7.8); соп нэ 0,2Р(0); ®с.оп (см. § 10.4).
По найденной сос проводится среднечастотный участок желаемой ЛАХ— асимптота с наклоном -20 дБ/дек влево и вправо от частоты среза до получения определенных запасов устойчивости /^(со) и 1^2 (®). Эти запасы могут быть заданными или определены по допустимой величине перерегулирования ст,% и требуемому запасу устойчивости по фазе у (рис. 10.3). Если Цсо)<-2ОдБ/дек, то уменьшается устойчивость САУ; если больше, то возникают трудности выбора КЗ. Если перерегулирование ст задано, то можно определить Рм — максимум Р (со), далее по величине Рм и заданному значению времени регулирования /р определить соотношение кп /соп (рис. 10.4). Тогда (0п = knltp, к = 1 + 5; при ст = 15 + 30% к = 1,3 + 2,5.
Сопряжение среднечастотной части с низкочастотной и построение высокочастотной части ЛАХ производят таким образом, чтобы при вычитании Дк(р) - Lp(p) = LK3(p) получалось в реализации наиболее простое КЗ. Обычно с этой же целью на практике низкочастотные и высокочастотные части стараются оставить без изменений. Здесь
Рис. 10.3
Рис. 10.4
267
юв «[(2ч-4)юс]ч-[(6ч-Ю)<ос].
После формирования желаемой ЛАХ и определения Ькз(ю) = = Дк (р) - Ар(р) проверяют соблюдение требуемых запасов устойчивости по фазе у=л-ср((о) (пост для L((o)§ Ly2, рис. 10.3). Если значение запаса устойчивости по фазе у не выдерживается, то необходимо расширить среднечастотный участок ЛАХ и вновь произвести проверку.
По виду ЛАХ КЗ Екз(со) на основании таблиц [2] определяется структура (вид передаточной функции) и параметры корректирующего звена последовательного типа (или его эквивалента). Пример КЗ ПД-звена и его ЛАХ (см. рис. 10.2) показаны на рис. 10.5, а, б, где
И'кз(р) = к\ ; Тд1 = ед; Т2 = кхТ„х, кх =	< 1. Для ЛАХ
(рис. 10.5, в): КЗ будет ПИД-звено с передаточной функцией:
(7]р+1)(7^р+1)_______ Ь^р2 л-^р+Х
ТхТ2р2 +[{Тх+Т2) + Тх2\р+Х аор2+а1р+1
где Тх - RXCX\ T2-R2C2, TX2-R2Cx; OQ-bQ-TxT2, сц-Ь^ + Т^; t\-= TX + T2. Здесь в КЗ (рис. 10.5, а) необходимо последовательно с R2 включить емкость С2, тогда его W(p) = WK3X(p) (рис. 10.5, г).
После определения параметров КЗ производится поверочный расчет переходного процесса в САУ и определение показателей качества по кривой переходного процесса. Если определенные показатели качества удовлетворяют заданным, то расчет САУ на этом заканчивают. Если нет, то проводится уточнение структуры и параметров КЗ в соответствии с расчетом. Изложенная процедура синтеза справедлива для типовых ВЧХ замкнутых САУ вида (рис. 10.6). ЭтиЛАХ характери
зуют следующими параметрами:
Рис. 10.5
268
_ ®_d_.	=	\ = 0*1
<•>„’	°	'	®0
®в
®п
%2 =
(02
CD0’
где X—основной коэффициент наклона; Ха, X] — дополнительные коэффициенты наклона; — основной коэффициент формы; %2 — дополнительный коэффициент формы.
Для САУ с г = 1, если X < 0,8,
Ха > 0,4, %1 > 0,5, то перерегулирование о в основном определяется Рм: ст = [1,18Рм-Р(0)]/Р(0). Однако на о влияет и Рт, увеличивая его величину на Дст<0,ЗРт; Рт ~ |1-Рм|- Общее перерегулирование ст[%] = [ст-/(/>м) + 0,3|Рт|]-100%. В табл. 10.1 приведены значения Рм и соответствующие им показатели качества ст, tp и К. Здесь же представлена зависимость ст от М (ст<[1,18М -Р(0)]/-Р(0)).
Этот метод синтеза справедлив для широкого класса систем, так как реальные Р (со) обычно соответствуют типовым.
Низкочастотная часть ЛАХ определяет конец переходного процесса, т. е. определяет точность САУ или ошибку регулирования. Высокочастотная часть ЛАХ определяет начало переходного процесса, который не сказывается на основных показателях качества.
Основной характер переходного процесса формирует среднечастотная часть ЛАХ, которая определяет перерегулирование ст [%], время регулирования (р, колебательность системы К и др. Необходимым признаком хорошо спроектированных САУ является прохождение среднечастотного участка с наклоном ЛАХ в -20 дБ/дек через (ос продолжительностью I более или равной 0,75 декады:
Таблица 10.1
	О	'р	Колебательность К	м	о, %
1,0	< 17	<3п/шп	1	1,1	13,8
1,2	<26	<4л/шп	<2	1,3	26,5
1,3	<32	<5л/<оп	<2	1,5	37,2
1,4	<38	<6п/ш„	<3	1,7	44,6
269
, СО, М+1	М-1	М
=	; т = 201g	; Л,2 = 201g (г = 1).
сй2 М-1	31 в м 2	М+1
Для облегчения процедуры синтеза корректирующих звеньев (устройств) введены типовые желаемые ЛАХ и им соответствующие Wx (р).
Обозначения типовых желаемых ЛАХ: 1 в - 20 дБ/дек; 2 в - 40 дБ/дек; 3 в-60дБ/дек. Обычно рассматривается пять классов (типов) желаемых ЛАХ (рис. 10.7):
ObI-2-2-2: Wx(P) = kJP(l + TiP)(l + T3Py,
Iв1-2-1-2: Wx(p) = kv(l + Т2р)/р(1 + 7]р)(1 + Г3р);
II в 1 - 3 -1 -2: Wx(p) = kv(l + Т2р)2/р(1 + TiP)2(1 + ТзРУ,
Ш = 1-2-1-3: Wx(P) = kv(l + T2P)/P(l + TiP)(l + T3p)2-
IVsl-3-l-3: Wx(p) = М + Т2р)2/р(1 + ад2(1 + ТзР)2.
Здесь 7] > Т2 > Т3.
Все типовые ЛАХ и желаемые передаточные функции полностью определяются четырьмя величинами: к„ <0, =1/7], со2 = 1/Т2, со3 =1/Г3; соответственно для ЛАХ: (L =201g к, при со =1) на частоте сос, CDi/C0c, СО3/СОС.
Метод типовых ЛАХ облегчает синтез и широко используется в инженерной практике (иногда применяют девять типов желаемых ЛАХ).
Задача синтеза всегда решается неоднозначно, т. е. структура (вид) передаточной функции и параметры корректирующего звена могут варьироваться в определенных пределах.
270
Синтез областей устойчивости связан с методом 2)-разбиений в плоскости одного, двух или нескольких параметров, влияние которых исследуется на устойчивость и качество САУ.
При синтезе области устойчивости заранее задаются и определяются параметры (в конечном итоге параметры УУ или КЗ) так, чтобы удовлетворить требования по запасу устойчивости и качеству переходных процессов в САУ с учетом вариации одного, двух или более параметров. Если варьируемых параметров три, то область устойчивости получается трехмерной, и тогда граница устойчивости представляет собой трехмерную поверхность.
Синтез САУ на основе ППП с помощью вычислительных машин (3-я группа методов синтеза) позволяет, варьируя передаточные функции УУ или корректирующих звеньев и значения их параметров в широких пределах, получить большое количество соответствующих кривых переходных процессов h (t) и значений среднеквадратичных отклонений выходной величины при случайных воздействиях. Поэтому выбор КЗ или УУ (Р) и значений варьируемых параметров их настройки может быть выполнен простым перебором возможных вариантов. По каждому варианту можно построить области устойчивости в пространстве варьируемых параметров и определить линии равных значений заданных показателей качества (/р, о, Кит. д.); произвести выбор оптимальной коррекции иногда непосредственно по h (Г); аналогично можно определить значение среднеквадратического отклонения в разных точках области устойчивости при наличии случайных воздействий.
§ 10.3. ОСОБЕННОСТИ СИНТЕЗА МНОГОМЕРНЫХ САУ
В многомерных САУ выходная величина у является вектором и представляет собой совокупность нескольких выходных переменных у,, поэтому многомерная САУ всегда многоконтурна.
Анализ статики и динамики многомерной САУ аналогичен, но более трудоемок по сравнению с анализом одномерной системы. Он эквивалентен случаю для одномерной САУ с несколькими внешними воздействиями. При этом знаменатель передаточных функций для всех переменных одинаков.
Определение точности, показателей качества и построение переходных процессов осуществляются независимо для каждой выходной переменной (на основе уравнений, передаточных функций, частотных характеристик).
Устойчивость исследуется по полной структурной схеме многомерной САУ.
Синтез многомерной САУ имеет существенные особенности, определяемые необходимостью одновременного удовлетворения требований по точности и качеству ПП для нескольких выходных перемен
271
ных, которые обычно взаимосвязаны через ОУ. Поэтому из-за противоречивости требований необходимо компромиссное решение, оптимумом которого является удовлетворение требований, предъявляемых ко всем выходным переменным. Если многомерная САУ состоит из автономных одномерных САУ, когда изменение любой из переменных не вызывает изменения остальных, то, хотя контуры управления связаны друг с другом, они с точки зрения динамики являются независимыми. Таким образом, многомерная САУ расчленена на ряд одномерных систем управления, синтез которых по отдельным выходным переменным ведется самостоятельно.
Для упрощения синтеза квазиавтономных САУ их взаимосвязанные контуры можно в первом приближении также принимать автономными (связи между у; слабые). Квазиавтономные САУ обычно имеют значительную разницу в быстродействии между различными у,., когда длительность ПП для одной переменной на порядок или более превышает длительность ПП другой. Тогда синтез САУ можно вести независимо по каждой у,-, предполагая постоянство других переменных. В порядке поверочного расчета проверяется влияние взаимных связей и при необходимости осуществляется уточнение коррекции. Может, например, оказаться, что с точки зрения статического режима переменные существенно взаимосвязаны, а при исследовании динамики они квазиавтономные.
Многомерная неавтономная (связанная) САУ может быть преобразована в автономную или квазиавтономную (с возможностью независимого синтеза отдельных контуров) путем введения специальных перекрестных компенсирующих связей (КЗ) между этими контурами. Достигается это за счет использования идей инвариантного управления каждой из выходных переменных САУ относительно остальных переменных. На рис. 10.8 приведена двухмерная система с одним ОУ. Для получения автономности здесь введены дополнительные КЗ и компенсирующие корректирующие воздействия по у{ и по у2 (варианты показаны пунктиром и штрихпунктиром на рис. 10.8). Уравнения САУ имеют вид (Е — единичная матрица):
у = (Е + WRY1 (WRx + Wf) + Gxx + Gff,
где (E + WR) — неособенная характеристическая матрица; Gx, Gf — соответственно передаточные матрицы по задающим и возмущающим воздействиям. Уравнения САУ при х, = х2 = 0 имеют вид:
У^р) = ^н(р)/;(р) + [1Е12(р) + ^к1(р)]у2(р);
У2(р) = К22(Р)Ш + [W2l(p) + ^к2(р)]у,(р),
где передаточные функции Wi2(jp), W2l(p) учитывают взаимные влияния контуров; 1Кк1 (р), WK2(p) — корректирующие связи между контурами. Здесь член Wn(p)y2 учитывает влияние на у, изменения у2,
272
Рис. 10.8
воспринимаемых yt как возмущение; аналогично W2l(p) отражает влияние у, на (воздействия J\, f2 приведены ко входу ОУ).
Условие автономности в САУ сводится к следующим равенствам:
WKl(p) = ~Wi2(p)-, WK2(p) = -W2l(p).
Откуда можно определить передаточные функции корректирующих звеньев КЗ 1, КЗ 2, осуществляющих перекрестные связи между контурами.
Для получения автономности в САУ обычно необходимо введение корректирующих воздействий по идеальным производным различного порядка. Кроме того, в этих выражениях могут присутствовать множители е''т, точная реализация которых невозможна. Поэтому практически можно достигнуть лишь приближенного выполнения условий автономности. Обычно стремятся принять структуру коррекции с одинаковыми или близкими условиями автономности по воздействиям хи/
Автономное управление — стандартное требование к САУ, предъявляемое в целях получения независимой настройки управляющих устройств по отдельным переменным, что упрощает наладку и эксплуатацию САУ.
Однако у многих САУ переход к автономному управлению сопровождается значительным ухудшением показателей качества по сравнению с оптимальной многомерной САУ связанного управления. Это происходит в случае, если связи между выходными переменными сильны и ими нельзя пренебречь. Тогда, если можно выделить одну из всех переменных, требования к динамике управления которой значительно жестче, чем у остальных, синтез осуществляется вначале только для этой переменной. Определение точности и качества переход-
18 А. А. Ерофеев
273
ных процессов для остальных переменных осуществляются после этого и при необходимости последовательным приближением уточняется коррекция. Если требования к выходным переменным САУ одного уровня, целесообразно использовать ППП и вести синтез на ЭВМ.
§ 10.4.	О СИНТЕЗЕ САУ С ОПТИМАЛЬНЫМ ПЕРЕХОДНЫМ ПРОЦЕССОМ
Под САУ с оптимальным ПП будем понимать систему, у которой е (оо) = 0, а ПП от x(t) = x(O)-ol(z) имеет о = 0 и происходит с минимально возможным zp = топ (с учетом физических ограничений). Такой ПП реализуется в САУ, если d^yfdt1 =а для любого /, где а — максимально возможное ускорение выходной переменной (рис. 10.9);
топ = 2(х(0)/а)|/2.
Тогда
2	/	\2 /	\
Уоа(!) = — (№)-a z-y- -1 Z-y- +^(Z-Ton)2-l(Z-Ton).
При i-»oo yon(z) = уоп(°°) = —~~—- = x(0), a zp°=0,84xon, если 5 = 0,05.
В операторной форме
Уоа(Р> = а(1-2е^п + е1П°’‘)/р3 =
Р
Передаточная функция замкнутой САУ с оптимальным ПП
, УМ 4	+	. А(р)
Won(p) =	=—-------------г------= у ;
х(р) С Р	Р
для разомкнутой САУ
w ( ) =	= _ konA(P) = woa(P)P2
Р°	f-konA{p) р>-копА(РУ
где коп = 4/т2„. Передаточная функция по ошибке W3e(p) = 1 - Жоп(р). Значение еоп(р) = х(р) - уоп(р) = а/коп-аА(р)/р3.
Вещественная частотная характеристика САУ
l-2cos - топ +cos сот0„ Роп(а>) = -квп-----;
со
1/2
, Роп(сос) = 0,5. ЛАХ САУ с оптимальным ПП
2	| а
при со. = — = ------
с°" топ 1х(0)
274
на частоте юСоп (L(co) = 0) имеет наклон примерно -20 дБ/дек (при (0 < 4сос).
Передаточные функции САУ с оптимальным ПП являются трансцендентными функциями от р, т. е. обыкновенные линейные САУ не являются оптимальными (гр > , топ). Однако выбором КЗ или УУ(Р) можно приблизить свойства реальной САУ к оптимальным. При этом кроме линейных КЗ используют псевдолинейные КЗ, а также нелинейные корректирующие устройства.
Псевдолинейные корректирующие звенья являются устройствами неминимально-фазового типа, т. е. их АЧХ и ФЧХ либо не зависят друг от друга, либо зависят неоднозначно. Псевдолинейные КЗ подразделяются на три группы, изменяющие: ФЧХ (АЧХ остаются неизменными); АЧХ (ФЧХ остаются неизменными); АЧХ и ФЧХ неоднозначным образом.
Псевдолинейные КЗ могут быть с +Дф(со), -Дф(со) и относятся к звеньям более сложного типа, чем линейные КЗ,
а именно содержат в своем составе различные логические блоки, нелинейные блоки, блоки сигнатуры, бистабильные блоки, блоки модуль-функ-ции и др. Псевдолинейные КЗ необходимо отличать от линейных КЗ неминимально-фазового типа, в которых имеет место только -Дф(ю).
Псевдолинейные КЗ также, как и линейные, могут включаться последовательно, параллельно в прямой канал управления САУ или в цепь обратной связи.
Нелинейные КЗ, или нелинейные корректирующие устройства, принципиально применяются для коррекции нелинейных САУ, а также оптимальных САУ, синтезированных по принципу максимума или
метода динамического программирования.
Синтез оптимальных САУ (2-я группа — аналитические методы синтеза) более полно рассматривается с учетом различных критериев оптимальности, например минимаксных критериев или критериев, связанных с маргинальными функционалами [1, 2, 5, 7].
§ 10.5.	ПРОЕКТИРОВАНИЕ САУ
Проектирование САУ и полный расчет — сложная инженерная задача, связанная с выбором ее элементов, статическим расчетом характеристик отдельных звеньев и статической точности САУ и с динамиче
275
18*
ским расчетом для получения требуемых запасов устойчивости и показателей качества. Решение этих задач не является однозначным. Например, САУ может быть реализована из различных по физической природе элементов; требуемые показатели качества могут быть обеспечены разнообразными корректирующими средствами и УУ.
Проектирование САУ сводится к проведению анализа и синтеза САУ. Так как обычно САУ не удовлетворяет требованиям устойчивости и предписанного качества работы, целесообразен синтез САУ.
Энергетические данные САУ — мощность, точность, режимы работы, максимальная скорость, напряжение, род тока и т. д. — являются исходными данными при выборе элементов САУ и проведения статического расчета.
Исходными данными инженерного динамического синтеза (расчета) являются:
1)	тип сигнала или вид возмущающего воздействия (регулярное — детерминированное — обычно единичное ступенчатое воздействие; случайное воздействие или комбинация воздействий);
2)	перерегулирование о [%] (обычно < 10 + 40%);
3)	время переходного процесса /р, иногда колебательность К< 1 4-3;
4)	запасы (соответствующие хорошо демпфированной САУ) по фазе у >(30-4-50°), по модулю h >0,2 4-0,4 или ДЬ>8 4-12дБ;
5)	статические и динамические параметры отдельных звеньев САУ в виде передаточных функций W](p).
Данные по четырем первым пунктам обычно являются заданными; последний определяется в результате предварительных расчетов.
Для следящих и астатических САУ, а также для САУ с программным управлением задают еще коэффициенты ошибок с0, q, с2, ... в соответствии с видом САУ. Задача синтеза САУ в общем случае заключается в составлении математического описания управляющего устройства для данного объекта управления при определенных требованиях к точности, качеству управления и условиям работы (характеристики внешних воздействий, требования к надежности, массе, габаритам, потребляемой мощности и т. д.). Большое число разнообразных требований не позволяют обычно все их объединить в одном критерии оптимальности и решить задачу синтеза САУ как строго математическую (вариационную задачу на экстремум этого критерия), хотя задача синтеза САУ есть всегда задача на оптимум, так как требуется создать оптимальное УУ (Р), наилучшим образом удовлетворяющее всем требованиям.
Практически синтез САУ разбивается на ряд этапов, каждый из которых решает часть задачи синтеза.
При отсутствии общего критерия оптимальности обычно производят расчет вариантов УУ (Р) и методом сравнения выбирают оптимальный.
Основные звенья обычно определены сразу по заданию на разработку САУ (это объект управления, исполнительные механизмы, чувствительные элементы, преобразователи, усилители и т. д.). Следова
276
тельно, структурная схема САУ в результате синтеза должна быть дополнена УУ (или КЗ) с учетом выполнения требований по устойчивости, качеству переходных процессов и точности в стационарных случайных режимах.
Порядок астатизма и коэффициент передачи к? САУ определяются исходя из требований к точности в установившихся режимах при детерминированных воздействиях. Если А:р-рср = [(5р/53)-1]| оказывается большим, то целесообразно поднять порядок астатизма (включением И- или ПИ-звеньев) и свести к нулю установившуюся ошибку. Поэтому величину Ар выбирают, исходя из соображений устойчивости и качества ПП в САУ. При этом повышения запасов устойчивости достигают, применяя управление по производным, т. е. реализуют, например, ПИД-управление. В САУ используется также повышение точности с применением неединичных обратных связей, масштабирования сигналов. Так как управляющие воздействия по основным внешним возмущениям fk улучшают качественные показатели переходных процессов, а введение этих компенсаций по fk позволяет значительно уменьшить кр, то, если имеется возможность достаточно просто измерить основное возмущение (или несколько из них) и если в результате введения компенсации возмущений существенно упростится замкнутый контур САУ, целесообразен переход к комбинированной САУ.
Г л а в а 11. ОСОБЫЕ САУ
К особым линейным САУ относят: САУ с запаздыванием, САУ с распределенными параметрами, САУ с переменными параметрами (нестационарные САУ), дискретные САУ.
§ 11.1. САУ С ЗАПАЗДЫВАНИЕМ
Если в линейной САУ имеется одно или несколько звеньев с запаздыванием, то такая САУ называется САУ с запаздыванием. САУ с запаздыванием описываются уравнением с запаздывающим аргументом, называемым также дифференциально-разностным уравнением:
d2y	dy	,	. ,
«6	+ ах	+а, у+ai y(t - т) = кх.
at	at
Член в левой части уравнения а3у(г-т) а3уе~рх, так как t-- т е-/п. Если хвх = xMejm или xBX = xMsin со t, то у = ,уме7“('~т) или у = yMsin со(/ - т).
277
В первом приближении в качестве звеньев с определенной величи-ной т могут быть представлены: ленточные транспортеры (r=l/v); печи; нагреватели; длинные электрические и акустические линии; тру-бопроводы; сумма малых постоянных времени, например, у N последовательно соединенных апериодических звеньев 1 -го порядка: т=NT, если 7J = Т2 = Т и т. д. В последнем случае
X , I
--р + 1
N )

или
==(1+ТрГ*’ 2im =е^>
(1 + 7р)	at—*®®
где N = 8.
Временные (разгонные) характеристики звена с запаздыванием, имеющие вид, представленный на рис. 11.1, а, б, в одинаковой степени приближения могут описываться дифференциальным уравнением 1-го порядка с запаздывающим аргументом или обыкновенным дифференциальным уравнением 2-го порядка. Тогда для них
Frw = 2« = _^e-r
х(й 7р + 1
ИЛИ
W(p) =-------------=------------------
TiY + Tip+l (Т3р+1)(Т4р+1)
Введение т в САУ первого порядка, которая без т устойчива при любых положительных значениях к нТ. причем ПП при f (t) = const всегда простая экспонента (колебания невозможны), коренным образом меняет свойства САУ. В САУ возникают колебания, ПП становится колебательным, и появляется возможность неустойчивой работы, причем чем т больше, тем сильнее проявляются эти особенности.
В общем случае передаточная функция САУ с запаздыванием представляется в виде произведения
We(p) = W0(p)W(p) = Ж0(р)е-^,
”	R( Di
где в W(p) т = Ут,-, a W0(p) =-----линейная часть САУ.
м	Ом
АФХ системы с запаздыванием:
»;(»=w*"=A(®)eW(0)’<OT!=
278
при ее построении каждая точка W0(J(&) сдвигается вдоль окружности по часовой стрелке на угол <р = -(от, где со — значение частоты в данной точке Wq(J(o). АФХ при со-э °° асимптотически стремится к началу координат, как к особой точке типа «фокус», если степень числителя АФХ меньше степени знаменателя (рис. 11.2, а). Окружность с радиусом R = 1 (рис. 11.2, б) есть АФХ звена с запаздыванием, так как	= А (со) = 1; ф (о>) =- от. Обратная АФХ
звена (7(уса) =	и здесь обход окружности с R = 1 при со —> оо про-
исходит против часовой стрелки.
Характеристическое уравнение замкнутых систем с запаздыванием (и с распределенными параметрами) является не алгебраическим, а трансцендентным: g(p) + /?(р)е-/и: = 0, где степень R (р) меньше или в крайнем случае равна Q (р) (возможны уравнения и более сложного вида). Запаздывание входит в свободный член характеристического уравнения: а^р” +aip"~i + ... +аяе~рт =0; здесь е-/п — оператор сдвига (на величину т).
Трансцендентное уравнение такого типа, как известно, имеет бесчисленное множество корней. Решение дифференциального уравнения можно записать в виде некоторых рядов и для затухания этого решения, т. е. для устойчивости САУ необходимо и достаточно, чтобы все
Рис. 11.2
279
корни трансцендентного характеристического уравнения имели отрицательные вещественные части, число которых бесконечно вследствии наличия е“рт.
Для систем с запаздыванием обычно из-за сложности не применимы алгебраические критерии: Вышнеградского, Рауса и Гурвица.
Для устойчивых линейных САУ 1-го и 2-го порядка с запаздыванием уже недостаточно только положительности коэффициентов характеристического уравнения.
Для САУ с запаздыванием критерии Михайлова, Найквиста и D-разбиения применимы в обычных формулировках, но вид годографов существенно меняется. Например, уравнение годографа Михайлова
D(yco) = <2(уа>) + 7?( jw)(cos шт - ysin сот).
Более удобным для исследования устойчивости оказывается критерий Найквиста, как наиболее простой для систем с запаздыванием.
Наличие звена с запаздыванием не меняет модуль Wc(Jo3), а вносит лишь дополнительный фазовый сдвиг, что приводит к закручиванию АФХ по часовой стрелке только в высокочастотной части. Таким образом, наличие т в общем случае ухудшает условия устойчивости, так как АФХ приближается к точке (-1; 0). Критическое время т = ткр, при котором САУ оказывается на границе колебательной устойчивости, определяется следующим образом (рис. 11.3). Проводится окружность с Л = 1 и находится точка А у И^.(/со) с т = 0, где со = соя, <р = -у1=-л+(Ояткр.
Условие совпадения (•) А с (•) (-1; 0) л-V! у _ =------= -. При нескольких т
<»,	(0я
за ткр берется наименьшее значение. Кроме графического способа оп-По И"с(» = Л0((о)еЛ’о(ш)| г=0 Ад (со) = 1. Далее определяется
при т = ткр: V|/j + (0яткр = л и т
кр
ределения ткр определяется = л~ Vi
^кр
возможен аналитический.
(О=(ОЯ, Фо=-Ф1 Например, пусть
при
= г; =
Тр+1
4 к1 -1
TTwF ’“я= т
к
_	_ л-Vj _ л - arctg V/c2 -1
-V! = -arctg ((0я7); T«p “	“ 1	’
280
Запаздывание т существенно влияет на запасы устойчивости САУ, обычно уменьшая их (рис. 11.4, а). Однако для некоторых САУ с АФХ второго рода возможно придание САУ свойств устойчивости при первоначально неустойчивой САУ без запаздывания (рис. 11.4, б). Поэтому в общем случае необходимо проводить исследования устойчивости.
Исследование устойчивости по ЛАХ аналогично; разница здесь в ФЧХ из-за введения дополнительного фазового сдвига:
ф(ю) = ф0(со)-ют, ф(ю)->-°о при Ю-»о°.
Оценку качества ПП наиболее удобно производить при помощи частотных критериев качества по А (ю), Р (ю) и т. д., причем для построения ПП могут также применяться аналитические и графоаналитические методы и ППП при использовании вычислительных машин.
Примеры и задачи
1.	Показать, что для САУ с запаздыванием второго порядка условие положительности коэффициентов ее характеристического уравнения не является достаточным для ее устойчивости.
2.	Показать, что для САУ с запаздыванием передаточная функция которой имеет вид:
W(p) = ke~v/(Тр+1), сокр=(*2-1) /Т,
ткр = Т arctg {к2
281
3.	Показать, что для САУ:
. 2tyWp+\)e~v О1, п,п„ с W(p) = —<-----------, со =8 1/с, тк_ =0,173с.
ХЮ“2р+1)(р+1) кр	кр
§ 11.2.	САУ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Линейные системы с распределенными параметрами описываются кроме обыкновенных дифференциальных уравнений еще и уравнениями в частных производных. Это системы с длинными линиями электро-, радиосвязи (телеуправление), электропередачи, линии с трубопроводами и т. п. В системах с распределенными параметрами учитывается факт пространственно-временного распространения сигналов, в отличие от САУ с сосредоточенными параметрами, где рассматриваются функции, зависящие только от одной переменной t (времени): у (О, и (г), х (г) и т. д. Состояние ОУ с распределенными параметрами описывается с помощью функций распределения [ вида Q (у, f) и т. п.], т. е. для них связи типа «вход—выход» у ОУ описываются дифференциальными уравнениями в частных производных, интегральными и более сложными функциональными уравнениями.
В общем случае САУ с распределенными параметрами описываются в операторной форме уравнениями вида:
[M,(pp+M2(p)]G(y,p)=o,
где М{, М2 — полиномы с постоянными коэффициентами; Q (у,р) — изображение переменной# (у, i); р = Э/ Э1; py = dj Эу (например, pt = Э/ Э/, см. ниже). Определение передаточных функций ОУ (звеньев) с распределенными параметрами здесь аналогично осуществляется при нулевых начальных условиях (слева по переменной t): q (х, 0) = 0; pq (х, 0) = 0,....
Как отмечалось (см. п. 3.3), передаточные функции ОУ с распределенными параметрами уже не являются дробно-рациональной функцией от аргумента «р» (как у ОУ-звеньев с сосредоточенными параметрами).
Например, для произвольной точки линии распространения сигнала I:
w(i v}=Q^iPL= PAQM’PyQU’P^- l
V,p) Q(f),p) W0,p),pe(0,p),...]’
где рассматриваются краевые условия первого рода (простейшего вида) [1, 12]. При этом на САУ с распределенными параметрами распространяются все положения линейной теории САУ. Например, уравнения длинной электрической линии на удалении /ив момент времени t:
282
+ Ri(l,f) = а, ®)+сэ4« +Gm(/,?) = O, (11.1) Э/ dt	dt dt
или относительно только одной переменной (w или г):
_ LC ^W_(RC + GLy	_ GR	z) = a> (Ц.2)
Э/	dt	at
_ LC -(Rc + GE) - GR i(l, t) = 0,	(11.3)
dr	dr	at
где /, и, i —текущие значения расстояния, напряжения и тока; L, С, R,G — индуктивность, емкость, сопротивление и проводимость на единицу длины. Это уравнения гиперболического типа — представляют собой волновые уравнения напряжений и токов в линии. Если рассматривать идеальный случай в линии без потерь на сопротивление и утечки, когда R = G « О, тогда получим уравнения (простейший случай волнового уравнения, см. п. 3.3):
d2u	д2и	d2i	d2i
"—	— LQ — •	—	_	,
э/2	dt2	di2	dt2
Для случая, когда L = G~Q (линия без индуктивности и без утечек) уравнения имеют вид:
Это уже не гиперболические волновые уравнения, а простейшие уравнения параболического типа (см. п. 3.3). Здесь функция распределения Q (у, t) отражает распределение напряжений вдоль линии, т. е. Q = и в точке у (0 < у < Г) в момент времени t (t > 0).
Тогда, используя функцию распределения, можно, например, записать:
Ц-ьсЦ И =	(11.4)
а/2	э<2	а/2
или в операторной форме (/>=Э/dt, Pi=d/dl):
p2Q = LCp2Q(l) и p2Q = RCpQ(2).	(11.5)
Решения уравнений (11.2), (11.3) имеют соответственно вид
М(/,р) = С^' + С^1; i(l, р) = G0(C2eY/ -С]е-у/),
283
где С},С2 —постоянные интегрирования; у = yJ(Lp+R)(Cp +G) —коэффициент распространения или волновая постоянная; Go =
= ^(Cp+G)/(Lp+R) — волновая проводимость; Zo = 1/GO— волновое сопротивление линии. Здесь характеристическое уравнение q2 -у2 =0 имеет два корня qi2 = + у. При R = G ~ 0 у = pjbC, Go = yjClL, Zo = L/C. Тогда в произвольной точке линии (/):
и{1, р) = и(0, р) ch у I - Zoi (0) sh у I; i (I, р) = i (0, р) ch у I - Gou(O) sh у I.
Если на конце линии I - 1П (1П — полная длина линии) подключена нагрузка — полное сопротивление ZH(p), то u(ln, р) = ZKi(la, р), а W(p)= и(/, р)/и(0, p) = l/(chy/n+ashy/n), где « = ZH/Z0; w(0,p)—значение напряжения в начале линии (/ = 0). При согласованной нагрузке ZH = Zo (а = 1) w(/n, р) = и(0, р)е“у, a W(p) = е~у/". Для линий без потерь: R = G » 0, при согласованной нагрузке W(p) = е~хр; при ZH = °° (а = 0, х.х.) м(/п, р) =u(0, p)/'ch у 1а - u(0, p)/ch тр или и(1, р) =
= и(0, р)/(е~хр+ ехр), a W(p) = l/(e~xp+ ехр). Здесь т = /п/с = = /п -JlC — время, а с = 1/VLC — скорость распространения волнового процесса (волн напряжения) вдоль линии (для воздушных линий с равна скорости света).
Решая, например, первое уравнение (1) из системы (11.5) для случая, когда конец линии замкнут накоротко, а х (?) = и (?) (вход), у (t) = и (?) (выход) на расстоянии от начала линии при краевых Q (0, ?) = и (?), 2 (/,?) = 0 и начальных условиях Q(y, 0) = Q0(y),
smy—(/-^)
Рб(Л 0 - 61 О’)|/=о, получим Q =---------, а передаточная функ-
sin с
0(1, о) S2n J~U~ У> е-р(НУс _~р(1-кУс
- гда а(А sm j—I е е
QM
Таким образом, передаточные функции ОУ-звеньев с распределенными параметрами являются трансцендентными фунциями комплексного переменного р. Заметим, что звено с запаздыванием (см. п. 3.3) является одним из простейших типов звеньев с распределенными параметрами. После решения уравнений в частных производных (с учетом граничных условий) получается, что системы с распределенными параметрами в целом описываются дифференциальными уравнениями аналогичного типа, как и для систем с запаздыванием. При этом без учета волновых явлений в длинных линиях аналогичные системы описываются обыкновенными дифференциальными уравнениями, по-
284
рядок которых на единицу выше, чем порядок дифференциального уравнения с запаздывающим аргументом. Поэтому исследование устойчивости и качества САУ аналогично системам с запаздыванием,
так как и здесь Wc(p) =
D(p)= = Q(p) + R(p)^.
Физически появление частных производных соответствует учету волновых явлений или гидравлического удара в трубопроводах, учету волно
вых процессов в длинных электрических линиях, т. е. рассматривается изменение различных процессов во времени и в пространстве. Если в уравнениях (11.2), (11.3) вместо и (I, f) и i (I, t) принять соответственно давление (напор) и расход жидкости в трубопроводе, а вместо L, С, R,G — их гидравлические аналоги, то при, например, R = G ~ 0, получим аналоги уравнений, описывающих процессы в гидравлических линиях. Подобную аналогию можно продолжить и для других звеньев (ОУ), например, теплообменников, паропроводов и т. п. Необходимо отметить, что аппроксимация САУ с распределенными параметрами посредством передаточных функций с сосредоточенными параметрами широко распространена при анализе различных сложных ОУ химической, металлургической, строительной промышленности, а также в электро- и теплоэнергетике.
Примеры и задачи
1.	Показать, что выражение для АЧХ звена соответствует е"^“, если его W (р) =	, а выражение для ФЧХ звена
И/(р) = У(1 + л/7>).
-arctg	+	,
если его
2.	Показать, что для звена с передаточной функцией W (р) =
= th(pr) = \ерт -е ^Де^ + е j в области малых значений сот АФЧХ соответствует выражение усот.
3.	Показать, что передаточная функция длинной линии электропередачи, как ОУ с распределенными параметрами, при условии, что R * О (G^O) и и(х, t)|	= u(t); i(x, t)\x=l=0 [в момент t = 0 подается
напряжение и (/)], имеет вид:
W(p, х) =	= [е<7(/'х) + е 4(1 Л) ]/Де'?/ + е ql j = chq (I - x)/chq /.
§11.3. САУ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ (НЕСТАЦИОНАРНЫЕ САУ)
Все рассмотренные выше САУ описывались дифференциальными уравнениями с постоянными коэффициентами и являлись стационарными. Однако широко распространены САУ, математическое описание
285
которых приводит к линейным дифференциальным уравнениям с переменными во времени коэффициентами:
dnv	dn~'v	dmx
^(Z)	+й1(Г) 2 + +ая(0^ = А)(0”-т-+ +bm(t)x,
Mt'	W4	Ctl
где oq, а„, bfr, ..., bm — коэффициенты-функции времени, заданные аналитически или графически. Переменные коэффициенты могут быть только в одном [например, апЧ(/) = ТХТ2.. .Tn_x(t)} или нескольких звеньях САУ. Обычно это объект управления, например, печь для сушки изделий (с течением времени изменяется t°, давление); ЛА, самолет (по мере выгорания топлива изменяется масса, момент инерции). Параметры звеньев САУ могут изменяться также из-за изменения во времени внешних условий работы — температуры, напряжения питания и т. п.
Переменность коэффициентов дифференциального уравнения САУ приводит к тому, что функциями времени оказываются передаточная функция системы W3(p,t) = R(p, t)/Q(p, t), частотная функция Ж,( j(f>, t) и переходные функции: h (t - v, v) = h (т, v), w (t - v, v) = w (r, v). Здесь через v обозначен момент подачи на САУ ступенчатого воздействия. Эти функции содержат в качестве параметра время t, поэтому они называются параметрическими (параметрическая передаточная функция и т. д.).
Рассмотрим переходную функцию: h (t - v, v) и функцию веса w (t - v, v), которые являются основными динамическими характеристиками САУ с переменными параметрами. Так как коэффициенты уравнения меняются с течением времени, то эти функции будут зависеть от момента v приложения 1 (?) или 5 (/) на входе. Например, на рис. 11.5, а приведен график изменения коэффициента а, и функций h (т, v), w (т, v), где т = t - v — текущее время. Обычно характеристики САУ рассматривают в трехмерной плоскости (рис. 11.5, б). Весовая функция при v = const как параметре дает нормальную весовую функцию САУ w (t - v, v) = w (т, v) — параметрическую функцию w(x, v) = -Э/г(т, v)/9v. При t = const как параметре получаем сопряженную весовую функцию w (t - v, v), которая также является параметрической; на рис. 11.5,6 это плоскость, параллельная оси v (здесь 0 - t _ у — реверс-смещение), т. е. w (0, t - 0.) Напомним, что функция веса в САУ с постоянными параметрами одна и не зависит от времени поступления внешнего воздействия.
Весовая функция для САУ с переменными параметрами является ее исчерпывающей характеристикой. По ее виду можно судить о качестве САУ, определить быстродействие, склонность САУ к колебаниям. Определение весовой функции здесь затруднено, так как переменность коэффициентов уравнения САУ во времени усложняет задачу исследования динамики. Только уравнения с переменными парамет-
286
Рис. 11.5
рами первого	+ a{(t)y ~	и второго [oj)(0J2j/A2 +
+ а1(/)ф’/Л + а2(0^ = А)(г)/(г)] порядков могут быть решены в общем виде. Уравнения более высоких порядков решаются методами численного интегрирования на вычислительных машинах.
Переходной процесс в нестационарных САУ может быть построен с помощью вещественной Р3(со, t) [или мнимой <Q3(o>, 0] частотных характеристик (как и в случае САУ с постоянными параметрами).
Например, построение переходного процесса по ВЧХ замкнутой системы осуществляется согласно формуле
,.. 2 7 _ .	, sin он ,
Л(/) =..Г Р3(и, t)-------da.
(о
Формула отличается от аналогичной для САУ с постоянными
параметрами тем, то сюда входит параметрическая ВЧХ Р3((0, t),
которая изменяется во времени. Построение переходной характерис-
тики ведется для ряда фиксированных значений времени Z,; строятся характеристики Р3(со, Z,), по которым затем находятся переходные характеристики Л, (?). Искомая характеристика h (?) САУ строится, как показано на рис. 11.6, по точкам кривых соответствующим значениям времени, для которых получены характеристики Р3(а>, tt).
Разработаны приближенные методы анализа САУ, например, метод последовательных приближений, численно-графические методы и некоторые другие. Однако при исследовании таких САУ важно по
287
требуемым показателям качественно произвести синтез параметров. Эти задачи наиболее полно можно решить только с применением ППП и средств вычислительной техники. Изменяя различные переменные параметры САУ по известным или приближенным законам, можно определить опасные точки, построить области устойчивости и линии равных значений показателей качества переходного процесса или среднеквадратичного отклонения выходной переменной при случайном воздействии и произвести исследования САУ в окрестностях этих опасных точек.
Синтез (как и анализ) нестационарной САУ упрощается и можно использовать все методы, разработанные для стационарных систем, если САУ рассматривать как квазистационарную.
Квазистационарная САУ— это система, параметры которой изменяются медленно по сравнению с быстродействием системы, так что приближенно можно считать параметры системы постоянными по времени [const (t)].
Квазистационарные системы обычно исследуют с помощью двух приближенных аналитических методов — метода замороженных коэффициентов и метода замороженных реакций. Решение сводится к многократному исследованию с постоянными коэффициентами известными способами.
Метод замороженных коэффициентов более прост, но менее точен. Выбирается ряд последовательных моментов времени, в которые переменные параметры принимают предельные и наиболее критические по влиянию на динамику системы значения (опасные точки). Для каждой из этих точек производится исследование САУ, причем параметры ее принимаются постоянными, т. е. «замороженными». Если качество переходных процессов в выбранных точках удовлетворяет предъявляемым требованиям, считается, что исходная система с переменными параметрами тоже будет удовлетворять этим требованиям.
Метод замороженных реакций более точен, но сложнее. Применяется он, когда в рассматриваемой САУ можно выделить одно звено с переменными параметрами; остальная часть системы является стационарной. Выбирается также последовательный ряд наиболее характерных по значениям переменных параметров моментов времени t = Vj и определяется переходная функция h(t-vhVj) звена с переменными параметрами. По каждой найденной переходной функции в окрестностях опасных точек определяется эквивалентная передаточная функция W3i(p), т. е. передаточная функция звена с постоянными параметрами, имеющего такую же переходную функцию. Следовательно, здесь САУ заменяется эквивалентной стационарной системой, описываемой передаточной функцией с постоянными коэффициентами.
Исследование необходимо провести для всех выбранных опасных точек, как и в случае метода замороженных коэффициентов. Метод более точен, так как эквивалентное звено в определенной мере учитывает в целом переменность параметров САУ.
288
Примеры и задачи
1.	Показать, что если нормальная функция веса описывается выражением w(z) = e<“Vo”“', z(vo = const), то функция веса САУ с непеременными параметрами w(Z-v, v) = e~a('~v)/7, а сопряженная ей функция веса равна е~“'° eav/z0 (t0 = const).
2.	Показать, что если САУ с переменными параметрами описывается уравнением
+ (0,4+0,7z) + у = (1+0,6z)/(Z), dr	dt
то ее передаточная функция с «замороженными» коэффициентами определяется выражением
„., ч 1 + 0,6z W(p,t) = -5------------.
p2+(0,4+0,7z)p+l
3.	Показать, что коэффициент ошибки c0(z) = ЫЦа + Ы), если САУ с переменными параметрами замкнута, имеет единичную отрицательную обратную связь и ее W(p,t)~a/(b+a+bt).
§ 11.4. ДИСКРЕТНЫЕ САУ
В книге дискретные САУ рассматривались, по мере возможности, параллельно с непрерывными САУ, так как методы их исследования подобны с учетом подстановок (типа p = q^T',z = rl и др.). Напомним, что к дискретным относят импульсные (с квантованием сигнала по времени), цифровые (квантование — по времени и по уровню) и релейные (квантование по уровню) САУ.
Аналогично непрерывным системам по передаточным функциям можно определить частотные характеристики дискретных САУ, а именно, осуществляя подстановку q = рТ = ja>T = у®, где со = а>Т — относительная частота (со =2 л/= 2л/ Т; со = d)T = 2п; z = е9= ерТ= ejmT= eJU> ) Здесь	соответствует мнимая ось j на плоскости q.
Следовательно, все частотные характеристики дискретных САУ как дискретных импульсных систем являются периодическими функциями со и укладываются в область до ±л при изменении со от - °® до + °® (рис. 11.7, а).
Области устойчивости имеют вид единичного круга на плоскости z (рис. 11.7, б) или в виде полосы ± л левее оси j на ^-плоскости (рис. 11.7, а); соответственно граница устойчивости — единичный круг (или ось j). Переход к частотным характеристикам по передаточным функ-
19 А. А. Ерофеев
289
циям осуществляется: в непрерывных САУ р = ja>, а в дискретных z =	= eJW, т. е. рассматриваются только точки в окружности |z| = 1.
С использованием w-преобразования (билинейное преобразование Мёбиуса) w = (z-l)/(z+1) или более удобного модифициро-2
ванного w = —(z-l)/(z+l) единичная окружность на z-плоскости отображается в мнимую ось на iv-плоскости (рис. 11.7, в, г); здесь z = = (l+7w/2)/(l - Tw/2). При z = = е>г = cos со 74 /sin со Т:
2	2 -
w = [2J sin со 77 (1+cos соТ)] /Т = - /tg (соТ/ 2) = — jk = Jk = jv = /со*.
Здесь X = 2Х / Т = со* — абсолютная псевдочастота; X — относительная псевдочастота. Область внутри |z| = 1 соответствует левой полуплоскости на w-плоскости (области устойчивости); при 0 < со < л имеем О < со* < оо. При малых частотах или медленно изменяющихся входных сигналах, когда со Т <2, получим, что Х = со = со*, так как tg (со 772) = = со 772. Именно в этом, а также в простоте построения ЛАЧХ и ФЧХ дискретных САУ заключается ценность w-преобразования. Таким образом, W(z) н> W(w). Подстановка w = /со*= Jk позволяет ис-
290
пользовать для дискретных САУ обычные частотные методы [по jy*(yX) ]. Здесь 1/pi-»z/(z-l)h->(w+l)/(2M’). При изменении (0 = 0+л/Г Л изменяется от 0 до а комплексная переменная w движется по оси 71	71
мнимых от 0 до />= (если - - < (о < —, то - «> < X < <», & -j°°<w< j°°).
Устойчивость дискретных С А У определяется аналогично при рас-
смотрении характеристического уравнения Z)(z) = 1 + W(z) = a^z” + + aIz"-1 + ... +a„_{z + a„ =0 замкнутой дискретной САУ с W3(z) = = Wz(z)/[1 + jy(z)]. Дискретная САУ устойчива, если корни zf D (z)
лежат внутри единичного радиуса |z,|<l в комплексной плоскости z. f. Т /(
Для обычной интерпретации делают подстановку: z = 11 + у w I / 1 ” jn \	/	\
---w или z = (l+/ХТ/2)/(1-/ХГ/2). При исследовании устойчивос-
2 )
ти дискретных систем используют прямой метод Ляпунова (по функ
ции Ляпунова), алгебраические (критерий Шур—Кона, Рауса—Гур-
вица) и частотные (Михайлова, Найквиста) критерии устойчивости. Все они формально являются обобщением аналогов критериев устой
чивости для непрерывных систем, причем частотные критерии здесь также предпочтительнее [построение характеристик дискретных САУ по W(jK) = Л(Х) ехр7Ф(Х) наиболее просто]. Например, (критерий Найквиста), если разомкнутая система устойчива, то условием устойчивости замкнутой системы является не охват амплитудно-фазовой частотной характеристики W(jto) или W*(jk) разомкнутой системы точки с координатами (-1; 0) (см. рис. 11.7). Здесь при [т Т] -»», Дли Г] —> 0 (асимптотическая устойчивость).
Характеристики линейных дискретных систем в отличие от непрерывных стягиваются не в начало координат, а в некоторую точку со = п. Чтобы дискретная САУ была асимптотически устойчивой, кор
ни ее характеристического уравнения должны лежать на z-плоскости, внутри единичной окружности jz|=l (см. рис. 11.7). Устойчивость дискретных САУ зависит от значения Т; при больших Т дискретная САУ может быть неустойчивой (0< Т < Гкрит). При Г—>0 дискретная САУ стремится к аналоговой. При адекватных структурах и параметрах дискретная САУ обычно менее устойчива. От значений Т зависит и качество дискретной САУ. При Т —> °° дискретная САУ неустойчива. Границу устойчивости определяет некоторый корень \zk I = 1, при всех других iz,_fc | < 1; корни же w, аналогично должны иметь отрицательные вещественные части для устойчивой дискретной САУ.
Определение запасов устойчивости дискретных С А У аналогично определению запасов устойчивости для непрерывных систем. Запас устойчивости дискретной САУ также характеризуется запасом устойчивости по фазе и модулю. Требования к запасам устойчивости дискретных САУ аналогичны требованиям непрерывных систем (у > >30+50°; Л>0,2+0,4; АГ>6+12 дБ).
291
19*
Качество переходных процессов в дискретных СА У исследуют с помощью аналогичных методов и показателей качества, как и в случае непрерывных систем.
Коррекция дискретных СА У сводится аналогично к увеличению запасов устойчивости и улучшению показателей качества. Для этого обычно используют два приема:
1) выбор периода Т или частоты квантования юк, влияющих на форму амплитудно-фазовой характеристики и соответственно на динамические свойства дискретных САУ. Чем выше значение шк, тем ближе по свойствам дискретная САУ к непрерывной системе. Значение Т обычно выбирают по соображениям устойчивости, точности и качества переходных процессов (а не по адекватности аналогового и дискретного представления сигналов);
2) на свойства дискретных САУ оказывает влияние форма выходного импульса с ЦАП, так как именно она через передаточную функцию формирующего элемента (ФЭ) Ифэ(р) определяет передаточную функцию приведенной непрерывной части (ПНЧ):
^нч(р) = ^Фэ(рЖч(р).
Изменяя форму импульсов с ЦАП, можно корректировать динамические свойства дискретных САУ. При простейшей форме передаточной функции фиксатора (экстраполятора) 1Кфэ(р) = Ц1-е~лГ)/р — для прямоугольных импульсов; следовательно,
где WK(p) — передаточная функция корректирующего устройства (КЗ).
Другие методы коррекции дискретных САУ аналогичны методам коррекции непрерывных систем: применяют линейные последовательные, параллельные корректирующие устройства, корректирующие устройства типа обратной связи. Дискретные КЗ также преобразуют входную величину х[пТ\ в выходную у[пТ\ в соответствии с предписанным алгоритмом. Их расчет производят аналогично, например, как (см. п. 10.2) алгоритм WK(z) = Wx(z)/Wp(z) или IVK(z) = 1Кзж(2)/(1-1Узж(2))Ж/2) , где Wx(z), 1Узж(г) —соответственно желаемые передаточные функции САУ; РУр(г) — передаточная функция исходной разомкнутой САУ. Линейные цифровые КУ (ЦКУ) подразделяют на три группы: фильтрующие, оптимизирующие и особые. В зависимости от вида ЦКУ могут быть рекурсивными и нерекурсивными. В рекурсивных ЦКУ *вых = Я*вх, *вых), а в нерекурсивных хвых = /(хвх).
Цифровые корректирующие устройства [например, интегрирующего типа с fV*(q) = ke4(e9 -1) и др.] иначе называют импульсными фильтрами. Их включают для коррекции дискретных САУ, что позволяет получить те же результаты, что и при использовании аналоговых
292
корректирующих устройств. Однако в реализации они значительно сложнее и поэтому применяются реже. Для коррекции нелинейных дискретных САУ так же, как и для непрерывных систем, используют псевдолинейные [с изменением А (со) и ф(ю) = const; с изменением ср(со) и Я (со) = const; с неоднозначным изменением Л (со) и ср(со)], а также нелинейные (компенсирующего и управляющего типов) корректирующие устройства.
Синтез алгоритмов управления и дискретных систем начинается с построения моделей ОУ и внешних воздействий (идентификации ОУ). Методы синтеза дискретных систем являются обобщением аналогов методов синтеза непрерывных систем: используются также временные и частотные методы. Временные (например, по критериям J20 = ^е2 [га Г]; А1 т=0
и др.) предписывают введение обратной связи, т. е. коррекцию собственных движений ОУ независимо от их свойств; частотные игнорируют собственные движения ОУ (по разомкнутой ЛАЧХ) и обеспечивают более простые алгоритмы. Здесь также используются понятия о типовых желаемых ЛАЧХ:
LK(X) = 201g LK(X); LK(X) = LJX) -Lp(X)
(ЛАЧХ типа 1 —2—1 —2 и др.) и типовых желаемых передаточных функциях №ж(г) = WK(z)Wp(z), откуда WK(z) = Wx(z)/ FEp(z).
Дискретные УУ обеспечивают желаемые переходные процессы только в дискретные моменты времени Т. Поведение ОУ внутри интервала Т определяется динамическими свойствами ОУ и Т должен быть таков, чтобы внутри него не было значительных колебаний ПП. Выбор интервала Т необходимо соотносить с особенностями собственных движений ОУ. Если внутри Т возникают колебания ПП, то для их устранения надо уменьшать значения Т. Это требует пересчета алгоритмов управления, начиная с новой дискретной модели ОУ. Запаздывание дискретного УУ зависит от трудоемкости (сложности) алгоритма управления, быстродействия и организации вычислительного процесса и управления.
Существуют три варианта исследования дискретных (цифровых) САУ.
1.	Точное исследование, при котором учитываются процессы квантования по уровню и по времени. Учет процессов квантования по уровню приводит к решению нелинейной задачи и проявлению таких особенностей, как появление периодических режимов в цифровых САУ [ЦСАУ]. При построении процессов в ЦСАУ определение оригинала по изображению у (z) может быть обеспечено обратным Z-преобра-зованием: у* (t) = Z~l[y(z)].
ЦСАУ являются периодическими системами; эффекты периодичности можно свести к минимуму выбором малого значения Т (чем Т меньше, тем меньше эффекты; со к = 1/ 7’). Для ЦСАУ, устойчивых в разомкнутом состоянии, при приближенном исследовании используют ме
293
тод гармонической линеаризации, когда ЦСАУ представляют в виде импульсного нелинейного звена (ИНЗ) и ПНЧ (ИНЗ осуществляет, например, АИМ). Это позволяет определить периодические режимы ЦСАУ. Трудоемкость этого метода значительно выше, чем в непрерывных системах. Нелинейность цифровых систем может определяться не только квантованием по уровню (ИНЗ), но и нелинейностью приведенной непрерывной части (ПНЧ).
Квантование по уровню влияет на устойчивость и качественные показатели переходного процесса ЦСАУ (особенно на низких частотах, т. е. когда имеет место наложение амплитудно-частотных характеристик).
Характеристика квантователя представляется в виде суммы релейных характеристик с зонами нечувствительности (см. Приложение, «аналог—цифра»); тогда коэффициент гармонической линеаризации для квантователя будет
где х,- = (2z- l)q/2 или х,- = iq определяет моменты переключения; q определяет вес единицы младшего разряда. В остальном метод гармонической линеаризации с использованием qj(A) остается прежним, как и для непрерывных систем (см. п. 3.3).
2.	При разрядности п > 8 характеристику квантования обычно заменяют линейной; тогда цифровая система превращается в линейную импульсную систему. Если непрерывная часть линейна, то система называется предельной импульсной системой. Анализ и синтез такой дискретной САУ ведется методами теории импульсных систем.
3.	Приближенный метод исследования дискретных систем, при котором цифровая система эквивалентируется непрерывной системой; это возможно, когда удовлетворяется 2-й вариант и соблюдается условие теоремы Котельникова—Шеннона (дискретное управление аппроксимируется непрерывным процессом). Из рассмотрения частотных характеристик можно вывести условия такой эквивалентности. Для систем с ЦАП и амплитудно-импульсной модуляцией [фиксатор нулевого порядка с у = Ти /Т = 1; №фЭ(р) = (1 - eY/,r)/р = (1 -еГрг)'р}-.
(Оу <сок -(0с.
В граничном случае сок = 2сос, а со у = сос, где С0у — частота внешнего воздействия, приведенного к входу импульсного элемента. При выполнении условий эквивалентности ЦСАУ будет реагировать на низкочастотные воздействия подобно непрерывной системе. Таким образом, при выполнении условий эквивалентирования в ЦСАУ, по существу, пренебрегают квантованием по уровню и по времени.
294
Эквивалентирование дискретных САУ аналоговым создает широкие возможности приближенного исследования дискретных САУ, позволяет использовать традиционные методы расчета. На практике это приводит к рассмотрению дискретных САУ как квазианалоговых: о)к S8o)p, где ©р— рабочая частота контура регулирования.
Формально передаточные функции дискретных динамических звеньев и САУ можно получить из непрерывных И^(р) заменой р на . 2 z-1	2
р = — —- = w и умножением полученного результата на —т. е.
2	(2г-1А
В численных методах этот прием соответствует методу трапеций. Возможны и другие упрощенные варианты, соответствующие в численных методах методам прямоугольников: способ прямой разности—
_	2 — 1
p = (z-l)/T и способ обратной разности— р =---с умножением
результата на 1/z. Здесь везде исходное р = In z/T
z = epT ~1 +рТ; z = l/e~pT =^1/(1-рТ);
Следует отметить, что наиболее простой способ получения разностных уравнений, описывающих дискретные САУ, использует апрок-симацию производных конечными разностями:
dy dt
(л+1)ДГ
иД/
= lim y&n + \)bt)~y(nba) _ y[n+l]-y[n] д«-»о Дг ~ м n J’
? («+l)Af
d У = = lim y((n+l)M)-y(nSt)
dt2 .	&t
n&t
d3y
(и+1)Дг
dt3
= д2Я«] =
= А3Я«] =
(ДО2
(y[n+2]-2y[n+l]+y[n]);
1 (ДО2
(y[ n + 3] - Зу [n+2]+2 y[n +1] - y[n\,

295
„	. l^pS + Ь2р2 +61Р+Д)
Так, если W(p) =	---~~~— ----то конечно-разностному
а3р + а2р2+а1р+а0
аналогу соответствует выражение а3 А3 у[п] + а2 А2 .у [и] + q Д у[п] + +«оУ[«]= 6зД3х[и] + ^Д2х[п]+/51Дх[и] + £|)х[п] или Л3у[и+3]+ А2у[п +
+ 2] + Aty[n +1] + Аоу[п]= В3х[п + 3] + В2х[п + 2] + В}х[п + 1]+ Вох[п],
где
2яз + 2д2 + «1 .
(Д/)3 (ДО2 Д/’
а?	cit	_	„
j =-----2 +—• л _---------аналогично и для Вл ч- с за-
(до3 (ДО2	(ДО3
меной а,- на Ь,.
Подобные процедуры применимы (с определенными особенностями) и для получения векторно-матричных разностных уравнений, например вида j[n+l]+C[n]j[«] = Z>[«]x[n], hg[0, 7V-1].
Проектирование дискретных САУ, также как и непрерывных, базируется на математическом описании САУ на основе методов: операторно-структурного (передаточных функций, частотных и временных характеристик); переменных состояния и структурно-топологических (графовых).
Операторно-структурный метод, основываясь на качественном исследовании решений системы дифференциальных уравнений САУ, по существу, оперирует с алгебраическими свойствами определенных функций, порождаемых этой системой уравнений. По глубине и степени завер
шенности развития этот метод занимает лидирующие позиции.
Метод переменных состояния базируется на матричном исчислении и вычислительных методах линейной алгебры. Этот метод широко применяют для исследования сложных многомерных, многосвязных САУ, а также в теории оптимальных, адаптивных, интеллектуальных САУ. Метод переменных состояния и операторно-структурный метод сильно взаимосвязаны, дополняют и качественно развивают друг друга. В практике проектирования дискретных САУ применяют переходы от уравнений состояния непрерывных систем к уравнениям состояния дискретных систем (и наоборот).
Структурно-топологические методы широко используют теорию графов в ее современных представлениях. Применение этих методов
в сочетании со структурными числами дает возможность получать эквивалентную передаточную функцию сложной многомерной САУ (САУ с перекрестными связями), проводить параметрический синтез и вести анализ различных сложных структур САУ.
В частности, к таким относятся дискретные системы с распределенными параметрами, которые имеют определенную специфику описания, приводящую к цепочечным схемам с перекрестными связями. Эта специфика связана с природой ОУ с распределенными параметрами — с несоблюдением для них принципа направленности звеньев.
296
При этом такой ОУ разбивается обычно на однородные звенья (типа двух-, четырехполюсников) с сосредоточенными параметрами, связанные посредством прямых и обратных перекрестных связей. Например, для длинной линии электропередачи (см. § 11.2) обычно однородное звено — Т-образная схема четырехполюсника с погонными комплексными сопротивлениями: последовательными и параллельным z2.
САУ для системно-сложных ОУ (типа ИСУ) обычно представляют собой иерархические многокритериальные, многоцелевые системы, состоящие из разноуровневых подсистем, часть из которых может решать различные задачи. Отметим, что иерархические системы состоят из п- уровней управления, следующих в порядке определенного приоритета друг за другом (от нулевого до и-ого); связи между уровнями как вертикальные, так и горизонтальные, обычно соответствуют выбору согласованных решений. Для таких систем применяют путь многоуровневой иерархии описаний, когда описание высшего уровня зависит от обобщенных и факторизованных переменных низшего уровня, а описание в целом отражает параметры, процессы и иерархию. При этом всегда существует значительная неопределенность в решении задач, т. е. существует «неопределенность цели». Выбор оптимальных или наилучших решений (с учетом различных ограничений) и формирование эффективных алгоритмов функционирования являются основными задачами построения ИСУ. В ТАУ преодоление проблемы неопределенности осуществляют путем введения условий — компромиссов, например, путем сведения многокритериальной задачи к однокритериаль-п
ной (типа свертки критериев Jr = У kjJj, где /с, — весовые коэффициен-1-1
ты; J, — локальный критерий; Jr — глобальный критерий), использования методов: уступок (ранжирование критериев >- J2 >... Jк, здесь >- — знак ранжирования), равных и наименьших отклонений -= ——:^->(|AJ//./io|®cost) и др. Для таких иерархических систем
"Л'О
обычно необходимо решать две главные проблемы — структурную (проблема стратификации) и координации (управления). Первая из них связана с оптимальной декомпозицией задач управления на различных уровнях, вторая — с оптимальной согласованностью действий подсистем разного уровня для достижения глобальной цели (координация по принципам: прогнозирования оценки и согласования взаимодействий и т. п.).
Следует отметить, что обычно процесс проектирования дискретных САУ и САУ для системно-сложных ОУ производят с использованием ЭВМ и различных современных ППП.
Примеры и задачи
1.	Определить тип формирующего устройства, если его передаточ-(1-z-1)
ная функция W(р) = -—(z-1), z = epT.
Тр2
2.	Показать, что для дискретной САУ с единичной отрицательной обратной связью передаточная функция замкнутой САУ относительно ошибки равна (z - l)(z - 0,5)/[(z - l)(z - 0,5)+0,3], если для САУ в разомкнутом состоянии W(z) = 0,3/(z - l)(z - 0,5), и равна ^z2 - г +0,3jДг2 - z +0,6j, если W (z) = 0,3/ (z2 - z+0,б1
3.	Показать, что Z-преобразование решетчатой функции f\n] = а • 1[и] соответствует az/(z-l), а Ди] = аш->аг/(г-1)2; и наоборот: F (z) =
=	-н>1[и], F(z) = z/(z-l)2
(Z-1)
4.	Показать, что передаточной функции:
1-z'1 фиксатора нулевого порядка соответствует выражение-------;
/ 7	Р
дискретной САУ 9/(z -0,9z) соответствует разностное уравнение у [и] - 0,9_и [и -1] = 9х [и - 2].
ПРИЛОЖЕНИЕ
Характеристики типовых нелинейных звеньев
Название	Вид		Название	Вид					Название	Вид	
Зона нечувствительности		1	Парабола нечетная (1), четная (3) и кусочнолинейная (2)	1 зА			F \ 1		Гистерезисная с зоной нечувствительности		F к
	ьУ	0 х		/ / / f			0	*				
Ограничение	1	Г к	Отрицательный гистерезис (постоянный)	)			Г —	—► ) к.		Люфт		—	к	^4-У / 45>*
	1 у	0	X		<—1_			0	*				
Ограничение с зоной нечувствительности		F к Л 0	х	Отрицательный гистерезис (переменный)			2	к		Упор	)	F к
						2 к					
				Л			X				/45°
Пороговая однозначная нечетная	/	к 0	х	Положительный гистерезис	1 ~ Ха			F		Пороговая с зоной нечувствительности		F к
				| 0			Ха х					0	*
Переменная структура		Г	Сухое трение	2					ьный зоной ьносги		С* к
									Положител] гистерезисе: нечувствител!		
							0	*			
	। т Х*	»	X								11 1	0	X
											
Аналог —цифра	2	7 к	Несимметричный нечетный гистерезис			2 А			Треугольная с опережением		7 к
											
		о X					0 м	X			0	*
											
299
СПИСОК ЛИТЕРАТУРЫ
1.	Теория автоматического управления /Под ред. А. А.Воронова. — М.: Высш. шк„ 1986. — 4.1. — 368 с.; Ч. 2. — 504 с.
2.	Топчеев Ю. И. Атлас для проектирования систем автоматического регулирования. — М.: Машиностроение, 1989. — 752 с.
3.	Справочник по теории автоматического управления/Под ред. А. А. К р а с о в с кого . — М.: Наука, 1987. — 712 с.
4.	Юревич Е. И. Теория автоматического управления. — Л.: Энергия, 1975. —415 с.
5.	Теория автоматического управления/Под ред. А. В. Н е т у ш и л а. — М.: Высш. шк„ 1976. — 4.1. — 424 с.; Ч. П. — 430 с.
6.	Попов Е. П. Теория линейных систем автоматического регулирования и управления . — М.: Наука, 1989. — 304 с.
7.	Бесекерский В. А., Попов Е. П.Теория систем автоматического регулирования. — М.: Наука, 1975. — 768 с.
8.	Первозванский А. А. Курс теории автоматического управления. — М.: Наука, 1986. — 616 с.
9.	Цыпкин Я. 3. Основы теории автоматических систем. — М.: Наука, 1977. — 548 с.
10.	Ерофеев А. А. Алгоритмы управления промышленных автоматических систем. — СПб.: Политехника, 1992. — 106 с.
11.	Математические основы теории автоматического регулирования/Под ред. Б. К. Чемоданова. — М.: Высш, шк., 1971. — 807 с.
12.	Воронов А. А. Введение в динамику сложных управляемых систем. — М.: Наука, 1985,— 697 с.
13.	Ерофеев А. А., Александров В. В., Поляков А. О., Смирнов Ю. М. Интеллектуальные системы управления. // Научно-технические ведомости СПбГТУ. — № 1 (3). — СПб.: СПб.ГТУ, 1996. — С. 53 — 62.
14.	Ерофеев А. А., Городецкий А. Е. Принципы построения интеллектуальных систем управления подвижными объектами. // Автоматика и телемеханика. — №9. —1997. — С. 101 —ПО.
15.	Ерофеев А. А., Поляков А. О. Интеллектуальные системы управления: Учебное пособие для вузов. — СПб.: Изд-во СПбГТУ, 1999. — С. 265.
16.	Ерофеев А. А., Поляков А. О. Интеллектуальные нечеткие технологии управления для контекстно-зависимых информационных потоков // СПбГТУ. №3(17). — 1999, С. 113—124.
17.	Ерофеев А. А. Интеллектуальные технологии в системах управления. // Научно-технические ведомости СПбГТУ. — № 3 (21). — 2000. — С. 25—34.
18.	Ерофеев А. А., Коваль С. Н. Интеллектуальное управление в системах: нечеткие технологии управления. Вестник СЗО Академии медико-технических наук. Выпуск № 3. — СПб.: Агентство «РДК — принт»; 2000. С. 172-188.
ОГЛАВЛЕНИЕ
От автора.............................................................. 5
Предисловие............................................................ 7
Глава 1. Основные понятия и общие принципы построения автоматических систем................................................................. 9
§1.1.	Основные термины и определения....................... —
§ 1.2.	Типовая функциональная схема САУ.................... 12
§ 1.3.	Принципы управления и классификация САУ.............. 14
§ 1.4.	Задачи ТАУ и характеристика процессов управления.... 29
Глава 2. Математические основы теории автоматического управления....... 30
§ 2.1.	Математические модели объектов управления и методы их идентификации............................................... —
§ 2.2.	Математическое описание САУ......................... 37
§ 2.3.	Линеаризация звеньев и систем....................... 39
§ 2.4.	Формы записи дифференциальных уравнений САУ......... 43
§ 2.5.	Временные и частотные характеристики................ 52
Глава 3. Динамические свойства звеньев САУ и их характеристики........ 64
§3.1.	Классификация динамических звеньев САУ............... —
§ 3.2.	Обыкновенные типовые динамические звенья САУ........ 67
§ 3.3.	Особые динамические звенья САУ...................... 89
Глава 4. Анализ одномерных САУ. Алгоритмические схемы САУ............ 110
§ 4.1.	Передаточные функции соединений звеньев [алгебра W(p)]	—
§ 4.2.	Передаточные функции замкнутой САУ................. 115
§ 4.3.	Правила преобразования структурных схем............ 118
§ 4.4.	Матрично-топологические преобразования структурных схем 121 § 4.5. Частотные характеристики замкнутой САУ (определение и построение................................................ 125
Глава 5. Стационарные динамические режимы САУ при случайных воздействиях ........................................................... 129
§ 5.1.	Случайные процессы................................... —
§ 5.2.	Стационарные случайные процессы в САУ.............. 137
Глава 6. Устойчивость САУ............................................ 142
§6.1.	Понятие об устойчивости линеаризованных САУ. Теоремы Ляпунова.................................................... —
§ 6.2.	Алгебраические критерии устойчивости............... 148
§ 6.3.	Частотные (графоаналитические) критерии устойчивости. 151
§ 6.4.	Устойчивость систем с трансцендентными и иррациональными звеньями............................................. 159
§ 6.5.	Области устойчивости САУ........................... 161
§ 6.6.	Обобщенный критерий устойчивости................... 167
Глава 7. Качество процессов управления............................... 169
§ 7.1.	Стационарные режимы САУ.............................. —
§ 7.2.	Способы повышения точности САУ..................... 171
§ 7.3.	Стационарные динамические детерминированные режимы САУ....................................................... 176
§ 7.4.	Коэффициенты ошибок в САУ.......................... 177
§ 7.5.	Качество переходных процессов в САУ.................. 181
§ 7.6.	Критерии качества переходных процессов. Частотные критерии 187
§ 7.7	Корневые критерии качества.......................... 192
301
§ 7.8.	Интегральные критерии качества....................... 196	£'
§ 7.9.	Методы расчета (построения) переходных процессов..... 202	ф
§ 7.10.	Чувствительность САУ................................ 207	£
Глава 8.	Коррекция свойств САУ...................................... 209	<
§ 8.1.	Виды коррекции......................................... —	№
§ 8.2.	Корректирующие звенья последовательного типа......... 211	~
§ 8.3.	Параллельные корректирующие звенья................... 217	»|
§ 8.4.	Способы увеличения запасов устойчивости САУ.......... 220	£
Глава 9.	Алгоритмы и программы управления в САУ.................... 224
§ 9.1.	Аналоговые (непрерывные) алгоритмы..................... —	i
§ 9.2.	Реализация аналоговых алгоритмов управления.......... 232	;
§ 9.3.	Дискретные алгоритмы ................................ 239	j
§ 9.4.	Реализация дискретных алгоритмов.................... 244
§ 9.5.	Многосвязные (многомерные) регуляторы............... 247
§ 9.6.	Нелинейные алгоритмы управления (базовые представления). 248	j
Глава 10. Синтез и проектирование САУ...............................   262
§ 10.1.	Задачи и методы синтеза............................... —	\
§ 10.2.	Графоаналитические (частотные) методы синтеза...... 265
§ 10.3.	Особенности синтеза многомерных САУ ..............  271
§ 10.4.	0 синтезе САУ с оптимальным переходным процессом....... 274	;
§ 10.5.	Проектирование САУ................................. 275
Глава 11. Особые САУ.................................................. 277
§ 11.1.	САУ с запаздыванием.................................. —
§ 11.2.	САУ с распределенными параметрами.................. 282
§ 11.3.	САУ с переменными параметрами (нестационарные САУ)..... 285
§ 11.4.	Дискретные САУ..................................... 290
Приложение................ ............................................... 299
Список литературы...................................................... 300	J
Анатолий Александрович Ерофеев
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Редакторы Е. М. Миронченкова, Е. В. Шарова Переплет художника М. Л. Черненко Технический редактор Т. М. Жилич Корректоры 3. С. Романова, Н. В. Соловьева Верстка Л. Н. Сергеевой
ЛР№ 010292 от 18.08.98
Подписано в печать 09.09.03.
Формат издания 60x90V16. Бумага офсетная. Гарнитура Times. Печать офсетная. Усл. печ. л. 19.0. Уч-m i 19.5. Тираж 2000 экз.
Заказ 3074.
ФГУП «Издательство “Полшсхника”». 191023, Санкт-Петербург, Инженерная ул., 6.
Отпечатано с оригинала-макета в ГП «Типография им. П. Ф. Анохина». 185005, г. Петрозаводск, ул. «Правды», 4.