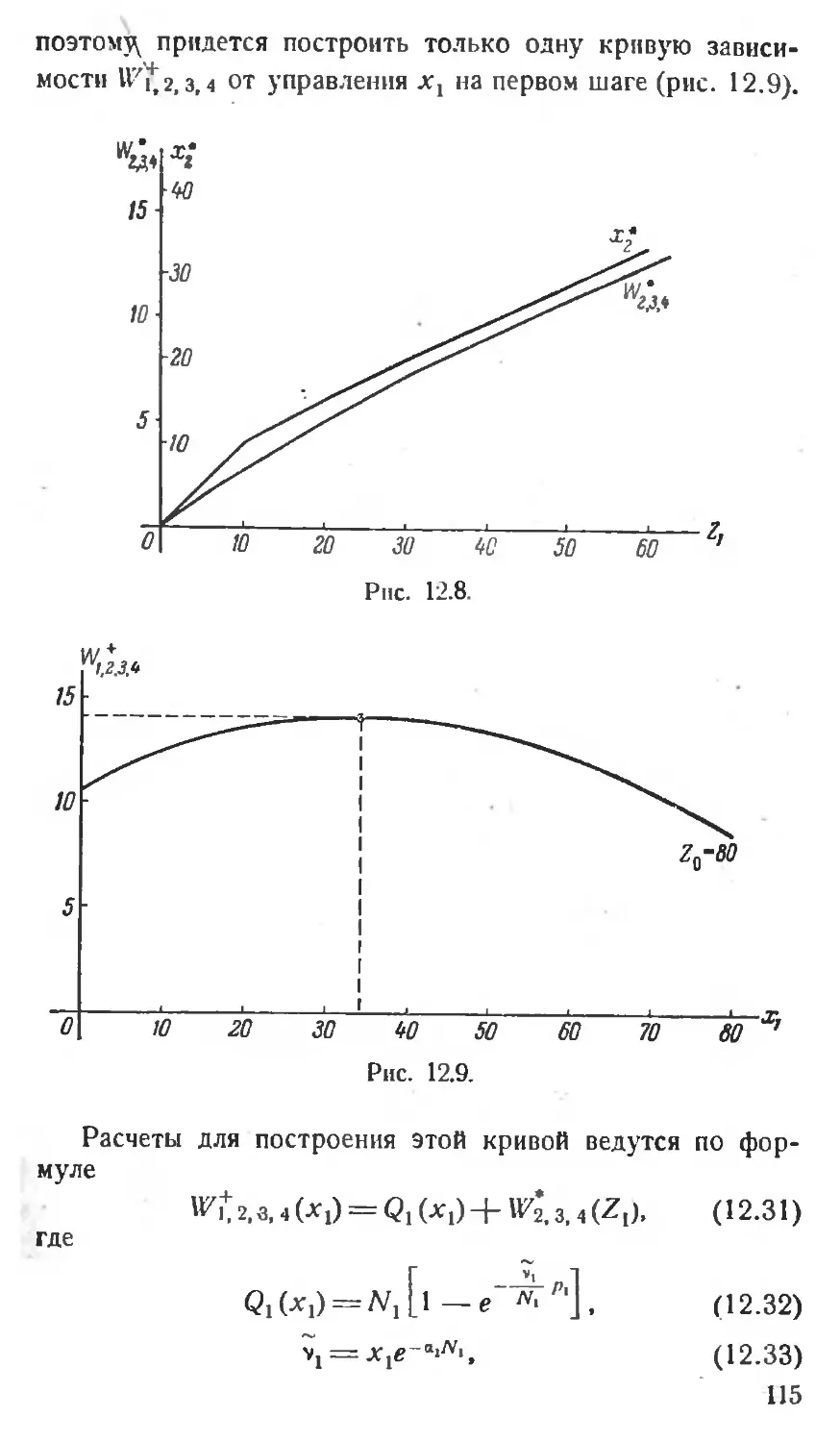
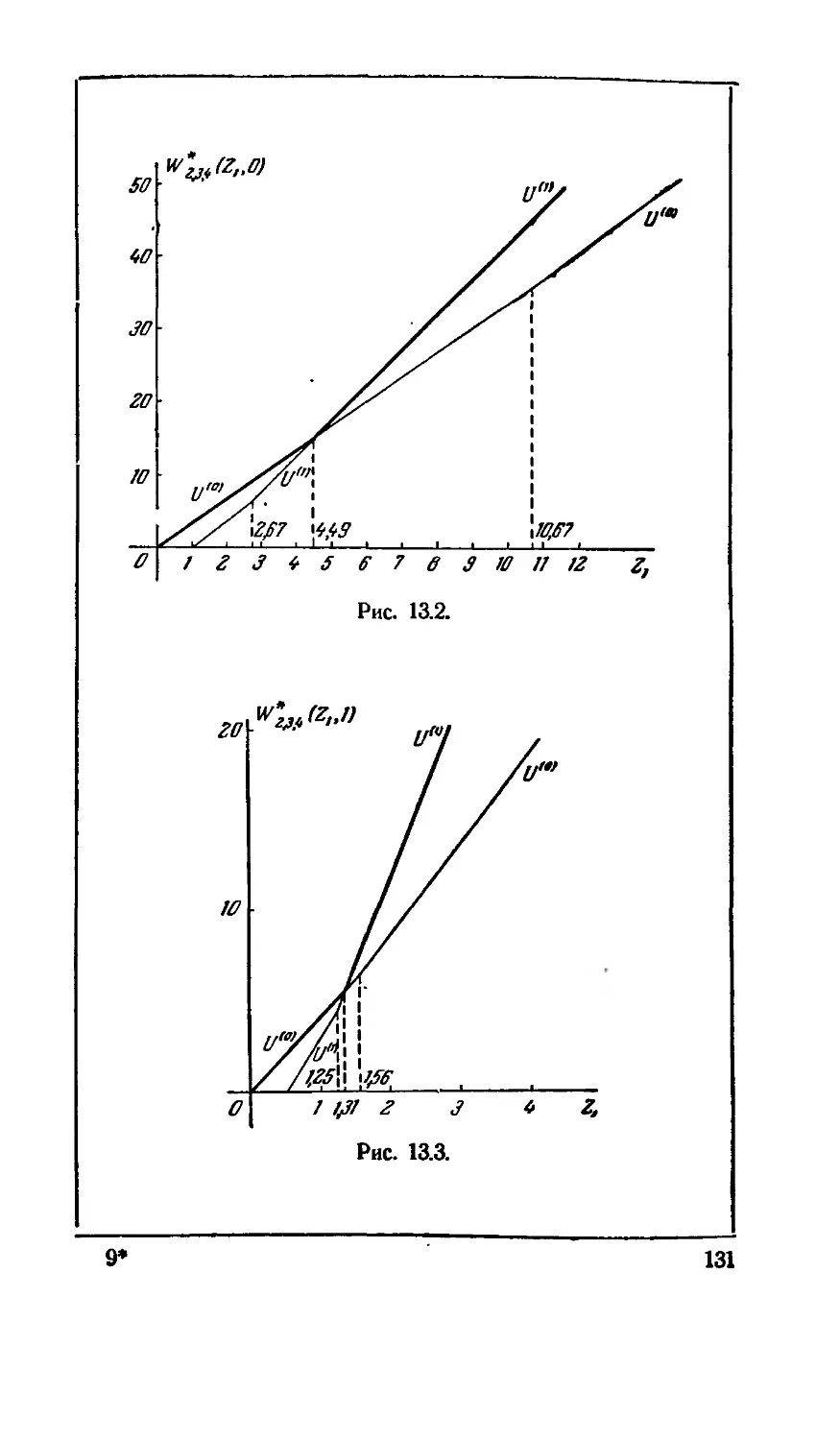
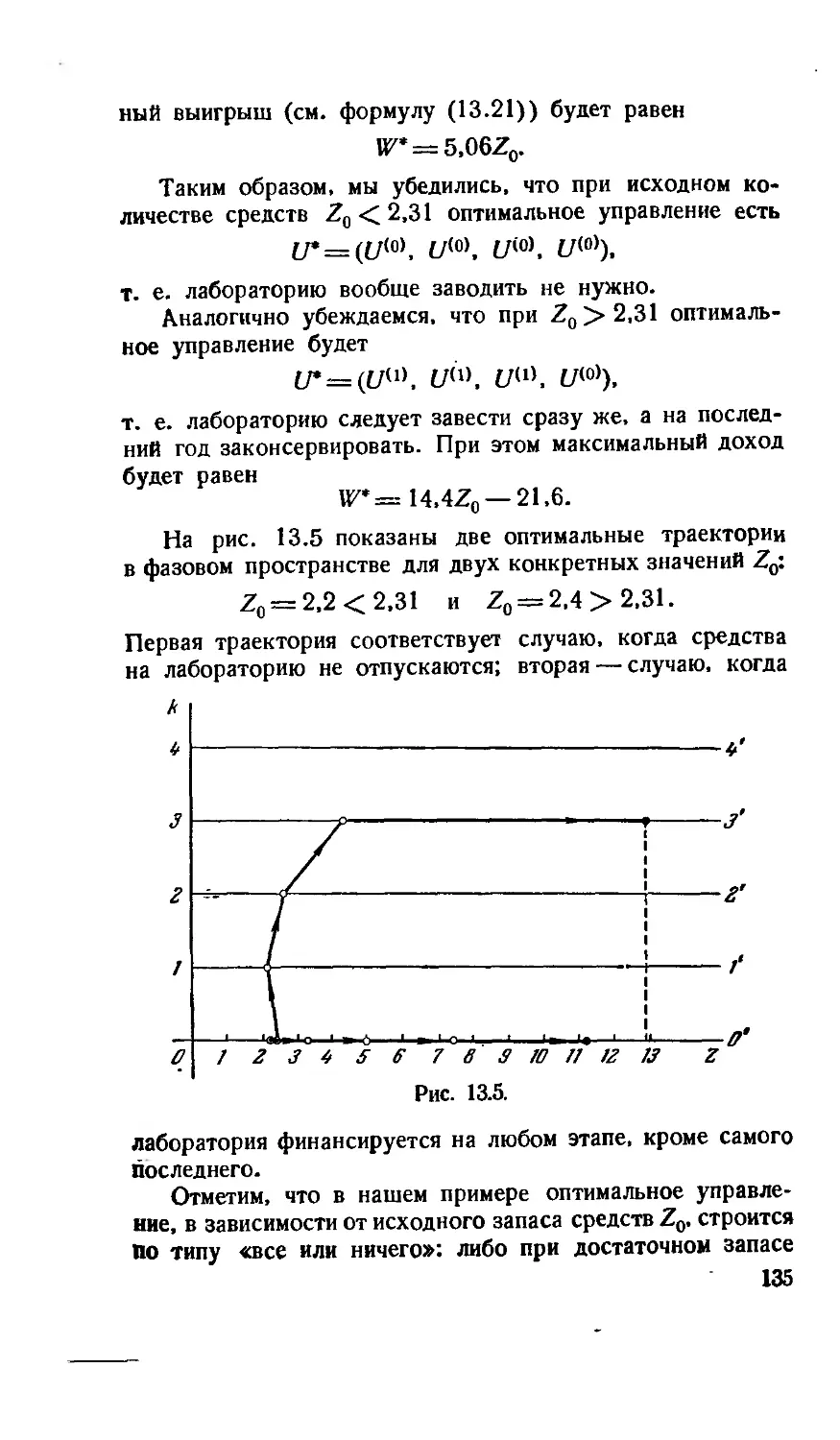
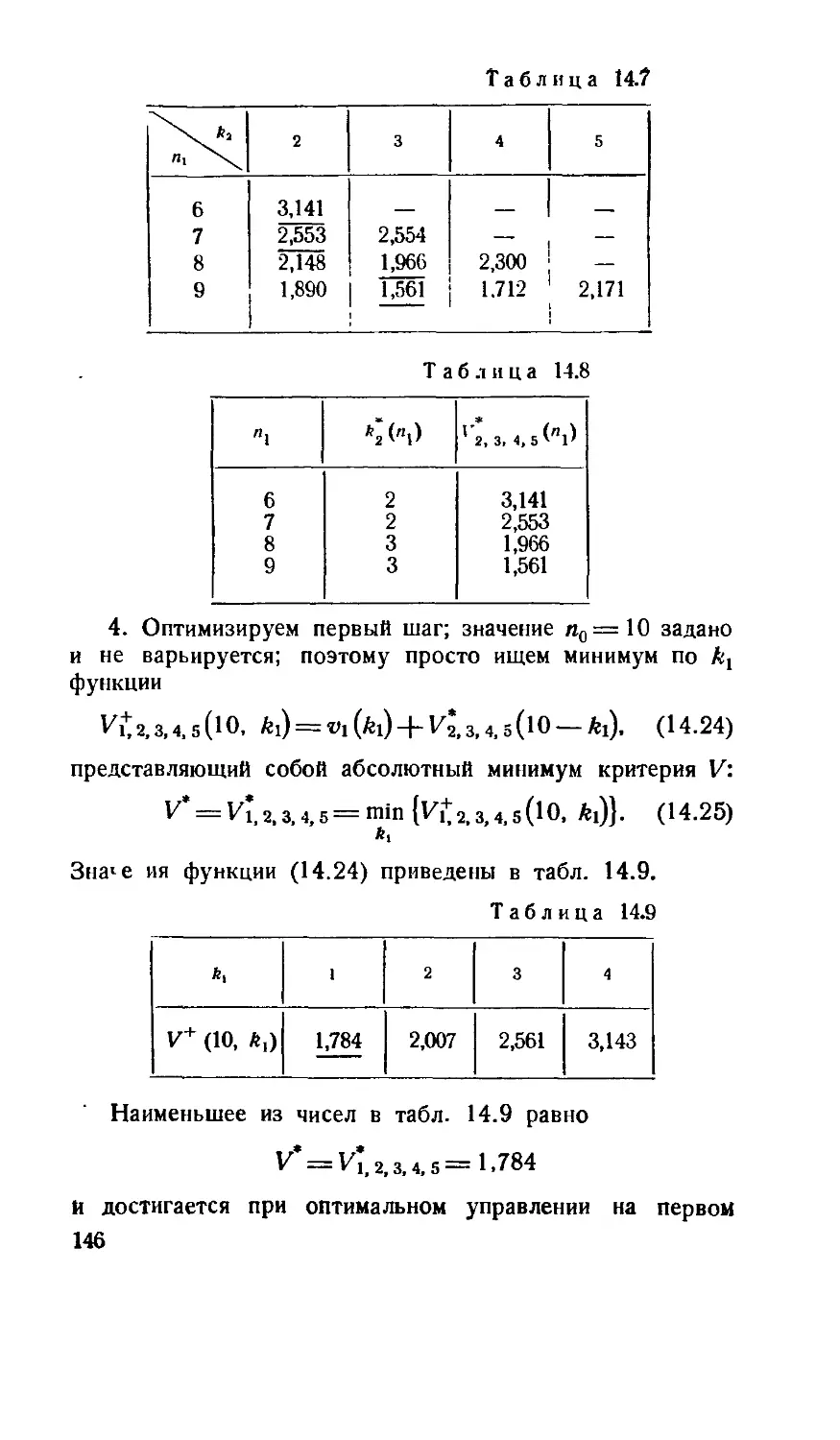
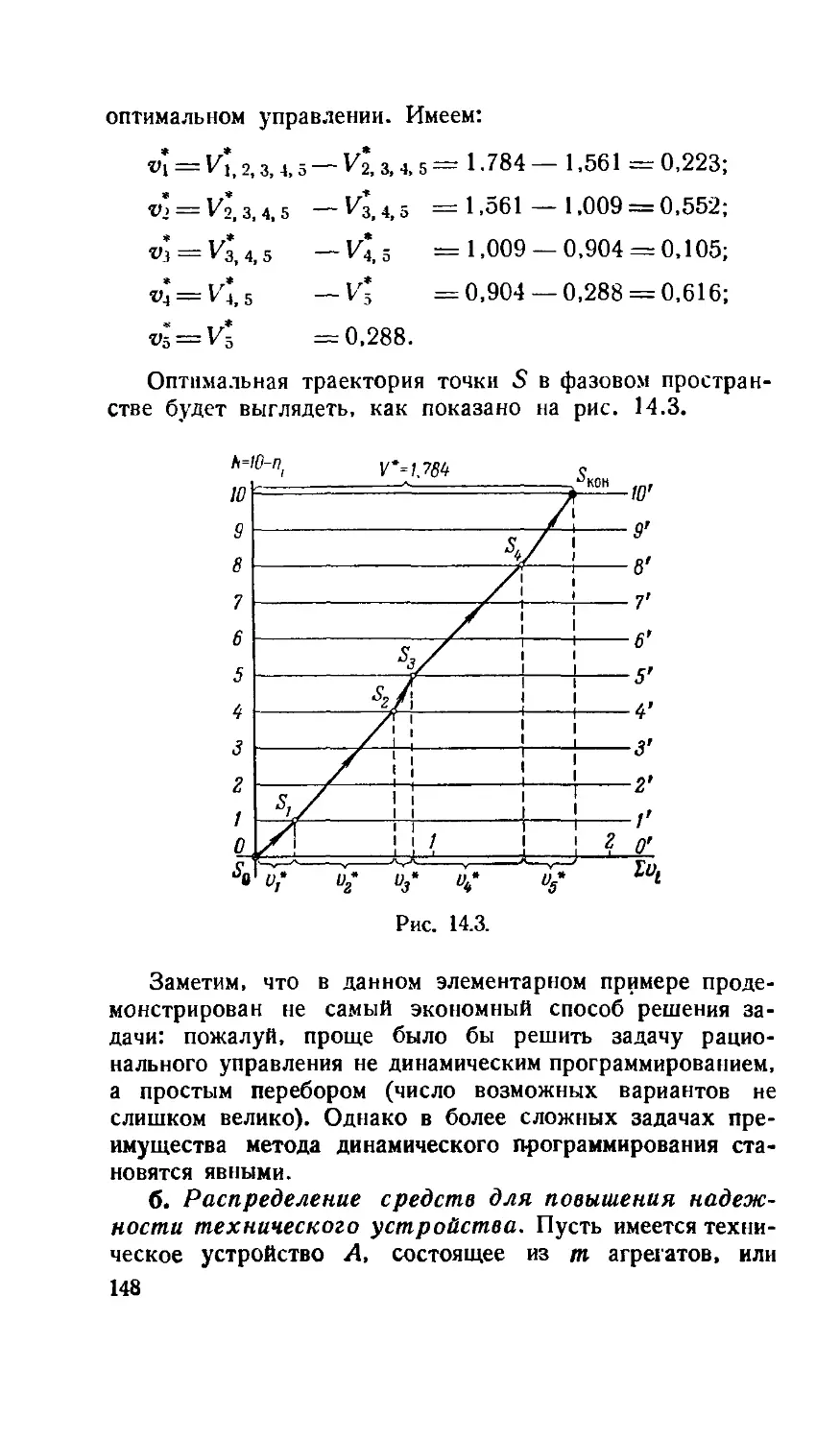
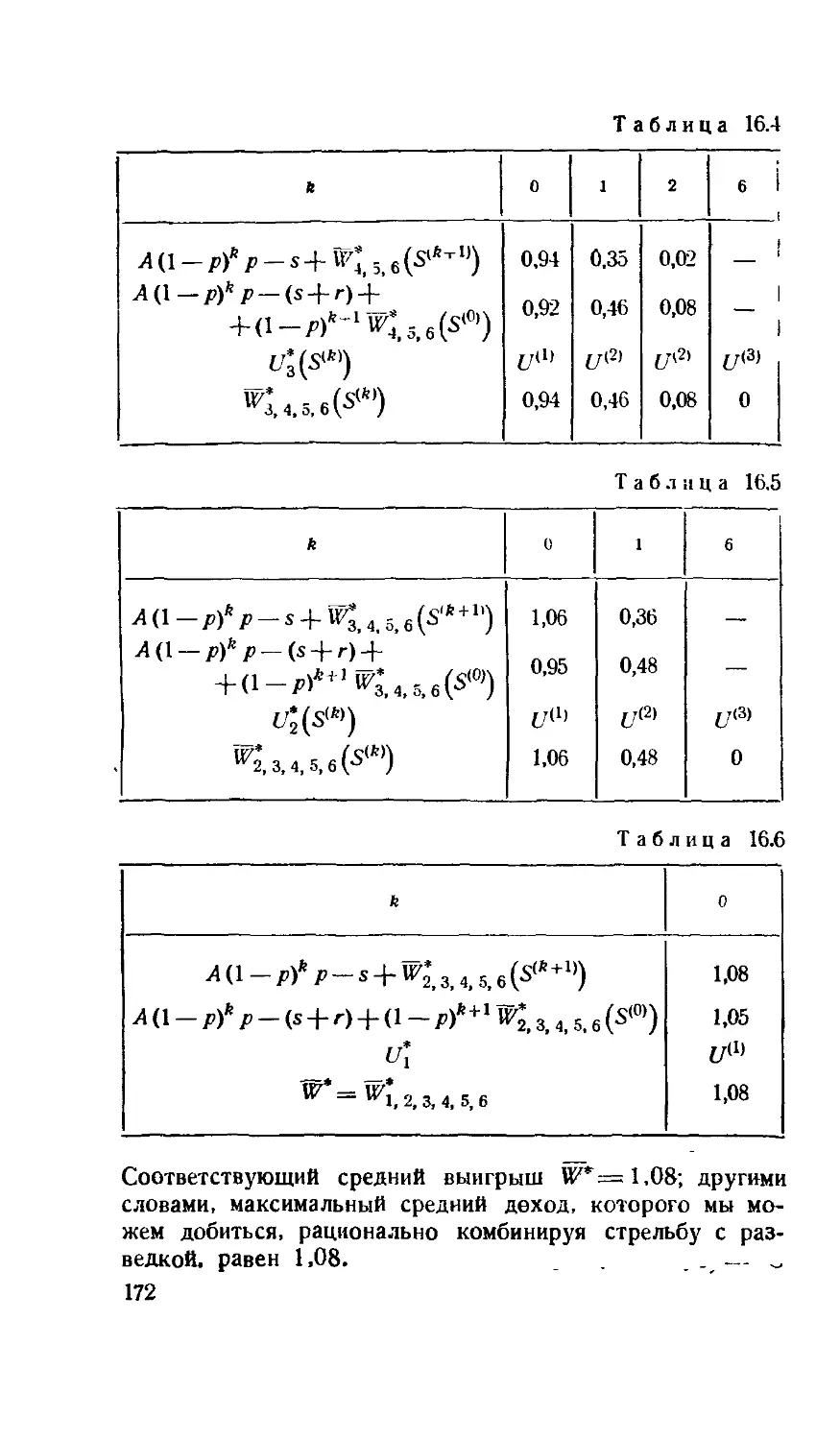
Теги: математика
Текст
Е-С.ВЕНТЦЕЛЬ
t
W4ftКОГО
кишмя
*' 'и
t. C ВLМИДЕЛЬ
ЭЛЕМЕНТЫ
ДИНАМИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
Мзда rt.'ibCTuo «нчука»
Ю С К Н А 10М
518
В 29
УДК 519.95
АННОТАЦИЯ
Динамическое программирование — недавно
возникший и интенсивно развивающийся раздел
математики, дающий методы для решения важ'
ных практических задач.. Речь идет о планиро-
планировании производственных или иных процессов, когда
управление ими осуществляется многоэтапным
путем ввиду их сложности. К таким задачам
молено отнести, например, выбор наивыгодней-
наивыгоднейшего профиля для проектирования железнодо-
железнодорожного пути (разбитого на ряд участков),
выбор наилучших размеров ступеней многосту-
многоступенчатой ракеты и многие другие.
В данной книге впервые в отечественной ли-
литературе делается попытка общедоступно из-
изложить основные идеи и методы динамического
программирования.
Книга представляет интерес для широкого
круга работников науки и производства, а также
для всех лиц, интересующихся развитием совре-
современной науки.
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Предисловие
В книге дается элементарное изложение метода дина-
динамического программирования, который рассматривается
как общий метод построения оптимального управления
различными видами физических систем. Книга предназна-
предназначена для инженеров, экономистов и научных работников
разных специальностей, занимающихся вопросами плани-
планирования, а также выбором рациональных параметров тех-
технических устройств. Автор не ставил себе задачей дать
строгое и последовательное изложение математической сто-
стороны метода, а стремился сделать его понятным и доступ-
доступным для широкого круга практических работников, не
имеющих специального математического образования и за-
заинтересованных главным образом в непосредственном
применении метода к интересующим их задачам. Такая
цель определила собой принятый стиль изложения: книга
почти не содержит строгих доказательств; объяснение
принципов метода ведется с опорой на многочисленные
практические задачи и примеры, из которых многие до-
доводятся до конкретного числового результата. Задачи
и примеры взяты из самых различных областей практики;
в изложении подчеркиваются общие черты, позволяющие
решать их сходными приемами.
Математический аппарат, применяемый в книге, несло-
несложен и нигде не выходит за пределы курса высшей мате-
математики, излагаемого во всех втузах, а по большей части
1* 3
не требует даже этого и сводится к несложным арифмети-
арифметическим и алгебраическим действиям. Однако для созна-
сознательного усвоения материала требуется известное напря-
напряжение мысли. Несколько непривычными для неискушен-
неискушенного читателя могут показаться применяемые при изложении
общие формулы, однако смысл этих формул и фигури-
фигурирующих в них обозначений подробно объяснен в тексте.
Для понимания двух последних параграфов (§§ 15 и 16)
требуется знакомство с элементарными понятиями теории
вероятностей.
Разобранные в книге конкретные задачи намеренно
выбраны очень простыми, чтобы громоздкие вычисления
не заслоняли существа метода. На практике, как правило,
приходится встречаться с более сложными задачами, для
решения которых требуется привлекать современную элект-
электронную вычислительную технику. Имея в виду необхо-
необходимость составления машинных алгоритмов, автор на про-
протяжении всей книги пользуется стандартной логической
схемой построения процесса поэтапной оптимизации и
стандартной последовательностью формул, облегчающей
составление программы для ЭВЦМ.
Автор сознательно ограничил себя рассмотрением
только дискретных задач динамического программирова-
программирования с конечным числом шагов т и оставил в стороне
предельные случаи, соответствующие м->оо и неограни-
неограниченному уменьшению длины шага. Однако отчетливое
усвоение идеи метода на элементарных задачах может
существенно облегчить читателю, желающему получить бо-
более глубокие знания, дальнейшее изучение предмета по
более солидным руководствам.
Е. Вентцель
1964 г.
$ L Задача динамического
программирования
Динамическое программирование (или, иначе,
намическое планирование») представляет собой особый
математический аппарат, позволяющий осуществлять опти-
оптимальное планирование управляемых процессов. Под «уп-
«управляемыми» разумеются процессы, на ход которых мы
можем в той или другой степени влиять.
Общеизвестно пристальное внимание, уделяемое сов-
современной наукой вопросам планирования во всех обла-
областях человеческой деятельности. Самая общая задача опти-
оптимального (наилучшего) планирования ставится следующим
образом.
Пусть предполагается к осуществлению некоторое''
мероприятие или серия мероприятий (короче, «операция»),
преследующая определенную цель. Спрашивается: как
нужно организовать (спланировать) операцию для того,
чтобы она была наиболее эффективной, т. е. наилучшим
образом удовлетворяла поставлениным перед ней требо-
требованиям?
Чтобы поставленная задача оптимального планирова-
планирования приобрела количественный, математический характер,
необходимо ввести в рассмотрение некоторый численный
критерий W, которым мы будем характеризовать качество,
успешность, эффективность операции.
Величина W, в зависимости от характера решаемой
задачи, может выбираться различными способами. Напри-
Например, при планировании деятельности системы промышлен-
промышленных предприятий в качестве критерия W может быть
(смотря по обстоятельствам) выбран общий годовой объем
продукции или же чистый годовой доход; критерием эффек-
эффективности работы транспортной системы может быть,
5
например, общий грузооборот или же средняя стоимость
перевозки тонны груза. Критерием эффективности бом-
бомбардировочного налета может быть, например, средняя
площадь причиненных разрушений или же среднее число
пораженных объектов, или же стоимость восстановитель-
восстановительных работ, которые придется выполнить противнику.
Вообще критерий эффективности в каждом конкрет-
конкретном случае выбирается исходя из целевой направленности
операции и задачи исследования (какой элемент управ-
управления оптимизируется и для чего).
Задача рационального планирования — выбрать такой
способ организации данной системы действий, чтобы обра-
обратить в максимум, (или минимум) какой-то критерий W.
Если в качестве критерия взята такая величина, увеличе-
увеличение которой нам выгодно (например, доход от группы
предприятий), то ее стремятся обратить в максимум. Если,
наоборот, величину W выгодно уменьшать, то ее стре-
стремятся обратить в минимум. Очевидно, задача минимиза-
минимизации критерия легко сводится к задаче максимизации (на-
(например, изменением знака критерия). Поэтому в дальней-
дальнейшем при рассмотрении задач планирования в общей
постановке мы часто будем говорить просто о «максими-
«максимизации» критерия W.
Дадим теперь количественную, математическую поста-
постановку общей задачи оптимального планирования.
Имеется некоторая физическая система S, состояние
которой с течением времени меняется. Процесс является
управляемым, т. е. мы имеем возможность в какой-то
мере влиять на его ход, выбирая по своему усмотрению то
или другое управление U. С процессом связана неко-
некоторая величина (или критерий) W, зависящая от приме-
примененного управления. Требуется выбрать такое управле-
управление U, чтобы величина W обратилась в максимум.
Современная математическая наука располагает целым
арсеналом методов, позволяющих решить задачу оптималь-
оптимального управления. Среди них особое место занимает метод
динамического программирования. Специфика этого ме-
метода в том, что для отыскания оптимального управления
планируемая операция разделяется на ряд последователь-
последовательных «шагов» или «этапов». Соответственно и самый про-
процесс планирования становится «многошаговым» и разви-
развивается последовательно, от этапа к этапу, причем каждый
раз оптимизируется управление только на одном шаге.
6
Некототорые операции естественно распадаются на
этапы; в других это членение приходится вводить искус-
искусственным путем.
Рассмотрим пример «естественно многоэтапной» опе-
операции. Пусть планируется деятельность некоторой системы
промышленных предприятий
Пх. П2 Пк
на некоторый период времени Г, состоящий из т хозяй-
хозяйственных лет (рис. 1.1).
В начале периода Т на развитие системы предприятий
выделяются какие-то основные средства К; кроме того,
функционирующие предприятия дают некоторый доход,
реализующийся в конце каждого года в виде чистой
прибыли.
В начале каждого хозяйственного года (т. е. в моменты
tv t2 tt tm) производится финансирование всей
системы предприятий, причем на каждое из них выделяется
какая-то доля средств, имеющихся к этому времени в рас-
распоряжении планирующего органа.
Обозначим х(р сумму, выделяемую в начале 1-го года
на долю предприятия Пу.
Ставится вопрос: как нужно распределить по пред-
предприятиям начальный капитал К и поступающие доходы
для того, чтобы к концу периода планирования Т сум-
суммарный доход от всей системы предприятий был макси-
максимальным?
Сформулированная задача представляет собой типич-
типичную задачу многоэтапного планирования.
Посмотрим, каковы могут быть подходы к решению
этой задачи.
Предположим, что распределение средств на /-м шаге
операции выполнено, т. е. мы выбрали определенное
7
управление Ut:
Формула A.1) читается следующим обрааом: управление L^
на /-м шаге состоит в том, что мы выделили предприя-
предприятию П, средства л;'^, предприятию П2 — средства xf\
и т. д.
Пользуясь широкоупотребительной терминологией, уп-
управление Ut можно представлять себе как вектор в
А-мерном пространстве, составляющие которого
равны л^1 >, xf> xfK
Рассмотрим всю совокупность управлений (выделенных
средств)
U у U2 Um A.2)
на от шагах операции как т векторов в А-мерном простран-
пространстве. Критерий эффективности W многоэтапной операции,
в качестве которого мы выбрали суммарный доход за т
лет, зависит от всей совокупности управлений A.2):
W^W{UV £/2 Um). A.3)
Ставится вопрос: как выбрать управление на каждом
шаге, т. е. как распределить средства для того, чтобы
величина W приняла максимальное значение?
Поставленная нами на конкретном примере задача легко
может быть обобщена.
Пусть планируется операция, распадающаяся на от
последовательных шагов или этапов. В начале каждого
(/-го) этапа нужно определенным образом выбрать имею-
имеющиеся в нашем распоряжении параметры
совокупность которых
образует управление на 1-м этапе.
Как нужно выбрать совокупность управлений
для того, чтобы некоторая величина W, зависящая от нее,
обратилась в максимум:
U2 £/m) = max?
Метод динамического программирования позволяет про-
производить такое оптимальное планирование поэтапно,
оптимизируя на каждом этапе только один шаг.
Вообще говоря, такой подход к нахождению оптималь-
оптимального решения не является единственно возможным. Задача
планирования многоэтапных процессов в принципе допу-
допускает и другое решение — непосредственное, при котором
все шаги объединяются в один.
Действительно, рассмотрим критерий W как функцию
от элементов управления на каждом шаге:
A.4)
Эта функция многих аргументов может быть исследована
на максимум, как таковая, без обязательного разделения
элементов управляния «по шагам». Для этого нужно найти
такую совокупность значений аргументов х1р (/= 1. 2,...
.... т; /=1, 2, ...), при которых функция A.4) до-
достигает максимума.
Казалось бы, чего проще? Нужно применить для нахож-
нахождения максимума классический прием: продифференциро-
продифференцировать функцию W по всем аргументам, приравнять произ-
производные нулю и решить полученную систему уравнений:
dW „ dW _„
U U
—о • — о -*HL-o rin
Однако эта простота обманчива.
Во-первых, когда шагов много, такой способ стано-
становится очень громоздким. Задача решения системы урав-
уравнений A.5) только в простейших случаях оказывается
легко разрешимой. Как правило, она очень сложна, и ча-
часто бывает легче непосредственно «нащупать» максимум
функции A.4), чем решать систему уравнений A.5).
9
Кроме того, указанный способ вовсе не гарантирует
нахождения решения! Напомним, что само по себе обра-
обращение производной в нуль не обеспечивает максимума
функции, и всегда требуется дополнительная проверка.
К тому же этот способ не дает возможности найти мак-
максимум, если он лежит не внутри, а на границе
области возможных значений аргументов (см., например,
рис. 1.2: абсолютный максимум функции W (х) достигается
не в точках хх, х2, хг, где производная равна нулю,
а в граничной точке х* области, в которой задана функ-
функция). Так что даже в тех ред-
редких случаях, когда систему
уравнений A.5) удается ре-
решить, отыскание абсолют-
абсолютного максимума требует це»
лой системы проверок, тем
™1 более сложной, чем больше
аргументов у функции.
Наконец, надо добавить,
'• что в ряде практических
задач функцию W вообще
нельзя дифференцировать;
например, когда элементы
V/fr)
х, х.
Рис. 1.2.
управления ху>, ху>, ...; х£>,
представляют собой не непрерывно изменяющиеся, а дис-
дискретные величины.
Все эти обстоятельства приводят к тому, что приме-
применение классических методов анализа (или вариационного
исчисления) к решению большинства задач планирования
оказывается неэффективным: оно сводит первоначально
поставленную задачу отыскания максимума к таким вто-
вторичным задачам, которые оказываются не проще исходной,
а зачастую и сложнее.
Вместе с тем решение многих таких задач может быть
существенно упрощено, если развернуть процесс плани-
планирования поэтапно, т. е. методом динамического програм-
программирования. Идея метода в том, что отыскание максимума
функции многих переменных заменяется многократным
отысканием максимума функции одного или небольшого
числа переменных.
Какие при этом применяются приемы, будет видно из
дальнейшего изложения.
10
§ 2. Принцип поэтапного
построения оптимального
управления
Итак, динамическое программирование есть поэтапное
планирование многошагового процесса, при котором на
каждом этапе оптимизируется только один шаг.
С первого взгляда может показаться, что сформулиро-
сформулированная идея довольно тривиальна. Действительно, что тут
мудреного: если трудно оптимизировать управление сразу
на протяжении всей операции, то разбить ее на ряд по-
последовательных шагов и оптимизировать отдельно каждый
шаг. Не так ли?
Вовсе не так1 Принцип динамического программиро-
программирования отнюдь не предполагает, что, выбирая управление
на одном отдельном шаге, можно забыть обо всех осталь-
остальных. Напротив, управление на каждом шаге должно вы-
выбираться с учетом всех его последствий в будущем. Дина-
Динамическое программирование — это планирование дально-
дальновидное, с учетом перспективы. Это не близорукое
планирование «вслепую» на один шаг («будь что будет,
лишь бы сейчас было хорошо»). Напротив, управление
на каждом шаге выбирается исходя из интересов операции
в целом.
Проиллюстрируем принцип «дальновидного» планиро-
планирования на примерах.
Пусть, например, планируется работа группы разно-
разнородных промышленных предприятий на период времени
т лет и конечной задачей является получение максималь-
максимального объема продукции некоторого класса С товаров
широкого потребления.
В начале периода имеется определенный запас средств
производства (машин, оборудования), с помощью кото-
которого можно начать производство товаров этого класса.
«Шагом» или «этапом» процесса планирования является
хозяйственный год. Пусть нам предстоит выбор решения
на закупку сырья, машин и распределение средств по
предприятиям на первый год. При «близоруком» поэтап-
поэтапном планировании мы приняли бы решение: вложить
максимальное количество средств в закупку сырья и пу-
пустить имеющиеся машины на полную мощность, стремясь
11
к максимальному объему продукции класса С к концу
первого же года.
К чему может привести такое планирование? К быст-
быстрому изнашиванию машинного парка и, как следствие,
к тому, что на втором году продукция упадет.
При дальновидном планировании, напротив, будут
предусмотрены мероприятия, обеспечивающие пополнение
машинного парка по мере его изнашивания. С учетом
таких капиталовложений объем продукции основного то-
товара С эа первый год будет меньше, чем мог бы быть,
но зато будет обеспечена возможность расширения про-
производства в последующие годы.
Возьмем другой пример. Процесс планирования в шах-
шахматной игре тоже распадется на отдельные шаги (ходы).
Допустим, что фигуры условно оценены тем или другим
числом очков соответственно своей важности; беря фигу-
фигуру, мы выигрываем это число очков, а отдавая — про-
проигрываем.
Разумно ли будет, продумывая шахматную партию на
несколько шагов вперед, всегда стремиться к тому, чтобы
на каждом шаге выигрывать максимальное число очков?
Очевидно, нет. Такое, например, решение, как «пожертво-
«пожертвовать фигуру», никогда не может быть выгодно с узкой
точки зрения одного-единственного хода, но может быть
выгодно с точки зрения партии в целом.
Так обстоит дело и в любой области практики. Пла-
Планируя многоэтапную операцию, мы должны выбирать
управление на каждом шаге, исходя не из узких интересов
именно этого шага, а из более широких интересов опе-
операции в целом, и далеко не всегда эти две точки
зрения совпадают.
Как же строить такое управление? Мы уже сформу-
сформулировали общее правило: в процессе поэтапного планиро-
планирования управление на каждом шаге должно приниматься
с учетом будущего. Однако из этого правила есть исклю-
исключение. Среди всех шагов существует один, который может
планироваться попросту, без «оглядки на будущее». Какой
это шаг? Очевидно, последний. Этот последний шаг,
единственный из всех, можно планировать так, чтобы он
как таковой приносил наибольшую выгоду.
Спланировав оптимальным образом этот последний
шаг, можно к нему «пристраивать» предпоследний, к этому
в свою очередь предпредпоследний и т. д.
12
Поэтому процесс динамического программирования
всегда разворачивается в обратном по времени направлении:
не от начала к концу, а от конца к началу. Раньше
всего планируется последний шаг. А как его спланировать,
если мы не знаем, чем кончился предпоследний? Очевидно,
нужно сделать разные предположения о том, чем
кончился предпоследний шаг, и для каждого из них
выбрать управление на последнем.
Такое оптимальное управление, выбранное при опре-
определенном условии о том, чем кончился предыдущий шаг,
мы будем называть условным оптимальным управ-
управлением.
Принцип динамического программирования требует на-
нахождения на каждом шаге условного оптимального управ-
управления для любого из возможных исходов предшествую-
предшествующего шага.
Продемонстрируем схему такой процедуры. Пусть
планируется /и-шаговая операция, и неизвестно, чем
кончился (т—1)-й шаг. Сделаем об этом ряд «гипотез»
или «предположений». Эти гипотезы мы обозначим:
Оговоримся, что буквой Sm'-i не обязательно обозначается
одно число: это может быть и группа чисел, характери-
характеризующих исход (т—1)-го шага, .а может быть и просто
качественное состояние той физической системы, в кото-
которой протекает управляемый процесс.
Найдем для каждого из предположений B.1) условное
оптимальное управление на последнем (т-м) шаге. Это
будет то из всех возможных управлений Um, при котором
достигается максимально возможное значение выигрыша
на последнем шаге.
Предположим, что для каждого из предположений B.1)
условное оптимальное управление Um на последнем шаге
найдено:
ifm(sS'-O: ul (sffi-0; • • •; u'm (&_& ... B.2)
Это означает, что последний шаг спланирован для
любого исхода предпоследнего.
Перейдем к планированию следующего от конца, пред-
предпоследнего шага. Снова сделаем ряд гипотез о том, чем
13
кончился предпредпоследний ((т — 2)-й) шаг:
Om-2. om-2 Ога-2. ••• (*■■$)
Поставим вопрос: как нужно выбирать для каждой из
этих гипотез условное оптимальное управление на (т—1)-м
шаге?
Очевидно, его нужно выбирать так, чтобы оно, сов-
совместно с уже выбранным управлением на последнем
шаге, обеспечивало максимальное значение крите-
критерия W на двух последних шагах.
Другими словами, для каждой из гипотез B.3) нужно
найти такое условное оптимальное управление на (т—1)-м
шаге t/m_iEm_2). чтобы оно, в совокупности с уже най-
найденным условным оптимальным управлением t/m(Sm_i),
давало максимально возможный выигрыш на двух послед-
последних шагах.
Очевидно, к (т— 1)-му шагу таким же точно способом
может быть присоединен (т — 2)-й и т. д. вплоть до
самого последнего (от конца) 1-го шага, с которого процесс
начинается.
Первый шаг, в отличие от всех других, планируется
несколько иначе. Так как мы обычно знаем, с чего
начинается процесс, то нам уже не требуется де-
делать гипотезы о том, в каком состоянии мы приступаем
к первому шагу. Это состояние нам известно. Поэтому,
учитывая, что все последующие шаги B-й, 3-й и т. д.)
уже спланированы (условно), нам остается просто спла-
спланировать первый шаг так, чтобы он был оптимальным
с учетом всех управлений, уже принятых наилучшим
образом на всех последующих шагах.
Принцип, положенный в основу построения такого
решения (искать всегда оптимальное продолжение процесса
относительно того состояния, которое достигнуто в дан-
данный момент), часто называют принципом оптималь-
оптимальности (см. [1]).
Общее объяснение способа построения оптимального
решения методом динамического программирования, кото-
которое было дано в настоящем параграфе, в силу самой
своей общности может показаться непонятным. Поэтому
следующие параграфы (§§ 3—5) мы посвятим решению
конкретных задач, на которых постараемся дать ему более
14
доходчивое истолкование. В дальнейшем, в § 6, мы снова
вернемся к общей постановке задачи, которая окажется
более понятной на фоне уже разобранных конкретных при-
примеров.
§ 3. Задача о наборе высоты
и скорости
Одной из простейших задач, решаемых методом ди-
динамического программирования, является задача об опти-
оптимальном режиме набора высоты и скорости летательным
аппаратом. С этой задачи мы и начнем изложение практи-
практических приемов динамического программирования, причем
в целях методической ясности условия задачи будут до
крайности упрощены.
Задача состоит в следующем. Самолет (или другой
летательный аппарат), находящийся на высоте Но и имею-
имеющий скорость Vo, должен быть поднят на заданную вы-
высоту Икон, а скорость его доведена до заданного значения
VK0H. Известен расход горючего, потребный для подъема
аппарата с любой высоты //, на любую другую Н2 > Ht
при неизменной скорости V; известен также расход го-
горючего, потребный для увеличения скорости от любого
значения Vl до любого другого V2 > Vl при неизменной
высоте Н.
Требуется найти оптимальный режим набора высоты
и скорости, при котором общий 'расход горючего будет
минимальным.
Решение будем строить следующим образом. Для
простоты допустим, что весь процесс набора высоты и
скорости разделен на ряд последовательных шагов (этапов),
и за каждый шаг самолет увеличивает только высоту
или только скорость.
Будем изображать состояние самолета с помощью точ-
точки на некоторой плоскости VOH, где абсцисса изображает
скорость самолета V, а ордината — его высоту Н (рис. 3.1).
Процесс перемещения точки S, изображающей состоя-
состояние самолета, из начального состояния So в конечное SK0H
изобразится на плоскости VOH некоторой ступенчатой
ломаной линией. Эта линия — траектория движения точки 5
на плоскости VOH — будет характеризовать управление
процессом набора высоты и скорости.
15
Очевидно, существует множество возможных управле-
управлений — множество траекторий, по которым можно перевести
точку 5 из So в SK0H. Из всех этих траекторий нужно
выбрать ту, на которой выбранный критерий W — расход
горючего — будет минимальным.
О V,
Рис. 3.1.
Чтобы построить решение методом динамического про-
программирования, разделим высоту Икон — Но, которую
нужно набрать самолету, на пх равных частей (например,
на шесть, см. рис. 3.2), а скорость VK0H — Vo. которую
требуется набрать, — на п2 равных частей (например, на
восемь). Разделим процесс набора высоты и скорости на
отдельные шаги и будем считать, что за один шаг само-
самолет может либо увеличивать высоту на величину
либо скорость — на величину
Д V — ■ Vkoh '
п2
Число частей nv n2, на которые делятся интервалы
^кон — ^о1 ^кон — IV принципиального значения не имеет
и может быть выбрано исходя из требований к точности
решения задачи. Пара чисел я1, п2 определяет собой общее
число шагов т многоэтапного процесса набора высоты
и скорости
/я = /jj —j— tiy.
16
соответствует свой расход горючего W. Нам нужно из
всех таких траекторий найти оптимальную — ту, на ко-
которой расход горючего минимален. Можно было бы, разу-
разумеется, перебрать все возможные траектории и в конеч-
конечном счете найти оптимальную, но это — очень громоздкий
путь. Гораздо скорее можно решить задачу методом ди-
динамического программирования по шагам. (
»ш
АН
[.
-20
10
12 13 13 И 15 lit Й
17 —|— it —|—13 —|— а —I— и —1— и —I—;«—|—/7-
8 В Ю II 12 13 К
/■* —|— w —I— w —|— да —|— « —i— * —I— // —|—is-
7 б в 7 в 10 II 10 8
-4—к —|—13 —I—is—|—/о—|—и —|—'•?■•—I—#4—го—4
"о
и
в
-+
10
с""
soi_
i
i
7
-10—V-
S
9
1
i
1
-в
-9
-II
8
-4-
10
-\-
10
4-
е
д
ю
9
4—
4-'-
12
1
1
1 V—
Рис.
9
-I И-
10
+-
«
4-и-
i
3.3.
to
J—/г-
■+--
4—
+
12
+
It
1
1
i
8
-4-
10
— М 1
в
-,7-f
1
7
-4
-и—|
10
-го—1
•
i
i
V
кон
Процесс состоит из т =14 шагов; будем оптимизи-
оптимизировать каждый шаг, начиная с последнего. Конечное со-
состояние самолета — точка SK0H на плоскости VOH—нам
задано. Четырнадцатый шаг непременно должен привести
нас в эту точку. Посмотрим, откуда мы можем пере-
переместиться в точку 5К0Н на четырнадцатом шаге.
Рассмотрим отдельно правый верхний угол прямо-
прямоугольной сетки (рис. 3.4) с конечной точкой SK0H. В точку
5К0Н можно переместиться из двух соседних точек (Вг и
В2), причем из каждой — только одним способом, так что
выбора условного управления на последнем шаге у нас
нет — оно единственно. Если предпоследний шаг привел
нас в точку By то мы должны двигаться по горизонтали
и тратить 17 единиц горючего; если в точку В2, — идти
18
no вертикали и тратить 14 единиц. Запишем эти мини-
минимальные (в данном случае просто неизбежные) расходы
горючего в специальных кружках, которые поставим
в точках Bv В2 (рис. 3.5). Запись «17» в кружке у Bt
означает: «если мы пришли в Bv то минимальный расход
кои
кон
13
Рис. 3.4.
Рис. 35.
горючего, переводящий нас в точку SK01I, равен 17 еди-
единицам». Аналогичный смысл имеет запись «14» в кружке
у точки В2. Оптимальное управление, приводящее к этому
расходу, помечено в каждом случае стрелкой, выходящей
из кружка. Стрелка указывает то направление, по кото-
которому мы должны двигаться из данной точки, если в ре-
результате предыдущей нашей деятельности оказались в ней.
Таким образом, условное оптимальное управление на -
последнем четырнадцатом шаге найдено для любого (В1
или В2) исхода тринадца-
тринадцатого шага. Для каждого
из этих исходов найден,
кроме того, минимальный
расход горючего, за счет
которого из данной точ-
точки можно переместиться
в 5К0Н.
Перейдем к планиро-
планированию предпоследнего
(тринадцатого) шага. Для
этого нам нужно рассмот-
рассмотреть все возможные ре-
результаты предпредпос-
леднего (двенадцатого) шага. После этого шага мы можем
оказаться только в одной из точек Cv С2, С3 (рис. 3.6).
Из каждой такой точки мы должны найти оптимальный
путь в точку SK0H и соответствующий этому пути мини-
минимальный расход горючего.
2* 19
Рис. 36.
Для точки Сх выбора нет: мы должны перемещаться
по горизонтали и тратить 15-f-17 = 32 единицы горючего.
Этот расход мы запишем в кружке при точке Cv а опти-
оптимальней (в данном случае единственный) путь из точки С1
снова пометим стрелкой.
Для точки С2 выбор есть: из нее можно идти в 5К0Н
через Вх или через В2. В первом случае мы израсходуем
13-f-17 = 30 единиц горючего; во втором 17 4-14 = 31
единицу. Значит, оптимальный путь из С2 вертикален
(отметим это стрелкой), а минимальный расход горю-
горючего равен 30 (это число мы запишем в кружке при
точке С2).
Наконец, для точки С3 путь в SK0H снова единствен-
единственный: по вертикали; обходится он в 12-f-14 = 26 единиц;
эту величину B6) мы и запишем в кружке при С3,
а стрелкой пометим оптимальное управление.
Таким образом, переходя от точки к точке справа
налево и сверху вниз (от конца процесса к его началу),
можно для каждой узловой точки рис. 3.3 выбрать услов-
условное оптимальное управление на следующем шаге, т. е.
направление, ведущее в 5К0Н с минимальным расходом
горючего, и записать в кружке при данной точке этот
минимальный расход. Чтобы найти из каждой точки опти-
оптимальный следующий шаг, нужно проследить два возмож-
возможных пути из этой точки: вправо и вверх, и для каждого
пути найти сумму расхода горючего на данном шаге и
минимального расхода горючего на оптимальном про-
продолжении, уже построенном из следующей точки, куда
направлен конец стрелки. Из двух путей выбирается тот,
для которого эта сумма меньше (в случае, если суммы
равны, выбирается любой из путей).
Таким образом, из каждой точки рис. 3.3 (см. стр. 18)
проводится стрелка, указывающая оптимальный путь из
этой точки (оптимальное условное управление), и в кружке
проставляется расход горючего, достигаемый при опти-
оптимальном управлении, начиная с этой точки до конца.
Рано или поздно такой процесс построения условных
оптимальных управлений заканчивается, дойдя до исход-
исходной точки So. Из этой точки, как из любой другой, ведет
стрелка, указывающая, куда нужно перемещаться, чтобы
дойти до 5К0Н оптимальным образом. После этого можно
построить всю оптимальную траекторию, перемещаясь
по стрелкам, уже от начала процесса к его концу.
20
На рис. 3.7 показан окончательный результат такой
процедуры — оптимальная траектория, ведущая из 50 в 5КОЯ
по стрелкам, т. е. имеющая из каждой точки оптимальное
продолжение. Эта траектория отмечена жирными кружками
MHWWS4raWS-f58W4-4*4VK-«2>-/S-O7Vff
W /f to f
Рис. 3.7.
и дополнительными стрелками. Число «139», стоящее
у точки 50, означает минимальный расход горючего W*.
меньше которого нельзя получить ни на какой траектории.
Таким образом, поставленная задача решена и опти-
оптимальное управление процессом набора высоты и скорости
найдено. Оно состоит в следующем:
на первом шаге увеличивать только скорость, сохраняя
неизменной высоту Ио, и довести скорость до V0-\-AV;
на втором шаге увеличить высоту до Н0-\-ЬН, сохра-
сохраняя скорость неизменной;
на третьем, четвертом и пятом шагах снова набирать
скорость, пока она не станет равной V0-f-4AV;
на шестом, седьмом и восьмом шагах набирать высоту
и довести ее до Я0+4ДЯ;
на девятом, десятом, одиннадцатом и двенадцатом
шагах снова набирать скорость и довести ее до задан-
заданного конечного значения Уков;
21
на последних двух шагах (тринадцатом и четырнадца-
четырнадцатом) набирать высоту до заданного значения Нкои.
Нетрудно на ряде примеров убедиться, что найденное
управление действительно является оптимальным, т. е.
что на любой другой траектории, ведущей из So в 5К0Н
расход горючего будет больше.
Рассмотренная здесь задача оптимального набора
высоты и скорости является простейшим примером, на
котором часто демонстрируют основную идею динамиче-
динамического программирования. Действительно, в нашей упро-
упрощенной постановке задача очень легко решается до конца
с помощью простейших приемов. Это объясняется сле-
следующими обстоятельствами. Во-первых, на каждом шаге
нам приходится выбирать не более чем между двумя
вариантами управления («набирать высоту» или «набирать
скорость»). Нахождение условного оптимального управле-
управления в каждой точке элементарно и сводится к выбору
более выгодного из этих двух путей. Во-вторых, в нашей
задаче очень просто произвести нумерацию шагов, начи-
начиная с конца. Действительно, каждая траектория состоит
из одного и того же числа шагов, и последним, есте-
естественно, оказывается тот, который непосредственно, пре-
преодолением одной (горизонтальной или вертикальной) сту-
ступени, приводит в точку 5К0Н; предпоследним—тот, после
которого до точки 5К0н остается только один шаг, и т. д. .
Такая упрощенная постановка задачи не вполне со-
соответствует действительности. Фактически летательный
аппарат может набирать (и зачастую набирает) высоту и
скорость одновременно.
Попробуем (опять-таки в упрощенном виде) поставить
задачу, где будет предусмотрен такой одновременный
набор, и посмотрим, к каким усложнениям методики это
приведет.
Вернемся к схеме рис. 3.3 и изменим ее так, чтобы,
кроме уже рассмотренных путей (вверх и вправо), из
каждой узловой точки сетки возможен был еще путь по
диагонали прямоугольника (одновременный набор высоты
и скорости). Поставим соответствующий расход горючего
по каждой диагонали (рис. 3.8).
Что отличает данную схему от прежней (см. рис. 3.3)?
Не только наличие, кроме двух возможных ранее упра-
управлений, еще третьего «по диагонали». Эту схему отличает
менее четкая нумерация шагов: в пределах каждого пря-
22
моугольника из нижнего левого угла в верхний правый
можно перейти и за два шага («вверх — направо» или
«направо — вверх») и за один шаг — по диагонали. По-
Поэтому в новой задаче непригоден такой простой принцип
последовательного перебора узловых точек, какой мы
приняли раньше (по числу шагов, оставшихся до конца),
а нужно принять какой-то другой.
И
"кон
w гв /г ге 13 г? и is w zi is ге /4
is- e го s 2i 7 w s го w
Ю Id В IS 10 IS II IB 10 JS II 24
K
II 20 S 20 10 20 a 20 13 23 П 24 « 21 12 29 10
! | | Ч1**) №-0 №
Рис. З.8.
Условимся нумеровать узловые точки не по числу
шагов, оставшихся до конца, а по признаку какой-либо
координаты. В качестве такой координаты можно взять,
например, «остаток скорости», VK0H — V, которую необ-
необходимо «добрать» за оставшееся время. При такой нуме-
нумерации точек «последним» будет тот шаг, который пере-
переведет точку 5 с вертикальной прямой (т — 1) — (т — 1)
(рис. 3.8) в точку 5К0Н (этот последний «шаг» может
состоять из нескольких ступеней); «предпоследним» — тот,
который переведет точку с прямой (т — 2) — (т — 2) на
прямую (т—1) — (т—1), и т. д.
На рис. 3.9 рассмотрен образец оптимизации процесса
при такой нумерации шагов (показаны только два послед-
последних шага). Условное оптимальное управление, как и ранее.
23
показано стрелками. Поясним процедуру построения упра-
управления.
Если мы оказались в любой точке на прямой (т) — (т),
проходящей через SKOH, то единственно возможный (он же
и оптимальный) путь выхода в
точку 5К0Н — по вертикали. Этот
0 путь показан на рис. 3.9 стрел-
-'7 —^ кои ками вдоль всей прямой (т) — (/и);
-'А. соответствующие расходы горю-
горючего показаны в кружках.
Предположим теперь, что в ре-
результате процесса набора высоты
и скорости мы оказались на пря-
прямой (т—1)—(т—1). Будем пере-
перебирать на этой прямой все точки
сверху донизу. Если мы оказа-
оказались в самой верхней точке, то
путь в точку 5К0Н отсюда един-
единственный (горизонтальный) и об-
обходится он в 17 единиц горючего
(записываем 17 в кружке и ставим
горизонтальную стрелку). Пере-
Переходим к следующей точке — вто-
второй сверху. Из нее на прямую
(т) — (т) — три пути. Первый
путь — вверх — направо — обхо-
обходится в 13 —j— 17 = 30 единиц го-
горючего; второй — по диагонали —
в 29 единиц; третий— направо —
вверх — в 31 единицу. Выбираем
диагональный путь, помечаем его
стрелкой, а соответствующий рас-
•29 единиц — ставим в кружок. Для третьей точки
сверху снова сравниваем три пути:
вверх (и далее по диагонали): 12+29=41 единица горючего;
по диагонали (и далее вверх): 25 -f-14=39 единиц » ;
направо (и далее вверх): 15+26=41 единица »
Выбираем оптимальный путь — по диагонали, отмечаем
стрелкой, записываем 39 в кружке. Для следующей — чет-
четвертой сверху — точки на прямой (т — 1) — (т—1) опти-
оптимальным будет путь вверх и т. д.
24
(rh-2)
ход-
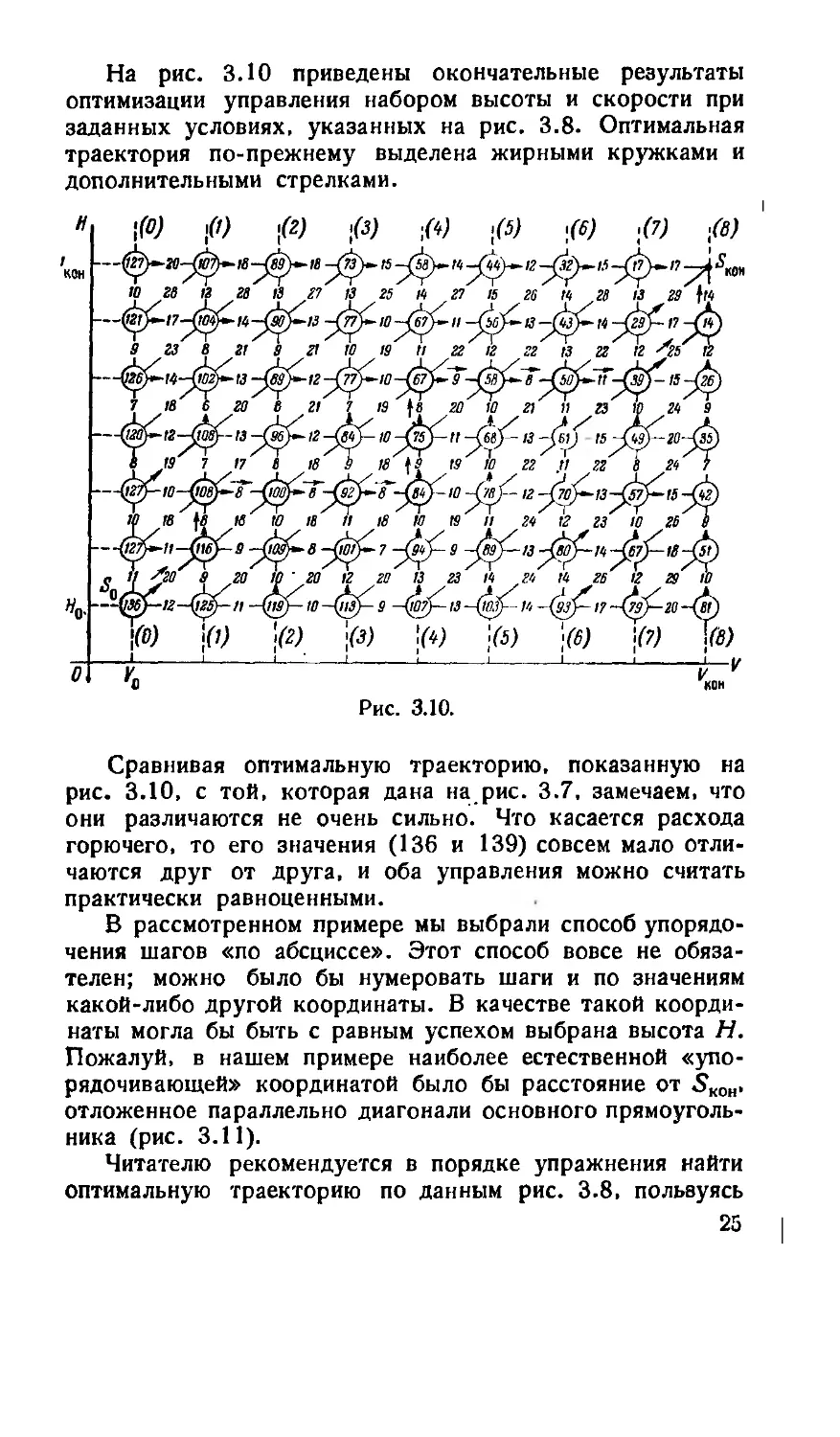
На рис. 3.10 приведены окончательные результаты
оптимизации управления набором высоты и скорости при
заданных условиях, указанных на рис. 3.8. Оптимальная
траектория по-прежнему выделена жирными кружками и
дополнительными стрелками.
Н
\(>) ft) \C) ;(*) >E) ,F) ,G) .fl)
25 « г? is гв п гв is гв
гг а гг и Ль
s гз в гг s я w i9 n гг
10 б 21 7 19 »8 20
г . гг в
% м ,г' '* ге г х '"
13 —(wf- i'i ~(язу~ I? ~(ш-го -ф
\ \ ( \
\@) \G) \B) \C) \(Ь) \E) \F) \G)
V '
ков
Рис. 3.10.
Сравнивая оптимальную траекторию, показанную на
рис. 3.10, с той, которая дана на рис. 3.7, замечаем, что
они различаются не очень сильно. Что касается расхода
горючего, то его значения A36 и 139) совсем мало отли-
отличаются друг от друга, и оба управления можно считать
практически равноценными.
В рассмотренном примере мы выбрали способ упорядо-
упорядочения шагов «по абсциссе». Этот способ вовсе не обяза-
обязателен; можно было бы нумеровать шаги и по значениям
какой-либо другой координаты. В качестве такой коорди-
координаты могла бы быть с равным успехом выбрана высота И.
Пожалуй, в нашем примере наиболее естественной «упо-
«упорядочивающей» координатой было бы расстояние от 5к0н.
отложенное параллельно диагонали основного прямоуголь-
прямоугольника (рис. 3.11).
Читателю рекомендуется в порядке упражнения найти
оптимальную траекторию по данным рис. 3.8, польвуясь
25
(т^-З) (m-2)
Тем способом упорядочивания шагов, который продемон-
продемонстрирован на рис. 3.11.
В разнообразных задачах динамического программиро-
программирования, где нет естественного разделения на шаги, принцип
этого разделения и упорядо-
упорядочивания шагов выбирается в
зависимости от удобства ор-
организации вычислительного
процесса, с учетом требуе-
требуемой точности решения зада-
задачи. Вообще интуитивно яс-
ясно, что при увеличении числа
ч
ч
ч
ч
\
\
ч
ч
ч
ч
ч
(т)
(т-1)
(т-г)
(т-3)
Рис. 3.11.
шагов точность решения
возрастает. В некоторых за-
задачах оказывается возмож-
возможным получить даже предель-
предельное решение при т —> оо; такое решение может представлять
теоретический, а иногда и практический интерес, однако
обычно бывает достаточно выяснить структуру оптималь-
оптимальною управления в общих, грубых чертах; при этом нет
необходимости сильно увеличивать число шагов. К тому же
при фактическом осуществлении управления чаще всего
приходится все равно отступать от строго оптимального
варианта, который может оказаться трудно выполнимым.
Поэтому мы не будем останавливаться на предельных
задачах управления, возникающих при т—>оо, а ограни-
ограничимся рассмотрением дискретной поэтапной схемы. Это
тем более имеет смысл, что во многих задачах хозяйствен-
хозяйственного планирования (а мы уделим подобным задачам большое
внимание) разделение на шаги не навязано извне, а естест-
естественно диктуется дискретной природой самого планирования
(план составляется, например, на год, на месяц и т. п., а не
меняется непрерывно в ходе производственного процесса).
§ 4. Задача выбора
наискорейшего пути
В предыдущем параграфе мы рассмотрели в простей-
простейшей постановке задачу оптимального набора высоты и
скорости. Здесь мы рассмотрим сходную по типу, но
все же несколько отличающуюся от нее задачу выбора
наискорейшего пути из одного пункта в другой.
26
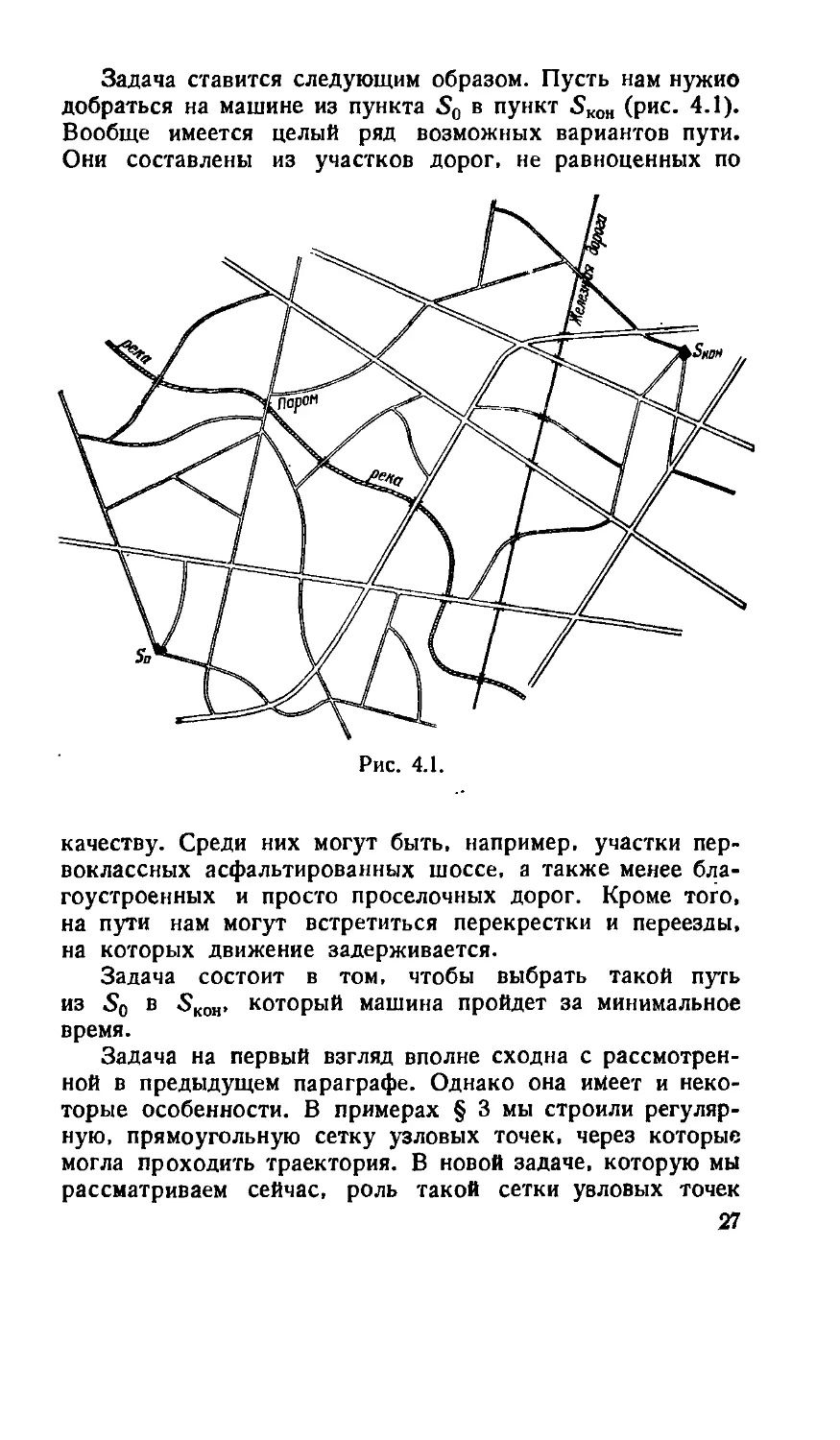
Задача ставится следующим образом. Пусть нам нужно
добраться на машине из пункта 50 в пункт 5К0н (рис. 4.1).
Вообще имеется целый ряд возможных вариантов пути.
Они составлены из участков дорог, не равноценных по
Рис. 4.1.
качеству. Среди них могут быть, например, участки пер-
первоклассных асфальтированных шоссе, а также менее бла-
благоустроенных и просто проселочных дорог. Кроме того,
на пути нам могут встретиться перекрестки и переезды,
на которых движение задерживается.
Задача состоит в том, чтобы выбрать такой путь
из So в 5к0Н, который машина пройдет за минимальное
время.
Задача на первый взгляд вполне сходна с рассмотрен-
рассмотренной в предыдущем параграфе. Однако она имеет и неко-
некоторые особенности. В примерах § 3 мы строили регуляр-
регулярную, прямоугольную сетку узловых точек, через которые
могла проходить траектория. В новой задаче, которую мы
рассматриваем сейчас, роль такой сетки узловых точек
27
могли бы играть естественно отмеченные «особые точки»
сети дорог — перекрестки и переезды, но они расположены
слишком нерегулярно, и их затруднительно «упорядочить
по шагам». Для того чтобы приближенно решить нашу
задачу методом динамического программирования, можно
ввести в нее искусственно некоторую «поэтапность».
Например, можно разделить расстояние D от 50 до SKOa
на т равных частей длиной ДО = — (рис. 4.2) и счи-
считать, что за каждый «шаг» процесса перемещения из So
в 5К0Н преодолевается т-я часть расстояния D (по напра-
направлению So— 5К0Н). Другими словами, каждый «шаг» пред-
представляет собой перемещение с одной из опорных прямых,
перпендикулярных So — 5К0Н. на соседнюю, более близкую
К "КОН"
Деля процесс на шаги таким образом, мы, естественно,
должны условиться, что перемещение от шага к шагу
допускается только в положительном направлении (т. е.
от 50 к SK0H, а не обратно); иными словами, после того
как определенный шаг пройден, возвращение обратно,
в ту же полосу между двумя опорными прямыми, не до-
допускается. Такое ограничение представляется достаточно
приемлемым для практики. Напомним, что в задаче § 3
мы встречались с еще более жестким ограничением: в ре-
режиме набора высоты и скорости допускалось перемещение
по обеим осям только в положительном направлении.
В задаче выбора наискорейшего пути введенное нами огра-
ограничение (в итоге каждого шага перемещаться только
«туда», по направлению 50 — 5К0Н, а не «обратно»)
является менее жестким, так как оно действует только
от шага к шагу, не внутри шага, и к тому же только по
одной оси (в случае надобности от этого ограничения можно
освободиться, но при этом решение сильно усложняется).
Итак, предположим, что путь из So в SKim разбит
на т шагов, в каждом из которых машина перемещается
с одной из опорных прямых (/)— (Г) на следующую по
порядку
(/-И) —
Проведенные нами опорные прямые пересекают дорож-
дорожную сеть в каких-то точках. Для решения задачи нам
должно быть известно время, требуемое для прохода
каждого участка пути, а также время задержки на каждом
28
перекрестке (переезде). На рис. 4.2 против каждого
отрезка пути проставлено соответствующее время прохода
(в минутах), а в кружке у каждого перекрестка (переезда) —
время ожидания машины в данном пункте.
Согласно количеству опорных прямых на рис. 4.2
процесс перемещения машины из 50 в 5КОН мы разделим
на семь шагов (т. е. примем т = 7) и начнем построение
оптимального пути с последнего (га-го) шага.
Наметим на опорной прямой (га—I) — (га—1) все
возможные положения машины в момент окончания пред-
предпоследнего ((га—1)-го) шага. Это будут гипотезы
о состоянии машины после (га—1)-го шага, -для каждой
из которых мы должны найти условное оптималь-
оптимальное управление на га-м шаге. На рис. 4.2 эти
возможные положения отмечены кружком с точкой внутри.
Из каждого такого положения мы должны выбрать опти-
оптимальный (кратчайший по времени) путь в точку 5КОН.
Рассмотрим сначала первую (сверху) из отмеченных
точек — точку А на прямой (га — 1) — (га—1). Из нее
в точку SK0H (в пределах полосы га-го шага) ведет один-
единственный путь, занимающий по времени 10 —J— 2 —J— 1 —J—
4-5+10 + 2 + 5 = 35 (минут).
Выбор этого пути представляет собой условное опти-
оптимальное управление при условии, что предыдущий шаг
привел нас в точку А. Отметим на рис. 4.2 этот опти-
оптимальный путь черной жирной линией, а у точки А выста-
выставим «флажок» с записанной на нем цифрой 35.
Жирная линия вместе с флажком означают следующее:
если, перемещаясь из So в 5К0Н, мы какими-то судьбами
оказались в точке А, то из нее мы должны двигаться
дальше по отмеченному черной линией маршруту и на
достижение точки SK0H затратим 35 минут.
Переходим к следующей точке (В) на прямой (га— 1) —
— (га—^ 1). Из нее в точку SKllH ведет одип-едипствепмый
путь, на который требуется 2 + 2 + 1+5+10 + 2 + 5 =
= 27 (минут). Число 27 также записываем на флажке
рядом с точкой В.
Для точки С путь снова единственный и продолжается
4 + 2 + 5=11 (минут).
Из точки К в SK0H есть два пути. 3 + 3 + 4 =
= 10 (минут) и 3 + 3 + 2+2 + 6=16 (минуг); из них
первый — скорейший; отмечаем его жирной линией и
записываем минимальное время A0) на флажке у точки К.
29
Рис. 4.2.
Продолжая таким же образом, находим для каждой
точки на прямой (т—1) — (т—1) оптимальное продол-
продолжение пути — условное оптимальное управление на /п-м
шаге.
После того как это выполнено, переходим к планиро-
планированию (т — 1)-го шага. Гипотезы о том, где может нахо-
находиться машина после предпредпоследнего {т — 2)-го шага,
отмечены треугольниками на прямой (т — 2) — (т — 2).
Для каждой из отмеченных точек мы должны найти
условное оптимальное управление, т. е. такой путь с пря-
прямой (т — 2) — (т — 2) на прямую (т—1) — (т—1),
который, совместно с уже оптимизированным
последним шагом, дает возможность достиг-
достигнуть SK0B за минимальное время. Чтобы найти
это условное оптимальное управление, мы должны для
каждой точки на прямой (от— 2) — (т — 2) перебрать все
возможные способы перехода на прямую (от— 1) — (т — 1)
и время, потребное на этот переход, сложить с мини-
минимальным временем последнего шага, записанным на флажке.
Из всех возможных путей выбирается тот, для которого
это суммарное время минимально; путь отмечается черной
линией, а время записывается на флажке у соответствую-
соответствующей точки.
В результате цепочки таких построений, перемещаясь
шаг за шагом с одной опорной прямой на другую, мы,
наконец, дойдем до исходной точки 50. Для нее мы опре-
определим оптимальный путь на прямую A) — A) и запишем
соответствующее минимальное время (87 минут) на флажке
у точки 50. Таким образом, все данные для построения
оптимального пути есть, так как для каждой из намечен-
намеченных точек (какими бы судьбами мы в ней ни оказались)
известно оптимальное продолжение пути. Чтобы построить
оптимальный путь из So в 5К0Н, нужно просто переме-
перемещаться по участкам дорог, отмеченным жирными линиями.
На рис. 4.2 оптимальная траектория из 50 в 5К0Н отмечена
жирной линией с пунктиром.
Таким образом, поставленная задача о выборе наиско-
наискорейшего пути между двумя заданными пунктами решена.
По поводу этой задачи можно высказать несколько со-
соображений, касающихся выбора числа шагов при построе-
построении решения методом динамического программирования.
С первого взгляда кажется, что для того чтобы реше-
решение было проще, желательно было бы иметь поменьше
31
шагов. Однако это не совсем так. Чем крупнее шаг, тем
труднее находить оптимальное решение на этом шаге,
тем больше существует вариантов перемещения с прямой
на прямую. В предельном случае, если бы мы рассмо-
рассмотрели только один шаг (/и=1), перед нами встала бы
исходная задача перебора всех возможных путей из So
в 5КОН во всей ее сложности.
Следует ли из этого, что в нашей конкретной задаче
нужно было бы еще увеличивать число шагов, сделать их,
например, не 7, а 20?
Тоже нет! Увеличение числа шагов за какие-то разум-
разумные пределы только усложнило бы процедуру построения
решения.
В том, что выбранное нами число шагов (т — 7)
довольно разумно, можно убедиться по тому, что нам
нигде не приходилось перебирать большого числа вариан-
вариантов перехода с прямой на прямую — этих вариантов ока-
оказывалось один, два, редко три, и найти среди них опти-
оптимальный было не слишком трудно. Если бы мы сильно
увеличили число шагов, т. е. чрезмерно измельчили
участки перехода, то в подавляющем большинстве случаев
с прямой на прямую вел бы один-единственный путь, и
никакой оптимизации не было бы. В конечном итоге мы
построили бы ту же оптимальную траекторию, но путем
более сложных расчетов.
§ 5. Непрерывная задача
прокладки оптимального пути
В § 4 была решена задача прокладки оптимального
пути из пункта So в пункт 5КОН при условии, что оба
пункта соединены какой-то сетью дорог и путь может про-
пролегать только по одной из дорог этой дискретной сетки.
На практике может встретиться и другая обстановка —
когда готовой дорожной сети не существует, а направле-
направление движения из каждой точки на плоскости может выби-
выбираться произвольно, например в пределах какого-то угло-
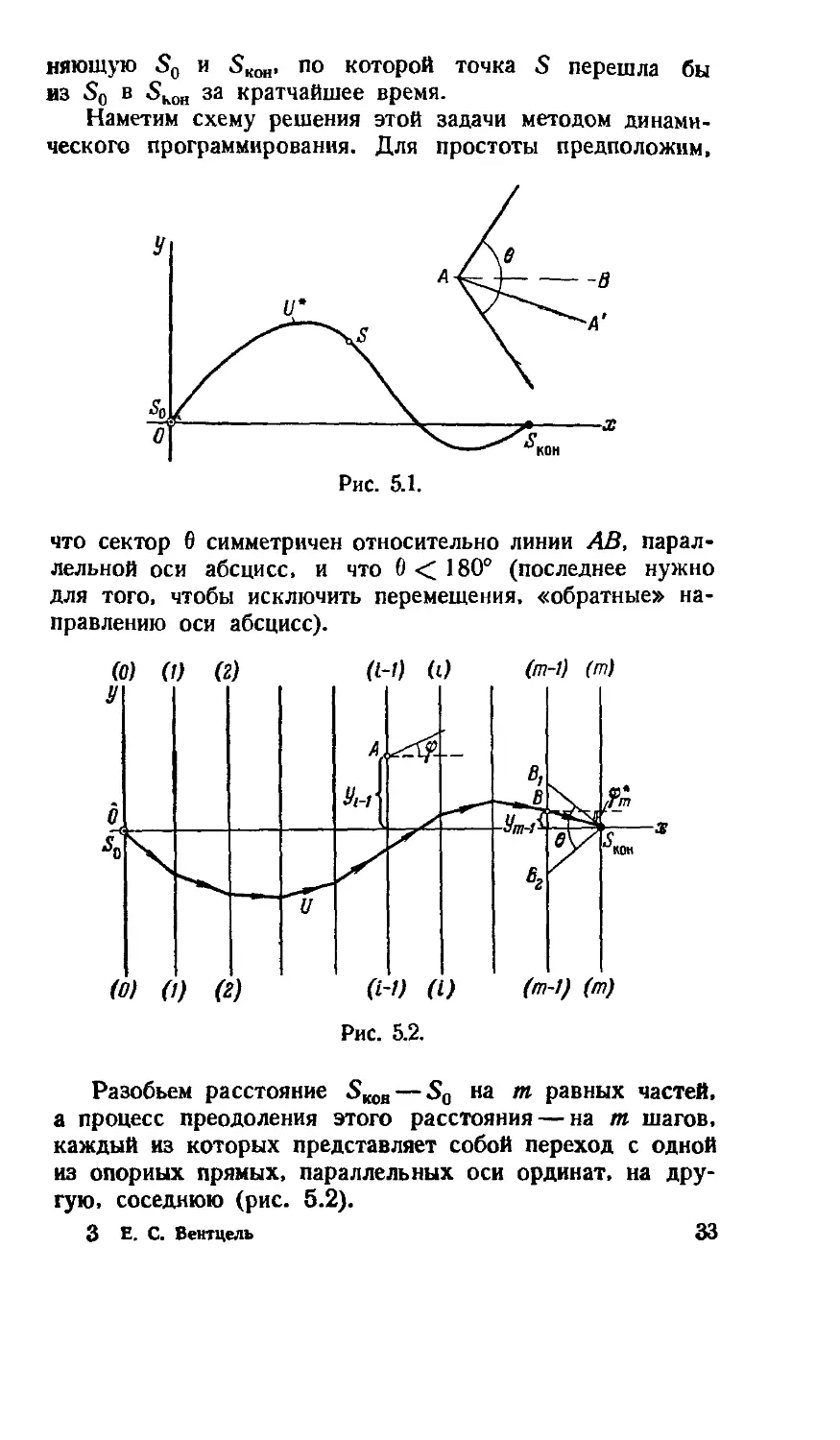
углового сектора 0 (рис. 5.1). При этом для каждой точка А
на плоскости хОу известна скорость перемещения из этой
точки по любому лучу АА' в пределах сектора в. Задача
состоит в том, чтобы найти такую траекторию U*. соеди-
32
няющую So и SKOH, no которой точка S перешла бы
из So в 5кон за кратчайшее время.
Наметим схему решения этой задачи методом динами-
динамического программирования. Для простоты предположим,
Рис. 5.1.
что сектор 6 симметричен относительно линии АВ, парал-
параллельной оси абсцисс, и что б < 180° (последнее нужно
для того, чтобы исключить перемещения, «обратные» на-
направлению оси абсцисс).
(О (г)
(l-l)
(т-1) (т)
— m -
и
\
Уп\
У
(о) 0) (г)
а-') (I)
Рис. 5.2.
(т-1) (т)
Разобьем расстояние SK0B — So на т равных частей,
а процесс преодоления этого расстояния — на т шагов,
каждый из которых представляет собой переход с одной
из опорных прямых, параллельных оси ординат, на дру-
другую, соседнюю (рис. 5.2).
3 Е. С. Вентцель 33
Если взять число шагов т достаточно большим, то
можно допустить, что на каждом шаге участок траектории
прямолинеен. Задача сводится к тому, чтобы для каждой
точки А на опорной прямой (i—1) — (i—1) определить
оптимальный угол ср (в пределах сектора 6), под которым
должна проходить точку А оптимальная траектория, т. е.
та, по которой мы должны двигаться из Л, чтобы достичь
5КОИ в минимальное время. Если положение точки А на пря-
прямой (i — 1)—(i—1) определять ее ординатой yt_v то услов-
условное оптимальное управление на /-м шаге будет предста-
представлять собой движение из точки А под углом <р* к оси
абсцисс, где с* зависит от у^,:
Будем планировать процесс перемещения, как всегда,
с последнего (m-го) шага. Предположим, что в результате
(т — 1)-го шага мы оказались в некоторой точке В на
прямой (т—1) — (т — 1) (рис. 5.2). Куда мы должны
двигаться дальше, чтобы оказаться в точке SK0H? Оче-
Очевидно, по прямой BSKOtl. Но направление этого движения
не для всех положений точки В на прямой (т—1)—(т—1)
находится в допустимых пределах. Для того чтобы по-
построить отрезок ВХВ2 возможных положений точки В,
откуда можно, при наших ограничениях, прийти в SK0H,
очевидно, нужно построить из точки 5КОИ «перевернутый»
сектор 6; границы его отсекут на прямой (т — 1) — (т — 1)
отрезок ВУВ2-
Итак, для каждой точки В отрезка ВХВ2 найдено
условное оптимальное управление — перемещение по пря-
прямой BSK0H под углом <fm к оси абсцисс, который зави-
зависит от ординаты ym_j точки В:
Тщ Тт \Ущ — 1/"
Зная скорость перемещения из точки В по этому на.
правлению, мы можем найти минимальное время выпол-
выполнения последнего шага:
Таким образом, для любой точки В на прямой (от—1) —
(от—1) условное оптимальное управление и соответствую-
соответствующее ему условное минимальное время от-го шага могут
34
быть определены. Зададимся несколькими значениями
ординаты ут_{.
yffLr yg!_i E.1)
и для каждого из них найдем условное оптимальное упра-
управление и условное минимальное время:
Если точки y^Li'-Ут-г " •' поставлены на отрезке ВХВ2
достаточно часто, то можно считать, что условное опти-
оптимальное управление и условное минимальное время найдены
для любого значения ym_r
Перейдем к планированию предпоследнего ((т—1)-го)
шага (рис. 5.3). Участок CjC2 возможных положений
@) A) B)
(И) п)
У
(б) A) B)
(Н) (I)
Рис. 5.3.
(т-2) (т-1) (т)
точки 5 в результате (т — 2)-го шага тоже определяется
«перевернутым» сектором 8; для того чтобы его построить,
нужно продолжить прямые SKmBl и SKOHB2 до пересечения
с прямой (т — 2) — (т — 2). Разместим на участке Cfi2
ряд опорных точек и для каждой из них найдем оптималь-
оптимальный путь в 5К0Н. Для точки С, этот путь ясен: он идет
по прямой CjSkoh. Проведем этот путь жирной линией и
вычислим соответствующее ему полное время Tm_i, m, рас-
расходуемое на выполнение двух последних тагов. Это время
35
равно сумме двух времен: времени tm_\ перемещения по
отрезку С1В1 и времени Тт перемещения из Bt в SK0H
(а оно было уже вычислено на предыдущем шаге). Анало-
Аналогично оптимальный путь из С2 в ShOH идет по прямой С^кон.
Возьмем на отрезке CjC2 любую внутреннюю точку С.
Для этой точки путь на прямую (от—1) — (т—1) уже
не единственный. Действительно, построив при точке С
сектор возможных направлений 6, мы видим, что в пре-
пределах этого сектора можно выбрать любой прямолинейный
пугь, ведущий из С в одну из точек отрезка BiB[.Какой же
из этих путей выбрать? Очевидно, тот путь CD, для кото-
которого суммарное время, идущее на оба последних
шага (CD и DSK(m), минимально. Обозначим это мини-
минимальное время Тт-\,т и заметим, что оно зависит от
ординаты ут_2 точки С. Беря целую гамму различных
положений точки С на отрезке СХС2 с ординатами у£'_2.
Ут'-2' • • •' найДем Для каждого из них оптимальное упра-
управление <р^_! и минимальное время Тлт_1 т достижения
точки SKoa:
7* ( (*) ^ т* ( <2) '\
т-1, т \Ут-2)\ ' т-\, т\Ут-2)'> ■ • •
После того как это сделано, переходим к планированию
(от — 2)-го шага и т. д.
В результате цепочки таких построений для каждой
точки на любой из опорных прямых будет выяснено услов-
условное оптимальное управление (найден угол ср*. под которым
должна проходить оптимальная траектория) и определено
соответствующее этому управлению минимальное время
достижения точки SK0H.
После того как процесс оптимизации доведен до
точки So, строится (уже от начала к концу) вся опти-
оптимальная траектория, которая из каждой точки идет под
оптимальным углом ф*.
На рис. 5.4 показан результат построения оптималь-
оптимального управления методом динамического программирования.
Оптимальная траектория отмечена жирной линией с пунк-,
тиром.
Заметим в заключение, что описанная методика по-
построения оптимальной траектории вовсе не зависит от
36
того, какая именно величина минимизируется — будь то
время Т перемещения из So в SKon, или расход горючего R.
или стоимость переезда С, или еще какой-нибудь крите-
критерий, выбранный в зависимости от характера решаемой
практической задачи. Например, при прокладке железно-
железнодорожного пути можно предпочесть тот маршрут, который
приводит к наименьшим затратам или наименьшему объему
(о) (О
@) О) (г)
земляных работ. При выборе траектории ракеты может
оказаться нужным минимизировать стартовый вес или
максимизировать скорость и т. д.
Заметим еще, что сектор возможных направлений 6,
который мы для простоты считали неизменным, может
меняться в зависимости от номера шага или, в общем
случае, от координат исходной точки А. В некоторых
практических задачах бывает, что направление скорости
в начальный момент или в конечный (или в тот и другой)
заданы заранее и меняться не могут. Это равносильно
тому, что сектор возможных направлений 6 в окрестно-
окрестности этих точек вырождается в одну прямую.
Опорные линии (/) — (/), которыми мы разделяли про-
процесс на этапы, вовсе не обязательно должны быть пря-
прямыми, параллельными одной из осей; их выбирают, исходя
из удобства построения решения. Если, например, задачу
удобнее решать не в декартовой, а в полярной системе
координат, линии (i) — (i) могут быть, в зависимости от
37
типа задачи, выбраны в виде пучка лучей, исходящих из
полюса О (рис. 5.5) или в виде концентрических окруж-
окружностей (рис. 5.6). Например, на рис. 5.7 показана схема
12)
м
A-1).
(г)
0)
Рис. 5.5.
о 0) (г) (i-i) (О
Рис. 5.6.
планирования вывода ракеты из точки So на поверхности
земли в заданную точку 5К0Н космического пространства,
выполненная в полярной системе координат. Полярные
Рис. 5.7.
координаты точки старта So заданы и равны (R3, i|>). Усло-
Условия вертикальности старта сужают сектор возможных
направлений 6 на первом шаге до одной прямой; условия
заданного направления конечной скорости г»кон наклады-
накладывают такие же ограничения на последний шаг; на проме-
промежуточных шагах ограничения, накладываемые на сектор
возможных направлений, выводятся из физических сообра-
соображений (например, из максимально допустимых поперечных
перегрузок ракеты).
§ 6. Общая постановка задачи
динамического программирования.
Интерпретация управления
в фазовом пространстве
После того как рассмотрен ряд конкретных задач
динамического программирования, дадим общую постановку
таких задач и сформулируем в общем виде принципы их
решения. В этом параграфе (и в следующем за ним § 7)
читателю, знакомому лишь с элементами высшей матема-
математики, придется столкнуться с не совсем привычной для
него записью формул и несколько необычной терминоло-
терминологией. Однако подчеркнем, что сознательное усвоение
именно этих параграфов очень существенно для понимания
метода: без такого общего подхода трудно будет увидеть
в дальнейшем изложении что-либо большее, чем набор
разнообразных примеров.
Рассмотрим следующую общую задачу.
Имеется некоторая физическая система S, которая
с течением времени может менять свое состояние. Мы
можем управлять этим процессом, т. е. тем или дру-
другим способом влиять на состояние системы, переводить
ее из одного состояния в другое. Такую систему S мы
будем называть управляемой системой, а мероприятия,
с помощью которых мы влияем на поведение системы,
управлением.
С процессом изменения состояния системы S связана
какая-то наша заинтересованность, выражающаяся численно
с помощью критерия W, и нужно организовать процесс
так, чтобы этот критерий обратился в максимум (мини-
(минимум) !).
Обозначим наше управление (т. е. всю систему меро-
мероприятий, с помощью которой мы влияем на состояние
системы 5) одной буквой U. Критерий W зависит от
этого управления; эту зависимость мы запишем в виде
формулы
W W(U F.1)
') В дальнейшем для краткости мы будем говорить только
о максимизации критерия, подразумевая, что «максимум» в любом
случае может быть заменен на «минимум».
39
Требуется найти такое управление U* («оптимальное упра-
управление»), при котором критерий W достигает максимума:
W* = max [W (£/)}. F-2)
v
Запись max читается: «максимум no U», а формула F.2)
v
означает: W* есть максимальное из значений, которые
лринимает критерий W при всех возможных упра-
управлениях U.
Однако задача оптимизации управления полностью еще
не поставлена. Обычно при постановке таких задач должны
быть учтены некоторые условия, накладываемые на
начальное состояние системы So и конечное состоя-
состояние SKOB. В простейших случаях оба эти состояния пол-
полностью заданы (как, например, в § 4, когда требовалось
перевести автомашину из пункта So в пункт SK0H). В дру-
других задачах эти состояния могут быть не заданы вполне
точно, а только ограничены какими-то условиями,
т. е. указаны область начальных состояний So и
область конечных состояний SKOtJ.
Тот факт, что начальное состояние системы So входит
в область So, мы будем записывать с помощью принятого
в математике «знака включения» £:
аналогично для конечного состояния:
"кон С "кон-
С учетом начальных и конечных условий задача опти-
оптимального управления формулируется следующим образом:
из множества возможных управлений U найти такое
управление if*, которое переводит физическую си-
систему S из начального состояния S0£S0 в конечное
^кон'б^кон так, чтобы некоторый критерий W(U)
обращался в максимум.
Дадим процессу управления геометрическую интерпре-
интерпретацию. Для этого нам придется несколько расширить наши
привычные геометрические представления и ввести понятие
о так называемом «фазовом пространстве».
Состояние физической системы S, которой мы упра-
управляем, всегда можно описать с помощью того или дру-
40
того количества численных параметров. Такими парамет-
параметрами могут быть, например, координаты физического тела
и его скорость; количество средств, вложенных в группу
предприятий; численность группировки войск и т. д. Эти
параметры мы будем называть фазовыми координатами
системы, а состояние системы изображать в виде точки S'
с этими координатами в некотором условном фазовом
пространстве. Изменение состояния системы S в про-
процессе управления будет изображаться, как перемещение
точки S в фазовом пространстве. Выбор управления U
означает выбор определенной траектории точки 5
в фазовом пространстве, определенного закона движения.
Фазовое пространство может быть различным в зави-
зависимости от числа параметров, характеризующих состояние
системы.
Пусть, например, состояние системы S характеризуется
только одним параметром — координатой х. Тогда изме-
изменение этой координаты будет изображаться перемещением
точки S по оси Ох (или по определенному ее участку,
если на координату х наложены какие-то ограничения).
В данном случае фазовое пространство будет одномер-
одномерным и представляет собой ось абсцисс Ох или ее уча-
участок, а управление интерпретируется законом движения
точки S из исходного состояния So £ So в конечное
(РИС. 6.1).
Область возможных состояний системы
(фазовое проЬтранство)
Рис. 6.1.
Если состояние системы S характеризуется двумя пара-
параметрами хх и х2 (например, абсцисса материальной точки
и ее скорость), то фазовым пространством будет плоскость
хх0х2 или какая-то ее часть (если на параметры xt и х2
наложены ограничения), а управляемый процесс будет
изображаться перемещением точки S из So£ So в SKOa £ SKoa
по определенной траектории на плоскости xfix2 (рис. 6.2).
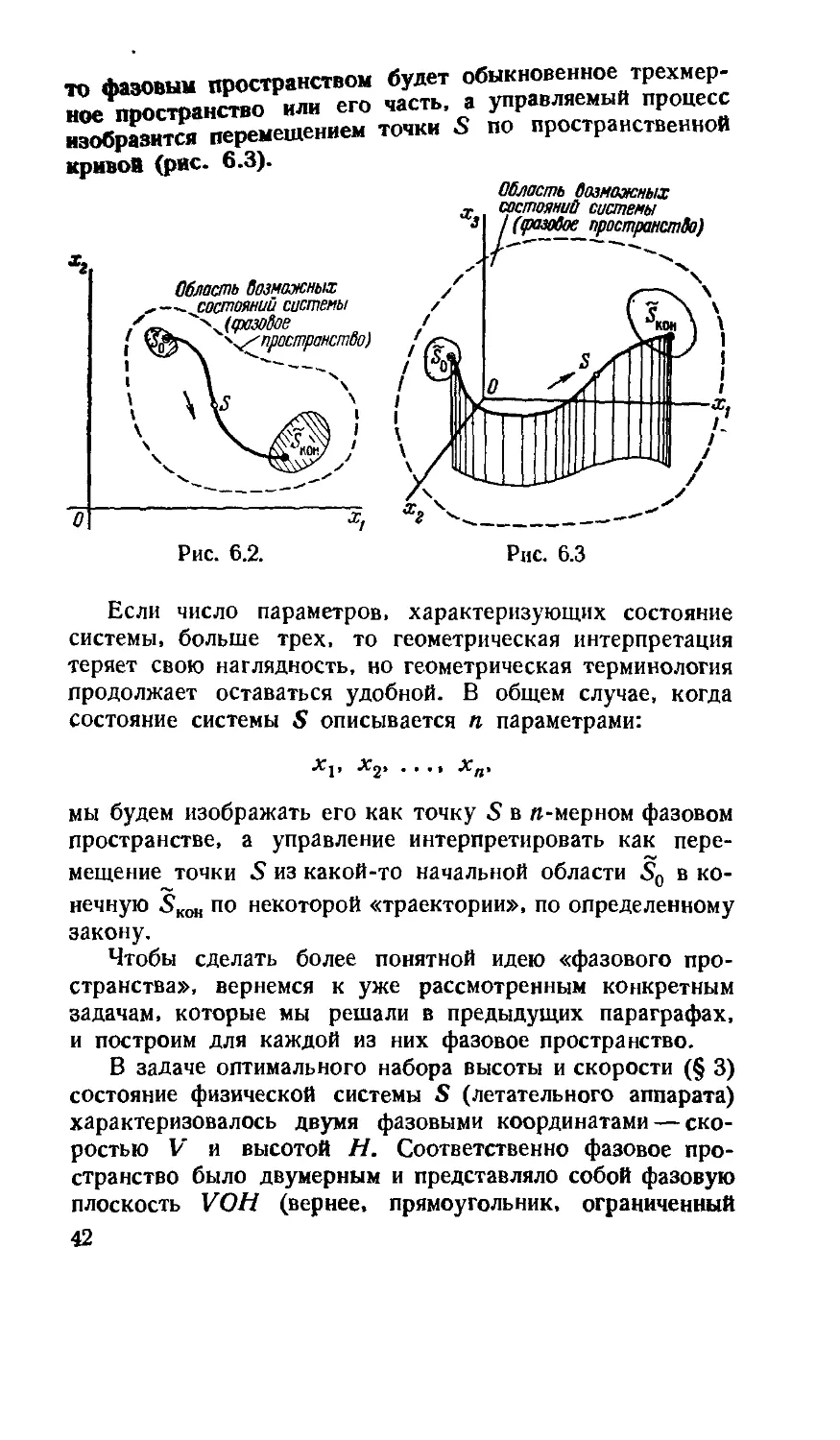
Если состояние системы характеризуется тремя пара-
параметрами xv x2, х3 (например, две координаты и скорость),
41
то фазовым пространством будет обыкновенное трехмер-
ISe пространство или его часть а управляемый процесс
изЫ5разится перемещением точки S по пространственной
кривой (рис. 6.3).
Область возможных
/состояний системы
(разовое пространство)
Область возможных
^--~ состояний системы
-^.(охзойое
?\ ^^пространство)
Рис. 6.2.
Рис. 6.3
Если число параметров, характеризующих состояние
системы, больше трех, то геометрическая интерпретация
теряет свою наглядность, но геометрическая терминология
продолжает оставаться удобной. В общем случае, когда
состояние системы S описывается п параметрами:
мы будем изображать его как точку 5 в «-мерном фазовом
пространстве, а управление интерпретировать как пере-
перемещение точки S из какой-то начальной области SQ в ко-
конечную SK0H по некоторой «траектории», по определенному
закону.
Чтобы сделать более понятной идею «фазового про-
пространства», вернемся к уже рассмотренным конкретным
задачам, которые мы решали в предыдущих параграфах,
и построим для каждой из них фазовое пространство.
В задаче оптимального набора высоты и скорости (§ 3)
состояние физической системы S (летательного аппарата)
характеризовалось двумя фазовыми координатами — ско-
скоростью V и высотой Н. Соответственно фазовое про-
пространство было двумерным и представляло собой фазовую
плоскость VOH (вернее, прямоугольник, ограниченный
42
абсциссами Vo, VKoa и ординатами Но, Нкон). Оптималь-
Оптимальное управление изображалось перемещением точки 5 по
оптимальной траектории на фазовой плоскости. Начальное
состояние 50(К0, //0) н конечное состояние 5K0H(VK0H, Нкои),
были вполне определены и представляли собой две
точки 50. 5К0Н на фазовой плоскости.
В задаче выбора наискорейшего пути (§ 4) физи-
физическая система S представляла собой автомашину, кото-
которую следовало перевести из начального пункта 50 в ко-
конечный 5К0Н за кратчайшее время. Здесь снова состояние
системы описывалось двумя параметрами jc nji (обычными
декартовыми координатами на плоскости), и траектория
точки 5 иа фазовой плоскости представляла собой самую
обычную траекторию движущейся точки (автомашины).
Непрерывная задача прокладки оптимального пути,
рассмотренная в § 5, ничем по постановке и по размер-
размерности пространства не отличается от предыдущей. Заме-
Заметим, что если бы оптимальный путь прокладывался не
в плоскости, а в пространстве (например, путь самолета
из одного пункта в другой), то фазовое пространство
стало бы трехмерным, а если бы при этом оптимизиро-
оптимизировался еще и режим изменения скорости — четырехмерным.
Во всех до сих пор рассмотренных примерах началь-
начальное и конечное состояния 50 и 5КОН были вполне опре-
определенными точками фазового пространства. Нетрудно
привести примеры задач, где эти состояния представляют
собой целые области So и 5КОН фазового пространства.
Пусть, например, нам требуется направить боевую
управляемую ракету из какой-то точки 50 на поверх-
поверхности земли в окрестность цели Ц так, чтобы она пора-
поразила эту цель. Очевидно, для этого нет надобности на-
направлять ракету в определенную точку 5ц, а достаточно,
чтобы она попала в заданную зону 5ц, окружающую
цель, размеры и форма которой определяются поражаю-
поражающим действием ракеты. Состояние ракеты в каждый мо-
момент времени будем изображать точкой 5 в шестимерном
фазовом пространстве (трн координаты, три составляю-
составляющих скорости). В начальный момент координаты ракеты
заданы; составляющие скорости равны нулю (точка 50
вполне определена). Что касается конечного состояния SK0B,
то оно определено не полностью: пространственные ко-
координаты должны находиться в пределах заданной зоны 5ц,
43
а на составляющие скорости никаких ограничений не
накладывается. Следовательно, область 5К0Н в шестимер-
шестимерном фазовом пространстве ограничена по координа-
координатам х, у, г и не ограничена по координатам V^, Vyt Vz.
Предположим теперь, что речь идет не о боевой,
а о пассажирской ракете; для нее точка приземления
полностью определена, а на составляющие скорости на-
накладываются самые жесткие ограничения; при этом об-
область 5К0Н существенно сужается.
В дальнейшем изложении мы встретимся с целым рядом
практических задач, где начальное состояние 50 и конеч-
конечное §кт представляют собой не точки, а целые области
фазового пространства.
Итак, сформулируем общую задачу оптимального
управления в терминах фазового пространства:
Найти такое управление U* (оптимальное упра-
управление), под влиянием которого точка S фазового
пространства переместится из начальной области So
в конечную область §кон так, что при этом кри-
критерий W обратится в максимум.
Поставленную общую задачу можно решать различ-
различными способамч — далеко не только методом динами-
динамического программирования.
Характерным для динами-
динамического программирования
является определенный ме-
методический прием, а именно:
процесс перемещения точки
5 из 50 в §кои разделяется
на ряд последовательных
этапов (шагов) (рис. 6.4), и
производится последова-
последовательная оптимизация каждо-
каждого из них, начиная с по-
Рис. 6.4. следнего. На каждом этапе
расчета ищется сначала
условное оптимальное управление (при все-
всевозможных предположениях о результатах предыдущего
шага), а затем, после того как процесс оптимизации до-
доведен до исходного состояния So, снова проходится вся
последовательность шагов, но уже с начала до конца,
44
х,
и на каждом шаге из множества условных оптималь-
оптимальных управлений выбирается одно.
Что же мы выигрываем с помощью такого поэтапного
расчисления процесса оптимизации? Выигрываем то. что
на одном шаге структура управления, как правило, ока-
оказывается проще, чем на всем протяжении процесса.
Вместо того чтобы один раз решать сложную
задач}', мы предпочитаем много раз решать за-
задачу относительно простую.
В этом — все существо метода динамического про-
программирования и все оправдание его применения на
практике. Если такого упрощения процедуры оптимиза-
оптимизации от разделения процесса на этапы не происходит, при-
применение метода динамического программирования теряет
свой смысл.
7. Общая формульная запись
решения задачи оптимального
управления методом динамического
программирования
В предыдущем параграфе мы сформулировали общую
постановку задачи динамического программирования и дали
этой задаче геометрическую интерпретацию, поставив ее
как задачу управления движением точки в фазовом про-
пространстве.
В настоящем параграфе мы попытаемся записать
в общем виде не только постановку, но и решение за-
задачи динамического программирования. Правда, формулы,
которые мы получим, будут по необходимости иметь
весьма общий, неконкретный вид, но для понимания
дальнейшего эти общие формулы окажутся 'полезными.
Перед тем как начать общую формульную запись
процесса динамического программирования, нам необхо-
необходимо уточнить природу критерия W, которым мы пока
что совсем не занимались.
Отметим, что во всех рассмотренных до сих пор
примерах критерий W обладал одним примечательным
свойством: значение этого критерия, достигнутое за весь
45
процесс, получалось простым суммированием частных
значений того же критерия и\, достигнутых на
отдельных шагах.
Действительно, общий расход горючего R на набор
высоты и скорости (см. § 3) представлял собой сумму
расходов горючего ri на отдельных шагах:
т
Я = 2 г,; G.1)
< = 1
общее время Т перемещения из одного пункта в другой
(см. § 4) представляло собой сумму времен преодоления
отдельных этапов tt:
m
Г = 2^ G-2)
i = l
и так далее.
Если критерий W обладает таким свойством:
W = 2 Щ> G-3)
1=1
т. е. складывается из элементарных значений того же кри-
критерия, полученных на отдельных шагах, то он называется
аддитивным.
В большинстве практических задач, решаемых мето-
методом динамического программирования, критерий W является
аддитивным. Если он в первоначальной постановке за-
задачи не аддитивен, то стараются так видоизменить эту
постановку или сам критерий, чтобы он приобрел свойство
аддитивности (см. далее, § 14).
Мы будем рассматривать только аддитивные задачи
динамического программирования и некоторые наиболее
элементарные из приводящихся к аддитивным.
Дадим постановку и общую схему решения задач ди-
динамического программирования с аддитивным критерием.
Пусть имеется процесс управления физической систе-
системой S, расчлененный на т шагов (этапов). В нашем рас-
распоряжении на каждом (i-м) шаге имеется управление Ut,
посредством которого мы переводим систему из состоя-
состояния Sf_,, достигнутого в результате ({—1)-го шага,
в новое состояние St, которое зависит от S^ и выбран-
46
ного нами управления Ut. Эту зависимость мы запишем
так:
Sl = Sl(.St_l. £/,). G.4)
рассматривая St как функцию двух аргументов Sl^1 и Ur
Заметим, что для применения метода динамического
программирования существенно, чтобы новое состояние Si
зависело только от состояния 5f_j и управления на
1-ы шаге Ut и не зависело от того, каким образом
система пришла в состояние St_x. Если это оказывается
не так, то следует «обогатить» понятие «состояния си-
системы», введя в него те параметры из прошлого, от ко-
которых зависит будущее, т. е. увеличить число измерений
фазового пространства.
Под влиянием управлений Uv U2 Um система
переходит из начального состояния So в конечное 5К0Н.
В результате всего процесса за т шагов получается
«доход» или «выигрыш»
tt/ = i>,(S,_r £/<), G.5)
1 = 1
где lwl(Si_v U() — выигрыш на 1-м шаге, зависящий,
естественно, от предыдущего состояния системы 5/_j
и выбранного управления U(.
Задана область начальных состояний §0 и конечных
состояний 5КОН- Требуется выбрать начальное состояние
So£So и управления U\. Ui Um на каждом шаге
так, чтобы после т шагов система перешла в область 5К0Н
и при этом выигрыш W обратился в максимум.
Опишем в общем виде процедуру применения мето-
метода динамического программирования к решению этой
задачи.
Для этого нам понадобится ввести некоторые новые
обозначения. Мы уже обозначили W — выигрыш за все
время процесса; wt — выигрыш за <-Й шаг. Поскольку
процесс динамического программирования разворачивается
с конца, нам придется ввести специальное обозначение
для выигрыша, приобретаемого за несколько последних
шагов процесса.
47
Обозначим:
Wm — выигрыш за последний шаг,
Wm_Um — выигрыш за два последних шага,
W/, i+i,.... т — выигрыш за последние (т — *+1) шага.
начиная с 1-го и кончая от-м.
Очевидно,
G.6)
1, ...,m = wt-\-wt+i'-\- ... -\-wm. ,
Как мы уже знаем, процесс оптимизации управления
методом динамического программирования начинается
с последнего (m-го) шага. Пусть после (т — 1)-го шага
система находится в состоянии Sm_v Так как последний
(m-й) шаг должен перевести систему в состояние Sm =
= ^кон 6 "^кон- то в качестве 5m_j можно брать не все
в принципе возможные состояния системы, а только те,
из которых за один шаг можно перейти в об-
область §ко„.
Предположим, что состояние 5m_t нам известно,
и найдем при этом условии условное оптимальное упра-
управление на от-м шаге; обозначим его t/mEm_i). Это — то
управление, которое, будучи примененным на от-м шаге,
переводит систему в конечное состояние Sm£SKm, при-
причем выигрыш на этом последнем шаге Wm достигает
своего максимального значения:
Wm(Sm_i)= max \Wm{Sm-i, Um)\. G.7)
Напомним смысл символической формулы G.7).
Wm(Sm-p Um) означает выигрыш вообще (не оптималь-
оптимальный) на последнем шаге; он зависит как от результата
предыдущего шага Sm_v так и от примененного на дан-
данном шаге управления Um. Из всех выигрышей Wm (Sm_1, Um)
при разных управлениях Vт выбирается тот выигрыш
^"(.Sj^j), который имеет максимальное значение; это
и означает запись max. Заметим, что в качестве управле-
лий Um мы должны брать только те, которые переводят
48
систему из заданного состояния Sm_x в состояние Sm,
принадлежащее области 5КОН.
Находя условное максимальное значение выигрыша
Wm(Sm-i), мы тем самым находим и условное оптималь-
оптимальное управление Um(Sm_i). Тот факт, что условный
максимальный выигрыш Wm(Sm-i) достигается при услов-
условном оптимальном управлении t/mEm_i), мы запишем
символически в виде
и в дальнейшем будем пользоваться такой записью для ука-
указания соответствия между условным максимальным выигры-
выигрышем и условным оптимальным управлением на каждом шаге.
Итак, оптимизация последнего шага при любом ре-
результате предпоследнего произведена, и найдено соот-
соответствующее условное оптимальное управление. Получен-
Полученный результат можно сформулировать так: в каком бы
состоянии ни оказалась система после (т — 1)-го шага,
мы уже знаем, что нам делать дальше.
Перейдем к оптимизации предпоследнего ((т—1)-го)
шага. Сделаем снова предположение, что в результате
(т — 2)-го шага система пришла в состояние Sm_2. Пусть
на (т—1)-м шаге мы применили управление t/m_t.
В результате этого управления мы на (т — 1)-м шаге
получим выигрыш, зависящий как от состояния системы,
так и от примененного управления:
»»-1 = «»«- 1 (««-г-" ^«- О- G-8)
а система перейдет в новое состояние Sm_v тоже зави-
зависящее от предыдущего состояния и от управления:
5m-i = 5m_1Em_2, Um^). G.9)
Но для любого результата (от— 1)-го шага следующий,
от-й шаг уже оптимизирован, и максимальный выигрыш на
нем равен
K,(Sm-i)=> «CEm-i (Sm_2. и„.1)У). G.10)
') Смысл записи G.10) следующий: выигрыш Wm есть функ-
функция состояния Sm_t> которое в свою очередь зависит от пре-
предыдущего состояния Sm_2 и примененного управления Um_x.
Так как для обозначения функциональной зависимости принято
пользоваться круглыми скобками, то в формулах типа G.10) мы
ставим круглые скобки внутри круглых.
4 Е. С. Вентцель 49
Введем в рассмотрение полный выигрыш на двух по-
последних шагах при любом управлении на (т — 1)-м
шаге и оптимальном управлении на m-м шаге.
Обозначим его W^-i, т\ знак «-|~» будет нам напоминать,
что это выигрыш при неполностью оптимизированном упра-
управлении, в отличие от знака «*», которым мы обозначали
выигрыш при полностью оптимизированном управлении.
Выигрыш Wm-\. m> очевидно, зависит от предыдущего
состояния системы Sm_2 и примененного на (т—1)-м
шаге управления Um_v Учитывая формулы G.8) и G.10),
получим следующее выражение для tt^-i, m'
W^m-l, m(Sm-2. Um-\) —
= wm.i{Sm-2. t/m-04-WmEm_,Em_2, £/„,_,))• G.П)
Нам нужно выбрать такое оптимальное условное упра-
управление на (от—1)-м шаге t/m_iEm_2). при котором ве-
величина G.It) достигла бы максимума:
{№+_,, mEm_2, t/m_i)}. G.12)
. (a) {
um-\
Так же, как и на предыдущем этапе оптимизации,
в качестве состояний 5т_2 после (от — 2) шагов нужно
брать не все возможные состояния системы, а только те,
из которых можно перейти в 5К0И за два шага.
Таким образом, найден максимальный условный вы-
выигрыш па двух последних шагах и соответствующее ему
оптимальное условное управление на (от—1)-м шаге:
Wm-I, m CSm-2)~£/m-l(Sm-2).
Продолжая точно таким же образом, можно найти
условные максимальные выигрыши на нескольких послед-
последних шагах процесса и соответствующие им оптимальные
условные управления:
W^m-2, m-1, m Eт_з) ~ Um-2 Eт_з).
Wm-З, т-2, т-1,т О^т-.}) ~ £/т-3 (<Sm-4)
И Т. Д.
Если мы уже оптимизировали (/ —|— 1)-й шаг для любого
исхода 1-го, т. е. нашли
Wl + l m{S,)~tA+l(.Sl).
50
то условная оптимизация /-го шага производится согласно
общей формуле
W*,l+l тE,_i) = шах [Wt.iM.. ..raE,_i. Ut)}. G.13)
где
Wf.l+1 mE/_i. £/,) =
^ч1 m(S,(S,_,. £/,)) G.14)
— выигрыш, достигаемый па последних шагах, начиная
с t'-го, при любом управлении на 1-м шаге и оптимальном
управлении на всех последующих; S, (S,^, Ut) — то со-
состояние, в которое переходит uicicmj из Sl_1 под влия-
влиянием управления Ut.
Таким образом, определяется условный максимальный
выигрыш на последних шагах, начиная с /-го, и соответ-
соответствующее оптимальное условное управление на 1-й шаге:
W*i,i+i «(S/_i) — LCEi_i). G.15)
Применяя последовательно, шаг за шагом, описанную
процедуру, мы дойдем, наконец, до первого шага:
W\... ,m(S,,)~£/i(So), G-16)
где So— каког-то начальное состояние системы, принад"
лежащее к области So возможных начальных состояний:
Остается выбрать оптимальным образом начальное со-
состояние системы So- Если начальное состояние So в точ-
точности задано (т. е. вся область So сводится к одной
точке So), то выбора нет, и So — So- Если же точка So
может свободно выбираться в пределах области §0, то
нужно оптимизировать выбор начального состояния, т. е.
найти абсолютный (уже не условный) максимальный вы-
выигрыш за все шаги:
W* m = max « . ., т (So)}. G.17)
где запись max означает: максимум берется по всем со-
стояниям So, входящим в область §0. Точку So. в кото-
которой достигается этот максимум, и следует взять в каче-
качестве начального сосюяния системы.
4* 51
Таким образом, в результате последовательного про-
прохождения всех этапов от конца к началу найдены: мак-
максимальное значение выигрыша на всех т шагах и соот-
соответствующее ему оптимальное начальное состояние про-
процесса
W* = W*i2 т~5*. G.18)
Но построено ли уже оптимальное управление? Нет
еще: ведь мы нашли на каждом шаге только услов-
условное оптимальное управление.
Чтобы найти оптимальное управление в окончательной
инстанции, мы должны снова пройти всю последователь-
последовательность шагоп — па этот раз от начала к концу. Этот
второй «проход по шагам» будет гораздо проще первого,
потому что варьировать условия уже не придется.
В качестве начального состояния системы берется So
(или просто So, если начальное состояние жестко фикси-
фиксировано). На первом шаге применяется оптимальное упра-
управление U\ (см. G.16))
&=&($). G.19)
после чего система переходит в новое состояние
G.20)
Теперь нужно выбрать оптимальное управление на втором
шаге. Мы уже оптимизировали его для любого результата
первого шага. т. е. знаем Ul(Si) (см. G.15)); подставляя
в него 5|. получим
Ul = ut(s:), G.21)
и так далее, пока не дойдем до оптимального управления
на последнем шаге
tf» = tfm(S»-i) G.22)
и конечного состояния системы
S*m = 5*он = S'n (S*m_i, U'm). G.23)
В результате всей этой процедуры находится, нако-
наконец, решение задачи: максимально возможный выигрыш W*
и оптимальное управление U*. состоящее из оптимальных
управлений на отдельных шагах (вектор оптимального
52
управления)
U* = (UIU*2 Ul). G.24)
Таким образом, в процессе динамического программи-
программирования последовательность этапов проходится дважды:
первый раз — от конца к началу, в результате чего нахо-
находится максимальное значение выигрыша №*, оптимальное
начальное состояние процесса So и условное оптимальное
управление на каждом шаге; второй раз — от начала
к концу, в результате чего находится оптимальное упра-
управление Ui на каждом шаге и конечное состояние системы
при оптимальном управлении SK0H.
Итак, нам удалось изложить в общем виде и записать
с помощью общих формул процесс динамического про-
программирования. Ввиду символической записи формул струк-
структура процесса представляется очень простой, но это —
ложное впечатление. При постановке конкретных задач
динамического программирования часто возникают труд-
трудности.
Эти трудности связаны, во-первых, с выбором группы
параметров хх, х2, ■ ■ ■, хп, характеризующих состояние
физической системы 5. Как уже было сказано, эти пара-
параметры нужно выбирать так, чтобы при заданном состоя-
состоянии S(xv х2, ..., хп) системы 5 в любой момент ее сле-
следующее состояние S fx'v x'2 х'У в которое она пере-
переходит под влиянием управления U, зависело только от
прежнего состояния S и управления U и не зависело от
«предыстории» процесса, т. е. от того, когда, как и
в результате каких управлений система пришла в состоя-
состояние 5. Если это оказывается не так, приходится те эле-
элементы прошлого, от которых зависит, будущее, включать
в совокупность параметров xv х2 хп, характери-
характеризующих состояние системы в данный момент. А это при-
приводит к увеличению числа измерений фазового простран-
пространства и, значит, к усложнению задачи.
Вторая трудность состоит в разумном «этапировании»
процесса. Необходимо так расчленить процесс перехода
из 50 в SK0H на шаги, чтобы они допускали удобную ну-
нумерацию и четкую последовательность действий. Эта задача
часто бывает далеко не простой. •
Как уже говорилось раньше, разделение процесса на
дискретные «шаги» не является обязательным признаком
53
метода динамического программирования. В принципе
всегда можно устремить длину шага к нулю и рассмотреть
предельный случай — «непрерывное» динамическое про-
программирование. Получить в конечном виде решение таких
непрерывных задач удается лишь в редких случаях, но
они имеют большое теоретическое значение при доказа-
доказательстве теорем существования, а также различных каче-
качественных снойств оптимальных решений (см. [1]). В нашем
элементарном изложении метода динамического программи-
программирования мы совсем не будем касаться этих предельных
случаев.
В дальнейших параграфах мы рассмотрим целый ряд
практических задач, подходящих под общую схему дина-
динамического программирования. Некоторые из этих задач
мы только поставим, для большинства набросаем схему
решения, а некоторые решим до конца. Одни задачи
сравнительно легко подойдут под общую схему, изложен-
изложенную в данном параграфе; над постановкой других при-
придется еще потрудиться. Имея в виду громоздкость вычи-
вычислений «вручную», легко понять, что до конкретного чис-
числового результата будут доведены только самые простые
задачи с небольшим числом параметров xv х2, ■■-, опре-
определяющих состояние системы. Однако нужно иметь в виду,
что совершенно теми же методами с помощью современ-
современных быстродействующих вычислительных машин можно
решать и гораздо более сложные задачи со значительным
числом параметров. Что же касается числа шагов т, то
для машинного расчета его увеличение вообще затрудне-
затруднений не доставляет: просто увеличивается время расчета
пропорционально числу шагов.
§ 8. Задача распределения
ресурсов
Среди практических задач, решаемых методом дина-
динамического программирования, многие имеют целью найти
рациональное распределение ресурсов по различным кате-
категориям мероприятий. К такому типу принадлежит, напри-
например, задача о распределении средств на оборудование,
54
закупку сырья и наем рабочей силы при организации ра-
работы промышленного предприятия; задача о распределении
товаров по торговым и складским помещениям; задача
о распределении средств между различными отраслями
промышленности; задача о распределении веса между раз-
различными агрегатами технического устройства и т. п.
Здесь мы рассмотрим одну из самых простых задач
распределения ресурсов, на которой легко продемонстри-
продемонстрировать особенности многих подобных задач.
Имеется заданное начальное количество средств Zo
(не обязательно в денежной форме), которое мы должны
распределить между двумя отраслями производства: I и II.
Эти средства, будучи вложены в отрасли I и II, приносят
определенный доход. Количество средств л;, вложенное
в отрасль I, за один год приносит доход f(x); при этом
оно уменьшается (частично тратится), так что к концу
года от него остается остаток, равный гу(х):
Аналогично количество средств у, вложенное в отрасль II,
приносит за год доход g(y) и уменьшается до
По истечении каждого года оставшиеся средства за-
заново распределяются между отраслями. Новых средств
не поступает, и в производство вкладываются все остав-
оставшиеся в наличии средства.
Требуется найти такой способ управления ресурсами —
какие средства, в какие годы и в какие отрасли вклады-
вкладывать, — при котором суммарный доход за период в т лет
обращается в максимум.
Будем решать задачу методом динамического програм-
программирования. Физическая система S, которой мы будем упра-
управлять, представляет собой группу предприятий с вложен-
вложенными в них средствами. Выигрыш W — доход от обеих
отраслей I и II за весь период. Задание — планировать
на т лет — дает естественное членение процесса на т ша-
шагов (этапов). Однако в целях ясности изложения мы будем
на каждом шаге различать два полушага или «звена».
На первом из них происходит перераспределение средств;
на втором — средства только тратятся и происходит обра-
образование дохода.
55
Выберем теперь численные параметры, с помощью
которых мы будем характеризовать ситуацию (состояние
системы).
Ситуацию перед началом 1-го этапа (до перераспреде-
перераспределения средств) условимся характеризовать количествами
средств
х', ,, \', ,,
оставшихся в отраслях I и П после предыдущего ((I — 1)-го)
шага;). Ситуацию после распределения средств (т. е. после
первого звена 1-го шага)
У будем характеризовать
количествами средств
xv yt,
вкладываемых в отрасли
I и II на данном шаге.
В результате второго
звена 1-го шага (расхо-
(расходования средств) эти зна-
значения уменьшатся и ста-
станут равными
В
-х
Рис. 8.1.
после чего мы перей-
перейдем к следующему шагу.
Изобразим состояние системы точкой 5 в фазовом
пространстве. Это пространство можно строить по-раз-
по-разному; в целях наглядности мы выберем его двумерным
(рис. 8.1).
По оси абсцисс Ох мы будем откладывать коли-
количество средств, вкладываемое в отрасль I; по оси орди-
ординат Оу— количество средств, вкладываемое в отрасль II.
Тогда фазовым пространством будет часть плоскости хОу,
лежащая внутри и на границах треугольника АОВ. Дей-
Действительно, для любого эгапа производства сумма средств,
вложенных в отрасли I и II, не может превосходить на-
начальный запас средств:
х~\-у <Z0;
(8.1)
') Это не относится к первому шагу, в начале которого нам
просто дано некоторое количество средств Zo.
56
кроме того, эти вложения неотрицательны:
*>0; у>0. (8.2)
Областью плоскости хОу, которая удовлетворяет усло-
условиям (8.1) и (8.2), является треугольник АОВ; это и есть
фазовое пространство, в котором может изменять свое
положение точка S, изображающая состояние системы.
Определим области So и SK0H начальных и конечных
состояний системы.
В начальный момент единственное, что мы знаем
о состоянии системы, это то, что сумма вложений в обе
отрасли равна начальному запасу средств:
Такому условию удовлетворяет любая точка отрезка АВ,
который и является областью 50 начальных состояний
системы. Что касается положения конечной точки SK0H,
то мы знаем только, что для нее
*>0. у>0, x-\-y<Z0,
т. е. область 5К0Н представляет собой весь треугольник
АОВ, кроме гипотенузы АВ.
Посмотрим, какой вид может иметь траектория точки S
в фазовом пространстве. Поскольку мы рассматриваем
дискретную задачу, эту траекторию будем изображать
в виде ломаной линии (рис. 8.2). На первом шаге, в отличие
от других, происходит только трата средств (перераспре-
(перераспределения нет). При этом из точки So с координатами (jelt у{)
мы переходим в точку М с координатами (х[, у'Х Так как
х[ <; xv yj <!}>,, то это звено траектории представляет
собой отрезок, направленный от точки So вниз и влево.
Следующий (второй) шаг разделяется на два звена: 2, и 22.
На первом звене 21 происходит перераспределение средств;
при этом х-\-у остается постоянным и, значит, точка S
перемещается по прямой, параллельной АВ, в точку N
с координатами (х2, у2). На втором звене второго шага
B2) снова происходит трата средств, и точка 5 переме-
перемещается вниз и влево, и так далее, пока через т шагов
не будет достигнуто конечное состояние 5К„Н — точка
с координатами (х'т, у'ту
57
Заметим, что звенья шагов неравноценны: управление
осуществляется только на первом звене каждого шага,
а на втором мы получаем доход. Управление Ul на 1-ы
в X
Рис. 8.2.
шаге (осуществляемое на первом звене /,) состоит в выборе
неотрицательных значений xt, yt таких, что
После этого мы получаем на втором звене 1-го шага (/2)
доход
«»/ = /(■*/) + «№ (8.3)
а точка 5. изображающая состояние системы, переходит
в новое положение с координатами
Требуется найти такое положение 5^ точки So на
прямой АВ и такую траекторию точки 5 в фазовом про-
пространстве, чтобы суммарный доход за все т шагов
W =
Щ
(8.5)
обращался в максимум.
Перед нами — типичная задача динамического програм-
программирования. Применим к ее решению общие приемы, изло-
58
женные в предыдущем параграфе. Чтобы сделать конкрет^
ное приложение общего метода как можно более понятным,
мы позволим себе, может быть, немного повторяться.
Как всегда, будем оптимизировать процесс распреде-
распределения средств, начиная с конца, причем сразу по обоим
звеньям каждого шага (учитывая, что второе из них
является неуправляемым).
Пусть перед т-и (последним) шагом мы находимся
в точке (x'm_v у'т_Х и нам предстоит перераспределить
средства, т. е. выбрать точку (хт, ут) такую, что
Хт
Заметим, что для решения этой задачи нам не тре-
требуется знания обоих чисел x'mV y'm_v а существенно
знать только их сумму, подлежащую перераспределению:
Перераспределение будет состоять в том, что мы вы-
выделим какую-то часть хт средств Zm_, и вложим ее
в отрасль I; количество средств ут, которое вкладывается
в отрасль II, автоматически определится из соотношения
Ут ~ *т-1 Хт-
Таким образом, на /га-шаге «управлением» является хт.
Мы должны найти на этом шаге условное оптимальное
управление, т. е. для любого значения 2Гт_, найти такое
количество средств x*m(Zm_iy вкладываемых в отрасль I,
при котором доход на т-и шаге, равный
Wm(Zm_v xm) = wm(Zm_l, xm), (8.6)
обращается в максимум:
vC(Zm-i)= max {Wm(Zm.v *,„)). (8.7)
') Так как состояние системы после каждого этапа характе-
характеризуется всего одним числом, мы могли бы выбрать наше фазо-
фазовое пространство одномерным, но тогда траектория выглядела бы
не так наглядно.
59
Запись max означает, что берется максимум
по всем возможным на данном шаге значениям управле-
управления хт; они неотрицательны н не превосходят общего
запаса средств Zm_v с которым мы пришли к дан-
данному шагу.
Выражая максимальный доход (8.7) на последнем шаге
через вложенные средства по формуле (8.3), получим
W*m{Zm-i)= max
Этому максимальному значению соответствует опре-
определенное условное оптимальное управление на m-м шаге
и задача условной оптимизации /га-го шага решена.
Перейдем к условной оптимизации предпоследнего
((/га—1)"го) шага. Пусть после (/га — 2)-го шага сохра-
сохранился запас средств
2т_2 = ^_а + У;_2- (8-9)
Найдем №'m-i,m{Zm-'i) — условный максимальный доход
за два последних шага. Пусть управление brm_1, приме-
применяемое на (т — 1)-м шаге, состоит в том, что мы вкла-
вкладываем в отрасль I средства хт_1 (а значит, в отрасль II —
средства ym-i = Zm_2 — xm_l). Соответственно этим вло-
вложениям на (т — 1)-м шаге мы получим доход
<»»-l(Zm-2. *«-l) = /(*«-!>+ *Bm_a— *„_,). (8.Ю)
и система перейдет в точку фазового пространства с коор-
координатами
<.-i = ?(*m-i): ^_1 = Ф(Ут_,) = ФBт.а-*т_1). (8.П)
Согласно общему принципу (см. § 7) для того, чтобы
оптимизировать условное управление на (т — 1)-м шаге,
нужно сложить доход на (т—1)-м шаге (8.10) при лю-
любом управлении хт_1 с уже оптимизированным доходом
на т-и шаге (8.8); получим суммарный доход на двух
60
последних шагах
Wm-1, ra(Zm_2. Хт_\) =
^(Zm_!). (8.12;
После этого найдем то управление хт_1 на (т—1)-м
шаге, при котором доход (8.12) обращается в максимум:
= max
n-2, *m-l)}. (8.13)
Напишем явное выражение Wm_i, m(Zm_2. xm_\) как
функции от обоих аргументов. Для этого подставим
в формулу (8.12) выражение (8.10):
1л/ . G о 1* «^ * '
" tn — lftn V*-*Ш — /* "^ ОТ — I/ "~~"
* (Zm_i). (8.14)
Но в правую часть (8.14) входит, кроме Zm_2 и xm_v
еще Zm_v Для того чтобы избавиться от этого «лишнего»
аргумента, вспомним, что запас средств Zm__j после
(т—1)-го шага зависит от запаса средств Zm_2, имев-
имевшегося к началу этого шага, и примененного на (т— 1)-м
шаге управления хт_1; согласно формуле (8.4)
*»-l = <P(*m-l)+<KZm-2 —■*»-!)■ (8-15)
Подставляя это выражение в формулу (8.14) и затем
(8.14) в (8.13), получим окончательно выражение услов-
условного максимального дохода на двух последних шагах:
= max [f{m_l) + g
+ Wm(<?(*ra_l) + <H^m-2— JCm-l))b (8-16)
где /, g, <p, <j> — вполне определенные, заданные функции
своих аргументов, a Wm(Zm-\) — функция, полученная
в результате условной оптимизации последнего шага;
в эту функцию (заданную формулой, графиком или табли-
таблицей) вместо аргумента Zro_l нужно подставить вели-
-чнну (8.15).
61
То значение хт_ v при котором достигается макси-
максимум (8.16), и есть условное оптимальное управление на
(т — 1)-м шаге
Таким образом, задача условной оптимизации управле-
управления на (т — 1)-м шаге решена: найден условный макси-
максимальный доход за два последних шага и соответствую-
соответствующее ему условное оптимальное управление — количество
средств, вкладываемых на (т — 1)-м шаге в отрасль 1:
Продолжая процесс условной оптимизации точно так же,
получим для любого (i-ro) шага условный максимальный
доход за все шаги, начиная с данного:
= max [Wt,t+i ,п(^_„ л-,)}, (8.17)
где
Wt.t + l m(Z,_,. Xl)=f(Xi)-\-g(Zl_1 — Xd +
*i — *i)). (8.18)
a Wi+i m(Zd — функция, уже построенная при опти-
оптимизации /-го шага: в эту функцию вместо аргумента Z,-
нужно подставить выражение
i- x;). (8.19)
Подставляя (8.18) r (8.17), получим явное выражение
(Ц,... т (Zi -i) через известные функции /, g, cp, ф,
i-i)— max
(8.20)
Этому условному максимальному доходу соответствует
условное оптимальное управление на £-м шаге:
Кш *{z'-r)~x'i(zi-i)- <8-21>
Когда таким образом мы произведем условную опти-
оптимизацию всех шагов, кроме первого (напомним, что он
62
качественно отличен от остальных, так как состоит только
из одного звена), нам остается оптимизировать управление
на этом первом шаге и наИти максимальный полный
выигрыш на всех шагах, зависящий, разумеется, от на-
начального запаса средств Zo:
() U...,«() (
Величина W\f 2, .,.,,„ (Zj) найдется по той же фор-
формуле (8.20), что и на остальных шагах:
= max
+ Vi'l ...,„ (? (Xl) + ■; (Zo — Xj))}. (8.23)
Вся особенность первого шага состоит в том, что исход-
исходный запас средств Zo не варьируется, а предполагается
известным. То значение управления х*, при котором
достигается максимум (8,23), представляет собой уже не
условно оптимальное, а просто оптимальное упра-
управление на первом шаге, которым и нужно пользоваться.
Это значение х* определяет абсциссу точки Sq на
отрезке АВ, с которой начинается оптимальная траекто-
траектория в фазовом пространстве.
Зная положение этой точки и снова проходя все шаги,
но уже в обратном направлении — от начала к концу, —
можно построить всю оптимальную траекторию точки 5.
Проследим, как пройдет эта траектория, по шагам и их
звеньям.
В начале первого шага точка S находится на отрезке АВ
и имеет координаты
После первого шага точка 5 перемещается в точку с коор-
координатами
сумма которых равна запасу средств после первого шага
На первом звене второго шага происходит перераспре-
перераспределение средств; точка 5 переходит в точку с коорди-
координатами
63
где x*(Z*^ — условное оптимальное управление на втором
шаге, в которое вместо Zl поставлено Z\. На втором
звене второго шага происходит трата средств, и точка 5
перемещается в точку с координатами
сумма которых равна оставшемуся к концу второго шага
запасу средств
и т. д. вплоть до последнего шага.
Таким образом будет найдено окончательное реше-
решение задачи: максимальный доход за все т шагов W" и
соответствующее ему оптимальное управление Xs =
= Х*(х*, л:* х*ту указывающее, какое количество
средств на каком этапе нужно выделять в отрасль I
(остаток автоматически отводится на отрасль II).
После того как рассмотрена конкретная задача дина-
динамического программирования, полезно снова вернуться
к общему изложению вопроса в § 7 и посмотреть, какое
конкретное воплощение получили в данной задаче введен-
введенные там общие понятия.
Систему этих соответствий мы запишем в виде таблицы,
разделенной на две части вертикальной чертой; слева от
черты мы будем писать ту величину, понятие или символ,
который применялся в общем случае; справа — соответ-
соответствующий ему аналог в нашем частном случае.
В общем случае
Физическая система S ,
т этапов (шагов)
Аддитивный критерий
т
где wL — выигрыш на /-м
шаге
В нашем частном случае
Группа предприятий с вло-
вложенными в них средствами
т лет
Общий доход за т лет
т
i=i
где wt —- доход от отраслей 1
и II на /-м шаге
64
Продолжение
В общем случае
Управление U t на i-м
шаге
Состояние системы после
/-го шага St
Состояние системы после
i-ro шага в зависимости от
ее состояния после (/—1)-го
шага к управления на i-м
шаге
Sl = Sl{Sl.l,Ul)
Выигрыш на (-м шкге в
зависимости от исхода
(/— 1)-го шага 5^_, и приме-
примененного на /-м шаге упра-
управления:
»,(Si-i. Ui)
Фазовое пространство
Область начальных состоя-
состояний системы So
Область конечных состоя-
состояний системы SKOa
U нашем частном случае
Количество средств л,-,
вкладываемое в отрасль I
Количество средств х\, у\,
оставшихся в отраслях I и II
соответственно; существенной
для планирования дальнейших
шагов является их сумма
zi = x't+y't
Zt^vixd + tyiZi-i-xt)
u>l(Zi-i, xi)=f{Xi)+g (Zi- 1-х-)
Треугольник АОВ (см.
рис. 8.1)
Отрезок АВ (см. рис. 8.1)
Треугольник АОВ (за исклю-
исключением гипотенузы) (см.
рис. 8.1)
5 Е, С. Вентцель
65
Продолжение
В общем случае
Оптимальное начальное со-
состояние системы
Оптимальное управление
U* = (U\, Ul, ...,U*m)
В нашем частном случае
Оптимальное количество
средств ATj- выделенное в пер-
первую отрасль, и определяемое
им количество средств
у* = Zo — x\, выделенное во
вторую отрасль
Оптимальное количество
средств по годам, выделяемое
в отрасль I:
л =(a:j,a:2, .... хт)
В дальнейшем изложении мы всюду будем следовать
общей схеме § 7, уже не сопровождая ее столь подроб-
подробными пояснениями.
9. Примеры задач
о распределении ресурсов
Для усвоения общего решения задачи о распределении
ресурсов, данного в предыдущем параграфе, полезно при-
применить его на конкретном материале. Здесь мы рассмотрим
два конкретных примера общей задачи о распределении
ресурсов, в каждом из которых зададимся вполне опре-
определенным видом функций f(x), g(y), <p(jc), ^(у), и до-
доведем каждый из примеров до численного результата.
Пример 1. Планируется работа двух отраслей
производства I и II на период т лет.
Количество средств л:, вложенное в отрасль I, дает
за один год доход
f(x) = x* (9.1)
и за счет этого уменьшается до
<р(лг)^=0,75лг. (9.2)
Количество средств у, вложенное в отрасль II, дает
за один год доход
g(y) = 2y2 (9.3)
66
и уменьшается до
ф(у) = 0.3у1). (9.4)
Требуется произвести распределение ресурсов Zo между
отраслями I и II на каждый год планируемого периода.
Решение. Условное оптимальное управление х*т
на последнем шаге (количество средств, выделенное
в отрасль I) находится как значение хт, при котором
достигает максимума доход на последнем шаге:
„_!)= max (
°<*m<Zm-l
)}-
где
=*!!,+2 (z^-
(9.5)
График функции
в зависимости от аргумента хт изображается при задан-
заданном Zm_1 некоторой параболой (рис. 9.1). Вторая произ-
производная функции wm по хт положительна, и поэтому
парабола обращена выпуклостью вниз. Максимальное зна-
значение может достигаться
только на границах проме-
промежутка @, Zm_lJ). Чтобы
определить, на какой именно
границе, подставим в фор- ZZ,
мулу (9.5)лг,„ = 0 и хт =
= Zm_v Получим в первом
случае (при дгт = О)
во втором случае (при
т 1Я~1 ^2
'т-1
0
Рис. 9.1.
Первая величина больше
второй; следовательно, не-
независимо от значения Zm_v максимум дохода на последнем
шаге достигается при лгт = О, т. е. условное оптимальное
') Единицы измерения дохода и вложенных средств не обяза-
обязательно должны быть одни и те же. Применение формул типа (9.1)
и (9.3) не противоречит принципам размерностей, если средства
и доход выражеиы во вполне определенных единнцах измерения.
*) Поэтому не имеет никакого смысла пытаться искать
максимум функции wm, приравнивая производную нулю.
67
управление x*m(Zml\ не зависит от Zml и всегда равно
нулю, а это значит, что в начале последнего года все
имеющиеся средства нужно вкладывать в отрасль II. Это
и естественно, так как доход от этой отрасли больше,
а затрата средств нас уже не интересует (следующего
шага не будет).
При этом оптимальном управлении последний год при-
принесет нам доход
Перейдем к распределению средств на (т—1)-й год.
Пусть мы подошли к нему с запасом средств Zm_2.
Найдем условный максимальный доход за два последних
года:
Но
■2m_i = 0,75д;т_1 + 0,3 (Zm_2 xm_x),
и следовательно,
W*m (Zm_,)= 2 [0.75*и_, + 0,3 (Zm_2- хт_{)J.
Отсюда получим
№'I-i.m(^ra-2)= max [xt
+ 2 ЮЛБх^ + 0,3 (Zm_2 - *m_,)]2}.
Выражение в фигурных скобках, коротко обозначае-
обозначаемое Wm-\,m< снова представляет собой полином второй
степени относительно хт_1 с положительной второй произ-
производной, а его график — параболу с выпуклостью вниз,
так что снова нужно исследовать на максимум только
крайние точки интервала (рис. 9.2):
В первом случае (при jcm_ t = 0) получим
Wm-i. m = 2Z^_2 + 2 @,3Zm_2J = 2,180Z^_2;
68
во втором случае (при xm_1 = Zm_2)
Wm-\. m = 4-2 4- 2 @.75Zm_ 2J = 2,125Z^_2.
откуда ясно, что максимум снова достигается при хт_1 = {
и равен №„,_!_m (Zm_2) = 2
последнем шаге нужно все
средства вкладывать в
отрасль II.
Перейдем к (т — 2)-му
шагу. Здесь нужно макси-
максимизировать полином второй
степени
4v/+ **2 ■
"/гн
_2, т. е. и на пред-
предт-Г, т
4-2,18[0,75*т_2 +
+ 0.3(Zm_3-*m_2)p.
Соответствующая парабола Рис. 9.2.
(как и на любом из шагов)
будет снова обращена выпуклостью вниз. Но на этот раз
максимум будет достигаться не на левой, а на правой
т-2, rn-I, m
Z Хт'г
Рис. 9.3.
границе участка (рис. 9.3). Действительно, полагая
Jtm_2 = O, получим
,18@,3Zm_3J«
а при Jcm_2 = Zm_
,18 @,75Zm_3J
Следовательно, условное оптимальное управление на
(т — 2)-м шаге будет
т. е. на этом шаге оптимальное управление состоит в том.
чтобы все имеющиеся средства вкладывать в отрасль I.
При этом мы получим условный максимальный доход
9
-2, m_ji m (Zm_3) ~ 2,23Zm_3-
Очевидно, на всех следующих этапах максимум всегда
будет достигаться, как и на рис. 9.3, на правом
конце отрезка. Действительно, для i<m — 2 функция
W»t«+i, ...,m будет иметь вид
где коэффициент С будет больше чем 2,18, так как он
с каждым шагом только увеличивается. Поэтому опти-
оптимальным условным управлением до самого первого шага
(включительно) останется
*i) = Zi_i (t = m — 2, т~3, ...),
а условный максимальный доход за все шаги, начиная
с /-го, будет
Wl t+l т (Zi-0 = Z^ + wUi т @.75Z|_,).
Таким образом, оптимальное управление найдено: оно
состоит в том, чтобы на всех шагах, кроме предпослед-
предпоследнего и последнего, вкладывать все средства в отрасль I,
а на двух последних шагах вкладывать все средства
в отрасль II. Заметим, что это решение получено неза-
независимо ни от числа шагов т, ни от исходного запаса
средств Zo.
Для того чтобы представить себе вид оптимальной
траектории в фазовом пространстве, аададимся конкрет-
конкретным значением числа шагов т. = 5 (производственный
процесс планируется на 5 лет). Оптимальная траектория
70
представлена на рис. 9.4. Оптимальный процесс управле-
управления средствами состоит в следующем. На первый год все
средства вкладываются в отрасль I и уменьшаются до 0,75 Zo.
На втором году — в ту же отрасль I и уменьшаются
циг.
wzB
Ofi2Z0
Рис. 9.4.
0,75Zo
до 0,56 Zo (перераспределения средств нет, и поэтому
второе звено второго шага пропадает). На третьем году
снова все средства вкладываются в ту же отрасль I и
уменьшаются до 0,42 Zo. На четвертом году политика
меняется: происходит перераспределение средств (наклон-
(наклонный участок траектории), все они вкладываются в отрасль II
и уменьшаются до 0,13 Zo. На последнем, пятом, году
снова все средства вкладываются в отрасль И; остаток
их в конце пятого года (и всего периода) будет равен 0,04 Zo.
При таком распределении средств за пятилетку будет
получен максимальный доход, равный
В данном примере оптимальное управление состояло
в том, чтобы на каждом шаге вкладывать все средства
либо в одну, либо в другую отрасль. Всегда ли это будет
так? Сейчас мы убедимся, что не всегда. Для этого
изменим вид функций f(x) и g(y).
Пример 2. Планируется деятельность двух отраслей
производства I и II сроком на 5 лет (т = 5). «Функции
траты средств» ср(х) = 0,75х и <J)(y) = 0,3y те же, что
и в предыдущем примере, но «функции дохода» f(x)
71
и g(y) заменены другими:
Требуется распределить имеющиеся ресурсы в размере
Zo = 2 между отраслями I и II по годам.
Решение. В предыдущем примере, в связи с очень
простым видом функций f(x) и g (у), решение было
дано в аналитическом виде; в данном примере построить
аналитическое решение трудно, и мы будем решать задачу
численно. Встречающиеся в задаче функциональные зави-
зависимости мы будем изображать с помощью графиков.
Пусть к началу пятого года количество средств равно Z4.
Чтобы найти условное оптимальное управление на пятом
шаге x*(Z4V нужно для каждого Z4 найти максимум
функции
w5 = 1 — *-
2 —[*-*
]. (9.6)
При фиксированном Z4 это — функция аргумента х5,
выпуклая кверху (рис. 9.5). Максимум этой функции
\
б)
Xх*
Рис. 9.5.
(в зависимости от значения Z4) может достигаться либо
внутри отрезка (О, Z^ (как показано на рис. 9.5, с),
либо на левом его конце (рис. 9.5, б).
Чтобы найти этот максимум, продифференцируем
выражение (9.6) по хъ. Если производная обратится в нуль
в некоторой точке внутри отрезка (О, Z^, то в этой
точке достигается максимум W; если вне — максимум
достигается при jc5=0.
72
Дифференцируя (9.6), имеем
^- = е-*- — 2e-2<z'-xJ = 0. (9.7)
На данном шаге уравнение (9.7) нам еще удастся
решить в буквенном виде; на дальнейших шагах анало-
аналогичные задачи мы будем решать численно. Из (9.7) имеем
_*5=ln2-2Z4 + 2x5; x5= 2Zf-ln2 . (9.8)
Из выражения (9.8) следует, что при Z4 > -^- ж 0,347
максимум достигается внутри отрезка (О, Z4), в точке
При Z4 <С -S-—~ 0,347 максимум достигается в левом
конце отрезка:
Итак, условное оптимальное управление на пятом шаге
найдено:
п т у 1п2
0 при Z4 < —£-.
2Z4
j *-
In2
Найдем условный максимальный доход за пятый год.
Он равен
-6V4/_|_e-4'b4-JI5V4/JJf (9.Ц)
или, подставляя (9.10) в (9.11),
1 -2Z 7 / lfl2
1 £ 4 При ^4 ^. к •
2 (9.12)
•1—-^\2еъ при Z4>—2~.
Так как нам придется много раз вычислять вели-
величину W$, удобно будет построить ее график в зависимости
73
от Z4 (рис. 9.6). На том же графике (но в другом мас-
масштабе) изобразим зависимость условного оптимального
управления на пятом шаге х* от Z4. Построением этих
двух графиков заканчиваются все наши дела, связанные
с пятым шагом. В дальнейшем, оптимизируя управление
т*
Х5
at
0,1 цг
0.3 ОМ
Рис. 9.6.
0,5 0,6
на четвертом шаге, мы будем только входить в эти гра-
графики с различными значениями Z4.
Переходим к четвертому шагу. Задачу его условной
оптимизации будем решать численно, задаваясь рядом
значений Z3 (запаса средств, оставшихся после третьего
шага). Чтобы не делать лишней работы, выясним, в каких
пределах может находиться Z3. Найдем самое большое
из возможных значений Z3. Оно будет достигнуто, если
на первых трех шагах все средства будут вложены
в отрасль I; при этом запас средств после трех лет
будет равен
^з Шах = Z0-0,753 = 0,844.
Наименьший запас средств соответствует случаю, когда
все средства на трех первых шагах будут вложены
в отрасль II:
= Z0. 0,33 = 0.054.
Итак, все возможные значения Z3 заключены на
участке от 0,054 до 0,844. Назначим на этом участке
74
опорные значения Z3:
Z3 = 0,l; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8 (9.13)
и для каждого из них найдем условное оптимальное
управление на 4-м шаге x*AZ^i и условный максимальный
доход на двух последних шагах Wii5(Z3). Для этого по-
построим серию кривых, изображающих выигрыш W£ 5
на двух последних ша- +
гах (при любом управле- wt.s
нии на четвертом и при 15
оптимальном—на пятом):
''2
-f Wl@,75X4+
-+0.3(Z3 —
где
= 2 —[е-'«+е-2<г'-^],
a Wl мы находим по гра-
фИКу рИС. 9.6, ВХОДЯ
в него с аргументом Z4 =
1,0
0,9
0,8
0,7
-0,6
Z,-0fi
Z.-0.4
1,-0,3
h-w
z.-o,i
0,1 0,2 0J 0,4 0J5 0,6 0,7 0,8 0J
Рис. 9.7.
Кривые зависимости №4>~з
от х4 (при заданном Z3)
представлены на рис. 9.7.
На каждой из этих кри-
кривых найдем точку с мак-
максимальной ординатой и
пометим ее кружком. Ор-
Ордината такой точки для
соответствующего кри-
кривой Z3 представляет собой условный максимальный выи-
выигрыш на двух последних шагах W4i 5 (Z3), а абсцисса —
условное оптимальное управление x*(Z3). Определив эти
величины для каждого значения Z3 из (9.13), построим
графики зависимостей W4>5(Z3) и x4(Zs) (рис. 9.8).
Построением этих двух кривых- мы покончили свои
расчеты с двумя последними шагами: вся информация
о них уже заключена в двух кривых рис. 9.8.
75
Переходим к третьему шагу. Область возможных
значений Z2 лежит между 2 ■ 0,32 = 0,18 и 2 ■ 0,752 = 1,12.
Задаемся в этом интервале рядом опорных значений Z2:
Z2=0,3; 0,5; 0,7; 0,9; 1,1
и для каждого из этих значений вычислим доход на
третьем шаге в зависимости от управления х3 на этом
шаге по формуле
w3(Z2, х3) = 2 — [е--«->-|-е-2<^-*.>].
Затем прибавим к нему уже оптимизированный доход на
0,3
0,2
0,1
сп 02 03 fl« 05 06 6,7 0,8
Рис. 9.8.
четвертом и пятом шагах W^ s(Z3), который мы опреде-
определим по графику рис. 9.8, входя в него со значением
Z4 = 0,75х3 + 0,3 (Z2 — лг3),
и получим величину
t 4,5 = wa (Z2, х8) + К 5@,75хз + 0,3 (Zo — х3)),
для которой снова построим графики зависимости от
х3 при фиксированном Z2 (рис. 9.9). На каждой из
этих кривых снова найдем максимум (на рисунке от-
отмечен кружком) и после этого построим зависимость
условного оптимального управления на третьем шаге jc^ и
76
t rto no л/, пс ne /1 no nn in i * 3
0.1 0,2 Q3 0.1 0.5 0.6 07 0.8 0.8 W U
Рис. 9.9.
О 0,1 0£ 0,3 0.1 05 0.6 07 0,8 0,9 1,0 Ц
Рис. 9.10.
соответствующего условию максимального дохода на
трех последних шагах №3,4,5 от Z2 (рис. 9.10).
Аналогично решается задача условной оптимизации
второго шага: варьируются значения Z, от 2-0,3 = 0,6
до 2-0,75=1,5:
Z, = 0,6; 0,9; 1,2; 1,5.
Доход на втором шаге будет
w2{Zv x£ = 2 — [e-x'-\-e-2&-*>'>].
К нему прибавляется условный максимальный доход №з, 4,5
по графику рис. 9.10 со входом
Z2 == 0,75х2 + 0,3 (Zj — х2);
получается величина W^z.^b, для которой снова строятся
графики (рис. 9.11). На каждой кривой находится мак-
максимум и строятся две кривые: х*2 (ZA и №* 3 4 5 (ZA
(рис. 9.12).
Осталось спланировать один первый шаг. Это — уже
более легкая задача, так как величина Zo, с которой мы
приступаем к этому шагу, точно известна (Zo = 2) и не
должна варьироваться. Поэтому для первого шага строится
только одна кривая зависимости W^2, з,4,5 от Х1(рис. 9.13),
где
Wt. 2, 3, 4, 5 = «1 (Zo. Xi) + Wl 3, 4, 5 (Zl) =
= 2 - [«-*■ + е-2 (Z>-*>'] + Wl, a, 4,5 (Z0,
а последний член находится по графику рис. 9.12 при
Zj = 0,75*! -f- 0,3 (Zo — Xj).
где Z0 = 2.
Определяя на единственной кривой рис. 9.13 максимум,
находим (уже не условное) оптимальное управление на
первом шаге х*=1,6 и соответствующий максимальный
доход за все пять лет
После этого, как всегда в методе динамического
программирования, нужно построить все оптимальное
78
0,5 1
Рис. 9.11.
15
-х,
0,1 02 0.3 ОЛ 0.5 0,6 0.7 0.8 Off 1,0 1.1 1,2 1.3 /.« 1,5 Z'
Рис. 9.12.
управление
= (х\, x*r x\, x*. x5
),
идя в обратном направлении: от первого шага к пятому.
Зная оптимальное управление на первом шаге
находим соответствующий ему запас средств к концу
первого шага:
Z\ = 0,75л:* + 0,3 (Zo — л:*) = 1,32.
Входя с этим значением Zx в график x*(Z) (си. рис. 9.12),
находим оптимальное управление на втором шаге:
х\ =1,02.
Остаток средств к концу второго шага будет
Z* == 0ЛЪх*2 + 0,3 (Z* — л:*) = 0,86.
С этим значением Z2 входим в график x\{Z^ (см. рис. 9.10)
и находим оптимальное
управление на третьем
шаге:
х\ = 0,62.
Остаток средств после
третьего шага будет
По графику рис. 9.8 на-
_^ i i_ ходим оптимальное упра-
0,5 1,0 1,5 2,0 ' вление на четвертом шаге
Pur Q 1Я v* П ЧП
После четвертого шага остаток равен
Z\ = 0,75л:'+ 0.3 (Z* — х4) = 0,30.
С этим значением Z4 входим в график x*5{Z\ (см. рис. 9.6)
и находим оптимальное управление на последнем шаге:
Итак, планирование процесса закончено. Найдено
оптимальное управление, указывающее, сколько средств
из имеющегося запаса Zo = 2 нужно вкладывать в отрасль I
по годам:
А'* = A,60; 1,02; 0,62; 0,30; 0).
Учитывая, что запасы средств перед началом каждого
года известны:
Z0 = 2;
= 1,32; Z2 = 0,
автоматически получаем количества средств, вкладываемых
по годам в отрасль II:
^=2;-^ = 0,30.
Таким образом, можно сформулировать следующие
рекомендации по оптимальному распределению средств.
Из имеющегося в начале периода запаса средств Zo = 2
и остающихся средств в конце каждого года нужно
вкладывать по годам в отрасли I и II следующие суммы:
Год
1
11
1-й
1,60
0,40
2-й
1,02
0,30
3-й
0,62
0,24
4-й
0,30
0,24
5-й
0
0,30
При таком планировании будет получен максимальный
доход за 5 лет, равный
W\, 2,3,4,5 = 4,35.
Остаток средств в конце периода будет равен
0,3 -0,30 = 0,09.
На рис. 9.14 изображена оптимальная траектория
в фазовом пространстве, соответствующая такому рас-
распределению средств. Точка So на гипотенузе треуголь-
треугольника АОВ изображает оптимальное начальное распределе-
распределение средств с резким преобладанием в сторону отрасли I.
Первое звено ломаной линии соответствует трате средств
за первый год. Следующие звенья объединяются попарно
6 Е. С Вентцель 81
и изображают перераспределение и трату средств на 2-м,
3-м, 4-м и 5-м годах. Последнее звежьлежит на оси Оу;
это значит, что на 5-м году производственного процесса
все средства вкладываются в отрасль II. Точка 5КОн изо-
изображает остаток средств Z5 = 0,09, получающийся при
оптимальном планировании.
§ 10. Видоизменения задачи
о распределении ресурсов
Рассмотренная в двух предыдущих параграфах задача
о распределении ресурсов имеет много видоизменений.
Некоторые из них сравнительно мало отличаются от про-
простейшей задачи, рассмотренной в § 8; другие настолько
отличаются от нее по своей словесной постановке, что
иногда трудно обнаружить в них общие черты. В данном
параграфе и в последующих (§§ 11, 12) мы рассмотрим
ряд вариантов подобных задач.
а. Распределение ресурсов по неоднородным эта-
этапам. В задаче § 8 этапы (шаги) были «однородными» в том
смысле, что средства х и у, вложенные соответственно
в отрасли I и II, на любом этапе давали один и тот же
доход и уменьшались одинаковым образом независимо
от номера этапа.
Естественным обобщением этой простейшей задачи
является случай, когда доход и убыль средств на раз-
различных этапах неодинаковы: средства х, у, вложенные
в отрасли I и II, дают на i-м шаге доход fi(x), ^(y)
и уменьшаются до срг(лг)^л\ ^(уХСу.
Как может возникнуть такая неоднородность? Различ-
Различными способами. Например, доходность может зависеть
от общего уровня развития производства, достигнутого
к определенному сроку; или же условия производства
(как, скажем, в сельском Хозяйстве) могут зависеть от
времени года.
Для решения задачи распределения ресурсов методом
динамического программирования это обстоятельство —
однородность или неоднородность этапов — совершенно
несущественно. Поскольку задача оптимизации управления
все равно решается по этапам, совершенно неважно,
одинаковы ли функции ft(x), gt(y), ^t(x), фг (у) на раз-
разных этапах или различны.
Общая схема решения сводится к последовательному
применению следующих формул для условного оптималь-
оптимального дохода на нескольких последних этапах:
-l (Zm-2 — *m-l> + Wm
m
с попутным определением условных оптимальных упра-
управлений:
После этого, как всегда, строится оптимальное управле-
управление, начиная с первого этапа и кончая последним. В этом
построении никакой разницы со случаем однородных
этапов нет.
6» 83
б. Задача О резервировании ресурсов. Задача ста-
ставится следующим образом. Имеется всего одна отрасль
производства и некоторый запас средств Zo, который
может вкладываться в производство не целиком, а ча-
частично резервироваться. Будучи вложено в производство
на г-м этапе, количество средств х дает доход ft(x) и
уменьшается до <?,-(>:)< х. Требуется рационально рас-
распределить имеющиеся и остающиеся средства по т эта-
этапам с тем, чтобы обратить в максимум общий доход W.
Нетрудно убедиться, что эта задача сводится к пре-
предыдущей. Действительно, резервированные средства можно
считать «вложенными» в некоторую ф ютивную «вторую
отрасль» производства, в которой средства не тратятся,
но и не дают дохода:
совершенно
С учетом этого условия задача решается
так же, как задача распределения ресурсов.
Траектория точки 5, изображающей состояние системы
в фазовом пространстве, будет иметь вид, представленный
на рис. 10.1. Участки «перераспределения средств» будут,
как и раньше, параллельны линии АВ, а участки «рас-
д ходования средств» — па-
параллельны оси абсцисс и
направлены влево. Послед-
Последнее звено ломаной всегда
будет лежать на оси
абсцисс, так как дальней-
дальнейшее резервирование средств
смысла не имеет.
Рассмотрим частный
случай задачи о резервиро-
резервировании, когда на всех эта-
этапах
0
Рис. 10.1.
т. е. вложенные средства
расходуются целиком. Тогда
задача резервирования средств сводится к нахождению
максимума следующей функции т аргументов:
(ЮЛ)
84
где xv x2, •-.» хт ограничены условиями
т
2j*f<zo-. A0.2)
лг,>0.
A0.3)
Если доход f[(x) (как это естественно предполагать)
представляет собой неубывающую функцию вложенных
средств х, то знак неравенства в формуле A0.2) можно
отбросить, так как в этих условиях расходовать не все
средства, а только их часть невыгодно.
Траектория точки 5 в фазовом пространстве будет
выглядеть, как показано на рис. 10.2, — каждый гори-
горизонтальный участок до- - у
ходит до оси ординат.
Сделаем некоторые
замечания по методу ре-
решения задачи. Выше мы
видели, что она свелась
к нахождению максимума z
функции A0.1). Может °
показаться, что тем са-
самым задача упрощена, но
это впечатление обманчи-
обманчивое. Ведь вообще задача 5",
нахождения максимума
функции многих аргу-
аргументов — не из легких. Рис. 10.2.
Вспомним (см. § 1), что
любая задача оптимального управления всегда сводится
к нахождению максимума (минимума) функции мно-
многих аргументов, и именно для того, чтобы избежать свя-
связанных с этим трудностей, мы прибегаем к методу динами-
динамического программирования. Приведя здесь формулу A0.1),
мы не имели в виду облегчить задачу динамического
программирования, сведя ее к задаче нахождения макси-
максимума функции A0.1). Наоборот, для решения задачи на-
нахождения максимума (минимума) функции типа A0.1)
с условиями A0.2) и A0.3) (где бы эта задача ни воз-
возникла), может оказаться наиболее подходящим именно
метод динамического программирования. Применением
этого метода в данном случае мы сводим многомерную
задачу нахождения максимума функции многих переменных
85
' х
к многократному нахождению максимума функции одного
переменного, что значительно легче.
Заметим, впрочем, что некоторые простейшие случаи
задачи резервирования средств допускают элементарное
решение и без применения метода динамического про-
программирования. К ним принадлежит, например, простей-
простейший случай, когда «функция дохода» на всех этапах
одна и та же:
причем средства на каждом этапе расходуются полностью:
<?i (*) = <&(*)= ••• = <?«(*) = °-
Можно доказать, что если функция f(x) — функция мо-
монотонно возрастающая и выпуклая вверх (рис. 10.3),
то максимум выражения
(Ю-1) достигается, когда
средства делятся поровну
между всеми этапами:
в. Задача о рас-
х пределении ресурсов
между несколькими
Рис. 10.3. (более чем двумя) от-
отраслями. Задача о рас-
распределении ресурсов допускает обобщение на случай,
когда средства распределяются не между двумя, а между
k отраслями:
I, II (Л),
причем для каждой (/-й) отрасли заданы: «функция до-
дохода»
выражающая доход, даваемый количеством средств х,
вложенным в J-ю отрасль на l-ы шаге, и «функция траты»
показывающая, до какой величины убывает количество
средств х, вложенное в J-ю отрасль на 1-м шаге.
86
Построим для этой задачи фазовое пространство.
В случае распределения средств по двум отраслям таким
фазовым пространством был треугольник АОВ (см.
рис. 8.1, 8.2 и т. д.). Для случая нескольких отраслей можно
в качестве фазового пространства рассмотреть многомер-
многомерное обобщение треугольника (которое принято называть
«симплексом»), а именно множе-
множество точек Л-мерного простран- ■ 3
ства, удовлетворяющих условиям: и
((/ =
(й)).)
A0-4)
В случае пространства трех из-
измерений (что соответствует рас-
распределению средств по трем от-
отраслям) симплекс будет иметь вид
треугольной пирамиды АВСО
(рис. 10.4), три ребра которой,
сходящиеся в начале координат,
равны Zo. Процесс распределения
средств, как и в двумерном слу-
случае, может быть разделен на звенья, соответствующие
«перераспределению средств» и «трате средств», причем
на первых звеньях точка 5 движется по плоскости, па-
параллельной ABC, а на вторых движется, удаляясь от
плоскости ABC в глубь симплекса.
Рис. 10.4.
11. Задача о распределении
ресурсов с вложением доходов
в производство
До сих пор во всех рассмотренных задачах о рас-
распределении ресурсов мы рассматривали «доход», прино-
приносимый производством, совершенно независимо от распре-
распределяемых основных средств (он даже мог выражаться
в других единицах, например ресурсы — в человеко-часах,
а доход — в рублях или в метрах ткани).
В данном параграфе мы рассмотрим тот случай, когда
доход может (полностью или частично) вкладываться
87
в производство вместе с основными средствами. Для этого,
разумеется, доход и основные средства должны быть при-
приведены к одному эквиваленту (например, к деньгам).
В зависимости от обстановки эта задача может ста-
ставиться различным образом, с разными критериями W.
Например, можно вкладывать в производство весь доход
или только некоторую его долю. Можно искать такое
управление, которое обеспечивает максимальный суммар-
суммарный чистый доход от т этапов. Можно искать и такое
управление, которое обращает в максимум общую сумму
средств (включая доход и сохранившиеся основные сред-
средства) после т этапов. Возможны и другие постановки
задачи. Здесь мы покажем схему решения методом дина-
динамического программирования нескольких простейших за-
задач такого типа.
а. Рассмотрим случай, когда доход вклады-
вкладывается в производство полностью, причем
максимизируется сумма всех средств (основ-
(основные средства плюс доход) после т-го этапа.
В данном случае критерий W представляет собой
сумму всех средств, сохранившихся в обеих отраслях
после т-го этапа, плюс доход, данный обеими отраслями
на этом этапе.
Рассматриваемый критерий W представляет собой
частный случай аддитивного критерия: он весь приобре-
приобретается на последнем этапе, т. е. W = wm, а на всех
предшествующих этапах его приращения wl равны нулю.
Так как все средства (и остаток основных, и доход)
вкладываются в производство и учитываются в крите-
критерии W на равных основаниях, то нам незачем здесь
вводить отдельно «функции дохода» /,(лг), gt(y) и «функ-
«функции траты» <р;(х)> фДу), а достаточно ввести две функции
Ft{x). Gt(y), A1.1)
показывающие, сколько средств (остаток основных плюс
доход) мы будем иметь в конце г-го этапа, вложив в на-
начале этого этапа количество средств х в первую отрасль
и у во вторую. Назовем функции Ft(x), Gt(y) «функ-
«функциями изменения средств» на i-м этапе. Заметим, что
возможно любое из соотношений:
Ft (х) < х; F, (х) = х, Ft(x)>x
(аналогично для
Рассмотрим фазовое пространство, соответствующее
данной задаче (рис. 11.1). Таким пространством будет
уже не треугольник АОВ (как в задачах без вложения
доходов), а весь первый квадрант хОу (средства могут
не только уменьшаться,
но и расти). Траектория
по-прежнему состоит из
ряда звеньев; каждому
. этапу (кроме первого) со-
соответствует пара звеньев:
первое — «перераспреде-
«перераспределение средств», когда
точка S перемещается
параллельно АВ; вто-
второе — «трата и приоб-
приобретение средств», на ко-
котором точка 5 может
W
О
двигаться в любом на- w
правлении. В отличие от рис. ц.1
всех предыдущих приме-
примеров, здесь получение «окончательного дохода» W связано
только с одним, самым последним, звеном т2, которое
на рис. 11.1 выделено жирной стрелкой.
В данном случае значение критерия W непосредственно
видно на чертеже — это сумма абсциссы и ординаты
точки 5К0Н, соответствующей конечному состоянию си-
системы. Таким образом, задачу оптимального управления
можно сформулировать так: выбрать такую траекторию
точки в фазовом пространстве, чтобы вывести ее в ре-
результате т-го шага на прямую Лкон Вкои, параллельную АВ
и отстоящую от начала координат так далеко, как только
это будет возможно. Значение критерия W изображается
отрезком, отсекаемым на каждой из осей прямой -^кон^кон-
Построим схему решения этой задачи методом дина-
динамического программирования без подробных словесных
объяснений, так как существо метода достаточно ясно
из предыдущего. На функции Ft(x), Ot(y) пока не будем
накладывать никаких ограничений.
1. Фиксируем исход (от—1)-го шага (сохранившиеся
средства плюс доход) Zm_1. Условное оптимальное упра-
управление х*т№т_Л — т0> при котором будет максимальным
суммарное количество средств (основные средства плюс
89
доход), — после от-го шага
«»Bm_I) = Z1BB1B_1). A1-2)
Но, учитывая формулы A1.1), можно написать
«m (Zm-l) = Fm (хт> + Gm (Zm-1 ~ *m)-
Условное оптимальное управление на т-м шаге
jc* (Z ,) найдется из условия
W;(Zm_,)= max {Fm(xm)+Gm(Zm_1-xJ}. A1.3)
°<z
2. Фиксируем исход (m — 2)-го шага Zm_2. Условное
оптимальное управление x*ml(Zm2\ находится из условия
№m-i,m(Zm-2)= max {w*m (Fm_! (xm
+ Gm_1(Zm_2-xm_1))} (П.4)
и т. д.
3. Фиксируем Z,_j. Условное оптимальное управление
x*(Ztl\ находится из условия
Wb+1 m(Zi-d =
= max {W*i+i ш^Д^ + ОД^.!-^))} A1.5)
И Т. Д.
4. Оптимальное управление на первом шаге х* и
максимальное значение выигрыша W* находятся из условия
= max
5. Исход первого шага при оптимальном управлении:
Z\ = F1{x\)-\-Gl{Zo-x\).
Оптимальное управление на втором шаге:
Х2 = Х2 (^р'
Исход второго шага при оптимальном управлении:
и т. д. до последнего шага.
90
Такова схема решения задачи методом динамического
программирования при любом виде функций изменения
средств Fi(x), Gi(y). Однако если на эти функции на-
наложить некоторые (очень естественные) ограничения, эта
схема может быть сильно упрощена.
Предположим, что все функции
Fi(x). О,(у) (/=1. ... т)
представляют собой неубывающие функции своих аргу-
аргументов (т. е. что при увеличении количества вложенных
средств сумма дохода и оставшихся средств к концу
этапа не может уменьшиться).
Покажем, что при этих условиях максимальный вы-
выигрыш на последнем шаге есть неубывающая функция
от исхода каждого шага (сумма средств в его конце).
Рассмотрим максимальный выигрыш при условии, что
сумма средств (остаток плюс доход) в конце (/—1)-го
этапа равна Zt_v Так как выигрыш приобретается только
на последнем этапе, то все равно, рассматривать ли этот
выигрыш за весь процесс, или только за последний этап,
или за все этапы, начиная с /-го. Выберем последнее:
будем рассматривать максимальный выигрыш за все этапы,
начиная с /-го, как функцию от Zt_v обозначая его, как
всегда,
№i, 1+1 т (Zi-i)-
Докажем, что эта функция неубывающая. Доказательство
будем вести методом полной индукции, но не от / к /-|- 1,
как это делается обычно, а наоборот, от 1-\- 1 к / (в соот-
соответствии с «обратным» ходом процесса динамического
программирования).
Предположим, что доказываемое свойство справедливо
для / -|- 1, т. е. функция
есть неубывающая функция своего аргумента Z, (это
значит: чем больше средств, включая доход и основные
средства, сохранилось к исходу /-го шага, тем больше
будет доход в конце). Докажем, что тогда неубывающей
функцией будет и
91
Действительно, согласно формуле A1.5), Wit i+\ m(Zi^i)
представляет собой максимум выражения
Покажем, что выражение A1.6) есть неубывающая
функция Zi-\\ тогда будет ясно, что и ее максимальное
значение №*, г+i m(Zi_i) с увеличением Z,-_i убывать
не может.
Зафиксируем какое-то значение Z/_b Пусть для этого
значения Z,-_i выражение A1.6) достигает максимума
по xt, равного №,-. /+i#.... т (Zt_i) при определенном упра-
управлении (распределении средств) л:,-. Придадим теперь вели-
величине Z,_! некоторое положительное приращение AZ;.
У нас образовался некоторый избыток средств, который
мы можем распределить между отраслями I и II, увеличив
количество средств, вложенных либо в одну, либо в другую
отрасль, либо в ту и другую сразу. Так как функции Ft(x),
Gt(y) неубывающие, то от такого «добавления»
средств каждое из слагаемых под знаком функции A1.6)
может только увеличиться; значит, и их сумма может
только увеличиться, а не стать меньше.
Что при этом будет с функцией A1.6)? Согласно
допущению это — функция неубывающая; значит, и при
увеличении Z;_i она уменьшаться не мсжет. Итак, пере-
переход от / -\- 1 к / доказан.
Покажем теперь, что наше свойство справедливо для
/ -\- 1 = т, т. е. для последнего шага. Это доказывается
очень просто. Выигрыш на последнем шаге при опти-
оптимальном управлении представляет собой максимум выра-
выражения
и, естественно, есть неубывающая функция от Zm_i (это
только что было показано для любого значения /, а значит,
и для i — m). Таким образом, Wm(Zm_\) есть неубываю-
неубывающая функция Zm_i, а значит, согласно принципу полной
индукции, и любой из выигрышей W*t> ;+i m(Z;_i) —
неубывающая функция, что и требовалось доказать.
Из доказанного вытекают очень простые рекомендации
по оптимальному управлению. Действительно, если окон-
окончательный выигрыш Wm представляет собой неубывающую
92
функцию от общей суммы средств, реализуемой на исходе
каждого шага, то оптимальное управление состоит
в том, чтобы на исходе каждого шага в отдельности
получать максимальное значение этой суммы средств.
Это значит, что в данном частном случае «интересы»
операции в целом совпадают с «интересами» каждого
отдельного шага. Рациональное планирование всей опе-
операции сводится к тому, чтвбы оптимизировать
каждый шаг в отдельности, не заботясь об
остальных.
Эта особенность приводит к тому, что процесс выра-
выработки оптимального управления сильно упрощается. Дей-
Действительно, больше нет надобности фиксировать результаты
каждого предыдущего шага и тянуть всю цепочку условных
оптимальных управлений от последнего шага к первому.
Можно непосредственно оптимизировать шаг за шагом
от начала к концу. На первом шаге взять такое упра-
управление jfj = x*y при котором обращается в максимум
сумма средств Zx:
Z\= max {FjCxJ + G^Zo — xx))\
0 < jr, < Zo
на втором — то управление х2 —х*2, при котором обра-
обращается в максимум Z2:
= max
и т. д. до конца.
Таким образом, при неубывающих функциях Ft (лг),
Ot(y) поставленная нами задача только по внешности
имеет вид задачи динамического программирования, а по
существу — гораздо проще ее.
Подобные «вырожденные» задачи динамического про-
программирования, где оптимальное управление состоит в том,
чтобы оптимизировать каждый этап, не заботясь об
остальных, нередко встречаются на практике. Если, не
обратив внимания на такую их особенность, решать их
все же методом динамического программирования, решение,
разумеется, получится верным, но потребует во много
раз больше времени, чем нужно.
Сделаем еще одно замечание. На первый взгляд может
показаться, что наложенное на функции Ft(x), G^y)
93
условие — чтобы они были неубывающими — выполняется
во всех практически мыслимых случаях. Однако можно
привести практические задачи, в которых оно не выпол-
выполняется. Рассмотрим, например, случай, когда одной из
«отраслей» производства является хранение скоропортя-
скоропортящихся товаров (овощей) на складе. Эта отрасль приносит
только убытки, связанные с потерями товаров при их
хранении. Обозначим Ft (лг) < х стоимость товаров, хра-
хранившихся на складе, в конце i-ro этапа, если в начале
этапа она была х. Всегда ли эта функция будет моно-
монотонной ? Нет, не всегда. iMo>kho представить себе такую
обстановку, когда при перегрузке склада свыше некоторого
критического значения функция F(x) начнет убывать
(например, за счет ухудшения условий хранения). В по-
подобных случаях приходится решать задачу по общей
схеме динамического программирования, как это было
показано выше.
б. Рассмотрим случай, когда в производство по-
прежнему вкладывается весь доход, но критерием W
является чистый доход на m-м этапе (сохранившиеся
основные средства не учитываются).
Пусть заданы «функции дохода» ft(x), g/(y) и «функ-
«функции траты» fi(x), tyi(y) для каждого этапа A=1, .... т).
Покажем, что если функции fm(x), gm(y)—«функции
дохода» на последнем этапе — неубывающие, то задача
сводится к рассмотренной в пункте а. а именно к макси-
максимизации суммарного выигрыша (оставшиеся средства плюс
доход) после (т—1)-го этапа. Действительно, условный
максимальный выигрыш на последнем шаге будет
uCBm-i)= max {fm(x)+gm(Zm^-xm)}. A1.7)
Можно доказать (аналогично тому, как было сделано
в пункте а), что функция Wm (Zm_{) есть неубывающая
функция своего аргумента, и ее максимум достигается
тогда, когда Zm_i достигает своего максимального зна-
значения. Таким образом, для нахождения оптимального упра-
управления достаточно решить задачу «а» для первых т — 1
шагов с функциями изменения средств
94
и затем отдельно найти оптимальное управление на ж-м
шаге, исходя из формулы A1.7).
Если функции Ft(x), Gt(y) (/=1, .... т—1) также
будут неубывающими, то задача, как и в предыдущем
случае, окажется вырожденной.
Если функции fm(x), gm(y) не являются неубывающими,
то сведение к задаче «а» становится уже невозможным и
приходится прибегать к общей схеме динамического про-
программирования. Читателю рекомендуется в качестве полез-
полезного упражнения набросать эту схему.
в. Рассмотрим случай, когда доход, получаемый на
каждом этапе, вкладывается в производство не полностью,
а частично, причем максимизируется полный чистый доход
на всех этапах плюс остаток средств после m-го этапа.
В этой задаче, как и в обычной задаче распределения
ресурсов, должны быть заданы «функции дохода»
/i(*). ft (У) ('=1. 2 «)
и «функции траты»
Ь(У)<Х> Ь(У)<У ('=1.2 т).
Кроме того, должны быть заданы «функции вложения»
? (/=1 т— 1),
показывающие, какая часть дохода £, полученного на /-м
этапе, вкладывается в производство на следующем,
(/-|- 1)-м, этапе.
В качестве фазового пространства рассмотрим уже
не первый квадрант хОу плоскости, а первый октант
хОу\ трехмерного пространства (рис. 11.2). По осям Ох
и Оу по-прежнему откладываются средства, находящиеся
в отраслях I и II; по оси О', — суммарный доход, при-
приносимый обеими отраслями. Область So начальных состояний
системы — по-прежнему гипотенуза АВ треугольника АОВ
в плоскости хОу. Все этапы, кроме первого, подраз-
подразделяются на два звена: на первом звене средства (сохра-
(сохранившиеся в обоих отраслях плюс определенная часть
дохода от предыдущего этапа) перераспределяются между
отраслями; на втором звене происходит трата средств и
приобретение дохода. На рис. 11.2 показаны два этапа:
первый состоит только из одного звена, второй —
из двух.
95
Рассмотрим величины лс*=<р1 (ж,) < х{, у{=<1>! {ух) < ух—
средства, сохранившиеся в отраслях I и II к концу пер-
первого этапа, где xv уг — координаты точки So—средства,
вложенные в отрасли I и II на первом этапе; £1==
=/i (-^i) + £"i (У1) — доход, принесенный обеими отраслями
на первом этапе. На первом
этапе точка S, изображаю-
изображающая состояние системы, пе-
перемещается из начального
состояния So — точки на ли-
. » нии АВ в плоскости хОу
с координатами (xv у,, 0)
— в точку К с координа-
координатами
Рис. 11.2. Затем на первом звене вто-
второго этапа Bj) происходит
вложение части дохода и перераспределение средств
между отраслями I и II. Точка 5 перемещается снова на
плоскость хОу в точку М с координатами (х2, у2, 0),
причем
Далее снова идет трата средств и приобретение дохода
(звено 22), затем опять перераспределение и т. д.
Наша задача—вывести точку 5, изображающую состоя-
состояние системы, на плоскость
с возможно ббльшим значением параметра С.
Набросаем схему решения задачи методом динамиче-
динамического программирования.
Заметим прежде всего, что если фиксирован исход
(£—1)-го этапа, то для следующего (/-го) существенна
только общая сумма перераспределяемых средств
и поэтому, несмотря на то. что состояние системы изо-
изображалось у нас точкой в трехмерном пространстве, мы
будем варьировать значения только одного параметра Zj_i.
«Управление» на 1-й этапе (так же, как и в ранее
рассмотренных задачах распределения ресурсов) будет
состоять в выборе величины дг, — количества средств,
вложенных в отрасль I на /-м этапе. Выигрыш W за весь
процесс естественным образом разбивается на т слагаемых:
^=»1 + «%+--+»«-1+«я. A1-8)
где wl при /=1, 2, .... т — 1 представляет собой
чистый доход, не вкладываемый в производство:
а на m-м шаге — весь чистый доход от m-го шага плюс
остаток вложенных средств:
Поэтапную оптимизацию будем вести по стандартной
схеме.
1. Фиксируем значение Zm_1 (сохранившиеся средства
плюс вкладываемая часть дохода), характеризующее исход
(т—1)-го шага. Условное оптимальное управление
jcm(Zm_j) на m-м шаге найдется из условия
№m(Zm_i)= max [wm] =
= max [fm {xm) -f- gm (Zm_ j — >
I Tm\ tit' I Tffll /n—1 m'i'
2. Фиксируем исход (га — 2)-го шага Zm_2. Чтобы
найти условное оптимальное управление на (/п—1)-м
шаге JCm_i(Zm_2). нужно максимизировать при заданном
Zm_2 сумму Wm-i, m следующих величин:
1) оставшийся (не вложенный в производство) доход
на (т— 1)-м шаге:
ш-1 = fm-l (-^m-l) + ёт-\ (Zm-2 ~ ^m-1) ~
7 E. С. Вентцель 97
2) выигрыш на последнем шаге при оптимальном
управлении
-1 От-1 (Хт-0 + ffm-l (Zm-2 — *,n-i) ))•
Таким образом, условное оптимальное управление на
(те—1)-м шаге находится как то значение xm_v при
котором достигается максимум величины IP'm-i, иГ-
_2)= max
3. Условное оптимальное управление x*(Z( Л на 1-
этапе найдется из соотношения
W/, m raB«_i)= max {
4. Оптимальное управление х\ на первом шаге и макси-
максимальное значение выигрыша W* находятся из условия
.3 m
= max
5. Исход первого шага при оптимальном управлении
z\=9i (*t)+*i (zo - *t> + «i (Л (*D
оптимальное управление на втором шаге:
исход второго шага при оптимальном управлении:
и т. д. до последнего шага.
Рекомендуем читателю самостоятельно набросать схему
решения следующих задач распределения ресурсов.
г. Оптимизировать распределение средств по двум
отраслям производства при следующих условиях: доход
вкладывается в производство . не полностью, а частично
(«функции вложения» /?,(;) (г—1, .... т—1) заданы);
максимизируется суммарный чистый доход за все этапы,
без учета оставшихся средств.
д. Оптимизировать распределение средств по двум
отраслям производства при следующих условиях: доход
вкладывается в производство не полностью, так как
известная доля его at{%) изымается в виде налога; остав-
оставшаяся часть вкладывается в производство; максимизируется
суммарное количество средств (основные плюс доход)
после /и-го этапа.
Не будет ли какая-нибудь из этих задач при некоторых
условиях вырожденной ?
§ 12. Другие разновидности задачи
распределения ресурсов
В данном параграфе мы рассмотрим несколько задач
из разных областей практики, принадлежащих, по суще-
существу, к той же категории «задач на распределение ресур-
ресурсов», но в которых необычная постановка не сразу на-
наводит на мысль о знакомой схеме. Рассчитывая, что
читатель уже овладел принципами динамического програм-
программирования, мы позволим себе при решении этих задач
отступить от стандартной системы обозначений, сохранив
неизменной лишь схему решения.
а. Задача о распределении веса между ступенями
космической ракеты. Предстоит спроектировать много-
многоступенчатую космическую ракету в пределах определен-
определенного стартового веса G. Кабина космонавта имеет задан-
заданный вес gK. Предполагается, что ракета будет иметь т
ступеней. Стартовый вес ракеты складывается из весов
7* ' 99
всех ступеней и кабины:
где G^ —вес t-й ступени.
Каждая ступень имеет какой-то запас горючего. После
израсходования горючего отработавшая ступень сбрасы-
сбрасывается и вступает в действие следующая.
Добавочная скорость Avt, которую приобретает ракета
за время работы двигателя /-Й ступени, зависит как
от веса самой ступени G, (определяющей запас горючего),
так и от веса того груза, который ей приходится нести:
Pt), A2.1)
где
Л = °<+1+°н2+ ••• +Gm + £V A2.2)
— вес «пассивного» груза, передвигаемого /-Й ступенью
ракеты.
Требуется найти наивыгоднейшее распределение веса
Q0=G — gK между т ступенями ракеты, при котором
скорость после сброса всех ступеней будет максимальна.
Задача похожа на один из вариантов задачи распре-
распределения ресурсов, а именно — задачу резервирования
средств (см. § 10, п. б). Действительно, т ступеней
ракеты можно представить себе как т этапов процесса
набора скорости. Перед каждым этапом мы должны решить:
какую часть находящегося в нашем распоряжении веса,
не истраченного до сих пор, мы истратим на данную
ступень, и какую мы резервируем для следующих. Однако
по сравнению с задачей резервирования средств, рассмо-
рассмотренной в § 10, данная задача имеет некоторую особен-
особенность: функция /, определяющая «доход» от одного этапа
набора скорости, зависит не от одного аргумента — «вло-
«вложенных» средств, а от двух — «вложенных» и «резерви-
«резервированных». Однако это не меняет метода решения и
даже не усложняет его сколько-нибудь существенно.
Обозначим Gl—вес, выделяемый на 1-ю ступень («упра-
(«управление» на i-m этапе); a Qi = Qo~(Oi + G2-(~ ...-J-O,) —
вес, резервированный на оставшиеся ступени. Величина Qt
аналогична сумме средств Zr остающейся в нашем рас-
распоряжении после 1-го этапа в задаче о резервировании
средств.
100
В новых обозначениях формулу A2.1) можно пере-
переписать так:
A2.3)
Фазовое пространство, так же как и в задаче о резерви-
резервировании средств, можно задать в виде треугольника АОВ
(рис. 12.1). На каждом этапе траектория доходит до
оси ординат («средства», выделенные на ступень, пол-
полностью расходуются).
Тогда So лежит на ли-
линии АВ, точка 5К0н —
в начале координат. •
Начнем, как всегда,
с последнего этапа. Лю-
Любой вес Qm_!. сохранив-
сохранившийся в результате пре-
предыдущих этапов, следует,
разумеется, полностью
отдать на m-ю ступень.
Условное оптимальное
управление на m-м шаге
будет
При этом будет приобретено условное максимальное
приращение скорости, соответствующее заданному Qm_x:
Фиксируем вес Qm_2. оставшийся после (т — 2)-го
этапа. Очевидно,
Qm-l — Qm-2 — Gm-V
Условное оптимальное управление на (т—1)-м этапе
G* _j (Ст_г) найдется как обращающее в максимум сумму
двух приращений скорости: Ai>m_i. достигнутой на
(т—1)-м этапе при управлении От_1, и &V*m — макси-
максимального приращения на т-и этапе:
и так далее.
101
Условное оптимальное управление на i-м шаге нахо-
находится из условия
После оптимизации первого шага (выбора веса первой
ступени G*) последовательность этапов, как всегда, про-
проходится вторично от начала к концу; в результате нахо-
находится совокупность оптимальных весов ступеней:
т
1 2 т' i=l I
придающая полезной ступени (кабине) максимальную
скорость
1, 2, ..., т'
б. Распределение средств поражения по оборо-
обороняющимся целям. В тех задачах распределения ресурсов,
которые встречались нам до сих пор, средства, выде-.
ленные на любом этапе, либо давали доход и за счет
этого тратились (полностью или частично), либо резерви-
резервировались, не давали дохода, но зато и не тратились.
Здесь мы рассмотрим своеобразную задачу, в которой
средства тратятся не только на том этапе, где они дают
«доход», но и на тех этапах, где они «дохода» не при-
приносят, причем интенсивность траты этих средств зависит
от того, сколько было вложено на данном этапе непо-
непосредственно действующих средств. Речь идет о распре-
распределении ресурсов со «взаимной поддержкой». В качестве
примера мы рассмотрим задачу о распределении средств
поражения по обороняющимся целям.
Задача ставится следующим образом: планируется
боевое воздействие определенными средствами поражения
(например, самолеты, ракеты, самолеты-снаряды) по
каким-то обороняющимся целям (например, корабли,,
зенитные орудия и т. п.). Цели эшелонированы по глу-
глубине территории на нескольких параллельных рубежах
обороны (рис. 12.2).
Перед тем, как выйти на данный рубеж, средства
поражения проходят зону действия огневых средств этого
102
рубежа, где подвергаются обстрелу со стороны последних.
Огневые средства каждого рубежа могут вести огонь
ODDDDDDDDDD
Цели 3-го рубежа
///
Зона
/
огневых
//////
рубежа
9999999 9
Цели 2-го рубежа
ууА Зона действия огневых средств 2-га рубежа у/у.
Цели 1-го рубежа
/////////////////////////
Зона действия огневых средств 1-го рубежа
S « 1 « П И
Средства параокения
Рис. 12.2.
не. только по средствам поражения, направляющимся непо-
непосредственно на цели данного рубежа, но и по тем сред-
средствам поражения, которые проходят через зону действия,
направляясь на более далекие цели, расположенные на
следующих рубежах.
103
Налет средств поражения планируется следующим
образом: они разделяются на последовательные «волны»;
первая волна направляется на цели 1-го рубежа, вторая —
на цели 2-го рубежа и т. д. Первая волна проходит
через зону действия огневых средств 1-го рубежа, несет
там известные потери, после чего оставшиеся средства
поражения атакуют цели 1-го рубежа, в результате чего
какая-то доля этих целей поражается, и их огневые сред-
средства выходят из строя. Таким образом, после налета
первой волны 1-й рубеж обороны оказывается частично
подавленным. Затем вступает в действие вторая волна;
она движется сквозь зону действия частично подавленных
огневых средств 1-го рубежа, теряет там некоторую" часть
своего состава, затем вступает в зону действия огневых
средств 2-го рубежа, снова теряет там некоторую часть
своего состава; оставшиеся средства поражения атакуют
цели 2-го рубежа и т. д.
Задача планирования налета ставится следующим
образом:
Распределить имеющиеся средства поражения
по волнам так, чтобы обратитъ в максимум сред-
среднее число пораженных целей на всех рубежах.
Поставленная задача по своему характеру напоминает
уже знакомую нам задачу распределения ресурсов («ре-
(«ресурсами» здесь являются средства поражения, «дохо-
«доходом» — пораженные цели), но отличается от нее двумя
особенностями.
Во-первых, средства поражения, выделенные для воз-
воздействия по целям того или другого рубежа, не только
выполняют свою прямую задачу (поражают цели), но и
выступают в качестве «поддержки» следующим волнам,
облегчая им преодоление предварительных рубежей
обороны.
Во-вторых, в отличие от всех ранее рассмотренных,
данная задача содержит элемент случайности. Дей-
Действительно, фактическое число пораженных целей и выве-
выведенных из строя средств поражения может оказаться тем
или другим в зависимости от случайных факторов (на-
(например, дальность обнаружения, точность стрельбы, отказы
аппаратуры и т. п.).
Задачи динамического программирования, содержащие
случайные факторы (так называемые «стохастические»
задачи) образуют особый класс и требуют особого под-
104
хода (см. § 15, 16). Однако в данном случае мы не
будем пользоваться этим общим подходом, а решим задачу
приближенно с помощью простейшего приема, часто при-
применяемого в подобных случаях: мы заменим все фигури-
фигурирующие в задаче случайные величины (число пораженных
целей на каждом рубеже, число выведенных из строя
средств поражения) их средними значениями (математи-
(математическими ожиданиями). Такой прием, сильно упрощающий
задачу, обычно дает сравнительно малые погрешности
в случае, когда число боевых единиц (целей, средств
поражения), участвующих в процессе, достаточно велико*).
Решение поставленной задачи распределения средств
поражения по обороняющимся целям проще будет рас-
рассмотреть на конкретном примере, задавшись определен-
определенным видом фигурирующих в ней функциональных зави-
зависимостей.
Пусть планируется налет п самолетов по средствам
ПВО (зенитным орудиям), расположенным на т рубежах
(рис. 12.3).
Всего на т рубежах имеется N орудий
т
N=J!,Nt. A2.4)
i=i
где Nt — число орудий, расположенных на i-м рубеже.
В нашем распоряжении имеется п самолетов, из ко-
которых должно быть сформировано т волн:
где щ (t=l, 2, .... т) — число самолетов, входящих
в состав 1-й волны и имеющих боевое задание воздей-
воздействовать по орудиям 1-го рубежа.
Предполагается, что волны формируются и получают
боевое задание заранее, и в процессе налета уже не пере-
перестраиваются. Каждая волна летит перед последующими
с некоторым упреждением по времени, так что к моменту
подлета следующей волны успевает уже выполнить свое
боевое задание.
') Пример задачи, решаемой не по «средним» характери-
характеристикам, а с действительным учетом случайности, дан в § 16.
105
Перед тем, как выйти на рубеж расположения орудий,
каждый самолет проходит зону действия орудий этого
рубежа, где подвергается обстрелу со стороны тех орудий
999999999999
'hi рубеж, N^ орудий
'У/У, Зона действия спудий U-го рубежа /
///У//////////////////////////////
9 9 9 9 9 9 9
3-й рубеж, N3 орудий
/Л/у/// Зона действия орудий 3-го рубежа /
YYYYYYYYY
2-й рубеж, Нг орудий
у//'/// Зона действия орудий 2-га рубежа
||| ||| ||| ||| ||| 1|| ||1
1-й рубеж, N, орудий
уууууу/ Зона действия орудий 1-го рубежа
9 9
шш
9
Y Y
^Ш
п самолетов
Рис. 12.3.
данного рубежа, которые имеют возможность стрелять
(т. е. находятся в пределах досягаемости и к данному
моменту не поражены). Атаковать орудия, расположенные
105
на данном рубеже, могут только те самолеты, которые
благополучно прошли зону действия орудия данного
рубежа и всех предшествующих.
Характеристики эффективности боевого воздействия
орудий по самолетам и самолетов по орудиям следующие.
1. Вероятность поражения одного самолета, пролетаю-
пролетающего зону действия орудий 1-го рубежа, выражается
формулой
V,= l — е—М. A2.6)
где Nf — среднее число орудий, сохранившихся непо-
непораженными на данном рубеже, at — коэффициент, зави-
зависящий от эффективности стрельбы орудий по само-
самолетам.
2. Среднее число орудий 1-го рубежа, поражаемых
волной самолетов, направленной по целям данного рубежа,
выражается формулой
где N[ — число орудий на i-ы рубеже, \1 — среднее число
самолетов в t-й волне, сохранившихся непоражен-
непораженными после прохода зон действия орудий данного
рубежа и всех предыдущих, pt — средняя вероятность
поражения одного орудия рубежа атакующим его само-
самолетом.
Требуется назначить состав волн, т. е. числа nv
л2, ..., пт так, чтобы обратить в максимум среднее число
пораженных целей на всех рубежах:
т
1F = 2 да,.
i=i
где Wi — среднее число пораженных целей 1-го рубежа.
Чтобы применить метод динамического программиро-
программирования, нужно прежде всего разделить планируемый про-
процесс на шаги (этапы). Это разделение можно сделать,
вообще говоря, разными способами; важно только в ходе
рассуждений четко представлять себе принятое опреде-
определение «шага» и не сбиваться с него на другое.
Мы будем разделять процесс на шаги, исходя из следую-
следующей (может быть, довольно искусственной) его схематизации.
107
Представим себе, что к зоне действия орудий /-го
рубежа подходит некоторое число самолетов Zt_v бла-
благополучно преодолевших все / — 1 предыдущих рубе-
рубежей обороны (это число Zt_x мы будем полагать равным
его среднему значению и допускать, таким образом,
не только целые, но и дробные «количества самолетов»).
Требуется эту величину — имеющиеся в нашем распоря-
распоряжении средства — разделить на две части: х% — самолеты,
направляющиеся на поражение орудий 1-го рубежа, и
у. = Zt_x — xt — самолеты, «резервированные» для пора-
поражения орудий последующих рубежей. Первые встретятся
с неослабленным огнем орудий i-го рубежа, вторые —
с огнем, уже ослабленным предшествующим воздей-
воздействием xt самолетов.
При такой постановке задачи мы узнаем в ней уже
знакомые признаки задачи о резервировании средств.
Наметим общую схему ее решения методом динами-
динамического программирования.
1. Фиксируем результат (т—1)-го шага: к зоне дей-
действия орудий m-ro рубежа подошло Zm_x самолетов.
Очевидно, все эти самолеты должны быть направлены
на поражение орудий т-го рубежа. Условное оптимальное
управление на fft-м шаге будет
Определим соответствующее условное максимальное
значение числа пораженных орудий т-го рубежа
W* (Z Л. Так как m-й рубеж еще не подвергался воз-
воздействию, на нем сохранились все Nm орудий:
Nm = Mm. A2.9)
Вероятность поражения каждого из выделенных само-
самолетов, согласно формуле A2.6). равна
Vm=\— «-*|Ч
а среднее число самолетов, которые благополучно пре-
преодолеют зону действия орудий этого рубежа, будет
108
\
Согласно формуле A2.7) эти самолеты поразят среднее
число орудий т-го рубежа, равное
@ 02-И)
где vm, как показывает формула A2.10), зависит от Zm_v
Таким образом, на m-м шаге найдены условное опти-
оптимальное управление A2.8) и условный максимальный
выигрыш A2.11).
2. Для планирования (т—1)-го шага фиксируем
результаты (т— 2)-го. Пусть к зоне действия орудий
(/и— 1)-го рубежа подошло Zm_2 самолетов; из них нужно
выделить хт_1 на цели (т—1)-го рубежа, а остальные
направить на /и-й рубеж сквозь зону действия орудий
(/и—1)-го рубежа.
Условное оптимальное управление x*m_l(Zm_^ найдется
из условия максимального выигрыша на двух послед-
последних шагах
W* (Z \ —
т-\, т\Гт-2)
-0)- <12Л2>
где Qm_i(#m_i)—среднее число целей, пораженных на
(/и—1)-м рубеже выделенными для этого хт_1 само-
самолетами; Zm_l — среднее число самолетов, которые по-
подойдут к зоне действия орудий т-го рубежа при таком
управлении (эта величина зависит как от управления
на (т — Г)-м шаге хт_х, так и от числа самолетов
ym = Zm_2 — xm_v выделенного на пролет зоны дей-
действия (т—1)-го рубежа).
По формуле A2.7) мы имеем
-h^p .1
— е Nm-t m 'J, A2.13)
где
Подсчитаем среднее число непораженных самолетов
второй («резервированной») группы, проходящей через
зону действия орудий (гп — 1)-го рубежа, чтобы быть
109
брошенной на m-й. При входе в зону действия их было
Z-m-Ъ Xm-V
Среднее число орудий, пораженных на (т—1)-м рубеже
хт_л самолетами, будет равно Qm-i(xm_l), определяе-
определяемому по формуле A2.13); следовательно, на (т—1)-м
рубеже сохранится среднее число орудий, равное
'Ч»-1 = .Vm_, - Qm_, (*„_,). A2.13)
Эти орудия своим огнем по «пролетающим» Zm_2 — хт_1
самолетам уменьшат их число в среднем до величины
^m-l = (^«-2-*m-l) • *~*т -1"'1»-1- 02.16)
Эту величину Zm_l. зависящую от Zm_2 и хт_х. нужно
подставить в формулу A2.12) и, варьируя управление хт_х,
найти максимальный условный выигрыш W*n_l т№т_Л
и соответствующее ему оптимальное условное управле-
НИе <-l(Zm-2)-
Ввиду сравнительной сложности фигурирующих в задаче
функций вряд ли имеет смысл пытаться искать максимум
аналитическим путем; придется построить серию кривых
зависимости величины
Wrm-l,m = Qm-l(*m-l) + WmBm-i). О 2- *?)
стоящей в фигурных скобках в правой части A2.12),
от jcto_v Каждая кривая будет соответствовать опреде-
определенному Zm_2, и на ней нужно будет найти точку с мак-
максимальной ординатой. Абсцисса этой точки будет пред-
представлять собой условное оптимальное управление на
(т—1)-м шаге x*m_\{Zm_\ а ордината — соответствую-
соответствующий ему условный максимальный доход W* . (Z Л
на двух последних шагах.
Далее будет оптимизироваться (т — 2)-й шаг и т. д.
3. Общие формулы для условного максимального вы-
выигрыша Wi, i+i, ..., m(^i-i) (и соответственно условного
оптимального управления jcj(Zj_i)) имеют вид
<i+i m(^-i)= max {Qi(Xi) + W*+i m(Zt)).
A2.18)
ПО
где
Q, (.v,.) = .V, [ 1 - е~~Ъ '"'' ] . A2.19)
y.=,Xle~*is'i, A2.20)
Z, =(Z,-_i — x,)<TvV\ A2.21)
N,=tW, — Ql(xl). A2.22)
4. Согласно общему правилу процесс оптимизации идет
вплоть до первого шага, после которого ищется опти-
оптимальное управление на каждом шаге:
х*, х* х*.
Однако найденные числа еще не представляют собой
(за исключением х*\ искомых оптимальных числеиностей
волн:
«?, «: «*,
1 2 т
так как они сформированы с учетом потерь самолетов
на всех предшествующих рубежах. Чтобы, пользуясь х*,
найти исходное число самолетов в 1-Я волне ft*, нужно
прибавить к х*. средние потери данной волны Ь* на всех
предшествующих рубежах.
Продемонстрируем процедуру оптимизации управления,
задавшись конкретными численными значениями параметров,
фигурирующих в задаче:
Число рубежей: т = 4.
Число самолетов: п — 80.
Число орудий на рубежах: Nl= 10; /V2— 12; /V3— 15;
N4=l0 (всего N= 10+ 12 -f-15+10 = 47).
Вероятности поражения орудия одним атакующим его
самолетом:
Характеристики эффективности огня средств ПВО по
самолетам:
0^ = 0,05; а2 = 0.04; а3=0,04; а4 = 0,05.
Ill
Найти оптимальные числа самолетов в волнах:
п\, п\, л*. п\,
при которых число пораженных орудий на всех рубежах
будет максимально.
Решение будем строить по этапам.
1. Условная оптимизация четвертого шага.
Задаемся рядом значений числа самолетов Z3, подошедших
к зоне действия орудий 4-го рубежа, например:
Z3=10, 20, 30, 40, 50,
и вычислим для них среднее число пораженных орудий
4-го рубежа по формуле
A2.11). Результаты рас-
расчета оформим в виде гра-
графика зависимости №4(Z3)
(рис. 12.4) Входя в этот
график при любом Z3,
мы сможем найти соот-
соответствующий условный
максимальный выигрыш
№4(Z3); что касается ус-
условного оптимального
управления, то оно про-
гО 30 W SO " сто равно
Рис. 12.4. *.
2. Условная оптимизация третьего шага.
Задаемся рядом значений числа Z2 самолетов, преодолевших
предыдущие два рубежа:
Z2=10, 15, 20, 25, 30, 40,
и для каждого из них подсчитаем выигрыш на двух по-
последних шагах: третьем — при любом управлении и четвер-
четвертом — при оптимальном:
Wl4 = Q3(x3)+w\(Z3). A2.23)
где
Z3 = (Z2-*3) «—*•; A2.24)
A2.25)
= N3[l—e к
112
Величина Q3(x3), входящая в A2.23), подсчитывается
по формуле A2.25), a W4(Z3) находится по графику
рис. 12.4, для чего нужно войти в него со значением Z3,
взятым из формулы A2.24).
Произведя вычисления по этим формулам для выбран-
выбранных значений Z, и ряда значений jc3. строим серию кри-
кривых для функции Н^4 в зависимости от х3 (рис. 12.5).
-25
5 10 20 30
Рис. 12.5.
■х.
9
8
7
6
5
it
3
г
1
0
хз
-40 /
/к
■30 /
/
■20 /
/ /^
10 / у'
/ У,
w го зо гг
Рис. 12.6.
На каждой из этих кривых отмечаем точку с максималь-
максимальной ординатой. Абсцисса этой точки — условное оптималь-
оптимальное управление x3(Z2), отвечающее тому Z2. к которому
относится кривая; ордината — соответствующий условный
максимальный выигрыш 1^3,4(^2)-
Строим на графике рис. 12.6 (в разных масштабах)
две кривые: зависимость Wz,i{Z2) и зависимость x3(Z2).
Задача условной оптимизации третьего шага решена.
3. Условная оптимизация второго шага.
Процедура совершенно аналогична и показана на рис. 12.7
и 12.8. Сначала строится серия кривых W2,3,4(x2), соот-
соответствующих разным значениям Zx (числа самолетов, подо-
подошедших к зоне действия орудий 2-го рубежа):
Zj=10, 20, 30, 40, 50, 60,
в зависимости от управления х2 на втором шаге.
8 Е, С. Вентцель
113
Вычисления ведутся по формуле
A2.26)
где
A2.27)
v2 = .v2e-»!-v'. A2.28)
а величина WziA(Z2) снимается с графика рис. 12.6 при
Z2 = (Zl — x2) е~ яАз, A2.29)
N2 = N, — Q2(x2). A2.30)
На каждой из построенных кривых (рис. 12.7) снова нахо-
находится максимум, и строятся зависимости его абсциссы
v г.зл
гог
10
Ю 20 30 U0 50
Рис. 12.7.
60
(условного оптимального управления на втором шаге) и его
ординаты (соответствующего выигрыша) от Zx (рис. 12.8).
Построением графика рис. 12.8 решена задача услов-
условной оптимизации второго шага.
4. Оптимизация первого шага. Значение Zo,
с которым мы приступили к оптимизации, задано:
114
поэтому придется построить только одну кривую зависи-
зависимости ^2,з,4 от управления xY на первом шаге (рис. 12.9).
IV*
"ад*
/5
10
х-
■30
20
10
10 20 30 40 50 60 '
Рис. 12.8.
О 10 20 30 W 50 60 70 80
Расчеты для построения этой кривой ведутся по фор-
формуле
WU.a.4(xd = Qi(Xi)-\-Wl3,t(Zl). A2.31)
где
A2.32)
A2.33)
115
а величина №2,3,4 (Zj) снимается с графика рис. 12.8 при
Z1 = (Z0 — *,)в-Д. A2.34J
A^A^-Q^jc,). A2.35)
На кривой рис. 12.9 отмечаем точку с максимальной орди-
ординатой и таким образом находим максимально возможный
выигрыш (среднее число пораженных орудий на всех четы-
четырех рубежах)
1^=1^,2,3,4=14,1
и оптимальное управление на первом шаге
*• ж 34.
5. Оптимизация всего процесса. Находим
оптимальное управление шаг за шагом с начала до конца.
Мы выделили в состав первой волны (на поражение ору-
орудий 1-го рубежа) лс* = 34 самолета, а остальные у' =
= 80 — 34 = 46 самолетов направили дальше.
К зоне действия орудий 2-го рубежа подойдет (см.
формулу A2.34)) число самолетов, равное
i\ A2.36)
где
Nl = Nl — Ql(xl), A2.37)
v* = x\e-a*N*.
Производя вычисления при а1 = 0,05, N, = 10, имеем
т. е. на 1-м рубеже будет поражено в среднем 5,6 ору-
орудия, а к зоне действия орудий 2-го рубежа подойдет
в среднем 37 самолетов из 46 «резервированных».
С полученным значением Z* = 37 войдем в график
рис. 12.8 и найдем оптимальное управление на втором
шаге
116
т. е. из 37 сохранившихся самолетов нужно выделить 23
на поражение орудий 2-го рубежа, а «резервировать»
у'= 37 —23 = 14.
Далее находим число самолетов, которые подойдут
к зоне действия орудий 3-го рубежа:
A2.39)
где
' 1). A2.40)
~;
Q2(x^ = N2ll-e ".й|. A2.41)
^==*^-«А«. A2.42)
Производя вычисления по этим формулам, найдем сред-
среднее число орудий, поражаемых на 2-м рубеже:
и среднее число самолетов, преодолевших первые два
рубежа:
Zz=10,7.
Со значением Z2=10,7 входим в график рис. 12.6 и на-
находим оптимальное управление на третьем шаге
т. е. на поражение орудий 3-го рубежа самолетов выде-
выделять вовсе не нужно! Этот с первого взгляда неожиданный
вывод представится вполне естественным, если учесть, что
стрельба по орудиям 4-го рубежа в условиях нашей задачи
гораздо более эффективна, чем по орудиям 3-го рубежа
(р3 = 0,4; р4=1), и поэтому имеет смысл, несмотря на
противодействие 3-го рубежа, резервировать все 10,7 само-
самолета для четвертой волны.
Из этих 10,7 самолета к зоне действия орудий 4-го
рубежа подойдет в среднем
Zl =£.е-*"- =5,9.
Все эти 5,9 самолета должны быть брошены на пора-
поражение орудий 4-го рубежа. Из них сохранятся непора-
117
женнымн в среднем
t4^=Zze =3,6 самолета,
и они поразят на 4-м рубеже в среднем
J\ 1
e "< P<J=3,1
орудия.
Процесс оптимизации закончен: найдено оптимальное
управление:
Л-; = 34; лг; = 23; *з = 0; лг* = 5,9.
Остается перейти от этих значений (количества само-
самолетов, выделяемых на данный рубеж из числа сохранив-
сохранившихся к данному рубежу) к значениям п*, п*у я*, и*, вклю-
включаемым в волны, формируемые в начале налета. Имеем
т. е. в первую волну нужно включить 34 самолета из 80.
В какой пропорции нужно разделить оставшиеся
46 самолетов между второй и четвертой волнами? Согласно
нашим расчетам после прохождения 1-го рубежа из 46
«резервированных» самолетов останется 37, из них 23
должны действовать по орудиям 2-го рубежа. Так как,
согласно условию, мы должны формировать волны заранее,
а не на границах рубежей, то очевидно, нужно разделить
46 «резервированных» самолетов между второй и четвер-
четвертой волнами в соотношении 23 : 14, т. е. включить во вто-
вторую волну 27 самолетов, а в четвертую — оставшиеся 19.
Итак,
п* -=34; п,;=г-27; п*,-=0; п\ = 19.
При таком оптимальном планировании будет поражено
максимально возможное среднее число целей, равное
из них на 1-м рубеже 5,6, на 2-м 5,4, на 3-м ни одной
и на 4-м 3.1.
Не представляет труда подсчитать также собственные
потери самолетов при выполнении боевого задания. Часть
этих потерь, а именно потери в «резервированных» само-
самолетах, мы уже вычислили в ходе расчета; к ним нужно
добавить еще потери в тех самолетах, которые, благо-
благополучно пройдя предшествовавшие рубежи, направляются
118
на поражение орудий данного рубежа. Среднее количество
этих потерь П; на г-м рубеже вычисляется по формуле
Применяя эту формулу, а также учитывая ранее най-
найденные потери в резервированных самолетах, получим
общие средние потери:
на 1-м рубеже
13,4 + 9.1 = 22.5;
на 2-м рубеже
8,8 + 3,3=12,1;
на 3-м рубеже
4,8;
на 4-м рубеже
2,3.
Итого из 80 самолетов при выполнении операции по по-
подавлению зоны ПВО будет потеряно в среднем 42; ценой
таких собственных потерь может быть достигнут макси-
максимальный «выигрыш» — поражено в среднем 14 орудий
противника.
Очевидно, такой неутешительный результат заставляет
задуматься о том, целесообразно ли вообще проводить
операцию по подавлению столь хорошо защищенных це-
целей, как в нашем примере", с помощью таких средств
поражения, как рассмотренные нами самолеты? Однако
рассуждения на эту тему выходят за рамки предмета
динамического программирования, тем более, что исход-
исходные численные данные, на которых мы строили решение,
выбраны из чисто методических соображений и не имеют
ничего общего с реальными.
Остановимся еще на одном вопросе. Поставленную
задачу о распределении средств поражения мы решаем
в предположении, что разделение самолетов на волны и
выдача боевого задания каждой волне производится зара-
заранее, и в ходе выполнения операции ее первоначальный
план не меняется.
В принципе задачу можно поставить и иначе: предпо-
предположить, что на подступах к каждому рубежу фактически
сохранившееся число самолетов (которое заранее в точ-
точности предсказать нельзя) каждый раз оптимальным об-
образом перераспределяется на две группы:«дна направляется
119
на поражение целей данного рубежа, а другая летит
дальше. При наличии быстродействующей управляющей
вычислительной машины такое оптимальное перераспреде-
перераспределение вполне возможно. Точное решение такой задачи
может быть построено общими методами решения сто-
стохастических задач динамического программирования (см.
§§ 15, 16). Однако в первом приближении можно вос-
воспользоваться следующим приемом.
В начале налета (до преодоления 1-го рубежа) ре-
решается задача динамического программирования, как это
было показано выше, и находится оптимальное управле-
управление на первом шаге х*. которое и осуществляется. Затем
обнаруживается, что ко 2-му рубежу подошло фактически
не Z\ самолетов, а другое число Zv Но ведь при реше-
решении задачи динамического программирования мы для ка-
каждого Zj нашли условное оптимальное управление x\(Z^)\
воспользуемся этой зависимостью и применим для факти-
фактически осуществившегося Zl это оптимальное управление
и т. д.
Естественно возникает вопрос: имеет ли смысл зани-
заниматься по ходу операции таким «перераспределением»,
т. е. велик ли выигрыш в среднем числе пораженных
орудий, покупаемый ценой такого усложнения управления?
Ответ на этот вопрос может быть дан, только если по-
построить более точную «стохастическую модель» боевых
действий (без замены случайных величин их математиче-
математическими ожиданиями), подобно тому как это делается
в §§ 15, 16.
в. Та же задача с другим критерием. При реше-
решении предыдущей задачи (б) мы предполагали, что цель
операции, выполняемой самолетами, — только поражение
обороняющихся целей (орудий), и чем больше будет по-
поражено этих орудий, тем лучше. Критерием W у нас
было среднее число пораженных целей.
Можно рассмотреть и другую задачу, когда п само-
самолетов преодолевают зону ПВО с тем, чтобы за ее пре-
пределами выполнить какую-то другую, основную боевую
задачу (например, бомбометание по промышленным объек-
объектам). Чтобы обеспечить максимально успешное выполнение
этой основной боевой задачи, и выделяется некоторое
количество самолетов для подавления средств ПВО.
В качестве критерия при оценке эффективности всей опе-
120
рации в данном случае целесообразно выбрать не среднее
число пораженных орудий, а среднее число самолетов Zm.
преодолевших все т рубежей ПВО и готовых к выпол-
выполнению дальнейших боевых действий:
W — 7
w — От-
т-
тданная задача имеет нечто общее с задачей о распре-
распределении ресурсов, когда максимизируется не доход,
а общее количество средств (см. § 116), и так же, как
и та, оказывается «вырожденной» задачей динамического
программирования.
Действительно, чтобы убедиться в этом, набросаем
схему решения задачи методом динамического програм-
программирования. Критерий, который нужно обратить в макси-
максимум, есть W = Zm — среднее число самолетов, благопо-
благополучно преодолевших все т рубежей.
1. Фиксируем Zm_v Условное оптимальное управление
на m-м шаге x*m(Zm_A уже не равно Zm_v а находится
из условия
W*m(Zm-i)= max \Zm{Zm_v xj],
0<<Z
где Zm(Zm_v jcm) — среднее число самолетов, преодо-
преодолевших m-й рубеж при заданном числе самолетов Zm_v
вступающих на этот рубеж, и управлении хт на этом
рубеже.
Совершенно ясно, что Zm есть неубывающая функция
Zm_f, стало быть, и Wm есть тоже неубывающая функ-
функция Zm_v
2. Фиксируем Zm_2. Условное оптимальное управление
на (т — 1)-м шаге x*m_1(Zm_^ найдется из условия
Wrm-i.mB«-s)= max {^(Zm_i(Zm_2,Jcm_,))},
где 2m_1(Zm_2, Jtm_i) — среднее число самолетов, преодо-
преодолевших первые т — 1 рубежей при заданном Zm_2 и
фиксированном управлении jcm_j. Ясно, что функция
Zm_j(Zm_2. JCm_i) есть неубывающая функция аргумента
Zm_2; следовательно, и №m(Zm_i(Zm_2. хз)) есть не-
неубывающая функция Zm_2, а значит, и Wm-i.m(Zm-2) —
тоже неубывающая функция.
121
3. Совершенно аналогичным способом убедимся, что
для любого (i-ro) шага выигрыш на всех оставшихся
шагах есть неубывающая функция числа самолетов Zt^v
подошедших к данному рубежу.
Отсюда выводим заключение: поставленная задача
является «вырожденной» задачей динамического програм-
программирования. Планировать нужно каждый шаг отдельно,
распределяя подлетевшие к данному рубежу самолеты
на две части — «на подавление средств ПВО» и «на про-
пролет дальше» так, чтобы обратить в максимум среднее
число самолетов, преодолевших данный рубеж (без-
(безотносительно к остальным).
13. Распределение ресурсов
с последействием
Рассмотренная в § 12 задача распределения ресурсов
отличалась той особенностью, что средства, выделенные
в одну «отрасль», выступали в качестве «поддержки» для
средств, выделенных в другую, увеличивая приносимый
ими доход. Эта поддержка сказывалась немедленно после
вложения соответствующих средств.
На практике могут встретиться и такие ситуации,
когда деятельность «поддерживающей» отрасли сказы-
сказывается не сразу после вложения в нее средств, а спустя
какое-то количество этапов. В общем случае увеличение
дохода «основной» отрасли зависит от того, сколько
времени прошло с момента вложения средств в «под-
«поддерживающую» отрасль.
Задачи такого рода имеют, по сравнению с ранее
рассмотренными, некоторую особенность: доход от «ос-
«основной» отрасли на данном этапе зависит не только от
состояния системы в данный момент (куда и сколько
вложено), а еще и от предыстории управляемого процесса
(куда, когда и сколько вкладывалось средств). Наличие
такого «последействия» (влияния прошлого на будущее)
вообще усложняет процесс планирования.
Ранее уже говорилось о том, что с наличием после-
последействия можно справиться, включая в настоящее состоя-
состояние системы те параметры из прошлого, которые суще-
существенны для будущего. При этом увеличивается количество
122
измерений фазового пространства и, следовательно, резко
возрастает количество вариантов состояний, которые
нужно перебрать в процессе оптимизации. Однако прин-
принципиальных трудностей такое решение не содержит.
Рассмотрим конкретный пример задачи на распреде-
распределение средств с последействием.
Планируется работа предприятия при исходном запасе
средств Zo вперед на период т лет. Количество средств х,
вложенное в предприятие, превращается через год (с уче-
учетом дохода и траты средств)' в какое-то другое количе-
количество средств F^0) (x), которое может быть меньше, равно
или больше исходного л\
Средства, имеющиеся в нашем распоряжении в начале
каждого года, мы можем по своему усмотрению либо
полностью вкладывать в производство, либо частично
расходовать на вспомогательные мероприятия, например
на содержание научной лаборатории, которая, проводя
исследования производственного процесса, через некото-
некоторое время после своей организации повышает доходность
производства, вследствие чего функция изменения средств
"' заменяется другой:
где k — количество лет, в течение которого лаборатория
уже существовала.
Функцию F '(jc) при любом k будем считать неубы-
неубывающей.
На содержание лаборатории, очевидно, нужно затратить
какие-то средства. Допустим, что эти средства — вполне
определенные (не зависят от нашего произвола) и равны
а (Л—1) на k-м году существования лаборатории (после
того как она работала уже k — 1 лет). При этом а @)
означает первоначальные затраты, потребные на создание
лаборатории и ее содержание в течение первого года.
Условимся считать, что если в течение какого-то года
средства на лабораторию не отпускаются, то она консер-
консервируется, достигнутый уровень доходности производства
сохраняется, а при новом вложении средств лаборатория
функционирует и повышает доходность прсиззодства так,
как если бы перерыва в финансировании не было.
«Управление» распределением средств на каждом шаге
.(перед началом каждого нового хозяйственного, года)
123
состоит в решении вопроса: отпускать деньги на лабо-
лабораторию или не отпускать? При такой упрощенной по-
постановке задачи на каждом шагу имеется выбор только
между двумя управлениями:
(/■ ' — не отпускать средств,
1/A) — отпускать средства.
Требуется найти такое управление в течение т. лет,
при котором общее количество средств, не вложенных
в лабораторию (чистый доход плюс оставшаяся часть
основных средств), к концу периода будет максимальным.
Будем решать поставленную задачу методом динами-
динамического программирования. Прежде всего нужно решить
вопрос: какими параметрами мы будем характеризовать
состояние системы после (i—1)-го шага (перед началом
i-ro хозяйственного года)?
Очевидно, одной величиной Zi_1—количеством средств,
находящимся в нашем распоряжении после (/—1)-го
шага, — обойтись не удастся, так как доход, который мы
получим на i-н шаге, зависит не только от того, каким
количеством средств мы располагали в начале года и
какое управление применили, а еще и от того, сколько
лет до сих пор работала лаборатория (при наших допу-
допущениях все равно — работала она непрерывно или с пере-
перерывами).
Придется характеризовать состояние системы после
шага двумя параметрами:
Zi_l — количество средств (основные плюс доход),
имеющихся в нашем распоряжении после (/ — 1)-го шага,
kl_l— количество лет. в течение которых функциони-
функционировала лаборатория перед началом /-го шага.
Состояние системы St_j после (I— 1)-го шага запишем
в виде вектора с двумя составляющими:
В качестве фазового пространства рассмотрим на пло-
плоскости ZOk (рис. 13.1) ряд прямых
0 — 0'; 1 —Г; 2 — 2'; ...; т — т.',
параллельных оси абсцисс; ординаты этих прямых равны
целым числам: 0, 1, 2, ... По оси абсцисс откладываются
распределяемые средства Z, по оси ординат — число лет
существования лаборатории к. Начальное состояние си-
124
стемы — вполне определенная точка So на оси OZ с абс-
абсциссой Zo (первоначальное количество средств). Если на
данном шаге средства на лабораторию не отпускаются,
точка на фазовой плоскости перемещается по горизонтали;
если средства на лабораторию отпускаются, точка пере-
перемещается с данной горизонтальной прямой на следующую
по порядку.
Область SKon конечных состояний системы предста-
представляет собой все фазовое пространство (совокупность пря-
прямых 0 — 0', 1 — 1' и т. д.). Выигрыш № = Zm есть не
О
I
г'
7'
О'
W
Рис. 13.1.
что иное, как абсцисса последней точки траектории 5К0Н.
Задача оптимального планирования сводится к тому, чтобы
вывести точку, изображающую состояние системы, в ко-
конечное состояние SK0U с наибольшей абсциссой (ордината
не имеет значения).
Наметим схему построения оптимального управления
методом динамического программирования. Представим
выигрыш W — Zm в виде суммы т слагаемых:
из которых все, кроме последнего, равны нулю. Будем
строить решение по стандартной схеме.
1. Фиксируем результат (т—1)-го шага, т. е. два
числа: количество средств Zm_t и число лет km^v
125
в течение которого уже работала лаборатория. Очевидно.
0<^fcm_!<^/n — 1. Рассмотрим и сравним доход на т-м
шаге, который мы получим при управлении U{0) (если не
отпустим денег на лабораторию) и при управлении
(если отпустим). В первом случае в производство будут
вложены все средства Zm_v и мы получим доход
Во втором случае в производство будут вложены не все
средства, а только те, которые останутся после финан-
финансирования лаборатории, и мы получим доход
•«U—1. **-i- ^<")='?(*—)Bm_,-a(*11,_l)). A3.2)
Так как функция /^m-i) неубывающая, то очевидно,
из двух доходов A3.1) и A3.2) первый всегда больше.
Таким образом, оптимальное управление на последнем
шаге есть Ui0) — не отпускать средств на лабораторию,
и это управление не зависит от исхода (т—1)-го шага
и;п=и'°\
а соответствующий максимальный выигрыш равен
wC(Zm_,. *m-i) = M*"»-')(Zm_i). A3.3)
2. Фиксируем исход (т — 2)-го шага. т. е. вектор
При управлении LJ( точка в фазовом пространстве
перейдет по горизонтали в точку Sm_x с координатами
Выигрыш за последние два шага (при оптимальном
управлении на последнем) будет
_2). Лт_2). A3.4)
или, пользуясь формулой A3.3),
A3.5)
126
При управлении £/( ' точка в фазовом пространстве
переместится с прямой km_2 — k'm_2 на следующую по
порядку прямую и попадет в точку Sm_l с координатами
В этом случае W^-i, m будет определяться формулой
_2-x{km_2)). Лт_2+1). A3.7)
или. учитывая A3.3),
). A3.8)
Оптимальное управление (t/( ' или t/L)) найдется сра-
сравнением двух выражений A3.5) и A3.8) и выбором мак-
максимального из них
= max*
3. Для любого (/-го) шага оптимальное управление
\U' или LJ ) найдется сравнением двух выражений
и выбором максимального из них
W/. i+i, .... m{Zi-\, /e/_i) =
liti + i «(ii ii ) | /tom
= max{ ,... , A3.9)
|«^л/ + 1 «B,-,. Л,_ь t/'1») |
где
WJi+i ».(z«--i- */-i. ^0)) =
') (£,-_,). Ai-i). A3.10)
-i) (Zf-_! _ а (Лг_,)). /?,-_, + 1). A3.11)
127
4. Оптимизация первого шага производится при ф|
рованном значении Zo и ko = O:
' 'U m(Zo,o,u'°),\
икси-
иксигде
Wt.t m(Z0. 0. t/@))= W\ m{F{0\Z0), 0), A3.13)
Wt.i m(Z0. 0, £/") =
= «^2 «.(^(Zo —o@)). 1). A3.14)
Оптимальное управление L/i на первом шаге будет £/@)
(не отпускать средств), если выражение A3.13) больше,
чем A3.14). Если наоборот, то оптимальное управление
будет GA) (отпускать средства1)).
5. Далее находится результат первого шага при опти-
оптимальном управлении: {Z\, k*\); затем оптимальное управле-
управление на втором шаге U?, и так далее, вплоть до послед-
последнего шага.
Продемонстрируем решение задачи на численном при-
примере.
Положим т = 4 и зададим функции F(k) (x) и
при 0 < k < 3:
(jc)=1,5jc; а@)=1;
\.6x; аA) = 0,5;
2x; а B) = 0,4;
= 3jc; аC) = 0,3.
1. Ha последнем шаге, как уже выяснено,
т. е. средств на лабораторию отпускать ие надо. При
этом оптимальном управлении выигрыш на четвертом шаге
для разных k будет равен
wftZa. 0)=1.5Z3;
3, 1)=1,6Z3;
a, 2) = 2Z3;
') Если выражения равны, то оба управления равноправны.
128
2. Оптимизируем третий шаг. Имеем
Wii{Z2. 0. Uv")=wUl.5Z2. 0) = 2.25Z2;
fa. 0, Ub)=W\{l,5(Z2-l), l) =
= 1.6A,5Z2—1,5) = 2,4Z2 —2,4.
Из этих двух выражений первое больше второго при
Z2<16; при Z2>16 — наоборот. Поэтому
при Z, < 16,
[24Z2_24 при ^>1б A3.15)
и соответственно
при Z2<16,
при Z2>16.
Далее имеем
l( {0)l >= 1.6 - 1,6Z2 = 2,
—0,5); 2) =
= 2A,6Z2 —0.8) = 3.2Z2—1,6.
Из этих двух выражений первое будет больше второго
при Z2 > 2,5. Поэтому
B,56Z2 при Z2<2,5,
^a.4(Z2. 1)= 2 п^и 72^9. A3.17)
13,2Z2—1,6 при Z2^-z,5
и соответственно
при Z, <2,5.
при ; ^13Л8)
Далее,
WZ*{Zb 2, U@))=U/4BZ2, 2) = 4Z2;
WtA{Z2. 2, UA))=tt/4B(Z2 —0,4), 3) = 6Z2 —2.4.
Из этих двух выражений первое больше при Z2 < 1,2.
второе — при Z2>1,2; следовательно,
DZ2 при Z2<1,2.
"^•HeZ,-2.4 при Z2>1.2 <13Л9>
и соответственно
[£/«» при Z2<1,2.
^зB2, 2) = f|fll 2 A3.20)
При £"Ч'&' **^ш
9 Е. С Вентцель 129
Полагать А2 = 3 уже не нужно, так как за два пер-
первых шага система не может прийти на прямую 3—3 .
3. Оптимизируем второй шаг. Имеем
и^з.4Bь 0, l/l0))=<4A.5Z,, 0),
или, пользуясь формулой A3.5),
Wi3,4(Zi. 0, </") =
—
3.375Z,
т.
3.6Z,—
Аналогично
U^3,4C
или, пользуясь
^3,4^,, 0, <
—
3.84Z, —3
т.
4
8Z, — 6,4
е.
2,4
при
при
при
0, U<1
формулой
/>)
84
е.
=
при 1
при
при
1,1
0=
1 A3
zi
2,
w.
•7)
,5(Z,-
< 16,
U0.5(Zx
■
-1)<2,5,
Z,<2|
Z,>2|-
i 10,67,
i 10,67.
-1). I).
»2,67,
^2,67.
Чтобы решить вопрос, какое из выражений A3.21)
или A3.22) больше, построим графики соответствующих
функций (рис. 13.2).
Каждая из кривых будет представлять собой ломаную
линию, составленную из двух прямых. Максимум этих
двух функций показан на рис. 13.2 жирной линией. Бук-
Буквами £/*0' и и^ помечены кривые, отвечающие соответ-
соответствующим управлениям. Ломаная линия, изображающая
максимум двух функций A3.11) и A3.12), токе состоит
из двух отрезков; точка перелома имеет абсциссу, рав-
равную 4,49.
Уравнение этой кривой будет
3,375Z, при Z1<4,49.
AZl±6A при ; <1323>
130
so
40
30
го
ю
о
и
.«-
ГО) У
У
г
го
w
о
1)
Zfi7
3 4
К.
у
i
5 6 7
Рис.
,(г„п
I
1 IjSl 2
Рис.
в
13.2.
Ifj
!
/
13.3.
L
/
3 10
/
/
3 <
(II ^
юл
и 12 г,
■> г.
131
и, следовательно,
[£/«» при Z,<4,49;
t/2(Z,. 0) = {/m) _ 7\ллп A3.24)
Далее находим
^3,4B1. I, Ul0))=wli4(\,6Z1. 1).
или, пользуясь формулой A3.7),
4,10Z1 при 1,6Z,<2,5,
т.е. при Z^l.56, A3.25)
5.12Z,—1,6 при Z,>1,56.
Далее,
^3,4B1. I, t/A))= ^,4A,6(^ — 0,5), 2),
или, пользуясь формулой A3.9),
6.4Z, —3,2 при 1.6Z,— 0,8 < 1,2,
т. е. при Zj< 1,25, A3.26)
9.6Z, —7,2 при Z,>1,25.
Выражения A3.25) и A3.26) представлены графически на
рис. 13.3. Максимум двух функций A3.25) и A3.26) по-
показан на рис. 13.3 жирной ломаной линией, уравнение
которой
^.lOZ, при Zj < 1,31,
3.6Z, — 7,2 при Z,^-
отсюда
при Z, < 1,31;
при Zj^-1,31.
,. A3.27)
A3.28)
Полагать /г, — 2 уже не нужно, так как за один пер-
первый шаг система не может прийти на прямую 2—2'.
4. Оптимизируем первый шаг. Имеем
o. 0, £/@))=
, 0),
132
или. пользуясь формулой A3.13).
Wt2,3,i{Z0. 0. t/@') =
5,06Z0 при l,5Z0<4,49,
т. е. при Zo<2,93, A3.29)
7,27Z0 —6.4 при Z0>2,93.
Аналогично
или, согласно формуле A3.17),
'6.14Z0 — 6,14 при 1.5Z0—1.5<1,31.
т. е. при ZO<1,87, A3.30)
14,4ZO —2,16 при
ZO>1,87.
Выражения A3.29) и A3.30) представлены графически
40
SO
го
ю
о
и
'"
Рис. 13.4.
на рис. 13.4. Жирной линией показан максимум этих двух
функций; уравнение этой линии
133
5,06Z0 при Zo<2,31.
[14.4Z0 —21,6 при Z0>2,31.
Отсюда оптимальное управление на первом шаге будет
при Z0<2.31.
при zl>2,31. <l3-32>
Таким образом, условная оптимизация каждого шага
выполнена.
5. Найдем теперь оптимальное управление за все четыре
года:
Рассмотрим два случая:
a) ZO<2,31;
6)ZO>2.31.
В случае а) оптимальное управление на первом шаге
будет U* — L/@), т. е. на первом году средств на лабора-
лабораторию отпускать не нужно. К концу первого года мы
будем иметь количество средств
Zl=l,5Z0<3.47;
при этом &! = (), т. е. 5i = A.5Z0. 0).
Чтобы найти оптимальное управление на втором шаге £/2,
обратимся к графику рис. 13.2. Так как Z\ < 3,47 < 4,49,
то оптимальное управление снова есть £/@):
т. е. и на втором году средств на лабораторию отпускать
не надо.
Находим результат второго шага при оптимальном
управлении:
Zz = 1 ,bZ\ = 2,25Z0 < 5.20; kl = 0;
S2 = B.25Zo, 0).
Из формулы A3.6) следует, что и на третьем шаге
оптимальное управление есть £/@) (не отпускать средств),
так как
Z2<5,20< 16.
Управление на последнем шаге стандартно: отпускать
средства на лабораторию не нужно. При этом максималь-
134
ный выигрыш (см. формулу A3.21)) будет равен
Таким образом, мы убедились, что при исходном ко-
количестве средств Zo < 2,31 оптимальное управление есть
т. е. лабораторию вообще заводить не нужно.
Аналогично убеждаемся, что при Zo>2,31 оптималь-
оптимальное управление будет
т. е. лабораторию следует завести сразу же, а на послед-
последний год законсервировать. При этом максимальный доход
будет равен
W*=HAZ0 — 21,6.
На рис. 13.5 показаны две оптимальные траектории
в фазовом пространстве для двух конкретных значений Zo:
Zo = 2,2 < 2.31 и Zo = 2,4 > 2.31.
Первая траектория соответствует случаю, когда средства
на лабораторию не отпускаются; вторая — случаю, когда
А
О
-*'
I
А
'о ■ 1 а '
/ 2 3 4 5 6 7 в' S Ю II К 13
Рис. 13.5.
лаборатория финансируется на любом этапе, кроме самого
последнего.
Отметим, что в нашем примере оптимальное управле-
управление, в зависимости от исходного запаса средств Zo. строится
По типу «все или ничего»: либо при достаточном запасе
135
средств нужно все время (кроме последнего года) держать
лабораторию, либо, если запас средств недостаточен, со-
совсем не заводить ее. Здесь ни при каких начальных усло-
условиях не может быть выгодным сначала накопить средства,
а потом вложить их в лабораторию.
Это связано с тем, что мы рассмотрели слишком не-
небольшое число шагов (т = 4). Можно предложить чита-
читателю такое упражнение: дополнить наши исходные дан-
данные, т. е. задать функции FD) (jc), F{5) (x), ... и рас-
расходы а D), а E) и попытаться получить такое решение,
при котором оптимальное управление будет «смешанным»:
на начальных шагах средства на лабораторию не отпу-
отпускаются, а потом это становится выгодным.
§ 14. Задачи динамического
программирования
с неаддитивным критерием
Все задачи динамического программирования, которые
мы рассматривали до сих пор, принадлежали к классу
«аддитивных» задач, т. е. таких, в которых максимизи-
максимизируется (минимизируется) критерий вида
т
W=^iwi, A4.1)
где wt — «выигрыш», приобретаемый на /-м этапе.
Вообще метод динамического программирования может
применяться и к «неаддчтивлым» задачам, в которых кри-
критерий не представляется в виде A4.1). Некоторые из них
сводятся к аддитивным простым преобразованием критерия.
Здесь мы рассмотрим наиболее простой вид задач, при-
приводящихся к аддитивным, а именно задачи с мультипли-
мультипликативным критерием.
^Мультипликативным-» мы будем называть критерий
(«выигрыш») W, если он может быть представлен в виде
произведения «выигрышей», достигаемых на отдельных
этапах:
т
W=да,а>2 ... wm = Ц да,. 04.2)
136
Очевидно, любой мультипликативный критерий W вида
A4.2) можно искусственно преобразовать к аддитивному,
если прологарифмировать выражение W:
т
lgW = 2lg^i A4.3)
1=1
и обозначить
A4.4)
Получим новый критерий
обладающий свойством аддитивности и обращающийся
в максимум (минимум) одновременно с W.
Рассмотрим два примера задач с мультипликативным
критерием.
а. Распределение п снарядов по т целям, которые
нужно поразить совместно. Пусть в нашем распоря-
распоряжении имеется и снарядов, которыми мы хотим поразить
т целей:
Ц,, Ц2, .... Ц, (т<п),
причем боевая задача состоит в том, чтобы поразить все
цели без исключения. Требуется так распределить
п снарядов по т целям, чтобы вероятность совместного
поражения всех целей W достигала максимума.
Будем рассматривать распределение снарядов как т-
этапную операцию, на каждом этапе которой происходит
выделение некоторого числа снарядов на определенную
цель. Обозначим kt число снарядов, выделенных на 1-ю
цель A=1, 2 т). Управление U будет состоять
в выборе чисел kv k2 km:
U = (kv k2 km). A4.6)
и требуется выбрать его оптимальным образом.
Допустим, что в процессе обстрела каждой цели рас-
расходуются все выделенные на нее снаряды и перераспре-
перераспределение средств не производится. Кроме того, предполо-
предположим, что отдельные цели поражаются выделенными на них
снарядами независимо друг от друга. Тогда вероятность
поражения всех т целей равна произведению вероятностей
ДО
поражения отдельных целей:
W = ![/>, (ft,).
где Pt{k^ — вероятность поражения 1-й цели выделенными
на нее kt снарядами.
Для решения поставленной задачи требуется задать
функции
Я,(£). P3(k) PM(k). A4.8)
характеризующие уязвимость целей и выражающие веро-
вероятность поражения каждой из них в зависимости от числа ft
выделенных на нее снарядов.
Если все эти функции одинаковы:
т. е. уязвимость всех целей одна и та же. то задача
становится тривиальной и сводится к тому, чтобы распре-
распределить снаряды по целям по возможности равномерно.
Если же цели неодинаковы по уязвимости, очевидно, ко-
количество снарядов, выделяемое по менее уязвимым целям,
должно быть относительно больше.
Прежде чем строить решение методом динамического
программирования, отметим некоторые его свойства.
Каждая из функций Р, (ft), очевидно, обращается в нуль
при ft = 0, т. е.
Pt @) = 0 при /=1,2 т.
поэтому, если не обстрелять хотя бы одну из целей, кри-
критерий W обратится в нуль. Отсюда следует условие
ft,>l (/=1. 2, .... т),
т. е. по каждой цели нужно выделить хотя бы один сна-
снаряд. Кроме того, выделяя снаряды по /-й цели, мы должны
помнить о том, что на оставшиеся т — / целей нужно не-
непременно резервировать хотя бы по одному снаряду; по-
поэтому каждая из величин kt ограничена не только снизу,
но и сверху:
l<ft(<n — m+l. (H.9)
Для того чтобы применить метод динамического про-
программирования, перейдем от мультипликативного критерия
A4.7) к аддитивному, прологарифмировав его при любом
138
основании (например, натуральном е):
A4.10)
2t
Чтобы не иметь дела с отрицательными числами, обо-
обозначим
\lnW\=V, |ln Я, (*,)!=«,(*,) A4.11)
и получим новый — аддитивный — критерий
У = 2М*д- A4.12)
Так как мы изменили знак критерия, то величину V
нужно уже не максимизировать, а минимизировать.
Таким образом, задача сводится к следующему: найти
управление О*, обращающее в минимум величину A4.12).
Полученная задача напоминает рассмотренную в § 10
задачу распределения ресурсов с резервированием. Дей-
Действительно, имеющиеся и снарядов можно рассматривать
как начальные средства, которые на каждом этапе опе-
операции делятся на две части: выделяемые и резервируемые,
причем выделяемые средства расходуются до конца. Осо-
Особенность данной задачи в том, что, во-первых, количество
средств, выделяемых на каждом этапе, может иметь только
целочисленные значения, ограниченные условием A4.9);
кроме того, «доход» V не максимизируется, а минимизи-
минимизируется.
В задачах распределения ресурсов мы, ради единооб-
единообразия, каждый раз в качестве фазового пространства рас-
рассматривали треугольник АОВ на плоскости хОу. Здесь
можно было бы сделать так же, но мы предпочтем другой,
более наглядный способ изображения процесса, при ко-
котором непосредственно видно не только управление, но
и получаемый «выигрыш».
Рассмотрим в качестве фазового пространства сово-
совокупность прямых, параллельных оси абсцисс: 0 — 0',
1 — V, ...,и — п' с целочисленными ординатами
(рис. 14.1). Точка S, изображающая состояние системы,
будет в процессе расходования снарядов перемещаться
с одной из этих прямых на другую. Если на данную цель
выделен только один снаряд, то точка 5 будет переме-
перемещаться на соседнюю прямую; если два — перескакивать
через прямую и т. д. Таким образом, по оси ординат
будет откладываться израсходованное к данному этапу число
снарядов N ^п. По оси абсцисс мы будем откладывать
накопленный за несколько этапов «выигрыш» 2^*-
Очевидно, начальное состояние системы 50 вполне оп-
определенно и совпадает с началом координат; область 5К0Н
N
t
3
г
i
JL
/
/
V
/
1 I
1 1
I !
1 1
°»
V-Lv,
У
°з
/
-—.—
°*
* v^
°s
>—л'
•at
nl
II
0'
Щ
Рис. 14.1.
конечных состояний системы представляет собой прямую
и — п' (на рис. 14.1 л = 9, тп = 5). Требуется найти та-
такое управление U (такую траекторию в фазовом прост-
m
ранстве), при котором абсцисса V = 2 <о1 конечной точки
5К0Н будет наименьшей.
Решим до конца поставленную задачу динамического
программирования, задаваясь определенными значениями п
и m и определенным видом функций Pt(k).
Положим число снарядов и = 10, число целей т = 5.
Функции Pi(k) зададим следующим образом:
Р, (ft) =1 — 0.2*;
P2(ft)= 1 — 2 -0,6*+0,2*;
Pa(ft)= I —0.1*;
pt (ft) = 1 — 0,7* — 0,5* + 0,2*;
= 1-0.5*.
A4.13)
140
Заметим, что из заданных пяти функций две (Р2 и Р^
обращаются в нуль не только при k = 0, но и при k = 1,
т. е. вторая и четвертая цели обладают значительно мень-
меньшей, по сравнению с первой, третьей и пятой, уязви-
уязвимостью; на эти цели нам придется выделять не меньше
чем по два снаряда:
Л2>2, А4>2. A4.14)
Перейдем от функций A4.13) к новым функциям
vi{k)=\\nPi(k)\ A=1. 2 5) A4.15)
и для упрощения дальнейших вычислений составим таб-
таблицу значений всех функций vt(k) (см. табл. 14.1).
Таблица 14.1
*
0
1
2
3
4
5
6
7
8
9
10
*Mft)
со
0,223
0,041
0,008
0,002
0,000
0,000
0,000
0,000
0,000
0,000
со
оо
1,139
0,552
0,298
0,169
0,098
0,058
0,034
0,020
0,012
со
0,105
0,010
0,001
0,000
0,000
0,000
0,000
0,000
0,000
0,000
V, (ft)
оо
со
1,204
0,616
0,358
0,222
0,143
0,094
0,063
0,043
0,030
»s(ft)
оо
0,693
0,288
0,134
0,065
0,032
0,016
0,008
0,004
0,002
0,001
Графики функций г>, (&)(/= 1 5) представлены
на рис. 14.2. Так как функции определены только для
целочисленных значений аргумента k. то линии на
рис. 14.2 показаны не кривыми, а ломаными.
Процесс планирования развернем по стандартной схеме.
В качестве величины, характеризующей исход 1-го шага,
будем рассматривать число и,- снарядов, оставшихся в на-
нашем распоряжении после выделения средств на 1-ю цель.
1. Фиксируем исход четвертого шага п4 — число сна-
снарядов, оставшееся в нашем распоряжении после выделе-
выделения снарядов на первые четыре цели. Определим границы,
в которых может находиться га4. На пятую цель нужно
оставить не менее одного снаряда:
и4>1.
141
На первые четыре цели было выделено не менее 1 -f-
-\-2-\-1 + 2 = 6 снарядов, осталось не более четырех.
Итак,
Очевидно, оптимальное управление на пятом шаге со-
состоит в том, чтобы все оставшиеся га4 снарядов выделить
на пятую цель:
kl(ll4) = IH- A4.16)
При этом значение критерия V, достигаемое на пятом
шаге, обращается в минимум и равно
Vl{n4) = v5(n4). A4.17)
Эта величина для любого значения «4 может быть най-
найдена из последнего столбца табл. 14.1. Запишем в новой
Ю
Рис. 14.2.
табл. 14.2 условное оптимальное управление на пятом
шаге kl (ra4) и значение критерия Vl(n,4), достигаемое
при этом управлении на пятом шаге.
Таблицей 14.2 исчерпывается задача оптимизации на
пятом шаге. Заметим, что здесь не имеет смысла строить
графики, так как возможные значения аргумента »4 цело-
целочисленные и их немного.
2. Зафиксируем п3 — число снарядов, оставшихся после
выделения средств на первые три цели. Определим границы,
142
Таблица 14.2
1
2
3
4
1
2
3
4
0,693
0,288
0,134
0,065
в которых лежит п3. На оставшиеся две цели — четвер-
четвертую и пятую — нужнорезервировать не меньше трех снаря-
снарядов, отсюда
га3 > 3;
с другой стороны, на первые три цели истрачено не
меньше 1 -\- 2 -J- 1 = 4 снарядов; осталось не больше шести.
Таким образом,
3 < га3 < 6.
Согласно стандартной процедуре нам нужно при каж-
каждом из возможных значений п3 минимизировать «выигрыш»
1Л£б за последние два шага при любом управлении на пред-
предпоследнем шаге и оптимальном управлении на последнем:
или, учитывая, что и4 = га3 — kv
Vt5{n3, luj = v4(k^ + Vs(na — k^. A4.18)
Условный оптимальный выигрыш К},5(яз) и условное
оптимальное управление ^(пз) найдутся из условия
К s (из) = min [Vt 5 (из. k4)}, A4.19)
где минимум берется по всем значениям числа выделенных
снарядов кА, допустимым при данном га3.
Пользуясь данными табл. 14.1 и 14.2 (в последнюю
нужно войти с га3 — k4 вместо га4), составим таблицу
с двумя входами для функции A4.18) (см. табл. 14.3).
Прочеркнутые графы табл. 14.3 соответствуют невоз-
невозможным, при данном п3, значениям kA. В каждой строке
таблицы подчеркнуто минимальное значение. Оно равно
143
У4,5(«з) и определяет условное оптимальное управление
на четвертом шаге &4(газ)- Сведем эти данные в табл. 14.3.
^\ft.
3
4
5
6
2
1,897
1,492
1,338
1,269
3
1,309
0,904
0,750
Табл
4
—
1,061
0,646
ица 14.3
5
■—
—
0,915
Таблица 14.4 решает полностью задачу оптимизации
четвертого шага.
Таблица 14.4
"з
3
4
5
6
*
М"з>
2
3
3
4
^,6(пз)
1,897
1,309
0,904
0,646
3. Оптимизируем третий шаг. Задаемся значениями га2,
для которых определяем границы. За первые два шага
истрачено не меньше трех снарядов; осталось не/ больше
семи.
На последние три шага надо резервировать не меньше
четырех снарядов; следовательно,
4<и2<7.
Строим таблицу с двумя входами значений функции
К*.s(. Аз)-г»3(А:з) + ^4,5(«2 — *з) A4.20)
(табл. 14.5) и ищем в каждой строке этой таблицы мини-
минимальное число:
*»
A4.21)
144
4
5
6
7
l
2,002
1,414
1,009
0,751
l
1,907
1,319
0,9N
Таб л
3
—
1,898
1,310
и ц а 14.5
4
—
—
1,897
Подчеркиваем в каждой строке минимальное число,
находим Аз («г) и V\ 4,5G*2) и записываем их в табл. 14.6.
Таблица 14.6
П2
4
5
6
7
*
1
1
1
1
* # v
Kg ^ S (П2)
2,002
1,414
1,009
0,751
Оптимизация третьего шага этим исчерпывается.
Аналогично оптимизируем второй шаг. Находим гра-
границы значений п{.
Строим таблицу с двумя входами значений функции
4l5(nl — k2) A4.22)
(см. табл. 14.7).
В каждой строке этой таблицы находим Минимальное
число:
A4.23)
Далее строим таблицу для оптимизации второго шага
(табл. 14.8).
10 Е. С. Вентцель 145
6
7
8
9
2
3,141
2,553
2,148
1,890
3
2,554
1,966
1,561
Таб л
4
—
2,300
1.712
и ц а 14.7
5
—
—
2,171
Таблица 14.8
Пъ
6
7
8
9
М»|>
2
2
3
3
*
4l.4.S<nl>
3,141
2,553
1,966
1,561
4. Оптимизируем первый шаг; значение по=Ю задано
и не варьируется; поэтому просто ищем минимум по Aj
функции
It 2, 3,4, 5 (Ю, *l) = 1»,(A:1) +1^2, 3.4, 5(Ю — ftl), A4.24)
представляющий собой абсолютный минимум критерия V:
V* = V\, 2, з, 4,5 = min {Vt, 2, з, 4, s (l0, ft,)}. A4.25)
3naie ия функции A4.24) приведены в табл. 14.9.
Таблица 14.9
V+ A0, ft,)
•
1,784
2
2,007
3
2,561
4
3,143
Наименьшее из чисел в табл. 14.9 равно
V' = V'Xi 2,3,4, s =1,784
и достигается при оптимальном управлении на первом
146
шаге
При этом вероятность W поражения всех целей дости-
достигает своего максимума:
W* = e~v* «0,168.
5. Проходя снова всю последовательность этапов от
начала к концу, находим безусловное оптимальное упра-
управление на каждом шаге, начиная с первого:
k\=\\ л* = 10 — Л* = 9.
Входя в табл. 14.8 при га, = 9, находим
&2 = &2(9) = 3; У2, 3, 4, 5= 1.561.
Далее имеем
га* = 9 — 3 = 6.
Входя в табл. 14.6 при ге2 = 6, найдем
Аз = й£F)=1; Vl, 4,5= 1.009.
Далее,
га* = 6—1=5;
из табл. 14.4 имеем
() 3; 1^4,5 = 0,904.
Далее,
га* = 5 — 3 = 2;
из табл. 14.2
2; Vl = 0,288.
Таким образом, оптимальное управление найдено:
£Г = A. 3, 1, 3, 2).
т. е. для достижения максимальной вероятности пораже-
поражения всех целей W нужно выделить на первую и третью
цели по одному снаряду, на вторую и четвертую цели —
по три снаряда, а оставшиеся два снаряда выделить на
пятую цель.
Для построения траектории в фазовом пространстве
нужно еще вычислить значения w* (/=1, 2, 3, 4, 5)
«выигрышей», достигаемых на отдельных этапах при
Ю» 147
оптимальном управлении. Имеем:
v\ = V\, 2, з, 4,5 — Vl з,4,5== 1.784— 1,561 = 0,223;
v> = Vl3,A,5 —^3.4,5 =1,561 — 1,009 = 0,552;
г»з = ^з,4,5 —^4,5 =1,009 — 0,904 = 0,105;
v*4 = V*,s —Vrl = 0,904 — 0,288 = 0,616;
vl = vl =0,288.
Оптимальная траектория точки 5 в фазовом простран-
пространстве будет выглядеть, как показано на рис. 14.3.
"в и.
Рис. 14.3.
Заметим, что в данном элементарном примере проде-
продемонстрирован не самый экономный способ решения за-
задачи: пожалуй, проще было бы решить задачу рацио-
рационального управления не динамическим программированием,
а простым перебором (число возможных вариантов не
слишком велико). Однако в более сложных задачах пре-
преимущества метода динамического программирования ста-
становятся явными.
б. Распределение средств для повышения надеж-
надежности технического устройства. Пусть имеется техни-
техническое устройство А, состоящее из т агрегатов, или
148
узлов
Av Av ..., Am
(рис. 14.4). Безотказная работа каждого из узлов необ-
необходима для работы устройства Л в целом. Агрегаты могут
Рис. 14.4.
выходить из строя, причем независимо одни от другого.
Надежность (вероятность безотказной работы) всего уст-
устройства равна произведению надежностей отдельных узлов
W=f[pl. A4.26)
г=1
где pt — надежность /-го узла.
Для повышения надежности всего устройства выделена
какая-то сумма средств Zo. Эти средства (выраженные
в деньгах, весах или иначе) могут быть произвольным
образом распределены между мероприятиями, повышаю-
повышающими надежность отдельных узлов. Для того чтобы по-
повысить надежность /-го узла с pt до Р > pt, необходимо
затратить сумму, равную ft (Р, pt).
Требуется так распределить отпущенные средства,
чтобы сделать надежность всего устройства макси-
максимальной.
Эта задача, как и предыдущая, тоже имеет мульти-
мультипликативный критерий, но отличается от нее тем, что
управление носит не дискретный, а непрерывный характер
и состоит в выделении на каждый узел (этап) определен-
определенной суммы средств xl{l=\, 2 т). После преобра-
преобразования критерия W к аддитивной форме логарифмиро-
логарифмированием перед нами будет обычная задача распределения
ресурсов с резервированием (причем в ее простейшей
форме, когда на каждом этапе расходуются до конца все
выделенные средства), с той разницей, что «доход» не
максимизируется, а минимизируется.
Рекомендуем читателю в качестве упражнения решить
задачу, распределения средств на повышение надежности.
149
При следующих конкретных данных:
= 0,97.
Л (
Л
Все функции /, (Р) определены только для Р> pt
(*=1 5).
/«5. Стохастические задачи
динамического программирования
На практике нередко встречаются такие задачи плани-
планирования, в которых заметную роль играют случайные
факторы, влияющие как на состояние системы S, так и на
пыигрыш W. В таких задачах управляемый процесс не
полностью определяется начальным состоянием So и вы-
выбранным управлением (Лав какой-то мере зависит от
случая. Условимся такие задачи планирования называть
«стохастическими» (вероятностными).
Некоторое представление о подобных задачах мы уже
получили в § 12, где отыскивалось оптимальное распре-
распределение средств поражения по обороняющимся целям.
В зависимости от случая число уцелевших к данному
рубежу средств поражения могло быть тем или другим,
т. е. состояние системы, в сущности, было случайным.
Однако при решении этой задачи иы ограничились рас-
150
смотрением только средних характеристик процесса,
т. е. решали ее не как стохастическую, а как обычную
задачу динамического программирования.
Такой прием, сводящийся к тому, что случайный про-
процесс заранее, еще до решения задачи, заменяется его
осредненной, не случайной, детерминированной моделью,
является приближенным и применим далеко не всегда. Он
дает неплохие результаты только в тех задачах, в кото-
которых управляемая система состоит из достаточно много-
многочисленных объектов (как в § 12: самолеты, орудия), и
несмотря на то, что состояние каждого из них меняется
случайным образом, в массе эти случайности взаимно по-
погашаются, нивелируются.
Во многих стохастических задачах планирования этот
прием не может быть применен; в одних он дает слиш-
слишком большие ошибки, в других и вовсе невозможен. И,
во всяком случае, всегда возникает вопрос: сильно ли
изменится оптимальное управление, если пренебречь слу-
случайностью и заменить стохастическую задачу детермини-
детерминированной? Чтобы ответить на этот вопрос, нужно уметь
решать стохастические задачи динамического программи-
программирования с учетом случайных факторов.
В настоящем параграфе мы дадим принципиальный
подход к таким задачам и наметим общую схему решения.
В следующем § 16 мы подробно разберем конкретный
пример.
Общая постановка стохастической задачи динамиче-
динамического программирования может быть описана следующим
образом.
Пусть имеется физическая система S, которая с тече-
течением времени меняет свое состояние. Мы можем в какой-то
мере воздействовать на этот процесс, направляя его в же-
желательную сторону, но контролируем этот процесс не
полностью, так как ход его, помимо управления, зависит
еще и от случая. Такой процесс мы будем называть «слу-
«случайным управляемым процессом».
Предположим, что с ходом процесса связана какая-то
наша заинтересованность, выражающаяся критерием («вы-
(«выигрышем») W, который нам желательно обратить в мак-
максимум. Критерий W является аддитивным:
W = 2iwl, A5.1)
151
где wt — «выигрыш», приобретаемый на /-м этапе про-
процесса.
Так как состояние системы S случайно, то случайным
оказывается и выигрыш wt на каждом этапе, и суммар-
суммарный выигрыш W.
Нам хотелось бы выбрать такое управление U. при
котором выигрыш W обращался бы в максимум. Но мо-
можем ли мы это сделать? Очевидно, нет: при любом нашем
управлении выигрыш W останется случайным. Однако мы
мзжем выбрать такое управление, при кот )ром с р е д н е е
значение случайного выигрыша W будет максималь-
максимальным. Обозначим среднее значение(математическое ожида-
ожидание) величины W буквой W:
W = M\W]. A5.2)
Учитывая формулу A5.1) и пользуясь свойством мате-
математического ожиданият), запишем W в виде
т
^ = 2 Щ, A5.3)
где wi — средний выигрыш на 1-й этапе.
Таким образом, в стохастических задачах вместо са-
самого критерия W, который случаен, рассматривается его
среднее значение W; этот критерий тоже аддитивен.
Задача динамического программирования сводится
к следующему: выбрать такое оптимальное управление U*.
состоящее из оптимальных управлений U\. if?, .... Um
на отдельных этапах, чтобы аддитивный критерий W об-
обратился в максимум.
Казалось бы, дело сводится к простой замене крите-
критерия; однако это не так. Разница между стохастической и
детерминированной схемами динамического программиро-
программирования гораздо глубже: она касается самой структуры
оптимального управления.
Действительно, вспомним общую схему динамического
программирования в детерминированных процессах, без
участия случайности (§ 7). Она состоит в следующем.
') Математическое ожидание суммы случайных величин равно
сумме их математических ожиданий.
152
Фиксируется состояние системы 5,_, после (/—1)-го
шага, и для каждого из таких состояний ищется услов-
условное оптимальное управление на /-м шаге. При этом со-
состояние системы после /-го шага S,- полностью опре-
определяется предыдущим состоянием Si^l и примененным
на 1-м шаге управлением £/,-:
£. = 5. (£._,, Ut). A5.4)
Равным образом выигрыш да, на /-м шаге полностью
определяется состоянием системы S,-_, в начале этого
шага и примененным управлением t/,-:
^. = ^(Si_1, U,). A5.5)
Так ли это будет в стохастических задачах? Нет, не
так. Состояние системы St после /-го шага не пол-
ностью определяется состоянием S;_, и управле-
управлением Uj, а зависит еще и от случая. Состояние S, при
заданных St-l и £/,- является случайным, а от задан-
заданных S|_i и и; зависит только распределение ве-
вероятностей для разных вариантов состояния 5,-.
Выигрыш w, на /-м шаге тоже не полностью опреде-
определяется предыдущим состоянием системы S,-_, и применен-
примененным управлением £/,-, а представляет собой случайную
величину, и от 5,_, и U{ зависит только распределение
вероятностей между его возможными значениями. Но так
как нас интересует не сам случайный выигрыш wit
а только его среднее значение на каждом шаге, эту слу-
случайную величину можно осреднить с учетом распределе-
распределения вероятностей и ввести в рассмотрение условный
средний в.ыигрыш на 1-й шаге при заданном
состоянии S,-_, после (/—1)-го шага и определенном
управлении на 1-й шаге U■:
w,E,_,. Ut). A5.6)
Мы будем предполагать, что как распределение ве*
роятностей для случайного состояния St, так и условный
средний выигрыш A5.6) зависят только от .S;., и Ut
и не зависят от «предыстории» процесса, т. е. от того,
каким образом, когда и в результате какого управления
система пришла в состояние Si_i J).
') Иначе говоря, управляемый процесс имеет марковский
характер.
153
Нашей задачей будет определить для каждого из воз-
возможных случайных исходов любого шага условное опти-
оптимальное управление на следующем шаге. Таким образом,
в стохастической схеме само оптимальное упра-
управление U* будет случайными будет каждый раз
осуществляться по-иному, в зависимости от того, как
развернется случайный процесс. Дело планирующего — не
выработать жесткую программу управления, а указать для
каждого шага то управление, которым следует
отвечать на любой случайный исход преды-
предыдущего шага.
В этом — коренная разница между детерминированной
и стохастической задачами динамического программиро-
программирования. В детерминированной задаче оптимальное управле-
управление является единственным и указывается заранее как
жесткая программа действий. В стохастической задаче
оптимальное управление является случайным и выбирается
в ходе самого процесса в зависимости от случайно сло-
сложившейся ситуации. Это — управление с «обратной связью»
от фактического состояния системы к управлению.
Обратим внимание еще на одно обстоятельство. В де-
детерминированной схеме, проходя процесс по этапам от
конца к началу, мы тоже на каждом этапе находили целый
ряд условных оптимальных управлений, но из всех этих
управлений в конечном счете осуществлялось только одно.
В стохастической схеме это не так. Каждое из условных
оптимальных управлений может оказаться фактически
осуществленным, если предшествующий ход случайного
процесса приведет систему в соответствующее состояние.
Как же найти условное оптимальное управление
£/*(S/_i) на l-ы шаге стохастического процесса? Это —
такое управление, которое, будучи применено на 1-й
шаге, обращает в максимум условный средний выигрыш
на всех последующих шагах: от i-го до т-го включи-
включительно. Как найти этот максимум? Совершенно анало-
аналогично тому, как мы делали в детерминированной схеме,
с той разницей, что вместо самого выигрыша, который
случаен, рассматривается его среднее значение.
Процесс планирования, как всегда, разворачивается,
начиная с последнего (т-го) шага. Фиксируется состояние
системы 5m_i после (т—1)-го шага, и при этом усло-
условии ищется то управление U*m(Sm_{), которое обращает
154
й Максимум средний условный выигрыш wm(Sm_l) на от-м
шаге:
/71
.1. Um)}. A5.7)
Когда найдена зависимость U*m(Sm_l) и п^, (•£„,_!)
от 5т_!, оптимизация последнего шага закончена. В ка-
какое бы состояние Sm_i случайно ни пришла система после
т—I шагов, мы уже знаем, что нам делать дальше и
какой максимальный средний выигрыш мы получим на
последнем шаге.
Затем оптимизируется (т — 1)-й шаг. Здесь дело об-
обстоит не так просто. Сначала зафиксируем состояние
Sm_2 после т — 2 шагов и найдем средний выигрыш
^m-i,mEm_2. £/m-i) на Двух последних шагах при лю-
любом управлении Um_1 на (т.— 1)-м шаге и при оптималь-
оптимальном управлении на последнем, которое нам уже известно.
Как найти этот средний выигрыш? Будем рассуждать
следующим образом. При заданном Sm_2 и любом упра-
управлении t/m_, состояние Sm_i будет случайным, но мы
знаем для него распределение вероятностей, зависящее
от S/n-2 и ^ш-1- Случайное состояние 5т-1 определяет
собой максимальный средний условный выигрыш на т-и
шаге Wm(Sm_i); осредним эту величину с учетом распре-
распределения вероятностей состояния Sm_v Получим «дважды
осредненный» максимальный условный выигрыш на т-и
шаге, зависящий уже не от 5m_j (по нему произведено
второе осреднение), а от 5т_2 и Um_v Обозначим этот
выигрыш
^Ж_2, Um_J. A5.8)
К нему нужно прибавить средний условный выигрыш
иа (т—1)-м шаге при управлении Um_x на этом шаге:
w«-i(S*-2. "m-i): A5.9)
получим
155
Найдем то управление на (т — 1)-м шаге, при кота-
ром величина A5.10) обращается в максимум:
= max \wm_,(Sm_2. Um_,)+ W{Sm_2. t/m_x)). A5.11)
"m-i
Обозначим это условное оптимальное управление
i/,,,_| Em_2). Таким образом, в результате оптимизации
(т — 1)-го шага найдены условное оптимальное управле-
управление £/,„_! (Sm_2) и соответствующий ему максимальный
средний условный выигрыш на двух последних шагах
"'т — 1, т Wm-2'"
Аналогичным образом оптимизируется любой /-й шаг.
Для каждого исхода /-го шага 5,- уже известен условный
максимальный средний выигрыш на последующих шагах:
W'i+i m(S,). A5.12)
Так как состояние St случайно и его распределение
зависит от 5,_! и Uit то можно случайный выигрыш
A5.12) осреднить с учетом распределения вероятностей St
и получить «дважды осредненный» выигрыш
Сложив его со средним выигрышем на 1-м шаге при лю-
любом управлении LJr получим
г_!, U0- A5.13)
Условное оптимальное управление на t-м шаге
найдется как то управление, при котором величина A5.13)
достигает максимума:
m
,_!) = max
+i m(Sl_l.Ut)\. A5.14)
Применяя формулу A5.14) последовательно на каждом
шагу, найдем условное оптимальное управление и
максимальный условный средний выигрыш на всех
шагах процесса до второго включительно. Оптимизация
156
первого шага имеет некоторые особенности, связанные
с тем, что исходное состояние So, как правило, случай-
случайным не является и его не нужно варьировать с учетом
распределения вероятностей1). Так как SQ не случайно,
то не случайным (вполне определенным) будет и оптималь-
оптимальное управление U\ на первом этапе, и средний выигрыш
с учетом этого этапа будет
W' = w'i.2.....m. A5.15)
Таким образом, процесс динамического программиро-
программирования завершен; найдено оптимальное управление
lf = (d[, UUSJ. Ul(S2) lfm(Sm_d). A5.16)
все элементы которого, кроме первого, являются случай-
случайными и зависят от состояния системы. Соответствующий
этому управлению максимальный средний выигрыш равен
A5.15).
Рекомендации по применению этого управления даются
в следующей форме: на первом шаге применять управле-
управление U\ и ждать результатов этого шага; на втором, в за-
зависимости от исхода 5t первого шага, выбирать оптималь-
оптимальное управление Uo(S{) и т. д.
§ 16. Пример стохастической
задачи динамического
программирования: совместное
управление стрельбой и разведкой
Рассмотрим элементарный пример стохастической за-
задачи динамического про!раммирования.
Производится стрельба по некоторой цели Ц. В на-
нашем распоряжении имеется т снарядов; для поражения
цели достаточно одного попадания. Выстрелы независимы;
') Для простоты изложения мы берем только тот случай,
когда SQ в точности известно.
157
вероятность попадания в цель при каждом выстреле
равна р. Каждый снаряд имеет значительную стоимость,
и поэтому нежелательно тратить снаряды впустую, по уже
пораженной цели. Мы имеем возможность, если хотим,
после каждого выстрела производить разведку (например,
посылать самолет-разведчик) и устанавливать, поражена
цель или нет; если поражена, мы прекратим стрельбу и
часть снарядов будет сэкономлена. Однако слишком
часто посылать разведку невыгодно, так как это дорого
обходится, а непосредственного ущерба цели при этом
мы не наносим. Возникает вопрос о разумном управле-
управлении процессом обстрела цели и разведывательных дей-
действий.
Очевидно, решение должно зависеть от стоимости сна-
снаряда, стоимости разведки, а также от ценности цели.
Пусть стоимость снаряда s; стоимость одной разведки г;
в случае поражения цели мы получаем «премию» А (вы-
(выражающуюся, например, стоимостью самой цели, или стои-
стоимостью восстановительных работ противника, или, нако-
наконец, нашим материальным ущербом, который удалось
предотвратить, поразив цель). Наша задача — спланировать
обстрел и разведку так, чтобы обратить в максимум
чистый «доход» от всей операции («доходы» от затрат
снарядов и посылки разведчиков, разумеется, считаются
отрицательными). Выбрать оптимальное управление — это
значит указать, когда (после каких по порядку выстре-
выстрелов) нужно посылать разведку и когда прекращать
стрельбу.
Физическая система, которой мы управляем, состоит
из информационного звена (разведчика) и средств пора-
поражения (снарядов). Процесс, протекающий в системе,
является случайным управляемым процессом, и задача
оптимизации должна решаться по стохастической схеме.
Критерием является средний «доход» W от всей серии
мероприятий (стрельба, разведка).
В данном примере мы имеем дело с дискретным слу-
случайным управляемым процессом, в ходе которого си-
система S скачками переходит из одного состояния в дру-
другое. Определим возможные состояния системы следующим
образом. Будем говорить, что система S находится в со-
состоянии 5(ft) @ <ft <m— 1), если стрельба по цели еще
не закончена, а с момента получения последних сведений
158
о цели произведено ровно k выстрелов1). Например,
«состояние 5@)» означает: только что произведена раз-
разведка, обнаружившая, что цель не поражена, и стрельба
продолжается. Очевидно, если стрельба еще не началась,
система тоже находится в состоянии 5* \ так как допод-
доподлинно известно, что цель не поражена. «Состояние 5C)»
означает, что с момента поступления последних сведений
о цели, состоящих в том, что цель не поражена, произ-
произведено три выстрела и еще не принято решение о пре-
прекращении стрельбы.
Если стрельба прекращена по любой причине (израсхо-
(израсходованы все снаряды, или обнаружено, что цель уже по-
поражена, или просто принято решение прекратить стрельбу),
то мы будем говорить, что система находится в состоя-
нии 5 •
Буквами 5<ft) c индексами вверху мы обозначаем раз-
различные возможные состояния системы. Не следует путать
их с обозначением St, которое у нас обозначает состоя-
состояние системы после /-го шага. В нашем процессе номер
шага вообще не будет совпадать с номером состояния.
В качестве фазового пространства рассмотрим точки
S(o), 5A), .... Slm-l), S(m) на оси абсцисс (рис. 16.1).
О S(o) S(n S(z> SC) S S
Рис. 16.1.
Переход системы скачком из одного состояния в дру-
другое будем изображать стрелкой, как показано на рис. 16.1.
Разделим процесс на шаги. Естественным «шагом»
в данном случае является «выстрел». Тот факт, что в дей-
действительности могут осуществиться не все т выстрелов,
не должен нас смущать: всегда можно после последнего
реально сделанного выстрела отсчитать мысленно еще не-
несколько фиктивных, так, чтобы общее число выстрелов
(действительных и фиктивных) было всегда равно т.
«Разведку» мы не будем считать за отдельный шаг,
') Заметим, что сведения о цели могут состоять только
в том, что «цель не поражена», так как в противном случае
стрельба была бы иемедлеиио прекращена.
159
так как иначе общее число шагов не было бы фиксиро-
фиксированным. Если после данного выстрела производится раз-
разведка, то мы будем относить ее к тому же шагу,
что и выстрел.
Таким образом, у нас будет три разновидности ша-
шагов: выстрел, выстрел с последующей разведкой и фик-
фиктивный выстрел.
Рассмотрим возможные управления на каждом шаге.
Если система находится в состоянии S т) — стрельба уже
прекращена,—то выбора нет, и единственно возможное (оно
же и оптимальное) управление будет: не стрелять. Если
же система находится в состоянии 5(Л) @ ^k ^т — 1).
то в нашем распоряжении имеется три варианта упра-
управления:
U —сделать шаг первого рода, т. е. выстрелить
и не посылать разведки,
B)
U —сделать шаг второго рода, т. е. выстрелить и по-
послать разведку,
U —сделать шаг третьего рода, т. е. прекратить
стрельбу и произвести фиктивный выстрел.
Условимся считать, что если разведка, выполненная
на предыдущем шаге, принесла известие «цель поражена»,
то стрельба сразу же прекращается, т. е. управление U 3
на следующем шаге является вынужденным.
Опишем движение точки 5, изображающей состояние
системы, в фазовом пространстве (рис. 16.1). Начальное
состояние системы So вполне определено и совпадает
с точкой 5 ° . Конечное состояние 5КОН точки вполне
определено и совпадает с точкой S m). Промежуточные же
положения точки 5 могут быть самыми разными, в за-
зависимости от примененного управления и успешности
стрельбы. Например, на рис. 16.2 изображена такая кон-
конкретная реализация случайного процесса: сначала делается
три выстрела без разведки; точка 5 скачками переме'
щается из S(o) в SA), 5B), 5C). После третьего выстрела
производится разведка; выяснено, что цель не поражена.
и точка S возвращается в состояние 5 . Затем произ-
производится еще четыре выстрела (точка перемещается в Sr ,
St2\ 5 , 54), посылается разведка, обнаруживает,
что цель поражена, и стрельба прекращается (точка S
160
перескакивает из 54 в 5(т ), после чего продолжается
отсчет фиктивных выстрелов, если они еще не все из-
израсходованы.
Каждая траектория, подобная только что изображен-
изображенной, состоит из т скачков (перемещений) в фазовом
пространстве, причем всем фиктивным выстрелам, произ-
произведенным уже при состоянии 5 т , соответствуют «скачки
на месте» с возвращением в ту же точку 5 . После
каждого шага, на котором было применено управление U "
(выстрел с последующей разведкой), точка 5 может
только либо вернуться в 5<0 (если разведка сообщила:
«цель не поражена»), либо перейти в 5 (если разведка
Рис. 16.2.
сообщила: «цель поражена», и принято решение прекра-
прекратить стрельбу). Заметим, что решение прекратить стрельбу
совершенно бессмысленно принимать после известия
«цель не поражена», так как, имея в виду прекратить
стрельбу при любом сообщении разведки, было бы ра-
разумнее вовсе не посылать ее и не производить бессмыс-
бессмысленных затрат г.
Перед нами стоит задача — выбрать оптимальное
управление на каждом шаге, т. е. указать, какое из трех
управлений U ' , U 2 , U3 нужно применять на данном
шаге в зависимости от исхода предыдущего шага. Оче-
Очевидно, оптимальное управление должно зависеть от па.
раметров задачи: числа снарядов т, вероятности попа-
попадания р, стоимости снаряда s, стоимости разведки г
и «премии» А. Заметим, что при некоторых соотноше-
соотношениях параметров задача решается тривиально. Например,
если s > рА< т. е. средняя стоимость одного снаряда
больше средней выгоды, которую он приносит при одном
выстреле, стрелять вообще не имеет смысла, т. е. на все^с
\\ Е. С- Вентцель Щ
шагах нужно применять управление U . Если г > А
или г > ms, то не имеет смысла производить разведку
и управление £/B) не должно применяться ни на од-
одном шаге.
Рассмотрим общий случай (при любых значениях па-
параметров) и построим схему решения задачи методом
динамического программирования.
Прежде всего установим, из каких состояний в какие
переходит система под влиянием определенных управле-
управлений U ' , U2 , U3 и какой при этом получается сред-
средний выигрыш.
Из состояния 5 т система больше никуда перейти
не может; единственное возможное (оно же и оптималь-
C)
ное) управление есть U ; выигрыш wt (и, разумеется,
средний выигрыш wt) при этом на любом t-м шаге ра-
равен нулю:
^E(m))-^E(m)) = 0. A6.1)
Если система находится в состоянии S (О <I k <; т — 1),
то ее дальнейшее поведение и выигрыш на 1-й шаге зави-
зависят от управления.
Предположим, что применено управление £/A) (вы-
(выстрел без разведки). Система переходит из 5 в сле-
следующее по порядку состояние 5 +1 , если только не кон-
кончились все снаряды; если на очередном выстреле
кончились снаряды, система переходит в состояние 5 .
Выигрыш, который мы при этом получим, не зависит
от того, перешла система в о или во .Он со-
состоит из двух слагаемых: не случайного и случайного.
Не случайное слагаемое отрицательно и равно — s (мы на-
наверняка теряем при выстреле стоимость снаряда). Слу-
Случайное слагаемое положительно и представляет собой
премию, которую мы иа данном выстреле можем полу-
получить, а можем и не получить. Премия будет получена
на данном шаге, если соответствующий выстрел окажется
успешным, поразит цель. Найдем вероятность этого со-
события. Чтобы цель была поражена данным выстрелом,
необходимо, во-первых, чтобы она не была поражена
предыдущими k выстрелами, выпущенными с тех пор,
как было получено известие «цель не поражена»; кроне
162
того, Ьна должна быть поражена именно данным выстре-
выстрелом. Вероятность этой совокупности событий равна
•С такой вероятностью данный выстрел принесет нам
«доход» в виде премии А; с вероятностью 1 —A —р)кр
он не принесет нам дохода, т. е. принесет «доход» 0.
Осредним значения Л и 0 с учетом их вероятностей;
получим средний доход от данного выстрела
Вычитая из него стоимость снаряда s, получим пол-
полный средний выигрыш, приобретаемый на одном i-м шаге
при исходном состоянии системы S и управлении (Z1 :
^(S(*\ Ull)) = A(l— pfp — s. A6.2)
Предположим теперь, что к системе, находящейся
в состоянии 5( , применено управление U 2 (выстрел
с разведкой). Дальнейшая судьба системы зависит от того,
какое известие сообщит разведка. Если это известие бу-
будет «цель не поражена», то система перейдет в состоя-
состояние 5@; если «цель поражена», то система перейдет
в состояние S . Вероятность первого из этих событий
равна A—р)к+\ второго 1—A—р) +1.
Подсчитаем средний выигрыш при применении управ-
управления U . Он складывается из достоверного расхода
(стоимости снаряда и разведки), равного —(s-j-r), и сред-
среднего дохода, равного А{\—р)кр; итого
wt{S(k\ £/B))=ЛA—/?)*/? —(s+r). A6.3)
Предположим, что к системе, находящейся в состоя-
состоянии S , применено управление U 3 (стрельба прекра-
прекращена). Точка 5 переместится в S , а выигрыш (как
фактический, так и средний) будет равен нулю:
w,(S(ft), U{3)) = 0. A6.4)
Опираясь на эти данные, будем строить процесс оп-
оптимизации управления. Начнем с ш-го шага. Пусть
после (т — 1)-го шага система находится в состоянии
163
$pi-i (He нужно смешивать это состояние с точкой S 1 !).
Может быть два случая: либо мы уже находимся в точке
(т)
5(т) (стрельба прекращена):
е<т>
либо стрельба еще не прекращена, и тогда мы можем
находиться в любой из остальных точек:
£„,_, = S(ft) @ <k Cm—1).
В первом случае единственно возможным (и, очевидно,
оптимальным) будет управление Uy :
U*m(S^) = U{3)- A6.5)
Во втором случае возможно только два управления: £/A)
и U (так как посылать разведку после последнего вы-
выстрела уже не имеет смысла). Найдем средний выигрыш
на последнем шаге для каждого из этих управлений.
Если мы применим управление U (выстрел без раз-
разведки), то средний выигрыш на т-и шаге будет (см. фор-
формулу A6.2))
wm{S(k\ U{1))=:A(l—p)kp — s (fc = 0, 1 m—1).
A6.6)
C)
Если мы применим управление U (прекратим стрельбу),
то средний выигрыш на т-м шаге будет
*я(!?\ t/C)) = 0. A6.7)
Условным оптимальным управлением на т-и шаге
Um\S ) будет то, при котором этот средний выигрыш
достигает. максимума:
W*m(S{k)) = max{A(l-p)kp — s; о}. A6.8)
Таким образом, если
ЛA— р)кр — s>0,
то нужно выбирать на т-и шаге управление U ; если же
/Л1
— управление U . Оптимизация последнего шага за-
закончена.
164
Перейдем к оптимизации {т — 1)-го шага. Пусть
после (т — 2)-го шага система находится в состоя-
состоянии 5,„_2. Здесь снова могут быть два случая: либо
стрельба прекращена, т. е.
с _ с<т>
*Лп-2— ^
либо она еще не прекращена:
Если 5m_2==5im>, снова единственно возможным управ-
управлением является U , а максимальный средний выигрыш
на двух последних шагах равен нулю:
Um-i{S )=U ; Um-I.m'i ) = 0. A6.9)
Найдем условное оптимальное управление и условный
максимальный средний выигрыш на двух последних ша-
шагах при 5m_2 = 5(*) (Ифт). Для этого рассмотрим сред-
средний условный выигрыш Wm-i.m на двух последних ша-
шагах при любом управлении на (т — 1)-м шаге
и оптимальном управлении на т-и шаге. Посмотрим,
во что обращается этот выигрыш при управлениях U ,
£/<2), £/<3) на {т—1)-м шаге, и выберем среди этих трех
значений наибольшее.
Мы знаем, что система после т — 2 шагов находится
в состоянии 5( . Применим к ней иа {т—1)-м шаге
управление £/A). При этом однозначно определяется со-
состояние системы после (т—1)-го шага:
а средний выигрыш на (т—1)-м шаге определится фор-
формулой A6.2). Поэтому мы можем сразу написать вы-
выражение
A6.10)
Предположим, что применяется управление (/B). Вы-
Выигрыш Wm-\.m будет складываться из выигрыша «>m-i
165
на (m— 1)-м шаге (см. формулу A6.3)) и дважды осреД-
ненного максимального выигрыша на последнем шаге Wm-
Его мы найдем следующим образом. При заданном со-
состоянии S после (т — 2)-го шага и управлении U
система с вероятностью A —/>)*+1 перейдет в состоя-
состояние 5 ° . и тогда максимальный средний выигрыш на по-
последнем шаге будет равен Wm (S ° ); с вероятностью 1 —
— A —р) она перейдет в 5 , и тогда выигрыш на по-
последнем шаге будет равен нулю. Осредняя эти два вы-
выигрыша с учетом их вероятностей, получим
1) ) — (\—р) w [S )
— /7)*+W*0Slo)). A6.11)
Наконец, при управлении U на (т—1)-м шаге
средний выигрыш за последние два шага будет равен
нулю:
i^m-i иE(''| £/C)) = 0. A6.12)
Найдем максимальное из трех значений A6.10), A6.11)
и A6.12): _
w m-l,i
'т-Л.тУ
= max
= тах
lk)
А A _ Р)лр - (s -Ь г) + A - />)V; E@)).
0
A6.13)
То из управлений £/A\ £/B\ £/C\ при котором дости-
достигается этот максимум, и есть оптимальное условное управ-
управление £/m-i(S(ft)) на (т.— 1)-м шаге.
Совершенно аналогично оптимизируется любой (/-й)
шаг A < I < т). Фиксируем исход (I — 1)-го шага St_v
Если
с _ с<т>
166
то дальнейшее управление будет U3 и выигрыш на всех
последующих шагах нуль. Если
S,_, = S(ft) @<ft<l—1).
то дальнейшее поведение системы и средний выигрыш
зависят от управления. Если на i-м шаге применено
управление £/A), то
- A6.14)
Предположим, что на i-м шаге к системе, находя-
(к\ B)
щейся в состоянии 5 (Ифт), применено управление U .
Средний выигрыш Wf+i m будет складываться из сред-
среднего выигрыша wt на i-м шаге (см. формулу A6.3))
и дважды осредненного максимального выигрыша ,,
на всех последних шагах, начиная с (i-j-l)-ro. Этот
дважды осредненный выигрыш найдем с помощью сле-
следующих рассуждений. При заданном состоянии 5 после
(i — 1)-го шага и управлении £/B на i-м шаге система
с вероятностью A—р)ь+х перейдет в 5@>, и тогда мак-
максимальный средний выигрыш на последних шагах, начи-
начиная с (i-f-l)-ro, будет W*+i m(S@)) (этот выигрыш
мы уже находили, оптимизируя (i-j-l)-ft шаг); с вероят-
вероятностью 1—A—р) +1 система перейдет в 5(т), и тогда
средний выигрыш на всех последующих шагах будет ра-
равен нулю. Осредняя эти два выигрыша с учетом их ве-
вероятностей, получим
m(S@))- A6.15)
167
Наконец, если на i-м шаге будет применено управ-
управление LJ3 , средний выигрыш на всех последующих ша-
шагах будет равен нулю:
Wt.i+i m(S{k\ Ui3))=-.O. A6.16)
Найдем максимальное из выражений A6.14), A6.15),
A6.16):
: max
A(\-p)k p-
+
|, i-rl
\
A6.17)
To управление — if \ if f или U{3\ — при котором дости-
достигается этот максимум, и есть условное оптимальное упра-
вление на 1-м шаге t/fE(ft)).
Оптимизация первого шага выполняется по тому же
принципу, с той разницей, что исходное состояние 5<0>
не случайно и гипотез о нем делать не нужно.
Если к системе, находящейся в состоянии 5<0>, на пер-
первом шаге применено управление (/'*, то она переходит
в состояние S , и средний выигрыш будет
lfL') = Ар — s-\-W2, з mW). A6.18)
Если будет применено if \ то
-p)W2.s m{Syv)). A6.19)
Если будет применено U{ \ то
Wi,2 т(&0). U'3)) — Q. A6.20)
168
Оптимальное управление на первом шаге находится
из условия
= max\Ap — (s + r) + {l—p)Wia m(S(U>). ■ A6-21)
i
Таким образом, построение оптимального управления
случайным процессом закончено.
Рассмотрим конкретный пример. Пусть т=6; /7 = 0,2:
s = 1; г = 0,4; /4 = 8. Определим оптимальное управление.
Проведем оптимизацию последнего (шестого) шага.
Если после пяти шагов стрельба уже прекращена (SF)),
то применяем управление £/'31 (не стреляем) и получаем
на шестом шаге средний выигрыш W(>EF)) = 0. Если
после пяти шагов достигнуто состояние S(k) @ <; k < 5),
то выбор оптимального управления определяется знаком
разности:
A(l—p)kp — s; A6.22)
если она больше нуля, применяется управление Um, если
меньше нуля — управление £/C). Вычислим значения раз-
разности A6.22) для различных значений k и сведем их
в таблицу (см. табл. 16.1). В той же таблице в двух
нижних строках приведем оптимальное управление на
шестом шаге Ue{^) и соответствующий максимальный
средний выигрыш №6(S(ft)). В последнем столбце той же
Таблицы поместим те же данные для случая 55 = 5F).
Таблица 16.1 содержит полные результаты оптимизации
последнего шага. Их можно сформулировать следующим
Таблица 16.1
k
A(l-p)kp-s
0
0,60
0,60
1
0,28
0,28
2
0,02
0,02
3
<0
ЩЗ)
0
4
<0
y&)
0
5
<o
0
6
0
169
образом. Если произошло уже Пять выстрелов и послед-
последние сведения о цели (цель не поражена) поступили только
что (& = 0) или за один выстрел до того (&=1), или за
два выстрела {k = 2), то нужно произвести последний
выстрел, причем без разведки (управление t/1'). Если же
со времени получения последних сведений о цели уже
выпущено три или более выстрелов, то следует прекра-
прекратить стрельбу.
Таким образом, наше оптимальное поведение на шестом
шаге в точности определено, как бы ни развернулись со-
события на предыдущих пяти шагах.
Оптимизировать управление на пятом шаге будем,
пользуясь формулой A6.13) и имея в виду, что функ-
функция №(;(S(ft)) при любом k уже имеется в табл. 16.1. Здесь
мы должны будем сравнить не два, а три числа, соот-
соответствующие трем управлениям; но так как одно из них —
соответствующее управлению £/(' — всегда нуль, то выпи-
выписывать будем только два из них. Если оба числа окажутся
положительными, выберем то управление, которое соот-
соответствует большему из них; если одно из чисел будет
положительным, другое — отрицательным, выберем то
управление, которое соответствует положительному числу;
если оба будут отрицательными, выберем управление 1/C).
Данные сведем в табл. 16.2.
Таблица 16.2
ft
A(l-p)*p-s + Wl(^>)
A{\-p)*p-(s-\-r) +
0
0,88
0,68
yd)
0,88
l
0,30
0,26
t/<«
0,30
2
0,02
<o
yd)
0,02
3
<o
<o
0
4
<0
<0
U&)
0
6
_
—
0
Оптимизация пятого шага выполнена. Вывод: после
четвертого шага ни при каких условиях не нужно посы-
посылать разведку. Если сведения о цели получены только что
или за один или два выстрела до этого, то нужно сде-
170
лать пятый выстрел (управление £/A)), если же с момента
получения последних сведений о цели сделано три или
больше выстрелов, нужно прекратить стрельбу.
Составим аналогичную таблицу для оптимизации упра-
управления на четвертом шаге (табл. 16.3).
f/;(s<*)>
0
0,90
0,90
l/W. t/<2>
0,90
l
0,30
0,34
t/<2>
0,34
Таблица
2
0,02
0,07
t/<2>
0,07
3
<o
<0
0
16.3
6
—
—
t/C)
0
Оптимизация четвертого шага выполнена. Вывод: если
после третьего шага система находится в состоянии 5<С)
(только что получены сведения о цели), то на четвертом
шаге одинаково выгодно любое из управлений t/A). l/2) —
сделать выстрел и посылать или не посылать разведку.
Если сведения о цели получены за один выстрел или за
два до того, оптимальное управление будет [/ ) — сделать
выстрел и послать разведку. Если сведения о цели полу-
получены за три выстрела, оптимальное управление (/•' —
прекратить стрельбу.
Оптимизация третьего и второго шага проведена
в табл. 16.4 и 16.5.
При оптимизации первого шага нет надобности варьи-
варьировать результаты предыдущего. Состояние системы перед
первым шагом есть 5<0). Поэтому в соответствующей таб-
таблице будет только один столбец, отвечающий 5 (см.
табл. 16.6).
Процесс оптимизации управления закончен. Найдено
оптимальное управление: безусловное — на первом шаге
и условное на всех остальных:
, _U*6(Ss)).
171
= (t/j = t/l). С/г"(Si).
Таблица 16.4
ft
Ail-pfp-,+ VPl%t{S*^
A A — p)k p — (s -f- r) -f-
i /j p)k~lW* - fS(C))
0
0,94
0,92
0,94
l
0.35
0,46
0,46
2
0,02
0,08
u&
0,08
6
—
(/<3>
0
Таблица 16.5
>1A
ЛA
-pi
-p)
4
W*
2, 3, 4,
^~ ^3, 4, 5, 6 (S )
С
1,06
0,95
1,06
l
0,36
0,48
0,48
6
—
0
k
A(l — p)k p — S 4" W^2 3 4 5 6
A(\ — p)k p — (s4-''L~(i — p)k+11
*--n,,.,,e
Таблица 16.6
^3,4,5.бE<0))
0
1,08
1,05
1,08
Соответствующий средний выигрыш W*=l,08; другими
словами, максимальный средний деход, которого мы мо-
можем добиться, рационально комбинируя стрельбу с раз-
разведкой, равен 1,08. _ . . . — ^
172
Посмотрим, как происходит реализация оптимального
управления.
На первом шаге мы всегда применяем управление Uw,
т. е. делаем выстрел и не посылаем разведки. В резуль-
результате этого система переходит в состояние 5A>. При этом
состоянии, как видно из табл. 16.5, оптимальным упра-
управлением является U ' — сделать выстрел и послать раз-
разведку. Если разведка сообщит «цель поражена», то
стрельба прекращается, т. е: на всех последующих ша-
шагах применяется управление £/!'. Если же разведка сооб-
сообщит «цель не поражена», то система переходит в со-
состояние 5@>. При этом состоянии, как видно из табл. 16.4,
на третьем шаге следует применять управление U (сде-
(сделать выстрел и не посылать разведки), в результате чего
система перейдет в состояние 5 .
Обращаясь к табл. 16.3, находим оптимальное упра-
управление на четвертом шаге U (выстрелить и послать раз-
разведку). Если будет сообщено «цель поражена», стрельба
прекращается на следующем же шаге. Если будет сооб-
сообщено «цель не поражена», то система переходит в со-
состояние 5<0); из табл. 16.2 находим оптимальное упра-
управление на пятом шаге £/A> (выстрелить и не посылать
разведки). В результате этого управления система перей-
перейдет в состояние 5A>. Из табл. 16.1 видно, что при этом
оптимальное управление на шестом шаге снова есть 1
Рис. 16.3.
На рис. 16.3 представлена траектория точки 5 в фа-
фазовом лространстве при найденном оптимальном управле-
управлении, построенная в предположении, что первая разведка
сообщила «цель не поражена», а вторая—«цель поражена».
173
В нашем примере оказалось, что в состав оптималь-
оптимального управления U* входят только управления t/A> н lf2).
а управление £/C> появляется только в случае известия
«цель поражена». Это не всегда будет так. При других
параметрах задачи управление £/<3) может оказаться вы-
выгодным и без получения известия «цель поражена». Ре-
Рекомендуем читателю в качестве упражнения найти реше-
решение задачи со следующими параметрами:
m = 5; P = Y' A=l' s~ "g: r~Y'
Приведем для сверки оптимальное управление, которое
должно получиться при решении этой задачи:
u'=(i/l\ иа\ uil\ t/C), t/C)).
Данная стохастическая задача оказывается в каком-то
смысле «вырожденной», так как оптимальное управление
не случайно.
Литература
1. Р. Б е л л м а н, Динамическое программирование, ИЛ, Москва,
1960.
2. «Современная математика для инженеров». Сб. под редакцией
Э. Ф. Беккенбаха, ИЛ, 1958.
3. Е. С. В е н т ц е л ь, Введение в исследование операций.
Изд-во «Советское радио>, 1964.
4. А, А. К р а с о в с к и й, Г. С. Поспелов, Основы автома-
автоматики и технической кибернетики, Энергоиздат, М. — Л., 1962.
Содержание
Предисловие 3
§ 1. Задача динамического программирования 5
§ 2. Принцип поэтапного построения оптимального управ-
управления 11
§ 3. Задача о наборе высоты и скорости 15
§ 4. Задача выбора наискорейшего пути 26
§ 5- Непрерывная задача прокладки оптимального пути . 32
§ б. Общая постановка задачи динамического программи-
программирования. Интерпретация управления в фазовом про-
пространстве 39
§ 7. Общая формульная запись решения задачи оптималь-
оптимального управления методом динамического программи-
программирования 45
§ 8. Задача распределения ресурсов 54
§ 9. Примеры задач о распределении ресурсов 66
§ 10. Видоизменения задачи о распределении ресурсов . . 82
§ 11. Задача о распределении ресурсов с вложением до-
доходов в производство 87
§ 12. Другие разновидности задачи распределения ресурсов 99
§ 13. Распределение ресурсов с последействием 122
§ 14. Задачи динамического программирования с неаддитив-
неаддитивным критерием 136
§ 15. Стохастические задачи динамического программиро-
программирования 150
§ 16. Пример стохастической задачи динамического про-
программирования: совместное управление стрельбой
и'разведкой 157
Литература 174
Вент цель Елена Сергеевна
ЭЛЕМЕНТЫ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
М., 1964 г., 176 стр. с илл.
Редактор А. П. Баеоа
Техн. редактор С. Я. Шкляр
Корректор О. А. Бутусова
Сдано в набор 20/V 1964 г. Подписано к печати 14/IX 1964 г.
Бумага 84х 1087s-» Физ.-реч. л. 5,5. Условн. иеч. л. 9,02.
Уч.-изд. л. 8,13. Тираж 16 500 эк». Т-12867. Цена книги 24 коп.
Заказ М 436.
Издательство «Наука».
Главная редакция физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ленинградская типография № 2 имени Евгении Соколовой
«Главполигдафпрома» Государственного комитета Совета
Министров СССР по печати. Измайловский проспект, 29.