Автор: Фиников С.П.
Теги: математика геометрия дифференциальная геометрия учебное пособие исторические сведения курс лекций для мгу
Год: 1961
Текст
С. П. ФИНИКОВ
ДИФФЕРЕНЦИАЛЬНАЯ
ГЕОМЕТРИЯ
Курс лекций, читанный на механическом
отделении механико-математического
факультета МГУ
Допущено, Министерством высшего и сред-
среднего специального образования РСФСР
в качестве учебного пособия для универси-
университетов и педагогических институтов
ИЗДАТЕЛЬСТВО
МОСКОВСКОГО УНИВЕРСИТЕТА
1961
ГЛАВА 1
ВВЕДЕНИЕ
§ 1. Понятие линии
Геометрическое место точек называется регулярным ку-
куском линии, если в достаточно малой окрестности каждой
точки оно представляет простую дугу.
Простая дуга определяется двумя условиями:
1. Топологически она эквивалентна отрезку прямой.
2. В каждой точке допускает касательную, которая непре-
непрерывно вращается при перемещении точки касания.
Остановимся на первом условии. Более точно оно выра-
выражается словами: простая дуга гомеоморфна отрезку прямой,
где под гомеоморфизмом понимается взаимно однозначное,
непрерывное соответствие точек дуги и отрезка прямой.
Следовательно, дуга АВ гомеоморфна отрезку аЪ, если
каждой точке m отрезка аЪ соответствует одна определенная
точка М дуги, и обратно, каждой точке М дуги соответствует
одна точка отрезка аЪ, и это соответствие непрерывно.
Понятие непрерывности — обычное: всякому положитель-
положительному числу г можно сопоставить положительное число h. так,
что если расстояние пары точек
jo расстояние соответствующих точек дуги
МГМ2 < е,
и наоборот.
Чтобы установить соответствие гомеоморфизма, достаточ-
достаточно дать параметрическое представление трех текущих коор-
координат точки М дуги АВ (рис. 1)
*i-M0. *. = М0. *• = /•(') A.1:1)*
* В обозначении формулы A.1 : 1) первая цифра означает главу, вти-
втирая — параграф и третья — порядковый номер формулы в этом параграфа.
так, чтобы при изменении параметра t от t=a до t=b точка
М(хи х2, Хз) пробегала дугу АВ.
Если функции ft (t) класса С1, т. е. допускают непрерыв-
непрерывные производные первого порядка и на отрезке ab эти произ-
водные в нуль одновремен-
но не обращаются
=(-^J, A-1:2)
Рис.
то дуга А В — гомеоморфна
отрезку ab.
Действительно, будем
рассматривать параметр t
как абсциссу точки
m = m(t)
прямой ab. Тогда система
A.1 : 1) будет определять
соответствие точек m на от-
отрезке ab точкам М на ду-
дуге АВ; при этом мы предпо-
предполагаем, что
а = m (a), b = m (b),
т. е. значения t=a и t=b соответствуют точкам а и b отрез-
отрезка ab.
Это соответствие однозначно в силу однозначности функ-
функций A.1: 1); оно непрерывно в силу непрерывности этих
функций класса С1. Оно будет взаимно однозначно, если каж-
каждой точке М дуги АВ соответствует одно значение параметра /
на отрезке ab (a^CtKb). Таким образом, вопрос сводится к
решению системы A.1 :1) относительно параметра t. Заме-
Заметим, что достаточно найти одно определенное значение
t (a<t < b), удовлетворяющее одному из уравнений A.1 : 1)
для точки М дуги АВ, чтобы этому значению по формулам
A.1 : 1) можно было найти вполне определенную точку М.
§ 2. Теорема анализа о существовании неявной функции
Теорема. Если функция F(x, у) — класса С (т. е. допу-
допускает непрерывные частные производные 1-го порядка), то
для существования неявной функции
y = f(x), A.2:1)
определяемой уравнением F(x, у) = 0, необходимо и достаточ-
достаточно существование начальной точки, т. е. пары чисел х0, у0.
удовлетворяющих условиям:
a) F(xo,yo) = Q,
Ь) F, (*,».)* О, ру = -^.
При этом неявная функция A.2:1) удовлетворяет условиям
/(*) = »•. -Т----Т-- A2:2)
ах г у
Прилагая эту теорему к системе A.1 : 1), мы видим, что
для начальной точки можно взять любое значение t=t0
(а < t0 < b) и три числа Xi, которые получаются, если в си-
систему A.1 :1) внести значение t=to. Координаты x^tf,
t=to, очевидно, удовлетворяют каждому уравнению системы
Л(**.0 = М0-*| = 0, A.2:3)
ибо значения *° отсюда и были получены; следовательно,
условие а) удовлетворено. Что касается условия Ь), то, диф-
дифференцируя обе части уравнения A.2:3) по параметру t (мы
определяем параметр t), получим
но в силу неравенства A.1 :2) по крайней мере одна из про-
производных ft (to) отлична от нуля:
Ш + 0.
Если это будет для t=l, то мы возьмем первое уравнение
A.1:1). Начальная точка будет тогда удовлетворить требо-
требованиям а) и Ь).
Следовательно, существует однозначная дифференцируе-
дифференцируемая функция
которая для jci=jcJ принимает значение t=t0 и в
окрестности точки (х\, to), не выходящей для х-
дуги АВ, а для t за пределы отрезка ab,
летворяет первому уравнению A.1 :1); э
удовлетворять и двум другим уравнениям A.1 : 1), ибо зна-
значения х%, х3 были подсчитаны для значений / (а<<<&) по
формулам A.1: 1).
Таким образом, геометрическое место точек (х\, х2, х3),
определяемых из уравнений A.1 : 1) для значений а<<<6,
удовлетворяет первому условию «простой дуги». Оно будет
удовлетворять и второму условию. Чтобы доказать это, надо
определить касательную к нашей линии. Это будет удобнее
сделать, пользуясь векторным представлением уравнений
кривой.
§ 3. Вектор как функция скалярного аргумента
Радиусом-вектором точки М называется вектор ОМ, со-
соединяющий начало координат О с точкой М; его обозначают
одной буквой М полужир-
полужирного шрифта
Рис. 2
Если задана прямоуголь-
прямоугольная (правая) декартова сис-
система координат, то единич-
единичные векторы осей обозна-
обозначаются буквами 1*!, i2, h или
короче i, j, k (рис. 2). В
этом случае компоненты ра-
радиуса-вектора по осям пря-
прямоугольной системы совпа-
совпадают с координатами точ-
точки М, конца вектора
M=ix +ly + kz. A.3:1)
Вектор М будет функцией параметра t, если для всякого
значения t в некотором интервале, например на отрезке
a < t < b, дано значение вектора М или его координат (ком-
(компонентов) .
Задание вектора М как функции параметра / записывает
ся в виде
М = М (t).
П.3:2)
Это эквивалентно заданию координат точки M(xi,X2,x3)— ком-
компонентов вектора
*, = М0 (t = 1,2,3). A.3:3)
Вектор равен нулю, если все его координаты равны нулю.
Переменный вектор называется бесконечно малым поряд-
порядка Л, если все его координаты — бесконечно малые порядка
не ниже А и одна из координат точно порядка h, т. е. если мо-
модуль вектора — бесконечно малая порядка А.
Переменный вектор стремится к пределу (постоянному
вектору), если разность между переменным вектором и пре-
пределом — бесконечно малая
НтМ@ = А, если lim {M(t) - А} = 0. A.3:4)
Если три функции A.3 : 3) — класса С. то и вектор A.3 : 2) —
класса С1.
Производной вектора по переменному параметру t назы-
называется предел отношения приращения вектора к приращению
независимого переменного при стремлении этого приращения
к нулю
ЖПт Пт\ A.3:5)
dt д<-о Д< д<-о Af
Если приложить эту формулу к вектору A.3:1), то полу-
получим
Л* A±JA^kA ^L + j lim 4L +
dt д<~о Д/
+ klim-^-,
или
— = i — + j-*L+k —. A.3:6)
dt dt dt dt
§ 4. Касательная к линии
Рассмотрим уравнение A.3:2) как уравнение линии в
пространстве. Возьмем две точки М и Mi (рис. 3), которые
соответствуют значениям t и ti=t-\-ht.
Тогда хорда, соединяющая точки М и Mi, определяет
вектор
который назовем приращением радиуса-вектора
Отношение приращения радиуса-вектора к приращению
независимого переменного At
ДМ
представляет вектор, лежащий на секущей MMi, но при ма-
малых значениях приращения At длиной больше хорды ММЬ
При переходе к пределу при At-*0 точка Mi, спускаясь но
дуге М\М, в пределе совпадает с точкой М, длина хорды ЛШ»
л дм мк\
обращается в нуль, но отношение — = —— может сохра-
сохранить конечное значение. По определению секущая в пределе
займет положение касательной ММ' к линии в точке М. На
этой касательной и будет
. - лежать вектор производной
dt
Д/
A.4:1)
Теорема. Производная
от радиуса-вектора текущей
точки кривой имеет направ-
направление касательной к кривой.
Если рассматривать в
уравнении A. 3 : 2) пара-
параметр t как время, то урав-
уравнение A. 3:2) будет опре-
определять положение точки М
во всякий момент времени t>
(a<ct<b), т. е. определять
закон движения точки М.
Приращение ДМ, или лучше дуга ^уММ\, определяет при
этом путь, пройденный точкой М за промежуток времени At.
Рис. 3
Поскольку предел отношения дуги к хорде равен единице, то
lim — = lim — =1. A.4:2)
Mi-m ММг м^м |ДМ| v '
Отсюда прямо следует, что модуль вектора производной
радиуса-вектора текущей точки по времени равен линейной
скорости точки. Действительно,
dfA * * ДМ
= lim—,
dt л<-о At
как мы видели, определяет вектор касательной.
С другой стороны,
dt
НшНшС
4<~0 At 4<->0\ WiWiWt At
= llm( mmi ¦ W""HI )=lim
есть линейная скорость точки при ее движении по дуге
Отсюда производная радиуса вектора по времени есть век-
вектор линейной скорости движения точки по линии.
Теперь мы можем закончить теорему о параметрическом
определении простой дуги.
Мы доказали, что параметрическое представление линии
A.1 : 1) функциями класса С с условием A.1 :2) топологи-
топологически эквивалентно отрезку прямой. Теперь мы можем пока-
показать, что линия A.1 : 1) удовлетворяет и второму условию:
в каждой точке допускает касательную, которая непрерывна
вращается при перемещении точки касания.
Действительно, по формуле A.3:6) вектор касательной
d!H^ JJ A.4:3)
dt dt dt dt '
имея координатами производные функций A.1 : 1) класса С1
(непрерывно дифференцируемых), будет непрерывно вра-
вращаться при изменении параметра t, т. е. при непрерывно»
перемещении точки М по дуге АВ.
§ 5. Правила дифференцирования векторных функций
1. Производная суммы равна сумме производных от
гаемых
± (Мх + М2) = ^ + ^ A.
at dt dt
Действительно, приращение суммы функций складывает-
складывается из приращений слагаемых
Л (М2 + М2) =
отсюда
Нш Д(м1 + м.) = ,.ш длч + Иш дм, = ш^
<о Д< Д< ) Л/ Л
2. Производная произведения вектора на скалярную функ-
функцию <p(t)
-А (срМ) = ^ М + <Р —. A.5:2)
dt VT ' Л Т dt
Действительно,
Л (<рМ) = (ф + Аф) (М + AM) — фМ = Лср (М + AM) +
•откуда
д* д< ' ' ' ' д< '
= lim —— ¦ lim (M + AM)
ДМ dtp w , dm
— =—!-Л14-ф—.
д<~о М dt dt
3. Производная скалярного произведения векторов
A ^ ^ A.5:3)
(MlM2) ^M2 + Ml^
dt dt dt
Действительно,
A (MxM2) = (Mx + AMJ • (M8 + AM2) —
= AMX (M2 + ЛМ2) +
откуда
dt
= lim A (MtMt) = lim^-1 • lim (M2 + AM8)
<о Д< <о Д< д<о
\t dt m ' x dt
4. Производная векторного произведения векторов
— Ш ум ) = rfMt w jyj _i_ до у dlAt A 5:4)
10
Действительно,
Л (Mi X М2) = (Mi + АМХ) X (М, + АМ8) ч-
- Мх X М2 = АМХ X (М2 + АМ2) + Мх X АМ2.
Отсюда
*»>L = НшА(Ml х Мг) - Hm *&¦ X Urn(М, + АМ8) +
at д(^о А/ д(^о А/ д(->о
^б A* A 'N " ' l" dt
5. Производная скалярного произведения трех векторов
± (м,МА) - (-^ ма) + (м, -SJ! м.)
Действительно,
(МхМ^з) = (Mi X М2) М3,
но по формуле A.5:2) имеем
~ № X М2) М3} = [^- (М, X М2)] М3 + (Mx X М2)
и по формуле A.5:4)
^Г(М1ХМ2)^ХМ2 + М1Х^
at at at
Соединяя вместе, получим
± (М1М2М3) = (^- X М2) М3 + (Мх X -^-) М3
или
d • * * i r>
6. Теорема о дифференцировании сложной функции:
если M = M(s) и s=f(t), то
dM = dM^ 15
dt ds dt v
Действительно,
lin, lim(
dt д<-*о Д< д(-*о\ As Д<
,. AM,. As dM ds
As At ds dt
§ 6. Основные теоремы дифференциального исчисления
Для векторных функций не имеет места ни теорема Рол-
ля, ни теорема Лагранжа. Действительно, теорема Ролля
утверждает: если дифференцируемая функция y=f(x) обра-
обращается в нуль для х=а и для х=Ь, то ее производная
dy •
fa =f (x) обратится в нуль для некоторого значения х=с,
где а <Сс <Ь. Для векторной функции A.3 :2), если ее истол-
истолковывать кинематически (как закон движения точки), то точ-
точка М может два раза пройти через начало координат (где
радиус-вектор М = СШ обращается в нуль) без того, чтобы
производная — , т. е. скорость движения, когда-либо обра-
dt
щалась в нуль. Например, можно пройти весь замкнутый
путь с постоянной скоростью.
Ряд Тэйлора. Ряд Тэйлора с остаточным членом можно
написать и для векторной функции. Для этого надо разло-
разложить в ряд Тэйлора каждую координату вектора и, умножив
на единичные векторы осей координат, сложить почленно.
Если функция
xl = fl(t) (t = 1,2,3),
класса С (имеет непрерывную производную порядка п) в
интервале (t, t-\-h) и в точке t существует производная по-
порядка п-\-\, то имеет место разложение
U V + h)- Ш = hi (t) +-^-fi @ + .-
A.6:1)
где
Л-+0
12
Выписывая эти разложения для t=l, 2, 3, т. е. для трех
координат вектора A.3:3), умножая их на соответствующие
векторы Ilt Is, i3 и почленно складывая, получим по формуле
A.6:1)
М(* + А) — М @ = AM @ + ~- М @ + ...
••¦+^м^ + 1т)Гф(а)' (
где
(л+1)
М@
м
В частности, для л=0 имеем теорему о конечном приращении
векторной функции
A.6:3)
ГЛАВА II
ФОРМУЛЫ ФРЕНЕ
§ 1. Длина дуги линии
Если линия задана параметрическим уравнением
то первая производная по параметру t
dfA _ jr.
dt ~ * '
B.1:1)
B.1:2)
определяет вектор касательной, т. е. вектор, определяющий
направление касательной в точке М.
При замене параметра t на новый параметр s
s = <?(t), -?_=,р(*)>0 B.1:3)
производная B.1:2) изменится. Согласно теореме о диффе-
дифференцировании сложной функции A.5:6) имеем
dt
dfA ds
ds dt '
B.1:4)
Мы видим, что направление вектора не меняется, но мо-
модуль вектора
dM\2 _ /dM\2 / ds \z
dt ) ~\ds)'(dt )'
dfA
ds
dfA
dt
ds
dt
B.1:5)
ds
делится на производную —=w(t).
at
14
При подходящем выборе функции y(t) модуль производ-
производной приводится к единице
т_ _ j
ds ~
Тогда вектор касательной
-^=т B.1:6)
ds
становится единичным. Обозначим его буквой х. Параметр s
будем называть длиной дуги линии. Из формулы B.1 : 5) при
[—) = 1 получим
\ ds /
ds \2
dt ) ~\кТ) '
или, если воспользоваться формулой A.3:6),
ds \2 / dx \2 / dy \2 / йг \2
))+)+
откуда
ds* = (dx)* + (dy)* + (dz)*. B.1 : 7)
Эта формула совпадает с формулой, получаемой в анали-
анализе при определении длины дуги как предела периметров, впи-
вписанных (или описанных) ломаных линий при неограниченном
увеличении числа сторон, когда каждая сторона ломаной
стремится к нулю.
§ 2. Формулы Френе
Уравнение B.1:6) определяет первый из инвариантных
единичных векторов, связанных с изучаемой линией.
Лемма 1. Производная единичного вектора перпендику-
перпендикулярна к самому вектору.
Рассмотрим единичный вектор
х = х (s),
по определению тождественно для всех значений параметра
имеем
х»=1. B.2:1)
1*.
Дифференцируя это тождество, получим
ds
B.2:2)
Скалярное произведение равно нулю; следовательно, векто-
dx
ры х и перпендикулярны.
ds
Лемма 2. Если единичный вектор
= m(t)
вращается около неподвижной точки О и независимое пере-
переменное t означает время, то модуль производной — равен
dt
скорости вращения.
Действительно, рассмотрим два положения вектора: Otnt
в момент времени t=0 и От% в момент времени t=At. Эти
два положения Ortii и От2 определяют равнобедренный тре-
треугольник miO/Пг (рис. 4).
Обозначим
Дер =^
угол при вершине треуголь-
треугольника. Поскольку треуголь-
треугольник miOm2 равнобедренный
с боковыми сторонами
От{ = От2 — 1, основание
m\tn% равно
тхт% = 2 sin —2. = | Д m |.
Вектор m\tn2, очевидно,
равен приращению Дш век-
вектора
Рис. 4
ш
От.
Производная радиуса-вектора m по времени t равна пре-
пределу отношения приращений
dm *. Am
— = hm —,
dt и-а А<
а модуль производной — пределу модуля отношения прира-
приращений
НО
dm
di
2sin
Д/
= lim
Am
M
lim
д/-*о At
Sifl ~2
Дх Д/-»0
2
2
f
M
2
lim
Здесь первый множитель имеет пределом единицу, как отно-
отношение синуса к его аргументу; второй — производную угла
поворота Дф по времени, т. е. быстроту вращения вектора:
lim
Д9-0
sinT
Отсюда
= 1,
dm
dt
lim—^~
д<~о ^
2
d/ '
d'f
~dT
что и доказывает лемму.
Приложим теперь эти леммы к исследованию векторов,
инвариантно связанных с кривой в заданной точке, и скаляр-
скалярных (числовых) инвариантов — модулей этих векторов.
§ 3. Главная нормаль и кривизна кривой
При определении первого инвариантного вектора, когда
мы рассматривали производную от радиуса-вектора текущей
точки кривой по параметру /, мы воспользовались модулем
этого вектора, чтобы выбрать инвариантный параметр на кри-
кривой, который имеет простое геометрическое истолкование —
длина дуги кривой. Мы получили его, требуя, чтобы модуль
производной равнялся единице
dm
ds
1.
B.3:1)
Дифференцируя еще раз по длине дуги s, мы получим но-
новый вектор
d*M
ds1
d-c
ds
2 Заказ 1874
17.
инвариантный и по направлению, и по модулю, ибо дифферен-
дифференцирование ведется по инвариантному параметру.
Обозначим через v единичный вектор, определяющий на-
направление этой производной, и через k — модуль ее. Тогда
получим первую из формул Френе
as
В силу леммы 1 вектор V, коллинеарный вектору
B.3:2)
ds
, пер*
иендикул ярен к вектору т
iv = 0.
B.3:3)
Прямые, проходящие через точку М кривой перпендику-
перпендикулярно к касательной называются нормалями кривой. В про-
пространстве к заданной прямой (касатель-
(касательной) в заданной точке (точке касания)
можно провести пучок перпендикуляр-
перпендикулярных прямых (нормалей). Все они лежат
в одной плоскости, которая называется
нормальной плоскостью линии (рис. 5).
—Вектор v определяет одну из норма-
нормалей кривой. Поскольку мы нашли ее пер-
первой, будем называть главной нормалью.
В силу леммы 2 модуль производной
единичного вектора
d-z
ds
показывает быстроту вращения вектора
касательной х при перемещении точки
касания М по кривой.
Точнее следует сказать: если прове-
провести из начала координат О (или любой
неподвижной точки) вектор, равный
вектору х в точке М кривой,
От = х,
то при перемещении точки М по кривой вектор От будет вра-
вращаться около неподвижной точки О. Если при этом точка М
движется по кривой равномерно, так что в единицу времени
проходит единицу пути, то скорость вращения вектора будет
характеризовать величину искривления кривой и называется
кривизной линии.
Рис. 5
18
Кривизна k пространственной кривой существенно поло-
положительна. '
§ 4. Бинормаль и кручение кривой
Имея два инвариантных вектора: вектор касательной и
вектор главной нормали, мы можем инвариантно определить
третий дополнительный вектор, как векторное произведение
двух первых
p = xXv. . B.4:1)
Поскольку модуль векторного произведения равен произ-
произведению модулей множителей (в нашем случае единичных
векторов), умноженному на синус угла между ними (в на-
нашем случае прямой угол), вектор Р будет тоже единичным
вектором. По свойству векторного произведения он перпен-
перпендикулярен к обоим векторам х и v. Как вектор, перпендику-
перпендикулярный к касательной, вектор ? определяет вторую нормаль,
или бинормаль. Три вектора х, v и р образуют трехгранник
(триэдр) той же ориентации (правой), как оси принятой си-
системы (декартовых) координат xi, х2, х3.
Этот подвижной трехгранник, или репер, сопровождающий
точку М при ее перемещении по кривой, называется подвиж-
подвижным трехгранником или трехгранником Френе. (Френе пер-
первый написал формулы для производных по длине дуги трех
векторов х, v, р.)
Уравнение B.3 :2) представляет первую из формул Фре-
Френе. Чтобы получить вторую; заметим, что всякий вектор про-
пространства, в том числе и вектор — , может быть разложен
as
на компоненты по трем независимым векторам х, v, p. По-
Поскольку производная единичного вектора — перпендику-
ds
лярна к вектору v, она по этому вектору компонента не имеет,
и мы можем положить
— =ач + с$. B.4:2)
ds
Между тем, дифференцируя тождество B.3:3), получим
dx , dbt п
v \-t = 0.
ds ds
2* 19
Внося сюда значения B.3:2) и B.4:2), получим
v k v + х (ах + eg) = О,
или в силу
Х2 _ va _ \t xp = О,
а + k = О, т. е. а = — k.
Если обозначить коэффициент с греческой буквой каппа х,
получим вторую формулу Френе
*L = _?x + xp. B.4:3)
Теперь последняя формула Френе получается непосредст-
непосредственным дифференцированием тождества B.4:1)
dS
dx
ds
dv
-r-
ds
внося сюда значения B.3:2), B.4:3), получим
или в силу
v,
ds
— XV.
B.4:4)
Уравнения B.3:2), B.4:3) и B.4:4) образуют систему
уравнений Френе [к которой можно присоединить уравнение
B.3:1)]:
B.4:5)
dm
ds Г°С%'
dx
ds
dv
= — kt
ds
ds
= — XV.
Кроме единичных векторов х, v, p, она содержит два ска-
скаляра k и х, которые являются инвариантами в силу инвари-
инвариантности формул Френе. Первый из них k является кривизной
20
линии, второй х называется кручением линии. Прилагая лем-
лемму 2 к уравнению B.4:4), получим
ds
Следовательно, абсолютная величина второго инвариан-
инварианта х равна скорости вращения бинормали.
Если кривизна k существенно положительна (по самому
определению), то кручение х может быть и положительным
и отрицательным. Чтобы определить кручение по величине и
по знаку, рассмотрим произведение трех векторов
(ЛГ М" ЛГ),
где штрихами обозначено дифференцирование по длине дуги.
Пользуясь формулами Френе B.4:5), имеем:
М' = х,
ЛГ = Ь, B.4:6)
М'" = k' v 4- k (- ?х + хр) - — ?*х + Ыч + ?хр.
Отсюда
ЛГ X ЛГ = х X (Ь) = ?р, (ЛГ X ЛГI = k2. B.4 :7)
(М'ЛГМ"') - (ЛГ X ЛГ) Ж'".= *р (— k2 х + k' v + ,
и =
' x m")* ¦
B.4:8)
Рассмотрим теперь приращение радиуса-вектора ДМ при
переходе из точки Nlo=t\(so) в точку М = JA(so-{-h). Разлагая
в ряд Тэйлора, получим
М0М - М E0 + А) - М (s0)
1-2
1-2-3
B.4:9)
где
или в силу B.4 :6)
lim<I>3(so,A) =
= Ах0+ |-^04--уф8'
B.4:10)
21
где в силу B.4 : 6)
lim Ф, = — #-т0 + k'4o + *охоРо- B-4 : * О
Первые два члена разложения B.4:10) лежат в плоско-
плоскости векторов х, v, которая называется соприкасающейся плос-
плоскостью. Третий член в своей главной части (бесконечно ма-
малая третьего порядка относительно Д«=А) содержит член
Л»
При движении по кривой в положительном направлении,
т. е. в сторону возрастания As=h>0, направление смеще-
смещения М0М относительно бинормали {30 зависит от знака круче-
кручения хо, ибо кривизна k всегда полЪжительна. Отсюда:
Теорема. Если кручение хо>О, то точка М переходит по
кривой с одной стороны соприкасающейся плоскости на дру-
другую в положительном направлении бинормали; если хо<0, то
в отрицательном.
§ 5. Соприкасающаяся плоскость
Определение 1. Порядком касания линии с плоско-
плоскостью в точке Мо называется наибольшее целое число, строго
меньшее порядка малости рас-
расстояния РМ точки кривой М
от плоскости в окрестности их
общей точки Мо, если за бес-
бесконечно малую первого поряд-
порядка принимать приращение дли-
длины дуги As=wAf<j/W (рис. 6).
Определение 2. Сопри-
Соприкасающейся плоскостью линии
в точке Мо называется плос-
плоскость, проходящая через точ-
точку Мо линии и имеющая с
ней в этой точке касание наи-
рис< 6 большего порядка.
Обозначим буквойпединич-
буквойпединичный вектор нормали к 4выбран-
ной плоскости, проходящей через точку Мо кривой. Тогда
расстояние d=PM точки от плоскости равно проекции радиу-
радиуса-вектора MqM на вектор нормали, т. е. скалярному произ-
произведению
22
Пользуясь разложением B.4:10), получим
B.5:1)
lim Ф8 = — ?§т0 + /г'очо
a) Если пх0 Ф0, т. е. касательная пересекает плоскость,
го порядок малости d равен 1, порядок касания равен нулю.
Линия пересекает плоскость.
b) Если
nxo = 0, nvo^O, B.5:2)
то первый член в разложении B.5:1) пропадает, порядок ма-
малости d определяется вторым членом
и будет равен 2. Порядок касания равен 1. Линия касается
плоскости.
Из равенства B.5:2) следует перпендикулярность векто-
векторов п и х0. Вектор касательной х0 проходит через точку Мо
плоскости и перпендикулярен к перпендикуляру п плоскости,
следовательно, лежит в плоскости.
Следствие. Линия касается плоскости, если ее касатель-
касательная лежит в этой плоскости.
с) Если
пх0 = 0, nv0 = 0,
то вектор перпендикуляра п к плоскости параллелен бинор-
бинормали Ро, плоскость содержит касательную и главную нормаль
линии.
Порядок малости d определяется третьим членом разло-
разложения B.5: 1)
-J пФ3 = -? *охвпРо = ?¦ Vo B.5 :3)
и равен 3; порядок касания равен 2. Это наибольший порядок
касания плоскости с кривой в общей точке, ибо произведение
B.5 :3) может обратиться в нуль только при условии, что
в этой точке обращается в нуль кривизна ko=0 или кручение
ко — 0, а это особенные точки линии.
Теорема. Соприкасающаяся плоскость проходит через ка-
касательную и главную нормаль; она имеет с кривой касание
второго порядка.
23
§ 6. Соприкасающаяся окружность
Определение. Соприкасающейся окружностью ли-
линии в точке Мо называется окружность, проходящая через-
точку Мо и имеющая с линией в этой точке касание наиболь-
наибольшего порядка.
Понятие порядка касания остается прежним. Определим
кратчайшее расстояние от точки М пашей линии до заданной
окружности. Для этого до-
^ статочно опустить из точ-
точки М перпендикуляр MQ
на плоскость окружности и
соединить основание пер-
перпендикуляра Q с центром
окружности С. Одна из то-
точек (Я, Р') пересечения пря-
прямой CQ с окружностью дает
кратчайшее расстояние PQ
от точки Q до окружности,
другая — наибольшее P'Q.
Соединяя точки Р и М, по-
получим прямоугольный тре-
треугольник с гипотенузой РМ.
Следовательно,
=* ~PQ* -j- QM*.
Рис. 7
Порядок малости РМ равен наименьшему из порядков мало-
малости PQ и QM. _^
a) Порядок малости QM — расстояния от точки М до пло-
плоскости— определяется порядком касания линии с плоскостью
(рис. 7). Наибольший порядок касания (второй) в обшей точке
линии достигается соприкасающейся плоскостью. Строим в
точке Мо соприкасающуюся плоскость; расстояние QM будет
бесконечно малым 3-го порядка по отношению к дуге
A = wAfoAf.
b) Теперь нам надо подсчитать порядок малости отрез-
отрезка PQ. Оба отрезка PQ и P'Q выражаются через CQ и радиус
окружности R:
PQ=CQ—R, P'Q=CQ+R;
но P'Q при М->М0 стремится к пределу 2#. Следовательно,
порядок малости PQ совпадает с порядком малости
B.6:1)
Отрезок CQ можно получить, проектируя на плоскость
(хо> vo) вектор CM — MqM—М0С. Пользуясь разложениями
B.4 : 10), B.4 : 11) и отбрасывая члены с вектором Р, получим
до бесконечно малых Л3 включительно
где M0C=Rv0; внося это в B.6:1), получим до ft3 включи-
включительно
= h*(\-Rkt) l-h*Rka.
Чтобы величина 6 была бесконечно малой 3-го порядка,
надо взять
1-#*0 = 0, т. е. ?0= ±-. B.6:2>
Тогда порядок малости б определится членом —h3Rko
и будет равен 3, т. е. такой же, как и порядок малости QA1.
Порядок малости расстояния РМ от точки М до окружности
тоже равен трем; порядок касания 2, и мы получаем сопри-
соприкасающуюся окружность.
Формула B.6: 2) показывает, что радиус соприкасающей-
соприкасающейся окружности равен радиусу кривизны, т. е. обратной вели-
величине кривизны. Центр соприкасающейся окружности назы-
называется центром кривизны.
§ 7. Кинематическая интерпретация
С каждой точкой кривой связан трехгранник Френе. Все
эти трехгранники — ортогональны, правые с единичными
векторами осей. Такие трехгранники все конгруэнтны. Поэто-
Поэтому мы можем рассматривать их как различные положения
одного трехгранника, перемещающегося вдоль кривой вместе
с его вершиной М, которая описывает кривую. При этом мы
будем рассматривать равномерное двил?ение, когда верши-
вершина М, описывая кривую, проходит в единицу времени едини-
единицу пути, т. е. будем полагать s=f.
Движение трехгранника Френе надо рассматривать как
движение твердого тела. Известно, что всякое перемещение
твердого тела можно разложить на два перемещения: 1) по-
поступательное, когда все точки тела перемещаются на один и
тот же вектор, и 2) вращательное, когда твердое тело совер-
совершает поворот около неподвижной оси. Такое разложение воз-
возможно и при инфинитезимальном смещении. В частности,
мгновенная скорость твердого тела разлагается на поступа-
поступательную и вращательную.
1. Скорость поступательного движения можно принять
равной скорости любой точки тела. Для движения трехгран-
трехгранника Френе скорость поступательного движения определяет-
определяется как скорость вершины трехгранника.
2. Если скорость поступательного движения вычесть из
скорости каждой точки тела, то полученное движение будет
Рис. 8
представлять вращение. Действительно, для второго компо-
компонента движения точка М — вершина трехгранника — не пе-
перемещается. Если при движении твердого тела имеется непо-
двнжКая точка, то в каждый момент движения найдется i<
неподвижная прямая — мгновенная ось вращения.
Можно наглядно представить эту операцию (рис. 8). Про-
Проведем из неподвижной точки, например начала координат,
векторы, равные (а следовательно, параллельные) единич-
единичным векторам осей трехгранника Френе. Новый трехгранник
имеет, очевидно, неподвижную вершину. При движении трех-
трехгранника Френе вдЪль кривой трехгранник с вершиной в на-
начале будет поворачиваться так, что его оси остаются парал-
параллельными осям трехгранника Френе.
Вектор скорости вращения определяется условиями:
а) модуль вектора равен производной —, где t — время
Ш
и ф — угол поворота,
26
b) вектор скорости вращения откладывается на оси вра-
вращения (или ей параллелен);
c) положительное направление определяется условием;
если ось вращения совпадает с третьей осью репера е3, то
вращение в положительном направлении идет от оси t\
к оси е2.
§ 8. Определение линейной скорости точки
по заданному вектору мгновенной скорости вращения
Предположим, что заданная скорость вращения отложена
на оси е3 ортогональной системы координат
следовательно, тело вращается около оси е3. Рассмотрим
точку т вращающегося тела, расположенную на оси ei на
расстоянии г от оси вращения
(рис. 9).
Если бы точка т = ге! рав-
равномерно вращалась с этой
скоростью, то она описывзла
бы окружность с центром О в
плоскости векторов (ei, ea)
в направлении от t\ к е2. По-
Поскольку скорость вращения
равна —, за время dt тело
at
повернется на угол d<p (в аб-
абсолютной мере углов) и точ-
точка т пройдет по окружности
радиуса г расстояние rdy; от-
отсюда линейная скорость точ-
точки m равна г — . Линейная
dt
скорость направлена по касательной к траектории в направле-
направлении движения, т.е. от ei к е2; а так как касательная к окруж-
окружности в точке m перпендикулярна к радиусу в точке касания,
то вектор линейной скорости точки m перпендикулярен к
вектору ei и параллелен вектору ег, а при положительном
вращении и одинаково направлен. Отсюда
V =
Рис. 9
dt
27
но
Эта формула
От.
B.8:1)
верна для определения линейной скорости любой точки /И
твердого тела
B.8 : 2)
где О — произвольная точка оси вращения (рис. 10).
Действительно, опус-
опустим из точки М перпен-
перпендикуляр на плоскость
(е1( е2) и пусть основа-
основанием перпендикуляра бу-
будет точка т на оси ei.
Очевидно, все точки пря-
прямой тМ, параллельной
оси вращения, вращают-
ся с одной и той же ли-
линейной скоростью, и ту
Рис. Ю же скорость получим по
формуле B.8:2).
Действительно, если
обозначить буквой R расстояние точки М от начала О и бук-
буквой 0 угол наклона вектора ОМ к оси е3, то по формуле
B.8:2) получим
v = V X О~М = е»-^. Х0М = e2tfsin О- -*L,
dt dt
так как вектор ег перпендикулярен к плоскости (е3, е^, ко-
которая содержит вектор ОМ, a Rsinb равно произведению мо-
модулей ОМ и е3, умноженному на синус угла между ними; из
прямоугольного треугольника ОтМ имеем
r=R sin6
и окончательно
v = е,г
dt
B.8:3)
Таким образом, линейная скорость точки v и скорость враще-
вращения V связаны соотношением B.8:2).
28
Если скорость вращения разложить на два компонента
то и линейная скорость v разложится на два компонента:
v - (vt + v.) х ом = vt х бм + v, х дм = Vl + vt.
§ 9. Компоненты вектора скорости вращения
трехгранника Френе
Уравнения Френе дают линейные скорости точек ти т^,
т3, лежащих на концах единичных векторов:
х = 6mlt v = 0mit р = 0та,
проведенных из начала координат параллельно касательной,
главной нормали и бинормали.
Разбиваем уравнения Френе на две подсистемы, сохраняя
в первой только члены с инвариантом k, а во второй только
с х.
Перваяподсистема Вторая подсистема
ds
4.4 ,
— --
B.9:1)
dx
ds
dv
ds
dp
ds
= 0,
= —XV.
B.9:2)
Мы рассматриваем только вращение трехгранника, или.
лучше, движение параллельного трехгранника с вершиной
в начале координат. Полагая (рис. 11)
От i = mlf Om, =
имеем для первой подсистемы
dnii « dnif
0/nsx=
dm,
ds
m8,
= 0.
B.9:3)
Последнее уравнение показывает, что точка /п3 стоит на
месте, а поскольку и точка О неподвижна, то осью вращения
служит ось Огпз (бинормаль). Следовательно, вектор скоро
вращения будет иметь вид
1 * dt
29
Внося это выражение в формулу B.8:2), получим для линей-
линейных скоростей B.9:3)
-a-*
откуда
dt
B.9: 4>
Вторая подсистема B.9 :2) приводит к уравнениям
as
^ = 0,
as
-5-=
as
B.9:5)
неподвижны точки тп.\ и О, ось вращения От» (касательная);
вектор скорости вращения имеет вид
dt
Внося эти выражения в формулу B.8:2), получим
—»
¦*-
30
откуда
-*.«„. V2 = xx.
Вторая подсистема приводит к вращению со скоростью
V2=xx. B.9:6>
Складывая оба компонента B.9:4) и B.9:6), получим
полную скорость вращения
Ф = Щ + хх. B.9 : 7>
Два компонента скорости вращения вместе со скоростью
поступательного движения, которая совпадает со скоростью
движения точки М по линии и равна х, позволяют хорошо
описать движение трехгранника.
В каждый момент трехгранник движется в положитель-
положительном направлении вектора касательной х. При этом первый
компонент скорости вращения &Р поворачивает касательную х,
т. е. направление скорости поступательного движения, около
бинормали, т. е. в соприкасающейся плоскости, и, таким об-
образом, в первом приближении позволяет точке М описывать
кривую. Второй компонент скорости вращения хх вращает
соприкасающуюся плоскость около касательной. Поступа-
Поступательное движение вдоль касательной и вращение около каса-
касательной придает перемещению трехгранника характер винто-
винтового движения, а для самой касательной напоминает закру-
закручивание нити, откуда и происходит название кручения дл»
инварианта х, определяющего.быстроту такого закручивания.
Двум знакам кручения соответствуют два направления
винтового движения. При положительном знаке хх трехгран-
трехгранник вращается около касательной от главной нормали к би-
бинормали, т. е. так, как ввинчивается обыкновенный буравчик.
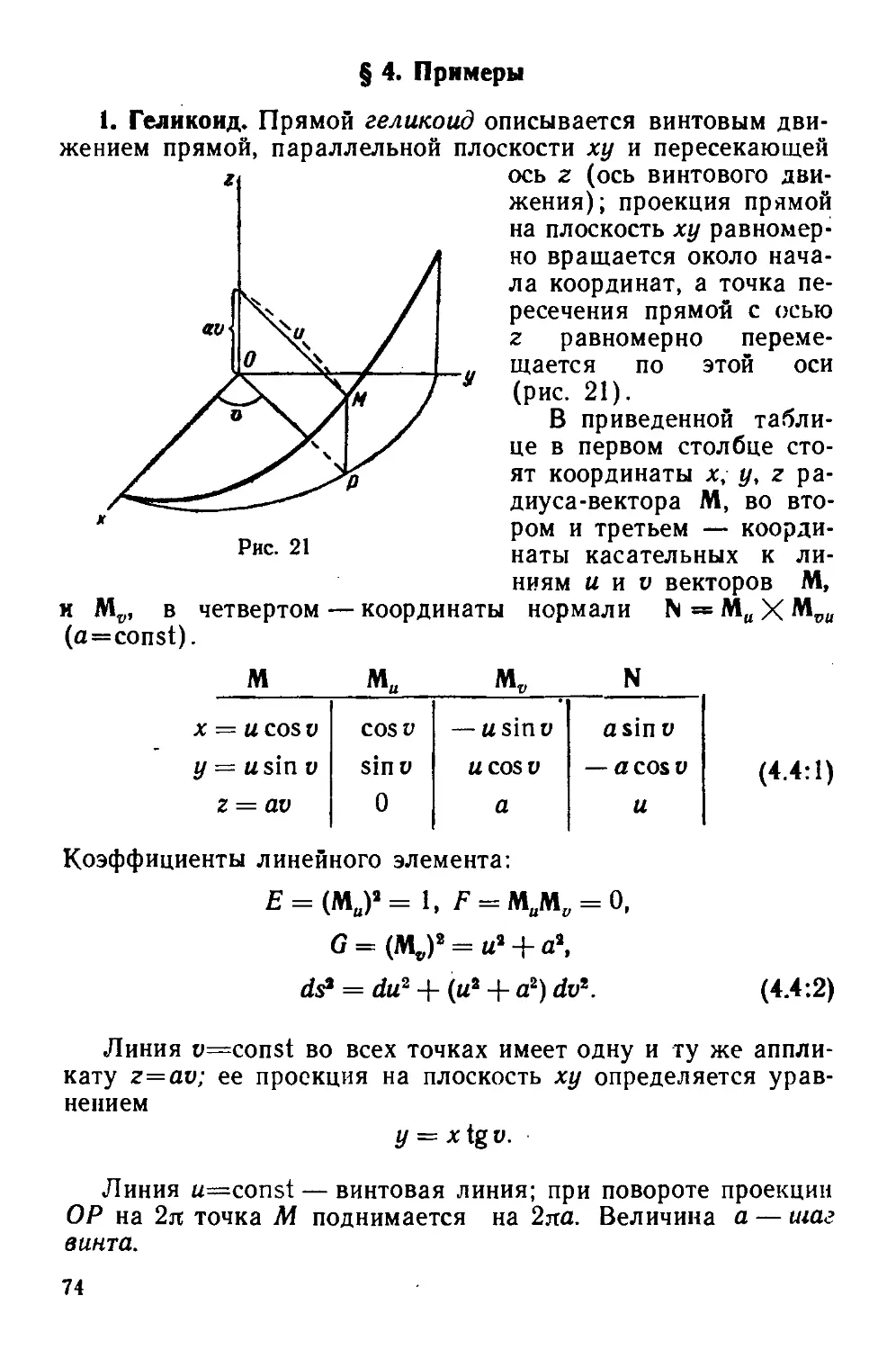
§ 10. Примеры интегрирования натуральных уравнений
кривой
Уравнения Френе B.4:5) содержат, кроме единичных
векторов х, v, p и их производных, только два инварианта k
и к. Теорема о существовании линии (и только одной с точ-
точностью до положения в пространстве) для заданных функ-
функциями длины дуги s двух инвариантов k и к— будет доказа-
доказана позднее B.12).
Уравнения
*«/(s), x = g(s), B.10:1>
определяющие линию, носят название натуральных уравнений
кривой, ибо не зависят от системы координат. Задача опре-
определения уравнений A.1 :1) в параметрическом виде для трех
текущих координат называется интегрированием натуральных
уравнений кривой.
Теперь мы рассмотрим несколько замечательных случаср
интегрирования натуральных уравнений.
Первый пример. Дано k—0.
Первое уравнение B.4 :5) запишется
dM _ dx
ds ' ds
Второе уравнение показывает, что
стоянное значение
х = х0 = const.
Интегрируя первое уравнение
М = xos -+- Мо>
0.
вектор х сохраняет по-
dM
~d7~^'
где Мт — постоянный вектор. Если обозначить
векторов
М (х, у, г), Мо (х0, у0, zQ), х (а, р, у),
получим
B.10:2)
координаты
то уравнение B.10:2) запишется в виде уравнений прямой
линии
х — хщ = у — yt = г—г, =g
a fi ¦ 7
Второй пример. Дано кручение х = 0. Теперь третье урав-
уравнение Френе будет
iL = 0Hp = po = const.
ds
Выберем оси неподвижной системы координат так, чтобы
единичный вектор Jj третьей оси был параллелен постоянному
вектору 00- Тогда векторы Ji, J2 будут перпендикулярны к би-
бинормали. Касательная t и главная нормаль v будут разла-
разлагаться только по векторам J^ J2. Обозначая буквой 6 угол
касательной t с вектором J,, можем записать
-с = J1cos6 -f- Jjsin6,
v = — Jx sin 0 -f J2 cos 6.
32
Внося эти значения в остальные уравнения Френе:
ds ds
получим
k =
df)
ds
B.10:3)
О
У
Рис. 12
Если кривизна задана уравнением B.10:1)
то, интегрируя, получим
где 60=const — начальное значение функции
3 Заказ 1874
B-10:4)
B.10:5)
33
Интегрируя уравнение
^L = , = j, cos (? + 0O) + J2 sin (? + 60), B.10 :6)
as
или
= Jt (cos «f cos 0o — sin <p sin Go) -f- J2 (sin <p cos Go -f cos <p sin 90),
получим (рис. 12)
M г- Мо = Jj (x cos 0o — у sin 0о) + J2 (x sin % + ycos %), B.10 :7)
где
s
Мо = const и х = J cos <p ds, у = J sin <f
Нетрудно заметить, что новые координаты
м = xjt + yj2)
где
ds
соответствуют переходу к новой системе координат, поверну-
повернутой на угол о. с началом в точке Mo=JiXo-|-J2}'o или, ина-
иначе, соответствуют перемещению плоскости вместе с кривой:
поступательно на вектор Mo=JiXo+J2l'o и повороту на
угол 60.
Теорема. Задание кривизны функцией длины дуги опреде-
определяет линию на плоскости с точностью до произвольного пере-
перемещения на плоскости.
Третий пример. Найти линии, у которых кручение пропор-
пропорционально кривизне с постоянным множителем пропорцио-
пропорциональности
x = lk, X = ctga = const. B.10 ; 8)
Составляем линейную комбинацию из первого и третьего
уравнений Френе
ds
34
В силу B.10:8) члены с вектором v сокращаются и мы полу-
получаем
— (Х-с + S) = 0 или — (xcosa-|-S'sin'a)= 0.
ds ds *
Поскольку производная равна нулю, вектор
п = х cos a -f p sin a
B.10:9)
будет постоянным; его квадрат равен единице, «мы его примем
за единичный вектор оси г.
Умножая почленно равенство B.10:9) на векторы х, v, f$
получим:
nx = cosa, nv = 0, n? = sina.
Первое равенство показывает, что касательная образует
постоянный угол а с осью г.
Спроектируем нашу линию на плоскость ху. Проектирую-
Проектирующие прямые (перпендикуляры, опущенные из точек кривой
Рис. 13
на плоскость ху) образуют' цилиндр, на котором лежит наша
линия. Так как все образующие цилиндра имеют направле-
направление оси z, то линия B.10: 8) пересекает все образующие ци-
цилиндра под постоянным углом я (локсодрома прямого ци-
цилиндра).
Разрежем цилиндрическую поверхность по двум образую-
образующим и развернем на плоскость. Тогда линия B.10:8) будет
пересекать под постоянным углом а все ординаты (прямые,
параллельные оси у, если развернутую плоскую направляю-
35
щую цилиндра принять за ось х); следовательно, после раз-
развертывания наша линия станет прямой.
Линии, определяющие кратчайшие расстояния на поверх
иости между двумя ее точками, называются геодезическими;
на плоскости это будут прямые линии. Когда наш лист бума-
бумаги навернем обратно на цилиндр, прямая amb (рис. 13) зай-
займет положение АМВ, но сохранит свойство определять крат-
кратчайшее расстояние в некоторой области поверхности и, сле-
следовательно, будет геодезической линией цилиндра.
Обозначим буквой s длину дуги AM, буквой а длину ду-
дуги АР. После развертывания они образуют вместе с отрезком
образующей цилиндра рт прямоугольный треугольник арт
с острым углом а при вершине т. Следовательно,
ар = am-sina, pm = am-cosa, B.10:10)
или o = s-sina, г — Z0 = s-cosa. B.10:11)
Радиус-вектор точки М можно представить суммой
М = Р + Р& = Р + п (г—г0). B.10:12)
Для координаты г—z0 мы имеем второе уравнение
B.10: 11), вектор п — единичный вектор оси z; остается толь-
только определить направляющую цилиндра
как плоскую линию. Для этого надо найти кривизну направ-
направляющей. Дифференцируя по длине дуги s равенство
М = Р -f ns-cosa,
получим
dP da ,
х = 1- n cos a.
da ds
Но — = T — единичный вектор касательной . к направляю-
аа
Ля
щей; между тем —-=sina в силу первой формулы B.10:11);
as
следовательно,
х = Tsina -fncosa.
Дифференцируя еще раз, получим
— = ^-sina, или hi = /CNsin2a.
as da is
Здесь v — главная нормаль линии (М), N — нормаль пло-
плоской кривой (Р); если К — кривизна плоской кривой — поло-
положительна, то N = v и
k = К sina а, или К = —— , B.10:13)
sin» a
что и требовалось найти.
Линии, определяемые уравнением B.10:8), которые мы
рассматривали, называются общими винтовыми линиями.
Замечательный специальный случай определяется урав-
уравнениями
k = const; x = const.
Отсюда по формуле B.10:13) кривизна К плоской на-
направляющей цилиндра будет тоже постоянна. Уравнения
B.10:4), B.10:5), B.10:6) второго примера легко теперь
интегрируются. Отбрасывая постоянные интеграции, имеем
ds
х = —j-sin(Ks), y = -l-cos(Ks),
А А
откуда
"•+*¦-?•
направляющая цилиндра — окружность.
Следовательно, линии постоянной кривизны и постоянного
кручения — винтовые линии круглого цилиндра, или обыкно-
обыкновенные винтовые линии.
Частным случаем обыкновенной винтовой линии для
<*= — будет окружность. Действительно, при а= — винто-
вая линия сечет образующие ортогонально и совпадает с на-
направляющей цилиндра.
§ 11. Эйлеровы углы
При интегрировании уравнений Френе B.4:5) дополни-
дополнительным затруднением является то, что координаты векто-
векторов х, v, p должны удовлетворять, кроме того, конечным со-
соотношениям, вытекающим из ортонормированности трехгран-
трехгранника Френе
x" = vl = pl=l, tv = vp = px = O. B.11:1)
37
Так как на девять координат векторов "с, v, $ накладывает-
накладывается 6 соотношений, то независимых координат, определяющих
поворот трехгранника
около начала О, останет-
останется три. Эйлер ввел эти
три угла.
Если два ортонорми-
рованных правых трех-
трехгранника имеют общую
вершину, то одним из
этих углов будет угол
между векторами треть-
третьих осей (рис. 14)
X = ^ е3Ое3 .
Линия § пересечения
плоскостей (еь ег) и
(e'ii е'г) будет перпендику-
перпендикулярна к обоим векторам
е3 и е'з, потому что она
лежит в плоскостях, пер*
пендикулярных одна из
рис 14 них к вектору е3, другая к
вектору е'3. Следователь-
Следовательно, повернув на угол %
около оси § второй трехгранник, мы совместим ось е'3 с осью е3.
Если предварительно повернуть первый трехгранник около
оси е3 на угол
Т 1 v9
а второй — около оси ь3 на угол
то будут совмещенными и оси ej
Остается выразить векторы (
е,
е2, е3 через
е2> ез
Для этого мы проведем еще векторы % ц' так, чтобы векторы
§, 4i e3 и §', *j', e^ определяли ортонормированные трех-
трехгранники.
Тогда последовательность преобразований, переводящая
репер (ei, e2, е3) в репер (e'F e2, е3), будет от трехгранника
(е^е^е,) к (§, % е3), затем к (§, ц', е^) и, наконец, к(е|,е^, tQ.
Каждый раз два соседних трехгранника имеют общую ось:
для первой пары — вектор е3. для второй — §, для тре-
третьей — ej.
38
В первой паре преобразуются векторы еъ еа в векто-
векторы §, г\ по правилу преобразования декартовых прямоуголь-
прямоугольных координат поворотом на угол ср:
§ = e1cos<f-f e2sin'f, ^ = — ej sin <p + е2 cos ®; (a)
во второй паре преобразуются % е3 в -ц', е, поворотом на
угол X:
4/ = qcosx + e,sinx; е^ = — qsin х + e3cosx; (b)
в третьей паре векторы §, rj' преобразуются eej, e^ пово-
поворотом на угол ф = ^ §OeJ:
ej = \cos ф-f *j'sirup; е2 = — §sirn()-f n^'costp. (с)
Исключая последовательно §, »j, ч', получаем сначала
Ч' = (— exsin(f -f e2 cos <f) cos x-f e3sinx,
eg = — (— ex sin <p -f e2 cos <p) sin x -f e3 cos x.
затем
ej = (e1cos<f-f easin<f)cos(() -f {( — ej^sin^-f e2cos<f) cosx-f
+ essinx}sini|i,
e'2 = — (ex cos <p -f e, sin <p) sin ф -f
-f {(— ex sin <p -f e2 cos <p) cos x -f вз sin x} cos ф,
наконец
ej=ex (cos <f cos ф — sin <f sin ф cos x) +
-f- e2 (sin <f cos ф + со5<р51пф cos x) + e8 sin ф sin %,
e'2 = — ex (cos <p sin ф -f sin <p cos ф cos x) —
— eg (sin <p sin ф — cos <p cos фсов х) + e3 cos ф sin x»
eg = exsin<f sinx — e2cos<f sinx + e3cosx. B.11: 2)
Если (e1, e2, e3) — векторы ортонормированного репера,
то для любых заданных углов <р, ф, % репер (ej, e2, е^) бу-
будет ортонормирован и таким образом в виде B.11:2) полу-
получим все единичные, прямоугольные правые трехгранники про-
пространства.
39
§ 12. Интегрирование натуральных уравнений
пространственной кривой
Обратимся теперь к уравнениям Френе B.4:5) и будем
искать трехгранник Френе в виде B11:2), полагая векторы
*[, е2, е^ равными х, v, 0 и принимая векторы е1, е2, е3
ва базисные векторы Jv Ja,' J3 неподвижной декартовой
системы координат:
х = Jx (cos <p cos ф — sin <p sin ф cos х) +
+ J2 (sin <р cos ф -f cos ? sin Ф cos X) + J3 sin ф sin %,
v= —Jx (cos <p sin ф-f- sin <p cos ф cos x) —
— J2 (sin <p з!пф — cos ф cos1^ cos x) -f J3 cos ф sin x,
P = Jx sin <p sin x — J2 cos <f sin x + J3 cos x-
B.12:1)
Тогда, обозначая через х, у, z текущие координаты точки М,
запишем первое уравнение B.4: 5), B.12: 1) в виде системы1.
dx
us
= cos <p cos ф — sin cp sin ф cos x.
-У- = sin <p cos ф + cos 9 sin ф cos у,
ds
-2- = sin ф sin x.
ds т Л
B.12:2)
Что касается второго уравнения Френе B.4:5), то в силу
шести конечных соотношений B.11:1) мы получим только
3 независимых уравнения. Дифференцируя третьи компонен-
компоненты векторов х и v и второй компонент вектора 0 получим:
dtp sin ф
ds sin x
—?- = k — x sin Ф ctg у,
ds
— = И COS ф.
ds r
B.12:3)
Система уравнений B.12:2), B.12:3) является системой
Коши для неизвестных функций х, у, z, <p, г|), х, ибо разрешена
относительно производных от неизвестных функций и имеет
40
регулярные правые части. Следовательно, система допускает
одно и только одно решение в виде регулярных функций:
x = x(s), y = y(s), z = z{s), <p = ?(s),
удовлетворяющих системам B.12:2), B.12:3) и начальным
условиям:
2 = го> X = Хо> для s = So
Начальные условия B.12:4) имеют простой геометриче-
геометрический смысл: координаты (х0, уо, z0) определяют начальную
точку Мо кривой, а эйлеровы углы (ф0, гро» Хо) по формулам
B.12:1) определят присоединенный репер.
Таким образом имеем теорему.
Теорема существования I. Если заданы кривизна и круче-
кручение в функциях длины дуги класса С1, то существует одна и
только одна линия с этими инвариантами, проходящая через
произвольно заданную точку Мо и обладающая в этой точке
заданным репером Френе.
Нетрудно обнаружить, что все это шестипараметрическое
семейство с параметрами х0, у0, z0, q>o, г|зо, Хо состоит из кон-
конгруэнтных линий. Действительно, очевидно, что кривизна и
кручение кривой не зависят от ее положения в пространстве
и при перемещении кривой, как одно целое, как твердое тело,
не меняются. Следовательно, при движении пространства
уравнения B.12:2), B.12:3) не меняются (ибо, кроме k и и,
других коэффициентов не содержат).
С другой стороны, два произвольных ортогональных трех-
трехгранника с единичными векторами осей правой ориентации
конгруэнтны. Допустим теперь, что система B.12:2),
B.12:3) определяет две кривые L и L' с начальными трех-
трехгранниками То и T'Q\ перенесем линию L со всеми ее трехгран-
трехгранниками Френе Т как одно целое так, чтобы начальный трех-
трехгранник То совместился с начальным трехгранником То. До-
Допустим, что после перемещения линия L займет положение
L*. Система B.12:2), B.12:3) при перемещении не меняется
и обе линии V и L*, как и раньше, будут удовлетворять одной
и той же системе уравнений, но, кроме того, после перемеще-
перемещения обе линии V и L* будут обладать одним и тем же началь-
начальным трехгранником Т*=Т^. Система Коши B.12:2), B.12:3)
41
при заданных начальных условиях B.12:4) имеет только
одно решение. Следовательно, линии U и L* совпадают.
Теорема существования II. Кривизна и кручение опреде-
определяют одну и только одну кривую до положения в простран-
пространстве.
Итак, если заданы две функции fi(s), f2(s) класса С1, из
которых первая существенно положительна, то существует
одна и только одна до положения в пространстве линия, кри-
кривизна и кручение которой в функциях от длины дуги будут
b = h(s), x = /a(s). B.12:5)
Действительно, интегрирование системы Коши B.12:2),
B.12:3) с произвольными начальными условиями B.12:4)
дает: первая группа B.12:2) — непосредственно координа-
координаты х, у, z текущей точки некоторой кривой L, вторая груп-
группа— эйлеровы углы <р, ф, % и по формулам Эйлера B.11:2).
если считать е1г е2, е8 за орты неподвижной ортогональ-
ортогональной декартовой системы координат, — единичные ортогональ-
ортогональные векторы е|, е?, е3', образующие правый трехгранник.
Из уравнений B.12:2) простым подсчетом получаем
+ {dyf + {dzf =
откуда следует, что ds есть элемент длины дуги постоянной
кривой L.
Уравнения B.12:3) были получены из уравнений Френе
B.4:5) и эквивалентны им, что можно проверить непосредст-
непосредственным подсчетом, дифференцируя систему B.11:2) и пола-
полагая ej = х, е2 = v, е^ = р.
Первое уравнение Френе показывает, что вектор ej яв-
является единичным вектором касательной кривой L.
Три уравнения второго столбца B.4 :5) показывают: пер-
первое, что единичный вектор е' является вектором главной
нормали, а скаляр k=fi(s) есть кривизна кривой L.
Поскольку
ез = ei X е^ = х X v,
вектор ej будет вектором бинормали, а коэффициент
v.=h(s) — кручением кривой L.
42
§ 13. Эволюта и эвольвента
Эволютой плоской кривой называется геометрическое ме-
место ее центров кривизны. По отношению к своей эволюте ис-
исходная кривая называется эвольвентой.
Если
M = M(s) B.18:1)
уравнение плоской кривой, v — главная нормаль (она лежит
в плоскости кривой, перпендикулярно к касательной; ее по-
положительное направление идет в ту сторону от касательной,
где расположена кривая; точки перегиба, где линия распола-
располагается по обе стороны от касательной, исключаются, так как
в точке перегиба кривизна обращается в нуль, а радиус кри-
кривизны — в бесконечность) и
k = — B.13 : 2)
Р
кривизна кривой (р—радиус кривизны), то центр кривизны
лежит на положительном направлении главной нормали на
расстоянии радиуса кривизны от точки кривой
M1 = M + pv. B.13:3)
Дифференцируя обе части уравнения B.13:3) по длине
дуги s кривой B.13:1), получим
dMi _ dM . dv , dp
~.— — —~.— ~r P т~ ~r * ~~.— >
ds ds ds ds
или по формулам Френе B.4:5) при к=0
ds ds
здесь в силу B.13:2) первые два члена правой части сокра-
сократятся и мы получим
ds ds
Если обозначить длину дуги эволюты буквой sb то
dMj dMi ds dp ds
dsi ds dsi ds dsi
откуда
x1 = ?V, J?-JL=et гдев=±1> B.13:4)
ds dsL
43
Отсюда следствие:
Следствие I. Касательная к эволюте совпадает с главной
нормалью исходной кривой.
Из формулы B.13:4) видно, что вектор касательной к
эволюте Ti и вектор главной нормали v кривой совпадают
с точностью до знака (е=±1).
Уравнение B.13:3) показы-
показывает, что точка М\ лежит на
главной нормали; в этой точке
эволюта касается нормали
кривой (рис. 15).
Второе уравнение B.13:4)
для е=+1 можно написать
в виде
d? _ <ki .
/о 1 q . ел
BЛЗ'5)
Рис. 15
откуда, интегрируя в пределах
от s=s' до s—s", получим
или, полагая
p" = M"M"v
— sj = w Af J
имеем
М\М\ = М"М\ — М'М\.
B.13:6)
Отсюда следствие:
Следствие II. Дуга эволюты равна разности радиусов кри-
кривизны эвольвенты в начале и в конце дуги.
Заметим, что изменение' знака параметра е имеет след-
следствием изменение знака s\, т. е. изменение положительного
направления на эволюте на противоположное.
Теорема. Одной эволюте соответствует однопараметриче-
ское семейство эвольвент.
Действительно, элементы эволюты М^ *i, si и эвольвенты
М, v, p, s связаны соотношениями B.13:3), B.13:4),
B.13:5). Интегрируя уравнение B.13:5), получим
р = «! + а, а = const, B.13:7)
где а — произвольное постоянное. Уравнение B.13:4) теперь
44
определяет вектор нормали эвольвенты. Полагая опять е=1,
получим
v = xlt B.13 : 8)
и уравнение B.13:3) определит однопараметрическое семей-
семейство эвольвент (параметр семейства — произвольное постоян-
постоянное а):
n = nl — (sl+.a)xl. B.13:9)
Действительно, дифференцируя по длине дуги si обе части
уравнения B.13:9), получим
dJU ds / , \ i_
— -r- — vi — {si + a) ki vx - xlt
• as dst
или
* — = - vi («i + a) ki.
ds,
Отсюда
x = — vx, ds = (sx + a) kjdSi. B.13:10
Первое уравнение B.13:10) хорошо согласуется с уравне-
уравнением B.13:8), ибо, перемножая векторно векторы т и v, по-
получим по формулам B.13:8), B.13:10)
Р = X X V = - VX X X! = ХХ X Vx = Рх,
так как для всех плоских кривых направление бинормали
одно и то же и совпадает с выбранным положительным на-
направлением перпендикуляра к плоскости кривой.
Дифференцируя теперь обе части уравнения B.13:8), по-
получим
— ktds = kl4lds1,
или в силу B.13 : 10)
i^k («х + a) kids! = kx Vxdsx
и
k («х -f a) = 1, т. е. р = sx -f a,
согласно с формулой B.13:7). Значит точка Mi, определяе-
определяемая уравнением B.13 :9), будет центром кривизны для эволь-
эвольвенты (М).
45
Таким образом, при изменении постоянного а имеем се-
семейство эвольвент. В соответствующих точках, т. е. при одном
и том же значении s, они имеют общую нормаль v, а радиусы
кривизны р отличаются на одну и ту же величину а. Из од-
одной эвольвенты получаются другие, если на всех нормалях
отложить один и тот же отрезок. Касательные в соответст-
соответствующих точках к различным эвольвентам параллельны, по-
поэтому их называют семейством параллельных кривых.
ГЛАВА III
ТЕОРИЯ ОГИБАЮЩИХ
§ 1. Огибающая однопараметрического семейства линий
на плоскости
1. Определение. Огибающей однопараметрического
семейства линий на плоскости называется кривая, которая
в каждой своей точке касается одной из линий семейства.
Такое семейство линий можно задать в параметрической
форме уравнениями
| C.1:1)
или М = М(*. а). C.1:2)
Здесь t — параметр, определяющий точку на линии, а — па-
параметр, определяющий линию семейства.
Поскольку огибающая в каждой своей точке касается од-
одной из линий семейства, то ее можно определить, если для
каждой кривой семейства, т. е. для каждого значения а за-
задать значение t
t = f(a), C.1:3)
определяющее ту точку линии, которая принадлежит огибаю-
огибающей. В этой точке вектор касательной к кривой семейства
a;=const.
dt '
и вектор касательной к огибающей совпадают. Вектор каса-
касательной к огибающей.получится, если будем дифференциро-
47
вать уравнение C.1 :2) по параметру а, принимая во внима-
внимание уравнение C.1 :3):
+ 1Н., M. = /(а). (з.1:5)
да па
Если касательные совпадают, то векторное произведение
этих векторов равно нулю
или
ЛЦ X Щ = 0.
По правилу векторного произведения двух векторов
получим
= 0. C.1:6)
Уе
а (а, <)
Если уравнение C.1:6) определяет функцию C.1 :3), то
внося полученное выражение t в уравнение C.1 :2), получим
уравнение огибающей..
2. Иногда более удобно задавать семейство, кривых одним
уравнением в неявной форме
F(x,y,a) = 0. C.1:7)
Мы будем предполагать, что это уравнение допускает пара-
параметрическое представление C.1:2), которое тождественно
удовлетворяет уравнению C.1:7).
Дифференцируя в этом предположении уравнение C.1: 7)
по t и по а, получим:
Если семейство C.1 : 7) допускает огибающую, то якобиан
C.1 :6) равен нулю, т. е. равен нулю определитель из коэф-
коэффициентов при Fx, Fy системы C.1 :8); следовательно, что-
чтобы система C.1:8) имела решения, ранг расширенной мат-
матрицы из коэффициентов при Fx, Fy и свободных членов
48
должен равняться единице, а это при xt yt ф 0 возможно
только при обращении в нуль Fa
Fu = 0. C.1:9)
С другой стороны, если уравнение C.1:9) имеет место,
то система C.1:8) относительно неизвестных Fx, Fy стано-
становится однородной и будет допускать только нулевые решения
Fx = 0, Fy=0, которые исключаются (особая точка). Таким
образом, из уравнения C.1:9) вытекает обращение в нуль
якобиана C.1:6).
Система уравнений
F(x,y,a) = 0, Fa(x,y,a) = O C.1:10)
определяет огибающую семейства кривых C.1 :7) при произ-
произвольном а. Если а закрепить, то первое уравнение C.1 :10)
определит линию семейства C.1:7), а второе уравнение опре-
определит точку, в которой эта кривая касается огибающей. Такая
точка называется характеристической. Геометрическое место
характеристических точек образует огибающую, если только
Fx и Fy не равны нулю одновременно, т. е. кроме особых
точек.
Заметим, что особая точка всегда удовлетворяет системе
C.1:8). Действительно, особая точка удовлетворяет системе
Fx = 0, Fy = 0, F = 0; C.1:11)
между тем полный дифференциал от обеих частей C.1:7)
дает
первые два члена обращаются в нуль в силу C.1: 1) и мы
имеем
но<*, как произвольный параметр, имеет дифференциал
da ф 0 следовательно,
и предложение доказано.
3. Пример. Найти огибающую од нопараметр инее кого се-
семейства окружностей
F (X,Y, s) - (X - х)* + (У -у)* - В* = 0, C.1:12)
где X, У —текущие координаты окружности, R — ее радиус,
х, у — координаты центра.
4 Заказ 1874 4Э
Параметром семейства окружности <x,=s возьмем длину
дуги линии центров
x = f(s), y='Hs), R = f(s). C.1:13)
Теперь
F.= — = -~2x'(X-x)-2y'(Y-y)-2RR'=0,
ds
где
x —
dR
ds
ds " ds
Сокращая на —2, получим нормальное уравнение прямой
x'(X-x)+y'(Y-y) + RR' = O, C.1:14)
ибо
(*')•+ОТ =1-
Прямая C.1 : 14) пер-
перпендикулярна к вектору ка-
касательной линии центров
C.1 : 13)
6
С = Ji* + S%y,
Рис. 16
откуда
Чтобы определить рас-
расстояние d прямой C.1 : 14)
от центра С(х, у), доста-
достаточно подставить в левую
часть нормального уравнения прямой C.1 : 14) вместо теку-
текущих координат X, Y координаты центра. Мы получим
d = RRf.
На чертеже (рис. 16) прямая C.1 : 14) изображается ли-
линией MiM2, касательная к линии центров—линией АВ. Если
расстояние СА прямой М1М2 от центра С меньше радиуса
R = CB, т. е.
d = RR' <#, т. е. R' < 1,
то прямая Fa =0 пересекает окружность F=0 в двух точках
М1 и М^ и окружность касается огибающей в двух точках.
50
Если
= RR' = Rt т. е. R'=i,
то прямая Fa касается окружности в точке В и две точки
пересечения Mi и М% сливаются в одну точку В. Можно по-
показать, что в этом случае порядок касания огибающей с
Рис. 17
Рис 18
окружностью повышается; окружность будет служить для
огибающей соприкасающейся окружностью (рис. 17).
Если
d = RRf > R, т. е. Rr > 1,
то прямая Fa=0 не имеет общих точек с окружностью; точ-
точки М\, М2 — мнимые сопряженные; семейство окружностей
не допускает огибающей (рис. 18).
§ 2. Понятие поверхности в дифференциальной геометрии
Прежде чем говорить об огибающей семейства поверхно-
поверхностей, надо определить понятие поверхности в дифференциаль-
дифференциальной геометрии. Мы будем следовать тем же путем, которым
мы шли при определении понятия линии,
Простой кусок поверхности
Определение. Простым куском поверхности называет-
называется геометрическое место точек, удовлетворяющее двум усло-
условиям:
51
a) оно гомеоморфно куску плоскости, например площади
прямоугольника;
b) в каждой точке допускает касательную плоскость,
непрерывно вращающуюся при перемещении точки касания.
а) Первое условие. Многообразие точек гомеоморфно кус-
куску плоскости.
Соответствие гомеоморфизма — взаимно однозначног
непрерывное соответствие. Чтобы установить такое соответ-
соответствие, достаточно дать параметрическое представление точек
поверхности функциями класса С1
M = M(u, i>), . C.2:1)
или
* = <р(и, о), у = Ии> v)> г = х(«. v), C.2:2)
где однозначные функции C.2:2) класса С допускают непре-
непрерывные частные производные по обоим аргументам с диффе-
дифференциальной матрицей ранга 2
ранг х« *« Z"
х„ ц„ г..
= 2. C.2 : 3)
Сопоставляя криволинейные координаты и, v точек по-
поверхности (в некоторой области) координатам (например,
декартовым) точек m(u, v) плоскости (в соответствующей
области), мы получим однозначное, непрерывное отображе-
отображение куска плоскости на рассматриваемую область поверхно-
поверхности. Отображение непрерывно в силу непрерывности функ-
функций C.2:2).
Чтобы доказать взаимную однозначность, надо сослаться
на теорему анализа — существования неявной функции.
II теорема существования неявной функции. Если система
уравнений
F1 (х, у, и, v) = 0, j .
Ft(x,y, u,v) = 0 j
допускает начальную точку
* = *о> У = Уо'> « = «о> » = »о> C.2:5)
удовлетворяющую системе C.2:4), и в окрестности началь-
начальной точки левые части уравнений C.2:4) —функции клас-
52
са С1 (непрерывные частные производные по всем аргумен-
аргументам) с неравным нулю якобианом
dFL dF2
ди
ди
dF,
dv dv
ФО,
то существует решение и только одно
u = h(x,y), v = f2(x,y)
C.2:6)
C.2:7)
с функциями класса С1, удовлетворяющее системе C.2:4) и
проходящее через начальную точку.
Опираясь на эту теорему, мы можем показать, что систе-
система C.2:2) может быть разрешена относительно параметров
и, v и, следовательно, каждой точке поверхности (х, у, г) в
рассматриваемой области соответствует только одна пара
значений (и, v).
Действительно, поскольку матрица C.2:3) ранга 2, суще-
существует определитель 2-го порядка, не равный нулю. Если это
будет определитель
ФО,
то мы возьмем систему C.2 :4) в виде
Fx (и, v; х,у) = <? (и, v) — x = O,
F2 (и, v; х, у) = (J) (и, v)—y=O.
C.2:8)
C.2:9)
Начальную точку C.2:5) построим, выбрав произвольную
пару значений и0, vq в рассматриваемой области и соответ-
соответствующие им значения Хо, у0 C.2:2). В окрестности этой точ-
точки определитель C.2:6) примет вид
dF2
ди
ди
dF2
dv dv
ди ди
dv dv
фО,
C.2:10)
так как при дифференцировании уравнений C.2:9) все четы-
четыре аргумента считаются независимыми, связанными только
уравнениями C.2:9). Определитель C.2:10) отличен от ну-
нуля в силу C.2:8).
53
Следовательно, в силу теоремы II существует решение
C.2 : 7). которое каждой паре значений (х, у) в соответствую-
соответствующей области сопоставляет пару значений (и, v), а эти послед-
последние по формулам C.2:2) дадут определенное значение г
и каждой точке (х, у, г) сопоставляется точка (аналитиче-
(аналитической) плоскости (и, v).
Таким образом, устанавливается непрерывно дифференци-
дифференцируемый гомеоморфизм и топологическая эквивалентность об-
области М(и, v) на поверхности соответствующей области
т(и, v) плоскости.
§ 3. Касательная плоскость
Ь) Второе условие. Многообразие в каждой точке допу-
допускает непрерывно вращающуюся касательную плоскость.
Определение. Касательной плоскостью в точке
(и0, vQ) называется плоскость, содержащая касательные ко
всем линиям на поверхности в точке (и0, vQ).
Рассмотрим полный дифференциал ¦ векторной функции
C.2:1)
dm = (MJ0 du + (МоH dv, C.3 : 1)
где
ди )и = и0
V = t'o V = Vq
Для всякой линии на поверхности, определяемой уравне-
уравнениями ч
u = h(t), v = f2(t), C.3:2)
где в правых частях стоят функции класса С1 с необращаю-
необращающимися одновременно в нуль в точке uo=/i(W' Vo=f2(to)
производными fi(to), h(U), вектор касательной в точке (и0, v0)
будет
/_dM_\ =(Mu) (du_\ + (jvy0(—) . C.3:3)
Эта производная не обращается в нуль в достаточно ма-
малой окрестности точки (и0, v0). В зависимости от выбора ли-
линии C.3:2), проходящей через точку (и0, v0), меняются толь-
только скалярные коэффициенты — производные:
du dfL(t) dv _ df, (t)
для t = ta.
dt dt dt dt °
54
Базисные векторы (МиH, (М^, H зависят только от выбран-
выбранной точки (и заданной поверхности). Из полученного равен-
равенства C.3:3) вытекает, что все касательные к линиям на по-
поверхности C.2: 1) в точке (и0, v0) лежат в плоскости, прохо-
проходящей через точку Мо и определяемой векторами (МиH, (MvH
если, конечно, эти векторы линейно независимы.
Независимость векторов (MuH, (NlvH вытекает из того, что
их векторное произведение не обращается в нуль
„ X М„ =
X
hyu + J3zu) X
J1 J2 J3
Xu Уи Zu
d(u, v)
d(u,v)
d(u,v)
0, C.3:4)
что вытекает из C.2:3).
Возвращаясь к нашему «второму условию» простого кус-
куска поверхности, мы видим, что поверхность C.2 : 1) с функ-
функциями C.2:2) класса С1 допускает в каждой точке (и0, vQ)
касательную плоскость и вектор, перпендикулярный к этой
плоскости, нормаль к поверхности, определяется векторным
произведением C.3:4)
N = Ма X
C.3:5)
оба множителя — производные функции класса С1 — непре-
непрерывны; отсюда при перемещении точки касания М(и, и) нор-
нормаль к поверхности, а вместе с ней и касательная плоскость
непрерывно вращаются. Имеем теорему:
Теорема. Уравнение
М = М (и, v)
C.3:6)
в области значений (и, v), где векторная функция (или ее
компоненты) непрерывна дифференцируема (класса С1) и
векторное произведение
отлично от нуля [матрица C.2 : 3) ранга 2], в окрестности
каждой точки представляет простой кусок поверхности.
55
§ 4. Область регулярности поверхности
Определение. Поверхность регулярна в области ?>,
если в достаточно малой окрестности каждой точки области
представляет простой кусок поверхности.
Теорема. Уравнение
F(x,y,z) = 0, C.4:1)
где функция F(x, у, г) класса С в некоторой области О и до-
допускает в этой области начальную точку (х0, уо> z0), удовлет-
удовлетворяющую уравнению C.4: 1), определяет поверхность, про-
проходящую через начальную точку и регулярную в области 0,
если частные производные Fx, Fy, Fz не обращаются в нуль
одновременно.
Действительно, допустим, что в точке (х0, уо, Zq) не равна
нулю производная
РАхо'Уо>го)ф0; C.4:2)
в силу непрерывности производной (функция F класса С1)
неравенство C.4 :2) будет сохраняться в некоторой окрестно-
окрестности этой точки. В достаточно малой окрестности уравнение
C.4: I) должно допускать решение класса С вида
z = f(x,y), C.4:3)
ибо 1) уравнение допускает начальную точку (хо, у0, г0) и
2) в этой точке производная C.4 : 2) отлична от нуля. После
этого можно взять любую точку этой окрестности с коорди-
координатами
они удовлетворяют уравнению C.4: 1) и принадлежат обла-
области О; все будет повторяться с той только разницей, что в
новой окрестности, возможно, поверхность будет представле-
представлена уравнением вида C.4:3), но разрешенным относительно
у или х.
§ 5. Огибающая однопараметрического семейства
поверхностей
Мы возвращаемся к теории огибающих и рассмотрим сна-
сначала семейство поверхностей, заданных уравнением в пара-
параметрической форме
Ni = Ni(u,v,a), Л^ХМ^О, C.5:1)
где функция М(ы, v, а) класса С относительно всех трех
56
аргументов; первые два и, v определяют точку на поверхно-
поверхности (криволинейные координаты на поверхности); третий
аргумент а определяет поверхность семейства.
По определению огибающая в каждой своей точке касает-
касается одной из поверхностей семейства; поэтому можно искать
огибающую в виде уравнения C.5: 1), где аргументы и, v, a.
связаны одним уравнением, например
а = /(ы, v). C.5:2)
Теперь огибающая определяется двумя уравнениями C.5: 1),
C.5:2), где независимыми переменными будут параметры
и, v. Ищем на ней касательные к координатным линиям
u=const и «=const.
dU dU C.5:3)
м . м дл
= "К + "»* т~ '
dv
дГЛ
ди '"" ' ' dv
дМ
здесь частная производная по независимому перемен-
ди
ному и при i>=const, причем аргумент а зависит от и по фор-
формуле C.5:2). Производные Mu, Nlv, ЛЦ—частные произ-
производные функции C,5 :1) по аргументам и, v, а в предположе-
предположении, что два других аргумента сохраняют постоянные зна-
значения.
Если в точке (и, v) огибающая касается поверхности се-
семейства C.5:1) со значением <z=ai, определяемым уравне-
уравнением C.5:2), то оба вектора C.5:3), касательные к огибаю-
огибающей, должны лежать в касательной плоскости поверхности
C.5:1) со значением a=ai, а потому будут перпендикулярны
к ее нормали
N = Ма X М„.
Ортогональность векторов выражается обращением в нуль
их скалярного произведения:
57
или
аи I
\ ov
= o.
C.5:4)
Отсюда, если скалярное произведение трех векторов не рав-
равно нулю, то
д& г\ да п
откуда
а = const
и мы получаем одну из поверхностей семейства C.5:1).
Если а не постоянно, то C.5:4) дает
(M0tMuMo)=0, C.5:5)
или обращение в нуль функционального определителя
Xv Уv
д (х, у, г)
д (и, V, а)
= 0.
C.5:6)
Теорема. Если уравнение C.5:6) определяет а как функ-
функцию параметров и, v в виде C.5: 2), то, внося это выражение
в уравнение C.5:1), получим уравнение огибающей семей-
семейства поверхностей C.5:1).
§ 6. Случай, когда семейство поверхностей
задано одним уравнением в неявной форме
Рассмотрим теперь ту же задачу определения огибающей
для случая задания семейства уравнением
F(x,y,z,a) = 0, C.6:1)
где по-прежнему а — параметр, определяющий поверхность
семейства, в рассматриваемой области функция F класса С2
по всем четырем аргументам и три производных Fx, Fy, Fz
не обращаются в нуль одновременно.
Для поверхности семейства, т. е. при постоянном а, ком-
компоненты вектора касательной к произвольной линии на по-
поверхности
¦zds = }vdx + J2dy -f J3dz C.6:2)
58
удовлетворяют уравнению, которое получится, если взять
полный дифференциал от обеих частей уравнения C.6:1)
Fxdx + Fydy + Fjiz = 0 C.6:3)
Следовательно, вектор нормали к поверхности C.6 :1) чбудет
N = J^, + V, + 33FZ, C.6:4)
ибо скалярное произведение tN в силу C.6:3) обращается
в нуль.
Для огибающей, которая определяется тем же уравнением
C.6: 1), если задать а подходящей функцией
а = /(*. у, z), C.6:5)
уравнение C.6: 3) запишется в виде
Fydy + Fzdz + Fada = 0. C.6:6)
В общей точке (точке касания огибающей с поверхностью
семейства) и в общем направлении (для общей касательной)
первые три члена уравнений C.6:3) и C.6:6) для огибаю-
огибающей и для поверхности семейства будут одни и те же.
Составляя разность левых частей уравнений C.6: 3)
и C.6 : 6), получим
F. d% = 0.
Если da=Q, то повторяя эти рассуждения для каждого на-
направления и каждой точки огибающей, получим
<z=const,
что недопустимо. Следовательно, надо принять
Fa = 0. C.6:7)
Обратно, если имеет место уравнение C.6:7). то уравне-
уравнения C.6:3) и C.6:6) в каждой общей точке огибающей и
поверхности семейства совпадают; следовательно, совпадают
нормали C.6:4), и огибающая касается поверхности семей-
семейства.
Таким образом, огибающая определяется системой
F(x, у, г, а) = 0, /v (х, у, z, а) = 0. C.6:8)
Если второе уравнение определяет а как функцию координат
х, у, г в виде C.6 :5), то, подставляя это выражение в урав-
уравнение C.6:1), получим уравнение огибающей.
59
§ 7. Характеристики и огибающая характеристик
Фиксируем значение а в уравнениях C.6 :8)
<z=ai.
Тогда яервое уравнение C.6:8) определит поверхность се-
семейства, а второе выделит на этой поверхности линию, кото-
которая принадлежит огибающей и вдоль которой огибающая ка-
касается поверхности a=ai семейства.
Линию прикосновения поверхности семейства с огибающей
называют характеристикой. Поскольку огибающая в каждой
своей точке касается какой-нибудь поверхности семейства, а
все точки касания лежат на характеристиках, то огибающая
образована геометрическим местом характеристик.
Огибающая характеристик. Однопараметрическое семей-
семейство линий в пространстве вообще не имеет огибающей, но,
поскольку характеристики лежат на одной поверхности, мож-
можно искать их огибающую, т. е. линию, которая в каждой своей
точке касается одной из линий семейства.
Допустим, что характеристика определяется системой
F(x, у, г, а) = О, F* (х, у, г, а) = 0 C.7:1)
при постоянном а, причем функция F(x, у, г, а) класса С2 по
всем четырем аргументам.
Поскольку каждая точка огибающей принадлежит одной
из линий семейства, можно определять огибающую той же
системой C.7:1), рассматривая а как функцию переменных
х, у, z
a = f(x,y,z). C.7:2)
Вектор касательной к характеристике
tde = }xdx + 32dy + Jjdz C.7:3)
определяется уравнениями, которые получаются при диффе-
дифференцировании уравнений системы C.7:1) при постоянном a
FJbt + Fydy + Fzdz = 0, )
Faxdx + Fa!/dy + Fazdz = 0.) " CJ:4)
Компоненты вектора касательной к огибающей характери-
характеристик определяются уравнениями, которые получаются диффе-
дифференцированием тех же уравнений C.7:1), но в предположе-
60
нии, что четвертый аргумент а есть функция C.7:2) от неза-
независимых переменных х, у, z:
Fxdx + Fydy + Fzdz + Fada = 0,
Faxdx + Faydy + Fazdz + Faada = 0. CJ:5)
В силу второго уравнения C.7:1) последний член первого
уравнения C.7:5) отпадает.
Рассмотрим характеристику семейства и огибающую ха-
характеристик в общей точке касания. Координаты х, у, z в этой
точке одни и те же в уравнениях C.7:4) и C.7:5); значе-
значения а, вычисляемые по формуле C.7:2), тоже должны сов-
совпадать. Наконец, в силу- совпадения касательных в точке ка-
касания можно считать дифференциалы dx, dy, dz в уравнениях
C.7:4), C.7:5) совпадающими. В таком случае первые
уравнения C.7:4), C.7:5) совпадают, а второе уравнение
C.7:5) отличается от второго уравнения C.7:4) только по-
последним членом. Таким образом, условие касания сводится
к равенству
/vda = 0.
Здесь, как и выше, обращение в нуль da=0 приводит к вы-
вырождению. Следовательно, надо принять
Fn = 0. C.7:6)
Обратно, если уравнение C.7:6) имеет место, то послед-
последний член второго уравнения C.7:5), как и первого, пропа-
пропадает. Системы C.7:4), C.7:5) совпадают, погибающая ха-
характеристик касается характеристики семейства. Имеем тео-
теорему:
Теорема. Семейство характеристик однопараметрического
семейства поверхностей
F(x, у, г, я) = 0, F* (х, у, г, а) = 0 C.7:7)
имеет огибающую, если уравнение
Л. (х, у, г, а) = 0 C.7:8)
определяет а как функцию от х, у, г в виде C.7:2). Уравне-
Уравнение огибающей получается, если выражение C.7:2) внести
в уравнения C.7:7).
61
§ 8. Ребро возврата огибающей
Определение. Огибающая характеристик однопара-
метрического семейства поверхностей называется ребром воз-
возврата огибающей семейства поверхностей. Это название объ-
объясняется следующей теоремой.
Теорема. Сечение огибающей семейства оо1 поверхностей
плоскостью, которая пересекает (не касается!) ребро возвра-
возврата огибающей, является плоской кривой с особой точкой в
точке пересечения ребра возврата.
Заметим, что линия
C.8:1)
имеет при ?=?<> особую точку, если
М(/0) = 0, М = -^-. C.8:2)
Если при этом
М (t0) Ф О,
то по формуле Тэйлора A.6:2) предел отношения хорды к
квадрату (AtJ при Д*->-0 будет равен второй производной
±(Д).
Следовательно, fH(t0) или вообще первая, не обращающаяся
в нуль производная, определяет касательную. Та же форму-
формула Тэйлора
мом = м (*0 + ДО - м (д = Ш- м <д + i|>-3 ф3 (/о, At)
показывает, что первый член правой части, который при до-
достаточно малом приращении Д? определяет проекцию смеще-
смещения МоМ на касательную МG0Л не меняет знака при измене-
изменении знака приращения Д?. Следовательно, кривая будет рас-
располагаться по одну сторону нормальной плоскости в точке
*=*о (для плоской линии по одну сторону нормали); подойдя
к точке Мо вдоль касательной МG0,), она как бы останавли-
останавливается и возвращается уже по другому пути назад. Отеюда
название точки возврата. Вернемся к доказательству теоре-
теоремы о ребре возврата огибающей. ¦ -. ; .¦
62
¦Поскольку оси координат у нас произвольны, мы можем
принять секущую плоскость за плоскость 2=0. Тогда уравне-
уравнение линии пересечения огибающей будет
F(x, у, О, а) = О, Fa (х, у, О, а) = 0. C.8:4)
Мы можем рассматривать а как независимый параметр, опре-
определяющий положение текущей точки (х, у,) на кривой
C.8:4). Дифференцируя уравнения C.8:4) по параметру а,
получим
da
da
C.8:5)
Если функции F и
д (х, у)
функционально независимы
фО в точке t = t0 C.8:6)
-и производная Faa отлична от нуля
Faa ф 0,
то система C.8:5) в точке t=t0 дает значения производных
— , —, не равные одновременно нулю. В точке пересечения
da da
с ребром возврата
Fn = 0,
при сохранении неравенства C.8 :6) система C.8 : 5) приво-
приводит к нулевым решениям — = 0, — = 0, . и тогда точка
d d
da da
линии C.8: 5) будет особой.
Исключение может быть только при понижении ранга си-
системы C.8:5), когда якобиан C.8:6) равен нулю; но тогда
касательная к ребру возврата
Tds = V* 4- hdy 4 hdz,
определяемая из уравнений C.7:5). которые теперь совпа-
совпадают с уравнениями C.7:4), приводит к пропорциональности
их dy dz
d.(F.F%) ~d(F,Fa) ~d(F.F.) '
д(у,г) д(г,х) »(х,у)
которая при обращении якобиана C.8:6) в нуль показывает,
63
что касательная к ребру возврата Т не имеет компонента
по оси 2 и, следовательно, лежит в секущей плоскости z=0.
Следовательно, линия пересечения огибающей семейства
поверхностей плоскостью z=0 в общей точке огибающей ха-
характеристик может и не иметь особой точки, но только тогда,
когда секущая плоскость z=0 касается ребра возврата.
§ 9. Огибающая семейства плоскостей
Рассмотрим семейство плоскостей
F = Ax + By + Cz+D = 0, C.9:1)
где коэффициенты А, В, С, D — функции параметра а. Диф-
Дифференцируя по параметру а, получим опять уравнение плос-
плоскости
Fa = Ах + By + Cz 4- D = 0. C.9:2)
Пересечение плоскостей C.9:1) и C.9:2) будет прямой, ко-
которая служит характеристикой плоскости C.9:1). Геометри-
Геометрическое место их, огибающая, будет, следовательно, линейча-
линейчатой поверхностью (поверхность, образованная движением
прямой линии).
Дифференцируем еще раз по параметру а:
Fa0l = Ax + By + Cz + D = 0. C.9:3)
Три уравнения C.9:1—3) определяют ребро возврата оги-
огибающей — пространственной линии, которая касается всех
прямых C.9 : 1—2).
Теорема. Ребро возврата огибающей однопараметрическо-
го семейства плоскостей — произвольная не плоская линия.
Возьмем произвольную пространственную линию
М = М (.s) C.9:4)
и рассмотрим семейство ее соприкасающихся плоскостей.
Если Р — призвольная точка соприкасающейся плоскости,
то вектор
перпендикулярен к бинормали (L Отсюда уравнение соприка-
соприкасающейся плоскости
F = (P-M)p = 0. C,9:5)
64
Здесь вектор Р имеет своими компонентами текущие ко-
координаты плоскости. Радиус-вектор М зависит от парамет^
pa s и определяется уравнением C.9 :4), вектор бинормали Р
тоже зависит от s и определяется уравнениями Френе. Пара-
Параметр s следует рассматривать как параметр, определяющий
нормальная
плоскость
i
a
центр
кривизны
Рис. 19
плоскость в семействе соприкасающихся плоскостей C.9:5).
Чтобы tfaftTH огибающую семейства C.9:5), надо дифферен-
дифференцировать это уравнение по параметру s
или в силу i$=
- — Fs = (P - M) v = 0.
C.9:6)
Это уравнение определяет плоскость, проходящую через ка-
касательную и бинормаль, так называемую спрямляющую плос-
плоскость. Плоскости C.9:5), C.9:6) пересекаются по касатель-
касательной, которая и будет характеристикой.
5 Заказ 1874
65
Огибающей характеристик будет, следовательно, исходная
кривая C.9:4), откуда и следует теорема, ибо кривая была
взята произвольно.
Надо заметить, что, кроме развертывающихся поверхно-
поверхностей, которые образованы касательными пространственной
кривой, огибающими семейства оо1 плоскостей будут кониче-
конические поверхности, у которых все касательные плоскости про-
проходят через вершину конуса и характеристиками служат об-
образующие конуса, и цилиндрические поверхности, у которых
все касательные плоскости параллельны одной прямой. У ко-
конических поверхностей ребро возврата вырождается в точ-
точку — вершину конуса, у цилиндрической поверхности ребро
возврата вырождается в несобственную точку.
Конические, цилиндрические и собственно развертываю-
развертывающиеся поверхности, и только эти поверхности, касаются каж-
каждой касательной плоскости вдоль образующей.
Как следствие имеем предложение: плоскости семейства
служат соприкасающимися плоскостями ребра возврата оги-
огибающей семейства .
§ 10. Огибающая нормальных и спрямляющих плоскостей
1. Семейство нормальных плоскостей линии C.9:4) опре-
определяется уравнением
f = (P_M)u = 0. C.10:1)
Дифференцируя по параметру семейства—длине дуги s
кривой, получим
Если умножить обе части на радиус кривизны кривой р = —
и заменить ta=I, то получим
(P-M)v-p=0. C.10:2)
Эта плоскость (рис. 19) параллельна спрямляющей плос-
плоскости C.9 :6), но, в отличие от нее, не проходит через верши-
вершину трехгранника Френе, точку кривой М; зато она содержит
центр кривизны кривой, точку С, ибо уравнение C.10:2)
удовлетворяется значением
Р = С = М + pv.
Линия пересечения плоскостей C.10:1) и C.10:2)—харак-
C.10:2)—характеристика плоскости C.10:1) проходит через центр кривиз
66
ны С параллельно бинормали. Эта прямая называется осью
кривизны. Огибающая нормальных плоскостей, геометриче-
геометрическое место осей кривизны, называется полярной поверхностью.
2. Семейство спрямляющих плоскостей определяется урав-
уравнением
F = (P- M) v = 0. C.10:3)
Дифференцируя по длине дуги s—параметру семейства, по-
получим
f,= (P-M).(-b + x^)--cv = 0. C.10:4)
Последний член обращается в нуль. Если обозначить проек-
проекции вектора М — Р = МР на векторы i, v, ? буквами
$ = (Р - М) 1, ij = (Р - М) v,
то уравнения C.10:3), C.10:4) дадут
?1 = 0, хС-#= 0. C.10:5)
Это уравнение характеристики в координатах g, i), t, относи-
относительно трехгранника Френе. Первое уравнение C.10:5) пока-
показывает, как и следовало ожидать, что характеристика лежит
на спрямляющей плоскости. Второе показывает, что
т. е. характеристика параллельна вектору мгновенной скоро-
скорости вращения
ф = ии + $k.
Огибающая спрямляющих плоскостей будет неподвижной
аксоидой.
ГЛАВА IV
ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ
§ 1. Первая квадратичная форма поверхности
Мы уже дали определение поверхности в дифференциаль-
дифференциальной геометрии. В окрестности каждой точки регулярной об-
области поверхность допускает параметрическое представление
М = М(и,о), D.1:1)
где вектор — функция, стоящая в правой части, класса С3 и
частные производные удовлетворяют неравенству
МвХМ„?=0. D.1:2)
Параметры и, v определяют положение точки М на поверхно-
поверхности, поэтому их называют координатами, обычно криволиней-
криволинейными координатами, так как координатные линии, т. е. линии,
вдоль которых одна из координат сохраняет постоянное зна-
значение, т. е. линии o=const или u=const, вообще будут кривы-
кривыми линиями.
Линия i»=const обычно называется линией и, а линия
u=const — линией о.
Координатная сеть называется правильной, если в данной
области каждая линия и пересекает в одной точке каждую
линию V. Условие D.1 :2) обеспечивает правильную сеть ко-
координатных линий.
Линия на поверхности в параметрическом представлении
определяется уравнениями
где функции (p(t), ty(t) класса С3 и первые производные их
одновременно в нуль не обращаются.
68
Полный дифференциал
dM = nju + N^dv D.1:4)
определяет касательные ко всем линиям D.1 :3) на поверхно-
поверхности; вектор касательной будет
dM _ м du* | м dv
где
-J--TW. 1Г=4('>- D-1:5)
Производные Мв, М^ определяют касательные к координат-
координатным ЛИНИЯМ O=COnst; U=COIlst.
Формула D.1:4) или D.1:5) показывает, что все каса-
касательные к линиям на поверхности, проходящим через точку
(и, v), лежат в одной (касательной) плоскости.
Вектор нормали определяется векторным произведением
N = MeXM*. D.1:6)
Дифференциал длины дуги любой линии D.1:3) на по-
поверхности определяется, если возвысить в квадрат левую и
правую часть равенства D.1:4)
ds* *= dM* = (MJ1 du1 + 2M/Л„ du dv + (Mv)* dv\
коэффициенты
E = (Ma)«, F = МаМ„, G = (M,I D.1:7)
зависят только от криволинейных координат и, v точки по-
поверхности и не зависят от уравнений линии D.1 :3). Поэтому
квадратичная форма
ds2 = Edu* + 2Fdu dv + Gdv* D.1:8)
называется линейным элементом поверхности. Это основная
метрическая форма поверхности. Она инвариантна в том
смысле, что не меняется при перемещении поверхности в про-
пространстве как твердое тело, не зависит от преобразования де-
декартовой системы координат. При замене переменных
и= ср(и*. и*), о = <|>(и*, v*), D.1:9)
где функции <р, if функционально независимы класса С3,
а("'р) ФО, D.1:10)
коэффициенты Е, F, G преобразуются подстановкой D.1 :9),
69
дифференциалы du, dv заменяются полными дифференциа-
дифференциалами:
-^- du*+^- dv*,
du* dv*
ди* dv*
D.1:11)
и линейный элемент D.1 :8) сохраняет свое значение.
Если обозначить модули векторов
|Mj = a, IMJ-6, D.1:12)
а угол между ними, т. е. угол, под которым пересекаются
координатные линии, буквой т> то из формулы D.1:7) по-
получим
? = 0*. G = b\ F = ab cos T, D.1:13)
откуда
EG-F* = a*b* A - cos1 у) = aW sin1 y. D.1:14)
Следовательно, коэффициенты Е, G и дискриминант
EG—F2 действительной поверхности — положительны и квад-
квадратичная форма D.1:8)—положительно определена. Сред-
Средний коэффициент F может быть и положительным и отрица-
отрицательным в зависимости от знака cosy, т. е. в зависимости от
того, будет ли координатный угол (т. е. угол поворота от век-
вектора Ма до вектора MJ острым или тупым.
Если f = —, т. е. координатные линии ортогональны, то
F = 0.
Заметим еще, что модуль векторного произведения D.1 :6)
равен произведению модулей множителей на синус угла меж-
между ними
| N | = ! Ма X М„ | = аб | sin т I = VEG-F*. D.1:15)
§ 2. Угол пересечения двух линий на поверхности
Рассмотрим две линии на поверхности в точке М(и, v):
*-мо. о-г, (<•).) D'2 )
70
Присвоим дифференцированию вдоль первой линии сим-
символ d, вдоль второй — символ б. Следовательно,
dv = }2(t)dt, bv = 'f'2(t*)bt*. |
Тогда единичные векторы касательных к этим линиям в
общей точке М будут:
<Ш м du . м dv ЫЛ м Ьи м bv .. „-.
= 1Ли— +Пь~Г • -Г=М«Т"+М»Т"' D.2:3)
ds " ds ' " ds ' bs u 8s ' v bs
Отсюда по известной формуле: скалярное произведение век-
векторов равно произведению модулей множителей на косинус
угла между ними, получим, обозначая буквой ф угол пересе-
пересечения линий D.2 :3)
(М„) +MaM,
ds bs V "' ds bs " ^ dsbs
, /щя \t dvmM bv
+ (JVU -dT ' V'
или с помощью обозначений D.1:7)
„„,. Еdulu + F (duly A-dvbu) +Gdvbv
cos <p -
где ;
8s1 = E (8u)» -f IF Ы lv + G (bv)*.
Отсюда условие ортогональности линий D.2: 1)
cos ф=0,
или ' ,, -; ¦' -^Щ-
Edulu + F(dubv + dvbu) +Gdvlv = 0. D.2:5)
Приложение. Ортогональная система линий на поверх-
поверхности.
Рассмотрим семейство линий на поверхности в области ее
регулярности
Ф(ы, v) = c, _ D.2:6)
где Ф — функция класса С2 и с — параметр семейства. Не-
Нетрудно заметить, что через каждую точку области проходит
одна и только одна линия семейства. Действительно, внося
в уравнение D.2:6) координаты (щ, Vi), определим параметр
71
c—Ci той единственной линии, которая проходит через эту
точку _ >
Присвоим этим линиям символ дифференцирования ft.
Дифференцируя равенство D.2:6) при постоянном с%, получим
ФиЪи + <bvbv = 0. D.2:7)
Будем искать линию, которая в каждой точке пересекает
линию семейства D.2:6) под прямым углом. Такая линия
называется ортогональной траекторией семейства D.2:6).
Если присвоить дифференцированию вдоль ортогональной
траектории символ дифференцирования d, то искомая линия
будет определяться уравнением D.2 : 5).
Исключая с помощью уравнения D.2:7) отношение диф-
дифференциалов 6и: 6v, получим
(«. v)-FOa(u, v))du +
+ {F<DV (и, v) - G<Dtt (и, V)} dv = 0. D.2:8)
В левой части стоит дифференциальный бином
А (и, v)du-\-B (и, v) dv.
Дифференциальный бином класса С1 допускает интегрирую-
интегрирующий множитель X (и, v) так, что
X [А (и, v)du + B {и, v) dv} = d4, Y = ? (и, v).
Таким образом, дифференциальное уравнение D.2:8)
имеет общий интеграл
?(«, v) = c, D.2:9)
где с — произвольное постоянное интеграции. Если рассмат-
рассматривать произвольное постоянное с как параметр семейства
кривых, то уравнение D.2:9) определит второе семейство
кривых так, что через всякую точку области будет проходить
одна линия семейства Ф и одна линия семейства Y, пересе-
пересекающихся под прямым углом.
Если рассматривать Ф и Т как новые криволинейные ко-
координаты на поверхности, то система координатных линий
Ф = const, Y = const
будет ортогональной, и линейный элемент поймет вид
ds1 = A* (dd))* + В2 (d4)*. D.2:10)
72
§ 3. Дифференциал площади поверхности
Рассмотрим координатную сеть линий на поверхности я
криволинейный четырехугольник, образованный линиями с
постоянными значениями координат и и и+Ди, v, и f+Ди, пе-
пересекающихся в точках М(и, v), МЦи+Ди, v), M2(u, $
+A) М(\& 4A) (рис. 20).
M(u,v)
Рис. 20
Хорды ММ\, ЛШг определяют векторы
Д„М = М (и + Ди, и) - М (и,
ДЩМ = М (и, v + Ди) — М (и,
их можно аппроксимировать векторами
а площадь криволинейного четырехугольника Л1Л1 |Af3Af2 пло-
площадью параллелограмма, построенного на векторах dM, 8M.
Площадь такого параллелограмма равна модулю векторного
произведения
= )MaXNK\dudv = VEG - Я dudv.
Отсюда дифференциал площади поверхности
dS = YEQ—F* du dv. D.3:1)
73
§ 4. Примеры
1. Геликоид. Прямой геликоид описывается винтовым дви-
движением прямой, параллельной плоскости ху и пересекающей
ось z (ось винтового дви-
движения); проекция прямой
на плоскость ху равномер-
равномерно вращается около нача-
начала координат, а точка пе-
пересечения прямой с осью
z равномерно переме-
перемещается по этой оси
(рис. 21).
В приведенной табли-
таблице в первом столбце сто-
стоят координаты х, у, z ра-
радиуса-вектора М, во вто-
втором и третьем — коорди-
наты касательных к ли-
линиям и и и векторов М,
и Nlv, в четвертом — координаты нормали N = Мц X Моц
(a=const).
D.4:1)
м
х = и cos v
у = usinv
z = av
Mu
COS V
sin и
0
— usini»
UCOSl»
a
N
a sine
— a cos v
и
Коэффициенты линейного элемента:
? = (МВ)«=1, JF = MttM?, =
G = (Лу* = и» + а\
ds1 = du2 + (и2 + a2) dv*.
D.4:2)
Линия i»=const во всех точках имеет одну и ту же аппли-
аппликату z=av; ее проекция на плоскость ху определяется урав-
уравнением
y = x\gv.
Линия u=const — винтовая линия; при повороте проекции
ОР на 2я точка М поднимается на 2па. Величина а — шаг
винта.
74
2. Поверхность вращения. Зададим в плоскости, проходя-
проходящей через ось z, произвольную линию
D.4:3)
координаты в плоско-
г = f{r),
где гиг — прямоугольные декартовы
ти rz и ось Or лежит на пере-
пересечении плоскости rz с коорди-
координатной плоскостью ху.
Рассмотрим поверхность
вращения, описанную линией
D.4:3), когда плоскость rz
вращается около оси z. Если
произвольную точку М линии
D.4:3) спроектировать на
плоскость ху, т. е. на ось Or
в плоскости, в точку Р с коор-
координатой по этой оси ОР=г и
обозначить угол поворота
(рис. 22)
^ хОР = <р,
то координаты точки Р будут
х = г cos у, у — rsincp D.4:4)
формулы перехода от полярных (г, ф) к декартовым (х, у)
координатам точки Р. Точка М имеет эти две координаты
(х, у) и еще третью координату z, определяемую уравнением
D.4:3). Имеем таблицу
Рис. 22
М
N
X = Г COS Cf
у = rsincp
z = f(r)
COScp
sin cp
f(r)
— rsincp
rcoscp
0
— rf cos cp
— r/sincp
r
D.4:5)
Коэффициенты линейного элемента:
E = (M,J = 1 + /2 (r), F =
, = О,
линейный элемент
ds2 = [ 1 + /2 (г)] dr2 + r2 df\ D.4:6)
координатные линии образуют ортогональную сеть.
75
Линии q)=const — сечения поверхности плоскостями, про-
проходящими через ось вращения, называются меридианами по-
поверхности вращения; они все между собой конгруэнтны »
представляют различные положения вращающегося профиля:
D.4:3).
Линии r=const — сечения поверхности плоскостями, пер-
перпендикулярными к оси вращения, ибо при постоянном
Рис. 23
Рис. 24
r=const и z=const. Они называются параллелями, ибо лежат
в параллельных плоскостях. Проекция такой линии на плос-
плоскость ху конгруэнтна самой линии и имеет уравнение
х> + у* = г*.
Это окружность с центром на оси вращения и радиусом г.
На рис. 23 и 24 изображены поверхности вращения посто-
постоянной отрицательной кривизны. Поверхность, данная на
рис. 24, называется псевдосферой.
3. Катеноид. Катеноидом называется поверхность враще-
вращения цепной линии около своего основания. Цепная линия есть
линия, форму которой принимает тяжелая цепь, если ее сво-
свободно подвесить за два конца (рис. 25).
76
При подходящем выборе осей цепная линия определяется
уравнением
г г_
r=-f (*• +е~ •)• D.4:7)
Если воспользоваться гипербо-
гиперболическими функциями: z
cht= е +е ,
cht
sht
то уравнение цепной линии
D.4 : 7) примет вид
г — a ch — .
а
Отсюда, дифференцируя, получим
dr = sh — -dz.
а
Следовательно,
sh —
а
Рис. 25
/2(г)=1 +
1
^ + 1
а г* —а*
г» _ п*
а а
и по формуле D.4:6) линейный элемент катеноида будет
ds* = 1- r2d<p*. D.4:8)
77
Если положить
и = Yr% —
D.4:9)
то
и линейный элемент геликоида D.4 : 2) совпадает с линейным
элементом катеноида.
§ 5. Изгибание поверхностей
Определение. Если между точками области V по-
поверхности 5 и точками области 0* поверхности S* можно
установить взаимно однозначное соответствие
и = <р (и*, v*), v = ty (и*, V*),
-^L^O D.5:1)
d(u*,v*) - v
так, что после подстановки вместо и, v этих функций линей-
линейный элемент ds2 первой поверхности совпадает с линейным
Рис. 26
Рис. 27
элементом второй, то говорят, что поверхности 5 и S* изомет-
ричны, или, что поверхность 5 налагается на поверхность 5*.
или, что поверхность 5* является изгибанием поверхности S,
78
а соответствие D.5:1) называется соответствием наложи-
наложимости.
Следовательно, геликоид налагается на катеноид и соот-
соответствие наложимости определяется формулами D.4 :9); при
этом линии i»=const, т. е. прямолинейные образующие гели-
геликоида налагаются на линии cp=const, т. е. меридианы катено-
катеноида, а линии u^const, т. е. винтовые линии геликоида, нала-
налагаются на линии r=const, т. е. параллели катеноида; а линия
и=0, т. е. ось ринтового движения геликоида, налагается на
линию г=0, т. е. горловую (минимальную) параллель кате-
катеноида (рис. 26 и 27).
Очевидно, бесконечная прямая (ось геликоида) не может
совместиться с окружностью длиной 2па наименьшей парал-
параллели катеноида; но проблема наложимости всегда рассмат-
рассматривается локально, т. е. наложение ограниченной области од-
одной поверхности на ограниченную область другой.
Изгибание называется непрерывным, если имеется непре-
непрерывное однопараметрическое семейство поверхностей, линей-
линейный элемент которых не зависит от параметра семейства так,
что с непрерывным изменением параметра поверхность, ме-
меняясь (изгибаясь), переходит от одной формы к другой.
§ в. Наложение развертывающейся поверхности
на плоскость
Примером непрерывного изгибания может служить изги-
изгибание развертывающейся поверхности. Развертывающейся
поверхностью мы назвали поверхность, образованную каса-
касательными пространственной кривой.
Рассмотрим кривую, описываемую точкой
Р = Р(р); D.6:1)
примем за параметр v длину дуги кривой (Р) и воспользуем-
воспользуемся формулами Френе
do do do
-4L=—xv. D.6:2)
do
Отложим на касательной т от точки Р отрезок длиной и.
Тогда развертывающаяся поверхность касательных кривой
(Р) будет определяться уравнением
М = Р -f их. D.6:3)
79
Здесь Р и -с — функции криволинейной координаты v, пара-
параметр и входит в уравнение D.6:3) явно.
Дифференцируя равенство D.6:3) почленно с помощью
формул D.6:2), получим
= -с dv -f х du -f uk* dv = x (du -f dv) -f vuk dv.
Розвышая обе части равенства в квадрат, получим
ds* = (du + du)* + u2k2 dv2. D.6:4)
„Линейный элемент D.6:4) зависит только от кривизны k ли-
линии D.6: 1). Между тем мы знаем B.12), что линия D.6:1)
определяется двумя инвариантами: кривизной k и кручением и;
произвольно заданные функциями длины дуги класса С, кри-
кривизна и кручение определяют пространственную линию до по-
положения в пространстве. Зададим же непрерывное семейство
линий кривизной и кручением в виде:
k =<f{v), х = сп|ф), D.6:5)
где v — длина дуги, <р(и) и i|>(i>)—функции класса С1 и
а — параметр линии в семействе кривых. Мы получим непре-
непрерывное семейство различных кривых и непрерывное семейство
различных развертывающихся поверхностей, зависящих от
параметра а; все поверхности независимо от значения пара-
параметра а имеют один и тот же линейный элемент D.6:4).
Будем стремить параметр а к нулю; поверхность D.6:3)
будет изгибаться, сохраняя свой линейный элемент D.6:4).
В пределе при а=0 линейный элемент D.6:4) не изменится,
ибо он не содержит параметра а, а кривая (Р) станет плос-
плоской, ибо кручение линии по формуле D.6:5) обратится в
нуль, и все ее касательные будут лежать в этой плоскости.
Линейный элемент D.6:4) не изменится, но он уже будет
принадлежать плоскости. Следовательно, развертывающаяся
поверхность наложится на плоскость. Если первоначально
взять обыкновенную винтовую линию с постоянной кривизной
и постоянным кручением, то после приведения кручения к ну-
нулю при а-*- 0 мы будем иметь плоскую линию постоянной
кривизны, т. е. окружность. Огибающая с ребром возврата
в виде обыкновенной винтовой линии, после того как отрезок
винтовой линии перейдет в окружность, наложится своими
двумя полостями — по одну и по другую сторону ребра воз-
возврата — на ту часть плоскости, которая лежит вне окружно-
окружности, покрыв ее два раза, ибо из внешней точки можно прове-
провести две касательные к окружности.
§ 7. Изгибание поверхности вращения в поверхность
вращения с сохранением меридианов и параллелей
Рассмотрим две поверхности вращения 5 н 5, определяе-
определяемые уравнениями D.4:3), D.4:4):
х = г cos со, х = г cos со,
i/ = rsincp, lj =7 sin ?,
z = f(r). г = 7G).
Потребуем, чтобы онн налагались так, чтобы меридианы
cp=const переходили в _мернднаны cp=const, а параллели
r=const — в параллели r=const.
Тогда соответствие наложимости должно быть вида
7=h(r), ?=?(<?), D.7:2)
откуда
dr = h (г) dr, d?=g (с?) d?. D.7:3)
При этом условии линейные элементы D.4:6) поверхностен
S я S должны совпадать
[ 1 + р G)] d? + 72 df = {1 + Р (г)] dr2 -!- г2 dec2, D.7:4)
или в силу D.7 : 2—3)
[ 1 +р(г)\ Л2 (г) dr2 -f Л2 (г) i2 (?) d?2 = [ 1 + /2 (г)] dr2 + r2 d?2.
Сравнивая коэффициенты при независимых дифференциалах
dr2, dcp2, получим
=1+/г(г), D.7:5)
= '. D.7:6)
Уравнение D.7 :6) можно переписать в виде
ft2 W 1 .
'2 г2(г) '
левая часть не меняется при изменении независимого пере-
переменного ф, правая часть не зависит от г. Следовательно, онн
обе равны одному и тому же постоянному. Возвращаясь к
обозначениям D.7:2—3),
6 Заказ 1874 81
Всегда можно выбрать знак А, так, чтобы
7= \г; D.7:7)
меняя в случае надобности знак ф и начало отсчета, получим
df = — d<p и <р = — <р. D.7:8)
А А
Внося значения D.7:7), D.7:8) в уравнение D.7:5) и
помня, что dz=f(r)dr, получим
или
откуда, интегрируя, имеем
Го
Получаем уравнения новой поверхности вращения S, на-
налагающейся на поверхность S:
г
x = lrcos j-,~y=lrsin^-, z= Г V^l — А.2 + /2(г) rfr. D-7:9)
Го
Постоянное Я можно рассматривать как параметр изгиба-
изгибания. Если Я<1, то радиусы параллели г становятся меньше
соответствующих радиусов г; поверхность становится уже;
при этом границы изменения угла <р = —-<р, которые соответ-
ствуют изменению
О < <р < 2ir,
становятся больше 2я, т. е. при изгибании поверхность сжи-
сжимается и «запахивается», т. е. близким к 2я значениям ф бу-
будут соответствовать после изгибания точки ф>2я, проходимые
уже по второму разу.
82
Если Я>1, то радиусы параллелей г становятся больше г,
зато полный обход 0<<р < 2ir будет соответствовать толь-
только части оборота второй поверхности: 0 < <р < 2гс.
Кроме того, при Я>1 разность 1—Я2 будет отрицательной
и, чтобы выражение под корнем в подынтегральной функции
для z D.7 : 9) не стало отрицательным, придется накладывать
ограничение
на тангенс угла наклона к оси г касательной к меридиану
исходной поверхности.
ГЛАВА V
ТЕОРИЯ КРИВИЗНЫ ПОВЕРХНОСТИ
§ 1. Кривизна линии на поверхности
Рассмотрим какую-нибудь линию на поверхности
М = М (u,v).
Дифференцируя по длине дуги этой линии, получим единич-
единичный вектор касательной
dM .. du . .. dv /с i . i\
т = —- = MU— 4-Mj,-—. E.1:1)
as ds ds
Вторичное дифференцирование дает по формуле Френе век-
вектор кривизны, т. е. вектор, отложенный в положительном на-
направлении по главной нормали, с модулем, равным кривизне
кривой
<5J:2>
^ d*u do
Чтобы освободиться от вторых производных —, —2 ,
умножаем обе части равенства на единичный вектор норма-
нормали п, т. е. проектируем вектор кривизны на нормаль к по-
поверхности.
Полагая
vn = cos&, E.1:3)
*я, E.1:4)
будем называть нормальной кривизной линии на поверхности
84
проекцию вектора кривизны на нормаль к поверхности
(рис. 28).
Имеем
ds*
Ddu2 -f 2D'dudv + D"dxfl
d7* '
E.1:5)
где
или, поскольку
n = —
1
u
E.1:6)
У EG — Л
можно писать
i
D =
N =
М„>
p.
1
<иУиги
Пасат. плоек,
поверхности
E.1:7)
Рис.28
лучим
и аналогично для D' и D".
Два последних члена разложения E.1:2) при умножении
на п пропадают, ибо
пМы = 0, пМ,, = 0.
Дифференцируя первое тождество по переменному и, по-
пыМы + пМыы = 0, или D + п„Мы = 0,
откуда
г\ жж г\/ жж it гу/ жж /|- I # о\
§ 2. Вторая квадратичная форма
Выражение, стоящее в числителе правой части формулы
E.1:5), называется второй основной квадратичной формой
поверхности
<р2 = Ddu- + 2D'dudv + D"dv*. E.2 : 1)
85
Нормальная кривизна кривой равна отношению двух квад-
квадратичных форм поверхности
* y2D'dudv + D"dt? E 2 • »
-f 2Fdudv 4- Gdb» '
Поскольку нормальная кривизна имеет внутреннее значе-
значение, не зависящее ни от выбора декартовой системы коорди-
координат или перемещения.поверхности в пространстве, ни от вы-
выбора криволинейных координат на поверхности, и такой же
внутренний смысл имеет линейный элемент ds2, то и вторая
квадратичная форма фг будет инвариантна в том же смысле,
как и первая квадратичная форма.
Заметим, что выражение E.2:2) однородно нулевого из-
измерения относительно дифференциалов du, dv, следователь-
следовательно, зависит только от их отношения du : dv, которое вполне
определено, если дана касательная E.1 : 1) кривой. Отсюда
следует теорема:
Теорема. Все линии на поверхности, проходящие через
точку Мо поверхности с общей касательной, имеют одну и ту
же нормальную кривизну.
Если обратить внимание на формулу E.1 :4), откуда сле-
следует
k=-^—, E.2:3)
cos a v
то можно усилить эту теорему. Поскольку ft , как угол глав-
главной нормали с нормалью к поверхности, определяет угол
соприкасающейся плоскости с нормалью к поверхности, то
при заданной соприкасающейся плоскости мы будем знать не
только касательную как пересечение касательной плоскости
с соприкасающейся, следовательно, знать нормальную кри-
кривизну kn линии, но по формуле E.2:3) с помощью угла ft
можем определить всю кривизну k линии. Отсюда имеем
следствие.
Следствие. Все линии на поверхности, имеющие в задан-
заданной точке заданную соприкасающуюся плоскость, имеют в
этой точке одну и ту же кривизну.
Среди всех Линий с общей соприкасающейся плоскостью
простейшей будет плоская линия, т. е. линия пересечения по-
поверхности этой плоскостью.
Рассмотрим теперь касательную х к поверхности и две
плоскости, секущие поверхность и проходящие через каса-
касательную х: одна нормальная плоекость, т. е. плоскость, про-
проходящая через нормаль, другая — наклонная, образующая с
первой угол ft.
86
Для нормального сечения угол наклона его ллоокости к
нормали поверхности равен 0 или я и с точностью до знака
ее кривизна равна нормальной кривизне, которая соответст-
соответствует этой касательной х;обозначим ее kn. Для второй плос-
плоскости этот угол равен &, а кривизна получается по форму-
формуле E.2:3). Введем теперь радиусы кривизны: для первой
kn = —, для второй &= —.Внося эти значения в уравне-
Рп Р
ние E.2:3) и освобождаясь от знаменателя, получим
р = рясс«&. E.2:4)
Радиус кривизны измеряет расстояние от точки М до цент-
центра кривизны С. Следовательно,
и формула E.2 : 4) запишется:
МС = МС„ cos &.
Это формула для катета МС прямоугольного треугольни-
треугольника, определяемого по гипотенузе МСп и прилежащему углу
Сп МС. Следовательно, в точке С треугольник имеет прямой
угол, и прямая СпС—перпендикуляр, опущенный из цент-
центра нормальной кривизны на наклонную (секущую) плоскость.
Теорема. Центр кривизны наклонного сечения является
проекцией на плоскость сечения центра кривизны нормально-
нормального сечения с той же касательной.
§ 3. Главные направления в точке поверхности
Перейдем теперь к исследованию изменения нормальной
кривизны при повороте касательной т в касательной плоско-
плоскости точки М.
Согласно обычаю радиус кривизны нормального сечения
поверхности берется с противоположным знаком
л *
Следовательно, при отрицательном знаке радиуса кривиз-
кривизны R нормального сечения центр кривизны лежит на норма-
нормали к поверхности в ее положительном направлении.
Исследование поведения всякой функции естественно на-
87
чинается с отыскания точек максимума и минимума функции.
Мы рассматриваем функцию
Ddu* + 2D'dudv,D"dV* E3:1)
в зависимости от направления касательной к линии на по-
поверхности, т. е. в зависимости от отношения дифференциалов
du : dv. Чтобы не иметь дело с дробями, освобождаемся от
знаменателей
Ddu2 + 2D'dudv + D"dv2 +
+ — (Edu2 + 2Fdudv + Gdv2) = 0. E.3 : 2)
Изменения отношения du: dv можно достигнуть, меняя
числитель t=du при постоянном знаменателе или знамена-
знаменатель T)=dv при постоянном числителе. Поэтому мы можем
дифференцировать обе части равенства E.3 :2) по перемен-
переменному | или по переменному ц; при этом, производную функ-
функции — будем полагать равной нулю, потому что экстремум
R
функции может быть только при обращении в нуль ее произ-
производной. Мы получим по сокращении на 2:
Ddu + D'dv + — (Edu + Fdv) = 0,
R E.3:3)
D'du + D"dv + — (Fdu + Gdv) = 0.
R
Каждое из этих уравнений вместе с уравнением E.3:2)
определяет отношение du:dv в точке экстремума и значение
функции — в этой точке'. Впрочем непосредственно видно,
R e
что из этих трех уравнений независимы только два: если
уравнения E.3:3) умножить первое на du, второе на dv и
сложить, то получим уравнение E.3:2).
Исключая из уравнений E.3:3) неизвестное —, полу-
получим уравнение
Ddu + D'dv Edu + Fdv
D'du + D"dv Fdu -f Gdv
= 0, E.3 : 4}
которое определяет те направления du: dv на поверхности,
которым соответствует экстремум нормальной кривизны.
88
Определение. Те направления в точке поверхности,
которые дают экстремум нормальной кривизны, называются
главными направлениями; соответствующие им экстремаль-
экстремальные значения R (или — ).— главными радиусами кривизны
R
(или главными кривизнами).
Теорема. В каждой точке всякой поверхности (кроме сфе-
сферы) существуют в касательной плоскости два действитель-
действительных, взаимно перпендикулярных главных направления. На
сфере главные направления неопределенны.
Надо доказать, что квадратное уравнение E.3:4) имеет
действительные корни для отношений —. Так как вопрос
0X1
существования главных направлений не может зависеть от
выбора координатных линий, то для облегчения выкладок бу-
будем считать координатную сеть ортогональной, т. е. будем
полагать F=0. Уравнение E.3:4) примет вид
(Ddu + D'dv) Gdv — (D'du 4 D'dv) Edu = 0,
или
ED'du* + (ED" - GD) dudv - GD'dv* = 0 E.3 :5)
и его дискриминант очевидно положителен
(ED" - GDJ + 4EGD'2 > 0,
ибо ?>0 и G>0.
Действительность главных направлений доказана. Чтобы
доказать ортогональность главных направлений, которые со-
соответствуют решениям — и — уравнения E.3:5), доста-
dv So
точно заметить, что произведение решений квадратного уран-
нения E.3:5) при D'=/=Q будет
du ш _ G
dv So E
откуда
Edubu + Gdvbv =* 0,
что при ^=0 совпадает с условием ортогональности D.2:5).
Если D'=0, то уравнение E.3 :5) принимает вид
(ED" — GD) dudv = 0 E.3 : 6)
89
и координатные линии du=0 и do=0'при F=Q ортогональны;
если же
ED" - GD = О, E.3 : 7)
то главные направления неопределенны.
§ 4. Линии кривизны
Определение. Линия, которая в каждой точке имеет
касательную главного направления, называется линией кри-
кривизны.
Следствие 1. Через каждую точку поверхности проходят
две линии кривизны.
Следствие 2. На каждой поверхности (кроме сферы) есть
два семейства линий кривизны; они всегда действительны и
образуют ортогональную сеть.
На сфере E.3:7) линии кривизны неопределенны.
Следствие 3. Обращение в нуль средних коэффициентов
двух квадратичных форм поверхности необходимо и доста-
достаточно, чтобы поверхность была отнесена к линиям кривизны.
Мы видели достаточность этого признака. Докажем необ-
необходимость. Если поверхность отнесена к линиям кривизны, то
уравнение E.3:4) допускает решения d«=0 и dv=0. Полагая
по очереди du=0 и dv=0, получим:
D'G — D"F = О, НЕ — DF = 0, E.4 :1)
их можно рассматривать как линейные однородные уравнения
относительно И и F. Такая система допускает только нулейые
решения D'=0, F=0, если только определитель системы
E.3:7) не обратится в нуль, что мы рассмотрим ниже в § G.
§ 5. Формулы Родрига
Вернемся к уравнениям E.3:3), которые дают повод к
хорошему геометрическому истолкованию.
Если Е, F, G заменить по формулам D.1 :7), a D, D', D"
по формулам E.1 :8), то легко заметить, что в первом урав-
уравнении выносится за скобку множитель Мц, а во втором М„
м„ {п„ du + n> - JL (м„ du + mv <fo)} = о,
du + n> - -L (м„ du + mv dv)} = o,
90
или
nv
v (dn — -L dn) = o,
n (dn - — ?/m) = 0.
E.5:1)
Последнее равенство — очевидное тождество: дифференциал
единичного вектора dn перпендикулярен к самому вектору
и касательный вектор dn перпендикулярен к нормали п.
Поскольку векторы М„, Мг,, п не компланарны, имеем
dn=— dn. E.5:2)
Уравнения E.3 :2) определяют главные направления du : dv
и главные радиусы кривизны R,, R2. Их следствие, уравнение
в полных дифференциалах E.5:2), имеет место для каждого
из главных направлений и соответствующего главного радиу-
радиуса кривизны R и только для этих направлений. Чтобы дать
геометрическую формулировку уравнению E.5:2), надо вве-
ввести понятие сферического изображения поверхности.
Рассмотрим поверхность
М = М (u, v)
и единичный вектор нормали п . Если провести из произволь-
произвольной фиксированной точки, например начала координат О, век-
вектор нормали п
От = m = п,
то конец этого радиуса-вектора, точка т, будет лежать на
сфере радиуса единицы с центром в начале координат. От-
Отсюда взаимно однозначное соответствие достаточно малок,
области поверхности и соответствующей области на сфере,
которое называется сферическим изображением- поверхности.
Уравнение E.5:2) теперь можно записать в виде
dm = — dn. E.5 :3)
R
Здесь dNi — инфинитезимальное смещение точки М на по-
поверхности в главном направлении, dm — соответствующее
смещение в сферическом отображении. Отсюда теорема:
91
Теорема. Главные направления поверхности параллельны
соответствующим направлениям в сферическом изображении
поверхности. Предел отношения этих смещений на сфере и
на поверхности равен главной кривизне этого направления.
Формулы Родрига E.5 :3) приводят к замечательной ха-
характеристике линий кривизны.
Теорема. Нормали к поверхности вдоль линии кривизны
и только вдоль линии кривизны образуют развертывающуюся
поверхность; ребро возврата при этом описывает соответст-
соответствующий главный центр кривизны.
Действительно, из уравнения E.5:2) следует
</М — Rdn = О, E.5 :4)
или
d(M — Rn) = dM-Rdn-ndR=-ndR. E.5:5)
Следовательно, главный центр кривизны
С = М — Rn E.5: 6)
при движении точки М вдоль линии кривизны! описывает ли-
линию, которая касается нормалей п к поверхности, а эти нор-
нормали тем самым образуют развертывающуюся поверхность.
Обратно, если нормали к поверхности образуют разверты-
развертывающуюся поверхность, то ребро возврата должно описывать-
описываться некоторой точкой нормали E.5 :6) при подходящем выборе
отрезка R. Дифференцируя равенство E.5:6) и требуя, что-
чтобы вектор касательной dC был коллинеарен вектору п , по-
получим E.5:5) и отсюда E.5:4), что эквивалентно равенству
E.5:2). Следовательно, смещение точки М идет по главному
направлению, и R — соответствующий главный радиус кри-
кривизны.
§ 6. Неопределенность главных направлений
Уравнение E.3:4) обратится в тождество и главные на-
направления будут неопределенны, если коэффициенты двух
квадратичньис форм поверхности будут пропорциональны
-° =-? = ?. E.6:1)
Е F G v
Уравнение E.3:1) показывает, что при этом кривизна нор-
нормального сечения по всем направлениям одна и та же. Урав-
Уравнение E.5:2) теперь будет иметь место для всякого смеще-
смещения dM. Следовательно, мы можем рассматривать уравне-
92
ние E.5:2), как уравнение в полных дифференциалах и раз-
разбить на два уравнения в частных производных
nu=-^Mu, ny = -LjVIo, E.6:2)
откуда, дифференцируя первое уравнение по v, второе по' и
и вычитая из одного другое, получим
Поскольку векторы Mu, M.v линейно независимы, коэффи-
коэффициенты обращаются в нуль:
±) =0, Ш =o.
Rlv \ Rlu
Следовательно, /?=const и уравнения E.6:2) можно заме-
заменить одним уравнением в полных дифференциалах
d (М - Rn) = 0,
откуда
М — Rn = А и М — А = Rn, A = const,
где А—произвольный постоянный радиус-вектор, и возвы-
возвышая обе части в квадрат, получим
(М - АK = Я2;
это означает, что радиус-вектор AM имеет постоянный модуль
и все точки М лежат на одном и том же расстоянии R от
точки А, т. е. поверхность является сферой радиуса R с цент-
центром в точке А.
§ 7. Полная и средняя кривизна поверхности
Система E.3:3) относительно неизвестных du, dv являет-
является однородной системой двух линейных уравнений с двумя
неизвестными. Такая система имеет нулевые решения, для
нас непригодные, если определитель системы не равен нулю.
Обращение его в нуль
D
D'
+
+
1
~R
1
R
Е
F
D'
D"
+
+
1
R
1
R
F
G
93
приводит к квадратному уравнению относительно главных
кривизн
(EG -P)-(—J+(DG+ D"E - 2FD1) -i- +
\ R I R
+ DD" - U2 = 0. E.7 :1)
Обозначая через R\, R2 два главных радиуса кривизны
нормальных сечений поверхности, получим по формулам
Вьета:
„ 1.1 2FD' -ED" -GD
п = = ,
Rt R3 EG-F*
1 DD"D'Z
~R~&~ ~ EG-F»
E.7:2)
Н и К называются соответственно средней и полной (гаус-
(гауссовой) кривизной поверхности. Это основные скалярные ин-
инварианты поверхности. Если говорят о поверхностях постоян-
постоянной кривизны, то имеют в виду полную кривизну поверхности.
Обращение в нуль средней кривизны #=0 выделяет замеча-
замечательный класс минимальных поверхностей, которые при за-
заданном контуре имеют наименьшую площадь.
Впервые получил эти инварианты, в другом виде, Эйлер.
§ 8. Формула Эйлера
Отнесем поверхность к линиям кривизны. Тогда D'=0,
F=0 и формула E.3: 1) примет вид
J_= fltf + W E8
R Edu* + Gdi* ' v
Главным направлениям соответствуют главные радиусы кри-
кривизны. Обозначим через R\ и R% соответственно главные ра-
радиусы кривизны направлений rfo=0 и du=0. Внося по очере-
очереди эти значения в равенство E.8: 1), получим:
-*- = -?-. ± = -^. E.8:2)
Ri Е ' R2 G У '
Исключая с помощью E.8:2) коэффициенты D, D" в форму-
формуле E.8: 1), получим
)+()\ E.8:3)
ds j ^ Л, \ ds ) v ;
94
Между тем по формулам D.2 :4) угол ф между касатель-
w du dv
ной —: — и главным направлением 6у=0 или 6«=0 опре-
определяется формулами:
cos<p= =—, cos I ф) =
ds у E bu \ 2 . / dsyG bu '
или
cos<p=ylT—, sincP = yrG—. E.8:4)
Внося эти значения в уравнение E.8:3), получим
1 cos8 ф . sin'tp _ о _.
~~Б~ = ~Б ' ~^~~- E.8:5)
Это и есть формула Эйлера. Она позволяет дать полную
картину изменения кривизны нормального сечения.
Будем предполагать, что главные радиусы кривизны^,R2
не равны между собой, и положим, учитывая знак,
Тогда, заменяя соз2ф на 1—sin^, получим:
— = — + sin2 <р(— —) ; — — > 0. E.8 : 6)
D D ID D I D D
Второе слагаемое правой части положительно; следова-
следовательно, наименьшее значение кривизны нормального сечения
(с учетом знака) будет при
при возрастании угла ф второе слагаемое возрастает, а вме-
вместе с ним возрастает и кривизна нормального сечения и до-
достигает наибольшего значения при ф= 1 , т. е. при sir^=l,
когда ,
_L = J_,/J х-\ = —
R Rx \R, Ri I R» '
Таким образом, если рассматривать кривизну нормально-
нормального сечения как алгебраическую величину, то экстремальными
значениями кривизны нормального сечения для главных на-
направлений будет один минимум и один максимум.
95
Иначе дело обстоит, если рассматривать перемещение по
нормали центра кривизны нормального сечения
С =,ЛГ+ Rn.
а) Если главные радиусы кривизны одного знака
1
К =
¦>0,
то, меняя в случае надобности положительное направление
нормали на противоположное, можно считать
Ri>R2>0.
Тогда по формуле E. 8: 5)
кривизна нормального сечения
для любого направления поло-
положительна, и центр кривизны
нормального сечения при вра-
вращении касательной будет про-
пробегать отрезок С] С2 положи-
положительной нормали между точка-
точками
d = М + #in и С2 = М + Rzti.
На рис. 29 в точке М по-
p1IC og верхность имеет положитель-
положительную кривизну; линии Р'МР"
и Q'MQ" касаются главных
направлений в точке М; Сх и С2 — главные центры кривизны.
Отрезок С\С2 содержит все центры кривизны нормальных се-
сечений.
Ь) Если кривизна
К = Ж<0'
мы будем считать Ri>0, R2<0, точки Сх и С2 будут располо-
расположены по разные стороны поверхности, а так как кривизна
нормального сечения в регулярной области не обращается в
бесконечность, то следует предположить, что центр кривизны
нормального сечения С, выходя из точки С\, будет поднимать-
подниматься, удаляясь от поверхности; найдутся направления (асимп-
(асимптотические), которые соответствуют нулевой нормальной кри-
кривизне и бесконечно удаленному центру кривизны; после этого
центр кривизны С будет приближаться к поверхности, подни-
поднимаясь уже по отрицательной нормали до точки С2.
96
о
Рис. 30
Рис 31
Г Заказ 1874
На рис. 30 в точке М полная кривизна поверхности отри-
отрицательна. С] и С2 — главные центры кривизны. Между С] и С2
нет ни одного центра кривизны нормального сечения. Они
расположены выше С2 и ниже Сь
с) Если кривизна поверхности
то одна из главных кривизн равна нулю
и центр кривизны нормального сечения пробегает полупря-
полупрямую от точки Ci в бесконечность (рис. 31).
§ 9. Индикатриса Дюпена
Наглядно можно представить изменение кривизны нор-
нормального сечения с помощью индикатрисы Дюпена.
Обозначим
incp E.9:1)
так, что если положить
где Ji, J2 — единичные векторы касательных главных на-
направлений в точке М поверхности, то точка Р будет все вре-
время лежать в касательной плоскости, так что расстояние ее от
точки касания М равно радиусу кривизны того нормального
сечения поверхности, которое проходит через касатель-
касательную МР.
Внося значения cosqp, sin ф по формулам E.9:1) в урав-
уравнение E.8:5), получим уравнение индикатрисы Дюпена в ви-
виде кривой 2-го порядка
-?¦ + -?.= 1,
отнесенной к осям.
Если К>0, то можно считать Ri>R2>0; индикатриса пред-
представляет каноническое уравнение эллипса с полуосями VR\>
V^Rz', главные направления эллипса совпадают с главными
направлениями поверхности (рис. 32).
98
Если К=
_1_
r!r»
<0 и
то индикатриса представ-
представляет гиперболу, вернее две сопряженные гиперболы. Если
положить
D пЪ D W
l\l — и , t\2 — — " >
то уравнение индикатрисы бу-
дет (рис. 33)
хг у2 ...
fl2 6» ~
Наконец, если
1
= 0 и
Рис. 32
то уравнение индикатрисы
— =1, или х = ± а,
а*
Рис. 33
представляет пару параллельных прямых. Одно из главных
направлений совпадает с асимптотическим направлением
(рис. 34).
7* 99
§ 10. Асимптотические линии
Асимптотической линией на поверхности называется ли-
линия, нормальная кривизна которой в каждой ее точке равна
нулю.
Рис. 34
По формуле E.1:4) нормальная кривизна линии обра-
обращается в нуль в двух случаях: 1) когда кривизна &=0; в этом
случае (если во всех точках линии кривизна равна нулю)
линия будет прямой; 2) когда
= 0, т.е. Ь= + —,
~ 2
Это показывает, что главная нормаль перпендикулярна к нор-
нормали поверхности и лежит в касательной плоскости, а по-
поскольку касательная плоскость всегда содержит касательную
к кривой, то касательная плоскость поверхности совпадает с
соприкасающейся плоскостью асимптотической линии, а нор-
нормаль к поверхности — с ее бинормалью.
Поскольку нормальная кривизна асимптотической линии
в каждой точке равна нулю, уравнение асимптотических ли-
линий поверхности получается обращением в нуль второй квад-
квадратичной формы E.2:1), которая стоит в числителе нормаль-
нормальной кривизны E.2:2)
D du* + 2D' dudv + D"dv* = 0.
E.10:1)
ioo
Дискриминант этой формы
DD" — D'2
стоит в числителе гауссовой кривизны E.7:2) при .положи
тельном знаменателе EG—F. Следовательно, уравнение
E.10:1) имеет действительные корни, и асимптотические ли-
линии существуют, образуя сеть линий, только в той области
поверхности, где ее кривизна отрицательна.
Пример. Найдем асимптотические линии геликоида. Под-
Подсчитывая коэффициенты второй квадратичной формы по фор-
формулам E.1 :7)
м
м„
X
У
г
получи\
«cos v
usiny
аи
i
cosy
sin у
0
— «sin у
ucosy
а
0
0
0
— sin у
cosy
0
— «cosy
— a sin у
0
VEG — Л = |/аа + а| ,
D = 0, D" = 0, D' =
a*
cosik —usmv
sin у «cosy
0 а
—sin у
cosy
0
— а
=— du dv,
и уравнение асимптотических линий
du dv = 0,
т. е. семейство «=const — винтовые линии и семейство
yr=const — прямолинейные образующие.
101
§ 11. Сопряженные семейства линий
Рассмотрим произвольную линию С на поверхности. Каса-
Касательные плоскости к поверхности в точках линии С образуют
однопараметрическое семейство плоскостей. Если обозначить
буквой Р текущую точку касательной плоскости к поверхно-
поверхности в некоторой точке М линии С, то ее уравнение запишется
(Р-М)п = 0, E.11:1)
где п — единичный вектор нормали к поверхности в точке М.
Если линия С задана уравнением D.1:3), то за параметр
семейства плоскостей можно принять а=*. т. е. параметр,
определяющий положение точки М на линии С.
Чтобы найти характеристику плоскости E.11 : 1), доста-
достаточно продифференцировать обе части уравнения E.11 : 1) по
параметру t; при этом текущие координаты плоскости и, сле-
следовательно, текущий радиус-вектор Р не дифференцируются:
Первый член обращается в нуль в силу ортогональности
вектора касательной к нормали п; имеем
at
(Рг_М)^- = 0. E.11:2)
Таким образом, характеристика касательной плоскости опре-
определяется уравнениями E.11:1), E.11:2). Первое уравнение
показывает, что вектор
Жр=Р-М=\ — , E.11:3)
Ss
как касательный вектор поверхности, может быть представ-
представлен производной радиуса-вектора точки поверхности, взятой
вдоль касательной к характеристике МР. Внося выраже-
выражение E.11:3) во второе уравнение характеристики E.11:2)
и отбрасывая множитель пропорциональности к, получим
Щ dn _„
8s dt ~ '
или, опуская дифференциалы 6s, dt и помня, что d — символ
102
дифференцирования вдоль линии С и б — вдоль характери-
характеристики, получим
SM dn = 0;
внося вместо 6М выражение D.1:4) и аналогично для dn,
получим
(Мв Ьи + М, bv) ¦ (n, du + nv dv) = 0,
или, пользуясь обозначениями E.1 :8),
bv'=O. E.11 :4)
В уравнение E.11 :4) символы дифференцирования d и 8
входят симметрично. Следовательно, если точку М смещать
в направлении Ш, то характеристика касательной плоскости
будет иметь направление dM.
Два направления dM и 8М, удовлетворяющие условию
E.11 :4), называются сопряженными.
Нетрудно заметить аналогию между условием ортогональ-
ортогональности D.2:5) и условием сопряженности E.11 :4). Повторяя
рассуждения D.2), придем к результату:
При произвольно заданном регулярном семействе линий
на поверхности
Ф(ы,1») = С E.11:5)
можно найти единственное второе семейство линий
4(u,v) = C E.11:6)
так, что через всякую точку области будут проходить по одной
линии каждого семейства, пересекающихся по сопряженным
направлениям.
Говорят, что такие два семейства линий E.11 :5 и 6) обра-
образуют сопряженную систему линий. Если координатные линии
u=const и u=const сопряжены, то уравнение E.11 :4) долж-
должно удовлетворяться значениями
du = 0, bv = 0.
Отсюда признак сопряженности координатных линий
D' = 0. . E.11:7)
Рассуждения E.4) следствия 3 (стр. 90) показывают, что
при отнесении поверхности к линиям кривизны E.4 : 1)
F=0, D'=0.
103
Следовательно, линии кривизны и только линии кривизны
образуют систему одновременно ортогональную и сопряжен-
сопряженную.
Наконец, если в условии сопряженности E.11:4) поло-
положить 6u=du, 6v=dv, то придем к уравнению асимптотических
линий E.10: 1). Следовательно, асимптотические линии сами
себе сопряжены.
ГЛАВА VI
ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
§ 1. Ортогональный репер, присоединенный к точкам
поверхности
Так же, как к каждой точке кривой присоединяется орто-
нормированный трехгранник Френе, так к каждой точке по-
поверхности можно присоединить прямоугольный трехгранник
с единичными векторами осей.
Две первые оси Jj, J2 располагаются в касательной пло-
плоскости, третья ось J3 совмещается с нормалью к поверхности.
Поскольку касательные к любой линии на поверхности
лежат в касательной плоскости, вектор
_ dM
Т ~~ ds
имеет компоненты только по осям Ji и J2. Следовательно,
вектор
dM = Madu + Mvdv F.1:1)
можно представить в виде
dto = шЧг + шЧг; F.1:2)
при этом компоненты со1, со2, очевидно, будут линейными фор-
формами дифференциалов du, dv:
= a1 du + b1 dv, j
F.1 :d>
105
Точно так же дифференциалы единичных векторов осей
J2, J3 будут:
= шх2 J2 -f
F.1:4)
Третьего компонента в правых частях нет, так как диффе-
дифференциалы единичных векторов перпендикулярны к самому
вектору и компонентов по этому вектору не имеют.
Следовательно,
= и>2 = <Мз =0.
F.1:5)
Кроме того, базисные векторы Jb J2, J3 попарно ортого-
ортогональны и единичны, например:
JjJj-O, J,2=J82=1. F.1:6)
Дифференцируя первое тождество, получим
JjdJi + hdh = h (<"!% + <"¦%) +
+ Jl (*%\ + Л) = 0.
Раскрывая скобки, убедимся, что в силу соотношений
F.1 :5, 6) останутся только квадраты векторов, и мы получим:
м =0;
(и,2 -)-
= 0.
= 0. <»з'+
F.1:7)
последние два тождества написаны по аналогии.
Следовательно, существуют только три линейно-независи-
линейно-независимые формы с двумя индексами, для которых мы даем выра
жения через дифференциалы du, dv в обозначениях Дарбу:
(и, = rdu + r' dv,
<u23 = pdu + р' dv
шз1 = qdu + q' dv.
F.1:8)
Здесь сопоставляются трем указателям 1, 2, 3 три после
довательные буквы латинского алфавита р, q, r. Если форма,
например, o>i2 несет две первые цифры, то сопоставляется
третья буква г. Коэффициенты при дифференциале dv снаб-
снабжаются штрихом. Переход от первой строки ко второй и тре-
106
тьей совершается круговой подстановкой, когда после указа-
указателя 3 снова идет указатель 1 и после буквы г снова буква р.
Линейный элемент поверхности получается возвышением
в квадрат дифференциала dtA
ds2 = dM2 = ((«ijj + uJJ2J = (uIJ + (uJJ. F.1: 9)
В силу ортогональности репера сохранились только квадра-
квадраты компонентов.
Если принять ортогональную систему координатных ли-
линий и, v а направить векторы Jx, J2 по касательным к ли-
линиям u=const и и= const, то форма w1 сохранит только диф-
дифференциал du, а со2 — только дифференциал dv. Меняя не-
несколько обозначения коэффициентов, будем писать:
F.1 : 10)
F.1:11)
§ 2. Нормальная и геодезическая кривизна линии
на поверхности
Рассмотрим произвольную линию на поверхности в обла-
области ее регулярности и обозначим буквой а угол наклона ее
касательной т к первой оси Jx (рис. 35). Тогда
т = Jx cos a 4- J2sina. F.2:1)
Отсюда, дифференцируя по длине дуги s этой кривой, по-
получим
dx djt . dj2 . 1 / . 1 • 1 1 /-» \ da
ds ds ds X ds
или, пользуясь формулами F.1:4),
2 „3
A
Ш2 Ш2 \ dz
—=- Ji И — J3 sin a + { - J,sina + J2cosa) ,
ds ds ) ds
или, выделяя члены с вектором J3,
ds
107
Левую часть можно преобразовать по формулам Френе
— — h
~ds' ~
и представить в виде вектора кривизны (отрезок, отложенный
на главной нормали в положительную сторону, равный кри-
кривизне кривой). В правой части
мы видим два слагаемых:
а) Второе слагаемое — лек-
лектор, отложенный по нормали;
следовательно, коэффициент
при единичном векторе J3 —
проекция вектора кривизны на
нормаль к поверхности, т. е.
нормальная кривизна кривой
<d,3coso 4- <«23s'n а
По формулам Дарбу F.1: 8),
F.1:7):
— и)!3 = (и3! = q du 4- q' dv,
Рис. 35
Следовательно,
cos a =
k —
Kn
Ddu*
—, Sina
ds
ds*
+ 2D' dudv +
D"
ds '
dv*
u)j3 = pdu + p'dv. F.2:3)
С другой стороны, сравни-
сравнивая формулы F.2:1) и
F.1 :2), получим:
F.2:4)
ds1
F.2:5)
или, пользуясь для а1, и2 выражением F.1 : 10), а для
формами Дарбу,
— (qdu 4- q'dv) adu + (pdu + p'dv) bdv =
2D' du dv + D"dv\
108
Отсюда
.?.= _,, ?1=р', & = ?=&-. F.2:6)
а о l
Ь) Первое слагаемое правой части F.2:2), тоже имеет
множителем единичный вектор
— Jl sin a + h cos а = Jx cos (— + а) -f
F.2:7)
Сравнивая с вектором касательной F.2:1), видим, что
вектор F.2:7) — тоже единичный вектор ч, но повернутый
в положительном направлении на —.
Коэффициент, который стоит при этом векторе, опреде-
определяет проекцию вектора кривизны на касательную плоскость.
Эта проекция называется геодезической кривизной линии и
обозначается
*,= ¦?- + ¦?' • <б'2:8)
* as ds
Нетрудно заметить, что da означает элементарный поворот
вектора касательной относительно трехгранника, wi2 — пово-
поворот самого трехгранника так, что сумма их дает полный по-
поворот касательной за время, в течение которого точка М сме-
сместилась на ds.
Если сохранить обозначение О за углом между вектором
главной нормали и нормалью к поверхности, то угол между
вектором главной нормали и касательной плоскостью будет
— —ft. Следовательно, геодезическая кривизна равна
kg = ksinb. F.2:9)
Теорема. Геодезическая кривизна линии на поверхности
зависит только от линейного элемента поверхности и уравне-
уравнения кривой относительно выбранного репера.
Действительно, первое слагаемое — зависит от угла a
между касательной и первой осью репера, т. е. определяете?
уравнением кривой и линейным элементом (выбранным ре-
пером). Покажем, что и второе слагаемое — определяется
as
коэффициентами линейного элемента.
109
Умножая первое уравнение F.1 : 4) на вектор J2, получим
<uj = J2dJx.
Пользуясь для простоты ортогональной системой коорди-
координатных линий и формулами F.1:9), F.1:10), заметим, что
единичные векторы репера будут
Ji = — Mu, J-> = — Mj,.
а о
Следовательно,
(V = 4- mJ mad -L + ± (Muadu + muvdv)),
b ( a a )
или в силу ортогональности координатных линий
М.М„ = 0 F.2:10)
имеем
щ2 = J- {MvtAuudu + MvtAuvdv\,
ab
но, очевидно,
а, дифференцируя по переменному и тождество F.2: 10), по-
получим
Мив Ми + Мв Мвг, = 0,
значит
Таким образом, имеем
2 1 да . , 1 дЬ , ,г, с% 11 \
(и, = —du -) du, F.2:11)
b dv a du
и геодезическая кривизна
t
g ds b dv ds ' a du ds
110
Следовательно, геодезическая кривизна линии зависит от
уравнения кривой на поверхности и линейного элемента по-
поверхности.
Следствие. При изгибании поверхности геодезическая
кривизна линий на поверхности не меняется.
§ 3. Геодезические линии
Определение. Геодезическими называются линии с
нулевой геодезической кривизной.
Следствие. Всякая прямая линия на поверхности будет
геодезической.
Действительно, кривизна прямой равна нулю /г=0, а сле-
следовательно, по формуле F.2:9) и геодезическая кривизнг
kg (и kn) равна нулю.
Из этой же формулы следует, что, кроме прямой, геоде-
геодезическими могут быть только те линии, у которых
sin& = 0, т. е. & = 0 или я.
В обоих случаях @ или я) главная нормаль с точностью до>
положительного направления совпадает с нормалью к по-
поверхности и соприкасающаяся плоскость проходит через нор-
нормаль к поверхности. Отсюда
Теорема. Соприкасающаяся плоскость геодезической ли-
линии проходит через нормаль к поверхности или неопределен-
неопределенна (случай прямой линии). Обратно, если соприкасающаяся
плоскость проходит через нормаль к поверхности, то линия —
геодезическая.
Уравнения геодезической линии. Чтобы определить на по-
поверхности геодезическую линию, надо к уравнению kg=0,
du
например, в форме F.2:12), добавить выражения для —>
as
—, исключая ш1, ш2 из уравнений F.2:4), F.1 : 10)
ds
F.3:1)
du dv
или, подставляя в первое уравнение значения —, -— из
1Н
да
ds
_ 1
b
да
dv
~dT
dv
ds
du
ds
a
_ 1
~~ b
1
a
COS a,
sina,
db
du
dv
ds '
второго и третьего,
d% 1 да 1 дЬ .
= cos a sin а,
ds ab ди аЬ ди
F.3:2)
du \ do 1 .
=—COS а, = —Sin а.
ds a as Ь
Если линейный элемент поверхности задан и, следователь-
следовательно, функции а, Ь (коэффициенты линейного элемента) изве-
известны, то для определения а, и, v надо проинтегрировать си-
систему обыкновенных дифференциальных уравнений F.3:2).
Это система Коши, разрешенная относительно производных
трех неизвестных функций и, v, а по независимому перемен-
переменному s.
Для системы Коши, если правые части —.регулярные
функции переменных и, v, а, имеет место теорема существо-
существования решения. Система Коши допускает решение и только
одно, удовлетворяющее системе F.3:2) и начальным усло-
условиям: неизвестные функции принимают значения
u = u0, v = v0, а.= а0 для s = s0, F.3:3)
если правые части системы F.3:2) регулярны в окрестности
точки (и0, i>o, ao. So).
Начальные значения F.3:3) допускают геометрическое
истолкование.
Теорема. Через' всякую точку поверхности М0(и0, v0) в об-
области ее регулярности под произвольным углом а0 наклона
касательной к первой оси репера проходит одна и только одна
геодезическая линия. .
Эту теорему можно сопоставить с теоремой на плоскости:
через всякую точку М0(х0, уо) по всякому направлению (под
произвольным углом наклона к оси х) проходит одна прямая.
Заметим, что второе предложение планиметрии: через каж-
каждые две точки плоскости проходит одна и только одна пря-
прямая — уже не всегда удовлетворяется для геодезических на
поверхности.
Если взять Сферу, то легко заметить, что геодезическими
будут плоские сечения сферы плоскостями, проходящими че-
через центр сферы С (окружности большого круга). Действи-
Действительно, нормаль к сфере совпадает с продолженным радиу-
радиусом; следовательно, плоскость окружности большого круга
всегда (во всех своих точках) проходит через нормаль к
сфере.
112
Для двух точек А и В, если они не лежат в концах одного
диаметра, можно провести одну плоскость ABC, где С —
центр сферы. Она определит одну замкнутую геодезическую
(окружность большого круга) и две дуги kjAB и \уАА'В, где
А' — точка, диаметрально противоположная точке А.
Если А и В — диаметрально противоположные точки сфе-
сферы, то центр С лежит на прямой АВ, и мы имеем пучок пло
скостей, каждая из которых сечет сферу по окружности боль-
большого круга, проходящего через точки А к В. Имеем однопа-
раметрическое семейство геодезических одной длины, соеди-
соединяющих точки А к В.
§ 4. Геодезическая линия как кратчайшее расстояние
между двумя точками поверхности
Обратимся теперь к условиям, при выполнении которых
дуга АВ геодезической осуществляет кратчайшее расстояние
между точками Л и Б по сравнению с другими линиями, про-
проходящими на поверхности между этими точками.
Проведем из точки А по всем направлениям пучок геоде-
геодезических линий с общей точкой А. К этому .семейству линий.
проведем семейство ортогональных траекторий. Мы получим
правильную ортогональную сеть линий, за исключением самой
точки А, через которую проходят все геодезические пучка А.
Чтобы исключить особую точку А, можно ограничить двумя
геодезическими линиями по обе стороны от геодезической АВ
и двумя ортогональными траекториями, из которых одну прп-
ведем через точку В, а другую сколь угодно близко от точ-
точки А, но так, чтобы точка А осталась вне рассматриваемой
области.
Будем предполагать, что в рассматриваемой области гео-
геодезические не пересекают друг друга, в частности, не пере-
пересекают геодезическую АВ. Примем эту сеть линий за коорди-
координатную сеть; пусть линейный элемент будет
ds2 = аЧиг + 6W. F.4:1)
Будем предполагать, что линии и—const будут геодезически-
геодезическими нашего семейства и линия v=0 — геодезическая АВ. Вы-
Выразим условие, что линии u=const геодезические; поскольку
вектор касательной совпадает с единичным вектором Jlt
угол а равен нулю; первое уравнение F.3:2) дает
t Заказ 1874 113
и линейный элемент принимает вид
ds* = [f (и) du]f + b4v*.
Если ввести вместо и новый параметр а посредством фор-
формулы
и
= j «Р (")
полагая <т равным нулю для ы=Ыо, т. е. для значения, соот-
соответствующего точке А, то линейный элемент примет вид
ds2 = do2 -f b2dv*. F.4:2)
Следовательно, а — длина дуги геодезической семейства, от-
отсчитываемой от точки А.
' Покажем, что геодезическая А В короче всякой линии, про-
проходящей внутри выделенной области, соединяющей точки
А и В.
Кривую сравнения можно выбрать так, чтобы она пересе-
пересекала каждую линию u=const, т. е. <r=const, только в одной
точке. Если бы она пересекала в двух точках, то можно было
бы ее спрямить, отбрасывая петли или заменяя отрезком ли-
линии u=const.
Таким образом, кривую сравнения можно определить, по-
полагая
0 = <!>(»). F.4:3)
где ф (а) — однозначная, кусочно непрерывная функция клас-
класса С. Длина дуги между точками А и В для кривой сравне-
сравнения определяется, если внести выражение F.4 : 3) в линейный
элемент F.4 : 2); мы получим
ds9 = da» + ЬЦ'г (a) da»,
откуда
ds = У\ + b2y2 (a) da,
i длина кривой сравнения между точками А, и В будет
V = f ]Л+бу*(о)*о, F.4:4)
•» с*
где е — значение параметра в в точке А% пересечения кри-
кривой сравнения с ортогональной траекторией геодезических
114
u=const, проведенной сколь угодно близко от точки А; в\ —
значение параметра а в точке В. Для всех линий AtB пре-
пределы интеграла F.4 : 4) — одни и те же; следовательно, наи-
наименьшее значение интеграла получится при наименьшем зна-
значении подынтегральной функции. Оба слагаемых под знаком
корня в подынтегральной функции положительны; первое
слагаемое остается постоянным; значит, наименьшее значение
интеграла получится при наименьшем" значении второго сла-
слагаемого. Поскольку оно не отрицательно, наименьшее значе-
значение будет нулем. Это заключение не изменится, если мы бу-
будем стремить е-»0-
Значит, рассматривая длину всей линии F.4:3) от точки
А до точки В, мы найдем наименьшей длины линию F.4:3),
удовлетворяющую равенству
или в силу b
f (а) = 0, т. е. ф (а) = С,
где с — постоянное. Чтобы линия проходила через точки А
и В, надо выбрать произвольное постоянное нулем
с = О, т. е. v = О,
и мы приходим к геодезической АВ. Теорема доказана.
Следует обратить внимание на те оговорки, при которых
теорема доказана:
a) Кривые сравнения протекали в достаточно малой окре-
окрестности выбранной геодезической.
b) Точка В расположена на геодезической не слишком да-
далеко от точки А так, чтобы геодезические, выходящие из точ-
точки А, не пересекали дугу А В.
Необходимость первого условия подтверждается приме-
примером винтовой линии на круглом цилиндре. Если развернуть
цилиндр на плоскость (рис. 36), то винтовая линия АСВ обра-
обратится в прямую, которая дает кратчайшее расстояние, одна-
однако на цилиндре отрезок образующей цилиндра АВ, конечно,
короче винтовой линии АСВ.
Необходимость второго ограничения показывает пример
сферы, где дуга окружности большого круга (геодезической)
дает кратчайшее расстояние только до тех пор, пока эта дуга
меньше полуокружности.
Вообще семейство геодезических, выходящих из точки А,
имеет огибающую. Если геодезическая АВ первый раз ка-
касается огибающей в точке А*, то А* называется точкой, со-
8» 115
пряженной точке А. Геодезическая АВ может определять
кратчайшее расстояние между точками А и В только в том
случае, если на дуге АВ нет точки А*; сопряженной точке А.
В
с
Рис 36
в
Рис 37
На чертеже (рис. 37) дуга АВ дает кратчайшее расстоя-
расстояние, дуга АА*В' не дает его, потому что на ней лежит точ-
точка А*, сопряженная точке А.
§ 5. Развертывание линии на плоскость
Как известно, геодезическая кривизна и, в частности, гео-
геодезические линии зависят только от линейного элемента по-
поверхности и при изгибании поверхности не меняютс? Таким
116
образом, если на поверхности построен треугольник из геоде-
геодезических линий, то при изгибании поверхности он сохраняет
все свои «внутренние» свойства. Если поверхность наложена
на плоскость, то геодезические станут прямыми и сумма
углов треугольника останется равной я. Однако не все по-
поверхности налагаются на плоскость. Мы увидим, что па плос-
плоскость налагаются только развертывающиеся поверхности.
Тем не менее мы можем развернуть на плоскость линию и
обнаружить, что после развертывания на плоскость геодези-
геодезическая станет прямой и вообще всякая линия сохранит толь-
только геодезическую кривизну.
Рассмотрим произвольную поверхность 5 и на ней линию L
с геодезической кривизной kg и нормальной kn. Рассмот-
Рассмотрим многообразие касательных плоскостей в точках линии L.
Огибающая этего однопараметрического семейства плоско-
плоскостей образована характеристиками, которые, как мы видели
E.10), проходят через точки касания этих плоскостей и пред-
представляют собой многообразие касательных к поверхности,
сопряженных в каждой точке касательным к линии L.
Развертывающаяся поверхность D, образованная этими ха-
характеристиками, в каждой точке линии L имеет ту же самую
касательную плоскость, что и поверхность S, стало быть ту
же самую нормаль. Линия L принадлежит и той и другой
поверхности: и поверхности 5 и развертывающейся поверхно-
поверхности D. Нормальная kn и геодезическая kg кривизна линии L
на поверхности 5 и на поверхности D будут совпадать. Но
поверхность D мы можем развернуть на плоскость. При этом
главная нормаль и вектор кривизны будут лежать в этой
плоскости, а нормалью будет служить перпендикуляр к пло-
плоскости; проекция вектора кривизны иа этот перпендикуляр
будет равна нулю. Значит после изгибания нормальная кри-
кривизна линии L будет равна нулю, а геодезическая кривизна
останется без изменения
и будет совпадать с кривизной той плоской линии L, в кото-
которую после изгибания обратится произвольная пространствен-
пространственная линия L.
Это построение принадлежит почетному академик}
АН СССР Леви-Чивита и дает наглядное представление внут-
внутренней геометрии произвольной линии на поверхности.
ГЛАВА VI!
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
§ 1. Внешнее дифференцирование линейных форм
Теперь мы возвращаемся к уравнениям F.1 : 1), F.1 :2),
F.1:4), которые определяют движения ортонормированного
трехгранника, чтобы исследовать совместность этих уравне-
уравнений для неизвестных функций М, Jlf J2> Js при заданных
формах а>\ а>1' (i, \— 1, 2 ,3).
Для этого нам придется рассматривать различные сме-
смещения (смещения по различным направлениям)
dM, dh (i= 1, 2, 3).
Будем обозначать различными символами дифференцирова-
дифференцирование по различным линиям, как это мы, например, делали при
определении косинуса угла пересечения двух линий на по-
поверхности D.2:3) или E.11:4).
Например, можно обозначить
следовательно,
* *= * G.1:1)
аи ov
df\=—t Wl=i?. G.1:2)
ди до
Поскольку дифференциал независимого переменного —
произвольное приращение этого переменного, мы нередко бу-
будем полагать аи—\, bv=\.
Рассмотрим уравнение F.1:2) для двух символов диф-
118
ференцирования (которые не обязательно совпадают со зна-
значениями G.1: 1)):
— 5
dM = m1 (d) Jt + ш* (d) Js,
Дифференцируя первое уравнение с символом дифферен-
дифференцирования б, а второе — с символом d и вычитая из нижнего
верхнее, получим:
d5M — 8dM = { doo1 (S) — Вш1 (d)} Jx + dJx ш1 (8) — 8JX ш1 (d) +
+ {dm1 C) — 8ш* (d) ) J2 + dJ2«>* C) - 8J,a> 2(d). G.1 : 3)
Если принять для символов дифференцирования значения
G.1:1), то
ди \ dv / дидо
'дП
дидо
Поскольку при дифференцировании функций по любым пере-
переменным а, р результат дифференцирования не зависит от по-
порядка дифференцированияпри любых значениях d и б, будем
считать
d EM) = 8 (dm)
и, следовательно, в левой части равенства G.1: 3) будет нуль.
Согласно первому уравнению F.1:4) имеем:
и аналогично для dJ2, 8J2.
Внося эти значения в правую часть равенства G.1 : 3) и
собирая члены с одинаковыми векторами 3lt J2, Js, получим:
Jx (doI (8) — 8Ш1 (d) + (<V (d) ш2 C) — ш,1 E) ш2 (d))} +
+ J2 (doJ E) — 8ш2 (d) + (<¦>!« (d) ш1 (8) -ш,2 (S) ш1 (d))} +
{(«.j» (d) ш1 (8)_mi» (8) ш1 (d)) + («)83(d)«J(8)_«)8» (8)ш« (d)))=0
G.1:4)
Здесь векторы Ji, J», J» линейно независимы (взаимно
перпендикулярны), следовательно, равенство G.1:4) может
119
быть удовлетворено только обращением в нуль коэффициен-
коэффициентов (фигурных скобок)
Жо1 (В) - So)i (d) + [«V (d) ш2 (S) — ш,1 E) оJ (d)] = 0 G.1:5)
и т. д.
§ 2. Внешнее произведение линейных форм
А. Нетрудно заметить, что выражение, стоящее в квадрат-
квадратных скобках G.1 :5), представляет определитель
Ш2 ( Ш ( ~ "' ( Ш ( ~ < (8) ю2 (8)
в каждой строке определителя стоят одни и те же формы со 2»
со2 с разными символами дифференцирования: в первой стро-
строке символ d, во второй—б. Такие определители мы будем обо-
обозначать символом
(8)
G.2:1)
и называть внешним произведением форм ©2 и со2.
Внешние произведения подчиняются следующим пра-
правилам:
1. Внешнее произведение меняет знак при перестановке
множителей:
К1»»»!-—[шХЧ. G.2:2)
ибо определитель в правой части равенства G.2:1) меняет
знак при перестановке двух столбцов.
Следствие. Внешнее произведение с двумя равными (или
пропорциональными) множителями равно нулю.
2. Функциональный множитель выходит за скобку внеш-
внешнего произведения:
[сршг1ш2] = ср [сй2'ш2], G.2 : 3)
ибо в определителе в правой части равенства G.2: 1) общий
множитель элементов одного столбца выходит за знак опре-
определителя.
3. Внешнее произведение подчиняется правилу дистрибу-
дистрибутивности:
К'+тД ш1] = [ш^ш1] + [свх'ш1], G.2:4)
12Q
ибо этому правилу подчиняются определители
Vs (d) + V (d), ш! (d)
V (d) ш1 (d)
mf (S) со1 (S)
(V (d) со1 (d)
©j» (S) CO1 (S)
В. Первые два члена в левой части равенства G.1 : 5)
dco1 (В) — В©1 (d)
представляют собой билинейную форму, т. е. линейную отно-
относительно форм с символом дифференцирования d и с симво-
символом дифференцирования б.
Действительно, допустим, что форма со' имеет вид F.1 :3).
Тогда
Отсюда
1 E) = ^
day1 (S) = da4u + db4v + a^dbu + b4bv,
Sm1 (d) = ЬаЧи + Ib4v + a4du + b4dv.
При вычитании последние два члена сократятся, ибо при
дифференцировании функций результат дифференцирования
не зависит от порядка дифференцирования, и мы получаем
1 (о) — Зш1 (d) =
G.2:5)
da1 du db1 dv
Ьа1 Ьи bb1 bv
Выражение, стоящее в левой части, называется внешним
дифференциалом формы со1 и обозначается
Doo1 = «to1 (S) — Зш1 (d). G.2 : 6)
Выражение в правой части G.2:5) называется значением
внешнего дифференциала.
Пользуясь для внешнего произведения обозначением
G.2: 1), получим
DoI ~ ЦаЫи] + \db4v].
Отсюда правило внешнего дифференцирования:
DoI = D (аЫи + Viv) = [da'du] + [db4v]. G.2 : 7)
121
Теперь мы можем переписать уравнение G.1 :4) в виде
Jx (DoI + К»ш8]) + J2 (D<o2 + К2 ш']) + J, ([m^m1] + [ш2»ш2]) = в,
откуда в силу линейной независимости векторов Jlf J2, Jj,
имеем:
+ К'ш2] = О,
D<o2 + [ш^ш1] = О,
[©!» о»1] + [ш23о»2] = 0.
В двух первых уравнениях перенесем второй член в пра-
правую часть с обратным знаком и одновременно переставим
множители с изменением знака; в третьем уравнении пере-
переставим в каждом произведении множители с изменением зна-
знака и одновременно у обоих членов изменим знак. Получим:
1 = [еЛвД
Do»2 =
!3] + [о»2о»23] = 0.
G.2:8)
Теперь нам надо дифференцировать внешним образом
уравнения F.1:4). Будет целесообразно предварительно
формулировать правила внешнего дифференцирования.
§ 3. Правила внешнего дифференцирования
1. Внешний дифференциал от полного дифференциала
равен нулю:
D (dM) = d (Ш) — 8 (dIA) = 0. G.3:1)
2. Внешний дифференциал от суммы форм равен сумме
внешних дифференциалов от слагаемых:
D (ш1 + о» *) = Do»1 + Do»2. G.3: 2)
Действительно,
D (о»1 + о»2) = do»!E) + do»2 E) — Вш1 (d) — 8о»2 (d) =
- {rf©1 (8) - В©* (d)} + {d©2 (8) — 8ш2 (d)) =
122
§ 4. Уравнения структуры
Дифференцируя внешним образом основные деривацион-
деривационные уравнения:
dIA = V1 + Vs. ш» = 0,
G.4:1)
G.4:2)
мы получили уравнения структуры:
DoI = [ш^а1],
DOJ = [(О1^!*],
[ш^/] + [ш2ш23] = О,
Do),» = [ш,
G.4:3)
G.4:4)
Это основные уравнения в теории поверхностей. Мы увидим
далее, что они не только необходимы, но и достаточны для су-
существования поверхности.
§ 5. Формулы Дарбу
Мы уже писали формы щ1 в обозначениях Дарбу F.1 :8).
Внося их в первое уравнение G.4 :4), получим
[drdu] -f [dr'dv] = [qdu + q'dv, pdu + p'dv],
или
— \dvdu] + — [dudv = (qp' - q'p) [dudv],
dv ou
или сокращая на [du dv] и меняя знаки:
123
и далее круговой заменой (р, q, r)
др до' . ,
я ~=qr'—q'r,
dv ди
%-- *?-=гр'-г'р.
dv du
G.5:2)
Два первых ' уравнения G.4:3) приводят к уравнению
[ср. F.2:11)]
<V = - JLiLdu + .-LILdv, G.5:3)
b dv a du
откуда, сравнивая с первым уравнением F.1 :8), имеем:
r = -±-%-, r' = -L^-. G.5:4)
b dv a du
Наконец, третье уравнение G.4: 3) дает
— aq' [dudv] — bp [dudv] = 0,
или
bp = —aq'. G.5:5)
Если исходить из двух квадратичных форм поверхности
ds2 = (ш1J + (ш2J = a2du2 + b2dv\ G.5 : 6)
или в силу
dtl
ds
и
dtl
ds
ds*
dj8
ds
dM
ds
ds ds
«VJi
ds2
^r ^2 J 2
ds
d
dM
' ds
Ddu* +
s*
O.1J!
ID'dudv -f
ds*
ds
D"dv*
t
ИЛИ
— adu (qdu -4- q'dv) ^- bdv( piu + p'dv) _ Ddu* + 2D'dudv -fr Wdv*
ds* ~ ds*
Отсюда в силу G.5 :5) имеем:
Л^—aq, ТУ' = bp', D' = bp=— aq'. G.5 :8)
124
Таким образом, знание двух квадратичных форм поверх-
поверхности позволяет вычислить значение всех форм <в', ш/. Дей-
Действительно, величины а, Ъ — коэффициенты первой квадра-
квадратичной формы. Уравнение G.5:4) позволяет вычислить ко-
коэффициенты г, f, т. е. форму и>12, а уравнения G.5:8) опре-
определяют через коэффициенты второй квадратичной формы по-
последние компоненты вращения р, р', q, q'.
§ 6. Уравнения Петерсона—Кодацци
Если с помощью уравнений G.5:4), G.5:8) исключить
р, q, г, р', q', г' в уравнениях G.5:1), G.5:2), то получим
непосредственно уравнения, налагающие условия на коэффи-
коэффициенты первой и второй квадратичных форм.
Уравнения G.5:2) принимают вид уравнений Кодацци*:
JL-(EL\ JLIЕ1Л — _ J_ JOL E 1 da D'
do \ b ) ди \ b I a du a b dv a
G.6 I 1)
d I D \ . d I D' \ _ 1 da D" 1 db D'
dv \ a ) du \ a ) b dv b a du b
Уравнение G.5: 1) дает уравнение Гаусса
/ t ли \
G.6:2)
\ (
ab dv \ b dv j ди { a du
Это основные единственные уравнения, связывающие коэф-
коэффициенты линейного элемента и второй квадратичной формы
поверхности.
§ 7. Теорема Гаусса о полной кривизне поверхности
Если обе части уравнения G.6:2) разделить на произве-
произведение ab и воспользоваться формулой E.7:2) для полной
кривизны поверхности, то получим
EGF* ~ ab { д \ а д ) d
EG—F* ~ ab { ди \ а ди ) dv \ b dv
G Г: 1)
откуда прямо следует знаменитая теорема Гаусса.
* Уравнения Петерсона—Кодатшч были получены К- М. Петерсоном
в 1953 г. вместе с полным доказательством теоремы существования поверх-
поверхности, определяемой двумя квадратичными формами. Кодацци независимо
опубликовал уравнения G.6:1) в 1956 г. Теорему существования поверх-
поверхности опубликовал Бонне в 1867 г.
126
Теорема. Полная (гауссова) кривизна поверхности зави-
зависит только от коэффициентов (и их производных первого и
второго порядка) линейного элемента поверхности, а потому
не меняется при изгибании поверхности.
Следствие 1. На плоскость налагаются только разверты-
развертывающиеся поверхности, конусы и цилиндры.
Действительно, гауссова кривизна плоскости равна нулю
/с=о.
Следовательно, у поверхностей, налагающихся на плоскость,
кривизна тоже равна нулю и все точки — параболические:
DD" - D'2 = 0. G.7 :2)
Имеется только одно (сдвоенное) семейство асимптотических
линий. Примем за линии t>=const (линии и) асимптотические
линии поверхности. Уравнение E.10:1) покажет, что в этом
случае
D = 0, U = 0. G.7 : 3)
Второе уравнение G.7 : 3) вытекает из уравнения G.7 :2).
Формулы E.1:8) позволяют переписать систему G.7:3) в
виде
пиМи = 0, nuMB = 0, п„п = 0. G.7:4)
Последнее уравнение следует из леммы 1 B.2).
Поскольку проекции вектора пц на три некомпланарные
направления Мв, М^, п равны нулю, то
пи = 0 и п = Ф (v) G.7 : 5)
и в уравнении касательной плоскости
(Р — М) п = 0
не только коэффициенты при текущих координатах векто-
вектора Р будут функциями одного параметра v, но и свободный
член
Л = Мп
не зависит от и. Действительно,
-Ц- = Мип + Мп„ = 0.
Здесь первый член правой части равен нулю, в силу ортого-
ортогональности касательной Ми и нормали п, а второй обращает-
обращается в нуль в силу G.7:5).
126
Таким образом, касательные плоскости поверхности G.7:3)
образуют однопараметрическое семейство плоскостей, и оги-
огибающая этого семейства, т. е. поверхность G.7:2), может
быть только развертывающейся, конусом или цилиндром.
§ 8. Наложимость поверхностей одной и той же постоянной
кривизны
Следствие 2. Каждая поверхность постоянной гауссовой
кривизны налагается на любую другую поверхность той же
самой постоянной кривизны так, что произвольная точка и
направление в этой точке совмещается с любой точкой и на-
направлением в точке другой (или той же самой) поверхности.
Рассмотрим произвольную поверхность постоянной гаус-
гауссовой кривизны К = const. Отнесем ее к полярно-геодезиче-
полярно-геодезической системе координатных линий. Берем произвольную точ-
точку О и произвольное направление, определяемое единичным
вектором е, выходящим из точки О и лежащим в касатель-
касательной плоскости поверхности в этой точке. Из точки О проводим
пучок геодезических линий и дополняем семейством ортого-
ортогональных траекторий. Если за параметр и взять длину геоде-
геодезической с началом в точке О, то линейный элемент поверх-
поверхности примет вид
ds2 = du2-i-b2dv2. G.8:1)
Будем предполагать, кроме того, что параметр v равен углу
наклона касательной к геодезической и = const в точке О к
выбранному вектору е. Для линейного элемента G.8 :1) урав-
уравнение Гаусса G.7:1) примет вид'
*--JLi» или-^+ЫС = 0. G.8:2)
Ъ дм2 ди*
Это уравнение интегрируется в квадратурах. Умножая обе
, дЬ
части уравнения на ои = — и рассматривая параметр и
аи
как одно независимое переменное, получим
du du
и после интеграции
FJ8 + Kb2 = V\ где V = / (v); G.8 : 3)
жроизвольная функция переменного v стоит вместо произ-
127
вольного постоянного, потому что при интегрировании по пе-
переменному и мы считаем v постоянным. Разрешая уравнение
G.8:3) относительно производной Ь =—.получим
аи
db .
= du.
а) Случай положительной кривизны /С= — >0.
/'-Ш
или
arcsin = -2— + V,
RV R
G.8:4)
но длина дуги замкнутой линии ы = const стремится к нулю
при и->0. Следовательно,
lim [bdv = lim Г RVsm I— + V^dv = ftfFsinV^v^O.
0 0 0
Поскольку при V=0 в силу G.8:4) получим'6=0, что исклю-
исключается, то
Vt = 0. G.8 :5)
С другой стороны, вращение вектора et вокруг нормали
определяется уравнением
н инфинитезимальное смещение в силу G.5:4) и G.8:1)
равно
dd
toj* = rdu+r'dv = ~^— dv,
а так как в точке О вращение определяется параметром 9,
128
то
ц—>о ди
Отсюда в силу G.8:4—5) имеем
дЬ
lim— = \im(Vcos— ) = V=\. G.8:6)
o ди u-o\ R 1 v
Таким образом, и вторая произвольная функция опреде-
определена, и линейный элемент не содержит никаких произвольных
величин
ds2 = du2 + R2 sin2 (—] dv\ G.8 : 7)
Мы взяли произвольную поверхность с кривизной
R*
и, выбрав произвольно точку О и вектор е, нашли вполне
определенный линейный элемент G.8:7). Следовательно, вся-
всякая другая поверхность с кривизной К = -г- с произвольной
точкой О' и вектором е' будет иметь тот же линейный эле-
элемент; значит, такие две поверхности налагаются произвольно
выбранными точкой О' и вектором е' на точку О и вектор е.
Ь) Случай отрицательной кривизны К = -— <0. Тогда
R
уравнение G.8: 3) после разрешения относительно Ьи = —
du
примет вид
db ,
- =du,
или
и, полагая
= sh х, 1 + I -— I = ch2 x, x = argsh — ,
RV \RVJ & RV
9 Заказ 1874 129
получим
chxdx
= ( dx = x = argsh
J S RV
Следовательно,
ds2 = du* + R*V* sh81— + Vx) dt;8. G.8:8)
Между тем первое требование
( V1) =RVshVt=0
)
\imb UmRVsh(
дает
и второе требование дает
R
Следовательно, опять вполне определенный линейный элемент
rfs2 = du* + R2 sh8 (—\ dv*, G.8:9)
откуда следует наложимость всех поверхностей постоянной
кривизны
причем произвольная точка О' второй поверхности и произ-
«ольный единичный вектор е' в точке О' совпадают с точ-
точкой О и вектором е первой поверхности.
ГЛАВА Vllf
ОПРЕДЕЛЕНИЕ. ПОВЕРХНОСТИ ДВУМЯ
КВАДРАТИЧНЫМИ ФОРМАМИ
§ 1. Преобразование пфаффовой системы уравнений
к каноническому виду
В предыдущей главе мы получили необходимые условия,
которым должны удовлетворять формы ш', щ , чтобы систе-
система F.1:2), F.1:4) определяла поверхность. Эти необходи-
необходимые условия G.4:3), G.4:4) вместе с тем будут и достаточ-
достаточными; но, чтобы доказать это, будет удобно предварительно
преобразовать их, представив в более общем каноническом
аиде. •
Введем обозначения:
(8.1 : 1)
= сМ-ш%- aAJ2
в2 = dJ2 — m^Jx — <o23Js,
в3 = dJ3 — СОз^! - OK2J2.
Дифференцируя внешним образом первое уравнение, получим
D60 = — [dV1] - [dJ2(o2] - ijpoI - J2Do)8.
Внося сюда значения
dlt = вх + «d^J, + mi»J,,
dJ2 = в2 + ш2'Jx + uJsj3
и D(ol, DaJ по формулам G.4:3), а так же используя третье
9* 131
уравнение G.4:3), получим
D60 = — [6Х] - [в8ш8]. (8.1 : 2)
Аналогично, дифференцируя внешним образом последние три
уравнения (8.1 : 1) и исключая дифференциалы dJ,-, а также
De>*, получим:
(8.1:3)
Систему (8.1 : 1—3) можно короче записать в виде:
вк = 0, DQk =— [в/шД 1фк = 0, 1, 2, 3. (8.1 : 4)
Система (8.1:4) имеет две независимые переменные —
криволинейные координаты на поверхности — и, v; их диф-
дифференциалы представлены формами и1, о>2. Все формы щ'
заданы линейными формами относительно дифференциалов
du, dv (или форм (о1, аJ) с коэффициентами в виде регуляр-
регулярных функций переменных и, v. Формы 0А, кроме того, содер-
содержат дифференциалы неизвестных функций Zj — координаты
вектора Ж(х, у, г) и три эйлеровы угла <р, 1|з, % B.11).
Вид системы (8.1:4) обнаруживает ее замечательное
свойство: квадратичные уравнения системы (внешние диф-
дифференциалы D8A ) обращаются в нуль в силу линейных урав-
уравнений системы 6А =0, ибо в каждом произведении правой
части один из множителей — линейная форма 6,- =0, которая
равна нулю в силу линейных уравнений системы. Такая си-
система называется вполне интегрируемой.
Рассмотрим вспомогательную аналитическую плоскость
независимых переменных и, v.
Теорема 1. Система @к =0 (8.1:4) позволяет определить
значения шести неизвестных функций Zj в произвольной точ-
точке аналитической плоскости Р(и, v), если даны их значения
в начальной точке Ро Zj = zj для и = и0, t>=t>o " задан путь
интеграции, т. е. даны функции:
ы=/1(^), v = f2(t), (8.1:5)
соединяющий точку Ро (для t = 0) с точкой Р\ (для t = tx).
Действительно, каждое из уравнений (8.1 : 1), т. е. каждая
из форм 6А, содержит дифференциал одной из шести неиз-
неизвестных функций; первое уравнение (8.1 :1), повторенное три
132
раза для трех координат х, у, z вектора М, определяет их
дифференциалы; три остальных определяют дифференциалы
эйлеровых углов d<p, dty, d%, ибо из девяти координат векто-
векторов Ji, J2, J3, связанных уравнениями ортогональности и
нормированием модулей, сохранятся только три независимые
величины. Все остальные формы ш\ ш| выражаются через
дифференциалы du, dv, которые на заданном пути (8.1:5)
будут иметь вид:
du = h (t) dt, dv = f2 (t) dt, /i = -$- • (8-l : 6>
at
После деления на дифференциал dt уравнения (8.1:1)
принимают вид системы Коши:
^L = Fj(t,zk), /, Л = 1 6. (8.1:7)
с начальными условиями:
г; = г° для t = 0. (8.1 : 8)
Система Коши имеет одно и только одно решение, удов-
удовлетворяющее начальным условиям. Это и доказывает теоре-
теорему 1.
§ 2. Теорема существования решения
вполне интегрируемой системы
Соединим начальную точку Ро регулярными путями со
всеми точками области; мы получим значения неизвестных Zj
во всех точках области. Однако это решение вообще зависит
от выбора путей интеграции.
Покажем, что для вполне интегрируемой системы получен-
полученные значения не зависят от пути интеграции.
Допустим, что мы имеем в односвязной области непре-
непрерывно дифференцируемое семейство путей
u = f1{t, a), » = /,('.«). (8-2:1)
соединяющих начальную точку Ро с некоторой точкой Р\. Зна-
Значения неизвестных функций zJt полученные интегрированием
по различным путям, выходящим из точки Ро и оканчиваю-
оканчивающимся в точке Р\, зависят от двух независимых переменных:
параметра t, определяющего положение точки на пути, и па-
параметра а, определяющего путь интеграции. Значит, решение
системы вообще имеет вид
133
Покажем, что для вполне интегрируемой системы неизве-
неизвестные функции Zj не зависят от а.
Введем два символа дифференцирования:
d = _d_ 8 д_
dt ' да '
В точках Ро и Р\ все пути сходятся, следовательно,
ш C) = 0 для t = О, т. е. в точке Ро, (8.2 : 2)
ш (В) = 0 для f = 1, т. е. в точке Р^ (8.2:3)
Формы 6Й в начальной точке Ро, где заданы начальные зна-
значения zk = zk, не зависят от параметра а, следовательно
для /=0, т. е. в точке Ро,
еА(8) = 0. (8.2:4)
С другой стороны, так как наши решения получены интег-
интегрированием вдоль пути, т. е. при изменении переменного t, то
в произвольной точке любого пути
6A(d) = 0. (8.2:5)
Напишем теперь в билинейной форме квадратичные урав-
уравнения (8.1 :4) для двух символов дифференцирования d и 6,
получим
dSk (S) - Ьв„ (d) = J] ^ (d) Sj E) _2 *kJ (8) ву. (d),
i
или в силу (8.2:5)
2Я/(<0еу(8), (8.2:6)
или, обозначая
вА(В) = ЯА, *к'(d) = рк'dt, (8.2:7)
получим из (8.2:6) систему Коши
с начальными условиями в силу (8.2:4)
ЯА = 0 для t = 0. (8.2 :9)
134
Система Коши, как известно, допускает одно и только
вдно решение, удовлетворяющее системе (8.2:8) и началь-
начальным условиям (8.2 :9); это решение очевидно. Поскольку си-
система (8.2:8) относительно Нк — линейно однородна, она
будет удовлетворена значением
Нк = 0 для всех значений t
Это очевидно удовлетворяет и начальным условиям (8.2:9).
По теореме Коши других решений нет.
Следовательно, в силу (8.2:7) во всех точках пути интег-
интегрирования будет
вА(В) = О. (8.2:10)
Между тем в силу линейной независимости форм 0ft относи-
относительно дифференциалов dzj мы можем разрешить однород-
однородную систему (8.2: 10) относительно dz,- и получим
Ьг; = 0,
т. е. найденное решение не зависит от параметра а.
Теорема 1. Для вполне интегрируемой системы решение,
получаемое интегрированием по произвольному пути, не за-
зависит от выбора пути интеграции.
Теорема 2. Вполне интегрируемая система уравнений до-
допускает решение и только одно, удовлетворяющее начальным
gCAOeUHM.
Более подробно эта же теорема формулируется так:
Теорема 3. Если, пфаффова система
вА = 0, ?=1 р, (8.2:11)
водержащая р уравнений и р неизвестных функций zjt мо-
может быть разрешена относительно дифференциалов р неиз-
неизвестных функций, а система внешних дифференциалов
= 0, k=\ p, (8.2:12)
будет алгебраическим следствием пфаффовой системы
(8.2 : 11) и после подстановки полученных из уравнений
(8.2:11) выражений dzf в систему (8.2:12) все уравнения
этой системы обратятся в тождества относительно неизвест-
неизвестных функций Zj независимых переменных х1 и их дифферен-
дифференциалов dx', то система (8.2 : 11) допускает решение
zj = FJ(x1,..., х")
и только одно, удовлетворяющее начальному условию
Zj = г/ для х1 =- xj.
1Э&
§ 3. Теорема существования поверхности
Мы доказали, что пять (шесть) линейных форм
«о», «о», о)8 =0, V, in,», a>3\ (8.3: 1)
заданных относительно двух независимых переменных и, v
и их дифференциалов du, dv и удовлетворяющих уравнениям
структуры G.4:3), G.4:4) и соотношениям F.1:5), F.1:7),
обеспечивают полную интегрируемость системы F.1:2),
F.1 :4) и существование решения.
Однако здесь встречается затруднение. Ниоткуда непо-
непосредственно не видно, что получаемые координаты векторов
репера действительно будут определять ортонормированный
трехгранник; и действительно, если начальный трехгранник
не будет ортогонален, то и трехгранники, определяемые реше-
решениями вполне интегрируемой системы, не обязаны быть орто-
ортогональными. Надо было бы доказывать, что полученные трех-
трехгранники при ортонормированном начальном репере будут
такими же; но в этом нет необходимости; с помощью эйлеро-
эйлеровых углов B.11 :2) и координат вершины трехгранника мы
можем представить все ортонормированные реперы евклидо-
евклидова пространства и вычислить компоненты действительных
инфинитезимальных смещений
си1, си2, и3, (V. <3. <V. (8.3:2)
которые несомненно удовлетворяют уравнениям структуры.
Среди этих смещений должны быть и те (8.3: 1}, которые
зависят от изменения переменных и, v при движении верши-
вершины по поверхности. Требуя совпадения формы (8.3:1) и
(8.3:2), мы получим пфаффову систему
ш' = < wtJ = mJ, i, / = 1, 2, 3. (8.3 : 3)
Она содержит 6 уравнений, 6 неизвестных функций: 3 коор-
координаты вершины и 3 эйлеровых угла при двух независимых
переменных. Дифференцируя внешним образом обе части
каждого уравнения (8.3:3), мы получим, пользуясь уравне-
уравнениями структуры, одни и те же выражения в левой и правой
части уравнения; только слева будут формы с титлами <»>', т[,
а справа те же формы, но без титлов. В силу уравнений
все полученные квадратичные равенства обращаются в тож-
136
дества. Следовательно, система вполне интегрируема, допу-
допускает решение и только одно, удовлетворяющее начальным
условиям. При этом мы прямо получаем координаты х, у, г
вершины и эйлеровы углы <р, 1|з, % как функции переменных
и, v, и все трехгранники будут ортонормированы, ибо других
эйлеровы углы не определяют. Остается показать, что поверх-
поверхность, определяемая координатами точек х, у, z и эйлеровыми
углами ф, if), х. действительно обладает двумя заданными
квадратичными формами:
ds2 = (а,1J + (а,2J, (а)
Ср2 = UIUI3 -\- UJUJS. (Ь)
Шесть неизвестных функций х, у, z, ф, if, % получены ин-
интегрированием пфаффовой системы (8.3 :3):
«>' = «),, ш/=о>/, i, j=\, 2, 3. (с)
Здесь формы
UI, UJ, UK = 0, IOj2, (D2S, U),1
построены, например, в виде F.1:10), F.1:8), F.2:11),
F.2 : 6) так, что выражения (а) и (Ь) будут заданными пер-
первой и второй квадратичными формами.
Линейные формы
Uj, <l>2,
выражаются через координаты х, у, z и эйлеровы углы ф, 1|з, %,
т. е. через элементы найденной интегрированием пфаффовой
системы (с) поверхности. Поскольку из (а), (Ь) и (с) следует
ср2 = ш1 ш^ -\- ш2 uJs,
то определенная интегрированием системы (с) поверхность
обладает заданными первой и второй квадратичными фор-
формами.
§ 4. Конгруэнтность поверхностей, определяемых
формами oj', щ' при различных начальных условиях
Лемма. Компоненты инфинитезимальных смещений репе-
репера инвариантны относительно движения пространства.
137
Движение пространства эквивалентно преобразованию де-
декартовой системы координат. Действительно, если простран-
пространство вместе с системой координат перемещается, то коорди-
координаты всех точек фигуры, отнесенной к этой системе коорди-
координат, сохраняются. Компоненты инфинитезимальных смещений
«*, Ш[! являются проекциями векторов dM, dij подвижно-
подвижного репера на векторы этого же репера. Как видим, преобра-
преобразование декартовой системы координат не может влиять на
величину этой проекции. Лемма доказана.
Рассмотрим теперь два решения, определяющие две по-
поверхности, которые относятся к одним и тем же формам
о>\ «в/, но с разными начальными трехгранниками То, То. Они
определяют двупараметрическое семейство трехгранников (Т)
и соответственно семейство (У). Перенесем в пространстве
все трехгранники (То, Т) как одно целое так, чтобы началь-
начальный репер То совпал с репером То; это всегда возможно, ибо
все реперы ортонормированы, следовательно, конгруэнтны.
Обозначим через (То. Т*), где Т'0=Т0, семейство трех-
трехгранников (Т*') после перенесения; начальный репер Т0=Т9
совпадает с начальным репером первого семейства.
Посмотрим, как определяется семейство трехгранников
(Т*). В силу инвариантности компонентов <«', щ' система
уравнений сохранится одна и та же и для трехгранников (Т)
и для (Т*). Начальные условия после совмещения трехгран-
трехгранников Т о=То тоже совпадают. Между тем вполне интегри-
интегрируемая система имеет одно и только одно определенное реше-
решение, удовлетворяющее начальным условиям. Следовательно,
после совмещения начальных реперов оба семейства (Т*) и
(Т) совместятся. Отсюда теорема:
Теорема 4. Формы «>', ш/, удовлетворяющие уравнениям
структуры, определяют поверхность и только одну до поло-
положения в пространстве.
§ 5. Определение поверхности двумя квадратичными
формами
Теперь мы выскажем теорему существования поверхности
в той форме, как ее доказал впервые Петерсон и затем Бонн*.
Теорема. Две квадратичные формы поверхности
?i = Ddua + 2D'dudv + D"dvi, I
138
удовлетворяющие уравнениям Гаусса и Петерсона—Кодацци,
определяют поверхность до положения в пространстве.
Ради простоты выкладок мы будем предполагать, что по-
поверхность отнесена к ортогональной системе координатных
линий
= a2du2 + b*dv\
\ (8-5:2>
Мы видели, что это всегда можно сделать D.2:9). Формы
«' запишутся:
а>3 = 0. (8.5:3)
Формула F.2:11) дает выражение для формы
Ш12= L*±.du + ±lLdv. (8.5:4)
Ь dv а ди
Формулы F.1:8) и G.5:8) дают возможность найти
1 D , D'
ш.1 = аи dv.
а а
(8.5:5)
Уравнения структуры G.4:3) удовлетворяются выбором
форм (8.5:4—5). Первое уравнение структуры G.4:4) при-
приводит к уравнению Гаусса G.6:2), два остальных — к урав-
уравнениям Петерсона—Кодацци G.6:1).
Таким образом, знание коэффициентов двух квадратич-
квадратичных форм (8.5:2) дает нам возможность построить формы
<«', щ1 (8.5 :3—5). Если коэффициенты основных квадра-
квадратичных форм удовлетворяют уравнениям Гаусса G.6:2) и
Петерсона—Кодацци G.6:1), то уравнения структуры
G.4 :3, 4) будут удовлетворены, и вполне интегрируемая си-
система (8.3:3) своими интегралами определит эйлеровы углы
и координаты х, у, z вершины М, описывающей поверхность.
Все остальные поверхности конгруэнтны полученной.
Задача интегрирования системы сводится к интегрирова-
интегрированию системы Коши. Примем координаты начальной точки
нулями
к, = vQ = 0.
139
Тогда путь интеграции можно задать равенствами:
и = tuv v = tvlt (8.5 : 6)
где ии Vi — произвольные постоянные координаты точки об-
области. Тогда
1 = aut dt, u>* =
да
= 0,
2 / l
\ b
1 дЬ
a du
D"
/ D , D \ ,,
= (т+-гУ1)dt-
dt,
is = (— "i + — f i)
\ a a I
(8.5:7)
и везде в коэффициентах сделана подстановка (8.5:6).
После интегрирования системы (8.5:7) можно положить
?=1, а координаты ut, yt заменить на и, и и рассматривать
их как независимые переменные.
ГЛАВА IX
приложения
§ 1. Минимальные поверхности
Определение. Минимальной называется поверхность,
которая при заданном контуре имеет наименьшую площадь.
Рассмотрим поверхность (М) и на ней заданный кон-
контур L. Отнесем поверхность к линиям кривизны и пусть ком-
компоненты инфинитезимальных смещений будут:
Тогда по формулам Родрига E.5: 3), если воспользовать-
воспользоваться уравнениями (9.1 : 1), получим:
^=-Lw\ *,> = А-^, . (9.1:2)
где Rt и /?2 — главные радиусы кривизны.
Допустим, что площадь поверхности (М), ограниченная
контуром L, — наименьшая по сравнению со всеми поверхно-
поверхностями (М*), проходящими через контур L и достаточно мало
от нее отличающимися.
Поверхность (М*) можно получить, откладывая на каж-
каждой яормали п поверхности (М) достаточно малый отрезок
где
ср = ср (U, V)
регулярная функция, обращающаяся в нуль на контуре L,
и е — постоянный параметр, достаточно малый, чтобы по-
верхность (М*) считалась мало отличающейся от поверхно-
поверхности (М); очевидно, радиус-вектор М* определяется урав-
уравнением
М* = М + е<рп. (9.1:3)
Площадь поверхности (М) должна быть наименьшей и в
том семействе поверхностей (М*1), которое получается при
е->0 и фиксированной функции q>(«, v). Поэтому в дальней-
дальнейшем мы можем пренебрегать степенями е, выше первой.
Дифференцируя равенство (9.1:3), получим
пренебрегая ds; отсюда в силу (9.1 :2)
+ -fj + V (i + ^-
Наконец, линейный элемент, если отбросить члены с ег,
будет
и элемент площади поверхности
а площадь поверхности
S* =
Ri R
Мы должны потребовать для минимума площади, чтобы про-
производная — в рассматриваемой точке обращалась в нуль,
at
а поскольку мы требуем, чтобы минимум площади осуществ-
осуществляла поверхность (М), которая соответствует значению е=0,
то надо потребовать
Y\R R
RiRt
x u,1"»* i = e,
142
или
Допустим, что существует область а внутри контура L та-
такая, что во всех ее точках
тогда мы выберем произвольную функцию q> так, чтобы она
равнялась нулю вне области а, а внутри ее была бы положи-
положительна; интеграл от существенно положительной подынтег-
подынтегральной функции будет строго положителен, т. е. не равен
нулю.
Следовательно, минимальная поверхность определяется
условием
или в силу E.7: 2)
2FD' — ED" -GD = 0. (9.1 : 5)
Отсюда теорема:
Теорема. Средняя кривизна минимальной поверхности
равна нулю.
Следствие 1. Полная (гауссова) кривизна минимальной
поверхности отрицательна.
Действительно, из равенства (9.1:4) следует
Следствие 2. Асимптотические линии на минимальной по-
поверхности действительны и ортогональны.
Первая половина предложения следует из (9.1:6). Если
поверхность отнести к асимптотическим линиям, то уравне-
148
ние асимптотической линии E.10 :1) должно допускать реше-
решения u=const и w=const, а это возможно только при
D = 0, D" = 0. (9.1:7)
Внося эти выражения в левую часть уравнения (9.1:5),
получим
2FD' = 0,
но обращение в нуль D' приводит к вырождению поверхно-
поверхности, ибо в силу (9.1 :7) вторая квадратичная форма тожде-
тождественно обращается в нуль и нормальная кривизна всякой
линии равна нулю.
Обращение в нуль F,
f = 0,
показывает, что координатные линии (теперь асимптотиче-
асимптотические) ортогональны.
Следствие 3. Сферическое изображение минимальных по-
поверхностей конформно.
Сферическим изображением поверхности называется изо-
изображение на сферу по принципу параллельности нормалей.
Следовательно, точке М поверхности сопоставляется точка п
сферы. Отображение называется конформным, если пары со-
соответствующих линий пересекаются под одинаковыми углами.
Для этого необходимо и достаточно, чтобы линейные элемен-
элементы ds2 и ds*2 двух поверхностей были пропорциональны
Edu2 + 2Fdudv + Gdv2 = X (E*du2 + 2F*dudv + G*dv2).
Действительно, при такой пропорциональности
Е = \Е*, F = IF*, G = lG*
в числителе и знаменателе выражения D.2:4) для косинуса
угла ф, под которым пересекаются линии du : dv и 6u : 6v, мно-
множитель К сократится и углы будут равны.
Если мы отнесем минимальную поверхность к линиям
кривизны, то будут иметь место равенства (9.1 :1, 2), которые
в силу (9.1 :6) принимают вид:
3 Л» J Ri .
и
dM = ш1^ + u>2J2, dn = — («Mi — <o2J2).
144
Отсюда получим линейные элементы поверхности ds2 и сфе-
сферы ds'2:
ds2 = (ш1J + КJ, ds'2 = -~ ( КJ + («•)}.
§ 2. Изгибание минимальных поверхностей
Теорема. Минимальные поверхности допускают непрерыв-
непрерывное изгибание с сохранением главных радиусов кривизны,
оставаясь все время минимальными.
Такое изгибание возможно только при условии, что глав-
главные направления в каждой точке поверхности меняются. Так
как они остаются взаимно перпендикулярными, то при изги-
изгибании поверхности главные направления поворачиваются.
Рассмотрим две минимальные поверхности S и S« с ком-
компонентами инфинитезимальных смещений трехгранника, по-
построенного на главных направлениях,
с одними и теми же радиусами главных кривизн
«ж. = К; К, = - К. (9.2 :1)
Эти формы будут:
«а1 = — , «ia = —; «а1 = —, Щ3 = — • (9.2 : 2)
А А А А
Если главные направления на второй поверхности повер-
повернуты на постоянный угол а = const относительно главных на-
направлений первой поверхности, то
0I = оI COS a -f- ОJ sin а, ш2 = —(О1 sin а -f- «>a COS а,
< = в1«, (9.2 : 3)
Шд1 = щ1 COS а -f- <»23 sin а» ша3 = — ""з1 sin a "Ь <°83 COS a.
Дифференцируя внешним образом, получим:
DuI = [uo^j1] = [«"ша1] COS a -f- [uI^!2] sin a =
= [— ш1 sin a 4- uJ COS a, a),1],
D<o* = [w1*»!2] = —{u^uVjsin a 4- [aI^!*] COS a =
= [ш1 COS a 4" <°s sin a, <»!*].
10 Заказ 1874 148
= [Ш31 COS a 4- u>a8 sin a, — u),1 sin a + u>a3 COS a] = [wj'a),*],
Dug1 = [ш,^1] = [mXl COS a +
4- [wj1^!8] sin a = [u>32 COS a — wta sin a, (Oj1],
DuTj8 = [ша1^!3] = — [«з^а1] sin a 4-
4- [ша1^!1] COS a = [ша1, <»iS COS a 4- <oga sin a].
Следовательно, формы <¦>', щ' в силу соотношений
(9.2:3) удовлетворяют уравнениям структуры G.4:3, 4), и
поверхность (М*) существует; она — минимальная в силу
уравнений (9.2:2); она налагается на поверхность (М), ибо
линейные элементы совпадают
(ds*)* = (ш1J + (">2)а = (u»1 COS a 4- <«asin a)a +
4- (— ш1 sin а + иJ cos aJ = (ш1J 4- (ша)а = ds*.
Соответствие наложимости устанавливается первыми
уравнениями (9.2:3).
Если положить
ш1 = adu, <оа = bdv,
ш1 = adu, <¦>* = bdv,
то первые уравнения (9.2:3) запишутся
adu = a cos a du 4- & sin a dw,
ftdw = — a sin adu -}- b cos a dw.
Если Яиц будут интегрирующими множителями дифферен-
дифференциальных биномов в правых частях, то достаточно положить
чтобы получить
f 1
! cos a du 4- b sin a dw),
"=}т(а|
v = 1 — (— a sin a du 4- b cos a dv).
146
Постоянные интеграции подобраны так, что точка u=0, w=0
поверхности S« соответствует точке и0, vq поверхности S.
Угол а можно рассматривать как параметр изгибания; при
изменении а поверхность S« непрерывно изгибается.
При а=0 она совпадает с поверхностью S.
При
к
имеем
Ш1 = U)S,
-3 _
=
<4,
-з _
-2
Линия и переходит в линию v.
При а= — получается ассоциированная поверхность
ша =
ут ут
Линии кривизны оJ=0, (о!=0 налагаются на асимптотиче-
асимптотические линии.
Действительно, асимптотические линии на поверхности S,
определяются уравнением
ш1 щ + ша J^ = О,
или по сокращении на — в силу (9.2 : 2)
R
Теорема. При наложении минимальной поверхности на
ассоциированную линии кривизны переходят в асимптотиче-
асимптотические линии и наоборот.
§ 3. Геодезические иа поверхностях вращения
Линейный элемент поверхности вращения
x = rcos<?, y = rsin<?, z = f(r)
имеет вид
147
Следовательно, в обозначениях F.1 :10)
a* = l+f>(r), Ь2 = г2
и уравнения геодезической F.3: 2) запишутся:
da sin а
dr cos а
sin«.
ds г
Деля почленно первое и третье уравнение на второе, мы
исключим параметр ds
_d*_ = _Jga d^^Vl+pjr) f (93:1)
dr r dr r
Первое уравнение интегрируется разделением переменных
ctgada + — =0,
откуда первый интеграл
г sin a --= ft = const, (9.3: 2)
Исключая из второго уравнения (9.3:1) с помощью первого
(9.3 : 2) угол а, получим
Л. =hl±±?lri (9.3:3)
dr ryr*—h*
(9-3:4)
Первый интеграл (9.3 :2) показывает, что в каждой точке
геодезической линии произведение радиуса параллели г на
синус угла наклона геодезической линии к меридиану посто-
постоянно (теорема Клеро).
Из неравенства
sina = A<l (9.3:5)
г
следует, что радиус параллели не может быть меньше пара-
148
метра h геодезической линии; если r=h, то sina=l, a=— и
геодезическая касается параллели.
Рассмотрим кусок поверхности между двумя параллелями,
для которых радиус параллели достигает минимума г=т и
максимума г=М. В этом интервале в силу (9.3 :5) не может
быть геодезической с параметром h>M.
1. Геодезическая с параметром h=M. Единст-
Единственное возможное значение радиуса параллели в точках этой
геодезической
г = М.
Параллель наибольшего радиуса — геодезическая линия (на-
(например, экватор на сфере).
2. Геодезические с параметром h между
т и М :
m<h<M.
Геодезическая пересекает наибольшую параллель г=М под
острым углом
sinaAJ <l.
По мере уменьшения радиуса параллели угол а геодезиче-
геодезической с меридианом
ft
sina = —
г
увеличивается и для r=h будет равен -—. Геодезическая ка-
касается параллели r=h, поворачивается назад, снова пересе-
пересекает наибольшую параллель г=М под тем же углом, но с
противоположным знаком, доходит до параллели г = h по
другую сторону наибольшей параллели (если параллель r=h
там существует), снова возвращается назад и т. д.
Колебанию геодезической от одной параллели r=h до
другой соответствует поворот поверхности на конечный угол
(9.3:4)
о =
(9-3:6)
ибо, хотя интеграл (9.3:6) не собственный, поскольку знаме
14Р
натель подынтегральной функции в точке r=h обращается в
нуль, но порядок малости
Yr2-h2 =(r-hJ (r + hJ
равен—, и интеграл сходится.
Если угол б соизмерим с я,
то геодезическая замыкается.
3. Л = т. Так же, как выше,
¦геодезическая подходит к па-
параллели г = т, но теперь под
знаком интеграла (9. 3 : 6) для
г = т не только знаменатель
обращается в нуль порядка
малости —, но и числитель
обращается в бесконечность,
ибо для наименьшей паралле-
параллели
= >¦ оо при Г->
h
Рис. 38
(касательная к меридиану па-
параллельна оси г). Нетрудно об-
обнаружить, что б стремится к
бесконечности. Следовательно,
геодезическая подходит асимп-
асимптотически к наименьшей па-
параллели r=m, совершая бес-
бесчисленное множество оборотов
по поверхности (рис. 38). Сама параллель r = m тоже геодези-
геодезическая линия.
4. Л=0. Геодезическая совпадает с меридианом.
§ 4. Геодезическое кручение
Мы рассматривали две основные квадратичные формы по-
поверхности: первая дает линейный элемент поверхности, вто-
вторая, если ее разделить на первую, определяет нормальную
кривизну линии на поверхности. При отнесении к ортого-
ортогональному реперу они имеют вид:
150
3 и>
По формулам Дарбу формы о>3, и>2 выражаются через
ф d d
фру ру фр
дифференциалы du, dv, но поскольку
du=J-u)i, dv=— и2,
а Ъ
мы можем представить их в виде:
(9.4:2)
= flu»I
Внося эти значения в третье уравнение G.2:8), получмм
а12 К ш2] 4- а21 [ш2 ш1] = 0.
Следовательно,
fl2i = а12, (9.4 : 4)
и в силу (9.4 :1)
«Pi = flu НI + 2ОИ»1»» 4- on (">2J- (9.4 :5)
Двумя формами (9.4:1) не ограничивается совокупность
квадратичных форм поверхности; например, линейный эле-
элемент сферы в сферическом отображении поверхности имеет
вид
Нас будет сейчас интересовать якобиан первых двух квад-
квадратичных форм
или
Ф = аи (п1J 4- (<к2 - «и) '»1'»2 - аи КJ, (9.4:6)
или в силу (9.4 :3)
4 ,.ч1 ,.ч2
(9.4:7)
Нулевые линий этой формы определяют главные направления
в касательной плоскости поверхности.
151
Действительно, сравнивая выражения E.2 : 2) и (9.4 :5)
для второй квадратичной формы и учитывая формулы
(9.4 : 2), получим
D D' D"
а2 аЬ Ь%
откуда прямо следует совпадение уравнения E.3:5) с урав-
уравнением
$ = 0.
Форма ф имеет непосредственный геометрический смысл:
это площадь инфинитезимального параллелограмма, по-
построенного на векторах
dJ3 =
ибо модуль векторного произведения совпадает с модулем
X dJa = Js
D31 ш32
Рассмотрим теперь, подобно отношению квадратичных
форм —, отношение
/g
Так же, как и отношение E.2 : 2), отношение (9,4 : 8) зависит
только от отношения форм и1 : и2, т. е. от направления каса-
касательной к кривой на поверхности. Чтобы выяснить геометри-
геометрический смысл отношения (9.4 : 8), мы можем фиксировать эту
касательную и совместить с ней вектор Jx. Тогда надо поло-
положить (о2=0 и мы получим
ds2 (о1
Так как
di% = Ш,^! + (Bj3J3,
то в силу (9.4 : 3)
J3 dJ2 - ш23 = оцш1. (9.4:9)
Поскольку вектор ^ совпадает с касательной, главная нор-
152
маль v и бинормаль р .чежат в плоскости J2, J3. Обозначим
буквой д угол, на который надо повернуть в положительном
направлении вектор v, чтобы он совпал с вектором J3. Тогда
J2 — vsinft —p cos 9,
J3 = vcos& + Psin&
и, дифференцируя по длине дуги ds, получим
-**- = -*-sin О- -^-cos&+(vcos8 + psinii)-^-,
ds ds ds ds
или по формулам Френе
-*А- = (_ Xk + xp) sin 8+xv cos »+(v cos » -f p sin b) JL ,
ds ds
ИЛИ
^*-= -<eAsin»-b(vcos»+psin»)/x+ —) (9.4:10>
ds \ ds /
ds G>i as
Аналогично геодезической кривизне
Rg == Л Sin и
второй компонент вектора (9.4 : 10) будем обозначать
. d»
и называть геодезическим кручением.
Для геодезической линии главная нормаль совпадает с
нормалью к поверхности и #=0; поэтому для геодезической
линии геодезическое кручение совпадает с ее кручением.
Поскольку геодезическое кручение
все линии на поверхности с общей касательной в точке по-
поверхности имеют в общей точке одну и ту же нормальную
кривизну и одно и то же геодезическое кручение.
Поэтому нормальная кривизна кривой на поверхности
равна кривизне геодезической линии с той же касательной,
15Э
а геодезическое кручение равно кручению этой геодезической.
Поскольку нулевые линии формы -ф определяют главные на-
направления, т. е. направления линий кривизны, то геодезиче-
геодезическое кручение линий кривизны равно нулю.
Для асимптотических линий соприкасающаяся плоскость
совпадает с касательной плоскостью и бинормаль — с нор-
нормалью к поверхности. Поэтому Ф= — и геодезическое кру-
кручение совпадает с кручением линии.
Если отнести поверхность к линиям кривизны, то
а« = 0, flu = — , а« = — ,
Kl К»
и согласно (9.4 :6)
¦>*(¦>»
ds* [ Я2 Rij ds*
и в силу E.8 :4)
Rx-Rt sjn(pC0S(p) (9.4:12)
где для асимптотических линий в силу (9.4:5) имеет место
уравнение
? !?=0. (9.4:13)
+ 0.
Rx R%
Отсюда прежде всего видно, что для двух асимптотических
направлений
tgcp=±l/ --?-.
•следовательно, геодезические кручения для асимптотических
линий в заданной точке равны по абсолютной величине и
противоположны по знаку.
Из соотношений (9.4:13) следует
со8*ф_ sin*<f _ cos*у + sin2ф 1 (9 44)
Ri ~ Ъ~3 R1 — R2 ~ Rx — Rt
154
Возвышая в квадрат формулу (9.4:12) для геодезическо-
геодезического кручения, в силу формул (9.4 :14) получаем
Отсюда теорема Эннепера. Кручения асимптотических ли-
линий в точке их пересечения равны по абсолютной величине
и противоположны по знаку, а их произведение равно полной
кривизне поверхности.
СОДЕРЖАНИЕ
Глава 1. Введение
§ 1. Понятие линии 3
§ 2. Теорема анализа о существовании неявной функции . 4-
§ 3. Вектор как функция скалярного аргумента 6
§ 4. Касательная к линии 7
§ 5. Правила дифференцирования векторных функций ... 9
§ 6. Основные теоремы дифференциального исчисления . . 12
Глава II. Формулы Фреие
§ 1. Длина дуги линии 14
§ 2. Формулы Фреие 15
§ 3. Главная нормаль и кривизна кривой 17
§ 4. Бинормаль и кручение кривой 19
§ 5. Соприкасающаяся плоскость 22
§ 6. Соприкасающаяся окружность 24
§ 7. Кинематическая интерпретация 25
§ 8. Определение линейной скорости точки по заданному век-
вектору мгновенной скорости вращения 27
§ 9. Компоненты вектора скорости вращения трехгранника
Фреие -. . 29
§ 10. Примеры интегрирования натуральных уравнений кривой 31
§ 11. Эйлеровы углы '. 37
§ 12. Интегрирование натуральных уравнений пространствен-
пространственной кривой 40
§ 13. Эволюта и эвольвента 43
Глава III. Теория огибающих
§ 1. Огибающая однопараметрического семейства линий на
плоскости 47
§ 2. Понятие поверхиести в дифференциальной геометрии . 51
§ 3. Касательная плоскость 54
§ 4. Область регулярности поверхности 56
§ 5. Огибающая одиопараметрического семейства поверхностей 56
§ 6. Случай, когда семейство поверхностей задано одним
уравнением в неявной форме 58
§ 7. Характеристики и огибающая характеристик 60
§ 8. Ребро возврата огибающей 62
§ 9. Огибающая семейства плоскостей 64
§ 10. Огибающая нормальных и спрямляющих плоскостей . 66
156
Глава IV. Общая теория поверхностей
§ 1. Первая квадратичная форма поверхности 68
§ 2. Угол пересечения двух линий иа поверхности .... 70
§ 3. Дифференциал площади поверхности 73
§ 4. Примеры 74
§ 5. Изгибание поверхностей 78
§ 6. Наложение развертывающейся поверхности иа плоскость 79
§ 7. Изгибание поверхности вращения в поверхность враще-
вращения с сохранением меридианов и параллелей 81
Глава V. Теория кривизны поверхности
§ 1. Кривизна линии на поверхности 84
§ 2. Вторая квадратичная форма 85
§ 3. Главные направления в точке поверхности 87
4. Линии кривизны 90
5. Формулы Родрига 90
6. Неопределенность главных направлений 92
7. Полная и средняя кривизна поверхности 93
8. Формула Эйлера 94
9. Индикатриса Дюпена 98
10. Асимптотические линии 100
§ 11. Сопряженные семейства линий 102
Глава VI. Внутренняя геометрия поверхности
§ 1. Ортогональный репер, присоединенный к точкам поверх-
поверхности 105
§ 2. Нормальная и геодезическая кривизна линии иа поверх-
поверхности 107
§ 3. Геодезические линии 111
§ 4. Геодезическая линия как кратчайшее расстояние между
двумя точками поверхности 113
§ 5. Развертывание линии иа плоскость 116
Глава VII. Основные уравнения теории поверхностей
§ 1. Внешнее дифференцирование лииейиых форм 118
§ 2. Внешнее произведение лииейиых форм 120
§ 3. Правила внешнего дифференцирования 122
§ 4. Уравнения структуры 123
§ 5. Формулы Дарбу 123
§ 6. Уравнения Петерсоиа—Кодацци 125
§ 7. Теорема Гаусса о полной кривизне поверхности . . 125
§ 8. Наложимость поверхностей одной и той же постоянной
кривизны 127
Глава VIII. Определение поверхности двумя квадратичными
формами
§ 1. Преобразование пфаффовой системы уравнений к кано-
каноническому виду 131
§ 2. Теорема существования решения вполне интегрируемой
системы : 133
157
§ 3. Теорема существования поверхности . . • 136
§ 4. Конгруэнтность поверхностей, определяемых формами
ш , о> / при различных начальных условиях 137
§ 5. Определение поверхности двумя квадратичными формами 138
Глава IX. Приложепия
§ 1. Минимальные поверхности 141
§ 2. Изгибание минимальных поверхностей 145
§ 3. Геодезические на поверхностях вращения 147
§ 4. Геодезическое кручение 150
Сергей Павлович Фиников
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Редактор В. С. Капустина
Технический редактор 7". А. Масленникова
Сдано в набор 14/ХН 1960 г. Подписано к печати 30/IX 1961 г.
Л-103939 Формат 60 X 9O'/i6. Печ. л. 10.
Уч.-изд. л. 6,58. „ Изд. № 1564.
Заказ 1874. Тираж 25 000. Цена 30 коп.
Издательство Московского университета, Москва, Ленинские горы
1 *
Типография Изд-ва МГУ, Москва, Ленинские горы