Автор: Эдвардс Р.Е.
Теги: анализ математика математический анализ функциональный анализ переводная литература издательство мир
Год: 1969
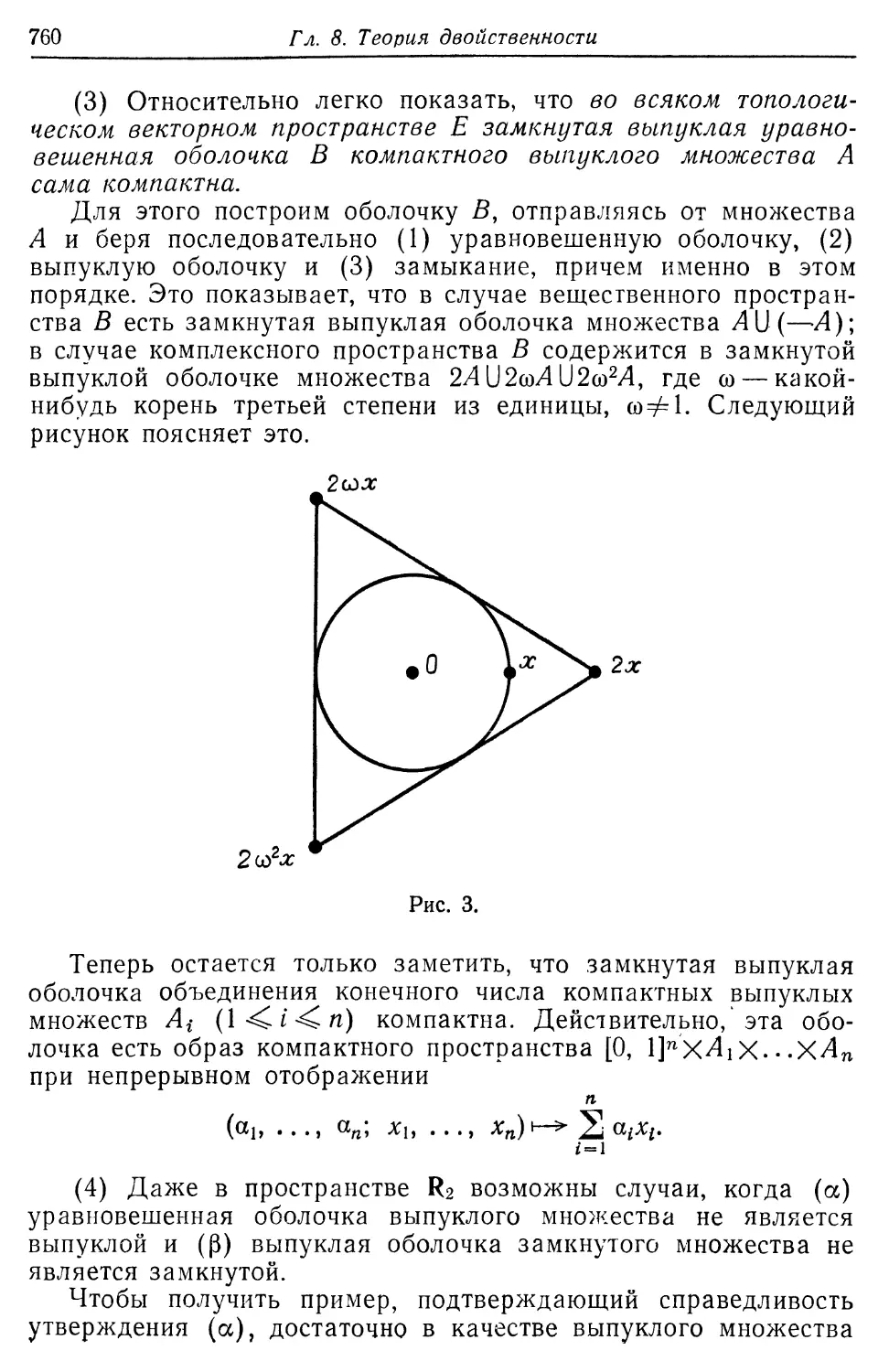
Текст
РЭдварде
Функциональный
анализ
ТЕОРИЯ
ПРИЛОЖЕНИЯ
FUNCTIONAL
ANALYSIS
THEORY
and
APPLICATIONS
R. E. EDWARDS
Institute of Advanced Studies
AUSTRALIAN NATIONAL UNIVERSITY
HOLT, RINEHART AND WINSTON
NEW YORK • CHICAGO • SAN FRANCISCO . TORONTO . LONDON
1965
Р. ЭДВАРДС
ФУНКЦИОНАЛЬНЫЙ
АНАЛИЗ
ТЕОРИЯ
И
ПРИЛОЖЕНИЯ
Перевод с английского
Г. X. БЕРМАНА и И. Б. РАСКИНОЙ
Под редакцией
В. Я. ЛИНА
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА 1969
УДК 517.43,519.55
Фундаментальный труд, в котором автору удалось со-
сочетать обстоятельное изложение современной теории топо-
топологических линейных пространств с широким показом
разнообразных приложений этой теории. Приложения эти
относятся к самым различным направлениям (абстрактные
эргодические теоремы, теория потенциала, методы суммиро-
суммирования, теория игр, ряды Фурье), но особое внимание автор
уделяет теории обобщенных функций. Изложение подробное
и ясное. Очень много упражнений и литературных ссылок,
Для чтения книги достаточна минимальная подготовка,
например в объеме общего курса математического анализа
и начал линейной алгебры. Однако она будет полезна
не только тем, кто захочет начать с нее изучение функцио-
функционального анализа, но и специалистам,
Редакция литературы по математическим наукам
Инд. 2-2-3
20-69
От издательства
Капитальный труд австралийского математика профессора
Р. Э. Эдвардса, предлагаемый вниманию читателя, отличается
своеобразием замысла, обстоятельностью изложения и сравни-
сравнительной элементарностью. Во многих отношениях эта книга
удачно дополняет известную монографию Н. Данфорда и
Дж. Шварца «Линейные операторы».
Профессор Р. Э. Эдварде написал предисловие к русскому
изданию и прислал несколько списков исправлений и добавле-
добавлений к английскому тексту. Издательство считает своим прият-
приятным долгом выразить ему признательность-,
Предисловие к русскому изданию
Я рад представившейся возможности высоко оценить усилия
переводчиков и редакторов, направленные на решение изнури-
изнурительной задачи перевода моей книги на русский язык. Не до-
довольствуясь формальным переводом, они внесли многочислен-
многочисленные ценные предложения, способствующие улучшению изло-
изложения.
Мой долг поблагодарить также проф. Лорана Шварца,
проф. Р. С. Филлипса, д-ра Ф. Смитиса и д-ра Я. Макдональда,
каждый из которых оказался настолько любезен, что написал
мне о некоторых из многочисленных опечаток, неясностей и тех-
технических пробелов, содержащихся в английском издании.
Основное изменение, которое повлекли эти замечания, со-
состоит в полном пересмотре доказательства теоремы 5.8.1 и сле-
следовавшего за ней в английском издании замечания, что привело
к появлению нового п. 5.8.2.
В русском издании имеются также некоторые добавления к
библиографии.
Я надеюсь, что в результате этих объединенных усилий книга
стала лучше и что она окажется полезной по крайней мере для
некоторых из моих русских коллег и в некоторой степени возна-
вознаградит их за ту пользу, которую я извлекаю из чтения англий-
английских переводов их работ.
Р. Э. Эдварде
Канберра
Февраль 1968
Предисловие
Классическая «Теория линейных операций» Банаха [1] со-
содержала значительную часть известных к моменту ее выхода в
свет фактов как «чистой» теории, так и приложений функцио-
функционального анализа. С тех пор и теория и приложения бурно раз-
развивались. Более современные книги по функциональному ана-
анализу в своем большинстве имеют уклон в сторону абстрактной
теории, оставляя приложениям роль упражнений для- читателя.
Другие же книги посвящены различным частным приложениям;
в них необходимая функционально аналитическая основа едва
затрагивается.
Я попытался в этой книге дать изложение ряда современных
исследований, в котором теория и приложения играют примерно
равную роль. Если чему и отдано предпочтение, так это, пожа-
пожалуй, приложениям. При этом я исходил из двух положений: во-
первых, из возможности разумного разделения функционального
анализа на «чистый» и «прикладной» (оставляя в стороне спор-
спорный вопрос о том, где проходит граница между ними); во-вто-
во-вторых, из целесообразности изложения, при котором обеим сторо-
сторонам уделяется равное внимание, отчего выигрывает каждая из
сторон. Мне представляется само собой разумеющимся, что при-
приложения абстрактных методов действительно полезны и как объ-
объединяющий фактор и как источник новых результатов и проб-
проблем. Кроме того, успешное усвоение предмета возможно лишь
при изучении общих теорем в тесной связи с их нетривиальными
приложениями.
Для достижения поставленной цели пришлось кое-чем по-
поступиться. Прежде всего в отношении охваченного в этой книге
материала ее нельзя рассматривать как исчерпывающий трак-
трактат ни по функциональному анализу, ни даже по топологическим
векторным пространствам. Достаточно сказать, что в ней либо
совсем не затрагиваются, либо только упоминаются такие вопро-
вопросы, как теория упорядоченных векторных пространств, тополо-
топологических алгебр, общая спектральная теория и топологические
тензорные произведения. Далее, стремление привести нетриви-
нетривиальные приложения избранных разделов абстрактной теории
воспрепятствовало тщательному изучению ее «внутренних» про-
Предисловие
блем. Так, например, оставлены в стороне многие вопросы, ка-
касающиеся общих структурных свойств топологических векторных
пространств. Нет также исчерпывающего исследования различ-
различных типов таких пространств. Фактически рассматриваются те и
только те свойства, которые на сегодняшний день оказались осо-
особенно полезными в приложениях. Если же в некоторых случаях
общая теория излагается в большем объеме, чем это необходимо
для последующих приложений, то причины кроются в личных
вкусах автора.
В приложениях аксиоматически построенных теорий редко
соблюдается та безупречность логического строения, которая
присуща самим этим теориям, и в некоторых случаях наруше-
нарушение логического порядка даже желательно. Так, будь это книга
по теории топологических векторных пространств самих по себе,
гл. 4 и 5 должны были бы почти наверняка следовать за
гл. 6—8. Хотя принятое расположение материала и не отвечает
требованиям строгой логики, тем не менее оно позволяет моти-
мотивировать введение некоторых классов топологических векторных
пространств, которое при другом порядке изложения могло бы
показаться надуманным. Общие результаты свободно приме-
применяются раньше их систематического рассмотрения, если предста-
представляется такая возможность и если не возникает опасности по-
порочного круга. В особенности это относится к результатам тео-
теории двойственности (гл. 8), которые применяются в гл. 4—7:
При изложении абстрактной теории я существенно использо-
использовал ряд имеющихся книг, а именно монографии Бурбаки, Гро-
тендика, Данфорда и Шварца и в меньшей степени Дэя, Тэйлора,
Кёте и Келли и Намиоки. Материал для приложений частично
обязан своим происхождением тем же источникам, но большая
его часть основана на сообщениях на различных семинарах, опуб-
опубликованных научных статьях и монографиях.
В список приложений, которые было бы желательно охватить,
но которые фактически не были здесь охвачены, безусловно, сле-
следует включить линейные аспекты анализа на многообразиях
(в том числе теорию потоков де Рама) и «теоремы конечности»
теории когомологий на комплексно аналитических многообра-
многообразиях. Следовало бы больше сказать о линейных аспектах теории
потенциала. Эти вопросы, кзк и многие другие, не были включе-
включены в книгу потому, что они требуют предварительного изучения
весьма громоздкого технического аппарата, значительная часть
которого выходит за рамки функционального анализа.
Проповедование одновременно двух различных точек зрения
всегда чревато опасностью, что ни одна из них не будет изложе-
изложена удовлетворительно. Более всего опасаюсь в этом смысле за
гл. 5. Функционально аналитический подход к теории линейных
Предисловие
дифференциальных уравнений в частных производных разраба-
разрабатывается в настоящее время с исключительной активностью.
Ввиду наличия обширной классической литературы по таким
уравнениям естественно было бы новые идеи и методы постоянно
сравнивать и сочетать со «старой» техникой. Для этого, однако,
пришлось бы включить в книгу массу материала, имеющего мало
или даже не имеющего никакого функционально аналитического
содержания. Опорой для моей позиции служат некоторые заме-
замечания Гординга, приведенные в начале гл. 5. Надеюсь, что эта
глава, несмотря на свои очевидные недостатки, передает дух со-
совсем недавно возникшей области приложений функционального
анализа.
Для удобства читателя в вводной главе (гл. 0) кратко изло-
изложены некоторые результаты теории множеств и общей топо-
топологии. Предполагается, что читатель знаком с основными
понятиями этих разделов математики и что ему известно беско-
бескоординатное определение векторного пространства. Знание клас-
классического анализа предполагается в весьма скромном объеме.
В частности, хотя знание интеграла Римана от непрерывных
функций по компактному интервалу обязательно, ссылки на ин-
интеграл Лебега сведены к минимуму вплоть до гл. 4, содержа-
содержащей полную и подробную его теорию.
После каждой главы следуют упражнения. Имеется в виду,
что читатель будет внимательно заниматься ими. Иногда упраж-
упражнения используются для сокращения основного текста путем вы-
вынесения в них доказательств вспомогательных результатов, но
чаще целью упражнений является расширение, развитие или
уточнение различных частей основного материала. Наиболее
сложные упражнения сопровождаются указаниями к решению.
Библиография не претендует ма полноту. На некоторые на-
названия нет никаких ссылок в тексте; они включены в список как
объекты для дальнейшего изучения в направлении, которое
обычно соответствует заглавию.
Конец доказательства отмечается символом |.
Кроме именного и предметного указателей, в книгу включен
также список часто употребляемых обозначений.
Пользуясь случаем, приношу свою искренюю благодарность
лицам, принимавшим участие в печатании рукописи: Дж. Чеп-
мэн из Редингского университета в Англии, М. Эдмондс и
С. Стаки из Института современных исследований при Австра-
Австралийском национальном университете. Каждая из них положила
много часов труда на мою книгу, за что я теперь с радостью
приношу им свою признательность.
Я благодарен редактору книги проф. Э. Хьюитту за под-
поддержку и советы, а также д-рам М. Данвуди и Б. Брэйнерду за
10 Предисловие
воодушевляющие замечания и ценные предложения, сделанные
ими после прочтения отдельных частей рукописи. Я хотел бы
также поблагодарить проф. Л. Гординга и д-ра Дж. А. Тодда
за разрешение процитировать в § 5.12 некоторые опубликован-
опубликованные высказывания первого из них.
Но больше всего я обязан, пожалуй, моей жене. Она проде-
проделала громадную обременительную работу по чтению корректур
и составлению указателей и библиографии. И еще я благодарен
ей за то (и это, быть может, самое главное), что она постоянно
ободряла меня в тех, к сожалению, весьма частых случаях,
когда у меня ничего не получалось так, как я бы того хотел.
я. э. э.
Канберра
Февраль 1965
ГЛАВА О
Предварительные сведения
из. теории множеств и топологии
0.0. Предисловие
Излагая в одной главе сводку основных сведений из теории
множеств и общей топологии, вряд ли можно сделать изложение
полным; трудно даже сохранить логическую последовательность.
Ярким примером отступления от идеальной схемы является от-
отсутствие всякого «традиционного» рассмотрения таких основных
множеств, как множество натуральных чисел, поле вещественных
и поле комплексных чисел. Напротив, предполагается, что чита-
читатель вполне знаком с алгебраической и топологической структу-
структурами, которыми обычно наделяются эти множества, даже если
они ему и не известны под таким названием. При этом, возмож-
возможно, нарушается логический порядок, однако такое изложение со-
соответствует той последовательности, в которой обычно препо-
преподают и изучают математику. Не будет большой ошибкой рас-
рассматривать эту главу как сводку понятий и необходимой техни-
техники, а не как логически связное изложение некоторых бурно раз-
развивающихся областей исследования.
0.1. Предварительные сведения из теории множеств
Мы придерживаемся «наивного» взгляда на теорию мно-
множеств, следуя, например, книге Халмоша [4]. Читатель, кото-
которого такой подход не удовлетворит, может воспользоваться кни-
книгой С а пс а [I]1) и собранной там библиографией. Обзорное
изложение аксиоматического подхода имеется в разделе «До-
«Добавление» в книге Келли [1]. Мы нигде не говорим о «клас-
«классах» в смысле, технически отличном от «множеств» (хотя, со-
согласно аксиоматике, иметь в виду такое различие иногда необхо-
необходимо во избежание логических противоречий). Дело в том, что
все классы, с которыми мы имеем дело, в действительности яв-
являются множествами в том специальном смысле этого слова,
который оно имеет в соответствующей аксиоматике.
0.1.1. Основные теоретико-множественные обозначения. Сим-
Символ ^ мы всегда употребляем для обозначения принадлежности.
1) Советскому читателю можно рекомендовать книгу Бурбаки [1].—
Прим, перев*
12 Гл. 0. Предварительные сведения
Запись х^А означает, что А — множество и что объект х яв-
является точкой (членом, элементом) множества Л, (Читатель, ве-
вероятно, отметит отождествление объекта с символом для его
обозначения, что является одной из форм наивного взгляда на
теорию множеств.) Отрицание утверждения х^А записывается
так: х фА9
Множества часто задаются определяющим их свойством. Эле-
Элемент принадлежит множеству тогда и только тогда, когда он
обладает указанным свойством. В соответствии с этим если Р —
некоторая функция высказываний, то через {х: Р(х)} обозна-
обозначается множество тех и только тех объектов х, для которых
истинно Р(х). Во избежание недоразумений (см. Келли [1,
стр. 14] *)) условимся подчинять эту символику следующему пра-*
вилу: между первой скобкой и двоеточием будем записывать
символ связанной переменной, который и тут, и в Р(х) может
быть заменен любым символом, отличным от всех тех, которые
наряду с х фигурируют в высказывании Р(х).
Конечные множества можно задать перечислением их элемен-
элементов, которые заключаются в скобки и разделяются запятыми
(если множество содержит более одного элемента). Так, например,
множество, составленное из элементов х, у, z (или объектов, обо-
обозначаемых этими буквами) записывается в виде {ху у, г). В част-
частности, {х} есть множество, состоящее из единственного элемента х.
Множество, не содержащее ни одного элемента, называется
пустым множеством и обозначается через 0. Его можно „опреде-
„определить как множество {х: хфх).
Пусть А и В— два множества. Отношение АаВ (которое чи-
читается «А содержится в В», или «В содержит Л», или «Л—под-
«Л—подмножество множества В», или «В — надмножество множе-
множества Л») означает, что каждый элемент множества Л принадле-
принадлежит множеству В. Это отношение может быть записано и так:
В id Л. Если АаВ и ВаС, то АаС. Одновременное выполнение
отношений АаВ и ВаА влечет за собой равенство Л=В. Не-
Непустое множество АаВ называется собственной частью множе-
множества В, если АфВ.
Под объединением множеств А и В понимается множество
{х: х^А или xgB (или выполнены оба эти условия)}, которое
обозначается через Л US. Объединение Л US — наименьшее мно-
множество, содержащее одновременно множества Л и В.
Пересечением множеств Л и В называется множество
{х: ХЕ/1 и *еВ},
которое обозначается через ЛПВ.
1) Во всех случаях, когда имеется русский перевод, номера страниц ука
зываются по нему. — Прим. перев.
0.1. Предварительные сведения из теории множеств 13
Для любого множества Л справедливы отношения 0сЛ,
Л110=Л, ЛП0 = 0.
Множества А и В называются непересекающимися, если
АПВ = 0. Систему множеств Л будем называть дизъюнктной,
если любые два множества А и В из Л либо совпадают, либо не
пересекаются.
Абсолютным дополнением множества А (обозначается через
~Л) называют множество {х: хфА). Относительным дополне*
нием множества А в множестве В называют множество В\А =
= йЛ(~Л).
Легко показать, что операции объединения и пересечения
множеств коммутативны и ассоциативны. Более того, для этих
операций справедливы дистрибутивные законы:
и формулы де Моргана
Х\(Х\А)=АПХ,
Х\(А{]В) = (Х\А)()(Х\В),
Х\(А(]В) = (Х\А) U (Х\В).
Часто возникает необходимость составления объединения и
пересечения множества множеств. Пусть Л —система множеств,
тогда объединение иИ-^ ^Л) есть по определению множество
{л:: х^Ау для некоторого А^Л}. Пересечение Г\{А:А^Л]
определяется как множество {х: xg Л для всел: А е Л). Гово-
Говорят, что (Лг)ге=/ есть семейство множеств, если каждому элемен-
элементу i некоторого множества индексов / поставлено в соответствие
множество Лг\ Для записи объединения семейства множеств
удобно пользоваться обозначениями
i^I) или \}Аи
а для пересечения — обозначениями
П {Aii i<=I) или П А{.
Формулы де Моргана имеют место и для бесконечных объ-
объединений и пересечений. Если Л ={Л, В}у то объединение
U {Л: А^Л) совпадает с множеством Л Об. Пусть Л—конеч-
Л—конечная система множеств, например {Л, Ву..., Х}\ тогда вместо
1){Л: Age Л} пишут A[jB[].. .[JX.
0.1.2. Упорядоченные пары и отношения. Свойство, опреде-
определяющее упорядоченную пару {хуу), можно сформулировать сле-
следующим образом: (х, у) = (х'у у') тогда и только тогда, когда
14 Гл. 0. Предварительные сведения
х — хг и у = у'. В теории множеств именно этим свойством и руко-
руководствуются при определении упорядоченной пары. Пусть
(х, у) —упорядоченная пара, тогда х называют ее первой коор-
координатой, а у— второй.
Отношением R называют некоторое множество, элементами
которого являются упорядоченные пары. Для обозначения при-
принадлежности пары (х, у) отношению R часто пользуются обо-
обозначением xRy.
Областью определения отношения R (записывается domR)
называют множество
{х: (ху у)^ R для некоторого у};
областью значений отношения R называют множество
{У- (х> У)е R Для некоторого х}.
Если R — отношение и А—некоторое множество, то множество
{у: xRy для некоторого х^А} обозначают через R[A] или R(A).
Множество R[domR] есть область значений отношения R.
Важным типом отношений является (декартово) произведе-
произведение АхВ двух множеств Л и В, которое определяется равен-
равенством
Некоторые подмножества такого произведения играют основную
роль в определяемом ниже понятии функции (п. 0.1.3).
Если R — отношение, то обратным отношением R~l называет-
называется множество
{(х,У): Q/, *)€=/?}.
Композицией отношений R и S (обозначается через RoS) назы-
называется множество
{(x,z): (x,y)^S и (y,z)^R для некоторого у}.
Композиция отношений не всегда коммутативна, т. е. отношения
RoS и SoRy вообще говоря, могут не совпадать.
Единичным, или диагональным, отношением в множестве X
(диагональю произведения ХхХ) называют множество
Д(Х) ={(*,*): х<=Х},
которое является подмножеством произведения ХхХ. Когда это
не вызывает недоразумения, вместо Д(Х) пишут Д.
Отношение R называют симметричным, если R = R~l, и анти-
антисимметричным, если Rf]R~l = 0. Будем говорить, что отношение
R рефлексивно, если Дс /?, где символ Д обозначает диагональ
в объединении области определения и области значений отноше-
отношения R. Отношение R называется транзитивным, если RoRczR,
0.1. П ред варите льные сведения из теории множеств 15
Рефлексивное, симметричное и транзитивное отношение назы-
называется отношением эквивалентности. Пусть R — отношение
эквивалентности и X = &omR\ тогда множество X можно разбить
на непересекающиеся классы эквивалентности по отношению
(или по модулю) R. Каждый такой класс эквивалентности есть
множество вида R(x)=R({x})y где х^Х. Любые два класса
эквивалентности либо совпадают, либо не пересекаются, и Х =
= U {#(*): х^Х}. Отношение R выражается на языке классов
эквивалентностей формулой
R=[){R(x)XR(x): xe=X}.
Обратно, если задано дизъюнктное семейство множеств (Л*)^!,
то, полагая
R= UiAiXAii is/},
получим отношение эквивалентности R с областью определения
X=\J{Ai): is/}.
Пусть заданы отношения R и S. Говорят, что отношение R
есть сужение отношения S, или, что то же, S есть продолжение
R, если Ra S. Если X cz dom /?, то сужение отношения R на
множество X — это множество
{(x,y): (x,y)e=R и х <ее X}.
0.1.3. Функции. Отношение f, обладающее тем свойством, что
(x,y)<=f и (х, г/') ее/=> */ = */'*),
называют функцией. Термины соответствие, преобразование, ото*
бражение, оператор являются синонимами слова «функция».
Если f — функция, то каждому элементу x^domf соответ-
соответствует такой единственный элемент у, что (x,y)^f. Этот эле-
элемент у называется значением функции f в точке х и обозначает-
обозначается через f(x) или fx. При этом говорят, что функция / отобра-
отображает или преобразует х в у.
Часто каждому элементу х^Х (тем или иным способом)
ставится в соответствие элемент гх. Множество {(jc, zx): xgX}
задает тогда некоторую функцию с областью определения X.
При этом говорят, что функция f преобразует х в zXi и записы-
записывают это так: f: x*—>zx (при этом предполагается, что х пробе-
пробегает множество X). Для обозначения функции f с областью
определения X и областью значений, содержащейся в множе-
множестве У (не обязательно с ним совпадающей), часто пользуются
1) =ф — знак логической импликации; А=гВ читается «из А следует
■о», «Л влечет В», «если А> то В». — Прим. перед,
16 Гл. 0. Предварительные сведения
обозначением f: X-+Yx). Общепринятый в настоящее время
взгляд на функцию очень близок к «операционному», о котором
мы только что говорили. При таком взгляде на функцию мно-
множество
{(*, f(x)): х^Х)
принято называть графиком функции f. С теоретико-множествен-
теоретико-множественной точки зрения понятия функции и графика совпадают.
В дальнейшем мы часто позволяем себе это безобидное раздвое-
раздвоение терминологии, хотя это и не общепринято. В частности, о
графике линейного оператора (п. 1.3.3) будем говорить там, где
основным рабочим определением служит операционное опреде-
определение этого оператора.
Функция f называется взаимно однозначной, если обратное
отношение frl также является функцией. Говорят, что f есть ото-
отображение на У, если область значений отношения f есть все мно-
множество У.
Если f — отображение, то множество f{A)={y: y = f(x) для _
некоторого х^А} называется образом множества А относитель-
относительно отображения f, а множество
Г(А)={х: f(x)eA)
— прообразом множества А относительно отображения f. Для
произвольных множеств А и В справедливы формулы
f(A{)B)czf(A)nf{B)9
Заметим, что во второй из приведенных формул равенство, во-
вообще говоря, не имеет места.
Существенного различия между функцией и семейством, или
проиндексированным множеством, нет. В последнем случае об-
область определения используется как удобная запись для задания
области значений функции. Таким образом, если / — множество
индексов, то семейство обычно обозначается через (a^ie^ или
просто (а{), когда множество / считается само собой разумею-
разумеющимся. Этот взгляд на семейство возник как очевидное обобще-
обобщение понятия последовательности, где в качестве множества ин-
индексов используется множество натуральных чисел или его
1) В оригинале в обоих случаях (i—>и ->) используется один и тот же
символ ->. Мы предпочли дифференцированные обозначения, так как они
помогают избежать неясности. — Прим. ред.
0.1. Предварительные сведения из теории множеств 17
конечное подмножество. Если семейство (а{) таково, что для ка-
каждого i элемент аг-еЛ, то говорят о семействе точек (элемен-
(элементов) из множества А.
Пусть f — вещественная или комплексная функция, опреде-
определенная на топологическом пространстве X (разд. 0.2). Носителем
функции f называют замыкание в X множества {х^Х: 1(х)ф0}.
Условимся обозначать носитель функции /через supp f.
Данное выше определение произведения двух множеств АхВ
(п. 0.1.2) тривиально распространяется на случай любого конеч-
ного числа множеств. Однако имеется потребность в определении
произведения любого семейства множеств (Х^е=/. Это произве-
произведение обозначается через UXi или ЩХ{: 1^1} и определяется
как множество всех таких наборов х=(Х{), что Xi&Xi для ка-
каждого ie/. Отображение я* произведения Х = ИХ{ на множе-
множество Xh определенное равенством т(х)=хи называется i-й про-
проекцией.
Если Xi=Y для каждого /g/, где У— фиксированное мно-
множество, то произведение ПХг- есть не что иное, как множество
всех отображений, определенных на / со значениями в У. Это
произведение иногда обозначают через У1.
0.1.4. Упорядоченные множества. Пусть X—множество;
рефлексивное и транзитивное отношение QczXxX называется
(частичным) упорядочением, или (частичным) отношением по-
порядка в Ху если ЙГШ~1==Д = Д(Х). Некоторые авторы (Келли
[1, стр. 29]!)) не требуют выполнения последнего условия, что не-
несущественно для случаев, с которыми мы будем встречаться.
Множество X, наделенное отношением порядка Q, будем назы-
называть (частично) упорядоченным множеством и обозначать ино-
иногда через (X, Q).
Там, где это не вызывает недоразумения, будем писать х^Су
(или эквивалентно у^х) вместо хпу и (Х,-^) вместо (X, Q) и
говорить, что ^ есть отношение порядка в X, или что множе-
множество X упорядочено отношением -*С В этих обозначениях спра-
справедливы соотношения
х<у и
где х, у, z — произвольные элементы множества X.
Пусть А — подмножество упорядоченного множества (X, <1).
Будем говорить, что элемент х е X мажорирует Л, или является
его мажорантой, если а^Сх для каждого элемента а^А. Если
же для любого элемента а^А имеет место отношение х^а, то
1) См. также Данфорд и Шварц [1, стр. 14]. — Прим. перев.
18 Гл. 0. Предварительные сведения
говорят, что х является минорантой, или минорирует множе-
множество А. Элемент х0 е X называется (наименьшей) верхней
гранью множества А а X, если х0 мажорирует А и хо^Сх для
любой мажоранты х множества Л. (Наибольшая) нижняя грань
множества А определяется аналогично. Для верхней грани мно-
множества А пользуются обозначениями sup Л, sup {л:: х ^ А} или
supjc; нижняя грань обозначается inM, inf{x: x^A) или inf x.
х^А х<=А
Каждое подмножество А а X имеет в X не более одной верхней
(нижней) грани.
Говорят, что ^ есть совершенное (или линейное) упорядоче-
упорядочение в X, если для каждой пары (х, у) gIX^ либо х-^у, либо
у-*Сх, т. е. Q\jQ~l—XxX. Множество X, наделенное отношением
совершенного порядка, называют совершенно (линейно) упоря-
упорядоченным, или цепью. Подмножество А упорядоченного множе-
множества (X, ^С) называется совершенно упорядоченным, если суже-
сужение отношения ^ на А есть совершенное упорядочение.
Упорядоченное множество (X, ^) называется индуктивным,
если каждое его совершенно упорядоченное подмножество А
обладает в X верхней гранью.
Пусть X — некоторая система подмножеств данного множе-
множества S. Важным примером отношения порядка в X является от-
отношение А ^СВ, определенное условиями А ^ X, В <= X и А а В.
При этом говорят, что X упорядочено по включению, или по воз*
растанию. Если Y cz X и объединение U{A' A<=Y) принадлежит
X, то верхняя грань sup У существует и равна этому объедине-
объединению. Противоположное отношение порядка, при котором А^СВ
означает Aid В, называют упорядочением по убыванию. Такой
порядок естествен, например, в множестве окрестностей некото-
некоторой точки топологического пространства (п. 0.2.2).
Элемент т^Х называется максимальным, если в X нет та-
такого элемента у, что т^Су и т-4=у.
0.1.5. Лемма Цорна. Для каждого элемента х индуктивно
упорядоченного множества X существует такой максимальный
элемент wgI, что х-^пг.
Лемма Цорна часто заменяет рассуждения, основанные на
таких принципах, как принцип трансфинитной индукции, теорема
Цермело о вполне упорядоченности, аксиома выбора. Краткое
изложение связей между некоторыми такими принципами можно
найти у Келли [1, стр. 53—59]1).
Сформулированную лемму мы будем называть, как это при-
принято, леммой Цорна, хотя этот результат установлен в 1923 г.
Р. Л. Муром и независимо от него Куратовским, а затем вновь
1) См также Райков [3, стр. 12—18]. — Прим. перев,
0.1. Предварительные сведения из теории множеств 19
открыт Цорном в 1935 г. и несколько позднее Тайхмюллером.
Бурбаки — один из первых, кто систематически пользовался лем-
леммой; ему и принадлежит это ее название. Более подробные све-
сведения по этому поводу содержатся в книге Розенбдюма
[1, стр. 21 и 150].
Некоторые авторы рассматривают вариант леммы Цорна, в
котором предположение индуктивной упорядоченности множе-
множества X заменяется более слабым требованием, чтобы каждое со-
совершенно упорядоченное подмножество в X обладало мажоран-
мажорантой в X. Доказательство этого варианта имеется, например, в
книгах Келли [1], Данфорда и Шварца [1]. Такое видоиз-
видоизменение леммы Цорна не существенно для тех случаев, где она
используется в этой книге.
0.1.6. Счетные множества. Мы редко будем пользоваться по-
понятием кардинального числа, однако без понятия счетности обой-
обойтись почти невозможно..
Два множества X и У называются равномощными, или имею-
имеющими одинаковую мощность (или одинаковое кардинальное
число), если существует взаимно однозначное отображение мно-
множества X на множество У.
Множество X бесконечно, если оно равномощно некоторой
своей собственной части; в противном случае множество X ко-
конечно.
Множество натуральных чисел N и его свойства предпола-
предполагаются известными. Для всякого «gN введем множество Nn =
= {m: /neN, m^Cn}. Легко видеть, что множество X конечно
тогда и только тогда, когда оно равномощно некоторому множе-
множеству Nn. В этом случае говорят, что множество X содержит
п элементов; оно может быть занумеровано в виде {хх, х2,..., хп)
или как семейство {Хк)х<к<п>
Множество X называется счетным, если оно равномощно
множеству натуральных чисел N. Если множество X счетно, то
его можно представить (вообще говоря, различными способами)
в виде последовательности (xv) ne=N. Будем говорить, что множе-
множество X не более чем счетно, если оно либо конечно, либо счетно.
Всякое подмножество не более чем счетного множества не
более чем счетно. Если область определения функции f не более
чем счетна, то такой же будет и область ее значений.
Пусть каждое из множеств А системы Л не более чем счет-
счетно; если система JL не более чем счетна, то таким же будет и
объединение \${А\ /lei}. Произведение двух (или любого ко-
конечного числа) не более чем счетных множеств — такое же мно-
множество. То же верно и относительно множества всех конечных
подмножеств не более чем счетного множества. Множество всех
20 Гл. 0. Предварительные сведения
подмножеств бесконечного множества уже не счетно. Множе-
Множество всех вещественных чисел также не счетно.
0.1.7. Направленные множества и сети. Под направленным
множеством мы понимаем упорядоченное множество (п. 0.1.4),
в котором любые два элемента обладают общей мажорантой.
Сеть1)—это семейство элементов, множество индексов кото-
которого направленно. Некоторые авторы, называют сеть обобщен-
обобщенной последовательностью.
Сети впервые были введены как обобщение последова-
последовательностей. Потребность в них возникла при изучении общих
топологических пространств и при исследовании понятия сходи-
сходимости.
Каждая последовательность есть сеть2). Множество окрест-
окрестностей произвольной точки в топологическом пространстве, упо-
упорядоченное по убыванию (см. конец п. 0.1.4), образует часто ис-
используемую сеть.
Нам понадобятся некоторые результаты и понятия, касаю-
касающиеся сетей.
Подсети. Сеть (уц)ц*=м называется подсетью сети (xJagel,
если для каждого IeL существует такой индекс ju^eM, что
соотношения \i' е М и (о/^-^х влекут за собой равенство у^> =
= хх для некоторого А/ ^ К.
Подсеть обобщает понятие подпоследовательности. Последо-
Последовательность может, однако, обладать подсетями, которые сами
не являются последовательностями.
Произведение направленных множеств. Рассмотрим две по-
последовательности вещественных чисел (хп) и (уп). Нетрудно
определить их произведение и сумму. Это будут соответственно
последовательности (хпуп) и (хп + уп). Такое определение оче-
очевидно и естественно, потому что множество индексов у обеих по-
последовательностей одинаково. В противном случае приходится
выбирать окольный путь, используя понятие произведения двух
направленных множеств индексов.
Пусть L и М — направленные множества. В произведении
L X М (и. 0.1.2) введем отношение порядка следующим образом:
(Х,\х) К (A/, \i')9 если А,<А/ и ц, < ц/. Легко проверить, что упо-
упорядоченное таким образом произведение L X М образует на-
направленное множество3).
1) В оригинале направленное семейство (directed family). — Прим. пё-
рев.
2) Имеется в виду; что натуральный ряд снабжен стандартным упоря-
упорядочением. — Прим. ред.
3) Теперь, например, сумму двух сетей вещественных чисел (х^),
можно определить как сеть (х^ + У\х){К,\л) ^LXM- — Прим. ред.
0.2. Предварительные сведения из общей топологии 21
0.2. Предварительные сведения из общей топологии
0.2.1. Определение топологии открытыми множествами. Пусть
X — множество. Под топологией в X понимают некоторую си-
систему % подмножеств из X, удовлетворяющую следующим
условиям:
A) 0 и X принадлежат £;
B) если U и U' принадлежат £, то и пересечение U[)U' при-
принадлежит £;
C) объединение любого семейства множеств из £ принад-
принадлежит £.
Элементы системы 2 называются открытыми множествами
(в, для) топологии 2, или %-открытыми множествами.
Пара (X, £), в которой X — множество и 2 — топология в
Ху называется топологическим пространством. Если % подразу-
подразумевается, то часто говорят об X как о топологическом простран-
пространстве.
Если % — топология в множестве X, то под (открытой) базой
топологии % понимают такую подсистему Л в 2, что каждый
элемент из % является объединением некоторого подмножества
элементов из JL. Предбазой (открытой предбазой) топологии %
называется такая подсистема 38 из £, что совокупность пересе-
пересечений конечных наборов множеств, принадлежащих 38, обра-
образует базу топологии Z.
Пусть (X, 2)—топологическое пространство. Окрестностью
точки j^gI называется любое подмножество из X, в котором
содержится открытое множество, содержащее х. Аналогично
окрестностью множества А а X называется всякое подмножество
из X, которое содержит открытое множество, содержащее А.
Подмножество в X тогда и только тогда принадлежит 2, когда
оно есть окрестность каждой своей точки.
Задание окрестностей точек в топологическом пространстве
полностью определяет его топологию. Это указывает на другой
метод введения топологии, которым мы часто будем пользо-
пользоваться. Он описан ниже, в п. 0.2.2.
Следует заметить, что одно и то же множество X может быть
топологизировано различными способами. Например, каждое
множество всегда может быть наделено нулевой, или антидис-
антидискретной, топологией {0, Х}\ другой крайний случай — это так
называемая дискретная топология, состоящая из всех подмно-
подмножеств множества X. Обе эти топологии являются экстремаль-
экстремальными в шкале сравнения топологией, описанной ниже, в п. 0,2.6.
0.2.2. Определение топологии с помощью окрестностей. Наи-
Наиболее удобный путь определения топологических векторных про-
пространств (§ 1.8) —это задание их топологии в терминах систем
22 Гл. 0. Предварительные сведения
окрестностей каждой точки. Составной частью определения то-
топологического векторного пространства является наличие связи
между его векторной и топологической структурами. Благодаря
этой связи система окрестностей каждой точки является соот-
соответствующим сдвигом системы окрестностей нуля. Это обстоя-
обстоятельство вынуждает нас рассмотреть и такой способ задания то-
топологии.
Пусть X — множество. Допустим, что задано множество 31
упорядоченных пар (x,N), где xeJ, а N— подмножество в X,
содержащее х. Предположим, что множество У1 удовлетворяет
следующим условиям:
(a) (х, X) е У1 для каждого элемента xgI;
(b) если (*,#') е51и (x,N") e= % то (х.ЛГПЛГ) е= $К;
(c) если {x,N)c=MhXz>N'zzN, то (*, N') е= 5П;
(d) если (х, N) e sJi, то существует такое множество N\
что (jc, iV') g?1 и (a:7, iV) e 9i для каждого элемента
*' е= #'.
Оказывается, система X, состоящая из всех таких подмно-
подмножеств UaX, что для элемента x^U пара (х, {/) принадлежит
ЭД, является топологией в X. Кроме того, окрестности точки х в
этой топологии X(по определению из п. 0.2.1) —это все те мно-
множества /V, для которых (х9 N) е ЭТ. Множество SR определяет,
таким образом, топологию X в X. Такое задание топологии на-
называется заданием топологии X с помощью окрестностей.
Пусть X — топологическое пространство, Шу — система всех
окрестностей некоторой точки хе! Подсистема 3&х называется
базой окрестностей1) в точке х (в заданной топологии), если
подмножество из X принадлежит %1Х тогда и только тогда, когда
оно содержит некоторое подмножество из $?х. Если для каждой
точки х топологического пространства X выбрана некоторая база
окрестностей Stх* то легко проверить, что выполняются следую*
щие условия:
(а7) хеЛ/ для каждого N^ffi/,
(b ) если N' и N" принадлежат 3&х, то существует такое
множество N<=&X1 что NczN'(]N"\
(d') если N^$x, то существует такое множество N'<=:$x,
что для каждого xf e N' множество /V содержит под-
подмножество, принадлежащее 38хг*
Обратно, если каждой точке хе! поставить в соответствие си-
систему 3£х подмножеств из X таким образом, что выполняются
условия (a7), (W) и (d7), то в множестве X' существует един-
1) Иногда 38х называют фундаментальной системой окрестностей точки
х. — Прим. перев.
0.2. Предварительные сведения из общей топологии 23
ственная топология, такая, что в каждой точке х система ЗРХ
есть база окрестностей этой точки.
Пример. Множество вещественных чисел R обычно наде-
наделяется топологией, в которой база открытых множеств состоит
из интервалов (а, 6), где а<Ь. Одна из баз окрестностей в точке
х образована всеми интервалами вида (х — р, х + р), где р>0.
Существует, разумеется, много различных баз окрестностей,
определяющих одну и ту же топологию. Мо-жно, например, огра-
ограничиться лишь р, пробегающими строго убывающую последова-
последовательность положительных чисел, стремящуюся к нулю; можно
далее в каждом случае заменить открытый интервал (х — р,
х+р) замкнутым интервалом [л: — р, х+р].
0.2.3. Замкнутые множества. Операция замыкания. Пусть
X — топологическое пространство. Множество А а X называется
замкнутым (в заданной топологии), если множество Х\А от-
открыто. Из этого определения вытекают следующие свойства
замкнутых множеств:
(а") 0 и X — замкнутые множества;
(Ь") любое пересечение замкнутых множеств замкнуто;
(с") объединение двух замкнутых множеств замкнуто.
Топологию можно определить заданием ее замкнутых мно-
множеств, которые должны удовлетворять условиям (а") — (с");
см., например, Келли [1, стр. 64].
Замыкание А множества А топологического пространства
X — это наименьшее замкнутое множество, содержащее Л, т. е.
(в силу (Ь")) А есть пересечение всех замкнутых множеств, со-
содержащих А. Легко проверить, что А есть множество тех и
только тех точек jcgI, каждая окрестность которых имеет не-
непустое пересечение с множеством А. Читатель легко заметит,
что множество А замкнуто тогда и только тогда, когда А=А.
Кроме того, справедливы соотношения
А=Л, А[)В=~АТГВ9
0=0, х=х, Т
Говорят, что множество А {всюду) плотно в X, если А=Х.
Топологию можно определить также в терминах операции
замыкания Лн->л, определенной для всех подмножеств из X и
удовлетворяющей приведенным выше условиям (среди которых
есть и зависимые от остальных). Этот способ определения топо-
топологии принадлежит Куратовскому [1, стр. 44]; см. также
Келли [1, стр. 68].
0.2.4. Внутренность множества. Это понятие двойственно по-
понятию замыкания. Пусть X — топологическое пространство и
А — подмножество б X. Внутренность множества Л, обозначае-
24 Гл. 0. Предварительные сведения
мую через А или int Л, можно определить как множество
Х\(Х\А), или, что то же самое, как наибольшее открытое мно-
множество, содержащееся в А (т. е. объединение всех открытых мно-
множеств, входящих в Л). Множество А открыто тогда и только
тогда, когда А=А.
0.2.5. Граница множества. Границей подмножества А тополо-
топологического пространства X называется множество всех тех точек
из Х} которые принадлежат одновременно замыканию множества
А и замыканию множества Х\А. Обозначается граница множе-
множества А через fr Л или dA. Эквивалентным определением границы
множества служит равенство
irA=A\A.
Очевидно, что UA — всегда замкнутое множество; кроме того,
А=А Ufi-Л, Л
0.2.6. Сравнение топологий. Пусть 2 и 2/ — две топологии
в множестве X. Говорят, что топология 2 слабее топологии 2',
или что топология 2' сильнее топологии 2, если % а 2', т. е.
если каждое 2-открытое множество является также и 2'-откры-
тым. Это эквивалентно утверждению, что всякая 2 -окрестность
любой точки х^Х является также ее ^^окрестностью, или что
каждое 2-замкнутое в X множество 2'-замкнуто.
Среди всех топологий в X нулевая — слабейшая, а дискрет-
дискретная (см. конец п. 0.2.1)—сильнейшая.
0.2.7. Индуцированные топологии и подпространства. Пусть
(X, 2)— топологическое пространство и У — подмножество в X.
Индуцированной топологией в У называется топология, в кото-
которой открытыми множествами по определению являются пересе-
пересечения У с 2-открытыми множествами из X. Индуцированная в
У топология обозначается через 2 | У.
Множество У топологического пространства X называется
(топологическим) подпространством в X, если оно наделено ин-
индуцированной топологией. Открытые (или замкнутые) множе-
множества в таком подпространстве часто называют относительно от-
открытыми (или относительно замкнутыми) множествами. Окрест-
Окрестности точки у подпространства У в индуцированной топологии
также иногда называют относительными окрестностями точки у.
0.2.8. Аксиомы отделимости. Постулаты, предполагающие>
существование в том или ином смысле «достаточного» запаса
открытых множеств (или замкнутых множеств, или окрестно-
окрестностей), известны под названием аксиом отделимости. Ниже мы
перечислим общепринятые постулаты такого рода.
Говорят, что топологическое пространство (Xt.Z) является:
0.2. Предварительное сведения из общей топологии 25
A) Т0-пространством, если для любой пары различных точек
х и у из X существует либо окрестность точки х, не содержащая
у, либо окрестность точки */,jH.e содержащая х, или, что то же
самое, либо хф{у), либо уф{х}\
B) Тгпространством, если каждое одноточечное множество
из X замкнуто, что равносильно следующему утверждению: для
любых двух различных точек х и у из X существуют окрестность
точки х, не содержащая у, и окрестность точки у, не содержащая
х (ср. с Го);
C) Т2-пространством (отделимым, или хаусдорфовым), если
любые две различные точки х и у из X имеют непересекающиеся
окрестности;
D) регулярным, если замкнутые окрестности каждой точки
xgX образуют базу окрестностей этой точки;
E) Тгпространством, если оно регулярно и является Тх-про-
Тх-пространством;
F) нормальным, если любые два непересекающихся замкну-
замкнутых множества обладают непересекающимися окрестностями;
G) Т^-пространством, если оно нормально и является Ггпро-
странством;
(8) вполне регулярным, если для каждой точки х<=Х и каж-
каждой окрестности N точки х существует непрерывная 1) функция
f: Х->[0, 1], удовлетворяющая условиям f(x)=O и f(y) = l для
X\N
y
(9) тихоновским, если оно вполне регулярно и является Тх-
пространством.
Легко проверяется выполнение следующих соотношений:
ТА^Т3^Т2^Тг^Т0;
полная регулярность^ регулярность.
Регулярное пространство не обязательно является Ггпрост-
ранством. Это следует из рассмотрения полуметризуемого про-
пространства, полуметрика которого не является метрикой (п. 0.2.21).
Существует также регулярное Г2-пространство, на котором каж-
каждая непрерывная функция постоянна (см. Келли [1, стр. 159]).
Для Ггпространств справедливы импликации:
нормальность :ф полная регулярность :=> регулярность =ф Т2.
Первая из этих импликаций нетривиальна и следует из леммы
Урысона (п. 0.2.12). Остальные импликации вытекают непосред-
непосредственно из определений.
0.2.9. Непрерывные отображения. Пусть X и У — топологиче-
топологические пространства и / — отображение пространсава X в Y
1) Понятие непрерывности вводится ниже. — Прим. ред.
26 Гл. 0. Предварительные сведения
(т. е. область определения f есть X, а область значений есть
подмножество в У; см. п. @.1.3). Отображение f называется не-
непрерывным, если множество f~l(V) открыто в X всякий раз, ко-
когда множество V открыто в У. Для этого достаточно, чтобы
f~l(V) было открытым множеством для каждого множества V,
принадлежащего некоторой открытой базе в У или даже откры-
открытой предбазе в У.
Отображение f называется непрерывным в точке xel, если
f~l(V) есть окрестность точки х всякий раз, когда V есть окрест-
окрестность точки f(x) (или, что то же, когда V принадлежит некото-
некоторой базе окрестностей точки f(x)).
Если в этих определениях область определения отображения
f не указана, то под ней подразумевается все пространство X.
Пусть f — отображение пространства X в пространство У и Л —
подпространство в X. Сужение f\A отображения / на А может
быть непрерывным (или непрерывным в точке xg^) и в том
случае, когда отображение f не обладает этим свойством. С дру-
другой стороны, непрерывность отображения / влечет непрерыв-
непрерывность сужения f\Ay где А — произвольное подпространство в X.
Пусть даны отображения /: X-+Y и g: Y-+Z (X, Y,Z— топо-
топологические пространства). Из непрерывности / и g следует не-
непрерывность композиции gof (которая отображает X в Z).
Отображение /: Х-+- У называется гомеоморфизмом простран-
пространства X в У, если оно взаимно однозначно, непрерывно и отобра-
отображение f~l непрерывно (как отображение подпространства f(X)
пространства У в X). Если f(X) = У, то отображение/называется
гомеоморфизмом пространства X на У. Топологические прост-
пространства X и У называются гомеоморфными, если существует
хотя бы один гомеоморфизм пространства X на У.
Отображение /: X-+Y называется открытым, если для каж-
каждого открытого множества V из X множество f(U) открыто в У.
Это равносильно требованию, чтобы для каждой точки хеХи
каждой окрестности U, принадлежащей некоторой базе окрест-
окрестностей точки х, множество f(U) было окрестностью точки f(x).
Взаимно однозначное отображение f пространства X на про-
пространство У является гомеоморфизмом пространства X на У то-
тогда и только тогда, когда отображение f непрерывно и открыто.
Если f не является отображением на, то следует различать
утверждения: «/ открыто как отображение пространства X в У»
и «f открыто, как отображение пространства X на f(X)>. Послед-
Последнее утверждение слабее первого. Например, если А* — подпро-
подпространство в У и f — вложение1) множества X в У, то /, рассма-
!) Если XczY, то вложением f: X->Y называется такое отображе-
отображение, что f{x) =х для х е X. — Прим. перев.
0.2. Предварительные сведения из общей топологии 27
триваемое как отображение пространства X в У, открыто тогда
и только тогда, когда X — открытое множество в У. В то же
время вложение / всегда открыто, если его рассматривать как
отображение X на f (X) =Х.
Другими словами, уточнение пространства, где находится
множество значений отображения /, существенно при выяснении
вопроса о том, является ли отображение / открытым или нет.
0.2.10. Полунепрерывные функции. Для определения полу-
полунепрерывности удобнее рассматривать функции, принимающие
свои значения в расширенной вещественной оси. Это множество,
обозначаемое через R, получается добавлением к вещественной
оси R двух различных точек —оо и Н-оо. Естественный порядок
на R распространяется и на R, а именно полагается, что
ОО<Г< + ОО
для каждого числа rgR. Заметим, что в R всякое подмноже-
подмножество обладает верхней и нижней гранями.
Не все операции в R распространимы на R. Договоримся
считать, что —(—оо) = +оо и —(-j-oo) ——оо; что как сложе-
сложение, так и умножение коммутативны всегда, когда они опреде-
определены; что для всякого вещественного числа г имеют место ра-
равенства
Г+ (—оо)= — оо, г+ ( + оо) = + оо
и
(—оо) + (—оо) =—оо, ( + оо) + ( + оо) = + оо,
а также, что
Г.( + оо) = +оо
Г • ( + (Х>) = ОО
Г» (—оо) =—оо
Г • (—оо) = + оо
О- (_оо)=(Ь
при
при
при
при
( + оо)
г>0,
г<0,
г>0,
г<0,
= 0.
С другой стороны, будем считать, что символы (—оо) + ( + оо),
(—оо) — (—оо), ( + оо) — ( + оо) лишены смысла.
_Обычная топология в R (см. конец п. 0.2.2) «продолжается»
fe R, если за базу окрестностей точки +оо принять совокупность
fccex интервалов вида (г, +оо], где re R, а за базу окрестностей
точки —оо — совокупность всех интервалов вида [— &о; г)% где
Пусть, как и_ раньше, X — топологическое пространство.
Функция f\ Х-+Я называется полунФпрершной снизу, если ее
28 Гл. 0. Предварительные сведения
значения принадлежат множеству R\{—оо}, и для любого числа
reR (или, что то же, rsR) множество
{х: х<=Х и f(x)>r)
открыто в X. Функция f: X-+R называется полунепрерывной
сверху, если полунепрерывна снизу функция —/.
Функция f: X->~R, полунепрерывная снизу и сверху, прини-
принимает свои значения в R и непрерывна, как функция /: А'-> R.
Верхняя (нижняя) огибающая1) семейства полунепрерывных
снизу (сверху) функций на X есть полунепрерывная снизу
(сверху) функция.
Сумма двух полунепрерывных снизу (сверху) функций —
полунепрерывная снизу (сверху) функция. То же верно и для
произведения двух положительных полунепрерывных снизу
(сверху) функций.
В гл. 4 нам понадобится следующая лемма:
Лемма. Пусть X — вполне регулярное топологическое прост-
пространство, Л — система подмножеств из X, содержащая базу
окрестностей каждой точки из X. Всякая положительная полу-
полунепрерывная снизу на X функция f есть верхняя огибающая мно-
множества G всех положительных непрерывных функций g: X->R,
каждая из которых равна нулю вне некоторого множества из
Л, и таких, что g^Cf (т. е. g(x) *Cf(x) для каждой точки jcgX).
Доказательство. Обозначим через fo верхнюю огибаю-
огибающую множества функций G. Очевидно, что fo-^-f- Пусть х0 — про-
произвольная фиксированная точка пространства X. Выберем такое
вещественное число г, чтобы г</(а:0). Из полунепрерывности
снизу функции f следует существование такой окрестности U
точки Хо, что f(x)>r для x^U. Не ограничивая общности, мож*
но считать, что U е Л (в противном случае можно сузить
окрестность U). Так как пространство X вполне регулярно, то
существует такая непрерывная функция g0: X -^ [0, 1], что
go(xo) = l и go{X\U)={O} (п. 0.2.8). Рассмотрим функцию
g: X->~R, определенную равенством g = rgo. Она непрерывна,
g(jto)=r, g обращается в нуль вне множества I)^ <А и £■</.
Следовательно, g^G, так что /о(*о) ^Sixo) =г. Так как г —
произвольное число, удовлетворяющее неравенству r<f(xo), то
fo(*o) <^f(xo), т. е. fo^f в силу произвольности хо.Щ
Как мы увидим в п. 0.2.18, всякое отделимое или регулярное
локально компактное пространство X вполне регулярно. В этом
*) Пусть (W/s/ — семейство числовых функций, определенных на мно-
множестве Е. Верхней огибающей sup fi (соотв. нижней огибающей inf ft)
семейства (fi) называют определенную на Е числовую функцию, значение
которой в каждой точке х ^ Е равно sup (ft (x)) /соотв. inf (fi (x) )\ .
0.2. Предварительные сведения из общей топологии 29
случае в качестве Л можно взять совокупность всех компакт-
компактных множеств пространства X; тогд# множество G будет со-
состоять из всех положительных непрерывных функций g: X—*R
(g^f) c компактными носителями.
0.2.11. Сети в топологическом пространстве. Пусть X — топо-
топологическое пространство. Наша цель — рассмотреть понятие схо-
сходимости и связанные с ним свойства, которыми может обладать
или не обладать сеть точек X, Для этой цели удобно пользо-
пользоваться терминологией Келли [1, стр. 96]1). Если (хх)—сеть
точек из X и А — множество в X, то будем говорить, что
A) сеть (а:^) в конечном счете попадает в множество Л,
если существует такой индекс Ло, что х^еЛ для каждого ин-
индекса X>V,
B) сеть (хх) часто бывает в множестве Л, если для каждого
индекса К существует такой индекс А'>Х, что хк>^А.
Пользуясь этими терминами, уже легко определить сходи-
сходимость сети и связанные с этим понятия.
Говорят, что сеть (хх) сходится к точке дс, или что х есть пре-
предел сети (хх), если (хх) в конечном счете попадает во всякую
окрестность U точки х. Записывается это следующим образом:
ИЛИ
Х\-+х при возрастании %.
Точка xgX называется предельной точкой (или точкой на-
накопления) для сети (хх), если х^ часто бывает во всякой окрест-
окрестности U точки х.
Ниже приводятся пять предложений, которыми мы будем в
дальнейшем часто пользоваться.
(a) Если сеть (хх) сходится к точке х, то и любая ее подсеть
(г/ц) также сходится к этой точке.
Это утверждение следует непосредственно из определений.
(b) Точка х является предельной для сети (хх) тогда и толь-
только тогда, когда существует подсеть (у^) сети (хк)9 сходя-
сходящаяся к х.
Действительно, пусть х — предельная точка сети (#х). Обо-
Обозначим через {£/} направленное множество окрестностей точки х
(упорядоченное по убыванию — п. 0.1.7) и рассмотрим произве-
произведение M = LX{U}y где L — направленное множество индексов сети
(х\). По условию каждой паре (A, U) соответствует такой индекс
^*=/(А,, U) >А,, что х\* ^ U. Полагая Уи^х^иь где |л =
= (^, (/) g M, получаем сеть (#д), являющуюся подсетью сети
1) В русском переводе книги Келли терминология несколько отличается
от принятой здесь. — Прим. ред.
30 Гл. 0. Предварительные сведения
(х). Легко проверить, что сеть (у^) сходится к точке х. Обрат-
Обратное утверждение тривиально. I _
(с) Точка xgX принадлежит замыканию А множества
Аа X тогда и только тогда, когда либо существует сеть точек
из А, сходящаяся к х, либо существует сеть точек из А, для ко-
которой х есть предельная точка.
Это утверждение также следует из определений.
(d). Топологическое пространство X отделимо (т. е. является
7^-пространством, или хаусдорфовым) тогда и только тогда, ко-
гда каждая сходящаяся сеть точек из X имеет не более одного
предела в X. Если X — отделимое пространство и х^-^х, то х
есть единственная предельная точка сети (х^).
Это утверждение легко следует из (а) и (Ь). (См. также
утверждение A) из п. 0.2.17.)
(е) Отображение f: X-+Y (X и У — топологические простран-
пространства) непрерывно в точке х тогда и только тогда, когда сеть-
(f{xx)) сходится к f(x) для любой сети (хх) из X, сходящейся
к х.
0.2.12. Лемма Урысона. Если X — нормальное топологическое
пространство и А, В — непересекающиеся замкнутые множества
в X, то существует такая непрерывная функция /: ^-^[О, 1], что
/(Л)={0> и f(B)={l}.
Доказательство можно найти в книге Келли [1, стр. 157]
или в книге Гильмана и Джерисона [1, стр. 43—44]1).
0.2.13. Теорема Урысона — Титце о продолжении. Если X —
нормальное топологическое пространство, А—замкнутое мно-
множество в X и функция /: Л ->[—1, 1] непрерывна, то существует
такая непрерывная функция g: Х-*[—1,1], что сужение g\A=f.
Из этой теоремы при тех же условиях относительно Л и X
вытекает, что каждая непрерывная функция /: Л-^R имеет не-
непрерывное продолжение на все пространство X.
Доказательство теоремы Урысона — Титце можно найти у
Келли [1, стр. 318], задача Я, или у Гильмана и Джери-
Джерисона [1, стр. 18—19]2). Титце установил этот результат для
метрических пространств; Урысон обобщил его на нормальные
пространства. Свойство, выражаемое теоремой Урысона —Тит-
—Титце,— характеристическое для нормальных пространств.
0.2.14. Топологии, определяемые семействами функций. Ино-
Иногда возникает необходимость наделения множества X такой то-
топологией, при которой становятся непрерывными одно или более
отображений множества X в некоторые топологические про-
пространства. Предположим, что задано семейство топологических
1) См. также Куратовский [1, стр. 132—133]. — Прим. перев.
*} См. также Куратовский [I, стр. 134—135]. — Яр«дс, п*рев>
0.2. Предварительные сведения из общей топологии 31
пространств (Yi) = (Yi)ie=I и что для каждого /g/ задано ото-
отображение fii X -у Уг. Рассмотрим такие топологии в множестве X
(если они имеются), при которых для каждого /е / отображение
f{: X-+Yt непрерывно.
Прежде всего заметим, что такие топологии существуют: на-
например, дискретная топология в X. Во-вторых, как сейчас будет
установлено, среди таких топологий существует слабейшая.
Пусть £ —одна из топологий, при которой для каждого /е/
отображение /*: X-^Y{ непрерывно. Если У* — открытое множе-
множество в У,-, то fr1 (Vi) — открытое множество в топологии 2. По-
Поэтому таким же будет всякое множество вида
где множество Vt открыто в Yt и Vi> = Y{ для всех £, кроме, быть
может, некоторого конечного (возможно пустого) набора индек-
индексов i. С другой стороны, легко проверить, что эти множества U
образуют базу открытых множеств некоторой топологии в X. Эта
топология, очевидно,— слабейшая среди всех тех топологий, при
которых каждое из отображений f{ непрерывно. Будем ее назы-
называть топологией, определенной заданным семейством отображе-
отображений (fi).
Пусть х — точка множества X. Множества вида
где при каждом i множество Л/г- есть окрестность точки fi(x) и
Ni=Yi для всех i, кроме, быть может, некоторого конечного (воз-
(возможно, пустого) набора индексов i, образуют базу окрестностей
точки х в топологии, определенной семейством отображений (fi).
0.2.15. Произведение пространств и произведение топологий.
Пусть (Хг) = (Xi) .s/ — некоторое семейство топологических про-
пространств. Образуем произведение множеств Х = ИХг (п. 0.1.3).
Пусть яг- есть /-я проекция произведения X на Х{. Топология в Ху
определенная семейством проекций яг-, называется произведе-
произведением топологий пространств Хг-. Множество X, наделенное такой
топологией, называется (топологическим) произведением семей-
семейства пространств (Х^, а сами пространства Хг-—-его сомножите-
сомножителями.
Каждая из проекций я* есть открытое отображение простран-
пространства X на Xt.
Отображение / топологического пространства S в произведе-
произведение ^непрерывно тогда и только тогда, когда каждое из отобра-
отображений яг-of; S-+Xt непрерывно.
Если каждый из сомножителей Хг произведения X — отдели-
отделимое пространство, то произведение X обладает тем же свойством*
32 Гл. 0. Предварительные сведения
Если Xi=Y для всех /, то произведение множеств Х = ПХг можно
отождествить с множеством Y1 всевозможных отображений /
в У. В этом случае произведение топологий в X иногда называют
топологией поточечной сходимости на /.
Стандартная топология пространства R71 (соответственно
О) — это произведение обычных топологий пространства R (со-
(соответственно С).
0.2.16. Факторпространства. Рассмотрим случай, когда X —
топологическое пространство, У— некоторое множество и / —
отображение X в У. В множестве Y естественно рассматривать
топологии, при которых отображение / непрерывно. Такие топо-
топологии существуют: например, нулевая топология в У. Для каждой
такой топологии V множество f~l(V) открыто в X для любого
^'-открытого множества V. Система 2 всех подмножеств V, для
которых f~l(V) открыто в X, образует топологию в У. Это силь-
сильнейшая среди топологий в У, относительно которых отображе-
отображение f непрерывно.
При изучении этой топологии удобно пользоваться следую-
следующим обозначением:
где Л — произвольное множество в X. Выполняются соотношения
A*idA, /(Л*)=/(Л), A**=A*.
Отметим следующие пять свойств нашей топологии.
A) Для каждого множества AczX имеет место равенство
f(X\A*)=f{X)\f(A).
B) Множество /(Л), где AczX, открыто тогда и только
тогда, когда открыто множество А*.
Первое утверждение следует из определений, второе из не-
непрерывности отображения /.
C) Отображение / открыто тогда и только тогда, когда
вместе с каждым открытым множеством U в X открыто и мно-
множество U*. Если / — открытое отображение и U пробегает базу
окрестностей точки ху то система множеств f(U) образует базу
окрестностей точки f(x).
D) Если / открыто и отображает X на У, то множество f(A)
замкнуто тогда и только тогда, цогда замкнуто множество Л*.
Действительно, в силу непрерывности отображения / из замк-
замкнутости множества f(A) следует замкнутость множества Л*.
С другой стороны, так как / — отображение на У, то из свой-
свойства A) вытекает справедливость равенства f(X\A*) = Y\f(Л).
Если множество Л* замкнуто, то из того, что отображение f от-
открыто, получаем, что множество Y\f(A) открыто и, следова-
следовательно, множество f(A) замкнуто.
0.2. Предварительные сведения из общей топологии 33
E) Отображение g пространства У в пространство Z непре-
непрерывно тогда и только тогда, когда отображение gof; X-+Z не-
непрерывно.
Утверждение непосредственно следует из определения тополо-
топологии 2 и непрерывности отображения /.
Используя описанную выше конструкцию, можно ввести по-
понятие факторпространства. Пусть X — топологическое простран-
пространство и R— отношение эквивалентности в X. Согласно п. 0.1.2,
множество X можно разбить на классы эквивалентности по мо-
модулю R. Множество всех классов эквивалентности, обозначаемое
обычно через X/R, называют, фактормножеством множества X
по модулю R. Если я— естественное отображение множества X
на X/R, то п(х) будет классом эквивалентности R(x). Фактор*
топологией в X/R называют сильнейшую топологию в множе-
множестве X/R, при которой отображение я: X-+X/R непрерывно.
В этом случае Л* является не чем иным, как множеством
R (A) = {у: (х, у)^ R для некоторого х е А}.
Если пространство X/R отделимо, то R1) замкнуто в произ-
произведении ХхХ. Если я — открытое отображение и 7?~замкнуто в
произведении ХхХ, то факторпространство X/R отделимо.
Наиболее важным для нас является случай, когда X — топо-
топологическое векторное пространство, а отношение R определяется
некоторым векторным подпространством L в X, т. е.
# = {(*> У)' x — y^.L, j^gI, j/gX}. .
В этой ситуации множество U* открыто всегда, когда открыто
множество U и, следовательно, из C) вытекает открытость ото-
отображения я. Таким образом, справедливо и утверждение D),
т. е. множество я (Л) замкнуто тогда и только тогда, когда замк-
замкнуто множество A + L.
0.2.17. Компактные пространства. Покрытием множества X
называют систему 2 (или иногда семейство (Л^)) подмножеств
в X, объединение которых совпадает с X. Покрытие 2' назы-
называется подпокрытием покрытия S, если каждое из множеств
системы 2' принадлежит 2.
Покрытие 2 топологического пространства X называется от-
крытым, если каждое множество из 2 открыто в X.
Систему 2 (или семейство (Лг)) подмножеств множества X
называют центрированной, если каждая непустая конечная под-
подсистема в 2 (или конечное подсемейство в (Лг)) имеет непустое
пересечение.
!) То есть множество пар (х,у) ^R. — Прим. перев,
34 Гл. 0. П р еде артельные сведения
Пусть X — топологическое пространство. Следующие четыре
утверждения эквивалентны.
(a) Каждое открытое покрытие пространства X содержит ко-
конечное подпокрытие.
(b) Если система 2 -(или семейство (Аг)) замкнутых мно-
множеств пространства X центрирована, то пересечение всех мно-
множеств системы 2( или семейства (^г)) непусто.
(c) Каждая сеть точек из X имеет в X предельную точку.
(d) Каждая сеть точек из X содержит сходящуюся подсеть.
Эквивалентность предложений (а) и (Ь) получается посред-
посредством перехода к дополнениям и использования формул де Мор-
Моргана (п. 0.1.1). Эквивалентность утверждений (с) и (d) устана-
устанавливается ссылкой на утверждение (Ь) из п: 0.2.11. Остается до-
доказать равносильность утверждений (Ь) и (с). Пусть (хх) — сеть
точек из X. Рассмотрим замкнутые множества Fx = {xx: Х'^Х}.
Так как-индекс X пробегает направленное множество, то система
(Fx) центрирована, и, следовательно, если верно (Ь), то суще-
существует точка х, принадлежащая всем /*\. Легко проверяется, что
х — предельная точка сети (лг^). Таким образом, (Ь) влечет (с).
Обратно, допустим, что выполняется условие (с), и пусть (/\)—
центрированная система замкнутых множеств в X. Обозначим
через L множество индексов X, а через / множество всех конеч-
конечных подмножеств i в L. Множество /, упорядоченное по вклю-
включению, направлено. По условию каждому i^I соответствует
точка хи принадлежащая пересечении^-= f| Uv ^ s /}. Из (с)
вытекает, что сеть (х{) обладает предельной точкой xsl Так
как каждое множество Р{ замкнуто и Руа Pi при ir =j i, то точка
igP,- для каждого i и, следовательно, хе ГК^\- X^L). Таким
образом, (с) ==> (d), что и требовалось доказать. |
Топологическое пространство X называется компактным1),
если оно обладает одним (и, следовательно, каждым) из указан-
указанных выше свойств (а) — (d).
Бурбаки [2] называет компактными пространства, которые
не только удовлетворяют приведенному определению, но еще и
отделимы.
Приведем некоторые основные свойства компактных про-
пространств.
A) Пусть X — компактное пространство. Если сеть (х}) то-
чек из X имеет не более одной предельной точки, то она схо-
сходится.
Так как пространство X компактно, то сеть (х}) обладает
предельной точкой х, которая единственна по условию. Остается
1) В советской литературе употребляется также термин бикомпакт-
. — Поим, пеоев.
ный. — Прим. перев,
0.2. Предварительные сведения из общей топологии 35
показать, что сеть (хх) сходится к х. Допустим, что это не так.
Тогда существуют такое открытое множество U, содержащее х,
и такая подсеть (у^) сети (**,), чю каждая точка ^еДУ.
Так как пространство X компактно, то сама сеть (#ц) обладает
подсетью BV), сходящейся к некоторой точке г. Множество
X\U замкнуто, и, следовательно, z^X\U; в частности, гфх.
Кроме того, z должна быть предельной точкой сети [х%), ибо
(zv) — ее подсеть. Это противоречит условию единственности пре-
предельной точки сети (*х), откуда и вытекает справедливость
утверждения A). |
Множество А топологического пространства X называется
компактным, если является компактным пространством в ин-
индуцированной топологии (п. 0.2.7). Множество А называется
относительно компактным (в X), если его замыкание А ком-
компактно.
Будем говорить, что топологическое пространство сигма-ком-
сигма-компактно (о-компактно), если оно представимо в виде счетного
объединения компактных множеств.
Легко видеть, что замкнутое множество в компактном про-
пространстве компактно и компактное множество в отделимом про-
пространстве замкнуто.
Теорема Больцано — Вейерштрасса (из курса математиче-
математического анализа) утверждает, что в пространствах Rn или О ком-
компактны те и только те множества, которые замкнуты и ограни-
ограничены.
B) Если X — компактное, а У— топологическое простран-
пространство и отображение f: X-+Y непрерывно, то множество f(X)
компактно в У. Если, кроме того, отображение f взаимно одно-
однозначно, a Y — отделимое пространство, Tof — гомеоморфизм про-
пространства X на f(X).
Пусть (Vi) — открытое покрытие множества Y0 = f(X). Систе-
Система (f~l{Vi)) является тогда открытым покрытием пространства
X и, следовательно, содержит конечное подпокрытие, например
{/-1(^г): i^ ^}>, Где J — конечное множество индексов. Система
(Vi).s/ образует тогда открытое покрытие множества Yo; по-
поэтому Уо компактно. Допустим теперь, что отображение f взаим-
взаимно однозначно, а У — отделимое пространство. Образ каждого
замкнутого (и, следовательно, компактного) множества из X
компактен и потому замкнут в У; следовательно, он замкнут и
в Уо. Получаем таким образом, что отображение f~l: Y0->X не-
непрерывно, так что отображение f является гомеоморфизмом про-
пространства X на Y0 = f(X). Ш
Следствием предложения4 B) является следующее полезное
замечание,
36 Гл. 0. Предварительные сведения
C) Пусть % и %'—две такие топологии в множестве X, что
(X %') —компактное, а (X, £) —отделимое пространство. Если
г<г7, то г = г/.
Действительно, тождественное отображение / пространства
(X, V) на пространство (X, Z) непрерывно (так как топология
к слабее топологии 3/) и взаимно однозначно. В силу предло-
предложения B) из компактности пространства (X, %') и отделимости
пространства (X, Z) следует, что f есть гомеоморфизм простран-
пространства (X, Z') на (X, £), т. е. топологии J и У совпадают. |
D) Всякое отделимое компактное пространство X нормально.
Пусть А и В — непересекающиеся замкнутые множества про-
пространства X. Если а^.А и Ь^В, то существуют непересекающие-
непересекающиеся открытые окрестности точек а и 6, например Na и Л^. Так как
множество В компактно, то ко-нечное число множеств 7V& обра^
зует покрытие множества В. Обозначим это объединение через
Va\ тогда Va — такое открытое множество, содержащее В, что
VattNa = 0. Так как множество А компактно, то конечное число
множеств вида Naj например множества N пу,..., A/fl/j, образует
покрытие множества А. Объединение U=\J{Na.: 1<л< п} от-
открыто и содержит множество А\ пересечение V= П{^: 1 -^^
также открыто и содержит множество В, причем
0
E) Пусть X — регулярное топологическое пространство и
А — компактное множество в X. Всякая окрестность U множе-
множества А содержит некоторую его замкнутую окрестность V. Ка-
Каждое компактное регулярное пространство нормально.
Действительно, так как пространство X регулярно, то для
каждой точки а е А найдется такая ее открытая окрестность Wa,
замыкание которой Wa содержится в U. В силу компактности
множества А конечное число гаких окрестностей Wa образует
покрытие множества Л, поэтому в качестве V можно взять объ-
объединение замыканий выбранных окрестностей Wa. Таким обра-
образом, справедливость первого утверждения установлена. Дока-
Докажем второе утверждение. Пусть А и В — непересекающиеся
замкнутые множества компактного регулярного пространства X.
Множество Х\В является тогда окрестностью множества А и
пб доказанному содержит его замкнутую окрестность U. Так
как замкнутые множества U и В не пересекаются, то таким же
образом можно установить существование не пересекающей U
замкнутой окрестности V множества В. Множества А и В обла-
обладают, следовательно, непересекающимися окрестностями U и V
соответственно, т. е. пространство X нормально. I
F) Если X — вполне регулярное топологическое пространство,
А — компактное множество в X и U — некоторая окрестность
0.2. Предварительные сведения из общей топологии 37
множества Л, то существует такая непрерывная функция
/: Х-ЧО, 1], что f(A)={l} и f(X\U)={0).
Каждой точке а^А соответствует такая непрерывная функ-
функция ga' Х->[0, 1], что ga(a) = l и ga(X\U) ={0}. Множество
{х: ga{x)> у} открыто, поэтому функция haX-+[0, 1], определен-
определенная соотношением
ha(x)=inf{2ga(x), 1},
непрерывна, равна нулю на множестве X\U и единице на неко-
некоторой окрестности Na точки а. Так как множество А компактно,
то найдется конечное число точек аг^А, /=1,2,... ,/z, для ко-
которых соответствующие окрестности Nai образуют покрытие
множества А. Для завершения доказательства достаточно поло-
положить f = sup {/ц: 1 ^ i ^ п}. |
Приводимый ниже результат является, вероятно, самым су-
существенным в теории компактных пространств.
G) Теорема Тихонова. Топологическое произведение семей-
семейства компактных пространств есть компактное пространство.
Доказательство. Пусть (Хг)Ш1 — семейство компактных
пространств и X — его произведение. Достаточно показать, что
если S — центрированная система множеств в X, то пересечение
[){А: А е 2} непусто. Не нарушая общности, можно считать,
что 2 — максимальная центрированная система множеств, ибо,
пользуясь леммой Цорна (п. 0.1.5), любую центрированную си-
систему можно расширить до максимальной. Из условия макси-
максимальности системы 2 вытекают следующие два утверждения:
(a) система S замкнута относительно конечных пересечений;
(b) всякое множество в X, пересекающее каждое множество
системы 2, само принадлежит системе 2.
При каждом фиксированном i система я*B) подмножеств
пространства Xt центрирована. Компактность пространства Х\
влечет существование точки х\ е Хи являющейся точкой прикос-
прикосновения1) каждого из множеств системы я* B). Поэтому если
и{ — некоторая окрестность точки хг-, то пересечение Ui(\7ti(A)
непусто для любого множества А е 2. Другими словами, мно-
множество яг1 (Ui) пересекает каждое множество системы 2. В силу
утверждения (Ь) множество яг1 (Ui) принадлежит системе 2, а
из (а) следует, что это верно для любого конечного пересечения
таких множеств. Однако совокупность конечных пересечений
1) Точка х называется тонкой прикосновения множества Л, если
в любой ее окрестности содержится хотя бы одна точка множества Л, т. е,
если х принадлежит замыканию Л. — Прим. ред.
38 Гл. 0. Предварительные сведения
множеств вида яг1^) образует базу окрестностей точки х =
= (Х{) в топологии произведения в X.
Таким образом, каждая окрестность точки х принадлежит си-
системе 2 и потому пересекает каждое множество системы S, т. е.
х является точкой прикосновения любого множества си-
системы 2. |
Замечание. Приведенное доказательство принадлежит
Б у р б а к и [2, гл. I, § 10, теорема 3]. Мы лишь отказались от упо-
употребления термина «ультрафильтр».
(8) Иногда удается выразить условие компактности в терми-
терминах обычных последовательностей.
В гл. 8 мы уделим некоторое время этому вопросу при изуче-
изучении одного специального класса топологических векторных про-
пространств. Отметим пока некоторые простые общие результаты
такого рода.
Рассмотрим следующие три утверждения относительно неко-
некоторого топологического пространства X.
(a) Каждая последовательность точек из X имеет предель-
предельную точку.
(b) Каждая последовательность точек из X содержит сходя-
сходящуюся подпоследовательность.
(c) Пространство X компактно.
Совершенно очевидно, что (Ь) влечет (а) и что (Ь) и (а)
эквивалентны, если X удовлетворяет первой аксиоме счетности
(т. е. каждая точка пространства X обладает счетной базой
окрестностей). Из определения компактности следует, что
(с) =ф (а); поэтому если X удовлетворяет первой аксиоме счет-
счетности, то из (с) вытекают и (а) и (Ь). Наконец, если простран-
пространство X удовлетворяет второй аксиоме счетности (т. е. обладает
счетной базой открытых множеств), то все три условия эквива-
эквивалентны. Доказательство этого утверждения предоставляется чи-
читателю. Заметим только, что можно начать со следующего на-
наблюдения: если пространство* удовлетворяет второй аксиоме
счетности, то всякое его открытое покрытие содержит вписанное
в него счетное открытое покрытие (говорят, что покрытие (В?)
вписано в покрытие (Лг), или есть измельчение покрытия (Лг),
если каждое из множеств Bj является подмножеством некото-
некоторого множества Аг).
0.2.18. Локально компактные пространства. Топологическое
пространство X называется локально компактным, если каждая
его точка обладает хотя бы одной компактной окрестностью.
Таким образом, всякое компактное пространство локально ком-
компактно; всякое дискретное пространство локально компактно;
всякое замкнутое подпространство локально компактного про-
0.2. Предварительные сведения из общей топологии 39
странства локально компактно. Каждое из числовых пространств
R" и О локально компактно, но не компактно.
Приведем некоторые свойства локально компактных про-
пространств, которыми (в явном или неявном виде) мы восполь-
воспользуемся в гл. 4.
A) Если локально компактное пространство X отделимо или
регулярно, то замкнутые компактные окрестности всякой точки
из X образуют базу ее окрестностей. В частности,
(a) всякое отделимое локально компактное пространство
регулярно;
(b) всякое открытое подпространство локально компакт-
компактного регулярного пространства также локально ком-
компактно и регулярно.
Для доказательства рассмотрим произвольную точку xg!
В силу локальной компактности X найдется компактная окрест-
окрестность ~Uо точки х. Пусть U — произвольная окрестность точки х.
Если пространство X регулярно, то существует замкнутая окре-
окрестность точки х, содержащаяся в пересечении Uf]Uo. Эта окре-
окрестность будет компактной (как замкнутое подмножество в Uo).
Этим установлена справедливость нашего утверждения для слу-
случая, когда локально компактное пространство регулярно.
Допустим теперь, что локально компактное пространство X f
отделимо. Обозначим через V внутренность пересечения U() Uq.
Множество V является окрестностью точки х, а его замыкание
V — отделимым компактным пространством. Далее, {х} и ^ХУ —
замкнутые непересекающиеся подмножества пространства V.
В силу утверждения D) из п. 0.2.17 в пространстве V существует
содержащаяся в V замкнутая компактная окрестность W точ-
точки х. Множество W является окрестностью точки х в V, и так
как V открыто в X, то W — окрестность точки х в X. Наличие
включения W а V a U завершает доказательство. I
B) Пусть X — локально компактное регулярное простран-
пространство, А — замкнутое компактное множество в X и U —окрест-
—окрестность множества А. Существует такая замкнутая окрестность V
множества А, что Va U. Кроме того, сиществиет такая непре-
непрерывная функция f: Х->[0, 1], что f(A) ={0} и f(X\V) ={1}. В ча-
частности, всякое локально компактное регулярное пространство
вполне регулярно, а отделимое локально компактное простран-
пространство является тихоновским пространством (т. е. оно вполне
регулярно и является ТГпространством).
Действительно, каждой точке х^А соответствует ее замкну-
замкнутая компактная окрестность Wx, содержащаяся в U. Так как
множество А компактно, то конечное число множеств Wx покры-
покрывает А, и их объединение является замкнутой компактной окре-
окрестностью V множества А. Подпространство V регулярно и
40 Гл. 0. Предварительные сведения
компактно и, следовательно, нормально (см. утверждение E) из
п. 0.2.17). Поэтому существует такая непрерывная функция
g: V->[0, 1], что g(A)={0} и g(V\int V)={1]. Положим
, , f g(x) при xezV,
nx)-\ 1 при xz=X\V.
Функция f непрерывна и удовлетворяет всем условиям нашего
предложения. I
Для локально компактных пространств имеет место теорема,
аналогичная теореме Тихонова @.2.12G)).
C) Пусть (Х{) — семейство локально компактных про-
пространств. Произведение X = YlX{ локально компактно тогда и
только тогда, когда все сомножители, кроме конечного числа, —
компактные пространства.
Доказательство этого предложения можно найти в книгах
Келли [1, стр. 199] и Б у р б а к и [2, гл. I, стр. 118].
D) Процессы компактификации. Имеется ряд конструкций,
цель которых — вложить данное пространство X в некоторое ком-
компактное пространство. Из таких конструкций нам понадобится
лишь самая простая и грубая.
Пусть задано топологическое пространство X. Рассмотрим
множество X*, получающееся добавлением к множеству X еще
одной точки, обозначаемой символом оо. Наделим X* топологией,
открытыми множествами которой являются все открытые множе-
множества из X, а также все множества вида Х*\К, где К — любое
замкнутое компактное множество из X. Полученное таким обра-
образом пространство X* называется (одноточечной) компатифика-
цией Александрова пространства X.
Компактность пространства X* почти очевидна. Действитель-
Действительно, если (Ui) — открытое покрытие пространства X*, то некоторое
Ui0 содержит точку оо. Множество X* \ £//0 компактно в Х\ по-
поэтому оно покрывается конечным числом множеств U{ и, следо-
следовательно, этим же свойством обладает и X*.
Ясно также, что топология, индуцированная в X, совпадает с
исходной топологией в X (т. е. X топологически вложено в X*)
и что X — открытое подпространство в X*.
Пространство X* отделимо тогда и только тогда, когда про-
пространство X отделимо и локально компактно.
Более подробно эти вопросы рассматриваются в книгах Кел-
Келли [1, стр. 202] и Бур баки [2, гл. I, стр. 119].
0.2.19. Для удобства перечислим необходимые нам в даль-
дальнейшем свойства локально компактных пространств, лежа-
лежащие в основе построения теории интегрирования, приведенной
в гл. 4,
0.2. Предварительные сведения из общей топологии 41
A) Всякое отделимое локально компактное пространство ре-
регулярно. Напомним также (п. 0.2.8), что регулярное Тгпростран-
ство отделимо.
B) Всякое регулярное локально компактное пространство
вполне регулярно.
Оба эти утверждения обсуждались в предыдущем пункте.
Легко проверить, что в регулярном локально компактном
пространстве совокупность всех компактных множеств содержит
базу окрестностей каждой точки. Поэтому из утверждения B)
и леммы п. 0.2.10 вытекает следующее утверждение.
C) Пусть X— регулярное локально компактное простран-
пространство. Каждая полунепрерывная снизу полооюительная числовая
функция f на X является верхней огибающей множества всех не
превосходящих f положительных непрерывных на X функций с
компактным носителем.
0.2.20. Паракомпактные пространства. В п. 0.2.17 компакт-
компактность была охарактеризована в терминах открытых покрытий.
В гл. 5 нам придется воспользоваться еще одним свойством то-
топологических пространств, связанным с поведением открытых
покрытий.
Покрытие (Ai) топологического пространства X называется
локально конечным, если каждая точка х е X обладает окрест-
окрестностью £7, пересекающейся лишь с конечным числом множеств
Ai (это число, вообще говоря, зависит от х и от U).
Топологическое пространство X называется паракомпактным,
если оно регулярно и в каждое его открытое покрытие можно
вписать локально конечное открытое покрытие.
Паракомпактные пространства можно разными способами
охарактеризовать в терминах покрытий. Эти способы описаны
у Келли [1, стр. 212]!), где получены также следующие два
результата.
A) Каждое паракомпактное пространство нормально.
B) Каждое полуметризуемое (п. 0.2.21) пространство пара-
компактно.
Нам важно будет установить еще одно свойство некоторых
открытых покрытий нормального пространства. Условимся на-
называть покрытие (А{) топологического пространства X точечно
конечным, если каждая точка xgJ принадлежит не более чем
конечному (зависящему от х) числу множеств Лг-.
C) Пусть X — нормальное топологическое пространство и
(U^i^j — его открытое точечно конечное покрытие. Существует
такое открытое покрытие (Уг-)?-е1 пространства X, что для каж-
каждого i е / имеет место включение V\ с V\.
х) См. также Бур баки [2, гл. I, § 10, п. 12].— Прим. перев.
42 Гл. 0. Предварительные сведения
При выполнении сформулированного отношения между по-
покрытиями (и{) и (Vi) иногда говорят, что покрытие (Vi) под-
подчинено покрытию (Ui). Это свойство покрытия (Vi), очевидно,
сильнее свойства «быть вписанным».
Рассмотрим сначала случай, когда покрытие {Ui} конечно.
Пусть / = {1, 2, ..., п}. Замкнутые множества F = X\U\ и F' =
= X\\J{Ui: \<iKn} не пересекаются; поэтому они обладают
непересекающимися открытыми окрестностями U и V\ соответ-
соответственно. Так как V\czX\U, то V\ czX\ U. Из того факта, что
X\(J{^' Kt^MjczVi, вытекает, что семейство {1Л, U2, ...
..., Un} образует открытое покрытие. Достаточно теперь повто-
повторить все рассуждение п— 1 раз.
Переходя к общему случаю, обозначим через 2 множество
всех функций щ определенных на / и удовлетворяющих следую-
следующим условиям: u(i) есть_либо множество Uu либо такое откры-
открытое множество Vu что ViCzUh и семейство (u(i))iGI образует
покрытие пространства X. В множестве 2 введем отношение по-
порядка -*С, полагая и^и' тогда и только тогда, когда u'(i)=u(i)
для всех тех индексов ie/, для которых u(i) ес^ь некоторое
Vi=hUi. Покажем сначала, что множество 2 индуктивно упоря-
доченно.
Пусть 5/ — линейно упорядоченное подмножество в 2. Опре-
Определим отображение а" равенством
Ввиду точечной конечности семейства (Ui) функция w"e2.
Кроме того, и" — верхняя грань множества 2' в 2.
В силу леммы Цорна @.1.5) множество 2 обладает макси-
максимальным элементом и*. Убедимся, что для каждого i значение
u*(i) есть некоторое Vi=U{; тем самым справедливость утвер-
утверждения C) будет установлена.
Допустим противное, т. е. что для некоторого / е / имеет
место равенство u*(j) = Uj, и рассмотрим множество
Гак как по доказанному утверждение справедливо для конечного
покрытия, то существует такое открытое множество Vj, что Fez
cz Vj и Vjd Uj. Если теперь определить функцию неравенст-
неравенствами u**(i)=u*(i) при гФ\ и u**(j) = Vj, то ^*<^** и и*фи**,
что противоречит максимальности элемента а*. Щ
Идея этого доказательства принадлежит Келли [1, стр. 230,
задача Ц].
Комбинируя A) и C), получаем следующее утверждение.
D) Пусть (Ui)—открытое покрытие паракомпактного про-
пространства X. Существует локально конечное открытое покрытие
0.2. Предварительные сведения из общей топологии А'б
(Vj) пространства X, обладающее свойством: каждому индексу
j соответствует такой индекс I, что Vj cz Ц^
Действительно, из паракомпактности пространства X выте-
вытекает существование локально конечного открытого покрытия
(£//), вписанного в покрытие (Ui). В силу C) существует такое
открытое покрытие (Vj), что включение VjCzUj справедливо
для любого /. Покрытие (Vj) локально конечно, и каждому /
соответствует такой индекс t, что V\ a U) a Ui (так как локрытие
([//) вписано в покрытие (£/,)). I
Рассмотренные свойства покрытий связаны с существованием
на X определенного вида семейств непрерывных функций. Се-
Семейство (fi) непрерывных числовых функций на топологическом
пространстве X называется (непрерывным) разбиением единицы,
если O^Cfi-Kl и 2/i=li причем это семейство локально ко*
нечно в том смысле, что каждой точке хе! соответствует такая
ее окрестность U, что fi(U) =0 для всех индексов t, за исключе-
исключением, быть может, конечного числа.
Из утверждений A_), D) и леммы Урысона 0.2.12 следует, что
таких разбиений единицы существует мною.
E) Всякому открытому покрытию (Ui) паракомпактного про-
пространства X соответствует такое разбиение единицы (fj), что для
каждого индекса j носитель функции fj содеронится в некотором
множестве U{.
Действительно, выберем т;акое открытое локально конечное
покрытие (Vj), что каждое Vj содержится в некотором множе-
множестве U^ Из C) вытекает существование локально конечного от-
открытого покрытия (Wj), подчиненного покрытию (Vj); поэтому
для каждого / имеет место включение WjCi Vj. Замкнутые мно-
множества Wj и X\Vj не пересекаются при любом /; следовательно,
в силу леммы Урысона существует такая непрерывная функция
gj' Х-+[0, 1], что gj(Wj)={\} и gj(X\Vj)={0}. Семейство (gj)
локально конечно, так что сумма 2 gj непрерывна, причем ясно,
что всюду 2 gj^ 1. Для завершения доказательства достаточно
положить
//-<?/B в/Г1.!
Для приложений, которые этот результат имеет в гл. 5,
важно заметить следующее: если X=Rn (или если X — открытое
подпространство в Rn, или вообще паракомпактное веществен-
вещественное дифференцируемое многообразие), то можно так опреде-
определить функции /j, чтобы они были бесконечно дифференцируе-
дифференцируемыми и обладали 'компактными носителями. В таком виде
44 Гл. 0. Предварительные сведения
утверждение E) может быть получено из первоначального с по-
помощью простого процесса регуляризации, описанного в гл. 5.
0.2.21. Полуметрики, метрики и ассоциированные топологии.
Полуметрикой на множестве X называется вещественная функ-
функция d, определенная на произведении ХхХ и удовлетворяющая
следующим условиям:
A) d(x9y)=d(y,x)>0;
B) d (ху z) К d (х, у) + d (у, z) (неравенство треугольника);
C) d(*,*)=0.
(х, у, z — произвольные точки множества X.)
Если, кроме того,
D) d(x,y)=0 влечет х = у, то d называется метрикой на X.
Некоторые авторы (например, Келли [1, стр. 161—162]) упо-
употребляют термин «псевдометрика» вместо «полуметрика».
Полуметрическим (метрическим) пространством называется
пара (X, d)y состоящая из множества X и полуметрики (метри-
(метрики) d на X.
Обычно об X говорят как о полуметрическом (метрическом)
пространстве, подразумевая при этом, что на X задана некото-
некоторая полуметрика (метрика) d.
Пусть (X, d)—полуметрическое пространство, х^Х и г—>
вещественное положительное число. Множество
B(x,r)={y\ j/gI и d(x,y)<r}
называют открытым шаром с центром х и радиусом г, а мно-
множество
B(x9r)={y: y^Xnd(x.y) <r}
— замкнутым шаром с центром вхи радиусом г. В дальнейшем
читатель убедится, что прилагательные «открытый» и «замкну-
«замкнутый» употребляются в этих определениях не случайно.
Если (X, d)—полуметрическое пространство, то из свойств
A) — C) следует, что множество пар (х, В(х, г)), где igI и
г>0, удовлетворяет требованиям (a'), (b'), (d') п. 0.2.2. Поэтому
существует единственная топология %а в X, в которой открытые
шары В(х> г) образуют базу окрестностей каждой точки xg!
Так как, кроме того, В(х, r)czB(x, r)cz.B(x, г') при гг>/*>0,
то замкнутые шары с центром в точке х и положительными ра-
радиусами также образуют базу окрестностей точки х.
Легко проверяется, что каждый открытый (замкнутый) шар
является открытым (замкнутым) множеством в топологии Zd,
что оправдывает их названия.
Из сказаннного выше, в частности, следует, что топология
%d регулярна. В качестве упражнения предлагаем читателю по-
показать, что топология %а ' на самом деле вполне регулярна.
0 3. Равномерные пространства 45
С другой стороны, топология Zd удовлетворяет аксиоме отде-
отделимости Го (п. 0.2.8) тогда и только тогда, когда d — метрика.
В этом случае топология %d является даже отделимой.
Пользуясь общими методами, описанными в п. 0.2.15, тополо-
топологию %>d можно определить как слабейшую топологию в X, при
которой непрерывны все функции dx: y*—>d(x,y)(dx: X->/?), ко-
когда х пробегает X.
Топологическое пространство (X, Z) называется полуметры-
зуемым (метризуемым), если существует такая полуметрика
(метрика) d на X, что Zd = %. Описанию таких пространств по-
посвящено довольно много работ (см., например, Келли [1,
стр. 169—177]), однако нас больше интересует несколько иная
задача, в которой вместо топологических рассматриваются так
называемые равномерные пространства (п. 0.3.5 и 0.3.6).
0.3. Равномерные пространства
0.3.1. Равномерная структура в множестве. Пусть ^ — мно-
множество и А = А(Х)—диагональ произведения ХхХ (п. 0.1.2).
Равномерной структурой в X называют систему Ж подмножеств
произведения ХхХ, удовлетворяющую следующим условиям:
(a) каждое множество U е Ж содержит диагональ А;
(b) если U е=Ж, то и~1^Ж;
(c) если U е Ж, то существует такое множество Uf e Ж,
что U'oU'aU;
(d) пересечение двух множеств из Ж также принадлежит Ж;
(e) всякое подмножество произведения XXX, содержа-
содержащее множество из Ж, само принадлежит Ж.
Множества системы 3? называются окружениями (диагонали
А) в равномерной структуре Ж. Подсистема & системы Ж на-
называется базой равномерной структуры Ж, если каждое множе-
множество произведения ^Х^,- содержащее элемент из 3&> принадле-
принадлежит Ж. База 35 равномерной структуры Ж обладает следую-
следующими свойствами:
(а') каждое множество В е Я? содержит диагональ А;
(Ь') если Ssf, то В содержит элемент из ЗВ\
(с') если В е ЗВ> то существует такой элемент Br e J*,
что В'оВ'аВ;
(d') пересечение двух элементов из 3& содержит элемент
из 35.
Обратно, пусть задана система J? подмножеств произведе-
произведения ^Х^, удовлетворяющая условиям (а7) — (d7).
Система всех тех подмножеств произведения ^Х^, которые
содержат хотя бы одно из множеств системы 35% есть равномер-
равномерная структура X, базой которой служит ^.
45 Гл. 0. Предварительные сведения
Пара (X, Ж), состоящая из множества X и равномерной
структуры I в1, называется равномерным пространством. Ко-
Когда это не вызывает недоразумений, говорят о «равномерном
пространстве X»; сравните с аналогичной вольностью, когда речь
идег о топологическом пространстве (п. 0.2.1).
Как и в случае топологий (п. 0.2.6), некоторые пары равно-
равномерных структур в множестве X можно сравнивать. Пусть Ж
и Ж' —равномерные структуры в множестве X. Будем говорить,
что Ж слабее Ж', или, что то же, что Ж' сильнее Ж/если Ж с: Ж'
(Ж и Ж' рассматриваются как подмножества множества всех
подмножеств произведения X X X). Существуют слабейшая
равномерная структура в Ху А именно структура, состоящая из
единственного окружения {X X X}, и сильнейшая равномерная
структура, а именно {U: A cz U а X X X}.
Исторически впервые изучалась равномерная структура,
возникающая при задании полуметрики d на X (п. 0.2.21).
База этой равномерной структуры состоит из множеств
Br = {(xyx') GlXX: d(xyx') < r},
где г — пробегает множество всех (строго) положительных чи-
чисел (или некоторое множество (строго) положительных чисел,
содержащее сколь угодно малые числа). Этот случай мы ис-
исследуем ниже более подробно (п. 0.3.5—0.3.7).
0.3.2. Топология^ определяемая равномерной структурой.
Пусть задано равномерное пространство (X, Ж). В множествеX
можно определить топологию 2, сопоставляя каждой точке
xg! базу . окрестностей, состоящую из множеств вида
U(x)={y: У^Х> (х,У)^У}> гДе U пробегает Ж. Обозначение
U(x) согласуется с принятым в п. 0.1.2, где для любого U cz
czXxX и любого АаХ через U(A) обозначалось множество
{у: //gX, (x, y)^ U хотя бы для одного х е Л}.
В то же время X X X можно снабдить топологией произве-
произведения (п. 0.2.15). При этом важно связать эту топологию с за-
заданной равномерной структурой в X. Если не оговорено про-
противное, мы будем считать, что X и произведение X X X
наделены указанными топологиями.
A) Если t/e Ж, то и внутренность множества U принад-
принадлежит Ж. Таким образом, открытые симметричные окружения
образуют базу равномерной структуры Ж.
B) Замыкание множества A cz X совпадает с множеством
f]{U(A): C/e$). Замыкание подмножества S произведения
ХхХ совпадает с множеством f\{U oS oJJ: f/eX}. Следова-
Следовательно, симметричные замкнутые окружения образуют базу.
0.3. Равномерные пространства 47
C) Из последнего предложения следует регулярность то-
топологии X. Топология £ отделима тогда и только тогда, когда
f]{U: (/еЗЕ} = Д. В этом случае равномерная структура и со-
соответствующее равномерное пространство называются отде-
отделимыми.
Каждому неотделимому равномерному пространству (X, X)
можно естественным образом поставить в соответствие ассо-
ассоциированное отделимое равномерное пространство. Множество
определяет отношение эквивалентности в множестве X. Рас-
Рассмотрим фактормножество X = X/R. Каждому окружению (/gI
сопоставим множество
0 = {{х, у): 3xei, yey, такие, что (*, y)'^U}1).
Множества U образуют базу некоторой равномерной струк-
структуры Ж в множестве X, причем равномерное пространство
(X, Ж) отделимо. Полученное таким образом отделимое равно-
равномерное пространство (X, X) называется ассоциированным с
пространством (X, X).
0.3.3. Равномерная непрерывность. Пусть (X, Ж) и (У, $) —
равномерные пространства и / — отображение пространства X
в У. Отображение / называется равномерно непрерывным, если
для каждого окружения Уе sJ) множество
{(x,x')zeXxX: (/(*),/(*')) e=V}
принадлежит Ж. Если при этом X и У наделить соответствую-
соответствующими топологиями, то отображение / становится непрерывным.
Обратное утверждение, вообще говоря, неверно.
Легко проверить, что композиция равномерно непрерывных
отображений также равномерно непрерывна.
0.3.4. Равномерная структура, определенная семейством
функций. Пусть задано множество X и семейство ((У* $ j))jE/
равномерных пространств. Существует такая слабейшая рав-
равномерная структура Ж в X, что при каждом i отображение ft
пространства (X, Ж) в (У*, $г-) равномерно непрерывно. Дей-
Действительно, конечные пересечения множеств вида
{(х, /)е!Х X: (U (х), U (*')) <= Vih
где Vi e fyi, образуют базу указанной равномерной структуры.
В качестве частных случаев этого общего метода можно
1) 3 — логический символ, который читается «существует» или «суще-
«существуют». — Прим. перев.
48 Гл. 0. Предварительные сведения
ввести индуцированную равномерную структуру в подмноже-
подмножестве X данного равномерного пространства У, а также произ-
произведение равномерных структур в множестве П^ь где ^ — рав-
равномерные пространства. Читатель может сравнить сказанное
с аналогичной ситуацией для топологических пространств
(п. 0.2.7 и 0.2.15). Топология, соответствующая произведению
равномерных структур, совпадает с произведением соответст-
соответствующих топологий. Топология, соответствующая индуцирован-
индуцированной равномерной структуре, совпадает с индуцированной то-
топологией.
0.3.5. Равномерные структуры и полуметрики. Пусть
(X, Ж) — равномерное пространство. Полуметрика d на мно-
множестве X (п. 0.2.21) равномерно непрерывна относительно про-
произведения равномерных структур в X X X тогда и только тогда,
когда для каждого е > 0 множество
£Л*,в = {(*, Х')€=ХХХ: d{xy х')<г)
принадлежит Ж.
С другой стороны, если заданы множество X и полумет-
полуметрика d на нем, то естественно рассмотреть равномерную струк-
структуру Жф база окружений которой состоит из указанных выше
множеств Ud, s- Это слабейшая равномерная структура в X,
при которой полуметрика d равномерно непрерывна относи-
относительно произведения равномерных структур в ХхХ. Отметим,
что равномерная структура Жа отделима тогда и только тогда,
когда d есть метрика. Равномерные структуры типа Заявляются
прототипами равномерных структур вообще.
Возникает естественный вопрос: каким условиям должно
удовлетворять равномерное пространство (X, Ж), чтобы $ = Э^
для некоторой полуметрики? В этом случае равномерное про-
пространство (X, Ж), или равномерная структура Ж, называется
полуметризуемой (или метризуемой, если d — метрика).
0.3.6. Полуметризационная лемма. Можно показать (Келли
[1, стр. 248], Бур баки [3, гл. IX, п° 4, стр. 7, предл. 2]), что
равномерное пространство полуметризуемо тогда и только
тогда, когда оно обладает счетной базой окружений.
Для нас наиболее важным является случай топологиче-
топологического векторного пространства. Доказательство сформулиро-
сформулированного утверждения для этого случая (похожее на доказа-
доказательство в общем случае) приводится в начале гл. 6.
0.3.7. Рассмотрим более общую ситуацию. Пусть на мно-
множестве X задано семейство полуметрик (di)mi. Множества
Udltel образуют базу равномерной структуры I в I Она яв-
является слабейшей из равномерных структур, для которых тож-
0.3. Равномерные пространства 49
дественное отображение пространства (X, Ж) в пространство
(X, Жа.) при каждом / равномерно непрерывно.
0.3.8. Можно показать, что всякую равномерную структуру,
заданную в множестве X, можно получить так, как это сделано
в п. 0.3.7. При этом (di) является семейством всех полуметрик,
которые равномерно непрерывны относительно произведения
равномерных структур в X X X. Отсюда следует, что всякое
равномерное пространство, рассматриваемое как топологиче-
топологическое, вполне регулярно.
0.3.9. Из сказанного в п. 0.3.8 в качестве следствия можно
получить следующий результат А. Вейля: всякое равномерное
пространство изоморфно (как равномерное пространство) под-
подпространству произведения полуметризуемых пространств (или
метризуемых пространств в случае, когда заданное равномер-
равномерное пространство отделимо).
Доказательство этого утверждения можно найти у Келли
[1, стр. 251] или у Б у р б а к и [3, гл. IX].
0.3.10. Топологические пространства, допускающие равно-
равномерную структуру. Из предыдущих результатов вытекает сле-
следующее утверждение.
Пусть (Ху £) — топологическое пространство. Для суще-
существования такой равномерной структуры Ж в Ху что соответ-
соответствующая ей топология совпадает с £, необходимо и доста-
достаточно, чтобы пространство (X, 2) было вполне регулярным.
В этом случае говорят, что топология 2 и топологическое про-
пространство (X, 2) допускают равномерную структуру, или рав-
номеризуемы. Из утверждения B) п. 0.2.19 вытекает, что ло-
локально компактные регулярные пространства равномеризуемы.
Если пространство (X, £) компактно, то равномерная
структура в X определяется однозначно. В этом случае всякое
непрерывное отображение пространства (X, Z) в равномерное
пространство равномерно непрерывно; любая полуметрика, не-
непрерывная на произведении X X X, равномерно непрерывна, и
каждое открытое множество произведения X X X, содержащее
диагональ А, принадлежит Ж.
Доказательство этих утверждений можно найти у Келли
[1, стр. 263—264] и Бур баки [2, гл. II, стр. 177—181].
0.3.11. Сети Коши и полнота. Так как равномерная струк-
структура дает возможность «нумеровать» окрестности различных
точек одним и тем же множеством индексов для всех точек,
то возникает возможность определения «малости» множеств
независимо от их положения. Пусть (X, X) — равномерное про-
пространство и (/gX. Говорят, что множество Аа X мало поряд-
порядка U (или, короче, и-мало)> если AxAczU. (Для уяснения
50 Гл. 0. Предварительные сведения
этого определения полезно рассмотреть случай, когда равномер-
равномерная структура Ж задается метрикой.)
Пользуясь понятием малости порядка С/, легко дать опре-
определение сети Коши (или, как иногда говорят, фундаментальной
сети). Сеть (xx)^L называется сетью Коши, если для каждого
окружения [/е$ существует такой индекс Xo=Xq(U), что
(хъ хх) е U для всех индексов Я и %\ следующих за V Дру-
Другими словами, «хвост» {х%\ Я>Яо} мал порядка U, если 10 до-
достаточно велико.
Пусть равномерная структура определена полуметрикой d.
Для того чтобы сеть (х%) была сетью Коши, необходимо и
достаточно, чтобы й{хъ ху) —>0, когда К и А/ возрастают не-
зависимо друг от друга.
Аналогичное предложение имеет место и в общем случае,
но при условии, что указанное соотношение выполняется для
всех равномерно непрерывных полуметрик.
Если в соответствующей топологии lim^ = x, то (хх) есть
Л.
сеть Коши. Всякая сеть Коши (хх) сходится к каждой своей
предельной точке (если такие существуют). Не всякая сеть
Коши сходится. (Достаточно рассмотреть незамкнутое под-
подпространство отделимого равномерного пространства.)
Равномерное пространстве (X, Ж) называется полным, если
в нем каждая сеть Коши сходится.
Замкнутое подпространство полного пространства полно.
Всякое полное подпространство отделимого равномерного про-
пространства замкнуто. Произведение равномерных пространств
будет полным тогда и только тогда, когда каждый сомножи-
сомножитель этого произведения является полным пространством. Для
того чтобы сеть в произведении пространств была сетью Коши,
необходимо и достаточно, чтобы ее проекция на каждый со-
сомножитель была сетью Коши.
Полуметризуемое равномерное пространство полно тогда и
только тогда, когда каждая его последовательность Коши схо-
сходится к некоторой точке этого пространства.
Равномерное пространство, удовлетворяющее этому усло-
условию, называется секвенциально полным. Существуют неполные
равномерные гТространства, которые все же являются секвен-
секвенциально полными.
Если (хк) — сеть Коши в X и отображение f: (X, $)-*(Х, *?))
равномерно непрерывно, то (f(#0) —сеть Коши в У.
0.3.12. Пополнение равномерного пространства. Процедура
вложения метрического пространства в качестве плотного под-
подпространства в полное метрическое пространство была исполь-
использована Кантором для построения вещественных чисел из ра-
0.3. Равномерные пространства 51
циональных. Эта конструкция, теперь общеизвестная, триви-
тривиально переносится на полуметрические пространства (см., на-
например, Келли [1, стр. 261]).
В некоторых случаях нам понадобится аналогичное по-
строение, но уже в применении к произвольному равномерному
пространству. Здесь можно было бы ограничиться ссылкой на
метод Кантора для полуметрических пространств и на резуль-
результат, сформулированный в п. 0.3.9. Однако мы проведем ука-
указанное построение, не опираясь на метод Кантора.
Пусть (X, Ж)—равномерное пространство. Пополнением
пространства (X, Ж) называется пара [(Х,Ж),[\, состоящая из
полного равномерного пространства (X, Ж) и равномерного изо-
изоморфизма f пространства X на некоторое подпространство,
плотное в X.
При построении пополнения мы следуем Бурбаки [2,
стр. 172—175], но вместо фильтров пользуемся сетями. Рассмот-
Рассмотрим множество X, состоящее из всех сетей Коши в простран-
пространстве X. Пусть U — симметричное окружение из Ж. Обозначим
через U множество пар ((**,), (#ц)), где (хх), (у^) —сети Коши
в X, обладающие следующим свойством: существуют такие Яо
и juio, что (хъ у у) е U для всех % > к0 и \i > \i0. Когда U про-
пробегает X, множества U пробегают базу окружений некоторой
равномерной структуры I в I. Легко проверить, что получен-
полученное равномерное пространство (X, Ж) полно. Обозначим че-
через f отображение, ставящее в соответствие каждому элементу
хе! одноэлементную сеть х=(х). Очевидно, f есть равномер-
равномерный изоморфизм пространства X на подпространство Х\ плот-
плотное в Х\ следовательно, [(X ,Ж, f] есть пополнение пространства
(Х,Ж). Равномерное пространство (X ,Х), вообще говоря, мо-
может не быть отделимым.
Если пространство (X, Ж) отделимо, то естественно попы-
попытаться построить отделимое его пополнение. Это можно сде-
сделать, заменяя пространство (X Л) ассоциированным с ним
отделимым пространством (Z, Ж) (п. 0.3.2). Оказывается, что
композиция gof отображения f с естественным отображением g
пространства X на X является равномерным изоморфизмом про-
пространства X на плотное в X подпространство Х\ Пара
[(Z, Ж), gof] является отделимым пополнением пространства
(Ху Ж). Более того, можно показать (Бурбаки [2, стр. 172]),
что отделимое пополнение определено однозначно с точностью
До равномерного изоморфизма; поэтому естественно говорить
просто об (отделимом) пополнении,
52 Гл. 0. Предварительные сведения
Следует заметить, что если пространство (X, Ж) не яв-
является отделимым, a Y—ассоциированное с ним отделимое
пространство, то Y равномерно изоморфно пространству X (от-
(отделимому пространству, ассоциированному с пространством X).
Другими словами, переход к ассоциированному отделимому
пространству может быть выполнен либо до, либо после опе-
операции ~ (см. Бур баки [2, стр. 177, упр. 5]).
Если равномерная структура Ж задана семейством полу-
полуметрик (di) (п. 0.3.7 и 0.3.8), то пополнение допускает не-
несколько более конкретное описание. Начнем с легко проверяе-
проверяемого замечания. Если (хк) и (у^) являются сетями Коши в X,
то сеть {di(x^y[x)) (где множеством индексов служит множе-
множество пар {k,\i)) есть сеть Коши; следовательно, существует
конечный предел
dt ((xk) (yj) = Hm dt (хх, yj.
Определенная таким образом функция Si является полу-
полуметрикой на X. Кроме того, равномерная структура Ж совпа-
совпадает с равномерной структурой, определенной семейством по-
полуметрик (di). Заметим, что di((x), (у)) =di(x, у) при
х,у^Х.
Легко проверить, что для каждого элемента xg! база
окрестностей точки х в X состоит из замыканий в X образов
окрестностей точки х^Х при отображении f (f: x^->x\ как
и выше).
Отделимое пространство X получается при отождествлении
тех сетей (х\) и (уц), для которых при каждом i выполнено
соотношение
(такие сети Коши (х^) и (у^) называются эквивалентными).
Пусть х и у — два класса эквивалентных сетей Коши (т. е. две
точки из X). Положим
где (л:^) и (у^)—произвольные сети из классов i и | соот-
соответственно. Семейство полуметрик (dt) определяет на X рав-
равномерную структуру Ж. Если X — отделимое пространство, то х.
и у эквивалентны (т. е. принадлежат одному и тому же классу.
эквивалентности из X) тогда и только тогда, когда для всех i
выполнено равенство di(x9 у) =0, т. е. х = у.
0.3.13. Предкомпактность. Равномерное пространство (X, Ж
называется предкомпактным, или вполне ограниченным, если
0.3. Равномерные пространства 53
для всякого окружения С/е$ существует конечное покрытие X
множествами, малыми порядка U. Другими словами, для каж-
каждого окружения U е Ж должно найтись такое конечное множе-
множество FczX, что X=U(F). Ясно, что подпространство предком-
пактиого пространства также предкомпактно. Если пространство
(X, Ж) не является предкомпактным, то можно построить после-
последовательность (хп)9 обладающую пр-и некотором U ^Ж тем
свойством, что Хпфи(хр) при р < п. Поэтому эта последова-
последовательность не обладает подсетью Коши.
0.3.14. Теорема. Равномерное пространство (X, Ж) предком-
пактно тогда и только тогда, когда каждая сеть в X обладает
подсетью Коши. Поэтому, для того чтобы (X, Ж) было пред-
компактным, достаточно, чтобы некоторое пополнение простран-
пространства (X, Ж) было компактным, и необходимо, чтобы каждое
пополнение пространства (X, Ж) было компактным.
0.3.15. Категории и теорема Бэра. Пусть X — топологическое
пространство и А — множество в ~Х. Множество А называется:
A) нигде не плотным в X, если внутренность его замыкания
пуста;
B) тощим множеством, или множеством первой категории
в X, если оно является объединением счетного семейства мно-
множеств, нигде не плотных в Х\
C) нетощим множеством, или множеством второй катего-
категории в X, если оно не является множеством первой категории
в X.
Мы увидим (см. также гл. 3 книги Келли и Намиока
[1]), что понятие категории широко используется в функцио-^
нальном анализе. Значение этого понятия во многом объяс-
объясняется следующей теоремой.
0.3.16. Теорема (Бэр). Пусть X — либо регулярное локально
компактное пространство, либо полуметризуемое полное равно-
равномерное пространство. Тогда дополнение ко всякому тощему
множеству в X всюду плотно (или, что то же, пересечение
счетного семейства всюду плотных открытых множеств также
плотно). В частности, X нетоще (в себе).
Доказательство можно найти в книге Келли [1, стр. 267].
Важную роль в функциональном анализе играет так на-
называемый принцип ограниченности (гл. 7), который опирается
на следующий результат.
0.3.17. Теорема. Пусть X — нетощее пространство, тогда по-
полунепрерывная снизу функция f на X, принимающая лишь ко-
конечные значения, ограничена сверху на некотором непустом
открытом подмножестве в X,
Доказательство. Множества Fn = {x: х^Х и f(x)^n]
замкнуты и образуют покрытие пространства X. Следователь-
54 Гл. 0. Предварительные сведения,
но, существует такой номер /г, что множество Fn имеет непу-
непустую внутренность, что и требовалось доказать. |
0.3.18. Полученный выше результат часто применяется к
случаю, когда всюду конечная функция f является верхней оги-
огибающей некоторого семейства (fi)i^i полунепрерывных снизу
на X функций. При этом делается вывод о существовании не-
непустого открытого множества AczX и такого числа с (< + оо),
чю
sup {/*(*): i^I и хе/1}<с.
0.3.19. Топологические группы. В гл. 4 и 10 мы будем иметь
дело с топологическими группами. Поэтому нам представляется
удобным перечислить здесь некоторые их элементарные топо-
топологические свойства.
Топологической группой называется множество X, наде-
наделенное:
A) структурой группы;
B) такой топологией, при которой групповые операции не-
непрерывны, т. е. отображение (ху у) н->х~1у произведения X X X
в X непрерывно.
Отсюда следует, что при фиксированном ае! отображе-
отображения х ь-> ах и х н-> crlx (а также отображения х н-> ха и х ь->
I—>хсгх) являются взаимно обратными гомеоморфизмами X на
себя. Кроме того, если V пробегает базу окрестностей точки е
(где е — единичный элемент группы X), то множества xU, а так-
также множества Ux пробегают базу окрестностей точки х.
Если каждой окрестности U точки е поставить в соответствие
подмножество
UL={(x,y): x-*ye=U)
произведения X X X, то всевозможные такие множества UL
образуют базу окружений некоторой равномерной структуры
в X. Из очевидного равенства UL[x] = xU следует, что тополо-
топология, определяемая этой структурой, совпадает с исходной то
пологией в X. Таким образом, пространство X равномеризуемо
и потому вполне регулярно (п. 0.3.8). Отсюда вытекает, что X
есть Ггпространство тогда и только тогда, когда оно отделимо.
Нужно заметить, что только что определенная равномерная
структура называется левой равномерной структурой в X. За-
Заменяя множества UL множествами
мы получим так называемую правую равномерную структуру
в X. Здесь UR[x]=Ux9 поэтому, как и ранее, полученная топо-
топология в X совпадает с исходной. Тем не менее, вообще говоря,
эти две равномерные структуры различны, хотя отображение
0.4. ТеореШ Асколи 55
хн->лг1 есть изоморфизм одной из них на другую. Однако эти
две структуры в X совпадают, если группа X коммутативна, а
также если пространство X компактно (п. 0.3.10).
Более детальное изучение этих равномерных, структур нам
не понадобится. Интересующиеся могут обратиться к книге
Б у р б а к и [2].
0.4. Теорема Асколи
Теорема4 Асколи является наиболее важным критерием ком-
компактности множества функций. В этой книге мы будем часто
на нее ссылаться.
0.4.1. Пусть Г, X—произвольные множества и Хт — сово-
совокупность всевозможных отображений множества Т в X. Если,
кроме того, Т и X — топологические пространства, то через
С(Т, X) будем обозначать множество всех непрерывных ото-
отображений из Хт.
0.4.2. Пусть Т — множество и X — топологическое простран-
пространство. Введем в Хт топологию простой (поточечной) сходимости.
Для этого каждому отображению fo^XT поставим в соответ-
соответствие базу окрестностей, состоящую из множеств вида
W(tu ..., tn; Uи ..., Un) = {f<=XT: f(tt)e=Uh i=l ..., п},
где п пробегает множество всех натуральных чисел, элементы t{
независимо друг от друга пробегают множество Г, a U{ при
каждом i является окрестностью точки fo(ti) в X. Эту топо-
топологию будем обозначать через xs.
0.4.3. Пусть Т—множество, X — равномерное пространство,
S cz Т и U—некоторое окружение равномерной структуры в X.
Для каждого f0 e Хт положим
V (L S, U) = {f<=XT: (f(t), fo(t))^U для всех <gS}.
Множества V(fo, S, £/), где f0 фиксировано, U пробегает мно-
множество всех окружений (или базу окружений), a S пробегает
некоторую фиксированную систему ® подмножеств в Г, обра-
образуют предбазу некоторой топологии т@ в множестве Хт. Эта то-
топология" называется топологией равномерной сходимости на
множествах, принадлежащих S, или просто © -топологией.
Если 3 состоит из одноточечных (или конечных) подмножеств
множества Г, то т@ совпадает с rs. В действительности rs — сла-
слабейшая из тех ^-топологий, для которых система ® ггокры-
вает Т (т. е. в случае, если пространство X отделимо, слабей-
слабейшая из всех отделимых ®-топологий).
0.4.4. Пусть Т — топологическое пространство. Особенно
важной является та в-топология, для которой система ®
56 Гл. 0. Предварительные сведения
состоит из всех компактных подмножеств пространства Т. Эта
топология обозначается через тс и часто называется тополо-
топологией компактной сходимости.
Важен также случай, когда ©={Г}, который порождает так
называемую топологию равномерной сходимости (на Г), обо-
обозначаемую через хи. Если пространство Т компактно, то тм = тс.
0.4.5. Каждая ^-топология в Хт равномеризуема. Действи-
Действительно, если S пробегает <3, a U пробегает Ж (где Ж— равно-
равномерная структура в Z), то семейство подмножеств
{(/, f0): (/, /0) efx XT, {f{t), fo(O) e £/ для всех (sS}
является предбазой окружений некоторой равномерной струк-
структуры и^ в Хт. Легко проверяется, что топология, определяемая
в Хт этой структурой, совпадает с исходной ©-топологией в Хт.
Через Ck(T,X), где k = c или k = u, мы будем иногда обо-
обозначать как топологическое пространство (С(Г, X),Xk)9 так и
равномерное пространство (С(Т,Х),ик).
0.4.6. Очевидно, что во всех случаях, когда Т — топологиче-
топологическое, а X — равномерное пространство, равномерная струк-
структура ис будет сильнее равномерной структуры uSi а тополо-
топология тс — сильнее топологии rs. Цель теоремы Асколи — выделить
некоторые множества в С(Г, X), в которых ис и us индуцируют
одну и ту же равномерную структуру, а тс и ts — одну и ту же
топологию. При этом существенную роль играет понятие рав-
равностепенной непрерывности.
0.4.7. Пусть Т — топологическое, а X — равномерное про-
пространство. Множество F из Хт называется равностепенно не-
непрерывным в точке t0 e Г, если для каждого окружения
U czX X X найдется такая окрестность TV точки t0 e T, что для
всех t e Af и f e F имеет место включение
(f(t),f{to))e=U.
Множество F cz Хт называется равностепенно непрерывным
(на Г), если оно равностепенно непрерывно в каждой точке
множества Т. В последнем случае множество F содержится
в С{Т,Х).
Теореме Асколи мы предпошлем несколько замечаний о
равностепенной непрерывности. Всюду в этих замечаниях бу*
дем предполагать (по меньшей мере), что Т — топологическое,
а X — равномерное пространство.
0.4.8. Лемма. Если множество F равностепенно непрерывно,
то его Xs-замыкание в Хт также равностепенно непрерывно.
Доказательство. Тривиальным образом следует из
определений, если вспомнить, что замкнутые окружения в
0.4. Теорема Ас ко ли 57
X X X образуют базу заданной равномерной структуры
(п. 0.3.2 B)). |
0.4.9. Предложение. Если множество F равностепенно не-
непрерывно, то us и ис (соотв. rs и тс) индуцируют в F одну и ту
же равномерную структуру (соотв. топологию).
Доказательство. Очевидно, достаточно показать, что
и8 и ис индуцируют в F одну и ту же равномерную структуру.
Пусть множество SczT компактно и U — окружение в ХхХ.
Возьмем такое симметричное окружение U\9 что U\ ° U\ ° UxczU.
Для каждого /еГ найдется такая окрестность Nt точки /, что
при t'^Nt и f^F. Так как множество 5 компактно, то можно
так выбрать точки t\, ..., tn, что окрестности Nt. будут по-
покрывать S. Легко проверить, что
(FxF)(]W(tl9 ..., tn\Ul)cz(FxF)nW(StU)9
откуда вытекает, что равномерная структура uc\F слабее рав-
равномерной структуры us\F\ следовательно, они совпадают. |
0.4.10. Следствие. Если F — равностепенно непрерывное мно-
множество, то его %8-замыкание и хс-замыкание (оба в Хт) совпа-
совпадают.
Доказательство. Пусть Fs и Fc — соответствующие за-
замыкания. Справедливость включения FcczFs очевидна. Из лем-
леммы 0.4.8 следует равностепенная непрерывность множества Fs;
но тогда из предложения 0.4.9 вытекает равенство топологий xs
и тс в F89 т. е.
|
Замыкание множества F в топологии xs\Fs совпадает с Fs. По
доказанному выше оно должно совпадать с замыканием F в то-
топологии Tcl/v Итак, имеем
(xsl^s)-замыкание F= (xc\Fs)-замыкание /\ т. е.
откуда следует включение FczdFs, что и требовалось доказать. |
0.4.11. Теорема (А скол и). Пусть Т — топологическое про-
пространство и X — равномерное пространство. Если множество
F <z: Хт равностепенно непрерывно-на Т и множество F(t) =
={f@- f ^ F} относительно компактно в X при каждом /gJ1,
то F относительно компактно в пространстве (Хт, тс).
Доказательство. Замыкание Fs множества F в тополо-
топологии т3 удовлетворяет тем же условиям, что и само множе-
множество F. Согласно теореме Тихонова, множество Fs относительно
58 Гл. 0. Предварительные сведения
компактно в пространстве {Хт, т6). Но тогда из предложе-
предложения 0.4.9 следует, что Fs относительно компактно и в тополо-
топологии тс. Наконец, из следствия 0.4.10 вытекает относительная
компактность множества F в пространстве (Хту тс).|
Иногда бывает полезным следующее частичное обращение
теоремы Асколи.
Предложение. Пусть Т — локально компактное пространство,
X — равномерное пространство и F — подмножество множества
С(Г, X). Если множество F относительно компактно в СС(Т, X),
то F(t) относительно компактно в X при каждом t^T и мно-
множество F равностепенно непрерывно.
До к аз а тел ь ств о. Так как отображение /»—>/(£) про-
пространства СС(Г, X) в X непрерывно при каждом £е7\ то мно-
множество F(t) как образ множества F при этом^ отображении отно-
относительно компактно при каждом /. Пусть F — замыкание мно-
множества F в пространстве СС(Г, X). Непрерывность отображения
£: FXT-+X, определенного формулой
следует непосредственно из локальной компактности простран-
пространства Т. Для каждого t e T равенство t*(f) =f(t) определяет ото-
отображение t*: F->X. Утверждение, что F равностепенно не-
непрерывно, равносильно утверждению^ что отображение / ь-> t*
пространства Т в пространство CU(F, X) непрерывно. Таким
образом, достаточно ограничиться доказательством последнего
утверждения.
Допустим, что отображение tt->t* не является непрерывным.
Тогда в произведении ХхХ существуют такое симметричное
окружение V2( = Vo V) и такая точка г^еТ, для каждой окрест-
окрестности которой N найдутся точка iN GiV и отображение fN e F,
такие, что
По условию предложения сеть_ (fN) обладает предельной точ-
точкой / е F. Так как множество F компактно, то, переходя при
необходимости к подсетям, можно считать, что сама сеть (fN)
сходится к f в F. Поэтому для всех достаточно малых окрестно-
окрестностей N имеем
Следовательно, для всех достаточно малых окрестностей N
(fN(tN),
0.4. Теорема Асколи 59
Поскольку сеть (fN, tN) сходится к (f, t) в пространстве
T, это противоречит непрерывности отображения g. |
0.4.12. Следствие. Если Т — локально компактное простран-
пространство, а X и F удовлетворяют условиям те_оремы 0.4.11, то мно-
множество F относительно компактно в пространстве (С(Т, X), тс).
Доказательство. Достаточно показать, что С (Г, X)
замкнуто в пространстве Хт, наделенном топологией тс. Но это
сразу следует из локальной компактности пространства Т. За-
Заметим, что в этом следствии условие локальной компактности Т
можно заменить любым условием, обеспечивающим непрерыв-
непрерывность на Т всякой функции f e Хт, все сужения которой на ком-
компактные подмножества КаТ непрерывны (например, условием
метризуемости пространства Г). |
Замечание. Многие встречающиеся в этой книге прило-
приложения теоремы Асколи относятся к случаю, когда F— множество
линейных форм на топологическом векторном пространстве или
сходящаяся последовательность линейных отображений одного
такого пространства в другое. В таких случаях предложение
0.4.9 и теорема 0.4.11 эквивалентны.
Отметим еще одно следствие теоремы. Пусть Т и X — равно-
равномерные пространства. Множество F а Хт называется равно-
равномерно равностепенно непрерывным, если для каждого окруже-
окружения VczXxX найдется такое окружение UczTxT, что при
fef и (t, f) e U имеет место включение
(f(t),f(f))e=V.
Ясно, что при этом каждое отображение из F равномерно не-
непрерывно.
0.4.13. Теорема. Пусть Т — предкомпактное равномерное про-
пространство, а X — отделимое равномерное пространство. Если
множество Fez Хт равномерно равностепенно непрерывно и для
каждого t еГ множество F(t) относительно компактно в X, то
множество F относительно компактно в пространстве
(СG\ X), ти).
Доказательство. Так как пространство Т предкомпактно,
то можно построить его компактное пополнение Т. Пусть X —
отделимое пополнение пространства X. В силу равномерной не-
непрерывности каждое отображение f e F допускает единственное
непрерывное продолжение до отображения f пространства Т в
пространство X. Легко убедиться в том, что множество F всех
таких ^продолжений равностепенно непрерывно на Г, а множе-
множество F(t) относительно компактно в X для каждого t&T.
Для завершения доказательства достаточно воспользоваться
60 Гл. 0. Предварительные сведения
теоремой 0.4.11 и рассмотреть затем сужения элементов множе-
множества F на Г. |
Отметим следующее полезное приложение предыдущего ре-
результата.
0.4.14. Предложение. Пусть Т — топологическое простран-
пространство, X — равномерное пространство, a F — такое равностепенно
непрерывное множество в Хт, что множество F(t) относительно
компактно в X для каждого t^T. Через Fc обозначим хс-замы-
кание множества F в Хт. Пусть далее (y{Gj — семейство комп-
комплексных непрерывных функций на пространстве (Fc, xc\Fc), от-
отделяющих точки множества Fc. Если (f%) — такая сеть элемен-
элементов из F, что lim^(/J существует для каждого индекса /g/,
А
то сеть (f%) сходится к некоторому элементу множества Fc в то-
топологии тс.
Доказательство. Из леммы 0.4.8 и теоремы 0.4.11 сле-
следует компактность множества Fc в топологии тс. Следовательно,
сеть {f%) обладает хотя бы одной тс-предельной точкой g e Fc.
С другой стороны, всякая такая предельная точка g удовлетво~-
ряет равенству \г (g) = lim ^ (f J (/ <= /) и потому определяется
к
однозначно. Наше предложение следует теперь из утверждения
A) п. 0.2.17. 1
0.4.15. Замечание. Если пространство Т локально ком-
компактно (или метризуемо), то предел g сети (/^) должен принад-
принадлежать множеству С (Г, X). Сравните со следствием 0.4.12.
О более общих формах теоремы Асколи см. Келли [1,
стр. 305—313] и В ада [4].
0.5. Теорема Брауэра о неподвижной точке
В § 3.6 в качестве отправной точки нам понадобится знаме-
знаменитая теорема Брауэра, которая заключается в следующем.
0.5.1. Теорема. Пусть В— замкнутый единичный шар с цен-
центром в начале координат пространства Rn. Тогда каждое непре-
непрерывное отображение f множества В в себя имеет по крайней
мере одну неподвижную точку, т. е. существует такая точка
хеВ, что f(x) =х.
0.5.2. Очевидно, что это чисто топологическая теорема. Ее
доказательство можно найти, например, в книге Лефшеца
[1, стр. 117—Н9]1). Аналогичное, но более близкое аналитику
доказательство более тонкого результата приведено в книге
Грейвса [1, стр. 145—150]. Там же содержатся и все необхо-
1) См. также Ху Сы-цзян [1, стр. 12].-— Прим. ред,
0.5. Теорема Б pay эра о неподвижной точке 61
димые предварительные сведения из комбинаторной топологии.-
Возможно «и чисто аналитическое доказательство, вероятно,
менее естественное (см., например, Данфорд и Шварц
[1, стр. 506-508]).
0.5.3. Теорема Брауэра останется справедливой, если заме-
заменить шар В топологическим пространством X, гомеоморфным В.
В частности, в качестве X можно взять замкнутый единичный
шар пространства О, который гомеоморфен замкнутому единич-
единичному шару пространства R2n. В § 3.6 используются оба эти
случая.
ГЛАВА 1
Векторные пространства
и топологические векторные пространства
1.0. Предисловие
Эта глава, в которой мы непосредственно переходим к ос-
основному предмету изучения, состоит из двух частей.
Первая из них включает в себя § 1.1 —1.7, в которых рас-
рассматриваются векторные пространства сами по себе без топо-
топологии. Первые четыре параграфа содержат сведения, известные
всякому читателю, знакомому с линейной алгеброй. Однако для
облегчения чтения мы все же приводим основные определения
и результаты. Содержание § 1.5—1.7 менее известно, поэтому
там изложение носит более детальный характер. Вопросы, за-
затронутые в § 1.1 —1.7, более подробно освещены в замечательной
книге Халмоша «Конечномерные векторные пространства»
[3]. Мы часто будем ссылаться на эту книгу, поэтому в настоя-
настоящей главе она будет обозначаться просто символом [X].
Вторая часть главы начинается с § 1.8, где вводятся топо-
топологические векторные пространства. В качестве дополнения к
этому параграфу можно предложить Бурбаки [7] и Тэйлора
[1]. В § 1.12 читатель вновь встретится с материалом, часть ко-
которого прекрасно излагается в книге Халмоша.
1.1. Векторные пространства [X, § 1, 2]
Читатель, вероятно, знаком с понятием конечномерного век-
векторного (или, что то же, линейного) пространства. Опуская в
обычном внутреннем (т. е. не использующем понятия базиса
или порождающего множества) определении конечномерного
векторного пространства требование линейной зависимости вся-
всякого достаточно большого конечного набора векторов, мы при-
приходим к общему понятию векторного пространства. Мы будем
иметь дело лишь с векторными пространствами над полем ве-
вещественных чисел R или над полем комплексных чисел С, при-
причем зачастую наши результаты и рассуждения не будут зави-
зависеть от того, какое из этих двух скалярных полей рассматри-
рассматривается. Поэтому поле скаляров будет вообще обозначаться че-
через К. Однако иногда важно иметь в виду, что поле К есть либо
R, либо С. Так как, в частности, наше К коммутативно, то мы
/./. Векторные пространства 63
не будем различать левое и правое векторные пространства над
К (см. Бур баки [4, стр. 184]).
Приведем формальное определение векторного пространства.
Непустое множество Е с двумя законами композиции, один из
которых внутренний, а другой внешний, с областью операто-
операторов1) К, называется векторным (или линейным) пространством
над /С, если выполняются следующие аксиомы.
A) Е — абелева группа относительно внутреннего закона
композиции, называемого сложением и обозначаемого симво-
символом + . Этот закон ставит в соответствие каждой паре (х, у)
элементов из Е их сумму х-\-у, также принадлежащую Е. То,
что Е с этим, законом композиции является абелевой группой,
означает, что выполняются следующие условия: сложение ассо-
ассоциативно и коммутативно-, существует такой элемент 0g£, что
для всех xg£ имеет место равенство х + 0 = х; для каждого
элемента xg£ существует противоположный элемент —х, для
которого справедливо соотношение х+(—х) = 0. В качестве не-
несложного упражнения можно доказать единственность элемента
0 и единственность для всякого xg£ противоположного эле-
элемента —х.
B) Внешний закон композиции представляет собой отобра-
отображение
(а, х) \—> ах
произведения КхЕ в Е, удовлетворяющее следующим условиям:
а(х + у) = ах + си/, (а + р) х = ах + $х,
, 1х = х,
где х, у — произвольные элементы из Е; а, |3 — произвольные
скаляры (т. е. элементы из К)', через 1 обозначается единичный
элемент поля /(. Для любого элемента xg£ справедливы ра-
равенства 0х = 0 и (—1)х = —х.
Более подробно теория векторных пространств излагается,
например, у Бурбаки [4], Тэйлора [1], Райкова [3]. Воз-
Возможно, что читатель по мере чтения нашей книги сочтет полез-
полезным обращаться к книгам этих и других .авторов.
Рассмотрим ряд примеров векторных пространств, часто
встречающихся в функциональном анализе. Все конечномерные
пространства по существу мало отличаются от пространства Кп
(которое обычно рассматривается как векторное пространство
над /С), поэтому мы не будем им уделять особого внимания. За-
Заметим лишь, что этот пример содержится как частный случай
(множество Т конечно) в примере 1.1.1. В функциональном
1) См. Бурбаки [2, стр. 55}. — Прим. ред.
64 Гл. 1. Векторные и топологические векторные пространства
анализе наиболее важными векторными пространствами являют-
являются функциональные пространства (т. е. пространства функций)
или пространства, получающиеся из них с помощью различных
общих конструкций (образование факторпространств, переход к
сопряженным пространствам и т. д.). Эти общие методы будут
изложены ниже.
1.1.1. Пример. Функциональные пространства могут быть опи-
описаны следующим образом. Возьмем произвольное множество Т
и образуем произведение Кт, элементами которого являются
функции f: T-+K. Превратим множество Кт в векторное про-
пространство над /С, положив х + у и ах равными соответственно
функциям t н->х(/) +y(t) и t*—>a-x(t) (знаки + и- в правых
частях обозначают операции поля К). Множество Кт с указан-
указанными операциями есть векторное пространство функций на Т.
Таким же образом могут быть описаны и векторные подпро-
подпространства (§ 1.2) пространства Кт и иногда даже его фактор-
пространства, если допустить некоторую вольность речи. Далее
мы увидим, что в случае, когда Т — топологическое простран-
пространство, векторные подпространства в Кт, состоящие из непрерыв-
непрерывных функций, играют фундаментальную роль в функциональ-
функциональном анализе. То же самое относится и к векторным подпростран-
подпространствам, выделяемым по другим признакам (см., например, гл. 4).
Если множество Т конечно и состоит из п элементов, то Кт
с точностью до изоморфизма (§ 1.3) совпадает с Кп — простран-
пространством n-членных упорядоченных наборов элементов из К с обыч-
обычным «покоординатным» определением сложения и умножения на
скаляры. Если множество Т счетно, то Кт изоморфно простран-
пространству KN (N — множество всех натуральных чисел), состоящему
из всевозможных бесконечных последовательностей, причем век-
векторные операции осуществляются снова «покоординатно». Про-
Пространство KN и его подпространства, наделенные топологией
или без нее, обычно называют пространствами последователь-
последовательностей; они сыграли важную роль в развитии функционального
анализа. (См. Ф. Рисе [1], Банах [1], О р л и ч [1], М а з у р и
Орлич [1], Кук [1, 2], где эти пространства рассматриваются
более подробно.)
1.2. Векторные подпространства, факторпространства,
произведения пространств [X, § 10—12, 18, 21]
1.2.1. Векторные подпространства. Пусть Е — векторное про-
пространство и L — множество в Е. Операции, .определенные в Е9
могут, вообще говоря, переводить элементы из L в элементы, не
принадлежащие L. Если такая возможность исключена, т. е. мно-
множество L замкнуто относительно сложения и умножения на ска-
1.2. Векторные пространства, факторпросгранства, произведения 65
ляры, то, сужая эти операции с Е на L, мы наделяем множество
L структурой векторного пространства. Множество LaE, замк-
замкнутое относительно операций векторного пространства Е и наде-
наделенное индуцированными из Е операциями, называется вектор-
векторным (или линейным) подпространством в Е. Тэйлор [1] и не-
некоторые другие авторы вместо «векторное подпространство» го-
говорят «линейное многообразие».
Введем некоторые обозначения. Пусть Л, В— множества
в Еу а М — множество в /С Положим
(векторная сумма множеств Л и В) и
С помощью этих обозначений можно так выразить необходимые
и достаточные условия того, что множество ЬсцЕ является век-
векторным подпространством в Е:
L + LczL,K-LczL A.2.1)
Наименьшим векторным подпространством в Е является множе-
множество {0}, где 0 — нулевой элемент пространства Е. Пересечение
любого семейства векторных подпространств в Е также является
векторным подпространством в Е. Пусть в Е задано множество
S. Наименьшее подпространство в Е, содержащее S, называется
подпространством, порожденным множеством S. Если S не
пусто, то подпространство, порожденное множеством S, состоит
п
в точности из элементов вида 2 аг-5г-, где а* е К, s,- e S
(l4^i^Cn), a n — произвольное натуральное число (зависящее,
вообще говоря, от рассматриваемого элемента). Некоторые ав-
авторы называют подпространство, порожденное множеством S,
линейной оболочкой множества S. Если линейная оболочка мно-
множества S совпадает со всем пространством Е, то говорят, что S
порождает Е или что S является системой образующих про-
пространства Е.
1.2.2. Примеры. A) Если в Кт (см. п. 1.1.1) взять только
ограниченные функции, то мы получим векторное подпростран-
подпространство В(Т) пространства Кт. Пусть Т — топологическое простран-
пространство. Множество всех непрерывных функций из Кт образует в
нем векторное подпространство, обозначаемое через С(Т). Ана-
Аналогично если М — некоторое подпространство в /С, то множество
Мт есть подпространство в Кт. Так, если К = С и M = R, то под-
подпространство RT состоит из всех вещественных функций на Т.
66 Гл. 1. Векторные и топологические векторные пространства
B) Пусть Е— заданное векторное подпространство в Кт и
То — некоторое подмножество в Т. Множество всех функций из
Еу равных нулю на Го, образует векторное подпространство в Е
(а потому и в Кт).
C) Более общим образом, пусть Е — векторное пространство
и (fi)—произвольное семейство линейных отображений (§ 1.3)
пространства Е в соответствующие векторные пространства F{.
Множество тех элементов х^Е, для которых при каждом i эле-
элемент fi(x) принадлежит заранее заданному подпространству в
Fiy образует векторное подпространство в Е. Из результатов
§ 1.4 следует, что всякое векторное подпространство в Е может
быть получено указанным способом.
1.2.3. Факторпространства. Перейдем к понятию факторпро-
странства. Пусть Е — векторное пространство и L — его вектор-
векторное подпространство.
Отношение x = y(modL), означающее, что х — у е L, яв-
является в Е отношением эквивалентности. Фактормножество
E/L можно наделить структурой векторного пространства. Пусть
xc = x + L и yc=y + L — классы эквивалентности, соответствующие
элементам х и у. Класс {х+у)с зависит только от хс и ус, по-
поэтому можно определить сложение классов следующим образом:
Хс + Ус"*2 (#+У)с- Аналогичным образом можно по определению
положить а*хс=(ах)с. Полученное таким образом векторное
пространство называется (векторным) факторпространством
пространства Е по подпространству (по модулю) L и обозна-
обозначается через E/L.
1.2.4. Примеры. A) Обозначим через L множество функций
из /Ст, равных нулю на некотором подмножестве ТоаТ. Тогда
пространство KT/L можно отождествить с пространством /(Го.
Если Т — топологическое пространство, а вместо Кт рассматри-
рассматривается С (Г), то аналогичное утверждение неверно: пространство
C(T)I(L(\C(T)), вообще говоря, не изоморфно пространству
С(Го). Более очевидно отсутствие топологического изоморфизма
между этими пространствами (п. 1.8.5 и 1.9.2).
B) В гл. 4 мы изучим различные стандартные пространства,
которые являются факторпространствами функциональных про-
пространств. Эти пространства играют основную роль в теории ин-
интегрирования и получаются с помощью следующего канониче-
канонического приема. Сначала рассматриваются векторное пространство
Е и полунорма (§ 1.6) р на Е. Ядро А^/г^О}) полунормы р
является подпространством в Е. Оказывается естественным ис-
использовать факторпространство E/N.
1.2.5. Произведение пространств. Пусть (Ei)i^I — семейство
векторных пространств над полем К. Произведение Е= Ц Et
1.2. Векторные пространства, факт о рпрост ранет ва, произведения 67
можно превратить в векторное пространство, если определить
в нем векторные операции следующим образом:
Полученное таким образом векторное пространство называется
произведением векторных пространств. Если, в частности, все
Ei = F, где F — фиксированное векторное пространство над /С, то
получается пространство F1. Если множества / и / равномощны,
то пространства F1 и FJ канонически изоморфны. Если множе-
множество / содержит п элементов, то вместо F1 пишут обычно Fn.
1.2.6. Гиперплоскости. Читатель вскоре заметит, что в функ-
функциональном анализе широко пользуются понятием линейной фор-
формы (или линейного функционала). Геометрическим двойником
линейной формы является гиперплоскость, к определению кото-
которой мы сейчас перейдем.
Будем называть векторное подпространство Е собственным,
если оно отлично от Е. Если пространство Е состоит более чем
из одного нулевого элемента, то в Е всегда существуют собствен-
собственные подпространства. Под {однородной) гиперплоскостью в век-
векторном пространстве Е понимается всякое его максимальное соб-
собственное векторное подпространство, т. е. такое собственное век-
векторное подпространство Я в £", что для любого векторного
подпространства V в Е, удовлетворяющего условию Н а V, либо
V=H, либо V=E.
Пусть Н — гиперплоскость в Я и х^Е\Н. В силу макси-
максимальности Н векторная сумма Н + Кх должна совпадать с Е.
Отсюда следует, что факторпространство Е/Н имеет размер-
размерность 1, т.е. порождается одним образующим элементом, отлич-
отличным от нулевого. Обратно, если Н — такое подпространство в Е$
что размерность Е/Н равна 1, то Н — гиперплоскость в Е.
Пусть пространство Е/Н имеет размерность 1 и элемент
х0 е Е/Н. Тогда каждому элементу xg£ соответствует такой
единственный скаляр а, что x^ax0(mod H). Рассмотрим эту
числовую функцию /: хь->а, определённую на Е. Очевидно, что
f(Х + У) = f(х) +f(У) и f(^*)=^f(*)i т. е. f есть линейная форма
(§ 1.3) на Е. Кроме того, /(*<>) = 1, /=£0, и
Н={хе=Е: f(x)=O} = f
Таким образом, полученная линейная форма f зависит от Xq и
от Я, но при изменении Хо функция / просто умножается на не-
ненулевой скаляр.
Обратно, если f — отличная от нуля линейная форма на Е, то
легко видеть, что # = ker /=/~1 ({0}) есть гиперплоскость в Е.
Из всего сказанного следует, что гиперплоскости в Е — это
те и только те множества из Е, которые имеют вид кег/, где
68 Гл. 1. Векторные и топологические векторные пространства
f — отличная от нуля линейная форма на Е. Таким образом, две
линейные формы определяют одну и ту же гиперплоскость тогда
и только тогда, когда они отличаются ненулевым скалярным
множителем.
1.2.7. Линейные многообразия. Линейным многообразием в Е
называется множество, получаемое сдвигом некоторого вектор-
векторного подпространства в Е, т. е. линейное многообразие в Е — это
множество V вида Xq + L, где L — некоторое векторное подпро-
подпространство в Е. Многообразие V однозначно определяет подпро-
подпространство L, но элемент xq определяется лишь с точностью до
слагаемого из L.
Иногда гиперплоскостью называют линейное многообразие
вида хо + Н, где Н — однородная гиперплоскостью Е. Всякая
такая гиперплоскость в Е есть множество вида
f ({«»={*е£: f(x)=a),
где f — отличная от нуля линейная форма на £, а а — число.
Если Н — гиперплоскость f~l({oc}) в вещественном векторном
пространстве, то множества f'1 ([a, +oo)), f~l((a, +<*>))>
f~l(—оо, а]) и f'l((—оо, а)) носят название полупространств.
определенных гиперплоскостью Н. Говорят, что множество А ле-
лежит (соответственно лежит строго) по одну сторону от Я, если
оно содержится в одном из полупространств f~l([a, +оо)) или
/!((—оо, а]) (соответственно в одном из полупространств
()) или/-Ч(-оо,а))).
1.3. Линейные отображения и линейные формы. Изоморфизм.
Графики [X, § 32, 13]
1.3.1. Линейные отображения и линейные формы. Пусть Е и
F — векторные пространства над Дг. Отображение и: E-+F на-
называется линейным отображением или линейным оператором,
если
и{ах+$у)=аи(х)+$и(у) A.3.1)
для любых х,у^Е и любых а, р е/С. В частности, когда F = K,
мы говорим о линейной форме или линейном функционале на Е.
Иногда приходится рассматривать более общую ситуацию,
когда область определения отображения и является векторным
подпространством L в Е. Тогда при определении линейности
отображения и следует в формуле A.3.1) 6j)aTb x и у из L. Так
как L само есть векторное пространство над /С, то здесь ничего
принципиально нового не возникает.
Вернемся к случаю, когда L совпадает с Е. Для любых двух
линейных отображений и и v можно обычным способом опреде-
определить их сумму — линейное отображение u + v. Обычным же обра-
1.3. Линейные отображения и линейные формы 69
зом определяется аи для любого числа а. Очевидно, чго таким
способом множество L(E,F) всех линейных отображений про-
пространства Е в F превращается в векторное пространство над /С
В частности, когда F = K, пишут Е* вместо L(E,K) и про-
пространство Е* называют алгебраическим сопряженным к Е1).
Легко заметить, что всякое отображение u^L(E,F) пре-
преобразует векторные подпространства (соответственно линейные
многообразия) LczE в векторные подпространства (соответ-
(соответственно линейные многообразия) u(L)czF. Если М — векторное
подпространство в /\ то u~l (M) — векторное подпространство
в Е. В частности, ker и = и~1({0})— векторное подпространство
в Е. Линейное отображение и взаимно однозначно тогда и толь-
только тогда, когда ker и = {0}. (В этом случае линейное отображение
и: E-^F называют мономорфизмом.)
Пусть Е — векторное пространство. Отображение aG L (£, Е),
т. е. линейное отображение пространства Ё в себя, часто назы-
называют эндоморфизмом пространства Е.
1.3.2. Изоморфизм [X, § 9]. Отображение u^L(E,F) назы-
называется мономорфизмом (или изоморфизмом в), если оно взаимно
однозначно, эпиморфизмом (или отображением на), если
u(E)=F, и изоморфизмом на, если оно является одновременно
и мономорфизмом и эпиморфизмом.
Векторные пространства Е и F называются изоморфными
(как векторные пространства над /С), если существует изомор-
изоморфизм Е на F.
Пусть дано отображение и^ L(E, F) и векторное подпро-
подпространство Lb£, такое, что u(L) ={0}. Этому отображению можно
поставить в соответствие отображение ис^ L(E/L, F), положив
ис(хс) — и(х), где хс — класс эквивалентности по модулю L, со-
содержащий элемент х. В частности, можно считать, что L = kevu\
тогда отображение ис будет взаимно однозначным. Таким обра-
образом, мы видим, что всякое линейное отображение и: E-+F опре-
определяет изоморфизм пространства E/kevu на и(Е). Эта про-
процедура перехода к факторпространству полезна во многих слу-
случаях.
1.3.3. График линейного отображения. Вернемся к ситуации,
когда и есть произвольное линейное отображение некоторого
подпространства LczE в F. Подпространство L называется, как
обычно, областью определения отображения и и обозначается
через Aomu. Область значений u(L), обозначаемую через im и,
называют также образом отображения и.
х) Халмош пользуется обозначением Ег вместо Е*. Мы резервируем сим-
символ £' для обозначения топологического сопряженного к пространству Е
(п. 1.9.4); следует избегать смешения этих обозначений.
70 Гл. 1. Векторные и топологические векторные пространства
Третье множество, которое появляется вместе с Аогпи и
\гпи, — это график отображения и, который представляет собой
множество всех элементов произведения ExF вида (л:, u(x))t
где х g dom и. Будем обозначать график отображения и через
gv и. Если отображение и: E-+F линейно, то его график является
линейным подпространством произведения ExF.
Пусть задано подмножество G произведения ExF. Естествен-
Естественно поставить вопрос: при каких условиях множество G является
графиком некоторого отображения и, определенного в £ и со
значениями в Z7? Несложные рассуждения показывают, что для
этого необходимо и достаточно, чтобы для каждого элемента
х^Е множество тех y^F, для которых (x,//)gG, содержало
не более одного элемента. Областью определения соответствую-
соответствующего отображения и будет множество всех элементов х^Е, для
которых существует по крайней мере один (и, следовательно,
только один) такой элемент y^F, что (х, у)<^ G. При этом для
каждого такого х элемент и(х) совпадает с у.
Отображение и будет линейным, если дополнительно пред-
предположить, что G есть векторное подпространство в произведении
EXF. Таким образом, для того чтобы множество Gcz ExF было
графиком некоторого линейного отображения и, определенного
в £ и со значениями в F, необходимо и достаточно, чтобы A) G
было векторным подпространством в произведении ExF и B)
из включения @,//)gG следовало бы равенство у = 0. Эта ха-
рактеризация графика линейного отображения будет использо-
использована позже при рассмотрении замкнутых линейных отображений
одного топологического векторного пространства в другое.
1.4; Линейная зависимость. Алгебраический базис.
Алгебраические дополнения [X, § 5—7]
1.4.1. Линейная зависимость. Пусть Е — векторное простран-
пространство над К. Семейство (ХгЬе/ элементов из Е называется ли-
нейно независимым, если из равенства
где F — любое конечное подмножество в / и а^/С, следуют ра-
равенства аг = 0 для fe/\ В противном случае семейство (хг) ш
называется линейно зависимым.
Очевидно, что свойство линейной зависимости или независи-
независимости семейства сохраняется, если его элементы каким угодно
образом переставлены. Каждое подсемейство линейно независи-
независимого семейства также линейно независимо. Ни один элемент ли-
1.4. Линейная зависимость 71
нейно независимого семейства не может быть нулевым, и
при 1Ф].
Если х е Е и хФО, то семейство {х}, состоящее из одного
элемента х, линейно независимо. Если Е = {0}, то в Е нет непу-
непустых линейно независимых семейств.
Взаимно однозначное линейное отображение преобразует ли-
линейно независимое семейство в линейно независимое семейство.
Приведем два простых, однако весьма полезных результата
о конечных линейно независимых семействах из £ и Е*.
1.4.2. Предложение. Пусть Е — векторное пространство над К
и (fi)i<i<n — конечное линейно независимое семейство линейных
форм из Е*. Линейная форма f является линейной комбина-
комбинацией 1) линейных форм fi (I ^Ci^Cn) тогда и только тогда, когда
В частности, если Г){кег/г: 1 <л-< я} = {0}, то формы fi A <л<1
*Сп) порождают пространство £*; следовательно, в этом случае
dim E*^n и dimE^Cn 2).
Доказательство. Последнее утверждение отчасти свя-
связано с содержанием п. 1.4.4—1.4.6. Однако мы помещаем его
здесь, так как оно является простым следствием первого утвер-
утверждения. Необходимость условия очевидна. Его достаточность мы
докажем индукцией по п. Допустим сначала, что /2 = 1. По усло-
условию из /i(a:)=0 следует f(x)=O, поэтому если /i = 0, то и f = 0;
так что f = O'f\. Если же fi¥=0, то существует такой элемент
е^Еу что fi(e) = I. Тогда для любого х е Е имеем fi(x —
— /1(х)в)=0 и, следовательно, f(x — fl(x)e)=0 для всех лге£.
Последнее равенство означает, что f = f(e)fi, чем завершается до-
доказательство для случая я=1.
Пусть теперь я> 1; предположим, что предложение справед-
справедливо для п—1. Если /п = 0, то доказывать нечего. Пусть /п=£0;
возьмем в Е такой вектор еп, что fn(en) = 1. К линейным формам
r = t-f{en)fn и rt-ft-fMfH A</<п-1)
применим предположение индукции. Из включения кег/иэ
П{кД 1^/^} легко следует, что
zDfl {ker/;: 1</<я-1}. A.4.1)
Действительно, если xef){ker^: 1</</г—1], то элемент
1) Элемент х е Е называется линейной комбинацией элементов */
п
A < / < п), если х = 2 а1хь Где а/ е /С. — Прим. перев,
2) Определение размерности dim £ см. в п. 1,4.4. — Прим. перев.
72 Гл. 1. Векторные и топологические векторные пространства
у = х — fn{x)en принадлежит пересечению ядер ker U по 1<л^
•</г—1, а также ядру формы fn (так как /п(£п) = 1)- Таким об-
образом, r/efl{kerft-: l^Ci^Cn}, и, следовательно, у е кег /. Но
тогда jc e кег /', что и доказывает A.4.1). В силу предположения
индукции получаем, что /' есть линейная комбинация линейных
форм f't A</^Аг—1). Отсюда следует, что f есть линейная
комбинация форм fi (l<^i^n)t что и требовалось доказать. |
Замечание. Более изящное, однако менее очевидное дока-
доказательство основывается на замечании, что всякая линейная фор-
форма, определенная на векторном подпространстве пространства Кп,
может быть продолжена до линейной формы на всем Кп. Исходя
из этого, можно рассмотреть линейное отображение и: £'->/(п,
задаваемое формулой и(х) = (fx (х),..., fn{x)), й продолжить на
все пространство Кп линейную форму g, определенную на под-
подпространстве и(Е) равенством g(u(x)) =f(x)l). После этого для
завершения доказательства остается воспользоваться тем, что
g, как и всякая линейная форма на /Сп, имеет вид
1.4.3. Предложение. Пусть Е — векторное пространство над /С
A) Если (fi) l<i<n—конечное линейно независимое семей-
семейство в Е*^ то в пространстве Е существует такое семейство
(Xi)l<i<n> ЧТ0
{1 при i — /,
О при i ф ] J
B) Утверждение A) останется справедливым, если в нем
поменять местами Е и Е*.
Доказательство. Утверждение A) докажем индукцией
по п. При я=1 оно тривиально. Предположим, что оно верно для
п\ установим его справедливость для п+1. Пусть линейные фор-
формы fi,... ,/n+i линейно независимы. Тогда и f\,..., fn обладают
тем же свойством. По предположению индукции в Е можно так
выбрать элементы Х\, ... xni чтобы fi(Xj)=dij> 1 ^л, j^С п.
Остается показать существование такого элемента xg£, что
fi{x)=0 при l^i^n и fn+\(x)=f--Oy и затем положить
хп+\ = -т ру. Но если такого элемента х нет, то
ker fn+i с= fl {ker ft: К i < п}.
J) Корректность такого определения формы g на и(Е) вытекает из усло-
условия, наложенного на ядра форм /, /i, .,,., /п. — Прим. ред.
1.4. Линейная зависимость 73
Тогда из предложения 1.4.2 следует, что /n+i есть линейная ком-
комбинация форм /ь ...,/п, а это противоречит линейной незави-
независимости форм /ь ..., fn+i-
Утверждение B) вытекает из A) и возможности вложения Е
в £** (п. 1.4.7). |
1.4.4. Алгебраический базис. Линейно независимое семейство
(ei)ien состоящее из элементов пространства £, называется
алгебраическим базисом в £, если множество {ег: i e /} поро-
порождает пространство Е (п. 1.2.1). Последнее условие равносильно
требованию, чтобы каждый элемент х е Е имел единственное
представление в виде суммы 2 aiei> где числа аг- отличны от
i «= /
нуля йе более чем для конечного множества индексов из / (это
конечное множество, вообще говоря, зависит от х).
Можно показать (см. Дэй [1, стр. 10, теорема 2]), что все
базисы в Е имеют одно и то же кардинальное число, которое
можно назвать размерностью пространства Е (обозначается
dimf). Доказательство относительно просто, если простран-
пространство Е конечномерно, и для этого случая мы будем считать его
известным". Понятие размерности бесконечномерного простран-
пространства будет редко использоваться, поэтому доказательство утвер-
утверждения для этого случая также .опускается. Отметим лишь такое
следствие: два векторных пространства над К изоморфны тогда
и только тогда, когда они имеют одну и ту же размерность.
В дальнейшем нам понадобится следующая теорема:
1.4.5. Теорема. Каждое векторное пространство £=£{0} обла-
обладает по крайней мере одним алгебраическим базисом. Более
того, если в Е задано произвольное линейно независимое семей-
семейство (#t)/e/, то в Е существует такой алгебраический базис
(xi)ie=j> что множество I содержится в /.
Доказательство опирается на лемму Цорна (п. 0.1.5).
Пусть L=(xi).(-IH L/=(yj)i^J—линейно независимые семей-
семейства элементов из Е. Будем писать L^CL't если /с=/ и уг==^г
при fe/. Таким образом, множество всевозможных линейно не-
независимых семейств из Е становится частично упорядоченным.
Легко убедиться в том, что оно индуктивно упорядочение Дей-
Действительно, пусть £а =(*?);€=/ —совершенно упорядоченное
множество линейно независимых семейств из £, где индекс а про-
пробегает некоторое множество Л. Положим /= [J /а. Если i^L
то /е/а по крайней мере для одного asi В силу совершен-
совершенной упорядоченности множества {La: a e А} все элементы хаг
такие, что / е 1а, совпадают между собой. В самом деле, если
fe/ и /е/|з, то либо La^Lj3» либо L^^L^. В первом случае
74 Гл. 1. Векторные и топологические векторные пространства
/ас/р и х? = х$ для всех /Е/а, во втором случае имеет место
аналогичное соотношение. Определим теперь элемент хг с по-
помощью равенства х.=х^, где а — любой из индексов, для кото-
которых ге/а. Семейство элементов Ь=(х{) . е/ линейно независимо
(опять в силу совершенной упорядоченности множества (La)a(-A)
и является верхней гранью множества (£а)а(_л. Таким образом,
индуктивная упорядоченность доказана.
Поэтому из леммы Цорна следует, что для всякого линейно
независимого семейства L =(л:г-Iе/ элементов пространства Е
найдется в Е такое максимальное линейно независимое семей-
семейство Л1 = (у/)/е/, что L^CM. Осталось только показать, что М
порождает Е. Обозначим через £о векторное подпространство
в Е', порожденное семейством Л1 Надо показать, что Е0 = Е. Пусть
ЕфЕ0. Возьмем элемент х0 е Е\Е0 и присоединим его к семей-
семейству М. Тогда получим такое линейно независимое семейство
ЛГ, что М^СМ' и МфМ', а это противоречит свойству макси-
максимальности семейства М. Отсюда следует, что Е0 = Е. |
Из теоремы 1.4.5 вытекают многочисленные следствия, с
двумя из которых мы сейчас познакомимся.
1.4.6. Предложение. Для всякого векторного пространства Е
над К справедливо неравенство dim E* ^> dim E. Если одна из
частей неравенства конечна, то имеет место равенство
Доказательство. Пусть (^)ie/—базис в Е (существо-
(существование хотя бы одного такого базиса следует из теоремы 1.4.5).
Для каждого i^I можно определить линейную форму е* е £*,
полагая ^(^/) = б// Для /^Л а затем линейно продолжая е* на
Е1). Легко видеть, что семейство (е*). линейно независимо
в £*. Из теоремы 1.4.5 (примененной к Е*) следует возможность
вложения (е!) в базис пространства Е*. Следовательно, dim E*
не меньше кардинального числа множества /, которое и есть
dim£.
Пусть теперь пространство Е конечномерно, dim Е = п и
(ei) l<i<n— базис в Е. Так же как и выше, построим линейные
формы е\ е Е*. Мы уже знаем, что формы е\ линейно независимы
в Е*. Кроме того, так как, очевидно,
П{кеге*: 1<
1) Пусть х = 2 aiei е Е' Тогда е* (х) = 2 a/eI (ey) — ai-"~ Прим. перев.
1.4. Линейная зависимость 75
то из предложения 1.4.2 вытекает, что формы е\ (l^i^n) по-
порождают пространство £*, т. е. образуют базис в £*. Таким об-
образом, dim E* — n. Если же dim£* конечна, то из доказанного не-
неравенства следует конечномерность Е и, следовательно, по уже
доказанному dim £* = dim E. I
Замечания. A) Семейство линейных форм (е!) в £*,
определенное по заданному линейно независимому семейству
(е{) в Е соотношениями е\{е^) — ^1р часто называют семейством,
дуальным к семейству (^). Пусть семейство {ег) образует базис
в Е\ если окажется, что семейство (eVj есть базис в Е* (это
всегда так в случае конечномерного £), то условимся говорить
о дуальных базисах в Е и £*. Это понятие симметрично относи-
относительно £ и Е* (см. п. Л.4.7, а также [X, § 15]).
B) Если векторное пространство £ конечномерно, то, как
это следует из предложения 1.4.6, пространства £ и £* изоморф-
изоморфны. Однако этот изоморфизм не является «каноническим», т. е.
он не определяется однозначно векторными структурами этих
пространств. Каждому базису (ег-) в £ соответствует свой изо-
изоморфизм и пространства £ на £*, определенный на базисе (ег)
равенствами и(е.} = е*. и затем линейно продолженный. Различ-
Различным базисам (в{) соответствуют, вообще говоря, различные изо-
изоморфизмы и. Выделение некоторого изоморфизма между £ и £*
на самом деле равносильно фиксации некоторой билинейной
формы на произведении £х£. Эта точка зрения лежит в основе
тензорной алгебры и классификации векторов и тензоров на
ковариантные и контрвариантные.
1.4.7. Вложение пространства Е в £** [X, § 14, 16]. Пусть £ —
векторное пространство над К. Алгебраическое сопряженное £*
также является векторным пространством, и можно говорить об
алгебраическом сопряженном ему пространстве £**. Если ка-
каждому х е £ поставить в соответствие линейную форму х** на
£*, определенную равенством
то получим каноническое линейное отображение х*->х** про-
пространства £ в £**. Это отображение взаимно однозначно, потому
что, как легко следует из теоремы 1.4.5, для каждого заданного
ненулевого элемента х е £ можно найти такую линейную форму
fe£*, что }(х)Ф0. Это позволяет отождествить элементы х и
*** и считать £ векторным подпространством в £**. В дальней-
дальнейшем мы без специальных оговорок будем считать элементы х
и х** совпадающими. В этом смысле пространство £ обычно
уже пространства £**; они, однако, совпадают, если £ конечно-
конечномерно,
76 Гл. 1. Векторные и топологические векторные пространства
В силу указанной симметрии часто пользуются более симме-
симметричным обозначением. Элементы пространства Е* обозначают
через х*,у*,...9 а вместо х*(х) пишут (х, х*). (У Халмоша
Аналогичная запись будет употребляться далее и в том слу-
случае, когда Е — топологическое векторное пространство, Е' — его
топологическое сопряженное.
1.4.8. Прямые суммы. Алгебраические дополнения [X, § 19,20].
Пусть Е — векторное пространство над /С, a L и М — его вектор-
векторные подпространства. Будем говорить, что пространство Е есть
(внутренняя) прямая сумма своих подпространств L и М, если
каждый элемент х е Е единственным образом представим в
виде
ae=L, be=M. A.4.2)
Это равносильно выполнению следующих условий:
{0}. A.4.3)
Если Е — прямая сумма подпространств L и М, то говорят, что
каждое из подпространств L и М есть алгебраическое дополне-
дополнение другого в Е (или относительно Е).
Из теоремы 1.4.5 непосредственно вытекает, что каждое век-
векторное подпространство в Е допускает по крайней мере одно
(вообще говоря, не единственное) алгебраическое дополнение.
Пусть выполнены соотношения A.4.3); тогда отображения
pL: x*-> а и рм: х^>Ь
принадлежат соответственно пространствам L{E,L)> и L(E, M),
причем
Рь + Рм=1 A.4.4)
где 1—тождественное отображение пространства Е на себя.
Кроме того, рь(х)=х тогда и только тогда, когда xgL, и
Рм(х)=х тогда и только тогда, когда х^М. Следовательно,
отображения pL и рм идемпотентны, т. е.
Р\ = Рь> Рм = Рм- A-4.4)
Таким образом, каждое из этих отображений является проекто-
проектором (т. е. линейным и идемпотентным отображением). Отобра-
Отображение pL называется проекцией пространства Е на подпростран-
подпространство L параллельно подпространству М.
Обратно, пусть р — проектор пространства Е. Обозначим че-
через L множество всех тех элементов х е Еу для которых р(х) =х\
тогда L есть векторное подпространство в Е. Отображение q =
= 1—р также является проектором пространства Е7 а множе-
1.4. Линейная зависимость 77
ство M = {xg£: <7 (*)=*} есть векторное подпространство в Е.
Для любого х е Е имеем
т. е. х — р(х)^М, следовательно, х = р(х) + q(x), так что
L M = E. Если далее х = р(х) =q(x)y то
x = p(x)=p(q(x))=p(x-p(x))=p(x)-p*(x)=O,
откуда следует, что £ГШ = {0}, значит, в силу A.4.3) простран-
пространство Е есть пряма сумма подпространств L и М. Легко про-
проверяется, что рь = р и pM = q>
1.4.9. Замечание. Мы показали, что каждое векторное
подпространство L в Е допускает дополнение и что это допол-
дополнение, вообще говоря, не единственно. Поэтому и проектор pL не
определяется однозначно подпространством L — нужно еще вы-
выбрать некоторое определенное дополнение М. Позже (в § 1.12)
мы увидим, что в пространстве Е со скалярным произведением
из всех дополнений к L естественно выделяется одно, а именно
ортогональное к L. Соответствующий проектор определяется
тогда однозначно подпространством L, как ортогональный про-
проектор. В общем случае такой выбор невозможен.
1.4.10. Несмотря на замечание 1.4.9, справедливо следующее
предложение.
► Пусть L — векторное подпространство векторного про-
пространства Е. Все его алгебраические дополнения в Е изо-
изоморфны, так как каждое из них изоморфно факторпро-
странству E/L.
Действительно, пусть E = L + M — прямая сумма. Из единст-
единственности разложения A.4.2) следует, что рм(х) зависит только
от класса эквивалентности хс элемента х по модулю L. Полагая
и(хс)=рм(х), получаем линейное отображение и факторпро-
странства E/L на М. Если и(хс)=0, то рм{х)=0, т. е. x e L и,
следовательно, хс есть нулевой элемент факторпространства E/L.
Таким образом, отображение и взаимно однозначно, поэтому и
есть изоморфизм E/L на М.
Замечание. Размерность факторпространства E/L назы-
называют коразмерностью (или факторразмерностью) подпростран-
подпространства L и обозначают через codimL.
1.4.11. Предложение. Пусть векторное пространство Е есть
прямая сумма векторных подпространств L и М. Тогда1)
A) dim Е = dim L + dim M,
1) Используемое- ниже понятие суммы кардинальных чисел определяется,
например, в книге Б у р б а к и [1]. — Прим. перев.
78 Гл. 1. Векторные и топологические векторные пространства
B) если dimL (соотв. dim E/L) конечно, то
dimE/L = dimE — dim! (соотв. dimL = dim£ — dim E/L).
Доказательство. A) Пусть (в*)/е/— базис в L. По тео-
теореме 1.4.5 его можно расширить до базиса (^)/е/ в £, где
/с/. Пусть М' — векторное подпространство в Е, порожденное
теми в\, для которых /g/\/. Легко видеть, что Е есть прямая
сумма L и М'. Из предложения 1.4.10 следует, что подпростран-
подпространства М и М' изоморфны и, следовательно, имеют одинаковую
размерность. С другой стороны, dim £ = card/, a card / = card /+,
+ card(/\/) = dim L + dim M' по определению размерности.
Итак, утверждение A) доказано.
B) Из предложения 1.4.10 вытекает, что dim£/L = dim M.
Это равенство дает возможность записать утверждение A) в
виде
dim Е = dim L + dim E/L.
Отсюда следует утверждение B). (Напомним читателю, что
с — п = с, если п — конечное, а с — бесконечное кардинальное
число.) |
1.4.12. Предложение. Пусть Е и F—векторные пространства
над К Если u^L(EyF)r то
dim Е = dim ker и + dim im и.
Доказательство. Обозначим через L подпространство
ker и. Известно (см. конец п. 1.3.2), что факторпространство
E/L изоморфно im и. Подпространство L допускает алгебраи-
алгебраическое дополнение М, которое также изоморфно E/L Из пред-
предложения 1.4.11 вытекает, что
dim£=dim L+dimAf = dimL + dim im a = dimker a + dim im a,
что и требовалось доказать. В
Замечание. Кардинальное число dim im u иногда назы-
называют рангом отображения и. В силу замечания следующего
ниже п. 1.4.13 можно сказать, что в предложении 1.4.12 содер-
содержится суть различных результатов, связанных с системами ли-
линейных уравнений и рангом соответствующих матриц.
1.4.13. Использование матриц для представления линейных
отображений. Пусть Е и F — векторные пространства над К и
ме L(EtF). Выберем в Е и F базисы (ei)i^I и (fj)fGJ соответ-
соответственно. Из основных свойств базисов и линейности отображе-
1.4. Линейная зависимость 79
ния и следует, что уравнение у = и(х) эквивалентно следующим
системам уравнений:
2
Числа at7 определяются по отображению и выбранным бази-
базисам с помощью следующих равенств:
и (et) = S atjff (i e= /).
Семейство (a£/)£€E//€E/,, являющееся элементом произведе-
произведения /CIXJ, обычно называют матрицей размера I X / (короче,
IXJ-матрицей), или матрицей с / строками и / столбцами. Если
card/ и card/ конечны и равны соответственно натуральным
числам m и п, то эта матрица записывается в виде следующей
прямоугольной таблицы:
и а12 ... аи
/тг1 а/тг2 • • • ат
Таким способом во всех случаях устанавливается взаимно
однозначное соответствие ^«->(at-j) между L(E,F) и всеми
/Х/-матрицами. Этот изоморфизм, разумеется, зависит от вы-
выбора базисов (е{) и (fj).
В случае, когда множества / и / конечны, это соответствие
часто используется при рассмотрении определенного круга за-
задач, необходимость решения которых вызвала к жизни целый
раздел алгебры (так называемую алгебру матриц). Ценность
этого метода заметно уменьшается, если / или / бесконечно. Тем
не менее если множества / и / счетны, то такие матрицы часто
используются при изучении линейных отображений пространств
последовательностей (см. Кук [1]). Подчеркнем, однако, что
указанный прием есть не что иное, как некоторое удобное согла-
соглашение для записи линейных отображений и манипуляций с ними.
Ни при каких обстоятельствах не следует отождествлять матри-
матрицы с линейными отображениями, потому что таким образом мы
лишаем первоначальное понятие линейного отображения его ло-
логического приоритета. Если бы существовало каноническое соот-
соответствие между линейными отображениями и матрицами, тогда
были бы еще какие-то основания для такого отождествления,
но такого канонического соответствия нет.
80 Гл. 1. Векторные и топологические векторные пространства
1.5. Поглощающие множества. Уравновешенные множества.
Выпуклые множества
Всюду в этом параграфе под Е понимается векторное про-
пространство над К.
1.5.1. Поглощающие множества. Множество S с Е называет-
называется поглощающим, если для каждого х^Е существует такое ве-
вещественное число а > 0, что ах е S. (Это определение несколько
отличается как от определения Бур баки [7, стр. 26], так и от
определения Тэйлора [1, стр. 24]. Однако в самом важном
случае, когда множество S выпукло и уравновешено (см. ниже),
все эти определения совпадают.)
1.5.2. Уравновешенные множества. Множество МаЕ назы-
называется уравновешенным, если ах ^ М для каждого х е М и ка-
каждого числа а е К, удовлетворяющего неравенству |а|^1
(Бур баки [7, стр. 25], Тэйлор [1, стр. 123]).
Так как пересечение уравновешенных множеств есть снова
уравновешенное множество, то для каждого множества в Е су-
существует наименьшее содержащее его уравновешенное множе-
множество в Е; оно называется уравновешенной оболочкой заданного
множества. Уравновешенная оболочка множества АаЕ есть не
что иное, как множество {ах: ае/С, |а| -^1, х^А}.
Заметим, что всякое уравновешенное множество содержит 0.
1.5.3. Выпуклые множества. Множество SaE называется
выпуклым, если A—а)х + <ху е S для всех x,y^S и для всех
а, удовлетворяющих неравенствам 0<1а<1. Пересечение вы-
выпуклых множеств есть выпуклое множество. Следовательно, для
каждого множества A cz E существует наименьшее содержащее
его выпуклое множество в Е. Оно называется выпуклой оболоч-
оболочкой множества Л. Выпуклая оболочка пустого множества также
пуста. Выпуклая оболочка множества А состоит из всех конеч-
конечных сумм вида 2 tyXj, гДе ^ — произвольные элементы из Л,
сс;<=[0, 1] и 2а*= 1.
i
Образ и прообраз выпуклого множества относительно ли-
линейного отображения также выпуклы.
Отметим, что выпуклая оболочка уравновешенной оболочки
множества А есть наименьшее выпуклое уравновешенное мно-
множество, содержащее Л; оно называется абсолютно выпуклой обо-
оболочкой множества Л. Абсолютно выпуклая оболочка множества
Л состоит из всех конечных сумм вида 2 «Л> где xt ^ Л, с^ ^ /С
1.6. Калибровочные функции и полунормы 81
Изучение свойств описанных здесь множеств облегчается,
если ввести в рассмотрение соответствующие вещественные
функции на £, служащие «уравнениями» этил множеств.
1.6. Калибровочные функции и полунормы
В настоящем параграфе под Е понимается векторное про-
пространство над К.
1.6.1. Калибровочная функция. Калибровочной функцией на
Е называют вещественную функцию g на Е, удовлетворяющую
следующим условиям:
g(x+y)<g(x)+g(y), A.6.1)
g(ax) = ag(x) A.6.2)
для произвольных х j g £ и любых вещественных чисел а ^ 0.
Очевидно, что g@)=0.
1.6.2. Полунормы. Калибровочная функция р на Е назы*
вается полунормой на Е, если для нее равенство A.6.2) выпол-
выполнено в усиленном виде
р{ах) = \а\р{х) A.6.2')
для любых xg£ и йроизвольных скаляров ос. Из справедливо-'
сти соотношения
следует, что полунорма принимает лишь неотрицательные зна-
значения.
Отметим также, что
\р(х)-р(у)\<р(х-у). A.6.3)
Опираясь на соотношения A.6.1) и A.6.2*), можно доказать
по индукции справедливость неравенства
A.6.4)
для любых %i^i E и щ е К.
1.6.3. Нормы. Полунорма р называется нормой на £, если
р{х) >0 для каждого хФО из Е. Норма элемента х обычно
обозначается через ||лс||. Для того чтобы отличать различные
нормы друг от друга, используются подстрочные индексы (на-
(например, Ы, и т. п.).
Мы покажем сейчас, каким образом калибровочные функ-
функции и полунормы служат для описания различных видов вы-
выпуклых множеств в Е.
82 Гл. 1. Векторные и топологические векторные пространства
1.6.4. Теорема. Пусть А— выпуклое поглощающее множе-
множество в Еу содержащее 0. Вещественная функция g на £, опре-
определенная равенством
сГ1*^}, A.6.5)
является положительной калибровочной функцией на Е и обла-
обладает следующими свойствами:
A) {хе=Е: g(x)<\}<=A,
B) Лс= {xe=£: g(*)<l}.
Обратно, если g — положительная калибровочная функция на
£, то каждое из множеств {х^Е: g(x)< I}, {xg£: g^(jc)^ 1}
является выпуклым и поглощающим и содержит 0.
Доказательство. Последнее утверждение тривиально в
силу условий, определяющих калибровочную функцию (п. 1.6.1),
Для доказательства остальных утверждений заметим, что
если множество А поглощающе, то множество {а > 0: a~!x G Л}
непусто. Следовательно, g(x) определено, а g(x)^>0. Из A.6.5)
непосредственно следуют соотношения A.6.2) и в силу выпук-
выпуклости множества А A.6.1).
Если g(x) < 1, то существует такое число а, что 0<а<1
и rtsl Так как 0е/1 и Л выпукло, то х = а(аг1х) + A —
— «HеА С другой стороны, если ^еД то а~хх^А при
а=1, следовательно, g(*);<l, что'и завершает доказатель-
доказательство. |
Функция g, определенная на Е равенством A,6.5), назы-
называется функционалом Минковского выпуклого поглощающего
множества А.
1.6.5. Доказанная теорема может быть дополнена следую-
следующим образом. Условимся говорить, что множество AczE от-
крыто (соответственно замкнуто) по лучам, если для каждого
элемента х^Е множество /х = {а>0: а~хх^А) открыто (соот-
(соответственно замкнуто) относительно интервала /=@, +оо). То-
Тогда верно следующее утверждение.
1.6.6. Следствие. Пусть А — выпуклое поглощающее множе-
множество из Еу содержащее 0, и g — его функционал Минковского.
Если множество А открыто (соответственно замкнуто) по лу-
лучам, то оно совпадает с множеством {xg£: g(x) < 1} (соот-
(соответственно {xe£: g(*)-^l})- В обоих случаях множество А
уравновешено тогда и только тогда, когда g — полунорма на Е.
Доказательство. Предположим, что множество А от-
открыто по лучам. Из теоремы 1.6.4 известно, что {х^Е: g(x) <
<l}cz А. Пусть теперь х^А, Тогда 1 е/^, и так как /* откры-
1.7. Аналитическая форма теоремы Хана — Банаха 83
то относительно /, то в 1Х найдется такое число а, что 0<а<
<1. Но тогда g(x) -<а<1. Таким образом, А={х<=Е:
g(x) < 1}.
Допустим, что А замкнуто по лучам. Известно, что A cz
cz{x^E: g{x)<^l}. Остается показать, что всякий элемент
х е £, удовлетворяющий условию а = g(x) •< 1, обязан при-
принадлежать множеству А. Рассмотрим два случая. Первый —
когда g(x) = 0. Тогда g(x) < 1 и из теоремы L6.4 следует, что
х^А. Второй — когда 0<£(л:)=а^1. Тогда в множестве 1Х
существует последовательность (ап), сходящаяся к а. Так как
ае/ и 1Х замкнуто относительно /, то а^1х. Из выпуклости
множества А следует, что
х = а(аГ1х) + A - аH & А,
что и требовалось доказать.
Если g — полунорма, то, как легко видеть, множества
{Е: g(x) < 1} и {xg£: g(#)-<П} уравновешены. Докажем
АЕ }
{ g() { g()} ур
обратное. Пусть А={х^Е: £(#)<!}, где g — положительная
калибровочная функция на Е. Нужно показать, что если А —
уравновешенное множество, то g—полунорма. Пусть х^Е и
е>0. Тогда (g{x) +г'х)х^А. Так как А — уравновешенное
множество, то . д ., аЛ , е А для а ф 0, а е К.
Поэтому
g(ax)<\a\(g(x) +e),
откуда в силу произвольности е вытекает, что
g(ax)<\a\g(x)
для любого числа а Ф 0.
Заменяя в последнем неравенстве а на а (а ф 0) и х на
ах, получаем
g{ax)> |a|g(*).
Таким образом, для всякого числа афО справедливо ра-
равенство g(ax) = |а|^(л:). Если же а == 0, то обе части равен-
равенства обращаются в нуль; следовательно, оно верно для всех
без исключения а, и функция g есть полунорма. В случае, ко-
когда А = {х^Е: g(x)^l}, доказательство аналогично. I
1.7. Аналитическая форма теоремы Хана —Банаха
Эта теорема вместе со своими многочисленными следствия-
следствиями является одним из центральных результатов функциональ-
функционального анализа. Здесь приводится одна из ее наиболее общих
форм, так называемая «аналитическая» форма, в отличие от
84 Гл. 1. Векторные и топологические векторные пространства
«геометрической» формы, приводимой в гл. 2. Теорема Хана—■
Банаха в аналитической форме справедлива для любого век-
векторного пространства, наделенного некоторой, калибровочной
функцией.
1.7.1. Теорема. A) Пусть Е — вещественное векторное про-
пространство, р — калибровочная функция на Е, L — векторное
подпространство в Е и f0— линейная форма на L, удовлетво-
удовлетворяющая неравенству
fo(x)<p(x) (*g=I). A.7.1)
Тогда существует такая линейная форма fe£*, что
f(x) = h(x) (jcsL), A.7.2)
f(x)^p(x) (*e£). A.7.3)
Если р — полунорма на Е, то неравенства A.7.1) и A.7.3) эк-
эквивалентны соответственно неравенствам
IfoWKpW ИД A.7. Г)
I/WKPW (*е=£). A.7.3*)
B) Если Е — комплексное векторное пространство, р — по-
полунорма на Е, a L и fo те же, что ив A), то справедливо ана-
аналогичное утверждение, получающееся заменой A.7.1) и A.7.3)
на A.7.1*) и A.7.3*) соответственно.
До ка з а те л ьство. Эквивалентность A.7.п) и A.7.м*) при
п = 1, 3 очевидна. Докажем сначала утверждение A), а затем
выведем из него B).
A) Применим лемму Цорна (п. 0.1.5) к множеству F всех
линейных форм f, для которых domf есть векторное подпрост-
подпространство в £, содержащее подпространство L, причем f\L = f0
и fKp на domf. По условию fo^F. Упорядочим множество F
следующим образом: запись f^Cg означает, что g есть продол-
продолжение f, т. е. domgZDdomf и g\domf = f. Легко проверяется,
что множество F индуктивно упорядочено. Раз это так, то из
леммы Цорна следует существование в F максимального эле-
элемента. Пусть f—максимальный элемент в F. Предложенное
Банахом [1, стр. 24—25] доказательство, которое мы сейчас
воспроизведем, показывает, что f обладает всеми требуемыми
свойствами. В действительности нужно лишь установить, что
domf = Е.
Допустим противное, т. е. что domf ф Е, и выберем элемент
Хо е £\dom f. Если л/, х" е dom f, то
/ (х") - f (*0 = / (*" - *0 < р {х" -х') = р \{х" + х0) + (- ^ - л:0)] <
1.7. Аналитическая форма теоремы Хана — Банаха 85
поэтому
Следовательно, числа
{— р( — х — лг0) — f{x):
Л = inf {p {x + xo) — f {х): х ^ dom /}
конечны, и ^4Л. Возьмем произвольное вещественное число у,
такое, что ^<у^Л. Тогда для любого x^domf имеем
p(x + xo)-f(x). A.7.4)
Положим M = Rx0+domf и определим форму /' на М с по-
помощью равенства
Г (х + Ш = /(*) + yl (x е= dom/, g e= R).
Очевидно, /' является линейной формой с областью опреде-
определения М id dom/ id L. Если теперь будет показано, что /' е Z7,
то максимальность / придет в противоречие с тем фактом, что
dom/ есть собственная часть М. Так как //|doin/ = /, то остается
проверить, что Г-</?. Если при 1Ф0 в A.7.4) заменить х на
1~1х, то получим
При £>0 из правой части этого неравенства следует, что
а при I < 0 из левой части вытекает, что
Итак, в обоих случаях имеем
f(*) +y£<p(* + £*o).
При | = 0 последнее неравенство очевидно. Таким образом,
У {х + &0) <р(х + 1х0) (х е dom/, £ ^ R),
т. е, f'Kp на М, что и завершает доказательство утвержде-
утверждения A).
B) Боненблуст и Собчик [1] показали, что утвержде-
утверждение B) следует из A) *). Пусть fo = uo + ivOy где и0 и v0 —
1) Независимо от них этот результат был получен Г. А. Сухомлиновым
(О продолжении линейных функционалов в комплексном и кватернионном
линейном пространстве, Матем, сб.., 3D5) A938), 353—358.). — Прим. перев.
86 Гл. 1. Векторные и топологические векторные пространства
вещественные линейные относительно вещественных скаляров
формы на L. Так как fo(ix) =ifo{x), то vo(x) =—uo(ix) и
fo(x) =uo{x) —iuo(ix).
Из A.7.1*) следует, что \ио(х)\ ^Ср(х) при всяком x^L. На
основании A) ио(х) можно продолжить до вещественной ли-
линейной (относительно вещественных скаляров) формы и на Е%
удовлетворяющей условию |м|<^р. Положим
f(x) = и(х)—iu(ix).
Тогда f является комплексной линейной формой на Е и /|L =
=/о. Остается показать, что выполняется неравенство A.7.3*).
Если х^Е и f(x) = reu (r^>Q,t вещественно), то
I / (х) I = e-»f (х) = f (е-«х) - Re / (е-"х) - и (е-"«х) <
что и требовалось доказать.
Теорема, таким образом, полностью доказана. I
1.7.2. Следствие (Хан [2]). Пусть Е — векторное простран-
пространство над К, р — полунорма на Е, L — векторное подпростран-
подпространство в Е, х0 е Е и
6 = inl{p(xo + у): уеД
Тогда на Е существует линейная форма f, удовлетворяющая
условиям
/
1.7.3. Систематическое изучение других следствий из теоре-
теоремы 1.7.1, относящихся к топологическим векторным простран-
пространствам, отложим до гл. 2. В ней и отчасти в гл. 3 будут даны
некоторые приложения и обобщения теоремы 1.7.1.
1.8. Топологические векторные пространства
Понятие топологического векторного пространства, к кото-
которому мы сейчас переходим, возникает при объединении поня-
понятий векторного и топологического пространств (§ 0.2) при ус-
условии, что эти структуры так взаимосвязны, что алгебраические
операции непрерывны.
1.8.1. Определение топологического векторного простран-.
ства. Под топологическим векторным пространством1) пони-
1) Приняты также термины топологическое линейное пространство и ли-
линейное топологическое пространство^ —■ Прим, перев%
1.8 Топологические векторные пространства 87
мается векторное пространство Е над /С, снабженное такой то-
топологией £, что непрерывны отображения1)
A) (х, у)*~->х + у произведения Е X Ев Е
и
B) (а, х) н-> ах произведения К X Е в Е.
Определенное таким образом топологическое векторное про-
пространство можно обозначать, например, символом (Е, £).
В действительности этим символом мы будем пользоваться,
если придется рассматривать одновременно несколько тополо-
топологических векторных пространств, полученных наделением данного
векторного пространства Е различными линейными тополо-
топологиями. В тех случаях, когда из контекста ясно, какой топологией
наделено векторное пространство £, мы будем обозначать
просто через Е и рассматриваемое топологическое вектор-
векторное" пространство. Прежде чем перейти к примерам, перечист
лим несколько почти очевидных следствий приведенного выше
определения.
1.8.2. Замечания. A) Возьмем произвольный, но фикси-
фиксированный элемент а^Е. Отображение х^-^х + а (сдвиг на а)
обладает обратным отображением хъ—>х—я. Следовательно, в
топологическом векторном пространстве каждый сдвиг являет-
является гомеоморфизмом этого пространства на себя. Поэтому его
топология вполне определяется системой окрестностей нулево-
нулевого элемента.
B) Условие A) п. 1.8.1 эквивалентно требованию непрерыв-
непрерывности сдвигов и непрерывности в точке @,0) отображения
(х,у)*->х + у.
C) Возьмем произвольное, но фиксированное число афО.
Отображение х^-^ах (гомотетия с коэффициентом а) обладает
обратным отображением хь—>а~1х. Следовательно, в топологи-
топологическом векторном пространстве каждая гомотетия с отличным
от нуля коэффициентом является гомеоморфизмом простран-
пространства на себя. Так как
ах - аохо = (а - а0) х0 + а0 {х - х0) + (а - а0) (х - х0),
то условие B) п. 1.8.1 эквивалентно требованию раздельной
непрерывности по каждой из переменных произведения ах и
непрерывности по обеим переменным этого произведения в точ-
точке @,0).
*) Топологию % в векторном пространстве Е, при которой непрерывны
отображения A) и B), мы будем иногда называть линейной топологией.—
Прим. перев.
88 Гл. 1. Векторные и топологические векторные пространства
D) Линейная топология векторного пространства может и
не быть отделимой, однако если это пространство является
Тгпространством (или даже 7^-пространством), то она отдели-
отделима. Действительно, пусть топологическое векторное простран-
пространство Е есть Го-пространство и хФу. Тогда существует окрест-
окрестность одной из этих точек, например точки х, не содержащая
другой точки, т. е. у. Как было установлено выше, сдвиг яв-
является гомеоморфизмом, поэтому существует такая окрестность
нуля (У, что у не принадлежит х + U. Так как вычитание х — у
непрерывно, то существует такая окрестность нуля V, что
V— V a U. Тогда множества х + V и у + V являются непере-
непересекающимися окрестностями точек х и у соответственно. Таким
образом, отделимость доказана. Ниже мы покажем, как с каж-
каждым неотделимым топологическим векторным пространством
можно естественным образом связать такое же отделимое про-
пространство.
E) Во всяком топологическом векторном пространстве Е
существуют (а) база окрестностей нуля, состоящая из уравно-
уравновешенных открытых множеств и (Ь) база окрестностей нуля,
состоящая из уравновешенных замкнутых множеств.
Действительно, как и во всяком топологическом простран-
пространстве, в Е существует база окрестностей нуля, состоящая из от-
открытых множеств. Пусть U — некоторая окрестность нуля. Из
непрерывности в точке @,0) отображения B) п. 1.-8.1 следует
существование такого числа е > 0 и такой открытой окрестно-
окрестности нуля V, что ахе U, если |а| ^е и хеУ. Пусть W —
уравновешенная оболочка множества eV (п. 1.5.2). Так как
множество V открыто, из непрерывности отображений A) и B)
п. 1.8.1 легко вытекает, что множество W открыто. Кроме того,
очевидно, что WaU; утверждение (а), таким образом, дока-
доказано.
Чтобы убедиться в справедливости утверждения (Ь), возь-
возьмем произвольную окрестность нуля U и покажем сначала, что
существует замкнутая окрестность нуля У, содержащаяся в U.
Из непрерывности отображений A) и B) п. 1.8.1 вытекает не-
непрерывность вычитания (х, у) у—>х — у в точке @,0). Следова-
Следовательно, можно найти такую окрестность нуля U\ что V— f/'cz
с: I). Тогда замыкание U' = V удовлетворяет нашим условиям.
Отсюда вытекает, что замкнутые окрестности нуля образуют
базу.
Как и при доказательстве утверждения (а), можно так по-
подобрать число е > 0 и окрестность нуля V\ чтобы уравнове-
уравновешенная оболочка множества eV\ которую мы обозначим через
W, содержалась в V. Множество W является_^равновешенной
окрестностью нуля. Так как V замкнуто, то W а V. Остается
1.8. Топологические векторные пространства 89
доказать, что замыкание W уравновешено, когда уравновеше-
уравновешено множество W. Пусть TV — окрестность нуля. Выберем (как
и при доказательстве утверждения (а)) окрестность нуля Л/',
уравновешенная оболочка которой содержится в ЛЛ
Если x^Wy то окрестность х—N' пересекает множество
W, т. е. #<= W + N'. Поэтому для |а|< 1 имеем
(множество W уравновешено). Так как это соотношение спра-
ведливо_для каждой окрестности нуля N, то ах е W> т. е. мно-
множество W уравновешено.
F) Из непрерывности отображения B) п. 1.8.1 непосред-
непосредственно следует, что в топологическом векторном пространстве
каждая окрестность нуля есть поглощающее множество.
«Прямая» часть следующего предложения вытекает из при-
приведенных здесь замечаний.
1.8.3. Предложение. В каждом топологическом векторном
пространстве Е над К существует база оЛ^ окрестностей нуля,
обладающая следующими свойствами:
A) каждое множество U е оЛГуравновешено ипоглощающе;
B) если U e J\T, aei(Ma^0, гоаУе ЛГ\
C) если U е= оЛГу то существует V ^ о#*, такое, что V + VczU;
D) если Uu U2^q4^9 to существует C/Gef, такое, что
Обратно, если в векторном пространстве Е над К задана
система подмножеств q/V9, удовлетворяющая условиям A) — D),
то существует одна и только одна такая топология % в Е, что
система оЛГ является базой окрестностей нуля, а (Е, X) есть
топологическое векторное пространство над /С.
Доказательство. Достаточно рассмотреть только «об-
«обратную» часть предложения. Единственность топологии £,
если она существует, следует из того, что в топологическом век-
векторном пространстве базу окрестностей всякой точки х можно
получить сдвигом на вектор х множеств, принадлежащих базе
окрестностей нуля (см. A) п. 1.8.2). С другой стороны, если
топология 2 определена указанным образом, то из свойств
A) — D) легко следует непрерывность отображений A) и B)
п. 1.8.1.1
1.8.4. Примеры. Приведем некоторые простые примеры то-
топологических векторных пространств, которые в дальнейшем
позволят нам построить с помощью ряда общих методов дру-
другие топологические векторные пространства.
A) Рассмотрим функциональное пространство /Ст, описан-
описанное в примере 1.1.1. Вначале будем считать, что Т — произволь-
произвольное множество.
90 Гл. 1. Векторные и топологические векторные пространства
Каждому конечному подмножеству F cz T и каждому числу
е>0 поставим в соответствие множество U(F, e)cz/(T, содер-
содержащее те и только те элементы х е Кт, для которых число
pF(x) = sup{|*(/)|: tezF]
удовлетворяет неравенству pF(x)<e. Легко проверяется, что
множества U(F, г) (где F и е изменяются независимо друг от
друга) удовлетворяют условиям предложения 1.8.3. Соответст-
Соответствующую линейную топологию в Кт часто называют топологией
поточечной (или простой) сходимости на Т. Это не что иное,
как топология произведения. Читатель заметит, что каждая
функция pF является полунормой на /Ст.
Ряд других примеров можно получить, переходя к вектор-
векторным подпространствам в Кт и наделяя их соответствующей ин-
индуцированной топологией.
B) Можно попытаться обо8щить пример A), заменяя си-
систему конечных подмножеств в Т некоторой другой системой
его подмножеств. Ес'ли пользоваться лишь конечными множе-
множествами, то получаемое пространство всегда будет векторным
топологическим, топология которого, вообще говоря, может ока-
оказаться неотделимой. Если же включить в рассмотрение и бес-
бесконечные подмножества Г, то в полученной топологии простран-
пространство Кт может не быть топологическим векторным простран-
пространством1). Так, например, если найдется хотя бы одна функция
х е Кт, неограниченная на некотором множестве F выбранной
системы, то условие ах-^О при а->0 не будет выполняться.
Это затруднение можно обойти, если рассмотреть в Кт под-
подпространство, скажем £, состоящее из тех функций х^Кт,
которые ограничены на каждом множестве F выбранной си-
системы.
Пусть, например, наша система содержит только одно мно-
множество— само Т. Тогда в качестве Е следует взять подпро-
подпространство в Кт, состоящее из всех ограниченных на Т функ-
функций. Мы будем обозначать это подпространство через В(Т)
или Вк(Т). Соответствующую топологию обычно называют
топологией равномерной сходимости на Т. Другие примеры
приводятся ниже, в пункте D).
C) Пусть Т — конечное множество. Тогда КТ = В(Т) (как
векторные пространства)-.' При этом, конечно, поточечная и рав-
равномерная сходимости совпадают. Если Т содержит п элемен-
элементов, то эта топология совпадает с обычной метрической топо-
топологией в Кп.
1) Однако при этом пространство Кт все Же может оказаться тополо*
гической группой относительно сложения.
18. Топологические векторные пространства 91
D) Рассмотрим теперь случай, когда Г — топологическое
пространство. Через С(Т) или СК(Т) будем обозначать век-
векторное подпространство в /Ст, образованное всеми непрерыв-
непрерывными /(-значными функциями на Т.
Если Т — компактное пространство, то С(Т)—векторное
подпространство в В(Т), и поэтому С(Т) можно топологизи-
топологизировать как подпространство в В(Т) (см. B)).
Если пространство Т не является компактным, то С(Т)
можно топологизировать с помощью системы всех компактных
множеств F аТ. В этой топологии, называемой топологией ком-
компактной (или локально равномерной, если Т — локально ком-
компактное пространство) сходимости на Т, а также компактно
открытой топологией, база окрестностей нуля состоит из мно-
множеств вида U(F,s), где F пробегает систему всех компактных
множеств в Т (или базу таких множеств), а е— строго поло-
положительные числа. Независимо от того, является ли Т компакт-
компактным пространством или нет, пространство Съа{Т) всех непре-
непрерывных, ограниченных функций на Т можно топологизировать
как подпространство в В(Т).
В гл. 4 и 5 мы займемся изучением других подобных при-
примеров.
E) Все предыдущие примеры можно обобщить, рассмотрев
функции, принимающие значение не в /(, а в произвольном то-
топологическом векторном пространстве X над К. Читателю пре-
предоставляется проделать это самостоятельно.
F) Пусть Т — интервал @,1) вещественной оси и р — ве-
вещественное число, р > 0. Через J?p обозначим множество всех
таких вещественных измеримых функций х на Т, что функция
\x\v интегрируема по Лебегу на интервале @,1). (Читатель,
не знакомый с понятием интеграла Лебега, может в этом при-
примере ограничиться непрерывными функциями. Подробное из-
изложение теории интегрирования дано в гл. 4.) Пусть Dv — по-
полуметрика на J^pt определенная равенством
Пространство <S>V, наделенное соответствующей этой полумет-
полуметрике топологией, является топологическим векторным простран-
пространством. Очевидно, Dp(x,y)=Np(x — у), где
1
f l 1
92 Гл. 1. Векторные и топологические векторные пространства
При /?>1 Np есть полунорма на J^v. При 0</?<1 это уже
не так.
G) Снова рассмотрим вещественные функции на интер-
интервале Т= @,1)- Обозначим через \х меру Лебега на веществен-
вещественной оси и зададим произвольно числа а > 0 и р > 0. Под £/а, р
будем понимать множество тех функций х е RT, для которых
ji-мера множества {/еГ: |*(/)|>а} не превосходит р. Мно-
Множества Ua, p можно взять в качестве базы окрестностей нуля
для некоторой топологии £ в RT. Окрестности всякой другой
точки х из RT могут быть получены с помощью сдвига. Таким
образом множество RT превращается в топологическое вектор-
векторное пространство. Топологию Z иногда называют топологией
сходимости по мере на Т.
Мы переходим теперь к некоторым общим методам, позво-
позволяющим из данных топологических векторных пространств по-
получать другие такие пространства.
1.8.5. Подпространства. Произведение пространств. Фак-
торпространства. Пусть L — векторное подпространство топо-
топологического векторного пространства Е. Подпространство L,
наделенное индуцированной топологией, очевидно, само есть
топологическое векторное пространство.
Пусть (Ei)iei — семейство топологических векторных про-
пространств и £= ЦБ,-— произведение векторных пространств
is/
(п. 1.2.5). Пространство £, наделенное произведением тополо-
топологий (п. 0.2.15), само становится топологическим векторным про-
пространством. Если, например, Е = К (рассматриваемому как то-
топологическое векторное пространство над К с обычной топо-
топологией) и / = Г — произвольное множество, то соответствующее
произведение является не чем иным, как пространством Кт с
топологией поточечной сходимости на Т (см. пример A)
п. 1.8.4).
Обратимся к факторпространствам. Пусть Е — топологиче-
топологическое векторное пространство и L — это векторное подпростран-
подпространство. Образуем факторпространство E/L (п. 1.2.3). Если E/L
наделить фактортопологией (п. 0.2.16), то получится топологи-
топологическое векторное пространство, называемое факторпростран-
стволе'пространства Е по подпространству L. Обозначим через
хс класс эквивалентности по подпространству L, содержащий
элемент х, а через / каноническое отображение х>—>хс про-
пространства Е на E/L. Отображение f линейно. Фактортопология
в E/L, как известно, сильнейшая из топологий, при которых f
непрерывно. База окрестностей нуля в E/L образуется теми
множествами WaE/L, для которых множества f~l{W) яв-
являются окрестностями нуля в Е.
/ 8 Топологические векторные пространства 93
Часто оказывается полезным следующее утверждение.
► Если множества (£/,-) образуют базу окрестностей нуля
в Е, то множества Wi = f(Ui) образуют базу окрестно-
окрестностей нуля в E/L.
Действительно, так как f~l(W{) zd £/г-, то W{ есть окрест-
окрестность нуля в факторпространстве. С другой стороны, пусть
W—некоторая окрестность нуля в E/L, тогда £/—f~l(W) яв-
является окрестностью нуля в Е. Следовательно, для некото-
некоторого i имеем Ui с= U. Так как f отображает Е на E/L, то
Отсюда следует, что множества W{ образуют базу окрестно-
окрестностей нуля, что и требовалось доказать.
Другими словами, естественное отображение f простран-
пространства Е на E/L открыто, или в терминологии § 1.9 естественное
отображение является гомоморфизмом топологического вектор-
векторного пространства Е на топологическое векторное простран-
пространство E/L.
Независимо от того, будет ли пространство Е отделимым
или нет, факторпространство E/L отделимо тогда и только
тогда, когда подпространство L замкнуто в Е. Действительно,
естественное отображение / пространства Е на E/L непре-
непрерывно, и подпространство L является его ядром. Далее про-
пространство E/L (как и всякое топологическое векторное про-
пространство) отделимо тогда и только тогда, когда его нулевой
элемент есть замкнутое множество. Таким образом, если E/L —
отделимое пространство, то подпространство L = kerf само зам-
замкнуто в Е как прообраз замкнутого множества при непрерыв-
непрерывном отображении.
Так как f(E\L) = (EIL)\f(L), то из замкнутости подпро-
подпространства L следует замкнутость f(L) в E/Lt a f(L) совпадает
с одноэлементным подмножеством в E/L, состоящим из од-
одного нуля.
Если пространство Е не отделимо, то можно получить от-
отделимое факторпространство E/L с помощью некоторого зам-
замкнутого подпространства L из Е. Естественно сделать это так,
чтобы отождествлялось возможно меньше различных элемен-
элементов из £, для чего .надо взять L возможно меныиим._Очевидно,
что наименьшее замкнутое_подпространство L равно {0}. По этой
причине пространство £"/{0} называется отделимым топологиче-
топологическим векторным пространством, ассоциированным с Е.
1.8.6. Уравновешенные и выпуклые множества в топологи-
топологических векторных пространствах. Рассмотрим некоторые по-
понятия, введенные в § 1.5 для векторных пространств, примени-
применительно к топологическим векторным пространствам.
94 Гл. 1, Векторные и топологические векторные пространства
Читатель может проверить, что в топологическом вектор-
векторном пространстве замыкание подпространства (соответственно
выпуклого множества, уравновешенного множества) является
множеством того же типа. Таким образом, замыкание ли-
линейной (соответственно выпуклой, уравновешенной) оболочки
всякого множества А в топологическом векторном простран-
пространстве Е — это наименьшее замкнутое подпространство (соот-
(соответственно замкнутое выпуклое множество, замкнутое урав-
уравновешенное множество) в Е, содержащее А. Мы называем
их соответственными замкнутыми оболочками множества
А в Е.
Заметим также, что всякая гиперплоскость в Е либо зам-
замкнута, либо всюду плотна (вследствие ее максимальности;
см. п. 1.2.6).
Рассмотрение топологий требует некоторых дополнений к
§ 1.3 и 1.4. Эти дополнения будут даны в § 1.9. В дальнейшем
нам понадобится одно новое понятие, определением которого
мы сейчас займемся.
1.8.7. Ограниченные множества в топологическом векторном
пространстве. Множество В в топологическом векторном про-
пространстве Е называется ограниченным, если для каждой ок-
окрестности нуля U в Е существует такое число а>0, что
BaaU.
Читатель может заметить, что для подмножеств простран-
пространства Кп понятия ограниченности и ограниченности по метрике
совпадают.
Отметим следующие два свойства ограниченных множеств.
A) Замкнутая уравновешенная оболочка ограниченного мно-
множества В также ограничена.
B) Объединение и векторная сумма конечного числа огра-
ограниченных множеств являются ограниченными множествами.
Утверждение A) непосредственно вытекает из замечания A)
п. 1.8.2. Следует предупредить читателя, что если пространство
Е не локально выпукло (§ 1.10), то выпуклая оболочка ограни-
ограниченного множества может и не быть ограниченной.
Что касается утверждения B), рассмотрим, например, век-
векторную сумму В = В'+В" двух ограниченных множеств В' и
В". Для заданной окрестности нуля U выберем (см. предложе-
предложение 1.8.3) такую уравновешенную окрестность нуля V, что
V+VaU. Из ограниченности В' и В" следует существование
таких чисел а', а">0, что B'aa'V, В"cz a"V. Полагая а =
= тах (а', а"), имеем Ва aV + aVcz a(V+ V) a at/, т. е. мно-
множество В ограничено.
Наконец, очевидно, что всякое конечное множество ограни-
ограничено.
1.8. Топологические векторные пространства 95
1.8.8. Примеры. Подмножество В пространства Кт ограни-
ограничено тогда и только тогда, когда при каждом /еГ ограничено
множество {|л;(/) |: ^gB}, т. е. если
sup{|*@|: xeeB}< +оо
для каждой точки /£Г. В пространстве В(Т) (пример B)
п. 1.8.4) множество ограничено тогда и только тогда, когда оно
равномерно ограничено, т. е. когда
sup{|jt(/) |: х<=В, /gJ1} < +оо.
1.8.9. Топологические векторные пространства как равномер-
равномерные пространства. Каждое топологическое векторное простран-
пространство Е можно наделить равномерной структурой (п. 0.3.1), у
которой база окружений диагонали А в ЕхЕ образована множе^
ствами вида A(U) ={(х, у): х — j/6 £/}, где U пробегает некото-
некоторую базу окрестностей нуля в Е. Таким образом, линейная то-
топология в Е однозначно порождает в Е равномерную структуру.
Поэтому не представляет большой опасности смешение тополо-
топологии топологического векторного пространства и его равномерной
структуры, и можно говорить о полноте топологического вектор-
векторного пространства. Вообще всякое понятие, относящееся к рав-
равномерной структуре (полнота, равномерная непрерывность
и т. д.), относится и к топологическим векторным пространствам.
1.8.10. Пополнение топологического векторного пространства.
Рассмотрим сначала случай, когда топологическое векторное
пространство Е отделимо. Как и для всякого отделимого равно-
равномерного пространства, для Е можно (п. 0.3.12) построить такое
полное равномерное пространство Е, что существует взаимно од-
однозначное отображение i: £->£, являющееся изоморфизмом
равномерного пространства Ё на плотное равномерное подпро-
подпространство i(E) в Ё. Более того, пространство Е однозначно с
точностью до изоморфизма определяется этими условиями (как
равномерное пространство).
Напомним следующую более или менее конкретную реали-
реализацию пространства Е. Точками в Е являются классы эквива-
эквивалентных сетей Коши, составленных из точек пространства £",
причем две такие сети Х= (л:*) и У= (t/j) эквивалентны, если для
всякой окрестности нуля U в Е и любых индексов i0 и /0 суще-
существуют такие индексы / ^ /о и / ^/о, что лгг- — Uj^U. Таким об-
образом, множество Е строится как фактормножество (f/R, где
е — множество всех сетей Коши Х=(Х{) из £, a R — указанное
отношение эквивалентности, Е= £*//?. Равномерная структура
в ^ вводится с помощью базы окружений диагонали, состоящей
из множеств вида W(U), где U пробегает базу окрестностей
96 Гл. 1. Векторные и топологические векторные пространства
нуля в £, a W(U)—множество таких пар (X, У) (Х=(х{)',
Y^ilh)—сети Коши в £), что Xi — t/j^U для произвольно
больших (и, следовательно, для всех достаточно больших) ин-
индексов i и /. Образы множеств W(U) при каноническом отобра-
отображении ef на &IR определяют базу окружений диагонали в рав-
равномерной структуре в Е.
Если Е — векторное пространство, то Е можно обычным об-
образом наделить векторной структурой. Обозначим, например, че-
через X+Y сеть (Xi + tjj) (это сеть Коши, множество индексов ко-
которой составлено из пар (i, /)). Тогда х + у будет классом по мо-
модулю R суммы X + Y.
Далее, если Е — топологическое векторное пространство, то
легко проверяется, что равномерная структура в Е дает^тополо-
дает^топологию, которая согласуется с векторной структурой в Е. Таким
образом, Ё становится топологическим векторным простран-
пространством. Если пространство Е отделимо, то Е обладает тем же
свойством. С помощью изоморфизма i можно вложить Е в Е.
Замыкание в Е окрестностей любой базы окрестностей нуля
в Е образует базу окрестностей нуля в Е. Всякое непрерывное
линейное отображение пространства Е в отделимое топологиче-
топологическое векторное пространство F обладает единственным непре-
непрерывным продолжением до элемента из ЬС(Е,У) (п. 1.9.4), и каж-
каждая непрерывная полунорма на Е однозначно продолжается до
непрерывной полунормы на Е. Если пространство Е не отде-
отделимо, то описанное выше построение можно применить к ассо-
ассоциированному отделимому пространству £"/{0}. Это предвари-
предварительное отождествление не вызывает каких-либо затруднений
при рассмотрении непрерывных линейных отображений или не-
непрерывных полунорм на Е.
1.9. Непрерывность линейных отображений. Изоморфизмы
и гомоморфизмы топологических векторных пространств.
Замкнутые линейные отображения
В этом параграфе всюду, где явно не оговорено противное,
Е и F обозначают топологические векторные пространства над
/С, а и — линейное отображение пространства Е в F, и е I(£, F).
1.9.1. Очевидно, что непрерывность отображения и в некото-
некоторой точке пространства Е равносильна непрерывности в нуле.
При этом отображение и непрерывно и, следовательно, равно-
равномерно непрерывно на Е.
Нет необходимости перечислять здесь те свойства непрерыв-
непрерывных линейных отображений одного топологического векторного
1.9. Непрерывность линейных отображений 9?
пространства в другое, которые являются частными случаями
простых результатов, справедливых для непрерывных отобра-
отображений одного топологического пространства в другое.
Рассмотрим важное свойство, не относящееся к указанному
типу свойств.
► Непрерывное линейное отображение и топологического
векторного пространства Е в топологическое векторное
пространство F переводит каждое ограниченное множе-
множество АаЕ в ограниченное в F множество В = и(А).
Пусть V — окрестность нуля в F. Тогда в силу непрерывности
отображения и множество U = u~l(V) есть окрестность нуля в Е.
Поэтому если A cz XU для некоторого Х>0, то Вс XV и, следо-
следовательно, В ограничено в F.
Линейное отображение пространства Е в F называется огра-
ограниченным, если оно переводит ограниченные множества в Е в
ограниченные множества в F. Естественно поставить вопрос,
верно ли обратное, т. е. будет ли всякое ограниченное отобра-'
жение непрерывным. Доказательство тривиально в случае, ко-
когда Е и F — полунормированные пространства (п. 1.10.2). Спра-
Справедливость обратного утверждения для другого вида прост-
пространств, так называемых борнологических пространств, является
менее очевидным фактом. Ниже, в § 7.3, мы вернемся к этому
вопросу.
1.9.2. Отображение u^L(E, F) называется изоморфизмом
пространства Е в F (как топологических векторных прост-
пространств), если оно является алгебраическим изоморфизмом про-
пространства Е в F (п. 1.3.2) и одновременно гомеоморфизмом про-
пространства Е в F. Линейное непрерывное взаимно однозначное
отображение и пространства Е в F есть изоморфизм простран-
пространства Е в F тогда и только тогда, когда оно является открытым
отображением Е ка и(Е).
Предлоги «в» и «на» употребляются здесь в таком же смыс-
смысле, как и в п. 1.3.2.
1.9.3. Пусть Е и F — топологические векторные пространства.
Отображение u^L(E, F) называется гомоморфизмом простран-
пространства Е в /% если оно непрерывно и открыто. Другими словами,
гомоморфизм и пространства Е в F — это изоморфизм фактор-
пространства E/ker и (п. 1.8.5) в F (или на и(Е)). Непрерывное
отображение u^L(E, F) будет гомоморфизмом пространства
Е в F тогда и только тогда, когда оно является открытым ото-
отображением пространства Е на и (Е).
Понятия изоморфизма и гомоморфизма можно применять и
в случае, когда область определения отображения и есть соб-
собственное векторное подпространство в Е. Непрерывность,
98 Гл. 1. Векторные и топологические векторные пространства
например, означает тогда непрерывность отображения и как
элемента множества L(domu, F).
Введем два новых обозначения, которыми мы будем в даль-
дальнейшем широко пользоваться.
1.9.4. Пусть Е и F— топологические векторные пространства.
Через Lc(£, F) будем обозначать подпространство в L(E, F)r
состоящее из всех непрерывных линейных отображений прост-
пространства Е в F. Если, в частности, F = K (К — поле скаляров), то
пространство LC{E, К) обозначается через Е\ Таким образом,
£' является подпространством в £*, состоящим из всех непре-
непрерывных линейных форм на Е. Пространство Ег называется топо-
топологическим сопряженным к Е. Обычно элементы пространства
Ег будут обозначаться через х\ у\ .... Значение линейной
формы х'&Е' в точке х^Е обозначается через х'(х) или, бо-
более симметрично, через (х, х') (ср. с замечанием п. 1.4.7).
1.9.5. Замечания. A) Вообще говоря, пространство Е'
значительно уже пространства Е*. Хотя Е* всегда отделяет
точки из Е (на этом основано вложение пространства Е в £**,
описанное в п. 1.4.7), Ef может этим свойством не обладать. Это
имеет место, например, когда Е не отделимо как топологическое
пространство, причем это не единственный и даже не самый ин-
интересный случай. Примером пространств, для которых Е' отде-
отделяет точки пространства £, служит широкий класс отделимых
локально выпуклых пространств, изучением которых мы зай-
займемся в § 1.10. В заключение заметим, что существует много
способов превратить Е/ в топологическое векторное простран-
пространство таким образом, чтобы каждая точка х^Е порождала эле-
элемент х'*-:>(х9х') пространства £". Соответствующее отображе-
отображение XI—»*" пространства Е в £", вообще говоря, может не быть
взаимно однозначным; в этом случае нельзя, конечно, вложить
с его помощью пространство Е в Е".
B) Используемые в этой книге обозначения и терминология
никоим образом не являются общепринятыми. Иногда вместо
топологического сопряженного пространства говорят о двой-
двойственном или дуальном пространстве. Некоторые авторы упо-
употребляют и другие^ названия; часто вместо нашего обозначения
Ег пишут Е* или Е. При обращении к другим источникам чита-
читатель должен во избежание недоразумений иметь все это в виду.
Мы придерживаемся терминологии, принятой Н. Бурбаки.
C) Нам понадобится подпространство в L(E, Z7), образован-
образованное всеми ограниченными линейными отображениями простран-
пространства Е в F. Это подпространство будет обозначаться через
Ьъ(Е, F). Заметим, что всегда имеет место включение: Lb(E, F)zd
zd Lc(£, F). Вообще говоря, это включение строгое, однако, как
читатель увидит в гл. 7, для важного класса топологических
1.9. Непрерывность линейных отображений 99
векторных пространств Е имеет место совпадение, т. е.
Lc(E,F)=Lb(E,F).
1.9.6. Конечномерные топологические векторные пространства.
В настоящем пункте мы докажем, что имеется единственный
способ превратить конечномерное векторное пространство в от-
отделимое топологическое векторное пространство.
Предложение. Пусть Е — отделимое топологическое вектор-
векторное пространство над К размерности п и (et) { ^ . < п — некоторый
алгебраический базис в Е. Тогда отображение и е L(Kn, £),
определяемое равенством
является изоморфизмом топологического векторного простран-
пространства Кп на топологическое векторное пространство Е.
Доказательство. Очевидно, что отображение и линейно,
непрерывно, взаимно однозначно и является отображением на.
Остается лишь показать, что отображение и открыто. Положим
11х||= sup 16,1
1 < i < п
для х = и(%), и пусть В и S — множества в £, определенные со-
соответственно условиями \\x\\ < 1 и Ы = 1. Так как отображение
и непрерывно, то S компактно. Поэтому в силу отделимости Е
множество S замкнуто. Нуль не принадлежит S, поэтому суще-
существует такая открытая окрестность нуля U в £, что пересечение
U(]S пусто. Не нарушая общности, можно считать, что окрест-
окрестность U уравновешена (замечание E) п. 1.8.2).
Покажем, что UczB. Если это не так, то найдется элемент
л:е U\B. Поскольку UOS = 09 то хфБ, так что 1М1>1. Поло-
Положим y = —j Тогда y^S. Кроме того, в силу уравновешенности
U и условия ||я||>1 элемент ys U, так что y&SOU, а это про-
противоречит выбору окрестности U. Щ
Заслуживают внимания три следствия.
► A) Всякое конечномерное подпространство отделимого
топологического векторного пространства замкнуто.
Действительно, это подпространство, будучи изоморфно при
некотором п пространству Кп, является полным.
► B) Всякое линейное отображение конечномерного отде-
отделимого топологического векторного пространства непре-
непрерывно.
► C) Пусть Е — топологическое векторное пространство,
Н — гиперплоскость в £, /<=£*, /=£0, <х^К и Я=/({а})
100 Гл. 1. Векторные и топологические векторные пространства
(п. 1.2.6 и 1.2.7). Гиперплоскость Н замкнута ~тогда
и только тогда, когда линейная форма f непре-
непрерывна. В этом случае f есть гомоморфизм пространства
Е на К.
Действительно, если линейная форма / непрерывна, то оче-
очевидно, что гиперплоскость Н замкнута. Докажем обратное.
Пусть гиперплоскость Н замкнута. Сделав в случае необходи-
необходимости сдвиг, можно считать, что Н— однородная гиперпло-
гиперплоскость, т. е. что а = 0. Так как Н замкнуто, то факторпростран-
ство Е/Н отделимо. Его размерность, очевидно, равна 1. Форма
/ определяет взаимно однозначное отображение пространства
Е/Н на К (п. 1.3.2). В силу B) это отображение есть изомор-
изоморфизм (рассматриваемых топологических векторных прост-
пространств), т. е. f есть гомоморфизм пространства Е на /(. |
Если Е — вещественное топологическое векторное простран-
пространство и H = f~l({a})—замкнутая гиперплоскость в Е, то множе-
множества f~l([a, +°°)) и f~l((—оо, а]) называются замкнутыми по-
полупространствами, определяемыми гиперплоскостью Н, а мно-
множества f ((а, + оо)) и f'1 ((—оо, а)) — открытыми полупро-
полупространствами, определяемыми этой гиперплоскостью.
Имеется важный критерий конечномерности отделимого то-
топологического векторного пространства, впервые установленный
Ф. Риссом для нормированных пространств.
Теорема Ф. Рисса. Для конечномерности отделимого тополо-
топологического векторного пространства Е необходимо и достаточно,
чтобы в Е существовала предкомпактная окрестность нуля.
Доказательство. Если пространство Е конечномерно,
то оно как топологическое векторное пространство изоморфно
пространству Кп для некоторого п, а потому локально ком-
компактно. Необходимость, таким образом, доказана.
При доказательстве достаточности воспользуемся рассужде-
рассуждениями Ж--П. Серра. Пусть U — предкомпактная окрестность
нуля в Е. Можно так выбрать конечное число точек хи ..., хп
в U, чтобы множества j^+yt/ покрывали U. Обозначим через
М векторное подпространство в Е, порожденное элементами хи
и рассмотрим факторпространство Е/М. Если f — естественное
отображение пространства Е на Е/М, то (п. 1.8.5) множество
W — f(U) есть окрестность нуля в Е/М. Так как отображение /
линейно и непрерывно, то оно равномерно непрерывно, так что
W предкомпактно. Из включения УсЛ1+у[/ вытекает, что
Wei i^W. По индукции можно получить, что для любого нату-
натурального числа k имеет место включение 2ftf с W. Поскольку
1.9. Непрерывность линейных отображений 101
W — окрестность нуля в Е/М, то E/M=W. Следовательно, про-
пространство Е/М предкомпактно. Так как подпространство М ко-
конечномерно и Е отделимо, то М замкнуто в Е\ поэтому Е/М от-
отделимо. Если пространство Е/М не сводится к нулевому эле-
элементу, то оно должно содержать подпространство, изоморфное
К, и потому не может быть предкомпактным.
Таким образом, Е/М содержит только нулевой элемент, и,
следовательно, пространство Е = М конечномерно. 1
1.9.7. Топологические прямые суммы и топологические до-
дополнения. Дополним содержание п. 1.4.8 некоторыми замеча-
замечаниями, касающимися топологических векторных пространств.
Пусть L — векторное подпространство в топологическом век-
векторном пространстве Е и М — какое-нибудь его алгебраическое
дополнение в Е. Известно, что отображение (а, Ь)ь-^а + Ь есть
алгебраический изоморфизм произведения LXM на Е. Очевидно,
что это отображение непрерывно. Если окажется, что оно обла-
обладает непрерывным обратным отображением, т. е. если оно есть
изоморфизм рассматриваемых топологических векторных про-
пространств, то будем говорить, что £ является топологической
прямой суммой подпространств L и М, а также что подпростран-
подпространства L и М служат друг для друга топологическими дополне-
дополнениями относительно пространства- Е. Обозначим через pL и рм
соответствующие проекторы. Для того чтобы пространство Е
было топологической прямой суммой подпространств L и Му
необходимо и достаточно, чтобы либо pLy либо рм было непре-
непрерывным отображением (в силу равенства рь + Рм=1 из непре-
непрерывности одного следует непрерывность другого). Для этого
необходимо (но, вообще говоря, не достаточно), чтобы оба под-
подпространства L и М были замкнутыми в Е.
Из результатов п. 1.9.6 следует
Предложение. Пусть L — векторное подпространство отдели-
отделимого топологического векторного пространства Е. Допустим, что
L замкнуто и codimL< + oo. Тогда всякое алгебраическое до-
дополнение М подпространства L в Е будет также и топологиче-
топологическим дополнением.
Доказательство. Пусть М — алгебраическое дополнение
подпространства L, я — естественная проекция пространства Е
на факторпространство E/L и пм — ее сужение на подпростран-
подпространство МсиЕ. Тогда пм' M-+E/L есть алгебраический изомор-
изоморфизм М на E/L и рм = я^1 о п. Поскольку Е отделимо и L замк-
замкнуто, то E/L — отделимое топологическое векторное пространство
конечной размерности codim L; поэтому из следствия B)
п. 1.9.6 вытекает, что отображение пм1 непрерывно. Так как я
непрерывно по определению топологии в E/L} то непрерывен и
проектор рм. |
102 Гл. 1. Векторные и топологические векторные пространства
1.9.8. Замечания. A) Отображение (a, b)y->a + b всегда
непрерывно, взаимно однозначно и является отображением на.
Иногда, чтобы установить, что алгебраическая сумма £ = L + M,
где L и М — замкнутые подпространства, есть топологическая
прямая сумма, можно воспользоваться теоремой обращения из
гл. 6. Так обстоит дело, например, в случае, когда Е — полное
полуметризуемое топологическое векторное пространство.
Существует другая возможность. Она опирается на то на-
наблюдение, что отображение pL' E-+-L имеет замкнутый график,
если L и М замкнуты в Е. После этого к паре Е и L применяют
(если возможно) теорему о замкнутом графике, из которой сле-
следует непрерывность отображения pLi так что прямая сумма
E = L + M оказывается топологической.
Подробнее эти вопросы будут изложены после знакомства с
соответствующими понятиями (гл. 6 и упр. 6.2).
B) Несмотря на замечание A), даже в случае, когда Е —
банахово пространство (а это один из самых благоприятных
случаев), существуют замкнутые подпространства L в £, кото-
которые не допускают ни одного топологического дополнения в Е
(см. Ньюмен [1], а также упр. 7.8).
C) Пусть топологическое векторное пространство Е есть
алгебраическая прямая сумма L + M. Тогда соответствующие
проекторы pL и рм являются открытыми отображениями про-
пространства Е на подпространства L и М соответственно. Действи-
Действительно, так как pLx = x, x^L, то для каждой окрестности нуля
U в Е имеем pL(U) ^> pL(L(]U) =U[)L. Если, кроме того, эта
прямая сумма является топологической, то pL (соответственно
рм) будет непрерывным открытым отображением пространства
Е на L (соответственно на М).
1.9.9. Замкнутые и предзамкнутые линейные отображения.
Пусть Е и F —*■ топологические векторные пространства над К.
Рассмотрим линейное отображение и, определенное на вектор-
векторном подпространстве domucnE и принимающее значения в F.
Пусть gr ua ExF — график отображения и (определенный в
п. 1.3.3).
Будем говорить, что отображение и замкнуто (как отображе-
отображение из Е в F), если его график gr и есть замкнутое векторное
подпространство в произведении ExF. Это понятие, вообще го-
говоря, зависит от пространств Е и F и от их топологий (а не
только от топологий, индуцированных ими соответственно на
dorn и и ixnu). Всякое допустимое1) сужение пространств Е или
F, а также всякое усиление их топологий увеличивает шансы
отображения и оказаться замкнутым.
1) Тр есть up затрагивающее множеств dom и и im и. — Прим. ред.
1.9. Непрерывность линейных отображений ШЗ
Наряду с условием замкнутости оказывается полезным рас*
сматривать еще одно, несколько ослабленное условие. Отобра-
Отображение и называется предзамкнутым (из Е в F), если оно обла-
обладает хотя бы одним замкнутым продолжением, т. е. если суще-
существует хотя бы одно такое замкнутое отображение v из Е в F,
что dom^crdoma и u = v\<loxnu. Ясно, что если отображение и
обладает таким продолжением v, то среди них существует наи-
наименьшее, а именно то отображение, графиком которого служит
gr и (замыкание gr и в произведении ExF). Это отображение
линейно; оно называется замыканием отображения и и обозна-
обозначается через гг. Существование отображения п и его область
определения (если п существует) зависят от Е и F и их топо-
топологий. Всякое сужение предзамкнутого отображения также
является предзамкнутым отображением.
Если отображение и замкнуто, то оно тем более предзамкнуто
и его замыкание п совпадает с и. Заметим, что если простран-
пространство F не отделимо, то не существует ни одного линейного пред-
предзамкнутого отображения^ из Е в F. Действительно, если уФО
и #se{0}, то @, j/)eE{@~0)} = {@, u(O))}czgru. Отсюда следует,
что множество gr и не может быть графиком.
В дальнейшем мы займемся изучением замкнутых линейных
отображений. Перечислим пока несколько их важных свойств.
1.9.10. Предложение. Пусть Е и F — топологические вектор-
векторные пространства и и — линейное отображение, определенное
в Е и принимающее значения в F. Для замкнутости отображения
и из Е в F необходимо и достаточно, чтобы выполнялось следую-
следующее условие: если сеть (хг) точек из dom и сходится к х е Е
и сеть (и(х{)) сходится к у е F, то х <= dom^ и у = и(х). В слу-
случае, когда dom и = Е, замкнутость отображения и равносильна
выполнению указанного выше условия при х--=0 (легко видеть,
что при этом у = 0). Если Е и F — метризуемые пространства, то
достаточно выполнения приведенного условия для последова-
последовательностей.
Доказательство. Предложение очевидно, так как сфор-
сформулированное условие является необходимым и достаточным
для того, чтобы gr и был замкнут в ExF. I
1.9.11. Предложение. Пусть Е и F — топологические вектор-
векторные пространства и и — линейное отображение из Е в F. Каждое
из следующих условий является необходимым и достаточным,
чтобы отображение и было предзамкнутым.
A) Если сеть (xi) точек из dom и сходится к нулю в Е и
сеть \и(хг)) сходится в F, то предел сети (u(Xi)) в F равен
нулю. Если Е и F — метризуемые пространства, то сети можно
заменить последовательностями.
104 Гл. 1. Векторные и топологические векторные пространства
B) Если (Uj) —база окрестностей нуля в £, то имеет место
равенство
Доказательство. Необходимость условия A) очевидна.
Действительно, если (хг) удовлетворяет указанным условиям
и y = \imu(Xi), то точка @, #) принадлежит замыканию gr и.
Так как это замыкание есть график (отображение и по предпо-
предположению предзамкнуто), то у = 0.
Обратно, предположим, что выполнено условие A). Доста-
Достаточно показать, что у{ = у2, если (х, у\) и (х, у2) принадлежат
gr и. Включение (х, уп) е gr и при п=1, 2 означает, что суще-
существует такая сеть (хг п) в dom и, что lim xt n = х и lim и (xt п) = уп.
i i
Разность сетей (х{)П) при я=1, 2 представляет собой такую
сеть (Xj) в dom и (вообще говоря, с другим множеством индек-
индексов), что \imXj = 0 и lim u(xj) =у\ — У2- Но тогда из условия A)
следует, что у\=уъ что и требовалось доказать. Таким образом,
условие A) является необходимым и достаточным.
Докажем необходимость условия B). Пусть множество
gr и — график. Если у принадлежит указанному в условии B)
пересечению и V — окрестность нуля в F, то y-\-V пересекает
каждое множество и(Ujf)dom и), т. е. для каждого / существует
такой элемент Xj e Ujf) dom и, что —y + u(Xj) e V. Отсюда вы-
вытекает, что (Xj, u(Xj)) e @, у) + (UjXV) и, следовательно, @, у)
принадлежит замыканию gr и. Так как множество gr и является
графиком, то у = 0, откуда и следует необходимость условия B).
Покажем, наконец, что условие B) достаточно. Множество
gr и есть векторное подпространство в ExF. Оно является гра-
графиком тогда и только тогда, когда из включения @, у) е gr и
вытекает, что у = 0. Пусть @, у) е gr и. J3to означает, что для
любых окрестностей нуля U и V в пространствах Е и F соответ-
соответственно существует такое х\ е Uf]dom и, что у — и(х}) ^V. Это
в свою очередь влечет за собой включение y^u(U[)domu) +V.
Так как это верно для любой окрестности нуля V в F, то
y^u(U[)dom и). В силу произвольности окрестности нуля U в
Е элемент у принадлежит пересечению, фигурирующему в усло-
условии B); следовательно, у = 0. |
1.9.12. Предложение. Пусть Е и F — топологические вектор-
векторные пространства и и — линейное отображение из Е в F. Спра-
Справедливы следующие утверждения.
A) Если dom u замкнуто в Е и отображение и предзамкнуто^
то и замкнуто,
1.9. Непрерывность линейных отображений 105
B) Если пространство F отделимо и и — непрерывное отобра-
отображение, то и предзамкнуто.
C) Если пространство F отделимо, dom и замкнуто в Е и
отображение и непрерывно, то и замкнуто.
D) Если Е — отделимое, a F — отделимое и полное простран-
пространство и и — замкнутое непрерывное отображение, то dom и замк-
замкнуто в Е.
E) Если отображение и взаимно однозначно и предзамк-
предзамкнуто (соответственно замкнуто), то отображение и~1 из F в Е —
предзамкнуто (соответственно замкнуто).
F) Если Е отделимо и полно, F отделимо, и замкнуто, а
и~1 существует и непрерывно, то im и замкнуто в F.
Доказательство. A) следует из предложений 1.9.10
и 1.9.11.
B) и C) вытекают соответственно из предложений 1.9.11
и 1.9.10.
D) Пусть элемент х принадлежит dom и. Тогда в dom и
существует сеть (х{), сходящаяся в Е к х. Так как отображе-
отображение и непрерывно, то сеть (u(Xi)) есть сеть Коши. Из полноты
пространства F следует тогда существование такого элемента
y^F, что y = limu(Xi). Отображение и замкнуто; следова-
i
тельно, х е dom и.
E) очевидно, так как gr u~l есть образ множества gr и
относительно отображения" (х9 у)*-^(у, х) произведения Е X F
в произведение Е X F. Но это отображение есть гомеоморфизм.
F) следует из D) и E) и из очевидного замечания, что
Im w = dom trl. |
1.9.13. Замечание. Из утверждения C) вытекает, в част-
частности, что если пространство F отделимо, то всякое отображе-
отображение u^Lc(E, F) замкнуто. Существует чрезвычайно важная
теорема, известная под названием теоремы о замкнутом гра-
графике, в которой для некоторого класса топологических вектор-
векторных пространств Е и F устанавливается справедливость обрат-
обратного утверждения. В дальнейшем мы уделим этому вопросу
большое внимание (§ 6.4—6.7 и 8.9).
Прежде чем заняться примерами, приведем еще одно пред-
предложение, которое часто позволяет избегать повторения доказа-
доказательств и получать без особого труда из одних примеров
другие.
1.9.14. Предложение. Пусть (E,s) и (F,t)—топологические
векторные пространства и и — линейное отображение с об-
областью определения D а Е и областью значений в F. Предпо-
Предположим, что (Ео, s0) и (Fo, t0) — такие топологические векторные
106 Гл. 1. Векторные и топологические векторные пространства
пространства, что Еосц.Е, so> s\E0, FQczF и to>t\Fo. Пусть,
наконец, и0 есть сужение отображения и на пересечение
ЕоГ№Г\и-1(Ро), рассматриваемое как отображение из Ео в Fo.
Тогда справедливы следующие утверждения:
A) если отображение и предзамкнуто, то таким же будет
отображение и$\
B) если и-—замкнутое отображение и u(D)c:Fq (г. е. об-
область определения отображения и^ совпадает с пересечением
£0ГШ), то отображение и0 замкнуто.
Доказательство. Пусть (X, X) — топологическое про-
пространство и А — множество в X. Временно условимся обозна-
обозначать через cl^/4 замыкание множества А в топологии £.
A) Пусть G0=gr^0 и G — grz/, так что
Go cz G П (Ео X FQ).
Тогда имеем
cU0 х ^oGo с: cl(S x t) | £o x FQGo = {EqXFo) П cl5 x tGo cz
c(£0X F
По предположению множество c\sXt G есть график; следова-
следовательно, множество c\SoxtQGo также является графиком, т. е.
отображение и0 предзамкнуто.
B) В этом случае справедливы равенства Go= (EoxFo) f]G
и clsxt G = G. Из включения, полученного при доказательстве
утверждения A), следует, что
cl5o х *oGo cz {Ео X Fo) П G = Go,
т. е. отображение Uq имеет замкнутый график. |
Обратимся к рассмотрению некоторых примеров. Прежде
всего ситуация, описанная в предложении 1.9.12B) (соответ-
(соответственно C)), часто возникает в анализе, и в каждом таком
случае мы имеем пример предзамкнутого (соответственно зам-
замкнутого) линейного отображения. В гл. 6 в связи с теоремой
о замкнутом графике будет описано несколько различных при-
примеров замкнутых линейных отображений (см. также упр. 8.10).
В большинстве примеров линейные отображения либо заведомо
непрерывны, либо оказываются таковыми на основании тео-
теоремы о замкнутом графике. В анализе довольно часто встре-
встречаются линейные отображения, предзамкнутые или замкнутые,
но не непрерывные. В связи с этим полезно рассмотреть ряд
примеров. Особенно важным их источником служат различ-
различного вида линейные дифференциальные операторы. Ими мы и
ограничимся.
Мы начнем с рассмотрения обыкновенных линейных диф-
дифференциальных операторов (содержащих производные только
по одной независимой переменной), которые, очевидно, проще
1.9. Непрерывность линейных отображений 107
дифференциальных операторов от многих независимых пере-
переменных.
1.9.15. Пример. Пусть Q — открытый интервал веществен-
вещественной оси. В примере D) п. 1.8.4 было ^определено векторное
пространство С(й), образованное всеми непрерывными функ-
функциями на Q, и была описана топология компактной (или ло-
локально равномерной) t сходимости на Q. Возьмем в качестве F
то же векторное пространство C(Q), наделенное более слабой
топологией, а именно топологией сходимости в среднем на
каждом компактном отрезке в Q. Эту топологию можно опре-
определить как слабейшую, при которой непрерывна каждая из
полунорм вида
где [а, Ь] — произвольный компактный отрезок в Q. Множества
вида
): j\g(x)\dx<e\9
где е > 0, образуют базу окрестностей нуля в этой топологии.
Пусть m — некоторое натуральное число. Возьмем в каче-
качестве Е пространство Cm-1(Q), образованное всеми функциями f,
m—1 раз непрерывно дифференцируемыми на Q (под нулевой
производной функции / понимают саму функцию /, т. е. C°(Q) =
= С(Й)). Наделим пространство Cm~l(Q) его «естественной»
топологией — слабейшей топологией, при которой непрерывна
каждая полунорма вида
где /<р) — р-я производная функции /, а К—компактное под-
подмножество в Q.
Отметим, что Е и Т7— метризуемые топологические вектор-
векторные пространства. Кроме того, оба они локально выпуклы
(§ 1.10), но ни одно из них не нормируемо. Впрочем эти факты
нам не понадобятся.
Пусть теперь а0, аь ..., ат — непрерывные функции на Q,
причем ат нигде на Q не обращается в нуль. Наше линейное
отображение а получаем специальным выбором области опре-
определения формального линейного дифференциального оператора
108 Гл. 1. Векторные и топологические векторные пространства
Именно будем считать, что D — область определения опера-
оператора и — состоит из тех и только из тех функций / е £, для
которых существует производная /(ш) на й и для которых
Для функций f <= D положим
0<<
Наша цель — доказать замкнутость отображения и из Е в F.
Для этого нужно показать следующее: если последователь-
последовательность (/п) из D такова, что в Е существует предел lim/n = f,
а в F — предел HmM(fn)=g, то feD и u(f)=g.
Возьмем произвольную, но фиксированную точку х0 е Q и
введем на С(й) интегральный оператор /, полагая
Оператор / является эндоморфизмом пространства C(Q), по-
поэтому можно образовывать его последовательные степени. Так
как функция ат непрерывна и нигде на Q не обращается в
нуль, то для всякой функции f e D производная /<те) непре-
непрерывна на Q и
.-. +(х~хо)т-1 ^1\)? +П{т)(х). A.9.1)
Так как
причем u(fn)->g в F и /„->/ в £, то
р < m
в смысле топологии в /ч Но тогда
р < m
в смысле поточечной (и даже локально равномерной) сходи-
сходимости на Q. Заменяя в формуле A.9.1) функцию / на fn и пере-
переходя к пределу при п—>оо, получаем
/м- 2 (*-*o)'^+
/ 9. Непрерывность линейных отображений 109
Так как выражение в квадратных скобках есть непрерывная
функция на Q, то из полученной формулы следует существо-
существование производной /<т) на Q. Кроме того,
p < m
т. e. |gDh u{f)=g, что и требовалось доказать. |
Стоит сделать несколько замечаний о другом подходе к
рассмотренной задаче, особенно в связи с приводимым ниже
примером 1.9.17. Если на коэффициенты а0, ..., ат налагать
дополнительные ограничения, то более тонкое исследование
дифференциального оператора и позволяет получить более
сильные результаты. Допустим, что интервал fi=(a, b) огра-
ограничен, и рассмотрим задачу, которая получается, если потре-
потребовать выполнения некоторых однородных граничных условий.
Здесь нам не понадобится точная формулировка этих условий,
поэтому обозначим их через fi, пока не расшифровывая их.
Не нарушая общности, можно считать, что уравнение u(f)=Q
с граничными условиями В не имеет других решений, кроме
нулевого, т. е. нуль не является собственным значением этой
однородной задачи (этого можно добиться заменой u(f) на
u(f)+cf, где с — соответствующим образом подобранная по-
постоянная). Условия гладкости, налагаемые на коэффициенты
а0, ..., ат, обеспечивают получение решений, непрерывно про-
продолжаемых на замыкание [а, Ь] множества Q.
Нам понадобится функция Грина рассматриваемой задачи
G(x,y). Эта функция обладает тем свойством, что для всех
j/Gfi функция хь-М7(л:,у) удовлетворяет условиям В и урав-
уравнению u(f)=O на каждом из интервалов (а, у) и (у>Ь). При
х = у соответствующие односторонние производные от G(x,y)
имеют особенности такого рода, что для заданной непрерывной
на [а, Ь] функции g решение / уравнения u(f)=g с граничными
условиями В дается формулой
f(x)=JG(x,y)g(y)dy. A.9.2)
Q
При этом интеграл представляет собой функцию, непрерывно
продолжаемую на [а, Ь] вместе с первыми т производными.
(Подробности см., например, в книге Коддингтон и Ле-
Левин со н [1, гл. 7]1).)
Возьмем теперь в качестве Е и F пространство С([а,Ь])
с равномерной нормой. Обозначим через D множество тех
') См. также В. В. Степанов, Курс дифференциальных уравнений,
гл. V, М., 1950. — Прим. перев.
110 Гл. 1. Векторные и топологические векторные пространства
удовлетворяющих условиям В функций f^E, первые m производ-
производных которых непрерывно продолжаемы на [а, Ь]. Легко пока-
показать, что отображение и, рассматриваемое^ как отображение с
областью определения Д замкнуто из Е в F. Действительно,
пусть fn^D, fn-+f в Е и u(fn)=gn-*g в F. Если в формуле
A.9.2) функции fug заменить соответственно на fn и gn и
перейти к пределу при л-*оо, то получится снова формула
A.9.2) с новыми fug. Отсюда следует, что fefl и u(f)=g.
Если нужно рассматривать решения, не удовлетворяющие
граничным условиям В, то поступают следующим образом.
Предположим, что условия В выражены в виде
где каждое Ls есть линейная форма относительно первых m— 1
(односторонних) производных функции f в точках а и Ь. Най-
Найдем решения еи ..., ег однородного уравнения u(f)=O, для
которых L8(et)=8st ПРИ М=1, ••-, г. Тогда решение / урав-
уравнения u(f)=g можно записать в виде
G(x, y)g(y)dy. A.9.2*)
В этом случае нужно так усилить топологию в Е, чтобы
каждая из линейных форм Ls стала непрерывной. Тогда можно
воспользоваться предыдущими рассуждениями, чтобы уже с
помощью формулы A.9.2*) (вместо A.9.2)) показать замкну-
замкнутость отображения и из Е в F, определенного на множестве D
тех функций /е£, ^дервые m производные которых непрерывно
продолжаемы на [а, Ь].
В книге Стоуна [1, стр. 424—530] в рамках теории гиль-
гильбертовых пространств (L2) весьма подробно изучаются линей-
линейные обыкновенные дифференциальные операторы первого и вто-
второго порядка.
На первый взгляд кажется, что этот метод может быть
использован для линейных операторов с частными производ-
производными; однако на самом деле здесь возникают некоторые ослож-
осложнения, которые отчасти объясняются тем, что соответствующие
функции Грина, как правило, имеют более сильные особенности
(см. пример 1.9.17).
1.9.16. Пример. Переходя к рассмотрению линейных опера-
операторов с частными производными, начнем с простейшего слу-
случая— с операторов первого порядка вида
1.9. Непрерывность линейных отображений 111
где аи ..., а<п и Ъ — заданные функции, непрерывные в обла-
области Q пространства Rn. Естественно в качестве Е и F взять
пространство C(Q), а за область определения D оператора и
принять пространство Cl(Q). Покажем сначала, что при таком
выборе £, F и D оператор и, вообще говоря, не замкнут, если п
больше 1 (в отличие от случая п=1).
Выберем функцию Л е С1 (Q) так, чтобы она всюду в Q
удовлетворяла уравнению
Рассмотрим на Q функции /г, определенные равенствами
fr = cproH (r=l, 2, ...),
где фг — такие непрерывно дифференцируемые функции одной
вещественной переменной, что существует локально равномер-
равномерный предел lim cpr = cp. Каждая из функций />, очевидно, при-
Г->оо
надлежит пространству С1 (£2). Далее в силу выбора функции Н
имеем
п п
Отсюда следует, что /г—>/=фоЯ в £ и u(fr)—*bf в F при
г->оо. Несмотря на это, функция f, вообще говоря, может не
быть непрерывно дифференцируемой на £2, т. е. может не при-
принадлежать D. Другими словами, оператор и в общем случае
не является замкнутым.
Пусть, например, в Q найдется хотя бы одна точка л:0, в
которой не все частные производные первого порядка от Н
равны нулю. Можно считать (вычитая, если надо, постоянную),
что Я(л:0)=0. Выберем последовательность фг так, чтобы ее
предел ф в некоторой окрестности точки £ = 0 удовлетворял ра-
равенству ф(£) = |||. Легко видеть, что функция f = yoH не диф-
дифференцируема в точке х0% и потому не может принадлежать
классу С1 ни в какой окрестности точки х0. Действительно, обо-
обозначим через L производную функции Н в точке хОу существую-
существующую в силу предположения H^Cl(Q). Если и функция фо#
дифференцируема в точке xOi то, обозначая ее производную
в Хо через L*, имеем
112 Гл. 1. Векторные и топологические векторные пространства
(|#|->0). Так как для достаточно малых g имеет место равен-
равенство qp(g) = |g|, то
\L(x)+o(\x\)\=L*(x) + o(\x\)
(| л:| —> 0). В силу линейности форм L и L* на Rn получаем
\L(x) | =L*(x) для всех х, т. е. L = 0, а это противоречит пред-
предположению, что в точке Хо не все первые частные производные
функции Н равны нулю.
Все же при сделанных предположениях оператор а яв-
является предзамкнутым. Действительно, пусть последователь-
последовательность fr(=D (r=l, 2, ...) такова, что />-*0 в £ и limu(fr) =
\\mgr = g в /\ Нужно показать, что g" = 0.
С этой целью возьмем произвольную, но фиксированную
точку х0 е Q. Рассмотрим непрерывную кривую, задаваемую
уравнением
() 0</
и удовлетворяющую условиям
при 0</<е и fe=l, 2, ..., /г. Тогда при 0<t<г имеем
откуда следует, что
fr (I d) ) - fr (Хо) = { [gr (I (О ) - Ь A (f) ) /r (| (/') )] df
0
для 0</<8. Переходя к пределу при г->оо, получаем
0=J g{W))df.
0
Так как функция g непрерывна, то g{l{t')) =0 при 0 < f < е*
Поэтому, полагая t'-+0, находим g(xo)=Oy откуда в силу про-
произвольности точки Хо£Й следует, что g = 0.
1.9.17. Пример. Рассмотрим весьма важный пример опера-
оператора— трехмерный оператор Лапласа Д, действующий на функ-
функциях с областью определения Q си R3. Как видно из примера
1.9.15, существенную роль играют функции Грина. Чтобы не
заниматься исследованием поведения этих функций на гра-
границе, мы построим изложение так, чтобы функции Грина
применялись только для ограниченных подобластей со обла-
1.9. Непрерывность линейных отображений 113
сти Q с гладкой границей <?со, таких, что со cz Q. Будем обо-
обозначать функцию Грина для области со через G(x,y) (см., на-
например, Келлог [1, стр. 236]). Рассмотрим прежде всего два
результата, относящихся к этой функции Грина.
A) Пусть feC2(Q). Обычное применение тождества Грина
приводит к формуле
I G{X>
A.9.3)
где ^G(o, dy—(лебегова) мера на R3, v — внешняя нормаль
к поверхности дсо, а а — поверхностная мера на дсо (ср. Кел-
Келлог [1, стр. 219]).
Для наших целей надо доказать формулу A.9.3) и в том
случае, когда известно лишь, Что всюду в Q существуют част-
частные производные—£- F=1, 2, 3) и функция А/= —4-4 ~ +
дх\ дх\ д*2
Ч т непрерывна на Q. Покажем методом аппроксимации,
что формула A.9.3) остается справедливой при этих более
слабых предположениях. Для доказательства возьмем функ-
функцию f*, совпадающую с функцией f на е-окрестности множе-
множества со (е > 0 достаточно мало, так что эта окрестность лежит
в £2), непрерывную на Rn и равную нулю вне некоторого огра-
ограниченного множества. Наш процесс аппроксимации будет
процессом регуляризации. Берется такая последовательность
(гп) положительных функций в C°°(Rn), что гп(х)=0 при
'*'>"/i и J J J гпМ^х= 1. Рассмотрим функции
J J lr(y)rn(x-y)dy=l J jr(x-y)rn(y)dy.
Каждая из этих функций принадлежит C°°(Rrt) и f*n(x)->f*(х)
локально равномерно благодаря непрерывности f. В частности,
f*n{x)->f(x) равномерно на со. Кроме того, Д/* = Д/ на некото-
некоторой окрестности множества со, и Д/ непрерывно на со. Легко
проверяется, что
откуда следует, что Д/* (х) -> Д/ (х) равномерно на со. Далее,
формула A.9.3) останется верной, если заменить / на Гп(п =
= 1, 2, ...). Переходя к пределу при п—> оо и пользуясь дока-
доказанной сходимостью, получаем A.9.3).
114 Гл. 1. Векторные и топологические векторные пространства
B) Пусть функция g^C(Q) в каждой точке области Q
удовлетворяет условию Липшица (или Гёльдера), т. е. каждой
точке Хо е Q соответствуют такие числа е>0, а>0 и М > О,
что
\g(x)-g(xo)\<M\x~xQ\a
при |л: — лго | <е. Рассмотрим функцию
G(x, y)g(y)dy.
Мы утверждаем, что в каждой точке области со функция f имеет
вторые частные производные и что всюду в со справедливо со-
соотношение kf = g. Действительно, так как G(x, у) отличается от
гармонической на Q функции на выражение —[4п\х — у\]~\ то
наше утверждение следует из теоремы III, приведенной на
стр. 156 книги Келлога [1].
Теперь мы можем перейти к рассмотрению основной задачи.
Возьмем в качестве Е пространство C(Q) в его естественной то-
топологии локально равномерной сходимости на Q. Пусть F — век-
векторное подпространство в С(£2), образованное теми функциями
из C(Q), которые удовлетворяют условию Липшица в каждой
точке области Q. Наделим F топологией, индуцированной топо-
топологией пространства C(Q). Рассмотрим оператор м = Д, область
опоеделения которого есть множество D тех функций / е £, для
1 d2f
которых существуют —~ (k=lt 2, 3), а функция Д/ непрерывна
дх
и удовлетворяет условию Липшица в каждой точке области Q.
Ясно, что и отображает D в F. Покажем, что и — замкнутое ото-
отображение из Е в F.
Пусть LeD (/i=l, 2, ...), fn->f в Е и gn = u(fn)->g в F.
В силу A) для любых п и х имеем
fn(x)=j J \G(x9y)&fn{y)dy+\ \fn{y) dG^yy) do (у).
Переходя к пределу при п->оо, получаем для
fW = J f JG(x, tj)g{y)dy+\ \f(i
д(о
Поверхностный интеграл в правой части является гармониче-
гармонической на со функцией от х. Поэтому в силу B) в каждой точке
области о) существуют вторые частные производные от / и Af = g
на со; следовательно, функция Д/ непрерывна на со и удовлетво-
удовлетворяет условию Липшица в каждой точке области со. Так как это
1.10. Локально выпуклые пространства 115
верно для любой подобласти указанного вида области £2, то
f e D и u(f) =g, т. е. отображение и замкнуто.
1.9.18. Замечания. Из примеров 1.9.16 и 1.9.17 видно, что
в связи с изучением линейных операторов в частных производ-
производных возникает целый ряд интересных задач. Какие линейные
операторы в частных производных с заданной областью опре-
определения замкнуты? Какие предзамкнуты? Можно ли конкретно
описать замыкание заданного предзамкнутого линейного опера-
оператора в частных производных? До сих пор отправной точкой мно-
многих исследований служит заданный формальный линейный опе-
оператор в частных производных вида
Р(*. д) = 2 ар(х)др,
\Р \<tn
где р = (/?!, ..., рп) — набор п неотрицательных целых чисел,
lpl = Pi+ ... +Рп>
и ар — заданные функции, определенные на некоторой области
Q в R". При этом возникают задача выбора области определе-
определения оператора Р(х,д), каковой выбор зависит в некоторой сте-
степени от поведения коэффициентов ар\ задача изучения опера-
оператора Р(х,д) как линейного отображения одного функциональ-
функционального пространства Е в другое функциональное пространство F\
наконец, задача исследования замыканий в различных смыслах.
Большинство современных исследований посвящено случаям, ко-
когда Е и F являются лебеговыми пространствами L?(Q) (см.,
например, Гальперин [1], Фуглид [1] и приведенную там
литературу, в частности Фридрихе [2, 3] и Л. Шварц [1]).
1.10. Локально выпуклые топологические векторные
пространства
Под локально выпуклым топологическим векторным про-
пространством (иногда говорят просто локально выпуклое простран-
пространство или даже выпуклое пространство) понимается топологиче-
топологическое векторное пространство £, в котором существует база
окрестностей нуля, состоящая из выпуклых множеств.
Причина, по которой важны локально выпуклые простран-
пространства, ясно обнаружится в следующей главе. Здесь же мы ука-
укажем на то, что в локально выпуклом пространстве существует
«достаточно много» открытых выпуклых множеств. Значение
этого факта станет понятным, когда пойдет речь о теореме
Хана — Банаха, из которой следует существование «достаточного
116 Гл. 1 Векторные и топологические векторные пространства
количества» непрерывных линейных функционалов на Е — до-
достаточного для отделения точек пространства Е и в действи-
действительности для представления всех замкнутых выпуклых мно-
множеств в Е. Практически это означает, что структуру локально
выпуклого пространства можно достаточно полно и хорошо опи-
описать в терминах непрерывных линейных форм, чего нельзя ска-
сказать о некоторых не локально выпуклых топологических вектор^
ных пространствах (например, о пространстве примера G)
п. 1.8.4 или о пространстве L?> @<р<1), о котором говорится
ниже, в п. 1.10.2).
В п. 1.8.4 уже приведено несколько примеров локально вы-
выпуклых пространств. Таковыми являются пространства в при-
примерах A) — D). Пространство примера E) локально выпукло,
если таковым является пространство Х\ пространство примера
F) локально выпукло при /?^> 1. Однако пространство примера
G) не является локально выпуклым. В самом деле, легко ви-
видеть, что в этом пространстве всякое непустое открытое выпук-
выпуклое множество совпадает со всем пространством (читателю ре-
рекомендуется проверить это).
Перечисленные примеры наводят на мысль, что топологию
локально выпуклого пространства можно определить с помощью
полунорм. Наша первая задача состоит в проверке этого пред-
предположения.
Прежде чем приступить к ее решению, отметим (это почти
очевидно), что подпространства, факторпространства и произве-
произведения локально выпуклых пространств сами являются локально
выпуклыми.
1.10.1. Локально выпуклые топологии и полунормы. Из за-
замечания E) п. 1.8.2 легко следует, что в локально выпуклом
пространстве Е всегда существует база окрестностей нуля, со-
состоящая из замкнутых (или открытых) выпуклых уравновешен-
уравновешенных множеств. (Например, пусть задана окрестность U. Выбе-
Выберем замкнутую уравновешенную окрестность U\ так, чтобы
U\ cz U. Из определения локально выпуклого пространства сле-
следует существование такой выпуклой окрестности нуля £/2, что
U2cz U\. Пусть, наконец, f/3 — такая замкнутая уравновешенная
окрестность, что f/3ci f/2. Тогда замкнутая выпуклая оболочка
окрестности £/3 содержится в U и, конечно, является окрест-
окрестностью нуля.)
Пусть Е — локально выпуклое пространство и (£/г)—база
замкнутых выпуклых уравновешенных окрестностей нуля. Обо-
Обозначим через pi функционал Минковского окрестности иг (§ 1.6).
Так как множество Их замкнуто, а значит, и замкнуто по лучам,
то из следствия 1.6.6 вытекает, что 1)\ совпадает с множеством
{хе£: pi(x) К 1} и что, кроме того, рг является полунормой на
1.10. Локально выпуклые пространства 117
Е. Очевидно, что каждая полунорма pi непрерывна в заданной
на Е топологии. Из определения полунорм pi видно, что тополо-
топология пространства Е — это топология, в которой база окрестно-
окрестностей нуля образована множествами вида
U{F, е) = {х<=Е: ft(*Xe для /eF},
где е>0, a F — произвольное конечное множество индексов и
Обратно, если Е — векторное пространство и (рг)—некото-
(рг)—некоторое семейство полунорм на £, то, как легко видеть, множества
U(F, е) образуют базу окрестностей нуля некоторой линейной
топологии в £, в которой Е локально выпукло. Семейство полу-
полунорм (pi) называется определяющим семейством полунорм со-
соответствующей топологии (или локально выпуклого простран-
пространства).
Стоит отметить, что различные определяющие семейства мо-
могут определять одну и ту же топологию.
Если возникает необходимость иметь дело с открытыми
окрестностями нуля, то каждое из неравенств Pi(x)-*Ce заме-
заменяют строгим неравенством рг(л:)<е.
Топология, определенная семейством полунорм (pi), отде-
отделима тогда и только тогда, когда для каждого хФО (ig£)
имеет место неравенство
sup pt(x)>0.
i
Пусть топология локально выпуклого пространства Е опре-
определена семейством полунорм (pi) и L — векторное подпростран-
подпространство в Е. Тогда топология подпространства L определяется по-
полунормами pi\L. Если семейство полунорм (pi) вместе с каж-
каждым конечным подсемейством содержит полунорму, мажорирую-
мажорирующую это подсемейство, то система полунорм
pi(xc) = mi{pi(x): х е= хс}
определяет топологию факторпространства E/L.
Сильнейшая локально выпуклая топология 1) заданного век-
векторного пространства. Среди всех локально выпуклых тополо-
топологий на заданном векторном пространстве Е существует силь-
сильнейшая. Эта топология (обозначим ее через /«,) обладает базой
окрестностей нуля, состоящей из всех выпуклых уравновешен-
уравновешенных поглощающих подмножеств W в Е. Хотя топология t^
редко встречается при решении задач, возникающих в анализе
(за исключением случая, когда Е конечномерно), все же
*) Под локально выпуклой топологией понимается линейная то-
топология, в которой векторное пространство локально выпукло. — Прим. пе-
рев.
118 Гл. 1. Векторные и топологические векторные пространства
некоторые ее свойства оказываются иногда полезными в общей
теории. (См., например, Келли и Намиока [1], в частности
задачи 6D, 6J, 14D и 20G.)
Возможно, самое важное из «экстремальных» свойств топо-
топологии toe заключается в том, что любая полунорма и любая ли-
линейная форма на£7оо-непрерывны. Так, если р — полунорма на £,
то множество {х^Е: р(х)<1} выпукло, уравновешено и погло-.
щающе и, следовательно, является /оо-окрестностью нуля, т. е.
полунорма р непрерывна в топологии /«>.
Таким образом, определяющим семейством топологии /<» слу-
служит семейство всех полунорм на Е. Полезно и поучительно,
однако, выявить наименьшее определяющее семейство. Примеры
таких семейств можно построить в терминах алгебраического
базиса в £, так же как и в случае конечномерного пространства.
Пусть (^eL — какой-нибудь алгебраический базис в Е.
Каждой строго положительной функции w на L поставим в со-
соответствие полунорму Nw на £, определенную формулой
Nw(x)= 2 w(X)-l\x(X)l
где через х обозначена такая скалярная функция на L с конеч-
конечным носителем, что х— 2 ^(^)ек- Покажем, что семейство
k <= L
полунорм Nw является определяющим для топологии ^оо.
Ввиду сказанного выше достаточно установить, что для ка-
каждого выпуклого уравновешенного поглощающего множества W
существует такая строго положительная функция w9 что W со-
содержит множество
Для построения функции w заметим, что из того факта, что мно*-
жество W является поглощающим, следует существование для
каждого X^L такого положительного числа w(X), что
wCk)e%^W. Пусть x^Uw для определенной таким образом
функции w. Так как при каждом h^L имеет место включение
ш(А,)£хе W, а множество W выпукло и уравновешено, то из со-
соотношения
х = Цх(Х)е1 = 2 w (Я)" x(K)-w {K)eK
следует, что хе^, что и требовалось доказать.
С помощью полунорм Nw покажем теперь, что пространство
(£, too) полно. Пусть (Хг)—сеть Коши в £ (в равномерной
структуре, определенной топологией too). Так как линейная фор-
форма л»—^Л(Я) является /оо-непрерывной при каждом XeL, то
существует конечный предел | (Л) = lim xi (Л) при любом ^et.
1.10. Локально выпуклые пространства 119
Остается показать, что определенная таким образом функция
| на L имеет конечный носитель и что х= 2 |(Я)еЛ< = Нт л^-,
в топологии too. Будем исходить из характеризации фундамен-
фундаментальности сети (лгг-) через полунормы Nw, т. е. из того факта,
что для каждой функции w существует такой индекс k = h{w)%
что для всех индексов /, / > /о имеет место неравенство
или
^ w AГ11 Stt (Я) -xj (Я) | < 1, /, / > /0.
Это неравенство останется справедливым, если заменить L лю-
любым его конечным подмножеством F. Делая такую замену, пере-
переходя к пределу при /->оо и снова расширяя F, получаем сле-
следующее неравенство:
2 ^(Я)"ЦП^)"-^(^I<1, t>h- A.10.1)
Отсюда вытекает, что
Пусть Т7 — конечный носитель функции х1о. Тогда имеет место
неравенство
|£(Л) |<^(Х), Ke=L\F. A.10.2)
Так как это справедливо для каждой функции w и соответствую-
соответствующего конечного множества, /\ то функция | обладает конечным
носителем. Действительно, в противном случае существовали бы
такие различные индексы Яп (я=1,2,...), что £(Хп)=£0. Опре-
Определим функцию w(k), положив ее равной 2-1\1(},пу\ при Я = ЯП,
м= 1, 2,..., и 1 при всех остальных Я. Тогда неравенство A.10.2)
не выполняется ни для какого конечного подмножества F в L.
Таким образом, £ обладает конечным носителем, и х = 1>1(Х)ек
есть элемент из Е, для которого £=£. Следовательно, неравен-
неравенство A.10.1) равносильно неравенству
Так как это верно для любого w, то x = /oo-lim дсг-, и полнота £
доказана.
Замечание. Топологию too не следует смешивать ни с
сильнейшей линейной топологией в Я, ни, с так называемой ко-
конечной топологией в Е. В последней топологии открытыми счи-
считаются те и только те множества £/, для которых пересечение
UC\F относительно- открыто в F (в единственной отделимой
120 Гл. 1. Векторные и топологические векторные пространства
линейной топологии в F) для каждого конечномерного вектор-
векторного подпространства F в Е. Подробнее об этих топологиях см.
у Ка кута ни и Кл и [1].
1.10.2. Полунормированные и нормированные пространства.
Рассмотрим случай, когда семейство (pi) состоит из одного эле-
элемента р. Пару (£, р) будем называть полунормированным век-
векторным пространством или нормированным векторным про-
пространством, если р — норма (т. е. р(х)>0 при хфО). В обоих
случаях одноэлементное семейство (р) определяет в Е локально
выпуклую топологию. Говорят, что полученное таким образом
локально выпуклое пространство полунормируемо (или норми-
нормируемо). Оно отделимо тогда и только тогда, когда р — норма.
Подпространства и факторпространства полунормируемых
пространств полунормируемы. Подпространства и факторпро-
факторпространства по замкнутым подпространствам нормируемых про-
пространств нормируемы.
Исторически самыми ранними примерами функциональных
пространств были нормируемые пространства.
За примерами обратимся к п. 1.8.4. Пространства В(Т) и
(Т) нормируемы. Пространство &* при р > 1 полунорми-
полунормируемо.
Отделимое пространство, ассоциированное с полунормиро-
полунормированным, нормируемо. В частности, при р^-\ нормируемо про-
пространство, асссоциированное с 9?v — так называемое лебегово
пространство, обычно обозначаемое через L? (гл. 4). Если
0<р<1, то пространство 3SV уже не локально выпукло
(п. 4.16.3).
Приведем еще несколько примеров нормированных прост-
пространств.
1.10.3. Примеры: пространства lp(T), c(f) и со(Т). Пусть
Г — произвольное множество и р^-l. Обозначим через 1р(Т)
векторное подпространство в Кт, образованное теми функциями
х, для которых
2 \x(t)\p< + oo.
Пространство 1р(Т) наделяется нормой (§ 4.2)
Иногда обозначают символом 1°°(Т) пространство, которое
мы до сих пор обозначали через В(Т) (пример C) п. 1.8.4).
Соответствующая норма записывается следующим образом:
Случай, когда множество Т конечно, не представляет особого
интереса. Если множество Т содержит, скажем, п элементов, то
1.10. Локально выпуклые пространства 121
все локально выпуклые пространства 1р(Т) изоморфны про-
пространству Кп (хотя, естественно, соответствующие нормы раз-
различны).
Если Т — счетное множество, то его можно отождествить с
множеством N натуральных чисел, а 1р(Т)—с известным про-
пространством последовательностей, суммируемых в р-й степени
l l(N)
Пространство iP(T) можно определить для любого р > О,
однако при 0 < р < 1 оно уже не будет локально выпуклым
(§ 4.2).
Отметим два важных подпространства в 1°°(Т). Первое из
них — это подпространство с(Т), состоящее из тех х^1°°(Т),
которые имеют конечный предел на бесконечности, т. е. для ко-
которых существует такое число | («предел x(t) при /стремящемся
к бесконечности»), что для любого е>0 множество {/ е Т: \x(t)—
— g| > e} конечно. Другое подпространство, со(Т) состоит из тех
х£с(Г), для которых предел на бесконечности (в указанном
выше смысле) равен нулю. Там, где это явно не оговаривается,
мы будем считать, что эти два подпространства наделены нор-
нормой, индуцированной нормой из 1°°(Т). Каждое из этих подпро-
подпространств замкнуто в 1°°(Т) (см. упр. 1.4) и, значит, является
банаховым пространством (п. 1.10.5).
В упр. 1.1 —1.4 устанавливаются некоторые основные свой-
свойства пространств /р(Г), с(Т) и Cq(T).
1.10.4. Примеры: пространства Харди Нр и пространства HLp.
Пусть D — открытый единичный круг в комплексной плоскости,
и пусть 0</?<оо. Обозначим через Нр множество голоморф-
голоморфных в области D функций /, для которых число
\ир
NP(f)-
конечно. При /? = оо требуем конечности числа
Afoo(/)= sup |/(z)|»
Если р^- 1, то Np является нормой на Нр. Это уже не имеет
места, когда 0 <р < 1. Однако из неравенства
h г*
|== sup \i^
L —3t
[см. Харди, Литтлвуд и Полна [1, F. 13—6)]; ср. с не-
неравенством D.2.4)] следует, что Np(f-g) есть метрика на Нр.
Это же неравенство показывает, что Нр при 0<р<1 есть
122 Гл. 1. Векторные и топологические векторные пространства
векторное пространство. При р ^ 1 это вытекает из неравенства
Минковского (п. 4.11.2):
Таким образом, Нр является нормированным векторным про-
пространством при /?^1 и метризуемым топологическим векторным
пространством при 0 <р < 1.
Ливингстон [1] показал, что при 0<р<1 пространство
Нр не является локально выпуклым. Для дальнейшего изучения
пространства Нр как топологических векторных пространств
можно рекомендовать работы' Тэйлора [3] и У о л тер с а [1, 2].
Многие глубокие свойства пространств Нр связаны с теорией
рядов Фурье (см. Зигмунд [1, 7.56] и [2, т. 1, стр. 431—452], а
также Гофман [1]).
Аналогичные пространства Hp(D) могут быть определены и
для более общих областей D. Однако при этом все усложняется,
так как окружности \z\ ==r приходится заменять линиями уровня
функции Грина для области D.
Другим пространством, связанным с областью D и имеющим
отношение к рассматриваемому кругу вопросов, является про-
пространство HLp(D), образованное голоморфными на D функция-
функциями, для которых конечно число
Под интегралом в правой части понимается верхняя грань
множества всевозможных интегралов J J | / \р dx dy, когда К
к
пробегает базу компактных подмножеств в D (ср. гл. 4). Множе-
Множество HLp(D) по-прежнему является векторным пространством;
пр есть норма на HLp(D) при /?>1, и npp(f — g) есть метрика
при 0 < р < 1.
Пусть D — открытый единичный круг с центром в начале
координат; тогда из равенства
1 2я
J J | f(z) \p dx dy= j r dr J \f(re*) \pdQ
D 0 0
вытекает
откуда следует, что Нр a HLp.
Доказательство полноты пространств Нр и HLp опирается
на некоторые неравенства. Пусть г0бО, и пусть число г > 0 на-
1.10. Локально выпуклые пространства 123
столько мало, что замкнутый круг Д(г0, г) с центром в точке г0
и радиусом г лежит в D. В силу формулы Коши
I/(*о) I<i£-J I/(г0 + reside.
О
При р^1 в силу неравенства Гёльдера имеем
2Я
<^ fl/(*<> +re"*) I'dB. A.10.3)
о
Это же неравенство справедливо и при р > 0, так как функция
|/|р — субгармоническая на D. Если обе части неравенства
A.10.3) умножить на rdr и затем проинтегрировать по г на от-
отрезке [0,/?], то получим
R 2я
4" Я21 / (г„) I" < ^г J r rfr f | / (zo + re"») 1^9 =
о о
А (го, ^
Следовательно, имеет место неравенство
\f(zo)\<(nR2rwnp(f).
Можно считать, что R <d(zOi D*), где d(zo,D*) — расстояние от
точки г0 до границы D* области D. Тогда для произвольной
точки z^ D получаем
|/(г)|<М2(г, D*)]-Upnp(f)*s:[d2(z, D*)Vlp Npif). A.10.4)
С помощью неравенств A.10.4) легко показать, что простран-
пространства Н? и HLp полны. В п. 1.12.1 (8) это подробно сделано для
случая р = 2. В упр. 1.5 читателю предлагается убедиться в ти-
типичности этого случая.
Другим следствием формулы A.10.4) является существова-
существование нетривиальных непрерывных линейных форм на простран-
пространствах Нр и HLp даже при 0</?<1. Это контрастирует с поло-
положением в случае общего пространства L? при 0 < р < 1
(п. 4.16.3).
1.10.5. Банаховы пространства. Под банаховым простран-
пространством мы будем понимать нормируемое топологическое вектор-
векторное пространство, которое является полным. Для наших целей,
вообще говоря, не столь уж важно, какой из возможных эквива-
эквивалентных норм наделено пространство. Поэтому мы рассма-
рассматриваем банахово пространство как нормируемое, а не как
121 Гл. 1. Векторные и топологические векторные пространства
нормированное. Однако для удобства рассматриваемые прост-
пространства задаются обычно вместе с нормой.
В книге Банаха [1] банаховы пространства названы «про-
«пространствами типа (В)». Этот термин встречается и у многих
других авторов.
Пространства В(Т), С(Т) (в случае когда Т — компактное
пространство) и Съа{Т) из примеров B) и D) п. 1.8.4 являются
банаховыми. Таковы же пространства 2>, ассоциированные с
пространствами 2?v (пример F) п. 1.8.4), и пространства 1р(Т)
из п. 1.10.3 при р> 1.
Всякое векторное подпространство банахова пространства
нормируемо. Всякое замкнутое векторное подпространство ба-
банахова пространства банахово.
Произведение конечного семейства {Ei)l<i<n банаховых
пространств само банахово относительно нормы
где x = (Xi)l<i<n^ Ц Ei (существует, конечно, много дру-
гих эквивалентных норм, которые можно использовать с тем же
успехом).
Факторпространство банахова пространства по его замкну-
замкнутому векторному подпространству также является банаховым
пространством. Докажем это. Пусть L — замкнутое векторное
подпространство банахова пространства Е. Как мы уже знаем
(п. 1.10.2) E/L — нормированное пространство с нормой
Из приводимой ниже леммы следует, что для полноты про-
пространства E/L необходимо и достаточно, чтобы всякий ряд
2*г (/г), для которого 2II** (я) II < + °°> сходился в E/L. Итак,
п п
пусть 2ll*c (я) 11< + °°; выберем элементы х(п)<~хс(п) так,
п
чтобы 2||*(я)||< + оо. В силу полноты пространства Е та же
п
лемма (или аналогичное прямое рассуждение) показывает, что
ряд 2*(я) сходится в Е. Обозначим сумму этого ряда через х\
таким образом, 11*— 2 *(л)||->0 при r-^оо. Наконец, из co-
coll п < г II
отношений
Uc- 2 * Л") HI (*-2 *("))< К it* - 2*(*)I-*Q
< < ^
/ tO. Локально выпуклые пространства 125
вытекает сходимость ряда ^jxc(n) к элементу хс из E/L. Таким
п
образом, остается доказать следующую лемму.
Лемма. Пусть (F,p)— полунормированное пространство. Для
полноты пространства F в равномерной структуре, определенной
полунормой р, необходимо и достаточно выполнение следующего
условия: если последовательность (уп) элементов из F такова,
что 2 р (уп) < + °°> т° ряд 2 Уп сходится в F.
п
Доказательство. Пусть F — полное пространство. В си-
силу неравенств
/n=r+k \ n=r+k
2 У< 2 Р(Уп)
1 I 1
2
г+1
и сходимости ряда 2лр(уп) последовательность (sr) частичных
п
сумм sr = 2 Уп есть последовательность Коши, поэтому (sr)
сходится в F.
Обратно, пусть выполнены условия леммы и (sj — последо-
последовательность Коши в F, Выберем по индукции натуральные
числа nk<nk+i так, чтобы элемент yk = sn — sn удовлетворял
неравенству р (^)< \/k2. Тогда ряд 2 Р (Ун) сходится и, еле-
k
довательно, ряд 2jyk сходится в F, а это означает сходимость
в F последовательности (snft). Но тогда последовательность (sn)
как последовательность Коши сходится в F. |
1.10.6. Топологическое сопряженное к полунормированному
пространству. Если (Е, р) — полунормированное пространство,
наделенное топологией, определяемой полунормой р, то его то-
топологическое сопряженное Ег состоит из тех и только тех ли-
линейных форм х*е£*, которые ограничены относительно ру т. е.
для которых конечно число
р* (*•) = sup {| <jc, х) |: х е= Е, р (х) < 1}.
Легко проверяется, что /?* есть норма на Е'. Мы будем назы-
называть ее естественной нормой на £'. Эта норма не определяется
однозначно топологией пространства Е. Однако если две различ-
различные полунормы р и q определяют в Е одну и ту же топологию
(т. е. р и q эквивалентны), то р* и q* эквивалентны, т. е. суще-
существует такое число с>0, что
ср* < q
126 Гл. 1 Векторные и топологические векторные пространства
Таким образом, нормы р* и q* определяют в Е' одну и ту же
топологию. Эта топология нормируема и называется канонически
ассоциированной с полунормированным пространством Е.
Важно отметить, что пространство Е' полно в структуре,
определяемой нормой /?*, и, следовательно, является банаховым
пространством.
Действительно, пусть (aQ — последовательность Коши в
(£', /?*). При любом х <= Е числовая последовательность ((х, л/))
будет, очевидно, последовательностью Коши. Следовательно, по-
последовательность [хг^ сходится к некоторому х*е£* в слабой
топологии а (Е*,Е) (п. 1.11.1). С другой стороны, для любого
заданного е>0 найдется такое число По — п0(г),что при т.п^-по
имеет место неравенство р* (х'т —- х'п)^,&. Таким образом, если
В = {х^Е: р(х)^С\} — единичный шар в £", то при т,п>п0 и
х^В имеет место неравенство
\<х. *;>-<*, <>|<е.
Пусть х и я>/10 фиксированы. Переходя в этом неравенстве
к пределу при т-*оо, получаем, что при всех х^В и всех
л> По
\(х,х')-(х, <>|<е. A.10.5)
Так как sup P*(*Q = k < + оо, то из A.10.5) следует, что при
п
любом хеВ имеет место неравенство ((х, х*) \^k + е, т. е.
р* (х*) < + оо, и потому х*^Е'. Обозначим х* через хг. Нера-
Неравенство A.10.5) показывает, что \(х, х' — х'п)\^& при п^п0 и
igB, или, что то же, р*(х' — х'п)^в при п^п0. Таким обра-
образом, х' = \\тх'п, что и доказывает полноту пространства (Ef, p*).
Замечание. Полученный результат есть частный случай
приводимого ниже предложения 1.10.9.
1.10.7. Колмогоровский критерий нормируемости. Критерий
Колмогорова (см. Колмогоров [1]) состоит в следующем:
отделимое топологическое векторное пространство Е норми-
нормируемо тогда и только тогда, когда в Е существует хотя бы
одно ограниченное открытое выпуклое множество.
Необходимость этого условия очевидна. Докажем его до-
достаточность. Пусть условие выполнено. Можно считать (совер-
(совершая в случае необходимости сдвиг), что в Е существует огра-
ограниченная открытая выпуклая окрестность нуля. Замыкание \V
этого множества является ограниченной выпуклой замкнутой
окрестностью нуля. Существует уравновешенная окрестность
нуля V, содержащаяся в W. Пусть U — замкнутая выпуклая
оболочка множества V. Множество U замкнуто, выпукло, ураз*
1.10 Локально выпуклые пространстве? 127
новешено и содержится в W, следовательно, оно ограничено.
Таким образом, множество U есть ограниченная замкнутая вы-
выпуклая уравновешенная окрестность нуля в Е.
Пусть р — функционал Минковского множества U (теорема
1.6.4). В силу следствия 1.6.6 U={x<=E: р(*)<1} и р — по-
полунорма на Е. Убедимся, что р определяет заданную в Е то-
топологию. Для этого достаточно показать, что множества вида
XV, где X > 0, образуют в Е базу окрестностей нуля. Для этого
в свою очередь достаточно проверить, что каждая окрестность
нуля U' в Е содержит некоторое XU. Так как U — ограничен-
ограниченное множество, то для некоторого а > О имеем U c= a U\ от-
откуда следует, что a~lUdU\ Тем самым нормируемость про-
пространства Е доказана х). Ц
Обозначим через {0} множество всех х^Е, удовлетворяю-
удовлетворяющих условию р(х)=0, т. е. множество fl &U: X > 0}. Оно сов-
совпадает с множеством f) {№' к > 0} для всякой ограниченной
окрестности нуля V в Е.
Отсюда следует, что критерий Колмогорова может быть
дополнен следующим образом.
► Топологическое векторное пространство Е нормируемо
тогда иг только тогда, когда в нем существует по край-
крайней мере одна такая ограниченная выпуклая окрест-
окрестность нуля U, что справедливо отношение
f]{XU: ^>0} = {0}.
Уильямсоном [1], [2] были недавно получены другие
критерии нормируемости.
1.10.8. Пространства непрерывных линейных отображений.
Вернемся снова к вопросу о различных способах топологиза-.
ции векторных подпространств пространства L(E, F), где F —
заданное топологическое векторное пространство. В наиболее
интересных случаях Е также является топологическим вектор-
векторным пространством, однако для общей теории это предполо-
предположение несущественно.
Для данных множества Л в £ и окрестности нуля V в F
положим
W(A,V)={us=L(E,F): и (А) с V].
Пусть выделена система © подмножеств А из £, обладаю-
обладающая тем свойством, что объединение любых двух множеств
из © содержится в некотором третьем множестве из ©, и
пусть Нг—векторное подпространство пространства L(E,F).
1) Так как Е по предположению отделимо, то р является нормой. В сле-
следующем абзаце Е уже не предполагается отделимым. — Прим. ред.
128 Гл. 1. Векторные и топологические векторные пространства
Мы превратим Я в топологическое векторное пространство с
базой окрестностей нуля, состоящей из множеств вида
Hf)W(A, V), где Л пробегает ©, а V—базу окрестностей
нуля в F. Полученную таким образом топологию в Я будем
называть топологией равномерной сходимости на множе-
множествах из системы ©, или коротко ^-топологией, и обозначать
через Г@.
Для того чтобы эта топология была линейной топологией
в Я, необходимо, чтобы каждое из множеств Hf)W(A,V) было
поглощающим в Я. Это возможно тогда и только тогда, когда
множество и(А) ограничено в F для каждого А е ©. Следо-
Следовательно, если система © задана, то наибольшее возможное
Я— это векторное подпространство L©(£, F) в £(£,£), со-
состоящее из тех и только тех линейных отображений u^L(EyF),
которые переводят каждое множество из © в ограниченное мно-
множество в F. Далее Г@ будет обозначать ©-топологию в
U(E,F).
Топология Г© отделима, если F отделимо и множество
U {^4: Я>0, ^eS} порождает Е. Очевидно также, что если
© d ©', то L® (£, F) => L& (£, F) и топология Г® | L& (£, F) сла-
слабее топологии Г©'. Пространство L©(£, Т7) ц топология Г@ не
изменяется, если каждое множество Л из © заменить его урав-
уравновешенной оболочкой. Если пространство F локально рыпукло,
то и при переходе к выпуклым оболочкам множеств Л из ©
пространство L©(£, F) и топология Т& не изменяются.
Особенно важным является тот случай, когда £ (так же
как и F)—топологическое векторное пространство, а © — си-
система всех ограниченных подмножеств в Е. Тогда мы будем
вместо L©(£, F) писать Ьь(Е, F) и топологию Г@ называть
сильной топологией. Линейные отображения, принадлежащие
Lb(E,F), называются ограниченными (ср. с п. 1.9.1).. Простран-
Пространство Lb(E,F) всегда содержит LC(E, F) (пространство всех не-
непрерывных линейных отображений £ в F).
Существенную роль играет другой крайний случай, когда ©
состоит из всех конечных подмножеств в £ (в частности, содер-
содержит все одноточечные подмножества в £). Тогда L®(E,F) =
= L(E, F) и Г© есть просто топология поточечной (или про-
простой) сходимости.
Читателю будет полезно запомнить, что множество @~ в
L<&(E,F) ограничено (в топологии Г@) тогда и только тогда,
когда для каждого множества Ле© множество \J{u(A): u^
^@~} ограничено в F. (В связи с этим см. также теорему 7.3.1
C).)
Если пространство F локально выпукло, то и топология Г©
локально выпукла,
1,10 Локально выпуклые пространства 129
1.10.9. Предложение. Пусть множество \}{ХА: Л > 0, ^gS}
порождает Е, a F— полное пространство. Тогда пространство
L® (E, F) полно (в равномерной структуре, определяемой топо-
топологией Т&).
Доказательство. Пусть (ui)—сеть Коши в L®(Ey F)
(в топологии 7'е). В силу предположений относительно системы
® для каждого элемента х^Е сеть (Ui(x)) есть сеть Коши в
F. Полнота F влечет существование при каждом х^Е предела
и(х) = \\шщ(х) в F. Определяемое таким образом отображе-
отображение и, очевидно, принадлежит L(E, F).
Так как (щ) есть сеть Коши, то для заданных множества
А е 3 и окрестности нуля V в F существует такой индекс i0,
что
щ(х)—и{{х) gI/
при х^А и I, j^-io. Окрестность V можно считать замкнутой.
Следовательно,
и (х) — щ (x) s V при х е Л и / ^ /0-
Отсюда, в частности, следует, что и (A) cz uio (A) + V. Так как
множество Uto(A) ограничено, то и множество и (А) ограничено.
Значит, отображение и принадлежит L® (£", F). Более того, из
предыдущего вытекает, что и — щ^ W (А, V) при /^/о» т. е.
Т&А\тщ = и. Полнота пространства Ls(£, F) доказана. В
1.10.10. Случай полунормированного пространства. В заклю-
заключение § 1.10 делаем несколько замечаний относительно того ча-
частного случая, в котором оба пространства Е и F топологизи-
рованы полунормами р и q соответственно.
В этом случае пространства Lb(E,F) и LC(E,F) совпадают.
Каждое из них состоит в точности из тех отображений и е
gL(£, F), для которых конечно число
n(u) = sup{q(u(x)): х <е= Е; р(лг)<1}.
Функция п является полунормой на LC(E, F), Если q — нор-
норма, то и п — норма. Заметим также, что если р и q заменить
эквивалентными полунормами р' и qr соответственно, то полу-
полунорма п заменится эквивалентной полунормой п'. Можно по-
поэтому сказать, что если пространства Е и F нормируемы, то
таково же и пространство LC(E, F).
Важно отметить, что если пространство F полно, то полным
будет и пространство LC(E, F). Это утверждение является ча-
частным случаем предложения 1.10.9.
Отсюда следует, что пространство LC(E, F) банахово, если
Е — полунормируемое, a F — банахово пространство.
130 Гл. 1. Векторные и топологические векторные пространства
Сходимость в LC(E, F) относительно рассмотренной выше
топологии называется часто «сходимостью в равномерной опе-
операторной топологии». Ее не следует смешивать с равномерной
сходимостью на Е, это равномерная сходимость на каждом ог-
ограниченном множестве в Е.
1.11. Слабые топологии в сопряженных пространствах
Подробное изучение этой темы будет проведено в гл. 7, но
нам удобно уже сейчас познакомить читателя с некоторыми
определениями и свойствами. Наши замечания уточняют и рас-
расширяют результаты п. 1.10.8, относящиеся к случаю F = К
1.11.1. Топологии o(E*,L). Пусть Е — векторное простран-
пространство без топологии, L — векторное подпространство в Е, Е* —
алгебраическое сопряженное пространства Е. Среди топологий
в £*, относительно которых каждая из функций х* (х, х*) не-
непрерывна при произвольном фиксированном x^L, существует
слабейшая. Эта топология обозначается через о(Е*, L) и назы-
называется слабой топологией в £*, порожденной подпространством
L. Топология g(£*, L) согласуется со структурой векторного
пространства £* и превращает £* в локально выпуклое про-
пространство. Базу окрестностей нуля в Е* образуют множества
вида
£/• (Л е) = {*• €= £•: | <*, х*) |<е для х с= F),
где е>0, a F — конечное подмножество в L. Семейство полу-
полунорм
/£(*•) = sup {|<х, х*)\: x<=F},
где F пробегает все конечные множества в L, является опреде-
определяющим для топологии о(Е*, L).
В случае, когда L = Е, говорят просто о слабой топологии в
£*.
Топология о(Е*9 Е) всегда отделима. Заметим, что Е* =
= L{E} К), а топология а(£*, Е) —не что иное, как 7©-тополо-
гия, где система © состоит из всех конечных подмножеств в Е
(п. 1.10.8).
1.11.2. Слабые топологии о(Е, М). Пусть снова Е — вектор-
векторное пространство, £* — его алгебраическое сопряженное. Пусть
М — векторное подпространство в Е*. Метод предыдущего пун-
пункта приводит к топологии а (£"**, М). Пользуясь вложением Е
в £** (п. 1.4.7), получаем индуцированную топологию а(Е, М),
которая называется слабой топологией в Ег порожденной под-
/.//. Слабые топологии в сопряженных пространствах 131
пространством М. Ее определяющее семейство полунорм обра-
образовано функциями
ро(х) = sup{|<*f x*)\: /ей},
где G пробегает все конечные подмножества в М.
Естественно, что топология а(Е, М) может быть определена
и без привлечения пространства £** и вложения Е в £**. Она
является слабейшей топологией в Е, при которой непрерывна
каждая линейная форма х *—> {х, #*), где х* — произвольный
фиксированный элемент из М.
Топология g(E, M), вообще говоря, не отделима. Топология
а(Е, £*), однако, всегда отделима.
1.11.3. Ослабленная топология топологического векторного
пространства. Пусть Е — топологическое векторное простран-
пространство и Е' — его топологическое сопряженное (п. 1.9.4). Про-
Пространство Е' является подпространством пространства £*, по-
поэтому можно рассмотреть в Е соответствующую топологию
а (£,£'). Она называется ослабленной топологией в Е. Это на-
название оправдано тем, что топология о(Е, Е') всегда слабее ис-
исходной топологии в Е.
-В исключительных случаях о(Е, Е') может быть и нулевой
топологией. Это имеет место, если Ef = {0} (например, если
Е =cS?pj 0<р< 1, или если Е—топологическое векторное про-
пространство, определенное в 1.8.4G)). Из теоремы Хана — Бана-
Банаха следует, что если Е — отделимое локально выпуклое про-
пространство, то топология о(Е, Е') отделима (см. следствие 2.2.6).
Замечание. «Двойственной» к топологии о{Е,Е') яв-
является топология о(Е\ £), индуцированная в Е' d £* тополо-
топологией о{Е*, Е). Топология а(£/, Е) всегда отделима.
В заключение сформулируем и докажем один полезный ре-
результат, касающийся слабых топологий.
1.11.4. Теорема. A) Пусть Е — векторное пространство. Мно-
Множество SaE* относительно компактно в топологии в(Е*,Е)
тогда и только тогда, когда оно слабо ограничено1), т. е.
когда
sup {\{x, x*)\: x*e=S}< + оо
для каждого х е Е.
B) Пусть Е — топологическое векторное пространство. Если
множество S а Е' слабо ограничено и равностепенно непрерыв-
непрерывно, то оно относительно компактно в топологии о(Е', Е).
Л) То есть ограничено в слабой топологии. Аналогичное замечание отно-
относится кб всем употреблениям слова «слабый». — Прим. pedt
132 Гл. 1. Векторные и топологические векторные пространства
Доказательство. A) Необходимость утверждения сле-
следует из общего принципа, согласно которому непрерывная чис-
числовая функция на компактном пространстве ограничена.
Достаточность условия вытекает из теоремы Тихонова
(п. 0.2.17) и того очевидного факта, что пространство Е*, наде-
наделенное слабой топологией, является замкнутым подпростран-
подпространством в КЕ (рассматриваемом в топологии произведения).
B) Равностепенная непрерывность множества S означает
существование в Е такой окрестности нуля_£/, что \{х, я*)|-<1
при хе(/ и х* е S. Слабое замыкание S множества SczE*
сохраняет это свойство, как и свойство быть слабо ограничен-
ограниченным. Далее из равностепенной непрерывности множества *? сле-
следует, что S с Е'. Остается воспользоваться утверждением A). I
1.11.5. Замечание. Если Е — полунормируемое простран-
пространство, то в Е' равностепенно непрерывны те и только те множе-
множества, которые ограничены относительно естественной нормы в
Ег (п. 1.10.6). Объединяя это замечание с утверждением B)
теоремы 1.11.4, можно получить некоторые важные результаты,
касающиеся слабой компактности слабо ограниченных мно-
множеств в различных функциональных пространствах и простран-
пространствах мер. Это будет сделано в гл. 4 (п. 4.10.3, 4.12 и 4.16).
1.12. Пространства со скалярным произведением.
Предгильбертовы пространства. Гильбертовы
пространства
В этом параграфе собраны те факты из элементарной тео-
теории гильбертовых пространств, которые используются далее в
этой книге и в то же время сами имеют приложения в функ-
функциональном анализе. Просто удивительно, насколько полезны-
полезными оказываются эти элементарные результаты. В настоящей
книге мы нигде не занимаемся по-настоящему глубоким изу-
изучением гильбертовых пространств и линейных операторов в
них. Этим вопросам посвящено много превосходных книг, среди
которых отметим лишь некоторые: Стоун [1], Рисе и Надь
[1], Кук [2], Халмош [2], Шмайдлер [1], фон Нейман
[1], Данфорд и Шварц [2]1). В книге Халмоша [X, гл. III]
имеется прекрасное изложение алгебраических основ теории.
Несмотря на то что книга посвящена конечномерному случаю,
большинство идей можно распространить на общий случай
(хотя отдельные результаты, или доказательства, или и то и
другое вместе такого обобщения не допускают).
]) См. также Ахиезер и Глазман [1]; Гохберг и Крейн
[1, 2] —Прим. перед,
1.12. Пространства со скалярным произведением 133
1.12.1. Исходные определения и примеры. [X, § 23, 26—30].
Пусть Е — векторное пространство над К (где К — либо R, ли-
либо С); /С-значная функция /, определенная на произведении
Е X Е, называется билинейной формой на £, если она линейна
по каждому аргументу. Если f(x, у) =f(y, х) для любых х, у
из Е, то говорят, что форма / симметрична. Под полуторали-
нейной формой на Е (терминология Гротендика) понимают та-
такую функцию /: Е X Е —> /С, что функция x\—>f(x,y) линейна
при каждом фиксированном у, а функция y*—^f(x, у) линейна
при каждом фиксированном х (черта сверху означает переход
к комплексно сопряженному числу). Последнее условие иногда
формулируют так: функция y^—^f(xyy) сопряженно линейна при
каждом фиксированном х. Если К = R, то понятия билинейно-
билинейности и полуторалинейности совпадают. Функция f: ЕхЕ—*К
называется эрмитовой, если f(x, у) =f(y, x) для любых х,
у е £. Если К = R, то эрмитовость и симметричность означают
одно и то же.
Скалярным (или внутренним) произведением на векторном
пространстве Е над К называется такая полуторалинейная эр-
эрмитова форма f на Е, что f(x,x)^0 для любого xg£ (f(x,x)
вещественно в силу эрмитовости f). Говорят, что скалярное
произведение строго положительно, если f(x, x) > 0 при
хфЪ.
Под пространством со скалярным произведением понимает-
понимается пара, состоящая из векторного пространства Е над К и ска-
скалярного произведения на Е. Обычно мы будем употреблять для
обозначения пространства со скалярным произведением просто
символ Е, а скалярное произведение обозначать через (х\у).
В книге Халмоша [X, § 59, 60] предлагаются названия унитар-
унитарное пространство и евклидово пространство для соответственно
комплексного и вещественного (конечномерного) пространства
со скалярным произведением.
Неравенство Коши — Шварца. Пусть (х\у)—скалярное
произведение на Е. При любых х,у^Е билинейная форма
(ах + $у\ах + ру) от переменных скаляров аир принимает
лишь неотрицательные значения. Отсюда с помощью неслож-
несложных рассуждений [X, § 64] получаем важное неравенство
\(х\у)\<(х\х)г(у\у)т. A.12.1)
Из этого неравенства следует, что функция N(x) = (x\xJ
является полунормой на Е. Каждое пространство со скаляр-
скалярным произведением можно, таким, образом, рассматривать как,
лолунормируемое топологическое векторное пространство.
134 Гл. 1. Векторные и топологические векторные пространства
Пространство со строго положительным скалярным произ-
произведением называется предгильбертовым пространством1); это
пространство, у которого ассоциированная полунорма N(x) =
= {х\х)х12 является в действительности нормой. В этом случае
вместо N(x) будем писать ||л:||.
Предгильбертово пространство, полное относительно ассо-
ассоциированной нормы, носит название гильбертова пространства.
Каждое гильбертово пространство является, следовательно, ба-
банаховым пространством.
Некоторые примеры и замечания. A) Пусть Т — произволь-
произвольное множество, р — положительная функция, определенная на
Т. Обозначим через 12{Т,р) множество тех элементов хе/Ст,
для которых 2 p(t) \x{t) |2 < + оо. Из неравенства Коши —
i е= Т
Шварца2) следует, что 12(Т,р) есть векторное подпространст-
подпространство в /Ст. Введем в 12(Т,р) скалярное произведение по формуле
(x\y) = tZTP(t)x(t)y(t).
Ряд в правой части сходится абсолютно (в силу того же нера-
неравенства Коши — Шварца). Ассоциированной полунормой слу-
служит, таким образом, функция
1
N(x) = \ 2 P(t)\x(t)
Функция N будет нормой тогда и только тогда, когда p(t) >0
при каждом /е Т.
Предоставляем читателю доказательство полноты простран-
пространства 12{Т,р). Таким образом, если p(t) >0 для каждого ^gT,
то 12(Т,р) есть гильбертово пространство. Пусть функция p(t)
не обладает указанным свойством. Обозначим через Го множе-
множество {/еГ: p(t)>0}. Существует естественное линейное ото-
отображение пространства 12(Т,р) на пространство /2(Г0,/?о), где
Ро = р\То, сохраняющее структуру пространства со скалярным
произведением. Ядро этого отображения состоит из всех тех
функций х^ 12(Т, р), которые обращаются в нуль на То.
Если р = 1, то 12(Т,р) совпадает с 12(Т) (п. 1.10.3).
!) Заметим, что у Бурбаки [7] предгильбертовым называется про-
пространство со скалярным произведением в терминологии автора. — Прим. пе~
рев.
2) Здесь уместнее воспользоваться неравенством Минковского
{
~-[1рим. перев,
1.12. Пространства со скалярным произведением 135
B) Замечательно, что всякое гильбертово пространство
изоморфно как пространство со скалярным произведением про-
пространству 12(Т) для некоторого соответствующим образом по-
подобранного множества Т (это будет доказано ниже; см. заме-
замечание (е) к следствию 1.12.5). При этом пространства 12(Т) и
/2(Г') изоморфны тогда и только тогда, когда множества Т и
Т' равномощны. Этот факт позволяет поставить в соответствие
каждому гильбертову пространству гильбертову размерность,
определяющую его с точностью до изоморфизма. Первоначаль-
Первоначально в определении гильбертова пространства требовали его се-
сепарабельности1) (как топологического пространства), что соот-
соответствует счетной гильбертовой размерйости.
C) Всякое конечномерное векторное пространство может
быть многими способами превращено в пространство со ска-
скалярным произведением. При этом получаются конечномерные
гильбертовы пространства (у которых алгебраическая и гиль-
гильбертова размерности совпадают).
D) Пусть Е— пространство со скалярным произведением и
ассоциированной полунормой N. Факторпространство E/kerN
является предгильбертовым пространством. Если рассматри-
рассматривать Е и E/kevN как топологические векторные пространства,
то последнее есть попросту отделимое пространство, ассоцииро-
ассоциированное с пространством Е (п. 1.8.5). Это следует из того фак-
факта, что множество кет N есть не что иное, как замыкание (в то-
топологическом векторном пространстве Е) множества {0}.
E) Всякое предгильбертово пространство Е превращается
в гильбертово, если его пополнить.
Приведем несколько более конкретных примеров.
F) Наряду с гильбертовым пространством последователь-
последовательностей /2 = /2(N) наиболее известным гильбертовым простран-
пространством, несомненно, является пространство функций, суммируе-
суммируемых в квадрате. Подробное изложение см. в гл. 4 (особенно
п. 4.11 и 4.12). Пока же мы ограничимся описанием лишь не-
некоторых относящихся сюда примеров предгильбертовых про-
пространств и пространств со скалярным произведением, не тре-
требующих знакомства с интегралом Лебега.
Для простоты будем считать, что Т — ограниченный интер-
интервал вещественной прямой. Возьмем на Т какую-нибудь ограни-
ограниченную непрерывную функцию р^О и рассмотрим множество
Е тех непрерывных ограниченных /С-значных функций х на Г,
для которых J p{t) \x(t) \2dt< + оо. (Наши ограничения на
1) Топологическое пространство называется сепарабельным, если оно
обладает счетным всюду плотным множеством. — Прим, перев.
136 Гл. 1. Векторные и топологические векторные пространства
функции р и х на самом деле в значительной мере излишни.
Нам они нужны для того, чтобы обеспечить существование ин-
интеграла в смысле Римана.) Из неравенства Коши — Шварца
для интегралов следует, что Е— подпространство в Д"г. Введем
в Е скалярное произведение по формуле
(x\y)= p(t)x(t)y(t)dt.
T
Очевидно, что вся эта процедура является «непрерывным»
аналогом построений, относящихся к 12(Т,р) (см. выше, пример
A)).
Построенное таким образом пространство Е со скалярным
произведением тогда и только тогда будет предгильбертовым
пространством, когда множество {/еГ: p(t) =0} нигде не
плотно в Г. Если функция р не равна тождественно нулю, то
пространство Е заведомо не полно. В действительности это
одна из причин неудовлетворительности римановой теории ин-
интегрирования.
Ясно, что приведенное построение можно видоизменить, за-
заменяя интервал Т какой-нибудь «простой» областью плоскости
или пространства. В гл. 4 даются гораздо более широкие обоб-
обобщения указанного построения.
G) Пространство Харды Я2 было определено в примере
1.10.4. Там же было доказано, что оно является банаховым
пространством относительно нормы 11/11 = Л/2(/), задаваемой
формулой
sup -L \\f(re*)fde\ .
11/11
Рассмотрим разложение функции / в ряд Тэйлора
Легко проверяется, что
-я гс=0
при 0<><1, откуда следует равенство
H/ll2=ikJ2.
0
1.12. Пространства со скалярным произведением 137
Сходимость ряда в правой части этого равенства является в
действительности необходимым и достаточным условием при-
принадлежности пространству Я2 функции f, для которой сп слу-
служат коэффициентами разложения в ряд Тэйлора. Это означает,
что Я2 становится гильбертовым пространством, если скаляр-
скалярное произведение определено следующим образом:
где сп и dn— коэффициенты разложения в ряд Тэйлора функ-
функций f и g соответственно. Так как полученный ряд сходится аб-
абсолютно, то имеет место равенство
(f\g)= lim ±-
10 ZJl
(8) Пространство HL2(D). Пусть D — некоторая область в
плоскости комплексного переменного z = х + iy. Как и в
п. 1.10.4, через HL2(D) обозначим пространство тех голоморф-
голоморфных в области D функций, для которых
J \\f(z)\2dxdy<+oo.
D
Введем в этом пространстве скалярное произведение по фор-
формуле
(/l£)=J \f{z)W)dxdy.
D
Так как рассматриваемые функции непрерывны, то полученное
пространство предгильбертово. На самом деле оно даже гиль-
гильбертово. Приведем подробное доказательство полноты про-
пространства HL2(D). Для этого воспользуемся неравенством
A.10.4) п. 1.10.4, переписав его следующим образом:
|^B)|<я~</-1ИЛ1, A-12.2)
где II/11 = (/IfJ и d—d(z, D*) — расстояние от точки z до
границы области D.
Из неравенства A.12.2) непосредственно следует, что по-
последовательность Коши (fn) в HL2(D) является также после-
последовательностью Коши относительно компактной (т. е. локально
равномерной) сходимости в D (см. пример D) п. A.8.4)).
Следовательно, в D существует локально равномерный пре-
предел / = limfn, причем функция f голоморфна в D, Остается
138 Гл. 1. Векторные и топологические векторные пространства
показать, что функция f^HL2(D) и что она является пределом
последовательности (/п) в смысле пространства HL2(D).
Так как (/п)—последовательность Коши, то она ограниче-
ограничена, т. е. sup||/rt|| = Af < + оо. Пусть К—компактное подмно-
п
жество в D\ тогда имеем
Фиксируя К и полагая /г->оо, получаем в силу локально рав-
равномерной сходимости неравенство
J
к
Так как число М не зависит от компакта /(, то f e#L2(D), ибо
J J | / р djc rfy = sup J \\f\2dxdy^M2< + oo.
в к к
Повторяя те же рассуждения для разностей fm — fn вместо fn
и имея в виду, что lim \\fm — fn\\ = 0> легко получаем
m, n -> оо
lim ||/ — /J| = 0, что и требовалось доказать.
Интересно, что HL2(D) является гильбертовым простран-
пространством, элементами которого являются сами функции, а не экви-
эквивалентные классы функций (как в случае L2). (В последнем слу-
случае «индивидуальные» функции получаются только тогда, когда
рассматриваемая мера дискретна — случай «обманный», в кото-
котором интеграл фактически является суммой.)
Неравенство A.12.2) и его аналог для HLp(D) при р> 1 по-
показывают, что на этих пространствах существует достаточно
много непрерывных линейных форм.
Для дальнейшего изучения пространства HL2(D) см.
упр. 1.7—1.11.
1.12.2. Ортогональность и ортогональные проекции [X, § 62—
67]. Элементы х и у пространства Е со скалярным произведе-
произведением называются ортогональными, если (х\у)=О. Говорят, что
множества А и В из Е ортогональны, если (а\Ь) =0 при а^А
hJg6. Для всякого множества A cz Е в Е существует наиболь-
наибольшее множество, ортогональное к Л. (Именно множество всех
тех элементов х^Е, которые удовлетворяют условию (х\а)=О
при каждом аеЛ.) Это множество называется ортогональным
дополнением множества Л в £ и обозначается через А1. Заметим,
что А1 — замкнутое подпространство в Е. Семейство (я*)/е/
элементов из Е называется ортогональным, если (Xi\Xj)=O при
1.12. Пространства со скалярным произведением 139
1Ф\, i, j e /. Иногда и про множество А говорят, что оно ортого-
ортогонально, если соответствующее ему семейство ортогонально, т. е.
если (х\у)=0 для х> у&А, хФу. Ортонормированным семей-
семейством (или множеством) называется ортогональное семей-
семейство, в котором каждый элемент удовлетворяет условию
\\х\[ = У(х | х) = 1. Таким образом, для ортонормированного се-
семейства (xt) имеем (Xi\x-j)= дц.
Вопросы, связанные с ортогональными проекциями, будем из-
излагать следуя Ф. Риссу; отправной точкой при этом подходе
служит некоторая экстремальная задача.
1.12.3. Теорема. Пусть Е — пространство со скалярным про-
произведением и М — полное (в равномерной структуре, индуциро-
индуцированной из Е) выпуклое подмножество в Е. Тогда для каждого
х^Е существует по меньшей мере один такой элемент т^М,
что
ll*-m||<||*-j/|| (y<=M).
При этом элемент m определяется однозначно с точностью до
слагаемого из подпространства {0}. Поэтому если Е предгиль-
предгильбертово, то m определяется однозначно заданием х и М.
Доказательство основано на тождестве Аполлония
справедливость которого для любых элементов а.Ь^с^Е легко
проверяется.
Положим 6 = inf{||x — у\\: у ^ М}. Возьмем такую последо-
последовательность точек (уп) в М, чтобы 6n=lk — уп\\ I&1)- Согласно
тождеству Аполлония,
Так как множество М выпукло, то -к (ут + Уп)е М, откуда
Следовательно,
Последнее неравенство показывает, что (уп) есгь последова-
последовательность Коши. В силу полноты М существует такой элемент
1) Символ ап\а означает, что последовательность (ап), убывая, стре-
стремится к а. г- Прим. перев.
140 Гл. 1. Векторные и топологические векторные пространства
т<=М, что уп-+т. Следовательно, ||х —m||= lim \\x — yn\\ = 6.
П ■> оо
Тем самым существование элемента т доказано.
Пусть т' — другой минимизирующий элемент из М. Согласно
тождеству Аполлония,
поэтому
Таким образом, \\т — т'|| = 0, т. е. т — т'е{0}. Если Е — пред-
предгильбертово пространство, то т = т'.
Эта теорема дает право на следующее определение. Пусть
заданы элемент х и подмножество М в Е, удовлетворяющее
условиям теоремы 1.12.3; всякий элемент meAf, обладающий
свойством, указанным в этой теореме, называется ортогональ-
ортогональной проекцией элемента х на множество М. Если пространство
Е предгильбертово, то ортогональная проекция х на М опреде-
определена однозначно. Употребление эпитета «ортогональная» оправ-
оправдано следующим предложением.
1.12.4. Предложение. Пусть М —выпуклое множество в про-
пространстве Е со скалярным произведением, и пусть х^Е.
A) Если OgM, то элемент ш^М будет ортогональной
проекцией х на М тогда и только тогда, когда
Re(x-m\y-m)^0 для уе=М. A.12.3)
B) Если 0gM« если М + МаМ, то элемент m^M будет
ортогональной проекцией х на М тогда и только тогда, когда
(a) Re(х-m \(/)<0 для у^М
и
(b) Re(x-m|/n) = 0.
C) Если М — векторное подпространство в £, то элемент
m е М будет ортогональной проекцией х на М тогда и только
тогда, когда х — me M1.
D) Если М — линейное многообразие в £, то элемент т^М
будет ортогональной проекцией х на М тогда и только тогда,
когда
(x — m\y — m) = 0 для у^М.
Доказательство. A) Справедливо тождество
IU - ^ И2 = I! (л: - т) - (^/ - т) ||2 =
= \\х - пг\\2 - 2Re{x - m \у - пг) + \\у - m\l2. A.12.4/
1.12. Пространства со скалярным произведением 141
Элемент m будет минимизирующим, т. е. неравенство
\\х-у\?>\\х-т\? для уеМ A.12.5)
будет выполняться тогда и только тогда, когда
2 Re (л;-~т| у - т)<,\\у - m\f для уеМ.
Пусть г/iG М и 0 < Я-< 1. Так как множество М выпукло и
содержит элемент 0, то y = fn + X(yi— т)^М. Поскольку эле-
элемент т — минимизирующий, то
- т \ у{ - т)<Я2|| ух-т ||2.
Деля обе части неравенства на Я и переходя к пределу при
Я->0, получаем
Re(х — т |у —
для любого элемента у е М, т. е. получаем неравенство A.12.3).
Обратно, пусть справедливо неравенство A.12.3). Тогда из
A.12.4) вытекает A.12.5), а это и означает, что т — минимизи-
минимизирующий элемент.
B)Пусть //igM. Из условия М + Ма М следует, что у —
= yi + m^ М. Если т — минимизирующий элемент, то (а) выте^
кает из доказанного неравенства A.12.3). С другой стороны, по-
полагая в A.12.3) // = 0, получаем Re(.*r — m|m)>0, откуда сле-
следует (Ь). Обратно, из (а) и (Ь) легко получается A.12.3).
C) Это утверждение сразу следует из B), так как если
М — подпространство, то —М = М.
D) Будем снова исходить из неравенства
2Re(х - т \z- m)<[[z- т ||2, г еМ,
характеризующего элемент т е М. Поскольку М — линейное
многообразие, то для произвольного элемента i/eM и произ-
произвольного скаляра а имеем г = ат+(\—а)у^М.
Для элемента z — tn=(l—а) (у — т) наше неравенство при-
принимает вид
т. е.
2 R е Я (х - т \ у - т) < | Я |211 у - т \ |2
для всех у е М и для всех чисел Я.
Повторяя рассуждения, использованные при доказательстве
утверждения A), получаем при Я>0
Re(х — т |у — т)<0, у^М,
а при Я<0
Re (л: — т\у — /л)>0, у е М.
142 Гл. 1. Векторные и топологические векторные пространства,
Следовательно,
Re (х - пг \ у - т) = 0, jg М.
Если поле скаляров — вещественное, то необходимость уже до-
доказана. В случае комплексного поля можно повторить приве-
приведенные рассуждения для чисто мнимого Я. Получим
Im (х — m | у — пг) = 0, у е М,
Последнее равенство вместе с предыдущим показывает, что
(х — m |r/~m) = 0, у^М.
Таким образом, необходимость доказана. Достаточность следует
из тождества A.12.4).|
1.12.5. Следствие. A) Пусть Е — пространство со скалярным
произведением и М — полное векторное подпространство в Е,
отличное от Е. Тогда в Е существует элемент аф О, ортогональ-
ортогональный к М. Если, кроме того, подпространство М замкнуто, то
элемент а можно выбрать так, чтобы ||а||>0.
B) Пусть Е — полное пространство со скалярным произведе-
произведением и (er)i<=; — некоторое ортонормированное семейство в Е.
Тогда в Е существует ортонормированное семейство (е^) te/, яв-
являющееся расширением заданного (т. е. J cz /) и полное в том
смысле, что для всякого Jte£ существует единственное семей-
семейство скаляров (£i)ie=/ такое, что ряд 2 hei сходится (слабо
i e /
сходится1)) к х в Е. При этом скаляры |г- определяются равен-
равенствами li=(x\ei) (i^I); ряд 2 hei сходится безусловно (т.е.
i €= /
по сети конечных подмножеств, множества /), любая его сум-
сумма #oo удовлетворяет условию х,— Хоо ^{0}, и имеет место равен-
равенство Парсеваля
IUIP= 2 |g,P= 2 l(*k)i2. A.12.6)
Доказательство. A) Возьмем элемент х е Е\М. Пусть
m — его ортогональная проекция на М. Положим а = х — пг.
Если ||я|| = 0, то включение х — а е М влечет дсеМ, что проти-
противоречит замкнутости подпространства М.
B) Множество всевозможных ортонормированных семейств,
являющихся расширениями заданного ортонормированного се-
семейства, можно частично упорядочить по включению. Это ча-
частично упорядоченное множество индуктивно (простая проверка
этого факта представляется читателю). По лемме Цорна
1) Говорят, что сеть (х o)o^s слабо сходится к элементу х^Е, если для
любого у^Е числовая сеть (ха — х \ у) oe=s сходится к 0. Если простран-
пространство Е гильбертово, то из следствия 1.12.6 вытекает, что слабая сходимость
сетей в Е соответствует сходимости в ослабленной топологии пространства Е.—
Прим. ред,
1.12 Пространства со скалярным произведением 143
(п. 0.1.5) это множество .имеет максимальный элемент, например
{ei)is=i* Легко видеть, что замкнутая" линейная оболочка М
множества {ei\ i е /} совпадает с Е. Действительно, в противном
случае, используя утверждение A), можно было бы это семей-
семейство расширить, что противоречит его максимальности.
Пусть х е Е. Если ряд 2 het слабо сходится к х в Е,
i e /
то для каждого индекса / s / имеет место равенство
(х\е,)= 2 ЬЫ*/),
i s /
откуда в силу ортонормальности семейства (ег) получаем, что
lj=(x\ej) для каждого / е /.
Пусть скаляры |г- определены указанным только что спосо-
способом. Для каждого конечного множества Sal положим
х$ = 2 hei- Имеем (снова в силу ортонормальности)
IU-*sll2 = IUII2- 2 1Ы2. A.12.7)
Следовательно,
\\XS\?= S U
откуда вытекает, что
Таким образом, ряд 2 I ^ I2 сходится. Если S с S7, то
i /
i е 5' \ S
Из сходимости ряда 2 I h I2 и из последнего равенства сле-
дует, что (xs) есть сеть Коши. Так как пространство Е полно,
то ряд 2 \&i сходится в Е. Пусть #оо — некоторая сумма этого
ряда. Сходимость ряда, определяющего элемент #оо, и ортонор-
мированность семейства (е*) влекут за собой равенство
(х — л:оо|вг)=0 для всех jg/. Так как линейная оболочка мно-
множества {ее i e /}, как мы уже видели, плотна в £, то элемент
х,— #оо ортогонален ко всем элементам пространства Еу т. е.
\\х — #оо 11= 0, или, что то же самое, х — Хоо е {0}. Переходя к пре-
пределу в равенстве A.12.7), приходим к A.12.6). I
Замечания, (а) Если Е — предгильбертово пространство,
то всякое полное векторное подпространство в Е замкнуто.
144 Гл. 1. Векторные и топологические векторные пространства
(Ь)Из утверждения B) вытекает, что ортонормированное
семейство в Еу замкнутая линейная оболочка которого совпадает
с Е, разумно называть ортонормированным базисом в Е. Мы
предпочитаем этот термин термину «полное ортонормированное
множество», так как слово «полный» употребляется и в других
значениях и это может привести к путанице.
(c) Если пространство Е отделимо, то можно утверждать не
только то, что х ss 2(* kf-)ej(mod{0}), но и что x = ^(x\ei)el.
i i __
(d) Пусть справедливы соотношения х = 2(* |^)^(тос1 {0})
и у == 2 {у I et) et (mod {0}). Тогда равенство Парсеваля допу-
i
екает следующее обобщение:
(х\у)= 2 {х\еь){упд> A.12.8)
i /
(е) Если пространство Е гильбертово, то отображение
х«—> ((х | ef)). е 7 определяет изоморфизм пространства £ на
гильбертово пространство /2(/).
1.12.6. Следствие. Пусть Е — полное пространство со скаляр-
скалярным произведением и f — непрерывная линейная форма на Е.
Тогда существует элемент а е Е, такой, что
f (*) = (*| а), хееЕ.
Для всякого такого элемента а имеет место соотношение
Следовательно, если пространство Е к тому же отделимо (т. е.
если Е — гильбертово пространство), то элемент а однозначно
определяется формой f.
Доказательство. Существование элемента а в случае
/ = 0 очевидно. Если же /^0, то множество Af = kerf есть замк-
замкнутое полное векторное подпространство в £, причем МфЕ. Из
следствия 1.12.5 вытекает существование такого ортогонального
к М элемента а\^Е, что i|aill>0. Таким образом, равенство
f(x)=O влечет равенство (x\ai)=0. Выберем элемент а2 так,
чтобы /(а2) = 1. Тогда для каждого х е Е имеет место равенство
f(x — f(x)a2)=0, поэтому f(x)(a2\ai) = (x\a\). Число {а2\а{) не
может равняться нулю (в противном случае, полагая х = аи по-
получили бы llaiH =0). Таким образом, f(x) = (хla),где а= , V ч.
Пусть а — некоторый элемент из £, такой, что f(x) — (x\a)
для всех xg£. Полагая в этом равенстве х = а, получаем
112. Пространства со скалярным произведением 145
следовательно, l|a||^||f||. Обратное неравенство llfli^||a|| выте-
вытекает из неравенства Коши— Шварца (см. A.12.1)). Таким об:
разом, ||я|| = ИЛ1. Для доказательства заключительного утвер-
утверждения заметим, что если а и а' соответствуют форме f, то раз-
разность а — а' соответствует нулевому функционалу. Значит,
||а — «'11 = 0, и в силу отделимости Е а = а\ |
Замечания. Пусть Е — полное пространство со скалярным
произведением. Из следствия 1.12.6 вытекает существование та-
такого сопряженно линейного отображения / пространства Е на
Er (E' — топологическое сопряженное к £), что для всех х,у^Е
(х,Цу))=(х\у).
Отображение / сохраняет норму. Часто, когда имеют дело с
гильбертовым пространством, используют отображение /, чтобы
явно не упоминать о пространстве Е'.
Существуют многочисленные приложения следствия 1.12.6,
многие из которых охватываются так называемым принци-
принципом проектирования, рассмотрением которого мы сейчас зай-
займемся.
1.12.7. Принцип проектирования. Как мы сейчас убедимся,
принципы, лежащие в основе следствия 1.12.6 и теоремы 1.12.3,
квивалентны применительно к замкнутым векторном подпро-
фанствам. Каждый из них можно охарактеризовать как прин-
ип проектирования; способ их применения можно назвать мето-
методом ортогонального проектирования. В конкретных примерах мы
будем от случая к случаю пользоваться то тем, то другим на-
названием.
Убедимся в том, что упомянутые в начале пункта принципы
эквивалентны. Пусть Е — полное пространство со скалярным
произведением. Рассмотрим следующие два утверждения.
A) Если М — замкнутое векторное подпространство в Е, то
каждый элемент xg£ может быть ортогонально спроектирован
на М, т. е. существует такой элемент т^М, что х— пг^М1.
B) Если М — замкнутое векторное подпространство в Е, то
каждую линейную непрерывную форму f на М можно предста-
представить в виде f(x) = (х\а), где а — некоторый элемент из М.
Так как всякое замкнутое векторное подпространство в Е
есть полное пространство со скалярным произведением (в ин-
индуцированной структуре), то рассуждения, использованные при
доказательстве следствия 1Л2.6, показывают, что A) влечет B).
Обратно, пусть верно B), и пусть М — замкнутое векторное под-
подпространство в Е, х — некоторый элемент из Е. Функция
y*->-(y\x) есть непрерывная линейная форма на М. В силу B)
существует такой элемент а еЛ1, что (у\х) = (у\а), у е М. По-
Последнее означает не что иное, как то, что х — а е М\ Таким об-
146 Гл. 1. Векторные и топологические векторные пространства
разом, B) влечет A), и, следовательно, они эквивалентны.
3 а м еч а н ияЛ По-видимому, Герман Вейль был одним из
первых, кто выделил принцип проектирования и показал, на-
насколько полезным он может быть в теории потенциала и в дока-
доказательствах теорем существования для линейных уравнений в
частных производных (см. Г. Вейль [1]). Первоначально Вейль
применил его к задаче Дирихле, однако затем этот метод был в
различных направлениях модифицирован и использован при ре-
решении более общих задач. Приложения такого рода довольно
подробно рассмотрены в гл. 5 (см. в особенности п. 5.13.2).
Здесь мы не можем заниматься этими приложениями, потому
что полнота пространств, в которыми приходится иметь дело,
может быть установлена лишь с помощью интеграла Лебега,
изучение которого отложено до гл. 4. Тем не менее общие черты
таких приложений, если пренебречь вопросами полноты и неко-
некоторыми другими тонкостями, можно обрисовать так скоро, что
трудно не поддаться искушению.
Пусть Q — область в R2 (случай п измерений требует лишь
формальных изменений) и f — функция, заданная в области Q и
на ее границе. В задаче Дирихле ставится вопрос о существова-
существовании гармонической в Q функции и, совпадающей на границе об-
области с функцией f. Уже давно было известно, что формально
функцию и можно получить, минимизируя так называемый инте-
интеграл Дирихле D (g) = J | | grad g |2 dx dyy когда функция g про-
бегает множество всех функций, совпадающих с / на границе.
Трудности строгого обоснования этого метода общеизвестны и
не'нуждаются в повторении. Рассмотрим в общих чертах, как
можно использовать здесь метод ортогонального проектиро-
проектирования.
Сначала нужно так выбрать пространство Е функций на Q
со скалярным произведением, чтобы функция / принадлежала £,
а интеграл D(g) совпадал с квадратом нормы g, т. е. чтобы
D(g) = (g\g). (Мы ограничиваемся рассмотрением лишь веще-
вещественных функций, так что пространство Е можно считать ве-
вещественным.) Выбрать такое скалярное произведение можно,
например, так:
(8\ I &) = J J grad Si • grad g2 dx dy.
Функции g, на которых квадрат нормы D{g) = ||g"||2, или, что то
же, норма \\g\\, достигает наименьшего значения, мы ищем среди
элементов линейного многообразия Мс£, образованного теми
функциями, которые на границе совпадают с /. Возникает зада-
1.12. Пространства со скалярным произведением 147
ча об ортогональном проектировании нуля на М. Если эта задача
разрешима, то из предложения 1.124D) следует, что миними-
минимизирующая функция (назовем ее и) удовлетворяет^ равенству
(u\g — &)=0, geM. Иначе говоря, (и\х) =0 для всякой функ-
функции /ig£c нулевыми значениями на границе.
В силу тождества Грина имеем формально
(и | К) = J J grad и • grad hdxdy = *
= J J hAudxdy- jh^ds,
Q Г
где Г — граница области D, а п — нормаль. Если функция h
равна нулю на границе Г, то
(а IЛ) — J" J hAudxdy.
Пусть это выражение обращается в нуль для всех функций h,
равных нулю на границе Г; тогда Да = 0, т. е. ^ — гармоническая
функция в Q. Таким образом, и действительно является реше-
решением задачи Дирихле с граничными условиями, определенными
функцией f.
Укажем только на три из многих очевидных серьезных про-
пробелов приведенного построения.
(а) Для того чтобы иметь дело с полным пространством со
скалярным произведением, надо еще пополнить - пространство
«гладких» функций g на й относительно структуры, определен-
определенной указанным выше скалярным произведением. Но тогда мы
сталкиваемся со второй трудностью.
(в) Какой смысл нужно приписать выражению «граничные
значения» применительно к элементам пополнения? В част-
частности, о каких элементах пополнения можно говорить как об
обращающихся в нуль на границе? Оказывается, что такими
элементами служат те функции, которые принадлежат замыка-
замыканию (в указанном пополнении) множества гладких в Q функций,
равных нулю в пограничных полосах (т. е. на множествах вида
Й\С, где С — переменное компактное подмножество в Q). Нет,
разумеется, никакой уверенности в том, что такая функция
имеет предельные (в смысле поточечной сходимости) гранич-
граничные значения, равные нулю.
(с) В предыдущих рассуждениях мы использовали формулу
Грина в виде
J j grad и • grad hdxdy = J J h • kudxdy.
143 Гл. 1. Векторные и топологические векторные пространства
Нам нужно, чтобы соотношение сохраняло силу для минимизи-
минимизирующей функции и и для всякой функции h из Е, имеющей ну-
нулевые граничные значения в обобщенном смысле. Очевидно, этот
вопрос требует тщательного рассмотрения. Действительно, пре-
прежде всего, нам известно лишь, что и — элемент пополнения, так
что даже существование лапласиана Аи вызывает серьезные со-
сомнения. Одной из главных заслуг Г. Вейля является то, что он
доказал, что из приведенного интегрального соотношения сле-
следует, что если подправить и на множестве лебеговой меры нуль,
то и будет иметь производные всех порядков и формула Грина
применима без всяких затруднений. Когда мы в гл. 5 приступим
к изучению линейных дифференциальных уравнений в частных
производных, мы дадим соответствующие формулировки в тер-
терминах распределений Шварца. Это позволит нам четко отделить
те части проблемы, которые легко поддаются разрешению с по-
помощью абстрактных методов, от тех, для решения которых тре-
требуется что-нибудь вроде леммы Г. Вейля. В то же время мы
рассмотрим значительно более сложные примеры применения
принципа проектирования.
1.12.8. Гильбертов сопряженный к непрерывному эндомор-
эндоморфизму. В п. 1.12.9 мы приведем еще один пример применения
принципа проектирования. Для этого нам потребуется понятие
гильбертова сопряженного а* к непрерывному эндоморфизму и
гильбертова пространства Е. Это понятие в свою очередь иллю-
иллюстрирует важность следствия 1.12.6. Как будет показано ниже,
понятие гильбертова сопряженного применимо не только к не-
непрерывным эндоморфизмам. Это понятие тесно связано с не-
несколько отличной идеей сопряженности, относящейся к эндо-
эндоморфизмам общих локально выпуклых пространств.
В этом пункте мы рассмотрим наиболее простой случай.
Пусть Е — гильбертово пространство и и — его непрерывный
эндоморфизм. Для заданного элемента у^Е линейная форма
непрерывна на Е. Согласно следствию 1.12.6, существует един-
единственный элемент у* е £, такой, что
(и(х)\у) = (х\У)
для всех х е Е. Отображение и*: у*->у*, очевидно, линейно, т.е.
является эндоморфизмом пространства Е. Эндоморфизм и* на-
называется гильбертовым сопряженным к эндоморфизму и,
В дальнейшем в этой главе всюду, где это не сможет вызывать
недоразумения, мы будем говорить просто «сопряженный» к и
вместо «гильбертов сопряженный» к и.
1.12. Пространства со скалярным произведением 149
Итак, а* определяется соотношением
(и(х)\у) = (х\и*(у)),
которое должно выполняться для любых х,у^.Е. Отсюда сле-
следует, что х)
Ни* II = Ы\
и
а** = и,
где и** = (а*)*, а также, что отображение и\—>и* есть сопря-
сопряженно линейное (п. 1.12.1) отображение пространства LC(E,E)
на себя. Понятие сопряженного эндоморфизма дает возмож-
возможность выделить два важных класса непрерывных эндоморфиз-
эндоморфизмов пространства Е: прежде всего —так называемые самосоп-
самосопряженные (непрерывные) эндоморфизмы и, характеризующиеся
соотношением а* = и\ затем — так называемые унитарные
эндоморфизмы и, характеризующиеся равенством и* = игх. Та-
Таким образом, непрерывный эндоморфизм и самосопряжен тогда
и только тогда, когда для всех х, у е Е имеет место равенство
(и(х)\у) = (х\и(у)).
(В действительности, как будет показано в § 8.11, условие не-
непрерывности можно опустить, так как оно является следствием
указанного тождества.) Аналогично непрерывный эндоморфизм
унитарен тогда и только тогда, когда он отображает Е на себя
и для любых х, у ^Е выполняется равенство
(и(х)\и(у)) = (х\у).
Несложное вычисление показывает, что последнее тождество
эквивалентно условию ||#(л;)|| = ||л;|| для любого ^££, т. е.
тому, что отображение и есть изометрия (т. е. сохраняет нор-
норму).
Самосопряженные и унитарные эндоморфизмы гильбертова
пространства играют важную роль в многочисленных прило-
приложениях, поэтому их теория глубоко разработана и изложена
во многих хорошо известных книгах. Для наших ближайших
целей достаточно беглого знакомства с этими понятиями.
1.12.9. Принцип проектирования и абстрактная эргодическая
теорема. Пусть Е — гильбертово пространство и и — его непре-
непрерывный эндоморфизм. Под абстрактной эргодической теоре*
мой подразумевают утверждение, что при определенных усло-
условиях средние арифметические степеней эндоморфизма //
1) Если и — эндоморфизм пространства Е, то по определению
IMI==sup{||«(*)||:|UKl}.
(См. п. 1.10.10.) -—Прим. перед,
150 Гл. 1. Векторные и топологические векторные пространства
поточечно сходятся к некоторому пределу, который необходимо
является непрерывным эндоморфизмом пространства Е. Ниже
(в § 9.13) будут рассмотрены некоторые из многочисленных ре-
результатов такого типа. Для более полного и детального озна-
ознакомления с этими вопросами читатель может обратиться к кни-
книге Данфорда и Шварца [1, стр. 699—774]. Здесь мы огра-
ограничимся одной теоремой для случая гильбертова пространства,
доказательство которой опирается только на принцип проек-
проектирования. В такой абстрактной форме результат был впервые
установлен (по крайней мере, для унитарных эндоморфизмов
и) фон Нейманом [6]. Приводимое ниже доказательство
принадлежит Ф. Риссу [7].
Теорема, которую мы собираемся доказывать, называется
«абстрактной» эргодической теоремой на том основании, что
она содержит как частный случай теорему под тем же назва-
названием, возникшую в статистической механике. В п. 1.12.10 мы
попытаемся кратко наметить переход от абстрактной формы
этой теоремы к ее конкретной реализации. Относительно обеих
формулировок см. подробнее Халмош [5] и Данфорд и
Шварц[1].
Будем считать, что эндоморфизм и удовлетворяет одному
из следующих условий:
(a) и — самосопряженный эндоморфизм и
c = sup{||an||: п = 1, 2, ...,}< + оо.
(b) и — унитарный эндоморфизм.
Заметим, что из условия (Ь) следует выполнение второго
условия из (а) с с = 1.
Теорема. Пусть Е — гильбертово пространство и и — его эн-
эндоморфизм, удовлетворяющий условию (а) или (Ь). Для лю-
любых двух натуральных чисел m < n определим эндоморфизм
Am n равенством
Ат п = (п-т)~1 2 uk.
т < k < п
Тогда существует поточечный предел Р = lim Am% n, т. е.
п—пг -> со
ппг > со
скользящие средние арифметические степеней эндоморфизма и
поточечно сходятся на Е. Предельный эндоморфизм Р яв-
является ортогональным проектором и удовлетворяет соотноше-
соотношениям
иР = Ри = Р.
Доказательство. Покажем вначале, что при каждом
х^Е существует предел Р {х) = lim Am, n (x).
П — Ш -> ОО
1.12. Пространства со скалярным произведением 151
Доказательство этого утверждения проведем в три этапа;
попутно выяснятся некоторые свойства отображения Р.
Заметим, что семейство отображений Ат>п равностепенно
непрерывно, так как
A) Пусть х=*и(у)—у для некоторого у^Е. Тогда
поэтому \\Ат)П(х)\\^2с\\у\\/(п — т). Отсюда следует существо-
существование предела Р(х) и равенство его нулю при каждом таком х.
То же самое справедливо для всех х, принадлежащих вектор-
векторному подпространству М в Е, порожденному элементами вида
и (у)— у.
B) Равностепенная непрерывность семейства Ат> п обеспе-
обеспечивает существование Р{х) и его равенство нулю для каждого
элемента х, принадлежащего замыканию М подпространства
М в Е.
C) В силу принципа проектирования если N— ортогональ-
ортогональное дополнение к М в Е, то каждый элемент хе£ можно за-
записать в виде х = а + Ь, где а е М и b e N. Так как существо-
существование предела Р(а) доказано, то достаточно доказать сущест-
существование Р{Ь). Для любого у^Е имеем (с учетом того, что
N — ортогональное дополнение к М, а и (у) —j/gM)
Из этого соотношения следует равенство u*(b)=b, которое
вместе с (а) или (Ь) приводит к равенству u(b)=b; тогда
Ат}П(Ь)=Ь для всех пар (т, /г), где т < п, и, следовательно,
Р(Ь) существует и равен Ь.
Таким образом, установлено существование поточечного
предела Р, а также то, что Р(х)=Ь для всякого элемента
х = а + Ь, где а^М и b^N. Последнее означает, что Р есть
ортогональный проектор пространства Е на N.
Так как каждое отображение Ат>п перестановочно с эндо-
эндоморфизмом и, то тем же свойством обладает и предел Р. Из
равенства АтгПи=Ат+\гП+\ следует, что Ри = Р, откуда Ри =
= иР = Р. Теорема полностью доказана. |
Замечание. Так как иР = Ру то для всякого х е Е эле-
элемент у = Р(х) инвариантен относительно эндоморфизма иу т. е.
У = и{у) = и2(у)=
Это свойство инвариантности часто (п. 1.2.10) довольно жестко
определяет природу элементов у.
152 Гл. 1. Векторные и топологические векторные пространства
Случай непрерывных средних. Как мы увидим в п. 1.12.10,
степени ип часто естественно вкладываются в непрерывное се-
семейство эндоморфизмов ии зависящее от вещественного пара-
параметра / (обычно интерпретируемого как время) и обладающее
полугрупповым свойством
ut+r = mur9 A.12.9.)
причем и = ии так что ип — ип. Для наших целей достаточно
считать, что эндоморфизмы щ определены для / > 0. Естест-
Естественно попытаться заменить использовавшиеся до сих пор ди-
дискретные скользящие средние Лт> п непрерывными скользящими
средними
\сЦ @<s<t) A.12.10)
и исследовать вопрос о существовании поточечного предела
отображений AStt при / — s—>оо. Мы покажем, что при неко-
некоторых слабых ограничениях эта задача может быть сведена к
предыдущему дискретному случаю и тем самым решена поло-
положительно.
Начнем с определения интегралов, которые фигурируют в
определении отображений ASit. Сделаем два предположения
относительно зависимости отображения щ от /. Во-первых, бу-
будем считать, что семейство (ut) слабо непрерывно, т. е. что
для каждой пары (х, у) элементов из Е функция t^—>(ut(x) \y)
непрерывна при / > 0. (Можно было бы потребовать и меньше,
а именно чтобы эта функция была измерима по Лебегу при
/ > 0.) Во-вторых, будем считать, что эта функция ограничена
при />0 (снова для каждой пары (х, у)). Отсюда в силу прин-
принципа ограниченности, с которым мы познакомимся в гл. 7,
следует существование такого числа с, что
\(щ(х)\у\<с\\х\\\\у\\
для t > 0 и х, у е Е, или, что то же самое,
\\Щ\\<С
Второе требование выражает, таким образом, ограниченность
семейства (ut). Итак, наши допущения таковы: семейство
{ut)t>o ограничено и слабо непрерывно.
Этих условий достаточно, чтобы обеспечить существование
t
интеграла J щй^=ю при любых t > s > 0 в следующем
L12. Пространства со скалярным произведением 153
смысле1). Для каждой пары х, у элементов из Е существует
интеграл Римана
t
B(x9y)=j(ut(x)\y)dl.
При каждом фиксированном х отображение y*—>B(x,y) есть
непрерывная линейная форма на Е, так как
t
По следствию 1.12.6 существует единственный элемент ге£,
такой, что В(х, у) = (г\у) для всех у<^Е, причем || г || ^
"*Cc(t — s)|M|. Элемент z естественно записать в виде
t t
z= \ ui(x)dl. Отображение х±-> \ u%{x)dli является, как легко
S S
видеть, эндоморфизмом пространства Е. Обозначим его через v;
очевидно,
Равным образом естественно обозначить эндоморфизм v через
t
j u^dl, что и приводит к желаемой интерпретации рассматри-
рассматриваемого интеграла как непрерывного- эндоморфизма простран-
пространства Е.
Важно заметить, что при нашем определении интеграла
t t
Т- J Uldl=j(Tui)dl A.12.11)
s s
И
t t
J uzds.T= J (uiT)dl A.12.12)
s s
для всякого непрерывного эндоморфизма Т пространства Е.
Докажем, например, первое из этих соотношений. Используя
определения интеграла и сопряженного эндоморфизма, полу-
получаем для произвольных элементов х, у е Е
t t
(Tv(x) \y) = (v (x) \T-(y))=j (Ы|(x) |Г (у))d%=\ (Тщ(х) |у) d%;
') Cm. § 8.14 и 8,15.
154 Гл. L Векторные и топологические векторные пространства
последнее выражение представляет собой скалярное произве-
произведение (v'(x)\y), где v'= J Tu%dl. Следовательно, Tv = v', от-
куда и вытекает справедливость формулы A.12.11).
Обратимся теперь к задаче существования поточечного пре-
предела непрерывных скользящих средних ASf t в предположении,
что семейство (tit) ограничено и слабо непрерывно, а эндомор-
эндоморфизм u = u\ удовлетворяет (как и выше) одному из условий (а)
или (Ь). Обозначим через А°т,п Дискретные скользящие сред-
средние эндоморфизма и. По доказанному существует поточечный
предел Р° = \\mA°mtn. Полагая
1
из A.12.10) -A.12.12) получаем, что
п
Лт, „ = (п- ту1 \щсЦ = Am, SS = SA°m, n
т
для любых двух натуральных чисел т <п. Таким образом,
предел \[тА1П}П существует и равен P°S = SP°. С другой сто-
стороны, если 0<5</ и если m = [s], n = [t] (квадратные скобки,
как обычно, обозначают целую часть), то
^ [t] t
As,t=-{t-sYl J uidl + (t-sTx J uidl + (t-sYx J mdl.
is] [s] [t]
Первое и третье слагаемые в правой части имеют норму, не
превышающую c(t — s)~\ и стремятся к нулю при f — 5—> оо.
Среднее слагаемое равно
{n-m){t-s) Amttt
и, поскольку {n — m)(t — s)~x-> 1 при / — 5->-оо, поточечно схо-
сходится к P°S. Таким образом,
lim As,t = P°S = SP° = P A.12.13)
t-s ->oo
в смысле поточечной сходимости.
Заметим, что из формул A.12.10) — A.12.12) следует пере-
перестановочность каждого ^(£>0) с каждым из эндоморфизмов
5, Р°, Р, A8tt @<,s<t). Далее, как легко проверить, исполь-
используя A.12.10) и элементарные свойства интеграла,
Put = P (t>OU A.12.14)
1.12. Пространства со скалярным произведением 155
Итак, для всех хе£ предел у = Р(х) = lim As>t{x) ин-
S-t "> ОО
вариантен относительно щ при каждом / > 0.
Если в A.12.14) заменить t на £ и взять среднее по g в ун-
тервале 5 < 2- < £, то получим
Р2 = Р. A.12.15)
Если эндоморфизм и* самосопряжен, то таким же будет
каждое ASjt и, следовательно, Р. Из формулы A.12.15) следует
тогда, что Р — ортогональный проектор. Если щ — унитарный
эндоморфизм, то это рассуждение не проходит — хотя по-преж-
по-прежнему верно, что Р является ортогональным проектором, —
нужно как-то изменить метод доказательства.
Один из путей преодоления возникшего затруднения, пред-
представляющий и самостоятельный интерес, заключается в сле-
следующем наблюдении: рассуждения, используемые в дискретном
случае, можно с самого начала так видоизменить, чтобы они
годились и для непрерывного случая. Действительно, полугруп-
полугрупповое свойство A.12.9) позволяет установить существование
и равенство нулю предела P(x\ = \imASit(x) для каждого х
вида иа(у) —у, где а>0 и уе£. То же верно, следовательно,
для х, принадлежащих замыканию М векторного подпростран-
подпространства М в Е, порожденного элементами вида иа(у)—у
(j/e£,a>0). Как и в дискретном случае, это следует из рав-
равностепенной непрерывности семейства ASit. Введем N — ортого-
ортогональное дополнение к М в Е— и представим каждый элемент
х^Е в виде суммы а + Ь, где аеМ и b^N. Элемент Ь орто-
ортогонален к каждому элементу вида иа(у)—уу где а > 0, //g£,
откуда вытекает, что ua(b)=b при каждом а > 0 и, следова-
следовательно, A8tt(b)=b при 0 < s </. Следовательно, Р(Ь) суще-
существует и равно 6, и потому Р(х) также существует и равно Ь.
Значит, Р есть ортогональный проектор пространства Е
на N.
Полученный для дискретного случая результат, таким об-
образом, полностью обобщается на непрерывный случай. Обра-
Обратимся теперь к обещанному примеру из статистической меха-
механики.
1.12.10. Пример из статистической механики. Эргодическая
теория отправляется от изучения статистического поведения
ньютоновой механической системы со многими степенями сво-
свободы. Движение такой системы можно описать в терминах фа-
фазового пространства, координатами которого служат обобщен-
обобщенные координаты и соответствующие обобщенные импульсы. Фа-
Фазовое пространство, которое мы будем обозначать через Q = {<?},
156 Гл. 1. Векторные и топологические векторные пространства
можно рассматривать как подмножество в Rn, где п обычно
очень велико. Ньютоновы уравнения движения определяют раз-
развитие системы во времени; если начальное состояние системы
(т. е. состояние в момент времени * = 0) представляется точкой
<7о е Q, то состояние в момент времени t представляется точ-
точкой qt e Q. Другими словами, движение системы представ-
представляется некоторой «траекторией» в Q, т. е. семейством qt точек
из Q. В случае систем с очень большим числом степеней сво-
свободы (например, макроскопического объема газа) начальное
состояние q0 практически никогда неизвестно. Поэтому мы вы-
вынуждены ограничиться статистической картиной рассматривае-
рассматриваемого процесса, представляющей среднее по неизвестным на-
начальным состояниям. Это связано с подсчетом математического
ожидания различных функций (например, полной энергии),
определенных на Q.
Физические соображения позволяют считать (и мы это бу-
будем делать), что отображение Tt: qo~+qt множества Q в себя
непрерывно. Физически очевидно также и выполнение полугруп-
полугруппового свойства Tt+y = TfTf. Знаменитая теорема Лиувилля
(Хин чин [1]) утверждает, Зто во всех случаях, когда га-
гамильтониан системы не зависит явно от времени, каждое пре-
преобразование Tt «сохраняет объемы». Точнее, если \х — лебегова
мера на Q, то \х [ГГ1 (S)\ = \i(S) для каждого измеримого под-
подмножества S в Q. При этом полная мера \x{Q) может быть как
конечной, так и бесконечной. В первом случае, нормируя ее
так, чтобы она стала равной единице, можно считать \х вероят-
вероятностной мерой на Q. Во втором случае можно считать \х отно-
относительной вероятностной мерой. В каждом из этих случаев
математическое ожидание некоторой функции х на Q выра-
выражается формулой
<*>= \xd\jL. A.12.16)
Q
(Здесь и далее мы вынуждены предполагать, что читатель хотя
бы бегло знаком с интегрированием по положительной, счетно
аддитивной мере. Изложенная ниже, в гл. 4, теория более чем
достаточна для наших целей.)
Такой прямой подсчет математического ожидания практиче-
практически неосуществим, и в статистической механике давно уже был
предложен другой подход. Очень кратко и грубо ход рассуж-
рассуждений можно описать следующим образом.
Рассматривается случай, когда «поток», т. е. семейство пре-
преобразований Ти параметризованное временной переменной /,
достаточно сильно «перемешивает» точки фазового прострац-
j.12. Пространства со скалярным произведением 157
ства Q. В этом случае разумно принять гипотезу, что средняя
по пространству (х) совпадает с пределом средних по времени
t
lim Г1 \ x{Tiq)dl. A.12.17)
Этот предел в силу предположенного свойства перемешивания
потока не должен зависеть от q. Предположение о том, что
имеет место «свойство перемешивания», аналогично так назы-
называемой эргодической гипотезе; впрочем, точно сформулировать
последнюю было бы затруднительно. Следует сказать, что
большинства ранних попыток сформулировать эту гипотезу
связано с привлечением постулатов, которые либо очевидным
образом не выполняются в большей части случаев, либо не под-
поддаются проверке, за исключением самых тривиальных случаев.
Большинство таких гипотез имело форму утверждений о харак-
характере отдельных орбит, и их проверка сталкивается с теми самы-
самыми трудностями, которые хотели обойти вначале.
Предел средних по времени A.12.17)- имеет физический
смысл. Если начальное состояние системы представлено точ-
точкой q, то ее состояние в момент времени / будет Ttq, а значе-
значение х в момент / будет x(Ttq). Для большинства систем вели-
величина x(Ttq) как функция от / испытывает крайне быстрые и
сильные флуктуации. Эти флуктуации происходят в течение
промежутков времени, ничтожно малых по сравнению со вре-
временем, необходимым для экспериментального измерения значе-
значения x(Ttq). Следовательно, действительно определяемая в ре-
результате опыта величина лежит значительно ближе к среднему
Г1 \x(Tiq)dl,
чем к мгновенному значению x(Ttq). Фактически / столь велико
в масштабах микровремени системы, что ошибка, связанная
с переходом к предельному выражению A.12.17), невелика.
Имеет ли предел средних по времени A.12.17) какое-ни-
какое-нибудь отношение к среднему по пространству A.12.16)—это
уже дело физика, а не чистого математика. Однако, как мы
увидим, первичная1 цель математика — исследовать вопрос о
существовании предела A.12.17)—ведет к получению некото-
некоторой информации о равенстве между величинами A.12.16) и
A.12.17).
С точки зрения математики значительный успех был до-
достигнут, когда Купмэн перенес внимание с самих операторов Т%
158 Гл. 1. Векторные и топологические векторные пространства
на индуцированные функциональные операторы щ, определяе-
определяемые равенством
ut{x){q) = x{Ttq), A.12.18)
указав при этом, что поскольку отображение Т% сохраняет
меру, то каждое щ можно рассматривать как изометрию ле-
лебегова пространства J?77 = о5^(C, ц.). Использованные здесь
обозначения вводятся в гл. 4: е2?р (Q, ц) обозначает векторное
пространство таких измеримых функций х на Q, для которых
\x\v интегрируемо относительно \i9 наделенное полунормой
Lq
Наиболее интересен случай, когда р = 2. Пространство <S?2 ока-
оказывается пространством со скалярным произведением
(х\у)= \ ху d\x.
Q
(Здесь рассматриваются только вещественные функции.) В гл.4
будет доказана полнота пространства J?2. Ассоциированное
отделимое пространство L2, элементами которого являются
классы функций, совпадающих всюду, кроме множества ji-меры
нуль, есть гильбертово пространство.
Изложенные соображения дают возможность применить ре-
результаты п. 1.12.9. Для этого надо положить Е = L2(Qy ji), а в
качестве и% взять отображение, определенное формулой
A.12.18). В результате получаем, что при каждом xeL2
скользящее среднее по времени
x{Tiq)dl A.12.19)
сходится в L2 к некоторому элементу у е L2 (т. е. к классу
эквивалентности, определяемому некоторой функцией из 2?2).
Кроме того, элемент у инвариантен в том смысле, что для ка-
каждого / имеет место равенство
A.12.20)
для почти всех точек ?eQ (т. е. для всех q, за исключением,
быть может, подмножества в Q нулевой pi-меры). При этом
если \x(Q) конечно, то
(х) = {У).
При некоторых условиях из свойства инвариантности
A.12.20) следует, что функция у (почти всюду) постоянна.
/ 12. Пространства со скалярным произведением 159
В частности, эта имеет место в том важном случае, когда вся-
всякое множество S с: Q, инвариантное в том смысле, что
5 = ГГ1E), удовлетворяет либо условию (я(S) =0, либо усло-
условию \x(Q\S) =0. В этом случае поток называется эргодическим
или метрически транзитивным. Таким образом, если мера
\x(Q) конечна и поток эргодичен, то при каждом х из 2?2 сколь-
скользящие средние по времени A.12.19) сходятся при t — s—*оо
в гильбертовом пространстве L2 к постоянной {х). Что ка-
касается типа сходимости, то это в точности то, на что можно
надеяться. Приведенное выше утверждение обычно называется
статистической эргодической теоремой.
Иллюстрация. Вернемся к дискретному случаю и допустим,
что |л(Q) = 1 - Пусть S — измеримое подмножество в Q и x(q) =
()—характеристическая функция множества 5. Тогда
(S). Далее
представляет собой долю времени (относительно всего интер-
интервала [0, я]), в течение которого точка фазового пространства,
изображающая состояние системы и находившаяся в началь-
начальный момент в состоянии q, будет принадлежать множеству S.
Теорема утверждает, что
lira Nn(q)
в средне-квадратичном. Это находится в полном согласии с
тем, что можно было бы ожидать. Легко показать (опираясь
на теорему Лебега о сходимости для интегралов), что для по-
почти всех q имеет место неравенство
lim sup Nn {q) > ц (S).
В связи с последним соотношением естественно поставить
вопрос: нельзя ли показать, что равенство lim Nn (q) = м- (S)
имеет место почти всюду, или, в более общей форме, нельзя
ли в нашей основной теореме сходимость в средне-квадратич-
средне-квадратичном заменить какой-нибудь другой сходимостью. Здесь мы мо-
можем лишь заметить, что Дж. Биркгоф [1] получил резуль-
результат, известный сейчас как индивидуальная (или поточечная)
эргодическая теорема. В этой теореме утверждается, что если
Tt сохраняет меру и xeJ?1, то приведенные выше средние по
времени почти всюду на Q поточечно сходятся, причем пре-
предел у инвариантен, принадлежит J?1 и {х) = (у), если мера
\i(Q) конечна, В последнем случае сходимость имеет место
160 Гл. 1. Векторные и топологические векторные пространства
также и по полунорме пространства J?1. Следствия из эргодич-
эргодичности потока те же, что и прежде.
Обе формы эргодической теоремы в дальнейшем были усо-
усовершенствованы, а их доказательства упрощены. Краткий об-
обзор этих вопросов можно найти у Халмоша [5] (см. также
приведенную там литературу), более подробное изложение у
Данфорда и Шварца [1, гл. VIII]).
Читателю, которого особенно интересуют приложения эрго-
дических теорем к статистической механике и, вообще, физи-
физическая сторона вопроса, полезно будет познакомиться с рабо-
работами Хин чин а [1] (где он найдет изящное доказательство
теоремы Биркгофа) и Тер-Хаара [1].
УПРАЖНЕНИЯ
1.1. Пусть Т — некоторое множество и р — число, удовлетворяющее не-
неравенствам l<Sp< + оо. Показать, что пространство lp (T) (пример 1.10.3)
полно относительно нормы
Пусть et — характеристическая функция одноточечного подмножества {/}
из Т. Показать, что каждый элемент х^.1р(Т) является пределом в lp (T)
сумм вида
где F пробегает частично упорядоченное по включению семейство конечных
подмножеств в Т.
1.2. Обозначения те же, что и в предыдущем упражнении. Пусть U —
непрерывная линейная форма на 1р = 1р(Т). Показать, что функция и, опреде-
определенная равенством
u(t) = U(et) (t<=T),
принадлежит lp\ где р'= оо при р= 1 и 1—т = 1 при 1 < р < оо. Вывести
Р Р
отсюда, что
U(x)= 2 ti{t)x(t)
t^ т
для каждого х^1р, причем ряд в правой части сходится абсолютно.
Доказать, что, обратно, каждый элемент u^lv' определяет таким образом
непрерывную линейную форму V на 1р и что норма этой линейной формы V
есть не что иное, как ||и||Р'.
(См. теорему 4.2.1.)
1.3. Показать на примере, что результат предыдущего упражнения ста-
становится неверным при /?— оо. (См. также упр. 1.19 и 1.21.)
1.С Пусть Т — произвольное множество и со(Т), с(Т)—пространства,
определенные в примере 1.10.3. Доказать, что оба они банаховы. Рассуждая,
как в последних двух упражнениях, показать, что пространство, сопряженное
Упражнения 161
к со, изоморфно ll=*ll(T). Двойственность между ними задается билинейной
формой
(х,у)- 2 x{t)y(t),
где х<= со и у <= Z1.
1.5. Провести подробно доказательства полноты пространств Н? и HL?
при Кр<оо(п. 1.10 4 и пример (8) п. 1.12.1).
Используемая при этом техника подсказывает следующий более общий
результат, который предлагается доказать читателю. Пусть X — секвен-
секвенциально полное топологическое пространство, (Afa)—семейство полунепре-
полунепрерывных снизу полунорм на X. Предположим, что каждой окрестности нуля
U в X соответствует такое число е>0, что из
jcgI, sup Na (х) ^ е =Ф х е= U.
а
Пусть далее Хо — векторное подпространство в X, образованное теми
элементами х^Х, для которых
a
Доказать, что Хо полно в равномерной структуре, определяемой полунор-
полунормой N на Хо.
1.6. Пусть Е — нормированное векторное пространство, в котором суще-
существует предкомпактная сфера (т. е. множество вида
{л: е Е: \\х — х0 II = г},
где г>0). Показать, что тогда Е конечномерно (ср. с теоремой Ф. Рисса,
п. 1.9.6).
1.7. Обозначения те же, что и в примере (8) п. 1.12.1. Показать, что
HL2(D) есть гильбертово пространство относительно скалярного произве-
произведения
(/1 g) - J J fg dx dy.
D
1.8. Обозначения те же, что и в предыдущем упражнении. Установить
справедливость следующих утверждений.
A) Если Z)=C (т. е. и — комплексная плоскость), то HL2(D) сводится
к нулевой функции.
B) Пусть D — некоторая область, Л — подмножество в Д не имеющее
ни одной предельной точки в Д и D' = D\A (предполагается, что D' — об-
область). Тогда каждый элемент из HL2{D') можно продолжить до элемента
из HL2(D).
[Указание. Для доказательства утверждения A) модифицировать
обычное доказательство теоремы Лиувилля, используя интегральную фор-
формулу для коэффициентов Тэйлора произвольной функции / из Н12{С). Чтобы
доказать B), представить / в окрестности произвольной точки гое=Л контур-
контурным интегралом по границе некоторого кольца с центром в z0 Устремляя
меньший радиус к нулю, показать, что Zo — устранимая особая точка.]
1.9. Обозначения те же, что и в предыдущих двух упражнениях. Пока-
Показать, что каждой точке l^D соответствует в точности одна функция
гь->/((г, I) из HL2(D), такая, что
-J
f(z)K[z,l)dxdy
162 Упражнения
для всякого элемента f^HL2(D). (Это — ядро Бергмана для D.) Пусть
(/п) —ортонормированный базис в HL'2(D). Показать, что
К {г, 6) - 23 £• (*) ЫБ).
и вывести отсюда, что
J
1.10. Обозначения те же, что и в предыдущем упражнении. Показать,
что" функция
обладает наименьшей нормой (равной КA, £)~1/2) среди всех функций
^HL2(D), удовлетворяющих условию /(£) = 1. (При этом предполагается, что
пространство HL2(D) не сводится к нулевой функции.) Элемент f% является,
таким образом, проекцией нуля на замкнутое выпуклое множество элементов
/е HL2(D), удовлетворяющих условию /(?•) = 1.
1.11. Обозначения те же, что и в предыдущих четырех упражнениях.
Пусть D — открытый единичный круг с центром в начале Выбрать числа
ап (я = 0, 1, 2, ...) так, чтобы функции tn(z)=anzn образовали ортонорми-
ортонормированный базис в HL2(D). Исходя из этого (или другим способом), пока-
показать, что ядром Бергмана будет в данном случае
1.12. Пусть Е — банахово пространство, F — нормированное простран-
пространство, и — линейный топологический изоморфизм Е на F, a v — такое линей-
линейное отображение пространства Е в F, что
Показать, что v — топологический изоморфизм Е на F.
1.13. Пусть (хп)—ортонормированный базис в гильбертовом простран-
пространстве Н и (уп)—последовательность, определенная соотношениями уп=*
= xn-\-zn. Если существует такое положительное число [х<1, что для всех
скалярных последовательностей (Jn) с конечным носителем выполнено не-
неравенство
'7
то каждый элемент х^Н единственным образом представим в виде сходя-
сходящегося ряда 2 %пУп> Для которого ^\1п\2 < + °°-
1.14. Пусть Е — топологическое векторное пространство, Л — открытое
множество в Е и В — выпуклая оболочка множества Л. Проверить, что
В — открытое множество.
1.15. Пусть Е — топологическое векторное пространство, А — выпуклое
множесхво в Е с внутренней точкой а, Ь — произвольная точка множе-
множества Л. Показать, что при 0^а<1 точка A — a)a + ab является внутренней
для Л.
Упражнения 163
1.16. Показать, что топологическое векторное пространство Е полуметри-
зуемо, если в Е существует ограниченная окрестность нуля. Привести пример
метризуемого топологического векторного пространства, в котором нет ни
одной ограниченной окрестности нуля.
1.17. Пусть Е — пространство со скалярным произведением, (еп)
(д=1, 2, ...)—ортонормированное семейство в Е} Л — подмножество в Я,
образованное элементами вида ет + теп, где т, п — натуральные числа и
т<п. Показать, что нуль принадлежит слабому замыканию множества Л,
но не принадлежит слабому замыканию никакого ограниченного подмноже-
подмножества в Л. (Из второго утверждения следует, что в Л не существует последо-
последовательности элементов, слабо сходящейся к нулю.)
Этот пример принадлежит фон Нейману.
1.18. Пусть (л:а)—ограниченная сеть в топологическом векторном про-
пространстве Е и Н — подмножество в Е\ такое, что порожденное им вектор-
векторное подпространство всюду плотно в сильной топологии в Е'. Показать,
что если lira {ха, хг) = 0 для каждого л:'^ Я, то lim ха = 0 в слабой топо-
a a
логии в Е.
Сформулировать и доказать аналогичное утверждение о слабой схо-
сходимости сильно ограниченной сети в пространстве, "сопряженном к нормиро-
нормированному пространству.
1.19. Пусть Г —некоторое множество. Обозначим через т{Т) множе-
множество всех (конечно) аддитивных скалярных функций [i, определенных на
всех подмножествах в Г, и таких, что конечна полная вариация
п
|| ^|| = sup ^\
где верхняя грань берется по всем конечным семействам непересекающихся
подмножеств {Tk)[^k^n множества Т.
Доказать следующие утверждения.
A) Относительно введенной выше нормы ш(Т) есть банахово про-
пространство.
B) Если каждому элементу fe Л (Т) поставить в соответствие функцию
множества |Х/, определенную равенством
то отображение и: /i—>[if есть линейная изометрия пространства Iх(Т)
в ш(Т)
C) Если \xz=m(T), то функция for *ь-> |i({f}) (fe Г) принадлежит Iх (Т)
И II full/. (Г) <И И-
D) Образом отображения м, определенного в B), является множество
шс(Т) элементов \х^ш(Т), обладающих следующими двумя свойствами:
(a) \х-т счетно аддитивна;
(b) существует такое не более чем счетное множество СсГ, что
\х(Х)=0 для всех множеств XczT, удовлетворяющих включению X аТ\С
E) Обозначим через то(Т) множество всех элементов |1ет(Г), таких,
что |x(F)=0 для всех конечных подмножеств F в Т. Пространство т(Т)
есть топологическая прямая сумма то(Т) и пгс(Т). В частности, и гпо(Т)
и шс(Т) —замкнутые векторные подпространства в пг(Т).
Замечания Если Т конечно, то очевидно, что mo(T) ={0}. С другой
стороны, если Т бесконечно, го тс(Т) есть собственное подмножество в
164 Упражнения
т(Т). Это следует из результатов, сформулированных в упр. 1.21, 1.24 и
1.25. Это можно вывести и из теоремы Хана — Банаха, установив существо-
существование так называемых обобщенных пределов, описанных в § 3.4.
1.20. Обозначения те же, что и в предыдущем упражнении. Пусть [х —
элемент пространства m(T) Показать, что всякая функция х^1°°(Т) с конеч-
конечной областью значений х(Т) (т. е. принимающая лишь конечное число значе-
п
нип) может быть записана в виде конечной суммы 2 %>k%Tk* где ^ "" числа>
(Tk)i^k<n~~конечное разбиение множества Г, а %т — характеристические
п*
функции множеств Tk. Показать далее, что значение суммы 2 £&М- (^&)
зависит лишь от самой функции х с конечной областью значений и не зависит
от способа ее представления. Общее значение всех таких сумм для задан-
заданного х обозначим через хd\i. Проверить, что отображение х\—> xd\x
т т
(для указанных х) линейно и что
|| \1 || = SUp
т
где верхняя грань берется по множеству всех функций с конечной областью
значений, таких, что
|| #|| =sup I х (t) | ^ 1.
Вывести отсюда, что этот интеграл имеет единственное непрерывное про-
продолжение на 1°°{Т) и что это продолжение линейно и удовлетворяет не-
неравенству
для х<==1°°(Т).
1.21. Обозначения те же, что и в предыдущем упражнении. Доказать,
что если каждому элементу \х^пг(Т) сопоставить непрерывную линейную
форму на 1°°(Т), определенную правилом х i—> х d\i, то тем самым
Т
получается линейная изометрия пространства пг(Т) на топологическое сопря-
сопряженное к пространству 1°°(Т).
[Указание. Для того чтобы представить заданную непрерывную ли-
линейную форму F на 1°°(Т) с помощью интеграла, рассмотреть функцию мно-
множества \х, определенную равенством \х{Х) =F(%X) для ХаТ.].
1.22. Обозначения те же, что и в предыдущих трех упражнениях. Дока-
Доказать следующие утверждения.
A) Всякое ограниченное по норме множество из ш(Т) относительно
компактно в топологии о(пг(Т), 1°°(Т)).
B) Ограниченная по норме сеть (цг) в пг(Т) тогда и только тогда удов-
удовлетворяет соотношению lim jx^ = 0 в топологии а (пг (Т), /°°(Г)), когда
'i n |д^ (X) =ш,0 для каждого подмножества X в Т.
i
[Указание. Воспользоваться упр. 1.18 и 1.21.]
Упражнения 165
Предварительные замечания. Следующие шесть упражнений
относятся к взаимосвязям между некоторыми элементами пространства
т(Т) и так называемыми у льтрафио летами на Т. Понятие фильтра введено
А. Картаном. Оно принято и систематически применяется в книгах Бурбаки.
При исследовании вопросов сходимости в топологических пространствах Бур-
баки использует фильтры вместо сетей. Хотя понятие фильтра интуитивно
гораздо менее ясно, чем понятие сети (по крайней мере для читателей, уже
привыкших к обычным последовательностям), тем не менее фильтры обла-
обладают некоторыми техническими преимуществами (см. вводные замечания
о фильтрах в книге Бурбаки [2}).
1.23. Пусть Т — множество; через 2Т обозначается множество всех под-
подмножеств в Т. Фильтром на Т называется непустое подмножество еГ
в 2Т, обладающее следующими свойствами:
A) всякое подмножество в Г, содержащее элемент из еГ, само принад-
принадлежит &';
B) пересечение двух множеств из £F принадлежит &';
C) пустое множество не принадлежит £F. Множество всех фильтров
на Т частично упорядочено по включению, т. е. фильтр *Г предшествует
фильтру of', в том и тол.ько в том случае, если каждое множество из аГ
принадлежит еГ'. Проверить, что множество всех фильтров на Т индуктивно
упорядочено и что, следовательно, каждый фильтр Т содержится в некото-
некотором максимальном фильтре. Этот максимальный фильтр на Т называется
ультрафильтром на Г.
Доказать следующие утверждения.
(a) Пусть Т — произвольное множество и A s 2Г. Тогда множество
{I: I g 2Г и X"Z) А) есть фильтр на Г, если А непусто. Если Т бесконечно,
то множество {X . X е 2Т и Т\Х конечно} есть фильтр на Т.
(b) Пусть Т — направленное множество Множество всех тех подмно-
подмножеств в Т, каждое из которых содержит некоторое множество вида St =
= {t' s T : t'^-t} (где t — элемент из Г), есть фильтр на Т.
(c) Если Т — топологическое пространство и t^T, то множество всех
окрестностей точки t есть фильтр на Т.
(d) Пусть Т — множество и/s?1. Множество всех подмножеств в Г, со-
содержащих точку t, есть ультрафильтр на Т. Ультрафильтры этого типа на-
называются тривиальными.
(e) Пусть Т — множество и U — ультрафильтр на Т. Если Л, В — под-
подмножества в Г и объединение А\]В<=2/, то по меньшей мере одно из мно-
множеств Л, В принадлежит V,
(f) Пусть Т — множество и гГ — фильтр на Г, обладающий следующим
свойством: для всякого подмножества А в Т либо Ле/, либо Т\А ^ *Г.
Тогда с^Г —ультрафильтр на Т.
(g) Если Г —конечное множество, то на Т имеются лишь тривиальные
ультрафильтры.
(h) Если Т — бесконечное множество, то в Г существует по крайней
мере один нетривиальный ультрафильтр.
1.24. Пусть Т — множество, X — отделимое топологическое пространство,
/ — функция, отображающая Г в X, такая, что f(T) относительно компактно
в X, и U—ультрафильтр в Т. Доказать, что существует в точности одна
точка xgI, обладающая тем свойством, что f~l(U) е2?для каждой окрест-
окрестности U точки xt и что эта точка х принадлежит f(T). Это х обозначим
через f*(U).
Пусть / и g — функции, отображающие Т в X, образы которых f(T) и
g(T) относительно компактны в X. Показать, что если функции fug совпа-
совпадают на некотором множестве, принадлежащем ультрафильтру U в Т} то-
г до = «• до.
166 Упражнения
[Указание. Показать, что система множеств f(A), А е= 2/, центриро-
центрирована (п. 0 2.17), и использовать тот факт, что f(T) содержится в компактном
подмножестве в X]
1.25. В упр. 1.24 взять в качестве X поле скаляров (вещественное или
комплексное) в обычной топологии. Пусть У>— ультрафильтр на Т. Показать,
что отображение f\—>f*(U) есть непрерывная линейная форма на 1°°(Т)
и что
(fg)* М = Г (Ю §* W
для /, g<==l°°(T).
[Указание. Сначала рассмотреть функции из 1°°(Т), принимающие
лишь конечное число значений.]
Замечания. Если множество Т бесконечно и U — ультрафильтр на
Т, содержащий фильтр дополнений к конечным подмножествам в Т, то
f*B/) есть своего рода обобщенный предел функции f(t) при t-> оо. Дру-
Другой подход к обобщенным пределам, опирающийся на теорему Хана — Ба-
Банаха, приведен в § 3.4.
1.26. Пусть Т — множество и т(Т) — пространство аддитивных скаляр-
скалярных функций множества на Г с конечной полной вариацией (см. упр. 1.19).
Обозначим через Ммножество тех элементов цеЕга(Г), которые принимают
только значения 0 и 1 и для которых \i(T) = \. Доказать, что множество М
компактно в топологии а(т(Г),/°°(Г)) (см. упражнение 1.22).
Показать далее, что если каждому ультрафильтру U на Т сопоставить
функцию множества |х, определенную для подмножеств X в Т равенствами
1 При IG U,
0 при X фи,
то тем самым между множеством М и множеством всех, ультрафильтров на
Т установится взаимно однозначное соответствие.
Замечание. Это соответствие может быть использовано для пере-
перенесения топологии с М на множество Г* всех ультрафильтров на Т. Множе-
Множество Т* становится при этом отделимым компактным пространством. Отож-
Отождествляя каждую точку t e= T с соответствующим тривиальным ультрафиль-
ультрафильтром Ut на Т (см. упр. 1.23), можно рассматривать Т как подмножество
в Т*. В то же время каждая функция / е 1°°(Т) продолжается до функции
f* на Т*.
1.27. В обозначениях предыдущего упражнения показать, что если
U — ультрафильтр на Г и [i — соответствующий ему элемент из Af, то
f d\x = /* (U) для каждого / е= /°° (Г). Интеграл понимается в смысле опре-
опреть
деления, данного в упр. 1.20. Доказать, что /* е= С (Г*).
[Указание. Достаточно проверить это равенство для функций / вида
п
f = 2 5fe%r » где ^к образует разбиение Т. Так как в точности одно мно-
множество Tk е= 2/, то \к (Tk) =\ и ц (Tk,) = 0 для k' ф k и, значит, f* (U) = gfe. ]
Замечание. Отображение f\—>f* является, таким образом, линейной
изометрией пространства /°°(Г) в С(Т*) и притом сохраняющей произве-
произведения.
1.28. В обозначениях упр. 1.26 показать, чго Т всюду плотно в Т*. Вы-
Вывести отсюда, что отображение /i—>/* является отображением простран-'
ства /"(Г) на С(Т*).
Упражнения 167
Замечания. Мы установили, таким образом, что Т* есть отделимое
компактное пространство, содержащее Т в качестве всюду плотного подмно-
подмножества и такое, что каждая функция /е/°°(Г) обладает единственным непре-
непрерывным продолжением /*еС(Г*). Отображение f\—>/* является линейной
изометрией пространства /°°(Г) на пространство С (Г*) и даже изоморфиз-
изоморфизмом (в любом разумном смысле) алгебры l°° (T) на алгебру С (Г*). Кроме
того, f*(T*)af(T). Можно показать, что множество Г* однозначно с точ-
точностью до гомеоморфизма определяется этими свойствами. Оно называется
компактафикацаей Стоуна — Чеха множества Т и иногда обозна-
обозначается через РГ. Пространство Т* индуцирует в Т дискретную топологию.
Стоуно-чеховская компактификация Г* может быть построена для лю-
любого вполне регулярного пространства Г, если в качестве исходного про-
пространства вместо /°°(Г) рассматривать Съа{Т). Вообще говоря, возможны
различные способы построения этой компактификации; один из наиболее
изящных опирается на теорию банаховых алгебр. Сущность этого подхода
состоит в доказательстве того, что всякая непрерывная линейная форма F
на пространстве Cbd{T), удовлетворяющая условиям F(\) = \ и F(fg) =
= F(f)F(g)> имеет вид F(f) =/*B/), где U — некоторый ультрафильтр на Т
(ср. с упр. 125). О подробностях см. Гильман и Джерисон [1] (в осо-
особенности гл. 6 и 7), Л ю м и с [1, стр. 75], Р и к к а р т [1, стр. 190].
ГЛАВА 2
Теорема Хана—Банаха
2.0. Предисловие
В предыдущей главе мы познакомились с теоремой Хана —
Банаха в так называемой аналитической форме, в которой она
применима к произвольному (не обязательно топологическому)
векторному пространству. В настоящей главе мы будем иметь
дело с топологическими векторными пространствами и увидим,
что в этой ситуации теорема Хана — Банаха многое может ска-
сказать о существовании непрерывных линейных форм, удовлетво-
удовлетворяющих некоторым условиям. Если ввести необходимые поня-
понятия, то все основные теоремы, приводимые ниже, следуют из
теоремы, установленной в § 1.7. Основные результаты этой
главы изложены в § 2.1. Между прочим заметим, что можно так
сформулировать геометрический вариант теоремы Хана —Ба-
—Банаха, что из него в свою очередь будет следовать ее аналитиче-
аналитическая форма, приведенная в п. 1.7.1 (см. упр. 2.19).
В § 2.2 исследуется так называемый принцип продолжения,
связанный с возможностью продолжения непрерывной линейной
формы с векторного подпространства на все рассматриваемое
топологическое векторное пространство.
Один из наиболее плодотворных методов применения тео-
теоремы Хана — Банаха — использовать эту теорему в виде прин-
принципа аппроксимации, который изложен в § 2.3. В последующих
главах приведены его многочисленные приложения; здесь же мы
ограничиваемся несколькими примерами, показывающими этот
принцип в действии.
В § 2.4 мы временно возвращаемся к вещественным вектор-
векторным пространствам и изучаем некоторые их подмножества, из-
известные под названием конусов. Задание выпуклого конуса опре-
определенного вида эквивалентно наделению пространства частич-
частичным порядком, который согласуется со структурой векторного
пространства. Это в свою очередь приводит к важному понятию
положительной линейной формы и теоремам о продолжении та-
таких форм.
В § 2.5 получают дальнейшее развитие идеи § 2.4 для случая,
когда вещественное пространство локально выпукло. Приводят-
Приводятся отдельные результаты, применяющиеся при функционально
21. Геометрическая форма теоремы Хана —Банаха 169
аналитическом подходе к некоторым разделам теории игр.
Даются также примеры из теории игр, в частности функцио-
функционально аналитические доказательства обобщенной теоремы Вил-
ля и основной теоремы теории игр.
Некоторые обобщения теоремы Хана — Банаха и ее след-
следствий нам удобнее отложить до гл. 3 (§ 3.3—3.5).
2.1. Геометрическая форма теоремы Хана— Банаха
Хотя результатам § 1.7 можно придать такую геометриче-
геометрическую форму, что они будут справедливы для произвольного век-
векторного пространства, здесь мы будем существенно пользоваться
предположением, что рассматриваемое векторное пространство
топологическое. Это предположение позволяет всюду, где это
возможно, сосредоточивать внимание на непрерывных линейных
формах и замкнутых векторных подпространствах. Оказывается,
что эти топологические рамки тесно связаны с ситуациями, воз-
возникающими в конкретных аналитических приложениях описы-
описываемой теории.
В общих чертах основной результат заключается в том, что
в локально выпуклом пространстве имеется достаточное коли-
количество непрерывных линейных форм для точного описания
структуры такого пространства в терминах линейных и топо-
топологических свойств его замкнутых подпространств и замкнутых
выпуклых подмножеств.
2.1.1. Теорема. A). Пусть Е — (вещественное или комплекс-
комплексное) топологическое векторное пространство, А — открытое вы-
выпуклое подмножество в Е и М — линейное многообразие в Е, не
пересекающее А. Тогда в Е существует замкнутая гиперпло-
гиперплоскость, содержащая М и не пересекающая А.
B). Пусть Е — вещественное топологическое векторное про-
пространство, А — открытое выпуклое подмножество в Е и L — век-
векторное подпространство в Е, не пересекающее А. Тогда суще-
существует такая непрерывная линейная форма f на Е, что
f(L)=0uf(A)>0,
т. е. f(x) = 0 для х из L и f(a) >0 для а из А.
Доказательство. A) Рассмотрим сначала случай, когда
Е — вещественное пространство. Можно считать, что М — век-
векторное подпространство в Е (этого всегда можно добиться с по-
помощью сдвига). В силу результатов § 1.6 можно считать, что
А={х^Е: р(х — х0) <1}, где х0 е Е, а р — положительная суб-
субаддитивная положительно-однородная функция на Я,
170 Гл. 2. Теорема Хана — Банаха
Так как множество А открыто, /? — непрерывная функция. Из
того, что МПЛ = 0, следует, что р(у — х0) > 1 для je! Опре-
Определим на множестве Af+Rx0 линейную форму / равенством
Если а>0, то
f(y - axQ) = а < а • р (|- - *0) = р {у - ах0);
если же а^О, то
Таким образом, во всех точках множества M+Rx0 справедливо
неравенство f-^-p. Так как р — положительная калибровочная
функция на £, то из аналитической формы теоремы Хана — Ба-
Банаха (теорема 1.7.1A)) следует, что f можно продолжить до
такой линейной формы f* на Е, что во всех точках к^Е будет
выполняться неравенство f*(x) -^ip(x), что влечет за собою не-
непрерывность формы /*. Далее, множество H — f*-l({0}) есть замк-
замкнутая гиперплоскость в £, содержащая множество М= (М-\- Rx0) П
П/ ({0}). Наконец, /*(г)=0 при любом 2Gfl; поэтому
= Г (г ~ х0) - 1 < р (г - х0) - 1,
откуда следует, что р(г — хо) ^ 1 при z e Я, т. е. что множество
А не пересекает Я, чем и завершается наше доказательство в
случае, когда Е — вещественное пространство.
Пусть Е — комплексное пространство. Сузим сначала поле
скаляров до вещественного и воспользуемся уже доказанным
результатом. Таким способом устанавливается существование
такой замкнутой вещественной гиперплоскости HqZdM, что
НоГ\А = 0. Так как М = Ш, то ШО есть замкнутая вещественная
гиперплоскость, содержащая М. Теперь достаточно положить
B) Применим утверждение A) к L вместо М. Получим од-
однородную гиперплоскость Я, которая в силу своей замкнутости
определяется уравнением / = 0, где f=f=O—непрерывная линейная
форма на Е. Так как Н zd L, то f(L)=O и, следовательно, Я не
пересекает А. Из того факта, что А —выпуклое множество, вы-
вытекает, что f(A) представляет собой вещественный интервал, не
содержащий нуля. Изменяя в случае надобности знак формы f,
получаем /(Л)>0. |
Существует не менее шести важных следствий доказанной
теоремы.
2.1. Геометрическая форма теоремы Хана — Банаха 171
2.1.2. Следствие. Пусть Е — вещественное топологическое век-
векторное пространство, А — открытое выпуклое множество в Е и
В— выпуклое множество в Е, причем А{~\В = 0. Существуют та-
такая непрерывная линейная форма \Ф0 на Е и такое веществен-
вещественное число а, что
f(A)<a, f(B)>a.
(Эти неравенства могут быть обращены заменой f на —/.)
Доказательство. Множество К=А—В открыто, вы-
выпукло и не содержит нуля. Следовательно (теорема 2.1.1), су-
существует такая непрерывная линейная форма 1Ф0 на £, что
/(/С)<0. Если a = sup{/(a): а^А}, то а конечно и
f(B)>a.
Поскольку, однако, /=£0, то /'—открытое отображение про-
пространства Е на R и, следовательно, в действительности имеет
место строгое неравенство /(Л)<а. I
2.1.3. Следствие. Пусть Е — вещественное локально выпуклое
пространство, А—замкнутое выпуклое, а К — компактное вы-
выпуклое множество в Е, причем А(]К = 0. Тогда существуют та-
такая линейная форма f=f=O на Е и такое вещественное число а,
что
f(A)<a, f(K)>a.
(Снова неравенства можно по желанию обратить.)
Доказательство. Существует такая открытая выпуклая
окрестность нуля U, что (A + U)[){K+U)=0. Применяя
следствие 2.1.2 к множествам А + U и К + U, мы получаем, что
существуют такая линейная форма / Ф 0 на Е и такое веще-
вещественное число а, что
U)<a,
Так как K+U — открытое множество и f — открытое отображе-
отображение пространства Е на R, то второе неравенство на самом деле
строгое, т. е. /(/(+£/)>а, откуда и следует наше утверждение. |
Замечание. Замкнутая гиперплоскость H = f~l ({а}) строго
отделяет множества А и К.
2.1.4. Следствие. A) Пусть Е — вещественное локально вы-
выпуклое пространство, А — замкнутое выпуклое множество в Е
и х^^Е\А. Тогда существует непрерывная линейная форма f
на Е, удовлетворяющая неравенству
f(xo)>supf(A).
В частности, множество А есть пересечение всех полупространств
пространства £, содержащих А.
172 Гл. 2. Теорема Хана — Банаха
B) Пусть Е—(вещественное или комплексное) локально
выпуклое пространство, А—замкнутое выпуклое уравновешен-
уравновешенное множество в Е и хо^Е\А. Тогда существует такая непре-
непрерывная линейная форма f на Е, что
\f(xo)\>sup\f(A)\.
Доказательство. A) Достаточно применить следствие
2.1.3, взяв К = {х0}.
B) Согласно A), существует вещественная непрерывная ли-
линейная форма и на Е, удовлетворяющая неравенствам
u(xQ)>ay
где а — некоторое вещественное число.
Так как множество А выпукло и уравновешено, то 0 е А и,
следовательно, а^О. Из неравенства и(А)-*Са и уравновешен-
уравновешенности множества А вытекает неравенство |и(Л)| <^ а. Этим за-
завершается доказательство утверждения B) в случае, когда про-
пространство Е вещественное. Если же оно комплексное, то опре-
определим комплексную линейную форму f на Е равенством
f(x)=u(x) — iu(ix),
где х е Е. Тогда и = Re f. Если х е А и / (х) = relt (г ^ 0, t веще-
вещественно), то е~цх также принадлежит А и, следовательно,
f(e-ux) = r. Так как 1(е~нх) — вещественное число, то f{e-~ux) =
= и (e~ltx)\ поэтому | / (e~lt) \ ^ а, откуда вытекает, что | / (А) |
С другой стороны,
2.1.5. Следствие. Пусть Е— (вещественное или комплексное)
локально выпуклое пространство, L—замкнутое векторное под-
подпространство в Е и х0^ Е\ L. Тогда существует такая непре-
непрерывная линейная форма f на £, что
/(L)=0, f(xQ)^O.
В частности, каждое замкнутое векторное подпространство в Е
есть пересечение всех содержащих его замкнутых гиперподпро-
гиперподпространств в Е.
Доказательство. Достаточно в следствии 2.1.4 положить
А — L или воспользоваться следствием 1.7.2 |
2.1.6. Следствие. Если Е — отделимое локально выпуклое про-
пространство, то точки пространства Е отделяются непрерывными
линейными формами на Е.
Доказательство. В силу предыдущего следствия если
О, то существует такая линейная форма / на Е9 что !(хо)ФО:
2.1. Геометрическая форма теоремы Хана — Банаха 173
мы используем тот факт, что подпространство £=*{()} замкнуто
в Е, ибо Е отделимо. Если Х\фх2, то xo = xi— х2ф0, и 1(х0)ф0
влечет !{х\)Ф\{х2). 1
2Л.7. Следствие. В локально выпуклом пространстве Е каж-
каждое замкнутое выпуклое множество слабо замкнуто.
Доказательство. Если Е — вещественное пространство,
то достаточно применить следствие 2.1.4A). Если же Е — комп-
комплексное пространство, то нужно сузить поле скаляров до веще-
вещественного и заметить, что слабая топология в Е совпадает с то-
топологией, определяемой вещественно-линейными формами. |
2.1.8. Приложение следствия 2.1.4 к линейной теории потен-
потенциала. Хотя это может казаться странным, систематическое изу-
изучение линейных аспектов теории потенциала стало проводиться
лишь совсем недавно. До последнего времени нелинейные ас-
аспекты (включая, например, квадратичные функционалы типа
взаимной энергии) казались более важными. Однако за послед-
последнее десятилетие линейные аспекты этой теории были в большой
общности рассмотрены Шоке и Дени [1, 2] и Хантом [1—3].
В качестве наглядного примера воспользуемся следствием 2.1.4,
чтобы установить связь между двумя основными принципами
теории потенциала — принципом мажорирования и принципом
выметания. Эти принципы давно известны как краеугольные
камни в ньютоновой и в некоторых других специальных теориях.
Мы в основном придерживаемся изложения Дени [1].
Нам понадобятся меры Радона, систематическое изучение
которых проводится в гл. 4. Так как число нужных здесь нетри-
нетривиальных фактов из теЬрии мер Радона невелико, то их привле-
привлечение не вызовет больших затруднений.
Пусть Т — отделимое локально компактное пространство.
Обозначим через C = Q(T) пространство вещественных непрерыв-
непрерывных функций на Г, а через оУС = оУС(Т) его подпространство,
образованное теми функциями /<=С, носители которых Sf ком-
компактны. Напомним, что S/— это замыкание множества тех точек
/ ^ Г, для которых /(/) =£0. Если наделить С локально равномер-
равномерной топологией; то оно становится локально выпуклым простран-
пространством. Что касается g/T, то нам будет достаточно ввести в нем
понятие секвенциальной сходимости. Именно,
будет означать, что
A) множество U [Sfn: /z=l, 2, ...} относительно компакт-
компактно в Г,
B) fn-^f равномерно на Т.
Легко проверяется, что оЖ всюду плотно в С,
174 Гл. 2 Теорема Хана — Банаха
Под (вещественной радоновой) мерой на Т понимают линей-
линейную форму \х на е/Г, непрерывную в том смысле, что fn —*► 0 вле-
влечет lim \i(fn) =0. Множество всех таких мер будет обозначаться
через М. Здесь для нас несущественно, что пространство М мо-
может быть отождествлено с топологическим сопряженным к о/С
относительно соответствующей локально выпуклой топологии
в <Ж{% 6.3). Важно, однако, отметить, что множество М содер-
содержится в алгебраическом сопряженном к пространству еЗГ; по-
поэтому мы имеем в М слабую топологию а(М,сзЯП, которую ино-
иногда называют широкой топологией1) в М.
Для наших целей полезно отождествить топологическое со-
сопряженное к С с некоторым подпространством в М. Подробно
мы будем говорить об этом в § 4.10; в общих чертах ход рас-
рассуждений таков. Пусть [i — мера, a U — открытое множество в
Т. Будем говорить, что мера [i обращается в нуль на /7, если
|li(/)=0 для всякой функции /, такой, что Sfd U. Можно пока-
показать, что для заданной меры \х существует наибольшее из от-
открытых подмножеств в Г, на которых ц обращается в нуль.
Дополнение к этому множеству называется носителем меры \х
и обозначается через 5Д. Положим
Mf = {fieM: S^ — компактно};
тогда Мс — векторное подпространство в М. Убедимся в том, что
пространство С (топологическое сопряженное к С) может быть
отождествлено с Мс.
Пусть L е С7; сужение ц, = /,|еЗГ, очевидно, является мерой.
Кроме того, непрерывность L на С означает существование та-
такого компактного множества К d T и такого числа с, что
Отсюда непосредственно вытекает, что мера \х обращается в
нуль на множестве Т\К\ следовательно, SnaK и ji ^ Мс.
С другой стороны, если [i^Mc, то \i(f)=\i(g) для функций
f, g е оЯГ, совпадающих на некоторой окрестности компактного
множества 5Д. Если f^C, то выберем какую-нибудь функцию
/о ^ Ж, совпадающую с / в окрестности носителя 5Ц меры \х, и
положим L(f) =ji(f0). Ясно, что L — корректно определенная
линейная форма на С; ее сужение на оЖ совпадает с \х. Легко про-
проверить, что форма L непрерывна на С. Остается добавить, что
в силу плотности е2Гв С каждый элемент из С однозначно опре-
определяется своим сужением на е2Г. Таким образом, каждый эле-
элемент из Мс однозначно продолжается сеЗГ на С, до элемента из
С, и каждый элемент пространства С получается таким
i....
1) См. Бурбаки [8, стр 74]. — Прим, перев.
2.1. Геометрическая форма теоремы Хана — Банаха 175
способом из единственного элемента пространства Мс. Тем са-
самым возможность отождествления пространства С и Мс показана.
В пространстве Мс можно ввести слабую топологию о(Мс,С),
которая, вообще говоря, сильнее топологии, индуцированной в
Мс топологией o{M,Jf).
Мера \х называется положительной (что записывается ^^0),
если для каждой неотрицательной функции f <=о/Г имеет место
неравенство \x(f) <> 0. Обозначим через М+ множество положи-
положительных мер и положим М+ —М+[)МС. Если мера \х е М+ про-
продолжена описанным выше способом на С (и ее продолжение
снова обозначено ц,), то при f^C и /^-0 имеет место неравен-
неравенство \i(f) >0.
Иногда удобнее пользоваться обозначением (f, \i) вместо
[i (/) (здесь [esTh \x e Af или [gCh [i£ 7WC).
Перечислим несколько почти очевидных свойств мер, кото-
которые нам понадобятся.
(a) Если X, \х^М и X = \i на открытом множестве UczT
(т. е. К — fx обращается в нуль на [/), то jut (/) = Я(jP) для всякой
функции f^oZT, обращающейся в нуль вне U.
(b) Если ii <= М+ м функции f, g ^С удовлетворяют нера-
неравенству f <g, TO \l (f) < |Л (g) .
(c) Если F — замкнутое подмножество в Г, то множество
замкнуто в М.
(d) £сла /С — компактное множество в Г, то множество
компактно в Мс.
Утверждение (а) следует из предложений 4.5.1 и 4.9.1, а
утверждение (Ь) содержится в вводных замечаниях § 4.6. Утвер-
Утверждение (с) непосредственно вытекает из определений. Для до-
доказательства (d) достаточно в силу (с) и теоремы 1.11.4 B) про-
проверить, что 2 — равностепенно непрерывное подмножество в С.
Возьмем произвольную функцию и ^g/T, удовлетворяющую усло-
условиям O^w^l на Е и и=\ на компактной окрестности К' мно-
множества К- Для всякой функции [еС и меры [iGll имеет место
равенство \i(f) =\i{fu). Далее, если /С/Х = 5и, то
поэтому из положительности \х следует, что при /gCh ц
176 Гл. 2 Теорема Хана— Банаха
Так как множество К" компактно, то отсюда вытекает, что мно-
множество 2 равностепенно непрерывно.
Связь 'с теорией потенциала основана на замечании, что в
теориях Ньютона, Рисса и Грина каждой функции /cigT, пред-
представляющей собой распределение массы или зарядов, ставится
в соответствие функция Gf^C, представляющая соответствую-
соответствующий потенциал. При этом отображение G определяется некото-
некоторым положительным ядром k(t,s)y а именно
Gf{t)=\k{ty s)f(s)ds.
Однако эта деталь сейчас не очень важна. Основные свойства
отображения G — это его линейность и положительность. По-
Последнее означает, что Gf S> 0 при f^-О. Положительность ото-
отображения G обеспечивает его непрерывность в том смысле, что
fn—-»0 влечет Gfn->0 в С. Действительно, пусть Л' — компактное
множество, содержащее Sfn для всех п, а функция и удовлетво-
удовлетворяет условиям и ^ 0 на Е и и = 1 на К. Тогда существует такая
последовательность чисел (ап), что ап->0и \fn\^Canu. Так как
отображение G положительно, то | Gfn j^Can • Ga, откуда сле-
следует, что Gfn-^O в С.
Непрерывность отображения G позволяет ввести сопряжен-
сопряженное к G отображение G' пространства Мс в Мг определяемое ра-
равенством
ц> = </, G'|i>f B.1.1)
где /&>лГи \х^Мс (подобным же образом определяется сопря-
сопряженное отображение в более общей ситуации, описанной в §8.6).
Таким образом, для заданной меры [igMc отображение
f-+(Gf,ii) есть мера; эта мера есть не что иное, как G'\i. Из
формулы B.1.1) следует непрерывность отображения G' при
топологиях o(MCi С) и g(M,g^T), а также положительность G',
которая означает, что G* {Nit) czM+.
Упомянутые выше два принципа теории потенциала можно
теперь сформулировать в терминах отображений G и G'. Пер-
Первый из них иногда называется также принципом максимума
Фростмана.
Принцип мажорирования. Если f и g — неотрицательные
функции из <ЗГи неравенство Gf •< Gg имеет место во всех точ-
точках множества 5/, то это неравенство справедливо во всех точ-
точках множества Т.
Второй принцип касается возможности применения процесса
выметания Пуанкаре.
Принцип выметания. Для любой меры цеМс+ 'и любого
относительно компактного открытого множества U аТ
2.1. Геометрическая форма теоремы Хана — Банаха 177
существует такая мера jj,*^jW+, что S^+czU, G'ji* = G'\k на U
и G V < G'\i на Т.
Мы не имеем возможности пояснять здесь общее значение
этих двух принципов. На эту тему имеется обширная литера-
литература, например, Валле-Пуссен [1], Фростман [1, 2],
Картан [5—7], Брело [1—3]. Чдтатель может такж$ обра-
обратиться к обзорной статье Оцуки [1], в которой приведен боль-
большой список литературы.
Для исследования связи между двумя принципами нам пона-
понадобится еще одно определение. Отображение G' называется
строго положительным, если G'ji^O при [ieMJ" и \хфО. Можно
показать, что для этого необходимо и достаточно, чтобы( для
каждого /gT имело место соотношение G'e/^O, где et — мера
Дирака, сосредоточенная в точке t, определяемая формулой
st(f)=f(t) для f^-Ж. Этот факт, однако, -использоваться не
будет.
В следующей ниже теореме выявляется тесная связь между
двумя принципами.
Теорема. Если отображение G' удовлетворяет принципу вы-
выметания, то G удовлетворяет принципу мажорирования. Если
отображение G' строго положительно, то справедливо и обрат-
обратное утверждение.
Доказательство. A) Пусть отображение G' удовлетво-
удовлетворяет принципу выметания, a f и g — неотрицательные функции
из Ж. Для каждого t е Т обозначим через е* меру вида, ука-
указанного в принципе выметания, если в нем положить jj, = sa, a
в качестве U взять множество тех точек Ig7, в которых
f(t) > 0. Из свойств меры г* и из равенства B.1.1) следует, что
Из утверждения (Ь) следует, что
Gf (t) = (Gf, e;> < (Gg, в)) = (г, G'e*>.
По определению MepbiG7e* правая часть последнего неравенства
мажорируется выражением
Таким образом, для каждой точки t^T имеем Gf(t) ^
что и означает справедливость принципа мажорирования.
B) Допустим теперь, что отображение G удовлетворяет
принципу мажорирования, а отображение G/ строго положи-
положительно. Для того чтобы вывести принцип выметания, мы сначала
запишем его в иной форме.
178 Гл. 2 Теорема Хана — Банаха
Положим А = G'(Mt) и А (К) = О'(М+ (К)) для каждого
компактного множества К а Т. Легко проверяется, что отобра-
отображение G/ удовлетворяет принципу выметания тогда и только
гогда, когда выполняется включение
AczA(U) + M+(T\U), B.1.2)
где U — любое относительно компактное открытое мно-
множество в Т.
Множество М+(Т\ U) выпукло и в силу (с) замкнуто в М.
Далее A(U)= \J{cB: с>0}, где B = G'B), а множество 2 опре-
определено так же, как ив (d), если там заменить К на U. Из (d)
следует, что множество 2 компактно в УИС, а из непрерывности
G' вытекает компактность множества В в М. Кроме того, так
как G7 — строго положительное отображение, то ОфВ. Оче-
Очевидно, что множество в правой части B.1.2) выпукло; из про-
простой леммы, которая будет доказана ниже, следует, что оно
замкнуто вМ. В силу следствия 2.1.4 это множество совпадает
с пересечением всех содержащих его замкнутых полупространств.
Чтобы установить включение B.1.2), а вместе с ним и прин-
принцип выметания, достаточно показать, что если функция h <=еЗГ
удовлетворяет неравенствам
(h,\i)>0 при ц£М
и
(К G'k)>0 при Х^
то
{К G'P) >0 для всех C е= Мс+. B.1.3)
Предположения, сделанные относительно функции /г, означают,
что
/г>0 на T\U
и
Gh>0 на U.
Положим
f = A" = sup(-A, 0), g = h+ = sup{hy 0).
Тогда SfCiU, и поскольку & = g — f, то
Gg—Gf=Gh>0 на 5/.
Из принципа мажорирования следует, что неравенство Gh^-0
выполняется всюду. Но тогда <G/i, C> > 0 для всех peAf^,
что совпадает с неравенством B.1.3). Таким образом, принцип
выметания доказан. |
Остается доказать справедливость следующей леммы.
2.2. Принцип продолжения 179
Лемма. Пусть В— компактное, а С — замкнутое подмноже-
подмножество в М+ и 0 ф. В. Тогда множество
А=Ц{сВ: с>О}[]С
замкнуто в М.
Доказательство. Надо показать, что если сеть (аг) в А
сходится вМк точке g, то g е А. Выберем сг- > 0, |Зг- е В и Yi^ С
так, чтобы аг=Сгрг + уг. Заметим сначала, что limsup*C;< +oo.
Действительно, в противном случае после перехода к подсетям
можно было бы считать, что Нт*сг-=+оо. Но
так что limp/ = 0; отсюда в силу замкнутости множества В сле-
следует, что OgB, а это противоречит нашему предположению.
Итак, lim sup £/<+оо. Переходя теперь к соответствующей
подсети, можно считать, что сеть (сг) сходится к с и в то же
время сеть (|Зг) сходится к р <= В. Тогда сеть \'г = а; — c$i схо-
сходится, и ее предел у принадлежит С. Следовательно, £ = £|3 +
+уеЛ, что и требовалось доказать. 1
2.2. Принцип продолжения
2.2.1. Теорема. Пусть Е — топологическое векторное прост-
пространство, S — подмножество в Е и g — скалярная функция, опре-
определенная на S. Для существования непрерывной линейной фор-
формы /, такой, что f\S = g, необходимо и достаточно, чтобы суще-
существовала такая непрерывная полунорма р на Е, для которой
неравенство
in I n \
B.2.1)
выполняется для любого конечного набора чисел
любого конечного набора {хьI<1<п точек из S.
Доказательство. Необходимость очевидна, ибо если су-
существует линейная форма /, удовлетворяющая условиям тео-
теоремы, то р=|/| есть полунорма, для которой справедливо соот-
соотношение B.2.1).
Докажем достаточность. Пусть L — векторное подпростран-
подпространство в £, порожденное множеством S. Каждый элемент х е L
п
имеет видл:= 2 аЛ> ГДе ссг- — число, a ^eS. Из соотношения
п
B.2.1) следует, что /о(#)= 2а*£(**) зависит только от х (и не
180 Гл. 2. Теорема Хана— Банаха
зависит от его представления). Очевидно, что определенная та-
таким образом функция fQ есть линейная форма на L, удовлетво-
удовлетворяющая неравенству \fo\^Cp. Теперь остается применить тео-
теорему Хана — Банаха (в аналитической форме), которая обеспе-
обеспечивает возможность продолжения /о до непрерывной линейной
формы f на Е. В
Замечания. Теорему 2.2.1 чаще всего приходится приме-
применять, когда 5 — векторное подпространство в Е (т. е. S = L) и
g— линейная форма на S. В этом случае B.2.1) просто озна-
означает, что форма g непрерывна на S. Далее продолжение всегда
может быть выбрано таким образом, чтобы непрерывная полу-
полунорма, мажорирующая \g\ на S, мажорировала бы и |/| на Е.
Читатель легко заметит, что теорема 2.2.1 применима к лю-
любому векторному пространству Е, наделенному топологией
а (£,£*).
Применим теорему 2.2.1 для доказательства теоремы Тёп-
лица, играющей значительную роль в изучении методов сумми-
суммирования.
2.2.2. Теорема (Теплиц). Пусть S и Т — произвольные мно-
множества, k — числовая функция на произведении SxT, такая,
что для каждого s<=S мнооюество {/<= Г: k(s, t)=£Q} конечно,
и пусть задана числовая функция у на S. Тогда для существова-
существования числовой функции х на Т, удовлетворяющей соотношению
y(s)= S k(s, t)x(t) (sgS), B.2.2)
необходимо и достаточно, чтобы для каждого конечного набора
чисел (ai)\^i^n u каждого конечного набора элементов
множества S из равенства
п
2a^(s,, 0 = 0 (tz=T) B.2.3)
следовало равенство
%aiy(Si) = 0. B.2 А)
Доказательство. Необходимость очевидна. Для доказа-
доказательства достаточности обозначим через Е векторное простран-
пространство тех числовых функций на Т, которые равны нулю всюду,
за исключением конечного подмножества в Т (причем это под-
подмножество зависит от рассматриваемой функции). По условию
функция us: t*—>k(s, t) принадлежит Е при каждом s^S.
Алгебраическое сопряженное к Е может быть отождествлено с
пространством Кт (под К понимается поле скаляров), если
2.2. Принцип продолжения 181
каждому xg/(t поставить в соответствие линейную форму
и*—^ ^u(t)x(t) на Е. Нам нужно найти такую,линейную форму f
te=T
на £, чтобы для каждого s е Е имело место равенство f(us) =
= y(s). Наделим пространство Е топологией о(Е,Е*). Из теоре-
теоремы 2.2.1 вытекает, что для существования такой линейной фор-
п
мы / необходимо и достаточно, чтобы из 2a^s=0 следовало
2at#(sj) = 0, где (аг) и Eг) — произвольные конечные наборы
соответственно чисел и элементов из S. Так как первое озна-
означает равенство нулю выражения
п
2
CiUs (t) = 2 <*i* (St, t)
* t — i
i-i
при каждом /еГ, то достаточность условия теоремы дока-
доказана. |
2.2.3. Следствие. Пусть S, Т и k те же, что и в теореме 2.2.2.
Множество числовых функций на S, имеющих вид B.2.2), для
некоторой функции х на Т замкнуто в пространстве Ks {К — по-
поле скаляров), наделенном топологией поточечной сходимости
на S.
Доказательство. Утверждение очевидно, так как если у
есть поточечный предел сети (уа) таких функций уа, что B.2.3)
влечет B.2.4) (с заменой у на уа), то этому же условию удовле-
удовлетворяет и функция у. 1
Замечание. Теорема 2.2.2 и следствие 2.2.3 останутся
справедливыми, если заменить числовые функции функциями
со значениями в произвольном векторном пространстве. Предо-
Предоставляем читателю сформулировать эти результаты для ука-
указанного случая.
2.2.4. Применение принципа продолжения к функции Грина.
Всюду в этом разделе через Q будет обозначаться фиксирован-
фиксированная ограниченная область в Rn (n^-2), а через F- (компакт-
(компактная) граница области Q в Rn. Классическая задача Дирихле
(первая граничная задача теории потенциала) состоит в нахо-
нахождении функции, гармонической вйи принимающей заданные
непрерывные граничные значения на F. Другими словами, для
заданной непрерывной вещественной функции f на F требуется
найти такую гармоническую в Q функцию Uf. что для каждой
точки /е/7
lim uf(x) = /(/).
Qx>t
182 Гл. 2. Теорема Хана —Банаха
Из принципа максимума для гармонических функций следует,
что решение, если оно существует, однозначно определяется
функцией /. Известно также, что в случае достаточно гладкой
границы F функцию щ при заданном f можно найти, исходя из
решений, соответствующих некоторым частным граничным зна-
значениям. Именно допустим, что для каждой точки xo<=Q изве-
известно решение U(x,xo), соответствующее граничным значениям
h(t,x0) функции А(л:, лго), определенной (для хфхо) форму-
формулой
( log\x-xQrl при /г = 2,
П УХ. Xq) = \ 9 „
[ \x-xo f~n при п > 2,
где через \х — хо\ обозначено евклидово расстояние между точ-
точками х и х0. Определим функцию Грина G(x,xQ) для области Q
равенством
G(X, Xo) =h(X, Xq)— U(X, Xq).
Как функция от х G является гармонической функцией в обла-
области Q\{a:o} и принимает нулевые граничные значения, Вблизи
точки х0 функция G имеет особенность такого же типа, как и
функция h(xyxQ). Применяя формулу Грина к области Q, полу-
получаем
uf (х0) = - со J f(t)dG (ty х0) da (О,
F
где (оп-- площадь (гипер) поверхности единичной сферы в R",
а — поверхностная мера на F, а д обозначает дифференцирова-
дифференцирование вдоль нормали к F. Разумеется, здесь еще надо многое сде-
сделать для наведения строгости. Рекомендуем посмотреть хорошо
известную книгу Келлога [1], в особенности стр. 236—
237.
Наша цель — выяснить, как теорема 2.2.1 может быть ис-
использована для доказательства существования функции Грина
G(x, х0). Фактически с помощью этой теоремы можно показать,
что функция G(x, xQ) существует для каждой ограниченной об-
области, является гармонической в Q\{x0} и обладает заданными
особенностями в точке x=xq, хотя граничное условие
lim G (x, Xq) = 0, /eF,
возможно, и не выполняется. Оно выполняется, если граница F
достаточно гладка. В противном случае, как установлено не-
недавними исследованиями, это условие заведомо нарушается.
Однако даже тогда оно выполняется для «большинства» точек
2.2. Принцип продолжения 183
границы F— исключительные точки образуют множество нуле-
нулевой меры, которое поэтому пренебрежимо в теории потенциала.
Эти результаты принадлежат Винеру, Перрону, Фростману, Вал-
ле-Пуссену и многим другим.
Для того чтобы применить теорему 2.2.1, введем банахово
пространство C(F) всех непрерывных вещественных функций на
F с обычными поточечными алгебраическими операциями и с
нормой, равной максимуму модуля рассматриваемой функции.
Обозначим через Е векторное подпространство в C(F), образо-
образованное сужениями на F функций, непрерывных на Q U F и гар-
гармонических в Q. Всякая функция /, принадлежащая Е, является
сужением единственной функции указанного вида, которая есть
не что иное, как функция щ (решение задачи Дирихле с гранич-
граничным значением /). Для заданной точки xogQ определим линей-
линейную форму L на £, полагая L(f)=Uf(xo) для f^E. Из принципа
максимума следует, что форма L непрерывна на Е (ее норма на
самом деле равна единице). Согласно теореме 2.2.1, форма L
обладает линейным и непрерывным продолжением L* на все
пространство C(F). Пользуясь формой L*, определим функции
U и G на Q следующим образом:
£/(*) = Г (АД
G(x) = hxi(x)-U(x),
где hp(y)=h(y, р) при уфр. Мы должны показать, что функции
U(x) и G(x) играют роль указанных выше функций U(x, x0) и
G{x,x0).
Помимо рассмотрения поведения функции f на границе, нуж-
нужно показать, что функция U— гармоническая bQ. Легко видеть,
что отображение х \-^hx области Q в C(F) непрерывно. Из не-
непрерывности формы L* на C(F) следует непрерывность функции
U на Q. Теперь, чтобы установить гармоничность функции U на
Q, достаточно показать, что в каждой точке xgQ величина
0(х) равна среднему значению функции U, взятому по любому
шару достаточно малого радиуса с центром в точке х. Пусть
В — шар с центром в х столь малого радиуса г, что 5сй.
Среднее значение т функции U на В вычисляется по формуле
где |ы — мера Лебега (т. е. d\i — элемент объема в Rn). Если
разложить В на конечное число подмножеств Bk достаточно ма-
малого диаметра и как-нибудь выбрать точки yk&Bhi то из
184 Гл. 2. Теорема Хана — Банаха
непрерывности функции U на Q вытекает, что этот интеграл от-
отличается от суммы
меньше, чем на любое наперед заданное е > 0. С другой сторо-
стороны, легко видеть, что разность
2 К @ и (я*) - -ц-щ- J а,
стремится к нулю равномерно относительно t^F, когда наи-
наибольший из диаметров множеств Bh стремится к нулю. Поэтому
в силу непрерывности формы L* на C(F) можно добиться, чтобы
модуль разности 5 — L*(z) не превосходил е, где z— элемент из
С(/7), определенный формулой
2 = -
j hy(t)dix(y).
Для каждого ^gF функция y*—>hy{t)=h(y,t) гармонична по
уЕЙи потому z(t)=h(x, t)=hx(t), т. е. 2 = /^. Таким образом,
если разбиение шара В достаточно мелко, то имеет место нера-
неравенство \s — L*(/ix)j<e, i. e. \s—U(x)\Ke, откуда следует,
что \т— U(x) |-<2e. Полагая е-^0, получаем m=U(x), что и
означает гармоничность функции U в Q.
Для того чтобы G-э-О во всех точках границы, требуется до-
достаточная гладкость некоторой части границы F. Здесь мы не
будем входить в эти вопросы.
Заметим, что из результатов гл. 4 вытекает возможность
представления формы L* интегралом по некоторой мере Радона
КХо на F. Мера ХХо положительна, ее общая масса равна 1. Соот-
Соответственно
J (x, t)dlXo(t),
и это служит определением функции G (х) = G (х, х0) независимо
от того, является ли граница F гладкой или нет. Последняя фор-
формула может быть записана в виде
G{x9 xQ) = U**°(x)-Ul*°(x),
23. Принцип аппроксимации 185
где (У6*0—потенциал (логарифмический при /г = 2, ньютонов при
га = 3) меры Дирака еХо в точке хо, a U Хо (х) — потенциал ме-
меры ХХо на F. Оказывается, что ХХо—это мера, получающаяся
применением к гХо процесса выметания Пуанкаре на границе F.
2.2.5. Принцип продолжения в таком виде, как он сформули-
сформулирован в теореме 2.2.1, наиболее прост в том смысле, что от иско-
искомого продолжения заданного функционала требуется только ли-
линейность и непрерывность. Ниже (в § 2.5 и 3.3) мы рассмотрим
аналогичные результаты, относящиеся к случаям, когда-на рас-
рассматриваемое продолжение накладываются дополнительные
ограничения. Последние связаны либо с частичным упорядоче-
упорядочением векторного пространства, либо с инвариантностью иско-
искомого продолжения относительно заданной группы автоморфиз-
автоморфизмов векторного пространства.
2.3. Принцип аппроксимации
В этом параграфе рассматривается роль теоремы Хана —
Банаха для обоснования некоторых общих приемов исследова-
исследования аппроксимационных задач. Это — одна из наиболее плодо-
плодотворных областей практического приложения названной тео-
теоремы.
Ситуация, с которой мы будем иметь дело, такова. Имеется
локально выпуклое пространство Е и некоторое множество S
в Е. Нужно найти условия, необходимые и достаточные для
того, чтобы заданный элемент xq^E можно было сколь угодно
точно аппроксимировать некоторой комбинацией элементов
из S. Допустимые комбинации могут быть трех видов:
A) Произвольные линейные комбинации, т. е. комбинации
п
вида 2 ^Л> где ^ — произвольные числа, а хг- — произволь-
произвольные элементы из S.
B) Произвольные выпуклые комбинации, т. е. комбинации
п
вида 2 «Л*, где ос* — такие положительные числа, что
п
2^ = 1, а Х{ — произвольные элементы из S.
C) Произвольные выпуклые уравновешенные комбинации,
п
т. е. комбинации вида 2 Рл> где числа рг- удовлетворяют ус-
п
ловию 2 I Pt I ^ 1» a^j — произвольные элементы из S.
18S Гл. 2. Теорема Хана — Банаха
Выражение «х0 аппроксимируется сколь угодно точно в Е
-комбинациями вида A) (соотв. вида B), C))» означает, что
х0 принадлежит замкнутой линейной оболочке (сооть. замкнутой
выпуклой оболочке, замкнутой выпуклой уравновешенной обо-
оболочке) множества S в Е. Соответствующие критерии могут быть
получены из следствий 2.1.4 A), B) и 2.1.5. Результат можно
сформулировать так.
2.3.1. Теорема. Пусть Е — локально выпуклое пространство,
S — подмножество в Е и х0^ Е. Тогда
(a) точка х0 является пределом (в Е) линейных ком-
комбинаций вида A) элементов из S тогда и только тогда,
когда каждая непрерывная линейная форма f на Е, удовле-
удовлетворяющая условию f(S)=O, удовлетворяет также условию
f(xo)=O;
(b) точка хо является пределом выпуклых комбинаций вида
B) элементов из S тогда и только тогда, когда для каждого ве-
вещественного непрерывного функционала f на Е выполнено не-
неравенство
f (*oK sup f(S);
(c) точка х0 является пределом выпуклых уравновешенных
комбинаций вида C) элементов из S тогда и только тогда,
когда для каждой непрерывной линейной формы [ на Е имеет
место неравенство
\f(xo)\<sup\f(S)\.
2.3.2. Замечания. A) Из теоремы 2.3.1 вытекает, что в ка-
каждом случае, когда аппроксимация возможна в смысле слабой
топологии в £", она возможна и в исходной топологии простран-
пространства Е. В частности, если (хп) — такая сеть элементов из Е, что
Птл;п = 0 в слабой топологии в Е (т. e. limf(xn)=O для каждой
непрерывной линейной формы f на Е), то можно построить та-
такую сеть (уг)у что Птг/г = 0 в исходной топологии простран-
пространства Е, причем каждый элемент ух является выпуклой комбина-
комбинацией конечного числа элементов хп.
B) Банах ввел понятия тотального множества и фундамен-
фундаментального множества в топологическом векторном простран-
пространстве Е. Множество S называется тотальным в Я, если для вся-
всякой непрерывной линейной формы / на £, для которой f(S)=O,
выполнено соотношение f(E)=O Множество S называется фун-
фундаментальным в Е, если наименьшее замкнутое векторное под-
подпространство в Е, содержащее S, совпадает с Е. В этих терми-
терминах теорема 2.3.1 (а) формулируется таким образом: множе-
множество S в локально выпуклом пространстве Е тотально тогда и
только тогда, когда оно фундаментально в Е.
2.3. Принцип аппроксимации 187
2.3.3. Теорема 2.3.1 имеет столь многочисленные полезные
приложения, что совершенно невозможно привести здесь даже
все характерные примеры. Л. Шварц [15] систематически ис-
использовал теорему 2.3.1 (а) для детального изучения семейства
функций е~ах (при различных значениях параметра а) в неко-
некоторых известных пространствах функций на полупрямой @, оо).
Читатель найдет в указанной работе пример использования
функционально аналитических методов для решения задач, воз-
возникающих в классическом анализе. Мы приведем несколько
примеров приложений более узкого типа, хотя тем не менее ка-
каждое из них типично для определенной категории задач.
2.3.4. Пример. Л. Шварц [3] очень изящно применил тео-
теорему 2.3.1( а), утверждающую тождественность тотальных и фун-
фундаментальных множеств в локально выпуклом пространстве, к
изучению специальных семейств непрерывных функций на Rn.
Обозначим через C(Rn) векторное пространство всех непре-
непрерывных вещественных функций на Rn. (Комплексные функции
могут быть изучены таким же образом.) Пространство C(Rn)
становится метризуемым локально выпуклым пространством,
если наделить его системой полунорм
Nk(f) = sup {\f(x)\: |* |<*}.
Эта система полунорм определяет компактно открытую тополо-
топологию, или топологию равномерной сходимости ка компактных
подмножествах пространства Rn. Для заданных функции
f<=C(Rn), числа ос >0 и точки 6 <= Rn обозначим через fa,b
функцию х*—> / (ах + b). Каждая функция fa> ъ принадлежит про-
пространству C(R??). Вначале выясним, при каких условиях на f
может оказаться, что семейство fa, ъ (а > О, J g Rn) не является
фундаментальным в C(Rn).
Теорема А. Пусть функция f^C(Rn) такова, что множество
функций fa,b (a>0,&ERn) не является фундаментальным в
C(R"). Тогда существует такой линейный дифференциальный
оператор с частными производными вида
где ри — неотрицательные целые числа и aPv ...,pn — веществен-
вещественные числа, не все равные нулю, что функция f является
обобщенным решением уравнения Lf = O, т. е. f является преде-
пределом в C(Rn) бесконечно дифференцируемых функций, удовле-
удовлетворяющих этому уравнению.
Доказательство. Используем тот факт (следствиезнаме-
(следствиезнаменитой теоремы Вейерштрасса о полиномиальной аппроксимации,
188 Гл. 2. Теорема Хана — Банаха
которая сама является частным случаем теоремы, устанавливае-
устанавливаемой в п. 4.9.5), что функции вида хр = хр{1 ... хрпп (где xh — коор-
координаты в Rn, a pk независимо друг от друга пробегают целые
неотрицательные числа) образуют фундаментальное множество
в C(Rn). Если множество функций /а, ь не является фундамен-
фундаментальным в C(Rn), то из теоремы 2.3.1 (а) следует существование
непрерывной линейной формы F на C(Rn), удовлетворяющей
условиям F=f=Q и F(fa6)=0 для всех а>0 и всех Ъ <= Rn. Так
как F=£0, то должен существовать такой одночлен х* (<7ь... ,qn),
где qk — неотрицательные целые числа, что Р(х^)Ф0. Положим
где p= (pu • • •, Pn) — всевозможные наборы целых чисел /?ь>0,
и определим оператор L формулой B.3.1); ясно, что L — нетри-
нетривиальный линейный дифференциальный оператор.
Теперь нам нужно обойти трудности, вызванные тем, что
функция / может не быть дифференцируемой. Возьмем некото-
некоторую бесконечно дифференцируемую функцию г на Rn, которая
обращается в нуль вне некоторого ограниченного множества, и
рассмотрим функцию
g(x)=$f{x + y)r{y)dVL{y)t B.3.2)
где через |ы обозначена мера Лебега на Rn. Функция g", очевид-
очевидно, бесконечно дифференцируема на Rn. Легко видеть, что из ра-
равенства F(fa, ъ) =0, где а > 0 и Ь е Rn, следует, что
F(g*.b) = 0 (a>0, 6eRtt), B.3.3)
Это утверждение легко установить, пользуясь непрерывностью
F и аппроксимируя функцию g в C(Rn) суммами вида
^!(х + ук)г{ук)\х{8к), где множества Sk образуют конечное
разбиение того ограниченного множества, на котором г отлично
от нуля, а уь, суть произвольным образом выбранные точки bS^.
Продифференцируем соотношение B.3.3) N раз по а и затем
положим а->0. В силу бесконечной дифференцируемости функ-
функции g и непрерывности формы F получим, что
Lg(b)=0
для всех b e Rn. Таким образом, функция g является решением
уравнения Lg = 0.
В заключение остается только заметить, что функция f мо-
может быть сколь угодно точно аппроксимирована в C(R7?) функ-
2.3. Принцип аппроксимации 189
циями вида B.3.2); действительно, если функция г удовлетво-
удовлетворяет условиям ^>0, J rt (у) d\i(y) = 1 и равна нулю вне неко-
некоторой окрестности нуля ut в Rn, где диаметры множеств £/?- стре-
стремятся к нулю при £*->оо, то gi~^f в C(Rn). Итак, теорема А до-
доказана. !
Имеет смысл пойти несколько дальше и выяснить, при каких
условиях множество всех функций, получающихся из функции /
движениями, не является фундаментальным. Движением в Rn
называется любое преобразование, принадлежащее группе, по-
порожденной сдвигами, вращениями вокруг начала координат и
гомотетиями с положительными коэффициентами с центром в
начале координат. Обозначим эту группу преобразований через
S. Если 5 — элемент группы S, а / — функция на Rn, то будем
обозначать функцию f о s через fs и говорить, что она получена
из функции f движением 5.
Теорема В. Пусть функция f^C(Rn) такова, что множество
всех функций, получающихся из нее движениями, не является
фундаментальным в C(Rn). Тогда существует такое целое число
т^>0, что функция f есть обобщенное решение полигармони-
полигармонического уравнения
Дт/ = 0, B.3 Л)
где через А обозначен оператор Лапласа на Rn.
Доказательство. Так как группа S содержит все сдвиги
и гомотетии с центром в нуле с положительными коэффициента-
коэффициентами, то по теореме А функция f является обобщенным решением
уравнения Lf = O, где L — дифференциальный оператор B.3.1) и
aP ... p = V Vй-• B-3-5)
pv >pn Pl\ ... pn\ ^ }
Так как группа S содержит все вращения,, то можно добиться,
чтобы форма F была инвариантна относительно вращений в
смысле, что F(gr) =F(g) для всех g e C(Rn) и всех вращений г.
Для этого рассмотрим множество G всех вращений как компакт-
компактную группу. (Ее топология может быть определена, например,
так: представим каждое вращение матрицей относительно неко-
некоторого фиксированного базиса в Rn и возьмем естественную то-
топологию, в которой сходимость означает сходимость каждого
элемента матрицы.) Пусть X— биинвариантная мера Хаара на
G (п. 4.0.8). Заменим F линейной формой Р, определенной ра-
равенством
= j F(gr)dX(r).
190 Гл. 2. Теорема Хана — Банаха
Легко видеть, что форма F* инвариантна относительно вращений
в описанном выше смысле; соответствующим выбором центра
вращения можно добиться того, чтобы Р*фО.
Обеспечив таким образом инвариантность формы F относи-
относительно вращений, рассмотрим форму
которая в силу B.3.5) равна
F[(XlXl+ ... +Xnxn)N].
Так как форма F инвариантна относительно вращений, то по-
последнее выражение является функцией от
что возможно только в том случае, если оно име^т вид
где -£ N— целое число; обозначим его через т. Но тогда ясно,
что уравнение Lf = O эквивалентно уравнению Дт/ = 0, что и тре-
требовалось доказать. |
Замечания. A) Если /г = 2, то группу G можно параметри-
параметризовать обычной угловой переменной 0, пробегающей интервал
(О, 2я). В этом случае
2Я
Если /г=1, то группа движений G состоит только из двух эле-
элементов (умножений на 1 и —1) и интегрирование по X означает
просто взятие среднего арифметического по этим двум эле-
элементам.
B) Если /г=1, то группа вращений G состоит лишь из тож-
тождественного преобразования. В этом случае получаем следую-
следующий результат: если множество функций fa> ь> где а пробегает
множество из R, имеющее нуль предельной точкой, а Ь — непу-
непустой открытый интервал (Ь\ Ъ") в R, не является фундамен-
фундаментальным, то сужение \\(ЪГ,Ъ") представляет собой многочлен
степени не выше т, где т зависит только от / (а не от интер-
интервала (&',&")). Доказательство мало отличается от доказатель-
доказательства теоремы А. При этом используется теорема Ролля для того,4
2.4. Дополнения к теореме 2.3.1 и ее дальнейшие приложения 191
чтобы показать, что если бесконечно дифференцируемая функ-
функция одного переменного обращается в нуль на множестве точек,
имеющем нуль предельной точкой, то такая функция и все ее
производные обращаются в нуле в нуль.
2.4. Дополнения к теореме 2.3.1 и ее дальнейшие приложения
До сих пор наше внимание было сосредоточено на части (а)
теоремы 2.3.1. В этом параграфе мы несколько дополним утвер-
утверждения (Ь) и (с) этой теоремы и приведем некоторые их при-
приложения.
Прежде всего утверждения (Ь) и (с) можно дополнить не-
независимыми от них утверждениями о возможности представле-
представления посредством рядов и интегралов элементов замкнутой вы-
выпуклой оболочки " (или замкнутой выпуклой уравновешенной
оболочки) некоторого заданного семейства элементов простран-
пространства Е. Рассмотрим вначале более простой случай рядов.
Пусть в пространстве Е задано семейство элементов (xt)t(=T,
где Т — произвольное множество. Обозначим через Iх (Т) бана-
банахово пространство числовых функций о на Т, для которых
l|ff|li= 2 I or (t) |< + oof
Примем следующее допущение:
(*) В Е/ существует такое тотальное подмножество F,
что для каждого элемента ore Л (Г) ряд 2 o(t)xt схо-
сходится в слабой топологии o(E,F) и Y\mf(xt) = 0 для
t->oo
каждого f^F (это означает, что lim sup |/(л:*)| = 0,
N t^T\N
где N пробегает упорядоченное по включению направлен-
направленное множество конечных подмножеств в Т).
2.4.1. Теорема. Пусть семейство (^)fSr в Ей тотальное под-
подмножество F в Е/ таковы, что выполняется допущение (*). Тогда
каждый элемент х замкнутой выпуклой оболочки А (соответ-
(соответственно замкнутой выпуклой уравновешенной оболочки В) мно-
множества {xt: t еГ} в Е можно представить в виде ряда
* = Дсг(О**. B.4.1)
где а — функция из Iх (Т), удовлетворяющая условиям а>0
и II а Hi < 1 (соответственно || а || i < 1). Кроме того, каждый
элемент х вида B.4.1), для которого || а Hi -< 1, принадлежит В.
Доказательство. Обозначим через Ло (соответствен-
(соответственно Во) множество тех функций а из Iх(Т), для которых а>0
192 Гл. 2. Теорема Хана —Банаха
и I|a||i-<1 (соответственно llalh^l). Множество Ао выпукло,
а множество Во выпукло и уравновешено. Ниже (теорема
4.1.2) мы увидим, что пространство Iх (J) может быть отождест-
отождествлено с сопряженным к банаховому пространству cq(T), обра-
образованному теми числовыми функциями на Г, которые стремятся
к нулю на бесконечности, и наделенному нормой, равной верх-
верхней грани модуля рассматриваемой функции. Из теоремы
1.11.4B) следует, что каждое из множеств Ло, Во относительно
компактно в топологии a(ll(T)t Со(Т)). Обозначим эту топо-
топологию через J". Очевидно, однако, что оба множества Ао и Во
замкнуты в топологии <?; следовательно, они оба компактны в
этой топологии.
Рассмотрим теперь линейное отображение и пространства
11(Т) в Е, определенное равенством и(о) = 2 o(t)xt. В силу
допущения (*) отображение и непрерывно для топологии J*
в 11(Т) и топологии o(E,F) в Е. Отсюда следует компактность
каждого из множеств и(Ао), и(В0) в топологии a(£, F), а также
их замкнутость в этой топологии (последняя отделима, так как
множество F тотально в Е').
С другой стороны, очевидно, что a(Е, F) -замыкание множе-
множества и(А0) (соответственно и(В0)) содержит А (соответствен-
(соответственно В). Следовательно, и (А 0) id А и u(B0)zdB, Наконец, оче-
очевидно, что и(Во) а Ву т. е. и(В0)=В, чем и завершается наше
доказательство. |
2.5.2. Замечания. A) Нет оснований ожидать, что
и(А0) czA. Ясно лишь, что если обозначить через А\ множество
тех функций ае/!(Г), для которых а>0 и ||a||i = l, то
u(Ai)czA и и(А\) плотно в Л (в топологии a(E,F)). Множе-
Множество А\, вообще говоря, не компактно в топологии <?> так что
мы не можем сделать вывода о замкнутости множества и(А\)
в топологии o(E,F) и, следовательно, о его совпадении с А.
Однако, может быть, удастся доказать равенство и(А{)=Ау
показав, что из условий oG/t0 и x = u(g)^ А следует ||a||i = l
(т. е. aGi4i)? Ответ на этот вопрос зависит главным образом
от того, насколько велико максимальное подмножество G в Е\
для которого ряд, определяющий и (а), сходится в топологии
о(Е, G), или, точнее, насколько велико множество G веществен-
вещественных функций g на Т вида g(t)=g(xt), где g^G. Действи-
Действительно, если ae/lo и х = и(о)^А, то для каждого функцио-
функционала gGF имеет место неравенство
и потому
2.5. Продолжение положительных линейных форм 193
2 o(t)e(t)>inf{e(t): ts=T) B.4.2)
для каждого g о G. Иногда удается показать, что неравенство
B.4.2) влечет за собой неравенство
и что, следовательно, aE/li и xgw^i).
В качестве простого примера рассмотрим случай, когда Г —
множество целых неотрицательных чисел, Е — пространство
непрерывных периодических вещественных функций веществен-
вещественного переменного с периодом 2я, наделенное топологией, опре-
определяемой равномерной нормой
*||x||==sup {\x(s) |: s вещественно},
а xt — функция sh->cos ts. Ясно, что в этом случае можно счи-
считать, что G = £/ и что F совпадает с множеством линейных
форм вида #н-> xfyffyds, где функция /, скажем, непре-
о
рывна и имеет период 2я. В формуле B.4.2) можно взять в ка-
оо
честве g линейную форму х\—>х@), что дает ^o(t)^l. Та-
ким образом, в этом случае можно утверждать, что замкнутая
выпуклая оболочка в Е функций xt состоит в точности из функ-
оо оо
ций вида х(s)= 2 <г@cos/5, для которых a(f)>0n 2tf@ =
= 1.
B) Аналогичный результат имеет место для соответствую-
соответствующих «непрерывных» семейств {xt)t^T, При этом обычно мно-
множество Т является локально компактным пространством, а
отображение t \—> х% непрерывно, причем limx^O (относи-
/->оо
тельно соответствующей отделимой топологии в Е). Простран-
Пространство 11{Т) можно тогда заменить пространством ограниченных
мер Радона на Т (гл. 4). Здесь мы не намерены углубляться
в вопрос, так как аналогичные рассуждения в сходной ситуа-
ситуации появятся при доказательстве теоремы 8.13.1 и 10.1.7.
2.5. Продолжение положительных линейных форм
2.5.1. Выпуклые конусы и частичное упорядочение. Пусть
Е — вещественное векторное пространство. Конусом в про-
пространстве Е называется такое его подмножество /(, что KKczK
194 Гл. 2. Теорема Хана — Банаха
для всякого числа Я > 0. Конус К называется заостренным,
если 0g/(, а заостренный конус — выступающим, если /С не
содержит никакого одномерного векторного подпространства
в Е. Конус /С, который является также выпуклым множеством
в Е, называется выпуклым конусом. Таким образом, подмноже-
подмножество /С в Е является выпуклым конусом тогда и только тогда,
когда Л/Сcz К для всякого Я>0 и /C+ZCcz/C. В этом случае
векторное подпространство в Е, порожденное выпуклым кону-
конусом /С, совпадает с множеством /С— К. Если конус /С заострен,
то /СП (—/С)—наибольшее векторное подпространство в £, со-
содержащееся в /С. Заостренный выпуклый конус /С будет вы-
выступающим тогда и только тогда, когда /СП (—/С)={0}.
Пусть векторное пространстве Е наделено частичным по-
порядком, записываемым «х^Су» (или, что то же, «у^-х»). Если
структуры векторного пространства и частичного порядка со-
согласованы так, что
A) х-*Су влечет x+*z^.y + z (x,y,z<= £),
B) соотношения Я^-0 и х^О влекут Кх^О AgR;xg£),
то пространство Е называется упорядоченным векторным про-
пространством. Предполагается, конечно, что частичный порядок
удовлетворяет обычным аксиомам: х^,х (рефлексивность), из
х^Су и yK-z следует x^Cz (транзитивность), из х^Су и
у^Сх следует х = у.
Если Е — упорядоченное векторное пространство, то оче-
очевидно, что так называемый положительный конус
Р = {х: хее.Еу х>0}
является выступающим заостренным выпуклым конусом в Е.
Обратно, если в Е задан выступающий заостренный выпуклый
конус Р, то можно определить частичный порядок в £, пола-
полагая х^-у, если х — у^Р. Этот частичный порядок превращает
Е в упорядоченное векторное пространство, причем это един-
единственная структура ^упорядоченного векторного пространства
в £, при которой Р совпадает с множеством положительных
(т. е. неотрицательных) элементов.
Естественно поставить вопрос, при каких условиях положи*
тельная1) линейная форма, заданная на векторном подпростран-
подпространстве упорядоченного векторного пространства Е, может быть
продолжена до положительной линейной формы на Е. Мы сна-
сначала получим результат (теорема 2.5.2), применимый в слу-
случае, когда Е — упорядоченное векторное пространство, а М —
«достаточно большое» векторное подпространство в Е. Отсюда
1) Напомним, что форма / называется положительной, если f(x)^O при
О. — Прим. nepeet
2.5. Продолжение положительных линейных форм 195
легко перейти к аналогичному результату (теорема 2.5.3), при-
принадлежащему М. Г. Крейну. Теорема Крейна 2.5.3 применима
к случаю, когда упорядоченное векторное пространство Е есть
также топологическое векторное пространство, а множество
Р[\М имеет внутреннюю точку.
2.5.2. Теорема. Пусть Е — упорядоченное векторное про-
пространство и М — векторное подпространство в Е, обладающее
тем свойством, что каждому элементу х е Е соответствует по
меньшей мере один такой элемент т^М, что х^Спг. Если f —
положительная линейная форма на М (относительно индуциро-
индуцированной структуры), то f можно продолжить до положительной
линейной формы f* на Е.
Доказательство. Определим функцию р на Е равен-
равенством
уе=М, у>х).
Из свойств множества М следует, что каждому х^Е соответ-
соответствуют такие элементы m, гп'^М, что т'^х^Ст. Отсюда вы-
вытекает конечность функции р; действительно, справедливо не-
неравенство
f(m')<Cp(x)<f(m).
Так как Р — выпуклый конус; то р служит калибровочной
функцией на Е (§ 1.6). Если ^еМ, то очевидно, что р(х) ^
^Cf(x). С другой стороны, если х, у е М и #> х, то f(y) ^f(x)
(так как форма / положительна на М)\ поэтому p(x)>f(jc)
для j^gM. Итак, если л:еМ, то имеет место равенство f(x)='
= р{х).
В силу теоремы 1.7.1A) на Е существует линейная форма
f*y являющаяся продолжением формы / и удовлетворяющая
условию f* (х) -< р (х) для х&Е. Если х>0, то f*(—х) -<
^p(—x)=ini{f{y): ye^M, у + х> 0}</@) =0. Таким образом,
f*(x)^0, и, следовательно, f* — положительная линейная
форма на Е. |
2.5.3. Теорема (М. Г. Крейн). Предположим, что Е —упо-
—упорядоченное векторное пространство с положительным конусом Р
и одновременно топологическое векторное пространство. Пусть
М — такое векторное подпространство в Е, что пересечение
МНР обладает по крайней мере одной внутренней для Р точ-
точкой х0. Тогда каждую положительную (относительно индуциро^
ванной структуры) линейную форму f на М можно продолжить
до непрерывной положительной линейной формы f* на Е.
Доказательство. Пусть U — такая уравновешенная
окрестность нуля в Е, xo+UdPt Если х^Е и число Я>0
196 Гл. 2. Теорема Хана —Банаха
таково, что x<=XU, то — г-х s U и, следовательно, хо~-^х& Р,
т. е. #<l?ao. Таким образом, условия теоремы 2.5.2 выполнены.
Из рассуждений, использованных при ее доказательстве, сле-
следует, что p(x)^Ckf(xo)y если x^W и X > 0. В силу теоре-
теоремы 2.5.2 форма / может быть продолжена до такой положи-
положительной линейной формы /* на Е, что /* (х) ^С р (х) для всех
х^Е. Значит, f*(x)^CXf(x0) при x^W и А, > 0. Из уравно-
уравновешенности окрестности U вытекает неравенство |/*(*)|^
^Ckf(xo) для x^U. Следовательно, форма /• непрерывна
на Е. |
2.5.4. Как уже говорилось в п. 2.2.5, можно искать аналогич-
аналогичные теоремы продолжения, в которых на заданные линейные
формы накладываются дополнительные ограничения и те же
требования предъявляются к продолжениям. Мы еще вернемся
к этому вопросу в § 3.3.
2,6. Некоторые результаты с приложениями к теории игр
Как будет показано ниже в этом параграфе, некоторые
основные принципы теории игр могут быть сформулированы в
терминах компактных выпуклых множеств и выпуклых конусов
в вещественных локально выпуклых пространствах. Примем
пока на веру, что приложения к теории игр действительно воз-
возможны, и займемся предварительно некоторыми абстрактными
результатами, в изложении которых мы будем следовать Б о-
ненблусту и Карлину [1]. Основополагающий принцип
теории игр в случае конечных дискретных игр, соответствую-
соответствующем конечномерному векторному пространству, может быть
сформулирован следующим образом. Пусть задана конечная
матрица (а^) с вещественными элементами; допустим, что
каждому набору чисел (qj)9 qt^O и 2<7/=1» соответствует
такой набор чисел (/?,), ft>0 и 2р*= 1» что
22
Тогда существует набор (pi) такого же типа, для которого не-
неравенство
справедливо для каждого набора (ft) указанного вида,
2.6. Некоторые результаты с приложениями к теории игр 197
Обобщение, которое мы имеем в виду, сводится к замене вы-
выражения
билинейной формой довольно общего вида, определенной на
произведении двух локально выпуклых пространств. Однако в
начале удобнее работать с одним таким пространством и его
топологическим сопряженным.
Всюду в этом разделе, где не указано противное, под Е и
F понимаются вещественные отделимые локально выпуклые про-
пространства с топологическими- сопряженными Е' и Р' соответ-
соответственно. Для обозначения значения линейной формы х' е Е' на
элементе х е Е будет удобно пользоваться симметричным сим-
символом (а:, л;').
Наша первая задача состоит в следующем. Допустим, что за-
заданы множество К в Е и выпуклый конус Г в Е\ Мы всегда бу-
будем предполагать, что конус Г слабо замкнут (т. е. замкнут в
топологии о(Е\ £)), хотя можно с таким же успехом заменить
эту топологию в Е' любой локально выпуклой топологией, кото-
которая согласуется с двойственностью между Е и Ег (т. е. относи-
относительно которой топологическое сопряженное к Е' совпадает с Е\
см. § 8.3). Будем считать, что выполнено следующее
Предположение. Каждому /еГ соответствует такое х ^К
(априори зависящее от х'), что (х, х') ^ 0.
Заключение, которое мы хотим вывести, таково.
Заключение. Существует такое х0 е /С, что (лг0, х') > 0 для
всех /gT.
Сначала мы покажем, что Заключение верно, если К — ком-
компактное выпуклое множество, затем покажем, что эти условия
на К могут быть видоизменены. Первый результат доказывается
сравнительно просто и уже охватывает некоторые приложения
к теории игр.
2.6.1. Теорема. Пусть К— выпуклое компактное подмноже-
подмножество в Е и Г — слабо замкнутый выпуклый конус в Е'. Если вы-
выполняется Предположение, то верно Заключение.
Доказательство. Рассмотрим множество
А={х<=Е: (х, *')>() для всех /еГ}
и покажем, что пересечение АПК не пусто. Очевидно, что множе-
множество А является заостренным выпуклым замкнутым конусом в Ё.
Допустим, что множество АПК пусто, тогда из следствия 2.1.3
вытекает существование такого функционала х'0&Е' и такого
вещественного числа а, что (х, х'0)>а при х^А я (х> х'0)<а
при х е К. Так как множество А содержит нуль, то из первого
неравенства следует, что сс<9. Поскольку А — конус, первое
198 Гл. 2. Теорема Хана —Банаха
неравенство влечет за собой также неравенство (х, х^)^О для
х^А. Докажем теперь, что jcjsr. Если это не так, то из след-
следствия 2.1.4 (примененного к Е' вместо Е) вытекает существова-
существование такого элемента с^Е, что (с, х^< inf {(с, х') .' х' е Г}. Так
как Г — конус, отсюда следует, что (с, х') ^ 0 для /еГ, т. е.
с^А и (с, Xq)<0, а это противоречит выбору функционала x'Qt
Следовательно, ^gF, Но тогда неравенство (х, x^<a<0
для х^К противоречит Предположению. Теорема доказана. |
Приведем сразу одну модификацию теоремы 2.6.1.
2.6.2. Теорема. Пусть подмножество К в Е удовлетворяет сле-
следующим условиям:
A) К компактно;
B) множество Q== (J %К выпукло;
C) не существует сегмента, соединяющего две точки из К
и содержащего нуль.
Пусть Г — слабо замкнутый выпуклый конус в Е'. Если вы-
выполняется наше Предположение, то справедливо и Заключение.
Доказательство теоремы 2.6.2 опирается на три леммы.
2.6.3. Лемма. Пусть К — компактное подмножество в Е, не
содержащее точки 0. Тогда множество Q = (J KK замкнуто.
К>0
(Если пространство Е неотделимо, то заключение леммы
Останется справедливым, если заменить условие 0 ф. К условием
{О}П/С=0.)
Доказательство. Если точка х из Е принадлежит замы-
замыканию множества Q, то существуют такие сети (Хг-) и (л:г) с оди-
одинаковым множеством индексов, что А,г-^0, ^е/(и НтЯ^ = х.
Так как множество К компактно, то найдется такая подсеть
{Уд), что предел у = \\шу^ существует и принадлежит К. Пусть
(\ij) — соответствующая подсеть сети (Х{). Тогда lim|i/#/= #.
Но уФО и, следовательно, существует такая непрерывная по-
полунорма р на Е, что р(у)Ф0 (если Е не отделимо, то это сле-
следует из тогот что ^{0}). Так как р{У])->р{у) и ^р(^) =
^РСм.^-^рМ, то существует, и притом конечный, предел
H = limjx/. Очевидно, ц,>0. Таким образом, \kj->\i и yj->y;
следовательно, tf-limOiy*//) — ^, откуда вытекает, что xeQ,
т. е. что множество Q замкнуто. 1
Замечание. Условие, что нуль не принадлежит множеству
Kt не может быть опущено в лемме 2.6.3. Действительно, пусть,
2.6. Некоторые результаты с приложениями к теории игр 199
например, £=R2, а множество К состоит из точек 0=@,0) и
хп=\п"\ (п + 2) 2)(п=1, 2, ..•)• Точка @, 1) не принадле-
принадлежит Q, тогда как точки ni/2xn принадлежат Q и образуют после-
последовательность, сходящуюся к точке @, 1). Следовательно, мно-
множество Q не замкнуто.
2.6.4. Лемма. Пусть множество К удовлетворяет условиям
A), B) и C) теоремы 2.6.2. Тогда существуют такое число
б > О и такой элемент х'о е Е\ что (х, x'oj ^ 6 для всех х е/0
Доказательство. В силу последней леммы множество Q
замкнуто, а по условию B) оно выпукло. Согласно C), если
х е /С, то элемент —х не принадлежит Q. Действительно, в про-
противном случае мы имели бы х=—Ху (у <= /С, Х> 0), откуда следо-
следовало бы, что х + Ху*=0, так что точка 0 = —т ^ + т~гт У ПРИ~
надлежала бы отрезку, соединяющему точки х и у из /С, что
противоречит C). Из следствия 2.1.3 вытекает существование
для каждого Хо^К такого функционала х'^Е' и такого веще-
вещественного числа а, что
{-х0, х')<а и (у, х')>а для #<=Q.
Полагая у = 0, получаем а<0 и, значит, (#0> х')>0. Так как
множество Q является конусом, то соотношение (у, х')>а
(y^Q) влечет неравенство (у, х')^0 для всех у^К- Теперь,
пользуясь компактностью множества /С, легко показать возмож-
возможность выбора таких элементов x'v ..., хгп из Е\ чтобы нера-
п
венство 2 (х> х'.)>0 было справедливо для всех х е /С. Пола-
/г
гая xj = 2 *J и снова пользуясь компактностью множества К,
мы видим, что нижняя грань множества чисел (л;, х'о^, где х
пробегает К, строго положительна. I
2.6.5. Лемма. Пусть множество К удовлетворяет условиям
A) — C) теоремы 2.6.2. Тогда в Е существует такое выпуклое
компактное множество Ко, что элемент хфО принадлежит Q
тогда и только тогда, когда Кх е /Со при некоторой % > 0.
Доказательство. Выберем функционал х'о и число б>0
так, чтобы (х, *о)^6 при х^К (по лемме 2.6.4 это можно
сделать). Ясно, что (х, х'0)>0, если xeQ и х ф 0. Пусть
/Со —пересечение множества Q с гиперплоскостью (x,xfy=*l.
Очевидно, что множество Ко замкнуто и выпукло. Если х е Q
и а: ^= 0, то ((#, Яо))* е Д^; если же Кх s /Co для некоторого
200 Гл. 2. Теорема Хана — Банаха
Л>6, то Xx^Q и, следовательно, xeQ. Остается только до-
доказать компактность множества Ко* Пусть х е /Со; тогда х = Куу
где Л>0 и у^К- Так как (#, ^)>б и (х, Хо)^1' то 1
Таким образом, множество Ко содержится в множестве (J
где ^i = 6. Отображение /: R X К~*Е, определенное правилом
{К f/)*—^^, непрерывно, поэтому оно переводит компактные
множества в компактные. Множество Ко содержится в образе
(относительно отображения /) компактного множества [0, \i] X К]
поэтому оно относительно компактно, а так как Ко замкнуто,
то и компактно. I
Доказательство теоремы 2.6.2. Теперь уже легко до-
доказать теорему 2.6.2. Если заменить множество К на множество
/Со, построенное в лемме 2.6.5, то выполняются условия теоремы
2.6.1. Следовательно, в Ко имеется такой элемент у0, что
(г/о, х')^>0 при лг^Г. В силу леммы 2.6.5 существует такое число
Я>0, что элемент хо = Хуо^К. Тогда и (лг0, х') >0 при лг^Г, что
и требовалось#доказать. |
Опираясь на теоремы 2.6.1 и 2.6.2, можно получить непосред-
непосредственное обобщение теоремы Билля из теории игр.
2.6.6. Теорема. Пусть Е и F — вещественные отделимые ло-
локально выпуклые пространства, L и М — множества в Е' и F'
соответственно, и пусть отображение и: L-+F обладает тем
свойством, что каждому у'^М соответствует некоторый элемент.
x'&lL, удовлетворяющий неравенству
<«(*')>/> >о.
Предположим также, что множество K=u(L) либо выпукло и
компактно, либо удовлетворяет условиям A), B) и C) тео-
теоремы 2.6.2 (где Е всюду заменено на F), и что множество
(J КМ выпукло и слабо замкнуто в F'. Тогда существует такой
элемент x'Q e L, что
(и(х'о), у')>0
для всех уг ^ М,
Доказательство следует из теоремы 2.6.1 или теоремы
2.6.2, если взять F в качестве £, K=u(L) и Г= (J хм. I
1
2.6J. Приложения к теории игр. Сейчас наша задача состоит
в том, чтобы задним числом мотивировать рассмотрение преды-
предыдущих результатов этого параграфа, показав их связь с теорией
игр. Сначала несколько слов по поводу этой теории (подробно
2.6. Некоторые результаты с приложениями к теории игр 201
с ней можно познакомиться по книгам фон Неймана и Мор-
генштерна [1] и Мак-Кинси []]).
Многие задачи теории игр можно сформулировать примерно
так. Рассматриваются два игрока, назовем их Л и В. «Игра»
(или отдельный «ход» в этой игре) сводится к выбору игроками
А и В соответственно элементов 5 и t из наперед заданных мно-
множеств S и Т. По «правилам игры» к концу игры, заключающе-
заключающемуся в выборе пары (s, /), игрок В выплачивает игроку А сумму
P(s, t), где Р — заранее заданная функция на SxT. Функция Р
может принимать и отрицательные значения (этим принимается
в расчет случай, когда игрок А «в проигрыше»). Здесь мы рас-
рассматриваем только игры «с нулевой суммой», в которых исклю-
исключены посторонние источники обогащения: на каждой стадии
один игрок выигрывает ровно столько, сколько другой проиг-
проигрывает.
Естественно возникает вопрос: всегда ли у игрока существует
«лучший» или «наиболее выгодный» выбор? Решая этот вопрос,
примем, например, сторону игрока А. Предположим на время,
что множества S и Т конечны, и введем следующие два числа:
^ (, t),
s t
W* = min max P(s, t\
t s
максимин и минимакс функции Р (определенной на SxT). До*
пустим, что элементы s е S и to^T таковы, что
E, t0).
s
Несложные рассуждения приводят к следующим выводам.
A) Если игрок А выберет s0, то он выиграет не менее, чем
W#, независимо от выбора игрока В. B) Если игрок В выберет
to, то игрок А ни в коем случае не выиграет больше, чем W*f и
при соответствующем выборе А может выиграть W*. Допуская,
что игрок А действительно выбрал s0, а игрок В выбрал tOi мы
получаем, что W# <C W*. (Разумеется, к тому же самому можно
прийти совершенно независимо от этой интерпретации. В самом
деле, minP(s', t')^P(s', t), следовательно, тем более min P(s\ П<
v v
^maxP(s, t); левая часть этого неравенства от / не зависит,
поэтому
minP(s', Г) < min max P (s, t)=W*;
t1 t s
202 Гл. 2. Теорема Хана — Банаха
в последнем неравенстве правая часть не зависит от 5, так что
W = maxminP(s', t')^W\)
Может оказаться, что W*=*W* = W. Тогда игрок Л, выбирая
So, может выиграть по меньшей мере W, в то время как игрок 5,
играя надлежащим образом (выбирая ^о), может помешать
игроку А выиграть более, чем W. Поэтому в очевидном смысле
50 представляет собой оптимальную стратегию для игрока А.
Аналогично t0 представляет оптимальную стратегию для игро-
игрока Д. Точку (so, U) можно назвать стратегической ссдловой точ-
точкой рассматриваемой игры. Мы видим, что точка (so, to) обла-
обладает следующими свойствами:
0, t)9
, tQ).
s
Таким образом, W^P{sOi t0) и W^P(sOi t0), т.е.
W = P(sOi t0)
P(s, to)^P(sOi g<P(s0, t). B.6.1)
Обратно, если выполняется соотношение B.6.1), то
maxP(s, to)^P(so, /0)<niinP(% t),
t
)
s t
поэтому
( )^{Oi )^(Oi t0)
s t t
И •
W* = minmaxP(s, /)<maxP(s, to)^P(so, to\
m t s s
т. e. №* < Я (so, foX №*. Так как всегда W**CW*, отсюда сле-
следует, что W* = W#sP(so, to). Другими словами, соотношение
B.6.1) характеризует (s0, fo) как стратегическую седловую, точ-
точку и, следовательно, s0 (соответственно to) как оптимальную
стратегию для игрока А (соответственно В).
Если мы теперь рассмотрим случай, когда множества S и Т
не являются оба конечными, то возникает отдельный предвари-
предварительный вопрос: являются ли величины
supinf P(s, t),
s t
inf supP(s, 0»
t s
2.6. Некоторые результаты с приложениями к теории игр 203
играющие роль W* и W* соответственно, конечными, и если это*
имеет место, то достигаются ли они?
Весьма важно, что даже в простейшем случае, когда множе-
множества S и Т конечны, числа W* и W*, вообще говоря, не совпа-
совпадают. Например, если 5 = Г={1,2} и РA, 1) =РB, 2) = 1,
РA, 2) =ЯB, 1) = — 1, то, очевидно, №* = —1 и W*= + l. При
этом не существует оптимальной стратегии, и в действительности
это скорее правило, чем исключение.
В связи с этим естественно возникает вопрос: нельзя ли в тех
случаях, когда обычных оптимальных стратегий не существует,
найти все же стратегии, рассчитанные на длинную последова-
последовательность игр и оптимальные в некотором «предельном» смысле?
Математически это можно интерпретировать заменой пары ин-
индивидуального выбора (s9t) парой (а, т), в которой о и т яв-
являются вероятностными мерами на множествах S и Т соответ-
соответственно. При этом платежная функция P(s,t) заменяется вели-
величиной
В (о, t)=JJpE, t)de(s)dx(ty).
S Т
Большинство интересных задач охватывается случаем, когда S и
Т — локально компактные пространства, г о а т— положитель-
положительные меры Радона на 5 и Г соответственно с общими массами,
равными единице. (Все эти понятия подробно рассматриваются
в гл. 4.) При этом ищутся оптимальные смешанные стратегии
0о и то, обладающие тем свойством, что
В (а, т0) < В (а0, т0) < В (а0, т) B.6.2)
(это условие совершенно аналогично условию B.6.1)). Основ-
Основная теорема теории игр утверждает, что при довольно широких
предположениях относительно множеств S, Т и функции P(s,t)
такие оптимальные смешанные стратегии оо и то существуют.
Мы докажем это, опираясь на теорему 2.6.6 и пользуясь неко-
некоторыми простыми свойствами мер Радона.
Пусть множества S и Т — компактные пространства (на прак-
практике это обычно компактные отрезки вещественной оси), а
P(s,t) — непрерывная функция на SxT. Из результатов гл. 4
вытекает, что интеграл, определяющий функцию В (о, т), сущест-
существует, конечен и может быть вычислен как повторный интеграл
с любым порядком интегрирования. В теореме 2.6.6 положим
E = C(S) и F=*C(T), где C(S) и С(Т)— банаховы пространства
1) То есть математическим ожиданием случайной величины Рш — Примк
ред.
204 Гл. 2. Теорема Хана — Банаха
вещественных непрерывных функций (с равномерными нормами)
на S и Т соответственно. Как будет показано в'§ 4.10, простран-
пространство Е' (соотв. /') может быть отождествлено с пространством
вещественных мер Радона о (соотв. т) на S (соотв. на Т). При
таком отождествлении мере о (соотв. т) сопоставляется линей-
линейная форма хь-> J х(s)da(s) (соотв. у*-> ) y(t)dx(t)) на иро-
s т
странстве C(S) (соотв. С(Т)). В качестве L (соотв. М) в теоре-
теореме 2.6.6 возьмем множество положительных мер Радона а
(соотв. т) на S (соотв. Т) с общей массой o(S) (соотв. т(Г)),
равной единице. Согласно теореме 4.10.3, каждое из множеств L,
М слабо компактно. Почти очевидно, что множество Г= \J ХМ
всех положительных мер Радона на Т является слабо замкну-
замкнутым выпуклым конусом в F\ Наконец, в качестве отображения
и, фигурирующего в теореме 2.6.6, возьмем отображение, пере-
переводящее меру о в функцию
>(s, t)da{s\
которая, как легко видеть, является элементом пространства F
(т. е. непрерывной вещественной функцией на Т).
Для того чтобы воспользоваться теоремой 2.6.6, нужно про-
проверить компактность в пространстве F = C(T) множества К=
= u(L). Если функция P(sJ) удовлетворяет на 5x7" неравен-
неравенству |РE,/)|<т, то ясно, что \o(t)\^Cm при (бГ и о е L.
Поэтому функции, принадлежащие множеству /С, равномерно
ограничены. Следующий шаг состоит в доказательстве их равно-
равностепенной непрерывности. Из непрерывности функции Р на про-
произведении SxT и компактности множеств S и Т легко следует,
что для заданных е > 0 и точки to^T существует такая окрест-
окрестность V точки tQ, что неравенство 1^E, t) —Р(s, t0) \^Севыпол-
\^Севыполняется для всех sgSh/gK Тогда неравенство \o(t)— 6(t0) |-<
<Се имеет место при всех /еУи о eL, что и доказывает равно-
равностепенную непрерывность функций из К в точке /о- В силу тео-
теоремы Асколи множество К относительно компактно в С (Г), по-
поэтому достаточно убедиться в его замкнутости. Но при фиксиро-
фиксированном ^еГ отображение a*->d{t), очевидно, непрерывно на L
(в слабой топологии). Так как L слабо компактно, то-множество
К = и(Ь) компактно в топологии простой сходимости в Г и, сле-
следовательно, замкнуто в этой топологии (ибо она отделима), а
значит, и подавно замкнуто в более сильной топологии равно-
равномерной сходимости на Т.
2.6. Некоторые результаты с приложениями к теории игр 205
В качестве последнего подготовительного шага покажем, что
максимин
f5(a, т)
и минимакс
W* = inf sup В (а, т)
т а
т а
конечны и достигаются.
Так как множества L и М слабо компактны, то таким же
будет и множество LxM в топологии произведения. Поэтому
достаточно доказать, что функция В (о, т) непрерывна на LxM
относительно топологии произведения. Действительно, тогда
функция ШВ(о, т) полунепрерывна сверху (и конечна) на t и
т
потому достигает конечного максимума W* на L. Аналогично
функция sup В (а, т) полунепрерывна снизу на М и достигает КО-
нечного минимума W*. Что касается непрерывности функции
В (о, т) на LxM, то она следует из того, что непрерывная на
SxT функция Р является равномерным пределом конечных
сумм вида
Po(s, t)=%ui(s)vi(t),
i = l
где и{ и Vi берутся из пространства C(S) и С(Т) соответственно.
(Если S и Т — компактные интервалы на вещественной прямой,
то это следует из теоремы Вейерштрасса о полиномиальной ап-
аппроксимации функций двух вещественных переменных. В общем
случае — из принадлежащего Стоуну обобщения теоремы Вейер-
Вейерштрасса, приведенного в п. 4.10.5.) Если функция Ро выбрана
так, что |Я — Л)|^е всюду на SxT, то для всех (a, t)<=LxM
справедливо неравенство, 5(а, т)— j J P^do-dx <e. С другой
5 Т
стороны, функция'
п
J J Ро do dx = 2j J Щ do • J vtdx
s т i-is т
непрерывна в точке (а, т) в топологии произведения. Следова-
Следовательно, и функция В (о, т) как равномерный предел непрерывных
функций непрерывна.
Применим теперь теорему 2.6.6. Так как билинейная форма
В (а, тН<и(а)э т)
приводит в двойственность пространства C(T)—F и F', то
сформулированное в § 2.6 Предположение означает в точности
206 Гл. 2. Теорема Хана — Банаха
то, что W* > 0, а приведенное там же Заключение означает
ровно то, что №*>0. Таким образом, для любой заданной не-
непрерывной функции Риз F>0 следует, что W* > 0. Посколь-
Поскольку здесь можно заменить функцию Р на функцию Р — k, где k —
вещественная постоянная (при этом функция В (а, т) заменяется
функцией В (о, т) — k), то те же самые рассуждения показывают,
что W* ^ k влечет W* > k. Отсюда непосредственно вытекает,
что Wx^-W* и, следовательно, W# = W*.
Итак, мы доказали, что для всякой игры, в которой множе-
множества S и Т компактны и платежная функция Р непрерывна, оп-
оптимальные смешанные стратегии существуют. Это фундамен-
фундаментальная теорема теорий игр. Подробное изложение теории
можно найти в уже упоминавшихся книгах фон Неймана и Мор-
генштерна и Мак-Кинси.
2.6.9. Замечания. Теорема о минимаксе, рассмотренная
в предыдущем пункте, была сформулирована Фаном [1] в еще
более общих терминах. Фан рассматривает случай, когда Е и
F— отделимые локально выпуклые пространства, Н и К — вы-
выпуклые компактные множества в Е и F соответственно, а /—■
вещественная непрерывная функция на произведении НхК,
Предполагается, что для каждой точки (хо, уо)^- НХК множе-
множества
ixeH: fix, #о)= sup fix', yo)\
[ *'€=Я j
И
е/0 fix*. */)= inf fixn,
выпуклы. Утверждается, что в этом случае справедливо ра-
равенство
sup inf /(*, у)= inf sup f(x, у).
Доказательство Фана опирается на одно обобщение теоремы
Какутани о неподвижной точке (п. 3.6.6).
УПРАЖНЕНИЯ
2.1. Пусть f=N —множество натуральных чисел. Рассмотрим простран-
пространство Co=co(N). Для данного комплексного числа q с вещественной частью
Re q>0 обозначим через xq элемент из с0, определенный равенством xq (t) =е~^К
Обозначим далее для всякого neN через уп элемент из с0, определенный
соотношением упУ)=№-1е-*. Показать, что каждое из семейств (xq)t (yn)
фундаментально в с0 (т. е. множество конечных линейных комбинаций эле*
ментов каждого из этих семейств плотно в Со).
Семейства (хя) и (уп) принадлежат также пространствам lp(N)t
1^Р< оо. Выяснить, являются ли они фундаментальными в этих лростран*
стЕах.
Упражнения 207
2.2. Пусть Е— векторное пространство, F — локально выпуклое простран-
пространство и L = L(E,F)—векторное пространство всех линейных отображений
пространства Е в F. Рассмотрим в L две топологии: A) топологию t\, имею-
имеющую базой окрестностей нуля семейство множеств вида
W{Ay V) = {u<=L: u(A)cz V},
где Л — произвольное конечное подмножество в Е, а V — окрестность нуля
в F; B) топологию ^ с базой окрестностей нуля, образованной множествами
W(A,U), где Л — снова конечное подмножество в Е, а (/ — слабая окрест-
окрестность нуля в F. Показать, что всякая линейная форма / на L, непрерывная
в топологии /i, непрерывна также и в топологии t2.
2.3. Пусть Е — векторное пространство, F — локально выпуклое простран-
пространство и / — линейная форма на L(E,F), непрерывная в топологии простой
сходимости. Показать, что найдутся такие конечные семейства (х.)
в Е и (ydi<i<n в F\ что
/(И)
для всех и ^L(E,F). Вывести отсюда, что форма / непрерывна в топологии
простой сходимости, если пространство F наделено слабой топологией
o(F,Ff).
2.4. Пусть Е — пространство целых функций одного комплексного пере-
переменного, наделенное топологией компактной сходимости (которая задается
семейством полунорм
Pn(f)= SUP
\t\<n
п=\, 2, ...). Для любой функции f^E и любого комплексного числа §
определим функцию f*^E равенством
/б @-/F0-
Показать, что если F — непрерывная линейная форма на Е и / gE, to
F0(g) =F(fz)—целая функция, порядок которой не превосходит порядка
функции /, и
Вывести отсюда, что система функций f| фундаментальна в Е, если
/(п)@) Ф О для я=0, 1, ... .
2.5. Пусть Е — пространство всех непрерывных комплексных функций
одного вещественного переменного, имеющих период 2я, с нормой ||/|| =
= sup|/@|. Показать, что Е — банахово пространство.
Для каждого вещественного числа а определим а-сдвчг функции
/е Е равенством
Пусть F — непрерывная линейная форма на Е. Положим F0(a)=F(fa), где
f — фиксированная функция из Е. Показать, что /г-й коэффициент Фурье
я
?oW = ^ J F0(a)e"inada
-я
функции Fo равен f{n) -F(eint).
208 Гл. 2. Теорема Хана — Банаха
Обозначим через Г/ замкнутое векторное подпространство в Е, порож-
порожденное всеми сдвигами/а функции /. Доказать, что eint^Tf тогда и только
тогда, когда f(n) Ф 0. Предполагая, что система функций eint фундамен-
фундаментальна в £, показать, что Tf=E тогда и только тогда, когда !(п)Ф 0 для
п=0, ±1, ±2, ... .
[Эта задача является аналогом для рядов Фурье теоремы Винера об
интегралах Фурье (см. Винер [1, стр. 101], Люмис [1, стр. 187—188], Р у-
дин [9, гл. 7}). См. также упр. 4.16 и 10.13. Со сдвигами связаны различные
задачи аппроксимации (см., например, Эдварде [1, 2, 12], Эгнью [1, 2]
и Л. Шварц [7,9, 11])\
2.6. Пусть Т — произвольное множество и La M — такие два векторных
подпространства в RT, что для каждого элемента х из М найдутся такие
элементы х' и х" из L, что х'^х^х". Показать, что всякая положительная
линейная форма / на L допускает положительное линейное продолжение
на М.
[Указание. Определить функцию р на М равенством
p(x)~ini{f(y):
и затем воспользоваться теоремой Хана — Банаха.]
2.7. Пусть Е — векторное пространство, наделенное топологией, в кото-
которой отображение х i—>Хх непрерывно в точке х=0 для всякого числа К.
Показать, что для существования на Е непрерывной в нуле линейной формы
/ Ф 0 необходимо и достаточно, чтобы в Е существовала выпуклая погло-
поглощающая окрестность нуля U Ф Е.
[Указание. Если линейная форма f существует, то множество
U={x & Е :\f(x)\<\} обладает указанными свойствами. Обратно, предположим
существование окрестности U. Пусть р — ее функционал Минковского; р —•
субаддитивная положительно однородная функция на Е, для которой
p(U)^l и р ф 0. Выберем такой элементно, что р(хо) = \. На подпростран-
подпространстве, порожденном элементом х0, определим линейную форму f0 равенством
foCkxo)=X. Применяя теорему Хана — Банаха, продолжим форму f0 до такой
линейной формы / на Е, что f(xo)=fo(xQ) = \ и f(x)^p(x). Форма / непре-
непрерывна в точке 0, так как f(x)^a при x^aU, а множество ail является
окрестностью нуля при каждом а>0. Так как отображение х I—>—х непре-
непрерывно в точке 0, то множество —aU также является окрестностью нуля.
Поэтому |/(*Жа при x&(aU) П (—£/)]
2.8. Пусть Е — вещественное предгильбертово пространство, К — полное
выпуклое множество в Е и х0 — точка из Е\К. Выберем точку а^К, нахо-
находящуюся на наименьшем расстоянии от х0, и положим
у lUo-air
Показать, что
(х\у)< (хо \у), х& К.
(Ср. со следствием 2.1.4.)
2.9. Пусть Е — конечномерное вещественное отделимое топологическое
векторное пространство, К — выпуклое множество в Е и х0 — граничная
точка множества К. Показать, что существует проходящая через х0 гипер-
гиперплоскость, являющаяся опорной для К.
(В вещественном векторном пространстве Е гиперплоскость Н назы-
называется опорной для множества А аЕ, если Н пересекается с Л и Л лежит
по одну сторону от Н.)
Упражнения 209
Замечание. Если пространство Е бесконечномерно, то приведенное
утверждение, вообще говоря, неверно, даже если К компактно, а хо — край-
крайняя точка множества К (см. Б у р б а к и [7, стр. 100]). _
[Указание. Рассуждения можно проводить для множества К (а не
К), т. е. предполагать, что К замкнуто. Рассмотреть последовательность
хп^Е\К, хп->х0. Применить упр. 2.8, пользуясь компактностью замкну-
замкнутого ограниченного множества в сопряженном пространстве.]
2.10. Пусть К — выпуклое множество в вещественном векторном про-
пространстве Е. Точка *е К называется окруженной точкой множества К (отно-
(относительно £), если для каждой точки у е Е существует такое число е>0,
что х+ау^ К при |а| ^ е. Это означает, что множество К — х поглощающе.
Показать, что если множество К обладает окруженными точками и все
они лежат по одну сторону гиперплоскости Я в Е, то само множество К
лежит по ту же сторону от Н.
2.11. Пусть К — выпуклое множество в вещественном векторном про-
пространстве Е. Обозначим через Кг множество всех окруженных точек мно-
множества К. Показать, что все точки множества Кн являются его окружен-
окруженными точками.
2.12. Пусть Е — вещественное векторное пространство и К— непустое вы-
выпуклое множество, все точки которого являются его окруженными точками.
Пусть далее V—векторное подпространство в Еу не пересекающее множе-
множества К. Показать, что в Е существует гиперплоскость, содержащая V и не
пересекающая К. (Ср. с теоремой 2.1.1.)
2.13. Пусть Е — вещественное векторное пространство, Ег — векторное
подпространство в Е, Я' — гиперплоскость в Е' и К -•выпуклое множество
в Е, такое, что Е' содержит по меньшей мере одну окруженную точку мно-
множества К относительно Е. Показать, что если К П Ег лежит по одну сторону
от Я', то существует такая гиперплоскость Яв£, что Н'=Н Г) Е' и К лежит
по одну сторону от Я.
[Указание. Пусть К% — множество окруженных точек множества К
относительно Е. Пользуясь упр. 2.11, показать, что Кг не пересекает #'. При-
Применить упр. 2.12, заменив К на Кг и V на Я'.]
2.14. Пусть Е — вещественное векторное пространство, Е — векторное
подпространство в Е и Я' — гиперплоскость в Е'. Пусть К — выпуклое мно-
множество в Е, причем множество К П Е' лежит по одну сторону от И''. Пред-
Предположим, что для каждого у е Е существует такой элемент х е Е\ что
х+ау^К для всех достаточно малых |а|. Показать, что существует такая
гиперплоскость Я в £, что Н'—Н{\ЕГ и множество К лежит по одну сто-
сторону от Я (Диксмье [3]). Это утверждение обобщает результат упр. 2.13.
[Указание. Рассмотреть множество всех пар (£*,Я*), где Е* — век-
векторное подпространство в £, Я* — гиперплоскость в Е* и К()Е* лежит по
одну сторону от Я*, причем E*zdE' и Я* П Е'=Н'. В этом множестве ввести
частичный порядок, считая, что (Еи #i)^ (£2, Я2), если EiCzE2 и H\<zlH2.
Проверить, что это частично упорядоченное множество индуктивно упорядо-
упорядочено. По лемме Цорна существует максимальный элемент (£о, Яо). Доста-
Достаточно показать, что Е0 = Е. Допустив противное, выбрать EQ таким образом,
чтобы dim(^Q^£0) = l, и положить Ко = Е'оП К. Переход к факторпространству
по модулю Яо сводит задачу к двумерной. Опираясь на результат упр. 2.9,
доказать существование такой гиперплоскости HfQ в Eq, что пара (£q, Яд)
«больше», чем пара (£о> Яо). Это будет противоречить максимальности по-,
следней]
2.15. Пусть Т — произвольное множество и G — полугруппа отображе-
отображений 11—> и • t множества Т в себя. Предположим, что существует левоцн-
210 Гл. 2. Теорема Хана —Банаха
вариантное среднее \х на G, т. е. положительная линейная форма на про-
пространстве всех вещественных ограниченных функций на G, инвариантная от-
относительно левых сдвигов и такая, что |i(l) = l.
Обозначим через Е векторное пространство всех ограниченных веще-
вещественных функций на Т. Для f^E и wgG положим fu = f ° и. Рассмотрим про-
произвольную функцию ge£, удовлетворяющую условию g>0. Обозначим через
Е' векторное подпространство в Е, порожденное функциями вида gUi где и
пробегает G, и через Е" векторное подпространство в Е, порожденное поло-
положительными функциями, мажорируемыми элементами из Е' (так что
Е'аЕ"<z:E). Допустим, что на Ef существует положительная линейная форма
ф ф о, инвариантная относительно G. Показать, что на Е" существует по-
положительная линейная форма Ф, инвариантная относительно G и такая, что
Ф (g) = 1 (Д и к с м ь е [3, теорема 8]).
Заметим, что левоинвариантное среднее ц всегда существует, если G —
абелева полугруппа или разрешимая группа (см. § 3.5 и упр. 3.12).
[Указание. Применить результат упр. 2.14 (заменив Е на Е") и до-
доказать существование такой положительной линейной формы со на Е'\ что
сужение со|£' отличается от ф лишь на неотрицательный постоянный мно-
множитель, так что можно считать co(gw) = l для всех u^G Ввести затем форму
Ф(/) =jn(o)(/w)), где отображение и\—>со(/м) рассматривается как веще-
вещественная ограниченная функция на G.]
2.16. Показать, что существует положительная конечноаддитивная функ-
функция множества т, определенная на всех подмножествах пространства R2,
такая, что т(£) = +°°для всякого неограниченного множества EczR2,
m(Q) = l для всякого квадрата Q со стороной 1, и инвариантная относи-
относительно всех изометрий пространства R2 (Д и к с м ь е [3, стр. 226]).
[Указание. В предыдущем упражнении взять в качестве Т простран-
пространство R2, в качестве G группу всех изометрий R2. Группа G разрешима, так
как если Gi — нормальная подгруппа сдвигов, то обе группы G{ и GjG\ абе-
левы. Положить £ = %<?, где %q— характеристическая функция множества Q.]
2.17. Пусть Е — произвольное нормированное пространство. Показать,
что существует такое отделимое компактное пространство 7*, что Е линейно
и изометрически изоморфно некоторому векторному подпространству про-
пространства С(Т). (Под С (Г), как обычно, понимается пространство непрерыв-
непрерывных скалярных функций на Г с нормой, равной максимуму модуля.) Пока-
Показать далее, что в случае, когда Е сепарабельно, пространство Т можно вы-
выбрать метризуемым. (Более общий результат приведен в упр. 6.17.)
[Указание. Взять в качестве Т единичный шар в сопряженном про-
пространстве и наделить Т топологией, индуцированной топологией о(Е'уЕ).]
2.18. Пусть Е и F — векторные подпространства векторного простран-
пространства G, причем каждое из них наделено локально выпуклой топологией. Рас-
Рассмотрим (линейную) топологию в E(]F, база окрестностей нуля которой об-
образована множествами вида U П V, где U и V — окрестности нуля в £ и
в F соответственно. Показать, что каждая непрерывная линейная форма на
Е П F имеет вид
( ') ( ')
где z е= Е П F, xr e= E' и у' е= Р.
[Указание. Рассмотреть линейное отображение /; z \—> (z, z) про-
пространства E(]F в произведение EXF и воспользоваться теоремой Хана —*
Банаха.]
2.19. Использовать упр. 2.13 для доказательства утверждения A) тео-
теоремы 1.7.1, т. е. для доказательства следующего факта. Пусть £ — веще-
вещественное векторное пространство, р — калибровочная функция на Et Ео —
Упражнения 211
векторное подпространство в Е и fo — линейная форма на EOt удовлетворяю-
удовлетворяющая условию /о (х)^р(х) при х^£. Тогда существует такая продолжающая
форму fo линейная форма f на £, что f(x)^p(x) при а;е£.
[Указание (модификация рассуждений Кли, сообщенная мне Д. Ферн-
ли-Сандером). Рассмотреть векторное пространство £XR, выпуклое мно-
множество
* = {(*, g): pW<9
в нем и однородную гиперплоскость Яо в векторном подпространстве £0XR,
определяемую равенством
Яо = {(*, £}: *e£0, M*H6>.
Проверить, что @,1)—окруженная точка множества /С и что пересечение
/СП (£oXR) лежит по одну сторону от Яо. Применить упр. 2.13 для построе-
построения однородной гиперплоскости, Я в £xR, по одну сторону которой лежит К.
Показать, что гиперплоскость Я определяется уравнением F(x,£)=Qt где
F — линейная форма на £xR, удовлетворяющая условию F@, 1)=—1. До-
Доказать, что форма f(x) =F(x, 0) удовлетворяет всем поставленным требова-
требованиям.]
ГЛАВА 3
Теоремы о неподвижной точке
3.0. Предисловие
Под теоремой о неподвижной точке мы будем понимать
утверждение, устанавливающее, что при некоторых условиях
отображение и множества Е в себя имеет хотя бы одну непо-
неподвижную точку, т. е. такую точку х'б£, что и(х) =х. К первым
теоремам такого типа относятся те, в которых Е — подмноже-
подмножество пространства Rn, а отображение и: Е-+-Е непрерывно. Так,
например, теорема Брауэра (§ 0.5) устанавливает существова-
существование неподвижной точки в случае, когда Е — замкнутый единич-
единичный шар в Rn, а и — непрерывное отображение. Ясно, что в лю-
любой подобной теореме о неподвижной точке Е можно заменить
любым его гомеоморфным образом.
Теоремы, ограничивающиеся лишь теми пространствами £,
которые являются подпространствами в Rn, редко применяются
в функциональном анализе, где обычно Е — бесконечномерное
подпространство некоторого функционального пространства.
Первая теорема о неподвижной точке, связанная с бесконечно-
бесконечномерными пространствами, появилась около 40 лет назад в книге
Биркгофа и Келлога [1]. Позднее Шаудер распространил
теорему Брауэра на случай, когда Е — выпуклое компактное
подмножество нормированного пространства. Вскоре после этого
Тихонов перенес результат Шаудера с нормированных про-
пространств на произвольные локально выпуклые пространства. От-
Отправной точкой в обоих случаях являлась теорема Брауэра.
Настоящую главу мы начнем с изложения двух теорем о не-
неподвижных точках, доказательства которых можно провести, не
прибегая к комбинаторной топологии. Первый результат (тео-
(теорема 3.1.1) относится к сжимающим (т. е. сокращающим рас-
расстояние) отображениям полного метрического пространства в
себя. Второй результат (теорема 3.2.1), принадлежащий Мар-
Маркову и Какутани, касается точек, неподвижных одновременно
относительно всех членов некоторого семейства непрерывных
отображений выпуклого компактного подмножества топологиче-
топологического векторного пространства в себя. Последний результат ис-
используется для получения одной теоремы типа Хана — Банаха
(п. 2.3.5).
3.1. Теоремы о неподвижной точке 213
В теореме Маркова — Какутани отображения должны удо-
удовлетворять условию, близкому к линейности. В доказательстве
Маркова [2] используется теорема Шаудера — Тихонова, однако
наше доказательство не прибегает к ней; оно близко к тому,
которое приводится у Какутани [1].
Наш третий главный результат (теорема 3.6.1) заключается
в упомянутой выше теореме Шаудера — Тихонова. В этой тео-
теореме ослабляется условие линейности, налагаемое на отображе-
отображения, поэтому она обладает большей общностью. Еще до Шау-
Шаудера (установившего эту теорему для сепарабельных банахо-
банаховых пространств в [3] и для произвольных банаховых пространств
в [6]) Биркгоф и Келлог [1] получили эту теорему для про-
пространств Сп[0, 1] и L2@, 1). Приложениями теоремы Шаудера—"
Тихонова к дифференциальным уравнениям занимались многие
авторы, среди которых первыми были Грейвс [2] и Лере [3].
Дальнейшее развитие эти приложения получили у Бон-
со л а [1].
3.1. Теоремы о неподвижной точке для сжимающих
отображений
Пусть Е— полуметрическое пространство, т. е. множество,
наделенное полуметрикой d, которая представляет собой веще-
вещественную функцию на ЕхЕ, такую, что
d(x,x)=0, d(x,y)=d(y,x)>0,
d(x1y)<d(x,z)+d(z1y)
для любых элементов х, у, гЪз Е (d — метрика, если выполняется
дополнительное условие d(x,y)=?=0 при хфу). Отображение
и: Е-^Е называется сжимающим отображением (или сжатием)
пространства Еу если существует такое число k, 0-^£<l, что
d(u(x),u(y))Kkd(x,y) для любых х,у^Е. Очевидно, что вся-
всякое сжимающее отображение непрерывно.
3.1.1. Теорема. A) Пусть (E,d)— полное полуметрическое
пространство и и — такое непрерывное отображение простран-
пространства Е в себя, что для некоторого натурального числа р ото-
отображение и? сжимающе. Тогда существует по крайней мере одна
точка jcg£, удовлетворяющая условию
d(u(x),x)=0. C.1.1)
Кроме того, если у ^Е — другая точка, такая, что d(u(y),у) = 0,
го d{xty)=0.
B) Если (Е, d) — полное метрическое пространство и отобра-
отображение, и удовлетворяет условиям части A), то оно обладает в
точности одной неподвижной точкой в Е,
214 Гл. 3. Теоремы о неподвижной точке
Доказательство. B) непосредственно следует из A).
Докажем вначале вторую часть утверждения A). Для этого за-
заметим, что равенство C.1.1) означает, что и(х)^{х}. Отсюда и
из непрерывности отображения и вытекает, что
и2 (х) е и ({х}) с {7(xj} а {*} = {*}.
По индукции получаем ир (х) е {х}. Аналогично ир(у)^{у}, сле-
следовательно,
d(x, y) = d(up(x), u"(y)Xk-d(x, у),
где k< 1, так как отображение и? сжимающе. Таким образом,
d(x, у) =0, что и утверждалось.
Для доказательства существования элемента х^Еу удовле-
удовлетворяющего условию C.1.1), рассмотрим сперва случай /?=1,
т. е. случай, когда само отображение и — сжатие. Возьмем про-
произвольную точку Хо е Е и определим последовательность (хп)
с помощью рекуррентного соотношения хп = и(хп-\)у /г=1,2,... .
Для любых натуральных чисел тип имеем
d{xn+mi xn) = d(un+m(x0), un(x0)Xknd(xm, x0)
и
d{xm, xo)<:d{xm, хт-г)+ ... +d(xu
^km~l d(xux0)+ ... +
Отсюда следует, что
Так как k< 1, то (хп) — последовательность Коши в Е. В силу
полноты Е последовательность (хп) сходится к некоторой точ-
точке х из Е. Тогда последовательность (и(хп))=*(хп+\), будучи
подпоследовательностью последовательности (хп), также схо-
сходится к х. Отображение и непрерывно, поэтому последователь-
последовательность (и(хп)) сходится к и(х)у откуда и следует равенство
C.1.1).
Перейдем к случаю, когда лишь отображение v = ut> сжимаю-
сжимающе. Повторим предыдущие рассуждения, заменяя везде и на v.
Получим, что существует точка х е Еу для которой d(v(x), x) =0.
Далее, для последовательности xn = vP-(xo) справедливы равен-
равенства и(хп) =u(v(xn-i))=v(u(xn-\)). Так как последователь-
последовательность (хп) сходится к а: и отображения и, v непрерывны, то
d(u(x),v(u(x)))=0. Но тогда
d{u{x)9 x)*£d(u{x), v(u(x))) + d(v(u(x)\ v{x)) + d(v(x), x) =
= d(v(u(x))9 v(x))<;kd(u(x), x),
откуда в силу условия k < 1 вытекает равенство d(u(x), x) =0. |
3.1. Теоремы о неподвижной точке 215
Замечания. Построение последовательности (хп) и иссле-
исследование вопроса о ее сходимости часто называют методом по-
следовательных приближений. Этот метод обычно фигурирует
под названием метода Пикара (см. Пикар [1]), хотя Пеано
[1] применял его раньше. Первая абстрактная формулировка ме-
метода принадлежит Банаху [2] и Каччиополи [1]. См. также
Канторович [1], Гёде [1], Кирк[1], Б р а у д е р [6—8],
Браудер и Петришин [1, 2].
Доказанная теорема о неподвижной точке представляет со-
собой лишь один из примеров применения такого рода техники.
Блестящее изложение других примеров можно найти в гл. X
книги Дьёдонне [13]. Недавно Эдельштейном [1, 2] были
получены обобщения самого принципа сжимающих отображе-
отображений. Одно из таких обобщений рассматривается в упр. 3.7.
Как мы сейчас убедимся на примерах, теорема 3.1.1, несмотря
на свою простоту, имеет полезные приложения в анализе.
3.1.2. Приложения к интегральным уравнениям. Пусть Т —
некоторый интервал вещественной оси. Обозначим через Е век-
векторное пространство ограниченных непрерывных функций
х: Т-+К (К — поле вещественных или комплексных чисел); Е —
становится полным метрическим пространством, если ввести
метрику d(x,y) = \\x — y\\, где
Предположим, что задана такая функция /: ТхТхК-+К, что
для каждого х е Е и каждого t ^Т функция
s\r-+f(t, 5, x(s))
интегрируема на Г, причем функция
t*-*jf(t,s,x(s))ds
т
ограничена и непрерывна на Т.
Рассмотрим произвольный элемент Je£ и определим ото-
отображение и пространства Е в себя формулой
u(x){t)=-lf(t,s, x(s))ds + b(t).
т
Неподвижная точка х отображения и является, очевидно, реше-
решением неоднородного и, вообще говоря, нелинейного интеграль-
интегрального уравнения
x(t)+lf(t,s,x(s))ds = b(t), C.1.2)
т
где х е Е.
216 Гл. 3. Теоремы о неподвижной точке
При соответствующих ограничениях и будет сжатием про-
станства £, и тогда существование и единственность принадле-
принадлежащего Е решения уравнения C.1.2) будет следовать из теоре-
теоремы 3.1.1.
Предположим, например, что f удовлетворяет неравенству
IW, st Z)-f(t, s, ?)\<F(tt 5) 16-Г I. C.1.3)
Тогда если хь х2^Е и У\~и{х\), у2 = и(х2\ то
d(yi, y2Xkd(xb х2\
где
й-sup/ J F(t, s)ds: t<=T\.
При k < 1 отображение и сжимающе и можно применить тео-
теорему 3.1.1.
Если ввести параметр Я («собственное значение») и заменить
f на hf, можно доказать существование и единственность реше-
решения х е Е уравнения
\ C.1.4)
для любого b^E и любого Я, такого, что &|Я|<1,
В случае, когда функция / имеет вид
f(t, s, l) = K(t, s)-S,
уравнение C.1.4) представляет собой неоднородное (линейное)
уравнение Фредгольма с ядром К. Таким образом, такое урав-
уравнение разрешимо по меньшей мере для достаточно малых Я.
В общем случае для некоторых Я и некоторых b уравнение не-
неразрешимо. Вопрос о разрешимости таких уравнений является
частью общей хорошо разработанной теории (см. Смитис [2],
Заанен [1], Дьёдонне [13]).
Интересен случай, когда Г —ограниченный интервал с кон-
концами а<р, ядро К ограничено на произведении ТхТ и /((/, s) =
= 0 при t < s. Тогда C.1.4) превращается в неоднородное (ли-
(линейное) уравнение Вольтерры
K(t, s)x(s)ds = b{t\ C.1.5)
а отображение и принимает вид
t
u(x)(t) = - Я | K{t, s)x(s)ds + b (*).
3.1. Теоремы о неподвижной точке 217
Предположим, что \K(t, s)\^.M, и построим последователь-
последовательность итераций хп = ип(х) и уп = ип(у) для произвольных двух
элементов х, у^Е. Можно доказать по индукции, что
причем коэффициент при d(x,y) в правой части неравенства
стремится к нулю при п-+оо. Таким образом, каково бы ни
было А,, существует такое натуральное число /?, что up— сжатие.
Вторая часть теоремы 3.1.1 обеспечивает существование и един-
единственность в Е решения уравнения C.1.5) для любого Я и любой
правой части Ъ е £. Отсутствие всяких ограничений на К являет-
является характерной особенностью уравнений типа Вольтерры.
Вскоре будет показано, что описанный выше метод можно
на разные лады варьировать. Мы накладывали на рассматри-
рассматриваемые функции такое сильное ограничение, как непрерывность,
чтобы избежать исследования вопросов существования интегра-
интегралов. Однако, используя развитую теорию интегрирования (гл. 4),
можно в качестве Е взять пространство Лебега JS?v (Г, |ы) и про-
провести подобное рассмотрение этого .случая.
Дальнейшие обобщения относятся к случаю, когда значения
функции а: на Г принадлежат некоторому полуметрическому про-
пространству, а значения функции f — некоторому полному то-
топологическому векторному пространству, топология которого
определяется полуметрикой. В таких обобщениях используется,
конечно, техника интегрирования векторнозначных функций. Чи-
Читатель может изучить эти вопросы самостоятельно после прочте-
прочтения соответствующих разделов гл. 8.
3.1.3. Приложения к дифференциальным уравнениям. С по-
помощью теорем о неподвижной точке для интегральных операто-
операторов можно доказывать по крайней мере локальное существова-
существование и единственность решений обыкновенных дифференциальных
уравнений типа
— = f(t х)
Основная идея состоит в следующем. Если f — непрерывная
функция, то решение этого дифференциального уравнения с на-
чальнымьГусловиями x(t0) =у0 (t0 и у0 заданы) есть не что иное,
как решение интегрального уравнения
t
x(t) = yo+ J f(s, x{s))ds.
и
Если функция / удовлетворяет условию Липшица по второму
аргументу, то применимы результаты п. 3.1.2. При этом если
218 Гл. 3. Теоремы о неподвижной точке
постоянная Липшица и длина выбираемого интервала измене-
изменения переменной t достаточно малы, то получается сжимающее
отображение. Отсюда следуют теоремы локального существова-
существования и единственности. Для объединения этих локальных реше-
решений в глобальное требуются уже отдельные рассуждения.
В недавнее время был получен более эффективный метод,
при котором вводится новое определение расстояния, зависящее
от постоянной Липшица. Этот метод, принадлежащий Белиц-
ком у [1], дает возможность доказывать непосредственно гло-
глобальную теорему существования. Вот описание этого метода.
Пусть F—банахово пространство и Т — вещественный интер-
интервал. Так как мы желаем интегрировать функции со значениями
в F, то на данном этапе надо предположить, что пространство F
конечномерно, ибо теория векторнозначных функций в бесконеч-
бесконечномерных пространствах излагается только в гл. 8. Как и рань-
раньше, рассмотрим дифференциальные уравнения
§- = Ш,х) C.1.6)
с начальным условием
x(to) = yo, C.1.7)
где to^T и yo^F наперед заданы. Под решением уравнения
C.1.6) будем понимать такую непрерывную функцию х: T-+F,
производная которой в каждой внутренней точке / интервала Т
равна f(t,x(t)). (Если пространство F бесконечномерно, то
возникает вопрос о выборе между слабой и сильной диффе-
ренцируемостью ^-значных функций. Настоящий метод приме-
применим к случаю, когда рассматривается сильная дифференцируе-
мость.) Пусть непрерывная функция /: TXF-+F удовлетво-
удовлетворяет условию Липшица
\\f(t, yi)-f{t, У2)\\<ЦУ1-уа\\,
где t е Т и уь у2 s /\ а число L не зависит от t, у\ и у2. Кроме
того, допустим, что функция f ограничена на каждом множе-
множестве вида Т X S, где В — ограниченное множество в F.
Предположим вначале, что интервал Т ограничен, и введем
в рассмотрение банахово пространство Е ограниченных непре-
непрерывных функций х: T-+F с нормой
где Я — фиксированное число, Х> 1.
Заметим, что ограниченными решениями задачи C.1.6),
C.1.7) являются те и только те элементы х е £, которые удов-
удовлетворяют условию
и (х) = х,
3.1. Теоремы о неподвижной точке 219
где отображение и определяется равенством
t
u(x)(t) = yQ+ jf(s,x(s))ds (te=T).
n
Очевидно, и есть отображение пространства Е в себя. Если мы
покажем, что и — сжатие, то на основании теоремы 3.1.1 дока-
докажем существование и единственность ограниченного решения
задачи C.1.6), C.1.7). То, что отображение и сжимающе, про-
проверяется в лоб, и мы дадим только набросок доказательства.
Предположим, что хх, х2 е Е. Тогда
t
[и (х{) - и (х2)] (t) = J [/ E, *, (s)) - / E, х2 (s))] ds
и
и, следовательно,
II [и (хг) - и(х2)] (t) || < L J II *i (s) - *2 (s) II dst
Ч
где It — интервал (to, t) или (/, t0) в зависимости от того, какое
из неравенств t > t0 или tKt0 имеет место. Правая часть не-
неравенства мажорируется выражением
• iv \X\ — X2)
Входящий в это выражение интеграл не превосходит
Таким образом, получаем
N [и (хх) - и (х2)] < ЯГ1 • N (хх - х2),
и так как X > 1, то отображение и сжимающе.
Остается рассмотреть случай неограниченного интервала Т.
Введем в рассмотрение такую возрастающую последователь-
последовательность (Tk) компактных интервалов, содержащих to в качестве
внутренней точки (относительно подпространства Г), что
^U^' Рассмотрим ограниченные решения для интерва-
интервале
лов Tk. Из доказанной единственности следует, что эти различ-
различные решения «складываются в одно целое», давая локально
ограниченное решение на всем интервале Т. Обратно, если х —
локально ограниченное решение на Г, то из доказанной выше
единственности вытекает, что сужение х \ Tk — единственное
ограниченное решение на 7V Так как это справедливо для
220 Гл. 3. Теоремы о неподвижной точке
любого k, то тем самым единственность решения на всем интер-
интервале Т доказана.
Для дальнейшего изучения абстрактных дифференциальных
уравнений рекомендуем Бур баки [13, гл. IV].
Следует отметить, что применение принципа сжимающих
отображений к дифференциальным и интегральным уравнениям
практически ограничивается случаями, когда функция f{t,y)
удовлетворяет условию Липшица по у. Для случаев, когда
условие Липшица не выполняется, необходима более сильная
теорема о неподвижной точке. Мы вернемся к этому вопросу
в § 3.6.
3.2. Теорема Маркова — Какутани
В этом параграфе изучается вопрос о существовании точек,
неподвижных относительно некоторых семейств непрерывных
отображений компактного выпуклого множества в себя.
3.2.1. Теорема. Пусть Е— отделимое топологическое вектор-
векторное пространство, К — непустое компактное выпуклое множе-
множество в Е и Г — некоторое семейство непрерывных отображений
множества К в себя, удовлетворяющее следующим двум усло-
условиям:
(а)' если и^Т, ху у^К и а, |3 — такие положительные
числа, что а + |3=1, то и(ах + $у) =аи(х) +§и{у)\
(Ь) существует такое натуральное число п и такие подсе-
подсемейства Тг семейства Г @<л</г—1), что
где 1 — тождественное отображение на /С, и каждой паре и\
и" е Гг-i соответствует такой элемент s e Г\-, что
u'u" = u"u's. C.2.1)
Тогда существует точка хо^К, такая, что и(хо)=хо для всех
отображений и^Т.
Доказательство проводится индукцией по п.
A) Рассмотрим случай я = 1. Из условия (Ь) вытекает, что
элементы множества Г попарно коммутируют. (Мы следуем
доказательству Бур баки [7, стр. 139—140].) Для каждого
элемента weT и каждого натурального числа г положим
иг=г-1 {\+и+ ...
Так как множество К выпукло, то иг(К)а К. Обозначим че-
через Г* множество тех отображений v, которые являются про-
произведениями конечного числа отображений иг. Каждое отобра-
отображение сеГ* удовлетворяет условию (а), элементы множе-
3.2. Теорема Маркова — Какутани 221
ства Г* попарно перестановочны и каждое v отображает мно-
множество К в себя.
Рассмотрим семейство множеств v(K), где v пробегает мно-
множество Г*. Каждое множество этого семейства компактно и
содержится в /С. Кроме того, если о'./еГ*, то a = aV =
= Л'£Г* и v(K)av'(K), v(К)civ"(К). Так как ни одно из
множеств v(К) не пусто и пространство Е отделимо, то {о(К)}—•
центрированная система замкнутых множеств в /С. В силу ком-
компактности множества К пересечение всех множеств v(K) со-
содержит по крайней мере одну точку х0. Докажем, что х0 удо-
удовлетворяет равенству и(хо)=хо для всех wgT.
Каково бы ни было натуральное число г, имеем Хо
таю что существует такая точка у^К, что
хо = г-1(у + и{у)+ ... + иг~1(у))9
откуда
Пусть V — уравновешенная окрестность нуля в Е и W — такая
уравновешенная окрестность нуля, что W-\-WczV. Так как
множество И = К — К компактное, то существует конечное число
точек аи^Н (l^Ck^im), таких, что Н содержится в объеди-
объединении множеств ak-\-W. Множество W поглощающе, поэтому
существует такое число а, 0 < а ^ 1, что aak ^W A ^ k ^ m).
Следовательно, аНa W + aWa W+Wcz V. Взяв г>а~\ ви-
видим, что и(х0)—х0 е V. Так как пространство Е отделимо и
V—произвольная уравновешенная окрестность нуля в Е9 то
и(х0) —хо = О, что и требовалось доказать.
B) Допустим теперь, что теорема верна, если Г удовлетво-
удовлетворяет условию (Ь) для некоторого фиксированного п. Покажем,
что теорема справедлива, если в условии (Ь) заменить п на
п+1. Рассмотрим последовательность
{} = Гп с= ... с= A cz Г0 = Г.
По предположению индукции теорема применима к Г\. Дру-
Другими словами, множество К\ тех точек из /С, которые остаются
неподвижными относительно элементов из Гь не пусто. Оче-
Очевидно, что множество К\ замкнуто и выпукло и потому ком-
компактно..
По условию если иг, и"^Г( = Го), то существует такой эле-
элемент sge Гь что u'u"=u"u's. Значит, иги"(х)=и"и'(х), если
Xi=Ku Следовательно, сужения и\К\ (и^Т) попарно пере-
перестановочны. Если далее иеГ, щ е Ti и хее Ки то uxu = uu\S
для некоторого 5 е Гь поэтому
щи (х) = uuxs (x) =5= ищ (х) =*и(х).
222 Гл. 3. Теоремы о неподвижной точке
Таким образом, п\(и(х)) = и(х) для х&Ки и, значит, суже-
сужение u\Ki отображает множество К\ в себя.
Теперь остается только применить A) к отображению
и\К\: Ki^r* Ki. В заключение получаем, что существует такой
элемент Хо^Ки что и(хо)*=хо для всех аеГ.
Теорема полностью доказана. |
3.2.2. Замечания. Имеются два особенно важных слу-
случая, когда предположение (Ь) выполняется.
A) Случай, когда Г — абелева полугруппа непрерывных
отображений множества К в себя, содержащая тождественное
отображение. Если последнее отображение не принадлежит
множеству Г, то его всегда можно присоединить к нему, не на-
нарушая остальных условий теоремы.
B) Случай когда Г — разрешимая группа взаимноодно-
взаимнооднозначных непрерывных отображений множества К в себя. На-
Напомним, что группа Г называется разрешимой, если она обла-
обладает композиционным рядом (Г*)о<*<л> таким, что Го=Г,
Гп = {1}, Гг+1 — нормальная ( = инвариантная) подгруппа в Гг и
факторгруппа 1УГ*+1 абелева (через {1} обозначена подгруппа,
состоящая из одного нейтрального элемента^. Так, например,
каждая абелева группа разрешима; группа гомотетий простран-
пространства R2 разрешима, хотя и не является абелевой; при /г^>3
ортогональная группа в Rn (и тем более группа гомотетий
в Rn) не разрешима. С результатами такого типа читатель
может познакомиться по книгам Дьёдонне [16] и Арти-
на [1].
Перейдем к рассмотрению некоторых приложений теоремы
3.2.1. Начнем с одного обобщения теоремы Хана —Банаха.
3.3. Одно обобщение теоремы Хана — Банаха
Рассматриваемый результат касается возможности продол-
продолжения линейных форм, подчиненных условию инвариантности
относительно соответствующего семейства автоморфизмов дан-
данного векторного пространства. Результат такого типа установ-
установлен Э г нью и Морсом [1].
3.1.1, Теорема. Пусть Е — векторное пространство, V — раз-
разрешимая группа автоморфизмов пространства Е или абелева
полугруппа эндоморфизмов пространства Е. Пусть L+- вектор-
векторное подпространство в Е, инвариантное относительно Г (т. el
u{L)aL для каждого меГ) и р — такая полунорма на £, что
рои^Ср для каждого йеГ. Тогда если f0 — линейная форма
на L, удовлетворяющая условиям
\Ш\<р(х) (хе=1) C.3.1)
ЗА. Обобщенные банаховы пределы 223
M«W) = /oM (xt=L,u^T), C.3.2)
то на Е существует такая линейная форма /, являющаяся про-
продолжением формы /о, что
I/WKpM (*e£) C.3.3)
f(u(x)) = f (х) (xeeE,u<= Г). C.3.4)
Замечание. Если Е — вещественное векторное простран-
пространство, то имеет место аналогичный результат, только полунор-
полунорма р заменяется калибровочной функцией (§ 1.6), а неравен-
неравенства C.3.1) и C.3.3) пишутся без модулей (ср. с утвержде-
утверждением A) теоремы 1.7.1).
Доказательство. Наделим алгебраическое сопряжен-
сопряженное £* к Е слабой топологией о(Е*,Е). Пусть К—множество
линейных форм / на £", являющихся продолжениями формы /о
и удовлетворяющих неравенству C.3.3). В силу теоремы 1.7.1
множество К непусто. Далее К компактно и выпукло. Оче-
Очевидно также, что К инвариантно относительно отображений
/*->/*, где
fu(x)=f(u(x))
для ибГ и х^Е. Теперь достаточно сослаться на теорему
3.2.1, взяв в качестве Г множество отображений вида f^-^fu
с «еГ. В результате получаем, что в К существует по край-
крайней мере одна такая линейная форма f, что fu~f для всех
иеГ. Форма / отвечает нашим требованиям. |
3.3.2. Замечание. Очевидно, что аналогичный результат
имеет место, если Г — множество линейных отображений про-
пространства Е в себя, удовлетворяющее условию (Ь) теоремы
3.2.1. Однако для большинства приложений вполне достаточно
приведенных двух случаев.
В оставшейся части главы займемся некоторыми приложе-
приложениями теоремы 3.3.1.
3.3.3. О различных обобщениях теоремы Хана — Банаха и о
средних на полугруппах (§ 3.5) см. Дан форд [3], В у д-
бери [1], Юд [1], Кли [3], Сильверман [1, 2], Ти йен [1],
Хьюитт и Росс [1, § 17]. У Сильвермана [1, 2] рассмот-
рассмотрена также теорема продолжения в случае упорядоченных
векторных пространств.
3.4. Обобщенные банаховы пределы
Банах [1, стр. 28, 29], опираясь на теорему Хана — Банаха,
Доказал существование инвариантного относительно сдвигов
обобщенного предела1 имеющего смысл для произвольных
224 Гл. 3, Теоремы о неподвижной точке
ограниченных функций на полуоси @, +оо) (или произвольных
последовательностей). Мы получим этот результат из теоремы
3.3.1, использование которой упрощает первоначальные рассуж-
рассуждения Банаха.
С этой целью возьмем в качестве Е вещественное векторное
пространство всех вещественных ограниченных функций на
(О, оо). Обозначим через L векторное подпространство в Et
состоящее из тех функций х на @, оо), для которых существует
конечный предел \imx(t). Этот предел примем в качестве ли-
нейной формы fo, определенной на L. Пусть Г—абелева полу-
полугруппа сдвигов х—>ха, где а>0 и xa(t)=x(t+a) t^@,oo).
Наконец, через р обозначим калибровочную функцию на £",
определенную равенством
x(t).
p()
t->oo
Легко проверяется, что все условия теоремы 3.3.1 выполняются.
Отсюда следует, что у линейной формы /о существует такое
продолжение f на £, что выполняются отношения C.3.3) и
C.3.4). Следуя Банаху, воспользуемся для f(x) обозначением
LimA:(/). Имеем
Umx{t) = l\mx(t) C.4.1)
для каждой ограниченной вещественной функции х на @, оо),
для которой существует предел в правой части равенства
C.4.1), и
Lim x(t + a) = Lim x (t) C.4.2)
*->оо t->oo
для каждой ограниченной, вещественной функции х на @, оо)
и любого а > 0. Кроме того, для каждой такой функции выпол-
выполнено неравенство
{)
t->oo t->oo
Из линейности формы Lim следует, что
lim inf x @ < Lim x (t) < lim sup x (t) C.4.3)
t->oo t->°o t->oo
для всякой ограниченной вещественной функции х на @, оо),
(Очевидно, C.4.3) влечет C.4.1).)
Точно такое же построение можно провести для ограничен-
ограниченных последовательностей вещественных чисел. Очевидным об'
разом можно продолжить форму Lim на комплексные ограни-
ограниченные функции на @, оо) (или на последовательности ком-
комплексных чисел),
3.5. Инвариантные средние на полугруппах 225
Отметим, что из существования обобщенных пределов сле-
следует, что не каждая непрерывная линейная форма на банахов-
ском пространстве /°° ограниченных последовательностей (с нор-
нормой, равной верхней грани модулей членов последовательности)
может быть представлена в виде
п) )
/1=1
где (сп)—некоторая числовая последовательность. Так, на-
например, если х — последовательность из /°°, для которой
x(k) = \ и х(п)=0 при пфк, то из равенства C.4.1) следует,
чт0 ск = 0 для всех k и линейная форма указанного вида дол-
должна всюду на /°° быть равной нулю. В то же время C.4.1) с
х= 1 показывает, что обобщенный предел не всюду равен нулю.
3.5. Инвариантные средние на полугруппах
Пусть вначале Т — произвольное множество, а Е— вектор-
векторное пространство ограниченных вещественных функций на Т.
Будем называть средним на Е всякую линейную форму М на £,
для которой
inf*<;W(A:)<sup.*; C.5.1)
т т
для каждого элемента х^Е. Если пространство Е содержит
постоянную функцию 1, то линейная форма М на Е будет сред-
средним на £ в указанном выше смысле тогда и только тогда, когда
форма М положительна (относительно структуры порядка, ин-
индуцированной в Е векторным пространством всех веществен-
вещественных функций на Г), т. е.
М(*)>0 для х>0 из Я
Если далее задано семейство отображений и множества Т
в себя, то это семейство порождает эндоморфизмы xv->xu =
= хоц пространства Е. Естественно рассмотреть те средние М
на £, которые инвариантны в том смысле, что М(хи) =М(х)
для всех х е Е и всех отображений и из заданного семейства.
При определенных условиях бывает удобно воспользоваться
теоремой 3.3.1 для доказательства существования таких инва-
инвариантных средних. Особый интерес представляет случай, когда
Т — полугруппа с мультипликативной записью закона компо-
композиции, а в качестве отображений и рассматриваются либо левые
сдвиги ti—>at, либо правые сдвиги t*—>ta, либо те и другие вме-
вместе. В этом случае через ах будем обозначать левый сдвиг
226 Г л 3. Теоремы о неподвижной точке
t*->x(at) функции х, а через ха — правый сдвиг t*->x(ta) той
же функции.
Среднее М называется левоинвариантным (соответственно
правоинвариантным, биинвариантным), если оно инвариантно
относительно левых (соответственно правых, двусторонних)
сдвигов.
Если теперь в качестве Е взять векторное пространство всех
ограниченных вещественных функций на Г и положить р(х) —
= sup х9 то из теоремы 3.3.1 следует существование биинва-
т
риантных средних, определенных для всех ограниченных веще-
вещественных функций на любой абелевой полугруппе Т.
Рассмотрим теперь более частный случай, когда Т — группа
(а не полугруппа). (Инвариантность относительно сдвигов
определяется так же, как и для полугрупп.) В этом случае мы
можем дополнительно рассмотреть эндоморфизм х i—>i про-
пространства £, определенный равенством x(t) =x(t~l). Если М —
среднее, то линейная форма М, определенная равенством
М(х) = М {х)
для любого элемента х е Еу также является средним. Пусть
М — левоинвариантное среднее; тогда среднее Ми определен-
определенное равенством М\(х) = М(л:/), где x/(t)=M(xt), как легко про-
проверить, биинвариантно. Левоинвариантность среднего М\ сле-
следует из соотношения (ах)' = х\ которое имеет место в силу
левоинвариантности среднего М. Правоинвариантность среднего
Mi вытекает из тождеств (х8)'=(х')8, {(x')s)~s=s~l{(x')~) и из
левоинвариантности среднего М.
Пользуясь этими замечаниями, легко, применяя теорему
3.3.1, показать существование по крайней мере одного биинва-
риантного среднего, определенного для всех ограниченных ве-
вещественных функций на группе Г, если'последняя разрешима.
Такие же рассуждения можно провести для пространства
всех вещественных непрерывных ограниченных функций на Г,
если Т — разрешимая топологическая группа.
Предостережение. Пусть Г —локально компактная
топологическая группа и М — инвариантное среднее (например,
левое) для всех ограниченных непрерывных вещественных
функций на Т. Не следует смешивать среднее М с интегралом
по левоинвариантной мере Хаара на 7, вводимой ниже, в
§ 4.18. Действительно, если группа Т не компактна, то суже-
сужение М на пространство е^Г(Г) вещественных непрерывных на Т
функций с компактными носителями равно нулю. В самом деле,
пусть *е/С(Г); можно считать функцию х положительной.
Выберем симметричное компактное множество KczT, вне ко-
3.6. Теорема Шаудера — Тихонова 227
торого функция х равна нулю. Если пространство Т не ком-
компактно, то можно так подобрать элементы ап^Т (я= 1, 2,...),
чтобы множества сп1К попарно не пересекались. Тогда для
всех /еГи всех натуральных чисел г
г
2 х (ant) < m = sup х.
п=\ Т
Применяя среднее М к обеим частям неравенства и используя
его левоинвариантность, получаем
M{m) = m-M A)
для всех натуральных чисел г. С другой стороны, так как х>0,
то М(х)^-0; следовательно, полагая гн->оо, получаем М(х) = 0,
т. е. М\<Ж(Т)=0.
Если, однако, пространство Т компактно, то, как можно по-
показать, левоинвариантное среднее М, определенное для всех
непрерывных вещественных функций на Г, совпадает с инте-
интегралом по левоинвариантной мере Хаара на Т.
Для дальнейшего изучения инвариантных средних на груп-
группах рекомендуем книгу Хьюитта и Росса [1, § 17]. Слу-
Случай инвариантных средних на полугруппах (не обязательно
абелевых) детально рассмотрен Диксмье [3]. (См. также
ссылки на литературу в п. 3.3.3.) Основной результат о суще-
существовании инвариантных средних на полугруппах, принадле-
принадлежащий Диксмье, приведен в упражнении 3.12. Результаты та-
такого рода можно использовать при доказательствах утвержде-
утверждений типа теоремы 3.3.1 (см. упр. 2.15 и 3.12).
3.6. Теорема Шаудера — Тихонова
Теорема Шаудера — Тихонова отличается от теоремы Мар-
Маркова— Какутани тем, что в ней участвует только одно отобра-
отображение и; зато, однако, на это отображение и не накладывается
никаких ограничений, кроме непрерывности.
3.6.1. Теорема (Ш а у дер — Тихонов). Пусть Е —отде-
—отделимое локально выпуклое пространство и К —непустое выпук-
выпуклое компактное множество в Е. Всякое непрерывное отображе-
отображение и множества К в себя обладает по крайней мере одной не-
неподвижной точкой.
Доказательство теоремы, заимствованное из книги Дан-
форда и Шварца [1, стр. 490—493], опирается на три лем-
леммы, наиболее сложная из которых, третья, является и самой
важной,
228 Гл. 3. Теоремы о неподвижной точке
Для краткости будем говорить, что топологическое про-
пространство обладает свойством неподвижной точки, если любое
непрерывное отображение этого пространства в себя обладает
по крайней мере одной неподвижной точкой.
Первые две леммы устанавливают, что некоторые подмно-
подмножества гильбертова пространства I2 обладают свойством не-
неподвижной точки. Гильбертовым кубом Q называется подмно-
подмножество пространства /2, образованное последовательностями х$
для которых | х (п) К — при всех /г. Легко проверяется, что
множество Q компактно и выпукло.
Лемма 1. Гильбертов куб Q обладает свойством неподвиж-
неподвижной точки.
Доказательство. Пусть и — непрерывное отображе-
отображение множества Q в себя и пп — проекторы, определенные ра-
равенствами
*Лх№-[ 0
Множество Qn — fin(Q) гомеоморфно замкнутому единичному
шару пространства Кп (К — поле вещественных или комплекс*
ных чисел). Так как яп о и — непрерывное отображение множе-
множества Qn в себя, то из теоремы Брауэра о неподвижной точке
(§ 0.5) следует существование такой точки хп е Qn cz Q, что
пп{и{хп)) =хп. Ввиду компактности множества Q некоторая
подпоследовательность (хПг) сходится к точке х е Q, Так как
то и(х) =х, что и требовалось доказать. |
Лемма 2. Каждое непустое замкнутое выпуклое подмноже-
подмножество К гильбертова куба Q обладает свойством неподвижной
точки.
Доказательство. В силу теоремы 1.12.3 для каждой
точки jcgQ существует единственная ближайшая к ней точка
f(x) из К. Отображение f непрерывно. В самом деле, если
хп-*х в Q и f (xn) 7*> f (x) t то ввиду компактности К некоторая
подпоследовательность f(xnk будет сходиться к точке у е /С,
отличной от f(x). Тогда
так что в пределе при &—юо будем иметь \\х — у\\ <1 \\х — f(x)\\9
что противоречит определению точки f{x). Таким образом, ото-
3.6. Теорема Шаудера — Тихонова 229
бражение /: Q-*/( непрерывно и на К совпадает с тождествен-
тождественным отображением.
Пусть теперь и — произвольное непрерывное отображение
множества К в себя. Тогда отображение и of: Q—► /( непрерывно
и потому в силу леммы 1 обладает неподвижной точкой x^Q.
Итак, u(f(x)) =х, откуда следует, что х е м(/() с: /С, так что х —
неподвижная точка отображения и. |
Лемма 3. Пусть Е — отделимое локально выпуклое про-
пространство, К — компактное выпуклое подмножество в £, содер-
содержащее по крайней мере две различные точки. Если отображе-
отображение и: К-+ К непрерывно, то в К существует такое собственное
замкнутое выпуклое подмножество К\, что t/(/Ci)cz /Сь
Доказательство. Так как множество К компактно,
а пространство Е отделимо и локально выпукло, то исходная и
ослабленная топологии пространства Е индуцируют в К одну
и ту же топологию. Поэтому отображение и: К-+К останется
непрерывным, если наделить К ослабленной топологией. Мно-
Множество К компактно и тем более слабо компактно, поэтому
отображение и будет равномерно непрерывным на К в ослаб-
ослабленной топологии.
Введем вспомогательные понятия. Скажем, что множество
GaE' определяет множество FczE', если для каждого f^F
и каждого е > 0 найдется такое конечное множество Go cz G
и такое число б > 0, что
\{и(х), f)-{u(y)f f>
если точки х, у е К удовлетворяют условию
| (г, g>|<6 для
Это условие в действительности означает, что отображение и не-
непрерывно в слабых топологиях g(E,G) \К и а(£1,/Г)|/С. Нам
понадобятся следующие три замечания.
A) Каждый функционал f^.E' определяется некоторым
счетным множеством G. Действительно, мы видели, что ото-
отображение хъ—>(и(х), f) равномерно непрерывно на К в ослаб-
ослабленной топологии, поэтому каждому натуральному числу п от-
отвечают такое конечное множество Gncz Er и такое число
бп>0, что | {и(*), /) - (и{у\ f) |< ^ для всех пар (х,у)&
s К X К, удовлетворяющим условию х — у е W(Gn, бп). Тогда
счетное множество G=\JGn определяет функционал f.
B) Из замечания A) непосредственно следует, что каждое
счетное множество FaE' определяется некоторым счетным
множеством GczE\ Однако верно более сильное утверждение.
230 Гл. 3. Теоремы о неподвижной точке
C) Каждый функционал /<=£' может быть включен в не-
некоторое счетное самоопределяющееся множество GczE'. В са-
самом деле, функционал / определяется некоторым счетным мно-
множеством G\ в силу замечания A); множество G{ определяется
(в силу замечания B)) некоторым счетным множеством G2;
множество G2 — некоторым множеством G$ и т. д., и доста-
/ оо \
точно положить G = {f} U (J
После этих замечаний продолжим доказательство.
Пусть а, Ъ — различные точки множества К. Выберем функ-
функционал f&E' так, чтобы {a,f) Ф {b,f)9 что возможно в силу
отделимости и локальной выпуклости пространства Е. Пусть
G={gk} — самоопределяющееся множество, содержащее f (за-
(замечание C)). Так как множество К ограничено, то можно счи-
считать, что | gk(К) I^-j Для всех &=1, 2, ... . Отобразим мно-
множество К в I2 с помощью отображения t, определенного равен-
равенством t(x)(k)={x9gh). Отображение t является непрерывным
отображением множества К на выпуклое компактное подмно-
подмножество Ко гильбертова куба Q. Так как t(aL=t(b), то Ко содер-
содержит по крайней мере две различные точки.
Поскольку множество G само себя определяет, композиция
v = touot~l есть однозначное отображение множества Ко в себя
(даже если t и не взаимно однозначно). Далее, отображение v
непрерывно. Действительно, пусть ро^Ко и 0<е<1. Выбе-
Выберем jV так, чтобы 2j~^r<e- Так как множество-G самоопреде-
k>N
ляющееся, найдется такое б > 0 и такое натуральное число т,
что
\{и(х), gk)-(u(y)9 A)|<-4, 1<£<W,
N2
для всех пар (х, у) е КХ К, удовлетворяющих условию
\(х — У> 8i)\< б> 1 </<т.\ Таким образом, если р е Ко и
lip — Poll < 6 и если х и у выбраны в К так, что t(x)=p и
Цу)==Ро, то в силу предыдущего неравенства имеем
II v(p)-v (ро) II2 - 21 {и (*), fo> - <а (у), gk) |2 =
k>N k<N k>N
откуда и вытекает непрерывность отображения v*
3.6. Теорема Ш ay дера — Тихонова 231
Лемма 2 позволяет теперь сделать вывод, что отображение
v обладает неподвижной точкой ро^Ко- Тогда u(t-l(p0))cz
cz t~l(po) =Ки причем К\ есть собственное выпуклое подмноже-
подмножество в К и u(K\)cz /Ci, чем и завершается доказательство
леммы. I
Иное доказательство см. у Сарымсакова [1].
Доказательство теоремы 3.6.1. Рассмотрим мно-
множество всех таких компактных выпуклых подмножеств К' с: /С,
что и(К')аК!> Если это множество упорядочить по убыванию,
то оно, очевидно, будет индуктивно упорядоченным. В силу лем-
леммы Цорна существует такое минимальное компактное выпуклое
подмножество /С* cz К, что и(К*)аК*. Из леммы 3 следует, что
/(* содержит только одну точку, которая и является неподвижной
для отображения и. |
3.6.2. Следствие. Пусть Е — отделимое локально выпуклое
пространство, удовлетворяющее следующему условию.
(*) Замкнутая выпуклая оболочка всякого компактного
множества в Е компактна.
Если А — непустое замкнутое выпуклое множество в Е и и — та-
такое непрерывное отображение множества А в себя, что множе-
множество и (А) относительно компактно в £, то отображение и обла-
обладает по крайней мере одной неподвижной точкой.
Доказательство. Обозначим через В выпуклую оболоч-
оболочку множества и (А) в £ и через К замыкание множества В в Е.
Очевидно, К с: А. Множество и(А) относительно компактно, по-
поэтому из условия (*) следует, что множество К компактно. Кро-
Кроме того, оно не пусто и выпукло. Так как /(с Л, то и (К) cz и (А).
Далее, u(A)czK по определению множества /(. Таким образом,
и(К)аК. Остается применить теорему 3.6.1 к отображению
и\К. I
Замечания. Приведенное выше условие (#) заведомо вы-
выполняется, если пространство Е полно или даже квазиполно (по-
(последнее означает, что каждое ограниченно замкнутое множество
в Е полно). Действительно, если Р — компактное подмножество
в Ей Q — его замкнутая выпуклая оболочка, то множество Q пред-
компактно (см. предложение 9.1.3). Далее, так как множество Р
ограничено, то таким же будет и множество Q. Если простран-
пространство Е квазиполно, то множество Q полно и потому компактно.
3.6.3. Одно приложение к дифференциальным уравнениям.
Пусть Г —интервал вещественной оси, F — конечномерное нор-
нормированное пространство и В — шар Jy — #oll^'> в /\ Рассмо-
Рассмотрим дифференциальное уравнение
•^-«/(f, х), x(tQ) = y0, C.6.1)
232 Гл. 3. Теоремы о неподвижной точке
где to^T и f: TxB-^F. Решением уравнения C.6.1) на Т бу-
будем называть функцию х: Т->В, обладающую в каждой точке
/gT производной, равной f(tyx(t)), и удовлетворяющую усло-
условию x(t0) =у0. Если функция / непрерывна и удовлетворяет усло-
условию типа Липшица по второй переменной, то, как было указано
в п. 3.1.3, методом сжимающих отображений доказывается суще-
существование и единственность решения уравнения C.6.1). Пеан о
[2] первый показал, что локальное решение этого уравнения су-
существует, хотя, возможно, и не единственно, если функция /
всего лишь непрерывна и ограничена, скажем \\f(t,y)\\^.M
(t^Ty у^В). Этот результат можно доказать, основываясь
на теореме Асколи (см., например, Колмогоров и Фомин
[1, стр. 108]). Ниже мы приведем доказательство, базирующееся
на тех же идеях, но использующее следствие 3.6.2.
Положим с = г/М и Г1 = ГП[/0 — c,to + c]. Введем банахово
пространство E = C(TUF) непрерывных функций х: T\->F с
нормой
II*II-sup {||jc(Oil: fe-71,}.
Каждому элементу х^Е сопоставим элемент и(х)^Еу опреде-
определенный равенством
t
u(x){t) = yo+\f{s, x(s))ds. C.6.2)
п
Если нам удастся установить, что отображение и обладает не-
неподвижной точкой х, то последняя и будет решением уравнения
C.6.1) на интервале ТхаТ.
Для доказательства существования неподвижной точки при-
применим следствие 3.6.2 к множеству Л, состоящему из тех точек
х&Е, для которых ||* — t/oll^f; здесь f/0 — постоянная функция,
принимающая значение у0 во всех точках интервала Т{. Про-
Проверим выполнение условий следствия 3.6.2.
Множество Л, очевидно, замкнуто и выпукло. Если /eTi и
5 принадлежит интервалу с концами t0 и /, то ||*(s) — yo\\ <>
для всякой функции xgA Так как ||f E, x(s)) || <1M на всей об-
области интегрирования в формуле C.6.2), то
Таким образом, отображение и переводит множество А в себя.
Докажем непрерывность отображения и на множестве А.
Если последовательность {xn)czA сходится в £ к точке хеД
то в силу равномерной непрерывности функции / на ТгхВ схо-
сходимость и(хп) (t) -+u(x) (/) в F имеет место равномерно относи-
относительно t^Ti. Итак, отображение и непрерывно на множестве Л,
3.6. Теорема Шаудера — Тихонова 233
Остается проверить, что множество и (А) относительно ком-
компактно в Е. Так как множество u(A)czA ограничено, а простран-
пространство F конечномерно, то достаточно (теорема Асколи) доказать,
равностепенную непрерывность множества и (А). Но если хеЛ
и t,t'& Tu то
\\u{x)(t)-u(x)(?)\\ = Uf{s, x{s))ds\^M\t-n
Таким образом, все условия следствия 3.6.2 выполнены, и тео-
теорема Пеано доказана.
Замечания. A) Налагаемое на F требование конечномер-
конечномерности существенно для справедливости теоремы.
B) Мы предположили, что /0 — внутренняя точка интервала
Т. Доказательство проходит и для концевых точек t0, если вне-
внести в него небольшие изменения.
3.6.4. Другое приложение к дифференциальным уравнениям,
На этот раз мы рассмотрим уравнение второго порядка
C.6.3)
на интеррале 0<^^Г с граничными условиями
х@) = х1 х(Т) = х2, C.6.4)
Следуя Бассу [1], докажем, что если f — ограниченная и не-
непрерывная функция на [0, TJxRXR, то задача C.6.3), C.6.4)
допускает по крайней мере одно решение.
Доказательство основано на следующем замечании. Если
ввести функцию
при
при
то всякое решение х интегрального уравнения
т
x(t) = Xl+ {x^]t -$G(t, s)f[s9 x(s), x'(s)]ds,
0
где штрих означает производную, является решением нашей за-
задачи.
Разрешимость интегрального уравнения может быть устано-
установлена с помощью следствия 3.6.2. Для этого возьмем в каче-
качестве Е банахово пространство непрерывно дифференцируемых
234 Гл. 3. Теоремы о неподвижной точке
на [О, Т] функций (на концах рассматриваются односторонние
производные) с нормой
sup {\x(t)\ + \x'(t)\}.
За А примем само пространство Е и отображение и определим
равенством
H(jc)(fl = *t+ (*'~*')' -JGQ, s)f[s, x(s), x'(s)]ds.
О
Легко проверяется, что и — непрерывное отображение простран-
пространства Е в себя. Чтобы можно было применить следствие 3.6.2,
остается только показать, что множество и(Е) относительно
компактно в Е. В силу теоремы Асколи для этого достаточно
доказать, что функции из множества и(Е) ограничены, так же
как их производные, причем множество производных равносте-
равностепенно непрерывно. Пусть |/|^М на [0, rjxRxR; полагая у =
= и(х)у имеем
МТ2
поскольку 0<G<r/4. Непосредственный подсчет показывает,
что
откуда
1/(*Ж lx2ZXl] +2MT
Таким образом, множество функций вида у = и(х), где х пробе-
пробегает Еу обладает всеми требуемыми свойствами, что и завер-
завершает доказательство.
Замечания. Относительно дальнейших приложений тео-
теорем о неподвижной точке к дифференциальным уравнениям см.
Кордуняну [1—4]. Следует отметить возможность приложе-
приложения к дифференциальным уравнениям и других функционально
аналитических принципов. См., например, Беллман [1], Мае-
сера и Шеффер [1—4] и приведенные там библиографии, а
также пример 7.2.6, ниже.
3.6.5. Приложение к рефлексивным банаховым простран-
пространствам. Пусть / — отображение банахова пространства Е в себя.
Обозначим через 1 тождественное отображение Е на себя. Воз-
Возникает вопрос, при каких условиях 1+/ является отображением
3.6. Теорема Шаудера — Тихонова 235
на. Если отображение f линейно, то, как хорошо известно, до-
достаточно выполнения условия ||/|| < 1. Действительно, в этом
оо
случае для любого элемента у^Е ряд 2 (—l)nfn(y) сходится
м = 0
в Е и имеет своей суммой элемент ху который удовлетворяет
условию x + f(x)=y. Мы, однако, применим следствие 3.6.2 к
случаям, когда отображение /, вообще говоря, нелинейно. Имен-
Именно, мы установим следующий результат.
A) Если слабо непрерывное отображение f переводит огра-
ограниченные множества в относительно слабо компактные и удо-
удовлетворяет соотношению
lim sup 1(^1 <1, C.6.5)
|| X || -> оо II Х II
то 1+/ есть отображение пространства Е на Е.
Для доказательства возьмем произвольную точку у ^Е. До-
Достаточно показать, что отображение и, определенное равенством
и(х)=у — /(*), обладает в Е неподвижной точкой. Мы сделаем
это, применив следствие 3.6.2 к пространству Е в его ослаблен-
ослабленной топологии. Обозначим через А шар {х: ||х|| <>}. Очевидно,
что в силу условий на отображение / сужение и\А непрерывно
и множество и (А) относительно компактно (и то и другое в
ослабленной топологии), каков бы ни был радиус шара г.
Остается добиться выполнения включения и {А) а А.
Положим
Л1(гН sup {||/(х) ||: || х ||< г}.
Из неравенства C.6.5) и локальной ограниченности отображе-
отображения f следует, что
Г->оо
С другой стороны, если ||л;|| О, то \\и(х) || •< \\y\\ +М(г). Итак,
если xg Л, то и и(х)^ А для достаточно больших г. Теперь для
завершения доказательства достаточно воспользоваться теоре-
теоремами 8.1.1, 8.3.5, 8.13.1 и следствием 3.6.2.
B) Если допустить, что пространство Е рефлексивно, то до-
доказательство упрощается, так как в этом случае из слабой не-
непрерывности отображения f следует, что / переводит ограничен-
ограниченные множества в относительно слабо компактные (каждое огра-
ограниченное множество будет относительно слабо компактно в силу
предположенной рефлексивности; см. § 8.4).
3.6.6. Теоремы Какутани и Фана о неподвижной точке. Ка-
к у т а н и [7] установил теорему о неподвижной точке для много-
многозначных отображений (т. е. для отображений, для которых
236 Гл. 3. Теоремы о неподвижной точке
образом точки является множество). Позднее Фан [1] получил
теорему, которая обобщает одновременно теорему Какутани
(с конечномерных на бесконечномерные пространства) и теоре-
теорему Шаудера— Тихонова. Мы приведем теорему Фана без дока-
доказательства. Она в этой книге не используется.
Теорема. Пусть Е — отделимое локально выпуклое простран*
ство, К — непустое выпуклое компактное множество в Е и f—•
многозначное отображение, которое каждому х^К ставит в со-
соответствие непустое выпуклое замкнутое множество f(x)czK.
Пусть далее отображение f полунепрерывно сверху в том смыс-
смысле, что если Хо е К и U — окрестность множества f(x0), то суще-
существует такая окрестность V точки лго, что множество f(x)czU
для каждого х е /СП V. Тогда существует точка х0 е /С, которая
является неподвижной для отображения f9 т. е. #о/()
3.7. Работы Лере и Шаудера
Еще в 1934 г. Лереи Шаудер [1] разработали и опублико-
опубликовали новый подход в теоремам о неподвижной точке. Мы не
ставим своей задачей воспроизвести здесь их результаты и от-
отсылаем интересующегося читателя к оригиналу. Все же пред-
представляет интерес знакомство с принципами, лежащими в основе
теории Шаудера — Лере, чтобы сравнить их с методами, кото-
которыми мы пользовались выше в этой главе.
Первым этапом в теории Шаудера — Лере было обобщение
понятия Брауэра о топологической степени, первоначально опре-
определенного лишь для отображений конечномерного простран-
пространства Е в себя. Шаудер и Лере распространили это понятие на
случай, когда Е — произвольное нормированное пространство.
Они исследовали (а) связь между разрешимостью уравнения
ВИДа x-f(x)=0
и топологической степенью отображения х*—>у = х — f(x) в точке
у = 0 и (Ь) инвариантность топологической степени при непре-
непрерывной деформации рассматриваемого отображения. Это иссле-
исследование было проведено в предположении, что отображение f
определено и непрерывно на замыкании ограниченного открьь
того множества Йс£и что множество /(Q) относительно ком-
компактно в Е.
*-fa(x)=0
Второй этап состоял в формулировке задачи в терминах раз-
разрешимости уравнения вида
я —М*)=0,
где ffl — элемент непрерывного семейства (fx) отображений опи-
описанного выше вида, Успех во многом зависит от семейства (/?,),
3.8. Теоремы о неподвижной точке 237
которое должно быть таким, чтобы для некоторого его элемента
fa вопрос разрешимости соответствующего уравнения
не представлял значительных трудностей.
Шаудеру и Лере удалось, действуя по только что описанной
программе, получить теоремы существования для дифферен-
дифференциальных уравнений в частных производных весьма общего
вида. Заметим, что второй этап потребовал большой изобрета-
изобретательности и глубокого предварительного изучения свойств весь-
весьма специальных (хотя все еще довольно общих) классов диф-
дифференциальных уравнений в частных производных. Краткое
изложение теории дано Мирандой [1, стр. 165 и далее]. Не-
Несколько упрощенное и сокращенное изложение, в котором ис-
используется лишь теорема 3.6.1 о неподвижной точке, дано в
книге Куранта и Гильберта [2, стр. 355—360].
Ясно, что принципы, используемые в методе Шаудера — Лере,
выходят за рамки тех, которые были использованы в этой главе.
Хотя применять их сложнее и труднее, тем не менее область их
приложений значительно шире.
Работа Лере и Шаудера явилась источником многочислен-
многочисленных обобщений и упрощений (см. Лере [3], Н а г у м о [1], А л ь т-
м ан [1, 2], Гр а на с [1], К л и [4], Браудер [7]).
3.8. Теоремы о неподвижной точке в упорядоченных множествах
Пикар в своей фундаментальной работе [1] указал на по-
полезность метода последовательных приближений при получении
теорем о неподвижных точках для отображений, которые преоб-
преобразуют упорядоченные множества в себя. Позднее этот метод^
был значительно развит Канторовичем [1]. Один из резуль-
результатов такого рода мы приведем здесь.
Предположим, что Е— (частично) упорядоченное множество
(п. 0.1.4). Допустим, что каждая ограниченная сверху возра-
возрастающая последовательность (хп) элементов из Е обладает в Е
верхней гранью и что каждая ограниченная снизу убывающая
последовательность (уп) элементов из Е обладает в Е нижней
гранью. Если при этих условиях х (соответственно у) есть верх-
верхняя (соответственно нижняя) грань последовательности (хп)
(соответственно (уп))> то будем писать хп\х* (соответственно
Уп\у). Читатель заметит, что тогда хп+\\х и уп+\\у.
Рассмотрим возрастающее отображение и: Е-+Е (т. е.
х"Су влечет и(х)^и(у)), такое, что из соотношений хп\х и
Уп\у следует, что и(хп)\и(х) и и(уп)\и(у) соответственно.
238 Гл. 3. Теоремы о неподвижной точке
3.8.1. Теорема. Пусть упорядоченное множество Е и отобра-
отображение и: Е-+Е удовлетворяют приведенным выше условиям.
Пусть далее существуют такие элементы *0, Уо s £", что
yo. C.8.1)
Определим последовательности (хп) и (уп) соотношениями
хп+1 = и (*„), уп+х = и (уп). C.8.2)
Тогда существуют такие точки х, у ^ Е> что
C.8.3)
причем х и у являются неподвижными точками отображения и.
Кроме того, если х* {соответственно у*)—неподвижная точка
отображения и такая, что х*^-хо (соответственно у*^Суо), то
х*^- х (соответственно у*-^у).
Доказательство. Из первого неравенства C.8.1) сле-
следует, что и(хо)-*Си(уо)\ из остальных неравенств C.8.1) по ин-
индукции получаем
х0 < хх < ... <хп Ку п '< yn_i < .. . <у0. C.8.4)
Таким образом, последовательность (хп) возрастает и ограни-
ограничена сверху элементом у0, поэтому хп\х для некоторого х^Е.
Аналогично уп\у для некоторого у^Е. Из C.8.4) вытекает, что
хп -*Сут при п^- т, что влечет х~*Сут для всех т и, следователь-
следовательно, х-*Су. Соотношения C.8.3) установлены. Так как хп\х, то
и(хп)\и(х). С другой стороны, хп+\\х и xn+i = u(xn), откуда сле-
следует, что х = и(х). Аналогичным образом получаем у = и(у).
Итак, х и у — неподвижные точки отображения и.
Пусть, наконец, х* — такая неподвижная точка отображения
и, что х* > х0. Тогда
Повторяя это рассуждение, приходим к тому, что х* ^> хп для
всех п, поэтому х* J> x. Таким же способом можно доказать, что
если у* — неподвижная точка отображения и, такая, что #*^*/о,
то у*-*Су. I
3.8.2. Пример. Рассмотрим отображение и описанного в
п. 3.1.3 типа, а именно
t
jf(s, x(s))dst C.8.5)
где rjо — вещественное число, f — функция на TxR, a T— интер-
интервал, содержащий точку t0. В C.8.5) х обозначает переменную
вещественную функцию на Г, а / — переменную точку интерва-
3.8 Теоремы о неподвижной точке 239
ла Т. Предположим, что / — такая вещественная измеримая на
TxR функция, что отображение x*—^f(t,x) возрастает при ка-
каждом (еГи
\f(t, C)\dt<
/'.
для каждого вещественного числа с. В качестве Е можно, на-
например, взять множество всех вещественных ограниченных из-
измеримых на Т функций, наделенное естественным порядком.
Легко проверяется, что множество Е удовлетворяет условиям
теоремы 3.8.1 и что и — возрастающее отображение множества £
в себя. Далее, если последовательность (хп) ограничена и моно-
монотонно сходится к л:, то и последовательность и(хп) таким же
образом сходится к и(х) (см. теорему 4.6.6). Для того чтобы
воспользоваться теоремой 3.8.1, остается только убедиться в
существовании элементов хо,уо^Е, удовлетворяющих условиям
C.8.1). Предоставляем это читателю.
Заметим, что при довольно слабых ограничениях на функцию
/ отображение и преобразует каждый элемент х^Е в непре-
непрерывную функцию. Если при этом функция f непрерывна, то из
соотношения и(х)=х будет следовать, что функция х удовле-
удовлетворяет дифференциальному уравнению
во всех внутренних точках интервала Т. Даже если функция f не
непрерывна, функция х удовлетворяет этому дифференциаль-
дифференциальному уравнению почти всюду на Т.
Упражнения
3.1. Пусть Е — банахово пространство, Л — открытое выпуклое множе-
множество в Е и / — непрерывное отображение множества А в себя. Пусть далее
отображение / непрерывно дифференцируемо на Л в том смысле, что каж-
каждой точке хеЛ соответствует такой непрерывный эндоморфизм Ах простран-
пространства £, непрерывно зависящий от точки яе=Л, что
f(x + h)-f(x)=Ax(h)+o(\\h\\) при
при этом о(||Л||) может зависеть от х. Допустим, наконец, что ||ЛХ||^Я для
всех *е=Л, где К<\.
Доказать, что отображение f обладает единственной неподвижной точ-
точкой в А.
[Указание. Доказать, что f — сжимающее отображение. Для этого
показать, что если t\—>x(t)—дифференцируемое отображение веществен-
вещественного интервала в Л, то
d с / /у\ \ л dx
f((t)) A
240 Гл. 3. Теоремы о неподвижной точке
так что
X
/Ы-/(*о)= J Axw^f
для всяких двух точек х0, х{^Л и любой лежащей в Л дифференцируемой
кривой th-*-x(t), такой, что *(O)=*o и x(l)=xi.]
Замечание. Условие выпуклости множества Л может быть ослаблено,
если имеется дополнительная информация относительно К\ такое ослабление
может быть также иногда достигнуто использованием результатов Э д е л ь-
штейна [1, 2].
3.2. Пусть Е — банахово пространство и Г — непрерывный эндоморфизм
пространства £, удовлетворяющий условию ||Г|| < 1. Применяя принцип сжи-
сжимающих отображений к сужению отображения и(х)^=Т(х) +у на шары пере-
переменного радиуса с центром в нуле, доказать, что отображение, обратное к
1 — Г, является непрерывным эндоморфизмом пространства Е с нормой, не
превосходящей A — ИГР).
Получить то же самое, рассмотрев так называемый ряд Неймана
П 0
[Указание. Отображение и есть сжатие шара с центром в нуле и ра-
радиусом г, если \\у\\^ A — IIГЦ)г.]
3.3. Пусть X, Y и Z — нормированные пространства, причем простран-
пространство X полно, и пусть f: X->Y и g: X -> Z — линейные отображения. Допу-
Допустим, что система уравнений
f(x)=y, g{x)=z
для заданных y^Y и zeZ обладает единственным решением х^Х, причем
это решение удовлетворяет условию
при некоторых постоянных р и q. Пусть F — такое отображение шара
S = {xs=X: |UHx<r}
в У, что
\\F{x)-F(x')\\Y<:%\\x-x\\x (x.je'eS)
для некоторого Я. Доказать, что система
f(x) = F(x), g(x)-z
допускает единственное решение x^Sf если qX<\ и
[Указание Рассмотреть отображение Г: S->X, определенное таким
образом, чтобы для каждого элемента ueS элемент х=Ти был единственным
решением системы
f(x)=F(u)9 g(x)=z.
Доказать, что при сформулированных условиях отображение Г: S->S сжи-
мающе, и воспользоваться принципом сжимающих отображений.]
Замечание. Этот метод был применен Кордуняну [5, теорема 1]
К задачам, связанным с обыкновенными дифференциальными уравнениями.
Упражнения 241
3.4. Подпространство У топологического пространства X называется
ретрактом пространства X, если существует непрерывное отображение
f:X->Y, оставляющее неподвижной каждую точку множества Y.
Показать, что Y обладает свойством неподвижной точки, если им обла-
обладает пространство X, a Y является ретрактом в X.
Замечание. Стоит отметить, что суть доказательства леммы 2 § 3.6
заключается в обосновании того факта, что всякое замкнутое выпуклое мно-
множество предгильбертова пространства является ретрактом любого компакт-
компактного множества, которое его содержит.
3.5. Пусть отделимое локально выпуклое пространство Е квазиполно
(т. е. каждое его ограниченное замкнутое множество полно), множество
А с= Е компактно и К — его замкнутая выпуклая оболочка в Е. Доказать,
что если А — ретракт в /С, то множество А обладает свойством неподвижной
точки.
[Указание. Доказать компактность множества К и затем применить
предыдущее упражнение вместе с теоремой Шаудера — Тихонова.]
3.6. Обозначим временно через F вещественное или комплексное поле
скаляров, а через К непрерывную функцию [О, 1]Х[0, \]XF->F, Для г^О
положим
М (г) - sup {I * (<, s, Е) |: 0<*<1, 0<s<l, |sf, 1Е|<л>.
Пусть
ее С ([0, l],F)
II а || = sup {\а @ |: 0 < t < 1}.
Доказать, что если М(ЦаЦ+г)^г для некоторого г^О, то уравнение
1
х @ + J К (/, s, x(s))ds = a (t) @ < t < 1)
о
обладает решением х^С([0, 1]. F).
Вывести отсюда, что указанное интегральное уравнение разрешимо для
всякой функции йе С([0, 1], F), если
lim inf/■■%(/-)< 1.
Г->°о
[Указание. Приспособить метод, использованный в п. 3.6.3.]
3.7. Пусть Е — метрическое пространство и f: Е -> Е — такое отображе-
отображение, что
d(f(x),f{y))<d(x,y)
для х, у^Е и хфу^. Допустим, что точка х0 е Е такова, что последователь-
последовательность (хп) итераций Xn = fn(x0) содержит подпоследовательность, сходя-
сходящуюся к точке х^^Е. Доказать, что х^ — единственная неподвижная точка
отображения / (Э д е л ь ш т е й н [2]).
[Указание. Единственность очевидна. Остальное доказывается от про-
противного. Пусть f(xco) фХоь. Рассмотрев функцию
d (f (x), f (у))
d (x, у)
на факторпространстве ЕХЕ/А (Л — диагональ произведения ЕуЕ), дока-
доказать существование такого числа г<\ и такой окрестности U точки (*»,
Г(•*«)), что
), f(y))<rd(x,y)
242 Гл. 3. Теоремы о неподвижной точке
для (х, у) е U. Выбрать число г'>0 настолько малым, чтобы
и
Г'< J<*(/(*oo)p*oo).
Выбрав подпоследовательность (хпА> сходящуюся к х^ показать, что
d(xn , хп + Л > г' при /г > &0 и что для А > /г > kQ имеет место неравенство
причем г -> 0 при Л->оо. Это дает требуемое противоречие.]
3.8. Пусть £ — топологическое векторное пространство, М — подмножество
в £ и (я^)— сильно ограниченная последовательность в £', порождающая
сильно плотное векторное подпространство в Е\ Пусть / — такое отображе-
отображение множества М в себя, что для некоторой точки х0 е М последователь-
последовательность итераций хп = fn (x0) содержит ограниченную подпоследовательность,
^имеющую слабую предельную точку х^ е М. Допустим, наконец, что
для всех х.у^Е и всех т, причем при х Ф у строгое неравенство имеет ме*
сто по крайней мере для одного значения т. Доказать, что Хоо — единствен-
единственная в М неподвижная точка отображения /.
[Указание. Ввести на Е метрику
и применить предыдущее упражнение.]
3.9. Пусть Е — топологическое векторное пространство, А — непрерыв-
непрерывный эндоформизм пространства £, такой, что его сопряженный А' обладает
последовательностью собственных векторов, каждый из которых принадле-
принадлежит собственному значению, модуль которого строго меньше 1. Допустим,
что эта последовательность сильно ограниченна, тотальна на £ и порождает
сильно плотное векторное подпространство в Е\ Пусть задан элемент у^Е.
Предположим существование такого элемента хо^Е, что последовательность
(Хп), определенная соотношением
обладает ограниченной подпоследовательностью, имеющей слабую предель-
предельную точку Хоо е Е. Доказать, что #«> — единственное содержащееся в Е ре-
решение уравнения х — Ах = у.
[Указание. Пусть хт — собственные векторы эндоморфизма А'. По-
Положить f{x) = Ax + y и применить упражнение 3.8.]
3.10. Пусть 1<р<оо, z/e=Z/(O, оо), К е L1 @, оо). Каждому эле-
элементу х е Lp @, оо) сопоставим функцию
t
Кх (t)= J x(t-s)K (s) ds.
См.- п. 0.2.21. — Прин. перев.
Упражнения 243
Показать, что К — непрерывный эндоморфизм пространства Lp (О, оо) и что
справедливо по крайней мере одно из двух следующих утверждений:
(а) для каждого х е Lp@, оо)
lim \\к»х 1Д
b) уравнение x — Kx=y имеет единственное решение x^Lp@, оо).
Примечание. Следует учесть относительную слабую компактность
ограниченных множеств в L? и тот факт, что пространство, сопряженное
к Lp> отождествимо с пространством Lp'% если \<р< оо и 1—у = 1. Эти
факты доказываются в гл. 4.
[Указание. Применить упр. 3.9, приняв за хт функции
11—> e~lm\
где Цт) — соответствующим образом подобранная последовательность ве-
вещественных чисел |
3.11. Пусть X— топологическая полугруппа, Cbd(X)—пространство ве-
вещественных ограниченных непрерывных функций на X. Положим af(x) =
= f(ax) для f^Cbd(X), a, xel Л евоинвариантное среднее на X — это та*
кая положительная линейная форма f\—> |я(/) на Сьй(Х), что fx(l) = l и
M'(a/)=M'(f) для всех aEl и всех f ^Cbd(X). [Правоинвариантное среднее
определяется аналогично с заменой левого сдвига af на правый сдвиг
fa(x)—f(xa)] Доказать, что для существования левоинвариантного среднего
на X необходимо и достаточно, чтобы полугруппа X удовлетворяла следую-
следующему условию:
если /i, ..., fn <= Сьа (X) и a\t ..., an e А", то
SUP (f,-„/, + ••• +fn-ajn)>°-
[Указание. Для доказательства достаточности рассмотреть векторное
подпространство L в Cbd(X), порожденное элементами вида / — af, и от-
открытое выпуклое множество /С, образованное теми элементами £, для кото-
которых sup g < 0. Применить теорему 2.1.1.]
Примечания. Этот результат принадлежит Д и к с м ь е [3, теоре-
теорема 1] и использован им для доказательства ряда утверждений относительно
существования или отсутствия инвариантных средних. Ср. с упр. 2.15.
3.12. Это упражнение посвящено одному из вариантов теоремы 3.3.1.
Пусть 5 — полугруппа с правоинвариантным средним, которое будем
обозначать через J ... ds. (Определение такое же, как и в предыдущем
упражнении, только вместо X рассматривается полугруппа, 5, наделенная
дискретной топологией.) Пусть Е — вещественное векторное пространство.
Предположим, что каждому элементу s^S поставлен в соответствие эндомор-
эндоморфизм Ts пространства Е таким образом, что Tss,= TSTS,, s, sf e S. Пусть
далее L — векторное подпространство в £, инвариантное относительно ка-
каждого эндоморфизма Ts и р — калибровочная функция на £, такая, что
p(Tsx)^p(x) для s ^ S, х е Е. Пусть, наконец, /0 — такая линейная форма
L, что
f о (*)</>(*), h{T,x)~ft(x) (s<=S,x<=L).
Доказать, что существует линейная форма f на £, удовлетворяющая усло-
условиям
/М<Р(*), f(Tsx) = f(x) (s<=S,xe=E)
и
f\L-f9.
244 Гл. 3. Теоремы о неподвижной точке
[Указание. Сначала так продолжить fo до линейной формы fi на Et
чтобы fi^p, затем положить
ь
f(x)-ffi(Tsx)ds.]
Замечания. Сравните это упражнение с упр. 2.15. Настоящий ре*
зультат менее тонок и применим только тогда, когда элемент g (из упр.
2.15) удовлетворяет условию Inf g>0. С другой стороны, этот результат
обладает более широкой областью применения. То, что в упр. 2.15 требуется
существование левоинвариантного среднего, объясняется тем фактом, что
эндоморфизм Т8 действует на функции х, определенные на множестве Q,
по правилу T8x=x°s9 где s — отображение множества Q в себя. Поэтому
TsTs,x— *°(s'°s), так что равенство TsTsr=Tss, выполняется, только если
полугрупповое произведение ss' означает s'° s (а не более привычное soS').
Это обращение порядка сомножителей и объясняет перестановку «левого»
и «правого».
ГЛАВА 4
Топологические сопряженные
к некоторым пространствам; меры Радона
4.0. Предисловие1)
Роль предисловия играет следующий параграф,
4.1. План главы
Пусть Г={/} — топологическое пространство. Наша цель —
подробно изучить некоторые весьма важные топологические
векторные пространства, являющиеся подпространствами про-
пространства Кт или их факторпространствами, и сопряженные к
ним пространства. Обычно мы будем считать, что Т локально
компактно; как правило, это предположение не является слиш-
слишком стеснительным. Хотя меры Радона и распределения Швар-
Шварца— понятия родственные, нам удобнее рассмотреть их по от-
отдельности в этой главе и в следующей.
Что касается мер Радона, то связанные с ними топологиче-
топологические векторные пространства строятся следующим образом.
Сначала берется «минимальное» пространство о%°(Г), состоя-
состоящее из непрерывных числовых функций на Г, имеющих ком-
компактный носитель. Если Т компактно, то это пространство со-
совпадает с более привычным банаховым пространством С(Т)
непрерывных числовых функций, наделенным естественной нор-
нормой
В пространстве <Ж(Т) вводится локально выпуклая топология
индуктивного предела, которая определяется лишь в § 6.3; тем
не менее мы можем пока пользоваться соответствующим опре-
определением секвенциальной сходимости во?Г(Т). Впоследствии
окажется, что линейные формы нае2Г(Г), непрерывные относи-
относительно этой сходимости, образуют топологическое сопряжен-
сопряженное к Ж(Т). Эти линейные формы и являются так называе-
называемыми мерами Радона на Т. Одна из наших задач — показать,
что каждая мера Радона, определенная таким образом, может
быть разложена в линейную комбинацию положительных мер
*) Параграфа с этим номером у автора почему-то нет. Мы включили его
для единообразия. — Прим, ред.
246 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Радона (т. е. таких мер, которые каждой положительной функ-
функции изo?t(T) ставят в соответствие положительное число) и что
действие всякой положительной меры Радона сводится к ин-
интегрированию относительно некоторой меры, понимаемой уже
как функция множества и определенной по крайней мере для
всех борелевских подмножеств в Т. Этим и объясняется тот
факт, что слово «мера» используется в названии объекта, ко-
который первоначально вводится как линейная форма на o/f(T).
По мере продвижения вперед мы будем вынуждены развить
теорию интегрирования относительно заданной положительной
радоновой меры \х на Т и тем самым выборочно изложим ре-
результаты данного Бурбаки чрезвычайно широкого развития
идей Даниэля и Ф. Рисса (см. Бурбаки [8]) с учетом незна-
незначительных вариаций, представленных в работе Эдварде [3];
см. также Хьюитт и Росс [1].
На первый взгляд естественно возникающая задача продол-
продолжения линейной формы \х с подпространства Ж(Т) на более
широкое подпространство пространства Кт кажется разреши-
разрешимой с помощью теоремы Хана — Банаха. И действительно,
такое решение возможно. Однако такое продолжение далеко
не единственно и, как правило, аналитически совершенно не-
неудовлетворительно, ибо оно приводит к интегралам по конечно
аддитивной мере, для которых нет мощной теоремы сходимо-
сходимости, характеристической для интегралов типа Лебега. Поэтому
мы используем конструктивное продолжение линейной формы,
несмотря на то что этот путь гораздо сложнее. В резуль-
результате мы приходим к пространствам Лебега LpG\ ji), ассо-
ассоциированным с данной положительной мерой Радона \х. Сле-
Следующим этапом является изменение этих пространств и их
сопряженных.
Мы начнем с изучения простого частного случая, когда про-
пространство Т дискретно; при этом все топологические ограничения
становятся излишними (все функции непрерывны, все мно-
множества открыты и т. д.) и в качестве объекта исследования вы-
выступают одни меры. Весьма важен случай T = N (N — множе-
множество натуральных чисел). В этом случае пространства Лебега
по существу сводятся к пространствам последовательностей /р.
Этот пример заслуживает отдельного рассмотрения ввиду его
относительной простоты. Это рассмотрение осуществляется в
§ 4.2. Изложение основных вопросов начинается с § 4.3.
4.2. Банаховы пространства 1р(Т) и со(Т)
Пусть Г —произвольное множество. Его можно рассматри-
рассматривать как локально компактное пространство в дискретной то-
топологии, что согласуется с общей схемой настоящей главы,
4.2. Банаховы пространства lp(T) и со(Т) 247
Пусть задано число р > 0. Обозначим через 1р(Т) подпро-
подпространство в Кт, состоящее из всех тех элементов х е /Сг, для
которых
В случае р — оо пространство 1°°(Т) состоит из тех и только тех
элементов хе/(т, которые ограничены, т. е. для которых
Предположим вначале, что 1<1р-<1оо, и определим сопря-
сопряженный показатель р' равенством h—-=1, причем р'=1
при р = оо и р' = оо при р = 1. Тогда из неравенств Гёльдера и
Минковского следует, что
x(t)y(t)\K\\x\\p-\\y\\p, D.2.1)
\\р + \\у\\р D.2.2)
для функций х, у е /Ст с конечным носителем. (См. также
п. 4.11.2.) С помощью очевидного предельного перехода по-
получаем, что формула D.2.1) остается справедливой, когда функ-
функции х и у принадлежат соответственно пространствам 1Р(Т)
и 1Р' G), а неравенство D.2.2) имеет место для х, у^1р(Т).
Из формулы D.2.2) следует, что отображение х\—> \\x\\v есть
норма на 1р(Т). Легко проверяется, что пространство 1р(Т)
банахово, если 1-^р^оо.
Пространство со(Т) можно определить как замыкание в
1°°(Т) множества функций х с конечным носителем. Оно также
является банаховым пространством, если его наделить нормой,
индуцированной нормой IUIU. Пространство со(Т) состоит из
тех и только тех функций х е Кт> которые обращаются в нуль
на бесконечности, т. е. обладают следующим свойством: каж-
каждому числу 8>0 соответствует такое конечное ( = компактное)
множество F в Г, что \x(t)\<z при t<=T\F.
Пусть теперь 0</?<1. Тогда рг отрицательно и неравен-
неравенство D.2.1) не/ имеет места. Соотношение D.2.2) также не-
неверно, ибо в действительности выполняется неравенство
Ip + llj/llp, D.2.2*)
причем равенство здесь имеет место только в случае, когда
х = ау для некоторого числа а (см. Хард и, Литтлвуд н
Полна [1, стр. 45 и 150]).
248 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Существует, однако, неполная замена соотношения D.2.2),
получаемая из элементарного числового неравенства
2Р~1 (ар + Ьр) < (а + Ь)р < ар + &р> D.2.3)
справедливого при 0<р<1 для чисел а, b^-О. Из этого не-
неравенства легко выводятся соотношения
D.2.4)
\\х + у\\р^2~~\\\х\\р + \\у\\р). D.2.5)"
Эти неравенства нельзя улучшить, так что при р < 1 отобра-
отображение х*—HUHp уже не является" нормой. Тем не менее №{Т)
будет полным метризуемым топологическим векторным ф
странством, если его наделить топологией, определяемой мет-
метрикой d(x9 y) = \\x-y\fp.
Если 0 < р < 1 и множество Т бесконечно, то полученное
таким образом топологическое векторное пространство /р(Т) не
является локально выпуклым. Чтобы в этом убедиться, доста-
достаточно построить ограниченное множество X в 1р(Т), выпуклая
оболочка которого У неограничена. Так как множество Т бес-
бесконечно, то можно выбрать такую последовательность (tn) эле-
элементов из Г, что tm4*tn для тфп. Пусть хп — элемент из
№(Т)9 принимающий значение 1 на tn и равный нулю для вся-
всякого t = tn. Тогда ||*п||р=1 и множество Х = {хп: п= 1, 2,...}
ограничено в 1*(Т). Выпуклая оболочка У множества X со-
содержит каждый из элементов вида
yn = j[(xi+ ... +хп).
Прямым подсчетом можно убедиться в том, что || уп \\р = пр .
Однако выражение пр стремится к бесконечности при я->оо;
следовательно, множество У неограничено в 1Р (Г).
Значительно более интересен случай 1^р<сю, для которого
имеет место следующий важный результат.
4.2.1. Теорема. Если 1^р<оо, то сопряженное к № может
быть отождествлено (как банаховское пространство) с про-
пространством 1рг таким образом, что при этом отождествлении
каждому элементу х' е 1р/ сопоставляется линейная форма
X'(x)~%x(t)x'(t). D.2.6)
teT
4.3 Пространство, сопряженное к &(Т); меры Радона 249
Доказательство. Для каждого t определим функцию
следующим образом:
1 при s = t,
0 при s¥=t.
Функция et принадлежит каждому из пространств /р. Так как
рфоо, то каждый элемент х&1? может быть записан в виде
сходящегося в № ряда 2 x(t)et.
Следовательно, если f — непрерывная линейная форма на /р
и если положить x'(t) = f(et), то
f{x)=%x(t)x'(t),
te=T
где ряд в правой части автоматически сходится для каждого
х е h. Более того, так как форма/ непрерывна, то
Выбирая соответствующим образом элемент х, легко видеть,
что #'^/р'. Обратно, пусть xr^.lpr. Тогда из неравенства
Гёльдера для сумм следует, что сумма в правой части равен-
равенства D.2.6) является непрерывной линейной формой на /р, нор-
норма которой совпадает с ||я'||Р'. I
Замечание. В случае р = оо теорема 4.2.1 неверна: про-
пространство, сопряженное к /°°, «содержит» Iх в качестве собствен-
собственного векторного подпространства.
4.2.2. Теорема. С помощью соотношения D.2.6) простран-
пространство, сопряженное к с0, можно отождествить (как банахово
пространство) с пространством I1.
Доказательство, Рассуждения весьма похожи на те,
которыми мы пользовались при доказательстве предыдущей
теоремы. Провести их предоставляется читателю (см. упр.
1.4). |
4.3. Пространство, сопряженное квЯГ(Г);
меры Радона
Всюду в оставшейся части настоящей главы через Т будет
обозначаться отделимое локально компактное пространство.
Если на Т будут накладываться еще какие-либо ограничения,
то это будет специально указываться. Под Ж{Т), или точнее
№К(Т), понимается векторное подпространство в Кт, состоящее
из непрерывных функций с компактным носителем. Поле скаля-
250 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
ров К — это R или С. При изучении линейных форм на ЖК{Т)
достаточно рассмотреть их поведение на e2TR (Г). Более того,
достаточно ограничиться исследованием вещественных линей-
линейных форм на e?fR(T). В дальнейшем мы будем пользоваться
символом о/Г(Т) для обозначения пространства e3TR (T).
Опишем теперь тот тип непрерывности линейных форм на
e2fV(T), который и характеризует их как меры Радона (ср. с
п. 2.1.8).
Определение. Пусть (хп) — последовательность (или сеть)
в оУСк(Т). Будем писать хп—*>0, если (а) существует компакт-
компактное множество £ в Г, содержащее носитель функций хп при каж-
каждом п9 и (Ь) последовательность (хп) равномерно сходится к
нулю на Т. В этом случае будем говорить, что (хп) сходится к
нулю в оуГк (Т).
Если функции хп принимают вещественные значения, то эта
сходимость, очевидно, не зависит от того, рассматриваются ли
хп как элементы нзс/Г(Г) или из о7Гс{Т).
4.3.1. Комплексной мерой Радона на Т называется линейная
форма ф нас2Гс(Г), непрерывная в следующем смысле: если
(хп) cze?tc(T) и хп—»0, то Нтф(д:п) =0. Если пространство
о%Гс(Т) заменить пространством^ (Г), рассматриваемым как
вещественное векторное пространство, то получим соответствен-
соответственно понятие вещественной меры Радона на Т.
Читатель легко проверит, что линейная форма ф на е2Гс(Г)
(соответственно нае2Г(Г)) тогда и только тогда удовлетворяет
условиям определения 4.3.1, когда каждому компактному мно-
множеству К в Т соответствует такое число тк, что
\у{х)\<тк\\х\\оо D.3.1)
для всякой функции x^(£Fc(T) (соотв. (Ж(Т)), носитель которой
содержится в К. Предвосхищая результаты § 6.3, можно указать
на существование ъ<Жс{Т) (соотв. во^(Т)) локально выпуклой
топологии, в которой непрерывность линейных форм равносильна
выполнению условия D.3.1). В соответствии с этим мы будем
говорить об определении 4.3.1 или об эквивалентном соотноше-
соотношении D.3.1) как об условии, выражающем непрерывность мер
Радона.
Легко видеть, что каждая вещественная мера Радона мо-
может быть так продолжена с Ж(Т) на ЖС(Г), что она становит-
становится комплексной мерой Радона, которая однозначно представима
в виде а-И"р, где а и р — вещественные меры Радона. Поэтому
достаточно рассмотреть подробно вещественные меры Радона.
4.3 Пространство, сопряженное к $С (Т); меры Радона 251
Менее очевидна возможность представления всякой веще-
вещественной меры Радона в виде разности двух положительных мер
Радона.
4.3.2. Теорема. Пусть К — вещественная мера Радона на Т.
Тогда существует единственная пара положительных мер Радона
К+ и Аг, обладающая следующими свойствами:
(a) Я = Х+ — Ат;
(b) если а и р— такие положительные меры Радона, что
Х = а — C, то а — Х+=р— К~ является положительной мерой
Радона на Т.
Говорят, что (а) представляет собою минимальное разложе-
разложение меры А,, а меры А,+ и Аг называют соответственно положи-
положительной и отрицательной частью меры А,.
Доказательство. Как легко видеть, единственность сле-
следует из условия (Ь).
Обращаясь к доказательству существования, положим для
каждого х из сЖ+ (Т) (множества положительных функций из
Ж(Т))
Ясно, что Х+(х)^0 и Х(х)^К+ (х). Покажем теперь, что
функция Я+ аддитивна на в^Г+(Г), т. е. что
для хи х2<=е7?+(Т). Если yi^QT+(T) и &<*, (/=1, 2), то
У\ + у2^ е/Г+ (Г) и уг + у2 ^ Х\ + хъ откуда непосредственно сле-
следует, что
+(
С другой стороны, пусть у е gT+ (Г) и у < xj + *2. Положим
г/! = sup (г/ — л:2, 0) и г/2 = i^f (г/, х2). Обе эти функции принадле-
принадлежат gT+ (Г) И
Таким образом,
^2) = Л (у).
Аддитивность К+ устанавливается теперь переходом к верхней
грани в правой части неравенства.
Аналогичными рассуждениями приходим к равенству
для > +()
Эти свойства позволяют продолжить линейным образом Х+
на все пространство еТ(Г). Действительно, каждая функция
252 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
2F() может быть многими способами представлена в виде
разности х\—х2/где хи х2&<2%*+(Т). В силу аддитивности зна-
значение К+(х\) —К+(х2) не зависит от этого разложения, и поэтому
его можно принять за определение %+(х). Таким образом, А,+
есть положительная линейная форма на о/Г (Г), положитель-
положительность которой обеспечивает выполнение условия D.3 1) 1). Итак,
^ — положительная мера Радона. Так как К+ (х) > К(х) для
х е е^Г+(Г), то линейная форма Х~ = %+ — К также является по-
положительной мерой Радона. Таким образом, пара (V, Аг) удо-
удовлетворяет условию (а).
Остается показать, что для этой пары справедливо (Ь).Если
Г) и у<ху то
Значит, Х+(х) ^Са(х), и, следовательно, мера а — Я+ положи-
положительна. Аналогично доказывается положительность меры
Р —Аг. I
Доказанная теорема позволяет нам ограничиться подробным
изучением лишь положительных мер Радона на Т, т. е. поло-
положительных линейных форм насЯГ(Г). Для краткости всюду в
оставшейся части главы вместо слов «положительная мера Ра-
Радона» будем говорить «положительная мера».
4.4. Некоторые примеры
Прежде чем перейти к весьма обширной теории интегриро-
интегрирования относительно положительной меры, приведем ряд при-
примеров мер Радона.
4.4.1. Атомарные меры. Пусть Т — отделимое локально ком-
компактное пространство. Обозначим через е* линейную форму на
в%*(Т) (или ее естественное продолжение нас^с(Г)), опреде-
определенную равенством
et{x)=x(t). D.4.1)
Мера et положительна. Ее часто называют мерой Дирака, со-
сосредоточенной в точке /. Физики часто, в случае когда Т есть
!) Действительно, пусть К — компактное подмножество в Т. На осно-
основании леммы Урысона (п. 0.2.12) существует функция у K(t) e <з%Г+(Г), нигде
не превосходящая единицы и равная единице на К. Из соотношения
верного для любой функции х е $С (Т), носитель которой содержится в К,
вытекает, что
- М« я+ (Ук)<l+ W < ы~ х+ (У к)-
Следовательно, соотношение D.3.1) имеет место при пг„ = Х+ (#jA — Прим.
перев.
4А Некоторые примеры 253
числовое пространство Rn, обращаются с мерой е* так, как если
бы она была функцией. Это частично оправдывается тем, что
при T=Rn мера е* в некотором смысле является пределом функ-
функций (точнее, слабым пределом в пространстве, сопряженном к
сЖ(Т), некоторой последовательности линейных форм, обладаю-
обладающих плотностями относительно меры Лебега; см. п. 4.4.3).
Более общим образом можно взять функцию [бСги попы-
попытаться определить меру Радона ji на Т формулой
|х(*Н2/@*@. D.4.2)
предполагая при этом, что ряд в правой части безусловно схо-
сходится для каждой функции х^о/^(Т). Тогда естественно ввести
обозначение
2 D.4.3)
причем этот ряд безусловно сходится в смысле слабой тополо-
топологии пространства, сопряженного ко?Г(Т). Меры такого вида на-
называются атомарными. Сходимость ряда D.4.2) эквивалентна
условию
2 l/WK+oo D.4.4)
для каждого компактного множества К из Г. (Подробнее см.
Бур баки [8, гл. V, § 5.10] и Эдварде [16, стр. 377—384].)
4.4.2. Меры Лебега. Пусть Т есть пространство Rn. Если
х^о?Г(Т) и Q — гиперкуб, вне которого функция х равна нулю,
то интеграл Римана
/.../*(*„ ..., tn)dtx... dtn-fx(t)dt
Q Q
существует, его значение не зависит от Q и может быть обозна-
обозначено просто через J x(t)dt. Этот интеграл как функция от х
является положительной мерой, которую мы назовем мерой
Лебега на Rn; впрочем, имя Лебега связано и с более общей
теорией интегрирования, о которой мы еще будем говорить.
Эта мера на Rn имеет особое значение в силу ее инвариант-
инвариантности относительно сдвигов. Мера Лебега на Rn — единственная
с точностью до постоянного множителя мера Радона на Rn, для
которой интегралы от всех сдвигов заданной функции
^GG^(Rn) равны между собой.
В более общем случае, когда Т — локально компактная
гРуппа, существует аналогичная единственная мера Радона на
** инвариантная относительно всех левых сдвигов. Это так
254 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
называемая левая мера Хаара на Т. Так же определяется правая
мера Хаара (§ 4.18). Меры Хаара широко используются при
исследовании различных функциональных пространств над
группами.
4.4.3. Плотности. Пусть Т—произвольное отделимое локаль-
локально компактное пространство, ji — заданная мера Радона на Г,
f — заданная непрерывная функция на Т. Легко видеть, что фор-
формула
v(x)=lx(fx) D.4.5)
определяет новую меру Радона v на Т. Ее обозначают через
f'\i. В действительности же (если, забегая вперед, воспользо-
воспользоваться результатами § 4.13) мера f*\i вполне определена для
всякой локально интегрируемой относительно \х функции /.
В таком случае говорят, что f*\x — мера с плотностью f отно-
относительно ix или что для меры v = f-\x функция f является произ-
производной по |ш и пишут f=-j^-- Круг вопросов, связанных с этой
ситуацией, довольно подробно изложен в § 4.13—4.15.
Пусть T=Rn и ji — мера Лебега. Утверждение (п. 4.4.1), что
мера Дирака st не является функцией, означает, что не суще-
существует никакой функции / (локально интегрируемой по мере Ле-
Лебега), для которой 8/ = f«ji. С другой стороны, как говорилось
в п. 4.4.1, можно найти такую последовательность (/п) непре-
непрерывных функций (даже функций из eT+(Rn)), что e* = lim fn - \х
в слабой топологии пространства,.сопряженного ко^(Кп). Дей-
Действительно, для этого достаточно взять такие непрерывные функ-
функции fn > 0, что
и /п = 0 вне шара с центром в точке /, радиус которого стремится
к нулю при п-^оо.
Другой распространенный способ выбора последовательности
(fn) таков:
МО = <Vr-l <'-"\
где \?—1\ —обычное расстояние между точками t и V, а числа
сп>0 выбраны так, чтобы \i(fn) = 1. Последовательность функций
(fn) поточечно сходится к нулю в точках, отличных от /, и к
Ч-оо в самой точке L Таким образом, последовательность \x(fnx)
сходится к x(t)=et(x) для каждого x^o?f(Rn).
4.4.4. Меры Лебега — Стилтьеса. Понятия, введенные в
п. 4.4.2, допускают ряд важных обобщений. Хотя эти обобщения
можно провести и для многомерных пространств, мы ограни-
ограничимся рассмотрением одномерного случая, чтобы избежать гро-
громоздких обозначений. Всюду в этом разделе Т будет обозначать
интервал в Я Наша цель —поставить в соответствие каждой
4.4 Некоторые примеры 255
функции / локально ограниченной вариации на Т (это понятие
определяется ниже) меру Радона на Т. Построенная таким об-
образом мера называется мерой Стилтьеса или Лебега — Стил-
льеса. Введенная в п. 4.4.2 мера Лебега получается на этом пути
как частный случай, когда исходная функция f определена ра-
равенством f(t)'=t, t^T. Достаточно рассмотреть случай, когда
функция / вещественна. Соответствующая мера Радона будет
тогда также вещественной.
Пусть f — вещественная функция на Т. Если / — содержа-
содержащийся в Т ограниченный интервал с концами ti-^t2y то будем
писать Д/(/)=/(/2)—f(h)- Пусть К— компактный подинтервал
в Т. Полной вариацией функции / на К называется величина
где верхняя грань берется по всем конечным семействам непере--
секающихся интервалов /Гс:/С Полная вариация Vf(K) может
равняться +оо. Если Vf(K)< + oo, то будем говорить, что / есть
функция ограниченной вариации на К. Если Vf(K) < + oo для
каждого компактного интервала К а Г, то говорят, что/ — функ-
функция локально ограниченной вариации на Т. Всякая монотонная
на Т функция является функцией локально ограниченной вариа-
вариации. То же справедливо и для разности двух таких функций.
Обратно, если / — функция ограниченной вариации на К, то она
может быть представлена в виде разности двух монотонных на
К функций (см., например, Натансон [1, стр. 238]). Отсюда
следует существование односторонних пределов функции / в
точках интервала Т и в его концах.
Первый шаг на пути определения меры Радона, соответ-
соответствующей функции /, состоит в определении интеграла Римана —
Стилтьеса по функции /, который сводился бы к интегралу Ри-
Римана в случае f(t)=t. Так как нам понадобится интеграл Ри*
мана — Стилтьеса лишь от непрерывных подинтегральных функ-
функций (фактически принадлежащих еЗГ(Г)), то мы ограничимся
лишь кратким обзором. Подробное изложение можно найти, на-
например, у Натансона [1, гл. VIII]. Пусть ХЕеТ(Г). Выберем
компактный интервал КаТу вне которого х обращается в нуль.
Если У/(/()< + оо, то, как можно показать, существует един-
единственное число i, обладающее следующим свойством: для задан-
заданного е>0 найдется такое б>0, что
<е
Г
Для любого конечного разбиеная интервала К на интервалы
и для любого выбора точек tr^Ir, если только наибольшая
Алина различных 1Г не превосходит 6. Если функция х обра-
256 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
щается в нуль вне К> то число i не зависит от выбора К. Число
i обозначается через RS- J xdf и называется интегралом Ри-
т
мана — Стилтьеса от функции х по интегрирующей функции f.
Легко видеть, что отображение
*h-^RS-J xdf
т
линейно и
RS-J xdf
где Ff(r) = sup Vf (К) — полная вариация функции / на Т. Это
к
отображение (назовем его \if) есть мера Радона, соответствую-
соответствующая функции /. Она также называется мерой Лебега — Стилтьеса
(или просто Стилтьеса) на Г, порожденной функцией f. Ясно,
что A/>0, если f монотонно возрастает.
Введем в рассмотрение более узкий класс интегрирующих
функций f. Значение этого класса станет ясным после того, как
читатель познакомится с § 4.13—4.15. Функция f на Г назы-
называется локально абсолютной непрерывной на Г, если для каж-
каждого компактного интервала Кcz T и каждого числа е>0 суще-
существует такое число б>0, что 2|Д/(/гI^8 Для всякого конеч-
г
ного семейства (/г) интервалов на К, сумма длин которых не
превосходит б. Если это условие выполняется для некоторого
отдельного /С, то будем говорить, что функция f абсолютно не-
непрерывна на К. В § 4.13—4.15 мы увидим, что это понятие есть
точный аналог понятия абсолютной непрерывности меры ji/ от-
относительно меры Лебега. Полезно отметить следующее: если,
функция f локально абсолютно непрерывна на Г, то она локально
равномерно непрерывна 1) и имеет локально ограниченную ва-
вариацию на Т. Существуют, однако, непрерывные функции ло-
локально ограниченной вариации, которые не являются локально
абсолютно непрерывными. Важность локально абсолютно не-
непрерывных функций в теории функции действительного пере-
переменного объясняется тем, что всякая такая функция почти всюду
дифференцируема, причем производная интегрируема и неопре-
неопределенный интеграл от нее (в смысле Лебега) восстанавливает
исходную функцию. В § 4.13—4.15 эти вопросы исследуются на
языке мер для произвольного локально компактного простран-
пространства Т.
1) Функция f называется локально равномерно непрерывной
если ее сужение /1К на каждое компактное множество /С равномерно не-
непрерывно.
4 5. Теория интегрирования 257
Другие свойства меры Лебега — Стилтьеса jli/ рассматри-
рассматриваются в примерах 4.5.6, 4.7.7, 4.7.8, 4.9.2 и 4.15.10.
4.5. Теория интегрирования относительно
положительной меры
Начиная отсюда и до конца § 4.10, через \х будет обозна-
обозначаться фиксированная положительная мера Радона на Т. Обра-
Обратимся к конструктивному продолжению функционала \х с <Ж(Т)
на более широкие множества вещественных или комплексных
функций на Т.
Первый этап продолжения сводится к определению так на-
называемого верхнего интеграла \х* для произвольной положи-
положительной функции на Т. В связи с этим удобно ввести в рассмо-
рассмотрение функции, принимающие и бесконечные значения. Перей-
Перейдем к подробному описанию того, как это можно сделать.
Множество вещественных чисел R расширяется с помощью
добавления двух бесконечных элементов, для записи которых
используются символы —оо и +оо соответственно. Это расши-
расширенное множество обозначается через R и упорядочивается сле-
следующим образом: на ' R сохраняем естественный порядок и
полагаем _—оо<а< + оо для всех cgR. Каждое непустое мно-
множество в R обладает верхней и нижней гранью. Что касается то-
топологии, то на R она остается без изменений, за базу окрестно-
окрестностей точки +оо берутся интервалы вида (а, +оо], «gR, аза
базу точки —оо — интервалы вида [—оо, а), а е R.
Легко видеть, что R — компактное пространство, в котором
R есть открытое плотное подпространство. Некоторые (но не
все) операции, определенные для вещественных чисел, могут
быть по непрерывности продолжены на R. Так, например, опе-
операции sup(x, у) и inf(#, у) непрерывны на RXR- Операция —х
может быть по непрерывности продолжена на все R. Операция
сложения х+у может быть по непрерывности продолжена на
(—оо, +оо] X (—оо, +оо] и на [—оо, +оо) X [—оо, +оо) таким
образом, что
оо) = (+ оо) + х= + оо При х=7^ — оо,
И
Х + {— оо) = ( — оо) + х=— оо При X Ф + оо.
Операции *+ = sup(*, 0), r- = sup(—x, 0) и |*|=sup(*, —x)
определены на R как и операции x*-\-xr и х+ — дг, которые яв-
являются не чем иным, как |д:| их соответственно. Имеет место
неравенство \х + у\ < |дг| + \у\ (если сумма х+у определена).
258 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Аналогично операция умножения ху по непрерывности продол-
продолжается на (й\{0}) X (Й\{0}) таким образом, что
+ оо при х>0,
оо при
, v / v foo при *>0,
— оо) = (—. оо) . Х = \ . .п
v ; v ' l + oo ПрИ Х<0.
Однако выражения 0- ( + «>), ( + оо) -0, 0- (—оо), (—оо) -0 уже
не определяются по непрерывности: условимся считать их рав-
равными нулю. Тогда равенство \ху\ = \х\ • \у\ имеет место всегда.
Наконец, равенство x(y + z) =xy + xz справедливо, если' каждая
из участвующих здесь операций определена. Действия с функ-
функциями, принимающими значения в R, подчиняются, конечно,
принятым только что соглашениям. Предположим далее, что по-
полунепрерывные снизу (соответственно сверху) функции со зна-
значениями в R никогда не принимают значения —оо (соответ-
(соответственно + оо). Непрерывная функция со значениями в R, бу-
будучи одновременно полунепрерывной снизу и сверху, принимает,
таким образом, значения в R (т. е. конечна).
Большую роль будет играть множество Ф = ФG1) положи-
положительных полунепрерывных снизу функций на Т. В силу наших
соглашений множество Ф устойчиво относительно сложения и
умножения на постоянные с >0 (см. также 0.2.19).
Для всякой функции ф£ф положим
[x*(cp)={sup|i(A:): х*=вИГ{Т), х < ф}. D.5.1)
Число jx*(cp) может равняться и +оо, но всегда неотрицательно.
Будем называть его верхним интегралом функции ср. Очевидно,
что
^(сФ)=сЧ1*(ф), D.5.2)
если с > 0, и
<, D.5.3)
если ф1 ^С ф2- Легко видеть, что для всякой положительной функ-
функции х из <?Ж(Т) имеет место равенство \i*(x) =\x(x).
Остальные результаты этого параграфа менее очевидны.
4.5.1. Предложение. Пусть Г — возрастающее направленное
семейство функций из Ф и фо = зир{ф: феГ}. Тогда
ix*(cpo)=sup{|i*(9): феГ}.
Доказательство. Левая часть рассматриваемого равен-
равенства, очевидно, не меньше правой, поэтому остается доказать об-
обратное неравенство. Для всякого заданного числа с<|1*(фо)
можно выбрать функцию х SG/T+ (Г), удовлетворяющую уело-
4 5. Теория интегрирования 259
виям х^Сфо и ii(x)=c'>c. Положим р = с' — с и выберем
компактное множество КаТ, вне которого функция х обра-
обращается в нуль, и функцию Xq из оЖ*+(Т), принимающую значе-
значение 1 во всех точках множества /(.
Пользуясь компактностью множества К и тем, что Г — воз-
возрастающая сеть, легко видеть, что для любого наперед задан-
заданного числа е>0 существует такая функция ф£Г, что ф^>х—
— еХо во всех точках множества К и потому всюду. Тогда име-
имеем jx*(cp) > \i(x)—s[i(x0) = с' — г\х(х0). Если число е выбрано
так, что eji(Xo) < Р, то |л*(ф) > с. Из того факта, что с—про-
с—произвольное число, удовлетворяющее неравенству с<м,*(ф0), сле-
следует справедливость нужного нам неравенства. I
4.5.2. Следствие. Для любых функций ф1 и ф2 из Ф
|Ы*(ф1 + ф2) = Ц*(ф1) + Ц*(ф2).
Доказательство. Каждая из. функций фг-, /= 1, 2, яв-
является верхней огибающей возрастающего направленного се-
семейства Г2- функций изе^Г+(Г), не превосходящих фг-. Следова-
Следовательно, функция ф1 + фг есть верхняя огибающая множества
Г = {хг + х2: ^еГь х2 е Гг}; поэтому наше следствие выте-
вытекает из предложения 4.5.1 и аддитивности меры \х. |
Распространим теперь определение верхнего интеграла [i*
на произвольные функции / на Т, принимающие значения в ин-
интервале [0, + оо] с R, полагая
li*(f) =inV(<p): феФ)Ф>|}.
Из предыдущих результатов-легко следует, что ^
V.*(U)<V>*(f2) при h<f2.
Мы подошли к двум фундаментальнейшим теоремам о схо-
сходимости.
4.5.3. Предложение. Если последовательность положитель-
положительных функций fn(n = 1, 2, ...), монотонно возрастая, сходится к
функции f, то верхние интегралы \i*(fn), монотонно возрастая,
сходятся к M*(f).
Доказательство. Из очевидных неравенств |л*(/) >
> p,*(fn+1)> \i*(fn) непосредственно следует, что последова-
последовательность \i*{fn) монотонно возрастает и сходится к пределу,
не превосходящему \x*(f). Таким образом, остается показать,
что \i*(f) <lim \i*(fn)- He нарушая общности, можно предполо-
предположить, что \x*(fn) конечно при каждом п. Мы докажем фактиче-
фактически следующее: для каждого е > 0 можно найти такую возра-
возрастающую последовательность фп е Ф, что fn <фп и ц*(фп)-^
260
Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
^M-*(M + е. После этого мы положим ср = limcpn1). Тогда
функция ф принадлежит множеству Ф, мажорирует функцию /\
и из предложения 4.5.1 следует, что [х*(ф) = lim \i*{q>n) ^
•< lim [a* (fn) + e. Далее, переходя в неравенстве \i*(f) 4^
< lim \i*(fn) +e к пределу при е->0, мы и получим наше пред-
предложение.
Для построения функций <ря выберем такие функции ф^ ^ Ф,
что /„<ф; и [t(fn)<\fD>'n)<V?(fn) + 2~nB. Покажем, что функ-
функции
удовлетворяют нашим требованиям. Прежде всего, очевидно,
что фд е Ф и /^Фд. Докажем по индукции неравенство
Ц*(фге)<И*(/п) + 8A-2-ге). D.5.4)
Оно справедливо для п=\. Так как Ф„+1 = зир(фп> Фп+i) и
4>n>f«. ф'ге+1 >/„+!>/„- то
^(«Р». Фа+1)>/«- D.5.5)
Далее,
Из D.5.5), D.5.3) и следствия 4.5.2 вытекает неравенство
Предполагая, что D.5.4) справедливо, получаем в силу выбора
т. е. неравенство D.5.4) остается справедливым, если заменить
м на Аг+1, и предложение полностью доказано. |
4.5.4. Предложение (лемма Фату). Если функции fn
{n=ly 2, ...) удовлетворяют неравенствам 0^/rt^ + oo, то
|x*(liminffn)<liminf|i'(fft).
Доказательство. Рассмотрим функции
1) Здесь предел понимается в смысле поточечной сходимости. — Прим.
перев.
4.5. Теория интегрирования 261
Эти функции положительны, монотонно возрастают и сходятся
к liminf/V Из предыдущего предложения следует, что
С другой стороны, FnKfm, поэтому \x*(Fn) ^Cix*(fm) при m>
> п. Значит,
что и требовалось доказать. |
4.5.5. Замечания. Если расширить множество Ф так, что-
чтобы оно содержало все полунепрерывные снизу функции на Г,
которые мажорируют хотя бы одну функцию* из <Ж(Т), то оп-
определение верхнего интеграла |ы*(/) годится для любой функ-
функции / из Ф независимо от того, положительна она или нет. Лег-
Легко видеть, что предложения 4.5.3 и 4.5.4 остаются справедливы-
справедливыми: первое — если |ы*(/п) > — °° для некоторых п, а второе —
если все функции fn, кроме, разве, конечного числа, мажори-
мажорируют функцию g", для которой jut* (g") > — сю. Без этих допол-
дополнительных ограничений предложения оказываются неверными.
4.5.6. Пример. Вернемся к ситуации, описанной в п. 4.4.4.
Пусть Т — интервал вещественной оси с концами а и b (a<.b)
и / — возрастающая функция на Т. Мы хотим вычислить
[^(XjI) для относительно открытых интервалов 1а Т. Пред-
Предвосхищая обозначения и терминологию последующих § 4.6 и
4.7, будем писать |л!(/) вместо М^(%7) и называть это число
внешней \хгмерой интервала /.
Предположим сначала, что /=(а, Р), где а<а^С$<Ь. Пока-
Покажем, что
0 при а = р,
(р_0)-/(а + 0) при а<Р. D'5-6)
Первое равенство очевидно, так как в этом случае /=0 и
%j = 0. Пусть а < Р; допустим, что х^(£Г+(Т) и х^С%г Тогда
х < 1 и х(а) =а:(Р) =0. Так как функция х непрерывна, то
для заданного е>0 найдется такое б > 0, что x(t)^e при
а</<а + б ир— б< ^< р. Но тогда
а+б р 3-6
4*fM = RS- j xdf = RS- J xdf + RS- jxdf + RS- J xdf^
|3G б
l) X/ — характеристическая функция множества {.—-Прим. перев.
262 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Полагая б~>0 и затем е->0, приходим к выводу, что
Чтобы доказать обратное неравенство, воспользуемся функ-
функцией xt график которой приведен на рис. 1. Для этой функции
a a a+6
Рис. 1.
имеют место соотношения
P--6
>- J xdf*
a+6
RS- J
Следовательно,
Полагая 6->0, получаем
a+6
откуда и вытекает равенство D.5.6).
Справедливость D.5.6) доказана пока только для случая
а < а ^ р < Ь. Если же a = а или р = b (или то и другое вме-
вместе), то предыдущее доказательство не проходит. Тем не менее
формула D.5.6) остается справедливой и в этих случаях. Это
можно установить, используя уже доказанный частный случай
в сочетании с предложением 4.5.3. Таким образом, формула
D.5.6) верна, если a^a-<p^6 и даже если а = — оо или
Ь = + оо (или и то и другое вместе). Более того, полученный
результат можно обобщить на случай, когда / — функция ло-
локально ограниченной вариации на Т, по крайней мере для ог-
ограниченных интервалов /. При этом используется представи-
представимость функции f в виде разности двух возрастающих функций.
Если а^Т и а-<р<6, то интервал / = [а, р) относительно-
открыт в Т. При р = а имеем / = 0 и |х* (/) = 0. Если р Ф а, то,
4.6. Пространство O2?1 + J?1 (Т, \i) 263
рассуждая, как и при доказательстве формулы D.5.6), полу-
получаем
^([я, Р)) = /(Р-О)-/(а) при aer,a<p<J, D.5.7)
Аналогично
^((а, b]) = f(b)-f(a + O) при b£=T, a<a<b. D.5.8)
Комбинируя эти результаты с аддитивностью верхнего ин-
интеграла \х* (Вытекающей из следствия 4.5.2), приходим к ра-
равенству
$((а, b)) = vrf{T) = f(b)-f(a), где Т = [а, Ь]. D.5.9)
Формулами D.5.6) — D.5.9) величина \i*f(I) определена для
всевозможных интервалов IczT, открытых относительно Т. Эти
соотношения можно распространить и на случай, когда / —
функция локально ограниченной вариации на Г, по крайней
мере если рассматриваемый интервал / ограничен.
Легче всего запоминается случай Т = R. Тогда для всех
открытых интервалов (а, |3), а < |3, имеет место равенство'
ц;((а, р)) = /(р-0)-/(а + 0).
Другим практически важным случаем является случай, ког-
когда Т = [а, Ь] — компактный интервал. Оказывается, что тогда
\х* является просто сужением на подинтервалы в Т верхнего
интеграла jj/\ где g — возрастающая функция на R, являю-
являющаяся продолжением функции / и определяемая следующим об-
образом: g(t)=f{a) при t<=(—oo,a) и g(t)=f(b) при /е
€= F, + оо).
4.6. Пространство 2>l = S>l(TJ jm) jm-интегрируемых функций
Сейчас мы воспользуемся верхним интегралом ju* (опреде-
(определенным пока только для положительных функций) для введе-
введения полунормы Ni на одном векторном подпространстве в Кт
и затем построим пространство^1, что сведется к пополнению
пространства Жк(Т) относительно структуры, определяемой
полунормой N\.
Для функции х^Кт (как обычно, К — это R или С) поло-
положим
Мг(х) =ц*(И).
Обозначим через ^к = <2?"кG\ \i) множество тех функций
х^Тк, для которых N\{x) < + оо. Из элементарных свойств
верхнего интеграла \х* следует, что <grlK — векторное подпро-
подпространство в Кт и Wi — полунорма в af^. Функция л: называется
264 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
[х-пренебрежимой, если N\(x)=O. Когда ясно, какая мера [г
имеется в виду, мы будем говорить просто «пренебрежимая»
вместо «|ы-пренебрежимая» .
Если А подмножество в Т и %А — характеристическая функ-
функция множества Л, то вместо \i*(%A) будем писать \х*(А). Число
[х*(Л) называется внешней \х-мерой множества А. Из элемен-
элементарных свойств верхнего интеграла \х* следует, что 0-^|1*(Л)^
< + оо, ус*(А) <\х*{В) при А а В
D.6.1)
Неравенство D.6.1) заведомо верно для конечных объедиле-
ний. Но тогда в силу предложения 4.5.3
= Нтц'(Л„) D.6.2)
для всякой возрастающей последовательности множеств Ап.
Из D.6.2) следует, что D.6.1) справедливо для любого не бо-
более чем счетного объединения множеств. Множества Л, харак-
характеристическая функция %А которых пренебрежима, называются
пренебрежимыми множествами. Из предыдущего следует, что
подмножество пренебрежимого множества пренебрежимо, и
всякое не более чем счетное объединение пренебрежимых мно-
множеств также является пренебрежимым.
Говорят, что некоторое свойство точек множества Т имеет
место \х-почти всюду (\х-п. в.), если множество тех точек из Г,
для которых это свойство неверно, ji-пренебрежимо. Как и
раньше, если ясно, какая мера \х имеется в виду, мы будем
употреблять выражение «почти всюду» (и сокращение п. в.)
вместо «|л-почти всюду». Если / и g — положительные функции
и неравенство f^g" имеет место почти всюду, то \х* (/) <^|ы* (g).
(Этим оправдывается эпитет «пренебрежимый».) Действитель-
Действительно, если А — пренебрежимое множество, на котором неравен-
неравенство f-^-g не выполняется, то неравенство
справедливо во всех точках, поэтому
у? (lim (g + n%A)) = lim |Г (g + nl
lim (|
Следовательно, если f и g положительны и f = g почти всюду,
то ii* (f) =|х*(г).
Далее, функция f пренебрежима тогда и только тогда, когда
/ = 0 почти всюду. В самом деле, если / = 0 почти всюду, то
4.6. Пространство J?1 + J?1 (T, \i) 265
|fl=O почти всюду, и по доказанному \х* (|/|) = \л*@) = 0.
С другой стороны, если ц/*(|/1) =0, то для всякого натураль-
натурального числа п множество точек, для которых \f\^ ггху очевидно,
пренебрежимо. Тогда и объединение этих множеств по л=1,
2,... также пренебрежимо. Таким образом, множество точек,
где [Ф0, пренебрежимо.
Теперь мы подошли к основному определению этого раз-
раздела.
4.6.1. Определение. Обозначим через J?1 = J2*1 G\ \i) замы-
замыкание подмножества е2Гс(П пространства <^"с = ^~сG\ мО отно-
относительно полунормы N{. Всякая функция, принадлежащая
^(Т, \х), называется ^-интегрируемой. Аналогично можно
ввести J?r как замыкание о/?к(Т) в o^~r. Читатель легко про-
проверит, что функции из J^r — это в точности вещественные функ-
функции из J?1.
Как мы уже знаем, неравенство
I^WI<iV,W D.6.3)
справедливо для х ^еЖ*{Т) = <Жъ{Т). Оно сохраняется и для
jcGgTcW Докажем это. Пусть x = u + iv, где и> uG?J(r).
Заметим, что если а и b — вещественные числа, то
| a + ib | = max {a cos г + Ъ sin r: r вещественно}.
Таким образом, имеем
| \х (х) | = | \х (и) + щ (v) | = max {\х {и) cos г + \х (v) sin r} =
= max\х(иcosr + v sinr)<\i| и + iv \ = \x(|x \) = N{(x).
В силу неравенства D.6.3) линейная форма \i допускает
единственное непрерывное продолжение с Jfc(T) на»?1, кото-
которое мы также будем обозначать через \л. Это продолжение \х
является линейной формой на 24, для которой неравенство
D.6.3) остается справедливым при х е J2?1.
Если функции / и g принадлежат Сг и почти всюду совпа-
совпадают, то они интегрируемы или неинтегрируемы одновременно.
Если они интегрируемы, то \i(f) = ^(g").
Пусть функции /, £€=СГ. Тогда |/| < \g\ + \f — g\ и по-
потому
Комбинируя это неравенство с тем, которое получится, если по-
поменять местами / и g, получаем
ЛМ/-£). D.6.4)
266 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
Отсюда следует, что отображение f ь-> р,*(|/|) равномерно не-
непрерывно на а?~с- Так как оно совпадает на оЖс(Т) с отобра-
отображением / н-^ \х (| /1), то
|i(l/l) = |i*(l/l) (f^^1). D.6.5)
В частности, \x(f) =jx*(f) для всякой положительной интегри-
интегрируемой функции.
Из неравенства D.6.4) следует также, что функция |/|
интегрируема, если интегрируема сама функция /.
4.6.2. Лемма. Функция ф еФ интегрируема тогда и только
тогда, когда ц«*(ф) < + оо. В этом случае ц,*(ф) = |ы(ф) 1).
Доказательство. В силу доказанного выше второе ут-
утверждение вытекает из первого. С другой стороны, если феФ
и jut* (ф) < + оо, то можно выбрать последовательность таких
функций хп е оЯГ (Т), что хп <^ ф и |ы* (ф) — [х(хп) ^ \/п. Так как
функция хп и ф — хп принадлежат Ф, то в силу следствия 4.5.2
получаем |л*(ф— *п) = ЛМф— хп) < 1/п, откуда следует инте-
интегрируемость функции ф. Справедливость обратного утвержде-
утверждения вытекает из определения о^с. i
Покажем теперь, что вещественные функции из J?1 обра-
образуют решетку2).
4.6.3. Предложение. Если вещественные функции f\ a f2 ин-
интегрируемы, то функции / = sup (/i, f2) и ^ = inf(/i, f2) также
интегрируемы.
Доказательство. Так как g = —sup(—fi, —f2), то до-
достаточно доказать интегрируемость функции f. Как известно,
функция \h\ интегрируема вместе с функцией А, поэтому най-
найдется такая интегрируемая функция р (например, —|fi| —
—1/2|), что U>p, i*-- 1,2. Тогда f — p = sup(/i — р, /2 — р), так
что можно считать функции f\ и f2 положительными. Далее для
заданного е > 0 можно выбрать такие функции ф^ ^ Ф, что
(pi^-fi и И'*(ф*)^!:х*(/г) + '2 8* ^ силу предыдущей леммы функ-
функции фг интегрируемы, следовательно, N\ (ф^ — ft) ^ -^ е* Кроме
того, из леммы 4.6.2 вытекает, что функция ф = sup (фЬ ф2)
интегрируема. Она, очевидно, мажорирует /. Из неравенства
х) Это утверждение остается справедливым и при некотором, расшире-
расширении класса Ф (п. 4.6.11).
2) Решетка — это частично упорядоченное множество, которое вместе
с любыми двумя^элементами содержит их верхнюю и нижнюю грани. У нас
принят также термин структура, но в этой книге слово «структура» исполь-
используется в другом смысле. — Прим. ред.
4.6. Пространство J?1 - J?x (T, \i) 267
следует, что Л^ф — /)^-|- + ■§- = е. Таким образом, функция /
аппроксимируема интегрируемыми функциями с любой точно-
точностью в смысле N\ и, значит, сама интегрируема. |
4.6.4. Следствие. Вещественная функция f интегрируема
тогда и только тогда, когда интегрируемы обе функции /+ =
= sup(/, 0) и f- = sup(—/, 0). В этом случае (/)(f+)
(f)
n)
В дальнейшем нам понадобится сходный результат, кото-
который не следует из предложения 4.6.3.
4.6.5. Лемма. Если f — положительная интегрируемая функ-
функция и с—число >0, то функция У = inf (/, с) интегрируема.
Доказательство. Для заданного е>0 найдем в мно-
множестве Ф такую функцию ф, что /^ф и м/*(ф) <C\x.*(f) + е. Из
интегрируемости функции / и леммы 4.6.2 вытекает неравенство
Ni (f—ф) ^ е. Функция ф' = inf (ф, с) принадлежит Ф и интег-
интегрируема. Далее, q/^f и
ф/-// = Ы(ф, c)-inf(/, с).
Если f^-c, то из последнего выражения следует, что с — с —
= 0 ^ ф — f. Если же /<с, то inf (ф, с) —f ^ ф — /. Таким обра-
образом, фг — /Г^Ф — /, поэтому N\ (ф7 — /') -^е. Так как фг — ин-
интегрируемая функция и е произвольно мало, то У интегри-
интегрируема. |
Это подводит нас к центральной теореме сходимости для
интегрируемых функций.
4.6.6. Теорема. Если последовательность вещественных ин-
интегрируемых функций \п (п=1, 2, ...) монотонно возрастает,
то функция f = lim/n интегрируема тогда и только тогда, когда
lim\i(fn) < + оо. В этом случае \i(f) = lim ^(fnI).
Доказательство. Рассматривая функции fn — f\ вместо
fn, можно свести доказательство к случаю, когда все функции
fn>0. Тогда для всех п имеет место равенство \i*(fn) = \л((п)>
и из предложения 4.5.3 следует, что \i*(f) =lim \x{fn)' Поэтому
достаточно показать, что функция f интегрируема, если \i*(f)<.
< + оо. Но тогда для любого заданного е>0 можно найти такую
функцию ф е Ф, что f4f и М<*(ф) ^ M«*(f) +e- В силу леммы
4.6.2 ф интегрируема, так что разности ф — fn положительны и
интегрируемы. Следовательно,
(/)< + оA) при п->оо.
1) См. п. 4.6.11, где указывается, что утверждение остается справедли-
справедливым при некотором ослаблении условий на функции /п.
268 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Так как / — fft^0, то
^1(/-/п) = |1'(/-/я)<|х'(ф-/я)<е + о A).
Таким образом, N\(f — fn) ^ 2е для достаточно больших л, от-
откуда и вытекает интегрируемость функции f. |
Следующая ниже теорема весьма важна; в частности, она
показывает, что 3?х получается из пространства g2Tc (T) попол-
пополнением его относительно структуры, определяемой полунор-
полунормой Ni.
4.6.7. Теорема. Если функции (fn) cz CT образуют последова-
последовательность Коши относительно полунормы Nu то из нее можно
извлечь подпоследовательность (fnk), которая почти всюду схо-
сходится к некоторой функции f, причем Ni(f — /п) ->0 при п-^оо.
В частности, пространство J?1 полно.
Доказательство. Выберем последовательность натураль-
натуральных чисел П\<п2<... так, чтобы имели место неравенства
#i (gk+i— gk) < 4~fer где gh=fnk- Пусть Ak — множество в Г, опре-
определенное неравенством \gk+i — gk|>2-fe. Тогда Ni(gk+i—£&)>
> 2-k\x*(Ak), откуда следует, что \i* (Ak) K2~h. Положим
Вк=1){А{: i>k). В силу D.6.1) \i*{Bk) <2~k+\ поэтому пере-
пересечение iV множеств Bk пренебрежимо. Если t еГ \ Л^, то не-
неравенство \gk+i(t)—gk(t)\<2~h имеет место для всех /г, сле-
следующих за некоторым kQ = ko(t). Отсюда получаем, что (gk(t))
есть числовая последовательность Коши для почти всех t. По-
Положим f(t) равным пределу последовательности (gk(t)) для та-
таких t и нулю во всех остальных точках. Из леммы Фату (пред-
(предложение 4.5.4) вытекает, что
tfitf-£ft) = |i'l/-g*l = |i'(Hm Iff,-& |)<
£->оо
< lim inf \i*(\gi-gk\)= lim inf N{ {gt - gk).
i i
i->oo
Так как (gk)—последовательность Коши, то последнее выра-
выражение стремится к нулю при /г-^оо. Теорема доказана. |
Заслуживают внимания два следствия.
4.6.8. Следствие. Пусть функция f, f и fn (л = 1, 2, ...) при-
принадлежат множеству Ст. Если fn-+f почти всюду и Ni(f — fn)->
-+0 при м-^оо, 70 \ = \f почти всюду.
Доказательство непосредственно следует из теоремы,
так как существует почти всюду сходящаяся к f подпоследова-
подпоследовательность последовательности (/n). I
4.6.9. Следствие. Для того чтобы функция f из Ст была инте-
интегрируема,
(а) не о б хо д им о существование такой сходящейся к f
почти всюду последовательности (хп) функций из сз/Гс(Г), кото-
4.6. Пространство J?1 = J?1 (Г, ц) 269
рая является последовательностью Коша относительно полу-
полунормы л/у,
(Ь) достаточно существование сходящейся к f почти
всюду последовательности (fn) функций из J?1, являющейся по-
последовательностью Коши относительно полунормы N\.
Доказательство. Утверждение (а) следует из опреде-
определения пространства J?1 как замыкания множества е%Гс{Т)
в <^с и из теоремы 4.6.7. С другой стороны, если имеет место
утверждение (Ь), то в силу той же теоремы существует такая
функция Y из Ст и такая подпоследовательность (/„J, что
fnk->ff почти всюду и N{ (f — fnk)~>^ ПРИ k->oo. Второе из
этих соотношений влечет за собой интегрируемость функций /',
а из первого вытекает равенство / = /' почти всюду. Отсюда сле-
следует интегрируемость функции /. |
Закончим этот параграф легко получающимся из следствия
4.6.9 предварительным результатом, который затем полностью
перекроется следствием 4.11.8.
4.6.10. Лемма. Если функции fug интегрируемы и ограни-
ограничены, то и функция h = fg интегрируема.
Доказательство. В силу утверждения (а) следствия
4.6.9 почти всюду имеет место равенство f = limxn, где (хп) —
последовательность ве2Гс(Г), являющаяся последовательностью
Коши относительно полунормы N\. Так как функция / ограни-
ограничена, то можно считать, что \хп\ <М для некоторого М. Выбе-
Выберем аналогичную последовательность (уп), аппроксимирующую
функцию g. Легко видеть, что zn = xnyn является в о/Гс(Т) по-
последовательностью Коши относительно полунормы N\, причем
эта последовательность почти всюду сходится к произведению
fg. Остается применить утверждение (Ь) следствия 4.6.9.1
4.6.11. Функции, определенные почти всюду. До сих пор на-
название «интегрируемая функция» мы сохраняли за теми функ-
функциями, которые всюду определены, всюду принимают конечные
значения и удовлетворяют признаку, сформулированному в на-
начале § 4.6. Как было замечено в связи с леммой 4.6.2 и теоре-
теоремой 4.6.6, эта точка зрения является излишне узкой. На самом
деле, исходя из функций, удовлетворяющих этим условиям, мы
естественным образом приходим к функциям, которые могуг
принимать бесконечные значения и тем не менее могут в неко-
некотором разумном смысле считаться интегрируемыми.
Поэтому удобно иногда применять эпитет «интегрируемая»
к функции /, удовлетворяющей следующим условиям: / опреде-
определена почти всюду и может принимать в некоторых точках бес-
бесконечные значения; существует такая всюду определенная и
всюду конечная интегрируемая (в старом смысле) функция g,
270 Гл. 4. Топологии сопряженные к некоторым пространствам; меры Радона
что f = g почти всюду. Если существует одна такая функция g,
то очевидно, что их существует много. Однако интегралы от них
принимают все одно и то же значение, которое мы и возьмем в
качестве \x{f).
За удобства, получаемые на этом пути, приходится распла-
расплачиваться. Функции, интегрируемые в указанном ролее широком
смысле, уже не образуют векторного пространства и даже не
образуют группы. На практике это не является серьезным пре-
препятствием, так как всякую такую функцию можно заменить дру-
другой, всюду определенной и конечной, не нарушая при этом соот-
соотношений между рассматриваемыми интегралами. Формальный
выход из возникающего затруднения лежит в использовании
факторпространства Ь\ вводимого в п. 4.11.10.
4.7. Интегрируемые множества, измеримые множества,
локально пренебрежимые множества
4.7.1. Интегрируемые множества. Множество АаТ назы-
называется интегрируемым (относительно положительной меры Ра-
Радона |ы), если интегрируема (относительно |ы) характеристи-
характеристическая функция %а- Из предыдущих результатов об интегрируе- -
мых функциях немедленно вытекают следующие основные свой-
свойства.
► A) Пусть множества Ап (м=1, 2, ...) интегрируемы и
Ап\А. Множество А интегрируемо тогда и только тогда,
когда lim |ы* (Лп)< + оо. В этом случае \х*(А) =lim \i*(An).
(Ср. D.6.2).)
► B)Если множества Ап (az=1, 2, ...) интегрируемы и
Ап\А, то интегрируемо и множество А, причем |д*(Л) =
Н*(Л)
ц()
► C) Если множества А и В интегрируемы, то и множества
АГ\В, А[)В; А\В интегрируемы.
► D) Всякое относительно компактное открытое множе-
множество и всякое компактное множество интегрируемы.
Утверждения A) и B) следуют из принципа монотонной
сходимости. Для доказательства утверждения C) заметим, что
Х^пв = Ха-Хв и Ха\в = Ха — Ха-Хв, а А 1)В= (А \ В) [) (В \ А) [}
\j(Af]B)=C[)C/[)C/\ где множества С, С и С" дизъюнктны и
интегрируемы, так что ХАив = Хс + Хс+Хс"э т. е. %a\jb является
суммой трех интегрируемых функций и потому сама интегри-
интегрируема. Утверждение D) следует из того факта, что характери-
характеристическая функция всякого относительно компактного открытого
множества принадлежит множеству Ф и имеет конечный верх-
верхний интеграл, а значит, интегрируема. Если множество К ком-
4 7 Интегрируемые множества 271
пактно, то оно обладает открытой относительно компактной
окрестностью U. Тогда множество U \ К относительно компакт-
компактно и открыто и, следовательно, интегрируемо. Множество К=
= U\ (U\K) интегрируемо в силу последней части утвержде-
утверждения C). I
За исключением того случая, когда само мнижество Т инте-
интегрируемо (т. е. мера \х ограничена, или конечна), дополнение к
интегрируемому множеству не является интегрируемым множе-
множеством. В связи с этим в п. 4.7.2 мы введем другое, более слабое
понятие, имеющее чисто локальный характер. Это понятие уже
устойчиво относительно перехода к дополнениям.
Множество или функция называются универсально интегри-
интегрируемыми, если они fx-интегрируемы относительно каждой поло-
положительной меры Радона \х на Т.
4.7.2. Измеримые множества. Множество АаТ называется
измеримым (относительно меры \х), если множество А[\К инте-
интегрируемо (относительно \х) для каждого компактного множе-
множества К а Т. Можно поэтому охарактеризовать измеримые Амно-
жества как «локально интегрируемые». Перечислим некоторые
свойства измеримых множеств.
► E) Множество А интегрируемо тогда и только тогда, ко-
когда оно измеримо и [л*(Л)< + оо.
Действительно, если множество А интегрируемо, то в силу
утверждений C) и D) интегрируемо и пересечение Л Л/С; при
этом, разумеется, [л*(Л)< + оо. Обратно, пусть множество А из-
измеримо и |1*(Л)< + оо. Тогда существуют такое пренебрежимое
множество N и такая возрастающая последовательность ком-
компактных множеств Кп (я=1, 2, ...), что Лс (\jKn)\JN и, зна-
п
чит, A = \J(A[)Kn)\J(AON)- Множество Af\N пренебрежимо и
п
потому интегрируемо. Каждое из множеств А[}Кп интегрируемо.
Эти множества образуют возрастающую последовательность, и
\i*{Af}Kn) <[л*(Л)< + оо. Поэтому множество \J(A[)Kn) =
= lim (АС\Кп) интегрируемо в силу A). Из C) следует теперь
интегрируемость множества А.
► F) Если множества А и Ап (п = \, 2, ...) измеримы, то
измеримы и множества Т\А, \J Ап, П Ап, lim supAn и
lim inf An.
Действительно, характеристическая функция %(т\а) п к =
= %к — Хк'%а по условию и по предложению D) есть разность
Двух интегрируемых функций; поэтому множество (Т\А)[)К
интегрируемо для каждого компактного множества К. Из C)
и D) следует, что всякое конечное объединение измеримых
272 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
множеств измеримо. В силу A) предел возрастающей последо-
последовательности измеримых множеств является измеримым множе-
множеством. Комбинируя эти два утверждения, получаем, что объеди-
объединение всякой последовательности измеримых множеств изме-
измеримо.
Измеримость пересечения (]Ап доказывается аналогичным
образом с использованием C) и B). Наконец, множества
lim sup Ап = f) (J An, lim inf An = (J f) An
измеримы в силу установленной измеримости объединений и пе-
пересечений.
► Всякое открытое множество и всякое замкнутое множе-
множество измеримы.
Это непосредственно следует из D). Действительно, если
F замкнуто, то F0K компактно и потому интегрируемо (К —
компактное множество в Г). Если U открыто, то U = T\F, где
F = T\U — замкнутое множество.
► (8) Пусть множества Ап (м=1, 2, ...) дизъюнктны и
измеримы и А = (J Ап. Тогда
Действительно, мы уже знаем, что ц,*(Л)^ 2 Н-*(Аг) незави-
п
симо от того, являются множества Ап дизъюнктными и измери-
измеримыми или нет. Остается доказать выполнение при заданных
условиях неравенства \С (Л)> 2 \i*(An). Оно тривиально, если
п
\х*(А) = +оо. Пусть \х*(А) < + оо. В силу E) и F) множества А
и Ап интегрируемы. Проинтегрировав равенство Ха^^Ха*
п
получаем наше утверждение.
4.7.3. Локально пренебрежимые множества. Множество
LczT называется локально пренебрежимым (относительно \х),
если множество L[)K пренебрежимо (относительно \х) для каж-
каждого компактного множества К а Т. Всякое локально пренебре-
жимое множество L измеримо. Пренебрежимые множества ло-
локально пренебрежимы, однако обратное, вообще говоря, не-
неверно. Это служит причиной многочисленных непринципиаль-
непринципиальных усложнений, возникающих, когда множество Т не является
«а-конечным» в следующем смысле.
Подмножество в Т называется \х-о-конечным, если оно со-
содержится в объединении не более чем счетного множества ин-
интегрируемых открытых множеств, или, что то же, в объединении
4 7. Интегрируемые множества 273
пренебрежимого множества и не более чем счетного множества
компактных множеств. Легко видеть, что всякое fx-a-конечное
локально пренебрежимое множество пренебрежимо. Поэтому
для ji-a-конечного (тем более, для a-компактного) множества Т
понятия «пренебрежимое» и «локально пренебрежимое» (относи-
(относительно \х) эквивалентны. В противном случае, вообще говоря,
существуют локально пренебрежимые множества L, для которых
|i*(L)>0. Для каждого такого множества обязательно \x*(L) =
= + 00 (так как в случае m,*(L)< + oo множество L было бы
jx-a-конечным).
По аналогии с терминологией, введенной в § 4.6, будем го-
говорить, что некоторое свойство точек из Т имеет место локально
почти всюду относительно jli (или ji-локально почти всюду),
если множество тех точек из Г, где это свойство не имеет места,
локально пренебрежимо относительно \х.
Ясно, что если каждое из множеств Ln (n=\, 2, ...) ло-
локально пренебрежимо, то то же верно и для всякого подмно-
подмножества объединения |J Ln.
4.7.4. Существенная внешняя мера. Понятие локальной пре-
небрежимости подсказывает введение следующей функции мно-
множества:
Д*(Л) = sup fti* (А П К): К компактно, К cz Т).
В обозначениях § 4.14 это не что иное, как существенный верх-
верхний интеграл Д*(%а). Поэтому назовем Д*(Л) существенной
внешней \х-мерой множества А. Множество L локально прене-
пренебрежимо (относительно \i) тогда и только тогда, когда fL*(L)=O.
Очевидно, также, что 0< р,*(Л)-< р,*(Л) •<+оо для всякого
множества ЛсГ и
^2Д*(ЛЛ) D.7.1)
п
для всякой последовательности (Ап) подмножеств в Т. Из ре-
результатов, которые будут получены в § 4.14, следует, что
\х*(А) =^*(Л), если множество Л открыто. Из тех же результа-
результатов вытекает, что тогда и только тогда множество А измеримо
иД*(Л)< + оо, когда существует такое интегрируемое множе-
множество В си А, что множество А\В локально пренебрежимо.
В этом случае Д*(Л) =fx*E); следовательно,
2й'(Лй), D.7.2)
если множества Ап (п = 1, 2, ...) дизъюнктны и измеримы.
4.7.5. Численная мера измеримых множеств. Как мы уже
видели, \х* и Д* являются счетно аддитивными функциями
274 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
множества, определенными на а-поле fx-измеримых множеств.
Вообще говоря, эти функции различны. Обозначим ограничения
их на измеримые множества через \х и р, соответственно. Измери-
Измеримое множество А, для которого \х(А) < + оо (соответственно
Д(Л)< + оо), является интегрируемым (соответственно суще-
существенно интегрируемым) множеством.
► (9) Для всякого множества А
\i*{A) = M{\x(U): U открыто, [/зЛ}. D.7.3)
Так как каждое U измеримо, то \x{U) = fx*([/)/B силу того что
in* — возрастающая функция множества, \х*{А) -dnf \x(U). При
доказательстве обратного неравенства можно, очевидно, счи-
считать, что \х*(А) < + сю. Тогда для заданного е>0 найдется
такая положительная полунепрерывная снизу функция ф^%д,
что ц/*(ф) ^Сц*(Л) +е. Множество V тех точек t, для которых
ср(/) > 1 — е, открыто. Кроме того, U zd А и %t/^(l — 8)-1ф.
Поэтому
Наше утверждение следует теперь из произвольности е.
4.7.6. Внутренняя мера. По аналогии с D.7.3) введем
^(Л) = sup {^(/C): К компактно, К с: А}. D.7.4)
Назовем \х*(А) внутренней \х~мерой множества А. Ясно, что
[л# — положительная возрастающая функция множества и
0<МЛ)<[Г(ЛК>х*(ЛК+оо. D.7.5)
Из счетной аддитивности \х на измеримых множествах легко
вывести, что
► A0) Если множества Av (м=1, 2, ...) дизъюнктны, то
► A1) Если множество А измеримо, то \i*(A) =р,(Л).
Для доказательства этого утверждения достаточно в силу
D.7.5) показать, что ц,*(Л)>р,*(Л), если А измеримо. Считая
это неравенство доказанным для относительно компактных мно-
множеств Л, Ихмеем
для каждого компактного мцожества /С Так как множество
ЛП/С интегрируемо, то \i*(A ПК)^- \л*{А). Беря верхнюю грань
по /С, получаем \х*(А) -^^.(Л). Таким образом, достаточно рас-
рассмотреть случай, когда множество Л относительно компактно и
измеримо. ВыберехМ такое открытое относительно компактное
множество Uy что U"Z>A. Тогда множество U\A интегрируемо,
4.7. Интегрируемые множества 275
и в силу утверждения (9) существует такое открытое множество
V, что VzdU\A и |ы(У)><ц(^/\Л)+8. Можно считать, что
Vcz U. Рассмотрим множество K=U\V. Легко видеть, что
/Сcz у4. Поэтому всякая точка прикосновения множества К при-
принадлежит множеству 1с[/и замыканию дополнения к V, сле-
следовательно, множество К кохмпактно. В равенстве V=
= (U\A)\J(A[)V) слагаемые в правой части не пересекаются,
поэтому
lx(V)=\x(U\A)+ii(Ar\V)
и, следовательно, ^(ЛЛУ) ^ е. Далее, A\K=A[)V. Таким об-
образом, К а Л, К компактно, и
Устремляя е к нулю, получаем требуемый результат. I
► A2) Множество А интегрируемо тогда и только тогда,
когда \х*(А) = ц,*(Л)< + оо. В этом случае общее зна-
значение внешней и внутренней мер равно [л(Л) =Д(Л).
Действительно, если множество Л интегрируемо, то в силу
A1) \х*(А) — Д(Л), что равносильно равенству \х*(А) = ц*(Л),
так как множество Л измеримо и fx-a-конечно. Обратно, пусть
\х%(А) =[х*(Л) < + оо. Тогда существуют такое множество XczA,
являющееся не более чем счетным объединением компактных
множеств, и такое множество YzdA, являющееся не более чем
счетным пересечением открытых множеств, что
Отсюда вытекает, что A*(У\Х)=0, т. е. множество Y\X пре-
пренебрежимо. Таким образом, А=Х[] (Л \ X), где множество
ЛЧ^с: Y\X пренебрежимо. Так как множество X измеримо,
то измеримо и множество Л. Поэтому \х*(А) < + оо, откуда в силу
утверждения E) следует интегрируемость множества Л. |
Завершим этот параграф двумя примерами, иллюстрирую-
ЩИхМи предыдущие результаты в терминах меры Лебега — Стил-
тьеса на интервале.
4.7.7. Пример. Воспользуемся обозначениями и результатами
п. 4.4.4 и 4.5.6 в предположении, что Т — вещественный интер-
интервал с концами a = inf Т и b = sup Г, a<b, и / — функция локально
ограниченной вариации на Г. Достаточно рассмотреть случай,
когда функция f возрастает; тогда ассоциированная мера Ле-
Лебега— Стилтьеса \if положительна. В п. 4.5.6 мы определили
М/) для каждого относительно открытого интервала I в Т.
Пользуясь этим определением и счетной аддитивностью меры
И/, легко найти меру \ij(I) любого интервала /с= Т. Читатель
заметит, что множество Т a-компактно (следовательно, понятия
276 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
|игпренебрежимости и ц,глокальной пренебрежимости экви-
эквивалентны) и что в данном случае нет никакого различия между
\х* и [х*.
Прежде всего если a<t<b, то одноточечное множество {t}
является пределом убывающей последовательности открытых
относительно компактных интервалов, замыкание которых ле-
лежит в Т. Из результатов п. 4.5.6 и из утверждения B) следует,
что
/(' + О)-/(*тО) при a<t<b. D.7.6)
Аналогично
/(а + 0)-/(а) при а с= 7\ D.7.60
f(b)-f(b-O) при Ь^Т. D.7.6-)
Рассмотрим теперь компактный интервал [а, |3], содержа-
содержащийся в Т. Пусть а<ос<^|3<6. Представим [ее, |3] в виде пересе-
пересечения убывающей последовательности открытых относительно
компактных интервалов (а\ Cх) с а < а! < C' < Ь. Из результа-
результатов п. 4.5.6 и из утверждения B) получаем
|xf([a, P]) = /(P + O)-/(a-O) при a<a<p<6. D.7.7)
Если ggT и a<C<6, то [a, p] = [a,jT> \ (р, р'), где р<р'<6.
Из аддитивности меры щ вытекает, что
М№. Р]) = /(Р + О)-/(а) при а<=Т, а<$<Ь. D.7.70
Аналогично
|xf([a, 6]) = /F)-/(a + 0) при 6gT, a<a<b, D.7.7/x)
/(a) при Г = [а, 6]. D.7.7^)
Эти результаты приводят к выводу, который полезно запом-
запомнить. Если ТаТ*, f* — функция, определенная на Р, и через
f обозначено сужение f*\T, то мера [Х/ я^ обязательно является
сужением меры \if* на подмножество Т. Например, если Г =
= [а, 6] и множество Т* открыто, то
тогда как
IV([а, 6]) = ГF + 0)-Г(а-0),
так что совпадение возможно, только если функция /* непре-
непрерывна справа в точке b и слева в точке а.
4.7.8. Пример. Пусть Т — вещественный интервал и \х — не-
некоторая мера Радона на Т. Мы теперь можем показать, что
\i = \if для некоторой функции / локально ограниченной вариа-
41. Интегрируемые множества 277
ции на Т. При этом можно считать, что мера \х положительна,
и функцию / можно выбрать так, чтобы она возрастала на Т.
Допустим сначала, что а==\п1Т gT. Пусть b — supT. Опре-
Определим функцию f следующим образом:
U([a, /)) при /еГ, t<b,
1 |i([a, b]) при t = b*=T.
Очевидно, / возрастает на Г, принимает конечные значения и не-
непрерывна слева во всех точках a<t<b. Если /gT и t<b, то
в силу результатов п. 4.7.7
O)-ff(a) при
0 при / = а,
причем ц,/([я, t)) совпадает с \х([а, /)), поскольку функция
непрерывна слева. Если t — b^T, то
Ь\).
Так как {&} = [а, 6] \ [а, Ь), то ^/({6}) =ц({6}) при Ь<=Т. Теперь
уже легко показать, что \if(x) =\х(х) для всякой функции
г^е/Г(Г). Для этого разобьем Г на подинтервалы [ty t') (и, воз-
возможно, {6}, если JgF), наибольшая длина которых стремится
к нулю. Функция х равномерно аппроксимируется конечными
линейными комбинациями характеристических функций таких
интервалов. Так как \if([t, t'))=\x([t, I')) (и \if({b})=\x({b}) при
b е Г, то (I- и ^/-интегралы от этих линейных комбинаций совпа-
совпадают. Переходя к пределу, получаем, что значения \х(х) и \if(x)
совпадают.
Допустим, наконец, что точка а не принадлежит множеству
Т. Выберем такую последовательность ап^Т, что ап\а. Опре-
Определим функцию f на Т следующим образом. Всякое /еГ удо-
удовлетворяет неравенству /^ ап для некоторого (в действитель-
действительности для многих) п. Для всех таких п числа
(А(К, t))-\i([an, аг))
не зависят от п (в силу аддитивности меры м,). Это общее их
значение и обозначим через f(t), если t<b. Если Ь^Т, то по-
полагаем f(b)=\x([au b]). Тогда при 0<а<$<Ь для достаточно
большого м имеем
, Р))-|1([ся, а)),
а это как раз и есть jx([a, |J)). В силу счетной аддитивности это
равенство справедливо и при р = 6. Если 6еГ, то
= / W - / (* - 0) = |i ([а„ 6]) - |i ([с„ 6)) =
278 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
С помощью рассуждений, аналогичных предыдущем, получаем,
что \х(х) =\xf{x) для каждой функции х изе/Г(Г), т. е. \x = \if.
4.8. Измеримые функции
Используя понятие измеримого хмножества и свойства таких
множеств (§ 4.7), можно ввести и исследовать понятие измери-
измеримости функций. Стандартные методы такого введения доступно
изложены в ряде книг по теории функций вещественного пере-
переменного и теории интегрирования (см., например Мак-Шейн
[1, гл. III], Г рей в с [1,гл.Х, § 4], Беркхилл [1, §2.12], Гофф-
ман [1, гл. 15], Натансон [1, гл. IV], Сакс [1, § 7, 8], Хал-
мош [1, гл. IV], Колмогоров и Фомин [1], Шилов [2,
гл. IV], Шилов и Гуревич [1, гл. III], Вулих [1, гл. VI]).
Приведем определения и основные свойства, предоставляя до-
доказательства читателю в качестве легких упражнений.
Начнем с вещественных функций /. Будем говорить, что ве-
вещественная функция измерима (точнее, ^-измерима), если мно-
множество тех точек /gT, для которых f(t) >а, измеримо при каж-
каждом вещественном а. (В этом определении с тем же успехом
можно использовать множества, для которых / > а, или f<a,
или f^Ca.) Это определение применимо к функциям, опреде-
определенным на любом заданном измеримом множестве А. Сумма и
произведение двух измеримых функций измеримы. Если функ-
функция f задана и измерима на измеримом множестве А и нигде
на А не обращается в нуль, то на множестве А измерима и функ-
функция 1//. Верхняя и нижняя огибающие, верхние и нижние пре-
пределы всякой (конечной или счетной) последовательности изме-
измеримых функций измеримы. Полунепрерывные функции изме-
измеримы. Всякая положительная измеримая функция является
пределом возрастающей последовательности измеримых функ-
функций, каждая из которых есть конечная линейная комбинация
характеристических функций измеримых множеств.
Комплексная функция называется измеримой, если измеримы
ее вещественная и мнимая части.
Две функции, локально почти всюду равные, измеримы или
неизмеримы одновременно.
Функция называется универсально измеримой, если она
(i-измерима для каждой положительной меры Радона \х на Т
Вот все об основных определениях и свойствах измеримых
функций. Покажем теперь, как понятие измеримости исполь-
используется в теории интегрирования: требование измеримости яв-
является существенной составной частью критерия интегрируе-
интегрируемости.4
4.8. Измеримые функции 279
4.8.1. Теорема. Функция f интегрируема тогда и только то-
тогда, когда
(а) аднцчтх + оо,
(Ь) функция f измерима.
Доказательство. Необходимость. Необходимость условия
(а) следует из самого определения интегрируемости (§ 4.6). Что
касается условия (Ь), то его необходимость вытекает из след-
следствия 4.6.9(а) и из измеримости непрерывных функций.
Достаточность. Пусть функция / удовлетворяет условиям (а)
и (о). Докажем интегрируемость функции /. Не нарушая общ-
общности, можно считать, что / — вещественная положительная
функция. Тогда функции fn = inf (/, п) измеримы, Ni(fn) -^
^С Ni(f) < + oo и последовательность fn, возрастая, сходится к
/. Таким образом (теорема 4.6.6), достаточно показать, что каж-
каждая из функций fn интегрируема. Другими словами, можно счи-
считать, что функция / ограничена и, более того, что 0^/<1. По-
Поскольку в силу условия (а) функция / обращается в нуль почти
всюду вне а-конечного множества, мы можем (еще раз опираясь
на теорему 4.6.6) свести рассуждения к случаю, когда функция^
f обращается в нуль вне интегрируемого множества Л. Возьмем
числа О = со<с\<.. .<сп= 1 и обозначим через Ak мложество
точек из Л, определенное неравенствами ck-i 4if<ch, Каждое
из множеств Ak измеримо и содержится в Л и потому интегри-
интегрируемо. Следовательно, функция
также интегрируема. Очевидно также, что g^-f^Cg + e%A, где
е — наибольшее из чисел (ck — c/t-i). Так как е можно взять
сколь угодно малым, то интегрируемость функции f вытекает
И8 соотношения Ni(f — g)<CNi(e%A)=E'\i(A). I
Замечание. Приведенная выше конструкция дает спо-
способ аппроксимации интеграла \x(f) or функции /, если послед-
последняя интегрируема и обращается в нуль вне интегрируемого
множества Л, причем Л можно разложить на измеримые под-
подмножества Ak, на каждом из которых колебание функции f мало.
Если выбрать произвольно точки tk в Aki то суммы вида
аппроксимируют \i(f). Это замечание в свою оче-
очередь подсказывает обозначения Г fd\i и J fd\i. В дальнейшем
А
мы будем иногда употреблять обозначения Г/ф и Г fd\x
вместо [i(f) и \i*(f) соответственно.
280 рлт 4, Топологии, сопряженные к некоторым пространствам; меры Радона
Обратимся теперь к знаменитой теореме Лебега о сходи-
сходимости.
4.8.2. Теорема (Лебег). Пусть вещественные функции fn
(п=\, 2, ...) измеримы, g— вещественная интегрируемая функ-
функция и для каждого п почти всюду имеет место неравенство
\fn\^>g- Тогда функции lim inf fn и lim sup/n интегрируемы и
справедливы неравенства
J (lim inf fn) d\x < lim inf J fn d\i.
J (lim sup fn) dp > lim sup J fn d\i.
Таким образом, если lim fn существует почти всюду, то
J (Нт/л)ф = Нт j fnd\i.
Доказательство. Прежде всего второе неравенство по-
получается из первого переменой знака. Рассмотрим функцию / =
= lim inf/n. Она измерима, и |/|-^g" почти всюду. Следова-
Следовательно (теорема 4.8.1), функция / интегрируема. Положим Fn =
= inf{fm: m^-n). Снова функции Fn измеримы, |Fn|^gf почти
всюду, и, значит, Fn интегрируемы. Далее, Kit/» функции
Fn-{-g положительны, интегрируемы и образуют возрастающую
последовательность, сходящуюся к f + g. Поэтому (предложение
4.5.3)
и так как мера |ш аддитивна, a \i(g) конечно, то \x(Fn) \\x(f).
Наконец, из неравенств Fn^Cfm (m > п) следует, что \i(Fn) <
^(fm) {m^n) и потому lim \x(Fn) < lim inf \i(fn). I
Рассмотрим некоторое общее свойство измеримых функций.
Начнем с важной теоремы о сходимости.
4.8.3. Теорема (Егоров). Пусть на интегрируемом мно-
множестве А определены и измеримы функции f и fn (м=1, 2, ...),
и пусть /п->/ почти всюду на А. Тогда эта сходимость почти
равномерна на А в следующем смысле: для каждого е>0 суще-
существует такое измеримое множество В а А (причем В можно
считать компактным), что \i(A\B)<e и fn-*-f равномерно
на В.
Доказательство. Можно считать, что /п->/ всюду на
А. Для любых двух натуральных чисел п и k обозначим через
Qn,k множество тех точек /еЛ, для которых
4.8. Измеримые функции 281
Множества Qn, и измеримы, Qn+i, u^Qn,и и f) Qn,A = 0. Следо-
п
вательно, ii(Qn,k) -*0 при п->оо. Поэтому можно так выбрать
числа nh, чтобы \i(pk)^2~ke, где Pk=zQnk^h- Если t^A\Pk,
то для всех т^- rtk имеет место неравенство
Достаточно положить S = A\(J/V (Если требуется, чтобы
k
множество В было компактным, то нужно просто сделать еще
один шаг: выбрать такое компактное множество К в б, чтобы
\х{В\К) было произвольно малым,) В
Укажем теперь, как аппроксимировать измеримые функции
«простыми» функциями.
4.8.4. Теорема. Пусть А—интегрируемое множество и функ-
функция f определена и измерима на А. Тогда f является на А почти
равномерным пределом (и тем более пределом почти всюду на
А) последовательности функций (/п), каждая из которых есть
конечная линейная комбинация характеристических функций ин-
интегрируемых подмножеств множества А.
Доказательство. Пусть (ап)—всюду плотная последо-
последовательность чисел (вещественных или комплексных). Обозначим
через АщР множество тех точек /еЛ, для которых
\f(t)—ап\^Ср~1. Все эти множества интегрируемы. Определим
множества Вп% р следующим образом:
В\,р — А\,р> Bn+it p = An+itр\ U Ak,p»
Эти множества также интегрируемы и образуют разбиение мно-
множества А для всякого фиксированного р (и переменного п). Для
каждого р можно так выбрать число пр, чтобы множество
А \ (J Вп> р имело меру, не превосходящую 2~р. Определим
п<пр
функцию /р, полагая ее равной ап на множестве Bn> p
(\4in4Lnp) и нулю во всех остальных точках. Очевидно, fp
являются функциями описанного в теореме вида, и неравенство
\f — fp\^P~l имеет место во всех точках множества Л, за
исключением, быть может, множества Np, для которого ii(Np)^.
<2~р. Множества N*q= (J Np удовлетворяют неравенствам
\x(N])^2]-q, и
\fp(t)-f(f)\<~ (t^A\N;, p>q).
Таким образом, fp-+f равномерно на А \ Nq, т. е. fp-*f почти
равномерно на А. В
282 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
4.8.5. Следствие (Лузин). Пусть функция f определена и
измерима на интегрируемом множестве А. Тогда для всякого
е>0 существует такое компактное множество К с; Л, что
\х(А \К) <е и сужение f\K непрерывно.
Доказательство. В силу теоремы 4.8.4 достаточно по-
показать, что наше утверждение справедливо в случае, когда
функция / является конечной линейной комбинацией характери-
характеристических функций интегрируемых подмножеств Аг в А
(\^Ci-tCn). Можно считать, что множества А{ дизъюнктны и
образуют разбиение множества А. Далее, компактные множе-
множества KiCiAi можно выбрать так, чтобы их объединение К удо-
удовлетворяло неравенству \х(А\К)^Сг. Ясно, что сужение f\K
непрерывно. В
4.8.6. Замечания. Очевидно, что справедливо и обратное
утверждение, т. е. каждая функция /, удовлетворяющая усло-
условию Лузина, измерима. Бур баки [8, гл. IV] при рассмотрении
функций со значениями в топологическом пространстве Г* бе-
берет условие Лузина в качестве определения измеримости функ-
функций. Два понятия измеримости совпадают, только бели про-
пространство Г* удовлетворяет некоторым условиям счетности.
Несомненно, что для функций, принимающих абстрактные
значения, критерий Лузина более целесообразен в качестве опре-
определения измеримости.
Сейчас мы вполне могли бы заняться вопросами, которыми
фактически займемся в § 4.11. Однако мы прервем изложение
общей теории интегрирования, чтобы показать, что некоторые
множества мер в точности представляют пространства, сопря-
сопряженные к пространствам непрерывных функций. Этот вопрос из-
излагается в § 4.10. В § 4.9 вводится подготовительное понятие
носителя меры.
4.9. Носитель меры
Пусть Т — локально компактное пространство и \х — поло-
положительная мера Радона на Т. Из предложения 4.5.1 следует,
что объединение всех открытых пренебрежимых множеств обра-
образует максимальное открытое пренебрежимое множество U. Точ-
Точка пространства Т принадлежит U тогда и только тогда, когда
она обладает пренебрежимой окрестностью. Дополнение F мно-
множества U называется носителем меры \х. Множество F всегда
замкнуто в Т. Точка t из Г. принадлежит множеству F тогда и
только тогда, когда у нее нет пренебрежимых окрестностей.
Пусть ji — комплексная мера Радона на Т. Носителем меры
\i будем называть носитель положительной меры
4.9. Носитель меры 283
где а и р — вещественная и мнимая части меры \х, а а = а+ — а
и Р = Р+ — Р~ — минимальные разложения мер аир (см. тео-
теорему 4.3.2). Носитель меры \л является, очевидно, объединением
носителей мер а+, а~, р+, (Г. Для удобства будем писать щ,
И-2> М-з» Ш вместо а+, а~~, р+, р~ и называть равенство
\X=\ll — \l2 + l[lZ— ^4
минимальным разложением меры [х.
4.9.1. Предложение. Пусть \х — комплексная мера Радона на
Т с носителем F. Открытое множество U в Т пренебрежимо (т. е.
содержится в T\F) тогда и только тогда, когда \x(f) = 0 для ка-
каждой функции / е^+(Г), носитель которой содержится в U.
Доказательство. Необходимость очевидна. Действи-
Действительно, если U пренебрежимо, то \i\(U) = 0 при й=1, 2, 3, 4.
Так как 0</ < HflU'Xy для ФУнкиий f^J!f+(T) с носителем,
содержащимся в U, то [л^(/) =0 (&=1, 2, 3, 4) и, следовательно,
и(/)=о.
Обратно, пусть jut(f) = 0 для всех функций /, удовлетворяю-
удовлетворяющих условиям теоремы. Это равенство имеет место и для веще-
вещественной и мнимой частей меры |i в отдельности. Поэтому (ср.
с доказательством теоремы 4.3.2) справедливы равенства
\ik(f) =0 при fe = l, 2, 3, 4. Функция %ц является верхней огибаю-
огибающей некоторой системы функций 1^Ж+(Т\ с носителями в £/,
и потому (предложение 4.5.1) \x+(U) = 0 при /г=1, 2, 3, 4. Та-
Таким образом, множество U пренебрежимо. В
Замечание. Если F — носитель положительной меры ji, то
вполне могут существовать ji-пренебрежимые непустые множе-
множества, содержащиеся в F. Например, если \х — мера Лебега на
R, то ее носителем служит само R (потому что всякое непустое
открытое множество имеет строго положительную меру). Од-
Однако пренебрежимые непустые множества все же существуют.
4.9.2. Пример. Пусть Т — вещественный интервал, f — функ-
функция локально ограниченной вариации на Г и \xf — соответствую-
соответствующая ей мера Лебега — Стилтьеса (п. 4.4.4, 4.5.6, 4.7.7, 4.7.8).
Найдем носитель S меры ji/. Множество U = T\S открыто от-
относительно Т. Предположим сперва, что функция f возрастаю-
возрастающая, так что |ы/>0. Для всякого ограниченного интервала /,
содержащегося в £/, имеем \xf(I)=0. Если в качестве / брать
одноточечные множества, то из результатов п. 4.7.7 следует не-
непрерывность функции / во всех точках множества U. Значит,
Функция / должна быть постоянной на каждой связной компо-
компоненте множества f/, т. е. функция f локально постоянна на U.
Обратно, если функция / локально постоянна на U, то ц./(£/) =0.
284 Гл. 4. Топологич. сопряженные к некоторым пространствам; меры Радона
Таким образом, носитель S меры ju/ есть дополнение в Т наи-
наибольшего открытого относительно Т множества t/ciT1, на кото-
котором функция f локально постоянна. То же самое имеет место и
для функций / локально ограниченной вариации. Это следует
из возможности разложения / на разность двух монотонно воз-
возрастающих функций или из предложения 4.9.1.
В качестве примера пусть Г = [а, Ь] и функция / постоянна
на каждом из интервалов (£г--ь £г) (l^-i^-tri), где а =
= co<ci<.. .<cm = b. Легко показать, что (см. Натансон [1,
гл. VIII, § 6, теорема 3]) для х?(Г)
ь
Это можно получить также на основании результатов п. 4.7.7.
Таким образом,
i
+ [f(b)-f(b-O)]sb.
Отсюда следует, что носитель S меры jm/ состоит из тех точек
с{ (l<t<m), в которых f(Ci + O) — f(c{ — 0)-=f0, точки а, если
f(a + 0)H(a)y и точки 6, если f(b)^f(b — O).
4.10. Пространство С(Т) и его сопряженное
Пусть Т — локально компактное пространство. Обозначим
через С(Т) векторное пространство всех комплексных, непре-
непрерывных функций на Г и наделим его топологией равномерной
сходимости на компактных подмножествах в Т.
Эта топология определяется полунормами
pK(x)=sup{\x(t)\: t<=Kh D.10.1)
где К пробегает некоторую заданную базу компактных подмно-
подмножеств в Т. Если Т компактно, то С(Т)—нормируемое и даже
банахово пространство с нормой lUIU.
Наша задача — показать, каким образом пространство, со-
сопряженное к С (Г), может быть описано с помощью комплекс-
комплексных мер Радона на Т. Такую же задачу можно поставить в слу-
случае, когда вместо С(Т) рассматривается векторное простран-
пространство вещественных непрерывных функций на Г. При этом можно
4.10. Пространство С(Т) и его сопряженное 285
иметь дело только с вещественными мерами Радона. Подробное
рассмотрение последней задачи предоставляем читателю.
4.10.1. Теорема. Пусть L — непрерывная линейная форма на
С(Т). Существует единственная комплексная мера Радона jm на
Т с компактным носителем, такая, что
x(t)dMt). D.10.2)
т
Обратно, если \х — комплексная мера Радона на Т с компактным
носителем, то формула D.10.2) определяет непрерывную линей-
линейную форму L на С(Т).
Доказательство. Обратное утверждение очевидно. Дей-
Действительно, если К — компактный носитель меры \i, то всякая
функция х^С(Т) интегрируема относительно \\х\ и, следова-
следовательно, относительно \ik (&=1, 2, 3, 4). Поэтому
\1 (X) = jl! (X) - \Х2 (X) + /Ц3 (X) - Щ4 (X)
является линейной формой на С (Г), а из соотношений
следует непрерывность линейной формы L, определенной фор-
формулой D.10.2).
Пусть теперь L — непрерывная линейная форма на С(Т).
Тогда найдется такое компактное множество К и такое число с,
что \L(x) \^Сс-рк(х) для всех х^С(Т). Пусть jm — сужение
линейной формы L на пространство <Ж(Т). Ясно, что \х — ком-
комплексная мера Радона на Т. Из предложения 4.9.1 вытекает, что
носитель \i содержится в К и, значит, является компактным мно-
множеством. Поэтому равенство L (х) = \л (х), справедливое по опре-
определению для всех х ^.<Ж{Т), продолжается на все х е С(Т) (обе
части этого равенства не изменяются при замене х на fx, где
/ — произвольная функция из е2Г+(Г), равная 1 на К). В
Установленный только что результат может быть сформули-
сформулирован следующим образом. Если через М(Т) обозначить век-
векторное пространство комплексных мер Радона на Т и через
МС(Т)—его векторное подпространство, образованное мерами
с компактными носителями, то пространство, сопряженное к ло-
локально выпуклому пространству С (Г), может быть отожде-
отождествлено с МС(Т), причем билинейной формой, приводящей эти
пространства в двойственность1), служит
= \i(x)= $ xdii, D.10.3)
См. § 8Л. — Прим. перев.
286 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
где х(=С(Т) и \1^МС{Т). Если Т компактно, то МС(Т)=М(Т)
и мы получаем классическую теорему Ф. Рисса в обобщенном
виде. История различных обобщений теоремы Рисса, которая
относится к случаю Г = [0, 1], весьма богата1). Некоторые исто-
исторические замечания читатель найдет в п. 4.10.7. В последнее
время рассматривалась возможность отказа от требования ло-
локальной компактности пространства Т (п. 4.10.7).
Стоит привести здесь два следствия только что установлен-
установленной двойственности. Первое из них — критерий слабой сходи-
сходимости в С (Г), второе — критерий слабой компактности в МС(Т).
4.10.2. Теорема. Для того чтобы последовательность (хп) в
С(Т) слабо 'сходилась к х^С(Т), необходимо и достаточно,
чтобы
(a) limxn = x поточечно в Г;
(b) для каждого компактного множества /(с: Т выполнялось
условие
sup{\xn(t)\: ts=K> /i=»l, 2, ...}< +оо.
Доказательство. Достаточность непосредственно сле-
следует из теоремы 4.8.2 и установленного выше совпадения про-
пространства, сопряженного к С (Г), с Мп(Т).
Необходимость условия (а) очевидна. Действительно, ото-
отображение x\—>x{t) при каждом fsT есть непрерывная линей-
линейная форма на С(Т) (соответствующей мерой является, конечно,
мера Дирака е*, сосредоточенная в точке t). Необходимость
условия (Ь) есть частный случай теоремы 8.2.2, так как всякая
слабо сходящаяся последовательность слабо ограничена. В
4.10.3. Теорема. Для того чтобы подмножество L простран-
пространства МС(Т) было относительно слабо компактным, достаточно
существования такого компактного множества К в Г, чтобы но-
носитель каждой меры \х из L лежал в К и чтобы
{sup{|^|(r): \i*=L}< +oo.
Если Т — а-компактное пространство, то это условие также и
необходимо.
Доказательство. Сформулированное условие равно-
равносильно равностепенной непрерывности множества L (рассматри-
(рассматриваемого как подмножество пространства, сопряженного к С (Г)),
поэтому множество L относительно слабо компактно (теорема
1.11.4B)). С другой стороны, если пространство Т а-компактно,
то С(Т) является пространством Фреше (§6.1 и пример 6.1.3),
1\ Доказательство самой теоремы Рисса см., ьапример, у Натансона
[1, стр. 258].
4.10. Пространство С(Т) и его сопряженное 287
поэтому достаточно воспользоваться следствием 7.1.2 и тем
фактом, что всякое относительно слабо компактное множество
слабо ограничено. В
Замечания. Если пространство С(Т) сепарабельно (на-
(например, если Т метризуемо и а-компактно) и множество L удо-
удовлетворяет сформулированным условиям, то теорема 4.10.3 сво-
сводится к утверждению, что из всякой последовательности (\хп)
элементов множества L можно извлечь подпоследовательность,
слабо сходящуюся к комплексной мере Радона, носитель кото-
которой содержится в К.
Если Т — компактный интервал вещественной оси, то это
утверждение тесно связано с так называемыми теоремами
Хелли, формулируемыми в терминах функций ограниченной ва-
вариации, причем здесь играет роль интеграл Римана — Стилгьеса.
Подробности см. у Натансона [1, стр. 242 и 254]. Для случая,
когда Т есть пространство Rn, этот результат был назван Валле-
Пуссеном принципом выбора и использовался им и Фростма-
ном в теории потенциала.
Заметим, что если Т — компактное пространство, то МС(Т) =
= М(Т)—банахово пространство относительно нормы \\\i\\ =
= \[х}(Т) или относительно эквивалентной нормы
x<=C(T), IUL<
В этом случае теорема утверждает, что множество L в М(Т)
относительно слабо компактно тогда и только тогда, когда оно
ограничено по норме. Существует много полезных приложений
этого принципа. Он используется в § 8.13 и затем в гл. 10 (см.,
в частности, теоремы представления Бернштейна и Бохнера в
§ 10.2 и 10.3 соответственно). Приводимый ниже пример служит
непосредственным приложением этого принципа.
4.10.4. Пример. Интеграл Пуассона гармонических функ-
функций. Рассмотрим представление с помощью интеграла Пуас-
Пуассона функций, гармонических на единичном круге D комплекс-
комплексной плоскости. Пусть Г —граница круга D, т. е. единичная
окружность. Мы исходим из того факта, что гармоническая на
D и непрерывная на D — DUT функция и имеет вид
*ф)= j P(z, t)u(t)da(t) (геД), D.10.4)
т
где а — положительная мера Радона на Г, определенная ра-
равенством
2Я
288 Гл. 4. Топологич. сопряженные к некоторым пространствам; меры Радона
(интеграл здесь — обычный интеграл Римана), и Р — ядро Пуас-
Пуассона
Р(г> 0 = Re 73J-
Схема доказательства равенства D.10.4) такова. Правая часть
(назовем ее V) является гармонической в D функцией. Стан-
Стандартными методами анализа показывается, что U(z)-+u(t),
когда точка z^D стремится к граничной точке t. Таким обра-
образом, разность и—U является гармонической функцией на D и
принимает всюду на границе нулевые предельные значения. Из
принципа максимума модуля следует тогда, что u=U всюду
в Д т. е. имеет место формула D.10.4).
Заметим теперь, что P(O,t) = \. Поэтому из D.10.4) вытекает
равенство
и@)= J u(t)da(t), D.10.5)
т
которое представляет собой не что иное, как известное «свой-
«свойство среднего значения» гармонических функций.
Если ввести меру \хи = и»а, то можно записать
и(г)=$Р(г9 t)]itt(t) (zeeD) D.10.6)
т
и
и@)= JrfMO- D.10.7)
т
Если и— положительная функция, то мера \хи положительна.
Пусть теперь и — гармоническая положительная функция на
D (не обязательно непрерывная, или даже определенная, на
Т). Положим ип (z) = и ( п* 1 j. Очевидно, что ип — гармони-
гармонические положительные на D и непрерывные на D функции. Обо-
Обозначим через \ьп = \*>и соответствующие им меры, В силу D.10.7)
и
поэтому все меры \in положительны. Согласно принципу выбора,
можно извлечь из последовательности (\хп) подпоследователь-
подпоследовательность, которая слабо сходится к некоторой положительной мере
\х на Т. При фиксированном z e D функция P(z, t) еС(Г). По-
Поэтому для выбранной подпоследовательности имеем
- J Р (^, t) фЛ it)->\p (Z, t) d\L (t).
4.10. Пространство С(Т) и его сопряженное 289
Очевидно, последовательность (ип) поточечно сходится к и на
D. Таким образом получаем формулу
u(z)=jP(z,t)dli(t) D.10.8)
т
— интегральную формулу Пуассона для функции и. Итак, эта
формула установлена для всякой положительной гармонической
на D функции и.
Если функция и не является положительной, то предыдущие
рассуждения не проходят. Меры \хп уже не обязательно поло-
положительны, и нельзя воспользоваться формулой D.10.7) для вы-
вычисления норм || \хп || = | \хп | (Г). Однако мера |шп во всех случаях
равна ип*а, поэтому
Таким образом, предыдущие рассуждения сохраняют силу, если
известно, что
2я
liminf [\u(rt)\da(t) = \imini-4- f \и(ге*<*) \dq>< + оо. D.10.9)
При этом, естественно, мера \х в окончательной формуле D.10.8),
вообще говоря, не будет положительной.
Легко видеть, что и, обратно, если формула D.10.8) имеет
место для некоторой меры \х на Г, то справедливо отношение
D.10.9). Действительно, так как Р ^ 0, то из D.10.8) следует,
что
J(Z, t)d\]L\(t).
т
Если 0<г<1 и ГеГ, то
и (rf) | da (Г) < J da (Г) J Р (/Г, 0 d | |x | (/).
Как легко показать, порядок интегрирования можно изменить,
так что правая часть неравенства равна
. t)da(f).
При фиксированных г_и t функция z*->P(rz, t) гармонична на
D и непрерывна на D. Внутренний интеграл, будучи средним
290 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
значением этой функции, есть не что иное, как Р@, t) = 1. Таким
образом, для всех г, удовлетворяющих условию 0<^г<1, имеем
J
КП
т. е. справедливо D.10.9).
Между прочим, мы доказали, что условие D.10.9) эквива-
эквивалентно условию
sup [\u(rt)\da(t)< + оо. D.10.9/)
0<г<1 J
Резюмируем:
► Для того чтобы функция и на D была представима в
форме D.10.8), где \i — мера Радона на Г, необходимо
и достаточно, чтобы функция и была гармонической
на D и удовлетворяла условию D.10.9/). Последнее
условие выполняется автоматически, если функция и
гармонична и положительна на D.
В заключение отметим, что подобные теоремы представле-
представления гармонических функций, определенных на других областях,
получаются с помощью сходных рассуждений (или в некото-
некоторых случаях с помощью конформных отображений из самой
формулы D.10.8). Такими рассуждениями доказываются ана-
аналогичные формулы для голоморфных функций, связанные с
именами Герглотца, Рисса, Неванлинны и др. Само представ-
представление D.10.8) принадлежит Эвансу, Брэю и Плеснеру.
4.10.5. Пространство С(Т) как алгебра; теорема Вейер-
штрасса— Стоуна. В этом и в следующем пунктах мы покажем,
каким образом понятие носителя меры в сочетании с теоремой
4.10.1 может быть использовано для выяснения структуры про-
пространства С(Г), принимая во внимание возможность перемно-
перемножать функции из С(Т) (т. е. здесь мы рассматриваем С(Т) как
алгебру, а не только как векторное пространство). В настоя-
настоящем пункте мы приведем доказательство знаменитой теоремы
Вейерштрасса — Стоуна о подалгебрах в С(Т), а в п. 4.10.6
займемся изучением замкнутых идеалов в С(Г).
Если Т — компактный интервал вещественной оси, то, не на-
нарушая общности, можно считать, что это отрезок [0, 1]. Класси-
Классическая аппроксимационная теорема Вейерштрасса утверждает,
что каждая вещественная непрерывная функция на Т является
равномерным пределом многочленов. Отсюда, очевидно, сле-
следует* возможность аналогичной аппроксимации непрерывных
комплексных функций. В своей (знаменитой теперь) открыв-
открывшей новые пути статье Стоун [2, стр. 466—469] начал изуче-
4 10 Пространство С(Т) и его сопряженное 291
ние далеко идущих обобщений теоремы Вейерштрасса, в кото-
которых Т — произвольное отделимое компактное пространство.
Всюду в этом пункте Т будет обозначать отделимое ком-
компактное пространство, CR (Т) (соотв. С(Т))—векторное про-
пространство над R (соотв. над С) вещественных (соотв. ком-
комплексных) непрерывных функций на Т и MR (Т) соотв.М(Т)) —
векторное пространство над R (соотв. над С) вещественных
(соотв. комплексных) ограниченных мер Радона на Т. Мы бу-
будем предполагать также, что каждое из пространств CR (T) и
С(Т) топологизировано с помощью равномерной нормы
||*|| = sup {|*(/) |; *е=71
Как мы знаем (теорема 4.10.1), MR(T) (соотв. М(Т)) можно
отождествить с пространством, сопряженным к CR (T) (соотв.
С{Т))
))
Подмножество Q в С(Т) называется отделяющим точки,
если для любых двух различных точек V и t" из Т существует
такая функция x(t), принадлежащая подмножеству Q, что
х(ПФх(П.
Пусть х (вещественная или комплексная) функция на Т.
Обозначим через Z(x) множество нулей функции х, т. е. Z(x) =
= {t^T: x(t) = 0}. Если F — множество таких функций, то че-
через Z(F) будем обозначать пересечение f){Z(x):x^F} мно-
множеств нулей элементов из F.
Напомним, что подкольцо в С# (Т) (соотв. С(Т))—это та-
такая аддитивная подгруппа А в CR (T) (соотв. С(Т)), для кото-
которой ху<=А при XG/1, у^А. Если, кроме того, Л —векторное
подпространство в CR (T) (соотв.С (Г)), то А — подалгебра в
Сц(Т) соотв. С(Т)). Говорят, что А — алгебра с единицей,
если А содержит постоянную функцию 1.
Вначале рассмотрим случай пространства CR (T). Наша за-
задача— доказать теорему, что всякая отделяющая точки подал-
подалгебра в CR(T), для которой Z(A) = 0, плотна в CR (Г). Из
этой теоремы будет получен аналогичный результат1) и для
С(Т) (Гельфанд и Шилов [1]). Некоторые весьма изящ-
изящные доказательства этого и связанных с ним результатов ис-
используют частичную упорядоченность множества CR(T) (см.,
например, Бур баки [8, гл. X], Гильман и Джерисон
[1, стр. 242], Какутани [1]). В приводимых нами рассужде-
рассуждениях, принадлежащих де Бранжу [1], частичная упорядо-
упорядоченность в явном виде почти не используется (хотя в неявном
') Но с важным дополнительным условием на подалгебру, состоящим
в том, что она вместе со всякой функцией содержит комплексно сопряжен-
сопряженную. — Прим. ред.
292 Г л 4. Топологии, сопряженные к некоторым пространствам; меры Радона
виде эта структура все-таки используется, поскольку она играет
роль в теории интегрирования).
С другой стороны, доказательство де Бранжа опирается
на теорему Крейна — Мильмана о выпуклых компактных мно-
множествах в топологическом векторном пространстве. Хотя до-
доказательство этой теоремы приводится лишь в гл. 10, ссыл-
ссылка на нее в этом месте не приводит к порочному кругу; тем
не менее имеет смысл хотя бы сформулировать эту теорему
здесь.
Пусть X — вещественное отделимое локально выпуклое про-
пространство и Q — выпуклое множество в X. Точка х е Q назы-
называется крайней (или экстремальной) для Q, если из равенства
х = ау + A— а) г для некоторого а, удовлетворяющего нера-
неравенству O^a^l, и некоторых у, z^Q следует, что х совпа-
совпадает с у или с z. Другими словами, х — концевая точка любого
отрезка, ее содержащего и целиком лежащего в Q. Теорема
Крейна — Мильмана (теорема 10.1.2) утверждает, что ком-
компактное выпуклое множество Q является замкнутой выпуклой
оболочкой множества своих крайних точек. В частности, если
Q ф {0}, то обязательно существуют ненулевые крайние точки
множества Q.
Эта теорема будет применена в следующей ситуации. Пусть
А — некоторое множество в CR (Т) и А0 — множество мер из
Мк (Г), обращающихся в нуль на функциях из множества А.
Обозначим через В замкнутый единичный шар в MR (T) и по-
положим Q=A°f]B. Наделим пространство Mr (T) слабой топо-
топологией, рассматривая его как топологическое сопряженное к
CR (T) (теорема 4.10.1). Из теоремы 4.10.3 следует компакт-
компактность множества В. Так как множество А° замкнуто, то множе-
множество Q компактно. Очевидно также, что Q выпукло. Следова-
Следовательно, к Q можно применить теорему Крейна — Мильмана.
В частности, если Q не сводится к {0}, то оно обладает крайней
точкой, отличной от нуля. Заметим, что в действительности для
всякой крайней точки X Ф 0 множества Q \\X\\ = 1. В самом де-
деле, если КФ0, то iXjj-esQ и потому ЛН|Л|| • щ + A -||А||) • 0.
Так как точка I крайняя, то Я = -щ- ф 0; следовательно, || Я || = 1.
Имея в виду эти предварительные замечания, докажем сле-
следующую лемму.
Лемма. Пусть К — крайняя точка множества Q и g — веще-
вещественная ограниченная универсально измеримая функция на Т,
для которой \ xgdX = 0 для всех х^А. Тогда существует
такое вещественное число k} что g*K=kh<
4.10. Пространство С(Т) и его сопряженное 293
Доказательство. Если X = О, то доказывать нечего.
Пусть J xgdX = 0 для xgA Равенство останется справед-
справедливым, если заменить g на a(g + b), каковы бы ни были веще-
вещественные числа а и Ь. Поэтому всюду далее можно считать, что
Введем меру X* = g-X и положим m = \\Х*\\. Если m = О, то
X* = 0 = 0• X и все ясно. Если же m = 1, то l=m=\gd\X\,
откуда в силу условия O^g"-<^1 следует, что g = 1 почти всю-
всюду, и потому X* = X = 1 • X.
Пусть теперь 0 < m < 1. Положим
X =— X -l~~v
Легко убедиться в том, что Х\у Х2 e Q. Следовательно,
= 1 и
J х dXx = m J л: ^Я* = m J л:^ dX = О
для хеЛ Значит, Xi e Q. Отсюда вытекает, что 1* =
е Л°. С другой стороны,
следовательно,
Далее, поскольку меры X и X* принадлежат Л°, это верно также
и для Х2. Таким образом, Х2 е Q. Из равенства
X = A — гп)Х2 + тЯ»!
и «крайности» меры Я следует, что либо X — Хи либо Я = Х2.
В каждом из этих случаев сразу получаем, что X = Х\. Поэто-
Поэтому g'X = X* = m^! == тЯ, как и утверждалось (только вместо
/г написано т). 1
Теперь мы можем доказать основной результат для CR (Г).
Теорема А. (Стоун). Пусть А — отделяющая точки подал-
подалгебра в CR (Г), такая, что Z(A) =0 (т. е. функции из А не
имеют ни одного общего нуля в Т). Тогда множество А всюду
плотно в CR (T).
Доказательство. Множество Л, будучи подалгеброй в
пространстве CR(T), является его векторным подпространст-
подпространством. Поэтому (теорема Хана — Банаха) Л плотно в CR (T)
тогда и только тогда, когда Л° ~ {0}, что равносильно условию
Q = {0}.
294 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Допустим, что Q не сводится к {0}. Тогда- из теоремы Крей-
на — Мильмана вытекает, как мы уже видели, существование
в Q по меньшей мере одной крайней точки X ф 0. Пользуясь
предыдущей леммой, мы покажем, что всякая такая мера д
является неотрицательным скалярным кратным меры е* для
некоторой точки t&T. Если это так, то x{t)= I xdX обраща-
обращается в нуль для всех х^А, потому что %^ Q аА°. Но тогда
t^Z(A), что противоречит условию.
Чтобы показать, что мера К должна иметь указанный вид,
заметим, что g-k(=Ao для g^A, так как множество А есть
подкольцо в CR (T). В силу доказанной леммы g'X = const «А,,
поэтому функция g постоянна на носителе меры К. Так как
множество А отделяет точки, то носитель меры К сводится к
одной точке, скажем t^T. Следовательно, А, = с-еь где число
с не может быть равно нулю, так как X Ф 0. Теорема полно-
полностью доказана. |
Из этой теоремы уже совсем легко получить аналогичный
результат для пространства С(Т).
Теорема В. Пусть А — отделяющая точки подалгебра в
С(Т), для которой Z(A) =0. Если вместе с каждой функцией
х функция х также принадлежит А, то множество А всюду
плотно в С(Т).
Доказательство. Из условия теоремы следует, что
Rex (= А и imx<=A при xgA Обозначим через Лк множество
вещественных функций из Л; множество Лк удовлетворяет ус-
условиям теоремы А. Следовательно, А% всюду плотно в Cr(T)
и потому А всюду плотно в С(Т).Ш
Замечания. Если Т — локально компактное, но не ком-
компактное пространство, то легко получить аналогичный резуль-
результат для пространства вещественных (или комплексных) непре-
непрерывных функций на Г, обращающихся в нуль на оо1). Надо
только продолжить все эти функции на пространство Т — ком-
пактификацию Александрова пространства Т — и рассмотреть
подкольцо в CR (T) (или С (Г)), порожденное объединением
Ли{1}. Мы заключаем, что справедливы прямые аналоги тео-
теорем А и В, только теперь Т — локально компактное простран-
пространство и рассматриваются лишь те непрерывные функции (веще-
(вещественные или комплексные), которые обращаются в нуль на оо.
Существует богатая литература по различным обобщениям
теоремы Вейерштрасса — Стоуна. Мы укажем лишь несколько
названий: Бур баки [6, гл. X], Арене [2], Кацлацский [1,
См. § 4.2. — Прим. пере*.
4 10. Пространство С(Т) и его сопряженное 295
2], Стоун [3], Хьюитт [3]; отметим также большую обзорную
статью Стоуна [1].
4.10.6. Замкнутые идеалы в С(Т). Приведем- здесь еще два
приложения понятия носителя меры и теоремы 4.10.1. В обоих
случаях пространство С(Т) будет рассматриваться как алгеб-
алгебра, где произведение ху означает функцию t\—>x(t)y(t). Легко
проверяется, что отображение (х,у)\—>ху произведения С(Т)Х
X С(Т) в С{Т) непрерывно, так что С(Т) является и тополо-
топологической алгеброй и топологическим векторным пространством.
Рассмотрим две задачи, связанные с этой дополнительной
структурой (см., например, Эдварде [7]).
Под характером1) на С(Т) понимается гомоморфизм X ал-
алгебры С(Т) на поле комплексных чисел С (фактически поле С
надо рассматривать здесь как алгебру над самим собою), т. е.
такое отображение X: С(Г)—>С, которое линейно, мультипли-
мультипликативно (Х(Х'у)—Х(х) *Х(у)) и не равно тождественно нулю.
Еслл через е обозначить постоянную функцию, принимающую
всюду значение 1, то, очевидно, Х(е) = 1. Первый из двух ре-
результатов, которые мы хотим доказать, формулируется следую-
следующим образом.
► (а) Если X — непрерывный характер на СG), то су-
существует единственная точка t e Г, такая, что
Х(х) =x(t) для всех функций х<=С(Т). Если про-
пространство Т компактно, то всякий характер на С(Т)
непрерывен и потому имеет указанный вид.
Обратное утверждение тривиально.
Второй наш результат относится к понятию идеала I в ал-
алгебре С(Т). Идеал I определяется следующими свойствами: / —
векторное подпространство в С(Т) и xl cz I для каждой .функции
х<= С(Т) (т. е. ху е / при хеС(Г) и t/e/). Например, если F —
некоторое множество в Г, то множество I(F) всех функций х е
^С(Г), которые обращаются в нуль на F, очевидно, представ-
представляет собой идеал в С(Т). При этом I(F) не изменится, если за-
заменить множество F его замыканием в Т. Кроме того, идеал
I(F) всегда замкнут в С(Т). Наша задача показать, что каж-
каждый замкнутый идеал в С(Т) можно получить таким образом,
если подходящим образом выбрать замкнутое множество F в Т.
Это утверждение можно доказывать по-разному. Пусть за-
задан идеал /. Обозначим через Z(I) множество всех общих ну-
нулей элементов из /. Очевидно, Z(I) —замкнутое подмножество
в Т и /cz/(Z(/)). Второй наш результат может быть сформу-
сформулирован следующим образом.
1) Употребляются также термины линейный мультипликативный функ-
функционал и просто мультипликативный функционал. — Прим. ред.
296 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
► (Ь) Для всякого замкнутого идеала I в С(Т) имеет
место равенство 1 = 1 (Z(I)).
Априори ясно, что если I = I(F) для некоторого замкнутого
множества F аТ, то F совпадает с Z(I). Мы, однако, не будем
использовать это замечание. Так как 1@) = С(£), то идеал /
является всюду плотным в С(Т) тогда (и, очевидно, только
тогда), когда элементы идеала / не имеют общих нулей в Т.
Доказательство утверждения (а). Пусть X—не-
X—непрерывный характер на С (Г). По теореме 4.10.1 существует
такая мера Радона ц на Г с компактным носителем /С, что
Х(х) = \i(x) для всех х^С(Т). Остается показать, что носи-
носитель К сводится к одной точке. Так как X ф 0, то множество К
не пусто. Пусть точка t принадлежит К и f — другая точка
множества К. Тогда существуют непересекающиеся открытые
окрестности U и V точек / и f соответственно. Так как t e К,
то можно подобрать такую функцию х^С(Т) с носителем в
U, что Х(х) Ф 0. Если носитель функции у<=С(Т) содержится
в V, то ху = 0, откуда Х(ху) = Х(х)Х(у) = 0 и, следовательно,
Х(у) = 0. Из предложения 4.9.1 следует теперь, что точка f не
принадлежит К, так что К — одноточечное множество {/}, а ме-
мера [i кратна мере е*. Коэффициент пропорциональности при этом
равен единице, так как X — гомоморфизм. Таким образом,
X(x)=et{x)=x{t).
Для доказательства второй части утверждения покажем,
что гиперплоскость Н, определенная равенством Х(х) =0, зам-
замкнута в СG), или, что то же самое, что Н не плотна в С(Т).
Действительно, если бы гиперплоскость Н была плотна в
С (Г), то она должна была бы содержать такой элемент хОу что
IUo — ^Ноо^у. Элемент х0 нигде бы в нуль не обращался, и
так как Т компактно, то функция 1/х0 принадлежала бы СG).
Из соотношения е = х0* A/х0) следовало бы, что 1 = Х(е) =
= Х(хо)ХA/хо) = 0-ХA/х0), а это невозможно. 1
Доказательство утверждения (Ь). Пусть / =
= /(Z(/)). Ясно, что /с/, поэтому остается только доказать,
что /с/. Для этого воспользуемся теоремой Хана — Банаха и
теоремой 4.10.1.
Пусть мера jj, принадлежит МС(Т) и обращается в нуль на
/, т. е. |i(/) =0 для каждого /е/. Нам надо показать, что |л
обращается в нуль на /. Так как / — идеал, то из наших пред-
предположений следует, что \i(jx)=O (/ е /, х^С(Т)). Отсюда
вытекает, что открытое множество U = T\Z(I) пренебрежимо
относительно меры \\i\. Действительно, если точка t принадле-
принадлежит [/, то существует функция / е /,• не обращающаяся в нуль
4 10. Пространство С(Т) и его сопряженное 297
в точке t и потому не равная нулю в некоторой окрестности V
этой точки. Тогда всякая функция у^С(Т) с носителем в V
может быть записана в виде у = jx, где х — некоторая функция
из С (Г), и, значит, \i{y) = 0. То, что множество U пренебрежи-
пренебрежимо относительно ||я|, следует из предложения 4.9.1. Носитель
К меры ji содержится в T\U = Z(I)y поэтому |я(л:)=0 для
всякой функции х е /, следовательно, функция х обращается в
нуль на Z(I). ■
Замечания. Естественно поставить вопрос: для каких
других алгебр функций остаются справедливыми утверждения
(а) и (Ь), в частности справедливы ли они для алгебр диффе-
дифференцируемых или голоморфных функций? Эти задачи требуют
намного более тонких рассуждений. Например, непосредствен-
непосредственный аналог утверждения (Ь) вообще оказывается неверным.
Случай дифференцируемых функций см. у Уитни [1] и
Шварца [11], а случай голоморфных функций — у К акут а-
ни [3] (см. также приведенные там ссылки) и Эдвардса [14].
4.10.7. Другой подход к изложению теории и некоторые ее
обобщения. Мы уже в достаточной степени разработали аппарат
теории интегрирования, и теперь удобно и уместно сказать
несколько слов о другом подходе к этой теории и сделать крат-
краткий обзор возможных ее обобщений. История развития теории
интегрирования довольно сложна; читатель найдет для себя
много интересного в разделе «Исторический очерк» в конце
книги Б у р б а к и [8].
В более ортодоксальном изложении теории интегрирования,
образцы которого даны Халмошем [1] и Саксом [1], поня-
понятие интеграла основывается на понятии меры как функции
множества, т. е. функции, определенной на некотором семей-
семействе подмножеств «основного пространства» Т и являющейся
по меньшей мере конечно аддитивной. В теориях, подобных ле-
лебеговой, эта мера предполагается счетно аддитивной. Во всех
случаях дело можно свести к рассмотрению положительных
мер.
Мы же, напротив, в качестве основного понятия взяли ин-
интеграл, определив его как линейную форму на некотором век-
векторном пространстве функций. При этом мы ограничились слу-
случаем, когда Т — локально компактное пространство, а функцио-
функциональным пространством служитеЗГ (Т). Эти ограничения можно
до-некоторой степени ослабить (см. Люмис [1, гл. III]; Сто-
Стоун [4], Бур баки [8, гл. IV, стр. 120 и далее], Шварц [21]).
Тот случай теоремы 4.10.1, в котором Г —компактное про-
пространство (с точки зрения техники наиболее легкий), можно
для удобства назвать теоремой представления Рисса, хотя при
этом не отдается должного многим авторам, труды которых
298 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
существенно способствовали тому, чтобы этот результат принял
современную форму. При нашем подходе к теории интегриро-
интегрирования теорема представления Рисса представляет собой почти
тавтологию. С другой стороны, нам пришлось извлекать из на-
нашего функционального определения интеграла соответствую-
соответствующую ему меру.
Альтернатива — принять более ортодоксальную, основанную
на понятии меры теорию интегрирования, в которой теорема
представления Рисса уже не является тавтологией. Образец
такого подхода дан Халмошем [1, § 56]. См. также Хью-
и т т [2], Хьюитт и Цукерман [1].
Вот*все, что мы хотели сказать о другом подходе.
Что касается дополнений и обобщений, рассмотрим сначала
теорему представления Рисса и различные способы ее доказа-
доказательства. Один из самых недавних и принципиально новых
методов доказательства этой теоремы принадлежит В а р а д а-
раяну [1]. Идея метода состоит в том, чтобы представить вся-
всякое компактное пространство Т в виде произведения компакт-
компактных пространств, каждое из которых настолько просто, что для
него теорема представления Рисса почти очевидна, а затем по-
показать, как распространить эту теорему на произведение.
Кроме того, можно искать обобщения этой теоремы, в ко-
которых ослабляется условие локальной компактности простран-
пространства Т. Многими авторами рассматривались аналоги теоремы
представления Рисса для случая, когда Т — впалне регулярное
пространство; отметим здесь лишь работы Хьюитт а [1, 6],
Гликсберга [1], Гоулда и Маховальда [2]. Последние
сводили задачу для вполне регулярного пространства Т к ком-
компактному случаю, вкладывая Т в его стоуночеховскую компак-
тификацию |37\ Сходные обобщения рассматривались Стоу-
Стоуном, Бурбаки (см. ссылки выше), Арен сом [3], Л ю м и-
с о м [4] и др.
Какие функционалы соответствуют конечно аддитивным ме-
мерам? Этот вопрос исследовался Фихтенгольцем и Канто-
Канторовичем [1], позднее Хьюитт ом и Иосидой [1] (см. так-
также Хьюитт [5]). Возможности использования аналогов теоремы
представления Рисса, в которых рассматриваются интегра-
интегралы по конечно аддитивным мерам, весьма ограничены. Конеч-
Конечно аддитивные меры иногда ведут себя просто дико. Вспомни-
Вспомните причины, побудившие нас в § 4.1 отказаться от обращения
к теореме Хана — Банаха в пользу трудоемкого, но «конструк-
«конструктивного» процесса, в результате которого мы пришли к счетно
аддитивным мерам.
Другой тип обобщений связан с заменой пространства
(Т) каким-нибудь другим векторным пространством функ-
4.10. Пространство С(Т) и его сопряженное 299
ций на Т. При этом в ряде случаев удается тем или иным об-
образом свести дело снова к исходному случаю. Однако это воз-
возможно далеко не всегда. Интересный пример, когда такое све-
сведение невозможно или, лучше сказать, удается лишь частич-
частично,— это случай, когда Т — группа и Ж(Т) заменяется век-
векторным пространством почти периодических функций на Т
(см. Хьюитт [9]).
Совсем иного рода обобщения возникают, когда простран-
пространство Т остается неизменным, но интегрируются векторные
(а не скалярные) функции, или же рассматриваются векторные
меры, или и то и другое вместе (если пространство значений
является алгеброй). Случай векторных функций и скалярных
мер представляет собой не столь уж коренное обобщение в от-
отличие от случая векторных мер и скалярных функций. Около
30 лет тому назад задача интегрирования векторных функций
по скалярной мере была очень популярна. Типичные исследо-
исследования такого рода относятся к интегралу Бохнера (Бохнер
[3]). Обзорное изложение теории интеграла Бохнера содержит-
содержится в книгах Хилле [1, гл. III], Хилле и Филлипса [1,
гл. III], Данфорда и Шварца [1, гл. III]. Жизнь показала,
однако, что более простые и удобные «слабые» теории интегра-
интеграла в равной мере полезны в большинстве приложений. В§ 8.14
мы приведем начальные сведения такой теории, трактуя ее с
точки зрения теории двойственности, на которую она в значи-
значительной мере опирается. Слабые интегралы будут использова-
использованы в § 8.13 и 10.1.
Что касается интегрирования по векторным мерам, здесь
опять встает вопрос о выборе отправной точки. Если мы рас-
рассматриваем меры, принимающие свои значения в Е, то можно
воспользоваться одним из следующих подходов.
A) Под мерой с самого начала понимается счетно адди-
аддитивная функция, определенная на соответствующим образом
подобранном классе подмножеств в Г.
B) Под мерой понимается удовлетворяющее соответствующим
ограничениям линейное отображение пространства Ж(Т) в Е.
Изложение первого подхода можно найти в книге Дан-
Данфорда и Шварца [1, гл. III и IV]. Линейные отображения,
о которых идет речь в B), естественно назвать £-значными
мерами Радона на Т. Вопрос, однако, заключается вот в чем:
каким условиям должно удовлетворять отображение, фигури-
фигурирующее в B), чтобы оно соответствовало (как и в скалярном
случае) мере в смысле A)? Ответ на этот вопрос в значитель-
значительной мере принадлежит Гротендику [1], который показал,
что, по крайней мере когда пространство Т компактно, искомое
условие заключается в том, чтобы отображение пространства
300 Г л 4. Топологии, сопряженные к некоторым пространствам; меры Радона
С(Т) в Е было компактным (= вполне непрерывным). Неко-
Некоторые аспекты этой задачи рассматриваются в п. 8.1.9 и 9.4.И.
Почти во всякой теории интегрирования числовых функций
существенно- используется естественное частичное упорядоче-
упорядочение вещественных функций. Важный вклад в выяснении роли
этой структуры принадлежит Мак-Шей ну [2] и Кристиа-
ну[1].
Читатель, желающий подробнее ознакомиться с теорией инте-
интегрирования векторных функций или теорией векторных мер, или
и с тем и другим, может обратиться к обзорной статье Гиль-
де бр ан дта [1].
Исторические замечания о теореме представления Рисса.
Еще в 1903—1904 г. Адамар [1] и Фреше [1—3] получили
теоремы представления для непрерывных линейных форм на
банаховом пространстве С = С [0, 1]. Однако в обоих случаях
имелись серьезные пробелы. В 1909 г. Рисе дал доказатель-
доказательство и формулировку теоремы, которые и теперь считаются
«правильными» и которые отличаются от современных лишь
использованием интегралов Римана — Стилтьеса вместо инте-
интегралов Лебега — Стилтьеса. Другие доказательства были за-
затем предложены самим Рисе ом ([4—6]) в 1911, 1914 и 1952 г.
соответственно и Хелли [1] в 1912 г.
Следующим важным шагом было обобщение теоремы на
пространства СG), где Т — компактное подмножество в Rn.
Это обобщение было дано Радоном [1]в 1913 г. Эта его
статья содержит, разумеется, и много других результатов,
Через 20 с лишним лет Банах в приложении II к моногра-
монографии Сакса [1] (опубликованной в 1937 г.) обобщил теорему
на случай компактного метрического пространства Г, исполь-
используя идеи Даниеля об «абстрактном» интегрировании. Сакс
[2] сам в 1938 г. занимался этим кругом задач.
Наконец, в 1941 г. Какутани [6] обобщил теорему на про-
произвольные компактные хаусдорфовы пространства, завершив
таким образом одну главу в истории рассматриваемого во-
вопроса.
Однако еще в 1938 г. Марков [1] сделал первую попытку
обобщить эту теорему на некомпактные пространства. Марков
рассматривал вместо С(Т) пространство ограниченных непре-
непрерывных функций на пространстве 7, которое хотя и нормаль-
нормально, но не является, вообще говоря, ^-пространством. В своей
работе Марков использовал конечно аддитивные меры. Анало-
Аналогичными вопросами в период 1940—1943 г. занимался
А. Д. Александров [1—3].
О более поздних работах, связанных с этой теоремой, мы
уже говорили.
4.11. Полунормы Np 301
4.11. Полунормы Np\ неравенства Гельдера и
Минковского; пространства Л£р и Lp
Вернемся к теории интегрирования (скалярных функций),
изложение которой мы временно прервали в конце § 4.8. Рас-
Рассмотрим «непрерывный» аналог пространств /*\ введенных в
§ 4.2. Пусть р—некоторое положительное число или оо (т. е.
+ оо). Положим // = 1, если р = оо, а во всех же остальных
случаях определим р' равенством 1—г=1. Всюду в этом
параграфе Т — локально компактное пространство, a ju — фик-
фиксированная положительная мера Радона на Т.
4.11.1. Для всякой (вещественной или комплексной) функ-
функции / на Т и всякого р =/= оо положим
при этом договоримся считать, что (+оо)а=+оо при а > 0.
Если р = 1, то Nv совпадает с определенной в § 4.6 полунор-
полунормой N\. Обозначим через ЗГя = ЗГя(Т, |ы) множеств'о всех функ-
функций /, для которых NP(f) < + оо. При р = 1 получаем про-
пространство о?~1 (§ 4.6). Тогда как N{ — полунорма на о?~1,
функция Np при /?<1 уже не является, вообще говоря, полунор-
полунормой на<^~р. Однако при р > 1 Np — полунорма. Это устанавли-
устанавливается с помощью неравенства Минковского, которое мы до-
докажем ниже. Но прежде чем это сделать, покончим с опреде-
определениями, рассмотрев случай р = оо.
При р = оо существуют по меньшей мере два возможных
определения. Эти два определения различны, если (Г, \х) не
о-конечно, и совпадают в противном случае. Согласно первому
определению, М»(/) есть существенная верхняя грань функции
|/|, т. е. наименьшее число m (возможно, + оо), для которого
неравенство \f\^Cm имеет место всюду, за исключением пре-
пренебрежимого множества (априори зависящего от т). Во вто-
втором определении (в котором используется обозначение JVoo)
JVoo(f) определяется как локально существенная верхняя грань
функции |/|, т. е. как наименьшее из чисел m (снова, возмож-
возможно, равное + оо), для которых неравенство |/|^т имеет ме-
место всюду, за исключением локально пренебрежимого множе-
множества (снова априори зависящего от гп). Очевидно, что всегда
Noo(f) ^CNoo(f). Это неравенство будет строгим для соответ-
соответствующих функций /, если в Т существует локально пренебре-
жимое, но не пренебрежимое множество (это условие и необ-
необходимо). Поэтому если (Т, [х) а-конечно, то оба определения
совпадают.
302 Гл. 4. Топологии сопряженные к некоторым пространствам; меры Радона
Соответствующие функциональные пространства <£Г°° =
= £Г°°(Г, |ы) и &ГОС=@~ОО(Т, \х) удовлетворяют соотношению
aF^czc^00, причем по крайней мере для о-конечных про-
пространств (Г, |ы) имеет место совпадение.
Замечание. Различие между ^°° от <гГ°° — это предве-
предвестник различия между пространствами @~х и @~1 (последнее мы
еще не успели ввести) и, более общо, различия между прост-
пространствами q7*v и Srv, 1 ^Ср < оо. По-видимому, надобность в
таком различии, появляющаяся во всяком случае лишь тогда,
когда (Г, \х) не а-конечно, наиболее ощутима при р = оо. Здесь
мы не будем заниматься исследованием указанного различия
для конечных р, отложив этот вопрос до рассмотрения произ-
произведения меры на функцию (§ 4.13).
Различие, о котором идет речь, по всей вероятности, впер-
впервые было замечено Б у р б а к и [8, гл. V]. _
Что бы мы ни выбрали в случае р = оо, ясно, что Л^ и Noo
являются полунормами на 3го0 и^0 соответственно.
Если пространство Т дискретно и \х сопоставляет единичную
массу каждой точке пространства Т, то @~р(Т, \х) совпадает с
№{Т)\ при этом полунорма Np совпадает с нормой ||-||р, опре-
определенной в § 4.2. Более того, в этом случае Nv не отличается
от Л/р, а &"& — от STv. Такое положение в действительности
имеет место всегда, когда мера \х атомарна (пример 4.4.1).
Подробнее см. Эдварде [16].
Из результатов § 4.2 и из только что сделанных замечаний
вытекает, что при 0 < р < 1 Np, вообще говоря, не является по-
полунормой на ЗГ'Р. Сейчас мы займемся изучением случая р > 1
и покажем, что в этом случае Nv — полунорма.
4.11.2. Неравенства Гёльдера и Минковского. Они записы-
записываются следующим образом:
Ni(fg)<NP(f)NP>(g) A<р<оо), (Н)
Ni(fg)<Nl(f)Noo(g) при ЛМ/К+оо, (НО
о), (М)
(MJ
Здесь f и g — произвольные функции на Т. Нам уже известна
справедливость неравенства (Н) для р=1 и /? = оо (см. формулу
D.6.3)), неравенства (М) для р = 1, а также неравенства (M«>).
Остается доказать неравенство (Н) для 1<р<оо, неравенство
(М) для 1</7<оо, а также неравенство (Hi).
4.11.3. Доказательство неравенства (Hi). Если
/)< + » то функция / обращается в нуль вне а-конечного
4.11. Полунормы Np 303
относительно \х множества Р. С другой стороны, неравенство
\g\ -*CNoo(g) имеет место всюду, за исключением локально пре-
небрежимого множества SczT. Но тогда неравенство \fg\ ^
^Noo{g) • if | не выполняется лишь на множестве PDS, которое
пренебрежимо. Таким образом,
т. е. неравенство (Hi) справедливо. I
4.11.4. Доказательство неравенства (Н) для
1</?<оо. Хотя здесь можно воспользоваться неравенством Гёль-
дера для конечных сумм, мы предпочитаем привести непосред-
непосредственное доказательство. Оно основано на элементарном число-
числовом неравенстве
У? 11Р'
*У<-у+? (х>0, у>0у A<р<оо), D.11.2)
убедиться в справедливости которого предоставляется читателю.
Не нарушая общности, можно считать, что пи один из множи-
множителей в правой части неравенства (Н) не равен нулю. Действи-
Действительно, в противном случае соответствующая функция (/ или
g) и, следовательно, произведение fg будут пренебрежимы.
Можно далее считать, что каждый из множителей в правой
части неравенства (Н) конечен. Напомним читателю наше со-
соглашение о том, что с-( + оо) = + оо при с>0 (§ 4.5).
Пусть теперь 0<Np(f)< + oo и 0<Np (g)< + oo. Запишем
неравенство D.11.2) для каждой точки t^T, положим
г- |/(/)|
Np(f) ' у Np,(g)
и применим к этим функциям верхний интеграл ^*. Так как
+ 1"
откуда и следует неравенство (Н). В
4.11.5. Доказательство неравенства (М) для
1</?<оо. Л1ожно считать, что функции f и g положительны, оба
слагаемых в правой части неравенства (М) конечны и
^p(/ + £)>° (так как в противном случае функции fug пре-
пренебрежимы и неравенство (М) выполняется тривиальным обра-
образом) Из неравенства (х f y)v < 2?>(xv+yv), справедливого при
х > 0 и у > 0, следует конечность числа Nv(f+g).
304 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Положим h = f + g. Тогда hp = hp"lf + hp~lg и [х*(/гр) <
<jx*(hp'lf) + \i*(hp~lg). Применяя неравенство (Н) к каждому
из слагаемых, получаем неравенство
I*' (hp) < [|Г {hp)V • [Np (/) + Np(g)]9
которое эквивалентно (М), так как 0 < \i* (hp) < + оо и
4.11.6. Следствие. Функции Np и N^ являются полунор-
полунормами на <?ГР A <р^оо) и о^°° соответственно.
4.11.7. Пространства J£p (Tf \i) и j£°°(T,ii). Аналогично
тому, как мы определили пространство J?1 в § 4.6, можно
определить пространство J?p = J?P(T, \i) (I ^p<oo) как замы-
замыкание в &*р относительно полунормы Np пространства о?Г(Т).
В случае р = оо пространства е55?оо=^оо(Г, р,) и ^0О=^0О(Г, jx)
определяются непосредственно как множества всех измеримых
функций в <^°° и о^00 соответственно. Эти пространства отнюдь
не совпадают с N^- и ^-замыканиями пространства ЛГ (Т).
Предоставляем читателю проверить, что теорема 4.6.7 и
следствия 4.6.8 и 4.6.9 остаются справедливыми, если заменить
<3?х и N\ на J?p и Np A<р<оо). Аналогичным образом
обобщается теорема 4.8.1 для всех р> удовлетворяющих нера-
неравенству l^p^oo (при р = оо имеют место два аналога,
причем оба справедливы). Таким образом, если о/И обозначает
множество всех измеримых функций, то J?p = ^р П о41 и J¥°° =
= qF°° П о^. Отсюда вытекает следующее ^утверждение: ком-
комплексная функция принадлежит J?p (или J?°°) тогда и только
тогда, когда этим свойством обладают ее вещественная и мни-
мнимая части. (В этой связи читатель может .заметить, что если
f = и + iVy где и и v — вещественные функции, то
4.11.8. Следствие. Если f<=J?p и gGi9"' A </><«>), то
fg e J?1, причем
\\i(fg)\<Ni(fg)<Np(f)Np>(g).
В случае р=1 можно заменить в предыдущей фразе J?°° на
J?°° и Nooig) на Noo(g).
Доказательство. Если функции / и g измеримы, то и
произведение fg обладает тем же свойством. Остается только
воспользоваться неравенством (Н) или (Hj). |
4 11 Полунормы Np 305
4.11.9. Интегрирование относительно комплексной меры Ра-
Радона. Если К — комплексная мера Радона на Г и
Я = Х\ — ^2 + /А,3 — /А<4
— ее минимальное разложение (см. теорему 4.3.2), то измери-
измеримость^ интегрируемость, пренебрежимость и локальная арене-
брежимость относительно % по определению эквивалентны тем
же свойствам относительно мер Ки (&=1, 2, 3, 4). В частности,
& (Я) = f| J¥l (lk). Для всякой функции / е= S (А,) полагаем
J fdl = J fdXx - | fdKi + i J fdl3- i J /rfV
Пространства S^CK) определяются аналогично. Если положить
1X1=^ + ^2 + ^3 + ^4, тОо^р^) =о2^(|Х|),- причем Л-измеримость
совпадает с |Х|-измеримостью. Из неравенства D.6.3) легко сле-
следует, что для всякой функции [Ео?7^) имеет место неравен-
неравенство
откуда
при /е^р(Я) и g^J^p'(X). Функция
является полунормой на пространстве J?p(X), и оно полно отно-
относительно структуры, определенной этой полунормой.
Как мы увидим в п. 4.15.6 и 4.15.13, некоторые формальные
преимущества имеет другое определение меры \К\. Оно заклю-
заключается в том, что мера \Х\ полагается равной (а2+р2I/а, где а
и р — вещественные меры Радона, для которых K = a + i$. Полу-
Получающаяся при этом полунорма эквивалентна предыдущей, а не-
неравенства (Я), (#i) и (М) остаются справедливы и при этом
новом понимании меры |>,|.
4.11.10. Пространство Jgp/ как подмножество сопряженного
kJSp . Пространства ZA Пусть 1 Кр ^ оо и q = p'. Пусть gG^
(или g^J2*°° при /7=1). На основании следствия 4.ГК8 функция
£_порождает непрерывную линейную форму Lg на gv (или на
9?°° при /7 = оо), определяемую равенством
306 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Более того, норма формы LgJ т. е. число
(или sup{|Lg(f)|: f eJ?°°, Noo(f) ^C 1}, при_/?=1), удовлетворяет
неравенству || Lg || < Nq (g) (или || Lg || < Noo(g) при /7=1). Дей-
Действительно, если р = оо, то при вычислении \\Lg\\ безразлично,
рассматривается ли Lg как линейная форма на J?°° или на»?00,
так как соответствующие нормы совпадают. В самом деле, с по-
помощью несложных рассуждений легко установить, что
g ( N^ig) при /7=1,
причем в общем случае нельзя заменить Noo(g) на Noo(g).
С другой стороны, каждой функции g e J?°° соответствует по
меньшей мере одна такая_функция g' (=J?°°, что g' = g локально
почти всюду и Noo(g') =Noc(g). Для всякой такой функции g'
имеем Lg(f)=Lg> (/) для каждой функции feJ?1. Это озна-
означает, что в случае р=\ мы получаем одно и то же множество
линейных форм на J?1, берем ли мы Lg с g eJ?°° или Lg с
g eJ?00. Уже один тот факт, что норма \\Lg\\ равна Noo(g), ka
не Noo(g), служит доказательством важности пространства о?30
и его полунормы Noo.
Во всяком случае, мы получили естественное линейное ото-
отображение g*—>Lg пространства <5?ч (или^?00 при р=\) в про-
пространство, сопряженное к J?p (или к J?°° при р = оо). Это ото-
отображение, вообще говоря, не является взаимно однозначным.
Его ядром служит множество всех тех функций g e Sq (или
из J?00 при р=1), для которых Nq(g)=-0 (или Noo{g)=0 при
/?=1). Это наводит на мысль рассмотреть ассоциированное фак-
торпространство, для того чтобы получить взаимно однозначное
отображение.
Это факторпространство, нужное для достижения взаимной
однозначности, — не что иное, как отделимое факторпростран-
факторпространство, ассоциированное с локально выпуклым пространством J?
(или J?°°), наделенным топологией, определяемой полунормой
Nq (или Noo). Это пространство обозначается обычно через Lq
(или L°°), а соответствующая норма —через ||«||д(или II-IU).
Все эти факторпространства являются банаховыми простран-
пространствами. Читателю следует помнить, что элементы пространства
1я (или L°°) —это, вообще говоря, не функции, а классы функ-
функций, совпадающих почти всюду (или локалыю почти всюду).
Если g есть элемент пространства e3?q (или <2>со), то через g
4.11. Полунормы Np 307
будет обозначаться соответствующий ему класс, являющийся
элементом в Lv (или в £°°).Эти определения и обозначения при-
применимы ко всякому q, удовлетворяющему неравенствам
1 <^4оо.
Возвращаясь к случаю, когда q~pf, мы видим, что форма
Lg зависит только от определенного функцией g класса из Ьч
(или из Е°° при /?=1), что дает линейное отображение g*—>Lg =
= ^g*- Это отображение взаимно однозначно по построению.
Следует заметить, что если g^Lv (или Ь°° при /?=1), то
L-(f)=[i(fg) зависит только от класса / из Lp (или из L°° при
/? = оо), определяемого функцией /. Таким образом, можно также
отобразить Ьч (или L°° при р = \) линейно и изометрично в про-
пространство, сопряженное к Lv (или к D при р=\).
Весьма важно исследовать, при каких условиях указанное
выше отображение «^-пространства (или L-пространства) в про-
пространство, сопряженное к пространству того же типа с сопря-
сопряженным показателем, является отображением на. Если форму-
формулировать эту задачу в терминах «^-пространств, то ничего
существенного потеряно не будет, так как соответствующие ре-
результаты в терминах L-пространств будут получаться очевидным
образом.
Оказывается, что при 1 <^/?<оо рассматриваемое отображе-
отображение есть отображение на. Напротив, при /? = оо мы получаем ото-
отображение на только в том тривиальном случае, когда простран-
пространство Т дискретно и конечно. Второе утверждение доказывается
намного легче и большого значения не имеет. Первое же утвер-
утверждение фундаментально. Если Т — ограниченный интервал ве-
вещественной оси, a [i — мера Лебега, то это утверждение пре-
превращается в результат, хорошо известный с первых дней возник-
возникновения функционального анализа. С тех пор этот результат
неоднократно обобщался. Первоначальное доказательство (см.,
например, Банах [1, стр. 54]) для случая, когда Т — интервал,
основывалось на свойствах абсолютно непрерывных функций.
Обобщения, вообще говоря, базируются на изучении свойств
абсолютной непрерывности счетно аддитивных функций множе-
множества. Отказ от а-конечности пространства (Г, |ы) приводит к не-
некоторым усложнениям.
Наше доказательство мы разобьем на несколько шагов. Вна-
Вначале рассмотрим частный случай р = 2. Так как J?2 — полное
пространство со скалярным произведением (§ 1.12), то искомый
результат в этом случае получается легко (§ 4.12). Следующим
шагом будет дальнейшее развитие теории интегрирования: ис-
исследование понятия абсолютной непрерывности и центральная
теорема в этой области — теорема Лебега — Радона — Никодима
(§ 4.13—4.15). Наконец, в § 4.16 мы покажем, как из этой
308 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
теоремы следует нужный нам результат. Попутно читатель уви-
увидит, что результаты §4.12 и теорема Лебега — Радона — Никоди-
ма играют важную роль и в других вопросах.
4.12. Пространство S2 и его сопряженное
Теперь мы в состоянии полностью понять утверждение о том,
что S2 является полным (вообще говоря, неотделимым) про-
пространством со скалярным произведением и что, следовательно,
ассоциированное с ним пространство L2 является гильбертовым
пространством. (Эти пространства не обязаны быть сепара-
бельными.)
То же самое верно и для пространств J2*2(А, \х) и L2(A, |ы),
где А — некоторое |ы-измеримое множество в Т. Мы уже рассмо-
рассмотрели случай, когда А совпадает с Г. В общем случае J?2(A, \i)
состоит из тех ^-измеримых функций /, которые определены на
А и для которых f*A\f(t) \2d\i(t) < + oo. Эти функции могут быть
как вещественными, так и комплексными. В зависимости от
этого J?2(А, \х) называют вещественным или комплексным про-
пространством. Определяя скалярное произведение формулой
где черта сверху означает переход к комплексно сопряженному,
мы сразу охватываем оба случая. Интегрируемость произведе-
произведения fg на множестве А непосредственно вытекает из следствия
4.11.8 при р = // = 2. Соответствующая полунорма определяется
равенством
N2.A(f) =
В силу замечания, предшествующего следствию 4.11.8, простран-
пространство с2^(А, |ы) полно относительно этой полунормы. Элементами
ассоциированного отделимого факторпространства L2(A, \х) слу-
служат классы эквивалентных функций. Две функции из J3?2(A, \х)
принадлежат одному и тому же классу тогда и только тогда,
когда они почти всюду равны на множестве А.
Опираясь на полученные сведения, читатель может рассмо-
рассмотреть результаты § 1.12 с изложенной выше точки зрения. Основ-
Основной результат сведется к следующей теореме.
4.12.1. Теорема. Если L — непрерывная линейная форма на
пространстве 272(Л, |ы), то существует такая функция g e
ц), что
4.13. Умножение меры на функцию 309
обратно, всякая функция g^J2*2(A, \i) порождает непрерывную
линейную форму L на J?2(A, \x), определенную указанной фор-
формулой. Кроме того, для всякой такой функции g имеет место
равенство
и
4.13. Умножение меры на функцию
Всюду в этом параграфе ^ — положительная мера Радона
на Т.
4.13.1. Пусть g — функция, определенная на Т. Для того
чтобы при каждой функции к^Ж+(Т) произведение gk было
|ы-интегрируемым, очевидно, необходимо и достаточно, чтобы
функция g была ^-интегрируемой на, каждом компактном мно-
множестве в Т. Функцию g, удовлетворяющую этому условию, бу-
будем называть локально ^-интегрируемой. Для такой функции g
произведение gk |ы-интегрируемо для любой функции k^o?f(T).
Если положить'
l(x) = \i(gx) (хе^(Г)), D.13.1)
то получится новая мера Радона К. Эта мера обозначается че-
через g-\i. Очевидно, мера g-[i вещественна (соотв. положитель-
положительна) тогда и только тогда, когда функция g вещественна (соотв.
положительна) локально почти всюду относительно [х. Следо-
Следовательно, каждое разложение вида g = gi — g2 + igs — ig*, где
gk — локально почти всюду положительные функции, влечет раз-
разложение 1 = К\ — ?1г + йз — &4, в котором меры Kk положительны.
Хотя мы этого и не будем доказывать, заметим, что, взяв g\ =
= (Reg)+, g2=(Reff)r, £з= (Im g)+, g4 = Img)-, мы получим
минимальное разложение меры К. Во всяком случае ясно, что
полученные таким образом меры Къ, мажорируют соответствую-
соответствующие положительные меры в минимальном разложении.
Наша задача — охарактеризовать те меры К на Г, которые
имеют вид g-\x. Полностью эта задача решается теоремой Ле-
Лебега — Радона — Никодима.
Начнем с перечисления некоторых свойств, которыми обла-
обладают меры вида g*\i. Теорема Лебега — Радона — Никодима
устанавливает, что, для того чтобы заданная мера имела указан-
указанный вид, достаточно, чтобы она обладала некоторым на первый
взгляд значительно более слабым свойством.
4.13.2. Предложение. Пусть X=*g-\x, где g — локально инте-
интегрируемая функция.
A) Если g^-О локально [i-почти всюду, то для каждой по-
положительной полунепрерывной снизу функции ф справедливо
3lO Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
неравенство Х*(ф) <^|Li*'(g4p); если функция ф \х-о-конечна1), то
имеет место равенство.
B) Каждое относительно компактное \л-непренебрежимое
множество ^-пренебрежимо. В частности, каждое ^-локально
пренебрежимое множество Х-локально пренебрежимо. Если про-
странство Т о-компактно, то каждое \1-пренебрежимов множе-
множество ^-пренебрежимо.
C) Если функция f ограничена, ^-измерима и обращается
в нуль вне некоторого компактного множества, то она Х-инте-
грируема и h(f) =\i(gf). В частности, если Р — множество, где
g=j=O, то множество Т\Р локально 1-пренебрежимо.
D) Если произведение gf ^-интегрируемо, то существует та-
такая i-интегрируемая функция f*, что f = f* локально К-почти
всюду и K(f*)=\i{gf).
E) Если функция f локально К-почти всюду равна Х-инте-
грируемой функции, то существует такая ^-интегрируемая функ-
функция /*, что f* = f локально l-почти всюду, произведение gf* ^-ин-
^-интегрируемо и равно локально \х-почти всюду функции gf и
Доказательство. В силу предыдущих замечаний можно
всюду считать, что ^0 и что, следовательно, мера Я положи-
положительна.
A) Обозначим через Рф множество всех функций х^Ж+(Т),
для которых х^ф. Так как мера К положительна и функция
gx |ы-интегрируема при любом х е Яф, то
К* (ф) = sup К (х) = sup ix (gx) < |ы* (g<p),
где х пробегает множество Рф. Не ограничивая общности, мож-
можно ограничиться доказательством равенства А,*(ф) ===|ы*(ёгф) для
случая, когда |ы*(ф)< + оо. Действительно, всегда можно счи-
считать, что ф = Птфп, где последовательность (фп) возрастает и
каждая функция фп |ы-интегрируем,а. Тогда нужный нам резуль-
результат вытекает из монотонной сходимости. Итак, допуская, что
функция ф |ы-интегрируема, можно так выбрать функции хп е
^Ж+(Т), что Xnfqp, функция ф мажорирует хп и \ь{Хп)\\ь*(ч)*
Отбрасывая в случае необходимости некоторые члены последо-
последовательности, можно считать (теорема 4.6.7), что хп\у ^-почти
всюду. Таким образом, gxn\g(p jli-почти всюду; тогда в силу мо-
ноТонной сходимости
что и требовалось доказать.
') Функция ф называется \\,-а-конечной, если она обращается в нуль на
дополнении к [i-a-конечному множеству (п. 4.7.3).
4 13. Умножение меры на функцию 311
B) Пусть N — относительно компактное |и-пренебрежимое
множество. Тогда можно найти такую убывающую последова-
последовательность ^-интегрируемых, полунепрерывных снизу функций
(фп), что функции фп мажорируют функцию %N и м*(фп) |0. От-
Отбрасывая в случае надобности некоторые члены последователь-
последовательности, можно считать, что фп|0 A-почти всюду. Можно также
предположить, что каждая функция фп обращается в нуль вне
некоторой фиксированной компактной окрестности множества
N. Тогда функция gw\ интегрируема и (например, в силу тео-
теоремы 4,8.2) \x*(gq)n) |0.- Пользуясь уже доказанным утвержде-
утверждением A), получаем, что Х*(фп) -*С м* (#фп) |0. Так как Х*(Л/)^С
•^^*(фп), то множество N Х-пренебрежимо. Остальная часть
утверждения B) непосредственно следует из уже доказанной
его части.
C) Пусть функция f обращается в нуль вне компактного
множества К. Тогда функции f и gf ^-интегрируемы (последнее
следует из локальной интегрируемости функции g и теоремы
4.8.1). В Ж(Т) можно выбрать такую последовательность (хп),
чтобы xn-+f ili-почти всюду. Можно также считать, что функ-
функции хп равномерно ограничены и обращаются в нуль вне фик-
фиксированной компактной окрестности множества К. Поэтому
можно принять, что gxn-+gf bJ2?'i{\i). В то же время (хп) яв-
является последовательностью Коши BJ2*l(h), так что (отбросив,
если нужно, некоторые ее члены) можно предположить, что
хп-+Г Х-почти всюду. Тогда из утверждения B) следует, что
/'=/ Х-почти всюду. Таким образом, функция / Х-интегрируема и
А, (/) = А, (П = Нт Я (хп) = Hm |i (gxn) = \i (gf),
что и требовалось доказать. Оставшаяся часть утверждения C)
является следствием уже доказанной части.
D) Пусть Р — множество тех точек, где g'=£0. Из утвержде-
утверждения C) вытекает, что множество Т \ Р локально Х-пренебре-
жимо. Так как функция fg ^-интегрируема, то множество S, на
котором fg=jf=O, является fi-a-конечным. Далее ScP и / = 0 на
P\S. Пусть функция /' равна f на S и равна нулю вне S. Это
равносильно тому, что f' = f на Р и f' = 0 вне Р. Тогда f' = f ло-
локально Х-почти всюду, и gf' = gf. Так как функция f ^-измерима
на Я, то функция /' также ^-измерима. Она равна нулю вне
|и-а-конечного множества S, поэтому // = lim/n |и-почти всюду,
где каждая функция fn является линейной комбинацией харак-
характеристических функций относительно компактных и-измеримых
множеств, на которых |fn|^lfl- Тогда Ig/nl^lg"/7! ^|g"/| и
gfn^gf fi-почти всюду. Из теоремы 4.8.2 следует, что gfn-**gf
Ъ^1A). С другой стороны, из утверждения C) вытекает, что
312 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
каждая из функций fn Я-интегрируема и Я(|/т — fn|)-
^(glf — fl)
Поэтому (fn) является последовательностью Коши в ^(Я).
Следовательно, в J&l(K) существует такая функция /*, что
fn-+f* в ^{(\). Отбрасывая в случае надобности некоторые
члены, можно добиться того, чтобы fn-*f* Я-почти всюду. Так
как /п-^Г и^-почти всюду, то из утверждения B) вытекает, что
/7 = /* локально Я-почти всюду и, следовательно, f = f* локально
Я-почти всюду. Наконец, так как gf' = gf, то из сходимости
/„-*/• в &(%) и gfn-+gf в^1(|ы) следует, что
Я (Г) = lim Я (fn) = lim ix (gfn) = ix (gf\
что и требовалось доказать.
E) Ясно, что без ограничения общности, можно считать
/^>0. Так как множество Т\Р локально Я-пренебрежимо, то
среди Я-интегрируемых функций, локально Я-почти всюду рав-
равных f, найдется по крайней мере одна, скажем Г, которая обра-
обращается в нуль вне Р. Из соотношения f — f/ локально Я-почти
всюду следует в силу утверждения C), что / = /7 локально
|и-почти всюду на Р, поэтому gf=gf локально |и-почти всюду.
Мы можем выбрать возрастающую последовательность функ-
функции (fn), Я-почти всюду сходящуюся к /', где каждая функция
fn ограничена, Я-измерима и равна нулю вне некоторого отно-
относительно компактного подмножества множества Р. В силу
утверждений B) из Я-измеримости функций fn вытекает их
^-измеримость (сначала на Р, потом на Г). В силу C) получаем
тогда, что k(fn)=\i(gfn) при каждом п. Так как последователь-
последовательность (fn) сходится монотонно, то Я(П =lim Я(fn) = lim \x(gfn).
Итак, мы показали, что вне некоторого Я-пренебрежимого мно-
множества j¥ выполняется равенство limfn = //, поэтому lim gfn = gf
вне множества PC\N. На множестве Р имеем g">0; следователь-
следовательно, из C) вытекает, что множество Pf)N локально |и-пренебре-
жимо. Таким образом, равенство lim gfnr=gf/ = gf имеет место
локально [1-почти всюду.
Все члены возрастающей последовательности gfn суть fi-ин-
тегрируемые функции, числа \x(gfn) =l(fn) мажорируются чис-
числом Я(Г)< + оо; поэтому монотонная сходимость последователь-
последовательности (gfn) влечет (^-интегрируемость функции lim gfn. Более
того,
f) (f
поэтому Л = lim gfn есть jui-интегрируемая функция, равная нулю
вне некоторого а-компактного множества. Определим функцию
f*, положив ее равной g"/* на Р и нулю вне Р. Тогда gf* = h
всюду и gf* = gf' = gf локально fi-почти всюду. Отсюда следует,
4.14. Существенно интегрируемые функции 313
что f* = f' = f локально Х-почти всюду. Так как функция /* обра-
обращается в нуль вне некоторого а-компактного множества, а функ-
функция Y Х-интегрируема, то /* = /' Х-почти всюду. Следовательно,
функция /* Я-интегрируема и
поскольку функция gf* = h (^-интегрируема и локально ji-почти
всюду равна gf. Все доказано. |
4.13.3. Замечания. Если пространство (Г, |ц) не а-ко-
нечно, то равенство в 4.13.2A), вообще говоря, не имеет места.
Таким образом, если функция g" локально |и-пренебрежима, но
не |и-пренебрежима, то M*(g)>0 и, кроме того, k*(l)=supK(k)
(где k пробегает функции из Ж+(Т), удовлетворяющие условию
й<1), a supk(k) =sup \x(gk) =supO = O<[x* (g). Хотя утвержде-
утверждения D) и E) раздражающе громоздки, эти недостатки, вообще
говоря, неизбежны. Тем не менее эти утверждения наводят на
мысль о введении модифицированного понятия интеграла, по-
позволяющего упростить их формулировку. Уже сейчас ясно (а
ниже это будет подтверждено), что вместо интегрируемости от-
относительно \х (или относительно К) нужна «существенная» ин-
интегрируемость (сводящаяся к равенству локально почти всюду
с некоторой интегрируемой функцией). Следующий параграф
посвящен развитию этой мысли. При этом схема изложения бу-
будет параллельна схеме, использованной при изложении обычной
теории интегрирования. Это позволит более удобно переформу-
переформулировать предложение 4.13.2.
4.14. Существенно интегрируемые функции
Модификации, которые мы намереваемся ввести, имеют
смысл для всякой положительной меры Радона [i на Г. При
этом мы почти дословно повторим рассуждения, использован-
использованные в § 4.6 и 4.11.
Начнем с определения существенного верхнего интеграла
Д*(/) для любой функции />0. Полагаем
£*(/) = sup К (fa*): KaT, К компактно}. D.14.1)
Ясно, что 0^ Д*(/) ^ М*(/) ^ +оо. Множество N локально пре-
пренебрежимо тогда и только тогда, когда ft*(z^v) =0. Очевидны
также следующие свойства: если функции f и g положительны
и /■<§" локально почти всюду, то Д*(/) ^Д*(£); если />0 и
а — положительное вещественное число, то jl*(af) =cc- (!*(/); для
любых двух положительных функций fug имеет место неравен-
неравенство £*(/ + £)< £•(/)+£*(£).
314 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
4.14.1. Предложение. Пусть f > 0. Равенство
Д'(/) = !*•(/) D.14.2)
выполняется, если либо (а) функция f полунепрерывна снизу,
либо (Ь) функция f равна нулю вне некоторого \х-о-конечного
множества.
Доказательство, (а) Пусть функция / полунепрерывна
снизу. По определению
Если k обращается в нуль вне компактного множества /(, то
k^Cftx, следовательно, \x(k) < м*(/хя) ^ Д*(/)- Отсюда выте-
вытекают неравенство \i*(f) •£ jl*(f) и справедливость формулы
D.14.2).
(Ь) По условию существует такая возрастающая последова-
последовательность компактных множеств (Кп), что f = lhnf%Kn fi-почти
всюду, поэтому \i*(f) = lim fi*(/%Kn), откуда непосредственно сле-
следует, что [i*{f) ^ &*(!)- Формула D.14.2) снова верна. 1
Для всякой комплексной функции f на Г определим N\ (f)
равенством Ni(f)=\i*(\f\). Тогда N\ (f) jC N{ (f) -<+oo, причем
функция Ni субаддитивна и Ni(af) = \a\N\(f) для любого комп-
комплексного числа а.
Обозначим через @~Х=@"Х(Т, \х) множество тех комплексных
функций / на Т, для которых N\(f)< +oo. Множество ЗгХ яв-
является векторным подпространством пространства Сг, содержа-
содержащим ^'1 = ^'1(Г, |ц), причем N\ является полунормой на STX. Со-
Соответствующая топология, вообще говоря, не отделима, так как
N\(f) =0 тогда и только тогда, когда / = 0 локально почти всюду.
4Л4.2. Предложение. Комплексная функция f на Т принадле-
принадлежит @~1 тогда и только тогда, когда существует функция f'^&~1,
локально почти всюду равная f; при этом N\(f) =Л/1(//).
Доказательство. Если существует функция // с указан-
указанными свойствами, то (предложение 4.14.1 (Ь))
(последнее равенство вытекает из_того, что / = /' локально почти
всюду). Это показывает, что /е^.
Пусть f/^3rX. Тогда существует такая возрастающая после-
последовательность компактных подмножеств (Кп) в Г, что N\(f) =
= lim \i*(\f\%Kn)- Обозначим через А объединение множеств KR.
Из монотонной сходимости |/|хял-"Ч/1ха следует, что
4.14. Существенно интегрируемые функции 315
поэтому функция f/:=f%A принадлежит @~х. Остается только до-
доказать, что f' = f локально почти всюду. В противном случае най-
найдется такое компактное множество КаТ\А, что а =
= М*AЛ%я)>0- Множество Ln = K[)Kn компактно, и
Так как множества К и Кп компактны и не пересекаются, то,
как легко показать, правая часть последнего равенства равна
(Подробное доказательство последнего утверждения приводится
в лемме 4.14.3.) Значит, справедливо соотношение
откуда вытекает неравенство
для достаточно больших п, что невозможно. |
4.14.3. Лемма. Пусть f>0 м К — объединение неперсекаю-
щихся компактных множеств К\ и Кг; тогда
Доказательство. Так как функция \х* субаддитивна, то
достаточно доказать, что правая часть этого равенства не пре-
превосходит левую.
Допустим, что ^* (/%#)< + °°- Для любого заданного е>0
можно выбрать такую полунепрерывную функцию ср, мажори-
мажорирующую f%K, что \х* (ф) < \х* (f%к) + е. Обозначим через Ux и U2
непересекающиеся окрестности множеств К\ и Д'2 соответст-
соответственно и положим ф^ФХ^, 92 = 9Xt/2- Обе эти функции полу-
полунепрерывны/ снизу, мажорируют f%K и /%„ соответственно, и
9i + Ф2 ^ Ф- Поэтому
= ^* (ф1 + ф2) < \х* (Ф) < [I* (f%K) + 6.
Полагая е->- 0, получаем требуемое ^равенство.
Теперь вводим пространство 2>l=2?l(T, |li) как замыкание в
$ГХ подпространства Же (Т) относительно топологии,
деленной полунормой N\. Для х^о^с(Т) имеем
316 Гл. 4. Топологии сопряженные к некоторым пространствам; меры Радона
откуда следует, что линейная форма \х обладает единственным
непрерывным продолжением на ~3?х9 которое обозначим через \х-
Тогда _ _
1ДШКЛМ/). (f^^1)* D.14.3)
и J?1 = J?1G\ \x) czJ?1. Далее, поскольку на пространстве
o9tc(T) выполняется равенство \i = \i и обе линейные формы
могут быть однозначно продолжены на J?1 по непрерывности
относительно полунормы Nb то
(f^^1)- DЛ4.4)
Заметим также, что
= f в &*1 tfe<^). D-14-5)
и, значит, то же самое справедливо для функции /eJ?4, по-
поэтому
^ D.14.6)
В формуле D.14.5) предел берется по направленному по
включению множеству компактных подмножеств К в Т.
Если множество S ^-измеримо, то \x(S) (определенное в
п. 4.7.5) равно ft* (%s), поэтому множество S измеримо и p,(S)<
< + оо тогда и только тогда, когда характеристическая функция
%s принадлежит J?1 (|и); в этом случае p,(S)=jI (%s)-
Сформулируем теперь аналог теоремы 4.8.1.
4.14.4. Предложение. Комплексная функция f на Т принадле-
принадлежит &х тогда и только тогда, когда она [i-измерима и
N(f)
(f)
Доказательство. Если ATi(f)< + oo, то (предложе-
(предложение 4.14.2) существует_функция /', для которой У = / локально
почти всюду и N\ (f ) =N\ (f) < + oo. Так как функция f измерима,
то измерима и функция /'. Следовательно (теорема 4.8.1), /'е
gS'1. Но тогда f'ei?1 и функция f, локально почти всюду рав-
равная f\ обладает тем же свойством.
Обратно, если функция /е^1, то JVi(/)< + oo по определе-
определению. Кроме того, для любого наперед заданного е>0 существует
такая функция k ^е/Гс(Г), что N\(f — k) < e. Снова восполь-
воспользуемся предложением 4.14.2. Пусть функция У такая же, как и
в первой части доказательства. Тогда N\ (/' — k) =N\ (f — &)<e.
Отсюда следует, что f'&JS?1 и, таким образом, функция /, бу-
будучи локально почти всюду равной функции /', измерима. |
4.14.5. Следствие. Для того чтобы комплексная функция f
на Т принадлежала пространству Л?\ необходимо и достаточно^
414. Существенно интегрируемые функции 317
чтобы существовала функция /' eJ?\ локально почти всюду
равная функции f.
Доказательство. Достаточность очевидна. Обратно,
если /eJ?i, то / измерима (предложение 4.14.4) и (предложе-
(предложение 4.14.2) существует функция //е<=5?1, локально почти всюду
равная функции /. Тогда /' измерима и, следовательно (тео-
(теорема 4.8.1), Гц&К |
Функции из^^Г, |и) называются существенно интегрируе-
интегрируемыми относительно |и, а р, — существенным интегралом. Из по-
последнего результата следует, что эти функции характеризуются
в точности так, как нам хотелось (см. замечание 4.13.3). Ясно
также, каким образом ввести пространства J?v(T, \x) при
1</?<оо. Предоставляем читателю самостоятельно убедиться
в том, что для видоизмененных таким образом понятий спра-
справедливы аналоги леммы Фату, теоремы 4.8.2 и результатов
§ 4.11. Наконец, все изложенное в п. 4.6.11 останется справед-
справедливым, если «интегрируемость» заменить на «существенная ин-
интегрируемость» и «почти всюду» — на «локально почти всюду».
Вернемся теперь к вопросам, поднятым в § 4.13, и, в част-
частности, к более удобной формулировке предложения 4.13.2 в тер-
терминах существенной интегрируемости.
4.14.6. Предложение. Пусть \х — положительная мера Радона
на Т, g— положительная локально ^.-интегрируемая функция,
Р — множество тех точек, где g'=£0, и X = gf • jut. Тогда
A) Каждое локально [i-пренебрежимое множество локально
^-пренебрежимо.
(Г) Множество Sа Т локально ^-пренебрежимо тогда и
только тогда, когда множество Pf]S локально [i-пренебрежимо.
B) Комплексная функция f на Т принадлежит J?1 (I) тогда
и только тогда, когда gf s J?1 (ц); при этом
*(/) = Й(£/). D.14.7)
C) для всякой положительной функции f на Т имеет место
равенство
D.14.8)
D) Комплексная функция f на Т локально интегрируема от-
относительно X=g'[x тогда и только тогда, когда fg локально ин-
интегрируема относительно [i; при этом /•Х==/- (g• \х) = (fg) • \х.
Доказательство. Ясно, что C) влечет (Г); из (Г) в
свою очередь вытекает A). Докажем сначала утверждение B),
а затем покажем, что из него следует C), Наше доказатель-
доказательство утверждения B) существенно опирается на утверждения
318 Г л 4. Топологии, сопряженные к некоторым пространствам; меры Радона
D) и E) и (последнюю часть) C) (т. е. на тот факт, что
Х*(Т\Р)=0) предложения 4Л3.2.
Предположим, что gf e J?1 (\х). В силу следствия 4.14.5 в
о2^(|и) найдется функция /i, равная gf локально |и-почти всюду.
Определим функцию /', полагая ее равной g~lh на Р и нулю во
всех остальных точках. Тогда f'=f локально |и-почти всюду на
Р, и так как Я*(Г\Р)=0, то // = / локально Х-почти всюду.
Кроме того, функция gf' = h принадлежит J?1 (\i), поэтому (пред-
(предложение 4.13.2 D)) существует в *S?[ (X) функция /*, равная f
локально Х-почти всюду, для которой X(f*) = [i(g"D-
Так как функция h = gf локально fi-почти всюду_равиа функ-
функции gf и f* = f локально Я-почти всюду, то /eJ?1^), откуда
следует равенство D.14.7). * Обратное утверждение получается
аналогичным образом из 4.13.2E).
Вывод C) из B) основывается на двух простых замечаниях,
относящихся к произвольной положительной мере Радона pi и к
произвольной положительной функции f. Первое из них состоит
в том, что
^ }
(подразумевается, что inf0=+oo и inf{ + oo}=+oo); при этом
соотношение h ^> f можно заменить соотношением h > / |и-почти
всюду. Второе замечание, которое непосредственно вытекает из
первого и из предложения 4.14.2, заключается в том, что
p,*(/) = inf{jx(ft): h^<S?l{)\), h^f локально pi-почти всюду}
с учетом тех же соглашений, что и выше. После этих наблю-
наблюдений остается только заметить, что если v — некоторая поло-
положительная функция, а и — функция, равная g~lv на Р и нулю
вне Р, то неравенство u^-f имеет место локально Х-почти всюду
тогда и только тогда, когда v^- gf локально |и-почти всюду.
В силу B) функция и принадлежит ^(Х) тогда и только тогда,
когда v^J?l(\i). В этом случае l{u) = \x{v). Следовательно,
что и означает справедливость утверждения C).
Остается доказать D). Функция / локально интегрируема
относительно меры X = g»[i тогда и только тогда, когда для каж-
каждой функции xGsTf?1) произведение fx интегрируемо относи-
относительно g • ,u. Так как х имеет компактный носитель и тем же
свойством обладает fx, то интегрируемость fx относительно меры
g • \х эквивалентна существенной интегрируемости fx относи-
относительно меры g-\x. В силу B) последнее имеет место тогда и
только тогда, когда функция gfx существенно интегрируема от-
4.14. Существенно интегрируемые функции 319
носительно |и. Это возможно (gfx имеет компактный носитель!)
тогда и только тогда, когда gfx интегрируема относительно \i.
Наконец, последнее означает не что иное, как то, что функция
gf локально интегрируема относительно |и. Далее по определе-
определению для всякой функции х^Ж(Т) имеем
В силу равенства D.14.7) и того факта, что функции fx и gfx
имеют компактный носитель, последний член равенства равен
(gf)-\x(x). Таким образом, f-l = f- (g - \х) = (fg) • \i, что и тре-
требовалось доказать. 1
Теорема Лебега — Радона — Никодима, которую мы дока-
докажем в § 4.15, утверждает, что достаточно выполнения одного
лишь условия A), для того чтобы положительная мера Я имела
вид g-\i для некоторой локально интегрируемой относительно
\х функции g^O. Таким образом, утверждение A) влечет все
остальные утверждения предложений 4.14.6 и 4.13.2. Предложе-
Предложение 4.14.6 имеет ряд следствий, которые нам понадобятся в
дальнейшем.
4.14.7. Сужение меры. Пусть \х — положительная мера на Т
и М — некоторое подмножество в Т. Функция g = %M локально
интегрируема относительно \х тогда и только тогда, когда мно-
множество М jii-измеримо. В этом случае к мере
Им^Хм'И D.14.9)
можно применить предложение 4.14.6. Мера \хм называется
сужением меры |и на множество М. В силу того же предложения
для каждого множества SaT имеет место равенство
^(S) = fl*0WnS). D.14.10)
Если множество S открыто, то D.14.1 (а)) вместо p^(S) можно
писать m^(S), откуда следует, что носитель меры \хм есть такое
наименьшее замкнутое множество S, что пересечение МП (T\S)
локально ^-пренебрежимо. В частности, если множество М замк-
замкнуто, то носитель меры \хм содержится в М. Кроме того, мно-
множество S тогда и только тогда ^м-измеримо, когда ^-измеримо
множество Mf]S. Функция / тогда и только тогда (Дм-измерима,
когда она ^-измерима на М.
4.14*8. Основной результат следующего п. 4.14.9 заключается
в том, что, пренебрегая локально пренебрежимыми множествами,
пространство Т всегда можно разложить в локально счетное
(см. ниже) объединение непересекающихся компактных мно-
множеств. Если пространство (Г, \х) а-конечно, то это доказывается
довольно легко. Однако нам понадобится не только этот случай.
320 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Система подмножеств в Т называется локально счетной, если
каждое компактное множество в Т пересекает не более чем счет-
счетное множество элементов этой системы.
4.14.9. Предложение. Пусть ус — положительная мера Радона
на Т. Существует локально счетная система Ж компактных под-
подмножеств в Г, обладающая следующими свойствами:
A) любые два различных множества, принадлежащие Ж.
не пересекаются;
B) для каждого множества X еЭ? и каждого открытого
множества £/, пересекающего Ху имеет- место неравенство
ГШ
);
C) множество Т \ (J{X: ХеЖ} локально ^-пренебрежимо.
Доказательство. Рассмотрим всевозможные системы
компактных подмножеств в Г, обладающие свойствами A) и
B). Такие системы существуют (например, система, состоящая
из одного компактного подмножества — носителя меры |и). Эти
системы можно частично упорядочить по включению, причем
очевидно, что полученная таким образом упорядоченность будет
индуктивной. Возьмем какую-нибудь максимальную систему
указанного вида и обозначим ее через Ж. Покажем, что $ —
локальная счетная система, удовлетворяющая условию C).
Пусть U — открытое относительно компактное множество.
Тогда для любого конечного числа множеств Xt из Ж справед-
справедливы неравенства 2^№ f] £/Хм,(£/)<4-°о, т. е. 2 \i(Xf\U)^.
i ЛеЭЕ
<^(£/)<+оо. Но тогда \х{Х[\1))>§ самое большее для счет-
счетного числа множеств X, откуда в силу B) следует, что си-
система Ж локально счетна.
Наконец, если множество N = T\ \J {X: XgX} не локально
(и-пренебрежимо, то найдется компактное множество /Сс:Л/, для
которого \х(К)>0. Сужение \хк = %к*\1 меры ji будет отлично от
нуля, и его носитель S будет непустым компактным множеством,
содержащимся в К. Тогда для всякого открытого множества £/,
пересекающего S, будем иметь
и, следовательно,
li(S(\U)>iiK(S[\U)>0.
Таким образом, система Xх = $ U{S} будет обладать свойствами
A) и B), откуда из максимальности системы Ж должно следо-
следовать, что S е Ж. Полученное противоречие доказывает наше
утверждение. |
4.15. Теорема Лебега — Радона — Никодима 321
4.15. Теорема Лебега—Радона—Никодима
Эта центральная теорема по существу сводится к предложе-
предложению 4.14.6 и его обращению (которое является более глубоким
результатом).
4.15.1. Теорема. Пусть К и \х — положительные меры Радона
на локально компактном пространстве Т. Для существования та-
такой локально интегрируемой относительно \х функции g^-О, что
X=g' |ы, необходимо и достаточно, чтобы каждое локально \x-npe-
небрежимое множество было локально %-пренебрежимым (т. е.
чтобы выполнялось условие A) предложения 4.14.6).
Доказательство. Необходимость уже была нами дока-
доказана (предложение 4.14.6).
Для доказательства достаточности заметим прежде всего, что
при сформулированных условиях ^-измеримость влечет Я-изме-
римость. Действительно, пусть S — ^-измеримое, а /(-компакт-
/(-компактное множество, тогда пересечение S0K также ji-измеримо. По-
Поэтому, как легко видеть, существует относительно компактное
множество PidSOK, являющееся пересечением последователь-
последовательности открытых относительно компактных множеств, такое, что
\х(Р\ (S0K)) —0. Следовательно, имеет место равенство
К(Р\ (SOК)) =0. Множество Р интегрируемо относительно вся-
всякой положительной меры Радона, откуда вытекает, что множе-
множество SO К Х-интегрируемо, так что множество 5 ^-измеримо.
Введем положительную меру р = |ы + Я. Тогда Кр и р-изме-
римость эквивалентна ^-измеримости. Пусть Л — некоторое ком-
компактное множество (или, более общим образом, некоторое р-ин-
тегрируемое множество). Отображение /*—^М/) является непре-
непрерывной линейной формой на пространстве <2Р2(Л,р), так как
<М |/1)< М I/ P)Vi • Нха)'2 <р(ЛI'2 ■ р( I/ ft
По теореме 4.12.1 существует такая функция фА е~2*2(Л, р), что
М/) = р(Фа/) (/е«2*(Л, р)).
Так как Х<^р, то, полагая фа = 0 вне множества Л, получаем, что
р-почти всюду O^qu^l.
Покажем теперь, что р-почти всюду фл< 1- Пусть Е — мно-
множество тех точек, где Фа= 1. Множество £, очевидно, содержится
в Л и р-интегрируемо. Пусть / = л/е, тогда
Я (Е) = Я Ы = р (ФлХ*) = Р Ы = Р (Е) - \х (Е) + X (Е).
Если р{Е) строго положительно, то \х(Е)=0 и Я(£")>0, что про-
противоречит нашим предположениям. Таким образом, р(£)=0, и
мы можем считать, что всюду 0^фА< 1.
322 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
Далее равенство X(f) =р(фл/) можно записать в виде
(f^^HA, p)),
откуда видно, что функция gA = ~rir~~ положительна и ц-изме-
рима и что
) D.15.1)
для всех таких функций /г, чтоA — фд)/г е J?2(/l, p). Читатель
заметит, что функция gA ja-интегрируема и равна нулю вне А.
Множество А можно представить в виде объединения возра-
возрастающей последовательности р-интегрируемых множеств (Лп),
на каждом из которых функция 1 —фА отлична от нуля. В соот-
соответствии с этим если h — ограниченная ^-измеримая равная
нулю вне некоторого множества Ап функция, то функция
A—Фа)^ принадлежит 5?2(Л, р) и к ней применима форму-
формула D.15.1). Если / — положительная (^-измеримая равная нулю
вне А функция, то функция hn = inf (f%A , ri\ ограничена, р-изме-
рима и равна нулю вне Ап\ кроме того, hn\f. Из монотонной схо-
сходимости hn\f и из формулы D.15.1), справедливой для h — hn
(п= 1, 2,...), следует равенство
V(f) = »(gJ). D.15.2)
Это равенство выполняется для любого р-интегрируемого множе-
множества А и для любой ^-измеримой положительной функции /, рав-
равной нулю вне А.
Воспользуемся теперь предложением 4.14.9. Пусть Ж — систе-
система, обладающая указанными там свойствами. Предыдущая
часть доказательства позволяет нам каждому множеству IgJ
сопоставить положительную ^-интегрируемую функцию gx, рав-
равную нулю вне X. Определим функцию g, полагая ее равной gx
на каждом множестве IgI и нулю на множестве N =
= T\\J{X: XgI}. Очевидно, что функция g положительна и
[д,-измерима. Пусть f — некоторая положительная ограниченная
(i-измеримая функция, равная нулю вне некоторого компактного
множества К. Множество тех Ху которые пересекают /С, не более
чем счетно, скажем Хи Х2, ... . Тогда
причем функции f%x Я- интегрируемы, а функции gx f |ы-инте-
грируемы. Из формулы D.15.2) и принципа монотонной сходи-
сходимости следует, что
D.15.3)
4.15. Теорема Лебега — Радона — Никодима 323
t
поскольку функция gf ^-интегрируема. В частности, функция g
локально интегрируема относительно \i, что следует из формулы
D.15.3), если в ней положить / = Хн (где Н — любое компактное
множество). Из этой последней формулы, верной для всякой
функции /езТ+(Г), следует, что k = g-\x, что и требовалось до-
доказать. |
4.15.2. Локальная абсолютная непрерывность. Взаимно син-
сингулярные меры. В случае когда две комплексные меры Радона К
и |ы взаимосвязаны так, что каждое локально jLi-пренебрежимое
множество является и локально Я-пренебрежимым множеством
то обычно говорят, что мера Я локально абсолютно непрерывна
относительно меры \х. Если К\ — Я2 + ^з — ^4 есть минимальное
разложение меры Я, то мера К локально абсолютно непрерывна
относительно меры jli тогда и только тогда, когда каждая поло-
положительная меры Ки локально абсолютно непрерывна относитель-
относительно меры |(li|, или, что то же самое, мера |Я| локально абсолютно
непрерывна относительно меры |ji|. В этом случае, как легко
следует из теоремы 4.15.1 X = g-ix, где g — комплексная локально
интегрируемая относительно jli (т. е. относительно |jli| по самому
определению) функция. Далее из предложения 4.15.3 (см. ниже)
вытекает, что если ji^-О, то в минимальном разложении меры К
участвуют меры Xk — gke^ где
8i = (Re g)+, g2 = (Re g)~, g3 = (Im g)+, g4 = (Im g)".
Наиболее важным является случай, когда мера К вещественна,
а мера |ы положительна. Этот случай и составляет содержание
предложения 4.15.3. Однако, прежде чем входить в подроб-
подробности, сделаем одно замечание по поводу определенной выше
локально абсолютной непрерывности и введем одно соотношение
между двумя мерами, которое, если можно так выразиться, яв-
является полной противоположностью локальной абсолютной не-
непрерывности. С помощью этого последнего понятия мы сможем
дополнить теорему Лебега — Радона — Никодима некоторым
утверждением, принадлежащим Лебегу (п. 4.15.7—4.15.9).
Начнем с одного замечания. Читателю могло показаться не-
несколько странным, что мы определили локальную абсолютную
непрерывность как выполнение импликации «р,*(£) = 0:ф Х*(Е) =
= 0». Казалось бы, более естественно называть меру К локаль-
локально абсолютно непрерывной относительно (положительной) ме-
меры |х, если выполняется некоторое свойство типа «Я*(£)->0 при
\х*(Е) ->0». Следующий результат несколько проясняет дело.
► Пусть заданы две меры Радона X и \х. Мера X локально
абсолютно непрерывна относительно меры \х тогда
и только тогда, когда для каждого компактного
324 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
множества К и каждого числа е > 0 существует такое
число 6>0, что \Ь\*(Е)<г при Еа К и |jli|*(£)<6.
Это последнее условие, касающееся множества /(, может
быть названо абсолютной непрерывностью на К. Локальная аб-
абсолютная непрерывность сводится, таким образом, к абсолютной
непрерывности на каждом компактном множестве К.
Действительно, если условие предложения выполнено, то вся-
всякое локально jLi-пренебрежимое множество локально Я-пренебре-
жимо, т. е. мера Я локально абсолютно непрерывна относитель-
относительно меры ]ы. При доказательстве обратного утверждения можно
считать, что меры Я и |ы положительны. Если это так и мера Я
локально абсолютно непрерывна относительно меры jli, то Я =
=g'\xi где функция g^O локально интегрируема. В частности,
функция g%K ^-интегрируема. Поэтому можно так выбрать
функцию f &уГ+Bп), чтобы \i*(\g — !\хк)< у. Для всякого мно-
множества Ecz К имеем к*(Е) = \х*(g%E)\ следовательно, |Я*(£)—
"■ Iх*(Не) К ~y • С другой стороны, справедливо неравенство
l^(f7LE)^-M\i*(E)i где М — максимум функции /. Таким образом,
неравенство Я* (Е) < -|- + М - \i* (E) имеет место для любого
множества Е cz К, откуда следует наше утверждение.
В приведенном рассуждении достаточно предполагать, что
множество К существенно Я-интегрируемо (но не обязательно
компактно), заменив повсюду Я* и j.i* на Я* и Д*.
Перейдем теперь к понятию сингулярности мер. Две ком-
комплексные меры Радона на Т % и jli называются взаимно сингу-
сингулярными (чужими (etrange) в терминологии Бурбаки), если су-
существуют непересекающиеся множества L и М, каждое из кото-
которых является несущим соответственно для мер К и jli; последнее
означает, что множества T\L и Т\М локально соответственно
К- и jn-пренебрежимы. (Читатель должен остерегаться смешения
утверждения, что множество L является несущим для меры h
в указанном выше смысле, т. е. что множество T\L локально
Я-пренебрежимо, с утверждением, что множество L является^
носителем или содержит носитель меры К. Носитель меры Я сов-
совпадает с наименьшим замкнутым множеством в Г, несущим
меру Я.) Если меры Я и jli взаимно сингулярны и Я локально аб-
абсолютно непрерывна относительно jli, то, очевидно, Я=0. Далее
если Я7 и jli, так же как и Я и jli, взаимно сингулярны, то %' + % и
(ы взаимно сингулярны. В оставшейся части параграфа введен-
введенное новое понятие будет многократно проиллюстрировано.
4.15.3. Предложение. Пусть jli — положительная, а Я — веще-
вещественная меры Радона на Тг и пусть мера Я локально абсолютно
4.15. Теорема Лебега — Радона — Никодима 325
непрерывна относительно меры \х и обладает минимальным раз-
разложением }, = %+ —%-. Тогда X = g-{iy x+ = g+-\x и Ar = g~-|Li, где
g — вещественная локально интегрируемая относительно \х функ-
функция. При этом меры Х+ wX~ взаимно сингулярны.
Доказательство. Поскольку мера X локально абсолютно
непрерывна относительно меры ji, то же самое справедливо и
для каждой из мер Х+ и Х~ в отдельности. Из теоремы 4.15.1 сле-
следует, что Х+ = р • jit и Х~ = q • \1У где pug — положительные ло-
локально интегрируемые относительно jli функции. Соответственно
X=g-.jLi, где функция g = p — q локально интегрируема относи-
относительно jli. Пусть Р и Q — множества, на которых /?•> О и q>0
соответственно. Мы утверждаем, что множество PflQ локально
jbi-пренебрежимо. Действительно, в противном случае найдется
такое компактное множество К и такое число с > 0, что \х(К) > О
и р ^ с, q ^ с на /С. Тогда меры
V» Р = (Ч - С1к)' V>
положительны и Х = а— р, причем меры а — h+ и C — %~~ не яв-
являются положительными. Это противоречит минимальности раз-
разложения Я = Я+ — %~. Таким образом, множество Pf)Q локально
jbi-пренебрежимо. Изменяя функции р и q на локально |ы-прене-
брежимом множестве, но не меняя при этом меры р-\х и q*\\,
можно добиться того, чтобы Pf]Q = 0. Но тогда функция g =
= р — q совпадает с р на Р, с —q на Q и равна нулю во всех
остальных точках. Отсюда следует, что p = g+ и ^ = g"~". Наконец,
множества Р и Q являются несущими соответственно для мер
K+ = g+4i и A,-=gr-|i. Так как эти множества не пересекаются,
то Я+ и X" взаимно сингулярны. |
4.15.4. Следствие. Пусть % и а — те же, что и в предложении
4.15.3. Тогда |Я|*A) =Д*( |g"|). В частности, если мера X огра-
ограничена (т. е. |Я|*A)<+оо), то функция g локально \х-почти
всюду равна некоторой функции go^£?l(\x) и \i*(\go\) = \k\(\).
4.15.5. Следствие. Пусть К —вещественная мера Радона на Т.
Тогда Т является объединением таких непересекающихся Х-из-
меримых множеств Р+ и Я_, что А+= \Х\р и Х~= \X\p_ так что
\Р
Доказательство. В предложении 4.15.3 положим jx =
= \Х\. Множества Р и Q, фигурирующие в доказательстве этого
предложения, являются не чем иным, как множествами
р { (П { 0} Р { 01 ( 0}
р
р+ = {g > (П = {g+ > 0} и Р- = {g < 01 = (g- > 0} соответственно.
Т \Х\ =X+ + l-= (g+ + g~) • |Я|, +l
N
+ {g g } {g ( }
Так как \Х\ =X+ + l-= (g+ + g~) • |Я|, то g++g~=l локально
^-почти всюду. Пусть N—множество, на котором не выполняет-
326 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
ся равенство g++g~=L и пусть N локально Я-пренебрежимо. Не
трогая функцию g на множестве T\N, заменим ее на множестве
N единицей. Тогда сохраняются равенства k+=g+- \K\ и Аг —
= g~» |Я| и уже всюду выполняется равенство g++g~=l. Следо-
Следовательно, в точках множества Р+, на котором g*~ = 0, функция g +
должна принимать значение 1. Таким образом, g+ = %Р+, и
аналогично g"~ = Xp_> поэтому Х+ = %р+ . \К\ = \К\ р+ и т. д. Мно-
Множества Р+ и Р- не пересекаются, а их объединение дает Т. Пред-
Предложение полностью доказано. I
4.15.6. Замечание. Пусть вещественная мера Радона X ло-
локально абсолютно непрерывна относительно меры |ы. Из след-
следствия 4.15.4 вытекает равенство h=g-\i, где g — вещественная
локально интегрируемая относительно |ы функция. В этом случае
значение |Я|*A) =Д*(|#|) равно
п (Л) = sup | Л, (*) I.
где х пробегает функции пространства g2Tc (T) (или
удовлетворяющие неравенству IUIU = sup|x(/) |^ 1. Если, одна-
однако, X — комплексная мера, то функция g комплексна, скажем
g = u + iv, и тогда значение |Я|*A) = Д* (| и\) +jT( \v j), вообще
говоря, больше, чем п(к). Тем не менее имеет место неравен-
неравенство п (X) > 2 2 | К Г A), так что п(Х) и | X \ * A) определяют экви-
эквивалентные нормы. Учитывая это замечание, часто отождест-
отождествляют пространство ограниченных мер, локально абсолютно не-
непрерывных относительно меры jli, с лебеговым пространством
L^j.i). Один из способов избежать разногласий — это пере-
переопределить меру |А,|, где Я=а + ф, положив ее равной ]Лх2 + Р2
(п. 4.15.13).
4.15.7. Разложение Лебега. Пусть заданы две комплексные
меры Радона Я и \х на Т. В теореме Лебега — Радона — Никоди-
ма исследуются условия, при которых мера К локально абсолют-
абсолютно непрерывна относительно \i. Покажем теперь, что меру X все-
всегда можно так разложить в сумму двух мер Х\ и Я2, что меры
h и jli будут взаимно сингулярными, тогда как мера %2 будет ло-
локально абсолютно непрерывной относительно jli.
4.15.8. Теорема. Пусть к и \х — две комплексные меры Радона
на Т. Существует единственное разложение
Я = Я1 + Я2, D.15.4)
где меры К\ и \х взаимно сингулярны, а мера Х2 локально абсо-
абсолютно непрерывна относительно \х.
Доказательство. Из определений п. 4.15.2 ясно, что если,
такое разложение существует, то оно единственно и что при до-
4.15. Теорема Лебега — Радона — Никодима 327
казательстве существования такого разложения достаточно огра-
ограничиться случаем, когда меры X и jli положительны. В этом слу-
случае мы можем применить доказательство теоремы 4.15.1, видо-
видоизменив его следующим образом.
Как и раньше, введем меру р = |ыН-^, и пусть А— произволь-
произвольное компактное множество. Докажем существование такой функ-
функции фл е 2?2 (А, р), что
) D.15.5)
для f^a2?2(A9p)'. По-прежнему можно считать, что 0-<фА-<1
и фА = 0 вне множества А. Пусть А\ (в доказательстве теоремы
4.15.1 обозначенное через Е)—множество тех точек, где фл=1, и
А2— остальная часть множества А. Теперь мы не можем пользо-
пользоваться локальной абсолютной непрерывностью меры К относи-
относительно |ы, чтобы показать, что р(А\) =0. Тем не менее из форму-
формулы D.15.5) следует, что
М А)=р Ыл) = р Ы = р (А) = НА)+и( А)
и, значит, |ы(^i) =0, т. е. множество А\ jLi-пренебрежимо.
С другой стороны, если множество Scz А2 таково, что \x(S) =
= 0, то
Поскольку на множестве S выполнено неравенство 1—Фа > 0,
то A,(S)=O.
Теперь введем в рассмотрение разбиение Ж множества Т на
компактные подмножества X (как и при доказательстве теоремы
4.15.1). Каждое из множеств X разложим надмножества Х\ и Х2
таким же образом, как выше было разложено множество А. Как
известно, множество N = T\\JX локально jn-пренебрежимо.
Введем множества Тг= \JX{[}N и T2=\J X2. Так как разбиение Ж
локально счетно, то множества Т\ и Т2 |ы-измеримы. Они не пере-
пересекаются, и их объединение равно Т. Если положить Кг—Х^п
^2 = Ат2, то, очевидно, Х = Я,1 + Я,2.
Множество Т\ локально ^-пренебрежимо, так как по дока-
доказанному jli(Xi)=O, а разбиение Ж локально счетно. Следователь-
Следовательно, меры К\ и jit взаимно сингулярны и Т\ — несущее множество
для меры Х\.
Покажем, наконец, что мера К2 локально абсолютно непре-
непрерывна относительно \х. Пусть S локально |ы-пренебрежимое, а
К — компактное множество. Тогда ^(Sfl/Cfl^)^ jbi(Sfl/C) =0 и
X*2(S[)K) =lk*{S[)Kf)T2). Так как компактное множество К
пересекает лишь счетное число множеств X, скажем Хп (п =
= 1,2,...), то множество 5Г\К(~}Т2 содержится в объединении
328 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
множеств Sf)Kf)XZ. Из того факта, что \i(SDKC\Xt2)=0 при ка-
каждом п, следует, что X*(Sf}KC\Xn2) =0 при любом п (как это
уже было доказано для Л, вместо XS), поэтому h(S [)К) = 0.
Таким образом, множество S локально ^-пренебрежимо, и ло-
локальная абсолютная непрерывность %2 относительно |ы доказана, i
4.15.9. Замечание. В тех же обозначениях теорема Лебе-
Лебега— Радона — Никодима показывает, что локально интегрируе-
интегрируемую относительно |ы функцию g в равенстве Я2 = ё"-|ы можно счи-
считать равной нулю вне множества Т^ т. е. на множестве Т\. При
этом
что служит явным представлением меры X в виде суммы двух
мер с несущими множествами Т\ и Т2 соответственно.
4.15.10. Функции вещественной переменной с локально огра-
ограниченной вариацией и локально абсолютно непрерывные. Приме-
Применяя теорему Лебега — Радона — Никодима и разложение Лебега
к мерам Лебега — Стилтьеса, можно установить связь этих тео-
теорем с некоторыми хорошо известными результатами теории
функций вещественной переменной. Будем пользоваться обозна-
обозначениями п. 4.4.4.
Пусть сперва функция f локально абсолютно непрерывна на
Т. Из примера 4.7.7 непосредственно следует, что ассоциирован-
ассоциированная мера |Ы/ локально абсолютно непрерывна относительно меры
Лебега на Т. Тогда из теоремы Лебега — Радона — Никодима
вытекает, что jLX/ = g" • jlx, где jli — мера Лебега на Г, a g— функция,
локально интегрируемая относительно ji. Так как функция f не-
непрерывна, то результаты примера 4.7.7 приводят к равенству
t
J g(s)ds,
D.15.6)
где а и / — точки интервала Т. (Следуя обычным соглашениям,
мы пишем в интеграле ds вместо d\i(s).)
Как известно из курса теории функций вещественной пере-
переменной (см., например, Натансон [1, стр. 272, теорема 2]),
функция J g{s)ds почти всюду обладает конечной производ-
а
ной, почти всюду равной функции g. Отсюда следует, что для
всякой локально абсолютно непрерывной функции f на Г почти
всюду существует производная f, почти всюду равная локально
4.15. Теорема Лебега — Радона — Никодима 329
интегрируемой на Т функции, которую можно также обозначить
через f, и что отношение
= f(a)+\f'(s)ds D.15.60
а
имеет место для любых двух точек из Т. Обратно (это очевид-
очевидно), формула D.15.6) справедлива, если / — локально абсолютно
непрерывная, функция на Т.
Легко проверить, что произведение двух локально абсолютно
непрерывных на Т функций fug обладает тем же сврйством,
причем равенство (fg)'=zf'g + fg/ имеет место почти всюду (точ-
(точнее, во всех точках, где существуют обе производные /' и g').
Интегрируя, получаем обычную формулу интегрирования по ча-
частям
ъ ь
= f(b)g(b)-.f(a)g(a)- J f'(t)g(t)dt D.15.7)
а а
для всякого компактного интервала [а, Ь]а Т.
Рассмотрим теперь более общий случай, когда известно толь-
только, что f имеет локально ограниченную вариацию на Т. Тогда в
силу замечания 4.15.9 имеет место разложение \Xf = o + g • |ы, где
g — локально интегрируемая (относительно |ы) функция и а —
мера, сингулярная относительно |ы. Аналогичный D.15.6/) пере-
переход от соотношения между мерами к соотношению между функ-
функциями в этом случае несколько усложняется. Так как этот ре-
результат в настоящей книге не используется, мы ограничимся
лишь наброском его доказательства. Подробное изложение мо-
можно найти в книге Натансона [1, гл. IX]. Первым и основным
шагом является установление того факта, что сингулярность
меры а относительно |ы означает выполнение в каждой точке t
отношения
для любой последовательности замкнутых множеств (Еп)у такой,
что для некоторой последовательности открытых интервалов
(/п), содержащих точку /, выполняются соотношения
0,
Это указывает на то, что своего рода обобщенная производная
меры а относительно \х равна нулю в точке t. (Доказательство
можно найти, например, у Мак-Шейна [1, стр. 381].)
330 [л. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Опираясь на этот результат, можно доказать, что аналогично
D.15.6') имеет место равенство
f(t)=S(t)+jf'(s)ds, D.15.6")
а
где функция f локально интегрируема и почти всюду равна
обычной производной от f, а функция S с локально ограниченной
вариацией сингулярна в том смысле, что S' = 0 почти всюду.
К этому результату можно прийти и обычным образом, исходя
из теории функций вещественной переменной и не прибегая к
мерам Лебега — Стилтьеса. (См., например, цитированную выше
книгу Натансона.)
4.5.11. Приложение теоремы Лебега—Радона—Никодима:
функции от мер. Наша задача — использовать теорему Лебега—
Радона — Никодима для придания смысла выражению Я (jlii,...
..., (in), где (\ii) к*<л— заданное семейство вещественных мер
на Г, а Н = Н(х\,..., хп) — заданная положительно однородная
функция на Rn. (Аналогично можно рассмотреть случай ком-
комплексных мер с функцией Я, определенной на О.) Положитель-
Положительная однородность означает, что
Я (а*!, ..., ахп) = а • Я (хи . .., хп)
для всех х= (хи . • •, #n)<= Rn и всех положительных чисел а.
Наше определение будет основываться на следующем пред-
предложении.
4.15.12. Предложение. Пусть Я и ц{ A ^i^Cn) те же, что и
выше. Выберем две положительные меры Радона Х\ и Х2 на Т
так, чтобы \\ii\^-kk A^л^я, 1-^&^2). Определим функции
fik условиями: \ii = fik'kh, функции fik Xk-измеримы и |f^|^l.
Функция Я(/1Ь ..., fni) локально интегрируема относительно А,!
тогда и только тогда, когда функция Я (fi2, ..., /пг) локально
интегрируема относительно h2f и в этом случае
..., Ы-Я*. D.15.3)
Доказательство. Положим ^ = ^i + ^2. Мы можем срав-
сравнить ситуацию с Kk (k=l или 2) и ситуацию с К. При этом кос-
косвенно сравниваются ситуации с ^ и Х2- Таким образом, можно
свести исследование к случаю 7и<Л2. Тогда X\=g-X2i где g
есть ^-измеримая функция и 0-<£-<1, и из предложения
4.14.6D) следует, что \n = fi\ -h = fa • (g - ta) = {fug) • X2. Поэтому
равенства fi2 = fug имеют место локально Я2-почти всюду и, сле-
следовательно, равенство
4.15. Теорема Лебега — Радона — Никодима 331
справедливо локально Я2-почти всюду. Опираясь еще раз на
предложение 4.14.6D), получаем, что локальная интегрируе-
интегрируемость функции //(/12,..., /пг) относительно Х2 эквивалентна ло-
локальной интегрируемости функции H(fn,..., /п1) относительно
g"*^2 = ^i, откуда и следует справедливость соотношения
D.15.8). |
Из доказанного предложения вытекает, что выражение
НGь . • • i fn) *k зависит только от функции Н и семейства мер
(\ii)\<i<n и не зависит от выбора положительной меры Я, удо-
удовлетворяющей условию ||Ы;|^Л для каждого I, и таких вспомо-
вспомогательных функций fi, что \ii = fi^K (существование функций fi
следует из теоремы Лебега — Радона — Никодима). Эту опреде-
определенную единственным образом меру мы будем обозначать через
Читатель легко проверит, что таким способом можно полу-
получить меры ц+, ц-, |jx| (при /г=1) и \i\ + \i2 (при п = 2), а также и
другие комбинации мер, например sup (jlh, \i2) и inf(jn, \l2), и
что эти определения не противоречат более прямым определе-
определениям, приведенным ранее.
4.15.13. Пример. Рассмотрим случай, когда
H(xv..., *„)=К
Поскольку Н ^ 0, то с помощью описанного выше метода при-
приходим к положительной мере
которая удовлетворяет соотношениям |p,i|^n, потому что
^Н(). Полагая К=\х и |n2 = fi-|Li, получаем
и, следовательно, (/^+... +f2nJ — 1 локально pi-почти всюду.
Обратно, пусть а—такая положительная мера, что |i/ = g"ra»
причем fff+...+^=l локально а-почти всюду. Тогда ||ij =
= I gi I' а ^ «, так что
т. е. pi = а. Далее ^ = Д. • \х = g{ • а = gr \i, a потому ft =
локально [л-почти всюду.
332 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Таким образом, для заданных мер \iu ..., \in существует
в точности одна такая положительная мера \i9 что щ = !г\1
A ^ / < п), причем f\ + ... + f2n = 1 локально ц,-почти всюду, т. е.
4.15.14. Приложение к поверхностным мерам. Пусть G —
ограниченное открытое множество в Rn с границей F, Е— вектор-
векторное пространство вещественных бесконечно дифференцируемых
функций на Rn, обладающих компактными носителями, % — мера
Лебега на Rn и х{ (/•</•< п) — координаты в Rn. Оператор част-
частного дифференцирования д\дх{ обозначим через Эг. Допустим,
что существует такое число М ^ О, что
\ DtudX
(u<=Ey 1</</г). D.15.9)
Это условие выполнено для всех достаточно простых ограничен-
ограниченных открытых множеств G. Например, оно справедливо, если
существует такое натуральное число г, что все (или даже только
«почти все») прямые, параллельные координатным осям, пересе-
пересекают F не более чем в г точках. Тогда можно воспользоваться
одним из стандартных доказательств формулы Грина. Во всяком
случае ясно, что D.15.9) представляет собой довольно грубый
в количественном отношении вид формулы Грина, когда гранич-
граничные значения функции и используются лишь для получения
оценки сверху. Мы покажем, как можно применить результаты
п. 4.15.13 для введения поверхностной меры на У7 и единичной
нормали, определенной почти всюду на F, а также для уточне-
уточнения формулы Грина.
Для этого введем банахово пространство C(F)} образованное
вещественными непрерывными функциями на F, с нормой, рав-
равной максимуму модуля на F. Обозначим через и0 сужение функ-
функции и^Е на F. Тогда и^-^щ есть линейное отображение про-
пространства Е в C(F), образ которого мы будем обозначать
через Ео.
Мы утверждаем, что Ео плотно в C(F). Это может быть уста-
установлено различными способами. С одной стороны, можно вос-
воспользоваться тем фактом, что, согласно одной из теорем Лебега,
каждая функция v^C(F) непрерывно продолжаема на Rn. Так
как F компактно, можно считать, что это продолжение обладает
компактным носителем. Теперь достаточно подвергнуть наше
продолжение v процессу регуляризации. Выберем такую после-
последовательность kn (n=l, 2, ...) положительных функций в £, что
I kndk—l и kn равна нулю вне некоторой окрестности нуля в
4.16. Пространства, сопряженные к J3?p и Lp (I <p^oo) 333
Rn, диаметр которой стремится к 0 при п->оо. С помощью не-
несложных рассуждений показывается, что функции г7п = г;*&п>
определенные равенствами
принадлежат Е и равномерно сходятся к г?, в частности (vnH-*v
bC(F).
С другой стороны, можно непосредственно использовать тео-
теорему Вейерштрасса — Стоуна (теорема А п. 4.10.5), применив ее
к подалгебре Ео в CG7)=CR (F).
Следующий этап рассуждений основывается на замечании,
что в силу формулы D.15.9) интеграл J Diti'dX зависит только
G
от по и линейная форма щ*—> Dtudk непрерывна на Ео (как
G
на подпространстве в C(F)).
Из теоремы Хана — Банаха и результатов § 4.10 вытекает су-
существование такой меры а* на F, что
J DtU'dX= J udat D.15.10)
G F
для и^Е. Далее из того факта, что Ео плотно в C(F), следует,
что мера О{ однозначно определяется областью G.
Наконец, как мы знаем из примера 4.15.13, на F существует
единственная положительная мераа = (о^+ ... +ог^J, для ко-
которой Gi = Ni-o (l^Ci^Cn), где вещественные функции Nt на F
таковы, что W?+ ... +Л^= 1 а-почти всюду. Эта мера а одно-
однозначно определяется областью G и является поверхностной ме-
мерой на F. Пользуясь ею, мы можем записать формулу D.15.10)
ц виде
J Diti-dX^ J uNtda. D.15.11)
G F
Это равенство выглядит уже в точности, как формула Грина.
Пока оно доказано лишь для функций и^Е. Однако его легко
продолжить (например, с помощью регуляризации) на все функ-
функции и, непрерывно дифференцируемые в некоторой окрестности
замыкания G области G.
4.16. Пространства, сопряженные к &р и Lp (l
Теперь можно дать полное обоснование утверждений (приве-
(приведенных без доказательства в § 4.11) относительно пространств,
334 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
сопряженных к <2>р и L?, где 1 ^Ср < оо. Теорема о представле-
представлении, которую мы хотим доказать, может быть сформулирована
применительно к любому из этих пространств. Мы выбираем
формулировку в терминах <2?р, добавляя в виде замечаний воз-
возможные варианты.
4.16.1. Теорема. Пусть \i — положительная мера Радона на
локально компактном пространстве Т и L — непрерывная линей-
линейная форма на J?p = J?p (T, \х), где 1^р<оо. Тогда в простран-
пространстве J?p = J2?p (Г, \х) существует такая функция gy что
D.16.1)
для всех функций f^J2?p. Для всякой такой функции g имеет
место равенство
NP' (g) = sup {|L (f) |: /e.2", Npif) < 1}. D.16.2)
В частности, элемент пространства Lp, соответствующий функ-
функции g, однозначно определяется формой L.
Доказательство. Непрерывность формы L означает су-
существование такого числа с^-0, что
\L(f)\<cNp(f) D.16.3)
для всех функций f^3?P. Пусть К — сужение формы L на про-
странствозТ(Г). Тогда в силу D.16.3) % — комплексная мера Ра-
Радона и потому, если ^i—Я2 + й3—Щ — минимальное разложение
меры А,, каждая из мер Ки удовлетворяет неравенству вида
D.16.3). Отсюда следует, что для любого открытого относитель-
относительно компактного множества U имеет место неравенство Я& (U) ^
\х ([/)р.Это означает, что для каждого k мера Ки локально
абсолютно непрерывна относительно ji и, следовательно, мера %
также локально абсолютно непрерывна относительно |ы. В силу
теоремы Лебега — Радона — Никодима K = g • jx, где g — локально
интегрируемая относительно (i функция. Таким образом,
MfHM/Hlitef) (!^еГ(Т)). D.16.4)
Поэтому для f^o^(T) имеетjviecTo неравенство \^(gf)\^cNp(f),
откуда легко следует, что NP'(g)< + оо. Изменяя значения
функции g на локально pi-пренебрежимом множестве, можно
добиться того, чтобы функция g принадлежала J?p. При этом
равенство D.16.4) не нарушится. Поскольку g^J2ppy можно
утверждать, что отображение f*—>\i(gf) есть непрерывная ли-
линейная форма на <S?P с нормой, равной Np>{g). Так как в/Г (Г)
плотно в J?p (p Ф оо), то продолжением по непрерывности ра-
равенства D.16.4) получаем D.16.1). |
4 16 Пространства, сопряженные к J£p и Lp A < р < с^335
4.16.2. Замечания. Можно сказать, что сопряженное к
пространство в его естественной норме отождествимо с простран-
пространством Lp. С другой стороны, так как непрерывные линейные
формы на J?p отождествимы обычным образом с непрерывными
линейными формами на Lp, to говорят, что пространством, со-
сопряженным к Lp, «является» пространство Lp . Теорему 4.16.1
можно также сформулировать в терминах 9?v и Lp (см. замеча-
замечания в § 4.11). Теорема 4.16.1 и ее варианты остаются верными
при р = оо лишь в самых тривиальных случаях.
4.16.3. Недостатки пространства Jg? при 0<р<1. Если
0<р<1, то J?p есть полное полуметризуемое топологическое
векторное пространство; Np больше не является полунормой,
однако (ср. D.2.4)) Np служит полуметрикой, инвариантной
относительно сдвигов и определяющей топологию в J?p. Как мы
сейчас покажем, в случае 0<р<1 теорема 4.16.1, вообще говоря
неверна.
В этом пункте компактное множество KczT будем называть
^-делимым, если существует такое с > 0, что для всякого нату-
натурального п>0 возможно разбиение множества К на такие ^-ин-
^-интегрируемые попарно не пересекающиеся множества А\, . . . ,Ап,
что A(ЛГХ— A </* < п). Меру |ы будем называть непрерыв-
непрерывной, если всякий компакт К!с= С, содержится в некотором |ы-дели-
мом компакте /(си Г. Можно доказать, что мера |ы непрерывна
тогда и только тогда, когда \i({t})=0 для любой точки t^T.
Докажем сейчас четыре утверждения, в каждом из которых
предполагается, что мера [х непрерывна и что 0 < р < 1.
► A) Всякое выпуклое множество в Л?р, содержащее вну-
трение точки совпадает с 9?v.
► B) Всякое замкнутое выпуклое поглощающее множе-
множество в 5?v совпадает с SB*.
► C) Не существует ненулевого непрерывного линейного
отображения пространства <2?р в какое бы то ни было ло-
локально выпуклое пространство (см. упражнения 4.29 и
4.33, а также Дэй [2]).
► D) Не существует ни одной ненулевой непрерывной ли-
линейной формы на <2?р.
Очевидно, что B) влечет C), откуда в свою очередь сле-
следует D). В силу теремы Бэра о категориях и полноты простран-
пространства S£v из A) вытекает B). Таким образом, остается дока-
доказать A).
Пусть множество A cz 9?v выпукло и имеет внутренние точки.
Для того чтобы установить равенство A^=S£V, достаточно
336 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
(упр. 1.15) показать, что множество А плотно в J?p. Можно счи-
считать (выполнив, если нужно, сдвиг), что множество А есть окре-
окрестность нуля. Докажем, что множество А содержит всякую огра-
ограниченную функцию [gS'p, обладающую компактным носителем.
Ясно, что множество всех таких функций плотно в 3?р. Для вся-
всякой такой функции / найдутся число УИ, такое, что |f|<M, и
^-делимое компактное множество /(, вне которого функция f рав-
равна нулю. Так как множество А есть окрестность нуля, то суще-
существует такое число d >0, что А содержит все функции J?p
п
для которыхNp(g)<d. Пусть К = [J Аг — разбиение, о котором,
идет речь в определении ^-делимости. Тогда
так что
Так как р < 1, то число Npp(fr) можно сделать сколь угодно ма*
лым для всех г, стоит только взять п достаточно большим. В ча-
частности, можно добиться, чтобы fr е А для 1 <1 г ^ п. В силу вы-
выпуклости множества А получаем [еЛ, что и требовалось дока-
доказать. |
Ситуацию, описываемую утверждениями A) —D), полезно
сравнить в той, которая имеет место (упр. 6.14) для сходных на
первый взгляд пространств //?, где 0 < р < 1 (упр. 4.29 и 4.33).
4.16.4. Возможно, что наиболее прямые практические след-
следствия теоремы 4.16.1 получаются из ее сочетания с теоремой
Хана — Банаха применительно к задачам линейной аппроксима-
аппроксимации, описанным в общих чертах в § 2.4.
Пусть 1 <^/7<оо и V—некоторое векторное подпространство
в <=2рр = J?/? (Г, |ы) или в ассоциированном отделимом простран-
пространстве />. Тогда замыкание подпространства V состоит из тех и
только тех элементов fo^J^p (или Lp), для которых имеет ме-
место равенство
n(fo£)=O, D.16.5)
где функция g ^J2pp/ удовлетворяет отношению
n(fe)=0 D.16.6)
для всех feV. Если V не является векторным подпространством,
то это же условие необходимо и достаточно для того, чтобы
функция /о была пределом в 9?v (или в Lv) конечных линейных
комбинаций элементов /gF,
4.17. Произведения мер и теорема Фубини 337
4.17. Произведения мер и теорема Фубини
Пусть Т и Т — отделимые локально компактные простран-
пространства *), Р = ТхТ/ — их произведение (которое является простран-
пространством того же типа). Пусть далее \х и \х' — положительные меры
Радона на Г и Г соответственно. Возьмем функцию / на Р и рас-
рассмотрим ее повторные интегралы относительно мер \х и \х'. При
этом априори надо учитывать порядок интегрирования. Далее
мы увидим, что меру-произведение на Р возможно определить
лишь единственным способом, другими словами, что порядок
интегрирования не играет роли при f GgT(P), в результате чего
мы приходим к некоторой положительной мере Радона на Р.
После этого неизбежен вопрос, в какой степени изменение по-
порядка интегрирования существенно, если f — функция более
общего характера. С другой стороны, можно поставить вопрос, ка-
каким образом этот «более общий» интеграл от функции f на Р от-
относительно меры произведения выражается через «частные» ин-
интегралы относительно мер \х и \i'. Ответ на этот вопрос дают тео-
теорема Лебега — Фубини и дополняющие ее результаты Тонелли.
(Вклад Фубини в этот результат ограничивается случаем инте-
интегралов Римана от вещественных функций; простейшая форма
этой теоремы для случая /^е/Г(Я) была известна еще Коши.)
4.17.1. Определение меры-произведения. Сначала мы рассмо-
рассмотрим случай, когда f &зЗГ(Р). Тогда функция ft: t't->-f(t, t')
принадлежит g^jT), и выражение
\>'{ft)=\f{U
вполне определено. Более того, легко видеть, что функция
tb-*\i'(ft) содержится в е/Г(Г), поэтому определен интеграл
J ц' (ft) ф @ = J ф (t) J / (t, t') ф' (f).
Если функция f положительнагтр повторный интеграл также по-
положителен. Поэтому отображение
щ: f^Jd|i(Oj/(ff Г№'(П D.17.1)
является положительной мерой Радона на Р.
1) Всюду в этом параграфе штрих (у Т') является лишь отличитель-
отличительным знаком. Мы временно отказываемся от соглашения, принятого в опреде-
определении 1.9.4 и используемого повсюду в этой книге.
338 Гл. 4 Топология, сопряженные к некоторым пространствам, меры Радона
Если обратить порядок интегрирования по \х и \if и поменять
ролями Т и Т\ то аналогичным образом придем к положитель-
положительной мере Радона я2 на Р
я2: /ь->/ф'('')/М nd[i{t). D.17.2)
Наша первая задача — показать, что меры щ и я2 в действи-
действительности тождественны. Эту меру мы и назовем (тензорным)
произведением \х ® \i' мер \i и \i' (или мерой-произведением).
Возможно и с логической точки зрения наиболее удовлетвори-
удовлетворительно доказывать совпадение мер Я1 и Я2, используя лишь инте-
интегралы от функций из пространств <£Г(Т) иеЗГ(Г'). Это проде-
проделано в работе Эдварде [3] следующим образом.
Если функция х (соотв. хг) принадлежит пространству е^Г(Г)
(соотв. е^Г(Г/)), то через х(&хг обозначается элемент простран-
пространства ойГ(Я), определяемый правилом (t,t')y—>x(t)x'(tf). Обозна-
Обозначим временно через g)F(T) ® о?Г{Т') векторное подпространство
пространства Ж(Р), порожденное такими функциями. Очевидно,
что при применении мер п\ и к2 к функции х ® Xх получается
одинаковый результат и, следовательно, то же самое имеет место
при применении этих мер к любому элементу из <Ж(Т)®Ж (Тг).
Поэтому достаточно показать, что подпространство е/Г(Г)®
®«3&?GV) в соответствующем смысле плотно в Ж(Р). Это может
быть доказано с помощью теоремы Вейерштрасса — Стоуна.
Альтернативный метод, в котором избегают явных ссылок
на теорему Вейерштрасса — Стоуна и который однако формаль-
формально весьма похож на предыдущий, заключается в следующем.
(Логически он менее удовлетворителен, ибо вводятся интегралы
относительно \х и \х' от разрывных функций). Выбирают такие
компактные множества К и К\ что функция f обращается в нуль
вне КХК'. Пользуясь компактностью, можно показать, что для
любого заданного числа е >0 множество К (соотв. К') может
быть разложено на такое конечное число универсально интегри-
интегрируемых множеств Ai (соотв. Л/), что
I f (*i, П - / (t2, t')\ < e (tu t2 e= Ai9 V е К%
(В действительности оба утверждения следуют из равномер-
равномерной непрерывности функции f на КХК', если воспользоваться
существованием единственной равномерной структуры на ком-
компактном пространстве КХК\ определяющей его топологию.)
Тогда множества Рц = At X Л/ образуют разбиение множества
4.17. Произведения мер и теорема Фубини
339
КхК'< Если точки (t\, t'\) и (fe, ^2) принадлежат какому-нибудь
Pijy то из неравенства треугольника следует, что
Выберем произвольно точки рц
jf(t,t:
для ('e/lj и
-. Тогда
Суммируя эти неравенства по i и /, приходим к неравенству
fit, f)
Изменяя порядок интегрирования, получаем, что интеграл
Г d\i(t) I / (t, f) d\i'(¥) удовлетворяет аналогичному неравенству.
Таким образом, оба повторных интеграла от функции f отли-
отличаются друг от друга не более чем на 4eji(/C),u/(/(/). Так как е
произвольно мало, оба интеграла равны, что и требовалось до-
доказать.
4.17.2. Полунепрерывные функции. Пусть ф — положительная
полунепрерывная снизу функция на Р. Каждая функция <pf: t'\r->
1—>ф(/, f) полунепрерывна снизу на Tf. Более того, представляя
функцию ф как верхнюю огибающую функций из Ж(Р) и поль-
пользуясь определением D.5.1), получаем, что функция tb—>ix'*(<pt)
полунепрерывна снизу на Т. Применяя, наконец, предложение
4.5.1, видим, что
fj\t, t')dn'(t'). D.17.3)
Аналогичные рассуждения показывают, что такое же равенство
получается, если в правой части изменить порядок интегри-
интегрирования.
4.17.3. Верхний интеграл от произвольных функций. Пусть
f — положительная функция на Р. Напомним читателю, что верх-
верхним интегралом от / (относительно некоторой положительной
меры) является по определению нижняя грань верхних инте-
интегралов от положительных полунепрерывных снизу функций,
340 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
мажорирующих /. Комбинируя это определение с замечаниями
п. 4.17.2, приходим к выводу, что всегда
я*(/)> /*ф(*)/*/(', ndvL'if). D.17.4)
Здесь снова можно изменить порядок интегрирования в правой
части.
Мы подошли к основной теореме.
4.17.4. Теорема (Лебег — Фубини). Пусть f — функция,
определенная на произведении Р = ТхТ' и интегрируемая отно-
относительно произведения мер я = |ы®|и/. Тогда функция ft: V ь—>
н-^/(£,/') интегрируема относительно \х' для \х-почти всех t^T.
Функция /ь-> f(ty V)d\xf(f), определенная для \х-почти всех
t еГ, интегрируема относительно \х и
М')Ф'(О- D.17.5)
То же самое справедливо, если поменять ролями Т и Т\
Доказательство. Не ограничивая общности, можно.счи-
можно.считать, что функция f положительна. Так как f интегрируема от-
относительно я, то можно выбрать убывающую последователь-
последовательность (фд) положительных полунепрерывных снизу функций на
Р, каждая из которых мажорирует функцию f, такую, что
lim (pn = f в J?J(P, я). Тогда функция g=lim(pn (сходимость по-
поточечная) интегрируема относительно я и f = g я-почти всюду.
Используя дважды монотонную сходимость, а также формулу
D.17.3), получаем
я (/) = lim я (Фп) = lim J * d\i (t) J * Фп (/, П ф' (V) =
git, t')d»'(Г). D.17.6)
Цалее функция gt измерима относительно \х' для каждого t e Г,
а функция tb->\ g(t, t')d\x'{t') измерима относительно |ы. По-
ггому из формулы D.17.6) вытекает интегрируемость gt отно-
:ительно \х' почти для всех / и интегрируемость относительно ^х
функции t'\—> g(t, f) d\i' (t')> определенной для почти всех t.
Наконец, формула D.17.4) показывает, что я-пренебрежимость
множества NczP влечет |ы/-пренебрежимость множества Nt =
= {f: f^T', (tytf)^N) для почти всех t^T. Следовательно,
t=gt для почти всех t, за исключением .а^пренебрежимого под-
подмножества в Т\ Наша теорема вытекает теперь из формулы
D.17.6) и предыдущих замечаний, i
4.17. Произведения мер и теорема Фубини 341
4.17.5. Замечание. Теорема терпит почти полный крах,
если заменить условие интегрируемости условием существенной
интегрируемости. Может случиться, что функция f существенно
интегрируема относительно я, тогда как функция ft не является
существенно интегрируемой относительно |х' ни для одного зна-
значения t. См., однако, следствие 4.17.12.
4.17.6. Обозначение. Вместо я(/) и n*(f) привычно и удобно
писать
J } f (/, f)ф(/)dW(П и //*/(*. ПФV)Ф'(П
соответственно. Читателю необходимо различать понятия «двой-
«двойной интеграл» и «повторный интеграл», так как иначе теорема
Лебега — Фубини лишается всякого смысла.
4.17.7. Следствие. A) Пусть f — положительная измеримая
относительно меры п = \х ® \х' функция, равная нулю вне
п-о-конечного множества. Тогда функции t*-^* f(t, t') ф/(f)
Г* v
и t'*-> I f(t9 t')d\k{t) измеримы относительно мер [i и \i' соот-
соотнно и
J p(f, n
ветственно и
B) Если функция f положительна и измерима относительно
меры я = [1®[х/, то функции **—>] f(t> t')d\i'(f) и ?\-*>
ъ—> f(t, t')d\i{t) измеримы относительно мер \л и \х' соответ-
соответственно и
j ff(t, t'
Доказательство. Можно считать, что / = lim/n, где
(fn) — возрастающая последовательность я-интегрируемых функ-
функций. Утверждение A) следует из теоремы 4.17.4 и из повторного
использования монотонной сходимости. Утверждение B) непо-
непосредственно вытекает из A), если его применить к функции
/Сэ ОХ/с(ОХ/с'(^)» гДе К и К! — производные компактные мно-
множества в Т и Т' соответственно. |
4.17.8. Теорема (Тонелли). Пусть f — измеримая относи-
относительно меры я = |1 ® ji7 функция, равная нулю вне некоторого
342 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
л-о-конечного множества. Если каждый из повторных верхних
интегралов
j*dii(t)f\f(t, П№'(П JV(Oj*l/('. t')\dvL(t)
конечен, то функция f п-интегрируема и к ней применима тео-
теорема 4.17.4.
Доказательство. Применить следствие 4.17.4 к функ-
функции |/|. ■
4.17.9. Измеримость относительно меры-произведения. Во
многих примерах теорема Тонелли используется для обоснова-
обоснования применимости теоремы Лебега — Фубини. Поэтому важно
иметь признаки измеримости относительно меры \i 0 \i'.
4.17.10. Предложение. Если g и g' — положительные функции
на Т и Т' соответственно, то имеет место равенство
J
D-17.8)
за исключением, быть может, случая, когда один из сомножите-
сомножителей в правой части равен 0, а другой оо.
Доказательство. Заметим, что в соответствии с согла-
соглашением 0»+оо = 0 (§ 4.5) формула Я*(а/) =а«Я*(/) имеет место
для любой положительной меры Я, любой функции /, удовле-
удовлетворяющей неравенствам О^/^Н-оо, и любого числа а, удо-
удовлетворяющего неравенствам 0-^а-^оо. [Если а= + оо, то
Я* (а/) равно 0 или Н-оо, в зависимости от того, является ли
функция / Я-пренебрежимой или нет; то же относится и к
<*V(f)-]
Обозначим через / двойной верхний интеграл в формуле
D.17.8). Из п. 4.17.3 следует, что
Согласно подготовительным замечаниям,
Аналогично
J * dp (/) } * g (t) g' (П dv! (f) = ц'* (g') ц* (g).
Таким образом, достаточно лишь доказать, -что
K\i4g)-V'4g'). D.17.80
Правую часть этого неравенства можно считать конечной.
Остается поэтому рассмотреть случай, когда оба множителя ко-
4.17. Произведения мер и теорема Фубини 343
нечны (все остальные варианты исключаются в силу наших
предположений). В этом случае правая часть формулы A4.17.8Г)
является нижней гранью произведений \х* (ф)^/*(ф/), где ф и
ф'— полунепрерывные снизу функции на Т и Т', мажорирующие
функции g и g' соответственно. Функция (t, О1—^ф@ф'(П по"
лунепрерывна снизу на произведении ТхТ' и мажорирует про-
произведение g{t)g'(t'). Достаточно теперь воспользоваться рас-
рассуждениями п. 4.17.2 и очевидным неравенством /-^л;*(ф®ф/)- I
4.17.11. Следствие. Пусть АаТ и А'аТ'. Произведение
АхА' пренебрежимо относительно меры \х ® \х', если либо
л*(А)=0 и >х/*(Л/)< + оо> либо м*(Л)< + оо и \i'*(A')=0.
4.17.12. Предложение. Если g и g/ — положительные функции
на Т и V соответственно, то
J J * g @ g' (П d\x (t) dp' (П - Д* (g) Д" (g'). D.17.9)
Доказательство. Пусть /С и /С' — произвольные компакт-
компактные множества в Г и Г соответственно. В силу предложения
4.17 10 имеет место равенство
J J * S V) %K d) g' (П %к. (П dv. (t) dW (П = ц* (g%K) и'* (g%,), D.17.9')
если только один из множителей в правой части не равен 0, а
другой +оо. Но если, скажем, M*(g"X/<r) =0, то интегрируемая
функция в двойном верхнем интеграле равна нулю вне множе-
множества, пренебрежимого относительно меры ji ® \х' (следствие
4.17.11), и потому равенство D.17.9') справедливо и в этом слу-у
чае. Таким образом, D.17.9') выполняется всегда. Утверждае-
Утверждаемый результат следует из определения существенного верхнего
интеграла D.14.1) и из того факта, что множества вида КхК'
образуют базу компактных подмножеств в ТхТ'. I
4.17.13. Предложение. Если функция g (соотв. g') измерима
относительно \х (соотв. |и/), а и — непрерывная на R2 функция,
то функция
u(g,g'Y. (U t')*-*u(g(t), g'(t'))
измерима относительно меры \х ® \х'.
Доказательство. Пусть К и /С' —компактные множе-
множества в Г и Г' соответственно. В силу критерия Лузина (след-
(следствие, 4.8.5) множество /С (соотв. К') можно так разбить на
компактные множества Кп (соотв. Кп) (/z=l, 2, ...) и множе-
множество N (соотв. N')9 пренебрежимое относительно меры \х
(соотв. \i)9 что сужения g\Kn (соотв. g'\Kn) непрерывны. Рас-
Рассмотрим множества Нт> п== КтХ Кп и обозначим через М
объединение множеств N X Кп> Кп X N' и Л^ X N' {п = 1, 2, ...),
344 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Множество М пренебрежимо относительно меры \i ® \i' (след-
(следствие 4.7.11). Множества Нтп (т, п=1, 2, ...) и М образуют
разбиение множества К X /С'. Поскольку сужения u{g, g')\Hmny
очевидно, непрерывны, то функция u(g, g') измерима относи-
относительно меры'|х®ц/, что и требовалось доказать. 1
4.17.14. Следствие. Если множества АаТ и A'zzJ' измеримы
(соотв. интегрируемы) относительно \х и \х', то множество АхА'
измеримо (соотв. интегрируемо) относительно \i<8>ii' и
fc A'). D.17.10)
Доказательство. Из предложения 4.17.13 следует изме-
измеримость множества АхА' относительно меры jli ® \х' в любом
из этих двух случаев. Если наши множества интегрируемы, то
формула D.17.10) вытекает из предложения 4.17.10, что показы-
показывает, между прочим, интегрируемость множества АхА/ относи-
относительно \i ® \xf. Для завершения доказательства остается вос-
воспользоваться предложением 4.17.12 и тем фактом, что мера из-
измеримого множества равна существенному верхнему интегралу
его характеристической функции (§ 4.7 и 4.14). 1
4.17.15. Следствие. Пусть А а Т и А' а Т'\ если А (соотв. А')
локально пренебрежимо относительно \х (соотв. ju/), то множе-
множество АхТ' (соотв. ТхА') локально пренебрежимо относитель-
относительно |Ы ® \jJ.
Доказательство. Это очевидно ввиду следствия 4.17.14
и в силу соглашения 0-+сх> = 0. |
4.18. Локально компактные группы и меры Хаара
В этом параграфе Т будет топологической группой (п. 0.3.19).
Это означает, что Т — группа в алгебраическом смысле и, кроме
того, топологическое пространство, причем эти две структуры
связаны так, что отображение (ttt')*-^>t-ltf произведения ТхТ
в Т непрерывно. Будем предполагать также, что пространство Т
отделимо. К топологическим группам относятся все конечные
группы; всякая группа может быть наделена дискретной тополо-
топологией, относительно которой она будет отделимой локально ком-
компактной топологической группой. Всякое отделимое топологиче-
топологическое векторное пространство является, конечно, топологической
группой, если не принимать во внимание умножение на скаля-
скаляры; эта топологическая группа коммутативна (абелева); она
локально компактна тогда и только тогда, когда рассматривае-
рассматриваемое пространство конечномерно. Так обстоит дело, например, с
пространствами Rn и О. Целые разделы классического анализа
4.18 Локально компактные группы и меры Хаара 345
основаны на том, что Rn — локально компактная группа. В дей-
действительности многие теории (например, значительная часть
гармонического анализа) зависят, за м'алым исключением, лишь
от этого свойства.
Множество комплексных чисел, по модулю равных 1, обра-
образует компактную коммутативную топологическую группу (с
умножением в качестве групповой операции и с обычной топо-
топологией), которая изоморфна факторгруппе R/2n (где групповая
операция — это сложение по модулю 2л, а топология — фактор-
топология обычной топологии в R). Разделы классического ана-
анализа, посвященные изучению функций одной или многих веще-
вещественных переменных, имеющих один или несколько периодов,
по существу сводятся к исследованию функций на R/2n или на
(R/2n)n. В частности, многие из основных результатов о рядах
Фурье (простых или кратных) зависят только от природы груп-
группы R/2jt (или ее степеней) как коммутативной топологической
группы. Подробное изложение тех свойств топологических групп,
которые раньше других привлекли внимание математиков, дано
Понтрягиным [1]. Более современный1) обзор основных по-
понятий теории топологических групп содержится в трактате Бур-
баки [2, гл. III]. Теория интегрирования на группе и связанные
с ней вопросы систематически изложены в книге Хьюитта и
Росса [1, § 15—20]2).
В нашем изучении топологических групп мы строго ограни-
ограничиваемся вопросами, относящимися к существованию инвари-
инвариантной меры (или, что то же, инвариантного интегрирования)
на локально компактной группе. Вклад функционального ана-
анализа в теорию локально компактных групп стал возможным бла-
благодаря исследованию различных пространств функций и мер,
более или менее тесно связанных с этой инвариантной мерой.
Во второй половине XIX в. конечные группы изучались
алгебраическими методами. Инвариантная мера на такой конеч-
конечной группе Т — это просто конечная сумма 2 £t (где 8* — мера
t<= т
Дирака, сосредоточенная в точке t) или положительные крат-
кратные этой суммы. Естественно, что анализ на конечной группе
весьма тривиален. Исторически следующий шаг состоял в срав-
сравнительно явном построении инвариантного интегрирования на
компактных группах Ли, которое в 1927 г. было осуществлено
Петером и Г. Вейлем. Этот случай заслуживает особого внима-
внимания, ибо группы Ли, естественно возникающие как группа пре-
преобразований, были первыми отличными от группы Rn и ее фак-
факторгрупп топологическими группами, которые обратили на себя
1) Но значительно менее глубокий. — Прим. ред.
2) См. также А. В е й л ь [1], Л ю м и с [1]. — Прим. ред.
346 Гл. 4. Топологич. сопряженные к некоторым пространствам; меры Радона
внимание. Построение инвариантного интеграла в этих случаях
облегчается благодаря существованию локальных координатных
систем. В 1934 г. фон Нейман установил существование инва-
инвариантного интегрирования на произвольных компактных группах
(в действительности даже существование среднего значения почти
периодических функций на произвольных группах). В 1933 г.
Хаар дал конструкцию инвариантной меры на любой локально
компактной группе, удовлетворяющей второй аксиоме счетности.
К последним, конечно, относится и группа Rn, инвариантная
мера на которой давно известна — это мера Лебега. К настоя-
настоящему времени метод Хаара видоизменен таким образом, что
стало возможным полностью отказаться от ограничений, связан-
связанных со счетностью. Установлено, что имеются по существу един-
единственные лево- (право-) инвариантные меры на любой отделимой
локально компактной топологической группе. Краткое, но насы-
насыщенное изложение многих затронутых здесь вопросов содержит-
содержится в книге А. В ей л я [1]. Некоторые недавние исследования
в этой области весьма подробно изложены в книгах Люмиса
[1], Наймарка [1], Хьюитта и Росса [1]. В последних трех
книгах широко используется функционально аналитическая тех-
техника. (См. также Бур баки [9, гл. VII, VIII].)
4.18.1. Определение мер Хаара. Вплоть до конца § 4,19 Т —
отделимая локально компактная топологическая группа. Среди
ненулевых положительных мер Радона на Т наиболее полезными
являются меры, в следующем смысле инвариантные относитель-
относительно сдвигов (левых или правых). Каждой функции f на Г и ка-
каждому элементу а группы Т поставим в соответствие новую
функцию, которую будем называть левым сдвигом f на элемент а
и обозначать через LJ или J. Эта функция определяется соот-
соотношением LJ(t)=af(t)—f(at). Правый сдвиг Raf или fa опреде-
определяется аналогично с заменой at на ia. Эти сдвиги, конечно, сов-
совпадают, если группа Т коммутативна. Под левоинвариантной
(инвариантной относительно левых сдвигов) мерой, или левой
мерой Хаара на Г, понимают ненулевую положительную меру
Радона \х на Г, для которой
li(Lax) = ii(x) D.18.1)
при всех х^Ж(Т) и а^Т. Правые меры Хаара определяются
аналогично с заменой Lax на Rax.
Сначала освободимся от необходимости отдельно рассматри-
рассматривать левую и правую меры Хаара. Определим отражение f функ-
функции f на Т равенством f{t)=f(t~l). Тогда, как легко видеть,
если [х — левая мера Хаара, то v=jli :х^-^\х(х) —правая мера
Хаара и обратно. Это позволяет рассматривать только левые
меры Хаара.
4.18. Локально компактные группы и меры Хаара 347
В терминах функции множества, определенной мерой \х, фор-
формула D.18.1) влечет за собой соотношения
для произвольного множества ЛсГ и произвольного элемента
а^Т. Обратно, формула D.18.1) вытекает из условия, что
\х{аА) = ju(Л) для всех компактных (или для всех открытых)
множеств Л с: Г. В частности, если jli — левая мера Хаара, а
множество N пренебрежимо относительно ji, то и множество aN
пренебрежимо относительно \х. Если функция /измерима относи-
относительно \х, то такой же будет и функция LJ. Для всякой положи-
положительной функции / имеют место равенства
V(Lj) = li*(f) и £*(LJ) = *•(/).
Функция / тогда и только тогда интегрируема (соотв. сущест-
существенно интегрируема) относительно \i, если тем же свойством
обладает Laf; в этом случае значения интегралов от указанных
функций одинаковы. Таким образом, инвариантность в форме
D.18.1) влечет за собой инвариантность в достаточно широком
смысле.
4.18.2. Существование и единственность мер Хаара. Основ-
Основными фактами теории мер Хаара являются следующие.
► A) Существует левая мера Хаара на Т.
► B) Если [I и \хг — две левые меры Хаара на Г, то ju/=
= C'\i, где с — некоторое число >0.
Мы не будем доказывать утверждений A) и B), отсылая чита-
читателя к книге Вейля (цитировавшейся выше) и к цитированным
выше книгам Халмоша [1], Най марка [1], Хьюитта и
Росса [1, §15, 16].
Аналогичные утверждения имеют место и для правых мер
Хаара.
Вообще говоря, нет никакого способа избежать неопределен-
неопределенности, возникающей из-за коэффициента пропорциональности
в B). Если, однако, Т — дискретная группа, то левую меру
Хаара можно нормировать условием, что она имеет в каждой
точке множества Т единичную массу. Если пространство Т ком-
компактно, то меру \х можно нормировать условием \i(T) = \. (Если
группа Т конечна и дискретна, то эти два выбора несовместны,
за исключением случая, когда группа Т сводится к одному ней-
нейтральному (единичному) элементу.)
Если r = R/2n, то нормирующее условие \х(Т)^=1 приводит к
интегралу Лебега (или Римана)
2Я
348 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
в котором х — функция вещественного переменного с периодом
2я. Интервал интегрирования @, 2я) может быть, конечно, за-
заменен любым другим интервалом длины 2я. В п. 4.18.6 и 4.18.7
мы приведем два менее тривиальных примера мер Хаара.
4.18.3. Основные свойства меры Хаара. Мы воспользуемся
утверждениями A) и B) п. 4.18.2 для того, чтобы вывести сле-
следующие важные свойства C) — F).
► C) Существует положительная непрерывная функция А
на Т, называемая модулярной функцией на Г, такая, что
D.18.2)
и такая, что если \х — левая мера Хаара на 7\ то
[i (Rax) = А (а) • (х (х),
т. е.
J x(ta)dii(t)^A(a)\ x(t)dix(t) D.18.3)
для всех функций х
► D) Если А — модулярная функция на Т и р — левая
мера Хаара на Г, то \х = А • \х, т. е.
J x(rl)dix(t)= j x(t)A(t)dii(t) D.18.4)
для всех х
E) Пусть А — модулярная функция на Г, \л и р — левая
и правая меры Хаара на Т соответственно. Тогда суще-
существует такое число с > 0, что p = cA'ji, т. е.
J = cj x(t)A(t)dix(t) D.18.5)
для всех функций х^.оЖ{Т). Кроме того, р(Ьах)==
= A(a)~1p(*), т. е-
J x(at)dp(t) = A(ayl | x(t)dp(t) D.18.6)
для всех функций х^о^(Т).
► F) Пусть \х — левая мера Хаара на Т. Тогда jn(£/)>0
для всякого непустого открытого множества U аТ и
\х(Т)< н-оо тогда и только тогда, когда группа Т ком-
компактна.
Доказательство. C) Пусть jli — левая мера Хаара на Г,
тогда отображение X: x*->ix(Rax) является ненулевой положи-
положительной мерой на Т. Так как RaLbX=LbRax, то левоинвариант-
ность меры \х влечет за собой левоинвариантность меры К.
4.18. Локально компактные группы и меры Хаара 349
В силу B) существует такое число Д(а)>0, что <к = А(а) -\х. Из
B) следует также, что любым двум левым мерам Хаара jli и yf
соответствует одна и та же функция А независимо от исходной
меры. Остальные свойства функции А очевидны.
D) Если [х-левая мера Хаара на Г, то v: x*-> \х (Ах) — не-
ненулевая положительная мера Радона на Т. Так как {Lax)w =
= Ra-ix, то формула D.18.2) приводит к соотношениям
= А (а) чх (/?,-, (Ах)) = А (а). А (а). v (А*),
причем последнее равенство вытекает из C). Таким образом,
мера v левоинварианта, и потому в силу B) существует такое
число с > 0, что v = c*\x. Заменяя х на х, получаем \х{Ах) =
— c\i(x). Выбирая функцию х с носителем, содержащимся в
сколь угодно малой окрестности элемента е, мы видим, что число
с должно равняться Д(е) = 1. Свойство D) доказано.
E) Заметим, что мера р левоинвариантна, поэтому из B)
вытекает, что она равна мере с*\л для некоторого числа с>0.
Из D) следует, что р = с*\л = сА' jut. Но тогда
р (Lax) = с (А • |i) (Lax) = с • \i (A • Lax) = сД (а). |i (La (Ax)) =
что и требовалось доказать.
, F) Достаточно рассмотреть случай, когда \х — левая мера
Хаара, так как «правый» случай совершенно аналогичен. Если
U — такое непустое открытое множество, что \x(U)=0, то ка-
каждое компактное множество К в Т может быть покрыто конеч-
конечным числом левых сдвигов aU, откуда в силу левой инвариант-
инвариантности меры \х следует, что \i(K)=0 для всех компактных мно-
множеств /С, т. е. jj, = O, что противоречит нашему предположению.
Если Т — компактное пространство, то |ыG')< + оо для
всякой положительной меры Радона |ы на Т. Обратно, если Т не
компактно и V — некоторая компактная окрестность элемента е,
то можно индуктивно определить элементы ап (п == 1,2,...) в Т
так, чтобы элемент ап не принадлежал объединению множеств
ctiV (l^Ci^Cn). Если U — окрестность элемента е, такая, что
U2а V, то множества anU не пересекаются. Их общая мера
строго положительна, поэтому \х(Т) = Н-оо. |
Замечания. С помощью предыдущих результатов можно
показать, что понятия локальной пренебрежимости (соотв. пре-
пренебрежимости, а-конечности) совпадают для всех мер Хаара
(и левых и правых). Что касается локальной пренебрежимости,
то это следует непосредственно из B) и E). Далее, так как А —
350 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
строго положительная и непрерывная функция, то из D.18.5)
вытекает, что
Р*(ф) = *.11*(Дф) D.18.7)
для всякой положительной полунепрерывной снизу функции ф
оо
на Т. Если множество N р-пренебрежимо, то МаМ= П Un,
n=l
где множества Un открыты, убывают и р*(£/Л)->0. Тогда функ-
функции %ц • Д ja-интегрируемы, и в силу монотонной сходимости
IX* (XAfД) = lim ix* fab) = Hm с~У (Un) = 0.
Таким образом, функция Д должна быть равна нулю ji-почти
всюду на М. Поскольку функция А нигде в нуль не обращается,
то \х*(М)=0 и, следовательно, \i*(N)=0. Так как D.18.7) экви-
эквивалентно соотношению
^(ф) = ^1р*(Д-1Ф), D.18.70
то [i*(N)=0 влечет p*(Af)=O. Таким образом, понятия пренебре-
жимости эквивалентны для всех мер Хаара.
Далее, если U — открытое множество и р*(£/)<+оо, то из
D.18.7) следует, что функция %VA |ы-интегрируема и потому рав-
равна нулю вне р-а-конечного множества. Так как функция Д ни-
нигде в нуль не обращается, то U должно быть |ы-ог-конечным. Та-
Таким образом, всякое p-or-конечное множество содержится в счет-
счетном объединении открытых множеств конечной р-меры и потому
является также и jLi-a-конечным. Обратное утверждение дока-
доказывается аналогично.
Так как локальная пренебрежимость означает одно и то же
для всех мер Хаара, то то же самое можно сказать об измери-
измеримости.
Интегральные соотношения D.18.3) — D.18.6) можно, конеч-
конечно, распространить на случаи, когда вместо х^Ж(Т) рассма-
рассматриваются более общие функции, а интегралы заменяются на
верхние или существенные верхние. В частности, эти соотноше-
соотношения могут быть сформулированы в терминах мер множеств. Рас-
Рассмотрение этих вопросов предоставляется читателю.
4.18.4. Унимодулярные группы. Группа Т называется унимо-
дулярной, если она допускает биинвариантную ненулевую поло-
положительную меру Радона, т. е. меру, которая является одновре-
одновременно левой и правой мерой Хаара. Это возможно тогда и толь-
только тогда, когда модулярная функция Д удовлетворяет условию
Д=1. Таким образом, всякая локально компактная коммутатив-
4.18 Локально компактные группы и меры Хаара 351
пая группа унимодулярна. Кроме того, полагая х=\ в формуле
D.18.3), видим, что всякая компактная группа унимодулярна.
Уравнение Д(а) = 1 во всех случаях определяет в Т замкну-
замкнутую инвариантную подгруппу G, а функция Л — алгебраический
изоморфизм группы T/G на подгруппу мультипликативной груп-
группы строго положительных вещественных чисел. Следовательно,
группа TIG коммутативна. Если Т — полупростая группа Ли, то
G = T, так что Т унимодулярна.
4.18.5. Относительно инвариантные меры. Комплексная мера
Радона X на Т называется относительно левоинвариачтной, если
существует такая комплексная функция D на Г, что
X(Lax) = D(a)-X(x) D.18.8)
для всех x^o/f(T). Относительно правоинвариантная мера
определяется аналогично равенством
где D'— комплексная функция на Т. Изучение относительно пра-
воинвариантных мер можно свести к изучению относительно
левоинвариантных мер, так как если р — относительно правоин-
вариантная мера, то мера Х = р относительно левоинвариантна,
поскольку формула D.18.8) справедлива при D(a) = D'(a~l). Это
следует из тождества (Lax)v = Ra-\x.
Пусть % — относительно левоинвариантная мера. Оставляя в
стороне тривиальный случай Х = 0, получаем из формулы D.18.8),
что функция D непрерывна, D(e) = \ и D(ah) = D(a)D(Ь). Сле-
Следовательно, мера a = D*X ненулевая, и
a (Lax) = %{D- Lax) = X[d(a)~l . La(Dx)] =
= D(a) • X(La(Dx)) = D{a)~l -D{a)X(Dx) = ax.
Таким образом, а — левоинвариантная мера. То же самое
справедливо для вещественной и мнимой частей меры а, а так-
также для положительной и отрицательной частей каждой из них.
Из B) следует, что а = с*\х, где |ы — произвольная левая мера
Хаара, а с — комплексное число, т. е. Х= (cD~l) *\х. Обратно,
всякая мера X такого вида, очевидно, левоинвариантна.
4.18.6. Пример. Рассмотрим группу Г, элементы которой —
упорядоченные пары вещественных чисел t=(a, 6), афО, с зако-
законом композиции
tt' = (aa', ab' + b),
где t = (a, b), t' = (a\ У). Группа Т топологизирустся как под-
подпространство в R2. Легко видеть, что группа Т локально ком-
компактна, но не компактна и не коммутативна. Элементы группы Т
352 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
можно рассматривать как взаимно однозначные отображения R
в себя. При этом элемент t=(a, b) интерпретируется как отобра-
отображение u^—^au + b. Закон композиции в Т согласуется с компози-
композицией соответствующих отображений.
Для определения левой меры Хаара на Т допустим, что вся-
всякая такая мера jli локально абсолютно непрерывна относительно
сужения на группу Т (рассматриваемую как подмножество в R2)
меры Лебега на R2, т. е. что существует такая функция F на R2,
что
\i{x)= J J x(at b)F(a, b)dadb
для всех х^Ж{Т). Подсчитаем функцию F, пользуясь левоин-
вариантностью меры jli.
Левоинвариантность меры \х означает, что соотношение
х (аоа, aob + b0) F (a, b)dadb= J J x (a, b) F (а, Ь) da db
справедливо для всех хЕбТ(Г) и всех элементов (а0, &0)е=Г.
Замена переменных Ь' = аф + Ь^ а'= аоа в левой части равен-
равенства приводит его к виду
J jx{a\ b')F(a^a't а (У - bo))a^da'db\
Для определения функции F получаем равенство
которое выполняется для почти всех (а,Ь). Допуская, что оно
име.ет место всюду, и полагая ао = а, bo = b, получаем
F{a, Ь) = ^г^- = const .a~2.
Можно проверить, что всякая функция F, определяемая этой
формулой, обеспечивает левоинвариантность -меры jli. Из свой-
свойства B) п. 4.18.2 следует, что
\i (х) = const • ^ х(а, b) a~2 da db,
где постоянная строго положительна.
Подсчитав левую меру Хаара на Г, мы можем использовать
формулу D.18.3) для определения модулярной функции Д. По-
Получаем А(а, Ь) = \а\. С помощью формулы D.18.5) находится
выражение для правой меры Хаара р:
р(*) = const J [ x(a, b)\a f1 dadb.
4.19. Групповые алгебры и свертка 353
4.18.7. Пример. Пусть Т — группа вещественных треугольных
матриц вида
где аФО и Ь — вещественные числа. Закон композиции— умно-
умножение матриц. Снова можно считать Т подмножеством в R2 с
индуцированной топологией. Получаем локально компактную
группу. Для определения левой меры Хаара, модулярной функ-
функции и правой меры Хаара можно воспользоваться методом, при-
примененным в предыдущем примере. Получаем, что левые меры
Хаара имеют вид
\х (х) = const Г Г х(а, b)a~2dadb,
модулярная функция равна
А (а, &) = а2,
так что для правых мер Хаара имеем
р (х) = const J J х (а, Ь) da db,
где функции на Т представлены как функции точки (a, b)^R2.
Другие примеры можно найти у Хьюитта и Росса
[1, A5.17)].
4.19. Групповые алгебры и свертка
При изучении конечных групп Т полезно рассматривать так
называемые групповые алгебры или групповые кольца. Под
групповой алгеброй понимают алгебру А над полем комплекс-
комплексных (или вещественных) чисел и такое отображение 6 группы Т
в А, что A) Q(tt')=Q(t)B(t') для произвольных элементов t и
V группы Г, B) О (Г) порождает Л и C) элементы 6@ линейно
независимы в А. Эти условия обеспечивают взаимную однознач-
однозначность отображения 6 и определяют А однозначно с точностью до
изоморфизма. Каждый элемент из А обладает единственным
представлением в виде 2 /@9@» гДе f — комплексная (или ве-
щественная) функция на Г. Если / и g — функции, соответствую-
соответствующие некоторым двум элементам из Л, то в силу A) произведе-
354 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
нию этих элементов в А соответствует функция f *g\ определяе-
определяемая равенством
Функция f *g называется сверткой функций / и g в заданном по-
порядке. Таким образом, одной из реализаций групповой алгебры
А служит алгебра комплексных (или вещественных) функций на
Т с поточечными сложением и умножением на скаляры и со*
сверткой в качестве умножения. При этом 9 — это отображение,
которое каждому <еГ ставит в соответствие функцию et, рав-
равную 1 в t и 0 на всех остальных элементах группы. Такая ал-
алгебра коммутативна тогда и только тогда, когда коммутативна
группа Т.
Другой способ реализации групповой алгебры заключается в
рассмотрении пар, каждая из которых состоит из функции f и
меры 2 /@ е/» гДе е* — мера Дирака, сосредоточенная в точ-
ке /. С точностью до положительного множителя мера \х = 2 в.
является (биинвариантной) мерой Хаара на Г, соответствующей
постоянной функции 1. Функции f соответствует мера f-[x. Если
а и р — меры, отвечающие соответственно функциям fug, то
мера, отвечающая функции f*g, обозначается через а* р.
Легко проверяется, что выражение меры а*р непосредственно
через аир имеет вид
т. е.
а*р(*) = а®р(Ж), D.19.1)
где л:--произвольный элемент изсуГ(Г) (т. е. произвольная ком-
комплексная функция на Г), а через х обозначена функция (tt')*—*-
*->x{tt') на ТхТ. В этой реализации отображение 9 перево-
переводит t в е*.
Попытаемся теперь распространить эти понятия на случай,
когда Т—некоторая отделимая локально компактная топологи-
топологическая группа. Опыт показывает, что при такой степени общно-
общности бесполезно характеризовать групповую алгебру условия-
условиями A) —C), как это делалось для конечной группы.
На практике соотношение D.19.1) используется в качестве
определения свертки для подходящего класса мер; групповые
алгебры, изучавшиеся до сих пор, представляют собой некоторые
алгебры мер со сверткой в качестве умножения.
При определении свертки мер, основанном на понятии сверт-
свертки функций, возникает, вообще говоря, некоторая неопределен-
4.19. Групповые алгебры и свертка 355~~
ность. Она появляется из-за того, что при выборе меры, отве-
отвечающей функции f, можно взять либо меру /«Я, где К — левая
мера Хаара на Г, либо меру /-р, где р — правая мера Хаара
на Т. Эта неопределенность исчезает в том и только в том слу-
случае, когда группа Т унимодулярна (например, когда Т—конеч-
Т—конечная группа); при этом, естественно, можно брать любую биин-
вариантную меру Хаара. Если группа не унимодулярна, то мы
будем пользоваться левой мерой Хаара.
Если группа Т не компактна и свертку определяют формулой
D.19Л), то следует соответствующим образом ограничить запас
мер аир, потому что функция х хотя и непрерывна, но не обла-
обладает, вообще говоря, компактным носителем. Исходя из всего
сказанного, сформулируем определение следующим образом.
4.19.1. Определение. A) Пусть а и р — положительные меры
Радона на Т. Будем говорить, что свертка а * р определена (су-
(существует), если для каждой функции хееУ(Г) функция х ин-
интегрируема относительно меры-произведения а ® р. В этом слу-
случае сверткой а*р называется положительная мера Радона на
Г, определенная формулой D.19.1).
B) Пусть а и Per- комплексные меры Радона на Г с мини-
минимальными разложениями a = ai — аг + /аз— ш*, P = Pi — Р2 +
+ *Рз— ^4- Будем говорить, что свертка а#р мер аир опре-
определена, если существует каждая из сверток ar * ps (г, s =
— 1,2,3,4). *В этом случае сверткой а*Р называется мера
4 \
2 crcs(ar*$s), где сг=1, — 1, i\ —i при г=1, 2, 3, 4. (Эта фор-
формула для определения свертки а*р — единственно возможная,
если требовать, чтобы форма а*р была билинейной.)
Определенная в A) (аир положительны) свертка а*р, оче-
очевидно, определена тогда и только тогда, когда для х^Ж+(Т)
интегрируема относительно a ® C функция х. В этом случае
функция х положительна, полунепрерывна снизу, и, следователь-
следовательно, из результатов п. 4.17.2 вытекает, что условие существования
свертки а*р можно записать в виде
f da(t) j\(tt')d$(t')= j*d$(t') j\(tt')da(t)< + оо
для х<=еТ+(Т).
Это условие можно в свою очередь сформулировать в терминах
мер аир, рассматриваемых как аддитивные функции измери-
измеримых подмножеств в Г. Для этого введем некоторые обозначения.
Для всякого подмножества Е в Т через Ё будем обозначать
подмножество произведения ТхТ, состоящее из пар (t,t')9 для
которых W е Е. Далее, по-прежнему считая, что а и, р —
356 Гл. 4. Топологич. сопряженные к некоторым пространствам; меры Радона
положительные меры Радона на Т, введем следующие три функ-
функции множества:
Очевидно, что каждая из этих функций есть возрастающая и
счетно субаддитивная функции множества.
4.19.2. Предложение. Пусть а и р— положительные меры Ра-
Радона на Т и yk (&=1, 2, 3)—определенные выше функции.
Тогда
A) y\(U) =y2{U) =ys(U) для каждого открытого множества
UcT;
B) свертка сс*р существует тогда и только тогда, когда
yi(U) =y2(U) =ys(U) < -f-oo для каждого открытого относитель-
относительно компактного множества U cz T;
C) свертка а * р существует тогда и только тогда, когда
для каждого компактного множества КаТ\ в этом случае для
всех таких множеств К имеют место равенства
уЛК)=у2(К)=уг(К);
D) свертка а * |3 существует тогда и только тогда, когда су-
существуют такие «сколь угодно большие» относительно компакт-
компактные множества А аТ, что
ini(yl(AIy2(A)iyz(A))< +oo.
(В условии D) имеется в виду, что всякое компактное мно-
множество КаТ содержится в некотором множестве Л, удовлетво-
удовлетворяющем сформулированным условиям.)
Доказательство. A) непосредственно следует из резуль-
результатов п. 4.17.2.
Для доказательства утверждения B) заметим, что каждая
функция х^Ж+{Т) удовлетворяет неравенству х ^ const %Uf где
U — открытое относительно компактное множество, и, обратно,
если U — открытое относительно компактное множество, то
Хи^Сх для некоторой функции x&lg№+{T). Остается сослаться на
критерий D.19.2).
C) Пусть К — компактное множество. Тогда Kc:Uf где
U — некоторое открытое относительно компактное множество,
так что Хз^%#. Функция %р полунепрерывна сверху и, еле*
4.19. Групповые алгебры и свертка 357
довательно, измерима относительно меры ос® р. Из A) вытекает
тогда, что функция %^ интегрируема относительно ос® р. По
теореме Фубини
Vi (К) = (а® Р)*(ЛГ) =Y2 (К) =Y3 (tf),
причем общее значение этих равенств не превосходит yi(£0 =
= (сс® р)*(#)< + сю.
Обратно, если U — относительно компактное открытое мно-
множество, то U а К, где K=U компактно. Поэтому выполнение
условия C) в силу B) влечет существование меры ос*р.
Наконец, с помощью аналогичных рассуждений можно по-
показать, что D) эквивалентно C). Предложение полностью до-
доказано. |
4.19.3. Следствие. Пусть ос, р, а', р'— положительные меры
Радона на Т. Тогда
A) Если а ^С ос' и р -< р', то из существования свертки
а' * р' следует существование свертки а * р, причем а * р <!
<а'*р'.
B) Если определены свертки а * Р и а'#р, то свертка
7)*р определена и равна а-»р + а7^р. Аналогично
а*(Р + Ю =а* р + а* р', £С/ш оба ^л^яа б правой части опре-
определены.
C) Свертка а * р существует, если одна из мер а} р имеет
компактный носитель либо если каждая из мер а, р ограничена.
В последнем случае мера а * р также ограничена и (а * Р) (Т) =
G-)р(Г)
()р
Доказательство. Все эти утверждения непосредственно
вытекают из определения 4.19.1A) и предложения 4.19.2, если
принять во внимание билинейную зависимость каждой из функ-
функций ук (А=1, 2, 3) от а и р. | ~
4.19.4. Следствие. Пусть а и р — комплексные меры Ра-
Радона на Т.
A) Свертка а*р определена тогда и только тогда, когда
определена свертка |а|*|р|, при этом
|а*р| <|а|»|р|.
B) Свертка а * р определена, если одна из мер а, р имеет
компактный носитель или если каждая из мер а, р ограничена.
Доказательство. Это непосредственно следует из опре-
определения 4.19.1B) и следствия 4.19.3. |
Рассмотрим теперь вопрос о том, останется ли определяющая
формула D.19.1) справедливой, если х будет более общей функ-
функцией.
4.19.5. Теорема. Пусть а и р — положительные меры Радона,
®р и свертка у^а^р определена.
358 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
A) Формула
D.19.3)
справедлива для всякой положительной полунепрерывной снизу
функции /, а также для всякой функции f ^> 0, которая у-изме-
рима и у-а-конечна.
B) Если функция f у-пренебрежима, то функция f п-прене-
брежима\ если функция f у-измерима, то функция f п-измерима.
C) Для всякой функции / > О выполняются неравенства
* da(t)ff (if) d$(n J^P(OjV(^)^@]<n*(f)<Y*(/).
D.19.4)
D) Для любой у-а-конечной функции f ^ О имеет место фор-
формула
Y* (/)=** (Л- D.19.5)
Доказательство. Если функция /^>0 полунепрерывна
снизу, то она является верхней огибающей тех функций х ^> О
из Ж, которые мажорируются функцией f. Функция f есть верх-
верхняя огибающая соответствующих функций х. Первая часть
утверждения (A) следует из результатов п. 4.5.1 и 4.17.2. Утвер-
Утверждение C) вытекает из A), если воспользоваться результатами
п. 4.17.3. Первая часть утверждения B) получается как частный
случай C). Что касается второй его части, то достаточно пока-
показать, что у-измеримость множества АаТ влечет я-измеримость
множества А. Пусть множество Я с: ТхТ компактно. Тогда най-
найдется такое компактное множество /С с: Г, что Н а К. Поэтому
имеют место равенства Л(]Н=ЖПКН= (АП/С) ~ П#. Множе-
Множество АПК у-интегРиРУем0'» значит, существует у-интегрируемое
множество S типа G6l), содержащее А[\К и такое, что множе-
множество 5\(ЛП/С) у-пРенебрежимо. Тогда множество 3\(АПК) ^
я-пренебрежимо. Множество S является множеством типа^ G~6
в ТхТ и потому я-измеримо. Таким образом, (ЛП/С)" я-изме-
римо, и то же справедливо для множества ЛТШ= (АПК) " Г\Н.
Итак, утверждение B) доказано.
Перейдем к утверждению D). В силу B) и принципа моно-
монотонной сходимости достаточно рассмотреть случай, когда f об-
обращается в нуль вне открытой относительно компактной окрест-
окрестности V элемента е. В силу C) достаточно показать, что у*(/)^
^ft*(f). При этом можно считать, что I = n*(f) < + оо. Для за-
]) Множество тала G& — это множество, представимое в виде пересечения
счетного семейства открытых множеств. — Прим. перев.
4.19. Групповые алгебры и г вертка 359
данного е>0 найдем такую полунепрерывную снизу функцию
Ф>/, что я*(Ф) </ + е. Пусть функция g, определенная на Г,
равна нулю вне V-V> а во всякой точке s^V-V принимает
значение'
Тогда g (t, t') = g (tf) <<D(*, *') на VxF и неравенство £<Ф
имеет место всюду на ГхГ. На множестве V-VzdV справед-
справедливо соотношение g(s)^f(s)\ следовательно, g > f всюду на
Т. Таким образом, /^g", и / ^ g 4Ф.
Мы утверждаем, что сужение g\(V • V) полунепрерывно снизу.
Поскольку g = 0 вне V -V, то функция g сама полунепрерывна
снизу. Пусть Sq^V'V и g(so)>e; возьмем такое с'>с, что
gEo)>^. Тогда на множестве LSoO(VXV), где_/,5 =
= {(f, t'): W = s}, имеем Ф(/, t')>c\ Множество LSo(](VXV)
компактно, а функция Ф полунепрерывна снизу. Поэтому
Ф(/, *')></_ на некотором открытом множестве \^, содержащем
^50П(^ X V). Если точка s достаточно близка к s0, то множе-
множество W будет содержать LS(]{VXV), так что значение g(s)
будет не меньше с'>с для всех sgI/«F, достаточно близких
к s0. Это означает, что сужение g\(V - V) полунепрерывно снизу.
Значит, справедливо неравенство y*(f)^y*(g)9 которое в силу
первой части утверждения A) равносильно неравенству я*(§)^
^я*(Ф)^/ + 8. Полагая е->0, получаем D). |
4.19.6. Следствие, (а) Если меры а а р ограничены, то у =
= а*р определена и ограничена, формула D.19 5) имеет место
для всех функций f ^ 0, а формула D.19.3) —для всех у-изме-
римых функций f ^> 0.
(Ь) Если свертка у = а*р определена и группа у-о-конёчна,
то равенство D.19.5) выполняется для всех функций f > 0, а со-
соотношение D.19.3) справедливо для всех у-измеримых функций
f>0.
Доказательство. Оба утверждения непосредственно сле-
следуют из предложений D) и A) теоремы 4.19.5, так как в лю-
любом из этих случаев всякая функция / будет v-оконечной. I
Об ассоциативности свертки. Пусть а, р и у — три меры Ра-
Радона на Т. Из существования сверток ос*р и (а*Р)*\' «е сле-
следует существования сверток р *,у и oc*(P#y)- Действительно,
первые две свертки определены при а = 0 независимо от того, ка-
каковы меры Р и у- Сейчас мы укажем, какими должны быть меры
а, р, у, чтобы имела место ассоциативность свертки.
4.19.7. Предложение. Пусть а, р и у — комплексные меры Ра-
Радона на Т. Если существуют свертки а * р, (a*p)*Y> P*Y u
360 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
ос* (Р*у)> т0
(a*p)*Y = a*(p*Y). D.19.6)
Доказательство. Достаточно рассмотреть случай, когда
все три меры положительны. Если х ^оЖ*+(Т), то значения
() () a* (P*Y) W Равны соответственно
x(tt't")dy(t").
Совпадение этих интегралов устанавливается повторным при-
применением результатов п. 4.17.2 в силу полунепрерывности снизу
функции x(tt't") на ТхТхТ. Таким образом, равенство рассма-
рассматриваемых двух мер доказано. I
4.19.8. Следствие. Операция свертки ассоциативна на мно-
множестве ограниченных мер Радона.
Доказательство вытекает из следствия 4.19.6(а) и пред-
предложения 4.19.7. |
Для практических целей это, вероятно, наиболее важный
случай.
4.19.9. Следствие. Если по крайней мере две из трех мер ос,
р и у обладают компактными носителями, то справедлива фор-
формула D.19.6). В частности, операция свертки ассоциативна на
множестве мер с компактными носителями.
4.19.10. Замечания. Пусть М(Т) (соотв. МС(Т))—мно-
МС(Т))—множество ограниченных (соотв. обладающих компактными носи-
носителями) мер Радона на Т. Последние два следствия показы-
показывают, что оба множества М и Мс являются алгебрами, если под
произведением мер понимается их свертка. В любом из этих
двух случаев t\—>et есть такое взаимно однозначное отображение
группы Т в рассматриваемую алгебру, что е/*е// = е^/. Поэтому
каждую из этих двух алгебр можно назвать групповой алгеброй
на Т. Если группа Т компактна, то обе алгебры совпадают.
В противном случае они структурно совершенно различны (даже
как топологические векторные пространства). На данном этапе
вряд ли можно предпочесть одну из этих алгебр другой. Как мы
увидим ниже, существует еще много других алгебр, которые
естественно называть групповыми.
4.19.11. Свертка функций. До сих пор свертка рассматрива-
рассматривалась как операция, применимая исключительно к мерам. Отожде-
Отождествляя функции с локально ji-абсолютно непрерывными мерами,
где \х — левая мера Хаара, понятие свертки можно распростра-
распространить и на функции. (Можно с таким же успехом воспользоваться
4.19. Групповые алгебры и свертка 361
правой мерой Хаара и получить параллельную теорию. При этом
различие между двумя теориями будет тривиальным.)
Пусть \х — некоторая фиксированная левая мера Хаара на
Т. Рассмотрим вначале свертку а*р, где a = f'\i, причем функ-
функция f локально интегрируема относительно \х. Эта свертка опре-
определена тогда и только тогда, когда определена свертка
lal*lPl = A/1 • ц) *]р|. В силу предложения 4.19.2B) так бу-
будет тогда и только тогда, когда
для каждого открытого относительно компактного множества U.
Далее в силу предложения 4.13.2A)
Таким образом, мера a *p определена тогда и только тогда, когда
fd\№')j%u(tt')\f(t)\dii(t)< + °°,
т. е. тогда и только тогда, когда
для каждого открытого относительно компактного множества
U аТ. Допуская, что это условие выполнено и что, кроме того,
/ = 0 вне некоторого |ы-сг-конечного множества (или что функция
\f\ полунепрерывна снизу), из теоремы Тонелли и Фубини по-
получаем, что для х У£(Т)
J rfp (П J x(s)f (st'-{) Д (Г) ф (s) =
причем функция ?\—>f (st'~~l)k(t') р-интегрируема для локаль-
локально (i-почти всех значений 5. Таким образом, функция g, локально
|я-почти всюду определенная формулой
d$(s), D.19.7)
локально интегрируема относительно |ы и (f-\i) *P = g-p. Ввиду
всего этого мы рассматриваем свертку /*р как функцию g",
определенную локально почти всюду формулой D.19.7).
Приведенные выше рассуждения можно повторить в предпо-
предположении, что не мера а, а мера р имеет вид f-\x. Это пр-иводит
362 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
нас к определению свертки а * / как функции й, определенной
локально pi-почти всюду формулой
t)da(s). D.19.8)
Из существования свертки а* |3 = а * (f • \х) следует локальная
интегрируемость относительно \х функции 1г.
Можно также рассмотреть случай, когда a = /-pi и Р = £чы,
где функции f и g локально интегрируемы относительно \х и каж-
каждая из них равна 0 вне некоторого |1-а-конечного множества
(или \f\, \g\ полунепрерывны снизу). Свертка а*р опреде-
определена тогда и только тогда, когда
f\f(t)\dii(t)f%u(s)\g(rls)\dix(s)< + oo DЛ9.9)
для каждого открытого относительно компактного множества
U а Т. При этом условии функция
h (t) = J /(ts)g(s-1)dii (s)=jf (s)g(s-4)ф(s) =•
= J f(ts~1)g{s)k(s)d\x(s) D.19.10)
локально jli-почти всюду определена, локально |х-интегрируема и
a* p= (fm\i) * (g"• jlx) =h • |x. Согласно предыдущему, естественно
рассматривать функцию h как свертку f*g функций / и g (в
указанном порядке). Вероятно, наиболее важен случай, когда
функции fug ji-интегрируемы. Тогда меры а=/-|ы и р=£-|ы
ограничены, свертка а * f$ определена и ограничена, так что
функция h [х-интегрируема. Фактически в этом случае
8). D.19.11)
Таким образом, пространство *2г?1 = с55'1 (Г, |ы) (или его фактор-
пространство Ll = Ll(T, [x)) представляет собой еще одну груп-
групповую алгебру, которая оказывается обычно удобнее всех.
Другие два часто встречающиеся случая свертки f*g рас-
рассмотрены ниже.
Заметим, что пространствооУС(Т) само образует алгебру от-
относительно свертки, если определить ее формулой D.19.10). Это
еще один пример групповой алгебры.
Замечание. Если пространство Т не является а-компакт-
ным, то условие, что fug равны 0 вне (i-a-конечного множества
(или что |f|, |g| —полунепрерывные снизу функции), не может
быть совсем опущено; подробности см. у Бур баки [9, гл. VIII].
4.19.12. Пусть fezJF1 и gezJZ'p A</?<оо) (или g <=JF~
при /? = оо). Из неравенства Гёльдера следует, что внутренний
интеграл в D.19.9) представляет собой ограниченную функцию
4.19. Групповые алгебры и свертка 363
от ty поэтому выполняется неравенство D.19.9). Следовательно,
определена свертка h = f*g. Кроме того, для х ^еЗГ(Г) имеем
\jhxdix\^f\x(t)\dlx(t)f\f(s)g(s-4)\dlx(s) =
= f\f(s)\dii(s) f\g(s-4)\\x(t)\dix(t).
В силу неравенства Гёльдера внутренний интеграл мажори-
мажорируется произведением Np(g)NP' (x). Отсюда следует, что Aej?*7 и
Npif'gXNAfiNpig). D.19.12)
Если р = оо, то можно заменить N^ig) на N^ig).
4.19.13. Пусть /е^"' и g^^p (т. е. A^gG^j. Тогда
левая часть D.19.9) равна
f %u(s)dix(s) flf^llgir'sjldixit),
где внутренний интеграл в силу неравенства Гёльдера мажори-
мажорируется величиной
Np,(/) • J %и (s)p ф(s) -Np(g)<+ 00.
Таким образом, свертка h = f*g определена. Далее, применяя
неравенство Гёльдера к правой части D.19.10), получаем, что
интеграл, определяющий А, существует всюду и h(t) мажори-
мажорируется произведением Np>(f) • Np(g). В частности, /*g<ec5?O0 и
£). D.19.13)
Действительно, из D.19.10), как можно показать, следует не-
непрерывность функции / * gt а при 1<р<оо f*g стремится к
нулю на бесконечности.
4.19.14. В силу D.19.12) пересечение J?lf)J?v образует ал-
алгебру относительно свертки. Если группа Т компактна, то это
пересечение совпадает с 9??, Все эти алгебры можно назвать
групповыми.
4.19.15. Свертка и сдвиг. Правый и левый сдвиги комплекс-
комплексной меры Радона а на элемент а^Т определяются формулами
(ОД(х) = аAв-.д), (ОД(х) = а(/?в-,*)
для jcGeT(r) или, что то же самое, формулами
(ОД* (Е) = а* (аЕ)9 (/?»* (Е) = а* (Еа),
где £ — произвольное множество в Т. Например, £^ = ea-ib.
Исходя из этого определения, легко проверить, что £а(/*Н')=а
364 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
= (Laf) • М* Для всякой локально интегрируемой относительно [х
функции /. Тем не менее различие в обозначениях вызвано тем,
что Lab = LaLby тогда как Ьаъ = ЬъЬ'а. В действительности сдвиг La
является сопряженным оператором к La-i относительно двой-
двойственности между <Ж{Т) и пространством мер на Т.
Из предложения 4.19.2 вытекает, что существование свертки
а*C всегда влечет за собой ^существование свертки (La<x)*p, при
этом {l'qo) * р = La (a * р). Аналогично из существования a * р
следует существование a*(/?ap), причем a * (Яа$) = Ra (a * р).
Таким образом, левый сдвиг коммутирует со сверткой слева,
а правый сдвиг — со сверткой справа. Эти свойства почти пол-
полностью характеризуют свертку (слева или справа), рассматри-
рассматриваемую как линейное отображение различных классов мер (или
функций) в себя. (Подробности см. в п. 5.11.3.)
4.19.16. Свертка как процесс сглаживания. Вернемся к фор-
формулам D.19.7) и D.19.8), определяющим функции /*р и cc*f
соответственно. Рассмотрим для определенности первую из них.
Если f непрерывна и для каждого компактного множества KT
имеет место неравенство
(ШК, з<=Т\А<),
где функция ф (которую можно взять полунепрерывной снизу)
Р-интегрируема и множество At р-пренебрежимо, то свертка
/*р определена. Далее интеграл D.19.7) существует для всех
/ и представляет собою непрерывную функцию от /. Поэтому
если выполнены сформулированные условия, то функция /*р
непрерывна. Таким образом, свертка с функцией f слева «сгла-
«сглаживает» меру р и превращает ее в непрерывную функцию f*p.
Если группа Т совпадает с R или с R/2jt, то можно пойти
дальше. В случае когда функция / обладает п непрерывными
производными, каждая из которых удовлетворяет тому же усло-
условию ограниченности сверху, что и сама функция f, свертка f*p
также будет иметь п непрерывны^ производных, причем опера-
операция дифференцирования перестановочна со сверткой:
(/*Р)' = /'*Р, (/*Р)" = Г*Р и т. д.
Если Т — произведение конечного числа групп R или R/2ji, то
справедливы аналогичные замечания относительно частных про-
производных. Такие же утверждения верны и для a*f.
Описанный процесс сглаживания полезен и интересен по сле-
следующим причинам. Так как е*Р=Р, то естественно ожидать,
что свертка f*p в некотором смысле сходится к р, если f соот-
соответствующим образом стремится к е; эти надежды оправды-
оправдываются, а смысл сходимости зависит в некоторой степени от огра-
4.19. Групповые алгебры и свертка 365
ничений, накладываемых на f и р. Рассмотрим несколько ти-
типичных случаев.
A) Если носители мер аг- содержатся все в фиксированном
компактном множестве и Нтаг=е в широкой топологии1), то
lim (с&г*Р)=р в той же топологии. Действительно, в силу сде-
сделанных предположений lim аг(Г) = 1. Кроме того, если х^<£Г(Т)%
то
Щ • Р (*) - Щ (Т) • Р (*) = J dat (t) j {x (t?) - x (?)} dp (?) = щ (z),
где
z it) ==
Функция z непрерывна, поэтому на компактном множестве, со-
содержащем носители всех мер а*, она совпадает с некоторой
функцией из е2Г(Г). Следовательно, lim аг-(г) =еB) =z(e) =0,
откуда и вытекает наше утверждение.
B) Применим утверждение A) к мерам вида аг-=/г|л, где
функции fi непрерывны и равны нулю вне фиксированного ком-
компактного множества, причем меры а* удовлетворяют всем
остальным условиям из A). Тогда непрерывные функции
fi*$ = bi сходятся в широкой топологии к р (т. е. меры 6г- • jli
СХОДЯТСЯ В ЭТОЙ ТОПОЛОГИИ К Р).
C) Рассмотрим случай, когда щ = ft • \х и р = g • \х, где g^J?p.
Допустим (ср. с п. 4.19.12), что каждая функция ft принад-
принадлежит J24, так что g£ = f£*ge»?7p. Пусть х^<Ж{Т) и ct =
= J ft d\x. Тогда
где модуль правой части не превосходит
I \ft(s)\dix(s)$ \g(s-4)-g(t)\\x(t)\dn(t).
Применяя к внутреннему интегралу неравенство Гёльдера, по-
получаем
| J (gt-ctg)xdn\^\ \ft(s)\Np(Ls-ig-g)dli(s).Np,(x),
откуда
^P(Si-<:{S)<j\f{(s)\Np(Ls.lg-g)dlx(s)=j\fi(s)\n(s)dlx(s).
•) См. п. 2.2.8. — Прим, перев.
366 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
Функция п ограничена, а именно \n(s) | ^ 2Np(g). При рФоо
она непрерывна и п(е)=0. Если для всякой окрестности V эле-
элемента е в Т выполняются условия
limsup J|fi(s)|dn(s)< + oo, D.19.14)
lim J
1 t\
t\v
то Np(gi — g)-^0. Другими словами, если семейство (fi) удо-
удовлетворяет указанным условиям и 1-^/?<оо, то \im(fi*g) = g
в смысле J?p при g^J^v. Это утверждение не имеет места при
/? = оо, хотя по-прежнему (fi * g) -> g слабо в «2700. См. также сле-
следующий случай D).
D) Рассмотрим, наконец, случай, когда аг = /г*|ы, где функ-
функции fi такие же, как и в C), и |3 = g*|i, где функция g непре-
непрерывна. Полагая gi = fi*g, получаем
\gi(t)-clS(t)\<
Если функции fi удовлетворяют условиям D.19.14) и их носи-
носители содержатся в фиксированном компактном множестве, то
fi*g-+g равномерно на компактных множествах. Это остается
справедливым и в том случае, когда g ограничена и функции fi
удовлетворяют лишь условиям D.19.14). Если, наконец, g огра-
ограничена и равномерно непрерывна, a fi удовлетворяют условиям
D.19.14), то fi*g-+g равномерно на Т.
4.19.17. Другие групповые алгебры. Мы привели не менее
пяти примеров групповых алгебр, соответствующих заданной
группе Г, а именно: М(Т) и МС(Т) (п. 4.19.10), ^1^^1(Т, ц)
и еЯГ(Г) (п. 4.19.11), ^1{\^р (п. 4.19.14). Опишем теперь спо-
способ построения бесконечного числа групповых алгебр, которые
также представляют определенный интерес.
Каждая из этих алгебр характеризуется некоторой весовой
функцией w, которая строго положительна на Г и имеет поло-
положительную нижнюю грань на каждом компактном подмножестве
в Г. Функция w может принимать значение +оо в некоторых
или во всех точках Г. Предположим далее, что существует такое
число ft>0, что w(tt')^kw(t)w(t') для всех точек t и tr из Т.
Оказывается, что алгебра, соответствующая функции wy не из-
изменится, если умножить w на строго положительное число. По-
4 19. Групповые алгебры и свертка 367
скольку это число можно выбрать так, чтобы новая функция
удовлетворяла условию
^(«')О@И0> D.19.15)
можно считать, что функция w с самого начала удовлетворяет
условию D.19.15). Такую функцию мы будем называть поло-
положительным подхарактером на Г.
Пусть задана функция w>0, удовлетворяющая условию
D.19.15). Обозначим через M{w) множество комплексных мер
Радона а на Г, для которых
Nw{a)= fwd\a\< + oo. D.19.16)
Множество M{w}, очевидно, является комплексным вектор-
векторным пространством, на котором Nw есть полунорма.
Проверим, что M{w) есть алгебра относительно свертки.
Пусть U — некоторое открытое относительно компактное мно-
множество в Г. В силу формулы D.19.15)
Так как нижняя грань функции w положительна на U *U, то
t')^ const w(t)w(n
причем постоянная, вообще говоря, зависит от U. Если а,
Р G М{ш}, то из теоремы 4.19.5A) и предложения 4.19.2C) сле-
следует, что свертка а * |3 определена. Кроме того, если у = а*Р|
то M^aMPl, поэтому (теорема 4.19.5A))
Nw(y)=fwd\y\=fd\a\(t)f w(
f d\a\(t) f w(t)w(t')d\№')==Mw(a)Nw(?>),
во всяком случае если функция w полунепрерывна снизу. Этот
вывод остается справедливым, если Т a-компактно (теорема
4.19.5D)) или если w имеет положительную нижнюю грань на
Т (тогда меры а и C обязательно ограничены, так же как и мера
Y, так что можно применить теорему 4.19.5D)). Следовательно,
во всех этих случаях а * Р е M{w} и
U<*)AUP). D.19.17)
Интересная подалгебра в M{w} получается, если рассмотреть
только те меры а^М{хю), которые локально абсолютно не-
непрерывны относительно меры \х. ЕЗсякую такую меру можно
368 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
записать в виде а=/-|ы, где / локально интегрируема относи-
относительно (я. Тогда, если функция w полунепрерывна снизу или
если Т является а-а-конечным (что необходимо в случае, когда
функция w имеет положительную нижнюю грань), Лимеем
wd\a\= j* w\f\dtx< + oo.
Отсюда следует, что / локально почти всюду равна функции f\
для которой wf^-S^di) и
Поэтому рассматриваемую подалгебру можно отождествить с
множеством J^{w} тех измеримых относительно меры \х функ-
функций f, для которых
NwiH-N^wfX + o*. D.19.18)
Функции /, такие, что Nw(f) = O, совпадают с ji-пренебрежимыми
функциями, и ассоциированное факторпространство L1 {w}
является нормированной алгеброй. Если w = l, то J?1 [w] и
Ll{w) сводятся соответственно к =5^(|ы) и Ll(\i).
Следует заметить, что множество Е тех точек /sT, в кото-
которых w(t) = + oo, является а-пренебрежимым для каждой меры
а е M{w} и что каждая функция f e 3?l{w} равна нулю |х-почти
всюду на Е.
4.19.18.-Пример. Положим T=R и w(t)~ ekU\ где k — веще-
вещественное число, k > 0. Тогда все наши требования выполняются.
4.19.19. Пример. Опять возьмем T=R, и пусть к — веществен-
вещественное число. Положим
+ оо при /^0,
еы при t > 0,
или
f + оо при £^0,
~~ 1 еыа при t > 0,
где k>0 и 0<а<1.
Эти функции w удовлетворяют всем поставленным требова-
требованиям. Каждая мера a^M{w} имеет носителем @, +оо), и каж-
каждая функция /eJ?1!^} равна нулю почти всюду на (—оо, 0).
Можно, таким образом, считать, что J?l{w} состоит из ц-изме-
римых на @, +оо) функций /, для которых
Nw(f)=j*ekt\f(t)\dtx(t)<
4.19. Групповые алгебры и свертка 369
где \х — мера Лебега на R+. Свергка таких двух функций fug
дается формулой
t
f*g(t)=jf(t-s)g(s)dii(s)
о
По отношению к сверткам функций на (—оо, +оо) эту свертку
называют иногда усеченной сверткой. Эта операция естественно
возникает при исследовании одностороннего преобразования
оо
Лапласа \ e~ptf{t)d\i(t), определенного для вещественных /?>£
о
(или для комплексных р с Re/?<>&).
4.19.20. Гомоморфизмы групповых алгебр. Изучение спе-
специальных видов алгебр (в частности, полных нормированных
коммутативных алгебр), среди которых много групповых алгебр
над коммутативными группами, показывает, что гомоморфизмы
таких алгебр на поле комплексных чисел играют решающую
роль. Эти гомоморфизмы играют роль, аналогичную роли не-
непрерывных линейных форм на локально выпуклом пространстве.
Оправдание этого замечания увело бы нас в сторону, поэтому
рекомендуем читателю книги Наймарка [1], Л ю ми с а [1] и
Риккарта [1]. Однако мы хотим показать, каким образом это
замечание, если принять его справедливость, приводит, по край-
крайней мере в случае некоторых групповых алгебр, к естественному
обобщению ряда и интеграла Фурье и преобразования Лапласа.
Пусть Г, как и раньше, — отделимая локально компактная
группа. Характером на Т называется такая комплексная функ-
функция % на Г, что
()U № ()(t') D.19.19)
Другими словами, % — это гомоморфизм группы Т на мульти-
мультипликативную группу С* отличных от нуля комплексных чисел.
Если функция х ограничена, то из D.19.19) следует, что
\x(t) | =1 для всех t, т. е. что % — гомоморфизм группы Т в муль-
мультипликативную группу комплексных чисел с модулем 1. Мы
будем иметь дело главным образом с непрерывными характе-
характерами (см., однако, упр. 4.22).
Легко видеть, что единственными непрерывными характе-
характерами на R являются функции вида %(t)=eict, где с — комплекс-
комплексное число. Если % — ограниченная функция, то с — вещественно,
и обратно. Непрерывные характеры на R/2n получаются из ука-
указанных, если в качестве с берутся целые числа.
Пусть % — характер на Т. В обозначениях п. 4.19.17 положим
и>=1х1 и построим ассоциированные алгебры M{w} и 3?x{w}y
370 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
которые теперь будем обозначать через М{у} и 9?х{у). Если % —
ограниченная функция, то получаем просто М uJ?1. Пусть % —
непрерывный характер. Тогда отображения
D.19.20)
являются гомоморфизмами в С алгебр М{%} и 9?х{у} соот-
соответственно. Если рассматриваемая алгебра не сводится к {0},
то соответствующий гомоморфизм есть гомоморфизм на С. [Дей-
[Действительно, достаточно показать, что алгебра не отображается
в {0}. Допустим противное. Если мера или функция а принадле-
принадлежит алгебре, то ей принадлежит и f*a для всякой функции
f^G%*(T). Из наших предположений вытекает, что %fda = 0
для всех функций /; следовательно, %«а = 0. Так как функция %
непрерывна и нигде в нуль не обращается, то а=.О в противо-
противоречие с допущением, что алгебра не совпадает с {0}.]
Более общим образом, можно взять множество S непрерыв-
непрерывных характеров и образовать алгебры
M{S}= П М(%), ^{5}= П -2* ДО-
X^S %<e=S
Тогда каждый характер, принадлежащий 5, с помощью формул
D.19.20) порождает гомоморфизм алгебры M{S} или 3?1{S}
на С. Особенно важен случай, когда S состоит из всех ограничен-
ограниченных непрерывных характеров. Тогда M{S} = M и <3?х {S} = «5571.
Естественно возникает вопрос: любой ли гомоморфизм ал-
алгебры M{S\ или J?l{S} на С получается только что описанным
способом? Вообще говоря, ответ отрицательный для M{S} и
утвердительный для J?1!*!?}. В частности, для T=R известно (Ру-
дин [9, § 5.3], Хьюитт и Росс [1]), что не все гомоморфизмы
М в С получаются таким способом. Окончательного ответа до
сих пор нет. С другой стороны, известно, что каждый гомомор-
гомоморфизм алгебры-!?1 на С получается с помощью некоторого огра-
ограниченного непрерывного характера на Т при условии, что груп-
группа Т коммутативна. Если T=R, то функция/, определенная фор-
формулой D.19.20) для всех ограниченных характеров х, совпадает
с классическим преобразованием Фурье функции f. Рассмотрим
вкратце алгебру J?l{w}.
Ради простоты ограничимся случаем, когда функция w всюду
конечна и локально интегрируема относительно |ы. (Некоторые
другие случаи, включая и описанные в примере 4.19.19, также
4.19. Групповые алгебры и свертка 371
могут быть исследованы приводимым ниже методом, если внести
соответствующие изменения.) Тогда еТ(Г) czJ?l{w} и из теоремы
Хана — Банаха и теоремы 4.16.1 легко получаем, что еТ(Г)
плотно в J?l{w} (относительно полунормы Nw). Алгебра J?l{w}
также полна. Если группа Т коммутативна, то алгебра *2?x{w},
как и все перечисленные до сих пор групповые алгебры, комму-
коммутативна. Относительно этого типа алгебр известно (Риккарт
[1, следствие C.1.7)]), что каждый их гомоморфизм непреры-
непрерывен. Таким образом, если обозначить через X некоторый гомо-
гомоморфизм алгебры J?l{w} на С, то
const Л^(/).
Если функция w удовлетворяет указанным условиям, то алгебра
J?l{w} инвариантна относительно сдвигов, т. е. если f^J?l{w}y
то LJ eJ?1 {w} для любого элемента а группы Т. Так как
гомоморфизм X не равен тождественно нулю, то можно найти
такую функцию /ееТ(Г), что X(f)ФО. Рассмотрим на Т функ-
функцию х, определенную равенством
Из свойств, которыми по условию обладает w, следует непре-
непрерывная зависимость La-if от а, поэтому функция % непрерывна.
Далее если группа Т коммутативна, то, как легко проверить,
V1/* Lb-if = L{abrif*f>
откуда
%(ab) = %{a)%(b\
т. е. % — непрерывный характер на Т. Кроме того,
^(a)(a). D.19.21)
Пусть теперь g^o?F(T). Свертка
fits'1)g(s)dvi(s)
может быть сколь угодно точно аппроксимирована bJ?]{w} ко-
конечными суммами
2
таким образом, что суммы 2 xC^gfoO^M*) стремятся
к i x{s)g{s)d\i(s). В силу непрерывности гомоморфизма X
372 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
является пределом сумм 2 X(Ls-if) • g(si)[i(Aiy Деление на
O приводит к равенству
Оно справедливо для каждой функции ^ео^(Г). Обе части
равенства непрерывны на J?l{w} (так как \%(s) |< const w(s))9
поэтому оно верно по непрерывности для всякой функции
J?l{w). Полученная таким образом формула
где f^^iw}, показывает, что гомоморфизм X имеет вид
D.19.20) в силу непрерывности характера %, удовлетворяющего
условию D.19.21). Обратно (это тривиально), всякий непрерыв-
непрерывный характер, удовлетворяющий условию D.19.21), порождает
непрерывный гомоморфизм алгебры J?l{w} на С вида D.19.20).
4.19.21. Пример. Пусть Т и w — те же, что и в примере
4.19.18. Тогда %{t) = eict9 где |el'^|^const • ek^K Таким образом,
|^й и
Если & = 0, то с — вещественно и f совпадает с классическим пре-
преобразованием Фурье функции f e *S?l{\\). В § 10.3 и 10.4 мы вер-
вернемся к теории преобразований Фурье на локально компактных
коммутативных- группах.
4.19.22. Замечания. Различные алгебры со сверткой над
локально компактной группой Г служат источником многих задач,
как решенных, так и нерешенных, касающихся структуры этих
алгебр. См. Сигал [1, 3], Рейтер [1—6], Р удин [1, 2, 5—7,
9], Хьюитт [И], Хьюитт и Росс [1], М а л я в е н [1—3].
Некоторые функциональные пространства А над Т ведут
себя так, что каждая ограниченная мера \х определяет на А
эндоморфизм, действуя как свертка. Например, каждая мера \х
определяет эндоморфизм Сц> р пространства />, где C^v\ — это
класс функций [i*f (которые почти всюду равны некоторой
функции из «S5^). Каждый гомоморфизм Сц, р непрерывен и
имеет норму, не большую, чем II [i \\ (полная масса меры \[х\).
Имеется ряд нерешенных задач, связанных с эндоморфизмами
С^р (см. Дьедонне [12, 12а]).
В гл. 5 мы кратко остановимся на свертках более общих
объектов (распределений), нежели функции и меры, ограничив-
ограничившись при этом случаем r=Rm,
4.20. Критерий А. Вейля 373
Несколько иной подход к сверткам и их свойствам исполь-
используется в книге Хьюитта и Росса [1, § 19, 20].
4.20. Критерий А. Вейля компактности в пространствах S?v
над группой
В этом параграфе Т — отделимая локально компактная
группа с левой мерой Хаара [х. Напомним читателю, что если
/ — функция на Г и а — элемент группы Г, то через af обозна-
обозначается левый сдвиг tb—>f{at) функции f. Критерий А. Вейля
формулируется следующим образом.
4.20.1. Теорема. Пусть 1-</?<оо. Для относительной ком-
компактности множества F в пространстве &v = 3?v(T, \x) необхо-
необходимо и достаточно, чтобы выполнялись следующие три условия:
A) sup{Wp(/): /gFX + oo;
B) для всякого е>0 существует такое компактное множе-
множество /(с Г, что
sup/ J \f\pdixi /E
\т\к
C) для всякого е>0 существует такая окрестность V ней-
нейтрального элемента группы Г, что для любого элемента ае U
Замечания. Условие A) означает ограниченность мно-
множества F в J2*v. Условие B) показывает, что функции множества
F «равномерно убывают к нулю на бесконечности» в смысле S£v.
Наконец, условие C) означает равностепенную непрерывность
множества F в смысле J2?v. Имеется, таким образом, очевидное
сходство с теоремой Асколи.
Доказательство. Необходимость является почти очевид-
очевидным следствием предкрмпактности (т. е. полной ограниченности)
множества F. Предкомпактность означает, что для любого за-
заданного е>0 существуют такие функции fi, ..., fn в /\ что вся-
всякая функция fef удовлетворяет условию /Vp(/ — fi)*Ce при
некотором зависящем от f индексе i A-<л-<п). Каждое из
условий A) — C) справедливо для всякого одноэлементного мно-
множества в -24 а потому и для любого конечного множества
{fb ...» fn}- Но тогда эти условия выполняются и для всякого
предкомпактного множества FaJfv.
Перейдем к доказательству достаточности. Для заданного
е>0 выберем компактное множество /С, удовлетворяющее нера-
неравенству из B), и пусть F* — множество функций вида f* = f%K,
где / пробегает F. В силу, C), выбрав достаточно малую
374 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
симметричную компактную окрестность [/нейтральногоэлемента
группы Т и такую функцию г ^ 0 во^(Т), что г=0 вне выбран-
выбранной окрестности U и J гф,= 1, и положив /**==/** г, получим
^р(Г-Г)<в D.20.1)
равномерно по f ^ F. Обозначим через F** множество всех функ-
функций /**, где f пробегает множество F. Функции /** равны нулю
вне компактного множества /(•[/. Далее из неравенства Гель*
дера и условия A) следует, что
М„ (Г*) < NP (Г) Np^ (г) < const Np (Г) < consf(tfp (/) + е) < const,
где постоянная, возможно, зависит от е. Условие C) влечет рав-
равностепенную непрерывность множества функций /**. По теореме
Асколи множество Z7** относительно компактно в С (Г), где Т —
компактификация Александрова пространства Т. Следовательно,
множество F** вполне ограничено в С(Т). Отсюда и из того
факта, что функции из Т7** равны нулю вне множества К* U, вы-
вытекает, что множество Т7** и подавно вполне ограничено в S>v.
Но тогда из D.20.1) следует, что множество F* вполне ограни-
ограничено. Условие B) аналогичным образом показывает, что само
множество F вполне ограничено. Наконец, поскольку 3?v — пол-
полное пространство, то F относительно компактно. I
, Замечание. А. В е й л ь [1, стр. 53] установил этот критерий
также и для р = оо, но под L°° он понимал пространство, обозна-
обозначаемое в этой книге Со(Г). По существу в этом случае приведен-
приведенный критерий совпадает с теоремой Асколи.
Теорема 4.20.1 для случая, когда Т — вещественная прямая,
была получена М. Риссом [1]. Цудзи [1] обобщил ее для
4.21. Слабая компактность в.?1; критерий Данфорда—Петтиса
Как мы уже знаем, в случае 1<р<оо относительно слабо
компактными множествами в *2?v являются попросту его ограни-
ограниченные множества. Это следует из теорем 4.16.1 и 1.11.4B). Ана-
Аналогичное утверждение для J?1 не имеет места, за исключением
тривиального случая^?1 =J?1(|i), где мера jx обладает конечным
носителем. С другой стороны, теорема 4.20.1 дает критерий ком-
компактности в каждом из пространств-?2', 1 < р < оо. Естественно
попытаться найти аналогичный критерий слабой компактности
в J?1.Такой критерий получен Данфордом и Петтисом [1,
теорема 3.2.1].
4.21. Слабая компактность в J3*1 375
В настоящем параграфе этот критерий будет изложен в ос-
основном по Дьёдонне [3]. Читателю рекомендуется также
познакомиться с подходом Гротендика [7, гл. V, стр. 27 и
далее]. Оба эти автора оказали влияние на схематическое изло-
изложение, приведенное Бур баки [8, гл. V, стр. 323, упр. 17].
Всюду в этом параграфе Т — отделимое локально компакт-
компактное пространство, \х — фиксированная положительная мера Ра-
Радона на Т. Для краткости мы 'будем часто писать <2?1 вместо
Мы облегчим себе задачу тем, что будем постоянно обра-
обращаться к результатам общей теории двойственности, в частности
к теоремам 1.11.4B), 8.2.2 и теоремам Шмульяна и Эберлейна
(§ 8.12). Будем надеяться, что читателя не смутит это забегание
далеко вперед.
4.21.1. Предложение. Пусть (fn) — последовательность функ-
функций из 3?х.
A) Если для каждого интегрируемого множества АаТ су-
существует конечный предел lim J fnd\i, то для любого заданного
е>0 существует такое б>0, что неравенство
sup [|/„|ф<е
п а
имеет место для каждого интегрируемого множества АаТ с
B) Если для каждого ^-конечного измеримого множества
АаТ существует конечный предел lim fnd\i, то для всякого
е>0 найдется такое компактное множество КаТ, что
sup | |/«|Ф^е.
п т\к
Доказательство (а). Вначале рассмотрим случай, когда
указанные пределы равны нулю.
A) Пусть L — множество в 24, образованное всеми функ-
функциями, равными почти всюду характеристическим функциям ин-
интегрируемых подмножеств в Т. Множество L замкнуто в 3?х и,
следовательно, является полным иолуметризуемым простран-
пространством. Таким образом (теорема Бэра), L нетоще.
Покажем прежде всего, что для каждого элемента /е^1
функция g*—> fgd\x непрерывна на L. Для этого заме-
заметим, что / является в J2*1 пределом ограниченных функций /\
376 Гл. 4 Топологии, сопряженные к некоторым пространствам; меры Радона
поэтому fgd\i служит равномерным пределом на L функций
[ Г&Ф. Очевидно, что функции J f*gd\x непрерывны на L, сле-
следовательно, непрерывна и функция J fgd\i.
Рассмотрим множество
:-Jq ДЛЯ
Оно замкнуто в L, и по условию L= \J{Ln: n^N). Так как L
нетоще, найдется такое натуральное число k, что Lk содержит
непустое открытое множество в L. Это означает, что существуют
такое интегрируемое множество АоаТ к такое число б > 0, что
неравенство
имеет место для всех интегрируемых множеств ЛсГ, удовле-
удовлетворяющих неравенству I \%А — %Ло|Ф^6. С другой стороны,
увеличивая, если нужно, число k, можно считать, что
^-^- при n^k.
Если теперь интегрируемое множество ВаТ таково, что
ВаАо и |хE)<6, то
поэтому, учитывая приведенное выше неравенство, имеем
J/.ф
-5* ДЛЯ
о
Это неравенство остается и подавно справедливым, если заме-
заменить функции fn на Re/n и Im/n. Заменяя множество В мно-
множествами Bri{Refn>0}, jBf1{Refn<0} и т. д., получаем
при [х(В)^Сд и ВаА0. Аналогичный результат имеет место и
для тех интегрируемых множеств BczT\AOi для которых
)
Если множество А интегрируемо и [л(Л)^6, то можно при-
применить предыдущие неравенства по очереди к множествам
4.21. Слабая компактность в J3?1 377
А(]А0 и Л\Л0 и получить, что \ \fn\d\i^.e для /г>&. Далее,
А
уменьшая 6, можно сделать так, чтобы неравенство имело место
и для п= 1, 2,..., k— 1. Итак, утверждение A) доказано.
B) Воспользуемся методом, аналогичным примененному при
доказательстве утверждения A). Вначале заметим, что суще-
существуют такая возрастающая последовательность компактных
множеств (Кг) и такое пренебрежимое множество Е, что все
функции fn равны нулю вне объединения двух множеств 5 =
= \jKr и Е.
Заменим теперь L множеством М всех функций, равных поч-
почти всюду характеристическим функциям измеримых подмно-
подмножеств в S. Положим
Полуметрики dr (r = 1, 2,...) превращают множество М в полное
полуметризуемое пространство. (Для доказательства полноты
надо использовать теорему 4.6.7 и диагональный процесс.)
Если функция fej?1 равна нулю почти всюду на Г \ 5, то
функция gy-> \fgd\i непрерывна на М. Для заданного е>0
существует такое число г, что 1/|ф^е. Функцию
т\кг
f^i^iKr) можно тогда аппроксимировать ограниченными функ-
функциями /* и т. д.
Применяя теорему Бэра, как и в доказательстве утвержде-
утверждения A), получим, что существуют такое измеримое множество
AqCiS, такие натуральные числа s и k и такое число б > 0, что
неравенство
^■| при
имеет место, если множество AaS измеримой |%л""~%л0К'Ц
Искомое заключение следует теперь из несложных рассу-
рассуждений, аналогичных тем, которые использовались в доказа-
доказательстве A). Действительно, увеличив (если нужно) число ky
добьемся того, чтобы неравенство J fnd\x
Ac
при всех п>й. Если множество В измеримо и BczT\Ks, то
8
-тг имело место
378 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
предыдущее неравенство можно применить к множеству А =
BU (/4of)/(s), для которого
откуда
jfndix
-| при
Это неравенство остается справедливым и при замене множе-
множества А множеством Aof] Ks. Так как А—объединение непересе-
непересекающихся множеств В и Л0П/(8, то
Следовательно,
J
j при
при
Поскольку последнее неравенство имеет место для каждого из-
измеримого множества BczT\Ks, то
J
при
t\ks
что
С другой стороны, для каждого п < k существует такое гп,
j l/ttl^^8'» это вытекает из того факта, чго функции
т\кг
fn ев 9?х равны нулю вне множества S. Таким образом, утвер-
утверждение B) доказано для множества К = КГ, где r = sup(rb ...
...,rft_bs).
(b) Рассмотрим теперь случай, когда фигурирующие в фор-
формулировке предложения пределы не предполагаются равными
нулю. В этом более общем случае достаточно рассмотреть лишь
A), так как метод доказательства B) тот же, что и при доказа-
доказательстве A).
Предполагая, что условия A) выполняются, покажем пре-
прежде всего, что для всякого заданного 8 > 0 существуют такое
число 6' > 0 и такое натуральное число &, что
f«-f»№<4 D.21.1)
при
4.21. Слабая компактность в J3?x 379
Действительно, в противном случае найдутся такое число
ео>О и такие последовательности (/пД {nt) и (Д-), что mt^iy
l
Но последовательность (g;) = (/m —fn) такова, что lim J gid\i = 0
А
для каждого интегрируемого множества А. Таким образом,
последнее неравенство противоречит утверждению A). Итак,
неравенство D.21.1) установлено.
Наконец, выбрав 8'Х) и k так, чтобы выполнялось нера-
неравенство D.21.1), выберем затем 8">0 так, чтобы
А
при ц(Л)^6"и n^Ck. Из этих неравенств и из D.21.1) следует,
что
\\fn
для всех я, если только [х(Л)^й = inf F', 8"), что и требовалось
доказать. |
4.21.2. Теорема (Данфорд — Петтис). Для того чтобы
подмножество Р пространства З?1 было относительно слабо ком-
компактно, необходимо и достаточно, чтобы выполнялись следую-
следующие условия:
A) sup{J
B) для всякого е > 0 существует такое б > 0, что неравенство
sup,
имеет место, если множество AczT интегрируемо и
C) для всякого е>0 существует такое компактное множе-
множество К с: Г, что
sup/ J |
I т\к
Доказательство. Докажем сначала необходимость. Не-
Необходимость условия A) следует из георемы 8.2.2. Далее пусть
множество Р относительно слабо компактно в 271, а условие B)
не выполняется. Тогда мы можем извлечь из множества Р
такую последовательность функции (/п) и найти такую после-
380 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
довательность интегрируемых множеств {Ап), что
|i (Д.К/Г1, j\fn\d\i>a>09
Ап
где а не зависит от п. Из теоремы Шмульяна (теорема 8.21.1)
вытекает существование подпоследовательности (§k)~(fn )>
слабо сходящейся к некоторой функции f &271. Тогда последо-
последовательность (f — gk) слабо сходится к нулю и приведенные выше
неравенства противоречат предложению 4.21.1A).
Аналогично может быть доказана необходимость условия C),
только на этот раз нужно сослаться на предложение 4.21.1B).
Докажем достаточность. Условие_ A) вместе с теоремой
1.11.4B) показывают, что замыкание Р множества Р в простран-
пространстве, сопряженном к 3?°°, компактно в слабой топологии этого
сопряженного пространства. Таким образом, все сводится к до-
доказательству того, что Р есть подмножество в J2?1. (Для полной
строгости следовало бы перейти от «271 к факторпространству/,1,
которое вкладывается в сопряженное kJ?°°.) Пусть L — непре-
непрерывная линейная форма на J?00, принадлежащая слабому за-
замыканию множества Р. В силу условия B) каждому е > 0 со-
соответствует такое б > 0, что если A(Л)^б и если функция
g^J?°° такова, что |g|^%A, то J fgd\x О для всех функ-
функций feP, и потому при тех же условиях |Mg)|^>8. С другой
стороны, ясно, что сужение A,=L^G) является мерой Радона
на Т. Поэтому если g^oT{T), \g\-4-%A и м,(Л)<6, то
Несложные рассуждения приводят к выводу, что мера К локаль-
локально абсолютно непрерывна относительно \х. По теореме Лебега —
Радона — Никодима (теорема 4.15Л) существует такая локально
интегрируемая функция f0, что A,=fo*M» Используя условие A),
можно показать, что функция fo интегрируема, т. е. fo^i?1. Та-
Таким образом,
для g^Q?f(T). Пользуясь еще раз тем, что |L(g)|^e при
geJ?00, |#|<Хл и IхИ)^*» легко установить, что соотношение
L{g)*~ ) fog dp справедливо для любой функции ge^*. От-
Отсюда следует, что форма L является (т. е. порождается) эле-
элементом /о^Д что и требовалось доказать. |
4.21. Слабая компактность в J3?x 381
Замечание. Для доказательства необходимости условия
A) мы воспользовались теоремой 8.2.2. Возможно и прямое до-
доказательство со ссылкой на теорему 4.21.1. См. предложение
4.21.8.
4.21.3. Следствие. Если множество PcZeS*1 относительно слабо
компактно в J?1, то такова же его замкнутая выпуклая уравно-
уравновешенная оболочка в &х.
Доказательство очевидно, так как если Р удовлетво-
удовлетворяет условиям теоремы 4.21.2, то и указанная оболочка тоже им
удовлетворяет. |
Помимо теоремы Данфорда — Петтиса, имеются и другие
важные следствия предложения 4.21.1.
4.21.4. Теорема. Пространство J?1 слабо секвенциально полно,
т. е. каждая последовательность, являющаяся последователь-
последовательностью Коши в слабой топологии в 9?х, слабо сходится в 9?х.
Доказательство. Пусть последовательность (fn) являет-
является последовательностью Коши в слабой топологии в «271, т. е.
для каждой функции g gJ?°° существует конечный предел
lim fng d\i. Тогда (опять теорема 8.2.2) последовательность
П->оо J
(fn) ограничена. Из утверждения A) предложения 4.21.1 сле-
следует, что если L — непрерывная линейная форма на i?00, опре-
определенная равенством
lim f fngd\i
tl->oo J
для geS'00, то мера Радона к=Ь\<£Г(Т) локально абсолютно
непрерывна относительно \i. (Ср. с доказательством теоремы
Данфорда—Петтиса.) Таким образом, в 9?х найдется такая
функция f, что
Ш-jfgdvL,
пока для ^ЕеТ(Г). Но, как и в доказательстве теоремы Дан-
Данфорда— Петтиса, можно показать, что это равенство выпол-
выполняется и для gG.?M, т. е. последовательность (fn) слабо схо-
сходится к / в J?1. I
Замечание. Лишь в тривиальном случае, когда носитель
меры \х конечен, пространство 3?1(\х) слабо полно (т. е. каждая
сеть Коши (в смысле слабой топологии) в <2?х слабо сходится
В следующей теореме будет установлена связь между сходи-
мостью и слабой сходимостью в &х%
382 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
4.21.5. Теорема. Последовательность (fn) сходится к f в
тогда и только тогда, когда
(Df«-S53r*/ слаб° eJ?l>
B) fn ' n^oo+f локально по мере, т. е. для каждого компакт-
компактного множества /С с Т и каждого числа е>0 имеет место соот-
соотношение
Доказательство. Докажем сначала необходимость. Не-
Необходимость условия A) тривиальна. С другой стороны, пусть
заданы компактные множество К d T и число е > 0. Положим
Лг = ^Г1 {\fn~~f |^е}' Тогда %А ^8~~1|^"~~AJ- Поэтому |д,(Лл)^
^e" I fn"-f \d\i->0, откуда и следует B).
Переходя к достаточности, заметим, что условие A) и
предложение 4.21.1B) показывают, что для всякого е>0
можно найти такое • компактное множество /Сс:Г, что
1/п-~ЛФ^е« ^ этом случае для доказательства соотноше-
ния in"* I достаточно доказать выполнение соотношения
>0 при az->oo. Но для любого а>0 имеет место
к
неравенство
поэтому в силу условия B) и предложения 4.21.1 A)
Hmsup
Полагая а->-0, заключаем, что fn-*f в «571. |
4.21.6. Следствие. Если fn-+f слабо в «271 и fn-+f почти всю-
всюду, то fn-+f в J?1.
Доказательство. Достаточно заметить, что из сходи-
сходимости fп к f почти всюду вытекает локальная сходимость по мере
fn-**f (см, теорему 4.8.3). Щ
4.21.7. Следствие. Пусть существует такое локально прене-
брежимое множество Гос=Г, что \i({t})>0 при каждом t^T\TQ.
Последовательность (fn) сходится к] в J?1 тогда и только тогда,
4.21. Слабая компактность в J371 383
когда fn-*f в слабой топологии eJ?1. Каоюдая слабая последо-
последовательность Коши в J?1 является последовательностью Коши.
Доказательство. Слабая сходимость влечет поточечную
сходимость на множестве T\Tq. В то же время
= J \g\dli
Т\Т0
для каждой функции jgS'1. Что касается последовательностей
Коши, то применима теорема 4.21.4. |
Замечание. Следствие 4.21.7 имеет силу, в частности,
когда Т дискретно. В случае T=N (N — дискретное простран-
пространство натуральных чисел) и 9?х — 11 этот результат принадлежит
Банаху [1, стр. 119].
Перейдем к доказательству еще двух критериев слабой схо-
сходимости последовательностей в-?71. В качестве отправной точки
нам понадобятся некоторые дополнительные следствия из пред-
предложения 4.21.1.
4.21.8. Предложение. Если последовательность (fn) в
такова, что для каждого а-конечного измеримого множе-
множества AczT существует конечный предел lim J fn d\i9 то
°° A
sup I |/я|ф<+°° и последовательность (fn) слабо сходится
в JZ*.
Доказательство. Применим к последовательности (fn)
предложение 4.21.1. Пусть нам известно, что интегралы J \fn\d\i
ограничны по п. Тогда, пользуясь утверждениями A) и B)
предложения 4.21.1 и тем фактом, что каждая функция g e=J?°°
может быть сколь угодно точно аппроксимирована конечными
линейными комбинациями характеристических функций %а>
легко доказать, что для каждой такой функции g существует ко-
конечный предел lim | fng d\x> т. е. что (/п) есть слабая последо-
вательность Коши в 9?{. Но тогда (теорема 4.21.4) эта последо-
последовательность слабо сходится в.?1, что и требовалось доказать.
Все, таким образом, сводится к проверке того обстоятельства,
что последовательность (fn) ограничена в J?1.
В силу предложения 4.21.1B) для этого достаточно доказать
ограниченность по п интегралов J \fn\d\x для каждого компакт-
к
ного множества KczT. В силу утверждения A) того же пред-
предложения это сводится в свою очередь к доказательству суще-
384 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
ствования такого измеримого множества DcK, что интегралы
П/^ф ограничены по я, а множество K\D может быть по-
D
крыто конечным числом измеримых множеств сколь угодно ма-
малой меры.
Мы покажем сейчас, что в качестве D можно взять множе-
множество тех точек t из /С, для которых |i(W)>0. Множество D, оче-
очевидно, счетно. Для любого заданного 6 > 0 существует такое ко-
конечное множество FczDy что \x(D\F)^6. Ограниченность по
п интегралов Г |/я|ф следует из утверждения A) предложе*
D\F
ния 4.21.1. С другой стороны, ограниченность интегралов Г | /л|ф
F
можно проверить непосредственно. При этом (рассматривая в
отдельности вещественную и мнимую части функции fn) можно
считать функции fn вещественными. Тогда в каждой точке t ^ F
имеет место равенство
где интегралы ограничены, так как (по условию) они обладают
конечным пределом при /г->оо. Таким образом, ограниченность
интегралов |/л|Ф установлена.
D
Последний шаг состоит в том, чтобы убедиться, что множе-
множество K\D может быть разбито в конечное объединение изме-
измеримых множеств, мера каждого из которых не превосходит б.
Это следует из приводимой ниже леммы. |
Лемма. Пусть S — произвольное измеримое множество, все
точки которого имеют нулевую меру, и пусть 0^C<jn(S).
Тогда существует такое интегрируемое множество MczS, что
p
Доказательство. В силу 4.7.6A1) мы можем так вы-
выбрать компактное множество /CczS, чтобы р<ц(/(). Поэтому
можно с самого начала считать множество S компактным.
Мы построим множества Мп, такие, что S zd Мх id M2 zd ...
и Р5^М'(М/2)<Р + ~> где a = \x(S). После этого останемся только
положить М =ПМЛ. В качестве множества Мх возьмем само
п
п
множество S. Допустим, что множества Ми ..., Мп уже построе-
построены. У каждой точки £е S существует такая окрестность Ut, что
U)^Ca/(п+\). Выберем конечное число таких окрестностей
4.21. Слабая компактность в J3?1 385
так, чтобы они покрывали S. Пусть, например, это будут окрест-
окрестности Ul9...,Um. Положим Vx = Vu V2=U2\Uh V3 = U3\(Ul[)
\]U2) и т. д. Множества Vi дизъюнктны и покрывают S. Следо-
Следовательно, множества Wi=Vif\Mn образуют разбиение множе-
множества Мп, и каждое Wt имеет меру, не превосходящую /A)
С другой стороны,
Отсюда легко следует, что можно так выбрать подсемейство в
(Wi), скажем Xi = Wil9 ..., Xr=Wir, что
Теперь достаточно положить Мп+\= \J{X): 1^
4.21.9. Теорема. Пусть оМ — такая система измеримых под-
подмножеств в Г, что для каждого о-конечного измеримого множе-
множества А и каждого числа 6 > 0 найдется такое множество М е о/И,
что )\(А\М) +fi(Af\,4)^<6. Для того чтобы последовательность
(fn)czJ?1 слабо сходилась в J?1, необходимо и достаточно, что-
чтобы выполнялись следующие три условия:
A) sup f |/„|ф<+ оо;
п J
B) для всякого г > 0 существует такое б > 0, что
sup Г|/Я|ф<е
Пусть Р = {1, 2,..., м}\ для QczP положим s(Q)= 2 I1
Тогда s(P)^p. Рассмотрим все те множества Q, для которых s(Q)^fi.
Существует лишь конечное число таких множеств (действительно, множе-
множество Р имеет только конечное число различных подмножеств). Среди таких
множеств Q существует минимальное, скажем Qo- Если s (Qo) больше
а
р -I -—г-, то можно удалить из Qo один элемент / и получить множество
Qi с Qo» Для которого
s (Qi) = (Q) М^) > (р + )
что противоречит минимальности множества Qo. Таким образом, C ^ s (Qo) ^
<РН ц-г, и если Q0 = {ij: l</<^}, то (Xj) = (W^) есть подсемейство
искомого вида.
386 Гл. 4. Топологич. сопряженные к некоторым пространствам; меры Радона
для каждого измеримого о-конечного множества A q
C) для каждого множества M^lq/H
lim I fni
существует и конечен.
Доказательство. Необходимость условия A) следует из
предыдущего предложения, условия B) — из предложения
4.21.1 A), а условия C) — из определения слабой сходимости, по-
поскольку
м
Докажем достаточность. Из условий B) и C) следует суще-
существование конечного предела lim J fnd\i для каждого измери-
°° А
мого с-конечного множества А. Тогда (предложение 4.21.1 B))
каждому е>0 соответствует такое компактное множество К^Т,
что для всех п имеет место неравенство J |/Л|ф^е. Пусть
т\к
g^J^ . Чтобы доказать существование конечного предела
lim fngd\it достаточно (в силу последнего замечания) дока-
доказать существование конечного предела lim | fngd\i для каждого
п к
к
компактного множества К. Функции g можно в J?°°(K) аппрок-
аппроксимировать конечными линейными комбинациями характери-
характеристических функций интегрируемых множеств А а К. Поэтому,
используя условие A) и свойства системы о/И, получаем, что
условие C) влечет сходимость последовательности i fngd\i
к
(к конечному пределу). Слабая сходимость последователь-
последовательности (fn) следует теперь из теоремы 4.21.4. |
Замечание. Пусть, например, Т — вещественный интервал,
а (х — сужение меры Лебега на Т. В качестве М можно взять
множество конечных объединений всех непересекающихся под-
интервалов в Т (или всех таких открытых (или замкнутых) под-
интервалов в Т). Таким образом, из теоремы 4.21.9 можно полу-
получить в качестве частного случая одну теорему, принадлежащую
Банаху (см. Банах [1, стр. 117]).
Завершим параграф результатом, который нам понадобится
в § 9.4. Впервые этот результат был получен Гротендиком
[4, стр. 139, предложение 3].
4.21. Слабая компактность в ^х 387
4.21.10. Теорема. Если последовательность (fn) eJ2?°° равно-
равномерно ограничена и локально по мере сходится к элементу f
(обязательно принадлежащему J?00), то
Urn |>„ф=|/г/ф
равномерно по h на всяком относительно слабо компактном мно-
множестве PczJ?1.
Замечание. На языке теории двойственности (гл. 8, в ча-
частности п. 8.3.3) заключение теоремы выражает тот факт, что
последовательность классов fn (элементов из L°°) сходится к
классу / в смысле топологии Макки t(L°°, L1).
Доказательство сводится к непосредственному примене-
применению теоремы 4.21.2. Для заданного е>0 выберем такое ком-
компактное множество КУ что
т\к
для всех AgP, где число с выбрано так, чтобы для всех п ло-
локально почти всюду выполнялось неравенство |fn|<c. Возьмем
затем 6 > 0, такое, что для всякого интегрируемого множества А
с |д,(Л)<6 имеет место неравенство
8
6<Г
для всех йеР.
В силу предположенной локальной сходимости по мере суще-
существует такое интегрируемое множество А а К, что \х(А)<6 и
fn-*f равномерно на К\А. Положим gn = f — fn и
oo
для всех п локально почти всюду \gn\<2c. Отсюда вытекает,
что для всех
T\K A K\A
388 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Последний член в правой части стремится к нулю при п->оо
в силу равномерной сходимости. Поэтому можно найти такое
число п0, не зависящее от А е Р, что при п> п0 неравенство
<е
имеет место для всех h е Р, что и требовалось доказать. |
4.22. Слабо компактные множества ограничейных мер
С этого момента через М(Т) будет обозначаться банахово
пространство ограниченных мер Радона на Т с нормой
Пространство М(Т) изоморфно сопряженному к С0(Г) (см.
упр. 4.45). Необходимое и достаточное условие того, чтобы мно-
множество AczM(T) было относительно компактным в слабой то-
топологии g(M, Co), может быть получено из общей теории: тео-
теорема 1.11.4B) показывает, что ограниченность множества А яв-
является достаточным условием, а поскольку Cq(T)—банахово
пространство, то из следствия 6.2.3 и теоремы 7.1.1 A)(Ь) выте-
вытекает, что это условие также и необходимо.
В этом параграфе мы рассмотрим критерий относительной
компактности в ослабленной топологии а(М9 ЛГ), которая (за
исключением тривиальных случаев) строго сильнее топологии
сг(Л1, Со). Всюду в этом параграфе, когда будет идти речь о сла-
слабой сходимости или относительной слабой компактности в связи
с элементами или подмножествами пространства М9 будет
иметься в виду ослабленная топология.
Приводимые результаты о пространстве М(Т) аналогичны
теореме 4.21.2. Они принадлежат Дьёдонне [14] и Г роте н-
дику [4, стр. 146, теорема 2, и стр. 151, лемма. 5]. Об аналогич-
аналогичных работах, относящихся к пространствам конечно аддитивных
и счетно аддитивных функций множества, см. Данфорд и
Шварц [1, стр. 458 и далее]. Доказываемые ниже утверждения
относительно пространства мер Радона будут использованы
в § 9.4.
Если пространство Съа{Т) наделено так называемой «стро-
«строгой топологией», то его сопряженное также можно отождествить
с М(Т). Компактность подмножеств пространства М(Т) в сла-
слабой топологии о(М(Т), Cbd(T)) изучалась в работах Кон-
вея [1, 2].
4.22.1. Теорема. Пусть А—ограниченное множество в М(Т).
Для того чтобы А было относительно слабо компактно в М(Т),
4 22. Слабо компактные множества ограниченных мер 389
необходимо и достаточно, чтобы выполнялось одно из следую-
следующих пяти {эквивалентных) условий.
A) Пусть (fn) — равномерно ограниченная последователь-
последовательность функций, каждая из которых измерима относительно всех
мер \х^А. Если fn-*f поточечно на Т, то I /ndjx-> I fd[x равно-
равномерно относительно [аеЛ.
(Г) То же, что и A), за исключением того, что сходимость
fn-^f предполагается локальной по мере относительно каждой
меры \х е А.
B) Если последовательность (fn) слабо сходится к нулю в
Со (Г), то \ fnd\x-+0 равномерно по \х^А.
C) Если (Un) — последовательность дизъюнктных открытых
множеств из Г, то ^([/п)->0 равномерно по f,isA
D) Выполняются следующие два условия:
(a) для каждого компактного множества /(с: Г и ка-
каждого е > 0 существует такое открытое множество U zd /С,
что \\л\ {U\ К)<г для всех \х^А\
(b) для каждого е>0 существует такое компактное
множество KczT, что \\х\(Т\К)< г для всех jigA
Замечание. Критерий D) поразительно похож на крите-
критерий относительной слабой компактности в 2х (или L1), содержа-
содержащийся в теореме 4.21.2. Действительно, в одном случае дело не-
непосредственно сводится к последнему критерию. Поскольку рас-
рассуждения, используемые при этом сведении, окажутся полез-
полезными при доказательстве настоящей теоремы и в гл. 9 (в част-
частности, в теореме 9.4.4), мы остановимся на них более подробно.
Допустим, что множество AczM{T) сепарабельно (в норми-
нормированной топологии). Мы утверждаем, что существуют ограни-
ограниченная положительная мера Радона \х на Т и изометрический
изоморфизм и пространства Ll(\i) на замкнутое векторное под-
подпространство L в М(Т), содержащее А. Для доказательства вы-
выберем в А плотное счетное множество мер {\хп} и числа сп > О
так, чтобы S^mIIm-azIK + °°- Тогда !■* = S^JHtzI есть ограничен-
ограниченная положительная мера Радона на Т. Отображение и опреде-
определим равенством u{fi) = h- \i, где ft — элемент пространства Ll(\i)t
a h — любой представитель класса ft. Ясно, что каждая мера \хп
абсолютно непрерывна относительно меры \х. Поэтому, согласно
теореме 4.15.1, множество u(Ll) содержит каждую меру \хп> Да-
Далее (см. замечание 4.15.6) отображение и является изометриче-
изометрическим изоморфизмом пространства Ll(\x) в М{Т). Так как про-
пространство Ll(\i) полно, то L = u(Ll) —замкнутое векторное под*
пространство в М(Т). Но тогда, поскольку L содержит каждую
меру jin, L содержит и множество 4,
390 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Теперь если А—относительно слабо компактное множество в
М(Т), то, используя теорему Хана — Банаха, чтобы установить
совпадение топологии e(L,L') с топологией, индуцированной в
L топологией g{M, AT), можно доказать, что множество А отно-
относительно слабо компактно в L, и обратно. Так как и — изомор-
изоморфизм Ll(\x) на L, можно заключить, что множество А относи-
относительно слабо компактно в М(Т) тогда и только тогда, когда
множество и~х(А) относительно слабо компактно в Ll(\i). Дру-
Другими словами, множество А относительно слабо компактно в
М(Т) тогда и только тогда, когда его можно записать в виде
{h-\x: h(=P), где Р — относительно слабо компактное множество
в <?>)•
Если ослабить требование сепарабельности множества Л, то
получится результат, основания которого лежат значительно
глубже. Мы приведем краткое описание этого результата в §4.23.
Доказательство теоремы 4.22.1. Очевидно, A') вле-
влечет A), так как поточечная сходимость следует из локальной
равномерной сходимости по всякой мере, и из A) вытекает B).
Временно обозначим через @) утверждение «множество А отно-
относительно слабо компактно в М(Т)». Тогда достаточно показать,
что @) влечет A), B) влечет C),C) влечет D) и D) вле-
влечет @), поскольку в этом случае мы получаем циклическую
схему
(a) @)=^>A/). Если (\'\ не имеет места, то должны суще-
существовать число 8 > 0, подпоследовательность (gn) последова-
последовательности (fn) и последовательность мер (\хп) из Л, такие, что
I {gn — f)dyin >8 Для всех п. Рассмотрим меру |х= 2 2~я|цл|.
1 J п
Легко проверяется, что gn-*-f локально по мере \i. Кроме того,
в силу приведенного выше замечания можно считать, что jnn =
= hn'\i, где множество {hn} относительно слабо компактно в
&х{\\). Поэтому предыдущее неравенство противоречит теореме
4.21Л0.
(b) B)=фC). Если C) не выполняется, то будет выполняться
неравенства \ln(Uk\\ >e для некоторого е>0, для некоторой
подпоследовательности (Uk \ последовательности ([/„) и некото-
некоторой последовательности мер (\in) из А. Тогда для каждого п суще-
существует такая функция fni принадлежащая оЖ{Т)аС0{Т) с но-
носителем в Uk , что |/rt|<;i и J fnd\in >е. Так как при этом
последовательность (fn) слабо сходится к нулю в С0(Г), то мы
приходим к противоречию с условием B),
4.22. Слабо компактные множества ограниченных мер 391
(с) C)=фD). Очевидно, достаточно ограничиться рассмотре-
рассмотрением случая, когда меры Радона вещественны. Допустим, напри-
например, что нарушено условие D) (а). Покажем, что тогда можно
по индукции построить убывающую последовательность (Vn) от-
открытых окрестностей множества /С, последовательность (Un)
открытых относительно компактных множеств и последователь-
последовательность мер (|ып) из Л, такие, что
и это даст противоречие с условием C). Действительно, пусть
построение было успешным вплоть до п-то шага. Тогда по усло-
условию существует такой элемент цп+1ЕЛ, что \\in+\\ (Vn\K)>z/2,
следовательно, Vn\K содержит такое компактное множество
Кп+и что \\1п+\\ (Кп+\)> е/2, и потому существует такое откры-
тое__относительно компактное множество W, что /Cn+idl^c:
c:WaVn\K и \\in+i\(W)> г/2. Поскольку (как легко выте-
вытекает из следствия 4.15.5; см. упр. 4,42) |цп+11 (W) =sup | p,n+i(S) |
Для измеримых множеств S czW, постольку при некотором та-
таком S имеет место неравенство | \in+\ (S) \ > е/2. Мы можем вы-
выбрать открытое множество Un+\ так, чтобы SczUn+ic:W и
чтобы |in+i(^n+i) сколько угодно мало отличалось от |in+i(S).
В частности, можно сделать так, чтобы \\in+i (Un+i) I > е/2. Те-
Теперь в качестве Vn+\ достаточно взять открытую окрестность
множества /С, содержащуюся в Vn и не пересекающую множе-
множества Un+\.
Аналогичными рассуждениями доказывается» что нарушение
условия D) (Ь) несовместимо с C).
(d) D)=ф@). В силу теоремы Эберлейна 8.12.7 для того,
чтобы показать относительную слабую компактность множе-
множества Л, достаточно установить, что каждая последовательность
(|лп) мер из А имеет слабую предельную точку. Используя
прием, описанный в замечании, предшествующем настоящему
доказательству, мы можем выбрать ограниченную положитель-
положительную меру Радона \х так, чтобы \in — hn • (л, и показать, что множе-
множество {hn} относительно слабо компатно в 9?1(\\), т. е. что {hn}
удовлетворяет условиям теоремы 4.21.2.
Условие A) этой теоремы выполнено, так как множество А
ограничено, а C) эквивалентно D)(Ь). Поэтому достаточно по-
показать, что j|Art|dji->0 равномерно по п, если множество
и
U открыто и |л(£/)~^0.
Действительно, допустим противное. Тогда, заменяя, если нуж-
нужно, (hn) соответствующей подпоследовательностью, получаем,
392 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
что для некоторого е > 0 и всех п
где (Un) — последовательность открытых множеств с \i(Un)<
< 2~п. Положим Vn= иСЛ- k^n). Очевидно, Vn — открытые
множества, Vn^Vn+u |i(Vn)-^0 и
J|Aft|d|i>e. D.22.1)
Заметим, что из условия D) (а) следует (если перейти к допол-
дополнениям) существование для каждого открытого множества V и
каждого а>0 такого компактного множества KaV, что
I |^m|d|i<a для всех т. Отсюда вытекает, что можно
так подобрать множества Кп cz Vn> что
J \hm\dli<2"n-h D.22.2)
для всех m. Введем множество Кп — Г\{Кк' \Kk^,n}. В силу
формулы D.22.1)
||Л„|ф= j- j >e- J \hn\d». D.22.3)
Так как
то из формулы D.22.2) следует, что
п
J I*.!
k = l
Согласно D.22.3), имеем
е-|е=4е. D.22.4)
Итак, множества /С* убывают, и ^(/С^—^О, поэтому их пере-
пересечение К — пренебрежимое множество. Из свойства D) (а) сле-
следует существование такого открытого множества U zd /С, что
J |Л„|
4.22. Слабо компактные множества ограниченных мер 393
для всех п. Так как К пренебрежимо, то
| | AJ4i<~e D.22.5)
и
для всех п. С другой стороны, множество U содержит /С; следо-
следовательно, оно содержит некоторое /(*• Тогда из соотношения
D.22.4) вытекает неравенство
J J £i
и к*
которое противоречит D.22.4). Полученное противоречие дока-
доказывает теорему. |
Замечание. Из результата, который будет установлен зна-
значительно позже (следствие 9.2.2), и из критерия B) настоящей
теоремы вытекает, что Множество AczM(T) относительно слабо
компактно тогда и только тогда, когда оно компактно в тополо-
топологии Макки т(ЛГ, Со) (п. 8.3.3).
4.22.2. Следствие. Ограниченная последовательность (\in) в
М(Т) слабо сходится тогда и только тогда, когда последователь-
последовательность (\in{U)) сходится (к конечному пределу) для каждого
открытого множества U из Т.
Доказательство. Очевидно, достаточно показать, что
множество {\хп} относительно слабо компактно. Для этого про-
проверим выполнение условия C) предыдущей теоремы.
Каждой мере }1еМ(Г) сопоставим элемент (л* ^ Iх, положив
\i*(n) =\i(Un). Если S — некоторое множество натуральных чи-
чисел, то
по условию последнее выражение сходится к конечному пределу
(при Аг->оо). Из предложения 4.21.8 вытекает слабая сходи-
сходимость последовательности (р,*) в I1. Поэтому множество {|x*J
относительно слабо компактно в Iх. Следовательно, по теоре-
теореме 4.21.2 для всякого е > 0 найдется гакое г, что
k>r
для всех п. Тем более неравенство k>r влечет |м
==\\*>n{Uk)\ <е для всех /г, откуда вытекает C). |
Замечание. Для случая, когда пространство Т метризуемо,
этот результат получен Дьёдонне [14, предложение 8], кото-
который, кроме того, показал, что условие ограниченности можно
394 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
отбросить. Доказательство этого результата мы опускаем, так
как в нашей книге он не потребуется.
4.22.3. Теорема. Обозначим через Q векторное пространство
функций на Т, порожденных характеристическими функциями
замкнутых множеств, обладающих счетной базой окрестностей.
Ограниченное множество АаМ(Т) относительно слабо ком-
компактно в М(Т) тогда и только тогда, когда
E) множество А относительно компактно в топологии
o(M,Q).
Замечание. Что касается топологии о(М, Q), то мы имеем
в виду, что каждая функция / е Q (и вообще каждая универ-
универсально измеримая и ограниченная функция / на Т) отожде-
отождествляется с линейной формой \х^—> I f d\i на М(Т).
Доказательство. Очевидно, достаточно доказать, что E)
влечет относительную слабую компактность множества А.
Покажем сначала, что задачу можно свести к случаю, когда
Т компактно. Для этого рассмотрим компактификацию Алек-
Александрова r* = rU{oo} пространства Т. Из упр. 4.40 будет видно,
что существует изометрический изоморфизм \х>—>ii* простран-
пространства М(Т) на замкнутое векторное подпространство NczM(T*)y
содержащее те меры Я из М(Г*), для которых множество {сю}
пренебрежимо (т. е. для которых Я({оо})=0). При этом изомор-
изоморфизме топологии o(M,Q) и o(N, Q*) соответствуют друг другу,
так как множество Q* определено относительно Г* так же, как
Q относительно Т. Далее, а(Л/, Q*) — это топология в Nt индуци-
индуцированная топологией g(M*, Q*), где М* = М(Т*). Итак, доказа-
доказательство можно свести к случаю, когда Т компактно.
Так и будем считать.
Сначала рассмотрим случай, когда Т — метризуемое про-
пространство; тогда каждое замкнутое множество в Т обладает
счетной базой окрестностей. Для того чтобы показать, что А
относительно слабо компактно, достаточно (теорема Эберлейна
8.12.7) убедиться в том, что из каждой последовательности
(\in)czA можно извлечь слабо сходящуюся подпоследователь-
подпоследовательность. Рассмотрим о(М, С)-замыкание А\ множества А. Так как
множество А\ ограничено, то o(M,Q) и с(М, Q) индуцируют в
А\ одну и ту же топологию. (Под Q здесь понимается равномер-
равномерное замыкание множества Q.) Так как (упр. 4.41) Qzd С = С(Т)У
то топология о(Му Q) сильнее топологии о(М,С). Поскольку
множество А\ ограничено, оно компактно в топологии о(М,С).
Пространство С(Т) сепарабельно (так как Т компактно и метри-
зуемо), поэтому о(М,С) индуцирует в А\ метризуемую тополо-
топологию. Следовательно, существует подпоследовательность (Хп) по-
последовательности (jLin), которая о(М, С)-сходится к некоторому
4.22. Слабо компактные множества ограниченных мер 395
пределу \х в А\. С другой стороны, так как А относительно ком-
компактно в топологии а(М, (?), то последовательность (Кп) имеет
по крайней мере одну предельную точку в этой топологии. Да-
Далее если Я— така'я предельная точка, то Я должна совпадать с [л.
Действительно, Я^ЛЬ и если V — некоторая а(М, С)-замкнутая
окрестность точки Я в топологии о (М/С), то Vf]A\ является
окрестностью Я в индуцированной топологии o(M,Q)\A\. Тогда
все элементы некоторой подпоследовательности (knk) принадле-
принадлежат V; поэтому предел \i содержится в V, откуда в силу отдели-
отделимости топологии о(М,С) следует, что Я = |л. Таким образом,
ц — единственная предельная точка последовательности (Яп) в
топологии а(М, С) и тем более единственная предельная точка
последовательности (Яп) в компактном пространстве, получаю-
получающемся при наделении а(М, ^)-замыкания множества А тополо-
топологией, индуцированной топологией о(Му Q). Отсюда следует, что
последовательность (Яп) сходится в топологии о(Му Q) к \х и
тем более (Яп) сходится к \х в топологии o(M,Q). Но тогда
(следствие 4.22.2) Яп->[1 слабо, что и требовалось доказать.
Перейдем к случаю, когда пространство Т (по-прежнему
предполагаемое компактным) не метризуемо. Мы рассмотрим
этот случай, опираясь на предложение 4.22.4 и следующее заме-
замечание относительно метризуемых факторпространств простран-
пространства Т.
Пусть Г* — некоторое отделимое факторпространство про-
пространства Г, я — естественное отображение пространства Т на
Г*. Отображение я одновременно непрерывно и открыто, поэтому
пространство Т компактно. Существует ассоциированное линей-
линейное отображение Р: М(Т)-*М(Т*), при котором (л* = Я(л есть
мера на Г*, определяемая формулой
Читатель может заметить, что если S* — замкнутое множество
в Г*, то S=n~l(S*)—замкнутое множество в Т. Кроме того,
если U* пробегает базу окрестностей множества S*, то множе-
множества U=n-l(U*) пробегают базу окрестностей множества S.
В частности, если пространство Г* метризуемо и S* — замкну-
замкнутое множество в Г*, то множество S = tc~1(S*) замкнуто и имеет
счетную базу окрестностей в Г. Из формулы, определяющей
меру |я* через [л, следует, что
J %s* dV? + J (Xs* ° я) Ф = J %s dV-
Поэтому отображение Р: \х-^\х* непрерывно в топологиях
a(Af, Q) и а(ЛР\ Q*), где М* = М(Т*) и Q* — то же для Г*, что
Q для Т. Таким образом, если А удовлетворяет условию E), то
396 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
то же справедливо для образа А* = Р(А); действительно, если
пространство Г* метризуемо, то образ Л* будет (по доказан-
доказанному) относительно слабо компактен в М(Т*).
Итак, для завершения доказательства теоремы 4.22.3 доста-
достаточно убедиться в справедливости следующего предложения. |
4.22.4. Предложение. Пусть Т — отделимое компактное про-
пространство и А—ограниченное множество в М(Т). Для относи-
относительной слабой компактности множества АаМ(Т) необходимо
и достаточно, чтобы для каждого метризуемого факторпростран-
ства Т* пространства Т образ А* = Р(А) множества А был отно-
относительно слабо компактен в М(Р).
Доказательство. Так как отображение Р банахова про-
пространства М(Т) в банахово пространство М(Т*)У очевидно, не-
непрерывно, то условие необходимо.
Перейдем к достаточности. Не ограничивая общности, можно
считать, что множество А выпукло, уравновешено и замкнуто
в топологии а(М, С).
Введем вспомогательное банахово пространство F, опреде-
определенное следующим образом. На пространстве Е=С(Т) рассмо-
рассмотрим полунорму р, равную функционалу Минковского множества
А° (п. 8.1.4). Образуем факторпространство E/kevp и обозна-
обозначим через F пополнение полученного нормированного простран-
пространства Е/кет р. Естественное отображение и пространства Е в про-
пространство F непрерывно, а его сопряженное и' отображает
единичный шар пространства F' на А.
Для доказательства относительной слабой компактности мно-
множества А в М(Т) (т. е. относительной компактности в тополо-
топологии о(Е\ Е")) достаточно показать (следствие 9.3.2), что ото-
отображение и слабо компактно (§ 9.2). Для этого достаточно (тео-
(теорема Эберлейна 8.12.7) убедиться в наличии слабой предельной
точки в F у всякой последовательности (u(fn))y где (fn) —про-
—произвольная последовательность элементов единичного шара про-
пространства Е = С(Т).
Пусть Т* — факторпространство пространства Т по отноше-
отношению эквивалентности «fn{U) =fn(t2) для всех п». Пространство
7* метризуемо. Его топология — это слабейшая топология, при
которой каждая функция на Г*, полученная из fn при фактори-
факторизации, .непрерывна. Далее пространство С(Т*) может быть отож-
отождествлено с замкнутым векторным подпространством в С (Г),
состоящим из тех функций /<=С(Г), для которых f{t\)=f(t2),
если fn(ti)=fn(t2) для всех п. Наша задача сводится, таким об-
образом, к доказательству того факта, то сужение v = u\C(T*)
слабо компактно, т. е. (опять следствие 9.3.2) что отображение
vr переводит замкнутый единичный шар В пространства Ff в
o{G\ G")-относительно компактное множество, где G' = M(T*) —
4.23. Теорема Какутани и ее следствия 397
пространство, сопряженное к G = C(T*). Однако, как легко про-
проверить, указанный образ v'(В) совпадает с Л*, что и завершает
доказательство предложения. |
4.23. Теорема Какутани и ее следствия
Нигде в этой книге не используется систематически и в пол-
полную силу естественный частичный порядок ни в множестве ве-
вещественных мер Радона на отделимом локально компактном
пространстве Г, ни в множестве непрерывных вещественных
функций на Т. Фактически было потрачено много усилий на
изучение этих аспектов теории интегрирования, а именно с точки
зрения общей теории (частично) упорядоченных векторных про-
пространств, в особенности тех, которые являются одновременно ба-
банаховыми пространствами. См., например, Бур баки [8, гл. II],
Н а к а н о [2], Биркгофф [2], Дан форд и Шварц [1,
стр. 428—431] и приведенную там литературу, Келли и На-
миока [1, приложение], Канторович, Вулих и Пинскер
[1], Вулих [1]. Одними из первооткрывателей в этой области
являются Ф. Рисе [8] и Какутани [5, 6]. Нас сейчас интере-
интересует основной результат работы Какутани [5] — абстрактная
характеризация вещественных пространств L1. Во второй из
указанных работ Какутани получен аналогичный результат для
вещественных пространств С(Т). Мы не будем останавливаться
на этой работе (см., однако, замечание B) п. 9.4.15).
4.23.1. Дадим сначала аксиоматическое описание рассматри-
рассматриваемой ситуации.
Во-первых, напомним читателю, что под упорядоченным век-
векторным пространством Е понимается вещественное векторное
пространство, (частично) упорядоченное (как множество) таким
образом, что выполняются следующие условия:
и -
и
и
Если, кроме того, структура порядка есть структура ре-
решетки, т. е. каждая пара элементов х и у из Е имеет верхнюю
грань xV{/ и нижнюю грань хЛу, то говорят, что Е есть век-
векторная решетка, или (по Бурбаки) пространство Рисса.
Если пространство Рисса Е наделено нормой, для которой
(N) Е — полное пространство;
(N') множество неотрицательных элементов замкнуто;
(N") хАу = 0^\\х + у\\ = \\х — у\\;
(L) х>0 и y>0z$\\x+y\\ = 11*Н + 1Ы1,
то Е называется абстрактным (L)-пространством.
398 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
Элемент е абстрактного (L)-пространства называется F-еди-
F-единицей (единицей Фрёйденталя), если
4.23.2. Теорема (К а кутан и). Всякое абстрактное (^-про-
(^-пространство Е изоморфно (и как нормированное векторное про-
пространство и как частично упорядоченное множество) некоторому
пространству Lr(S, а), где S — отделимое локально компактное
пространство, а о — положительная мера Радона на S. При этом
пространство S можно взять вполне несвязным (единственными
связными множествами в S являются одноточечные множества).
Если Е обладает F-единицей, то S можно взять еще и ком-
компактным.
3 а меч а ни я. Здесь Ir(S, a)—вещественное векторное про-
пространство (классов эквивалентности) вещественных о-интегри-
руемых функций на S с обычной нормой, частично упорядочен-
упорядоченное следующим соглашением: />g тогда и только тогда, когда
/ > g почти всюду для некоторой (и, следовательно, для вся-
всякой) функции f (соотв. g"), взятой из класса / (соотв. g). Случай,
когда Е обладает /^единицей, рассмотрен в статье Какутани
[5], тогда как более общая теорема приведена в статье Каку-
Какутани [6] как относительно простое обобщение частного случая.
Полное доказательство теоремы довольно длинно, и мы не будем
приводить его здесь.
Заметим, что этот результат является кульминацией не-
нескольких упражнений Бур баки [8, стр. 41, упр. 12 и 13,
стр. 194, упр. 10]. При принятом там подходе пространство S
оказывается отделимым локально компактным пространством
Стоуна. Последнее означает, что замыкание каждого открытого
множества снова открыто, откуда ввиду других условий, кото-
которым удовлетворяет S, следует, что S вполне несвязно.
4.23.3. Приложение к пространствам мер. Рассмотрим мно-
множество MR (T) вещественных ограниченных мер Радона на от-
отделимом локально компактном пространстве Т. Легко показать
(используя результаты этой главы), что MR(T) есть абстракт*
ное (L)-пространство. По теореме Какутани пространство
Mr (Г) изоморфно пространству ^(S, g) для соответственным
образом подобранных S и а. Отсюда вытекает много следствий;
одно из них и имелось в виду в замечаниях после формулировки
теоремы 4.22.1.
4.23.4. Следствие. Пусть А — относительное слабо компакт*
ное множество в М(Т). Существует такая положительная мера
[io ^М(Т)У что каждая мера \х^А имеет вид |л=/-|ло» где / —
некоторая функция из 3?Х(Т, ц0).
4.24. Замечания о теоремах выпуклости 399
Доказательство. Из теоремы 4.22.1, очевидно, следует,
что множество А можно считать состоящим только из положи-
положительных мер. Далее в силу теоремы Лебега — Радона — Нико-
дима 4.15.1 достаточно показать, что каждая мера из А абсо-
абсолютно непрерывна относительно некоторой меры jn0.
Выберем S и о так, чтобы пространство Мц(Т) было изо-
изоморфно Lr(S, сг). При этом изоморфизме множеству А будет
соответствовать некоторое относительно слабо компактное мно-
множество Pa Ll(S, а). Применяя теорему 4.21.2 к множеству Я,
получаем, что существует такая убывающая последовательность
(Кп) компактных множеств в S, что каждый элемент'из Р имеет
представителем функцию /, равную нулю вне объединения мно-
множеств Кп- Можно считать, что о(Кп)>0 при каждом п. Опреде-
Определим функцию f0 на S следующим образом:
/о-2 п-*о(КпГ1Хк-
Функция /о положительна и а-интегрируема. Каждый элемент
множества Р имеет представителем некоторую функцию f, кото-
которая является в 3?X{S, о) пределом последовательности (fn),
определенной соотношением
fn = inf (f, nfQ).
Пусть |io — элемент из MRG), соответствующий функции f0;
тогда каждый элемент (л е А служит в MR (Г) пределом после-
последовательности (\in), для которой \хп ^ ftfio. Отсюда сразу сле-
следует, что мера \х абсолютно непрерывна относительно \i0. |
4.24. Замечания о теоремах выпуклости
Подробное изложение тех разделов теории интегрирования,
которые используются в этой книге, закончено. Сделаем ряд за-
замечаний о двух специальных результатах, играющих централь-
центральную роль при изучении линейных операторов, действующих из
одного пространства Лебега в другое. Речь идет о так называе-
называемых теоремах выпуклости М. Рисса и Марцинкевича. Опишем
их кратко.
Пусть S и Т — отделимые, локально компактные пространства
с положительными мерами Радона а и т соответственно. Рас-
Рассмотрим линейный оператор /, который предполагается перво-
первоначально определенным на некотором общем векторном под-
подпространстве D каждого из пространств Лебега Lv(S, а). Пока-
Показатель р и все другие показатели, которые встретятся ниже,
предполагаются лежащими в интервале [1, оо]. В качестве под-
подпространства D можно, например, взять пространство X(S)
400 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
или, что часто бывает более удобным, множество линейных ком-
комбинаций характеристических функций а-интегрируемых мно-
множеств в S. В любом случае D должно быть плотным в L?(Sy о)
при /?<оо. Далее предполагается, что область значений опера-
оператора / состоит из функций (или эквивалентных классов функ-
функций), которые т-измеримы и т-почти всюду конечны. Говорят,
что / есть оператор (сильного) типа (р, q), если существует та-
такое число* С, что
Vf\\q<C\\f\\v
где
U
Наименьшее из всех таких чисел С обозначается через || / Цр, q
и называется (сильной) (р, ц)-нормой оператора /. Если такого
С не существует, то полагают ||/||Pf g = oo. Если D плотно в
Lp(S, а), то, как легко показать, / есть оператор типа (/?, q)
тогда и только тогда, когда он допускает непрерывное продол-
продолжение до оператора из Lp(S, о) в Lq(T, т).
Первая теорема о выпуклости, доказанная впервые М. Рис-
сом [2], утверждает справедливость неравенства
где
Pi Р2 Я Я\ Я2
причем правая часть неравенства D.24.1) считается равной оо,
если либо l|/llPli<7lt либо || / ||А q2 обращаются в оо.
Различные доказательства, варианты, обобщения и прило-
приложения этой теоремы читатель может найти у Данфорда и
Шварца [1], Зигмунда [2, гл. ХН и имеющиеся там при-
примечания], Хард и, Литтлвуда и Полна [1, гл. VIII], Кот-
ля р а [1, 2], А. В е й л я [1, гл. II и VI], Торина [1, 2], Стейна
[1]. Отметим, в частности, обобщение на сублинейные операторы,
полученное Кальдероном и Зигмундом [6]. Оператор /
называется сублинейным, если
\Hh+f2)(t)\<\Jfi(t)\ + \Jf2(t)\ т-почти всюду.
В п. 10.4.11 указан один хорошо известный и полезный способ
применения этой теоремы.
Вторая теорема выпуклости, принадлежащая Марцинке-
в и чу [1], относится к операторам / слабого типа. Говорят, что
/ есть оператор слабого типа (р, q), q<oo, если существует та-
такое число С, что
o>0).
4 24. Замечания о теоремах выпуклости 401
Слабый тип (р, оо) по определению совпадает с (сильным) ти-
типом (р, оо). Наименьшее допустимое значение С обозначается
через w\\J\\Piq и называется слабой (р, q)-нормой оператора /.
Если / не является оператором слабого типа (р, q), то полагают
w || / lip, q = oo. Очень просто показывается, что оператор типа
(/?, q) является также оператором слабого типа (р, q). Без ка-
каких-либо ограничений обратное утверждение неверно. Теорема
выпуклости Марцинкевича представляет собой замечательное
частичное обращение указанного результата. Именно, она
утверждает, что имеет место неравенство
,,, w\\ I%uqi-w\\If-^ D.24.2)
где
+
В D.24.2) число К зависит от ри qu p2, q2 и t9 однако остается
ограниченным при фиксированных ри qu р2, 42, когда / изме-
изменяется между 0 и 1.
Доказательства, варианты, обобщения и приложения можно
найти у Зигмунда [2, гл. XII и имеющиеся там примечания],
отляра [1, 2], Кальдерона и Зигмунда [3, 4], Стейн а
ТИЗи Дж. Шварца [1].
Вообще говоря, свойства оператора /, определяемые его сла-
ЛэШ типом, являются более глубокими, чем те, которые опре-
определяются сильным типом. Понятие слабого типа, по-видимому,
впервые вошло в анализ со ставшей теперь знаменитой рабо-
работой Харди и Литтлвуда [1]. В простейшем чслучае там
утверждается, что сублинейный оператор /, определенный для
интегрируемых функций / вещественной переменной равенством
x+h
//(*) = sup
h>0
будет типа (р, р) при Кр ^ оо и слабого типа A, 1) (но не
сильного типа A, 1)). Аналогичные результаты справедливы
для функций нескольких вещественных переменных (см. 3 и г-
мунд [2, гл. I и XII]) и даже в более общих ситуациях (см.
Смит [1] и Раух [1]). Такие результаты имеют первостепенное
значение в более глубоких разделах гармонического анализа,
теории функций комплексного переменного и эргодической
теории.
402 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
УПРАЖНЕНИЯ
В следующих ниже упражнениях всюду, где не указано противное, Г —
отделимое локально компактное пространство, [i — положительная мера Ра*
дона на Т и измеримость и интегрируемость рассматриваются относитель'
но \i.
4.1. Пусть ф — положительная полунепрерывная снизу функция на Rn,
\i — положительная мера Радона на Rn. Показать, что функция
полунепрерывна снизу.
[Указание. Использовать предложение 4.5.1.]
4.2. Показать, что ц = а + р, где а и Р — положительные меры Радона,
причем а — непрерывная мера (т. е. а(й)=0 для каждой точки /е Г), а
Р— атомарная мера (п 4 4.1).
[Указание. Для каждого компактного множества /С ci T имеем
2 V (W) < + °°- Рассмотреть меру Р = 2 ^ (W) 1
mк t&T
4.3. Пусть \i — 2 tn(t) &t — положительная атомарная мера Радона на Т.
*е= т
Показать, что для всякого множества AczT имеет место равенство
4.4. Показать, что все подмножества в Г, а значит, и все функции на Т
измеримы относительно всякой атомарной положительной меры Радона
на Т.
4.5. Лебегова лестница. Пусть А — интегрируемое множество, / — веще-
вещественная ограниченная измеримая на А функция, и пусть |/|^Л1 Под
лестницей будем понимать такой конечный набор чисел (Wo<£<>i» что
-М = 1о<1х< ... </„ = М.
Введем множества
Ak = {tt=A: lk_x<f{t)<lk)
и положим
е= sup (lk-lk i
Показать, что
lk\i (Ak) <[е|л (A).
A k=\
4.6. Показать, что
r* r* f*
(/ + g) d\i == f d\i+ \ g d\x
j J J
для любых двух положительных измеримых функций fug.
4.7* Неравенство Йенсена. Вещественная функция F на [0, оо) называет-
называется выпуклой, если
Упражнения 403
для любых двух конечных наборов положительных чисел (аи) и (хи) при
условии, что а\+ ... +ап = 1.
Пусть F — положительная возрастающая выпуклая на [0, оо) функция.
Показать, что если интегрируемое множество А удовлетворяет условию
ц(А)>0 и / — положительная измеримая функция на А, то
F \\()
L A
где под F( + оо) подразумевается
lim F (х) = sup Z7 (*) < + оо.
[Указание. Обозначим через М множество тех положительных изме-
измеримых функций / на Л, для которых неравенство выполнено. Показать, что
множество М устойчиво относительно перехода к пределу по всякой возра-
возрастающей последовательности его членов. Далее рассмотреть функции, яв-
являющиеся конечными линейными комбинациями характеристических функций
интегрируемых подмножеств в Л.]
4.8. Пусть / и А те же, что и в упр. 4.7. Показать, что при
р
А
Показать также, что если ц (Л) = 1, то
Г J
L A
J /^<log Г efd\i.
А А
Замечание. Первый результат может быть получен из неравенства
Гёльдера (§ 4.11).
4.9. Пусть мера ц ограничена, 0<p<q и / — положительная функция на
Т. Показать, что
± JLL JL
4.10. Пусть 0 < р < 1. Введем на пространстве eS?p — <S>p{Jy ц) полу-
полуметрику
Убедиться в том, что О3?р — векторное пространство, а полуметрика cfp опре-
определяет на Jg>P линейную топологию. Показать, что пространство J£p полно
относительно этой полуметрики.
4.11. Доказать, что если мера \х ограничена и 0 <р < q, то ^р zd Jg*^
причем вложение t3?q в ^^ непрерывно.
4.12. Рассмотрим гильбертово пространство L2@, 1) (относительно меры,
являющейся сужением меры Лебега с R на @,1)) и линейное отображение
5 пространства L2@, 1) в себя, переводящее класс х в класс (fx)} где [ —
заданная ограниченная и измеримая на @,1) функция. Доказать следующие
Утверждения.
A) Отображение S непрерывно и l|S||=tf«>(/).
404 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
B) Сопряженному к S* отображению соответствует функция f.
C) Отображение 5 унитарно тогда и только тогда, когда 1/@1=1 по-
почти всюду на @, 1).
D) Отображение S~l существует и непрерывно тогда и только тогда,
когда функция /~! существенно ограничена.
E) Спектр отображения 5 не пуст, т. е. существуют такие скаляры Я,
что оператор 5 — XI не обладает непрерывным обратным отображением
(/ — тождественный эндоморфизм пространства L2@, 1)).
F) Если множество f~l ({X}) пренебрежимо для каждого скаляра Я, то
отображение 5 не имеет собственных векторов.
4.13. Доказать, что всякая положительная интегрируемая относительно
положительной меры Радона \х функция является Ji-почти всюду пределом
возрастающей последовательности (fn), где fn — положительные ограничен-
ограниченные универсально измеримые и равные нулю вне некоторых компактных мно-
множеств функции.
[Указание. Воспользоваться тем фактом, что множество F положи-
положительных интегрируемых относительно меры \i функций с указанными свой-
свойствами устойчиво относительно образования пределов возрастающих после-
последовательностей. Принять во внимание также, что всякое ^-интегрируемое
множество отличается от некоторого содержащегося в нем множества типа
FGl) лишь на ji-пренебрежимое множество.]
4.14. Пусть ц = 2 /я @ 8*— атомарная мера Радона. Показать, что
для всякой положительной (конечной или бесконечной) функции /.
4.15. Пусть X— вещественная мера Радона на Г, 5 — ее носитель и
/е5. Показать, что справедливо по крайней мере одно из следующих трех
утверждений.
A) X+(U)>0 и X~(U)>0 для каждой окрестности U точки / (т. е. точ-
точка / принадлежит носителю меры Х+ и носителю меры Х~).
B) Существует такая окрестность Uo точки /, что
Я, (X) = Я+ (X)
для всякого измеримого множества X с £/0, тогда как X{U)=X^(U)>0 для
всякой окрестности U точки t, такой, что U cz Uo (в частности, точка t при-
принадлежит носителю меры Х+).
C) Существует такая окрестность Uo точки /, что
для всякого измеримого множества X с [/о, тогда как
Я(£/)=-АГ (U) <0
для всякой окрестности U точки t, такой, что UczU0 (в частности, точка t
принадлежит носителю меры Х~).
- 4.16. Исследовать аналоги результатов упр. 2.5 для случая, когда вме-
пространства непрерывных периодических функций рассматриваются про-
нства Lp(—jt,Jt) (относительно меры Лебега), 1^р< оо .
сто
странства
*) Множество типа Fa — это множество, представимое в виде обьедине-
ния счетного семейства замкнутых множеств. — Прим. перев.
Упражнения 405
4.17. Пусть съ ..., сп — вещественные или комплексные числа, jli — мера
Лебега на R", g —функция из е%Гс (Rn), удовлетворяющая условию
Показать, что в $£с (R") существуют такие непрерывно дифференцируемые
функции fh ..., fn, что
где tk — координаты в Rn.
[Указание. Свести задачу к случаю, когда все си равны нулю. За-
Затем применить индукцию по п.]
4.18. Пусть [i — мера Лебега на Rn и % — мера Радона на Rn, относи-
относительно инвариантная относительно сдвигов. Доказать существование таких
вещественных или комплексных чисел си ..., сп, что
[Указание. Если Я = 0, то утверждение очевидно. Пусть X Ф 0 и
X(fa) = D(a)X(f). Показать, что £>@)=1, D (а + b) = D (a) D F), D непре-
непрерывно дифференцируемо и -_-— = ckD, где ck — некоторые числа. Следова-
Следовательно, Я \-^-)==сЛAI если функция f^^c(Rn) непрерывно дифферен-
цируема. Воспользоваться предыдущим упражнением.]
4.19. Определить все вещественные меры Радона на вещественной пря-
прямой, относительно инвариантные относительно гомотетий t\—>at, где а про-
пробегает множество всех ненулевых вещественных чисел.
4.20. Пусть Т — локально компактная группа, \х — левая мера Хаара на
Т и Кр< оо. Если f ^J?p' и g t=J?p, то функция f*g локально почти
совпадает с некоторой непрерывной функцией. Показать также, что при К
<р< оо эта непрерывная функция стремится к нулю на бесконечности.
4.21. Пусть Т — локально компактная группа и Е — такое подмножество
в Т, что (!*(£) >0, где \х — левая мера Хаара. на Т. Доказать, что множе-
множество Е • Е~1 является окрестностью нейтрального элемента группы Т.
[Указание. Можно считать Е компактным. Рассмотреть функцию
Показать, что f непрерывна и отлична от нуля на нейтральном элементе ]
4.22. Пусть Т — локально компактная группа и % — характер на Т. По-
Показать, что если % измерим (относительно левой меры Хаара), то он непре-
непрерывен.
[Указание. Вначале воспользоваться упр. 4.21 для доказательства ло-
локальной ограниченности характера %. Затем выбрать функцию g^K(T) так,
чтобы x~1gAd\i ф 0, и рассмотреть функцию g * %.]
4.23. Пусть R—вещественная прямая и ц — мера Лебега на ней. Возь-
Возьмем функцию k e J£x (R) и рассмотрим эндоморфизм 5 пространства
J2?2(R), определенный соотношением Sf = k*f. Показать, что
406 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
A) отображение S непрерывно на eS?2 (R) и HSll^Ari(£);
B) спектром отображения S служит множество k(R), где
есть преобразование Фурье функции k\
C) комплексное число К является собственным значением отображения
5 тогда и только тогда, когда равенство k(s)=X имеет место на некотором
множестве положительной меры.
Замечание. Используя равенство Парсеваля, можно доказать, что
\\S\\=Noo(k).
4.24. Пусть Р — относительно слабо компактное множество в «g71 =
= JS*1 {T, \i). Пусть далее (fn) — ограниченная последовательность в J3*00,
которая локально по мере сходится к пределу / (необходимо принадлежа-
принадлежащему „25700). Показать, что
lim f gfn d\i = f gf d\i
n J J
равномерно по g s P.
В последующих четырех упражнениях предполагается известным тот
факт (следствие из теоремы 8.2.2), что в локально выпуклом пространстве
каждая слабо сходящаяся последовательность ограничена в исходной топо-
топологии.
4.25. Пусть 1<р< оо. Показать, что последовательность (fn) <=:jg^P слабо
сходится к / в этом пространстве тогда и только тогда, когда выполнены
следующие два условия:
A) sup ЛГР (/„)< +оа;
п
B) lim fn d\i— f da для каждого интегрируемого множества А.
" А X
Показать, что /п->/ слабо „в J271 тогда и только тогда, когда выпол-
выполнены следующие два условия:
п
B0 lim fnd\i= f da для каждого измеримого множества А.
п А А
4.26. Показать, что fn->f слабо в JS?1 тогда и только тогда, когда вы-
выполнены следующие три условия:
п
B) lim I fnd\i= I f da для каждого интегрируемого множества Л;
А А
C) для каждого е>0 существует такое интегрируемое множество /С, что
()
up I |fft|d|Ji<e.
п т<к
sup
4.27. Пусть Т — вещественный интервал и а — сужение меры Лебега на
Т. Показать, что fn->f слабо ъ J2?1 тогда и только тогда, когда выпол-
выполняются следующие четыре условия:
(Ю sup Nx (fn) < + <*>;
п
Упражнения 407
B") lim fnd\i~ f d\i для каждого ограниченного интервала (a, b)czT;
п J J
а а
C) то же, что и в упр. 4.26;
D) для всякого е>0 существует такое б>0, что sup | fn \ й\л для ка-
" А
ждого интегрируемого множества Л с \i(A)<6.
[Указания. Необходимость условий A), B), B') и B") следует из
замечания, предваряющего эти упражнения, и из определения слабой сходи-
сходимости. Необходимость условий C) и D) вытекает из теоремы 4.21.2. Доста-
Достаточность сформулированных условий доказывается во всех случаях приме-
применением результата упр. 1.18 к соответствующим образом выбранному мно-
множеству Я с tS>o°\
4.28. Показать, что единичный шар пространства J2?1 = <2*х (Т, ц) отно-
относительно слабо компактен тогда и только тогда, когда носитель меры \i ко-
конечен (в этом случае пространство J3?1 конечномерно).
[Указание. Пусть 5 — носитель меры [Л. Показать сначала, что
МШ)>0 для каждой точки /g5. Используя теорему 4.21.2, доказать суще-
существование такого числа 6>0, что \*>({t})>6 для каждой точки fe5, затем
доказать, что множество 5 локально конечно и существует такое компакт-
компактное множество /(с:7\ что Т\К локально пренебрежимо. Следовательно, мно-
множество S=S [}K конечно.]
Замечание. Как мы увидим в гл. 8, пространство <2*1 рефлексивно
(т. е. каждая непрерывная линейная форма на (J2?lY = J2?°° представима
в виде g i—> fg d\i, где / — некоторая функция из „g71) тогда и только
тогда, когда единичный шар пространства <2*х относительно слабо компак-
компактен. Предыдущее упражнение показывает, что это возможно тогда и только
тогда, когда пространство C2?l конечномерно. В противоположность этому,
как показывает упр. 4.16, пространство J3?p рефлексивно при \<р< оо.
4.29. Пусть Ц — непрерывная положительная мера Радона на отделимом
локально компактном пространстве Т и 0</?<1. Показать, что всякая поло-
положительная линейная форма L на еЗ?р = OS?P (T, ц) тождественно равна
нулю.
[Указание. Рассмотреть сужение k=L\$£(T). Показать, что положи-
положительная мера Радона К локально абсолютно непрерывна относительно ц
и, следовательно, имеет вид X = g • ц, где g — функция, локально интег-
интегрируемая относительно \i. Показать затем, что g = 0 локально ц-почти
всюду.]
4.30. Пусть Е — пространство Рисса (п. 4.23.1) и / — линейная форма на
£, относительно ограниченная в том смысле, что для каждого эле-
элемента #>0 из Е множество {f(y): у^Е, О^у^х] ограничено. Показать, что
форма f есть разность двух положительных линейных форм на Е.
[Указание. Видоизменить соответствующим образом рассуждения, ис-
использованные при доказательстве теоремы 4.3.2.]
4.31. Пусть Е — пространство Рисса, наделенное линейной топологией
с базой окрестностей нуля, образованной такими множествами W, что из
отношений лге W и О^у^х следует, что y^W. Показать, что всякая огра-
ограниченная линейная форма на Е относительно ограничена.
4.32. Пусть Е — пространство Рисса, наделенное линейной топологией, и
пусть задано некоторое подмножество N в Е, элементы которого будем на*
зывать «пренебрежимыми». Предположим, что выполнено следующее уело-
408 Гл. 4. Топологии, сопряженные к некоторым пространствам; меры Радона
вие: каждому ограниченному множеству В аЕ соответствует такая последова-
последовательность чисел сп > 0, что если (хп} —• произвольная последовательность
элементов из В, то можно найти такой элемент i/g£ и такую последователь-
последовательность (zn) пренебрежимых элементов из £, что
для всех натуральных т.
Показать, что всякая относительно ограниченная линейная форма на Et
равная нулю на всех пренебрежимых элементах, ограничена. "
[Указание. В силу упр. 4.30 достаточно рассмотреть положительную
линейную форму / на Е. Если форма f неограничена, то существует такое
ограниченное множество Вс£, что множество f(B) неограниченно. Выбрать
элементы хп^В так, чтобы \f(xn)\>c~l и, следовательно, f (\ ^п\)> с~1.
Показать, что это приводит к противоречию.]
4.33. Опираясь на упр. 4.31 и 4.32, сравнить результат упр. 4.29 с ре-
результатом, полученным в п. 4.16.3.
[Указание. Заметим, что если (/п) — ограниченная последователь-
последовательность в J2*p и 2j cpn < + °о, то ряд £±сп\]п\ почти всюду сходится к ко-
конечному пределу, так как
т \Р т
V с \f и <r V /.Pif \p
jLd n I '
и, значит,
4.34. Показать, что всякая интегрируемая функция почти всюду равна
разности двух положительных интегрируемых полунепрерывных снизу функ-
функций. (Ср. Рисе иНадь [1, стр. 40].)
4.35. Пусть Т — отделимое локально компактное пространство [0, + оо)
и а>0. Показать, что множество функций е~ап (лг =1,2, ...) тотально в
Со(Г), и вывести отсюда, что множество функций вида e~atP (/), где /> —
многочлен, плотно в С0(Г).
4.36. Пусть Т и а — те же, что и в предыдущем упражнении. Показать,
что множество функций вида Р (/) • е~ , где Р — многочлен, плотно в
Со(Г).
4.37. Показать, что при а>0 и 1^5р<оо множество функций вида
e~atP (/), где Р — многочлен, плотно в Lp @, оо). Показать, что то же спра-
справедливо для функций вида е~а Р (t).
4.38. Пусть Г —интервал в Rn, fx — положительная мера Радона на Г.
Под ступенчатой функцией будем понимать конечную линейную комбина-
комбинацию характеристических функций ограниченных подинтервалов в Т.
Доказать, что функция / ц-интегрируема тогда и только тогда, когда
выполнено следующее условие: для каждого е>0 существуют такие после-
Упражнения 409
довательности (sn)n-^\ и (s^) ступенчатых функций, что
для я>1 и
2^ J sn <fy < + оо, 2j J s^
4.39. Пусть \i — положительная мера Радона на отделимом локально
компактном пространстве Г, и пусть s — конечно аддитивная функция мно-
множества, определенная (и конечная) для всех ^-интегрируемых подмножеств
в Г и такая, что ц(Лп)->0 влечет s(/4n)-»0. Доказать, что существует
такая положительная локально (^-интегрируемая функция / на Г, что
s(A)=jfdii.
[Указание. Определить положительную меру Радона а на Т сле-
следующим образом. Если g— непрерывная вещественная функция на Г, рав-
равная нулю вне компактного множества К с: 7\ то положить o(g) равным пре-
пределу сумм вида ^jCks(Ak) при max (рк — ^_j) -> 0, где
k &
с = max | g|, -c = £0<£i< ••• <cn = c+\,
Показать, что a(U)^s(U)y если U — открытое относительно компактное мно-
множество Следовательно, мера а локально абсолютно непрерывна относитель-
относительно ц. Использовать теорему Лебега — Радона — Никодима.]
4.40. Пусть Т — отделимое локально компактное пространство и 7** =
= Г U{°°} — его компактификация Александрова (п. 0.2.18D)). Показать, что
существует изометрический изоморфизм \i\—> у.* пространства ограниченных
мер Радона на Т на подпространство N пространства всех мер Радона
на Г*, состоящее из тех мер X на Г*, для которых \К\ ({оо}) =0.
4.41. Пусть Т — локально компактное пространство. Показать, что вся-
всякая непрерывная функция на Г, стремящаяся к нулю на бесконечности, яв-
является пределом конечных линейных комбинаций характеристических функ-
функций %а компактных множеств Л с: Г, обладающих счетной базой окрестно-
окрестностей.
4.42. Пусть % — вещественная мера Радона на отделимом локально ком-
компактном пространстве Т. Доказать, что для всякого измеримого множества
S czT имеют место соотношения
Х+ (S)-supX(M), Я" (S) - - inf к (М),
где М пробегает все измеримые подмножества в S.
[Указание. Воспользоваться следствием 4.15.5.]
410 Гл. 4. Топология, сопряженные к некоторым пространствам; меры Радона
4.43. Пусть Г —отделимое локально компактное пространство, М(Т) —
пространство ограниченных мер Радона на Т. Доказать, что пространство
М секвенциально слабо полно, не прибегая к теореме Какутани 4.23.2.
[Указание. Использовать прием, изложенный в замечании, идущем
вслед за теоремой 4.22.1.]
4.44. Показать, что пространство М(Т) рефлексивно тогда и только тог-
тогда, когда множество Т конечно (обозначения те же, что и в предыдущем
упражнении).
[Указание. Использовать упр. 4.28.]
4.45. Пусть Т — отделимое локально компактное пространство и С0(Т) —
банахово пространство непрерывных скалярных функций х на 7\ стремя-
стремящихся к нулю на бесконечности (в том смысле, что множество
{* е= Т: | х (t) | > е}
относительно компактно в Т для каждого е>0), причем норма на Со(Т)
определена равенством
Показать, что пространство, сопряженное к С0(Т), может быть отождест-
отождествлено с М(Т), если каждой мере цеМ(Г) поставить в соответствие линей-
линей(), р
ную форму х i—> х d\x на С0(Г).
Т
Замечание. Это — «непрерывный аналог» теоремы 4.2.2. Относительно
«природы» ассоциированной сопряженной нормы на М(Т) см. замечание
4.15.6. Из теоремы 1.11.4B) следует, что ограниченные по норме подмноже^
ства в М(Т) относительно компактны в топологии сг(М, Со).
ГЛАВА 5
Распределения и линейные дифференциальные
уравнения в частных производных
5.0. Предисловие
В предыдущей главе мы весьма подробно изучили объекты
(меры Радона), представляющие собой по существу непрерыв-
непрерывные линейные формы на некоторых топологических векторных
пространствах непрерывных функций. Непрерывность этих ли-
линейных форм рассматривалась относительно равномерной схо-
сходимости функций, подчиненных тому условию, что носители этих
функций лежат в произвольном, но фиксированном компактном
множестве. В этой главе мы хотим изучить линейные формы,
первоначально определенные лишь для бесконечно дифференци-
дифференцируемых функций и непрерывные в более слабом смысле. Новый
тип непрерывности линейных форм связан с расмотрением функ-
функций, носители которых лежат в произвольном, но фиксированном
компактном множестве и которые сходятся равномерно вместе
со всеми своими производными. Такие линейные формы и пред-
представляют собой распределения (или обобщенные функции1)),
введенные Л. Шварцем.
Распределения, введенные таким (или эквивалентным) спо-
способом, являются обобщением как понятия функции, так и поня-
понятия меры, и на них можно распространить некоторые операции,
применимые к функциям и мерам. Самое главное, распределения
можно дифференцировать сколько угодно раз, причем операция
дифференцирования непрерывна. Отсюда следует, что в число
естественных уравнений, содержащих распределения, заведомо
входят все линейные дифференциальные уравнения в частных
производных с постоянными коэффицинтами (и даже с коэффи-
коэффициентами, которые являются функциями, если только эти функ-
функции удовлетворяют определенным условиям гладкости, завися-
зависящим от типа рассматриваемых распределений). Расширение
сферы изучения таких уравнений дало мощный импульс разви-
развитию теории, и в настоящее время это процветающая область ис-
исследований. Мы постарались достаточно широко осветить неко-
некоторые аспекты этой теории. Надеемся, что в итоге нам удастся
1) В русской литературе чаще используется термин обобщенные функ-
функции, которым обычно и переводят distributions. Нам будет удобно использо-
использовать оба термина сразу. — Прим. ред,
412 Гл. 5. Распределения и дифференциальные уравнения
мотивировать изучение распределений и одновременно побудить
читателя следить за современными исследованиями в области
прикладного функционального анализа.
Введение обобщенных функций в дифференциальные урав-
уравнения естественно предполагает, что в качестве решений допус-
допускаются объекты, которые, даже будучи функциями, не являются
гладкими, например поточечно дифференцируемыми в обычном
смысле. Допускать это кажется на. первый взгляд в корне оши-
ошибочным, но, немного поразмыслив, нетрудно видеть, что гакое
изменение точки зрения не лишено смысла. Если обычная функ-
функция рассматривается как обобщенная, то это означает, что она
характеризуется не своими значениями в отдельных точках, а
своими «средними» значениями, которые проявляются после
умножения ее на произвольную «пробную» функцию и последую-
последующего интегрирования. Эти пробные функции «должны» быть бес-
бесконечно дифференцируемы и обладать компактными носителями.
Фактически пробные функции образуют функциональное про-
пространство, а обобщенные функции определяются как линейные
формы на этом пространстве. В настоящее время, когда пы-
пытаются применить математику к естественным наукам, наблю-
наблюдаемые величины измеряют именно такими «средними», а не
значениями в отдельных точках. В классической теории поля
хорошо известно, что дифференциальные уравнения в частных
производных могут быть всегда заменены соотношениями, со-
содержащими интегралы. В теории распределений уравнение в
частных производных выражает точно такое же соотношение и
потому ближе к реальной действительности, чем при старом
толковании дифференциальных уравнений.
Хорошим аккомпанементом к настоящей главе послужит чте-
чтение книг из следующего списка: Шварц [1, 2], Гельфанд и
Шилов [2, 3], Хёрмандер [7], Фридман [1], Гельфанд
и Виленкин [1], Бремерман [1], Гальперин [3], Ши-
Шилов [3]. Особого упоминания заслуживает учебник Куранта
и Гильберта [2J, в котором после изложения обширной части
классической теории дифференциальных уравнений делается
превосходный переход к современной теории этих уравнений.
См. также Данфорди Шварц [2].
5.1. Распределения
Определение понятия обобщенной функции на Rn или на
открытых подмножествах QczR77, данное Л. Шварцем [1, 2],
строится по образцу определения меры Радона на Rn (п. 4.3.1),
которая вводится как линейная форма на Ж(Rn), удовлетво-
удовлетворяющая некоторому условию непрерывности. При введении рас*
5.1. Распределения 413
пределений мы переходим от Ж(&) к его векторному подпро-
подпространству S)(Q), наделяя последнее более сильной топологией,
чем индуцируемая из Ж{п). В силу теоремы Хана — Банаха
некоторое усиление топологии неизбежно, если мы хотим иметь
среди непрерывных линейных форм на 2)(Q) объекты, более
общие, чем меры Радона на Q.
Грубо говоря, этот процесс может быть описан в физических
терминах следующим образом. Вещественные меры Радона на
R3 можно считать математическими объектами, описывающими
такие распределения электрических зарядов, магнитных «заря-
«зарядов» или гравитационных масс, которые представляют собой
«простые полюсы». Эта точка зрения подтверждается всем раз-
развитием теории потенциала за последние 30 лет. Однако в мате-
математической физике принято вводить наряду с распределениями,
описываемыми мерами Радона, некоторые их идеализированные
пределы, а именно распределения, представляющие собой
«мультиполи» различных видов. Распределения Шварца можно
рассматривать как математические объекты, соответствующие
самым общим распределениям зарядов или масс, включая «муль-
«мультиполи» сколь угодно большого и даже бесконечного порядка.
Для описания условия непрерывности, характеризующего
распределения, удобно, как и в § 4.3 для мер, ввести предвари-
предварительно понятие сходимости последовательностей в S)(Q). За-
Задача превращения £D(Q) в локально выпуклое пространство,
сопряженное к ксугорому реализуется так определенными рас-
распределениями, будет решена позже в терминах индуктивных
пределов (§ 6.3, пример 2).
Мы увидим, что распределения обладают производными лю-
любого порядка, не зависящими от порядка дифференцирования, и
что операция дифференцирования непрерывна. Вследствие этого
теория дифференциальных уравнений с частными производными
как будто получила новую жизнь: использование распределений
ставит новые проблемы и предлагает новые методы для их ре-
решения. За последнее десятилетие в этой области был достигнут
большой прогресс. Исторически многие из основных идей, отно-
относящихся к распределениям, первоначально возникли при изуче-
изучении так называемых «слабых решений» дифференциальных урав-
уравнений с частными производными, и развитие систематической
теории явилось результатом труда многих авторов1).
Мы попытаемся не только изложить основные идеи, сами по
себе представляющие большой интерес для функционального
анализа, но и показать, как эти новые идеи в сочетании
') Впервые обобщенные функции в явной форме ввел Соболев [2] в
1936 г. — Прим. перев.
414 Г л 5. Распределения и дифференциальные уравнения
с общими теоремами функционального анализа открывают но-
новые подходы и новые точки зрения на задачи анализа.
В п. 5.11.5 мы приведем дальнейшие ссылки на литературу.
5.1.1. Обозначения. В дальнейшем всюду через Q будет обо-
обозначаться открытое подмножество в Rn, а через хи ..., хп —
независимые переменные в R*. Через 2){п) будет обозначаться
векторное подпространство в Ж{й), образованное всеми функ-
функциями, обладающими на п частными производными любого по-
порядка и обращающимися в нуль вне некоторого компактного
подмножества в Q (зависящего от рассматриваемой функции).
Дифференциальный оператор -^—(k=l. ..., п), действующий
в 3){О>), будет обозначаться через dk. Оператор df1 ... д„п обо-
обозначается через д?> где р— набор целых неотрицательных чисел
(Ри •••> Рп), а \р\=р\ + ... + Рп — порядок оператора д*. Так
как каждая функция из £D(Q) принадлежит классу C°°(Q), то
д — коммутирующие между собой эндоморфизмы пространства
(Q)
()
Пусть 5 — подмножество в Й; через £D(Q, S) обозначается
подпространство в S)(Q), образованное теми функциями
ф£2)(й), носитель которых содержится в 5. Определим на
C°°(Q) положительную функцию Nsm, полагая
где т !> О — целое число и Scz Q. Ясно, что jVm(qp)< + oo> если
S относительно компактно в Q (т. е. Sf]Q компактно) и
C(Q) или при произвольном 5 если фей)(й). Функции
qp()
Nm и Nm=Nm совпадают на 2)(Q, 5).
Если S относительно компактно в Q, то Л^т и Nm являются
нормами на 2)(п, 5), что дает возможность превратить
£D(Q, S) в полное метризуемое локально выпуклое простран-
пространство, т. е. в пространство Фреше1).
Если S пробегает базу относительно компактных подмно-
подмножеств в Q, то N^ определяют в С°°>(Й) топологию, в которой
C°°(Q) также является пространством Фреше. Топология, ин-
индуцированная в 3){Q), не является топологией, относительно ко-
которой сопряженное к 2D(Q) совпадает с пространством распре-
распределений на Q. Несколько позже мы увидим, что таким способом
получаются только распределения, имеющие компактные носи-
носители в Q. Нужную нам топологию на 3)(п) мы получим, обра-
образуя индуктивный предел пространств Фреше 3)(Q, 5), когда 5
пробегает базу относительно компактных (или компактных) под-
См. § 6.11. — Прим. ред.
5.1. Распределения 415
множеств в Q (§ 6.3). Тем не менее нормы Nm позволяют опре-
определить понятия секвенциальной сходимости и ограниченности
в &(Q), которые, как будет позже показано, совпадают с соот-
соответствующими понятиями, определенными топологией индук-
индуктивного предела (п. 6.6.1 и 7.4.3).
Приведем определение этих понятий. Говорят, что последо-
последовательность (q)n)czS)(Q) сходится в 3) (Q) к нулю, если (а)
ПтЛ/т(фп) =0 для каждого т >0 и (Ь) существует такое отно-
п
сительно компактное (или компактное) множество S a Q, что
{уп)а3)(п, S). Аналогично множество ВаЗ)(п) называется
ограниченным eg)(Q), если (а) зир{Л^т(ф): фЕВ}< +оо для
каждого т>0 и (Ь) ВаЗ){п, S) для некоторого относительно
компактного (или компактного) множества S a Q. Другими сло-
словами, последовательность (фп) сходится к нулю в £D(Q) (соотв.
множество В ограничено в @){п)) тогда и только тогда, когда
существует такое относительно компактное (или компактное)
множество ScQ, что все фп (соотв. В) попадают в iZ>(£2, 5)
и фп-^0 (соотв. В ограничено) в смысле пространства Фреше
0>{Q; S).
5.1.2. Определение распределений. Теперь можно ввести
определение распределения на Q: распределением, или обоб-
обобщенной функцией, на Q называется такая линейная форма X
на iZ)(Q), что сужение X\£D(Q, S) непрерывно на пространстве
Фреше k>(Q, S) для каждого относительно компактного (или
компактного) подмножества ScrQ. Очевидно, в условии опре-
определения можно считать, что S пробегает базу относительно ком-
компактных (или компактных) множеств в Q. Эквивалентное усло-
условие: НтА'(фп)=0 для каждой последовательности фп->0 в
3t)(Q)\ или еще: X переводит каждое ограниченное подмноже-
подмножество в iZ>(Q, S) (S — произвольное относительно компактное
множество в Q) в ограниченное числовое множество.
Как и в случае мер, каждое распределение X на Q вполне
определяется своими значениями на вещественных функциях из
@)(п). Более того, X может быть всегда записано в виде A + iB,
где А и В — распределения на £2, которые являются веществен-
вещественными в том смысле, что они принимают вещественные значения
на вещественных функциях лз 3)(Q). Однако в отличие от мер
вещественное распределение не является, вообще говоря, раз-
разностью двух положительных распределений. Действительно,
легко показать (Л. Шварц [1, стр. 28—29]), что распределение
X на Q положительно (т. е. Х(ф) > 0 для ф> 0 из 3)(й)) тогда
и только тогда, когда X — положительная мера Радона на Q.
Обозначим через 3)'(п) множество всех распределений на
й. Это множество является векторным подпространством алгеб*
416 Гл. 5. Распределения и дифференциальные уравнения
раического сопряженного к £D(Q)* Учитывая наличие двойствен-
двойственности между 3){п) и &'{&), мы часто будем писать (ср, X)
вместо Х()
5.2. Меры и функции как распределения
Пусть К — произвольная мера Радона на Q. Очевидно, что
сужение L = K\S)(Q) —распределение на Q. Кроме того, L опре-
определяет % однозначно, так как каждая функция ф£^)(й) яв-
является пределом в £D(Q) некоторой последовательности
(фп) cz 2D{Q). Действительно, достаточно воспользоваться про-
процессом регуляризации, который заключается в следующем.
Возьмем такую последовательность (гп) положительных функ-
функций из 2)(Q), носители которых являются уменьшающимися
окрестностями нуля, что \rnd\i=l (jx—мера Лебега на Rn);
если положить ф равным нулю вне Й, то функции
Ф/i (*) = rn*V W = J гп (У) q(x-y) dp (у)
принадлежат 2){п) и ф — фп-^0 в
Так как соответствие X^-^L взаимно однозначно, то можно
безбоязненно отождествить меру К с распределением L и не де-
делать разницы в обозначениях.
Если функция / локально интегрируема относительно \х на
Q, то предыдущее замечание можно применить к мере f-\i на Q.
В этом случае мера определяет только класс функций / (отли-
(отличающихся от f на функцию, пренебрежимую на Q). Таким об-
образом, каждую локально интегрируемую функцию f на Q (или,
точнее, каждый класс таких функций) можно отождествить с
распределением на Q, определенным соотношением
В случае непрерывных на Q функций соответствие между
функциями и обобщенными функциями уже взаимно однозначно.
Примеры распределений на Q, которые не являются ни функ-
функциями, ни мерами (после описанного выше отождествления),
можно получить дифференцированием и делением распределений
этих частных видов. Указанные операции будут определены в
§ 5.4 и 5.5.
5.3. Сходимость распределений
Пространство iZ)'(Q), рассматриваемое как сопряженное к
3){п), можно наделить по крайней мере двумя естественными
топологиями: A) слабой топологией а{3)\3)) и B) сильной то-
5 3 Сходимость распределений 417
пологией ${££>', 3)). В § 1.11 мы уже встречались с общим опре-
определением слабой топологии а. Параллельное исследование то-
топологии C на языке общей теории двойственности будет прове-
проведено в § 8.4. Тем не менее в нашем частном случае мы расска-
расскажем о топологии C достаточно для того, чтобы можно было
пользоваться этим понятием, и перечислим затем некоторые ее
свойства. Справедливость этих свойств вытекает из общих тео-
теорем, доказываемых в § 8.4.
По определению база окрестностей нуля в топологии C =
= C(й)/, SD) образована полярами 5°, где В пробегает систему
ограниченных подмножеств в £D(Q). Другими словами, если
(Xi) —сеть распределений на й и X — некоторое распределение
на Q, то соотношение \imXi = X в топологии |3 означает, что
i
limsup{|;r(q>)-X,((p)|: qp€EB} = 0
i
для каждого ограниченного подмножества В в <2)(Q). Зна-
Значение этого условия становится более ясным, если принять во
внимание некоторые характерные особенности ограниченных
множеств в 2D(Q), которые мы сейчас напомним. В каждой из
топологий а или |3 пространство 2)'(Q) является отделимым и
локально выпуклым.
Сделаем теперь несколько замечаний о природе ограничен-
ограниченных множеств в £D(Q). Топология пространства 2){п) будет
описана в примере B) п. 6.3.3. В § 6.6 будет показано, что мно-
множество Bcz3)(Q) ограничено тогда и только тогда, когда суще-
существует такое компактное множество KczQ, что В содержится
и ограничено в пространстве Фреше 3)(Q, К). Другими словами,
должны выполняться следующие два условия:
(a) ф = 0 на Q \ К для каждой функции феВ;
(b) sup (|(?рф(х) |: х <= £2, ф£Й}< + оо для каждого набора
р=(р\, ..., рп) (где, как обычно, ри ^ 0 — целые числа).
Пример. Пусть л = 1 и (/*) — сеть функций из L\0C(Q) !).
Обозначим через k некоторое неотрицательное целое число, и
пусть для каждого i функция F{ есть fe-кратный неопределенный
интеграл от /V Приведенный выше критерий ограниченности
множества в 2){Q) позволяет сделать следующий вывод: сеть
(/,-) слабо (соотв. сильно) сходится в 3)'(Q), если для каждого
компактного множества KczQ сеть (/%•) слабо (соотв. сильно)
сходится в Ll(K). Фактически в этом случае все распределения
локально представимы как пределы последовательностей (/*),
сходящихся в указанном смысле. Это обстоятельство служит
основанием для некоторых других подходов к теории обобщен-
*) См. п. 5.13.4. — Прим. перев.
418 Гл. 5. Распределения и дифференциальные уравнения
ных функций1). Те же идеи можно развить и в многомерном
случае.
Имея в виду приведенную выше характеризацию ограничен-
ограниченных множеств, перечислим ниже ряд важных свойств прост-
пространств &(Q) и &'(Q).
A) 2)(Q)—бочечное пространство (§ 6.2 и п. 6.3.3). Это
означает, что каждое замкнутое выпуклое уравновешенное по-
поглощающее множество в 2){Q) является окрестностью нуля в
2D{Q), или, что то же самое (теорема 7.1.1), каждое слабо огра-
ограниченное множество в 3)'{О) равностепенно непрерывно и тем
более сильно ограничено.
B) SD(U)—монтелевское пространство (п. 8.4.7), т. е. каж-
каждое ограниченное замкнутое множество в £D{Q) компактно. До-
Доказательство этого свойства опирается на приведенную выше
характеризацию ограниченных множеств в 2)(Q) и на теорему
Асколи. Отсюда следует (теорема 8.4.8 и A)), что топология
пространства 2)(Q) и слабая топология а(<®, 3)') индуцируют
одну и ту же топологию в каждом ограниченном множестве В
в S)(Q) и что слабая и сильная топологии совпадают на каж-
каждом (слабо или сильно) ограниченном множестве в 0'(Q).
В частности, всякая слабо сходящаяся последовательность
в 2)(п) (соотв. в 3)'{Q)) сходится в 3){п) (соотв. сильно
сходится). Более того, пространство 3)'{п), наделенное
сильной топологией р, также является монтелевским (теоре-
(теорема 8.4.11).
C) 2)(Q)—рефлексивное пространство (§ 8.4, в частности
теоремы 8.4.2 и 8.4.5), и поэтому 2)'(Q), наделенное топологией
|3, является бочечным пространством (теорема 8.4.3). Рефлек-
Рефлексивность пространства S)(Q) означает, что каждая линейная
форма L на S57(Q), непрерывная в топологии C, может быть за-
записана (и притом единственным образом) в виде L(X) =X(qp)
для некоторого фЕ®(£2) и что сходимость сети {сра} в 2D(Q)
равносильна тому, что соответствующая сеть {La} (La(X) =*.
=^(фа)) линейных форм на 3)'{0>) равномерно сходится на
каждом ограниченном множестве в iZ>'(Q).
D) 2D(Q)—борнологическое пространство (§ 7.3, теоремы
7.3.2 и 7.3.3A)). Это означает, что каждое выпуклое уравнове-
уравновешенное множество в 2)(Q), поглощающее каждое ограниченное
множество в iZ>(Q), является в S)(Q) окрестностью нули. Сле-
Следовательно (теорема 7.3.1, замечание (а)), линейная форма X
на S)(Q) принадлежит 3)'{п) тогда (и только тогда), когда
sup(|Х(ф) |: феВ}< + оо для каждого ограниченного множе-
множества В2)(Й)
1) См. Минусинский и Сикорский [1]. — Прим. пере в.
5.4. Дифференцирование распределений 419
E) 3)'(fi)—полное пространство в сильной топологии р.
Это следует из D) в силу утверждения п. 8.4.13.
5.4. Дифференцирование распределений
Пусть /г=1, Q — открытый интервал вещественной оси и
f — локально абсолютно непрерывная функция на й. Интегри-
Интегрированием по частям получаем
. /') = J /'фФ=- f
где qpeS5(Q), а /'— производная функции f (производная f
определена почти всюду и локально интегрируема на Q); вне-
интегральный член, возникающий при интегрировании по ча-
частям, равен нулю, потому что ср обращается в нуль вне некото-
некоторого компактного подинтервала в Q. Таким образом, f как рас-
распределение на Q удовлетворяет условию
<ф, П=-(ф/, f)
для любого cp()
Это наблюдение используется для определения производной
любого распределения X на Q, т. е. в общем случае мы назы-
называем производной д?Х распределение, задаваемое условием
<Ф', дрХ)-(-1Iр\(д%Х)
для всех фе2)(й). Ясно, что д*Х действительно является рас-
распределением на Q, так как отображение <р ^—■> д^у является не-
непрерывным эндоморфизмом пространства 2)(Q). Поскольку ото-
отображение ф ь-> ^Рф переводит ограниченные множества в &(Q)
в ограниченные множества, то отображение Х^-^д^Х непрерывно
как в слабой, так и в сильной топологиях в 3)'(п).
В более «высокой» терминологии действие отображения д?
на распределения совпадает с точностью до числового множи-
множителя (—1)|Р| с отображением, сопряженным к д?\ 2D(Q)->
Ф
()
В качестве примера рассмотрим распределение X, равное
еа — мере Дирака, сосредоточенной в точке й£Й. В одномер-
одномерном случае получаем
—(ф'> еа>=—ф'(а)
для всех <p&3)(Q). Так как в Ж{п) можно выбрать такую схо-
сходящуюся к нулю последовательность (фпЬ что последователь-
последовательность чисел Ф^(а) к нулю не стремится, то распределение деа
не является мерой (и тем более не является функцией)^.
420 Гл. 5. Распределения и дифференциальные уравнения
В физических терминах обобщенная функция типа д^га соответ-
соответствует «мультиполю», сосредоточенному в точке а.
Много других примеров можно найти в книге Гельфанда
и Ш и л о в а [2, стр. 35—56].
Предостережение. Снова рассмотрим случай, когда
Q — открытый интервал. Еслр / — локально интегрируемая
функция на Q, имеющая локально ограниченную вариацию, но
не локально абсолютно непрерывна/! Не Q, то обычная произ-
производная /' (которая почти всюду определена и локально инте-
интегрируема на п) приводит к обобщенной функции на й, которая,
вообще говоря, отличается от производной df обобщенной функ-
функции, порожденной функцией /. Например, возьмем Q = R, и пусть
f — функция Хевисайда
при #<0,
при х^О.
Тогда производная f равна 0 почти всюду и, таким образом,
определяет нулевую обобщенную функцию. Однако df опреде-
определяется равенствами
— оо 0
т. е. <?f = eo — мера Дирака, сосредоточенная в нуле.
5.5. Умножение и деление распределения на функцию.
Псевдофункции
5.5.1. Если f e C°°(Q), то отображение фь->/чр является непре-
непрерывным эндоморфизмом пространства 3)(Q); поэтому можно
определить произведение функции f и распределение X на Q
как результат применения к X отображения, сопряженного к
отображению фн-^fq). Другими словами, fX — это распределение
на Q, определенное равенством
для фЕЙ)@). Отображение (f, X)*->fX билинейно; оно непре-
непрерывно по обеим переменным в произведении топологии про-
пространства Фреше на C°°(Q) (п. 5.1.1) и сильной топологии в
<Ю'(О). Более того, пользуясь обычным правилом дифференци-
дифференцирования произведения ftp, получаем, что то же правило спра-
справедливо и для fX, а именно
откуда немедленно следует формула Лейбница.
5.5. Умножение и деление 421
Если на X наложить дополнительные ограничения, то произ-
произведение fX можно определить для более общих функций /. На-
Например, в случае, когда X — мера, произведение fX опреде-
определяется для любой функции /, локально интегрируемой по мере
Я. В § 5.8 мы введем понятие распределения конечного порядка
т (т 1> 0 — целое число); при этом окажется, что для гаких
распределений X произведение fX определяется для любой функ-
функции /eCm(Q), причем fX также есть распределение конечного
порядка, не превышающего т.
Проблема определения fX при возможно более широких
условиях представляет большой интерес как для квантовой фи-
физики, так и для чистой математики (см. Кениг [2] и Л.Шварц
[19]).
5.5.2. Теперь мы подошли к действию, обратному умноже-
умножению,— к делению, т. е. к решению уравнения
fX=At E.5.1)
где неизвестно 1е2);(й) и заданы А е SD'(Q) и функция f
на Q. Можно, конечно, искать решение в 2Dfm{&) (§ 5.8), но для
определенности и простоты мы ограничимся изучением случая,
когда на X не наложено никаких ограничений, a /eC°°(Q).
Из результатов § 5.6 будет видно, что эта задача носит ло-
локальный характер, по крайней мере поскольку речь идет о тео-
теоремах существования.
С другой стороны, в случае пф\ изложение значительно
усложняется (см. Шварц [1, стр. 121 —126]). Поэтому начнем
с одномерного случая.
5.5.3. Деление. Случай л = 1. Независимо от размерности п
если функция f нигде на Q не обращается в нуль, го решение
задачи тривиально. В этом случае feCoo(Q) и единственным
решением уравнения E.5 1) является распределение f~lA.
Допуская, что / обладает нулями, рассмотрим сначала слу-
случай, когда эти нули изолированы и каждый из них имеет конеч-
конечный порядок. Если это условие нарушается, то уравнение E.5.1),
вообще говоря, неразрешимо. Однако при п=\ указанное усло-
условие на практике редко нарушается, так что о нем много гово-
говорить не приходится. К сожалению, этого нельзя сказать о случае
п>\.
Итак, допустим, что нули функции / изолированы и имеют
конечный порядок. Локальный характер задачи позволяет свести
ее к случаю, когда Q содержит только один нуль конечного по-
порядка функции f. Совершая, если надо, сдвиг, можно считать,
что Q является окрестностью нуля и f = xmg, где т — порядок
единственного нуля х = 0 функции /, а функция g <= C°°(Q) нигде
б нуль не обращается. Так как деление на § всегда возможно,
422 Гл. 5. Распределения и дифференциальные уравнения
то мы можем ограничиться исследованием случая деления на
одночлен хту что в свою очередь сводится к повторному деле-
делению на х. Таким образом, мы пришли к рассмотрению простого
уравнения
хХ=А. E.5.2)
Если А —функция из C°°(Q), то разрешимость уравнения E.5.2)
будет следовать уже из разрешимости уравнения хХ=1.
Если уравнение E.5.2) разрешимо, то оно имеет бесконечное
множество решений. Разность S между двумя любыми реше-
решениями удовлетворяет однородному уравнению
xS = 0. E.5.3)
Если S удовлетворяет уравнению E.5.3), то S(xy) —0 для любой
функции cp^^)(Q). С другой стороны, если ^>^Ф(п) иф@) =
= 0, то ф^Хф, где ф — некоторая функция из «25(Q). В действи-
действительности функция ф однозначно определяется по функции г|) с
помощью соотношений ф@)=г|/@) и ®(х) =х-1\\-)(х) при хФО.
Соответственно с этим S(\|))=0 при г|)@)=0, и поэтому распре-
распределение S должно быть кратно 8 (мере Дирака в 0). Обратно,
любое S, кратно 8, S = cey является решением уравнения E.5.3).
Между прочим, следует отметить, что аналогичные рассужде-
рассуждения показывают, что решения уравнения xmS = 0 являются в точ-
точности распределениями вида S = Т срдре.
р <т
Теперь остается только рассмотреть вопрос о существовании
какого-нибудь решения уравнения E.5.2) и изучить его свой-
свойства. Если X — искомое решение, а ф и -ф удовлетворяют изло-
изложенным выше условиям, то Лг(г|))=Л(ф). Это равенство опреде-
определяет X на векторном подпространстве Я={фЕ^)(й): г[>@) =
= 0}c:iZ>(Q), которое является гиперплоскостью в 55 (Q). Из
явного вида зависимости г|) от ф следует, что limi|) = 0, если
1im<p = 0 (в обоих случаях в 3){п)). Поэтому если мы опреде-
определим X на Н соотношением X(ф) =Л(ф), то X будет непрерывно
в топологии, индуцированной в Н топологией пространства
3)(Q). Из теоремы Хана — Банаха вытекает, что линейная фор-
форма X обладает по крайней мере одним непрерывным продолже-
продолжением на 2D(Q), причем любое такое продолжение является эле-
элементом из 55'(Q), удовлетворяющим уравнению E.5.2). Таким
образом, существование решения доказано.
Путем повторного деления на х получаем, что уравнение
хтХ=А E.5.4)
обладает при заданном A&2)'(Q) бесконечным числом реше-
решений, любые два из которых отличаются на обобщенную функцию
5.5. Умножение и деление 423
типа 2 срдре (пустую сумму, как обычно, считаем равной
нулю).
Ниже мы увидим, как выразить явно некоторые решения
уравнения E.5.4) через распределения одного нового типа.
5.5.4. Деление. Случай п > 1. Предполагать, что нули функ-
функции / изолированы, здесь совершенно нереально, так как это не
имеет места даже в таких простых случаях, когда / — многочлен.
Тем не менее разрешимость уравнения E.5.1) может быть уста-
установлена для функций f, принадлежащих достаточно широким
классам, важным в приложениях.
Начнем с того, что деление возможно, когда f = xh. В этом
случае можно приспособить доказательство, проведенное выше
для случая п=\ и f = x.
Если можно делить на каждую из конечного числа функций,
скажем fi,..., fr, то можно делить и на произведение f=f\ • /2. • •
... fr.
Деление возможно на любую функцию feC°°(Q), обладаю-
обладающую тем свойством, что если у нее и есть нули, то /, d\fy..., dnf
не имеют общих нулей. В этом случае задачу можно решать
локально в окрестности каждого нуля функции / и локально из-
изменить координаты таким образом, чтобы задача сводилась к
делению на хп. Так, например, возможно деление на любой
многочлен вида /(х) = (сх+\х I2)"*1 ... (сг + \х |2)"Ч где Cj — от-
отличные от нуля числа.
Функции \х\т, вообще говоря, не удовлетворяют предыду-
предыдущим условиям, а это наиболее важные среди всех делителей.
Уже по одному этому стоит сделать значительное отступление
и ввести технический аппарат, необходимый для исследования
вопроса о делении на эти функции. Во всяком случае, применяе-
применяемая здесь техника приводит к новым важным примерам обоб-
обобщенных функций и заслуживает внимания сама по себе.
Что касается решения задач общей теории деления, см.
Лоясевич [1, 2] и Хёрмандер [4].
5.5.5. Конечные части расходящихся интегралов. Для просто-
простоты рассмотрим сначала одномерный случай (az=1).
Предположим, что т^-1. Поточечное деление единицы на
функцию х™ приводит к фукции х~т. Последняя не является
локально интегрируемой ни на каком открытом множестве, со-
содержащем начало координат, и, таким образом, не определяет
обобщенной функции ни на одном таком открытом множестве.
Несмотря на это, существует, как известно, бесконечное множе-
множество решений X уравнения хтХ=1. (Если 0<т< 1, то реше-
решениями служат функции х~т + се, где с — произвольная постоян-
постоянная.) Мы увидим далее, что при т> 1 все же можно определить
424 Гл 5. Распределения и дифференциальные уравнения
обобщенную функцию, связанную с функцией х~т. Мы будем
называть ее конечной частью функции x~m.
Неудивительно, что определение распределения, соответ-
соответствующего функции х~т, тесно связано с изучением (вообще
говоря, расходящегося) интеграла j Гтфф как функционала
от ф£Й). Разработка соответствующей техники для исследова-
исследования расходящихся интегралов, по-видимому, принадлежит Ада-
Адама р у [2], который применил ее к уравнениям с частными про-
производными.
Наша цель — изложить общие идеи для случая произвольной
размерности п. Однако в отдельных примерах часто бывает по-
полезным отдельно рассматривать случаи п=\ и п>\, так как
это значительно упрощает вычисления.
Обозначим через р строго положительную переменную, кото-
которую будем затем предполагать стремящейся к нулю. Иногда
нам будет удобно заменять р на ^ = log(l/p), так что / веще-
вещественно и стремится к +оо. Под б(р) будем понимать шар (от-
(открытый или замкнутый, безразлично) в Rn с центром в начале
координат и радиусом р. Наконец, положим А (Р) = Rn\S(p).
Начнем с исследования расходящихся интегралов типа
| fd\i, где функция / интегрируема на А (Р) для любого р > 0.
(Это означает, что интеграл f d\i Г расходится из-за плохого по-
поведения интегрируемой функции / лишь в начале координат.
При желании можно аналогично рассмотреть случай, когда f
ведет себя плохо в любой другой точке из Rn.)
Основная идея заключается в том, чтобы при некоторых огра-
ограничениях на / получить равенство
E.5.5)
Аф)
где /(Р) — функция специального вида, неограниченная при
Р-vO, в то время как предел F@) =lim F(P) существует и ко-
C>0
(
нечен. На компоненту /(Р) — бесконечную часть — будут заранее
наложены такие сильные ограничения, чтобы существовало не
более одного разложения вида E.5.5). При этом конечной
частью интеграла f d\i называют число ^@) и обозначают его
через
]) F Р.— первые буквы английских слов finite part (конечная часть).—
Прим. ред.
55. Умножение и деление 425
Распределение F.P./ мы определим затем с помощью соот-
соотношения
если правая часть этого равенства существует для каждого
фЕЙ)и представляет собой непрерывную функцию от ср.
Первое, что требует внимания, — это уточнение вида допу-
допустимых бесконечных частей /(Р) и проверка единственности раз-
разложения E.5.5). Мы .требуем, чтобы бесконечная часть /(C)
была конечной линейной комбинацией степеней |3~\ где % — ком-
комплексное число, ХФО, Re К > 0, и, возможно, логарифмического
члена log(l/P), т. е.
S(jL + Blog|, E.5.6)
где сумма конечна, а коэффициенты Ah и В комплексные. Если
ввести переменную / = log A/C), то
/(*"') = 2 Л***' +BU E.5.60
k
В соответствии с этим E.5.5) запишется в виде
ке^ +Bt + F{e'*\ p = e"'. E.5.50
Аф) k
Перейдем теперь к вопросу о единственности представления
E.5.5). Этот вопрос является хитро замаскированной формой
следующей задачи. Пусть задана функция g(t), определенная
для вещественных t и представимая по крайней мере одним спо-
способом, в виде
S Pr V) + ро V) + Bt + h @, E.5.7)
Г = \
где
A) a!>a2> ... >аЛГ>0;
B) РгУ)Ф0 (г = 0, 1, ..., Л^), Pr(t) является конечной ли-
линейной комбинацией функций е{& с вещественными % и в Ро
нет ни одного члена с ^ = 0;
C) В — комплексное число;
D) limft(f) существует и конечен.
Нужно доказать, что ar, Pr, В и h однозначно определяются
заданием функции g. (В действительности нам нужно лишь убе-
убедиться в единственности предела lim h(t). Ниже показывается,
426 Гл. 5. Распределения и дифференциальные уравнения
как вычисляются неизвестные элементы, причем нахождение h
оставляется .на самый конец.)
Подсчет неизвестных основан на следующем замечании. Если
P(t) есть конечная сумма вида 2^С/е15/' где gj — веществен-
вещественные числа и РA)ФО, то lim sup [ P (t) |>0. Чтобы доказать
это, воспользуемся формулой
2Т
Г 1
Пт * Г eWdt = \ Л
1 при 1 = 0,
при вещественном
(Здесь и в некоторых других местах мы будем часто писать dt
вместо d\x(t) — элемента меры Лебега на R1.) Из этой формулы
следует, что
2Г
lim f P{t)e-^dt
-^.4- ой J
Kf при l = lf для некото-
некоторого /,
0 при всех остальных
вещественных £.
E.5.8)
Таким образом, если бы lim sup |P (t) | = 0, то все Kj = O, что
привело бы к противоречию с условием P(t)
Продолжая определять неизвестные элементы в выражении
для g(t), заметим сначала, что ai — единственное веществен-
вещественное а, для которого
0<lim sup e~at \g(i) |< + oo,
где предел берется при t-++oo. Это следует непосредственно
из условий A)—D) и предварительного замечания, сделанного
непосредственно перед их формулировкой.
Определив таким образом ai, можно найти Pi. Действитель-
Действительно,
Теперь можно применить формулу E.5.8) к Р\ вместо Р, заме-
заметив, что
lim •
Это приводит к определению чисел £j и Kj в конечном разложе-
разложении 2 Я/в^' функции P\(t) и потому к определению самого Рх.
5.5. Умножение и деление 427
Если ai и Р\ известны, то а2 и Р2 определяются аналогично
по известной функции g{t) — e~aitPi(t).
Продолжая рассуждать таким образом, находим ai,..., ajv,
Л,..., PN. Так как P0 + h ограничена при t-+- + 00, то В опреде-
определяется из равенства
В= lim t^lg-Iie^
L
Воспользуемся еще раз формулой E.5.8), интегрируя функ-
функцию [g— 2—Bt], гДе 2 обозначает (уже определенную)
сумму S^Pf Так как (в силу B)) P(t) равно конечной
г
сумме SCge'*', гДе С0=0 и (в силу D)) Л(^) =L+o(l), то
lim jr [g — S"~ Bt\dt = L.
Число L — это именно то, что требовалось найти. Заметим, одна-
однако, что Ро (а потому и h) вполне определяются (опять в силу
E.5.8)) равенством
2Г
где | — отличное от нуля вещественное число.
Теперь можно обоснованно ввести формальное определение
конечной части интеграла.
Определение. Допустим, что функция f на Rn интегрируема
на А (р) для любого р > 0. Если имеет место разложение E.5.5),
где бесконечная часть /(Р) имеет вид E.5.6), и если существует
конечный предел lim F(P), то по определению
3>о
F.P. f
В качестве дополнения отметим, что при п—\ особый интерес
представляют конечные части F.P. J fd\i и F.P. J fd\i. Они
0 —оо
определяются как F.P. \ gd\i, где g=f на @, +<х>), g" = 0 на
(—оо,0) и g = 0 на @, +оо), g = f на (—оо, 0) соответственно.
428 Гл. 5. Распределения и дифференциальные уравнения
Замечания. Очевидно, что если f интегрируема, то
F.P. [ I d\i существует и совпадает с J f d\i. Вообще если су-
существует и конечно главное значение в смысле Коши 1)
P.V. f/d|i*lim f/ф,
то конечная часть существует и имеет то же значение. При п — \
имеет место формула
+ оо О
F.P. J/dii-F.P. J fdii + F.P. J fd\i9
0 —oo
если оба члена в правой части существуют.
5.5.6. Один простой признак существования F.P. \ fdji. Всюду
ниже будем считать, что функция / интегрируема на Л(р) для
любого р>0. Пусть далее для некоторого (а поэтому для
любого) числа ро>О справедливо равенство
f=%Ap.KxPr-* + gt E.5.9)
р, л
где г = \х\ и g интегрируема на Вф0). В этом выражении по
существу всегда можно положить р0 = 1 и допустить, что сум-
суммирование распространяется только на пары (/?, Я), удовлетво-
удовлетворяющие условию Ipl^Re^ — n. Действительно, что касается
последнего замечания, то при Re Л — |р\ < п член хрг~1 интегрируем
на В = 5A), так как | xpr~K |^riPl"ReX, и потому его можно от-
отнести к функции g. Если 0<р<р0, то из E.5.9) получаем
А®) А (Ре) Р<г<[3о
C) £3
А (|3о)
Величина j fd\i постоянна, а интеграл J gd\i стремится
A (|3o) P<r<C0
к конечному пределу \ gd\i при р->0. Поэтому остается рас-
3
') P. V.— первые буквы английских слов principal value (главное зна-
значение). — Прим. ред.
5.5. Умножение и деление 429
смотреть интеграл J Г^ ... 1 ф, который является конеч-
конечной линейной комбинацией интегралов вида
J xprkdix(x). E.5.10)
Мы увидим, что эти интегралы как раз и определяют вид беско-
бесконечной части.
Обозначим через S единичную сферу |#| = 1 в Rn, и пусть
а — поверхностная мера на ней. Хорошо известна формула
Зо
J F(x)dvL(x)~\ rn~* drJF (rу) da (у)
3<r<3o 3 5
(она легко выводится, скажем, для непрерывных функций F).
Из нее непосредственно следует, что интеграл E.5.10) равен
Зо
р J Л-\р\-п + \ »
з
где
" ypda(y).
Пренебрегая множителем WPi получаем интеграл, который при
р-^0 либо имеет конечный предел, либо обладает логарифми-
логарифмическим полюсом, либо ведет себя как A/C)^~ |0'~n в зависи-
зависимости от того, будет ли Re X— |р|—п < 0, =0 или > 0.
Отсюда следует, что разложение E.5.5) возможно и чго
при сделанных предположениях относительно f существует
F. P. fd\i. При л=1 справедлив несколько более общий
аналогичный результат (в правой части E.5.9) можно добавить
степени х~т> где т — натуральное число). Доказательство почти
дословно повторяет только что приведенное.
Для наиболее простых функций f легко найти разложение
E.5.9) и тем самым представить F. P. J f d\i в виде сходящихся
интегралов (подсчет которых, конечно, также может быть за-
затруднительным).
5.5.7. Распределения-псевдофункции. Пусть /-—функция,
удовлетворяющая условиям п. 5 5.6. Тогда, как легко видеть,
если f допускает разложение вида E.5.9), го всякая функция
вида /ф (феО) обладает тем же свойством. Более того, если
430 Гл. 5. Распределения и дифференциальные уравнения
к «g-части» в E.5.9) отнести все локально интегрируемые сла-
слагаемые, то нетрудно показать, что суммирование распростра-
распространится не более чем на конечное множество пар (/?Д), не зави-
зависящих от ф. Соответствующие коэффициенты APtXi как это будет
доказано в дальнейшем, являются конечными линейными комби-
комбинациями частных производных (Э^ф(О) порядка |/?|<jV, где N
зависит только от /. Сформулированные утверждения легко про-
проверить, если воспользоваться формулой Тэйлора
ф(*)- 2 аМо^ + оОяГ1).
\P\<N
где N— любое натуральное тело, а через р\ обозначается выра-
выражение Р\\ Р2\ ...Put-
С помощью этой формулы можно установить, что конечная
часть F.P. / fcpd\i существует для каждого фЕЙ) и допускает
представление в виде
—liml" J
/фф-
Для каждого Р > 0 выражение в квадратных скобках является
линейным функционалом по ф, который, очевидно, определен и
непрерывен на SBN =*3N(iC) (§ 5.8). Так как 2>N — бочечное
пространство, то точечный предел этих линейных форм — функ-
функционал фь-^F. P. J/чрф — непрерывен и линеен на55^. Это озна*
чает, что отображение
J E.5.11)
есть распределение на Rn порядка не выше N. Это рас-
распределение обозначается через F.P./. Такое же обозначение упо-
употребляется во всех тех случаях, когда линейная форма E.5.11)
определена и непрерывна на 3). При этом соответствующее рас-
распределение на Rn обозначается через F.P./. Полученные таким
способом распределения называются псевдофункциями.
В одномерном случае (лг = 1) можно (при соответствующих
ограничениях на f) определить аналогичным образом псевдо-
оо
функции F.P.(/)*>0 и F.P. (/)*<() с помощью формул F. P. J /<рф и
0
F. P. j /ф ф, соответственно.
5.5. Умножение и деление 431
5.5.8. Пример. Вычислим F.P.jr"w в одномерном случае, где
т — натуральное число. Если ф£Й), то при малых х имеет ме*
сто разложение
где g — интегрируемая функция. Поэтому при |3 > О
Mm-p-l
Аф)
где F(p) имеет конечный предел при р-^0. Таким образом,
|1о
Аф)
E.5.12)
что и представляет собой явное выражение, определяющее
¥.V.x~m.
Если в E.5.12) заменить ф на -ф=л:тф, то сумма и слагаемое,
содержащее log-тг, тождественно обращаются в нуль при р > 0.
Кроме того,
J лГтг|) dx = j q>dx
АФ) Аф)
стремится к J фйл; = (ф, 1) при р->0. Таким образом,
(л:тФ, Р.Р.л:~т) = (ф, 1>
для любого фЕ®, откуда следует, что
A:mF.P.Arm=l.
Другими словами, X = F.P.A:-m есть решение уравнения
Аналогичными рассуждениями можно доказать, что (незави-
(независимо от размерности п) Х = ¥.Р.г~т есть решение уравнения
5.5.9. Пример. В случае п=\ часто удается подсчитать ко-
конечные части с помощью повторного интегрирования по частям.
В качестве примера* докажем формулу
FtPfje-,e-ilMl£lI. E.5.,з)
432 Гл. 5. Распределения и дифференциальные уравнения
Если ipei1, то
dx С dx
В каждом из интегралов справа произведем интегрирование по
частям.
После некоторых преобразований получаем формулу
Аф)
ОО
- J q/(- A:)l
y—J
при р—>0. Таким образом,
или
(Ф, F.P.x-)=-
что эквивалентно равенству E.5.13).
Дословно повторяя предыдущие рассуждения, можно пока-
показать, что
~ F. Р. х~т = - mF.P. jc"-1
dx
для любого натурального числа /п. Последнее равенство пред-
представляет собой обобщение известной формулы дифференциро-
дифференцирования степени с положительным показателем.
5.5.10. Пример. При п > 1 часто интегрирование по частям
по единственной переменной можно заменить применением фор-
формулы Грина к области /1(C). (В действительности, поскольку
подинтегральное выражение содержит в качестве множителя
элемент из Ф, естественно применять формулу Грина к шаро-
шаровому слою S(P') ПЛ (|3) ) Этот прием часто применяется для
подсчета конечных частей, в особенности для функций, завися-
зависящих только от г= 1x1,
5 5. Умножение и деление 433
Допустим, что фей) и функция F принадлежит, скажем,
классу С2 на Rn\{0}. Тогда формула Грина (полученная в
п. 4.15.14) может быть записана в виде
А О) 5 <|3)
где через 5(C) обозначена сфера с центром в нуле и радиусом C,
а через ар — поверхностная мера на ней. Если частные произ-
производные по г обозначить штрихами, то это последнее равенство
примет такой вид:
J (Ф AF - F Дф) ф = - Г J [Ф № F' № - F Ш Ф' (ру)] Лт (у),
А (Р) 5
где S = SA) и (т = (т1. В частности, если F зависит только от г,
то
(Ф AF - F Дф) ф = - Р*-1/" (Р) J
/(у): E.5.14)
Выбрав подходящим образом функцию F = F(r), можно ис-
использовать E.5.14) для подсчета конечных частей различных
простых функций от г, которые не локально интегрируемы.
Пусть, например, нужно подсчитать F.P.r~2. Если п > 2, то
г~2 локально интегрируема и F.P.r-2 = r~2. Мы укажем прием,
пригодный для любого п. Первый шаг заключается в подборе
функции Т7, удовлетворяющей условию AF = r~2 при гфО (опера-
(оператор Лапласа понимается здесь в классическом смысле). Если
F зависит только от г, то AF = r~~n+1 -r—(rn~lF)y поэтому в каче-
качестве F можно взять функцию, определенную следующим обра-
образом:
(п — 2)~1logr при
-jlog2r при n = 2.
Эта функция локально интегрируема.
Применив E.5.14) к выбранной таким-образом функции Fy
получим
А C) А ф)
где
/ (Р) = р*-1/?' (р) J Ф фу) da (у) - р*-^ (р) J Ф' фу) do (у).
434 Гл. 5. Распределения и дифференциальные уравнения
Если п>2, то $п~гР'ф) и р/|~1/7(р) стремятся к 0 при р->0.
Поэтому
2 1 E.5.15)
Здесь лапласиан понимается в смысле теории распределения.
Если я = 2, то p/2-1f/(P)=-log(l/p) и p/2~1f(p)->0 при
р-»0, поэтому
/(РН - log j . J
Таким образом,
log
Аф) S
= log ■«-' Ф (°) f da{y)+ [ F- Дфй[х + оA).
p j J
Так как ] de = 2я, то
(Ф, F.P.r-2> = lim Г f ф-^--2яф@)log-] =<Аф, F>, E.5.16)
и поэтому
F.P.r~2= ^A(logV) (л = 2). E.5.17)
Здесь опять лапласиан понимается в смысле теории обобщен-
обобщенных функций. Формула E.5.16) позволяет удостовериться в том,
что г2 F.P. г~2= 1.
Другие примеры читатель может найти в книге Гельфан-
да и Шилова [2, стр. 62—132].
5.6. Сужение распределений; локализация;
носитель распределения
Пусть Q и Q'— открытые подмножества в Rn и йс Q'. Пред-
Предположим, что X^SD (Q). Мы хотим определить сужение X на
Q. Для этого заметим, что каждая функция фЕ2)(Й) обладает
естественным продолжением до элемента из ^(£У). Таким про-
продолжением служит функция фг на Q', равная ф на Q и нулю во
всех остальных точках множества Q'. Тогда фн-^ф' является не-
непрерывным линейным отображением пространс!ва^)(Й) bS)(Q/).
Образом пространства 2)(Q) относительно этого отображения
является множество тех функций из ^)(£У), носители которых
содержатся в Q. Оператор сужения распределений с £У на Й по
определению сопряжен к отображению cpi—>ц>'. Таким образом,
5.6. Сужение распределений 435
сужение X\Q есть распределение на Q, определенное пра-
правилом
для фе25(Й). Отображение Х*->Х\п линейно и непрерывно
(как в слабых, так и сильных топологиях в 2)(Q') и 3){п)).
Пусть X &2)'(Q')\ будем говорить что X равно нулю на Q, и
писать «Х = 0 на Q», если X|Q = 0, т. е. если (ф, Х)=0 для каждой
функции ф£Й)(йА), носитель которой содержится в Q. Это со-
соответствует соглашению для случая мер (§ 4.9; напомним, чтр
(§ 5.2) 2)(Q) плотно в!(Й)),
Обратная задача — восстановление распределения по его
локальным составляющим — решается в терминах открытых по-
покрытий и разбиений единицы. Каждое открытое множество
QczR" (как и всякое подпространство в Rn) паракомпактно и
потому нормально (п. 0.2.20). Будучи локально компактным, Q
обладает тем свойством, что в каждое его открытое покрытие
можно вписать покрытие, состоящее из открытых относительно
компактных подмножеств в Q. Пусть (Q*)—произвольное от-
открытое покрытие множества Q. В силу только что приведенных
двух свойств множества £2 существует такое локально конечное
открытое покрытие (Qj) множества £2, что каждое из множеств
Qy относительно компактно в Q и содержится в некотором Qt-.
5.6.1. Предложение. Пусть Q — открытое множество в Rn и
(Qt) —некоторое открытое покрытие множества Q. Тогда суще-
существует такое семейство (ср^) функций из 2)(Q), что
(a) ф;>0 и supp 9j содержится в некотором Йг-;
(b) сумма 2 ф; локально конечна1) и всюду на Q равна
единице.
Если покрытие (Йг) локально конечно и каждое из множеств
п{ относительно компактно в й, то можно считать, что множе-
множество индексов функций ф-/ такое же, как и у (Q*).
Доказательство. Из сделанных нами предварительных
замечаний следует, что всегда можно найти такое локально ко-
конечное покрытие (Qy), что каждое Q'f относительно компакт-
компактно в Q и Qy содержится в некотором Й*. Так как Q параком-
паракомпактно, то мы можем найти такое открытое покрытие (QJ') с та-
таким же множеством индексов, как и у (Q^), что Q" czQJ. В силу
нормальности Q и леммы Урысона (п. 0.2.12) для каждого / су-
существует такая непрерывная функщш а;- на Q, что O^c%j<lr
а;=1 на О/'иа/ = 0 вне п'г Так как Qy' и граница множества il]
1) См п. 0.2.20. — Прим. перев»
436 Гл. 5. Распределения и дифференциальные уравнения
компактны и не пересекаются, го они находятся на положитель-
положительном расстоянии 8j друг от друга. Заменим функцию otj ее регу-
регуляризацией |3j = ct;-*rj, где функция rj^2)(Rn) положительная
ее носитель содержится в шаре с центром в нуле и радиусом у б/,
причем Гг#ф=1. Тогда pi^iZ5(Rn), 6j > 0 на й'' и носи-
тель функции р^ содержится в Q'czQ.. Сумма 2 Р/» таким обра-
образом, локально конечна на Й и всюду строго положительна; в
силу локальной конечности 2jP/^^>(R )• Функции фу =
отвечают всем поставленным требованиям. 1
Семейство (ф^) вида, описанного в предложении 5.6.1, назы-
называется разбиением единицы в @)(Q), соответствующим покры-
покрытию (Qt). Такие разбиения единицы используются при решении
задачи восстановления обобщенной функции по ее локальным
составляющим.
5.6.2. Предложение (принцип локализации). Пусть
Й — открытое множество в Rn и (Йг) — открытое покрытие мно-
множества Й. Предположим, что (Xt)— такое семейство распреде-
распределений, что Xi^2)'(Qi) и Xi\Qi\)Qj = Xj\Qi(]Qj, если пересечение
ЙгПй?- непусто. Тогда существует единственное распределение
X на й, такое, что Аг|Йг=Хг для каждого L
Доказательство. Пусть (Q^)—такое локально конечное
открытое покрытие множества й, что каждое Й^ относительно
компактно в Й и Q/jczQi при некотором и Определим распреде-
распределение Х'} на й^, положив Х'; = Х{ |й, для всякого такого ин-
индекса £, что ЦзэЙу. Из предположенной согласованности се-
семейства (Х{) следует корректность введенного определения. Вы-
Выберем такое разбиение единицы (qpj) в Й)(Й), что suppqpjCi^
для каждого /. Любую функцию ф из 3)(Q) можно представить
в виде суммы
Ф = 2 (фф/)»
где число слагаемых справа конечно. Следовательно, если рас-
распределение X существует, то
X (ф) = 2 X (фф/) = 2 Х] (ф/ф),
/ /
откуда вытекает, что Х~ однозначно определяется заданием се-
семейства (^г-).
5.7. Обобщенные функции с компактными носителями 437
Обратно, эта формула определяет распределение X на Й.
Если supp(pc:Qt, то suppqp7(pc:k2 ЛИ', и так как ^ = ZJQ'.,
то X'j (ф/ф) = А'Дфф). Таким образом, равенство
Xt (Ф) = 2 ^ (ф/ф) = S а:; (ф/ф) = * (Ф)
справедливо для любой функции фЕ^(й), носитель которой
содержится в й*. Другими словами, Xi = X\Qh что и требовалось
доказать. |
5.6.3. Следствие. Пусть Й — открытое множество в Rn и
(Qi) — произвольное семейство открытых подмножеств в Й. Если
распределение X на Q равью нулю на каждом йг, то оно равно
нулю на (jQi. В частности, для каждого распределения Хе
i
E^ffi) существует наибольшее открытое подмножество
U cz Й, на* котором X равно нулю.
Относительно замкнутое множество F = Q\U называется
носителем распределения X и обозначается через supp X.
Читатель, вероятно, заметил, что если X — мера Радона на
й, то это определение носителя согласуется с тем, которое при-
приведено в § 4 9.
Необходимо отметить следующие соотношения:
supp fZc:(supp /) П (supp X).
Кроме того, значение X (ф) зависит лишь от сужения функ-
функции ф на любую окрестность носителя supp X, т. е. X (фь) = X (ф2У,
если функции ф! и ф2 совпадают на некоторой окрестности но-
носителя распределения X. Если сеть распределений (Х() слабо
сходится к X, причем supp Хгар для всех /, где F — относи-
относительно замкнутое подмножество в Q, то supp X a F.
5.7. Обобщенные функции с компактными носителями
Обобщенные функции из <3>'(й), имеющие компактные носи-
носители, можно рассматривать как элементы сопряженного к про-
пространству С°°(й), наделенному топологией, описанной в п. 5.1.1,
относительно которой С°° (Q) — пространство Фреше.
Действительно, метод регуляризации показывает, что &(Q)
плотно в С°°(Й). Таким образом, любая непрерывная линейна^
форма L на С°°(й) вполне определяется своим сужением X на
^(й), которое является элементом из ЗУ (Q). Непрерывность
формы L означает, что существуют такое компактное множе-
множество /(cQ и такое целое число m ^ 0, что
|L(/)|<constsup{|dp/U)|: x<eeK, lp
438 Гл. 5. Распределения и дифференциальные уравнения
для feC°°(Q). Следовательно,
| JT (<р)|< const sup {\дР у(х)\: х(=К* I р\<т} = const Wm(<P)
для фе2)(Й). Отсюда следует, что supp Xcz К и распределе-
распределение X имеет порядок -<т (§ 5.8). Обратно, если распределение
Xg2);(Q) имеет своим носителем компактное множество /(, то
X обладает естественным непрерывным продолжением на про-
пространство C°°(Q), например можно положить
X(f)=X(af)
для всех feC°°(Q), где а — любая функция из ®(Й), равная
единице на некоторой окрестности множества /С (В пределах
этого класса выбор а несуществен в силу предположения
supp Ic /С)
Если Ig2)'(Q) обладает компактным носителем /СсЙ, то
X есть сужение на Q распределения Y^3)/(Rn)i носитель кото-
которого есть /С. Действительно, нужно только положить
для каждого cp^2)(fln), где ф* — любая функция из (),
совпадающая с ф на некоторой окрестности множества /С На-
Например, мы можем раз и навсегда выбрать функцию aG2)(Q),
равную единице на некоторой окрестности множества /С, и затем
положить ф* = а(ф|Й). Тот факт, что распределения на Q, обла-
обладающие компактным носителем, могут быть таким способом
продолжены до распределений на Rn с тем же компактным но-
носителем, часто упрощает работу с такими распределениями.
5.8. Распределения конечного порядка
Пусть т>0 — целое число и S)m(Q)— множество таких
функций фнайс компактными носителями, что все производные
<Э^, для которых \p\Km, непрерывны. Таким образом, 2D°(Q) =
?(&) и й5(Й)=П^т(Й). Последовательность (фп) изЗ>т(п)
>0
называется сходящейся к нулю в 2)т(п), если носители функ-
функций фп лежат в некотором компактном множестве /С, не завися-
зависящем от п, и ПтдРфп=0 равномерно на Q для каждого р с
\р\<т.
С помощью регуляризации легко видеть, что 3D(Q) плотно
в 3)m(Q). Поэтому пространство, сопряженное к 2Dm(Q), можно
отождествить с некоторым подмножеством в 2)'(п), т. е.
Распределение X из £D' (Q) принадлежит 3)'m(Q) тогда и только
тогда, когда оно непрерывно на 3)(Q) в смысле введенного по-
понятия сходимости в 0m(Q). Другими словами, X принадлежит
5.8. Распределения конечного порядка 439
2)'m(Q) в том и только в том случае, когда для каждого ком-
компактного множества KczQ существует такое число ск^-0, что
для всех фЕ^(Й) с носителем в К. Про такие распределения
говорят, что их порядок не превосходит т. Будем говорить так-
также, что порядок распределения X равен т, если X есть рас-
распределение порядка, не превосходящего т, но не является рас-
распределением порядка, не превосходящего т\ для т! < т.
Так, например, распределения на Й порядка 0 (или, что то
же, порядка, не превосходящего 0) совпадают с мерами Радона
на Й. Порядок распределения д^гх (где х — произвольная точка
в Й) равен \р\. Если порядок обобщенной функции X не пре-
превосходит т, то порядок ее производной д?Х не превосходит
т+\р\. Если порядок распределения X не превосходит т и
feCm(Q), то определено распределение fX и его порядок не
превосходит т.
Пусть <S^(Q)= (J £$'m(Q)— множество обобщенных функ-
ций на й, имеющих конечный порядок. На Й всегда существуют
обобщенные функции, порядок которых не конечен. Например,
пусть (хп) — последовательность точек в й, не обладающая пре-
предельной точкой в й, и (сп)— произвольная последовательность
ненулевых чисел. Тогда ряд 2 спдРпгХп сходится в З)'(п)
п
(слабо или сильно, не имеет значения), и если sup| рп\= + оо,
то порядок суммы — распределения X — бесконечен.
Как было замечено в § 5.7, любое распределение с компакт-
компактным носителем имеет конечный порядок. Ниже мы приведем ин-
интересную и важную структурную теорему для распределений
конечного порядка. В частности, эта теорема применима к рас-
распределениям с компактными носителями. Более того, она приме-
применима к сужениям любого распределения iG^'ffi) на относи-
относительно компактные открытые множества в Й. Из этой теоремы
следует, что всякое распределение ХеЙ'(й) локально (хотя,
возможно, и не глобально) равно конечной сумме производных
от мер Радона.
5.8.1. Теорема. Пусть IgS)%(Q). Тогда X равно конечной
сумме
, % E.8.1)
где av — меры Радона на Й. Если, кроме того, X обладает
компактным носителем /С, то можно считать, что suppap содер-
содержатся о некоторой заранее заданной окрестности множества /(.
440 Гл. 5. Распределения и дифференциальные уравнения
Обратно, любая такая конечная сумма производных порядков
\p\^Cm oj мер Радона является элементом пространства 2)'m(Q).
Доказательство. Последнее утверждение очевидно.
Остальные утверждения теоремы докажем в два этапа.
(а) Вначале допустим, что X обладает компактным носите-
носителем /Сс: Q. Тогда (ср. с § 5.7) если U — компактная окрестность
множества /С, то X удовлетворяет неравенству
\Х (Ф)| < coust Num (Ф) (Фе=^ (Q)). E.8.2)
Пусть s — число наборов /?, составленных из п неотрицательных
целых чисел с \р\ -^ш. Обозначим через Е произведениеs бана-
банаховых пространств С0(Й) (см. упр. 4.45). Относительно топо-
топологии произведения Е представляет собой банахово простран-
пространство. Рассмотрим непрерывное линейное отображение /: iZ)(Q)-*-
-v£, определенное с помощью равенства /ф= (дрф)| Р |<т.
В силу соотношения E.8.2) непрерывный линейный функционал
| определяется на подпространстве E0 = J3)(Q) формулой
|(/ф)=Х(ф). Из теоремы Хана — Банаха и упр. 4.45 следует
существование такого семейства (ар)\ р\^т ограниченных мер
Радона на Q, что supp av с= U и ?• является сужением на Ео ли-
нейнего функционала
I р\ <т
Другими словами,
для всех фб2)(й), т. е.
\р\<т
(Ь) Переходя к общему случаю, рассмотрим на Q разбиение
единицы (Ui)i<=T, образованное такими функциями ^g2)(Q),
что supp щс1п0 где относительно компактные открытые мно-
множества Qi составляют локально конечное покрытие множества
п{ (см. предложение 5.6.1). Теперь к каждому распределению
щХ, i^I, можно применить доказанную часть (а) нашей тео-
теоремы и получить
2
\p\<m
где a,itP — такие меры на Й, что supp аг-, v с: Й*. В соответствии
с этим
5.8. Распределения конечного порядка 441
Так как а*, р с: п{ и покрытие (£2$)ге=7 локально конечно, го
сумма Д] aitf)m локально конечна, поэтому
р 2 *, р
является мерой на Q. Таким образом, мы снова приходим к фор-
формуле E.8.1) для X, что и требовалось доказать. I
5.8.2. Замечания и дополнения. Иногда оказываете^ полез-
полезным (см., например, теорему Л' из п. 5.17.1) иметь аналог тео-
теоремы 5.8.1, в котором меры ар заменяются гладкими функциями.
Интересно иметь и такие аналоги этой теоремы, применимые
к любому распределению на Q. Коротко остановимся на этих
вопросах.
A) Пусть т и k — неотрицательные целые числа и
X ^2)'m(Q). Мы утверждаем, что распределение X представимо
в виде конечной суммы производных порядка не более
m + k(n + 2) от функций из Ck(Q).
Для доказательства этого утверждения в силу теоремы
5.8.1 достаточно рассмотреть случай, когда Х = а является ме-
мерой и т = 0.
Вначале допустим, что а обладает компактным носителем
KczQ, тогда (ср. с E.8.2))
|a((p)|<constsup|cp| (ф€=«2Г(О)) E.8.3)
к
(здесь в силу специальных свойств распределений, порожден-
порожденных мерами, можно "вместо sup|qp|, где U — окрестность мно-
множества /С, писать просто sup|qp|). Обозначим через б диффе-
дифференциальный оператор д\ ... дп; тогда из элементарной фор-
формулы
*1 *п
Ф(л:)= J ..'.
—оо
вытекает, что
соотношение E.8.3) влечет неравенство
|а(ф)| < const || 6<р Hi (фе2)@)).
Из этого неравенства, георемы Хана — Банаха и теоремы
4.16.1 следует существование такой функции geL°°(Rn), что
т. е.
a = 6g на Q.
442 Гл. 5. Распределения и дифференциальные уравнения
Заменим g на ug, где функция и из 2)(Q) равна 1 на некоторой
окрестности множества К и нулю вне заданной окрестности U
множества /С. Повторное применение формулы Лейбница приво-
приводит к равенству
а= 2 dqgq на Q, E.8.4)
\q\<m
где функции gq принадлежат L°°(Rn) и обращаются в нуль вне
U. Заданному набору q поставим в соответствие функции
fq,r (r = 0, 1>2,...) с помощью формул
q,r-id\i (r=l,2, ...).
Заметим, что каждая из функций fQt r обладает носителем,
содержащимся в множестве вида Ln, где L — ограниченный
снизу интервал в R. Легко проверяется, что /7>reCr(Rrt), 6fqt0 =
= gq и 6fq,r = fq,r-i (r=l, 2, ...)• В частности, gq =
так что E.8.4) может быть переписано в виде
Ц %tk. E.8.5)
Заменим, наконец, fq через vfq, где функция v из ()
равна 1 на некоторой окрестности множества /С, причем supp v
содержится-в заданной окрестности U множества /С. Применяя
еще раз формулу Лейбница, получим из E.8.5)
%, E.8.6)
где функции fp принадлежат C°°(Rn) и носитель функции fp
содержится в заданной окрестности U множества /C = suppa.
Мы доказали требуемый результат в предположении, что supp a
компактен.
Отказываясь от этого предположения, рассмотрим разбиение
единицы {Ui)iei, такое же, как и на этапе (Ь) доказательства
теоремы 5.8.1. Тогда в силу E.8.6) имеем
2 д%р, E.8.7)
t
где t = n(k + 2)yfi)P<=Ck(Rn) и suppfi р <= Q,. Сумма 2^,Р=
L
Р
5.8. Распределения конечного порядка 443
локально конечна на Й, и потому fp^Ch(Q). Таким образом,
из E.8.7) следует, что
а= 2и,а= 2 д%, E.8.8)
что и требовалось доказать.
B) Предыдущие результаты могут быть распространены на
любое распределение X^SD(Qt) с тем лишь исключением, что
конечные суммы, вообще говоря, заменяются локально конеч-
конечными суммами, содержащими производные сколь угодно высо-
высокого порядка.
Если Xg^JQ), to из части (а) доказательства теоремы
5.8.1 следует, что
щХ= 2 дрщ
где щ — такие же функции, как и в части (Ь) доказательства
теоремы 5.8.1, а аг->р— такие меры на Й, что supp ait Р с: Q{. Со-
Совокупность неотрицательных целых чисел т{ может, вообще
говоря, быть неограниченной (i пробегает множество /). Таким
образом, имеем
2
{ ч
l|pl<mi
где, как и выше, суммы 2 Щ, Р локально конечны и пред-
ставляют собой меры на Q. Кроме того, семейство. (ар) также
локально конечно. (Если Н — компактное подмножество в Q,
пересекающее множества suppap для бесконечного числа раз-
различных значений р\, р2, ... индекса /?, то должны существовать
такие индексы iu t2, ... из /, что m^^lp/l и Н пересекает
множества supp a^, P/c= Qijt Так как \pj\ должно неограниченно
возрастать вместе с /, то множество {ij\ /=1, 2, ...} неограничен-
неограниченно, что противоречит локальной конечности системы Qt.) Итак,
J = 2<3Pv E-8-9)
р
т. е. мы выразили X через локально конечную сумму производ-
производных от мер av на Q.
Продолжая, можно представить каждую из мер ар, входя-
входящих в выражение E.8.9), в виде конечной суммы производных
от функций, как в E.8.8), т. е.
E.8.10)
444 Гл. 5. Распределения и дифференциальные уравнения
где t = n(k + 2)9 gp,q^Ck(Q) и suppgp,<,czsuppap. Из формул
E.8.9) и E.8.10) следует, что
X=%d'fn E.8.11)
г
где
fr = 2 gpt q>
причем суммирование в последнем выражении распространяется
на те пары (р, q), для которых p + q = r и |<7| ^ я(&4-2). Таким
образом, supp/vcz(J suppap, где объединение распространяется
на те наборы /?, для которых p=-r — q при некотором q, удовле-
удовлетворяющем неравенству \q\^,n(k + 2). Отсюда вытекает, что
frGCft(Q) и сумма в правой части равенства E.8.11) локально
конечна (каждое компактное подмножество в Q пересекает не
более чем конечное число множеств suppfr). Поэтому E.8.11)
представляет собой выражение распределения X в виде локально
конечной суммы производных (порядки которых, вообще говоря,
сколь угодно велики) от функций из Ch(Q).
5.9. Восстановление распределения по его первым производным
Пусть X — распределение на Q} и пусть каждая частная про-
л v дХ
изводная okX = -^- задана, а именно равна распределению
Ак на Q. Что в этом случае можно сказать об X? При каких
условиях система уравнений dkX = Ah (l^k*Cn)t где Ah за-
заданы, разрешима относительно X?
Что касается первого вопроса, то практически наиболее ва-
важен и интересен случай, когда про Ak известно, что они яв-
являются функциями fk (локально интегрируемыми на Q). Наряду
с явным способом решения системы dkX = fk (I < k <л) нас
интересует также, будет ли каждое решение X этой системы
функцией. Рассмотрим сначала случай, когда fk непрерывны.
5.9.1. Предложение. A) Если распределение X на области Q
удовлетворяет уравнениям
то X — постоянная функция на Q.
B) Если распределение X на п удовлетворяет уравнениям
5.9. Восстановление распределения 445
где fu — непрерывные функции на Q, то X — такая функция
fGC'fQ), что dhf=fh (l^-k^Cn) в обычном смысле. Следова-
Следовательно,
X
/М-/(*о)= \[fxdt,+ ... +fndtn],
х0
где интеграл берется по любой спрямляемой дуге в Q, соединяю-
соединяющей точки х0 и х.
C) Если все частные производные д^Х распределения X на
Q являются непрерывными функциями на Q, то X — функция
класса C°°(Q).
Доказательство. Начнем с утверждения B) Рассмотрим
покрытие области Q открытыми шарами В. Пусть а — центр
шара В. Определим функцию gB на В соотношением
г1
ёв(х)= J f\{tb x2> .... xn)dtx +
+ J hfau '2. х3, ..., xn)dt2+ ... + J fn(au ..., ая_1э tn)dtn.
Все пути интегрирования предполагаются лежащими в б, а по-
потому ивЙ. Ясно, что функция gB непрерывна. Можно показать
(см., например, Л. Шварц [1, стр. 62—63]), что g^Cl(B) и
dhgB = fk на В. (Мы не приводим здесь подробного доказатель-
доказательства этого утверждения, так как из описанного ниже в п. 5.11.1
общего метода следует другое доказательство утверждения B);
см., например, E.11.2) и E.11.5).) Если выполняется утвержде-
утверждение A), то разность св = Х — gB постоянна на В. Тогда fB = gB +
+ св^. С1 (В) и, кроме того, \в~!вг—^ всюду на пересечении
ВПВ\ если ВПВ'Ф0. Отсюда следует, что fB являются суже-
сужениями на В такой функции f^C{(Q), что X = f на Q, что и тре-
требовалось доказать.
Так как dhf = fh всюду (т. е. в каждой точке из Q), то функ-
функция f восстанавливается интегрированием выражения [f\dt\ + ...
... + fndtn] вдоль произвольных спрямляемых дуг в Q.
Остается доказать утверждение A). Предположим, что
X^l2D'{Q) удовлетворяет на Q уравнениям dkX = 0 (k — 1,
2, ..., п). Пусть со — произвольное подмножество в Й, являю-
являющееся произведением п открытых интервалов в R1, и пусть
Х^=Х\и>. Тогда, очевидно, dkX(d=0, &=1,2,.. ,'п на со. Те-
Теперь достаточно доказать, что Ха — постоянная функция на со,
так как тогда (покрывая область Q множествами вида со) полу-
получим, что функция X постоянна на Я. Таким образом, мы свели
446 Гл. 5. Распределения и дифференциальные уравнения
все к случаю, когда сама область Q является произведением
открытых интервалов в R1.
Условия dkX = 0 на Q, й=1, 2, ..., п, означают, что ^(ф)=0,
если ф£®B) имеет вид
п
Ф== ^j ^^ф^ E.9.1)
для некоторых ф^е2)(й). Очевидно, что всякая функция та-
такого вида удовлетворяет равенству
)ф = 0, E.9.2)
где \х — мера Лебега на Rn. Если верно обратное утверждение,
то Х(ц))=6 для всякой функции фб2)(Й), удовлетворяющей
условию 1q (ф)=0, где Ь — постоянная функция на Q, все зна-
значения которой равны единице. Отсюда следует, что Х = с«1о,
где с — некоторое число, что и требовалось доказать.
Мы предоставляем читателю доказать, что из E.9.2) выте-
вытекает E.9.1), если функции принадлежат S)(Q), где Q — произ-
произведение п открытых интервалов в R1. Этот результат очень легко
доказать в случае, когда м=1. Общий результат получается с
помощью индукции по п.
Утверждение C) следует из повторного применения B).|
5.9.2. Замечания. Случай, когда в B) функции fk предпо-
предполагаются лишь локально интегрируемыми (или локально инте-
интегрируемыми в р-й степени) на Q, не удается исследовать таким
прямым способом. Вместо этого нужно использовать понятие
свертки двух распределений и некоторые результаты о свертках
функций, принадлежащие Соболеву и сходные с результатами,
приведенными в § 9.5.
Схема доказательства будет изложена в § 5.11 после введе-
введения понятия свертки распределений.
Остановимся теперь коротко на второй проблеме, а именно
на существовании решения системы уравнений д^Х=Ак A -^ k^
</г), где Ah заданы. Очевидно, что необходимым условием раз-
разрешимости этой системы уравнений является выполнение си-
системы условий
diAh — dhAt^0 {Ki, k<n). E.9.3)
Доказательство достаточности этих условий далеко не три-
тривиально, особенно когда область Q отлична от всего Rn. Мы
приведем только окончательный результат.
5.10. Свертка распределений на Rn 447
5.9.3. Теорема. Пусть на Q заданы обобщенные функции
Ah (I Kk<Cn). Для существования решения Х^£$'@) системы
уравнений
dhX=Ak (Kk<n) E.9.4)
необходимо и достаточно, чтобы выполнялось условие E.9.3).
Если это условие выполнено, то решение системы E.9.4) един-
единственно с точностью до постоянных слагаемых.
Доказательство. Мы отсылаем читателя к книге
Л. Шварца [1, стр. 60, теорема VI] для случая, когда Q = Rn.
В случае произвольного Q (могущего быть произвольным веще-
вещественным дифференцируемым многообразием класса С°°) эта
теорема следует из теоремы де Рама [1, стр. 153, теорема 17],
которая содержится также в книге де Рама и Кодайры
[1, стр. 40, теорема С]. I
5.9.4. Замечание. Характер решения X системы E.9.4) в
предположении, что оно существует, исследуется в § 5.11.
5.10. Свертка распределений на Rn
Свертку распределений на Rn можно, как и для мер (§ 4.19),
определить на основе прямого или тензорного произведения рас-
распределений. Здесь мы рассмотрим только тот случай, когда в
свертке X * У по крайней мере одно из распределений X, У обла-
обладает компактным носителем; в этом случае рассуждения суще-
существенно упрощаются.
Более подробное изложение вопросов, связанных с понятием
свертки, можно найти в книгах Л. Шварца [1, гл. IV; 2,
гл. VI]. Другой подход к определению свертки обобщенных
функций описан в работах Шев а лле [1], Хираты [1], С и-
р а и с и [1], Иосинаги и Огаты 1], Сираиси и Хираты
[1, 2] (см. также упр. 7.19).
Как и в случае мер, определим свертку X*Y — Z, полагая
Z(cp) равным общему значению функции X(X){Y^y)[^(x+y)]} и
У(у){Х{х)[<((х + у)Ъ Для ф е= 2>=&(Rn). Через Yiy)[<p(x+y)] здесь
обозначен результат (функция от х) применения распределения
У к функции у*->ц(х + у) е 9D.Аналогичный смысл имеют и дру-
другие обозначения. Так же как и в случае мер, ни одно из выше-
вышеприведенных выражений не имеет смысла, если X и У — произ-
произвольные распределения. Однако в случае, когда одно из рас-
распределений X, У (скажем, X) обладает компактным носителем,
то смысл имеют оба выражения: первое — поскольку функция
УаЛф (# + £/)] е С°° как функция от л: и потому к ней можно при-
применить X, второе — потому что Х(х)[ц(х + у)] ^2) как функция
от у и, следовательно, к ней можно применить У.- Наша цель
показать, что в этом случае оба выражения равны. Для этого
448 Гл. 5. Распределения и дифференциальные уравнения
обозначим их соответственно через 2'(ф) и Z"(cp). Очевидно,
что для заданного ф £'(ф) и ^"(ф) билинейны как функции от
(X, У). В силу теоремы 5.8.1 распределение X можно предста-
представить в виде конечной суммы производных д^а, где а — меры
Радона с компактным носителем. Таким образом, достаточно
рассмотреть случай, когда X само равно д^а. При этом если
положить Х = а, то равенство Z' (q)—Z" {($) равносильно ра-
равенству Z'(dvq) =Z"(d^). Так как дРу^2) при фей), то до-
доказательство сводится к рассмотрению случая, когда Х = а есть
мера с компактным носителем. Другими словами, надо пока-
показать, что
/ У {у) [ф (х + У)] da (х) *= Y{y) [ J Ф (х + у) da (x)],
где Уe 2)'=£D'(Rn), фе^) и а — мера с компактным носите-
носителем. Если распределение Y также обладает компактным носи-
носителем, то можно опять воспользоваться теоремой 5.8.1, чтобы
свести доказательство к случаю, когда У — мера с компактным
носителем. Тогда нужное нам равенство вытекает из свойств
произведения мер (§ 4.17).
Пусть Y не обладает компактным носителем. Тогда У можно
представить в виде сильного предела последовательности рас-
распределений (Yn) с компактными носителями, скажем Yn = anY,
где ап е 5D и ап= 1 на шаре в Rn с центром в нуле и радиусом
п. Тогда
Yn {у) [ф (X + У)] ~> У{у) [ф (X + у)]
равномерно по х, пробегающим любое компактное множество
(при этом соответствующие функции у*-><р(х+у) попадают в не-
некоторое ограниченное подмножество в 3D), и
J Yn (у) [ф (х + у)] da (х) -> J У(у) [Ф (х + у)] da (x).
В то же время так как ф (х + у) da (x) e «2^, то
Уп(у) [/ ф(* + У) da (а:)] -> У^ [ J q>(* + #) rfaU)].
Таким образом, нужное нам равенство получается предель-
предельным переходом.
Теперь легко понять, как определяется свертка X * Y * Z * ...
любого конечного числа распределений, если все они, кроме,
быть может, одного, обладают компактными носителями. Такие
свертки подчиняются законам коммутативности и ассоциатив-
ассоциативности. (Если ослабить ограничения, наложенные на носители,
то ассоциативность может нарушиться.) Более того, свертка
X % У билинейна по переменным X, У, если хотя бы одно из рас-
распределений Ху У обладает компактным носителем.
5.10. Свертка распределений на Rn 449
Легко убедиться в справедливости следующих формул:
е*Х = Х для любого Х<=^',
др (X * У) = (дрХ) *Y = X*(dp У),
если хотя бы одно из распределений X, Y обладает компактным
носителем;
дрХ = (дре)*Х для любого J[ef,
Отсюда следует, что дифференцирование представляет собой
особый случай свертки с распределением д^е, носитель которого
равен {0}. Таким образом, уравнение типа свертки А *Х = В, где
А и В заданы, а X — неизвестное распределение, причем А об-
обладает компактным носителем, содержит в себе как частный
случай все линейные дифференциальные уравнения в частных
производных с постоянными коэффициентами; уравнение типа
А # Х — В включает в себя и некоторые виды интегральных урав-
уравнений.
Предоставляем читателю проверить, что
supp (X * У) cz (supp X) + (supp У),
если хотя бы одно из множеств в правой части компактно; в
частности, supp (X* У) компактен, если носители обоих распре-
распределений X и У компактны.
Что касается непрерывности свертки X * У по каждому мно-
множителю, то легко проверяется, что Х{ # У->- X * У в сильной топо-
топологии в 2)\ если supp X{ содержатся в некотором фиксированном
компактном множестве (не зависящем от i) и Х{-*Х в сильной
топологии в 2)'. Аналогично можно показать, что X *Yi-+X *Y
в сильной топологии в Я)\ если X обладает компактным носи-
носителем и 7г->У в сильной топологии в SD'.
Для доказательства, например, первого соотношения рас-
рассмотрим функции
Если slippy лежат в фиксированном компактном множестве и
Ф пробегает ограниченное подмножество Bcz£Dt то функции
ipi обладают равномерно ограниченными носителями и г|зг- сильно
сходятся в S)(Rn, S) (где 5 — соответствующее ограниченное
множество) к Х{х)[ц)(х+у)], если Х{-*Х в сильной топологии.
Отсюда следует, что j** У(ф)-> X* У(ср) равномерно относи-
относительно феб, так что Xi*Y-+X *Y в сильной топологии в 3)\
Справедливость второго соотношения устанавливается анало-
аналогичными рассуждениями.
450 Гл. 5. Распределения и дифференциальные уравнения
Если в качестве X взять функцию рей), то р* У является
(распределением, порожденным) функцией
принадлежащей С°°. Аналогично если peS5w и Y^£D'm, то
р * У является непрерывной функцией
Если У обладает компактным носителем, то supp (р*У) также
компактен. Пользуясь результатами предыдущего абзаца, мож-
можно показать, что в 3) можно выбрать такие функции рп (м=1,
2, ...) с носителями в любой наперед заданной окрестности
нуля, что обобщенные функции рп будут сильно сходиться к е.
(Нужно только потребовать, чтобы выполнялись соотношения
I pnd\i= 1 и рп = 0 вне шара с центром в нуле и радиу-
радиусом 1/п.) Тогда рп * У сходится к У сильно в 55' для любого эле-
элемента У е 55'.
Если У обладает компактным носителем /С, то рп * У яв-
являются функциями в 55, носители которых содержатся в произ-
произвольной наперед заданной окрестности множества К. В част-
частности, 55 сильно плотно в 55' (предполагается, что функции из
9D отождествляются с распределениями, которые они порож-
порождают). Здесь мы вновь сталкиваемся с понятием регуляризации,
или сглаживания, введенным в п. 4.19.16 для мер. В связи с
этим отметим формулу
где фЕЙ), Уе55' и f — произвольная интегрируемая функ-
функция с компактным носителем.
Наконец, можно заметить, что наш способ определения
свертки X*Y, когда хотя бы одно из распределений X, У обла-
обладает компактным носителем, может применяться и в более об-
общем случае, когда множества /4 = suppX и supp У = В таковы,,
что для каждого компактного множества /Cc:Rn подмножество
(AxB)[)R в RnXRn также компактно; здесь К = {{х, у) е
^RnXRn: х + у^К\ (ср. с рассуждениями в § 4.19 для мер).
Это имеет место, например, если оба множества suppZ и supp У
содержатся в полупространствах вида Х\^-аи ..., хп S> an.
Этот случай важен в связи с преобразованием Лапласа. Вводные
сведения по затронутым здесь вопросам применительно к одно-
одномерному случаю содержатся в книге Гарни [1, стр. 154—168].
Используя свертки и простые свойства элементарных реше-
решений уравнения Лапласа, можно исследовать ряд более тонких
свойств распределений.
5.11. Другие свойства распределений 451
В следующем параграфе мы приведем примеры, в которых
используется комбинированная техника. Перед этим мы про-
продолжим изучение вопросов, с которыми мы уже встречались в
§ 5.9.
О небольшом, но важном обобщении понятия свертки см.
упр. 5.19.
5.11. Другие свойства распределений
5.11.1. Снова о восстановлении распределений по производ-
производным. Нас интересуют сейчас обобщенные функции X на Q, о ко-
которых известно, что их частные производные дкХ есть функции
fk (&=1, 2, ..., п). Поскольку наша цель состоит в том, чтобы
определить, является ли при этих условиях X функцией или нет,
то поставленная задача имеет локальный характер. Однако, к
сожалению, задача не сводится сразу к случаю, когда носитель
suppX компактен и потому X обладает продолжением, принад-
принадлежащим S)/ = ^)/(Rn). Все же независимо от того, компактен
ли носитель suppX или нет, первый шаг заключается в отыска-
отыскании явного вида решения X системы уравнений dhX = fk
(/е=1, ..., п).
Метод решения этой системы зависит от того, существует
или нет распределение Е на Rn, удовлетворяющее уравнению
Д£ = е, E.11.1)
п
где Д=2^1 —оператор Лапласа. Такая обобщенная функ-
функция Е называется фундаментальным решением1) уравнения
Д« = 0, или еще фундаментальной функцией оператора Д.
Если Е задано, а X обладает компактным носителем и яв-
является решением системы уравнений dkX = fk (k=l, 2, ..., /г),
то
2 (dkE) * h = S (dkE) * (dkX) = 2 dk (dkE) * X =
т. e.
*= 2 (<?*£)*/*. E.11.2)
Очевидно, E.11.2) выполняется, если fk = dkX — произволь-
произвольные распределения (не обязательно функции) при условии, что
X (а потому и fk) обладает компактным носителем. Равенство
!) Позднее мы подробно исследуем фундаментальные решения линейных
уравнений с частными производными — см. § 5.12, 5.14 и 5.18.
452 Гл 5. Распределения и дифференциальные уравнения
E.11.2) представляет собой явное выражение решения X. Если
носитель распределения X не является компактным, то приве-
приведенные выше вычисления не проходят. Действительно, распреде-
распределение Е, удовлетворяющее уравнению E.11.1), не может при
этом обладать компактным носителем, так что мы заранее не
знаем, имеют ли рассматриваемые свертки смысл.
[Отсутствие у уравнения АЕ = е решений с компактным носи-
носителем вытекает из следующего замечания: если А и В— распре-
распределения, носители которых компактны, и 5A) =0, то А *5A) =
= 0. Теперь достаточно положить А=Е и 5 = Де. Доказатель-
Доказательство приведенного замечания несложно. Выберем относительно
компактные открытые окрестности U и V множеств supp Л и
supp В соответственно. Тогда
А*ВA)=А*В(<р)=А(х){В(у)[<р(х + у)Ъ
для любой функции ф^^5, равной единице на U+V. Для вся-
всякой такой функции ф и любого x^U функция y*-^q>(x+y)
равна единице на V, так что В(у)[ц)(х-\-у)] = ВA) для xg(/. Но
тогда
А{х){В{у)[у(х + у)}} = А{х){ВA)} = А(\) • ВA) = АA) • 0 = 0,
что и требовалось доказать.]
Чтобы обойти возникшее затруднение, выберем произволь-
произвольную функцию /ig2), равную единице на некоторой окрестности
нуля, и рассмотрим распределение F = hE. Оно обладает ком-
компактным носителем, и
AF = (ДА) • Е + 2 2 dkh • dkE + h . Д£.
fci
Далее Е можно выбрать так, чтобы оно было функцией класса
С°° на Rn\{0}. Так как Ah = dhh = 0 на некоторой окрестности
нуля, то первые два члена правой части равенства являются
функциями из С°° и их носители содержатся в supp/i, т. е. они
принадлежат SD. Поскольку h-AE = h-E = h@) «8 = 8, то
Д/7 = е + ^, E.11.3)
где ^g2), supp £ си supp h и функция £ равна нулю на некото-
некоторой окрестности нуля. Распределение F является так называе-
называемым параметриксом оператора Д; его носитель в отличие от но-
носителя фундаментального решения Е компактен1).
х) Мы воспользуемся понятием параметрикса при исследовании линей-
линейных дифференциальных операторов в частных производных (п. 5.18.4).
5Л1. Другие свойства распределений 453
В случае Q = Rn, заменяя в предыдущих вычислениях Е на
F, получаем
X=-t*X+%dkF*fk9 E.11.4)
где —£*Х есть функция класса С°° (так как ^ей)).
Если Q произвольно, то для локального исследования X на
Q как функции от fk можно воспользоваться равенством вида
E.11.4). Для этого предположим, что coi и со —открытые отно-
относительно компактные подмножества в Й, причем coi cz со. Возь-
Возьмем некоторую функцию ае^), равную единице на со, с носи-
носителем в Q. Тогда аХ можно продолжить до распределения У
на Rn, обладающего компактным носителем. Далее продолжим
afk до функции gk на Rn, имеющей компактный носитель. Тогда
X и У совпадают на со, так же как fk и gh. Таким образом,
dkY=gk на со. Если мы теперь в качестве носителя функции h
возьмем такую малую окрестность нуля V, что cdi + Vczcd, to
на озь Следовательно, если заменить X и fk на У и gk соответ-
соответственно, то равенство E.11.4) будет выполняться. Это позволяет
судить о характере функции У на coi, а поэтому и о характере X
на о)ь Таким образом определяется локальное поведение рас-
распределения X.
Так как первое слагаемое в правой части E.11.4) принадле-
принадлежит 3), то во всех случаях локальная природа распределения X
определяется поведением свертки
dkF*f = dk(F*f)
или
dkE*f = dk(E*f),
тде / — функция, обладающая компактным носителем. Поскольку
речь идет о локальном поведении, то различие между Е и F =
= hE несущественно. Таким образом, достаточно исследовать
только dkE*f, где / — функция с компактным носителем (обя-
(обязательно интегрируемая).
Возможности дальнейшего исследования зависят от природы
выбранного фундаментального решения Е. Естественно, что Е
определяется неоднозначно: к Е можно добавить любое распре-
распределение Н на Rn, являющееся гармоническим в том смысле, что
АЯ = 0. Можно показать (лемма Г. Вейля, см. п. 5.18.4 и также
Л. Шварц [1, стр. 136]), что любая гармоническая обобщенная
функция Н является в действительности гармонической функ-
функцией в обычном смысле, так что И е С°°. В таком случае тот
член в dhE*f, который возникает за счет этой компоненты
454 Г л 5. Распределения и дифференциальные уравнения
функции Е, сам принадлежит классу С°° и поэтому для нас несу-
несуществен. Таким образом, нас устраивает любое распределение
£", удовлетворяющее равенству Л£" = е.
Вероятно, наиболее простым из таких распределений яв-
является распределение £", определенное формулами
£ =
— [(/г — 2) сол] 1 г2 п при п>2,
- BЯГ1 log (I/r) при /г = 2, E.11.5)
х • F(jc) при лг = 1,
где У — функция Хевисайда на R1,
О при
У(*|-Ц при х>0,
г = | х | = (х\ + ... + х2J и о)п — площадь поверхности единич-
единичной сферы в Rn. (Использованная здесь техника совершенно не
обязательна в случае п=1. Для этого случая имеется более пря-
прямой метод. Мы включаем случай п=\ в наше рассмотрение
только для того, чтобы показать возможность единого подхода.)
Во всех случаях Е—функция класса С°° на Rn\{0}; при п = 1,
кроме того, Е — всюду непрерывная функция. Проверка того, что
£", определенное формулами E.11.5), удовлетворяет равенству
АЕ = е для случая /г = 1, тривиальна. При п^-2 эта проверка
опирается на формулу Грина для простых областей и доста-
достаточно гладких функций. Мы набросаем доказательство для слу-
случая п>2.
В п. 4.15.14 мы получили формулу Грина
J dku • d\i = J и dok = J uNk do
Q F F
для любой достаточно простой ограниченной области в Rn с
границей F и любой функции и класса С1 на некоторой окрест-
окрестности множества Q; здесь N=(NU ..., Nn)—единичная нор-
нормаль к F и а — поверхностная мера на F. Полагая в этой фор-
формуле и = ср • dfeip, получаем
фа^г]) d\x = ф • dktyNk do,
Q п F
где ф принадлежит классу С1 и г|) — классу С2 на некоторой
окрестности множества Q. Суммируя по k, меняя местами ф и г|>
и затем вычитая, получаем (в обычных обозначениях)
I (ф • Дф —1|). Дф)ф = J (ф • grad ф — ф • grad ф) • Af • do,
5.11. Другие свойства распределений 455
где ф и гр — функции класса С2 на окрестности множества Q.
Возьмем в этой формуле в качество Q круговое кольцо а < г =
= |#|<Р, где а>0 и множество {х: г < |3} содержит носитель
функции фей), a ty = r2~n. Тогда ф и gгadф равны нулю на
внешней стороне сферы |*|=р и Лф=0 на Q. Таким образом,
получаем
- J г2~п Дф d\x = J [ф • grad (r2~n) - г2~п • grad ф] N • da,
где 5а — сфера с центром в нуле и радиусом а. При а-^0
левая часть этого равенства стремится к — "* \ r2~n&(pd\x =
=—(ф, Л(г2~п)). Стандартные рассуждения показывают, что
правая часть стремится к (п — 2)сопф@). Отсюда следует, что
А(г2~п)= — (п — 2)сопе в смысле обобщенных функций, т. е.
имеет место первая из формул в E.11.5). Случай п=2 рассма-
рассматривается аналогичным образом.
Следующий шаг — исследование природы 'распределения
функции дкЕ. При п=1 тривиальной проверкой устанавливается,
что дЕ является функцией У. Рассмотрим случай п>2. В точках
хфО у Е существует обычная частная производная, равная
— (x)~lxkr~n при п > 2 и Bcoi)X/tr-2 при п = 2. Естественно ожи-
ожидать, что эти локально интегрируемые функции порождают рас-
распределение dkE, т. е. что
для всех ф^^5 при п > 2 (и аналогичная формула для п = 2).
Это действительно так, и доказательство проходит одинаково
для я = 2 и п > 2.
Мы проведем доказательство для случая п > 2. Нужно пока-
показать, что
J = (п - 2)
J dkq>
для каждой функции фей). Выберем число р настолько боль-
большим, чтобы носитель функции ф содержался в шаре с центром
в нуле и радиусом р. Так как обе подинтегральные функции
интегрируемы, то результат не изменится, если проинтегрировать
их в слое Q: а < г < р, где а > 0, и положить затем а \ 0.
К интегралам по слою можно применить формулу Грина, заме-
заметив, что в классическом смысле
дн (ф • r2~n) = r2~ndky —(п — 2) лг*ф • г~п
456 Г л 5. Распределения и дифференциальные уравнения
всюду в слое. Отсюда
J dkcp • r2~n d\x = J dk (г2-*ф) d\x + (п - 2) J xk<pr~n d\i,
Q
где первый член справа в силу формулы Грина есть
n do
a
(Sa — сфера с центром в нуле и радиусом а). Если а|0, то
этот поверхностный интеграл стремится к нулю, откуда и выте-
вытекает искомая формула.
На заключительном этапе покажем, что каждый член
dkE%f (где f интегрируема и обладает компактным носителем)
является локально интегрируемой функцией. При п=\ это оче-
очевидно, потому что дЕ есть ограниченная функция У, и потому
E*f — ограниченная и непрерывная функция. Если п^>2, то
дкЕ, как уже было доказано, есть произведение постоянной на
функцию xkr-n = g. Поэтому достаточно лишь показать, что
функция g *f локально интегрируема. Так как Ig"!^/*11, то до-
достаточно показать локальную интегрируемость функции rx-n*f.
При этом можно считать, что функция f^O интегрируема и об-
обладает компактным носителем, содержащимся, скажем, в шаре
Бр. Для любого а > 0 имеем
J (Г*"» * f) d\l = J dv. (X) J f (У) | X - у I' -" 4l (y) =
= \f(y)d\i(y)j\x-y\x-ndlx(x),
где внутренний интеграл равен
J |г|1-"
ва-\у\ в<*+\у\
Следовательно,
откуда следует, что функция rl~n*f локально интегрируема.
Таким образом, мы показали, что если распределение X на
Q таково, что дкХ — функции (k= 1,..., /г), то X — также функ-
функция на Q.
Если о функциях fh имеется дополнительная информация, то
и о локальных свойствах X можно сказать больше. Теорема
9.5.10 служит одним из источников таких сведений. Она как раз
5.11. Другие свойства распределений 457
содержит утверждения о функции rx~n*f. Если в этой теореме
положить Х = п—1, то получаем следующие выводы:
(a) Если каждая функция fk имеет локально интегрируемую
р-ю степень, 1 •</?*<+оо, 0<^<+оо, < Г» то ^'я
степень функции X локально интегрируема.
(b) Если р> п и р-я степень каждой функции fk локально
интегрируема, то X — непрерывная функция.
Используя принадлежащее Соболеву уточнение теоремы
9.5.10, эти результаты можно усилить; более подробно об этом
можно прочитать у Л. Шварца [2, стр. 37—40] и Д е н и и
Лионса [1, теорема 2.1]. Оказывается возможным доказать
следующие утверждения.
(а') Если 1 < р ^С +оо, то в (а) можно брать q, такое, что
п ^ . , 1 1 1
0 < я < +оо и = —.
^ р я n
(c) Если р = п> 1, то X е Lfoc (Q) для любого конечного г.
Аналогичные проблемы возникают, если известны все част-
частные производные д^Х порядка \q\^Ch. К этим вопросам отно-
относятся так называемые теоремы вложения Соболева [1, 1а].
Соболев обозначает через WpPiQ)^ пространство функций
/eLioc(S), для которых 5«/eLP(Q), где |q|^A. Наиболее
простая из его теорем вложения утверждает, что если Q ограни-
ограничено и п < ph, то W{p] czCb{Q) (где Cb(Q)— пространство огра-
ограниченных непрерывных функций на Q). Мы не будем явно ис-
использовать этот интересный результат, поэтому ограничимся
лишь замечанием, что если h четно, то его можно вывести из
теоремы 9.5.10 (с), пользуясь пар'аметриксом Р, вводимым ниже
в доказательстве теоремы А п. 5.11.3.
Все эти результаты относятся к локальным свойствам рас-
распределения X. Поэтому естественно поставить вопрос о возмож-
возможности установления результатов, касающихся глобальных
свойств распределения X, предполагая, что каждая производная
dkX принадлежит Lp(Q) для некоторых значений р. Особый ин-
интерес представляют собой следующие две проблемы.
A) Для каких областей Q в Rn из соотношений
ЛГе=<2Г'@), dkX^L2(Q) (fe=l, 2, ..., п) E.11.6)
вытекает существование такой константы с = с(Х), что
е L«(Q), причем предполагается, что п > 2 и q = _2 ?
B) Для каких областей Q cz Rn, обладающих конечной ме-
мерой, из соотношений E.11.6) следует, что IgL2(Q)?
Два типа областей Q, характеризующиеся условиями A) и
B), называются соответственно областями Соболева и обла-
458 Гл. 5. Распределения и дифференциальные уравнения ,
стями Никодима. Очевидно, любая область Соболева, имеющая
конечную меру, является областью Никодима. Обратное утвер-
утверждение не имеет места.
Некоторая связь между областями Иикодима и граничными
задачами для линейных дифференциальных уравнений с част-
частными производными ясна уже из книги Куранта и Гиль-
бе р та [1, гл. VII]. (См. также Д е н и и Л и о н с [1, гл. I, § 10]
и следующий ниже п. 9.12.2.)
Про обобщенные функции X на Q, удовлетворяющие соотно-
соотношениям E.11.6), говорят, что они принадлежат {обобщенному)
пространству Беппо Леей BL(Q). При этом пересечение
L2(Q)flBL(Q) обозначается через <S\* (Q). Последнее простран-
пространство будет играть важную роль в этой главе при изучении ли-
линейных дифференциальных уравнений с частными производ-
производными (§ 5.13).
Читатель, вероятно, заметит, что если Q обладает конечной
мерой, то Q есть область Соболева в том и только в том случае,
если BL(Q)cz L^(Q), и Q есть область Никодима тогда и только
тогда, когда BL(Q) cz&x^ (Q). Можно показать (упр. 6.12 и
6.13), что области Соболева и Никодима с конечной мерой могут
быть охарактеризованы неравенствами, весьма эффективно «вы-
«выражающими специальные функционально-аналитические свой-
свойства этих областей.
Детальный разбор этих вопросов можно найти у Дени и
Лионса [1, гл. I]. См. также Фуглид и Шварц [1].
5.11.2. Ограниченные множества распределений. Мы рассмо-
рассмотрим здесь критерий ограниченности подмножеств S в 3)'(Q),
где Q — данное открытое подмножество в Rn. Как было указано
в 5.3A), понятия слабой ограниченности, сильной ограничен-
ограниченности и равностепенной непрерывности для подмножеств про-
пространства 2D'(Q) совпадают. Поэтому можно говорить просто
об ограниченности.
Начнем с необходимых условий ограниченности множества
2. Пусть со — произвольное открытое относительно компактное
множество в Q (это означает, что со ограничено и его замыка-
замыкание со в Rn содержится bQ). Тогда со находится на расстоянии
г > 0 от границы множества Q. Если X, Ycz£D'{Q), причем но-
носитель У содержится в шаре Вг радиуса г с центром в начале,
то можно определить свертку X * У, считая ее элементом про-
пространства 2D'((u). Действительно, если ф^^)(со) и у е ВГ1 то
носитель функции ху—>у(х+у) лежит в Q, и, таким образом,
Х(х)[у(х + у)] определено. X(X)[q>(x+y)] как функция от у при-
принадлежит классу С°° на Вг. Так как suppyc:Br, то
^(у)№*)[ф (*+*/)]} имеет смысл.
5.11. Другие свойства распределений 459
Свертка X* У определяется сх помощью равенства Х#У(ф) =
= Y(y){X(X)[(p(x+y)]}. Читатель может проверить, что такой же
результат получится, если подсчитать X(x){Y(y)[q)(x+y)]}, где вы-
выражение в фигурных скобках есть элемент из 2)(Q) (см.
упр. 5.19).
Таким же образом свертка X*f*g имеет смысл для всех
Л'^Е и всех распределений / и g, носители которых'лежат в
достаточно малой (зависящей от Q и со) окрестности нуля U,
причем X*f*g eiZ)'(co). Из этого определения следует, что если
fug фиксированы, а X пробегает ограниченное множество
2с=^£>'(!Я), то значения X*f*g пробегают соответственно огра-
ограниченное множество в .2)'(со). Наша задача — доказать обратное
утверждение. Это обращение и будет первым из двух критериев
ограниченности.
Теорема А. Пусть Q — открытое множество в Rn, 2 — некото-
некоторое множество в &'(£1). Для того чтобы 2 было ограниченным
в &'(Q), необходимо и достаточно, чтобы выполнялось следую-
следующее условие: для любого открытого относительно компактного
множества со cz Q существуют такое целое число пг^-О и такая
окрестность нуля U в Rn, что множество
ограничено в SD'(и>) для всех f и g из 2Dm(U).
Доказательство. Необходимость тривиальным образом
следует из предыдущих замечаний.
Доказательство достаточности опирается на существование
и свойства фундаментальной функции итерированного опера-
оператора Лапласа Ak. В частности, используется тот факт, что суще-
существует распределение Е на Rn, удовлетворяющее уравнению
AkE = e, причем можно выбрать Е в виде \x\2h~n(A log|л: +В).
Явные формулы (для нас не представляющие интереса) можно
найти у Л. III в а р ц а [1, стр. 48]. Пусть задано произвольное т\
тогда, выбрав k достаточно большим, можно добиться, чтобы
Е принадлежало Ст. Составим с помощью Е параметрикс P=fE,
где feg), f=l на некоторой окрестности нуля и supp/czG.
Тогда P€E2)m(U) и
где | принадлежит 2D(U)cz 3)m{U).
Уменьшим, если это необходимо, U до таких размеров, что-
чтобы все появляющиеся ниже свертки были определены на со.
Тогда на со будет справедливо соотношение
460 Гл. 5. Распределения и дифференциальные уравнения
Повторяя рассуждения, получаем
X = X * I * £ + 2Ak{X * g * Р) + A2k(X * Р * Р).
Так как | и Р принадлежат 2Dm(U), то по предположению ка-
каждая из тройных сверток в правой части равенства пробегает
ограниченное множество, когда X пробегает 2. Кроме того, опе-
операторы Ak и A2h переводят ограниченные множества в ограни-
ограниченные. Следовательно, 2 ограничено в iZ)'(Q), что и требова-
требовалось доказать. |
Замечания. Очевидно, что справедливо аналогичное
утверждение с заменой множества 2#/#g' множеством вида
2 * /i * ... *fs>
где 5 фиксировано. Для доказательства можно применить пре-
предыдущие рассуждения, видоизменив их соответствующим обра-
образом для сверток с большим числом членов, или воспользоваться
самой теоремой А, проведя индукцию по 5.
К теореме А примыкает один сходный критерий.
Теорема В. Пусть Q — открытое подмножество в Rn, 2 — под-
множество в £D'(Q). Для того чтобы 2 было ограниченным в
£Df (Q), необходимо и достаточно, чтобы выполнялось следующее
условие: каждому относительно компактному открытому в Q
множеству со соответствует такая окрестность нуля U, что мно-
множество S*f ограничено в 2)*'(со) для каждого f^3)(U).
Доказательство. Необходимость очевидна. Достаточ-
Достаточность будет установлена, если показать, что выполняются усло-
условия теоремы А. Главное — доказать, что 2)(U) можно расширить
до 3)m(U) для некоторого конечного т, не нарушая при этом
ограниченности множеств. Так как задача имеет локальный ха-
характер, доказательство для случая Q=Rn типично. Отложим
рассмотрение этого случая до п. 7.8.2, где он послужит иллю-
иллюстрацией некоторых общих принципов функционального ана-
анализа. |
Замечание. Теоремы А и В, как и, за исключением незна-
незначительных деталей, приведенные доказательства, принадлежат
Л. Шварцу [2, гл. VI, стр. 47—52].
5.11.3. Линейные отображения, перестановочные с операцией
дифференцирования. С помощью теоремы В п. 5.11.2 мы полу-
получим центральную теорему о непрерывных линейных отображе-
отображениях и: SD-+2)', удовлетворяющих некоторым простым усло-
условиям. Эта теорема, принадлежащая Л. Шварцу [2, гл. VI,
стр. 53—54], инспирирована рядом аналогичных результатов, со-
содержащихся в ней в качестве частных случаев.
С самого начала развития функционального анализа боль-
большой интерес вызывали отображения, которые Вольтерра назвал
5.11. Другие свойства распределений 46 J
операторами замкнутого цикла. Это операторы, переводящие
функции в функции и перестановочные со сдвигами. Другими
словами, такой оператор и преобразует функцию / (одной или
нескольких вещественных переменных) некоторого заданного
типа в другую такую функцию g = u(f) и обладает тем свой-
свойством, что сдвиг функции / переходит после применения опера-
оператора и в такой же сдвиг функции g. Очевидно, что если L —
функция, подобранная соответствующим образом по заданному
классу функций /, то u(f)=L*f является непрерывным опера-
оператором описанного типа. В приведенном ниже примере 6.4.9 полу-
получен результат, из которого следует, что для класса рассматри-
рассматриваемых там функций верно и обратное утверждение, т. е. ка-
каждый оператор и указанного вида представим в виде свертки.
Эти и многие подобные результаты (см. ссылки в примере 6.4.9)
суть следствия теоремы Л. Шварца, из которой при довольно
слабых ограничениях на и следуют многие другие интересные и
полезные результаты.
Теорема. Пусть и: Й)-+Й)г — непрерывное линейное отобра-
отображение. Тогда следующие четыре условия эквивалентны:
A) и перестановочно с операцией дифференцирования\
B) и перестановочно со сдвигами;
C) и перестановочно со свертками;
D) существует такое распределение L на Rn, что
u(f)=L*f (fez&).
Доказательство. Пусть f— функция на R и х — точка из
Rn. Обозначим через txf сдвиг функции /, определенный пра-
правилом y-*f(y + x). Действие сдвига tx на распределения опре-
определяется таким образом: (f, txX) = {t-xf, X) для / е25 и X <= 2D'.
Важно отметить, что
в смысле пространства 3), где |Е2)ие обозначает k-й единич-
единичный вектор в Rn. Аналогично
8->0
в смысле пространства <£>\ если Ig^.
Эти замечания показывают уже, что из B) следует A).
Для доказательства того, что A) влечет B) и, следовательно,
эквивалентно B), достаточно установить, что для любой пары
элементов f и g из 2) выражение
F(x) = (txg,u(txf))
462 Гл. 5. Распределения и дифференциальные уравнения
не зависит от х. Покажем, что, действительно, dkF=0 для ка-
каждого k= 1, 2,..., п. Дифференцируя, имеем
dkF(х) = (-£rk{txg\ и(tj)) + (txgi JL[и (tj)]),
где, например, через -Q^itxe) обозначен элемент из Ф, опреде-
определяемый как
lim e (tx+eeg-txg).
е->0
Аналогичное замечание относится и к ^—[u(txf)]. Мы не будем
останавливаться на этом, чтобы не прерывать нить доказатель-
доказательства, однако легко проверить, что определенное таким образом
-Q^{txg) совпадает с dktxg и что
В силу A) последний член равен dh[u(txf)]y поэтому второе сла-
слагаемое в выражении для dkF(x) равно
-{dktxg, u(tj))
и, следовательно, dhF = Oy что и утверждалось.
Таким образом, утверждения A) и B) эквивалентны.
Докажем теперь импликацию B)=фC). С этой целью аппро-
аппроксимируем в 2) свертку f*g суммами Римана ^t_Xjf • g(xr) • Axr.
г
Из непрерывности отображения и и утверждения B) следует,
что
u(f*g) = lim2it-Xru(f)-g(xr).Axr в 36*.
Предел справа есть не что иное, как u(f)*g. Таким образом,
uif*g) =u(f)*g, т- е. справедливо C).
Из D), как легко видеть, вытекает каждое из утверждений
A), B) и C). Поэтому для завершения доказательства теоремы
достаточно установить импликацию C)z^D). Для этого рассмо-
рассмотрим произвольную последовательность (fr) с: 3), сходящуюся в
£)' к е. Если g е 3), то fr*g-+g в 3). Из C) следует тогда, что
lim и (fr) * g = lim и {fr * g") = и (g)
в SB' для любого je^,
В силу теоремы В п. 5.11.2 последовательность Lr = u(fr)
ограничена в 3)' и, следовательно, содержится в некотором
равностепенно непрерывном подмножестве в 3)'. Поэтому эта по-
5.11. Другие свойства распределений 463
следовательность имеет в &)' слабую предельную точку L. Но
тогда L*g = lim(Lr*g) =u(g). Тем самым D) доказано. I
Замечания. Из утверждения D) следует, что отображение
и обладает естественным продолжением с пространства 3) на
пространство (С00)' всех распределений с компактными носите-
носителями. Это продолжение удовлетворяет условию C), т. е.
u(X*Y)=u(X)* У.
С другой стороны, если известно, что C) выполняется в этой
более сильной форме, то A) и B) становятся тривиальными
следствиями отсюда, так как dkX = dk&* X и 1хХ = гх*Х для про-
произвольного распределения X.
Накладывая на и дополнительные ограничения, можно полу-
получить из доказанной теоремы различные следствия. Приведем не-
некоторые из них.
Следствие 1. Если отображение и удовлетворяет всем усло-
условиям теоремы и, кроме того, supp u(f)cz suppf для всех f^3),
то и — линейный дифференциальный оператор в частных про-
изводных с постоянными коэффициентами:
u(f)= 2 cpdpf.
Ip-<m
Обратно, всякий такой оператор и обладает сформулированны-
сформулированными свойствами.
Доказательство. Обратное утверждение очевидно. Для
доказательства прямого утверждения используем построение L
как предела последовательности Lr = u(fr), Поскольку можно
считать, что все носители supp fr содержатся в сколь угодно ма-
малой окрестности нуля U в Rn, то то же самое верно и для L.
Фактически отсюда вытекает, что suppLc:{0}. Но в таком слу-
случае L является линейной комбинацией производных ч(Э^8 и по-
потому отображение и имеет вид, указанный в следствии. I
Приводимое ниже следствие используется в примере 6.4.9, где
дается более прямое доказательство (хотя основные идеи в
основном те же).
Следствие 2. Пусть непрерывное линейное отображение
и: L1-*Lp A^/7^оо) перестановочно со сдвигами. Тогда
u(f)=L*fy
где L^Lv при р > 1 и L — ограниченная мера Радона при /7=1.
Справедливо и обратное утверждение, почти тривиальное.
Доказательство. Рассмотрим сужение отображения и
на 3). (Мы отождествляем функцию из 3) с классом (элементом
из L1), который она определяет.) Тогда распределение L из
утверждения D) обладает тем свойством, что L % / является
464 Гл. 5. Распределения и дифференциальные уравнения
(обобщенной функцией, порожденной) классом из L?, Обозна-
Обозначая этот класс через L * /, имеем
||L* f||p < const Il/Ць
Если f пробегает такую последовательность (fr)cz3), что
/г^0> [/гф=1 и fr(x) = 0 при |*|>1/г, то последователь-
последовательность L*fry сходясь к L в j2)', ограничена в L?. При р>1 огра-
ограниченные подмножества в Lp относительно слабо компактны, и
потому последовательность L*fr обладает в Lv слабой предель-
предельной точкой. Эта предельная точка не может быть отличной от
L, так что L^Lp. Это рассуждение не проходит при /7=1. Но
тогда вместо L1 можно взять более широкое пространство огра-
ограниченных мер Радона. В этом пространстве последовательность
L*fr обладает слабой предельной точкой и поэтому L — огра-
ограниченная мера Радона.
Таким образом, u(f) =L * f, где L e Lp при /7>1 и L — огра-
ограниченная мера при /7=1; в обоих случаях предполагается, что
/ей). Но отображение fi—>L*/ в обоих случаях непрерывно на
L1, а 3) плотно в L1, поэтому из непрерывности отображения и
следует, что равенство u(f)=L*f сохраняется для любого
О некоторых сходных результатах см. Эдварде [9].
Замечание. Рассматривая круг вопросов и идей, свя-
связанных с последней теоремой, нельзя не упомянуть теорему о
ядре Л. Шварца, которая относится к непрерывным линейным
отображениям и: 2)-^2)', для которых не предполагаются вы-
выполненными условия A), B) или C). Теорема утверждает, что
каждому отображению и соответствует ядро, т. е. такое распре-
распределение К на произведении 3)ХЗ), что
где /®g — функция
(*, У) *-*/(*)
Эта теорема, конечно, является более общей, чем приведен-
приведенная в тексте, и служит основным инструментом для предста-
представления широкого класса функциональных операторов и. По-
Подробное обсуждение этой теоремы можно найти у Л. Швар-
Шварца [18], Эренпрейса [16], Гельфанда и Вилен-
к и н а [1].
5.11.4. Имеются и другие приложения методов, описанных в
п. 5.11.1—5.П.З.. Одно из них — характеризация в терминах
свойств сверток X*f тех обобщенных функций Ху которые яв-
являются аналитическими функциями (Л. Шварц [2, стр. 54]).
Другое приложение — применение этих методов к теореме пред-
5.11 Другие свойства распределений 465
ставления Рисса для субгармонических функций (Л. Ш в а р. ц
[2, стр. 74—78]). См. также упр. 7.17—7.27.
5.11.5. Небольшой привал для обзора и ориентировки. Мы
располагаем теперь основной и достаточно общей информацией
о распределениях, чтобы (а) набросать в общих чертах различ-
различные обобщения и видоизменения рассматриваемой теории, с ко-
которыми читатель, возможно, пожелает ознакомиться по другим
руководствам, и (Ь) перейти к применению обобщенных функ-
функций к теории линейных дифференциальных уравнений в частных
производных. Эта новая тема начнется в § 5.12, а сейчас зай-
займемся пунктом (а).
Как мы отмечали в § 5.1, имеется много подходов к теории
обобщенных функций. Наряду с уж„е указанными работами см.
Темп л [1], Лайтхилл [1], Себаштьян э Сильва [2],
Кёниг [1], Микусинский [1, 2], Гординг и Лионе [1],
Гальперин [3], Гельфанд и Шилов [2]. Последняя моно-
монография заслуживает особого упоминания за детальное рассмо-
рассмотрение вычислительных аспектов теории обобщенных функций.
Второй том этой монографии (Гельфанд и Шилов [3]) по-
посвящен теоретическим и функционально-аналитическим аспек-
аспектам теории.
К одному типу обобщений относятся те, в которых «основное
пространство» Rn заменяется каким-нибудь более общим объек-
объектом. Если заменить Rn вещественным дифференцируемым много-
многообразием класса С°°, то потребуются лишь незначительные видо-
видоизменения. Соображения по этому вопросу разбросаны по кни-
книгам Л. Ш в а р ц а [1, 2]. Детальное изложение приводится в книге
де Рама [1]. В действительности де Рам рассматривает слу-
случай, объединяющий этот тип обобщений с другим, в котором
распределения действуют на дифференциальных формах произ-
произвольной степени, а не на функциях: это так называемые потоки,
введенные и исследованные де Рамом. Еще более широкие обоб-
обобщения принадлежат М. Риссу [1] и Эренпрейсу [1].
У М. Рисса в качестве основного пространства взята локально
компактная абелева группа. Эренпрсйс за основное пространство
берет общее отделимое локально компактное пространство и по-
показывает, как можно построить теорию, во многом параллель-
параллельную теории Шварца. В теории Эренпрейса нет, конечно, заранее
заданных дифференциальных операторов в частных производ-
производных, аналогичных д^ Вместо них предполагаются заданными
некоторые операторы «локального типа», которые играют роль
dk и на которые никаких ограничений, кроме нескольких общих
постулатов, не накладывается.
Одним из мощных побудительных мотивдв для обобщений
типа Рисса и Эренпрейса является стремление обеспечить
466 Гл. 5. Распределения и дифференциальные уравнения
достаточный «простор» для разумного обобщения понятий диффе-
дифференцирования и преобразования Фурье (см. Эренпрейс [2—8]).
Следует упомянуть также исследование Минусинским
[3—5] его операционного исчисления. Хотя объем этих иссле-
исследований никоим образом не идет в сравнение с теорией распре-
распределений, оба аппарата имеют много общего и ставят аналогич-
аналогичные задачи функционально-аналитического характера.
К другому типу обобщений относятся те, в которых вместо
скалярных распределений (т. е. непрерывных линейных форм на
3)) рассматриваются непрерывные линейные отображения
пространства SD в заданное топологическое векторное про-
пространство Е. Такие объекты носят название Е-значных рас-
распределений. Исследование такого обобщения для случая мер
Радона, о котором упоминалось в п. 4.10.7, проводится в § 8.14.
Детальное рассмотрение для случая распределений см. у
Л. Шварца [4—6].
Интересно отметить, что стимулом для последнего типа об-
обобщений послужило развитие квантовой теории поля. В этой
области довольно неохотно пришли к допущению, что перемен-
переменные поля могут быть представлены операторно-значными рас-
распределениями. В результате здесь, а также в квантовой меха-
механике частиц использование обобщенных функций позволило уза-
узаконить некоторые действия, которые до этого казались довольно
подозрительными. Однако справедливости ради следует отме-
отметить, что использование обобщенных функций в теории поля
ставит не меньше задач, чем их решает. Относительно подроб-
подробностей, доступных математикам, см. Л. Шварц [14], Вайт-
ман [1] и Фридрихе [1].
Мы уже упоминали о том, как расширилась область примене-
применения гармонического анализа с использованием обобщенных
функций. В этом отношении теория распределений развивает
идеи, восходящие к Бохнеру [1]. В § 5.15 мы вернемся к этой*
теме.
5.12. Линейные дифференциальные уравнения
в частных производных
Оставшаяся часть этой главы целиком посвящена некоторым
современным достижениям в теории линейных дифференциаль-
дифференциальных уравнений в частных производных. Читатель, знакомый с
классической теорией дифференциальных уравнений в частных
производных, обнаружит, что переход от классического к со:
временному методу не является «непрерывным».
По-видимому, не будет ошибкой сказать, что первой внешней
причиной для развития теории обобщенных функций послужил
5.12. Линейные дифференциальные уравнения 467
именно ряд работ по линейным дифференциальным уравнениям
в частных производных. Эти работы относятся к периоду,
который можно бы назвать переходным. Типичным примером
работ этого периода служат книга Соболева [1] и некоторые
разделы книг Л. Шварца [1, 2]. Что касается упомянутого от-
отсутствия «непрерывности», приведем слова Гординга [4]:
«Многие плодотворные проблемы в этой области (т. е. в
теории линейных дифференциальных уравнений в частных произ-
производных с постоянными коэффициентами) обязаны своим возник-
возникновением теории обобщенных функций, а не классической фи-
физике, и это показывает, что новая теория не обязана заниматься
решением старых задач, чтобы оправдать свое существование.
Вполне достаточно, если она поставит и решит новые задачи».
Мы рекомендуем читателю прочитать доклад Гординга, из
которого взята цитата1).
Одно из самых удивительных свойств новой теории — это
фундаментальная роль, которую играют в ней неравенства
(§ 5.14 и 5Л9). Приведем снова слова Гординга:
«Когда какая-либо задача, касающаяся линейных дифферен-
дифференциальных операторов с частными производными, уже сформули-
сформулирована в терминах абстрактной теории, все, что остается, — это
доказать некоторое неравенство; большая часть новых результа-
результатов, по существу, содержится в таких неравенствах».
При установлении подобных неравенств часто (хотя и не
при всех обстоятельствах) бывает полезным воспользоваться
преобразованием Фурье. Это служит дополнительным поводом
для обобщения преобразования Фурье на распределения. На-
Набросок такого обобщения мы дадим в § 5.15.
Одним из самых ранних методов, базирующихся в конечном
счете на неравенствах, является метод ортогонального проекти-
проектирования, принадлежащий Герману Вейлю. Первоначально этот
метод предназначался для решения задачи Дирихле (первая
краевая задача) для уравнения Лапласа. С тех пор этот метод
был значительно обобщен многими авторами. Этот вопрос рас-
рассматривается в § 5.13. Абстрактные обоснования этого метода
лежат в простых свойствах гильбертовых пространств, приведен-
приведенных в гл. 1. Современное изложение этого и сходных методов
имеется у Гарни [1].
В настоящем параграфе мы сформулируем несколько задач
теории линейных дифференциальных уравнений в частных про-
производных, к которым будем обращаться в последующих пара-
параграфах этой главы.
]) Русский перевод доклада напечатан в УМН, I960, т. XV, вып. 1 (91),
стр. 137—152. — Прим. перев.
468 Гл. 5. Распределения и дифференциальные уравнения
Что касается линейных дифференциальных уравнений в част-
частных производных, необходимо подчеркнуть следующее. Нас
прежде всего интересуют функционально-аналитический подход
и содержание современной теории. У нас нет возможности
рассматривать аспекты, требующие детального анализа в класси-
классическом духе. Например, используя метод ортогонального проек-
проектирования в § 5.13, мы не интересуемся интегральными пред-
представлениями фигурирующих там операторов Грина. Конечно,
такой бесцеремонный подход не* ставит своей целью преумень-
преуменьшить интерес и важность этих задач. Несомненно, некоторые
читатели захотят восполнить пробелы. Что касается приведен-
приведенного примера с операторами'Грина, можно рекомендовать чита-
читателю обратиться к работе Гарни [1] и к литературе, которая
там указана.
Тот факт, что проблемы, которые мы имеем в виду, можно
трактовать с различных точек зрения, одна из которых носит
по преимуществу функционально-аналитический характер, а вто-
вторая принадлежит в основном классическому анализу, хорошо
иллюстрируется на примере задачи Дирихле, рассмотренной на
стр. 283—299 книги Эпштейна [1].
Нужно отметить еще вот что. Мы нигде подробно не оста-
останавливаемся на уравнениях с переменными коэффицентами,
кроме тех случаев, когда методы, используемые для исследова-
исследования уравнений с постоянными коэффициентами, подходят и для
уравнений с переменными коэффициентами. Читатель, интере-
интересующийся более общим случаем, может обратиться к статьям,
упоминаемым в соответствующих местах, и к книге X ё р м а н-
дера [7]. Последняя книга содержит почти весь материал на-
настоящей главы, а также много сверх того.
5.12.1. Определения, обозначения и предварительные заме-
замечания. Пусть Р (х, Z) =Р(хи ..., дсп, Zb ... , Zn) — многочлен от
неизвестных Zb...,Zn, коэффициенты которого являются ком-
комплексными функциями, определенными и локально интегрируе-
интегрируемыми в области Йс Rn, где через х= (хи ... 9хп) обозначается
переменная точка в Q. Таким образом,
Р(х, Z)= 2 ap(x)Zp,
\р\<пг
7р = 7р\ 7рп
Как многочлен относительно Z P(x> Z) имеет степень не
выше т. Мы будем говорить, что степень многочлена равна (точ-
(точно) /п, если существует такой индекс р с \р\=т, что функция ар
не является пренебрежимой в Q.
5 12. Линейные дифференциальные уравнения 469
Если вместо Z= (Zb ..., Zn) формально подставить д =
= (ди ..., дп)у то получаем линейный дифференциальный опера-
оператор в частных производных (на £2)
Р(х,д)= Ц ар(х)др9 E.12.0)
порядок которого равен степени многочлена Р(ху Z). Случай
т = 0 не представляет интереса, поэтому будем считать всюду,
что т > 1.
Начиная с § 5.14 мы будем пользоваться преобразованием
Фурье, в связи с чем удобно иногда представлять линейные диф-
дифференциальные операторы в виде многочленов от операторов
Dk= Bni)"ldh вместо самих dh.
Тогда полиному Р(ху Z) соответствует линейный дифферен-
дифференциальный оператор в частных производных
Р(х> D)= S ap(x)Dp. E.12.00
\p\<rn
В каждом отдельном случае мы будем пользоваться тем обо-
обозначением, которое нам покажется удобнее.
Говорят, что линейный дифференциальный оператор в ча-
частных производных имеет постоянные коэффициенты, если ар—
постоянные функции на Q. Такой оператор обычно обозначается
просто через P(D). В этом случае естественно считать, что
Q = Rn, хотя это вовсе не обязательно. Действительно, при п > 1
решения уравнения P(D)X=A в открытом множестве Q, вообще
говоря (даже при Л=0), не продолжаются до решений того же
уравнения на всем Rn: рассмотрите, например, гармонические
в некоторой области функции, которые являются в ней реше-
п
ниями уравнения P(D)X = 0y где Р (D) = А = —4я2 2 D\ — опе-
оператор Лапласа иа Rn.
В зависимости от природы коэффициентов ар можно рас-
рассматривать Р(ху D) как непрерывное линейное отображение раз-
различных подпространств пространства 3)'(Q) в себя. При этом
соответственно изменяется интерпретация так называемых*фор-
называемых*формальных, или лагранжевых сопряженных к P(xyD). Формаль-
Формальный (лагранжев) сопряженный оператор P(x,D) — это линейный
дифференциальный оператор в частных производных, характе-
характеризуемый тем свойством, что
f P{x9 D)f-gd\x= f f • Р{х9 D)g-d\i E.12.1)
Q Q
470 Гл. 5. Распределения и дифференциальные уравнения
для любых /, §ей)(Й). Если воспользоваться обозначением
(,) теории распределений, то условие E.12.1) равносильно
соотношению
{Р(х, D)f, £> = </, P(x, D)g). E.12.1')
Переходя к явным выражениям, получаем
P(x,D)g= 2 (-lf]Dp(apg) E.12.1")
для g^2)(Q). В правой части равенства оператор Dp следует,
вообще говоря, интерпретировать в смысле обобщенных функций,
хотя иногда, например при ар е Cp'(lQ), оператор Dp можно по-
понимать в классическом смысле.
Приведенная выше формула определяет оператор P(xyD)
через его действие на функции из&(£1). Если воспользоваться
формулой Лейбница, чтобы выразить правую часть равенства
E.12.1") в виде
2 bpDpg,
\Р\<т
то выражение для Ьр будет содержать каждое ар вместе с про-
производными Dvav, где |</|^|р|. Таким образом, если функции ар
не подчинить некоторым условиям гладкости, то P(x,D) не бу-
будет оператором того же типа, что и Р(х, D), так как его коэффи-
коэффициенты не будут локально интегрируемыми функциями. Положе-
Положение может быть исправлено, если наложить на ар дополнитель-
дополнительные ограничения.
Например, если все ар е C°°(lQ), то оператор P(xyD) непре-
непрерывно отображает пространство Ф(£1) в себя, поэтому P(xyD)
можно продолжить до непрерывного эндоморфизма простран-
пространства £D'(Q). Это продолжение задается формулой E.12.Г7), если
заменить в ней g на произвольный элемент X из 2)'(Q). Ана-
Аналогично если ар е Cpi+^(Q), где k — заданное целое число, то
оператор Р(х, D) непрерывно отображает пространство £D{Q) в
3)h{Q)y поэтому P(x,D) можно продолжить до непрерывного
отображения пространства 3)'h{Q) в <2)'(Q). Это продолжение
задается очевидным образом с помощью выражения E.12.Г7).
В каждом из этих случаев формула E.12.1') продолжается
по непрерывности до равенства
{Р(х, D)f, X) = {f, P(x, D)X), E.12.1'")
справедливого для /g=^(Q) и для Ig^(Q) и 1е^(Й)
соответственно.
Предыдущие замечания о продолжении оператора Р(х, D)
можно рассматривать как частные примеры общих результатов
5.12. Линейные дифференциальные уравнения 471
о сопряженных отображениях (§ 8.6), если принять во внимание
некоторые специальные свойства пространства й)(£2), отмечен-
отмеченные в § 5.3 (см. также п. 8.4.7).
Здесь следует отметить, что определенный выше сопряжен-
сопряженный оператор Р отличается от того, которым пользуется
Хёрмандер [1]. Он работает с гильбертовым сопряженным
оператором Р, вводимым в п. 5.14.4. Однако различие между
ними не слишком глубокое. Оно является результатом исполь-
использования гильбертова скалярного произведения (\)ь-> вместо би-
билинейной формы (,), приводящей в двойственность простран-
пространства 3>(Q) и g)'(Q).
Исследование линейного дифференциального уравнения
P(x,D)X = A, E.12.2)
где А задано, в частности соответствующего однородного урав-
уравнения
P(x,D)X = 09 E.12.3)
тесно связано с развитием математической физики и приклад-
прикладной математики и восходит к временам Эйлера, Даламбера и
семьи Бернулли. В те времена, которые можно назвать класси-
классической эпохой, предполагалось, что А — функция на Q (обычно
непрерывная и всегда локально интегрируемая). Решения иска-
искались среди функций, принадлежащих С (£2), удовлетворяющих
(в классическом смысле) всюду на Q уравнению E.12.2). Впер-
Впервые от условий гладкости отказались в теории обыкновенных
дифференциальных уравнений (одна независимая переменная,
п=\). И тогда стала очевидной польза абстрактных методов,
основанных на теории гильбертова пространства. В этой связи
читателю можно рекомендовать работу Стоуна [1, гл. IX], где
эти абстрактные методы излагаются довольно подробно как
часть спектральной теории эндоморфизмов гильбертова про-
пространства.
Другой подход, близкий к тому, который мы собираемся
предложить, излагается в гл. 7 и 9 книги Коддингтона и
Левинсона [1]. Этот подход заключается в том, что диффе-
дифференциальному уравнению вместе с граничными условиями при-
придается вид эквивалентного интегрального уравнения, к которому
можно применить общую теорию Рисса компактных эндомор-
эндоморфизмов; см. гл. 9, в частности § 9.12.
Оба эти метода существенно отличаются от метода ортого-
ортогонального проектирования, который излагается в § 5.13. Прежде
всего метод ортогонального проектирования применим даже к
сингулярным задачам (хотя, конечно, получаемые при этом
результаты не так сильны), тогда как (см. упомянутую книгу
472 Гл. 5. Распределения и дифференциальные уравнения
Коддингтона и Левинсона) метод, основанный на теории Рисса,
можно непосредственно применить только к более простому ре-
регулярному случаю, а при переходе к сингулярному случаю
нужны дополнительные рассуждения.
Абстрактные методы проникли в теорию дифференциальных
уравнений в частных производных (случай /г>1) совсем не-
недавно. Большая часть аппарата, который мы собираемся изло-
изложить, была разработана в течение последних 20 лет, причем
многое было сделано за последнее десятилетие. Введение новых
методов само по себе выдвинуло много новых идей, которые
затем впитала в себя теория обобщенных функций.
Например, так называемые слабые решения уравнения
E.12.2), где А—локально интегрируемая функция, были вве-
введены как такие локально интегрируемые функции X на Q, для
которых
J P(x, D)f.Xd\i= J Afd[i
Q Q
для любого [g2)(Q). Из E.12.V") следует, что это равно-
равносильно рассмотрению тех распределений — решений X уравнения
E.12.2), — которые являются (локально интегрируемыми) функ-
функциями. В то же время, конечно, использование таких обобщен-
обобщенных решений требовало иной формулировки граничных усло-
условий. Гарни [1] систематически пдльзуется слабыми реше-
решениями.
Фундаментальная статья Г. В ей л я [1] хорошо иллюстрирует
этот этап развития теории, когда обобщение было на полпути
к завершению. Нежелание порывать все связи со старой класси-
классической теорией послужило причиной чрезвычайно плодотворной
и важной части работы Вейля, а именно доказательства того,
что всякое слабое решение уравнения Лапласа (после измене-
изменения его на некотором пренебрежимом множестве) является клас-
классическим решением класса С°°. Это обстоятельство привело к
определению и исследованию класса так называемых гипоэллип-
тических линейных дифференциальных операторов в частных
производных, а именно тех операторов Р(х, D), для которых из
локального выполнения соотношения Р(х9 D)X^C°° вытекает
такое же соотношение и для самого X. Мы подробно остано-
остановимся на этом вопросе в § 5.18.
Далее мы увидим, что одномерный случай является совер-
совершенно исключительным, а не только более легким для исследо-
исследования: если коэффициенты ар и А — гладкие функции, то при
гг=1 единственными обобщенными решениями уравнения
E.12.2) оказываются классические функция. Это далеко не так
при м>1; мы убедимся в этом, например, в п. 5.12.2.
5.12 Линейные дифференциальные уравнения 473
Ясно, что все определенные выше операторы Р(х, D) яв-
являются операторами локального типа в том смысле, что
suppP(x, D)Xcz supp X. Оказалось, что это свойство является
характеристическим. Этот результат установил Петре [1], рас-
рассмотревший гомоморфизмы пучков ростков С°°-функций на диф-
дифференцируемых многообразиях. Для изучаемых здесь отобра-
отображений это свойство выполняется.
В оставшейся части § 5.12 хмы ограничимся изучением линей-
линейных дифференциальных операторов в частных производных с
постоянными коэффициентами. Остановимся коротко на неко-
некоторых задачах для одномерного случая, который во многих от-
отношениях слишком прост, чтобы быть типичным, но тем не менее
является источником нетривиальных задач для многомерного
случая. Некоторые из этих задач будут сформулированы в по-
последующих параграфах.
5.12.2. Предварительный обзор примеров и задач. Как уже
было сказано, мы ограничимся здесь рассмотрением уравнения
P(D)X=A E.12.4)
с постоянными коэффициентами и соответствующего ему одно-
однородного уравнения
P(D)X = 0. E.12.5)
Здесь P(D)— 2 clpDp, где ар — постоянные, причем m ^> 1
\P\<m H
и арф0 по крайней мере для одного индекса р г \р\=т.
Даже когда коэффициенты ар являются совершенно произ-
произвольными гладкими функциями, одномерный случай необыкно-
необыкновенно прост по своей структуре. Предположив, что ат не равно
нулю ни в одной точке открытого множества £2; можно показать
(см. Л. Шварц [2, стр. 126 и далее]), что все обобщенные функ-
функции, служащие решениями уравнения E.12.5), обязательно яв-
являются гладкими функциями и потому решениями в классиче-
классическом смысле. То же самое справедливо и для уравнения E.12.4),
если А — гладкая функция. Однако к этому нужно добавить, что
если ат равно нулю в какой-нибудь точке открытого множества,
о котором идет речь, то уравнение E.12.4) может вообще не
иметь ни одного решения в классе обобщенных функций. Рас-
Рассмотрим, например, уравнение
На открытом множестве Q = R1\{0} его решениями являются
функции
ае х2 при х < О,
be х2 при х > О,
474 Гл. 5. Распределения и дифференциальные уравнения
где а и b — постоянные. Других решений это уравнение не имеет.
Легко видеть, что не существует ни одной обобщенной функции,
которая была бы решением на какой-нибудь открытой окрест-
окрестности нуля.
В случае, когда коэффициенты постоянны, нетрудно описать
решения уравнения более точно. Допустим, что п=1 и А — не-
непрерывная функция на интервале Qc R1. Оператор P(D) можно
представить в виде произведения (D — X\)mi...{D — Яг)тг, где
Х{ (i = l, 2,..., г)—различные комплексные числа, тг- —нату-
—натуральные числа и т = т{ + .. , + тг. Так как
D (е-2пЛхХ) = е-ыи ф _ я) X,
то легко видеть, что единственными обобщенными решениями
уравнения (D — К)Х=А будут функции
где а — постоянная, а хо — некоторая фиксированная точка ин-
интервала Q. Повторное применение этих рассуждений приводит
нас к следующим выводам.
A) Пусть n=l, a Q — интервал в R1; пусть линейный диффе-
дифференциальный оператор с постоянными коэффициентами Р (D) =*
= 2 apDP имеет порядок m (т. е. атФ0). Тогда оператор
р
P(D)—гипоэллиптический в том смысле, что если со — произ-
произвольный подинтервал в Q и А есть С°°-функция на со, то суже-
сужение любого решения X уравнения E.12.4) на со также принад-
принадлежит классу С°° на со. Если А е C°°(Q), то все решения урав-
уравнения E.12.4) принадлежат C°°(Q) и потому являются класси-
классическими функциями.
В частности, получаем также следующее утверждение.
B) При выполнении условий утверждения A) каждое ре-
решение однородного уравнения E.12.5) является конечной линей-
линейной комбинацией решений вида x^e27tikx, где К — нуль порядка q
многочлена Pup удовлетворяет условию р < q.
Поставим теперь следующий вопрос: что изменится в утвер-
утверждениях A) и B), если размерность п больше единицы? Рас-
Рассмотрим каждое из утверждений в отдельности.
(а) Если п>1 и на оператор P(D) не наложено дополни-
дополнительных ограничений, то утверждение A) неверно. Это побуж-
побуждает нас ввести в рассмотрение класс операторов P(D), которые
будем называть гипоэллиптическими и которые заслуживают
особого внимания. Мы рассмотрим их несколько ниже. А пока
5.12. Линейные дифференциальные уравнения 475
приведем пример оператора, который не является гипоэллипти-
ческим.
Начнем с замечания, что если £2 = Rn и X — решение уравне-
уравнения E.12.5), то и К*Х также является его решением для любого
распределения К с компактным носителем. (Это свойство очень
близко к свойству, характеризующему линейный дифферен-
дифференциальный оператор в частных производных с постоянными ко-
коэффициентами (см. п. 5.11.3).)
Положим п = 2 и
Если [GC'fR1) и функция g определена на R2 равенством
то g^Cl(R2) и P(D)g = 0 поточечно. Поэтому функция g удо-
удовлетворяет тому же уравнению в смысле обобщенных функций.
Допустим теперь, что функция f лишь локально интегри-
интегрируема. Тогда g обладает тем же свойством и потому порождает
распределение на R2. Покажем, что P(D)g = 0 в смысле обоб-
обобщенных функций. Для этого возьмем какую-нибудь регуляри-
зирующую последовательность г{ в S) = S)(R2) и положим G* =
= £*/%-. Непосредственным подсчетом получаем
Gi(xu x2)=Fi(xl—x2),
где
Fi(x)=- J jfMrM-y, y'-x)dydy\
Очевидно, Fi^Coc{Rl) и Gz-^ C°°(R2). В силу сказанного выше
P(D)Gi = 0 при каждом и Если t-^oo, то G^g в 3)'(Ц2). Так
как всякий линейный оператор в частных производных с посто-
постоянными коэффициентами-является непрерывным эндоморфизмом
пространства S)'(Rn), то P(D)g = 0.
С другой стороны, ясно, что если на / не накладывать других
ограничений, кроме локальной интегрируемости, то функция g
может не принадлежать Cl(R2). Более того, так как DpX =
= (D*e)*X является решением, если Л" —решение, то с по-
помощью g можно получить распределения произвольно высокого
порядка, являющиеся решениями уравнения P(D)X = 0. Поэтому
P(D) не является гипоэллиптическим оператором. Другой при-
пример приводится в упр. 5.3.
(Ь) Ответ снова отрицательный: при п>1 прямой аналог
утверждения B) неверен, так как экспоненциальные одночлены
2iix принимают сейчас вид функций
476 Гл 5. Распределения и дифференциальные уравнения
где Я=(Яь ..., Хп)—точка из О. Пример, приведенный в
пункте (а), показывает, что «большинство» решений рассматри-
рассматриваемого здесь уравнения не являются конечными линейными
комбинациями таких экспоненциальных одночленов независимо
от выбора, точек Я из О.
Оказывается, однако, что множество всевозможных конеч-
конечных линейных комбинаций экспоненциальных одночленов плотно
в множестве всех решений. Этот вопрос будет нами рассмотрен
в первой из ряда задач, которые мы сформулируем и изучим
(задача 1 п. 5.12.3).
Плотность в множестве всех решений множества решений,
являющихся конечными линейными комбинациями экспонен-
экспоненциальных одночленов, приводит к следующей задаче. Может ли,
и если может, то при каких условиях, множество всех полино-
полиномиальных решений обладать этим свойством плотности?
В п. 5.12.3 мы сформулируем эту задачу под номером V. Ниже
(п. 5.16.4) мы увидим, что эта задача также весьма плодотворна.
Посмотрим теперь, как ее частный случай связан с теорией
функций комплексного переменного.
Опять положим п — 2 и, как обычно, отождествим точки из
R2 и комплексные числа. Пусть Q — область в R2 и Н(Q) —мно-
—множество функций, определенных и голоморфных в Q. Каждая
функция f e U (Q) порождает распределение (фактически меру)
/ • (lx, где \х — сужение на Q меры Лебега на R2. Так как функция
/ непрерывна, то соответствие f<-+f*\i взаимно однозначно; по-
поэтому H(Q) можно рассматривать как векторное подпростран-
подпространство в 2)'(Q). В качестве дифференциального оператора возьмем
где z — независимая комплексная переменная X\ + ix2i a z —
комплексное сопряженное к z.
Легко видеть, что всякая функция f^Cl(Q), для которой
P(D)f = 0 всюду на £2, является элементом из Я(й). Покажем,
что то же самое верно и для любой обобщенной функции X, ко-
которая является решением уравнения P(D)X = 0. Под этим мы,
конечно, подразумеваем то, что всякое такое решение X порож-
порождается локально интегрируемой функцией /, которая лишь на
пренебрежимом множестве отличается от некоторой функции из
H(Q). Мы достигнем нашей цели, слегка изменив процесс ре-
регуляризации, использованный выше в пункте (а).
Если бы Q совпадало со всем R2, то мы попытались бы
аппроксимировать X функциями вида X*riy где (гг), как и
выше, — регуляризирующая последовательность, выбранная из
5 12. Линейные дифференциальные уравнения 477
2). Если, однако, X определено только на Q, то нужны дополни-
дополнительные рассуждения.
Воспользуемся следующим замечанием: достаточно показать,
что сужение функции X на каждое относительно компактное от-
открытое подмножество со си £2 является элементом множества
Я (со). Зафиксировав любое такое со, предположим, что г{ вы-
выбраны так, что их носители содержатся в шаре с центром в нуле
и радиусом с, где 2с — расстояние между со и границей области
Q. Для фиксированной точки х <= со носитель функции
yv~^ri(x— у) лежит в Й, поэтому определена функция fi(x)=*
= Х(У)[г{(х — у)]. Очевидно, определенные таким образом функ-
функции fi принадлежат С°°(со), и нетрудно проверить, что U-+X
в й)'(со) при i->oo. Как и следовало ожидать, функции fi удо-
удовлетворяют на со уравнению P(D)fi = 0. Действительно,
для любой фиксированной точки х<=со, где через Rx обозначена
функция yy-^ri(x— у). [Эта формула выводится немедленно,
если она уже доказана для частного случая P(D) =dk. Для этого
же случая достаточно проверить, что fi(x) = (Rx, X) и что раз-
ностное отношение ^ , где п — малое приращение коорди-
координаты xk при переходе от х= (хи .. „, xk, ..., хп) к х'=(хи ...
A -.., ^п),сходится в iZ)(to) к функции^/1—> dkrt (x — #) =
]
Таким образом, мы показали, что X является в 2)'(ю) пре-
пределом последовательности функций (/г) из С°°(со), удовлетво-
удовлетворяющих на со равенству P(D)Д- = 0. Поэтому каждая функция
fi принадлежит Я (со). Если мы теперь сумеем показать, что
равномерная структура, индуцированная в Я (со) равномерной
структурой в й)'(со), не слабее структуры локальной равномер-
равномерной сходимости (а потому тождественна ей), то отсюда будет
следовать, что (fi) — последовательность Коши в последней рав-
равномерной структуре. Но очевидно, что Я (со) полно, следова-
следовательно, ХеЯ(оз).
Сравнение нужных нам двух равномерных структур легко
осуществить, если немного модифицировать интегральную фор-
формулу Коши. Пусть /^Я(со); рассмотрим открытый круг с цен-
центром в точке хо^со и со столь малым радиусом с>0, что соот-
соответствующий замкнутый круг содержится в со. Согласно инте-
интегральной формуле,
с / ч _ 1 с f (x) dx
x — z
478 Гл 5. Распределения и дифференциальные уравнения
для |г_я0|<г < с. Возьмем любую функцию q <= ^(R1), такую,
+ ОО
что ее носитель лежит в интервале \JC> с) и J Q(r)dr== 1.
— оо
Если \z — Хо1<-пг, то
■ v d\i (x) _
(О 0)
где \х — мера Лебега на R2 и
о
Так как q (| х — х0 |) = 0 при | х — х0 К -^ с и | а: — х01 > ^, то, как
легко проверить, множество I gz: \ z — x01<тс Г ограничено в
). Следовательно, если ft — последовательность Коши в
), то (fi) будет последовательностью Коши и в структуре
равномерной сходимости на круге | z — х0 К "о" с- Так как каждое
компактное подмножество в со можно покрыть конечным числом
таких кругов, то требуемое сравнение равномерных структур
осуществлено.
Итак, мы знаем теперь, что любое решение в 3)' (п) уравне-
уравнения P(D)X = -Qg X = 0 принадлежит #(Й), т.. е. является голо-
голоморфной функцией на Q. Поэтому если Q — односвязная об-
область, то по теореме Рунге любое решение X является (в H(Q)
и тем более в ЗУ(Q)) пределом многочленов от комплексного
переменного z = X\ + ix2, т. е. от полиномиальных решений этого
уравнения. Другими словами, в этом примере можно в (приве-
(приведенной ранее без доказательства) аппроксимационной теореме
заменить экспоненциальные одночлены одночленами в обычном
смысле. Дальнейшее исследование возможности такой замены
в общей ситуации (п. 5.16.4) приводит к довольно широким
обобщениям теоремы Рунге.
Теперь можно более точно сформулировать несколько есте-
естественных задач, которые вытекают уже из беглого рассмотрения
приведенных выше примеров. В остальных параграфах этой
главы мы займемся решением этих задач.
512. Линейные дифференциальные уравнения 479
5.12.3. Формулировка задач 1 и Г.
Задача 1. Пусть заданы открытое множество £2cRn и
P(D)—линейный дифференциальный оператор в частных про-
производных с постоянными коэффициентами. При каких условиях
каждая обобщенная функция X^SDf{Q), удовлетворяющая
уравнению P(D)X = 0, является в 3)г(п) пределом конечных ли-
линейных комбинаций экспоненциальных одночленов, являющихся
решениями этого уравнения?
Задача Г. Пусть Q и P{D)— те же, что и в задаче 1. При ка-
каких условиях каждое решение iG^fQ) уравнения P(D)X = 0
является в £D'(Q) пределом многочленов, являющихся решения-
решениями этого уравнения?
Естественно также поставить аналогичные вопросы, заменив
3)'(Q) каким-нибудь другим пространством, например про-
пространством C°°(Q).
В каждом из этих случаев известны достаточные условия,
обеспечивающие возможность желаемой аппроксимации, но не
совсем ясно, в какой .степени эти условия также и необходимы.
Частичное решение этих вопросов изложено в § 5.16.
5.12.4. Существование фундаментальных решений. Формули-
Формулировка задачи 2. Пусть Q — открытое подмножество в Rn, t —
точка в Q и P(D) —линейный дифференциальный оператор в
частных производных. Под фундаментальным решением в О от-
относительно точки t оператора Р (D) понимают такое распреде-
распределение Et&2>'(Q)9 что
P(D)Et = su E.12.6)
где (как и всегда) 8/ — мера Дирака, сосредоточенная в точке L
Если, как мы и будем в дальнейшем Предполагать, £2 = Rn,
коэффициенты оператора P(D) постоянны и Ео = Е— фундамен-
фундаментальное решение относительно начала координат, т. е. если
P(D)E = sy E.12.7}
то Et = Et*E будет фундаментальным решением относительно
точки /. Итак, в этом случае достаточно рассматривать только
решение Е = ЕОу которое далее будем называть просто фунда-
фундаментальным решением или фундаментальной функцией опера-
оператора P(D).
Если P(D)—гипоэллиптический оператор, то всякое его
фундаментальное решение Е является функцией класса С°° на
Rn \ {0}. Вне начала координат P(D)E — 0 поточечно. В любой
окрестности начала координат фундаментальное решение Е яв-
является обычно сингулярным в том смысле, что вместо P(D)E = 0
имеет место P(D)E=^e. По этой причине в старину о Е говорили
как о фундаментальном решении линейного дифференциального
уравнения в частных производных P(D)E = Q. Конечно^ Е — как
480 Гл. 5. Распределения и дифференциальные уравнения
распределение на Rn — не является решением этого однородного
уравнения.
Значение фундаментальных решений довольно ясно уже из
§ 5-11, где мы видели, как существование и свойства фундамен-
п
тального решения оператора Лапласа А = 2 д| сильно влияют
на общие вопросы теории обобщенных функций. Фундаменталь-
Фундаментальным решением оператора Д служит функция, определенная фор-
формулой E.11.5). Рекомендуем читателю вернуться к § 5.11 и
проследить за рассуждениями, с помощью которых устанавли-
устанавливается, что функция Еу определенная этой формулой, играет
роль фундаментального решения оператора Д. Замена равенства
P(D)E = 0, справедливого на Rn \ {0} в классическом смысле,
на E.12.7), справедливое глобально в смысле обобщенных функ-
функций, является итогом преобразований, включающих формулу
Грина и последующий переход к пределу, с которыми мы встре-
встречались в § 5.11 и с которыми будем еще часто встречаться в
рассуждениях, основанных на классической Интерпретации вы-
выражения P(D)E.
Имеется еще один случай, когда знание фундаментального
решения и его свойств играет важную роль при изучении опе-
оператора P(D). Так как оператор P(D) перестановочен со сверт-
свертками, то из E.12.7) следует, что решение уравнения P(D)X = A
задается равенством Х = Е*А, по крайней мере когда А обла-
обладает компактным носителем.
Ясно, что желательно иметь теорему существования фунда-
фундаментального решения, поэтому мы формулируем следующую за-
задачу.
Задача 2. Доказать существование фундаментального ре-
решения для возможно более широкого класса линейных
дифференциальных операторов в частных производных типа
P(D).
Эта задача будет рассмотрена и решена в § 5.14 с использо-
использованием преобразования Фурье и теории функций комплексного
переменного, следуя методу, разработанному Мальгранжем
[1, гл. II, § 1]; см. также Л. Шварц [8, сообщение 2].
Другой метод доказательства и более детальное изучение
свойств фундаментального решения (в частности, для гипоэл-
липтических операторов) составляют предмет изучения § 5.18.
5.12.5. Разрешимость уравнения P(D)X = А. Формулировка
задачи 3. Как мы увидим, даже частично решение задач 1 и 2
позволяет получать довольно глубокие результаты относительно
разрешимости уравнения P(D)X = A. Мы сформулируем сле-
следующую задачу.
5.13. Метод ортогонального проектирования 481
Задача 3. Выяснить, справедливы или нет соотношения
D)C = C~ P(DJ)' = 2)' и т. п.
В § 5.17 будет указан ряд положительных решений этой за-
задачи. Там же приводятся ссылки для дальнейшего изучения этой
задачи. Приводимые в § 5.17 результаты получены в основном
Мальгранжем [1, гл. II, § 3] и независимо Эренпрейсом.
5.13. Метод ортогонального проектирования и его развитие
Цель настоящего параграфа — детально показать,-каким об-
образом можно использовать метод ортогонального проектирова-
проектирования в пространствах со скалярным произведением, описанный в
§ 1.12, при решении граничных задач типа Дирихле и Неймана
для линейных дифференциальных уравнений в частных произ-
производных. По-видимому, впервые этот метод и его приложения
были разработаны Г. Вейлем [1]. Набросок подхода Вейля
был приведен в п. 1.12.7. Впоследствии этот метод претерпел
изменения и обобщения в работах многих авторов. Мы придер-
придерживаемся изложения Гарни [1], Л. Шварца [8, сообщение 11
и далее; 10] и Л и о н с а [1].
Всюду в этом параграфе через Q обозначается открытое под-
подмножество в Rn. Без ограничения общности можно считать Q
связным (и, следовательно, областью в Rn). Все функциональные
пространства B)(Q), Lp(Q), L]0c(Q) и т. д.) могут и будут рас-
рассматриваться как подпространства в iZ)'(Q).
Начнем с попытки описать метод в общих чертах." Централь-
Центральную роль будет играть пространство У, удовлетворяющее соот-
соотношению
2){Q)a Vc®'(Q) E.13.1)
и наделенное структурой пространства со специальным образом
подобранным скалярным произведением (\)v- Пространство V
будет выбираться (по мере возможности) таким образом, чтобы
заранее заданный формальный оператор Р = Р(х, д) можно было
истолковать, как такое линейное отображение Р: V-+3)'(Q,), что
и ogF, E.13.2)
Метод заключается в том, что мы стараемся выразить гра-
граничные условия в терминах соответствующих векторных под-
подпространств N в V. При этом не будем особенно заботиться о
том, чтобы выраженные таким образом граничные условия были
явно эквивалентны условиям, выраженным в классических тер-
терминах и применимым к гладким функциям. Этот вопрос можно
отделить от остальных и рассмотреть независимо. В настоящей
книге из-за недостатка места ему уделено гораздо меньше
482 Гл. 5. Распределения и дифференциальные уравнения
внимания, чем он того заслуживает. Наши замечания, относя-
относящиеся к этому вопросу и связанным с ним задачам, мы отклады-
откладываем до п. 5.13.9, где будет собран ряд таких утверждений. Во
многих случаях их доказательство увело бы нас в сторону, по-
поэтому мы ограничимся лишь ссылками на соответствующую ли-
литературу.
Основная цель этого параграфа — установить существова-
существование и единственность решения системы
uzeN, Pu=f
и коротко изучить функционально-аналитическую природу за-
зависимости решения от свойств функции /. Эта система решается
с помощью принципа проектирования, установленного в п. 1.12.7,
откуда и название параграфа. В частных случаях эта задача
сводится к абстрактным формулировкам задачи Дирихле, кото-
которая решается развитием методов, набросанных в п. 1.12.7.
Переходим к точному описанию пространства V. Всюду в
этом параграфе V будет пространством одного и того же стан-
стандартного типа.
5.13.1. Выбор пространства V. Пусть заранее заданы функ-
функции /?о, • • •, Рп, которые всюду неотрицательны и локально ин-
интегрируемы на Q.
Определим V как множество тех функций (или, точнее, клас-
классов функций) / на Q, для которых
/ei^Q), WgL|0C(Q) (й=1, 2, ..., п) E.13.3)
и
pWf <= L2 (Q), pfdj gL2(Q) (Л—1, 2 п). E.13.30
Определим на V скалярное произведение (f\g)v равенством
п
(/ I g) у = (р ЛI рП\, + 2 «Ч/1 /Л4> =
Л = 1
п
= | Pofg Ф + 2 J Pkdkf • dkg ф. E.13.4)
Q k=\ Q
Так как функции /?0> ...» Рп локально интегрируемы на Q, то
S4Q) с= V. Более того, если /gF,to pf e= Lfoc(Q) и p}j2fs= L2(Q),
так что функция pof = pl0/2 • pl0/2f локально интегрируема. Анало-
Аналогично функции pkdkf локально интегрируемы. Поэтому если
^(С) ТО
J P^kf • <Э*Ф Ф = ~ (Ф, dh
п
5.13. Метод ортогонального проектирования 483
в смысле обобщенных функций. Следовательно, соотношение
E.13.2) выполнено для
f Pr%P E.13.5)
1 /2=1
Некоторые замечания относительно природы пространства V
приводятся в п. 5.13.9.
5.13.2. Формулировка и решение задачи Дирихле— Неймана.
Рассмотрим ситуацию, описанную в п. 5.13.1. Наша цель — изу-
изучить уравнение Ри = 0, где Р — оператор, заданный равенством
E.13.5). К этому уравнению нужно добавить граничные условия
смешанного типа Дирихле — Неймана. Сформулируем эти гра-
граничные условия в абстрактном виде.
Пусть Q — граница области Q и 2 — некоторое подмножество
в Q. Обозначим через Vs —замыкание в V множества тех функ<
ций i/eV, которые (почти всюду) равны нулю на пересечении
области Q с некоторой окрестностью множества S в Rn (эта
окрестность, вообще говоря, может зависеть от v). Читатель, ве-
вероятно, заметит, что 2D(Q)cz Vs. Принадлежность к Vz выра-
выражает в некотором обобщенном смысле свойство функции обла-
обладать нулевыми граничными значениями на части 2 границы Q.
К этому вопросу мы еще вернемся.
Для формулировки граничных условий Дирихле — Неймана
нужно разделить й на два множества £ld и Qn. Для краткости
будем писатьVo вместо Vь . Введем следующие два условия:
d
(Bd) и с= Vo,
(Вп) uz==V, P«eL2(Q),
(Ри | v)L2{Q) = (и | v)v для v e= Vo.
Говорят, что функция и удовлетворяет на Qd условию Дирихле,
если она удовлетворяет условию (Bd).
Введем, наконец, два подпространства в V, а именно
E.13.6)
и
N = {и е= V: Pue= L2(Q) и и удовлетворяет (Bd) и (Вп)}. E.13.6')
Таким образом, Af — такое подмножество пересечения VoOH, что
(Pu\v)L4Q) = (u\v)v для os70. (бЛЗ.б^)
Принадлежность к N определяется выполнением некоторого
глобального условия (принадлежность к VqOH) и условия
484 Гл. 5. Распределения и дифференциальные уравнения
E.13.6"). Как мы позднее увидим, соотношение E.13.6") имеет
характер граничных условий.
Задачу Дирихле — Неймана можно сейчас сформулировать
в следующих терминах: пусть задана функция /eL2(Q); тре-
требуется решить систему
«gJV, Pu = f. E.13.7)
Существование и единственность решения. Пусть функция
f^L2(Q) задана. Допустим, что
A) Vq полно в структуре, индуцируемой в Vq структурой про-
пространства V, и
B) Vocz L2(Q) и существует такое число с, что
\\v\\L*W<c\\v\\v для v<==V0. E.13.8)
Тогда существует, и притом единственное, решение системы
E.13.7).
Доказательство. Чтобы доказать существование, вос-
воспользуемся принципом проектирования. Пусть v e Vq, тогда из
неравенства E.13.8) следует, что
I (/1 ^ W) I2 < II / libra IIv ifc.fl» <const IIv Pp
где постоянная может зависеть от f и не превосходит c2\\ffL4Qy
Так как Vq полно, то в силу условия A) и результатов п. 1.12.7B)
существует такой элемент и е Vq, что
(f\v)L4Q) = (u\v)v Для veeVo F.13.9)
Если в первом равенстве положить v = q>^3)(£l) и воспользо-
воспользоваться соотношением E.13.2), то получим
(Лф)^(а) = (и|фO = (ф, Ри\
(Ф, /> = (Ф, Ри\
откуда следует, что Pu=f. Остается только проверить, что вы-
выполняется E.13.6"). Но в E.13.9) можно теперь положить / =
= Ри, откуда немедленно вытекает E.13.6").
Докажем единственность. Разность z двух решений системы
E.13.7) удовлетворяет условиям z^Ncz Vq и Pz = 0. Но тогда
в силу F.13.6")
0
для всех не Vq. Полагая v = z, имеем ||г||у = 0, откуда, согласно
E.13.8), llzH^-O, т. е. z=0. I
5.13. Метод ортогонального проектирования 485
5.13.3. Чистая задача Дирихле. Читатель может заметить,
что если выполняется E.13.8), то условию (Вп) удовлетворяет
всякая функция «еУ, для которой PweL2(iJ), если равенство
(Ри\ v)L2{Q) = (u\v)v
справедливо для всех v из некоторого подмножества, плотного в
Vo. Далее можно показать, что если Q^ = Q и функции /?0, •••
..., рп подчинены некоторым условиям, то уже £D{Q) плотно
в Vo (см. Гарни [1, стр. 94—97], где рассматривается частный
случай). В силу E.13.2) подпространство TV сводится просто к
множеству тех функций и^ Vo, для которых Ри<= L2(Q), а си-
система E.13.7) приводится к системе
Это и есть чистая задача Дирихле с нулевыми граничными зна-
значениями. Граничные условия здесь однородны и линейны, тогда
как рассматриваемое уравнение в частных производных не яв-
является однородным.
Рассмотрим теперь задачу
asV, u — ge=VOi Pu = 0, E.13.10)
которая опять является чистой задачей Дирихле. На этот раз
граничные условия неоднородны, а линейное дифференциальное
уравнение в частных производных однородно. В случае Р = —Л
получается точный аналог классической задачи Дирихле для
гармонических функций с заданными граничными значениями.
Как показано в упр. 5.8, задачу такого вида можно свести к од-
одной из задач типа E.13.7). Но мы хотим показать, что к этой
задаче можно подойти прямо и решать ее более простым спосо-
способом и при меньшем числе предположений. В частности, нам не
понадобится ни явно предполагать выполнение условия E.13.8),
ни вводить Vo указанным выше способом.
Допустим только, что пространство V определено так же, как
в п. 5.13.1. Тогда имеет место следующая теорема существо-
существования.
(а) Пусть Vo"—векторное подпространство в V, полное в
структуре, индуцированной из V, и такое, что «25 (Q) cz Vo. Тогда
для каждой заданной функции geF система E.13.10) допус-
допускает по крайней мере одно решение.
Доказательство. В силу теоремы 1.12.3 и предложения
1.12.4 существует ортогональная проекция на Vo элемента g\
которую мы обозначим через g'. Положим u=g — g'. Тогда
«eV, u — g = —g' e Vo и (u\w)v = 0 для всех w e Vo. Полагая
^ = qpeiZ5(Q) и пользуясь соотношением E.13.2), получаем
Ри = 0. Таким образом, и — решение системы E.13.10). |
486 Гл. 5. Распределения и дифференциальные уравнения
Кроме того, справедлива следующая теорема единствен-
единственности.
(Ь) Пусть 3)(Q) плотно в векторном подпроаранстве Vo про-
пространства V, причем Vo отделимо в индуцированной структуре.
Тогда для каждой заданной функции g^V система E.13.10)
имеет не более одного решения.
Доказательство. Разность z двух решений системы
E.13.10) удовлетворяет условиям ге^о и Pz = 0. Тогда из
E.13.2) следует, что (г|ф)^ = 0 для всех qpe^)(Q). Так как
SD(Q) плотно в Vo, то ||z 1/^ = 0. Поэтому из отделимости под-
подпространства Vo вытекает, что г = 0, что и требовалось дока-
доказать. 1
Рассмотрим весьма важный частный случай. Полагая ро = О
и /?i = .. . = рп = 1, получаем Р = —А. Пространство V представ-
представляет собой в этом случае пространство классов функций
/ е L\QC (Q), для которых 5й/е12(й) при &=1, ..., п. Скаляр-
Скалярным произведением на V служит
а квадрат нормы
\\f\\i=
является обычным интегралом Дирихле.
В силу свойства минимальности расстояния для ортогональ-
ортогональной проекции решение системы E.13.10), существование кото-
которого установлено выше в (а), характеризуется соотношениями
u^V, и — g e Vo, D(u)^D(w) для ше1^, w — g^Vo.
Другими словами, если принадлежность элемента к Vo озна-
означает, что он обладает нулевыми граничными значениями в не-
некотором обобщенном смысле, то и минимизирует D(w) по срав-
сравнению с функциями w ^ V, совпадающими с ^ на границе.
Риман предложил использовать это свойство минимальности
для доказательства теоремы существования. Разница с приве-
приведенным выше подходом заключается в том, что он рассматри-
рассматривал значения D{w), когда w пробегает все те функции класса
C!(Q), которые непрерывны на Q и совпадают на й с заданной
непрерывной функцией на Q. Нет нужды приводить здесь хо-
хорошо известные затруднения, которые возникали при попытках
осуществить предложение Римана. На эти трудности указали
еще Вейерштрасс и Адамар. Сегодняшняя техника обходит эти
5.13. Метод ортогонального проектирования 487
трудности за счет изменения смысла понятий «решение» и «гра-
«граничные значения». Но из-за нового определения граничных зна-
значений приходится исключать некоторые случаи, когда класси-
классическое решение существует. Рассмотрим пример, приведенный
Адамаром, когда Q — единичный круг с центром в начале ко-
координат пространства R2 и g— следующая функция:
где р и 0 — полярные координаты. Функция g непрерывна на Q
и гармонична в Q, но D(g) = +oo. Таким образом, g не принад-
принадлежит V, поэтому наша теорема существования здесь неприме-
неприменима. Метод доказательства Римана также несовершенен, так
как можно показать, что не существует таких функций w, кото-
которые непрерывны на Q, принадлежат Cl(Q) и совпадают с g на
границе и для которых D(w)<-\-oo.
В заключение отметим, что ни один из методов, основанных
на рассмотрении интеграла Дирихле, не сравним по полезности
с методами совсем другого рода, разработанными Винером, Пер-
Перроном и другими для этой частной задачи. В гл. 7 книги Эпш-
тейна [1] имеется прекрасный обзор различных подходов к
решению классической задачи Дирихле (метод выметания Пер-
Перрона, метод, основанный на применении интегральных уравне-
уравнений, и метод Римана). В этом обзоре реабилитируется доказа-
доказательство существования, предложенное Риманом, и исследуется
связь между абстрактным определением граничных условий и
их классическим определением в случае областей с достаточно
гладкими границами (там же, стр. 196—198).
5.13.4. Продолжение п. 5.13.1, Наша задача теперь — приме-
применить результаты, полученные в п. 5.13.2 и 5.13.3, к ситуации,
описанной в п. 5.13.1. Для этого мы должны исследовать отде-
отделимость и полноту пространства Vo- В действительности мы при-
приведем достаточные условия того, что объемлющее пространство
V полно. Так как Vo замкнуто в V, то полнота пространства V
влечет за собой полноту пространства Vo-
Всюду в этом пункте предполагается, что функции /?0, ..., рп
удовлетворяют следующему условию:
/V ■••./>*> РТХ* ->Рп1 E.13.11)
локально интегрируемы на Q.
Что касается отделимости, то заметим, что из E.13.11) сле-
следует, что ри>0 почти всюду на Q для &=1, ..., п. Таким обра-
образом, если функция fsl/ удовлетворяет равенству ||f||v = 0, то
д/г/ = О для &=1, ..., п. Следовательно, / — постоянная функция
с на Q. Тогда из равенства ||fllv = 0 вытекает, что \c\2( pQdix = 0.
488 Г л 5. Распределения и дифференциальные уравнения
Если функция р0 не является пренебрежимой, то с = 0 и потому
/ = 0. Таким образом, V, а значит, и Vo отделимы, если р0 не-
пренебрежима. Но даже если р0 — пренебрежимая функция, то
все же Vo может быть отделимым (при этом, конечно, V таким
не будет) в силу обобщенных граничных условий, которым удо-
удовлетворяют элементы пространства Vo-
Если ess info/?о>О, то имеют место включение V0c:L2(Q)
и неравенство E.13.8).
Вернемся к вопросу о полноте. Она будет установлена с по-
помощью нескольких лемм, некоторые из которых представляют
и самостоятельный интерес.
Пространство *2*\ос {&) локально интегрируемых функций на
Q является полуметризуемым локально выпуклым простран-
пространством, если наделить его полунормами
где К пробегает произвольную базу (Kj) компактных подмно-
подмножеств в Q. Полнота ^\ос (Q) легко следует из теоремы 4.6.7. Ас-
Ассоциированное отделимое пространство (элементами которого
являются классы функций, совпадающих почти всюду на Q),
обозначаемое через L{OC(Q), есть пространство Фреше. Поэтому
мы можем рассматривать L{OC(Q) как подпространство в Z)'(Q).
Наш основной вывод будет таков:
Предложение. Если условия E.13.11) выполнены, то про-
пространство V полно.
Для доказательства нам понадобятся некоторые леммы, каж-
каждая из которых является частным случаем результатов, полу-
полученных Дени и Лионсом [1, стр. 308, теорема 1.1; стр. 311,
теорема 2.2].
Лемма А. Если (Ха) — такая сеть в 35' (Q), что при каждом
k=l, 2, ..., п сеть {dkXa) является сетью Коши в сильной то-
топологии 35' (Q), то в 35' (Q) существует такое X, что lim dkXa = dkX
а
при k=l, ..., п.
Доказательство. Пространство 35'(п) полно, так как
оно является сильным сопряженным к некоторому борнологи-
ческому пространству (здесь к 35(Q)) (§ 7.3 и теорема 8.4.13).
Следовательно, Yk = lim dkXa существует в 35'(п) для каждого k.
а
Поскольку операция дифференцирования непрерывна, то
djYk = limd/d^a- lim dkdjXa = dkY,
a
5.13. Метод ортогонального проектирования 489
для &, /=1, ..., п. Таким образом (теорема 5.9.3), существует
такое ief^Q), что Yk = dkX, что и требовалось доказать. |
Лемма В. Обозначим через М векторное подпространство
в 2$'{Q), состоящее из тех распределений X на й, для которых
dkX^L\QQ{Q) при &=1, ..., п. Тогда М полно относительно
структуры, определенной полунормами
рк (X) =%МК (dkX) = 2 J | дкX | ф,
где К пробегает произвольную базу (Kj) компактных подмно-
подмножеств в Q. Ассоциированное отделимое пространство М' есть
факторпространство М/С, где через С обозначено пространство
постоянных функций на Q. Кроме того, М- — пространство
Фреше.
Доказательство. Ясно, что М — полуметризуемое ло-
локально выпуклое пространство относительно указанной струк-
структуры. В силу предложения 5.9.1 достаточно доказать полноту М.
Пусть (Хп) — последовательность Коши в М, тогда (лемма А)
существует такая обобщенная функция X на Q, что dkXn-*dhX
в 2D'(Q) при k=l, ..., п. При каждом k\ однако, (dkXn) есть
последовательность Коши в LJ0C(Q), а потому сходится в этом
пространстве, причем ее пределом может быть только дкХ. Та-
Таким образом, dhX принадлежит L\Oc(Q) и является пределом по-
последовательности (dhXn) в этом пространстве. Итак, (Хп) схо-1
дится в М к Хч что и устанавливает полноту пространства М. |
Третья и последняя лемма гребует нескольких предвари-
предварительных замечаний. Из результатов, полученных в § 5.11, выте-
вытекает, что каждый элемент пространства М принадлежит L\OC(Q).
Поэтому в М можно рассмотреть структуру, определяемую по-
полунормами
где К пробегает некоторую базу компактных подмножеств в Q.
На факторпространстве МЛ = М/С имеются две структуры: одна
определяемая полунормами рк, которую можно назвать
/^-структурой, и другая, определяемая полунормами qKi которую
можно назвать ^-структурой. Полнота относительно р-структуры
уже была доказана в лемме В. Полноту относительно ^-струк-
^-структуры (которая, очевидно, сильнее р-структуры) установить
проще. Предоставляем это читателю.
Лемма С. На М* р- и q-структуры тождественны.
Доказательство. Рассмотрим тождественное отображе-
отображение {М\ q) на {М\ р). Оно взаимно однозначно и непрерывно.
490 Гл. 5. Распределения и дифференциальные уравнения
Так как оба пространства являются пространствами Фреше, то
наше утверждение следует из теоремы об открытом отображе-
отображении (например, в форме 6.4.4). |
Замечание. Мы будем использовать лемму С в следую-
следующей форме. Если (fn)—последовательность Коши в М относи-
относительно р-структуры, то существует такая числовая последова-
последовательность (сп), что (fn + Cn) —последовательность Коши (и по-
потому СХОДИТСЯ) В Lloc(^).
Доказательство предложения. Предположим, что
(fn) — последовательность Коши в V. Заметим прежде всего, что
для любого компактного подмножества /(ciQ и любого k =
= 1, ..., п справедливо неравенство Коши — Шварца
Следовательно, в силу условия E.13.11) Vcz M и структура
самого пространства V сильнее структуры, индуцируемой в V
/^-структурой пространства М. Поэтому из замечания после лем-
леммы С следует существование такой числовой последовательности
(сп), что (fn + c-n) сходится в L\OC(Q). В то же время, конечно,
из полноты М вытекает существование такого элемента fa е Му
что limdkfn = dkfaBL\oc(Q) для каждого k\ fa принадлежит
Lioc(Q).
Так как (pl^2dkfn) — последовательность Коши в L2(£l)y то
(лемма Фату 4.5.4) можно утверждать, что для каждого k в
действительности p)l2dkfa принадлежит L2(Q) и является в этом
пространстве пределом последовательности (Pk2dJn).
Если функция ро пренебрежима, то доказывать нечего: тогда
fn-+fa в V. Итак, нужно рассмотреть случай, когда функция р0
не является пренебрежимой.
Из того факта, что (/п)—последовательность Коши в V,
следует также, что (Pq/2/J является последовательностью Коши
в L2(Q). Поэтому можно воспользоваться теоремой 4.6.7, видо-
видоизмененной так, как это указано в п. 4.11.7, чтобы ее можно
было применить к L2(Q), а затем (опять с помощью леммы Фату)
заключить о существовании такой функции fb на Q что
Pl/2fn-*Plo/2fb в LHQ).
Так как (fn + cn) сходится в L}OC(Q), то для доказательства
существования подпоследовательности (ffr + cfr) = (fn +cn^t схо-
сходящейся почти всюду на Q, можно воспользоваться теоремой
4.6.7. (Символ fn используется здесь для обозначения предста-
5.13. Метод ортогонального проектирования 491
вителя класса /Я/.. Просим читателя простить нам эту вольность
здесь и в других местах, так как более точная запись была бы
слишком громоздкой.) Тогда последовательность элементов
Ро/2К "J~ Po/2cr сходится на £2 почти всюду. Но р10/2Гг сходится в
L2(Q) к pQ2fb,и, таким образом, существует такая подпоследова-
подпоследовательность (f") = (f'n \ что Plo/2f" сходится почти всюду на Q к
Отсюда следует, что (pj/2c") сходится на п почти всюду и
потому (функция ро не является пренебрежимой) сходится по-
последовательность (c'f).
Следовательно, fs сходится в Lioc (Q) и почти всюду на Q
к некоторому пределу /.
Так как pl0/2f" -> p\j2f почти всюду на Q и одновременно та
же последовательность (p{Q/2f") сходится почти всюду на Q к
/?Q/2/b, то p\{2f и p\j2fb совпадают (как классы функций), так что
Поскольку f" сходится к f в L\0C{Q) и тем более в i^'(Q),
то dj"->dj в cS^(Q). Но dkf" (как подпоследовательность по-
последовательности dkfn) сходится в Lioc(Q) к д^.Поэтому dkf и
dkfa совпадают (как классы функций) для каждого k.
Наконец, pff^ -> pl0/2f и pfd/^->pfdkf в L2(Q)
ff* p\jf и pfdj^p^dj в L(Q) для ft-1,
2, ..., п. Так как feL[0C(Q), то fel/ и служит в этом про-
пространстве пределом подпоследовательности (/^) последователь-
последовательности (fn). Поскольку (fn) — последовательность Коши в V, то
из общих соображений следует, что (fn) сходится к f в V.
Таким образом, каждая последовательность Коши в V схо-
сходится в V, что и доказывает наше предложение. I
Замечание. Доказательство значительно упрощается, если
на ро и pk наложить некоторые ограничения. Наиболее труден
был случай, когда функция ро хотя и не является пренебрежи-
пренебрежимой, но не достаточно далеко ушла от пренебрежимых функций,
для того чтобы можно было сделать вывод о сходимости (/п)
в Lioc(Q) непосредственно из того факта, что (/п) —последова-
—последовательность Коши в V. Если предположить, что р^1—локально ин-
интегрируемая функция, то такое заключение возможно и дока-
доказательство проходит без осложнений.
5.13.5. Оператор Грина. Пусть выполнены те же предполо-
предположения, что и в п. 5.13.1, 5.13.2. Введем отображение G: L2(Q)-+
->Nt которое каждому |gL2(Q) ставит в соответствие решение
492 Гл. 5. Распределения и дифференциальные уравнения
u=Gf системы E.13.7). Очевидно, С —линейное отображение.
Из рассуждений, приведенных в п. 5.13.2, следует, что
\\Gf\\v<cl\f\\L2{Q)
для /gL2(Q), ve=V0. E.13.12)
Последнего соотношения достаточно, чтобы охарактеризовать
Gf в Vo. По определению G имеем
PGf = f для f<z=L2(Q). E.13.13)
Из единственности решения задачи Дирихле — Неймана сле-
следует, что
u для i/GJV. E.13.14)
Таким образом, если N наделить структурой, определяемой ска-
скалярным произведением
(и | и% = (и | и% + (Ри | Pu')L4Q)t
то Р будет изоморфизмом (алгебраическим и топологическим)
пространства N на £2(Q), обратным к которому является G.
Если в E.13.12) положить v = Gf и воспользоваться соотно-
соотношением E.13.8), то получаем, что Gf \ f)L2(Q) вещественно и
(Gf\f)L4Q)>c-2\\Gf\\l2(Q) для ft=L2(Q). E.13.15)
Если же в E.13.12) положить v = Gg% где ^gL2(Q), to
(Л (W
Отсюда следует, что G — самосопряженный эндоморфизм
пространства L2(Q). Тогда из E.13.15) вытекает, что G — не-
непрерывный эндоморфизм пространства L2(Q), поскольку
(^<c2||f||L2(Q) для fe=L4Q). E.13.16)
Более того, G — строго положительный самосопряженный эндо-
эндоморфизм пространства L2(Q).
Как было замечено,
7<c||flUQ) Для f^L2(Q), E.13.17)
поэтому в силу E.13.8)
\\Gv\\v^c2\\v\\v для v<=V0. E.13.18)
Мы будем называть G оператором Грина системы E.13.7).
Поскольку из допущений, сделанных в п. 5.13.2, следует, что
Vqcz L2(Q), to можно рассмотреть сужение на Vq оператора G,
5.13. Метод ортогонального проектирования 493
которое будем обозначать через $?. Так как оператор G отобра-
отображает L2 на N а 1/0, то можно считать ^ эндоморфизмом про-
пространства 1/0. Тогда из E.13.12) вытекает, что
= {v\v')L2 для vt v' e Vo- E.13.19)
В силу E.13.18)
\\&v\\v^c2\\v\\v для tiG|/0, E.13.20)
т. е. отображение ^ непрерывно. В то же время из E.13.19)
вытекает, что § — положительный, самосопряженный эндомор-
эндоморфизм. Он является алгебраическим изоморфизмом пространства
Vo в N cz Vo, причем
■•V для t>GFD, E.13.21)
■и для us=N, Pu<= Vo. E.13.22)
5.13.6. В некоторых случаях вложение пространства Vo в L2
не только непрерывно (что выражается неравенством E.13.8)),
но даже компактно (= вполне непрерывно). В последнем случае
& — компактный эндоморфизм пространства Vo, так как <£? =
= Go/, где отображение G: L2->V0 непрерывно, a i: Vo->L2 —
компактное вложение. Если, кроме того, Vq — гильбертово про-
пространство, то общая теория компактных эндоморфизмов таких
пространств дает информацию о § и его собственных векторах
(или собственных функциях в случае линейных дифференциаль-
дифференциальных операторов в частных производных).
Общая теория компактных линейных отображений рассма-
рассматривается в гл. 9, а упомянутый ее аспект — в § 9.12.
5.13.7. Для того чтобы облегчить ссылки в следующем пункте,
мы перечислим здесь .простые условия, достаточные для того,
чтобы можно было применять результаты п. 5.13.2 и 5.13.5.
Во-первых, для полноты пространства Vo достаточно предпо-
предположить, что
Ро» • • • > Рп> Р\ » • • •» Рп loc №)ш (O.lo.ll)
Во-вторых, чтобы обеспечить вложение VoCzL2(Q) и выпол-
выполнение соотношения E.13.8), достаточно предположить, что
т0 = ess inf Q pQ > 0, E.13.23)
причем тогда неравенство E.13.8) имеет место с постоянной
5.13.8. Уравнение Pu + Xu—f. Иногда представляет интересна
только уравнение Pu=f, но и уравнение Pu + Xu=ft где X —ска-
—скаляр (вещественный или комплексный).
494 Гл, 5. Распределения и дифференциальные уравнения
Например, если рассматривается волновое уравнение
— = Д[/
dt2 '
где Д — оператор Лапласа в трехмерном пространстве, го первый
шаг часто заключается в отыскании простых гармонических ре-
решений U(x, t)=u(x)eikt. При этом требуют, чтобы функция и
удовлетворяла так называемому метагармоническому уравнению
где Х=—k2. Это уравнение в качестве частного случая (^ = 0)
содержит уравнение Лапласа.
Абстрактное рассмотрение уравнения Pu + Xu = f разбивается
на два этапа. На первом этапе X предполагается вещественным
положительным. Тогда мегод ортогонального проектирования
применим без всяких изменений. Фактически этот метод гораздо
легче применить при Х>0, чем при Я = 0 (в случае Х>0 более
вероятно выполнение условий, перечисленных в п. 5.13.7). На
втором этапе используются некоторые простые свойства эндо-
эндоморфизмов гильбертова пространства, чтобы расширить семей-
семейство G\ ассоциированных операторов Грина (полученное на пер-
первом этапе для Х>0) на некоторые комплексные X. Семейство
Gx, расширенное таким образом, продолжает разрешать ассо-
ассоциированную систему E.13.7) (где Р заменено на Р + Х). Не
имея возможности подробно исследовать семейство G^, мы отсы-
отсылаем читателя к работе Гарни [1].
В этом пункте достаточно предположить выполнение условия
E.13.11). Тогда пространство V определяется так же, как в на-
начале п. 5.13.1, так что соотношение E.13.5) имеет место. Про-
Пространство V может быть или не быть полным или отделимым.
Обозначим через VK пространство, построенное так же, как V,
с той лишь разницей, что ро заменяется на ро + Х. Тогда Vkcz Vy
VkczL2(Q) и скалярное произведение на VK определяется ра-
равенством
Если заменить V на Vk и взять v e V\ то неравенство E.13.8)
имеет место с постоянной с, не превосходящей Х~Х1>. Если заме-
заменить теперь Р на Р + Х, то будет выполнено и соотношение
E.13.2).
Так как неравенство
+ X'
справедливо для 0<Х<Х' и />0, то все VK совпадают как мно-
множества, и их равномерные структуры тождественны. Поэтому
5.13. Метод ортогонального проектирования 495
вместо Vх будем писать V+. Структура самого пространства V+
сильнее структуры в 1/+, индуцированной структурой простран-
пространства V.
Обозначим через Vo замыкание в V+ множества функций
из V+t каждая из которых обращается в нуль на пересечении Q,
с некоторой окрестностью множества Q^. Множество Vo не шире
множества Vo. Соответствующие граничные условия можно за-
записать в следующем виде:
(PU\ V)L2{Q) = (U\ V)Y ДЛЯ O
Соответственно имеем
N+ = {u^ H+: и удовлетворяет (в%) и (Вп)}.
Читатель заметит, что Н+аН и N+aN.
Применяя результаты п. 5.13.2 и 5.13.5 к новой ситуации,
обозначим через G% и &% соответствующие операторы Грина.
Они обладают следующими свойствами, первое из которых ха-
характеризует функцию Gxf'
В последних трех неравенствах символом ||Г]|А|В обозначается
норма линейного оператора Т: А-+В, тле А, В — нормированные
пространства1). Так как
то Gx—непрерывный положительный самосопряженный эндо-
эндоморфизм. В действительности эндоморфизм G% строго положи-
положителен, ибо при Gxf = O имеем f=(P + X)G\f = O. Таким образом,
)>0 при /sL2(Q), f^O.
\\Т\\л,в = sup{||7a|U: \\а\\А^ 1}. — Прим. перев.
496 Гл 5. Распределения и дифференциальные уравнения
Из приведенных выше тождеств вытекает связь между раз-
различными Gx при Л,>0, наличие которой весьма существенно для
второго этапа —расширения семейства Gx. Если f^L2 и Х>0,
Я0>0, то
GKf =Gi(P + Яо) GjJ = Gi [{P + Л) - (Л -
- (Я -
и потому ввиду равенства и = GkJ e Af+ имеем
Gk-Gko= -(X-X0)GiGh при А>0, Я0>0.
В частности, операторы Gx (Я>0) перестановочны. Кроме того,
h)GKfix E.13.24)
при Я>0, Я0>0.
Как мы сейчас увидим, это соотношение позволит нам рас-
распространить определение операторов Gx с положительных i на
комплексные значения Я.
Лемма. Пусть Е — полное пространство со скалярным произ-
произведением и Т — положительный самосопряженный эндоморфизм
пространства Е. Если у—комплексное число, не являющееся ве-
вещественным строго отрицательным, то A+y^) существует и
представляет собой непрерывный эндоморфизм пространства Е.
Доказательство. Число y можно записать в виде
Y = ct + /p, где а и C — вещественные числа, причем либо A)
р^О, либо B) 0 = 0, а>0. Так как (Tf \/) = (f\ Tf) —веществен
ное число, то для любого элемента f e E имеем
Таким образом,
H(l+Y7')fll2
Если [| /1| ф 0, то отсюда следует, что
где / = || Tf H/II /1|. Правая часть неравенства не меньше, чем
P2(a2 + p2)~1||f||2. При р = 0, а^О это выражение не меньше,
чем ||/|р. Следовательно, в любом из случаев A), B) имеем
E.13.25)
где C=C(y)>0. Итак, в любом случае образ М оператора
\+уТ замкнут в £. С другой стороны, М плотно в Е. Действи-
Действительно, если g — элемент из Е} ортогональный к М, то в силу
соотношения ({l+yT)f\g) =0 имеем (/| A + yT)g) =0 для всех
5.13 Метод ортогонального проектирования 497
f, т. е. || A -+- v^) ёГН = 0. Но тогда из неравенства E.13.25), спра-
справедливого как для у> так и для у, получаем, что ||g1l = 0. Плот-
Плотность множества М в Е вытекает теперь из теоремы Хана —
Банаха. Поэтому М должно совпадать с£и, значит, E.13.25)
означает, что (I+y^) — непрерывный эндоморфизм простран-
пространства Е. |
Расширение семейства G^. Пусть R_ — множество веществен-
вещественных чисел г ^С 0, С — множество комплексных чисел. Наша за-
задача— определить G% для ^gC\R..
Для любого A,^C\R_ можно многими способами так вы-
выбрать число Яо>О, чтобы разность Я— Яо не была вещественной
строго отрицательной. Пусть такое Яо выбрано. Так как Gu —
положительный самосопряженный эндоморфизм пространства
L2, то в силу предыдущей леммы оператор
определен и является непрерывным эндоморфизмом простран-
пространства L2.
Воспользуемся теперь соотношением E.13.24) и определим
Gx равенством
Gk = GxQU + (Л- Ао) Gio]~l = [1+ (Я- Яо) GK]~l Ол.. E.13.26)
определение согласуется с уже известным определением
Л для случая, когда Я вещественно и строго положительно (это
седует из соотношения E.13.24), установленного для Я>0 и
Яо>О). Легко проверяется, что этот метод определения G% не
зависит от выбора Я0>0, такого, что разность Я —Яо отлична
от всех вещественных строго отрицательных чисел. (Здесь опять
проверка использует соотношение E.13.24).)
Покажем теперь, что из E.13.26) следует, что функция G*
голоморфна на C\R_ в том смысле, что для каждой пары
(f, g) (=L2xL2 комплексная функция Я»—>(GjJ|g)L2 голоморфна
на C\R_. Действительно, пусть Я^С\^_; выберем Яо, как ука-
указано выше. Тогда если h'^k + e, с достаточно малым |е|, то в
определении G\> можно воспользоваться тем же самым Яо. По-
Положим временно Г=1 + (Я — Я0)О^. Если fug принадлежат
L2, то в силу E.13.26)
(G^f\ g)L2-(GJ\ g)L2 = (GK0(T + еСкУ1 f\ g)L,--(GK0T
Если |e| настолько мало, что | г \ • || GiQ\\L2 L2<|r~ 11^2^2» то ряд
498 Гл. 5. Распределения и дифференциальные уравнения
сходится в смысле нормы [| • \\Li L, и его сумма есть не что иное,
как (r + eGaJ- Следовательно,
(Gx'/I g)L>-(GJ\ g)L>= 2(~1Гen(GxJ-l(T-lGjf\ g\n
где ряд в правой части сходится при достаточно малых |е|.
Таким образом, голоморфность Gx в некоторой окрестности точ-
точки X установлена.
Теперь из принципа аналитического продолжения следует,
что соотношения E.13.24) выполняются, когда оба числа К и
Яо принадлежат C\R_ (расширение области допустимых зна-
значений для К и %о может быть проведено последовательно).
Наконец, пусть A,eC\R_ и feL2. Покажем, что u = GJ
есть решение системы
ue=N+, (P + X)u = f. E.13.70
Достаточно доказать, что для всех таких К и всех пар (Д
eL2Xi2 имеет место соотношение
L E,13.27)
Левая часть для всех фиксированных fug голоморфна на
C\R_. Известно, что соотношение справедливо, если % — веще-
вещественное строго положительное число. Принцип аналитического
продолжения обеспечивает справедливость равенства для лю-
любого X е C\R_. С другой стороны, известно что для Хо>О GkJ
отображает L2 в jV+; поэтому если в E.13.26) взять Яо>О, то из
этой формулы следует, что G\ f e N+ при А, е C\R_ h|gL2.
5.13.9. Замечания о пространствах V и о граничных условиях.
Начнем с некоторых замечаний о природе элементов простран-
пространства V. Как уже говорилось в п. 5.13.1, множество V состоит из
классов функций f ^Lioc(Q), таких, что
A) dkfe=L\0C(Q) для 6=1, 2, ..., п,
B) pfft=L2(Q), p^dkft=L2(Q) для й=1, 2, ..., п.
(а) Природа элементов пространства V при л=1. В этом
случае, как мы увидим, все исследование может быть проведено
без явного упоминания об обобщенных функциях или о каких-
нибудь «слабых» производных.
Область Q есть сейчас просто ограниченный или неограни-
неограниченный линейный интервал (а, C). Вместо ро, pi будем употреб-
употреблять более обычные обозначения ц, р.
5.13. Метод ортогонального проектирования 4S9
Пространство V по определению есть множество таких клас-
классов фуНКЦИЙ f^Lloc(Q), ЧТО
Здесь df интерпретируется пока в смысле обобщенных функций,
но мы увидим, что элементы пространства V можно считать
функциями и интерпретировать их производные как обычные,
существующие почти повсюду.
Действительно, поскольку класс 3/eLioc(Q), то класс f со-
содержит в точности одну непрерывную функцию, которую также
будем обозначать через f и которую возьмем в качестве пред-
представителя этого класса. Более того, эта функция — представи-
представитель f — будет даже локально абсолютно непрерывной1) на Q,
так что на Q существует такая локально интегрируемая функ-
функция /', что
х
/(*)-/(*')= J/'Ф (*, Jt'eG). E.13.28)
Непрерывная функция f почти всюду на Q обладает обычной
производной, почти всюду на Q равной f. Разумеется, однознач-
однозначно определен лишь класс функции /', но, какую бы функцию
f мы ни выбрали в качестве представителя класса, py*f и qi/2f
должны принадлежать пространству 3?2(п).
Все эти выводы следуют из результатов п. 4.15.10, из которых
также вытекает, что df (обобщенная функция, служащая про-
производной класса локально абсолютно непрерывной функции f)
есть (класс функций) f.
Если выбрать непрерывные (и, следовательно, локально аб-
абсолютно непрерывные) функции f и g, представляющие два эле-
элемента из V, то соответствующим скалярным произведением
будет
В силу этих замечаний, как мы уже говорили, можно, не огра-
ограничивая общности, рассматривать элементы пространства V как
функции на Q. Впредь будем придерживаться этого соглашения.
Как было установлено в п. 5.13.2 и 5.13.3, разрешимость и
единственность решения различных граничных задач требуют
!) Под этим понимается, что / абсолютно непрерывна в обычном смысле
на каждом компактном подинтервале в Q.
500 Гл. 5. Распределения и дифференциальные уравнения
полноты и отделимости некоторых подпространств в V. Несмотря
на общие результаты п. 5.13.4, случай я«= 1 заслуживает спе-
специального рассмотрения.
Начнем с замечания, что задача становится почти тривиаль-
тривиальной (при м=1), если функция q пренебрежима: тогда дифферен-
дифференциальное уравнение сводится к уравнению (pf')' = O. Поэтому
впредь будем предполагать, что функция q не является прене-
брежимой на Q.
Пусть норма элемента / е V равна нулю. Тогда
Если р>0 почти всюду на Q, то первый интеграл равен нулю,
только если /' = 0 почти всюду. В этом случае из E.13.28) сле-
следует, что / — постоянная на Q. Из равенства нулю второго ин-
интеграла следует, что f = 0. Таким образом, V отделимо, если
р>0 почти всюду на Q; это свойство является наследственным
для любого векторного подпространства в V.
Пусть / — некоторый подинтервал в Q. Предположим, что
р"ф< + оо. Тогда в силу E.13.28) и неравенства Коши —
Шварца
[ /M-7Uo)l<| I Р^ФП/Ни (*, хое=1) E.13.29)
и поэтому также
[ f Г (х, хое=1). EЛ3.30)
Если, кроме того, функция q не является пренебрежимой на /,
то (упр. 5.4)
lf(x)\<UjqdliY1+np-1diiJ2'\-\\f\\v (же/). E.13.31)
В частности, если функция q не является пренебрежимой на Q
и р~{ локально интегрируема на Q, тс каждому достаточно боль-
большому (а значит, и любому) компактному интервалу Kc^Q co-
ответстует такое число тКу что
\f(x)\<mK\\f\\v (x&K). F.13.310
Далее если функция q не яляется пренебрежимой на Й и р~1
интегрируема на й, то существует такое число т, что
II/Ик UeQ). F.13.3Г)
5.13. Метод ортогонального проектирования 501
Опираясь на эти неравенства, относительно просто показать,
что V полно, если q не является пренебрежимой и р~1 — локаль-
локально интегрируемая функция. Этот результат доказан в п. 5.15.4
для любых п и при более слабых предположениях.
(Ь) Природа элементов пространства V при я>1. Резуль-
Результаты, установленные в п. 5.11.1, показывают, что любая обоб-
обобщенная функция f^2)'(Q), удовлетворяющая условию A),
принадлежит L\0C(Q). При этом для соответствующих областей
Q (например, для всех областей Никодима) неравенства
essinf pk>0 (&= 1, 2, ..., п)
влекут включение VaL2(Q).
С другой стороны, последнее включение тривиально для лю-
любой области Q, если
ess infQ p0 > 0.
Особенно важен случай
Получаемое при этом пространство V обозначается через cfl^Q);
это — гильбертово пространство со скалярным произведением
Если
essinfpr>0 (r = 0, 1, ...» n\
то Fcicf^Q), причем V обладает более сильной равномерной
структурой. Если, кроме того,
ess sup pr < + оо (г = 0, 1, ..., /г),
то пространства V и «^(Q) вместе с их равномерными структу-
структурами совпадают (хотя их скалярные произведения могут не
совпадать).
Различные структурные свойства пространства У = ^12(й) и
его подпространств f/2 исследуются в книге Гарни [1] (см.,
в частности, стр. 87—101). Некоторые из результатов этой ра-
работы относятся к функциям /eLioc(^), про которые известно
только, что они удовлетворяют A), и поэтому эти результаты
можно применить к пространству V независимо от выбора р
Типичным результатом такого рода служат соотношение
г.
502 Гл. 5. Распределения и дифференциальные уравнения
и утверждение, что если / — вещественная функция из 1/, то
/, f- и |/| тоже принадлежат V.
(с) Природа граничных условий при я=1. Как было пока-
показано в пункте (а), каждый элемент u^V можно считать ло-
локально абсолютно непрерывной функцией на Q=(a, C). Из опре-
определения E.13.6) подпространства Н следует, что если меЯ,
то —д(р ди) +qu e L2(Q), откуда, так же как и в (а), вытекает,
что класс ди содержит в точности одну такую функцию и\ что
функция ри' локально абсолютно непрерывна; тогда ри' имеет
почти всюду производную g, и —(pu)' + qu есть класс функции
g. Таким образом, решения системы E.13.7) можно рассматри-
рассматривать теперь как локально абсолютно непрерывные функции и,
для которых при некотором выборе и' функция ри' локально
абсолютно непрерывна и функция —(pu')' + qu почти всюду
равна f.
Опишем теперь подпространство У0 = У^ . В данном случае
d
Qd есть одно из множеств 0, {а}, {C}, {а, C). Если Qd = 0, то о
характере Q<j говорить нечего. Во всех остальных случаях до-
достаточно рассмотреть случай aeQd и исследовать, как это
условие выражается в терминах поведения на границе функции
и е Vq. Допущение, что a e Qd, означает, что а>—оо.
Если предположить, что J p~~l ф < + оо для некоторого
a
(а значит, и для всех) хоей, то из неравенства E.13.29)
пункта (а) вытекает, что для каждого и е Vq предельное гра-
граничное значение
и(а) = Нти(х)
существует и конечно. Если, кроме того, функция q не является
пренебрежимой на Q, то можно воспользоваться неравенством
E.13.31) пункта (а), из которого следует, что м(а)=0 при
и е Vq. Будет ли какой-нибудь элемент и е V, удовлетворяющий
равенству и(а)=0у принадлежать Vq или нет, зависит от пове-
поведения р и q в окрестности точки а.
Выясним теперь смысл соотношения и е N, снова полагая
Й(/ = {а}« Если и^Н и ugK, to
(и | v)v = J (pw'o' + quv)d\x,
(pu | y)^2(Q) = J [- (ри')' + qu] v
5.13. Метод ортогонального проектирования 503
По определению и е N тогда и только тогда, когда и е Vo,
Pu^L2(Q) и (u\v)v= (Pu\v)l\q) для всех v e W Последнее
равенство означает, что
J pu'v' ф = — Г (ри')' ^ Ф-
Если [а, Ь] — компактный подинтервал в Q, то, интегрируя по
частям, получаем
ь ъ
\ (ри')' v ф = [pu'v]ba — J pu'v' d\i.
а а
Следовательно, и & N тогда и только тогда, когда и е 1/о,
Pue=L2(Q) и
lim [р//^]^ = 0 для v e Fo-
а ^ а, 6 ^ р
Таким образом, при весьма слабых ограничениях на р и q
часть соотношения и ^ N, касающаяся поведения и на границе,
сводится к условиям
lim и (х) = 0, lim р (х) и' {х) = 0,
т. е. к двум настоящим граничным условиям для и. (Напоми-
(Напоминаем, что и' должно быть выбрано так, чтобы функция ри! была
локально абсолютно непрерывна на Q).
Аналогичные замечания можно сделать, поменяв местами
а и C.
Если Qd = {a, C}, то получаем следующие граничные условия:
если же Q<j = 0, to граничные условия имеют вид
lim p (х) и' (х) = lim p (х) и' (х) = 0.
х^а *>МЗ
(d) Природа граничных условий при я>1. В этом случае
прежде всего возникает вопрос: как ведут себя на границе эле-
элементы пространства У0 = У^, где Qd — заданное подмноже-
подмножество в й?
A) Прежде всего заметим, что если f g V, то принадлеж-
принадлежность f к Vo является в действительности ограничением на пове-
поведение / только в непосредственной близости от Q^. Точнее, пусть
U — произвольная окрестность множества Я<* в Rn, и пусть а —
такая принадлежащая Cl(Q) функция, что а и dha (&=1,
504 Гл. 5. Распределения и дифференциальные уравнения
2, ..., п) ограничены на Q и а=1 на Qf]U. Мы утверждаем, что
если f^V, то f^V0 тогда и только тогда, когда afeVo. В са-
самом деле, если / е V, то а/ и A—a)f принадлежат У; более
того, функция A — a)f равна нулю на Qf]U и потому, конечно,
принадлежит Vq. Далее из равенства af—f—A—a)f следует,
что af е Уо при f е V<j. Обратно, если f е V и a/ е 1/0, то из
равенства / = а/+ A — а)/ вытекает, что / е VV Наше утвержде-
утверждение доказано.
Легко видеть, что если функции /, g e V таковы, что f = g
на Q\/C, где /С — произвольное компактное подмножество в Q,
то / и g одновременно либо принадлежат Vo, либо нет. Действи-
Действительно, выберем функцию aGC'(Rn) так, чтобы а и d^a (k =
= 1, 2, ..., п) были ограниченными и чтобы а = 0 на К и а=1
на некоторой окрестности U множества Q. В этом случае af =
= ag на Q и [е^о тогда и только тогда, когда afeV0, а geVo
тогда и только тогда, когда ag €= Уо-
B) Поведение на границе элементов пространства Vq
подробно исследовалось только для случая
рг=1 (г = 0, 1, ..., п)у 7 = ^Ь@) и QjeQ
(чистая задача Дирихле). Но полученные при этом результаты
применимы и тогда, когда
0 < ess inf pr < ess sup pr < + oo
Q Q
для каждого г. В этом случае <^(Q) плотно в Vq, поэтому
]/p = ^[2(Q)r замыканию <S^(Q) в ^(Q). (Доказательство см.
в книге Г ар ни [1, стр. 97].)
Детальное исследование элементов пространства c?l2(&) про-
проведено у Л. Шварца [8, сообщения 12 и 13, часть 1], а также
у Д ени и Л ионса [1, гл. 1, § 7]. Основной результат следую-
следующий: если: граница Q достаточно гладка, то существует непре-
непрерывное линейное отображение &: ^b(Q)-> l}oc(Q, a), которое
на функциях класса С°° на некоторой окрестности множества Q
в Rn совпадает с оператором сужения на Q. (Через а здесь обо-
обозначается поверхностная мера на Q.) Кроме того, пространство
i^!,2(Q) совпадает с множеством тех функций f^^l2(^)> для
которых bf = O. О некоторых более общих результатах такого
рода см. Кальдерон [1].
Совпадают пространства ^^(Q) и ^b(Q) или «ет, не имеет
особого значения. Совпадение имеет место тогда и только тогда,
когда Rn\Q имеет нулевой объем (см. Л. Ш в а р ц [8, сообще-
5.13. Метод ортогонального проектирования 505
ние 15]). В этом случае нет свободы выбора пространства Vo
из п. 5.13.3.
C) Обращаясь к рассмотрению условия (Вп)у допустим сна-
сначала, что Qd = Q и £D(Q) плотно в Vo (см. B) выше). При этом
следует ожидать, что условие
)L4Q) = (u\v)v для ve=V0
будет выполняться для любой функции и е Vo, такой, что
Pu^L2(Q). В силу E.13.2) указанное соотношение выполняется
для уей)(й). Поэтому если имеет место E.13.8), так что обе
части равенства непрерывны по v^L2(Q), то наше соотношение
действительно выполняется для всех ие Уо- В этом случае
и система E.13.7) эквивалентна системе
и е= V09 Pu=fy
т. е. чистой задаче Дирихле.
D) Чисто формальный подход к смыслу условий (Вп) связан
с использованием формулы Грина, что дает
(u\v)v= J роИйф + 2 Jpkdku-dkvd\i =
= J Pouvdix- J ^dk(pkdku)- vd\i+ J ^Nkpkdku- v do,
Q k
где a — поверхностная мера на Q и N = (Nu ..., Nn) — единичная
нормаль к Q. Соответственно
{и \v)v = (Pu\ v)L,{Q) + J / J[ Nkpkdku\ v da.
q \ ь J
Таким образом, соотношение we N означает формально, что
К PL2(Q) и
= 0 для v(=V.
I
Так как функция v ^ Vo принимает нулевые значения на Q<*, то
можно считать, что последняя формула сводится к требованию,
что
!^Nd Q на пп.
506 Гл. 5. Распределения и дифференциальные уравнения
Если pk — отличная от нуля постоянная, не зависящая от k, то
это соотношение означает равенство нулю на Qn производной
по нормали от функции и. Это — граничная задача Неймана.
5.13.10. Замечания. Методы, которыми в этом параграфе
исследовались некоторые линейные дифференциальные уравне-
уравнения в частных производных второго порядка, могут быть рас-
распространены на некоторые типы уравнений более высокого по-
порядка. (См. Вишик [1], Лионе [1].) Простой пример такого
рода приводится в упр. 5.24.
5.14. Существование фундаментального решения.
Обсуждение задачи 2
Пусть заданы область QczRn и линейный дифференциаль-
дифференциальный оператор в частных производных
Р(х, D)= 2 ap(x)Dpt E.14.1)
\р\<т
где ар — заданные (достаточно гладкие) функции на Q. Тогда
Р(х, D) можно применить к любому распределению на Q. Обо-
Обозначим через Р полученный таким образом эндоморфизм про-
пространства S)'(Q). Ниже, в § 5.17, будет рассмотрен вопрос о
разрешимости уравнения
РХ=Р(х, D)X=A E.14.2)
для любого заданного A ^&'(Q). Пока что нас интересует слу-
случай, когда А = га, где а — некоторая точка в Q. Напомним, что
в этом случае решение X уравнения E.14.2) называется фунда-
фундаментальным решением оператора Р(ху D) относительно точки а.
Техника, разработанная при исследовании фундаментальных
решений линейных дифференциальных операторов Р в частных
производных с постоянными коэффициентами, излагаемая в этом
параграфе, не может быть прямо использована для исследова-
исследования случая, когда А имеет более общую природу или когда ко-
коэффициенты ар(х) в E.14.1) переменны. Этим объясняется то,
что эта частная задача изучается отдельно. Несколько иной и
более конструктивный подход рассматривается ниже, в п. 5.18.3.
(См. также Хёрмандер [7].)
Тем не менее методы, описанные в этом параграфе, хорошо
переносятся на случай, когда А обладает в Q компактным но-
носителем. Это очевидно, когда Q = R" и ар постоянны, ибо тогда
из Р(Х)=г следует, что Р(Х*А)=А.
Результаты настоящего параграфа в значительной мере осно-
основываются на работах Мальгранжа [1], переработанное изло-
изложение которых содержится у Л. Шварца [8]. Большая часть
приводимого здесь материала перекрывается содержанием ра-
5.14. Существование фундаментального решения 507
боты Хёрмандера [1], подходу которого будет уделено вни-
внимание в п. 5.18.3. Важные результаты Эренпрейса [2, 3, 10,
11] относятся скорее к общему уравнению E.14.2), и потому мы
обратимся к ним ниже, в § 5.17.
5.14.1. Описание метода. В отличие от методов, описанных
в п. 5.18.3, метод, используемый в этом параграфе, по своей
природе относится к методам «чистого существования». Он слу-
служит ярким подтверждением важности той роли, которую играют
неравенства в современной (функционально аналитической) тео-
теории линейных дифференциальных уравнений, о которой уже упо-
упоминалось в § 5.12.
Целесообразно предварительно привести описание общих
принципов, используемых при доказательстве существования
решения уравнения E.14.2), где Р — линейный дифференциаль-
дифференциальный оператор в частных производных.
Абстрактную ситуацию можно описать следующим образом.
(a) ё — такое локально выпуклое пространство, содержащее
Q) в качестве плотного подпространства, что вложение
2)(Q) в & непрерывно. В силу этого каждый элемент простран-
пространства (%', топологического сопряженного к &\ представим в точ-
точности одним распределением 1е®А(й) и потому <§' можно
(алгебраически) отождествить с некоторым подпространством
в 2>'(Q).
(b) Q: &(Q)->& (соотв. Р: %'->3'{О)) — такое линейное
отображение, что
(Ф, PX) = (Q<p, X) для q>e=3f(Q)f X е= Г. E.14.3)
(с) А е -2J'(Q) — такое распределение, что
для q>e=3f(Q), E.14.4)
где р — некоторая непрерывная полунорма на &\
(А) Заключение состоит в том, что существует элемент
Xg^, удовлетворяющий соотношению E.14.2).
В наших рассуждениях Р будет линейным дифференциаль-
дифференциальным оператором в частных производных с постоянными коэффи-
коэффициентами вида
P{X) = P{D)X= S apDpX, E.14.5)
|p|<m
a Q — его формальным сопряженным, т. е. линейным дифферен-
дифференциальным оператором в частных производных с постоянными ко-
коэффициентами вида
Qy = Q(D)y= S M-1)|P|Z)V E.14.6)
\p\<m
Таким образом, Q{D)=P(D) (п. 5.12.1),
508 Гл. 5. Распределения и дифференциальные уравнения
В этом случае оказывается возможным установить неравен-
неравенство E.14.4). Для дальнейшего удобно сформулировать в виде
леммы результат, к которому приводят описанные выше общие
принципы в частном случае.
Лемма. Пусть задано конечное число непрерывных линей-
линейных отображений Kk: £${Q)->Lrk, где каждое из rk удовлетво-
удовлетворяет условиям 1 ^С г&<оо. Предположим, что Р — линейный диф-
дифференциальный оператор в частных производных с постоянными
коэффициентами, такой, что для фей)(й) справедливо нера-
неравенство
I! Ф ll^oo < const ^
Тогда если А—ограниченная мера Радона на Q, то уравнение
РХ = А имеет своим решением распределение X вида
f^Lk для каждого k и линейные отображения A,*: Lk->£$' (Q)
определены отношениями
(h<P, g) = (ф> bkg)
для ф£^(й) и g^b\
Доказательство. В качестве векторного пространства
& возьмем &(Q) и наделим <§ топологией, определяемой одной
полунормой
Так как А—ограниченная мера, то
| (ф, А) | < const || ф Н^оо < const N (Рф).
Таким образом, Рф»—>(ф, А) —непрерывная линейная форма на
векторном подпространствеР(.®(£2)) в <%. В силу теоремы Ха-
Хана— Банаха эта линейная форма обладает непрерывным про-
продолжением на <§. Рассматривая линейное отображение ф»—>(^ф)
пространства 8 в произведение J\brk и еще раз применяя тео-
теорему Хана — Банаха, получаем, что каждая непрерывная линей-
линейная форма на & имеет вид
5.14. Существование фундаментального решения 509
г
где fk^ L k при каждом k. Таким образом, для произвольного
Х) = (Ф, РХ),
где X = ^u%'kfk. Отсюда получаем, что А=РХ, что и требова-
требовалось доказать. |
Из упр. 8.34—8.39 будет видно, что описанные выше методы
легко обобщаются.
5.14.2. Формулировки вспомогательных неравенств и теоре-
теоремы существования. Мы укажем здесь два метода доказатель-
доказательства теоремы, второй из которых является менее общим и эф-
эффективно применим только к ограниченным областям Q, но пред-
представляет интерес в связи с другими вопросами (п. 5.19.3). Оба
метода используют неравенства и приводят к одинаковым общим
заключениям, отличающимся лишь в деталях. В обоих случаях
исследование завершается доказательством разрешимости урав-
уравнения E.14.2) для случая, когда Л—заданная ограниченная
мера Радона на Q, при этом решение X оказывается распреде-
распределением на Q порядка не более п+\. Дополнительные рассужде-
рассуждения позволяют перейти к случаю, когда А — более общее рас-
распределение. Но мы отложим этот вопрос до § 5.17, где он будет
подробно рассмотрен.
A) Первый метод опирается на вспомогательное неравен-
неравенство, в доказательстве которого к функциям из 3 = 28{JHn) при-
применяется преобразование Фурье. Вот это неравенство.
Неравенство А. Пусть Q=pO — линейный дифференциальный
оператор в частных производных с постоянными коэффициен-
коэффициентами. Существуют такие же операторы Lu ..., Ln+{ порядка не
более п-\-\ и линейная форма % на Rn, обладающие тем свой-
ствому что для любого е>0 найдется такое число c(Q, /г, е),
что
llplLO(Qf , ) 2l[
к — 1
для каждого фЕЙ). (Все пространства Лебега Lv строятся от-
относительно меры Лебега \i на Rn.)
Это неравенство и его доказательство, которое мы приводим
в п. 5.14.3, принадлежат Мальгранжу (см. Л. Шварц [8, сооб-
сообщение 2]; ср. Мальгранж [1, гл. I, предложение 1]).
Теперь можно воспользоваться леммой п. 5.14.1, положив
Q = P, Я^ф = еЕп '^ф, гл = 1, r'k = оо. Заключением будет сле-
следующая теорема существования.
510 Гл. 5. Распределения и дифференциальные уравнения
Теорема А. Пусть РФО — линейный дифференциальный опе-
оператор в частных производных с постоянными коэффициентами,
пусть задано е>0, и пусть Lu ..., Ln+i и % связаны с операто-
оператором Q = P, как в неравенстве А. Если Q — произвольная область
в Rn и А —ограниченная мера на Q, то уравнение E.14.2) обла-
обладает решением X вида
я + 1
где функции fh (или, лучше сказать, их классы) таковы, что
е~~е|А'//г е L°° (Q). В частности, порядок X на Q не превосходит
п+\ (фактически X явлется сужением на Q некоторого распре-
распределения на Rn порядка не выше п+\).
Замечание. Так как всегда можно продолжить А до огра-
ограниченной меры Радона на Rn, то, не нарушая общности, можно
с самого начала считать, что Q = Rn.
B) Для второго метода нужны два вспомогательных
неравенства. Эти неравенства в совокупности дают результат,
по существу эквивалентный неравенству А в случае, когда
Q ограничено и фе2)(Й). Первое из этих двух неравенств
принадлежит Хёрмандеру [1, теорема 2.1] и заключается в сле-
следующем.
Неравенство В. Пусть Q — то же, что и в неравенстве А. То-
Тогда существует такое число c(Q, d)y что
для каждого qp ^ 2Dy диаметр носителя которого не превосхо-
превосходит d.
Доказательство этого неравенства можно провести, не поль-
пользуясь преобразованием Фурье (Хёрмандер [1, § 2.6]) или ис-
используя его (Хёрмандер [1, теорема 2.1]). Мы приведем пер-
первое доказательство.
Преобразование Фурье будет использовано при доказатель-
доказательстве второго неравенства, которое оценивает ||qp||L°° через ||ср|к.2.
Неравенство В'. Для каждого натурального числа г> — п
id
существует такое число С(п, г), что
для всех ср
5.14. Существование фундаментального решения 511
Если область Q ограничена и имеет диаметр d, то из двух
предыдущих неравенств следует, что
L<c(Q, п, r, d)
для ф ^ 55. В силу этого из леммы 5.14.1 вытекает
Теорема В. Пусть Q — ограниченная область в R", РфО —
линейный дифференциальный оператор в частных производных
с постоянными коэффициентами и А—ограниченная мера Ра-
Радона на Q. Тогда уравнение E.14.2) обладает решением X вида
где г — наименьшее натуральное число, большее, чем -^ пу
a g^L2(Q)\ в частности, порядок X не больше п + % если п
четно, и не больше п+1, если п нечетно.
Замечания. Прежде чем доказывать неравенства, из кото-
которых вытекают теоремы А и В, следует отметить, что последние
можно улучшить. Известно, например, что всегда существует
фундаментальное решение X оператора P(D), являющееся ко-
конечной линейной комбинацией производных порядка не выше
\-^п +1 от функций из L?<>c (Q) и (что еще важее) такое, что
I*gG Lioc (й) для g e L2 с компактным носителем. См. М а л ь-
гр а и ж [1, стр. 21, 22], Л. Шварц [8, сообщение 3, теорема 2,
и сообщение 3 bis, стр. 3—17], Хёрмандер [5].
Другие свойства фундаментального решения будут рассмо-
рассмотрены в § 5.18.
5.14.3. Доказательство неравенства А. Начнем с
перечисления нескольких свойств преобразования Фурье при-
применительно к функциям из 2D. Все факты, которые нам нужны,
представляют собой частные случаи результатов § 10.3 и 10.4.
Однако в силу специальных свойств функций из 2) возможны
более прямые и простые их доказательства.
Пусть функция ф принадлежит £D\ ее преобразование Фурье
Ф представляет собой функцию, определенную первоначально
на Rn формулой
J Ф (х)е-^'Ы11(х), E.14.7)
J
где через \х обозначена мера Лебега на Rn и
п
512 Гл. 5. Распределения и дифференциальные уравнения
Иногда бывает удобнее использовать для обозначения преобра-
преобразования Фурье функции ф символ ф но сейчас в этом нет необ-
необходимости.
Так как ср обладает компактным носителем, то интеграл в
E.14.7) сходится абсолютно, даже если заменить точку £ из Rn
точкой £ —£ + ni из О. Отсюда следует, что Ф можно рассматри-
рассматривать как целую аналитическую функцию на О. В качество та-
таковой Ф однозначно определяется своим сужением на Rn.
В дальнейшем нам понадобится неравенство
> EЛ4.8)
справедливое для £i = £i + nr)i, где ^ и г\\ — вещественные числа,
причем |rji|^a.
Интегрируя по частям в E.14.7), получаем, что функция Ф
быстро убывает на Rn в том смысле, что
lim р
для каждого многочлена р на Rn; в частности, функция Ф инте-
интегрируема (относительно (я). Теперь нетрудно доказать формулу
обращения
\ E.14.9)
которая представляет собой частный случай леммы 10.4.5.
Для нас одним из самых важных свойств преобразования Ф
является равенство Парсе валя
E.14.10)
которое доказано в п. 10.4.4 для достаточно общего случая.
Кроме того, нам понадобится тот факт, что преобразование
Фурье для Q(D)(p есть Q(%)-(b(l). Это можно вывести из
E.14.7) повторным интегрированием по частям.
При доказательстве неравенства А воспользуемся упомяну-
упомянутыми свойствами преобразования Фурье и одной леммой из тео-
теории функций одного комплексного переменного, принадлежащей
Мальгранжу [1, гл. I, лемма 1] (ср. Хёрмандер [1,
лемма 2.1]).
Лемма. Пусть f и g— целые функции комплексного перемен-
переменного, a q(z)=zm + cizm-l+ ... +cm — такой многочлен с ком-
комплексными коэффициентами и коэффициентом 1 при старшем
члене, что f — qg. Тогда для любого заданного г>0 м для всех
комплексных чисел г0 выполняется неравенство
m- sup |/B)|. E.14.11)
|К2
614. Существование фундаментального решения 513
Доказательство. Разлагая q на линейные множители и
применяя индукцию по т, получаем, что достаточно рассмотреть
случай q(z)=z — a (случай т = 0, <7=1 тривиален).
Пусть |г0 —а|>г; тогда
IfQgp)!
г
и неравенство E.14.11), очевидно, выполняется. Если |2 — я[=г,
то
|e_UML<r-i. sup
Г |z-a|<r
В силу принципа максимума модуля это неравенство выпол-
выполняется для всех 2о, удовлетворяющих условию |г0 — а|<г. Для
любого такого г0 имеем |г —го|<^2г при |г — я|О. Таким об-
образом, наше неравенство выполняется и в этом случае. Поэтому
оно справедливо для всех г0, что и требовалось доказать. I
Теперь можно приступить к доказательству неравенства А.
Если фе2), то из E.14.9) следует, что
и поэтому
||cp||too<Cn.SupJ(l+|i1|n+l+ ... +||„Г1)ФШ|, E.14.12)
где
Так как Q=f=O, то линейным преобразованием координат можно
добиться, чтобы
где Qo(S)—многочлен по £i степени не более m — 1, коэффи-
коэффициентами которого служат функции от fe» • • •» £п» и b=zb(Q)—•
число, отличное от нуля. В силу леммы имеем
ПН sup I QCCi. ГЖСь ГI,
IC6l<2
где в правой части неравенства £i — комплексное число и
== (£г,. • •» ?п). Аналогичным образом получаем
i—It l<2mr
для /г == 2, ..., п.
514 Гл. 5. Распределения и дифференциальные уравнения
Функции Q(£)O(£) и S"+1Q(£)O(£) служат преобразованиями
Фурье соответственно для Qqp и /)?+1Q(p. Беря в E.14.8) в каче-
качестве ф поочередно ф, Qq> и Dk+kQty, получаем из E.14.12)
неравенство
/г=1
где 8 = 4ятг сколь угодно мало вместе с г. Это и есть неравен-
неравенство А, где К{х) =хи £/г = Dk*1 (k= I, ..., я) и Ln+\ = 1 (тожде-
(тождественный оператор). С учетом выполненного нами линейного
преобразования координат неравенство А тем самым установ-
установлено и в общем случае. I
5.14.4. Доказательствонеравенства В. Приводимые
здесь рассуждения основаны на одной лемме (Хёрмандер [1,
§ 2.6]), из которой неравенство В выводится с помощью индук-
индукции по порядку т оператора Q.
Отправляясь от многочлена Q(£)= 2 Ьр^р9 введем много-
член
и запишем тождество
Q(DHw)«*!Q(D)9 + Qi(D)<P. E.14.13)
которое следует из формулы Лейбница.
Далее будем писать Q и Q\ вместо Q(D) и Q\(D) соответ-
соответственно.
Лемма. Пусть
Тогда
II Q1Ф \\L2 < 2/nrf, || <2ф ||l2, E.14.14)
где ф£2) a m — степень многочлена Q.
Доказательство. Обозначим через Q оператор, L2-coj
пряженный к Q. Наш оператор Q (совпадающий с оператором Q
из статьи Хёрмандера) есть такой линейный дифференциаль-
дифференциальный оператор в частных производных с постоянными коэффи-
коэффициентами, что
E.14.15)
где ф, фе^). В частности,
5.14. Существование фундаментального решения 515
Читатель, вероятно, заметил, что Q, Qi, Q и Q\ перестановочны,
так как их коэффициенты постоянны, и что, кроме того,
II QcplHQqpll^
С помощью E.14.13) получаем
где временно опущен индекс L2. Таким образом,
II Qi<P IP = (Q (*tf) I Qi<p) - (х&у | Q&) = Qi{x{q) | Qq>)
Заменяя в E.14.13) Q на Qb находим, что
II Qi<p IP = UiQi9 + Qn91 <2ф) - (*1<2ф I Qi9) -
$ - (^РФ I Qx<p).
Отсюда с помощью несложных оценок и неравенства Коши —
Шварца получаем
II Qi4P IP ^^ ^1II Qi4P II - II Qcp II -Ь || Qncp || -1| Qcp || -I- rf! . || Qcp И -1| Qicp II —
I -b II Qncp || -1| СЗср ||. E.14.16)
Утверждение леммы очевидно при m = 0, ибо тогда Qi = 0. До-
Допустим, что лемма справедлива для многочленов Q степени, не
превосходящей m—1, где т> 1. Тогда если степень Q не пре-
превосходит т, то степень Q\ не превосходит m— 1 и в силу индук-
индуктивного предположения
Кг^т-1Н1<21Ф II.
Подстановка этой оценки в E.14.16) дает
Другими словами, неравенство установлено для многочленов
Q степени, не превосходящей т, что и требовалось доказать. 1
Для вывода неравенства В сначала с помощью линейного
преобразования координат добьемся того, чтобы
Q(i) = ft&r+ 2 bPip с ьфо.
|р|<т, р ф (т, 0, ...,0)
Повторным применением леммы с поочередной подстановкой
вместо Q операторов Qi, Qn,... (заканчивая, таким образом,
скалярным оператором Ь-т\) приходим к неравенству В. |
5.14.5. Доказательство неравенства В'. В силу
E.14.9) для Ц)^Ф имеем неравенство
516 Гл. 5. Распределения и дифференциальные уравнения
из которого в свою очередь с помощью неравенства Коши —
Шварца вытекает, что
где
с(п, г)--
Величина с(п,г) конечна при г>-^п. Функция A + |£|2)ГФ(|)
является (г—натуральное число) преобразованием Фурье от
(l""~r) Ф» гДе чеРез Д> кзк обычно, обозначен оператор Лап-
2/2 2\
ласа —4л; (D\ + ... + D«). Таким образом, пользуясь равен-
равенством Парсеваля E.14.10),'приходим к неравенству
5.15. Преобразвание Фурье распределений
Теперь мы хотим перейти к изучению линейных дифферен-
дифференциальных операторов в частных производных с постоянными ко-
коэффициентами с помощью методов, опирающихся на преобра-
преобразование Фурье. Классическое преобразование Фурье определено
для функций, на скорость роста которых на бесконечности на-
накладываются жесткие ограничения. Эти ограничения очень за-
затрудняют, если не делают невозможным, удовлетворительное
использование преобразования Фурье. Выход — в определении
преобразования Фурье по крайней мере для некоторых распреде-
распределений. Одно из таких обобщений принадлежит Л. Шварцу. Оно
применимо к функциям, которые, грубо говоря, имеют степенной
порядок роста на бесконечности. Это преобразование обладает
большой гибкостью и удобно в обращении. Другое определение
преобразования Фурье, принадлежащее Эренпрейсу и примени-
применимое ко всем обобщенным функциям, правда за счет некоторой
потери гибкости, будет кратко описано в конце параграфа.
5.15.1. Пространство с^ = <^(Rrt) и его фурье-образ. Опреде-
Определим 3? = & (Rn) как векторное подпространство в Coo=Coo(Rn),
образованное теми функциями mgC00, для которых числа
Sm(u) = sup{(l+\x\)m\Dpu(x)\: \p\<m, xe=R*}
конечны при всех т=1,2,... (или, что то же, для произвольно
большого т)\ ср. с примерами в § 6.1. Нормы Sm на простран-
пространстве & определяют в нем линейную топологию, относительно
которой, как легко проверить, & есть пространство Фреше. Более
5.15. Преобразование Фурье распределений 517
того, 9 —монтелево пространство (§ 8.4), г. е. каждое огра-
ограниченное замкнутое подмножество в 9 компактно. Эго —прямое
следствие теоремы Асколи.
Очевидно, что <3* = ^(Rtt) есть векторное подпространство
в^и что топология пространства 9 индуцирует в SD топологию,
которая строго слабее топологии индуктивного предела в про-
пространстве SD. Легко видеть, что в £D можно выбрать такие после-
последовательности (рп), что \\т$пи=*и в 9> для каждого и е 9, Ta-
ким образом, 2) плотно в 9>.
Основным моментом в теории Шварца обобщенного преоб-
преобразования Фурье является то, что это преобразование переводит
пространство 9> в себя. Сейчас мы в этом убедимся.
Так как каждая функция и из 9 интегрируема, то ее преоб-
преобразование Фурье
\ E.15.1)
есть непрерывная функция от gs Rn. (Как обычно, \х — мера Ле-
Лебега на Rn.) Справедливо более сильное утверждение. Так как
функция и убывает быстрее любой отрицательной степени функ-
функции |*| при |*|->оо, то функция й принадлежит С°° и ее част-
частные производные можно подсчитать, производя дифференцирова-
дифференцирование под знаком интеграла.
С другой стороны, так как каждая частная поризводная от
и интегрируема, то с помощью повторного интегрирования по ча-
частям получаем, что функция fi(g) убывает быстрее, чем любая
отрицательная степень функции |£| при |£|->оо.
Из этих двух замечаний следует, что ЗГ отображает 9* в себя.
Несложные оценки, проводимые после интегрирования по частям
и дифференцирования под знаком интеграла, показывают, что
ST — непрерывный эндоморфизм пространств 9.
Нам сейчас важно удостовериться в том, что ЗГ в действи-
действительности является (алгебраическим и топологическим) автомор-
автоморфизмом пространства 9.
Для этого введем на 9 преобразование $Г~Х с помощью сле-
следующего равенства:
gr-xv (х)» J е+™Х'Ч F) d\k (g). E.15.2)
Согласно формуле обращения,
для
В § 10.4 аналогичный формуле обращения результат уста-
установлен при гораздо более слабых ограничениях на и и v для
518 Гл. 5. Распределения и дифференциальные уравнения
случая, когда Rn заменяется более общей группой. В том част-
частном случае, который рассматривается здесь, эта формула сле-
следует из стандартных свойств несобственных интегралов.
Таким образом, ЗГ—алгебраический автоморфизм простран-
пространства 5^, обратным к которому служит &~~х (отсюда и обозначе-
обозначение). Отображения ST и £Г~Х отличаются только знаком в экспо-
экспоненциальном множителе. Поэтому непрерывность ЗГ~Х устанав-
устанавливается так же, как непрерывность ЗГ. Таким образом, ЗГ
обладает непрерывным обратным отображением &~~~1, и, значит,
ЗГ — автоморфизм, что и требовалось доказать.
Заметим еще, что, поскольку уже установлено, что ^" — не-
непрерывное взаимно однозначное отображение пространства
Фреше 9> на себя, то ничего не стоит установить непрерывность
обратного отображения #"~1, ссылаясь на теорему об открытом
отображении (п. 6.4.4).
Нам понадобятся еще две формулы. Если mg^hP — много-
многочлен на Rn, то Рм е ^ и имеет место соотношение
E.15.3)
Более того, P{D)u^9}, и имеет место соотношение
E.15.4)
В силу линейности достаточно доказать эти формулы для слу-
случая, когда Р — одночлен, Р(х)=х*.
При этом условии наши соотношения получаются соответ-
соответственно с помощью дифференцирования под знаком интеграла
и интегрирования по частям.
Последнее свойство преобразования ЗГ, которое нам понадо-
понадобится, выражается равенством Парсеваля
J u-vd\i= J (&*и) • {4Tv)dyL, E.15.5)
справедливым для и, иеУ, Так же как и формула обращения,
это равенство в § 10.4 доказано при значительно более слабых
ограничениях (см., в частности, равенство A0.4.7)). Для рассма-
рассматриваемых здесь функций это соотношение может быть устано-
установлено классическими методами.
5.15.2. Пространство 4У' = £Pr (Rn) медленно растущих рас-
распределений. Мы определили 2)' как топологическое сопряженное
к зЬ. Таким же образом определим пространство ^?/=^?/(Rn) как
топологическое сопряженное к S^(Rn). Так как топология про-
пространства У индуцирует в 3) топологию, более слабую, чем то-
пологя индуктивного предела в 3)> то сужение каждого элемента
X € 9>' на 2) определяет распределение на Rn. Так как 2> плот-
5.15. Преобразование Фурье распределений 519
но в 9, то X вполне определяется своим сужением на 2D. По-
Поэтому можно рассматривать 9Г как векторное подпространство
в 2D'. Элементы пространств 9' называются медленно растущи-
растущими распределениями на Rn. С топологическим векторным про-
пространством 9 проще обращаться, чем с 3), так как оно является
пространством Фреше, а не индуктивным пределом таких про-
пространств. Как легко следует из теоремы Асколи, %— монтелев-
ское пространство (каждое ограниченное замкнутое подмноже-
подмножество в 9 компактно). Поэтому все результаты A) — E), уста-
установленные в § 5.3 для 3) и 3)', справедливы и для 9 и 9'. При
этом, конечно, подразумевается, что 9Г наделено слабой или
сильной топологией, определяемой двойственностью между 9
и 9'. Поэтому, в частности, каждое из пространств 9 и 9Г (по-
(последнее рассматривается в сильной топологии) полное, бочеч-
бочечное и борнологическое. Кроме того, пространство 9 рефлексив-
рефлексивно, т. е. каждая сильно непрерывная форма на 9' может быть
единственным образом записана в виде X*—>(и, X), где и — соот-
соответствующим образом подобранный элемент из 9, и сходимость
сети {иа} в 9 равносильна равномерной сходимости на сильно
ограниченных подмножествах в 9Г соответствующей сети {La}
линейных форм La{X) = (иа, X). Очевидно, что 9' как подпро-
подпространство в 2D' инвариантно относительно частных дифферен-
дифференцирований и умножения на функции / класса С°° степенного
роста на бесконечности.
5.15.3. Преобразование Фурье медленно растущих распреде-
распределений. Мы намереваемся использовать равенство Парсеваля
E.15.5) для распространения преобразования Фурье ^ с про-
пространства 9 на 9'. Общим принципом, лежащим в основе такого
распространения, является переход к отображению, сопряжен-
сопряженному к данному линейному отображению одного локально вы-
выпуклого пространства в другое, — процесс, в общем случае рас-
рассматриваемый в § 8.6.
Так как @~—непрерывный эндоморфизм пространства 9, то
для фиксированного Xg/ отображение v*->{8Tv, X) есть не-
непрерывная линейная форма на 9Г. Поэтому по определению 9*
существует такой однозначно определенный элемент ЗГ'Х, что
для всех v из 9. Мы получаем, таким образом, алгебраический
эндоморфизм ST' пространства 9\ называемый сопряженным к
$Г. В силу следствия 8.6.6 отображение ST' непрерывно в силь-
сильной и слабой топологиях в 9'. Из утверждения (d) § 8.6 и из того
факта, что 3~(9) =9, вытекает, что &~' — взаимно однозначное
отображение. В то же время поскольку 9 — рефлексивное
520 Гл. 5. Распределения и дифференциальные уравнения
пространство и У — взаимно однозначное отображение, го из тео-
теоремы 8.6.13 следует, что &"(&') =9*'. Таким образом, и7"' —вза-
—взаимно однозначное линейное непрерывное (сильно и слабо) ото-
отображение пространства 9" на себя. Так как отображеие ^~1
обладает теми же свойствами, что и #", то сопряженным к нему
служит ({F')-x. Отсюда следует, что отображение (ST')-1 также
(сильно и слабо) непрерывно. Итак, %Ff— (алгебраический и то-
топологический) автоморфизм пространства 9)Г (которое рассма-
рассматривается либо в слабой, либо в сильной топологии).
Для отображения &~~{ и его сопряженного (^"-1)/ = <Г/-1
имеем следующее определяющее соотношение:
Если в этой формуле заменить v на &~v и затем v на v и, значит,
на {q7~v)v to в результате получим равенство
(б, Х)^(Жх), &*гХ), E.15.6)
где временно положено
Каждый элемент и^.99 порождает медленно растущее рас-
распределение и может быть с ним отождествлен (аналогичная си-
ситуация возникает, когда произвольная локально интегрируемая
функция порождает распределение). Если теперь заменить X на
и в E.15.6) и сравнить получающееся соотношение с равенством
Парсеваля E.15.5), то мы увидим, что ff~\u=!Fu для mg^, По-
Поэтому, начиная с этого момента, будем писать &~Х вместо fF\X и
в случае медленно растущих распределений. Мы будем называть
SFX преобразованием Фурье распределения X. (Возможно, луч-
лучше было бы назвать ^Х преобразованием Фурье — Шварца.)
Как и раньше, вместо @~Х иногда будем употреблять символ X.
Таким образом, &~Х определено для каждого JfG/ как
единственное медленно растущее распределение, для которого
равенство Парсеваля
1 E.15.7)
выполняется при всех yG^. В действительности $ГХ — един-
единственное распределение (даже если не накладывать ограничений
на его рост), для которого соотношение
С^Ф, *>-<ф, £~Х) E.15.8)
имеет место при всех tp^S). [В самом деле, если равенство
E.15.8) выполняется для фей), то в силу того факта, что ST —
автоморфизм пространства 9>i распределение X непрерывно в
15. Преобразование Фурье распределений 521
топологии, индуцированной в 3) топологией пространства 9У и
поэтому X обладает единственным непрерывным продолжением
с SD на 9> т. е. является медленно растущим распределением.
Равенство E.15.8) по непрерывности продолжает оставаться
верным, если заменить в нем ф любым элементом и (=9*. Полу-
Получающаяся при этом формула эквивалентна равенству E.15.7),
если положить u = @~v.]
Из наших построений следует, что ST—автоморфизм про-
пространства 9* (в слабой или сильной топологии).
Мы уже отмечали, что 9 можно рассматривать как вектор-
векторное подпространство в 9'. Из рефлексивности и из теоремы
Хана — Банаха вытекает, что 9 плотно в 9'. Из того обстоятель-
обстоятельства, что равенство Парсеваля послужило нам в качестве опре-
определяющего соотношения для отображения 5Г применительно к
9\ следует, что это отображение получено продолжением ЗГ по
непрерывности с 9 на 9'.
В силу этого замечания формулы E.15.3) и E.15.4) продол-
продолжают оставаться справедливыми, если заменить в них и на про-
произвольный элемент X е 9)Г. (При этом нужно лишь заметить, что
операции частного дифференцирования и умножения на много-
многочлен непрерывны на 9'.)
Ниже мы укажем способ дальнейшего распространения этих
равенств на случай, когда свертка P(D)X = P(D)s*X заменяется
более общей сверткой S*X.
5.15.4. Связь между отображениями пространства Rn и пре-
преобразованием Фурье. Пусть Я— взаимно однозначное отображе-
отображение пространства Rn на себя, которое вместе с обратным отобра-
отображением Я принадлежит классу С°°. Тогда Я порождает преоб-
преобразования ## и Я* соответственно функций и распределений,
определяемые равенствами
(и, Н'Х) = (Н.и, X),
где и пробегает множество 3D (или при желании 9\ если X —
медленно растущее распределение). Если функция / локально
интегрируема на Rn, то ее можно считать обобщенной функцией.
При этом обощенная функция Я*/, вообще говоря, порождается
функцией и может быть с нею отождествлена. Однако эта функ-
функция в большинстве случаев отлична от Я*/, чем и объясняется
различие в положении звездочки и обозначениях.
Простыми, но важными примерами отображений Я являются
сдвиги Га, где а — точка из Rn и Тах = х — а, и гомотетии Ях, где
— вещественное число и Н%х = Хх. Эти отображения вместе с
522 Гл. 5. Распределения и дифференциальные уравнения
вращениями исчерпывают все примеры отображений, которые
нам понадобятся в дальнейшем.
В частности, H-\^f = J (ср. с п. 4.18.1); поэтому положим
X=H*-iX для любого распределения Х^З)'. Наша задача —
найги зависимость преобразования Фурье распределения Н*Х от
преобразования Фурье распределения X. Сначала мы сделаем
это для сдвигов, & затем — для случая, когда Н — линейный
автоморфизм пространства Rn (например, гомотетия Ях).
Если f — локально интегрируемая функция и и е 3), то с уче-
учетом инвариантности меры \х относительно сдвигов имеем
<И, faf) = (Ta*U, f) = J U (X - п) f (x) d\L (x) -
причем последний член есть не что иное, как {«, Г_а*/). Таким
образом,
faf=T-a*f. E.15.9)
Аналогичные рассуждения показывают, чго
£ГТат==:е-2та.1^п E.15.10)
для пеб^. Чтобы подсчитать <&"ТаХ для X е &\ применим
дважды формулу Парсеваля и соотношение E.15.10):
т. е.
&~Т*аХ == еШа*ЗГх. E.15.11)
Формулы E.15.9) —E.15.11) в совокупности полностью охва-
охватывают случай сдвигов.
Пусть теперь Я — линейный автоморфизм пространства Rn.
Вывод формулы, аналогичной E.15.9), опирается в этом случае
на формулу замены переменных в кратном интеграле. Для авто-
автоморфизма Н эта формула принимает следующий простой вид:
где через detH обозначен определитель матрицы преобразова-
преобразования Я, записанного в каноническом базисе пространства Rn. До-
Доказательство этого результата можно найти в любом из много-
5.15. Преобразование Фурье распределений 523
численных учебников по анализу. Если ограничиться лишь пре-
преобразованиями Н = Н^ так что |det #| = |Я|П, то этот результат
легко получается повторным использованием формулы для
одномерного случая, или же использованием характерной для \х
инвариантности относительно сдвигов. Действительно, из фор-
формулы
/о7>о# = /о#о7>, где й = Я"](а),
и инвариантности \х относительно сдвигов следует, что равенство
\i'(f) = [i(f ©Я) определяет \х' как меру Радона на Rn, инвариант-
инвариантную относительно сдвигов. Следовательно, \i'=D(H)[iy где
D (Я) — строго положительная функция от Я. Ясно, что D (НН') =
= D(H) -D(H') для любых двух автоморфизмов Я и Н' и что
D(I) = 1, где / — тождественный автоморфизм пространства Rn;
таким образом, функция d(X) =D(Hx) удовлетворяет условиям
d(l) = l и d{Kh/) =d('k)d('k/) для любых двух ненулевых веще-
вещественных чисел i и АЛ Теперь легко показать, что d(\) = \\\h, где
к — некоторое вещественное число. Таким образом, равенство
выполняется для всех интегрируемых функций f и всех веще-
вещественных чисел ^=т^0. Теперь уже нетрудно подобрать так функ-
функцию /, чтобы получить равенство k — —п.
Из общей формулы замены переменных под знаком инте-
интеграла следует, что
H*f = \detH\-lH;lf E.15.12)
(ср. Л. Шварц [2, формула (VII, 6; 14)]).
Аналог формулы E.15.10) основан на том же правиле пре-
преобразования интегралов и на введении сопряженного к Н ото-
отображения Я7, являющегося автоморфизмом пространства Rn
(отождествленного с сопряженным к Rn посредством билинейной
п \
формы х • |= 2 *k\k) и определяемого тождеством Нх» ^=Х'Н%.
fe=i /
Заметим кстати, что (Н~1)' == (Я')~ . Таким образом, получаем
,и = \ det Я Г1. Н;1'<&~и E.15.13)
для и е 9*.
Наконец, из E.15.13) следует формула
Srrfx-lfeiHr1 Н:У3~Х E.15.14)
для Zg^'. Доказательство такое же, как и при выводе
E.15.11) из E.15.10).
524 Гл. 5. Распределения и дифференциальные уравнения
Читатель может заметить, что если 1б^и @~Х — функция,
то из E.15.14) и E.15.12) вытекает равенство
E.15.140
Если далее X — функция, то аналогичным образом получаем
ll E.15.14")
Эта формула служит обобщением формулы E.15.13). Ср.
Л. Шварц [2, формулы (VII, 6; 15) и (VII, 6; 16)] для случая,
# = #ъ когда Н' = Н.
5.15.5. Однородные функции и распределения. Обычно гово-
говорят, что функция / на Rn однородна степени р, если #/*/ = | Я ff
для любого вещественного отличного от нуля числа %. Для рас-
распределения X, порожденного функцией / (которая предполагает-
предполагается локально интегрируемой), это условие в силу E.15.12) и того
факта, что det #х=Яп, эквивалентно требованию
Условимся называть распределение X однородным степени р,
если последнее соотношение выполняется для всех отличных от
нуля вещественных X. Если X — однородное распределение сте-
степени р, то из E.15.14) следует, что @~Х — однородное распреде-
распределение степени —п—р.
5.15.6. Функции и распределения, инвариантные относительно
вращений. Выделим из всех автоморфизмов пространства Rn
вращения R требованием, чтобы равенство /?л: •/?£=#•£ выпол-
выполнялось тождественно по х и |. Это эквивалентно условию /?'=*.
= R~l, из которого следует, что det#=±l. Иногда подразделяют
вращения на так называемые собственные и несобственные. Пер-
Первые— это те, детерминант которых равен +1. Нам такое раз-
различие не понадобится.
Говорят, что функция / инвариантна относительно вращений,
если R*f=f для всех вращений R. Ясно, что инвариантными от-
относительно вращений являются те и только те функции, которые
представимы как функции лишь от \х\. Распределение X инва-
инвариантно относительно вращений (в том смысле, что
(Rji% X)-(u9 X)
для всех вращений R и всех и^Ф) тогда и только тогда, когда
R*X = X для всех вращений R. Так как R' = R~l и |det/?| = 1, то
из E.15.14) следует, что медленно растущее распределениеXин-
распределениеXинвариантно относительно вращений в том и юлько в том случае,
когда его преобразование Фурье SFX обладает тем же свой-
свойством,
5.15. Преобразование Фурье распределений 525
В п. 5.15.8 мы увидим, что предыдущие простые замечания,
касающиеся однородности и инвариантности относительно вра-
вращений, полезны при подсчете преобразований Фурье некоторых
функций и распределений.
5.15.7. Вопросы согласованности. В теории, которую условно
можно назвать «классической», имеется несколько определений
преобразования Фурье функции или меры. Эти определения за-
зависят от ограничений, которые накладываются на рассматривае-
рассматриваемую функцию или меру. Два наиболее старых определения при-
применимы одно к интегрируемым функциям и ограниченным ме-
мерам, другое к функциям, интегрируемым в квадрате. Рассмотрим
первое из них.
Пусть / — интегрируемая на Rn функция; ее преобразование
Фурье @~f принято определять как непрерывную функцию на
Rn, определенную с помощью абсолютно сходящегося интеграла
Наше определение 2Г на пространстве 9 является, очевидно, су-
сужением этого определения. Мы уже отмечали, что определение
преобразования Фурье — Шварца согласуется с данным элемен-
элементарным определением, когда это преобразование применяется к
функциям из 9*. Совершенно аналогичные рассуждения показы-
показывают, что эта согласованность имеет место и для интегрируемых
функций вообще. Действительно, каждая интегрируемая функ-
функция f является в «5*1 = J^1 (R", \i) пределом последовательности
(ип) элементов из 9. Тем более, \imun = f в 9'. Из сходимости
в 9?х следует, что lim!Fun={Ff равномерно на Rn. Из сходи-
сходимости в 9/ вытекает, что \im£run=£Tif в 9\ где мы временно
восстановили индекс «1» у @~и чтобы выделить преобразование
Фурье — Шварца. Из этих двух соотношений получаем, что @~\f
является (распределением, порожденным) функцией #7, что и
доказывает наличие согласованности, о которой мы говорили.
Рассуждения совершенно аналогичны и в том случае, когда
вместо интегрируемой функции f рассматривается ограниченная
мера Радона Я. При этом преобразование Фурье определяется
как абсолютно сходящийся интеграл
$)-X(g)-J e-WdMx)-
Пусть теперь f — функция из i?2(Rn). Тогда интеграл Фурье
в обычном смысле не существует. Выход из затруднения в этом
случае дает теория Планшереля, которая будет подробно рас-
рассмотрена в § 10.4,
526 Гл. 5. Распределения и дифференциальные уравнения
Если в пересечении 9?х(\9?2 взять некоторую последователь-
последовательность (fn), сходящуюся в S2 к /, то функции Tfn будут схо-
сходиться в 572. Класс (элемент из L2), определяемый предельной
функцией, зависит только от класса функции / (и не зависит от
выбранной последовательности); он и принимается в качестве
ST]. Уже сам этот предельный переход убеждает нас в наличии
согласованности с @"\f. К этому заключению можно прийти,
пользуясь равенством Парсеваля, которое справедливо при лю-
любом определении.
В классической теории имеется еще ряд определений, а имен-
именно относящихся к функциям, принадлежащим i?p для 1</?<2.
Эти определения получаются интерполяцией (с помощью тео-
теоремы выпуклости Рисса или другим методом) между предыду-
предыдущими определениями для р—\ и р = 2. Это также согласуется с
определением Шварца; доказательство такое же, как и выше.
Преобразованием Фурье функции из 3?^ A < р < 2) в этом слу-
случае служит класс функций, принадлежащий Lv', где—Ь—= 1.
См., например, для одномерного случая Титчмарш [1, гл. IV].
Самая неудобная черта любой из этих теорий — жесткие
ограничения, которые накладываются на скорость роста на бес-
бесконечности рассматриваемой функции f, и никакие изменения
допустимых значений показателя р в &v не приносят значитель-
значительного улучшения. Бохнер [1] был, по-видимому, первым, кто
нарушил традицию и показал, как можно определить преобразо-
преобразование Фурье для функций /, имеющих степенной рост на беско-
бесконечности. Как мы сейчас увидим, идея Бохнера неявно исполь-
использует некоторое обобщенное дифференцирование, поэтому прак-
практическая ценность его схемы была ограничена отсутствием в то
время необходимой техники. Сравнительно недавно были введе-
введены определения преобразования Фурье для функций f, имеющих
экспоненциальный рост на бесконечности (см., например, Кар-
леман [1], Титчмарш [1]). Эти определения основаны на ис-
использовании методов комплексного переменного и, вообще го-
говоря, обладают рядом недостатков, так как определенное таким
образом преобразование теряет некоторые из основных свойств
преобразования Фурье. Мы оставляем в стороне определения,
основанные на теории комплексного переменного, и остановимся
немного на методе Бохнера.
Идея Бохнера относилась к случаю /1=1, рассмотрением ко-
которого мы и ограничимся. Для начала предположим, что
f — интегрируемая функция. Ее преобразованием Фурье можно
считать непрерывную функцию
5.15. Преобразование Фурье распределений 527
Положим Fod) =F(I) и определим Fh индуктивно с помощью
формулы
о
Легко проверяется, что
Fk(l)=jf(x)Ek(h x)dp(x), E.15.15)
где
\^ J ^Mll E.15.16)
Выражение E.15.15) можно переписать в виде
+1
Fk(l)= j f(x)Ek(lf x)dp(x) +
-1
+ jf(x)(~2mxrke-2nilxdii(x) + Pk-.i(&, E.15.17)
\x\>\
где под Pr понимается многочлен степени не выше г.
Теперь не представляет труда восстановить F=F0 no Fk. Дей-
Действительно, так как функция F непрерывна (в силу интегри-
интегрируемости /), то Fk принадлежит классу Ск и
F = ^±. E.15.18)
Наблюдение Бохнера заключалось в следующем: во-первых,
сумма первых двух членов в правой части равенства E.15.17)
определена как непрерывная функция от |, если функция
A +1 х |)~ / интегрируема; во-вторых, если обозначить эту сумму
через Fk (£), то, поскольку Ри-л — многочлен степени не выше
k—1, равенство E.15.18) можно заменить равенством
, E.15.19)
когда f интегрируема.
Бохнер обратил внимание на то, что равенство E.15.19) мо-
может быть использовано для определения F, когда функция / сама
не является интегрируемой, но A +| х \)~ f обладает этим свой-
свойством. Тем самым мы сталкиваемся по сути дела с задачей об-
обобщенного дифференцирования, так как функция Fk, вообще го-
говоря, не будет обладать k производными (ни даже одной) в
классическом смысле. С другой стороны, становится понятным,
528 Гл. 5. Распределения и дифференциальные уравнения
каким образом удовлетворительная техника обобщенного диф-
дифференцирования способствует обобщению понятия преобразова-
преобразования Фурье.
Здесь следует также отметить, что предложенное Бохнером
определение имеет такие же недостатки, как rf некоторые более
ранние определения. Эти недостатки сказываются при переходе
от Fh к F*k. Например, связь между Fin сдвигами функции f или
с операцией взятия свертки / с другими функциями или мерами
не столь очевидна, не столь проста, как этого хотелось бы (см.
п. 5.15.4).
Если сравнить определение, предложенное Бохнером, с опре-
определением Шварца, то, считая производные, фигурирующие в
E.15.19), производными в смысле обобщенных функций, легко
установить, что F, определенное равенством E.15.19), действи-
действительно является преобразованием Фурье — Шварца @~f = f для
функции /. Таким образом, трудности, возникающие при исполь-
использовании определения Бохнера, лишь кажущиеся. Но нужно по-
помнить, что к этому выводу можно прийти, только используя пре-
преобразование Фурье — Шварца.
Вопрос согласованности заслуживает того, чтобы рассмотреть
его более подробно. Предположим, что функция (l + \x\)~hf ин-
интегрируема, Fk — функция, представляющая собой сумму первых
двух интегралов в правой части E.15.17), и F — обобщенная
функция, определенная равенством E.15.19). Так как функция
Fl ограничена и непрерывна, то очевидно, что F — медленно рас-
растущая обобщенная функция. По условию / — тоже медленно рас-
растущая обобщенная функция. Таким образом, преобразование
Фурье — Шварца / = &*\ определено и также является медленно
растущей обобщенной функцией. Наша задача — показать, что
F и f совпадают. Для этого достаточно доказать, что
для любого и из плотного в 9* подмножества. Применяя клевой
части этого равенства определение дифференцирования в смысле
теории обобщенных функций, а к правой части — равенство Пар-
севаля, видим, что задача сводится к доказательству тож-
тождества
для м, пробегающих плотное в Ф множество. Это множество со-
состоит из обратных преобразований Фурье функций v из 2). Та-
5 15. Преобразование Фурье распределений 529
ким образом, нам нужно показать, что для любого ug® спра-
справедливо равенство
IF' F"k(|) ф (s) = If {
E.15.20)
Для этого рассмотрим соотношения
\ 1Г !г*Ф(£) = 0 для 0<г<&, E.15.21)
dc.
где г и k — целые числа. Формула E.15.21) получается при по-
повторном интегрировании по частям с учетом финитности
функции v.
Приступая к доказательству соотношения E.15.20), напоми-
напоминаем, что
" *k—i (ь> х) »
где Pk-\(l,x)—многочлен от | степени не выше k—1, коэффи-
коэффициенты которого суть непрерывные функции от хфО.
Пользуясь соотношениями E.15.21), получаем, что внутрен-
внутренний интеграл в правой части E.15.20) повторным интегрирова-
интегрированием по частям может быть преобразован в интеграл
или при хФО в интеграл
Теперь разобьем область интегрирования во внешнем интеграле
на интервал |я|<1 и его дополнение и подставим первое из при-
приведенных выше двух выражений во. внутренний интеграл, где
|я|<1, а второе в интеграл на дополнительном множестве
|д:|> 1. К каждому из повторных интегралов, полученных таким
образом, можно применить теорему Фубини — Тонелли, чтобы
оправдать изменение порядка интегрирования. В результате в
правой части E.15.20) получаем выражение
(-0* J^-.фЦ Jf(
Очевидно, что член в квадратных скобках есть не что иное, как
F*k(Q. Таким образом, E.15.20) доказано,
530 Гл. 5. Распределения и дифференциальные уравнения
5.15.8. Некоторые примеры. Читатель, по-видимому, заметил,
что теория Шварца не дает способов быстрого подсчета преобра-
преобразований Фурье конкретных функций или распределений. Поло-
Положение здесь не лучше и не хуже, чем при классической интерпре-
интерпретации. Ниже мы перечислим несколько простых примеров, вычис-
вычисления преобразований Фурье функций или распределений, для
которых не существует преобразования Фурье в классическом
смысле. Некоторые из этих примеров нам понадобятся в даль-
дальнейшем.
В число полезных результатов, конечно, следует включить
формулы E.15.3) и E.15.4), обобщенные таким образом, чтобы
и можно было заменить любой медленно растущей обобщенной
функцией (см. конец п. 5.15.3).
Из очевидного равенства
^8=1 E.15.22)
и из E.15.4) непосредственно вытекают следующие частные ре-
результаты:
&~{Ор) = 1Ру E.15.23)
с^(Ае) = — 4л:2[ g |2, E.15.24)
где Л — оператор Лапласа в Rn.
Одномерный случай. Следующие ниже примеры, возможно,
в слегка измененном виде содержатся в гл. 3 книги Лайтхил-
л а [1]; см. также Л. Шварц [2, стр. 113—114], Гельфанд и
Шилов [2, гл. II,«в частности стр. 189—219].
Обозначим через Н функцию Хевисайда, т. е. характеристи-
характеристическую функцию интервала @, оо). Первая из формул, которая
будет установлена, даст нам преобразование Фурье функции
хаН, где —1 < а < 0. Вот она:
+1)8еп1Bя|1|)-«-1. E.15.25)
Здесь и далее а! = Г(а+1) — гамма-функция, определяемая, как
обычно, интегралом
при Rea>—1 и его аналитическим продолжением при всех
остальных значениях а.
Пользуясь E.15.25) и тождеством
5.15. Преобразование Фурье распределений 531
легко получить, что
&*(\х |а)= - 2а! sin ^ . Bя| g |)"а E.15.26)
для — 1 <а<0.
В качестве третьего примера докажем равенство
oT(logU|) = -i-F. Р.||Г1-(у + 1оё2я)е, E.15.27)
где у — постоянная Эйлера.
Прежде чем перейти к доказательству формул E.15.25) —
E.15.27), скажем несколько слов об условиях применимости фор-
формул E.15.25) и E.15.26). Первая из них будет доказана в пред-
предположении, что а — вещественное число, —1<а<0. В против-
противном случае по крайней мере одно из выражений хаН\1\~а~1
нельзя определить как распределение. Однако обычно эту труд-
трудность обходят, заменяя указанные выражения соответственно
псевдофункциями F. Р. (хан) и F. Р. || Г", после чего фор-
формулу E.15.25) можно распространить на комплексные значения
а с помощью аналитического продолжения.
Аналогичные замечания можно сделать и по поводу E.15.26).
Доказательство формулы E.15.25). Так как в Ф'
то
& (хаН) = lim 4Г (xae~txH).
С другой стороны, при £>0 функция xae~txH интегрируема, и по-
потому в силу согласованности ее преобразованием Фурье яв-
является функция
с
J
о
которая, как показывает подсчет, равна
при этом для дробных степеней комплексных чисел взято их
главное значение. Полагая /->0 (^>0)г получаем в пределе
правую часть формулы E.15.25). I
Доказательство формулы E.15.26). Метод доказа-
доказательства формулы E.15.26) уже был указан. Нужно только
принять во внимание общее правило, что преобразование Фурье
от X есть {&~X)V I
632 Гл. 5. Распределения и дифференциальные уравнений.
Доказательство формулы E.15.27). Так как в SP'
а-»0
то из формулы E.15.26) следует, что
и|)
При этом мы воспользовались разложениями
(-а)\ = 1-уа + О(а2),
сТ1 sin ^- = ^[1 + 0 (a2)],
Bя)а-] = BлГ' [1 + a log2n+O(а2)].
Таким образом,
а [е- 2(- a)! sin -^-. Bл)| £ Г']"' -
= ае -1 [1+ (у + In 2я)а + О (а2)]| | Г1.
Проводя несложное интегрирование по частям, получаем, что
в У
a-»0
Таким образом,
z a->0
-5-lim
z a-»0
например, в смысле У. Поэтому для доказательства E.15.27)
Г
достаточно показать, что lim Xa = F. Р. 11 Г (известно, что пре-
дел существует).
Легко проверяется, что
F Р 1 t 1"'= ^ (sgn g - log [ 6 I)
С другой стороны, если и ^2), то
5.15. Преобразование Фурье распределений 533
Интеграл преобразуется с помощью интегрирования по частям
по отдельности в интервалах (—оо, 0) и @, оо). В результате
получаем
<и, Ха) - - J и'F)а~!(бв- 1)ФF)+ J *'(-
Р о
При а->0 это выражение стремится к
оо оо
- JV (I) log | ф (£)+J «'(-£) log
о о
<iif F. Р.1БГ1).
Г1
Соответственно lim Xa = F. P.| g Г1, во всяком случае, слабо в
а-»оо
SP', чго и требовалось доказать. Таким образом, E.15.27) дока-
доказано. В
Функция |#|-а в многомерном случае. Рассмотрим функцию
(|л;|~ана Rn. Она локально интегрируема при Rea<ft. Поскольку
она инвариантна относительно вращений, то ее преобразование
Фурье обладает тем же свойством (п. 5.15.6). Далее, так как
\х\~а — однородная функция степени —а, то из результатов
п. 5.15.5 следует, что ее преобразование Фурье — однородная
функция степени a — п.
Можно показать, что для некоторых значений а (по крайней
мере для тех, у которых Rea>2-n) of (| х \~а) есть функция.
Если это считать доказанным, то однородность и инвариантность
относительно вращений определят преобразование Фурье с точ-
точностью до постоянного множителя. Таким образом, это преобра-
преобразование должно быть функцией Сп,а\ I \а~п, где Сп>а — число,
зависящее только от п и а. Величину Сп,а можно определить,
пользуясь равенством Парсеваля E.15.7). Полагая в нем
и = ехр(—я|л:|2), получаем, что &~v = exp(—я|||2), откуда
—л: 2
— a
d) •
Для других значений а нужно воспользоваться аналитическим
продолжением и псевдофункциями. См. Л. Шварц [2, стр.113
и далее].
534 Гл. 5. Распределения и дифференциальные уравнения
5.15.9. Формула замены. Название принадлежит Л. Ш в а р цу
[2, стр. 124]. Имеются две формулы замены, из которых нам по-
понадобится только одна — формула, в которой свертка с по-
помощью преобразования Фурье заменяется обычным произведе-
произведением:
* X) - <3TS • <ЗГХ. E.15.28)
Формула превращается в классическую, если 5 и X—интегри-
X—интегрируемые функции или ограниченные меры, так как тогда пре-
преобразование Фурье можно определить в классическом смысле
с помощью абсолютно сходящихся интегралов; при этом фор-
формула E.15.28) становится следствием теоремы Фубини— Тонел-
ли. Очевидно, однако, что E.15.28) не имеет смысла, если S и
X — произвольные медленно растущие обобщенные функции.
Л. Шварц [2, стр. 124] приводит ряд достаточных условий
справедливости этой формулы; некоторые другие условия
имеются в работах Эдварде [4] и Хирата и Огата [4].
Нам достаточно будет рассмотреть случай, когда S обладает
компактным носителем и X — медленно растущее распределе-
распределение. Докажем при этих условиях формулу E.15.28).
A) В силу теоремы 5.8.1 распределение S есть конечная
сумма членов вида D^X, где Я— мера Радона, обладающая ком-
компактным носителем. Пользуясь линейностью, нетрудно прове-
проверить нашу формулу для случая, когда S = Dvk.
С другой стороны, если S имеет такой вид, то из E.15.4) сле-
следует, что
Х] = <&* [Dp (Я * X)] « 1Р • gT (Я * X)
Таким образом, доказательство сводится к проверке формулы
в случае 5 = Я.
B) Выберем в 9> некоторую сеть (щ), сходящуюся в &' к X.
(Здесь достаточно даже слабой сходимости.) Тогда для каждого
i имеем
(&~ (Я * щ) = <&"к • <&"иь
что является следствием классических интегральных представле-
представлений преобразования Фурье и теоремы Фубини — Тонелли.
Так как Я обладает компактным носителем, то из формулы
(v9 Я * щ) = (р * Я, ut)
непосредственно следует, что Я* ^->Я*Х слабо в 9". Следова-
Следовательно,
5.15. Преобразование Фурье распределений 535
слабо в &'. В то же время так как Х = \\тщ, то щ
(оба предела в смысле слабой сходимости в ЗРГ). Переходя к
пределу, получаем
Таким образом, формула E.15.28) при сделанных нами пред-
предположениях установлена.
5.15.10. Теорема Пэли—Винера и «теорема о носителях»
Лионса. Указанные теоремы играют основную роль в теории
линейных дифференциальных уравнений в частных производ-
производных. Хотя в теореме Лионса не содержится никакого упомина-
упоминания о преобразовании Фурье, но ее доказательство и ее прило-
приложения тесно с ними связаны. Теорема Пэли — Винера является
центральной теоремой гармонического анализа.
У нас теперь достаточно сведений о преобразовании Фурье,
чтобы сформулировать эти результаты. Обе теоремы будут при-
приведены здесь без доказательства.
Теорема Лионса о носителях. Пусть X и Y — распределения
на Rn, обладающие компактными носителями. Тогда замкнутая
выпуклая оболочка множества supp (X* У) совпадает с вектор-
ной суммой замкнутых выпуклых оболочек множеств supp X a
supp У.
Эту теорему и ее доказательство можно найти в работе
Лионса [4].
В своем первоначальном виде теорема Пэли — Винера
(Пэли и Винер [1, стр. 12],\3игмунд [2, т. II, стр. 408])
дает характеризацию функций одного комплексного перемен-
переменного, получающихся как преобразование Фурье функций из
L2(R!) с компактными носителями. Л. Шварцу [2, стр. 128]
удалось освободиться от условия принадлежности к L2 и рас-
распространить теорему на случай нескольких переменных. В та-
таком виде теорема более естественна и полезна.
Вначале сделаем несколько замечаний о преобразовании
Фурье Х = @~Х распределения X на Rn, обладающего компакт-
компактным носителем, содержащимся в гиперкубе с центром в нуле и
стороной 2с. Мы знаем, что X есть конечная сумма производных
D^X, где % — мера Радона на Rn с компактным носителем. Да-
Далее, как было замечено в п. 5.15.7, преобразование Фурье от X
является (распределением, порожденным) функцией
Х(|) = J e-2^'xdX(k).
Согласно E.15.4) в обобщенной форме, преобразование Фурье
от X представляет собой конечную сумму функций вида |рЯ(|).
536 Гл. 5. Распределения и дифференциальные уравнения
Таким образом, X можно продолжить до целой функции на О,
которая на Rn имеет степенной порядок на бесконечности.
Кроме того, так как меру X можно выбрать так, чтобы ее
носитель содержался в гиперкубе с центром в нуле и стороной
2с' для любого с'>с, то для £>^Сп имеем
Л-1
Отсюда
Другими словами, целая функция X есть функция экспонен-
экспоненциального типа не выше 2пс.
Теорема Пэли — Винера в формулировке Шварца сводится
к утверждению, что условия, которым удовлетворяет X, харак-
характеризуют ее как преобразование некоторого распределения с
компактным носителем.
Теорема Пэли — Винера — Шварца. Пусть X принадлежит
9*'. Для того чтобы распределение X обладало компактным но-
носителем, содержащимся в гиперкубе с центром в нуле и сторо-
стороной 2с, необходимо и достаточно, чтобы его преобразование
Фурье X было целой функцией экспоненциального типа не
выше 2пс.
Другая формулировка:
Для того чтобы функция F на Rn была преобразованием
Фурье распределения на Rn, имеющего компактный носитель,
заключенный внутри гиперкуба с центром в нуле и стороной 2су
небходимо и достаточно, чтобы A) F имела на Rn степенной
рост на бесконечности и B) F можно было продолжить до целой
функции на О экспоненциального типа не выше 2лс.
5.15.11. Заканчивая изложение теории обобщенного преобра-
преобразования Фурье, следует упомянуть теорию Эренпрейса [7].
Введем в рассмотрение пространство D = ST(£D) всех функ-
функций, являющихся преобразованиями Фурье функций, принадле-
принадлежащих S) = S)(Rn). Элементы из D естественно рассматривать
как функции п комплексных переменных, и как таковые они
представляют собой в точности те целые аналитические функции
на О экспоненциального типа, которые быстро убывают на Ra.
Такая характеризация этих функций следует из теоремы Пэли —
Винера — Шварца. Пространство _Z) топологизируется требова-
требованием, чтобы У было гомеоморфизмом пространства 3) на D.
5.16. Рассмотрение задачи 1 537
Нетрудно описать эту топологию непосредственно в терминах
самих' функций из D, но для наших целей это не потребуется.
Пользуясь теоремой о замкнутом графике, можно проверить, что
SF'1 — непрерывное отображение пространства D в 2), откуда
вытекает, что ЗГ — топологический изоморфизм пространства 3)
на IX Поэтому преобразование Фурье для произвольных обоб-
обобщенных функций можно определить как отображение (@~~1)\
причем результат такого преобразования будет элементом из
D'. Другими словами, преобразование Эренпрейса STT опреде-
определяется для Т е 3)' равенством
для каждого f g D. Сравните это определение с определением
преобразования Шварца из п. 5.15.3, где Т — медленно расту-
растущее распределение. Эти определения согласуются. Подробности
см. уЭренпрейса [7] и Гельфанда и Шилова [2, гл. II].
Как будет замечено в п. 5.17.3, Эренпрейс использует свое
определение преобразования Фурье для исследования уравнений
в свертках, частным случаем которых являются линейные диф-
дифференциальные уравнения в частных производных.
Но за общность подхода, принадлежащего Эренпрейсу, при-
приходится расплачиваться невозможностью локально сравнить два
элемента из D\ как это можно делать с распределениями Швар-
Шварца. Это происходит потому, что новые пробные функции (эле-
(элементы из D) не могут равняться нулю на непустом открытом
множестве, не обращаясь при этом в нуль всюду.
5.16. Рассмотрение задачи 1
Здесь мъ1 приведем несколько результатов, относящихся к ре-
решению задачи 1 из п. 5.12.3. Возможны различные подходы к ре-
решению этой задачи. Хотя мы подробно рассмотрим лишь часть
имеющихся в настоящее время результатов, полученных одним
из этих подходов, впоследствии мы прокомментируем и другие
подходы и успехи в решении этой задачи. Для наших целей, ве-
вероятно, лучшее — придерживаться изложения Мальгранжа
[1], или Л. Шварца [8], или обоих. Систематическое исследова-
исследование вопроса содержится в книге Хёрмандера [7].
5.16.1. Замечания о степенных рядах. При решении задачи 1
и подобных более общих вопросов Мальгранж использует неко-
некоторые нетривиальные свойства степенных рядов от нескольких
неизвестных (или переменных), причем эти ряды могут быть
сходящимися или формальными.
538 Гл. 5. Распределения и дифференциальные уравнения
Для решения самой задачи 1 применяются только некото-
некоторые из этих результатов. Мы коротко расскажем о тех свой-
свойствах степенных рядов, которые нам понадобятся.
Сначала рассмотрим формальные степенные ряды от п не-
неизвестных. Основные определения и свойства таких рядов чита-
читатель может найти у Бурбаки [5, стр. 64—82]. Мы ограничимся
рассмотрением рядов с коэффициентами из поля комплексных
чисел С. Можно следующим образом построить алгебру Fn
формальных степенных рядов от п переменных (с коэффициен-
коэффициентами из С). Как обычно, обозначим через р набор п целых чисел
Pk^O, \4^k^n. Таким образом, если /—множество неотри-
неотрицательных целых чисел, то р е Iй. Через \р\ обозначается сумма
Pi + ... + Рп- Элементами алгебры Fn являются семейства/= (ар),
где индекс р пробегает множество Iй и каждое ар есть комп-
комплексное число; как множество Fn есть просто С(/п). Множество
Fn как некоторая степень (см. конец п. 0.1.3) множества С об-
обладает естественной структурой векторного пространства над
С. Превратим Fn в алгебру следующим образом. Для каждого
р обозначим через X? элемент из Fn, представляющий собой се-
семейство (aq)f для которого aq равно 1 при q = p и 0 при цфр.
Тогда f=(ap) можно формально представить в виде суммы
2 CLPXP. Произведение X? и Хч по определению равно Хр+<*.
Операцию умножения распространяют на произвольные пары
элементов из Fn, постулируя ее билинейность относительно фор-
формальных сумм. Другими словами, если f=(uv) и g={bp), то
произведение fg есть (ср), где
£Р= 2 я А'
r+s = p
Очевидно, что это продиктовано тем, что под (ар) пони-
понимается «степенной ряд» вида
от п неизвестных, причем умножение этих рядов производится
формально по правилу Коши. Приведенное выше формальное
определение дает возможность избежать определения в матема-
математических терминах того, что понимается иод «неизвестными».
Ряды ^jupXpt которые до сих пор строились формально,
можно считать рядами элементов из Fn, сходящимися относи-
относительно топологии покоэффициентной сходимости, т. е. относи-
относительно локально выпуклой топологии в Fn, в которой база
окрестностей нуля состоит из множеств {(ар): | ар К е для р е /},
где е — произвольное число >0, а / пробегает все конечные под-
подмножества в /п. Таким путем Fn превращается в отделимое ло-
5.16. Рассмотрение задачи 1 539
кально выпуклое пространство; легко проверить, что Fn на са-
самом деле есть пространство Фреше; кроме того, Fn— топологи-
топологическая алгебра. Пространство, сопряженное к Fnj можно отож-
отождествить с ЖAп) (векторным пространством комплексных функ-
функций на /п, обладающих конечными носителями; при этом Iй
рассматривается как дискретное пространство). При таком отож-
отождествлении элемент м=(мр) g J(/n) порождает линейную
форму
(ар) ь-> 2 tipap.
Если f = (ap)=%apXpe=Fn и £=(£,, ..., Сп)—точка из О,
то имеет смысл поставить вопрос об абсолютной сходимости
рядов комплексных чисел 2^Р, где £р = £^ ... £рпп. Обозна-
Обозначим через CFn множество тех f&Fn, для которых указанные
ряды комплексных чисел абсолютно сходятся при каждом £ из
некоторой окрестности нуля в О. Такие / будем называть схо-
сходящимися степенными , рядами от п неизвестных. Естественно
обозначить через /(£) сумму ряда ^ар£,р, если £чтаково, что
2 аР£>Р— абсолютно сходящийся ряд из комплексных чисел.
Очевидно, что CFn — всюду плотная подалгебра в Fn (так
как она содержит все конечные ряды, т. е. все многочлены от
п неизвестных).
Как алгебру Fn можно отождествить с алгеброй ростков го-
голоморфных в нуле функций (см. пример 3 § 6.3). Однако топо-
топология пространства Fn индуцирует в CFn топологию, которая
строго слабее топологии индуктивного предела, определяемой
в § 6.3.
Теперь можно описать результаты относительно Fn и CFn,
необходимые для понимания подхода Мальгранжа к задаче 1
и к аналогичным вопросам.
Теорема а. Пусть /, g\, ..., gr принадлежат CFn. Для того
чтобы ряд f содержался в идеале алгебры CFUi порожденном
элементами gu ..., gry достаточно (и, очевидно, необходимо),
чтобы f принадлежал идеалу в Fny порожденному элементами
gu •. •» gr- Другими словами, если уравнение
относительно hj разрешимо в Fn, то оно разрешимо и в CFn.
Теорема b (лемма Крулля), Каждый идеал в Fn замкнут.
Доказательства этих теорем см. в трудах семинара Кар-
Карта на [3, сообщение XI, теорема III, следствие, и теорема IV,
540 Гл. 5. Распределения и дифференциальные уравнения
следствие]. В дополнение к этим «локальным» теоремам имеется
еще «глобальная» теорема, принадлежащая К а р т а н у [4].
Теорема с. Пусть /, g\, ..., gr— целые функции на О и для
каждого а^Сп элемент f(a + £) из CFn принадлежит идеалу
в Fn, порожденному элементами g"i(a + £), ..., g"r(a + £) из CFn.
Тогда f принадлежит идеалу, порооюденному в алгебре всех це-
целых функций элементами gu ..., gY, т. е. существуют такие це-
г
лые функции hr на О, что / — 2 A/g/,
Для общих проблем, которые рассматривал Мальгранж, тео-
теоремы а, Ь и с используются в полную силу. Для изучения за-
задачи 1, что является нашей главной целью, нам нужны только
теорема b для главных идеалов (т. е. для идеалов с одной обра-
образующей) и случай г=\ в теоремах а и с. Эти частные случаи
являются легкими, но тем не менее не очевидными.
Приведем еще одно замечание о представлении пространства,
сопряженного к Fn. Если f~lZjupXp принадлежит CFn, то ар~
можно выразить через f с помощью обычной формулы Тейлора
где в правой части через f обозначена функция, определяемая
сходящимся степенным рядом f (ее область определения — не-
некоторая окрестность нуля в О). Такая функция существует не
для любого f из Fnj но мы можем определить d^f(O) через ар
с помощью вышеприведенных формул. Это означает, что дей-
действие обобщенной функции д?е как линейной формы на Fn опре-
определяется равенством
Из всего того, что было сказано о топологическом сопряжен-
сопряженном к Fn, следует, что его можно отождествить с векторным
пространством распределений, носитель которых есть {0}. Любое
такое распределение однозначно представимо в виде конечной
линейной комбинации производных д^г от меры Дирака е, со-
сосредоточенной в начале координат.
5.16.2. Предварительные сведения об уравнениях в свертках.
Пользуясь описанными в п. 5.16.1 свойствами степенных рядов,
можно получить некоторые результаты об уравнениях, в которые
входят свертки распределений, обладающих компактными носи-
носителями; это приводит к решению задачи 1. Связь между распре-
распределениями с компактными носителями и степенными рядами осу-
осуществляется с помощью преобразований Фурье,
5.16. Рассмотрение задачи 1 541
Как мы видели в п. 5.15.10, если X — распределение на Rn,
имеющее компактный носитель, то его преобразование Фурье
X есть целая функция на О (или продолжается до такой функ-
функции). Поэтому ее можно отождествить с рядом Тейлора в нуле,
который является элементом из CFn, причем это соответствие
взаимно однозначно. С другой стороны, если Y — другое такое
распределение, то преобразование Фурье от Х*У есть X*Y.
Следовательно, это преобразование переводит свертки в обыч-
обычные произведения, и эта процедура дает возможность с по-
помощью теорем об идеалах в Fn и в CFn получить инфомацию
об уравнениях в свертках.
Перейдем к осуществлению этой программы. Для краткости
будем писать С°° вместо C°°(Rn) и С'00 вместо C/co(Rn). Под
C'°°(Rn) понимается пространство распределений с компактными
носителями.
Лемма 1. Пусть Л, В е С/о° и условие
(a) g — многочлен и A *g = 0
влечет за собой условие
(Р) Я*£ = 0.
Тогда В принадлежит идеалу в CFn, порожденному элементом
А. Обратно, если В принадлежит этому идеалу, то (а) :ф (Р).
Доказательство. Пусть М — идеал в Fn, порожденный
элементом А. В силу теоремы а п. 5.16.1 достаточно доказать,
что В принадлежит М. По теореме b п. 5.16.1 идеал М замкнут
в Fn. Таким образом, можно воспользоваться теоремой Хана —
Банаха и свести вопрос к доказательству того, что любая не-
непрерывная линейная форма на Fn, аннулирующая М, аннули-
аннулирует и В. Переходом к преобразованию Фурье импликация
(а) гф (Р) сводится к следующему утверждению: пусть X — про-
произвольная обобщенная функция тина P(D)e, где P(D)—произ-
P(D)—произвольный линейный оператор в частных производных с постоян-
постоянными коэффициентами. Тогда если Л-Х = 0, то В-Х = 0. Таким
образом, А *Х = 0 влечет, в частности, (В, Х) = A, В-Х)=0. Дру-
Другими словами, если (Лф, Х) = 0 для всех ф из 2) = 2)(Rn), то
(Б, ,Y)=0. Однако в силу природы X утверждение, что (Лф, Х) =
= 0 для всех ф из 2), эквивалентно утверждению, что (Л/7,Х)=0
для всех F из Fni т. е. что X аннулирует М. Но, как было заме-
замечено, такие X порождают пространство, сопряженное к Fn. От-
Отсюда следует нужное нам утверждение.
Так как рассуждения можно обратить, то это показывает,
что импликация (а) =ф (Р) и необходима для того, чтобы В при-
принадлежал идеалу в CFnt порожденному элементом Л. |
542 г л 5. Распределения и дифференциальные уравнения
Лемма 2. Пусть Л= (Ль ..., К)—точка из О. Если А и
В — распределения на Rn, имеющие компактные носители, то
для того, чтобы B = FA для некоторой функции F, голоморфной
в какой-нибудь окрестности точки X, необходимо и достаточно^
чтобы условие
(a') g — многочлен и A*(ge2i%a'x) = О
влекло за собой условие
Доказательство. Эту лемму можно свести к лемме 1,
рассмотрев А' = e~2niK'xA и В' = e~2nilxB. Нужно учесть только
при этом, что A/(^)=A(X + t)), Я'(£)=£(*, + £) и
А * (ge2ntb.X) = ешьх(А' * g), E.16.1)
причем равенства остаются справедливыми, если заменить А и
А' соответственно на В и В\ |
С помощью этих двух лемм получаем два главных вспомо-
вспомогательных результата.
Предложение 1. Пусть А и В — распределения, имеющие
компактные носители. Для того чтобы B = FA, где F — некоторая
целая функция на О, необходимо и достаточно, чтобы для лю-
любой точки ^еСп имела место импликация (а') =ф ((З7). (Обо-
(Обозначения те же, что и в лемме 2.)
Доказательство. Необходимость непосредственно сле-
следует из необходимости условия леммы 2. Обратно, если импли-
импликация (а') :ф (р7) имеет место для любой точки X, то из доста-
достаточного условия леммы 2 вытекает, что B = FxAy где FK — неко-
некоторая функция, голоморфная в некоторой окрестности точки %.
Применение теоремы с п. 5.16.1 показывает, что B = FA для не-
некоторой целой функции F на С71. |
Предложение 2. Пусть P(D)—линейный дифференциальный
оператор в частных производных с постоянными коэффициен-
коэффициентами, F=P(D)e и X — распределение с компактным носителем.
Для существования такого распределения Y с компактным но-
носителем, что P(D)Y = X, необходимо и достаточно, чтобы X/F
была целой функцией на О.
Доказательство. Необходимость очевидна, так как
X = P(D)Y, тде Y имеет компактный носитель, эквивалентно
X=FY, где У — целая функция.
Для доказательства достаточности предположим, что Х =
zxF-G, где G — целая функция на О. Известно, что X — целая
функция на R* экспоненциального типа и степенного роста на
бесконечности (п» 5,15,10), В соответствии с теоремой Пэли —
5.16. Рассмотрение задачи 1 543
Винера-—Шварца (п. 5.15.10) достаточно показать, что целая
функция G = X/F— экспоненциального типа и степенного роста
на Rn.
Исключая тривиальный случай P(D)=0, можно считать
(после предварительного линейного преобразования координат),
что F—многочлен вида
m
* (bp • • •» b ) === СЪ\ "Г 2j «1 Г V'2> * • • » Ь^»
где с — отличное от нуля комплексное число и Fr—многочлены
на О. Теперь нужные нам свойства функции G сразу же вы-
вытекают из леммы п. 5.14.3. 1
Замечания. Допустим, что Xg2), а остальные условия
леммы оставлены без изменений. Тогда X = P(D)Y для неко-
некоторого Y ^3). Действительно, как мы уже знаем, У можно вы-
выбрать из С/о°. Пользуясь теоремой А § 5.14, выбираем фундамен-
фундаментальное решение Е оператора P(D). Тогда* из равенства Х =
= P(D)Y получаем, что Е*Х= У, откуда в силу принадлежности
X к 3) следует, что У принадлежит СООПС'ОС = 2).
Можно получить другие варианты предложения, если вос-
воспользоваться замечаниями в конце п. 5.14.2, в силу которых Е
можно выбрать так, чтобы свертка £*А принадлежала L\Oc
если h e L2 обладает компактным носителем. Таким образом,,
если известно, что X имеет компактный носитель и DpXeL?Oc,
для |/?|^&, то Y( = E*X) можно выбрать так, чтобы удовле-
удовлетворялись те же условия. Напомним, что
5.16.3. Решение задачи 1. Мы приведем несколько вариантов
решений в зависимости от рассматриваемых пространств функ-
функций или распределений.
Теорема А. Пусть п —выпуклая область в Rn, a P(D) — ли-
линейный оператор в частных производных на Rn с постоянными
коэффициентами. Каждая функция f из C°°(Q), удовлетворяю-
шдя на Q уравнению P(D)f = 0, является в C°°(Q) пределом ко-
конечных линейных комбинаций экспоненциальных многочленов,
удовлетворяющих тому же уравнению.
Доказательство. Предположим, что X^C'°°(Q) аннули-
аннулирует все экспоненциальные многочлены g, удовлетворяющие
уравнению P(D)g = 0. Достаточно показать (теорема Хана —
Банаха), что Л' аннулирует любое решение /eC°°(Q) этого
544 Fa. 5. Распределения и дифференциальные уравнения
уравнения. По условию (e2Kix'xg, Х) = 0э если ХеО, g — мно-
многочлен и
Другими словами, соотношение
влечет равенство
X * (e2ni^xg) = 0.
Поэтому в силу предложений 1 и 2 п. 5.16.2 X = P(D)Y, или, что
то же, X = P(D)Y, где У— некоторое распределение с компакт-
компактным носителем.
Далее, так как Q выпукло, то из теоремы о носителях Лион-
са (п. 5.15.10) следует, что supp Y cz Q. Итак, если /eC°°(Q) и
P(D)f=0 на Q, то (f, *) = </, P(D) Y) = (Р(D), У> = <0, У>=0,
что и требовалось доказать. |
Теорема А'. Теорема А остается справедливой, если всюду
заменить O(Q) на Ck{Q) (fe = 0, 1, 2, ...).
Доказательство. Достаточно регуляризовать f, получая
таким образом решение /^еС00^), и применить теорему А. I
Теорема А". Теорема А остается справедливой, если всюду
заменить O(Q) на 3>'(Q) или на D/fe(Q) (й = 0, 1, 2, ...).
Доказательство. Можно повторить доказательство тео-
теоремы А, имея в виду, что теперь X принадлежит 2)(Q) или
£Dh(Q). Следовательно, в силу замечаний, следующих за дока-
доказательством предложения 2 п*. 5.16.2, можно выбрать У соответ-
соответственно из Ф или 2)k. |
Эти фундаментальные результаты принадлежат Мальгранжу
(см. Мальгранж [1, стр. 24—26] или Л. Шварц [8, сообще-
сообщение 1]). Недавно Мальгранж получил более простое доказатель-
доказательство теоремы А для случая Q=Rn.
5.16.4. Дополнения. Занимаясь решением задач 1 и Г (а так-
также задачи 3, см. § 5.17), Мальгранж получил более глубокие ре-
результаты, чем те, что мы изложили. Ниже мы попытаемся дать
краткий обзор некоторых из них.
В п. 5.12.2 было указано, что голоморфные функции (одного
комплексного переменного) можно считать решениями уравне-
уравнения P(D)X = 0, где (в наших обычных обозначениях) п = 2 и
P(D) = (d\ + id2). Там же отмечалось наличие связи между ре-
решением задачи V для этого случая и теоремой Рунге. Последний
результат может быть сформулирован следующим образом,
5 16. Рассмотрение задачи 1 545
► Если область Q cz R2 односвязна, то всякое решение f
уравнения
в Q является пределом решений уравнения P(D)g = O,
принадлежащих ^'(R2) (всякое решение этого уравне-
уравнения, принадлежащее ^'(R2), является многочленом от
комплексной переменной z = x\ + ix2).
Очевидно, что это есть усиление теорем типа А, А' и А" (для
специального оператора P(D)) по крайней мере по двум причи-
причинам: A) ослаблено условие выпуклости, которое накладывалось
на Q, и B) экспоненциальные многочлены заменены обычными
многочленами. Эта частная теорема иллюстрирует характер ре-
результатов, полученных Мальгранжем для довольно широких
классов линейных дифференциальных операторов в частных про-
производных P(D) и областей Q в Rn. Следует отметить также, что
Мальгранж рассматривает даже более общие случаи, когда
Q — область в бесконечно дифференцируемом многообразии М
(а не в Rn).
За отсутствием места мы не будем излагать здесь форма-
формализм, который предшествует такого рода обобщениям.
В предложении 4, стр. 66, и в теореме 6, стр. 73, работы [1]
Мальгранж приводит достаточные условия, которым должны
удовлетворять P(D) и область Q в М, чтобы каждая функция
feC°°(Q), удовлетворяющая уравнению P(D)f = 0 в Q, была в
С°°(п) пределом решений уравнения P(D)g = 0 в М. В пред-
предложении 8, стр. 68 (там же), доказано, что при некоторых об-
обстоятельствах эти достаточные условия оказываются также и
необходимыми.
Ограничения, налагаемые там на P(D), довольно сложны и
среди прочего включают предположение, что P(D) —эллипти-
—эллиптический оператор в том смысле, что он обладает фундаменталь-
фундаментальным решением, которое является вещественно-аналитической
функцией всюду, кроме начала. Условие, которому подчиняется
Q, было впервые введено Гротендиком [8]. Оно равносильно
требованию, чтобы M\Q не обладало связными компонентами,
относительно компактными в М. Эти результаты частично рас-
рассмотрены также у Шварца [8, сообщение 3 bis].
Применяя подобные результаты к случаю, когда М — неком-
некомпактная риманова поверхность (см. Мальгранж [1, стр. 75—
77]), получаем принадлежащий Беенке и Штейну [1] ва-
ригнт теоремы Рунге для таких поверхностей, из которого в
свою очередь следует, что всякая такая поверхность есть много-
многообразие Штейна. Это — важнейший результат, из которого вы-
вытекают многочисленные следствия.
546 Гл. 5. Распределения и дифференциальные уравнений,
5.17. Решение задачи 3
Опираясь на результаты § 5.14 и 5.16, мы можем, следуя
Мальгранжу [1, гл. III, § 3], изложить некоторые вопросы,
связанные с задачей 3, т. е. с задачей о разрешимости уравне-
уравнения P(D)X = A.
Мы ограничимся подробным изложением того случая, когда
Q — выпуклая область в Rn; в п. 5.17.4 мы коротко остановимся
на том, что известно для более общего случая (см. также X ё р-
м а н д е р [7]).
Всюду в этом параграфе P(D) обозначает отличный от нуля
дифференциальный оператор в частных производных с постоян-
постоянными коэффициентами.
5.17.1. Случай, когда Q выпукло. Так же как и в п. 5.16.3,
мы приведем несколько теорем, каждая из которых связана с во-
вопросом о разрешимости уравнения P(D)X=A. Эти теоремы от-
отличаются друг от друга рассматриваемыми пространствами
функций или распределений.
Теорема А. Пусть k — целое неотрицательное число или оо
и Q — выпуклая область в Rn. Если f принадлежит Ch+n+l(Q),
то уравнение P(D)g = f разрешимо в О(й). (Если /г = оо, то
под k + n+l понимается оо.)
Доказательство. Исчерпаем область Q возрастающей
последовательностью (оог) выпуклых открытых множеств, каж-
каждое из которых относительно компактно в Q и сог_1 с сог, соо = 0.
В силу предложения 5.6.1 можно выбрать такое разбиение еди-
единицы аг в SD, чтобы носитель функции аг лежал внутри Q\©r.
Соответственно / = 2/г>где fr = arf^Ch+n+l и suppfr cz Q\cor.
г
По теореме А п. 5.14.2 существует фундаментальное решение
оператора P(D), порядок которого не превосходит п+\\ обозна-
обозначим его, например, через Е. Тогда так как Р(Ь)Е = г9 то
E*f<=C* и
Формально решение данного уравнения P(D)g = f запишется в
виде g = 2 {Е * /г). Однако, вообще говоря, ряд 2 (£*/>) не
г г
будет сходиться в Ck(£l). Теперь воспользуемся теоремой А'
п. 5.16.3, которая позволяет имитировать принадлежащий Мит-
таг-Лефлеру метод построения мероморфной функции с заранее
заданной главной частью. (Этот метод описан в любом учеб-
учебнике по теории функций комплексного переменного.) Так как
P(D) (E *fr) =0 на о)г, то из указанной теоремы А7 следует, что
5.17. Решение задачи 3 547
в Cft(cor) можно с любой степенью точности аппроксимировать
E*fr конечными линейными комбинациями экспоненциально-
полиномиальных решений данного линейного дифференциаль-
дифференциального уравнения в частных производных. В частности, можно вы-
выбрать такое решение ри для которого функция E*fr — pr и ее
частные производные до й-го порядка включительно (или до
r-го порядка включительно при й = оо) по абсолютной величине
не будут превосходить 2'г равномерно на ©r-i.
Ряд 2 (Е * fr — рг) сходится в Ck(Q). Обозначим его сумму
г
через g\ тогда
Оператор P(D) понимается здесь в смысле теории обобщенных
функций. В классическом смысле его можно трактовать только
при k>m (где т— порядок P(D)). |
Замечание. Любое улучшение оценки порядка решения
Е приводит к соответствующему усилению теоремы А, в котором
п+\ заменяется порядком решения Е. Известно, что таким пу-
путем п+\ можно фактически заменить на I-g-nJ-f-1 (см. замеча-
замечание в конце п. 5.14.2).
Следствие. Если Q — выпуклая область в Rn, то Р (D) C°° (Q) =
= C°°(Q) (причем P(D) можно понимать здесь в классическом
смысле).
Теорема А'. Пусть sX) — целое число (фоо) и Q — выпук-
выпуклая область в Rn. Если А е 35's (Q), то существует решение X
уравнения P(D)X = A, принадлежащее &'s+n{n+3)(Q). В частно^
Доказательство. В силу 5.8.2A), положив там k = n+l,
достаточно рассмотреть случай, когда A — Dvf, где |/?|^s +
+ п(п + 3) и feCn+1(Q). Полагая в предыдущей теореме Аг = О,
получаем существование непрерывной функции g на Я, удовле-
удовлетворяющей уравнению P(D)g=f. Тогда P(D) (D^g) =DvP(D)g =
s=Dvf=A, поэтому можно положить X = Dpg; порядок X не пре-
превосходит \р\. |
5.17.2. Соотношение P(D)g)'(u) =9)'(Q). Полное рассмотре-
рассмотрение необходимых и достаточных условий для выполнения этого
соотношения проведено в книге Хёрмандера [7, гл. III]. До-
Доказательство опирается на один из вариантов теоремы Пэли —
Винера — Шварца. В частности, в этой книге доказано, что ука-
указанное соотношение выполняется для любого выпуклого Q. Из
наших предыдущих результатов вытекает только частичное
548 Гл 5. Распределения и дифференциальные уравнения
решение, так как мы вынуждены предполагать, что P(D)— гипо-
эллиптический оператор. Операторы такого типа будут рассмо-
рассмотрены подробно ниже, в § 5.18. Пока же будем считать, что это
означает существование фундаментального решения Е уравне-
уравнения P(D)E = e, принадлежащего C°°(Rn\{0}).
Теорема А". Если Q — выпуклая область в Rn и P(D) —ги~
поэллиптический оператор, то P(DJ)'(QJ)'(Q)
Доказательство. С помощью разбиения единицы (аг),
введенного выше в доказательстве теоремы А, любую заданную
обобщенную функцию А можно представить в виде суммы 2 ^»
г
где Аг = агА обладает компактным носителем, содержащимся в
Q\cor, Тогда Е*АГ принадлежит С°°(сог) в силу условий, кото-
которым удовлетворяет Е, и того обстоятельства, что Лг = 0 на юг.
Далее
что равно нулю на сог. По теореме А' п. 5.16.3 свертка Е*АГ мо-
может быть с любой степенью точности аппроксимирована в
С°°(со,) конечными линейными комбинациями экспоненциальных
многочленов рг, удовлетворяющих уравнению P(D)pr=0. В част-
частности, можно так выбрать /?г, чтобы ряд 2(£ * Ат — рГ) сходился
г
в 2)'(Q). Пусть X — сумма этого ряда. Тогда
что и требовалось доказать. |
Замечания. При п — \ любой оператор P(D)=f=0 будет ги-
поэллиптическим. При п > 2 оператор Лапласа P(D)=& гипо-
эллиптический. Оба эти утверждения вытекают из E.11.5).
При м = 2 из формулы -0^z~l = m (Л. Шварц [1, стр. 49])
следует, что Р (D) = -^г- = д{ + id2 — гипоэллиптический оператор.
5.17.3. Для случая, когдаЙ = Кп и вместо P(D)e рассматри-
рассматривается распределение с компактным носителем, Мальгранж
[1, гл. II, § 2] получил ряд результатов такого же общего типа,
как теоремы А, А' и А". Имеются также аналоги результатов,
изложенных выше в § 5.16.
Все основные результаты этого рода были независимо по-
получены Эрен прей сом [2, 3, 10, 11], который называет рас-
рассматриваемую задачу проблемой деления. Он может пользо-
пользоваться таким названием с большим основанием, чем мы,
поскольку его обобщенное понятие преобразования Фурье
5 17. Решение задачи 3 549
менимо к произвольному распределению на Rn (см. наши заме-
замечания в конце § 5.15).
Как и следовалр ожидать, результаты, касающиеся общих
уравнений, содержащих свертки, часто бывают менее точными,
чем аналогичные теоремы для линейных дифференциальных
операторов в частных производных.
Весьма удивительно, что теорема, аналогичная теореме А",
для операторов с переменными аналитическими коэффициентами
оказывается неверной. Впервые это было установлено Г. Леви
в 1957 г. с помощью следующего примера. Пусть в R3
Q и со— два непустых открытых подмножества в R3 и шей.
Тогда существует такая функция (на самом деле множество
всех таких функций нетоще в ^(R3)) / в ^(R3), что уравнение
Р(х, D)g = f на со не имеет решения gG^fo). Полное иссле-
исследование этого совершенно неожиданного факта было дано в
1960 г. Хёрмандером, за что он и получил одну из Филдсовских
медалей 1963 года. См. Хёрмандер [7, гл. VI].
5.17.4. Остается еще проблема разрешимости уравнения
P(D)X=A, рассматриваемого на невыпуклых открытых множе*
ствах Qcz Rn, где А —заданное распределение на О, некоторого
специального типа. Подробное исследование этой задачи чита-
читатель может найти у Л. Ш в а р ц а [8, сообщение 3] и у М а л ь-
гранжа [1]. В работе Мальгранжа особое внимание следует
обратить на теорему 4, стр. 27, и предложение 7, стр. 68.
Можно доказать эквивалентность следующих, условий.
A)
B)
C) Для каждого компактного множества KczQ найдется
такое компактное множество К' а й, что из соотношений
IeC/O°(Q), supp P (D) X с К
следует, что
supp X cz К'.
Более того, если P(D) —гипоэллиптический оператор, то пре-
предыдущие три условия эквивалентны следующему:
D) P(DKS'(Q)~&'(Q).
Если оператор P(D) эллиптический (в том смысле, что он обла-
обладает фундаментальным решением Е, которое является веще-
вещественно-аналитической функцией на Rn\{0}, то все четыре усло-
условия выполняются для любого открытого множества Й в R71,
550 рЛщ 5. Распределения и дифференциальные уравнения
Эти факты, возможно, указывают ни то, что, по крайней мере
для указанного ограниченного класса операторов, условие вы-
выпуклости в теоремах А, А' и А" является следствием недостат-
недостатков принятых методов доказательства, опирающихся на ре-
результаты § 5.16, где выпуклость и другие ограничения на Q, не-
несомненно, существенны.
5.18. Дальнейшие свойства фундаментальных решений.
Гипозллиптические и гиперболические операторы
и уравнения
5.18.1. Конструктивный подход к построению фундаменталь-
фундаментального решения. Приведенным в § 5.14 доказательствам существо-
существования фундаментального решения произвольного линейного диф-
дифференциального оператора P = P(D)=£=0 в частных производных
с постоянными коэффициентами присущи две характерные чер-
черты, а именно (а) фундаментальная роль неравенств в сочетании
с теоремой Хана — Банаха и (Ь) необязательность использова-
использования преобразования Фурье даже в его классической форме, при-
применимой к функциям из 3) = £D(Rn).
Возможен и другой подход, более конструктивный, не обла*
дающий чертами (а) и (Ь). Одно из преимуществ этого подхода
в том, что, будучи относительно явным, он позволяет получить
дальнейшие важные свойства фундаментальных решений. Для
более подробного знакомства с этим методом, набросок кото-
которого следует ниже, рекомендуем заметки Г о р д и н г а [5] (и
указанную там литературу), подготовленные для конференции
по функциональному анализу, состоявшейся в апреле 1961 г. в
Лондоне. Многие фундаментальные работы в этой области вы-
выполнены Хёрмандером [1], хотя Хёрмандер больше руко-
руководствовался теорией гильбертова пространства, чем теорией
обобщенных функций. Однако для нашего обзора эта разница
не имеет значения. Заметки Гординга, о которых говорилось
выше, будем обозначать через [Г]. Читателю следует обратить
внимание на то, что у Гординга символ Dh отличается от нашего
множителем 2я. Описываемая ниже техника построения фунда-
фундаментального решения оператора P(D) сводится к представлению
обратного преобразования Фурье при помощи процесса класси-
классического интегрирования для тех частных случаев, которые мы
рассматриваем.
Следует также напомнить вытекающее из E.15.7) опреде-
определяющее свойство преобразования Фурье, выраженное равен-
равенством Парсеваля, а именно _
<Ф> *>-<Ф. *> E.18.1)
для фе^ и Х&&".
5.18. Дальнейшие свойства фундаментальных решений 551
Допустим, что оператор P(D) обладает медленно растущим
фундаментальным решением Е. С помощью преобразования
Фурье получаем, что определяющее свойство фундаментального
решения
эквивалентно равенству
P(t)-E(t)=U E.18.2)
откуда формально Е(%) = 1/Р(|). Требуется построить £, удовле-
удовлетворяющее этому соотношению. Это построение сводится к ис-
использованию различных методов «суммирования» некоторых вы-
выражений, содержащих расходящиеся интегралы.
Заменим в E.18.1) ф на ф и X на Е, предполагая, что Е —
медленно растущее распределение. Получаем
(Ф) £) = <(ф)у, Ё).
Поскольку мы приняли формально, что £(g) = 1/P(g), то нам
следует рассмотреть выражение
(-|I^§- E.18.3)
как функцию от переменной ф, пробегающей 3). Это — отправная
точка при построении фундаментального решения операто-
оператора P(D).
5.18.2. Суммирование интеграла /(ф). Начнем со следующего
замечания. Допустим, что у нас есть такой способ интерпрета-
интерпретации интеграла /(ф) для каждого ф е 3), что интеграл оказывает-
оказывается непрерывным по ф. Тогда будет существовать такая единст-
единственная обобщенная функция Е (хотя пока и не ясно, что она
является медленно растущей), что /(<p) = (cp, E). Если теперь
заменить ф на Р(—D)(p и сделать естественное предположение,
что наша интерпретация выражения /(ф)=/(Р(—£>)ф)— просто
(абсолютно сходящийся) интеграл I ф(— |)ф(|), то мы придем
к заключению, что
и потому P(D)E — £, т. е. Е будет фундаментальным решением.
Таким образом, все зависит от отыскания подходящей и есте-
естественной интерпретации интеграла /()
552 Гл. 5. Распределения и дифференциальные уравнения
В некоторых частных случаях, конечно, ничего придумывать
и не требуется. Таково, например, положение с метаполигамони-
ческим оператором
для Х>0 и любого натурального к > у п. В этом случае E.18.3)
существует как (абсолютно сходящийся) интеграл Лебега и все
ясно. Действительно, можно даже непосредственно определить Е
как непрерывную функцию
|_&т, E.18.4)
являющуюся обратным преобразованием Фурье интегрируемой
функции l/P&) = l(\l\2 + X)K
Если отбросить осторожность, то выражение E.18.4) можно
принять за исходное также и в других случаях. К возникающему
при этом интегралу нужно применить такой же прием суммиро-
суммирования, который имелся в виду для /(ф). (Применение последнего
дает некоторые преимущества при рассмотрении деталей: напри-
например, хотя обе функции е2л{х'* и ф(—|), очевидно, продолжаемы
до целых аналитических функций от | е О, последняя стремится
к нулю при Reg->-oo, в то время как первая этим свойством не
обладает. Этот факт существен при рассмотрении вопросов схо-
сходимости.) В квантовой теории поля таким приемом обычно поль-
пользуются для построения так называемых потенциалов Грина; на-
например, в относительно простом случае скалярных и псевдоска-
псевдоскалярных мезонных полей соответствующим оператором будет опе-
оператор Клейна — Гордона, а именно
где А — оператор в трехмерном пространстве координат Х\, х2, *з,
с — скорость света, х4 — временная координата, \i = 2nmc/h,
m — масса мезона и h — постоянная Планка.
Один из полезных способов интерпретации интеграла /(ф)
основан на том, что ф можно продолжить до целой аналитиче-
аналитической функции на О, а 1/Р можно аналогично продолжить до
мероморфной функции на О. Так как все трудности возникают,
по-видимому, из-за слишком быстрого роста функции 1/Р на ве-
вещественном подпространстве RnczO и, в частности, из-за воз-
возможности существования вещественных нулей, то естественно по-
попытаться использовать теорию комплексных функций в связи с
переносом «пути интегрирования» в интеграле E.18.3) с веще-
5.18. Дальнейшие свойства фундаментальных решений 553
ственной в комплексную область. Имея это в виду, возьмем точ-
точку ц е Rn и рассмотрим интеграл
Если мы сможем показать, то /т, определено и непрерывно на
и что
сводится к Г ф (— | + гп) d\i (g), то тем самым будет установлено
существование такой обобщенной функции JE^, что
Теперь уже нетрудно показать, что правая часть этого равенства
не зависит от г) и потому равна ф@) = (ф, е). Таким образом,
P(D)Ey] =e и E^ — фундаментальное решение. В то же время
наше построение фундаментального решения Ец позволяет часто
получать полезные сведения о носителе функции Е^.
5.18.3. Существование фундаментального решения общего
оператора P(D)=£0. Найдем приемлемую для нас интерпрета-
интерпретацию интеграла /(ф), не накладывая на Р дополнительных огра-
ограничений. Оказывается, этого можно достичь, полагая
(-6)тйр E-18-6)
где Г=(|2, ..., ln)^Rn-\ ix'-мера Лебега на R^1 и Г(Г) —
путь в комплексной ^i-плоскости, выбранный следующим обра-
образом. Зафиксируем произвольное б > 0, и пусть S — полоса
О ■< Im gi ■< 6. Подобрав координаты так, чтобы Р (I) = с%™ + ...,
где m — степень многочлена Р, разложим его на множители
m
P(g) = £ П (Si ~" zk)y где гк = гкA')—алгебраические функции от
g'. Пусть Ah — круг в комплексной gi-плоскости с центром в г&
m
и радиусом б и А= U Л^,. Наконец, пусть F(g/)—нижняя грань
k= 1
множества S\(SflA). Хотя, вообще говоря, F(g') зависит от gr
не непрерывно, все же можно показать, что внутренний интеграл
В E.18.6) — измеримая функция от §'.
554
Гл. 5. Распределения и дифференциальные уравнения
Из построения контура Г(|') следует, что
\Р(Ъ)\>\с\6т
для g'e Rn~l и |i e Г (Ю- Пользуясь этим неравенством, нетруд-
нетрудно (хотя и довольно утомительно) проверить, что интеграл в
E.18.6) определяет непрерывную линейную форму на SD и что
Рис. 2.
/(ф)»=/(Р(—£))ф) сводится к Jq>(-£)d|xE) (в силу теоремы
Коши, примененной к ф(—|ь— |') как к функции от |ь при ка-
каждом фиксированном |'е Rn). Таким образом доказывается су-
существование фундаментального решения Е.
Относительно применения предыдущих формул представле-
представления фундаментального решения Е см. работу Аграновича [1]
который использует этот метод в различных задачах деления и
аппроксимации.
5.18.4. Гипоэллиптические операторы. Рассмотрим следующие
утверждения относительно оператора P(D).
A) Если X(=2)'(Q)y At=C°°(Q) (Q — открытое подмноже-
подмножество в Rn) и P(D)X=A на Й, то X<=C°°(Q).
B) Существует фундаментальное решение Е оператора P(D),
принадлежащее C°°(R?1\{0})'.
Мы утверждаем, что эти предложения эквивалентны.
Действительно, в силу результатов § 5.14 о существовании
фундаментального решения, A) влечет B).
Обратно, пусть справедливо B) и выполнены условия утвер-
утверждения A). Покажем, что X<=C°°(Q). Пусть е > 0. Выберем та-
такое a,^S)(B^) (Ве —открытый шар с центром в нуле и радиу-
5.18. Дальнейшие свойства фундаментальных решений 555
са е), что а=1 на некоторой окрестности нуля. Рассмотрим £* =
= аЕ. По формуле Лейбница
DPE* =
Соотношения qK-p и дфр означают, что Qk^-Pk для
<Ся и qu < Ph по крайней мере для одного такого k. Для всякого
такого q на некоторой окрестности нуля D^~^a = 0, поэтому
IP Km q < p
Цфр
(Через / обозначено второе слагаемое в правой части.) Так как
а=1 на некоторой окрестности нуля, то a •e = e. Кроме того,
внутренняя сумма в правой части представляет собой элемент из
3)(В&), поскольку DP-<*a = 0 на некоторой окрестности нуля и по
нашему допущению Е е C°°(Rn\{0}). Таким образом, / ek2)(Be)<
Подводя итог, получаем, что
, E.18.7)
где Е* = аЕ обладает носителем, содержащимся в Вг. Действи-
Действительно, Е* представляет собой пример параметрикса для P(D),
т. е. такой аппроксимации фундаментального решения, носитель
которой компактен. Следовательно, £*, так же как и £, принад-
принадлежит C°°(Rn\{0}).
Так как supp E*cz Вв и supp/cz бе, то можно (см. упр, 5.19)
рассмотреть свертку с Е* обеих частей равенства P(D)X = A.
Пользуясь ассоциативностью и соотношениями E.18.7), полу-
получаем, что
Х==£%Л-/* J на йе1). E.18.8)
Свертка f*X принадлежит C°°(Qe), потому что f^3). Для
дальнейшего изучения слагаемого Я**/ рассмотрим произволь-
произвольное открытое относительно компактное множество £Ус: (QeN и
такую функцию Ре®, что supp p cz Q и р= 1 на Q'. Из очевид-
очевидного равенства Л = рЛ+A — р)Л следует, что
£% А = Е** (РЛ) + Е* * [A - Р) А] = Y + Z
Так как A^C°°(Q) и supppczQ, то р/4 s SD\ следовательно,
У> С другой стороны, supp[l —Р)Л]с Rn\Q'. Откуда и
х) Смысл обозначения Qe см. в упр. 5.19. — Прим. перев.
556 Гл. 5. Распределения и дифференциальные уравнения
из того факта, что Е* е C°°(Rn\{0}), легко получается, что
ZeCoo(fi/). Таким образом, первый член в правой части
E.18.8) и вместе с ним и X принадлежат С°°(£У). Так как это
имеет место для любого открытого относительно компактного
множества Q'c: (£2в)б, то, полагая 6->0 и е->0, устанавливаем
включение X е С°°(Й), что и требовалось показать. Эквивалент-
Эквивалентность утверждений A) и B) доказана. I
Читатель может заметит, что A) эквивалентно кажущемуся
более сильным утверждению
(Г) Если X, Ле=Ф'(£2), P(D)X=A на Й, юс Q и А |со е=
<sC°°(<d), то Х|сое С°°(со).
Эквивалентность утверждений A), (Г) и B) дает основания
для следующего определения. Оператор P(D) называется гипо-
гипоэллиптическим, если он удовлетворяет одному (а значит, и ка-
каждому) из условий A), A') и B).
Примеры. При п=\ любой оператор P(D)=f=0 гипоэллипти-
ческий. (Условия A) или B) легко проверяются с помощью
элементарных свойств обыкновенных линейных дифференциаль-
дифференциальных уравнений с постоянными коэффициентами.) Пусть п = 2\
тогда оператор (теплопроводности) P(D)=d\ — д\ гипоэллипти-
ческий, так как он обладает фундаментальным решением
^, E.18.9)
где// — функция Хевисайда на R1:
Оператор Р {D) = id\ + 62 также гипоэллиптичен. При любом п
будет гипоэллиптическим оператор Лапласа Д, обладающий эле-
элементарным решением, пропорциональным U'|2-n при д>2 и
log|x| при п = 2. Другие примеры приводятся в упр. 5.20.
Естественно попытаться найти необходимые и достаточные
условия, которым нужно подчинить многочлен Р(^) для того,
чтобы оператор Р(D) был гипоэллиптическим. Хёрмандером
[1, теоремы 3.3 и 3.4] получены различные такие условия; на не-
некоторых из них мы остановимся. Другие критерии такого типа
принадлежат Эренпрейсу [2], который рассматривал опера-
операторы со свертками, более общие, чем наш оператор P{D).
Следующие два эквивалентных (Хёрмандер [1, теоре-
теорема 3.3]) условия (а) и (Ь) достаточны для того, чтобы оператор
P(D) был гипоэллиптическим.
(а) Каждому а>0 соответствует такое число Ь =
что РA + щ)Ф0 при I, tigeR", |т||<а и \1\>Ь.
5.18. Дальнейшие свойства фундаментальных решений 557
(Ь) Для каждого а>0
lim inf |Р(| + /лIв +°°.
|€=r", £-»«> lie Rn\y\\>a
С другой стороны, Гор д и н г [Г, § 11] показал, что если опе-
оператор P(D) гипоэллиптичен, то
(а7) существуют такие числа с > 0 и d > 0, что
если I, r\ e Rn удовлетворяют равенству Р
Так как {аг) влечет (а), то получаем, что
► Условия (а), (а') и (Ь) эквивалентны между собой; каж-
каждое из них необходимо и достаточно для того, чтобы опе-
оператор P(D) был гипоэллиптическим.
При доказательстве достаточности условия (Ь) Хёрмандер
пользовался методами, изложенными выше в п. 5.18.2. Коротко
наметим его конструкцию фундаментального решения Е. С этой
целью примем интерпретацию E.18.6) интеграла /(ф), заменяя
путь интегрирования Г(£') контуром С(£')> устроенным следую-
следующим образом. Как и выше, сначала выберем координаты так,
чтобы P(£) = cg|n+ ...» где сФО. В соответствии с условием (Ь)
существует такое г > 0, что | Р (|) J > 1 для | е Rn и 111 > г. От-
Отсюда следует, что существует такое число г* > 0, что |Я(|ь |') |^
^ 1 для любого ^ Е У?11 с |g'|-^r и для любого комплексного
h c l^i|>r*- Поэтому контур С(|') представляет собой веще-
вещественную ось комплексной gi-плоскости, если ||'!>г; если же
||'| <г, то C(g') есть вещественная ось, в которой отрезок
[—л*, г*] заменен нижней полуокружностью, построенной на этом
отрезке как на диаметре. В этом случае \РA) |^ 1 для всех £,
входящих в E.18.6). Суть доказательства сводится к показу
того, что получаемое фундаментальное решение Е удовлетворяет
условию B). За подробностями отсылаем читателя к Хёрман-
деру.
В дополнение заметим, что Петровский [1] указал чисто
алгебраическое условие эллиптичности, а именно
(с) Ро(Ь)ФО для geR", %ФО,
где Ро(£)= 2 Ср\р — главная часть1) многочлена РA).
В заключение наших замечаний о гипоэллиптичности опера-
операторов добавим, что Джон [1] доказал существование фунда-
фундаментального решения для операторов P(D), удовлетворяющих
1) См. п. 5.19.2. — Прим. перее.
558 Гл. 5. Распределения и дифференциальные уравнения
условию (с). Исследованием гипоэллиптических операторов
Р(х,D) с переменными коэффициентами класса С°° занимались
(наряду с другими) Мальгранж [2], Хёр манде р [3, 7],
Гординг и Мальгранж [1], Т р е в [5] и П е т р е [2].
5.18.5. Гиперболические операторы. Вернемся к равенству
E.18.5), которое благодаря некоторым свойствам многочлена
РA) служит инструментом для изучения фундаментальных ре-
решений заданного оператора P(D).
Начнем с предположения, что существуют точка r\ e Rn и
вещественное число /о, для которых выполнено условие
(*) РA + Иц)ФО для ^еГ и t^tQ.
Мы утверждаем, что
► Фундаментальное решение Е, определенное с помощью
соотношения E.18.5), в котором ц заменено на tr\ с лю-
любым t > t0, обладает носителем, содероюащимся в полу-
полупространстве
Доказательство этого утверждения основано на следующей
лемме.
Лемма. Пусть выполнено условие (*), и пусть Pq—главная
часть многочлена Р\ тогда Ро{щ)фО и
\P(l + Ui\)\>\Po(ii\)\(t-tQ)m E.18.10)
для I e Rn и вещественных /> t0. Кроме того, существуют такие
числа а > 0 и Ь > 0, что
\P(l + itr\)\>a[\+\l\ + (t-tb)]b E.18.11)
для |eRn и t>t0.
Доказательство этой леммы см. в [Г, § 11].
Из неравенств, фигурирующих в лемме, следует, что соот«
ношение E.18.5) эффективно определяет не зависящее от t при
/>/0 фундаментальное решение оператора P(D). Таким обра-
образом, для фей) имеет место равенство
(ер, ^-/фС-б-^рУ^) (*>'о).
Пусть теперь носитель К функции ф содержится в открытом мно-
множестве R^Xtf^. Тогда существует такое число с > 0, что г\-х^> с
для х^К. Полагая t—to + s, где s>0, и замечая, чю
518 Дальнейшие свойства фундаментальных решений 559
где
получаем (ф, Е) = (фв, Е). Но поскольку ц-х^- с(>0) на носи-
теле К функции ф, то легко установить, что | (ф, Е) | = О (е~2ЯС5).
Полагая s->oo, получаем, что для любой функции ф, носитель
которой лежит в Rn\# , справедливо равенство (ф, £)=0. Та-
Таким образом, Е = 0 на Кп\Нц, т. е. supp ЕаНц, что и требова-
требовалось доказать. |
Отметим попутно, что Гор дин г [1] показал, что соотноше-
соотношение (supp E) П#_п = {0} эквивалентно соотношениям Р0(щ)ф0 и
Р(^ + Ик\)ФО для | е Rn и достаточно больших вещественных t.
Условимся называть оператор P(D) гиперболическим, если
он обладает фундаментальным решением, носитель которого
содержится в некотором собственном конусе с вершиной в на-
начале.
Из установленного только что результата вытекает, что для
гиперболичности оператора P(D) достаточно существования та-
такого непустого открытого множества Q cz Rn и такого веществен-
вещественного числа t0, что
Р{1 + Иц)Ф0 для £е= Rn, r) GE Й и вещественных t>t0. E.18.12)
Гордин г [Г, § 11] показал, что если оператор Р (D) гипер-
гиперболичен и координаты выбраны так, что supp E содержится в
полупространстве *i<iO, то
E€=R"f T|ERB, P(l + it\) =
h2l, .... hnl)>- E.18.13)
Более того, при таком выборе координат E.18.13) эквивалентно
соотношению E.18.12).
Таким образом, оператор P(D) гиперболичен тогда и только
тогда, когда выполнено условие E.18.12), что дает нам доста-
достаточно тонкий и простой критерий гиперболичности.
Пользуясь этим критерием или зная явное выражение для
фундаментального решения, легко проверить гиперболичность
операторов в следующих примерах. При /г=1 оператор P(D) =
= —д\ гиперболичен, так как носитель его фундаментального
решения Е = Н(х{) содержится в полупрямой Xi>0. При п = 2
(волновой) оператор P(D) — d\ — д\ гиперболичен, так как но-
носитель его фундаментального решения
Е = \ Н {хх) {Н (хг + х2) + Н (хх - х2)}
содержится в множестве Х\^0, |Л'2|^^1.То же самое справед-
справедливо для волнового оператора в случае любого числа пере-
переменных,
560 Гл. 5. Распределения и дифференциальные уравнения
5.19. Характеризация некоторых типов линейных
дифференциальных операторов в частных производных
с помощью неравенств и отношения порядка
Мы уже неоднократно подчеркивали, что современная теория
линейных дифференциальных операторов в значительной мере
основывается на использовании неравенств в сочетании с общими
принципами функционального анализа. В настоящем параграфе
мы выделим важный класс операторов с помощью неравенств и
связанных с ними отношений частичного порядка.
Заметим, что два важных класса линейных операторов в ча-
частных производных — эллиптические и гиперболические — ха-
характеризуются именно таким способом (определение эллиптиче-
эллиптического оператора еще не вводилось, гиперболические операторы
были определены в п. 5.18.5). Хёрмандер [1] нашел характе-
ризацию эллиптических операторов, а Трев [2—4] — гиперболи-
гиперболических. Работа Хёрмандера содержит также характеризацию
гипоэллиптических операторов (определенных в п. 5.18.4), го-
гораздо более сложную, чем дЛя эллиптических операторов. Мы
коротко изложим исследования Хёрмандера по эллиптическим
операторам и еще более коротко — часть результатов Трева о
гиперболических операторах, оставляя в стороне случай гипо-
гипоэллиптических операторов. Читатель, вероятно, заметил, что по-
последние два типа операторов были охарактеризованы почти алге-
алгебраически способами, описанными в п. 5.18.4 и 5.18.5 соответ-
соответственно.
Хотя во всех случаях исследования проводились так, чтобы,
по крайней мере частично, их можно было применить к операто-
операторам с переменными коэффициентами (см. Хёрмандер [7]),
мы ограничимся рассмотрением случая постоянных коэффи-
коэффициентов.
Характеризация как эллиптических, так и гиперболических
операторов будет дана с помощью соответствующего отношения
частичного порядка: силы в случае Хёрмандера и доминирова-
доминирования в случае Трева, Рассмотрим каждое из этих понятий в от-
отдельности.
5.19.1. Сила операторов. Всюду ниже термином оператор бу-
будем пользоваться для обозначения линейного дифференци-
дифференциального оператора в частных производных с постоянными
коэффициентами (хотя последнее условие не всегда необхо-
необходимо).
В излагаемых здесь исследованиях Хёрмандера, всюду огра-
ограниченных рамками пространства L2, необходимо различать так
называемые минимальный и максимальный операторы Ро и Р,
5 19. Характеризация некоторых типов операторов 561
соответствующие заданному дифференциальному оператору
\P\<m
apDp.
Минимальный оператор Pq. Рассмотрим P(D) как отображе-
отображение пространства 2D(Q) в L2(Q). Легко показать (Хёрман-
дер[1, лемма 1.4]), что P(D)—предзамкнутое отображение про-
пространства L2(Q) в себя (замыкание его графика в L2(Q)X
XL2(Q) также является графиком). По определению минималь-
минимальный оператор Ро— это замыкание этого отображения. Другими
словами, область определения оператора Ро, которую впредь бу-
будем обозначать через domP0, состоит из тех и только тех
u^L2(Q), для которых P(D)u (в смысле обобщенных функций)
принадлежит к L2(Q) и для которых в 3){Q) существует по
крайней мере одна такая последовательность (<рп), что фп-^и и
P(D)qn-+P(D)u в L2(Q). Для всякого такого элемента и зна-
значение Ро^ по определению равно P(D)u.
Максимальный оператор Р. Пусть P(D)= 2 (~l)lp| apDp —
\p\<m
оператор, сопряженный (относительно гильбертовой структуры
в L2(Q)) оператору P(D) и Ро— соответствующий ему мини-
минимальный оператор. Тогда максимальным оператором Р, соответ-
соответствующим оператору P{D)y называется оператор, сопряженный
(относительно структуры гильбертова пространства L2(Q) к Pq.
Другими словами, Р — такое отображение L2(Q) в L2(Q)y об-
область определения которого dom P образована теми mgL2(JJ),
для которых P(D)u (в смысле теории обобщенных функций)
принадлежит L2(Q); для всякого такого элемента и имеет место
равенство Pu = P(D)u.
Определения Хёрмандера операторов Ро и Р полезно допол-
дополнить замечаниями, принадлежащими Фуглиду [1].
Употребляемое Хёрмандером понятие силы операторов совпа-
совпадает с понятием включения применительно к областям опреде-
определения минимальных операторов. Более точно, пусть заданы два
оператора P(D) и Q(D) и область Q cz Rn; будем говорить, что
оператор P(D) сильнее, чем Q(D), на Й, и писать P(D)^>Q(D)
на Q, если dom Po cz dom Qo.
Так как Ро и Qo — по определению замкнутые операторы, то
из результатов п. 6.4.11 получаем необходимое и достаточное
условие того, что P(D) сильнее, чем Q(D), а именно неравенство
110ои|Р<С(||и|р + ||Рои|р), E.19.1)
где С — некоторая постоянная, и — произвольный элемент из
dom Ро, а нормы берутся в L2(Q). С другой стороны, в силу
562 Гл 5. Распределения и дифференциальные уравнения
определения domPo и dom Qo это неравенство эквивалентно не-
неравенству
||д№)|р<С(|||р + ||Рф)||2) E.19.2)
для всех фЕ^(й). Действительно, пусть выполнено E.19.2).
Если и е dom Po, то существует такая последовательность
(фп) с: iZ)(Q), что срп-+и и P(D)q)n~+Pou в L2(Q). Тогда и<з
E.19.2) следует, что последовательность (Q(D)q)n) сходится в
L2(Q) и, поскольку оператор Q(D) предзамкнут, предел этой
последовательности равен Qou. Таким образом, полагая ф = фп
в E.19.2) и переходя к пределу при л->оо, получаем E.19.1).
Если область Q ограничена, то, как известно (неравенство В
п. 5.14.2; Хёрмандер [1, теорема 2.1]),
II Ф II < const ||Р (Я) ф ||
для фЕЙ)(й). Поэтому в этом случае отношение P(D)^> Q(D)
на Q влечет за собой неравенство
II Q (Я) ФII < С ||Р (Я) ф ||. E.19.3)
для фЕЙ5(й). Постоянная С здесь может, вообще говоря, от-
отличаться от постоянной в E.19.2). Обратно, E.19.3) влечет
E.19.2) независимо от того, будет ли область Q ограничена или
нет. Таким образом, в случае ограниченной области Q отноше-
отношение P(D)^Q(D) на Q выполняется тогда и только тогда, когда
неравенство E.19.3) справедливо для любого ф е 3)(Q).
Итак, мы, описали хёрмандерово отношение силы с помощью
неравенств.
Заметим, между прочим, что если всюду заменить минималь-
минимальные операторы Pq и Qo на максимальные Р и Q, то получится
несколько иное понятие силы. Оно будет выражаться неравен-
неравенством E.19.1), если в нем заменить PQ и Qo соответственно на
Р и Q и постулировать его справедливость при каждом
и е dom P. Однако в этом случае, вообще говоря, невозможно
перейти от E.19.1) к E.19.2).
5.19.2. Определение эллиптических операторов. Рассмотрим
оператор P(D)= 2 apDp степени т (т. е. оператор, для кото-
\р]<т
рого арф0 по крайней мере для одного значения р с \р\=т).
Обозначим через р(|) главную часть многочлена P(g), т. е. его
однородную часть степени m
P(SH 2 aPlp.
1 р |=m
Следуя классической терминологии, назовем оператор P(D)
эллиптическим, если
р(%)фО для |е=1Г, |^=0. E.19.4)
5.19. Характеризация некоторых типов операторов 563
Из E.19.4), очевидно, вытекает условие (Ь) п. 5.18.4, поэтому
всякий эллиптический оператор является гипоэллиптическим
(чем последнее название и оправдывается). Обратное неверно:
оператор теплопроводности P(D) = d\ — <?!, как мы видели в
п. 5.18.4, гипоэллиптичен, однако он не является эллиптическим,
потому что для него р (I) = — 2^.
Для того чтобы охарактеризовать эллиптические операторы в
терминах силы, нужно это последнее понятие выразить алгебраи-
алгебраически, поскольку само определение эллиптического оператора
дано в алгебраической форме. Мы это сейчас сделаем, следуя
Хёрмандеру[1, теорема 2.2]. Из алгебраического определения
силы непосредственно вытекает нужная нам характеризация
эллиптичности оператора (Хёрмандер [1, теорема 2.4]).
5.19.3. Алгебраическое описание силы. Докажем справедли-
справедливость следующего утверждения.
► Пусть Q — ограниченная область в Rn. Для того чтобы
P(D)^- Q(D) на Q, необходимо и достаточно, чтобы вы-
выполнялось одно из следующих двух условий:
%Щ<+°°, E.19.5)
Шг<+°°, E.19.6)
где
причем суммирование производится по всем р (конечно,
для заданного Р только конечное число членов отлично
от нуля)\ Q°(g) определяется аналогичным образом по Q.
Доказательство. A) Предположим, что P(D)^Q(D)
на Й, и докажем, что E.19.5) следует из E.19.3). Для этого
возьмем произвольную функцию /е2)(й) и применим E.19.3)
к ф(х) =ег$'хf(х). Повторным использованием формулы Лейб-
Лейбница получаем
и аналогичную формулу, в которой Р заменено на Q. Временно
положим
564
Гл. 5. Распределения и дифференциальные уравнения
Тогда из E.19.3) вытекает, что
/р.
S /р., Q(P) (l)Q{q)(l) < С2 2 /р. ,Р
(Р)
р, я
Р>Я
E.19.7)
Эти суммы не содержат других (отличных от нуля) членов, кро-
кроме тех, для которых |р| и \q\ мажорируются наибольшим из
порядков операторов Р и Q, скажем N. Пусть z=(zp), ,^N —
такой набор комплексных чисел, что zp = zq, если q получается
из р перестановкой. Квадратичная форма
2 /*.
I р К /v
-i
(здесь
2
и второе равенство вытекает из равенства Парсеваля) строго по-
положительна, за исключением случая, когда zp = 0 для всех р. От-
Отсюда следует, что
Полагая ^P =
)» получаем из E.19.7)
откуда в силу неравенства Коши — Шварца вытекает неравен-
неравенство
которое эквивалентно E.19.5).
B) Пусть теперь выполнено E.19.6). Докажем справедли-
справедливость неравенства E.19.3). Для этого напомним, что в случав
ограниченной области Q в силу леммы п. 5.14.4
E.19.8;
для каждого р и каждого
Положим
Ф (I) = Bя)~ 2 n J е-И-х ф (я) сЦх (х).
5.19. Характеризация некоторых типов операторов 565
С помощью равенства Парсеваля получаем соотношение
цд(д)Ф1р=/|дШ121ФШ12ФШ,
правая часть которого, согласно E.19.6), мажорируется числом
Р
Последнее снова в силу равенства Парсеваля равно
Р
Наконец, в силу E.19.8) имеем
откуда и вытекает неравенство E.19.3), что и требовалось до-
доказать. Ш
5.19.4. Характеризация эллиптических операторов. Очевидно,
что если оператор P(D) эллиптический в смысле условия
E.19.4), описанного в п. 5.19.2, то неравенство E,19.6) справед-
справедливо для любого многочена Q, степень которого не превосходит
степени m многочлена Р. Таким образом, P(D) сильнее, чем
любой такой оператор Q(D). Обратно, если P{D) сильнее, чем
любой такой оператор Q(D), то из E.19.5) следует, что рA)фО
для 1Ф0 из Rn, т. е. что оператор P(D) эллиптичен.
Таким, образом,
► оператор P(D) эллиптичен тогда и только тогда, когда
P(D)^- Q(D) для любого оператора Q, порядок кото-
которого не выше, чем порядок оператора Р.
Это и есть нужная нам характеризация эллиптических операто-
операторов в терминах силы.
5.19.5. Замечание. Всякий эллиптический оператор P(D)
и подавно гипоэллиптичен. Поэтому существует фундаменталь-
фундаментальное решение Е оператора P(D), принадлежащее C°°(Rn\{0}). На
самом же деле из эллиптичности оператора P(D) можно вывести
(см. Л. Шварц [1, стр. 138—143] и приведенные там ссылки,
а также Хёрмандер [1, теорема 3.5]), что в качестве фунда-
фундаментального решения Е можно выбрать некоторую вещественно-
аналитическую на Rn\{0}' функцию. Отсюда и из соображений,
приведенных в п. 5.18.4, получаем, что все эллиптические опе-
операторы обладают следующим свойством.
566 Гл. 5. Распределения и дифференциальные уравнения
A*) Пусть X, А е 2$' и А — вещественно-аналитическая
функция на открытом множестве йс Rn. Тогда если P(D)X=A,
то и X — вещественно-аналитическая функция на Q.
Таким образом, эллиптический оператор, определенный клас-
классическим образом в п. 5.19.2, удовлетворяет условию, аналогич-
аналогичному условию A) п. 5.18.4, использованному для определения
гипоэллиптического оператора. Автору неизвестно, верно ли об-
обратное утверждение, т. е. следует ли из A*) эллиптичность
оператора P(D). Конечно, при п=1 оба класса операторов со-
совпадают.
5.19.5. Отношение доминирования Трева и характеризация
гиперболических операторов. Здесь мы бегло коснемся части ре-
результатов Трева, которые выражаются с помощью (частного
случая) введенного им понятия доминирования. Приводимая
здесь часть, хотя и невелика, но вполне типична. Наши замечания
ограничиваются случаем линейных дифференциальных опера-
операторов в частных производных с постоянными коэффициентами.
Пусть Q—открытое подмножество в Rn и Pi(D) (/e/), Qj(D)
(/ g /) — два семейства операторов. Говорят, что семейство
(Pi(D)) (экспоненциально) равномерно на Q доминирует семей-
семейство (Qj(D)), если для каждого ограниченного множества ogQ
и каждого е > 0 существует точка fteCn (или, что все равно,
h e Rn), такая, что
sup || e-*'hQj (D) ф ||L2 < е sup || e~*-hPt (D) <p \y
для всех (р£2)((о).
Это понятие, так же как хёрмандерово понятие силы, приво-
приводит к отношению частичного порядка между операторами. В от-
отличие от хёрмандеровой силы доминирование оказалось мало
связанным с эллиптичностью. Однако, как это следует из иссле-
исследований Трева, доминирование тесно связано с гиперболич-
гиперболичностью (а также с параболичностью, которую мы совсем не рас-
рассматриваем).
В частности, Трев показал [4, теорема 2.1], что оператор
P(D) гиперболичен тогда и только тогда, когда он равномерно
доминирует все операторы Dp с \р\-*Спг (гпу как обычно, — поря-
порядок оператора Р (£))). Эта же теорема содержит квазиалгебраи-
квазиалгебраическую характеризацию гиперболических операторов, подобную
той, которая была приведена в п. 5.18.5.
. Результаты такого рода еще раз демонстрируют первостепен-
первостепенную важность роли, которую играют в современной теории ли-
линейных дифференциальных операторов в частных производных
априорные неравенства.
5.20. Работы Ф. Э. Браудера 567
5.20. Работы Ф. Э. Браудера
Предыдущий обзор задач, связанных с линейными диф-
дифференциальными уравнениями в частных производных, был сде-
сделан с точки зрения теории обобщенных функций и поэтому так
тесно привязан к работам «европейских» математиков (Маль-
гранжа, Лионса, Л. Шварца, Гординга и др.)- Было бы непра-
неправильно сделать отсюда вывод, что это единственый или даже
лучший подход. И действительно, Ф. Э. Браудер, выдающийся
представитель американской школы, разрабатывает и пропове-
проповедует несколько иной подход, полное и подробное изложение ко-
которого мы здесь не можем привести.
Использование теории распределений позволяет формулиро-
формулировать рассматриваемые задачи в терминах непрерывных опера-
операторов, действующих в весьма сложных локально выпуклых про-
пространствах. Метод Браудера, возникший под влиянием идей
Дж. фон Неймана, применим к замкнутым, не обязательно не-
непрерывным операторам, действующим в относительно простых
пространствах. В работе Браудера [1] содержится весьма
общее и глубокое изложение аналогов ряда результатов § 8.6
и 8.7 для замкнутых операторов с всюду плотной областью опре-
определения, причем для очень широкого класса локально выпуклых
пространств. Формулировка одного из таких результатов для
случая банаховых пространств дана в теореме 8.7.9, утверждаю-
утверждающей, что замкнутый линейный оператор с всюду плотной обла-
областью определения, действующей из банахова пространства Е в
другое такое пространство Z7, является отображением на тогда и
только тогда, когда его сопряженный обладает непрерывным
обратным оператором.
Общая черта двух подходов состоит в том, что оба они сво-
сводят теоремы существования к соответствующим априорным не-
неравенствам. Работа [1] задумана как введение к ряду работ,
посвященных приложениям к линейным дифференциальным
уравнениям в частных производных. Публикация этих приложе-
приложений начата Браудером [1а] и будет продолжена в последую-
последующих статьях, которые будут выходить под одним и тем же об-
общим названием.
УПРАЖНЕНИЯ
5.1. Пользуясь тем, что (при я=1) размерность множества S обычных
решений уравнения P(D)X = 0 конечна, дать прямое доказательство утвер-
утверждения B) п. 5.12.2 (Гординг и Лионе [1, стр. 33]).
[Указание. Воспользоваться тем, что топология, а поэтому и рав-
равномерная структура отделимого конечномерною топологического векторного
пространства единстренны. Принять во внимание, htq если X ен $}' является
568 Гл 5. Распределения и дифференциальные уравнения
решением уравнения P(D)X = 0 ифЕ^, то свертка ф * X служит обычным
решением того же уравнения.]
5.2. Пусть п = \ и P(D) = Dm+ .... Показать, что Р (D) X = е тогда
и только тогда, когда X — такая функция из С°° (Rrt\{0}), что
О ПрИ 0 </ < /72,
(—2ni)m при j = m.
Такие функции возникают в теории обыкновенных линейных дифферен-
дифференциальных уравнений, где Х(х — у) обычно называют функцией Грина ука-
указанного уравнения. (Гординг иЛионс [1, стр. 33])
5.3. Пусть Хь Xe^'fR1) и X — элемент из &'(R2), определенный ра-
равенством
т. е.
( J / (*ь *2) dx2, X,) + (J / (хь х2) dxu
для /^^(R2). Доказать, что D\D2X = 0. Это показывает, что оператор Г^Ог
не является гипоэллиптическим.
5.4. Обозначения и предположения те же, что и в п. 5.13.1 и 5.13.9(а).
Рассмотрим случай п=\ и £2= (а, р), где а>—оо. Допустим, что q не
л:
является пренебрежимой функцией и Р~ d\i < + оо для некоторго (а по-
а
этому для всех) л;£Й. Доказать, что каждому ограниченному интервалу
/Q соответствуют такие числа Mi и NIt что
sup
sup I/WK^II/II
Показать, что
A) существует конечный предел lim / (д:) при любом / ^ V;
B) если fn->f в V, то для любого ^eQ последовательность /rt равно-
равномерно стремится к f на [а, Ь];
C) Пт/(л:) = 0 для каждого / е= ^ (^ — замыкание ^ (Й) в V).
х^а v \ v
Р
Аналогичные результаты справедливы, если Р < + оо и р d\x < + оо
я'
при некотором (а поэтому при всех) х ее Й.
5.5. В обозначениях п. 1.13.9 (а) показать, что при п—1 множество V
полно, если р, р~ и q принадлежат ^\ос (Q) и функция ^ не является
пренебрежимой на Q. (См. также замечания в конце п. 5.13.4.)
5.6. В обозначениях п. 5.13.9 (а) (случай /г = 1) положим
Va=\f&V: /(a)-. li
Показать, что
A) Vq отделимо, если р > 0 почти всюду на Q;
Упражнения 569
л
B) если р" d\i < + оо для некоторого (а поэтому для всех) хеЙ,
а
то Va замкнуто в V (и, следовательно, полно, если V полно); доказать также,
что сходимость (соотв. ограниченность) в Va влечет за собой равномерную
сходимость (соотв. ограниченность) на (а, х0) для каждого х0 ^ Q.
5.7. Обозначения те же, что и в § 5.13. Доказать, что если Е = L2 (Q),
то функция
достигает своего наибольшего значения по ugF при v = G/, причем это наи-
наибольшее значение равно (Gf \ f)E = || Gf ||j>.
5.8. Допущения те же, что и в § 5 13 Доказать, что при заданных
/ е L2(Q) и g ^H единственное решение системы
u-ge=N, Pu = f
задается равенством
+G(fP)
причем это решение принадлежит подпространству
Замечание. Для оператора Р = — А + Х у Гординга [5, стр. 12—
13] изложен другой подход к решению задачи. Ограничения, которые Гор-
динг накладывает на / и g, отличаются от наших, а граничные условия фор-
формулируются в терминах замыкания QJ (Q) в V.
Обозначения и предположения в упр. 5.9—5.15 те же, что и в п. 5.13.8.
5.9. Рассмотрим в качестве Е пространство L2(Q)=L2. Опираясь на оп-
определяющее свойство операторов G^, показать, что G^f—G-J, если ugF
при v e V.
5.10. Воспользовавшись равенствами E.13.24), проверить соотношение
для X е C\R_; производные берутся в смысле нормированной топологии
на пространстве эндоморфизмов в Е.
5.11. С помощью равенства E.13.26) доказать, что оператор Gi само-
самосопряжен, если рассматривать его как эндоморфизм пространства Е или про-
пространства Vi, где X — вещественное строго положительное число.
5.12. Доказать, что отношение
остается справедливым для Х^С \ R_.
5.13. Рассматривается ситуация, описанная в п. 5 13 8.
Пусть E=L2=L2(Q) и А, = <х + ф принадлежит C\R_. Доказать следую»
щие неравенства.
A) Если а + ро>О и (а + роГ1 ezj?1 (Q), то
B) Если а > 0, то
570 Гл. 5. Распределения и дифференциальные уравнения
C) Если а>0ир/;'еУ (Q), то
nwnL,< I я \-ц Pi%mL*
D) Если а<0 и р=^=0, то
E) Если а < 0, р Ф О и р^1 е= J?x (Q), то
H^x/t^dPI^ + laP^Dlpi-'gl/b
5.14. Показать, что в Z.2
HmXGx/-f
при А,->оо вдоль любого луча, отличного от отрицательной вещественной
полуоси.
5.15. Рассматривается ситуация, описанная в п. 513.8. Доказать, что
задача
п
ue=N, Ри + Хи + 2 ckdku = /
разрешима для любого заданного fel2; если
[Указание. Записать уравнение в виде
5.16. Исследовать волновое уравнение
дХ _ д2Х Х( r)\ = f(\
dt dt2 ~ ' {Х' } ' W
с помощью такой i^'-значной функции / \—> Xt, что
д\у ^2^_п у_*
~dt)At аТ2""' л°~г'
Предполагая, что Xt и / — медленно растущие распределения, воспользоваться
преобразованием Фурье для формального доказательства равенства
где Et — обратное преобразование Фурье от ехр [— 4я2£2/], а именно
ехр [— x2/4t].
5.17. Показать, что уравнение
где а > 0, обладает единственным решением X е &" при заданном А е с?*'.
В частности, Х = 0 является единственным решением в <$" уравнения
Упражнения 571
5.18. Доказать, что единственными медленно растущими решениями ура-
уравнения АЛ" = 0 являются многочлены, но в & существуют и другие реше-
решения этого уравнения.
5.19. Пусть Q — непустое открытое подмножество в R". Выберем е>0
настолько малым, чтобы множество'пг = {л; е Q: d (х, Q) > е} было непусто
(Q —граница множества Q). Пусть ^е^'(й), Be^jR") и supp В содер-
содержится в шаре В (О, е) с центром в нуле и радиусом е. Доказать, что" если
ф£^ (йе), ТО фуНКЦИЯ
принадлежит & (п) и формула
<Ф,Л*Б)«(х, Л)
определяет свертку А * В как элемент из &' (Qe).
5.20. Пусть Е — локально интегрируемая на Rn функция, зависящая
только от | л: | *= г и принадлежащая С2(^\{0}). Пусть далее Е удовле-
удовлетворяет следующим соотношениям:
- \)Г1 ^--ХЕ=0 при г>0,
dr2
dr n
n
(где wn*= 2л; 2 IT I — j — площадь единичной сферы в Rn). Убедиться в
том, что Е является фундаментальным решением оператора —А + Я.
[Указание. Рассуждать, как в § 5.11J
Замечания. Если п^2 и Я не является вещественным числом ^0,
то в качестве функции Е можно взять
оо 1
/» -рг \1Ъ — 3)
г„Л, /„ о\п~1 Л^—2 п—art (ft <W j±
[wn \n — zj.'j a e \t —i) at,
1
где а2 = % и Re a > 0; при п=*3 это выражение сводится к е~аг1\т. При
п = 1 и Я ф 0 можно положить Е = е"а'х '/2а, где а2 = Я.
Отсюда следует, что оператор — А 4- Я является гипоэллиптическим,
если Я не является вещественным числом ^0.
5.21. Обозначения те же, что и в п. 5.13.1. Пусть 0 < ess inf/?г ^
п
< ess sup pr < + °° @ <Г г ^ /г). Доказать, что следующие подмножества
п
будут плотными в пространстве V:
A) С°°(Й)П^;
B) множество функций из пересечения С°° (Q) П V', обладающих ограни-
ограниченными носителями.
[Указание. В первом случае воспользоваться теоремой Хана — Ба-
Банаха и гипоэллиптичностью оператора —А + 1; см. предыдущее упражнение.]
Замечания. Так как А —* гипоэллиптический оператор, то аналогич-
аналогичные рассуждения показывают, что даже при ро—0 (остальные условия
572 Гл. 5. Распределения и дифференциальные уравнения
сохраняются) функции с ограниченными носителями из пересечения С°° (Q) (] V
образуют плотное в V множество. Под V здесь понимается BL(Q) —
пространство Беппо Леей (Дени и Лионе [1]), образованное теми
функциями /е L}0C(Q), для которых dhf&L2(Q) при£=1, .... п, и на-
наделенное скалярным произведением
fe-i
5.22. Пусть Q — область в Rn и Р — многочлен на Rn вида
такой, что Р (I) > О при ^ g R" и ^ 0. Для любых / и g из Q) (Q) положим
\р\ = т Q
Доказать (например, с помощью преобразования Фурье), что существует
такое число с > 0, что
1
для / €= @ (Q), где || /|lm - 4- (/1 /)'Д, и т. п.
Допустим теперь, что область Q ограничена. Показать, что из неравен-
неравенства В п. 5.14.2 следует существование такого числа со>О, что
для fe^(Q).
5.23. Обозначения и предположения те же, что и в упр. 5.22. Доказать,
что пополнение Е пространства Q) (Q) относительно нормы ||«||р можно ото-
отождествить с подпространством пространства %™2 (Q) таких функций (или
классов функций) /eL2(Q), для которых dpf^L2(Q) при каждом р с \р\ — т.
5.24. Обозначения и предположения те же, что и в других предыдущих
упражнениях. Показать, что для заданного g e %™2 (^) найдется такое и е
<= ф (Q), что
u — g^E и Р(д)и = 0 на Q.
[Указание. Воспользоваться методом ортогонального проектирова-
проектирования.]
5.25. Пусть Q — некоторая область в Rn. Доказать, что если f — веще-
вещественная функция на Q и f и dkf локально интегрируемы на Й (k — 1, .,,
..., п), то то же самое справедливо для /+ и
где а — характеристическая функция того множества; где />0.
Показать также, что если g удовлетворяет тому же условию, что и f, то
sup (f, g) и inf (f, g) обладают частными производными первого порядка, яв-
являющимися локально интегрируемыми функциями.
Упражнения 573
Заключить, что если / — вещественная функция, принадлежащая BL(Q)\h
/r = inf [sup (/, ~r), r],
то fr e BL (Q) и dkfr = (dkf)fin где Рг ~ характеристическая функция того
множества, где |/|</-. Показать также, что
lim/> = / в BL(Q).
Г->оо
5.26. Пусть Xg^' (Q) — такая обобщенная функция, что kkX e Q}r (Q)
при некотором фиксированном т и произвольно больших Л. Доказать, что
X €= С°° (Q) (Л. Шварц [2, теорема XIX, стр. 47] ).
[Указание. Воспользоваться техникой, введенной в п. 5.11.2.]
5.27. Пусть Хе^' (й), и пусть при некотором m имеет место следую-
следующее условие: для каждого ограниченного открытого множества со, для ко-
которого со с: Q, существует такая окрестность нуля U, что X * а е С°° (со) для
а s=Q)m{U). Показать, 4ToXeC°°(Q) (Л. Ш в а р ц [2, теорема XXI, стр. 50]).
[Указание. То же, что и для предыдущего упражнения.]
ГЛАВА 6
Теоремы об открытом отображении
и замкнутом графике
6.0. Предисловие
Теоремы, фигурирующие в названии этой главы, восходят к
начальному периоду развития функционального анализа (Ба-
(Банах [1]), когда они были доказаны для полных метризуемых
топологических векторных пространств. В этом случае они зву-
звучат так.
► Пусть Е и F — полные метризуемыв топологические век-
векторные пространства. Непрерывное линейное отображе-
отображение и пространства Е на F открыто. Линейное отображе-
отображение v пространства F в Е, обладающее замкнутым гра-
графиком, непрерывно.
С тех пор, особенно в последние годы, первоначальные доказа-
доказательства этих теорем подвергались тщательному анализу. Эти
исследования, помимо того, что они интересны сами по себе,
были вызваны еще и желанием применить эти теоремы в других
современных разделах математики (теория интегрирования, рас-
распределения Шварца, потоки Де Рама, уравнения в частных про-
производных и т. п.), где приходится привлекать топологические
векторные пространства все более общего вида. В частности,
оказалось, что метризуемость менее существенна, чем можно
было ожидать.
В данной главе изучаются некоторые типы топологических
векторных пространств, имеющие в настоящее время важное зна-
значение, а именно: метризуемые, бочечные и ультрабочечные про-
пространства. (Значение этих пространств выявится еще и в даль-
дальнейшем, в гл. 7 и 8.) Кроме того, здесь рассмотрен способ обра*
зования пространств с помощью индуктивного предела.
В этой главе мы приводим только часть материала, касаю-
касающегося теорем об открытом отображении и замкнутом графике.
Дело в том, что в настоящее время эти вопросы можно излагать
двояко: (а) для общих топологических векторных пространств,
не обязательно локально выпуклых, и (Ь) для локально выпук-
выпуклых пространств1). Последний случай лучше рассмотреть неза-
1) Результаты § 6.5 и 6.6, возможно, составляют исключение из этой
дихотомии. Они применимы к некоторой смешаной категории локально вы-
выпуклых и не локально выпуклых пространств, поскольку опираются в основ-
основном на метризуемость.
6.1. Полу мет ризу емые топологические векторные пространства 575
висимо от (а), но в тесной связи с теорией двойственности. По-
Поэтому исследование случая (Ь) нужно отложить до гл. 8. Успеху
в этом направлении мы обязаны в значительной мере Птаку1)
[1—4] и Р а й ко в у [1, 2].
Что касается (а), т. е. случая, когда пространства не обяза-
обязательно локально выпуклы, то здесь положение менее удовлетво-
удовлетворительно. Некоторые недавние исследования в этом направлении
принадлежат В. Робертсону [1]. В отличие от случая локаль-
локально выпуклых пространств здесь пространство £ сохраняет некото-
некоторые «следы» метризуемости и доказательства более «традици-
онны», так как они явно используют «категорные рассуждения».
Настоящая глава содержит все, что мы намерены сказать о слу-
случае (а).
Здесь уместно сделать несколько замечаний относительно
предположения полноты пространств Е и F в теоремах об откры-
открытом отображении и замкнутом графике. В случае (а) в новейших
результатах полнота пространства F явно не фигурирует. От
полноты Е также можно отказаться, но только за счет дополни-
дополнительных предположений, которые по сути дела являются «само-
«самообманом», ибо дают возможность заменить пространства Е и F
их пополнениями. Напротив, в случае (Ь) условие полноты Е
(даже более сильное, чем обычное) является весьма существен-
существенным, а относительно пространства F необходимо сделать еще и
другие предположения.
Из этих общих замечаний видно, что первоначальная сим-
симметрия между пространствами Е и F утеряна. Однако обе эти
теоремы излагаются параллельно: теорема об открытом отобра-
отображении формулируется для и: £->/% а теорема о замкнутом
графике — для v: F-+■ Е. В дальнейшем при выборе обозначений
мы руководствуемся этим замечанием.
Другое изложение различных форм теорем об открытом ото-
отображении и замкнутом графике можно найти в книге Келли
и Намиоки [1, § 11 и задачи 1 ID, 12E, 13F, 13G, 181, 18J,
19В и 20J].
6.1. Полуметризуемые топологические векторные пространства
и пространства Фреше
Если топологическое векторное пространство Е обладает
счетной базой окрестностей нуля, то ассоциированная равномер-
равномерная структура имеет счетную базу окружений, поэтому в силу
1) Птак пользуется терминами «открытое отображение» и «почти от-
открытое отображение» в смысле, несколько отличном от нашего. В примене-
применении к отображению и: Е -> F определение Птака совпадает с нашим, если
в последнем заменить Е на u(E)t
576 Гл. в. Теоремы об открытом отображении и замкнутом графике
п. 0.3.6 эта равномерная структура полуметризуема. Если, кроме
того, пространство Е отделимо, то его равномерная структура
метризуема. Приведем здесь доказательство леммы 0.3.6 для
случая топологического векторного пространства.
6.1.1. Теорема. Для того чтобы равномерная структура
(а следовательно, и топология) топологического векторного про-
странства Е была полуметризуема, необходимо и достаточно,
чтобы в Е существовала счетная база окрестностей нуля. В этом
случае его равномерную структуру можно определить с по-
помощью полу метрики dy инвариантной относительно сдвигов,
т. е. такой, что d{x, y)—d(x— у, 0).
Доказательство. Необходимость очевидна. Докажем
достаточность. Пусть (Vn)—счетная база окрестностей нуля.
Построим по индукции другую базу (Un) уравновешенных
окрестностей нуля так, чтобы U\CiVi и
при п > 1. Определим на Е функцию g > 0 следующим образом:
со
0 при xg f)Uny
2~k при xg[/,\[/h1,
1 при x^E\U{.
Очевидно, g"@)=0. Исходя из g, определим функцию f с по-
помощью соотношения
р
2
i = l
где нижняя грань берется по всевозможным конечным системам
р
(Xi)l<i<p(p неограничено), для которых х= 2 **• Ясно, что
функция / положительна и субаддитивна и что f^Cg.
Докажем, что /^yg. Для этого индукцией по р покажем,
р
что х = S Х( влечет
р
*±g(x). F.1.1)
6.1. Полуметризуемые топологические векторные пространства 577
Справедливость соотношения F.1.1) очевидна при /7 = 1. Пусть
//>1; допустим, что неравенство F.1.1) установлено для всех
/?<//. Положим
Если а = 0 или а^у, то неравенство F.1.1) остается справед-
справедливым, если заменить р на //. Это следует из того очевидного
факта, что g-< 1. Допустим, чтоО<а< у. Пусть h — наиболь-
наибольшее из натуральных чисел г, для которых
а
(пустые суммы считаются равными нулю). Имеем тогда
a 2 ff(^)>
следовательно,
Так как h—1<// и р' — h<p\ то по индуктивному предполо-
предположению
аналогично
С другой стороны, (
Пусть k — наименьшее натуральное число, для которого
2~k -^>a. Из определения функции g" и из предыдущих неравенств
следует, что k > 1, 2 xt e f/fe, 2 ** ^^ихЛе [/л. Таким об-
разом, элемент * — ( 2 *Л + *л + ( 2 ^) принадлежит множе-
\i<h } \i>h j
ству Uk+Uk+Uk> которое содержится в D_i. Но тогда
g(x)<21~fe<2a, откуда следует, что неравенство вида F.1.1)
справедливо и при разбиении х в сумму // слагаемых. Индукция
окончена и неравенство F.1.1) установлено,
578 Гл. в. Теоремы об открытом отображении и замкнутом графике
Таким образом, f^-jg', отсюда вытекает, что Uk содержит
все те элементы xg£, которые удовлетворяют неравенству
f(x) <2~h~l; в то же время при |3>0 множество {х е Е: f(x)-^$}
содержит Uk, для которых 2~fe<p. Следовательно, d(xy у) =
= f(x— у) —полуметрика, определяющая равномерную струк-
структуру в Е. Щ
Замечания. A) Приведенное выше рассуждение принад-
принадлежит Б у р б а к и [3, гл. IX]. Его можно приспособить к равно-
равномерным пространствам так, чтобы получить доказательство
леммы 0.3.6.
B) Если пространство Е локально выпукло, то полуметрику
можно построить непосредственно. Возьмем базу окрестности
нуля (Un), образованную открытыми (или замкнутыми) выпук-
выпуклыми уравновешенными множествами. Пусть рп — функционалы
Минковского множеств Ип\ тогда полуметрику d можно опре-
определить равенством
d(xt y) =
C) Наиболее важными и исторически первыми метризуе-
мыми (соотв. полуметризуемыми) топологическими векторными
пространствами являются нормированные (соотв. полунормиро-
полунормированные) пространства. Они, конечно, локально выпуклы.
D) Следуя Бурбаки, будем называть пространством Фреше
всякое метризуемое полное локально выпуклое пространство.
Каждое банахово пространство является пространством Фреше.
Так называемые (F)-пространства по Банаху [1, гл. III] —
это полные метризуемые, но не обязательно локально выпуклые
пространства. В п. 6.1.3 и 6.1.4 мы приведем несколько важных
конкретных примеров пространств Фреше, не являющихся ба-
банаховыми.
Факторизация полуметризуемых пространств. Пусть Е — по-
луметризуемое топологическое векторное пространство, М—
векторное подпространство в £ и / — естественное отображение
пространства Е на Е/М. Так как / преобразует базу окрестностей
нуля пространства Е в базу окрестностей нуля пространства
Е/М, то по теореме 6.1.1 пространство Е/М полуметризуемо (и
потому метризуемо тогда и только тогда, когда подпростран-
подпространство М замкнуто в Е). Кроме того, существует такая положи-
положительная субаддитивная функция x*—>N(x) на Еу что N (х — у)
есть полуметрика, определяющая равномерную структуру в Е.
Определим на Е/М функцию /V' по формуле
6.1. П олу мет ризу емые топологические векторные пространства 579
Функция N' положительна и субаддитивна. Если мы для каж-
каждого е>0 введем множества
Ue = {xt=E: N(x)<e}
то, как легко проверить, /(£/в)=£/е. Отсюда следует, что мно-
множества Ue образуют базу окрестностей нуля в фактортопологии
в Е/М\ поэтому полуметрика, соответствующая функции N',
определяет равномерную структуру в Е/М.
Из этих замечаний можно вывести следующий Еажный ре-
результат.
6.1.2. Теорема. Если Е — полное полуметризуемое топологи-
топологическое векторное пространство и М — векторное подпространство
в Е, то факторпространство Е/М полно и полуметризуемо.
В частности, если Е — пространство Фреше и М — замкнутое
векторное подпространство в Е, то факторпространство Е/М
есть пространство Фреше.
Доказательство. Второе утверждение непосредственно
вытекает из первого. Для доказательства первого утверждения
рассмотрим последовательность Коши (gn) в пространстве Е/М.
Для того чтобы установить сходимость последовательности (|а)
в Е/М, достаточно показать, что некоторая ее подпоследователь-
подпоследовательность сходится. Нам дано, что W(gw-—in)-^0 при /п, /г-^оо.
Выберем подпоследовательность \Пк так, чтобы
Полржим ал = 5я —%п и выберем ak e f~l (ЫЛ) так, чтобы
Тогда ^jN(ak)< + оо. Из субаддитивности функции Af еле*
дует, что частичные суммы
sk = a{+ ... +ak
образуют последовательность Коши в Е. Так как Е — полное
пространство, то последовательность (sk) сходится к некоторому
элементу в Е. Естественное отображение / пространства Е на
Е/М непрерывно, поэтому последовательность (f{sk)) сходится
в пространстве Е/М. Но /(^) — ai+ ••• +a£s==£rt ~~ ln , от-
580 Гл. 6. Теоремы об открытом отображении и замкнутом графике
Замечание. В общем случае факторпространство полного
топологического векторного пространства по векторному подпро-
подпространству (замкнутому или нет) может и не быть полным.
Контрпример имеется у Кёте [4]; см. также Гротендик [7,
стр. 145, упр. 5].
6.1.3. Примеры. Если Т — сг-компактное локально компакт-
компактное пространство, то пространство С(Т) всех непрерывных чис-
числовых функций на Т становится пространством Фреше, если
наделить его топологией локально равномерной сходимости (т. е.
топологией равномерной сходимости на компактных подмноже-
подмножествах пространства 71, называемой иногда компактно-открытой
топологией). Определяющая система полунорм получится, если
взять базу Кп (я=1, 2, ...) компактных множеств в Г и поло-
положить
pn(x)=sup\x\.
Если подчинить пространство Т более сильным ограничениям,
то различные важные подпространства пространства С(Т) ста-
становятся пространствами Фреше, если наделить их индуцирован-
индуцированной или более сильной топологией. Вот примеры.
(a) Если Т — открытое подмножество комплексной плоскости
(или вообще комплексное аналитическое многообразие), то про-
пространство голоморфных на Т функций образует замкнутое под-
подпространство в С(Т) и, следовательно, есть пространство Фреше
в индуцированной топологии.
(b) Если T=Rn или является открытым подмножеством в
Rn, то пространство С°°(Т) всех бесконечно дифференцируемых
функций на Т образует векторное подпространство в С(Т). Оно
не замкнуто в С(Т) и поэтому в индуцированной топологии не
является пространством Фреше. Однако С°°(Т) становится про-
пространством Фреше, если усилить в нем топологию до топологии
локально равномерной сходимости функций вместе со всеми
частными производными. Обозначим через t\, ..., tn координаты
bR"h через k — набор (ku ..., kn) целых неотрицательных чи-
чисел, и пусть dft —дифференциальный оператор
*/?■ ...a/*"'
Систему определяющих полунорм для указанной топологии з
С°°(Т) образуют функции
pr(x) = sup {|d*(/)|: | /1 ^ г, kx+k2+ ... +&„<г},
где г=1, 2, ... . Пользуясь локальными координатами, можно
аналогичным образом топологизировать пространство С°°(Т)
6.1. Полу мет разу емые топологические векторные пространства 581
для всякого вещественного дифференцируемого многообразия
Т класса С°°. Если Т — риманово многообразие, то можно выде-
выделить в С°°(Т) гармонические функции. Они образуют замкнутое
подпространство в С°°(Г), которое является поэтому простран-
пространством Фреше в индуцированной топологии.
(с) Векторным подпространством в C°°(Rn), играющим важ-
важную роль в теории распределений Шварца, является простран-
пространство ^(Rn) тех функций хе C°°(Rn), для которых конечна каж-
каждая из величин
(r=l, 2, ...). Функции Sr являются полунормами на простран-
пространстве 5^(Rn), которое будет пространством Фреше относительно
топологии, определяемой этими полунормами. Пространство
^(Rn) содержит множество S)(Rn) функций из C°°(Rn), имею-
имеющих компактные носители. Множество S)(Rn) всюду плотно в
&{Rn). (См. § 5.15; а также Л. Шварц [1, 2].)
6.1.4. Примеры из теории суммируемости. Пусть N — множе-
множество натуральных чисел. Обозначим через С векторное про-
пространство всех числовых (комплексных) последовательностей
(т. е. функций на N). Относительно топологии поточечной схо-
сходимости С есть пространство Фреше, которое фактически со-
совпадает с пространством C(N) п. 6.1.3. Пусть А — бесконечная
матрица, т. е. скалярная функция на произведении NXN. Обо-
Обозначим через D(A) множество тех хе№, для которых ряд
2<Д(т, п)х(п) сходится при каждом т. Множество D(А) яв-
п n
ляется, очевидно, векторным подпространством в С , а матрица
А определяет линейное отображение иА пространства D(A) в
CN, которое каждому элементу x^D(A) сопоставляет последо-
последовательность у = иА(х), определенную соотношениями
//(т)=ЦЛ(т, п)х(п) (m c= N). F.1.1)
п
При соответствующих условиях (которые будут перечислены
ниже, в примере 7.2.4) отображение иА переводит сходящиеся
последовательности в сходящиеся и, возможно, некоторые рас-
расходящиеся последовательности в сходящиеся. В этом случае мы
имеем нетривиальный способ сопоставить обобщенный предел
некоторым расходящимся последовательностям, т. е. мы имеем
тогда то, что (несколько странно) называют методом суммиро-
суммирования1), ассоциированным с матрицей Л. Такие методы сумми-
]) Это название объясняется тем, что впервые преобразования такого
типа возникли в теории суммирования расходящихся рядов (при этом пре-
преобразованию с матрицей А подвергается последовательности частичных сумм
ряда). —Я/ш*. ред.
582 Гл. 6. Теоремы об открытом отображении и замкнутом графике
рования представляют большой интерес, а аппарат функцио-
функционального анализа оказывается весьма полезным инструментом
при их исследовании (см. Цел л ер [1—4], Мазур и Орлич
[1], Т э т ч е л [1]). Укажем здесь несколько полезных пространств
Фреше, связанных с методами суммирования. Здесь и ниже мы
приводим примеры применения общих теорем функционального
анализа. Книга Целлера [4] с ее обширной библиографией
служит стандартной ссылкой по этой тематике. См. также
Кук [1, 2].
Как обычно, через /°°,' с и с0 будем обозначать соответственно
прос1ранство ограниченных, сходящихся и сходящихся к нулю
последовательностей. Относительно нормы
пространство /°° банахово, а с и с0 — его замкнутые подпро-
подпространства.
Зададимся матрицей А и обозначим через В (А), С (А) и
Со(А) множества в D(Л), образованные теми последовательно-
последовательностями х, для которых иА(х) принадлежит соответственно про-
пространствам /°°, с и с0. Таким образом, имеют место включения
С о (А) cz С(А) а В(А) a D(A)\ все эти множества являются
векторными подпространствами в CN.
Для данной последовательности х и данного натурального
числа k обозначим через skx k-сечение последовательности х,
определенное соотношениями
| х(п) при /г<Аэ
* v } { 0 при п > k.
Очевидно, что sk (x) e D(A) и что
lim u
поточечно для каждого x()
В качестве полунорм, определяющих естественную тополо-
топологию в CN, возьмем функции
РпМ = \х(п)\ (/1=1, 2, ...). F.1.2)
Введем еще другие функции, которыми будем пользоваться в
теории суммирования как полунормами на D(A). Положим
FЛ.З)
= sup
н
A(mt n)x(n)
6.1. П олу мет ризу емые топологические векторные пространства 583
для л;еС% натуральных чисел т. Ясно, что qAf m — полунорма
на D(А). Введем также функцию
^M4!M*)L< + «> (xsD(A)). F.1.30
Пространство В(А) совпадает с множеством тех x^D(A)t для
которых qA(x)< + oo, причем qA — полунорма на В (А).
Рассмотрим в пространстве В (А) топологию ТА, определяе-
определяемую системой полунорм /?n, qA>m и qA> где m и п независимо
друг от друга пробегают множество N. Основной результат со-
состоит в следующем.
► A) Если В (А) наделить топологией ТА, то оно стано-
становится пространством Фреше. Векторные подпространства
С (А) и Со (А) замкнуты в В (А) и, следовательно, яв-
являются пространствами Фреше в индуцированной топо-
топологии.
Доказательство. Замкнутость подпространств С (А) и
Со (Л) в В (А) следует из того, что подпространства с и с0 замк-
замкнуты в /°°. Остается доказать, что пространство В (А) дол но от-
относительно топологии ТА. Пусть (Xi) есть ГА-последовательность
Коши в В (А) и yi = uA(Xi). Тогда (уг) есть последовательность
Коши в /°° и, следовательно, существует такой элемент у е /°°,
что \\у — г/г11оо->-0 при /->оо. В то же время (хг) есть последо-
последовательность Коши в CN относительно топологии поточечной
сходимости, поэтому в CN существует поточечный предел
х= limjty. Положим
sup 1 2 A(m, n)[xi(n) — Xf(n)] =Rm,i, /•
k | n^. k
Тогда для каждого m имеет место равенство
lim Rmt{tj = O,
которое является следствием того факта, что (Xi) есть последо-
последовательность Коши. Полагая /->оо, получаем
sup
k
2 A(m, n)[xi(n)-x(n)] -/?„.,. F-1.4)
где lim Rmti = 0 для каждого m. Отсюда следует, во-первых
ельно
\imyi.
i
(при фиксированном г), что последовательность х принадлежит
D(A) и, во-вторых, что поточечно
584
Гл. 6. Теоремы об открытом отображении и замкнутом графике
Но Ух-+у в /°°, поэтому у = иА(х).,Следовательно, последователь-
последовательность х принадлежит В (А) и иА(х{) -+иА(х) в /°°. Отсюда вы-
вытекают поточечная сходимость х{~+ху сходимость в /°° иА(хг) ->
-+иА(х) и соотношение F.1.4), где \imRmti = 0 для каждого т.
Это означает сходимость Хх~+х в смысле топологии ТА. Пол-
Полнота пространства В (А), таким образом, установлена. I
Рассмотрим теперь множество КА = К тех натуральных чисел
п, для которых
sup| A(m9 /г)
Очевидно, значение иА(х) зависит только от сужения х\К. Да-
Далее всегда имеет место неравенство
\А(ш9 n)\pn(x)^2qAtm(x).
Поэтому для всякого п е КА существуют такое число а = а(А, п)
и такое натуральное число m = m(n)y что
Pm(x)<a.qAtm(x). F.1.5)
В качестве следствия получаем:
► B) Пусть В*(А)—множество тех последовательностей
лее В (Л), для которых x\N\KA = 0. Тогда топология ТА
индуцирует в В*(А) топологию, совпадающую с топо-
топологией, определяемой полунормами qA и qA,m (m=l,
2, ...,). В частности, если /Ca = N, to обе эти топологии
совпадают в В (А).
Аналогичное утверждение имеет место, когда А — матрица с
финитными строками, т. е. когда каждому m соответствует такое
число пш, что А(т, п)=0 при п>пт. В этом случае D(A)=CN;
кроме того, тогда
Я а. т№<$ (А, т). sup рп (х), F.1.6)
где
2 \А(т, п)\.
т
Таким образом:
► Если А — матрица с финитными строками, то топология
ТА совпадает с топологией, определяемой полунормами
Ца и рп (п=\, 2, ...).
Важно заметить, что все предыдущие результаты без особых
затруднений могут быть перенесены на случай, когда рассматри-
рассматриваются одновременно последовательность матриц Аг (г=1,
2, ,..) и определенные ими методы суммирования. По опре-
6.2. Бочечные пространства 585
делению полагаем тогда/) {Аи А2, .. .) = f]D(Ar)f B(AU Аъ.. .) =
г
= Р|В(ЛГ) и т. д.) Множество К а заменяем множествОхМ
г
К(Аи Аъ ...) = р\К(Аг)> а топологию ТА — топологией Т(Аи
г
А2, ...)» определяемой полунормами рп, qAr, qAfi m, где nt m, r
пробегают независимо друг от друга множество натуральных
чисел. При этом справедливы аналоги утверждений A), B) и
C). Доказательства повторяют приведенные с очевидными ви-
видоизменениями.
В примерах 6.4.10, 7.2.4 и замечании C) после предложения
9.3.9 мы вернемся к обсуждению этих вопросов.
6.2. Бочечные, инфрабочечные и ультрабочечные пространства
Бур баки [7, стр. 143] был первым, кто выделил среди ло-
локально выпуклых пространств класс пространств, обладающих
некоторыми важными свойствами банаховых пространств и про-
пространств Фреше, без предположения метризуемости. Эти про-
пространства характеризуются свойствами некоторых своих подмно-
подмножеств, которые Бурбаки назвал бочками. Сами пространства
были названы им бочечными.
Бочкой в топологическом векторном пространстве Е будем
называть всякое его замкнутое выпуклое уравновешенное и по-
поглощающее подмножество. Топологическое векторное простран-
пространство Е называется бочечным, если оно локально выпукло и
каждая бочка в Е является окрестностью нуля. Читатель мо-
может заметить, что в каждом локально выпуклом пространстве
существует база окрестностей нуля, состоящая из бочек.
Часто оказывается полезным следующее более слабое свой-
свойство. Локально выпуклое пространство называется инфрабочеч-
ным, если каждая бочка в Е, поглощающая всякое ограниченное
множество в £, есть окрестность нуля в Е.
Другая характеризация бочечного пространства, без явного
упоминания о бочках, дается теоремой 6.2.1B). Эта иная фор-
формулировка в значительной мере обязана своим существованием
наличию третьего типа пространств, который будет введен ниже.
Для не локально выпуклых пространств В. Робертсон
[1, стр. 249] ввел и исследовал свойство ультрабочечности. По-
Попытки определить это свойство в терминах некоторых подмно-
подмножеств (аналогичных бочкам) оказались затруднительными. По
этой причине и для удобства ссылок в дальнейшем мы включим
его точное определение в часть A) теоремы 6.2.1. В части B)
586 Гл. 6. Теоремы об открытом отображении и замкнутом графике
этой теоремы будет дана аналогичная характеризация бочечных
пространств.
Укажем, кстати, «крайний» пример: векторное пространство
Е, наделенное сильнейшей локально выпуклой топологией /«>
(п. 1.10.1), бочечно.
6.2.1. Теорема. A) Топологическое векторное пространство
(Е, t) ультрабочечно тогда и только тогда, когда всякая линей-
линейная топология /' в Е, обладающая базой окрестностей нуля из
t-замкнутых множеств, слабее топологии /.
B) Локально выпуклое пространство (Е, /) бочечно тогда
и только тогда, когда каждая локально выпуклая топология f
в Е, обладающая базой окрестностей нуля, образованной (-замк-
(-замкнутыми множествами, слабее топологии /.
Доказательство. A) Это определение.
B) Пусть пространство (Е, /) бочечно и топология V обла-
обладает указанными свойствами. Пусть V—/'-окрестность нуля;
она содержит /'-окрестность куля, скажем V, которая является
/-замкнутой. Так как топология /' локально выпукла, то V со-
содержит уравновешенную и выпуклую /'-окрестность нуля V".
Тогда /-замыкание /'-окрестности V" есть бочка в (Е, /) и по-
потому /-окрестность нуля. Так как /-замыкание окрестности V"
содержится в У'и тем более в V, то V есть /-окрестность нуля.
Таким образом, топология /' слабее топологии /, и, следова-
следовательно, условие B) выполняется.
Обратно, пусть пространство (£, /) удовлетворяет условию
B) и Л— произвольная бочка в Е. Множества вида аА, где
а>0, образуют базу окрестностей нуля для некоторой локально
выпуклой топологии /', удовлетворяющей условиям утвержде-
утверждения B). В соответствии с этим топология V слабее топологии
/, откуда следует, что бочка А есть /-окрестность нуля. Итак,
(Е, /) — бочечное пространство. I
Замечания. A) Из теоремы 6.2.1 легко следует, что всякое
локально выпуклое ультрабочечное пространство бочечно. Для
локально выпуклых пространств справедливы следующие импли-
импликации:
ультрабочечность =ф бочечность =ф> инфрабочечность
Пример, приведенный у В. Робертсона [1, стр. 256] и при-
принадлежащий Вестону, показывает, что бочечное пространство
может и не быть ультрабочечным.
B) В п. 7.1.1 и 8.9.6 мы еще встретимся с другими важными
и интересными характеризациями бочечных пространств. Сейчас
мы продолжим исследование свойств и приведем ряд важных
примеров рассматриваемых пространств,
6.2. Бочечные пространства 587
6.2.2. Теорема. Всякое нетощее топологическое векторное про-
пространство {см. п. 0.3.15) ультрабочечно. Всякое нетощее локально
выпуклое пространство бочечно.
Доказательство. Второе утверждение непосредственно
следует из первого, Допустим, что (Е, /) — нетощее топологи-
топологическое векторное пространство и что /'— некоторая линейная
топология в Е, обладающая базой окрестностей нуля, образован-
образованной /-замкнутыми множествами. Пусть U — некоторая /'-окрест-
носгь нуля. Покажем, что U есть /-окрестность нуля. Из свойств
топологии f вытекает существование такой уравновешенной
/-замкнутой /'-окрестности нуля У, что 1/+Vcz U. Так как про-
пространство Е есть объединение множеств вида nV (я=1, 2, ...),
каждое из которых /-замкнуто, и пространство (Е, /) нетоще,
то существует такое п, что /-внутренность множества nV не
пуста. Множество V содержит тогда некоторое множество вида
x+W, где xs£h W—/-окрестность нуля. Из соотношений
UzdV+V=*V+ (—V) r> W+ (-W)
следует, что U есть /-окрестность нуля. Топология V\ таким об-
образом, слабее топологии /. I
6.2.3. Следствие. Всякое полное по лу мет ризу е мое топологи-
топологическое векторное пространство ультрабочечно.
Замечание. Очень важно (§ 6.3 и п. 8.3.7), что нетощие
топологические векторные пространства — не единственные уль-
ультрабочечные пространства. В этом большая практическая цен-
ценность этого понятия. Заметим также, что существуют полные
ультрабочечные, но не метризуемые топологические векторные
пространства. Это следует из того, что произведение любого
числа полных метрических пространств является бэровским про-
пространством (Б у р б а к и [7, стр. 146, упр. 7]).
6.2.4. Теорема. A) Пусть Е и F— топологические векторные
пространства и f — непрерывное линейное открытое отображение
Е на F. Если Е — ультрабочечное (соотв. бочечное) пространство,
то и F — ультрабочечно (соотв. бочечно). В частности, любое
факторпространство ультрабочечного (соотв. бочечного) про-
пространства ультрабочечно (соотв. бочечно).
B) Пусть Е — топологическое векторное пространство, Е —
его пополнение и F — векторное подпространство в Е, содержа-
содержащее Е. Если пространство Е ультрабочечно (соотв. бочечно), то
и пространство F ультрабочечно (соотв. бочечно).
Доказательство. В каждом из этих случаев достаточно
рассмотреть только ультрабочечный случай. Для бочечных про-
пространств доказательство аналогично.
688 Гл. 6. Теоремы об открытом отображении и замкнутом графике
A) Пусть 5 и /— исходные топологии пространств Е и F
соответственно. Допустим, что линейная топология ? обладает
базой окрестностей нуля, образованной /-замкнутыми множе-
множествами V. Тогда множества f~l(V) -s-замкнуты и образуют-базу
окрестностей нуля для некоторой топологии s\ Так как про-
пространство Е ультрабочечно, то топология s' слабее топологии
s. Таким образом, каждое из множеств f~l(V) есть s-окрестность
нуля. Поскольку отображение / открыто, то множество f(f~l(V))
есть /-окрестность нуля. Из включения f(f~l(V)) cz V вытекает,
что тем же свойством обладает и V. Следовательно, тополо-
топология /' слабее топологии /, и поэтому пространство F ультрабо-
ультрабочечно.
B) Пусть /— исходная топология пространства £, f — топо-
топология пространства Е и V — линейная топология в F, обладаю-
обладающая базой окрестностей нуля, образованной множествами V,
замкнутыми в топологии t\F. Мы покажем, что множество V
есть окрестность нуля в топологии t\F. Множества V0E яв-
являются /-замкнутыми и образуют базу окрестностей нуля неко-
некоторой топологии в £. Так как Е — ультрабочечное пространство,
то эта топология слабее топологии /. Поэтому каждое множе-
ство V0E содержит /-окрестность нуля, так что множество
V0E (замыкание в Е) есть /-окрестность нуля. Следовательно,
множество V[)E[)F_ является ?^-окрестностью нуля. Тогда тем
более множество V()F есть/^-окрестность нуля. Но V(]F=V1
ибо множество V замкнуто в топологии f\F. Таким образом, V
есть /[.Р-окрестность нуля. |
6.2.5. Теорема. Произведение любого числа бочечных (соотв.
инфрабочечных) пространств бочечно (соотв. инфрабочечно).
Мы нигде существенно этим результатом не пользуемся, по-
поэтому его доказательство перенесено в упр. 7.23.
6.2.6, В общем случае замкнутое векторное подпространство
бочечного пространства может не быть бочечным (в индуциро-
индуцированной топологии). Это следует из упр. 6.17 и 6.18. Второе из
этих упражнений доказывает существование полных (неметри-
зуемых) отделимых локально выпуклых пространств, не являю-
являющихся бочечными (см. также замечание D) после теоремы
7.3.3). Однако если Е бочечно, а М — векторное подпространство
в Е, допускающее топологическое дополнение, то подпростран-
подпространство М бочечно (упр. 6.19).
Существуют неполные нормированные векторные простран-
пространства, которые нетощи и потому бочечны (упр. 6.23). Существуют
также нормированные векторные пространства, которые бочечны
и тощи (Бурбаки [7, стр. 273, упр. 10]).
6.3. Индуктивные пределы пространств 589
6.2.7. Прежде чем перейти к дальнейшим примерам бочечных
пространств, мы немного уклонимся в сторону. Мы рассмотрим
в высшей степени важный процесс образования так называемых
индуктивных пределов. Этот процесс позволяет по заданному
семейству топологических векторных пространств построить но-
новое топологическое векторное пространство и служит эффектив-
эффективным средством исследования топологических векторных прост-
пространств, естественно возникающих в теории обобщенных функций.
6.3. Индуктивные пределы пространств
Пусть Е{ (i е /) — семейство топологических векторных про-
пространств, Е — векторное пространство, фг-: Е{-+Е— линейные
отображения и £ = (Jcpi (£"/). Среди локально выпуклых тополо-
i
гий в £, относительно которых непрерывны все отображения фь
существует сильнейшая; назовем ее Э~. База окрестностей нуля
в топологии Э~ образована теми выпуклыми поглощающими
множествами WczjE1, для которых множество <pj~l(W) является
окрестностью нуля в Ег при каждом и (Линейность топологии Т
вытекает из того, что множество W выпукло и -^-W + ^W dW.
Это свойство может нарушиться, если опустить условие локаль-
локальной выпуклости.) Топологию ST в Е называют индуктивным пре-
пределом топологий пространств Е{ (или индуктивной топологией)
относительно отображений ф{. Пространство Е, наделенное то-
топологией ZT, называют индуктивным пределом семейства топо-
топологических векторных пространств Е{ относительно отображений
фг-. Бур баки [7, стр. 84] ограничивается случаем локально вы-
выпуклых пространств Еи который, конечно, практически наиболее
важен. См. также Себаштьян э Сильва [1].
В том частном случае, когда каждое Ег — векторное подпро-
подпространство в Я, а фг-: Е{->Е — вложение, мы будем говорить о
внутреннем индуктивном пределе. В п. 7.3.5 мы увидим, что мно-
многие локально выпуклые пространства представимы в виде вну-
внутренних индуктивных пределов полунормированных пространств.
Определенные таким образом индуктивные пределы близки
к прямым пределам, используемым в алгебре. Они вводятся па-
параллельно с так называемыми проективными, или обратными,
пределами. Их подробное описание в применении к группам и
модулям (для нужд теории когомологий) имеется у Стин-
рода и Эйленберга [1, гл. VIII]. (См. также Келли
и Намиока [1, стр. 9—11 и задача 81, 16С, 19А, 19В
и 22С])
Приведем ряд важных примеров индуктивных пределов,
590 Гл. 6. Теоремы об открытом отображении и замкнутом графике
A) Пространство Ж(Т). Обозначения те же, что и в § 4.1.
Пусть 5 — относительно компактное подмножество в Т. Через
Ж(Т, S) обозначим множество тех функций [еТ(Г), носитель
которых содержится в S. Каждое из множеств Ж(Т, S) есть
подпространство в Ж(Т) и пространство Ж(Т) есть объединение
подпространств Ж(Т, 5г), где семейство (Si) —база относитель-
относительно компактных подмножеств в Т (т. е. каждое множество Si
относительно компактно и каждое относительно компактное мно-
множество в Т содержится в некотором множестве Si). Если каж-
каждое из подпространств Ж(ТУ S) наделить равномерной нормой
то оно становится банаховым пространством.
Выбрав базу (Si) относительно компактных множеств в Т9
мы можем наделить пространство Ж(Т) индуктивной топологией
относительно вложений фг подпространств Ж (Г, 5г) в Ж (Т).
Несложно показать, что полученная таким образом индуктив-
индуктивная топология не зависит от выбора базы (Si) относительно
компактных множеств. Достаточно только заметить, что при
S a S' топология пространства Ж (Г, S') индуцирует в Ж (Т, S)
исходную топологию.
Согласно общей теореме 6.3.2, сопряженное к пространству
Ж(Т), топологизированному как индуктивный предел банаховых
пространств, совпадает с пространством мер Радона, опреде-
определенных в § 4.3.
B) Пространство пробных функций в теории распределений.
Вернемся к ситуации, описанной в § 5.1, и воспользуемся вве-
введенными там обозначениями. Нашей первой задачей будет ин-
интерпретировать 2D(Q) как индуктивный предел. Как мы видели
в § 5.1, каждое из подпространств 2D(Q> S) пространства 20 (Q)
(S — относительно компактное множество в Q) является про-
странстом Фреше, если наделить его топологией, определяемой
полунормами
Nm(f) = suv{\dpf(x)\: xe=Q, |/>|<m},
где пг пробегает все (или достаточно широкое) множество на-
натуральных чисел. Если (S2)—база относительно компактных
множеств в Q, то 3(Q) = (J^(S, St). Обозначим через фг- вло-
i
жение подпространства 2D(Q, St) в <2)(Q) и наделим простран-
пространство 2D(Q) индуктивной топологией, определяемой простран-
пространствами 2D(Q, Si) и отображениями Ф*. Легко проверить, что по-
полученная таким образом топология в действительности не зави-
зависит от выбора базы (Si). В частности, можно воспользоваться
соответствующим образом подобранной счетной базой (Si). Та-
6.3. Индуктивные пределы пространств 591
ким образом, пространство 3)(Q) является индуктивным пре-
пределом последовательности пространств Фреше.
Аналогично пространство £Dm(Q) (m — натуральное число
или 0; см. § 5.8) можно топологизировать как индуктивный пре-
предел последовательности банаховых пространств 3)т(п, Si)
По теореме 6.3.2 сопряженное к SDm(Q) совпадает с прост-
пространством 3)'т(п) @<w<oo).
Нетрудно указать определяющее семейство полунорм для
индуктивной топологии в Я)т(п) при O^m-^оо. Один из спо-
способов сделать это (Л. Шварц [1, стр. 67]) состоит в выборе
такой фиксированной последовательности (Qr),>0 открытых от-
относительно компактных в Q множеств, что Qo = 0, QrczQr+\ и
Q= (J Qr. Каждой возрастающей последовательности s=(sr)
неотрицательных целых чисел и каждой убывающей последова-
последовательности 8=(ег) строго положительных чисел, стремящихся к
нулю, сопоставим полунорму
Ns,e(<p) = supsup {еГ1 |<Эрф(л:)|: xEQ\Qr, |p|^5r}.
Утверждается, что NSi 8 образуют определяющее семейство по-
полунорм для S)(Q), причем при /тг<оо аналогичную роль играют
полунормы NS) е, для которых sr = m при всех г.
Докажем это утверждение для случая т = оо. Начнем с почти
очевидного замечания, что /VSj 8 непрерывно на SD(Q). Для этого
достаточно проверить, что для каждого компактного множества
KczQ сужение NSi 8|S)(Q, К) непрерывно, а это совершенно оче-
очевидно. Кроме того, мы должны показать, что если U — замкну-
замкнутая выпуклая окрестность нуля в индуктивной топологии, то
можно так выбрать 5 и е, что U будет содержать каждую функ-
функцию фей)(й), для которой Л^>8(ф)< 1. Множество U обладает
тем свойством, что для каждого г найдется такое целое sr 1> 0
и такое бг>0, что U содержит каждую функцию фе2)(Й) с но-
носителем в йг+2, удовлетворяющую неравенству |<Эрф|^бг при
\p\^Csr. Можно считать, что с возрастанием г числа sr возрас-
возрастают, а 8, убывают. Выберем и зафиксируем положительные
функции |3Г в 3)(Q) так, чтобы 2рг=1 на йи носители функций
г
рг содержались в Qr+2\£2r. Функцию ф можно записать тогда
в виде суммы следующего ряда:
г
причем этот ряд конечен для каждого фе2)(Й). Так как U —
выпуклое и замкнутое множество, то ф принадлежит U, если
для всех г функции 2г+1ргф принадлежат (Л
592 Гл. б. Теоремы об открытом отображении и замкнутом графике
Производная с?Р(|Згф) является конечной линейной комбина-
комбинацией производных д*$г и д^ф с |?|-<|/?| и |<7'|<|/?|. Так как
произведение ргф рассматривается только для значений функ-
функции ф на Qr+2\Qn то несложные рассуждения показывают, что
для каждого г найдется такое число kr, что соотношение
р г для x^Q\Qr и |/?|<sr
влечет соотношение
|2г+1Eр(ргФ)|<Мг Для |/7|<5г.
Поэтому если выбрать ег так, чтобы krer^C6r, то в силу нера-
неравенства Л/^^ф)^ 1 имеем 2г+1ргфе U для всех г, откуда выте-
вытекает, что фе(/, что и требовалось доказать. |
Другой способ выбора определяющего семейства полунорм
описан у Гординга и Л ион с а [1, стр 21].
Тот факт, что индуктивная топология в 3)т(п) определяется
полунормами NS} 8, позволяет установить некоторые важные
следствия, три из которых мы здесь приведем.
(а) Пусть S — относительно компактное множество в Q. Ин-
Индуктивная топология пространства SDm(Q) индуцирует в про-
пространстве SDm(u, S) его исходную топологию.
Доказательство. Существует такой индекс r* = r*(S),
что S с Qr*. Для функции фе2)ш(й, 5) имеем тогда
Ns, в (ф) = - sup sup {еГ1 | <5рф (х) \: х е- Q \ Qn \ р \ < sr}.
0<<*
Используя результаты § 5.1, легко установить, что сужения
A^JSHQ, 5)
определяют в 0m(Q, S) его исходную топологию. 1
(Ь) Множество в S)m(Q) ограничено в индуктивной тополо-
топологии тогда и только тогда, когда оно содержится и ограничено
в 2Dm{Q, S) для некоторого относительно компактного множе-
множества S в Q. (См. также упр. 6.24.)
Доказательство. Из определения индуктивной тополо-
топологии следует, что всякое ограниченное множество в S)m(Q, 5)
ограничено в индуктивном пределе. В силу (а) для доказатель-
доказательства обратного утверждения достаточно показать, что всякое
ограниченное множество В в &m(Q) содержится в некотором
подпространстве S)m(Qy S). В противном случае можно выбрать
точки xreQ\Qr и функции фгеВ так, чтобы уг(хг)Ф0. Если
положить Ег = г-1 |фг(хг) |, то полунорма NSf E будет неограничена
на В, а это противоречит предположению ограниченности мно-
множества В в 3)m(Q). |
6 3. Индуктивные пределы пространств 593
(с) Пространство 2Dm(u) полно.
Доказательство. Пусть (ср;) — сеть Коши в 3)ш(Q). Это
означает, что для каждой полунормы NSt 8 из определяющего се-
семейства найдется такой индекс /0, что
F.3.1)
для индексов i, /, следующих за to. [Привычнее вместо 1 в пра-
правой части неравенства F.3.1) видеть наперед заданное малое
число ^>0, но это в точности то же неравенство F.3.1), в кото-
котором е заменено на te=(teo, teu •..)•]
Выбрав соответствующим образом 5 и е, можно показать,
что сеть Eрсрг) локально равномерно сходится на Q для каж-
каждого р (или при т<оо для каждого р с \р\^Ст). Поэтому су-
существует такая функция феСт(й), что (?Pcp^-><9pcp локально
равномерно для каждого р. Применяя неравенства F.3.1) для
случая s = @, 0, ...), получаем, что носитель функции ф ком-
компактен и, следовательно, фей)т(й). Тогда для всякой последо-
последовательности 8
| (pi (х) — ф/ (х) | ^ гг для х
при /, /, больших некоторого io. Полагая /->оо, получаем
I Ф/(*) —ф(*) 1^8г для xGQ\Qr
при i ^ i0. Так как функция фг-0 имеет компактный носитель, то
|ф(*)|<еГ на Q\Qr
для достаточно больших г. Так как последовательность 8 про-
произвольна, то носитель функции ф компактен. Действительно, в
противном случае существуют такие точки хг£Й\йп что
(р(хг)Ф0, а это противоречит полученному неравенству, если
взять гГ = у[ q(xr) |. Таким образом, функция ф принадлежит
{)
Остается показать, что Птф; = ф в индуктивной топологии.
Для этого достаточно доказать, что Л^6)£(фг — ф) ^ 1 для до-
достаточно больших индексов i при произвольном выборе 5 и е.
Но это следует из неравенства F.3.1) и из поточечной сходимо-
сходимости на Q сети (<3рфг) к <9^ф для каждого р. Это становится более
очевидным, если выписать неравенство F.3.1) в явном виде:
I dpcpi(x) - др<$1 (х) |<ег для JC^Q\Qr и |/7|<5г.
Полнота, таким образом, доказана. I
Замечания. A) Если пространство Т а-компактно, то те
же рассуждения применимы к пространству Ж(Т)У которое фор-
формально совпадает с 2)°.
594 Гл. 6. Теоремы об открытом отображении и замкнутом графике
B) Утверждения (а) и (Ь) неверны для произвольных счет-
счетных внутренних индуктивных пределов пространств Фреше.
Контрпример к (а) приведен ниже, в C). В § 6.5 мы увидим, что
утверждение (Ь) остается справедливым для довольно широкого
класса индуктивных пределов. При этом используются рассуж-
рассуждения более общего характера.
C) Пространства функций, голоморфных на некотором
замкнутом множестве. Если Q — открытое множество в комп-
комплексной плоскости (или, более общим образом, некоторое комп-
комплексное аналитическое многообразие), то пространство H(Q)
голоморфных на Q функций естественно топологизируется то-
топологией локальной равномерной сходимости (см. пример
6.1.3(а)). Допустим теперь, чго Т — замкнутое подмножество
комплексной плоскости (или некоторого комплексного аналити-
аналитического многообразия). Принято говорить, что функция / (при-
(принимающая комплексные значения) голоморфна на Г, если она
определена и голоморфна на некотором открытом подмножестве
плоскости (или многообразия), содержащем Т. Это открытое
множество зависит от /. Полезно (см., например, Гротендик
J5, 6]) наделить множество этих функций структурой локально
выпуклого пространства.
Первая трудность заключается в том, что само по себе это
множество не является даже векторным пространством ввиду
того, что его элементы — это функции с различными областями
определения. (Это вызывает затруднения с определением нуле-
нулевого элемента и вычитанием.) Однако эту трудность можно
обойти простой факторизацией по некоторому отношению экви-
эквивалентности. Если Q — открытое множество, содержащее Г, то
через Н(Q) будем обозначать векторное пространство голо-
голоморфных на Q функций. Пусть / и /' — функции, принадлежа-
принадлежащие соответственно пространствам И (Q) и #(£У). Будем гово-
говорить, что они эквивалентны, если они совпадают на некотором
открытом множестве, содержащем Т. Класс эквивалентности по
этому отношению, содержащий данную функцию /, будем на-
называть ростком (голоморфной) функции / на Т. Множество всех
таких росткоз функций на Т образует векторное пространство.
Алгебраические операции определяются, как обычно, с по-
помощью выбора представителей с общей областью определения.
Например, для того, чтобы составить сумму двух ростков функ-
функций, скажем / и g, выберем представителей f и g соответственно
в / и g с общей областью определения (так, если /0 и g0— лю-
любые два представителя, то пусть f и g суть сужения функций
[о и go соответственно на область (dom/0) П (domgo)). По опре-
определению f+g—это росток функции f + g.
6.3. Индуктивные пределы пространств 595
Обозначим через Н(Т) векторное пространство ростков
функций на Т. Возьмем некоторую базу (п{) открытых мно-
множеств, содержащих Т. Пусть срг- при каждом i — отображение
пространства H(Q{) в Я (Г), которое переводит функцию /е
е Н (Q) в ее росток /. Тогда пространство Н (Т) можно наделить
индуктивной топологией относительно отображений срг-, где ка-
каждое из пространств #(йг) топологизировапо указанным выше
способом.
Если множество Т оказывается настолько широким, что вся-
всякая функция из H(Q) (Q zd Г, Q открыто), обращающаяся в нуль
на Г, равна нулю всюду на некотором (сколь угодно малом)
открытом множестве, содержащем Г, то можно считать элементы
из Н(Т) функциями, определенными на Т. Однако в том важном
частном случае, когда Т сводится к одной точке, такой взгляд
на элементы из Н(Т) совершенно неверен.
Читатель может также заметить, что пространство Н(Т)
представимо как индуктивный предел банаховых пространств,
по крайней мере если Т относительно компактно. Для этого до-
достаточно воспользоваться пространствами Hbd(&i) ограниченных
голоморфных функций на йг. Пространства Hbd(Qi) наделяются
топологией равномерной сходимости на Q/, а множества йг про-
пробегают базу открытых относительно компактных множеств, со-
содержащих Т. Вместо пространств НЪа{^г) можно даже исполь-
использовать пространства функций, голоморфных на йг- и непрерывно
продолжаемых на Q{. Если множество Т относительно компакт-
компактно, то любой выбор упомянутой выше базы (йг-) приводит к од-
одной и той же топологии в Н(Т).
Замечания. Приведенные выше примеры A) и B) — это
примеры внутренних индуктивных пределов (каждое Е{ — век-
векторное подпространство в Е, а срг-— соответствующие вложения).
Существуют и другие специальные индуктивные пределы, напри-
например строгие внутренние индуктивные пределы (Б у р б а к и [7,
стр. 87]), и даже еще более специальные, например YF-простран-
YF-пространства Дьёдонне и Шварца [1]. Сейчас же мы рассмотрим
основные свойства, общие всем индуктивным пределам.
6.3.1. Теорема. Всякий индуктивный предел бочечных (соотв.
инфрабочечных) пространств есть бочечное (соотв. инфрабочеч-
ное) пространство.
Доказательство. Пусть Е — индуктивный предел про-
пространств Ei относительно отображений ср*.
Если А — бочка в Е, то множества фг!(Л) будут бочкой в Еи
поэтому фг!(/1) — окрестность нуля в Ег. Следовательно, А—•
окрестность нуля в индуктивной топологии. Случай инфрабо-
инфрабочечных пространств исследуется аналогично. |
596 Гл. 6. Теоремы об открытом отображении и замкнутом графике
6.3.2. Теорема. Пусть Е — индуктивный предел пространств
Et относительно отображений срг-. Пусть далее F — локально вы-
выпуклое пространство и отображение и: E-*~F линейно. Отобра-
Отображение и непрерывно тогда (и только тогда), когда отображение
#офг-; Е{-*Р непрерывно для каждого L
Доказательство. Пусть V — выпуклая окрестность нуля
в F. По условию множество U=u~l(V) таково, что "ф^1 (U) —
окрестность нуля в Ех для каждого L Так как множество U вы-
выпукло и поглощающе, то оно — окрестность куля в Е. |
(См. также Макаров [1], Словиковский [1—3], Ко м у-
6.3.3. Некоторые примеры. Рассмотрим возникающие в тео-
теории обобщенных функций пространства 3^@) и ^m(Q), превра*
щенные в локально выпуклые пространства описанным в при-
примере B) способом. Каждое из них есть индуктивный предел
пространств Фреше (во втором примере даже банаховых про-
пространств). Поэтому (следствие 6.2.3 и георема 6.3.1) эти про-
пространства бочечны. То же самое верно и для пространства Ж (Г),
топологизированного так же, как и в примере A). Ни одно из
этих пространств не метризуемо, за исключением Ж(Т) в случае
компактного множества Т (когда Ж(Т) — банахово простран-
пространство). Для доказательства неметризуемости всех остальных про-
пространств можно воспользоваться теоремой § 6.5.
6.4. Некторые теоремы об открытом отображении
и замкнутом графике
Начнем с общей леммы, характеризующей те свойства мет-
метризуемости, которые существенны для рассматриваемых ниже
теорем.
6.4.1. Лемма. Пусть X — полное полу мет ризу емое простран-
пространство, У — равномерное пространство и d — некоторая полуметри-
полуметрика в X. Через Вг(х) обозначим открытый шар в X с центром в х
и раду сом г > О, через кх и я г—проекции произведения ХхУ
соответственно на X и У. Пусть S — замкнутое подмножество
произведения XxY, обладающее следующими свойствами: для
каждого г > 0 существует такое окружение Т {равномерной
структуры в У), что соотношение (х, у) е 5 влечет включение
F.4.1)
Тогда для всех г>0, е>0 и (х, у) eS имеют место включения
nY(S П я-' (Вг+е(*))) => nY(S П п? (В, (*)))=> Г (у). F.4.2)
Если, кроме того, множество ny{S) плотно в Y, то ny(S) = i'.
6.4. Некоторые теоремы 597
Доказательство. Эта лемма принадлежит Келли [1,
стр. 270] и доказывается в два этапа, первый из которых вспо-
вспомогательный. Если АаХ, то для краткости множество
nY(S(]n~l(Ay) будем обозначать через SY(A).
A) Для заданных множеств А с: X и элемента y^SY(A)
существует множество.Вcz У произвольно малого диаметра, удо-
удовлетворяющее условиям АПВФ0 и j/GSy(B).
Действительно, пусть г>0. Возьмем симметричное окружение
У, такое, что из отношения (x,y)^S следует F.4.1). Выберем
элемент у' е Sy(/4) i"\T(y) и затем элемент а^А так, чтобы
(а, у') gS. Тогда у' принадлежит множеству У*(у'), которое со-
содержится в SY(Br(a))t и шар Вг(а) имеет диаметр 2г. Поэтому
остается только взять В = Вг(а) с достаточно малым г.
B) Покажем, что
Пусть А0 = Вг(х). По индукции выберем множества АпаХ
так, чтобы Ап[)Ап+\Ф0, диаметр множества Ап был меньше
е/2п+2 и j/GyDn). Такой выбор возможен в силу A). В ка-
каждом из множеств ЛпПЛп+1 возьмем по элементу хп. Легко ви-
видеть, что
d(xn, хп+р)< ^n+i + ••• + 2п+р ^"^Г
для любого натурального р, так что (хп) есть последователь-
последовательность Коши. Поскольку пространство X полно, то последователь-
последовательность (хп) сходится к некоторой точке а е X. Ясно также, что
d(xy a)<r + s. Возьмем некоторую окрестность U точки а. Так
как у ^SY{An)y то каждая окрестность N точки у содержит не-
некоторую точку у/е5у(Лп). Поэтому существует такая точка
х'еЛп, что (^,s')eS. Имеем
d(x'y a)^d(xn9 x') + d(xny a) < диаметр (Ап) + -£г.
Отсюда следует, что при достаточно больших п xr e U и у' е
eSy((/),T. e.yeSr([/).
Если Л/ — произвольная окрестность точки г/, то SY(U) пере-
пересекает Л/. Поэтому существуют такие точки х" е [/ и t/" e Л^,
что (^.^JeS, т. е. SH (£/Х^)=£0. Так как множество S за-
замкнуто, то (a,y)^S. Таким образом, из а^Вг+г(х) следует, что
у GSy(Bm(x)), что и требовалось доказать.
Если, наконец, множество яуE) плотно в У, то для всякого
элемента у €= У можно выбрать точки Х\ и у\ так, чтобы
598 Гл 6. Теоремы об открытом отображении и замкнутом графике
(xb//i)eS и у<=У{у\). Тогда из соотношений F.4.2) следует,
что f/eny(S).|
Из этой леммы можно получить разные теоремы об открытом
отображении и замкнутом графике, применимые к топологиче-
топологическим группам (Келли [1, стр. 281], Хусейн [4]).
Мы перейдем, однако, к случаю топологических векторных
пространств.
Обозначения. С этого момента впредь до п. 6.4.7 Е и F — то-
топологические векторные пространства, Ео— векторное подпро-
подпространство в Е, Fo— векторное подпространство, плотное в F,
и: Eq-^F и v: Fo ->£ — линейные отображения. (Время от вре-
времени Eq будет предполагаться совпадающим с Е9 или FQ— сов-
совпадающим с /\ или и то и другое вместе.) Отображение и назы-
называется почти открытым, если множество u(E0(MJ) (замыкание
берется в F) является окрестностью нуля в F для всякой окрест-
окрестности нуля U в Е. Отображение v называется почти непрерыв-
непрерывным, если множество v~l(U) есть окрестность нуля в F для ка-
каждой окрестности нуля U в Е. Читатель может заметить, что
если и(Е0) нетоще в F, то отображение и почти открыто, и если
Fo нетоще в F, то отображение v почти непрерывно.
6.4.2. Теорема. Пусть Е — полное полу мет ризу емое простран-
пространство. Тогда справедливы следующие два утверждения (обозна-
(обозначения и терминология описаны выше).
(a) Если график отображения и замкнут в произведении
ExF и и почти открыто, то и есть открытое отображение Ео на F
(т. е. u(E0)=F и и переводит относительные окрестности нуля
в Ео в окрестности нуля в F).
(b) Если график отображения v замкнут в произведении
FxE и v почти непрерывно, то F0 = F и отображение v непрерыв-
непрерывно (т. е. множество v~l (U) есть окрестность нуля в F для всякой
окрестности нуля U в Е).
Доказательство, (а) В лемме 6.4.1 положим Х = Е, Y=F
и S = Qvu = {(x,u(x)): xg£0}. Тогда множество, обозначаемое
нами через 5у(Л) или яуEП я (Л)), является не чем иным,
как и(Е00А), где А — некоторое множество в Е. Легко также
видеть, что условие, выраженное соотношением F.4.1), эквива-
эквивалентно предположению, что и — почти открытое отображение.
Замкнутость графика отображения и в ExF означает, что 5 —
замкнутое подмножество в произведении ExF. Наконец^ в силу
леммы 6.4.1 и переводит относительные окрестности нуля в Ео
в окрестности нуля в F, т, е. и — открытое отображение Ео
на /\
6.4. Некоторые теоремы 599
(b) Вторично воспользуемся леммой 6.4.1. На этот раз в ка-
качестве 5 возьмем множество {(v(y), у): у е Fo}> т. е. отражение
относительно диагонали графика отображения у. В этом слу-
случае SY(A)=v~l(A).
В остальном доказательство такое же, как и в случае (а).1
6.4.3. Следствие. Пусть Е — полное полу мет ризу е мое про-
пространство, F — отделимое пространство. Всякое непрерывное
почти открытое линейное отображение и: E-+-F есть открытое
отображение пространства Е на F.
Доказательство. В этом случае Е0 = Е, и поскольку и
непрерывно, а пространство F отделимо, то график отображе-
отображения и замкнут в произведении ExF. |
Перейдем теперь к следующему этапу, когда на F наклады-
накладываются ограничения, позволяющие исключить явные требования
и почти открытости и и почти ^непрерывности v.
6.4.4. Теорема. Пусть Е — полное полу мет ризу емое простран-
пространство.
(a) Пусть график отображения и замкнут в произведении
ExF. Если пространство F ультрабочечно и и(Е0) совпадает с
F или нетоще в F, то и — открытое отображение на F.
(b) Пусть график отображения v замкнут в произведении
FxE. Если пространство F ультрабочечное и Fo совпадает с F
или нетоще в F, то F0 = F и отображение v непрерывно.
Доказательство. В силу теоремы 6.4.2 достаточно уста-
установить, что если U — уравновешенная окрестность нуля в £, то
каждое из множеств V = u(E00U)y W=vl(U) является окрест-
окрестностью нуля в F. Выберем такую уравновешенную окрестность
нуля U\ в £, что U\ + U\cz U, и определим множества V\ и W\
с помощью U\ так же, как множества U и W определены с по-
помощью U. Имеем
u(E0)czU{nVl: n=l, 2, ...}
,: /i=l, 2, ...}.
Если множество и(Е0) нетоще в F, то для некоторого п множе-
множество nV\, а следовательно, и само множество V\ имеет внутрен-
внутренние точки. Аналогично доказывается такое же утверждение о
множестве Wu если множество Fo нетоще в F. Так как каждое
из множеств V\.n W\ уравновешено, то множества 1Л + 1Л и
Wi + W7! являются окрестностями нуля в F. Но V\ + V\czV и
W\ + W\c:W9 поэтому множества V и W действительно суть
окрестности нуля в /\
600 Гл. 6. Теоремы об открытом отображении и замкнутом графике
Допустим теперь, что и(Е0) =*F и что пространство F ультра-
бочечно. В этом случае замечаем, что множества V, получаю-
получающиеся, когда U пробегает систему окрестностей нуля в £, обра-
образуют базу окрестностей нуля некоторой линейной топологии в
F. Каждое множество V замкнуто в исходной топологии про-
пространства F, поэтому из ультрабочечности F следует, что полу-
полученная топология в F слабее исходной (теорема 6.2.1A)).
Каждое из множеств V является, таким образом, окрестностью
нуля в F. Если пространство F ультрабочечно и F0 = F, то ана-
аналогичным образом доказывается, что множество W является
окрестностью нуля в F. I
Замечания. A) Можно попытаться отбросить в теоре-
теореме 6.4.4 (а) условие полноты пространства Е за счет наложения
дополнительных ограничений на отображение и. В. Роберт-
сон [1] показал, что это действительно можно сделать, потребо-
потребовав, чтобы отображение и удовлетворяло некоторому условию,
обеспечивающему возможность соответствующим образом про-
продолжить отображение и на пополнение пространства Е. К этому
продолжению затем применяется утверждение (а) в приведен-
приведенной здесь форме.
B) Если в утверждениях (а) или (Ь) предположить допол-
дополнительно, что пространство Е локально выпукло, то ультрабо-
чечность пространства F можно заменить на бочечность.
C) Если пространство F (соотв. Е) не является отделимым,
то (а) (соотв. (Ь)) становится неверным просто потому, что
тогда никакое отображение и (соотв. v) не может иметь замк-
замкнутого графика в произведении ExF (соотв. FxE). Можно по-
попытаться обойти эту трудность следующим образом.
Рассмотрим сначала случай (а). Образуем отделимое фак-
торпространство Fc = F/{0}. Пусть / — естественное отображение
F на Fc. Возьмем отображение uc = fou вместо отображения и.
Так как отображение f открыто и непрерывно, то оно переводит
нетощие множества в нетощие. Если пространство F бочечно или
ультрабочечно, то таким же будет и пространство Fc (теоре-
(теорема 6.2.4A)). Если график отображения ис замкнут в ExFr, то
мы можем заключить, что отображение ис открыто, т. е. что мно-
множество u(Eof)U) +{0} является окрестностью нуля в /\ когда
U есть окрестность нуля в Е. Поэтому если и(Е0П{0} zd {0}, го
отображение и будет открытым. _
В случае (Ь) образуем факторпространство Ес = Е/{0}. Пусть
е — естественное отображение Е на Ес\ рассмотрим отображение
vc = eov вместо отображения v. Если график отображения vc
замкнут в FxEc, то оно непрерывно, откуда следует также не-
непрерывность отображения v.
6.4. Некоторые теоремы 601
D) Теорема 6.4.4 уже содержит формы теорем об открытом
отображении и замкнутом графике, применимые к полным ме*
тризуемым топологическим векторным пространствам и приве-
приведенные в начале главы. Это непосредственно вытекает из след-
следствия 6.2.3.
Важен частный случай, когда отображение и предполагается
взаимно однозначным.
6.4.5. Теорема (об обратном операторе). Пусть Е, Ео,
F и и те же, что и в теореме 6.4.4 (а). Если отображение и взаим-
взаимно однозначно, то и(Е0) =F и и~1 есть непрерывное отображение
пространства F в Е.
Доказательство. Из теоремы 6.4.4 (а) следует, что и —
открытое отображение Ео на F. Так как отображение и взаимно
однозначно, то это эквивалентно утверждению, что отображение
игх существует и непрерывно на F. I
Замечание. Как это следует из замечания B), следую-
следующего за теоремой 6.4.4, если Е еще и локально выпукло, то до-
достаточно, чтобы F было бочечным.
6.4.6. Следствие. Пусть векторное пространство'Е становится
полным полу мет ризу емым топологическим векторным простран-
пространством при наделении его каждой из двух топологий t, ¥. Допу-
Допустим также, что для любых двух различных точек х и xf из Е
существуют неперсекающиеся t-окрестность U точки х и t'-ок-
рестность V точки х\ Тогда топологии tut' отделимы и совпа-
совпадают.
Доказательство. Пусть и — тождественное отображение
(£, t) на (Е',У). Применим теорему 6.4.5 к случаю, когда £, £0
и F — одно и то же множество. Из свойств топологий t и V\ ко-
которыми они обладают по условию, непосредственно следует, что
график отображения и замкнут в произведении ЕхЕ (наделен-
(наделенном произведением топологий t и ¥). Отсюда уже вытекает от-
отделимость топологии f. Так как и — взаимно однозначное ото-
отображение Е на £, то отображение и~1 непрерывно. Другими
словами, топология t слабее топологии ¥, Аналогично устанав-
устанавливаем, что топология / слабее топологии ¥. Следовательно, то-
топологии t и ¥ совпадают и отделимы. |
Замечание. Требования,предъявляемые к топологиям / и
t\ выполняются, если они сравнимы и более слабая топология
отделима (ср. Банах [1, стр. 35, теорема 6]). Они выполняются
и тогда, когда на Е существует разделяющее точки множество
линейных форм, каждая из которых непрерывна в обеих тополо-
топологиях (упр. 6.3). Такое положение вещей имеет место, например,
если Е — полупростая коммутативная банахова алгебра с
602 Гл. 6. Теоремы об открытом отображении и замкнутом графике
единицей. При этом разделяющее точки множество линейных
форм состоит из гомоморфизмов, определяемых максимальными
идеалами в Е. Следовательно, норма на такой алгебре един-
единственна с точностью до эквивалентности. (См. Люмис [1,
стр. 102], а также Рик-карт [1, стр. 75]*).)
6.4.7. Легко видеть, что теорема об обратном операторе в при-
применении к полным метризуемым топологическим векторным про-
пространствам эквивалентна как теореме об открытом отображе-
отображении, так и теореме о замкнутом графике, если в формулировки
этих теорем ввести некоторые ограничения. Для таких про-
пространств эти три теоремы образуют почти неразделимую тройку.
Для топологических векторных пространств более общего типа
это уже не так и теорема об обратном операторе в общем случае
подчинена двум другим.
К теоремам об открытом отображении и замкнутом графике,
так же как и к теореме об обратном операторе (к последней в
неявном виде), мы вернемся в § 6.7 и затем в гл. 8.
Рассмотрим здесь несколько примеров приложения предыду-
предыдущих общих теорем. Другие иллюстрации приведены в конце
главы в качестве упражнений.
6.4.8. Пример. Пусть / — компактный интервал [а, Ь] вещест-
вещественной оси, Q = /X/ (плоский квадрат) и К — некоторая функ-
функция на Q. Для определенности и простоты допустим, что функ-
функция К непрерывна. Однако читатель легко сможет проверить, что
это условие можно ослабить. Пусть С(/)—пространство непре-
непрерывных функций на /. Оно является банаховым пространством,
если наделить его равномерной нормой
Пусть А,— некоторое число. Формула
K(t9 s)x(s)ds
определяет линейное отображение и пространства С(/) в себя
у = и(х). Непрерывность отображения и очезидна. Действитель-
Действительно, если m — максимум модуля функции К на Q, то
\\и{х)\\^{\+т\Х\)Л\х\\.
Если т|Я|< 1, то и — взаимно однозначное отображение на,
что можно установить многими способами. (Например, посколь-
!) Более сильный результат о единственности нормы в полупростой (во-
(вообще говоря, некоммутативной) банаховой алгебре имеется в недавней ра-
работе Джонсона [1]. — Прим. ред,
6.4. Некоторые теоремы 603
ку m|A,|< 1, то и — сжимающее отображение, и мы можем вос-
воспользоваться общими результатами п. 3.1.2.) Поэтому из теоре-
теоремы об обратном операторе следует непрерывность отображения
и~К Это означает (если учесть результаты гл. 4), что каждой
точке i^I соответствует такая мера Радона \xt на /, что един-
единственное решение х уравнения и(х) =у задается формулой
у (s) d\it (s) (t <~ /).
Аналогичные рассуждения применимы и к другим простран-
пространствам, кроме С(/). Можно, например, заменить / любым локаль-
локально компактным пространством, наделенным положительной ме-
мерой Радона [х. Вместо С(/) можно взять 9?2{1, \л) (или, что то же
самое, ассоциированное отделимое пространство L2(/, \x)). Если
допустить, что /(<= 3?2(Q, \i ® jut), то приведенная выше формула
определяет непрерывное линейное отображение и пространства
i?2(/, jut) в себя. Полагая
и предполагая, что mlk\ < 1, снова получаем, что и — сжимающее
отображение. Вывод тот же — обратное отображение игх не-
непрерывно.
6.4.9. Пример. Рассмотрим так называемые мультипликаторы
Фурье. Пусть все рассматриваемые функции определены на ве-
вещественной оси и имеют период 2я. Построим пространство Ле-^
бега относительно сужения меры Лебега на интервал (—я, +я).
Если функция х <= 3х, то ее п-й коэффициент Фурье определяет-
определяется выражением
\x{t)e~M
dt
для я = 0, ±1, ±2,... .
Допустим теперь, что в 2?1 выделены два подмножества X
и У. Последовательность (fn) (/г = 0, ± 1, ±2,...) называется
мультипликатором Фурье типа (X, У), если выполнено следую-
следующее условие: для всякой функции х^Х последовательность
(fr}X(n)) совпадает с последовательностью (у(п)) для некоторой
функции у из У (зависящей, конечно, от х). Задача описания
мультипликаторов типа (X, У) рассматривалась при различном
выборе множеств X и У, например X=Y = C (С — множество не-
непрерывных периодических функций); Х = 3?\ У = Я??\ X = Y=3?p
(см. Зигмунд [1, 2], Качмаж-Штейнгауз [1], Эд-
Эдварде [6]).
604 Гл. 6. Теоремы об открытом отображении и замкнутом графике
В некоторых случаях можно добиться успеха, пользуясь про-
простыми общими рассуждениями. Проиллюстрируем это на при-
примере X = «2?1, Y = &p (Эдварде [6]).
Ключ к решению вопроса содержится в наблюдении, что у за-
зависит (с точностью до пренебрежимых функций) только от
класса, определяемого функцией х. Таким образом, мультипли-
мультипликатор (fn) типа (З?1, 3?v) определяет отображение простран-
пространства L1 в L?, переводящее класс, определенный функцией х, в
класс, определенный функцией г/, где fnx(n) — y(n) для всех я.
Так как сходимость в L1 или в L*>, очевидно, влечет за собой
сходимость соответствующих коэффициентов Фурье для всякого
фиксированного п, то легко видеть, что график отображения и
замкнут. Линейность отображения и очевидна. Теорема о замкну-
замкнутом графике обеспечивает непрерывность отображения и.
Другое существенное свойство отображения и — его пере-
перестановочность со свертками (или, что в случае непрерывности
отображения и приводит к тому же самому, его перестановоч-
перестановочность со сдвигами). Если снова рассматривать и как отображе-
отображение «2?1 в 9?v, то это означает, что
u(k **) = u(k)* х
для k,x^9?x. Допустим теперь, что k пробегает такую ограни-
ограниченную в 3?х последовательность (&г), что kr*x-*x в 2£х при
г->оо. Тогда в силу непрерывности отображения и последова-
последовательность hr=u(kr) будет ограничена. Поэтому в 3?
и (л:) = lim и (kT * х) = lim hT * х.
При р>1 последовательность hr обладает слабой предельной
точкой h е 3?р и, значит, h % / является предельной точкой по-
последовательности hr*x в смысле поточечной сходимости, по
крайней мере если функция х непрерывна. Отсюда следует, что
для непрерывной функции х имеет место равенство и(х) =й * х,
которое в силу непрерывности отображения и остается верным
для всех х е 271. (В этой связи напомним читателю теоремы
1.11.4 и 4.16.1.)
При р=\ предыдущие рассуждения не проходят, так как
ограниченные множества в 3?х не являются относительно слабо
компактными. Однако этим свойством обладает пространство
ограниченных мер Радона, и мы можем вложить 3?х в это про-
пространство. При этом получаем тот же результат, только теперь
А —ограниченная мера Радона.
Если взять преобразование Фурье соотношения u(x)=h*x9
то мы увидим, что последовательность (fn) должна быть после-
последовательностью коэффициентов Фурье некоторой функции из 9?р
при р > I или некоторой ограниченной меры Радона при p=U
6.4. Некоторые теоремы 605
Это необходимое условие, как легко видеть, является также до-
достаточным, и мы тем самым имеем полное решение задачи для
этого случая.
Относительно других примеров см. Эдварде [6], а также
упр. 9.10.
6.4.10. Пример. Воспользуемся обозначениями примера 6.1.4.
Пусть А—матрица с финитными строками и иА — соответствую-
соответствующее линейное отображение пространства CN в CN . В приме-
примере 6.1.4 мы ввели пространство В (А) и показали, что оно есть
пространство Фреше в топологии ГА, определяемой полунормами
Рп W = \х (п) |,
А(т, п)х(п)
(x) = \\uA(x)\\oo.
Мы утверждаем, что если А — матрица с финитными строками и
отображение иА взаимно однозначно, то топология ТА совпадает
с топологией, определяемой одной полунормой qA. Этот резуль-
результат дополняет утверждение C) примера 6.1.4. Вообще, справед-
справедливо следующее утверждение.
► A) Пусть А — матрица с финитными строками, L — век-
векторное подпространство в В (А), замкнутое относительно
полунормы qA (например, В (А), С (А) или С0(А)), и
пусть Q — ядро сужения иА\L. Топологии TA\L и qA\L
индуцируют в факторпространстве L/Q одну и ту же
фактортопологию, г. е. для любых пит существуют та-
такие числа ап и рт, что для к^Ь
inf | jc(п) + z(п) |< ап • || иА(х)L, F.4.3)
Q
inf sup 2j A(m9 n)(x(n) + z(n)) <pm-|IM*)IL- F.4.4)
- - k
При этом L полно и полунормируемо относительно топо-
топологии qA\L, a L/Q банахово относительно qA\L. Если
отображение иА взаимно однозначно, то топология TA\L
совпадает с топологией, определяемой нормой qA\L.
Доказательство. Вначале покажем, что пространство L
полно относительно qA. Пусть (л:г) —^-последовательность Ко-
ши в L. Последовательность yi:=uA(xi) сходится в /°° к некото-
некоторому элементу у. Так как А — матрица с финитными строками,
то из теоремы Теплица (п. 2.3.2) следует, что у = иА(х), для не-
некоторого элемента xgCn, Элемент х принадлежит В(А), и
qA(Xi — х) = \\уг — г/||оо->0. Следовательно, х принадлежит под-
подпространству L, и полнота доказана,
606 Гл. в. Теоремы об открытом отображении и замкнутом графике
В факторпространстве L/Q мы можем рассмотреть любую из
следующих двух топологий: фактортопологию, определенную то-
топологией TA\L> или фактортопологию, определенную нормой qA.
Так как подпространство L ^А-замкнуто в В (А), то оно тем бо-
более ГА-замкнуто. Таким образом, L/Q есть пространство Фреше
относительно первой из этих топологий. Но по доказанному
L/Q — банахово пространство относительно второй из тополо-
топологий. Тождественное отображение непрерывно и потому открыто
(теорема 6.4.4(а)), так что обе эти топологии совпадают.
Остальные утверждения непосредственно следуют из уже до-
доказанного. |
Этот результат приводит к интересным следствиям, если
комбинировать его с принципами ограниченности, рассматривае-
рассматриваемыми в гл. 7. Непосредственным приложением этого результата
служит аналог теоремы Теплица, которой мы пользовались в
предыдущем доказательстве.
► B) Пусть А — такая матрица с финитными строками, что
НтЛ(/п, п) = 0 (/1=1, 2, ...) F.4.5)
т
и соотношения
SG/1,
т
= 0 (л-1,2,...) F.4.6)
влекут 5 = 0. Тогда иА отображает СH(Л) на с0, т. е. для
каждого у е с0 существует такой элемент х <s CN, что
v , n)x(n) = y(m) (т = 1, 2, .. .)•
Доказательство. Соотношение F.4.5) показывает, что
Со(Л) содержит каждую финитную последовательность х (т. е.
последовательность с конечным носителем). Пусть Fa с0 — мно-
множество значений отображения иА. В силу утверждения A) про-
пространство С0(А) полно относительно полунормы qA(x) =
= \\ua(x)\\oo', следовательно, как это вытекает из F.4.3), множе-
множество F есть замкнутое векторное подпространство в Cq. С другой
стороны, так как соотношения F.4.6) влекут 5 = 0, то из георемы
Хана — Банаха следует плотность множества F в с0. Таким об-
образом, F = c0. I
6.4.11. Приложение к одной теореме Хёрмандера. Восполь-
Воспользуемся здесь теоремой о замкнутом графике для доказательства
результата, установленного Хёрмандером [1, теорема 1.1] и
примененного им в теории линейных дифференциальных уравне-
уравнений в частных производных, уже описадной нами в § 5,19*
6.4. Некоторые теоремы 607
Предположим, что Е, F\ и F2— полные метризуемые тополо-
топологические векторные пространства. (Требуется лишь, чтобы про-
пространства £, F\ и F2 были такими, чтобы можно было применить
теорему о замкнутом графике к линейному отображению замк-
замкнутого векторного подпространства в ExF\ в F2. В § 5.19 каждое
из этих пространств банахово.) Пусть щ (i= 1,2)-—-линейное
отображение Е в Ff (не обязательно, чтобы область определения
отображения п{ совпадала с Е). Предположим следующее:
A) отображение их замкнуто,
B) отображение и2 предзамкнуто,
C) dom u\ с= dom u2.
Докажем, что для каждой окрестности нуля V2 в F2 существуют
такие окрестности нуля U и V\ соответственно в Е и Fu что
u2(dom и, Л U П ^f1 (Vx))cz Vr F.4.7)
Заметим, что в случае банаховых пространств Е, Fx и F2 за-
заключение сводится к утверждению существования такой постоян-
постоянной с^>0, что неравенство
или, что то же, неравенство
(возможно, с другой постоянной с), имеет место для всех
х е dom г/i.
Доказательство соотношения F.4.7). Пусть G —
график отображения и\, рассматриваемый как подпространство
в ExFx. В качестве такового он является полным метризуемым
топологическим векторным пространством в силу замкнутости
графика отображения их (допущение A)). Рассмотрим линей-
линейное отображение v графика G в F2, определенное формулой
v((x,ui(x))=u2(x)
для xedom^i. Такое определение корректно в силу допуще-
допущения C). Соотношение F.4.7) равносильно утверждению, что ото-
отображение v непрерывно. Так как все рассматриваемые простран-
пространства полны и метризуемы, то наша задача сводится к доказа-
доказательству замкнутости отображения v (теорема 6.4.4).
Пусть (г&) — сеть точек из Gy сходящаяся к точке ге G, так
что zh=(xh, Hi(Xft)), z={x,tii(x)), ^e dom мь (xh) — сеть в
dorn^i, Xk->x в Е и Ui(xh)-+U\(x) в F\. Допустим, кроме того,
что v(Zh)-+q в F2. Нам надо показать, что q — v{z). Таким об-
образом, нам известно, что
608 Гл. 6. Теоремы об открытом отображении и замкнутом графике
в F2y и мы хотим установить, что q = u2(x). Но мы знаем, что
справедливы соотношения
х — xk e dom п\ с dom и2
и
и2 (х — xk) = и2 (х) — и2 (xh) -^ и2 {х) — q
в F2. В силу предложения 1.9.11 A) и допущения B) получаем
желаемый результат, а именно равенство и2{х)—? = 0, что и
завершает доказательство. I
6.5. Некоторые результаты о последовательностях
полных полуметризуемых топологических векторных
пространств
Следующие результаты являются в некоторой степени резуль-
результатами «смешанного» типа. Они имеют отношение и к теореме
об открытом отображении и к принципам ограниченности, кото-
которые будут изложены в гл. 7. Эти результаты подсказаны одним
упражнением Бур баки [7, стр. 181, упр. 13]; см. также Гро-
тендик [1, стр. 16, теор. А].
6.5.1. Теорема. Пусть Е — топологическое векторное простран-
пространство, a F, Fn (лг =1,2,...) — полные метризуемые топологические
векторные пространства, причем F отделимо. Пусть, далее, ото-
отображения и: F-+E и ип: Fn-+E (я =1,2,...) непрерывны и ли-
линейны. Основное наше предположение таково:
u(F)cz(jun(Fn). F.5.1)
При этих условиях существует число п, обладающее следую*
щими свойствами: u(F)czun(En)\ если Un — окрестность нуля в
Fn, то множество U = u~] (ип@п)) есть окрестность нуля в F.
То же заключение справедливо, если E — F и и — тождественное
отображение пространства £, а предположение F.5.1) заменено
оо
условием, что множество (J un (Fn) нетоще в F.
/г=1
Доказательство (по Бур баки, там же). Пусть Нп —
векторное подпространство произведения FxFn, образованное
теми парами (у,уп), для которых и (у) =ип(уп). Подпростран-
Подпространство Нп замкнуто в произведении FxFn и потому полно и полу-
метризуемо. Пусть Рп — естественная проекция произведения
FxFn на Ft Из соотношения F.5.1) следует, что
f-ОрпШ.
6.5. Некоторые результаты 609
Тогда при некотором п множество Рп(Нп) нетоще в F. Следова-
Следовательно, отображение Рп почти открыто. Из следствия 6.4.3 выте-
вытекает тогда, что Рп есть открытое отображение Нп на F, что и до-
доказывает теорему. |
Покажем сейчас, что для некоторых ограниченных множеств
в Е имеет место аналогичный результат. В доказательстве ис-
используется интересная идея, сводящаяся к наделению вектор-
векторного подпространства в Е, порожденного ограниченным множе-
множеством, структурой полуметризуемого пространства с своей соб-
собственной топологией (не обязательно совпадающей с топологией,
индуцированной из Е). Эта идея принадлежит Бур баки (там
же, стр. 165, лемма 1). Мы, однако, слегка ослабим сделанные
тан предположения.
6.5.2. Лемма. Пусть А—ограниченное выпуклое уравнове-
уравновешенное секвенциально полное и секвенциально замкнутое под-
подмножество топологического векторного пространства Е. Обозна-
Обозначим через ЕА векторное подпространство в Е, порожденное мно-
множеством А. Определим функцию р на ЕА равенством
p(x) = inf{r>0: х^гА}.
Тогда р — полунорма на ЕА {если Е отделимо, то норма), отно-
относительно которой пространство ЕА полно. Топология в ЕА, опре-
определенная полунормой р, сильнее, чем топология, индуцирован-
индуцированная в ЕА топологией из Е.
Доказательство. Легко проверить, что множество А
определяется в-пространстве ЕА соотношением р(х) *С\. Мно-
Множества вида еЛ (е>0) образуют базу окрестностей нуля в то-
топологии, определяемой полунормой р. Из этого и из ограничен-
ограниченности множества А в Е следует, что топология в ЕА, определен-
определенная полунормой р, сильнее топологии, индуцированной из Е.
Отсюда же следует и то, что р — норма на ЕА, если Е отделимо.
Остается доказать /7-полноту пространства ЕА. Пусть (хп)—-
^-последовательность Коши в ЕА. Тогда sup p(xn) = k< + оо,
п
так что хп е&Л. Множество kA так же, как и Л, секвенциально
полно в Е. Так как пространство Е индуцирует в ЕА топологию,
более слабую, чем его р-топология, то найдется такой элемент
x^kA, что хп->х в Е. Так как (хп) есть ^-последовательность
Коши, то
р(хт-хп) = гтгП-^0 при m, п->0.
Имеем тогда (хт — хп)/ет>п е А. Полагая m-^оо и используя
секвенциальную замкнутость множества А в Е, получаем
(х — хп)/еп& Л, где гп = п~1 + Hmsup8m>ft->0 при п-+оо. Та-
т>оо
ким образом, х^ЕА и р(х — хп)-+0} т. е. хп-+х в ЕА.
610 Гл. в. Теоремы об открытом отображении и замкнутом графике
Замечание. Если Е отделимо, то секвенциальная полнота
множества А влечет его секвенциальную замкнутость.
6.5.3. Теорема. Пусть А— ограниченное выпуклое уравнове-
уравновешенное секвенциально полное и секвенциально замкнутое под-
подмножество топологического векторного пространства Е. Пусть
далее Fn (/г = 1, 2,...)—полные полу мет ризу емые топологиче-
топологические векторные пространства и ип: Fn-^F— непрерывные ли-
линейные отображения. Если
Aa\Jun(Fn), F.5.2)
то существует такое п, что для каждой окрестности нуля Un
в Fn при некотором \i = \k(Un)s>0 имеет место соотношение
A^n-un(Un). F.5.3)
Доказательство. Определим пространство ЕА так же,
как в лемме 6.5.2. В теореме 6.5.1 положим F = EA и возьмем
в качестве и вложение F в Е. Из F.5.2) следует F.5.1). Из той
же теоремы 6.5.1 вытекает, что множество wl(un(Un)) есть
окрестность нуля в f и потому поглощает множество А. Соот-
Соотношение F.5.3) установлено. 1
Полезно привести один частный случай теоремы 6.5.3 в отри-
отрицательной форме.
6.5.4. Следствие. Пусть Е, Еп и ип — те же, что и в тео-
теореме 6.5.3, и Е — секвенциально полное пространство. Пусть
AczE — ограниченное выпуклое уравновешенное множество, для
которого при каждом п существует такая окрестность нуля
Un в Fn, что множество un(Un) не поглощает А. Тогда в про-
странстве Е найдется элемент х, не принадлежащий un(Fn),
являющийся пределом в Е последовательности элементов из А.
Доказательство. Применить теорему 6.5.3 к секвен-
секвенциальному замыканию множества А. |
Мы закончим этот параграф аналогом теоремы 6.5.3, в ко-
котором каждое из пространств Fn заменено его ограниченным
подмножеством.
6.5.5. Теорема. Пусть А (соотв. Ап) —ограниченное выпуклое
уравновешенное секвенциально замкнутое и секвенциально пол-
полное подмножество топологического векторного пространства
Е (соотв. ЕПу л=1, 2,...), и пусть ип\ Еп-+Е — непрерывное
л»
линейное отображение. Если множество (J ип(Ап) поглощает
п= 1
множество Л, то существуют такое п и такое \х>0, что
A cz \i-un(An).
6.5. Некоторые результаты 611
Доказательство. Воспользуемся теоремой 6.5.3, полагая
Fn= (En)A (ср. с леммой 6.5.2). Сужение vn = un\Fn является
непрерывным отображением Fn в Е. Из условия 1еоремы следует
оо
включение А с: (J vn(Fn). Из теоремы 6.5.3 вытекает существо-
/г=1
вание такого п, что множество А поглощается множеством
vn(Un), где Un — любая окрестность нуля в Fn. В таком случае
можно взять Un=An, откуда и следует теорема. |
6.5.6. Пример. Займемся одной задачей, связанной с функ-
функциями многих комплексных переменных. Этот вопрос наряду
с рядом аналогичных вопросов примерно так же изложен в ра-
работе Эдварде [11].
Пусть М — комплексное аналитическое многообразие. Обо-
Обозначим через Н(М) пространство всех функций, голоморфных
на М. Это комплексное векторное пространство становится ло-
локально выпуклым, если наделить его топологией равномерной
сходимости на компактных подмножествах в М. Если много-
многообразие М а-компактно, то Н(М) —пространство Фреше. Пусть
А — множество в М, тогда Н(М)-оболочкой множества А в М
называется множество всех таких точек т0 <= М, что
|z(mo)|<sup|z(m)|
А
для всякой функции ^()
Допустим, что S и Т — комплексные аналитические многооб-
многообразия, каждое из которых а-компактно. Пусть далее f: S-+T —
локально аналитический изоморфизм; тогда образ S'=f(S) яв-
является областью в Т.
Для заданной функции x^H(S) может существовать или
не существовать область D в Г, содержащая S' в качестве соб-
собственной части, и такая функция y^H(D), что x=yof. Если
такая функция у существует, то она однозначно определяется
по х (функция / фиксирована заранее) и может быть названа
голоморфным продолжением функции х в D относительно /.
Область D априори может зависеть от функции х. Суть нашего
примера заключается, однако, ^доказательстве того факта, что
если указанное продолжение возможно для всякой функции
x^H(S), то фактически существует единая область Д продол-
продолжение в которую возможно для любой функции х. Точнее, мы
докажем следующее утверждение.
► Пусть для каждой функции x^H(S) существует такая
область D d Г, что
D=>S\ D*S', F.5.4)
612 Гл. 6. Теоремы об открытом отображении и замкнутом графике
и такая функция y^H(D), что
x = yof. F.5.5)
Тогда область D со свойствами F.5.4) может быть вы-
выбрана независимо от х и так, что представление F.5.5)
возможно для каждого x^H(S). Кроме того, для каж-
каждого компактного множества К a D найдется такое ком-
компактное множество Ко с: S и такое число с ^ 0, что
функцию у из #(£>), удовлетворяющую F.5.5), можно
выбрать так, чтобы имело место неравенство
sup|*/(/)|<csupU(s)|. F.5.6)
t e К 5 е /Со
Наконец, в S существует по крайней мере одно компакт-
компактное множество /Со, Н {S)-оболочка которого некомпактна.
Доказательство. Так как каждое а-компактное много-
многообразие сепарабельно, то существует такая последовательность
(Dn) областей, удовлетворяющих условию F.5.4), что всякая
область Д удовлетворяющая условию F.5.4), содержит некото-
некоторое Dn. В теореме 6.5.1 положим E = F = H(S) и в качестве и
возьмем тождественное отображение; примем Fn=H(Dn)y и
пусть ип — отображение, определенное равенством
Ясно, что ип — непрерывное линейное отображение пространства
Fn в /\ В силу основного предположения F является объедине-
объединением всех un(Fn). Из теоремы 6.5.1 вытекает, что при некото-
некотором п отображение ип открыто и F = un(Fn). Это дает первое
утверждение, если мы возьмем D равным Dn для указанного /г,
а также оценку F.5.6). Кроме того, при таком выборе D су-
существует точка /, общая для области D и границы области S'
относительно Т. Выберем такую последовательность Eг-) в S,
чтобы ^=Пт/Eг). Для К в F.5.6) выберем компактную окрест-
окрестность точки /, содержащую все точки f(Si). Тогда |#(s/)|^
<; с sup | х(s)\ для всех I и всех x^H(S). Если заменить те-
перь функцию х ее k-и степенью (£=1, 2; ...), затем извлечь
корень &-й степени и устремить k к бесконечности, то получим
для всех i и всех x^H(S). Таким образом, Я(S)-оболочка мно-
множества /Со содержит последовательность (^г). Но поскольку /
непрерывно и /Eг)-^^, а точка t не принадлежит множеству
S/==f(S)) то последовательность ($*) не может иметь предельной
6.6. Ограниченные множества 613
точки в 5, так что указанная оболочка множества Ко неком-
некомпактна, что и требовалось доказать. |
6.6. Ограниченные множества в пространствах3)т(п) и oPf(T)
A) Мы хотим с помощью теоремы 6.5.3 заново получить ре-
результаты § 6.3B), касающиеся ограниченных подмножеств про-
пространств S)m(Q) (Q — открытое множество в Rn; m — натураль-
натуральное число, 0 или оо; под SD°°(Q) подразумевается £D(Q); см.
§ 5.1, 6.3) и Ж(Т), где пространство Т а-компактно (см. § 4.3
и 6.3). Секвенциальная полнота этих пространств следует из ре-
результатов § 6.3. Мы здесь приведем несколько иные рассужде-
рассуждения, не использующие определяющих систем полунорм.
Так как каждая мера Дирака принадлежит сопряженному
пространству, то очевидно, что всякая последовательность Коши
(или даже слабая последовательность Коши) поточечно схо-
сходится на Q (или на Т). Далее если точка х пробегает любое
компактное множество К в Q (или в Г), то мера Дирака ех, ко-
которая как функция от х слабо непрерывна, пробегает слабо ком-
компактное множество в сопряженном пространстве. Поскольку
(п. 6.3.3) рассматриваемые пространства бочечны, то указанное
множество мер Дирака гх равностепенно непрерывно. По тео-
теореме Асколи последовательность Коши (/п) в каждом из про-
пространств 3)m{Q), Ж(Т) равномерно сходится на компактных
подмножествах в Q (или в Т).
В случае пространства £Dm(Q) те же рассуждения проходят,
если заменить гх производными д^гх (\р\^Ст). Тогда получаем,
что при каждом таком р последовательность (<Эр/п) сходится
локально равномерно на Q.
Поэтому для установления секвенциальной полноты доста-
достаточно показать, что предельная функция f имеет компактный
носитель в Q (или в Т). (Непрерывность функции / и ее рас-
рассматриваемых производных следует из локально равномерной
сходимости.)
Чтобы показать это, мы должны предположить, что прост-
пространство Т а-компактно (это условие автоматически выполняется
для любого множества Q в Rn). При этом условии допустим,
что функции fn не обращаются в нуль вне никакого общего ком-
компактного множества в Q (или в Т). Тогда в силу а-компактности
множества Т можно так выбрать последовательность (xk) точек
из Q (или из Г), чтобы она не имела предельной точки в Q (или
в Г) и чтобы fn (х^ = скф0, где П\<п2<.. . — натуральные
числа. Последовательность линейных форм о^1гх =kk слабо
сходится к нулю в сопряженном пространстве (каждое компакт-
614 Гл. 6. Теоремы об открытом отображении и замкнутом графике
ное множество в Q (или в Т) содержит не более чем конечное
число точек xk). Так как наши пространства бочечны, то эта по-
последовательность линейных форм равностепенно непрерывна.
Ввиду того что (fn) —последовательность Коши, h(fn) -> 0 при
k -»- оо равномерно относительно п. (Здесь мы снова применяем
теорему Асколи к последовательности Коши (/п), образующей
предкомпактное множество.) Но это невозможно, так как
%k (fn \ = 1 для всех k. Полученное противоречие доказывает
наше утверждение.
Теперь применение теоремы 6.5.3 дает следующее предло-
предложение.
B) Пусть В— ограниченное подмножество пространства
3)m(Q) (или Ж(Т), где Т о-компактно). Тогда существует та-
такое компактное множество К в Q (или в Г), что множество В
содержится и ограничено в 2)m(Q, К) (или в Ж(Т, /()).
Замечания, (а) Дьёдонне и Шварц дали другое
доказательство, пригодное для /./^пространств (см. их работу
[1, стр. 70]). Относительно пространства Ж(Т) см. также Бур-
баки [8, гл. III, стр. 79, упр. 2].
(Ь) Верно ли утверждение B) для Ж(Т), когда пространство
Т не предполагается а-компактным? Оказывается, существует
патологическое не а-компактное локально компактное простран-
пространство 71, для которого утверждение B) ложно. Этот пример при-
принадлежит Бурбаки [8, гл. III, стр. 79, упр. 3]. Можно дока-
доказать, что для такого пространства Т индуктивная топология в
Ж(Т) (§ 6.3) является не чем иным, как топологией равномер-
равномерной сходимости на Г, поэтому ограниченные множества в
Ж(Т)—это прорто множества, определяемые неравенствами
11/11 =sup{|f(/)|: t(=T}<c.
Несмотря на эту вычурность, остается справедливым, что
пространство, сопряженное к Ж(Т), состоит из тех линейных
форм [я на Ж(Т), для которых сужение \л\Ж(Г, К) непрерывно
для каждого компактного множества /(cz Г, т. е. состоит из мер
Радона на Т (определенных в § 4.3). Действительно, это яв-
является следствием общего свойства индуктивных пределов, вы-
выражаемого теоремой 6.3.2. Оказывается, что каждая мера Ра-
Радона на указанном причудливом пространстве Т обладает ком-
компактным носителем (Бурбаки [8, стр. 94, упр. 4]).
В силу сказанного призываем читателя к осторожности при
использовании бурбакистского термина «сильная топология»
(Бурбаки [8, стр. 79, упр. 4]) для пространства мер, в слу-
случае когда Т не а-компактно; оно, вообще говоря, не согласуется
6.7. Другой вариант теоремы о замкнутом графике 615
с использованием этого термина в теории двойственности (§8.4).
Если, однако, Т а-компактно, то никаких расхождений не воз-
возникает.
6.7. Другой вариант теоремы о замкнутом графике
Мы хотим доказать довольно специальную теорему, имеющую
общее как с теоремой о замкнутом графике, так и с результа-
результатами § 6.5. (См. также Гротендик [1, стр.' 17, теор. В].)
6.7.1. Теорема. Пусть F — индуктивный предел семейства пол-
полных полуметризуемых топологических векторных пространств,
Е—индуктивный предел последовательности Еп (п=\, 2, ...)
полных полуметризуемых топологических векторных пространств
относительно отображений ип\ Еп-+Е. Если график линейного
отображения v: F-+E замкнут (или даже секвенциально замк-
замкнут), то отображение v непрерывно1).
Доказательство. Начнем с двух предварительных за-
замечаний. Во-первых, если F — индуктивный предел семейства
(Fi) полных полуметризуемых топологических векторных про-
пространств относительно отображений Д-, то непрерывность ото-
отображения v: F-+E означает непрерывность отображения
v°fi'. F{~^E для каждого индекса и Так как отображение
fi\ Fi-+F непрерывно и график отображения v (секвенциально)
замкнут, то таким же будет и график отображения г/о/,-, Таким
образом, достаточно ограничиться случаем, когда само, про-
пространство F полно и полуметризуемо.
Во-вторых, переходя к факторпространствам Ёп = E/ker ип
и факторотображениям2) йп' Еп-+Е и используя отображения
йп для переноса топологии из пространства Еп (которое является
полным и полуметризуемым) в пространство йп(Еп)=ип(Еп),
мы видим (на основании упр. 6.20), что достаточно рассмотреть
случай, когда Е — внутренний индуктивный предел векторных
подпространств Еп относительно вложений. При этом каждое
подпространство Еп полно и. полуметризуемо и естественно
оо
Е= \J Еп. F.7.1)
Л n=i
1) Если Е — внутренний индуктивный предел, то достаточно, чтобы для
всякой сходящейся к нулю в F последовательности (*/&), для которой после-
последовательность (v(yh)) сходится в некотором Еп к пределу х, имело место
равенство x—v(y).
2) Если х е Еп и * —представитель класса х, то факторотображение
й-п- Ёп~>Е определяется равенством йп(х) = ип(х). — Прим. перев.
616 Гл. 6. Теоремы об открытом отображении и замкнутом графике
Эти упрощения позволяют представить график G отображе-
отображения v следующим образом:
G={J{GO(FXFn)}=[jGn> F.7.2)
где Gn = G(](FxEn). В топологии произведения пространство
FxEn полно и полуметризуемо.
Предполагая график G секвенциально замкнутым в произве-
произведении FxE, покажем вначале, что множество Gn секвен-
секвенциально замкнуто (и потому замкнуто) в произведении FxEn.
Действительно, пусть (zk)—последовательность элементов из
Gn> сходящаяся к z^FxEn, Тогда
(Ук^Р> v(yk)z=Fn),
По предположению уи~^У в F и v(yk)-^x в Еп. Тем более,
v(yk)-+x в Я Следовательно, zk-+z в произведении FxE, от-
откуда "б силу секвенциальной замкнутости множества G в FxE
следует, что зеС, т. е x = v(y). Таким образом, z=(y, v(y)),
где y^F и v(y) =х е ЕПу т. е. z e GC\ (FxEn) =Gn, откуда и
следует замкнутость множества Gn в FxEn.
Таким образом, множество Gn как замкнутое подпростран-
подпространство произведения FxEn полно и полуметризуемо.
Рассмотрим теперь проекции Рп'- Gn-*F. Они непрерывны,
а соотношение F.7.1) влечет равенство
й
Из теоремы 6.5.1 следует существование такого пу что F=
= Pn(Gn), откуда v(F)czEn.
Легко проверяется, что v, рассматриваемое как линейное ото-
отображение пространства F в £п, имеет замкнутый график. Надо
просто воспользоваться тем, что множество G секвенциально
замкнуто в FxE, и вспомнить, что топология пространства Еп
сильнее, чем топология в ЕП1 индуцированная из Е. По теореме
о замкнутом графике для полных полуметризуемых топологи-
топологических векторных пространств (теор. 6.4.4 (Ь) и следствие 6.2.3)
отображение v: F-+En непрерывно; тем более оно непрерывно
как отображение пространства F в Е. Теорема доказана. |
Предыдущая теорема приводит к соответствующему вариан-
варианту теоремы об открытом отображении.
6.7.2. Теорема. Пусть F — индуктивный предел семейства пол-
полных полуметризуемых топологических векторных пространств а
Е — индуктивный предел последовательности Еп (п=1, 2, .,.)
6.7. Другой вариант теоремы о замкнутом графике 617
полных полуметризуемых топологических векторных пространств
относительно отображений ип:"Еп-+Е. Если и — линейное ото-
отображение пространства Е на F, график которого секвенциально
замкнут в произведении ExF, то и открыто.
Доказательство. Вначале сведем нашу задачу к слу-
случаю, когда отображение и взаимно однозначно. Для этого обо-
обозначим через М ядро отображения и и рассмотрим ассоцииро-
ассоциированное отображение и факторпространства Е/М на F, -опреде-
-определенное равенством й(х) =и(х), где х — произвольный элемент
класса х по модулю М. Отображение и взаимно однозначно.
Согласно упр. 6.20, факторпространство Е/М удовлетворяет тем
же условиям, что и пространство Е. Поэтому, если считать до-
доказанной нашу теорему для 4 случая, когда отображение и
взаимно однозначно, отображение и факторпространства Е/М
на F открыто. Так как естественное отображение тс: Е->Е/М
открыто и и = йотс, то и отображение и пространства Е на F
открыто. Таким образом, достаточно рассмотреть случай, когда
отображение и взаимно однозначно.
Пусть и — взаимно однозначное отображение. Введем в рас-
рассмотрение отображение v = u~l пространства F в Е. Так как по
предположению график отображения и секвенциально замкнут
в произведении ExF, то, как легко проверить, график отобра-
отображения v секвенциально замкнут в произведении FxE. Следова-
Следовательно, по теореме 6.7.1 отображение v: F-+E непрерывно. Но
это означает, что отображение и пространства Е на простран-
пространство F открыто, что и требовалось доказать. |
Замечания. A) Если фигурирующие в теоремах 6.7.1 и
6.7.2 пространства Ей F локально выпуклы (в индуктивной
топологии), то естественно выяснить, как эти теоремы относятся
к теоремам об открытом отображении и замкнутом графике для
именно этого типа пространств, т. е. к теореме 8.9.3., Поставлен-
Поставленный вопрос требует уточнения хотя бы потому, что индуктивный
предел семейства совершенно полных1) (даже банаховых) про-
пространств может не быть полон (Кёте [5, гл. V], Г рот ен дик
[7, стр. 145, упр. 4]).
B) Условия, наложенные на F, хотя и кажутся существен-
существенными ограничениями, в действительности очень слабые. Как мы
увидим в п. 7.3.5, всякое секвенциально полное и борнологиче-
ское пространство F является внутренним индуктивным преде-
пределом семейства полных полунормируемых пространств (даже ба-
банаховых, если F отделимо).
C) Теоремы 6.7.1 и 6.7.2 приходится иногда применять
к случаю, когда пространства Е и F заменены их сильными
См. п. &.9Л. — Прим. перев,
618 Г л 6. Теоремы об открытом отображении и замкнутом графике
сопряженными Е' и F' соответственно. В связи с этим возникает
вопрос: при каких условиях Ег и Fr являются индуктивными
пределами соответствующего типа? Ответ на этот вопрос будет
дан в п. 8.4.14.
D) Пусть Е и F — LF-пространства (см. Дьёдонне и
Шварц [1]) и и — непрерывное линейное отображение про-
пространства Е в F. Если и есть отображение на /\ то оно открыто.
Однако и(Е) может быть замкнутым подпространством в F без
того, чтобы и было открытым отображением пространства Е
на и(Е). Птак [7] исследовал условия, достаточные для того,
чтобы и, рассматриваемое как отображение пространства Е на
и(Е), было открытым при условии, что и(Е)—замкнутое под-
подпространство в F. Полученные при этом результаты Птак при-
применил к доказательству теорем существования для уравнений,
содержащих свертки (ср. Мальгранж [1]).
6.7.3. Свойство «секвенциально замкнутого графика» Бур-
баки. В связи с интегрированием векториозначных функций
Бур баки [9, гл. VI, стр. 18] (см. также § 8.16 ниже) ввел по-
понятие секвенциально замкнутого графика. С другой стороны, это
понятие в значительной мере вызвано к жизни теоремой 6.7.1.
Говорят, что отделимое локально выпуклое пространство F
обладает свойством секвенциально замкнутого графика, если
всякое линейное отображение v пространства F в банахово про-
пространство X, график которого секвенциально замкнут в произ-
произведении FxX, непрерывно.
Из теоремы 6.4.4 (Ь) и следствия 6.2.3 вытекает, что каждое
пространство Фреше обладает свойством секвенциально замк-
замкнутого графика. Из теоремы 6.7.1 следует, что этим свойством
обладает и индуктивный предел пространства Фреше. В § 8.16
мы заново, другим способом (принадлежащим Бурбаки) полу-
получим тот же результат.
6.8. Приложения к топологическим базисам
В § 1.4 мы рассмотрели понятие алгебраического базиса век-
векторного пространства Е — такого семейства (аг) элементов из
£, что каждому элементу х^Е отвечает такое единственное се-
семейство скаляров (£г)> отличных от нуля только для конечного
(зависящего от х) множества индексов i, что х = 2 ^а$. Такие
алгебраические базисы всегда существуют.
Если Е — бесконечномерное топологическое векторное про-
пространство, то алгебраические базисы практически бесполезны
при решении задач, связанных с топологией в Е. (Для примера
рассмотрите случай базиса для R над полем рациональных чи-
6.8. Приложения к топологическим базисам 619
сел.) Поэтому пытаются изменить понятие базиса таким обра-
образом, чтобы с самого начала привлечь топологию пространства
Е. Для таких топологических базисов имеют смысл бесконечные
суммы с обычной оговоркой о сходимости. ,
Мы ограничимся здесь подробным изучением счетных тополо-
топологических базисов, некоторым образом занумерованных в после-
последовательность. К сожалению, в общем случае даже вопрос о
существовании топологического базиса (счетного или нет) вы-
вызывает значительные трудности. Однако в классическом анализе
для конкретных функциональных пространств такие базисы до-
достаточно часто существуют.
Мы коснемся здесь только некоторых сторон поднятого во-
вопроса; относительно других аспектов см. ссылки.
6.8.1. Пусть Е — топологическое векторное пространство. То-
Топологическим базисом в (или для) Е мы называем последова-
последовательность (еп) элементов из £, обладающую следующим свой-
свойством: каждому элементу х^Е отвечает такая единственная
последовательность чисел (gn), что ряд 2|/Ai сходится и имеет
п
своей суммой элемент х. Если потребовать только слабой схо-
сходимости ряда к элементу х> то топологический базис называется
слабым.
Слово «топологический» часто опускается. Его употребляют,
чтобы подчеркнуть тот факт, что речь идет не о базисе в алгеб-
алгебраическом смысле (§ 1.4).
Таким образом, последовательность (еп) является (слабым)
топологическим базисом в Е, если существует такая последо-
последовательность (е*п) в £*, что * = 2(*э е*п) £п для каждого х^.Е,
п
где ряд (слабо) сходится в £, а последовательности (еп) и (е*)
биортогональны в том смысле, что
Vm» еп) ~ *т, п*
Функционалы е*п могут принадлежать или не принадлежать про-
пространству Е'. Этим вопросом мы вскоре займемся. В любом слу-
случае функционалы е*п называются коэффициентными функциона-
функционалами, определяемыми (или ассоциированными с) базисом (еп).
6.8.2. Базис Шаудера. Базисом Шаудера (соотв. слабым ба-
базисом Шаудера) в Е называется топологический (соотв. слабый
топологический) базис в £, все ассоциированные коэффициент*
ные функционалы которого непрерывны на Е.
В этом случае мы будем обозначать д-й коэффициентный
функционал через е'а вместо е*п- Очевидно, что последователь-
620 Гл. 6. Теоремы об открытом отображении и замкнутом графике
ность (е£) образует топологический базис в £', если Е' наделено
слабой топологией g(E\ E).
Замечания. A) Понятие топологического базиса банахова
пространства восходит к Шаудеру [3]. Как мы увидим, всякий
слабый топологический базис банахова пространства есть баз-ис
Шаудера (относительно исходной нормированной топологии).
Ш а уд ер [3, 5] построил топологический базис для простран-
пространства С[0, 1] и показал, что некоторая ортогональная система
функций, {система Хаара) образует топологический базис в
Lp@, 1) при 1^/?<оо. Идея топологического базиса много-
многократно подвергалась обобщениям (см., например, Маркуше-
вич [1,2], Арсов [1], Арсов и Эдварде [1], Эдварде [13]).
Комментарии и ссылки можно найти у Данфорда и Швар-
Шварца [1, стр. 18 и 84], Дэя [1, стр. 115—124], Банаха [1,
стр. 95—99 и 206], Тэйлора [1, стр. 207 и 220]; см. также
С и н г е р [7, 8].
B) Нетрудно видеть, что существуют биортогональные си-
системы (еп) и (е^), такие, что (еп) не образует слабого тополо-
топологического базиса. Пример дан в упр. 7.15. Тем не менее биорто-
биортогональные системы представляют некоторый самостоятельный-
интерес. Тонкое исследование их свойств можно найти у Дьё-
донне [15]. Классической в теории ортогональных рядов яв-
является книга Качмажа и Штейнгауза [1]. Больше не бу-
будем на этом останавливаться.
6.8.3. Примеры. A) Пусть Е — гильбертово пространство,
(еп)— ортонормированный базис в Е (п. 1.1.2). Тогда (еп) —
топологический базис в Е. Сепарабельиые гильбертовы про-
пространства (сепарабельность служит необходимым и достаточ-
достаточным условием, обеспечивающим существование счетного орто-
нормированного базиса) образуют единственный известный
общий класс конкретных топологических векторных про-
пространств, в которых существование топологического базиса не-
несомненно.
Очевидно, что всякое топологическое векторное простран-
пространство, допускающее топологический базис, сепарабельно. Однако
остается нерешенной следующая задача: всякое ли сепарабель-
ное банахово пространство обладает хотя бы одним топологи-
топологическим базисом?
B) В каждом из пространств последовательностей с0 и
№ A ^С/?<оо) элементы еп, определенные равенствами en(k) =
= бпй» образуют топологический базис. Пространство /°°, не бу-
будучи сепарабельным, не обладает топологическим базисом (от-
(относительно нормированной топологии), хотя элементы еп обра-
образуют в нем базис относительно топологии а(/°°, Iх),
6 8. Приложения к топологическим базисам 621
C) Рассмотрим функциональные пространства С и Lp
A-^/7<оо) на окружности (или, что то же, соответствующие
пространства периодических функций на прямой). Обозначим
через еп функции t*—>eint (или их класс).
Глубоким результатом теории рядов Фурье является уста-
установление того факта, что функции еп (п = 0, ±1, ±2, ...) обра-
образуют топологический базис в пространствах Lp, 1</?<оо (см.
Зигмунд [2, том I, стр. 423]). Напротив, они не образуют то-
топологического базиса ни для одного из пространств С, L1, L°°"
(упр. 7.15 и 7.16)
При изучении основных сойств функций еп под суммой
2\tfin понимается lim 2 lnen-
-оо N->oo \n\KN
D) Весьма легко (упр. 6.15) построить неограниченное число
нормированных векторных пространств Е и топологических ба-
базисов в Е, таких, чтобы ни один из ассоциированных коэффи-
коэффициентных функционалов не был непрерывным.
6.8.4. Некоторые общие задачи. Пусть Е — заданное тополо-
топологическое векторное пространство. Рассмотрим следующие три
утверждения.
A) Всякий топологический базис в Е является базисом
Шаудера.
B) Всякий слабый топологический базис в Е является бази-
базисом Шаудера (теорема о слабом базисе).
C) Всякий слабый базис Шаудера в Е является топологи*
ческим базисом (и тем самым базисом Шаудера).
Банах [1, стр. 95—96] доказал утверждение A) для бана-
банаховых пространств и заметил (там же, стр. 206), что для бана-
банаховых пространств справедливо и утверждение B). Ньюнс [1,
стр. 431—432] распространил утверждение A) на пространства
Фреше, а Ар сов [2] расправился со случаем полных метризуе-
мых топологических векторных пространств. Совсем недавно
Бессага и Пелчинский [1] установили B) для пространств
Фреше, а в работах Арсов и Эдварде [1] и Эдварде [13]
рассмотрены различные обобщения утверждения A) для неко-
некоторых индуктивных пределов пространств Фреше с использова-
использованием результатов § 6.5. Дьёдонне [15] доказал утверждение
C) для бочечных пространств Е.
6.8.5. Мы хотим привести здесь в лице теоремы 6.8.6 ре-
результат Бессаги и Пелчинского. Наше доказательство основы-
основывается на справедливости утверждения C) для бочечных про-
пространств Е, которая устанавливается в примере 7.2.2. Здесь
достаточно заметить, что если (еп)—слабый базис Шау-
Шаудера в Е9 то соответствующие коэффициентные функционалы по
622 Гл. 6. Теоремы об открытом отображении и замкнутом графике
предположению принадлежат Е'. Если обозначить их через (е'п),
то для каждого элемента хе£ имеем
оо
где ряд слабо сходится. Теперь можно применять результаты
примера 7.2.2.
6.8.6. Теорема. Если Е — пространство Фреше, то справедливо
утверждение B).
В силу п. 6.8.5 достаточно показать, что если (еп) —слабый
топологический базис в пространстве Фреше Е, то каждый из
ассоциированных коэффициентных функционалов непрерывен на
Е. Для этого мы обобщим рассуждения, использованные Бана-
Банахом [1, стр. 95—96]. При этом нам понадобится несколько вспо-*
могательных лемм.
В конечном счете в леммах рассматриваются два топологи-
топологических векторных пространства Z и Е и последовательность не-
непрерывных линейных отображений ип\ Z-+E (п=1, 2, ...). Мы,
однако, начнем с леммы, относящейся исключительно к про-
пространству Е и слабой секвенциальной сходимости в нем.
Лемма 1. Пусть Е — полное отделимое локально выпуклое
пространство, (ain)—двойная последовательность, (bt) и
(ап) —последовательности элементов из Е. Допустим, что
(a) lim ain = bi в слабой топологии в Е при каждом i\
П->оо
(b) lim ain = ап равномерно по п.
г-»оо
Тогда в Е найдется такой элемент а, что \iman = a в слабой
П->оо
топологии в Е и lim Ьг — а в Е.
г-»оо
Доказательство. Пусть U — произвольная замкнутая
выпуклая уравновешенная окрестность нуля в Е. В соответ-
соответствии с предположением (Ь) найдется такая сходящаяся к нулю
последовательность (ег) положительных чисел, что
1 F.8.1)
для всех п. Если xf e U0 (п. 8.1.4), то
для всех ft, так что
\(ат-ап, /)К1(^ОТ-^, *'I + 2е,.
Отсюда и из условия (а) следует, что ((аПу х'))—последова-
х'))—последовательность Коши для каждого элемента /g(/°, Множества U0
6.8. Приложения к топологическим базисам 623
образуют покрытие пространства Е'. Так как (ап) —слабая по-
последовательность Коши в £, то она слабо сходится в Е" к неко-
некоторому элементу а. Нам нужно показать, что элемент а при-
принадлежит Е.
Для этого воспользуемся следующим замечанием. Пусть
(сп) — произвольная слабо сходящаяся к нулю последователь-
последовательность элементов из Е. Рассмотрим множество таких финитных
числовых последовательностей К= Щп)), что К(п) > 0 для всех
пи 2Цп)=1. Пусть г—произвольное натуральное число. Обо-
п
значим через Lr множество тех Х=(Х(я)), носитель которых со-
содержится в множество {п>г}. Мы утверждаем, что для всякого
е > 0 можно выбрать такую последовательность X е Lr, что
где U — любая наперед заданная окрестность нуля в Е. Чтобы
доказать наше утверждение, рассмотрим в Е выпуклую обо-
оболочку G элементов сп с п>г. По условию нуль принадлежит
слабому замыканию множества G и потому принадлежит так-
также и замыканию множества G в исходной топологии. С другой
стороны, каждый элемент множества G представим в виде
суммы 2Мм)ся cleLr, т. е. имеет место наше утверждение.
п
Из соотношения F.8.1) следует, что
Так как U — выпуклая окрестность, то для всякой последова-
последовательности leir имеем
2 Я (п) (ain - Ьг) -SMn)fl» + ^e BtU.
п п
Применяя предыдущее замечание к последовательности £„ =
= 0in — bi, можно так выбрать Kn e Lr, что
В этом случае
п
Таким образом, для х'е U0 имеет место неравенство
+r-K F.8,2)
624 Гл. 6. Теоремы об открытом отображении и замкнутом графике
Если положить sri = 2 Ki (п) ап> то> как легко проверить,
п
1Гт sTi = а в слабой топологии в Е". Итак, для л:' е С/0 спра-
ведливы отношения
\<srt-a9 x')\^%Ki(n)\(an-a, x')l =
■ s
n>r
Kt(n)\(an-a, x') |< sup {| <an - a,
причем последовательность в правой части неравенства стре-
стремится к нулю при г-+оо, так как ап-+а в слабой топологии
в Е".
Из неравенства F.8.2) вытекает, что
\(а, x')-(bh *'>1<е, F.8.3)
для xr e U0. Поэтому если х' и у' принадлежат U0, то
Отсюда следует, что сужение на U0 линейной формы х'н-> (а, л:')
непрерывно в топологии, индуцированной в U° топологией
a(£/, E). Но тогда (по теореме 8.5.1) элемент а принадлежит
Е, поскольку пространство Е по условию полно.
Доказательство завершается ссылкой на теорему 8.1.5 о би-
полярах, которая в сочетании с неравенством F.8.3) влечет со*
отношение а — bi^EiU. А это означает, что \1шЬ{ = а в Е. |
Введем теперь ^некоторые обозначения. Пусть Z—топологи-
Z—топологическое векторное "пространство, Е — локально выпуклое про-
пространство, ип: Z-+-E (п—\, 2, ...)—последовательность непре-
непрерывных линейных отображений. Через Z&, Zwc и Zc обозначим
векторные подпространства в Z, состоящие из тех г, для кото-
которых последовательность (un(z)) соответственно ограничена,
слабо сходится и сходится в Е. Очевидны соотношения
Zc cz Zwc a Zbd Z.
Сделаем следующее
► Предположение. Если для сети (г{) в Zb существует
limun(zi)e E равномерно по п, то сеть (Z{) сходится eZ.
Наконец, определим топологию в Zb следующим образом.
Выберем некоторую систему полунорм {ри}, определяющую топо-
топологию в Е. Каждой полунорме ра поставим в соответствие полу-
полунорму
qa(z) = sup {pv(un(z)): /i=l, 2, ...},
6.8. Приложения к топологическим базисам 625
определенную на Zb. Система полунорм qa по определению об-
образует определяющую систему полунорм указанной топологии
в Zb. Для краткости будем эту топологию в Zb обозначать че-
через t.
Лемма 2. В предыдущих -обозначениях пусть Е — полное
пространство, и пусть выполнено сформулированное предполо-
предположение. Тогда пространство Zb полно в топологии t.
Доказательство. Пусть (гг)—/-сеть Коши в Zb.
Это означает, что
где lim 8^= 0 для каждого а. Так как пространство Е полно, то
для каждого п в Е существует lim ип(г(). Тогда, согласно пред-
предположению, существует lim zt = z в Z. Остается показать, что*
2gZ6 и что lim qa{z — 2()==0 для каждого а.
i
Если положить хп = lim un{zb), то из соотношения F.8.4) сле-
следует, что
РаК-ия(**))<е?' F.8.5)
где lim е^ = й для каждого а. Выберем и зафиксируем индекс /0
так, чтобы е^ ^ 1. Тогда
Pa (*n) < Pa ("я (**.))+!.
откуда в силу того факта, что Zio^Zb, получаем, что последо
вательность хп ограничена в Е. Но- xrt = lim^rt(^) есть не что
иное, как un(z), ибо отображение ип непрерывно. Ограничен-
Ограниченность' последовательности хп означает, что z e Zb. Переписывая,
наконец, соотношение F.8.5) в виде qa{z — Z\) ^ &и получаем
z = t-\im Z{. I
Лемма 3. Пусть обозначения и предположения те же, что и
в лемме 2. Тогда пространство Zc t-замкнуто в Zb и потому пол-
полно в топологии, индуцированной топологией t.
Доказательство. Пусть (гг)—сеть в Zc, /-сходящаяся
к некоторому элементу z s Zb. Мы должны показать, что
z e Zc. По условию
626 Гл 6. Теоремы об открытом отображении и замкнутом графике
где lime? = O при каждом а. Для заданных а и е>0 выберем
и зафиксируем индекс i так, чтобы е^<е/4. Тогда
Pa (Um (?) -Un(*))<J*+Pa (Um fa) - Un fa) )
равномерно по m и п. Так как элементы гг принадлежат Zc, то
немедленно получаем, что
если тип достаточно велики. Таким образом, (un(z)) —после-
—последовательность Коши и потому сходится в Е. Следовательно,
Лемма 4. При тех же условиях, что и в лемме 2, подпро-
подпространство Zwc t-замкнуто в Zb и потому t-полно.
Доказательство. Допустим, что каждый элемент Z\
принадлежит Zwc, z^Zb и t-\\mzi = z. Мы должны показать,
что z = Zwc.
Для этого применим лемму 1 к последовательности ain =
— unfa). Так как z,- e Z«,c, то слабый предел \\main*=bi суще-
п
стует в Е для каждого L Далее если мы положим an = un(z),
.то условие t-\\mZi = z означает, что Mm ain = an в Е равномерно
относительно п. Из леммы 1 следует, что последовательность
(an) = (un(z)) слабо сходится в £, т. е. z ^ Zwc. |
Доказательство теоремы 6.8.6. Пусть Е — простран-
пространство Фреше и (еп) —слабый топологический базис в Е. Мы хо-
хотим показать, что каждый коэффициентный функционал непре-
непрерывен на Е. Для этого воспользуемся леммой 4 и теоремой об
обратном операторе.
В качестве Z возьмем пространство /CN (К — поле скаляров,
N — множество натуральных чисел) в топологии произведения.
Пусть ип — отображение, определенное соотношением
п
ип (z) = 2 z (k) ek.
Так как епФ0 (как элемент топологического базиса), то для
заданного п существует такой индекс а = а(п), что $ = ра(еп)Ф
ФО. Имеем
\z(n)\^2$-{qa(z). F.8.6)
Поскольку пространство /(N полно, то сформулированное выше
предположение выполняется. Из леммы 4 следует, что про-
6.8. Приложения к топологическим базисам 627
странство Zwc /-полно. Кроме того, так как пространство Е мет-
ризуемо, то таким же будет и каждое из подпространств Z&,
Zc и Zwc. Пространство Zwc есть, таким образом, пространство
Фреше.
Рассмотрим теперь линейное отображение и: ZWC-*E, опре-
определенное равенством
Последовательность (un(z)) слабо сходится к u(z), поэтому из
очевидного неравенства
pa(tfB))<sup pa(un(z))
п
следует, что
откуда вытекает непрерывность отображения и. С другой сто-
стороны, поскольку (еп)—слабый топологический базис в Е, то
и — взаимнооднозначное отображение Zwc на Е.
Так как Е и Zwc — пространства Фреше, то по теореме 6.4.5
об обратном операторе отображение и~1 непрерывно.
Заметим, что в разложении х=^^пеп
Из соотношения F.8.6) следует непрерывность координатного
функционала z\—>z(n) на Zwc\ поэтому из установленной непре-
непрерывности отображения и~х вытекает непрерывность п-то коэф-
коэффициентного функционала x*—>ln. I
6.8.7. Возможные обобщения. Ясно, что, помимо уже упомя-
упомянутых в п. 6.8.4 обобщений, предыдущее доказательство можно
приспособить к случаю, когда (еп) есть, так сказать, базис сла-
слабой суммируемости.
Пусть, например, существует такое семейство суммирующих
множителей Хпь, что каждому элементу х е Е отвечает такая
единственная последовательность чисел (£п), что
x = \lm^Xnklkek F.8.7)
п k
в слабой топологии в Е. При этом предполагается, что ряды
2^/ife£fc£fc сами слабо сходятся в Е для каждого п.
Можно тогда попытаться положить
Для многих хорошо известных методов суммирования Xnk = 0
при k > ko. Тогда сходимость каждого из рядов F.8.7), как и не-
628 Гл. 6. Теоремы об открытом отображении и замкнутом графике
прерывность отображения ип: /CN~^£, обеспечены, и нужно по-
посмотреть, выполняется ли сформулированное выше предположе-
предположение в случае, когда %Пк = 1 при kKn и 0 при k > п (см. F.8.7)).
Предоставляем читателю исследовать все указанные возмож-
возможности.
Что касается дальнейших работ, посвященных базисам, см.
Резер фор д [1, 2], Д эвис [1], Сандер [1], Мак-Артур [1].
УПРАЖНЕНИЯ
6.1. Пусть Т — отделимое локально компактное пространство, \i — поло-
положительная мера Радона на Т и f — такая функция на Г, что произведение
fg интегрируемо для каждой функции g e Jg>P (T, \х). Воспользоваться тео-
теоремой о замкнутом графике для доказательства того, что / е J^p (Г, \х),
где, как обычно, р' определяется равенством 1—7 = 1. (Ср. с упр. 7.1.)
6.2. -Доказать, что если пространство Фреше "есть алгебраическая пря-
прямая сумма замкнутых векторных подпространств L и Af, то оно является и
топологической прямой суммой L и М.
6.3. Пусть Е— векторное пространство, которое становится простран-
пространством Фреше, если наделить его любой из двух топологий / и t'. Если су-
существует разделяющее точки множество линейных форм, каждая из кото-
которых непрерывна в любой из топологий t и /', то топологии t и /' совпа-
совпадают.
6.4. Пусть функция /eC°°(Rn) такова, что если « g ^, то произведе-
произведение fu e <&*. Показать, что для каждого р модуль производной dpf мажо-
мажорируется некоторым многочленом.
6.5. Пусть Е и F — полные полуметризуемые топологические векторные
пространства, Gn (я=1, 2, ...)—произвольные отделимые топологические
векторные пространства. Допустим, что при каждом п отображение
fn'.F->Gn линейно и непрерывно и что отображения fn разделяют точки
из F. Показать, что отображение и: Е -> F непрерывно, если при каждом п
непрерывно отображение fn°u>: E~>Gn.
6.6. Пусть Е и F — полные метризуемые топологические векторные про-
пространства, Gn (n==l» 2, ...)—произвольные топологические векторные про-
пространства, ип\ E-^-Gn (соотв. vn\ F->Gn)—непрерывные линейные отобра-
отображения. Если для каждого элемента х^Е существует такой единственный
элемент y=f(x)^F, что
ОяЫ-ИяМ A=1,2, ...),
то / — непрерывное линейное отображение пространства Е в F.
6.7. Пусть Q — ограниченный открытый интервал вещественной прямой,
/0 G Й и р, g б С (Й), где Q = [a, b]. Рассмотрим дифференциальное уравне-
уравнение
х" 4- рх' + qx = y.
Обозначим через Bh пространство тех функций /, для которых непрерывны
и ограничены на Q функции f, f, ..., f(fe), и наделим Bk нормой
Шл~8ир{|/(л)@1: '6=0, ()</*<£:}.
Основываясь на общеизвестных теоремах существования и единственности ре-
решения дифференциальных уравнений указанного вида, показать, что для каж-
Упражнения 629
дого у^В° существует единственное решение приведенного дифференциаль-
дифференциального уравнения, удовлетворяющее начальным условиям x(to)=x'(to)=O Пусть
Е— подпространство в В2, определяемое этими начальными условиями.
Рассмотрим отображение и: £~>£°, задаваемое равенством
и (Х) = х" + pxf + qx.
Показать, что и — непрерывное отображение Е на В0. Доказать, что отобра-
отображение иг1: В°-+Е непрерывно и что отображение игх\ В0 -> В1 компактно
(т. е. переводит единичный шар пространства В0 в относительно компактное
множество в В1).
6.8. Обозначения предыдущего упражнения. Исследовать, что произойдет,
если начальные условия x(t0) =х'(/о) =0 заменить граничными условиями
х(а) =х(Ь)=0. Показать, в частности, что отображение и~х существует, если
q(t) <0 для t e п.
6.9. Пусть Е — бесконечномерное полуметризуемое локально выпуклое про-
пространство, (<Хп) и ((Зп) —такие две последовательности положительных чисел,
что lim an = lim (Зп = +©о. Показать, что существуют такая последователь-
последовательность (хп) в пространстве Е и такая линейная форма f на £, что
— 0,
Следующие четыре упражнения основаны на работе Дени и Лионса [1].
6.10. Обозначения п. 5.11.1. Доказать, что пространство BL(Q) полно от-
относительно нормы, определяемой равенством
[Указание. Воспользоваться методом доказательства леммы А п. 5.13.4.]
6.11. Пусть й-область в^и tlq2 (Q) = BL (п) П Lq ($). Показать, что
\ 2 (^) "" банахово пространство относительно нормы
где норма || и Hi определена так же, как и в предыдущем упражнении.
6.12. Пусть п > 2, Q — область в Rn, имеющая конечную меру, и q=
3=2n/(n — 2). Показать, что Q есть область Соболева тогда и только тогда,
когда существует такое число S(Q), что
inf \\u + c\\ q <S(Q)\\u\\
c=const L W> 1
для «e^f2(Q).
[Указание. Образовать факторпространства (^\г2^) = Е в BL (Q)
(по модулю постоянных функций) и рассмотреть тождественное отображе-
отображение Е в BL'(Q). Это отображение есть отображение на тогда и только тогда,
когда Q является областью Соболева Использовать теорему об обратном
операторе. Показать далее, что образ пространства Е плотен в BL'(Q). См.
упр. 5.25.]
630 Гл. 6. Теоремы об открытом отображении и замкнутом графике
6.13. Пусть область Q в Rn имеет конечную меру. Показать, что ^есть
область Никодима тогда и только тогда, когда существует такое число
что
Ud\L
Й
для и е txL2 (Q).
(Это - неравенство Пуанкаре. Наименьшее допустимое значение Р (О)
называется постоянной Пуанкаре области Q.)
[Указание. Доказательство такое же, как и в предыдущем упражнении,
с заменой 2^2(Q) на %[* (£).]
Результаты упр. 6.11—6.13, а также их доказательства, принадлежат
Дени и Л и о н с у [1, теоремы 5.1, 5.3).
6.14. Пусть 0<р< оо и Нр—пространство, определенное в п. 1.10.4. По-
Показать, что для каждого компактного подмножества К открытого единичного
круга с центром в начале координат комплексной плоскости полунорма
p
К
непрерывна на Нр.
[Указание. Воспользоваться полнотой пространства Нр (п. 1.10.4) и
теоремой о замкнутом графике.]
6.15. Пусть Е— бочечное пространство, (еп)/— базис Шаудера в Е с ассо-
ассоциированными коэффициентными функционалами (e^). Допустим, что суще-
существует такое число г > 0, что для каждого х е Е имеет место неравенство
2 КХ.Ф1 *»< + «.
п
На множестве чисел t, удовлетворяющих условию \t\^r, определим функ-
функцию х* равенством х (/) = 2 (*» вл) ^* Пусть (thjj — такая последова-
п
тельность попарно различных вещественных чисел, что 0 < I tu I ^ г и tk ->*«>,
где 0>< I ^оо I < г. Для каждого х е Е положим
1 *| - sup | *•('*)!•
k
Проверить, что || • II — норма на Е. Пусть Ео — соответствующее нормиро-
нормированное пространство Показать, что (еп) —топологический базис в Ео, такой,
что ни один из ассоциированных коэффициентных функционалов не является
непрерывным на Ео.
6.16. Пусть Е — банахово пространство и Т — непрерывное линейное ото-
отображение Е на ll = ll(N). Показать, что Е — прямая топологическая сумма
М + ker 71, где М — некоторое замкнутое векторное подпространство в Е.
6.17. Обобщить результаты упр. 2.17 следующим образом.
Пусть Е — отделимое локально выпуклое пространство. Выберем такое
семейство (Ui) окрестностей нуля в Е, что гомотетические образы множеств Ui
образуют базу окрестностей нуля. Обозначим через Qi поляру (п. 8.1.4) окре-
окрестности Ui в Е'. Каждое из множеств Qi есть отделимое компактное про-
пространства в топологии, индуцированной топологией о(Е',Е). Рассмотрим ото-
отображение и пространства Е в произведение Р = JJ С (Qi) банаховых про-
Упражнения 631
странств C(Qi), которое каждому х^Е сопоставляет элемент произведения Р,
i-я координата которого является элементом C(Qi), получаемым сужением
на Qi функции х' \—> {х, х') на Е'.
Проверить, что и — изоморфизм пространства Е в Р.
Вывести отсюда, что каждое отделимое полное локально выпуклое про-
пространство Е изоморфно замкнутому векторному подпространству произведе-
произведения банаховых пространств, причем это произведение является бочечным про-
пространством.
6.18. Пусть Т — произвольное множество, рассматриваемое как дискр'ет-
ное топологическое пространство, и пусть £/£ (Т)—векторное пространство
всех скалярных функций на Г с конечными носителями. Наделим Ж (Т) то-
топологией, определяемой полунормами
Np (x) = sup p(t)\x (t) |
где р — произвольная положительная функция на Т.
Доказать, что пространство £&(Т) полно. Рассмотреть множество
A = jxt
и показать, что если Т несчетно, то пространство Ж (Т) не бочечно.
(Этот пример принадлежит Бурбаки [7, стр. 145, упр. 5].)
6.19. Показать, что всякий гомоморфный образ бочечного пространства
бочечен, т. е. если Е — бочечное пространство и существует открытое непре-
непрерывное линейное отображение и пространства Е на локально выпуклое про-
пространство F, то F бочечно.
Вывести отсюда, что если Е бочечно и М — векторное подпространство
в Е, имеющее в Е топологическое дополнение, то М бочечно.
6.20. Пусть Е — индуктивный предел пространств Е{ относительно отобра-
отображений фг, М — векторное подпространство в Е, и пусть факторпространство
F=E/M наделено фактортопологией. Положим Mi = <рг~ (М), и пусть про
странства Fi = Ei/Mi также наделены фактортопологией. Обозначим через fi
и / естественные отображения Ei на F,- и Е на F соответственно. Определим,
наконец, отображения грг: Fi->F соотношением
Проверить, что F есть индуктивный предел пространств Fi относительно
отображений г|)г-.
Заметить, что если подпространство М замкнуто в Е} то подпространство
М{ замкнуто в Ег при каждом /.
6.21. Пусть X — топологическое пространство и У — нетощее множество
в X. Показать, что если рассматривать У как подпространство в X, то оно
нетоще в себе.
6.22. Показать, что всякий алгебраический базис бесконечномерного ба
нахова пространства Е несчетен.
6.23. Пусть Е — банахово пространство, в котором существует бесконеч-
бесконечная последовательность (ап) линейно независимых элементов, порождающих
векторное подпространство, плотное в Е (скажем, £=/1). Продолжить (ап) до
алгебраического базиса (at). , где / — некоторое множество, содержащее
множество N натуральных чисел. Согласно предыдущему упражнению, мно-
множество / несчетно. Выберем последовательность попарно различных индексов in
(л=1, 2, ...) из /\N. Пусть Fh — векторное подпространство в £, порожденное
632 Гл. 6. Теоремы об открытом отображении и замкнутом графике
теми пг с /, отличными от всех in, и а{ с 1</1<й. Проверить, что
каждое из подпространств Fh плотно в Е, однако отлично от Е. Показать
также, что для некоторого k подпространство Fu нетоще в Е. Для всякого та-
такого k подпространство Fu есть неполное нормируемое векторное простран-
пространство, являющееся бочечным.
Эта конструкция принадлежит Бурбаки [7, стр. 145—146, упр. б].
сю
[Указание. Заметив, что Е=* U F^, воспользоваться теоремой Бэра
0.3.16 и упр. 6.21J
6.24. Установить результат (Ь) из § 6.3, B), не используя явно полу-
полунорм Ns, e.
[Указание. Пусть В — ограниченное подмножество в Q)m (Q). Если
носители элементов множества В не содержатся в фиксированном компакт-
компактном подмножестве из Q, то должна существовать такая последовательность
точек (хп\ из Q и такая последовательность (фп) функций из В, что верхняя
грань
I
конечна для каждой функции ф е Q)m (Q) и в то же время неограничена на В.
Пользуясь бочечностью пространства &т (Q), прийти к противоречию.]
6.25. Пусть Е — нормированное пространство и А—подмножество в £,
обладающее следующим свойством: существует такое число А, > 1, что для
каждого х ^Е с \\x\\ < 1 найдется а е А с \\х — а|| ^ Х~1. Доказать, что для
каждого элемента х^Е с lUil^l существует такая последовательность
точек из Л, что
6.26. Используя предыдущее упражнение, доказать, что всякое замкнутое
линейное отображение и банахова пространства Е в банахово пространство F
непрерывно.
[Указание. Опираясь на теорему о категориях, показать, что при неко-
некотором k множество
A = {xs=E: \\u(x)\\^k)
плотно в замкнутом единичном шаре пространства Е. Применить предыдущее
упражнение, взяв, скажем, Х=2.]
ГЛАВА 7
Принципы ограниченности
7.0. Предисловие
Общая сквозная тема этой главы — обсуждение результатов,
утверждающих, что если некоторое множество линейных или
билинейных отображений одного или нескольких топологических
векторных пространств в другое ограничено в каком-то смысле,
то оно будет ограничено в некоем более сильном смысле. Эта
ограниченность в более сильном смысле будет часто заключаться
в равномерности того или иного рода, не фигурирующей в ис-
исходных предпосылках, почему результаты рассматриваемого
типа иногда называют принципами равномерной ограниченности.
Эти принципы применимы лишь к некоторым категориям тополо-
топологических векторных пространств. Понятия бочечных и ультра-
ультрабочечных пространств, введенные в гл. 6, до некоторой степени
обязаны своим возникновением анализу доказательств этих
принципов, первоначально применявшихся только к банаховым
или полным метризуемым пространствам.
Мы получим четыре главных принципа ограниченности ли-
линейных отображений, представленных соответственно теоремами
7.1.1, 7.1.3, 7.3.1 и 7.4.3. Эти теоремы отличаются как типом про-
пространств, к которым они применимы, так и типом ограничен-
ограниченности, предполагаемой по условию. Так, например, в § 7.1 рас-
рассматриваются случаи, когда поточечная ограниченность влечет
равностепенную непрерывность (бочечные и ультрабочечные
пространства), тогда как § 7.3 посвящен переходу от сильной
ограниченности к равностепенной непрерывности (борнологиче-
ские и инфрабочечные пространства). Из главных принципов вы-
вытекает великое множество следствий приспособленных к более
или менее конкретным ситуациям. В § 7.7 рассмотрен случай
билинейных отображений.
Таким образом, естественно появляется еще один класс ло-
локально выпуклых пространств: борнологические пространства,
вводимые в § 7.3.
Некоторые вопросы, связанные с содержанием настоящей
главы, но не затронутые в ней, рассматриваются в работах Сар*
джента [2] и Хенстока [1].
634 Гл. 7. Принципы ограниченности
7.1. Принципы ограниченности для бочечных
и ультрабочечных пространств
Независимо друг от друга Орлич [1], Гельфанд [1] и
Бозанке и Кестельман [1] показали, -ito всякая полуне-
полунепрерывная снизу полунорма р на банаховом пространстве Е не-
непрерывна. Эберлейн [3] заменил полунепрерывность снизу
свойством Бэра. (Говорят, что функция р на топологическом про-
пространстве Е со значениями в некотором топологическом про-
пространстве обладает свойством Бэра, если существует такое то-
тощее подмножество М в Е, что сужение р\(Е\М) непрерывно;
см. Банах [1, стр. 17].) Мехди [1] показал, что р непрерывна,
если Е — нетощее топологическое векторное пространство и мно-
множество {х: xg£; /?(#)^1} обладает свойством Бэра (см. Ба-
Банах [1, стр. 16], Кур а то в с кий [1, стр. 93]). Как мы увидим в
дальнейшем, существование любого такого принципа оправды-
оправдывается возможностью разнообразных приложений, не говоря уже
о том, что они интересны и сами по себе.
Перечисленные выше исследования опирались только на тео-
теорему Бэра о категории и аналогичные соображения, поэтому
указанные результаты остаются в силе для полных метризуемых
топологических векторных пространств.
Несомненно, Бурбаки имел в виду этот принцип, когда
вводил бочечные пространства [7, стр. 143]. В самом деле,
очень просто доказывается (теорема 7.1.1), что локально вы-
выпуклое пространство Е бочечно в том и только в том случае,
когда каждая полунепрерывная снизу полунорма на Е непре-
непрерывна. Этот результат мы будем называть принципом Орлича —
Гельфанда — Бозанке — Кестельмана, сокращенно принципом
ОГБК.
Непосредственным поводом для введения нового класса ло-
локально выпуклых пространств для Бурбаки послужила теоре-
теорема 6.3.1, которая показывает, что существует много неметризуе-
мых локально выпуклых пространств, для которых справедлив
принцип ОГБК. Такие пространства не укладываются в рамки
первоначальной теории.
Мы сформулируем также аналогичный принцип ограничен-
ограниченности для ультрабочечных пространств.
Общие принципы ограниченности изложены в п. 7.1.1—7.1.5,
7.3.1, 7.4.3, 7.4.4 и 7.7.4—7.7.9.
Наш первый результат выражает в аналитической форме
принципы ограниченности для пространств рассматриваемого
типа и даже представляет собой характеризацию в аналитиче-
аналитических терминах бочечных и инфрабочечных пространств.
7.1. Принципы ограниченности 635
7.1.1. Теорема. A) Локально выпуклое пространство Е бочеч-
но тогда и только тогда, когда выполняется одно из следующих
двух эквивалентных условий:
(a) всякая полунепрерывная снизу полунорма на Е непре-
непрерывна (принцип ОГБК);
(b) всякое слабо ограниченное подмножество в Е* равносте-
равностепенно непрерывно.
B) Пусть Е — ультрабочечное топологическое векторное про-
пространство и f — такая положительная полунепрерывная снизу
функция на Е, что для любого ^Gi( (К — поле вещественных
или комплексных чисел) и любых х, у е Е
f(Xx)<A(Kf(x))y
f(x-y)<B{f(x),f(y))9
где А и В— функции, определенные на /CXR+ и RH.xR|. соот-
соответственно и удовлетворяющие условиям
A(K,t)-+O, B(s,t)-+O
при %, s и t, стремящихся к нулю. Тогда функция f непрерывна
в нуле.
C) Локально выпуклое пространство Е инфрабочечно тогда
и только тогда, когда либо каждая ограниченная полунепрерыв-
полунепрерывная снизу полунорма на Е непрерывна, либо каждое сильно
ограниченное подмножество в Ef равностепенно непрерывно.
Замечания. В пункте C) под ограниченностью полунор-
полунормы понимается ее ограниченность на каждом ограниченном под-
подмножестве в Е, а под сильной ограниченностью множества
SaE'— его ограниченность в сильной топологии в Е\ Сильная
топология в Е' определена в п. 1.10.8 (надо положить там F = K).
Таким образом, S сильно ограничено тогда и только тогда, когда
sup {| (х, х') |: х е В, х' е S) < + оо для каждого ограниченного
подмножества В в Е.
Доказательство. A) Прежде всего заметим, что в силу
результатов § 6.1 бочки в Е — это множества, определяемые со-
соотношением р(х)^.\, где р — полунепрерывная снизу полу-
полунорма на Е.
Утверждение пункта (а) непосредственно вытекает из этого
замечания и определения бочечного пространства (§ 6.2).
Что касается (Ь), то читатель может заметить, что поскольку
пространство Е' в его слабой топологии локально выпукло, то
достаточно рассмотреть только те слабо ограниченные множества
В', которые слабо замкнуты, выпуклы и уравновешены. Тогда
(§ 8.1) поляра В/о в Е множества Bf является бочкой в Е. Кроме
того, В/ = В/0°, Поэтому если пространство Е бочечно, то В'0 —
636 Гл. 7. Принципы ограниченности
окрестность нуля в Е и, следовательно, Bf равностепенно непре-
непрерывно. Обратно, если Т — бочка в Е, то ее поляра Т° в Е' слабо
ограничена. Если (Ь) выполяется, го Т° равностепенно- непре-
непрерывно и Т°° — окрестность нуля в Е. Но Т = Т°° (теорема 8.1.5),
и потому Е — бочечное пространство
C) Это утверждение доказывается аналогично. Читатель
может заметить, что если бочка в Е определена соотношением
р(х)^С 1, то функция р ограничена в точности тогда, когда ука-
указанная бочка поглощает каждое ограниченное подмножество
в Е. Если множество В' сильно ограничено в Е', то В/о есть боч-
бочка в Е, поглощающая каждое ограниченное множество; если Т—
бочка в £, поглощающая ограниченные множества, то Т° сильно
ограничено в Ег.
B) Пусть е>0. Положим
Множество VB замкнуто, так как f — полунепрерывная снизу
функция. В силу остальных условий, которым удовлетворяет f,
множества Уг образуют базу окрестностей нуля некоторой ли-
линейной топологии в Е. Если пространство Е ультрабочечно, то
эта топология слабее исходной. Таким образом, каждое У8 яв-
является окрестностью нуля в £, что и требовалось доказать. |
Наиболее часто встречающаяся форма использования прин-
принципа ОГБК заслуживает отдельного рассмотрения.
7.1.2. Следствие. Если Е — пространство Фреше, то всякая
полунепрерывная снизу полунорма на Е непрерывна и всякое
слабо ограниченное подмножество в Ег равностепенно непре-
непрерывно.
Обратимся теперь к одной из обобщенных форм теоремы
Банаха — Штейнгауза. Первоначальная формулировка этой тео-
теоремы для банаховых пространств приведена в книге Банаха [1],
7.1.3. Теорема (Банах — Штейнгауз). Пусть Е и F —
топологические векторные пространства, причем Е ультра-
ультрабочечно.
Если множество & непрерывных линейных отображений Е в
F ограничено в каждой точке пространства Е, то £Г равносте-
равностепенно непрерывно. То же заключение справедливо в случае,
когда Е бочечно, a F локально выпукло.
Доказательство. Предположим, что V пробегает си-
систему замкнутых окрестностей нуля в F. Каждой такой окрест-
окрестности V сопоставим множество
V=(\{u-l{V): ие=ЗГ}.
Так как 3^ ограничено в каждой точке, то V* — поглощающее
множество. Из непрерывности каждого wef следует, что У*
7.1. Принципы ограниченности 637
замкнуто в Е. Множества V* можно принять за базу окрестно-
окрестностей нуля некоторой линейной топологии в Е. Поскольку про-
пространство Е ультрабочечно, а множества V* замкнуты, то эта
топология слабее, чем исходная топология в £", следовательно,
каждое такое У* является окрестностью нуля в Е. Таким обра-
образом, ST — равностепенно непрерывное множество.
Если F локально выпукло, то каждую окрестность V можно
считать выпуклой. Тогда каждое V* обладает тем же свойством.
Следовательно, V* — бочка в Е, откуда вытекает, что V* — окре-
окрестность нуля в Е, что и требовалось доказать. |
Замечание. Если пространство F локально выпукло, то
предпосылка ограниченности следует из условия
для каждого x'^F'. Достаточность этого на вид более слабого
условия вытекает из теоремы 8.2.2.
7.1.4. Следствие. Пусть либо Е ультрабочечно, либо же Е
бочечно, a F — локально выпуклое пространство, и пусть в обоих
случаях пространство F квазиполно1). Пусть далее {ui)i^I —
сеть непрерывных линейных отображений пространства Е в F,
ограниченная в каждой точке из Е. Тогда множество Ео тех
х^Е, для которых существует в F предел lim щ(х) = и (х), есть
замкнутое векторное подпространство в Е, отображение и не-
непрерывно на Ео и и = lim щ равномерно на каждом, предкомпакт-
i
ном ( = вполне ограниченном) подмножестве в Ео. Наконец, если
сеть заменить последовательностью (ип), то достаточно, чтобы F
было секвенциально полным.
Доказательство. В силу теоремы 7.1.3 множество ото-
отображений {иг) равностепенно непрерывно. Ясно, что Ео — век-
векторное подпространство в Е. Из равностепенной непрерывности
следует, что если х — точка прикосновения множества ЕОу то
(щ(х)) — сеть Коши в F. Так как эта сеть ограничена в F, a F
квазиполно, то в F существует и(х) =*Мтщ{х). Таким образом,
Ео замкнуто. Равномерная сходимость на предкомпактных
множествах в Ео является прямым следствием теоремы
Асколи. I
В заключении этого параграфа рассмотрим одно из приложе-
приложений теоремы Банаха — Штейнгауза к билинейным отображе-
отображениям. Сформулируем сначала более общую теорему.
!) Определение квазиполноты приводится в § 7.4; квазиполнота означает,
что полны ограниченные замкнутые множества, и потому вытекает из пол-
полноты. Предварительное использование здесь этого термина не должно бес-
беспокоить читателя.
638 Гл. 7. Принципы ограниченности
7.1.5. Теорема. Пусть Е — полуметризуемое, a G — произволь-
произвольное топологическое векторное пространство. Предположим, что
либо (а) Е ультрабочечно, либо (b) E бочечно и G локально вы-
выпукло. Пусть Т — произвольное топологическое пространство,
удовлетворяющее первой аксиоме счетности. Множество £Г ото-
отображений произведения ЕхТ в G равностепенно непрерывно в
том и только в том случае, когда выполняются следующие ус-
условия:
A) для каждого mgJ и каждого t^T xb—>u(x,t\ есть
линейное непрерывное отображение пространства Е в G;
B) для каждого х^Е множество отображений t\—>u(x, I)
{и е 5Г) равностепенно непрерывно в каждой точке простран-
пространства Т\
C) для каждой пары (x,t)^ ЕхТ множество {u(x,t):
и е &~\ ограничено в G.
Доказательство. Необходимость очевидна, причем без
всяких особых ограничений на Е, G или Г.
Докажем достаточность. Начнем со следующего наблюдения.
Если Р — топологическое пространство, удовлетворяющее первой
аксиоме счетности, G — равномерное пространство и #"—мно-
#"—множество отображений пространства Р в G, то ST равностепен-
равностепенно непрерывно в заданной точке р^Р тогда (и только тогда),
когда для каждой последовательности рп-+р множество суже-
сужений отображений и е У на множество {р, ри Ръ - - •} равносте-
равностепенно непрерывно в точке р. Применяя это наблюдение к Р =
= ЕхТу мы видим, что достаточно рассмотреть случай, когда
пространство Т компактно. В этом случае условия B) и C)
влекут ограниченность в G множества
Sx = {u(xJ): t<=Tiuz-P'}
при каждом х е Е. Действительно, в силу B) каждой точке
/еГ соответствует такая ее открытая окрестность Nu что
u(x,t) — u(x,t')^W при t'^Nu где W — заданная уравнове-
уравновешенная окрестность нуля в G. Так как Т компактно, то можно
так выбрать точки t\ (l^Ci-*Cn) в Г, чтобы Nti покрывали Г.
В силу C) множество
{и{х, t): t = tt (I <
ограничено в G и потому содержится в kW для некоторого
Но тогда Sxcz(k-{-l)W. Отсюда следует, что множество Sx огра-
ограничено в G, что и требовалось доказать.
В силу условия A) и теоремы 7.1.3 множество линейных
отображений х\->и(х, t) (t ^Tfu^@~) равностепенно непре-
непрерывно. Таким образом, для любой окрестности нуля W в G и
7.2. Некоторые приложения и примеры 639
произвольной пары (xOi t0)^ ЕхТ существует такая окрестность
U ТОЧКИ Х0, ЧТО
и(х, /) — u(xq, t)ezW
при MGf и /g?1. Еще раз используя B), получаем, что суще-
существует окрестность N точки t0, для которой
и(х0, t)—u(x0, /0)е W
при MGf h^eJV. Но тогда
при «Gf, t^N, ^еУ, чем и завершается наше доказатель-
доказательство. |
7.2. Некоторые приложения и примеры
Приведем несколько непосредственных приложений резуль-
результатов § 7.1.
7.2.1. Пример. Начнем с небольшой Теоремы, которая будет
для нас шагом на пути к теореме 8.2.2, служащей ее обобще-
обобщением.
Пусть Е — произвольное полунормированное векторное про-
пространство и А— слабо ограниченное подмножество в Е, т. е.
sup | х'(х) |< + оо
для каждого х' ^Е\ Тогда множество А ограничено, т. е. огра-
ограничено числовое множество р(А), где р — полунорма, опреде-
определяющая топологию пространства Е.
Действительно, заметим, что Ег есть банахово пространство
с замкнутым единичным шаром S, представляющим собой мно-
множество тех х', для которых
\х'{х)\<р{х) (хе£).
В силу теоремы Хана — Банаха
/>(*)= sup U'(x)|. G.2.1)
Каждый элемент х&Е порождает на Ег непрерывную линейную
форму х' ь-> хг (х). В силу наших условий элементы множества А
порождают подмножество в Е", ограниченное в каждой точке.
Заменив в следствии 7.1.2 Е на Е', получим, что указанный образ
множества А равностепенно непрерывен. В силу G.2.1) это озна-
означает, что множество р(А) ограничено.
Как уже было сказано, в теореме 8.2.2 будет доказано, что
слабая ограниченность эквивалентна ограниченности в любом
локально выпуклом пространстве.
640 Гл. 7. Принципы ограниченности
7.2.2. Пример. Вернемся к задаче C), поставленной в
п. 6.8.4 в связи с обсуждением одного результата, который ис-
использовался в качестве вспомогательного предложения при до-
доказательстве теоремы 6.8.6.
Рассматриваются топологическое векторное пространство Е
и слабый базис Шаудера (еп) в Е. Наша задача доказать, чт«
► Если пространство Е бочечно и ряды
2 <(*)«„ G-2.2)
слабо сходятся к х для каждого х е Е, то они сходятся
к х в исходной топологии в Е.
Доказательство. Воспользуемся теоремой 7.1.3, положив
в ней F = E и
ия(х)=
ТП=\
Если пространство Е полунормировано (и, значит, применим
пример 7.2.1), то из слабой сходимости ряда G.2.2) следует огра-
ограниченность последовательности (ип(х)) при каждом х^Е.
Однако, забегая вперед, можно воспользоваться теоремой 8.2.2,
в которой доказывается, что в любом локально выпуклом про-
пространстве каждое слабо ограниченное множество ограничено.
Тогда из теоремы 7.1.3 следует, что множество отображений
{ип} равностепенно непрерывно.
Если х принадлежит векторному подпространству ЕоаЕ,
порожденному векторами еП9 то очевидно, что ип(х)-+0 в исход-
исходной топологии.
Из слабой сходимости ряда G.2.2) к х следует, что Ео слабо
плотно в Е. Но тогда, согласно теореме Хана — Банаха, Ео
плотно в Е.
Пусть V — выпуклая окрестность нуля в Е. В силу равносте-
равностепенной непрерывности множества отображений {ип} существует
такая окрестность нуля U в Е, что un{U)ci-^V для всех п. Для
заданного элемента х&Е можно так выбрать точку х0 е Ео,
чтобы х — Xo&U и, значит, ип (х) е ип (х0) + у V для всех п.
Так как х0 е Ео, то ип (х0) е-^-У для всех п > п0. Следовательно,
ип(х)&; V при п > п0, откуда и вытекает сходимость ряда G.2.2)
к х в исходной топологии, что и требовалось доказать. |
7.2.3. Пример. Рассмотрим некоторые свойства коэффициен-
коэффициентов Фурье периодических функций вещественного переменного,
7.2. Некоторые приложения и примеры 641
принадлежащих различным функциональным пространствам.
В этом примере предполагается, что все функции имеют период
2я. Пространства Лебега &v строятся относительно сужения
меры Лебега на некоторый интервал длины 2я, скажем
(—я, +я). Если х — интегрируемая функция, то ее коэффи-
коэффициенты Фурье определяются равенством
x{t)e~intdt,
где п — любое целое число (положительное, отрицательное или
нуль).
Согласно знаменитой лемме Римана — Лебега,
lim x{n) = 0
\п\->оо
для х^З?1. Покажем, что это наилучший возможный результат
в следующем смысле.
► Пусть заданы такая последовательность положительных
чисел (ak), что lima^ = 0, и такая последовательность
(nk) целых чисел, что lim \nk\= +00. Тогда существует,
функция х^3?х, для которой
lim sup |ifa)l = + 00. G.2.3)
Фактически множество функций х, удовлетворяющих
условию G.2.3), есть нетощее множество в 9?х.
Допустим, что, какова бы ни была функция х^3?\ условие
G.2.3) не имеет места. Тогда
будет конечно и поэтому функция р будет полунормой на 5? \
причем во всяком случае полунеперывнои снизу. Но тогда в силу
следствия 7.1.2 функция р -непрерывна, т. е. существует такое
число с, что
для всех k и всех jte^1. Выбрав последовательность (хг) так,
чтобы N(xr)^C 1 и хг{п)-+\ при г->оо для каждого п, мы полу-
получим, что \/аи^с для всех k. А это противоречит условию
642 Гл. 7. Принципы ограниченности
lim ak = 0. Более сильное «категорное» утверждение анаЛОГИЧ-
й-^oo
ным образом получается из обобщения следствия 7.1.2, содержа-
содержащегося в теореме 7.5.1. |
Доказательство легко переносится со случая 2х на случай
<<)
► Если (ak) — такая последовательность положительных
чисел, что
ak = 0(nkUp/) (^->оо)>
то существует функция х е 3?v, для которой выполняется
G.2.3); совокупность таких функций х образует нетощее
множество в 9?v.
(Здесь р' определяется равенством 1—, = 1, причем р'=\
при р = оо и jt/=+oo при р=1.) Это утверждение служит как бы
противовесом к теореме Хаусдорфа — Юнга — Рисса, в котсрэй
утверждается, что если ^g^, l-^Cp-^2, то х е 1р\ т. е.
Таким образом, эта теорема в некотором смысле лучшая из
возможных.
Закончим этот пункт обсуждением следующей проблемы:
► Для каких последовательностей (сп)
S |с„*(и) |<+оо G.2.4)
для всех х
Рассмотрим сначала случай р=\. Очевидно, что условие
G.2.5)
достаточно. Что оно является также необходимым, легко полу-
получается, как и выше, применением следствия 7.1.2 к подходящей
последовательности {хг)а9?х.
Случай р>\ более сложен. Автору неизвестно никаких не-
необходимых и достаточных условий для этого случая, которые
были бы легко проверяемы. Следствие 7.1.2 показывает, что
справедливость G.2.4) для каждого x^.3Sv эквивалентна суще-
существованию такого числа &, что
21 ся*(л)| <*-#,(*) G.2.6)
7.2. Некоторые приложения и примеры 643
для х <= SB* (причем независимо от того, будет ли р > 1 или
нет). Пусть F — произвольное конечное множество целых чисел.
Положим
2 се™
Тогда из G.2.6) получаем, что
Njf {sF)<k, G.2.7)
т. е. множество функций sF ограниченно в Sp\ Можно показать
также, что G.2.6) эквивалентно следующему утверждению:
► Для любой последовательности 0П, удовлетворяющей
условию |0П|^1 для всех п, (Qncn) есть последователь-
последовательность коэффициентов Фурье некоторой функции из 9?р\
если р<+оо; если же р= + оо, то из G.2.6) следует,
что (Qncn) есть последовательность коэффициентов Фурье
некоторой меры.
Отсюда вытекает, что (cn) G /2 (ср. Зигмунд [2, т. II,
стр. 333]). Ясно, что, выбирая соответствующим образом х^З??,
можно с помощью G.2.6) показать, что
Но очевидно, что это неравенство далеко не является доста-
достаточным условием.
7.2.4. Пример. Приложения к теории суммирования. Вернемся
к вопросам, о которых шла речь в примерах 6.1.4 и 6.4.10, и по-
посмотрим, как принципы ограниченности помогают решить неко-
некоторые задачи, возникающие в теории суммирования. Мы будем
пользоваться обозначениями, введенными в упомянутых при-
примерах.
Естественно поставить следующий вопрос: каким необходи-
необходимым и достаточным условиям должна удовлетворять матрица
Л, чтобы она переводила сходящиеся последовательности в схо-
сходящиеся последовательности (т. е. чтобы с а С (А)) или чтобы
она переводила сходящиеся к нулю последовательности в после-
последовательности, также сходящиеся к нулю (т. е. чтобы соаСо (А))?
В первом случае интересно также знать, когда сохраняются пре-
пределы при преобразовании, определяемом матрицей А. Ответы на
эти и другие подобные вопросы известны (Кук [1]).
Для решения этих вопросов можно плодотворно использовать
принципы ограниченности. Исследуем условия, при которых
со с: Со (Л). Докажем следующие предложения.
644 Гл. 7. Принципы ограниченности
► A) Для того чтобы матрица А преобразовывала каждую
сходящуюся к нулю последовательность в ограниченную
последовательность, т. е. чтобы CoczB(A), необходимо
и достаточно, чтобы
sup 2| Л (m, /i)|< + оо. G.2.10)
m n
В этом случае А переводит каждую ограниченную после-
последовательность в ограниченную последовательность, т. е.
1°°аВ(А), и
IIиа (х) Поо < const IUIU (а: е /°°).
► B) Чтобы матрица А переводила каждую сходящуюся к
нулю последовательность в последовательность, сходя-
сходящуюся к нулю, т. е. чтобы cocz Co (А), необходимо и до-
достаточно, чтобы А удовлетворяла условию G.2.10) и
чтобы, кроме того,
НтЛ(т, /i) = 0 (n= 1, 2, ...). G.2.11)
m
Доказательства. Что касается утверждения A), то оче-
очевидно, что G.2.10) влечет включение l°°czB(A) и неравенство
\\иА(х) lloo^ const ||л;||оо для хе/°°. Обратно, предположим, что
cocz В (А), так что иА отображает с0 в /°°. Тогда
QA,m(x) = sup 2 A(m, n)x(n)
k n^k
конечно для любого m и любого х <= с0. Ясно, что qAi m есть полу-
полунепрерывная снизу полунорма на с0 и потому (следствие 7.1.2)
непрерывна. Отсюда получаем, что отображение д:i—>иА(х) (ш)
непрерывно для каждого т. Так как иА(х) по условию принад-
принадлежит /°°, то в силу этого же следствия отображение
*|—>sup | иА(х)(т) | непрерывно на с0, поэтому
m
sup
i A(m, n)x(ri)\<L const|| x\
для х ^ с0. Отсюда вытекает G.2.10).
Необходимость отношений G.2.10) и G.2.11) для утвержде-
утверждения B) очевидна. Обратно, если эти условия выполняются, то
иА непрерывно отображает с0 в /°°, и иА(х) принадлежит с0, если
последовательность х финитна (обладает конечным носителем).
Множество таких х плотно в с0, а с0 замкнуто в /°°, поэтому иА
отображает Со в с0, что и требовалось доказать. |
Интересно отметить (в дальнейшем н^м это понадобится)
одну характеризацию представимости линейных отображений
пространства /°° в себя с помощью матриц.
7.2. Некоторые приложения и примеры 645
► C) Для того чтобы линейное отображение и простран-
пространства 1°° в себя имело вид и — иА, где А — некоторая мат-
матрица, необходимо и достаточно, чтобы отображение и
было непрерывно в слабой топологии в а(/°°, Iх).
Доказательство. Если и — иА для некоторой матрицы Л,
то выполняется G.2.10). Тогда если у = и(х) hse/1, to
2 У {ш) s (пг) = 2 s (т) 2 А (т, п) х (п) = 2 х (п) t (n)9
m m n n
где
^(я) = 2Л(т, ri)s(m).
m
Но в силу G.2.10)
-2ls(m)l2li4(m, n)l<const2|s(m)|,
m /г т
т. е. /е/1. Таким образом, непрерывность отображения иА в
топологии g(/°°, Z1) доказана.
Обратно, предположим, что и непрерывно в этой топологии.
Так как каждое хе/°° можно записать в виде х = 2 # (^)^rt>
где ряд сходится в топологии а(/°°, Z1), то
п
где ряд сходится,в том же смысле. В частности,
и (х) {ш) = ^х (п) • и {еп) (ш) == 2 А (т, я) х {п\
п п
где
Л(т, п) = и(еп)(пг).
Итак,
чем утверждение C) и доказано. |
В примере 6.1.4 мы ввели топологию ТА, относительно кото-
которой отображение иА пространства В (А) в /°° (или С (А) в с, или
Со (Л) в Со) непрерывно. С другой стороны, в силу A), если иА
отображает пространство с0 в /°°, то иА непрерывно относительно
нормированных топологий (и также в силу C) относительно сла-
слабых топологий). Фактически всякий раз, когда па отображает
векторное подпространство Е пространства D(A) в векторное
подпространство F пространства CN и Е и F наделены линейны-
линейными топологиями некоторого весьма общего типа, отображение
иА: E-+F автоматически непрерывно. Точнее;
646 Гл. 7. Принципы ограниченности
► D) Пусть Е — векторное подпространство в D(A) и F —
векторное подпространство в CN, причем Е и F наделены
структурами топологических векторных пространств, удо-
удовлетворяющими следующим условиям:
(a) F отделимо, и каждое y^F является пределом
своих конечных сечений sky\
(b) E ультрабочечно, и его топология сильнее, чем
топология поточечной сходимости.
Тогда если иА (Е) с: F, то иА непрерывно отображает
Е в F.
Доказательство. В силу (Ь) и следствия 7.1.4 отображе-
отображение х\—>иА(х) (пг) непрерывно на Е для каждого т. Пусть
uk: E-+F (&=1,2,...)— отображение, определяемое й-м сече-
сечением элемента иА(х), tik{x)—skuA{x). В силу (a) lim uk = uA по-
поточечно в Е. Если Fk — подпространство в F, образованное теми
y^F, для которых y = sky (т. е. у(п)=0 при n>k), то Fu ко-
конечномерно и может быть наделено единственной отделимой
линейной топологией. Обозначим ее через Т. Топология Т совпа-
совпадает с топологией, определяемой любым тотальным множеством
линейных форм на Fk, например линейными формами у*—^у(т)
(пг= 1, 2,..., k). В силу предварительных замечаний uk непре-
непрерывно относительно топологии Т. С другой стороны, так как F
отделимо, то топология Т должна совпадать с топологией, ин-
индуцированной топологией пространства F. Таким образом, uh
непрерывно отображает Е в F. Используя опять тот факт, что
пространство £ ультрабочечно, получаем, что поточечный предел
иА последовательности (uk) есть непрерывное отображение
(а также, что множество отображений {uk} равностепенно непре-
непрерывно), что и требовалось доказать. |
Замечание. Если дополнительно потребовать, чтобы F
было локально выпуклым, то достаточно предполагать, что в (а)
Shy*->y слабо в Z7, а в (Ь) — что пространство Е бочечно. Дей-
Действительно, если F локально выпукло, то из слабой сходимости
sky к у следует (теорема 8.2.2) ограниченность последователь-
последовательности sky в F. Таким образом, совокупность отображений uh
ограничена в каждой точке, и предыдущие рассуждения про-
проходят. К тем же самым заключениям приводят и некоторые дру-
другие ограничения, налагаемые на Е и F (упр. 7.4). Для случаев,
когда Е и F — банаховы пространства, сходные результаты были
получены Целлером [3].
Приведем еще одно приложение принципов ограниченности.
Покажем, что для широкого класса методов суммирования,
включающего и обычные, существуют неограниченные последо-
последовательности, которые можно преобразовать в сходящиеся.
7.2. Некоторые приложения и примеры 647
► E) Пусть Af (i'=l, 2, ...)—матрицы, для которых
lim Ai(mt n) существует и конечен G.2.12)
m
(/, «=1, 2, ...)
и
lim sup Л, (от, л) = 0 (/=1,2,...), G.2.13)
п m
Тогда пространство С(Аи Л2,♦ ..) содержит неограни-
неограниченные последовательности.
Доказательство. Мы будем пользоваться обозначениями
примера 6.1.4. Положим К = Ка1 П Кл2 П ••• • Если К конечно, то
утверждение тривиально, так как тогда С=С(А\9А2, ...) содер-
содержит всякую последовательность, обращающуюся на К в нуль.
Предположим, что К бесконечно. Пусть С* — множество тех
х е С, которые равны нулю вне К. В силу A) и B) и заключи-
заключительных замечаний примера 6.1.4 С есть пространство Фреше
относительно топологии, индуцированной топологией Т =
= Т(Аи А2,.. .)> поэтому замкнутое подпространство С* в С
также является пространством Фреше относительно топологии
Т\С*, которая определяется полунормами
Кроме того, в силу G.2.12) еп s С* при я е /С, и можно выбрать
последовательность таких п, стремящуюся к бесконечности.
Предположим теперь, что Ccz/°°. Тогда функция IMU ко-
конечна для xg С*. Так как отображение x*-*-\x(n) | непрерывно
на С* для каждого п, то из следствия 7.1.2 вытекает, что полу-
полунорма XI—HML непрерывна на С*. Однако, согласно G.2.13),
qAlt m(en) = I At(m, n)\^at(n),
где lim a,-(ft) = 0, откуда
n
<lA.{er) = SViV\Ai{m» яI~>0 при /г->оо.
1 m
Итак, в этом случае еп-*0 в С*, и потому ||еЛЦоо-*0 при п^К,
стремящемся к бесконечности. Но это противоречит тому факту,
что 1кэт11оо = 1 для всех п. Полученное противоречие и доказывает
наше утверждение. I
Замечание. Если вместо G.2.12) предположить, что
lim Л,(га, л) = 0 (/, л= 1, 2, ...)•
m
то аналогичным образом можно показать, что С0(Ль А2,...) со-
содержит неограниченные последовательности. Это имеет место,
648 Гл. 7. Принципы ограниченности
например, если Аг — итерированные арифметические средние
или итерированные абелевы средние.
7.2.5. Пример. Совпадение классов слабо ограниченных и
равностепенно непрерывных множеств в пространстве, сопря-
сопряженном к бочечному, будет использовано сейчас для получения
одного результата, в свою очередь применяемого при исследо-
исследовании ограниченности решений дифференциальных уравнений
(см. следующий пример).
Пусть X — векторное пространство конечной размерности п,
и пусть (Ка) — некоторое семейство функций вещественного пе-
переменного t > О, принимающих значения в L (X, X), где L (X, X) —
пространство эндоморфизмов пространства X. Если в X выбран
некоторый базис, то каждый эндоморфизм /Са(/) представляется
в виде матрицы, ij-й элемент которой будет обозначаться через
Ka,ij{t). Предположим, что каждая функция Ка,ц интегри-
интегрируема по мере Лебега на интервале @, +°о).
Обозначим через С0([0, оо),Х) пространство непрерывных
векторных функций на [0, оо) со значениями в X, стремящихся
к нулю на бесконечности. Предположим, что
sup
а
а Но
J Ka(t)v(t)dt < + oo G.2.14)
II
для каждого феС0([0, оо), X), где через j /Са(^)ф(О^ обозна-
о
чен элемент из X, t'-я координата которого равна
/-10
В качестве нормы в неравенстве G.2.14) можно взять любую
норму в конечномерном векторном пространстве X. Для опре-
определенности возьмем норму, определенную равенством
где li — координаты вектора х относительно выбранного в X ба-
базиса. Соответствующей нормой на L (X, X) будет
ЦМЦ-sup S
где (Mfj) — матрица, представляющая эндоморфизм М.
Наша задача — показать, что из G.2.14) следует, что
оо
sup Г
G.2.15)
7.2. Некоторые приложения и примеры
649
Для этого рассмотрим С0([0, оо),Х) как банахово простран-
пространство с нормой
11Ф11= sup |
i,t>0
Тогда условие G.2.14) означает, что
со
sup sup У ( Ка, и (О Ф/ @ dt
a I , z
<+оо
G.2.16)
для каждого ф= (фь ..., <рп) из С0([0, оо), X). Далее для ка-
каждого а и каждого /
i о
есть непрерывная линейная форма, а условие G.2.16) означает,
что множество этих линейных форм, получающееся при измене-
изменении а и i, слабо ограничено. Отсюда следует, что это множество
линейных форм равностепенно непрерывно, т. е. существует та-
такое не зависящее от а и i число А, что
/ о
для всех i и всех а. Поскольку ф^- могут меняться независимо
друг от друга, можно заключить, что
для всех а и всех /. Итак,
/
i
для всех а, откуда и следует G.2.15). |
Замечание. Если предположить, что каждое Ка, и принад-
принадлежит ^'(О, оо) и G.2.14) выполняется для всякого ф с ф,- G
ei?p@, оо), l^i-^n, то имеет место аналогичный результат,
а именно
SUP j\\Ka(t)f dt <+oo.
650 Гл 7. Принципы ограниченности
7.2.6. Пример. Пусть X — то же, что и в предыдущем примере.
Рассмотрим Х-значные решения дифференциальных уравнений
и
С
It
А:
ф:
ib:
• = ,
[0,
[0,
[0,
-A{t)x
4(/)хН
00)-*
оо)->
оо)Х
: + Ф(
х,
t)
х),
X),
X.
G
G
.2.
.2.
17)
18)
где
Для простоты предположим, что каждая из функций Л, <р, \|) не-
непрерывна.
Следуя Беллману [1], покажем, что если для каждого
ф£ С0([0, оо), X) все решения уравнения G.2.17) ограничены,
то и все решения уравнения G.2.18) также ограничены при усло-
условии ограниченности функции я|).
Доказательство использует тот хорошо известный и легко
проверяемый факт, что решения уравнения G.2.17) имеют вид
0
где функция U: [0, оо)-> L(X, X) есть решение системы
-§-= Л (/)£/, £/@) = /
(/ — тождественный эндоморфизм пространства X). Из этого
факта и из наших предположений следует, что функция
О
ограничена по />0 для каждого фб5 С0([0, оо), X). Далее из
предыдущего примера вытекает, что
t
sup J I С/ (О С/ (О II Л' = С < + оо. G.2.19)
Возвращаясь к уравнению G.2.18) и полагая x(t) = U(t)y(t),
получаем, что у удовлетворяет уравнению
7.3. Борнологические пространства 651
Следовательно, любое решение х уравнения G.2.18) удовле-
удовлетворяет соотношению
t
x(t)=U (t) у @) + J U (t) U (Г)'1 У (f, x (f)) dt' =
0
t
= U (t) x @) + [ U (t) U (tTl У (Г, x (П) dt'.
о
Теперь U(t)x@)y являясь решением уравнения G.2.17) с
Ф = 0, по условию ограничено при t^-О. Кроме того, если
H(t9x(t))\\ < при />0,
то в силу G.2.19)
It || t
f U {t) U (t')~l Ф (f, х (О) df < m [ I U (t) U (tT1 II dt' ^mC,
J II J
о II о
откуда вытекает, что решение x(t) ограничено при />0, что и
требовалось доказать. |
7.3. Борнологические пространства
Определение борнологических пространств напоминает опре-
определение бочечных и инфрабочечных пространств, приведенное
в § 6.2. Локально выпуклое пространство Е называется борноло-
гическим, если каждое выпуклое уравновешенное множество
А а Еу поглощающее каждое ограниченное подмножество в Е,
является окрестностью нуля в Е. Читатель может заметить, что
такое А не является бочкой, так как А может и не быть замк-
замкнутым; с другой стороны, предполагается, что А поглощает ка-
каждое ограниченное множество, а не только каждое одноточечное
множество. Известно, что существуют бочечные пространства,
не являющиеся борнологическими (см. замечание C) после тео-
теоремы 7.3.3); с другой стороны, теорема 7.3.2 приводит к при-
примерам борнологических пространств, которые не являются бо-
бочечными. Однако из следствия 7.4.2 вытекает, что всякое полное
борнологическое пространство бочечно. Отсюда немедленно сле-
следует, что всякое борнологическое пространство инфрабочечно.
Часть B) приводимой ниже теоремы представляет собой тре-
третий принцип ограниченности.
7.3.1. Теорема. A) Локально выпуклое пространство Е борно-
логично тогда и только тогда, когда каждая ограниченная полу-
норма на Е (т. е. полунорма, ограниченная на каждом ограни-
ограниченном подмножестве в Е) непрерывна.
652 Гл. 7. Принципы ограниченности
B) Пусть Е— борнологическое и F — произвольное локально
выпуклое пространство. Если £Г— сильно ограниченное множе*
ство линейных отображений пространства Е в F, то &~ равно-
равностепенно непрерывно. То же самое заключение справедливо, если
Е инфрабочечно и каждое отображение из ЗГ непрерывно (ср. с
теоремой 7.1.1 C)).
Доказательство. A) Пусть пространство Е борноло-
гично и р — ограниченная полунорма на Е. Тогда множество
А = {х^ Е: р(х)^С1} выпукло, уравновешено и поглощает ка-
каждое ограниченное множество. Следовательно, А — окрестность
нуля, и потому полунорма р непрерывна. Обратно, если множе-
множество А обладает всеми указанными свойствами, то его функ-
функционал Минковского р есть ограниченная полунорма. Ее непре-
непрерывность означает, что А (которое во всяком случае содержит
множество {х^Е: р(х)< 1}) есть окрестность нуля.
B) Для доказательства утверждения B) нужно применить
определение борнологического пространства к множеству
где V — произвольная выпуклая уравновешенная окрестность
нуля в F; утверждение, что множество $Г сильно ограничено,
означает, что множество Л, которое заведомо ограничено и урав-
уравновешено, к тому же поглощает каждое ограниченное подмноже-
подмножество в Е. Вторая часть утверждения следует из того наблюдения,
что если каждое отображение из ЗГ непрерывно, то Л — бочка. |
Замечания, (а) Для того чтобы ЗГ было сильно ограни-
ограниченным, достаточно, чтобы выполнялось следующее условие.
C) Какова бы ни была последовательность хп-^0 в Е и по-
последовательность ип&&~, последовательность ип(хп) ограни-
ограничена в F.
Действительно, предположим, что C) выполняется. Если
множество ЗГ не является сильно ограниченным, то в £ суще-
существует такое ограниченное множество В, что множество
{и(х): j:gB,me ЗГ} неограничено в F. Но тогда существуют та-
такие последовательности уп^В и апе£Г, что последователь-
последовательность ип(уп) неограничена в F, и затем такая последователь-
последовательность чисел Яп-^0, что Кп^п(Уп) все еще неограничена в F. По-
Полагая хп = 'КпУп, мы приходим к противоречию с условием C).
(Ь) Из B) вытекает следующее утверждение: если Е — бор-
борнологическое, a F — локально выпуклое пространство, то всякое
ограниченное линейное отображение и: E-+F непрерывно.
(Обратное утверждение справедливо и тривиально для любых
двух топологических векторных пространств Е и F.) Если про-
7.3. Борнологические пространства 653
странство F полно, а Е борнологично, то из предложения 1.10.9
следует, что LC(E,F) полно в сильной топологии. В частности,
если Е борнологично, то Е/ совпадает с пространством Е огра-
ограниченных линейных форм на Е. Связь между Е' и Е в общем
случае рассмотрел Сирота [1]. Он доказал, что Е' = Е тогда
и только тогда, когда топология Макки х) т(£, Е') борнологична.
Наш следующий шаг состоит в том, чтобы описать некото-
некоторые общие типы борнологических пространств.
7.3.2. Теорема. Всякое по лу мет ризу е мое локально выпуклое
пространство борнологично. Точнее, если Е — полуметризуемое
топологическое векторное пространство, то каждое уравновешен-
уравновешенное подмножество в Е, поглощающее каждую сходящуюся к
нулю последовательность, есть окрестность нуля.
Доказательство. Пусть множество А а Е удовлетворяет
условиям теоремы и U\ id U2 =>... — база- окрестностей нуля.
Если бы А не было окрестностью нуля, то отношение AzDrVn
было бы неверным для любого п и любого г > 0. Поэтому суще-
существовала бы такая последовательность хпфА, что xn^n^lUn.
Но тогда последовательность уп = пхп сходилась бы к нулю, а
А ее не поглощало. |
7.3.3. Теорема. A) Индуктивный предел борнологических
пространств есть борнологическое пространство.
B) Факторпространство борнологического пространства по
любому векторному подпространству есть борнологическое про-
пространство.
Доказательство. A) Пусть Е—индуктивный предел
борнологических пространств Е{ относительно отображений ср*.
Пусть АаЕ — выпуклое уравновешенное множество, погло-
поглощающее каждое ограниченное подмножество в Е. Тогда для
каждого i множество At = фГ{(Л) си Et выпукло и уравновеше-
уравновешено. Далее если В{ ограничено в Eh то фг(#г) ограничено в Е, а
потому поглощается множеством А и, следовательно, Вг- погло-
поглощается множеством А{. Значит, А{ есть окрестность нуля в Е{.
Но тогда А — окрестность нуля в Е.
B) Предположим, что пространство Е борнологично. Пусть
М—векторное подпространство в Е и f — естественное отобра-
отображение Е-+Е/М. Предположим, что А — выпуклое уравновешен-
уравновешенное множество, поглощающее ограниченные множества в Е/М.
Если BczE ограничено, то f(B) ограничено в Е/М. Поэтому
f(B)czXA при некотором X и, следовательно, BaKf-l(A), от-
См. п. 8.3.3. — Прим. перев.
654 Гл. 7. Принципы ограниченности
куда вытекает, что f~l(A)— окрестность нуля в Е. Но отобра-
отображение / открыто и f(f~l(A))cz: А. Таким образом, А — окрест-
окрестность нуля в Е/М. I
Замечания A) Последние две теоремы легко приводят к
примерам борнологических пространств, которые не являются
бочечными.
B) Можно доказать, что произведение П Et борнологиче-
i £= /
ских пространств есть борнологическое пространство, если про-
произведение К1 борнологично (Бурбаки [7, стр. 158, упр. 186]).
Поэтому (теорема 7.3.2) произведение счетного числа борноло-
борнологических пространств есть борнологическое пространство.
Вопрос о борнологичности пространства К1 рассматривался
давно (хотя, естественно, терминология использовалась другая).
Его связь с теорией меры была установлена и исследована
Уламом [1] и Макки [5]. Новый подход к этому вопросу был
недавно предложен Симонсом [1], который показал, что про-
пространство R7 борнологично тогда и только тогда, когда каждый
б-ультрафильтр на / тривиален (Ь-ультрафилътром на множе-
множестве / называется фильтр на /, устойчивый относительно счет-
счетных пересечений; фильтр на / называется тривиальным, если он
порождается каким-нибудь одноточечным подмножеством в /).
C) Борнологичность пространства CR(T) (пространства ве-
вещественных непрерывных функций на Г, наделенного тополо-
топологией локально равномерной сходимости) исследовалась Н а х-
бином [2] и Сиротой [1] (см. также Маховальд и
Гоулд [1]). Это же пространство (и его комплексный аналог)
исчерпывающе описано Уорнером [1], который установил
связь между свойствами пространства Т и следующими свой-
свойствами'пространства Cr(T): быть метризуемым, борнологиче-
ским, бочечным, инфрабочечным, полным, квазиполным, сепара-
бельным, пространством Фреше, пространством Монтеля, ре-
рефлексивным, полурефлексивным, ядерным, (DF)-пространством 1)
и т. п.
В предположении, что Т вполне регулярно, Н ахбин [2] и
Сирота [1] независимо друг от друга доказали, что:
a) CR(T) бочечно в том и только в том случае, если для
каждого некомпактного замкнутого множества S а Т суще-
существует такая функция f^CR(T)y что sup| f @1= °°;
m s
1) Локально выпуклое пространство Е называется (DF)-пространст-
(DF)-пространством, если оно обладает фундаментальной последовательностью ограничен-
ограниченных множеств и если каждое сильно ограниченное множество МпЕ\ яв-
являющееся счетным объединением равностепенно непрерывных множеств»
само равностепенно непрерывно. — Прим. перев.
7 3. Борно логические пространства 655
(b) CR (Г) борнологично тогда и только тогда, когда Т яв-
является Q-пространством в смысле Хьюитта (т. е. вещественно-
компактным пространством в терминологии Гильмана и
Джерисона [1, гл. 8]).
Можно построить пространство 7\ обладающее первым свой-
свойством, но не обладающее вторым; для него пространство CR(T)
бочечио, но не борнологично; это Т есть некоторое пространство
трансфинитных чисел.
D) Замкнутое векторное подпространстйо борнологического
пространства не обязательно борнологично (ср. п. 6.2.6). Дей-
Действительно, Бур баки [7, стр. 278, упр. 216] построил пример
бочечного борнологического пространства, обладающего замк-
замкнутым векторным подпространством, которое не является ин-
фрабочечным; это подпространство секвенциально полно и по-
потому (в силу следствия 7.4.2 (d)) не может быть борнологиче-
ским (см. также Кёте [5, гл. V]).
7.3.4. Приложение. В силу теоремы 7.3.3A) и § 6.3 простран-
пространства Ж(Т) в теории интегрирования и S)m(Q) (O^Cm^Loo) в
теории распределений являются борнологическими.
7.3.5. Борнологические пространства и индуктивные пределы.
Из теорем 7.3.2 и 7.3.3A) следует, что индуктивный предел
нормируемых пространств является борнологическим. Рассмо-
Рассмотрим теперь частичное обращение этого утверждения.
Пусть (E,t)—произвольное локально выпуклое простран-
пространство, a (Bi)— такое семейство выпуклых уравновешенных огра-
ограниченных подмножеств в Е, что каждое ограниченное подмно-
подмножество в Е поглощается каким-нибудь Вг. Рассмотрим векторное
подпространство
Его можно считать полунормированным пространством, в кото-
котором множества гВ{ (s > 0) образуют базу окрестностей нуля
(см. лемму 6.5.2). Если Е отделимо, то £г- номировано. Далее
если Bi секвенциально полно (в топологии t), то и Е{ полно.
Обозначим через f{ вложение Е{ в Е. Если Ег наделяется только
что описанной полунормированной топологией tiy то fi непрерыв-
непрерывно (поскольку множество В{ /-ограничено). Таким образом,
можно рассмотреть пространство (Е, ?)—индуктивный предел
пространств (Eiy t{) относительно вложений fi. Ясно, что топо-
топология t слабее топологии tr\ в самом деле, так как множество В{
/-ограничено, любая ^-окрестность нуля U в Е содержит множе-
множество efl» для некоторого е > 0, поэтому U П Ег есть ^-окрестность
нуля для каждого и
656 Гл. 7. Принципы ограниченности
Легко видеть, что если топология / борнологична !), го / и
/' совпадают. Действительно, пусть V—произвольная ^-окрест-
^-окрестность нуля. Тогда для каждого / найдется такое а* > 0, что
V П Е{ zd щВг. С другой стороны, если В /-ограничено, то суще-
существуют такой индекс i и такое А, > 0, что BczXBi и, следова-
следовательно, В с: Xa{~xV. Таким образом, V поглощает каждое /-огра-
/-ограниченное множество. Окрестность V можно считать выпуклой и
уравновешенной, и так как пространство (Е, /) борнологично по
условию, то V есть /-окрестность нуля. Итак, топология f слабее
топологии /, и, значит, топологии / и /' совпадают.
Читатель может заметить, что из предыдущих рассуждений
вытекает, что независимо от того, борнологично ли (Е, /) или
нет, подмножество в Е является /-ограниченным тогда и только
тогда, когда оно /'-ограничено.
Таким образом, мы получили следующий результат.
► Всякое борнологическое пространство Е является вну-
внутренним индуктивным пределом полу нормируемых про-
пространств {нормируемых, если Е отделимо, полных полу-
полунормируемых, если Е секвенциально полно, и банаховых,
если Е отделимо и секвенциально полно).
7.4. Некоторые результаты о секвенциально полных
и квазиполных пространствах
Говорят, что топологическое векторное пространство Е сек-
секвенциально полно (соотв. квазиполно), если в Е каждая после-
последовательность Коши сходится (соотв. каждое ограниченное
замкнутое подмножество в Е полно). Так как каждая после-
последовательность Коши ограничена, то всякое квазиполное тополо-
топологическое векторное пространство секвенциально полно. Обрат-
Обратное утверждение неверно. Это видно на примере любого локаль-
локально выпуклого секвенциально слабо полного пространства Еу не
являющегося рефлексивным (скажем, на примере пространства
L1): если такое пространство наделить топологией о(Е,Е'), то
оно будет секвенциально полно, но не квазиполно, потому что
если х" — элемент из Е'\ не порождаемый элементом из Е, то
х" служит а (£", Е') -пределом ограниченной сети (хг) в Е, и
тогда (слабо) замкнутая выпуклая оболочка в Е множества
{xi} (слабо) ограничена и (слабо) замкнута, но не (слабо)
полна.
Из приводимого ниже результата вытекает важное свой-
свойство секвенциально полных пространств, лежащее в основе
дальнейших принципов ограниченности.
') То есть пространство (EJ) борнологично. — Прим. перед.
7.4 Некоторые результаты 657
7.4.1. Предложение. Пусть Е — топологическое векторное
пространство и Q — секвенциально замкнутое выпуклое подмно-
подмножество в £, такое, что для некоторого C > 0 выполняется соот-
соотношение
Q=3 [J{aQ: |a|<p}.
Пусть, далее, подмножество А а Е выпукло, уравновешено и сек-
секвенциально полно. Тогда если множество Q поглощает каждую
точку из А, то оно поглощает множество А.
Доказательство. Введем в рассмотрение пространство
ЕА, определенное в лемме 6.5.2. Это пространство полно и полу-
полунормировано, а потому бочечно.
Множества eQf)EA, где 8 > 0, образуют базу окрестностей
нуля некоторой локально выпуклой топологии t в ЕА. Так как
топология пространства ЕА сильнее, чем топология, индуциро-
индуцированная из Е, и Q секвенциально замкнуто в £", то t обладает
базой окрестностей нуля,- состоящей из множеств, замкнутых
относительно полунормированной топологии в ЕА. Таким обра-
образом (теорема 6.2.1 B)), топология t слабее полунормированной
топологии. В частности, QdEA есть окрестность нуля в ЕА, т. е.
QDEA =э сА при некотором с > 0, и потому Q поглощает А. |
7.4.2. Следствие. Пусть Е — произвольное секвенциально пол-
полное топологическое векторное пространство.
(a) Если множество QaE секвенциально замкнуто, вы-
выпукло, уравновешено и поглощающе, то оно поглощает каждое
ограниченное выпуклое уравновешенное подмножество в Е.
(b) Всякая бочка в Е поглощает каждое ограниченное вы-
выпуклое уравновешенное подмножество в Е.
(c) Если Е инфрабочечно, то оно бочечно.
(d) Если Е борнологично, то оно бочечно.
Доказательство, (а) Пусть АаЕ—ограниченное вы-
выпуклое уравновешенное множество. Тогда его замыкание А есть
ограниченное выпуклое уравновешенное секвенциально полное
множество. В силу предложения 7.4.1 Q поглощает А, а зна-
значит, и А.
(b) Это утверждение тривиально следует из (а).
(c) Пусть Е инфрабочечно и, значит, локально выпукло.
Тогда в силу (Ь) всякая бочка в Е поглощает каждое ограни-
ограниченное множество и потому в силу инфрабочечности Е является
окрестностью нуля, т. е. Е — бочечное пространство.
(d) Следует из (с), поскольку всякое борнологическое про-
пространство инфрабочечно. I
Следствие 7.4.2 позволяет установить еще два принципа огра-
ограниченности.
658 Гл. 7. Принципы ограниченности
7.4.3. Теорема. Пусть Е и F — локально выпуклые простран-
пространства, причем Е секвенциально полно и инфрабочечно и Ф~ — мно-
множество непрерывных линейных отображений пространства Е в
F, ограниченное в каждой точке пространства Е. Тогда вГ равно-
равностепенно непрерывно.
Доказательство. В силу следствия 7.4.2 (с) это утвер-
утверждение есть частный случай теоремы 7.1.3. |
Замечание. Сравнивая приведенную теорему с теоремой
7.3.1 B), мы видим, что дополнительное условие секвенциальной
полноты, которому удовлетворяет £, позволяет ослабить требо-
требования, предъявляемые к £Г, а именно заменить сильную ограни-
ограниченность на ограниченность в каждой точке.
Для (лишь) секвенциально полных пространств Е справед-
справедлив более слабый принцип ограниченности.
7.4.4. Теорема. Пусть Е — секвенциально полное локально вы-
выпуклое пространство, F — локально выпуклое пространство и
£Г — множество непрерывных линейных отобраокений Е в F.
Если &~ ограничено в каждой точке, то оно сильно ограничено,
т. е. множество £Г(В)={и{х)\ и^@~,х^В} ограничено в F
для всякого ограниченного подмножества В в Е. В частности,
каждое слабо ограниченное подмножество в Ег сильно ограни-
ограничено.
Доказательство. Пусть V — произвольная замкнутая
выпуклая уравновешенная окрестность нуля в F. Рассмотрим
множество /С= П {u~l(V): «Ef}. Достаточно показать, что К
поглощает любое заранее заданное 'ограниченное подмножество
ВаЕ. Так как #" ограничено в каждой точке, то множество К
поглощающе. Из непрерывности каждого и е ЗГ следует, что
множество К замкнуто. Оно является также выпуклым и урав-
уравновешенным, так как V обладает этими свойствами. Таким об-
образом, К—бочка в Е. Из следствия 7.4.2 (Ь) вытекает, что К
поглощает каждое ограниченное подмножество в Е, что и тре-
требовалось доказать. |
Замечание. Сильная ограниченность подмножества &~ в
Lr(E,F), определенная указанным в формулировке теоремы
образом, равносильна ограниченности £Г относительно сильной
топологии в LC(E,F). Напомним, что по определению (п. 1.10.8)
эта топология обладает базой окрестностей нуля, состоящей из
множества вида
W(B,V)={ue=Lc(E,F): u{B)c=lV),
где В пробегает ограниченные подмножества в Е, а V — произ-
произвольную базу окрестностей нуля в F. Если F^=K (К—поле ска-
7.5. Принципы ограниченности 659
ляров), то Lc(£,J7) =£'. Сильная топология в Ег будет часто
встречаться в гл. 8, где она обозначается через р (£',£).
7.5. Принципы ограниченности для полных
полуметризуемых пространств
Рассмотрим некоторые вытекающие из результатов § 6.5
уточнения принципа ОГБК для пространства Фреше (след-
(следствие 7.1.2).
7.5.1 Теорема. Пусть F— полное полуметризуемое топологи-
топологическое векторное пространство, А — выпуклое ограниченное за-
замкнутое уравновешенное подмножество в F, и пусть для ка-
каждого п fn — полунепрерывная снизу функция на F, обладающая
следующими свойствами:
n (X) + fn (У), L (А,*) < fn (*),
если А, е/<", |А,|^1, х, y^F и fn(x), fn(y) конечны.
Тогда либо
(a) при некотором п функция fn конечна и непрерывна на F^
либо
(b) fn(x) = + oo для всех п и всех х, принйдлежащих мно-
множеству SczFy такому, что F\S тоще1) в F.
Аналогично либо
(а7) множество fn(A) ограниченно для некоторого п,
либо
(Ь7) для некоторого #еЛ, fn(x) = +oo при всех п.
Доказательство. Утверждения (а) и (Ь) следуют из
теоремы 6.5.1, а утверждения (а7) и (I/) — из теоремы 6.5.3.
Проведем доказательство для случая первой пары.
Рассмотрим множество Fn = {x^ F: fn(*)<+oo}. Оно яв-
является векторным подпространством в F. Определим топологию
в Fn с помощью метрики d(x,y)+fn(x — y), где d — метрика,
определяющая топологию в F\ при этом вложение ип: Fn-+F
становится непрерывным. Так как функция fn полунепрерывна
снизу, то пространство Fn полно. Применим теперь теорему 6.5.1,
полагая в ней E = F и и равным тождественному отображению.
Тогда если (Ь) не выполняется, то существует такое /г, что
F = un(Fn)=Fn и ип устанавливает топологический изоморфизм
между пространствами F и Fn, т. е. выполняется (а).
') В частности, само S нетоще в F.
660 Гл. 7. Принципы ограниченности
Доказательство дизъюнкции «(а') или (Ь')>> аналогично. |
Полезно сформулировать теорему 7.5.1 в «геометрическом»
виде.
7.5.2. Теорема. Пусть F и А— те же, что и в теореме 7.5.1.
Пусть Тп (/2=1,2,...) — ограниченные замкнутые выпуклые
уравновешенные подмножества в F. Тогда
оо
A) если (J Тп — поглощающее множество, то некоторое Тп
п= 1
есть окрестность нуля в F\
со
B) если (J Тп поглощает Л, то некоторое Тп поглощает А.
Доказательство. Положим
fn(x)=inf{r >0: х<=гТп),
причем будем считать fn(x) = + oo, если Тп не поглощает х.
Функции fn удовлетворяют условиям теоремы 7.5.1, и Тп =
= {лсе/7: fn(jcLl}. Если выполняется A), то (Ь) неверно и,
значит, выполняется (а), тогда Тп есть окрестность нуля. Ана-
Аналогичным образом если выполняется B), то (Ь7) неверно и, зна-
значит, верно (а7), а поэтому Тп поглощает А. В
7.6. Приложение теоремы 7.5.1 к суммированию
рядов Фурье
Предположим, что для каждой пары положительных целых
чисел (К j) определена последовательность чисел akj(n) (n =
= 0, ±1,...). Рассмотрим ряды Фурье периодических функций
(обозначения те же, что и в примере 7.2.3).
Для любого xgS71 положим
fki(x)= %akl(n)x(n) , G.6.1)
п
предполагая, что
%\akf(n)\<+oo G.6.2)
п
для каждой пары (&,/); пусть, кроме того,
*Н sup |/*,(*) |. G.6.3)
Может случиться так, что ahj(n) будет иметь вид sk(n)eltjn>
где sk(n) — суммирующие множители и ^- — некоторые точки
интервала-периода. В этом случае G.6.1) представляет резуль-
результат суммирования ряда Фурье функции х в точке tj с помощью
7.6. Приложение теоремы 7.5.1 661
заданного процесса суммирования. Обычно в этом случае
\\msk(n) = \ для каждого п и, следовательно,
Ит|аЛ/(л)|-1 G.6.4)
k
для каждого / и каждого п.
Мы хотим установить следующий результат.
► Предположим, что выполнены G.6.1) — G.6.3) и, главное,
что для каждой функции х, принадлежащей одновремен-
одновременно всем пространствам 9?? A^Ср<+оо), существует
такое j (возможно, зависящее от х), что
Ш<+оо. G.6.5)
Тогда существуют такое /, такое р A ^/? < +оо) и такая
функция у^сЗ?р'( (-—7=1), что для каждого п у(п)
есть предельная точка последовательности (akj(n))k=\, 2,....
Для доказательства заметим, что совокупность функций х,
удовлетворяющих «главному» предположению, образует полу-
метризуемое топологическое векторное пространство с тополо-
гией,определяемой полунормами Np (p пробегает любую после-
последовательность, стремящуюся к +оо, например р-—1,2,. ..). Ясно,
что каждая функция fj удовлетворяет условиям теоремы 7.5 1.
Так как «главное» предположение исключает случай (Ь) этой
теоремы, то справедливо (а). Это значит, что существуют такие
/ И /?, ЧТО
fi(x) ^const'Np(x),
т. е.
fkj(x)<const-Np(x),
где постоянная не зависит от k. В силу обращения неравенства
Гёльдера1), полагая
У kit =Sat/(n)e«
П
(/ фиксировано), получаем Np* (yk)^Cconst. Так как //>1, то
последовательность (yk) имеет слабую предельную точку
у^3?р , откуда и вытекает наше утверждение. 1
Если выполняется G.6.4), то таким способом можно дока-
доказать существование функции х, принадлежащей всем 9?v
A^/?<оо) одновременно, ряд Фурье которой расходится во
всех точках любого наперед заданного счетного множества.
Такие же рассуждения по существу без изменений мож-
можно применить к случаю рядов Фурье на любой компактной
1) См., например, упр. 7.2. — Прим. перев.
662 Гл. 7. Принципы ограниченности
абелевой группе и даже до некоторой степени на неабелевых
компактных группах. Возможны также обобщения, связанные
с рассмотрением других ортогональных систем функций.
7.7. Принципы ограниченности для билинейных отображений
Перенесем теперь внимание с линейных отображений одного
топологического векторного пространства в другое на билиней-
билинейные отображения произведения ExF двух топологических век-
векторных пространств в третье топологическое векторное простран*
ство G. При изучении таких отображений или их семейств также
оказываются полезными принципы ограниченности.
Пусть f — билинейное отображение произведения ExF в G.
Для х^Е и y^F обозначим через fx. элемент из L(F, G),
определенный правилом y*-*f(x,y), а через f.v элемент из
L(E, G), определенный правилом лсь->f(x, у). Важно делать раз-
различие между непрерывностью отображения / (рассматриваемого
как функция на ExF, т. е. как функция двух переменных) и
так называемой раздельной непрерывностью (непрерывностью
по каждой переменной в отдельности, когда другая переменная
фиксирована). Последняя означает, другими словами, что fx.
принадлежит LC(F,G) для каждого х е Е и fy принадлежит
Lc(£, G) для каждого y^F. Очевидно, что непрерывность вле-
влечет раздельную непрерывность.
Аналогичное различие существует между равностепенной
непрерывностью и раздельной равностепенной непрерывностью
применительно к некоторому множеству #" билинейных отобра-
отображений. Рассматриваемые нами принципы ограниченности часто
связаны с отношением между"этими двумя понятиями.
Прежде чем перейти к нашим основным результатам, сде-
сделаем два замечания. Первое из них представляет собой «поло-
«положительное» утверждение, а второе — «отрицательное» утвер-
утверждение о связи между равностепенной непрерывностью и
раздельной равностепенной непрерывностью.
Положительное утверждение. Хотя это утверждение и пред-
представляет собой частный случай более общих результатов (в ча-
частности, теорем 7.7.3 и 7.7.8), его все же полезно рассмотреть
отдельно, поскольку оно позволяет делать заключения о били-
билинейных отображениях, исходя из свойств линейных отображе-
отображений. Помимо того, предположение полунормируемости рассма-
рассматриваемых пространств соответствует истории развития вопроса.
Тот факт, что оно здесь не по существу, нас пока не трогает.
Пусть топологии пространств £, F и G определены с по-
помощью полунорм /?, q и г соответственно, причем Е полно (и по-
потому бочечно), и пусть ЗГУ — семейство билинейных отображений
7.7. Принципы ограниченности для билинейных отображений 663
произведения ExF в G, Тогда если SF раздельно равностепенно
непрерывно, то оно равностепенно непрерывно. Фактически до-
достаточно лишь предположить, что A) для каждого y^F ото-
отображения f.y непрерывны на £ и B) для каждого х е Е множе-
множество {fx.: f^&~} равностепенно непрерывно на F.
Доказательство. Из условия B) следует, что
N(x) = sup{r[f(x, у)]: /е<^, ysf
конечно. Поэтому N — полунорма на Е. В силу A) полунорма
/V полунепрерывна снизу на Е. Так как Е бочечно, то N непре-
непрерывна (теорема 7.1.1 A)). А это» означает, что ЗГ равностепен-
равностепенно непрерывно на ExF. 1
Отсюда в качестве следствия вытекает, что всякое раздельно
непрерывное билинейное отображение f непрерывно (£, F и G
те же, что и выше).
Отрицательное утвеждение. Мы намереваемся показать, что
нет никаких надежд на то, что рассмотренное выше следствие
можно обобщить на любые пространства. Это покажет пример,
в котором Е будет бочечным пространством, F — пространством
Фреше, G — полем скаляров, а билинейная форма /, будучи раз-
раздельно непрерывной (и даже Е-гипонепрерывнсй в смысле, опре-
определяемом ниже), не будет непрерывной. Причиной этого, как мы
узнаем из теоремы 7.7.9, является неполуметризуемость про-
пространства Е.
Вот наш пример: возьмем Е = Ж^ (N) с топологией индук-
индуктивного предела (она описана в примере A) § 6.3; мы полагаем
Т равным множеству натуральных чисел N; индекс R означает,
что рассматриваются только вещественные функции на N, хотя
это ограничение роли не играет). В качестве F возьмем про-
пространство RN в топологии произведения. Оно есть пространство
Фреше. Роль G играет поле R вещественных чисел. Билинейную
форму определим равенством
S x(t)y(t).
Форма f является Е-гипонепрерывной, т. е. f(x,y)-*0 при
у-+0 равномерно по х, пробегающим любое ограниченное под-
подмножество в Е (поэтому тем более f(x,y) непрерывна по у при
каждом фиксированном х). Действительно, ограниченность мно-
множества А в Е (п. 6.6, B)) влечет существование такого натураль-
натурального числа п и такого числа с > 0, что x(t)=0 при t>n и
\x(t)\<c при всех /, причем это верно для всех х&А. Таким
образом, если задано р > 0, то \f(x,y)\<p при х^А и
^j \ y(t)\<CC1p. Это заведомо остается верным, если х^А и
664 Гл. 7. Принципы ограниченности
\y(t)\<p/nc при t^Cn. Множество V, состоящее из тех y^F,
которые удовлетворяют последним неравенствам, является
окрестностью нуля в F. Следовательно, неравенство \f(x,y)\<p
имеет место для х^А и у е 1/, что и означает £-гипонепрерыв-
ность формы /.
Остается показать, что форма f не является непрерывной на
ExF. В самом деле, допустим, что / непрерывна на ExF. Тогда
существуют окрестность нуля U в Е, конечное множество Н d N
и число р > 0, такие, что
S x(t)y(t) <1,
=N
если хе(/и \y(t) I < Р Для / е Н. Но тогда
| 2 x(t)y(t)\<p-4up\y(t)\
для всех xg[/ и всех i/eRN. Отсюда следует, что каждое
x^U равно нулю вне Я, что невозможно, так как // конечно
(поскольку U — окрестность нуля в Е). Таким образом, форма/
не является непрерывной. |
7.7.1. Гипонепрерывность. Приведенное выше отрицательное
утверждение показывает, что, даже если на Е и F наложены
какие-то ограничения, раздельная непрерывность, вообще говоря,
не влечет за собой непрерывности; в то же время оно указывает
на наличие некоего промежуточного свойства (гипонепрерыв-
ности), которое уже следует из раздельной непрерывности. При-
Приведем общее определение этого свойства.
Рассмотрим сначала одно билинейное отображение /: ЕХ
XF-+G. Легко проверяется, что следующие три условия экви-
эквивалентны.
(a) Для каждой окрестности нуля W в G и каждого ограни-
ограниченного множества А в Е существует такая окрестность нуля V
в F, 4Tof(AxV)a W.
(b) Образ каждого ограниченного множества А в Е относи-
относительно отображения x*—>fx. является равностепенно непрерыв-
непрерывным подмножеством в LC(F, G).
(c) Отображение y*—>f.y есть непрерывное отображение F в
LC(F,G), где пространство LC(F,G) наделено своей сильной
топологией.
Если какое-нибудь из этих условий (а поэтому и каждое из
них) выполняется, то говорят, что билинейная форма f является
Е-гипонепрерывной. Множество ЗГ билинейных отображений
произведения ExF в G называется равностепенно Е-гипонепре-
рывным, если условие (а) выполняется для каждого \^.$Г, при-
7.7. Принципы ограниченности для билинейных отображений 665
чем указанную там окрестность нуля V можно выбрать незави-
независимо от f e У.
Аналогичным образом можно определить F-гипонепрерыв-
ность и равностепенную f-гипонепрерывность.
Наконец, отображение f называется гипонепрерывным (соотв.
множество ЗГ называется равностепенно гипонепрерывным),
если 5Г является одновременно Е- и /^-гипонепрерывным (соотв.
равностепенно Е- и ^-гипонепрерывным).
7.7.2. Предварительные замечания. Ниже будет достаточно
формулировать предложения, касающиеся (той или иной) рав-
равностепенной гипонепрерывности множества &~, так как соответ-
соответствующие утверждения о (той или иной) гипонепрерывности
одного билинейного отображения f получаются как частный
случай при #" = {/}. .
Очевидно, равностепенная £-гипонепрерывность множества
£Г влечет равностепенную непрерывность множества {fx.: f^&~}
при каждом фиксированном х^Е. Следовательно, равностепен-
равностепенная гипонепрерывность множества $Г влечет его раздельную
равностепенную непрерывность. С другой стороны, также оче-
очевидно, что из равностепенной непрерывности множества У сле-
следует его равностепенная гипонепрерывность (отсюда гипо1)).
Далее если пространство Е полунормируемо, то равностепенная
^-гипонепрерывность эквивалентна равностепенной непрерыв-
непрерывности.
Несколько менее очевидны следующие утверждения.
► A) Если множество ЗГ равностепенно Е-гипонепрерывно
и А и В — ограниченные подмножества соответственно в
Е и F, то (а) У равностепенно непрерывно на AxF и
(b) U {f (А X В): f e &"} есть ограниченное подмноже-
подмножество в G.
► B) Если множество ЗГ равностепенно гипонепрерывчо,
то оно равностепенно равномерно непрерывно на Ах В,
где А и В — произвольные ограниченные подмножества
соответственно в Е и F.
Доказательства. Проверку утверждения A) предостав-
предоставляем читателю. Набросаем доказательство утверждения B).
Так как множество А—А ограничено в £, то для заданной
окрестности нуля W в G можно выбрать в Е и F соответственно
такие окрестности нуля U и V, чтобы f[(A—A)xV\aW и
f(UXB)cz W. Предположим, что х и х + а принадлежат Л, у и
у + Ь принадлежат S^eVhJgV. Тогда
, y + b)-f(x4 у) =f(x, b) +f(a, у) +/(а, b).
io (греч.) — под, внизу. — Прим. ред.
666 Гл. 7. Принципы ограниченности
Первый член справа содержится в W, так как (х, Ь) <=Лх1Л
и можно считать, что А содержит 0, так что А а А —А. Второй
член содержится в W, потому что (а, у)^ UxB. Третий член
также содержится в W, поскольку (a, b) e UxB. Таким образ-
зом, f(x + a,y + b) — f(x,y)<=W+W+W, a W+W+W— произ-
произвольно малая окрестность нуля в G. Таким образом, множе-
множество ST равностепенно равномерно непрерывно на АхВ. |
Обозначение. В дальнейшем нам понадобится одно обозна-
обозначение. Пусть &~— множество билинейных отображений произве-
произведения ExF в О. Через <£ГХ- мы будем обозначать множество
{fx.: f g= q?~} (x^E), а через <&~-у —множество {f.y: f^<&~}
(ye/7). Таким образом, <&~х. есть подмножество в L(F, G), и
о^.^ — подмножество в L(E, G).
Утверждение, что У раздельно непрерывно, т. е. что каждый
элемент f^&~ раздельно непрерывен, равносильно утвержде-
утверждению, что &~х a LC(F9 G) для каждого х е Е и 2Г.уа Lc(Ey G) для
каждого y^F. Аналогично раздельная равностепенная непре-
непрерывность множества ЗГ означает что^"Л. есть равностепенно не-
непрерывное подмножество в LC(F, G) для каждого х е Е и <&~.у
есть равностепенно непрерывное подмножество в Lc(Ey G) для
каждого у Ef.
Прежде чем переходить к подробному изложению дальней-
дальнейших результатов, имеет смысл остановиться на некоторых, так
сказать, «тактических» приемах, которые мы будем использо-
использовать. Исследование принципов ограниченности для билинейных
отображений не носит такого прямого характера, как в случае
линейных отображений. Наиболее сильная форма принципа, ко-
который мы имеем в виду, для линейных отображений звучит так:
«поточечная ограниченность влечет равностепенную непрерыв-
непрерывность» (теорема 7.1.3). Для билинейных отображений этот прин-
принцип лучше всего рассматривать как совокупность частных ре-
результатов, некоторые из которых являются вовсе не принципами
ограниченности, а скорее предложениями, устанавливающими
связь между различными видами равностепенной непрерывности
для соответствующих типов пространств. Теорема 7.7.3, предло-
предложение 7.7.4, теорема 7.7.5 и следствие 7.7.6 служат примерами
таких результатов. Комбинируя эти результаты с принципами
ограниченности для линейных отображений, можно получить
принципы ограниченности для билинейных отображений (см.,
например, теор. 7.7.7—7.7.9).
7.7.3. Теорема. Пусть F ультрабочечно (или бочечно, если G
локально выпукло). Если (a) &~x.cz LC(F, G) для каждого х^Е
и (Ь) 9~ у -Ь равностепенно непрерывное подмножество в LC(E, G)
7.7. Принципы ограниченности для билинейных отображений 667
для каждого у е F, то %Г — равностепенно Е-гипонепрерывное
множество.
Доказательство. Пусть W—произвольная окрестность
нуля в F и А — произвольное ограниченное подмножество в Е.
Можно считать, что W замкнуто, уравновешено и, кроме того,
выпукло, если G локально выпукло.
Если фиксирован элемент y^F, то из (Ь) следует, что в Е
существует такая окрестность нуля Uy, что f(x,y)^W для
x^Uy и f e У. Так как А поглощается окрестностью UUy то
существует такое X > 0, что
Следовательно, если положить
V(A9 W) = {ys=F: /(Л, y)czW для
то каждое множество V(A, W) будет в F поглощающим.
Кроме того, из (а) следует, что V(A, W) замкнуто в F. Итак,
V(A, W) уравновешено всегда и выпукло, если W выпукло.
Таким образом, если G локально выпукло, то каждое
V(A, W) есть бочка в F, а потому окрестность нуля в F, что и
означает, что ЗГ равностепенно £-гипонепрерывно.
Если же пространство G не локально выпукло, го замечаем,
что множества V(A, W) (где А и W переменны) образуют базу
окрестностей нуля некоторой линейной топологии / в F, причем
каждое из этих множеств замкнуто в F. Так как пространство F
ультрабочечно, то мы опять приходим к выводу, что каждое
V(A, W) есть окрестность нуля в Fy т. е. множество У равносте-
равностепенно £-гипонепрерывно. 1
Замечание. Если пространство Е полунормируемо, то из
указанной теоремы следует, что множество ST равностепенно не-
непрерывно. Вот обобщение того результата, о котором шла речь
вначале.
7.7.4. Предложение. Предположим, что Е, F и G — локально
выпуклые пространства, причем Е инфрабочечно. Если множе-
множество ST раздельно непрерывно и равностепенно Е-гипонепрерыв-
ноу то оно равностепенно гипонепрерывно.
Доказательство. Достаточно показать, что !Г равно-
равностепенно F-гипонепрерывно, т. е. что если В — ограниченное под-
подмножество в F и W — окрестность нуля в G, то множество
[/={хе£: f(x%B)d W для fe-Т}
668 Гл. 7. Принципы ограниченности
есть окрестность нуля в Е. Можно считать, что W — бочка в G;
тогда из раздельной непрерывности отображения / следует, что
U — бочка в Е. Далее так как SF равностепенно £-гипонепре-
рывно, то U поглощает ограниченные подмножества в Е, откуда
в силу инфрабочечности пространства Е вытекает нужный нам
результат. |
Замечания. Читатель может сравнить этот результат с
георемой 7.3.1 B) для линейных отображений. Как мы уже от-
отмечали, заключение предложения справедливо, если Е полунор-
полунормируемо, причем тогда F и G могут быть произвольными топо-
топологическими линейными пространствами.
Для линейных отображений предположения бочечности или
ультрабочечности области определения позволяют получать
сильнейшие возможные результаты, в данном случае — равно-
равностепенную непрерывность. Однако два предыдущих результата
говорят лишь о равностепенной гипонепрерывности. Наше отри-
отрицательное утверждение показывает, что в общем невозможно
получить более сильный результат. Оказывается, что при полу-
получении наиболее сильных результатов для билинейных отображе-
отображений существенна полуметризуемость, как видно из следующих
двух теорем.
7.7.5. Теорема. Пусть Е — полуметризуемое, a G — произволь-
произвольное топологическое векторное пространство, Т — топологическое
пространство, удовлетворяющее первой аксиоме счетности. Пред-
Предположим, что либо (а) Е ультрабочечно, либо (b) E бочечно и
G локально выпукло. Пусть &~ — множество таких отображений
произведения ЕхТв G, что отображение f.t: xt—>f(x,t) линейно
для каждого t еГ и каждого f e &~. Тогда если ST раздельно
равностепенно непрерывно, то оно равностепенно непрерывно.
Доказательство основано на теореме 7.1.5. Очевидно,
что условия A) и B) этой теоремы выполняются. Остается
только проверить, что £Г поточечно ограничено. Пусть (xq, t0) —
произвольная точка произведения ЕхТ. В силу равностепенной
непрерывности по х для произвольной окрестности нуля W в G
найдется такая окрестность нуля U в Е, что
f(x,to)(= W для хе= U и f е=#-.
Существует такое число X, что xo^XU, поэтому
f(x0, to)e=:XW для [eJ.
Отсюда следует, что множество {/(*о, ^о): f e &"} ограничено в
G, что и требовалось доказать. 1
7.7.6. Следствие. Пусть Е и F — полу мет ризу емые топологи-
топологические векторные пространства и G —топологическое векторное
7.7. Принципы ограниченности для билинейных отображений 669
пространство. Предположим, что либо (а) Е — ультрабочечно,
либо (Ь) Е бочечно и G локально выпукло. Тогда если &~ — раз-
раздельно равностепенно непрерывное множество билинейных ото-
отображений произведения ExF в G, то оно равностепенно непре-
непрерывно.
Доказательство непосредственно вытекает из теоре-
теоремы 7.7.5. |
Замечание. Если предположить, что F полунормируемо,
то можно не требовать, чтобы Е было полуметризуемым; заклю-
заключение следует тогда из теоремы 7.7.3, если в ней поменять ме-
местами Е и F.
Теперь у нас достаточно предварительных сведений, чтобы
перейти к принципам ограниченности для множеств билинейных
отображений.
7.7.7. Теорема. Предполооюим, что либо (а) Е и F ультра-
бочечны, либо (Ъ) Е и F бочечны и G локально выпукло, тогда
если $Г — раздельно непрерывное и поточечно ограниченное мно-
множество, то оно равностепенно Е-гипонепрерывно.
Доказательство. Воспользуемся теремОй 7.7.3. Доста-
Достаточно проверить, что ЗГ.У есть равностепенно непрерывное под-
подмножество в LC(E, G) для каждого y^F. Но это следует из по-
поточечной ограниченности в силу теоремы 7.1.3. |
7.7.8. Теорема. Предположим, что Е и F бочечны и G локаль-
локально выпукло. Тогда если $Г — раздельно непрерывное и поточеч-
поточечное ограниченное множество, то оно равностепенно гипонепре-
рывно.
Доказательство следует из теоремы 7.7.7 и предложе-
предложения 7.7.4. 1
Еслц добавить к нашим предположениям полуметризуемость,
то получится принцип ограниченности в «сильной» форме, а
именно
7.7.9. Теорема. Предположим, что Е it F полуметризуемы и
ультрабочечны (или бочечны, если G локально выпукло). Тогда
если SF — раздельно непрерывное и поточечно ограниченное мно-
множество, то оно равностепенно непрерывно.
Доказательство. Достаточно воспользоваться теоремой
7.1.3, которая от поточечной ограниченности позволяет перехо-
переходить к раздельной равностепенной непрерывности, и следствием
7.7.6. 1
Замечание. Теорема остается справедливой (при тех же
ограничениях на #~), если Е ультрабочечно (или бочечно при
670 Гл. 7 Принципы ограниченности
локально выпуклом G) и F полунормируемо и полно. Это также
следует из теоремы 7.7.3, если в ней поменять местами Е и F.
7.7.10. Пределы сходящихся последовательностей билинейных
отображений. Так же как в случае линейных отображений (см.,
например, следствие 7.1.4), с помощью принципов ограничен-
ограниченности можно устанавливать непрерывность того или иного вида
для пределов поточечно сходящихся последовательностей (или
поточечно ограниченных сходящихся сетей) билинейных отобра-
отображений. Случай последовательностей проще лишь в том отноше-
отношении, что поточечная сходимость последовательности влечет ее
поточечную ограниченность. Тем не менее мы ограничимся рас-
рассмотрением только этого случая.
Пусть (fn)—поточечно сходящаяся последовательность раз-
раздельно непрерывных билинейных отображений произведения
ExF в G. Очевидно, что предел / этой последовательности есть
билинейное отображение произведения ExF в G. Каждый из
результатов 7.7.6—7.7.9 приводит к утверждению о непрерыв-
непрерывности предела / при соответствующих условиях на Е и F. Мы не
намерены перечислять все возможные теоремы. Достаточно за-
заметить, что, например, / будет непрерывным по совокупности
переменных, если выполнены условия теоремы 7.7.9. Если же
имеют место условия теоремы 7.7.7, то / будет £-гипонепре-
рывным.
7.7.11. Случай индуктивных пределов. Для билинейных ото-
отображений существует аналог теоремы 6.3.2.
Предположим, что Е {соотв. F) — индуктивный предел про-
пространств Ех (соотв. Fj) относительно отображений q^ (соотв. i|)j),
G— произвольное локально выпуклое пространство и f — би-
билинейное отображение произведения ExF в G. При этих усло-
условиях для непрерывности отображения f необходимо и достаточ-
достаточно, чтобы для каждой пары индексов (i, j) отображение
произведения EiXFj в G было непрерывно.
Необходимость этого условия очевидна, так как каждое из
отображений ср* и i|?j непрерывно. Для доказательства доста-
достаточности рассмотрим произвольную окрестность нуля W в G. По
условию для каждой пары (/, /) можно выбрать такие окрест-
окрестности нуля Ui и Vj в Е{ и Fj соответственно, что
М,^-(#))<= W При XG^HJ/G Vj.
Таким образом, f(x,y)&W, если x^lJy^Ui) и у J
i I
а также если х и у принадлежат соответственно U и V, где U —
7.8. Некоторые приложения 671
выпуклая оболочка объединения {Jtyi(Ui), a V—выпуклая обо-
оболочка объединения {Jtyj{Vj). Так как q>fl (U) содержит Uif то
U есть окрестность нуля в Е. Аналогичным образом устанавли-
устанавливается, что V — окрестность нуля в F, откуда и следует непре-
непрерывность отображения /. |
Разумеется, имеет место аналогичное утверждение о равно-
равностепенной непрерывности множества билинейных отображений
на EXF.
7.7.12. Другая формулировка теоремы 7.7.9. Существует за-
замечательная формулировка теоремы 7.7.9 в терминах линейных
отображений.
Пусть Е и F— полуметризуемые бочечные пространства и
и: E-+F'— линейное отображение, непрерывное для исходной
топологии в Е и слабой топологии g(F'9 F) в F\ Тогда в Е суще-
ствует такая окрестность нуля U, что множество u(U) равно-
степенно непрерывно в F'.
Действительно, рассмотрим билинейную форму / на Е X F,
определенную равенством
Из свойств отображения и следует, что форма/ раздельно не-
непрерывна; поэтому в силу теоремы 7.7.9 форма / непрерывна. Та-,
ким образом, существуют такие окрестности нуля U и V в Е и F
соответственно, что \f (Ux V) |^ 1, а это означает, что u(U)a
czV°, т. е. что множество u(U) равностепенно непрерывно. I
Очевидно, что эти рассуждения обратимы, так что приведен-
приведенное выше утверждение относительно линейных отображений про*
странства Е в F' действительно эквивалентно теореме 7.7.9.
7.8. Некоторые приложения
7.8.1. Пример. Суммирование двойных рядов. Рассмотрим во-
вопрос о суммировании двойных числовых рядоз 2^(т, п), где m
и п пробегают независимо друг от друга множество N натураль-
натуральных чисел. При этом будем пользоваться суммирующими множи-
множителями, т. е. последовательностью (//,) функций на произведении
NxN, удовлетворяющих следующим условиям:
fk>09 Iifk(m,n)<+ oo, limfk(m, я)=1. G.8.1)
k
Назовем обобщенной суммой ряда ^z(mt n) предел^
Нт 2/*("*„ ri)z(m, я),
672 Гл. 7. Принципы ограниченности
если он существует и конечен. Возникает вопрос о согласован-
согласованности: при каких ограничениях на двойные последовательности г
обобщенная сумма существует и совпадает с обычной суммой.
Здесь мы рассмотрим один из вариантов этой задачи (ср. Бур-
баки [7, стр. 193, упр. 10]).
Обозначим через Е пространство тех последовательностей лс,
для которых ряд ^jx(m) сходится к (конечной) сумме s(x).
Если наделить пространство Е нормой
II х\\= sup 2 x(m)
но оно становится банаховым пространством, содержащим про-
пространство Iх в качестве всюду плотного подпространства.
Поставим следующий вопрос: при каких дополнительных
ограничениях на последовательность (fh)
limSMm, n)x{m)y{n)
k
существует и равен произведению s(x)s(y) для каждого х^Е
и каждого у е Z1? Если мы положим
Uk (*> #) = 2 /* (m, п) х (m) у (п),
и(х, y) = s(x)s(y)
для х е Е и у е Z1, то наш вопрос сведется к такому: при каких
условиях последовательность uh сходится к и в каждой точке
произведения 5Х/1? Очевидно, что все uk и и являются билиней-
билинейными формами на Exlx. Используя G.8.J), легко также пока-
показать, что lim uk — u на произведении llXlx (для чего достаточно
и удобно предположить, что х ^ 0 и у > 0).
Мы хотим доказать, что
► Предел \imuk(xt у) существует и конечен для каждой
пары (х,у)^ Exl1 тогда и только тогда, когда
-оо; G.8.2)
p
k, n m
в этом случае
и на EX Iх.
Доказательство. Осуществляется повторным примене-
применением теоремы 7.7.9 и связанных с ней замечаний из п. 7.7.10.
7.8. Некоторые приложения 673
Прежде всего, как легко заметить, сходимость в любом из
пространств Еу Iх влечет поточечную сходимость на N. Отсюда
следует, что каждая конечная сумма
и*,р(*, у)** 2 fh{mt n)x{m)y(n)
• т<р
п<р
раздельно непрерывна (и даже непрерывна) на Exlx. Более
того,
М*> У)** Hm uktP(x, у)
р->оо
для любого k и любой пары (х, у)^ Exl1..
Первое обращение к геореме 7.7.9 показывает, что если на
Exl1 существует поточечный предел u = limuhj то совокупность
отображений uh (&=1, 2, ...) равностепенно непрерывна. С дру-
другой стороны, так как uk поточечно сходятся к и на 1ХХ1\ то из
их равностепенной непрерывности (с учетом очевидной непре-
непрерывности отображения и) следует их поточечная сходимость к
и на Е X Iх.
Таким образом, поточечная сходимость и^-^и на Exl1 имеет
место тогда и только тогда, когда uh равностепенно непрерывны.
Следовательно, остается показать, что Uk равностепенно непре-
непрерывны тогда и только тогда, когда выполняется соотношение
G.8.2).
Так как Е и Iх — нормированные пространства, то uk равно-
равностепенно непрерывны тогда и только тогда, когда их нормы, т. е.
числа
ограничены по k. Итак, нам нужно показать, что
^ = suP2lMm, n)-fk(m + l, n)\. G.8.3)
п т
Для этого рассмотрим отображение х*—>х\ определенное
равенством
Оно представляет собой линейную изометрию пространства Е
на подпространство с в /°°, образованное сходящимися после-
последовательностями из /°°. Отображение, обратное к этой изометрии,
определяется равенством х(т)=х'(т) — хг(т—1), если усло-
условиться, что jc/(O)=O. Отсюда получаем, что Съ, есть верхняя
грань сумм
2 Mm, n)[x'{m)-x'{m-\)]y{n\
т% п
674 Гл. 7. Принципы ограниченности
где х'—-пробегает единичный шар пространства с, г у— единич-
единичный шар пространства Iх. Представляя теперь двойную сумму в
виде повторной (что возможно в силу абсолютной сходимости
ряда), имеем
mf n)-fk(m + l, n)]x'(m).
n m
Верхняя грань по у модуля этого выражения равна
sup 12 [Ы/я, n)-fk(m + l, n)]x'(m) ,
п ( m
а верхняя грань последнего выражения по х' равна
sup 21 fk(m, n)-fk{m+\, n) |;
n m
т. е. правой части равенства G.8.3), что и требовалось доказать.
7.8.2. Приложение к исследованию ограниченных множеств
распределений. В качестве второго приложения теоремы 7.7.9
заполним пробел, оставленный в п. 5.11.2, а именно докажем
приведенную ниже теорему, которая утверждает гораздо боль-
больше, чем требуется в п. 5.11.2 (там говорится только об ограни-
ограниченности в ЗУ множества 2*f*g для каждой пары (/, g)e
^2Dm(Q) X3)m(Q)). За исключением явной ссылки на теоре-
теорему 7.7.9, приводимое нами доказательство такое же, как у
Л. Шварца [2, гл. VI].
Теорема. Пусть 2 — подмножество в SD', обладающее тем
свойством, что для каждого [£2) множество
ограничено в £D\ Тогда для любого компактного множества
Kcz Rn и любого открытого относительно компактного множе-
множества QczRn существуют такое целое число /л>0« такое число
с > 0, что
sup{U*/*g(x)|: IeS, xe=K}<cNm(f)Nm(g) G.8.4)
для f, ge=35m(Q), где
Доказательство. Для каждого X обозначим через Fx
билинейное отображение произведения 3)нХЗ)н в С(/(),опреде-
С(/(),определенное с помощью равенства FX{U ё) =^*/*ff, гДе &н есть
сокращенный символ для S)(Rn, Я), Н — компактная окрест-
окрестность множества Q и С (К) —обычное банахово пространство не-
7.8. Некоторые приложения 675
прерывных на К функций, норма которых равна максимуму их
модуля на /С Важно иметь в виду, что 2)н — пространство Фре-
ше (см. пример (Ь) п. 6.1.3).
Сначала докажем, что из ограниченности в 3)' множества
2*f для каждого f е 2) вытекает, что совокупность всех Fx,
где ^gS, раздельно равностепенно непрерывна. Действительно,
пусть f e SDw Рассмотрим линейные отображения Uy'- ^h-*
->С(/С), определенные равенствами
(Y*g) \K,
где Y=X*f и X пробегает множество 2. Ясно, что множество
{У: XgS} ограничено в &'. Очевидно также, что каждое ото-
отображение uY непрерывно. Далее множество {uY: IgU} поточеч-
поточечно ограничено, поскольку (а) если g^&H, то совокупность
функций y*—>g(x — у) образует ограниченное подмножество в
i2), когда х пробегает множество К, и (Ь) множество {У: IgE}
ограничено в & по условию. Из теоремы 7.1.3 следует, что
{uY' X е 2} равностепенно непрерывно на 3)н- Из симметрич-
симметричности Fx(f,g) относительно fug следует, что {Fx: X еИ} раз-
раздельно равностепенно непрерывно.
Теперь, снова применяя уже к {Fx> IeS} теорему 7.7.9, при-
приходим к выводу, что множество {uY* ^e2} равностепенно не-
непрерывно на &нХ&н- Это означает, что существуют такие чис-
числа m и с, для которых неравенство G.8.4) выполняется, если
f и g принадлежат 2DH. Остается показать, что на самом деле /
и g из 3)m(Q) могут быть выбраны независимо друг от друга.
Пусть f, g^2)m(Q). С помощью регуляризации можно ап-
аппроксимировать f и g в смысле пространства 2Е>™ соответствен-
соответственно последовательностями /л=/*г^ и gk = g*rk, лежащими в 3)н-
Тогда в силу G.8.4)
\X*fk*gu{x)\<cNm{fh)Nm{gk\
где 1^И,л:е/(и А,й=1,2,.., . Пусть h фиксировано и k->-оо.
Тогда Nm(gh)-*Nm(g), и поскольку X*fh принадлежит С°°, то
X*fh*gk(x) -+Х*fh*g(x) для каждого х. Отсюда следует, что
\X*fh*g(x)\<cNm (h) Nm (g) G.8.5)
для IeS, x^K и /z=1,2, ... . Эти рассуждения показывают,
что в G.8.5) мы можем заменить fh любым элементом из 3)н,
причем g~- произвольный элемент из <2)m(Q).
Допустим (это не уменьшает общности), что Q симметрично
относительно нуля. Обозначая через Z свертку X*g и заменяя
в G.8.5) fn на ф, где cpeS)(Q), получаем, что
676 Гл. 7. Принципы ограниченности
Таким образом,
\(<p,txZ)\<c'Nm(<p),
где tx обозначает сдвиг на х. Следовательно, порядок обобщен-
обобщенной функции txZ на Q не превосходит m для каждого х е /С Но
тогда в G.8.5) можно перейти к пределу при /z->oo. При этом
левая часть неравенства стремится к \Х #f *g(x) |. Окончатель-
Окончательно, получаем неравенство G.8.4), что и требовалось доказать. I
УПРАЖНЕНИЯ
7.1. Пусть f — такая функция на R (R — вещественная прямая), что функ-
функция fg локально интегрируема (по мере Лебега) и существует конечный пре-
предел
п
lim In (g) = lim | fg d\i
n n J
для каждого ^gC0(R). Доказать, что функция / интегрируема.
7.2. Пусть Т — локально компактное пространство и \i — положительная
мера Радона на Т. Предположим, что g — такая функция на Т, что fg интег-
интегрируема относительно \х для каждого /е С3?р (\х), где р — некоторое задан-
заданное число 1 ^ р ^ оо , Используя бочечность пространства J3?p (\л), доказать,
что geJP'M, где j+ у= 1. (Ср. с упр. 6.1.)
7.3. Допустим, что для каждого натурального числа п выбраны семейство
(№А точек отрезка [0, 1] и семейство чисел (с^).^... так, что
x(t)dt= J} cV>x(t(»>) = Sn(x) A)
О
для всех многочленов х степени, не превосходящей п, причем для каждой не-
непрерывной на отрезке [0, 1] функции х существует конечный предел lim Sn (x).
п
Показать, что
2 К)|
1
HmSn(jf)= f x(t)dt B)
П J
О
для каждой функции х, непрерывной на [0, 1].
Доказать также, что если равенство A) выполняется для всех многочле-
многочленов х степени не выше п и если все числа с^ положительные, то спра-аед*
либо равенство B).
7.4. Обозначения примера 7.2.4 D). Предположим, что
Упражнения 677
а) пространство Е бочечно и координатные функционалы !) на Е непре-
непрерывны;
(b) координатные функционалы на F непрерывны;
(c) для линейных отображений пространства Е в F справедлива теорема
о замкнутом графике.
Доказать, что если и л (Е) a Fy то иА есть непрерывное отображение Е в F.
7.5. Пусть Е—бочечное пространство, F — топологическое векторное про-
пространство, и пусть для линейных отображений пространства Е в F справед-
справедлива теорема о замкнутом графике. Пусть, кроме того, L — тотальное под-
подмножество в F' и (пг) —такяя сеть элементов из LC(E,F), что для каждого
х^Е сеть (Ui(x)) ограничена и сходится в топологии a(F, L). Определим ото-
отображение и: E->F, полагая
u(x)~o(F, L)-limu.(x).
i г
Доказать, что семейство отображений {иг} равностепенно непрерывно и ото-
отображение и: Е -> F непрерывно.
Если (иг) — счетная последовательность, то достаточно ограничиться тре-
требованием, чтобы сеть (Ui(x)) была o*(F, L)-сходящейся для любого х&Е
(остальные условия при этом прежние).
7.6. Пусть 1^/?<оо, 1 ^S g < оо, Q — открытое подмножество в Rn и
(fn)—последовательность элементов из L?(Q). Предположим, что для каж-
каждого х е 1р ряд
сходится в пространстве &' (Q) распределений на Q к пределу, принадлежа-
принадлежащему пространству L*(Q). Доказать, что данный ряд сходится в L^(Q) для
каждого х^ 1р.
[Указание. Воспользоваться упр. 7.5, а также тем фактом, что каждый
элемент х^1р является в этом пространстве пределом своих конечных сече-
сечений.]
7.7. Пусть E=Ll(—л, п) (мера Лебега) и еп — класс, определяемый функ-
функцией eint, n=0, ±1, ±2, «... Для каждой функции х&Е рассмотрим ее
л-й коэффициент Фурье
Пусть Р — некоторое множество целых чисел. Обозначим через Е[Р] множе*
ство тех х ^Е, для которых £(п)=0 при п (£ Р. Обозначим через Q дополне-
дополнение к Р в множестве всех целых чисел.
Показать, что Е будет прямой суммой пространств Е[Р] и E[Q] в том и
только в том случае, когда характеристическая функция множества Р яв-
является преобразованием Фурье некоторой меры на [—я, л].
7.8. Обозначения упр. 7.7. Говорят, что Р есть множество Сцидона
(Зигмунд [1, стр. 139]; см. также § 8.8 ниже), если всякая ограниченная
измеримая функция из Е[Р] почти всюду на [—л, л] совпадает с непрерывной
функцией.
Доказать, что если Р — бесконечное множество Сцидона, то E[Q] не до*
пускает топологического дополнения в Е.
То есть функционалы х ь-> х(п). —Прим. перев*
678 Гл. 7. Принципы ограниченности
7.9. Обозначения упр. 7.7. Доказать, что элементы еп М?) образуют
в Е[Р] слабый базис тогда и только тогда, когда ряд
сходится для каждого х^Е[Р] и каждой ограниченной измеримой функции g
на [—я, я].
7.10. Пусть Т — отделимое локально компактное пространство и |ы — по-
положительная мера Радона на Т. Рассмотрим последовательность функций
Кг (/=1, 2, ...) на 7, каждая из которых принадлежит J2?s = CS?S (Г, \i)
при некотором s = sr > 1. Предположим, что
lim Г Krfd\i= J / d%
для каждой функции f из некоторого тотального подмножества в<%* (Г), где
мера Радона Я на Т не представима в виде X = h • \х с h^c3?q и q > 1. До-
Доказать, что существует такая функция
что
sup Krg d\i
+ оо.
7.11. Применить упр. 7.10 к исследованию сходимости и суммируемости
обычных рядов Фурье.
7.12. Пусть Е — топологическое векторное пространство, А — выпуклое
уравновешенное секвенциально слабо полное и слабо ограниченное подмноже-
подмножество в Е''. Доказать, что А сильно ограничено в Е' (ср. К ел л и [1, стр. 241, 242,
замечание в конце задачи М]).
[Указание. Рассмотреть банахово пространство^, построенное таким
же образом, как в лемме 6.5.2, только вместо фигурирующего там простран-
пространства Е взять пространство £', наделенное слабой топологией.]
7.13. Пусть Q — открытое множество в R" и (ft) —ограниченное в 9}' (Q)
семейство локально интегрируемых на Q функций. Доказать, что для каждого
компактного множества /CczQ существуют такое целое число ш^О и такая
постоянная М, что
sup
' la
М sup {| дРу (х) |: х s Q, | р\ < пг)
при всех ф е Q)m (Q, К) (где 3)m (Q, К) — множество тех функций ф s Cm,
носители которых содержатся в К).
[Указание. Воспользоваться тем фактом, что ^ — бочечное простран-
пространство, и теоремой 7.1.1 (в).]
7.14. Пусть X — обобщенная функция на R'2, обладающая тем свойством,
что X * ф е Lp iyC) для каждого ф g ^ (r"). Доказать, что существуют
такое целое число k^O и такие функции /, g^Lp, что J=*f + A g. При
/i=l Д можно заменить на д (Л. Ш в а р ц [2, стр. 59]).
[Указание. Пусть В — пересечение пространства & с замкнутым еди«
ничным шаром в L?'. Множество {X*ty : if>e В} ограничено в &. Пользуясь
предыдущим упражнением, показать, что для каждого компактного множества
/С значение (\f, X * ф) ограничено по if> е 5 для каждой функции (р ^ ^^
Упражнения 679
носитель которой содержится в К, так что 1*фег для каждой такой
функции ф. Для завершения доказательства следует воспользоваться форму-
формулами п. 5.П.2.]
7.15. Доказать, что функции еп: t\—> eint не образуют топологического
базиса в пространстве С непрерывных вещественных функций, имеющих пе-
период 2я (с обычной нормой || х || = sup | x(t) |).
7.16. Доказать, что классы, определяемые функциями еп (см. предыдущее
упражнение), не образуют топологического базиса в пространстве Ll(—я, я).
7.17. Пусть 1^/?^ оо, X — некоторое распределение на Rn. Доказать, что
Х*ф е= Lp = Lp (Яп) для каждого ф е @ = Щ (Rn) тогда и только тогда, когда
X является конечной линейной комбинацией производных от функций из L*
(Л. Ш в а р ц [2, стр. 57, теор. XXV]).
[Указание. При доказательстве необходимости приведенного условия
показать, что Т: ф I—> X*q> есть непрерывное отображение пространства <& в
Lp. Для этого достаточно рассмотреть сужение отображения Т на Of (R", К)
(К компактно) и использовать теорему о замкнутом графике. Показать, что
для каждого компактного К существует такое целое число т^О, что Х*ф^ L?
для ф е= Q)m (Rn, К). Воспользоваться затем техникой п. 5.11.2.]
. 7.18. Пусть X — распределение на Rn. Доказать, что свертка Х*у является
непрерывной функцией для каждой непрерывной функции ф с компактным но-
носителем в том и только в том случае, когда X — мера (Л. Ш в а р ц [2, стр. 48,
теор. XX]). Способ доказательства, который мы предлагаем ниже, отличается
от способа Шварца.
[Указание. При доказательстве необходимости ввести отображение
Т: ф1—>Х*у пространства @° в С. Показать, что Т непрерывно, и рассмотреть
сопряженное отображение V пространства Мс (пространство мер, обладаю-
обладающих компактным носителем) в М (пространство всех мер). Доказать, что
Т'(<х,*$) =а*Г'р для а, реЛ!с, и вывести отсюда, что существует такая мера
jiE A1, что Т'а. — jx * а для всех а е= Мс.]
7.19. Пусть X и Y — распределения на Rn. Говорят, что определена сверт-
свертка Шевалле (Ш е в а л л е [1]), если (X * <р) (Y * г|)) е= L1 = L1 (Rn) для ф,
-ф е= %$ — 3) (Rn). Доказать, что если это условие выполняется, то существует
такое единственное распределение Z — X* У, что
J
для ф, г|) е= @F, где \i — мера Лебега на Rn.
[Указание. Воспользоваться теоремой п. 5.11.3 о непрерывных линей-
линейных отображениях из & в Qf\ перестановочных со сдвигами.]
7.20. Убедиться в справедливости следующего утверждения: если X и
Y — распределения на Rn, носители которых А и В таковы, что пересечение
Л Г) (К — В) компактно для каждого компактного множества /(c=Rn, то опре-
определена свертка X* Y в смысле Шевалле. (Ср. с § 5.10.)
Доказать также, что если X и Y — меры, то понятие свертки Шевалле
X* Y согласуется с понятием свертки, выделенным в § 4.19.
7.21. Пусть l^p^oo и X — распределение на Rn. Показать, что свертка
Шевалле (упр. 7.19) X*Y определена для каждого Y^Lp тогда и только
тогда, когда X есть конечная линейная комбинация производных от функций
из Lp'. Доказать также, что свертка Шевалле X *Y определена для любой
ограниченной меры Y тогда и только тогда, когда X есть конечная линейная .
комбинация производных от функций из L°°<
680 Гл. 7. Принципы ограниченности
[Указание. При доказательстве необходимости показать сперва, что
X *y*ty^ L*>' для ф, г|з е @ Затем дважды воспользоваться упр. 7.17.]
7.22. Пусть Т — произвольное множество, F — множество числовых функ-
функций на Г, обращающихся в нуль вне некоторого конечного подмножества в Т.
Предположим, что
sup
5@/@
i Т
для любой числовой функции g на Т. Доказать, что существует такое конечное
подмножество Го в Г, что все функции из F обращаются в нуль на T\Tq.
7.23. Пусть Т — произвольное множество, (Ef)t€=T— семейство бочечных
пространств. Доказать, что произведение Е— Jj£* также является бочечным.
Доказать аналогичное утверждение для инфрабочечных пространств.
[Указание. Воспользоваться критерием A) (Ь) или вторым условием
части C) теоремы 7.1.1. При этом отождествить сопряженное к Е с векторным
подпространством в JJ Е^у образованным теми семействами л/ = (л^), для
которых х\ = 0 всюду, кроме, быть может, конечного подмножества в Т
(зависящего от х'). Двойственность определяется формой
Если В — слабо (соотв. сильно) ограниченное множество в Е\ то такова же
каждая проекция множества В. Следовательно, все упирается в доказатель-
доказательство того факта, что существует такое конечное подмножество То в Г, что
х[ = 0 для всех ^'еВи всех t <=T\T0. При доказательстве этого утвержде-
утверждения воспользоваться предыдущим упражнением.]
7.24. Пусть (Хг) — последовательность распределений на Rn, обладающих
тем свойством, что множество {сгХг) слабо ограничено в 3ff для любой по-
последовательности чисел (сг). Показать, что не существует точек в Rn, общих
для носителей всех Хг.
7.25. Пусть и — непрерывное линейное отображение пространства С°° в $г',
перестановочное со всеми сдвигами. Доказать, что существует такое распреде-
распределение L с компактным носителем, что
n(/)-W
для / е= С~.
[Указание. Воспользоваться результатами п. 5.11.3 и предыдущего
упражнения.]
7.26. Обозначим через ®с множество распределений на Rn с компакт-
компактными носителями, отождествимое с сопряженным к С00. Показать, что всякое
линейное отображение и: Q) -> £^, перестановочное со сдвигами и непрерыв-
непрерывное в топологии сх(^, С00), представимо в виде u(f)=L*f для некоторого
[Указание. Рассмотреть сопряженное к и отображение и воспользовать-
воспользоваться предыдущим упражнением.]
7.27. Пусть А е ^', Bg^', и пусть внутренность множества supp В не-
непуста. Показать, что соотношение
А * & с В * ^
Упражнения 681
справедливо тогда и только тогда, когда А е В * &с. (Через А ♦ @ обозначено
множество всех сверток вида Л* /, где / пробегает пространство <&\ подобным
образом определяются и остальные аналогичные символы.)
[Указание. Доказательство достаточности тривиально. Действительно,
если ЛеВ* ^, то А * & cz В * В- Для доказательства необходимости по-
построить пример такого линейного отображения и: Q) -> в'с, что A* f=B* u(f),
и показать, что результат предыдущего упражнения применим к этому ото-
отображению и.]
ГЛАВА 8
Теория двойственности
8.0. Предисловие
Настоящая глава посвящена теории двойственности (в осо-
особенности двойственности между локально выпуклым простран-
пространством Е и его топологическим сопряженным Е') и ее приложе-
приложениям. Типичная и фундаментальная задача этой теории, впервые
поставленная и решенная Макки, заключается в определении
всех локально выпуклых топологий в заданном векторном про-
пространстве £, для которых топологическое сопряженное совпадает
(как векторное пространство) с наперед заданным векторным
подпространством алгебраического сопряженного Е*. Другие
вопросы, затронутые в этой главе, связаны с изучением* ли-
линейных отображений, их сопряженных и вторых сопряженных,
вторых сопряженных пространств, рефлексивности и различ-
различных топологий в сопряженных пространствах. Мы хотим проил-
проиллюстрировать эти понятия приложениями к задачам классиче-
классического анализа, теории интегрирования и теории обобщенных
функций.
Последняя часть главы посвящена некоторым аспектам тео-
теории векторных мер Радона и теории интегрирования векторных
функций. Отчасти эти разделы можно рассматривать как при-
примеры использования идей теории двойственности. В то же время
они представляют собой обобщение некоторых результатов, по-
полученных в гл. 4 для скалярных мер Радона и интегралов от
скалярных функций.
Ряд интересных приложений общей теории двойственности
к изучению пространств распределений можно найти в работах
Хирата [1] и Иосинага и Огата [1].
8.1. Дуальные пары и слабые топологии
Под дуальной парой понимают пару (£, Е') векторых про-
пространств (над одним и тем же полем К) вместе с билинейной
формой (х, х') на ЕхЕ'. Дуальная пара определяет линейное
отображение /: Е-*Е'* по формуле
8.1. Дуальные пары и слабые топологии 683
и линейное отображение /': Е'-+Е* по формуле
Говорят, что билинейная форма (*, х') приводит пространства Е
и Е в двойственность. Двойственность называется отделимой по
Е (соотв. по £')> если отображение f (соотв. /') взаимно одно-
однозначно. В последнем случае естественно считать Е векторным
подпространством в Е'* (соотв. Ег векторным подпространством
в £*). Двойственность отделима, если она отделима и по Е
и по Е'.
Наиболее важен случай, когда Е — топологическое векторное
пространство и Е' — его топологическое сопряженное, а в каче-
стве {х, х') берется х'(х). Такая двойственность всегда отдели-
отделима по Е'. Если Е отделимое ( = хаусдорфово) локально выпук-
выпуклое пространство, то двойственность отделима (по Е). Описан-
Описанная двойственность оказывается полезной, вообще говоря,
только для локально выпуклых пространств.
Мы уже пользовались понятием слабой топологии для.случая
топологических векторных пространств. Вообще если простран-
пространства Е и Е' находятся в двойственности (т. е. образуют дуаль-
дуальную пару), то о{Е,Е') (соотв. g(E\E))—слабейшая топология
в Е (соотв. в £'), при которой непрерывна каждая линейная
форма х*-> (х9 я'), где х' е Е' (соотв. х*»—> (х, х'), где хе£).
Обе эти топологии локально выпуклы. Топология а (Е,Е') (соотв.
о(Е\ Е)) отделима, если двойственность отделима по Е (соотв.
по Е'). Если Е — топологическое векторное пространство и Е' —
его топологическое сопряженное, то а(£, £') называется ослаб-
ослабленной, топологией в Е (или ослабленной топологией, ассоцииро-
ассоциированной с исходной топологией в Е). Если Е — локально выпук-
выпуклое пространство, отделимое в исходной топологии, то о(Е,Е')—•
отделимая топология. Топология о(Е,Е') всегда слабее исход-
исходной топологии.
Наша первая теорема показывает среди прочего, что всякую
дуальную пару можно получить, исходя из некоторого локально
выпуклого пространства.
8.1.1. Теорема. Пусть векторные пространства Е и Ег нахо-
находятся в двойственности. Класс линейных форм на Е (соотв. на
Е'), непрерывных в топологии о(Е, Е') (соотв. о(Е\ £)), совпа-
совпадает с классом линейных форм вида хь-> (х, х') (соотв.
х'*-> (х,х'))9 где х' (соотв. х) есть произвольный фиксирован-
фиксированный элемент из Е' (соотв. из Е).
Доказательство непосредственно следует из предложе-
предложений 1.4.2. |
Нам понадобятся некоторые сведения о слабых топологиях,
определяемых двойственностью между подпространствами и
684 Гл. 8. Теория двойственности
факторпространствами в Е или в Е'. Предположим, что Е и Е'
находятся в двойственности и М — векторное подпространство
в Е. Если М°аЕ' — ортогональное к М множество, т. е. множе-
множество всех таких элементов х' е Е\ что (х, х')=0 для каждого
яеМ, то пару (М,Е'/М°) можно привести в двойственнность
с помощью билинейной формы
(х, *') = <*. *0,
где х е М, а х' — класс эквивалентности по модулю М°, содер-
содержащий элемент х'. Аналогично можно привести в двойственность
и пару (Е/М, АР).
8.1.2. Предложение. Топология о(Е,Е') индуцирует в под-
подпространстве М топологию о(М,Е'/А1°). Топология о(Е/М, М°)
является фактортопологией топологии о(Е,Е') по модулю М.
Доказательство. Первое утверждение непосредственно
вытекает из следующего замечания. Если элементы х\ (I —
= 1,2,..., /г) принадлежат Е' и определяют классы эквивилент-
ности х\ п'о модулю М°, то окрестность
в топологии о(М, Е'/М°) совпадает с пересечением подпростран-
подпространства М и окрестности
в топологии о(Е,Е').
Второе утверждение менее просто. Условимся обозначать че-
через а топологию о (Е/М, М°), а через q фактортопологию в
Е/М, индуцированную топологией о(Е,Е'). Пусть / — естествен-
естественное отображение пространства Е на Е/М. Так как (по определе-
определению) (f (х), х') = (х, х') для х'^М°у то отображение / непре-
непрерывно в топологиях о(Е,Е') и а. Следовательно, топология а
слабее топологии q. Докажем обратное. Пусть х[^ Е' (t'=l, 2,...
..., п) и U= W(x'{,..., х'п). Достаточно показать, что f(U)~
окрестность нуля в топологии а.
С этой целью рассмотрим векторное подпространство L в Е\
порожденное М° и элементами х'г Выберем какое-нибудь алге-
алгебраическое дополнение Р к М° относительно L. Подпространство
Р будет конечномерным. Пусть размерность его равна тку'
(/=1,...,т) — базис в Р. Как линейные формы на М сужения
t/y I M линейно независимы. Действительно, если линейная фор-
форма у' = 2 к^у' принадлежит М°, то из соотношения М°[\Р = {0}
i
8.1. Дуальные пары и слабые топологии 685
вытекает, что у' = 0 и, следовательно, Xj = O для всех /. Поэтому
для каждого элемента j^e£ найдется такой элемент х0 е М, что
(х + х0, г/у) = 0 для всех /. Пользуясь разложением L в прямую
сумму L = iW° + P, имеем
откуда
(ху ^[)^{х + х^ х\) для *=1, ..., /г.
Если элемент £ е £/М таков, что |(g, ^)|^1 для всех f, то g =
= /(х) при некотором xg£ и (g, ^) = (#, ^) по определению.
Поэтому
откуда следует, что х + х0 s (/. Так как д:0 е М, то
т. е. l^f(U). Таким образом, f(U) содержит все такие элемен-
элементы £, для которых
sup|<i, 01 <!•
Поскольку последнее множество является окрестностью нуля в
топологии а, то это верно и для множества f(U). |
Из доказанного предложения вытекает следующее утвержде-
утверждение.
8.1.3. Следствие. Пусть N — векторное подпространство в Е'.
Для того чтобы топология o{E/N°,N) была фактортопологией в
Е/№, индуцированной топологией о(Е,Е'), необходимо и до-
достаточно, чтобы подпространство^ было слабо замкнуто в Е'.
Доказательство. Пусть N — слабое замыкание подпр£-
странства N. Обозначим через М ортогональное дополнение к N,
тогда M = N°=_(N)° и M° = N. Согласно предыдущему предложе-
предложению, o(E/M,N) есть фактортопология в Е/М, индуцированная
топологией, о{Е,Е'). С другой стороны, если ЫФМ, то топология
o(E/M,N) строго сильнее топологии о(Е/М, N), откуда и выте-
вытекает сформулированное следствие. 1
8.1.4. Полярные множества. Мы уже пользовались обозначе-
обозначением М° для подпространства, ортогонального к векторному под-
подпространству М. Удобно обобщить это понятие на произвольные
множества в любом из пространств дуальной пары (Я, Е').
Делается это так. Пусть А — некоторое подмножество в Е.
Полярой А0 множества А (относительно заданной дуальной
686 Гл. 8. Теория двойственности
пары) называется множество
4° = {*'€=£': \(х, *')К1 для хе=А}.
Очевидно, что поляра Л° всегда а(£, £')-замкнута, выпукла и
уравновешена. Если В — множество в Е\ то его поляра В° в Е
определяется симметрично, а именно
B° = {x(=zE: \(х9 *'>1<1 Для х'е=В}.
Пусть Е — топологическое векторное пространство. Если не
указано противное, то, говоря о полярах подмножеств простран-
пространства Е или Е', мы будем иметь в виду поляры относительно ду-
дуальной пары (£, £"'), где Ег — топологическое сопряжен-
сопряженное к Е.
Из теорем 2.4.1 (с) и 8.1.1 вытекает важный результат:
8.1.5. Теорема (о б и пол я р е). Пусть (£, Е')—дуальная па-
пара и А—подмножество в Е. Биполяра ЛОО=(Л°H множества А
совпадает с о (Е, Е')-замкнутой выпуклой уравновешенной обо-
лочкой в Е множества А. (Справедлив также двойственный ре-
результат для множеств из £"'.)
Замечание. Из теоремы 8.2.1 (которая является просто
иной формулировкой следствия 2.2.7) вытекает, что в дуальной
паре (£, £'), ассоциированной с локально выпуклым простран-
пространством £, биполяра Л00 множества Л из Е совпадает с замкнутой
выпуклой уравновешенной оболочкой в Е множества А.
8.2. Свойства ослабленной топологии локально выпуклого
пространства
Этот параграф начнем с того, что сформулируем результат,
уже полученный ранее (следствие 2.2.7) с помощью теоремы
Хана — Банаха.
8.2.1. Теорема. Выпуклое подмножество А локально выпук-
выпуклого пространства Е замкнуто тогда и только тогда, когда оно
слабо замкнуто (т. е. замкнуто в ослабленной топологии в Е)щ
С понятием ограниченного множества связано еще одно об-
общее свойство локально выпуклой топологии и ассоциированной с
ней ослабленной топологии.
8.2.2. Теорема. Подмножество А локально выпуклого про-
странства Е ограничено тогда и только тогда, когда оно слабо
ограничено.
Доказательство. Так как ослабленная топология слабее
исходной, то ограниченность влечет слабую ограниченности
8.3. Топологии, согласующиеся с двойственностью 687
Прежде чем доказывать обратное утверждение, напомним,
что оно уже было получено (пример 7.2.1) для полунормирован-
полунормированных пространств. Поэтому мы постараемся свести общий случай
к этому частному.
Пусть U — произвольная замкнутая выпуклая уравновешен-
уравновешенная окрестность нуля в Е. Достаточно показать, что если А —
слабо ограниченное множество, то множество р(А), где р —
функционал Минковского множества £/, ограничено. Множество
N = p~l@) есть замкнутое векторное подпространство в Е. Обра-
Образуем факторпространство E = E/N и определим на Ё функцию^,
полагая р(х)=р(х), где х — произвольный элемент, принадле-
принадлежащий классу х. Функция р есть норма на Я, поэтому достаточ-
достаточно установить ограниченность множества р(А). Всякая непре-
непрерывная относительно р линейная форма / на Е порождает ли-
линейную форму g на £, такую, что g(x) = f(x). Из соотношений
I g (х) | = I / (*) К const р (x) = const р (х)
следует непрерывность формы g на Е. По условию множество
g(A) ограничено, следовательно, ограничено и множество f(A).
Таким образом,, множество А слабо ограничено в полунормиро-
полунормированном пространстве £, поэтому остается лишь сослаться на
пример 7.2.1. |
8.3. Топологии, согласующиеся с заданной двойственностью
Обратимся теперь к проблеме Макки. Пусть задана дуаль-
дуальная пара (£, Е'). Каким образом могут быть охарактеризованы
те локально выпуклые топологии в £, относительно которых то-
топологическое сопряженное к Е совпадает с £'? Такие топологии
существуют, причем слабейшей среди них является а(£, £').
Мы покажем, что среди них существует и сильнейшая и что
любая другая такая топология находится «между» этими двумя.
Решение этой проблемы будет сформулировано в терминах
так называемых ^топологий в Е, где @ — система слабо ограни-
ограниченных подмножеств в Ег. Эти топологии определяются совер-
совершенно аналогично тому, как в п. 1.10.8 определялись топологии
в подмножествах пространства L(E,F). Если задана система @,
то в качестве базы окрестностей нуля соответствующей тополо-
топологии 7© принимаются множества вида eS° и всевозможные их
конечные пересечения; здесь е>0, SgS, a
S° = {xz=E: \(x, *'I<1 Для x'*=S]
есть поляра в Е множества S. Если © — направленное по вклю-
включению множество (этого всегда можно добиться без изменения
688 Гл. 8 Теория двойственности
топологии Г©), то множества eS° (e > 0) образуют базу окрест-
окрестностей нуля топологии Г© .
Топология Г© может быть описана как топология равномер-
равномерной сходимости на множествах, принадлежащих ©, если рассма-
рассматривать элементы пространства Е как функции на £". Более
того, если Е— локально выпуклое пространство и Ег — его топо-
топологическое сопряженное, то исходная топология пространства Е
является топологией вида Г©, а именно топологией, которая по-
получается, если в качестве © берется система всех равностепенно
непрерывных подмножеств в Е'.
Читатель может заметить, что топология Т® не изменится,
если заменить каждое из множеств S системы © его слабо
замкнутой выпуклой уравновешенной оболочкой в Е'.
8.3.1. Теорема (Макки — Бурбаки). Пусть {Е,Е') — ду-
дуальная пара, отделимая по Ег (т. е. можно считать, что Е' cz E*).
Пусть далее © — направленное по включению множество слабо
ограниченных выпуклых уравновешенных подмножеств в Е\
причем © устойчиво относительно гомотетий. Тогда топологиче-
топологическое сопряженное к Е относительно топологии Г© совпадает с
объединением слабых (т. е. а(£*, Е)-)замыканий в Е* множеств
S из ©•
Доказательство. Главное здесь — доказать, что если и
принадлежит указанному подпространству в £*, то и непрерыв-
непрерывно в топологии Г© и обратно.
Если и принадлежит слабому замыканию множества S, то
ясно, что
l|4
для всех x^S°. Так KaKS0 есть по определению Т©-окрестность
нуля в £, то и непрерывно в топологии Г©.
С другой стороны, если и непрерывно в топологии 71©, то най-
найдется такое множество S е ©, что |и(х)|«<1 для всех x^S°.
Так как множество S выпукло и ограничено, то по теореме 8.1.5
и принадлежит а(Е*, Е) -замыканию множества S. 1
Замечание. Из теоремы Хана — Банаха следует, что Е'
плотно в Е* относительно топологии а (Я*, Е)у поэтому Е* можно
считать пополнением пространства Е' относительно топологии
о(Е\Е).
8.3.2. Теорема. Пусть (Е,Е') — дуальная пара, отделимая по
Е'. Локально выпуклые топологии в £*, согласующиеся с задан-
заданной двойственностью, совпадают с топологиями типа 7^ где& —
некоторая направленная по включению система слабо компакт-
8 3. Топологии, согласующиеся с двойственностью 689
ных выпуклых уравновешенных подмножеств в Е\ такая, что
объединение \JS порождает пространство Е'.
Доказательство. Если топология Т в Е согласуется с
двойственностью, то Г = Т©, где © состоит из всех слабо ком-
компактных множеств вида S=U°, где U пробегает базу окрест-
окрестностей нуля в топологии Г, образованную Г-замкнутыми вы-
выпуклыми уравновешенными множествами.
Обратно, пусть© — система указанного вида. К © можно
добавить все гомотетические образы ее элементов» не изменяя
топологии Г©. Тогда © будет покрывать пространство Е\ сохра-
сохранив все остальные свойства. Топология а(£*,£) отделима и ин-
индуцирует в Е' топологию g(E', E)y поэтому из а(£'/, ^-ком-
^-компактности множества S следует его а (Е*,Е) -замкнутость. По
теореме 8.3.1 сопряженное к Е относительно топологии Г® равно
объединению (J S, которое по условию совпадает с Е'. |
8.3.3. Топология Макки х(Е,Е') и топология Аренса х(Е\Е).
Из теоремы 8.3.2 следует, что среди локально выпуклых тополо-
топологий в £, согласующихся с заданной двойственностью, существует
сильнейшая — это топология Г®, где © состоит из всех слабо
компактных выпуклых уравновешенных (или всех слабо ком-
компактных выпуклых) множеств в Е'. Эта топология называется
топологией Макки и обозначается т(£, Е'). Локально выпуклая
топология Т в Е согласуется с двойственностью тогда и только
тогда, когда
о(Е,Е')<Т<%(ЕуЕ'). (8.3.1)
Если Е — локально выпуклое пространство и Е' — его тополо-
топологическое сопряженное, то соотношение (8.3.1) выполняется, сле-
следовательно, для исходной топологии в Е. Обычно имеют место
строгие неравенства. Для некоторых важных типов локально вы-
выпуклых пространств имеет место равенство Т = т(Е, £'). Такие
пространства называются относительно сильными (см. теор. 8.3.5).
Пусть Е — топологическое векторное пространство и Ег —
его топологическое сопряженное. Арене [1] ввел топологию в
£", база окрестностей нуля которой образована полярами А0 ком-
компактных выпуклых уравновешенных множеств А из Е. Мы бу-
будем называть ее топологией Аренса в Е' и обозначать п(Е\ Е).
Топология Аренса, конечно, локально выпукла и слабее топо-
топологии Макки %(Е',Е) (так как каждое компактное множество
в £ относительно компактно в ослабленной топологии а (£,£')).
Так как топология Аренса к(Е\ £), очевидно, сильнее топологии
о(Е\ Е), то она согласуется с двойственностью между Е и £'.
690 Гл. 8. Теория двойственности
8.3.4. Теорема. Пусть Е — локально выпуклое пространство.
A) Множество А в Е ограничено тогда и только тогда, когда
оно ограничено относительно какой-нибудь локально выпуклой
топологии, согласующейся с двойственностью между • Е и Е/
(а потому относительно всех таких топологий).
B) Выпуклое множество в Е замкнуто тогда и только тогда,
когда оно замкнуто относительно какой-нибудь локально вы-
выпуклой топологии, согласующейся с двойственностью между Е
и Е' (а потому и относительно всех таких топологий).
C) Бочки в Е совпадают с полярами слабо ограниченных
множеств из Ег.
Доказательство. Утверждение A) следует из теоре-
теоремы 8.2.2, так как всем таким топологиям соответствует одна и
та же ассоциированная ослабленная топология а(£, Е'). Утвер-
Утверждение B) аналогичным образом получается из следствия 2.2.7
и теоремы Хана — Банаха. Для доказательства утверждения C)
допустим, что Т — бочка в Е. Так как множество Т поглощающе,
то поляра Т° слабо ограничена. Замкнутость, выпуклость и урав-
уравновешенность множества Т влекут за собой в силу теоремы 8.1.5
равенство Т = Т°°. С другой стороны, ^сли М— слабо ограничен-
ограниченное множество в Е', то его поляра Т=М°, очевидно, есть замкну-
замкнутое выпуклое уравновешенное поглощающее множество в Е, т. е.
бочка в Е. 1
8.3.5. Теорема. Если локально выпуклое пространство Е либо
A) бочечно, либо B) полунормируемо, то оно относительно
сильно.
Доказательство. A) Если Е —бочечное пространство, то
всякое слабо ограниченное множество в Е' равностепенно непре-
непрерывно. Это тем более верно для всякого слабо компактного мно-
множества в Е'. Поляра всякого такого множества является по-
поэтому окрестностью нуля в исходной топологии в Е, которая,
следовательно, сильнее топологии т(£, £'), а потому совпадает
с ней.
B) Пусть W — произвольная уравновешенная окрестность
нуля в £ в топологии т(£, Е'). Тогда (теорема 8.3.4A)) мно-
множество W поглощает всякое подмножество в Еу ограниченное в
исходной топологии. Так как пространство Е борнологично
(теор. 7.3.2)* то W — окрестность нуля в исходной топологии.
Последняя, таким образом, сильнее топологии %{ЕУЕ') и потому
совпадает с ней. 1
8.3.6. Пример применения теоремы 8.3.2. Пусть Т — отдели-
отделимое локально компактное пространство, jix — ограниченная поло-
положительная мера Радона на 7, А — выпуклое подмножество в S700,
Мы хотим доказать, что
8.3, Топологии, согласующиеся с двойственностью 691
► Если функция х е 9?°° принадлежит замыканию множе-
множества А в топологии аE?°°, 271), то в А существует такая
последовательность (хп), что хп^х в 3?v для каждого
р, удовлетворяющего неравенствам 1^/?< + оо (Гро-
тендик [7, стр. 67, упр. 6]).
Здесь имеется в виду обычная двойственность между 9?°° и 571,
определяемая с помощью равенства
(х, х') = / x(t)x'(t)dMt).
т
Обозначим через Sp' замкнутый единичный шар в JS?P' (отно-
(относительно полунормы NP'). Так как р < + оо, то р! > К и потому
множество Sp/ компактно в топологии o{J2?p % J?p). Так как мера
(я ограничена, то Sp' czJ3*1; по этой же причине aS?00cz0S?p и,
следовательно, топология аE?1,«2?о°) индуцирует в J?p' тополо-
топологию, более слабую, чем топология a (J?p, J?p). Таким образом,
множество Sp компактно в топологии o(J2*1, =5^°°). Пусть систе-
система в состоит из множеств Sp A ^ р < + оо). По доказанному
и по теореме 8.3.2 топология Г© в &°° согласуется с двойствен-
двойственностью между 9?°° и З?1. С другой стороны, топология Ге совпа-
совпадает с топологией 7V, где ®r ={Sl, S2,...}; это вытекает из
ограниченности меры ji. Топология Г©, таким образом, метри-
зуема. Наше утверждение следует теперь из теоремы 8.3.4 B). 1
См. также упр. 8.5—8.7.
8.3.7. Топология т(Е, Е*). Пусть Е — векторное пространство
над полем К и Е* — его алгебраическое сопряженное. Рассмо-
Рассмотрим топологию Макки т=т(£, Е*) и покажем, что она совпа-
совпадает с сильнейшей локально выпуклой топологией в Е (п. 1.10.1).
Временно обозначим последнюю топологию через /.
Так как топология т локально выпукла, то x^-t. С другой
стороны, существует база окрестностей нуля в топологии ty со-
состоящая из выпуклых уравновешенных поглощающих множеств
А, каждое из которых /-замкнуто. Так как топологическое со-
сопряженное к Е относительно топологии t (т. е. £*) то же самое,
что и относительно т, то (теор. 8.3.4 B)) каждое множество А
замкнуто в топологии т. Поляра К=А° множества А есть выпук-
выпуклое уравновешенное слабо замкнутое и слабо ограниченное мно-
множество в £*, поэтому (теор. 1.11.4A)) она слабо компактна.
.Следовательно, поляра К0 множества К есть т-окрестность нуля
в £. По теореме о биполяре К° = А00=А, т. е. топология t слабее
топологии т. Таким образом, топологии t а т совпадают, что и
требовалось доказать. |
692 Гл. 8. Теория двойственности
Отсюда непосредственно вытекает, что пространство Е бочеч-
но в топологии т. Действительно, каждая полунорма на Е непре-
непрерывна (в топологии /, а потому и в топологии т).
С помощью последнего замечания можно получить пример
тощего бочечного локально выпуклого пространства (см. заме-
замечание после следствия 6.2.3). В самом деле, пусть Е=Ж(К)
(пространство всех финитных числовых последовательностей).
Пространство Е есть объединение счетной совокупности конечно-
конечномерных векторных подпространств Еп (я= 1, 2,...), каждое из
которых т-замкнуто (ибо т — отделимая топология). Ясно так
же, что каждое из подпространств Еп нигде не плотно в Е. Та-
Таким образом, пространство Е (наделенное топологией т) тоще и
бочечно.
8.3.8. Читатель может заподозрить, что топологии т=т(£, £"*)
и g = g(E, £*) совпадают. Хотя это и верно для конечномерных £,
в общем случае это не так. Чтобы убедиться в этом, допустим,
что dim£ = oo, и выберем в Е какой-нибудь алгебраический ба-
базис (е*)/еЕ/, так что множество / бесконечно. Пусть (е*) — дуаль-
дуальная система векторов в Е*. Если ввести обозначения x{i) = (xy e*y
для jte£hx* (i) = (eiy х*) для г* е £*, то каждое х представимо
в виде конечной суммы 2 х (I) et и каждое х* представимо в
виде 2 x*(i)e* причем ряды слабо сходятся в Е*.
Возьмем произвольную конечную положительную функцию /
на / и рассмотрим полунорму
р«= 2/@1*@1
на Е. Эта полунорма т-непрерывна. Если бы топологии т и а
совпадали, то в £* существовали бы такие элементы х*у ..., х*п
и такое число с ^ 0, что
= с sup Л 2 x*{i)x(\
I \i e /
для всех ^g£. В частности, для элемента л: из £, ортогональ-
ортогонального к х*т (l^m^n), p(x) должно было бы равняться нулю.
Так как f(i)>0 Для всех U то р(х)=0 тогда и только тогда,
когда х = 0. Таким образом, соотношения (л;, xln)^® {l^m^n)
влекли бы равенство х = 0. Отсюда, однако, следовало бы, что
dim E ^Сп, — противоречие.
К топологии т мы еще возвратимся в п. 8.10.13.
8.4. Сильная топология fi(E', E) и рефлексивность 693
8.4. Сильная топология $(Е\Е) и рефлексивность.
Монтелевы пространства
Всюду в этом параграфе Е— локально выпуклое простран-
пространство, Е' — его топологическое сопряженное.
Пользуясь обозначениями § 8.3, определим так называемую
сильную топологию ${Е\ Е) в Е' как топологию Г&, получаю-
получающуюся, если в качестве © взять систему всех ограниченных под-
подмножеств в Е. Другими словами, база окрестностей нуля тополо-
топологии Р(£1/, Е) образована полярами В°, где В пробегает систему
всех ограниченных множеств в Е. Естественно, что та же топо-
топология Р(£', Е) получается, если В пробегает лишь базу ограни-
ограниченных множеств в Е (например, все ограниченные замкнутые
выпуклые уравновешенные подмножества в Е).
Читатель может заметить, что если пространство Е полунор-
полунормируемо, то топология C(£1/, Е) определяется естественной нор-
нормой на Е' (п. 1.10.6).
В общем случае топология §(Е\ Е) не согласуется с двой-
двойственностью между Е и Е', т. е. не каждая линейная форма на
Е', непрерывная в топологии $(Е\Е), порождается некоторым
элементом из Е. Например, если E = co(N) (пространство сходя-
сходящихся к нулю числовых последовательностей, наделенное норми-
нормированной топологией, определяемой нормой || *|| = sup| х{п) \\,
то пространство Ег изоморфно пространству 11{Щ (теор. 4.2.2).
Сильная топология в 11{Щ определяется обычной нормой на
/*(N) (§ 4.2); следовательно, топологическое сопряженное к Е'
отождествимо с пространством /°°(N) (теор. 4.2.1), которое го-
гораздо «шире», чем само Е.
8.4.1. Полурефлексивные пространства. Следуя Бур баки
[7, стр. 238], будем говорить, что отделимое локально выпуклое
пространство Е полурефлексивно, если каждая сильно непре-
непрерывная линейная форма на Е' порождается некоторым элемен-
элементом пространства Е. Если пространство Е отделимо, то оно ото-
отождествимо (как векторное пространство) с подпространством в
Е" (§ 8.7; ср. замечание 1.9.5 A)). Поэтому если Е — полуреф-
полурефлексивное пространство, то имеет место изоморфизм Е" = Е в
смысле векторных пространств, где Е"— топологическое сопря-
сопряженное к Е\ наделенному сильной топологией р (£',£).
Из теоремы 8.3.1 вытекает следующий критерий полурефлек-
полурефлексивности.
8.4.2. Теорема. Отделимое локально выпуклое пространство Е
полурефлексивно тогда и только тогда, когда каждое ограничен-
ное подмножество в Е относительно слабо компактно.
694 Гл. 8. Теория двойственности
Примеры. Из следствия 1.12.6 легко вывести, что всякое гиль-
гильбертово пространство полурефлексивно. Теорема 4.2.1 показы-
показывает, что пространства 1р(Т)у 1 < р < оо, полурефлексивны. Ана-
Аналогично полурефлексивность пространств Lp(T, ji), 1<р<оо,
следует из теоремы 4.16.1. Так как в каждом из этих случаев
пространства нормируемы, то они в действительности даже ре-
рефлексивны в смысле приводимого ниже определения (см. заме-
замечание после теор. 8.4.5). Монтелевы пространства1) служат
примерами ненормируемых и даже неметризуемых полурефлек-
полурефлексивных пространств.
8.4.3. Теорема, Если пространство Е полу рефлексивно, то его
топологическое^ сопряженное Е' бочечно в своей сильной топо-
топологии.
Доказательство. Наделим Е' топологией Р(£', Е). По
условию его сопряженное алгебраически отождествимо с про-
пространством Е. Поэтому (теор. 8.3.4 C)) бочки в Е' — это поляры
слабо ограниченных подмножеств Е. Но последнее в силу утвер-
утверждения A) этой же теоремы означает, что бочки в Ег являются
окрестностями нуля, т. е. Е' бочечно. 1
8.4.4. Рефлексивные пространства. Если пространство Е полу-
полурефлексивно, то Е и Е" могут быть отождествлены как вектор-
векторные пространства. Что можно сказать об их топологиях? Про-
Пространство Е имеет свою исходную топологию, а в Е" можно рас-
рассмотреть топологию 7V, где через в' обозначена система всех
сильно ограниченных подмножеств в Е\ Так как исходная топо-
топология в Е совпадает с топологией Г@„ где ®i состоит из всех
равностепенно непрерывных множеств в Е\ то ясно, что исход-
исходная топология в Е, вообще говоря, слабее топологии Г@/. Снова
следуя Бурбаки [1, стр.239], будем говорить, что простран-
пространство Е рефлексивно, если оно полурефлексивно и, кроме того,
топология 7V совпадает с исходной топологией в £, т. е. Е и
Е" могут быть отождествлены как топологические векторные
пространства (а не только как векторные пространства).
Имеет место следующая теорема, параллельная теореме 8.4.2.
8.4.5. Теорема. Пространство Е рефлексивно тогда и только
тогда, когда оно полурефлексивно и бочечно.
Доказательство. Если пространство Е полурефлексивно,
то слабо ограниченные множества в Ег сильно ограничены
(теор. 8.3.4 A), примененная к пространству Ег в сильной топо-
топологии). Поэтому (теор. 8.3.4C)) бочки в Е совпадают с поля-
полярами сильно ограниченных множеств в Е\ т. е. они являются
]) См. ниже п. 8.4.7. — Прим. перев*
8.4. Сильная топология Р(£', Е) и рефлексивность 695
окрестностями нуля в Е". Таким образом, пространство Е бу-
будет рефлексивно тогда и только тогда, когда бочки в Е являются
окрестностями нуля, т. е. тогда и только тогда, когда Е — бочеч-
бочечное пространство. |
Замечание. Эта теорема показывает, что для бочечных
пространств нет разницы между полурефлексивностью и ре-
рефлексивностью. Далее, если пространство Е нормируемо и полу-
полурефлексивно, то его единичный шар (будучи ограниченным)
относительно слабо компактен (теор. 8.4.2) (или, что эквива-
эквивалентно, его замкнутый единичный шар слабо полон). Тогда про-
пространство Е полно и потому бочечно (теор. 6.2.2). Таким обра-
образом, для нормируемых пространств нет разницы между полу-
полурефлексивностью и рефлексивностью — именно потому, что при
этом замкнутый единичный шар слабо компактен (или, что то
же самое, слабо полон).
8.4.6. Следствие. Если пространство Е рефлексивно, то ре-
рефлексивно и Е' в своей сильной топологии.
Доказательство. По теореме 8.4.3 пространство Е' бо-
бочечно в своей сильной топологии. Полурефлексивность простран-
пространства Е' в этой топологии есть непосредственное следствие ре-
рефлексивности пространства £*, которая означает совпадение Е
как топологического векторного пространства с сильным сопря-
сопряженным к Е\ Таким образом, пространство Е' рефлексивно. |
Исторические замечания. Понятие рефлексивности для нор-
нормируемых пространств вырабатывалось постепенно. Банах, Ка-
кутани, Шмульян и Эберлейн — все внесли свой вклад в это
дело. В книге Данфорда и Шварца [1, гл. 5, § 4, а также
стр. 501] приведен обзор относящихся сюда результатов этих и
других авторов.
8.4.7. Ограниченно компактные пространства и монтелевы
пространства. Будем говорить, что топологическое векторное
пространство Е ограниченно компактно, если каждое его огра-
ограниченное множество относительно компактно. Как следует из
теоремы Ф. Рисса из п. 1.9.6, не существует нормируемых огра-
ограниченно компактных пространств, отличных от конечномерных.
Однако пространство C°°(Q) (где Q — область в Rn или вообще
вещественное дифференцируемое многообразие класса С°°) огра-
ограниченно компактно. Таково же пространство #(Q) (где Q — об-.
ласть комплексной плоскости или вообше комплексное аналити-
аналитическое многообразие), образованное голоморфными функциями
на Q и наделенное топологией локально равномерной сходи-
сходимости. Пространство C°°(Q) бесконечномерно, так же как и,
вообще говоря, пространство Н{п),
696 Гл. 8. Теория двойственности
Бур баки [7, стр. 240] называет монтелевым пространством
(пространством Монтеля) всякое отделимое локально выпуклое
бочечное ограниченно компактное пространство. Пространства
C°°(Q) и H(Q) монтелевы. Монтелевы и пространства 2D(Q, S)
(множество SczQ относительно компактно), а также 2D(Q) и
^(Rn), возникающие в теории обобщенных функций (§ 5.1, 6.3
и 5.15).
Из предыдущих результатов этого параграфа следует, что
всякое ограниченно компактное локально выпуклое простран-
пространство полурефлексивно и что всякое монтелево пространство ре-
рефлексивно.
Отметим также следующее свойство ограниченно компактных
топологических векторных пространств.
8.4.8. Теорема. Пусть Е— ограниченно компактное тополо-
топологическое векторное пространство. В каждом равностепенно не-
непрерывном множестве Q из Е' слабая и сильная топология сов-
совпадают. Если, кроме того, Е — отделимое локально выпуклое
пространство, то в каждом ограниченном множестве В из Е
ослабленная и исходная топологии совпадают.
Доказательство. Оба утверждения следуют из теоремы
Асколи. Например, если сеть (х^) точек множества Q слабо схо-
сходится к / g Q, то эта сходимость равномерна на каждом огра-
ограниченном множестве в Е, т. е. lim х\ = л/ в смысле сильной топо-
топологии р (£',£). I
8.4.9. Следствие. Пусть Е — монтелево пространство и Q —
слабо ограниченное множество в Е'. Тогда в Q слабая и сильная
топологии совпадают. В частности, всякая слабо сходящаяся по-
последовательность в Е' сходится сильно.
Доказательство. Это непосредственно следует из теоре-
теоремы 8.4.8, так как пространство Е одновременно ограниченно ком-
компактно и бочечно, а из последнего свойства вытекает равносте-
равностепенная непрерывность слабо ограниченного множества Q. |
8.4.10. Одно приложение. В каждом из пространств S5(Q) и
(R) (§ 5.1, 6.3 и 5.15) всякая слабо сходящаяся последова-
последовательность сходится. В каждом из пространств 2)'(Q) и ^'(Rn)
(§ 5.3 и 5.15) всякая слабо сходящаяся последовательность схо-
сходится сильно.
8.4.11. Теорема. Если Е монтелево, то монтелево и его топо-
топологическое сопряженное Е' в сильной топологии.
Доказательство. Так как Е полурефлексивно, то Е' бо-
бочечно в сильной топологии (теор. 8.4.3), Далее если Q — сильно
84 Сильная топология р(£', Е) и рефлексивность 697
ограниченное множество в Е\ то его сильно замкнутая выпуклая
оболочка Р также сильно ограничена. Так как пространство Е
рефлексивно, то множество Р слабо замкнуто (теор. 8.3.4). Из
бочечности пространства Е следует равностепенная непрерыв-
непрерывность и потому слабая компактность множества Р (теор. 1.11.4).
Следовательно (следствие 8.4.9), множество Р сильно компакт-
компактно. Поэтому множество Q сильно относительно компактно. Та-
Таким образом, пространство Ег ограниченно компактно в топо-
топологии $(Е\ Е) и, значит, монтелево в сильной топологии. |
8.4.12. Приложение. Пространства 2D'(Q) и &'(Rn) монтеле-
вы, если каждое из них наделить сильной топологией.
8.4.13. Сильная полнота пространства Е\ Из замечания (Ь)
после теоремы 7.3.1 вытекает, что
всякое борнологическое пространство сильно полно.
Этот результат, вероятно, наиболее важен из всех утвержде-
утверждений такого сорта. Полезно отметить также, что для всякого ин-
фрабочечного пространства Е пространство Ег сильно квази-
квазиполно. Фактически последнее утверждение справедливо для
любого пространства LC(E,F), где F — произвольное локально
выпуклое пространство 1). Действительно, рассмотрим произволь-
произвольную сильную сеть Коши (щ) в LC(E, F), лежащую в сильно огра-
ограниченном замкнутом подмножестве Н пространства LC(E,F).
Нам уже известно (предложение 1.10.9), что сеть (щ) сильно
сходится к некоторому элементу weLb(£,f), так что остается
лишь доказать непрерывность отображения и на Е. Поскольку
множество Н сильно ограничено, а пространство Е инфрабочеч-
но, то Н равностепенно непрерывно, откуда легко следует не-
непрерывность отображения и.
8.4.14. Сильное сопряженное как индуктивный предел. В за-
замечании C) после теоремы 6.7.2 мы указали на важность во-
вопроса: при каких условиях пространство Ег в сильной топологии
есть индуктивный предел (последовательности или в более об-
общем случае семейства) пространств Фреше? Как мы сейчас
покажем, этот вопрос связан с более широким вопросом: при ка-
каких условиях пространство Е' борнологично или бочечно?
Ниже мы будем обозначать через 6 сильную топологию
'Е)
)
Начнем с построения некоторой индуктивной топологии % в
Е\ а затем выясним связь между топологиями C и Я.
1) Пространство F следует здесь предполагать полным (предложение
1.10.9), a LC(E, F) — наделенным топологией равномерной сходимости на
ограниченных множествах из Е, — Прим. перев.
698 Гл. 8. Теория двойственности
Пусть (Ui) — семейство окрестностей нуля в £, гомотегиче-
ские образы которых образуют базу в нуле. Обозначим через Р*
поляру в Е' окрестности Uiy а через Gt- = (J o,Pt векторное под-
а >0
пространство в Е', порожденное полярой Яг-. Так же как и в
лемме 6.5.2, превратим G7- в банахово пространство с единичным
шаром Р{, и пусть Яг- — соответствующая топология в G*. Тогда
(Е',Х) есть индуктивный предел пространств (GuKi) относитель-
относительно вложений Gi в Е\ Пространство (£', I) является, таким обра-
образом, внутренним индуктивным пределом банаховых пространств.
Если Е — метризуемое пространство, то можно считать, что ин-
индекс i пробегает множество натуральных чисел, и мы имеем
дело лишь с последовательностью пространств (G2-, Яг). Во всех
случаях пространство (Е\ X) одновременно борнологично и бо-
чечно.
Так как Яг- — сильно ограниченное множество, то топология
P|GZ- слабее топологии V, следовательно, во всех случаях топо-
топология р слабее топологии К. Основная задача — определить усло-
условия, при которых p = /L
Если предположить, что Е — инфрабочечное пространство, то
получаются некоторые интересные упрощения.
8.4.15. Предложение. Если пространство Е инфрабочечно, то
(a) подмножество в Ег ^-ограничено тогда и только тогда,
когда оно Х-ограншено;
(b) пространство (Е\ р) борнологично тогда и только тогда,
когда р = Х.
Доказательство, (а) Так как топология р слабее топо-
топологии Я, то достаточно показать, что всякое р-ограниченное мно-
множество Н в Е' является и ^-ограниченным. Пространство Е ин-
фрабочечно, поэтому (теор. 7.1.1 C)) множество Н равностепен-
равностепенно непрерывно и, следовательно, содержится- в некотором
множестве вида аРг-, где а > 0. Но тогда множество Н погло-
поглощается каждой ^-окрестностью нуля, т. е. ^-ограничено.
(Ь) Мы должны показать, что если (£7, р)—борнологическое
пространство, то топология X слабее топологии р. Если V — вы-
выпуклая, уравновешенная ^-окрестность нуля, то (по утвержде-
утверждению (а)) она поглощает все р-ограниченные множества. Так как
пространство (Е', р) борнологично, то V есть р-окрестность нуля.
Таким образом, топология X слабее топологии р. I
Непосредственное применение теоремы 6.2.1 B) приводит к
следующему аналогу утверждения (Ь) последнего предложения.
8.4.16. Предложение. Если пространство (Е\ р) бочечно и
обладает базой ^-замкнутых ^-окрестностей нуля, то Х=р.
8.4. Сильная топология $(Е', Е) и рефлексивность 699
Правильные пространства. Отвлекаясь немного в сторону, мы
можем сейчас сформулировать необходимые и достаточные усло-
условия бочечности пространства (Е\ C). Для этого нам понадобится
следующее определение. Отделимое локально выпуклое про-
пространство Е называется правильным (Дьёдонне и Шварц
[1, стр. 78], Бу р б а к и [7, гл. 4, стр. 244, упр. 10]), если каждое
о(Е", .Р)-ограниченное подмножество из Е" содержится в
а(Е", Е') -замыкании некоторого ограниченного множества из Е.
8.4.17. Предложение. Пространство (Е\ р) бочечно тогда и
только тогда, когда оно правильно.
Доказательство. Если пространство (£', Р) бочечно, то
всякое о(Е", E') -ограниченное множество Q равностепенно не-
непрерывно, т. е. Qcz (В°)°, где В— ограниченное множество из Е,
а поляра (В0H множества В0 взята в Е". Считая (это не умень-
уменьшает общности) множество В выпуклым и уравновешенным,
получаем, что В°° совпадает с а(Е'\ £')-замыканием множе-
множества В. Пространство Е, таким образом, правильно.
Обратно, пусть пространство Е правильно и А —бочка в
(Е\ р). Тогда ее поляра Л° в Е" является а(Е", Е') -замкнутой.
По условию существует такое ограниченное множество В в Е,
что А0 содержится в о (£", Е') -замыкании множества В. Но
тогда множество А°° содержит поляру 5°, которая есть р-окрест-
ность нуля. Так как множество А есть Р'-бочка, то А=А0о1 так
что А есть р-окрестность нуля. Следовательно, пространство
(Е\ р) бочечно. |
Подведем итог предыдущим результатам.
► A) Пространство (Е\ р) бочечно тогда и только тогда,
когда Е правильно.
► B) Если пространство Е инфрабочечно, то (Е\ р) борно-
логично тогда и только тогда, когда 1 = р, и в этом слу-
случае (Е\ р) также бочечно. Отсюда следует, что равенство
Я = р влечет правильность пространства Е.
Как мы сейчас покажем, для пространств Фреше верно и об-
обратное утверждение.
8.4.18. Предложение. Если Е — пространство Фреше, то ра-
равенство А, = р имеет место тогда и только тогда, когда простран-
пространство Е правильно. В этом случае сильное сопряженное Е' есть
внутренний индуктивный предел последовательности банаховых
пространств.
Доказательство. Нужно доказать только, что Я== р, если
£—-правильное пространство Фреше. Ввиду предложений 8.4.16
и 8.4.17 достаточно установить, что выполнены условия предло-
предложения 8.4.16. Приводимое ниже доказательство принадлежит
Бур баки [9, гл. 6, стр. 76? лемма 1],
700 Гл. 8 Теория двойственности
Пусть (Ui) — убывающая последовательность замкнутых, вы-
выпуклых уравновешенных множеств в £, образующая базу окре-
окрестностей нуля в Е. Пусть далее V — выпуклая уравновешенная
Я-окрестность нуля в Е\ Для каждого i найдется такое число
аг- > 0, что а.[/°. c-rF. Обозначим через Ап выпуклую оболочку
множества (J {а,.£/°Г* 1<л^/г] и через W объединение мно-
множеств Ап. Множество W выпукло, уравновешено, поглощающе и
содержится в у V. Замыкание W множества W в топологии р
есть бочка в этой топологии и, значит, р-окрестность нуля. Те-
Теперь достаточно установить, что множество W содержится в V,
отсюда в силу выбора множества V будет следовать выполне-
выполнение условий предложения 8.4.16.
С этой целью возьмем некоторую точку х\ не принадлежа-
принадлежащую V. Каждое из множеств Ui компактно в слабой топологии
о(Е\ЕI поэтому таково же и множество Ап. Так как точка хг
не принадлежит множеству 2Ап, то в Ап (поляра взята в Е) най-
найдется такая точка хп, что (хп, х')=2. Если у'— произвольный
элемент из Е\ то у' е U°k при некотором k и потому | (хп, у'Л | ^
^а^1 для п > k. Отсюда вытекает, что последовательность (хп)
слабо ограничена и, следовательно, ограничена в Е. Пусть Н —
выпуклая уравновешенная оболочка множества {хп} в Е. Поля-
Поляра Н° множества Н является C-окрестностью нуля в Е\ поэтому
ее поляра Я00 в Е" компактна в топологии о{Ег',Е'). Следова-
Следовательно, последовательность (хп) обладает в Е" о(Е'\ Е')-пре-
Е')-предельной точкой х", для которой, очевидно, имеет место равен-
равенство (х", х')=2. Кроме того, х" принадлежит всем полярам Ап
(в Е"), так что х" е W° (поляра в Е"). Но тогда хг не принад-
принадлежит множеству W00 и, следовательно, не принадлежит и
о(Е\ Е") -замыканию множества W. Тем более х' не принадле-
принадлежит р-замыканию множества W, х' ф. W. Таким образом, Wa V,
что и требовалось доказать. 1
См. также Келли и Намиока [1, теорема 22.15 и зада-
задача G, стр. 221], Шефер [4, стр. 153], Ко мура [1].
8.4.19. Таким образом, мы видим, что обе теоремы 6.7.1 и
6.7.2 остаются справедливыми, если всюду заменить простран-
пространства Е и F сильными сопряженными Е' и F' правильных (напри-
(например, рефлексивных) пространств Фреше. (Подробности см. в
упр. 8.44 и 8.45.)
8.5. Теорема Банаха — Гротендика
Если Е — локально выпуклое пространство и Е' — его топо-
топологическое сопряженное, то, как известно, линейная форма на
8.5. Теорема Банаха — Гротендика 701
Е' тогда и только тогда порождается элементом из Е (т. е. имеет
вид *'н-> (*,*') для некоторого х из £), когда она слабо непре-
непрерывна. Во многих приложениях бывает удобно иметь критерий,
более приспособленный для некоторых конкретных типов про-
пространств Е. Условимся обозначать через j(x) линейную форму
на Е\ определяемую элементом из Е, т. е. форму вида х'*->
8.5.1. Теорема (Банах — Гротендик). Пусть Е — полное
локально выпуклое пространство. Линейная форма и на Е' имеет
вид j(x) для некоторого х е Е тогда и только тогда, когда суже-
сужение и | U° слабо непрерывно для каждой окрестности U из не-
некоторой базы окрестностей нуля в Е.
Доказательство. Необходимость утверждения триви-
тривиальна.
Для доказательства достаточности обозначим через F множе-
множество всех линейных форм и на £', сужение которых u\S на ка-
каждое множество вида 0° слабо непрерывно. Систему всех таких
подмножеств обозначим через 2. Если S^S и u^F, то u(S)
ограничено и мы можем рассмотреть в F топологию Г2 , превра-
превратив, таким образом, F в локально выпуклое пространство. Мы
хотим доказать, что j(E)=F.
Прежде всего легко показать, что множество j(E) замкнуто
в F. Действительно, если иг=]'(х^ и (щ) — сеть Коши в /(£"), то
и (xt) будет сетью Коши, и можно воспользоваться полнотой
пространства Е. Достаточно, таким образом, доказать плотность
множества j(E) в F. Если тогда удастся установить, что сопря-
сопряженное к F совпадает с Е\ то из теоремы Хана — Банаха будет
вытекать плотность множества j(E) в F. Действительно, любой
элемент х' е Е\ для которого x'(j(x))=0 при всех х^Е, удо-
удовлетворяет равенству х' = 0, так что и(х')=0 для всех и ^F.
В силу теоремы 8.3.2 достаточно показать, что каждое множе-
множество S = U° компактно в топологии o(F',F). Так как каждое та-
такое множество а (Е\ Е) -компактно, то остается проверить, что
обе эти топологии индуцируют в S одну и ту же топологию. Пер-
Первая из этих топологий сильнее второй, поэтому надо только про-
проверить, что о(Е\ F) \S^o(E\ E) \S. Но о(Е', F)\S — слабейшая
топология в S, относительно которой каждая функция u^F не-"
прерывна на S. По определению F она слабее топологии
о(Е\ E)\S. Доказательство теоремы закончено. I
Замечания. A) Если пространство Е отделимо, то отобра-
отображение / взаимно однозначно, что позволяет отождествить х с
j(x) и считать Е вложенным в множество F, которое само есть
подмножество в Е'*,
702 Гл. 8. Теория двойственности
B) Если пространство Е не является полным, то предыдущие
рассуждения показывают, что F можно отождествить с /(£"), где
отображение / обычным образом продолжено на пополнение.
8.5.2. Следствие. Пусть Е—полное отделимое локально вы-
выпуклое пространство. Линейная форма и на Е/ принадлежит
множеству j(E) тогда и только'тогда, когда \imu(x'n)=0 для
Л ->оо
каждой равностепенно непрерывной последовательности (х'п),
слабо сходящейся к нулю в Е\
Доказательство. Необходимость утверждения очевидна.
Докажем достаточность. Читатель может заметить, что если про-
пространство Е содержит счетное тотальное множество, то тополо-
топология о(Е',Е) индуцирует в каждом равностепенно непрерывном
множестве из Е' метризуемую топологию. Отсюда и из теоре-
теоремы 8.5.1 следует, что we/ (Е), если и (л£) -> и {х) для каждой
последовательности (л£) с: S, слабо сходящейся к хг. Остается
показать, что последнее утверждение следует, в свою очередь,
из своего частного случая при х' = 0.
Если S — выпуклое уравновешенное множество и сужение
u\S слабо непрерывно в нуле, то в Е' существует такая слабая
окрестность нуля Wy что I m(x') 1*С тг8 Для Xf^S{\W. Если
х'о — точка множества S и х' е (x'Q + IF) П 5, то xr s S, /-xjs
<=W и
Не нарушая общности, можно считать, что W — выпуклая и
уравновешенная окрестность. Тогда х'-^еЯ^, откуда •п-(*/ —
- х'о) е W{\ 5, так что
поэтому
Этим доказана непрерывность сужения u\S в точке х'о. Таким
образом, из слабой непрерывности сужения u\S в нуле следует
его слабая непрерывность на S. I
8.6. Сопряженные отображения
Пусть Е и F — векторные пространства (над одним и тем же
полем К) у а £* и F* — их алгебраические сопряженные. Тогда
(£,£*) и (F,F*) являются дуальными парами, отделимыми со-
8.6. Сопряженные отображена. 703
ответственно по £* и F* (пара (£, £*) фактически является «наи-
«наибольшей» из дуальных пар (£,£'), отделимых по Е').
Пусть и: E-+F— линейное отображение. Тогда соотношение
определяет линейное отображение и*\ /7*->£*. Отображе-
Отображение и* называется алгебраическим сопряженным к отображе-
отображению и.
Можно попытаться обобщить этот процесс «сопряжения» на
произвольные дуальные пары {Е,Е') и (F,Ff), отделимые со-
соответственно по Е' и F'. Пусть задано линейное отображение
и: E-+F. Прежде всего, надо выяснить, для каких элементов
у/е/7/ линейная форма x*—>{u(x)f у') порождается некоторым
элементом из £', т. е. непрерывна в топологии о(Е, E'). Множе-
Множество таких у' образует векторное подпространство D' в F\ и
можно определить сопряженное отображение и!\ D'-*E't по-
полагая
(и(х),у') = (х,и'(у')) (8.6.1)
для y'^D' и х^Е. Отсюда следует, что элемент и'{у'), если
он существует, совпадает с и*{у'). Другими словами, D' — это
множество всех тех у\ принадлежащих F/czF*y для которых
и*(у') попадает в Е\ и u' = u*\D'. Читатель может заметить, что
равенство D' = F' имеет место тогда и только тогда, когда ото-
отображение и слабо непрерывно, т. е. непрерывно в топологиях
о{Е,Е') и o{F,F'). Если, кроме того, рассматриваемые дуаль-
дуальные пары отделимы по Е и по F и отображение и: E-+F слабо
непрерывно, то можно построить отображение и"=(и')\ при
этом мы получим в точности отображение и. (Если отображение
и слабо непрерывно, то и отображение и! автоматически обла-
обладает этим свойством.)
Сказанное выше имеет два важных приложения. Оба они
относятся к локально выпуклым пространствам. Рассмотрение
этих приложений проведем в два этапа.
A) Пусть Е и F — локально выпуклые пространства, Е/ и
F' — их сопряженные. Если и: E-^F — непрерывное линейное
отображение, то оно слабо непрерывно, так что отображение и'
определено всюду на F'.
Действительно, для всякого элемента yr e F' линейная форма
ху-Цм(лг), у') непрерывна на £ в исходной топологии и потому
непрерывна и в ослабленной топологии о(Е, Е') (по определе-
определению последней).
B) Обратимся теперь к более общему случаю, когда Е и
^-—топологические векторные пространства и линейное отобра-
704 Гл. 8. Теория двойственности
жение и определено не обязательно всюду на Е. Мы предпола-
предполагаем, таким образом, что область определения отображения и
содержится в£, а его область значений — в F. Мы не требуем
даже непрерывности отображения и в его области опреде-
определения.
При исследовании этого случая удобно воспользоваться гра-
графиками. Для этого приведем пространства ExF и F'ХЕ' в
двойственность с помощью билинейной формы
Знак минус употребляется здесь лишь для удобства.
Рассмотрим поляру (grw)° графика gvu отображения и от-
относительно только что определенной двойственности. (grw)°ecTb
подмножество в F'xE', образованное теми парами («/', *'), для
которых
для x^domu. Возникает вопрос: когда само множество (gru)°
есть график? Так как (grw)°, очевидно, есть векторное подпро-
подпространство в F'xE', то ответ таков: тогда и только тогда, когда
@>х')^(цти)° влечет х'=0. Это означает ровно то, что соотно-
соотношение xr e (dom£/)° (здесь (domw)° — поляра множества dom и
относительно дуальной пары (£, £')) влечет равенство ^ = 0, а
это (теорема Хана — Банаха) равносильно слабой плотности
dom а в Е.
Таким образом, множество (grw)° есть график тогда и толь-
только тогда, когда множество dom и слабо плотно в Е. Если это
условие выполнено, то {gv иH есть график некоторого (обяза-
(обязательно линейного) отображения с областью определения в Ff и
областью значений в Е'. Его область определения совпадает с
множеством тех у' е F', для которых существует элемент х' е Е',
такой, что (х,х') — (и(х),у')=0 для всех x^domu. Обращаясь
к уже рассмотренному случаю doma = £, видим, что полученное
отображение есть не что иное, как сопряженное отображение-м'.
Мы сохраним это название и обозначение и для случая, когда
множество dom и только слабо плотно в Е.
Окончательно: сопряженное отображение и' существует (т. е.
(grw)° есть график) тогда и только тогда, когда множество
domw слабо плотно в Е\ если отображение и! существует, то об-
область его определения совпадает с множеством тех у' е F\ для
которых линейная форма х>—>{и (х), у') слабо непрерывна на
dom u\ для всякого у/ е dom и' существует такой единственный
элемент х/ е Е\ что
8 6. Сопряженные отображения 705.
для х е dom и, причем этот х/ и есть элемент и'(у'). Таким обра-
образом, отображение и! вполне определяется соотношением
<*,к'(/)> = <"(*). У0.
имеющим место для х е dom и и у' е dom г/
Заметим, что отображение и' слабо замкнуто, ибо множество
(grw)° слабо замкнуто.
Следует отметить, что если Е и F — топологические вектор-
векторные пространства, а Е' и F'— их топологические сопряженные,
то отображение и! замкнуто относительно любых топологий в
F' и £', согласующихся с двойственностями между £и£'и ме-
между F и F' соответственно. Если, кроме того, пространство Е
локально выпукло, то отображение и' определено (т. е. множе-
множество dom и слабо плотно в Е) тогда и только тогда, когда мно-
множество dom и плотно в £ (в заданной топологии в Е). В этом
случае можно также сказать, что элемент у' принадлежит dom и'
тогда и только тогда, когда линейная форма х*->(и(х),у') не-
непрерывна на dom и в топологии, индуцированной топологией,
заданной в Е.
Всюду в оставшейся части этого параграфа мы будем иметь
дело со случаем, когда (£, Е') и (/\ F') —дуальные пары, отде-
отделимые соответственно по Е' и F\ а и: E-+F — слабо непрерыв-
непрерывное линейное отображение. При этом выполняются и часто при-
применяются следующие соотношения.
(a) Если А а Е и В с= F\ то
и (АH = и'~1 (Л°), гГ1 (В°) = и' (В)°. (8.6.2)
(b) Если AczE и BcF, то
' (B°) с Л°, (8.6.3)
причем обратное верно, если В — выпуклое уравновешенное
слабо замкнутое множество.
(с) ^ = (kerttT=k-'({0})]°,
(d) Множество и(Е) слабо плотно в пространстве F тогда
и только тогда, когда отображение и' взаимно однозначно; если
рассматриваемые дуальные пары отделимы, то множество
u'(F') слабо плотно в Е' тогда и только тогда, когда отображе-
отображение и взаимно однозначно. Если нет отделимости по Е и F, то
вместо взаимной однозначности следует требовать выполнения
условия
706 Гл. 8. Теория двойственности
Доказательство. Доказательство утверждения (а) сво-
сводится к жонглированию формулой (8.6.1) и определейием йоля-
ры (п. 8.1.4). Утверждение (Ь) следует из теоремы 8.1.5 о бипо-
ляре. (с) есть частный случай (a), a (d) следует из (с). 1
Хотя пока мы рассматривали абстрактные дуальные пары и
их слабые топологии, задачи, относящиеся к отображениям и и
и\ довольно конкретны. Наибольший интерес представляет слу-
случай, когда Е и F — локально выпуклые пространства, Е' и F' —
их топологические сопряженные, и мы хотим для этого случая
связать свойства отображения и относительно исходных тополо-
топологий со свойствами относительно слабых топологий, возникающих
при рассмотрении дуальных пар (Е, Е') и (F,Ff). Эта задача
нетривиальна, и мы посвятим ей всю оставшуюся часть на-
настоящего параграфа.
Как мы уже отмечали, из непрерывности линейного отобра-
отображения и: E-+F следует его слабая непрерывность (так что ото-
отображение и'\ F'-^E' определено). Обратное утверждение, во-
вообще говоря, не имеет места, однако в двух приводимых ниже
теоремах содержатся некоторые результаты в этом направлении.
8.6.1. Теорема. Пусть Е и F — локально выпуклые простран-
пространства и и: E-^F— слабо непрерывное линейное отображение.-
Тогда
A) отображение и непрерывно в топологиях т(Е,Е') и
t(F,F);
B) отображение иг непрерывно в топологиях k(F',F) и
*(£',£);
C) отображение и ограничено.
Доказательство. A) Если множество V есть т-окрест-
ность нуля в Т7, то оно содержит множество вида /С0, где К— вы-
выпуклое уравновешенное слабо компактное множество в F'. Так
как отображение и' слабо непрерывно, то множество Н = и'(К)
выпукло, уравновешено и слабо компактно в Е', поэтому множе-
множество U~H° есть т-окрестность нуля в Е. Из соотношения
u~1(V)zd U следует, что u~l(V) есть т-окрестность нуля в £, т. е.
что отображение и непрерывно.
B) Доказательство непосредственно вытекает из формулы
(8.6.3) и из того факта, что непрерывное отображение и перево-
переводит всякое выпуклое уравновешенное компактное множество из
Е в аналогичное множество из F.
C) Отображение у' ° и непрерывно для каждого элемента yr ^
ef. Если А—ограниченное множество в £, то таким же будет
и множество у'ои(А). Отсюда вытекает слабая ограниченность,
а значит (теор. 8.2.2), ограниченность множества и(А) в /\ Сле-
Следовательно, отображение и ограничено. I
8.6. Сопряженные отображения 707
8.6.2. Теорема. Пусть Е и F— локально выпуклые простран-
пространства и W.E-+F — слабо непрерывное линейное отображение.
Отображение и непрерывно в каждом из следующих двух слу-
случаев:
A) пространство Е относительно сильно (например, бочечно
или полуметризуемо (теор. 8.3.5));
B) пространство Е борнологично.
Доказательство. A) Утверждение следует из части A)
предыдущей теоремы, так как топология x(F,F') сильнее исход-
исходной топологии в F.
B) Это утверждение вытекает из части C) предыдущей тео-
теоремы и из замечания (Ь), следующего за георемой 7.3.1. I
Для абстрактных дуальных пар следующий результат играет
основополагающую роль.
8.6.3. Предложение. Пусть (£,£') и (F,F') —отделимые ду-
дуальные пары и и: E-^F— слабо непрерывное линейное отобра-
отображение. Отображение и пространства Е на и(Е) слабо открыто
тогда и только тогда, когда множество и'IF') слабо замкнуто
в Е'.
Доказательство. A) Вначале предположим, что ото-
отображение и взаимно однозначно, т. е. что множество и'(F')
слабо плотно в Е'. Покажем, что в этом случае и является сла-
слабым изоморфизмом пространства Е на и(Е)=М тогда и только
тогда, когда и' (Ff) =E'.
Если и — слабый изоморфизм пространства Е на М, то ото-
отображение и~1 непрерывно в топологиях o(F,F')\M и о(Е,Е').
Поэтому для заданного элемента х'^Е' линейная форма
уь—>(и~1 (у)у х') на М непрерывна в топологии а(/7, F')\M. По
теореме Хана — Банаха она является сужением на М некото-
некоторого элемента yr e F'. Таким образом, для элементов у е М
имеем
Пусть х^Е; полагая в последнем равенстве у = и(х), полу-
получаем {х,х') = {и(х),у'), т. е. и'(у')=х'. Таким образом, и' есть
отображение пространства F' на £', что и требовалось доказать.
Допустим обратное, т. е. что и' отображает Fr на Ег (откуда
следует взаимная однозначность отображения и). Тогда для
каждого конечного семейства (xj) в Е' найдется такое же се-
семейство (jyty в F\ что u'(yty = x't для каждого /. Неравен-
Неравенства \(и(х), ^)|<1 эквивалентны неравенствам | (х, *J)|^1,
откуда вытекает, что и — слабый изоморфизм пространства Е
на и(Е)ч
708 Гл. 8. Теория двойственности
B) В общем случае, когда отображение и не взаимно одно-
однозначно, введем в рассмотрение ядро N отображения и и взаимно
однозначное отображение v: E/N-+F, индуцированное отобра-
отображением и. Утверждение «и— слабо открытое отображение про-
пространства Е в F» означает, что отображение v — изоморфизм
пространства E/N в F относительно фактортопологии о(Е, E')/N
в E/N и топологии o{FyFf). Но в силу предложения 8.1.2 это
означает, что v — слабый изоморфизм пространства E/N в F от-
относительно слабых топологий в E/N и F. По уже доказанному
это эквивалентно утверждению, что vr отображает F' на № (по-
(последнее пространство является сопряженным к E/N). С другой
стороны, имеет место равенство u'—[ovf, где i — вложение под-
подпространства № в Е'. Таким образом, если и: E->F— слабо от-
открытое отображение, то и'(F/)=i{№)—№1 причем это множе-
множество слабо замкнуто.
С другой стороны, если множество u'(F') слабо замкнуто в
Е\ то из соотношения u'(F')° = N следует, что u'(F')=№, т. е.
что v'(F')=№\ следовательно, и: E-+F — слабо открытое ото-
отображение. |
Замечание. Так как абстрактные дуальные пары совер-
совершенно симметричны, то предложение 8.6.3 приводит к аналогич-
аналогичным утверждениям относительно слабо непрерывных линейных
отображений пространства F' в Е'. Примером такого результата
является утверждение B) приводимого ниже следствия.
8.6.4. Следствие. Пусть (Е,Е') и {F,Ff)—отделимые дуаль-
дуальные пары и и: E-+F — слабо непрерывное линейное отобра-
отображение.
A) Отображение и является слабым изоморфизмом тогда и
только тогда, когда u'(F')s=E' (т. е. иг есть отображение на).
B) Тогда и только тогда u(E)=F (т. е. и есть отображение
«а), когда иг — слабый изоморфизм пространства F/ в Е'.
8.6.5. Предложение. Пусть Е и F—-отделимые локально вы-
выпуклые пространства, Е/ и Fr — их топологические сопряженные,
и: E-^F и v: F'-^E' — линейные отображения. Тогда для
утверждений
(a) и непрерывно,
(b) и слабо непрерывно,
(c) v слабо непрерывно,
(a) v сильно непрерывно
справедливы импликации
(а)=МЬ)
(c)^(d).
Доказательство. Импликация (а)=^(Ь) уже доказана,
8.6. Сопряженные отображения 709
Докажем вторую импликацию. Так как v слабо непрерывно, то
можно считать, что v = u' для некоторого слабо непрерывного
отображения и\ E-+F. Для доказательства сильной непрерыв-
непрерывности v достаточно показать, что для каждого ограниченного
множества А а Е существует такое ограниченное множество
BczF, что u'(B°)czAo. Но отображение и слабо непрерывно, по-
поэтому множество и (А) слабо ограничено и, следовательно
(теор. 8.2.2), ограничено в F. Достаточно положить В = и(А). |
8.6.6. Следствие. Пусть Е и F — отделимые локально выпук-
выпуклые пространства. Er и F' — их топологические сопряженные.
Тогда всякое непрерывное линейное отображение и простран-
пространства Е в F слабо непрерывно, а его сопряженное uf и слабо и
сильно непрерывно.
» 8.6.7. Следствие. Пусть Е и F — отделимые локально выпук-
выпуклые пространства, причем F полурефлексивно. Тогда всякое
сильно непрерывное линейное отображение v: F'-^E' слабо не-
непрерывно.
Доказательство. Импликация (a)z^>(b) из теоре-
теоремы 8.6.5 показывает, что v непрерывно при топологиях o(F\F")
и о(Е', Е"). Так как F полурефлексивно, то o(F',F")=g(F',F).
Наконец, очевидно, что топология в(Е',Е") сильнее топологии
о(Е'9Е). I
8.6.8. Теорема. Пусть Е и F — отделимые локально выпуклые
пространства с топологическими сопряженными Е/ и F/ соответ-
соответственно и и: E-+F — непрерывное линейное отображение. Для
того чтобы и было открытым отображением пространства Е на
и(Е), необходимо и достаточно, чтобы
(a) и было слабо открытым отображением Е в F (т. е. чтобы
множество и'(F') было слабо замкнутым в F' (теор. 8.6.3)) и
(b) каждое равностепенно непрерывное множество в Е', со-
содержащееся в u'(F'), было образом некоторого равностепенно
непрерывного множества в F' относительно и'.
Доказательство. Введем обозначения N = u~l@), Х =
= E/N, Y = u(E). Пусть v—взаимно однозначное отображение
X на У, определяемое отображением и. Сказать, что и — откры-
открытое отображение пространства Е в F, по определению равносиль-
равносильно утверждению, что v — изоморфизм пространства X на У.
В силу предложения 8.1.2 утверждения «а —слабо открытое ото-
отображение в» и «v — слабый изоморфизм на» эквивалентны. Да-
Далее в силу того же предложения X' отождествимо с №. Равно-
Равностепенно непрерывными множествами в X' являются те равно-
равностепенно непрерывные множества в Е', которые содержатся в №,
а равностепенно непрерывные множества в Y'*=F'IY° — это
710 Гл. 8. Теория двойственности
образы (относительно естественного' отображения F' на F'jY°)
равностепенно непрерывных множеств из F'.
Пусть теперь и— открытое отображение пространства Е на
и(Е), так что v — изоморфизм. По предложению 8.6.5 оба ото-
отображения v и v~l слабо непрерывны, так что v — слабый изо-
изоморфизм. Это означает, что и— слабо открытое отображение
пространства Е в F. Из того факта, что v — слабый изоморфизм,
вытекает, что множество v'(Y') слабо плотно и слабо замкнуто
в Х\ т. е. v'(Y')=X' и u'(F')=№. Так как v — изоморфизм, то
всякое равностепенно непрерывное множество в X' есть образ
некоторого равностепенно непрерывного множества из У относи-
относительно v\ т. е. каждое равностепенно непрерывное множество из
Е\ содержащееся в N°=uf{F'), является образом некоторого
равностепенно непрерывного множества из F' относительно и'.
Таким образом, (а) и (Ь) необходимы для того, чтобы и было
открытым отображением пространства Е в F.
Обратно, предположим, что (а) и (Ь) выполнены. В силу (а)
отображение v — слабый изоморфизм, так что v'(Y')=X', т. е.
u'(F')=№. Утверждение (Ь) означает, что всякое равностепенно
непрерывное множество в X'является образом некоторого равно-
равностепенно непрерывного множества из У' относительно v'. Эго
в свою очередь показывает, что v — изоморфизм (в силу соот-
соотношения, двойственного (8.6.3)). Таким образом достаточность
условий (а) и (Ь) установлена, что и завершает доказательство
теоремы. |
8.6.9. Следствие. Пусть Е и F — отделимые локально выпук-
выпуклые пространства с топологическими сопряженными Е/ и F', и—
непрерывное линейное отображение пространства Е в F. Для
того чтобы отображение и было изоморфизмом Е в Fy необходи-
необходимо и достаточно, чтобы каждое равностепенно непрерывное мно-
множество в Ег было образом некоторого равностепенно непрерыв-
непрерывного множества из Fr относительно и'.
Доказательство. Если и изоморфизм пространства Е в
F, то и — слабый изоморфизм Е в F (теор. 8.6.8), поэтому
(предл. 8.6.3) множество u'(F') слабо замкнуто в £'. Так как
отображение и взаимно однозначно, то uf(Ff) слабо плотно в Е\
следовательно, ur(Ff) —Е'. Остается применить теорему 8.6.8 (Ь).
Необходимость доказана.
Обратно, если и удовлетворяет сформулированным условиям,
то u'(F')=E'y поэтому отображение и взаимно однозначно. Да-
Далее (предложение 8.6.3) и — слабо открытое отображение про-
пространства Е в F. Таким образом, и удовлетворяет условиям (а)
и (Ь) теоремы 8.6.8; следовательно, и — изоморфизм простран*
ства Е з F. |
8 6. Сопряженные отображения 711
8.6.10. Следствие. Пусть Е и F — отделимые локально выпук-
выпуклые пространства, причем F относительно сильно (например,
метризуемо или бочечно). Непрерывное линейное отображение и
пространства Е в F открыто тогда и только тогда, когда оно
слабо открыто.
Доказательство. Прежде всего «открыто» влечет «слабо
открыто» (теор. 8.6.8). Докажем оставшуюся часть следствия.
Если и — слабо открытое отображение пространства Е в F, то по
следствию 8.6.4 отображение и' есть слабый изоморфизм про-
стр.анства F' на и' (Fr). С другой стороны, если множество А' а
a ur (F') равностепенно непрерывно как множество в Е\ то
оно относительно слабо компактно, поэтому множество В' =
— и'-х(Аг) относительно компактно в Fr. Так как пространство/7
относительно сильно, то В' равностепенно непрерывно в F'. Из
равенства А' = и'(В') следует выполнение условия 8.6.8 (Ь). Та-
Таким образом, и — открытое отображение пространства Е в F. В
8.6.11. Следствие. Пусть Е и F — отделимые локально выпук-
выпуклые пространства, и — непрерывное линейное отображение про-
пространства Е в F. Для того чтобы и было открытым отображе-
отображением пространства Е на плотное векторное подпространство в
F, необходимо и достаточно, чтобы отображение и' было взаимно
однозначно, чтобы множество и' (F') было слабо замкнуто в Е*
и чтобы прообраз всякого равностепенно непрерывного множе-
множества из Е' относительно и* был равностепенно непрерывен в F\
Доказательство. Достаточно воспользоваться теоремой
8.6.8 и тем фактом, что множество и(Е) плотно тогда и только
тогда, когда отображение и' взаимно однозначно. В
Посмотрим теперь, как выглядят предыдущие результаты в
важном частном случае пространств Фреше или Банаха. Возни-
Возникающие при этом упрощения частично основаны на следующей
лемме.
8.6.12. Лемма. Пусть Е—полное полуметризуемое, a F — по-
луметризуемое локально выпуклое пространство и Аа Е' — рав-
равностепенно непрерывное слабо замкнутое выпуклое уравнове-
уравновешенное множество. Построим банахово пространство Еа (ср. с
леммой 6.5.2). Если и: E->F — непрерывное линейное отображе-
отображение и пересечение u'(F')()A замкнуто в Еа для каждого Л, то
множество u'(F') слабо замкнуто в Е'.
Доказательство. В силу теоремы 8.10.5 (доказатель-
(доказательство которой совершенно не зависит от приводимых здесь рассу-
рассуждений) достаточно показать, что для каждого А множество
K~uf(F')()A слабо замкнуто в Е'. Так как топология о(Е',Е)
712 Гл. 8. Теория двойственности
отделима, то доказательство сводится к установлению слабой
компактности множества /С Итак, пусть множество К выпукло,
уравновешено и замкнуто в Е'а. Множество F' есть объединение
последовательности (Сп) слабо компактных выпуклых уравно-
уравновешенных множеств (например, поляр базы окрестностей нуля
в F). Следовательно, множество Кп=А О и'(Сп) выпукло и
уравновешено в йи слабо компактно в Е/ (поскольку отобра-
отображение и' слабо непрерывно). Множество Кп,таким образом,зам-
оо
кнуто в £#. Далее имеем (J пКп — Е'к* Так как Е% нетоще в
1
/г=1
себе, то некоторое Кп есть окрестность нуля в £#. Умножая Сп
на соответствующее положительное число, получаем
K<^Kn = u'{Cn)[\Aczu'(F')[\A = K.
Таким образом, /( = /(„, откуда в силу слабой компактности Кп
следует слабая компактность /С. Лемма полностью доказана. |
8.6.13. Теорема. Пусть Е и F — пространства Фрейхе и и: £->
-+F— непрерывное линейное отображение. Тогда следующие
условия эквивалентны:
A) и — открытое отображение пространства Е в F\
B) и — слабо открытое отображение пространства Е в F\
C) множество и(Е) замкнуто в F;
D) и' — слабо открытое отображение пространства F' в Е'\
E) множество и' (р') слабо замкнуто в Е'\
F) множество u'(F') сильно замкнуто в Е'.
Доказательство. A) эквивалентно B) в силу следствия
8.6.10, так как всякое векторное подпространство в F, будучи
метризуемым, является поэтому относительно сильным. A) экви-
эквивалентно C) по теореме об открытом отображении в форме
6.4.4 (а), так как всякое замкнутое подпространство простран-
пространства Фреше само является пространством Фреше. C) эквива-
эквивалентно D) в силу предложения 8.6.3, примененного к и', по-
поскольку (и')'г = и и векторные подпространства в Е и F слабо
замкнуты тогда и только тогда, когда они замкнуты. B) эквива-
эквивалентно E) снова в силу предложения 8.6.3. Таким образом,
эквивалентность утверждений A) — E) доказана. Из E) три-
тривиально вытекает F).
Наконец, импликация F)гфE) следует из леммы 8.6.12, так
как если множество u'(F') сильно замкнуто в £', то оно удо-
удовлетворяет условиям этой леммы. Действительно, пусть и'(F')
сильно замкнуто в Е'. Всякое множество А указанного в лем-
лемме 8.6.12 вида содержится в поляре некоторой окрестности нуля
U в £, и если последовательность (х'п) с: u'(F')(} А сходится к
8 6. Сопряженные отображения 713
х' в Е'А, то х! — х'п е ХпА, где А,п-^0. Всякое ограниченное мно-
множество Bcz E поглощается окрестностью U, поэтому л;^-**' рав-
равномерно на В. Таким образом, х'п-*х' сильно в Е'\ следователь-
следовательно, х' ^u'{F'). Так как множество А слабо замкнуто и х'п-> х'
слабо, то /gA Отсюда следует, что х' е ^'(F') Л А, т. е. мно-
множество u'(F')()A слабо замкнуто.
Теорема полностью доказана. |
8.6.14. Замечание. В общем случае F) следует из следую-
следующего условия:
G) и'— сильно открытое отображение пространства F' в Е'.
Если, кроме того, Е и F — банаховы пространства, то такими
же будут и их сильно сопряженные Е/ и F', и поэтому (теорема
об открытом отображении) F) влечет G). Таким образом, спра-
справедливо
8.6.15. Следствие. Если Е и F~ банаховы пространства и
и: Е -> F — непрерывное линейное отображение, то все условия
A) — G) эквивалентны. Поэтому, в частности,
(a) и есть отображение на F тогда и только тогда, когда
иг — сильный изоморфизм в;
(b) и' есть отображение на тогда и только тогда, когда и —
изоморфизм в.
Перечислим еще некоторые следствия (ср. Банах [1,
стр. 126—129]).
8.6.16. Следствие. Если Е и F — пространства Фреше и
и: E-^F — непрерывное линейное отображение, то следующие
два условия эквивалентны:
(8) и' есть взаимно однозначное отображение и иг~х перево-
переводит равностепенно непрерывные множества из и'{F') в равно-
равностепенно непрерывные множества из Е'\
(9) u(E)=Fuu'(F/) = (u-l@))°.
Если, кроме того, Е и F — банаховы пространства, то условие
(8) эквивалентно следующему условию:
(9) и' есть сильный' изоморфизм в.
Доказательство. Пусть выполнено (8). Так как отобра-
отображение и' взаимно однозначно, то и(Е) плотно в F. Из второй
части утверждения (8) следует, что и' переводит слабо замкну-
замкнутые векторные подпространства в такие же подпространства
(теор, 8.10.5). В частности, подпространство и'(F') слабо замк-
замкнуто. Таким образом, выполнено E), поэтому имеет место и C).
Следовательно, u(E)=F. Наконец, из слабой замкнутости
714 Гл. 8. Теория двойственности
и'(F') вытекает его совпадение с множеством {и~1@))°. Таким
образом (8) влечет (9).
Обратно, если выполнено (9), то отображение и' взаимно
однозначно (так как и — отображение на). Из второй части
утверждения (9) следует слабая замкнутость множества и'(F')
и тем самым выполнение условия E); поэтому имеет место A).
Оставшаяся часть утверждения (8) вытекает из теоремы
8.6.8(Ь). |
8.6.17. Следствие. Пусть Е и F — пространства Фреше и
и: E-^F —непрерывное линейное отображение. Тогда следую-
следующие два условия эквивалентны:
A0) u'(F')=E' и и(Е) = (и'~1@))о\
A1) и есть изоморфизм в.
Доказательство. Пусть выполнено условие A0). Так
как и'(F')=E\ то и — взаимно однозначное отображение, и по-
потому имеет место E). Но тогда выполнены условия A) и, сле-
следовательно, A1). Обратно, если имеет место условие A1), то
множество ur {F') слабо плотно (поскольку отображение и
взаимно однозначно). Так как из A1) следует A), то выполнено
E), т. е. ur (F') слабо замкнуто в Е'\ значит, и {Ff)—Ef. Далее
из того, что и — изоморфизм в и Е — полное пространство, сле-
следует C). Но тогда множество и(Е) слабо замкнуто и совпадает
с множеством (и'~1(О)H. В
8.6.18. Следствие. Пусть Е и F — пространства Фреше и
и: E-+F— непрерывное линейное отображение. Тогда
(a) и есть взаимно однозначное отображение на тогда и
только тогда, когда и' — взаимно однозначное отображение на;
(b) если и — изоморфизм в и отображение и' взаимно одно-
однозначно, то оба они являются отображениями на;
(c) если и и иг являются отображениями на, то оба они
взаимно однозначны.
Доказательство, (а) Пусть и — взаимно однозначное
отображение на, тогда множество и'(F') слабо всюду плотно.
Так как выполнено C), то имеет место E); следовательно, и'
есть отображение на. Поскольку и — отображение на, то и' —
взаимно однозначное отображение.
Обратно, если иг — взаимно однозначнее отображение на,
то множество и(Е) всюду плотно. Так как, кроме того, выпол-
выполнено E), то имеет место C), поэтому и есть отображение на.
Отображение и взаимно однозначно, потому что и' есть отобра-
отображение на.
8 7. Второе сопряженное 715
(b) Из того факта, что и — изоморфизм в, следует замкну-
замкнутость множества и(Е) в F. Так как отображение и' взаимно
однозначно, то множество и(Е) всюду плотно, следовательно,
и есть отображение на. Из той же взаимной однозначности ото-
отображения и следует слабая всюду плотность множества u'(F').
Далее из A) вытекает E), поэтому и/— отображение на.
(c) Если одно из отображений и или иг есть отображение на,
то другое взаимно однозначно. В
8.7. Второе сопряженное пространство и второе сопряженное
отображение
Пусть Е — отделимое локально выпуклое пространство, Е' —
его топологическое сопряженное. В § 8.4 мы определили силь-
сильную топологию ${Е\ Е) в Е\ Будем впредь обозначать через
Е" топологическое сопряженное к Е' в этой топологии. Про-
Пространство Е" называют вторым сопряженным1) к Е. Суще-
Существует естественное отображение / пространства Е в £", кото-
которое каждому х е Е ставит в соответствие линейную форму
х'*-*-(х, х') на Е\ очевидно, принадлежащую Е". Как легко
видеть, отображение / линейно и взаимно однозначно. Оно есгь
отображение на Е" тогда и только тогда, когда пространство Е
полурефлексивно (§ 8.4). Обычно принято отождествлять Е с его
образом j(E) в £". Если Е — нормированное пространство, то
таким же будет и Е' и р (£',£), совпадая с нормированной то-
топологией. Пространство Е" при этом также нормируемо, а ото-
отображение j сохраняет норму.
В пространстве Е" можно рассматривать по меньшей мере
две топологии типа Г®. Первая из них, которую мы будем обо*
значать через Те (е — первая буква слова equicontinuous (рав-
(равностепенно непрерывный)), соответствует случаю, когда © —
система всех равностепенно непрерывных подмножеств в Е'.
Вторая, которую мы будем обозначать Tb (b — первая буква
слова bounded (ограниченный)), соответствует случаю, когда
® — система всех сильно ограниченных подмножеств в Е'. База
окрестностей нуля в топологии Те получается, если взять
g(E", E')-замыкания базы окрестностей нуля в исходной топо-
топологии в £, образованной выпуклыми уравновешенными множе-
множествами. Аналогично база окрестностей нуля в топологии Ть по-
получается, если взять а(£//, Е') -замыкания поляр в Е сильно
ограниченных подмножеств из Е'. Отсюда непосредственно сле-
Дует, что топология Тъ всегда мажорирует топологию Те. Если,
однако, пространство Е борнологическое, то Те и Ть совпадают.
1) У автора strong bidual. — Прим. перев.
716 Гл. 8. Теория двойственности
[Действительно, пусть IF-г-окрестность нуля в Е" в топологии
7V Можно считать, что W есть о(£", £") -замыкание поляры
В'° в Е некоторого сильно ограниченного множества В' из Е'.
Если множество В cz E ограничено, то его поляра В° поглощает
В\ так что В'° поглощает В, т. е. WOE поглощает В. Так как
пространство Е борнологично, то Wf]E есть окрестность нуля
в Е\ обозначим ее через U. Таким образом, W и> £/, следова-
следовательно, WjpU (замыкание в топологии о(Е'\ Е')). Так как
W=W, a U есть Т^-окрестность нуля, то и IF будет 7е-окрест-
носчью нуля. Последнее означает, что Ть^СТе и ^потому Tb = Te.]
В общем случае пространство Е не является* плотным в Е"
относительно топологии Те (тем более относительно 7^). На-
Например, £ = со, Е' = 1\ Е"у=1°°. Как мы, однако, видели выше, Е
плотно относительно топологии o(E/f, E'). Действительно, Е"
есть объединение о{Е'\ Ег) -замыканий ограниченных подмно-
подмножеств из Е.
Если Е — нормированное пространство, то последнее утвер-
утверждение можно уточнить.
► Единичный шар В нормированного пространства Е
о(£"', Е')-плотен в единичном шаре В" пространства Е".
Действительно, согласно теореме о биполяре (теор. 8.1.5), до-
достаточно показать, что из соотношения ||*"||^ 1 вытекает, что
\(х"9 *'>Юир{1(х, х*): IUIKD,
т. е. что
|<х", j^KII*!.
Но это следует из определения нормы ||*"||.
До сих пор при рассмотрении абстрактных отделимых дуаль-
дуальных пар (£, Ef) и (F. F') мы так определяли второе сопряжен-
сопряженное и" к слабо непрерывному линейному отображению и: E-+F,
чтобы оно оказывалось линейным отображением пространства
Е в F, совпадающим с и. Ниже мы покажем, что если Е и F —
отделимые локально выпуклые пространства и и: E-+F — не-
непрерывное линейное отображение, то естественно продолжить
и" до линейного отображения пространства Е" в F'\ сужение
которогр на Е совпадает с и,
8.7.1. Предложение. Пусть Е и F — локально выпуклые про-
странства, и — слабо непрерывное линейное отображение про-
пространства Е в F. Тогда отображение и' непрерывно в топологиях
Р(Р, F) и p(£'f E).
Доказательство. Достаточно показать, что отображение
и переводит ограниченные множества в ограниченные. Но это
очевидно, ибо в Е и в F слабо ограниченные множества совпа-
8 7. Второе сопряженное 7\7
дают с ограниченными, а слабо непрерывное отображение и
переводит слабо ограниченные множества в слабо ограничен-
ограниченные. |
Поэтому можно попытаться определить и" как отображение
Е" $ F" с помощью равенства
(и"(х")9 У') = (х"у и'Ь/))9 (8.7.1)
предполагая, что оно выполняется для всех y'^F' и всех
х"^Е". Это определение и в самом деле корректно. Дей-
Действительно, предложение 8.7.1 показывает, что форма у'*—*
н—>(х", и'(у')) непрерывна относительно топологии Р (/*"', F) для
каждого х" е Е"\ следовательно, она имеет вид у'*—>{у", у') для
некоторого однозначно определенного у" из F". Этот элемент
у" и есть и"(х"). Будем и дальше называть и" вторым сопря-
сопряженным к отображению и. Очевидно, отображение и" линейно
и и"\Е = и.
8.7.2. Предложение. Пусть Е и F — отделимые локально вы-
выпуклые пространства, и— непрерывное линейное отображение
пространства Е в F. Тогда его второе сопряженное и" непре-
непрерывно в Ть-топологиях и в Те-топологиях на Е" и F".
Доказательство. Достаточно показать, что и* переводит
сильно ограниченные (соотв. равностепенно непрерывные) мно-
множества из F' в сильно ограниченные (соотв. равностепенно не-
непрерывные) множества из Е'. Для сильно ограниченных мно-
множеств это утверждается предложением 8.7.1. С другой стороны,
если V — окрестность нуля в F, то U = u~l(V) есть окрестность
нуля в Е. Так как u(U) cz V, то в силу (8.6.3) u'{V°) cz U°, по-
поэтому u'(V°) —равностепенно непрерывное множество в Е\ что
и требовалось доказать. В
Замечание. Из равенства (8.7.1) следует, что отображение
и" непрерывно в слабых топологиях о(Е", Е') и а(/г//, F'). От-
Отсюда в силу а{Е", Е') -плотности пространства Е в Е" получаем,
что и" — единственное продолжение по непрерывности отобра-
отображения и относительно этих слабых топологий.
Если Е и F — нормированные пространства, то предложе-
предложение 8.7.2 допускает следующее уточнение.
► Если Е и F — нормированные пространства, то отобра-
отображение иу->и" пространства LC(E, F) в LC(E", F") сохра-
сохраняет норму.
Так как Е изометрично отображается в Е" и иг'\Е — и, то до-
достаточно показать, что l|w"||^ ||и||. Имеем
(^a y')\- iu"ii<i, ii/iKD-
= sup
718 Гл. 8. Теория двойственности
Мы знаем, что каждый элемент х", для которого ||лу/||<1 1, есть
о(Е", £')-предел элементов х^Е, для которых IU||-< 1. Поэтому
= sup{\(u(xI y')\:
что и требовалось доказать. В
В заключение параграфа приведем один результат, относя-
относящийся к банаховым пространствам, который демонстрирует по-
полезность второго сопряженного пространства и второго сопря-
сопряженного отображения и ведет к некоторым интересным прило-
приложениям.
8.7.3. Теорема. Пусть Е и F — банаховы пространства, и —
непрерывное линейное отображение Е на плотное векторное
подпространство в F, G и Н — сильно замкнутые векторные
подпространства в Е\ Обозначим через G\ векторное подпро-
подпространство u'-l(G) в F', через v сужение иг на G\, рассматривае-
рассматриваемое как линейное отображение G\ в G. Кроме того, предполо-
предположим, что выполняется следующее условие:
(*) Подпространство Н содержит и'(Ff) и содержится в
объединении слабых замыканий в Е' ограниченных
подмножеств из u'(F').
Рассмотрим также условия
(a) u(E)=F;
(b) u'(F')=H;
(c) и'(F') замкнуто (слабо ила сильно) в Е'\
(d) и' есть сильный изоморфизм пространства F' в Е'\
(e) для каждого элемента у" е F" существует такой элемент
zr e G', что v'(z') —y"\ G\, или, что то же самое, существует та-
такой элемент х" ^.Е", что и"(х") \G\=y"\G\.
Тогда
A) (а)О(ЬLФ(сL
B) если Gzdu/(F/)i то все пять условий (а) — (е) эквива-
эквивалентны.
Доказательство. Из теоремы 8.6.13 следует эквивалент-
эквивалентность условий (а), (с) и (d), причем условие (с) может быть
взято в любой формулировке.
Если имеет место (с), то из (*) следует (Ь). Обратно если
выполнено (Ь), то множество «/(/7/)=Я сильно замкнуто в Е',
поэтому справедливость (d) вытекает из теоремы о замкнутом
графике. Таким образом, условия (a) -^ (d) эквивалентны.
Остается показать, что из них вытекает (е) и что они вытекают
из (е) при условии Gzdu'(F'), т. е. Gi = F\
8.7. Второе сопряженное 719
Вначале заметим, что для каждого zf e G' существует (тео-
(теорема Хана — Банаха) по меньшей мере один такой элемент
%" е Е", что z'—x"\G, и для всякого такого х" имеет место ра-
равенство v'{z!) =u"(x") \G\. Фактически формула
(х\и'(у')) = (и"(х"\у') (8.7.2)
имеет место для y'&F'. С другой стороны, для каждого y'&G\
(z't v(y')) = <^(z'), </'),
или
<*", u'W)) = (v'(z'\tf). (8.7.3)
Сравнение формул (8.7.2) и (8.7.3) приводит к искомой фор-
формуле. Отсюда видна эквивалентность двух формулировок усло-
условия (е).
Наделим G и G\ топологиями, индуцированными сильными
( = нормированными) топологиями соответственно в Е' и F'.
Заметим при этом, что (так как G замкнуто и и' сильно непре-
непрерывно) оба пространства G и G\ банаховы. С другой стороны,
очевидно в силу (d), что v — изоморфизм пространства G\ в G,
а при GX = F' верно и обратное. Далее из следствия 8.6.15 (Ь)
вытекает, что v есть изоморфизм пространства G\ в G тогда и
только тогда, когда ^/(g') — Gi. Пространство G'\ совпадает (тео-
(теорема Хана — Банаха) с множеством сужений элементов из F"
на G\. Это утверждение с учетом предыдущих замечаний завер-
завершает доказательство теоремы. В
8.7.4. Следствие. Если Е и F — банаховы пространства и и—
непрерывное линейное отображение Е на векторное подпростран-
подпространство, плотное в F, то u(E)=F тогда и только тогда, когда
u"(E")=F".
Доказательство. Положим G = E/ и положим Я равным
сильному замыканию подпространства и'(F') в Е'. Теперь
остается применить теорему. В
Замечание. Как мы увидим в § 8.8, рассмотрение соот-
соответствующего подпространства G в Е/ вместо самого этого про-
пространства дает значительные практические преимущества, глав-
главным образом потому, что часто легче работать с G', чем с Е".
8.7.5. В качестве иллюстрации к теореме 8.7.3 рассмотрим
следующую ситуацию. Пусть Е — банахово пространство,
п)/еГ—семейство элементов из Е\ где Т—произвольное мно-
множество индексов. Предположим, что
lim e\ = 0 слабо в £' (8.7,4)
720 Гл. 8 Теория двойственности
(предел берется в предположении, что множество Т наделено
дискретной топологией). Обозначим через и отображение про-
пространства Е в со(Т)=Р, которое каждому элементу х^Е ста-
ставит в соответствие семейство
Легко проверяется, что сопряженное отображение иг переводит
X^F' = ll(T) в ^X(t)eft9 причем ряд слабо безусловно сходится
в Е'. Простой и удобный способ обеспечить взаимную однознач-
однозначность отображения и! и, следовательно, плотность и(Е) в F —
это предположить существование такого семейства (et)t^T в Е,
что
(et> et') = \t> (US71). (8.7.6)
В этом случае утверждение, что элемент х' е Е' принадлежит
u'(F'), означает, что 2 \ifiu *')!<+ °°- Если G — сильно
te= T
замкнутое векторное подпространство в Е', содержащее все ert,
то G\ = u'-X(G) есть не что иное, как пространство F[ = ll(T).
Далее если /gC, to v'(z') есть семейство z' = ((e' z'\)
принадлежащее пространству F" = l°°(T). Если теперь восполь-
воспользоваться теоремой 8.7.3, то и получим следующий результат.
8.7.6. Теорема. Пусть Е — банахово пространство, (eft) —
семейство элементов из Е\ удовлетворяющее соотношениям
(8.7.4) и (8.7.6), G — сильно замкнутое векторное подпростран-
подпространство в Е', содержащее все e't, и Н — сильно замкнутое вектор-
векторное подпространство в Е', содержащее множество
(8.7.7)
и само содержащееся в объединении слабых замыканий в Ег
ограниченных подмножеств из Л. Попустим, что семейства ху
определенные формулой (8.7.5), где х пробегает Е, образуют
множество, плотное в со(Т). Тогда следующие утверждения
эквивалентны:
A) семейства х, где х, пробегает пространства £, исчерпы-
исчерпывают со(Т);
B) 2 I (ри х')\< + °° для каждого элемента х' е Я;
t е т
C) Л замкнуто (слабо или сильно) в Е'\
D) существует такое число k^0t что для каждого
имеет место неравенство
11 е Т
8 7. Второе сопряженное 721
E) каждое семейство р из 1°°(Т) может быть записано в виде
для некоторого zr e G'.
Аналогичный результат можно получить, если исходить из
предположения, что для некоторого р, 1 ^С/?<оо, все семейства
х лежат в пространстве №(Т) и образуют в нем плотное под-
подпространство. Для этого в теореме 8.7.3 нужно положить /7 =
= 1р(Т). Тогда F' = lp'(T)[^ + y=\} и F"zdIp(T). Мы прихо-
приходим к следующей теореме.
8.7.7. Теорема. Пусть Е— банахово пространство, (e't} —
такое семейство элементов из Е\ удовлетворяющее соотношению
(8.7.6), что для каждого х^Е семейство (8.7.5) принадлежит
1р(Т)ч G — сильно замкнутое векторное подпространство в Е\
содержащее множество1)
2 We'f. h^lP'(T)\ (8.7.8)
tT j
и само содержащееся в объединении слабых замыканий в Е'
ограниченных подмножеств из Л. Допустим, что семейства х,
определенные формулой (8.7.5) (х пробегает Е), образуют мно-
множество, плотное в 1р(Т). Тогда следующие утверждения экви-
эквивалентны:
A) семейства Я, где х пробегает £, исчерпывают 1р(Т)\
B) 2 I (вь х') 1Р < + °° для каждого элемента х' е Я;
C) Л замкнуто (слабо или сильно) в Е'\
D) существует такое число k ^ О, что для каждого X^lp' (T)
имеет место неравенство
S МО<|;
при /7=1 в левой части этого неравенства должно стоять
sup U @1;
E) семейства z' = ((e't, г')) , где z' пробегает G\ исчер-
исчерпывают пространство 1р(Т).
В § 8.8 мы увидим, что приведенные выше теоремы могут
быть применены к некоторым задачам гармонического анализа.
1) Из наших предположений следует слабая безусловная сходимости в
Е' ряда ^ А, (/) e't для каждого К е lp (T),
ts=T
722 Гл. 8. Теория двойственности
8.7.8. Перейдем теперь к рассмотрению некоторых обобще-
обобщений утверждения (а) из следствия 8.6.15. Эти обобщения можно
делать в двух направлениях; первое из них относится по-преж-
по-прежнему к банаховым пространствам, но отображение и уже не
предполагается непрерывным. Второе связано с попытками от-
отказаться от условия, что Е и F— банаховы пространства. Обоб-
Обобщениями первого вида занимался Рота [1], но гораздо более
подробное изложение вопроса дано Браудером [1], чьи иссле-
исследования относятся к обобщениям обоих типов и послужили ему
основой для изучения линейных уравнений в частных произрод-
ных (§ 5.20). Работа Браудера объемиста и довольно сложна;
мы ограничимся рассмотрением случая банаховых пространств.
8.7.9. Теорема. Пусчь Е и F— банаховы пространства, и —
линейное отображение с плотной в Е областью определения D,
и пусть график G отображения и замкнут в ExF. Тогда u(D) =
= F в том и только в том случае, если сопряженное отображение
и' обладает непрерывным обратным, т. е. в том и только в том
случае, если существует такое число £>0, что
\\u'(y')\\>k\\y'\\ {y'^D'\ (8.7.9)
где D' a F' — область определения отображения и'.
Замечание. Случай, когда E = F есть гильбертово про-
пространство, был рассмотрен Хёрмандером [1] и использован
им в теории линейных уравнений, в частных производных. Его
доказательство существенно опирается на специфику этого част-
частного случая.
Доказательство. Введем в рассмотрение линейное ото-
отображение v, определенное на графике G отображения и, полагая
v(x, u(x)) =u(x) (xgD).
Так как график G замкнут в ExF, то он образует банахово
пространство с индуцированной нормой. Очевидно, что v — не-
непрерывное отображение пространства G в F и что v(G) -u(D).
Таким образом, u(D)—F тогда и только тогда, когда v(G)=F.
Из следствия 8.6.15 вытекает, что v(G) =/7 тогда и только тогда,
кргда v' есть сильный изоморфизм пространства F' в G', т. е.
тогда и только тогда, когда существует такое число с > 0, что
\WW)W>c\W\\ (^П (8.7.10)
Далее Gr есть факторпространство произведения E'xF',
причем элементу (а\ Ъг) ^E'xF' соответствует элемент z'=
= f(a\ b') из G', определяемый правилом
(х, и{х))>-> (х, а') + (и (х), У) (х € D),
8.7. Второе сопряженное 723
и норма ||г'|| равна нижней грани сумм вида На'Н + НЬ'Н, когда
(а\ Ь') пробегает множество f~l(z'). С другой стороны, если
y'^F', то элемент z'=v'(y') определяется соотношением
((х, и(х)), z') = ((x, u(x))t v'(y')) =
= (v (х, и (х)), /) =
= <m(jc), у') (x&D).
Если теперь подробно расписать соотношение (8.7.10), то по-
получим
inf {|| а'Ц+11 &'II: <*, а') + (и(х), Ь*) = (и(х\ у') для x&D)>c\\t/l
или
inf{||a' || + \\b' ||: (х9 а') = (и{х\ tf-Ъ') для xez D}>c\\y'\\.
Условие
(jc, а") = (и (jc), / - 6Г) для л: g= D
означает, что w'—yr — b'^ D' и (лс, а') — (х, u'(w'))> для x^D.
Так как множество D плотно в £, то последнее условие равно-
равносильно условию а'=и'(йу'). Соответственно неравенство (8.7.10)
эквивалентно неравенству
ini{\\u'(w')\\ + \\y'-w'\\: w'<= D')^c\\y'\\ (у'z= F'). (8.7.11)
Соотношение (8.7.11), очевидно, влечет за собой неравенство
(8.7.9), ибо если y'^D'y то нижняя грань в (8.7.11) не превос-
превосходит ||м'(#')Ц (берем w' — y'). Обратно, пусть верно неравен-
неравенство (8.7.9); проверим справедливость соотношения (8.7.11).
Оно тривиально в случае у' = 0. Кроме того, если неравенство
(8.7.11) имеет место для некоторого у\ то оно продолжает быть
верным, если заменить уг на \у\ где К — любое отличное от нуля
число. Таким образом, остается проверить, что неравенство
(8.7.11) имеет место при ||г/'|| = 1. Допустим, что это не так. То-
Тогда найдутся такие последовательности (/J e f' и (ш^е/У,
что
Отсюда следует, что |] и'(а^)||^ l/n и
так что
724 Гл. 8. Теория двойственности
Таким образом,
что противоречит неравенству (8.7.9). Теорема полностью дока-
доказана. |
8.8. Некоторые приложения
Следуя Хьюитту, Цукерману и Хелсону, мы покажем, как
можно применить теоремы 8.7.3, 8.7.6 и 8.7.7 к некоторым за-
задачам гармонического анализа.
A) Лакунарные ряды Фурье. Рассмотрим функции веще-
вещественного переменного с периодом 2я, или, что то же, функции,
определенные на единичной окружности S комплексной плоско-
плоскости. Воспользуемся обозначениями примера 7.2.3. Если / —
функция или мера на S, то под f понимается ее преобразование
Фурье (последовательность коэффициентов Фурье f(n), /г = 0,
±1, ±2, ...). В дальнейшем Т будет обозначать некоторое мно-
множество целых чисел — положительных или отрицательных.
Функцию или меру / называют Т-спектральной, если f(n)=O
для всех целых пу не принадлежащих Т. Лемма Римана — Ле-
Лебега показывает, что сужение на Т преобразования Фурье,
и(х) =х\Т, отображает L1 в Со(Т). Как хорошо известно и
легко проверяется, множество u(Ll) плотно в Со(Т). Непрерыв-
Непрерывность отображения и: L1-+cq(T) доказывается тривиально.
Уже давно было обнаружено, что если множество Т очень
редко расположено среди множества целых чисел, то Г-спек-
тральные функции или меры обладают некоторыми из ряда
вон выходящими свойствами. Более точно, множество Т назы-
называется лакунарным, если
T = {±nk; /5=1, 2, ...}, где пк>0,
Тригонометрический ряд, ненулевые гармоники которого обра-
образуют такое лакунарное множество, сам называется лакунарным.
Один из типичных результатов, относящихся к таким рядам,
принадлежит Сцидону (Зигмунд [1, стр. 139]) и состоит в том,
что лакунарный ряд Фурье ограниченной функции абсолютно
сходится. Другой результат, установленный Банахом (Зиг-
(Зигмунд [1, стр. 215]), гласит, что если множество Т лакунарно,
то и отображает L1 на со(Т). Качмаж и Штейнагуз [1,
8.8. Некоторые приложения 725
стр. 250—255], Хьюитт и Цукерман [2] и независимо автор
настоящей книги показали без всяких явных предположений
лакунарности Г, что теоремы типа Сцидона и Банаха могут
быть объединены и обобщены на основе функционально-анали-
функционально-аналитического подхода. Две теоремы эквивалентности Хьюитта и
Цукермана [2, теоремы 2.1 и 6.1] непосредственно следуют
из наших теорем 8.7.6 и 8.7.7. »
Действительно, положим в теореме 8.7.6 E = L\ так что Е'=
= L°°. В качестве е\ возьмем элемент из L°°y определяемый функ-
функцией eriu от s. Роль G будет играть пространство С непрерыв-
непрерывных на 5 функций, так что G' совпадает с пространством М мер
Радона на S. В качестве et возьмем элемент из L1, определяемый
функцией Bn)~leits от 5. Ясно, что w'(/r/)c:C=G. Обозначим че-
через —Т множество целых чисел —/, где / пробегает Т. В каче~-
стве Н можно взять либо множество (—Г)-спектральных эле-
элементов из L°°, либо множество (—Г)-спектральных элементов из
С. В любом из этих случаев выполнение условия (*) из теоремы
8.7.3 есть следствие свойства (С, 1)-суммируемости рядов
Фурье. Ниже, при записи условия B) теоремы 8.7.6, мы восполь-
воспользуемся, однако, тем очевидным фактом, что отображение /*->/',
где f'(s)=f(—s), есть изоморфизм (слабый и сильный) про-
пространства L°° на себя, переводящий множество (—Г)-спектраль-
(—Г)-спектральных элементов в множество Г-спектральных элементов. Наконец,
отметим, что отображение v' также определяется как сужение
преобразования Фурье на множество Т.
С учетом принятых обозначений и сделанных замечаний тео-
теорема 8.7.6 дает первую теорему Хьюитта — Цукермана, утвер-
утверждающую эквивалентность следующих пяти условий (если А —
множество функций или мер на S, то символом А\Т мы обозна-
обозначаем множество сужений на Т преобразований Фурье элементов
из А):
(a) 11\Т
(b) 2lf@K+°° для каждой Т-спектральной функции
t&T
f <= L°° (или для каждой Т-спектральной функции fsC);
(c) множество функций 2 k(t)eltsy где X пробегает простран*
*<ЕЕ Т
ство 11(Т), замкнуто (слабо и сильно) в L°°;
(d) существует такое число k > 0, что для каждого элемента
2 WOKA-supl 2 4t)eits
tT \tT
(e)
726 Гл. 8. Теория двойственности
Вторая теорема Хьюитта — Цукермана аналогичным обра-
образом слвдует из теоремы 8.7.7, если мы придадим соответствую-
соответствующий смысл символам. Короче, положим' Е = С, так что Е'=М,
G = L\ р = 2, а в качестве Н возьмем множество (—Г)-спектраль-
(—Г)-спектральных элементов из LK За ert примем меры с плотностями e~its.
Наконец, и рассматривается как отображение пространства С
в 12(Т). В результате получаем эквивалентность следующих че-
четырех условий:
(а') С\Т = 1ЦТ);
(Ь') 2 lf(OI2< + °° для каждой Т-спектральной функции
t €= Т
f^M {или для каждой Т-спектральной функции f из L1);
(с') множество функций 2 k{t)elts, где Я пробегает /2(Г),
£€= Т
замкнуто {слабо и сильно) в М\
(d') существует такое число &^0, что для каждого элемента
/2(Г)
J
Ms
В силу равенства Парсеваля условие (d') означает, что
для каждой Г-спектральной функции fsi2. В силу теоремы
о замкнутом графике это, в свою очередь, равносильно утвер-
утверждению, что каждая Г-спектральная функция из L1 (соотв. каж-
каждая Г-спектральная мера) принадлежит L2 (соотв. имеет в ка-
качестве плотности функцию из L2). Дальнейшим исследованием
этих вопросов занимался Рудин [3; 9, гл. 5].
B) Обратимся теперь к некоторым частичным аналогам
предыдущих результатов, применимым к интегралам Фурье, и
рассмотрим одну проблему, исследованную Хелсоном [4].
Начнем с несколько более общей ситуации, чем та, которая рас-
рассматривалась в связи с преобразованиями Фурье.
Пусть S и Т — локально компактные пространства с поло-
положительными мерами Радона ds и dt соответственно. Через
LX{S) и Ll{T) обозначим соответствующие лебеговы простран-
пространства, а через СоE) и С0(Т)—соответствующие банаховы про-
пространства непрерывных на S и Г функций, стремящихся к нулю
на бесконечности. Пространства C0(S) и С0{Т) имеют в качестве
сопряженных пространства ограниченных мер Радона M(S) и
М(Т) соответственно. Пространство Ll(S) вкладывается в
M{S), если каждому классу /е Ll(S) поставить в соответствие
8 8. Некоторые приложения 727
меру с плотностью f относительно ds\ аналогично Ll(T) вкла-
вкладывается в М(Т).
Возьмем в качестве ядра функцию k на SxT, которая не-
непрерывна, ограничена и для которой
lim*(.s,0 = 0 слабо в L°°E). (8.8.1)
t~*oo
Положим в теореме 8.7.3 E = D(S), F=C0(T) и и(х)=у, где
у@=J k(s, t)x(s)ds. (8.8.2)
В соответствии с этим E' = L°°(S) и F' = M(T). Сопряженное ото-
отображение и\ определяемое равенством х' = и'(у'), где
x'(s)=j k(s, t)dy'(t\ (8.8.3)
переводит меру у'^М(Т) в функцию хг из L°°(S). В качестве
G возьмем C0(S) (или, точнее, множество элементов из L°°(S)y
определяемых функциями из СоE)), так что G\ состоит из та-
таких мер у' ^М(Т), что определяемая ими по формуле (8.8.3)
функция х' стремится к нулю при s-^oo. Множество только что
описанных элементов у' из М(Т) обозначим через М0(Т). Тогда
G' = Af(S), и для г'еС элемент v'(z') будет функцией
f k(s9 t)dz'(s) от t. Роль пространства Н в теореме 8.7.3 нас
не интересует, так как оно никак не связано с теоремой Хел-
сона, которую мы хотим получить. Основное наше заключение
состоит в утверждении, что в теореме 8.7.3 условие (а) влечет
(е). Чтобы применить этот результат, заметим, что каждая уни-
универсально измеримая функция C на Т определяет элемент из
F" = M(T)', который переводит меру /леМ(Г) в число
\i(t)dm(t). В соответствии с этим получаем следующий ре-
результат.
Теорема Хелсона. Если и отображает Ll(S) в С0(Г), то для
каждой универсально измеримой функции р на Т существует
такая мера \х в M(S), что
J р @ dv @ = J dv (t) J k E, 0 Ф (s) (8.8.4)
для всех геМо(Г).
Результат Хелсона можно получить еще одним способом
в том частном случае, когда S — вещественная прямая, ds —
мера Лебега, Г —подмножество вещественной прямой, которое,
не ограничивая общности, можно считать замкнутым, di — суже-
сужение на Т меры Лебега и k(s, t)=e-2ztist. Тогда и(х)=х\Т, где
728 Гл. 8 Теория двойственности
х — обычное преобразование Фурье функции х, а и' сводится к
обычному обратному преобразованию Фурье. Пространство
М0(Т) можно рассматривать как множество тех мер Радона на
вещественной прямой, носитель которых содержится в Г и об-
обратное преобразование Ф>рье которых стремится к нулю на бес-
бесконечности. Если v принадлежит МО(Т)У то ясно, что.тем же
свойством обладает и e2niatv для любого вещественного а. Из со-
соотношения (8.8.4) следует, что v-почти всюду ${t) =
= k(s, £)<4i(s), и из теоремы Хелсона вытекает, что это
утверждение имеет место для каждой меры vGM0(r), если
Ъ\Т = С0(Т).
Остальные результаты Хелсона заключаются в доказатель-
доказательстве того, что последнее равенство возможно лишь тогда, когда
М0(Т)={0}. Действительно, пусть Мо(Т) содержит меру v^=0,
и пусть К а Г —носитель меры v. Множество К не может быть
счетным, так как в этом случае обратное преобразование Фурье
меры v имело бы вид 2 cne2nttnS, где 0<2l^«l<+ °°, но ни
п п
одна функция такого вида не стремится к нулю при 5—^оо. От-
Открытое дополнение множества К есть объединение последова-
последовательности непересекающихся интервалов (ап, bn) (an<6n). Вы-
Выберем в К точку /0, отличную от всех ап и Ьп. Тогда \v\(t0 — е9
to)>O для каждого е>0. В противном случае интервал
(to — е, t0) содержался бы в некотором (ап, Ьп), что влекло бы
за собой соотношения an<to^bn. Но to^K, поэтому t0 не
меньше 6П, равенство же to = bn также невозможно в силу вы-
выбора to. Аналогично можно показать, что |v|(/o, ^o + £)>O для
каждого е>0. Теперь возьмем в качестве |3 функцию
( О
ко- ,
О при t<tOt
при t>tQ.
Для непрерывной функции f(t)= e~2nistd\x(s) должно было бы
f(t)=O для значений t, сколь угодно близких к ^0 слева от него,
и f(t) = l для значений t9 сколь угодно близких к ^о справа от
него, что невозможно. Мы заключаем вместе с Хелсоном:
► Если Ll\T = Co(T), то Мо(Г)={О}, т. е. Т не является
носителем ни одной отличной от нуля меры Радона, пре-
преобразование Фурье которой стремится к нулю на бес-
бесконечности.
Относительно дальнейшего развития этих идей см. К а х а н
и Салем [1] и Рудин [4]. Современное изложение вопроса
имеется в гл. 5 книги Р уди на [9].
8.9. Еще раз о теоремах об открытом отображении 729
8.9. Еще раз о теоремах об открытом отображении
и замкнутом графике
Как было обещано, мы снова возвращаемся к этой теме. На
этот раз сосредоточим наше внимание на случае локально вы-
выпуклых пространств. В теоремах § 6.4 условие метризуемости
налагалось на одно из рассматриваемых пространств, в то
время как на другое пространство ограничения такого рода не
налагались. В случае локально выпуклых пространств положе-
положение гораздо лучше: здесь возможен и желателен новый и неза-
независимый подход. В исследование этого случая значительный
вклад внесли Птак [1—4], Коллинз [1], В. Робертсон [1],
А. П. Робертсон и В. Робертсон [1]. Работа В. Р о-
бертсона убедительно наводит на мысль, что пространство Е
должно удовлетворять некоторому условию полноты (см. заме-
замечание A) после теоремы 6.4.4). Необходимость такого ограни-
ограничения подтверждается анализом Птака, который показывает,
что требование некоторой полноты, более сильной, чем обычная,
является естественным. См. также С лов и ков с кий [4, 5],
X у с е й н [2, 3], П т а к [8], К ё т е [7], Л. Шварц [22], Райков
[2], Ма ртино [1].
8.9.1. Совершенно полные и Вг-полные пространства. Пусть
Е — локально выпуклое пространство. Множество М в Ег на-
называется почти слабо замкнутым, если Mf]U° слабо замкнуто
в Ef для каждой окрестности нуля U в Е. Так как
при Ua V, то, очевидно, эквивалентное условие таково: Mf]Ua
слабо замкнуто в Ег для каждой окрестности U некоторой базы
окрестностей нуля в Е.
Понятие почти слабой замкнутости будет подробно изучено
в следующем параграфе. Пока же мы перефразируем теорему
8.5.1 в форме, которая служила бы обоснованием некоторых
дальнейших определений.
Как известно, гиперплоскость Яв£' представима (многими
способами) в виде множества {xf е Е': и(х')=0}, где и — отлич-
лый от нуля элемент из Е'*. При этом гиперплоскость Н слабо
замкнута тогда и только тогда, когда и слабо непрерывно. Это
утверждение остается справедливым, если «слабо замкнуто»
заменить на «почти слабо замкнуто», а слабую непрерывность
формы и — на слабую непрерывность сужения u\U° для каж-
каждой окрестности U. ,
Действительно, если сужение u\U° слабо непрерывно, то пе-
пересечение Hf)U° слабо замкнуто, т. е. Н почти слабо замкнуто.
Докажем обратное. Пусть Н почти слабо замкнуто. Положим
733 Гл. 8. Теория двойственности
Н(а) =-{л:'<= Е'\ и(х')=а}у так что Н = Н@). Для каждой окрест-
окрестности нуля U либо пересечение U°f]H(a) пусто, либо найдется
принадлежащий ему элемент у'. В последнем случае
Отсюда следует, что каждое множество Я (а) почти слабо замк-
замкнуто. Допустим, что u\U° не слабо непрерывно. Тогда при не-
некотором А,>0 для каждой слабой окрестности нуля W в Ег най-
найдется такой элемент я'е W(]U°9 что \и(х') |>Х. С другой сто-
стороны, множество и°С\Н[-^^\ слабо замкнуто и не содержит
нуля. Существует, следовательно, такая слабая окрестность
нуля W в £', что
(H. (8.9.1)
Мы знаем, однако, что имеется такой элемент х' ^WC\U°, что
\и(х')\>К. Пусть р = У2м(*'). Тогда |р|<^- и $x'€=W(]U°.
В то же время и (р*') == -j Я и потому рл;' s Я (-j Л j. Таким обра-
образом, рл:' е W П U° П Я (у ^)» что противоречит соотношению
(8.9.1). Утверждение полностью доказано.
Теперь из теоремы 8.5.1 вытекает, что полнота пространства
Е необходима и достаточна для того, чтобы в Ег каждая почти
слабо замкнутая гиперплоскость была слабо замкнута. Этот
результат служит основанием для введения следующих опре-
определений.
Пространство Е называется совершенно полным (В-полнота
Птака), если каждое почти слабо замкнутое векторное подпро-
подпространство М в Е' слабо замкнуто. Птак ввел также Вг~полные
пространства как пространства, для которых это же условие
выполняется для слабо плотных векторных подпространств М
в Ef (в этом случае, конечно, М = Е').
Исследования Птака, которых мы здесь полностью не вос-
воспроизводим, показывают, что
A) пространство Е совершенно полно тогда и только тогда,
ко?,да каждое непрерывное почти открытое линейное отображе-
отображение и пространства Е на отделимое локально выпуклое про-
пространство F открыто;
B) пространство Е Вг-полно тогда и только тогда, когда
каждое взаимно однозначное почти непрерывное линейное ото-
отображение и пространства Е на отделимое локально выпуклое
пространство открыто.
8 9. Еще раз о теоремах об открытом отображении 731
Ниже мы ограничимся доказательством утверждений A) и
B) лишь в части «только тогда», которая, естественна, яв-
является наиболее важной с точки зрения приложений.
Заметим здесь, что Коллинз [1] ввел понятие совершен-
совершенной полноты несколько другим образом. Эквивалентность его
и нашего определений установлена Келли [4, теор. 4]. В то же
время Келли ввел понятие гиперполноты, которая, как он пока-
показал (там же), эквивалентна условию, что каждое почти слабо
замкнутое выпуклое уравновешенное множество в Е' слабо
замкнуто. См. также Сингер [6], А. П. Робертсон [1].
Отправной точкой для нас будет служить одна общая тео-
теорема, принадлежащая Птаку [3]. Ситуация будет та же, что и
в лемме 6.4.1, поэтому мы воспользуемся аналогичными обозна-
обозначениями: если S — подмножество произведения ExF, A — под-
подмножество в Е, то полагаем
8.9.2. Теорема. Пусть Е и F— локально выпуклые простран-
пространства, S — такое замкнутое векторное подпространство в ExF,
что 7iF(S)=F. Допустим, что Е — совершенно полное простран-
пространство и для каждой окрестности нуля U и Е множество SF(U)
есть окрестность нуля в F. Тогда само множество SfF(U) тоже
есть окрестность нуля в F. Если, кроме того, множество
X = nE(S П Яр1 @)) равно {0}, то предыдущее заключение верно,
если пространство Е Вг-полно.
Доказательство. Пусть Z — множество таких элементов
(х\у') из E'xF', что (х, xf) + {у, у') = 0 для всех (x,y)^S. Обо-
Обозначим через Q множество тех элементов х'^Е\ для ко-
которых (х\ у') е Z при некотором yf e F''. Пусть, наконец,
X = пЕ(S П я @)) = {ш£: (jc, 0)е= S}. Множество Q — вектор-
векторное пространство в Е', X — векторное подпространство в Е. Пер-
Первым шагом будет доказательство того, что Q00 = X°.
Вначале докажем, что Q а Х°. Пусть /gQ, тогда найдется
такой элемент у' е Ef, что (х', yf) e Z, т. е. (х, х') + {у, у') =0 для
всех (х9 у) eS. Если х е X, то (х, 0) е S, тогда (х, х') = (х, х') +
+ фуу'}=0у т. е. / g Г, что и требовалось доказать. Если же
некоторый элемент х е Q° не принадлежит X, то (дс, 0) не при-
принадлежит S. Так как множество S замкнуто, то найдется такой
элемент (xf, y')<^Zy что (*, х') + (у, у')ф0, т. е. (*, х')ФО. Это
противоречит предположению, что х е Q0, ибо условие (xf, yf) e
gZ означает, что xr e Q. Таким образом, Q°czA'. Из получен-
йых соотношений Qcz Х° и Q°c: X следует, что Qoo=^°1
732 Гл. 8. Теория двойственности
На втором шаге доказательства с помощью совершенной
(или Вт-) полноты пространства Е установим слабую замкну-
замкнутость множества Q. Отсюда и из того факта, что Q = Q00, будет
следовать, что Q — X°.
Пусть U — произвольная окрестность нуля в Е. Докажем,
что множество QC\U° слабо замкнуто. Тогда слабая замкнутость
множества Q будет следствием совершенной полноты простран-
пространства Е или его 5г-полноты, если заранее известно, что Х = {0}.
Пусть (#9~- сеть в Q П £/°, слабо сходящаяся к х'. Нам нужно
показать, что х'^ Q[}U°. Так как U° — слабо замкнутое множе-
множество, то, очевидно, х/ е U°. Для каждого индекса i найдется та-
такой элемент y\^F\ что (*J, #J)eZ; следовательно,
<*.*!> + <»• «О-° (8-9-2>
для всех (x,i/)gS. Мы видим, что функция /(#) = lim(z/, z/')
определена и конечна для каждого элемента у ejii?(S) =/г.
Ясно также, что / — линейная форма на F. Теперь достаточно
показать, что форма / непрерывна: тогда она совпадает с неко-
некоторым элементом у' из-Т7'. Переходя к пределу в (8.9.2), полу-
получаем (а:, х') + (у, #')=0 для всех (x,y)^S, поэтому (/,(/')£Z,
т. е. /gQ.
Чтобы доказать непрерывность формы f, воспользуемся пред-
предположением, что множество V=SF(U) есть окрестность нуля в F.
Всякий элемент у е V есть предел некоторой сети (у$) элемен-
элементов из SF(U). Для каждого индекса / найдется такой элемент
Xj<=U, что (Xj,yj)&S. Из (8.9.2) следует тогда, что для всех
/ числа (yjt у>) = — (х^ x'ty по модулю не превосходят единицы
(так как xJg(/°), Фиксируя I и заставляя / неограниченно воз-
возрастать, получаем, что |(у, yj)|^l для всех и Устремляя те-
теперь i к бесконечности, получаем, что |/(у)|^1. Так как это
справедливо для каждого г/ g V, то форма f непрерывна.
Таким образом, нами установлено, что Q = X°. На последнем
этапе докажем, что
SF(U)cz2'SP{U).
Допустим, что элемент уо принадлежит первому множеству, но
не содержится во втором. Так как г/о не принадлежит множеству
SFBU), то можно выбрать такой элемент хо^Е, что (xo,yo)^S.
Тогда множества 2/7 и х0 + X не пересекаются. Поэтому (след-
(следствие 2.2.4) можно в U0 найти такой элемент х\ что число
+ xt x')\: х<=Х]
будет больше единицы. Так как X — векторное подпространство,
то х' <=X°=Q, и элемент у' можно взять таким, чтобы {х',у')^
8 9 Еще раз о теоремах об открытом отображении 733
eZ, поэтому (дс, х') + (у, у')=0 для всех (х, y)^S. Если
y^SF{U), то x<=U можно выбрать так, чтобы (x9y)^S. Из
(8.9.2) следует тогда, что
Это соотношение останется по непрерывности справедливым,
если заменить у на у0. С другой стороны, так как (*0, #o)sS, то
откуда вытекает, что | (yQi у') | = | (х0, х') | > m > 1. Мы пришли
к противоречию. Теорема полностью доказана. ■
Теперь уже легко привести соответствующие формулировки
теорем об открытом отображении и замкнутом графике.
8.9.3. Теорема. Пусть Е и F — локально выпуклые простран-
пространства и и— почти открытое линейное отображение векторного
подпространства Ео пространства Е на Fy график которого
замкнут в EXF. Тогда
A) если пространство Е совершенно полно, то и открыто]
B) если пространство Е Вг-полно и и взаимно однозначно,
то и открыто.
Доказательство. В теореме 8.9.2 возьмем в качестве 5
график отображения и
S = {(xyu(x)): x^Eo}.
Тогда
Отсюда непосредственно вытекает требуемый результат. |
8.9.4. Теорема. Пусть Е и F*—локально выпуклые простран-
пространства, причем Е Вг-полно, и v — линейное отображение простран-
пространства F в £, обладающее замкнутым в FxE графиком. Тогда
если отображение v почти непрерывно, то оно непрерывно.
Доказательство. В качестве S в теореме 8.9.2 возьмем
отражение графика v относительно диагонали
S = {(v(y),y): y&F).
Множество S замкнуто в ExF. Имеем
SF(U)=v-l(U), nF{S)=F
и
Искомый результат непосредственно следует из теоремы 8.9.2. I
734 Гл. 8. Теория двойственности
8.9.5. Замечания. A) Напомним читателю, что если про-
пространство F бочечно, то всякое отображение и подпространства
Eq на F почти открыто и всякое линейное отображение v про-
пространства F в Е почти непрерывно. См. доказательство теоре-
теоремы 6.4.4.
B) Поскольку речь идет о локально выпуклых простран-
пространствах, постольку из приведенных теорем вытекают полученные
нами ранее результаты (см. теоремы 6.4.2—6.4.4), если считать
известным тот факт, что всякое полное полуметризуемое про-
пространство совершенно полно. Этот факт будет доказан в сле-
следующем параграфе.
C) Налагая дополнительные ограничения на отображение
и (или v), можно переформулировать теоремы 8.9.3 и 8.9.4 для
случая, когда пространство Е обладает пополнением, которое со-
соответственно либо совершенно полно, либо 5г-полно (ср. с за-
замечанием A), следующим за теоремой 6.4.4).
D) Комбинируя теоремы 8.9.3 и 8.9.4 с предложениями
8.10.7 и 8.10.11, можно получить другие формы'теорем об откры-
открытом отображении и замкнутом графике, которые оказываются
полезными для некоторых приложений. (См. упр. 8.41—8.43, а
также Гротендик [9].)
8.9.6. В связи с теоремой 8.9.4 интересно отметить, что бочеч-
бочечные пространства могут быть охарактеризованы с помощью тео-
теоремы о замкнутом графике в классе всех локально выпуклых
пространств. Махов ал ьд [1] показал, что локально выпуклое
пространство F бочечно тогда и только тогда, когда всякое замк-
замкнутое линейное отображение пространства F в произвольное
банахово пространство Е является непрерывным.
Используя аналогичные рассуждения, можно установить, что
локально выпуклое пространство F инфрабочечно тогда и только
тогда, когда для каждого банахова пространства Е всякое замк-
замкнутое ограниченное (т. е. переводящее ограниченные множества
в ограниченные) линейное отображение пространства F в Е не-
непрерывно.
8.9.7. В теореме 8.9.3 совершенную (или Вг-) полноту про-
пространства Е нельзя заменить обычной полнотой, даже если
Eq = E и F — банахово пространство. Следующий ниже пример
убеждает нас в этом.
Пусть Е — бесконечномерное банахово пространство, норми-
нормированную топологию которого обозначим через t. Пусть too —
сильнейшая локально выпуклая топология в Е (п. 1.10.1). Мы
показали (там же), что (£", t^) —полное пространство.
В качестве и возьмем тождественное отображение простран-
пространства (£", /оо) в (£, /). Очевидно, и — непрерывное отображение
на. Так как пространство (£, /) отделимо, то график отображе-
8.10. О совершенно полных пространствах 735
ния и замкнут. Далее отображение и почти открыто. Действи-
Действительно, если tt? — выпуклое уравновешенное поглощающее мно-
множество в Е, то ^-замыкание множества u(W)*=W есть бочка в
(£, t) и потому ^-окрестность нуля.
Несмотря на это, отображение и не является открытым.
В противном случае всякое выпуклое уравновешенное и погло-
поглощающее множество в Е было бы /-окрестностью нуля. В част-
частности, всякая линейная форма на Е была бы непрерывной. Но
это неверно. В самом деле, возьмем произвольную бесконечную
последовательность линейно независимых элементов (ап) из Е.
Можно считать, что ||ап|| = 1 для каждого п. Последовательность
(ап) может быть расширена до алгебраического базиса в Е. Ли-
Линейную форму на Е можно определить любыми наперед задан-
заданными значениями на элементах базиса. В частности, существует
линейная форма / на Е, такая, что f(an) = я для п= 1, 2,.... Оче-
Очевидно, эта форма f не является непрерывной.
С помощью этого построения мы получаем пример отдели-
отделимого полного бочечного (§ 6.2) локально выпуклого простран-
пространства Е, которое тем не менее не является Вг-полным и тем более
совершенно полным. Более прямое построение см. в п. 8.10.13.
8.10. О совершенно полных пространствах
В сопряженном пространстве Е' можно рассмотреть тополо-
топологию, относительно которой класс замкнутых множеств совпадает
с классом почти слабо замкнутых множеств в смысле п. 8.9.1.
Такую топологию естественно назвать почти слабой топологией
в Ег. В случае когда Е — банахово пространство, эту топологию
принято также называть ограниченно слабой. Этот случай рас-
рассматривал Дьёдонне [6]; см. также Данфорд и Шварц
[1, стр. 463]. Никоим образом не ясно, будет ли такая топология
локально выпуклой в общем случае. Тем не менее для полуме-
тризуемых локально выпуклых пространств Е это так, и мы это
докажем. Сейчас мы слегка изменим наш подход к задаче и по-
попытаемся найти те локально выпуклые топологии в £', которые
индуцируют в каждом из множеств U° ту же топологию, что и
слабая топология а{Е', Е). Таких локально выпуклых топологий
обычно бывает много. Мы рассмотрим три из них:
A) топологию Тс = к(Е',Е) (п. 8.3.3), база окрестностей нуля
которой образована полярами выпуклых уравновешенных ком-
компактных подмножеств в Е\
B) топологию Тр, база окрестностей нуля которой образо-
образована полярами предкомпактных подмножеств в Е {так как урав-
уравновешенная выпуклая оболочка предкомпактного множества
предкомпактна, то топология не изменится, если взять базу,
736 Гл. 8. Теория двойственности
образованную полярами выпуклых уравновешенных предком-
пактных подмножеств в Е);
C) топологию Г*, база окрестностей нуля которой образо-
образована выпуклыми уравновешенными почти слабо замкнутыми по-
поглощающими множествами W, поляры которых W° предкомпакт-
ны в Е.
Очевидно, что
ТС<ТР<Т*. (8.10.1)
С другой стороны, если пространство Е квазиполно, то ТС=ТР
(ибо тогда замыкание всякого предкомпактного множества в Е
компактно). Птак показал [1, F.9)], что топология Т* — силь-
сильнейшая из локально выпуклых топологий в Е\ которые индуци-
индуцируют в каждом из множеств U° ту же топологию, что и слабая
топология о(Е\Е). Так как это утверждение нам не понадобит-
понадобится, то мы опускаем его доказательство. Однако важно заметить,
что топология Тс в Е' согласуется с двойственностью между Е и
Ег (теор. 8.3.2).
Наша первая задача — установить совершенную полноту вся-
всякого пространства Фреше. Доказательство основывается на
одной лемме, принадлежащей Дьёдонне и Шварцу [1,
стр. 84, лемма].
8.10.1. Лемма. Пусть (Un)n>0 {Uo = E) —убывающая после-
последовательность окрестностей нуля локально выпуклого простран-
пространства Е и W — почти слабо открытое подмножество в Е\ содер-
содержащее точку 0. Тогда для каждого п ^ 0 существует такое ко-
конечное множество BnaUni что если Ап= U В , то A°nf] f/° с: W
для п^- 1.
Доказательство. Воспользуемся индукцией по п. Выбе-
Выберем такое конечное множество Во, что В° П U] cz W (это возмож-
возможно, ибо W почти слабо замкнуто); тогда A\f\U]cz W. Пусть
теперь п > 1 и множества Вр определены для р^п— 1 так, что
выполнено соотношение A°nflU°ncz W. Множество Я = U°n+l П
П(£/Ч\№) слабо замкнуто и потому слабо компактно. Если не
существует конечного множества BnaUn с требуемыми свой-
свойствами, то для каждого конечного множества BczUn множе-
множество (Ап[) В)°() U°n+l не содержится в Wy так что множества
А°п{\В°(\Н непусты. Эти множества слабо замкнуты и образуют
«убывающую» сеть. В силу слабой компактности этих множеств
найдется точка х'о, общая всем множествам А°п[\В°[\Н (В ко-
конечно, В a Un). Так как Un есть объединение своих конечных
8.10. О совершенно полных пространствах 737
подмножеств Б, то элемент x'Q принадлежит А°п {]U°n()H. Но по-
последнее множество пусто, ибо Н a E'\W и A°nf]U°nczW. Полу-
Полученное противоречие показывает, что индуктивный процесс мо-
можно продолжить, что и завершает доказательство. I
8.10.2. Следствие. Пусть Е — полуметризуемое локально вы-
выпуклое пространство. Тогда всякое почти слабо открытое под-
подмножество W в Е', содержащее нуль, содержит 7^-окрестность
нуля.
Доказательство. В предыдущей лемме последователь-
последовательностью (Un) может служить база окрестностей нуля в Е. Ясно,
оо
что множество Р = (J Ап предкомпактно в Е9 так что Р° есть
Гр-окрестность нуля. При каждом п имеют место соотношения
W^> A°n П U°n zdP°zd U°n. Множества U°n образуют покрытие про-
пространства Е\ Таким образом, WzdP0, что и требовалось дока-
доказать. |
8.10.3. Следствие. Пусть Е—полное полуметризуемое локаль-
локально выпуклое пространство. Тогда всякое почти слабо открытое
подмножество W в Е\ содержащее нуль, содержит Тс-окрест-
ность нуля.
Доказательство. Полнота Е влечет равенство Tc = TPi
так что остается воспользоваться следствием 8.10.2.
8.10.4. Следствие. Пусть Е — полуметризуемое локально вы-
пуклое пространство. Подмножество L в Ег почти слабо замкну-
замкнуто тогда и только тогда, когда оно Тр-замкнуто. Если, кроме
того, Е полно, то L почти слабо замкнуто тогда и только тогда,
когда оно Тс-замкнуто.
Доказательство. Как известно (предложение 0.4.9), то-
топология Тр индуцирует в каждом из множеств U° ту же тополо-
топологию, что и слабая топология о(Е\Е). Отсюда в силу Гр-замкну-
тости множества L следует его почти слабая замкнутость.
Обратно, пусть множество L почти слабо замкнуто и х'о —
Точка его Гр-замыкания. Легко видеть, что при сдвигах почти
слабо замкнутые множества переходят в такие же множества.
Поэтому если элемент х'о не принадлежит L, то найдется почти
слабо открытое множество W, содержащее нуль и не пересекаю-
пересекающее множества L — x'^ Из следствия 8.10.2 вытекает, что точка 0
не принадлежит Гр-замыканию множества L — х'0> т. е. х'о не при-
принадлежит Гр-замыканию множества L. Полученное противоре-
738 Гл. 8. Теория двойственности
чие показывает, что х'о принадлежит Гр-замыканию L, что и
означает Гр-замкнутость множества L. |
8.10.5. Теорема. Пусть Е — полное полуметризуемое локально
выпуклое пространство. Для слабой замкнутости выпуклого мно-
множества L из Е' достаточно (и необходимо), чтобы L было почти
слабо замкнутым. В частности, пространство Е совершенно пол-
полно (и даже гиперполно).
Доказательство. Если множество L почти слабо замкну-
замкнуто, то в силу предыдущего следствия оно 7>замкнуто. Но топо-
топология Тс согласуется с двойственностью между Е и Е\ так что
остается только применить теорему 8.3.4 B). |
Замечание. Теорема 8.10.5 была доказана, К р ей но м и
Шмульяном [1] для банаховых пространств. Для векторных
подпространств (вместо выпуклых подмножеств) этот результат
был ранее анонсирован Бур баки [12]. В данной здесь форму-
формулировке теорема принадлежит Дьёдонне и Шварцу [1]; им
же принадлежит и ее доказательство. Некоторые ^обобщения
были получены Кёте [1].
Приведем еще несколько свойств совершенно полных про-
пространств.
8.10.6. Предложение. Пусть Е — локально выпуклое простран-
пространство с топологией Т и Т' — такая локально выпуклая топология
в £, что Т^СТ' ^Сх(Е, Е'). Если пространство Е совершенно
(соотв. Вг-) полно в топологии Г, то оно совершенно (соотв. Вг-)
полно и в топологии Т'.
Доказательство. Топологическое сопряженное к Е% от-
относительно V совпадает с Е'. Пусть М — почти слабо замкнутое
относительно V векторное подпространство в Е'. Тогда множе-
множество Mf]V° слабо замкнуто для любой Т'-окрестности нуля V
в Е. Так как топология Тг сильнее Г, то и M[\U° слабо замкну-
замкнуто для любой Г-окрестности нуля U в Е. Из совершенной пол-
полноты пространства Е в топологии Т следует слабая замкнутость
множества М. Таким образом, пространство Е совершенно полно
относительно топологии Т\ Доказательство Вг-полноты анало-
аналогично. |
8.10.7. Предложение. Топологическое сопряженное Е' к про-
пространству Фреше Е совершенно полно относительно всякой ло-
локально выпуклой топологии Г, удовлетворяющем условиям
Т<Т<(Е\Е)
Доказательство. Пространством, сопряженным к Ег в
топологии Гс, будет Е. Предыдущий результат позволяет нам
ограничиться рассмотрением случая Т = ТС. Пусть М — почти
слабо замкнутое векторное подпространство в £, т. е. множество
8.10. О совершенно полных пространствах 739
МО V° слабо замкнуто для любой окрестности нуля V в Е'. Это
означает, что для всякого выпуклого уравновешенного компакт-
компактного множества К в Е множество МОК слабо замкнуто. Мы
должны установить, что подпространство М слабо замкнуто, т. е.
(следствие 2.2.7) что М замкнуто в Е. Если х — точка прикосно-
прикосновения множества М, то она является точкой прикосновения и
множества МОК для некоторого выпуклого уравновешенного
компактного множества К в £. (Возьмем в М какую-нибудь по-
последовательность (хп), сходящуюся к х. Замкнутая выпуклая
уравновешенная оболочка К точек хп и х предкомпактна и, сле-
следовательно, в силу полноты Е компактна. Таким образом, х при-
принадлежит замыканию множества МОК-) Так как множество
МОК слабо замкнуто и тем более замкнуто, то х е КОМ с: М.
Предложение полностью доказано. |
8.10.8. Предложение. Пусть Е u F — локально выпуклые пра-^
странства и и— линейное отображение пространства Е в F.
A) Если и — почти открытое отображение и Е — совершенно
полное пространство, то и пространство F совершенно полно.
B) Если и — почти открытое отображение url({0})a({0}) и
пространство Е Вг-полно, то и F Вг-полно.
Доказательство, Рассмотрим сопряженное отображение
и' пространства F' в Ег. Так как и почти открыто, то и(Е) плот-
плотно в F, поэтому и' взаимно однозначно. Пусть М — почти слабо
замкнутое подпространство bFh L = u'(M). Тогда M=u'~l(L).
Если мы покажем, что L слабо замкнуто в Е\ то из слабой не-
непрерывности отображения и' будет следовать слабая замкну-
замкнутость множества М в F'. Кроме того, из дополнительного ограни-
ограничения на и в B) вытекает, что М слабо плотно в Ff и, следова-
следовательно, L слабо плотно в Е'. ^Множество М слабо плотно тогда
и только тогда, когда М° = {0} аналогично для L\ из формулы
(8.6.2), заменяя и на и', получаем также
Таким образом, доказательство каждого из утверждений A), B)
сводится к проверке того, что почти слабая замкнутость вектор-
векторного подпространства М влечет слабую замкнутость множе-
множества L. Так как пространство Е совершенно (или Вг-) полно, то
достаточно доказать почти слабую замкнутость множества L.
Для этого возьмем произвольную окрестность нуля U в Е. По
условию множество V—u(U) есть окрестность нуля в F, поэтому
множество М 0 V0 слабо замкнуто. Можно считать, что окрест-
окрестность U выпукла, уравновешена и замкнута. Тогда в силу соот-
соотношения V=u(U), формулы (8.6.3) и следующего за ней
740 Гл. 8. Теория двойственности
замечания имеем /7° = ^/(V°). Отображение и' взаимно однознач-
однозначно, поэтому L Л 1/° = н'(Л1 Л Vе). Из слабой непрерывности ото-
отображения и' и слабой компактности множества М П V° вытекает
слабая компактность и, следовательно, слабая замкнутость мно-
множества LCW0, что и требовалось доказать. |
8.10.9. Следствие. Факторпространство Е/М совершенно пол-
ного локально выпуклого пространства Е по любому векторному
подпространству М совершенно полно.
Доказательство. Достаточно в предыдущем предложе-
предложении положить F — E/M и взять в качестве и естественное отобра-
отображение пространства Е на F. |
8.10.10. Предложение. Для того чтобы локально выпуклое
пространство Е было совершенно полным, (а) необходимо, чтобы
факторпространство Е/М по каждому векторному подпростран-
подпространству М в Е было Вг-полным\ и (Ь) достаточно, чтобы факторпро-
факторпространство Е/М по каждому замкнутому векторному подпро-
подпространству М в Е было Вг-полным.
Доказательство, (а) вытекает из следствия 8.10.9.
Докажем (Ь). Пусть N — почти слабо замкнутое векторное
подпространство в Е''. Рассмотрим факторпространство F = E/№.
Его сопряженное F' можно отождествить с №°— слабым замы-
замыканием N в £'. Поэтому достаточно показать, что N почти слабо
замкнуто относительно F\ т. е. доказать слабую замкнутость
множества N Л V0 в F' для каждой окрестности нуля V в F. Но
V есть проекция некоторой окрестности нуля U в Е, так что
множество Aff] V° = Nf) U° слабо замкнуто з Е' (по условию),
поэтому оно тем более слабо замкнуто в F'. |
8.10.11. Предложение. Всякое замкнутое векторное подпро-
подпространство Е локально выпуклого Вг-полного пространства F
само Вг-полно.
Доказательство. Рассмотрим вложение и подпростран-
подпространства Е в F и его сопряженное и'. Отображение и' представляет
собой сужение каждой линейной формы с F ка Е. Пусть L —
слабо плотное и почти слабо замкнутое векторное подпростран-
подпространство в Ег и М = и' ~l(L). Так как и—изоморфизм, тс и' — ото-
отображение на (см., например, следствие 8.6.4). Покажем вначале,
что множество М слабо плотно в F'y т. е. что М° = {0}.
Допустим, что уо^М0. Если уо не принадлежит Е = и(Е), то
в силу замкнутости подпространства Е найдется такой элемент
y'&F\ что (и(Е), у') *=0 и (уоу у') = \- Из первого соотношения
следует, что &'(#') =0, так что и'(у') si и потому у'^М. Но
тогда второе соотношение противоречит предположению, что
8.10. О совершенно полных пространствах 741
у0 е М°. Таким образом, у0 е Еу т. е. в Е найдется такой элемент
хо, что уо = и(хо). Тогда 0 = (у0, М) = (хОу и'(М)). Если x'el, то
х'=и'(у ) при некотором г/7 (и! есть отображение «а). Этот эле-
элемент у' должен принадлежать множеству М, откуда получаем
(xo,L)=O. Так как подпространство L слабо плотно в Е\ то
хо^{О}. Из непрерывности и следует, что элемент уо = и(хо) так-
также принадлежит {0}. Таким образом, множество М слабо плотно
в F'.
Теперь покажем, что множество М почти слабо замкнуто
в F'. Пусть V—произвольная окрестность нуля в F. Легко про-
проверить, что множество
содержится в множестве
и' {и-1 (VH П L) = и' (U0 П L) с: и'~{ (L) = М,
где
есть окрестность нуля в Е. Поэтому
Так как подпространство L почти слабо замкнуто в Е', то U° f) L
слабо компактно. Из слабой непрерывности отображения и' сле-
следует слабая замкнутость в F/ множества V0 П М и тем самым
почти слабая замкнутость множества М.
Итак, мы показали, что множество М слабо плотно и почти
слабо замкнуто. Так как пространство F Вг-полно, то M = F\ Из
того факта, что и' есть отображение на, вытекает равенство L =
— Е', откуда следует, что подпространство Е Бг-полно, что и тре-
требовалось доказать. |
8.10.12. Предложение. Пусть Е и F — отделимые локально
выпуклые пространства, и — взаимно однозначное открытое
почти непрерывное линейное отображение пространства Е на
замкнутое векторное подпространство пространства F. Тогда
если пространство F Вг-полно, то таким же будет и Е.
Доказательство. Множество F0 = u(E) есть векторное
подпространство в F. В силу предложения 8.10.11 пространство
^о Sr-полно. Рассмотрим отображение v — u~l пространства Fo
на Е. Отображение v непрерывна и почти открыто. Кроме того,
график отображения v замкнут, ибо пространства Fo и Е отде-
отделимы и v непрерывно. По теореме 8.9.2 B) отображение v от-
открыто. Таким образом, и — изоморфизм пространства Е на Fq,
742 Гл. 8. Теория двойственности
поэтому Е имеет те же свойства, что и FOi т. е. пространство Е
Br-полно. |
8.10.13. Пример полного, но не £г-полного пространства. Зай-
Займемся топологией т, введенной в п. 8.3.7, т. е. топологией %(Е, £*),
которая, как это установлено в п. 8.3.7, совпадает с сильнейшей
локально выпуклой топологией на заданном векторном про-
пространстве Е. Отправной точкой нам будет служить следующая
Лемма. Пространство Е полно в топологии т.
Этот результат принадлежит К а плану [1]. Наше доказа-
доказательство близко к данному Птаком [1, стр. 69—70].
Доказательство. Рассмотрим в Е какой-нибудь алгеб-
алгебраический базис (ei)i^I и дуальный базис (я?) в £*. Пусть у —
элемент т-пополнения Е пространства Е. Покажем, что у е Е.
Каждая линейная форма е\ т-непрерывна на £, и ее можно
(единственным образом) продолжить по непрерывности на Е.
Пусть / — множество тех индексов /, для которых (у, *^0
Покажем прежде всего, что множество / конечно.
Положим
ut-
ei ПРИ
*
—Чг- ПрИ
Каждое xg£ представимо в виде х = 2 ^U)eh гДе числа
#(/) = (#, £*) отличны от нуля для индексов i из некоторого ко-
конечного подмножества F=FxczI. Таким образом, имеем
х{1) при i^F(](I\J),
x(i)
при
Отсюда следует, что семейство (м*) слабо ограничено в £"*. То же
самое верно и для выпуклой оболочки Я этого семейства. Мно-
Множество Я (теор. 1.11.4 A)) относительно слабо компактно в £*,
следовательно, поляра Я0 есть т-окрестность нуля в Е,
Для я е £" положим
|<**1>Г
Функционал р как полунорма на Е является т-непрерывным, сле-
следовательно, р можно по непрерывности продолжить на Ё.
S.JO. 0 совершенно полных пространствах 743
Далее элемент у является пределом некоторой сети (ха) то-
точек из £, так что р(у) = lim р(ха). Поэтому в Е можно найти
а
такой элемент ж, что р{у — x)^.-w. Отсюда следует, что (х, е*^Ф
для i е /. Конечность множества / доказана.
Пусть *о = .2 (У, е])е(<ЕЕЕ. Тогда (xQ, е]) = (у9 е]) для is/.
Для остальных индексов i обе части равенства равны нулю; сле-
следовательно, оно имеет место для всех L
Обозначим через М векторное подпространство в £"*, поро-
порожденное векторами е*.. Мы знаем теперь, что (у, х*) = {хо,х*)
для всех х* е М. Наша цель показать, что это равенство спра-
справедливо для всех л:* е Е*. Легко видеть, что каждый элемент
х* е £* принадлежит множеству вида
Q = {/sr:|(^/)|<af для /е=/},
где числа аг- соответствующим образом подобраны. Функция
явля.ется полунормой на Е, причем Q есть поляра множества, на
котором q(x) ^1. Как и всякая полунорма на £, полунорма q
непрерывна, следовательно, множество Q равностепенно непре-
непрерывное. Так как у^Еу то сужение линейной формы х**—^(уух*)
слабо (т. е. о(Е*, £")-) непрерывно на Q. Нам надо только пока-
показать, что (у, х*) = (хо, х*) для всякого х* из каждого такого мно-
множества Q. Так как это равенство имеет место на М и обе его
части непрерывны, то достаточно убедиться в том, что множество
М П Q плотно в Q. Но это есть простое следствие теоремы о би-
поляре, которое сводит решение задачи к доказательству соот-
соотношения
\(х,
Q и л; g £, т. е. к доказательству того, что
<7(*)<sup{|<*, z*)\: 2*sMflQ}
для х е Е. Но действительно,
где числа 0г = 6г(л:) удовлетворяют неравенству |8<(х) |-^1. Пра-
Правая сторона последнего равенства равна (х, г*) для элемента
г* = 2at-9/eJ (сумма конечна), который, очевидно, принадлежит
М П Q. Это завершает доказательство. |
Теперь мы можем привести пример полного локально выпук-
выпуклого пространства, которое не является 5г-полным.
744 Гл. 8. Теория двойственности
Пусть Е — векторное пространство Iх (N) и Т — его обычная
нормированная топология. Тогда (£, Т) как банахово простран-
пространство бочечно.
Пространство /OO = /OO(N), топологическое сопряженное к
(£, Г), явлется, очевидно, собственным векторным подпростран-
подпространством в Е*. Следовательно, топология т в Е строго сильнее,
чем Т. Покажем теперь, что
(a) 1°° слабо плотно в £*;
(b) /°° почти слабо замкнуто в Е*.
Из двух этих утверждений следует, что пространство (£", т)
не Вг-полно, хотя и полно (в силу предыдущей леммы).
Утверждение (а) тривиально, так как /°° тотально над Е.
Рассмотрим (Ь). Пусть сеть (х!) принадлежит пересечению
/°° П U° и слабо сходится в Е* к элементу х*, где U—некоторая
т-окрестность нуля в Е, Нам надо показать, что х* е Z00, Сеть
(х?), очевидно, слабо ограничена в £*, т. е. sup |(дг, х*)|< + оо
для каждого х^Е. Так как пространство (ЕУТ) бочечно, то
множество (л:!} ограничено по норме в /°°, т. е.
Но тогда, рассматривая элементы х\ как принадлежащие про-
пространству /°°, сопряженному к (£, Г), получаем (теор. 1.11.4 A)),
что сеть (х*.) обладает слабой предельной точкой в 1°°, которая
не может не совпасть с х*. Таким образом, х* е /°°, что и требо-
требовалось доказать.
Замечание. Левин [2] исследовал условия В-полноты
ультрабочечных и бочечных пространств.
8.11. Теорема Хеллингера — Теплица
В этом параграфе мы изложим подход к теоремам о замкну-
замкнутом графике и открытом отображении (в форме, по существу
совпадающей с теоремами 8.9.4 и 8.9.3), который возник при
попытке проанализировать и обобщить теорему, доказанную
Хеллингером и Тёплицем. Эта теорема в своей первоначальной
форме относится к самосопряженным эндоморфизмам гильбер-
гильбертова пространства. Различные эквивалентные формулировки
этого первого результата принадлежат многим авторам. Некото-
Некоторые обобщения этого результата получены в работах Эдварде
[8] и Т э й л о р [2]. Мы, однако, будем в основном следовать из-
изложению П т а к а [2].
Всюду в этом параграфе Е и F — локально выпуклые про-
пространства, и — линейное отображение пространства Е в F, ко-
которое не предполагается непрерывным. Поэтому область опре-
8.11. Теорема Хеллингера — Теплица 745
деления Dr сопряженного отображения и' является, вообще го-
говоря, собственным векторным подпространством в F' (§ 8.6). Во
всех рассматриваемых теоремах утверждается непрерывность
или ограниченность отображения и на основе определенных
свойств множества D\ возможно, при соответствующих ограни-
ограничениях на Е и F. Сама теорема Хеллингера — Теплица относит-
относится к случаю, когда известно, что D' тотально (т. е. слабо плот-
плотно) в F'.
Отправной точкой служит выражение свойства замкнутости
графика отображения и в терминах свойств области D'. Впервые
этот прием, по-видимому, использовал Птак [1, теорема C.7)].
8.11.1. Предложение. Если график отображения и замкнут,
то множество D' тотально. Если пространство F отделимо, то
верно и обратное.
Доказательство. Если множество D' тотально и про-
пространство F отделимо, то проверить, что график отображения и
замкнут, очень просто. Действительно, пусть (Х{)—сеть, сходя-
сходящаяся к нулю в Е, и пусть yi = u(Xi) сходится к у в Г. Тогда для
каждого элемента //'gD' имеют место равенства (ууу') =
= lim(#i, y') = lim(u(Xi), y/) = \im(xi, u'{y'))=0. Так как D' то-
тотально и F отделимо, то у = 0. Это означает, что график отобра-
отображения и замкнут в ExF.
Обратно, пусть график G отображения и замкнут в ExF.
Пусть уо — элемент в F, ортогональный к множеству D'. Нужно
показать, что уо = О. Это будет сделано, если мы установим, что
(О, yo)^G. Действительно, если @, у о) не принадлежит G, то
(так как график G замкнут) найдется такой элемент (х', #')е
f=E'xF\ что (G, (х',у'))=0 и (@, у0), (х', у'))фО. [Здесь мы
пользуемся тем, что сопряженное к ExF может быть отожде-
отождествлено с E'xF\ причем двойственность определяется билиней-
билинейной формой
<(*, у), (*
Из первого соотношения следует, что у/ е D\ из второго — что
(у0уу')ф0. Так как по нашему предположению элемент уо орто-
ортогонален к D', то мы приходим к противоречию. Предложение
тем самым доказано. I
Выясним теперь, что можно сказать в случае, когда D'=Ff.
Основной результат содержится в следующем предварительном
предложении.
8.11.2. Предложение. Пусть D'=F' и V — любая замкнутая
выпуклая уравновешенная окрестность нуля в F. Тогда множе-
множество U = u~l(V) замкнуто в Я,
746 Гл. 8. Теория двойственности
Доказательство. Пусть точка xQ e E не принадлежит U.
Покажем, что х0 не принадлежит замыканию множества U. Так
как элемент и(х0) не лежит в У и У выпукло, уравновешено и
замкнуто в /\ то в Т7' можно выбрать такой элемент #'е V0, что
\(и(хо),у')\> I. Тогда |(*о, и'(у')) |> 1, и так как /еГ, то
| (С/, и'(*,')> 1 = 1 {u(U)t y*)\ = \{V, /Ж К
Таким образом, х0 не принадлежит слабому замыканию множе-
множества U, что и требовалось доказать. |
8.11.3. Теорема. Пусть D' = F'. Тогда
(a) отображение и ограничено;
(b) если пространство Е борнологично, то отображение и не-
непрерывно;
(c) если отображение и почти непрерывно, то оно непре-
непрерывно.
Доказательство. Из условия D' = F' следует, что ото-
бражение и переводит ограниченные множества из £ в множе-
множества, слабо ограниченные в Т7, поэтому (теор. 8.2.2) отображение
и ограничено. Утверждение (а), таким образом,доказано.Утвер-
образом,доказано.Утверждение (Ь) вытекает из (а) и из того, что пространство Е борно-
логично (см. замечание (Ь) после теоремы 7.3.1). Для доказа-
доказательства (с) достаточно вспомнить определение почти непре-
непрерывности и воспользоваться предложением 8.11.2. |
Установим теперь некоторые отношения между свойствами
слабого замыкания множества D' и свойствами отображения и
и пространства Е.
8.11.4. Предложение, (а) Если отображение и непрерывно, то
D' почти слабо замкнуто в F'.
(Ь) Если Е —бочечное пространство, то D' почти слабо
замкнуто в F'.
Доказательство, (а) Надо показать, что множество
D' П V0 слабо замкнуто в F' для каждой окрестности нуля V в F.
Так как отображение и почти непрерывно, то множество U—
= url(V) есть окрестность нуля в Е. Из соотношений
вытекает, что (/ci(a/(Z)/n V°))° и, следовательно,
Пусть элемент у' принадлежит слабому замыканию множе
ства D' П V°- Нам нужно показать, что ^ е Dr П V°. Так
8.11. Теорема Хеллингера — Теплица 747
множество V0 слабо замкнуто, то для этого достаточно убедить-
убедиться в том, что y'^D'. Для произвольных элементов хи •••, хп из
Е и произвольного е>0 обозначим через W(xu...,xn; e) мно-
множество всех тех элементов х' е £/°, для которых
sup \(xh х')-(и{хг\ />|<е.
1 < i < п
Это множество, очевидно, слабо замкнуто в £"'. Оно непусто, по-
поскольку из того факта, что у' принадлежит слабому замыканию
множества D' Г) У0, вытекает существование такого элемента
2/еО'П V0, что
\{u(xt), z'-
Так как z'eD' и z'e У°, то «'(г7) е= G°. Кроме того,
*)> z'> + а,е =
где |аг-К 1, откуда следует, что и'(г')^. W(xu . .., jcn; e).
Таким образом, система множеств вида W(x\,...txn\ г) яв-
является центрированной (п. 0.2.17). Так как поляра U0 слабо ком-
компактна, то существует точка х'^1)°, принадлежащая всем
W(xu ..., хп\ г). Это означает, что равенство {и(х), у') = (х, х')
имеет место для всех х е Е, т. е. у/ е D\ что и требовалось до-
доказать.
Наконец, (Ь) следует из (а). Действительно, если простран-
пространство Е бочечно, то всякое отображение и почти непрерывно (так
как и~1 (V) бочка в Е). В
8.11.5. Теорема, (а) Пусть Е — Вг-полное пространство и и —
почти непрерывное линейное отображение пространства Е в F.
Тогда следующие три условия эквивалентны:
A) отображение и непрерывно;
B) D' = F'\
C) множество D' тотально.
(Ь) Если Е бочечно и F Вг-полно, то для всякого линейного
отображения и пространства Е в F условия A), B) и C) экви-
эквивалентны.
Доказательство. Если пространство Е бочечно, то вся-
всякое линейное отображение и пространства Е в F почти непре-
непрерывно. Таким образом, (а) влечет (Ь).
Докажем (а). Импликация B) гф C) тривиальна. Если про-
пространство F Бг-полно, то в силу предложения 8.11.4(а) верна
обратная импликация. Следовательно, B) и C) эквивалентны.
Из A) тривиальным образом вытекает C). Обратная имплика-
импликация дается теоремой 8.11.3(с). |
748 Гл. 8. Теория двойственности
8.11.6. Замечания. В силу предложения 8.11.1 часть (Ь)
теоремы 8.11.5 дает эквивалентные теоремы о замкнутом гра-
графике, получающиеся, если в формулировке теоремы 7.8.9 поме-
поменять местами Е и F и вместо ы рассмотреть отображение
v: F-+E. В конце параграфа мы обратимся к вопросу о том,
как получить теорему об открытом отображении из этой форму-
формулировки теоремы о замкнутом графике. Таким образом, в пре-
пределах одного этого параграфа мы дадим замкнутое изложение
обеих теорем.
Перейдем теперь к формулировке обобщенной теоремы Хел-
лингера — Теплица, которая непосредственно вытекает из тео-
теоремы 8.11.5(Ь).
8.11.7. Теорема. Пусть S — тотальное множество в F' и f —
такое отображение множества S в Е', что для каоюдого х е Е
найдется элемент у е F, такой, что
(x,№) = (y,s) (ssS). (8.11.1)
Если пространство F отделимо, то элемент у однозначно опре-
определяется элементом х и определенное таким образом отображе-
отображение и: х*—> у линейно. Если,кроме того, Е бочечно, a F Вг:полно,
то и — непрерывное отображение пространства Е в F.
Доказательство. Первое утверждение очевидно. Из со-
соотношения (8.11.1) следует, что D' содержит S, поэтому D' — то-
тотальное множество. Это же соотношение показывает, что u'(s) =
= f(x) для seS. Для доказательства второго утверждения
остается воспользоваться теоремой 8.11.5 (b). I
8.11.8. Замечания. A) Полагая S = D' и f = u', видим, что
теорема 8.11.7 содержит в себе теорему 8.11.5 (Ь), т. е. содержит
одну из форм теоремы о замкнутом графике.
B) В своем первоначальном виде теорема Хеллингера —
Теплица относилась к случаю, когда E = F есть гильбертово про-
пространство, а условие, аналогичное (8.11.1), формулировалось в
терминах скалярного произведения на Е. Известно (следствие
1.12.6), что в гильбертовом пространстве Е существует такой со-
сохраняющий норму сопряженно-линейный изоморфизм / про-
пространства Е на Е\ что
(х, Jy) = {x\y)
для всех х, у е Е. Гильбертово сопряженное и* характеризуется
соотношением
(и{х)\у)-{х\и'(у))9
т. е. отображения и* и и' связаны следующим образом;
U ~ /~~ °U °Jt U — J ° U ° J" •
8.11. Теорема Хеллингера — Теплица 749
Область определения D' отображения uf тотальна, если то-
тотальна область определения отображения а*. Поэтому условие
(8.11.1) записывается в виде следующего равенства:
(x\f(s)) = (y\s) (s<=S), (8.11.2)
где теперь / — отображение тотального подмножества 5 про-
пространства Е в S. Тогда отображения f и и* совпадают на S.
Полученный результат можно сформулировать следующим об-
образом.
► Пусть и — эндоморфизм гильбертова пространства. Если
его гильбертов сопряженный и* имеет тотальную область
определения, то эндоморфизм и непрерывен. В част-
частности, всякий самосопряженный эндоморфизм и непре-
непрерывен. [При этом подразумевается, что область опреде-
определения и есть все пространство.)
Заслуживают внимания следующие два следствия из тео-
теоремы 8.11.7.
8.11.9. Следствие. Пусть Е, F и G — локально выпуклые про-
пространства, причем G отделимо. Допустим, что Р — такое мно-
множество непрерывных линейных отображений пространства F в
F, что если у е F и р(у) = 0 для всех р е Р, то у = 0. Пусть, да-
далее, g — такое отображение множества Р в множество непрерыв-
непрерывных линейных отображений пространства Е в G, что для каж-
каждого х<=Е существует элемент у е F, такой, что
g(p)(x)=p(y) для всех р^Р.
Тогда элемент у однозначно определяется элементом х и опре-
определенное таким образом отображение и: х ■—>у линейно. Если,
кроме того, Е бочечно, a F Вг-полно, то отображение и непре-
непрерывно.
Доказательство. Применить теорему 8.11.7 к случаю,
когда множество S образовано композициями zr ° р, где р про-
пробегает множество Р, a z'—множество G\ и f(s) = z'°g(p) при
5 = z' о р. |
8.11.10. Следствие. Пусть Е, F и G — три локально выпуклых
пространства, причем G отделимо, a F — векторное подпро-
подпространство в GT, где Т — некоторое множество. Допустим, что для
каждого t^T отображение е?: y^-^y(t) пространства F в G
непрерывно. Пусть, далее, h — такое отображение множества Г
в множество непрерывных линейных отображений пространства
Е в G, что для каждого'х е Е функция t^—>h(l)(x) принадле-
принадлежит F. Этот элемент из F обозначим через и(х). Тогда и есть
линейное отображение пространства Е в F. Если, кроме того,
пространство Е бочечно, a F Вг-полно, то и непрерывно.
750 Гл. 8. Теория двойственности
Доказательство. Воспользуемся предыдущим след-
следствием, взяв P = {&t' t^T), где 8^ — непрерывное линейное ото-
отображение пространства F в G, определенное равенством
e,t(y)=y(t), и положив по определению g"(/?)=/*@ Для Р = &г-
Тогда соотношения
имеют место тождественно похе£иреР. Условия следствия
8.11.9 выполняются, и мы получаем нужный нам результат. |
В оставшейся части этого параграфа указывается, каким
образом, исходя из теоремы 8.11.5 (или, точнее, из ее след-
следствия— теоремы 8.9.4), можно быстро вывести две формы тео-
теоремы об открытом отображении применительно к линейному
отображению и пространства Е в F. Удобнее сделать это в два
этапа, на первом из которых отображение и предполагается
взаимно однозначным.
8.11.11. Теорема. Пусть и — взаимно однозначное линейное
отображение пространства Е в F, почти открытое на FQ = u(E)
и обладающее графиком, замкнутым в ExF0. Если пространство
Е Вг-полно, то и есть открытое отображение пространства Е
на и(Е).
Доказательство. Мы хотим применить теорему 8.9.4
к обратному отображению v = u~\ которое является линейным
отображением пространства Fo в £. Легко проверить, что из
ограничений на и следует замкнутость графика отображения v.
Далее отображение v почти непрерывно, ибо отображение и
пространства Е на Fo почти открыто и для всякого множества
U из Е имеет место соотношение v~l(U) zdu(U). Теперь, заме-'
нив в теореме 8.9.4 F на Fo, получаем, что v непрерывно, а это
и означает, что отображение и пространства Е на Fo открыто. I
8.11.12. Теорема. Пусть и — линейное отображение простран-
пространства Е в F, почти открытое на F0 = u(E) и обладающее замкну-
замкнутым графиком в ExF0. Если пространство Е совершенно полно,
то отображение и пространства Е на и(Е) открыто.
Доказательство. Это следует из предыдущего резуль-
результата, если перейти к факторпространству Е/кети, учитывая
(предложение 8.10.10(а)), что это факторпространство Вг-полно.
Легко проверить, что факторотображение удовлетворяет усло-
условиям теоремы 8.11.11. |
8.12. О слабой компактности
Так как ослабленная топология локально выпуклого про-
пространства, вообще говоря, не удовлетворяет первой аксиоме
счетности, то априори не ясно3 в какой мере слабая компакт*
8.12. О слабой компактности 751
ность может быть выражена в терминах последовательностей.
Мы займемся этим вопросом и среди прочего приведем два ре-
результата, принадлежащих соответственно Шмульяну и Эбер-
лейну.
8.12.1. Теорема (Шмульян). Пусть Е— метризуемое ло-
локально выпуклое пространство, (хп) — относительно слабо ком-
пактная последовательность в Е. Тогда из последовательности
(хп) можно извлечь слабо сходящуюся подпоследовательность.
Доказательство. Мы можем заменить Е векторным
подпространством, порожденным элементами хп, и считать, та-
таким образом, что Е сепарабельно. В таком случае пусть Uh
(k=l, 2, ...)—база окрестностей нуля в Е. Множества Ul
слабо компактны в Е', и их объединение совпадает с Е'. Каждое
из множеств Ul слабо метризуемо и, следовательно, слабо сепа-
сепарабельно (так как оно слабо компактно). Поэтому пространство
Е' тоже слабо сепарабельно. Пусть {х^— последовательность,
плотная в Е\ Так как последовательность (хп) относительно
слабо компактна, то для каждого / числовая последова-
последовательность ((хп, х£)) содержит сходящуюся подпоследова-
подпоследовательность. С помощью диагонального процесса можно извлечь
из (хп) такую подпоследовательность (уп), для которой предел
\\т(уп, л^) существует и конечен при каждом L Отсюда еле-
п
дует, что относительно слабо компактная последовательность
(уп) обладает по крайней мере одной слабой предельной точкой
и, следовательно, слабо сходится. |
8.12.2. Замечание. Эта теорема остается справедливой,
если Е — строгий индуктивный предел метризуемых локально
выпуклых пространств1). Действительно, тогда относительно
слабо компактная последовательность (хп), будучи ограничен-
ограниченной, попадает в одно из определяющих индуктивный предел
метризуемых пространств, к которому применимы предыдущие
рассуждения. Более того, проведенное доказательство прохо-
проходит в случае существования последовательности (Uk) окрест-
окрестностей нуля в Е, пересечение которых сводится к {0}.
Наш следующий результат основан на простой лемме о не-
непрерывных функциях на компактном пространстве Т. Обозначим
(как всегда) через С(Т) пространство непрерывных функций
на Г, рассматриваемое как банахово пространство с нормой,
равной максимуму модуля. Иногда возникает необходимость
1) Определение строго индуктивного предела локально выпуклых про-
пространств см. у Б у р б а к и [7, стр. 87—88}. — Прим. перев.
752 Гл. 8. Теория двойственности
рассмотреть на С(Т) также и топологию поточечной сходимости.
Обозначим соответствующее локально выпуклое пространство
через СР(Т).
8.12.3. Лемма. Пусть Т — компактное пространство и Я—
множество в С(Т). Если f0 принадлежит замыканию Я в СР(Г),
то существует такое счетное множество Яо а Я, что f0 принад-
принадлежит замыканию Яо в СР(Т).
Доказательство. Пусть заданы натуральные числа m
иди функция f^C(T). Через W(f, m, n) обозначим множе-
множество всех тех точек (^)i<i<OTH3 Tm, для которых
sup lf(/,)
1 <i<
Каждое из этих множеств открыто. Когда функция f пробегает
Я, эти множества покрывают пространство Тт. В силу его ком-
компактности найдется конечное множество Ят?пс= Я, для которого
соответствующие множества W(f, m, n) покрывают Тт. В каче-
качестве Яо достаточно теперь взять объединение всех таких Нт> п. |
8.12.4. Теорема. Пусть Е — метризуемое локально выпуклое
пространство, Я — некоторое множество в Е и х0 е Е. Тогда
(a) если точка х0 принадлежит слабому замыканию множе-
множества Я, то она принадлежит слабому замыканию некоторого
счетного подмножества Яо в Я;
(b) если множество Я слабо относительно компактно и xQ
принадлежит слабому замыканию множества Я, то существует
последовательность (хп) а Я, слабо сходящаяся к х0.
Доказательство, (а) Как и в доказательстве теоремы
8.12.1, пространство Е' есть объединение последовательности
слабо компактных множеств (Tk). Всякий элемент простран-
пространства Е можно рассматривать как элемент пространства C(Th).
Применяя к каждому Tk лемму 8.12.3, легко получаем нужный
результат.
(Ь) Согласно (а), множество Я можно считать счетным. Как
и при доказательстве теоремы 8.12.1, Е' будет слабо сепара-
бельным. Пусть (xty — последовательность, сла-бо плотная в Е\
Для каждого i можно извлечь из множества Я такую последо-
последовательность (яп), что
Нгп<ая, *;> = <х0, <>.
С помощью диагонального процесса построим такую последова-
последовательность (уп) с: Я, что
){ ') всех *•
8.12 О слабой компактности 753
Так как множество Н относительно слабо компактно, то по тео-
теореме Шмульяна существует подпоследовательность (хп) после-
последовательности (уп)> которая слабо сходится к некоторому эле-
элементу из Е. Так как последовательность (л;£) слабо плотна в Е\
то этим пределом может быть только элемент х0. Теорема пол-
полностью доказана. |
8.12.5. Замечание. Часть (Ь) доказанной теоремы также
может быть распространена на строгие индуктивные пределы
метризуемых локально выпуклых пространств. Рассуждения про-
проводятся так же, как в замечании 8.12.2.
Ниже мы приводим теорему Эберлейна, доказательство ко-
которой опирается на другую лемму, относящуюся к простран-
пространству С(Т).
8.12.6. Лемма. Пусть Т — компактное пространство и Н —
подмножество в С(Т). Если каждая последовательность элемен-
элементов из Н имеет предельную точку в СР(Т), то поточечное замы-
замыкание Н множества Н в Кт компактно относительно поточечной
сходимости и содержится в С(Т).
Доказательству. Из теоремы Тихонова вытекает ком-
компактность множества Н в топологии поточечной сходимости. Та-
Таким образом, остается доказать, что Н содержится в С(Т).
Допустим противное, т. е. что найдется функция и^Н, ко-
которая разрывна в некоторой точке а еГ. Тогда можно по ин-
индукции построить такие число d>0, последовательность
(tn) а Т и последовательность (/п) с; Я, что будут справед-
справедливы следующие соотношения:
\u{tn)-u(a)\^d9 (8.12.1)
\fm{tn)-L(a)\<j (m<n), (8.12.2)
U(U-L(UI<|, U(a)-fm(a)|<f (m>n). (8.12.3)
Пусть f — предельная точка последовательности (fm) в CV(T)
и b — предельная точка последовательности (tn) в Т. Тогда из
неравенства (8.12.2) получаем при п->оо
Переходя к пределу при т->оо, находим, что
/(a)l<f. (8.12.4)
754 Гл. 8. Теория двойственности
Переход к пределу в (8.12.3) при т-*оо дает
и
|и(а)-/(а)|<|. (8.12.6)
Отсюда и из (8.12.5) вытекает, что неравенство
имеет место для бесконечного множества чисел п. Из послед-
последнего неравенства и из (8.12.4) следует неравенство
которое вместе с (8.12.6) влечет за собой неравенство
для бесконечного множества чисел /г, что противоречит соотно-
соотношению (8.12.1). Мы получили противоречие, чем лемма и до-
доказана. 1
8.12.7. Теорема (Эберлейн). Пусть Е — отделимое ло-
локально выпуклое пространство и Я— подмножество в Е. Если
(а) каждая последовательность элементов из Я обладает пре-
предельной точкой в Е и (Ь) замкнутая выпуклая оболочка мно-
множества Я полна в топологии т(£, Е'), то множество Н относи-
относительно компактно в Е.
Доказательство. Из условия__(а) следует предкомпакт-
ность множества Я. Его замыкание Н будет компактным тогда
(и только тогда), когда оно полно. Поэтому достаточно пока-
показать, что слабое замыкание множества Я слабо полно. Это сво-
сводит все к случаю, когда в пространстве Е рассматривается то-
топология а (Я, Ег).
Пусть Я*— слабо замкнутая выпуклая оболочка множества
U. По условию (Ь) множество Я* полно в топологии т(Е, Е').
Если Е — пополнение пространства Е в топологии т(Е, £'), то
множество Я* (будучи полным) замкнуто в Е и, следовательно,
слабо замкнуто в Е (ибо Я* выпукло). Теперь достаточно по-
показать, что слабое замыкание множества Я в Ё слабо ком-
компактно (это замыкание содержится в Е). Доказательство этого
факта в свою очередь сводится к рассмотрению случая, когда
пространство Е полно в топологии т(£, Е').
8.12. О слабой компактности 755
Множество //, очевидно, ограничено и потому относительно
слабо компактно в Е'*. Таким образом, остается доказать, что
всякая линейная форма и на Е\ принадлежащая слабому за-
замыканию множества Н в £'*, принадлежит Е. Если множество
КаЕ' слабо компактно, то сужение и\К принадлежит поточеч-
поточечному замыканию множества Нк сужений х\К (хеЯ). Из усло-
условия (а) вытекает тогда, что каждая последовательность в Нк
обладает предельной точкой в Ср(/С). Из леммы 8.12.6 следует,
что множество Нк относительно компактно в СР(К). Поэтому
сужение и\К непрерывно на К. Остается применить теорему
8.5.1. |
8.12.8. Следствие. Пусть Т — компактное пространство. Мно-
Множество На С(Т) относительно слабо компактно тогда и только
тогда, когда оно ограничено и относительно компактно в СР(Т).
В этом случае каждая последовательность в Н содержит слабо
сходящуюся подпоследовательность.
Доказательство. Необходимость очевидна.
В силу теоремы Эберлейна для .доказательства достаточ-
достаточности надо только показать, что всякая последовательность
(fn) элементов из Н обладает слабой предельной точкой в С(Т).
Последовательность (/п) относительно компактна в СР(Т). По-
Поэтому в силу следующей ниже леммы 8.12.9 можно извлечь из
(fn) подпоследовательность (g"n), сходящуюся в СР(Т). Из тео-
теоремы 4.10.2 следует тогда, что последовательность (gn) слабо
сходится в С (Г). Таким образом, последовательность (/п)
имеет слабую предельную точку в С(Т). |
8.12.9. Лемма. Пусть Т — компактное пространство и <5—
система подмножеств из Г, которая покрывает Т. Обозначим
через С© (Т) пространство непрерывных функций на Г, наде-
наделенное топологией равномерной сходимости на множествах из
®. Тогда всякая относительно компактная последовательность
(fn) в С© (Т) содержит подпоследовательность, сходящуюся в
С© (Г).
Доказательство. Пусть Н — компактное замыкание по-
последовательности (fn) в С© (Г). Топология в С© (Г) и тополо-
топология равномерной сходимости на каком-нибудь плотном подмно-
подмножестве пространства Т индуцируют в Н одну и ту же топологию.
Поэтому достаточно найти подпоследовательность, которая схо-
сходится поточечно на каком-либо плотном подмножестве в Т. Да-
Далее, не ограничивая общности, в качестве © можно взять мно-
множество одноточечных подмножеств в Г; тогда С®(Т)=СР(Т).
Допустим сначала, что пространство Т метризуемо. Тогда оно
сепарабельно, и мы можем считать, что (/г) —плотная в Т после-
последовательность. Поэтому множество /У метризуемо в топологии
756 Рл. 8. Теория двойственности
поточечной сходимости на точках U. Отсюда с помощью диаго-
диагонального процесса получаем нужный нам результат.
Рассмотрим общий случай. Пусть Г*— факторпространство
пространства Т по отношению «fn(t) =fn{t') для всех п». Про-
Пространство Т* компактно, метризуемо, и его топология — сла-
слабейшая из топологий, при которых каждая из функций fn непре-
непрерывна на Т*. Кроме того, пространство СР(Т*) может быть
отождествлено с замкнутым векторным подпространством в
СР(Г), поэтому последовательность (/п) можно отождествить
с некоторой относительно компактной последовательностью в
СР(Т*). Таким образом, задача сведена к уже рассмотренному
случаю, когда пространство Т метризуемо, и тем самым лемма
доказана. 1
8.12.10. Замечания. У Данфорда и Шварца [1,
стр. 466] приводится для банаховых пространств утверждение,
являющееся своего рода комбинацией теорем 8.12.1 и 8.12.7.
Даже для случая банаховых пространств установление теорем
Шмульяна и Эберлейна происходило постепенно; см. стр. 503—
504 книги Данфорда и Шварца [1]. Распространение этих
результатов на случай более общих пространств было проведено
Коллинзом [1], Дьёдонне и Шварцем [1] и Гротен-
диком [1]. На две последние работы оказало влияние изложе-
изложение рассматриваемых вопросов в книге Бур баки [7, стр. 232,
упр. 136; стр. 233, упр. 156], которому мы и следуем в нашей
книге. См. также Гроте н дик {7, гл. V, стр. 17—19].
Шмульян дал другое «счетное» условие слабой компактности
выпуклых множеств К в банаховом пространстве, а именно
чтобы каждая убывающая последовательность непустых замк-
замкнутых выпуклых подмножеств из К имела непустое пересече-
пересечение. Доказательство можно найти у Данфорда и Шварца
[1, стр. 470]. Этот результат опубликован впервые в работе
Шмульяна [3]. Другое доказательство принадлежит Кли [2].
См. также Дьёдонне [5].
Обобщая работы Джеймса, Прайс [1] показал, что под-
подмножество А полного вещественного локально выпуклого про-
пространства компактно тогда и только тогда, когда каждая форма
х' е Е' достигает своей верхней грани на Л в некоторой точке
множества А.
См. также Корсон и Линденштраус [1].
8.13. Теорема Крейна
В общем виде теорема формулируется следующим образом.
8.13.1. Теорема. Пусть Е — отделимое локально выпуклое
пространство, А—компактное подмножество в Е и В — замкну-
8.13. Теорема Крейна 757
тая выпуклая оболочка А в Е. Множество В компактно тогда а
только тогда, когда оно полно в топологии т(£, Е').
Доказательство. Если В компактно, то оно полно и по-
потому тем более полно в топологии т(£, Е').
Пусть теперь множество В полно в топологии т(£, £'). То-
Тогда оно предкомпактно, и, следовательно, множество В ком-
компактно тогда и только тогда, когда оно полно. Значит, доста-
достаточно показать, что множество В слабо компактно (или даже
относительно слабо компактно). Это означает, что можно с са-
самого начала считать, что исходной топологией в Е является
топология а(£, Е').
Так как множество В т-полно, то оно замкнуто в т-пополне-
нии Е пространства Е, откуда следует^что множество В (в силу
своей выпуклости) слабо замкнуто в Е.
Таким образом, достаточно показать, что В относительно
слабо компактно в Е. В соответствии с этим можно считать
пространство Е т-полным, и наша задача сводится к доказа-
доказательству слабой относительной компакт-ности множества В.
Согласно теореме Эберлейна, достаточно показать, что каж-
каждая последовательность элементов из В имеет слабую предель-
предельную точку в Е. Таким образом, без всякого ущерба можно пред-
предположить, что пространство Е сепарабельно в топологии т. (На-
(Напомним читателю, что замкнутые векторные подпространства из
Е совпадают в топологиях т и а.)
Подводя итог, видим, что наша задача сводится к следую-
следующему: пусть Е — полное отделимое сепарабсльное локально вы-
выпуклое пространство, А — слабо компактное подмножество в Е
с замкнутой выпуклой оболочкой В. Нужно показать, что мно-
множество В относительно слабо компактно. Мы сделаем это, ис-
пользуя представление точек множества В в виде интегралов
по А.'
Рассмотрим множество А как компактное пространство в
слабой топологии. Пусть \х — вещественная мера Радона на Л.
Покажем, что интеграл
&== j xd[x(x) (8.13.1)
принадлежит множеству В. Априори такой интеграл является
элементом пространства £'* (алгебраического сопряженного к
£'), задаваемым правилом
(п. 8.14.1). Все свойства этого интеграла, которые нам понадо-
понадобятся, непосредственно следуют отсюда.
758 Гл. 8. Теория двойственности
Утверждение, что линейная форма b принадлежит простран-
пространству Е, означает, что эта форма на Е' слабо непрерывна. Как
только это будет установлено, из очевидного неравенства
(b, *')<sup (Х9 х'), (8.13.2)
справедливого для меры \л > 0 с общей массой 1, сразу будет
следовать, что b e В.
Слабую непрерывность b как линейной формы на Е' легко
установить с помощью теоремы 8.5.1. Действительно, так как
пространство Е сепарабельно, то слабая топология в U° (U—
окрестность нуля в Е) метризуема. Непрерывность сужения
b | U° является тогда непосредственным следствием теоремы Ле-
Лебега 4.8.2.
Таким образом, формула (8.13.1) задает отображение t мно-
множества М нормированных положительных мер Радона на А
в множество В. Покажем теперь, что t есть отображение на.
В самом деле, если элемент b принадлежит множеству В, то он
есть предел выпуклых комбинаций 2 Ctxif где £*^0, 2^ = 1
i
и Xi e А. Каждая такая сумма может быть представлена инте-
интегралом вида (8.13.1), где \i — сумма масс с% в точках х\. Так как
\х — нормированная положительная мера Радона, то \\ е М.
Множество М слабо компактно, поэтому ясно, что отображение
t непрерывно в слабой топологии в М и в топологии о(Е, Е').
Следовательно, t отображает М на В.
Из слабой компактности множества М и непрерывности ото-
отображения t следует, что множество B = t(M) слабо компактно.
Теорема Крейна тем самым полностью доказана. |
8.13.2. Следствие. Пусть Е — отделимое локально выпуклое
пространство, квазиполное в топологии %{Е, Е'), Т—компакт-
Т—компактное пространство, t*—>x(t)—слабо непрерывное отображение
пространства Т в Е и \л — мера Радона на Т. Пусть далее
X{t)dp(t)
является элементом из Е'*. Тогда
(a) элемент х0 принадлежит замкнутой выпуклой уравнове-
уравновешенной оболочке в Е множества \\[i\\'X(T)\
(b) если jj, — положительная мера с общей единичной мас-
массой, то элемент xQ принадлежит замкнутой выпуклой оболочке в
Е множества х(Т).
Доказательство. Множество А=х(Т) слабо компактно.
Пусть В и К суть соответственно его замкнутая выпуклая и
8.13. Теорема Крейна 759
замкнутая выпуклая уравновешенная оболочка в Е. Множество
К есть уравновешенная оболочка множества В. По теореме
Крейна В слабо компактно; следовательно, слабо компактно
также и множество К.
Ясно, что хо принадлежит слабо замкнутой выпуклой урав-
уравновешенной оболочке множества Ц|л||«Л в Е'*. Так как мно-
множество К слабо компактно, то оно слабо замкнуто в £'*. По-
Поэтому указанная оболочка в Е'* совпадает с соответствующей
оболочкой в Е. Таким образом, Xq e |||л|| •/(, и (а) доказано.
Часть (Ь) является частным случаем доказанного утвержде-
утверждения, поскольку неравенство
(хо, *')<sup (*(*), х')
*е= Т
имеет место для каждого элемента хг е Е\ так что в силу след-
следствия 2.2.4 элемент -хо принадлежит множеству В. |
8.13.3. Следствие. Пусть А — подмножество отделимого про-
странства Е, квазиполного в топологии х(Е, Е'). Обозначим
через В замкнутую выпуклую оболочку множества Л, а через
К его уравновешенную замкнутую выпуклую оболочку. Тогда
В=П xdix(x):
К = I I xd\x(x): \x вещественна, \ ф= 1 1.
U A J
Доказательство. Достаточно воспользоваться след-
следствием 8.13.2 и заключительной частью доказательства теоремы
Крейна, видоизменив его очевидным образом, в случае мно-
множества К. 1
8.13.4. 3 а м е ч а н и я. A) Для случая банаховых пространств
теорема Крейна изложена у Данфорда и Шварца [1,
стр. 471], которые называют ее теоремой Крейна — Шмульяна,
отмечая, что сначала Крейн доказал ее для сепарабельных
банаховых пространств [1], а затем условие сепарабельности
было снято в совместной работе Крейна и Шмульяна
[1]. Приведенное нами доказательство для пространств более
общего вида принадлежит Гротендику [7, гл. V, стр. 22].
B) Имеется менее тонкая форма теоремы Крейна, которая
доказывается гораздо легче. Она заключается в следующем:
в квазиполном локально выпуклом пространстве Е замкнутая
выпуклая оболочка В компактного множества Аа Е также
компактна. Действительно, легко видеть, что множество В пред-
компактно и ограничено, и наше утверждение следует из квази-
квазиполноты пространства Е,
760
Гл. 8. Теория двойственности
C) Относительно легко показать, что во всяком топологи-
топологическом векторном пространстве Е замкнутая выпуклая уравно-
уравновешенная оболочка В компактного выпуклого множества А
сама компактна.
Для этого построим оболочку Б, отправляясь от множества
А и беря последовательно A) уравновешенную оболочку, B)
выпуклую оболочку и C) замыкание, причем именно в этом
порядке. Это показывает, что в случае вещественного простран-
пространства В есть замкнутая выпуклая оболочка множества А[}(—А);
в случае комплексного пространства В содержится в замкнутой
выпуклой оболочке множества 2Л 112соЛU2oA4, где со — какой-
нибудь корень третьей степени из единицы, co^l. Следующий
рисунок поясняет это.
Рис. 3.
Теперь остается только заметить, что замкнутая выпуклая
оболочка объединения конечного числа компактных выпуклых
множеств Af (I-*Ci ^C n) компактна. Действительно, эта обо-
оболочка есть образ компактного пространства [0, l]nX^iX.. .ХЛП
при непрерывном отображении
п
^1л|, • , ,, U'fii лц» • • • > *"п) ^d ^i^l*
D) Даже в пространстве R2 возможны случаи, когда (а)
уравновешенная оболочка выпуклого множества не является
выпуклой и (C) выпуклая оболочка замкнутого множества не
является замкнутой.
Чтобы получить пример, подтверждающий справедливость
утверждения (а), достаточно в качестве выпуклого множества
8.13. Теорема Крейна 761
взять любой отрезок, не проходящий через нуль. Примером,
иллюстрирующим утверждение (C), служит замкнутое множе-
множество {(п, п~1): п=\, 2, ...}. Его выпуклая оболочка — это за-
заштрихованная часть плоскости на приведенном ниже рисунке.
Верхняя горизонтальная прямая состоит из точек прикоснове-
прикосновения выпуклой оболочки, которые ей не принадлежат.
B,1/2)
E) В следствии 8.13.2(а) множество Т можно считать лишь
локально компактным, если предположить, что lim x(/)=0
t ->оо
слабо. Далее если множество Т дискретно, то достаточно таких
предположений: функция x(t) ограничена, lim (х {t), х') = 0
t->oo
для каждого элемента х' некоторого подмножества НаЕ\ то-
тотального над Е (т. е. разделяющего точки из Е), и пространство
Е квазиполно. Действительно, тогда ряды 2j\i(t) x(t) сходятся
в Е для каждого элемента \х из 11(Т). Этот вопрос мы уже рас-
рассматривали в § 2.5.
8.13.5. Пример. Пусть Т — вещественная прямая, E = L°°(T)
(для меры Лебега) и x(t)—элемент из L°°(T) (т. е. класс),
определяемый функцией вещественного переменного s^->e^its.
Представим себе, что пространство Е наделено слабой тополо-
топологией a(L°°, L1). Тогда функция t\—>x(l) ограничена и слабо не-
непрерывна и lim x(t) = O в слабой топологии (по лемме Римана-—
Лебега). Если \х — некоторая ограниченная мера Радона на Г,
то интеграл x(t)d\i(t) существует как элемент из Е и яв-
является фактически элементом из L°°(T), т. е. классом ограничен-
ограниченной непрерывной функции
которая есть в точности преобразование Фурье меры \х. Преды-
Предыдущие общие рассуждения показывают, что каждый элемент
замкнутой выпуклой оболочки в Ь°° множества экспоненциаль-
экспоненциальных функций e~iU (t — вещественно) имеет вид \х (или, точнее,
762 Гл. 8. Теория двойственности
есть класс функции fi), где \х— положительная мера, для кото-
которой I" ф(/)<1. При этом можно утверждать даже большее, а
именно что \d\x(t)=l. По-видимому, наиболее быстрый путь
доказательства этого утверждения — продолжить функцию x(t)
на компактификацию Александрова пространства Г, полагая
х(оо)=0 (на мысль воспользоваться таким приемом наводит
лемма Римана — Лебега). Затем можно непосредственно при-
применить следствие 8.13.2 (Ь).
Этот пример примыкает к теме, которая будет рассмотрена
в § 10.3, а именно к теореме Бохнера о представлении положи-
положительно определенных функций. Существенный пробел, имею-
имеющийся пока в наших рассуждениях, заполняется теоремой
Крейна — Мильмана, из которой следует, что непрерывные по-
положительно определенные функции совпадают с точностью до
множителя с элементами замкнутой выпуклой оболочки мно-
множества экспоненциальных функций e~its.
8.14. Интегрирование векторных функций
Как было возвещено в п. 4.10.7, оставшаяся часть главы
будет посвящена некоторым аспектам теории интегрирования
векторных функций относительно скалярных мер Радона и свя-
связанной с нею теории интегрирования скалярных функций отно-.
сительно векторных мер Радона. В § 8.13 мы слегка коснулись,
первой из этих теорий. К сожалению, почти нигде больше в на-
нашей книге эти теории не используются. Тем не менее они вполне
заслуживают внимания, так как служат обширным и процве-
процветающим полем приложения общей теории двойственности, где
еще многое предстоит сделать.
Задачи, возникающие при интегрировании векторных функ-
функций, обычно параллельны соответствующим задачам (гл. 4) для
числовых функций и естественным образом приводят к поня-
понятию векторных мер Радона, которые рассматриваются как не-
непрерывные линейные отображения пространства непрерывных
функций в отделимое локально выпуклое пространство. Основ-
Основные вопросы настоящей главы, относящиеся к мерам Радона,
концентрируются вокруг теоремы типа Лебега — Радона — Ни-
кодима. Ниже, в п. 9.4.14, мы подробнее остановимся на роли
векторных мер Радона как непрерывных линейных бтображений.
Всюду на протяжении оставшейся части главы, если не ука-
указано противное, Т будет обозначать отделимое локально ком-
компактное пространство, \х— положительную меру Радона на Г и
Е — отделимое локально выпуклое пространство. Предпола-
8.14. Интегрирование векторных функций 763
гается также, что термины «измеримость», «интегрируемость»,
«сг-компактность», «почти всюду», «пренебрежимость» и т. д.
относятся к мере jut. Без существенного ограничения общности
можно считать Е вещественным векторным пространством (если
Е— комплексное векторное пространство, то сужение на поле
вещественных чисел не вносит никаких принципиальных изме-
изменений).
Перед нами стоит задача рассмотреть возможность образо-
образования интеграла
где / — заданная (удовлетворяющая соответствующим усло-
условиям) функция на Т со значениями в Е. Как обычно, под инте-
интегралом вида f ф, взятым по измеримому подмножеству М
м
в Г, по определению понимают интеграл %Mf d\i, где ^ — ха-
характеристическая функция множества М.
Как уже было сказано в п. 4.10.7, имеются два подхода к ре-
решению этой задачи. Один из них обычно называется «слабой»
теорией (мы предпочитаем употреблять эпитет «скалярный»),
а другой — «сильной» теорией, которая в случае банаховых про-
пространств связана с именем Бохнера. Изложение теории Бохнера
можно найти в книгах Хил л е [1, гл. III], ХиллеиФиллипс
[1, гл. III], Данфорд и Шварц [1, гл. III]. Бур баки [8,
гл. IV] предлагает подход, строго параллельный применяемому
им подходу к теории интегрирования числовых функций (по
существу воспроизведенному нами в гл. 4) и приводящий к тем
же выводам.
Все названные авторы — Хилле, Данфорд и Шварц и Бур-
баки [8, гл. IV] — уделяют также внимание различным «сла-
«слабым» теориям. Мы приведем здесь лишь краткий обзор некото-
некоторых аспектов этой тематики, причем наше изложение отличается
в деталях от изложения любого из перечисленных выше авторов
и ставит своей целью получить теорию типа Бохнера, служащую
естественным и действенным инструментом для случая про-
пространств Фреше. Однако за пределом этой категории про-
пространств слабая теория определенно проще и все еще удовле-
удовлетворяет большинству требований. В случае общих отделимых
локально выпуклых пространств Е нам представляется более
простым начать со слабой, или скалярной, теории. (Если про-
пространство Е не является локально выпуклым, то возникает
ряд новых задач; см. Грамш [1], Пжеворска-Ролевич
и Ролевич [1].)
764 Гл. 8. Теория двойственности
Всюду, где не указано противное, через / будет обозначаться
функция на Т со значениями в Е.
8.14.1. Различные определения понятия измеримости и ин-
интегрируемости. Как мы уже говорили, все понятия распадаются
на две категории: скалярные понятия (иногда называемые ела-
быми\ см., однако, замечание A) ниже) и сильные понятия.
Приведем сначала точные определения, а затем снабдим их не-
некоторыми комментариями.
(а) Скалярные понятия. Будем говорить, что функция
f: Т->Е скалярно обладает свойством Р (например, свойство
измеримости, интегрируемости или существенной интегрируе-
интегрируемости), если для каждого элемента хг из пространства Ег (то-
(топологического сопряженного к Е) числовая функция х*of обла-
обладает свойством Р.
Если функция / скалярно существенно измерима, то инте-
интеграл fd\x вводится как единственный элемент z пространства
Е'* (алгебраического сопряженного к £'), определяемый с по-
помощью соотношения _
(г, х')=|(*/о/)Ф, (8.14.1)
справедливого для всех х'^Е'. Вместо xf°f мы будем иногда
писать (f, x') или fxr.
Так как пространство Е отделимо, то его можно отожде-
отождествить с некоторым векторным подпространством в Е'*. Часто
возникает вопрос: принадлежит ли \ fd\i пространству Е или
какому-нибудь другому векторному подпространству в Е* (на-
(например, второму сопряженному £")? Мы уделим этому вопросу
значительное внимание.
Если функция / скалярно интегрируема, то она тем более
скалярно существенно интегрируема; в этом случае вместо \ f d\i
мы будем писать J / ф.
Некоторые авторы рассматривают ситуацию, возникающую,
если взять векторное подпространство L в Е\ отделяющее точки
из £, и требовать от функции fx/ существенной интегрируемости
при каждом х' из L. Тогда интеграл Г f d\i определяется априори
как элемент из L*. Эта ситуация, хотя и кажется более общей,
сводится, однако, к уже описанной^ если наделить Е слабой
топологией а(£, L), относительно которой топологическое со-
сопряженное к Е совпадает с L, Ввиду этого оставим в стороне
вариант с заменой Е' на L
8.14. Интегрирование векторных функций 765
(b) Измеримость. Мы исходим из теоремы Лузина 4.8.5.
Будем говорить, что функция / измерима, если для каждого
интегрируемого множества AczT (или, чго то же, для каждого
компактного множества AczT) и каждого числа е>0 суще-
существует такое компактное множество К а Л, что \х(А\К)<& и
сужение f\K непрерывно.
Очевидно, что измеримость в этом смысле (которую часто
называют «сильной», хотя мы и будем избегать употребления
этого термина) влечет за собой скалярную измеримость (см.
ниже замечание B)).
По поводу истории вопроса и соответствующей литературы,
связанной с понятием измеримости, см. замечание после тео-
теоремы 8.15.2.
(c) Интегрируемость. Функция f, отображающая Т в Е, на-
называется интегрируемой (соотв. существенно интегрируемой),
если она измерима (см. (Ь)) и, кроме того,
соотв. |*(р°/)ф<+ оо) (8.14.2)
для каждой непрерывной полунормы р на Е.
Мы получим, очевидно, эквивалентное определение, если
ограничимся любой системой непрерывных полунорм р на про-
пространстве £, определяющей его топологию.
Как и в случае измеримости, этому понятию интегрируемо-
интегрируемости часто предшествует эпитет «сильная». Мы, однако, как и
выше, будем избегать пользоваться этим эпитетом.
Очевидно, что интегрируемая (соотз. существенно интегри-
интегрируемая) функция f скалярно интегрируема (соотв. скалярно су-
существенно интегрируема). Далее (теор. 8.15 2) мы получим ча-
частичное обращение этого утверждения, разумеется, при соот-
соответствующих ограничениях на Е.
Замечания. A) Ясно, что понятие измеримости в неко-
некоторой степени зависит от топологии, заданной в Е. Вопрос о
том, в какой степени, далеко не тривиален.
Особенно важно выделить измеримость, соответствующую
ослабленной топологии о(Е, £'); мы будем называть ее слабой
измеримостью. Многие авторы отдают это название измери-
измеримости, которую мы здесь назвали скалярной. Опасность сме-
смешения этих понятий усугубляется еще и тем, что слабая непре-
непрерывность (т. е. непрерывность в топологии а(£, Е')) и скаляр-
скалярная непрерывность, действительно, совпадают. Однако для
измеримости эти два понятия следует четко различать.
Слабая измеримость, очевидно, влечет за собой скалярную.
Обратное же неверно, как показывает следующий пример
(Бур баки [9, гл. VI, стр. 81, упр. 12]). Пусть Г = [0, 1], |я — мера
706 Гл. 8. Теория двойственности
Лебега, Е—некоторое гильбертово пространство с ортонорми-
рованным базисом (е*)/€= т. Определим функцию / равенством
f(t)=et. Эта функция скалярно нренебрежима и тем более ска-
скалярно измерима. Тем не менее функция f не является слабо из-
измеримой. Для доказательства рассмотрим компактное множе-
множество К а Г, обладающее тем свойством, что сужение (f(t) \x) \К
непрерывно для всех х из Е. Легко видеть, что этим свойством
обладают только конечные множества К. Если теперь функция /
слабо измерима, то должны существовать множества К указан-
указанного выше вида, для которых число \х(Т\К) сколь угодно мало,
а это противоречит конечности множества К.
Этот пример служит полезным уроком еще и в другом от-
отношении. Пусть множество АаТ не является измеримым, и
пусть g = %Af- Функция t^^\\g(t)\\ не будет измеримой, несмотря
на то что g (так же как и /)—скалярно пренебрежимая и, сле-
следовательно, скалярно измеримая функция. Таким образом, при-
применение непрерывной полунормы к скалярно измеримой функции
может дать неизмеримую функцию.
По этой причине мы будем следовать терминологии Бурбаки,
отдавая ей предпочтение перед обычной.
B) В противовес отрицательным результатам, указанным в
замечании A), ниже мы увидим (§ 8.15), что для метризуемых
пространств Е имеется важная положительная связь между из-
измеримостью и скалярной измеримостью.
C) В связи с примером, рассмотренным в замечании A),
стоит отметить следующий простой результат: непрерывная (ска-
(скалярная или векторная) функция от измеримой (скалярной или
векторной) функции снова измерима.
D) Скалярная интегрируемость до некоторой степени также
зависит от топологии пространства Е. Для иллюстрации этого
факта рассмотрим следующую ситуацию (Бурбаки [9, гл. VI,
стр. 80, упр. 5]). В качестве Е возьмем пространство C(R) ком-
комплексных непрерывных функций на R, наделенное топологией
локально равномерной сходимости. В качестве Т возьмем R, а в
качестве \х — меру Лебега. Пусть f(t) — функция (элемент изЕ),
определенная правилом !•»—^ e~2nit^. Очевидно, f ограничена и
скалярно измерима, ибо каждый элемент сопряженного про-
пространства Е' порождается некоторой мерой Я на R, обладающей
компактным носителем, причем
преобразованию Фурье меры X. Из этой формулы вытекает сла-
слабая непрерывность функции f. Однако очевидно, что функция /
не является скалярно интегрируемой.
8.14. Интегрирование векторных функций ?6?
Исследуем возможности, которые появляются, если простран-
пространство Е наделить одной из следующих трех топологий: (а) ослаб-
ослабленной топологией о=^о(Е, £'), (Ь) слабой топологией а' =
о(Е,Ж), (с) слабой топологией о" = о(Е, 3>). Через Ж и SD
здесь обозначены соответственно пространство непрерывных и
пространство бесконечно дифференцируемых комплексных функ-
функций на R с компактными носителями, причем функция g из ка-
каждого пространства отождествляется с мерой g-\i. Как и в
общем случае, скалярная измеримость и интегрируемость озна-
означают в топологии а то же, что и в исходной топологии. Сопря-
Сопряженное к Е относительно топологии о' (соотв. а") совпадает с
Ж (соотв. 2D), поэтому функция f склярно измерима (и даже
слабо непрерывна) в каждом случае. Она не является скалярио
интегрируемой ни относительно а, ни относительно а', поскольку
существует функция §gJ, преобразование Фурье которой
не интегрируемо относительно \х. С другой стороны, функция g"
jn-интегрируема для всякой функции ^е2), так что / скалярно
интегрируема относительно о".
Приведем теперь два простых результата, дающих достаточ-
достаточные условия принадлежности интеграла пространству Е.
8.14.2. Лемма. Пусть функция f скалярно существенно инте-
интегрируема, М — подмножество в Г, несущее меру jut (т. е. такое,
что множество Т\М локально пренебрежимо), То — измеримое
подмножество в М, такое, что / = 0 локально почти всюду на
М\Т0, и пусть т = \хх(Т0) < + оо. Тогда z= f d\x принадлежит
множеству m-Г, где Г — слабо замкнутая выпуклая оболочка в
Е'* множества f{T0).
Доказательство. В силу следствия 2.2.4A) достаточно
показать, что неравенство
<z, *')<m.sup{</(/), х'): t<=T0}
имеет место при каждом хг е £'. Из определения z вытекает, что
(z, х') = J (f (t), x') ф (t) =]%M(f (t), x') 4i (/).
Существенная интегрируемость функции fx> влечет существова-
существование такого а-конечного измеримого множества S с То (S может
зависеть от л:'), что /v^U локально почти всюду на множестве
768 Г л 8. Теория двойственности
M\S. Таким образом,
(г, *'J
</ф(*)-sup
причем первый множитель в правой части не превосходит
\Хх(Т0) (так как 5 а-компактно и содержится в Го; см. п. 4.7.6),
а второй множитель не превосходит sup {(f(t), х'): t^T0}. Лем-
Лемма полностью доказана. |
8.14.3. Предложение. Допустим, что для пространства Е вы-
выполняется следующее условие:
(*) замкнутая выпуклая оболочка всякого компактного
(соотв. слабо компактного) множества в Е полна в то-
топологии т(£, £').
Тогда если в Т существует такое компактное множество К,
что сужение f\K непрерывно (соотв. слабо непрерывности / = 0
локально почти всюду на Т\К, то элемент f d\i принадлежит
пространству Е.
JXo к аз а тел ьств о. Согласно предыдущей лемме, элемент
2= J fd\i принадлежит множеству тТ, где т = ц(/С) (\х(К) обя-
обязательно конечно) и Г—-слабо замкнутая выпуклая оболочка в
Е'* множества / (/С) U {0}. Поэтому достаточно показать, что
ГаЕ.
По теореме Крейна 8.13.1 замкнутая выпуклая оболочка в Е
множества /(/С) 0{0} слабо компактна, ибо из свойств / выте-
вытекает, что множество f(K), а вместе с ним и множество f(K) U {0}
компактно (соотв. слабо компактно). Таким образом, его обо-
оболочка в Е слабо замкнута в Е'* и потому совпадает с Г, чго и
требовалось доказать. |
Замечания. A) Наш результат подсказан одним резуль-
результатом Бур баки [8, гл. III, стр. 96] и является простым его
обобщением. Читатель может заметить, что условие (*) обяза-
обязательно выполняется (в любой из форм), если пространство Е
квазиполно, так как замкнутая выпуклая оболочка слабо ком-
компактного множества ограничена и замкнута и потому полна в
исходной топологии в£и тем^олее в топологии т(£, Е'). (Дело
в том, что последняя топология сильнее исходной и, кроме того,
имеет базу окрестностей нуля, образованную множествами,
замкнутыми в исходной топологии; см. предложение 9.1.5.)
8.14. Интегрирование векторных функций 769
B) Иногда удобнее иметь дело непосредственно с комплекс-
комплексным локально выпуклым пространством Е (т. е. не прибегая к
сужению поля скаляров). В этом случае в формулировках ана-
аналогов леммы 8.14.2 и предложения 8.14.3 следует вместо замкну-
замкнутых выпуклых оболочек говорить о замкнутых выпуклых уравно-
уравновешенных оболочках. Однако если функция / удовлетворяет
условиям предложения 8.14.3, то нет необходимости изменять
условие (*). Действительно, замкнутая выпуклая уравновешен-
уравновешенная оболочка множества f(K)l){0} является не чем иным, как
замкнутой выпуклой оболочкой уравновешенной оболочки В мно-
множества f(/C)U{0}, и множество В компактно, если /(/С) U{0} ком-
компактно (слабо или в ином смысле). (Множество В есть образ
пространства Sx (f(K) U {0}) при непрерывном отображении
(а, х)|—>ах, где S — множество скаляров а, удовлетворяющих
неравенству |а| ^ 1.) Читатель может заметить, что в видоиз-
видоизмененном таким образом предложении 8.14.3 фактически опери-
оперируют уже не с положительными мерами (i, а с произвольными
комплексными мерами Радона на Т.
8.14.4. Рассмотрим теперь действие на интегралы непрерыв-
непрерывных линейных отображений и и непрерывных полунорм. В пер-
первом случае пусть F — другое отделимое локально выпуклое про-
пространство и и— непрерывное линейное отображение простран-
пространства Е в F. Пусть ur\ F'-*Ef— сопряженное к и отображение.
Введем разновидность второго сопряженного ur*\ E'*->Ff*,
определяемую соотношением
(и* (г), />-<*, и'ЬП), (8.14.3)
где у'<^ F' и ze£'*. Заметим, что и'*\Е" = и" и и'*\Е = и.
8.14.5. Предложение; Пусть Е и F — отделимые локально вы-
выпуклые пространства и и— непрерывное линейное отображение
Е в F. Если функция f — отображающая Т в Е — скалярно су-
существенно интегрируема, то какой же будет функция uof (ото-
(отображающая Т в F). При этом имеет место равенство
(8.14.4)
Доказательство. Пусть g = uof. Тогда для у' из F'
функция
существенно интегрируема, так как таким свойством обла-
обладает /, а х' = и'(у') е£'. Функция g, таким образом, скалярно
770 Гл. 8. Теория двойственности
существенно интегрируема. Кроме того, из (8.14.3) следует, что
= (](uof)dp, у'),
откуда вытекает равенство (8.14.4). | ^
Замечание. Если откуда-нибудь известно, что J
(соотв. е£), то в формуле (8.14.4) отображение и'* можно за-
заменить на и" (соотв. на и). В следующей ниже теореме 8.14.15
приводится уточнение предложения 8.14.5. Эта теорема спра-
справедлива, если Е в F полны, а и лишь замкнуто.
Имея дело с полунормами, удобно пользоваться продолже-
продолжением всякой полунормы р на Е до функции на Е'* (принимаю-
(принимающей, возможно, и значения +оо), определяемой формулой
//*B) = sup{|<z, x'H я'еП (8.14.5)
где W — поляра в Ег множества {х ^ Е: р(х)^С\}. Если прене-
пренебречь тем, что р'* может принимать в некоторых точках из Е'*
значение +оо, то эта функция может быть названа полунормой
на Е'*. Во всяком случае, из следствия 2.1.4 B) вытекает равен-
равенство рп\Е=*р, если р — непрерывная полунорма на Е.
8.14.6. Предложение. Пусть f — скалярно существенно инте-
интегрируемая функция. Тогда для всякой непрерывной полунормы
р на Е имеет место неравенство
(ро/)ф. (8.14.6)
Доказательство. Это почти очевидно: если x'^W, то
\(Jfdix, х')| = и
8.14. Интегрирование векторных функций 771
откуда и следует (8.14.6), если взять верхнюю грань по всем
Замечание. Если известно, что /фбЯ, то в неравен-
неравенстве (8.14.6) можно заменить р'* на р.
Хотя результаты, содержащиеся в предложениях 8.14.3—
8.14.6, элементарны, ими уже можно воспользоваться, чтобы
проиллюстрировать значение интегрирования векторных функ-
функций. Это будет сделано в следующем пункте. Позднее мы при-
приведем другие примеры, демонстрирующие полезность более тон-
тонких общих теорем.
8.14.7. Приложение к исследованию голоморфных векторных
функций. Использование голоморфных векторных функций яв-
является в настоящее время общепринятым приемом в различных
разделах функционального анализа. Читатель сможет в этом
убедиться, если не поленится просмотреть книгу Хилле [1]или
Данфорда и Шварца [1] (мы могли бы упомянуть и другие
книги). Как это можно было предвидеть на основании теории
скалярных голоморфных функций, в исследовании голоморфных
векторных функций огромную роль играют интегральная форму-
формула типа Коши и ее следствия. Оказывается, что в случае вектор-
векторных функций из наличия такой интегральной формулы следует,
что слабая голоморфность влечет сильную, чего разумно было и
ожидать. Мы докажем это, не прибегая к результатам, выходя-
выходящим за рамки слабой или скалярной теории.
Пусть Е — отделимое локально выпуклое пространство, Q —
область комплексной плоскости, f — отображение Я в Е. Беря
определение голоморфности в самом слабом смысле, мы будем
называть функцию / голоморфной на Q, если функция х' of голо-
голоморфна на Q (в обычном для скалярных функций смысле) при
каждом х' е Е'. Для того чтобы введенное понятие представляло
интерес, Е должно быть комплексным векторным пространством:
если Е — вещественное пространство, то хг о f — вещественная
функция; будучи голоморфной, функция x'of будет постоянна
на й, следовательно, и f будет постоянной.
Мы покажем, каким образом могут быть получены следую-
следующие довольно неожиданные результаты, в предположении, что Е
удовлетворяет условию (#) предложения 8.14.13.
A) Голоморфная на Q функция f имеет производные всех
порядков в каждой точке области Q, причем эти производные
принадлежат Е и сами голоморфны на Q.
B) Вышеуказанные производные представимы интегральной
формулой, в точности аналогичной известной формуле для б
ных комплексных функций.
772 Гл. 8. Теория двойственности
C) Имеет место разложение Тэйлора, которое сходится в Е
в некоторой окрестности каждой точки области Q.
Как только эти факты будут установлены, многие другие
свойства голоморфных функций, известные для комплексных
функций, можно будет получить с помощью стандартных
рассуждений. Доказательства могут быть предоставлены чита-
читателю; см. упр. 8.15—8.17.
Чтобы доказать указанные выше утверждения, прежде всего
покажем, что всякая голоморфная функция непрерывна (причем
это имеет место для любого локально выпуклого простран-
пространства Е). Действительно, так как скалярная функция x'of голо-
голоморфна, то существует такое число М = М(х')9 что
\x'of(t)-x'of(t0)\^M-\t-t0\
для to^Q и t, достаточно близких к t0. Таким образом, семей-
семейство элементов из Е
(t-to)-l{f(t)-f(tQ)},
получаемое, когда t пробегает достаточно малую проколотую
окрестность точки t0, слабо ограничено. Но тогда (теор. 8.2.2)
это семейство ограничено в Е. В частности, lim f(t) =f(t0) в Е
при t ->- to.
Убедившись в непрерывности функции /, мы можем ввести
интеграл Коши. Пусть to e Q и с — кусочно непрерывно диффе-
дифференцируемая замкнутая кривая в й\{/о}, индекс (число враще-
вращений) которой относительно точки t0 равен +1. Рассмотрим ин-
интеграл
Из непрерывности f и условия (*), наложенного на £, следует в
силу предложения 8.14.3, что q&E.
Сопоставляя определение интеграла (см. формулу (8.14.1)) с
интегральной формулой Коши для скалярных функций, полу-
получаем непосредственно, что <7=f(^o). Таким образом, интеграль-
интегральная формула Коши для функции f получена.
Рассмотрим теперь разностное отношение
Представим его в виде
8.14. Интегрирование векторных функций 773
где, например, с — положительно ориентированная окружность с
центром в точке t0 и такого малого радиуса г > О, что соответ-
соответствующий замкнутый круг лежит в £2, причем точка гФг^ лежит
в открытом круге. Используя предложения 8.14.3 и 8.14.6, при-
приходим к заключению, что интеграл
является элементом пространства Е и, кроме того, пределом Ц\
при t-*to. Следовательно, производная Г (/о) существует как
элемент пространства Е и допускает представление в виде
Здесь, так же как и в самой интегральной формуле Коши, кон-
контур с может быть заменен любой кусочно непрерывно дифферен-
дифференцируемой замкнутой кривой Q\{70}, индекс которой относи-
относительно точки t0 равен +1.
Фиксируя в последней формуле контур с и допуская локаль*
ное изменение точки t0, заключаем, что сама производная голо-
голоморфна. Действительно, скалярная функция
голоморфна при каждом х' e Е\
С помощью простой индукции по п = 0, 1,2,... (как и в ска-
скалярном случае) доказывается, что все производные функции /
существуют как элементы пространства Е и также голоморфны
на Q. Утверждения A) и B), таким образом, доказаны.
Из интегральной формулы
dt
f (o)~"^TJ (tto)
получаемой индукцией по п, можно вывести неравенства Коши
где М — верхняя грань значенийp(f(t)) на окружности \t — t0\ =
= /-; при этом предполагается, что замкнутый круг радиусом г с
центром в ^о лежит в Я. (Здесь р — любая непрерывная полу-
полунорма на Е\ неравенство получается, если еще раз воспользо-
воспользоваться предложением 8.14.6.)
774 Гл. 8. Теория двойственности
Из этих неравенств вытекает, что частичные суммы ряда
Тэйлора
я-0
образуют последовательность Коши. С другой стороны, слабая
сходимость этого ряда следует из классической скалярной тео-
теории. Сопоставление этих фактов приводит к утверждению C).
Намеченная нами программа выполнена.
Замечания. A) Дальнейшее развитие и систематическое
исследование пространств голоморфных векторных функций чи-
читатель может найти у Гротендика [5, 6].
B) Предыдущая техника до некоторой степени применима
и в случае дифференцируемых векторных функций веществен-
вещественного переменного (см. Л. Ш в а р ц [17], Эв а р д с [15] и упр. 8.14)в
Этот вопрос играет важную роль в теории векторных распреде-
распределений (Л. Шварц [4—6]; см. также И и но [1]).
8.14.8. Теперь пора получить некоторые аналоги предложе-
предложения 8.14.3, в которых ограничения на / слабее, чем в предполо-
предположении 8.14.3, но зато ограничения на Е сильнее. Мы будем
избегать использования измеримости и интегрируемости, с кото-
которыми в общем случае иметь дело довольно трудно.
Пусть f — скалярно существенно интегрируемая функция и
z = J / ф — элемент из Е'*. Утверждение, что z принадлежит вто-
второму сопряженному Е", означает просто, что линейная форма
на Е\ определяемая элементом г, а именно форма
является на Е' сильно непрерывной. В этом случае мы будем
называть \ fd\i интегралом Гельфанда (см. Гельфанд [2]).
Если та же линейная форма слабо непрерывна на Е', то эле-
элемент z будет принадлежать самому пространству Е. Будем тогда
говорить, что fd\x есть интеграл Петтиса (Петтис [2]).
Приведем два сравнительно простых результата, относя-
относящихся к интегралам Гельфанда и Петтиса.
8.14.9. Предложение. Пусть f—- такая скалярно существенно
интегрируемая функция^ что для каждого компактного чноже-
Д/4. Интегрирование векторных функций 775
ства КаТ замкнутая выпуклая оболочка в Е множества f(K)
слабо компактна. Тогда [fd\i^E"t т. е. (f d\i является интегра-
интегралом Гельфанда:
Доказательство. Из леммы 8.14.2 следует, что элемент
принадлежит множеству Г, т. е. слабо замкнутой выпуклой обо-
оболочке в Ег множества f(K). Однако замкнутая выпуклая обо-
оболочка в Е множества f(K) (назовем ее Го) является также и
слабо замкнутой выпуклой оболочкой Е множества /(/С), по-
поэтому она слабо компактна. Множество Го, таким образом, слабо
замкнуто в Е'*. Так как множество Го и слабо плотно в Г, то
Го-Г, т. е. zKt=E.
Функция / скалярно существенно интегрируема, поэтому эле-
элемент z= \ fd\i является слабым пределом в Е'* сети (zK)y где
компактные множества К частично упорядочены по включению.
В то же время для каждого х' е Е' имеют место неравенства
*) К ]
откуда следует, что элементы zK содержатся в некотором огра-
ограниченном множестве В из Е. Поэтому для завершения доказа-
доказательства достаточно вспомнить, что слабое замыкание в Ef* вся-
всякого ограниченного множества из Е содержится в £". I
8.14.10. Следствие. Если пространство Е полу рефлексивно и
f — скалярно существенно интегрируемая и локально ограничен-
ограниченная функция, то f d\x<=E.
Доказательство. В этих условиях Е" = Е (как множе-
множества) и, кроме того, каждое ограниченное множество из Е слабо
относительно компактно в Е. |
Если Е — нормированное пространство, то имеют место более
сильные результаты.
8.14.11. Предложение, (а) Если пространство Е нормируемо
и функция f скалярно существенно интегрируема, то \ f d\x e E"9
т. е. f d\x является интегралом Гельфанда.
776 Гл. 8. Теория двойственности
(Ь) Если Е— рефлексивное банахово пространство и функ-
функция f скалярно существенно интегрируема, то \ f d\i^E9 т. е.
\ f d\i является интегралом Петтиса.
Доказательство. Очевидно, что (Ь) следует из (а).
Чтобы установить (а), достаточно показать, что полунорма
сильно непрерывна на Е'. Так как Ег банахово и потому бочеч-
но, то необходимо только проверить полунепрерывность снизу
полунормы q. Другими словами, мы свели все к доказательству
того, что множество в Е\ определенное неравенством q{x') ^ 1,
сильно замкнуто. Но это следует непосредственно из леммы
Фату 4.5.4. |
Замечания. A) Доказательство утверждения (а) сохра-
сохраняет силу, если сильное сопряженное Ег бочечно и метризуемо.
Однако если Е — пространство Фреше, то сильное сопряженное
Ег метризуемо тогда и только тогда, когда Е — банахово про-
пространство, поэтому в этом направлении возможность обобщений
ограничена.
B) Часть (Ь) безусловно применима, если Е — гильбертово
пространство. Идея интегрирования функций со значениями в
гильбертовом пространстве уже применялась в п. 1.12.9 таким
же точно образом, как и здесь,
C) Несложно привести примеры, в которых Е — банахово
пространство, / — скалярно существенно интегрируемая функция,
элемент \ f d\i принадлежит £", однако не принадлежит Е. Так
(Б у р б а к и [9, гл. VI, стр. 80, упр. 7]), пусть Т = [0, 1], ji — суже-
сужение на Т меры Лебега, Е — пространство Со сходящихся к
нулю последовательностей, f — функция, определенная равен-
равенством
где /n=@,n-1). Здесь £'=/'. Легко видеть, что для х' из I1
функция
д n
функция
принадлежит пространству 9?Х(Т, \х). Таким образом, / скалярно
интегрируема. Далее z = \ fd\i — элемент из Е" = 1°°, определяе-
определяемый равенством z(n) = 1 для всех п9 — очевидно, не принадлежит
пространству E = Cq.
8.14. Интегрирование векторных функций 777
8.14.12. Замечания и примеры. Следствие 8.14.10 может быть
применено к случаю, когда f отображает Т в пространство F\
сопряженное к некоторому локально выпуклому пространству F;
к этому вопросу мы позднее вернемся (теор. 8.16.1). Если пред-
предположить, что пространство F бочечно и F' наделено своей сла-
слабой топологией o(F',F), то пространство Fr будет полурефлек-
полурефлексивно. Действительно, сопряженным к F' будет F, и ассоцииро-
ассоциированная сильная топология в F (т. е. топология равномерной
сходимости на слабо ограниченных подмножествах из F') будет
совпадать с исходной топологией в г, ибо из бочечности F сле-
следует равностепенная непрерывность слабо ограниченных под-
подмножеств из F'.
Из указанного следствия вытекает, что fd\i&F\ если про-
пространство F бочечно и функция /: Т -> F' скалярно существенно
интегрируема (в том смысле, что функция (у, f) существенно ин-
интегрируема для каждого элемента у е F) и локально слабо огра-
ограниченна (т. е. множество f(K) слабо ограниченно в F' для ка-
каждого компактного подмножества К из Г).
Пример 1. Произведение мер. Полученный только что резуль*
тат более чем достаточен для обоснования нового определения
произведения двух мер (ср. § 4.17).
Пусть S и Т — два отделимых локально компактных про-
пространства, Р — их произведение, а и р— меры соответственно на
S и Т. Как известно, пространство Р=Ж{Р) бочечно (п. 6.3.3).
Его сопряженное F' совпадает с пространством М(Р) всех мер
Радона на Р. Эти утверждения, естественно, остаются справед-
справедливыми, если повсюду заменить Р на S или на Г.
Пусть PgM(T) hvsgS; обозначим через SP элемент про-
пространства М(Р), определенный соотношением
Рассмотрим функцию f, отображающую S в M(P)=F' и опре-
определяемую равенством /(s)=sp. Элемент (g, ep), очевидно, при-
принадлежит пространству Ж(Р), поэтому функция / слабо непре-
непрерывна и ограничена. Допустим, что а—положительная мера
(играющая роль \х в общей теории); ясно, что функция / ска-
скалярно интегрируема относительно а. Из наших общих результа-
результатов следует тогда, что J /rfaGF'= М(Я), Из определения инте-
интеграла непосредственно вытекает, что \ fda есть не что иное, как
произведение мер а®р.
778 Гл. 8. Теория двойственности
Условие положительности меры а, естественно, совершенно
излишне, и от него легко освободиться.
Пример 2. Свертка мер. Аналогичным образом можно рас-
рассмотреть и свертку двух мер (§ 4.19). Пусть здесь S = T — отде-
отделимая локально компактная группа. Для заданной меры (i
определим левый сдвиг Lt$ с помощью равенства
<& W= J gd(L$)= J g{rlt
для g^X(T) и рассмотрим функцию f(t) = Lt-i$y отображаю-
отображающую Т в F'=M(T). Снова (полагая временно меру а положи-
положительной) мы видим, что функция / скалярно непрерывна и что
для скалярной существенной интегрируемости (эквивалентной
здесь в силу скалярной непрерывности скалярной интегрируе-
интегрируемости) необходимо и достаточно, чтобы для каждой функции
Ji£(T) имело место неравенство
f da @
П
<+ оо.
Если мера р также положительна, то это есть в точности
условие, использованное в § 4.19 для доказательства существо-
существования свертки а* р. При выполнении этого условия свертка
а#р есть не что иное, как
Если, с другой стороны, мера р не положительна, то весьма
правдоподобно, что интеграл f da может существовать (т. е.
функция f может быть скалярно интегрируемой), если даже
свертка а*р не определена (а так будет тогда и только тогда,
когда не определена свертка а*|р|). Во всяком таком случае
мы приходим к обобщению определения свертки.
Возвращаясь к общей теории, рассмотрим теперь несколько
результатов для Е и f частного вида, причем ограничения на /
выражаются с помощью условий, близких к' интегрируемости.
8.14.13. Предложение. Допустим, что пространство Е квази-
квазиполно и функция f удовлетворяет следующим двум условиям:
A) f скалярно локально интегрируема и элемент
\ fd\i= J hKd\i
к
принадлежит Е для каждого компактного множества К а Г;
У*
B) I (р о f) d\i < + оо для каждой полунормы ру принадле-
8.14. Интегрирование векторных функций 779
жащей семейству полунорм, определяющих, топологию про-
пространства £.
Тогда f скалярно существенно интегрируема и I gfdp^E
для всякой функции g е 3?°°. Кроме того, элемент gf d\i яв-
является пределом в Е сети \ gfd\i (упорядочение по включению).
к
Доказательство распадается на две части.
(a) Если функция / удовлетворяет условиям A) и B), то она
скалярно существенно интегрируема и элемент J /ф является
пределом в Е сети J /ф.
к
(b) Если / удовлетворяет условиям A) и B), то \ gfdp^E
к
для каждого компактного множества К и каждой функции
0 ё= Я?00
Как только это будет доказано, для завершения доказатель-
доказательства останется лишь воспользоваться утверждением (а), заме-
заменив в нем / на g]c
Для доказательства утверждения (а) введем zK= \ f d\x.
к
В силу предложения 8.14.6 и следующего за ним замечания для
любых двух компактных множеств К и К\ где KczK\ имеют
место следующие неравенства:
(р°Л-х*Ф<J (р
Из первого ряда неравенств следует, что сеть (zK) ограничена,
а из второго — что она сеть Коши. Так как пространство Е
квазиполно, то в £ существует предел z=\imzK. Условие B)
влечет за собой скалярную существенную интегрируемость функ-
функции f, так что для всякого элемента xr e Е/ выполнены соотно-
соотношения
B, *') = lim (гК9 х') = lim J (f9 х') ф = J (/, хг) ф,
780 Гл. 8. Теория двойственности
из которых вытекает, что z= J f ф. Утверждение (а), таким
образом, доказано.
Что касается утверждения (Ь), то функция gf скалярно су-
существенно интегрируема для всякой функции g e «2^°°, поэтому-
интеграл I gf d\i вполне определен. Докажем принадлежность
к
этого интеграла к Е. Допустим, что функция g обращается в
нуль на множестве Т\К. Обозначим через G множество всех тех
функций g^2°°, которые обращаются в нуль на Т\К и для
которых gfd\x= \ gfd\k^E. По условию A) множество G со-
к
держит все характеристические функции компактных множеств
Не К.
Если М — любое измеримое множество из /С, то М есть пре-
предел почти всюду возрастающей последовательности компакт-
компактных множеств HnczM. Как мы знаем ап = \fd\i^E. Если
m < /г, то в силу предложения 8.14.6 имеем
Р К - ап) < f (Ч - ХЯт) (Р ° /) Ф < J * {%м ~ ^ят) (Р ° /) Ф-
Последнее выражение стремится к нулю при т->оо (в силу
монотонной сходимости). Тогда в Е существует предел а = \\таГ1,
который (можно повторить рассуждения, использованные при
доказательстве утверждения (а)) должен быть не чем иным,
как j jd\i. Таким образом, множество G содержит характерн-
характерном
стические функции всех измеримых подмножеств из К; следова-
следовательно, G содержит также векторное подпространство Go, поро-
порожденное такими функциями.. _
Если теперь функция g принадлежит 2?°° и обращается в
нуль на множестве Т\К, то оно является равномерным преде-
пределом последовательности (gn) элементов из Go. Полагая Ьп =
= \ gnfd\i, легко видеть, что {Ьп) есть последовательность
Коши, которая сходится в Е. Ее предел совпадает с | gfd[xy что
доказывается с помощью рассуждений, аналогичных использо-
использовавшимся выше. Таким образом, g e G, и утверждение (Ь) до-
доказано. |
Замечания. A) Если заданное пространство Е полуре-
полурефлексивно и функция / скалярно существенно интегрируема и
8.14. Интегрирование векторных функций 781
удовлетворяет условию A) предложения 8.14.13, то можно так-
также показать, что J gfd\x e Е для каждой функции g e 2?°°. Тот
же вывод остается справедливым, если вместо рефлексивности
пространства Е предположить его слабую секвенциальную пол-
полноту и допустить, что обращающаяся в нуль вне а-конечного
множества функция / скалярно существенно интегрируема и удо-
удовлетворяет условию A). Действительно, последовательность
(ап), появляющаяся в части (Ь) предыдущего доказательства,
есть слабая последовательность Коши, поэтому если простран-
пространство Е слабо секвенциально полно, что всегда имеет место для
полурефлексивного пространства Еу то можно заключить, что
J /фе£для всякого относительно компактного измеримого
м
множества М.
Равным образом, рассматривая введенную выше последова-
последовательность (bn)t мы видим, что I gfd\i^E аля любой функции
g^3?°°, обращающейся в куль вне а-конечного множества.
Здесь опять нам нужна только слабая секвенциальная полнота.
Поэтому если функция f обращается в нуль вне а-конечного
множества, то достаточно этого последнего условия (вместо
полурефлексивности).
Пусть пространство Т не а-конечно. Рассмотрим сеть
^ = J gf Ф
к
элементов из Е. Так как функция / скалярно существенно инте-
интегрируема и jg «2?о°, то есть (ск) слабо ограничена и потому
ограничена. Если Е полурефлексивно, то его сопряженное Е'
бочечно в своей сильной топологии (теор. 8.4.3), так что сеть
(ск) попадает в равностепенно непрерывное множество из со-
сопряженного пространства Е/ и, следовательно, обладает слабой
предельной точкой 2, которая сильно непрерывна на Е'. Полу-
Полурефлексивность пространства Е влечет принадлежность z к Е.
И во всяком случае z должен равняться интегралу gfd\i*
B) Следуя Бур баки [9, гл. VI, стр. 84, упр. 19], функцию
f:T->E будем называть скалярно вполне интегрируемой, если
она скалярно существенно интегрируема и J gfd\x e E для каж-
каждой функции g e «2700. Предложение 8.14.13 и замечание A)
дают, таким образом, достаточные условия скалярной вполне
интегрируемости функции /. Позднее мы вернемся к этому
782 Г л 8. Теория двойственности
вопросу (конец § 9.3) и увидим, что скалярно вполне интегри-
интегрируемые функции обладают рядом замечательных свойств.
Следующий результат — один из основных в теории инте-
интегрируемых функций, в особенности когда пространство Е подчи-
подчинено условию метризуемости (§ 8.15).
8.14.14. Теорема. Пусть Е — полное пространство, и пусть
функция f удовлетворяет следующим условиям:
A) qhu локально почти сепарабельнозначна, т. е. каждое
компактное множество КаТ содержит такое пренебрежимое
множество N, что множество f(K\N) образует сепарабельное
подпространство в Е\
B) она скалярно измерима-,
C) J *(pof)d\\ < +oo для каждой непрерывной полунормы
р из некоторого семейства полунорм, определяющих тополо-
топологию в Е.
Тогда z=
Доказательство. Согласно последнему предложению,
достаточно показать, что f d\x^ E для каждого компактного
множества /С Ввиду условия A), не нарушая общности, можно
считать пространство Т компактным и множество f(T) сепара-
бельным. Более того, заменяя повсюду Е замкнутым векторным
подпространством, порожденным множеством /(Г), можно счи-
считать, что пространство Е само сепарабельно и полно.
Очевидно, из условий B) и C) следует, что функция / ска-
скалярно существенно цнтегрируема. _
Для доказательства того, что 2 = fd\i^E, достаточно
(теорема 8.5.1) показать, что для всякого равностепенно непре-
непрерывного множества Q из Е/ сужение z\Q слабо непрерывно. Так
как пространство Е сепарабельно, то слабая топология про-
пространства Е' индуцирует в Q метризуемую топологию. Таким
образом, факт, который нужно доказать, заключается в следую-
следующем: если х'п (я= 1, 2, ...) и х/ — точки из Q и х'пслабо сходит-
сходится к х\ то (-г, x/n^-^(zy x'). Из слабой сходимости х'п к х' сле-
следует, что функции (/, х'п} сходятся к функции (f, л/) поточечно
на Т. Кроме того, так как множество Q равностепенно непре-
непрерывно, то существует такая непрерывная полунорма р на Е, что
Q лежит в поляре множества, определяемого соотношением
8.14. Интегрирование векторных функций 783
р(х)^1. Тогда |(/, ^)|^P°/> и из условия C) и теоремы Ле-
Лебега 4.8.2 о сходимости следует, что
<*• О = J </. К) 4* -* J </. *') Ф = <*. *')>
что и требовалось доказать. |
8.14.14'. Следствие. Если Т локально• сепарабельно (напри-
(например, локально метризуемо), f существенно интегрируема и Е
полно, то f скалярно вполне интегрируема.
Доказательство. Так как вместе с f и произведение gf
при geS700 удовлетворяет всем нашим условиям, то достаточно
показать, что / d\x^.E. Существенная интегрируемость функции
f влечет за собой выполнение условий B) и C) теоремы 8.14.14,
поэтому остается проверить, что /—.локально почти сепарабель-
нозначная функция.
Для этого воспользуемся измеримостью f, согласно которой
для всякого компактного множества Kcz T существует такая по-
последовательность (Нг) компактных множеств, содержащихся в
/(, что \\m\i(K \ Нг) = 0 и сужение f\Hr непрерывно для ка-
г
ждого г.
Так как пространство Т локально сепарабельно, то множество
Нт сепарабельно, и таким же будет его образ f(Hr). Полагая
#= [JHri видим, что множество N = K\H пренебрежимо и мно-
г
жество
сепарабельно. Таким образом, условие A) теоремы 8.14.14 вы-
выполняется. |
В качестве приложения теоремы 8.14.14 докажем обещанное
уточнение предложения 8.14.5 (ср. Данфорди Шварц [1,
стр. 170, теор. 20]).
8.14.15. Теорема. Пусть Е и F — полные отделимые локально
выпуклые пространства, и — замкнутое линейное отображение
Е в F и f — отображение Т в Е со значениями в dom и. Допустим
также, что функции f и g = uof локально почти сепарабельно-
значны и скалярно измеримы и
[ (p°f)d\x<+ оо (соотв. J (q о g) d\i < + оо\
784 Гл. 8. Теория двойственности
для каждой непрерывной полунормы р (соотв. q) из семейства
полунорм, определяющих топологию пространства Е (соотв. F).
Тогда /фе domи и
и(] fd
Доказательство. График G отображения и замкнут в
F и, следовательно, полон. Рассмотрим отображение h про-
пространства Т в Gj определенное равенством
Так как обе функиии f я g локально почти сепарабельнозначны
и скалярно измеримы, то это же верно и для функции А. Дей-
Действительно, нужно только заметить, что (по теореме Хана — Ба-
Банаха) каждая непрерывная линейная форма на G имеет вид
(ху и(х))*->(х, хг) + (и(х), у') (хе dom и)
для некоторой (не обязательно единственной) точки (л/, у')^
^E'xF'. Кроме того, каждой непрерывной полунорме г на (?
соответствует такая пара полунорм (/?,?), что
для х g dom м. Последнее следует из того, что полунормы вида
(х, у)ь-^р(х)+q(y) определяют топологию произведения EF
Отсюда вытекает что
]*
оо
для всякой непрерывной полунормы г на G.
В силу теоремы 8.14.14 Г Афеб. Это означает, что при не-
некотором лее dom и имеет место равенство hd\x = (xt u(x)). По
определению интеграла (п. 8.14.1)
j(h(t), (*', y'))dii(t) = (x, х*) + (и(х), у')
для каждого элемента (xr,y')^E'xF'. Но
<А@, (*', y')) = (f{t), x') + (g(t), у'),
поэтому
(J/ф, x') + (J gdp, /)-(х, х') + (и(х), у')
8.15. Случай, когда пространство Е метризуемо 785
для всех х' е Е' и у' е Z7'. Следовательно, л: должен совпасть с
I fd\\, а и(х) — с \ gd\i. Таким образом, | /ф^с!отм и
и[\ /ф) = I gd\i, что и требовалось доказать. |
Замечания. Если Е и F — пространства Фреше, то наши
предположения о функциях / и g = uof сводятся просто к их ин-
интегрируемости и к соотношению f(T) а dom и. В этой форме
теорема приведена у Данфорда и Шварца [1, стр. 170].
8.15. Случай, когда пространство Е метризуемо
Существенно, что измеримость функции / в теореме 8.14.14
•не предполагается. Для~ полноты картины выясним, хотя бы до
некоторой степени, связь между скалярной измеримостью и из-
измеримостью для случая, когда пространство Е метризуемо. Ни
в каком другом общем случае такой простой связи не суще-
существует.
Начнем с замечания, что теорема Егорова 4.8.3 справедлива
и для функций со значениями в метризуемом пространстве Е.
Действительно, рассмотрим на пространстве Е метрику d, опре-
определяющую его топологию. Пусть А — интегрируемое множество
и измеримые функции fn (я=1, 2, ...) и | таковы, что fn-*f
почти всюду на А. Рассмотрим числовые функции gn = d(fny f).
Они измеримы, и gn-+0 почти всюду на А. По теореме 4.8.3
для заданного е>0 найдется такое измеримое множество В а А
(которое можно считать компактным), что |ы(Л\6)<е и gn->0
равномерно на В. Тогда и сходимость fn-**f равномерна на В.
Таким образом, теорема Егорова для векторных функций до-
доказана.
Нам понадобятся две вспомогательные леммы.
Лемма 1. Допустим, что Е — локально выпуклое простран-
пространство, S — сепарабельное подпространство в Еу р — непрерывная
полунорма на Е, U — подмножество в Et определенное соотно-
соотношением р(х) ^ 1. Тогда существует такое счетное подмноже-
подмножество W поляры U0, что
p(x)=sup{\(x,
для каждого jcgS.
Доказательство. Очевидно, достаточно показать, что
p(x)<q(x)
для xeS, где q(x) —указанная верхняя грань. Пусть последо-
последовательность (ат) плотна в S. По теореме Хана — Банаха для
786 Гл. 8. Теория двойственности
каждого m имеет место равенство
p(am) = sup{\(amt *'): x'
Поэтому в U0 можно выбрать такую последовательность (x'mr^ ,
что
^K) = sup|<am, x'mn)\.
Положим W={x'mn: m, n=l, 2, ...j. Ясно, что
для всех т. По заданному е>0 k'x^S можно найти такое
что р(х — ат) <е и
Так как, очевидно, q ^С р, то q{am) ^q(x)+q(x — am)<q(x) -\-e>
Таким образом, р(х) ^С q(x) + 2е и, значит, р(х) ^С q(x) ввиду
произвольной малости г. Щ
Лемма 2. Пусть Е — локально выпуклое пространство, f —
скалярно измеримая и локально почти сепарабельнозначная
функция со значениями в Е. Тогда для любой непрерывной по-
полунормы р на Е функция р о f измерима.
Доказательство. Так как измеримость — свойство ло-
локальное, то с самого начала можно предполагать функцию /
сепарабельнозначной. По лемме 1 в Е' найдется такая последо-
последовательность (л^\ что
p(/(O) = sup|(f(O> х'п)\
П
для всех t. Утверждение леммы следует теперь из того, что по
условию каждая из функций (f, x'n) измерима. I
Будем для удобства называть простой функцией (со значе-
значениями в Е) всякую функцию f со значениями в Е, представимую
в виде конечной линейной комбинации функций %м#: t\—> %M(t)a,
где а — элемент из £ и М — измеримое подмножество в Т. Каж-
Каждая простая функция, очевидно, измерима. Заметим, что про-
простая функция f, обращающаяся в нуль вне измеримого множе-
множества S, представимая в виде конечной линейной комбинации
функций вида %м<2, где М — измеримое подмножество множе-
множества S.
Теперь мы можем установить первый из двух основных ре-
результатов, связывающих измеримость и скалярную измери-
измеримость,
8 15. Случай, когда пространство Е метризуемо 787
8.15.1. Теорема. Для того чтобы функция f со значениями в
локально выпуклом пространстве Е была измерима,
A) достаточно, чтобы для каждого компактного множества
К существовала последовательность (fn) простых функций,
почти всюду на К сходящаяся к f;
B) необходимо в случае метризуемости Е, чтобы для каж-
каждого компактного множества К существовала последователь-
последовательность (fn) простых функций, сходящихся к f почти равномерно
на К.
Доказательство. A) Если такая последовательность
существует, то по теореме Егорова сходимость fn-+f почти рав-
равномерна на /С, и измеримость / следует из определения
(п. 8.14.1 (Ь)).
B) Опять в силу теоремы Егорова достаточно построить по-
последовательность (/п) простых функций, почти всюду на К схо-
сходящуюся к f.
Из измеримости f вытекает существование такого пренебре-
жимого множества N а: К и таких компактных множеств
Кга К (г=1, 2, ...), что K\N=\jKr и сужение /|/Сгнепре-
г
рывно для каждого г. Пусть d—метрика, определяющая топо-
топологию пространства Е. Определим функции fn следующим об-
образом.
Для каждого i^n существует такое конечное разбиение
)</<<7 множества Кг на измеримые множества, на каж-
каждом из которых d-колебание функции / не превосходит */п. Вы-
Выберем произвольно в Atj точки tij и положим
(/(*//) при tf=Aih 1</<я, 1</<<&,
' I 0 в противном случае.
Каждая из функций fn проста, причем, очевидно, fn-+f на
K\N. 1
Приведем теперь основную теорему настоящего параграфа.
8.15.2. Теорема. Для измеримости функции f со значениями
в метризуемом локально выпуклом пространстве Е необходимо
и достаточно, чтобы выполнялись следующие два условия:
(a) функция f локально почти сепарабельнозначна;
(b) функция f скалярно измерима.
Доказательство. Если / измерима, то условие (Ь) вы-
выполняется тривиально.
Условие (а) следует из части B) предыдущей теоремы. Та-
Таким образом, оба условия необходимы.
Докажем обратное. Пусть выполнены условия (а) и (Ь). По-
Покажем, что функция / измерима. Пусть /С —произвольное
788 Гл. 8. Теория двойственности
компактное множество. Так как изменение значений функции f
на пренебрежимом подмножестве в К не влияет на ее измери-
измеримость, то можно считать множество f(K) сепарабельным. По-
Построим теперь последовательность (/п) простых функций, почти
всюду на К сходящуюся к /.
Пусть (хп)—последовательность, плотная в f(K)> и (pk) —
возрастающая последовательность полунорм, определяющих то-
топологию пространства Е. Из леммы 2 следует, что множества
измеримы. Для каждого k имеет место равенство К=У]Аъп. Рас-
п
смотрим множества
Bki^Aku Bkn=Akn\ \}{Bki\ j<n}
при п>1. При каждом k множества Bkn измеримы и образуют
разбиение множества /С Введем функции
и
Каждая из функций ghi проста. Легко проверить, что
Р* (f (О-А ('))<■£■
для всех t ^ К и всех k. Поэтому для всех h < k и всех /еД'
имеет место неравенство
Рл(/@-г*@)<}. (8.15.1)
Кроме того,
lijn gki = gk
поточечно на Л'. По теореме 8.15.1A) функция gh измерима.
Из неравенства (8.15.1) следует равномерная сходимость'gk-+f
на /С. Измеримость функции f вытекает теперь либо из теоремы
8.15.1A), либо, проще, из определения 8.14.1 (b). I
Замечания. Для банаховых пространств теорема 8.15.2
получена Петтисом [2] (см. также X и л л е [1, стр. 54], X и л л е
и Филлипс [1, стр. 86] и Данфорд и Шварц [1, стр. 166]).
Очень легко привести примеры, показывающие, что условие (а)
существенно, т. е. что существуют скалярно измеримые функ-
функции, которые не локально почти сепарабельнозначны.
8.15. Случай, когда пространство Ё метризуемо
Свойство измеримых функций, описываемое теоремой
8.15.1B), часто принимается за определение измеримости; так
сделано у Хилле [1, стр. 54], у Хил ле и Филлипса [1,
стр. 87] и уДанфорда и Шварца [1, стр. 120].
Теорема 8.15.2 по существу не отличается от предложения 12
на стр. 21 книги Бур баки [9, гл. VI]. Ниже нам понадобится
аналогичный результат для функций со значениями в слабом
сопряженном к сепарабельному пространству Фреше (Бур-
баки [там же, стр. 21, предл. 13]).
8.15.3. Предложение. Пусть Е — сепарабельное пространство
Фреше, f — отображение Т в слабое сопряженное E'w. Тогда если
f скаАярно измерима, то она слабо измерима. Кроме того, если
Е — сепарабельное нормированное пространство, то функция
11/1!: t^\\f(t)\\ измерима.
Доказательство. Пусть D — счетное множество, плотное
в £, и (Vn) —убывающая база окрестностей нуля в £, образо-
образованная выпуклыми уравновешенными открытыми множествами.
Множества Тп = f~~l(Vn) возрастают и покрывают Т. Каждое из
множеств
Sx = {t<=T: \{x,
измеримо. Так как множество D П Vn плотно в Vn9 то
откуда следует измеримость множеств Тп.
Выберем теперь произвольное компактное множество К в Т
и произвольное число е>0. Можно найти такой индекс п и та-
такое компактное множество К) а КГ\Тп, что fx[/C\(^СПТП)]<С
<е/4 и \х[(КС\Тп)\К\]<е/4. Так как каждая из функций (х, f)
измерима, то найдется такое компактное множество /С2с:/Сь
что jj (/Ci\/C2)<s/2 и сужение (х9 f)\K2 непрерывно для каж-
каждого JfGfl.
Множество / (/С2) ^ f(Tn) cz V°n равностепенно непрерывно,
поэтому топологии а(£</, Е) и о(Е\ D) индуцируют в /(/G) одну
и ту же топологию. Отсюда следует, что сужение /|/B слабо не-
непрерывно. Из того факта, что
вытекает слабая измеримость функции /.
Предполагая теперь Е нормированным и сепарабельным,
можно считать V\ открытым единичным шаром IUH<1 в Е. Вы-
Выбирая множество Kz так же, как и выше, получаем, что сужение
790 Гл. 8. Теория двойственности
(л:, /)|/<2 непрерывно для каждого элемента x^DCiVi. Из соот-
соотношения
ll/(/)ll=sup{|<*, f(t))\: xeDOVi),
которое имеет место для каждого ty следует, что функция ||/||
полунепрерывна снизу на /С2. Но так как это верно для всех ком-
компактных множеств /Gcz Кг для которых мера \л(К\К2) сколь
угодно мала, то функция ||/|| измерима. I
8.16. Функции со значениями в Е'.
Свойство секвенциально замкнутого графика
Рассмотрим кратко задачу интегрирования функции /, ото-
отображающей Т в пространство Е\ сопряженное к локально вы-
выпуклому пространству Е. Обозначим через Erw отделимое ло-
локально выпуклое пространство, получаемое наделением Е' сла-
слабой топологией о(Е\ Е). _
Мы намерены прежде всего показать, что fd\i е Е, если Е
обладает свойством секвенциально замкнутого графика, а функ-
функция /: Т -> E'w скалярно существенно интегрируема. Затем мы
приведем некоторые важные примеры пространств Я, обла-
обладающих свойством секвенциального замкнутого графика. Пер-
Первый из названных результатов мы сравним с полученным выше
в п. 8.4.12.
Напомним читателю (п. 6.7.3), что по определению отдели-
отделимое локально выпуклое пространство Е обладает свойством сек-
секвенциально замкнутого графика, если непрерывно всякое линей-
линейное отображение пространства Е в банахово пространство F,
график которого в ExF секвенциально замкнут. Как отмечалось
в п. 6.7.3, всякое пространство Фреше и всякий индуктивный
предел таких пространств обладают свойством секвенциально
замкнутого графика. Другие примеры и иное доказательство
второго из этих утверждений приведены ниже.
Наш первый результат является принадлежащим Бур баки
[9, гл. VI, стр. 18, теор. 1] обобщением одной теоремы для бана-
банаховых пространств, на которую указали Гельфанд и Данфорд.
8.16.1. Теорема. Если пространство Е обладает свойством
секвенциально замкнутого графика и функция f: T-+Ew ска-
скалярно существенно интегрируема, то I fd\i e E'.
Доказательство. Надо доказать, что линейная форма
8.16. Функции со значениями в Ег 791
непрерывна на Е. На самом деле мы докажем большее, а имен-
именно что непрерывно линейное отображение и: E-*Ll, ставящее
в соответствие каждому х элемент и{х), равный классу (эле-
(элементу из L1), определяемому функцией (xi f).
Для этого, поскольку пространство Е обладает свойством
секвенциально замкнутого графика, достаточно показать, что
график отображения и секвенциально замкнут. Допустим, что
последовательность (хп) сходится к нулю в -Б и что соответ-
соответствующая последовательность (gn) = (н(хп)) сходится в L1 к g.
Надо показать, что £ = 0. Так как л^-^-О, то (хп, /)-^0 пото-
поточечно. С другой стороны, поскольку In сходится к § в L1, то
можно так выбрать функции gn и g из соответствующих клас-
классов In и £, чтобы некоторая подпоследовательность (gnk) пото-
поточечно сходилась к g. Так как функции gnk и (xnk, f) принадле-
принадлежат одному и тому же классу,, то они почти всюду совпадают.
Но тогда g = 0 почти всюду, следовательно, 1=0. 1
Перейдем ко второй части нашей программы и докажем
устойчивость свойства секвенциально замкнутого графика отно*
сительно образования индуктивных пределов.
8.16.2. Предложение. Пусть Е — отделимый индуктивный пре^
дел пространств Е\ относительно отображений fim Тогда если
каждое из пространств Е{ обладает свойством секвенциально
замкнутого графика, то Е также обладает этим свойством.
Доказательство. Пусть X— банахово пространство и
и: Е -> X — линейное отображение, график которого секвен-
секвенциально замкнут,. Для доказательства непрерывности отображе-
отображения и (необходимо и) достаточно показать непрерывность каж-
каждого из отображений Uof^ Е\-^Х. Так как каждое из отобра-
отображений \с Ei-^E непрерывно, то график отображения Uof{
секвенциально замкнут. Непрерывность ио\{ следует из того,
что каждое из пространств Е{ обладает свойством секвенциаль-
секвенциально замкнутого графика. 1
8.16.3. Следствие. Всякий отделимый индуктивный предел
пространств Фреше обладает свойством секвенциально замк-
замкнутого графика.
8.16.4. Следствие. Сильное сопряженное к правильному про-
пространству Фреше обладает свойством секвенциально замкнутого
графика.
Доказательство непосредственно следует из предложе-
предложений 8.4.18 и 8.16.2.
8.16.5. Замечания. Интересно, что всякое пространство,
обладающее свойством секвенциально замкнутого графика,
792 Гл. 8. Теория двойственности
является бочечным. Поскольку этот результат нам не понадо-
понадобится, его доказательство мы опускаем.
Добавим еще следующее замечание к теореме 8.16.1. Пусть
пространство E'w полурефлексивно (т. е. каждое слабо огра-
ограниченное подмножество в Е' слабо относительно компактно;
это условие выполняется, например, если Е бочечное). Тогда и^
теоремы 8.14.10 следует, что \d\x <= Е\ если функция /: Г->
-> E'w скалярно существенно интегрируема и локально слабо
ограничена.
8.17. Теорема Данфорда—Петтиса
Основной результат этого параграфа— теорема об инте-
интегральном представлении некоторых линейных отображений про-
пространства Ll = Ll(Ty jn) в пространство Е;, сопряженное к ло-
локально выпуклому пространству Е, на которое наложены опре-
определенные ограничения. Для случая, когда Е—сепарабельное
банахово пространство, а (Г, jn) является интервалом в Rn с ин-
индуцированной на нем мерой Лебега, этот результат был полу-
получен Данфордом и Петтисом [1, теор, 2.1.6]. Для произ-
произвольного а-конечного пространства (Г, \х) доказательство при-
приводится в книге Данфорда и Шварца [1, стр. 541, геор. 6].
В нашем изложении мы придерживаемся подхода Б у р б а к и
[9, гл. VI, стр. 42—43], предварительно исследуя непрерывные
линейные отображения пространства Е в Г°° (или, что эквива-
эквивалентно, в L°°). Относительно других исследований в этой области
см. Динкуляну [1—8], А. Ионеску Тулча и К. Ионес-
ку Тулча [1—3], К. Ионеску Тулча [1], Динкуляну и
Фояш [1], Богданович [1—3].
Теорему Данфорда — Петтиса можно рассматривать как об-
обобщение на векторные функции того факта, что сопряженное к
L1 отождествимо с L°° (см. теорему 4.16.1 и замечания 4.16.2).
Задача состоит в том, чтобы определить множество функций
(или классов функций), отображающих Т в Е', каждое из кото-
которых будет в некоторой степени играть роль пространства Ь°° и
сводится к последнему, если Е одномерно.
Векторный аналог пространства L°°, который оказывается
полезным во многих случаях, определяется следующим обра-
образом Рассмотрим £', наделенное слабой топологией о(Е\ £), и
введем векторное пространство Л£, скалярно измеримых отобра-
отображений f: Т -> E'w, локально почти всюду равных некоторому ото-
отображению Т в £"', значения которого принадлежат равносте-
равностепенно непрерывному подмножеству в Е', Факторпространство
8.17. Теорема Данфорда —Петтиса 793
пространства А& по подпространству скалярно локально пре*
небрежимых функций обозначим через А&. Если пространство
Е нормировано, то скалярно измеримая функция /: Т-+Е' при-
принадлежит А& тогда и только тогда, когда
#„ A1/11) ^locess supH/WIK+oo.
Тогда левая часть этого выражения есть полунорма на А&, ко-
которую, если Е сепарабельно, можно считать определенной и на
факторпространстве Ае* и индуцирующей в нем норму.
Пространство Л^ банахово_относительно этой нормы. Если
Е не сепарабельно, то число №о A1/11), вообще говоря, зависит
не только от класса в А&, определяемого функцией /. Если Е —
сепарабельное пространство Фреше, то каждая функция /еЛя'
слабо измерима (предложение 8.15.3).
Когда нам понадобится отметить различие между функцией
[еЛ£'И классом (элементом из Ае), ею определяемым, то
последний будет обозначаться через /,_Для скалярных функций
естественную проекцию пространства 3?°° на L°° будем обозна-
обозначать через я. При попытках установить связь между Аег и не-
непрерывными линейными отображениями пространства Е в Е°°
неизбежно возникнет вопрос о частичном обращении проекции
я. Этот процесс мы будем называть лифтингом, или восстано-
восстановлением (relevement в терминологии Бурбаки).
Более точно, пусть [gAf. Введем Xf — элемент простран-
пространства Lc(£, L°°), определяемый равенством
Xf(x) = n({x, /». (8.17.1)
Ясно, что Xf зависит только от класса f функции f. Переходя
к факторпространству, получаем линейное отображение X:
f>—>Xf пространства АЕ/ в Lc(Ey L°°). Читатель может заметить,
что если пространство Е нормировано, то имеет место соотно-
соотношение
Одна из наших основных задач — показать, что при некоторых
условиях X есть отображение на. Соотношение (8.17.1) приводит
тогда к частичному обращению проекции я. Имея это в виду,
обратимся к проблеме лифтинга.
Лифтинг. Пусть М — векторное подпространство в L°°. Бу-
Будем говорить, что М восстановимо, если существует такое ли-
линейное отображение % подпространства М в i?00, называемое
794 Гл. 8. Теория двойственности
восстанавливающим для Му что композиция я ° X есть тожде-
тождественное отображение на М и
для каждого элемента / е М. Восстановление сводится, таким
образом, к выбору соответствующего представителя для каж-
каждого класса функций из М.
8.17.1а. Лемма. Каждое сепарабельное подпространство М
из L°° восстановимо.
Доказательство. Пусть D — счетное множество, плотное
в М, и D'— множество всех конечных линейных комбинаций
элементов из D с рациональными коэффициентами. Множество
D' счетно. Запишем базис в D' над полем Q рациональных чи-
чисел в виде последовательности hn (я= 1, 2,...). Для каждого п
можно выбрать такую функцию h'n ^ «5"°°, что n(hn) = hn- Через
л/ обозначим единственное Q-линейное отображение простран-
пространства D' в &°°, определяемое равенствами 'k'(hn)=hn. Ясно, что
композиция я о?/ равна тождественному отображению в D'\
кроме того, для каждого h из Dr и всех точек t, за исключением
локально пренебрежимого множества N(h), имеет место нера-
неравенство
Множество N=[J{N(h): h^D'} локально пренебрежимо. Обо-
Обозначим через X(h) функцию h'\ определенную равенствами
А/(А) @ п(ри te=T\N,
0 при t^N.
Очевидно, X является таким Q-линейным отображением на D\
что я о X совпадает с тождественным отображением на D\ и для
всех h e D' и /еГ имеет место неравенство
Так как D' плотно в М и пространство 3?°° полно относительно
полунормы JVoo, то отображение К может быть продолжено по
непрерывности до восстанавливающего отображения для М. |
Замечание. Проблема лифтинга является краеугольным
камнем многих попыток изучения интегрального представления
линейных функционалов и операторов на пространствах вектор-
векторных функций. Дальнейшее обширное и тонкое исследование
этих вопросов, которое мы не приводим из-за отсутствия места,
8.17. Теорема Данфорда —- Петтиса 795
показывает, что в большинстве случаев условие счетности нельзя
ослабить. (См. Махарам [1], А. Ионеску Тулча [1],
А. Ионеску Тулча и К. Ионеску Тулча [2—7], До-
ногю [1], Динкуляну [8].)
Мы лишь дополним предыдущую лемму доказательством
того факта (Бур баки [9, гл. VI, стр. 92, упр. 18]), что если_Г
метризуемо (и локально компактно), то само пространство Ь°°
и, следовательно, каждое его векторное подпространство восста-
восстановимы относительно всякой положительной меры \х на Г. Хотя
это обобщение интересно и полезно, тем не менее оно, к сожа-
сожалению, не позволяет полностью освободиться от условия сепара-
сепарабельности в основных результатах этого параграфа.
8.17.1Ь. Лемма. Если Т — локально компактное простран-
пространство, каждое компактное подпространство которого метризуемо,
и [I — произвольная положительная мера Радона на Т, то про-
пространство L°°=Zoo(r, (!) восстановимо.
Доказательство. Предложение 4.14.9 позволяет нам, не
ограничивая общности, считать, что Т компактно и метризуемо.
Предполагая это, выберем метрику d, определяющую тополо-
топологию в Т.
Выберем также такую последовательность пп (я=1, 2, ...)
конечных разбиений пп= (Ап>k)i<k<k пространства Т на инте-
интегрируемые множества, что
A) каждое из множеств AUik является объединением неко-
некоторых из множеств An+\,h\
B) limmax (диаметр Antk) = 0.
п k
Каждому интегрируемому множеству А и каждой интегри-
интегрируемой функции / поставим в соответствие число
/ ф при \х {А) > О,
А
О при (л (Л) = О*
Читатель может заметить, что |1л(/) зависит только от клас-
класса /, определяемого функцией f, поэтому можно писать |1л(/)«
Положим
S
Если f — существенно ограниченная функция, то Xn(f)-
римая функция, удовлетворяющая неравенству
796 Гл. 8. Теория двойственности
Суть доказательства сводится к установлению того факта,
чю
(8Л7.3)
почти всюду для каждой существенно ограниченной и измери-
измеримой функции /. Допустим, что это так. Тогда доказательство
возможности восстановления пространства L°° может быть про-
проведено следующим образом.
Обозначим через Lim обобщенный предел, определенный для
всех ограниченных числовых последовательностей в § 3.4. Если
/ существенно ограничена и измерима, то функция Я(/)(/) =
= LimXn(/)(O определена для каждого t и удовлетворяет не-
неравенству
IM/) (О К 11/11.
Далее, из (8.17.3) следует, что h(f) (i)=f(t) почти всюду, от-
откуда вытекают измеримость функции X(f): t*->%(f) (t) и равен-
равенство я (X(/))=/. Другими словами^ отображение К: /»—>Л(/) яв-
является восстанавливающим для L°°.
Таким образом, все упирается в доказательство справедли-
справедливости соотношения (8.17.3). В действительности мы докажем
(8.17.3) при более слабых предположениях, чем интегрируе-
интегрируемость функции f. Для этого вначале установим одно неравен-
неравенство.
Пусть g— произвольная интегрируемая функция и а — про-
произвольное положительное число. Каждому натуральному п по-
поставим в соответствие множество Вп, являющееся объединением
тех множеств An>k, для которых
J
An,k
и пусть B==(Jj3rt, т. е. В есть объединение всех множеств AUjk
п
(изменяются оба индекса п и k), для которых справедливо по-
последнее неравенство. Из условия A) следует, что BnczBn+i.
Если, кроме того, обозначить через 2Г суммирование по тем ин-
индексам fee[l, kn], для которых множества Ап,н содержатся в
Вп, то имеем
откуда следует, что
8 17. Теорема Данфорда — Петтиса 797
Заметим далее, что если пренебречь теми из множеств Ап,к,
которые пренебрежимы, то Вп — это множество тех точек t, для
которых Яп(£)(/)>а. Следовательно, если обозначить через
D множество всех тех точек /, для которых Kn{g) (/)> а при
некотором п, то
\i (D)< a J £ф. (8.17.4)
Если функция / непрерывна (а следовательно, и равномерно
непрерывна), то из условия B) тривиально следует, что
kn(f) ->f равномерно на Т. Теперь для заданной интегрируемой
функции / выберем такую последовательность (fr) непрерывных
функций, что | f — fr \d\x->0 и \imfr = f почти всюду. Отбрасы-
вая в случае надобности некоторые члены последовательности,
можно считать, что ^рг<+оо, где Pr=J grd\i и gr = f — fr-
г
Определим множество Dr no gr так же, как множество D было
определено по g. Тогда Dr — это множество всех тех точек t,
для которых при некотором п справедливо неравенство
K(gr)(t)> а. Из (8.17.4) следует, что
Если D's = \J{Dr: г>5], то ^(Z^cr^, где р;= 2 Рг стре-
мится к нулю при 5-^оо. Если t^L T\DSj то для всех п и всех
г>5 имеет место неравенство Xn(gr) A)<а- Поэтому
Первый член в правой части не превосходит \Xn(gr) (О I» следо-
следовательно, если t e T\DS, то для всех п и всех г <> 5 имеем
Пользуясь тем, что \imfr = f вне пренебрежимого множества N,
предположим, что t еГ \ (D's [} Л/'), и выберем r^- s так, чтобы
\fr(t)-f(t)\<a.
Теперь тот факт, что Kn(fr) -*-fr при re-voo, показывает, qTo
limsup| ЛЛ(f)(/) -f @ l<2a
для t<=T\(D's[)N). Так как ji(D^)->0 при s-^oo, то левая
часть только что полученного соотношения не превосходит 2а
всюду, за исключением пренебрежимого множества Na, которое
798 Гл. 8. Теория двойственности
может зависеть от а. Так как это верно для любого а > 0, то
этим доказано соотношение (8.17.3), а с ним и лемма. |
Вооружившись этими леммами, мы можем сформулировать
и доказать первый из наших главных результатов.
8.17.2. Теорема. Пусть и— такое непрерывное линейное ото-
отображение пространства Е в L°°, что подпространство и(Е) вое-
становимо. Тогда
(a) существует такая функция [gA^, что u=Xfi г. е.
и(х)=п((х, /)) для каждого элемента х^Е\
(b) если пространство Е нормировано,, то функцию f в (а)
можно выбрать так, чтобы
sup ||/ (t) || HI и II; (8.17.5)
(c) если пространство Е сепарабельно и f — функция из (а),
то класс f однозначно определен;
(d) если пространство Е сепарабельно, то имеют место
утверждения (а) и (с) и X является линейным взаимно одно-
однозначным отображением пространства АЕ, на LC(E, L°°) и при-
притом изометрией, если пространство Е вдобавок нормировано.
Доказательство, (а) Надо показать, что существует та-
такая функция feAE', что и(х)=п({х, /)) для всех х. Пусть
Я — восстанавливающее отображение для и(Е). Для каждого
t^T отображение хь—>Х(и(х)) (t) есть непрерывная линейная
форма на Е. Поэтому найдется такой элемент f(t) ^E', что
при всех х. Тем самым функция /, отображающая Т в £', опре-
определена. Так как %{и{х)) ^2>о°, то f скалярно измерима. Из не-
непрерывности отображения и следует, что прообраз U относи-
относительно и единичного шара.из L°° есть окрестность нуля в Е, по-
поэтому для х е U и / еГ имеем
\ = \l(u(x)) (t)\^Noo(u (*))< 1.
Отсюда следует, что f(T) cz U°t и поэтому f gAs/. Наконец,
п((х, f))=n[l(u(x))] = u(x),
что и требовалось доказать.
(Ь) Пусть функция / построена так же, как в (а). Из соот-
соотношения (8.17.2) следует, что
sup || f(t) ||,
8.17. Теорема Данфорда —Петтиса 799
С другой стороны, поскольку X — восстанавливающее отображе-
отображение, то для каждого t e T
I {x, f (t)) I = I Я (и (х)) (t) | < N.. (и (х)) < ||и|| • \\x ||.
Отсюда вытекает неравенство ||/(OII-^ IMI» а тем самым и ра-
равенство (8.17.5).
(с) Нужно только показать, что если для всех х
то функции / и /* локально почти всюду совпадают. Пусть S —
счетное множество, плотное в Е. Из приведенного выше равен-
равенства, примененного к каждому х из S, следует существование
такого локально пренебрежимого множества /V, что (х, 7@) —
= (х, f*@) Для всех -^^5 и t^T\N. Так как множество S
плотно в £, то равенство f = f* выполняется на T\N.
(d) Если пространство Е сеиарабельно, то таким же будет
и и(Е). Поэтому (лемма 8.171а) подпространство и(Е) вос-
восстановимо и, значит, справедливы утверждения (а) и (с). Сле-
Следовательно, X — линейное взаимное однозначное отображение
на. Допустим, что пространство Е еще и нормировано. Из (Ь)
следует, что ||u|| > iV<»(II/II) для того класса / (единственного
.согласно (с)), для которого u = Xf = X(f). Противоположное не-
неравенство iVoo(II/II) ^ 11^11 доказано еще в (8.17.2). Таким обра-
образом, имеет место равенство, и X есть изометрия. 1
8.17.3. Остальные наши главные результаты будут получены
из теоремы 8.17.2 с помощью следующей билинейной формы В/,
ассоциированной с элементом Xf и определяемой формулой
Bf (x, g)=jg(t)- {x, f (t))ф(t), (8.17.6)
gG2"! иле£ Эту формулу можно переписать в таком виде:
Вf(x, g) = {g, Xf(x)), (8.17.7)
где скобки в правой части относятся к обычной двойственности
между U и L°°. Имеется еще и другая форма записи Bf:
Bf(x, g) = {x, Yf(g)\ (8.17.8)
где
Yf(g)=j gfdix (8.17.9)
является линейным отображением пространства Lx в Е'. Что
касается интерпретации интеграла (8.17.9), заметим, что функ-
функция gf: T-+E' скалярно интегрируема, a J gf d\x e E't поскольку
800 Гл. 8. Теория двойственности
непрерывна линейная форма х*-*- \ g • {х, f)d\x на £, что обес-
обеспечивается существованием такого локально пренебрежимого
множества N аТ, что множество f(T\N) равностепенно непре-
непрерывно в Ег.
Остальные рассуждения можно провести в общих терминах.
8.17.4. Пусть Е и F — локально выпуклые пространства и Е'
и F* — их сопряженные. Будем обозначать через Ew и E's
пространство Е' соответственно в слабой и в сильной тополо-
топологии; аналогичный смысл имеют обозначения F*w и F's, Пусть
В — раздельно непрерывная билинейная форма на ExF. Мы
можем тогда написать
В(х, у) = (х, BR(y)) = (y, BL{x))y
где BR (соотв. BL) является непрерывным линейным отображе-
отображением F в E'w (соотв. Е в F'w). Обратно, каждое отображение Вв
(или BL) указанного типа порождает таким образом раздельно
непрерывную билинейную форму В. Это соответствие линейно
и взаимно однозначно.
Для непрерывности билинейной формы В (по совокупности
переменных) необходимо и достаточно, чтобы отображение BL
переводило некоторую окрестность нуля из £ в равностепенно
непрерывное множество из F' или чтобы BR обладало аналогич-
аналогичным свойством, если поменять местами Е и F. В случае когда
пространство F нормированное, непрерывность формы В влечет
непрерывность отображения Bl'- Е-> F'Si и обратно.
Таким образом, если обозначить через ВС(Е, F) пространство
непрерывных билинейных форм на произведении ExF и через
Le(E, F')—пространство линейных отображений пространства
Е в Z7', каждое из которых переводит некоторую окрестность
нуля из Е (зависящую от рассматриваемого отображения) в
равностепенно непрерывное множество из F\ то соответствие
B*—>BL есть взаимно однозначное отображение пространства
BC(E,F) на Le(E,F'), в то время как соответствие B\->BR яв-
является взаимно однозначным отображением пространства
ВС(Е, F) на Le(F9 E'). Далее Le(E, F') есть всегда подпростран-
подпространство пространства LC{E, F's), причем Le(E, F')=* LC{E, Z7^)» если
F нормировано. Если Е и F — нормированные пространства, то
указанные выше линейные отображения являются изометриями.
Теперь применим эти замечания к случаю, когда F = Ll и В
есть билинейная форма В/, определенная в (8.17.6). В резуль-
результате получаем, что теореме 8.17 2 можно придать любую из сле-
следующих двух эквивалентных форм.
817. Теорема Данфорда — Петтиса 801
8.17.5. Теорема. Пусть Е— сепарабельное локально выпуклое
пространство. Тогда каждая непрерывная билинейная форма В
на произведении ExL1 представила в виде (8.17.6), где f — не-
некоторая функция из Кег\ при этом класс /, соответствующий
функции /, определяется однозначно. Если пространство Е нор-
нормировано, то соответствие В <-> f есть изометрия.
8.17.6. Теорема (Данфорд — Петтис). Пусть Е — сепа-
сепарабельное локально выпуклое пространство. Тогда каждое ото-
отображение v e Le(L\ Е') представило в виде v(g) = Yf(g) =
= J gfd[i, где f — некоторая функция из Л^. Класс f, соответ-
соответствующий функции /, определяется однозначно. Если простран-
пространство Е нормировано, то это утверждение справедливо для каж-'
дого непрерывного линейного отображения v: U-+E' (простран-
(пространство Е' наделено сильной топологией), причем соответствие
v «*-> / является изометрией.
Замечания. A) Среди^ ранних рабог по этим вопросам,
кроме статьи Данфорда и Петтиса [1], следует отметить
работы Гельфанда [2], Бохнера и Тэйлора [1] и Кан-
Канторовича и Вулиха [1].
B) Интересно и важно отказаться, насколько это возможно,
от условия сепарабельности в теоремах 8.17.5 и 8.17.6. Резуль-
Результаты п. 8.17.4 позволяют переходить от одной теоремы к другой,
поэтому мы ограничимся обобщением теоремы 8.17.6. Укажем
два таких обобщения.
8.17.7. Допустим, что пространство Т (локально компактно
и) локально метризуемо. Тогда, как мы видели в лемме
8.17.1 (Ь), пространство L°° восстановимо. Пусть v e Le(L\ E'),
и пусть отображение и: Е ->■ L°° определено равенством
Тогда из теоремы 8.17.2(а) следует, что и(х) =л((х, /)) для
некоторой функции |еЛ£/. Соответственно для каждого эле-
элемента gG^1
a (g) = J gf dV"
Таким образом, часть теоремы 8.17.6, связанная с существо-
существованием, остается справедливой. Однако теперь у нас нет уве-
уверенности в единственности класса f. Знание отображения и
определяет (я, f) лишь локально почти всюду для каждого х^Е.
8.17.8. Заключение п. 8.17.7 остается справедливым, если Е—'
банахово пространство и v(Lx) сильно сепарабельно в Е\ что
имеет место, например, если L1 сепарабельно (Данфорд и
802 Гл. 8. Теория двойственности
Шварц [1, стр. 542, следствие 7], Бур баки [9, гл. VI, стр. 93,
упр. 19]).
Доказательство этого утверждения основывается на том, что
рассматриваемую ситуацию можно свести к такой, где приме-
применима теорема 8.17.6. Это сведение основывается, в свою очередь,
на двух простых леммах.
Лемма А. Пусть Е— нормированное векторное пространство,
G — сильно сепарабельное и сильно замкнутое векторное под-
подпространство в Е'\ Тогда существует линейная изометрия j
подпространства G на замкнутое векторное подпространство
сильного сопряженного £о, где Eq — замкнутое сепарабельное
векторное подпространство в Е,
Доказательство. Выберем в G сильно плотную после-
последовательность (<а£) и затем такую последовательность (ап) в
£, что
Пусть Eq — замкнутое векторное подпространство ч Е, порож-
порожденное элементами ап (п=1, 2, ...). Легко проверить, что
11*1 = sup \{аП9 х')\
п
для каждого х' е G.
Отображение / определим следующим образом. Если х' е G,
то в качестве j(x') возьмем элемент из Ео> определенный ра-
равенством
Другими словами, j(x') =х'\Е0. Имеем тогда
= sup{|(r/, x')\: у^Е,
Последнее выражение равно \\х'\\ при xf^G. Таким образом, /
есть изометрия пространства G в Eq. Так как / линейно, то
j(G) есть сильно замкнутое векторное подпространство в Ео. I
Лемма В. Пусть Е — нормированное векторное пространство,
М — сильно сепарабельное векторное подпространство в Е; и
I — непрерывная линейная форма на М. Тогда из Е можно из-
извлечь такую последовательность (хп), что
l(x') = lim{xnt х')
п
для х' е М.
8.17. Теорема Данфорда — Петтиса 803
Доказательство. Согласно теореме Хана — Банаха, g
есть сужение на М некоторого функционала д/'е/?". Далее х"
принадлежат о(Е", Е')-замыканию некоторого ограниченного
подмножества В из Е. Топология о(Е", Е') \В сильнее топологии
а(£, М)\В, а топология о(Е, М)\В иолуметризуема, так как
множество М сильно сепарабельно. Отсюда следует существова-
существование такой последовательности (хп) элементов из Ву что
<*„, х')->(х", *') = 6(*Т
для х' е М. |
Теперь мы можем обратиться к доказательству основного
утверждения. Пусть v — такое непрерывное линейное отображе-
отображение пространства L1 в Я', что подпространство v(V) сильно
сепарабельно. Пусть далее G — сильное замыкание подпростран-
подпространства v(Ll) в Е'. Согласно лемме А, существуют такое сепара-
бельное замкнутое векторное подпространство 2?о в Е и такая
линейная изометрия / подпространства G на сильно замкнутое
векторное подпространство в Е^ что j(x')~x'\E0 для каждого
дг'е G. Рассмотрим композицию /о v как непрерывное линейное
отображение пространства L1 в Eq. Так как Ео сепарабельно,
то по теореме 8.17.6 существует такая функция |0ЕА /, что
= J
Положим f = j~lof09 так что функция / отображает Т в G cz Er
и \\f(t) II ^ ||и||. Остается только проверить, что /еАе/, т. е.
(с учетом нам уже известного) что f скалярно измерима.
Для этого допустим, что х^Е. Тогда форма х' •—>(;:, хГ)
непрерывна на G и форма у'*—>(х, Г1 (у')) непрерывна на
j(G)czE'Q. Подпространство /(G) сильно сепарабельно, и по
лемме В существует такая последовательность (уп) элементов
из £о, что
{х, ГЧу')) = \ш{Уп, У')
п
для yr e /(G). Иначе
для /gG. Полагая здесь *' = /(/)• получаем, что
Так как функция f0 скалярно измерима, го измерима каждая
из функций (уп, /о/. Поэтому измерима и функция (^, f), что и
требовалось доказать, 1
804 Гл. 8. Теория двойственности
8.18. Пространства j£pE и LPE
В гл. 4 мы ввели пространства числовых функций 9?v и Lv
и нашли их сопряженные. В связи с этим мы пришли к теореме
Лебега — Радона — Никодима для числовых мер. В этом и в
следующих двух параграфах мы рассмотрим аналогичные за-
задачи для векторных функций и мер. Векторный характер рас-
рассматриваемых функций и мер порождает много дополнитель-
дополнительных осложнений. Немногие из известных «векторных» резуль-
результатов обладают такой законченной формой, как аналогичные
результаты для числовых функций и мер.
Определение пространств, аналогичных пространствам «2??
и Lp, особых затруднений не вызывает. Всюду ниже Т — отдели*
мое локально компактное пространство, jn — положительная
мера Радона на Г, Е — отделимое локально выпуклое простран-
пространство.
При 1 </?<оо через •27j? = J^e(T9 |ы) будем обозначать век-
векторное пространство всех таких измеримых функций g, отобра-
отображающих Г в £, что функция Nog принадлежит пространству
2?р = 2?р(Г, jn) для каждой непрерывной полунормы N на Е.
Через Lj? = LPE{T, \x) обозначаем факторпространство про-
пространства J?£ по подпространству пренебрежимых функций.
(Так как мы часто будем иметь дело с векторными и число-
числовыми функциями одновременно, то стрелочка в «g» должна
напоминать читателю, что этот символ обозначает функцию со
значениями в Е. Стрелкой противоположного направления бу-
будем пользоваться для обозначения функций, принимающих зна-
значения в Е\)
Если /? = оо, то J?£ =-£?£ (Г, \i) обозначает векторное про-
пространство всех измеримых функций g: Т-^Е, почти всюду со-
совпадающих с ограниченной функцией (т. е. функцией, область
значений которой есть ограниченное множество в Е). Фактор-
пространство пространства J?£ по подпространству пренебре-
пренебрежимых функций обозначается через /.£=/,£ (Г, Ц-).
Можно также говорить о пространствах J3?PE и L|, анало-
аналогичных пространствам &? и L^, где интегрируемость заменена
на существенную интегрируемость и «почти всюду» на «локально
почти всюду». В большинстве случаев мы будем предоставлять
читателю делать необходимые видоизменения.
Заметим, что если в качестве Е берется пространство F'WJ
слабо сопряженное к некоторому локально выпуклому про-
пространству F9 то не следует смешивать «5^ с пространством Др,
8 18 Пространства J3?PE и LE 805
введенным в § 8.17. Во-первых, в общем случае неверно, что
каждая функция из Л/?' измерима относительно топологии
а(/7/, F). Во-вторых, функция из J?i? может не быть локально
почти всюду равной функции, множество значений которой
равностепенно непрерывно. Однако, как это видно из предло-
предложения 8Л5.3, если Е — сепарабельное пространство Фреше, то
Kf* и J?^ совпадают при Е = F'w.
8.18.1. Случай банаховых пространств. Если Е — банахово
пространство, то на <3?Е можно ввести полунорму
] при 1 </,<«>,
ess sup \\g(t) || при /? = оо.
Переходя к факторпространству, получаем соответствующую
норму на Ье-
Построение теории интегрирования в случае банаховых про-
пространств и исследование пространств LE было начато Бохне-
ром [3] и продолжено многими авторами, например Данфор-
дом и Петтисом [1], Бохнером и Тэйлором [11,
Филлипсом [2], Петтисом [2], Биркгофом [4],
Дьёдонне [8—11], причем мы упоминаем лишь некоторых.
Большинство описаний интеграла Бохнера (см,, например,
X и л л е [1], Данфорд и Шварц [1]) отличается от принятого
нами. Последнее ближе к изложению Б у р б а к и [8, гл. IV,
стр. 144 и 228].
Можно показать (см. упр. 8.28, 8.29), что (если Е — бана-
банахово пространство, то)
(a) пространство З'е полно, a Le банахово;
(b) простые функции вида
(где ak^E и множества Ah (которые можно считать непересе-
непересекающимися) интегрируемы) плотны в J?£ при 1</?<оо.
Главная задача в теории пространств Le — найти сопряжен-
сопряженное пространство. Вспомогательной является задача выяснения
условий рефлексивности пространства Lpe- Многие авторы спо-
способствовали решению этой задачи. К ним, кроме указанных
выше, относятся Мурье [1], Форте и Мурье [1] и Чат-
герджи (неопубликованные заметки).
806 Гл. 8. Теория двойственности
По аналогии со случаем числовых функций можно ожидать,
что (LeY ** L& при 1<4/?<оо, где число р' определено равен-
равенством /?-1 + //~1 = 1 и Е' — сильное сопряженное к Я, само яв-
являющееся банаховым пространством. При этом ожидаемом
отождествлении имеется в виду двойственность относительно
билинейной формы, которая получается при переходе к фактор-
пространствам из билинейной формы
Можно также ожидать, что LPE будет рефлексивным при
1 < р < оо, если таким же будет Е.
Вообще говоря, эти ожидания оправдываются, по крайней
мере, при выполнении некоторых условий сепарабельности. Мы
не располагаем местом, чтобы рассмотреть эти вопросы; упо-
упомянем лищь, что часто от этих ограничений можно отказаться
(см. литературу, цитированную в замечании после леммы
8.17.1 (а), а также в п. 8.20.4 и 8.20.5 ниже).
Как и в числовом случае, многое здесь основывается на тео-
теоремах типа Лебега — Радона — Никодима. В этом параграфе
исследуется самый простой случай, а именно когда /?=1. Сле-
Следующий параграф будет посвящен теоремам типа Лебега — Ра-
Радона — Никодима, которые служат трамплином к исследованию
случая р>1.
Прежде чем перейти к детальному изложению, сделаем два
простых отрицательных наблюдения.
Если пространство Е не сводится к нулевому элементу, то
утверждение, что (££)'« Li', неверно для р = оо, если оно не-
неверно для числовых функций. Это вытекает из следующего за-
замечания. Если выбрать в Е такой элемент а, что ||а|| = 1, то ото-
отображение, ставящее в соответствие элементу g<=3?v функцию
t\—>a-g(t) из J^pe, является изометрическим изоморфизмом про*
странства J?p в .2?%, Отсюда следует, что (Lp)'« Lp\ если
(Li)' ~ Lps,
Точно так же, если пространство Е не тривиально, рефлек-
рефлексивность пространства Le влечет рефлексивность пространства
Е. Действительно, предыдущие рассуждения показывают, что
пространство Le всегда содержит изоморфную копию про-
пространства Е в качестве замкнутого векторного подпространства
(при ЕФ{0}), а замкнутое векторное подпространство рефлек-
рефлексивного банахова пространства само рефлексивно.
Мы сейчас сформулируем и докажем результат, который
определяет пространство, сопряженное к L%, для довольно об-
общего случая,
8.18. Пространства J?| и LPE 807
8.18.2. Теорема. Пусть Е — банахово пространство.
A) Если g e J?lE и f е Ля'> то функция (g, f) существенно
интегрируема и
Поэтому при факторизации каждая функция f e Ля/ опреде-
определяет с помощью правила
непрерывную линейную форму на l)E с нормой, не превосходящей
Й
B) Допустим, что выполняется одно из следующих трех
условий:
(a) пространство £_ сепарабельно;
(b) пространство L°° восстановимо (п. 8.17.7);
(c) пространство L1 сепарабельно.
Тогда для каждой непрерывной линейной формы F на l)E су-
существует такая функция f е Л#', что 11/@11^11^11 и F полу-
получается из f способом, описанным выше в A).
C) Допустим, что пространство Е сепарабельно. Сопоста-
Сопоставим каждому элементу f из Ля/ непрерывную линейную форму
P(f) на Ье, получаемую при переходе к факторпространству,
отправляясь от любой функции f из класса f. Тогда р есть ли-
линейная изометрия пространства Ля/ на сильно сопряженное
к LlE.
Доказательство. A) Пусть К—произвольное компакт-
компактное подмножество в Т. Измеримая функция g является на К
пределом последовательности простых функций gn (теор. 8.15.1);
поэтому (gn, f) ->■ (gj f) на /С. Скалярная измеримость функций
/ влечет измеримость каждой из функций (gn, f) и, следова-
следовательно, измеримость функции (g, /). Остальное вытекает из не-
неравенств
I {g(t)> T(t)) К Иг (ОН • ll?@IKIlJ@ll • л^со(Й).
второе из которых имеет место локально почти всюду.
808 Гл. 8. Теория двойственности
B) Пусть F— заданная непрерывная линейная форма на
Ье- Обозначим через v непрерывное линейное отображение про-
пространства L1 в Е\ определяемое равенством
где gx— элемент в L#, являющийся классом функции ()
где g — некоторая функция из класса g e LK Неравенство
IMI-^ \\F\\ очевидно. При выполнении условий (а), (Ь) или (с)
мы ссылаемся соответственно на теорему 8.17.6, на п. 8.17.7
или на п. 8.17.8. В каждом из этих случаев существует такая
функция Те-Лд', что <
для всех g e Я?1 и всех jtg£. В силу линейности сужение F
на множество классов простых функций получается из ото-
отображения
переходом к факторпространству. Результат (Ь) п. 8.18.1 и не-
непрерывность F позволяют распространить этот вывод на произ-
произвольный элемент из Ье-
C) Из утверждения B) следует, что р есть отображение на.
Так как пространство Е сепарабельно, то класс f однозначно
определен линейной формой F\ следовательно, р — взаимно од-
однозначное отображение. Кроме того, из неравенства, получен-
полученного в A), вытекает, что
В соответствии с этим имеем
поэтому llp(f)ll = llfll, т. е. р — изометрия. ■
Замечания. В случае C) можно даже утверждать, что
функция f слабо измерима ( = измерима относительно о(Е\ Е))
(предл. 8.15.3). Следовательно, если пространство Е сепара-
сепарабельно и рефлексивно (в этом случае Е' как пространство, сопря-
сопряженное к которому сепарабельно, автоматически сепарабельно),
то / будет сильно измерима (теорема 8.15.2) и потому будет
принадлежать пространству J^^. Однако, если пространство
Е рефлексивно, оно может и не быть сепарабельным. Это еле-
8.18. Пространства JZ'e и LE 809
дует из некоторых результатов Филлипса [2]. Хотя наше
доказательство будет использовать следствие 8.19.5, удобно уже
здесь рассмотреть случай, когда Е рефлексивно.
8.18.3. Теорема. Пусть Е — рефлексивное банахово про-
странство. Если F — непрерывная линейная форма на LE, то
существует такая сально измеримая ограниченная функция
f: T-+E', что
для всех g e J3?{E и N^iWfW)** \\F\\. Таким образом, (Le)' « Z,?/.
Доказательство. Если функция gG^1 фиксирована,
то соответствие л;ь—^(gx) есть непрерывная линейная форма
на Е. Поэтому найдется такой единственный элемент m(g) е £"',
что
Очевидно, что
поэтому т есть непрерывное линейное отображение простран-
пространства L1 в Е\ Так как Е рефлексивно, то таким же будет и его
сильно сопряженное Е'. Поэтому из следствия 8.19.5 вытекает
существование такой сильно измеримой функции /: Т-+Е\ что
ft < \\F\\ и
для всех х и всех g e 2х. Так как множество конечных линей-
линейных комб]
чаем, что
ных комбинаций функций вида gx плотно в Ь]в, то легко полу-
, Г>ф
для гсех g e J&e. Из этой формулы следует, что
||F||<locesssup||f(OII
<■
и, следовательно, ||/7H=iVoo(II/II). I
Замечания. Филлипс [2, теорема 5.1] по-другому про-
проводит решающий шаг в приведенном выше доказательстве, не
810 Гл. 8. Теория двойственности
прибегая при этом к следствию 8.19.5, Теорема Филлипса 5.1 —
это наша теорема 8.19.4,
8.19. Векторные меры
Для исследования сопряженного к LlE нам понадобятся
меры, принимающие значения в заданном отделимом локально
выпуклом пространстве и некоторые аналоги теоремы Лебега —
Радона — Никодима. В этом параграфе мы ограничимся изло-
изложением лишь тех сведений по этим вопросам, которые необхо-
необходимы для наших целей. Дальнейшую информацию по этой те-
тематике можно найти в работах Динкуляну [1—8], Динку-
ляну и Фояш [1], А. Ионеску Тулча и К Ионеску
Тулча [1—3], Ионеску Тулча [1], Богданович [1—3].
Как и в случае числовых мер, меру можно рассматривать либо
как линейное отображение, определенное на пространстве Ж (Г),
либо как функцию множества, определенную на некотором
классе подмножеств в Т. Бурбаки последовательно придержи-
придерживается первой точки зрения, которой и мы до сих пор придержи-
придерживались в этой книге. Мы намерены сохранить эту линию и в
случае векторных мер, однако надо иметь в виду, что вторая
точка зрения имеет много приверженцев и в некоторых отноше-
отношениях имеет свои преимущества. В п. 9.4.14 мы подробно иссле-
исследуем связь между обеими точками зрения.
Систематическое изложение принятого нами подхода можно
найти в книге Данфорда и Шварца [1, стр. 345—357]. Дин-
Динкуляну [4, 5] рассмотрел более общие определения векторных
мер.
Определим меру Радона со значениями в Е (или, короче,
Е-значную меру Радона) (где Е — произвольное отделимое ло-
локально выпуклое пространство) как непрерывное линейное ото-
отображение m пространства Ж(Т) в Е. Непрерывность означает,
что lim m(gn) =0 в смысле пространства £, если последователь-
последовательность непрерывных функций (gn) с компактными носителями,
содержащимися в некотором компактном (не зависящем от п)
подмножестве из Г, сходится равномерно к нулю.
->
Пример. Пусть /: Т-*Е — скалярно локально интегрируемая
функция. Можно попытаться определить соответствующую меру
Радона m со значениями в £, полагая
(8.19.1)
8.19. Векторные меры 811
для g<=y*?(T). Для того чтобы определенный таким образом
элемент m(g), априори принадлежащий пространству E'*zdE,
принадлежал Е и непрерывно зависел от g", нужны дополни-
дополнительные ограничения. Из результатов § 8.14 вытекают различ-
различные условия, достаточные для этого. Из теоремы 8.14.14 сле-
следует, что таким достаточным условием служит, например, пол-
полнота пространства Е, измеримость функции / и локальная
интегрируемость функции ||/||.
В связи с этим примером естественно поставить следующую
задачу: найти условия (если возможно, необходимые и доста-
->
точные), которым должна удовлетворять £-значная мера т,
чтобы быть мерой указанного выше вида. Ответ будет в опре-
определенной степени зависеть от требований, предъявляемых к
функции /, например требуется ли, чтобы / была измерима или
лишь скалярно измерима. В дальнейшем мы встретимся и с той
и с другой возможностью. -
Если мера m имеет вид (8.19.1), то, вообще говоря, суще-
существует очевидное продолжение меры пг на более широкий класс
функций, чем Ж(Т), Заслуживает рассмотрения вопрос о воз-
возможности такого продолжения для мер т, не являющихся уже
мерами такого специального вида. Этот вопрос легче поддается
исследованию в том частном случае, когда Е является слабым
сопряженным к некоторому локально выпуклому пространству/
Этот случай будет рассмотрен в п. 8.19.7.
8.19.1. Продолжение векторных мер Радона. Пусть m — мера
Радона со значениями в отделимом локально выпуклом про-
пространстве Е. Существует естественный и простой способ про-
продолжения меры m с Ж{Т) на более широкий класс функций.
Применяемая при этом техника очень сходна с той, которой мы
пользовались при определении интеграла от функции со зна-
значениями в Е относительно числовой меры Радона (п. 8.14.1).
Числовая функция g на Т называется существенно интегри-
интегрируемой относительно т, если существенно интегрируема каж-
каждая из числовых мер Радона л:'от', где *' пробегает Е\ Обозна-
Обозначим через 3?(пг) пространство всех таких функций.
Если g ^2?(пг), то под m(g) понимается элемент простран-
пространства Е'*, определяемый соотношением
812 Гл. 8. Теория двойственности
для каждого х'^Е'. Это определение, очевидно, согласуется
с первоначальным определением, когда g^y£(T).
Ясно, что пространство 3? (т) содержит все ограниченные
универсально измеримые функции с компактными носителями.
Если (gn)—равномерно ограниченная последовательность функ-
функций из 3?(т), обращающихся в нуль вне некоторого компакт-
компактного множества (не зависящего от п), и на Г существует пото-
поточечный предел £ = Пт£п, то
m(g) = \\mm(gn) (8.19.2)
п
слабо в £'* (т. е. в топологии а(£'*, £'))• Это непосредственно
следует из теоремы Лебега о сходимости.
Важную роль играет частный случай, когда мера пг скалярно
локально абсолютно непрерывна относительно некоторой по-
положительной меры Радона \х на Г, что означает локальную
[х-абсолютную непрерывность каждой из числовых мер х' о пг.
В этом случае 3?(пг) содержит все функции из S?°°(\i) с ком-
компактными носителями. Кроме того, если функция g локально
пренебрежима относительно [л, то m(g)=0. Соотношение
(8.19.2) будет иметь место, если существует такое число с > О
и такое компактное множество К, что
I gn I ^ о локально почти всюду,
g"n = 0 локально почти всюду на Г\/С,
g~\\mgn локально почти всюду.
Получив продолжение меры т, значения которого лежат в
£'*, естественно попытаться определить условия, при которых
m(g) принадлежит пространству Е(аЕ'*). Приведем два ре-
результата, относящихся к этой задаче.
->
8.19.2. Пусть пг — мера Радона со значениями в Е, обладаю-
обладающая тем свойством, что для некоторого компактного множества
К в Т множество
{m(g): geJTVr, К), |?|<1} (8.19.3)
относительно слабо компактно. Покажем, что m(f)^E для
всякой функции f <= 3? (m), которая всюду ограничена и равна
нулю на Т\К.
8.19. Векторные меры 813
Действительно, пусть Л — множество всех тех функций
f^3?(m), которые обращаются в нуль на Т\К и для которых
|/| < 1. Введем множество В=А[)Ж(Т). Нам дано, что мно-
множество т(В) относительно слабо компактно в Е. Мы хотим по-
показать, что т(А) а Е. Достаточно установить, что множество
т(А) содержится в слабом замыкании в Е'* множества т(В).
Так как множество т(В) выпукло и уравновешено, то мы при-
придем к тому же, если докажем, чтр поляра т(В)° содержится в
т(Л)°. Соотношение х'^т(ВH означает, что
для всех g e В, т. е. что сужение на К положительной меры
\x'otn\ имеет общую массу, не превосходящую единицы. Но то-
тогда для всякой функции /еЛ, очевидно, \\ fd(xf ° т) ^1, от-
откуда следует, что хг е т (Л)°. |
Замечания. Предыдущее доказательство принадлежит
Бур баки [9, гл. VI, стр. 34]. Сходный результат можно полу-
получить иначе, исходя из общих свойств „слабо компактных линей-
линейных отображений (п. 9.4.14).
Для всякого такого продолжения продолженная мера т с
помощью формулы
т (Л) = т (%л)
порождает функцию множества со значениями в Е. Такое опре-
определение меры применимо ко всякому подмножеству Л в Г, ха-
характеристическая функция которого принадлежит 2' (т) и ко-
которое содержится ,в некотором компактном множестве. К, для
которого множество (8.19.3) относительно слабо компактно в
Е. Таким образом, полученная функция множества будет по
крайней мере слабо счетно аддитивна. Подробнее об этом бу-
будет сказано в п. 9.4.14.
8Л9.3. Продолжение возможно и в другом важном случае,
а именно когда множество
М--
■.{m(g):
содержится в некотором ограниченном секвенциально полном
подмножестве в Е. Тогда, как это сейчас будет доказано, мера
814 Гл. 8. Теория двойственности
m продолжается на S?l=2'l(ii) таким образом, что в резуль-
результате' получается непрерывное линейное отображение простран-
пространства Ll = Ll(ix) в £.
Действительно, если указанное условие выполняется, то мно-
множество М будет ограничено, секвенциально полно, выпукло и
уравновешено. Для всякой функции gJi£(T)
Для произвольного элемента h пространства 9?х можно выбрать
в Ж(Т) такую последовательность (gn), что lim N\(h— g>n)=0
и Ni(gn) ^N\(h). Отсюда следует, чго каждый элемент m(gn)
принадлежит Nx{h) »М и m(gi[— m(gj) ^ PifAf, где p*j-*O при
i, /->оо. Так как множество М и, следовательно, его образ при
всякой гомотетии являются секвенциально полными, то в Я су-
шествует х = \\mm(gn). Такие же рассуждения показывают, что
х зависит только от Л, а не от выбора последовательности (gn)<
Можно, таким образом, считать, что
Из ограниченности множества М в Е следует, что числовая
мера Радона х'огп при каждом х' имеет вид qv°|i, где ф^—
ограниченная измеримая функция. Отсюда вытекает, что
для /ig^1 и х*^Е'. Это соотношение годится для одвознач-
ного определения m(h). Оно также указывает на то, что m(h)
зависит только от класса ft функции /г, так что можно перейти к
факторпространству L1 и рассматривать m как линейное ото-
отображение L1 в Е. Непрерывность этого отображения является
следствием предыдущих рассуждений, поскольку из них выте-
вытекает, что m (h) е М при Nx (h) < 1. 1
Читатель может заметить, что в случае относительной слабой
компактности множества М в Е предыдущее условие выполняет*
ся и, кроме того, отображение rn\ L1 —>Е слабо компактно (§9.2).
Исходя из этого замечания, мы можем сформулировать первый
из нескольких результатов типа теоремы Лебега — Радона — Ни-
кодима. Его можно рассматривать, как один из вариантов тео«
ремы Филлипса [2, теор. 5.1 и 5.2]; существенно, что этот же
результат появляется еще раз в виде теоремы 9.4.7, доказывае-
доказываемой с помощью несколько иных методов. Для сравнения с фор-
8.19. Векторные меры 815
мулировкой Филлипса заметим, что мы получим условия на
меру т, эквивалентные условиям п. 8.19.2, если заменить множе-
множество М на множество
где А — относительно компактное универсально измеримое под-
подмножество в Т.
8.19.4. Теорема. Пусть m — такая мера Радона со значениями
в £, что множество
относительно слабо компактно в Е. Тогда существует такая ска-
лярно измеримая функция /: Т->£, что f(T)czMu
(g) = / gfdp
для каждого gei?1. Если пространство Е, кроме того, метри-
зуемо и квазиполно, то функцию f можно считать измеримой.
->
Доказательство. В соответствии с п. 8.19.3 меру m мо-
можно продолжить на i?1, и это продолжение после перехода к
факторпространству можно рассматривать как слабо компакт-
компактное линейное отображение пространства L1 в Е.
Рассмотрим теперь семейства я= (Аи), ^fe<tt, образованные
относительно компактными (или fx-интегрируемыми) универсаль-
универсально измеримыми множествами Akt для которых \i(Ah)>0. Такие
семейства я можно частично упорядочить. Будем говорить, что
я' > я, если объединение множеств из яг содержит объединение
множеств из я и если каждое множество из л/ либо содержится
в некотором множестве из я, либо не пересекается ни с одним из
множеств из я. Множество всех семейств я становится таким об-
образом направленным множеством. Каждому семейству я поста-
поставим в соответствие функцию /я: Т-*-Е, а именно
Функция fn измерима и, очевидно, принимает значения в Л7, так
как М выпукло и уравневешено и m(Ak)\i{Ak)^ M при ка-
каждом k.
816 Гл. 8. Теория двойственности
Как было отмечено в п. 8.19.3, существует такая ограничен-
ограниченная jx-измеримая функция ф^„ что хг ° щ = qy • pi. Следовательно,
С помощью рассуждений, похожих на те, которые были исполь-
использованы в лемме 8.171 (Ь), можно проверить, что.
->
Пгп^/Л(/), х'\ = срх, {t)
я
локально почти всюду.
С другой стороны, так как множество М слабо компактно, то
сеть (fn(t)) обладает при каждом t слабой предельной точкой.
Пусть такая слабая предельная точка f(t) выбрана для каждо-
каждого t. Предыдущее равенство показывает, что (/, х') = ух, локаль-
локально почти всюду для каждого х\ Таюш образом, f скалярна изме-
измерима и принимает свои значения в М. Кроме того, при каждом
хг имеем
(m (g), х') = J gd (х' о т) = J g%, dp = J g • (/, x') ф,
поэтому
> (g) = J
что и доказывает первую часть теоремы.
Для завершения доказательства надо показать, что метризуе-
метризуемость и квазиполнота пространства Е влекут измеримость функ-
функции /. Для этого достаточно доказать, что множество f(K\N)
сепарабельно для каждого компактного множества К а Т и со-
соответствующим образом подобранного пренебрежимого множе-
множества N из К- Это в свою очередь будет следовать из относитель-
относительной компактности множества
S = {m(A): А а К и [х-интегрируемо (или [х-измеримо)}.
Множество S является образом множества 2 = {хл: А а К}
из Sx относительно т. По теореме 4 21.2 множество 2 относи-
относительно слабо компактно в «271. Как мы увидим в гл. 9 (след-
(следствие 9.4.5), слабо компактное линейное отображение т: Ц-+Е
119. Векторные меры 817
переводит 2 в относительно компактное подмножество в Е, что и
требовалось доказать. 1
Для полурефлексивных пространств Е отсюда непосредствен-
непосредственно вытекает следующее, уже использованное в доказательстве
теоремы 8.18.3 следствие.
8.19.5. Следствие. Пусть Е — полу рефлексивное локально вы-
выпуклое пространство, m — такая мера Радона со значениями в
Е, что множество
ограничено в Е. Тогда существует такая скалярно измеримая
-> ->
функция /: Т-+Е, что f(T)czM и
= J gf d\k
для gG^1. Если, кроме того, пространство Е метризуемо, то
функция f измерима.
8.19.6. Уточнение теоремы 8.19.4 и следствия 8.19.5. Просма-
Просматривая доказательство теоремы 8.18.3, мы видим, что изучение
пространства, сопряженного к LpEi приводит к рассмотрению
векторных мер т, принимающих значение в сопряженном про-
пространстве Е', удовлетворяющих условию п. 8.19.2 и обладающих
конечной рг-вариацией (которую мы сейчас определим). Для тя-
ких мер Ф и л л и п с [2, теор. 5.5 и следствие 5.6] получил уточ-
уточнения теоремы 8.19.4 и следствия 8.19.5. Эти уточнения особенно
важны для случая, когда пространство Е/ рефлексивно. Это
имеет место тогда, когда само Е рефлексивно, и в этом послед-
последнем случае результаты Филлипса приводят к полному описанию
пространства, сопряженного к Lj?% (там же, теорема 5.7). Мы
сформулируем здесь эти уточненные результаты; доказательства
читатель может найти в работе Филлипса.
Пусть Е — банахово пространство и 1-^/?<оо. Будем гово-
говорить, что мера Радона m со значениями в Е имеет конечную
р-вариацию, если она удовлетворяет условию п. 8.19.2 и если,
кроме того,
где верхняя грань берется по всем конечным семействам (Л&),
состоящим из попарно не пересекающихся относительно ком-
компактных универсально измеримых множеств Ah из Г, для кото»
рых \i(Ah)>0.
818 Г л 8. Теория двойственности
Результаты Филлипса, второй из. которых непосредственно
следует из первого, могут быть сформулированы следующим
образом.
A) В предыдущих обозначениях пусть пг—мера Радона со
значениями в £, скалярно локально ^-абсолютно непрерыв-
наяу обладающая конечной р-вариацией и такая, что множество
\ т(А) . |[т(ЛI1 ^
относительно слабо компактно при каждом п. Пусть, далее, про-
пространство (Т, jli) а-конечно. Тогда существует такая измеримая
функция f: Т-+Е, что
для всех ^-интегрируемых множеств А при р > 1 или для всех
^измеримых множеств А при /7=1, и 1акаяу что
B) Пусть Е— рефлексивное банахово пространство, m—-
мера Радона со значениями в Е, которая скалярно локально
\х-абсолютно непрерывна и обладает конечной р-вариацией.
Пусть, далее, пространство (Г, jli) а-конечно. Тогда справедливы
все заключения утверждения A).
8.19.7. Меры со значениями в сопряженном пространстве.
Как отмечалось в п. 8.196, изучение пространства, сопряженного
к L% приводит к мерам со значениями в Ег. Поэтому мы наме-
намерены подробно рассмотреть этот частный случай.
Пусть Е — локально выпуклое пространство и Ег — его сопря-
сопряженное. Через E'w обозначим векторное пространство Ег, наде-
наделенное топологией о(Е',Е). Пространство Ew имеет своим со-
сопряженным пространство Е. Рассмотрим меру Радона m со зна-
чениями в Ew. Мере m поставим в соответствие числовые меры
Радона Хот, определенные равенством gd(x° m) = (x, m(g)),
где g^X{T). Функция g называется существенно интегрируе-
интегрируемой относительно т, если она существенно интегрируема отно-
относительно каждой из мер хот. В этом случае m(g) является
8.19. Векторные меры 819
элементом пространства Е =((EwY) , таким, что
(xt i
для всех х<= Е.
Нас опять будут интересовать условия, при которых m(g)
принадлежит £', а не только пространству £* zd E'. Естественно
воспользоваться результатами п. 8.19.1 и 8.19.3, где Е заменено
на Ew. Однако на практике обычно случается, что простран-^
ство Е бочечно, а тогда справедлив более сильный результат.
8.19.8. Предложение. Если пространство Е бочечно и m — ме-
мера Радона со значениями eE'w, то m(g)^E' для каждой суще-
существенно интегрируемой относительно m функции g.
Доказательство мы разделим на несколько шагов.
A) Так как отображение m: eyf(T)->E'w непрерывно и про-
пространство Е бочечно, то множество m(G) равностепенно непре-
непрерывно в Е' для всякого ограниченного подмножества G в Ж(Т).
Следовательно, найдется такая окрестность нуля U в Е, что
I Jgtf (*от)[<1 (8.19.4)
для g e G и х ^ U.
Пусть теперь g —существенно интегрируемая относительно
m функция, ограниченная и равная нулю вне некоторого ком-
компактного множества К с: Т. Покажем, что m(g)^E'. Для этого
заметим, что если К—произвольная положительная мера, отно-
относительно которой функция g измерима, то g является пределом
в i?!(X) такой последовательности (gn) из Ж(Т), что |gw|^
<sup|g|=c и gn = 0 вне некоторой компактной окрестности Ко
множества К. Возьмем в качестве G множество всех тех функций
из Ж(Т), которые обращаются в нуль вне Ко и равномерно огра-
ограничены по модулю числом с\ в качестве К возьмем меру |*о/п|.
Тогда из (8.19.4) следует, что
| J gd (х о ш)
для
Это показывает, что линейная форма х н-> (х, m (g)) непрерывна
на Е и, следовательно, m(g)^ Е\
820 Гл 8. Теория двойственности
B) Предположим теперь, что функция g существенно инте-
интегрируема относительно m и обращается в нуль вне счетного объ-
объединения компактных множеств Кп (я= 1, 2, ...), которые можно
считать возрастающими /Cncz/(n+i. Определим функцию gn сле-
следующим образом:
(л/ 8{t) при tEEiK« и \8(t)\<n,
\ 0 в противном случае.
В силу A) m(gn)^ E' для каждого п. Кроме того, для каждого
х е Е из теоремы Лебега о сходимости следует, что
(х, m (gn)) = J gnd {x о m) -► J grf (* о m) = (x, m (g)).
Так как пространство Е бочечно, то последовательность m(gn)
образует равностепенно непрерывное множество в Е\ поэтому
слабый предел этой последовательности m(g) непрерывен на Е.
Следовательно, и в этом случае m(g) ^E'.
C) Пусть, наконец, функция g лишь существенно интегри-
интегрируема относительно т. Каждому компактному множеству S в Т
сопоставим функцию gs = ^°Xs- Согласно B), имеем m(gs)^ E'
для каждого S. Кроме того,
К*. m(gs))\^$\gs\d\xom\^ $\g\d\xom\<+oo.
Пользуясь еще раз бочечностью пространства Е, приходим к вы-
выводу, что все элементы m(gs) попадают в некоторое равносте-
равностепенно непрерывное и потому слабо компактное подмножество в
Ег. Если множества S частично упорядочить по включению, то
сеть (m(gs)) будет иметь слабую предельную точку xr e E'. Для
заданного х функция g обращается в нуль локально почти всюду
относительно меры \хогп\ вне некоторого а-компактного множе-
множества S: поэтому
(х, mfe5))->(x,
Отсюда непосредственно следует, что (дс, m(g)) = (x, x') для ка-
каждого х9 так что m (g) =х' е Е'. |
8.19.9. Замечание. Если мера m скалярно локально абсо-
абсолютно непрерывна относительно р,, то из предложения 8.19.8
следует, что m(g)^E' для всякой функции gei?00^!), которая
8.19. Векторные меры 821
обращается в нуль вне некоторого компактного подмноже-
подмножества в Т.
8.19.10. Теорема Лебега — Радона—Никодима для мер со
значениями в Ew. Если функция /: T->E'W скалярно локально
интегрируема относительно |х, то можно попытаться определить
£ш-значную меру Радона т с помощью формулы
т(ё)= j gfdp (££=еТ(Г)) (8.19.5)
(ср. с (8.19.1)). Согласно теореме 8.16.1, мера пг, заданная соот-
соотношением (8.19.5), действительно является отображением про-
пространства Ж(Т) в Е\ если Е обладает свойством секвенциально
замкнутого графика. Далее "из определяющего равенства
{ху пг {g)) =*J g • (х,
следует, что отображение g*—>m(g) пространства Ж(Т) в Ew
непрерывно. Таким образом, если пространство Е обладает свой-
свойством секвенциально замкнутого графика, то формула (8.19.5)
определяет меру Радона пг со значениями в Ew Как мы видели
в § 8.16, всякое пространство Фреше обладает свойством секвен-
секвенциально замкнутого графика.
Мы рассмотрим сейчас задачу отыскания достаточных (а если
возможно, и необходимых) условий, при которых заданная мера
пг имеет вид (8.19.5). Простоты ради будем обозначать меру,
определенную формулой (8.19.5), через f-\x и говорить, что такая
мера локально абсолютно непрерывна относительно jx, распро-
распространяя таким образом- терминологию, которой мы пользовались
в случае числовых мер.
Очевидным необходимым условием того, что мера пг имеет
вид (8.19.5), является скалярная локальная абсолютная непре4
рывность относительно \х меры /л, т. е. локальная абсолютная
непрерывность относительно \i каждой из мер хот. В таком
случае элемент m(g) определен для всякой g^2?l(\i)t имеющей
компактный носитель (замечание 8.19.9). Заманчиво предполо-
предположить, что если Е—банахово пространство, то нужное нам необ-
необходимое и достаточное условие состоит в следующем.
Условие A). Для каждого компактного множества КаТ и
каждого числа е >0 существует такое число б = б(/(, е)>0, что
822 Гл. 8. Теория двойственности
\\m(g)\\4ie для всякой функции gs^fn), обращающейся в
нуль вне К и такой, что I Igldix^8'
Однако (Петтис [2, стр. 303, пример 9.4]) существуют
меры т, удовлетворяющие условию A) и тем не менее не имею-
имеющие вида /«pi. Известно также (Биркгоф [3, стр. 377, при*
мер 7]), что существуют меры вида f • ja, которые не удовлетво-
удовлетворяют условию A).
Дьёдонне [11, теор. 1] соформулировал условие, которое
представляется удовлетворительным во всех отношениях. Его
идеи получили дальнейшее развитие в книге Б у р б а к и [9,
гл. VI, стр. 35—41]. Нам понадобится несколько видоизмененная
формулировка условия Дьёдонне.
Условие B). Для любого заданного е>0 и любого компакт-
компактного множества КаТ существует такое компактное подмноже-
подмножество К! с: /(, что \i(K\K') < г и множество
, К') и
относительно слабо компактно в Е',
Рассуждения п. 8.19.2 показывают, что если мера m удовле-
удовлетворяет условию B), то множество элементов m{g), которое по-
получается, когда g пробегает все функции из S£(m), обращаю-
обращающиеся в нуль вне К' и такие, что \g(t) |^ 1, также относительно
слабо компактно в Е'.
Наша задача—показать далее, что условие B) и скалярная
локальная абсолютная непрерывность относительно \х меры m
достаточны для того, чтобы мера пг была локально абсолютно
непрерывной относительно \i.
<•
8.19.11. Предложение. Пусть мера Радона m на Т со значе-
значениями в Ёш скалярно локально абсолютно непрерывна относи-
тельно \i и удовлетворяет условию B). Тогда мера пг локально
абсолютно непрерывна относительно (х, т. е. существует такая
скалярно локально интегрируемая функция /: T->EW> что
m (g) = J gfd\i
для каждой функции g e 3?°°{\к), обладающей компактным но-
носителем.
8.19. Векторные меры 823
Доказательство разобьем на несколько этапов.
A) Пусть е и К заданы и К' выбрано согласно условию B).
Воспользуемся теоремой 8.19.4, заменив в ней Е на E'w, T на К!
и pi на ее сужение на К!. Из этой теоремы следует существование
функции fK,: Kr~+EWi образ которой относительно слабо компак-
компактен в E'w и для которой
== J gfK,d\i,
какова бы ни была функция gG^1, обращающаяся в нуль
вне /('.
B) Исчерпаем множество К возрастающей последователь-
последовательностью компактных множеств Кп и пренебрежимым множест-
множеством N, причем каждое из Кп является множеством типа множе-
множества К', фигурирующего в A). Множество К, таким образом,
разбивается на множества An = Kn\Kn-\ и N, где /Со=0. В си-
силу A) для каждого п существует такая скалярно измеримая
функция fn: An~>Ew с слабо относительно компактным образом,
что
для функций g e 3?1, обращающихся в нуль вне АПш
Так как мера пг локально абсолютно непрерывна относи-
относительно fx, то из формулы
(х, m(g))= I gd{xom)
следует, что m(g)=09 если g обращается в нуль вне .V.
Определим теперь функцию /я, положив ее равной fn на Ап
(м=1,2,...) и нулю на N. Очевидно, функция fK: K->E'W ска-
скалярно измерима. Кроме того, для всякой функции g^3?x(\\),
обращающейся в нуль вне некоторого Ап или вне N, имеет место
равенство
J
Если g"e«2?00(pi) и g обращается в нуль вне А", то
где go обращается в нуль вне N. Так как мера m локально абсо-
абсолютно непрерывна относительно |ы, то из результатов п. 8.19.1
824 Гл. 8. Теория двойственности
следует, что
m{g) = m {go) + 2m(g%An)- Цm(g%Afl\
причем ряд сходится в E'w. Поскольку для каждого п имеет ме-
место равенство
то в силу слабой сходимости указанного ряда следует, что ряд
(х, Тк) dp
сходится для каждого х е Е. Так как это верно для всякой функ-
функции g^S>co(\x)i которая обращается в нуль вне /С, то функция
(х, 1к) интегрируема на К при каждом х. Поэтому
(х, m (g)) = 2 (х> m (8%aJ) = S J ^ХлЛ ' <Я /^) Ф =
= | g B Хлд) • <^> W Ф = | g • <x,
где для обоснования перемены порядка интегрирования и сум-
суммирования надо воспользоваться теоремой Лебега 4.8.2. Таким
образом, для любой функции g e 2?°°(\л), обращающейся в нуль
вне /С, имеет место соотношение
m (g) = J g//^ ф.
C) На заключительном этапе разобьем пространство Т на
объединение компактных множеств Кг и локально пренебрежи-
мого множества N'. Каждое компактное множество пересекает
не более чем счетное число множеств К{. Полагая функцию /
равной fK. на множестве К% при каждом i и равной 0 на N', по-
лучаем такую скалярно измеримую функцию /: Т->Ет что
т (8) = J g/ Ф
для каждой функции geS'^dx), обращающейся в нуль вне не-
некоторого Кг-
Пусть теперь К — произвольное компактное множество и
функция g е 9?°°(\\) обращается в нуль вне К. Тогда g = 2
и из результатов п. 8.19.1 следует, что
т (g) =
8 19. Векторные меры 825
Этот ряд сходится в E'Wi причем суммирование распространяется
на не более чем счетное число тех индексов i9 для которых Ki
пересекает /С. С помощью рассуждений, похожих на использо-
использованные на втором этапе, получаем, что функция ,(л\ А интегри-
интегрируема на К при каждом х. Таким образом, функция / скалярно
локально интегрируема и
= J gfd\x
для каждой функции g e 3?°°(\\), обладающей компактным но-
носителем. |
Справедливо следующее частичное обращение последнего
результата.
8.19.12. Предложение. Пусть Е — сепарабельное пространство
Фреше и m — мера Радона со значениями в Ёт вида f • jx, где
f — скалярно локально интегрируемая относительно \х функция.
Тогда мера m скалярно локально абсолютно непрерывна относи-
относительно \i и удовлетворяет условию B).
Доказательство. Так как xom=(x,f)'\i, то ясно, что
мера m локально абсолютно непрерывна относительно \х.
Проверим выполнение условия B) п. 8.19.10. Пусть К—про-
К—произвольное компактное подмножество в Т и е > 0. В силу опре-
определения слабой измеримости и в силу предложения 8.15.3 суще-
существует такое компактное множество К'с= /С, что \i(K\K/) < e и
сужение f\K слабо непрерывно. Множество /(/С'), таким обра-
образом, слабо компактно и потому равностепенно непрерывно, т. е.
содержится в поляре U0 некоторой окрестности нуля U в Е. Но
тогда если g е <£Г (Г, /СО и J | g \ d\x < 1, то для x^U имеем
I <х, m (g)) I = | J г . {x,/) dvi
/)
g
Отсюда следует, что m(g)^ f/0, и так как £/° относительно слабо
компактно, то условие B) выполняется. 1
Комбинация последних двух результатов дает следующую
теорему.
8.19.13. Теорема. Пусть Е—сепарабельное пространство Фре-
<- г
шс\ m — произвольная мера Радона на Т со значениями в Ew.
<- <- <-
Для того чтобы мера m была представима в виде m = /.|i, где
826 Гл. 8. Теория двойственности
f — некоторая скалярно локально интегрируемая функция, необ-
необходимо и достаточно, чтобы мера m была локально абсолютно
непрерывна относительно \х и удовлетворяла условию B).
8.19.14. Предыдущие результаты имеют связь с некоторыми
общими понятиями, введенными Гротендиком [1, стр. 145 и
след.] и развитыми в работах Сингера [2—4].
Для простоты и для определенности будем предполагать, что
Т — компактное, а Е — банахово пространство. Упомянутые об-
общие понятия Гротендика приводят в этом случае к рассмотрению
£^-значных мер Радона m на 7\ которые являются «интегра-
«интегралами» в том смысле, что существует такая линейная непрерыв-
непрерывная, форма U на С(Т, Е), что
= (x, m(g)) teGEeT, *€=£). {8.19.6)
(Через С(Т,Е) здесь обозначается пространство непрерывных
функций g: T-+E с нормой ||g|| = sup \\l(t) ||.)
С другой стороны, мера m называется мажорированной
(Дьёдонне), если существует такая положительная мера Радо-
Радона тл на Г, что
J (8.19.7)
Кроме этих двух ограничений, введем еще одно постулирую-
постулирующее существование такой положительной меры Радона \х и такой
ограниченной скалярно измеримой функции /: Т—>EWy что
m(g)= j gfdtx (g€=e%T). (8.19.8)
Ясно, что из соотношения (8.19.8) вытекает (8.19.6), если по-
положить
Так же очевидно, что из (8.19.8) вытекает (8.19.7). Из дока-
доказательства предложения 8.19.11 следует (в силу компактности Г),
что (8.19.7) влечет (8.19.8).
Таким образом, соотношения (8.19.7) и (8.19.8) эквивалентны
и влекут за собой (8.19.6). С другой стороны Сингер (там же)
установил, что из (8.19.6) вытекает (8.19.7), так что все эти три
условия эквивалентны.
8.20. Сопряженное к LPE 827
8.20. Сопряженное к Le в случае, когда Е — банахово
пространство и 1 < р < оо
В § 8.18 для некоторых важных случаев мы описали про-
пространство, сопряженное к L^. Теперь мы обратимся к аналогич-
аналогичной задаче для пространств L% 1</?<оо. Всюду в этом пара-
параграфе мы будем предполагать, что пространство Е банахово.
Через р' будем обозначать показатель, сопряженный показателю
/?, так что р~1 + р'~ = 1.
8.20.1. Пусть F—непрерывная линейная форма на L%
Можно с таким же успехом рассматривать форму F как форму
на пространстве -?£, чтобы не усложнять обозначения. Наша4 за-
задача — изучить векторную меру Радона, ассоциированную с
формой F.
A) Если задана функция g^3i?(T), то. отображение
x*—>F(gx) является непрерывной линейной формой на £, по-
поэтому существует такой элемент m(g)^E\ что
Wm{g)\\<\\FhNp(g).
<- f
Таким образом, m есть мера Радона на Т со значениями в Ew.
На самом деле мера m является даже £'-значной мерой, где Е'
наделено своей сильной топологией.
B) Для фиксированного элемента х из Е отображение
g*—>F(gx) является непрерывной линейной формой на SS'9, по-
поэтому существует такая функция hx e J2?p, что
C) Комбинируя A) и B), получаем, что хо m = hx* jn, и, сле-
следовательно, мера m скалярно локально абсолютно непрерывна
относительно ji. Далее, J2*p аЛ?(т). Если jgS'p, to из опре-
определения m(g) (п. 8.19.7) следует, что
(х, m(g)>- J gd(xom) = J ghxd\i = F(gx).
Таким образом, соотнесения из A) продолжаются на все функ-
функции g из 2?р,
828 Гл. 8. Теория двойственности
D) Наша следующая задача — установить ограниченность
^-вариации меры т. Точнее, мы утверждаем, что
\\
S\\m(Ak)\\p' ^ „ г. |,Р'
НА*)*'-1 ^" "
для каждой конечной системы попарно непересекающихся инте-
интегрируемых множеств Ak с |л(/Ц)> 0.
Действительно, пусть элементы xk e E удовлетворяют усло-
условиям || xk ||^1, и пусть ^ — скаляры. Тогда имеют место соот-
соотношения
IS £*<**, m(Ak))\
Заменяя lh на ^-|л(Л^) р, получаем
"<^f m(Ak))\ <|| F || • [Si 6* \PV-
Варьируя xu и замечая, что р'1р = р'—1, получаем нужное нам
неравенство.
E) В качестве примера на применение неравенства Гёльдера
из D) можно получить, что
если интегрируемые множества Ah образуют разбиение множе-
множества А.
F) Введем теперь положительную функцию множества 5,
определяемую для всех интегрируемых множеств соотношением
5 (А) = sup 2II т Ш ||,
где верхняя грань берется по всем конечным разбиениям мно-
множества А на интегрируемые множества Ak. Из E) следует, что
Докажем аддитивность функции's. Пусть А=А' U Л", где
Л'ПЛ" = 0. Если множества At образуют разбиение множе-
множества Аг и множества А"— разбиение множества А", то взятые
вместе* они образуют разбиение множества Л, поэтому
8.20. Сопряженное к LPE 829
Так как суммы в правой части могут быть выбраны сколь угодно
близкими к s(A') и s(A") соответственно, то
s(A) >s(A')+s(A").
С другой стороны, если множества Ak образуют разбиение мно-
множества Л, то АкГ\А' образуют разбиение множества А', а
Ah f)A" — разбиение множества А". Так как мера т аддитивна,
то
(A"[}A
•
Последний член в правой части может быть сделан сколь угодно
близким к s(A), поэтому s(A') +s(A")^- s(A). Аддитивность, та-
таким образом, установлена.
G) Из утверждения F) можно вывести (упр. 4.39), что су-
существует такая положительная локально интегрируемая функ-
функция L, что
А
для всех интегрируемых множеств Л. В частности, так как
||т(Л)|| <5(Л), то для всех интегрируемых множеств Л имеем
А
Отсюда уже легко получить
для каждой функции g^Ji£(T) (в действительности для каждой
функции g ej?°°(|ji), обладающей компактным носителем).
(8) Теперь уже нетрудно показать, что мера т, которая, как
уже доказано, скалярно локально абсолютно непрерывна отно-
относительно (ы, удовлетворяет условию B) п. 8.19.10. Действительно,
так как функция L измерима, то по любым заданным компакт-
компактным множествам KczT и числу е>0 можно найти такое ком-
компактное множество К'а /С, что \х(К\К')< е и сужение L\K' не-
непрерывно. В частности, функция L ограничена на К\ скажем
£<с. Тогда если §^Ж(Т,К/) и Г |§-|ф<1, то из последнего
результата утверждения G) следует, что
830 Гл. 8. Теория двойственности
Теперь достаточно вспомнить, что всякое ограниченное по норме
множество в Ег слабо относительно компактно.
(9) Предложение 8.19.11 показывает далее, что существует
такая скалярно локально интегрирумая функция /: Т-**Е\ что
(8.20.1)
для каждой функции g e 3?°°(\х)у обладающей компактным но-
носителем. Из сравнения предложения 8.19.11 с утверждением B)
следует, что (x,f) = hx локально почти всюду при каждом х, по-
поэтому _
для каждого х
Так как каждая функция g из gv является в 3?* пределом
последовательности (gn), где каждая из функций gn принадле-
принадлежит 5?°°(|1), имеет компактный носитель и удовлетворяет нера-
неравенству |g"n|^|g"|, то, исходя из соотношения (8.20.1), простым
предельным переходом можно установить справедливость этого
отношения для всех функций g из 3?
В силу G)
для каждого х^Е и каждого интегрируемого множества Л, от-
откуда
локально почти всюду для каждого х е Е.
Из сопоставления (8.20.1) и C) вытекает, что
и по линейности что
/4j)=J4J, Г)Ф (8.20.2)
для любой простой функции g из S"e. Поэтому для всякой такой
функции g имеет место неравенство
11Л1-ЛМ5)- (8-20.3)
8 20. Сопряженное к LPE 831
8.20.2. Получив формулу (8.20.2) для простых функций
gG^, естественно ожидать и надеяться на то, что она в
действительности останется верной для всех функций g из сЗ*е-
Однако если на / не налагается дополнительных ограниче-
ограничений, то нельзя быть даже уверенным в том, что правая часть
равенства (8.20.2) определена (т. е. что функция (gj) интегри-
интегрируема). Сомнения немедленно рассеиваются, если известно, что
ибо тогда, как легко видеть, функция (g, f) измерима для всякой
функции g e J3?\.
Как мы сейчас покажем, если пространство Е сепарабельно,
то указанные трудности можно преодолеть.
A0) Если пространство Е сепарабельно, то функция f слабо
измерима (т. е. измерима как отображение Т в E'w), функция
11/11 измерима и
jJfdii = \\Ff. (8.20.4)
Действительно, из предложения 8.15.3 следует справедли-
справедливость первых двух утверждений, поэтому остается лишь доказать
(8.20.4). Вначале покажем, что левая часть не превосходит
правую.
Для этого достаточно показать, что
для каждого компактного множества Ко cz 7*. Чтобы это уста-
установить, в свою- очередь достаточно доказать, что это неравен-
неравенство имеет место, если заменить Ко компактным множеством
/Ccz/Co, для которого \1(Ко\К) произвольно мало. При этом
множества К можно выбирать так, чтобы функции Ц/Щ/С были
непрерывны, а функции f\K — слабо непрерывны. В силу этих
свойств непрерывности величина J || / ||р d\i не превосходит верх-
к
ней грани сумм вида
832 Гл. 8. Теория двойственности
где (Ah) обозначает произвольное разбиение множества К на
интегрируемые множества, a tk — произвольным образом вы-
выбранную точку из Ah. Далее достаточно рассматривать только
«произвольно мелкие» разбиения. Написанная выше сумма в
свою очередь не превосходит верхней грани сумм вида
где Хи — произвольно выбранные элементы из £, удовлетворяю-
удовлетворяющие условию НлгьИ •< 1. Эта сумма не превышает верхней грани
величин
JL L Г
где gft подчинены ограничению 2l I& f^i^k) ^ !• Рассматривая
произвольно мелкие разбиения, получаем; наконец, что послед-
последнее выражение не превосходит верхней грани выражений
\\{g, f)dm ,
где g = 2j ^k^kXAk "~ простые функции, удовлетворяющие усло-
условию Np(g) К 1. Из (8.20.3) следует, что
к
С другой стороны, из формулы (8.20.2) вытекает, что
1
\F (gj||*T[J*T'
и, значит,
Таким образом, для сепарабельных пространств Е формула
(8.20.4) доказана.
Так как изменение функции / на локально пренебрежимом
множестве несущественно, то можно следующим образом поды-
подытожить полученные результаты для случая сепарабельных про-
пространств.
8.20.3. Теорема. Пусть Е — сепарабельное банахово простран-
пространство и F — непрерывная линейная форма huJS^e, 1<р<оо. Тогда
существует такая слабо измеримая функция /: Т ~> E'w, что
(8.20.5)
8.20. Сопряженное к LE 833
для каждой функции g e J2?e и
1
f ]V. (8.20.6)
Обратно, всякая слабо измеримая функция /, для которой ко-
конечна правая часть в (8.20.6), определяет с помощью соотноше-
соотношения (8.20.5) непрерывную линейную форму F на ~5?£, для кото*
рой справедливо равенство (8.20.6).
Замечание. Непрерывную линейную форму на Le всегда
можно получить (переходя к факторпространству) из непрерыв-
непрерывной линейной формы на J?e- Поэтому излишне останавливаться
на формулировке наших результатов для Ье-
8.20.4. Случай, когда пространство Е рефлексивно. Если к
условиям теоремы 8.20.3 добавить рефлексивность простран-
пространства £, то Е\ обладая сильно сепарабельным сопряженным,
само будет сильно сепарабельно. Тогда слабо измеримая функ-
функция / даже сильно измерима (теорема 8.15.2) и потому принад-
принадлежит •29j£. Следовательно, если Е — сепарабельное рефлексив-
рефлексивное банахово пространство, то (Le)' ^ Le1* Более того, если
известно, что пространство Е рефлексивно, то условие сепара-
сепарабельности можно опустить, воспользовавшись результатами Фил-
липса, приведенными в п. 8.19.6.
Действительно, если пространство Е рефлексивно, то таким
же будет и его сопряженное Е' (в своей сильной топологии), по-
поэтому из утверждений C) и D) п. 8.20.1 и утверждения B)
п. 8.19.6 (где Е заменено на Е ) следует, что если пространство
(Г, |я) а-конечно, то существует такая функция / ^ ^е'* что
А
для всех интегрируемых множеств А и
Из этих двух свойств функции / легко вытекают соотношения
(8.20.5) и (8.20.6). Это дает следующий результат.
8.20.5. Теорема. Пусть Е — рефлексивное банахово простран-
пространство, (Г, \х)—о-конечное пространство и 1</?<оо. Тогда за*
ключения теоремы 8.20.3 останутся справедливыми, даже если
слабую измеримость 'функции f заменить ее сильной измери-
измеримостью. В частности, (LeY « LE^
834 Гл. 8. Теория двойственности
Замечания. A) См. Мурье [1] и Форте и Мурье [1].
B) Дэй [3] установил тот же результат для любого равно-
равномерно выпуклого банахова пространства Е.
C) Из того факта, что имеет место представление (8.20.5),
где / — сильно измеримая функция, следует, между прочим,
утверждение, что всякая скалярно измеримая функция
/: T->E'W, удовлетворяющая равенству (8.20.6), локально почти
всюду равна сильно измеримой функции. Здесь предполагается,
что Е— рефлексивное банахово пространство. Аналогичный ре-
результат можно найти в книге Бур баки [9, гл. VI, стр. 95,
упр. 25].
D) Исследование возможностей интегрального представле-
представления различных типов линейных операторов на Ьре привлекло
большое внимание. Эти и относящиеся к ним вопросы рассмо-
рассмотрены в работах Динкуляну [1—8], Динкуляну и Ф о я ш
[1], А. Ионеску Тулча и К. Ионеску Тулча fl—3].
УПРАЖНЕНИЯ
8.1. Пусть Е— полунормированное векторное пространство и Е'— его
сопряженное. Доказать, что сильная сепарабельность пространства Ег влечет
сепарабельность пространства Е. Показать, что обратное утверждение в об-
общем случае неверно.
8.2. Пусть Е — локально выпуклое пространство, В — ограниченное мно-
множество в Е. Доказать, что если В0 сильно сепарабельно в Е' (и, следовательно,
Е сильно сепарабельно), то множество В сепарабельно в исходной тополо-
топологии в Е.
[Указание. Множество В можно считать замкнутым, выпуклым и урав-
уравновешенным. Примените упр. 8.1 к полунормированному пространству Ев (ср.
с леммой 6.5.2).]
8.3. Пусть Е — сепарабельное рефлексивное полунормированное простран-
пространство. Доказать, что каждое ограниченное множество в Е слабо полуметри-
зуемо.
[Указание. Показать, что Е' сильно сепарабельно.]
8.4. Пусть Е~- рефлексивное полунормированное пространство, (хп) —
ограниченная в Е последовательность. Доказать, что (хп) обладает слабой
сходящейся подпоследовательностью.
[Указание. Применить упр. 8.3 к замкнутому векторному подпростран-
подпространству в Е, порожденному элементами хп, или воспользоваться теоремой Шмуль-
яна 8.12.1.]
8.5. Обозначения и условий примера 8.3.6. Кроме того, допустим, что мно-
множество Л ограничено и 1^р<оо. Доказать, что функция f принадлежит замы-
замыканию множества Л в топологии а („5^°°, J§*1) тогда и только тогда, когда
существует такая последовательность (fnj элементов из А, что fn->f ъ J~/?p.
[Указание. Необходимость доказана в примере 8.3.6. Для проверки до-
достаточности следует заметить, что сходимость fn ■**• / во2?р влечет сходимость
J gfn d\i-> ] gf d\i
для функций g из плотного в J2? множества.]
Упражнения 835
8.6. Обозначения и условия предыдущего упражнения. Показать, что если
функция f принадлежит о (t2?o°, ^^-замыканию множества Л, то суще-
существует такая последовательность (fn) czA, что /п->/ почти всюду.
[Указание. Воспользоваться упр. 8.5.]
8.7. Результат упр. 8.6 получен в предположении, что мера \х ограничена.
Показать, что он остается верным, если пространство (Т, \х) а-конечно.
[Указание. Пространство Т является объединением пренебрежимого
множества и последовательности (Кг) компактных множеств. Применить
упр. 8.6 к пространствам (Кг, \х | Кг) и использовать диагональный процесс]
8.8. Пусть Е и F — локально выпуклые пространства, и — линейное ото-
отображение Е в F и и* — его алгебраическое сопряженное. Рассмотрим следую-
следующие условия:
A) и непрерывно;
B) и ограничено;
C) u*(F')czEf.
Доказать, что C)=ЬB), A) ==> B) и A)=^>C). Вывести отсюда, что если
пространство Е борнологично, то все три условия равносильны. (Для случая
полунормированных пространств см. Макки [1, teor. II.4].)
8.9. Пусть Е — векторное пространство, р и q — две полунормы на Е. Обо-
Обозначим через Ер и Eq соответствующие топологические сопряженные, каждое
из которых является подпространством в Е*. Доказать, что для существования
такого числа с, что р(х) ^ cq(x) для всех х е £, необходимо и достаточно,
чтобы EpCzEfq. (Этот результат для случая нормированных пространств по-
получен Фихтенгольцем [1].)
8.10. Пусть Е и F — локально выпуклые пространства и м-—линейное
отображение, определенное на векторном подпространстве D из Е и принимаю-
принимающее значения в F. Показать, что отображение и\ рассматриваемое как отобра-
отображение F''->£', всегда замкнуто, если пространства F' и Е' наделены слабыми
топологиями.
8.11. Пусть Е — полное отделимое локально выпуклое пространство, ко-
которое не является полурефлексивным, и Е" — его второе сопряженное. Пока-
Показать, что Е тоще в Е".
8.12. Пусть Е — бесконечномерное банахово пространство. Доказать су-
существование взаимно однозначного непрерывного линейного отображения и
пространства /°° в Е. (Макки [2, теор. 1.1].)
[Указание. Показать, что можно указать такие бесконечномерные под-
подпространства (£ = )Мо=>М, zdM2=> ... в £ и такие элементы #п(я>1) из
£, что хп е Мп_{ \Мп и \\хп\\^\/п2. Рассмотреть отображение и: | ->
8.13. Пусть Т — отделимое локально компактное пространство, \i — поло-
положительная мера Радона на Т, Е — нормированное векторное пространство,
/ — такая функция на Т со значениями в Е, что
для каждого х'<=Е'. Доказать существование такого числа с>0, чте
для х' е £'.
836 Гл. 8. Теория двойственности
Исследовать возможности распространения этого результата на более
общие отделимые локально выпуклые пространства £ (ср. с упр. 8.24}.
[Указание. Рассмотреть полунорму N (х') = | (f, xr) | d\i и восполь-
воспользоваться леммой Фату.]
8.14. Рассмотрим функции ф вещественного переменного. Если ф — ска-
скалярная функция, то говорят, что она локально Липшице ва, если отношение
ограничено при а^ ti <t2^ b, для любых вещественных чисел а и 6, удов-
удовлетворяющих условию а < Ь (лричем верхняя и нижняя грани отношения мо-
могут зависеть от а и Ь). Это определение по сути дела применимо и к случаю,
когда функция ф принимает значения в некотором топологическом векторном
пространстве Е.
Пусть Е — квазиполное отделимое локально выпуклое пространство, f —
функция на R1 со значениями в £, п — целое неотрицательное число. Предпо-
Предположим, что при каждом хг е Е' функция х' ° / обладает локально липшицевой
п-й производной. Доказать, что функция f имеет п-ю производную в смысле
топологии в £ и что эта п-я производная локально липшицева.
[Указание. Воспользоваться индукцией по п, опираясь на теорему
8.3.4A). Для перехода от п к п + 1 положить
х {h) = /Г1 [D»f (t + h)- Dnf (t)]
и рассмотреть элементы [х(h) —x(k)](h — k)~l, где 0, h, k попарно различны.]
8.15. Пусть Е — отделимое локально выпуклое пространство, удовлетво-
удовлетворяющее условию (*) предложения 8.14.3, / — функция со значениями в Е, го-
голоморфная в области Q комплексной плоскости, р — непрерывная полунорма
на Е. Показать, что если с — такое число, что p°f^c на Q, то либо
A) ро fz=c на й,
либо
B) p°f <с на Q.
Замечание. Если р° /= | х' ° / |, где х'^Е\ то сформулированный ре-
результат может быть усилен следующим образом: |#'°/| не допускает локаль~
ного максимума в Q, если только функция x'°f не постоянна на Q.
[Указание. См. п. 8.14.7. Вначале показать, что
о
при to^Q п достаточно малых г !> 0. Показать затем, что множество точек
/е Й, для которых р °f(t) = с одновременно открыто и замкнуто в п.]
8.16. Обозначения и предположения предыдущего упражнения. Кроме того,
допустим, что область Q относительно компактна. Доказать, что если k — та-
такое число, что
lim sup
для каждой точ&и s границы Q области Q, то_р° f(t) ^ k для t s Q.
[Указание. Определить функцию g на Q, полагая
g(t)= lim sup p°f(t').
t'&Q tf*t
Упражнения 837
Заметить, что функция g полунепрерывна сверху, g^k на Q и £=Р°/ на Q.
Функция g примет свое наибольшее значение, скажем т, в некоторой точке
из п. Воспользовавшись предыдущим упражнением, показать необходимость
неравенства т ^ k]
8.17. Пусть ф — скалярная функция, голоморфная на открытом единичном
круге с центром в начале координат комплексной плоскости. Показать, что
при 1 ^ р < оо выражение
[2я
о J
Up
есть возрастающая функция от г для 0 ^ г < 1.
Замечание. Этот результат является основным в теории пространства
Харди Нр. Для дальнейшего изучения этих пространств см. Зигмунд [2,
т. 1, гл. VII], Данфорд и Шварц [1, стр. 391, 406] и Уолтере [1,2].
[Указание. Применить предыдущее упражнение.]
8.18. Пусть Е, F и G — локально выпуклые пространства, Т — отделимое
локально компактное пространство с положительной мерой Радона [i. Предпо-
Предположим, что е и f — функции, отображающие соответственно Т в Е и Т в F>
и В — непрерывное билинейное отображение произведения Е X F в G. Опре-
Определим функцию g : Г-> G равенством
g()
Доказать, что
(a) если е и f измеримы, то такова же функция g\
(b) если е скалярно измерима, / измерима, а пространство F метризуемо,
то g скалярно измерима.
Показать, далее, что в (Ь) достаточно предположить раздельную непре-
непрерывность билинейной формы В.
8.19. Пусть Т и \х те же, что и в предыдущем упражнении, и Я— банахо-
банахова алгебра. (Это означает, что Е — комплексное банахово пространство с
таким билинейным отображением (х, у) I—> ху произведения ЕхЕ ву Еу что*
(ху) z = x (yz) и || ху ||< || х II • || у || для х, у, г е= Е.)
Показать, что если / е JgpE и g e «SPjg' (определения см. в § 8.18), то
j \\f(t)g(t)\\dii(t)<Np(f)-Np,{g).
8.20. Пусть Е — банахова алгебра, 71=R1 и \i — мера Лебега на Т. Пока-
Показать, что если функции f и g принадлежат Jg*xE, то функция s ь-> f (t - s) g (s)
принадлежит JgxE для почти всех t, и что если положить
= J f(t-s)g(s)d\i(s)
для таких t и положить /г=Ов противном случае, то h e ^ХЕ. Можно назвать
h сверткой f и g, h = f*g. Пространство Jg'E является, таким образом, ба-
банаховой алгеброй. (Относительно полноты см. п. 8.18.1.)
Исследовать случай, когда Т — локально компактная группа и ц — левая
мера Хаара на Т.
838 Гл. 8. Теория двойственности
8.21. Пусть Е — топологическое векторное пространство, U— окрестность
нуля в £, £/° —ее поляра в Е'. Обозначив через Е'ц векторное подпростран-
подпространство в Е\ порожденное полярой U0. Показать, что Ец является банаховым
пространством, если в качестве его замкнутого единичного шара взять мно-
множество U0, при этом норма задается соотношением
|| *' || = inf {Я > 0: x'e=XU°}
для х е Ец.
8.22. Пусть Е — топологическое векторное пространство, Е' — его тополо-
топологическое сопряженное. Векторное подпространство D в Е' называется опре-
определяющим подпространством в Е\ если выполняется следующее усло-
условие: существует семейство (Ui) окрестностей нуля в Е, гомотетические образы
которых образуют базу окрестностей нуля в Е, обладающее тем свойством, что
для каждого i существует такое число а* > 0, что множество D f) U°t слабо
плотно в ctjf/j-. Доказать, что это возможно тогда и только тогда, когда
р( (х) < аГ1 sup {| (х, х) |: / е D П U]}
для всех х&Е, где Pi — функционал Минковского замкнутой выпуклой урав-
уравновешенной оболочки множества Ui в Е.
Доказать, что если Е — отделимое локально выпуклое пространство, то
всякое определяющее подпространство в Е' отделяет точки из Е.
8.23. Пусть Е — локально выпуклое пространство и D — секвенциально
сильно замкнутое определяющее подпространство в Е'. Показать, что если
множество Ас=Е таково, что
sup {| (*, х?) |: х <= А) < + оо
для каждого xr gD, то Л ограничено в Е.
[Указание. Используя предыдущие два упражнения, показать, что мно-
множество А поглощается замкнутой выпуклой уравновешенной оболочкой каж-
каждого из множеств /7г-.]
8.24. Пусть Е — отделимое локально выпуклое пространство, D — секвен-
секвенциально сильно замкнутое определяющее подпространство в Е'. Пусть далее
Т — отделимое локально компактное пространство, \i — положительная мера
Радона на Г и (fa\ — семейство функций, отображающих Т в Е. Пусть, на*
конец,
up Г|(/а>
а J
sup
a
для каждого xf e D. Показать, что существует база окрестностей нуля U в Е,
для каждой из которых существует такое число с — си, что
sup | | (fa, x') I
a J
для /EDf]C/°. Ср. с упр. 8.13.
[Указание. Рассмотреть полунорму
a J
на Ец П D, где Ui — множество из упр. 8.22.]
Упражнения 839
8.25. Пусть Е — секвенциально полное отделимое локально выпуклое про*
странство, Т — отделимое локально компактное пространство, \х — положи-
положительная мера на Г и f:T->E— скалярно локально интегрируемая функция*
Допустим, что
A) ф/ d\i.^ E для каждой функции ф<=е%Г(Г),
B) J | (/, x')\d\i< + oo для х' €= D,
где D — секвенциально сильно замкнутое определяющее подпространство в Е\
Доказать, что ф/ d\i е Е для каждой функции q>^C0(T) и „цто соответствие
ф|—> ф/ d\i есть непрерывное отображение пространства С(Т) в Е. Вы-
Вывести отсюда, что | (f, x') | dpi < + оо для каждого элемента х'^Е'.
[Указание. Используя упр. 8.24, показать, что если феС0(Г) являет-
является равномерным пределом последовательности ф^е^ (Г), то интегралы
/фя ф образуют последовательность Коши в Е.]
8.26. Пусть Е — банахово пространство, D — сильно замкнутое определяю-
определяющее подпространство в Е\ (ап) —последовательность элементов из Е. Допу-
Допустим, что 2 I (а«> *') I < °° Для х' е D. Показать, что ряд 2 I М а/г схо"
дится в Е для каждого элемента ^sc0 и что соответствие
является непрерывным отображением пространства с0 в Е.
[Указание. Это упражнение является частным случаем предыдущего.]
8.27. Пусть Т — отделимое локально компактное пространство с положи-
положительной мерой Радона \i на нем, (ип)—последовательность элементов из
J2?1 = Jg*1 (Ту ц). Положим f (n)= fun d\i. Показать, что если (ап) — такая
последовательность положительных чисел, что 2 ап I f (п) I < + °° Для каж-
каждой функции f е Со (Г), то ряд 2 ап$пип сходится в J2?1 для каждой после-
довательности скаляров (Рп), такой, что |Зп->0 при я->оо.
Аналогичным образом показать, что если ип^С0 (Г) и ^ап\ё (п)\ < + °°
для каждой функции я е «571» то РЯД 2 an$nUn сходится в С0(Г), если
рп->0 при п->оо. Здесь предполагается, что Т является носителем меры \х.
Примените эти результаты к случай, когда Г== [0, 1], \i — сужение меры
Лебега на Г и un(t)=tn. Докажите, что тогда и только тогда
\ f(t)
tndt
oo для каждой функции /<=С [0, 1], когда V
/1+1
< -t- оо.
[Указание. Воспользоваться упр. 8.26, положив
840 Гл. 8. Теория двойственности
8.28. Пусть Е — банахово пространство и 1 ^р^оо. Показать, что про-
пространство JS*^ банахово.
[Указание. Видоизменить доказательство для случая скалярных функ-
функций.]
8.29. Пусть Е — банахово пространство, Kip<oo. Показать, что простые
функции (п. 8.17.1) образуют множество, плотное в J3?PE.
Следующие ниже четыре упражнения касаются связи между ограничен-
ограниченностью относительно структуры порядка и непрерывностью линейных форм и
отображений,, определенных на топологических пространствах Рисса. Система'
тическое изучение этого вопроса в рамках общей теории упорядоченных век-
векторных пространств предпринято Ш е ф е р о м [1—3] и Кистом [1].
8.30. Пусть Е — локально выпуклое пространство, (Хп)—такая числовая
последовательность, что ряд 2 №п\ сходится, и (хп)—ограниченная после-
последовательность в Е. Доказать, что частичные суммы ряда 2 ^пХп образуют
последовательность Коши в Е.
Некоторые определения. Пусть Е — пространство Рисса (= векторная ре-
решетка; см. п. 4.23.1). Множество AczE называется ограниченным отнеси-
тельно структуры порядка (или, короче, о-ограниченным х)), если оно
содержится в некотором отрезке
[*', х"] - {х €= Е: х*<х<х"),
где *', х"е£; это равносильно существованию такого элемента а^Е, что
| х | ^ а для каждого х^А. Множество А называется о-выпуклым, если из
соотношений х^А, у^Е и | у | ^ х следует, что у^А.
Под топологической векторной решеткой будем, понимать вектор-
векторную решетку £, которая является также и топологическим векторным про-
пространством, причем A) множество Е+ = {#е Е- х > 0} замкнуто в£и B) су-
существует база окрестностей нуля в Е, образованная о-выпуклыми множествами.
Локально выпуклой топологической векторной решеткой (или,
короче, локальна выпуклой решеткой) будем называть топологическую
векторную решетку, топология которой локально выпукла (ор. Б и р к г о ф
[2, стр. 238 и далее]?.
В топологической векторной решетке всякое о-ограниченное множество
ограничено. Обратное, вообще говоря, неверно. Это видно, например, из рас-
рассмотрения пространства lp (\ ^ p <оо) с обычной топологией и с обычным
порядком.
Если Е и F — векторные решетки и и: E->F, то говорят, что отображе-
отображение и положительно (и пишут и>0), если u(E+)aF+. Отображение и
называется о-ограниченным, если оно переводит всякое о-ограниченное
множество из Е в о-ограниченное множество из F. Эти термины применимы,
в частности, к линейным формам на вещественной векторной решетке (т. е.
к векторной решетке, «базисное» векторное пространство которой веще-
вещественно).
8.31. Пусть Е — топологическая векторная решетка. Доказать, что всякая
ограниченная линейная форма на Е о-ограниченна. Показать, что обратное
утверждение также верно, если пространство Е секвенциально полно и ло-
локально выпукло.
[Указание. При доказательстве второго утверждения можно считать,
что рассматриваемая линейная форма f ^ 0 (см. следующее упражнение)).
1) о-—первая буква английского слова order (порядок). — Прим. ред.
Упражнения 841
Если форма / не является ограниченной, то существует такая ограниченная
последовательность (хп), что \f(xn)\^n2. Показать, что можна считать
хп ^ 0, и затем рассмотреть ряд 2 п~2хп\ использовать упр. 8.30.]
8.32. Пусть Е — топологическая векторная решетка. Показать, что всякая
о-ограниченная линейная форма / на Е может быть представлена в виде раз-
разности /=f+ — f- двух положительных линейных форм, причем если форма /
ограничена (соотв. непрерывна), то и формы /+ и /~ можно считать ограни-
ограниченными (соотв. непрерывными).
Вывести отсюда, что топология а (£,£') обладает базой окрестностей
нуля, образованной о-выпуклыми множествами, и что если пространство Е
отделимо и локально выпукло, то положительные линейные формы на Е от-
отделяют точки из Е.
[Указание. Определить /+ для х ^ 0, положив
Показать, что определенная таким образом функция /+ аддитивна на Я+ и,
значит, может быть продолжена по линейности на Е. Ср. с методом, исполь-
использованным в гл. 4 для мер Радона.]
8.33. Пусть Е — локально выпуклая секвенциально полная решетка, F —
топологическая векторная решетка, u\E->F — о-ограниченное линейное ото-
отображение. Доказать, что и ограничено (и потому непрерывно, если простран-
пространство Е борнологично, a F локально выпукло).
[Ука'зание. Пусть (хп) —ограниченная последовательность в Е и уп**
s=u(xn). Надо показать, что последовательность (уп) ограничена в F. Восполь-
Воспользоваться упр. 8.30 и показать, что для всякой последовательности (Хп) с
N
2 I А,,1* | < + °° СУММЫ 2 ^пУп ограничены по N.]
'1
Некоторые определения. Пусть X и Y — топологические векторные про-
пространства и Т, Т\, ..., Тп—непрерывные линейные отображения простран-
пространства X в Y. Обозначим через N замыкание в Y множества {0}сиУ. В последую-
последующих трех упражнениях будет рассмотрено некоторое условие, которое назовем
условием А. Оно распадается на две части, первая из которых формулируется
следующим образом:
(А1) Если х е= X и Тих = 0 для 1 < k < л, то Tx<=N.
Рассмотрим векторное подпространство V в Кп, образованное элемен-
элементами (Т\Х, ..., Тпх), когда х пробегает X. Согласно (А1), можно определить
линейное отображение L: V->Y/N, полагая
£ (Уи • • •» Уп) = Тх (mod N),
если (уи ..., уп) = (Г,*, •.., Тпх) е= V.
Вторая часть условия А формулируется так:
(А2) Отображение L: V-+Y/N непрерывно (V рассматривается как под-
подпространство произведения Ynt наделенного топологией произведения).
8.34. В только что приведенных обозначениях пусть пространство Y ло-
локально выпукло, и пусть выполнено условие А. Доказать, что
R(T')czR(T[)+ ... +R(T%, (8.34.1)
где «Ry> означает «образ», а штрихи —сопряжение, так что Tf$ Т^
суть отображения Y' в X'.
842 Гл. 8. Теория двойственности
[Указание. Взять произвольный элемент у'<^У и рассмотреть линей-
линейную форму на V, которая переводит (Т{х, ..., Тпх) в (Тх, у'). С помощью
теоремы Хана — Банаха продолжить ее на Yn.]
8.35. Во введенных перед упр. 8.34 обозначениях пусть Y'° = N и простран-
пространство V борнологично. Показать, что если имеет место соотношение (8.34.1), то
выполнено условие А.
[Указание. Сначала доказать, что выполнено условие (А1), так что
можно определить L. Показать затем, что V определено на всем пространстве
У'. Использовать теорему 8.П.З.]
8.36. Рассмотреть предыдущие два упражнения в случае полунормирован-
полунормированного пространства Y. Показать, в частности, что если р — полунорма на У,
определяющая его топологию, то для существования такого числа с, что
необходимо и достаточно, чтобы для каждого элемента y'^Y' можно было
указать такой набор элементов у[, ..., уп е Y\ что
k
n
Здесь \\у'\\ обозначает норму элемента у' в пространстве У, сопряженном к У
относительно р, т. е.
Замечание. Случай, когда X—Y, п=\ и Т — тождественное отобра-
отображение, тесно примыкает к содержанию § 8.6 (см., в частности, следствие 8.6.9).
Ср также с техникой, использованной в § 5.14.
8.37. Пусть Е — гильбертово пространство, А и В — два непрерывных эн-
эндоморфизма в £, Л* и В* — их гильбертовы сопряженные (п. 1.12.8). Предпо-
Предположим, что существует такое число k < 1, что
\(Ax\Bx)\<k\\Ax\\-\\Bx\\ (X€=E).
Доказать, что («R» обозначает «образ»)
[Указание. Вначале показать, что
|| Ах || < const || Ах + Вх || (х е= Е).
Затем незначительно видоизменить методы, примененные в предыдущих трех
упражнениях.]
8.38. Пусть Q — открытое множество в Rn, P(D)—линейный дифферен-
дифференциальный оператор в частных производных с постоянными коэффициентами и
1 ^ р <оо. Показать, что уравнение
Упражнения 843
тогда и только тогда разрешимо при каждом (peLp (Q)y когда
для всех « g ^ (Q) (постоянная может зависеть от P(D), Q и р).
[Указание. Применить упр. 8.34—8.36, положив X = Q) (Q) со своей
собственной топологией, Y' = 3) (Q) с нормой, индуцированной из Lp(Q), n=\t
Т TP(D)]
8.39. Обозначения те же, что и в упр. 8.38. Предположим, что множество Q
ограничено и оператор P(D) имеет на Rn фундаментальное решение Е, при-
принадлежащее Lfoc (Rn). Показать, что заключения упр. 8.38 справедливы для р,
удовлетворяющего неравенствам 1 ^ р <оо и р ^ q.
[Указание. Оценить сверху функцию f—E*(p (ф полагается равным
нулю вне Q).]
Замечания. В § 5.14 было показано, что при р=2 условия упр. 8.38
выполняются для любого оператора P(D)=^Ot причем даже для неограничен-
неограниченного множества Q.
8.40. Пусть Е — нормированное векторное пространство, Е' — его сопря-
сопряженное, Е" — его второе сопряженное. Будем считать, что Е вложено в Е"\
Обозначим через 2 и 2" замкнутые единичные шары соответственно в Е и E"g
Из теоремы 8.1.5 о биполяре следует, что 2 о(Е", £')-плотно в 2".
Привести пример, показывающий, что, несмотря на это, 2", вообще го-
говоря, содержит элементы, которые не являются а(£", £')-пределами последо-
последовательностей в Е.
[Указание. Рассмотреть пространство E — Ll(T, jj,), соответствующим
образом подобрав Т и \х. Или, иначе, рассмотреть пространство Е=С0(Т), где
Т — соответствующим образом подобранное отделимое локально компактное
пространство. Пользуясь теоремой Бэра о категориях 0.3.15, показать, что су-
существует «много» ограниченных универсально измеримых функций на Г, не
являющихся пределами последовательностей непрерывных на Т функций.]
8.41. Пусть Е — рефлексивное пространство Фреше. Доказать, что про-
пространство Е' совершенно полно в своей сильной топологии и что всякое сильно
замкнутое векторное подпространство в Е' является £г-полным в индуциро-
индуцированной топологии.
8.42. Пусть Е — рефлексивное пространство Фреше, V—векторное под-
подпространство b£'hF — бочечное пространство. Предположим, что и — линей-
линейное отображение подпространства V на F, график которого замкнут в произ-
произведении Е' X F, наделенном произведением исходной топологии в F и сильной
топологии в Е'. Показать, что отображение и открыто (топология в V индуци-
индуцируется сильной топологией из Е').
8.43. Пусть Е — рефлексивное пространство Фреше, F — бочечное про-
пространство и v\ F-> Е' — линейное отображение, график которого замкнут в
произведении F X Е\ наделенном произведением исходной топологии в F и
сильной топологии в Е'. Показать, что отображение v непрерывно.
Замечание. Сравните результаты последних двух упражнений с ре-
результатами Гротендика [9].
8.44. Пусть Е и F — рефлексивные (или правильные) пространства Фреше
и и — линейное отображение пространства Ег на F'. Допустим, что график ото-
отображения и замкнут в произведении Е' X Fr относительности произведения
сильных топологий |3(£', Е) и fi(F't F). Доказать, что отображение и открыто
в сильных топологиях.
844 Гл. 8. Теория двойственности
[Указание. Воспользоваться теоремой 6.7.2 и предложениями 8.4.17 и
8.4.18.]
Замечание. Этот результат и результат следующего упражнения были
использованы Мальгранжем [1] при изучении уравнений, содержащих
свертки.
8.45. Пусть Е и F — рефлексивные пространства Фреше и v: F'-^E'— ли-
линейное отображение, график которого секвенциально замкнут в произведении
F' X Е' относительно произведения сильных топологий. Показать, что отобра-
отображение v непрерывно в сильных топологиях.
8.46. Пусть Е — банахово пространство, М — замкнутое подпространство
в Е. Показать, что если Е рефлексивно, то таким же будет и факторпростран-
ство Е/М.
Замечание. Существуют рефлексивные пространства Фреше Е, обла-
обладающие такими замкнутыми векторными подпространствами М, что фактор-
пространство Е/М не является рефлексивным (см. Кёте [5, гл. V]). Отсюда
следует существование ограниченного подмножества в Е/М, не являющегося
образом никакого ограниченного подмножества в Е относительно канониче-
канонического отображения и пространства Е на Е/М, и это несмотря на то, что и —
непрерывное открытое отображение пространства Е на Е/М1 (См. также Бур-
баки [7, стр. 278, упр. 216].)
8.47. Показать, что всякое сепарабельное банахово пространство Е изо-
изоморфно факторпространству пространства Iх.
Вывести отсюда существование такого замкнутого векторного подпро-
подпространства М в Z1, что V-/M содержит слабо сходящуюся к нулю последователь-
последовательность, не являющуюся образом никакой слабо сходящейся к нулю последова-
последовательности в Iх относительно канонического отображения Iх на 1Х/М.
Этот пример принадлежит Гротендику [7, стр. 129 упр. 4].
[Указание. Для доказательства первой части выбрать в Е такую по-
последовательность (ап) с ||flnllel, которая порождает плотное в Е подпро-
подпространство. Рассмотреть отображение
пространства Iх в Е.
Для доказательства второй, части применить полученный результат к се-
парабельному банахову пространству Е, в котором существует слабо сходя-
сходящаяся к нулю, но не сходящая к нулю последовательность, и воспользоваться
следствием 4.21.7.]
8.48. Пусть Е и Е; — векторные пространства в двойственности и @ — воз-
возрастающая направленная система слабо ограниченных подмножеств в Е, объе-
объединение которых совпадает с Е. Рассмотрим в Е' топологию Г@ (§ 8.3). Пусть
Mi и М2 — векторные подпространства в Е', Показать, что Мх и М2 имеют одно
и то же замыкание (относительно Т@) тогда и только тогда, когда а(Е, М{) и
о(Е, М2) индуцируют в каждом Ле@ одну и ту же топологию. (Люкс ем-
бург [2].)
8.49. Пусть Е, Е; и @ — те же, что и в предыдущем упражнении, и М —
векторное подпространство в Е'. Показать, что замыкание М (относительно
Г@) совпадает с множеством всех элементов *'€=£', сужения которых х'\А
непрерывны в топологии а(Е} М)\А для каждого Ле<2>. (Люксембург
й-)
Упражнения 845
8.50. Пусть Е — бочечное пространство, F — векторное пространство,
и: Е->• F — линейное отображение и F' — векторное подпространство в F*
(алгебраическом сопряженном к F). Предположим, что B>—такая система
подмножеств в F*y что каждое множество А^& содержится в слабо замкну-
замкнутой выпуклой уравновешенной оболочке в F* некоторого слабо ограниченного
подмножества из F'. (Эпитет «слабый» относится здесь к топологии сг(/7*, F).)
Показать, что непрерывность отображения и в топологии а(/\ F) влечет
его непрерывность в топологии Г@ в F.
8.51. Пусть Т — отделимое локально компактное пространство, ()
пространство всех мер Радона на Т. Предположим, что Е— бочечное про-
пространство и и: E->gM (T) — линейное отображение, непрерывное в широкой
топологии о(<*М(Т)у £&(Т)) в <Jl(T). Показать, что
lim
для каждого компактного множества КаТ.
[Указание. Воспользоваться предыдущим упражнением.]
ГЛАВА 9
Теория компактных операторов
9.0. Предисловие
Эта глава посвящается систематическому изложению неко-
некоторых общих результатов, касающихся компактных линейных
отображений одного локально выпуклого пространства в дру-
другое. В последних параграфах излагается уже почти классиче-
классическая теория Рисса. Первоначально эта теория применялась к
банаховским пространствам, и это все еще наиболее обычная
сфера ее приложения. Мы увидим, однако, что некоторые ре-
результаты естественным и полезным образом обобщаются на бо-
более общие типы локально выпуклых пространств.
9.1. Компактные и предкомпактные множества
В этом параграфе приводится несколько элементарных тео-
теорем о компактности и предкомпактности подмножеств локально
выпуклого пространства.
9.1.1. Предложение. Пусть (£*, Е')—дуальная пара. Множе-
Множество А в Е слабо ограничено тогда и только тогда, когда оно
слабо предкомпактно.
Доказательство. Это очевидно. |
9.1.2. Предложение. Пусть Е — локально выпуклое простран-
пространство. Множество А в Е предкомпактно тогда и только тогда,
когда (а) Л ограничено и (Ь) индуцированная в А равномерная
структура совпадает с индуцированной слабой равномерной
структурой.
Доказательство. Условия достаточны, так как Л, будучи
слабо ограниченным, слабо предкомпактно (предложение 9.1.1).
Необходимость условия (а) тривиальна.
При доказательстве необходимости условия (Ь) можно пред-
предположить, что Е отделимо и полно. Тогда предкомпактность
множества А означает его относительную компактность в Е. В то
же время Е можно рассматривать как подмножество простран-
пространства С(Е') непрерывных числовых функций на пространстве Е\
наделенном своей слабой топологией. Пусть U — произвольная
9.1. Компактные и пред компактные множества 847
окрестность нуля в Е; тогда поляра U0 слабо компактна. Так
как исходной равномерной структурой в Е является структура
равномерной сходимости на полярах U°, то A\U° (множество
сужений на U0 функций на Ег, определяемых элементами из А)
относительно компактно в CU(U°). В силу теоремы, обратной
к теореме Асколи (п. 0.4.11, предложение), множество А \ U°
равностепенно непрерывно. Но тогда из предложения 0.4.9 сле-
следует, что равномерная структура в А \ U0 совпадает с структурой
равномерной сходимости в U0. Отсюда уже легко вытекает усло-
условие (Ь). |
9.1.3. Предложение. Пусть Е — локально выпуклое простран-
пространство, А — предкомпактное подмножество в Е. Тогда выпуклая
уравновешенная оболочка множества А предкомпактна.
Доказательство. Это непосредственно вытекает из опре-
определения предкомпактности. I
9.1.4. Следствие. Пусть Е — локально выпуклое простран-
пространство, А — предкомпактное подмножество в Е и В — замкнутая
выпуклая уравновешенная оболочка множества А. Для того
чтобы оболочка В была компактна, необходимо (а в случае от-
отделимости пространства Е и достаточно), чтобы она была
полна. |
Замечание. Это — слабая форма теоремы Крейна (§ 8.13).
Доказательство этой теоремы в такой форме намного проще;
см. замечание 8.13.4B).
9.1.5. Предложение. Пусть Е — локально выпуклое простран-
пространство, А — полное подмножество в Е. Тогда множество А полно
в любой локально выпуклой топологии Т, более сильной, чем
исходная топология, и обладающей базой окрестностей нуля,
образованной множествами, замкнутыми в исходной топологии.
Доказательство. Обозначим через То исходную тополо-
топологию в Е. Пусть (Хг) — произвольная сеть Коши в Л в топологии
Т. Тогда (х^ тем более является сетью Коши в топологии То.
Так как множество А полно, то в Л существует точка х, к кото-
которой сеть (Xi) сходится в топологии То. Достаточно показать, что
(х^ сходится к х в топологии Г. Пусть V—произвольная Го-
замкнутая Г-окрестность нуля. По условию х{ — Xj e V для всех
достаточно больших i и /. Считая i фиксированным, а у устрем-
устремляя к бесконечности, получаем, что х\ — х <= V для всех доста-
достаточно больших i, откуда и следует нужный нам результат. В
9.1.6. Следствие. В локально выпуклом пространстве всякое
слабо полное множество полно.
9.1.7. Следствие. Пусть Е — локально выпуклое пространство,
А — предкомпактное подмножество в Е, В — замкнутая выпук-
848 Гл. 9. Теория компактных операторов
лая уравновешенная оболочка множества А. Для того чтобы
множество В было компактно, необходима .и достаточно, чтобы
оно было слабо компактно.
Доказательство. Это вытекает из следствий 9.1.4 и
9.1.6. 1
9.1.8. Следствие. В локально выпуклом пространстве каждое
слабо компактное множество является полным.
9.1.9. Предложение. Пусть Е — локально выпуклое простран-
пространство, А и В — подмножества в Е. Тогда
A) если А компактно и В замкнуто, то А + В замкнуто;
B) если А и В компактны и выпуклы, то выпуклая оболочка
С объединения А[]В компактна.
Доказательство. A) Если х не принадлежит А + В, то
компактное множество х — Л не пересекается с В. Но тогда су-
существует такая окрестность нуля [/, что (х — A)+U и В не пе-
пересекаются, т. е. x+U не пересекается с А+В. Таким образом,
А + В замкнуто.
B) Множество С есть замыкание множества D, состоящего
из элементов вида %а+ A —Х)Ь, где ае Л, b e В и^е/=[0, 1].
Отображение (X, а, Ь)\—>Ха+ (I—%)Ь произведения IxAxB
в Е непрерывно, и поэтому его образ D компактен. В топологи-
топологическом векторном пространстве замыкание компактного мно-
множества компаюно, откуда и следует нужный нам результат.
(Действительно, пусть (G2) образуют открытое покрытие мно-
множества D = C. Для любого х^С существуют индекс i=i(x) и
такая замкнутая окрестность нуля Ux, что G^ содержит x+Ux.
Совокупность внутренних точек множеств x+Ux, где х пробегает
D, покрывает D; поэтому конечное число таких множеств, ска-
скажем множеств Xk + Uxk, покрывает D. Так как последние мно-
множества замкнуты, то их объединение покрывает D = C. To же
самое справедливо и для соответствующих Gi(Xk\. Отсюда сле-
следует, что С компактно.) |
9.2. Определение и некоторые свойства
компактных линейных отображений
Пусть Е и F — топологические векторные пространства,
и: E-+F — линейное отображение.'Будем говорить, что отобра-
отображение и компактно (соотв. предкомпактно), если существует та-
такая окрестность нуля U в Е9 что множество u(U) относительно
компактно (соотв. предкомпактно) в F. Из компактности сле-
следует предкомпактность; оба понятия совпадают, если F квази-
квазиполно»
9.2. Определение компактных отображений 849
Для случая, когда Е и F — локально выпуклые пространства,
введем понятие слабой компактности линейного отображения
и: E-+F. Будем говорить, что и слабо компактно, если суще-
существует такая окрестность нуля U в Е, что множество u(U) отно-
относительно слабо компактно в F.
Очевидно, что каждый из приведенных выше трех видов
компактности влечет за собой непрерывность.
Замечания. Компактные операторы часто называют впол-
вполне непрерывными. Исследование компактных линейных операто-
операторов в топологических векторных пространствах было начато
Ка кутан и [4] и Иосидой [1] в связи с эргодической теорией
(§ 9.13).
Отдельные примеры компактных линейных операторов по-
появились гораздо раньше. Гильберт [1] выразил это понятие
в терминах билинейных форм на /2; приводимое нами определе-
определение принадлежит Ф. Риссу и было дано им для банаховых про-
пространств.
Определение Гильберта относится к ограниченным эндомор-
эндоморфизмам и пространства /2 и равносильно следующему- свойству:
(Н) Отображение и переводит слабые последовательности
Коши в сходящиеся последовательности.
Рассмотрим это свойство применительно к произвольным не-
непрерывным линейным отображениям и: E-+F, где Е, F — ло-
локально выпуклые пространства, причем F отделимо. Прежде
всего если и переводит ограниченные множества в относительно
компактные, то, как легко видеть, и удовлетворяет свойству (Н).
Действительно, если отображение и непрерывно и (хп) —слабая
последовательность Коши в Е, то (уп) = (и(хп)) —слабая после-
последовательность Коши в F. Далее множество {хп} ограничено, и
потому множество {уп} относительно компактно. Отсюда следует,
что последовательность (уп) обладает в точности одной пре-
предельной точкой, а потому сходится.
С другой стороны, если каждая ограниченная последователь-
последовательность в Е содержит слабую подпоследовательность Коши, F
метризуемо или квазиполно и отображение и удовлетворяет
условию (Н), то и переводит ограниченные множества в относи-
относительно компактные.
Действительно, предположим, что А—ограниченное подмно-
подмножество в Е. Докажем, что и (А) относительно компактно в F.
Если F метризуемо, то достаточно показать, что каждая после-
последовательность (уа) в и (А) обладает сходящейся подпоследова-
подпоследовательностью. Если F квазиполно, то достаточно доказать, что
и (А) предкомпактно, т. е. что любая последовательность
(Уп) в и (А) обладает подпоследовательностью Коши. Пусть
850 Гл. 9. Теория компактных операторов
уп = и(Хп), хп^А. В силу предположенных свойств пространства
Е последовательность (хп) обладает слабой подпоследователь-
подпоследовательностью Коши (xnk). Но тогда из условия (Н) следует, что по-
последовательность (ynk) сходится в F.
Из приведенных замечаний следует, что если Е — нормиро-
нормированное пространство, обладающее указанными выше свой-
свойствами, a f — то же, что и выше, то условие (Н) равносильно
компактности.
Пространство Е удовлетворяет указанным свойствам, если
либо A) ограниченные подмножества в Е слабо метризуемы
(например, если Ег сильно сепарабельно), либо B) Е — рефлек-
рефлексивное банахово пространство (например, гильбертово простран-
пространство, или />(Г, ц), где 1</?<оо); что касается случая A), см.
также упр. 8.2—8.4.
В настоящем и следующих параграфах будут изложены две
центральные теоремы (9.2.1 и 9.3.1) весьма общего характера,
которые в полной общности были получены Гротендиком
[4] (см. также Бур баки [7, гл. IV, стр. 209, упр. 12]). Каждая
из этих теорем содержит в качестве частных случаев ряд более
ранних результатов, принадлежащих различным авторам. Обе
теоремы будут часто использоваться в § 9.3 и 9.4. Вот первая
из этих теорем.
9.2.1. Теорема. Пусть (Е, Е') и (F, F')—отделимые дуаль-
дуальные пары, © — система слабо ограниченных подмножеств в Е,
<&' — система слабо ограниченных подмножеств в F\ и: E-+F —
слабо непрерывное линейное отображение и иг — его сопряжен-
сопряженное. Тогда следующие шесть условий эквивалентны.
A) Для каждого /1е6 множество и {А) предкомпактно в
топологии Г@/.
(Г) Для каждого А''е®' множество и'(А') предкомпактно
в топологии Г@.
B) Для каждого ^g6 сужение и\А равномерно непре-
непрерывно в слабой топологии в Е и топологии Г@, в F.
B') Для каждого Af'е<5' сужение и'\А' равномерно непре-
непрерывно в слабой топологии в Fr и топологии 7@ в Е\
C) Для каждого А ^ <& и каждого Л'е©' сужение били-
билинейной формы (и(х), у') = {х, и'(у')) на АхА' равномерно не-
непрерывно относительно произведения слабых топологий.
(Зг) То же, что и C), только рассматривается произведение
слабой топологии в А и сильной топологии в А' {или наоборот).
Если каждое множество /1g6 (соотв. А' ее®') выпукло
и уравновешено, то в B) (соотв. в B')) можно заменить рав-
равномерную непрерывность на непрерывность в" нуле.
9.2. Определение компактных отображений 851
Из каждого из предыдущих условий вытекает, что
sup{|<tt(*), у')\: ^еД у'<=А'}< +оо
для всех А е ® и всех А/ е ®'.
Наконец, если каждое из множеств /1еб слабо компактно,
то каждое из предыдущих условий влечет за собой условие
D) Если /1g6 li (хп)—последовательность элементов из
А, слабо сходящаяся в Е, то последовательность (и(хп)) яв-
является Т ^-сходящейся в F.
Если, кроме того, Е — метризуемое пространство, то D) экви-
эквивалентно всем предыдущим условиям.
Доказательство длинновато, поэтому имеет смысл сна-
сначала набросать его план. Прежде всего мы докажем, что
(a) ОЖ20;
(b) B')=ИГ).
Тогда в силу симметрии будем также иметь A/)=^>B) и
B)z^(l). Таким образом, эквивалентность первых четырех
условий будет доказана. Далее покажем, что
(c) B)=МЗ);
Щ C0 # B).
(Импликация C) =ф C') тривиальна.) Отсюда будет следовать
эквивалентность первых шести условий.
Замена равномерной непрерывности на непрерывность в нуле
(в случае, когда А или А' выпуклы и уравновешены) основана
на следующем простом замечании; если G — векторное про-
пространство, Я — выпуклое уравновешенное подмножество в G,
то две локально выпуклые топологии в G индуцируют в Н одну
и ту же равномерную структуру в том и только в том случае,
если они индуцируют одни и те же относительные окрестности
нуля (ср. упр. 9.2).
Очевидно, что C) влечет ограниченность множества
{(и(х), у')\ хбД у'еЛ'}, так как равномерная непрерывность
сохраняет предкомпактность.
Последним шагом доказательства служит проверка утвер-
утверждений
(е) A)=М4);
которые доказываются при указанных дополнительных предпо-
предположениях.
Итак, приступим к доказательству импликаций (а) — (f).
(а) Каждое из множеств А/ представляет собой равно-
степено непрерывное множество функций на F, наделенном
852 Гл. 9. Теория компактных операторов
топологией 7V. Таким образом, в каждом множестве А' слабая
равномерная структура совпадает со структурой равномерной
сходимости на подмножествах из F, предкомпактных в топологии
7V. Из предложения 9.1.2 следует, что каждое множество А'
предкомпактно относительно такой структуры. С другой сто-
стороны, A) означает, что отображение и! непрерывно, а значит,
равномерно непрерывно в топологии «предкомпактной сходи-
сходимости» в F' и топологии Т& в Е'. Так как при равномерно не-
непрерывном отображении образ предкомпактного множества
предкомпактен, то из A) следует B').
(j) Это непосредственно следует из отмеченной равномерной
непрерывности и повторного применения предложения 9.1.2.
(c) Импликация B) :ф C) вытекает из тождества
(«D 0l>-<tt(*2). </2> = M*i-*2)> ^> + <Х*2)> #-4$-(9.2.1)
(d) Если выполняется C'), то для заданных е>0, А и А'
существует такая слабая окрестность нуля W в Е> что если
хь х2 еД Хг^е^и/Е А', то | (и (*i), у') - (и (х2), /)|<е,
т. е. и(х1) — и(х2)^гА/0. А это и означает, что выполняется
условие B).
(e) Предположим, что множество А слабо компактно. Если
справедливо A), то и (А) предкомпактно в топологии 7V. В то
же время если (хп) а А — слабая последовательность Коши, то
из B) следует, что (и(хп)) есть последовательность Коши в то-
топологии 7V. Поэтому если последовательность (хп) слабо схо-
сходится, то множество {хп} относительно слабо компактно, следо-
следовательно (так как и слабо непрерывно), и множество {и(хп)}
является относительно слабо компактным. Но тогда последова-
последовательность (и(хп)) обладает слабой предельной точкой в F. Так
как (и(хп)) —последовательность Коши в топологии 7V, то она
сходится в F в топологии 7V, т. е. имеет место импликация
A)=^D).
(f) Допустим теперь, что каждое множество А слабо ком-
компактно, пространство Е метризуемо и условие D) выполняется.
Докажем, что имеет место условие A). Для этого достаточно
доказать, что если (хп) с: Л, то можно найти такую подпосле-
подпоследовательность (xnk), что {и(хп^) сходится bFb топологии Г®'.
В силу теоремы Шмульяна 8.12.1 из (хп) можно извлечь под-
подпоследовательность (xnk), слабо сходящуюся в Е. Теперь
остается применить условие D) к этой подпоследовательности.
Итак, теорема 9.2.1 доказана. |
9.2.2. Следствие. Пусть Е—метризуемое локально выпуклое
пространство, в — система слабо компактных подмножеств в
£, А/ — слабо ограниченное подмножество в Е'. Тогда
9.2. Определение компактных отображений 853
A) Множество Ат предкомпактно в топологии 7© тогда и
только тогда, когда всякая слабо сходящаяся последователь-
последовательность в А равномерно сходится на Аг.
B) Множество А' предкомпактно в топологии т(Е'у Е) тогда
и только тогда, когда всякая слабо сходящаяся последователь-
последовательность в Е равномерно сходится на А'.
C) Если Е — пространство Фреше, то для относительной
компактности множества А/ в топологии %(Е', Е) необходимо и
достаточно, чтобы каждая слабо сходящаяся последовательность
в Е равномерно сходилась на А'.
Доказательство. A) В теореме 9.2.1 положим E — F, и
равным тождественному отображению, @' = {Л'} и воспользуемся
эквивалентностью (V) и D).
B) В условии A) в качестве © возьмем систему всех слабо
компактных выпуклых подмножеств в Е, так что 7© =%[Е\ Е).
C) В силу B) достаточно показать, что если множество А'
предкомпактно в топологии т, то оно относительно компактно
в этой же топологии. Но так как Е — пространство Фреше, то
слабо ограниченное множество А/ равностепенно непрерывно
(следствие 7.1.2); отсюда вытекает, что т-замыкание множества
А' является т-полным. Таким образом, А' относительно ком-
компактно в топологии т. I
В случае нормированных пространств из теоремы 9.2.1 можно
получить два важных результата.
9.2.3. Следствие. Пусть Е и F — нормированные пространства.
Линейное отображение и: E-+F предкомпактно тогда и только
тогда, когда его сопряженное и* предкомпактно (в сильных,
т. е. в нормированных, топологиях в F' и Е').
Доказательство непосредственно следует из эквива-
эквивалентности условий A) и (У) теоремы 9.2.1, если в качестве ©
взять систему всех ограниченных подмножеств в Е, а в качестзе
©'— систему всех сильно ограниченных, (т. е. ограниченных по
норме) подмножеств в F\ I
Замечание. Так как пространство Е' всегда полно, то
отображение и' предкомпактно тогда и только тогда, когда оно
компактно. Для случая банаховых пространств Е и F* этот ре-
результат принадлежит Ш а удеру [4] (см. также Какутани
[2] и следствие 9.6.3).
9.2.4. Следствие. Пусть Е и F — нормированные простран-
пространства. Линейное отображение и: E-+F является предкомпактным
в том и только в тем случае, если сопряженное отображение и'
переводит сильно ограниченные (т. е. ограниченные по норме)
и а(/7/, F)-сходящиеся сети (yf?) аз F' в сильно сходящиеся (т. е.
сходящиеся по норме) сети (и'(у^) из Е\
854 Гл. 9. Теория компактных операторов
Доказательство. Это непосредственно вытекает из эк-
эквивалентности условий A) и B') теоремы 9.2.1, если учесть, что
сильную топологию в Е' можно определить как топологию 7V,
где &' — система всех выпуклых ограниченных подмножеств
из Е. I
Замечания. Если пространство F сепарабельно, то доста-
достаточно потребовать, чтобы отображение и* переводило сильно
ограниченные и слабо сходящиеся последовательности из F' в
сильно сходящиеся последовательности из Е'. (Напомним, что
из сепарабельности F следует, что топология o(F',F) индуци-
индуцирует метризуемую топологию в каждом сильно ограниченном
подмножестве в F'.) Для сепарабельных банаховых пространств
этот результат принадлежит Гельфанду [2].
Мы закончим этот параграф тремя результатами, относя-
относящимися к множествам компактных или предкомпактных линей-
линейных отображений одного топологического векторного простран-
пространства в другое.
9.2.5. Теорема. Пусть £, F, G— отделимые топологические
векторные пространства.
(a) Если u^Lc(E, F) — компактное (соотв. пред компактное)
отображение и v e LC(F, G), то отображение vu e LC(E, G)
компактно (соотв. предкомпактно).
(b) Пусть и е LC(E, F) и v e LC(F, G). Если отображение v
компактно (соотв. предкомпактно), то отображение vu^Lc (E, G)
компактно (соотв. предкомпактно).
Доказательство, (а) Пусть U— такая окрестность нуля
в Я, что множество u(U) относительно компактно (соотв. пред-
предкомпактно) в F. Тогда множество vu(U)=v(u(U)) обладает
тем же свойством в качестве подпространства в G, так как ото-
отображение v непрерывно (соотв. равномерно непрерывно).
(Ь) Пусть V — такая окрестность нуля в F, что множество
v(V) относительно компактно (соотв. предкомпактно) в G. Так
как и непрерывно, то существует такая окрестность нуля U в £,
что u(U) cz V. Но тогда vu(U), будучи подмножеством в v(V),
относительно компактно (соотв. предкомпактно) в G. |
9.2.6. Теорема. Пусть Е — полунормированное пространство
и (щ)—сеть в LC(E, F), сильно сходящаяся к u^Lc(E, F).
Тогда если каждое отображение щ предкомпактно, то и также
предкомпактно.
Доказательство, Пусть В — единичный шар в £ и V —
произвольная окрестность нуля в /\ В силу сильной сходимости
9 3. Теорема о слабо компактных отображениях 855
можно выбрать такое f, что и(х) — щ(х) е V для xgB. Так как
множество иг(В) предкомпактно и и(В) cz щ(В) + V, то отсюда
следует, что и множество и (В) предкомпактно. 1
Замечания. A) Под сильной сходимостью в Lc(Е, F)
(например, в теореме 9.2.6) понимается сходимость в смысле
сильной топологии в LC(E, F), т. е. равномерная сходимость на
ограниченных подмножествах из Е (п. 1.10.8) (ср. определение
сильной топологии на сопряженном пространстве в § 8.4).
Любопытно, что для случая, когда Е и F— нормированные
пространства, чаще всего употребляется неудачная терминоло-
терминология, в которой эта сильная топология в LC(E, F) называется
равномерной операторной топологией, — несмотря на то что
равномерность относится только к ограниченным подмножествам
из Е (а *не к самому пространству Е). Более того, так называе-
называемая сильная операторная топология — это топология поточеч-
поточечной сходимости! Наконец, употребляется еще термин слабая
операторная топология, сходимость в которой — это поточечная
сходимость в случае, когда F наделено ослабленной топологией
a(F, Г).
B) Последние две теоремы обладают аналогами, в которых
компактность (или предкомпактность) заменена слабой ком-
компактностью. Эти аналоги мы приведем после нашей второй об-
общей теоремы в качестве теорем 9.3.6 и 9.3.7 соответственно. Ана-
Аналогом следствия 9.2.3 служит следствие 9.3.3.
9.3. Теорема о слабо компактных линейных отображениях
Этот параграф посвящен доказательству второй общей тео-
теоремы, утверждающей эквивалентность некоторых условий, на-
налагаемых на линейное отображение и: E-+F или на сопряжен-
сопряженные ему отображения. Она отличается от теоремы 9.2.1 заменой
предкомпактности на слабую компактность.
9.3.1. Теорема. Пусть Е и F — отделимые локально выпуклые
пространства, <S— система ограниченных подмножеств в Е,
Н — векторное подпространство в Е", порожденное слабыми
замыканиями в Е" множеств А из системы ©, и: E-+F — не-
непрерывное линейное отображение, и пусть Е а Н. Рассмотрим
следующие' условия:
A) Для любого /IgS множество и (А) относительно слабо
компактно в F.
B) u"{H)c^F.
Bа) и" переводит равностепенно непрерывные подмножества
в И {рассматриваемые как подмножества сопряженного к про-
пространству (£', Т®)) в относительно слабо компактные подмно-
подмножества в F,
856 Гл. 9. Теория компактных операторов
(За) Отображение и' непрерывно в топологиях %(F\ F) и Г@.
(ЗЬ) Отображение и' непрерывно в топологиях g(F\ F) и
о(Е'9 Н).
D) Отображение и' переводит слабо компактные подмно-
подмножества из F/ в о (Е\ Н) -компактные подмножества в Е\
Dа) Отображение и' переводит равностепенно непрерывные
слабо замкнутые подмножества из F/ в о (Е', Н)-компактные
подмножества в Е\
Имеют место следующие утверждения.
(i) A) & B) & Bа) & (За) & (ЗЬ)=>D)=>Dа).
(и) Если F — квазиполное пространство, то все предыдущие
условия эквивалентны.
Доказательство. Так как доказательство довольно
длинно, то мы снова набросаем сначала план. Начнем с дока-
доказательства импликаций
(a) (Л)=>Bа),
(b) Bа) #B),
(c) B)=ФA).
Отсюда будет следовать, что условия A), B) и Bа) эквива-
эквивалентны. Далее мы докажем, что
(d) (За)=ФBа), (ЗЬ)=ФB),
(e) Bа)=>Cа),
(f) B)=Ф(ЗЬ).
Тем самым будет доказано, что условия A), B), Bа), (За),
(ЗЬ) эквивалентны. В заключение будет показано, что
(g) Cb)#D)#Da),
(h) Da) + (квазиполнота /?)==> B).
(a) Предположим, что условие A) выполняется. Пусть А
принадлежит ®. Множество и (А) относительно слабо компакт-
компактно в F. Пусть А будет о(Н, Е') -замыканием множества А. Так
как отображение^ и" непрерывно в топологиях g(E", E') и
а(/7//, F7), то и"(А) содержится в o(F'\ Ff)-замыкании множе-
множества и{А). Следовательно (так как множество и(А)_ относи-
относительно слабо компактно в F), отсюда следует, что и"(А) содер-
содержится в o(F, F') -замыкании множества и (А) и потому относи-
относительно слабо компактно в F. Так как множества А образуют
базу равностепенно непрерывных подмножеств в Я, то имеет
место условие Bа).
(b) Доказывается аналогично.
(c) Предположим, что выполняется условие B). Равносте-
Равностепенно непрерывные подмножества из Н являются относительно
9.3. Теорема о слабо компактных отображениях 857
компактными в топологии а (Я, Е'). Если Леб, то.4 czAoof]H
и А°° равностепенно непрерывно и компактно в топологии
о(Е", Е'). Как уже было отмечено, отображение и" непрерывно
в топологиях о{Е'\ Е') и o(F", F'). Таким образом, B) влечет
относительную слабую компактность в F множества и(А) =
= и"(А). А это и есть A).
(d) Предположим, что выполняется условие (За). Если
Де6, то существует такая т(/7/, F)-окрестность нуля V, что
u'(V) с=Л°. Соотношение
<*", и'(у')) = {и"(х"),у') (9.3.1)
1°°
показывает тогда, что \(u"(xf'), у') \ < 1 для /е/1° /
Итак, и"(х") gF, и множество и"(А°°) относительно слабо ком-
компактно в F. (Читатель помнит, конечно, определение топологии
x(F\ F) и тот факт, что она согласуется с двойственностью ме-
между F и F'.) Так как множества А°° образуют базу равносте-
равностепенно непрерывных множеств в Е" (относительно топологии Г@
в £'), то условие Bа) выполняется.
Аналогичным образом доказывается импликация (ЗЬ) =^> B).
(e) Предположим, что выполняется условие Bа). Если /1е6,
то А0 есть 7@-окрестность нуля, и так как Л с: Л00, то множе-
множество А равностепенно непрерывно. Следовательно, и"(А) отно-
относительно слабо компактно в F. Но тогда из соотношения
(х, и'{у')) = (и"(х), у') следует, что и'(у')-+0 в топологии Г@
при #'->0 в топологии x{F',F), т. е. имеет место (За).
(f) Предположим, что выполняется B). Из равенства (9.3.1)
непосредственно вытекает, что отображение и' непрерывно в то-
топологиях g(F', F) и g(E', H).
(g) Очевидно, что (ЗЬ) =^> D) и D) =^> Dа).
(h) Предположим, что выполняется Dа). Пусть множество
В cuF' равностепенно непрерывно и слабо замкнуто в F'. Тогда
множество и'{В) является в(Е', Я)-компактным. Поэтому топо-
топологии а{Е\ Н) и о(Е\ Е) индуцируют в и'(В) одну и ту же
топологию. Отсюда следует, что сужение и'\В непрерывно в то-
топологиях o(F'y F) и о(Е\ Е). Поэтому если /еЯ, то и"(х") —
= х" °и' является линейной формой на F\ сужения которой на
равностепенно непрерывные множества слабо непрерывны. По-
Поэтому существует такая слабая окрестность нуля W в F\ чго
для г/'ее W0B
Из замечания B) к^теореме 8.5.1 вытекает, что и"(х") принад-
принадлежит пополнению F пространства F. Далее так как отображе-
отображение и" непрерывно в топологиях а(£", Е') и а(/7//, F'), ю и"(х")
принадлежит слабому замыканию в F некоторого множества
858 Гл. 9. Теория компактных операторов
и (А), где /1g6. Поскольку множество и(А) ограничено в /\
то можно считать, что множество А, а значит, и и (А) выпуклы
и уравновешены. Но тогда слабое замыкание множества и (А)
в F совпадает с его замыканием в естественной топологии про-
пространству F (как пополнения F). Если F квазиполно, то замы-
замыкание множества и (А) в F совпадает с его замыканием в У7, и
поэтому ^(/)gF. Таким образом, условие B) выполняется.
Теорема 9.3.1 полностью доказана. |
9.3.2. Следствие. Пусть Е и F — два отделимых локально
выпуклых пространства, и: E-^F — непрерывное линейное ото-
отображение. Тогда следующие два условия эквивалентны:
A) отображение и переводит ограниченные подмножества
из Е в относительно слабо компактные подмножества в F\
B) и"{Е") czF,
и каждое из них влечет выполнение условия
C) и' переводит равностепенно непрерывные подмножества
из F/ в подмножества из Е\ относительно компактные в тополо-
топологии в о(Е', Е").
Если F квазиполно, то все три условия равносильны.
Доказательство непосредственно вытекает из теоремы
9.3.1, если в этой теореме в качестве © взять систему всех огра-
ограниченных подмножеств в Е. В
9.3.3. Следствие. Пусть Е — нормированное векторное про-
пространство, F — банахово пространство, и: E-+F — непрерывное
линейное отображение. Отображение и слабо компактно тогда
и только тогда, когда и' слабо компактно (как отображение ба-
банахова пространства Fr в банахово пространство Е').
Доказательство. Отображение и тогда и только тогда
слабо компактно, когда выполняется условие A) предыдущего
следствия. С другой стороны, в этом случае условие C) того же
следствия означает, что и' — слабо компактное отображение ба-
банахова пространства F/ в банахово пространство Е'. |
Замечания. Доказательство эквивалентности условий A)
и B) следствия 9.3.2 для случая сепарабельных банаховых про-
пространств принадлежит Гантмахер [1], а для случая несепара-
бельных пространств — Накамуре [1]. То же относится к
следствию 9.3.3. Если Е — нормированное пространство, то усло-
условие A) означает, что и — слабо компактное отображение. Та-
Таким образом, в этом случае и слабо компактно тогда и только
тогда, когда и" (Е") cz F.
9.3.4. Теорема. Пусть Е — отделимое локально выпуклое про-
пространство, © — некоторая система ограниченных подмножеств
в Е. Тогда следующие условия эквивалентны.
9.3. Теорема о слабо компактных отображениях 859
A) Если F— отделимое локально выпуклое пространство и
и: E-+F— непрерывное линейное отображение, переводящее
ограниченные множества в относительно слабо компактные, то
и переводит множество из системы © в предкомпактные множе-
множества в F.
A') То жеу что и A), только F предполагается банаховым
пространством.
B) Каждое из множеств у!е6 предкомпактно в топологии
Т равномерной сходимости на равностепенно непрерывных вы-
выпуклых уравновешенных а(£/, Е")-компактных подмножествах
из Е'.
Bа) Каждое равностепенно непрерывное выпуклое уравно-
уравновешенное а(£', Е")-компактное подмножество из Е/ предком-
предкомпактно в топологии Т @.
Доказательство. Условия B) и Bа) эквивалентны в
силу теоремы 9.2.1 (надо в ней положить E = F и взять в ка-
качестве и тождественное отображение). Очевидно, что {\)d${V).
Далее, покажем, что '(Г)=фB). Пусть ^g6 и Ет — про-
пространство Е, наделенное топологией Т.
Заметим, что топология Т согласуется с двойственностью
между Е и Ег (теорема Макки 8.3.2). В силу упр. 6.17 простран-
пространство Ет изоморфно векторному подпространству произведения
полных полунормированных пространств. Поэтому достаточно
показать, что любое непрерывное линейное отображение и про-
пространства Ет в полное полунормированное пространство F пе-
переводит А в предкомпактное множество. При этом можно счи-
считать, что F отделимо, т. е. банахово.
Так как топология Т слабее исходной топологии в Е, то и —
непрерывное отображение Е в F\ далее и' переводит слабо
замкнутые и равностепенно непрерывные подмножества из Ff
в слабо замкнутые и равностепенно непрерывные подмножества
в {Ет)', т. е. в компактные в топологии о(Е',Е") подмножества
из Е'. Но тогда (теорема 9.3.1) и переводит ограниченные под-
подмножества из Е в относительно слабые компактные подмноже-
подмножества из F. Следовательно, в силу (I7) множество и(А) пред-
предкомпактно в F.
Остается показать, что B) влечет A). Можно считать, что
пространство F в условии A) является полным. Пусть и — ото-
отображение, удовлетворяющее условиям из A),и^е6. Нужно
показать, что множество и (А) предкомпактно. По условию А
предкомпактно в топологии Т\ поэтому достаточно доказать, что
и — непрерывное отображение Ет в F, т. е. что и' переводит
равностепенно непрерывные выпуклые уравновешенные слабо
компактные подмножества из Fr в равностепенно непрерывные
860 Гл. 9. Теория компактных операторов
о(Е\ Е") -компактные подмножества из Е'. Но так как отобра-
отображение и: E-^F непрерывно, то и' переводит равностепенно не-
непрерывные множества в равностепенно непрерывные множества,
откуда в силу теоремы 9.3.1 следует, что и' переводит слабо ком-
компактные подмножества из F' в о(Е/, Е") -компактные подмно-
подмножества из Е', что и требовалось доказать. В
Замечание. Если каждое множество /4g6 является
слабо компактным, то в условиях A), (Г) и B) можно заме-
заменить «предкомпактность» на «компактность». Действительно,
предкомпактное и слабо компактное множество предкомпактно
и слабо полно, а потому предкомпактно и полно и, следова-
следовательно, компактно.
9.3.5. Следствие. Пусть Е — отделимое локально выпуклое
пространство. Тогда следующие условия эквивалентны:
A) Если F — отделимое локально выпуклое пространство и
и: Е-+ F — непрерывное линейное отображение, переводящее
ограниченные множества в относительно слабо компактные мно-
множества, то и переводит слабые последовательности Коши в по-
последовательности Коши.
(!') То же, что и A), только F предполагается банаховым.
B ) Каждая слабая последовательность Коши в Е является
последовательностью Коши в топологии Т.
Доказательство. Достаточно воспользоваться теоремой
9.3.4, предполагая, что ® состоит из всех множеств вида А-=
=--{хп), где (хп)—слабая последовательность Коши в Е. Надо
только заметить следующее: если G — отделимое локально вы-
выпуклое пространство, (zn)—слабая последовательность Коши
в G и Р — множество всех точек zn, то Р предкомпактно тогда
и только тогда, когда (zn) является последовательностью Коши.
Действительно, если (zn) — последовательности Коши, то, оче-
очевидно, Р — предкомпактное множество. С другой стороны, если
Р предкомпактно, то его замыкание Р в пополнении G простран-
пространства G является компактным. Слабая равномерная структура
в Р совпадает со структурой, индуцированной естественной струк-
структурой пространства G, поэтому (zn) есть последовательность
Коши в исходной структуре пространства G. |
9.3.6. Теорема. Пусть Е, F и G — локально выпуклые про-
пространства, причем Е нормируемо, и пусть u^Lc(E, F), а
v e LC(F, G). Тогда отображение vu <= LC(E, G) слабо компакт-
компактно, если (а) отображение и слабо компактно или (Ь) отображе-
отображение v слабо компактно.
9.3. Теорема о слабо компактных отображениях 861
Доказательство. Легко проверить справедливость со-
соотношения
Если выполнено условие (а), то из следствия 9.3.2 вытекает,
что и"(Е") czF. Так как v"\F = v, то (vu)"(E") c= G. Но тогда
из замечания после следствия 9.3.3 вытекает, что отображение
vu слабо компактно. Если выполнено условие (Ь), то из приве-
приведенного выше соотношения следует, что (vu)"(E") a v"(F"),
причем v" (F") a. Q (в силу следствия 9.3.2). Но тогда, как и
в первом случае, отображение vu слабо компактно. |
9.3.7. Теорема. Пусть Е — нормированное пространство, F —
отделимое квазиполное локально выпуклое пространство. Пред-
Предположим, что сеть (щ) с Lc(Ey F) сходится к отображению и
в сильной топологии пространства Lc(Ey F). Тогда если каждое
щ слабо компактно, то и отображение и обладает тем же свой-
свойством.
Доказательство. Известно (следствие 9.3.2), что
и"(Е") cz F для каждого /, и нужно показать, что и"(Е") a F.
Пусть V — произвольная выпуклая уравновешенная окрестность
нуля в F. Можно выбрать такой индекс i, что и(х) —щ(х) е V
при IMI -< 1. Предположим, что V слабо замкнуто. Так как и"
получается из отображения и продолжением по непрерывности
в слабой топологии, то и" (х") — и" (х") е V при \\х"\\ -< 1, где
через V обозначено замыкание в Е" множества V. Из сильной
сходимости сети (щ) следует, что для некоторого i0 и некото-
некоторого ограниченного замкнутого подмножества HaF Ui(B)czH
для всех i& io, где через В обозначен единичный шар в Е. Если
i и / достаточно велики, то для \\х"\\ ^ 1 имеем
Отсюда следует, что(и"(*")) (^h) —сеть Коши в Н. Так как
F квазиполно, то lima"(л;") cyiuecTByet в Я и тем более в F.
Поскольку F, а потому и F" отделимы, этот предел есть не что
иное, как и"(х"). Следовательно, и"(Е") с: У7, что и требовалось
доказать. I
Некоторые примеры и дополнения, Банаховы пространства
Со и Iх сепарабельны, поэтому
(a) единичный шар в с0 слабо метризуем\
(b) единичный шар в Iх метризуем в топологии а (I1, с0).
Кроме того, из теоремы 4.21.2 легко следует, что
(c) каково бы ни было множество индексов /, всякое слабо
компактное множество в Iх (I) компактно.
862 Гл. 9. Теория компактных операторов
Прямое доказательство. Достаточно показать (тео-
(теорема 8.12.7), что из любой относительно слабо компактной по-
последовательности (хп) в /*(/) можно выбрать сходящуюся под-
подпоследовательность! Поэтому можно считать, что / — счетное
множество, и, таким образом, иметь дело с пространством Iх.
Применим теперь утверждение (Ь), выбрав из (хп) подпоследо-
подпоследовательность (уп)9 сходящуюся в топологии о{1\ Со). Легко по-
показать, пользуясь относительной слабой компактностью после-
последовательности (хп), что (уп) сходится также в топологии
Опираясь на эти замечания, докажем следующее
9.3.8. Предложение. Пусть I — произвольное множество ин-
индексов, Е — отделимое локально выпуклое пространство, и:
СоA)-+Е — непрерывное линейное отображение. Тогда если
и слабо компактно, то оно компактно.
Замечание. См. также предложение 9.4.13.
Доказательство. В силу следствия 9.3.2 слабая ком-
компактность отображения и означает, что и' переводит равносте-
равностепенно непрерывные множества из Е' в относительно слабо ком-
компактные подмножества пространства Iх {I). Но тогда в силу (с)
и' переводит равностепенно непрерывные подмножества из Ег
в относительно компактные подмножества пространства /*(/).
Пусть V—некоторая окрестность нуля в Е, (хп)—последова-
(хп)—последовательность в СоA) с |Un|| ^ 1. Известно, что (и(хп)) обладает
слабой предельной точкой у^Е. Поэтому если W — произволь-
произвольная слабая окрестность нуля в Е и п — произвольное целое
число, то существует такое целое число N > пу что и (xN) — у е W.
Рассмотрим множество упорядоченных пар i=(n, W), частично
упорядоченное обычным образом, и множество элементов вида
a{ = xN. Сеть (а(аг)) будет слабо сходиться к у, а потому будет
слабой сетью Коши в Е. Так как ,
(at - ah и' (у')) = (и {at - a,)9 у'),
то (а,-) — сеть Коши относительно структуры поточечной сходи-
сходимости в u'(V°). Так как множество и'(V°) относительно ком-
компактно и ||аг|| ^ 1, то из предложения 0.4.9' следует, что (аг-)
есть сеть Коши относительно структуры равномерной сходимости
в u(V°). Это означает, что (и(аг).) есть сеть Коши ъЕ. Поскольку
сеть u(a,i) слабо сходится к у е £", то и(п{) -+у в Е, откуда сле-
следует, что у есть предельная точка в Е последовательности
(и(хп)). Таким образом, отображение и компактно. I
9.3.9. Предложение. Пусть 1 — произвольное множество ин-
индексов, Е — отделимое локально выпуклое пространство, и пусть
линейное отображение и: 1°° (/)->£ непрерывно в топологиях
9.3. Теорема о слабо компактных отображениях 863
а(/°°, Iх) и о(Еу Е'). Тогда и переводит замкнутый единичный
шар пространства 1°°A) в компактное подмножество в Е.
Доказательство. Пусть S — замкнутый единичный шар
в /°°. Множество S компактно в топологии а(/°°, Z1), поэтому
A=u(S) слабо компактно в Е. С другой стороны, So — единич-
единичный шар в Со — слабо плотен в S, и, следовательно, u(S0) слабо
плотно в А. Так как множество u(S0) выпукло, отсюда вытекает,
что u(S0) плотно в А. Применяя предложение 9.3.8 к сужению
и|£0, которое является слабо компактным отображением, полу-
получаем, что u(S0) относительно компактно в Е. Следовательно,
А — компактное множество в £", что и требовалось доказать. |
Замечания. A) Как показывают приведенные выше рас-
рассуждения, сужение ио = и\соA) переводит единичный шар Socz
czco(I) в относительно компактное подмножество в Е. Поль-
зуясь теоремой 9.2.1, получаем, что по переводит равностепенно
непрерывные подмножества из Ег в предкомпактные (т. е. в дан-
данном случае в относительно компактные) подмножества в Iх (/).
B) Примеры таких отображений и возникают при рассмо-
рассмотрении семейств элементов (аг)^/из Е, обладающих тем свой-
свойством, что ряд 2^@^' слабо сходится в Е для каждого
sg/°°(/). [Заметим в скобках, что если мы имеем последова-
последовательность (ап) и если Е слабо секвенциально полно, то доста-
достаточно предположить, что ряд ^js(n)an слабо сходится в Е для
п
каждого s е с0. Если Е полурефлексивно, то это более слабое
предположение оказывается достаточным и для произвольных
семейств (а*)-] Из указанного свойства следует, что 2l (at, х') К
< + оо для каждого xr e Ег\ отсюда вытекает, что отображе-
отображение и, определенное равенством
непрерывно в топологиях а(/°°, I1) и в(Е,Е'). Применим теперь
к и предложение 9.3.9 и замечание A). Так как иг переводит
х'<=Е' в семейство {{а{, х')), то из замечания A) следует (на-
(например, в силу теоремы 4.21.2), что для всякой окрестности нуля
U в Е и всякого е > 0 существует такое конечное множество
F а /, что
равномерно по х\ пробегающему множество U0. Поэтому если
U — выпуклое уравновешенное замкнутое множество, то
864 Гл. 9. Теория компактных операторов
для всякого конечного множества индексов Р, F с: F' с: /, и вся-
всякого s^lSq. Поэтому конечные частичные суммы 2 s(i)at обра-
образуют ограниченную сеть Коши в Е. Если Е квазиполно, то ряд
2 s {i)at безусловно сходится в Е для каждого se/°°(/) (см.
также предложение 9.3.10). Что касается компактных матричных
преобразований некоторых типов пространств последовательно-
последовательностей (ср. примеры 6.1.4, 6.4.10 и 7.2.4), см. Сарджент [3].
C) В качестве примера применения предложения 9.3.9 к
теории суммирования приведем доказательство одной теоремы,
принадлежащей Шуру. Речь идет о матрицах Л, переводящих
последовательности, сходящиеся к нулю, в такие же последова-
последовательности; см. примеры 6.1.4, 6.4.10 и 7.2.4. Теорема Шура за-
заключается в следующем.
► Для того чтобы матрица А переводила каждую сходя-
сходящуюся к нулю последовательность в сходящюуся к нулю
последовательность, необходимо и достаточно, чтобы
Пт2|Л(т, л) | = 0.
m n
Действительно, достаточность этого условия очевидна, так
как ясно, что оно влечет справедливость соотношений G.2.10)
и G.2.11) в утверждениях соответственно A) и B) примера
7.2.4. Обратно, предположим, что матрица А обладает указан-
указанным свойством, и пусть и = иА есть соответствующее линейное
отображение. Как известно из примера 7.2.4, отображение и мо-
можно продолжить до некоторого непрерывного линейного отобра-
отображения пространства /°° в себя, причем (в силу части C) того же
примера) и непрерывно в топологии а(/°°, Iх). Из предложения
9.3.9 и утверждения A) приведенного выше замечания вытекает,
что и переводит единичный шар пространства с0 в относительно
компактное подмножество Р в Со (поскольку известно, что и ото-
отображает Со в подпространство Со пространства /°°). Поэтому мо-
можно рассматривать Р как подмножество пространства непрерыв-
непрерывных функций на компактном пространстве N*, образованном
множеством натуральных чисел N с присоединенной к нему бес-
бесконечно удаленной точкой оо (компактификация Александрова).
При таком взгляде на Р получаем, что из относительной ком-
компактности Р следует его равностепенная непрерывность в оо.
Следовательно, для заданного е>0 должно существовать такое
натуральное число т0, что при m>m0 неравенство \y(m)\^Cs
имеет место для всех j/eP,t. e.
2 A(mt п)х{п)\
п I
9.3. Теорема о слабо компактных отображениях 865
для m>m0 и для лгесо, удовлетворяющих условию lUIU^l.
Фиксируя пг> т0 и варьируя х, видим, что указанное неравен-
неравенство эквивалентно неравенству
2|Л(т, м)|<е (т>т0).
п
Таким образом, соотношение (9.3.1) доказано. I
Приложение к скалярным вполне интегрируемым функциям.
Теперь мы рассмотрим некоторый непрерывный аналог предло-
предложения 9.3.9, следуя при этом Гротендику [4, в частности
следствие из предл. 3 и теор. 5], а также Бур баки [9, гл. VI,
стр. 84—85, упр. 19 и 21].
9.3.10. Предложение. Пусть F — отделимое локально выпук-
выпуклое пространство, и: LOO = LOO(T, ц) -> F — линейное отображение,
непрерывное в топологиях o(L°°,L]) и o(F,Ff). Тогда
(a) и — слабо компактное отображение банахова простран-
пространства L°° в F;
(b) uf переводит равностепенно непрерывные подмножества
из F' в относительно компактные в топологии o(L\ L°°) подмно-
подмножества из L1; _
(c) если ограниченная последовательность (fn) в 3?°° сходит-
сходится локально по мере1) к ffE^00), то u(fn) сходится в F к u{f).
Доказательство. Единичный шар в L°° компактен в то-
топологии o(L°°,L1)] отсюда следует справедливость утвержде-
утверждения (а). Поэтому утверждение (Ь) вытекает из следствия 9.3.2.
Для доказательства утверждения (с) рассмотрим формулу
Применение утверждения (Ь) в сочетании с критерием Данфор-
да—Петтиса (теорема 4.21.2) показывает, что u(fn)-*u(j) в F
(т. е. в смысле равномерной сходимости на равностепенно не-
непрерывных подмножествах из F'). Подробности предоставляются
читателю. |
Интересная разновидность отображений и типа фигурирую-
фигурирующих в последнем предложении возникает при рассмотрении
скалярно вполно интегрируемых (в терминологии Бур баки,
там же) функций Ф: T-+F (см. также замечание B) после
предложения 8.14.13). Напомним, что функция Ф нязывается
скалярно вполне интегрируемой, если она скалярно существенно
интегрируема и J /Ф^ц^^для каждой функции f^2?°° (или,
1) То есть сходится по мере на каждом компактном множестве /(с7.«-
Прим. перев.
866 Гл. 9. Теория компактных операторов
что то же, для каждой ограниченной ji-измеримой функции f).
Обозначим через иф отображение пространства L°° в F, опреде-
определяемое равенством
где f — произвольная функция из класса /. Рассмотрим также
линейное отображение Vf^: F'-+Ll (где Ф — скалярно сущест-
существенно интегрируемая функция), ставящее в соответствие ка-
каждому элементу /eF; класс, определяемый функцией (Ф, х').
Легко проверить, что, для того чтобы функция Ф была ска-
скалярно вполне интегрируемой, необходимо и достаточно, чтобы
она была скалярно существенно интегрируемой и чтобы отобра-
отображение иф было неперывным в топологиях a(F\F) и o(L\L°°).
Далее, если Ф — скалярно вполне интегрируемая функция, то
имеет место тождество
для / е L°° и х' е F'. В частности, иф непрерывно в топологиях
o(L°°yLl) и o(F,F'), причем vo является отображением, сопря-
сопряженным к иф.
Таким образом, предложение 9.3.10 применимо к иф (и пред-
представляет собой обобщение одной из теорем Орлича). Однако
справедливо более сильное утверждение.
9.3.11. Предложение. Предположим, что функция Ф: Т-+Р
скалярно вполне интегрируема. Обозначим .через л систему под-
подмножеств Н в F\ обладающих тем свойством, что всякая после-
последовательность элементов из Н содержит подпоследовательность,
которая является слабой последовательностью Коши. Обозначим
через Fn пространство F, наделенное топологией Тл (г. е. топо-
топологией равномерной сходимости на множествах из системы я).
Тогда иф как отображение пространства L°° в Fn предкомпактно.
Доказательство. В силу теоремы 9.2.1 нам нужно дока-
доказать, что vo (Н) предкомпактно в U для каждого ^ея. Для
этого достаточно убедиться в том, что если [хг^ есть последова-
последовательность элементов" из Я, то существует такая подпоследова-
подпоследовательность (х'п V что Vt^fx^ \ сходится в L1.
По условию из (л£) можно выбрать подпоследовательность,
являющуюся последовательностью Коши. Так как аф непрерыв-
непрерывно в топологиях o(F\F) и а(/Л/,°°), то (o(^)) = (Afe) является
слабой последовательностью Коши в L1 и потому слабо сходится
9.3. Теорема о слабо компактных отображениях 867
в L1 (теорема 4.21.4). Далее hk есть класс, определяемый функ-
функцией (Ф, хгп ), а эти функции сходятся поточечно. Отсюда (след-
(следствие 4.21.6) вытекает, что последовательность (hk) сходится
в LK |
Является открытым вопрос о том, всегда ли отображение
иф\ L°°-+-F (где F рассматривается в своей исходной топологии)
предкомпактно. Однако из предложения 9.3.11 следует положи-
положительный ответ на этот вопрос для ряда важных частных случаев.
9.3.12. Следствие. Если Ф: T-+F — скалярно интегрируемая
функция, то отображение иф: L°°-+F является предкомпактным
в каждом из следующих случаев:
(a) F — сепарабельное пространство;
(b) F — рефлексивное банахово пространство;
(c) F — метризуемое пространство и Ф — измеримая функ-
функция.
Доказательство. В случаях (а) и (Ь) нужно только за-
заметить, что всякое равностепенно непрерывное подмножество Н
в F' принадлежит я, откуда следует, что я-топология сильнее,
чем исходная топология в /:. В случае (а) это так, поскольку ка-
каждое такое множество Н относительно компактно и метризуемо
в слабой топологии. В случае (Ь) надо применить теорему
Шмульяна 8.12.1 к банахову пространству F'.
Перейдем теперь к случаю (с). Предположим сначала, что
пространство Т а-компактно. В силу теоремы 8.15.2, не нарушая
общности, можно считать, что Ф — сеперабельнозначная функ-
функция, так что F можно заменить сепарабельным векторным под-
подпространством, порождаемым множеством Ф(^), и воспользо-
воспользоваться случаем (а).
Если пространство Т не а-компактно, то применим метод,
сводящий доказательство к рассмотрению а-конечного случая.
Замкнутый единичный шар Во пространства С0(Т) плотен отно-
относительно топологии a(L°°, L1) в единичном шаре В простран-
пространства L°°. Поэтому ввиду непрерывности отображения и в топо-
топологиях a(L°°, L1) и a(F, F') достаточно показать, что иф(В0) яв-
является предкомпактным множеством в F. [Читатель может за-
заметить, что иф(В) является слабым замыканием множества
иф{Во) и потому в силу выпуклости служит также замыканием
множества иф(В0).] Для этого, в свою очередь, достаточно по-
показать, что для каждой последовательности (fn) из Во множе-
множество {иф{!п)} предкомпактно в F. Но все функции fn обращаются
в нуль вне a-компактного подмножества в Т\ отсюда и следует
то, что требуется доказать. I
868 Гл. 9. Теория компактных операторов
Как показывает один результат, анонсированный Б у р б а к и
(там же, стр. 86, упр. 25), предложение* 9.3.11 и его следствие
принимают поразительный вид, если на пространство F нало-
наложить некоторые дополнительные ограничения.
9.3.13. Предложение. Если F — сепарабельное слабо секвен-
секвенциально полное пространство Фреше, то всякая скалярное суще-
существенно интегрируемая функция Ф: T-+F скалярно вполне
интегрируема. В частности, иф переводит единичный шар из L°°
в относительно компактное подмножество в F, а ъф переводит
равностепенно непрерывные подмножества из Fr в относительно
компактные подмножества в L1.
Доказательство. Доказательство проводится в три шага.
Первые два из них относительно просты и представляют собой
доказательство сформулированного предложения в случае, когда
пространство (Г, \х) а-конечно.
На шаге A) мы докажем, что J Ф ф g F для всякого ком-
к
пактного подмножества К а Т. Так как функция /Ф скалярно
существенно интегрируема, если Ф обладает тем же свойством
и f е 3?°°, то иф (/) е Л если / е J?T, где Л?? — множество
функций из 3?°° с компактными носителями. Далее, на шаге B)
будет доказано, что иф(?) ^ Fy если /eJ^o0, где =5^0° —множе-
—множество тех функций из i?00, которые обращаются в нуль вне а-ко-
нечных множеств. Наконец, на шаге C) мы рассмотрим случай,
когда f — произвольная функция из 3?°°.
A)В силу теоремы 8.15.2 функция Ф измерима. Заданное
компактное множество К можно записать в виде ( (J Кп ] U N, где
каждое множество Кп компактно и N — пренебрежимое множе-
множество, причем сужение Ф\Кп непрерывно. Тогда
J Ф d\x = lim J Ф d\i
в топологии a(F7*, F'). С другой стороны, из предложения 8.14.3
следует, что хп == J Ффе? для каждого п. Кроме того, (хп)
является слабой последовательностью Коши в F и потому слабо
сходится к некоторой точке х е F. Этот предел х должен совпа-
9.3. Теорема о слабо компактных отображениях 869
дать с I Фй\х (что доказывается применением к ним обоим про-
к
извольного функционала /eF7) т. е. J
__ к
B) Пусть теперь f^J?™. Изменяя значения функции f на
некотором пренебрежимом множестве, можно считать, что / рав-
равна нулю вне объединения возрастающей последовательности
компактных множеств (/Сп). Полагая fn = hK » получаем в силу
K
A), что хп = J /„ФфЕ F. Далее очевидно, что последователь-
последовательность (хп) сходится к J /Фф в топологии e{Ff*,F'). Теперь для
завершения доказательства на этом шаге достаточно воспользо-
воспользоваться слабой секвенциальной полнотой пространства F так же,
как это было сделано на шаге A).
C) Здесь мы воспользуемся отображением vo и докажем,
что. оно переводит любое заданное равностепенно непрерывное
подмножество Я из Р в подмножество из L1, относительно ком-
компактное в слабой топологии. Считая это доказанным, обозначим
через fs функцию /%s, где f—функция из i?°°, а 5 — а-конечное
множество. Тогда fs^J?™, и в силу B) иф(/5) = J /Фф е F.
s
Далее
<«Ф(/5). jO = (h> 'ф (*0> = J / • (ф, х') • Ф
5
для каждого S. Из теоремы 4.21.2 очевидным образом следует,
что Г fhd\i-> fhd\inpn возрастании S, причем сходимость здесь
s
равномерна по А, пробегающим произвольное множество из i?1,
относительно компактное в слабой топологии. Следовательно,
в силу предположенного нами сеть (xs), где xs = ^ф(/5), являет-
является сетью Коши в F. Из полноты пространства F вытекает суще-
существование предела х сети (х$). Поэтому для каждого xr e F'
имеем
(х, х') = lim (xSt x') — lim J / - (Ф, *'> ф = J/ • (Ф, х') ф,
s
откуда следует, что х= J fOd\i. Таким образом, последний инте-
интеграл принадлежит пространству Т7, и наше предложение дока-
доказано,
870 Гл. 9. Теория компактных операторов
Остается показать, что если Н — равностепенно непрерывное
множесто в F', то множество й = иф(Н) относительно компактно
в L1 в слабой топологии. В силу теоремы Эберлейна 8.12.7 доста-
достаточно доказать, что для любой последовательности (хг^ с: Н по-
последовательность (уф(х'п)) обладает слабой предельной точкой в
L1. Так как пространство F сепарабельно, то И слабо метри-
зуемо. Множество Н относительно слабо компактно в F\ по-
поэтому из последовательности (х'п) можно извлечь подпоследова-
подпоследовательность (г/^), слабо сходящуюся в F\ скажем, к х\ Покажем,
что последовательность (^)==(^ф(^)) слабо сходится в
L1 к h = vo(x'). Это означает, что
для каждой функции / е i?00. Так как обе функции (Ф» У'п)
и (Ф, х) вместе обращаются в нуль вне объединения некото-
некоторого а-конечного и локально пренебрежимого множества, то
можно считать, что /^J?o°. В этом случае соотношение, спра-
справедливость которого нам нужно доказать, приобретает простой
вид
где, как это известно из B), иф (f)^F. Но это соотношение яв-
является тривиальным следствием слабой сходимости последова-
последовательности (yQ к х\ ■
В этом месте читателю стоит посмотреть упр. 9.14.
9.4. Условия Данфорда — Петтиса и Дьёдонне.
Слабо компактные и компактные линейные отображения
пространств L1 и С
В своей совместной работе [1] Данфорд и Петгис (на-
(наряду с другими результатами) провели систематическое иссле-
исследование теорем представления для компактных и слабо компакт-
компактных линейных отображений пространства L1 в банахово про-
пространство F. Недавно Гротендик [4] исследовал эти вопросы
с некоторой более общей точки зрения. Он показал, что многие
из полученных ранее результатов вытекают из того факта, что
пространство E — L1 удовлетворяет условиям, эквивалентным тем,
о которых идет речь в теореме 9.3.4. Кроме того, он показал, что
аналогичная ситуация возникает в случае, когда Е есть про-
пространство L°° или С(Т) (пространство непрерывных функций на
9.4. Условия Данфорда — Петтиса и Дьёдонне 871
отделимом компактном пространстве Г), и использовал этот ре-
зультат при изучении векторных мер.
В этом параграфе мы намереваемся привести обзор некото-
некоторых из этих идей; при этом будем в основном опираться на ука-
указанную выше работу Гротендика, а также воспользуемся неко-
некоторыми идеями из книги Б у р б а к и [9, гл. VI].
Всюду, где не оговорено противное, Е — отделимое локально
выпуклое пространство; 2 — система всех выпуклых уравнове-
уравновешенных подмножеств в Е, компактных в топологии о(Е, Е')\
2'— система всех выпуклых уравновешенных равностепенно не-
непрерывных подмножеств в Е', компактных в топологии о(Е', Е")\
Г2, —топология в Е, база окрестностей нуля которой образо-
образована полярами S0 множеств S из системы 2'. Аналогичная топо-
топология Г2 в Е/ совпадает с топологией Макки х(Е', Е) (п. 8.3.3).
Из теоремы 9.3.4 следует эквивалентность следующих трех
свойств пространства Е.
(DPi) Всякое непрерывное линейное отображение простран-
пространства Е в отделимое квазиполное локально выпуклое простран-
пространство F, переводящее ограниченные множества в множества, от-
носителъно компактные в слабой топологии, переводит каждое
множество из И в относительно компактное множество в F.
(Эквивалентное свойство получится, если считать здесь F бана-
банаховым пространством.)
(DP2) Каждое множество А из 2 предкомпактно в тополо-
топологии Г2,#
() Каждое множество из 2' предкомпактно (или, что
эквивалентно, относительно компактно) в топологии %(Е\Е).
Подобным же образом из следствия 9.3.5 вытекает эквива*
лентность следующих трех свойств пространства Е.
(SDPj) Всякое непрерывное линейное отображение про-
пространства Е в отделимое квазиполное локально выпуклое про-
пространство F, переводящее ограниченные множества в множества,
относительно компактные в слабой топологии, переводит слабые
последовательности Коши в сходящиеся в F последовательности
(или, что эквивалентно, в последовательности Коши в F). Экви-
Эквивалентное свойство получится, если считать здесь F банаховым
пространством.
(SDP2) Каждая слабая последовательность Коши в Е яв-
является последовательностью Коши в топологии Г2,.
(SDP3) Каждое множество из 2Г предкомпактно (или, что
эквивалентно, относительно компактно) в топологии равномер*
ной сходимости на слабых последовательностях Коши из Е.
Читатель сам может получить множество других эквивалент-
эквивалентных условий, например, из теоремы 9.2.1.
872 Гл. 9. Теория компактных операторов
Как уже было замечено, анализ, проведенный Гротенди-
ком [4], показал, что результаты Данфорда и Петтиса о линей-
линейных отображениях пространства L1 опирается на тот факт, что
пространство E = Ll удовлетворяет эквивалентным между собой
условиям (DPi) — (DP3), а пространство Е = С(Т) обладает экви-
эквивалентными друг другу свойствами (SDPi) — (SDP3), причем
последнее обстоятельство весьма важно при изучении векторных
мер. В связи с этим Гротендик ввел следующее определение.
Говорят, что отделимое локально выпуклое пространство Е
обладает свойством (DP) {свойством Данфорда — Петтиса)
[соотв. (SDP) (строгим свойством Данфорда — Петтиса)], если
Е удовлетворяет одному из эквивалентных условий (DPi) —
(DP3) [соотв. (SDPi) —(SDP3)].
9.4.1. Замечания. A) Если Е и F — локально выпуклые
пространства и и: E-+F — непрерывное линейное отображение,
то следующие два утверждения эквивалентны (ср. с условием
(SDP0):
(a) отображение и переводит слабые последовательности
Коши в последовательности Коши;
(b) отображение и переводит ограниченные слабо метризуе-
мые множества в предкомпактные множества.
Таким образом, если выполняется условие (а) и А— огра-
ограниченное слабо метризуемое множество, то А слабо предком-
пактно (в силу ограниченности). Будучи слабо метризуемым,
множество А обладает тем свойством, что всякая последователь-
последовательность элементов из А содержит слабую подпоследовательность
Коши, которую отображение и переводит в последовательность
Коши. Таким образом, любая последовательность элементов из
и (А) обладает подпоследовательностью Коши, откуда и следует
предкомпактность множества и (А), т. е. (а)=ф>(Ь).
Пусть теперь выполняется условие (Ь) и (хп)— слабая после-
последовательность Коши в Е. Тогда множество S = {xn} ограничено
и слабо метризуемо (упр. Д11). По условию множество u(S)
предкомпактно. Так как отображение и непрерывно, то (и(хп)) —
слабая последовательность Коши в F. Будучи предкомпактной,
эта последовательность обязана быть последовательностью Ко-
Коши в F. Поэтому из (Ь) следует (а). Таким образом, оба условия
действительно эквивалентны.
B) В замечании A) мы использовали тот факт (упр. 9.11),
что в равномерном пространстве Е всякая последовательность
Коши образует полуметризуемое подпространство (метризуемое,
если Е отделимо). Если Е — отделимое локально выпуклое про-
пространство, справедлив более сильный результат, которым время
от времени мы будем пользоваться, а именно: замкнутая выпук-
выпуклая уравновешенная оболочка множества точек последователь-
9.4. Условия Данфорда — Петтиса и Дьёдонне 873
ности Коши метризуема. В качестве следствия из этого утвер-
утверждения получаем, что всякое линейное отображение простран-
пространства Е в локально выпуклое пространство F, переводящее схо-
сходящиеся к нулю последовательности в сходящиеся (необходимо
к нулю) последовательности, переводит последовательности
Коши в последовательности Коши (упр. 9.12 и 9.13). Очевидно,
этот результат применим и тогда, когда одно из пространств £,
F наделено своей ослабленной топологией.
C) Если пространство Е полно (или даже квазиполно в то-
топологии т(Е, £"')), то без всяких существенных последствий в
условиях (DPi) — (DP3) под 2 можно понимать систему всех
компактных подмножеств в Е. Более того (см. замечание после
теоремы 9.3.4), в условии (DP2) в этом случае можно заменить
«предкомпактность» на «компактность».
9.4.2. Примеры. Класс полурефлексивных пространств Ещ об-
обладающих свойством (DP), совпадает с классом ограниченно
компактных пространств (п. 8.4.7).
Действительно, пусть полурефлексивное пространство Е об-
обладает свойством (DP). Рассмотрим тождественное отображение
и: E-*F = E. Оно переводит ограниченные множества в множе-
множества, относительно компактные в слабой топологии (теоре-
(теорема 8.4.2), и потому переводит ограниченные множества в отно-
относительно компактные; следовательно, пространство Е ограничен-
ограниченно компактно.
Обратно, пусть Е — ограниченно компактное пространство.
Убедимся в том, что выполняется условие (DPi).-Действительно,
каждое множество /1g2 ограничено, а потому относительно
компактно, и, следовательно, множество и (А) относительно ком-
компактно, если отображение и непрерывно. (Так же легко было бы
проверить выполнение условия (DP2).)
Мы видим, таким образом, что единственными полурефлек-
полурефлексивными банаховыми пространствами, обладающими свойством
(DP), являются конечномерные пространства. С другой стороны,
монтелевы пространства С°°(Й), #(Й), 55 (Q, S), &{п) и 2)'(Q)
все обладают свойством (DP) (см. снова п. 8.4.7).
Заметим также, что всякое ограниченное компактное про-
пространство обладает свойством (SDP).
Все эти примеры довольно «грубы»; следующая ниже теоре-
теорема 9.4.4 гораздо интереснее как сама по себе, так и по своим
следствиям.
9.4.3. Некоторые общие свойства. Здесь собран ряд общих
утверждений, касающихся свойств (DP) и (SDP).
(а) Пусть (Е{) —семейство локально выпуклых пространств,
каждое из которых обладает свойством (DP) (соотв. (SDP)).
874 Гл. 9. Теория компактных операторов
Тогда произведение E=J\Ei также обладает свойством (DP)
(соотв. (SDP)).
Доказательство. Рассмотрим, например, случай, когда-
все пространства Ех обладают свойством (DP). Покажем, что
выполняется условие (DP), в своей на вид самой слабой форме
(DPi). Пусть и: E-+F — линейное непрерывное отображение и
ji — естественное отображение пространства Е{ в Е\ тогда ото-
отображение Ui — uo]^ Ei~+F непрерывно. Так как F— банахово
пространство, то из непрерывности и следует, что Ui=j=0 лишь
для конечного множества значений индекса и Поэтому доста-
достаточно ограничиться рассмотрением случая, когда число сомножи-
сомножителей в произведении конечно. Если и переводит ограниченные
множества в множества, относительно компактные в слабой то-
топологии, то это имеет место для каждого отображения иг. Тогда
по условию щ переводит множества из 2; B< — система выпук-
выпуклых уравновешенных <*(£,, £{)-компакных подмножеств в Ег) в
относительно компактные множества в F. Так как топология
в(Е,Е') является произведением топологий сг(£\, £Т), то отсюда
вытекает, что и переводит множества из 2 в относительно ком-
компактные подмножества в F. |
(b) Пусть пространство Е обладает свойством (DP) (соотв.
(SDP)) и Н — векторное подпространство в Е, имеющие тополо-
топологическое дополнение в Е. Тогда Н также обладает свойством
(DP) (соотв. (SDP)).
Доказательство. По условию существует непрерывная
проекция я пространства Е на Н. Если непрерывное линейное
отображение и: H-+F переводит ограниченные множества в
множества, относительно компактные в слабой топологии, то
отображение v = uoji\ E-+F линейно, непрерывно и переводит
ограниченные множества в множества, относительно компактные
в слабой топологии. Если множество АаН выпукло, уравнове-
уравновешено и а(#, Н') -компактно, то оно о(Е, Е') -компактно. Так
как Е обладает свойством (DP), то множество и (A) =v(A) от-
относительно компактно в F, и потому Н обладает свойством (DP).
Аналогичным образом доказывается, что подпространство Н бу-
будет обладать свойством (SDP), если этим свойством обладает
пространство Е. |
Замечание. Для произвольных векторных подпространств
Н в Е утверждение (Ь), вообще говоря, неверно.
(c) Пусть Е и F — полные отделимые локально выпуклые
пространства и Е обладает свойством (DP). Если f — непрерыв-
непрерывное билинейное отображение произведения Ex F в топологиче-
топологическое векторное пространство G и последовательности (хп) и (уп)
9.4. Условия Данфорда — Петтиса и Дьёдонне 875
слабо сходятся соответственно вЕиЕкхиу^то f(xn, уп) слабо
сходится к f{x,y) в G.
Доказательство. Достаточно рассмотреть случай, когда
G —скалярное поле и f — непрерывная билинейная форма на
произведении ExF. В этом случае можно считать, что f(x, у)—
= (х,и(у)), где и — непрерывное линейное отображение про-
пространства F в ^сильное сопряженное к Е. Если х'п = и(у^ то
последовательность х'п будет сходиться к х'=и(у) в топологии
а (£',£"), и нам достаточно показать, что (хп, х'п)->(х, х') при
п-^оо. Так как Е обладает свойством (DP), то, согласно теоре-
теореме 9.2.1, достаточно убедиться в том, что A) замкнутая выпук-
выпуклая уравновешенная оболочка А множества {хп} слабо компакт-
компактна в £ и B) а(£', Е") -замкнутая выпуклая уравновешенная обо-
оболочка А' множества |х^} является о(Е\ £//)*компакты°й-
Справедливость утверждения A) непосредственно вытекает
из теоремы Крейна 8.13.1. Для доказательства утверждения B)
можно воспользоваться сначала той же теоремой Крейна, чтобы
убедиться в том, что замкнутая выпуклая уравновешенная обо-
оболочка множества \уп) в F слабо компактна, а затем непрерыв-
непрерывностью отображения и. |
(с') Для того чтобы банахово пространство Е обладало свой-
ством (DP), необходимо и достаточно, чтобы (хп, л£)->0, если
последовательность (хп) слабо сходится к нулю в Е и последо-
последовательность (*д) сходится в топологии о{Е\ Е"). Очевидно, к
приведенным условиям можно, ничего не изменив, добавить
условие, что х'п—>0 в топологии о(Е', Е").
Доказательство. Необходимость ясна из (с). Докажем
достаточность. Если пространство Е не обладает свойством
(DP), то (теорема 9.2.1) существует такая последовательность
(хп), слабо сходящаяся к нулю в Е, и такое о(Е\ £")-компакт-
£")-компактное множество А' а Е', что (хп) не сходится к нулю равномерно
на А'. Следовательно, должны существовать такое число е>0
и такая последовательность (д£) элементов из А', что
\{хп> хп)\'>г для всех п' ^ силу теоремы Шмульяна 8.12.1, при-
примененной к банахову пространству Ег, можно считать, что по-
последовательность (*д) сходится в топологии о(Е', Е"). А это
противоречит условию. Таким образом, достаточность дока-
доказана. |
Замечание. Брэйс [1] изучил банаховы пространства Е,
для которых из слабой сходимости хп-*х в Е и сходимости
х'п-> х' в топологии о{Е\ Е") вытекает, что (хп, х'п)->(х, х').
876 Гл. 9. Теория компактных операторов
(d) Если пространство Е метризуемо, то (SDP2)z^> (DP2).
Если, кроме того, пространство Е слабо секвенциально полно,
то условия (DP2) и (SDP2) эквивалентны.
Доказательство. Пусть /IgE. Для доказательства пред-
компактности множества А в топологии 7V достаточно показать,
что из любой последовательности (хп) элементов из А можно
выбрать такую подпоследовательность, что множество ее эле-
элементов будет предкомпактно в топологии 7V. Множество элемен-
элементов {хп} относительно компактно в слабой топологии; поэтому из
теоремы Шмульяна 8.12.1 следует, что (хп) содержит слабо схо-
сходящуюся подпоследовательность. Но тогда из условия (SDP2)
вытекает, что эта последовательность является последователь-
последовательностью Коши и, значит, предкомпактна в топологии 7V. Таким
образом, (SDP2)=^(DP2).
Пусть теперь пространство Е метризуемо, слабо секвен-
секвенциально полно и обладает свойством (DP2). В Е каждая слабая
последовательность Коши (хп) слабо сходится и множество {хп}
относительно компактно в слабой топологии. В силу условия
(DP2) множество {и(хп)} относительно компактно в F. Но тогда
из непрерывности отображения и вытекает, что последователь-
последовательность (и(хп)) слабо сходится в F, а потому сходится и в ис-
исходной топологии в F. Это и означает справедливость условия
(SDP2).|
(d') Для того чтобы метризуемое локально выпуклое про-
пространство Е обладало свойством (DP), необходимо и доста-
достаточно, чтобьС в Е всякая слабо сходящаяся к нулю последова-
последовательность (хп) сходилась к нулю равномерно на каждом мно-
множестве из Z' (т. е. в топологии 7V).
Доказательство следует из теоремы 9.2.1 и определения
свойства (DP). (Ср. с доказательством утверждения (с').) I
Нам понадобится также следующий общий результат (Г ро-
роге нд и к [4, предл. 1, следствие], Бур бак и 9, гл. VI, стр. 94,
упр. 22с]).
(e) Если пространство Е инфрабочечно и его сильное сопря-
сопряженное Ег обладает свойством (DP), то само Е также обла-
обладает этим свойством.
Доказательство. Если пространство Е' обладает свой-
свойством (DP), то каждое множество из 2' предкомпактно в топо-
топологии 7V, где 2" — система всех выпуклых уравновешенных
равностепенно непрерывных о(Е",Е'") -компактных подмножеств
в Е". Поэтому в силу теоремы 9.2.1 каждое множество из 2"
предкомпактно в топологии 7V (или, точнее, в топологии в Е",
база окрестностей нуля которой образована полярами S0 в Е"
9.4. Условия Данфорда — Петтиса и Дьёдоннб 8?7
множеств S е 2'; эта топология индуцирует в Е топологию Гг).
Теперь остается убедиться в том, что 2 с: 2", т. е. что каждое
множество Ле2 является о{Е", Е'")-компактным. [Читатель
может заметить, что множество Л, будучи ограниченным в £",
равностепенно непрерывно в пространстве Е", сопряженном к
Е'.] Так как пространство Е инфрабочечно, то сильная тополо-
топология в Е" индуцирует в Е его исходную топологию, поэтому каж-
каждая форма из Е'" является продолжением некоторой формы из
Е'. Но тогда топология о(Е", Е"') индуцирует в А топологию
более слабую, чем та, которая индуцируется топологией
о(Е, Е'). В последней топологии множество А компактно по
определению, так что А компактно и в топологии о{Е'\ Е'"). |
Прежде чем приступить к одному из ключевых результатов
Гротендика [4, теорема 1], напомним, что через CQ(T) обо-
обозначается банахово пространство непрерывных на отделимом
локально компактном пространстве Т функций, обращающихся
в нуль на бесконечности. Норма в этом пространстве опреде-
определяется как максимум модуля рассматриваемой функции.
9.4.4. Теорема. Пусть Т — отделимое локально компактное
пространство, \х — положительная мера Радона на Т. Тогда
каждое из пространств С0(Т) и L1 = L1G1, \i) обладает свой-
свойством (SDP), а потому (в силу 9.4.3(d)) и свойством (DP).
Доказательство. Мы рассмотрим подробно случай про-
пространства Со(Г), а для пространства L1 лишь ограничимся ука-
указаниями, как этот случай можно свести к предыдущему.
(а) Случай пространства С0(Г). Нам нужно пока-
показать, что если (/п)—слабая последовательность Коши в С0(Т),
то последовательность J fndX равномерно сходится на каждом
ограниченном по норме и компактном в топологии о(М, М')
подмножестве Н банахова пространства М ограниченных мер
Радсна на Т. То, что (/п) —последовательность Коши, означает,
что функции fn равномерно ограничены, скажем \fn(t)\ ^c для
всех п и всех ty и что последовательность fn(t) поточечно схо-
сходится к некоторой функции /(/). Нам нужно показать, что
\ fndk-> \ fdl (при п-+оо) равномерно по X, пробегающим
множество Н. Для этого достаточно установить, что сходимость
равномерна относительно любого счетного подмножества в Н.
Другими словами, можно считать, что множество Н счетно и
относительно компактно в слабой топологии. В силу замечания,
предшествующего теореме 4.22.1, задача сводится к случаю,
когда H = {h-a: h<=P}, где а — некоторая ограниченная поло-
положительная мера и Р — подмножество в 3?1{<х), относительно
878 Гл. 9. Теория компактных операторов
компактное в слабой топологии. Надо показать, что Г fnh da ->
->\fhda равномерно по h e P. Но в силу теоремы Егорова 4.8.3
этот результат следует из георемы 4.21.10.
(Ь) Случай пространства /Л На основании 9.4.3(d)
нужно только показать, что L1 обладает свойством (DP). Сла-
Слабая секвенциальная полнота пространства L1 установлена в тео-
теореме 4.21.4.
В силу 9.4.3 (е) достаточно показать, что банахово простран-
пространство L°° обладает свойством (DP).
Здесь мы вынуждены сослаться на известные результаты,
выходящие за рамки этой книги. Пространство L°° представляет
собой пример коммутативной банаховой алгебры с инволюцией.
Из теории таких алгебр (Люмис [\н стр. 114], Риккарт [1,
стр. 190, теор. 4.2.2]) следует, что L°° изометрически изоморфно
пространству C(S)t где S — некоторое отделимое компактное
пространство, причем указанный изоморфизм сопоставляет ве-
вещественным функциям из L°° вещественные функции из С(S)<
Отсюда в силу (а) следует, что L°° обладает свойством (DP).|
Замечание. Из последнего абзаца вытекает, что если Т —
вполне регулярное топологическое пространство, то банахово
пространство Cbd{T) всех ограниченных непрерывных на Т функ-
функций (с нормой, равной верхней грани модуля рассматриваемой
функции) тоже обладает свойствами (DP) и (SDP). Действи-
Действительно,
где рГ есть компактификация Стоуна — Чеха пространства Т
(ср. с упр. 1.28).
Рассмотрим некоторые следствия предыдущей теоремы.
9.4.5. Следствие. Пусть и — слабо компактное линейное ото-
отображение пространства С0(Т) [или Щ в квазиполное отделимое
локально выпуклое пространство Р. Тогда
A) отображение и переводит множества, относительно ком-
компактные в слабой топологии, в относительно компактные мно-
множества',
B) отображение и переводит слабые последовательности
Коши в сходящиеся последовательности.
Доказательство. Для доказательства утверждения A)
достаточно заметить, что и С0(Т) и L1 обладают свойством (DP)
и что во всяком банаховом пространстве выпуклая уравнове-
уравновешенная оболочка каждого относительно слабо компактного
множества относительно слабо компактна. Это утверждение вы-
вытекает из теоремы Крейна 8.13,1. Для случая пространства
9.4. Условия Данфорда — Петтиса и Дьёдонне 879
О можно вместо теоремы Крейна воспользоваться теоремой
4.21.2.
С другой стороны, утверждение B) следует из того факта,
что как Со (Г), так и D обладают свойством (SDP). |
Замечание. Относительно случая L1 см. Дан форд и
Шварц [1, стр. 547, теор. 12].
Свойство (DP) и композиция слабо компактных линейных
отображений. Пусть X, Е и F— отделимые локально выпуклые
пространства, причем Е обладает свойством (DP) и F квази-
квазиполно. Предположим также, что отображения v: Х-+Е и и:
E-+F линейны и непрерывны и переводят ограниченные мно-
множества в относительно слабо компактные множества. Тогда ото-
отображение1) uv: X-+F переводит ограниченные множества в от-
относительно компактные.
В частности, если X и Е — нормированные пространства, то
(при сохранении других условий) отображение uv компактно,
если каждое из отображений и и v слабо компактно. Относи-
Относительно случая, когда X = E = F = Ll, см. книгу Данфорда и
Шварца [1, стр. 549, следствие 13], а также упр. 9.18.
Аналогичным образом если Е обладает свойством (SDP)
(причем X, F, и и v удовлетворяют тем же условиям, что и
выше), то отображение uv переводит слабые последовательно-
последовательности Коши в сходящиеся последовательности. То же заключение
справедливо, если X (а не Е) обладает свойством (SDP).
В частности, если X и Е — нормированные пространства и по
крайней мере одно из них обладает свойством (SDP), то отобра-
отображение uv переводит слабые последовательности Коши в сходя-
сходящиеся последовательности, если каждое из отображений и и v
слабо компактно.
9.4.6. Другие пространства, обладающие свойствами (DP) и
(SDP). Опираясь на теорему 9.4.4, можно показать, что свой-
свойствами (DP) и (SDP) обладают некоторые другие важные про-
пространства.
(a) Пусть Т — нормальное топологическое пространство, я—
некоторая система подмножеств в Т,Сп(Т) —пространство функ-
функций, непрерывных на Т и ограниченных на каждом множестве,
принадлежащем я. Если Сп(Т) наделено топологией, равномер-
равномерной сходимости на каждом множестве из я, то получающееся
локально выпуклое пространство обладает свойствами (DP) и
(SDP).
(b) Пусть Т — отделимое локально компактное пространство,
(л — положительная мера Радона на Т, я — система относи-
1) Здесь uv = u ov. — Прим. ред.
880 Гл. 9. Теория компактных операторов
тельно компактных и ^-измеримых подмножеств в Т. Обозначим
через Ln — Ln(T, \x) пространство (эквивалентных классов) та-
*
ких ^-измеримых функций /, что Г | /1 d\i < +00 для каждого
р
множества Рея. Наделим пространство Ln(T, \x) топологией,
определяемой полунормами /»-->j | / |ф. Тогда пространство
р
Ln обладает свойствами (DP) и (SDP).
Доказательство. Докажем подробно лишь утверждение
(а). Доказательство утверждения (Ь) вполне аналогично и ис-
аользует часть теоремы 9.4.4, относящуюся к пространству U.
Не нарушая общности, можно считать, что всякое множество
Рея замкнуто, а я представляет собой направленное по вклю-
включению множество. Для доказательства утверждения (а) доста-
достаточно показать, что если (/г) —слабая последовательность Коши
(или слабо сходящаяся сеть точек некоторого слабо компактного
подмножества) в Е = СПу то (/г) равномерно сходится на каж-
каждом равностепенно непрерывном о(Е\ Е") -компактном множе-
множестве A'czE'.
Так как множество Аг равностепенно непрерывно, то суще-
существует такое Р^л, что, полагая
(/ = {/еСя: 1/ЙК1 для /еР},
имеем A'zjk'U0 для некоторого k > 0.
Пусть ^ — непрерывное линейное отображение пространства
Сл в пространство C^d(P)=/7, ставящее в соответствие каждой
функции /еСл ее сужение f\P. Так как пространство Т нор-
нормально, то в силу теоремы Урысона 0.2.13 и отображает мно-
множество U на единичный шар пространства F. Соответственно
и' является взаимно однозначным линейным отображением про-
пространства F' в Е\ отображающим единичный шар в F' на по-
поляру U° множества U. Следовательно, каждый элемент xr e А'
является образом в точности одного элемента у'€= F' относи-
относительно отображения и'.
Докажем далее, что множество и'~1 (А') является o(F', F")-
компактным. Для этого достаточно показать, что и' есть изо-
изоморфизм пространства Fr в Ег (где Е' наделено своей сильной
топологией). Это будет установлено, если мы покажем, что
существует такое ограниченное множество ВаЕ, что и (В)
плотно в единичном шаре пространства F. Но в силу той
же теоремы Урысона можно в качестве В взять множество тех
функций / е Сл, абсолютное значение которых нигде не пре-
превосходит 1,
9.4. Условия Данфорда —Петтиса и Дьёдонне 881
Выбрав таким образом множество В, покажем, что предел
lim(/t-, х') существует равномерно по /еЛ'. Действительно,
(ft,x') = (u(f{), у'),
где у' = и'~х(х'). Поскольку и непрерывно, то (u(fi)) является
слабой последовательностью Коши (или слабо сходящейся
сетью из слабо компактного подмножества в F). Искомая рав-
равномерная сходимость следует из того факта, что пространство
F = Cbd{P) обладает свойствами (DP) и (SDP) (см. замечание
после теоремы 9.4.4). |
(с) Пусть Q — открытое подмножество в Rn и Cm(Q) —про-
—пространство пг раз непрерывно дифференцируемых на Q функций
(наделенное топологией равномерной сходимости на Q частных
производных dvf при каждом фиксированном р с \ р \ ^С пг
(гл. 5). Тогда пространство Cm(Q) обладает свойствами (DP)
и (SDP).
Доказательство. Не нарушая общности, можно считать,
что Q является областью. Действительно, Cm(Q) изоморфно
произведению ПСт(Йг), где йг— связные компоненты множе-
множества £2, и можно воспользоваться утверждением 9.4.3(а).
Кроме того, мы будем считать, что область Q выпукла. Без
этого условия доказательство несколько усложняется: прихо-
приходится использовать разбиение единицы для того, чтобы свести
общую задачу к случаю, когда область Q выпукла.
Рассмотрим Cm(Q) как векторное подпространство произве-
произведения Е= II Ер (каждое EP = C(Q)) относительно изомор-
физма, переводящего / в семейство (dpf)lp]<m. В силу 9.4.3(а)
и 9.4.3 (Ь) достаточно показать, что пространство Cm(Q) имеет
в Е топологическое дополнение, т. е. что существует непрерывная
Проекция пространства Е на Cm(Q). Возьмем произвольную
точку t0 e Q и обозначим через С™ (Q) векторное подпростран-
подпространство в Ст(й), образованное теми функциями [ECffl(Q), для
которых dPf(to)=O при \р\<пг. Тогда подпространство С™@)
имеет в Cm(Q) конечную коразмерность. Поэтому достаточно
указать непрерывную проекцию я пространства Е на CcT(Q).
Такая проекция я получается, если положить n((fp)) = (gp),
где семейство (gp) определено следующим образом. Если
\р\=пг, то g"p=/P. Пусть gp определено для всех p = k, где
0kKm, и ^ — индекс с \q\=k—1. Положим
= J [
[^" i V , +
Ut
882 Гл. 9. Теория компактных операторов
где ^ = (?1 + 1, q2> •••> Яп\ <7" = (<7i> ?2+1»-ч ?п) и т. д. суть
такие индексы р, что \p\=k. Интегрирование произво-
производится здесь по отрезку, соединяющему точки t0 и /, что воз-
возможно, так как область Q выпукла. (Это и есть то место в до-
доказательстве, которое вызывает трудности, если не предпола-
предполагать выпуклости- Q.) Шаг за шагом проверяется, что gP{to)=O
при \р\<т * dkg{Pl,..., Рп) = S{Pv ...t Pk+lf ..„ Рпу откуда и следует,
что я — непрерывная проекция пространства Е на CcF(Q). I
(d) Из теоремы 9.4.4 и теоремы 4.23.2 (которая в настоящей
книге не доказывается) следует, что пространство М(Т) ограни-
ограниченных мер Радона* на отделимом локально компактном про-
пространстве Т обладает свойствами (DP) и (SDP).
Теорема Данфорда, Петтиса и Филлипса. В качестве прило-
приложения теоремы 9.4.4 мы хотим привести доказательство одной
важной теоремы представления, принадлежащей Данфорду
и Пет тису [1, теор. 3.1.7] и позднее видоизмененной Фил-
липпсом [2, теор. 5.2]. Излагаемое здесь доказательство в зна-
значительной мере совпадает с тем, которое набросано Бур баки
[9, гл. VI, стр. 95, упр. 24]. Св. также А. Ионеску Тулча и
К. Ионеску Тулча [3].
9.4.7. Теорема. Пусть F — банахово пространство, Т — отде-
отделимое локально компактное пространство, \х — положительная
мера Радона на Т и и — слабо компактное линейное отображе-
отображение пространства Ll = Ll(T, \x) в F. Тогда суьцествует такая из-
измеримая функция /: T-+F, что
A) 11/@ II < Ы для <еГ;
B) функция f слабо компакт позначна (т. е. f(T)—относи-
f(T)—относительно слабо компактное подмножество в F);
C) u(g)=jgfdti для ge^.
Обратно, если измеримая функция f: T-+F удовлетворяет
условию B) (или локально почти всюду равна такой функции),
то соотношение C) определяет слабо компактное линейное ото-
отображение и: L1 ->■ F.
Доказательство теоремы довольно длинно, и мы его
разобьем на ряд шагов. На первом и наиболее важном шаге
мы покажем, что если и слабо компактно, то оно допускает
представление C), где / — измеримая функция, удовлетворяю-
удовлетворяющая условию A). На втором шаге мы докажем, что после из-
изменения на локально пренебрежимом множестве (что всегда
возможно сделать, не затрагивая условия A)) функция / будет
принимать значения в некотором относительно слабо компакт-
компактном подмножестве в F. Таким образом, утверждение B) будет
9.4. Условия Данфорда — Петтиса и Дьёдонне 883
доказано. На последнем шаге устанавливается справедливость
обратного утверждения.
Шаг I. Допустим, что в случае, когда пространство Т ком-
компактно, требуемое представление возможно. В общем случае,
как известно (предложение 4.14.9), пространство Т представляет
собой объединение локально пренебрежимого множества N и
локально счетного семейства- непересекающихся компактных
множеств Ki. Если наше допущение справедливо, то для каж-
каждого i существует такая измеримая функция /г-: /(г-> Т7, что
ИЫ01К IN для teKi и
и (ё) = J
для каждой функции g e 571, равной нулю на T\Kv Положим
(Ш при t<=Ku
П) 1 0 при /eiV
Определенная таким образом функция f: T-+F измерима,
11/@ II <\\и\\ для /еГ, и
J г/Ф
для всех geS71. Другими словами, общий случай сводится к
случаю, когда Т компактно. Итак, будем считать пространство
Т компактным.
Из компактности Т следует, что L°° a L1 и замкнутый еди-
единичный шар В из L°° ограничен в L1. Поэтому множество и (В)
относительно слабо компактно в F. Кроме того, В компактно
в топологии o(L\ L°°), и потому, так как L1 обладает свойством
(DP), множество и (В) относительно компактно в F. В частности,
и (В) сепарабельно, следовательно, u(Ll) также сепарабельно.
В силу сказанного можно всюду заменить F замкнутым век-
векторным подпространством, порожденным множеством u(Lx), и
с самого начала считать, что F сепарабельно и u(Ll) плотно в/7.
Обозначим через А замыкание в F образа единичного шара
из L1 относительно отображения и. Множество А слабо ком-
компактно. Так как пространство F сепарабельно и метризуемо, то
Fr слабо сепарабельно (как объединение слабо компактных и
слабо метризуемых, а потому слабо сепарабельных множеств
V°n\ где (Vn) —счетная база окрестностей нуля в F). Таким
образом, существует последовательность (л/J, тотальная в F'.
Отсюда получаем, что множество А слабо метризуемо метрикой
884 Гл. 9. Теория компактных операторов
Действительно, эта метрика определяет в Л отделимую тополо-
топологию, более слабую, чем та, что индуцируется в Л топологией
o{F, F'). Так как множество А компактно в последней тополо-
топологии, то указанные топологии в А совпадают. Зная, что множе-
множество А компактно и метризуемо в топологии а(/7, F'), заключаем,
что оно сепарабельно в этой топологии.
Введем теперь нормированное пространство Z, состоящее из
точек пространства F\ для которого Л° служит единичным ша-
шаром. Множество А можно тогда отождествить с единичным ша-
шаром пространства Z'. В силу теоремы Хана —Банаха Z изомет-
рично и изоморфно пространству С (Л), где А наделено тополо-
топологией, индуцированной топологией а(/7, F'). Так как А компактно
и метризуемо, то пространство Z сепарабельно. Действительно,
по теореме Вейерштрасса — Стоуна (п. 4.10.5) если (ап)—по-
(ап)—последовательность, плотная в Л, то подалгебра в С (А), порож-
порожденная функциями q>n(x) =d(x, an), плотна в С (А).
Отображение и можно, таким образом, рассматривать как
линейное отображение пространства L1 в Z\ где Z — нормиро-
нормированное сепарабельное пространство. Очевидно, что и: LX->Z'
непрерывно. По теореме Данфорда — Петтиса 8.17.6 существует
такая скалярная измеримая функция /: T->Z' (Z' a F как век-
векторное подпространство), что
для gG,?1. Скалярная измеримость функции / означает, что
функция xof измерима для каждого 2gZ, т. е. для каждого
z^F'. Таким образом, функция /: T-+F скалярно измерима,
и так как пространство F сепарабельно, то (теорема 8.15.2)
функция f: T-*~F измерима.
Остается показать, что можно так выбрать функцию /, чтобы
всюду выполнялось неравенство \\f(t) || ^ ||wj|. Из самой фор-
формулы представления непосредственно следует, что \{f(t)9x')\ ^
<-1М1 для каждого хг с ||*'|К1 и каждого <еГ\ Nxf, где Nxf —
локально пренебрежимое множество. С другой стороны, как мы
уже видели, единичный шар в F' слабо сепарабелен. Отсюда
следует, что существует такое локально пренебрежимое мно-
множество N, что | {f(t), х') |-< ||и|| для всех t^T\N и всех х'
с 1ИК1. Итак, ||/@ !|< Hull для всех te=T\N. Если теперь
переопределить функцию f(t), полагая ее равной нулю для t^N,
то левая часть формулы представления не изменится, и опреде-
определенная таким образом функция f будет удовлетворять всем на-
нашим требованиям.
Шаг II. Для доказательства того факта, что функцию f
можно выбрать так, чтобы она удовлетворяла условию B),
9.4. Условия Данфорда — Петтиса и Дьёдоннё &8о
больше чем достаточно убедиться в справедливости следующего
утверждения.
Если функция /: T-+F измерима и скалярно локально ин-
интегрируема, а множество
Q = j ti{A)~l J /ф: А интегрируемо, ц(Л)>о1
содержится в F, то в Г существует такое локально пренебре-
жимое множество N, что f(T\N) содержится в замыкании мно-
множества Q в F. (Здесь "достаточно ограничиться предположением,
что F — отделимое локально выпуклое пространство.)
Докажем это утверждение. Представим Т в виде объедине-
объединения локально пренебрежимого множества No и локально счет-
счетного семейства (Ki) непересекающихся компактных множеств
(см. предложение 4.14.9). Очевидно, достаточно показать, что
для каждого i существует такое пренебрежимое множество^
NiCzKi, что f(K{\Ni) a Q. [Напомним читателю, что каждое
компактное подмножество в Т пересекает не более чем счетную
совокупность множеств Кг]
Так как / измерима, то для каждого i множество Кг можно
представить в виде объединения последовательности таких ком-
компактных множеств (Нп) и такого пренебрежимого множества
Л", чю сужения f\Hn непрерызны. Следовательно, достаточно
показать, что f(Hn\Mn) a Q для некоторого пренебрежимого
множества Мп с Нп.
Предположим поэтому, что множество И компактно и суже-
сужение f\H непрерывно. Докажем, что f(H\M) cz Q для некоторого
пренебрежимого множества МаН. Для этого определим М как
множество таких точек /бЯ, что \x(H[]U) =0 для некоторой
окрестности U точки /. Множество М открыто относительно Н
и потому измеримо. Множество М пренебрежимо. Действительно,
если L — компактное подмножество в М, то для каждой точки
t e L найдется такая ее открытая окрестность Uu что
\x(H(MJt)=O. Так как конечное число множеств Ut покрывает
L, то L содержится в объединении конечного числа пренебре-
жимых множеств H[)Ut и потому само пренебрежимо. Так как
это справедливо для произвольного компактного множества
L а М, то само множество М пренебрежимо.
Если теперь /еЯ\М, то \х(Н[)М)>0 для любой окрест-
окрестности U точки t. Так как сужение f\H непрерывно, то принад-
принадлежащие Q интегралы
tx(H[)U)-1 J /ф
H[\U
Гл. 9. Теория компактных Операторов
сходятся к f(t), когда окрестность U неограниченно стягивается
к точке. _
Таким образом, f(H\M) a Q, что и требовалось доказать.
Шаг III. Пусть f: T-+F — измеримая функция, почти всюду
равная функции, удовлетворяющей условию B). Нам нужно
показать, что соотношение C) определяет и как слабо компакт-
компактное линейное отображение пространства L1 в F. При этом можно
считать, что сама f удовлетворяет условию B). Но тогда мно-
множество f(T) слабо ограничено, а потому ограничено в F. Из
теорем 8.14.14 и 8.15.2 следует, чго соотношение C) опреде-
определяет и как линейное отображение пространства L1 в F. Наша
задача показать, что и слабо компактно.
В силу условия B) и теоремы Крейна 8.13Л существует
выпуклое уравновешенное слабо компактное множество Р, со-
содержащее /(Г). Если gs S71, J | g \d\i ^ 1 и Jt7 G Р°, то
J I 8 I •
I (и (г). *'> I = | J S • <Д *'> •
Из теоремы о биполяре вытекает, что u(g) ^ Р00 = Р. Следова-
Следовательно, 2/ переводит единичный шар пространства L1 в подмно-
подмножество из Р, т. е. отображение и слабо компактно. |
Замечания. Эта теорема приводится в книге Данфор-
да и Шварца [1, стр. 545, теор. 10] при дополнительном усло-
условии, что u(L1) сепарабельно.
Последняя часть доказательства на шаге I может быть ис-
использована в более общей ситуации, а именно когда F — ло-
локально выпуклое пространство и и — отображение единичного
шара из U в подмножество некоторого компактного выпуклого
уравновешенного множества Аа F, которое метризуемо в инду-
индуцированной топологии. В результате получаем существование
представления C), в котором функция / скалярно измерима и
такова, что л/of локально существенно ограниченна для каж-
каждого jc'eF. Более подробно см. Данфорд и Шварц [1,
стр. 537, теор. 2].
Располагая теоремой 9.4.7, относительно легко получить
условия, которым должна удовлетворять функция / для того,
чтобы соответствующее отображение и: U -> F было компактно.
Этот вопрос тоже рассмотрен в работе Данфорда и Пет-
тиса [1, теор. 3.1.2] (см. также Данфорд и Шварц [1,
стр. 546, следствие 11]).
9.4.8. Теорема. Пусть F, Т и \х те же, что и в теореме 9.4.7.
Если линейное отображение и: U ->• F компактно, то существует
такая измеримая функция f: T-+F, что 11/@ II ^ IHI всюду на
9.4. Условия Данфорда — Петтиса и Дьёдонне 887
Т% множество f(T) относительно компактно в F и
(9.4.1)
для g^.3!x. Обратно, если функция /: T-+F измерима а ло-
локально почти всюду равна функции, множество значений кото-
которой относительно компактно в F, то формула (9.4.1) определяет
компактное линейное отображение и: Ll-+F.
Доказательство. Докажем прямое утверждение. Из
теоремы 9.4.7 вытекает существование такой измеримой функ-
функции f, что 11/@11^11^11 всюду на Т и имеет место формула
(9.4.1). В силу результата, полученного на шаге II предыдущего
доказательства, существует такое локально пренебрежимое мно-
множество /V, что f(T\N) а Я, где Н—компактное замыкание об-
образа единичного шара в L1 относительно и. Теперь достаточно
переопределить функцию /, полагая f(I\f)=O.
Что касается доказательства обратного утверждения, то
можно считать, что множество f(T) относительно компактно.
В этом случае применимы такие же рассуждения, как на шаге
III доказательства теоремы 9.4.7, если под Р понимать замкну-
замкнутую, выпуклую, уравновешенную оболочку множества f(T) в F.
В результате получим, что u(g) е Р, если g е 9?х и Г | g \d[i ^ U
откуда и вытекает компактность отображения и. 1
Условие Дьёдонне. Условия Данфорда — Петтиса в неко-
некотором смысле представляют собой аксиоматизацию довольно
глубоких свойств относительно слабо компактных линейных ото-
отображений, действующих на пространствах непрерывных или
интегрируемых функций (см. следствие 9.4.5). Для пространств
непрерывных функций Гротендик [4, стр. 157—161] получил
другое подобное свойство и подверг его аналогичной аксиома-
аксиоматизации. Он назвал его свойством Дьёдонне (коротко, свой-
свойством (D)). Прежде чем применять свойство (DP) простран-
пространства Со(Г) к изучению векторных мер Радона, рассмотрим
новое свойство в общих терминах, так как оно также имеет не-
некоторое отношение к векторным мерам.
9.4.9. Предложение. Пусть Е— отделимое локально выпук-
выпуклое пространство, &~ — множество сетей в Е, каждая из кото-
которых слабо (т. е. в топологии а(£", F/)) сходится в Е". Пусть
далее Н — векторное подпространство в Е", порожденное про-
пространством Е и пределами сетей из ЗГ. Тогда следующие свой-
свойства пространства Е эквивалентны.
A) Всякое непрерывное линейное отображение и простран-
пространства Е в полное отделимое локально выпуклое пространство F,
Гл. 9. Теория компактных операторов
переводящее сети из SF в слабо сходящиеся сети в F, переводит
ограниченные сети в относительно слабо компактные множества.
(Г) То же, что и A), только F — банахово пространство.
B) Всякое непрерывное линейное отображение и: E-+F
(пространство F такое же, как в A)), для которого и" (Н) с: У7,
удовлетворяет условию и"(Е") a F.
B') То же, что и B), только F — банахово пространство.
C) Всякое равностепенно непрерывное выпуклое урав-
уравновешенное о (Е', Н)-компактное множество в Е' является
о (£А, Е") -компактным.
Доказательство. В доказательстве несколько раз бу-
будет применяться следствие 9.3.2. Очевидно, что A)=ф(Г) и
B)=фB').
(a) A) Ф%> B). Допустим, что справедливо утверждение A)
и выполняются условия утверждения B). Пусть (хг)—элемент
из #". По условию (Х{) слабо сходится в Е" к некоторому
х"^Н.. Тогда сеть и(х{) = и"(хг) слабо сходится к и"(х") в F,
так как отображение и" непрерывно в топологиях а(£", Е') и
o(F", F') и по предположению и"(Н) czF. Таким образом, ото-
отображение и удовлетворяет условиям утверждения A) и, следо-
следовательно, переводит ограниченные множества в относительно
слабо компактные. Отсюда получаем (следствие 9.3.2), что
u"(E")aF, т. е. справедливо утверждение B). Итак, (l)z^B).
Так как все рассуждения обратимы, то AL$ B).
(а') Аналогично доказывается эквивалентность утверждений
(П и B0-
(b) B/)z^C). Действительно, пусть А'а Е' — равностепенно
непрерывное выпуклое уравновешенное о(Е', Н) -компактное
множество, и пусть выполняется утверждение B). Нам нужно
показать, что множество А' о(Е\ £")^компактное, или, что то
же самое, что оно относительно компактно в топологии
в(Е\Е"). Обозначим через р функционал Минковского поляры
Л'°; он является полунормой на Е. Образуем факторпростран-
ство E/ker р, для которого р является нормой, и пополним это
факторпространство до банахова пространства F. Пусть и —
естественное отображение Е в F. Обозначим через В замкнутый
единичный шар в F'. Легко проверить, что и'(В) zdA'. Поэтому,
воспользовавшись еще раз следствием 9.3.2, видим, что А' отно-
относительно компактно в топологии о(Е\ Е"). Следовательно, до-
достаточно показать, что и" отображает Е" в F. Так как простран-
пространство Е удовлетворяет условию B), то это будет вытекать из со-
соотношения и"(Н) а Т7, которое мы сейчас докажем. В силу тео-
теоремы Хана —Банаха Е плотно в // относительно топологии
Макки т(#, Е'). Из условий, которым удовлетворяет А\ следует,
9.4. Условия Данфорда — Петтиса и Дьёдонне 889
что сужение и"\Н непрерывно в топологии т(#, Е') и той топо-
топологии в Т7", для которой базой окрестностей нуля служат поляры
в F" равностепенно непрерывных подмножеств из F'. Эта топо-
топология в F" индуцирует в F его исходную топологию. Так как
и"(Е) a F и F полно, то и"(Н) с: F, что и требовалось доказать.
(с) C)=фA). Действительно, пусть и: E^F— такое непре-
непрерывное линейное отображение, что u"(H)czF. Нам нужно по-
показать, что если Е удовлетворяет условию C), то и переводит
ограниченные множества в относительно слабо компактные. Из
следствия 9.3.2 вытекает, что и' отображает равностепенно не-
непрерывные подмножества В'a F' в множества, относительно
компактные в топологии о(Е\ Е"). Из соотношения u"(H)czF
следует, что отображение и' непрерывно в топологиях a(F\ F)
и о(Е\ //), откуда получаем, что множество и'(В') относительно
компактно в топологии о(Е', Н). Но тогда в силу утверждения
C) и'(В') относительно компактно в топологии о(Е', Е ).
И гак, мы получили следующую схему импликаций:
т. е. все эти условия эквивалентны. |
Замечание. Предложение 9.4 9 можно сформулировать
по-другому, заменив множество %Г множеством 2 ограниченных
подмножеств в £ и часть утверждения A), относящуюся к #~,
словами: «...переводящее множества А е 2 в относительно слабо
компактные подмножества в F...» При этом Н заменяется на
векторное подпространство в £", порожденное пространством Е
и слабыми замыканиями в Е" множеств, принадлежащих 2.
Однако специального доказательства предложения 9.4.9, моди-
модифицированного таким образом, не требуется, так как оно вы-
вытекает из первоначальной формулировки, если взять в качестве
& множество всех сетей (Хг), которые A) слабо сходятся в Е"
и B) состоят из элементов, принадлежащих некоторому мно-
множеству из 2.
Основываясь на предложении 9.4.9, введем следующее опре-
определение. Говорят, что пространство Е обладает свойством Дьё-
Дьёдонне (= свойством (D)), если для него выполняются эквива-
эквивалентные условия предложения 9.4.9, где в качестве ЗГ взято
множество всех слабых последовательностей Коши в Е. В этом
случае пространство Н называется бэровским подпространством
первого класса в Е".
Замечание. Конечно, можно ввести свойство Дьёдонне
относительно любого множества сетей #", удовлетворяющего
условиям предложения 9.4.9. Ясно, что чем меньше множество
•У, тем сильнее ассоциированное с ним свойство Дьёдонне.
890 Гл. 9. Теория компактных операторов
Примеры. A) Каждое полурефлексивное пространство об-
обладает свойством Дьёдонне, поскольку в этом случае EczHa
czE" = E, так что Н=Е" и должно выполняться условие B)
предложения 9.4.9.
Если Е полно и слабо секвенциально полно, то оно может
обладать свойством Дьёдонне, только будучи полурефлексив-
полурефлексивным. Действительно, тождественное отображение и простран-
пространства Е на себя переводит слабые последовательности Коши в
слабо сходящиеся последовательности и потому (если Е обла-
обладает свойством Дьёдонне) ограниченные множества в относи-
относительно слабо компактные. Это означает, что пространство Е по-
полурефлексивно (теорема 8.4.2).
В частности, пространство L1 обладает свойством Дьёдонне
только тогда, когда оно конечномерно. Это видно из теорем
8.4.2 и 4.21.2, ибо L1 полурефлексивно лишь в упомянутом три-
тривиальном случае.
B) Если ограниченные множества в Е слабо метризуемы
(например, если Е — нормированное пространство, сопряжен-
сопряженное Ef к которому сильно сепарабельно), то Е обладает свой-
свойством Дьёдонне. В самом деле, в этом случае H = F" (E" в лю-
любом случае есть объединение о(Е", Е') -замыканий ограничен-
ограниченных подмножеств из £), и потому снова выполняется условие
B) предложения 9.4.9.
C) Произведение пространств, каждое из которых обладает
свойством Дьёдонне, также обладает этим свойством (ср. со
свойствами (DP) и (SDP); см. п. 9.4.3(а) и (Ь)). Если про-
пространство Е обладает свойством Дьёдоние, то им обладает и
каждое векторное подпространство НаЕ, имеющее топологи-
топологическое дополнение в Е. Доказательства этих утверждений ана-
аналогичны предыдущим.
Перейдем теперь к основному результату (Гротендик
[4, стр. 160, теор. 6]).
9.4.10. Теорема, (а) Если Т — отделимое локально компакт-
компактное пространство, то пространство С0(Т) обладает свойством
Дьёдонне. Фактически справедливо даже более сильное утвер-
утверждение: если и — непрерывное линейное отображние простран-
пространства Со (Г) в полное отделимое локально, выпуклое простран-
пространство F, то следующие утверждения эквивалентны:
A) и слабо компактно;
B) u"(%A)^F для каждого замкнутого подмножества
Лс=Г;
B') и"(%А) g/7, если множество А обладает счетной базой
окрестностей;
9.4. Условия Данфорда — Петтиса и Дьёдонне 891
C) и переводит всякую ограниченную возрастающую после-
последовательность из Со (Г) в слабо сходящуюся последователь-
последовательность в F.
(Ь) Если Q — открытое подмножество в Rn, то Cm(Q) обла-
обладает свойством Дьёдонне.
Доказательство, (а) Ясно, что A) влечет C), по-
поскольку всякая последовательность элементов из С0(Г), удовле-
удовлетворяющая условиям утверждения C), будучи слабой последо-
последовательностью Коши, переводится в силу непрерывности отобра-
отображения и в слабую последовательность Коши в F.
Далее A) влечет B) в силу следствия 9.3.2, а из B) три-
тривиально следует B/)-
С другой стороны, B') эквивалентно утверждению, которое
получится, если в B/) считать, что А—открытое множество,
являющееся объединением последовательности замкнутых мно-
множеств. Если А удовлетворяет этому условию, то %А является
пределом в Со(Т)" ограниченной возрастающей последователь-
последовательности функций из Со(Г). Отсюда следует, что C)гфB/).
Для завершения доказательства остается установить, что
B')=ФA)> Для чег0 нужно убедиться в том, что пространство
Е = С0(Т) удовлетворяет какому-нибудь из эквивалентных
утверждений A) — C) предложения 9.4.9, где в качестве ЯГ
взято множество ограниченных монотонно возрастающих после-
последовательностей функций из Со (Г). Но тогда // совпадает с про-
пространством, обозначенным в теореме 4.22.3 через Q. Из этой же
теоремы вытекает справедливость условия C) предложения
9.4.9, что и завершает доказательство утверждения (а).
(Ь) В силу утверждения C), предшествующего настоящей
теореме, с учетом доказательства утверждения 9.4.6 (с) доста-
достаточно показать, что C(Q) обладает свойством Дьёдонне. Фак-
Фактически мы покажем, что пространство £ = C(Q) удовлетворяет
условию C) предложения 9.4.9.
Если £=C(Q), то Е' является пространством мер Радона на
Q с компактными носителями, а Н — множеством функций на
Q, служащих пределами поточечно сходящихся локально равно-
равномерно ограниченных последовательностей функций из С{п).
Так как Е — пространство Фреше (и потому бочечно), то вся-
всякое равностепенно непрерывное множество А'а Е' можно отож-
отождествить с ограниченным подмножеством пространства М(К),
где К—некоторое компактное множество в Q. Если далее мно-
множество А' а(Е\ Я)-компактно, то из теоремы 4.22.3 следует,
что А слабо компактно в М(К). Всякая сильно непрерывная ли-
линейная форма на Ег обладает непрерывным сужением на М(К),
поскольку, как легко проверить, последовательность, сходящаяся
892 Гл. 9. Теория компактных операторов
к нулю в М(К), сильно сходится к нулю в Е'. Отсюда вытекает,
что топология а(Е\Е") индуцирует в М(К) более слабую то-
топологию, чем о(М, М'), и, следовательно, А' относительно ком-
компактно в топологии g(E\ E"). Тем самым условие C) прове-
проверено. |
В этом месте читателю рекомендуется посмотреть упр. 9.14.
Имеет смысл выписать отдельно одно свойство непрерывных
линейных отображений, действующих на пространстве, обла-
обладающем свойством Дьёдонне.
9.4.11. Теорема. Пусть пространство Е обладает свойством
Дьёдонне, F — полно и слабо секвенциально полно и и: E-+F —
непрерывное линейное отображение. Тогда и переводит
(a) слабые последовательности Коши в слабо сходящиеся
последовательности,
(b) ограниченные множества в множества, относительно
слабо компактные.
Доказательство. Из непрерывности отображения и
следует (для любых Е и Z7), что оно переводит слабые после-
последовательности Коши в последовательности такого же вида.
Если F — слабо секвенциально полное пространство, то слабые
последовательности Коши в F слабо сходятся. Отсюда вытекает
свойство (а). Если Е обладает свойством Дьёдонне, то свой-
свойство (Ь) следует из уже доказанного свойства (а).|
9.4.12. Замечания. Если известно, что пространство Е об-
обладает и свойством Дьёдонне и свойством (DP) (или SDP),
например если £=С0(Г), то справедливы еще более замеча-
замечательные утверждения о всяком непрерывном линейном отобра-
отображении и: E-+F (где F — полное и слабо секвенциально полное
пространство).
Именно,
если Е обладает свойством Дьёдонне и свойством (DP), то
и переводит
(c) относительно слабо компактные множества в относи-
относительно компактные*,
а если Е обладает свойством Дьёдонне и свойством (SDP),
то и переводит
(d) слабые последовательности Коши в сходящиеся после-
последовательности;
(e) ограниченные и слабо метризуемые множества в относи-
относительно компактные множества.
Утверждение (е) показывает, что, рассматривая простран-
пространства £, в которых каждое ограниченное множество слабо мет-
ризуемо, имеет смысл выделять все те пространства £, сопря-
сопряженные к которым сильно сепарабельны. Приведем один иа ре-
9.4. Условия Данфорда — Петтиса и Дьёдонне 893
зультатов, принадлежащих Гротендуку [4, стр. 170,
предл. 15]).
9.4.13. Предложение. Пусть Е и F — полные, отделимые ло-
локально выпуклые пространства, причем в Е каждое ограничен-
ограниченное множество слабо метризуемо. Тогда справедливы следую-
следующие утверждения.
A) £ обладает свойством Дьёдонне.
B) Всякое непрерывное линейное отображение и: E-+F,
такое, что и(хп)-+0 в F, если последовательность (хп) слабо
сходится к нулю в Еу переводит ограниченные множества в от-
относительно компактные множества.
C) Если F обладает свойством (DP), то всякое непрерывное
линейное отображение и: E-+F, переводящее ограниченные
множества в относительно слабо компактные, переводит ограни-
ограниченные множества в относительно компактные; каждое равно-
равностепенно непрерывное и относительно компактное в топологии
а(£/, Е") подмножество в Е/ является относительно сильно ком-
компактным.
Доказательство. Утверждение A) уже было рассмот-
рассмотрено в примере B), предшествующем теореме 9.4.10.
Докажем справедливость утверждения B). Пусть А — про-
произвольное выпуклое уравновешенное ограниченное подмноже-
подмножество в Е. Так как А слабо метризуемо, то по условию сужение
и\А непрерывно в нуле. Но тогда из выпуклости и уравновешен-
уравновешенности множества А следует, что сужение и\А равномерно непре-
непрерывно. Всюду здесь в А рассматривается топология, индуци-
индуцированная слабой топологией. Так как А слабо предкомпактно,
то и (А) предкомпактно, а потому относительно компактно.
Наконец, если и переводит ограниченные множества в отно-
относительно слабо компактные и Е обладает свойством (DP), то
и переводит относительно слабо компактные множества в отно-
относительно компактные. В частности, и переводит слабо сходящие-
сходящиеся последовательности в сходящиеся. Но тогда в силу утвержде-
утверждения B) и переводит ограниченные множества в относительно
компактные. Остальная часть утверждения C) следует из теоре-
теоремы 9.3.4, если в ней под ® понимать систему всех ограниченных
подмножеств в Е. Читатель может заметить, что если множество
А'аЕ' о(£', Е") -компактно, то оно полно в этой структуре, а
потому и сильно полно; итак, если множество А' сильно предком-
предкомпактно, то оно относительно сильно компактно. I
Замечание. Гротендик [4, стр. 171, теор. 10] доказал,
что заключения предложения 9.4.13 справедливы, если простран-
пространство Е является факторпространством или замкнутым векторным
подпространством пространства cq. См. упр. 9.16,
894 Гл. 9. Теория компактных операторов
9.4.14. Приложения к векторным мерам Радона. В § 8.19
.(см. замечание после п. 8.19.2) мы говорили о задаче расшире-
расширения области определения векторной меры Радона. Как уже
было отмечено, существует подход к этой задаче, отличный от
примененного в § 8.19 и существенно использующий результаты
общей теории слабо компактных линейных отображений. Послед-
Последние результаты уже приведены в предыдущей части настоящего
параграфа. Поэтому мы можем описать этот другой подход.
Всюду ниже будем предполагать, что локально выпуклое
пространство Е полно. Для простоты будем считать, что основ-
основное отделимое пространство Т компактно; тогда пространство
Ж(Т) =С0(Т) = С(Г) банахово. Выражение «мера Радона» будет
означать «скалярная мера Радона на Г». В остальном обозна-
обозначения те же, что и в § 8.19. В частности, через m обозначается
£-значная мера Радона на 7\ т. е. согласно нашему определе-
определению, m — непрерывное линейное отображение пространства
С(Т) в Е. Идеи, аналогичные тем, которые излагаются здесь,
описаны в книге Данфорда и Шварца [1, стр. 527—536] для
случая, когда Е — банахово пространство; мы занимаемся теми
же задачами, но в несколько более общей постановке.
->
(А) Предположим сначала, что отображение m непрерывно.
Тогда очевидно, что для каждого х' е Е' линейная форма
m(f), х')
на С(Т) является мерой Радона на Т. Далее если отождествить
пространство С{Т)\ сопряженное к С (Г), с пространством М(Т)
мер Радона на Т (теорема 4.10.1), то отображение т\ сопряжен-
сопряженное к т, переводит хг в меру тхг.
В дальнейшем нам понадобится второе сопряженное С(Т)" =
= М(Т)'. Простое «конкретное» описание этого второго сопря-
сопряженного неизвестно, однако одно его важное замкнутое вектор-
рое подпространство можно описать как пространство £/(Т) ограни -
ченных универсально измеримых функций g на Т. Всякая такая
функция g отождествляется с элементом пространства М(Т)\
определяемым правилом Лн-> Г gdX, так что мы будем писать
Ясно, что С(Т) — замкнутое векторное подпространство в U(T).
Хотя элемент m(g) определен только для случая, когда
g&C(T)cz U(T)} элемент m"(g) определен для каждого ge
9.4. Условия Данфорда — Петтиса и Дьёдонне 895
и характеризуется соотношением
<m"(§)> *')-(g, m'(*')>-\gdm'x,,
которое выполняется для каждого fe U(T) и каждого х' &Е'9
причем m"(g)^E". В соответствии с общей теорией (§ 8.7) эле-
элемент tn"{g) определяется как а (£", Е') -предел сети (т(/г)), где
сеть (fi)cz С(Т) ограничена и сходится к g в топологии g(C", M).
Последнее требование предполагает, что lim/< = g> поточечно
на Г. Кроме того, по теореме Лебега 4.8.2 последовательность
(gi) сходится к g в топологии о(С",М) тогда и только тогда,
когда она ограничена и поточечно сходится к g на Т.
Обозначим временно через m совокупность всех универсально
измеримых подмножеств в Т. Эта совокупность является а-алге-
брой (т. е. она устойчива относительно взятия счетных объедине-
объединений и перехода к дополнениям). Совокупность m содержит все
борелевские1) подмножества в Т. Для М^т положим \х(М) =
= т"(Хм)^Е". Таким образом, получаем функцию множества,
определенную на т, со значениями в Е". Для каждого я'е£'
имеем
откуда следует, что функция множества \х слабо счетно аддитив-
аддитивна. Отсюда в силу теоремы Петтиса (см. Данфорд и Шварц
[1, стр. 346]), доказательство которой приводится ниже в пунк-
пункте (В) (где рассматривается Е вместо £""), следует, что функция
множества jli счетно аддитивна.
Теперь уже легко показать, что функция множества |л осуще-
осуществляет представление функционала пг в том смысле, что
где интеграл \ g(t)d\i(t) можно определить для любого je
е V(Т) как элемент из Е'\ являющийся пределом в топологии
о (£", Е') лебеговых сумм вида
Если g — комплексная функция, то удобно рассматривать отдель-
отдельно вещественную и мнимую части функции g. Если функция g
1) Подмножество В топологического пространства Е называется боре-
левскам, если оно принадлежит а-алгебре, порожденной открытыми множе-
множествами. — Прим. перев,
896 Гл. 9. Теория компактных операторов
вещественна, то лебегова сумма определяется приведенной выше
формулой для каждого конечного набора вещественных чисел
со< С\ < ... < сп, такого, что интервал [с0, сп)у содержит все
значения функции g, причем
Если взять последовательность таких «лесенок» (сг), для кото-
которых sup (с,- — Ci_i)->09 то лебеговы суммы аппроксимируют ин-
интеграл. Доказательство этого утверждения хорошо известно и
элементарно в случае числовых мер (упр. 4.5).
Последние замечания наводят на мысль о частичном обра-
обращении этого построения, когда задана некоторая счетно адди-
аддитивная функция множества jli со значениями в Еу определенная
на всех борелевских подмножествах из Т. Тогда в силу полноты
пространства Е формула m(/) = J fd\i определяет непрерывное
линейное отображение пространства С(Т) в Е (подробнее см.
пункт (В) ниже).
Читатель может, однако, заметить одну неприятную вещь:
отправляясь от меры пг, мы пришли к счетно аддитивной вектор-
векторной функции множества, такой, что
->
m (/) =
однако нам известно лишь, что \к принимает значения в Е'\ a
вовсе не в Е. Как мы сейчас увидим, это неприятное свойство
симптоматично для тех отображений т, которые не слабо ком-
компактны.
(В) Случай слабо компактных отображений т. Рассмотрим
следующие свойства меры Радона пг со значениями в простран-
пространстве Е:
A) т — слабо компактное отображение-,
B) т"(%А)^Е// для каждого замкнутого множества АаТ
(или для каждого замкнутого множества АаТ, обладающего
счетной базой окрестностей)-,
B') т"(С")аЕ;
C) т' переводит равностепенно непрерывные подмножества
из Е* в множества, относительно компактные в топологии
g(M\ M);
->
D) m переводит ограниченные возрастающие последователь-
последовательности из С(Т) в последовательности, слабо сходящиеся в Е\
9.4. Условия Данфорда — Петтиса и Дьёдонне 897
D0 m — переводит слабые последовательности Коши из
С(Т) в последовательности, слабо сходящиеся в Е\
E) m перевод относительно слабо компактные множества
из С(Т) в множества, относительно компактные в Е.
Мы утверждаем, что
(a) свойства A) —D0 эквивалентны-,
(b) каждое из свойств A) — D') влечет свойство E).
Действительно, из теоремы 9.4.10 следует, что свойства A),
B) и D) эквивалентны, а из теоремы 9.3.2 — эквивалентны свой-
свойства A), B0 и C). Таким образом, свойства A), B), B0, C)
и D) эквивалентны. Далеее из D0 тривиально вытекает свой-
свойство D). G другой стороны, D) эквивалентно свойству B0, ко-
которое влечет за собой D0, так как всякая слабая последователь-
последовательность Коши в С{Т) слабо сходится в C(T)"t а поэтому перево-
переводится отображением и" в последовательность, которая слабо
сходится в Е"\ следовательно, из B0 вытекает D0- Таким обра-
образом, утверждения A) — D0 эквивалентны. Наконец, поскольку
С(Т) обладает свойством (DP), то A) влечет за собой E). В
Мы хотим показать еще, что если m—слабо компактное ото-
отображение, то функция множества \х, о которой известно, что она
слабо счетно аддитивна, является на самом деле счетно аддитив-
аддитивной. Пусть (Мп)—последовательность попарно непересекающих-
оо
ся универсально измеримых подмножеств в Т и М = {jMn. До-
оо
кажем, что ряд ^j\*>(Mn) сходится в Е к сумме \i(M). (Нам из-
вестно только, что этот ряд слабо сходится в Е к сумме \х{М).)
Пусть фе!00. Положим ап = \х(Мп) и
(/0xAf @.
Функции gr (r=l,2,...) принадлежат пространству U(T). По-
Последовательность gr ограничена и сходится на Т поточечно к
п
замечаний пункта (А) следует, что m"(gr)
-*m"(g) в топологии о(ЕуЕ'). Поэтому, в частности, ряд
2 ф(я)Ял слабо сходится в Е для каждого ф е /°°. Из предложе-
п
ния 9.3.10 (или, так как пространство Е квазиполно, из замеча-
замечания B) после предложения 9.3.9) гюлучаем, что ряд 2 ял
898 Гл. 9. Теория компактных операторов
сходится в £, т. е. что ряд ^Ецл(Мп) сходится. Так как этот ряд
п=[
слабо сходится к \л(М), то его сумма и должна быть не чем
иным, как (я(М) (пространство Е по условию отделимо). Этим
теорема Петтиса доказана.
Обратно, пусть задана счетно аддитивная функция множе-
множества [х со значениями в Еу определенная на некоторой а-алгебре
moc:m подмножеств в Т, содержащая все борелевские множе-
множества. Пусть Uo(T)czU(T) — пространство всех щ-измеримых
ограниченных комплексных функций g на Т. (Под щ-измери-
мостью функции g понимается следующее ее свойство: если g' и
g" — соответственно вещественная и мнимая части функции g,
то прообраз всякого вещественного интервала относительно ка-
каждой из функций g'-и g" принадлежит т0.) Поскольку Е по усло-
условию полно, то легко показать, что интеграл
v (8) = /
существует как элемент из Е для каждого gG U0(T). Действи-
Действительно, в силу полноты Е этот интеграл существует как предел
в Е лебеговых сумм, описанных выше в пункте (А). В частности,
сужение m отображения v на С(Т) является линейным отобра-
отображением пространства С(Т) в Е и v = m"\ U0(T). Так как т" не-
непрерывно в топологиях о(С'\С) и а(£", £') и замкнутый еди-
единичный шар в С" является а (С", С) -компактным множеством,
отсюда непосредственно вытекает, что т -г- слабо компактное
отображение пространства С(Т) в Е. Легко видеть, что вектор-
векторная функция множества, полученная из отображения га спосо-
способом, описанным выше в пункте (А), есть не что иное, как Mepaji,
с которой мы начали рассуждения.
Таким образом, можно сказать, что существует взаимно одно-
однозначное соответствие между слабо компактными линейными ото-
отображениями пространства С(Т) в отделимое локально выпуклое
и полное пространство Е и счетно аддитивными мерами, прини-
принимающими значения в Е и определенными на о-алгебре универ-
универсально измеримых подмножеств в Г, содержащей все борелев-
борелевские множества (или, что то же самое, все открытые или все
замкнутые множества в Т). Этот результат принадлежит Гро-'
тендику [1, стр. 167, предл. 14].
Отметим, наконец, что из условия Bа) теоремы 9.3.1 следует,
что если отображение m слабо компактно, то соответствующая
функция множества \х является слабо компактнозначной, г. е.
jx(m) относительно слабо компактно в £,
9 4. Условия Данфорда — Петтиса и Дьёдонне 899
->
Другой подход к исследованию случая, когда отображение га
слабо компактно, имеется в работе Бартла, Данфорда и
Шварца [1].^
(С) Случай, когда отображение m компактно. В этом случае
можно воспользоваться теоремой 9.2.1, взяв в качестве © систему
ограниченных подмножеств в Е, а в качестве ©'— систему
равностепенно непрерывных подмножеств в Ег. Тогда если
Q — равностепенно непрерывное подмножествоо в Е\ то множе-
ство P = {mxf'- x'^Q} относительно компактно в М(Т). Предо-
Предоставляем самому читателю в качестве упражнения показать, что
отсюда следует предкомпактность в Е множества \х(т) и, следо-
следовательно, его относительная компактность, поскольку простран-
пространство Е квазиполно. Эту ситуацию будем характеризовать сло-
словами «функция множества jli компактнозначна» (ср. с ситуацией
пункта (В)).
Как и в (В), справедливо обратное утверждение: если функ-
функция множества jli компактнозначна, счетно аддитивна и прини-
принимает свои значения в квазиполном пространстве £, то ra.(f) =i
= fd\i — компактное линейное отображение пространства С(Т)
в Е (это легко следует из теоремы Крейна 8.13.1) и функция
множества, полученная из га с помощью способа, описанного в
пункте (А), есть не что иное, как сама функция \х.
9.4.15. Замечания. A)Динкуляну [1—7] и Динкуля-
ну и Фояш [1] рассмотрели много разновидностей векторно-
значных и операторнозначных мер в свете их использования для
интегральных представлений линейных операторов, действующих
из пространств функций, определенных на Г и принимающих
значения в £, в пространство F (пространства Е и F предпола-
предполагаются у них банаховыми).
B) Довольно большое число работ посвящено непрерывным
линейным отображениям пространства C(S) для того весьма ча-
частного случая, когда 5 — отделимое компактное пространство
Стоуна. (Топологическое пространство S называется простран-
пространством Стоуна, если замыкание всякого открытого множества в
S также открыто.)
Гротендик [4, стр. 168, теор. 9 и следствие 1] показал, что
в пространстве M(S) (ограниченных мер Радона на S) всякая
а(М, С) -сходящаяся последовательность слабо сходится (т. е.
сходится в топологии а(М,М')). В качестве следствия отсюда
вытекает, что каждое непрерывное линейное отображение про-
900 Гл. 9. Теория компактных операторов
странства C(S) в полное отделимое сепарабельное локально вы-
выпуклое пространство является слабо компактным.
Рассуждения Гротендика опираются на некоторые другие
интересные свойства пространства C(S) в частности на тот
факт, что если C(S) — замкнутое векторное подпространство не-
некоторого банахова пространства X, то C(S) допускает топологи-
топологическое дополнение в X. Это свойство характеризует простран-
пространство C(S) среди других банаховых пространств (см. Нахбин
[3]„ Гуднер [1] и Келли [3]).
Важно, конечно, иметь способ распознавать пространства,
изоморфные C(S). Тут на помощь приходит теорема Какутани,
параллельная принадлежащей ему же теореме 4.23 2, являющей-
являющейся абстрактной характеризацией пространства L1.
Абстрактным (Ж)-пространством называется пространство
Рисса Е, наделенное нормой, удовлетворяющей всем условиям
п. 4.23.1, за исключением условия (L), которое заменяется сле-
следующим условием:
(М) если х>0 и у>0, то \\х V */|| = sup(IU||, \\y\\).
Единицей е абстрактного (М)-пространства называется эле*
мент, обладающий следующими двумя свойствами:
(U) е>0 и 1И = 1;
(U') если \\х\\<19 то х<е.
Какутани [6, теор. 2] показал, что если Е—абстрактное
(М)-пространство с единицей е, то Е изометрично и изоморфно
(линейно и относительно порядка) пространству С^(Г), где Т —
некоторое отделимое компактное пространство, единственное с
точностью до гомеоморфизма. Здесь CR (T)—вещественное ба-
банахово пространство вещественных непрерывных функций на Т
с нормой ||/|| = sup{\f(t) \: /бГ}ис естественным частичным по-
порядком (f •<£ означает, что f(t)^Cg(t) для всех /еГ),
С другой стороны, можно показать (Бур баки [8, гл. IV,
стр. 43, упр. 13f]), что Cr (T) является вполне решеточным про-
пространством (т. е. обладает тем свойством, что всякое его не-
непустое мажорированное подмножество обладает верхней
гранью) тогда и только тогда, когда Т — пространство Стоуна.-
Таким образом, всякое вполне решеточное абстрактное
(М)-пространство с единицей изометрично и изоморфно про-
пространству Cr(S) для некоторого отделимого компактного про-
пространства Стоуна S, которое определяется однозначно с точно-
точностью до гомеоморфизма среди всех отделимых компактных про-
пространств.
Приведем два важных примера.
(а) Е = 1°°A), где / — произвольное множество (рассматри-
(рассматриваемое как дискретное пространство). Соответствующее этому
9.5. Интегральные операторы 901
случаю пространство S является компактификацией Стоуна —
Чеха множества^/.
(b) E—L =L°°(T, jli), где Т — отделимое локально компакт-
компактное пространство, а |л — положительная мера Радона на Т. Чи-
Читатель может убедиться сам (упр. 9.17), что вещественные эле-
элементы пространства Ь°° образуют вполне решеточное абстракт-
абстрактное (М) -пространство с единицей. Элемент / из Е°° является
вещественным, если его класс имет своим представителем веще-
вещественную функцию; отношение f^g для вещественных элемен-
элементов / и g имеет место тогда и только тогда, когда соответствую-
соответствующие им представители — функции / и g — удовлетворяют усло-
условию f(t)^.g(t) локально почти всюду.
9.5. Интегральные операторы и ядерные представления
Многие из первых примеров компактных линейных отобра-
отображений возникали в связи с решением интегральных уравнений и
задач, выражающихся в форме интегральных уравнений. Соот-
Соответствующие линейные отображения преобразуют одно функцио-
функциональное пространство в другое и имеют вид
у = и(х),
y(t)=jk(t,s)x(s)do(s), (9.5.1)
где s и /—переменные точки двух отделимых локально компакт-
компактных пространств S и Т с положительными мерами Радона а и т
соответственно и k — заданная функция, называемая ядром и
определенная на произведении TxS. Всюду в дальнейшем мы
будем считать, что ядро k измеримо относительно меры т®т
При соответствующих условиях, примерам которых посвящена
первая половина этого параграфа, формула (9.5.1) определяет
и как непрерывное линейное отображение пространства 2>(S, a)
в Ьч(Т, т), или пространства C(S) в С(Т), или других известных
функциональных пространств друг в друга. При некоторых огра-
ограничениях на k отображение и будет компактным. При изучении
этих вопросов мы не будем различать функцию и ее класс (кото-
(который может быть элементом из Lp(S, а) или из L^(Ty %)). Предо-
Предоставим самому читателю в необходимых случаях различать эти
понятия.
Во второй части этого параграфа мы коротко остановимся
на обратной задаче, а именно на представлении данного отобра-
отображения и в виде (9.5.1). Вообще говоря, эта задача более тонкая.
Некоторые первые работы в этой области принадлежат Дан-
форду и Петтису [1, особенно часть 3]; см. также Дан-
форд и Шварц [1, стр. 544, следствие 9]. В обеих работах
902 Гл. 9. Теория компактных операторов
сматриваются отображения из 2> в Ьч. Ядерные представления
слабо компактных или компактных линейных отображений про-
пространства СE) в банахово пространство исследовались Барт-
лом [1], Бартлом, Данфордом и Шварцем [1] и В а-
д о й [1] в очень общей постановке. Мы коротко остановимся и на
их работах.
Интегральные операторы такого вида, как в (9.5.1), и соот-
соответствующие им интегральные уравнения возникают в связи с
дифференциальными уравнениями как в обыкновенных, так и в
частных производных, а также в теории потенциала. В большей
части мы будем вынуждены предоставлять читателю подробный
анализ этих связей; см., например, Смитис [2], Курант и
Гильберт [1, 2], Коддингтон и Левинсон [1]. Однако
в § 9.12 мы наметим такой подход к изучению дифференциаль-
дифференциальных уравнений с помощью компактных линейных отображений,
при котором ядерные представления отображений играют второ-
второстепенную роль.
В первой и более конкретной части наших исследований мы
будем пользоваться некоторыми неравенствами Юнга, которые
опираются на непрерывность отображений вида (9.5.1), преобря
зующих пространство Lp(S, а) в Ь<*(Тут).
9.5.1. Теорема, (а) Пусть 0<а<+оо, 0<Ь<+оои
т-ess sup | J ! k (t9 s) \a da (s)ja = Mx < + oo, (9.5.2)
a-esssu'p{ j\k(t, s)\bdx{t)Y =M2< + oo. (9.5.3)
Тогда определенное равенствами (9.5.1) отображение и есть не-
непрерывное линейное отображение пространства Lp (S, а) в
L<i(T, т), если
и тогда
t ь_ _ь_
||и||<М, *Af/. (9.5.5)
(b) Пусть 1^а^ + оо и имеет место неравенство (9.5.2)»
Тогда и есть непрерывное линейное отображение пространства
La'(S> a) в L°°G\ т) и ||и|КМ,.
(c) Пусть 1 ^ Ь ^ + оо и имеет место неравенство (9.5.3).
Гогйа и есть непрерывное линейное отображение пространства
Ll{S, о) в Lb(T, т) и ||и||<М2.
(а7) Пусть a{S) и х(Т) конечны и неравенства (9.5.2) и (9.5.3)
имеют место при 0<a< + oof 0< & < + оо. Тогда и есть не-
9.5. Интегральные операторы 903
прерывное линейное отображение пространства Lp E, а) в Lq (Г, т),
ее ни существует такое число qx ^ q, что
(Ь') Пусть а E) и %(Т) конечны и неравенство (9.5.3) имеет
место при 1^а^ + оо. Тогда если
то и есть непрерывное линейное отображение пространства
LP(S, а) в LQ(T, т) и
(с') Пусть a(S) и х(Т) конечны и неравенство (9.5.3) имеет
место при 1^6^ + оо. Тогда если 0<^^6, то и есть непре-
непрерывное линейное отображение пространства L1 (,S, а) в Lq G1, т) и
Доказательство, (а) Из неравенства Гёльдера следует,
что (для любой положительной меры \х)
если 0<а, р, ..., Y< + °° и — + J+ ••• +7=1' (°ДН0 или
несколько из чисел а, р, у» • • • могут равняться +оо, при этом
соответствующий интеграл в правой части заменяется на ess sup.)
Положим
1 = 1 1:=1_А 1 = 1-1
а <7'Р a aq 9 у р q '
Тогда равенство (9.5.4) позволяет воспользоваться неравен-
неравенством Гёльдера, из которого следует, что для почти всех t
X
\y(t)\< | {\k(t, s) \T\x{s) fr\{\k{t, s) f Й"Й} x
{\x(s) \P(i~tyde(s)^{ | \k(t, s)\b\x(s) \pda(s)\~ X
x{j\k(t, s)\ada(s)Y {j\x(s)\pda(s)Y <
r , ,-L ± JL
<{j\b(t,s)f\x(s)\pdo(s)\q -Af/» - (H^yv.
904 Гл. 9. Теория компактных операторов
На последнем шаге мы воспользовались неравенством (9.5.2).
Из полученного неравенства следует, что
ад PQ
||jc||pv j dx(t)\\k(t, s)\b\x(s)\pdo(s)
Л± Ж.
aq pq
Отсюда вытекает нужный нам результат, так как
* !_А и £. + £„!_£ + £
(Ь) Если а>1 и справедливо (9.5.2), то из обычной формы
неравенства Гёльдера получаем, что для почти всех t
откуда и следует требуемый результат.
(с) Если Ь%\, имеет место (9.5.3) и x^Ll(S, a), то можно
выбрать такое z^Lb'(T, т), что ||z||6,= 1 и
\\y\\b=\y{t)z(t)dx{t).
Но тогда в силу неравенства Гёльдера
\\y\\b=\ z(t)dx(t)j k(t, s)x(s)do(s) =
= j x(s)da{s)j k{t, s)z(t)dx(t)^
< J \x(s)\do(s) ■ ||z \\b, • { J \k(t, s) fdx(t)}T,
откуда и следует нужное нам утверждение.
(а') Для пространств S и Т с конечной мерой непрерывность
из Lp в Z/1 влечет за собой непрерывность из 1/ в Lq, если
qx^q- Пусть p^j удовлетворяют условию (9.5.4'), тогда
р \а) q a ^
Определим q2 с помощью отношения f—J— = 1 — — и рас-
рассмотрим два случая.
9.5. Интегральные операторы 905
Допустим сначала, что —>1——. Тогда 0<^2< + °° и
<7i^<72- В силу (а) и непрерывно отображает if в Lq\ а по-
поэтому оно тем более непрерывно преобразует if в LQl и if в If.
Во втором случае — ^ 1 — — и можно применить утвержде-
утверждение (Ь').
(Ь') Пусть 1<а< + оо, -.^1——и k удовлетворяет нера-
неравенству (9.5.2). В силу (Ь) и непрерывно отображает if' в L°°.
Так как — < 1 — — ^-^г» то а'^р. Поэтому из того факта,
что рассматриваемые пространства S и Т имеют конечную меру,
следует, что
J 1_
M{a(S)a/ p\\x\\P9
что и требовалось доказать.
(с') Если 1^6^ + оо и k удовлетворяет неравенству (9.5.3),
то из (с) следует, что и непрерывно отображает L1 в Ьъ. Так
как q ^ b и пространства S и Т имеют конечную меру, то и
непрерывно отображает L1 в Lq и
-L -L L ±
~ )я"ь М2\\х\\{.
Теорема полностью доказана. |
Что касается компактности отображения и, то здесь имеют
место два относительно простых результата.
9.5.2. Предложение. Пусть пространства S и Т компактны и
функция k непрерывна на пространстве TxS. Тогда отображе-
отображение и, определенное равенством (9.5.1), является компактным
отображением пространства C(S) в С (Г), пространства Lp(S) в
С(Т), пространства C(S) в L<i(T) и пространства L?(S) в L<*(T)9
если 1<р<+оо и 0< <7<+оо.
Доказательство. Так как вложения С в Z/ и Lp в L1 не-
непрерывны для любого г > 0 и любого /?5> 1, то достаточно пока-
показать, что и — компактное отображение пространства Ll(S) в
С(Т). Пространства S и Т можно наделить равномерными струк-
структурами, определяющими их топологии, и непрерывность функ-
функции k влечет за собой ее равномерную непрерывность. Поэтому
очевидно, что и преобразует единичный шар пространства V E)
906 Гл. 9. Теория компактных операторов
в ограниченное и равностепенно непрерывное множество про-
пространства /Сг. В силу теоремы Асколи это множество относи-
относительно компактно в С(Т).Щ
Замечание. Более глубокий результат содержится в пред-
предложении 9.5.17.
9.5.3. Предложение (Банах). Пусть S и Т — компактные
пространства, 14/"< +оо м
_i_
Af =| J j\k(t9 s)\rao{s)dx{t)y <+ оо. (9.5.6)
Тогда, если
(9.5.7)
то и компактно как отображение пространства Ьр E, а)
в LQ(Tyx).
Доказательство. Так как р^г', то //<>, откуда,
поскольку o{S) конечно, получаем, что
<ll*||, ■{ J|*(*f s)\rda(s)y -const.
Так как q^r и т(Г) конечно, то
\\у Wg^constWyWr^constWxWp. { j dx(t)j\k(t, s)\rda(s)\r
< const M-\\x\\p. Г9.5.8)
Отсюда следует, что и — непрерывное отображение пространства
Lp в ZA
Если функция k(t,s) непрерывна, то компактность отображе-
отображения и вытекает из предложения 9.5.2. В противном случае мы
аппроксимируем в Lr(TxSy%<8) в) функцию k(t, s) непрерывны-
непрерывными ядрами ki{t,s), замечая, что из (9.5.8) вытекает сильная схо-
сходимость соответствующих отображений щ к и, и применяем сле-
дующую^ниже простую лемму. 1
9.5.4. Лемма. Если сеть (щ) предкомпактных линейных ото-
отображений нормированного векторного пространства Е в тополо-
топологическое векторное пространство F сходится к отображению и в
сильной топологии в Lc(£, F) (т. е. сходится равномерно на
ограниченных подмножествах из Е)у то и — предкомпактное
отображение.
9.5. Интегральные операторы 907
Доказательство. Пусть В— единичный шар в Е и V —
произвольная окрестность нуля в F. Выберем / так, чтобы и(х) —
— Ui(x)^V для xgB. Так как множество и{(В) предком-
пактно, то тем же свойством обладает и множество <u(B)cz
czUi(B) + V. Следовательно, отображение и предкомпактно.|
9.5.5. Замечание. Читатель может легко проверить, что
если 5 и Г не компактны, но k обладает компактным носителем,
то предложения 9.5.2 и 9.5.3 остаются справедливыми.
Следующий ниже результат менее очевиден.
9.5.6. Теорема. Пусть o(S) и т(Г) конечны.
. (а) Пусть k удовлетворяет неравенствам (9.5.2) и (9.5.3) при
0 < а ^ + оо и 0<6<+оо. Если существует такое q\ ^ qy что
(9.5.9)
то определенное равенством (9.5.1) отображение и компактно
как отображение пространства L^(S, а) в Ь^(ТУ т).
(Ь) Пусть 1<а<1+оо и k удовлетворяет неравенству
(9.5.2). Если 0</?<+оо, 0<<7<+оо w 1 < 1 - If T0 и яв-
является компактным отображением пространства L? (S, а) в
LHL)
Доказательство, (а) Так как т(Т) конечно, то достаточ-
достаточно показать, что и компактно как отображение пространства
Ьр в Lq\ если р и q\ удовлетворяют (9.5.9). Определим число ах
равенством
±
1 CL\
Тогда 0<ai<+oo и соотношение (9.5.9) можно переписать
в виде
р \а ) qx a
при некотором d > 0. Так как #i — 6 > 0, то а\<а.
Положим
{& При |&|^Аг,
0 при \k\> п9
где лг = 1, 2,..., и пусть ггп — отображение, определяемое яд-
ядром kn. Так как функция /гп ограничена и o(S) и т(Г) конечны,
то ип является компактным отображением пространства Lp в
Lq\ Это следует из предложения 9.5.3, если взять там любое
908 Гл. 9. Теория компактных операторов
конечное число r^- max(p\ qi). Теперь в силу леммы 9.5.4 до-
достаточно показать, что
\\u(x)-un(x)\\qi^MJx\\p,
где Мп—>0 при п->оо.
Теорема (9.5.1) (а) позволяет считать, что
где
М1п = т-ess sup | J | k (tt s) - kn (*, s) f' do (s) p",
JL
M2w = a-esssupj j\k(t, s)-kn{t, s)\bdx(t)Y .
Так как \k — kn\^\k\y то последовательность Ni\ ограничена.
С другой стороны, так как а{<ау то можно положить а — а{ =
= с>0. Тогда, поскольку \k — kn\ — либо нуль, либо величина,
большая, чем п, имеем
l*-ft»r</r'l*-ftnle<*-W,
и поэтому
Afi<T-esssup
при az~>oo. Утверждение (а) полностью доказано.
(Ь) Доказательство этого утверждения аналогично доказа-
доказательству предыдущего, надо только воспользоваться теоре-
теоремой 9.5.1A/). ■
9.5.7. Рассмотрим сейчас одно полезное уточнение предложе-
предложения 9.5.2, ослабив условие непрерывности функции k. Будем го-
говорить, что функция k квазиравностепенно непрерывна в точке
t0 е Г, если для любого е > 0 существуют такое множество
SqCzS и такая окрестность U точки t^ что cr(So)<e и
\HU s)-k(tOy s)\<b
при (*,s)<= f/X(S\S0).
9.5.8. Теорема (Канторович). Пусть a(S) и т(Г) конечны,
ядро к удовлетворяет неравенству (9.5.2) при некотором а > 0
и k квазиравностепенно непрерывно в каждой точке t gT. Тогда
если — < 1 , 0</?^+оо, то и — компактное отображение
пространства Lv{S,a) в СЪа{Т)х).
') Ctd(T) — пространство ограниченных непрерывных функций на Г с
нормой \\y\\ = sup{\y(t)\:t еГ}.
9.5. Интегральные операторы 909
Доказательство! В силу теоремы 9.5.6(Ь), где положено
*7 = оо, достаточно показать, что и отображает пространство Lv
в Cbd(T). Выберем число с так, чтобы 1 < с < а, — <1— —.
В теореме 9.5.1 (Ь') возьмем T = {t}y q= + oo и т равным мере
единичной массы, сосредоточенной в точке t, а в качестве ядра
возьмем разность k(t,s) — k(tOys). Тогда из равенства
-У (to) = J {£ Л 5) - 6 (/о, s)} х (s) do (s)
получаем, что
\y(t)-y(to)\<{j\k(t9 s)-k(tOi s)fda{s)}T.\\x\)p.
Докажем, что первый множитель в правой части равенства стре-
стремится к нулю, когда t-^tQ. Этот множитель не превосходит
/ |... ГЛЛЧ-/J|... fda\T.
S\Sr J I So I
Первый член в этом выражении не превосходит 8'(r(S)c, если
t e U, а второй член в силу неравенства Гёльдера не превос-
превосходит
J| ... Г^а)а Л j da\ c
Правая часть этого неравенства стремится к нулю, когда е->0,
потому что >0. Таким образом, теорема доказана. |
С CL
9.5.9. С помощью последней теоремы можно установить не-
некоторые свойства ядер типа потенциала.
Пусть пространство S = T является некоторым ограниченным
множеством D в Rn и а = т является сужением на D я-мерной
меры Лебега. М. Рисе ввел потенциалы порядка а @<а^дг),
порожденные ядром
(это — обобщение ньютоновского потенциала в Rn, определяе-
определяемого ядром г2'п). Формальное частное дифференцирование со-
соответствующих потенциалов приводит к рассмотрению более
общих ядер
k(tf s) = B(ty s)|f-sr\ (9.5.10)
где В — ограниченная и непрерывная при гфэ функция и
0 < К < п.
910 Гл. 9. Теория компактных операторов
Теперь мы коротко остановимся на вытекающих из некоторых
предыдущих результатов свойствах интегральных операторов,
содержащих ядра такого вида. Так как функция В и множе-
множество D ограничены, то неравенства (9.5.2) и (9.5.3) имеют место
при Ха < п и Kb < n соответственно. (Без дополнительных огра-
ограничений на поведение B(t,s) вблизи диагонали l = s ни одно из
этих условий не выполняется для D = Rn.)
Приведем сейчас интерпретации теорем 9.5.1 (а7), 9.5.1 (с7) и
9.5.8 для рассматриваемого нами случая.
9.5.10. Теорема. Пусть D — ограниченное подмножество в Rn
k — ядро (9.5.10), причем функция B(tys) всюду ограничена и
непрерывна при t=f=s. Пусть далее и — отображение, определен-
определенное формулой (9.5.1), где T = S = D, а а и т — меры Лебега.
(а) Если 1<р^+оо, 0<#<+оо и
то и — непрерывное отображение пространства Lp(D) в Lv(D).
(b) £с./Ш 0<<7<-г-, то и —непрерывное отображение про-
пространства Ll(D) в L<i(D).
(c) Если р> _. , то и — компактное отображение про-
пространства Lp(D) в Cb(D).
Доказательство, (а) Воспользуемся теоремой 9.5.1 (а7),
полагая в ней
и 6 =
где 0 < а < 1, 0< р < 1 будут выбраны позднее. Предположим
временно, что ^0 = niax(^, p). Тогда выбор qx определяется ра-
равенством ^/i = <7оA + Y)> гДе 0-^Y< +oo. Отсюда получаем, что
(ср. 9.5.40
где
1 _1_ Л1 I
Соотношение
I__L
р qQ
9.5. Интегральные операторы 9J1
эквивалентно соотношению
<+1
Так как 1 >0, то
что и есть (9.5.11). Таким образом,
1 1 Л А
!1
где г>0 и не зависит от а, р и у, Итйк,
Остается только проверить, что можно так выбрать а, р и у,
чтобы выполнялось неравенство /?■</*. Это легко проверяется;
поэтому наше утверждение (а) следует из теоремы 9.5.1 (а7).
(b) Берем в теореме 9.5.1 (с7) в качестве Ь число, удовлетво-
удовлетворяющее неравенствам а<й<т-> 1^6< + °°, сколь угодно
близкое к j- (т> О и превосходящее q.
(c) Чтобы применить теорему 9.5.8, нужно подобрать чис-
числа а так, чтобы а<-г-, 0<р^ + оо, — < 1 . Ясно, что это
л р а
можно сделать, если р>0 и — < 1 , т. е. р> «-.
Теорема полностью доказана. |
9.5.11. Замечания. Некоторые другие результаты такого
же типа, как и те, с которыми мы пока имели дело в этом пара-
параграфе, включены в главу в качестве упр. 9.18—9.22.
Сейчас мы приведем несколько замечаний и ссылок на дру-
другие исследования интегральных преобразований, которые непо-
непосредственно не связаны с основной темой этой главы.
Исследование интегральных операторов было очень плодо-
плодотворным и послужило темой обширной специальной литературы.
Кроме литературы, посвященной специально интегральным урав-
уравнениям (см. ссылки в начале параграфа), читатель может по-
посмотреть соответствующие места у Заанена [1], а также у
Данфорда и Шварца [1]. В примерах, которые мы до сих
пор изучали, предполагается, что рассматриваемые интегралы
912 Гл. 9. Теория компактных операторов
существуют (по крайней мере почти всюду) как интегралы
Лебега — Стилтьеса, т. е. что эти интегралы абсолютно сходятся.
Но некоторые важные для анализа интегральные преобразова-
преобразования не удовлетворяют этому условию: они являются сингуляр-
сингулярными и существуют (возможно, почти всюду) как главные зна-
значения Коши. В этом направлении см. Котляр [1, 2], Кальде-
рон и Зигмунд [1, 3—5], Коидзуми [1] и приведенные в
этих работах ссылки, а также Ароншайн и Шептицкий
[1] и Кор отков [1].
Одним из наиболее важных примеров сингулярного инте-
интегрального преобразования служит преобразование Фурье, если
рассматривать его как преобразование, определенное для не-
некоторых неинтегрируемых функций; см., например, Титчмарш
[1] и Б ох нер [1]. В гл. 10 мы рассмотрим пример такого преоб-
преобразования. В некотором смысле этот пример представляет собой
простейший случай («/Лслучай») этой задачи для локально ком-
компактных абелевых групп.
Сравнительно недавно был весьма подробно описан другой
важный пример такого типа преобразований — преобразование
Гильберта. Исследование интегралов Фурье приводит к изуче-
изучению пребразования Гильберта для одномерного случая, ядром
которого служит
(См. Титчмарш [1] и указанные там ссылки.) Для получения
результатов в этом случае сперва использовали методы теории
функций комплексного переменного. Если размерность п> 1, то
преобразование Гильберта встречается и в теории потенциала
и фактически порождает различные интегральные преобразова-
преобразования с ядрами
k (t, s) = 11 — s Г" • i
где со принадлежит некоторому узкому классу функций, опреде-
определенных на единичной сфере пространства Rn. Методы теории
функций вещественного переменного (включающие также слу-
случай п = 1) рассмотрены у К о т л я р а [1]; см. также К о и д з у-
м и [2] и приведенные там ссылки.
Важным инструментом во всех этих исследованиях служит
понятие сильных и слабых типов отображений (подмножеств)
пространства L? в L?, теорема выпуклости Рисса — Торина для
сильных типов преобразований (Данфорд и Шварц [1,
стр. 560 и далее] и Котляр [1]) и аналогичная интерполяцион-
интерполяционная теорема Марцинкевича и Зигмунда для слабых типов пре-
преобразований (Зигмунд [3], Котляр [1], Коидзуми [1]).
9 5. Интегральные операторы 913
См. также п. 4.2.4. Что касается неравенства Соболева (теоре-
(теорема 9.5.10) и его обобщения, см. Аранда, Каттанео и
Окл а н д ер [1].
9.5.12. Теперь мы приступаем ко второй части программы,
которую мы наметили осуществить в этом параграфе. Прежде
чем перейти к ядерному представлению линейных отображений
пространства C(S) в С(Г), приведем некоторые результаты,
связанные с отображениями отделимого локально выпуклого
пространства Е довольно общего типа в пространство С(Т).
Основным источником этих результатов является работа Вады
[3]. Он рассматривает случай, когда пространства S и Т не обя-
обязательно отделимы и локально компактны. Мы же ограничи-
ограничиваемся исследованием случая, когда S и Т отделимы и локально
компактны. Как обычно, через C(S) (соотв. С(Т)) обозначается
пространство непрерывных комплексных функций на S (соотв. Г),
наделенное топологией локально равномерной сходимости. Для
краткости вместо С(Т) мы часто будем писать F. Тогда сопря-
сопряженное пространство F' отождествимо с пространством ком-
комплексных мер Радона на Т, обладающих компактными носите-
носителями.
Начиная с этого момента, всюду в этом параграфе через и
будет обозначаться непрерывное линейное отображение про-
пространства Е в F = C(T). Сопряженное отображение и'\ F'-+E'
непрерывно в топологиях o(F\F) и о{Е',Е). Обозначим через
е* меру Дирака в точке / и будем рассматривать эту меру как
элемент из F", полагая l(t) -=и'(et). Тогда | есть отображение
пространства Т в Е\ непрерывное в топологии о(Е\Е). Как бу-
будет доказано ниже, отображение и и некоторые его свойства вы-
выражаются в терминах отображения |. Начнем с того, что спра-
справедливы следующие равенства:
и потому для и имеет место формула
(9-5.12)
Очевидно, что если заданное линейное отображение и: £-> С(Т)
представимо в виде (9.5.12) для некоторого отображения
|: Т-+Е', то I определяется однозначно. Несколько менее оче-
очевидно следующее утверждение.
5.9.13. Предложение. Линейное отображение и бочечного про-
пространства Е в С(Т) непрерывно тогда и только тогда, когда су-
существует непрерывное в топологии о(Е\Е) отображение
|: Т-+Е', для которого выполняется равенство (9.5.12).
914 Гл. 9. Теория компактных операторов
Доказательство. В силу предыдущих замечаний остает-
остается только показать, что если Е и I удовлетворяют условиям
предложения, то отображение и, определяемое равенством
(9.5.12), непрерывно.
Непрерывность | влечет за собой а (£', Е) -компактность мно-
множества £(/() для любого компактного множества К а Т. Тогда
если Е бочечно, то ЦК) равностепенно непрерывно. Поэтому в Е
существует такая окрестность нуля U, что g(/C)cz U° и, следова-
следовательно, |m(jc)(/)|^C1 для х ^ U и t ^ К, а это и означает, что
отображение и: Е-^С(Т) непрерывно. |
В следующем ниже предложении мы увидим, как слабая ком-
компактность отображения и зависит от свойств отображения Е.
9.5.14. Предложение. Пусть Е — отделимое локально выпук-
выпуклое пространство, и: E-+F=C(T) — непрерывное линейное ото-
отображение и I: Т->Е' — отображение, для которого справедливо
соотношение (9.5.12). Для слабой компактности отображения а
необходимо и достаточно, чтобы отображение g обладало сле-
следующим свойством: в Е' существует такое выпуклое, уравнове-
уравновешенное, равностепенно непрерывное и слабо замкнутое подмно-
подмножество Q, что I отображает Т в Eq (где Eq — банахово простран-
пространство U {aQ: а > 0}, в котором Q служит единичным замкнутым
шаром) и непрерывно в топологии o(Eq> (EqY).
Доказательство. Сначала покажем, что доказательство
сводится к случаю, когда £ — нормированное пространство. Если
и слабо компактно, то существует такая замкнутая выпуклая
уравновешенная окрестность нуля U в Е, что u(U)— относитель-
относительно слабо компактное множество в F. Положим N=f\{n~]U: n —
= 1,2,...}, и пусть Е — факторпространство E/N, наделенное
нормой, получающейся при факторизации функционала Минков-
ского окрестности U. Если / — естественное отображение про-
пространства Е на £, то u — voj, где отображение v: E-+F слабо
компактно. Если наше предложение выполняется для нормиро-
нормированных пространств, то существует такое непрерывное в топо-
топологии о{Ё\ Ё") отображение |г. Т-*~Ё\ что
для x = j(x). Тогда, отождествив Ег с Eq, можно положить Q =
= [/° (где U0 — поляра в Е') и | = |,.
Обратно, если g обладает указанным свойством, то можно по-
повторить предыдущее построение, положив U = Q° (U будет окре-
окрестностью нуля в £"), и получить выражение u = voj. Если предло-
предложение верно для случая нормированных пространств, то v будет
9 5. Интегральные операторы 915
слабо компактным отображением и потому и также будет обла-
обладать этим свойством.
Таким образом, достаточно рассмотреть случай, когда Е—
нормированное пространство, что и будет предполагаться
дальше. Для этого случая условие, касающееся |, равносильно
непрерывности этого отображения в топологии в{Е', Е").
Если и слабо компактно, то (теорема 9.3.1) и' непрерывно
в топологиях o(F\ F) и о(Е', Е")\ отсюда непосредственно сле-
следует, что отображение g непрерывно в топологии о(Е\ Е").
Обратно, предположим, что \ непрерывно в топологии
о(Е\ Е"). Нужно доказать (опять теорема 9.3.1), что и' непре-
непрерывно в топологиях o(F\ F) и о(Е\ Е").
Для этого нужно показать, что
ф (9.5.13)
для каждого ц е F', т. е. для каждой меры Радона \л на Г, обла-
обладающей компактным носителем. Для доказательства существо-
существования этого интеграла и его принадлежности к пространству Е\
которое наделяется топологией g(E\ E"), можно воспользо-
воспользоваться непрерывностью | в этой топологии и предложением
8.14.3. По определению интеграла для любого х"^.Е" имеем
(х
", l(t))dix\t).
В частности, заменяя х" на произвольный элемент хе£, в силу
(9.5.12) получаем
(*, jtdli)=j (х, I (t)) din (t)=\u (x) (t) ф (t) =
= (и (х), \i) = (х, и' (\i)),
откуда следует (9.5.13).
Если сеть (\ц) сходится к \х в топологии а(/7/, Z7), то из
(9.5.13) и непрерывности g в топологии о(Е', Е") вытекает, что
что и доказывает непрерывность отображения и'. 1
В дополнение к последнему предложению приведем резуль-
результат, выражающий зависимость между компактностью отобра-
отображения и и свойствами отображения |.
916 Гл. 9. Теория компактных операторов
9.5.15. Предложение. Пусть Е, и и \ те же, что и в предло-
предложении 9.5.14. Для компактности отображения и необходимо и
достаточно, чтобы | обладало следующим свойством: суще-
ствует такое выпуклое, уравновешенное, равностепенно непре-
непрерывное и слабо замкнутое подмножество Q в Е', что | преобра-
преобразуем Т в Eq и является непрерывным в нормированной топо-
топологии в Eq.
Доказательство. Если g удовлетворяет указанному
условию, то из теоремы Асколи следует, что u(U) относительно
компактно в F=C(T)y где U — такая окрестность нуля в Е, что
QcU°.
Обратно, пусть и компактно и U — такая окрестность нуля
в Е, что u(U) относительно компактно в F=C(T). В силу пред-
предложения, следующего за теоремой Асколи (п. 0.4.11), из
(9.5.12) следует, что для каждого /еГ
sup| (х, №) I = sup| и(х) (t)\ < + оо,
что означает, что g отображает Т в Eq, где Q есть U0. Из того
же предложения (п. 0.4.11) следует, что u(U) равностепенно
непрерывно в каждой точке to^T. Поэтому для любого s>0
найдется такая окрестность W точки tOy что
\u(x)(t)-u(x)(tQ)l<e
для /Gf и ^g(/, В силу (9.5.12) и определения Q = U° это
означает, что g(f)—l{t0) ee-Q для t^Wt т. е. g непрерывно
в нормированной топологии в Eq. 1
Всюду далее мы будем предполагать, что E = C(S), и поль-
пользоваться последними двумя предложениями для получения
ядерных представлений слабо компактных и компактных линей-
линейных отображений и: C(S) ~>С(Г) при условии о-компактности
пространства Т.
9.5.16. Предложение. Пусть Т — о-компактное пространство
и и — непрерывное линейное отображение пространства Е =
= C(S) в F = C(T). Для того чтобы и было слабо компактным,
необходимо и достаточно, чтобы существовали такое компактное
подмножество /CczS, такая функция k на ТхК и такая поло-
положительная мера Радона о на Kt что
= I k(t9 s)x(s)do(s), (9.5.14)
к
причем k удовлетворяет следующим трем условиям:
A) функция s*—>k(t9 s) о-интегрируема при каждом t^T\
9.5. Интегральные операторы 917
B) функция
j k(t9 s)do{s)
непрерывна для каждого борелевского подмножества В в К\
C) для каждого компактного подмножества К' в Т
sup \\k{t, s)\do{s)
тк i
oo.
9.5.17. Предложение. Если S, Т и и — те же, что и в преды-
предыдущем предложении, то отображение и компактно тогда и
только тогда, когда оно допускает представление вида (9.5.14),
где ядро k удовлетворяет вышеприведенному условию A), а
также условию
D) Jim j\k(t, s)-k(t0, s)\do(s) = 0
для каждого t0 e Т.
Доказательство предложения 9.5.16. Достаточ-
Достаточность вытекает из равенства u = vojy где / — отображение про-
пространства C(S) в С (К), получаемое сужением на К функций,
определенных на S, a v — отображение пространства С (К) в
С(Г), определяемое правой частью равенства (9.5.14), где в ка-
качестве х можно взять любой элемент из С (К). Слабая компакт-
компактность отображения и будет следовать из слабой компактности
отображения и, так как/ переводит выбранные соответствующим
образом окрестности нуля в C(S) в ограниченные подмножества
в С (К). С другой стороны, для доказательства слабой компакт-
компактности отображения и достаточно убедиться (теорема 9.4.10) в
том, что и"(g) принадлежит F (а не только F") для каждой
функции g на /С, которая служит поточечным пределом ограни-
ограниченной последовательности в С (К), Легко проверить, что
v"(g) —как раз тот элемент.из F'\ который определятся функ-
функцией / ь-> J k(t, s) g(s) do(s). Таким образом, все сводится к
к
доказательству непрерывности этой функции. Однако из B) и
C) следует, что эта функция обладает непрерывным сужением
на К', если g является равномерным на К пределом конечных
линейных комбинаций характеристических функций борелев-
ских множеств В а К. Так как пространство Т локально ком-
компактно, то рассматриваемая нами функция непрерывна на Т9
Достаточность, таким образом, доказана.
918 Гл. 9. Теория компактных операторов
Докажем необходимость. Предположим, что отображение и
слабо компактно. Тогда существует такое компактное множество
К a S, что если
£/ = {хеСE): И«)|<1 Для sg/(},
го u(U) содержится в некотором слабо компактном подмно-
подмножестве Р в С(Т). Положим
A = (\{n-lU: n=l, 2, ...} = {xe=C(S): x\K = 0}.
Тогда и(А) а(){гг1Р: п=\, 2, ...}, а так как Р ограничено, то
это пересечение равно {0}. Таким образом, u = vojy где / — суже-
сужение на К функций из C(S), a v — слабо компактное отображение
пространства С(К) в С(Т). В силу предложения 9.5.14 суще-
существует такое непрерывное в топологии 2j = o(C(K)', С (К)") ото-
отображение |: Т->С(КУ, что v(x){t) = (xf g(*)> для х*=С(К) и
t&.T. Итак, для xe^C(S) имеем
где l(t) для каждого t есть мера Радона на К.
Так как пространство Т а-компактно, то оно является объ-
объединением последовательности компактных множеств (Тп). Но
тогда в силу непрерывности | множества 1(Тп) слабо компактны
в С(К)' = М(К). Из следствия 4.23.4 вытекает существование
на К положительной меры Радона ап, относительно которой
каждый элемент из %(Тп) является абсолютно непрерывным.
Полагая
легко видеть, что каждый элемент множества Ь,(Т) абсолютно
непрерывен относительно о. Поэтому из теоремы Лебега — Ра-
Радона— Никодима следует, что символически d[l(t)](s)=k(t,s)X
Xdo(s), где k(t, s) как функция от s при каждом / является
а-интегрируемой. Таким образом,
u(x)(t)= k(t, s)x(s)da(s),
J
К
и остается только показать, что k обладает свойствами B) и C).
Для этой цели рассмотрим подмножество L в С(К)' = М(К),
состоящее из мер вида /»а, где / является а-интегрируемой
функцией. Каждая ограниченная и а-измеримая функция g на
К определяет непрерывную линейную форму на L и потому яв-
9.6. Дальнейшее развитие теории 919
ляется сужением на L некоторого элемента х" из С (К)". Если
t (= Г, то
а" (*") @ = <""(*"), */> = <*"> о/(е/)> =
= <*",£(*)> = <*", ft,-а),
где /^ — функция s^—>k{t, s). Так как kt-o^Lt то
/с
С другой стороны, отображение v слабо компактно, поэтому
v"{x") принадлежит F=C(T). Таким образом, интеграл
J g(s)k{t, s)da(s) является непрерывной функцией от / для
к
каждой ограниченной и a-измеримой функции g. Отсюда в ка-
качестве частного случая следует условие B), если под g пони-
понимать характеристическую функцию множества В.
Кроме того, v" преобразует ограниченные подмножества из^
С (К)" в относительно слабо компактные и, значит, ограничен-
ограниченные подмножества в F=C(T). Отсюда следует, что если К'—
произвольное компактное подмножество в Г, то
s) da (s)
g(s)k(t,
к
ограничены в совокупности, когда t пробегает мно-
множество К\ а g — множество всех a-измеримых функций, удовле-
удовлетворяющих на К условию \g\^ 1.
Таким образом, условие C) выполняется, и предложение
9.5.16 полностью доказано. 1
Доказательство .предложения 9.5.17. Это предло-
предложение представляет собой простое развитие предложения
9.5.16 и его доказательства, так что подробности предостаз-
ляются читателю. Достаточность очевидна. Что касается необ-
необходимости, то здесь нужно воспользоваться предложением
9.5.16 для обоснования представления (9.5.14). Условие D) по-
получается тогда либо из предложения 9.5.15, либо из теоремы
Асколи. Напомним читателю, что £(/) есть мера kt*G, поэтому
C) выражает непрерывность отображения | в нормированной
топологии пространства ограниченных мер Радона на К> I
9.6* Дальнейшее развитие теории
компактных линейных отображений
Почти во всех книгах по функциональному анализу уделяется
внимание теории Рисса — Шаудера линейных отображений вида
1—и, где отображение и компактно. Эта теория обычно пред-
920 Гл. 9. Теория компактных операторов
шествует подробному изложению спектральной теории отобра-
отображений и. Первоисточниками служат работы Ф. Рисса [2] и
Шаудера [4]. Среди книг на эту тему отметим следующие:
Б ан а х [1, гл. VI], Тэй л ор [1, гл. 5 и 6], Ц а а н е н [1, гл. II] и
Дьёдонне [13, гл. И]. Этот список, конечно, не является ис-
исчерпывающим.
Естественно, что первоначально все результаты формулиро-
формулировались для банаховых пространств. Уже полученные в этом слу-
случае результаты были достаточно общими для того, чтобы вклю-
включать в себя многие важные приложения. Однако процесс
обобщения продолжался, что оказалось полезным и для прило-
приложений (п. 9.10.6). Эти обобщения были начаты Л. Шварцем
[13]. Наше изложение в значительной мере следует курсу Гро-
тендика [7]. См. также Келли и Намиока [1, задачи
21А—21D].
Ключевые теоремы этой теории распадаются на две группы
и содержатся соответственно в п. 9.6.5—9.6.8 и 9.10.1—9.10.4.
Из теорем первой группы следует, что во многих случаях с точ-
точностью до конечномерного подпространства добавление к изо-
изоморфизму компактного линейного отображения не изменяет
некоторых важных его свойств (например, открытости отображе-
отображения или замкнутости образа). Результаты второй группы приме-
применяются в спектральной теории компактных эндоморфизмов и,
г. е. в исследовании свойств семейства эндоморфизмов ХЛ—и,
где К — произвольное число. Эта теория содержит так называе-
называемую теорию Фредгольма [1] и исследует случай, когда и
допускает ядерное представление (§ 9.5). Спектральная теория
более общих линейных отображений в нашей книге не затраги-
затрагивается. Этим вопросам посвящена обширная литература; см.,
например, Данфорд и Шварц [1, гл. VII] и Лорх [1].
9.6.1. Предложение. Пусть Е и F — отделимые локально вы-
выпуклые пространства и и: E-+F— непрерывное линейное ото-
отображение. Если отображение и компактно, то таким же будет и
его сопряженное и' в топологиях n(F\ F) и к(Е\ Е). (Эти топо-
топологии определены в § 8.10.)
Доказательство. Пусть U — такая окрестность нуля в
£, что множество K = u(U) относительно компактно в Z7, тогда
иг(К°)а U°. Так как К° — окрестность нуля в топологии
k(F\ F), а множество U0 равностепенно непрерывно и слабо
компактно, то U0 компактно в топологии к(Е\ £), что и требо-
требовалось доказать. 1
Естественно выяснить, при каких условиях отображение и'
является сильно компактным, если отображение и компактно.
9.6. Дальнейшее развитие теории 921
9.6.2. Предложение. Пусть Е— отделимое локально выпук-
выпуклое пространство. Следующие три условия эквивалентны.
A) Если АаЕ — компактное выпуклое уравновешенное
множество, то в Е существует такое ограниченное замкнутое
выпуклое уравновешенное множество В, содержащее Л, что А
компактно в нормированном пространстве Ев.
B) Для любого отделимого локально выпуклого простран-
пространства F и любого линейного компактного отображения и; F-+E
сопряженное отображение и' сильно компактно.
C) То же, что и B), только F— банахово пространство.
Доказательство, Так как импликация B)=^>C) оче-
очевидна, то остается доказать, что
(а) A)=фB); (Ь) C)=фA).
(а) Предположим, что условие A) выполняется. Пусть ото-
отображение и: F-+E линейно и компактно. Тогда существует та-
такая окрестность нуля V в F, что u(V) относительно компактно
в Е. Пусть A=u(V). Так как окрестность V можно считать вы-
выпуклой и, уравновешенной, то из A) следует, что существует
такое ограниченное замкнутое выпуклое уравновешенное мно-
множество В, содержащее А, что А компактно в Ев. Докажем те-
теперь, что и'(В0) сильно относительно компактно в F'.
Каждый элемент у' из и'(В0) можно записать в виде у'=
= w/(a:/), где х'—некоторый элемент из В0. Сужение х'\Ев при-
принадлежит единичному шару в (Ев)\ который является слабо
компактным, а поэтому (предложение 0.4.9) компактным в то-
топологии равномерной сходимости на компактных подмноже-
подмножествах из Ев. С другой стороны, если сеть (х[) такова, что
х'.\Ев->х'\Ев равномерно на компактных подмножествах из
Ев, то
равномерно по у е У, так как множество A = u(V) компактно
в Ев. Отсюда получаем, что сеть и' (хг^ сходится равномерно на
ограниченных подмножествах из F, т. е. в пространстве F/ схо-
сходимость ur (xty ->и' (х') сильна. Следовательно, множество и'{В0)
сильно относительно компактно и утверждение (а) доказано.
(Ь) Пусть выполняется C), множество А с= Е — такое же,
как в утверждении A), F=EA — банахово пространство пи —
компактное линейное вложение пространства F в Е. В силу C)
отображение и'\ Е/ ->(ЕА)' сильно компактно. Поэтому суще-
существует такое ограниченное множество Вс£, что и'(В0) сильно
относительно компактно в {ЕА)\ Ясно, что множество В можно
922 Гл. 9. Теория компактных операторов
считать замкнутым выпуклым уравновешенным и содержащим
А. (Расширение множества В только уменьшает В0.) Докажем,
что А компактно в Ев. Для этого достаточно показать, что Е
и Ев индуцируют в А одну и ту же топологию, а поскольку
множество А выпукло и уравновешено, то достаточно только
убедиться в том, что Е и Ев индуцируют в А одинаковые окрест-
окрестности нуля.
Так как топология пространства Ев сильнее, чем топология,
индуцируемая топологией пространства Е, то достаточно огра-
ограничиться доказательством следующего утверждения: если сеть
(Xi) d А такова, что и(Хг)->0 (т. е. хг-+0 в £), то Х{-+0 в Ев.
Для любого х' <=Е' имеем (и(Х{)> л/), т. е. (xi} u'(x'))->0 для
каждого хг. Отсюда *t-->0 поточечно на и'(В°). Так как ||**||а^
< 1 и и'(В0) сильно относительно компактно в {ЕА)\ то из
предложения 0.4.9 следует, что (xit u/(x/))->0 равномерно от-
относительно х' е i5°. Полагая
имеем С{-*0 и \(и(Х{), х')\*Сс{ для х'<=В°. Так как и— вло-
вложение, то это означает, что | (хи х') | ^ С\ для xf e В°. Мно-
Множество В выпукло, уравновешено и замкнуто в £, а эти нера-
неравенства показывают, что Xi e с{ • В; следовательно, ||хг||Б -^ сг-.
Таким образом, х{-+0 в ЕВу что и требовалось доказать. |
9.6.3. Следствие. Пусть Е — отделимое, a F — метризуемое
локально выпуклое пространство. Если линейное отображение
и: E-+F компактно, то сопряженное отображение и' сильно
компактно.
Доказательство. Достаточно показать, что условие A)
предыдущего предложения остается справедливым, если F за-
заменить на £, которое по условию метризуемо. Это следует из
приводимой ниже леммы. I
9.6.4. Лемма. Пусть F — метризуемое локально выпуклое про-
пространство и А — ограниченное множество в F. Тогда в F суще-
существует такое ограниченное замкнутое выпуклое уравновешенное
множество В, содержащее Л, что нормированное пространство
FB индуцирует в А ту же равномерную структуру, что и F.
Доказательство. Можно считать, что множество А вы-
выпукло и уравновешено. Тогда достаточно показать, что инду-
индуцируемые окрестности нуля в обоих случаях одни и те же, т. е.
что если V\, V2y ... — база окрестностей нуля в /% то для каж-
каждого Х>0 при некотором п имеем Af)VnczXB. Так как мно-
множество А ограничено в jF, то существуют такие положительные
9 6. Дальнейшее развитие теории 923
числа A,t-->oo, что Aczf]KiVi. Выберем числа щ^'кх так, чтобы
WjAt-^О» и положим В=П|ы?Кг-. Если А,>0, то ?w < A,jli; для
i
/>г0. Тогда ЛсА,^!/,- (*^*о), и существует такое п, что
7яс: f] M*iVi- Таким образом, ЛЛ Уп с А^У* для всех i, т. е.
i < «о
AfWnd'kB, что и требовалось доказать. I
Обратимся теперь к основным теоремам, относящимся к ком-
компактным операторам. Эти теоремы являются обобщением тео-
теорем Рисса и обязаны своим возникновением некоторым важным
типам интегральных уравнений.
9.6.5. Теорема. Пусть Е и F— два отделимых локально вы-
выпуклых пространства, и и v-~ такие линейные отображения про-
пространства Е в F, что
A) и есть изоморфизм пространства Е на замкнутое век-
векторное подпространство в F\
B) v компактно.
Тогда w = u-{-v является открытым отображением простран-
пространства Е на w(E), подпространство w(E) замкнуто в F, а ^({О})
конечномерно.
Доказательство. Пусть U — такая замкнутая выпуклая
уравновешенная окрестность нуля в Еу что множество v(U)
относительно компактно в F. Положим N=w~l({0}) и U\ = Ut\N.
Тогда u(Ui)=—v(U{) a v(U), т. е. множество u(Ux) относи-
относительно компактно в F и поэтому предкомпактно. Так как и
есть изоморфизм, то U\ предкомпактно. Таким образом, 1)\ есть
относительная окрестность нуля в N, следовательно, jV — конеч-
конечномерное подпространство (и. 1.9.6).
Пусть М — некоторое топологическое дополнение в Е к под-
подпространству N. Такое дополнение существует, так как N ко-
конечномерно (п. 1.9.7). Тогда сужения ио = и\М, vo = v\M и wo =
= w\M удовлетворяют условиям A) и B), если в этих услосиях
заменить Е на М.
Далее
w(E) = w(M + N) = w (М) = w0(AT),
ш-1 ({0}) = М П W1 ({0}) = M[)N = {0},
т. е. отображение w0 взаимно однозначно. Таким образом, до-
достаточно ограничиться случаем, когда отображение w взаимно
однозначно, и показать, что w есть изоморфизм пространства Ь
на некоторое замкнутое векторное подпространство в F. Это
означает, что если (хг)—такая сеть в £, что w(xt) сходится
в F% то (хг) обладает предельной точкой в Е. Действительно,
924 Гл. 9. Теория компактных операторов
если это условие выполняется, то из взаимной однозначности
отображения w следует, что сеть (хг) имеет только одну пре-
предельную-точку и потому сходится. Перейдем к проверке этого
условия.
Обозначим через р функционал Минковского окрестности
нуля U и рассмотрим два возможных случая.
(a) Пусть (р(Х{)) обладает конечной предельной точкой.
Опуская некоторые члены (т. е. переходы к подсети), можно
считать, что сеть (р(#г)) ограничена, скажем р(Х{) ^т. Тогда
Xi^mU и множество элементов {v(Xi)} относительно компактно.
Следовательно, сеть (и(х{)) обладает предельной точкой, а по-
потому сеть и(Х{) =w(Xi)—v(X{) обладает предельной точкой у.
Так как множество и(Е) замкнуто, то у = и(х) при некотором х,
а так как и — изоморфизм, то х есть предельная точка сети .(я»).
(b) Допустим теперь /?(*г-)->оо Покажем, что на самом
деле такое невозможно. Действительно, если р(Х{) ->оо, то
w(xl)/p(Xi) ->0, и тогда из части (а) следует, что сеть Хг1р{хг)
обладает предельной точкой х\ следовательно, р(х) является
предельной точкой сети р(х{/р(х{)) = 1, и поэтому р(х) = \. Од-
Однако в то же время w(x) является предельной точкой сети
w(Xi/p(Xi)) =w(Xi)jp(Xi), поэтому w(x)=0. Так как отображе-
отображение w взаимно однозначно, то равенства р(х) = 1 и w(x)=0
противоречат друг другу.
Теорема полностью доказана. I
9.6.6. Теорема. Пусть Е и F — отделимые локально выпуклые
пространства, и и v - линейные отображения пространства Е в
F. Предположим, что
Aа) и — слабо открытое отображение пространства Е на F\
(lb) каждое замкнутое выпуклое уравновешенное компакт-
компактное подмножество в F содержится в образе относительно и та-
такого же подмножества в Е;
B) отображение v компактно.
Тогда w = u + v — слабо открытое отображение пространства Е
на замкнутое векторное подпространство в F и w(E) имеет ко-
конечную коразмерность в F.
Доказательство. Идея доказательства заключается в
том, чтобы наделить пространства Ег и Fr их х-топологиями и
применить предыдущую теорему к отображениям и' и vf, опи-
опираясь на результаты § 8.6. Заметим, что х-топологии согла-
согласуются с двойственностью между Е и Е' и F и F'.
В силу предложения 9.6.1 отображение vr компактно, а из
предложения 8.6.3 следует, что ur (Fr) слабо замкнуто в тополо-
топологии к(Е\ Е). Отображение и' непрерывно в х-топологиях, по-
поскольку если // — компактное выпуклое уравновешенное под-
9.6. Дальнейшее развитие теории 925
множество в Е, то К — и(Н) есть подмножество в F, обладающее
теми же свойствами, а из соотношений (8.6.3) вытекает, что
и'(К°) аН°. Кроме того, из условия AЬ) и следствия 8.6.9 (где
вместо Е и F нужно рассмотреть Ег и F\ наделенные х-тополо-
гиями) получаем, что ^'-изоморфизм в х-тонологиях. Таким об-
образом, иг и vr удовлетворяют условиям предыдущей теоремы.
Отсюда следует, что w' = u' + v' является открытым отобра-
отображением пространства F' на замкнутое подпространство в Ег и
w' обладает конечномерным ядром. Поэтому w'(F') слабо замк-
замкнуто в Ег и, следовательно (предложение 8.6.3), w слабо от-
открыто. Так как wr открыто, то оно слабо открыто (теорема
8 6.8) и (w')'=w. Применяя еще раз предложение 8.6.3, полу-
получаем, что w(E) замкнуто в F. Наконец, из того факта, что
w(E) замкнуто в /vвытекает, что w(E) есть подпространство,
ортогональное к ядру отображения w\ а потому имеет конечную
коразмерность, что и требовалось доказать. I
9.6.7. Теорема. Пусть Е и F — пространства Фреше, и и v —
непрерывные линейные отображения пространства Е в F. Если
u(E)=F и отображение v компактно, то w = u + v является от-
открытым отображением пространства Е на замкнутое векторное
подпространство конечной коразмерности в F.
Доказательство. По условию отображение и открыто,
а потому тем более слабо открыто (теоремы 6.4.4 (а) и 8.6 8).
Допуская, что выполняется условие AЬ) теоремы 9.6.6, ви-
видим, что тогда отображение w слабо открыто и, следовательно
(теорема 8.6.13), открыто.
Условие AЬ) заведомо выполняется, если отображение и
взаимно однозначно, а это наиболее важный случай. Если же
это не так, то нужно воспользоваться приводимой ниже леммой
9.6.9. ■
Отметим тем временем еще один результат, вытекающий из
теорем 9.6.5 и 9.6.6.
9.6.8. Теорема. Пусть Е и F — отделимые локально выпуклые
пространства, и — изоморфизм Е на F, и пусть линейное отобра*
женив v: E-+F компактно. Тогда w = u + v — открытое отображе-
отображение пространства Е на замкнутое векторное подпространство
конечной коразмерности в F и размерность подпространства
w~x ({0}) конечна.
Доказательство. Это следует из теорем 9.6.5 и 9.6.6. |
Замечание. Позднее будет доказано (следствие 9.7.2),
что на самом деле
dim ш*" ({0}) = codim w {E) (< оо).
925 Гл. 9. Теория компактных операторов
Это следствие применимо к случаю, когда E = F и и — тожде-
тождественное отображение. Ясно также, что общий случай сводится
к этому частному.
Остается рассмотреть лемму, необходимую для доказатель-
доказательства теоремы 9.6.7.
9.6.9. Лемма. Пусть Е и F— метризуемые топологические
векторные пространства, причем Е полно, и — линейное непре-
непрерывное открытое отображение пространства Е на F. Тогда каж-
каждое компактное множество К из. F является образом относи-
относительно и некоторого компактного множества Н из Е.
Доказательство. Введем инвариантную метрику d на
Е и обозначение |M|=d(#, 0). Для элементов y^F положим
||*/|| = inf{|U||: xg£, u(x) = yl
Метрика \\ух—у2\\ определяет в F топологию, которая (поскольку
отображение и открыто) совпадает с исходной топологией. Рас-
Рассмотрим множества
В(Уо, r) = {y(=F: \\y-yQ\\<r}.
Компактное множество К можно покрыт^ конечным числом
множеств вида Bt = B(yi, 2), причем можно считать, что у^К.
Так как и — отображение яа, то можно выбрать х{^Е так,
чтобы Уг = и(Хг). Аналогичным образом можно выбрать конеч-
конечное число таких точек уц е В if] К, что множества Вц = В(у^у 2~2)
покрывают Вг-ПК, и таких точек Хц в £, что u(Xij)=yij и
l\Xij — Xi\\<2~1- Продолжая таким же образом,, так выберем ко-
конечное число точек yijk^ Bijf)K, что множества Bijk =
= В {уцк, 2~3) покрывают В{)[)К, и таких точек Xijh e £, что
u{xijh)=yijh и \\xiik — хц\\<2~2. Этот процесс можно продол-
продолжать неограниченно.
Пусть H0 = {Xi, X{j, Xi^, ...}. Для любого элемента х из Л/о
можно найти такую пару (/, /), что
II *!!<++
и такую тройку чисел (/, /, &), что
wx^Xijkw<jr+jr+ ... =-V,
и т. д. Таким образом, Но предкомпактно, и потому в силу пол-
полноты Е замыкание Н множества Но компактно. Кроме того,
9.7. Эндоморфизмы векторных пространств 927
множество и(Н0)={уи yijy yijki ...} плотно в К. Так как отобра-
отображение и непрерывно, то и(Н) замкнуто и
и (Я) = ЦНо) = К,
что и требовалось доказать. 1
Замечание. Приведенное доказательство принадлежит
Ж.-П. Серру.
9.7. Эндоморфизмы векторных пространств
Как обычно, под эндоморфизмом векторного пространства
мы понимаем линейное отображение этого пространства в себя.
Настоящий параграф посвящен некоторым чисто алгебраиче-
алгебраическим результатам, связанным с ядрами и образами степеней
некоторого эндоморфизма.
9.7.1. Предложение. Пусть Е — векторное пространство, и —
его эндоморфизм, Еп — ядро отображения ии, 1п — образ ото-
отображения ип; здесь п — целое неотрицательное число, Ео =
=={0}, 10 = Е. Тогда справедливы следующие утверждения.
A) Последовательность (Еп) либо строго возрастает, либо
строго возрастает до некоторого индекса р, а затем стабилизи-
стабилизируется.
B) Последовательность Aп) либо строго убывает, либо
строго убывает до некоторого индекса q, а затем стабилизи-
стабилизируется.
C) Если обе последовательности (Еп) и (!„) стабилизи-
стабилизируются, то p = q. Полагая в этом случае Eoo = Ev=\]En, 1^ =
= /р=П/п, получаем, что Е совпадает с прямой суммой E^-j-
+ /оо, сужение ^Е^ нильпотентно, а сужение и\1 оо является
автоморфизмом пространства /«>.
Доказательство. Имеем En+m—(um)-l(En) и /т+эт=»
= um(In). Так как отображения ип и и перестановочны, то Еп
и 1п устойчивы относительно и. Поэтому En+i = u"](En) содер-
содержит Еп и аналогичным образом /n+i cz/п. Таким образом, мо-
монотонность очевидна. Если для некоторого п справедливо ра-
равенство Еп = Еп+и то (um)-l(En)^(um)-l(En+l), т. е. Еп+т =
— En^m+i, и потому последовательность (£7) стабилизируется
при /^ п. Аналогичные рассуждения справедливы и для по-
последовательности (/*). Таким образом, A) и B) доказаны.
Для доказательства C) покажем сначала, что q < р. Для
этого достаточно доказать, что из соотношений Еп=^Еп+] и 1пФ
Ф1п+\ следует, что /n+i=£/n+2 Допустим, что 1п+\ = 1п+2, и пусть
ип(х)^1п. Тогда ип+1(х) принадлежит /n+i, а потому и 1п+2.
928 Гл. 9. Теория компактных операторов
Следовательно, найдется такое jg£, что ип+х (х) = ип+2(у). То-
Тогда ип+1(х — и(у))=0 и так как Еп = Еп+и то ип(х — и(у))=0,
т. е. ип(х) = un+l(y) e /п+ь Таким образом, /п = /п+ь что про-
противоречит условию. Тем самым доказано, что q <1 р. Аналогич-
Аналогичным образом доказывается, что p*Cq\ следовательно, если р и
? определены, то p = q.
Считая, что числа р и q определены, покажем, что ^ооП/оо^
= {0}. Всякий элемент этого пересечения имеет вид х = иР(у) и
удовлетворяет равенству up(x)=0. Таким образом, и2Р(у)=0,
откуда в силу равенства Ev = Е2р получаем, что up (у) = 0, т. е.
дг = О. Пусть и — эндоморфизм факторпространства Е/Е^, полу-
получаемый из и переходом к факторпространству. Так как £оо =
= Ер'=Ер+и то отображение и взаимно однозначно. Мы утверж-
утверждаем, что и есть отображение на. Применяя первую часть утвер-
утверждения C) к отображению и (для которого р = 0), получаем,
что если бы и не было отображением на, то последовательность
образов йп(Е1Еоо) была бы строго убывающей. Отсюда следо-
следовало бы, что последовательность ип(Е) + £сх> =/п + £«> также
должна строго убывать. Но это противоречит предположению,
что последовательность /п стабилизируется. Таким образом,
отображение и есть автоморфизм. Аналогичное утверждение
справедливо и для йр, в частности й^ отображает Е/Еоо на себя.
Отсюда следует, что uv(E) +ЕОО = Е, т. е. 1ОО + ЕОО = Е, так что Е
есть прямая сумма подпространств Е^ и /оо.
Наконец, утверждение, что и есть автоморфизм, означает,
что сужение и|/оо также является автоморфизмом, а так как
иР(Еоо) ={0}, то очевидно, что сужение и\Е<х> нильпотентно, что и
завершает доказательство. I
9.7.2. Следствие. Пусть Е и и — те же, что и в предложе-
предложении 9.7.1. Предположим, что выполняется утверждение C) этого
предложения и что подпространство E^ конечномерно. Тогда
dim ^({O}) =codim u(E).
Доказательство. В силу C) достаточно проверить это
равенство отдельно для и\Есо и м|/оо. В первом случае равенство
проверяется элементарно, так как по условию £оо конечномерно.
С другой стороны, во втором случае обе части равенства равны
нулю, так как и\1оо есть автоморфизм. |
9.7.3. Замечание. Пусть Е и и — те же, что и в предло-
предложении 9.7.1. Предположим также, что последовательность (Еп)
стабилизируется и р — наименьший номер, начиная с которого
Еп+\ = Еп. Тогда, как известно, сужение и\Еоо нильпотентно.
Пусть k — наименьшее натуральное число, для которого
uh(Eoo) ={0}. Мы утверждаем, что k = p.
9.8. Собственные значения и спектр 929
Действительно, up(Ev)={0\ по определению подпространства
Ер. Равенство Еоо = Ер следует из стабильности последователь-
последовательности (Еп), начиная с п = р. Поэтом// и^(Еоо) = {0} и, следова-
следовательно, k ^C р. Далее если бы k было меньше р, то из равен-
равенства ^(Еоо) вытекало бы, что EooCzEk и, следовательно, Яоо =
= Ek (так как последовательность Еп возрастает). Но EOO = EV,
значит, Ev = Ek. Так как последовательность (Еп) возрастает, то
Eh = Eh+\ =... = Ev = Ev+\ =...,
что противоречит определению числа р. Таким образом, k = p,
что и требовалось доказать.
9.8. Собственные значения и спектр
Пусть и — эндоморфизм векторного пространства Е. Соб-
Собственным значением эндоморфизма и называется такое число X,
что и(х) =Хх при некотором хФО из Е. Таким образом, если че-
через 1 обозначать тождественный эндоморфизм пространства £,
то X— собственное значение тогда и только тогда, когда отобра-
отображение Х\—и не является взаимно однозначным. Если X— про-
произвольное число, то ядро отображения Х\ — и называется соб-
собственным подпространством эндоморфизма и, соответствующим
числу X. Если X не является собственным значением, то соответ-
соответствующее ему собственное подпространство есть {0}.
Под алгебраическим спектральным значением эндомор-
эндоморфизма и понимается такое число К что отображение XI—и не
имеет обратного в алгебре всех эндоморфизмов пространства Е\
другими словами, это означает, что либо Х\—и — не взаимно
однозначное отображение (т. е. что X — собственное значение
отображения и), либо XI—и не является отображением на.
(Возможно, что оба случая имеют место одновременно.) Таким
образом, всякое собственное значение является алгебраическим
спектральным; обратное, вообще говоря, неверно, однако верно,
если пространство Е конечномерно.
Пусть Е — топологическое векторное пространство и и — его
непрерывный эндоморфизм. Число X называется (топологиче-
(топологическим) спектральным значением эндоморфизма и, если отобра-
отображение Х\—и не является обратимым в алгебре LC(E) всех не-
непрерывных эндоморфизмов пространства Е.
Обозначим через во{и), аа{и) и а (и) соответственно множе-
множество всех собственных значений, всех алгебраических спектраль-
спектральных значений и спектральных значений эндоморфизма и. Мы
будем называть множества оа(и) и о (и) соответственно алгеб-
алгебраическим спектром и спектром эндоморфизма и. Ясно, что
всегда
О0(и) CZ Oa{u) CZ 0{и)ч
930 Гл. 9. Теория компактных операторов
Как было замечено, <то(^)=аа(^), если & конечномерно. В этом
случае также и оа(и)=о(и) (каждый эндоморфизм конечномер-
конечномерного пространства Е непрерывен в любой отделимой линейной
топологии в Е). Кроме того, если Е — полное метризуемое топо-
топологическое векторное пространство, то оа(и) =о(и) для любого
непрерывного эндоморфизма и пространства Е: это следует из
георемы об обратном операторе (теорема 6.4.5). (Тем не менее
Oq(u) может отличаться от оа(и), если пространство Е беско-
бесконечномерно.)
Обозначим через £\, п и 1\у п соответственно ядро и образ ото-
отображения (АЛ—и)пу где X — произвольное, а п > 0— целое
число, и положим Ек = [J Ек>п и /х= f) /я, п. Тогда Ек | есть
>0 >0
собственное подпространство эндоморфизма и, соответствующее
числу X. Подпространство £\ называется спектральным подпро-
подпространством эндоморфизма а, соответствующим числу X. При
А,=0 введенное только что подпространство совпадает с тем, ко-
которое фигурирует в предложении 9.7.1. Размерность подпро-
подпространства Е% (которая, конечно, может быть и бесконечной) на-
называется спектральной кратностью числа А,.
Из элементарной линейной алгебры известно, что если Е —
конечномерное пространство и поле скаляров алгебраически
замкнуто, то Е является прямой суммой подпространств £\, где
Я пробегает все собственные значения эндоморфизма и. Множе-
Множество этих собственных значений совпадает с множеством нулей
так называемого характеристического многочлена Р(А,) =
= det(XI—и), степень которого равна dim E, а спектральная
кратность собственного значения X (т. е. dim£\) равна крат-
кратности X как нуля многочлена Р.
9.8.1. Предложение. Пусть Е — векторное пространство, и —
его эндоморфизм Если ХФк\ то Е^а /х .
Доказательство. Пусть х е Еъ т. е. (XI — и)п(х) =0
при некотором п. Нам нужно показать, что х= (АЛ—и)т(у)
при всех т и некотором у (возможно, зависящем от т).
Пусть G векторное подпространство в £, порожденное эле-
элементами х, и(х), и2(х), ... . Подпространство G устойчиво от-
относительно отображения и и dim G -^ п. Сужение u\G является
эндоморфизмом в G, и X — его единственное собственное значе-
значение, поэтому (Х'\—u)\G — обратимый эндоморфизм подпро-
подпространства G. То же самое справедливо для сужения
(VI— u)m\G при любом т. Но так как dim G конечна, то
(Х'\—и)т отображает G на себя, и поэтому найдется такое у%
что х= (Х'1—и)т(у), что и требовалось доказать. 1
9.9. Некоторые результаты о спектрах эндоморфизмов 931
9.9. Некоторые результаты о спектрах эндоморфизмов
В настоящем параграфе мы коснемся некоторых общих
утверждений, относящихся к спектрам непрерывных эндомор-
эндоморфизмов и топологического векторного пространства Е. Наиболее
простой случай возникает тогда, когда Е—банахово простран-
пространство. Как будет видно из предложения 9.9.3, общий случай ино-
иногда можно свести к этому частному случаю.
9.9.1. Предложение. Пусть Е — банахово пространство. Тогда
LC(E) является банаховым пространством относительно нормы
\и\\= sup || и (х) || = sup || и (х) ||.
11|| < 1 ЦхЦ-1
Множество обратимых элементов из ЬС(Е) открыто и содержит
все те элементы и из LC(E), которые удовлетворяют неравен-
неравенству \\и— 1||<1.
Доказательство. Первое утверждение тривиально. До-
Допустим сначала, что и— элемент из LC(E), удовлетворяющий
условию \\и—1||<1. Тогда ряд 2 A—и)л сходится в LC(E)
>0
и умножение его справа или слева на и=1 — A—и) приводит
к 1, откуда следует, что и — обратимый элемент из LC(E).
Пусть далее и0 — обратимый элемент из LC(E), а и — эле-
элемент из ЬС(Е), удовлетворяющий условию
И - "о|| <К1 Г- (9-9-1)
Докажем, что отображение и обратимо. Действительно,
и = ио-(ио-и) = ио[1 - V (и0 - и)].
Так как норма произведения двух эндоморфизмов не превосхо-
превосходит произведения их норм, то второй сомножитель обратим в
силу (9.9.1) и уже рассмотренного случая. Первый сомножитель
uQ обратим по предположению, следовательно, и обратим как
произведение двух обратимых эндоморфизмов, что и требовалось
доказать. I
9.9.2. Следствие. Если Е — банахово пространство и и — его
непрерывный эндоморфизм, то о (и) есть компактное числовое
множество и для любого Х^о(и) выполнено неравенство
\К\<\\и\\.
Доказательство. Спектр о (и) является прообразом
множества необратимых элементов из ЬС(Е) относительно ото-
отображения Яь-^ 1\ — и. В силу предложения 9.9.1 это множество
замкнуто. Так как отображение X*-^h\ —и, очевидно, непрерыв-
непрерывно, то множество о (и) замкнуто. Если число К удовлетворяет
932 Гл. 9. Теория компактных операторов
условию \Х\> Цм||, то XI —и = Х{\ — Х~1и). Тогда из неравенства
ЦЛ,—1^г|| -< 1 и предложения 9.9.1 следует, что отображение 1 —Х~1и
обратимо, т. е. X не принадлежит а(и). Остальная часть след-
следствия очевидна. Я
Замечание. Если пространство Е не является нормирован-
нормированным, то о (и) может не быть ни ограниченным, ни замкнутым.
Однако иногда можно получить некоторую информацию о мно-
множестве а (и), пользуясь следующим предложением.
9.9.3. Предложение. Пусть Е — топологическое векторное про-
пространство, F — векторное подпространство в £, наделенное более
сильной линейной топологией, чем индуцированная из Е, и ] —
вложение подпространства F в Е. Пусть далее и: E-^F— не-
непрерывное линейное отображение. Тогда
A) Спектр произведения \и в ЬС(Е) совпадает со спектром
и\ в LC(F), за исключением, быть может, Х = 0.
B) Если ХфО принадлежит этому общему спектру, то соб-
собственное подпространство (соотв. спектральное подпространство)
отображения и\ —то же, что и у \и.
Доказательство. Пусть ХФО. Докажем, что если XI—
— \и обратимо в LC(E), то то же самое справедливо и для
XI — и\ в LC(F). Обратное утверждение доказывается анало-
аналогичными рассуждениями. Если разделить на X и заменить и на
—Х~1и, то достаточно установить обратимость отображений
l+ju и l+uj.
Пусть l+ju обратимо в LC(E)\ тогда его обратное отображе-
отображение можно записать в виде l + v, где ugLc(£). Имеем
O. (9.9.2)
Из первого равенства вытекает, что v=jw, где w = —u(\+v)—
непрерывное линейное отображение пространства Е в F. Заме-
Заменяя v в (9.9.2) на jw, получаем
j(u + w + ujw) =j(u + w + wju) =0.
Так как отображение / взаимно однозначно, то
и + w + ujw = u + w + wju = 0.
Умножая обе части этого равенства справа на /, видим, что
UJ + WJ+ (Uj) (Wj) =UJ + Wj+ (wj) (Uj) =0,
откуда следует, что l+wj является обратным к \+uj в LC(F).
Утверждение A), таким образом, доказано.
Переходя к утверждению B), предположим, что число ХфО
принадлежит спектру эндоморфизма uj. Соответствующее соб-
собственное подпространство эндоморфизма uj является пересвче-
9 10. Спектральная теория компактных эндоморфизмов 933
нием подпространства F с соответствующим собственным под-
подпространством эндоморфизма \и. Последнее подпространство со-
содержится в F, так как из ju(x)=Xx вытекает, что x = X-lju(x)^
е F. Таким образом, эти собственные подпространства совпа-
совпадают. Аналогичные рассуждения показывают, что ядро в Е ото-
отображения (XI —ju)n и ядро в F отображения (XI —щ)п совпа-
совпадают, так как с точностью до множителя Хп эти отображения
могут быть записаны в виде l+jun и 1+ип/, где ип\ E-+F —
соответствующим образом выбранное линейное отображение.
Совпадение спектральных подпространств следует теперь из
определений. |
9.9.4. Следствие. Пусть Е — отделимое топологическое вектор-
векторное пространство и и — его эндоморфизм, обладающий следую-
следующим свойством: существуют такая окрестность нуля U в Е и та-
такое ограниченное выпуклое уравновешенное подмножество В в
Е, что u(U) а В и нормированное векторное пространство Ев
полно. Тогда множество о (и) компактно. В частности, указанное
заключение справедливо, если отображение и компактно.
Доказательство. Будем различать два случая.
Сначала допустим, что 0 не принадлежит спектру а (и). Тогда
и является изоморфизмом пространства Е на себя; следователь-
следовательно, В — окрестность нуля в Е, и потому пространства Е и Ев
изоморфны. В этом случае можно воспользоваться следствием
9.9.2.
С другой стороны, если Og0(w),tob силу предложения 9.9.3,
примененного к F = EBi за возможным исключением нуля, спектр
а (и) эндоморфизма .и в LC(E) совпадает со спектром непрерыв-
непрерывного эндоморфизма и] банахова пространства Ев. Если спектр
последнего эндоморфизма обозначить через а', то а' компактно
в силу следствия 9.9.2, и
Следовательно, множество
ограничено и замкнуто и потому компактно, что и требовалось
доказать. I
Дальнейшие сведения о спектрах компактных эндоморфиз-
эндоморфизмов содержатся в следующем параграфе.
9.10. Спектральная теория компактных эндоморфизмов
Мы переходим к обобщению результатов Ф. Рисса, относя-
относящихся к компактным эндоморфизмам. Для банаховых про-
пространств эти результаты изложены Ф, Риссом в работе [2J, в
934 Гл. 9 Теория компактных операторов
затем обобщены Л е р э [2] на случай локально выпуклых про-
пространств.
9.10.1. Теорема. Пусть Е — отделимое локально выпуклое про-
пространство, и — его компактный эндоморфизм и а=1+и. Поло-
Положил!,
Е~ = U (уТ' ({0}), EL = U (v'nTl ({0}),
п>0
П °в(£). '»= П
Тогда справедливы следующие утверждения.
A) у — открытое отображение пространства Е на замкнутое
векторное подпространство v(E), коразмерность которого конеч-
конечна и равна размерности ядра ir1 ({0}) отображения v.
\2) Пространство Е является топологической прямой суммой
подпространств £<» и /«>; размерность подпространства Еоо ко-
конечна-, подпространства Е^ и Л» устойчивы относительно отобра-.
жений и и v; сужение v\Eoo нильпотентно, а сужение v\Ioo яв-
является топологическим автоморфизмом пространства /«,;
(9.10.1)
codim v (E) = codim v' (Ef) = dim v~l ({0}) = dim v'~l ({0})< + oo;
(9.10.2)
/ ° / °
-Coo == /oo> 1 сю == -tl oo'y (y.lU.OJ
dim £oo = dim eLKoo. (9.10.4)
C) Следующие условия эквивалентны:
(a) отображение v взаимно однозначно;
(а') отображение vf взаимно однозначно;
(b) v — отображение на;
(Ъ') vr — отображение на;
(c) v — топологический автоморфизм;
(V) v' — топологический автоморфизм.
D) Последовательности Еп= (vn)~{ ({0}) a In = vn(E) (n =
= 1, 2, ...) стабилизируются, и наименьшее натуральное число р,
для которого En+i = En при п^р, является также и наимень-
наименьшим натуральным числом р, для которого 1пН = 1п при п^ р.
Это же р является наименьшим натуральным числом, для кото-
которого ур(£оо)={0}.
Доказательство теоремы довольно длинно, и мы разо-
разобьем его на несколько шагов.
Шаг A). Сначала покажем, что последовательность ядер
Еп= (^n)~4{n}) стабилизируется. Для этого выберем в Е такую
9.10. Спектральная теория компактных эндоморфизмов 935
окрестность нуля U и такое компактное выпуклое уравновешен-
уравновешенное множество Л, что u(U)cz A cz E. Тогда ЕА— банахово про-
пространство и вложение /: ЕА-±Е компактно. Отображение и
определяет непрерывное линейное отображение и0: Е-+ЕА и uoj
компактно. В силу предложения 9.9.3 достаточно доказать наше
утверждение для случая, когда и заменено на uoj. Другими сло-
словами, доказательство сводится к случаю, когда Е— банахово
пространство. Воспользуемся методом от противного. Допустим,
что последовательность Еп строго возрастает. Тогда можно най-
найти такую последовательность (г/п), что уп е Еп+\, ||ynll = l и рас-
расстояние уп от Еп не меньше 2~\ Действительно, Еп — замкнутое
подпространство в £П+Г» выберем ае Еп+\\Еп, расстояние d от
а до Еп отлично от нуля, поэтому для наперед заданного г > О
можно так выбрать г е £п, что d< \\a — z\\ <d(l + e). Полагая
уп=(а — z)/\\a — г||, легко проверить, что ||^Л11 = 1 и расстояние
от уп до Еп не меньше A+е)-1. Выбранная последовательность
(уп) такова, что при m <п
где x = v(yJ + (l-v)(yn)sEm.HT2LK,\\u{yn)--u(ym)\\'^2l при
тфп. Так как ||уп|| = 1, а отображение и компактно, то мы
приходим к противоречию, откуда вытекает, что последователь-
последовательность (Еп) стабилизируется.
Шаг B). Сопряженным к v будет v/=\f + u\ где и' — ком-
компактный энодоморфизм пространства Е\ наделенного топологией
к(Е'у Е) (предложение 9.6.1). Из шага A) вытекает, что после-
последовательность ядер En = (v'n) ({0}) стабилизируется.
Шаг C). Так как v'n={vn)' и vn= A+и)я= 1 +ип, где
ип — компактный эндоморфизм, то (теорема 9.6.8) vn — открытое
отображение пространства Е на замкнутое подпространство 1п
конечной коразмерности, являющееся ортогональным дополне-
дополнением к подпространству {vn)'~l ({0}) = (v'n) ({()})«=£?«. В силу
шага B) последняя последовательность также стабилизируется.
Таким образом, последовательность подпространства In = vn(E)
стабилизируется и 1^= Q 1п является замкнутым подпростран-
ством конечной коразмерности. Из шага A) и предложения
9.7.1 вытекает, что последовательности Еп и 1п стабилизируются,
начиная с некоторого п = р, Е^^ Ер, /те = 1Р и Е есть алгебраиче-
алгебраическая прямая сумма подпространств £оо и /оо. Так как подпро-
подпространство /оо замкнуто и обладает конечной коразмерностью, то
указанное разложение на прямую сумму — топологическое. Да-
Далее (снова в силу предложения 9.7.1) сужение v\Eoo нильпотент-
но, а сужение и [А» есть алгебраический автоморфизм. Из
936 Гл. 9. Теория компактных операторов
теоремы 9.6.8 вытекает, что сужение v\Ioo есть открытое отобра-
отображение /оо на себя, следовательно, v\Ioo есть топологический изо-
изоморфизм.
Утверждение D) теоремы 9.10.1 следует тогда из предложе-
предложения 9.7.1 и замечания 9.7.3.
Шаг D). Справедливость равенств (9.10.1) следует из того,
что v(E) замкнуто в £, и того, что v'(E') слабо замкнуто, по-
поскольку v'(E') замкнуто в топологии к(Е\Е). Равенства (9.10.2)
вытекают из следствия 9.7.2. Чтобы получить соотношения
(9.10.3) и (9.10.4), достаточно применить (9.10.1) и (9.10.2) к
степеням vn отображения v, имея в виду, что £IOO = £P, I^^Ip
и т. д.
Итак, утверждения A), B) и D) доказаны.
Рассмотрим утверждение C). Заметим, что из (9.10.2) сле-
следует эквивалентность (а) и (Ь), а также (а') и (Ь'). С другой
стороны, так как отображение v открыто, то (а) и (Ь) влекут
(с); обратное очевидно. Аналогичным образом получаем, что
(а7) и (Ь') эквивалентны (с'). Итак, (а), (Ь) и (с) эквивалент-
эквивалентны друг другу.
То же самое справедливо и для (а'), (Ь') и (с'). Остается
лишь заметить, что (Ь) и (а7) эквивалентны в силу (9.10.2).
Теорема полностью доказана. В
Теперь можно получить некоторые важные свойства спекгра
компактного эндоморфизма.
9.10.2. Теорема. Пусть Е — отделимое локально выпуклое про-
пространство и и — его компактный эндоморфизм.
A) Всякое отличное от нуля значение ^е о (и) является соб-
собственным значением эндоморфизма и, причем соответствующее
спектральное подпространство £\ имеет конечную размерность,
равную размерности соответствующего -спектрального подпро-
подпространства Ек эндоморфизма и'.
B) Эндоморфизмы и и и' имеют одинаковые отличные от
нуля собственные значения с одной и той же спектральной крат-
кратностью.
C) Спектральные многообразия £\ (X=f=O) топологически не-
независимы, т. е. для каждого ХфО существует такое замкнутое
векторное подпространство в Е, содержащее все £V с У ф 0 и
X ф А', которое пересекается с £\ лишь в {0}.
D) Спектр а (и) компактен и не имеет предельных точек, от-
отличных от 0 (т. е. множество о (и) либо конечно, либо представ-
представляет собой последовательность, сходящуюся к нулю).
Доказательство. Воспользуемся теоремой 9.10.1, заме-
заменив в ней и на U==—K~lu и v на V=k~l(kl — и). Если К е о(и),
9.10. Спектральная теория компактных эндоморфизмов 937
то V не является изоморфизмом пространства Е на себя. Так как
в любом случае отображение V открыто (теорема 9.10.1 A)), то
это означает, что либо (а) V не взаимно однозначно, либо (Ь)
V не есть отображение на. Если выполняется (Ь), то
codim V(E)> 0; поэтому (теорема 9.10.1A)) dim V~l ({0}) > 0 и,
следовательно, имеет место (а). Итак, справедливо (а), т. е. X—
собственное значение эндоморфизма и. Остальная часть утвер-
утверждения A), так же как и B), вытекает из равенств (9.10.2).
Для доказательства утверждения C) следует лишь заметить,
что из предложения 9.8.1 и теоремы 9.10.1 следует, что под-
подпространство /х в Е как раз и обладает нужными нам свой-
свойствами.
Докажем утверждение D). Компактность спектра а (и) вы-
вытекает из следствия 9.9.4. Чтобы получить остальное, допустим,
что ХфО и ^Ga(«). Как известно (теорема 9.10.1 B)), простран-
пространство Е есть топологическая прямая сумма подпространств £\ и
/ь каждое из которых устойчиво относительно эндоморфизма и.
Пусть п\ и и2 — сужения отображения и соответственно на £\ и
1^ Легко проверить, что о (и) = а (и\) []а (и2). Из утверждения A)
и из того факта, что сужение (XI—и) |£\ нильпотентно (теоре-
(теорема 9.10.1 B)), следует, что a(u\)={X}. С другой стороны, опять
в силу A), спектр о(и2) компактен. Кроме того, X не принадле-
принадлежит спектру о(и2). Действительно, в противном случае 1% будет
содержать ненулевой собственный вектор х, который соответ-
соответствует собственному значению X, причем х е EKi что невозможно,
так как £\ Л /х={0}. Итак, X — изолированная точка спектра о(и).
Теорема полностью доказана. I
9.10.3. Альтернатива Фредгольма. Из теоремы 9.10.2A) сле-
следует, что для всякого ХФ0 имеет место в точности одно из сле-
следующих двух утверждений:
(a) существует такое х'ФО, что и' (х')=Хх';
(b) для каждого у^Е уравнение Хх — и(х)=у имеет в Е
единственное решение х, непрерывно зависящее от у.
Далее в силу теоремы 9.10.1C) при каждом ХфО справед-
справедливо в точности одно из утверждений (а'), (t/), получаемых из
предыдущих заменой Е на Е' и и на и'.
Это было впервые установлено Фредгольмом для случая,
когда и—компактный интегральный оператор типа Гильберта —
Шмидта (см. § 9.5, а также Смитис [2, стр. 51, 52], Банах
[1, гл. X]).
Рискуя ломиться в открытые ворота, мы перефразируем не-
некоторые части теорем 9.10.1 и 9.10.2 в несколько измененной
форме, которая более удобна при изучении интегральных ураз-
нений и одновременно помогает яснее представить себе суть дела,
938 Гл. 9. Теория компактных операторов
Пусть, как и раньше, и — компактный эндоморфизм простран-
пространства Е. Рассмотрим эндоморфизм 1 — \iu = v с переменным зна-
значением параметра ji, который играет роль k~l в предыдущих
обозначениях. Основные результаты можно сформулировать так.
9.10.4. Теорема. Пусть Е — отделимое локально выпуклое
пространство и и — его компактный эндоморфизм. Для каждого
числа \х существует такое целое число пц ^ 0, что
A) по = О; совокупность чисел \х, для которых мц > 0, либо
конечна, либо (если она бесконечна) ее можно расположить в
последовательность (|ir), такую, что lim|jxr| = +оо.
Г->оо
B) Ядра отображений 1 — \iu и V — \iuf конечномерны и
имеют оба размерность пд. Пусть (di)i<i<n — базис ядра ото-
отображения 1 — \хи, a (aj) — базис ядра отображения
V — \xu'. " " "
C) Для данного у е Е [соотв. yr ^ E') уравнение
= y (9.10.5)
(соотв. х'-w'(x') = yT) (9.10.50
разрешимо относительно х в Е (соотв. относительно хг в Е')
тогда и только тогда, когда
(у, а{> = 0 (9.10.6)
(соотв. (ah #'} = 0) (9.10.60
для 1 -^л^Яд. Если эти условия выполняются, то множество ре-
решений х (соотв. х') уравнения (9.10.5) (соотв. (9.10.50) обра-
образует в Е (соотв. в FJ) линейное многообразие размерности мц.
Точнее, если х0 (соотв. xfy— решение уравнения (9.10.5) (соотв.
(9.10.50), т0 любое другое его решение имеет вид хо+ 2 aiai
соотв. x'Q + 2 aia'i)> г^е аг — числа. Обратно, каковы бы ни
были числа аи указанная сумма является решениен рассматри-
рассматриваемого уравнения.
D) При любом [х, для которого %=0, отображения 1 — [iu
и Г — \ки' являются топологическими автоморфизмами про-
пространств Е и Ег соответственно.
9.10.5. Потенциально компактные эндоморфизмы. Мы назы-
называем потенциально компактным непрерывный эндоморфизм и,
некоторая степень которого компактна. Легко видеть, что свой-
9 JO. Спектральная теория компактных эндоморфизмов 939
ства A) и D) теоремы 9.10.2 остаются справедливыми для вся-
всякого такого эндоморфизма и.
Действительно, пусть отображение и?, где р — некоторое на-
натуральное число, компактно. Почти очевидно, что если Х^а(и),
то ^еа(И- Применяя к эндоморфизму up теорему 9.10.2D),
получаем, что спектр а (и) компактен и не имеет отличных от
нуля предельных точек. Так как из (К1 — и)п(х) =0 вытекает,
что (№4 — uv)n(x)=01 то Ex{u)aEKp(uv). Таким образом, из
теоремы 9.10.2 A), примененной к up, следует, что подпростран-
подпространство Ех(и) конечномерно. Другие аналогичные свойства см. в
упр. 9.24.
Читатель может заметить, что если пространство Е обладает
строгим свойством Данфорда — Петтиса, то всякий слабо ком-
компактный эндоморфизм и является потенциально компактным, так
как и2 — компактное отображение (замечание B) после след-
следствия 9.4.5).
9.10.6. Замечания. A) Прежде чем закончить изложение
общих фактов, следует упомянуть о работе Депри [1], где при-
приведено полное исследование линейных отображений, близких к
тождественному в различных смыслах (например, отображений
с конечномерными ядрами, или с образами конечной коразмер-
коразмерности, или таких, которые являются открытыми отображениями
на свой образ). Также уделялось внимание линейным отображе-
отображениям, у которых последовательность итерированных ядер (или
итерированных образов) стабилизируется.
Свойства линейного отображения, описанные в утверждении
B) теоремы 9.10.1 совместно со свойствами стабилизации после-
последовательностей (Еп) и Aп) кратко называют иногда свойствами
Рисса. Если выполняется свойство стационарное!и, то линейное
отображение иногда называют конечным. Отображения такого
типа и их спектральные свойства были подробно изучены для ба-
банаховых и гильбертовых пространств. См., например, Хойзер
[1—3], Тэйлор [4], Кар аду с [1, 2], Гохберг [1—3], Ни-
Никольский [1].
B) Элегантное изложение теории Рисса для нормированных
пространств содержится в гл. 11 книги Дьёдонне [13]. Там
приводятся также указания на возможные обобщения на отобра-
отображения вида v = f — гг, действующие из пространства Е в F, глеи
компактно, а / — изоморфизм; см., в частности, задачи в конце
§ 11.3 в упомянутой книге Дьёдонне.
C) Как уже было сказано и как будет показано в § 9.11 и
9.12, общая теория, изложенная в § 9.6 и далее, находит наи-
наиболее широкое применение в случае, когда Е и F — банаховы
пространства. Приложения, в которых пространства Е и F — бо-
более общего типа, являются и более новыми, и более трудными.
940 Гл. 9. Теория компактных операторов
Блестящее приложение эта теория получила в теории гомологии.
К сожалению, из-за большого объема необходимых предвари-
предварительных сведений мы не можем останавливаться на этом в на-
нашей книге. В типичной для теории гомологии теореме конечности
утверждается, что группы когомологий Hn(X1F) (рассматривае-
(рассматриваемые как векторные пространства над полем комплексных чисел)
конечномерны, если X — компактное комплексно-аналитическое
многообразие, F — когерентный аналитический пучок над X, а
п — произвольное неотрицательное целое число. Доказательство
этого утверждения, использующее, в частности, теорему 9.6.7,
имеется в трудах семинара Кар та на (Париж, 1953—1954 гг.),
сообщения XVI и XVII.
9.11. Спектральная теория компактных эндоморфизмов
гильбертова пространства
Всюду в этом параграфе, если не оговорено противное, через
Е будет обозначаться гильбертово пространство со скалярным
произведением (х\у) и нормой ||а:||. Как известно (см. замечания
к следствию 1.12.6 и п. 8.11.8), существует такое сопряженно-
линейное и сохраняющее норму отображение / пространства Е
на Е\ что соотношение
(9.11.1)
выполняется тождественно по х,г/Е Е.
Пусть и — непрерывный эндоморфизм пространства Е. Как
и в п. 8.11.8, обозначаем через и* гильбертово сопряженное к и.
Оно определяется равенством
(и(х)\у) = (х\и*(у)) (9.11.2)
для х,у^Е. Отображение и* связано с сопряженным и! соотно-
соотношением u* = J-xu'J'. Эндоморфизм и называется самосопряжен-
самосопряженным, если и* = и, т. е. если
(и(х)\у) = (х\и{у)) (9.11.3)
тождественно по х, у е Е.
Некоторые элементарные спектральные свойства самосопря-
самосопряженных эндоморфизмов непосредственно вытекают из (9.11.3).
Так, поскольку в силу (9.11.3) скалярное произведение (и(х) \х)
вещественно, то всякое собственное значение самосопряженного
эндоморфизма и вещественно. Если, кроме того, и — положи-
положительный самосопряженный эндоморфизм, то его собственные
значения суть неотрицательные вещественные числа.
Из (9.11.3) также следует, что собственные векторы само-
самосопряженного эндоморфизма и, принадлежащие различным соб-
9 11. Спектральная теория компактных эндоморфизмов 941
ственным значениям, ортогональны. Наконец, для самосопря-
самосопряженного эндоморфизма и с помощью (9.11.3) и несложных рас-
рассуждений по индукции легко получить, что ип(х)=0 влечет
и(х) = 0. / Следовательно, спектральное подпространство
(J кег(и — Х\)п совпадает с собственным подпространством
кег(а — XI) (здесь X— любое вещественное число).
Мы хотим применить теорему 9.10.2 к компактному самосо-
самосопряженному эндоморфизму и пространства £, чтобы установить
некоторые характерные для рассматриваемого случая факты.
Эти факты вытекают из следующего ниже предварительного ре-
результата. Последний представляет интерес и сам по себе, так
как его доказательство служит примером применения вариаци-
вариационного метода определения больших (по модулю) собственных
значений эндоморфизма и.
9.11.1. Лемма. Всякий компактный самосопряженный эндо-
эндоморфизм иФО гильбертова пространства Е обладает по крайней
мере одним собственным значением ХфО.
Доказательство. Эндоморфизм и, очевидно, непрерывен.
Так как он самосопряжен и иФО, то число
Я= sup \(u(x)\x)\
||*1Ы
строго положительно. Ввиду того что (и(х)\х) вещественно, мо-
можно считать (заменяя, если нужно, и на —и), что X = sup(u(x) \х).
н*ц=1
Возьмем такую последовательность (хп), что IUn|| = l и
(и(хп) \хп)-^Х. Так как эндоморфизм и компактен, то можно
считать, что последовательность и(хп) сходится, скажем, к г.
Тогда числовая последовательность
II и (хп) - Ххп ||2 = || и (хп) ||2 - 2Х (и (хп) | хп) + А21| хп If
сходится к ||г||2 — X2, откуда ||г|| > X. Из того, что | (и(х) \х) \^С
<Л||д;||2 при всех х, следует, что | (и(х) \у) \KX\\x\\ \\y\\ при всех
х и у. Отсюда вытекает, что ||и(л:)|| <1^ ||х|| при всех х. Следова-
Следовательно, ||г||= lim \\и(хп)\\КК откуда ||г||=Л, и потому \\и(хп) —
— Ххп\\-+0. Но тогда xn-^X~]z, в силу чего u(xn)-^'k~lu(z), a
это означает, что u(z) =Xz, т.е. что z — собственный вектор эндо-
эндоморфизма и, соответствующий собственному значению X. Лемма
полностью доказана. |
Перейдем к основной теореме.
9.11.2. Теорема. Пусть Е — гильбертово пространство и и —
его компактный самосопряженный эндоморфизм. Тогда
942 Гл. 9. Теория компактных операторов
A) Спектр о (и) эндоморфизма и состоит из вещественных
чисел. Спектр о(и) не пуст, если иЧ=$. Если и — положительный
самосопряженный эндоморфизм, то о (и) состоит из неотрица-
неотрицательных чисел. В любом случае ненулевые точки спектра о (и)
являются собственными значениями эндоморфизма и. Собствен-
Собственное подпространство эндоморфизма и, соответствующее любому
собственному значению К, совпадает со спектральным подпро-
подпространством эндоморфизма иу соответствующим тому же К. Соб-
Собственные подпространства эндоморфизма и, соответствующие
различным собственным значениям, ортогональны.
B) Отличные от нуля собственные значения эндоморфизма
и (если они существуют) могут быть занумерованы в виде конеч-
конечной или бесконечной последовательности К\, Л2,..., которая в
том случае, когда она бесконечна, удовлетворяет условию
lim Kk = 0. Если ифО, то существуют отличные от. нуля собствен-
fe->oo
ные значения. Если 0 является спектральным значением эндо-
эндоморфизма и (что всегда имеет место, если Е бесконечномерно),
то мы включаем его в указанную последовательность в каче-
качестве Ко. Каждое собственное подпространство, соответствующее
отличному от нуля собственному значению, конечномерно.
C) Полагая Eh = kev(u — Xhl) при fe = 0, 1, 2,..., получаем,
что Е есть гильбертова прямая сумма подпространств Eh (fe =
= 0, 1,2,...). Если Pk — ортогональный проектор на Ek, то ка-
каждое Pk перестановочно сии
и= 2 hPk= 2 hPk, (9.11.4)
1= 2 Pk, (9.11.5)
' = 0 при кфк\ (9.11.6)
Замечания. Соотношения (9.11.5) и (9.11.6) позволяют
сказать, что последовательность (Pk)k^o ортогональных проек-
проекторов является разложением единицы (тождественного эндомор-
эндоморфизма). Тот факт, что Ри перестановочны с и и справедливо
(9.11.4), можно выразить так: последовательность (Ph) есть раз-
разложение единицы, соответствующее эндоморфизму и, или так:
соотношение (9.11.4) есть спектральное разложение эндомор-
эндоморфизма и.
Доказательство теоремы 9.11.2. Утверждения A) и
B) вытекают из предварительных замечаний в начале парагра-
параграфа и из теоремы 9.10.2.
Если показать, что Е есть гильбертова прямая сумма под-
подпространств Ekt то остальная часть утверждения C) получается
сразу.
911. Спектральная теория компактных эндоморфизмов 943
Пусть М — векторное подпространство в £, порожденное объ-
объединением всех Ek с k > 0. Нужно показать, что его ортогональ-
ортогональное дополнение М1 совпадает с Е0=кет и. В силу A) подпро-
подпространство Ео содержится в М1. Поэтому мы должны только по-
показать, что u(ML) ={0}. Если это не так, то из леммы 9.11.1 сле-
следует существование такого числа ХфО и такого элемента хФО
в M1i4To и(х)=Кх. Но тогда X совпадает с некоторым Кк при
k > 0 и соответственно х должен принадлежать Eh. Так как Ей
и М1 ортогональны, это противоречит условию хФО. Теорема
полностью доказана. |
9.11.3. Дополнения к теореме 9.11.2. Об уравнении
и(х)-кх~у (9.11.7)
можно (предполагая, что условия теоремы 9.11.2 выполняются)
утверждать следующее.
(а) Если К отлично от всех %н (* = 0, 1, 2, ...), то уравнение
(9.11.7) обладает единственным решением
2 (Я*-ЯГЧг/. (9.11.8)
>0
(b) Если X = %h при некотором h > 0, то уравнение (9.11.7)
имеет решение тогда и только тогда, когда Рпу = 0; в этом случае
решение имеет вид
2
НФЪ.
где а — произвольный элемент из Eh = ker(u — A^l).
(с) Если Я = 0, то уравнение (9.11.7) обладает решением
тогда и только тогда, когда Р0у = 0 и 2 ^k2\\Pky\t< + °°;
в этом случае решение имеет вид
2
fe>0
где а — произвольный элемент из £0 = ker и.
Проверку этих утверждений предоставляем читателю в каче-
качестве упражнения. В случаях (а) и (Ь) не требуется прибегать
к каким-нибудь критериям сходимости, так как соответствующие
ряды тривиально сходятся в Е.
Приведем еще одну формулу для решения в случае (а).
В силу (9.11.7) для решения х получаем выражение х = — h~l +
+ fk~lu(x). Если в и(х) подставить вместо х его выражение через
944 Гл. 9. Теория компактных операторов
ряд (9.11.8), то получаем
'2 $й <9-"-9>
fe>c
При вычислениях надо иметь в виду, .что иР0 = 0.
Следует указать и на другое толкование равенства (9.11.4).
Оно зависит от выбора ортонормированного базиса в каждом из
Eh при k > 0. Положим по = О и выберем натуральные числа пи
(k > 0) и векторы в{ (i= 1, 2,...) в Е таким образом, чтобы си-
система (е^), nk-\<i^Cnky образовывала ортонормированный ба-
базис в Ek (k> 0). Тогда dlmEh = nh — Пи-\. Рассмотрим последо-
последовательность (я9, составленную из «повторений» элементов по-
последовательности (hk)k>o в соответствии с правилом
Ki = kk при nk-i<i^.nk.
Последовательность (Я*), если она бесконечна, сходится к нулю.
Кроме того, вместо (9.11.4) и (9.11.5) имеем
и(х)=2оК(х\еде1 (9.11.40
2 (x\ei)ei. (9.11.50
i >о
Справедливо и обратное: если задана .сходящаяся к нулю
числовая последовательность (%\) и (е.) — ортонормированное
семейство в Е, то формула (9.11.4') определяет компактный
эндоморфизм пространства £, собственными значениями кото-
которого я*вляются числа Яг, а собственными векторами — векто-
векторы ег-. Полученное отображение и является самосопряженным
тогда и только тогда, когда все числа Я/ вещественны; и являет-
является положительным самосопряженным эндоморфизмом тогда и
только тогда, когда все Я/ положительны. Как будет показано в
п. 9.11.6, случай, когда Я/ не являются вещественными, соответ-
соответствует компактному нормальному эндоморфизму простран-
пространства Е.
9.11.4. Случай, когда пространство Е не является полным.
В некоторых приложениях используются предыдущие резуль-
результаты (во всяком случае те из них, которые сохраняются) для
случая, когда пространство Е есть (не обязательно полное)
предгильбертово пространство. Рассмотрим эту ситуацию под-
подробнее.
Всюду ниже в этом параграфе Е — предгильбертово про-
пространство, Е — его пополнение, которое является гильбертовым
9.11. Спектральная теория компактных эндоморфизмов 945
пространством. Пусть и — компактный (и, следовательно, непре-
непрерывный) эндоморфизм пространства Е, самосопряженный в том
смысле, что (9.11.3) справедливо для любых ху у е Е.
В теореме 9.10.2 не требуется полноты пространства £, по-
поэтому утверждения A) и B) теоремы 9.11.2 остаются верными,
если опустить условие полноты пространства Е. В лемме 9.11.1
нигде не используется полнота пространства £, ее возможное от-
отсутствие компенсируется компактностью эндоморфизма и.
В силу этого остается справедливым, что Ео является ортого-
ортогональным дополнением в Е к подпространству (J Ek.
Однако прежде чем рассматривать ортогональные проекторы
Ph на £ft, необходимо сделать некоторые замечания.
Проектирование на векторное подпространство предгильбер-
предгильбертова пространства возможно только тогда, когда рассматривае-
рассматриваемое векторное подпространство полно. Это имеет место для под-
подпространств Ek при k > 0, так как каждое из них конечномерно.
Таким образом, Pkx определено для каждого k > 0 как элемент
в Е. Если (это общий случай) Ео бесконечномерно, то Рох может
не быть элементом из Е (а только элементом из Е, принадлежа-
принадлежащим замыканию пространства Ео в Е). Подойдем теперь к этому
вопросу с другой'стороны. Если х&Е задано, то можно рассмо-
рассмотреть ряд 2 PkX. Так как Pk ортогональны, то частичные сум-
k> о
мы 2п= 2 Pk% этого ряда образуют последовательность
0<k<n
Коши в Е. Последовательность частичных сумм (гп) будет в Е
(хотя, возможно, не в Е) сходиться к некоторому г. Тогда эле-
элемент х — г = х0 из Е должен нам заменить Рох. Относительно
элемента хо мы можем сказать, что он ортогонален к объедине-
объединению (J Ek, но, вообще говоря, неизвестно, принадлежит ли х0
пространству E0 = ker и.
Таким образом, мы имеем
х = хо+ 2 Pkx9 (9.11.4")
k> о
где Хо ортогонально к (J Ek и Phx e Ek при k >0. Всякое такое
k>0
разложение единственно для любого заданного х. Вообще го-
говоря, ни хо, ни сумма 2 Рн* не принадлежат £, хотя это
имеет место в том случае, когда Ео конечномерно (и тем более,
если само Е конечномерно). С другой стороны, если известно,
что хое£", то *о^£о,(так как Ео — ортогональное дополнение
946 Гл. 9. Теория компактных операторов
к (J Ek в Е\. К сожалению, в общем случае соотношения
k>0 I
(9.11.4) и (9.11.5) не выполняются.
В свете предыдущих замечаний довольно удивительно, что
формулу (9.11.9), куда не входят х0 и у0, можно сохранить. Этот
факт опирается на одно замечание, которое представляет собой
частный случай следующей леммы.
Лемма. Пусть Е — предгильбертово пространство, и — его
компактный самосопряженный эндоморфизм. Пусть Eh и Рь
определены для k > 0 так же, как и выше. Тогда для любой
ограниченной числовой последовательности (lh) ряд 2 \bPkX
сходится в Е при х^и(Е). Более того, для любого такого х
имеем
лг= 2
k>0
Доказательство. Пусть x = u(z) для некоторого
Если tn и sn являются соответственно конечными частичными
суммами рядов 2 \kP хх и 2 \kPkz> то из того, что каждое
Pk перестановочно с и, следует, что tn~u{sn). Теперь так как Ph
ортогональны, то (sn) есть последовательность Коши, и потому
она ограниченна в Е. Следовательно, и (tn) — также последова-
последовательность Коши. Но эндоморфизм и компактен, поэтому (tn)
обладает сходящейся подпоследовательностью. Так как (/п) —
последовательность Коши, то она сходится в Е. Таким образом,
первое утверждение доказано.
Из равенства (9.11.4") следует, что х = хо+ 2 Я/г*, откуда
в силу уже установленной сходимости ряда 2 Pk* получаем,
что хо&Е, и, значит, х0 е ker и = Е0. Так как Ео — ортогональ-
ортогональное дополнение к (J Ek9 то
k>0
откуда вытекает, что хо = О, чем доказано и второе утверждение
леммы. |
Вернемся к равенству (9.11.9). Из соотношения (9.11.7)
(однозначная разрешимость которого не вызывает сомнений)
получаем
(h-h)~l Pky при
9.11. Спектральная теория компактных эндоморфизмов 947
Далее так как у + Хх = и(х) принадлежит и(Е), то из доказанной
леммы следует, что
k>0
Заменяя здесь Pkx на его выражение через Р^у и решая получен-
полученное уравнение относительно х, получаем (9.11.9). Заметим, что
сходимость ряда в (9.11.9) следует из предыдущих рассуждений.
9.11.5. Приложение к интегральным уравнениям. Остановимся
коротко на интегральном операторе у = и(х) вида
y(t)= $ Kit, s)x(s)ds,
О
где написано ds вместо d\x(s) (\х — мера Лебега на веществен-
вещественной прямой). Таким образом, ядро K(t, s) определено на квадра-
квадрате [О, 1]Х[О, 1] в R2.
В зависимости от характера функции K(t,s), которая во
всяком случае предполагается измеримой относительно меры Ле-
Лебега на R2, существует несколько естественных подходов к иссле-
исследованию оператора и. Например, можно исследовать и как эндо-
эндоморфизм гильбертова пространства L2 = L2([0, I], ji); в этом слу-
случае критерий компактности оператора и следует из предложений
9.5.2, 9.5.3 и 9.5.8. Или можно рассматривать и как эндоморфизм
банахова пространства С = С[0, 1] непрерывных числовых функ-
функций на [0, 1] с равномерной нормой ||х||оо = sup {\x(t) |: / ^ [О, 1]}.
В этом случае, для того чтобы убедиться в том, что и действи-
действительно есть энодоморфизм пространства С, достаточно, очевидно,
выполнения следующих двух условий:
1
lim J
j\K(t, s)\ds< + oo при /e=[0, 1], (9.11.10)
о
l
= 0 при to<z=[O, 1], (9.11.11)
В этом случае
sup Г
^[oi] j
Из теоремы Асколи и соотношений (9.11.10) и (9.11.11) выте-
вытекает, что и — компактный эндоморфизм пространства С.
Кроме этих двух привлекательных точек зрения, мы факти-
фактически рассмотрим в некотором смысле «смешанную» постановку
948 Гл. 9. Теория компактных операторов
вопроса, в которой и — эндоморфизм предгильбертова простран-
пространства, и воспользуемся результатами (п. 9.11.4), характерными
для этого случая.
Наше предгильбертово пространство, которое обозначим че-
через Е, представляет собой векторное пространство С, наделенное
скалярным произведением, индуцированным на С как на под-
подмножество в L2, т. е.
1
{x\y)=\x{t)JJf)dt.
о
Для применения предыдущей теории мы должны потребовать,
чтобы эндоморфизм и был самосопряженным. Для функции К
это означает, что
О- (9.11.12)
во всех точках {t,s) квадрата [О, 1]Х[0, 1]. В этом случае гово-
говорят, что ядро К является эрмитово симметричным.
При переходе от банахова пространства С к предгильберто-
вому пространству Е соотношения (9.11.10) и (9.11.11) могут
оказаться недостаточными для того, чтобы эндоморфизм и был
компактным. (Читатель заметит, что топология в Е слабее то-
топологии в С.) В силу ряда причин, о которых скажем позднее,
мы вынуждены наложить на К довольно сильные ограничения,
для того чтобы обеспечить компактность и как отображения
пространства Е в С (и тем более компактность и как отображе-
отображения из Е в Е). Достаточным условием для этого является (как
легко проверить с помощью неравенства Коши — Шварца и тео-
теоремы Асколи) выполнение отношений
1
j\K{t, s)\2ds<+ оо для *€=[0, 1] (9.11.13)
1
lim \\K(t, s)-K(t0, s)\2ds = 0 для t0 е= [0, 1]. (9.11.14)
Соотношения (9.11.12) — (9.11.14) позволяют воспользоваться
всей предыдущей теорией. Однако благодаря «смешанному»
характеру нашего примера имеется возможность слегка уточ-
уточнить лемму п. 9.11.4. Как было сказано, из (9.11.13) и (9.11.14)
вытекает не только то, что и — компактный эндоморфизм про-
пространства Е, но и то, что и — компактное отображение из Е в С.
Доказательство заключается в том, чтобы показать, что для
9 11. Спектральная теория компактных эндоморфизмов 949
любого х^и(Е) и любой ограниченной числовой последова-
последовательности (Ik) ряд 2 ikPkX сходится в С (и тем более в Е).
Более того, то же самое справедливо и для рядов, получаю-
получающихся заменой каждого Pk (ортогонального проектора на ко-
конечномерное* собственное подпространство Ей, соответствующее
собственному значению Xk) на ортогональный проектор Qk на
любое векторное подпространство в £&.
Посмотрим, что дает такое уточнение леммы.. Пусть
n>k — nk-i = dim Eh при fe>0, где по = О. Выберем в Eh некоторый
ортонормированный базис (фг), где nk-i<i"Cnh. Теперь удобно
заменить последовательность Xk различных ненулевых собствен-
собственных значений эндоморфизма и на последовательность, содержа-
содержащую число Хи повторенным nk раз. Другими словами, заменим
(kk) на последовательность (Кг), где А^ = Лг- для nk-i<i^.nk. и
k=l, 2, .... Таким же образом перейдем от (gft) к последова-
последовательности (li) «с повторениями». Если воспользоваться этими
обозначениями, то ряд 2 %kPk* принимает вид
k>0
L К — 1
k>0 '
Мы получаем ряд 2j |*(*1ф*)фо члены которого объединены в
конечные суммы так, как это указано квадратными скобками.
Обычно, конечно, эти скобки отбросить нельзя. Но в данном
примере это возможно, так как мы можем перейти от Pk к Q&.
Это означает, что при любом выборе конечных подмножеств
в интервалах (пк~и Пи] «ряд со скобками» 2 Г 2 hix\(Pi){
k>Q [_« e=Ik
сходится в С. Разлагая каждый член на вещественную и мни-
мнимую части и соответствующим образом выбирая /ft, получаем,
что ряд со скобками, составленный из абсолютных величин
|£г(*1фг)фг(О |, сходится для каждого t из [0, 1]. Таким обра-
образом, мы приходим к заключению, что ряд 2 £i(* 1ф*)фг схо-
сходится абсолютно и равномерно на [0, 1].
Опираясь на результаты п. 9.4.11, приходим к следующему
заключению.
(а) Пусть ядро К удовлетворяет соотношениям (9.11.12) —
(9.11.14). Если ХФО и отлично от всех Хи то для каждой непре-
непрерывной функции y(t) уравнение
1
-- J K(t, s)x{s)ds-Xx(t)
о
950 Гл. 9. Теория компактных операторов
обладает единственным непрерывным решением x(t)y выражае-
выражаемым формулой
х (t) - - ЯЛ @ + Я 2 Я, (Я, - Я)' (у | <р,) ф£ (f)f
i>0
ряд в правой части сходится абсолютно и равномерно по
/е[0, 1]. {Числа Яг- и функции фг- являются соответственно от-
отличными от нуля собственными значениями и собственными
функциями, выбранными и занумерованными описанным выше
способом.)
Теперь перейдем к другим свойствам интегральных урав-
уравнений.
(Ь) Предположим, что ядро К удовлетворяет соотношениям
(9.11.12) —(9.11.14). Тогда
1 1
]Я?< \dt f\K(t, s)\4s<+ oo.
i > 0
Доказательство. В силу неравенства Бесселя, приме-
примененного к функции /ь->K{t, s) и к ортонормированной системе
(фг-), для каждого п имеем
0 < i < л I 0
Из эрмитовой симметричности ядра К и из того, что фг- — соб-
собственная функция, соответствующая собственному значению Яг-,
следует, что суммы в левой части неравенства совпадают с сум-
суммами 2 Я? | ф{. (s) |2. Нужное нам неравенство получается те-
теперь, если проинтегрировать неравенство
О < i < п
1
^ J I K(t, s) 12dt no s и воспользоваться ортонормированностью
о
системы (фг), теоремой Фубини — Тоннели и, наконец, соотно-
соотношениями (9.11.13) и (9.11.14) (из которых следует, что интеграл
J \K{t> s)fds ограничен по /).|
о
(W) Пусть выполняются условия утверждения (а) и функция
" t% s) непрерывна при каждом фиксированном 5. Тогда
911. Спектральная теория компактных эндоморфизмов 951
ряд 2 М|ф/(О|2 равномерно сходится и его сумма равна
1
j\K(t, s)?ds.
О
Доказательство. Рассмотрим итерированное ядро
1
H{t, s)=j Kit, DKih s)dt
0
Читатель может заметить, что
1
причем функция H(t, t) непрерывна в силу (9.11.14). Так как-
K(t, s)—непрерывная функция от t, то функция t^—>H(ty s)
при фиксированном 5 является элементом образа и(Е). Из лем-
леммы 9.11.4 (уточненной описанным выше способом) следует, что
на,
i > 0
i > 0 Lo
где ряд сходится абсолютно и равномерно. Легко видеть, что
1
J H(f^ s) Фг- (^) dt' = Цч>1 E)i следовательно,
H(t, 5) ЕТ^
где ряд сходится для каждой пары (s, t). Полагая t=s, полу-
получаем, что ряд 2 ^|фН012 сходится к непрерывной функции
H(t, t). В силу теоремы Дени эта сходимость равномерна, что
и требовалось доказать. 1
(с) Предпосылки те же, что и в (Ь'). Утверждается, что для
каждого ХфО, отличного от всех собственных значений А,*, ряд
сходится абсолютно и равномерно по совокупности переменных
(t, s). Кроме того, решение х уравнения, фигурирующего в (а),
имеет вид
*(<)=»- Я у@ + J Rk(t, s)y(s)ds.
952 Гл. 9. Теория компактных операторов
Доказательство. Воспользуемся формулой для реше-
решения, полученной в (а). Имеем (снова в силу уточненной леммы)
, s)y(s)ds
0 i > О О
где ряд сходится, абсолютно и равномерно. Из тождества
Л (Л/ — А) г" Л == A A>i (Л; — Л)
получаем следующую формулу:
х @ = - АГху (О — Л" J /С (*, 5) у (s) ds +
о
+ AT22Л?(А,,-А,)
I
"
г>0 О
Поэтому достаточно показать, что ряд, определяющий
/?ь(/, 5), сходится абсолютно и равномерно по совокупности пе-
переменных (t, 5), так как тогда можно поменять местами инте-
интегрирование и суммирование: J V = Jj J •
Согласно (Ь'), ряд 2А»||ф/ (^) |2 равномерно сходится. С дру-
другой стороны,
inf | А* - А, | = с>0.
Из неравенства Коши — Шварца получаем, что для сумм, со-
содержащих любое конечное число слагаемых, справедливо нера-
неравенство
откуда и следует доказываемое утверждение. I
(d) Предпосылки те же, что и в (W). Утверждается, что
1
lirn I \K(t, s)-
""^^ 0 I 0 < i <n
равномерно относительно t.
ds-
9.11. Спектральная теория компактных эндоморфизмов 953
Доказательство. Непосредственный подсчет показы-
показывает, что
1
ds =
О < i < п
= j\K(t, s)fds-
О 0 < i < п
Наше утверждение следует тогда из (br). I
Замечание. Отсюда, в частности, вытекает, что K(ty s)
является пределом в смысле L2 (над квадратом [0, 1]Х[0х1])
частичных сумм ряда 2 VP* @ Фг E)- Однако, вообще говоря,
эгот ряд может не сходиться поточечно на этом квадрате (см.
С м'ити с [2, стр. 126]). В силу хорошо известной теоремы Мер-
сера поточечная сходимость имеет место в случае, когда эндо-
эндоморфизм и, определяемый ядром /С, является положительным
и самосопряженным. Доказательство этого утверждения мы
приводить не будем, отсылая читателя к Дьёдонне [13,
стр. 399], С мити су [2, стр. 128] или Заанену [1, стр. 534]
(см. также К а дота [1]).
9.11.6. Компактные нормальные эндоморфизмы. Рассмотрим
вкратце вопрос, упомянутый в конце п. 9.11.3, а именно воз-
возможность отказаться от условия самосопряженности, которому
до сих пер должно было удовлетворять и. Для простоты ограни-
ограничимся случаем, когда и — компактный эндоморфизм гильбертова
(а не предгильбертова) пространства Е.
Основное заключение 'состоит в том, что спектральное раз-
разложение, выражаемое соотношениями (9.11.4) —(9.11.6), воз-
возможно для тех компактных эндоморфизмов и, которые нор-
нормальны в том смысле, что мим* перестановочны. Ясно, что это
условие существенно, так как всякий эндоморфизм и, предста-
вимый в виде суммы (9.11.4), где Ри — перестановочные ортого-
ортогональные проекторы, очевидно, нормален.
Прежде чем перейти к интересующему нас обобщению, не-
необходимо сделать одно замечание, относящееся к уже извест-
известному случаю (когда и — самосопряженный эндоморфизм). Если
воспользоваться спектральным разложением эндоморфизма и,
то ясно, что
F(u)= 2 F(Xk)Pk (9.11.15)
k>0
для всякого многочлена F от вещественного переменного; здесь
для
2 *Лля
954 Гл. 9. Теория компактных операторов
через F(u) обозначается эндоморфизм ^jcnun. С другой сто-
стороны, если F — ограниченная комплексная функция, определен-
определенная на S = o(u)\{0} = {ku Яг, ••.}, то ряд 2 F{%k)Pkx схо-
k>0
дится для каждого х е Е и, таким образом, служит определе-
определением эндоморфизма пространства Я, который мы будем обозна-
обозначать также через F(u), Легко проверить, что
p(^)|. (9.11.16)
k>0
В частности, следует, что отображение F(u) компактно, если
(эндоморфизм и компактен) и lim F(Kk) = 0. Далее если это
последнее условие выполняется, то функция F может быть не-
непрерывно продолжена на компактное множество о (и) и, значит,
на всю вещественную ось. Но тогда функцию F можно аппрокси-
аппроксимировать равномерно на а (и) многочленами (теорема Вейер-
штрасса). Следовательно, F(u) является пределом в LC(E) мно-
многочленов от и. Это применимо и к тому частному случаю, когда
функция F равна 1 в точке ^иОв точке hk' при кфИ\ что со-
соответствует случаю F(u)=Pk. Таким образом, каждое Р&, где
&>0, является пределом многочленов от и (из предыдущих рас-
рассуждений даже следует, что эти многочлены могут быть вы-
выбраны так, чтобы их постоянный член равнялся нулю, но для
наших целей это неважно).
Теперь вернемся к случаю, когда эндоморфизм и компактен
и нормален. Положим
Щ = j {и + и*), и2 = -ji(u- u*)t
что соответствует выделению вещественной и мнимой частей
комплексного числа. Так как эндоморфизмы и и и* перестано-
перестановочны, то U\ и и2 самосопряжены. Из компактности эндомор-
эндоморфизмов и и и* вытекает компактность эндоморфизмов щ ц.и2.
Запишем разложение единицы, соответствующее эндоморфиз-
эндоморфизмам ип (/1=1, 2), в виде такого семейства Рп,к (^ вещественно)
ортогональных проекторов [если К не принадлежит спектру
о{ипI что РпЛ'РПу%,=0 при КФУ и
2j Рп, \ ~
А
Решающим является то обстоятельство, что каждое Pi,^ пе-
перестановочно с каждым Рг, v Это следует из того, что, как было
доказано выше, Рп, %, является пределом многочленов от unt a
9.1 L Спектральная теория компактных эндоморфизмов 955
щ и и2 перестановочны между собой, поскольку и — нормальный
эндоморфизм.
Благодаря этому, полагая
для каждого комплексного l = K+i\i (А, и \х — вещественные чис-
числа), получаем, что Р% образуют семейство ортогональных проек-
проекторов, причем РъРу = 0 при 1Ф1' и Р^ФО, кроме того случая, ко-
когда £ принадлежит множеству a(ui) +io(u2) (которое является
счетным). Далее
и = и, + ш2 = 2 ЯР ик + 12 [хР2>
что может быть записано в виде
Таким образом, семейство (Р^) образует разложение единицы,
соответствующее эндоморфизму и. Читатель может заметить,
что каждое Р% с £=£0 является пределом многочленов от и и */*,
а потому перестановочно с каждым из и и */*; то же самое спра-
справедливо и для Ро(которое равно 1— 2 Pi). Итак, мы полу-
\ 1фо I
чили нужное нам спектральное разложение эндоморфизма и.
Те же самые рассуждения можно использовать для случая
произвольного конечного числа перестановочных нормальных
эндоморфизмов, что приводит к одновременному спектральному
разложению рассматриваемых эндоморфизмов. Можно даже
рассмотреть бесконечное множество перестановочных непрерыв-
непрерывных нормальных эндоморфизмов, хотя здесь суммы придется
заменить интегралами. Для решения этой задачи требуются бо-
более сложные методы. Случай самосопряженных эндоморфизмов,
которые не являются непрерывными, еще более сложен и слу-
служит предметом изучения целого раздела теории гильбертовых
пространств. Все эти исследования лежат вне рамок нашей кни-
книги; читатель может познакомиться с ними, например, по следую-
следующим работам: Стоун [1], Рисе и Надь [1], Кук [2], Хал-
мош [2] (образец более ранних подходов), Люмис 1], Год-
м а н [5], Р и к к а р т [2], Б у р б а к и [10, гл. I] (образец современ-
современного подхода, основанного на использовании банаховых алгебр),
ГохбергиКрейн[1, 2].
956 Гл. 9. Теория компактных операторов
9.12. Дифференциальные уравнения в частных производных
и компактные линейные отображения
В п. 5.13.6 мы указывали на возможность использования ком-
компактных линейных отображений одного топологического вектор-
векторного пространства в другое в теории линейных дифференциаль-
дифференциальных уравнений в частных производных. В настоящем параграфе
мы немного продвинемся в этом направлении.
Мы будем придерживаться обозначений, принятых в § 5.13.
Повторим их здесь для удобства читателя.
Через й обозначается область в Rn, через \х — мера Лебега
на Rn; ро, • > Рп — положительные измеримые функции на й,
удовлетворяющие условиям
р0, .... pn<=^{0C(Q). (9.12.1)
Через V обозначается пространство (классов эквивалент-
эквивалентности) таких функций / на Q, что
l
f9dkfe=Lll0C(Q); pjf, p}dJ^L2(Q) A<*<л). (9.12.2)
В пространстве V можно ввести скалярное произведение
(f I g\ = {pjf I pjg\% „ + 21 (pjdj I pjdkg\t (Q). (9.12.3)
Очевидно, что 3)(Q) cz V.
Наш линейный дифференциальный оператор в частных про-
производных Р = Р(х, д) обладает тем свойством, что
(9.12.4)
для оеУ и фе2)(Й), причем скобки в правой части равен-
равенства относятся к двойственности между 3)(Q) и S)'(Q). Отсюда
следует (п. 5.13.1), что Р есть отображение пространства V в
3) (Q), определяемое равенством
Pf = Pof+%dk(Pkdkf). (9.12.5)
Для определенности рассмотрим задачу Дирихле; следуя
п. 5.13.2, обозначим через Vo замыкание множества SD(U) в V.
Предположим (ср. E.13.8)), что пространство Vq полно й
\\v\kw<e-\\v\\y (v&VQ). (9.12.6)
Как и раньше, через Л^ обозначим множество тех и ^ Vo> для
которых Ри& L2(Q). Заметим, что в силу (9.12.6) множество N
9.12. Дифференциальные уравнения 957
полно относительно структуры, определяемой скалярным произ-
произведением
(Q). (9.12.7)
Условия, достаточные для того, чтобы выполнялось соотно-
соотношение (9.12.6), приводятся в п. 5.13.4. Напомним, чго если вы-
выполняется (9.12.1) и если, кроме того,
РГ1,4..., /^eJ^Q), (9.12.8)
то V, а потому и Vo являются полными. Из части п. 5.13.9(Ь)
следует, что если
тт = ess inf pr>О @<г<я), (9.12.9)
го V — подпространство в ^(Q), структура которого сильней,
чем индуцированная из последнего пространства. Если при этом
ess sup pr < + оо @ < г ^ я),
то V и (^(Q) совпадают как множества и их структуры экви-
эквивалентны.
Заключительное требование, которое позволит воспользо-
воспользоваться теорией компактных операторов, заключается в том, что-
чтобы отображение вложения Уо в L2(Q) было компактным. Ясно,
что если выполняется (9.12.9), то для этого достаточно, чтобы
вложение ^(Q) (или же c3^2(Q)) в L2(Q) было* компактным.
Приведем три группы простых условий, обеспечивающих выпол-
выполнение этого требования. Случаю п=\ будут посвящены несколь-
несколько отдельных замечаний.
9.12.1. Компактность вложения Vo в L2(Q). Сформулируем
последовательно те три результата, о которых говорилось выше,
затем приведем их доказательства.
(a) Пусть область Q ограничена и выполняется (9.12.9). То-
Тогда вложение Vo в L2(Q) компактно.
Этот результат и его доказательство принадлежат Гор-
Гордин г у [2].
(b) Пусть выполняется (9.12.9) и
sup fess inf /?(Л = + оо,
к V Q\/c У
где К пробегает систему компактных подмножеств в Q. Тогда
вложение V в LU(Q) компактно.
(См. Лионе [1, предл. 4.3].)
(с) Пусть jx(Q)< +оо, выполняется (9.12,9) и Q обладает
следующим свойством**
958 Гл. 9. Теория компактных операторов
(S) существует такое число q>2, что ^(Q) c= Lq (Q). Тогда
вложение V в L2(Q) компактно.
Этот результат и его доказательство принадлежат Дени и
Лионсу [1, гл. I, теор. 9.1]. Ниже, в п. 9.12.2, мы еще остано-
остановимся на свойстве (S).
(d) Как мы видели в п. 5.13.4, случай п= 1 можно рассматри-
рассматривать отдельно и более элементарно. Подробнее изучение этого
случая предлагается читателю в качестве упражнения. Отметим
только пару простых результатов.
(сГ) Если \x(Q)< +oo, функция р0 не является пренебрежи-
мой и pj eoSf1 (Q), то вложение V в Cbd(Q) компактно. (Здесь
Cbd(Q) —банахово пространство ограниченных непрерывных на
й функций с равномерной нормой.) Если, кроне того, и область
Q ограничена, то вложение V в C(Q) компактно.
(d") Если ji(Q)<+oo, p~l^J2?x(Q) и V\—множество тех
функций f из V, которые стремятся к нулю на левом (правом)
конце области Q, то вложение \\ в Съа(&) компактно
Поскольку |л(й)< Н-оо, то компактность вложений, рассма-
рассматриваемых в (dr) или (d"), влечет за собой компактность рас-
рассматриваемых вложений как отображений в L2(Q).
Без всяких ограничений на Q легко получить, что вложе-
вложение V в L2(Q) компактно при гао>О и pj~l e *S?\0C (Q); это уточ-
уточняет утверждение (Ь). Читателю стоит также ознакомиться с ре-
результатами Хёрмандера [1, § 2.9] о компактности оператора,
обратного к линейному дифференциальному оператору в частных
производных с постоянными коэффициентами. Эти результаты
преподносятся там в контексте, несколько отличном от нашего.
Доказательство утверждений (Ь) и (с) опирается на крите-
критерий Вейля компактности в пространствах Лебега; см. § 4.20.
Всюду в последующем если f — функция на Q, то через /* бу-
будем обозначать функцию на Rn, равную / на Q и нулю вне Q.
Через В обозначается замкнутый единичный шар в &l*(Q\ Для
краткости условимся обозначать через Ill/llli норму функции f
в с?Ь^)> через <$ пространство ^Ь(Q) и через Lp пространство
L(R)
Доказательство утверждения (а). Из условия
(9.12.9) для mr (O^Cr^n) следует, что V — подпространство в
<% с более сильной структурой, чем та, что индуцируется из про-
пространства 8\ поэтому Vo — подпространство в «З^(й) с более
сильной топологией, тем та, что индуцируется из последнего про-
пространства. В соответствии с этим достаточно показать, что вло-
вложение =3*1.2 (Q) в L2(Q) компактно.
9 12. Дифференциальные уравнения 959
Для этого докажем, что для заданной последовательности
(fk) элементов пересечения B(]&l*(Q) существует подпоследо-
подпоследовательность, сходящаяся в L2(Q). Так как 2D — 3)(Q) плотно в
<2^(Q), то ясно, что достаточно рассмотреть случай, когда (fk)
состоит из элементов пересечения В Г) SD.
Введем преобразования Фурье
Fh (£) - J e-Wfk (х) ф (х) - J е-™*'*Гк (х) ф (jc).
Мы знаем, что
поэтому существует подпоследовательность (fkp), слабо сходя-
сходящаяся в L2(Q). Так как Q ограничено, то из теоремы Асколи сле-
следует, что последовательность (Fk ) сходится локально равно-
равномерно на Rn. В силу равенства Парсеваля
- J \Fkp{l)-Fq j
\ll>R
Применяя еще раз равенство Парсеваля, получаем (имея в виду,
4To/fte=iZ>(Q))
dih \fLt m < BnR)~2 HI fk HI
С другой стороны, для любого заданного R имеем
J \Fkp(t)-Fkq(l)\4ix(l)-+O при р, ?-
в силу локально равномерной сходимости. Таким образом, полу-
получаем, что (fk ) есть последовательность Коши и потому сходится
bL*(G).| p
Доказательство утверждения (с)» Докажем сна-
сначала (с), так как это удобнее.
960 Гл. 9. Теория компактных операторов
По условию Va&, причем топология в V сильнее, чем та,
что индуцируется из пространства &, поэтому достаточно дока-
доказать компактность вложения'<*? в L2(Q), или, что эквивалентно,
доказать, что В*— образ В при отображении/ь—> /* — компак-
компактен в L2.
Из условия (S) и теоремы о замкнутом графике следует су-
существование такого числа С, что
Для / gB из неравенства Гёльдера, полагая r=q/(q — 2), по-
получаем
J 1П2Ф = J
(О)
Так как q>2 и fx(Q) конечног то для произвольного е>0
J |/*|2ф<е (fGB),
если компактное множество К достаточно велико.
Таким образом, по заданному е > 0 можно выбрать такое
множество К! с: й, что
Выбрав е и К', зафиксируем затем такое компактное множество
iC'cQ, что int К" 35 /Сг. Тогда существует такое число 6/ =
= в'(е)>0> что
Если через Th обозначить сдвиг на h, то
Фиксируя е (а значит, и /Г, К" и (V), выберем такую функцию
Ф е2)(й), что 0<ф< 1 и ф= 1 на К'\ пусть теперь
С(е)= sup И^фЦ^со.
После простого подсчета получаем, что
§ = ф/*еГ[2и'г) и ||g|U 0?в)<С(е) (/efl).
9.12. Дифференциальные уравнения 961
Далее
В силу равенства Парсеваля
II Thg - g |g, = J | e2*^ - 1 p I G (I) I2 rf|x (g),
где G— преобразование Фурье функции g. Так как |A«g|^
^|A|-ISI и I^-IKC'I/I для вещественных t, то, снова
пользуясь равенством Парсеваля (только в обратном напра-
направлении), получаем
II Thg-g\l^C'2\ h I2 J || p • I G
и потому
II 7*Afir - ff it, ^c • i л I • с (в).
Следовательно,
для всех f^B и всех I/H^d7. Правая часть этого неравен-
неравенства в свою очередь не превосходит е при /еВ, |А|^б, где
Таким образом, В* удовлетворяет критерию Вейля. Утверждение
полностью доказано. |
Доказательство утверждения (Ь). Снова покажем,
что 5* удовлетворяет критерию Вейля. Как и раньше, заменим V
на &.
Для заданного е > 0 существует такое компактное множество
/Сс: Q, что ро > 8 почти всюду на Q\K. Тогда для f ^ В
-1 J
Q Q\7C
и потому
J |П2Ф<е при fes-B.
чп\к
962 Гл. 9. Теория компактных операторов
Теперь можно воспользоваться второй частью критерия Вей-
ля таким же образом, как и в предыдущем доказательстве. I
9.12.2. Об условии (S). Если п>2 и q = 2n/{n — 2) (>2), то
условие (S), примененное к областям в Rn конечной меры, ха-
характеризует так называемые области Соболева; см. замечания
в п, 5.11.1. Роль этого условия в исследовании функций Беппо
Леви давно известна (см. библиографию в работе Дени и
Л и он с а [1]). Посмотрим, как это условие фигурирует в иссле-
исследовании дифференциальных уравнений в частных производных.
9.12.3. Об операторе Грина *§. Вернемся к вопросам, затрону-
затронутым в начале § 9.12. Пусть й, pr (О^Сг^Сп) и V таковы, что
вложение пространства Vo в L2(Q) компактно. Пусть далее вы-
выполняется (9.12.6) и Vo —гильбертово пространство. Таково же
будет и Ny наделенное скалярным произведением (9.12.7). Если
G обозначает то же, что и в п. 5.13.5, и S = G\ Vo, то S7 есть ком-
компактный положительный самосопряженный эндоморфизм про-
пространства Vo. Таким образом, к *§ можно применить теорию
§ 9.11.
В результате получаем, что ^ обладает собственными значе-
значениями, которые можно расположить в виде последовательности
X'k (£=1,2,...), где ku > 0 и Хь. f +oo; соответствующие соб-
собственные функции оператора $ образуют тотальное множество
в Vo. Это множество можно записать в виде последовательности
ид (&= 1, 2, Г. .), повторяя, если нужно, Къ. несколько раз, чтобы
uk соответствовало числу А*, т. е.
Последовательность (uk) можно ортонормировать в L2(Q), после
чего получаем
(Щ I Ui)V = (Xi^Ui I Ui)V = К №Ui I Ul)v = Xi (Ui I Ufh (Q)
(последнее равенство следует из E.13.19)). Таким образом,
(ut\ui)v = Wu. (9.12.10)
Пространство S)(Q) плотно в L2(Q), поэтому и Vo, содер-
содержащее S)(Q), плотно в L?(Q). Так как (ик) образует в L2(Q)
ортонормированный базис, то [Xk 2uk) образует ортонормирован-
ный базис в Vo. Кроме того (п. 5.13.3), соотношения
ие=1/0, и=£0, tfu = Xklu (9.12.11)
эквивалентны соотношениям
«GJV, и ф 0, Pw=Xkuy (9.12.12
9.12. Дифференциальные уравнения 963
и потому Xk и uk являются собственными значениями и собствен-
собственными функциями (в смысле, обычном при исследовании диффе-
дифференциальных уравнений) оператора Р, рассматриваемого как
отображение пространства N в L2(Q). (Сужение оператора Р на
N сводится, как мы видели раньше, к наложению граничных
условий на допустимые решения.)
Наконец, (Xk + Xf) 2 uk образуют ортонормированный базис
в N относительно структуры, определенной скалярным произве-
произведением (9.12.7).
Если наложить на рг и f соответствующие требования глад-
гладкости, то uk (а на самом деле и все решения задачи Дирихле —
Неймана) также будут «гладкими»; например, если все рг и /
принадлежат C°°(Q), то то же самое справедливо и для ик\ это
следует из соотношения trk = ^lPuk.
Формально легко показать, что ядром оператора Грина <£?,
если представить его в виде интегрального оператора
gu(x)=j&(x, y)u(y)d\i(y)t (9.12.13)
является функция
&(х, y) = %^uk(x)lljy). (9.12.14)
k
При неформальном рассмотрении получаем, что такое представ-
представление возможно, когда рг достаточно гладки. Для того чтобы
формально получить (9.12.14) из (9.12.13), нужно только вос-
воспользоваться соотношением
(см. E.13.19)), произвести указанное почленное интегрирование
и воспользоваться тем, что последовательность (uk) ортонорми-
рована в L2(Q), и соотношением (9.12.10).
Естественно, что положение с (9.12.13) облегчается, когда из-
известно, что сумма в (9.12.14) сходится в соответствующем смыс-
смысле (например, сходится в L2(QxQ; м-® |ы); это может быть про-
проверено заранее, если только известен характер скорости роста
Хъ. Но это уже другая задача, углубляться в которую мы не
будем.
Дьёдонне [13, § 11.7] приводит подробный обзор одномер-
одномерного случая, в частности, так называемой задачи Штурма — Лиу-
вилля. Использованный там метод заключается в переходе от
заданного дифференциального уравнения и граничных условий
к эквивалентному интегральному уравнению, к которому можно
применить те же рассуждения, которые использовались в
п. 9.11.5.
964 Гл. 9. Теория компактных операторов
9.13. Снова об эргодических теоремах
В п. 1.12.9 мы рассмотрели'эргодическую теорему о средних
для некоторых эндоморфизмов гильбертова пространства и го-
говорили о ее связи со статистической механикой. Было указано,
что эргодические теоремы различных видов получены для про-
пространств более общих, чем гильбертовы, и было обещано, что
мы еще вернемся к этой теме. Сейчас мы можем это сделать.
Сформулируем и докажем одну общую теорему, из которой
можно получить несколько важных и интересных частных слу-
случаев.
9.13.1. Теорема. Пусть Е — отделимое локально выпуклое про-
пространство, и — его непрерывный эндоморфизм и
Допустим, что
(a) множество {Ап{х)\ /г=1, 2, ...} относительно слабо ком-
компактно в Е для каждого х е Е;
(а7) множество {Ап} равностепенно непрерывно;
(b) Mm п~1ип(х) =0 в слабой топологии для каждого х<=Е.
п
Положим Л/ = кегA—и) и R = im(l—и). Тогда
A) Е — топологическая' прямая сумма подпространств N uR\
B) если я — проектирование Е на N параллельно Л, то
lim Ап {х) = я (л:) в слабой топологии для каждого х е Е.
п
Наконец, если условие (Ь) выполняется при замене слабой
топологии исходной, то то же самое справедливо и для утвер-
утверждения B).
Доказательство. Пусть х е Е. Обозначим через х0
какую-нибудь слабую предельную точку последовательности
(Ап(х)) {х0 существует в силу (а)). Тождество
и условие (Ь) показывает, что х0 е N.
Покажем далее, что х — лгое Л. Действительно, пусть
ортогонально к Л. Если бы разность х — хо не принадлежала Л,
то х'о можно было бы выбрать так, чтобы (х — х0, jcJ)=1.. Но
(A-и)ип(х), *о> = о и потому (ип(х), х'о) =* (ип+г(х), х'о), откуда
следует, что (\(х)> хо) = (л:» хо) ПРИ всех п- Но тогда, переходя
к пределу, находим, что <л:0, х'0) = (х9 х'о), т. е/<дс-дс0, ^)==0.
Получили противоречие, следовательно, х—лгое/?.
9.13. Снова об эргодических теорецах 965
Убедимся в справедливости соотношения N Л Л = {0}. Прежде
всего если z^R, то из предыдущего тождества и условия (Ь)
следует, что An(z)-+0 в слабой топологии. В силу (а') это
остается справедливым для каждого геЯ. С другой стороны,
если 2GiV, то u(z)=z и потому An(z)=z при всех п. Отсюда
получаем, что единственное г, общее подпространствам N и
R, — это нуль.
Так_как х = (х — х0) + хОу то Е есть алгебраическая прямая
сумма Д и N. Более того, лг0 однозначно определяется заданием
ху поэтому (Ап(х)) обладает единственной слабой предельной
точкой и поэтому слабо сходится к слабому пределу я(х), где
я—проектирование Е на N параллельно R. Из условия (а7) сле-
следует теперь, что я непрерывно. Таким образом, прямая сумма
E — N + R является не только алгебраической, но и топологиче-
топологической.
Если условие (Ь) выполняется в смысле исходной топологии,
то An(z)-+0 в том же смысле, для z^R. Следовательно, и B)
выполняется в смысле исходной топологии. |
Приведем несколько замечаний по поводу последнего резуль-
результата.
9.13.2. Если пространство Е бочечно, то из (а) следует (а'),
так что последнее условие можно опустить.
9.13.3. Пусть Е — нормированное векторное пространство, и —
его слабо компактный эндоморфизм, степени которого ип обра-
образуют равностепенно непрерывное множество. Полагая
где
D 1 + и + ...ип~2
видим, что множества {Вп} и {Ап} равностепенно непрерывны,
причем из слабой компактности и вытекает условие (а). Кроме
того, условие (Ь) выполняется в исходной топологии. Таким об-
образом, и заключение B) имеет место в исходной топологии.
Эта форма теоремы для случая банахова пространства Е
принадлежит И о с и д е [1]. См также Д а н ф о р д [2].
9.13.4. Заметим, что если и — компактное отображение, то R
замкнуто в Е (теорема 9.10.1). То же самое верно, если Е — нор-
нормированное векторное пространство и и — потенциально ком-
компактный эндоморфизм (т. е. некоторая положительная степень
эндоморфизма и компактна); см. упр. 9.24.
9.13.5. Допустим, что Е — нормированное векторное простран-
пространство и условие (Ь) усилено требованием, чтобы n-1lknll-^0.
966 Гл. 9. Теория компактных операторов
Тогда если z^R, то г = л: — и(х) при некотором х и потому
An(z) = (x — un(x))/n. Отсюда
Если далее 1 — и — изоморфизм пространства Ё на R (что рав-
равносильно замкнутости подпространства R в случае, если Е— ба-
банахово пространство), то
для каждого z^R. Так как Ап(у)=у при всех п и всех y^
то из разложения
х=п(х)+л'(х),
где я' — проектирование Е на R параллельно N, следует, что
Ап (х) = п(х) + Апп' (х),
и поэтому
II Ап (х) - я(х) ||< const ±±Ш . ||Я' (*) ||<ай . ||* ||,
где limart = 0. Таким образом, в этом случае
Нт||Д,-я||-0.
Естественно, что из условия /z|knll ->0 следует выполнение
условия (а').
УПРАЖНЕНИЯ
9.1. Пусть F — отделимое локально выпуклое пространствр и А—такое
множество в F, что либо A) А относительно компактно в F, либо B) F квази-
квазиполно и А предкомпактно в F. Доказать, что слабая и исходная топологии в А
совпадают.
Вывести отсюда, что если Е — топологическое векторное пространство и
а: Е — F — непрерывное линейное отображение, причем либо (а) и компактно,
либо (b) F квазиполно и А предкомпактно, то а переводит всякую слабо схо-
сходящуюся к х ограниченную в F сеть (Xi) в сеть, сходящуюся в F к и(х).
9.2. Пусть Е и F — локально выпуклые пространства, Лсг£и BcnF — вы-
выпуклые уравновешенные множества и / — билинейная форма на Е X F. Дока-
Доказать, что
(a) еслл сужение f \ А X В непрерывно в точке @, 0), то оно непрерывно;
(b) если А предкомпактно, В компактно и /1А X В непрерывно в точ-
точке @, 0), то f\AxB равномерно непрерывно." (Г р о т е н д и к [7, стр. 95/
упр. 4].)
9.3. Пусть Е и F — локально выпуклые пространства, и: E->F — слабо
непрерывное линейное отображение и @ — система ограниченных выпуклых
уравновешенных подмножеств в Е. Доказать эквивалентность следующих двух
утверждений.
A) и(А) предкомпактно для каждого множества /1е@,
Упражнения 967
B) (и(х),у') \АхВ непрерывно в точке @, 0) в произведении слабых
топологий для каждого множества ^е<э и каждого выпуклого уравнове-
уравновешенного слабо замкнутого и равностепенно непрерывного множества BczF'.
[Указание. Воспользоваться теоремой 9.2.1 и предыдущим упражне-
упражнением.]
9.4. Пусть Е — сепарабельное банахово пространство. Доказать эквива-
эквивалентность следующих двух утверждений.
A) Каждое слабо компактное множество в Е компактно.
B) Если Птл'п = 0 в слабой топологии^ в Е и lim^ = 0 в слабой топо-
топологии в Е\ то (хп> х'п) -» 0.
[Указание. Применить упр. 9.3, взяв в качестве @ множество всех
слабо компактных подмножеств из Еу F=Ey и в качестве и — тождественное
отображение пространства Е на себя.]
9.5. Пусть Е и F -■- локально выпуклые пространства, причем в Е все огра-
ограниченные множества слабо метризуемы (как это имеет место в случае, когда
Е' сильно сепарабельно). Пусть далее u:E-*F— слабо непрерывное линей-
линейное отображение. Доказать, что^
(a) ~и переводит ограниченные подмножества из Е в предкомпактные под-
подмножества в F тогда и только тогда, когда \imu(xn)=0 в F, если limxn = 0
в слабой топологии в Е. (Ср. с предложением 9.4.13B).)
(b) Если, кроме того, каждое слабо компактное подмножество в F ком-
компактно, то и переводит ограниченные множества в предкомпактные.
9.6. Пусть Е — нормированное векторное пространство, в котором каждое
ограниченное множество слабо метризуемо. Показать, что если в Е каждое
слабо компактное множество компактно, то dim E <оо .
[Указание. Применить утверждение (Ь) упр. 9.5, полагая F=E и беря
в качестве и тождественное отображение пространства Е]
9.7. Пусть Е — бесконечномерное банахово пространство, сопряженное к
которому Ег сильно сепарабельно. Доказать, что существуют такие последо-
последовательности (хп) в £ и (х'п) в Е\ что (хп\ слабо сходится к нулю, {х^ слабо
сходится к нулю и (хпУ x'^j = 1 для всех п.
[Указание. Воспользоваться упр. 9.4 и 9.6.]
9.8. Пусть Е — банахово пространство. Доказать эквивалентность следую-
следующих двух утверждений.
A) Каждая последовательность (л;^) элементов из Е', слабо сходящаяся
к нулю, сходится к нулю в топологии а(£', Е").
B) Каждое непрерывное линейное отображение и пространства Е в от-
отделимое полное сепарабельное локально выпуклое пространство F слабо ком-
компактно.
[Указание. Воспользоваться теоремой 9.2.1 и теоремой Эберлейна.]
9.9. Пусть Е и F — отделимые локально выпуклые пространства, причем F
лолуюефлексивно, и и: E-^-F — непрерывное линейное отображение. Показать,
4tou"(E")czF.
9.10. Рассмотреть задачу о факторпоследовательностях Фурье, введенных
в примере 6.4.9. Показать, что если, (/п)—факторпоследовательность типа
(С, Lp) (I </?<°o, С — пространство непрерывных периодических функций),
то (fn) является также факторпоследовательностью типа (L°°, L?).
[Указание. Воспользоваться упр. 9.9, считая, что £ = С, F = Lp пи —
отображение, определяемое последовательностью (/п). Заметить, что каждая
968 Гл. 9. Теория компактных операторов
функция из L°° почти всюду равна ограниченной универсально измеримой
функции и что функции последнего типа образуют подпространство в Е".]
9.11. Пусть Е— равномерное пространство и (хп)—последовательность
Коши в Е. Показать, что подпространство S = {xn} полуметризуемо как равно-
равномерное пространство.
[Указание. Показать, что индуцированная в 5 структура обладает счет-
счетной базой окружений диагонали.]
9.12. Пусть Е — отделимое локально выпуклое пространство, (хп)—по-
(хп)—последовательность Коши в Е, А — замкнутая, выпуклая уравновешенная обо-
оболочка в Е множества {хп}. Показать, что индуцированная в А равномерная
структура метризуема. (Г р о т е н д и к [7, гл. V, стр. 24, упр. 1].)
[Указание. Свести задачу к случаю lirnxn = 0. Затем воспользоваться
следствием 8.13.3 и теоремой Крейна.]
9.13. Пусть Е и F — отделимые локально выпуклые пространства, и: £->
-> F— линейное отображение. Показать, что если и секвенциально непрерыв-
непрерывно в нуле, то оно переводит последовательности Коши в последовательности
Коши. (Г р о т е н д и к [7, гл. V, стр. 24, упр. 2])
[Указание. Пусть (хп)—последовательность Коши в Е, А— замкну-
замкнутая, выпуклая уравновешенная оболочка в Е множества {хп}. Пользуясь
упр. 9.12, показать, что сужение и\Л непрерывно в нуле, так что и\А равно-
равномерно непрерывно.]
9.14. Пусть Т — отделимое локально компактное пространство, (ш — поло-
положительная мера Радона на Т и F — банахово пространство. Предположим, что
функция Ф: T~>F скалярно существенно интегрируема (п. 8.14.1). Показать,
что для того, чтобы Ф была скалярно вполне интегрируемой (см. замеча-
замечание B) после предложения 8.14.13), необходимо и достаточно, чтобы
Ф а*ц е Е для каждого замкнутого множества Л си Г (или для каждого
А
замкнутого множества АаТ, обладающего счетной базой окрестностей).
(Г р о т е н д и к [4, стр. 162, предл. 13].)
[Указание. Необходимость тривиальна. При доказательстве достаточ-
достаточности показать сперва, пользуясь предложением 8.14.11 и теоремой о замкну-
замкнутом графике, что u(f) = /Ф d\i — непрерывное отображение Ь°° в F". Заме-
Заметить, что единичный шар Во в С0(Т) является e{L°°, L1)-плотным в единичном
шаре пространства L°°. Из непрерывности отображения и следует, что и ото-
отображает Со(Г) в F, так как каждая функция из С0(Т) является равномерным
пределом конечных линейных комбинаций характеристических функций %а-
Остается показать, что сужение и на С0(Т) является слабо компактным ото-
отображением лространства С0(Т) в F, и затем воспользоваться теоремой 9.4.10.]
9.15. Пусть Т, \х, F и Ф удовлетворяют условиям упр. 9.14. Привести при-
пример, из которого бы следовало, что дополнительное условие
f /Ф d\i ( « | /ф d\x) е= F для каждой функции / <= Со (Т)
не является достаточным,для того, чтобы функция Ф была скалярно вполне
интегрируемой.
[Указание. Пусть F=c0, Г —некоторое отделимое локальное компакт-
компактное, но не компактное пространство, а мера ц такова, что существует после-
последовательность Aп) таких непересекающихся интегрируемых множеств, что
|я(/п) > 0, и каждое компактное подмножество из Т пересекает только конеч-
Упражнения 969
яое число множеств In. Рассмотреть функцию Ф, определенную с помощью
равенства
X/ @ ,
9.16. Пусть Е—банахово пространство, изоморфное факторпространству
пространства с0. Доказать следующие утверждения.
A) Е обладает свойством Дьёдонне.
B) Всякое непрерывное линейное отображение пространства Е в отдели-
отделимое полное локально выпуклое пространство F, переводящее слабо сходящие-
сходящиеся последовательности в сходящиеся, является компактным.
C) Е обладает свойством (DP).
D) Всякое слабо компактное линейное отображение пространства Е в от-
отделимое локально выпуклое пространство является компактным.
E) Каждое множество из £', относительно компактное в топологии
<з(Е', Е"), является сильно относительно компактным.
F) Всякая последовательность Коши в Е' в топологии о(Е\ Е") сильно
сходится.
[Указание. Воспользоваться предложением 9.4.13 и критерием Данфор-
да — Петтиса для Iх]
9.17. Пусть Т — отделимое локально компактное пространство, ц — поло-
положительная мера Радона на Т. Пусть L# = L% (Г, ц) — пространство классов
эквивалентности ограниченных измеримых вещественных функций на Т, ча-
частично упорядоченное с помощью отношения t^g, означающего, что /^^
локально .почти всюду. Показать, что Л^—полная решетка (см. замечание
B) в конце п. 9.4.14). _
[Указание. Ясно, что всякое конечное подмножество из L^ имеет
верхнюю грань, поэтому достаточно убедиться в том, что всякая мажориро-
мажорированная возрастающая сеть (Д) обладает верхней гранью. Заметить, что отно-
отношение f^g имеет место тогда и только тогда, когда \ fh dp ^ gh d\i
для каждой положительной функции/ге^1 (ц). Рассмотреть линейные формы
на e2?1 (д), определяемые классами //, и воспользоваться теоремой 4.16.1.]
9.18. В обозначениях § 9.5 предположим, что
Kt II со ч dx (t) < + оо,
L (S, о)
где через Kt обозначена функция s\—>k(t, s) на S. Показать, что и — слабо
компактное отображение пространства L1 E, а) в Ll(T, т), так что и2 — ком-
компактное отображение пространства L]E, а) в Ll(T, т). (Есть контрпримеры,
показывающие, что само и может не быть компактным.)
9.19. В обозначениях теоремы 9.5.10 показать, что если D ограничено и
B(t, s) ограничено на D X Д то « — непрерывное отображение пространства
L*>(D) в Lp(D), 1 < /?<оо.
9.20. Пусть 1 < р <оо и
f \k(tt s)f
j
Показать, что и — компактное отображение пространства Lp(S, а) в Lp(T, t).
970 Гл. 9. Теория компактных операторов
9.21. В обозначениях теоремы 9.5.10 предположим, что D — ограниченное
подмножество в Rn и
где 0 ^ А, < п и В ограничено на D X D. Известно (упр. 9.19), что и — непре-
непрерывный эндоморфизм пространства Lp (D) для l^p^oo. Пусть теперь
1 ^ р < оо. Показать, что для заданного е > 0 существует такое б > 0, что
соотношения
влекут неравенство
\yfd[i<e.
м
9.22. Пусть D, k, В и X — те же, что и в упр. 9.21. Показать, что и — ком-
компактный эндоморфизм пространства Lp (D) при 1 < р <оо.
[Указание. Используя упр. 9.20, рассмотреть сначала случай, когда
р>п/(п — X). Затем исследовать случай, когда 1 < р < /г/А,, рассмотрев со-
сопряженный эндоморфизм и' пространства Lp'(D) и пользуясь следствием 9.2.3.
Если %<—п, то все доказано. Остается в заключение разобрать случай
г- п < Я < /г, воспользовавшись упр. 9.21.]
9.23. Пусть Е — гильбертово пространство и и — такой его эндоморфизм,
что
для некоторого ортонормированного базиса (ег) в Е. Доказать, что это соот-
соотношение справедливо для любого ортонормированного базиса в Е и что и
компактно. Вывести из теоремы 9.11.2, что если и — нормальный эндоморфизм
и Xi — его отличные от нуля собственные значения (повторенные с учетом их
кратности), то
Замечания. Неравенство 2 ' ^ I2 ^ HI u Ш2 справедливо для всякого
i
эндоморфизма и с ||| и \\\ < + оо независимо от того, является ли и нормаль-
нормальным или нет; этот результат принадлежит Шуру [1]; см. также Заанен [1,
стр. 353]. Близкая теорема Лалеско (Л а л е с к о [1], Георгину [1], X и л л е,
Тамаркин [1]) утверждает, что если и=и'и", где ||| и' \\\ < + оо и ||| и" |||<
< + оо, то 2 I ^i I ^ \W u' HI' ''I u" HIj cm- также упомянутую выше работу
3 а а н е н а. Относительно связи между компактными интегральными операто*
рами и и операторами, для которых ||| ип \\\ < + оо при некотором п, см.
За анен [1, стр. 360].
9.24. Пусть Е — нормированное векторное пространство, « — такой его
эндоморфизм, что up компактно при некотором натуральном р (п. 9.10.5). По-
Показать, что v = l — и переводит ограниченные замкнутые множества в замкну-
Упражнения 971
тые множества. Вывести отсюда, что v перводит замкнутые векторные подпро-
подпространства в замкнутые векторные подпространства.
9.25. Пусть Е — рефлексивное банахово пространство, и — непрерывное
линейное отображение пространства L1 в сильное сопряженное Е''. Показать,
что существует такая сильно измеримая функция /: Т->Е\ что ||/(/)|| ^||и!|
и (g) = J gf d\i
для каждого g e eS?l.
[Указание. Применить теорему 9.4.7, заметив, что поскольку и непре-
непрерывно и Е рефлексивно, то отображение и: D->E' слабо компактно.]
ГЛАВА 10
Теорема Крейна — Мильмана и ее приложения
10.0. Предисловие
В этой главе рассматривается важная георема о выпуклых
компактных множествах, принадлежащая Крейну и Миль-
м а н у [1]. Она синтезирует в абстрактной форме несколько тео-
теорем представления, полученных первоначально в классическом
анализе методами, затемнявшими их общее происхождение. По-
видимому, наиболее важными из этих теорем представления
являются теорема Бохнера о положительно определенных функ-
функциях и теорема Бернштейна о вполне монотонных функциях.
Подход Крейна—Мильмана к теореме Бохнера позволил (и это
не единственное его достоинство) распространить эту теорему на
локально компактные абелевы группы, что впервые было сдела-
сделано Кар таном и Годманом [1]. Первым, кто показал, как
можно аналогичным образом подойти к теореме Бернштейна,
был Шоке [1, гл. VII]. Мы обратимся к этим приложениям в
последних параграфах этой главы. Ни одно из „этих приложений
не является непосредственным. Необходимость предварительного
изложения большого числа сведений привела к тому, что, не-
несмотря на то что теорема Крейна — Мильмана тесно связана с
кругом идей, изложенных в § 8.13, мы уделили этой теореме от-
отдельную главу.
10.1. Крайние точки и теорема Крейна — Мильмана
Всюду в этом параграфе Е— вещественное топологическое
векторное пространство. Пусть А—выпуклое подмножество в Е.
Открытым отрезком , в А называется подмножество вида
{A—k)a + Xb: 0<Х<1}, где а и Ь — различные точки множе-
множества А.
Теорема Крейна — Мильмана связана с понятием крайней
точки выпуклого множества А. Точка х0 е А называется край-
крайней, если она не содержится ни в одном открытом отрезке мно-
множества Л. Это равносильно тому, что из соотношений
10.1. Крайние точки 973
следует либо Хо — а, либо Хо = Ь. Теорема показывает, каким обра-
образом в определенных случаях множество А может быть пред-
представлено с помощью своих крайних точек.
Для доказательства теоремы нам понадобится несколько бо-
более общее понятие. Замкнутое подмножество В выпуклого мно-
множества А в Е называется крайним подмножеством в Л, если из
соотношений
ае=А, 6е=Л, Ха+ A — %)Ь е= Я, 0<Я<1,
следует, что точки а и Ъ принадлежат множеству В. Легко про-
проверить, что одноточечное множество {xq} является крайним под-
подмножеством в А тогда и только тогда, когда х0 — крайняя точка
множества А.
Нам понадобится следующая вспомогательная лемма.
10.1.1. Лемма. Пусть Е — вещественное топологическое век-
торное пространство, А — непустое выпуклое замкнутое компакт-
компактное множество в Е, f — непрерывная линейная форма на Е и C =
= inf/(/4). Тогда B=A[)f~l({$}) является непустым компактным
крайним подмножеством в А.
Доказательство. Из линейности и непрерывности формы
f следует, что В—выпуклое замкнутое множество. Так как А
компактно, то и его замкнутое подмножество В компактно. Фор-
Форма /, будучи непрерывной, достигает своей нижней грани на ком-
компактном множестве Л, т. е. множество В непусто. Остается дока-
доказать, что В — крайнее подмножество в А. Пусть A—Х)а +
+ Я6 е В, где а^А, b g/1 и 0 < Л < 1. Если, например, точка а
не принадлежит множеству В,' то f(a)> |3 и поэтому
что противоречит условию A—Х)а + ХЬ s В. Таким образом,
аеВ; аналогичным образом устанавливается, что Ь^ВУ что и
требовалось доказать. |
10.1.2. Теорема (Крейн —Мильман). Пусть Е — веще-
вещественное отделимое локально выпуклое пространство, А —непу-
—непустое выпуклое компактное множество в Е. Тогда А является зам-
замкнутой выпуклой оболочкой в Е множества своих крайних точек.
Доказательство проведем в два шага.
(а) Каждое непустое крайнее подмножество X в А содержит
крайнюю точку множества А,-
Действительно, пусть SB — совокупность всех крайних под-
подмножеств в Л. В силу леммы 10.1.1 совокупность SB не-
непуста. Упорядочим SB по отношению zd (см. конец п. 0.1.4).
Мы утверждаем, что SB индуктивно упорядочено. В са-
самом деле, если. 2? — совершенно упорядоченное подмножество
974 Гл. 10 Теорема Крейна — Мильмана
в 96, то множество Y= f] {X: Ig^} непусто, так как множе-
множество А компактно. Легко также видеть, что У— нижняя грань
подмножества & в 96, В силу леммы Цорна 0.1.5 множество 86
обладает минимальным элементом, скажем У. Остается дока-
доказать, что У — одноточечное множество. Пусть это не так, тогда
У должно содержать по крайней мере две различные точки х и у.
Гак как пространство Е отделимо и локально выпукло, то на Е
существует такая непрерывная линейная форма /, что f(x)<f(y).
В силу предыдущей леммы Z= У П /~][inf f(Y)] есть непустое, не
содержащее у, крайнее подмножество в А. Таким образом, Z —
такое крайнее подмножество в Л, что Z а У, Z ф У, что противо-
противоречит минимальности У. Поэтому У — одноточечное множество,
что и требовалось доказать.
(Ь) Пусть В — выпуклая оболочка в Е множества всех край-
крайних точек множества А. Тогда В — выпуклое компактное множе-
множество^ содержащееся в А. Мы должны показать^ что множество
А\В пусто. Допустим противное, что х0^ А\В. В силу теоре-
теоремы Хана — Банаха существует такая линейная форма / на Е,
что inif(B)>f(x0). Но тогда W = A П f~l[ini f(A)] будет непу-
непустым крайним подмножеством в Л, которое не пересекает мно-
множества В (лемма 10.1.1). Поэтому в силу (а) множество W бу-
будет содержать крайние точки множества Л, что невозможно, так
как ГПЗс W()B = 0. ■
Замечания. Другую, несколько более общую формулиров-
формулировку теоремы Крейна — Мильмана см. у Данфорда и Швар-
Шварца [1, стр. 477, 504]. Первое доказательство этой теоремы при-
принадлежит Крейну и Мильману [1], а усовершенствован-
усовершенствованное— Мильману и Рутману [1]. Другое доказательство
принадлежит Годману [4], причем в нем чувствуется несо-
несомненное влияние доказательства, предложенного Бур баки
[7, стр. 108]. Мы привели доказательство, принадлежащее Кел-
ли [1]. См. также Агжери [1].
Что касается конкретных пространств, то Арене и Келли
[1] установили вид крайних точек замкнутого единичного шара
в замкнутом векторном подпространстве пространства С(Т)
(Т — компактное пространство) и применили свой результат к
доказательству одной теоремы Банаха (Банах [1, стр. 145],
Стоун [2, стр. 469]) об изометрическом изоморфизме между
пространствами С(Т) и С (Г').
Существует частичное обращение теоремы Крейна — Миль-
Мильмана, которое мы приводим ниже. Отметим, что, помимо тех
приложений, которые рассматриваются в этой главе, теорема
Крейна — Мильмана и ее частичное обращение имеют интерес-
интересные приложения к изучению двойных стохастических матриц и
субстохастических матриц (Кендалл [1]).
10.1. Крайние точки 975
Рассмотрим упомянутое выше обращение и некоторые допол-
дополнения к теореме Крейна — Мильмана.
10.1.3. Предложение. Пусть Е— отделимое локально выпук-
выпуклое пространство, К — компактное множество в £", замкнутая вы-
выпуклая оболочка которого А компактна. Тогда каждая крайняя
точка множества А принадлежит множеству /С.
Доказательство. Пусть х — крайняя точка множества А.
Если U — замкнутая выпуклая уравновешенная окрестность
нуля в Е, то существует конечное число таких точек аг- <= К
A<л-<п), что множества аг- + £/ покрывают К> Пусть А\ —
замкнутая выпуклая оболочка множества К [)(щ + и)\ каждое
Ai компактно. Выпуклая оболочка объединения множеств Ah
будучи компактной, содержится в А и, содержа К, должна совпа-
п
дать с А. Следовательно, х = 2 Kxi* ГДе л'г^^г, ?w ^ 0 и
как х — крайняя точка множества Л, то она дол-
жна совпадать с некоторой точкой х\. Таким образом, xiy
и поэтому х е /(+(/. Так как К замкнуто, a U произвольно, то
х^К, что и требовалось доказать. 1
10.1.4. Замечания и примеры. A) Даже если dim £ конечна,
множество крайних точек выпуклого компактного множества А
может не быть замкнутым. Например, пусть E=R3 и А — выпук-
выпуклая оболочка объединения окружности {(x,y,z): г = 0, х2-\-у2 —
— 2jc = 0} и двух точек @,0,1) и @,0,—1). Легко видеть, что
начало координат не будет крайней точкой множества Л, но бу-
будет пределом последовательностей таких точек.
B) Компактное выпуклое множество А может не быть вы-
выпуклой оболочкой своих крайних точек. Например, пусть Е = 1°°.
Обозначим через еп элемент пространства £, определенный ра-
равенствами
*W~l0 при кФп.
В качестве множества А возьмем замкнутую выпуклую оболочку
в Е множества точек п~хеп (я=1,2,.. .). Из предложения 10.1.3
можно вывести, что крайними точками множества А являются
точка 0 и точки п~1еп (п= 1,2,...). Далее множество А компакт-
компактно и содержит все точки х= 2 n~lknen, где (Хп) — любая по-
следоЕательность, такая, что Хп > 0 и 2 Ал= 1. Если все Хп > 0
п>\ *
то ясно, что х не может принадлежать выпуклой оболочке край-
крайних точек множества А (всякая точка выпуклой оболочки
976 Гл. 10. Теорема Крейна — Мильмана
является финитной последовательностью (т. е. последователь-
последовательностью с конечным носителем)).
C) Замкнутое некомпактное выпуклое множество А может
не иметь ни одной крайней точки. Например, пусть Е = с0 и А —
замкнутый единичный шар в Е. Пусть х — произвольный элемент
множества А. Рассмотрим два случая. Сначала предположим,
что х обладает конечным носителем, скажем х(п)=0 при п>г.
Определим элементы а м Ь следующим образом:
а(п)-\
-'- при п>г;
Ь(п) =
П
х(п) при п
- — при п>г.
Ясно, что а, Ь^А, афЪ и х=^-(а + Ь), так что х не являете*!
крайней точкой множества А. Пусть теперь х не облагает кон£Ч
ным носителем. Выберем г так, чтобы \х(п) \--C2~1 при п >
определим элементы а и Ь следующим образом:
а{п) =
Ь(п) =
х(п), если
2х (п), если n>r n n четно,
О, если п>г и п нечетно;
х(п), если п <г,
О, если п > г w n четно,
2х(п), если п>г и п нечетно.
Тогда снова а, бе Л, афЬ и л: = у(а + &), т. е. х не является
крайней точкой множества А.
D) Пусть Г — отделимое локально компактное пространство,
М(Т) — пространство вещественных ограниченных мер Радона
на Т. Пространство М(Т) можно считать сопряженным к С0(Т)
и наделить соответствующей слабой топологией. Множество
М\{Т) положительных мер из М(Т), имеющих общую массу,
не превосходящую единицы, компактно и выпукло.
Покажем, что крайними точками множества М1+{Т) яв-
являются 0 и меры Дирака е* (/еГ). В самом деле, ясно, что О
есть крайняя точка множества М1+(Т). Пусть [хфО — ненулевая
крайняя точка этого множества. Достаточно показать, что но-
носитель К меры |i сводится к одной точке. Пусть К содержит
10.1. Крайние точки 977
точки t\ и t2, причем t\=ht2. Выберем непересекающиеся окрест-
окрестности U\ и U2 точек U и t2 соответственно. Тогда m = \(U
удовлетворяет неравенству О < m < 1. Положим
Тогда, очевидно, а, реМ!+(Г), аф$ и (ш = та-Ь A — т) р, что
противоречит тому, что точка |я крайняя. Следовательно, множе-
множество К сводится к одной точке.
Аналогичные рассуждения показывают, что если простран-
пространство Т компактно, то множество положительных мер с общей
массой, равной единице, компактно и выпукло и его крайние точ-
точки являются мерами Дирака е*. Этот результат полезен в свете
следующей ниже теоремы 10.1.7, так как он в некотором роде
является ее дополнением.
Обратимся сейчас к теореме о крайних точках выпуклого
подмножества упорядоченного векторного пространства. Эта
Чорема иногда оказывается полезной при приложениях теоремы
й — Мильмана.
Теорема. Пусть Е— упорядоченное векторное про-
Е+— множество его полжительных элементов, Р — не-
подмножество в Е+. Точка jcgP называется Р-минималь-
НСй (или просто минимальной, если Р = Е+)У если из соотношений
у е Я, у <jc
следует, что у отличается от х лишь числовым множителем.
Предположим, что нам заданы непустое выпуклое множество
Ас: Р и вещественная функция f, определенная на Р, причем вы-
выполняются следующие условия:
A) если xg/1, у е Р и у-^-х, то у и х — у принадлежат мно-
множеству А;
B) если К > 0 и х, у, Хх и х+у принадлежат множеству Я, то
C) если хеЛ и f(x) = 0, то лг = О;
D) /(х)< 1 для каждого х из А;
E) если х&А и f{x)=£O, то x/f(x)e=A.
Тогда
(a) о — крайняя точка множества Л;
(b) отличные от нуля крайние точки множества А совпадают
с Р-минимальными точками х, принадлежащими множеству А и
удовлетворяющими равенству f(x) = l.
Доказательство. Так как Л непусто, то из A) следует,
что 0g A.
978 Г л 10. Теорема Крейна — Мильмана
(а) Предположим, что 0 = Ъ:+A—К)у для некоторых х, у
из Л, 0-<А,-<1. Тогда из B) следует
С другой стороны, из E) вытекает, что /(Л)>0. Отсюда полу-
получаем
Если ХФО, то f (х) =0 и потому в силу C) х = 0. Аналогично если
1 —а^О, то у = 0, и если 0 < К < 1, то х = у = 0. В любом случае
справедливо по крайней мере одно из двух равенств х = 0 или
£/ = 0, откуда следует, что 0 — крайняя точка.
(Ь) Заметим, что если хФО есть крайняя точка множе-
множества Л, то, поскольку х принадлежит отрезку, соединяющему
точки 0 и x/f(x) (в силу C) и D)), точка х должна совпадать с
x/f(x) и, значит, f(x) равно единице.
Предполагая по-прежнему, что хфО — крайняя точка мно-
множества Л, докажем, что х есть Р-минимальная точка. Пусть
(/еРи у-^Сх. Мы можем исключить тривиальные случаи у = 0
или у = х. В силу (I) у и х — у принадлежат Л и отличаются от
нуля. Тогда в силу C) и E) элементы
— У — х~~ У _ х~~ У
и~"ТШу V~ f(x-y) - i-f(y)
принадлежат Л. Но 0<f(y)<l и
С / . Л .. I /1
Так как х — крайняя точка, то либо x = u = y/f(y), либо x=^v =
= (х — «/)/A—f(y))- В любом случае y = f(y)xt т. е. точка #
Р-минимальна.
Обратно, пусть Я-минимальная точка л: принадлежит А и
/(х) = 1. Докажем, что х — крайняя точка множества А. В самом
деле, предположим, что х = аа+A — а) 6, где О-^а-^1 и
а, Ь^А. Тогда аа-^х, и если афО, то из Р-минимальности точ-
точки х следует, что а = Хх, где X — некоторое число '^0. [ЕслиА,<0,
то одновременно а-^0 и а^>0, т. е. а = 0; тогда л:—A—а)Ь\
если а=1, то это противоречит условию хФ0\ если а=£1, то
[(ft) = A —a)~lf(x) = A — а)-1> 1, что противоречит условию
D), так как JgA] Далее из B) и D) вытекает, что 1 1^-f(a) =
= Xf(jt)=X, поэтому 0<А,<1.
Аналогичным образом получаем, что если а=£1, то b = iix, где
0<ц<1.
Итак, если 0 < а < 1, то х = аХх+ A — а)\лх, откуда 1 =аА,+
+ A—а)\х. Поэтому A, = ji=l и, следовательно, х = а = Ь. Если, с
другой стороны, а = 0 (или ее = 1), то х = а (или х = Ь). Поэтому
10 1. Крайние точки 979
во всех случаях х совпадает с а или с b (или с обеими точками),
откуда следует, что х— крайняя точка. Теорема полностью до-
доказана. ■
10.1.6. Интегральные представления с крайними точками.
Снова предположим, что Е— отделимое вещественное локально
выпуклое пространство и А— непустое компактное выпуклое
подмножество в Е. Обозначим через е(А) множество крайних
точек множества А. Теорема Крейна — Мильмана утверждает,
что каждая точка х0 из А является в Е пределом выпуклых ком-
га п
бинаций 2 ltxh где хг е е(А), К{ > 0 и 2 h = 1 • С другой сто-
i — \ i — \
роны, мы видели (замечание A) п. 1*0.1.4), что е(А) может не
быть компактным множеством. Если е(А) компактно, то можно
показать, что каждая точка множесгва А является центром
масс некоторой положительной меры на е(А) с общей массой,
равной единице. Более общим образом справедлива следующая
теорема.
10.1.7. Теорема. Пусть Е — отделимое вещественное локально
выпуклое пространство, квазиполное в топологии %(Е,Е')\ А —
непустое компактное выпуклое подмножество в Е; е(А)—мно-
е(А)—множество крайних точек множества А. Тогда А совпадает с множе-
множеством точек xq^E вида
хо= j xd\i(x), A0.1.1)
где \х — положительная мера Радона на е(А) {замыкание в Е)
с общей массой, равной единице.
Доказательство. Множество В = е(А) компактно. Обо-
Обозначим через М множество положительных мер Радона на В с
общей массой, равной единице. Множество М как подмножество
в С(В)' слабо компактно. Из следствий 8.13.2 и 8.13.3 вытекает,
что отображение jbt>—>m(\i)= / xdix{x) отображает М в замкну-
замкнутую выпуклую оболочку С в Е множества В, и это отображение
непрерывно в слабой топологии в М (как подмножества сопря-
сопряженного к С (В)) и в топологии а(Е,Е/). Таким образом, с одной
стороны (так как В ci A), m(M)aA, с другой стороны, множе-
множество пг(М) слабо замкнуто в Е. Но в силу теоремы Крейна —
Мильмана гп(М) плотно в А. Следовательно, т(М)=Ау что и
требовалось доказать. 1
Замечание. Приведем один из вариантов последней тео-
теоремы.
Если Т — отделимое локально компактное пространство и f —
такое слабо непрерывное отображение пространства Т в Е, что
980 Гл. 10. Теорема Крейна — Мильмана
e(A)cz f(T)y то каждый элемент х0 множества А допускает пред-
представление Хо= I f{t)d\k(t), где \к — положительная мера Радона
т
на Т общей массой не более единицы.
Эту теорему об интегральном представлении можно допол-
дополнить следующим образом.
10.1.8. Предложение. Пусть условия и обозначения те же, что
и в теореме 10.1.7. Если х0 не является крайней точкой множе-
множества Л, то существует такое представление A0.1.1), в котором
Ц ({*(>}) =0.
Доказательство. Рассмотрим какое-нибудь представле-
представление A0.1.1). Если предположить, что ^ = 8^ (мера Дирака в точ-
точке х0), то m = ii({xo})< 1. Тогда мера
положительна, имеет общую массу, равную единице, и \({хо})
= 0. Далее
J xdv(x) = (l —m)~l J х d\x(x) — m(\ —
= A — m)lXQ — m A — m)lx0~ xQ,
т. е. мера v осуществляет нужное на*м представление. Задача,
таким образбм, сводится к доказательству того, что существует
по крайней мере одно представление A0.1.1) с \1фгх..
Воспользуемся тем, что точка х0 не является крайней. В мно-
множестве А найдутся такие точки а и b и такое число Ку 0 < Я < 1,
что л'о=A—k)a + Xb. Из теоремы представления получаем, что
а = J х da (x), b = J
где аир — положительные меры на В с общей массой, равной
единице. Отсюда получаем представление A0.1.1), где jn =
= A —А,)а + А,р. Так как афЬ, то одновременно а({х0}) и р({х0})
не могут равняться единице (в противном случае аир одновре-
одновременно равнялись бы еХа следовательно, а и & не были бы различ-
различными). Поэтому по крайней мере одно из чисел а({х0}) или
р({лг0}) меньше единицы, откуда следует, что то же самое верно
и для
Предложение полностью доказано. 1
Замечания. Шоке [2—8] рассмотрел вопросы существо-
существования и единственности интегральных представлений точек вы-
10.2. Приложения к теореме Бернштейна 981
пуклого конуса через его крайние точки. См. также Шоке и
Мейе [1], Фелпс, Бишоп и де Лю [1], Бонсол [2], Б аде
[1], Гуд н ер [2], Пек [1].
10.2. Приложения к теореме Бернштейна
Всюду в этом параграфе Т обозначает аддитивно записывае-
записываемую абелевую полугруппу с нейтральным элементом 0, а Е —
вещественное векторное пространство RT. Если наделить Е топо-
топологией поточечной сходимости на Т, то Е становится отделимым
локально выпуклым пространством. Итерированные разностные
операторы — это эндоморфизмы пространства Е, определяемые
соотношениями
d°x = х, d\x (t) = x(t + a)-x {t)
где a, ai,».., an+i — некоторые элементы из Т. Для краткости
будем иногда писать dn вместо d2 ...,fl .
Функцию х, принадлежащую E = RT, будем называть вполне
монотонной, если (—l)ndnx^0 для /г = 0, 1, 2, .... Совокуп-
Совокупность М таких функций есть выпуклое подмножество в Е.
10.2.1. Пример. Пусть 7"=R+, где сложение понимается в
обычном смысле. Легко видеть, что если функция х непрерывна
при t^O и бесконечно дифференцируема при t > 0, то она впол-
вполне монотонна тогда и только тогда, когда (—l)nx^(t)^0 при
я = 0, 1,2,... и при £>0. Из рассматриваемой ниже теоремы
Бернштейна следует, что всякая вполне монотонная функция на
R+ бесконечно дифференцируема при t > 0, хотя в точке t = 0
она может быть разрывной и иметь простой скачок.
Немного сокращая рассуждения Шоке [1, гл. VII], применим
теорему Крейна — Мильмана для того, чтобы получить -инте-
-интегральное представление вполне монотонных функций, в случае
Т = R+ сводящееся к теореме Бернштейна.
Если функция х вполне монотонна, то x(t + а) — #(/)<0 и
потому х(а)^л:@). Отсюда легко следует, что множество Мо
тех вполне монотонных функций х, для которых л:@)^1, яв-
является компактным выпуклым множеством в Е. Наш метод за-
заключается в использовании теоремы 10.1.5 для нахождения
крайних точек множества Мо с последующим обращением к тео-
теореме 10.1.7. С этой целью упорядочим Е соглашением, что л:</у,
если у — х^М. Далее в теореме 10.1.5 положим Р = М = Е*+9
А=М0 и f(x)=x@). Теперь нужно найти минимальные элементы
множества МОу удовлетворяющие условию х@) = 1. Мы докажем,
982 Гл. 10. Теорема Крейна — Мильмана
что такими элементами являются так называемые экспоненци-
экспоненциальные функции, определение которых сейчас приведем.
Неравная тождественно нулю функция и: T~>R называется
экспоненциальной на Г, если она удовлетворяет функциональ-
функциональному уравнению
u(t + t')=u(t)u(f) A0.2.1)
и неравенствам
0<и@<1, A0.2.2)
где / и f — произвольные точки из Т. Отсюда следует, что и @) ^=
= 1. Кроме того,
(- lTdnav ...tanU(t) = u(t) ■ (I - U(ai)) . . . (\ - U(an)),
т. е. функция и вполне монотонна и/iE Мо.
10.2.2. Пример. Вернемся к примеру 10.2.1, где T=R+y в ко-
котором легко определить экспоненциальные функции. Действи-
Действительно, если и — не обращающаяся в нуль экспоненциальная
функция, то ее можно продолжить до характера на R, полагая
и(—t)=u(t)~l (t>0). Так как и — убывающая функция от- ty
то она должна иметь вид us(t)=e-st для некоторого числа-5>0.
Пусть, с другой стороны, функция и обращается в нуль при не-,
котором / > 0. Положим ta=ini{t> 0: u(t)=0}; тогда u(t)==O
при />/о- Если /р>0, то из соотношения uBt0) =u(t0J следует,
что u(to)=O. Таким образом, u(t)=0 при / > t0 и а(/)>0 при
/1 \ 2
0-<^<^0. Но тогда соотношение «(^0) =м( ^о) противоречиво.
Значит, ^о = О, и и совпадает с функцией
1 при * = 0,
Следовательно, экспоненциальными функциями на R+ являются
функции us @ ^Cs ^С оо).
10.2.3. Предложение. Пусть х—-такой М-минимальный эле-
элемент множества Мо, что #@) = 1. Тогда х — экспоненциальная
функция на Т.
Доказательство. Положим
где а — некоторый наперед заданный элемент из Т. Тогда
Х\ е Му х2^М и х = Х\ + х2. Из минимальности элемента х сле-
следует существование такого числа Ха, что 0^^а-^1 и x2 = Kaxt
т. е. x(t + a) =XaX(t) для всех t^T. Полагая ^ = 0, получаем, что
да = л:(а). Таким образом, функция х удовлетворяет условию
10 2. Приложения к теореме Бернштейна 983
A0.2.1). С другой стороны, A0.2.2) следует из того, что х@) = 1
и х ^ М. Доказательство закончено. 1
Теперь можно доказать основной результат.
10.2.4. Теорема. Крайними для множества Мо являются точ-
точка 0 и экспоненциальные функции на Т. Множество S экспонен-
экспоненциальных функций компактно в топологии поточечной сходи-
сходимости на Г, и каждая вполне монотонная на Т функция х до-
допускает представление
J u{t)dm{u), A0.2.3)
где m—положительная мера Радона на S.
Доказательство. Ясно, что множество S компактно.
В силу предложения 10.2.3 множество крайних точек множе-
множества Мо содержится в SU{0}. Возможность представления
A0.2.3) непосредственно вытекает из теоремы 10.1.7. Остается
показать, что каждая экспоненциальная функция и является на
самом деле крайней точкой множества Мо. Для этого восполь-
воспользуемся предложением 10.1.8.
Пусть и0—экспоненциальная функция, не являющаяся край-
крайней точкой множества Мо. Тогда в силу предложения 10.1.8
uo{t)= j u(t)dm(u)9 A0.2.4)
5
где т({щ}) =0. Если t и е> 0 заданы, то замкнутое множество
{u^S: u(t)^- Uo(t) +e} является m-пренебрежимым. Действи-
Действительно, если мера этого множества равна /?, то
(w0 (О Г = ^о (nt) = J w (nt) dm (и)= \и (tf dm (и) > /? • (w0 @ + в)",
5 5
откуда следует (если л—^оо), что /? = 0. Таким образом, u(t)^C
^Uo(t) для почти всех и. Так как из A0.2.4) вытекает, что
1=^0@)= I dm (и), то снова в силу A0.2.4) получаем
J (uo(t) -u(t))dm (и) = uo(t)- \ u(t)dm (u) = 0.
Подинтегральная функция почти всюду положительна, следова-
следовательно, u(t)=uo(t) почти всюду. В силу непрерывности щ(() =
= u(t) для всех u^suppm. Отсюда следует, что supp m сво-
сводится к одной точке, которой может быть только щ. Это протчво-
984 Гл. 10. Теорема Крейна — Мильмана
речит тому, что т({и0}) =0. Теорема тем самым полностью до-
доказана. |
10.2.5. Следствие (Бернштейн). Пусть х — вполне моно-
монотонная функция на R+. Существуют такая ограниченная поло-
положительная мера Радона ju на R+ и такое число с^-0, что
) f 00.9.5)
для t > 0, где
1 при * = 0,
Доказательство. Как мы видели в примере 10.2.2, мно-
множество S состоит из функций e-st(s e R+) и и^- Остается приме-
применить теорему 10.2.4. |
10.3. Приложения к теореме Бохнера
Бохнер [1] был первым, кто систематически исследовал не-
непрерывные положительно определенные функции вещественного
переменного. К этим исследованиям он пришел в результате изу-
изучения интегралов Фурье. По Бохнеру, непрерывная (комплекс-
(комплексная) функция ф на R называется положительно определенной,
если неравенство
2 2 ф('р-^)*Л>0 A0.3.1)
выполняется для всех конечных наборов {tp)\^p<^n чисел из R
и всех конечных наборов комплексных чисел (гр),^ ^п. Легко
видеть, что функция ф эрмитово симметрична, т. е.
ф@=ф@^фР0. (Ю.3.2)
и ограничена:
1ф@Кф@). (Ю.з.з)
Если предполагать функцию ф непрерывной, то условие A0.3.1)
равносильно требованию
Ф*И@)= J j<p(ti-t2)f(ti)f(fidtldt2>0 A0.3.4)
для каждой функции f^o/f = g3T(R). Если же предполагается
ограниченность функции ф, то условие A0.3.1) равносильно тре-
требованию, чтобы соотношение A0.3.4) выполнялось для всех
функций /eS'^R). Условие A0.3.4) применимо к любой ло-
локально интегрируемой функции ф, и поэтому мы его примем В ка-
J0.3. Приложения к теореме Бохнера 985
честве определения положительной определенности функций (не
обязательно непрерывных).
Легко проверить, что если \х— положительная ограниченная
мера Радона на R, то функция
A0.3.5)
(обратное преобразование Фурье меры \х) непрерывна и положи-
положительно определена. Основной результат Бохнера состоит в
установлении справедливости обратного утверждения: каждая
непрерывная положительно определенная функция на R одно-
однозначно представима в таком виде. Доказательство Бохнера ис-
использует глубокие, далеко не тривиальные свойства преобразо-
преобразования Фурье. Теорема Бохнера использовалась (Купер [1, 2])
при изучении однопараметрических групп унитарных эндомор-
эндоморфизмов гильбертова пространства. Различные авторы (Купер
[3], Кр а м [1]) детально изучали представления, пригодные и для
разрывных положительно определенных функций. Мы не будем
останавливаться на этих обобщениях, наша задача — показать
возможность применения теоремы Крейна— Мильмана и ее
следствий к доказательству самой теоремы Бохнера. Если го-
говорить точнее, из теоремы Крейна — Мильмана непосредственно
выводится только лишь та часть теоремы Бохнера, которая свя-
связана с существованием, что же касается единственности, то она
выводится из других соображений.
Доказательство такого типа дано в работе Карта на
и Годмана [1], Этот метод доказательства позволил распро-
распространить теорему Бохнера на функции, определенные на группе.
Очевидно, что понятие положительно определенной функции со-
сохраняет смысл, если заменить R на произвольную группу Т. Для
того чтобы сохраняли смысл непрерывность и условие A0.3.4),
надо предположить, что группа Т отделима и локально компакт-
компактна. Годман [4] и независимо от него Гельфанд и Рай-
Райков [1] исследовали случай некоммутативных групп. Возникаю-
Возникающие в этом случае трудности подтверждают ту точку зрения,
что «естественной» сферой действия теоремы Бохнера является
класс отделимых локально компактных абелевых групп. Во вся-
всяком случае, мы ограничимся этим случаем. Очевиден также и
аналог представления A0.3.5): по-видимому, функции е2яЫ заме-
заменятся ограниченными непрерывными характерами на 71, и мо-
можно надеяться превратить эту совокупность характеров в
отделимое локально компактное пространство, несущее меру [i.
Как мы увидим, эти наши надежды полностью оправдаются.
Следует отметить, что теорема Крейна — Мильмана не яв-
является единственным функционально аналитическим инструмент
986 Гл. 10. Теорема Крейна — Мильмана
том для доказательства этой общей формы теоремы Бохнера.
Иной метод доказательства основан на теории коммутативных
нормированных алгебр и был открыт несколькими авторами не-
независимо друг от друга и почти одновременно в самом начале
второй мировой войны — в тот период, когда отсутствие связи
мешало обмену научной информацией. Подробное изложение
этого подхода легко доступно; см., например, Л ю м и с [1], Н а й-
марк [1], Рудин [9], Бур баки [10, гл. II].
С точки зрения обобщения теоремы Бохнера на локально
компактные абелевы группы намного более ранний результат
Гер г л отца [1J о положительно определенных последователь-
последовательностях представляет собой тот частный случай, когда Т — ди-
дискретная аддитивная группа целых чисел. Существует, однако,
чувствительный барьер, отделяющий случай, когда Т — дискрет-
дискретная или компактная группа, от общего случая, который значи-
значительно более сложен. Случай компактных групп относительно
проще, даже если эти группы не являются абелевыми.
Основная трудность теперь (как и во многих других прило-
приложения теоремы Крейна — Мильмана) состоит в отыскании край-
крайних точек соответствующего выпуклого множества. В рассматри-
рассматриваемом нами примере в качестве Е можно взять пространство
всех эрмитово симметрических функций из 1°°(Г), в качестве
А — множество тех непрерывных положительно определенных
функций ф (отождествляемых со своими классами в L°°(T))y для
которых ф@)^ L Затем нужно доказать, что крайними для
множества А являются точка 0 и ограниченные непрерывные ха-
характеры на Т. Если это будет установлено, то уже относительно
легко получить теорему Бохнера с помощью теоремы 10.1.7.
Для опознавания крайних точек неким «квазиалгебраиче-
«квазиалгебраическим» способом устанавливается связь между непрерывными по-
положительно определенными функциями и унитарными представ-
представлениями рассматриваемой группы. Эта идея почти одновременно
и независимо появляется, с одной стороны, у Картана и Год-
мана, с другой — у Гельфанда и Райкова1). Эта связь весьма
существенна и является источником почти всех известных ре-
результатов, касающихся положительно определенных функций
на группах.
После этого затянувшегося вступления перейдем к подроб-
подробному изложению вопроса.
10.3.1. Характеры. Всюду ниже T = {t} обозначает локально
компактную абелеву группу в аддитивной записи с нейтральным
элементом 0. Выберем и зафиксируем меру Хаара на Т (§ 4.18),
соответствующий интеграл будем обозначать через / ... dt.
1) Результаты последних полнее и опубликованы на год раньше. — Прим.
перев.
10.3. Приложения к теореме Бохнера 987
Характером на Т называется представление группы Т в
мультипликативную группу отличных от нуля комплексных чи-
чисел. Другими словами, характер на Т — это такая комплексная
функция х на 71, что х@) = 1 hj((U t2) = %(t{)%(t2) Для ti,t2<= Т.
Множество характеров само образует группу относительно по-
поточечного умножения. Обозначим через Т подгруппу, образован-
образованную ограниченными непрерывными характерами на Т. Обычно
Т записывают аддитивно (несмотря на то что законом компози-
композиции является поточечное умножение). Группа Т называется
дуальной к Т. Если t еГ; то вместо t(t) будем писать [t, t], где
t^T. Таким образом:
[0, ?]=1, [t{ + t2, i] = [tb ?]•['*?], [t% f, + ?2] + [/, ?iM', t2\
а из ограниченности следует, что |[/, ?]|==1, так что [—tyt]=-
— [Uf\ = [U—1\- Отсюда вытекает, что каждый характер t^T
есть непрерывная положительно определенная функция на Т.
Ниже мы увидим, что Т можно естественным образом наде-
наделить структурой локально компактной абелевой группы так, что
и группа Т будет (изоморфна как топологическая группа) ду-
дуальной к Т. Доказательство этого утверждения тривиально, если
Т — аддитивная группа вещественных чисел, или ее факторгруп-
факторгруппа по модулю 2я (или по любому другому отличному от нуля
модулю), или конечное произведение таких групп. Этими слу-
случаями исчерпываются все приложения в кассическом анализе.
10.3.2. Унитарные представления. Унитарным представлением
группы Т называется пара (H,U)y состоящая из гильбертова
пространства Н и гомоморфизма U: t*—>U(t) группы Т в муль-
мультипликативную группу унитарных эндоморфизмов простран-
пространства Я. О пространстве Н говорят как о пространстве предста-
представления, а о его размерности — как о размерности представления.
Ниже в тех случаях, когда противное явно не оговорено, под
термином «представление» будет пониматься унитарное пред-
представление (см. замечания в п. 10.3.9).
Представление (Я, U) отделимой локально компактной груп-
группы Т называется непрерывным (соотв. измеримым), если для
каждого х^Н числовая функция t*—>(U(t)x\x) непрерывна
(соотв. измерима относительно меры Хаара на Т). Это равно-
равносильно требованию, чтобы для каждой пары х, у элементов из
Я функция tv->(U(t)x\y) была непрерывна (соотв. измерима).
Непрерывные одномерные представления группы Т имеют вид
U(l)=%(t) '1, где 1—тождественный эндоморфизм, а %^Т.
Как уже говорилось, наша задача частично заключается в
том, чтобы установить связь между непрерывными представле-
988 Г л 10. Теорема Крсйна — Мильмана
ниями группы Т и непрерывными положительно определенными
функциями на Т. При этом решающий момент — выделить те
представления, которые соответствуют крайним точкам некото-
некоторого выпуклого множества положительно определенных функ-
функций. Оказывается, что соответствующим свойством представле-
представления является его неприводимость, к определению которой мы
переходим.
Неприводимость. Пусть (H,U) — представление группы 7\
Рассмотрим следующие три утверждения.
(a) В Н не существует отличного от {0} и И замкнутого век-
векторного подпространства, инвариантного относительно каждого
эндоморфизма U(t) (t^T).
(b) В Н не существует ортогонального проектора Р, отлич-
отличного от 0 и I и перестановочного с каждым эндоморфизмом
U(t) (/е=Г).
(c) Не существует нормальных непрерывных эндоморфизмов
Л пространства Н, отличных от Х\ (X—число) и перестановоч*
ных с каждым эндоморфизмом U(t) (t^T).
Напомним читателю, что непрерывный эндоморфизм А про-
пространства Н называется нормальным, если он перестановочен со
своим сопряженным. Таким образом, каждый самосопряженный
и каждый унитарный эндоморфизм нормален.
Очень просто показать, что утверждения (а) и (Ь) эквива-
эквивалентны (см. упр. 10.1). Тривиальна также и импликация (с)=^
гф (Ь). Однако то, что из (Ь) следует (с) и, следовательно, все
три условия эквивалентны, доказывается далеко не тривиально.
Доказательство опирается на спектральную теорию непрерыв-
непрерывных нормальных эндоморфизмов. Мы будем без доказательства
считать эти условия эквивалентными и пользоваться любым из
них как определением неприводимости представления (Я, U).
Доказательство этой эквивалентности можно найти во многих
книгах, например в книге Р исс а и Н а дя [1, гл. VII] или Л о р-
ха [1]. Имеется также весьма элегантный подход к этому дока-
доказательству, использующий общую теорию коммутативных бана-
банаховых алгебр с инволюцией, см. Люмис [1, гл. V, в частности
стр. 129—137].
Примеры. Всякое одномерное представление, очевидно, не-
приводимо. Как мы сейчас увидим, любое неприводимое пред-
представление абелевой группы Т одномерно. Если группа Т не яв-
является абелевой, то, вообще говоря, ее неприводимые представ-
представления могут быть и не одномерными (см. упр. 10.3—10.5).
Основное следствие неприводимости. Всякое неприводимое
представление абелевой группы Т одномерно.
Действительно, так как U — гомоморфизм абелевой группы Г,
то U(s)U(t)= U(st)= U(ts)= U(t) U(s). Таким образом, каждое
10.3. Приложения к теореме Бохнера 989
U(s) есть нормальный эндоморфизм пространства Я, переста-
перестановочный с каждым U(t). Поэтому из неприводимости предста-
представления вытекает, что f/(s) =g(s) 1, где I(s) — некоторое число.
Далее из неприводимости следует условие (а), из которого в
свою очередь вытекает, что для всякого элемента хФО из Я зам-
замкнутое векторное подпространство в Я, порожденное элемен-
элементами U(t)x (/еГ), совпадает с Я. Но тогда пространство Я
одномерно. |
Перейдем теперь к изучению связи между измеримыми пред-
представлениями и положительно определенными функциями.
Если (Я, U) — измеримое унитарное представление группы Т
и h — некоторый элемент из Я, то (U(t)h\h) — ограниченная по-
положительно определенная функция на 7, непрерывная, если
представление непрерывно. Основным техническим моментом в
рассматриваемой теории является тот факт, что справедливо
обратное утверждение, т. е. что каждой положительно опреде-
определенной функции из L°°(T) соответствует измеримое унитарное
представление группы Г, с помощью которого эта функция мо-
может быть получена описанным выше образом. Опишем подроб-
подробнее это соответствие.
Пусть ф — заданная положительно определенная функция
на Т. Для функций /, g ЕеТ = оЯГ(Г) положим
t2. A0.3.6)
Из A0.3.4) вытекает, что (f|g)ф — положительная эрмитова по-
луторалинейная форма на Ж. Пусть N^ = {f ^Ж: (/|/)ф = 0}.
Очевидно, Л^ф — векторное подпространство в Ж, и потому мо-
можно образовать факторпространство Жц> = Ж/Ыц. Обозначим че-
через /ф элемент пространства Ж<$, определяемый функцией f. Вы-
Выражение (/1 g") ф зависит только от fv и £ф, и поэтому его можно
использовать в качестве определения скалярного произведения
(/ф|£ф)ф. Таким образом, Жц становится предгильбертовым про-
пространством, пополнение которого обозначим через Яф. Унитар-
Унитарные эндоморфизмы пространства Яф, которые образуют вторую
компоненту представления, соответствующего функции ф, полу-
получаются с помощью операторов сдвига в пространстве Ж: если
f g Г и f е Т, то через ft обозначим f-сдвиг функции f, опреде-
определяемый равенством MO=f(^ — 0- Читатель без особого труда
проверит, что ft e Л^ф при /е Л^ф, так что класс ffs=(f^ зависит
только от класса /ф. Можно, таким образом, определить эндо-
эндоморфизм £/Ф@ пространства Жу, полагая Uy(t)fv=ff для ка-
каждого !^ЖУ проверить, что эндоморфизм С/Ф(£) унитарен в Ж®,
и продолжить £/ф@ по непрерывности до унитарного эндомор-
эндоморфизма пространства Яф. Не представляет труда доказать, что
J93 Г л 10. Теорема Крейна — Мильмана
t*->Uq(t) есть представление группы Г, так что пара (Яф, £/ф)
представляет собой унитарное представление группы Т. Это
представление непрерывно. Действительно, достаточно прове-
проверить, что (ft\f)q> — непрерывная функция от t для каждой функ-
функции \^Ж, но это ясно из соотношения A0.3.6).
Если ясно, какая функция ф имеется в виду, то часто вместо
Я(Г, £/ф, (|) ф,... пишут просто Я, U, (|),. .. .
Используя только что проведенное построение, можно полу-
получить важный результат, принадлежащий Гельфанду и Райкову.
10.3.3. Теорема. Пусть ср — такая положительно определенная
функция на Г, что для некоторого числа k
f*y*f@)^k(\\f\dtJ A0.3.7)
для всех функций ]<=Ж, обращающихся в нуль вне некоторой
заранее заданной окрестности нуля в Т: Тогда ф локально почти
всюду на Т равна непрерывной положительно определенной
функции.
Доказательство. Допустим, что условие A0.3.7) выпол-
выполняется для всех функций /, обращающихся в нуль вне окрест-
окрестности нуля Vo в Т. Для каждой окрестности нуля V в Г, удовле-
удовлетворяющей условию V cz Vo, возьмем такую положительно опре-
определенную обращающуюся в нуль вне V функцию gv ^ Ж, что
gvdt=l. Упорядочение окрестности V по отношению и> при-
приводит нас к направленному множеству. Сеть (g-£) слабо сходится
в Н. Действительно, из A0.3.7) следует, что эта сеть ограничена
в Н\ поэтому достаточно показать, что Пт(/Ф|^^) существует и
конечен для каждой функции 1^Ж (совокупность классов /ф
плотна в Я). Имеем
jgv(t2)dt2j (pVi-
где внутренний интеграл является непрерывной функцией от t2;
поэтому, в силу выбора функций gv указанный предел суще-
существует и равен / cpfdt. Предположим, что h является слабым пре-
пределом в Я сети (g^). В силу уже доказанного
10.3. Приложения к теореме Бохнера 991
Далее U(t)g^ слабо сходится к U(t)h в Я, откуда с помощью
прямого подсчета получаем, что
Таким образом, равенство
W)dt A0.3.8)
справедливо для всех функций / и g из Ж. Продолжая его по
непрерывности и заменяя /ф любым элементом из //, получаем
(с помощью теоремы Хана — Банаха), что множество элементов
вида U(t)h(t <=Т) тотально в Н. Далее, заменяя в A0.3.8) /<р
на /г, получаем
или, что то же самое,
№\h)=j(U(t)h\h)g(t)dt {g
Левая часть этого равенства, как было доказано, равна
/ dt откуда следует, что локально почти всюду
= (U(l)h\h), A0.3.9)
причем правая часть этого равенства есть непрерывная положи-
положительно определенная функция на Т. В
10.3.4. Следствие. Всякая положительно определенная функ-
функция, существенно ограниченная на некоторой окрестности нуля
в Т, локально почти всюду равна непрерывной положительно
определенной функции.
Каждый элемент пространства L°° содержит не ^более одной
непрерывной функции, поэтому ограниченную непрерывную
функцию можно отождествить с ее классом в L°°. Кроме того,
если ф — непрерывная положительно определенная функция, то
ПфПоо = ф@) (см. A0.3.3)). Из следствия 10.3.4 вытекает, что
множество Ро непрерывных положительно определенных функ-
функций ф, для которых ф@) -^ 1, слабо компактно в L°°. Очевидно,
также, что Ро выпукло. Поэтому к Ро можно применить теорему
Крейна — Мильмана. Основная задача теперь — найти крайние
992 Гл. 10. Теорема Крейна — Мильмана
точки множества Яо- Для этого воспользуемся теоремой 10.1.5.
В этой теореме возьмем в качестве Е множество всех эрмитово
симметрических функций из L°°, в качестве Е+ — все положи-
положительно определенные функции из L°°, в качестве Р — множество
всех непрерывных положительно определенных функций из L°°,
кроме того, положим А = Р0 и /(ф)=ф@). Ясно, что условия
A) — E) теоремы 10.1.5 выполняются, откуда следует, что край-
крайними для Ро являются: (а) точка 0 и (Ь) Р-минимальные точки
множества Ро, для которых ~ф@) = 1. Читатель может заметить,
что элемент ф£Р является Р-минимальным тогда и только
тогда, когда каждая непрерывная положительно определенная
функция г|), для которой функция ф — г|) положительно определе-
определена, отличается от ф лишь числовым множителем. Крайние точки
определяются теперь следующим предложением.
10.3.5. Предложение. Непрерывная положительно определен-
определенная функция ф, для которой ф@) = 1, является Р-минимальной
тогда и только тогда, когда соответствующее ей унитарное пред-
представление (Яф, f/ф) неприводимо, что в свою очередь х) означает,
ЧТО ф£Г.
Доказательство, (а) Пусть ф — Я-мипимальная точка и
ф @) = 1. Обозначим через Q проектор в Я, перестановочный со
всеми U(t). Тогда
ф(t) = (U(t)h\h)^{U(t)h\QU(t)h) + (U(t)h\h- QU(t)h) =
где Q'=l— Q. Здесь мы воспользуемся тем, что Q и Q' пере-
перестановочны с U(t), и тем, что (Sh\h) = (Sh\Sh) для всякого про-
проектора 5 во всяком гильбертовом пространстве. Оба члена в пра-
правой части последнего равенства являются непрерывными функ-
функциями из Ро, поэтому Р-минимальность точки ф влечет существо-
существование такого числа с, что
(U{t)Qh\Qh)=c-{U{t)h\h).
Пользуясь еще раз тем, что Q перестановочно с каждым U(t),
последнее равенство можно записать в виде
(U{t)h\Qh)=c- (U(t)h\h).
Как было обнаружено при доказательстве теоремы 10.3.3,
множество элементов вида U(t)h (/e T) тотально в Я, следова-
следовательно, Qh — с • h. Но так как Q — проектор, то либо с = 0, либо
с=1, т. е. представление (Я, U) неприводимо.
]) Это первое место, где существенно используется коммутативность
группы Г,
10.3. Приложения к теореме Бохнера 993
(Ь) Допустим обратное, т. е. что (Я, U) — неприводимое
представление, ifeP и ф — \|)gP. Мы должны доказать, чго
-ф = с»Ф, где с — некоторое число. Пусть /е Ж. Тогда из отноше-
отношения ф-1|)ЕР следует, что (/^|/ф)ф ^ {ftlM- Таким образом,
(f*|g*) Ф определяет ограниченную эрмитову полуторалинейную
форму на Я; поэтому существует такой ограниченный самосо-
самосопряженный эндоморфизм А пространства Я, что
(f IЛ - (АГI *ф) (А В е «ЯГ). (Ю.3.10)
Далее,
С помощью аналогичных преобразований получаем
(ли @ Г | яф) = (и (о Г | V) = (VI £/ @ Г)
следовательно,
Отсюда вытекает, что U(t)A=AU(t)9 т. е. что эндоморфизм А
перестановочен с U(t). Из неприводимости представления (Я, U)
следует, что А = сЛ и поэтому
* | А% = (ЛС/ (ОА|А) = с • (С/ @ А | А) = с
где (Л{У(/)А|А) продолжаемо по непрерывности в силу соотно-
соотношения A0.3.10). Таким образом, ^ = £«ф, что и требовалось до-
доказать.
(с) В заключение воспользуемся коммутативностью груп-
группы Т. Эта коммутативность влечет перестановочность эндомор-
эндоморфизмов U(t). Поэтому если представление (Я, U) неприводимо,
то каждый эндоморфизм [/(/) с точностью до числового множи-
множителя совпадает с тождественным, т. е. t/@==x@1- Но тогда
X — ограниченный непрерывный характер на Г, а потому U —
непрерывное унитарное представление. Следовательно, ф@ =
-A/@А|А)=х@(А|А)=ф@)-х@- Если Ф@) = 1, то Фе=7.
Обратно, если ф — ограниченный непрерывный характер, то из
построения пространства Я следует, что оно одномерно, а пред-
представление (Я, U) неприводимо. I
994 Гл. 10. Теорема Крейна — Мильмана
Теперь мы знаем, что множество крайних точек множества
Ро совпадает с множеством Т'=Т1){0} с Pod L°°. Применяя тео-
теорему Крейна — Мильмана, получаем:
► Всякое слабо замкнутое выпуклое множество в L°°, со-
содержащее 0 и все ограниченные непрерывные характеры
на Г, содержит и множество Ро.
Теорема Бохнера получается с помощью теоремы 10.1.7, по-
поэтому еще надо показать, что Т можно превратить в отделимое
локально компактное пространство.
10.3.6. Предложение, (а) Множество Т' слабо замкнуто в Ро
и, следовательно, компактно в слабой топологии в L°°.
(b) Множество Т локально компактно в слабой топологии
пространства L°°,
(c) В Т слабая топология пространства L°° совпадает с то-
топологией равномерной сходимости на компактных подмноже-
подмножествах из Т.
Доказательство. Для доказательства всех трех утвер-
утверждений достаточно показать, что если сеть (ti) в Т слабо схо-
сходится в L°° к пределу ф=£0 из Ро, то /;->Ф равномерно на ком-
компактных подмножествах из Т. Так как <р=£0, можно так выбрать
[gJ, чтобы [ fdt=£O. Положим <pi(t)=[t, U\ Тогда
%*f @ = J % (t - П f (П dV = q>, @ J W) f (П dt'« ct • ф, @,
где числовая сеть (ci) сходится к f(pdt=£O. Из первого выра-
выражения для фг*/(О следует, что фг^/->ф^/ поточечно на Т. Так
как, кроме того, функции фг равномерно ограничены, то множе-
множество функций {фг*/} равностепенно непрерывно. Действительно,
в силу инвариантности меры Хаара
Таким образом (предложение 0.4.9), фг-^/-^ф^/ равномерно на
компактных подмножествах из Г, что и требовалось доказать. 1
Замечания. Топология в Г, определяемая локально равно-
равномерной сходимостью на Г, была введена Понтрягиным
[1, гл. V] и часто называется его именем. Легко проверить, что
топологизированная таким образом группа Т является отдели-
отделимой топологической группой.
10.3. Приложения к теореме Бохнера 995
Важным следствием предложения 10.3.6 является следующее
обобщение знаменитой леммы Римана —Лебега.
10.3.7. Предложение. Если f — интегрируемая на Т функция,
то ее преобразование Фурье
т
принадлежит С0(Т) (пространству непрерывных комплексных
функций на f, стремящихся к нулю на бесконечности). Кроме
того, когда f пробегает пространство 3?Х(Т), то функции f обра-
образуют векторное подпространство в C0(f), плотное относительно
топологии равномерной сходимости на Т.
Доказательство. Так как f — равномерный предел
функций
f(t)[t7T]dt,
К
где К — компактное множество в 7\ то из предложения 10.3.6(с)
следует, что функция / непрерывна на f. Кроме того, для за-
заданного е>0 существует такая открытая окрестность нуля W
в^ Г', что в силу самого определения слабой топологии в L°°
|/(/)| <е при t^T'\W. Пользуясь еще раз предложением
10.3.6, получаем, что K=T'\W является компактным множе-
множеством в Т. Так как \f(t) \ <е для t ^ f\/C, то /^ С0(Т).
Для доказательства оставшейся части предложения предпо-
предположим, что каждая функция / определена на компактном про-
пространстве Г^ГЩО} (предложение 10.3^6) и удовлетворяет усло-
условию /@)=0. Каждая такая функция f принадлежит простран-
пространству С(Т). Заметим также, что преобразование Фурье функции
f является функцией, комплексно сопряженной к fj что пре-
преобразование Фурье свертки f*g (п. 4.19.12) равно f*g. Отсюда
и из теоремы Вейерштрасса — Стоуна (теорема В п. 4.10.5) сле-
следует, что функции вида %+f, где К — комплексная постоянная и
f&2?l(T), образуют плотную подалгебру в С(Т'). Теперь уже
непосредственно ясно, что функции f образуют в Со(Т) плотную
подалгебру, которую можно отождествить с множеством функ-.
ций из С(ГГ), обращающихся в нуль в точке 0. I
Замечание. Хотя для каждой функции f^2*l(T) функ-
функция f на f и стремится к нулю на бесконечности, можно пока-
показать, что если Т не компактно (т. е. Т не дискретно), то суще-
существует интегрируемая функция f на Г, преобразование Фурье
996 Гл. 10. Теорема Крейна — Мильмана
которой стремится к нулю сколь угодно медленно, когда ? стре-
стремится к бесконечности. См. упр. 10.8.
Наша цель совсем близка.
10.3.8. Теорема. Если ф — локально существенно ограничен-
ограниченная измеримая положительно определенная функция на Г, то
существует такая единственная ограниченная положительная
мера Радона ji на f, что локально почти всюду на Т
Если функция ф непрерывна, то это равенство справедливо для
всех точек t еГ.
Доказательство. В силу следствия 10.3.4 при доказа-
доказательстве существования меры \i можно считать, что функция ф
непрерывна. Тогда если ф@)=0, то ф=^0, и можно положить
\х = 0. Если же ф@)=£0, то можно считать, что ф е Ро- Существо-
Существование меры \х следует из теорем 10.1.5, 10.1.7 и предложе-
предложения 10.3.5.
Доказательство единственности сводится к проверке того
факта, что ц = 0, если
для всех tmT. Если воспользоваться теоремой Лебега—Фу-
бини 4.17.4, то из этого условия вытекает, что
для всех интегрируемых функций f на Т. Равенство jlx = 0 следует
тогда из утверждения о плотности в предыдущем предло-
предложении. ■
10.3.9. Замечания. Классическая теория представлений
первоначально применялась к конечным группам; при этом
обычно говорили о матричных представлениях или, что то же
самое, о представлениях с помощью обратимых эндоморфизмов
конечномерного векторного пространства Я. Конечно, Н можцо
превратить в гильбертово пространство многими способами.
Можно показать (Маак [1, § 4, 30]), что всякое ограниченное
представление такого вида эквивалентно унитарному представ-
представлению, если соответствующим образом наделить Н структурой
гильбертова пространства.
После того как было обнаружено существование меры Хаара
для отделимых компактных групп, значительная часть теории
была распространена на представления таких групп; слЧ.
А- В ей л ь [1, гл. IV и V]. В этой книге все еще рассматриваются
10.4. Теорема Планшереля 997
конечномерные представления. М а а к [1] пользовался аналогич-
аналогичной техникой для произвольных групп, опираясь на существова-
существование среднего для почти периодических функций и на связь по-
последних с ограниченными представлениями. Небольшое пред-
представление о методе Маака дается в упр. 10.7. В упомянутой
выше книге А. Вейля (гл. IV) доказывается, что всякое измери-
измеримое конечномерное представление отделимой компактной группы
непрерывно, а всякое конечномерное представление отделимой
локально компактной группы, содержащейся в пространстве L*>,
ограничено. Таким образом, для отделимых компактных групп
всякое измеримое конечномерное представление эквивалентно
непрерывному унитарному представлению, поэтому можно огра-
ограничиться рассмотрением только этих последних.
Опыт показывает, что для отделимых локально компактных
групп все еще удобнее рассматривать унитарные представления,
правда, допуская при этом возможность бесконечномерных пред-
представлений.
Основное следствие неприводимости для конечномерных
представлений было получено с помощью леммы Шура
(упр. 10.5 и 10.6). Эта лемма не допускает прямого обобщения
на бесконечномерные представления. Основным препятствием
для этого служит тот факт, что, к сожалению, не всякий эндо-
эндоморфизм бесконечномерного пространства обладает собствен-
собственными значениями.
Явный подсчет неприводимых унитарных представлений за-
заданной некоммутативной группы является обычно задачей пер-
первостепенной важности. Такие представления группы вращений
в R3 тесно связаны со сферическими гармоническими функциями,
но изложение этого вопроса достаточно сложно; см. М а а к
[1, § 48]. Аналогичная задача для группы Лоренца представляет
интерес как для физиков, так и для математиков. Интересующе-
Интересующемуся этими вопросами читателю можно рекомендовать гл. XV
книги Любарского [1].
Нахождение крайних точек множества Яо в случае абелевой
группы и доказательство теоремы 10.3.8 может быть осущест-
осуществлено более коротким путем, если воспользоваться теоремой
представления Шоке (см. замечания в конце п. 10.1.8), не при-
прибегая при этом к общей теории представления. См. Бью с и и
Ма л тиз [1].
10.4. Теорема Планшереля и закон двойственности
Непосредственное применение теоремы Крейна —Мильмана
затруднительно. Мы, однако, используем теорему Бохнера, как
это сделано у Картана и Годмзиа [1]. Это приводит
998 Гл. 10. Теорема Крейна — Мильмана
к обобщению понятия преобразования Фурье (до этого опре-
определенного только для функций, интегрируемых на Т) на функ-
функции с интегрируемым квадратом на Т. В качестве следствия мы
получим закон двойственности Понтрягина, который гласит, что
группа Т=(Т)~ (с точностью до изоморфизма топологических
групп) совпадает с Т.
В частности, если Т есть аддитивная группа Rn, то резуль-
результаты» которые мы получим, перекрывают те, которыми пользо-
пользовались в различных местах гл. 5, в частности в п. 5.15.1. Напом-
Напомним читателю, что там для исследования некоторых свойств
преобразования Фурье — Шварца медленно растущих распре-
распределений мы пользовались равенством Парсеваля для функций
весьма частного вида.
Начнем с одного уточнения теоремы Бохнера, вытекающего
из нее и в действительности ей эквивалентного.
10.4.1. Теорема. Нормировкой меры Хаара на Т можнр до-
добиться того, чтобы преобразование Фурье ф каждой непрерывной
положительно определенной функции qp^j?1^) принадлежало
пространству 3?Х(Т) и чтобы была справедлива формула обра-
обращения
/ A0.4.1)
Доказательство. Обозначим через Р] множество непре-
непрерывных положительно определенных функций из 9?Х{Т). Из-
Известно (теорема 10.3.8), что каждой функции ф^Р1 соответ-
соответствует такая единственная ограниченная мера Радона ^ф на Т,
что
/ ПФФ@. (Ю.4.2)
причем мера |д,ф положительна. Таким образом, нужно показать,
что можно так нормировать меру Хаара m на Г, что цф=ф«т.
Задача заключается в том, чтобы доказать существование
меры m на Г, такой, что |Хф = ф«т для каждой функции фЕР1,
и проверить, что она нетривиальна и инвариантна относительно
сдвигов. Это и будет нужная нам нормированная мера Хаара.
Из A0.4.2) легко получить, что
1*ф(Г) (ю.4.3)
для всех f^2?](T). Далее если соотношение A0.4.3) выпол-
выполняется для всех / из некоторого множества, плотного в 3?Х(Т),
то отсюда следует A0.4.2). Таким образом, цф — единственная
ограниченная мера Радона на 7\ для которой соотношение
10.4. Теорема Планшереля 999
A0.4.3) выполняется для всех f^2?l(f) или для всех / из не-
некоторого множества, плотного в 3?Х{Т). Из равенства A0.4.2)
вытекает также, что |Ыф(Г) = ф@).
Характеризация меры |ыф с помощью A0.4.3) позволяет нам
заключить, что
■V^ = Ф" • 14 = Ф • IV, (Ю.4.4)
где ф, ф' е Р1. Изучим теперь это соотношение, варьируя ф' со-
соответствующим образом.
Возьмем в Р1 такую сеть (ф£), что ф^О, J ф^Л=1 и функ-
функции ф^ обращаются в нуль вне некоторой окрестности нуля, ко-
которая становится произвольно малой для достаточно больших и
(Например, ф-= /,*/> где f^oTf+iT), J ftdt=l и функции U
обращаются в нуль вне произвольно малых окрестностей для
достаточно больших i). В частности, сеть мер (ф£Л) сходится
широко к мере Дирака е, сосредоточенной в нуле. Если в
A0.4.4) можно положить ф'=е, то задача тривиальна. Очевидно,
что этого нельзя сделать, если Т не дискретно. В этом случае
можно воспользоваться предельным переходом. Действительно,
пусть ф' пробегает сеть (ф^). Так как cp*f — ограниченная непре-
непрерывная функция на Г, то
Ф*ф; (/) = Ф*Ф/*/ @) -> ф*/ @) = цф (f).
Далее, меры \i # /(Г) = Ф*Ф^@)->ф@) остаются ограниченными,
поэтому из предложения 10.3.7 вытекает, что сеть М-ф^ слабо
сходится к [лф в сопряженном к С0(Т). С другой стороны,
\i / = ф • \х г для каждого и Применяя еще раз предложение
10.3.7, видим, что можно так выбрать функцию ф в Я1, что ф
не может принимать значений, сколь угодно близких к нулю, на
некотором компактном множестве в Т. Так как сеть (ф • jlx Л
слабо сходится, то сама сеть Лх А должна широко сходиться
к некоторой обязательно положительной мере m на Т. Тогда
u =limix / = Нтф-Ц/ в слабой топологии сопряженного к
С0(Т), так что [Хер является широким пределом сети (ф • jli /\ т. е.
|1Ф= ф • т.
Так как мера цф ограничена, а функция ф непрерывна, то ф
интегрируема относительно т. Теперь вместо A0.4.3) получаем
1000 Гл. 10. Теорема Крейна — Мильмана
соотношение
<р*/@)= \$fdm% A0.4.5)
которое справедливо для всех феР1 и всех f^3?l(T) и одно-
однозначно определяет меру т. Очевидно, что тфО.
Для доказательства инвариантности меры т относительно
сдвигов удобно обозначить через S векторное подпространство
в 2?Х(Т), порожденное множеством РК Так как обе части ра-
равенства A0.4.5) билинейны по совокупности переменных (ф, f),
то соотношение A0.4.5) справедливо для cpeS и [eS. Под-
Подпространство S содержит все функции вида u*v,rReu,v^J?(T)y
поэтому S плотно в 9?Х(Т). Следовательно, в силу предложения
10.3.7 множество преобразований Фурье функций из 5 плотно
в Со (Г) относительно топологии равномерной сходимости на Т.
Если далее в равенстве A0.4.5) умножить каждую из функций ф
и / на характер аеГ, то левая часть этого равенства не изме-
изменится, а потому
(t-u)f(t-u)dm(I)=J4(f)f{T)dm(t) A0.4.50
для ф, f e S.
Пусть теперь g e Ж(Т). В S можно выбрать функцию ф так,
чтобы она не обращалась в нуль на некоторой окрестности но-
носителя функции g. Тогда g = yh для некоторой функции Н^Ж(Т).
Эта функция h является равномерным пределом некоторой по-
последовательности (/„), где fn^S. Соответственно g" = lim<pfrt
в топологии равномерной сходимости на Т. В то же время
причем известно, что функция в правой части интегрируема от-
относительно меры т. Но тогда в силу теоремы 4.8.2
\g(f-a)dm(t) = \im f ф(?- u)fn(f - u)dm(f).
Из A0.4.5/) следует, что правая часть этого выражения не за-
зависит от а. Таким образом, мера m действительно инвариантна
относительно сдвигов. 1
10.4.2. Замечание. Если феР1, то положительность меры
^ф=ф./п означает, что непрерывная функция ф положительна.
Таким образом, если функция ф непрерывна, положительно опре-
определена и интегрируема, то функция ф непрерывна, положительна
и интегрируема,
104. Теорема Планшереля 1001
10.4.3. Следствие. Если точки /'=£/" принадлежат Г, то суще-
существует такой характер t е Г, <*го [/', /] =£ [Г7, /].
Доказательство. Достаточно показать, что если t'=f=Oy
то существует такой характер F, что [/', /j=£l. Как и при доказа-
доказательстве теоремы 10.4.1, построим функцию феР1 так, чтобы
Ф @) = 1 и ф(//)=0. Тогда из формулы обращения A0.4.1) сле-
дует,^что соотношение [t\ ?]=1=[0, /] не может выполняться при
всех /, что и требовалось доказать. В
10.4.4. Сейчас с помощью теоремы 10.4.1 мы получим некото-
некоторый вариант равенства Парсеваля, который в свою очередь по-
послужит основанием для доказательства теоремы Планшереля.
Предположим, что f't=g>l(T)fJ>2(T)y и рассмотрим свертку
<p = f*/. Функция ф непрерывна —свойство, которым обладает
свертка любых двух функций из 3?2(Т) и которое вытекает из
неравенства Коши — Шварца. Как свертка двух интегрируемых
функций функция ф интегрируема. Кроме того, она положи-
положительно определена; следовательно, ф е РК Ее преобразование
Фурье есть ф = /•/ = |f |2. Из теоремы 10.4.1 следует тогда, что
fe=&2(f) и
/ /J (Ю.4.6)
Далее если /, g е= &1(Т)(]2?2(Т), . то равенство A0.4.6)
остается справедливым, если / заменить на f + ag, где а — про-
произвольное комплексное число. Поэтому получаем
A0.4.7)
это и есть равенство Парсеваля для рассматриваемого класса
функций fug.
Теперь можно без труда развить теорию Планшереля. Пусть
f е= S2(J). Выберем последовательность (/п) с: SX{J) [\&2(Т),
сходящуюся в 3?2(Т) к /. Из A0.4.6) следует, что Qn) —после-
—последовательность Коши в &2(Т). Следовательно, существует такая
функция FeS72(Г), что fn-+F. Функция F определяется одно-
однозначно с точностью до пренебрежимых множеств, т. е. класс F
определяется однозначно. Заметим, что F определяется одно-
однозначно не только последовательностью (/п), но и заданием функ-
функции /: это следует из равенства A0.4.6), если применить его к
разности Уп — ?п элементов двух произвольных аппроксимирую-
аппроксимирующих последовательностей (/£) и (/£). Кроме того, равенство
1002 Гл. 10. Теорема Крейна — Мильмана
A0.4.6) дает в пределе соотношение
\\f?dt=\\F?dt.
Очевидно также, что класс F зависит только от класса /. Таким
образом, переход от f (или /) к F определяет отображение и
пространства 22{Т) (или L2(T)) в L2(T). Ясно, что и— линей-
линейное и изометрическое отображение; оно представляет собой про-
продолжение преобразования Фурье: если /е^(Г)П^2(Г), то F
является не чем иным, как классом, определяемым функцией /.
Поэтому будем обозначать через / и класс и (допуская «воль-
«вольность речи») представителя F этого класса. Равенства A0.4.6)
и A0.4.7), таким образом, справедливы для функций / и g из
3?2{Т). Чтобы отличать это преобразование, условимся назы-
называть u(f) преобразованием Фурье — Планшереля функции f.
Для завершения картины покажем, что и отображает L2(T)
на L2(f). Обозначим через Q образ пространства L2(T) относи-
относительно отображения и. Так как и— изометрия и пространство
L2(T) полно, то Q замкнуто в L2(T). Поэтому для установления
равенства Q = L2(f) достаточно показать, что Q плотно в L2(f).
Это вытекает из следующей леммы.
10.4.5. Лемма. Пусть Fe 2l(T) (]&2(Т). Тогда функция
(f).[ty t]dt
принадлежит пространству 2£2{Т), причем ]=-F почти всюду.
Доказательство. Если g^X(T), то
J F'udt = J F(i)df J J(t) • [t, t]dt = J f(t)^Jt)dt
и потому
(последнее равенство получается из A0.4.6), если заменить f
на g"). Из этого неравенства вытекает, что f e 9?2{Т). Примени
равенство A0.4.7), получаем, что
для всех функций g^X(T). Множество всех g плотно в С0(Г),
поэтому f=F почти всюду. I
Подытожим наши результаты,
tO.4. Теорема Планшереля 1003
10.4.6. Теорема. Преобразование Фурье — Планшереля опре-
определяет унитарное отображение пространства L2(T) на L2(T)>
причем унитарность этого отображения выражается конкретно
формулой A0.4.7).
10.4.7. Замечание. Из леммы 10.4.5 следует, что всякая
функция F^ 9?X(T) Л2?2(Г) почти всюду равна преобразованию
/ некоторой ограниченной непрерывной функции f из 2?2(Т). От-
Отсюда непосредственно вытекает, что любая свертка H = F*G>
где F, G^J?1^)!!^2^), равна (всюду) преобразованию не-
непрерывной ограниченной функции h^2>x{T), Это замечание
окажется полезным при рассмотрении закона двойственности.
С помощью теоремы выпуклости Рисса (§ 4.24) легко пока-
показать, что преобразование Фурье можно продолжить до преобра-
преобразования пространства Lp(T) в Lv'(t), где \<р<2 и /г1 + р/~1 = 1
(упр. 10.26).
10.4.8. Закон двойственности. Если / е Г, то отображение
fn->[/, Ц представляет собой ограниченный непрерывный харак-
характер группы Г, причем различным t соответствуют рааличные ха-
характеры на Т. Это позволяет нам рассматривать Т как под-
подгруппу в Т. Более того, заменив в предложении 10.3.6 группу Т
на Г, легко получаем, что топология в группе Т (рассматривае-
(рассматриваемой как дуальная к Т) индуцирует в Т исходную топологию.
Так как группа Т локально компактна, а потому полна, то она
замкнута в Т. Закон двойственности утверждает, что Т = Т. Он
будет установлен, если мы покажем, что Т плотна в Т.
Предположим, что группа Т не является плотной в Т. Тогда
существуют такая точка to^T.n такая окрестность нуля N в Т,
что to + 2N не пересекает Т. В этом случае можно так выбрать
функцию F ^Ж+(Т)У чтобы F=t=O и ^ = 0 вне N. Тогда функция
F*F положительна, не равна тождественно нулю и равна нулю
вне N + N. Функция G(t)=F*F(t — ?0) не равна тождественно
нулю, но тем не менее равна нулю на Т. В силу замечания 10.4.7
существует такая функция g е «2м G*), что
откуда [?(?)[*, t]dt*=O для всех /еГ, а потому (упр. 10.10)
g = 0 почти всюду. Но тогда G==0 на Т% что невозможно. I
1004 Гл. 10. Теорема Крейна — Мильмана
10.4.9. Обратное преобразование Фурье. Установленное со-
впадение групп Т и Т позволяет нам поменять местами Г и Г
во всех результатах § 10.3 и 10.4. Первое, что можно извлечь
отсюда, это возможность определения преобразования Фурье из
Т в Т как преобразования, которое переводит функцию F на f
в функцию
на Т. Теорема 10.4.1 подсказывает возможность еще более три-
тривиальной замены: если в написанном только что интеграле за-
заменить [t, f] на [ty Г], то получается преобразование, которое по
крайней мере для некоторых функций, является обратным к пре-
преобразованию Фурье f*—*f.
Учитывая это, обозначим через #" изучавшееся до сих пор
преобразование Фурье f*—>f и определим преобразование ^~, пе-
переводящее функции на Г в функции на Г, с помощью формулы
WF (/) = J F (?) [t, i] di. A0.4.8)
Первоначально преобразование ЗГ определено только для функ-
функций F е &Х(Т)\ его свойства могут быть получены из соответ-
соответствующих свойств преобразования ЗГ. В частности, из теоремы
10.4.1 следует, что если f — непрерывная положительно_ опреде-
определенная функция из Я?1(Т), то F=T]<=gx(T) и f = ^F, т. е.
f = gr<^f. Фактически (упр. 10.14) несложные рассуждения по-
показывают, что формула
f = ^T^f A0.4.9)
справедлива (в смысле почти всюду) для всякой функции
f€=z&l(T), ЧТО T\f=-&x(f).
Ввиду теоремы Планшереля 10.4.6 естественно надеяться, что
формула A0.4.9) будет иметь место для всех функций /е,2?2(Г).
Исследуем подробнее этот вопрос.
Прежде всего, меняя местами Г и Г, с помощью рассуждений,
использованных при доказательстве теоремы 10.4.6, получаем,
что 2F можно продолжить с пересечения 9?Х(Т)[\&2{Т) до уни-
унитарного отображения пространства 2?2G) на 9?2(Т). Отсюда
вытекает, что STSF есть непрерывный эндоморфизм пространства
272(Г); поэтому для установления справедливости формулы
A0.4.9) для всех /е^2(Г) достаточно проверить ее для функ-
функций f, принадлежащих такому множеству из 2>2(Т), что всевоз-
всевозможные конечные линейные комбинации его элементов образуют
104' Теорема Планшереля 1005
множество, плотное в S2{T). Обозначим через М множество
образованное всеми непрерывными положительно определен-
определенными интегрируемыми функциями на Г, вместе с их сдвигами.
Тогда, как уже было отмечено, формула A0.4.9) справедлива
для всех feM. Остается показать, что М порождает векторное
подпространство, плотное в 9?2{Т).
В силу теоремы Хана — Банаха достаточно показать, что
если g^.3?2(T) и f*g = O для всех непрерывных положительно
определенных и интегрируемых функций f, то g = 0 почти всюду.
Пусть V — компактная окрестность нуля в Т. Возьмем такую
симметричную окрестность нуля V, что V + V'cz,V. Затем вы-
выберем такую обращающуюся в нуль вне V функцию k e Ж+(Т),
что kdl—\. Функция fv = k*k непрерывна, положительно
определена, интегрируема, положительна и fvdt—\. Легко
показать, что fv*g-+g в g'l(T), когда окрестность V стяги-
стягивается к точке. Но так как /V*g = 0 для всех V, то g = 0 почти
всюду.
Таким образом, мы доказали, что формула A0.4.9) выпол-
выполняется в смысле почти всюду для всех f ^.S?2{T). Точно такими
же рассуждениями устанавливается, что
F^^^F A0.4.90
имеет место в смысле почти всюду для всех F е 3?2(Т). Тем са-
самым полностью доказано, что &~ является обратным преобразо-
преобразованием Фурье.
10.4.10. Замечания о формуле обращения. Как уже было от-
отмечено, легко показать, что формула
/@= Jf(Ol', Udf A0.4.10)
справедлива^поточечно почти всюду, если функция f^S?l(T)
такова, что J^.9?l(f). Если \^.9?2(Т), то эта формула имеет
место в ином смысле: в этом случае равенство A0.4.9) означает,
что если последовательность Fn^=J2?1(T)(]a2?2(T) сходится в
S2(f) к /, то функции
являющиеся элементами пространства С0(Г), сходятся в
3?2(Т) .к I
Автору неизвестно никаких вполне удовлетворительных ре-
результатов относительно формулы обращения в каком-нибудь
1006 Г л 10. Теорема Крейна — Мильмана
более тонком поточечном (всюду или почти всюду) смысле. Труд-
Трудности возникают даже в случае IT=Rn. To, что при рассмотрении
общего случая приходится сталкиваться с трудностями, и не
удивительно, потому что даже в классических результатах для
71 = R1 на функцию / накладываются ограничения типа локальной
ограниченности вариации, которые используют свойства упоря-
упорядоченности пространства R1. См. Эдварде и Хьюитт [1].
Несмотря на сказанное выше, для рядов и интегралов Фурье
можно относительно легко воспроизвести различные классиче-
классические процедуры суммирования. Чтобы найги суммирующие мно--
жители, построим функции sv (так же как функции /> в
п. 10.4.9), где V пробегает базу компактных окрестностей нуля
в 7\ Каждая из функций sv положительна, непрерывна, инте-
интегрируема, положительно определена и обращается в нуль вне V.
(Во многих задачах последнее условие может быть ослаблено
и заменено условием, что
lim J svdt^O
v т\и
для каждой окрестности нуля U в Т.) Нормируем функции sv
условием
Преобразование Sv = §v будет положительной непрерывной
интегрируемой положительно определенной функцией. Относи-
Относительно легко показать, что
limsv*/ = / A0.4.11)
v
в смысле S^(T), если ]^9?v(J) и 1</?<<х>; если же /? = оо,
то это соотношение остается справедливым в смысле слабой то-
топологии в S>OO(TI определяемой двойственностью между 3?°°(Т)
и 3?1(Т). Если / — ограниченная и непрерывная функция, го это
соотношение выполняется в смысле локальной равномерной схо-
сходимости или в смысле равномерной сходимости, если / — огра-
ограниченная равномерно непрерывная функция.
С другой стороны, если )^SX{T), то преобразование функ-
функции sv *~f, а именно Svf есть интегрируемая функция. Поэтому
в силу формулы обращения A0.4.10) равенство
Sv(Df(f)[t, f]di A0.4.12)
справедливо для всех (еГ, Следовательно,
/-lim j Sv(/)/(?)[t, i]dl A0.4.13)
Упражнения 1007
в смысле 9?Х(Т). Это равенство выполняется также и в поточеч-
поточечном смысле в каждой точке непрерывности функции f.
Читатель может также заметить, что если f^2>2(T)y то функ-
функция Svf и в этом случае интегрируема (как произведение двух
функций из 3?2{Т)). Поэтому снова справедливо равенство
A0.4.12), в то время как A0.4.13) выполняется, если предел по-
понимать в смысле 3?2(Т), и выполняется в поточечном смысле
в каждой точке непрерывности функции f. To же самое верно и
при 1</?<2, если преобразование Фурье функций f^3?P(T)
определить так, чтобы f e 9?v' (T).
Короче говоря, при указанных условиях теория суммируе-
суммируемости вполне удовлетворительна.
10.4.11. Разное. В этой главе мы определили преобразование
Фурье-для функций из 3?1{Т) и 3?2(Т). Пользуясь полученными
результатами и теоремой выпуклости М. Рисса (см., например,
§ 4.24), можно продолжить преобразование Фурье и дальше до
непрерывного линейного отображения Lv(T) в Lp/ (T) для
1<р<2 и р' = р/{р—1). Классический случай такого продолже-
продолжения применяется к обычным рядам Фурье и подробно изложен
в книге Зигмунда [2, т. II, гл. XII]. Общий случай отделимых
локально компактных абелевых групп рассмотрен А. Вейлем
[1, гл. VI]. При 1</?<2 фурье-образ пространства Lv(T), во-
вообще говоря, не совпадает со всем пространством If' (f).
Для случая классических групп мы рассмотрели в § 5.15 про-
продолжение преобразования Фурье на произвольные медленно
растущие распределения. Естественно попытаться обобщить тео-
теорему Бохнера на положительно определенные распределения;
это сделал Л. Ш в а р ц [2, теор. XVIII].
Имеется много интересных и нерешенных задач, связанных
с тонкими вопросами гармонического анализа, даже если огра-
ограничиться случаем R1 или группой Rl/2n вращений окружности.
Обзор таких задач приведен у Хыоитта [11] и Рудина [9].
Несколько таких задач указано в упражнениях в конце главы.
Наконец, следует отметить, что естественная задача обобщения
римановой теории общих тригонометрических рядов и интегра-
интегралов одного вещественного переменного (Зигмунд [2, т. I,
гл. IX й т. II, гл. XVI) остается почти полностью открытой.
УПРАЖНЕНИЯ
10.1. Пусть Е— гильбертово пространство, А— его непрерывный эндомор-
эндоморфизм, М — замкнутое векторное подпространство в Е и Р — ортогональный
проектор на М.
Показать, что А (М) а М и А* (М) а М тогда и только тогда, когда
РА=АР.
1008 Гл. 10. Теорема Крейна — Мильмана
10.2. Привести пример векторного пространства Е, его разложения в пря-
прямую сумму E^M+N и такого эндофоризма и пространства Еу что если Р —
проектирование на М параллельно /V, то и(М)аМ, однако иР Ф Ри. (Ср.
с предыдущим упражнением.)
10.3. Привести пример непрерывного унитарного представления неабелевой
компактной неприводимой группы Г, размерность которого больше единицы.
10.4. Пусть Т — аддитивная группа вещественных чисел по модулю 2л.
Для sef определим эндоморфизм U(s) пространства L2 (Т) как отображение,
переводящее класс функций / в класс функции t\—>f(t — s). Пусть Я —замк-
—замкнутое векторное подпространство в L2(f)> инвариантное относительно сдвигов
(т. е. U(s)H a H для каждого sef). Показать, что (Я, U) является непре-
непрерывным унитарным представлением группы Т. Если ф {0}, то это представле-
представление неприводимо тогда и только тогда, когда Я состоит из числовых кратных
функции eint для некоторого целого п.
Рассмотреть эту же задачу, заменив Т аддитивной группой вещественных
чисел, и показать, что если Я Ф {0}, то представление (Я, U) не может быть
неприводимым.
10.5. Пусть Е и F— векторные пространства и t и с^Г —неприводимые
множества эндоморфизмов пространств Е и F соответственно. (Неприводи-
(Неприводимость множества % означает здесь справедливость следующего условия: не
существует отличного от {0} и Е векторного подпространства в Е% инвариант-
инвариантного относительно каждого эндоморфизма из %.) Пусть А Ф 0—-такое лг
нейное отображение пространства Е в Fy что
т. е. для каждого Ге^ существует такое 5g^, что TA = AS, и для к;
дого S ^ % существует такое Ге^ что выполнено то же соотношение 1
казать, что А — изоморфизм пространства Е на F. (Это одна из форм лемг
Шура.)
10.6. Пусть Е — конечномерное векторное пространство над полем komi
лексных чисел, t — неприводимое множество его эндоморфизмов. Показать
что если Т — эндоморфизм пространства Е, перестановочный с %> т. е. тако"
что t • Т — Т • t (см. предыдущее упражнение), то существует такое.комплекс
ное число А/, что Т==Х\.
Следовательно, если множество % еще и коммутативно (т. е. любые два
элемента в t перестановочны), то dim£=l.
10.7. Пусть Т — группа, обладающая правоинвариантным средним (§ 3.5),
т. е. такой положительной линейной формой \i на пространстве всех ограни-
ограниченных комплексных функций на Г, что р,A) = 1 и \i(fs) =№(f), где ls(t)=f(ts).
Пусть *i—>A(t) —ограниченное представление группы Т с помощью непрерыв-
непрерывных эндоморфизмов гильбертова пространства Я, т. е. A (s/) = A (s) A (Z)
и sup || А (/) || < + оо. Показать, что это представление эквивалентно уни-
t&T
тарному представлению, т. е. что существует такой автоморфизм »S простран-
пространства Я, что SA(t)S~l унитарно при каждом t gT.
[Указание. Рассмотреть скалярное произведение на Я, определенное
равенством
(x\y)t-]il(A(t)x\A(t)y)];
показать, что это произведение при некотором с > 0 удовлетворяет нера-
неравенствам
Упражнения 1009
Для того чтобы доказать существование автоморфизма S пространства //, та-
такого, что (х \ у) i=* (Sx \ Sy) для х, У&.Н, требуются некоторые сведения, кото-
которые в нашей книге не излагаются.]
10.8. Пусть Т — отделимая локально компактная абелевая группа, Т — ее
дуальная группа, р — такая строго положительная функция на Т, что
inf{p(?): ^е П=0, и Q — некоторое непустое открытое множество в Т. Пока-
Показать, что на Т существует такая непрерывная интегрируемая функция / с носи-
носителем в Q, что
[Отметим, что если нижняя грань функции р положительна на каждом ком-
компактном множестве в Т, то приведенное выше равенство можно записать в
виде
V4» P(t)
[Указание. Воспользоваться методом от противного, рассмотрев по-
полунорму
пространстве непрерывных функций, обращающихся в нуль вне некоторого
ыбранного относительно компактного непустого открытого подмножества в Q.]
10.9. Пусть Т — отделимая локально компактная абелева группа; Т — ее
альная группа. Доказать, что
(a) если группа Т дискретна, то группа Т компактна;
(b) если группа Т компактна, то группа Т дискретна.
Замечание. В силу закона двойственности п. 10.4.8 оба условия яв-
являются необходимыми и достаточными.
10.10. Пусть Т и Т те же, что и в упражнении 10.9. Пользуясь предложе-
предложением 10.3.7, доказать следующую теорему единственности: если \i — ограни-
ограниченная мера Радона на Г и обратное преобразование Фурье
при всех t ^ 7\ то jw = O.
Доказать, что, обратно, из этой теоремы единственности следует, что пре-
преобразования f (/ е сЗ?{ (Т)) равномерно плотны в С0(Г).
10.11. Пусть Т — отделимая, локально компактная абелева группа. Пока-
Показать, что произведение двух непрерывных положительно определенных функ-
функций на Т есть снова положительно определенная функция.
10.12. Пусть Т — отделимая, локально компактная группа и / е Jg*
(Г), где 1 ^ р^ оо и p"ljrp'~l = \. Показать, что функция
непрерывна и положительно определена на Г,
1010 Гл. 10. Теорема Крейна — Мильмана
10.13. Пусть Т — отделимая локально компактная абелева группа и
f^L2(T). Показать, что конечные линейные комбинации сдвигов функции /
тогда и только тогда образуют в L2(T) плотное множество, когда множество
нулей функции f локально пренебрежимо.
[Указание. Воспользоваться теоремой Хана — Банаха и равенством
Парсеваля.]
Замечания. Для случая Т=И} результат принадлежит Винеру [1,
стр. 100], хотя его доказательство совершенно другое. Если Т не компактно и
рф2, то решение задачи для Lp (T) значительно труднее. При р=1 решение
известно (Винер [1, стр. 97—99] для T=Rl\ для более общих групп Т можно
применить метод, основанный на теории банаховых алгебр; см., например, Л ю-
мис [1]). Для случая р= оо известно решение для случая слабой топологии
(X ел сон [1]). Для других значений р известные результаты носят довольно
обрывочный характер (см. Сигал [2], Э г н ь ю [1], [2] и Эдварде [4]). Сход-
Сходные задачи рассматривались и в других пространствах; см., например,
Л. Шварц [9] и [11].
10.14. Пусть Г —отделимая локально компактная абелева группа. До-
Допустим, что / е J2?1 (Т)— функция, преобразование Фурье f которой интегри-
интегрируемо. Доказать, что равенство
справедливо почти всюду на Т.
10.15. Пусть Т — отделимая локально компактная абелева группа и
/ е JS*1 (Т). Доказать, что если f > 0, то функция f положительно опреде-
определена, и обратно.
10.16. Установить аналоги для J^2 результатов последного упражнения.
10.17. Пусть Т — отделимая а-компактная локально компактная абелева
группа, удовлетворяющая первой аксиоме счетности. Допустим далее, что
каждая функция из С0(Т) является преобразованием Фурье некоторой функ-
функции f e oS?l (Т). Доказать, что Т — конечная группа.
Замечание. Ср. с аналогичным результатом в Эдвард с [5], гдз
нет условия счетности. См. также Эдварде [10] и Хелсон [4].
10.18. Пусть T=R\ Определить суммирующие множители 5n(g)(gef),
получающиеся с помощью процесса, описанного в п. 10.4.10, исходя из функ-
функций sn на Ту определенных следующим образом:
<а) Sn{t) = [-^rj'
(b) s"{t)=n(l+n>t>)'>
(Это приводит к методам суммирования, связанным соответственно с именами
Чезаро, Абеля — Пуассона и Гаусса.)
10.19. Пусть Т — отделимая локально компактная абелева группа, (\ii)—■
ограниченная по норме сеть ограниченных мер Радона на Г и [i — ограничен-
ограниченная мера Радона на Т. Доказать, что lim^^j-A в слабой топологии в сопря-
сопряженном к Со(Г) тогда и только тогда, когда Пт£ц = ,й в слабой топологии в
сопряженном к J^x (Г),
Упражнения ЮН
10.20. Пусть Г —отделимая локально компактная абелева группа, (Р,) —.
такая сеть непрерывных положительно определенных интегрируемых функций
на Т, что ПтР* = 1 на Г, причем sup {| -Р/ (?) |: / е/, fe71}< + oo, где /—.
направленное множество, пробегаемое индексом и Пусть далее F — ограни-
ограниченная непрерывная функция на 7\ Положим
Показать, что F является преобразованием Фурье ограниченной меры Радона
на Т тогда и только тогда, когда множество функций {/*} принадлежит про-
пространству Jgx (Г), и ограничено в нем.
10.21. Пусть 7 —группа вращений окружности G=R72rt), так что 7
является аддитивной группой целых чисел. Пусть далее F — функция на Т
вида
где а — мера Радона на Г и
A(k)-itt
A(k) \b
при k>0.
Показать, что если аФЬ, то F не является преобразованием Фурье ни одной
меры Радона на Т.
10.22. Заимствуем обозначения и терминологию из упр. 1.19—1.28. Пусть
miCzm(T)—множество положительных аддитивных функций множества ц,
удовлетворяющих условию \i(T) = 1. Убедиться в том, что
(a) множество mi выпукло и компактно в топологии, индуцированной то-
топологией о(т(Т), 1°°(Т)).
(b) множество крайних точек множества гп\ совпадает с множеством М
(определенным в упр. 1.26).
Вывести отсюда, что каждой функции \х^.тх соответствует такая положи-
положительная мера Радона \х* на Т* с общей массой, равной единице, чго
для / е /°° G*) (Т* и f* определяются так же, как в упр. 1.27 и 1.28).
[Указание. При доказательстве последней части воспользоваться тео-
теоремой 10.1.7.]
Замечание. Существование такой формулы представления вытекает
также из изоморфизма между £°°(Г) и С(Т*), установленного в упр. 1.28.
Кратко говоря, аддитивным функциям множества с конечной полной вариа-
вариацией на Т соответствуют меры Радона на Т*.
10.23. Пусть Т — отделимая компактная абелева группа, и при каждом п
пусть сп —такая комплексная функция на дуальной группе ?, что 2 \cn(i)\<
?
п
J
< + оо Предположим далее, что lim cn = с поточечно на Т. Определим
функцию sn на Т с помощью равенства
f
fef
1012 Гл. 10. Теорема Крейна — Мильмана
Пусть, наконец, 1 ^ р < оо. Доказать эквивалентность следующих трех усло-
условий:
A) существует конечный предел lim 2 сп @ / @ Для каждой функции
п
f&Lp-Lp(T);
B) SUplUftl р> < + <*>;
/г L
C) существует слабый предел lim sn в Lp' = Lp' (T).
п
Показать также, что любое из этих условий влечет за собой каждое из
следующих двух:
D) для каждой функции /gL^ существует равномерно по /еГ предел
lim ^ cn(f)f(f)[t,i];
E) существует такая функция 5 е Lp' (Г), что s =c.
Замечание. Если Т — группа вращений окружности, 1 < р < оо и
При 'f I
пК) @ при |?|>я,
то из условия E) вытекают все остальные: в этом случае sn является п-\\
симметрической частичной суммой ряда Фурье функции s, а известно, что
sn->s в L. Это уже не имеет места для р = 1. (См. Зигмунд [2, том II,
стр. 266].)
10.24. Сформулировать и доказать аналоги результатов предыдущего
упражнения для случая, когда Lp (T) заменяется на С(Т) и Lv' — na M(T)
( = пространство мер Радона на Т).
10.25. Исследовать возможные обобщения результатов упр. 10.23 и 10.24
на случай, когда группа Т не компактна (а лишь отделима, локально компакт-
компактна и абелева).
10.26. Опираясь на теорему выпуклости Рисса (§ 4.24), показать, что пре-
преобразование Фурье можно продолжить до непрерывного линейного отображе-
отображения пространства Lp (Т) в L*'(T) для 1 < р < 2 и /г1 +//ч = 1.
[Указание. Заметить, что указанное преобразование, определенное пер-
первоначально на УС (Т), является в то же время оператором сильных типов
A, оо) и B,2).]
Библиография')
Агжери (Aggeri J. С.)
1. Les fonctions convexes continues et le theoreme de Krein — Milman,
С R., 262 A966), A229—A232.
Агранович М. С.
1. Об уравнениях в частных производных с постоянными коэффициента-
коэффициентами, УМН, 16 A961), вып. 2, 27—93.
Адам ар (Hadamard J.)
1. Sur les operations fonctionelles, С. #., 136 A903), 315—354.
2. Le Probleme de Cauchy et les Equations aux Derivees Partielles, Her-
Hermann et Cie, Paris, 1932.
Александров А. Д.
1. Additive set functions in abstract space, I, Мат. сб., 8 A940), 307—348.
2. Additive set functions in abstract space, II, Мат. сб. 9 A941), 563—628.
3. ^'Hitive set functions in abstract space, III, Мат. сб., 13 A943), 169—
238.
Альтман (А 11 m a n M.)
1. An extension to lotally convex spaces of Borsuk's theorem on antipo-
antipodes, Bull. Acad. Polon. Sci., 6 A958), 293—295.
2. Continuous transformations of open sets locally convex spaces, Bull.
Acad. Polon. ScL, 6 A958), 297—301.
Амброз (Ambrose W.)
1. Lectures on Topological Groups, Unpublished lecture notes, Univ. of
Michigan, Ann Arbor, 1943.
2. Measures on locally compact topological groups, Trans. Am. Math. Soc,
61 A947), 106—121
Аранда, Каттанео, Окландер (Aranda P. J., Cattaneo E. P.,
Ok lander E.)
1. A proof of the continuity of potential operators (исп.), Math. Notae, 20
A965), 54—64.
Арене (А г e n s R. F.)
1. Duality in linear spaces, Duke Math. /., C), 14 A947), 787—794.
2. Approximation in, and representation of, certain Banach algebras, Am.
J. Math., 71 A947), 763—790.
3. Representation of functional by integrals, Duke Math. /., 17 A950),
499—506
АренсДелли (A r e n s R. F., К e 11 у J. L.)
1. Characterization of the space of continuous functions over a compact
Hausdorff space, Trans. Am. Math. Soc, 62 A947), 499—508.
Ароншайн, Шептицкий (Aronszajn N, Szeptycki P.)
1. On general integral transformations, Math. Ann., 163 A966), 127—154.
l) Звездочкой отмечены работы, добавленные при переводе. Для перевод-
переводных книг в круглых скобках указан год оригинального издания. — Прим. ped.
1014 Библиография
Ар сов (Arsove M. G.)
1. Similar bases and isomorphisms in Frechet spaces, Math. Ann., 135
A958), 283—293
2. The Pa ley — Wiener theorem in metric linear spaces, Pacific J. Math.,
10 A960), 365—379.
Арсов, Эдварде (Arsove M. GM Edwards R. E.)
1. Generalized bases in topological linear spaces, Studia Math., 19 A960),
95—113.
Артин (Artin E.)
1. Геометрическая алгебра. «Наука», М., 1969 A957).
Ахиезер Н. И., Глазман И. М.
1. Теория линейных операторов в гильбертовом пространстве B-е изд.),
«Наука», М., 1966.
Б аде (Bade W.)
1. Functional Analysis Notes. University of California, Berkeley, 1957 (не
опубликовано).
Бак (Buck R. С.) (редактор)
1. Studies in Modern Analysis, Studies in Mathematics, 1, The Math As-
soc. of America, Prentice-Hall, Inc., Englewood Cliffs, N. Y., 1962.
Банах (Banach S.)
1. Operations Lineaires, Monografie Mathematyczne, I, Warszawa, 1932.
(Украинский перевод: Курс функционального анал1зу, «Радянська шко-
школа», КиТв, 1948.)
2. Sur les operations dans les ensembles abstraits et leur applications aux
equations integrates, Fund. Math., 3 A922), 133—181.
Барт л (В art le R. G.)
1. On compactness in functional analysis, Trans. Am. Math. Soc, 79 A955),
35—57.
Бартл, Данфорд, Шварц (Bartle R. G., Dunford N.«
Schwartz J.)
1. Weak compactness and vector measures, Can. J. Math., 7 A955), 289—
305.
Басе (Bass R.)
1. Contributions to the theory of nonlinear oscilations, Vol. IV (ed.
S. Lefschetz), p. 208.
Б е л и ц к и й (В i e I i с k i A.)
1. Une remarque sur la methode de Banach-Cacciopoli-Tikhonov, Bull. Acad.
Polon. ScL, 4 A956), 261—268.
Беллман (Bellman R.)
1. On an application of the Banach-Steinhaus theorem to the study of
boundedness of solutions of nonlinear differential and difference equa-
equations, Ann. Math., 49 A948), 515—522.
Бенке, Штейн (Behnke H., Stein K.)
1. Entwicklung analytischer Functionen auf Riemannschen Flachen, Math.
Ann., 120 A948), 430—461.
Бергман (Bergmann S.)
1. Sur les functions orthogonales de plusieurs variables complexes avec
les applications a la theorie des fonctions analytiques, Mem. Sci Math.
Fasc, CVI, Paris, 1947.
Беркхилл (Burkhill J. C.)
1 The Lebesgue Integral, Cambridge Tracts in Math, and Math Phys.,
№ 40, Cambridge Univ. Press.. N. Y., 1951.
Берс, Джон, Шехтер (Bers L., John F., Schechter M)
1*. Уравнения с частными производными, «Мир», М., 1966 A964).
Бессага. Пелчинский (Bessaga G., Pelczynski A)
1. Spaces of continuous functions (IV), Studia Math., 19 (I960), 53—62.
Библиография 1015
Бёрлинг (Beurling A.)
1. On the spectral synthesis of bounded fonctions, Ada Math., 81 A948),
225—238.
2. Sur les spectres de fonctions, Analyse Harmonique, Colloq. Intern. Cent-
Centre Nail Rech. Sci., 15 A949), 9—29.
Бёрлинг, Дени (Beurling A., Deny J.)
1. Espaces de Dirichlet. I. Le cas elementaire, Ada Math., 99 A958), 203—
224.
2. Dirichlet spaces, Proc. Nat. Acad. Sd. USA B), 45 A959), 208—215.
Биркгоф Г. (Birkhof f G.)
1. Moore-Smith convergence in general topology, Ann. Math. B), 38
A937), 39—56.
2. Теория структур, ИЛ, Е., 1952 A948).
3. Integration of functions with values in a Banach space, Trans. Am.,
Math. Soc, 38 A935), 357—378.
Биркгоф Дж. (Birkhoff G. D.)
1. Proof of the ergodic theorem, Proc. Nat. Acad. Sci. USA, 17 A931),
656—660.
Биркгоф Дж., Келлог (Birkhoff G. D., Kellog O. D.)
1. Invariant points in function space, Trans. Am. Math, Soc, 23 A922),
96—115.
Бишоп, Лю (Bishop E,de Leew K.)
1. The representations of linear functional by measures on sets of extre-
extreme points, Ann. Inst. Fourier, 9 A959), 305—331.
Б лед coy, Mope (B 1 e d s о е W.W., Morse A. P.)
1. Product measures, Trans. Am. Math. Soc. A), 79 A955), 173—215.
Богданович (Bogdanowicz W. M.)
LA generalisation of the Lebesgue — Bochner — Stieltjes integral and a
new approach to the theory of integration, Proc. Nat. Acad. Sci. USA,
53 A965), 492—498.
2. Integral representation of linear continuous operators from the space
of Lebesgue-Bochner summable functions into any Banach space, Proc.
Nat. Acad. Sci. USA., 54 A965), 351—354.
3. Integral representation of multilinear continuous operators from the
space of Lebesgue-Bochner summable functions into any Banach space,
Bull. Am. Math. Sqc, 72 A966), 317—320.
4. An approach to the theory of Lv spaces of Lebesgue — Bochner sum-
summable functions and generalized Lebesgue-Bochner-Stieltjes integrals,
Bull. Acad. Polon. Sci. Math. Astronom. Phys., 13 A965), 793—800.
5. Integral representation of linear continuous operators on Lp spaces of
Lebesgue-Bochner summable functions, Bull. Acad. Polon. Sci. Math.
Astronom. Phys., 13 A965), 801—808.
Боголюбов Н. Н., Владимиров B.C.
1. О некоторых математических вопросах квантовой теории поля, Ме-
Международный математический Конгресс в Эдинбурге 1958, Физматгиз,
М., 1962.
Боголюбовы Н, Ширков Д В.
1. Введение в теорию квантованных полей, Гостехиздат, М., 1957.
Бозанке, Кестельман (Bosanquet L. S., Kestelman H.)
1. The absolute convergence of a series of integrals, Proc. London Math.
Soc. B), 45 A939), 88-97. *
Бонеблуст, Карлин (BohnenblustF., KarlinS.)
1. On a theorem of Ville — Theory of games, Annals of Math. Study, v. 24,
155-160-
1016 Библиография
Боненблуст, Собчик (Bohnenblust F., Sobczyk A.)
1. Extentions of functionals on complex linear spaces, Bull. Am. Math.
Soc, 44 A938), 91—93.
Бонсол (Bonsall F. F.)
1. Lectures on Some Fixed Point Theorems of Functional Analysis, Tata
Institute, Bombay, 1962.
2. On the representation of points of a convex set, /. London Math. Soc.t
38 A963), 332—334.
Бохнер (Bochner S.)
1. Лекции об интегралах Фурье, Изд-во АН СССР, М, 1962 A932).
2. Dirichlet problem for domains bounded by spheres, Ann. Math., Study
№ 25, Princeton, 1950, 24—45.
3. Integration von Funktionen, deren Werte die Elemente einer Vectorau-
mes sind, Fund Math., 20 A933), 262—276.
Бохнер, Мартин (Bochner S., Martin W. T.)
1. Функции многих комплексных переменных, ИЛ, М., 1951 A948).
Бохнер, Тэйлор (Bochner S., Taylor A. E.)
1. Linear functionals on certain spaces of abstractly valued functions, Ann
Math. B), 39 A938), 913—944.
Бохнер, Чандрасекхаран (Bochner S, Chandrasekharan K.)
1. Fourier Transforms, Ann. Math., Study № 19, Princeton, 1949.
Бранж (de Branges L.)
1. The Stone —Weierstrass theorem, Proc. Am. Math. Soc, 10 A959),
822—824.
Браудер (Browder F. E.)
1. Functional analysis and partial differential equations. I, Math. Ann.%
138 A959), 55—79 (русский перевод: Математика, 4:3 A960), 79-
106); II, Math. Ann., 145 A961/62), 81—226.
2 On the spectral theory of elliptic differential equations, I, Math. Ann.t
142 A961), 22—130.
3. Approximation by solutions of partial differential equations, Am. J.
Math. A), 84 A962), 134—160.
4. Analyticity and partial differential equations, I, Am. J. Math. D), Ы
A962), 666—710.
5. Variational boundary value problems fo'r quasi-linear elliptic equations
of arbitrary order, Proc. Nat. Acad. Sci. USA A), 50 A963), 31 —
37.
6. Nonexpansive nonlinear operators in a Banach space, Proc. Nat. Acad.
Sci. USA, 54 A965), 1041—1044.
7. Nonlinear operators in Banach spaces, Math. Ann., 162 A965/66), 280—
283.
8. Nonlinear elliptic functional equations in nonreflexive Banach spaces,
Bull. Am. Math. Soc, 72 A966), 89-95.
Браудер, Петришин (Browder F. E., Petryshyn W. V.)
1. The solution by iteration of functional equations in Banach spaces,
Bull. Am. Math. Soc, 72 A966), 566—570.
2. The solution by iteration of nonlinear functional equations in Banach
spaces, Bull. Am Math. Soc, 72 A966), 571—575.
Брело (Brelot M)
1. La theorie moderne du potentiel, Ann. Inst. Fourier, 4 A954), 113—140
2. Elements de la Theorie du Potentiel. Cours de Sorbonne, Paris, 1959.
3. Lectures on Potential Theory Tata Institute, Bombay, 1960.
4*. Основы классической теории потенциала, «Мир», М., 1964.
Бремерман (Bremermann H.)
1. Распределения, комплексные переменные и преобразования Фурье,
«Мир», М., 1968 A965).
Библиография 1017
Брэйс (Brace J. W.)
I. Transformation in Banach spaces. Dissertations, Cornell Univ. Press,
Ithaca, N. Y., 1953.
Бурбаки (Bourbaki N.)
1. Теория множеств, «Мир», М., 1965.
2. Общая топология. Основные структуры, «Наука», М., 1968.
3. Общая топология. Топологические группы. Числа и связанные с ними
группы и пространства, «Наука», М, 1969.
4. Алгебра. Алгебраические структуры. Линейная и полилинейная ал-
алгебра, Физматгиз, Мм 1962.
5. Алгебра. Многочлены и поля. Упорядоченные группы, Физматгиз, М.,
1965.
6. Алгебра. Модули, кольца, формы, «Наука», М., 1966.
7. Топологические векторные пространства, ИЛ, М., 1959.
8. Интегрирование. Меры, интегрирование мер, «Наука», М., 1967.
9. Integration. Chapitres VI—VIII, Hermann et Cie, Paris, 1244- A956),
1281 A959), 1306 A963).
10. Theorie Spectrales. Chapitres I, II, Hermann et Cie, Paris, 1332 A967).
II. Sur certains espaces victoriels topologiques, Ann. Inst. Fourier, 2 A950),
5—16 (Русский перевод: Математика, 2 : 2 A958).)
12 Sur les espaces de Banach, С /?., 206 A938), 1071 — 1074.
Бьюси, Мальтиз (BucyR. S., Maltese G.)
1 Extreme Positive Definite Funktions and Choquet's Representation Theo-
Theorem, /. Math. Anal. Appl., 12 A965), 371—377.
В а д a (W a d a J.)
1. Positive linear functional on ideals of continuous functions, Osaka
Math. /., 11 A959), 173—185.
2. Strict convexity and smoothness of normed spaces, Osaka Math. J., 10
A958), 221—230.
3. Weakly compact linear operators on function spaces, Osaka Math. /.,
13 A961), 169—183.
4. On P*Spaces and Equicontinuity, Proc. Japan. Acad.y 42 A0) A966),
714—718.
Вайтман (Wightman A. S.)
1. Les problemes mathematiques de la theorie quantique des champs, Colloq.
Intern. Centre. Nat. Rech. Sci., Lille A957).
Валбрук (WaelbroeckL.)
1. Les espaces a bornes complets. Colloque sur l'Analyse Functionelle, Lou-
vain, 1960, 51—55, Librairie Universitaire, Louvain, 1961.
Балле Пуссен (de la Va Нее Poussin C.)
1. Les Nouvelles Methodes de la Theorie du Potential et le Probleme Gene-
Generalise de Dirichlet, Act. Sci. Ind. 578, Hermann et Cie, Paris, 1937.
Варадараян (V a r a d a r a j a n V. S.)
1. On a theorem of F. Riesz concerning the form of linear functionals,
Fund. Math., 46 A958), 209—220.
ВейльА. (W i e 1 A.)
1. Интегрирование в топологических группах и его применения, М., ИЛ,
1950 A940).
2. Sur les espaces a structure uniforme, Act. Sci. Ind. 551, Hermann et Cie,
Paris, 1937.
В ей ль Г (Weyl H.)
1. The method of orthogonal projection in potential theory, Duke Math. /.,
7 A940), 411—444.
Вейс (Weiss G.)
1. Analisis armonica en varias variables. Teoria de los espacios //P, Cursos
у Seminar, de Mat., Fasc. 9, Universidad de Buenos Aires, 1960.
1018 Библиография
Вендель (WendelJ.)
1. Left centralizers and isomorphismus of group algebras, Pacific J. Math.,
2 A952), 251—261.
В е с т о н (WestonJ.D.)
1. On the representation of operators by convolution integrals, Pacific J.
Math., D), 10 A960), 1453—1468.
2. The representation of linear functionals by sequences of functions, /. Lon-
London Math. Soc, 33 A958), 123—125.
Вехаузен (WehausenJ. V.)
1. Transformation in topological linear spaces, Duke Math. /., 4 A938),
157—169.
Вильямсон (Williamson J. H.)
1. Two conditions equivalent to normability, /. London Math. Soc, 31
A956), 111—113.
2. A third condition equivalent to normability, /. London Math. Soc, 32
--A957), 231—232.
3. Linear transformations in arbitrary linear spaces, /. London. Math. Soc,
28 A953), 203—210.
4. Compact linear operators in linear topological spaces, /. London Math.
Soc, 29 A954), 149—156.
Винер (Wiener N.)
1. Интеграл Фурье и некоторые его применения, Физматгиз, М., 1963
A933).
В и н е р, П э л и (W i e n e r N., Р а 1 е у R. Е. А. С.)
1. Преобразование Фурье в комплексной области, «Наука», М., 1964 A934).
В и ш и к М. И.
1. Метод ортогональных и прямых разложений в теории эллиптических
дифференциальных уравнений, Мат. сб., 25 A949), 189—234.
В и ш и к М. И., Э с к и н Г. И
1*. Эллиптические уравнения в свертках в ограниченной области и их
приложения, ШН, 22 A967), вып. 1, 15—76.
2*. Нормально разрешимые задачи для эллиптических систем уравнений
в свертках, Мат. сб., 74 A16): 3 A967), 326—356.
Вудбери (WoodburyM. А.)
1. Invariant functionals and measures, Bull. Am. Math. Soc, 56 A950),
172, Abstract 168t.
В у л и x Б. 3.
1*. Краткий курс теории функций вещественной переменной, «Наука», М.,
1965.
2*. Введение в теорию полуупорядоченных пространств, Физматгиз, М,
1961.
Гальперин (Halperinl.)
1. Closures and adjoints of linear differential operators, Ann. Math., D),
38 A937), 880—919.
2. Function spaces, Can. J. Math., 5 A953), 273—288.
3. Введение в теорию обобщенных функций, ИЛ, М., 1954 A952).
Гантмахер В. Р.
1. Uber schwache totalstetige Operatoren, Мат. об., 7 D9) A940), 301—308.
Г арни (Garnir H. G.)
1. Les Problems aux Limites de la Physique Mathematique, Birkhauseer
Verlag, Basel-Stuttgart, 1958.
ГельфандИ. М.
1. Sur un lemme de la theorie des espaces lineaires, Записки Харьковского
матем. о-ва, D), 13 A936), 35—40.
2 Abstrakte Funktionen und lineare Operatoren, Мат. сб., 4 D6) A938),
235—286.
Библиография 1019
ГельфандИ. М,Виленк и нН. Я.
1. Обобщенные функции. 4. Некоторые применения гармонического ана-
анализа. Оснащенные гильбертовы пространства, Физматгиз, М., 1961.
ГельфандИ. М,Райков Д. А.
1. Неприводимые унитарные представления локально бикомпактных групп,
Мат. сб., 13 E5) A943), 301—316.
ГельфандИ. М., Р а й к о в Д. А., Шилов Г. Е.
1*. Коммутативные нормированные кольца, Физматгиз, М., 1960.
ГельфандИ. М., Шилов Г. Е.
1. Uber verschiedene Methoden der Einfuhrung der Topologie in die Menge
der maximalen Ideaie eines normierten Ringes, Мат. сб., 9 E1) A941),
25—40.
2. Обобщенные функции. 1. Обобщенные функции и действия над ними,
Физматгиз, М., 1958.
3. Обобщенные функции. 2. Пространства основных и обобщенных функ-
функций, Физматгиз, М., 1958.
Георгиу (Gheorgiu R.)
1. Sur l'equation de Fredholm. These, Paris, 1928.
Герглотц (HerglotzG.)
1. Uber Potenzreihen mit positivem reelen Teil in Einheitskreis, S.-B*
Sachs. Acad. Wiss., 63 A911), 501—511.
Гёде (Gohde D.)
1. Zum Prinzip der Kontraktiven Abbildung, Math. Nachr., 30 A965),
251—258.
Гильберт (HilbertD.)
1. Grundzuge einer allgemeinen Theorie der linearen Integralgleichungen,
I—VI, I, Nachr. Akad. Wiss. Gottingen, Math-Phys., A904), 49—91; II,
там же A905), 213—259; III, там же A905), 307—338; IV, там же
A906), 157—227; V, там же A906), 439—480; VI, там же A910),
355—417.
Гильдебрандт (HildebrandtT. H.)
1. Integration in abstract spaces, Bull. Am. Math. Soc, 59 A953), 111—139.
Гильман, Джерисон (Gillman LM Jerison M.)
1. Rings of Continuous Functions, D. Van Nostrand Co., Inc., Princeton,
N. J., 1960.
Гликсберг (Gliksbergl.)
1. The representation of functionals by integrals, Duke Math. /., 19 A952),
253—261.
Годман (GodementR.)
1. L'Analyse Harmonique dans les Groupes non Abeliens, Suppl. au Colloq.
Anal. Harmonique, Nancy, 1952.
2. Extension a un groupe quelconque des theoremes tauberiens de N. Wie-
Wiener et d'un theoreme de A. Beurling, С /?., 223 A946), 16—18.
3. Theoremes tauberiens et theorie spectrale, Ann. Sci. Ecole Norm. Sup.,
C), 64 A947/48), 119—138.
4. Les fonctions de type positif et la theorie des groups, Trans. Am. Math.
Soc, 63 A948), 1—84.
5. Sur la theorie des representations unitaires, Ann. Math. B), 53 A951),
68—124.
Гординг (Garding L)
1. Linear hyperbolic partial differential equations with constant coefficients,
Ada Math,, 35 A950), 1—62.
2. Dirichlet's problem for linear elliptic partial differential equations,
Math. Scand., 1 A953), 55—72.
3. Задача Кощи для гиперболических уравнений, ИЛМ М, 13вЬ
1020 Библиография
4. Some Trends and Problems in Linear Partial Differential Equations,
Proc. Intern. Congr. Math. Edinburgh, 1958, Cambridge Univ. Press,
London, 1960. (Русский перевод: УМН, 15 A960), вып. 1, 137—140.)
5. Distributions and their applications to paitial differential equations.
Lecture notes. Conf. on Functional Analysis, London, 1961.
6. Dirichlet's problem and the vibration problem for linear elliptic partial
differential equations with constant coefficients. Proc. Symp. on Spectral
Theory and Differential Problems, Stillwater, 1951.
Гордин г, Лионе (Garding L., Lions Y. L.)
1. Functional analysis, Nuovo Cimento, 14, SerX A959), Supplement, 19—66.
Гордин г, Мальгранж (Garding L., Malgrange B)
1. Operateurs differentiels partiellement hypoelliptiques, C. R., 247 A958),
2083—2085.
Гоулд (Gould G. G)
1. On a class of integration spaces, /. London Math. Soc, 34 A959),
161—172.
Гоулд, Маховальд (Gould G. G., Mahowald M.)
1. Quasi-barrelled locally convex spaces, Proc. Am. Math. Soc, 11 A960),
811—816.
2. Measures on completely regular spaces, /. London Math. Soc, 37 A962),
103—111.
Гофман (Hoffman К.)
1. Банаховы пространства аналитических функций, ИЛ, М., 1963.
Гоффман (GoffmanC.)
1. Real Functions, Holt. Rinehart and Winston, Inc., N. Y., 1953.
Гохберг И. Ц.
1*. О линейных уравнениях в пространстве Гильберта, ДАН СССР, 76
A951), 9-12.
2*. О линейных уравнениях в нормированных пространствах, ДАН СССР,
76 A951), 477—480.
3*. О линейных операторах, аналитически зависящих от параметра, ДАН
СССР, 78 A951), 629—632.
Г о х б е р г И. Ц., К Р е й н М. Г.
1*. Введение в теорию линейных несамосопряженных опароторов, «Нау-
«Наука», М., 1965.
2*. Теория вольтерровых операторов в гильбертовом пространстве и ее
приложения, «Наука», М., 1967.
Грамш (Gr'amsch В.)
1. Integration und holomorphe Funktionen in lokalbeschrankten Raumen,
Math. Ann., 162 A965/66), 190—210.
Гранас (GranasA.)
1. Extension homotopy theorem in Banach spaces and some of its appli-
applications to the theory of nonlinear equations, Bull. Acad. Polon. ScL 7
A959), 387—394.
Грейвс (Graves L. M)
1. The Theory of Functions of Real Variables, 2d. ed., McGraw-Hill Book
Co., Inc., N. Y.f 1956.
2. Topics in the functional calculus, Bull. Am. Math. Soc, 41 A935)
641—662; Errata, ibid., 42 A936), 381—382.
Гротендик (GrothendieckA.)
1. Produits Tensoriels Topologiques et Espaces Nucleaires, Mem. Am. Math.
Soc, № 16, 1955.
2. Sur la completion du dual d'un espace vectoriel localement convexe,
С R., 230 A950), 605—606.
3. Criteres de compacite dans les espaces generaux, Am. J. Math., 7\
A952), 168-186.
Библиография 1021
4. Sur les applications lineaires faiblement compactes des espaces du type
C(K), Can. J. Math., 5 A953), 129—173.
5. Sur certains espaces de fonctions holornorphes, I, /. /. die reine u. ang.
Math., A), 192 A953), 35—64.
6. Sur certains espaces de fonctions holomorphes, II. /. /. die reine u. ang.
Math., B), 192 A953), 77—95.
7. Espaces Vectoriels Topologiques, Instituto de Matematica Рига е Apli-
cada. Universidade de Sao Paulo, S2o Paulo, 1954.
8. Sur les espaces de solutions d'une classe generale d'equations aux deri-
vees partielles, /. Ann. Math, II A952/53), 243—280.
9. Sur les espaces (F) et (DF), Sum. Brasil. Mathematicae, 3 A954),
57—123. (Русский перевод: Математика, 2:3 A958), 81—127.)
Г у д н e p (G о о d n е г D. В.)
1. Projections in normed linear spaces, Trans. Am. Math. Soc, 69 A950),
89—108.
2. The closed convex hull of certain extreme points, Proc. Am. Math. Soc,
15 A964), 256—258.
ГурарийВ. П.
1*. Спектральный анализ ограниченных функций на полуоси, Теория
функций, функциональный анализ и приложения, Харьков, 5 A967),
210—231.
2*. О спектре функций на полуоси, Функциональный анализ и его при-
приложения, 1 A967), вып. 3, 88—89.
Даниэль (D a n i е 11 P. J.)
1. A general form of integral, Ann. Math., B), 19 A917/18), 279—294.
Данфорд (Dunford N )
1. Integration and linear operations, Trans. Am. Math. Soc, 40 A936),
474—494.
2. Spectral theory, I. Convergence to projections, Trans. Am. Math. Soc,
54 A943), 185—217.
3. Direct decompositions of Banach spaces, Bol. Soc. Mat. Мех., 3 A946),
1-12.
Данфорд, Петтис (Dunford N., Pettis B. J.)
1. Linear operators on summable functions, Trans. Am. Math. Soc, 47
A940), 323—392.
Данфорд, Шварц (Dunford N., Schwartz J. T.)
1. Линейные операторы. Общая теория, ИЛ, М., 1962.
2. Линейные операторы. Спектральная теория, «Мир», М., 1966.
Дворецкий, Роджерс (Dvoretzky A., Rogers С. А.)
1. Absolute and unconditional convergence in normed linear spaces, Proc
Nat. Acad. Set. USA, C), 36 A950), 192—197.
Д е н и (D e n у J.)
1. Potential theory. Lecture notes, London Math. Soc. Intern. Conference
(Easter, 1961).
Д е н и, Лионе (D e n у J., Lions J. L.)
1. Les espaces du type $e Beppo Levi, Ann. Inst. Fourier, 5 A953/54),
305—370.
Депри (DepritA.)
1. Contributions a l'etude de l'algebre des applications lineaires continues
d'un espace localement convexe separe. Theorie de Riesz — theorie spec-
trale, Acad. Roy. Belg. Classe Sci. Mem., Collection in 8°, 31 A959), №2.
Джерисон, Рудин (Jerison M., Rudin W.)
1. Translation-invariant functionals, Proc. Am. Math. §oc} C), 13 A962),
417-423-
1022 Библиография
Джон (John F.)
1. General properties of solutions of elliptic partial differential equations,
Symposium on Spectral Theory and Differentia] Problems, Mathematics
Dept. Oklahoma Agricultural and Mechanical College, Stillwater, Okla-
Oklahoma A951), 113—175.
Джонсон (Johnson В. Е.)
1. The uniqueness of the (complex) norm topology, Bull. Am. Math. Soc.t
73 A967), № 4, 537—539.
Диксмье (DixmierJ.)
1. Sur un theoreme de Banach, Duke. Math. /., 15 A948), 1057—1071.
2. Sur les bases orthonormales dans les espaces prehilbertiens, Ada ScL
Math. Szeged., 15 A953), 29—30.
3. Les moyennes invariantes dans les semi-groupes et leurs applications,
Ada Sti. Math. Szeged, 12 A950), 213—227.
Динкуляну (Dinculeanu N.)
1. Sur la representation integrale des certains operations lineaires, I, C. A.,
245 A957), 1203—1205.
2. Sur la representation integrale des certains operations lineaires. II, Com-
posito Math., 14 A959), 1—22.
3. Sur la representation integrale des certains operations lineaires. Ill,
Proc. Am. Math. Soc, 10 A959), 59—68.
4. Mesures vectorielles sur les espaces localement compacts, Bull. Math.
Soc. Sd. Math. Phys. Rep. Populare Roumaine (N. S.), 2 A958),
137—164.
5. Mesures vectorielles et operations lineaires, С R., 246 A958), 2328—2331.
6. Remarks on the integral representation of vector measures and linear
operations on L , Rev. Math. Pures Appl., 7 A962), 287—300.
7. Integral representation of vector measures and linear operations, Studia
Math., 25 A965), 181—205.
8. Vector measures, VEB Deutscher Verlag der Wissenschaften, Berlin,
1966.
9*. Integrarea pe spatii local compacte, Edit. Acad. Populare Romane,
Bucuresti, 1965.
Динкуляну, Фояш (Dinculeanu NM Foias C.)
1. Sur la representation integrale des certaines operations lineaires, IV,
Operateurs lineaires sur l'espace L§ Can. J. Math., 13 A961), 529—556.
Доногю (DonoghueW. Fr., Jr.)
1. On the lifting property, Proc. Am. Math. Soc, 16 A965), 913—914.
Дьёдонне (Dieudonne J.)
1. La dualite dans les espaces vectorielles topologiques, Ann. Sd. Ecole
Norm. Sup., C), 59 A942), 107—139.
2. Recent developments in the theory of locally convex vector spaces,
Bull. Am. Math. Soc, 59 A953), 495—512.
3." Sur les espaces de Kothe, /. Anal. Math., 1 A951), 81—115.
4. Sur les espaces de Montel metrisables, C. R., 238 A954), 194—195.
5. Sur un theoreme de Smulian, Arch. Math., 3 A952), 436—440.
6. Natural homomorphisms in Banach spaces, Proc. Am. Math. Soc, A),
1 A950), 54—59.
7. Sur le theoreme de Lebesgue-Nikodym, Ann. Math., 42 A941), 547—555.
8. Sur le theoreme de Lebesgue-Nikodym, II, Bull. Soc. Math. France, 72
A944), 193—239.
9 Sur le theoreme de Lebesgue-Nikodym, III, Ann. Univ Grenoble, 23
A947-1948), 25-53.
10 Sur le theoreme de Lebesgue-Nikodym, IV, /. Indian, Math. Soc. 1$
A951), 77-86.
Библиография 1023
11. Sur le theoreme de Lebesgue-Nikodym, V, Can. J. Math., B), 3 A951),
129—139.
12. Sur le produit de composition, Сотр. Math., A), 12 A954), 17—34.
12a. Sur le produit de composition, II, J. Math. Pures Appl, C), 29 A960),
275—292.
13. Основы современного анализа, «Мир», М., 1964.
14. Sur la convergence des suites de mesures de Radon Anais Acad. Bra-
sll. Cienc, 23 A951), 21—38.
15. On biorthogonal systems, Mich. Math. J., 2 A954), 7—20. (Русский
перевод: Математика, 3:4 A959), 133—145.)
16 La Geometrie des Groupes classiques, Springer-Verlag, Berlin, Vienna,
1955.
Дьёдонне, Шварц (Dieudonne J., Schwartz L.)
1. La dualite dans les espaces (F) et (LF), Ann. Inst. Fourier, 1 A949),
61—101. (Русский перевод: Математика, 2:2 A958), 77—117.)
Дэви с (Davis W. J.)
1. Dual generalized bases in linear topological spaces, Proc. Amer. Math,
Soc, 17 A966), 1067—1069.
Дэй (Day M. M.)
1. Линейные нормированные пространства, ИЛ, М., 1961.
2. The spaces Lp with 0<р<1, Bull. Am. Math. Soc, 46 A940), 816—823.
3. Some uniformly convex spaces, Bull. Am. Math. Soc, 47 A941),
504—507.
3 а а н е н (Zaanen A. C.)
1. Linear Analysis, North Holland Publ. Co., Amsterdam, 1953.
2. A note on the Daniell-Stone integral, Colloq. sur TAnalyse Conctionelle,
Louvain A960), 63—69. Librairie Universitaire, Louvain A961).
Зигмунд (Zygmund H. S.)
1. Trigonometrical Series. Monografje Matematyczme, V, Warszawa-Lwow,
1935. (Русский перевод: Тригонометрические ряды, ГОНТИ, М. — Л.,
1939.)
2. Тригонометрические ряды, т. 1 и 2, «Мир», М., 1965.
3. On a theorem of Marcinkiewicz concerning interpolation of operations,
/. Math., 35 A956), 223—248.
И и н о (lino)
1. Sur les derivations dans les espaces vectoriels topologiques sur les
corps des nombres complexes, I—III, Proc Japan Acad., 35 A959),
343—348, 530—535; 36 A960), 27—32.
Ионеску Тулча А (I о n e s cu T u 1 с е а А.)
1. On the lifting property. V, Ann. Math. Statist, 36 A965), 819—828.
2. Sur le relevement fort et la disintegration de mesures, C. R., 262 A966),
A617—618.
Ионеску Тулча А., Ионеску Тулча К- (Ionescu Tulcea A.,
Ionescu Tulcea C.)
1. On the decomposition and integral representation of continuous linear
operators, Ann. Math. Рига Appl, D), 53 A961), 63—87.
2. On the lifting property. I, /. Math. Anal. Appl, 3 A961), 537—546.
3. On the lifting property. II, Representation of linear operators on Spaces
LrE (l<r< oo), /. Math. Mech., 11 A962), 773—795.
4. Abstract ergodic theorems, Proc Nat. Acad. Sci. USA., 48 A962),
204—206.
5. Abstract ergodic theorems, Trans. Am. Math. Soc, 107 A963), 107—124
6. On the lifting property. Ill, Bull Am. Math Soc, 70 A964), 193—197.
7. On the lifting property. IV, Disintegration of measures, Ann. Inst. Fou-
Fourier (Grenoble), 14 A964), 445—472.
1024 Библиография
ИонескуТулчаК. (IonescuTulceaC.)
1. On the lifting property and disintegration of measures, Bull. Am. Math.
Soc, 71 A965), 829—842.
Иосида (I osida К.)
1. Mean ergodic theorem in Banach spaces, Proc. Imp. Acad. Tokyo, 14
A938), 292—294.
2*. Функциональный анализ, «Мир», М, 1967 A965).
Иосинага, Огата (Yoshinaga К., Ogata H.)
1. On convolutions, /. Sci. Hiroshima Univ., 22 A958), 15—24.
И се к и (Iseki К.)
1. On a theorem on function spaces of A. Grothendieck, Proc. Japan.
Acad., 33 A957), 605—607.
2. On complete orthonormal sets in Hilbert space, Proc. Japan. Acad., 33
A957), 450—452.
Исеки, Kacaxapa (Iseki K-, Kasahara S.)
1. Some properties of convex sets in linear spaces, Rev. Fac. Cien. Lisboa
Univ. B), 3 A954/55), 238—242.
Кадота (Kadota Т. Т.)
1. Term-by-term differentiability of Mercer's expansion, Proc. Am. Math.
Soc, 18 A967), 133—135.
Какутани (KakutaniS.)
1. Two fixed-point theorems concerning bicompact convex sets, Proc. Imp.
Acad. Tokyo, 14 A938), 242—245.
2. A proof of Schauder's theorem, /. Math. Soc. Japan., A), 3 A951),
228—231.
3. Rings of analytical functions. Lectures on Functions of a Complex Vari-
Variable, Univ. of Michigan Press, Ann. Arbor A955), 71—83.
4. Iteration of linear operators in complex Banach spaces, Proc. Imp.
Acad. Tokyo, 14 A938), 295—300.
5. Concrete representations of abstract (L)-spaces and the mean ergodic
theorem, Ann. Math. B), 42 A941), 523—537.
6. Concrete representations of abstract (M)-spaces (A characterization of
the space of continuous functions.), Ann. Math. B), 42 A941), 994—
1024.
7. A generalization of Brouwer's fixed point theorem, Duke Math. J., 8
A941), 457—459.
Какутани, К л и (К a k u t a n i S., К 1 e e V. L.)
1. The finite topology of a linear space, Arch. Math., Fasc. 1, 14 A963),
55—58.
Какутани, Кодайра (KakutaniS., KodairaK.)
1. Ober das Haarsche Mass in der lokal bikompakten Gruppe, Proc. Imp.
Acad. Tokyo, 20 A944), 444—450.
Кальдерон (CalderonA. P.)
1. Lebesgue spaces of differentiable functions and distributions, Proc. ol
Symposia in Pure Mathematics, IV, Am. Math. Soc. A961), 33—49.
Кальдерон, Зигмунд (С а 1 d e г б л А. Р., Zygmund A.)
1. Singular integral operators and differential equations, Am. J. Math., 79
A957), 901—921.
2. On the theorem of Haussdorff-Young and its extensions, Ann. Math.%
Study, 25, Princeton A950), 166—188.
3. On singular integrals, Ada Math., 88 A952), 85—139.
4. On singular integrals, Am. J. Math., 78 A956), 289—309.
5. Algebras of certain singular operators, Am. J. Math., 78 A956),
310—320.
6. A note on the interpolation of sublinear operations, Am. J. Math., 78
A956), 282-288.
Библиография 1025
Канторович Л В.
1. The method of successive approximations for functional equations, Ada
Math., 71 A939), 63—97.
Канторович Л. В., А к и л о в Г. П.
1*. Функциональный анализ в нормированных пространствах, Физматгиз,
М., 1959.
Канторович Л. В., Вулих Б. 3.
1. Sur la representation des operations lineaires, Compositio Math., 5
A938), 119—165.
Канторович Л. В., Вулих Б. 3 , П и н с к е р А. Ф.
1. Функциональный анализ в полуупорядоченных пространствах, Гостех-
издат, М. — Л., 1950.
К а п л а н (Kaplan S.)
1. Cartesian products of reals, Am. J. Math., 74 A952), 936—954.
Капланский (KaplanskyJ.)
1. Functional Analysis, Surveys in Applied Math. IV, 3—30, John Wiley
and Sons., Inc., N. Y., 1958.
2. The structure of certain operator algebras, Trans. Am. Math. Soc, 70
A951), 219—255.
3. The Weierstrass theorem in fields with valuations, Proc. Am. Math. Soc.t
1 A950), 356—357.
Карадус (Caradus S. R.)
1. Operators of Riesz type, Pacific J. Math., 18 A966), 61—71.
2. Operators with finite ascent and descent, Pacific, I. Math., 18 A966),
437—449.
Карлеман (CarlemanT.)
1. L'integrale de Fourier et questions qui s'y rattachent, Publications Sci-
entifiques de l'lnstitut Mittag-Leffler, Uppsala, 1944.
Картан (CartanH.)
1. Seminaire, Ecole Norm. Sup., 1953/54.
2. Sur la mesure de Haar, С R., 211 A940), 759—762.
3. Seminaire, Ecole Norm Sup., 1951/52.
4. Ideaux et modules de fonctions analytiques de variables complexes,
Bull. Soc. Math. France, 78 A950), 28-64.
5. Sur les fondements de la theorie du potentiel, Bull. Soc. Math. France,
69 A941), 71—96.
6. Theorie du potentiel newtonien: energie, capacite suites de potentiels,
Bull Soc. Math. France, 73 A945), 74—106.
7. Theorie generale du balayage en potentiel newtonien, Ann. Univ. Gre-
Grenoble, 22 A946), 221—280.
Картан, Годман (Cartan H., Godement R.)
1. Theorie de la dualite et analyse harmonique dans les groupes Abeliens
localement compacts, Ann. Sci. Ecole Norm. Sup., C), 64 A947), 79—99.
Кахан (Kahane J.-P.)
1*. Sur un theoreme de Paul Malliavin, C. #., 248 A959), 2943—2944.
Кахан, Салем (Kahane J.-P., Salem R.)
1. Sur les ensembles lineaires ne portant pas de pseudomesures, C. /?.,
243 A956), 1185—1187.
2*. Ensembles parfaits et series trigonometriques, Hermann, Paris, 1963.
Кацнельсон (KatznelsonJ.)
1*. Sur un theoreme de Kahane et Salem concernant les ensembles parfaita
symetriques, С #., 254 A962), 2700—2702.
Качмаж, Штейнгауз (Kaczmarz S, Steinhaus H.)
1. Теория ортогональных рядов, Физматгиз, M.t 1959 A935).
1026 Библиография
Каччиоиоли (CaccioppoliR.)
1. Un theorema generale sull'esistenza di elemente uniti in una transforms-
zione funzionale, Rend. Ace. Naz. Lincei, 11 A930), 794—799.
Келли (Kelley J. L.)
1. Общая топология, «Наука», М., 1968 A955).
2. Convergence in topology, Duke Math. /., 17 A950), 277—283.
3. Banach spaces with the extension property, Trans. Am. Math. Soc, 72
A952), 323—326.
4. Hypercomplete linear topological spaces, Mich. Math. /., 5 A958)»
235—246. (Русский перевод: Математика, 4:6 A960), 79—92.)
5. Note on a theorem of Krein and Milman, /. Osaka Inst. of Sci. Tech., 3,
A951), 1—2.
Келли, Намиока и др. (Kelley J. L, N a mi ok a I. and co-aut-
co-authors)
1. Linear Topological Spaces, D Van. Nostrand Co., Inc., Princeton, N. J.,
1963.
Келлог (Kellog O. D.)
1. Foundations of Potential Theory, Frederick Ungar Publishing Co., N. Y.,
1929.
К е н д а л л (К e n d a 11 D. G.)
1. On infinite doubly stohastic matrices and Birkhoff's problem. Ill, /. Lon-
London Math. Soc, 35 A960), 81—84.
Кёниг (KonigH.)
1. Neue begrundung der theorie der distributionen von. L. Schwartz, Math.
Nach. C), 9 A953), 129—148.
2. Multiplikation von distributionen, Math. Ann., 128 A955), 420—452.
Кёте (Ко the G.)
1. Uber zwei Satze von Banach, Math. Z., 53 A950), 203—209.
2. Zur theorie der kompakten operatoren in lokalconvexen Raumen, Port.
Math., 13 A954), 97—104.
3. A theoria dos espacos localemente convexos e as suas appligacoes 9 Ana-
lise, Acad. da Cien! de Lisboa, 1954.
4. Die Quotientenraume eines linearen vollkommenen Raumes, Math. Z.,
51 A947), 17—55.
5. Topologische lineare Raume, Springer Verlag, Berlin, Vienna, 1960.
6. Une caracterisation des espaces bornologiques, Colloq. sur PAnalyse
Functionnel Louvain (I960), 39—45 Librairie Universitaire, Louvain
A961).
7. General linear transformations of locally convex spaces, Math. Ann.,
159 A965), 309—328.
Кир к (Kirk W. A.)
1. A fixed point theorem for mappings which do not increase distances,
Am. Math. Monthly, 72 A965), 1004—1006.
Кист (Kist J.)
1. Locally o-convex spaces, Duke Math. J., 25 A958), 569—582.
Кларксон (ClarksonJ. A.)
1. Uniform by convex spaces, Trans. Am. Math. Soc, 40 A936), 396—414.
Кли (К lee V.)
1. Convex sets in linear spaces, Duke Math. /., 18 A951), 443—466.
2. Convex sets in linear spaces. II, Duke Math. /., 18 A951), 875—
893.
3. Invariant extensions of linear functionals, Pacific J. Math., 4 A954),
37—46.
4. Leray-Schauder theory without local convexity, Math. Ann., 141 (I960),
286—296. Corrections: 145 A962), 464—465.
Библиография 1027
Коддингтон, Левинсон (Coddington E. A., Levinson N.)
1. Теория обыкновенных дифференциальных уравнений, ИЛ, М., 1958
A955).
Коидзуми (Koizumi S)
1. On the singular integrals. 1—VI, Proc. Japan. Acad., 34 A958), 193—
198, 235—240, 594—598, 653—656; 35 A959); 1—6, 323—328.
2. On the Hilbert Transform, I, II, /. Fac. Sci. Hokkaido Univ., Ser. I, 14
A959), 153—224; 15 A960), 93—130.
Коллинз (Collins H. S)
1. Completeness and compactness in linear topological spaces, Trans. Am
Math. Soc, 79 A955), 256—280.
Колмогоров А. Н.
1. Zur Norrnierbarkheit eines allgemeinen topologischen linearen Raumes,
Studia Math., 5 A934), 29—33.
Колмогоров А. Н., Фомин С. В.
1. Элементы теории функции и функционального анализа, изд. 2-е,
«Наука», М., 1968.
Комура (KomuraY.)
1. Some examples on linear topological spaces, Math. Ann., 153 A964),
150—162.
К о н в е й (С о n w а у J. B.)
1. The strict topology and compactness in the space of measures, Bull.
Am. Math. Soc, 12 A966), 75—78.
2. The strict topology and compactness in the space of measures. II, Proc.
Am. Math. Soc, 126 A967), 474—486.
Кордуняну (CorduneanuC.)
1. Sisteme differentiale care admit solu(ii marginite, Analele §tiint. Univ.
«Al. I. Cuza», Iasi, B), 8 A957), 1—20.
2. Une application du theoreme du point fixe a la theorie des equations
differentielles, Analele Stiint. Univ. «Al. I. Cuza», Iasi, B), 4 A958),
43—47.
3. Sur la stabilite conditionelle par rapport aux pertubations permanentes,
Ada. Sci. Math. Szeged, 19 A958), 229—236.
4. Asupra exis^entei solutiilor marginite pentru unele sisteme differentiale
neliniare, Acad. RPR Fil. Iasi Stud. Cere. $ti. Mat., 11 A960), 271—
282.
5 Sur certains systemes differentiels non-lineaires, Analele §tiint Univ.
«A 1. I Cuza», Iasi, 6 A960), 257—260.
Коревар (KorevaarJ.)
1. Distributions defined by fundamental sequences. I—V, Proc. Ned. Acad.
Wet., A, 58 A955).
Коротков В. Б.
1. Интегральные операторы с ядром Карлемана, Дифференциальные
уравнения, 2 A966), 252—256.
Корсон, Линденштраус (С о г s о n H H., Lindenstrauss J.)
1 On weakly compact subsets of Banach spaces, Proc. Am. Math. Soc.t 17
A966), 407—412.
Костюченко А. Г.
1*. Асимптотическое распределение собственных значений эллиптических
операторов, ДАН СССР, 158 A964), 42—45.
2*. Асимптотика спектральной функции для сингулярного дифференциаль-
дифференциального оператора 2т-порядка, ДАН СССР, 168 A966), 276—279.
3*. Асимптотическое поведение спектральной функции самосопряженных
эллиптических операторов, 4-я летняя математическая школа, Кшв,
«Наукова думка» A968), 42—118.
1028 Библиография
Костюченко А. Г., Л е в и т а н Б М.
1*. Об асимптотическом поведении собственных значений операторной за-
задачи Штурма — Лиувилла, Функциональный анализ и его приложе-
приложения, 1 A967), вып. 1, 86—96.
Котляр (Collar M)
1. Lectures notes on integral operators, Universidad de Buenos Aires,
Facultad de Cienecjas Exactas u Naturales, Departarnento de Matemati-
cas, Buenos Aires, 1959.
2. A unified theory of Hilbert transforms and ergodic theorems. Rev. Mat.
Guyana, 1 A955), 105—167.
К р а м (CrumM. M.)
1. On positive definite functions, Proc. London Math. Soc, B4), 6 A956),
548-560.
К р е й н М. Г.
1. О некоторых вопросах геометрии выпуклых ансамблей, принадлежа-
принадлежащих линейному нормированному и полному пространству, ДАН CCCPt
14 A937), 5—8.
К р е й н М. Г., Al и л ь м а н Д. П.
1. On extreme points of regularle convex sets, Studia Math., 9 A940),
123—138.
К р е й н М. Г., Шмульян В. Л.
1. On regularly convex sets in the space conjugate to a Banach space,
Ann. Math., B), 41 A940), 556—583.
Кристиан (Christian R. R.)
1. On integration with respect to a finitely additive measure whose values
lie in a Dedekind complete partially ordered vector space. Dissertation,
Yale University Press, New Haven, Conn., 1954.
Кук (Cooke R. G.)
1. Бесконечные матрицы и пространства последовательностей, Физматгиз,
М., 1960 A950).
2. Linear Operators, The Macmillan Co., N.' Y., 1953.
Купер (Cooper J. L. B.)
1. One-parameter semigroups of isometric operators in Hilbert space, Ann.
Math., 48 A947), 827—842.
2. Symmetric Operators in Hilbert space, Proc. London Math. Soc, 50
A948), 11—55.
3. Positive definite functions of a real variable, Proc. London Math. Soc,
C7), 10 A960), 53—66.
Курант, Гильберт (Courant R., Hilbert D.)
1. Методы математической физики, т. 2, ГИТТЛ, М. —-Л., 1945 A937).
2. Методы математической физики, т. 2. Уравнения с частными произ*
водными, «Мир», М., 1964 A962).
Куратовский (KuratowskiC.)
1. Топология, т. 1, «Мир», М., 1966 A966); т. 2, «Мир», М., 1969 A968).
Лав (Love E. R)
1. A Banach space of distributions (I), /. London Math. Soc, 32 A957),
483—498.
Л айтхилл (Li gh thill M. J.)
1. An Introduction to Fourier Analysis and Generalized Functions, Cam-
Cambridge Univ. Press, N. Y., 1958.
Лалеско (LalescoT.)
1 Une theoreme sur les noyeaux composes, Bull. Acad Roumalne A915),
271—272.
Ламадрид (Gil de Lamadrid J.)
1, Completion of semmormed ьрасеъ and the Daniell process ot extending
an integral, Math. Mag., 33 A959/60), 199—210.
Библиография 1029
Л евин В Л.
1 Об одном классе локально выпуклых пространств, ДАН СССР, 145
A962), 35—38.
2 Условия 5-полноты ультрабочечных и бочечных пространств, ДАН
СССР, 145 A962), 273—276.
Л е р э (I. е г а у J )
1. Hyperbolic Differential Equations, Princeton, N. J., 1953.
2 Valeurs propres et vecteurs propres d'un endomorphisme completement
continu d'un espace vectoriels a voisinage convex, Ada Sci. Math. Sze-
Szeged., 12 A950), 177—186.
3. La theorie des points fixes et ses applications en analyse, Proc. Intern.
Congress Math, Combridge, Mass. A950), 202—208. (Русский перевод:
Математика, 4 : 5 A960), 737—783.)
Лерэ, Шаудер (LerayJ., SchauderJ.)
1. Topologie et equations fonctionelles, Ann Sci. Ecole Norm Sup, C),
51 A934), 45—78. (Русский перевод: УМН, 1 A946), № 3—4, 71—95)
2*. A priori estimates for differential operators in Loo norm, Illinois J.
Math, 8 A964), № 1, 112—124.
Лефшец (Lefschetz S.)
1 Introduction to Topology, Princeton Univ. Press, Princeton, N. Y., 1949.
2. Алгебраическая топология, ИЛ, М, 1949 A942).
Ливингстоун (Livingstone A. E.)
1. The space Нр, 0<р<1, is not normable, Pacific J. Math., 3 A953),
613-616.
Лионе (L i о n s J. L.)
1. Problemes aux limites en theorie des distributions, Ada Math., 94
A955), 13—153.
2. Supports de produits de composition, C. R., 232 A951), 1530—1532.
3. Supports de produits de composition, C. R., 232 A951), 1622—1624.
4. Supports dans la transformation de Laplace, / Anal. Math., 2 A952/53),
369—380.
5 Problemes aux limites de type mixte, Second colloq. sur les equations
aux derivees partielles, Bruxelles, 1954.
6. Sur quelques problemes aux limites relatifs a des operateurs differentiels
elliptiques, Bull Soc. Math. France, 83 A955), 225—250.
7. Sur le problemes aux limites du type derivee oblique, Ann. Math., B),
64 A956), 207—239
8. Operateurs de Dclsarte et Problemes Mixtes, Bull. Soc. Math. France,
84 A956), 9—95.
9. Problemes mixtes abstracts, Proc. Intern Congr. Math., Edinburgh, 1958;
Cambr. Univ Press, N. Y., 1960.
Лорентц, Вертейм (Lorentz G. G, Wertheim D. G.)
1. Representation of linear functional on Kothe spaces, Can. J. Math., 5
A953), 568—575.
Л op x (Lo r ch E. R.)
1 Spectral Theory, Univ. Texts in the Math. Sciences, Oxford Univ. Press,
N. Y., 1962.
Л о я с е в и ч (L о j a s i e w i с / S.)
1 Division d'une distribution par une fonction analytique de variables reol
les, С /?., 246 A958), 683—686.
2. Sur le probleme de la division, Studia Math., 18 A959), 87—136.
Л ю (d e L e e u w К )
1*. On Lp multiplies, Ann. Math., 81, № 2 A965), 364—379
Лю, Кацнельсон (deLceuwK.KatznelsonY)
'l* Functions that operate on non-self-adjoint algerbras, /. d'Analyse Math.,
11 A963), 207-219.
1030 Библиография
Л ю, Миркил (deLeeuwK., Mirkil H.)
1. Majorants dans Loo des operateurs differentials a coefficient constant
С R., 254 A962), 2286—2288.
Любарский Г. Я.
1. Теория групп и ее приложения в физике, Гостехиздат., М., 1957.
Люксембург (LuxembuigW. A. J.)
1. Banach Function Spaces, Proefschrift, Delft, 1955.
2. On closed linear subspaces and dense linear spaces, Proc. Intern. Symp.
on Linear Spaces, Jerusalem (July, 1960), 307—318.
Люксембург, Заанен (Luxemburg W. A. J., Zaanen A. C.)
1. Conjugate spaces of Orlicz spaces, Koninkl Ned. Acad. Wet., A B) 59
A956), 217—228.
Л ю м и с (L о о m i s L. H.)
1. Введение в абстрактный гармонический анализ, ИЛ, М., 1956 A953).
2. Abstract congruence and the uniqueness of Haar measures, Ann. Math.,
B), 46 A945), 348—355.
3. Haar measure uniform structures, Duke Math. /., 16 A949), 193—
208.
4. Linear functional and content, Am. J. Math.t 76 A954), 168—182.
Люстерник Л А., Соболев В. И,
1. Элементы функционального анализа, изд. 2-е, «Наука», М., 1965.
Маак (MaakW.)
1. Fastperiodische Funktionen, Die Grundlehren der Math. Wiss, Band LXI,
Springer-Verlag, Berlin, 1950.
Мазур, Орлич (Mazur S., Orlicz W.)
1. On linear methods of summability, Studia Math., 14 A955), 129—160
Майерс (MyersS. B.J
1. Normed linear spaces of continuous functions, Bull Am Math. Soc. 56
A950), 233—241.
Макаров В. М.
1. Индуктивные пределы нормированных пространств, Вестник Ленингр
унив., 20 A965), № 13, 50—58.
Мак-Артур (McArthurC. W.)
1. The Weak Basis Theorem, Colloq Math., 17 A967), 71—76.
Макки (MackeyG W.)
1. Note on a theorem of Murray, Bull. Am. Math. Soc, D), 52 A946)
322—325.
2. On infinite dimensional linear spaces, Trans Am. Math. Soc, 57 A945),
155—207.
3. On convex topological linear spaces, Trans. Am. Math. Soc, 60 A946),
519—537.
4. Functions on locally compact groups, Bull. Am. Math. Soc, 56 A950),
385—412.
5. Equivalence of a problem in measure theory to a problem in the theory
of vector lattices, Bull. Am. Math. Soc, 50 A944), 719—722.
Мак-Кинси (McKinseyY. С. С.)
1. Введение в теорию игр, Физматгиз, М, 1960 A952).
Мак-Шейн (М с S h a n e E. Y.)
1. Integration, Princeton Univ. Press, Princeton, N. J., 1947.
2. Order Preserving Maps and Integration Processes, Ann. Math. Study,
№ 31, Princeton Univ. Press, Princeton, N. J., 1953.
Мальгранж (Ma lgrange В.)
1. Existence et approximation des solutions des equations aux derivees par-
tielles et des equations de convolution, These, Paris, 1956
2 Sur une classe d'opcratours differentials hypoelliptiques, Bull. Sop. Math.
France, 85 A957), 283-306.
Библиография 1031
3. Sur les equations de convolution, Rend. Sent. Math. Univ. Torino, 19
A959/60), 19—27.
Малявен (M a 11 i a v i n P.)
1. Sur Timpossibilite de la synthese spectrale dans une algebre de fonctions
presque periodiques, C. R., 248 A959), 1756—1759.
2. Sur rimpossibilite de la synthese spectrale sur la droite, C. R., 248
A959), 2155—2157.
3. Impossibility de la synthese spectrale dans les groupes abeliens non
compacts, Publ. Math. Inst. Hautes Etudes Sci. Paris, A959), 61—68.
Марков A. A.
1. On mean values and exterior densities, Мат. сб., 4 A938), 165—191.
2. Некоторые теоремы об абелевых множествах, ДАН СССР, 10 A936),
311—314.
Маркушевич А. И.
1. О базисе (в широком смысле слова), ДАН СССР, 41 A943), 241—243.
2. О базисе в пространстве аналитических функций, Мат. сб., 17 A945),
211—252.
М а р 1 и н о (М а г t i n e a u А.)
1. Sur le theoreme du graphe ferme, С. R., 263 A966), A 870—871.
Марцинкевич (М а г с i n к i e w i с z J.)
1. Sur Interpolation d'operations, C. R., 208 A939), 1272—1273.
Массера, Шеффер (Massera J. L., SchafferJ. J.)
1. Linear differential equations and functional analysis. I, Ann. Math., 67
A958), 517—573; II. Equations with periodic coeficients, Ann. Math., 69
A959), 88—104; III. Lyapunov's second method in the case of conditio-
conditional stability, Ann. Math., 69 A959), 535—574; IV, Math. Ann., 139
A960), 287—342.
2*. Linear differential equations and function spaces, Academic Press,
N. Y.-London, 1966. (Готовится русский перевод в изд-ве «Мир».)
Махарам (Maharam D.)
1. On a theorem of von Neumann, Proc. Am. Math. Soc, 9 A958),
987—994.
Маховальд (Mahowald M.)
1. Barrelled spaces and the closed graph theorem, /. London Math. Soc,
36 A961), 108—111.
Мехди (Mehdi M. R.)
1. Continuity of seminorms on topological vector spaces, Studia Matht 18
A959), 81—86.
Мидзохата (MizohataS.)
1. Hypoellipticite des equations paraboliques, Bull Soc. Math. France, 85
A957), 15—50.
Микусинский (MikusinskiJ.)
1. Une definition de distributions, Bull. Acad. Polon. Sci., Cl. Ill, 3 A955),
589-591.
2. Sur la methode de generalisation de M. Laurent Schwartz et sur la con-
convergence faible, Fund. Math., 35 A948), 235—239.
3. Sur les fondements du calcul operatoire, Studia Math., 11 A949), 41—70.
4. L'anneau algebrique et ses applications dans l'analyse fonctionelle, Ann.
Univ. Mariae Curie-Sklodowska, II A), Sect. A A947), 1—48; III A),
Sect. A A949), 1—82.
5. Operational Calcus, Pergamon Press, Inc., N. Y., 1959. (Русский пере-
перевод 1-го издания: Операторное исчисление, ИЛ, М., 1956).
Микусинский, Сикорский (Mikusinski J., Sikorski R)
1. Элементарная теория обобщенных функций, вып. 1, ИЛ, М., 1959
A958); вып. 2, ИЛ, М., 1963 A962).
1032 Библиография
М и л ь м а н Д П., Р у т м а н М. А.
1. Об одном уточнении теоремы о полноте системы крайних точек регу-
регулярно выпуклого множества, ДАН СССР, 60 A948), 25—27.
Миранда (М i г a n d а С.)
1. Уравнения с частными производными эллиптического типа, ИЛ, М.,
1957 A955).
М о р с (М о г s e A. P )
1. Squares are normal, Fund. Math., 36 A949), 35—39.
Myp (Mo ore E. H.)
1 Definition of limit in general integral analysis, Proc. Nat I. Acad. ScL
USA, 1 A915), 628.
M у р, С м и т (М о о r e E H.f S m i t h H. L.)
1. A general theory of limits, Am. J. Math., 44 A922), 102—121.
Мурье (Mourier Edith)
1. Elements aleatoires dans un espace de Banach, Ann. Inst. Henri Poin-
care, 13 A952), 161—244,
Нагумо (Nagumo M.)
1. Degree of mapping in convex linear topological spaces, Am. J. Math., 73
A951), 497—511.
НаймаркМ. А.
1. Нормированные кольца, Гостехиздат, М, 1956.
2*. Нормированные кольца,.изд. 2-е, «Наука», М., 1968.
Накамура (Nakamura М.)
1. Complete continuities of linear operators, Proc. Japan Acad., 27 A951),
544_547.
Накано (NakanoH)
1. Topology and Topological Linear Spaces, Maruzen Co., Ltd., Tokyo, 1951.
2. Modern Spectral Theory, Maruzen Co., Ltd., Tokyo, 1950.
Натансон И. П
1. Теория функций вещественной переменной, Гостехиздат, М., 1957.
Нахбин (NachbinL.)
1. Topological Vector Spaces, Rio de Janeiro, 1948.
2. Topological vector spaces of continuous functions, Proc Nat. Acad. Set
USA, 40 A954), 471—474
3. A theorem of the Hahn-Banach'type for linear transformations, Trans.
Am. Math. Soc, 68 A950), 28—46.
Нейман (von Neumann J.)
1. Mathematical Foundations of Quantum Mechanics, Princeton Univ.
Press, Princeton, N J., 1955
2. On complete topological spaces, Trans. Am. Math. Soc, 37 A935)
1—20
3. Functional Operators, Princeton Univ. Press, Princeton, 1933—35
4 The uniqueness of Haar's measure, Мат. сб., 1D3) A936), 721—734.
5. Lectures on Invariant Measures, Princeton Univ., 1940 (неопублико-
вано).
6. Proof of the quasi-ergodic hypothesis, Proc. Nat. Acad. ScL USA, 18
A932), 70-82.
Нейман, Моргенштерн (von Neumann J., Morgenstern O.)
1. Theory of Games and Fconomic Behaviour, 2d. e'd., Princeton Univ.
Press, Princeton, N J., 1947.
H и к о д и м (N i k о d у m О.)
1. Sur une generalisation des integrates de M. J. Radon, Fund. Math., 15
A930), 131-179.
Никольский С М.
1*. Линейные уравнения в пинейных нормированных пространствах, Из$.
АН СССР, сер. матем., 7 A943), Ц7—16§.
Библиография 1033
Ниренберг (NirenbergL.)
1. Remarks on strongly elliptic partial differential equations, Comtn. Pure
Appl. Math., 8 A955), 649—675.
Ньюмен (Newman D. J.)
1. The non-existence of projections from Iх to tf1, Proc. Am. Math. Soc, 12
A961), 98—99.
H ь ю н с (N e w n s W. F.)
1. On the representation of analytical functions by infinte series, Phil
Trans. Roy. Soc. London, (A), 245 A953), 429—468.
О р л и ч (О г 1 i с z W )
1 Beitrage zur Theorie der Orthogonalentwicklungen, Studia Math., 1
A928), 1—39.
Орлич, Птак (OrliczW., PtakV)
1. Some remarks on Saks spaces, Studia Math, 16 A957), 56—68.
Оцука (Ohtsuka M.)
1. On potentials in locally compact spaces, /. Sci. Hiroshima Univ., B), 25
A961), 135—353.
Паламодов В. П.
1*. Линейные дифференциальные операторы с постоянными коэффициен-
коэффициентами, М., «Наука», 1967.
Пеан о (Peano G.)
1. Integration par series des equations differentielles lineaires, Math. Ann.,
32 A888), 450—456
2. Demonstration de l'mtegrabilite des equations differentielles ordinaires,
Math. Ann., 37 A890), 182—228.
Пек (Peck N. Т.)
1. Representation of functions in C(X) by means of extreme points, Proc.
Am. Math. Soc, 18 A967), 133—135.
Петре (Peetre J.)
1. Une characterisation abstraite des operateurs differentiels, Math. Scand.,
7 A959), 211—218; 8 A960), 116—120.
2. Theoremes de regularite pours quelques classes d'operateurs difieren-
tiels, Medd. Lunds Univ. Mat. Sent., 16 A959).
Петришин (PetryshynW. V)
1*. On non-linear P-compact operators in Banach space with applications
to constructive fixed-point theorems, /. Math. Anal Appl., 15 A966),
228—242.
Петровский И. Г.
1. Sur l'analyticite des solutions des systemes d'equations differentiels,
Мат. сб., 5 A939), 3—68.
2. О некоторых проблемах теории уравнений с частными производными,
УМН, 1 A946), вып. 3—4, 44—70.
Петтис (Pettis В. J.)
1. On continuity and openness of homomorphism in topological groups,
Ann Math., 52 A950), 293—308.
2. On integration in vector spaces, Trans. Am. Math. Soc, 44 A938),
277—304.
3. Differentiation in Banach spaces, Duke Math. J., 5 A939), 254—269.
Пжеворска-Ролевнчч, Ролевич (Przeworska-Rolewicz D.,
R о 1 e w i с z S )
1. On integrals of functions with values in a complete linear metric space,
Siudia Math, 26 A966), 121—131.
П и к a p (P i с а г d E.)
1. Mcmoire sur la theorie des equations aux derivees partielles et la met-
jiode des approximations secassives, /. Math., D), 6 A890), 145—210,
1034 Библиография
Планшерель (Planchercl M.)
1 Contributions a l'etude de la representation d'une fonction arbitraire par
les integrates definies, Rend. Circ. Mat. Palermo, 30 A910), 289—335.
Плесси (du P less is N.)
1. Concerning the validity of finite difference operations, /. London Math.
Soc, 34 A959), 208—214.
Понтрягин Л. С.
1. Непрерывные группы, ГИТТИ, М., 1954.
Пр айс (Price G. В.)
1. The theory of integration, Trans. Am. Math. Soc, 47 A940), 1—50.
Прайс Дж. (Pryce J. D.)
1. Weak compactness in locally convex spaces, Proc. Am. Math. Soc., 17
A966), 148—155.
П т а к (Р t a k V )
1. Completeness and the open mapping theorem, Bull. Soc. Math. France,
86 A958), 41—74. (Русский перевод: Математика, 4:6 (I960), 39—67.)
2 The Principle of Uniform Boundedness and the Closed Graph Theorem,
Ceh. Mat. Z., 12 A962), 523—528
3. On the closed graph theorem, Ceh. Mat. Z., 9 A959), 523—527. (Рус-
(Русский перевод: Математика, 4:6 A960), 69—72.)
4 О полных топологических линейных пространствах, Ceh. Mat. Z., 3
A953), 285—290, 301—364.
5. On a theorem of W. F. Eberlein, Studia Math., 14 A954), 276—284.
6 Weak compactness in conver topoological linear spaces, Ceeh. Mat. Z.y
4 A954), 175-186.
7. Some open mapping theorems in (LF)-spaces and their application to
existence theorems for convolution equations, Math. Scand., 16 A965),
75—93.
8. Some metric aspects of the open mapping and closed graph theorems,
Math. Ann., 163 A966), 95—104.
Радон (Radon J.)
1. Theorie und Anwendungen der absolut additiven Mengenfunktionen,
S.-B. Akad. Wiss. Wien, 128 A913), 1295—1438.
P а й к о в Д А.
1. Гармонический анализ на коммутативных группах с мерой Хаара и
теория характеров, Труды Матем. ин-та АН СССР, 14 A945), 1—86.
2. Двусторонняя теорема о замкнутом графике для топологических ли-
линейных пространств, Сибирский мат. ж. B), 7 A966), 353—372.
3. Векторные пространства, Физматгиз, М., 1962.
4. Теоремы о замкнутом графике и полнота топологических линейных
пространств, Тр. 4-го Всесоюзного матем. съезда, т. II, «Наука», Л , 1964.
Ракоч (Rakotch E.)
1. A note on contractive mappings, Proc. Am. Math. Soc, C), 13 A962),
459- 465.
Рам (de Rham G.)
1. Дифференцируемые многообразия, М., ИЛ, 1956.
Рам, Кодайра (de R h a m G., К о d a i r a К-)
1. Harmonic Integrals, Inst. for Advanced Study, Princeton, N. J., 1950
Payx (Rauch H. E.)
1. Harmonic and analytic functions of several variables and the maximal
theorem of Hardy and Littlewood, Can. J. Math., 8 A956), 171—183.
Резерфорд (RetherfordJ. R.)
1. t^*-bases and bw*-bases in Banach spaces, Studia Math., 25 A964/65),
65—71.
2. Shrinking bases in Banach spaces, Am. Math. Monthly A966), 841— 84Q.
Библиография 1035
Рейтер (Reiter H.)
1. Ober Z^-Raume auf Gruppen. I, Monatsh. Math,, B), 58 A954), 73—76.
2. Ober Z^-Raume auf Gruppen. II, Monatsh. Math, C), 58 A954),
172—180.
3. Investigations in harmonic analysis, Trans. Am. Math. Soc, 73 A952),
401—427.
4. On a certain class of ideals in the L!-algebra of a locally compact Abe-
lian group, Trans. Am. Math. Soc, 75 A953), 505—509.
5. Contributions to harmonic analysis, Ada Math., 96 A956), 254—263.
6. Contributions to harmonic analysis. Ill, /. London Math. Soc., 32
A957), 477—483.
Риккарт (Rickart С. Е.)
1. General Theory of Banach Algebras, D. Van Nostrand Co., Inc., Prin-
Princeton, N. J., 1960.
Рингроуз (RingroseJ. R.)
1. A note on uniformly convex spaces, /. London Math. Soc, 34 A959),
92.
Рис (Riss J)
1. Elements de calcul differentiel et theorie de distributions sur les groupes
abeliens localement compacts, Ada Math., 89 A953), 46—105.
Рисе М. (Riesz M.)
1. Sur les ensembles compacts de fonctions sommables, Ada ScL Math
Szeged., 6 A933), 136—142.
2. Sur le maxima des formes bilineaires et sur les fonctionelles lineaires,
Ada Math., 49 A926), 456—497; Trans Am. Math. Soc, 83 A956),
482—492.
P и с с Ф. (R i e s z F.)
1. Les systemes d'equations a une infinite d'inconnues, Gauthier-Villars,
Paris, 1913.
2. Ober lineare Funkfionalgleichungen, Ada Math., 41 A918), 71—98.
(Русский перевод: УМН, 1 A936), 175—199.)
3. Sur les operations fonctionelles lineaires, C. #., 149 A909), 974—977.
4 Sur certains systemes singuliers d'equations integrates, Ann. ScL Ecole
Norm. Sup, C), 28 A91 i), 33—62.
5. Demonstration nouvelle d'un theoreme concernent les operations fon*
ctionelles lineaires, Ann. Sd. Ecole Norm. Sup., C), 31 A914), 9—14.
6. Sur la representation des operations fonctionelles lineaires par des in-
integrales de Stieltjes, Proc Roy. PhysioL Soc Lund, 21 A6) A962),
145—151.
7. Sur la theorie ergodique, Comm. Math. Helv., 17 A945), 221—239.
8. Sur quelques notions fondamentales dans la theorie generale des opera-
operations lineaires, Ann. Math., B), 41 A940), 174—206. (Русский перевод-
УМН, 1:2 B) A946), 147-178.
Рисе Ф., Секефальви-Надь (Riesz F., Sz-Nagy В.)
1. Лекции по функциональному анализу, ИЛ, М., 1954.
РобертсонА. П. (Robertson А. Р.)
1. Hypercomplete spaces, Deux. Colloq. Г Anal. Fonct., Louvain, A9G4),
57—60.
Робертсон А. П., Робертсон В. (Robertson A. P., Robert-
Robertson W.)
1. On the closed graph theorem, Proc. Glasgow Math. Assoc, 3 A956),
9-12.
2. Тополо1ические векторные пространства, «Мир», М., 1967 A964).
Робертсон В (Robertson W.)
1 Completions of topological vector spaces, Proc London Math. Soct C),
8 A958), 242- 257,
1036 Библиография
Рогозинский (RogosinskiW. W.)
1. Continuous linear functionals on subspaces of L*> and C, Proc. London
Math. Soc, B), 6 A956), 175—189.
2 Linear extremum problems for real polynomials and trigonometric poly-
polynomials, Arch. Math., 5 A954), 182—190
3. Linear extremum problems for real polynomials and trigonometric poly-
polynomials. Corrigenda, Arch. Math., 6 A955), 87.
4. On finite systems of linear equations with an infinity of unknowns,
Math. Z., 63 A955), 97—108.
5. Extremum problems for polynomials and trigonometric polynomials,
/. London Math. Soc, 29 A954), 259—275.
Розенблюм (RosenbloomP.)
1. The Elements of Mathematical Logic, Dover Publications, N Y,
1960.
Ройден (RoydenH.L.)
1. On a paper of Rogosinski, /. London Math Soc. 35 A960), 225—228.
Рота (Rota G. C.)
1. Extension theory of ordinary differential operators. Thesis, Yale Univ.
Press, 1956.
Рудин (Ru d i n W.)
1. The automorphisms and endomorphisma of the group algebra of the
unit circle, Ada Math., 95 A956), 39—55.
2. Representation of functions by convolutions, J. Math. Mech., 7 A958),
103—116
3. Fourier-Stieltjes transforms of measures on independent sets, Bull. Am.
Math. Soc, 66 A960), 199—202.
4. Trigonometric series with gaps, /. Math. Mech., 9 A960), 203—228.
5. Independent measures on Abelian groups, Pacific J. Math, 9 A959),
195—209.
6. Measure algebras on Abelian groups, Bull. Am. Math Soc, 65 {Ш59),
227—247.
7. Closed ideals in group algebras, Bull. Am. Math. Soc, 66 A960)
81—83.
8. Projections on invariant subspaces, Proc Am. Math Soc, C), 13 A962),
429—432.
9. Fourier Analysis on Groups, Interscience Publ. Inc., N. Y., 1962.
Сакс (Saks S.)
1. Теория интеграла, ИЛ, М., 1949 A937)
2. Integration in abstract metric spaces, Duke Math. /., 4 A938), 408-
411.
Сандерс (S a n d e r s В. L.)
1. On the existence of Schauder decomposition in Banach spaces, Proc
Am. Math. Soc, 16 A965), 987—990.
Cane (Suppes P.)
1. Axiomatic Set Theory, D. Van Nostrand Co, Inc., Princeton, N J., 1960.
Сарджент (S a r g e n t W. L. С.)
1. Some sequence spaces related to /p spaces, /. London Math. Soc, 35
A960), 161 — 171.
2. On some theorems of Hahn, Banach and Steinhaus, /. London Math.
Soc, 28 A953), 438—451
3. On compact matrix transformations between sectionally bounded BK-spa-
ces, /. London Math. Soc , 41 A966), 79—87.
Сарымсаков Т. А.
1 Краткое доказательство теоремы А. Н. Тихонова, У МИ, 20 A965), 4
A24), 172-173
Библиография 1037
Себаштьян эСильва (Sebasti2oeSilvaJ.)
1. Su certi spazi localmente convessi importanii per le applicazioni, Rend.
Math. Univ. Roma E), 14 A955), 388—410. (Русский перевод: Мате-
Математика, 1-1 A957), 60—77)
2. Sur une construction axiomatique de la theorie des distributions, Univ.
Lisboa. Revista Fac. Ci. B), 4 A955), 79—186; 5 A956), 169—170.
Сигал (SegalI.E.)
1. The group ring of a locally compact group. I, Proc. Nat. Acad. Sci.
USA, G), 27 A941), 348—352.
2. The span of translations of a function in a Lebesgue space, Proc. Nat.
Acad Sci. USA, G), 30 A944), 165—169.
3. The group algebra of a locally compact group, Trans. Am. Math. Soc,
61 A947), 69—105.
4. The class of functions which are absolutely convergent Fourier trans-
transforms, Ada Sci Math. Szeged., 12 A950), 157—161.
Сильвермэн (Silverman R. J)
1. Invariant linear functions, Trans. Am. Math. Soc, 81 A956), 411—
424.
2. Means on semigroups and the Hahn-Banach extension property, Trans.
Am. Math. Soc, 83 A956), 222—237.
Симоне (Simons S.)
1. The bornological space associated with R1, J. London Math. Soc, 36
A961), 461-473.
С и н г е р (Singer I.)
1. On a theorem of J. D. Weston, /. London Math. Soc, 34 A959),
320—324.
2. Sur les applications lineaires integrales des espaces de fonctions conti-
continues. I, Rev. Math Pares Appl, 4 A959), 391—401.
3. Sur les applications lineaires integrales des espaces de fonctions conti-
continues a valeurs vectorielles, Ada Math. Acad. Sci. Hung., 11 A960),
3-13.
4. Sur les applications lineaires integrales majorees des espaces de fon-
fonctions continues, Ada Acad. Naz. Lined. Rend. Cl. Sci. Fis. Mat. Nat.,
B7), 8 A959), 35—41.
5. Sur une classe duplications lineaires continues des espaces LPF
(l<p<oo), Ann. Sci. Ecole Norm. Sup. C), 77 A960), 235—256.
6. Completness and &y*-topologies, Arch. Math., 15 A964),, 42—45.
7. Bases in Banach spaces. I—III: I, Roumaine. Stud. Cere Mat, 14
A963), 533—585; II, там же, 15 A964), 157—208; III, там же, 16
A964), 675—725.
С и р а и с и (S !i i r a i s h i R.)
1. On the definition of convolutions for distributions, /. Sci. Hiroshima
Univ., Ser A, 23 A959), 19—32.
С и р а и с и, X и р а т a (S h i r a i s h i R., H i r a t a Y.)
1. On partial summability and convolutions in the theory of vector valued
distributions, / Sci. Hiroshima Univ , Sen A, 23 A960), 535—562.
2. Convolution maps and semi-group distributions, /. ScL Hiroshima Univ.,
Ser. A-l, 28 A964), 71—78.
Сирота (S h i г о t a T.)
1. On locally convex vector spaces of continuous functions, Proc. Japan
Acad., 30 A954), 294—299.
Словиковский (Slowikowski W.)
1. Extensions of sequentially continuous linear functionals in inductive
sequences of (F) -spaces, Studia Math., 26 A966), 193—221.
2 On extensions of sequentially continuous functionals to distributions,
Bull Acad. Polon, ScL, Ser. Math Astronom. Phys.f 13 A965), 411—414.
1038 Библиография
3. An example of a linear functional with no extension to a distribution,
Bull. Acad. Polon. ScL, Ser. Math. Astronom. Phys., 13 A965), 415—419.
4. On the continuity of inverse operators, Bull. Am. Math. Soc, 67 A961),
467—470.
5. Quotient spaces and the open map theorem, Bull. Am. Math. Soc.y 67
A961), 498—500.
Смит К- (Smith К. Т.)
1. A generalization of an inequality of Hardy and Littlewood, Can. J.
Math., 8 A956), 157—170.
С м и т и с (S m i t h i e s F.)
1. A note on completely continuous transformations Ann. Math., C), 38
A937), 626—630.
2. Integral Equations, Cambridge Tracts in Math, and Math. Phys., D9),
Cambridge Univ. Press, N. Y., 1958.
Соболев С. Л.
1. Некоторые применения функционального анализа в математической
физике, Л., 1950.
2. Methode nouvelle a resoudre le probleme de Chauchy pour les equations
lineaires hyperbolique Мат. сб., A), 43 A936), 39—72.
3. Об одной теореме функционального анализа, Мат. сб., 4 A938), 471 —
498
Стейн (Stein Е. М.)
1. Interpolation of linear operators, Trans. Am. Math. Soc, 83 A956),
482—492.
2. On limits of sequences of operators, Ann, Math., A), 74 A961), 140—170.
Стинрод, Эйленберг (Steenrod N.. Eilenberg S.)
1. Основания алгебраической топологии. М., Физматгнз, 1958 A952).
Стоун (S tone М. Н.)
1. Linear Transformations in Hilbert Space, Am. Math. Soc. Colloq. Publi-
Publications, 15, N. Y., 1932.
2. Applications of the theory of Boolean rings to general topology, Trans.
Am. Math. Soc, 41 A937), 375—481.
3. The generalized Weierstrass approximation theorem, Math. Mag., 21
A947/48), 167-183, 237—254.
4. Notes on integration, I—IV, Proc Nat. Acad. Sci. USA, 34 A948),
336—342, 447—455, 483—490; 35 A949), 50—58.
Такенухи (Takenouchi O)
1. Sur les espaces lineaires localement convexes, Math. J. Okayama Univ.,
A), 2 A952), 57—84.
2. Une demonstration directe d'un theoreme de M. G. W. Mackey, Kodai
Math. Sem. Rep., C/4) A951), 49-50.
Такер (Tucker D. H)
1. A representation theorem for a continuous linear transformation on a
space of continuous functions, Proc Am. Math. Soc, 16 A965), 946—953.
Тем п л (Temp 1 e G.)
1. Generalized functions, Proc. Roy. Soc, A, 228 A955), 175—190.
2. Theories and applications of generalized functions, /. London MatK
Soc, 28 A953), 134—148.
Tep-Xaap (TerHaarD.)
1. Foundations of statistical mechanics, Rev. Mod. Phys. C), 27 A955),
289—338.
Ти йен (Ti Yen)
1. The Hahn-Banach theorem and the least upper bound property, Trans.
Am. Math. Soc, 90 A959), 523—526.
Титчмарш (Titchmarsh E. C.)
1. Введение в теорию интегралов Фурье, Гостехиздат, 1948.
Библиография 1039
Тихонов А. Н.
1. Ein Fixpunktzatz, Math. Ann., Ill A935), 767—776.
Толстов Г. П.
1. Об абстрактном интеграле, рассматривавшемся С. Банахом, Мат. сб.,
57 A962), 319—322.
То р и н (Th о г i n G. О.)
1. An extension of a convexity theorem due to M. Riesz, Comm. Sem.
Math. Univ. Lund., D), A939).
2. Convexity theorems, Comm. Sem. Math. Univ Lund., (9), A948). (Рус-
(Русский перевод: Математика, 1 :3 A957), 41—78.)
T p e в (TrevesF.)
1. Domination et problemes aux limites du type mixte, С R., 245 A947),
2454—2457.
2. Domination et operateurs hyperboiiques, С R., 246 A958), 680—683.
3. Domination et operateurs paraboliques, C. R., 246 A958), 867—870.
4. Relations de domination entre operateurs differtntiels. These. Paris,
1958; Ada. Math., 101 A959), 1—139.
5. Operateurs differentiels hypoelliptiques, Ann. Inst. Fourier, 9 A959),
1—73.
6. Differential equations in Hilbert space, Proc. Symp. Pure Math., Am.
Math. Soc, IV A961), 83—89.
Тьюки (TukeyJ. W)
1. Convergence and Uniformity in Topology, Ann. Math. Study, № 2,
Princeton Univ. Press, Princeton, N. J., 1940.
Тэйлор (Taylor A. E.)
1. Introduction to Functional Analysis, John Wiley and Sons, N. Y., 1958.
2. Extensions of a theorem of Hellinger and Toeplitz, Math. Z., 66 A956),
53—57.
3. Banach spaces of functions analytic in the unit circle, Studia Math., 11
A950). 145—170. 12 A951), 25—30
4. Theorems on aspect, descent, nullity and defect of linear operators, Math
Ann., 163 A966), 18—49.
Тэтчелл (Tatchell J. B.)
1. A note on matrix summability of unbounded sequences, /. London Math.
Soc, 34 A959), 27—36.
У и л я м с о н (W i I I i a m s о n J. H.)
1. Two conditions equivalent to normability, /. London Math. Soc, 31
A956), 111—113.
2. A third condition equivalent to normability, J. London Math. Soc, 32
A957), 231—232.
3. Linear transformations in arbitrary linear spaces, /. London Math. Soc,
28 A953), 203—210.
4 Compact linear operators in linear topological spaces, /. London Math.
Soc, 29 A954), 149—156.
У и т н и (W h i t n e у Н.)
1. On ideals of differentiable functions, Am. J. Math., 70 A948), 635—658.
(Русский перевод: Математика, 10:4 A966).)
Ул ам (Ul a m S )
1. Zur Masstheorie in der allgemeinen Mengenlehre, Fund. Math., 16
A930), 140—150.
Уолтере (Walters S. S.)
1. The space Hp with 0<p<l, Proc. Am. Math. Soc, 1 A950), 800—805.
2 Remarks on the spaces H»4 Pacific J. Math., 1 A951), 455—471.
Уорнер (Warner S.)
1. The topology of compact convergences on continuous function spaces,
Duke Math. J., 25 A958), 265—282.
1040 Библиография
Фан (F a n Ky)
1. Fixed point and minimax theorems in locally convex topological linear
spaces, Proc. Nat. Acad. Sci. USA, 38 A952), 121—126.
2*. A generalization of Tichonoff's fixed point theorem, Math. Ann., 142
A961), 305—310. (Русский перевод. Математика, 9:4 A965).)
Фелпс (Phelps R. R.)
1. Лекции о теоремах Шоке, «Мир», М, 1968 A966).
Ф и л л и п с (Phillips R. S.)
1. On linear transformations, Trans. Am. Math. Soc, 48 A940), 516—541.
2. On weakly compact subsets of a Banach space, Am. J. Math., 65 A943),
Ю8—136.
Фихтенгольц Г. М.
1. Sur les fonctionelles lineaires, continues an sens generalised, Мат. сб.,
4 D6), A938), 193—214.
Фихтенгольц Г. М., Канторович Л. В.
1. Sur les operations dans l'espace des fonctions bornees, Studia Math., 5
A934), 69—98.
Форте, Мурье (F о r t e t R., M о u r i e r E.)
1. Loi des grandes nombres et theorie ergodique, С R., 232 A954), 923.
Фредгольм (Fredholm Y.)
1. Sur une classe d'equations fonctionelles, Ada Math., 27 A903), 365—390.
Фреше (Frechet M.)
1. Sur les operation lineaires, I—III: I, Trans Am. Math. Soc, 5 A904),
493—499; II, там же, 6 A905), 134—140; III, там же, 8 A907),
433—446.
Фридман (Friedman A.)
1. Generalized Functions and Partial Differential Equations, Prentice-Hall,
Inc., Englwood Cliffs, N. J., 1963.
Фридрихе (Friedrichs K. O.)
1. Mathematical Aspects of the Quantum Theory of. Fields, Interscience
Publ., Inc., N. Y., London, 1953.
2. On differential operators in Hiibert spaces, Amer. J. Math., 61 A939),
523—544.
3. The identity of strong and weak extensions of differential operators,
Trans. Am. Math. Soc, 55 A944), 132—151.
Фростман (Frost man О.)
1. Potentiel d'equilibre et capacite des ensembles avec quelques applica-
applications a la theorie de fonctions, These, Lund, 1935.
2. Sur le balayage des masses, Ada Szeged., 9 A938), 43—51.
Ф у г л и д (F u g I e d e В.)
1. Extremal Length and Closed Extensions of Partial Differential Opera-
Operators, Jul. Gjellerups Boghandel, Kobenhavn, 1960.
Фуглид, Шварц Л. (Fuglede В., Schwarts L.)
1. Un nouvean theoreme sur les distributions, C. R., 263 A966), A899—901.
Халмош (HalmosP.)
1. Теория меры, ИЛ, М., 1953 A950).
2. Introduction to Hiibert space and the Theory of Spectral Multiplicity,
Chelsea Publ. Co., N. Y., 1951.
3. Конечномерные векторные пространства, Физматгиз, М., 1963 A958).
4. Naive set Theory, D Van Nostrand Co., Inc., Princeton, N. J., 1960.
5. Лекции по эргодической теории, ИЛ, М., 1959 A956).
Хан (Hahn H.)
1. Ober Folgen linearen Operationen, Monatsch. Math. Phys., 32 A922),
3-88.
2 Ober lineare Gleichungsysteme in linearen Raumen, /. /\ Math., 157
A927), 214—229.
Библиография 1041
X а н т (Hunt G. А.)
1. Markoff processes and potentials, I—III: I, Illinois J. Math., 1 A957),
44—93; II, там же, 1 A957), 316—369; III, там же, 2 A958), 151-213.
(Русский перевод имеется в книге: Хант Дж. А, Марковские про-
процессы и потенциалы, ИЛ, М, 1962)
Хард и, Литлвуд (Hardy G. H, Littlewood J.)
1. A maximal theorem with function-theoretic applications, Ada Math., 54
A930), 81 — 116.
X a p д и, Литлвуд, Полна1
1. Неравенства, ИЛ, М , 1948.
Хелли (Hell у Е.)
1. Uber lineare Funktionaloperationen. S.-B. Akad. Wiss. Wien, KX 121 Ha
A912), 265-297.
Хеллингер, Теплиц (Hellinger E., Toeplitz O.)
1. Grundlagen fur eine Theorie der unendlichen Matrizen, Math. Ann., 69
A910), 289—330.
Хелсон (Helson H)
1. Spectral synihesis of bounded functions, Ark. Mat., 1 A951), 497—502.
2. On the ideal structure of group algebras, Ark. Mat,, 2 A952), 83—
86.
3. Isomorphisms of group algebras, Ark Mat., 2 A953), 475—487.
4. Fourier transforms on perfect sets, Stuclia Math., 14, A954/55),
209—213.
Хенсток (Н e n stock R.)
1. Difference sets and the Banach-Steinhaus theorem, Proc. London Math.
Soc, 13 A963), 305—321.
Хёрмандер (Hormander L)
1. К теории общих дифференциальных операторов в частных производ-
производных, ИЛ, М, 1959 A955).
2. On the interior regularity of the solutions of partial differential equa-
equations, Comm. Pure Appl. Math., 11 A958), 197—218. (Русский перевод:
Математика, 7 : 1 A963), 66—78.)
3. On the interior regularity of the solutions of boundary problems, Ada.
Math., 99 A958), 225—264.
4. On the division of distributions by polynomials, Ark. Mat., 3 A958),
555—568. (Русский перевод: Математика, 3:5 A959), 117—130.)
5. Local and global properties of the fundamental solutions, Math. Scand.,
5 A957), 27—39.
6. Definitions of maximal differential operators Ark. Mai., 3 A958),
501—504.
7. Линейные дифференциальные операторы с частными производными,
«Мир», М., 1965 A963).
8. Hypoelliptic convolution equations, Math. Scand., 9 A961), 178—184.
9. On the range of convolution operators, Ann. Math., B), 76 A962),
148—170. (Русский перевод: Математика, 6:3 A962), 37—65.)
Хилле (Hi lie E.)
1. Функциональный анализ и полугруппы, ИЛ, М, 1951.
Хилле, Тамаркин (Hille E., TamarkinJ. D.)
1. On the characteristic values of linear integral equations, Ada Math., 57
A931), 1—76.
X и л л е, Ф и л л и п с (Н i 11 e E., Phillips R. S )
^.Функциональный анализ и полугруппы, ИЛ, М., 1962.
Хинчин А. Я.
1. Математические основы статистической механики, М. — Л., 1943.
Полна = Пойа. — Прим. ред.
1042 Библиография,
X и р а т а (Н i r a t a Y.)
1. On convolutions in the theory of distributions, /. Sci. Hiroshima Univ.,
Ser. A, 22 A958), 89—98.
Хирата, Огата (HirataY., Ogata Й.)
1. On the exchange formula for distributions, /. Sci. Hiroshima Univ.,
Ser. A, 22 A958), 147—152.
Хойзер (HeuserH.)
1. Ober die iteration Rieszcher operatoren, Arch. Math., 9 A958), 202—
210.
2. Ober eigenwerte und eigenlosungen symmetrisierbar finiter operatoren,
Arch. Math., 10 A959), 12—20.
3. On the spectral theory of symmetric finite operators, Trans. Am. Math.
Soc, 94 (I960), 327—336.
ХуСы-цзян (Sze-TsenHu)
1. Теория гемотопий, «Мир», М., 1964 A959).
Хусейн (HusainT.)
1. S-Spaces and the open mapping theorem, Pacific. J. Math., A), 12
A962), 253—271.
2. The open mapping and closed graph theorems in topological vector spa-
spaces, Oxford University Press, 1964.
3. Minimal-type locally convex spaces, Math. Ann., 159 A965), 44—50.
4. Introduction to topological groups, W. В Saunders, Philadelphia, 1966.
Хусейн, Маховальд (Husain Т., Mahowald M.)
1. Barrelled spaces and the open mapping theorem, Proc. Am, Math. Soc.,
C), 13 A962), 423—424.
Хьюитт (Hewitt E)
1. Linear functionals on spaces of continuous functions, Fund. Math., 37
A950), 161—189.
2. Integration on locally compact spaces, I, Univ. Wash. Publ. Math.,
B), 3 A952), 71—75. "
3. Certain generalizations of the Weierstrass approximation theorem, Duke
Math. /., B), 14 A947), 419—427.
4. Rings of real-valued continuous functions, Trans. Am. Math. Soc, A),
64 A948), 45—99.
5. A problem concerning finitely additive measures, Mat. Tidssk., В A951),
81—95.
6. Integral representation of certain linear functionals, Ark. Mat., A1), 2
A952), 269—282.
7. The role of compactness in analysis, Am. Math. Monthly, F), 67 A960),
499-516.
8. The assymetry of certain algebras of Fourier-Stieltjes transforms, Mich.
Math. J., 5 A958), 149—158.
9. Linear functionals on almost periodic functions, Trans. Am. Math. Soc,
74 A953), 303—322.
10. Representation of functions as absolutely convergent Fourier-Stieltjes
transforms, Proc. Am. Math. Soc, D), 4 A953), 663—670.
11. Abstract Harmonic Analysis, Surveys in Applied Mathematics, IV,
107—168; Wiley and Sons, Inc., N. Y., 1958. (Русский перевод: Мате*
матика, 4 : 4 A960), 75—133.)
12. Two notes on measure theory, Bull. Am. Math Soc, 49 A943), 719—721.
Хьюитт, Иосида (Hewitt E., Yosida K.)
1. Finitely additive measures, Trans. Am. Math. Soc, A), 72 A952),
46-66.
Хьюитт.Росс (H e w i 11 E., R о s s К. А.)
1. Abstract Harmonic Analysis, I, Grundlehren der Math. Wiss., Band 115,
Springer-Verlag, Heidelberg, 1963.
Библиография 1043
Хьюитт, Цукерман (Hewitt E., Zuckerman H. S.)
1. Integration in locally compact spaces. II, Nagoya Math. /., 3 A951),
7—22.
2. Some theorems on lacunary Fourier series, with extensions to compact
groups, Trans. Am. Math. Soc, A), 93 A959), 1—19.
3 Finite-dimensional convolution algebras, Ada Math, 93 A955), 67—
119.
4 The ^-algebra of a commutative semigroup, Trans. Am. Math. Soc, A),
83 A956), 70—97.
5. Structure theory for a class of convolution algebras, Pacific J. Math.,
A), 7 A957), 913—941.
Целлер (Zeller К.)
1. Allgemeine Eigenschaften von Limitierungsverfahren, Math. Z., 53
A951), 463—487.
2. FK-Raume und Matrixtransformationen, Math. Z., 58 A953), 46—48.
3. Matrixtransformationen von Folgenraumen, Univ. Roma 1st. Naz. Alta
Mat. Rend. Mat. e App., E), 12 A953), 340—346.
4. Theorie der Limitierungsverfahren, Ergebnisseder Mat., N. F., Heft 15,
Springer-Verlag, Berlin-Vienna, 1958.
Ц у д з и (T s u j i M.)
1. On the compactness of space Lp (p>0) and its application to integral
equations, Kodai Math. Sem. Rep., A951), 33—36.
Шатуновский С. О.
1*. Ввведение в анализ, Одесса, 1932.
Шаудер (SchauderJ)
1. Das Anfangswertproblem einer quasilinearen hyperbolischen Differen-
tialgleichung zweiter Ordnung in beliebiger Anzahl von unabhangigen
Yeranderlichen, Fund. Math., 24 A935), 213—246.
2. Equations du type elliptique, problemes lineaires, Enseign. Math., 35
A936), 126-139.
3. Zur Theorie stetiger Abbildungen in Funktionaloperatoren Math. Z., 26
A927), 47—65.
4. Uber lineare, vollstetige Funktionaloperatoren, Studia Math., 2 A930),
183—196.
5. Eine Eigenschaft des Haarschen Orthogonalsystemes, Math. Z., 28
A928), 317—320.
6. Die Fixpunktsatz in Funktionalraume, Studia Math., 2 A930), 171—
180.
Шварц Д ж. (Schwartz J. I)
1. A remark on inequalities of the Calderon-Zygmund type for vector-va-
vector-valued functions, Comm. Pure Appl. Math., 14 A961), 785—799.
Шварц Л. (Schwartz L )
1. Theorie des Distributions. I, Hermann, Paris, 1950.
la. Theorie des Distributions. I, 2d. ed., Hermann, Paris, 1957.
2. Theorie des Distributions. II, Hermann, Paris, 1951.
3 Sur certains families non-fundamentales de fonctions continues, Bull.
Soc. Math. France, 12 A944), 141—145.
4. Distributions a valeurs vectorielles, I, Ann. Inst. Fourier, 7 A957),
1—141.
5. Distributions a valeurs vectorielles, II, Ann. Inst. Fourier, 8 A959),
1—207.
6. Espaces de fonctions differentiables a valeurs vectorielles, /. Anal
Math., 4 A954/55), 88—148.
7. Sur une propriete de synthese spectrale dans les groupes non-compacts,
С /?., 227 A948), 421—426.
1044 Библиография
8. Equations aux derivees partielles, Seminaire Inst. Henri Poincare,
1954/55; Paris, 1955.
9. Theorie generate des fonctions moyenne-periodiques, Ann. Math, 48
A947), 857—929.
10. Problemes aux limites dans les equations aux derivees partielles ellipti-
ques, Second Coll. sur les equations aux derivees partelles, C. B. R. M.,
Bruxelles, 1954.
11. Analyse et synthese harmoniques dans les espaces de distributions, Can.
J. Math., D), 3 A951), 503—512.
12. Les equations devolution liees an produit de composition, Ann. Inst*
Fourier, 2 A950), 19—49.
13. Homomorphismes et applications completement continues, C. R., 236
A953), 2472—2473.
14 Mathematica у Fisica Cuantica, Lecture notes, Universidad de Buenos
Aires, 1958.
15. Etude dts somes d'exponentielles reelles, Hermann, Paris, 1943.
16. Approximation d'une fonction quelconque par des sommes d'exponen-
d'exponentielles imaginaires, Ann. Fac. Set Univ. Toulouse, 6 A943), 111 — 174.
16a Etude des sommes d'exponentielles, Act. Sci. et Ind. (959), Paris, 1959.
(Эта работа содержит результаты работ [15] и [16].)
17. Une lemfne sur la derivation des fonctions vectorielles d'une variable
reelle, Ann. Inst. Fourier, 2 A950), 17—18.
18. Theorie des noyaux, Proc Intern. Congr. Math., Cambridge, Mass., I
A950), 220—230. (Русский перевод: Математика, 3:3 A959), 69—79.)
19. Sur l'impossibilite de la multiplication des distributions, C. /?., 239
A954), 847—848.
20. Some Applications of the Theory of Distributions, Lectures on Modern
Math., Vol 1, N. Y., London A963), 23-58.
21. Mesures de Radon sur des espaces topologiques arbitraires, Sem. Inst.
Henri Poincare, 1955/56, Paris, 1965
22. Sur le theoreme du graphe ferme, C. R., 263 A966), A 602—605.
Шварц С. (Schwa rz S.)
1. On weak and strong extensions of partial differential operators with
constant coefficients, Ark. Math., 3 A958), 515—526.
Шевалле (ChevalleyC.)
1. Theory of Distributions, Lectures at Columbia Univ., Columbia Univ.
Press, N. Y., 1950/51.
Шефер (Schaef er H.)
1. Halbgeordnete lokalkonvexe Vektorraurne, Math. Ann., 135 A958),
115—141; 138 A959), 259—286; 141 A960), 113—142.
2. Topological Vector Spaces, Macmillan Co., N. Y., 1966.
Шехтер (S ch ech t e r M.)
1. Some Lp estimates for partial differential equations, Bull. Am. Math.
Soc, 68 A962), 470—474.
HI и л о в Г. Е.
1. Однородные кольца функций, УМН, 6:1 D1) A951), 91—137.
2*. Математический анализ. Специальный курс, Физматгиз, М., 1961.
3*. Математический анализ. Второй специальный курс, М., «Наука», 1965.
Шилов Г. Е., ГуревичБ Л
1*. Интеграл, мера и производная, «Наука», М., 1964.
Шмайдлер (S ch m e i d 1 е г W.)
1. Lineare Cperatoren in Hilbertschen Raum Teubner, Verl. Stuttgart, 1954,
Шмульян В. Л.
1. О регулярно замкнутых и слабо компактных множествах в простран-
пространствах типа (В), ДАН СССР, 18 A938), 403—406.
% Ober linear^ topologische Raume, Мат. сб., 7D9) A940), 425—448,
Библиография 1045
3. О принципе вкладок в пространства типа (В), Мат. сб., 5 D7), A939),
317—328.
Шоке (Choquet G.)
1. Theory of Capacities, Univ. Kansas Press, Lawrence, 1954.
2. Unicite des representations integrates au moyen des points extremaux
dans les cones convexes reticules, C. R., 243 A956), 555—557.
3. Existence des representations integrates au moyen des points extremaux
dans les cones convexes, C. R., 243 A956), 699—702.
4. Limites projectives d'ensembles convexes et elements extremaux, C. R.,
250 A960), 2495—2497.
5. Le theoreme de representation integrate dans les ensembles convexes
compacts, Ann. Inst. Fourier (Grenoble), 10 A960), 333—344.
6. Representations integrates dans les cones converxes sans compacte, С R.y
253 A961), 1901 — 1903.
7. Axiomatiques des mesures maximales. Applications aux cones convexes
faiblement complets, C. #., 255 A962), 37—39.
8. Etude des mesures coniques. Cones convexes saillants faiblement com-
complets sans generatrices extremales, C. R., 255 A962), 445—447.
Шоке, Д е н и (С h о q u e t G., D e n у J.)
1. Aspects lineaires de la theorie du potentiel, C. R., 243 A956), 222—225,
764—767.
Шоке, Мейе (Choquet G., Meyer P.-A.)
1. Existence et unicite des representations integrates dans convexes com-
compacts quelconques, Ann. Inst. Fourier (Grenoble), 13 A963), 139—154.
Шрейдер Ю. A.
1. Об одном примере обобщенного характера, Мат. сб., 29G1), A951),
419—426.
Шур (Sen ur I.)
1. Uber die charakterische Wurzeln einer linearen Substitution mit em
Anwendung auf der Theorie der Integralgieichungen, Math. Ann., 66
A909), 488—510.
Эберлейн (EberleinW. F.)
1. Weak Compactness in Banach spaces. I, Pros. Nat. Acad. Sci. USA, 33
A947), 51—53.
2. Banach-Haussdorff limits, Proc. Am. Math. Soc, E), 1 A950), 662—665.
3. Closure, convexity and linearity in Banach spaces, Ann. Math., 47
A946), 688—703.
Эгнью (A g n e w R. P.)
1. Spans in Lebesgue and uniform spaces of translations of step functions,
Bull. Am. Math. Soc, D), 51 A945), 229—233.
2. Spans in Lebesgue and uniform spaces of translations of peak functions
Am. J. Math., 67 A945), 431—436.
Э г н ь ю, М о р с (AgnewR. P, MorseA. P.)
1. Extensions of- linear functional, with applications to limits, integrals
measures and densities, Ann. Math., 39 A938), 20—30.
Эдварде (EdwardsR. E.)
1. On functions whose translates are independent, Ann. Inst. Fourier 3
A951), 31—72.
2. On convex spans of translates of functions on a group, Proc. London
Math. Soc, C), 3 A953), 222—242.
3. A theory of Radon measures on locally compact spaces Ada Math.
89 A953), 133—164.
4. The exchange formula for distibutions and spans of translates Proc.
Am. Math. Soc, 4 A953), 888—894.
5. On the functions which are Fourier transforms, Proc. Am, Math, $ос.ш
5 A954), 71-78.
1046 Библиография
6. On factor functions, Pacific /. Math., 5 A955), 367—378.
7. Note on two theorems about function algebras, Mathematica, 4 A957),
138—139.
8. The Hellinger-Toeplits theorem, /. London Math. Soc, 32 A957),
499—501.
9. Representation theorems for certain functional operators, Pacific J.
Math., 7 A957), 1333—1339.
10. Bounded functions and Fourier transforms, Proc. Am. Math. Soc, 9
A958), 440—446.
11. Simultaneous analytic continuation, /. London. Math. Soc, 34 A959),
264—272.
12. Approximation theorems for translates, Proc. London Math. Soc, C),
9 A959), 321—342.
13. Integral bases in inductive limit spaces, Pacific J. Math., 10 A960),
797—812.
14. Algebras of holomorphic functions, Proc. London Math. Soc, C), 7
A957), 510—517.
15. Derivatives of vector-valued functions, Mathematica, 5 A958), 58—
61.
16. The stability of weighted Lebesgue spaces, Trans. Am. Math. Soc, 93
A959), 369—394.
Эдварде, Хьюитт (Edwards R. E., Hewitt E.)
1. Pointwise limits for sequences of convolution operators, Ada Math., 113
A965), 181—218.
Эдельштейн (Edelstein M.)
1. An extension of Banach's contraction principle, Proc Am. Math. Soc,
12 A) A961), 7—10.
2. On fixed and periodic points under contractive mappings, /. London
Math. Soc, 37 A962), 74—79.
Э п ш т е й н (E p s t e i n B.)
1. Partial Differential Equations, McGraw-Hill Book Co., Inc., N. Y.t
1962.
Эренпрейс (EhrenpreisL.)
1. The Theory of Distributions for Locally Compact Spaces, Mem. Am.
Math. Soc, № 21, 1956.
2. Solution of some problems of division. I—III, Am. J. Math., 76 A954),
883—903; 77 A955), 286—292; 78 A956), 685—715.
3 Analytic functions and the Fourier transform of distributions. I, Ann.
Math., 63 A956), 129—159; //, Trans. Am. Math. Soc, 89 A958),
450-483.
4. Mean periodic functions, Am. J. Math., 78 A955), 292—328.
5. General theory of elliptic equations, Proc Nat. Acad. Sci. USA, A),
42 A956), 39—41.
6. The division problem for distributions, Proc Nat. Acad. Sci. USA, 42
A956), 756—758.
7. Completely inversible operators, Proc Nat. Acad. Sci. USA, 42 A956),
945_946.
8. Theory of infinite derivatives, Am. J. Math., 81 A959), 799—845.
9. A new proof and extension of Hartog's theorem, Bull. Am. Math. Soc,
67 A961), 507—509.
10. Analytically uniform spaces and some applications, Trans. Am. Math.
Soc, 101 A961), 52—74.
11 A fundamental principle for systems of linear differential equations
with constant coefficients and some of its applications, Proc. Intern.
Symp. Linear Spaces (Yerusalem, I960), 161—174: Pergamon Press,
N. У, 1961,
Библиография 1047
12. On the theory of kernels of Schwartz, Proc. Am. Math. Soc, 7 A956),
713-718.
Эренпрейс, Маутнер (Ehrenpreis L, Mautner F. J.)
1. Some properties of distributions on Lie groups, Pacific J. Math., 6
A956), 591—606.
2. Some properties of the Fourier transform on semisimple Lie groups. II,
Trans. Am. Math. Soc, 84 A957), 1—55; III, там же, 89 A959),
431—484.
Юд (Yood В.)
1. On fixed points for semigroups of linear operations, Proc. Am. Math.
Soc, 2 A951), 225—233.
Именной указатель
Агжери (Aggeri J. С.) 974, 1013
Агранович М. С. 554, 1013
Адамар (Hadamard J.) 300, 424, 487
Александров А. Д. 300, 1013
Альтман (Altman M.) 237, 1013
Амброз (Ambrose W.) 1013
Аранда (Aranda P. J.) 913, 1013
Арене (Arens R. F.) 294, 298, 689,
974, 1013
Ароншайн (Aronszajn N.) 912, 1013
Арсов (Arsove M. G.) 620, 621, 1014
Артин (Artin E ) 222, 1014
Ахиезер Н. И. 132, 1014
Баде (Bade W.) 981, 1017
Бак (Buck R. С) 1014
Банах (Banach S.) 7, 64, 124, 186,
215, 223, 300, 307, 383, 386, 574,
578, 601, 620, 621, 622, 634, 636,
695, 713, 724, 725, 920, 937, 974,
1014
Бартл (Bartle R. G.) 899, 902, 1014
Басе (Bass R.) 232, 1014
Белицкий (Bielicki A.) 218, 1014
Беллман (Bellman R.) 234, 1014
Бенке (Behnke H.) 545, 1014
Бергман (Bergmann S.) 1014
Беркхилл (Burkhill J. С.) 278, 1014
Бернулли (Bernoulli) (семья) 471
Берс (Bers L) 1014
Бессага (Bessaga G.) 621, 1014
Бёрлинг (Beurling A.) 1015
Биркгоф Г. (Birkhoff G.) 397, 805,
822, 840, 1015
Биркгоф Г. Д. (Birkhoff G. D.) 159,
212, 213, 1015
Бишоп (Bishop E.) 981, 1015
Бледсоу (Bledsoe W. W) 1015
Богданович (Bogdanowicz W. М.)
792, 810, 1015
Боголюбов Н. Н. 1015
Бозанке (Bosanquet L. S.) 634, 1015
Боненблуст (Bohnenblust F.) 85, 196,
1016
Бонсол (Bonsall F. F.) 213, 981, 1015
Бохнер (Bochner S.) 299, 466, 526,
527, 528, 763, 801, 805, 912, 984,
985, 1015, 1016
Бранж (de Branges L.) 291, 292, 1016
Браудер (Browder F. E.) 215, 237,
567, 722, 1016
Брело (Brelot M.) 177, 1016
Бремерман (Bremmermann H.) 412,
1016
Брэй (Bray H. E.) 290
Брэйнерд (Brainerd B.) 9
Брэйс (Brace J. W.) 875, 1017
Бурбаки (Bourbaki N.) 8, 11, 19, 34,
38, 40, 41, 48, 49, 51, 52, 55, 62,
63, 77, 80, 98, 134, 164, 165, 174,
209, 220, 246, 253, 282, 291, 294,
297, 298, 302, 345, 346, 364, 375,
397, 398, 538, 578, 585, 587, 583,
589, 595, 608, 609, 614, 618, 631,
632, 654, 655, 672, 693, 694, 696,
699, 738, 751, 756, 763, 765, 766,
768, 776, 781, 789, 790, 792, 795,
802, 805, 810, 813, 822, 834, 844,
850, 865, 868, 871, 876, 882, 900,
995, 974, 986
Бьюси (Bucy R. S.) 997, 1017
Вада (Wada J) 60, 902, 1017
Вайтман (Wightman A. S.) 466, 1017
Валбрук (Waelbroeck L.) 1017
Балле Пуссен (de la Vallee Pous-
sin C.) 177, 183, 287, 1017
Варадараян (Varadarajan V. S ) 298,
1017
Вейерштрасс (Weierstrass K.) 487
Вейль A. (Weil H ) 49, 345, 346, 374,
400, 996, 997, 1007
Вейль Г. (Weyl H.) 146, 148, 345, 467,
472, 481, 1017
Вейс (Weiss G) 1017
Вендель (Wendel J) 1017
Вертейм (Wertheim D. G.) 1018
Вестон (Weston J. D.) 586, 1018
Вехаузен (Wehausen J. V.) 1018
Виленкин Н. Я. 412, 464, 1019
Именной указатель
1049
Винер (Wiener N.) 183, 208, 487, 535,
1010, 1018
Вишик М. И. 506, 1018
Владимиров В. С. 1015
Вольтерра (Volterra V.) 460
Вудбери (Woodbury M. А) 223, 1018
Вулих Б. 3. 278, 397, 801, 1018, 1025
Гальперин (Halperin I.) 115, 412, 465,
1018
Гантмахер В. Р. 858, 1018
Гарни (Garnir H. G.) 430, 467, 468,
472, 481, 485, 494, 501, 504, 1018
Гельфанд И. М. 291, 412, 420, 434, 464
465, 530, 537, 634, 774, 790, 801,
854, 985, 986, 990, 1018, 1019
Георгиу (Gheorgiu В.) 970, 1019
Герглотц (Herglotz G.) 290, 986, 1019
Гёде (Gohde D.) 215, 1019
Гильберт (Hilbert D.) 237, 412, 458,
849, 902, 1019
Гильдебрандт (Hildebrandt Т. Н.) 30,
1019
Гильман (Gillman L.) 30, 167, 291,
655, 1019
Глазман И. М. 132, 1014
Гликсберг (Gliksberg I.) 298, 1019
Годман (Godement R.) 955, 972, 974,
985, 986, 997, 1019
Гординг (Garding L.) 9, 10, 465, 467,
550, 557, 558, 559, 567, 568, 569,
592, 957, 1019, 1020
Гоулд (Gould G. G.) 298, 654, 1020
Гофман (Hoffman К.) 122, 1020
Гоффман (Goffrnan С.) 278, 1020
Гохберг И. Ц. 132, 939, 955, 1020
Грамш (Gramsch В.) 763, 1020
Гранас (Granas A.) 237, 1020
Грейвс (Graves L. М.) 60, 213, 278,
1020
Гротендик (Grothendick A) 8, 133,
299, 375, 386, 388, 545, 580, 594,
608, 615, 617, 734, 756, 759, 774,
826, 843, 844, 850, 865, 870, 871,
872, 876, 877, 887, 890, 893, 898,
899, 900, 920, 968, 1020, 1021
Гуднер (Goodner D. В.) 900, 981, 1021
Гурарий В. П. 1021
Гуревич Б. Л. 278, 1045
Даламбер (d'Alambert J.) 471
Данвуди (Dunwoody M) 9
Даниэль (Daniell P. J.) 246, 1021
Данфорд (Dunford N.) 8, 17, 19, 61,
132, 150, 160, 223, 227, 299, 374,
388, 397, 400, 412, 620, 695, 735,
756, 759, 763, 771, 783, 785 788
789, 790, 792, 801, 805, 810, 837
870, 872, 879, 882, 886, 894, 895,'
899, 901, 902, 911, 912, 920, 965,
974, 1014, 1021
Дворецкий (Dvoretzky A.) 1021
Дени (Deny J.) 173, 457, 458, 488,504,
572, 629, 630, 958, 962, 1015, 1021,
1045
Депри (Deprit A) 939, 1021
Джеймс (James R. С.) 756
Джерисон (Jerison M.) 30, 167, 291,
602, 655, 1019, 1021
Джон (John F.) 557, 1014, 1022
Джонсон (Johnson В. Е.) 1022
Диксмье (Dixmier J.) 210, 227, 243,
1022
Динкуляну (Dinculeanu N.) 792, 795,
810, 834, 899, 1022
Доногю (Donoghue W. Fr., Jr.) 795,
1022
Дьёдонне (Dieudonne J.) 215, 216, 222,%
372, 375, 388, 393, 595, 614, 618,
620, 621, 699, 735, 736, 738, 756,
805, 822, 826, 920, 939, 953, 963,
1022, 1023 ,
Дэвис (Davis W. J.) 628, 1023
Дэй (Day M. M.) 8, 620, 834, 1023
Заанен (Zaanen A. C.) 102, 216, 911,
920, 953, 970, 1023, 1030
Зигмунд (Zygmund H. A.) 122, 400,
401, 535, 603, 621, 643, 677, 724,
837, 912, 1007, 1012, 1023, 1024
Иино (lino) 774, 1023
Ионеску Тулча A. (Ionescu Tulcea A.)
792, 795, 810, 834, 882, 1023
Ионеску Тулча К. (Ionescu Tulcea С.)
792, 795, 810, 834, 882, 1023, 1024
Иосида (Iosida К.) 298, 849, 965, 1024
Иосинага (Yoshinaga К.) 447, 682,
1024
Исеки (Iseki К.) 1024
Кадота (Kadota Т. Т.) 953, 1024
Какутани (Kakutani S) 120, 212, 213,
235, 291, 297, 300, 397, 398, 695,
849, 853, 900, 1024
Кальдерон (Calderon А. Р.) 400, 401,
504, 912, 1024
Канторович Л. В 215, 237, 298, 397,
801, 1025, 1040
Каплан (Kaplan S ) 742, 1025
Капланский (Kaplanskv J.) 294, 1025
Карадус (Caradus S. R.) 939, 1025
1050
Именной указатель
Карлеман (Carleman Т.) 526, 1025
Карлин (Karlin S.) 196
Картан (Cartan H.) 164, 177, 539,540,
940, 972, 985, 986, 997, 1025
Касахара (Kasahara S.) 1024
Каттанео (Cattaneo E. Р.) 913, 1013
Кахан (Kahane J-Р.) 728, 1025
Кацнельсон (Katznelson J.) 1025, 1030
Качмаж (Kaczmarz S.) 603, 620, 724,
1025
Каччиополи (Caccioppoli R.) 215, 1026
Келли (Kelley J. L.) 8, 11, 12, 17, 18,
19, 23, 29, 30, 40, 41, 42, 44, 45,
48, 49, 51, 53, 60, 118
Келлог (Kellog О. D.) 113, 114, 182,
212, 213, 1026
Кендалл (Kendall D. G.) 974, 1026
Келельман (Kestelman H ) 634, 1015
Кёниг (Konig H.) 421, 465, 1026
Кёте (Kothe G ) 8, 580, 617, 655, 729,
738, 844, 1026
Кирк (Kirk W. A.) 215, 1026
Кист (Kist J.) 840, 1026
Кларксон (Clarkson J. A.) 1026
Кли (Klee V.) 120, 211, 223, 237, 756,
1026
Кодайра (Kodaira R.) 447, 1027
Коддингтон (Coddington E. A.) 109,
471, 902, 1027
Коидзуми (Koizumi S.) 912, 1027
Коллинз (Collins H. S.) 729, 731, 756,
1027
Колмогоров А. Н. 126, 232, 278, 1027
Комура (Komura Y.) 596, 700, 1027
Конвей (Cunway J. 3.) 388, 1027
Кордуняну (Corduneanu C.) 234, 240,
1027
Коревар (Korevaar J.) 1027
Коротков В. Б. 912, 1027
Корсон (Corson H. H.) 756, 1027
Костюченко А. Г. 1027
Котляр (Cotlar M.) 400, 401, 912,
1028
Коши (Cauchy A.) 337
Крам (Crum M. M.) 985, 1028
Крейн М Г. 132, 195, 738, 759, 955,
972, 974, 1020, 1028
Кристиан (Christian R R) 300 1028
Кук (Cooke R. G.) 64, 79, 132, 582,
643, 955, 1028
Купер (Cooper J. L. В ) 985, 1028
Купмэн (Koopman В. О) 157
Курант (Courant R) 237, 412, 458,
902, 1028
Куратовский (Kuratowski С.) 18, 23,
30, 634, 1028
Лав (Love E. R.) 1028
Лайтхилл (Lighthill M. J.) 465, 530,
1028
Лалеско (Lalesco T.) 970, 1028
Ламадрид (Gil de Lamadrid J.) 1028
Лебег (Lebesgue H.) 9, 323
Леви Г. (Lewy H.) 549
Левин В. Л. 744, 1029
Левинсон (Levinson N.) 109, 471, 902,
1027
Лерэ (Leray J.) 213, 236, 237, 934,
1029
Лефшец (Lefschetz S.) 60, 1029
Ливингстоун (Livingstone A. E.) 122,
1029
Линденштраус (Lindenstrauss J.) 756,
1027
Лионе (Lions J. L.) 457, 458, 465, 481,
488, 504, 506, 535, 567, 572, 592,
629, 630, 957, 958, 962, 1020, 1021,
1029
Литтлвуд (Littlewood J. E.) 121, 247,
400, 401, 1041
Лоренц (Lorentz G. G.) 1029
Лорх (Lorch E. R.) 920, 988, 1029
Лоясевич (Lojasiewicz S ) 423, 1029
Лю (de Leeuw R.) 981, 1030
Любарский Г. Я. 997, 1030
Люксембург (Luxemburg W. A. J.)
844, 1030
Люмис (Loomis L. H.) 167, 208, 297,
298, 345, 346, 369, 602, 878, 955,
986, 988, 1010, 1030
Люстерник Л. А. 1030
Маак (Maak W.) 996, 997, 1030
Мазур (Mazur S) 64, 582, 1030
Майерс (Myers S. B.) 1030
Макаров В. М. 596
Мак-Артур (McArthur С. W.) 628,
1030
Макдональд (McDonald J.) 5
Макки (Mackey G. W.) 654, 682, 687,
835, 1030
Мак-Кинси (McRinsey Y. С. С.) 201,
206, 1030
Мак-Шейн (McShane E. Y.) 278, 300,
329 1030
Малтиз' (Maltese G) 997, 1017
Мальгранж (Malgrange В ) 480, 481,
506, 509, 511, 512, 537, 539, 540,
544, 545, 546, 548, 549, 558, 567,
618, 844, 1020, 1031
Малявен (Malliavin P.) 372, 1031
Марков A. A. 212, 300, 1030
Маркушевич А. И. 620, 1031
Именной указатель
1051
Мартин (Martin W. Т.) 1016
Мартино (Martineau A.) 729, 1031
Марцинкевич (Marcinkiewicz J.) 399,
400, 1031
Массера (Massera J. L.) 234, 1031
Маутнер (Mautner F. J) 1047
Махарам (Maharam D.) 795, 1031
Маховальд (Mahowald M.) 298, 654,
734, 1020, 1030, 1042
Мейе (Meyer P. A.) 981, 1045
Мехди (Mehdi M. R.) 634, 1031
Мидзохата (Mizohata S.) 1031
Минусинский (Mikusinski J.) 418, 465,
466, 1031, 1032
Мильман Д. П. 972, 974, 1032
Миранда (Miranda С) 237, 1032
Миркилл (Mirkill H ) 1030
Миттаг-Лефлер (Mittag-Lefler) 546
Моргенштерн (Morgenstern О.) 201,
206, 1033
Морс (Morse А. Р.) 222, 1015, 1032
Мур (Moore E. Н.) 18, 1032
Мурье (Mourier Edith) 805, 834, 1032
Нагумо (Nagumo M.) 237, 1032
Надь см. Секефальви-Надь
Наймарк М. А. 346, 347, 369, 986, 1032
Накамура (Nakamura M.) 858, 1032
Накано (Nakano H ) 397, 1032
Намиока (Namioka J.) 8, 53, 70, 118,
397, 575, 589, 920, 1026
Натансон И. П. 255, 278, 284, 286,
287, 328, 329, 1032
Нахбин (Nachbin L.) 654, 900, 1032
Неванлинна (Nevanlinna R.) 290
Нейман (von Neumann J.) 132, 150,
201, 206, 346, 567, 1032
Никодим (Nikodym О.) 1033
Никольский С. М. 939, 1033
Ниренберг (Nirenberg L.) 1033
Ньюмен (Newman D. J.) 102, 1033
Ньюнс (Newns W. F.) 621, 1033
Огата (Ogata H.) 447, 534, 682, 1024,
1042
Окландер (Oklander E.) 913, 1013
Орлич (Orlicz К.) 64, 582, 634, 866,
1030, 1033
Оцука (Ohtsuka M.) 177, 1033
Паламодов В. П. 1033
Пеано (Peano G.) 215, 232, 1033
Пек (Peck N. Т.) 981, 1033
Пелчинский (Pelczyriski A.) 621, 1033
Перрон (Perron) 183, 487
Петер (Peter F.) 345
Петре (Peetre J ) 473, 558, 1033
Петришин (Petryshyn W. V.) 215,
1016, 1033
Петровский И. Г. 557, 1033
Петтис (Pettis В. J.) 374, 774, 788,
792, 801, 805, 822, 870, 872, 882,
886, 901, 1021, 1034
Пжеворска-Ролевич (Przeworska-Ro-
lewicz D.) 763, 1034
Пикар (Picard E.) 215, 237, 1034
Пинскер А. Г. 397, 1025
Планшерель (Plancherel M.) 1001,
1034
Плеснер А. И. 290
Пойа (Polya G.) 121, 247, 400, 1041
Понтрягин Л. С. 345, 994, 1034
Прайс (Price G. В.) 756, 1034
Прайс Дж. (Pryce J. D.) 1034
Птак (Ptak V.) 575, 618, 729, 730, 731,
736, 742, 744, 745, 1033, 1034
Пэли (Paley R. Е. А. С.) 535, 1018
Радон (Radon J.) 300, 1034
Райков Д. А. 63, 575, 729, 985, 986,
990, 1019, 1034
Ракоч (Rakotch E.) 1035
Рам (de Rham G.) 8, 447, 465, 574,
1035
Раух (Rauch H. E.) 401, 1035
Резерфорд (Retherford J. R.) 628, 1035
Рейтер (Reiter H.) 372, 1035
Риккарт (Rickart С. Е.) 167, 369,371,
602, 878, 955, 1035
Рингроуз (Ringrose J. R.) 1035
Рис (Riss J.) 1035
Рисе М. (Riesz M.) 374, 399, 400, 465,
1007, 1035
Рисе Ф. (Riesz F) 64, 132, 139, 150,
246, 290, 300, 397, 408, 695, 846,
849, 919, 920, 933, 955, 988, 1035,
1036
Робертсон А. П. (Robertson А. Р.)
729, 731, 1036
Робертсон В. (Robertson W.) 575, 585,
586, 600, 1036
Рогозинский (Rogosinski W. W.) 1036
Роджерс (Rogers С. А.) 1021
Розенблюм (Rosenbloom P.) 19, 1036
Ройден (Royden H. L.) 1036
Ролевич (Rolewicz S.) 763, 1034
Росс (Ross К. А.) 223, 227, 246, 345,
346, 347, 353, 370, 372, 373, 1043
Рота (Rota G. С.) 722, 1036
Рудин (Rudin W.) 208, 370, 372, 726,
728, 986, 1007, 1036
Рутман М. А. 974, 1032
1052
Именной указатель
Сакс (Saks S.) 1036
Салем (Salem R.) 728, 1025
Сандерс (Sanders В. L.) 628, 1037
Сапе (Suppes P.) 11, 278, 297, 300,
1037
Сарджент (Sargent W. L. С.) 633,
864, 1037
Сарымсаков Т. А. 231, 1037
Себаштьян э Сильва (SebastiSo e Sil-
va J.) 465, 589, 1037
Секефальви-Надь (Sz-Nady В.) 132,
408, 955, 988, 1036
Серр (Serre J.-P.) 100, 927
Сигал (Segal I. E.) 372, 1010, 1037
Сикорский (Sikorski R.) 418, 1032
Сильвермэн (Silverman R. J.) 223,
1037
Симоне (Simons S.) 654, 1037
Сингер (Singer I.) 620, 731, 826, 1037
Сираиси (Shiraishi R.) 447, 1045
Сирота (Shirota T.) 653, 645, 1038
Словиковский (Slowikowski W.) 596,
729, 1038
Смит (Smith H. L.) 401, 1032
Смитис (Smithies F.) 5, 216, 902,937,
953, 1038
Соболев В. И. 1030
Соболев С. Л. 413, 446, 457, 467, 1038
Собчик (Sobczyk A.) 85, 1016
Стаки (Stuckey S.) 9
Стейн (Stein E. М.) 400, 401, 1038
Степанов В. В. 109
Стинрод (Steenrod N.) 589, 1038
Стоун (Stone М. Н.) ПО, 132, 205,
290 295, 297, 298, 471, 955, 974,
1038
Сухомлинов Г. А. 85
Сцидон (Szidon) 724, 725
Тайхмюллер (Teichmuller) 19
Такенути (Takenouchi О.) 1038
Такер (Tucker D. Н.) 1038
Тамаркин (Tamarkin J. D.) 1042
Темпл (Temple G.) 465, 1039
Tep-Xaap (Тег Нааг D.) 160, 1039
Теплиц (Toeplitz О.) 744, 1041
Ти йен (Ti Yen) 223, 1039
Титце (Titze) 30
Титчмарш (Titchmarsh Е. С.) 526,
912, 970, 1039
Тихонов А. Н. 212, 1039
Тодд (Todd J. A.) 10
Толстов Г. П. 1039
Тонелли (ТопеШ L.) 337
Торин (Thorin G. О) 400, 1039
Трев (Treves F) 558, 560, 566, 1039
Тыоки (Tukey J. W.) 1039
Тэйлор (Taylor A. E ) 8, 62, 63, 80,
122, 620, 744, 801, 805, 920, 939,
1016, 1039
Тэтчелл (Tatchell J. В.) 582, 1039
Уильямсон (Williamson) 127 1039
Уитни (Whitney H.) 297, 1039
Улам (Ulam S.) 654, 1039
Уолтере (Walters S. S.) 122, 837,
1040
Уорнер (Warner S.) 654, 1040
Урысон П. С. 30
Фан (Fan Ky) 206, 236, 1040
Фелпс (Phelps R. R.) 981, 1040
Фернли-Сандер (Fearnly-Sander D.)
211
Филлипс (Phillips R. S.) 5, 299, 763/
788, 789, 805, 809, 810, 814, 815,
817, 818, 833, 882, 1040
Фихтенгольц Г. М. 298, 835, 1040
Фомин С. В. 232, 278, 1027
Форте (Fortet R.) 805, 834, 1040
Фояш (Foias С.) 792, 810, 834, 899,
1022
Фредгольм (Fredholm Y) 920, 1040
Фреше (Frechet) 300, 1040
Фридман (Friedman A.) 412, 1040
Фридрихе (Friedrichs К. О.) 115, 466,
1040
Фростман (Frostman О.) 117, 183,
287, 1040
Фубини (Fubini G.) 337
Фуглид (Fuglede В.) 115, 458, 561,
1040
Хаар (Нааг А.) 346
Халмош (Halmos P.) И, 62, 69, 76,
132, 133, 150, 160, 278, 297, 298,
347, 955, 1040
Хан (Hahn H ) 86, 1041
Хант (Hunt G. А.) 173, 1041
Харди (Hardy G. Н.) 121, 247, 400,
401, 1041
Хелли (Helly E.) 1041
Хеллингер (Hellinger E.) 744, 1041
Хелсон (Helson H.) 724, 726, 727, 728,
1010, 1041
Хенсток (Henstock R.) 663, 1041
Хёрмандер (Hormander L.) 412, 423,
468, 471, 506, 507, 510, 511, 512,
513, 537, 546, 547, 549, 550, 555,
557, 558, 560, 561, 562, 563, 565,
606, 722, 958, 1041
Именной указатель
1053
Хилле (Hille E.) 299, 300, 763, 771,
788, 789, 805, 970, 1041, 1042
Хинчин А. Я. 156, 160, 1042
Хирата (Hirata Y.) 447, 534, 682, 1042
Хойзер (Heuser H.) 939, 1042
Хусейн (Husain Т.) 598, 729, 1042
Ху Сы-цзян (Sze-Tsen Ни) 60,
1042
Хьюитт (Hewitt E.) 9, 227, 246, 295,
298, 299, 345, 346, 347, 353, 370,
372, 373, 724, 725, 1006, 1007,
1042, 1043
Целлер (Zeller К.) 582, 646, 1043
Цорн (Zorn M.) 19
Цудзи (Tsuji M.) 374, 1043
Цукерман (Zuckerman H. S.) 298, 724,
725, 1043
Чандрасекхаран (Chandrasekharan K-)
1043
Чаттерджи (Chatterji) 805
Чепмэн (Chapman J.) 9
Шаудер (Schauder J.) 212, 213, 236,
237, 620, 853, 919, 920, 1029, 1043
Шварц Дж. (Schwartz J. T.) 8, 17,
19, 61, 132, 150, 160, 227, 299,
388, 397, 400, 401, 412, 620, 695,
735, 756, 759, 763, 771, 783, 785,
788, 789, 792, 802, 805, 810, 837,
879, 886, 894, 895, 899, 901, 902,
911, 912, 920, 974, 1014, 1041,
1043
Швярц Л. (Schwartz L.) 5, 115, 187,
208, 297, 411, 412, 413, 415, 421,
445, 447, 453, 457, 458, 459, 460,
461, 464, 465, 466, 467, 473, 480,
481, 504, 506, 509, 511, 516, 517,
523, 524, 528, 530, 533, 534, 535,
537, 544, 545, 548, 549, 565, 567,
573, 574, 581, 591, 595, 614, 618,
674, 678, 679, 699, 729, 736, 738,
1040, То43
Шварц С. (Schwartz S.) 1044
Шевалле (Chevalley С.) 447, 679 1044
Шептицкий (Szeptycki P.) 912, 1013
Шефер (Schaefer H.) 700, 840, 1044
Шеффер (Schaffer J. J.) 234, 1031
Шехтер (Schechter M.) 1044
Шилов Г. Е. 278, 291, 412, 420 434
465, 530, 537, 1019, 1044 1045
Ширков Д В. 1015
Шмайдлер (Schmeidler W.) 132 1045
Шмульян В. Л. 695, 738, 75l', 756
759, 1028, 1045
Шоке (Choquet G.) 173, 972, 980, 981
1045
Шрейдер Ю. А. 1045
Штейн (Stein К.) 545, 1014
Шгейнгауз (Steinhaus H) 603, 620
724, 1025
Шур (Schur I.) 864, 970, 1045
Эберлейн (Eberlein W. F.) 634, 695,
751, 1045
Эванс (Evans) 290
Эгнью (Agnew R. Р.) 208, 222, 1010,
1046
Эдварде (Edwards R. Е.) 5, 208, 246,
253, 295, 297, 302, 338, 464, 534,
603, 604, 605, 611, 620, 621, 725,
744, 774, 1006, 1010, 1014, 1046
Эделыитейн (Edelstein M) 215, 240,
241, 1046
Эдмондс (Edmonds M ) 9
Эйленберг (Eilenberg S.) 589, 1038
Эйлер (Euler L.) 471
Эпштейн (Epstein В.) 468, 487, 1046
Эренпрейс (Ehrenpreis L.) 464, 465,
466, 481, 507, 516, 536, 537, 548,
556, 1046, 1047
Эскин Г. И. 1018
Юд (Yood В.) 323, 1047
Предметный указатель
абсолютная непрерывность 323, 324
локальная 323
абсолютно выпуклая оболочка 80
абстрактное (L)-пространство 397
— (М)-пространство 900
алгебра банахова 837
— топологическая 295
алгебраический базис 73
алгебраическое дополнение 76
— сопряженное (пространство) 69
(отображение) 703
аксиома счетности вторая 38
первая 38
аксиомы отделимости 24
альтернатива Фредгольма 937
ассоциированное (об отделимых рав-
равномерных пространствах) 47
— (об отделимых топологических век-
векторных пространствах) 93
база окрестностей 22
— равномерной структуры 45
— топологии 21
базис алгебраический 73
— дуальный 75
— ортонормирозанный 144
— слабой суммируемости 627
— топологический 619
— Шаудера 619
слабый 619
банахова алгебра 837
банахово пространство 123
бесконечная часть 424
билинейная форма 133
симметричная 133
биортогональность 618
биполяра 686
борелевское множество 896
борнологическое пространство 651
бочка 585
бочечное пространство 585
быстро убывает (о функциях) 512
бэровское подпространство первого
класса 889
в конечном счете попадает (о сетях)
29
векторная решетка 397
— сумма множеств 65
векторное подпространство 65
порожденное 65
— пространство 63
упорядоченное 194, 397
векторные пространства изоморфные
69
верхняя грань 18
локально существенная 301
наименьшая 18
существенная 301
— огибающая 28
вещественно-компактное простран-
пространство 655
взаимная сингулярность (о мерах)
324
вложение 26
внутренность 23
восстановимость 793
восстановление 793
восстанавливающее отображение 794
вполне монотонная функция 981
— непрерывное отображение 849
второе сопряженное (отображение)
715
(пространство) 715
выпуклая комбинация 185
— оболочка 80
— уравновешенная комбинация 185
выпуклость (функций) 402
гиперболичность 559
гиперплоскость 67
— однородная 67
— опорная 208
гиперполнота 731
гипонепрерывность 664, 665
гипонепрерывность равностепенная
664, 665
гипээллиптичность 474, 556
главная часть (многочлена) 562
Предметный указатель
1055
главное значение (в смысле Коши)
428
гильбертов куб 228
■*— сопряженный 148
гильбертово пространство 134
голоморфное продолжение 611
голоморфность 771
гомеоморфизм 26
— на 26
гомоморфизм 97
гомотетия 87
граница 24
график 16, 70
группа абелева 63
— разрешимая 222
— топологическая 54
— унимодулярная 350
групповая алгебра 353, 360
групповое кольцо 353
движение 189
двойственное пространство 98
двойственность 683
— отделимая 683
диагональ 14
доминирование 566
дополнение абсолютное 13
— относительное 13
допускает равномерную структуру (о
пространствах) 49
дуальная группа 987
—- пара 682
дуальное пространство 98
— семейство линейных форм 75
евклидово пространство 133
единица абстрактного (М)-простран-
(М)-пространства 900
— Фрёйденталя 398
задача Дирихле 485
— Дирихле — Неймана 480
— Штурма — Лиувилля 963
закон двойственности 1003
— — Понтрягина 998
замкнутая оболочка 94
замыкание 23
— отображения 103
значение 15
идеал 295
идемпотентность 76
измельчение (о покрытиях) 38
измеримость 271, 305
— слабая 765
— сильная 765
изометрия 149
изоморфизм на 69
— в 69, 97
инвариантность относительно враще-
вращений 524
индуктивная топология 589
индуктивный предел 589
внутренний 589
строгий внутренний 595
интеграл Бохнера 299
— верхний 258
— Гельфанда 774
— Коши 772
— Петтиса 774
— Пуассона 287
— Римана — Стилтьеса 255, 256
— существенный 317
— существенный верхний 273, 313
интегральная формула Пуассона 289
интегрируемость 305, 765
— локальная 309
— сильная 765
существенная 765
— 317, 765
итерированный разностный оператор
981
инфрабочечное пространство 585
калибровочная функция 81
канонически ассоциированная (о то-
топологиях) 126
кардинальное число 19
квазиполнота 231, 656
квазиравностепенная непрерывность
908
класс 11
— эквивалентности 15
компактификация 40
— Александрова 40
— одноточечная 40
— Стоуна — Чеха 167
компактное отображение 848
компактнозначность 899
композиция 14
конечная топология 119
— часть 424
конечное (о линейных отображениях)
939
конус 193
— выпуклый 194
— выступающий 194
— заостренный 194
— положительный 194
коразмерность 77
коэффициентный функционал 619
коэффициент Фурье 603
1056
Предметный указатель
крайнее подмножество 973
критерий А. Вейля 373
— Данфорда — Петтиса 374
— Колмогорова 126
лагранжев сопряженный 469
лакунарность 724
лебегова лестница 402
— сумма 895, 896
лебегово пространство 115, 120
левоинвариантное среднее 209—210
лемма Крулля 539
— полуметризационная 48
— Римана — Лебега 641
(обобщенная) 995
— Урысона 30
— Фату 260
— Цорна 18
— Шура 997, 1008
лестница 402
линейная зависимость 70
— комбинация 71, 185
— независимость 70
— оболочка 65
— форма 68
относительно ограниченная 407
линейное многообразие 65, 68
— подпространство 65
— пространство 63
—"топологическое пространство 86
линейный функционал 68
лифтинг 793
локальная пренебрежимость 305
— счетность 320
локачьно абсолютно непрерывная
(векторная мера) 821
— выпуклая решетка 840
топология 117
■— сильнейшая 117
локально выпуклое пространство 115
— конечное семейство функций 43
— липшицева функция 836
— почти всюду 273
■— почти сепарабельнозначная (функ-
(функция) 782
— сепарабельное пространство 783
мажоранта 17
мажорирует 17
максимальный элемент 18
максимин 201
матрица 73
мера 246
— атомарная 253
— биинвариантная 350
•— векторная 810
мера внешняя 261, 264
— внутренняя 274
— Дирака 177, 252
— конечная 271
— конечной р-варнации 817
— Лебега 253
— Лебега — Стилтьеса 254, 256
— локально абсолютно непрерывная
821
— мажорированная 826
—- непрерывная 335, 402
— ограниченная 271
— относительно левоинвариантная
351
правоинвариантная 351
— положительная 175, 252
— -произведение 338
— Радона 250
векторная 762
вещественная 240
комплексная 250
£-значная 810
— скалярно локально абсолютно не-
непрерывная 812
— Стилтьеса 255, 256
— существенная внешняя 273
— Хаара 254. 346
левая 254, 346
левоинтриантная 346
правая 254, 346
метагармоническое уравнение 494
метод выметания Перрона 487
— ортогонального проектирования 467
— Пикара 215
— последовательных приближений
215
— Римана 487
— суммирования 581
Абеля — Пуассона 1010
Гаусса 1010
Чезаро 1010
метрика 44
метрическое пространство 44
минпмакс 201
минимальное разложение меры 251,
283
миноранта 18
минорирует 18
множества непересекающиеся 13
множества равномощные 19
множество И
— бесконечное 19
— борелевское 895
— всюду плотное 23
•— второй категории 53
— выпуклое 80
Предметный указатель
1057
множество замкнутое 23
— — по лучам 82
— измеримое 271
— индексов 16
— индуктивное 18
— интегрируемое 270
— компактное 35
— конечное 19
— линейно упорядоченное 18
— локально пренебрежимое 272
— максимальное открытое пренебре-
пренебрежимое 282
— малое порядка V 49
— направленное 20
— не более чем счетное 19
— несущее (меру) 324
— нетощее 53
— нигде не плотное 53
— ограниченное 94
— открытое 21
по лучам 82
— относительно замкнутое 24
открытое 24
— первой категории 53
— плотное 23
— поглощающее 80
— почти слабо замкнутое 729
— пренебрежимое 264
— проиндексированное 16
— пустое 12
— слабо ограниченное 131
— совершенно упорядоченное 18
— Сцидона 677
— счетное 19
— шпа Gb 358
— тотальное 186
— тощее 53
— универсально интегрируемое 281
— упорядоченное 17
— уравновешенное 80
— фундаментальное 186
— частично упорядоченное 17
— jLi-cr-колечное 272
— [7-малое 49
модуль 15, 33, 65
модулярная функция 348
мономорфизм 69
монтелево пространство 696
мощность 19
мультипликатор Фурье 603
надмножество 12
находятся в двойственности (о про-
пространствах) 683
неприводимость 1008
неравенство Бесселя 950
неравенство Гельдера 302
— Иенсена 402
— Кош и 773
— Коши — Шварца 133
— Минковского 302
— Пуанкаре 630
— треугольника 44
— Юнга 902
нижняя грань (наибольшая) 18
нижняя огибающая 28
норма 81
— естественная 125
— равномерная 291
нормальный эндоморфизм 953
нормированное пространство 120
нормируемое пространство 120
носитель 17, 282, 437
область значений 14
— Никодима 457—458
— определения 14
— Соболева 457
обобщенная последовательность 20
— сумма (ряда) 671
— функция 411, 415
обобщенный предел 166, 223
образ 16, 69
объединение 12
ограниченно компактное пространство
695
— слабая топология 735
ограниченность 635
— в D(Q) 415
— сильная 635
— относительно структуры порядка
840
однородность 524
— положительная 330
окрестность 21
— множества 21
— относительная 24
— точки 21
окружение 45
о тератор 15, 560
— Гильберта— Шмидта 937
— гиперболический 559
— гипоэллиптический 474, 556
— Грина 492
— замкнутого цикла 461
— Клейна — Гордона 552
— линейный 68
— локального типа 473
— максимальный 561
— минилальный 561
— (сильного) типа (/?, q) 400
— слабого типа (/?, q) 400
1058
Предметный указатель
оператор сублинейный 400
— эллиптический 545, 562
определяющее подпространство 838
отделяющее точки (о множестве
функций) 291
определяющее семейство полунорм
117
оптимальная смешанная стратегия 203
— стратегия 202
относительно сильное пространство
689
ортогональное дополнение 138
ортогональность 138
ортонормированный базис 144
ортонормированное семейство 139
открытый отрезок 972
отношение 14
— антисимметричное 14
— диагональное 14
— единичное 14
— обратное 14
— порядка 17
частичное 17
— рефлексивное 14
— симметричное 14
— транзитивное 14
— эквивалентности 15
отображение 15
— замкнутое 102
— линейное 68
— на 16, 69
— непрерывное 26
в точке 26
— ограниченное 97, 128
— открытое 26
— предзамкнутое 103
— равномерно непрерывное 47
— сжимающее 213
— строго положительное 177
отражение 346
отрезок 840
отрицательная часть меры 251
ослабленная топология 683
п. в. 264
параметрикс 452
пересечение 12
платежная функция 203
плотность меры 254
подмножество 12
подпокрытие 33
подпространство 65
подпространство собственное 67
подсеть 20
подхарактер положительный 367
покрытие 33
покрытие вписанное 38
— локально конечное 41
— открытое 33
— подчиненное 42
— точечно конечное 41
полная вариация 163, 255, 256
полная ограниченность 52
полнота (о семействе) 142
— секвенциальная 656
положительная часть меры 251
положительно определенная функция
984
положительное отображение (реше-
(решеток) 840
полултетрика 44
полуметрическое пространство 44
полунорма 81
полунормированное пространство 120
полунормируемое пространство 120
полунормы эквивалентные 125
полупространство 68
— замкнутое 100
— открытое 100
полурефлексивность 693
полуторалинейная форма 133
поляра 686
по одну сторону гиперплоскости 68
пополнение 51
порожденное (о подпространствах)
65
порядок (дифференциального опера-
оператора) 469
порядок распределения 439
потенциал Грина 552
потенциально компактный эндомор-
эндоморфизм 938
поток 156
— метрически транзитивный 159
— эргодически транзитивный 159
последовательность 16
постоянная Пуанкаре 630
почти всюду 264
почти непрерывность 598
почти открытость 598
— слабая топология 735
— слабо замкнутое (множество) 729
правильное пространство 699
предбаза топологии 21
предгильбертово пространство 134
предел 29
— обобщенный 166, 223
предкомпактное отображение 848
предкомпактность 52
представление 987
— измеримое 987
— непрерывное 987
Предметный указатель
1059
представление неприводимое 988
пренебрежимость 305
преобразование 15
— Гильберта 912
— Лапласа 369
— Фурье 370, 511
— Фурье (распределений) 520
— Фурье — Планшереля 1002
— Фурье —Шварца 520
— Эренпрейса 537
приводит в двойственность (о били-
билинейных формах) 683
принцип аппроксимации 185
— выбора 287
— выметания 176
— локализации 436
— мажорирования 176
— максимума Фростмана 176
— ОГБК 634
— Орлича — Гельфанда — Бозанке—
Кестельмана
—- продолжения 179
— проектирования 145
проблема деления (распределений)
548
продолжение 15
проектор 76
проекция 17, 76
— ортогональная 140
произведение 14, 17
— векторных пространств 67
— внутреннее 133
— декартово 14
— мер 338
— направленных множеств 20
— равномерных структур 48
— скалярное 133
— скалярное строго положительное
133
— топологий 31
— топологическое 31
производная (в смысле теории меры)
254
— (распределения) 419
прообраз 16
простая функция 786
пространство Беппо Леви 458, 572
— Монтеля 696
— представления 987
— Рисса 397
— со скалярным произведением 133
— Стоуна 398, 899
— Фреше 578
— Харди 136, 121
противоположный элемент 63
прямая сумма 76
псевдометрика 44
псевдофункция 430
равенство Парсеваля 142, 512 518
1001
равно нулю на п (о распределениях)
4d5
равномеризуемость 49
равномерная операторная топология
855
— равностепенная непрерывность 59
— структура 45
—- — индуцированная 48
левая 54
метризуемая 48
полуметризуемая 48
правая 54
равномерное пространство 46
вполне ограниченное 52
метризуемое 48
отделимое 47
полное 50
полуметризуемое 48
предкомпактное 52
равномерное пространство секвенци-
секвенциально полное 50
равностепенная непрерывность 56
в точке 56
разбиение единицы 43, 436
раздельная непрерывность 662
разложение единицы 942
разложение Лебега 326
размерность 73
размерность гильбертова 135
— представления 987
ранг 78
распределение 411, 415
— инвариантное относительно вра-
вращений 524
— медленно растущее 519
— однородное 524
— £-значное 466
регуляризация 416
ретракт 241
рефлексивность 694
решение слабое 472
решетка 266, 397
— векторная 397
— локально выпуклая 840
— топологическая векторная 840
росток 594
ряд Неймана 240
самосопряженность 149
самосопряженный эндоморфизм 940
свертка 837
1060
Предметный указатель
свертка определена 355
— (мер) 355
— (распределений) 447
— существует 355
— усеченная 369
— (функций) 354, 360
— Шевалле 679
свойство Бэра 634
—- Данфорда — Петтиса 872
— Данфорда — Петтиса строгое 872
— Дьёдонне 887, 889
— неподвижной точки 228
— Рисса 939
— секвенциально замкнутого графика
618
— среднего значения 288
— (D) 887, 889
— (DP) 872
— (SDP) 872
связанная переменная 12
сдвиг 87
— левый 346, 363
— правый 346, 363
секвенциальная сходимость 173, 245
семейство 13, 16
— направленное 20
■— ортогональное 138
— ортонормированное 139
— полное 142
— центрированное 33
сепарабельность 135
сети Коши эквивалентные 52
сеть 20
— Коши 50
— фундаментальная 50
сжатие 213
сила (оператора) 561
сильная операторная топология 855
— сходимость 855
— топология 693
сильнее (об операторах) 561
— (о равномерных структурах) 46
— (о топологиях) 24
сильнейшая линейная топология 119
— локально выпуклая топология
117
сингулярное интегральное преобразо-
преобразование 912
система дизъюнктная 13
— локально счетная 320
— образующих 65
— Хаара 620
скалярно вполне интегрируемая функ-
функция 781
•— локально абсолютно непрерывная
мера 812
скалярно (о каких-либо свойствах)
764
слабая операторная топология 855
— сходимость 142
слабее (о равномерных структурах)
46
— (о топологиях) 24
слабо компактное отображение 859
сложение 63
собственная часть 12
собственное значение 929
— подпространство 929
совершенно полное пространство 730
согласуется с двойственностью (о
топологиях) 197
соответствие 15
сопряженное (отображение) 702
сопряженный лагранжев 469
— формальный 469
спектр 929
— алгебраический 929
спектральная кратность 930
спектральное значение 929
— значение алгебраическое 929
— значение топологическое 929
— подпространство 930
— разложение 942
среднее 225
— биинвариантное 226
— левоинвариантное 226, 243
— правоинвариантное 226, 243
степенной ряд сходящийся 539
формальный 538
стратегическая седловая точка 202
строго по одну сторону гиперплоско-
гиперплоскости 68
структура 266
сужение 15
— (меры) 319
сумма 63
суммирующий множитель 627, 660
существенно интегрируемая функция
811, 818
сходимость в О) (Q) 415
— в 9т (О) 438
— секвенциальная 173, 245
сходится (о сетях) 29
тензорное произведение мер 338
теорема Асколи 57
— Банаха (о компактности) 906
— Банаха — Гротендика 701
— Банаха — Штейнгауза 636
— Бернштейна 981, 984
— Бессаги — Пелчинского 622
— Биркгофа 159
Предметный указатель
1061
теорема Больцано — Вейерштрасса
35
— Бохнера 984, 996
— Брауэра 60
— Бэра 53
— Вейерштрасса — Стоуна 290
— Вейля 200
— Гельфанда — Райкова 990
— Данфорда — Петтиса 379, 801
— Данфорда — Филлипса 882
— Егорова 280
— Какутани 398
— Какутани (о неподвижной точке)
235
— конечности 940
— Канторовича 908
— Крейна 195, 756
— Крейна — Мильмана 292, 973
— Крейна — Шмульяна 759
— Лалеско 970
— Лебега (о сходимости) 280
— Лебега — Радона — Никодима 321
(для векторных мер) 821
— Лебега — Фубини 340
— Лионса о носителях 535
— Лиувилля 156
— Лузина 282
— Макки — Бурбаки 688
— Маркова — Какутани 220
— Марцинкевича 401
— о минимаксе 201
— о поляре 686
— о замкнутом графике 598
— о сжимающих отображениях 213
— об обратном операторе 601
— об открытом отображении 599
— о слабом базисе 621
— о ядре 464
— представления Рисса 297
Шоке 997
— Пэли — Винера 535
— Пэли — Винера — Шварца 536
— Петтиса 895
— Планшереля 997
— Ф. Рисса 100, 286
— Стоуна 293
— Тихонова 37
— Теплица 180, 606
— Тонелли 341
— Фана 236
— Филлипса 810, 815
— Хана 86
— Хана — Банаха (аналитическая
форма) 84
(геометрическая форма) 169
— Хаусдорфа — Юнга — Рисса 642
теорема Хелли 287
— Хеллингера — Теплица 744, 745
обобщенная 748
— Хелсона 727
— Хьюитта — Цукермана первая 725
вторая 726
— Шаудера— Тихонова 227
— Шмульяна 751
— Шура 864
— Урысона — Титце 30
— Эберлейна 754
— Эгнью —Морса 222
— Шаудера —Лерэ 236
теоремы вложения 457
теория Фредгольца 920
тождество Аполлония 139
топологическая векторная решетка
840
— прямая сумма 101
топологический базис 619
слабый 619
топологическое векторное простран-
пространство 86
— дополнение 101
— линейное пространство 86
— подпространство 24
— пространство 21
— — вполне несвязное 398
регулярное 25
компактное 34
локально компактное 38
метризуемое 45
нормальное 25
отделимое 25
паракомпактное 41
полуметризуемое 45
равномеризуемое 49
регулярное 25
сепарабельное 135
а-компактное 35
тихоновское 25
хаусдорфово 25
— сопряженное 98
топологические пространства гомео-
морфные 26
топология 21
— антидискретная 21
— Аренса 689
— дискретная 21
— индуктивная 589
— индуцированная 24
— компактно открытая 91
— компактной сходимости 56, 91
— конечная 119
— линейная 87
сильнейшая 119
1062
Предметный указатель
топология локально выпуклая 117
сильнейшая 117
— — равномерной сходимости 91
— Макки 689
— нулевая 21
— ограниченно слабая 735
— определенная семейством отобра-
отображений 31
— ослабленная 131, 683
— поточечной сходимости 32, 55, 90,
128
— почти слабая 735
— простой сходимости 55, 90, 128
— равномеризуемая 49
— равномерная операторная 855
— равномерной сходимости 56, 90
— на множествах из системы
© 128
принадлежащих © 55
— сильная 128, 693
операторная 855
— слабая 130
— — операторная 855
порожденная подпространст-
подпространством 130
— сходимости по мере 92
— широкая 174
точка крайняя 292, 972
— накопления 29
— окруженная 209
— предельная 29
— прикосновения 37
— экстремальная 292
ультрабочечное пространство 586
ультрафильтр 165, 654
— тривиальный 165
универсальная интегрируемость 271
унитарное представление 987
— пространство 133
унитарность 149
упорядоченная пара 13
упорядочение 17
— линейное 18
— по включению 18
— по возрастанию 18
— по убыванию 18
— совершенное 18
упорядочение частичное 17
упорядоченное векторное простран-
пространство 194, 397
уравнение Вольтерры 216
— Фредгольма 216
уравновешенная оболочка 80
условие Гёльдера 114
— Дирихле 483
условие Дьёдонне 822
— Липшица 114
фактормножество 33
факторпространство 32, 66, 92
— векторное 66
факторразмерность 77
фактортопология 33
фильтр 165
форма положительная 194
формальный сопряженный 469
— степенной ряд 538
формула замены 534
— обращения 512
формулы де Моргана 13
фундаментальная система окрестно-
окрестностей 22
— функция 451
фундаментальное решение 451, 479
относительно точки 479
фундаментальная функция 479
функционал линейный 68
— — мультипликативный 295
— Минковского 82
— мультипликативный 295
функциональное пространство 64
функция 15
— абсолютно непрерывная 256
— Беппо Леви 962
— взаимно однозначная 16
— Грина 568
— интегрируемая 265
— конечная 258
— локально абсолютно непрерывная
256
интегрируемая 309
— — ограниченной вариации 255
равномерно непрерывная 256
— модулярная 348
— ограниченной вариации 255
— почти периодическая 299
— полунепрерывная сверху 28
— полунепрерывная снизу 27
— пренебрежимая 264
— сопряженно линейная 133
— ступенчатая 408
— существенно интегрируемая 317
— измеримая 278
— универсально измеримая 278
интегрируемая 271
— Хевисайда 420, 530
— эрмитова 133
— ^-измеримая 278
— ^-интегрируемая 265
— ц-а-конечная 310
Предметный указатель
1063
функция ii-прнебрежимая 264
фурье-образ 516
характер 295, 369, 986
характеристический многочлен 930
центр масс 979
центрированная система 33
цепь 18
шар замкнутый 44
— открытый 44
экспоненциальная функция 932
эллиптичность 545, 562
эндоморфизм 148, 927
— самосопряженный 149
— унитарный 149
эпиморфизм 69
эргодическая гипотеза 157
— теорема 150, 964
абстрактная 149
индивидуальная 159
статистическая 159
эрмитово симметричная функция 984
В-полнота Птака 730
Вг-полное пространство 730
(DF)-пространство 654
^-единица 398
Н (М) -оболочка 611
^-сечение (последовательности) 582
(L)-пространство абстрактное 397
LF-пространство 595
о-выпуклость 840
о-ограниченность 840
(р,^)-норма (сильная) 400
(р,^)-норма (слабая) 400
Q-пространство 655
Г-спектральность (функций или мер)
724
Го-пространство 25
^-пространство 25
Г2-пространство 25
Гз-пространство 25
^-пространство 25
ш0-измеримость 898
©-топология 55, 128, 687
б-ультрафильтр 654
ц-делимость 335
[х-а-конечность 310
Указатель обозначений
За немногими временными исключениями приводимые ниже обозначе-
обозначения сохраняют смысл, придаваемый им на указываемой странице. Некото-
Некоторые символы (например, А) в соответствии с традицией играют сразу не-
несколько ролей; та роль, которую они играют в данный момент, обычно
вполне ясна из контекста.
Общие теоретике*-множественные обозначения
е, &, {х:Р(х)}у {х}, 0, с, =>, U, П, (J, f), ~, \ 12, 13
(х, у), R[A]=R(A), domR, A X Я, R'\ R*S, Ь=Ь(Х) 13
С — множество комплексных чисел
Сп — произведение п экземпляров С
N — множество натуральных чисел
Nn — произведение п экземпляров N
R — множество вещественных чисел
R72 — произведение /г экземпляров R
Общие топологические обозначения
J, A = intA Л=1гЛ = дЛ 23,24
Прочие обозначения
(в том числе обозначения функциональных пространств)
А1 138
Л°, А°° 686
В (Г), Вк (Т) 65, 90
BL (Q) 458
Р (F, Е) 693
С (Г), СК(Т) 65, 91
СЫ(Т) 91
Со (Г) 410
СЦ(Т) 291
САП Си (Т) 56
Cm(Q), C°°(Q) 107, 580
Dp 469
др 115, 414
Д (диагональ) 14
Д (оператор Лапласа в R72) 480
Указатель обозначений Ю65
□ (волновой оператор) 552
#(G), &{&, S) 414
&'(&) 415
@m (Q), 0W (Q, 5), ^/m (Q), &'F (Q) 438, 439
#[, (Q) 504
£', E" 98
£*, £и* 69, 75
?[, (Q) 501
£J>=*&_P(T, pi) 263, 301
<ГР = £ГР(Т, |i) 302
Ф(Г) 258
/, 7 (класс эквивалентности функций, обычно по модулю пренебрежи-
пренебрежимых или локально пренебрежимых функций) 306, 793
gr 16, 70
Нр, HLp 121, 122
Я (Q) 594
КТ 64
5Г (Г), $TR G1) ЙГС (Г), ЙГ, (П 249 - 251
(Ж1 {Т, S) 590
<з# (Г) ® Ж (П 338
к (£, F) 689
Р(Т) 120
2(^, Р) 134
P jg?f{T ) 265, 304
304, 317
, p), (\ pi) 306
^}0C(Q), Ljoc(Q) 488 _
£>l(Ty pi), Lg G\ pi), ^g (Г, |x), LpE (T, |x) 804
^() 811
()
(, f) 69
Lb (E, F) 98
Lr (£, Z7) 98
L^(£, f) 128
Л£,, Л^ 792, 793
M(T) 174, 388
МЛ Л 285
pi ® pi' 338
jli* 258, 264
pi* 273
pi+ 274
pi+, pi- 251
||x| 282
Np 263, 301
ЛГР 301, 314
|p| = P,+ ... +p«, p! = Pi!p2! ...ря! (для /7 e Nn) 414
(^ 516, 581
tf" 518
a(£'f L) 130
a(E, pi) 130
a(£, F), a(£', £) 131, 683
1066 Указатель обозначений
Т (группа характеров) 987
Т® 128
т (£, £') 689
и (замыкание отображения и) 103
(х, **) 76
\х, х') 98, 682
X (преобразование Фурье) 515, 520, 995
X*Y (свертка) 355, 361, 362, 447
|| • \\р 120, 247, 306
(|) (скалярное произведение) 133
х • у (евклидово скалярное произведение векторов х, i/gR") 511
Оглавление
От издательства . . , • . « , 5
Предисловие к русскому изданию б
Предисловие 7
Глава 0. Предварительные сведения из теории множеств и топологии 11
0.0. Предисловие 11
0.1. Предварительные сведения из теории множеств 11
0.2. Предварительные сведения из общей топологии 21
0.3. Равномерные пространства 45
0.4. Теорема Асколи 55
0.5. Теорема Брауэра о неподвижной точке 61
Глава 1. Векторные пространства и топологические векторные про-
пространства , 62
1.0. Предисловие 62
1.1. Векторные пространства [X, § 1, 2] 62
1.2. Векторные подпространства, факторпространства, произведе-
произведения пространств [X, § 10—12, 18, 21] 64
1.3. Линейные отображения и линейные формы. Изоморфизм. Гра-
Графики [X, § 32, 13] 68
1.4. Линейная зависимость. Алгебраический базис. Алгебраиче-
Алгебраические дополнения [X, § 5—7] 70
1.5. Поглощающие множества. Уравновешенные множества. Вы-
Выпуклые множества 80
1.6. Калибровочные функции и полунормы 81
1.7. Аналитическая форма теоремы Хана — Банаха 83
1.8. Топологические векторные пространства 86
1.9. Непрерывность линейных отображений. Изоморфизмы и го-
гомоморфизмы топологических векторных пространств. Замкну-
Замкнутые линейные отображения 96
1 10. Локально выпуклые топологические векторные пространства 115
1.11. Слабые топологии в сопряженных пространствах 130
1.12. Пространства со скалярным произведением. Предгильбертовы
пространства. Гильбертовы пространства 132
Упражнения 160
Глава 2. Теорема Хана—Банаха ? , s 168
2.0. Предисловие 168
2.1. Геометрическая форма теоремы Хана — Банаха 169
2.2. Принцип продолжения ,,..,,,,.,»*<• 179
1068 Оглавление
2.3. Принцип аппроксимации 185
2.4. Дополнения к теореме 2.3.1 и ее дальнейшие приложения . . 191
2.5. Продолжение положительных линейных форм 193
2.6. Некоторые результаты с приложениями к теории игр .... 196
Упражнения 205
Глава 3. Теоремы о неподвижной точке 212
3.0. Предисловие .212
3.1. Теоремы о неподвижной точке для сжимающих отображений 213
3.2. Теорема Маркова — Какутани 220
3.3. Одно обобщение теоремы Хана — Банаха , 222
3.4. Обобщенные банаховы пределы 223
3.5. Инвариантные средние на полугруппах 225
3.6. Теорема Шаудера — Тихонова 227
3.7. Работы Лерэ и Шаудера 236
3.8. Теоремы о неподвижной точке в упорядоченных множествах . 237
Упражнения 239
Глава 4. Топологические сопряженные к некоторым пространствам;
меры Радона 245
4.0. Предисловие < . , в 245
4.1. План главы 245
4.2. Банаховы пространства lp(T) и со(Т) 246
4.3. Пространство, сопряженное к й*(Г); меры Радона .... 249
4.4. Некоторые примеры 252
4.5. Теория интегрирования относительно положительной меры . . 257
4.6. Пространство J?1 = J?1^» \i) ^-интегрируемых функций * . 263
4.7. Интегрируемые множества, измеримые множества, локально
пренебрежимые множества 270
4.8. Измеримые функции 278
4.9. Носитель меры 282
4.10. Пространство С(Т) и его сопряженное 284
4.11. Полунормы iVp; неравенства Гёльдера и Минковского; про-
пространства Jgv и Lp 301
4.12. Пространство J?2 и его сопряженное 308
4.13. Умножение меры на функцию 309
4.14. Существенно интегрируемые функции 313
4.15. Теорема Лебега — Радона — Никодима 321
4.16. Пространства, сопряженные к Jgv и Lp A ^ р < ooj . . . 333
4.17/ Произведения мер и теорема Фубини 337
4.18. Локально компактные группы и меры Хаара 344
4.19. Групповые алгебры и свертка 353
4.20. Критерий А. Вейля компактности в пространствах J2?v над
группой 373
4.21. Слабая компактность в J?1; критерий Данфорда — Петтиса 374
4.22. Слабо компактные множества ограниченных мер 388
4.23. Теорема Какутани и ее следствия 397
4.24. Замечания о теоремах выпуклости 399
Упражнения * < * . . . * , 402
Оглавление 1069
Глава 5. Распределения и линейные дифференциальные уравнения
в частных производных ._ 411
5.0. Предисловие 411
5.1. Распределения 412
5.2. Меры и функции как распределения 416
5.3. Сходимость распределений 416
5.4. Дифференцирование распределений 419
5.5. Умножение и деление распределения на функцию. Псевдофунк-
Псевдофункции 420
5.6. Сужение распределений; локализация; носитель распределения 434
5.7. Обобщенные функции с компактными носителями 437
5.8. Распределения конечного порядка 438
5.9. Восстановление распределения по его первым производным 444
5.10. Свертка распределений на Rn 447
5.11. Другие свойства распределений 451
5.12. Линейные дифференциальные уравнения в частных производ-
производных 466
5.13. Метод ортогонального проектирования и его развитие . . . 481
5.14. Существование фундаментального решения. Обсуждение за-
задачи 2 506
5.15. Преобразование Фурье распределений 516
5.16. Рассмотрение задачи 1 537
5.17. Решение задачи 3 546
5.18. Дальнейшие свойства фундаментальных решений. Гипоэллип-
тические и гиперболические операторы и уравнения .... 550
5.19. Характеризация некоторых типов линейных дифференциальных
операторов в частных производных с помощью неравенств и
отношения порядка 560
5.20. Работы Ф. Э. Браудера 567
Упражнения 567
Глава 6. Теоремы об открытом отображении и замкнутом графике. . 574
6.0. Предисловие 574
6.1. Полуметризуемые топологические векторные пространства и
пространства Фреше * . 575
6.2. Бочечные, инфрабочечные и ультрабочечные пространства . . 585
6.3. Индуктивные пределы пространств 589
6.4. Некоторые теоремы об открытом отображении и замкнутом
графике < 596
6.5. Некоторые результаты о последовательностях полных полумет-
ризуемых топологических векторных пространств ...... 608
6.6 Ограниченные множества в пространствах @т(п) и Ж(Т) 613
6.7. Другой вариант теоремы о замкнутом графике 615
6.8. Приложения к топологическим базисам 618
Упражнения 628
Глава 7. Принципы ограниченности 633
7.0. Предисловие ... ... 633
7.1. Принципы ограниченности для бочечных и ультрабочечных про-
пространств . , , ( ♦ , , 634
1070 Оглавление
7.2. Некоторые приложения и примеры 639
7.3. Борнологические пространства 651
7.4. Некоторые результаты о секвенциально полных и квазипол-
квазиполных пространствах 656
7.5. Принципы ограниченности для полных полуметризуемых про-
пространств 659
7.6. Приложение теоремы 7.5.1 к суммированию рядов Фурье . . 660
7.7. Принципы ограниченности для билинейных отображений . . . 662
7.8. Некоторые приложения 671
Упражнения 676
Глава 8. Теория двойственности 682
8.0. Предисловие 682
8.1. Дуальные пары и слабые топологии 682
8.2. Свойства ослабленной топологии локально выпуклого про-
пространства 686
8.3. Топологии, согласующиеся с заданной двойственностью . . . 687
8.4. Сильная топология $(Е\ Е) и рефлексивность. Монтелевы про-
пространства 693
8.5. Теорема Банаха — Гротендика 700
8.6. Сопряженные отображения 702
8.7. Второе сопряженное пространство и второе сопряженное ото-
отображение 715
8.8. Некоторые приложения 724
8.9. Еще раз о теоремах об открытом отображении и замкнутом
графике 729
8 10. О совершенно полных пространствах . 735
8.11. Теорема Хеллингера — Теплица 744
8.12. О слабой компактности 750
8.13. Теорема Крейна 756
8.14. Интегрирование некоторых функций 762
8.15. Случай, когда пространство Е метризуемо 785
8.16. Функции со значениями в Ег. Свойство секвенциально замкну-
замкнутого графика 790
8.17. Теорема Данфорда — Петтиса • 792
8.18. Пространства J?PE и L§ 804
8.19. Векторные меры 810
8.20. Сопряженное к L^b случае, когда Е—банахово пространство
и 1 < р < оо 827
Упражнения 837
Глава 9. Теория компактных операторов 846
9.0. Предисловие 846
9.1. Компактные и предкомпактные множества 846
9.2. Определение и некоторые свойства компактных линейных ото-
отображений 848
9.3. Теорема о слабо компактных линейных отображениях . . . 855
9.4. Условия Данфорда — Петтиса и Дьёдонне. Слабокомпакт-
Слабокомпактные и компактные линейные отображения пространств L1 и С 870
9.5. Интегральные операторы и ядерные представления . т . . 901
Оглавление 1071
9 6. Дальнейшее развитие теории компактных линейных отобра-
отображений 919
9.7. Эндоморфизмы векторных пространств 927
9.8. Собственные значения и спектр 929
9.9. Некоторые результаты о спектрах эндоморфизмов 931
9.10. Спектральная теория компактных эндоморфизмов .... 933
9.11. Спектральная теория компактных эндоморфизмов гильбертова
пространства . . . 940
9.12. Дифференциальные уравнения в частных производных и ком-
компактные линейные отображения 956
9.13. Снова об эргодических теоремах 564
Упражнения 966
Глава 10. Теорема Крейна—Мильмана и ее приложения 972
10.0. Предисловие 972
10.1. Крайние точки и теорема Крейна — Мильмана 972
10.2. Приложения к теореме Бернштейна 981
10.3. Приложения к теореме Бохнера 984
10.4. Теорема Планшереля и закон двойственности 997
Упражнения 1007
Библиография 1013
Именной указатель 1048
Предметный указатель 1054
Указатель обозначений 1064
Р. Эдварде
ФУНКЦИОНАЛЬНЫЙ
АНАЛИЗ
Редактор В. И. Авербух
Художник А. Д. Смеляков
Художественный редактор В. И. Шаповалов
Технический редактор Т. А, Мирошина
Сдано в производство 14/IV 1969 г.
Подписано к печати 9/Х 1969 г.
Бумага № 3 60x907i6 = 33,50 бум. л.
67 печ. л. Уч.-изд. л. 63,95 Изд. № 1/4260-
Цена 4 р. 59 к. Зак. 156.
ИЗДАТЕЛЬСТВО „МИР"
Москва, 1-й Рижский пер., 2
Ленинградская типография № 2
имени Евгении Соколовой
Главполиграфпрома
Комитета по печати
при Совете Министров СССР.
Измайловский проспект, 29,