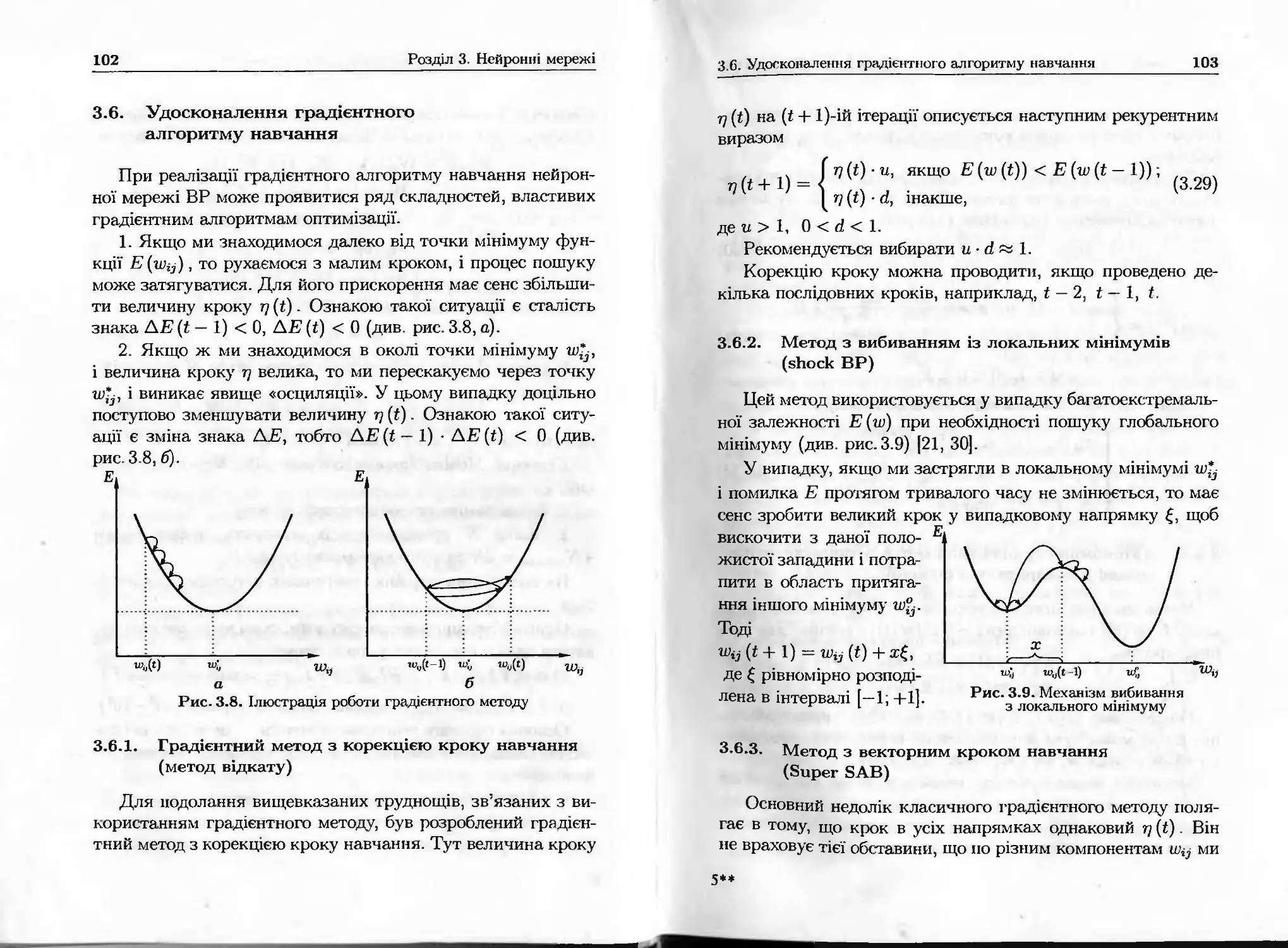
Автор: Зайченко Ю.П.
Теги: навчальний посібник інтелектуальні системи проектування нейронні мережи градієнти
ISBN: 966-8407021-0
Год: 2004
Текст
Зайченко Ю.П.
ОСНОВИ
проектування
інтелектуальних
систем
Міністерство освіти і науки України
Зайченко Ю.ГІ.
ОСНОВИ
ПРОЕКТУВАННЯ
ІНТЕЛЕКТУАЛЬНИХ СИСТЕМ
Рекомендовано Міністерством освіти і науки України
як навчальний посібник для студентів
вищих навчальних закладів
Київ 2004
»^¥ДК 004.^9(075.8)
ББК-&Зт843я73
>/3 17
Рекомендовано Міністерством освіти і науки України
як навчальний посібник для студентів вищих навчальних закладів
(лист МЦ/18.2-768 від Ц 04.2004 р.)
Рецензенти: д.т.н., проф. Бідюк П.І. (Національний технічний
університет України «КПІ»):
д т.н., засл. проф. Волков О А. (Національний авіа-
ційний університет України);
д-т.н., проф. Теленик С.Ф. (Національний техніч-
ний університет України «КШ»);
д.т.н., проф. Тоценко В Г. (зав. відділом Інститута
проблем реєстрації інформації НАН України).
З 17 Зайченко Ю.П. Основи проектування інтелектуаль-
них систем. Навчальний посібник. — КТгТЗидавничий
Дім”«Слово», 2004Г— 352 с.
I8ВN 966-8407-21-0
В посібнику розглянуто актуальні напрямки робіт в галузі інтелектуальних
систем. Розглянуто задачі і методи навчання та самонавчання в інтелектуальних
системах. Велику увагу приділено важливому напрямку в галузі ІС-пітучним ней-
ронним мережам. Розглянуто та проаналізовано методи навчання нейромереж:
генетичний, градієнтні методи, метод спряжених градієнтів та інші. Крім класич-
них нейромереж в посібнику розглянуто новий перспективний клас нейроме-
реж— нечіткі нейромережі, їх властивості, алгоритми навчання та самонавчання.
Застосування нечітких мереж ілюструється численними прикладами в задачах
класифікації, кластер-аналізу та прогнозування в макроекономіці. Розглянуто
також перспективний метод самоорганізації моделей складних систем — так зва-
ний метод МГУА, а також його новий варіант — нечіткий МГУА, запропонова-
ний в роботах автора. Ці методи дістали широке використання в задачах
моделювання та прогнозування.
Особливістю навчального посібника є те, що він містить багато прикладів
застосування методів ІС иейронних мереж та МГУА в задачах класифікації та
.моделювання в економіці, які є оригінальними і раніше в монографіях не вис-
вітлювались.
Підручник розраховано насамперед на студентів ВНЗ різних напрямів,
зокрема «Комп’ютерні науки», «Прикладна математика», він буде корисний та-
кож і спеціалістам, що займаються розробкою та експлуатацією систем штучного
інтелекту.
І8ВМ 966-8407-21-0
© Ю.П. Зайченко, 2004
© Видавничий Дім «Слово», 2004
ПЕРЕДМОВА
Навчальний посібник «Основи проектування інтелекту-
альних систем» підготовлено на базі курсу лекцій з цієї
дисципліни, які автор протягом майже 10 років читає
для студентів напряму «Комп’ютерні науки» спеціальності
«Інтелектуальні системи прийняття рішень» в економіці і бі-
знесі в Інституті прикладного системного аналізу при НТУУ
«КПІ».
У посібнику розглянуті важливі напрями робіт у галузі
інтелектуальних систем (ІС), а саме моделі й методи розпі-
знавання образів і класифікації, моделі і алгоритми навчан-
ня та самонавчання в ІС. Богато уваги приділено розгляду
основних напрямів робіт в галузі нейронних мереж, включа-
ючи НМ зі зворотним поширенням помилки, методи і алгори-
тми навчання нейронних мереж, нейронні мережі Хопфілда,
Хемінга, нейронна мережа Кохонена та алгоритми її самоор-
ганізації. Значна увага приділена розгляду нечітких інтеле-
ктуальних систем та нечітких нейромереж, основам їх фун-
кціонування та застосування.
4
ПЕРЕДМОВА
Четверта глава присвячена цікавому та перспективному
напряму в галузі систем штучного інтелекту — індуктивно-
му методу самоорганізації складних систем, так званому «ме-
тоду групового урахування аргументів» (МГУА). Тут роз-
глянуті основні принципи та ідеї МГУА, поліноміальний та
комбінаторний алгоритми МГУА, їхні властивості. Крім тра-
диційних алгоритмів МГУА, у посібнику розглянуто нові ал-
горитми МГУА з нечіткою логікою. В цьому розділі відобра-
жені оригінальні результати автора по нечіткому алгоритму
МГУА та його застосуванню для прогнозування макроеко-
номічних показників. Остання глава посібника присвячена
викладенню основ еволюційного моделювання та генетичних
алгоритмів і їх застосуванню в розробці моделей складних ін-
телектуальних систем прийняття рішень, зокрема в задачах
розпізнавання образів та класифікації.
Слід зазначити, що в навчальному посібнику, крім тра-
диційних та широко відомих напрямів робіт в різних галузях
систем штучного інтелекту, знайшли відображення також до-
слідження автора в галузі нейронних мереж, нечітких інте-
лектуальних систем та нечіткого методу самоорганізації та їх
застосування в сфері прогнозування в макроекономіці.
Навчальний посібник розраховано на студентів напряму
«Комп’ютерні науки», він буде корисним і для фахівців, що
працюють в області систем штучного інтелекту.
Професор НТУУ «КПІ» Зайченко Ю.П.
ВСТУП
Основні поняття та визначення.
Основні напрямки робіт в галузі
систем штучного інтелекту
Сучасний етап розвитку систем підтримки прийняття рі-
шень характеризується все більшою інтелектуалізацією про-
цесів прийняття рішень, причому процес автоматизації твор-
чих процесів прийняття рішень йде як ушир, так і углиб, охо-
плюючи все нові та нові сфери, які раніше вважалися цілком
прерогативою людини.
Зараз існує багато визначень системи штучного інтелекту.
Дамо одне з них, не претендуючи на вичерпну повноту.
Системою штучного інтелекту називається людино-ма-
шинна система, яка використовується для автоматизації про-
цесів творчої діяльності людини в різних сферах, зокрема
прийнятті рішень.
Зробимо коротенький огляд історії робіт в галузі систем
штучного інтелекту (ШІ).
Термін штучний інтелект (агіійсіаі іпіеііі^епсе) вперше
був запропонований в 1956 році на семінар із аналогічною
назвою в Дартмутському коледжі в США [5|. Семінар було
присвячено розробці методів розв’язання логічних задач (в
протилежність обчислювальним).
І2
6
ВСТУП
Невдовзі після визнання ШІ окремою галуззю науки від-
булося її розділення на 2 напрямки робіт — нейрокібернсти-
ку та кібернетику «чорної шухляди» (Ьіаск Ьох) [5]. Основну
ідею першого напрямку можна сформулювати таким чином:
єдиний в світі об’єкт, здатний мислити — цс людський мозок,
тому будь-який об’єкт (система), яка має на мсті реалізувати
процеси мислення, повинна відтворювати структуру мозку.
Отже нсйрокібсрнстика орієнтована на апаратно-прог-
рамне моделювання структур, подібних до структури люд-
ського мозку.
Основою для цього напрямку робіт були дослідження ней-
рофізіологів по вивченню структури та функцій мозку. В ре-
зультаті цих досліджень з’явилися перші наукові роботи по
штучним пейронним мережам, які складаються з множини
(набору) нейроподібних елементів.
Перші дослідження нейронних мереж були виконані Мак-
Калоком (1956р.) та Фр. Розенблатом (1962р.). Фр. Розсн-
блат створив нейронну мережу, яка моделювала роботу си-
стеми людського зору — «око-зоровий центр мозку» — і отри-
мала назву перцептрон (від латинського слова «регссрііо» —
сприйняття). Перцептрон складається з 3-х типів нейронів:
5-елемснтів (сенсорних), що перетворюють оптичні сигнали
на електричні; Л-елементів (асоціативних), які оброблюють
сигнали від 5-слсмснтів і виконують аналіз зорової інформа-
ції; Я-елсментів (реагуючих), які виконують класифікацію.
Проведені Фр. Розенблатом досліди з перцептроном показа-
ли його здатність розпізнавати прості геометричні фігури, а
також латинські букви. Тобто, перцептрон дійсно може слу-
жити моделлю роботи зорової системи людини. Ці піонер-
ські дослідження Фр. Розснблата були підхоплені багатьма
вченими в різних країнах світу і дали початок новому на-
уковому напряму з нейронних мереж. Проте згодом, після
наступних досліджень були виявлені суттєві недоліки три-
шарового перцептрона, зокрема його нездатність виконувати
функції абстрагування та екстраполяції зображень, за якими
ВСТУП
7
проводилися навчання, на інші подібні зображення, а також
відсутність інваріантності до зсуву та повороту зображень
(об’єктів). Теоретичні дослідження математиків Мінського та
Новікова показали суттєво обмеженість можливостей перце-
птронів, зокрема по розпізнаванню зображень. В результаті
весь напрямок по нейромережам перцептронного типу був
підданий нищівній критиці з боку математиків, і роботи в
напрямку нейромереж були необгрунтовано припинені на 10
років.
Лише в середині 80-х років вони були знову відновлені, і
зараз цей напрямок переживає новий бум.
У 1980-х роках в Японії в рамках проекту ЕОМ 5-го по-
коління був створений перший нейрокомп’ютер. На цей чаз
обмеження по ємності пам’яті та швидкодії комп’ютерів бу-
ли практично зняті. З’явилися так звані «трансп’ютери» —
мікроЕОМ з великим числом паралельних процесорів. Вони
почали широко використовуватися в нейромережах
Можна виділити 3 підходи до створення нейронних.ме-
реж: 1) апаратний; 2) програмний; 3) гібридний.
Апаратний підхід базується на розробці інтегральних
схем, в яких відтворюється структура нейронноі мережі. В
останні роки з’явилось багато фірм, які розробляють та виго-
товляють нейрочіпи, де реалізована паралельна архітектура
нейромережі.
Програмний підхід пов’язаний з розробкою програмних
моделей нейромереж на звичайних ЕОМ. Основною областю
застосування нейрокомп’ютерів стали системи розпізнавання
образів.
Кібернетика «чорної шухляди». В основу цього підходу
покладено такий принцип: «Не суттєво, як влаштована інте-
лектуальна система. Головне, щоб на задані вхідні стимули
(сигнали) вона реагувала так само, як і людський мозок».
Цей напрямок спочатку був орієнтований на пошук алгори-
тмів рішення інтелектуальних задач на існуючих на той час
комп’ютерах.
1**
8
ВСТУП
Суттєвий внесок в становлення нової науки (напрямку)
внесли такі вчені, як МакКарті, автор першої мови програ-
мування для задач штучного інтелекту — ЛІСП, та М Мін-
ський, автор ідеї та винахідник фрейма та фреймової моделі
представлення знань.
В середині 60-х та 70-х років проводились інтенсивні по-
шуки моделей та алгоритмів, здатних вирішувати інтелекту-
альні творчі задачі. В 60-і роки народилась ідея лабіринтного
пошуку, з’явились перші програми для гри в шахи та шашки.
60-70-і роки — це епоха розвитку евристичного програмува-
ння. Родоначальниками цього цікавого напрямку були вчені
Ньюелл, Саймон та Шоу, які розробили систему СР8 (^епегаї
ргоЬІет воіуєг) — загальний вирішувач задач. Ця система бу-
ла з успіхом застосована для пошуку доведень теорем з ев-
клідової геометрії на основі системи аксіом.
Програма СР8 при пошуку доведень теорем використовує
так звані «евристики» — це прийоми для скорочення числа
вариантів просмотру, якими користується людина. Програма
СР8 виявилась дуже ефективною і знайшла доведення не
тільки всіх теорем планіметрії, а майже усіх теорем з розділу
математичної логіки — обчислення висловлювань.
Евристичне програмування та ідеї програми СР8 були з
успіхом використані і в інших розділах математики, зокре-
ма математичної логіки, для автоматичного пошуку доведень
теорем в 70-і роки. В цей же час Робінсон розробив метод
резолюцій, який дозволяє автоматично доводити теореми з
наявного набору аксіом. На основі методу резолюцій Альбер
Кальмерое в 1973 р. створив мову логічного програмування
ПРОЛОГ. Одночасно радянський математик Ю.С.Маслов
запропонував метод зворотного висновку, який дозволяє зна-
йти рішення логічних задач, рухаючись від кінця (наслідку)
до початку (посилання).
Приблизно в цей же час суттєвий прорив в галузі ШІ було
зроблено в США, де в середині 70-х років на зміну пошуку
універсальних алгоритмів мислення виникла ідея моделюва-
ВСТУП
9
ти конкретні знання фахівців-експертів. В США з’явились
перші експертні системи (ЕС), що базуються на знаннях, бу-
ли створені ЕС МУСШ (1976) та БЕКОНАЬ (1978); в ре-
зультаті яких виник та почав застосовуватися новий підхід
до вирішення задач ШІ, заснований на представленні знань.
Наприкінці 70-х років у сферу штучного інтелекту актив-
но вторгається Японія, яка об’явила про початок проекту
ЕОМ 5-го покоління. Цей проект був розрахований на 10 ро-
ків і об’єднав зусилля кращих молодих спеціалістів провідних
компаній Японії в галузі комп’ютерів.
В результаті було створено перший нейрокомп’ютер та
перші інтелектуальні роботи.
Історія досліджень в галузі штучного інтелекту в Радян-
ському Союзі.
В 1954 році в СРСР в МДУ ім. Ломоносова почав пра-
цювати перший семінар «Автомати і мислення» під керівни-
цтвом академіка А.А. Ляпунова. Проводяться численні робо-
ти в царині розпізнавання зображень, мови.
В 1974 році створено Наукову Раду з проблеми штучно-
го інтелекту при Президії АН СРСР, яку очолив академік
Г.С. Поспелов. З ініціативи Ради було започатковано 5 ком-
плексних наукових проектів під керівництвом провідних вче-
них в сфері ШІ, а саме:
ДІАЛОГ — роботи по розумінню натуральної мови — ке-
рівник А.П. Єршов;
СИТУАЦІЯ — ситуаційне керування — керівник Д.О. Пос-
пелов;
БАНК — створення банків даних та знань — керівник
Л.Т. Кузін;
КОНСТРУКТОР — автоматизація конструкторського
проектування — керівник О.І. Половінкін;
ІНТЕЛЕКТ РОБОТА — проектування інтелектуальних
роботів — керівник Д. Охоцімський.
В 80-і роки проводяться активні дослідження в галузі екс-
пертних систем. В 1988 році створено асоціацію штучного
Р
10
ВСТУП
інтелекту в СРСР, до складу якої увійшли понад 300 вче-
них. Президентом асоціації було обрано професора Д О. Пос-
пелова, відзначаючи його винятковий вклад в розвиток бага-
тьох напрямків в галузі ШІ
В Україні наукові дослідження у сфері штучного інтеле-
кту сконцентрувалися в Інституті кібернетики ПАНУ. Тут
в 70-80-ірр. проводили роботи по створенню нових методів,
алгоритмів розпізнавання зображень професори В.А. Кова-
левський, М.І. Шлезінгер, В.І. Рибак та інші. В сфері роз-
пізнавання мовних сигналів значний внесок зробив профе-
сор Т.К. Вінцюк. Результати їх робіт відомі далеко за межа-
ми України. Значний внесок в розвиток ряду перспективних
напрямків досліджень в сфері ШІ зробив академік НАНУ
О.Г. Івахненко та його учні, які ще в 70-і роки розробили нові
алгоритми навчання та самонавчання розпізнаючих систем,
що знайшли відображення в численних монографіях.
Особливо слід відзначити вклад О.Г. Івахненка в створен-
ня принципово нового методу індуктивного моделювання
складних систем — МГУА, який вже понад ЗО років з успіхом
використовується не тільки в Україні, але й у провідних за-
рубіжних країнах (США, Японія, Німеччіна) для розробки
моделей складних інтелектуальних систем.
В галузі моделювання мислення та психіки цікаві дослі-
дження були виконані під керівництвом академіка М.М. Амо-
сова, де було розроблено одну з перших моделей психіки та
мислення з урахуванням емоціональної сфери. Слід визна-
чити значний внесок в галузь нейронних мереж та нейро-
комп’ютерів вчених Кібернетичного центру НАНУ, зокрема
Е.М. Куссуля, Б. Резніката інших. В області розробки інтеле-
ктуальних систем планування дій на протязі багатьох років
плідно працює В.П. Гладун.
В останні 2 роки вченими Кібернетичного центру започа-
тковано нову комплексну програму НАН України «Образний
комп’ютер», основні цілі якої — розробка та впровадження
комп’ютерів, заснованих на принципах ШІ, які будуть здатні
ВСТУП
11
оперувати не тільки даними в числовій формі, а й образа-
ми — візуальними та мовними. Керівник програми — профе-
сор Т.К. Вінцюк.
Як видно з цього огляду історії розвитку штучного інтеле-
кту, на даний час це перспективна галузь науки, що швидко
розвивається та має багато напрямків.
Виділимо деякі основні з них напрямків.
1. Представлення знань, маніпуляція знаннями та ство-
рення експертних систем.
2. Спілкування, комунікації «людина-машина».
3. Розпізнавання образів.
4. Навчання та самонавчання.
5. Планування дій, пошук розв’язків задач.
6. Нейронні мережі.
7. Самоорганізація, методи евристичної самоорганізації.
8. Генетичні алгоритми та еволюційне моделювання.
9. Автоматизація конструювання та проектування нових
виробів, пошук винаходів за допомогою ЕОМ.
Дамо коротеньку характеристику деяких з цих напрямків.
1. Представлення знань та маніпулювання знання-
ми. В рамках цього напрямку вирішуються задачі, пов’яза-
ні з формалізацією та представленням знань в пам’яті інте-
лектуальної системи (ІС). Для цього розробляються спеці-
альні моделі представлення знань та мови для опису знань.
Вивчаються джерела, з яких ІС може видобувати знання, і
розробляються процедури, за допомогою яких можливе отри-
мання нових знань. Проблема представлення знань для ІС
дуже актуальна, оскільки ІС — це системи, що спираються
на знання про відповідну предметну сферу.
Для того, щоб користуватися знаннями, необхідно ІС
навчити маніпулювати ними. В рамках цього напрямку
будуються засоби поповнення знань, вивчаються системи
класифікації знань, розробляються процедури узагальнення
знань і формування на їх основі понять. Створюються ме-
тоди правдоподібного виводу нових знань на основі наявних
І ♦ **
12
ВСТУП
з використанням різних правил висновку. Даний напрямок
глибоко пов’язаний із створенням експертних систем.
2. Спілкування. В коло задач цього напрямку входить
проблема розуміння зв’язних текстів на обмеженій та не-
обмеженій природній мові, розуміння мови, синтез мови, тео-
рія комунікацій «людина-машина». До цього ж кола проблем
належать задачі формування пояснень дій інтелектуальної
системи, які вона повинна дати на запит людини. На базі
досліджень в цій сфері створюються методи побудови лінгві-
стичних процесорів, систем діалогового типу.
3. Сприйняття та розпізнавання образів. Розпізна-
вання образів, класифікація відносяться до однієї з найважли-
віших властивостей інтелекту як природного, так і штучного.
Термін розпізнавання образів відноситься в рівній мірі як
до процесів сприйняття та пізнання, так і до класифікації
об’єктів, що спостерігаються.
Метою створення автоматизованих систем розпізнавання
образів є автоматизація процесів сприйняття і пізнання об’єк-
тів, що пов’язано з пошуком, ідентифікацією, класифікацією
та описом образів на основі аналізу реальних даних. В зада-
чі розпізнавання образів можна виділити 2 етапи: 1) аналіз
вхідних об’єктів, їх опис у вихідному просторі ознак, пошук
інформативних ознак, достатніх для правильного розпізна-
вання, та перехід до опису об’єктів у просторі інформатив-
них ознак; 2) класифікація об’єкта, тобто віднесення його до
одного з класів. Для цього розробляються відповідні вирі-
шальні правила класифікації. Слід відзначити, що вхідна ін-
формація про вхідні об’єкти може мати самий різний хара-
ктер: зображення (плоскі та об’ємні), мовні сигнали, електри-
чні, оптичні та інші види сигналів, чисельні послідовності то-
що, деякі сценарії.
4. Навчання. Одна з суттєвих особливостей людського
інтелекту — це здатність до навчання. Під навчанням розу-
міється накопичення досвіду вирішення задач і перенос його
на інші задачі, які досі не вирішувалися.
ВСТУП
13
Для того, щоб це стало можливим, необхідно створити ме-
тоди формування умов задачі по опису проблемної ситуації,
або в результаті спостережень за нею, навчитися переходу від
відомих рішень (розв’язків) часткових задач (прикладів) до
вирішення загальної задачі; створити прийоми (засоби) де-
композиції початкової задачі на більш малі задачі так, щоб
вони виявилися відомими для системи. На цей час існує 2
основних напрямки у сфері навчання ІС (2 типи моделей на-
вчання): перший напрямок базується на асоціативній моделі
навчання, згідно з якою будь-яке навчання є встановленням
асоціативних зв’язків в нейроноподібних структурах; другий
напрямок базується на лабіринтній моделі навчання, згідно
з якою навчання — це процес пошуку напрямку руху в ла-
біринті можливих варіантів (напрямків руху) з оцінюванням
перспективності руху в даному напрямку за деякими локаль-
ними критеріями оцінки.
Важливий клас задач становлять так звані задачі само-
навчання, або навчання без вчителя (поп-еирегуівесі Іеаг-
піп^). До цього класу задач належать задачі кластеризацїї
або кластер-аналізу (сіиеіег-апаїузіз). Ці задачі формулюю-
ться так: є якась вибірка (множина) об’єктів, класифікація
яких невідома, треба розбити цю множину на деякі підмно-
жини (кластери) так, щоб максимізувати (або мінімізувати)
вибраний критерій кластеризацїї. При цьому використовує-
ться вибрана метрика відстані між об’єктами, які належать
до одного кластера.
5. Планування дій рішення задач. Функціонування
багатьох ІС носить цілеспрямований характер (наприклад,
автономні інтелектуальні роботи). Типовим прикладом тако-
го функціонування являється рішення задач планування до-
сягнення поставленої мети із деякої фіксованої вихідної ситу-
ації. Результатом вирішення задачі повинен бути план дії —
частково упорядкована послідовність дій.
Такий план нагадує деякий сценарій (граф), в якому в
якості відношення між вершинами виступають відношення
типу: «ціль — підціль», «ціль — дія», «дія — результат».
14
ВСТУП
Довільний шлях у цьому сценарії, який веде від вершини,
що відповідає початковій ситуації, в довільну цільову верши-
ну визначає план дій.
Пошук плана дій виникає в ІС лише тоді, коли вона зустрі-
чається з нестандартною ситуацією, для якої апріорі нема ві-
домого заздалегідь набора дій. Усі задачі побудови плана дій
можна розділити на 2 класи, яким відповідають різні моделі:
планування в просторі станів (88-проблема) та планування в
просторі задач (РВ-проблсма).
В першому випадку (88-проблема) вважається заданим
деякий простір ситуацій. Опис ситуацій включає стани зов-
нішнього світу та стани ІС. Ситуації утворюють деякі уза-
гальнені стани, а дії ІС призводять до зміни актуалізованих
в даний момент станів. Серед узагальнених станів виділя-
ють початкові стани (зазвичай один) та кінцеві (цільові). 88-
проблема полягає в пошуку шляху, який веде із початкового
стану в один із кінцевих.
При плануванні в просторі задач (РВ-проблема) ситуація
інша. Простір утворюється в результаті введення на множині
задач відношень типу: «частина — ціле», «задача — підзада-
ча», «загальний випадок — частковий випадок». Проблема
планування полягає в пошуку такої декомпозиції вихідної
задачі на підзадачі, яка б приводила к підзадачам, розв’я-
зок яких відомий. Цей метод (підхід) приводить до хороших
результатів тому, що часто рішення задачі має ієрархічну
структуру. Пошук планування в просторі задач полягає в
послідовному зведенні початкової задачі до все більш про-
стих доти, поки не будуть отримані лише елементарні задачі.
Частково впорядкована сукупність таких задач і складає рі-
шення початкової задачі. Дскомпозицію задачі на альтерна-
тивні підмножини підзадач зручно представляти у вигляді
І/АБО-графа. В такому графі будь-яка вершина, крім кінце-
вої, має або кон’юнктивно зв’язані з нею дочірні вершини («I-
вершини»), або диз’юнктивно зв’язані («АБО-вершини»). В
окремому випадку при відсутності «І-вершини» маємо граф
ВСТУП
15
простору станів. Кінцеві вершини являються або заключни-
ми (їм відповідають елементарні задачі), або тупиковими.
Початкова вершина (корінь І/АБО-графа) представляє со-
бою вихідну задачу. Мета пошуку на І/АБО-графі — пока-
зати, що початкова вершина розв’язна. Розв’язними являю-
ться ті заключні «І-всршини», у яких розв’язні усі дочірні,
або «АБО-всршини», у яких розв’язна хоча б одна дочірня.
Розв’язний граф складається з розв’язних вершин і вказує
спосіб розв’язання (розв’язності) для початкової вершини.
Наявність тупикових вершин приводить до нерозв’язних вер-
шин. Нерозв’язними вважаються тупикові І-вершини, у яких
нерозв’язна хоча б одна дочірня, та АБО-всршини, у яких
нерозв’язні усі дочірні.
Існує багато алгоритмів в просторі задач. Розглянемо, на-
приклад, метод ключових операторів. Нехай задана задача
(А, В}, де А — вихідна задача, В — кінцева задача, і нехай ві-
домо, що оператор / обов’язково входить в її рішення. Такий
оператор називається ключовим. Нехай для застосування /
потрібно мати стан С, а результат його застосування є / (С).
Тоді І — вершина породжує 3 дочірні: (А,С)-, та
(/ (С), В), із яких середня являється елементарною задачею.
Далі до задач (А, С) та (/ (С), В) також шукають ключові
оператори, і вказаний процес редукції повторюється доти, по-
ки це можливо. В результаті вихідна задача розбивається на
впорядковану сукупність підзадач (елементарних), для ко-
жної з яких розв’язок розв’язання відомий.
6. Нейронні мережі. Нейронні мережі — один з най-
більш популярних напрям-
ків робіт в області інтелек-
туальних систем, який веде
свій відлік часу з появи пер-
цептрона Фр. Розенблата.
Нейронні мережі складаю-
ться з великого числа
нейроподібних елементів —
Рис. 1. Структура нейрона
16
ВСТУП
формальних нейронів. Кожний нейрон має декілька вхідних
зв’язків-синапсів і один вихідний зв’язок-аксон (див. рис. 1).
Кожний зв’язок (г,7) характеризується своєю вагою
якщо на г-му вході подано сигнал х*, то через синапс (г,у)
на вхід т-го нейрона поступає сигнал ХіН}^. Сигнали на вхо-
ді 7-го нейрона сумуються і сумарний сигнал дорівнює 8у =
= 52 ХіНІгз.
і—І
Вихідний сигнал 7-го нейрона у* визначається як уі =
= / (8г) , де / — так звана «функція активації» спрацьову-
вання нейрона. Найчастіше використовується функція акти-
вації типу:
а) сигмоїд і
/№1=^(5,) = ^^;
б) релейна функція
1, якщо 5^ > Т^\
0, в протилежному випадку,
де Т — поріг спрацьовування нейрона;
в) пропорційно-релейна функція
/ф) = <
кЗ], якщо |5д| < Т, к =
1, якщо5д>Т;
—1, якщо 5^ < — Т.
Нейронні мережі (НМ) складаються із довільного числа
шарів із нейронів, мають різну структуру одного із наступних
типів (див. рис. 2):
1. з послідовними зв’язками;
2. з перехресними зв’язками;
3. із зворотними зв’язками
Найбільш відомою є нейронна мережа з послідовними
зв’язками типу «Васк ргора^аііоп» — зворотного поширен-
ня (помилки) (див. рис.З).
ВСТУП
17
Уі
-®----Ук
Рис. 2. Типові структури нейромереж
Ук
Рис. 3. Нейронна мережа
«Васк ргора^айоп»
Така мережа має в найпро-
стішому випадку 2 шари нейро-
нів:
1. «скритий» шар нейронів
{А}д=і,7 ;
2. вихідний шар {Ук}к=тк •
На вхід подається сигнал
Х = [жі]і=і5ї+Г і на виході отри-
муємо ¥ = [з/*]а.=їтк’ •
НМ зворотного поширення характеризується матрицями
зв’язків-
а) вхідних XV= ЦіУ^Ц , і = 1,п+1, і = 1, 7;
б) вихідних ХУ0 = Ц ІУД Ц , і = ЇГ7, к - Т^К.
Сигнал на виході т-го нейрона скритого шару визначає-
ться так
'>>=/№)•
Київського
і політехнічного ЙіСГл.’угу З
18
ВСТУП
Д6 7і+1
І=1
а на виході нейронів вихідного шару
Ук = 9 (8к),
Де 7
^к = ^З^ук-
Ї=1
Функції / (5?) і д (8к) — функції активації нейронів відпо-
відного шару. Найчастіше приймається / = д.
Таким чином нейронна мережа здійснює нелінійне пере-
творення входів у виходи: V — р (X), або Р : X —» V, де Е —
відповідна функція трансформації, яка реалізується нейро-
мерєжею.
При заданій архітектурі НМ (тобто число входів і число
нейронів скритого шару — та число виходів К) поведін-
ка нейромережі повністю визначається її вагами Шо- Ваги
нейромережі можуть навчатися (тобто Корегуватися) в про-
цесі навчання мережі, коли на вхід подаємо один за одним
вхідні вектори X), х2,..., хп, спостерігаємо на виході сигнали
¥і, ¥2,..., ¥п і порівнюємо їх з бажаними значеннями вихо-
дів
Ваги змінюються так, щоб отримати мінімум середнього
квадрату помилки апроксимації:
71
є2 = V IIй* - ¥* (-)ІІ2 -*тіп-
* IV
Існують різні алгоритми навчання НМ, які відрізняються
складністю, швидкістю збіжності. Вони будуть розглянуті
нижче. Основними перевагами НМ, які забезпечили їм ши-
роке використання в ІС, являються такі:
а) універсальність, тобто нейромережа є «універсальним
апроксиматором», яка здатна реалізувати будь-яку функцію
трансформації: „, .
Р Г(ті,ж2,...,хп).
вступ
19
Ця універсальність підтверджується відповідною теоре-
мою. Для будь-якої неперервної функції /?(хі,х2, - . . ,Хп) ,
яка відповідає ряду досить простих вимог, існує нейронна
мережа типу ВР, що реалізує це відображення з довільною
точністю, тобто IIР (х) - д (х)||2 < є, де д(х) — функція, яка
реалізується НМ.
б) гнучкість, простота навчання нейромереж шляхом на-
вчання ваг з використанням універсальних алгоритмів.
7. Генетичні алгоритми та еволюційне моделюва-
ння. Основний постулат (ідея) еволюційного моделювання
полягає в заміні проблеми побудови моделі складної системи
моделюванням її еволюції.
Еволюційне моделювання базується на трьох основних ме-
ханізмах еволюції живих організмів:
1) схрещування батьківських осіб і генерація нащадків,
2) дія мутацій;
3) селекція, відбір найкращих нащадків.
Процес починається із задання початкової популяції осо-
бин [\¥1 [0] , . . . , IV/У [0]]
Процес еволюційного моделювання — ітераційний про-
цес, на кожній ітерації якого на батьківську популяцію
[\У] [п],..., XV/V [п]] діють послідовно 3 вищевказаних меха-
нізми, в результаті ми отримуємо нову популяцію нащадків
[1У1 [п + 1] , . . . . [п + 1]]
Всі нащадки 'щ [п + 1] оцінюються за деяким критерієм
«пристосовності» РІ (йіпезз іпсіех) і серед них відбираються
/V найкращих, які і утворюють нову популяцію (п+1)-ї ітерації
Процес повторюється багато разів Кожна ітерація тут на-
зивається «епохою». Процес еволюційного моделювання за-
кінчується при виконанні однієї з умов зупинки:
1) Пітер > пзад) де Пітер — ЧИСЛО Ітерацій алгоритму; Ї1зад —
задане число.
2) Р (и\ (п)) > Езвд, де Е,яд — задане значення критерій РІ
На цих же механізмах базуються і численні генетичні
алгоритми оптимізації, які знайшли широке застосування в
комбінаторних задачах оптимізації в ІС.
20
ВСТУП
Зазначимо основні переваги еволюційного моделювання:
а) універсальність, простота реалізації;
б) здатність знаходити глобально оптимальні рішення при
п —» оо.
А основний недолік — високі обчислювальні витрати, які
пов’язані з реалізацією методу, а також наявність деяких па-
раметрів, які необхідно підбирати експериментально, зокре-
ма розмір популяції N.
Розділ 1
ОСНОВИ МАТЕМАТИЧНОЇ ТЕОРІЇ
РОЗПІЗНАВАННЯ ОБРАЗІВ
1.1. Основні етапи розвитку й аналіз сучасного
стану розпізнавання образів
До середини 70-х р.р. розпізнавання як самостійний нау-
ковий напрямок досяг такої стадії розвитку, що з’явилися пе-
редумови створення математичної теорії розпізнавання обра-
зів. Однієї з передумов з’явилася розробка й узагальнення
ряду моделей і алгоритмів розпізнавання образів. До їхнього
числа відносяться [19]:
1. Моделі, засновані на використанні принципу поділу (Я-мо-
делі);
2. Статистичні моделі розпізнавання образів;
3. Моделі, засновані на використанні методу потенційних
функцій;
4. Моделі обчислення оцінок близькості (голосування);
5. Моделі, засновані на обчисленні висловлень.
Дамо їх коротку характеристику.
Моделі, засновані на використанні принципу по-
ділу. Вони розрізняються головним чином завданням класу
поверхонь, серед яких вибирається набір поверхонь, що як
найкраще розділяють елементи різних класів.
Статистичні моделі. Засновані на використанні апарата
статистичної теорії прийняття рішень. Застосовуються в тих
випадках, коли відомі, чи можуть бути визначені імовірнісні
характеристики класів, наприклад, функції розподілу.
Моделі, засновані на методі потенційних функцій
(П-моделі). Базуються на запозиченій з фізики ідеї потенці-
алу, обумовленого для будь-якої точки простору і залежного
22
Розділ 1. Основи математичної теорії розпізнавання образів
від розташування джерела потенціалу. Як функція прина-
лежності об’єкта класу використовується «потенційна функ-
ція» — усюди позитивна і монотонно спадна функція відстані
(Айзерман, Браверман, 1970 р).
Моделі обчислення оцінок близькості (голосуван-
ня) — Г-моделі. Ці моделі засновані на принципі часткової
прецедентності. Аналізується близькість між частинами ра-
ніше класифікованих об’єктів і об’єктів, які необхідно розпі-
знати. Наявність близькості служить частковим прецедентом
і оцінюється за заданим правилом. По набору оцінок близь-
кості виробляється загальна оцінка розпізнавального об’єкта
для класу, що і є значенням функції приналежності об’єкта
класу.
Моделі, засновані на обчисленні висловлень (апа-
раті математичної логіки). Ознаки об’єктів описуються
як логічні перемінні, а опис класів мовою ознак представля-
ється у формі бульових співвідношень (ФАЛ).
1.2. Короткий екскурс в історію
розпізнавання образів
Протягом тривалого часу переважна більшість додатків
теорії розпізнавання образів була зв’язана з погано форма-
лізованими галузями — медициною, геологією, соціологією,
хімією і т.д. Тому на першому етапі розвитку розпізнавання
з’явилася множина методів і алгоритмів, що були застосо-
вані без серйозних теоретичних обґрунтувань для рішення
практичних задач При дослідженні задачі на базі правдо-
подібних міркувань пропонувався нестрогий, але змістовно
розумний метод рішення і заснований на ньому алгоритм, об-
ґрунтування якого проводилося безпосередньо в експеримен-
ті з задачами. Алгоритми, що приносили успіх при рішенні
визначених практичних задач використовувалися надалі, не-
зважаючи на відсутність математичного обґрунтування.
Тому другий етап розвитку теорії розпізнавання образів
відрізнявся прагненням, з одного боку, ставити і вирішувати
1.2. Короткий екскурс в історію розпізнавання образів
23
задачу вибору в конкретній ситуації найкращого алгоритму,
а з іншого боку — переходити від опису окремих некоректних
алгоритмів до опису принципів їхнього формування, тобто
будувати уніфіковані описи для множини евристичних, але
успішно вирішуючих реальні задачі процедур.
Потреба в синтезі моделей алгоритмів розпізнавання
образів визначалася необхідністю фіксувати клас алгоритмів
при виборі оптимальної чи хоча б прийнятної процедури рі-
шення конкретної задачі. У свою чергу побудова таких моде-
лей породила інтерес до власне математичних властивостей
алгоритмів розпізнавання і, особливо, до проблем строгого
обґрунтування.
Перехід до моделей розповсюджених алгоритмів не при-
вів ні до створення універсальної моделі, ні до формалізації
вибору моделі для рішення конкретної задачі розпізнавання
образів, але і він дозволив ставити і вирішувати в рамках
визначеної моделі задачу вибору алгоритму, екстремального
по показниках якості чи класифікації прогнозу. У більшості
практичних випадків клас таких задач невеликий, тому що
в практичних випадках при синтезі моделей алгоритмів роз-
пізнавання образів, описі класів і виборі ознак об’єкта роз-
пізнавання необхідно було б використовувати значний обсяг
апріорної інформації, яку можна одержати лише при наяв-
ності точної моделі досліджуваних об’єктів і явищ.
Надалі, на третьому етапі, був запропонований алгебраїч-
ний підхід до задач розпізнавання образів (ЖуравльовЮ.І.,
1978, 1989р.), що забезпечує ефективне дослідження і кон-
структивний опис проблеми розпізнавання, у тому числі за-
гальне визначення алгоритму розпізнавання образів, у рамки
якого укладаються всі існуючі типи алгоритмів.
В основі алгебраїчного підходу лежить ідея індуктивного
породження математичних об’єктів за допомогою узагальне-
ного індуктивного визначення.
Виділяються базисні алгоритми і моделі розпізнавання
образів і вводяться операції над ними, що дозволяють по-
слідовно породжувати нові моделі.
24
Розділ 1. Основи математичної теорії розпізнавання образів
1.3. Математична постановка задачі
розпізнавання образів
Нехай дана множина М об’єктів {<а}; на цій множині є
розбивка на кінцеве число підмножин (класів) £1к, к = 1,т
ТП
(і.і)
/с=1
Розбивка визначена не цілком — заданий лише деякий на-
бір інформації Іо (Рі, Рг, • • •, Рт) про класи Рд.
Об’єкти задаються значеннями деяких ознак х^, і = 1, N
(цей набір завжди той самий для всіх об’єктів, розглянутих
при рішенні задачі). Сукупність значень ознак визначає
опис об’єкта І(ш) — {хі,Х2, , тлг} .
Варіанти задання значень ознак:
0,
1.
2.
х, - 1,
Д,
якщо ознака не виконується;
якщо ознака виконується;
якщо інформація про ознаку не задана.
Х3 Є {0,1,2,..., й,} — дискретна ознака;
3. X] Є (а, Ь) — інтервал; а, Ь — довільні числа.
Значення ознаки х^ є випадковою величиною з деякою
функцією розподілу Р (х?).
Опис об’єкта І (щ) = {ті (<д), т2 (ш),.. .,х^ (<д)} назива-
ється стандартним, якщо кожний х? (о;) приймає значення
з множини припустимих значень. Задача розпізнавання зі
стандартною інформацією полягає в тому, щоб для дано-
го об’єкта ш і набору класів Рд; А: = 1,т за інформацією
Іо (Рі, Рг, • •, Рт) й описом /(ш) обчислити значення преди-
катів Р Є Р*), к = 1, т.
Інформація про входження об’єкта ш в який-небудь клас
представляється у вигляді так званого інформаційного векто-
1.3- Математична постановка задачі розпізнавання образів
25
ра 7 (о>) = {/і (о>), /2 (о>), - - -, Іт М} , Де Ік (^) несе інформа-
цію про приналежність об’єкта ш до класу £1к
1, си Є
Ік М = * 0, ш <£ Сік',
Д, ЯКЩО невідомо Ш Є Гік або ц} £1к-
Стандартною інформацією Іо (Г2і, Г2г, • - • > &т) називається
сукупність множин виду {/ (<Ді)(<А-„)} і {Л («+0 ,,
...,Іт (ш)} , для яких передбачається, що серед інформацій-
них векторів немає вектора виду (Д, Д,..., Д).
Апріорна інформація в задачі розпізнавання з непересі-
чними класами часто задається у вигляді так званої таблиці
навчання Т^:
Таблиця 1.1.
Таблиця розпізнавання
Об'єкти розпізнавання Ознаки Класи
її Х^ ...
ш. Діл й1.2 . а?3 ... 0,
... ... ... ...
«41 0,2 «4 «4«
«*4 «41 ац.2 °Ч3 °п,<у
«4+11 ач+1-2 ... ап+м ап+іл О2
... ... ...
Шг, «4.1 «4,2 «4Л °т,.П
... ... ...
«*4 ,+і «4„’|+1.1 «4„,_, + 1.2 ^.,+1^ ... «4-іпл
и)Гги «4-і «4-2 «4з аг,„.К
X ь, Ь2 ... ь, ... ь»
2і
26
Розділ 1. Основи математичної теорії розпізнавання образів
1.4. Синтез евристичного алгоритму
розпізнавання образів
Проілюструємо побудову моделі розпізнавання образів на
прикладі формалізації задачі побудови поділяючої поверхні
між класами (тут висувається гіпотеза, що опис приналежно-
сті до різних класів може бути здійснено поверхнями досить
простого виду; наприклад, гіперплощинами).
Припустимо, що в якості поділяючої поверхні є гіперпло-
щина, яка задана у вигляді:
N
а^Хі + адг+1 = 0. (1.2)
7=1
Нехай множину об’єктів розділено на два класи Пі і П2,
причому Пі Г) П2 = 0 і відомо, що об’єкти 51,52,..., Зт
належать класу Пі, а об’єкти 5то+і, 5т+2,..., — класу
П2. Об’єкти 8і в загальному випадку нерівнозначні, тому
вводяться їхні чисельні характеристики 7 (шг) = 7г — ва-
ги об’єктів. Таким чином, алгоритм РО характеризується
набором параметрів Оі,а2,... , а#+і коефіцієнтів гіперпло-
щини в (1) і набором ваг {7г}- Процес РО для І (ш) =
= {ті (и>) , т2 (а?), ..,Хрі (ш)} провадиться наступним чином.
Позначимо
N
/ (ті (и>), т2 (о;),..., Тдг (а/)) = а7ж7 + а/У+і = 0. (1.3)
7=1
Розділимо об’єкти і^і, ш2,... ,шт на дві множини 0“ і П*,
де
Є П*, якщо / (І (о;,)) > 0,
о>і Є И~, якщо / (/ (о,і)) < 0.
Аналогічно шт+1, .., му разділимо на дві множини і .
1 4. Синтез евристичного алгоритму розпізнавання образів
27
Розглянемо величини
Г(П*) = Е іМ і Г(Я-)= £ 7(и,.) (1.4)
і аналогічно
Г(^) = Е і Г(Я2-)= Е (1-5)
Обчислимо функцію / (/ (5)). Зпівставимо о? з двома чи-
слами Гі (ш) і Г2 (ш) — значеннями функції приналежності З
класам і П2 відповідно.
Якщо / (/ (ш)) > 0, то
Г(ПП . х Г(П^)
Г|Н= г(п+)+г(О 1 Г2И = г(п+)+г(п+)
При /(І(ш)) <0
Г(ПГ) : Г / Ч _ Г )
1Н г(пГ)+г(02-) 2(ш) Г(пг) + Г(п2).
По числах Гі (ш) і Г2 (ш) приймаються рішення про зара-
хування ш в Пі чи П2. Ця процедура задається вирішальним
правилом. Визначимо клас вирішальних правил, обумовле-
них параметром <5 > 0 :
якщо Гі (ш) — Г2 (ш) > <5, то 8 є Пі;
якщо ?! (ш) — Г2 (ш) < —6, то 8 Є П2;
якщо |Гі (ш) — Г2 (ш)| <5, то рішення не приймається, і
алгоритм відмовляється від класифікації 8.
Побудована модель ґрунтується на наступних гіпотезах
[6,91:
1. Елементи класів Пі і П2 можуть бути розділені гіпер-
площиною (чи, принаймні, їх велика частина),
2. Елементи класів нерівнозначні по важливості, і міру
їхньої важливості можна виразити деяким числом 7 (шЦ =
= 7і — вагами.
2*
28
Розділ 1. Основи математичної теорії розпізнавання образів
1.5. Алгоритм розпізнавання на основі
обчислення оцінок (АОО)
Алгоритм розпізнавання АОО заснований на принципі
прецедентності чи часткової прецедентності. Він порівнює
опис об’єкта І (о/), що розпізнається, з матрицею Т^<т і при-
ймає рішення про те, до якого класу варто віднести цей
об’єкт. При цьому рішення виноситься в результаті обчислен-
ня ступеня подібності цього об’єкта з тими об’єктами, прина-
лежність яких до заданих класів відома. Для цього алгоритм
порівнює останній рядок матриці Т^-тп з кожним з попередніх
рядків за визначеним критерієм близькості.
Опис алгоритму АОО. Розглянемо основні ідеї алгори-
тму АОО.
1. Нехай задані стандартні описи об’єктів {иД , € Пд і
{й1,}, шг Пд, к — 1,т. Потрібно визначити приналежність
пред’явленого для розпізнавання об’єкта о/ до якого-небудь
із класів Пд. Якщо введено критерій близькості деяких ча-
стин опису І (о/) до відповідних частин {7 (с<л)} і {/ (оЦ}, то
можна сформувати узагальнений критерій близькості об’єк-
та ш' до відповідних класів об’єктів О*.. У найпростішому ви-
падку узагальнений критерій визначають у вигляді суми час-
ткових критеріїв, що відносяться до окремих частин опису.
У результаті, характеристику виду Г, (о/) = Г, — Гг, де Гг
і Г, — значення відповідної близькості о/ др {о/,} і {й),} при-
родно вважати значенням функції приналежності об’єкта ш'
класу Пк- Величина Гг (о/) = Гг (ц/, £ік) називається оцінкою
об’єкта а)' по класу Пд.
Описи об’єктів {а/} , пред’явлених для розпізнавання, пе-
реводяться алгоритмом розпізнавання в числову матрицю
оцінок Г = {Г,}Мхгп. Ця процедура включає 2 етапи- спо-
чатку підраховується оцінка ш' по кожному рядку магриці
1.5. Алгоритм розпізнавання на основі обчислення оцінок
29
Тдг.т, а потім ці оцінки використовуються для одержання су-
марних оцінок по кожному з класів Пк.
2. Розглянемо процедуру побудови оцінок Г, (о/), вико-
ристовувану в тестових алгоритмах АОО. В основі тестових
алгоритмів лежить поняття «теста».
Тестом матриці Т^т називається сукупність таких стов-
пців тгі,т(2,... ,х1д, що після видалення з матриці Т^<тп всіх
стовпців за винятком зазначених х31,х]2,... ,Хдч, в отрима-
ній матриці Тдг-9,тп будь-які два рядки, що належать різним
класам, будуть різні.
Тест називається тупиковим, якщо ніяка його частина
не є тестом (тобто тупиковий тест — це такий тест, що не
можна видалити з нього жодного стовпця (ознаки) без втрати
здатності до розпізнавання).
Нехай {Ттеуп} — множини усіх тупикових тестів матриці
Тіу.т І Т — (х1і,хі2,...,х1ч') Є {Ттуп} . ВИДІЛИМО В ОПИСІ рОЗ-
пізнаваного об’єкта І (у/) = (Ьі,..частину [Ьі}, ЬІ2, ч..,
..., Ьід} , що відповідає ознакам хг,, хІ2,..., хід і зіставимо її з
усіма частковими описами ,аіід} об’єктів матри-
ці 7дгіТО, де і = гк_і + 1... гк, к = 1, т (г0 = 0).
Підрахуємо число збігів — Гу (о/, П*.), що являє собою чи-
сло рядків цього класу, близьких до розпізнаваного рядка
по тесту Т. Аналогічно обчислюється оцінка иУ по інших те-
стах (для кожного класу). Величина
Г(^,П,) = —----------V гт(^,^) (1-6)
Г*. — Гь-1 *—у
* к 1 тє{7„.и„}
являє собою оцінку об’єкта ш' по класу $їк.
Відомі різновиди тестових алгоритмів, у яких при фор-
муванні оцінок Гу (ц/, П*.) враховуються розходження в пока-
зниках «важливості» окремих рядків матриці Т^<т й ознак,
включених у стандартні описи.
22
зо
Розділ 1. Основи математичної теорії розпізнавання образів
(1.7)
Для цього використовуються числові коефіцієнти — ваги
ознак і ваги об’єктів. Найчастіше ці ваги задаються за допо-
могою експертних оцінок.
Для тестових алгоритмів була запропонована наступна мі-
ра важливості ознак — «інформаційна вага» (Дмитрієв):
1 11 г(ІЧ.т) ’
де г (IV, т) — загальне число тупикових тестів матриці 7\,то;
гХі (IV, т) — число тупикових тестів матриці Тк,т, що містять
ознаку X].
Якщо враховуються ваги ознак Р (37), Р (х?),..., Р (х^)
і ваги об’єктів матриці — 7 (шД ,7 (шг),... ,7 (шг), то
кожен збіг часткового опису {Ь41, ЬІ2,..., об’єкта з час-
тковими описами {ац1,аіІ2,...,ацч} об’єктів з що від-
повідає деякому тесту Т, оцінюємо величиною
Гт (иУ, шД = 7 (шД • (Р (тгД + Р (хІ2) + ... + Р (хгД) . (1.8)
У результаті оцінка об’єкта по класу П*. приймає насту-
пний вигляд:
Г(ш'А) = 1 У £ Гт(иЛ«,)
Тє{Ттуп} з=гк_1+1
(1.9)
Перехід від тестових алгоритмів до АОО зв’язаний з роз-
ширенням видів підмножин множини ознак, за якими прово-
диться зіставлення невідомого об’єкта з об’єктами з і
побудовою ефективної формули обчислення оцінок Г (иУ, ПД
для різних випадків завдання підмножин множини ознак (в
АОО вони називаються «опорними множинами» алгоритму
розпізнавання). У тестових алгоритмах як опорні множини
використовуються множини тупикових тестів.
В АОО розглядаються два випадки визначення опорних
множин:
1.5. Алгоритм розпізнавання на основі обчислення оцінок
31
1. Наявність обмежень на систему опорних множин алго-
ритму.
2. Відсутність обмежень на систему опорних множин ал-
горитму.
У першому випадку найбільш розповсюдженими є систе-
ми опорних множин, складених із усіх підмножин множини
ознак заданої довжини д, д = 2,..., N — 1.
Розглянемо повний набір ознак {а?і,х2,... ,Ждг} і виді-
лимо систему підмножин множини ознак (систему опорних
множин алгоритму) Хі, х2,..., %к- Видалимо довільний набір
ознак з рядків ... ,<х>Гтп,ш' і позначимо отримані рядки
через 5ш2, ..., 8шГт, 8иУ.
Критерій близькості дозволяє оцінити подібність рядків
8ш, і 8ш'. Він полягає ось у чому. Нехай усічені рядки мі-
стять д перших ознак, тобто 8ші = {щі, аі2,..., а^} і 5ш' =
— {^і, Ь2,..., . Тоді рядки 8ші і 8ш' вважаються схожими,
якщо виконується не менше, ніж 6 нерівностей виду:
Іаі - Ьі\ < 7 = М- (1-Ю)
Величини £і,£2, ... ,£д, 6 входять як параметри в модель
класу алгоритмів типу АОО. (Звичайно £і = £2 = ... = = £).
Розглянемо процес обчислення оцінок по підмножині 51.
Для інших підмножин вона аналогічна. У матриці виді-
ляються стовпці, що відповідають ознакам, що входять у 5і
(інші стовпці викидаються). Перевіряється близькість рядка
8\іУ з рядками 51^, і = 1,г,, а отже, і приналежність до
класу П! (за критерієм (1.10)).
Число рядків цього класу, близьких до класифіковано-
го рядка 5іш' за обраним критерієм (1.10), позначимо через
(ш', П(). Аналогічно обчислюються оцінки для всіх інших
класів:
2**
32
Розділ 1. Основи математичної теорії розпізнавання образів
Ці операції проводяться для всіх опорних множин 51,...,
... ,8п і для кожної з них обчислюють відповідні оцінки
близькості:
Г51 (ц/,£21),...,Г5<,(ц/,£2„1),
ц = ІЛ-
Величини
Г$Л (ь/, £2*.) = Г51 (о/, £2*) + Г$2 (а/, £2*) + ...
ч (1 121
... + Г5Д^,£2Ц = ^Г5Да/.£2,) ’
11=1
являють собою оцінки рядка а/ для відповідних класів по
системі опорних множин алгоритму 8д. На підставі аналізу
цих величин приймається рішення або про віднесення об’єкта
иУ до одного з класів £2^, к — 1,т, або про відмовлення від
розпізнавання.
Вирішальне правило може приймати різні форми:
1. Або розпізнаваний рядок відноситься до класу з макси-
мальною оцінкою;
2. Або ця оцінка буде перевищувати оцінки для всіх інших
класів не менше, ніж на визначену граничну величину т?і;
3. Або величина відношення відповідної оцінки до суми
оцінок для всіх інших класів не менш деякого порога %•
Визначення класу АОО зводиться до формалізації насту-
пних етапів процедури розпізнавання:
1. Виділяється система опорних множин алгоритму, за
якими провадиться аналіз розпізнаваних об’єктів;
2. Уводиться міра близькості на множині часткових описів
об’єктів;
3. Задаються правила:
а) правило обчислення оцінки для пар об’єктів за значен-
ням ступеня подоби еталонного і розпізнаваного об’єктів;
б) правило формування оцінок по фіксованій опорній мно-
жині для кожного з еталонних класів на основі оцінок для
пар об’єктів;
1.5. Алгоритм розпізнавання па основі обчислення оцінок
33
в) правило формування сумарної оцінки для кожного з
еталонних класів по всіх опорних множинах;
г) правило прийняття рішень на основі сумарних оцінок,
що забезпечують віднесення невідомого об’єкта до одного з
класів чи відмовлення від класифікації даного об’єкта.
Якщо будувати обчислювальну процедуру за приведеним
описом алгоритму, то при великій кількості опорних множин
потрібен значний обсяг обчислень. Так при виборі як системи
опорних множин усіх підмножин множини ознак потужно-
сті д число опорних множин дорівнює С1^, а число додан-
ків у формулі, що визначає величину , дорівнює
(Л - Гі_і) • С^.
Відомі два методи, комбінація яких дозволяє одержати
прості формули для практично важливих моделей АОО (за
умови, що використовуються граничні функції близькості,
що приймають значення 0 і 1) і Р (5) = Р (х41) 4- Р (хІ2) +...
(тд) (вага опорної множини дорівнює сумі ваг вхідних
у нього ознак).
Перший метод, запропонований Журавльовим (1978) [6],
використовує властивість оцінок для класифікації по опорній
множині 8У, V = 1, т.
Тут використовується оцінка виду
Г (о/, П*.) =--—--х
Ті - Д_і
х У? 7 (^і) + Ріг + • - + Рі.д) В8„ (ш, ші) ,
де її,..., — сукупність номерів ознак, що визначають опор-
ну множину В8гі — функція близькості часткових описів
об’єктів Зуїд' і 8уи,. що приймає значення 1 чи 0, у залежності
від числа виконаних нерівностей виду
І«ї “У < & З = ЇЇ9-
2і
34
Розділ 1. Основи математичної теорії розпізнавання образів
1.6. Метод розпізнавання образів на основі
статистичної теорії прийняття рішень
Нехай маємо К класів: 14, к — І.К. Позначимо: Р (X |14)
— імовірність того, що X належить к-му класу (умовна щіль-
ність зображення); рк— апріорна імовірність появи зображен-
ня к-го класу; X— зображення, що спостерігаються (об’єкти).
Спостерігаємо Х3. Необхідно визначити приналежність
його до якогось класу. Для цього обчислюється [3]
рґсіхї Р(Х3\УкуРк _ Р(Х3\Ук)-Рк
р \Ук |лу) =--——---------- —-------------, (113)
1 £Р(ХДИ)-Рг
І=1
(1.13) — функція правдоподібності. Далі приймається рішення:
Х3 Є Ук, якщо Р(Х3\Ук)-рк = тахР(ХДЦ)-А (1.14)
і=1,К
(на основі принципу максимуму правдоподібності)
Недолік: звичайно невідомі Р (X 114 ), відомий лише клас
законів розподілу імовірностей (сімейство законів з різними
параметрами)
р(х,К) = х(^,^), к = ТУк.
Нехай тк — ризик, зв’язаний з помилковою класифікацією
об’єктів розпізнавання, що належать класу Ук (тобто ситуа-
ція, коли об’єкт із 14 помилково віднесли до іншого класу).
Позначимо Імовірність ПОМИЛКИ Р,мм (Ук).
Середній ризик розпізнавання [3,19]
к
к=1
Середня помилка розпізнавання к-го класу визначається
в такий спосіб
РпОМ(Ук)= У Р(Х\Ук)<іх. (1.15)
ХєУк
1.6. Метод розпізнавання образів на основі статистичної теорії ... 35
Необхідно знайти вирішальне правило О (X, 14), при яко-
му \У —> шіп .
О(Х.П)
Для одномірного закону розподілу (X — скаляр) із умови
Р (X |У]) = Р (X |І4) знаходимо значення величини (І*. Далі
приймається рішення
Хп Є Ц, якщо Хп < (Г;
Хп Е У?, якщо Хп > (1*.
Якщо Гі Гг . 7^ гк, то границя буде визначатися з
урахуванням ваг
В (X, 14) : Хп Е Ук, якщо гк Р (Х„ |І4) = тах.
к
Нехай Гі > гк, тоді сГ визначається з виразу:
гі-Р(Х\Уі) = гк-Р(Х\Ук). (1.16)
Якщо попадаємо в точку, в якій виконується рівність
(1.16), то відмовлення від ухвалення рішення
Цей підхід широко застосовувався в 70-і роки для розпі-
знавання радіолокаційних сигналів.
Сфера застосування теорії статистичних рішень при роз-
пізнаванні образів обмежена тим, що її методи припуска-
ють відомими умовні щільності імовірності. При вирішенні
практичних задач точне чисельне значення цих імовірностей
одержати дуже складно. Однак принципово завжди можна
одержати наближене значення щільності розподілу імовірно-
стей, визначивши відносну частоту, з якою з’являється кожне
зображення. На практиці обмежуються скінченним і порівня-
но малим числом зображень, за якими оцінюються невідомі
розподіли.
Відповідно до теорії статистичних рішень, навчання мо-
жна розглядати як знаходження або приблизну оцінку щіль-
ностей розподілу імовірностей у просторі описів.
У процесі розпізнавання оцінюються і зіставляються отри-
мані умовні щільності імовірностей кожного образу для тієї
точки векторного простору, що відповідає досліджуваному
2**«
36
Розділ 1. Основи математичної теорії розпізнавання образів
зображенню. При навчанні передбачається, що зображен-
ня навчальної послідовності досить повно представляють
розглянуті образи. Цс припущення дозволяє допустити, що
щільності імовірностей, побудовані по навчальній послідов-
ності, близькі до істинних.
Істотним обмеженням методів теорії статистичних рішень
є складність практичної реалізації. Якщо щільності імовір-
ностей не вдається представити аналітично, то, навіть якщо
вони відомі, необхідно зберігати в пам’яті їхні значення для
кожної точки п-мірного простору. Обсяг необхідної пам’яті
при цьому такий великий, що побудова машин, що розпізна-
ють, заснованих на обчисленні коефіцієнта правдоподібності,
практично неможлива. Тому часто передбачається, що хара-
ктер розподілів відомий (наприклад, нормальний розподіл),
але невідомі його параметри (наприклад, математичне споді-
вання, дисперсія), тобто закони розподілу задаються з точні-
стю до параметрів. У цьому випадку задача навчання істотно
спрощується і складається лише у визначенні невідомих па-
раметрів. Часто прагнуть сформулювати такі правила, що
були б прості в реалізації, але по надійності наближалися до
методу, заснованому на статистичних рішеннях, тобто до ме-
тоду коефіцієнтів правдоподібності.
Рішення, отримані згідно баєсовському правилу при пев-
ному правилі апроксимації щільності імовірності, збігаються
з рішеннями, отриманими на підставі порівняння евклідових
відстаней між зображеннями в перетвореному просторі.
1.7. Метод потенційних функцій
У роботах М. Айзермана, Е. Бравермана, Л. Розоноера в
журналі «Автоматика і телемеханіка» («АіТ» 1964, №6, 9, 12;
«АіТ» №11, 1965; а також АйзерманМ.А., БравсрманЕ.М.,
РозоносрЛ.І. Проблема навчання машин розпізнаванню зов-
нішніх ситуацій — У зб.: Автоматичні системи, що самонавча-
1 7 Метод потенційних функцій
37
ються Наука, 1966) були розроблені і досліджені алгоритми
розпізнавання, в основу яких покладені так звані потенцій-
ні функції. Запропоновані авторами алгоритми базуються на
основній гіпотезі про характер функцій, ідо розділяють мно-
жини, які відповідають різним образам [1].
1.7.1. Геометрична інтерпретація методу
Для спрощення, але без обмеження спільності, розгляне-
мо задачу РО для двох класів Ц, У2-
Будемо вважати, що в просторі вхідних описів кожному
вхідному зображенню 8 (х) відповідає єдина точка простору
X. Припустимо, що класи Ц і 14 не перетинаються. Це озна-
чає, що в просторі вхідних описів X існує, принаймні, одна
функція, яка цілком розділяє множини зображень, що нале-
жать різним образам. Ця функція Ф (х) повинна приймати
значення Ф (х) > 0 в точках, що відповідають зображенням
образа Ц і Ф (х) < 0 для х Є Ц. У загальному випадку таких
поділяючих функцій може бути багато. У процесі навчання
системі, що розпізнає, послідовно пред’являють зображення,
яким відповідають точки простору X. При цьому відомо, до
якого класу Ц чи 14 належать показані зображення. Метод
потенційних функцій зв’язаний з наступною процедурою.
При показі (пред’явленні) у ході навчання деякого зображе-
ння 8к (ж), якому відповідає точка Хк в просторі X, з ним
зв’язується функція V (х, Хк), задана на всьому просторі X і
залежна від Хк як від параметра. Така функція називається
потенційною. Навчальній послідовності 8 = {51,8?,.... 5д.} і
точкам X], х2,. .,х*. простору X відповідає послідовність по-
тенційних функцій V (х, хі), [7 (х, х2),...,[/ (х, х*,), що вико-
ристовується для побудови поділяючої функції Ф (х) за допо-
могою визначальних правил. Правила формування функцій
повинні бути такими, щоб у міру збільшення числа пред’яв-
лених зображень функція Ф (х) наближалася б до однієї з
поділяючих функцій.
38
Розділ 1 Основи математичної теорії розпізнавання образів
Метод потенційних функцій припускає існування в про-
сторі X системи функцій (х) ,1 = 1,2,..., що дозволяють
для кожної пари поділяючих множин знайти такс X, при яко-
му поділяючу функцію можна було б представити у вигляді:
N
Ф(х) = 22сі<а(х). (117)
ї=і
Якщо в просторі X існує повна система функцій, то (х)
можна вважати її елементами і будь-яка функція цієї системи
може бути представлена у вигляді нескінченного ряду
оо
ф(х)= 52с«^(х). (і-і8)
г=і
Однак нам бажано, щоб поділяюча функція (згідно (1-17))
розкладалася в ряд із скінченним числом членів N 3 цього
випливає, що поділяючі функції в просторі X повинні бути
досить гладкими і не мати великого числа екстремумів у ма-
лій області. Використовуючи (1.17) можна ввести в розгляд
//-мірний простір 2, на який відображається вихідний про-
стір X. Кожній точці простору X ставиться у відповідність
точка простору 2 відповідно до співвідношення 2г — <рг (х),
і = \Х.
Внаслідок умови (1.17) поділяюча функція Ф (х) відобра-
N
жається в лінійну функцію 52 аг^і (х) в просторі 2 і має на-
і=1
ступну властивість:
N
Ф (х) = Сі2і (х) > 0, якщо х Є Ц;
(119)
Ф (х) — Сі2і (х) < 0, якщо х Є У2.
І=1
У зв’язку з тим, що функції, що розкладаються по систе-
мі (х), лінсаризуються в просторі 2, останній називають
спрямляючим простором.
1.7. Метод потенційних функцій
39
1.7.2. Алгоритм розпізнавання, заснований
на методі потенційних функцій
В якості потенційної функції приймається скалярна фун-
кція двох векторних аргументів вигляду
оо
Ф (х) = ^2 «г • <Рі (х) • (Х*)> (12°)
і=1
де ірі (х) — лінійно-незалежна система функцій: — дійсні
числа, відмінні від 0 для всіх і, я* — точка, що з’являється в
ході навчання.
Передбачається, що <рг (х) й І/ (х, х*) обмежені для х Є
Є Ц О Ц. Нехай у процесі навчання пред’являються зобра-
ження 5і, 52,.. , Зк, яким відповідають точки хь х2,..., хй в
просторі X. Кожна з точок належить Уі чи Ц. Будемо вва-
жати множину Ц позитивною, а У2 — негативною. З появою
першої точки хі будується потенційна функція Пі (х), рівна
потенціалу, що відповідає точці хі, який береться з відповід-
ним знаком:
С7,(х) = ] С7<Х’Х,)' якио ХЄІ‘; (1.21)
—V (х, хі), якщо х Є У2.
Далі нехай після г-го пред’явлення побудовано потенціал
ПДх).
На наступному (г +1) -му кроці навчання показується то-
чка Хі+1 . У результаті можливі 4 випадки:
1. Хі+і Є И;С7і(хі+1) > 0;
2. Хі+і Є У2; 1/і (хі+і) < 0;
3. х.+1 є Уі;Ді(хі+і) < 0;
4 Хі+і є Ді (х»+і) > 0.
У випадках 1 і 2 алгоритм правильно класифікує зобра-
ження 5і+і. У цьому випадку приймається
Пі+1 (х) = Уі (х). (1.23)
40
Роїділ 1. Основи математичної теорії розпізнавання образів
У 3 і 4 випадках є помилка класифікації і необхідна коре-
кція потенційної функції.
Для випадку 3 приймаємо
Пі+І (х) = Ні (х) + Д(х,Хі+1). (1.24)
Для випадку 4 приймаємо
ї/і+1 (х) = 1/і (х) - П (х, хі+1). (1.25)
Побудований після г-го кроку потенціал можна записати
в такий спосіб:
^і(х) = У2 П(х,хк)- £2 ^(х>х<?), (1-26)
Х*.(_)ЄЦ Х,(_)ЄР2
де хд;(_) — точки, що належать образу Ц, підстановка яких
у попередній потенціал приводила до помилки класифікації;
аналогічно х9(_), точки, що належать образу Ц, які були по-
милково класифіковані.
У роботах авторів було розроблено кілька алгоритмів РО,
заснованих на методі потенційних функцій [1,3].
Розходження між варіантами алгоритму зводиться в
основному до вибору законів корекції поділяючої функції від
кроку до кроку.
Перший алгоритм. Будемо вважати, що побудовано
функцію Фі (х), а на (г + 1)-му кроці пред’явлена т. х,+1,
для якої відомо дійсне (необхідне) значення функції Ф (хг+і).
Воно повідомляється вчителем. Тоді функція Фі+1 (х) будує-
ться за наступним правилом:
Фі+і (х) = Ф, (х) + аг+і-
(1.27)
[єщп Ф (Хі+і) - ЄЩП Фг (Хі+1)] 17 (X, Хі+1) ,
де Ф(хг+і) — дійсне значення поділяючої функції в т Хі+і;
аг+і — будь-яка послідовність чисел, що задовольняє наступ-
1.7. Метод потенційних функцій
41
ним умовам:
00 00
а’—* о, 52а»= °°> 52< °°-
і=1 »=1
Наприклад, а, = с)і,с = сопзі.
Збіжність алгоритму обґрунтовується наступною теоре-
мою, доведення якої див. [Айзерман М.А., Браверман Е.М.,
Метод потенційних функцій у задачі відновлення характери-
стики функціонального перетворювача по струмах, що ви-
падково спостерігаються], [« АіТ», № 12,1964].
ТЕОРЕМА 1. Нехай х, — послідовність незалежних ви-
падкових точок з X, а Р(хг) — послідовність імовірностей
їхньої появи.
Нехай Ф (х) — функція, що задовольняє умові (1.17)
N
ф(х) = 52Сі,рі
г=1
Тоді послідовність функцій Ф,(х) (г = 1,2,...), що визна-
чаються рекурентним співвідношенням (1.27) при і —> оо за-
довольняє умові:
Р < Іііп [ |Ф(х) — Фг(х)| • Р(х)(1х = 0 > = 1. (1-28)
(і-ооУ )
Другий алгоритм. Як і раніше, покладемо Фо(х) = 0.
фі+і (х) = Фі (х) + у • [Ф (хі+і) - Фі(хі+і)]-Р (х,хі+і), (1.29)
де Л — довільна позитивна константа, що задовольняє умові
Л = - шах (7 (х,х‘), (1.30)
де Ф (хі+і) — дійсне значення поділяючої функції на т. хі+і.
Збіжність цього алгоритму підтверджується наступною
теоремою.
42
Розділ 1. Основи математичної теорії розпізнавання образів
ТЕОРЕМА 2. Нехай виконуються ті ж умови, що й у
теоремі 1. Тоді послідовність функцій Фі (х) (і = 1,2,...),
які визначаються рекурентним співвідношенням (129) при
і —> оо задовольняє умові
Р< ,1пп / |Ф(х) - Фі (х)|2 • Р(х)гіх = 0 > = 1.
(1-31)
Наведені алгоритми можна використовувати і для послі-
довних наближень коефіцієнтів с7 у представленні поділяю-
чої функції ЛГ
ф (х) = 52 (х)
і=і
за формулами
N
8І§П Ф (хі+1) - 5І£П ^2 С^і (Хі+1)
і=1
-¥>і(хі+і), (1.32)
з =
N
ф(хі+о - 52
І=1
(хі+і) >
(1.33)
Дані алгоритми є алгоритмами статистичної оптимізацїї,
окремими випадками методу СКГ. Описаним алгоритмам мо-
жна дати зручну геометричну інтерпретацію, використовую-
чи для цього процес навчання. Будемо вважати, що в просто-
рі X існує поділяюча поверхня Ф (х), яка може бути пред-
ставлена розкладанням (117), причому така, що виконую-
ться умови (1.19). Тоді в спрямляючому просторі існує поді-
ляюча площина з направляючим вектором V, що проходить
1.7. Метод потенційних функцій
43
через початок координат:
оо
така, що
якщо х Є Ц;
якщо х Є 14;
(1.34)
Відобразивши множину У2 симе-
трично відносно початку координат,
одержимо множину V — Ц О У2, Де
У2* — відображення множини У2 (див.
рис. 1.1). Множини Уі і У2 можуть
бути розділені площиною з направ-
ляючим вектором V (Ут2 = 0) за
УМОВИ, ЩО оо
Vу 2 = Уі2і > 0, при
Рис. 1.1. Побудова
множини У2’
2 Є V.
Іншими словами множини Ц і 14 розділяються цією пло-
щиною за умови, що об’єднана область V лежить по один
бік від неї. Поставимо у відповідність послідовність М точок
{хі,х2,... ,хр} із простору X, що належать множинам Ц і
У2, І ПОСЛІДОВНІСТЬ М ТОЧОК {2і,22, - -. , 2р} з У = Уі О У2.
Потенційна функція може бути представлена в спрямляючо-
му просторі 7 як скалярний добуток двох векторів 2,2*, де
7г — аг^г (х) і 7* — ацр.(х*). (1.35)
Тоді вирази (1.20) для потенційної функції можна пред-
ставити в наступному вигляді:
Щх,х‘) = 2-2*. (1.36)
Тепер вирази (126) можна переписати так:
Пр(2)= £ 2 2д,
2,_єМ*
(1.37)
44
Розділ 1 Основи математичної теорії розпізнавання образів
де 2д_ — точки з послідовності М*, пред’явлення яких у про-
цесі навчання призвело до виправлення помилок.
Якщо з послідовності точок М* вилучити всі точки, що
не призвели до виправлення помилок, а точки, що залиши-
лися, (необхідні для виправлення помилок) перенумерувати
підряд, то вираз (1-37) можна переписати в такий спосіб:
*:(Р)
Пр(2) = 2 • У 2т, 2т є М*‘, (1.38)
771—1
де М** — множина точок, що включають у себе тільки ті то-
чки, які супроводжувалися виправленням помилок, що від-
булися протягом перших р пред’явлень
Виправлення помилки в точці 2 Є V буде відбуватися за
умови 1/р (2) < 0.
На підставі цього можна стверджувати, що (к + 1)-е ви-
правлення помилки відбудеться, якщо
к
2а.+і 52 2т < 0. (1.39)
771=1
Тепер роботу алгоритму можна пояснити в такий спосіб.
Поява першої точки 2] з множини М* приводить до побудови
в спрямляючому просторі площини Пі (2) = (2, 2і) = 0 з на-
правляючим вектором 2]. У випадку, якщо наступна точка з
М* лежить у тому ж підпросторі (просторі), куди орієнтова-
ний направляючий вектор 2г, то помилка буде відсутня і при
цьому положення ПОДІЛЯЮЧОЇ ПЛОЩИНИ І вектор 21 не зміню-
ються, і провадиться пред’явлення наступного зображення.
Як тільки пропонована точка потрапить у протилежний пів-
простір, відбувається виправлення помилки.
При цьому направляючий вектор площини V, побудова-
ний до цього кроку, складається з вектором точки, яка
потребувала виправлення, і сумарний вектор приймається
за новий направляючий вектор (див. рис. 1.2, де показаний
1.7. Мегод потенційних функцій
45
випадок, коли виправлення
помилки було вже потрібно
на 2-му кроці. Тут новий
направляючий вектор дорів-
нює 2і + 22). У загальному
випадку, після к виправлень
помилок направляючий век-
тор поділяючої площини
Рис. 1.2. Випадок, коли виправлення
помилки вже потрібно на 2-му кроці
дорівнює
к
^2 (ДЄ 2т Є М*) .
т=1
(1-40)
Після певного числа пред’явлень зображень з навчальної
послідовності одержимо площину, що проходить через поча-
ток координат спрямляючого простору, яка приймається за
поділяючу площину. На цьому навчання закінчується. У про-
цесі розпізнавання для кожної нової точки підраховується
значення С/ (ж), а рішення приймається за знаком /7 (х).
1.7.3. Збіжність алгоритму потенційних функцій
і умова його зупинки
У [1] доведено 2 теореми, в яких стверджуються дуже ва-
жливі властивості алгоритмів, заснованих на методі потен-
ційних функцій. Перша з них стверджує, що число виправ-
лень помилок в алгоритмах скінченне, а в другій доводиться
збіжність цих алгоритмів.
ТЕОРЕМА 3. Нехай М — довільна нескінченна послі-
довність точок {хі, х2,..., хр} простору X, що належать мно-
жинам Ц і Ц. Припустимо, що існує функція Ф (х) така, що
ґ > £, якщо х Є V];
Ф(х) = ч 4 1.41)
[ < — £, якщо х є Ц.
Крім того, ця функція може бути представлена розклада-
нням (1-17). Нехай /7 (х,х*) обмежена на Ц СІ У2. Тоді існує
46
Розділ 1. Основи математичної теорії розпізнавання образів
ціле число А:, що не залежить від вибору послідовності Л/, та-
ке, що при використанні методу потенційних функцій число
виправлень помилок не перевершує к, де
зир у/1/ (х, х*).І'£сі/аі
хєУіиУ2 V І=1
(1.42)
хєЦиі^
Наведена теорема не доводить збіжності функції Ьтр (х),
формованої відповідно до алгоритму поділяючої функції, то-
му що вона не накладає ніяких обмежень на статистику пре-
д’явлення зображень у процесі навчання.
Насамперед, для правильного поділу множин 14 і 14 не-
обхідна досить представницька навчальна послідовність. Це
означає, що точки, які відповідають зображенням з навчаль-
ної послідовності, повинні бути досить добре розкидані по
множинах 14 і 14-
ТЕОРЕМА 4. Нехай множини 14 й 14 у просторі X такі,
що існує поділяюча функція, що задовольняє умові (1-41),
яка може бути представлена розкладанням (1.17). Нехай
функція І/ (х, х*) обмежена при х Є 14 014- Припустимо, що
появи зображень з навчальної послідовності — по суті неза-
лежні випадкові події, і яким би не було п, до п-го кроку ал-
горитму існує строго позитивна імовірність виправлення по-
милки за умови, що до цього кроку не відбулося повного по-
ділу МНОЖИН 14 І 14- Тоді з імовірністю, рівною 1, для кожної
реалізації алгоритму знайдеться таке скінченне число т, що
пт (х) =
> 0,
< 0,
якщо х Є 14;
якщо х Є 14-
(1.43)
Тобто процес поділу множин з імовірністю Р — 1 здійсню-
ється за скінченне число кроків.
1.8. Синтез екстремальної моделі (алгоритму) РО
47
1.8. Синтез екстремальної моделі (алгоритму) РО
Серед множини математичних задач, що виникають на
рівні моделей РО, варто виділити задачу синтезу математи-
чної моделі (чи алгоритму), оптимальної за якістю розпізна-
вання образів у даному класі моделей. Звичайно задається
спосіб побудови об’єктів кожного класу оцінювання для ал-
горитму з даного класу моделей, а також, яку частку об’є-
ктів він класифікує правильно (тобто відносить до задано-
го класу). Отримана величина усереднюється по класам і є
функціоналом якості РО. Завдання полягає в тому, щоб для
заданого класу моделей знайти алгоритм (модель) з макси-
мальним значенням функціонала якості (ФЯ) [19]
9?(Л) = ф(?}. (1.44)
1. Наприклад, може бути заданий наступний закон пород-
ження класів і 12г- Нехай описи І (ш) об’єктів 8 є набо-
рами числових ознак {аі (5),..., ап (5)} = а (5), де —оо <
а.і (5) < +оо, і — 1,п. Нехай у п-вимірному просторі задані два
нормальних розподіли з математичним сподіванням ті, т.2 і
дисперсією &1, Провадиться випадковий вибір точок (опи-
сів) і розігрується за заданими законами клас, у який вони зара-
ховуються. Після цього об’єкт 8, занесений, наприклад, у клас
12і з імовірністю р, зараховується до навчальної вибірки, а з
імовірністю (1 — р) — до контрольної, те ж саме виконується
і з об’єктами з класу 12г- Нехай сформовані таким чином на-
вчальні і контрольні вибірки. У навчальну вибірку зарахова-
ні об’єкти 511,512,..., 8іт Є 12і і 821,822, >821 Є 12г, а в кон-
трольну вибірку — 531,5з2, і 8^ Є 12] і 641,842,..., 8±и Є 12г-
У моделі будується алгоритм А, що за описами І (5ц),...,
- ..,1 (8іт), І (821(821) дає максимальне значення ФЯ
9?(Л) = де ір'А — число об’єктів з контрольної вибірки,
правильно класифікованих алгоритмом Л, </?" = и + V — за-
гальне число об’єктів у контрольній вибірці.
48
Розділ 1. Основи математичної теорії розпізнавання образів
2. Більш стандартним є підхід, у якому при фіксованій
початковій інформації /о і моделі потрібно знайти алгоритм,
що дозволяє максимально точно класифікувати дану сукуп-
ність Зі, і — 1,771 контрольних об’єктів, приналежність яких
класам Н2, • - , відома. Природно, що інформація типу
Зі Є ІД і Зі Є іїк не вводиться в алгоритм. Зокрема, можна
сформувати наступний клас задач синтезу експерименталь-
ної моделі (алгоритму) розпізнавання.
Нехай дані описи об’єктів І (5і), І (52) (Зт) із кла-
су $7! і ЦЗт+і), І(Зт+2), • • •, І (Зд) з класу П2, де І (&) =
(хц, хі2,..., хцу). Будується /?-модель, розбивка провадиться
гіперплощиною
N
/ (х) = = 0. (1-45)
7=1
Параметрами моделі є невідомі коефіцієнти аі,а2, , адчі,
вирішальне правило таке: якщо / (/(5і)) > 0, то Зі Є ІД,
якщо / (І (Зі)) < 0, то З, Є И2. Виписавши ці умови для всіх
об’єктів 5і, 32,..., 8т, • -чЗд, ми одержимо систему лінійних
нерівностей з невідомими аі, а2,..., ал+і :
а]Жц + ... + а//Хідг + <^+і > 0;
+ • + а^Хтіу + адг+1 > 0;
Оі^т+і,і + - - + аічхт+і'іу + ^N+1 < 0;
(1-46)
Оі + • • - + а^Хдіи + а N41 < 0.
Для синтезу шуканого алгоритму потрібно знайти макси-
мальну сумісну підсистему в (1.46). Вирішивши її, одержимо
шукані значення параметрів , а2,..., адг+і-
Розділ 2
МОДЕЛІ ТА АЛГОРИТМИ НАВЧАННЯ
ТА САМОНАВЧАННЯ В ЗАДАЧАХ
РОЗПІЗНАВАННЯ ОБРАЗІВ
2.1. Класифікація моделей навчання.
Формальна модель навчання
Навчання — це одна з невід’ємних властивостей будь-якої
інтелектуальної системи (ІС), як природної, так і штучної,
яке полягає в нагромадженні досвіду на основі рішення по-
передніх задач і узагальненні його на нові задачі, що раніше
не зустрічалися. Існує 3 класи моделей навчання, що базую-
ться на ідеях когнітивної психології.
Моделі навчання (з погляду психології) такі:
1. Модель навчання, що використовує механізм утворення
умовних рефлексів (рефлекторна модель І.П. Павлова);
2. Асоціативна модель навчання. Вона заснована на асо-
ціативній теорії навчання, відповідно до якої процес навчан-
ня трактується як процес настроювання асоціативних зв’яз-
ків у нейроподібних мережах.
3. Лабіринтна модель навчання. Вона використовує ідеї
когнітивної психології. Процес навчання в ній складається в
евристичному пошуку в лабіринті можливих альтернатив і
оцінюванні руху по лабіринту на основі локальних критеріїв.
Формальна модель навчання
Розглянемо формальну модель навчання [19].
Задано:
а) множину вхідних сигналів — навчальну вибірку {а:і, а?2,
...,, х^і ) ,
б) відповідну множину виходів {уь у2,..., уп} = ¥ь.
3і
50
Розділ 2 Моделі та алгоритми навчання та самонавчання
Є шукане відображення (класифікація) рь (рь С Хе х У^),
відоме тільки вчителю, що здійснює відображення %£ —» Уе-
Задано також множину відображень {//,} Є Р з деякого класу
Р Хь ~~* ^ь), Щ° будуються системою в процесі навчан-
ня. Крім того, заданий критерій навчання = ІіАрь, /ь),
що залежить від ступеня близькості класифікації Д, отрима-
ної системою в результаті навчання, до дійсної класифікації
вчителя рі.
Таким чином, задачу навчання £ можна формально запи-
сати як деяку оптимізаційну модель, обумовлену п’ятіркою
Ь = {Хс,¥ь,рь,/,Іь), (2.1)
де її — критерій якості навчання, що залежить від змісту
задачі; іе — множина відображень, що задається на Хе х У£,
які будуються системою в ході навчання.
Вводиться поняття алгоритму А, що вирішує задачу на-
вчання £, а також поняття алгоритмічної складності С(А, її)
алгоритму А в залежності від розмірності задачі п. Потрібно
знайти такий А*, для якого С (Л*, п) тіп .
Найбільш розповсюдженим способом навчання є навчан-
ня за прикладами.
Задаються приклади (навчальна послідовність)
Рі) ,(Х2,У2,Рї) , • Лхп,Ук,Річ)}
Необхідно знайти таку класифікацію /* Є Р, яка б набли-
жалася до класифікації вчителя ре і мінімізувала використо-
вуваний критерій якості навчання Д(рь,/*) на навчальній
і перевірочній вибірці X — Хе и Хт, де X? — перевірочна
вибірка.
Математична модель задачі навчання в цій постановці має
вигляд
пііп Іе(рі.,Г)
2.2. Алгоритм навчання за Байєсом
51
2.2. Алгоритм навчання за Байєсом
Оскільки алгоритми навчання і самонавчання за Байєсом
зв’язані з тими самими ітсраційними процедурами, приведе-
мо постановку задачі послідовного навчання за Байєсом |3]
Задачею навчання є оцінка невідомих параметрів розподі-
лів за навчальними зображеннями. Припустимо, що нами по-
будована оцінка для невідомого параметра В на п-ому кроці
навчання, а також відома апостеріорна щільність для пара-
метра В по (п— 1) попереднім спостереженням, що позначимо
через Р (£?|Х„_і,..., ХО .
Якщо на п-ому кроці спостерігається зображення Хп, то
апостеріорну щільність на цьому кроці можна визначити по
рекурентній формулі Байєса
Р(В|Х1,Х2>...,ХП) =
Р1(ХП|В)Р(В|Х1,Х2,...,ХП 1) (2.2)
^(Хп)
Кін розглянув задачу байєсівського навчання за парамет-
рами багатовимірного нормального розподілу. Було доведено,
що при необмеженому збільшенні числа показів адаптивний
байєсівський фільтр наближається до оптимального фільтра.
Основні труднощі застосування байєсівського підходу
зв’язані з визначенням апостеріорних імовірностей. У своїй
книзі Кін показав [3], що деякі класи розподілів мають
чудову властивість: при збільшенні числа спостережень вид
апостеріорного закону Р(В|Хі, Х2,...,Х„) не змінюється і
збігається з апріорним розподілом (В). На кожному кроці
навчання відбувається лише перерахування параметрів цих
розподілів. Такі розподіли називаються «відтворюючими».
До них, зокрема, відносяться нормальний розподіл, біноміаль-
ний, Пуассона, розподіли Релєя й Уішарта.
З*
52
Розділ 2. Моделі та алгоритми навчання та самонавчання
Спрегінс вирішив цю задачу в більш загальному випадку.
Він довів, що скінченний обчислювальний алгоритм для ре-
курентного визначення Р(В|Хі,... , Хп) може бути побудо-
ваний тільки в тих випадках, коли розподіл / (В|Х!,..., Хп)
має достатні статистики у вигляді т-мірного вектора від ре-
зультатів спостережень Хі, Хг,..., Хп, що можна записати
Р(В|Х„...,Х„) = . .
= Р(В,В*|Х„Х2........Х„)9(Х1,...,Х„),
де д (Хі, ..., Хп) не залежить від В; В* — оцінка невідомого
сигналу В за вибіркою.
Друга теорема, доведена цим же автором, стверджує, що
відтворююча апостеріорна щільність Р(В|ХІ;..., Хп) існує
тоді і тільки тоді, коли спостереження Хі, Хг,..., Хп допу-
скають достатню статистику.
У наступній табл. 2.1 приведені основні типи відтворюю-
чих розподілів, де |^| — визначник матриці .
Перш ніж перейти до задачі навчання без вчителя, зроби-
мо наступне зауваження. Дуже важливим є правильна поста-
новка задачі. Дійсно, якщо бажано, щоб система виконувала
яку-небудь класифікацію, то це тривіально, тому що будь-
який пристрій із входами і виходом при будь-яких станах
виходу реалізує деяку класифікацію.
Правильною виявляється постановка задачі навчання і
розпізнавання без вчителя з погляду статистичної теорії рішень.
Постановка задачі. Нехай є т джерел, позначених
V], Ц,..., Ут, причому в кожен момент часу активне тіль-
ки одне з них. Цс джерело генерує /-вимірний вектор-
зображення Хд.. Нехай Рг0 — імовірність активності г-го дже-
рела і Ріо не залежить від к.
Припустимо, що послідовність спостережень Х1,Хг,...,
..., Х„ надходить на вхід класифікуючої системи і потрібно
прийняти рішення про приналежність Х^ з мінімумом ризику.
2.2. Алгоритм навчання за Байєсом
53
& X ч Л Н Ядро функції правдоподібної: гі 1 ЙЗ ?2 • В,п \ (1 — В] —... — В,п 1 ) В" ехр [-Вт] іД 1 «1? й •—І СЧ 1 X «|е« іДІ Їй І»е* СІ 1 о X к 1 є*. 1 іД е І іД 1 с сч . іД 1 (X, -Чсч сч | В" ехр[—ВС„] X' II сі С) та , і о, ф &3 В. і М. - В
< е е хехр
оюних розподілів Апостеріорний розподіл Р(В|Х1,...,Х„) г>ета 3 с 3 Г Г амма Багатовимірний в Я 2 2 с о । КОМПОЗИЦІЯ Уііпарта-Гаусса Гамма Гамма Розподіл Пірсопа, тип 8
ОВНІ типи відтворі Діапазон зміни параметра ВЄ [0,1] V/ об п =б В Є (0,+ оо) [’н] = а В, Є (-оо,+оо) Ві — позитивно визначена симет-| рнчпа матриця В2 = [^2.] (оо+‘оо-) 3^0 т 4; 6 со В Є (0,+ оо) ’8 иі со
б Характер спостерігаємих величин годиниць г - п пулів г, одиниць і — 1,т п подій за час т п векторів X, х..=^£х. Вї X* і; X IX 17^ • 1с И к II —'1 Є х ю ІХ§=“0 у хипяихітєоп и п позитивних X, п векторів X, X. Є(-В,+В) Мп — тпах|Х,|
Закон розподілу Р(Х|В) Біноміальний і с І і і Пуассопа Багатовимірний ь' 3 3 І а 0 І відомим середнім В Багатовимірний нормальний з невідомим середнім і матоииею коваоіанії II =1 д II '•м Релея Експоненціальний Прямокутний з невідомим середнім
54
Розділ 2. Моделі та алгоритми навчання та самонавчання
З появою Хд, можливе настання однієї з т непересічних подій,
що утворюють повну групу (X*,, V]), (Хк, У2), • • •, (Х&, Цп).
Якщо Р (Ц) = Рі, то для всіх к
ТП
Р(Х,) = £>(Х,|Ц)Ц. (2.4)
Припустимо, що Р(Х/с|Ц) характеризується деякою під-
множиною параметрів Вг, тоді
В = Ві х В2 х ... х Вт х Вт+і, (2.5)
де
Вт+і = {Рі}і=І^, (2.6)
звідси т
Р (Хк) = Р (Х*|В) = £ Р (Хк|Вг) Рг. (2.7)
і=1
Оскільки множина В невідома, то задачу самонавчання
можна розглядати як задачу оцінки параметрів В зі змішаної
вибірки.
Виникає питання, коли при заданому чи обчисленому на
практиці Р(Х^) рівняння Р (X*.) = Р(Х*,|В) має єдине рі-
шення для В?
Така задача називається «ідентифікацією змішаної вибір-
ки». Були сформульовані достатні умови ідентифікованості
деяких сімейств розподілів, зокрема біноміального і нормального.
Однак існування рішення для рівняння Р(Х^) = Р(Х^|В)
не дає відповіді, як знайти це рішення, тобто як побудува-
ти послідовність функцій {/п (Хд.)} , що збігається до Во, де
Во — шукане значення параметрів.
Були сформульовані достатні умови для одержання по-
слідовності {/п (Х^)} , що збігається до Во, коли апостеріор-
ні імовірності /(В|Х) визначаються по формулі Байєса. Ці
умови можна сформулювати так:
а) відоме число джерел — т;
2.2. Алгоритм навчання за Байєсом
55
б) закон розподілу {Е (Хк|Ц)}і=ї^ відомий з точністю до
параметрів Вг\
в) на В та X накладені обмеження, достатні для іденти-
фікації Р(Х^|В);
г) на В та X накладені додаткові обмеження для одержа-
ння спроможних оцінок для В.
Нехай вид функції Г(Х^|^,В7) невідомий. Тоді імовірні-
сний простір по кожній з І осей квантується на д +1 ділянок,
тобто будується деякий аналог гістограми.
Нехай р* — /-мірний вектор (ррРг, • - чРІ), тоді Рк ~ імо~
вірність того, що Хд; Є Ц потрапить в інтервал [6^., ^1+1]
У загальному випадку X*, — послідовність ІТ-мірних ве-
кторів, що складається з IV повідомлень від одного джерела,
ТОбТО' х4 = {1м)^. (2.8)
Позначимо Уп = {Хі, Хг,..., Хп} .
Якщо по кожній з осей зробити розбиття на § рівнів, то
весь простір розіб’ється на д1 кубиків чи зон, усередині ко-
жного з яких щільність постійна Довільний може потра-
пити в один з д1 кубиків чи в частину простору, що лишилася.
Зони будемо позначати /€, £ — 1,2,... ,д1,д1 4-1. У цьому
випадку ТДХ^-ІВі) апроксимується поліноміальним розподі-
лом з вектором параметрів
В. = (РІ,Р2>-- ,Рд<,Рд< + 1) ,
ч‘
дер‘,+1 = 1- Ер«-
Частота появи X*. в кожній із зон задається вектором з
цілочисельними компонентами
№ = [м/сі, Мі2, . . - , 1^ + 1]
?‘+1
де Е = №.
€=1
з**
56
Розділ 2. Моделі та алгоритми навчання та самонавчання
Тоді умовна пильність X*;, що належить до г-го класу, за-
дається поліноміальним розподілом
РІХ.ІИ.В.) = 7 П (2.9)
е=1
Таким чином, сім’я поліноміальних розподілів характери-
зується т (</ + 1) параметрами, які необхідно визначати по
змішаній вибірці Ця задача вимагає дуже великих обчислю-
вальних ресурсів. Якщо є додаткова інформація про те, на-
приклад, що усі Р (Х^Щ-, ВЦ ідентичні і відрізняються лише
зсувом {оі}і=ї-^ щодо центра до, то число невідомих параме-
трів, яке потрібно визначити, складе д1 + 2 т.
Позначимо тепер для будь-якого джерела Ц і даного ви-
рішального правила гЦХ^) : Р{гЦХ&) Щ} — умовний ризик
класифікації X*. є Ц. Тоді середній ризик Р(гіЩ) є умовні
втрати, усереднені по усім X*,, к — 1,п.
Вираз для безумовного ризику за результатами всіх спо-
стережень має вигляд
771
Я(и|¥п_1) = ^Я(п|Ц)Рі =
І=1
Р(и(Хп)|Ц)-Р(Хп|Ц,ВІ)-РіЙХ
де ¥п-і — {Хі, %2, • • • > *п~1}
р(В|¥п_1)ав,
(2.10)
Якщо матриця штрафів має антидіагональний вид, а
Р(В|¥п_і) — апостеріорна щільність для В, то оптимальна
вирішальна функція, мінімізуюча середній ризик,
{Ц, якщо Р(Х„, V, |¥„_і) =
= 5цр{Р(Хп,И !¥„_!)};
V,, інакше,
(2П)
2.2. Алгоритм навчання за Байєсом
57
тобто спостерігаємий Х„ відноситься до того класу У3, для яко-
го апостеріорна умовно-вибіркова щільність Р(ХП,^|УП_1)
виявляється максимальною. Вирішальна функція (2.11) збі-
гається з вирішальною функцією, для якої точно відомі зна-
чення параметрів В7.
На кожному кроці відбувається переоцінка невідомих
{В,}=у^. Для мінімізації середнього ризику потрібно
обчислити Р (В |¥п_ і) на основі апріорної інформації (умови
а — в), а також інформації про розподіл Р(В)
Р(В |¥п_і) =
Р(ХП_І|В)Р(В |¥п-2)
Р(Хп_!і¥п_2)
Р(Х„_1 |В)Р(В |¥п_2)
/ Р(Хп_і |В)Р(В|¥п_2)с!В’
(В)
(2.12)
де Хп-! — поточне зображення; ¥п_2 = п_2 ;
Р (В |¥п_2 ) — апостеріорна щільність на (п — 2) кроці.
Використовуючи (2.7) і (2.12), одержимо
£ріР(Хп_1|Ц,Ві)Р(В |¥п_2)
Р (В |¥п_1) = . (2.13)
/12 ргР (Хп_! Іи, В,) Р (В |¥п_2 )с®
і=1
На рис. 2.1 представлені блок-схеми алгоритмів двох ти-
пів систем, що самонавчаються, мінімізуючих середній ризик
(імовірність помилки) у класі послідовних байєсівських про-
цедур.
У першому випадку вид сімейства розподілів відомий, у
другому — невідомий і апроксимується поліноміальним роз-
поділом. Для забезпечення збіжності й однозначності знайде-
них оцінок для В необхідно виконання умов а — г (див. вище
в даному розділі).
Оскільки для оцінки Р (В |¥п ) використовуються байєсів-
ські процедури, то для їх реалізації потрібно виконання тих
58
Розділ 2. Моделі та алгоритми навчання та самонавчання
же умов, що необхідні для байєсівського навчання з учителем
(наявність достатніх статистик для Р (В |¥п)).
Вирішальне правило, мінімізуюче умовний ризик, реалі-
зується при обчисленні
т
£ріР(хп_1щ,ві)Р(в |У„_2)
Р(В ІУп-х) = —---------------------------------• (214)
/ Е РгР (Хп_! |Ц, Ві ) Р (В І¥п_2 )гіВ
і=1
Були визначені достатні умови ідентифікації для сімей-
ства Р — <Р Х^ /V, {РВ, т- І > ____ одномірних поліномі-
IIIі 1 '«-1.93 ) і=1,т
альних розподілів (т — загальне число класів; N — число
послідовних показів зображень з одного класу).
Достатньою умовою для ідентифікації такого сімейства є [3]
N > 2т - 1.
1 — блок обчислення суми £Рі-Р(Хп|В,);
І=1
2 — інтегрування по параметру В,;
З — блок обчислення апостеріорних імовірностей;
4 — блок обчислення
5,7 — пристрій прийняття рішень,
6 — блок обчислення функцій правдоподібності.
Рис. 2.1. Блок-схема самонавчання
2.3- Імовірнісні ітеративні алгоритми навчання
59
2.3. Імовірнісні ітеративні алгоритми навчання
Замість визначення невідомих умовних щільностей роз-
поділу Р{Х|И} , що потребує великого обсягу інформації і
є надзвичайно трудомістким, значно простіше відновити не-
відому вирішальну функцію (класифікацію) вчителя. Даний
підхід заснований на роботах К.С. Фу (США) та Л.З. Цип-
кіна (СРСР).
В роботах Ципкіна, Фу та інших авторів був розробле-
ний цілий клас ітеративних імовірнісних алгоритмів навчан-
ня (або параметричної адаптації) [31].
Тут мета навчання трактується як відновлення невідомої
вирішальної дискримінантної функції в процесі навчання.
Нехай є деяка вирішальна функція Г(х, с), параметри
с = [сД якої невідомі. Нехай спостерігається зразок X, для
якого істинна класифікація є С(Х), а класифікація системи
визначається вирішальною функцією Р(Х, с).
Тоді помилка розпізнавання дорівнює є = V(X) — К(Х, с).
Задамося деяким функціоналом
(2(Є) = <2(У(Х.)-Г(Х,СУ) =
= (У(Х) -Г(Х,с))2*, (2.15)
де к = 1,2,...
Нехай К(х, с) відноситься до одного з наступних класів:
1. Р(х, с) = стх;
2. Г(х,с) = с[х + хтС2х, де х = [яДі=ї^; сх = [сД —
невідомий вектор; С2 = ||су|| — невідома матриця;
к
3. Г(х,с) = £сі(#(х).
І—1
Мета навчання: відновити невідомі параметри с за на-
вчальною вибіркою, використовуючи деякий критерій І(с).
З***
60
Розділ 2. Моделі та алгоритми навчання та самонавчання
Задамося в якості критерія /(с) наступним інтегральним се-
редньоквадратичним критерієм.
І (с) = Мх&(У, ?(*,<»} =
- У <2(У, Г(х,с)) -р(х,У)гіх —+ тіп. (216)
Ох
Якщо б сумісні щільносте розподілу р(х, У) були відомі,
то для знахождення шуканих параметрів с* = [с*] можна бу-
ло б застосувати стандартні методи оптимізації, наприклад,
метод градієнтного спуску
с [п] = с [п - 1] - 7 [п] УСІ (с [п - 1]),
п = 1,2,..., 1 '
<9/(с) І
І с=с[п— 1]
де УСІ (с [п - 1]) = єгасі [7 (с [п - 1])] =
7 [тг] — величина кроку.
Умови збіжносте алгоритму (2.17) такі:
оо
7 [тт]---» 0; 2 7 [п] = оо.
п—»оо '
п=0
Тоді послідовність с [пі ----» с*, де с* = [с*] — істинні
значення параметрів.
У випадку ж, коли спільні щільності Р(х,У) — невідо-
мі (а цей випадок найчастіше і має місце на практиці), ви-
користовуються ітеративні імовірнісні алгоритми навчання,
що базуються на методі стохастичної апроксимації (який
був запропонований Кіфером, Вольфовіцем і розвинений
Дворецьким). Ципкін у 60-і роки розробив клас алгоритмів
параметричної адаптації на основі метода стохастичної апро-
ксимації. Отже, нехай потрібно знайти
тіп І (с) = Мх {(£ (х. с)} = / (х, с) р (х V) гіх,
2.3. Імовірнісні ітеративні алгоритми навчання
61
причому р(х, V) невідомі; <2(х, с) — деякий опуклий функціо-
нал від помилки класифікації (V (X) — Г (X, с)) ; с — неві-
домий вектор параметрів.
Припустимо, ми спостерігаємо реалізації випадкового про-
цесу — зображення X [1], X [2],..., X [п — 1], і за (п— 1) крок
навчання побудована оцінка с[п — 1]. Тоді на п-му кроці при
спостереженні X [п] алгоритм пошуку буде мати вигляд
с [п] = с [п - 1] - Г [п - 1] (X [п], с [п - 1]), (2.18)
де Г [п] — деяка квадратна матриця діагонального виду
' 7і(«) 0 0 С '
0 72 (п) • - 0 0
Г[п] = . . . 1
0 0 7к-і (”) 0
1 0 0 0 7л- (п)
де т,- (п) — величина кроку ПО 7-й компоненті Су. В окремо-
му випадку т,- [п] — у [п], 'Уі — 1, к . Умови збіжності для
імовірнісного алгоритму навчання (2.18) такі [31]:
1. 7 [п]----> 0;
ті—>оо
£ 7 И = (2 19)
оо
52 72 Н < оо,
п=0
крім того, додаткові умови:
2. іп£ \мх |(с - с*)т Х7СР (х, с)}] > 0,
якщо є < ||с — с*|| < |, де є > 0;
3. (х,с) \7С<2 (х, с)} < ії (1 + стс), .
де (1 > 0.
62
Розділ 2 Моделі та алгоритми навчання та самонавчання
Умова 2) — необхідна умова мінімуму <2(х, с) у точці с*,
а умова 3) означає, що норма градієнта ||\7с<2(х, с)|| повин-
на бути обмежена зверху деякою квадратичною функцією.
У випадку, коли обчислити градієнта \7сф (х, с) аналітично
важко, то можна скористатися різницевими схемами. Тоді за-
даємося зсувами Д^ по кожній з осей і і обчислюємо
(х[п],с[п- 1]) =
С} (х [п], с [п — 1] + Д^е^) — <2 (х [п], С [п — 1])
д; ет
(2.22)
де Єу — орт у-й осі.
У даному випадку умови збіжності приймуть наступний
вигляд [31]:
1. 7 [ті]---> 0;
п—»оо
Е 7 [п] = оо;
~п=°г 1 (2.23)
^2 7 [тг] Д [?г] < оо;
к
=Е
71=0
2. (с - с*)Т (<5+ (х, с) - (х, с))
к • ||с - с*|| • ||3+ (х,с) - (х,с)||, (2.24)
де к >
з. ц<г+ (х,с) - а. (х,с)ц < лис-с-ц + в,
де С}+ (х, с) = <2 (X [її], с [п - 1] + Д^е^),
<2- (х, с) = <2 (X [п], с [тг - 1] - Д^).
При виконанні зазначених умов послідовність с [п] при
п —> оо збігається до шуканого вектора параметрів с* по імо-
вірності, тобто
Ііт Р {||с Іп] — с*||2 > є} = 0
п—»ос
(2.25)
2.3. Імовірнісні ітеративні алгоритми навчання
63
(2.26)
і в середньоквадратичному
Ііпі Л/ {Це [тг] — с*||2} = 0.
п—>оо
Використовуючи клас алгоритмів навчання (2.18) і зада-
ючи різні види (^, можна побудувати різні відомі алгоритми
навчання й адаптації. Наприклад,
1. Для методу потенційних функцій, де
к
припустимо, що
2
к
(2.27)
к
Тоді можна знайти
(х, с) _ |
8с3 ।
І відповідний алгоритм адаптації буде виглядати так
(2.28)
N
і=і
де п = 0,1,2.3,..., V [?г] = V (х [п]) — класифікація вчителя.
2. Для перцептрона вирішальна функція така
/ к \
(2.29)
де в (а) - деяка гранична функція, наприклад, виду
1, якщо а > 0;
в (а) =
0, якщо а 0.
64
Розділ 2. Моделі та алгоритми навчання та самонавчання
Тоді алгоритм навчання перцептрона буде таким
Сі [?і] = сг [п
1] + 7 [п]
52 сі і«- ш (х Н)
1=1
(2.30)
де в' (а) = <
1,
-1,
якщо фі (х [п]) > 0;
інакше.
Умови збіжності цих алгоритмів будуть аналогічними.
Правила зупинки алгоритмів. У випадку, якщо вико-
ристовується детермінований алгоритм навчання (2.17), за-
снований на обчисленні \7СІ (є [п]), то збіжність с [ті] до є* —
монотонна, і правило зупинки алгоритму виглядає так
Де (п) = Це [п] — с [п — 1] || < є.
При імовірнісних алгоритмах навчання спостерігаються
випадкові реалізації, і гладкої кривої І (с [ті]) уже не буде.
Тому треба усереднити с [п] на деякому інтервалі N і далі
використовувати метод ковзного середнього.
Позначимо с [А’] = ^2 с [т] •
т=(к—1)М+1
Тоді правило зупинки таке:
|с [А: + 1] с [А’] | Є()оп*
Можна використовувати інші правила зупинки, напри-
клад, порівнювати не значення с [п], а величини градієнтів.
Тоді умови зупинки будуть такими-
а) ||Ч7(с[п])|| < єі;
б) |^с£(с[п])||<є2:
в) Д/с [ті] = | / (с [її] - 7(с [п — 1])| < єз-
2.3. Імовірнісні ітеративні алгоритми навчання
65
Задачі навчання з обмеженнями. Розглянемо тепер
задачу навчання при наявності обмежень. Нехай відповідна
задача оптимізації має вигляд
тіп І (с) = Мх {<2 (х, с)} (2.31)
с
при умовах
Мх {к (х, с)} = С (с) = 0, (2.32)
де к (х, с) = [Лі (х, с)]і=г^ — вектор-функція. Причому І (с)
і С (с) — неможливо обчислити, тому що невідомі щільності
розподілу р (х, і/).
Будуємо функцію Лагранжа
£(с,А) = 7(с) + ЛтС(с)= г х
\ \ \ > (2.33)
= Мх {£(х,с) + Атк (х,с)} ,
Будемо шукати сідлову точку (с°, А0) функції Ь (с, А), та-
Щ° Ь (с°, А0) = тах тіп Ь (с, А).
Пошук шуканих с° і А0 здійснюємо, використовуючи імо-
вірнісний алгоритм навчання.
На п-ій ітерації одержимо
с [п] = с [п - 1] - 7 [п] {^с<2 (х [п] ,с [п - 1]) +
4-Не (х [тг], с [п — 1]) А [п — 1]} ,
де Не (х, с) = [— гесіан.
І І -І 1=1,771,2=1,П
Одночасно будемо шукати і вектор множників Лагранжа
А = [А,] відповідно формулі
А [п] = А [п — 1] +- 71 [п] к (х [п], с [т? — 1]). (2.35)
Умови збіжності будуть такими ж, як і умови для задач
без обмежень (2.18), (2.19).
66
Розділ 2. Моделі та алгоритми навчання та самонавчання
2.4. Самонавчання в інтелектуальних системах.
Постановка задачі кластер-аналізу.
Критерії і метрики кластер-аналізу
Розглянемо тепер задачі навчання без вчителя (чи зада-
чі самонавчання). Методи самонавчання одержали широке
поширення в інтелектуальних системах, зокрема — в експер-
тних системах розпізнавання образів і класифікації і т.д.
У системах розпізнавання образів і класифікації відповід-
ний клас задач навчання без вчителя одержав назву кластер-
аналізу (тобто мимовільного розбиття вихідної вибірки на
компактні підмножини чи кластери).
Кластер-аналіз. Постановка задачі. Критерії яко-
сті і метрики кластер-аналізу. Нехай задана множина
спостережень Х-= {Х1; Х2,..., Хп} , де X; = , і = 1, N.
Потрібно розбити вибірку X- на непересічні підмножини —
кластери 5і,..., 8к так, щоб забезпечити мінімум (екстре-
мум) деякого критерію (функціонала якості), тобто: знайти
такі 8 — {5і, 52,..., 5/с} . Р (5) —» пип (гпах).
Можливі різні види критеріїв (функціоналів) розбивки.
Зазначемо, что ця задача тісно зв’язана з визначенням деякої
метрики в просторі ознак.
Розглянемо найбільш широко використовувані функціо-
нали якості розбивки:
1. Коефіцієнт розбивки Р, що визначається таким чи-
де Є [0; 1] — деякий ступінь приналежності г-го об’єкта
7-му кластеру. Діапазон зміни Р Є [|; 1] , де п — число об’є-
ктів, к — число кластерів.
2 4. Самонавчання в інтелектуальних системах
67
2. Індекс чіткості:
КГ — 1
ЯРІ = —--------, ИРІ Є [0; 1], (2.37)
К — 1
де К — число класів (кластерів); Р — коефіцієнт розбивки.
3. Ентропія розбивки:
К п
н 5252
>=і і=і
- 1п (?е0)
п
Н Є (0;1п/<).
(2 38)
4. Нормалізована ентропія розбивки:
Н
1 — К/п
п 1п К \
71 — К /
(2.39)
Н, Є
де 71 — число ТОЧОК.
5. Модифікована ентропія:
Н2 = Д, Н2 Є (б; —Д) . (2.40)
ІП К \ 71 — К /
6. Другий функціонал Рубенса:
1 /1 ” \ /1
Р2 = - І — тахта, 4- тіптахш,,- І , Р2 є ( —; 1
2\пз 3 і з І \К
(2 41)
7. Третій функціонал Рубенса (другий індекс чіткості):
1УР2І = КНР2ІЄ(О-,1). (2 42)
Оскільки вихідна інформація задається у вигляді матри-
ці X, то виникає проблема вибору метрики. Вибір метрики
— найбільш важливий фактор, що впливає на результати
кластер-аналізу. У залежності від типу ознак використову-
ються різні міри близькості (метрики).
Нехай маємо зразки X, й Хк у 7\Г-мірному просторі ознак.
Основні метрики, використовувані при кластеризації,
приводяться в таблиці 2 2.
68
Розділ 2. Моделі та алгоритми навчання та самонавчання
Таблиця 2.2.
Основні піни метрик
Найменування метрики Тни ознак Формула для оцінки міри блізькості (метрики)
Евклідова відстань Кількісні
Міра подібності Хеміпга Номінальні (якісні) N де п"к- число співпадаючих одиничних ознак у зразків X, і Хк
Міра подібності Роджерса-Таїнмото Номінальні шкали Ні; И|#г Пк ) і де пХ - число співпадаючих одиничних ознак у зразківX, і Хк ; п, п*-загальне число одиничних ознак у зразків X, і Х„ відповідно
Манхеттепська метрика Кількісні } 1
Відстань Махалопобіса Кількісні = (Хо - - хм), де - коваріаційна матриця вибірки: * = {Х1,Ха ..,х„}
Відстань Журавльова Змішані Л,к=уі‘к. де Ій=( п ЯКЩ0 ’* /у •* такте
Існує велика кількість алгоритмів кластсризації, що ви-
користовують різні метрики і критерії розбивки. При цьому
число класів (кластерів) або задається апріорі, або визнача-
ється в процесі роботи самого алгоритму.
Одним з перших алгоритмів кластсризації був дисперсій-
ний алгоритм мимовільної розбивки Ю.П. Зайченко (див
журнал «Автоматика» №5, 1966). В цьому алгоритмі число
класів не задане, і воно визначається в процесі роботи алго-
ритму.
2.5. Дисперсійний алгоритм самонавчання
69
2.5. Дисперсійний алгоритм самонавчання
(мимовільної класифікації)
з незаданим числом класів
Можливість рішення задачі самонавчання при невідомо-
му числі класів була уперше висловлена в статті Волохо-
ва В.С. і Зайченко Ю.П. «Дисперсійний метод мимовільної
розбивки простору зображень на компактні множини» у
журналі «Автоматика», 1966, №5.
Пізніше було опубліковано теоретичне обґрунтування і
розвиток цього алгоритму.
2.5.1. Формулювання критерію мимовільної розбивки
Розглянемо наступний приклад. Нехай Аі, Аг,.. -, А# —
деякі об’єкти, агрегати і т.д., кожний з яких характеризує-
ться своїми параметрами Хі = (ггн, Хц,..., хпг). Припустимо,
що схожим за властивостями об’єктам відповідають близькі
значення параметрів.
Потрібно розбити {А,}, і — 1,?/ на ряд підмножин, що
включають «близькі» об’єкти, причому керування кожною
множиною об'єктів можна проводити індивідуальним керу-
ючим пристроєм.
У такому випадку виникають втрати Ь (т)), унаслідок то-
го, що різні об’єкти керуються одним пристроєм. Величина
цих втрат залежить від ступеня розходження між об’єктами
однієї підмножини (класу), де ступінь розходження може, на-
приклад, визначатися дисперсією
Г> [Х-= {ХД, г = ЇДУ] =
і "
= ултУІІх'-х<.Л
1=1
70
Розділ 2. Моделі та алгоритми навчання та самонавчання
Можна було б керувати кожним об’єктом Аг за допомогою
окремого керуючого пристрою, і тоді усі втрати £ (/;) будуть
дорівнювати нулю Однак це економічно невигідно, тому що
виготовлення й експлуатація керуючих пристроїв зв’язані з
певними витратами, що позначимо IV (к). Виникає задача
компромісного настроювання, що приводить до необхідності
мінімізації функціонала виду
Г{£[£>(?0], IV (к)}.
В окремому випадку функціонал Р позначає загальні ви-
трати, і тоді він приймає досить простий вигляд
Р=Ь[П (А}] + IV (к). (2.43)
Мінімізація (2.43) являє собою мету мимовільної розбивки
при невідомому числі к класів.
Вид функцій Ь [£) (=¥-)] і IV (к) задається вчителем і може
варіюватися в залежності від задачі. Можна вказати лише
загальний характер цих функцій. IV (к) монотонно зроста-
юча функція цілочисельного аргументу, а втрати Ь [£> (>¥-)]
монотонно зростають з ростом дисперсії.
к
Оскільки £> (Х-) = 52 £* (^т) убуває з ростом к, а IV (к)
і=1
зростає, то мінімум функціонала Ь [О (X-)] + ЇУ (к) може до-
сягатися як на кінцях інтервалу [1, /V], так і у середині його.
Сформулюємо задачу самонавчання в наступному вигля-
ді. Вихідну множину Х- = {8і, 82, ., 8м} потрібно розбити
на такі непересічні підмножини ^¥2, - -, А*, щоб мінімізу-
вати сумарні витрати
(Аг \
22 £>(*?) І + IV (к). (2.44)
І=1 /
2.5. Дисперсійний алгоритм самонавчання
71
2.5.2. Теоретичні основи алгоритму розбивки
Формулюється гіпотеза «компактності» про те, що зо-
браження 51, . . . , 8і усередині кожної підмножини розміщені
щільною групою.
Як міру компактності пропонується використати диспер-
сію £> (Лї) = £> [{5іг}}, Г = 1,Пі] , оцінка якої по вибірці до-
рівнює п.
'Н 1
Г—1
Чим менше О {Хі) при заданому тим більш компактна
множина Хг-
Нехай задана множина Х-= {51, 82, - - -, <$л}
Потрібно розбити А7-на к підмножин Х-і.Хг,...,Хц так,
к
щоб забезпечити мінімум ^2 В (Хі)Рі. Назвемо таку розбивку
1=1
оптимальною і позначимо
к
тіп 52Г(^)Рг = Л(/с).
і=1
Існує і доведена наступна лема:
При збільшенні числа класів середня дисперсія монотонно
зменшується, тобто А (к 4-1) < А (А;) .
Якщо N — число зображень, то А (/V) = 0.
Нехай Ф — матриця коваріацій множини X- Тоді
Г> (^-) = ІгФ,
де ігФ — слід матриці Ф. Цікаво установити вид поділяючих
границь між класами при оптимальній розбивці.
На це питання дає відповідь теорема 1.
72
Розділ 2. Моделі та алгоритми навчання та самонавчання
ТЕОРЕМА 1. Оптимальні поділяючі границі між мно-
жинами Х? є гіперплощинами, а самі X? — опуклі множи-
ни. Нормаллю до гіперплощини між Хт і Ху служить вектор
Су = — /4,, де І Ді — центри множин X? І Ху відповідно.
Отже, для завдання поділяючої границі необхідно визна-
чити два параметри: нормаль С и одну точку на гіперпло-
щині.
Основою для пропонованого далі алгоритму розбивки є
теорема 2.
ТЕОРЕМА 2. Нехай Ф — матриця коваріацій деякої
множини; Сі — найбільший власний вектор матриці Ф. Тоді
оптимальна поділяюча границя при розбивці X- на дві під-
множини задається наступним рівнянням
Ф12 (8) = С^8 - Є = 0,
де в — такий поріг, що
В(Ху : С|8 Є) +Г>(^2 : С^8 > 0) = тіп . (2.45)
Теорема 2 указує, что гіперплощина проходить нормально
Сі, причому через таку точку 0, що сума дисперсій в утворе-
них при цьому підмножинах Ху і X? виявляється мінімаль-
ною.
2.5.3. Оптимальна розбивка упорядкованої множини
Перш ніж вирішувати задачу оптимальної розбивки в за-
гальному випадку при К > 2, розглянемо спочатку однови-
мірний випадок.
Нехай ($і,..., вм) = X-— упорядкована множина точок
на ЧИСЛОВІЙ ОСІ, тобто 51 < 52 • • • < 5уу. Потрібно розбити
к
Х-на такі Х^,..., Хц, щоб забезпечити мінімум
ї=і
Назвемо таку задачу одновимірною задачею оптимальної
розбивки.
2.5. Дисперсійний алгоритм самонавчання
73
•Якщо Аг П X] = 0, то очевидно,
= ;г Е (* - 8^)2- <2ле>
Щ Г=1
Ця задача еквівалентна наступній. На інтервалі
(51,...,5уу) розставити к — 1 різних порогів 01,..., 0^-1
так, щоб досягався мінімум функції
к
^Г>(^С [0І-1Л)),
1=1
де [0і_і, 0і) — інтервал, відкритий праворуч.
Приймаємо 0о = 8і, а вк > 8р/.
Сформульовану вище задачу можна вирішити методом
послідовної оптимізації чи динамічного програмування [3].
2.5.4. Алгоритм мимовільної розбивки
на незадане число класів
Використовуючи теорему 2, можна легко поширити за-
пропонований вище алгоритм рішення одновимірної задачі
на багатовимірний випадок. Для цього знайдемо для матриці
Ф всієї сукупності вектор Сі і визначимо проекції всіх точок
на цей напрямок.
Нехай тії — проекція 8і на Сі, і = 1, N. Тоді щ =
= 0^8,. Визначивши проекції всіх точок вихідної множи-
ни на Сі, приводимо задачу до одновимірного випадку.
Багатовимірність простору зображень враховується при об-
численні дисперсій у підмножинах X?, а саме
1 №
о {х,№ с, є «,)[ = 77 ЕII8'. - 8‘«ІГ- <2-47)
У результаті X- розбивається паралельними гіперпло-
щинами, що проходять через точки 0і,... ,0^-1 нормально
до найбільшого власного вектора Сі матриці Ф. Пороги
4і
74
Розділ 2. Моделі та алгоритми навчання та самонавчання
визначаються відповідно до описаного вище ал-
горитму.
У зв’язку з тим, що уже після першої розбивки найбільші
власні вектори в утворених підмножинах Хі і Х^ можуть не
співпадати з Сі, недоцільно проводити розбивку в одному
напрямку більше, ніж на два класи.
Тому процес розбивки при к > 2 варто звести до послі-
довної дихотомії. Багаторазово застосовуючи алгоритм опти-
мальної дихотомії, можна одержати розбивку на будь-яке чи-
сло класів.
Однак алгоритм оптимальної дихотомії салі по собі ще
не забезпечує оптимуму при розбивці на к класів. Тому ви-
пливає оптимізувати процес розбивки, увівши деякий крите-
рій об’єднання. Цей критерій повинен залежати від £(£)) і
XV (к) Нехай після розбивки на к класів X? і Ху — сусідні
підмножини. При об’єднанні X? і Ху дисперсія може лише
зрости, тому що
О (Хт) + (Ху) <П(Х,Ц Ху),
а функція вартості зменшиться, тому що ЛЮ = IV (к — 1) —
XV (А;) < 0.
Тому якщо величина Д£ (7?) + ДІУ (к) менше нуля, то
втрати за рахунок збільшення дисперсії компенсуються змен-
шенням вартості на утримання класів, а тому X? і Ху доціль-
но об’єднати. Як критерій об’єднання приймемо відношення
Тоді правило об’єднання можна записати в наступно-
му вигляді
якщо Д£(£>) ДЖ (А:) ДЬ(Г>) >Т(г), то збережемо вихідну розбивку; И (2.48)
і ДІТ (А;) <1 иь жини слід об'єднати,
2.5. Дисперсійний алгоритм самонавчання
75
де Т (г) — деякий поріг, що залежить від номера кроку. Якщо
покладемо Т = 1, то правило об’єднання буде діяти, почи-
наючи з першого кроку, після кожної чергової розбивки. У
такому випадку процес формування множин закінчується в
той момент, коли після деякого об’єднання ми одержимо ті ж
самі множини, що були до початку розбивки на цьому кроці.
Ясно, що такий вибір порога не може привести до найкра-
щої розбивки, оскільки залишається можливість застрягти
на проміжному мінімумі функціонала вартості, не довівши
розбивку до кінця. Можна рекомендувати вибір перемінного
порога з наступних міркувань. Оскільки на перших кроках
має сенс провести розбивку на якомога більше число класів,
поріг Т вибирається так, що Т < 1. Далі процес розбивки
повинен змінитися протилежним процесом — об’єднанням, а
тому Т має зростати від кроку до кроку, поки не досягне
свого сталого значення Т — 1. (Як функцію Т (г) можна ви-
брати, наприклад, Т (г) = 1 — е~г, де г — номер кроку).
Регулюючи величину Т = Т (г) , можна одержувати різні
співвідношення між режимами розбивки й об’єднання класів.
Опишемо коротенько алгоритм формування класів:
а) обчислюється матриця коваріацій Ф вихідної множини;
б) визначаються ІгФ, Сі і Ах;
в) знаходимо проекції точок 8і,..., 8уу на Сі;
г) робимо оптимальну дихотомію в напрямку Сі й одер-
жуємо ДВІ ПІДМНОЖИНИ Ху І
д) перевіряємо сусідні підмножини (класи) за критерієм
об’єднання (2.48).
На другому кроці пункти а-д повторюються незалежно
з кожною із утворених на попередньому кроці підмножин і
т.д. Процес закінчується в той момент, коли на деякому кроці
процедури розбивки й об’єднання будуть цілком компенсува-
ти одна одну, а множини придбають сталі границі.
4*
76
Розділ 2. Моделі та алгоритми навчання та самонавчання
Цей алгоритм робить попереднє формування класів і, від-
повідно до термінології А.Г. Івахненко, реалізує «самонавчан-
ня по входах», тобто розбиває вихідну множину на класи
безвідносно вихідним реакціям системи. Надалі при надхо-
дженні нової інформації положення границь уточнюється.
Був запропонований також алгоритм корекції границь на ба-
зі методу стохастичної апроксимації. Відбувається адаптація
границь того класу, у котрий попадає чергова точка. Такий
процес можна назвати «самонавчанням по виходах» (тобто
по реакції самої системи, що розпізнає).
Отже, процес самонавчання природним образом розпа-
дається на два етапи: спочатку «самонавчання по входах»
(де одночасно використовується вся апріорна інформація),
а потім «доучування» системи по виходах при надходжен-
ні поточної інформації. Застосування такого комбінованого
алгоритму значно скорочує повний час самонавчання, тому
що деякі дослідники експериментальним шляхом установи-
ли, що рекурентні алгоритми самонавчання, якщо не викори-
стовувати апріорну інформацію, сходяться занадто повільно.
Крім того, кінцевий результат при використанні рекурентних
алгоритмів типу стохастичної апроксимації залежить від по-
чаткового стану (початкового положення границь) і від по-
рядку надходження поточної інформації, якщо вона викори-
стовується однократно.
При цьому існує велика імовірність «застрягти» на про-
міжному локальному екстремумі. Комбінований метод само-
навчання вільний від такого недоліку, оскільки на першому
етапі всі точки обробляються паралельно. Тому використан-
ня комбінованого алгоритму самонавчання значно розширює
можливості самонавчання і коло його застосувань для пра-
ктичних задач
2.6. Агломеративний ієрархічний алгоритм кластер-аналізу
77
2.6. Агломеративний ієрархічний алгоритм
кластер-аналізу
Загальна схема всіх алгоритмів цього класу така: форму-
ється послідовність порогів {ф < (І2 < Ф-} , що зв’язана з по-
будовою дерева кластеризації. Починається з кластеризації,
при якій кожна точка є окремий кластер.
На першому кроці поєднуються ті точки, міра близькості
ЯКИХ не перевищує ф, тобто
(1 (Хі, Х^) ф.
На другому кроці поєднуються ті, у яких поріг близькості
не перевищує сІ2 і т.і. доти, поки всі точки не об’єднаються в
один клас, чи на деякому рівні число кластерів буде стабілі-
зовано, і при цьому всі точки усередині класу задовольняти-
муть порогові (1Г.
Насамперед, для побудови правила останова буде вико-
ристане поняття мінімальної дистанційної розбивки 5 (е) =
— {5і (е), 52 (е),..., 8Г (е)} , де е — еталон
5і (еі) = ї (х, Єї) тіп(1 (х, е,)
і при цьому наступний крок
52 (е2) = 5і О < х : <1 (х, е2) < тіп с? (х, е,)
5уу (е/у) = 5і Я ... П 5іу-і П |х : гі(х,е/у) тіп<ї(х,е,)|.
Розбивка 5* називається незмгщеною, якщо ця розбив-
ка з точністю до множини міри нуль збігається з мінімаль-
ною дистанційною розбивкою, породжуваною векторами
78
Розділ 2. Моделі та алгоритми навчання та самонавчання
середніх Пі
Є3 (5 ) = ~~ >
“7 1=1
де Ху — сукупність точок, що належать Зр, щ — число точок
в Зр
Правильною кластєризацгєю називається незміщена роз-
бивка точок вибірки на кластери 3* — {5{, 3%,, 3^} , для
якої виконуються наступні умови:
1. визначені оцінки середніх (5*);
2. найбільша внутрішньокластерна відстань на множині
кластерів менше найменшої міжкластерної відстані, тобто
такі, = г/,пах < тій г/„,
*
де сіі — відстань між точками одного кластера: =
= шах |хь — ху|; гіу — відстань між різними кластерами
гіу може бути визначено різними способами:
— як максимальна відстань між парою точок з цих кла-
стерів: ск = тах |хь - хгІ:
х*Є5і, хгє5л
— як відстань між центрами кластерів: гіу = |єі — е^|,
Єі = 52 хь ез обчислюється аналогічно.
’ хкЄ5,
Опис алгоритму кластеризацїї
Початковий етап. Задано послідовність < й2 <
< <к„} = <7, початковий набір середніх е° = [є?, е^,..., е^], де
е° — хг, і — 1, N. Початкове розбиття 3° = {5і,52,...,5^},
__________________ N
де 59 = Хі, г = 1Л, СІ 5° = X
і=1
1-а ітерація: 1. Визначимо розбиття 3^ — |5Р\ 3^\ ...,
шляхом відшукання точок х7, найближчих до цен-
2.0. Агломсратишіий ієрархічний алгоритм кластер-аналізу
79
тра е°, і їх об’єднання в один клас
5*,) =
аг§ тіп д, (хЛ, є,) = х^
х*.ЄХ,хк/е®
А [б/ (х,, е°) гіі] , (тоб то х7 0);
хі,
якщо такого х7 нема,( х5 = 0);
.....................; (2.49)
якщо
А
якщо
аг^тіп гі(хье°) = х,
х^єХг.х^/еО
л
=
р
=х\сип;
хР,
якщо Ху = 0;
Цей крок повторюємо доти, поки не отримаємо: Х^4-1 —
їй т
= Х\ 5' 1 — 0, де М — число кластерів, отриманих в ре-
і=і
зультаті 1-ої ітерації.
3. Обчислюємо центри нових кластерів
— ^Х", якщо х7 ± 0, = {Хр,х^;}
Хр, якщо х^ = 0,
Р = ЇЛІ.
На 2-ій ітерації поєднуємо сусідні кластери, відстань між
якими менше С?2.
у(і) = е(і) =
Ур ЄР
4**
80
Розділ 2. Моделі та алгоритми навчання та самонавчання
т-о ітерація (г > 1) : Послідовно за рекурентними фор-
мулами знаходимо нову розбивку 8^ = ^5^ 5^ \
шляхом злиття найближчих кластерів і визначення їх цен-
трів (змінні г-го рівня ієрархії).
5^-1)и55;-1)
якщо уУ ' — аг£ шіп сі
і>р
(г-1) (Г-1Л <
•У р ї «У зр і
якщо = 0,
р — 1, Аг,
де Аг — число кластерів, отриманих після г-ої ітерації.
Обчислюємо змінні г-го рівня ієрархії (центри)
(г-1) , (г-1)
ПрУр + п>ру)р
Пр • Ь п^р
якщо / 0 і 8^ = б^-1) СІ
уО-О '
•У р і
якщо 5,р-1) = 0,
Р = 1,М-
Продовжуємо виконувати ітерації доти, поки не почне ви-
конуватися умова 8^ = 8^г~1^ (тобто, коли відстань між ко-
жною парою кластерів не стане > (1Гп або всі кластери не
зіллються в один).
ЛЕМА. Нехай для заданого кластера внутрішньокла-
стерна відстань с? = <1Гп (дорівнює максимальному гранично-
му значенню), тоді при реалізації алгоритму сума відхилень
8<г) = <
ур
А
Уї
А
, 8^~1} + 0; (2.50)
(2.51)
2.6. Агломеративний ієрархічний алгоритм кластер-аналізу
81
поточних середніх (центрів кластерів) на 7-тій ітерації від де-
яких істинних еталонних значень кластерів, що визначається
в такий спосіб:
і=і
строго убуває, тобто £)г_і > Сг, і починаючи з деякого номе-
ра гтах, стає рівною нулю, тобто у^ —* е* при і —> гтах, V]
(ІУГ — число кластерів, отриманих в результаті г-ої ітерації).
Наслідком з цієї леми є теорема, що встановлює достатню
умову збіжності ДО НЄЗМІЩЄНОЇ розбивки 8* = {5'1,5'21 •••>
...,5^}.
ТЕОРЕМА: Нехай вибірка А-допускає правильну кла-
стеризацію щодо множини є (5'*) = {еі (5і*) ,е? (5*),...,
... ,е/у (5*)} , де е_і (5*) — центр кластера 5*, причому ма-
ксимальне граничне значення с/Гп знаходиться в наступних
межах
тах < ЛГп і'иііпі
(2.52)
де с/тах — максимальна внутрішньокластерна відстань, а
Стіп —• мінімальна міжкластерна відстань при даній роз-
бивці.
Тоді цей алгоритм за скінченне число кроків гтах збіга-
ється до незміщеної розбивки 8*, а центри у^™1^ = е7 (5*)
незалежно від вибору значень д.\ < <І2 < сІГп.
Зауважимо, що тут основним є вибір гі,п, який би задо-
вольняв нерівності (2.52).
Якщо вибірка А- не допускає правильної кластериза-
ції, то даний алгоритм сходиться до кластеризації 8 =
= 15і, §2, • , 8^} , у якій задані центри класів є найбільш
репрезентативними точками.
43
82
Розділ 2. Моделі та алгоритми навчання та самонавчання
2.7. Алгоритм самонавчання на основі
методу потенційних функцій
Розглянемо задачу розбивки множини точок на два класи
у функціональному просторі на основі методу потенцій-
них функцій. В якості міри близькості між точками X, і X*,
вводиться узагальнена відстань
р(Х£,Х*) =
= у/к (х2) Х£) + К (X*, X*) - 2К (Хг, ХД
де К (X, V) — так звана потенційна функція
N
К(Х,¥) = £а^(Х)^(¥).
Отже, 7=1
Р(Х£,ХЛ) =
N
£А2[^(Хг)-^(Х,)]2.
І=1
(2.53)
(2-54)
(2.55)
У найпростішому випадку, коли (X,) = Ту, ми прихо-
димо до евклідової відстані.
Далі передбачається, що розбивка простору £1Х здійснює-
ться поверхнею виду / (X) = 0.
Усі Х£, для яких / (Хг) > 0, відносять до класу А, а всі X*,,
для яких / (Х^.) < 0. — до класу В. Вводиться функціонал
від / (X) виду
К (X)) = рАМ [р2 (X, ¥) |Х. ¥ Є А] +
+рвМ [р2 (Х,У) |Х,¥ є В] ,
де, наприклад,
М[р2(Х,¥)|Х,¥є А] =
/ / р2 (X, ¥) р (X, ¥) с/ХсГ¥
_ /(Х)>0/(¥)>0____________________
І / р(Х,У) ОХсГУ
ДХ)>0/(¥)>0
(2.56)
(2.57)
2.7. Алгоритм самонавчання на основі методу потенційних функцій 83
де М — знак математичного сподівання;
М [р2 (X, V) |Х,У є А] - середній квадрат відстані між то-
чками класу А.
В якості поділяючої функції / (X) пропонується шукати
таку, котра відповідає мінімуму функціонала (2.56). Зміст
цієї вимоги полягає в мінімізації середнього квадрата відстані
по всіх множинах точок.
Існує і доведена теорема, яка стверджує, що якщо фун-
кціонал є функцією від моментів, що диференцюється, або
якщо екстремум К досягається на деякій поділяючій поверх-
ні, то він же досягається і на поділяючій функції / (X), що є
поліномом г-того ступеня, [1]
г
/(Х) = £(Сг,Х‘), (2.58)
1=0
де дК дК
1~ дМ1А дМ^’
71і — вектор при непарному і і число при парному і\
(С4,Х‘) — скалярний добуток.
Для функціоналу виду (2.56) поділяюча поверхня в
спрямляючому просторі (для точки X = {гу} справедли-
вий вираз [з, = Хуїру (X)]) має вигляд
/ (X) = (С, X) — а,
де дК дК МА Мв
~ дМА дМВ ~ РА РВ
— вектор нормалі до гіперплощини;
П_МІ_МІ
2^, 2Й'
Згадана теорема свідчить про те, що при заданій метри-
ці (узагальнена відстань) оптимальна границя буде лінійною.
(2.59)
(2.60)
(2-61)
4***
84
Розділ 2. Моделі та алгоритми навчання та самонавчання
Для вирішення задачі була запропонована рекурентна про-
цедура, заснована на методі стохастичної апроксимації. Ця
процедура допускає реалізацію як у вихідному, так і в спрям-
ляючому просторі.
Нехай у процесі навчання з’являються точки Хі, Х2,.. -,
..., Хп. У процесі роботи алгоритму по цих точках будуються
функції Р% (х) і ?в (х) •
Поділяюча функція на п-ому кроці має вигляд
Г (X) = (X) - (X) - (а" - апв). (2.62)
Якщо на (п + 1)-ому кроці з’явилася точка Хп+1, то при-
ймається рішення, що:
Хп+і Є А, якщо /(Х„+1) > 0;
, - (2.63)
Хп+1 є В, якщо /(Х„+1) < 0.
Тоді (п + 1)-наближення поділяючої функції /"+1 (X) бу-
дується за наступним правилом:
а) якщо Хп+і Є А, то
г;+1 (X) = Г2 (X) + 7н+і (^ (X, Хп+1) - В2 (х))> (2-64)
«Г = «д + 7пд (Рд (Х„+І) - 2а"), (2.65)
Г^+1(Х)-^(Х), а^=апв- (2.66)
б) якщо Хп+і Є В, то
г;+'(х) = г;(х),
РГ ‘ (X) = Гв (X) + 7»+і (К (X, Х„+1) - Гі (X)), (2.67)
йв+1 = + 7пв (Рв (Хп+і) — 2ав),
де і !
7п = 0 < є < - (2.68)
2.8. Рекурентні алгоритми самонавчання ...
85
Аналогічний алгоритм має місце і для перцептронноі ре-
алізації в спрямляючому просторі Пг.
Була також доведена збіжність оцінок, що будуються, Гд,
йд, а# до оптимальних значень, тобто при п —> оо
Ма, гп
Ра
Мв_
Рв
Ма.
?Ра
М2В
ІРІ
(2.69)
УП
ав ~*
Метод потенційних функцій неявно використовує інфор-
мацію про характер розподілів і може бути використаний, ко-
ли справедлива гіпотеза про «компактність». У противному
разі він приводить до таких же помилок, як і інші методи, що
використовують як міру близькості монотонно спадну фун-
кцію (чи опуклий функціонал) від відстані поточної точки до
центру.
2.8. Рекурентні алгоритми самонавчання на основі
методу стохастичної апроксимації
Розглянемо таку задачу самонавчання. Потрібно розби-
ти початковий простір ознак на такі непересічні області
^і,.. ,щоб мінімізувати наступний функціонал (сере-
дній ризик розпізнавання)
N
^Рк / рй(8,и1,и2,...,и/у)Р(8//с)£/8, (2.70)
к=і 4
де Гк (8, II], її2,..., ІІдг) — функція втрат при класифікації
8 Є А*, Іїі,..., ІІдг — параметри областей Х-і,..., Х-м, напри-
клад. середні; рк — апріорні імовірності класів
Мінімізація (2.70) еквівалентна мінімізації середніх втрат
при розпізнаванні.
Було доведено, що для того, щоб функціонал, що задає-
ться формулою (2.70) був мінімальний, необхідне виконання
86
Розділ 2. Моделі та алгоритми навчання та самонавчання
наступних умов |311:
N г
] ^1/тгь(8.и1,и2,...,и^р(8)а8 = о,
Ь=1 **' (2.71)
^(8) = ^(8.Иі ,ід,...,ад-
—7^(8, ІІі,ІІ2, ..,ІДу),
де (8,и) — градієнт Рк (8,11) по ТГТО, — границя
між областями Х^ і Хк.
Для переходу від інтегрування по області Хк до інтегрува-
ння по всьому простору ГД вводяться характеристичні фун-
кції (
І 1, якщо 8 Є Хк\
єь(8,ід,ід,...,ад = { ’ *’
І 0, якщо 8 £ Хк.
Тоді (2.71) буде мати наступний вигляд
г
^Рк / [Єк(8,ІД,и2,...,ІДу)-
Ь=1 Па
(8, ІД, ІД,..., П„) Р (8) <28] = 72)
N
= ^М5{єк (8,ІД,ІД,...,ІДД.
к=1
^І/тгь(8>и1,и2,...)^)} = о.
Оскільки в (2.72) невідомо Р (8), то вирішити рівняння
щодо шуканих параметрів областей Хл,..., Х-^ не представ-
ляється можливим. Тому пропонується адаптивний алгоритм
для знаходження оцінок ІД,..., ІДу, який базується на засто-
суванні стохастичної апроксимації.
Нехай на (п — 1)-ому кроці побудовані оцінки для пара-
метрів ІД [п — 1],..., ІДу [п — 1]. Тоді якщо на п-ому кроці
2.8. Рекурентні алгоритми самонавчання .
87
надходить 8„, то
Щ [п] = ІЛп [п - 1] - 7т [п] -
N
• 52 <8"’ иі [п - і], • • -, [П - І]) х (2.73)
Ь=1
хУцт/ц (Зп.Иі [п - 1]. «Илт [п - 1])} •
Якщо 8П попадає в область то всі єт (8п, Уі, • •, Щг),
за винятком (8П, Тії [п — 1],..., ГТ/у [п — 1]), дорівнюють
нулю.
У цьому випадку алгоритм самонавчання (2.73) набуде
наступного вигляду
[п] = Пщ [п 1] 7т [^]
^тГа8п,иі[п-1ь...,Сдг[п-1]), (2 74)
т = 1, N
Чудова особливість даного підходу полягає в тому, що,
вибираючи різні функції ризику /ц (8, II), можна одержати
з (2.73) як відомі до теперішнього часу, так і нові алгоритми
самонавчання рекурентного типу [31].
Це дозволяє вважати алгоритм самонавчання (2.73) най-
більш універсальним рекурентним алгоритмом самонавчан-
ня, відомим дотепер. Критерій же у вигляді функції ризику
Гк (8, V) повинен задавати вчитель.
Варто підкреслити, що всі рекурентні алгоритми самона-
вчання страждають спільним істотним недоліком. Вони схо-
дяться до того чи іншого стаціонарного рішення в залежно-
сті від початкового стану, наприклад, початкового положен-
ня границь.
Розділ З
НЕЙРОННІ МЕРЕЖІ
3.1. Структура та математична модель мережі
3.1.1. Нейронні мережі зі зворотним розповсюдженням
Загальновизнаними нейронними мережами, іцо найбільш
широко використовуються, є так звані мережі зі зворотним
розповсюдженням («Ьаск ргора§аІіоп»).
Ці мережі прогнозують стан фондової біржі, розпі-
знають почерки, синтезують мову з тексту, управляють
автомашиною. Ми побачимо,
що зворотне розповсюджен-
ня скоріше відноситься до
алгоритмів навчання, а не
до архітектури мережі. Таку
мережу правильніше називати
мережею з прямою передачею
сигналів.
На рис. 3.1 наведена класи-
чна трьохрівнева архітектура
нейронної мережі.
Позначимо: Я1* — (/-мірний
простір.
Рис. 3.1. Архітектура нейронної
мережі ВР
Вхідній вектор X = {Х1,Т2, . . . ,Т/у}, ^N+1 = 1; вихідний
вектор у = {уі,у2, • • • Ум}-
Нейронна мережа виконує функціональне перетворення,
яке може бути представлено як у = Р (х), де х = {х,}, і =
= 1, /V; у = {уд.} , к = 1,М
Схований шар насправді може складатися з декількох ша-
рів, проте можна вважати, що достатньо розглядати лише
3.1. Структура та математична модель мережі
89
три шари для опису цього типу поведінки. Для нейронної ме-
режі з N вхідними вершинами, 7 вершинами схованого шару
та М вихідними вершинами величини у* задаються так:
(7 \
£ = (3.1)
7=1 /
Тут — вихідна вага зв’язку від вершини і схованого
шару до вершини к вихідного шару; д — функція (яка буде
визначена пізніше), виконуюча відображення /ї7 —» В!.
Вихідні сигнали вершин схованого шару /г7, 7 = 1,7 зада-
ються так: , N х
+ >=ЇД. (3.2)
\і=1 /
Тут И'Т — вхідна вага зв’язку (г, Д; — величина по-
рогу (вага від вузла, що має постійний сигнал, рівний 1, до
вузла д); Хі — сигнал на виході г-го вхідного вузла; сг — так
звана функція «сигмоїд», що задається так:
(«)
Функція а в (3.2) називає-
ться функцією активації ней-
ронної мережі, іноді її назива-
ють «функцією запалювання»
нейронної мережі.
Функція д у рівнянні (3.1)
може бути такою ж самою, що
Рис. 3.2. Графік функції о (х)
і а (х), або іншою В нашому викладі ми будемо приймати д
функцією вида ст, або одиничною функцією, тобто неліній-
ною. Необхідно, щоб функція активації була нелінійною і ма-
ла обмежений вихід, тобто була обмеженою. Графік функції
о (х) наведено на рис. 3.2.
90
Розділ 3 Нейронні мережі
3.1.2. Нейронні мережі прямої дії
Дія мережі прямої дії визначається двома факторами:
— архітектурою мережі;
— величинами ваг.
Кількість вхідних і вихідних вузлів визначається апріорі
та, по суті, є фіксованою. Число схованих вузлів є змінним і
може настроюватися (регулюватися) користувачем.
До теперішнього часу це настроювання залишається по-
ки «мистецтвом», хоча були запропоновані в літературі різні
методи установлення числа схованих вузлів та видалення не-
потрібних.
Після визначення (задання) архітектури мережі, власне
значення ваг визначають її поведінку.
Кажуть, що мережа «навчається», якщо ваги змінюю-
ться так, щоби досягти бажаної цілі. Тут слід мати на увазі,
що термін «навчання», запозичений з біології, в мережі озна-
чає просте настроювання множини параметрів.
3.2. Градієнтний алгоритм навчання
нейронної мережі
Першим алгоритмом навчання, який було розроблено для
навчання мережі Васк Ргора§аііоп (ВР), являвся градієн-
тний метод навчання.
Нехай критерій навчання мережі, що має 3 шари (один
прихований шар), такий
м
е м = 22 - уі м)2 тіп (3-4)
1=1
де Д — бажане значення г-го виходу нейромережі, у, (уу) —
фактичне значення г-го виходу нейромережі ВР для вагової
матриці = [XVі; XV0] .
3.2. Градієнтний алгоритм навчання нейронної мережі
91
Тобто критерій є (лу) являє собою середній квадрат по-
милки апроксимації.
Нехай функції активації для нейронів прихованого шару
52 + Идг+іу І та нейронів вихідного шару ук =
(і \
52 А^И^0 ) — однакові і представляють собою функцію
і=і /
«сигмоїд» (3.3).
Для такої функції похідна дорівнює
о' (т) — о (т) • (1 — о (х)).
(3.5)
Розглянемо градієнтний алгоритм навчання нейронної ме-
режі.
Алгоритм навчання Я-мережі
1. Нехай XV (п) — поточне значення матриці ваг. Алгоритм
має такий вигляд
XV (тг + 1) = XV (п) - 7п+і^и,е (XV (п)),
де 7П — розмір кроку на п-й ітерації.
2. На кожній ітерації спочатку ми навчаємо (коригуємо)
вхідні ваги а
(п + 1) = (п) - (з-б)
V к=1 7
(XV0))} • Щ (XV)' • (1 - к3 (XV)) • Хі.
3. Знаходимо (навчаємо) вихідні ваги
®=-2(4-№т)№(^)х . (м)
X (1 - ук (XV0)) к3,
92
Розділ 3. Нейронні мережі
И<° (п + 1) = (п) - 7п+і^®, (3.9)
де Хі, і = 1, N + 1 — входи НМ, ук, к = 1, М — виходи НМ,
Ну, 7 = 1,7 — виходи прихованого шару.
4. п = п + 1 та переходимо на наступну ітерацію.
Зауваження: Так званий алгоритм навчання з пам’яттю
має вигляд:
XV (п + 1) = XV (п) - А (1 - о) (XV (п)) -
—ОІЧууЄ (XV (п — 1)),
де А — швидкість навчання, а Є [0,1] — параметр забування.
Градієнтний метод є першим запропонованим алгоритмом
навчання, він простий в реалізації, але має такі недоліки:
— повільно збігається;
— знаходить лише локальний екстремум.
3.3. Побудова рекурентного виразу
для обчислення похідних помилок
Розглянемо градієнтний метод навчання нейронної мере-
жі ВР. Нехай необхідно мінімізувати критерій:
1 / \ 2
’ (310)
Р з
де у^ — реальний вихід т-го нейрона вихідного шару N ней-
ронної мережі при поданні на вхід р-го образу; — бажаний
вихід.
Мінімізація проводиться за методом градієнтного спуску,
що означає побудову ваг наступним чином
гоц (і) = (І - 1) + Агс0,
^4 = -ч—(з-іі)
3.3. Рекурентний вираз для обчислення похідних помилок
93
де и>^ — ваговий коефіцієнт зв’язку г-го нейрона (п — 1)-го
шару з 7-им нейроном п—го шару; 0 < у < 1 — коефіцієнт
швидкості навчання. Тоді
_дЕ_=дЕ_ ду™ дз^
ди$ ду^п} дз^} ди)^ ’
де у у — вихід 7-го нейрона п-го шару; 5; — зважений сумарний
вхідний сигнал 7-го нейрона.
Очевидно, що
4
(3.12)
,(«)„("-1)
(3.13)
8у}' Т°
— Якщо функція активації 7-го нейрона має вигляд
& = №), то ^ = /'(8>).
СІІ&д
В окремому випадку, якщо / = а — сигмоїд, то
= /'(«,) = Й'(1-%)-
азу
Третій МНОЖНИК = у(П-1).
Що ж стосується першого множника в (3.12)
він легко розкладається через виходи нейронів наступного
(п + 1)-го шару таким чином
9Е _ у^ дЕ (1ук дзк _ у^ дЕ дук (п+1)
ду3 к &Ук ду3 дук йзк ™зк
Тут сумування ведеться по нейронах (п + 1)-го шару.
Введемо нову змінну
й(п) дЕ ау]
дуд д.з^
Отримаємо рекурентну формулу для обчислення величи-
ни п-го шару через величини ^"+1) наступного шару (ди-
вись нижче рис. 3.3.) К
(3.15)
(3.16)
к=1
94
Розділ 3. Нейронні мережі
Для вихідного шару п = N маємо
Рис. 3.3. Фрагмент шару п
структури НМ ВР
Тепер можна записати алгоритм градієнтного спуску
(3.11) в наступному вигляді
(3.18)
Іноді для надання процесу
корекції ваг деякої інерційно-
сті для згладжування різких
стрибків, якщо рухатись по
поверхні, використовується зна-
чення на попередній іте-
рації (і — 1). В цьому випадку
величина ДгГу(і) буде мати ви-
гляд
Д*4п) (0 = (і-1)-
-(1- ^"М"-1^)), (3-19)
де /X Є [0,1].
Опис алгоритму навчання Васк Ргора^аііоп
Таким чином, повний алгоритм навчання НМ за допомо-
гою процедури зворотного поширення включає наступні кро-
ки [21].
Нехай на вхід НМ поданий один з можливих образів
х= {хі}і=ї7-
1. Покладемо = Хі, і = 1,1.
2. Розраховуємо послідовно значення виходів для п-го ша-
ру (п=1, IV) !
5ЇП) = (3.20)
2=1
„<"> = / ; (3.21)
3 3. Рекурентний вираз для обчислення ПОХІДНИХ помилок
95
3. Розраховуємо величини для нейронів вихідного ша-
ру. Визначаємо
4. Використовуючи рекурентну формулу, розраховуємо
через і Дш^+1) для всіх попередніх шарів п —
= N-1, N-2,..., 1.
5. Коректуємо ваги в НМ відповідно до процедури
ЧП) (0 = - !) + (*) • (3.22)
На цьому ітерація і закінчується.
6. Розраховуємо Е = Е (ш (і))
Якщо Е (ш (і)) < є^ад, то СТОП.
Інакше йдемо на крок 1 (і + 1) ітерації.
Даний алгоритм розрахунку величин 6^ ілюструється на
рис. 3.4, 3.5, 3.6, 3.7.
96
Розділ 3. Нейронні мережі
3.4. Прискорення збіжності алгоритмів
навчання нейронних мереж.
Алгоритм спряжених градієнтів
Як показано вище, алгоритм навчання мереж типу «Ьаск
ргора§аііоп» — це реалізація класичного методу найшвидшо-
го спуску. Цей алгоритм навчання відносно простий у реалі-
зації і застосуванні, що і пояснює його широке використання
в області нейромереж Однак у нього є два слабкі місця:
1) він повільно сходиться;
2) метод ефективний тільки при пошуку точок локального
мінімуму.
Тому були розроблені інші більш ефективні методи навча-
ння, що є альтернативою методу градієнта: метод спряжених
градієнтів і метод, заснований на генетичній оптимізації.
Метод спряжених градієнтів
Метод спряжених градієнтів (СГ) дає поліпшення швид-
кості збіжності в порівнянні з методом найшвидшого спуску.
Однак, як і метод найшвидшого спуску, він є методом ло-
кальної оптимізації.
У нейронних мережах цільова функція (ц.ф.), яку необ-
хідно мінімізувати, — це середня помилка на всій множині
навчальних зразків. Вона дорівнює
т м
Ее (УЮ = £ Е - Уц (^)Л (3-23)
4=1 Ь=1
де і = 1,Т — множина навчальних зразків.
Для тришарової мережі з N вхідними вузлами, схова-
ними вузлами і М вихідними вузлами вектор ваг XV містить
N.7 + М^ компонент.
З 4. Алгоритм спряжених градієнтів
97
У формулі (3.23) М — число вихідних вузлів, {гі41, ф2,...,
— бажаний вихід для навчального зразка і, а
Уі (^) = {&! С^У), Уі2 С^) .'•••> (^)І - реакція (вихід-
ний сигнал мережі) на зразок і.
Алгоритм СГ, як і більш загальний алгоритм спряжених
напрямків, набув застосування в області оптимізації завдя-
ки широкому класу проблем, для яких він забезпечує збі-
жність до оптимального рішення за скінченне число кроків.
Це суттєве поліпшення в порівнянні з методом найшвидшого
спуску, що вимагає нескінченного числа ітерацій для пошуку
мінімуму функції У
Спряжені напрямки. Назва походить від використан-
ня спряжених векторів. У векторному просторі вимірності І)
множина векторів {Рь Рг, - • •,Рр} утворює множину спря-
жених напрямків щодо матриці А, якщо
Р,АР; = 0, для, і / у, (3.24)
де А — позитивно визначена матриця розміром О х Е.
Вектори, що задовольняють (3.24), називають А-спря-
женими.
Виникає питання: яким чином алгоритм СГ досягає збіж-
ності за кінцеве число кроків і на яких задачах? Припустимо,
що нам необхідно мінімізувати функцію
Г (УУ) = (Ь - АУУ)Т (Ь - АУУ), (3.25)
де Ь і УУ — Р-вимірні вектори, а матриця А£,х£) визначена
вище. Отже, ми маємо квадратичну функцію. Припустимо,
що ми шукаємо ітераційно оптимальний вектор УУ*, що мі-
німізує Е (УУ), і починаємо пошук з початкової точки УУо-
Вибираємо ненульовий вектор рі, який служить напрямком
пошуку на наступній ітерації, при цьому не важливо, яким
чином були обрані УУ0 і Рі Задамо УУі як наступний вектор
УУ^УУо + арь (3.26)
5'
98
Розділ 3. Нейронні мережі
де скаляр а вибирається так, щоб мінімізувати Е'(\¥о + о,Рі).
Зараз ми підходимо до головному пункту. Оптимальний на-
прямок, у якому необхідно рухатися на наступній ітерації, -
це напрямок, у якому потрібен тільки один крок безпосере-
дньо в точку оптимального рішення IV*, і він повинен утво-
рювати А-спряжену пару з вектором рр
Оптимальний напрямок — це УУ* — тому умова,
що (XV* — ЛУї) є А-спряжений напрямок, еквівалентна твер-
дженню, що повинна виконуватися умова
(ЛУ* - УУО Арі = 0.
Звичайно, у цій точці ми не знаємо оптимального рішен-
ня XV*, у противному випадку нам би не треба було ніякого
алгоритму. Однак ця умова важлива з наступної причини. У
Гамірному просторі є рівно 2? — 1 незалежних векторів, що
утворюють А-спряжену пару з вектором рі-
Таким чином, нам буде потрібно тільки скінченне число
напрямків, щоб знайти оптимальне рішення.
Алгоритм спряжених напрямків систематично конструює
множину А-спряжених векторів. Через максимум £) кроків
алгоритм знайде оптимальний напрямок, і збіжність буде за-
безпечена.
Тут ми опустили важливе питання визначення задачі
одномірної мінімізації по скаляру о. Для задач у формі (3.25)
така мінімізація виконується безпосередньо й утворить ча-
стину класичного алгоритму СГ, хоча для більш загальних
проблем ця задача аж ніяк не тривіальна.
У розглянутій задачі навчання Н-мережі не існує в явній
формі рівняння (3.25), і, зокрема, ми не маємо явного виразу
для матриці А, хоча градієнт помилки VЕ може виконувати
цю роль.
Помітимо, що в рівнянні (3.25) — АУУ є множник, про-
порційний градієнту функції Е (\У).
3.4. Алгоритм спряжених градієнтів
99
Отже, для квадратичних функцій Е (XV) метод спряже-
них градієнтів забезпечує збіжність за скінчене число кроків.
Проте для функцій загального вигляду скінченна збіжність
більш не гарантується.
Необхідно усвідомлювати, що алгоритм СГ, подібно ме-
тоду градієнтного спуску, забезпечує знаходження лише ло-
кально оптимальних рішень. Проте, метод дає значне приско-
рення збіжності в порівнянні з методом найшвидшого спуску.
Опис алгоритму. Крок 0. Покласти К — 0. Ініціалізу-
вати ваговий вектор XV і обчислити градієнт С = щасі Е(ХУ)
Покласти вектор початкового напрямку ^д)= —
Крок 1. Знайти скаляр а*, що мінімізує Е (XV + ар),
для чого можна використовувати метод Фібоначчі чи золо-
того перетину. Покласти
XV (К + 1) = XV (/<) + а*р (Е) (3.27)
Крок 2. Якщо Е(ХУ (К + 1)) < єприп, де єпрпп — при-
пустима точність досягнення мінімуму, то 8ТОР. Інакше —
обчислити новий напрямок
С (А; + 1) = 8гаа Е (XV (к + 1)).
(3.28)
Крок 3. ЯкщоТїТофДА: + 1) = 0, то новий вектор на-
ПРЯМКУ гаді)- +
' + ' цс(* + і)||’
інакше покласти _
С(К + 1)ТС(К + 1)
р С (Е)т С (/<)
та обчислити новий вектор напрямку
-С(к + 1)+0р(к)
к+1 ||—С(А; + 1) +/?р(/с)|Г
Крок 4. Замінити р (к) нар (к + 1) та С (к) на С (к + 1).
Перехід на крок 1 наступної ітерації.
5*
100
Розділ 3. Нейронні мережі
3.5. Генетичний алгоритм навчання
нейронної мережі
Цей алгоритм є алгоритмом глобальної оптимізацїї. У ньо-
му використовуються наступні механізми [13,20]:
1. схрещування батьківських пар (сгозз-оуєг), генерація
нащадків;
2. мутація (дія випадкових впливів);
3. природний добір кращих (селекція).
Мета навчання — мінімізація середньоквадратичної по-
милки м
Я(ху) = ^£(4-уДХУ))2,
/.-=1
деХУ = [ХУ;,ХУо], XV; = Н||, Х¥о = ||^||.
Задається початкова популяція з N особин
[ХУі (0),...,ХУ,(0),...,ХУ;у (0)]
Будь-яка особина представляється відповідними вагами.
Для кожної особи обчислюємо індекс придатності (Гііпезз
Іпсіех) і оцінюємо якість прогнозування
ГІ (XV,) = С - Е (XV,) -> тах,
де С — константа.
Схрещування батьківських пар. При виборі батьків вико-
ристовується імовірнісний механізм. Позначимо Рі — імовір-
ність вибору г-го батька:
Г/(ХУД0))
11 N
Е ГІ (ХУДО))
1=1
Потім здійснюється схрещування обраних пар.
Можна застосовувати різні механізми схрещування.
Наприклад: для першого нащадка беруться непарні компо-
ненти з вектора першого батька, а парні компоненти з ве-
ктора другого батька, для другого нащадка навпаки — парні
3.5. Генетичний алгоритм навчання нейронної мережі
101
компоненти з вектора першого батька, а непарні компоненти
з вектора другого батька. Це можна записати таким чином
ХУ< (0) ф АУ, (0) -> \Уг (1) + (1),
ЛУ, - ’
, _ Г Юу (0), якщо ] = 2т;
1 'Шкз (0), якщо і — 2т — 1,
,п _ Г (°)» ЯКЩ° І = 2т’>
[ Шу (0), якщо у = 2т — 1,
т = 1,
Береться батьківських пар і генеруються N нащадків.
Дія мутацгй.
и'ц («) = (п) +£(«).
де £ (п) = а • е~ап, а = гапдот Є [—1; +1].
Селекція. Можна використовувати різні механізми селе-
кції.
1. Повна заміна старої популяції на нову.
2. Вибір N кращих із всіх існуючих особин /Ірод+
+^потомк — за критерієм максимуму ГІ.
На цьому одна ітерація генетичного алгоритму закінчує-
ться.
Описані ітерації повторюємо доти, поки не почне викону-
ватися одна з наступних умов зупинки:
а) тах ГІ (ш, (А:)) ГІзад, де ГІзад — задане значення ГГ,
І
б) к N303, де Узаа — задана кількість ітерацій (103 —104).
Основна перевага генетичного метода — це те, що він до-
зволяє знаходити глобальний мінімум, проте він має такі не-
доліки:
— він потребує значних обчислювальних витрат;
— ряд параметрів визначається експериментально, напри-
клад; N — розмір популяції; а — показник загасання мутацій.
102
Розділ 3. Нейронні мережі
3.6. Удосконалення градієнтного
алгоритму навчання
При реалізації градієнтного алгоритму навчання нейрон-
ної мережі ВР може проявитися ряд складностей, властивих
градієнтним алгоритмам оптимізації.
1. Якщо ми знаходимося далеко від точки мінімуму фун-
кції Е , то рухаємося з малим кроком, і процес пошуку
може затягуватися. Для його прискорення має сенс збільши-
ти величину кроку т] (і). Ознакою такої ситуації є сталість
знака ДЕ (і — 1) < 0, ДЕ (і) < 0 (див. рис. 3.8, а).
2. Якщо ж ми знаходимося в околі точки мінімуму
і величина кроку т] велика, то ми перескакуємо через точку
і виникає явище «осциляції». У цьому випадку доцільно
поступово зменшувати величину т) (і). Ознакою такої ситу-
ації є зміна знака ДЕ, тобто ДЕ (і — 1) • ДЕ (і) < 0 (див.
Рис. 3.8. Ілюстрація роботи градієнтного методу
3.6.1. Градієнтний метод з корекцією кроку навчання
(метод відкату)
Для подолання вищевказаних труднощів, зв’язаних з ви-
користанням градієнтного методу, був розроблений градієн-
тний метод з корекцією кроку навчання. Тут величина кроку
3.6. Удосконалення градієнтного алгоритму навчання
103
ц (і) на (і + 1)-ій ітерації описується наступним рекурентним
виразом
т](і+ !) =
Т] (і) • Л, якщо Е (щ (і))
т] (і) • (і, інакше,
де и > 1, 0 < (1 < 1.
Рекомендується вибирати и д, « 1.
Корекцію кроку можна проводити, якщо проведено де-
кілька послідовних кроків, наприклад, і — 2, І — 1, і.
Я(лЦі-І)); , х
К (3.29)
3.6.2. Метод з вибиванням із локальних мінімумів
(зИоск ВР)
Цей метод використовується у випадку багатоекстремаль-
ної залежності Е (л>) при необхідності пошуку глобального
мінімуму (див. рис. 3.9) |21, ЗО].
У випадку, якщо ми застрягли в локальному мінімумі л\*-
і помилка Е протягом тривалого часу не змінюється, то має
сенс зробити великий крок у
•• г
вискочити з даної поло-
жистої западини і потра-
пити в область притяга-
ння іншого мінімуму л>°-.
Тоді
ггу(і+ 1) = л^-(і) + а;£, _
де £ рівномірно розподі-
лена в інтервалі [—1; +1].
випадковому напрямку щоб
Рис. 3.9. Механізм вибивання
з локального мінімуму
3.6.3. Метод з векторним кроком навчання
(Зирег ЗАВ)
Основний недолік класичного градієнтного методу поля-
гає в тому, що крок в усіх напрямках однаковий т] (і). Він
не враховує тієї обставини, що по різним компонентам ми
5**
104
Розділ 3. Нейронні мережі
можемо знаходитися на різній відстані від шуканої точки мі-
німуму (тобто по одним компонентам далеко, а по іншим —
близько).
Тому Аішеісіа і сіа Зііуа розробили метод з векторним кро-
ком пошуку, який вони назвали Зирег ЗАВ. У цьому методі
пошук відбувається відповідно до виразу
Юу (і) = іУу (і - 1) - (0 ^’г)у1(п-1), (3.30)
де
| («-І)’ якщо ® > 0;
(1) “ І % (1 - 1). і, якщо « . < о, (3.31)
и > 1, 0 < (і < 1.
Зміна ваг відбувається відповідно до виразу
Шу (<) = і
(І - і) - (І) ^П)уг(П П,
якшо 8Е(1-
шг] {і — 1), інакше.
0;
і
(3.32)
3.6.4. Автономний градієнтний метод з апроксимацією
рельєфу квадратичної функції
Нехай ми знаходимося в точці V/ (і). Розраховуємо граді-
єнт \7Е (ту (і)) і антиградієнт —\?Е (V/ (і)) і робимо два про-
бних кроки = (і) + Х7Е ?
іу2 = (£) — (\у) .
Обчислюємо Е (лу) , Е (^) і Е (тл^) . Далі, припускаючи,
що Е (\у) може бути апроксимована параболою, знаходимо
по трьох точках V/. иг1 і лу2 точку мінімуму.
Основний недолік методу полягає в тому, що функція
Е (\у) може мати значно складніший вигляд, і тому цю про-
цедуру апроксимації доводиться повторювати багаторазово,
що вимагає великих обчислювальних витрат.
3.7. НМ, які самооргаиізуються. Алгоритм навчання Кохонена
105
3.7. НМ, які самооргаиізуються.
Алгоритм навчання Кохонена
3.7.1. Навчання на основі збігів. Закон навчання Хебба
У 1949 р. канадський психолог Д. Хебб опублікував книгу
«Організація поведінки» (В. НеЬЬ «Ог^апіхаііопаї ВеЬауіоиг»),
у якій він постулював правдоподібний механізм навчання на
клітинному рівні в мозку [20, ЗО].
Основна ідея Хебба полягала в тому, що коли вхідний си-
гнал нейрона, що надходить через синапгичні зв’язки, викли-
кає спрацьовування нейрона, то ефективність такого входу в
термінах його здатності сприяти спрацьовуванню нейрона в
майбутньому повинна збільшуватися.
Хебб припустив, що зміна ефективності повинна відбува-
тися саме в синапсі, що подає цей сигнал на вхід нейрона
призначення. Пізніші дослідження підтвердили цей здогад
Хебба. Хоча останнім часом були відкриті інші механізми
біологічного навчання на клітинному рівні, у визнання за-
слуг Хебба піонерського характеру цей закон навчання був
названий у його честь.
Закон навчання Хебба належить до класу законів навча-
ння по змаганню.
Лінійні асоціативні елементи.
На рис. 3.10 представлена архіте-
ктура нейронної мережі (НМ), що
складається з нейронів, що нази-
ваються «лінійними асоціаторами».
Вхідний вектор у лінійному
асоціаторі — це вектор X = {ж,},
і = 1,п, що вибирається з про-
стору ВІДПОВІДНО до деякого
розподілу р (X).
Рис. 3.10. Шар лінійних
асоціативних елементів
5’
106
Розділ 3. Нейронні мережі
Вихідний вектор V обчислюється з вхідного X за насту-
пною формулою
¥ = ХУХ,
де XV = ЦіОцІІ — матриця ваг п х т; XV — (ХУі, ХУ2,.. -, ХУт),
XV,- — стовпці матриці XV, XV,- = (Щ^-, • • • > ^п>)т — ве-
ктор ваг.
Позначимо через ¥' = {у^} — бажаний вихід. Основна
ідея лінійної асоціативної НМ полягає в тому, що мережа
повинна навчатися на парах вхід-вихід
(Х1,¥1),(Х2,¥2),...,(Хг,¥г).
Коли на вхід НМ подається вхідний сигнал X*,, то бажа-
ний ¥' повинен дорівнювати Ук- Якщо на вхід мережі пода-
ний вектор Хь + £ (де £ — достатньо мале), то вихід повинен
дорівнювати Ук + є (тобто на виході повинні одержати ве-
ктор, близький до Ук- )
Закон навчання Хебба виглядає таким чином
= ^ + укіхкі, (3.34)
де Хкі — це і-а компонента вектора Х^.; у^- — ^-а компонента
вектора Ук-
У векторному вигляді вираз (3.34) запишеться в такий
спосіб
Х¥"еи’ = ХУоМ + Хь¥£ = ХУоМ + УкХ-1- (3.35)
Щоб реалізувати цей закон навчання в процесі навчання уво-
дяться відповідні компоненти У’к = [уь7], що показані стріл-
ками на рис. 3.10.
Передбачається, що перш ніж почати навчання, усі
— 0. Тоді в результаті показу навчальної вибірки
(Хі,¥!),..., (Х£,,¥ь) кінцевий стан матриці XV задається
так
XV = ¥!Х[ + ¥2Х£ + ... + ¥ГХ£. (3.36)
3.7. НМ. які самоорганізуються. Алгоритм навчання Кохонена
107
Це рівняння (3.36) називають «формулою суми зовні-
шнього добутку» для XV. Ця назва виходить з того факту,
ЩО ¥ЬХ* — це зовнішній добуток.
Переформулювання закону Хебба у вигляді суми зовні-
шнього добутку дозволяє провести додаткові дослідження
можливостей цього закону забезпечити асоціації пар векторів
(ХіЛ*).
Перший висновок полягає в тому, що коли вектори
{Хі,Хг,... ,Хь} ортогональні і мають одиничну довжину,
тобто є ортонормованими, то тоді
Ук - ХУХЬ (3.37)
Іншими словами, лінійна асоціативна НМ реалізує бажане
перетворення вхід-вихід.
Це наслідок властивості ортонормованості
ХТХ^ = <50 = ^’ (3.38)
Тоді ь
ХУХ, = ^Х^Х, = ¥*. (3.39)
Т=1
Але проблема полягає в тому, що умова ортонормованості
дуже жорстка (насамперед необхідно, щоб Ь п ).
Далі ми обмежені вимогою ||Хі|| = 1. Було б набагато
корисніше, якби вдалося зняти це обмеження. Ця мета може
бути досягнута, але не в лінійній асоціативній НМ. Тут, якщо
вектор Х^. не є ортонормованим, то з’являється помилка від-
творення Ук на виході
ь
УЖк = 52 ¥ГХ*ХЬ = + 52 ^Х?ХЬ = ¥*. + 7]. (3.40)
г=1 г^к
Бажано домогтися того, щоб г] було мінімально. Для того,
щоб досягти у = тіп чи забезпечити ?/ = 0, необхідно перейти
до асоціативної мережі з нелінійними елементами.
5***
108
Розділ 3. Нейронні мережі
3.7.2. Змагальне навчання
Змагальне навчання використовується в задачах самона-
вчання, коли немає класифікації вчителя.
Закони навчання, що відносяться до категорії змагальних,
мають таку властивість, що виникає змагальний процес між
деякими чи всіма обробними елементами НМ. Ті елементи,
що виявляються переможцями змагання, одержують право
змінювати свої ваги. У той час, ті що програли , свої ваги не
змінюють (чи змінюють за іншим правилом).
Змагальне навчання відоме як «навчання Кохонсна» [23].
Навчання Кохонсна істотно відрізняється від навчання за
Хсббом чи за алгоритмом ВР тим, що в ньому використо-
вується принцип самоорганізації (у противагу принципу кон-
трольованого навчання з учителем) [22].
Змагальний закон навчання має довгу і складну істо-
рію. Наприкінці 60-х — початку 70-х р.р. Стефан Гроссберг
(ЗісрЬеп СгоззЬег^) запропонував цілу множину змагальних
схем навчання НМ. Інший дослідник, що займався пробле-
мами змагального навчання був, ван дер Мальсбург (уап сісг
Ма1зЬиг§). Закон навчання ван дер Мальсбурга був засно-
ваний на ідеї, що сума ваг, зв’язаних із входами для різних
обробних нейронів єдиного вхідного елемента, повинна зали-
шатися постійною в процесі навчання, тобто якщо одна з ваг
(чи декілька) збільшується, то інші повинні зменшитися.
Після значних досліджень і вивчення робіт Гроссберга,
ван дер Мальсбурга та інших Тойво Кохонен прийшов до
висновку, що головна мета змагального навчання повинна
складатися в конструюванні набору векторів, що утворять
множину рівноймовірних представників з деякої фіксованої
функції щільності розподілу р (X) вхідних векторів.
І хоча закони навчання цього типу були незалежно отри-
мані багатьма дослідниками, саме Т. Кохонен був першим,
3.7. НМ, які самоорганізуються. Алгоритм навчання Кохонена
109
хто звернув увагу на питання про рівноймовірності. Саме
завдяки цій ідеї і всесвітньому поширенню книги Т. Кохонена
«Самоорганізація й асоціативна пам’ять» («8еИ-Ог§апі/аІіоп
апсі Азвосіаііуе Мстогу»), його ім’я стало зв’язуватися з да-
ним законом навчання |23].
3.7.3. Закон навчання Кохонена
На рис. 3.11 приведена базова структура шару Кохонсна.
Шар складається з N обробних елементів, кожний з
яких одержує п вхідних сигналів
Ті,а?2, - - -,хп з нижчого шару, що
є прямим передавачем сигналів.
Входу Хі і зв’язку (і, у) припишемо
вагу Шу.
Кожен обробний елемент шару
Кохонсна підраховує свою вхідну
інтенсивність Іу у відповідності з
формулою
І, = Г>(\У,,Х), (3.41)
де XV, = .. - ,шп^)т і X = (хь^г,... ,жп); 79(\У^,Х)
— деяка міра (метрика) відстані між і X
Виділимо два найбільш загальні види функції 79 (ЛУ,-, X) :
1) Евклідова відстань:
Г>(ДУ,Х) = ||ЛУ - Х||;
2) Сферична дугова відстань
7? (\У, X) = 1 — \УТХ = 1 - соз 0, (3.42)
де \УТХ — скалярний добуток, причому передбачається, що
ІІ^ц = ||хц = і.
110
Розділ 3. Нейронні мережі
У даному викладі, якщо не зазначено інше, ми будемо
використовувати евклідову відстань £)(Х,\У). При реалі-
зації закону Кохонена, як тільки кожен обробний елемент
(нейрон) підрахував свою функцію Д, між ними відбувається
змагання, мета якого — знаходження елемента з найменшим
значенням Іу (тобто І,тіп). Як тільки буде знайдений перемо-
жець такого змагання, його вихід покладається рівним 1.
Вихідні сигнали всіх інших елементів покладаються рівними 0.
У цей момент і відбувається навчання по Кохонену.
Навчальні дані для шару Кохонена приблизно складаю-
ться з послідовності вхідних векторів {X} , що витягаються
випадково з фіксованою щільністю розподілу імовірностей
р (X). Як тільки черговий з векторів X вводиться в мережу,
обробні елементи Кохонена починають змагатися між собою,
щоб знайти переможця, для якого досягається тіп £) (X, И^).
з
Тоді для нейрона-переможця і* вихід встановлюється 2* — 1,
а для всіх інших = 0, ) і*.
У цей момент відбувається зміна ваг відповідно до закону
навчання Кохонена
= + а (Х _ (3 43)
де 0 < а < 1.
Даний закон можна переписати в наступному вигляді:
пеш _ / С1 ~ Для переможця і = /;
Очевидно, що при такому законі навчання ваговий вектор
У?і рухається від до вхідного вектора X. На початку
процесу навчання а ~ 1, а потім у міру розвитку процесу
навчання зменшується до величини а = 0.1.
Далі слід зазначити подібність навчання за Кохоненом і
статистичного процесу визначення «/с-середніх».
3.7. НМ, які самоорганізуються. Алгоритм навчання Кохонена
111
Х-середні для фіксованого набору векторів {Х^Хг,...,
.7. ,Хь}, котрі обрані випадково з деякої генеральної сукуп-
ності з фіксованою щільністю розподілу імовірностей р (х),
складають множину к векторів {ХУЬ ХУ2,..., XV*;} таких, що
мінімізується наступний функціонал
ь
тіпХ^ІХ^Х,)), (3.45)
' І=1
де XV (Хг) — вектор XV, найближчий до X,.
На закінчення, необхідно підкреслити, що навчальний за-
кон Кохонена в загальному випадку не генерує множину рів-
ноймовірних вагових векторів, тобто множину таких векто-
рів, що X, який вибрано випадково, відповідно до щільності
розподілу імовірностей р буде мати рівну імовірність вияви-
тися найближчим до кожного з вагових векторів XV?.
3.7.4. Оцінка щільності розподілу імовірностей
Як вже відзначалося вище, ми прагнемо домогтися того,
щоб отримати вектори XV, , що самі були б приблизно рівно-
імовірні з точки зору найближчого сусідства стосовно векто-
рів X, що витягаються з з деякою щільністю розподілу
імовірностей р (т) . Іншими словами, для довільного вектора
X, витягнутого з 3?” з імовірністю р (X), бажано, щоб імо-
вірність того, що X виявиться найближчим до XV,, повинна
приблизно дорівнювати для усіх г = 1, N.
Існує кілька підходів для вирішення проблем, що вини-
кають при реалізації базового закону навчання Кохонена
[22,23].
1. Перший підхід називається Васііаі Зргоиііщ;; («радіальні
паростки»). Він є найкращим для евклідової та аналогічних
їй метрик (відстаней). Всі вагові вектори XV, = спо-
чатку вибирають так, що (0) ~ 0. Усі вхідні вектори X
112
Розділ 3. Нейронні мережі
спочатку помножуються на деякий малий позитивний ска-
ляр /3. Процес починається з р, близького до 0 Це забезпечує
близькість вхідних векторів X до векторів В міру розви-
тку процесу Р повільно збільшується, поки не досягне значен-
ня Р = 1. Як тільки це відбувається, вагові вектори «виштов-
хуються» зі своїх початкових значень і рухаються за вхідни-
ми векторами. Ця схема працює досить добре, але звичайно
декілька вагових векторів будуть відставати від процесу й у
підсумку виявляться зайвими, що сповільнює процес навчання.
2. Інший підхід (підхід «додавання шуму») полягає в то-
му, щоб додати рівномірно розподілений шум до векторів
даних X, що полегшує ефект досягнення р(Х) > 0 у всій
області Рівень (інтенсивність) шуму спочатку вибирають
досить великим, щоб вектори шуму були набагато більшими,
ніж вектори даних X. Але в міру розвитку процесу навча-
ння рівень шуму поступово знижується. Цей підхід працює
правильно, але він виявляється ще повільнішим, ніж підхід
«Еасііаі Зргоиіпщ». Тому підходи «Касііаі Зргоиїіпц» і «до-
давання шуму» вирішують проблему представлення складно
представимих законів з малою імовірністю розподілу в де-
яких областях, але вони не вирішують проблеми рівноімо-
вірного позиціювання векторів \У7.
У цілому, базовий закон навчання Кохонена приведе до
надлишку при розміщенні векторів XV3 у тих областях, де
висока щільність розподілу імовірностей (РІ) р (X), і до не-
стачі векторів XV, в областях, де щільність р (X) мала.
3. Ідея, що була запропонована Опале Оееіело, — це вмон-
тувати «свідомість» (чи пам’ять) у кожен елемент к, щоб здій-
снити моніторинг (контроль) за історією успішних результа-
тів (перемог) кожного нейроелемепту. Якщо обробний еле-
мент Кохонена виграє змагання істотно частіше, ніж раз
(часу), тоді його «свідомість» виключає цей елемент зі зма-
3.7. НМ, які самооргаиізуються. Алгоритм навчання Кохонена
113
гання на якийсь час, тим самим даючи можливість елемен-
там з перенасиченої області переміщатися в сусідні ненасиче-
ні області. Такий підхід часто працює дуже добре й у змозі
породити досить гарний набір рівноімовірних вагових векторів.
Основна ідея механізму «свідомості» — це відстеження
частки часу Д, протягом якого обробний елемент ] виграє
змагання. Ця величина може бути обчислена локально ко-
жним обробним елементом за формулою
Д(і + і) = Д(О + /?(^-Д(О)- (3.46)
Відразу ж після того, як закінчене змагання і визначене
поточне значення (0 чи 1), константа (3 вибирається ма-
лим позитивним числом (типове значення /З = 10“4 = 0,0001)
і обчислюється частка Д. Далі визначається поточне значе-
ння «зсуву» :
= 7 (| - Л) , (3.47)
де 7 — позитивна константа (порядку 7 ~ 10).
Далі здійснюється корекція ваг. Однак, на відміну від зви-
чайної ситуації, у якій ваги змінюються тільки для одного
обробного елемента-переможця З = 1, тут проходить окре-
ме змагання для визначення обробного елемента, що має най-
менше значення величини
РС%,Х)-Ь7. (3.48)
Елемент, що виграв, далі коректує свої ваги відповідно до
звичайного закону навчання Кохонена.
Роль члена зсуву полягає в наступному. Для елементів Д
які часто виграють, величина Д > і < 0, тому для них
величина 29(5¥,,Х) — Ь:І зростає в порівнянні з £)(АУ7, X),
тоді як для елементів, які рідко виграють, Д С Ь3 > 0
і Р('\У;, X) — Ь3 зменшується, що підвищує їхні шанси на
перемогу.
114
Розділ 3. Нейронні мережі
3.7.5. Розвиток алгоритму Кохонена
У 1982 р. Т. Кохонен запропонував ввести в базове пра-
вило змагального навчання інформацію про розташування
нейронів у вихідному шарі. Для цього нейрони вихідного ша-
ру упорядковуються, утворюючи одновимірні чи двовимірні
решітки. Розташування нейронів у таких решітках маркіру-
ється векторним індексом і = (г’ьїг). Таке упорядкування
природним образом уводить відстань між нейронами |г — Д -
Модифіковане правило змагального навчання Кохонена
враховує відстань нейронів від нейрона-переможця [22,30]
Щ (і + 1) = ІУ,- (і) + а(і) (X - А (гі (і,/)), (3.49)
де А — функція сусідства, А (<7 (г, 7*)) дорівнює 1 для нейрона-
переможця з індексом і* і поступово убуває в міру збільше-
ння відстані д,, наприклад, за законом
А (гі) = е-гі2/й2.
Як темп навчання а, так і радіус взаємодії 7? поступово
зменшується в процесі навчання, так що на кінцевій стадії
навчання ми повертаємося до базового закону адаптації вагів
ТІЛЬКИ НеЙрОНІВ-перемОЖЦІВ, Н (і) = Н()Є~к1.
На відміну від газоподібної динаміки при індивідуально-
му підстроюванні нейронів, навчання по Кохонену нагадує
натягування еластичної сітки прототипів на масив даних з
навчальної вибірки. В процесі навчання еластичність сітки
поступово зменшується.
У результаті ми одержуємо не тільки квантування входів,
але й упорядковуємо вхідну інформацію у вигляді однови-
мірної чи двовимірної топографічної карти Кохонена. На цій •
сітці кожен багатомірний вектор має свою координату, при-
чому чим ближче координати двох векторів на карті, тим
ближче вони й у вихідному просторі.
/
3.7. НМ, які самооргапізуються. Алгоритм навчання Кохонсна 115
Така топографічна карта дає наочне уявлення про стру-
ктуру даних у багатовимірному вхідному просторі, геометрію
якого ми не в змозі уявити собі іншим способом. Візуалізація
багатовимірної інформації є головним застосуванням карт
Кохонена [22,23].
Зауважемо, що у відповідності з загальним життєвим прин-
ципом «безкоштовних обідів не буває» топографічні карти
зберігають відношення близькості лише локально, тобто
близькі на карті області близькі й у вихідному просторі,
але не навпаки (див. рис. 3.12). У загальному випадку не
існує відображення, що понижує і СЛ О
розмірність і зберігає при цьому (,---
відношення близькості глобально. / С/ ' О
На рис. 3.12 стрілкою показана \ • /
область порушення неперерв-
ності відображення: близькі на —О—
площині точки відображаються Рис. 3.12. Приклад порушення
на протилежні кінці карти. неперервності відображення
Зручним інструментом візуалізацїї є розфарбування то-
пографічних карт аналогічно тому, як це робиться на зви-
чайних географічних картах. Кожна ознака породжує своє
розфарбування карти — за величиною середнього значення
цієї ознаки в даних, що потрапили в даний осередок.
Зібравши воєдино карти всіх цікавлячих нас ознак, одер-
жимо топографічний атлас, що дає інтегральне уявлення про
структуру багатовимірних даних. Мережі, що самонавчаю-
ться. Кохонена широко використовуються для передобробки
даних при розпізнаванні образів у просторі дуже великої роз-
мірності. У цьому випадку, щоб процедура була ефективна,
потрібно спочатку зкомнресувати вхідну інформацію тим чи
іншим способом:
1) або понизити розмірність, виділивши значимі ознаки;
2) або зробити квантування даних.
Розділ 3. Нейронні мережі
116
Розглянемо звичайний алгоритм навчання Кохонена
И4Ді + 1) =
= ^,40+« (<))*>
(3.50)
де у-п — вихід і-го нейрона попереднього шару;
1,
<
0,
якщо Я (У^,у(п_1) = тіп£) (\Уі,у(п-1))) ;
інакше.
При використанні навчання за алгоритмом Кохонена існує
практика нормалізації вхідних образів
(351>
а також ініціалізації вагових коефіцієнтів Ініціалізація
вагових коефіцієнтів випадковими значеннями може приве-
сти до того, що різні класи, яким відповідають щільно розпо-
ділені вхідні образи або зіллються, або, навпаки, роздрібня-
ться на додаткові підкласи у випадку близьких образів того
самого класу.
Для запобігання цього явища використовується метод
опуклої комбінації. Його суть полягає в тому, що вхідні нор-
малізовані образи піддаються перетворенню виду
+ (3.52)
де а (і) — коефіцієнт, що змінюється в процесі навчання від
одиниці до нуля.
У результаті цього спочатку на входи мережі подаються
практично однакові образи, а з часом вони усе більше збіга-
ються до вихідних.
3.7. НМ, які самоорганізуються. Алгоритм навчання Кохонена
117
Вагові коефіцієнти на кроці ініціалізації встановлюються
рівними и>о — де п — розмірність вектора вагів для ней-
ронів ініціалізуючого шару.
На основі розглянутого методу будуються Н-мережі осо-
бливого типу — так званні «карти ознак, що самооргані-
зуються» (яе1£-ог§апі7Іп£ (еаіиге шарв) Для них після ви-
бору із шару п нейрона і з мінімальною відстанню =
= £) У^п-0) навчається за формулою (3.50) не тільки
цей нейрон, але і його найближчі сусіди, розташовані в околи-
ці радіуса В. Величина В на перших ітераціях дуже велика,
так що навчаються спочатку всі нейрони, але з часом В змен-
шується до 0. Таким чином, чим ближче кінець навчання,
тим точніше визначається група нейронів, що відповідають
кожному класу образів.
Експериментальні дослідження алгоритму самона-
вчання Кохонена. Розглянемо результати використання
алгоритму Кохонена в задачі розпізнавання букв.
Після навчання на еталонних та зашумлених зразках (при
5% рівні шуму) було проведено експерименти по розпізнаванню
для 5 літер: А П Р 0 Л;
для 10 літер: ФЬІВАПРОЛДЗ;
для 25 літер: ЙЦУКЕНГШЩЗХЬФЬІВА ПРОЛДЯЧСМ;
для 32 літер: ЙЦУКЕНГШЩЗХ'ЬФЬІВА ПРОЛДЖЗЯЧСМИТЬБЮ
При цьому рівень шуму змінювався від 0% до 25%. Нижче
наведені таблиці, які показують кількість правильно розпі-
знаних літер А П Р О Л в % для різних вихідних алфавітів,
також в таблицях наведено середній відсоток правильного
розпізнавання.
118
Розділ 3. Нейронні мережі
Таблиця 3.1.
Кількість вірно розпізнаних зображень для алфавіту
з 5 літер при навчанні за еталонними зразками
Шум, % А П р о л Ср.,%
0 100 100 100 100 100 100
5 100 100 100 100 100 100
10 100 100 100 100 100 100
15 100 100 100 100 100 100
20 100 100 100 100 100 100
25 100 100 100 100 100 100
Таблиця 3.2.
Кількість вірно розпізнаних зображень для алфавіту
з 5 літер при навчанні за зашумленими зразками
Шум,% А п Р О Л Ср.,%
0 100 100 100 100 100 100
5 100 100 100 100 100 100
10 100 95 100 100 100 99
15 100 90 95 95 100 96
20 100 85 95 90 95 93
25 100 85 85 85 90 89
Таблиця 3.3.
Кількість вірно розпізнаних зображень для алфавіту
з 10 літер при навчанні за еталонними зразками
Шум,% А П р 0 л Ср,%
0 100 100 100 100 100 100
5 100 100 100 100’ 100 100
10 100 100 100 100 100 100
15 100 100 100 100 100 100
20 100 100 100 100 100 100
25 100 100 100 100 100 100
Таблиця 3.4.
Кількість вірно розпізнаних зображень для алфавіту
з 10 літер при навчанні за зашумленими зразками
Шум, % А П Р О Л Ср.,%
0 100 100 100 100 100 100
5 100 100 100 100 100 100
10 100 90 90 95 100 95
15 100 90 85 90 95 92
20 100 85 85 85 90 89
25 95 70 75 85 85 82
3.7. НМ, які самоорганізуються. Алгоритм навчання Кохонена
119
Таблиця 3.5.
Кількість вірно розпізнаних зображень для алфавіту
з 25 літер при навчанні за еталонними зразками
Шум,% А П Р О Л Ср.,%
0 100 100 100 100 100 100
5 100 100 100 100 100 100
10 100 100 100 100 100 100
15 100 95 100 100 100 99
20 100 90 95 95 100 96
25 100 90 95 85 95 93
Таблиця 3.6.
Кількість вірно розпізнаних зображень для алфавіту
з 25 літер при навчанні за зашумленими зразками
Шум, % А П Р 0 л Ср.,%
0 100 100 100 100 100 100
5 100 90 100 100 100 98
10 100 65 90 85 100 88
15 100 60 80 80 90 82
20 100 45 80 55 80 72
25 95 35 70 зо 75 61
Таблиця 3.7.
Кількість вірно розпізнаних зображень для алфавіту
з 32 літер при навчанні за еталонними зразками
Шум,% А П Р О Л Ср.,%
0 100 100 100 100 100 100
5 100 100 100 100 100 100
10 100 100 100 100 100 100
15 100 95 100 100 100 99
20 100 90 95 90 100 95
25 100 85 95 85 95 92
Таблиця 3.8.
Кількість вірно розпізнаних зображень для алфавіту
з 32 літер при навчанні за зашумленими зразками
Шум, % А П Р О Л Ср.,%
0 100 100 100 100 100 100
5 100 85 90 95 100 94
10 100 60 85 90 100 87
15 100 45 65 90 90 78
20 100 40 60 80 80 72
25 90 20 40 70 75 59
120
Розділ 3. Нейронні мережі
3.8. Застосування НМ у задачах
прогнозування в макроекономіці
Одним з найпоширеніших застосувань нейронної мережі
ВР є прогнозування макроекономічних процесів, а також ін-
ших часових випадкових процесів.
Особливості прогнозування економічних процесів в еконо-
міці перехідного періоду полягають в такому
1. Процеси, що прогнозуються, відносяться до класу не-
стаціонарних процесів, параметри яких змінюються з часом.
Це особливо характерно для країн з перехідною економікою.
2. Макроекономічні процеси тісно пов’язані один з одним,
проте характер цієї залежності між прогнозованим процесом
та вхідними складний, і вигляд цієї залежності, як правило,
невідомий особі, що приймає рішення.
3. Вихідна інформація про ці процеси неповна, як прави-
ло, недостовірна і обмежена в часі (так звані короткі виборки).
За цих обставин неможливо використати для прогнозува-
ння класичні методи статистичного аналізу, зокрема, кореля-
ційний та регрссійний, для яких необхідно, щоб процеси були
стаціонарні, і був відомий вигляд залежності між вхідними
та вихідними процесами.
Тому для задач прогнозування нестаціонарних часових
процесів з невідомою структурою прогнозуючої моделі пер-
спективним являється використання нейронних мереж, які
не потребують знання виду математичної залежності і дуже
просто настроюються шляхом навчання та корекції вагів
Вагові коефіцієнти мережі
Відомо, що вагові коефіцієнти відіграють роль пам’яті /^ме-
режі. Зрозуміло, обсяг пам’яті прямо пропорційний кількості
цих коефіцієнтів, а оскільки ми маємо справу з мережами
3.8. Застосування НМ у задачах прогнозування в макроекономіці 121
ВР фіксованої архітектури, то можна сказати, що при фіксо-
ваній кількості входів і виходів мережі цей обсяг залежить
тільки від числа внутрішніх шарів і розмірності прихованого
шару.
На жаль, не існує чіткого правила завдання значень цим
двом параметрам. їхній вибір залишається мистецтвом ба-
лансування між достатністю і надмірністю.
Проте, вибір необхідного обсягу пам’яті варто робити з
огляду на: розмір вікна, кількість входів і виходів мережі,
а також діапазон значень прогнозованої величини, оскільки,
чим більше діапазон значень, тим більше пам'яті потрібно
для чіткого запам’ятовування цих коливань. Безумовно, до-
бір параметрів обсягу пам’яті краще робити експериментально.
Розглянемо підходи до навчання //-мереж, що використо-
вують технологію ковзного вікна [13,14].
Підхід перший. Полягає в мінімізації сумарної помил-
ки на вікні навчання, що мало ефективно, тому що при та-
кому алгоритмі ми дійсно одержимо не мережу-оракул, а
мерсжу-апроксиматор.
Справа в тому, що
— У вікно можуть попадати нерспрезентативні пари-
приклади з іншого закону взаємовпливу.
— Закон взаємовпливу в межах вікна може різко змінюва-
тися. Отже, будуть існувати пари, на яких неможливо мінімі-
зувати помилку окремо, тобто неможливо підібрати мережу,
добре навчену під кожну з таких пар.
Таким чином, оскільки //-мережа — це все-таки універ-
сальний апроксиматор, мінімізація помилки на всіх зраз-
ках може привести до перенавчання мережі. Ми одержимо
мережу-функцію, що апроксимує тренувальну послідовність,
у тому числі і нерспрезентативні точки. Мережа не відкриє
закон взаємовпливу і, як наслідок, не зможе зробити якісний
6і
122
Розділ 3. Нейронпі мережі
прогноз. Область застосування такого алгоритму навчання
звужена до прогнозування параметрів з невеликим діапазо-
ном значень. Однак якісно спрогнозувати показник, що має
відношення до економіки перехідного періоду, з таким підхо-
дом дуже проблематично.
Другий підхід. Полягає в мінімізації помилки на ко-
жній парі-прикладі вікна в порядку їхнього проходження.
Проте рухаючись ітеративно по вікну, мережа буде забува-
ти інформацію, отриману від перших точок вікна на той час,
коли дійде черга навчатися на останніх.
Третій підхід. Полягає в мінімізації помилки на кожній
парі-прикладі вікна, але з тасуванням цих пар по визначе-
ному закону, що змінюється в залежності від прогресу на-
вчання. Приведені нижче результати експериментів свідчать
про високу ефективність такого підходу в порівнянні з ін-
шими підходами. Можна навіть говорити про нього як про
найбільш адекватний. При такому алгоритмі ми автомати-
чно застраховані від ефекту перенавчання Я-мережі, тому
що вона просто не стане навчатися на нерепрезентативних
парах-прикладах.
Прогнозувати майбутнє, виходячи з закону, укладеного
в парах-прикладах, а не наступне значення функції з упо-
рядкованого ряду попередніх її значень — ось мета навчання
//-мережі.
Опис алгоритму навчання //-мережі
Розглянемо алгоритм навчання нейромережі ВР для за-
дач прогнозування в макроекономіці, розроблений в роботі
|13|.
Насамперед, необхідно відзначити, що даний алгоритм
складається з двох модулів: модуля тасування пар-прикладів
і модуля генетичного алгоритму глобальної оптимізації.
^.8 Застосування НМ у задачах прогнозування в макроекономіці 123
Алгоритм тасування пар-прикладів
Завдання алгоритму полягає в тому, щоб змусити //-ме-
режу запам’ятати всі приклади і перетворитися в модель,
що представляє собою «чорну шухляду», що вміє на парах-
прикладах правильно зіставляти входу потрібний вихід. При
цьому важливо не перенавчити мережу. Виражаючись обра-
зно — мережа повинна увібрати в себе тільки основний зміст,
закладений у парах-прикладах, і пропустити непотрібні по-
дробиці, що засмічують пам’ять.
Тут можна провести паралель зі здатністю людини вико-
ристовувати аналогію при прийнятті рішень у ситуаціях, не
знайомих їй раніше.
Насамперед, варто сказати, що цей алгоритм відноситься
тільки до пар-прикладів, до кожної з яких у свою чергу за-
стосовується алгоритм оптимізацїї, обраний користувачем.
Схема алгоритму тасування точок на вікні:
1. До кожної пари-прикладу застосовується алгоритм оп-
тимізацїї, у результаті якого ми одержуємо ваговий вектор,
при якому помилка на даній парі-прикладі менше чи дорів-
нює заданій £ (XV). Таким чином, перший раз пройшовши
по вікну послідовно по кожній парі-прикладу, ми одержуємо
ваговий вектор IV
2 Далі, використовуючи отриманий XV, ми ще раз про-
ходимо по вікну і складаємо масив помилок, що відповідає
парам-прикладам, у результаті одержуючи деяку схему прі-
оритетів за значеннями помилок.
3. Тепер ми знову проходимо по парах-прикладах оптимі-
зуючим алгоритмом, але вже не послідовно, а у відповідно-
сті зі значеннями масиву помилок. А саме, починаємо з пари,
якій відповідає найбільша помилка, і закінчуємо парою з най-
меншою помилкою. При цьому пари, на яких наданій ітерації
6*
124
Розділ 3. Нейронні мережі
досягнута задана точність, у навчанні не приймають участь.
Після цього кроку ми одержуємо новий ваговий вектор Ж і
переходимо до пункту 2.
4. Навчання закінчується по досягненні заданої точності
на кожній парі-прикладі, або якщо перевищена припустима
задана користувачем кількість ітерацій алгоритму тасування.
Модифікація генетичного алгоритму
У пропонованому генетичному алгоритмі [13, 14], як і в
інших алгоритмах цього класу, існує стандартний набір па-
раметрів, що варіюються: розмір популяції, рівень мутації,
алгоритм зміни рівня мутацій.
Модифікація даного алгоритму складається в застосуван-
ні спрощеної схеми зміни рівня мутацій. Користувач задає
початковий і кінцевий рівень мутацій в умовних одиницях і
кількість ітерацій алгоритму, за яку рівень мутацій зменши-
ться з початкового значення до кінцевого. При цьому змен-
шення рівня мутацій відбувається за лінійним законом ви-
гляду у = кх + Ь.
Результати експериментів
Як підтвердження правильності вибору нами третього
підходу приведемо зведені таблиці результатів експеримен-
тів для різних алгоритмів навчання [13].
Вихідні дані, прогнозоване значення, лагові періоди, тип
і параметри Я-мережі були ідентичні в цих експериментах.
Розходження складалося винятково в тому, що створена ав-
торами програма Віаск Огасіе РготМ (ВРО) використовує
при навчанні третій підхід, а альтернативні програми — пер-
ший підхід.
3.8- Застосування НМ у задачах прогнозування в макроекономіці 125
Вихідні дані: П’ять показників економіки України
(агрегат МО, агрегат М2, індекс оптових цін |ІОЦ], індекс
споживчих цін |ІСЦ], кредити, вкладені в економіку [КВВЕ])
представлені у вигляді часових рядів. Дані охоплюють період
з 01.01.1995 по 01.12.1997, виміри провадилися щомісяця. За
прогнозовану величину був узятий показник ІСЦ (див. табл. З 9)
Таблиця 3.9.
___________Фрагмент вихідних даних__________
№ ДАТА МО М2 ЮЦ ІСЦ КВВЕ
1 01.01.95 4,70 2,00 29,20 21,20 2,10
2 01.02.95 15,40 13,20 11,40 18,10 13,40
3 01.03.95 18,70 8,00 9,30 11,40 10,10
Лагоеа модель Н-мережі: Вхід (М0[-7], М2[-7], ЮЦ[0],
КВВЕ[-7], ІСЦ|0]), вихід (ІСЦ[+1|).
Схема експерименту: Використовується ковзне вікно роз-
міром 12 пар-прикладів, що становить 12 місяців, потрібно
прогнозувати 13-у точку. Здвигаючи вікно з одиничним кро-
ком, спрогнозуємо 11 точок. В якості критерію оптимізації
навчального алгоритму використовується точність прогно-
зу — СКП (середньоквадратична похибка).
Параметри мережі: Число входів —5, число виходів—1,
розмірність внутрішнього шару — 10, точність навчання па-
ри-приклада — І.е—5.
Параметри генетичного алгоритму пакета ВОР: Розмір
популяції — 40, початковий рівень мутацій у — 320, кінце-
вий рівень мутацій — у = 20, передбачуване число ітерацій
на вікні 1000, закон зміни рівня мутацій — лінійний.
Зведені результати експериментів по навчанню нейроме-
режі при різних алгоритмах навчання наведені в табл. 3.10,
а результати прогнозування за цими алгоритмами навчання
представлені в табл. 3 11.
б2
126
Розділ 3. Нейронні мережі
Таблиця 3.10. Результати навчання Я-мережі
Значення СКП повіконно №1 №2 №3 №4 №5 №6
Алгоритм навчання Ямсрсжі ВР 0.01001 0,0005 0,00017 0,00011 0,0036 0,0001
ВР суо 0,01758 0,01688 0 01578 0,01212 0,0035 0 00127
ВР МІ Ьаск 0,08545 0 05997 0,07233 0,07759 0 08534 0,07547
ВР ГаІІ Ьаск суо 0.09106 0,06115 0,04839 0,05092 0.05001 0,03832
ВР уссіог «Іер 0 0 0 0 0 0
ВР УССІОГ 5Ієр СУО 0.00206 0.00334 0 00287 0,00255 0,00179 0.00072
ВР яіюск 0.01259 0 00565 0,00054 0,00943 0.00171 0,00112
ВР нііоск єуо 0.08801 0.04254 0,03813 0,03491 0.03113 0.02847
НЛ суо 0.06618 0,04055 0,03973 0.04308 0,04422 0.03408
НсигізЬіс НЛ 0,07061 0.10169 0,10971 0,11653 0,11831 0,11226
НеигізЬіс НЛ суо 0,00728 0.01384 0,01852 0.01079 0.015'1 0,00844
ВО РВО ВР 0,09296 0,06322 0.056 0,05212 0,05097 0,04258
ВО РВО СЕН 0.08877 0.05.318 0,04984 0.04853 0,0489 0,03028
ВО РВО СЕИ 1 ВР 0,0793 0.0508 0,0478 0,0461 0.0446 0,0295
Значення СКП повіконно N•7 N•8 №9 №10 N•11 Су маСКО
ВР 0.00941 0 00404 0,00046 0,00086 0,00632 0 0356
ВР е\о 0,00725 0 00562 0 00471 0.00404 0.00579 0 09451
& ВР ГаІІ Ьаск 0.0758 0 07996 0.07768 0.07525 0,08004 0 84486
ВР Гнії Ьаск єуо 0.03548 0,03315 0,03654 0,0338 0,03769 0,51651
Д ВР уссіог ьіер 0 0 0 0 0,00001 0,00001
ЄН ВР сесіог 8ІЄр СУО 0,00262 0,00389 0,00301 0.00157 0,00156 0,02588
= ВР вііоск 0,00875 0.01279 0,00413 0.01162 0,00853 0,07684
£ ВР нЬоск суо 0,02046 0.02046 0,02046 0,02046 0.02046 0,36546
Г НЛ СУО 0.02023 0 027 0,03022 0.02356 0.02488 0.39373
£ Нсигійііс НЛ 0,11599 0 11461 0 18192 0.17575 0.18347 1,40083
о. Нсигіаііс НЛ суо 0.00749 0 0078 0 01978 0.02143 0,0128 0,14386
ВО РВО ВР 0.02884 0 02731 0 02716 0.01811 0 00893 0 46819
* ВО РВО СЕН 0,02535 0 02767 0,02436 0.02144 0.02295 0,44127
ВО РВО СЕХ 4 ВР 0.0217 0 02507 0,02551 0.02428 0.02042 0 41508
Таблиця 3.11. Результати прогнозів Я-мережі
Номер прогнозованої точки 13 14 15 16 17 18
Реальне значення ІСЦ 2 1.5 1,2 0.9 2.2 1.2
ВР 2 61693 16.7802 4.06173 -0.29532 -1 4108 0,73349
£ ВР суо -2.5154 18,484 1,4729 0.30536 0,89443 -0,23587
о- ВР ГаІІ Ьаск 1,60667 5.4299 3.66196 3.49016 3,1931 3,53568
? ВР ГаІІ Ьаск суо 1.88306 3 51883 3.45194 3.24742 3.18056 3,55969
ВР УЄСІОГ 8Юр -0.38615 6 9876 0 14191 -0,05191 1,04855 0 81644
х ВР УССІОГ віср СУО -2.59518 20 5864 7 77759 7.07751 1,82606 -0 15846
£ ВР «Ііоск -1.57723 21 2383 13.4517 -0.34041 1.63206 0.08989
х НЛ суо 1.04974 3 20592 1 70183 1.13786 0 9054 1 09172
= Сігкі НЛ 23.8441 4.06094 3.39974 1.46598 1,85068 2,41256
Я, Сігісі НЛ суо -0.18824 23.85 -0.40545 3.33762 2.79692 4.79724
£ во рко вр 0.20638 3.63169 0.20638 1,65343 0,84505 1.28644
< ВО РВО СЕЬ 0,48119 1.83151 1,26425 0.73327 0,76671 1,15991
ВО РВО ПЕК • ВР 0.4431 1.55333 1.13124 0,63042 0.59576 1.11238
З .4. Застосування НМ у задачах прогнозування в макроекопоміці 127
Номер прогнозованої точки 19 20 21 22 23
Прогнозні значення 1СЦ Реальне значення ІСЦ 0,1 0,8 0,8 0,1 0.1
ВР 0.83411 2.9649 1.02889 2,86605 1.61711
ВР суо 1,23837 1 49985 0,95191 0.90922 4,40915
ВР ГаІІ Ьаск 3 42473 1 69144 2,88601 3 08078 3.26891
ВР ГаІІ Ьаск суо 3 49103 2.56382 3.10869 3.26143 2.96084
ВР уссіог ьіер 1 75377 13 4115 0.89207 0.43113 2,33873
ВР уєгіог .чі ер єуо 1 09559 1 02163 0,88354 0,49311 2.27434
ВР »Ьоск 1.52497 0.52189 0.5441 0,68132 1.4407
НЛ суо 1.32837 -0,643 1,01506 2.12583 1,74362
ста нл 3,93228 23,85 0.80862 2,55357 1,63993
Сігісі НЛ єуо -0.08866 9.39836 0,77528 1.19131 1,31284
БОРНОВР 1,71371 0,22254 0.47426 0,61324 1,49207
ВОРВОСЕN 1,3411 0,35309 0,48425 0,74165 0,92018
БОРНО СЕІЧ + ВР 1,40165 0,38367 0,52715 0,5687 0,76824
Номер дельти прогнозу Бека 13 Гк’Иа 14 ОсНа 15 Пеііа 16 Осіїа 17 Г)е11а 18
ВР 1 61693 15.2802 2.86173 1 19532 3.6108 0.46651
ВР суо 4,5154 16,984 0,2729 0.59464 1.30557 1.43587
2 ВР ГаІІ Ьаск 0.39333 3,9299 2,46196 2,59016 1.2931 2,33568
§ § ВР ГаІІ Ьаск суо 0.11694 2.01833 2.25194 2,34742 0 98056 2.35969
§ £ ВР УСС ІОГ 8іер 2,38465 5,4876 1.05809 0,95191 1,15145 0,38356
о-'* ВР УССІОГ 8іср СУО 4,59518 19,0864 6.57759 6.17751 0.37394 1..35846
- о ВР зЬоск 3.-57723 19.7383 12.2517 1.24041 0.56794 1,11011
.2с НІ єуо 3.04974 1,70592 0.50183 0.23786 1.2946 0.10828
є ь Сігіа Н.1 21,8441 2 56094 2,19974 0.56598 0.34932 1,21256
Сігкі НЛ єуо 2.18824 22.35 1,60545 2.43762 0.59692 3,59724
2 ВО РНО ВР 1,79362 2,13469 0,99362 0,75343 1,35495 0,08644
ВОРНОСЕК 1,51881 0,33151 0,06425 0,16673 1,43329 0,04009
БОРНО СЕН ьВР 1,5569 0,05333 0,06876 0,26958 1,60424 0,08762
Номер дельти прогнозу Осіїа 19 Ос На 20 ПеНа 21 ІЛсНа 22 Осіїа 23 Тоїаі Осіїа
ВР 0,73411 2.1649 0,22889 2.76605 1.51711 35,44255
ВР суо 1.13937 0.69985 0.15191 0.80922 4.30915 32,21687
§ л ВР ГаІІ Ьаск 3,32473 0,89144 2.08601 2,98078 3.16891 25.456
5 с ВР ГаІІ Ьаск суо 3.39103 1,7682 2,30869 3,16143 2,86084 23.56069
3 2 ВР «есіог їіїср 1,65377 12.6115 0.09207 0,33113 2,23873 28.34627
.„о ВР УССІОГ 5іер СУО 0 99559 0.22163 0.08354 0,39311 2 17434 42.03729
= § ВРяІюск 1.42497 0,27512 0,2559 0.58132 1 1407 42.3637
= 2 НЛєуо 1.22837 1.44299 0,21506 2.02583 1 64 162 13.4541
о Сігкі НЛ 3 83228 23.05 0.00862 2 45357 1 53993 59.61704
Сігкі НЛ суо 0,18866 8,59836 0.02472 1.09131 1 21284 43,89136
2 БОРНОВР 1,61371 0,57746 0,32574 0,51324 1,39207 11,53898
ВО РНО СЕІЧ 1,2411 0,44681 0,31575 0,64165 0,82018 7,02026
БОРНО СЕН+ ВР 1,30165 0,41633 0,27285 0,4687 0,66824 6,76819
6**
128
Розділ 3. Нейронні мережі
Умовні позначки:
ВР — алгоритм Васк Ргора§аііоп;
єуо — еволюційний;
Еаіі Ьаск — з методом відкату;
Неигівіісб — з евристикою;
вЬоск — шоковий метод;
Ш — метод Хука-Дживса;
ВО РНО — позначення стосується результатів, отриманих
за допомогою ВОРго™;
СЕN — генетичний алгоритм.
В усіх експериментах використовувався механізм ковзно-
го вікна — розмір вікна навчання — 12 точок, 13 точка була
прогнозна, і по ній оцінювалася якість прогнозу. Далі вікно
здвигалося на 1 точку вперед, і процес навчання повторю-
вався.
Висновок
Проаналізувавши результати, можна зробити кілька ва-
жливих висновків.
При використанні підходу з мінімізацією сумарної функції
помилки //-мережа, як правило, перенавчається і, не дивля-
чись на відмінну якість навчання, прогнозовані значення да-
лекі від реальних. Іншими словами — якісне навчання ще не
означає успіх при прогнозуванні(див.табл. 3.11).
Запропонований в [13] алгоритм тасування точок автома-
тично виключає можливість перенавчання і, незважаючи на
відносно погану якість навчання, дає на порядок кращі ре-
зультати при прогнозі, ніж результати навчання за іншими
алгоритмами, що використовують перший підхід.
Застосування спрощеної схеми зміни мутацій у генетично-
му алгоритмі збільшує швидкість збіжності і не впливає на
ЯКІСТЬ П]ЮГНОЗУ-
3.9. Нейронна мережа Хопфілда та її застосування
129
3.9. Нейронна мережа Хопфілда
та її застосування
Відродження інтересу до нейронних мереж зв’язано з ро-
ботою Хопфілда (1982 р.). Ця робота пролила світло на ту
обставину, що запозичені з природи мережі з нейроноподі-
бних елементів можуть бути використані для обчислюваль-
них цілей. Дослідники з багатьох галузей знання одержали
стимул для подальших досліджень цих мереж, переслідуючи
при цьому двояку мету: краще розуміння того, як працює мо-
зок, та застосування мозгоподібних властивостей цих мереж
для рішення проблем, що не піддаються рішенню традицій-
ними методами.
3.9.1. Ідея рекурентності
Нейронна мережа Хопфілда — це приклад мережі, яку
можна визначити як динамічну систему з ОС. у якої вихід
однієї цілком прямої операції служить входом наступної опе-
рації мережі, як показано на рис. 3.13 [20].
Мережі, що працюють як системи зворотного зв’язку, на-
зиваю гься «рекурентними мережами». Кожна пряма опе-
рація мережі називається ітерацією. Рекурентні мережі,
Рис. 3.13. Принципова схема виконання прямої ітерації
6і
130
Розділ 3. Нейронні мережі
подібно будь-яким іншим нелінійним динамічним системам,
здатні виявляти цілий спектр різних поведінок. Зокрема,
один можливий зразок поведінки — це те, що система мо-
же бути стійкою, тобто вона може сходитися до єдиної фі-
ксованої (нерухомої) точки. Коли нерухома точка є входом у
таку динамічну систему, то на виході будемо мати ту ж саму
точку. Таким чином система залишається зафіксованою в то-
му ж самому стані. Можливі періодичні цикли чи хаотична
поведінка.
Було показано, що мережі Хопфілда стійкі. У загальному
випадку може бути більше однієї фіксованої точки. Те, до
якої фіксованої точки буде сходитися мережа, залежить від
вихідної точки, обраної для початкової ітерації.
Нерухомі точки називаються атракторами. Множина то-
чок (векторів), що притягаються до визначеного атракто-
ру в процесі ітерацій мережі, називається «областю притя-
гання» цього атрактора. Множина нерухомих точок мережі
Хопфілда — це її пам’ять. У цьому випадку мережа може
діяти як асоціативна пам’ять. Ті вхідні вектори, що попада-
ють у сферу притягання окремого атрактора, є зв’язаними
(асоційованими) з ним.
Наприклад, атрактор може бути деяким бажаним обра-
зом. Область притягання може складатися з зашумлених чи
неповних версій цього образа. Є надія, що образи, що смутно
нагадують бажаний образ будуть згадані мережею як асоці-
йовані з даним образом.
3.9.2. Бінарні мережі Хопфілда
На рис. 3.13 зображена схема обробки інформації в мере-
жі Хопфілда. Вхідні і вихідні вектори складаються з «-1»
і «+1» (замість «—1» може бути використане «0») Є симет-
рична вагова матриця, що складається з цілих чисел з нуля-
3.9. Нейронна мережа Хопфілда та її застосування
131
ми по діагоналі = ||г%|| Вхідний вектор X помножується
на вагову матрицю, використовуючи звичайне матрично-
векторне множення. Однак тільки 1 компонента вихідного
вектора V = [у?] використовується на кожній ітерації. Ця
компонента, що може бути обрана випадково, подається на
пороговий елемент, чий вихід або —1, або +1. Відповідна ком-
понента вхідного вектора заміняється на це значення і, та-
ким чином, утворить вхідний вектор для наступної ітерації.
Ця процедура відома як «асинхронна корекція» [20]. Процес
продовжується доти, поки вхідні і вихідні вектори не стануть
однаковими (тобто поки не буде досягнута нерухома точка).
Цей алгоритм описаний нижче.
3.9.3. Опис алгоритму
• Обчислити компоненти вихідного вектора Уі, ] = 1,п, за
формулою
(3.53)
ґ —1. якщо х < 0,
де Т (т) = <!
( 1, якщо х > 0.
• Виконати асинхронну корекцію, тобто
1) почати з вхідного вектора (ті, х2, - ., хп);
2) знайти у, відповідно до формули (3 53);
3) замінити (ті. Тг,. , хп) на (уі, х2, х3,..., хп) = У і по-
дати на вхід;
4) повторити процес, щоб знайти у2, у3 і т.д. (у, можуть
вибиратися випадково).
• Повторювати кроки 2—3 доти, поки вектор V = (уі,у2,
- -., уп) не перестане змінюватися. Кожен крок зменшує ве-
личину енергії зв’язків
Е = 152 52 гсіуХіХ^, (3.54)
7—1 7 = 1
6***
132
Розділ 3. Нейронні мережі
так що забезпечується збіжність до нерухомої точки (атра-
ктору).
Асинхронна корекція і нулі на діагоналі матриці XV га-
рантують, що енергетична функція (3.54) буде зменшуватися
з кожною ітерацією. Асинхронна корекція — особливо істо-
тна для забезпечення збіжності до нерухомої точки. Якщо
ми допустимо, щоб весь вектор коректувався на кожній іте-
рації, то можна одержати мережу з періодичними циклами
як термінальними станами, а не з нерухомими точками.
3.9.4. Зразки поведінки
Саме вагова матриця відрізняє поведінку одній’ мережі
Хопфілда від іншої, так що виникає питання: «Як визначити
цю вагову матрицю?»
Відповідь — треба задати визначені вагові вектори, що
називають екземплярами. Є надія, що ці екземпляри будуть
фіксованими точками результуючої мережі Хопфілда. Хоча
це не завжди так. Для того, щоб екземпляри були атракто-
рами, вагову матрицю XV = ||шу|| треба задати так [20, ЗО):
{^
(355)
0, для і = і,
де А — число заданих екземплярів, а ХІг = {т^, ,т^2,...,
— &-ий екземпляр.
Якщо екземпляри векторів утворять множину ортого-
нальних векторів, то можна гарантувати, що коли вагова ма-
триця вибирається як показано вище, то кожен екземпляр ве-
ктора буде нерухомою точкою. Однак у загальному випадку
3.9. Нейронна мережа Хопфілда та її застосування
133
для того, щоб екземпляри приводили до нерухомих точок,
ортогональність не обов’язкова.
3-9.5. Застосування мережі Хопфілда
Мережа Хопфілда може зокрема використовуватися для
розпізнавання образів. Але число розпізнаваних образів не
занадто велике внаслідок обмеженості пам’яті в мережах
Хопфілда. Далі приведені результати дослідження її роботи
при навчанні на 4 буквах російського алфавіту.
Вихідні образи:
рввввввввр
□□
□□□□□□а
ввррррррвв
вввввввррр
вввввввррр
вврррррррр
вввввврррр
вввввввррр
вврррввврр
ввсрррвврр
вврррввврр
вввввввррр
вввввврррр
ввррррррвв
ввррррррвв
ввррррррвв
ввррррррвв
ввррррррвв
ввррррррвв
ввррррррвв
ввррррррвв
Дослідження проводилося таким чином: послідовно збіль-
шуючи зашумленість кожного з 4 образів, вони подавалися
на вхід мережі Хопфілда. Результати роботи мережі приве-
дені в табл.3.12.
Таким чином, НМ Хопфілда прекрасно справляється із
задачею розпізнавання образів для експериментів з перекру-
чуванням на 0 — 40%. У цьому діапазоні всі еталони розпі-
знаються без помилок (іноді виникають незначні перешкоди
для 40% зашумлення).
При 45 — 55 — 60% зашумлення образи розпізнаються не-
стабільно, часто виникає «переплутування» і на виході НМ
з’являється зовсім інший еталон або його негатив.
Починаючи з 60% на виході системи починає з’являтися
негатив образа, що тестується, іноді частково перекручений
(при 60 - 70%).
134
Розділ 3. Нейронні мережі
3.9. Нейронна мережа Хопфілда та її застосування
135
Образ, що тестується Відсоток зашумлення образу Вигляд перекрученого образа Результат розпізнавання
50% □□□□□□а вгахтаавпов ввшввввов □□□□ВВОЕИЗП □□□□ввппоп □□□ввввпоо □□□вппвопп □□ввппввпа □□вппоовпа □аввввввва □аввваввва ввпоогизавв ввооааповв
60% □вввапвта □В^ВВВВВОГ] □□□вваооов □□□вввввпп вввввпгювв □□□□□□ввоо всппвввовв ввпвавоввс □□вовввпш □□ввсаввво [.іпвввввасіо [завввввопа □□ввввоооо □□ВВВВОВОЦ □□ввповаоп □□□□□□ввоп □□вопвввап □□□□□авеста □□вввввваа □□ввввввш
70% □□ВСОВВЙОВ □ввавпппаа □□□ввввввв вооавввасв □ввваоввав ввоввапвва □ввпввввоо ввпвввоапа ^□□□□вавап в□□□□впарв □□□□□□□□□а □□□□□□□□□□ □□□ввввввв вааавввввв ввааравввв ввввапрввв ввввввпаав ВВВВВВВРПО □□□□□□□□□□ □□□□□□□□□а
80% □□□□ваваав □впааоппав □□вввввввв впсаввавав ВВРРПВВОВВ впвваврввв врввввсрпо ввввовпвов □всваооова □□□□□□□вас □□□□□□□□□а □□□□□□□□□□ □□□ввввввв ВСРПВВВВВВ вввшовввв ввввааповв ввввввааав вввввввааа □□□□□□□□□а □□□□□□□□□а
□□□вввввпп □□в вв в □□□
90% □врввввапп □□ВВВ1.1ВВПР1 □□ВВОПВВПО всзввавввш вапповвваа □□□□□□ввав □□□□ввввпп □□свввввап □□ВВВВОПІЗО □□ввввоопо □□вввопваа □□ввставвоа □□всавввас □□□□□вввос □□□□ввввіза □□□ВВВВВОЦ
100% □іиввввопи □□вввваапс □оввввпппп □□ввваовпа □□ввопввоп □□ввппввпо □□ваовввоа □□□□□вввсга □□□□ввввш □□□вввввпс □□ввввваао □□ввввоаап □□вввваапп □□вввопвас □пввооввсзо □□ввповвпа □□ваавввоа □□□□□вввса □□□□ВВВВРС □□□вввввао
136
Розділ 3- Нейронні мережі
3.9- Нейронна мережа Хопфілда та її застосування
137
Образ, що тестується Відсоток зашумлення образу Вигляд перекрученого образа Результат розпізнавання
60% □□□а ВВЦВОГ1ВПОГ] □□□□□а □ввповсовв васввввпво ввиаоопввв □□□□а ввооаооввв ввооовоовв ВВС ІІ.ШВС11ШВ
всвовввпвв воавввпосп □вапооосво вввавввввв □□□вооваов ВВІ1ВВВВІМВ ввасососав вваоапсовв ввввоаппвв вввппопавв
65% □ввваваопв □ввпваввпа ввоаповввв □ввпвопввв □ввпаввппа □□□□ВВВПВВ вавпвввпва ввпвппвпвв □ввпвваапв □вввввааав □□ВВВВВВВВ □□□□вввввв ввппппвввв ввоаваасвв вваовввпаа ввоавввопа ввппвсппвв ввапаовавв □□□□вввввв □□ВВВВВВВВ
70% □впввваяав □ввпввввпв ввппапвввв □□□вппаво □ваввпвааа □□ввввппва вавввпаавв ввппввввпв ваосвавввв □ввваовавв ввввоовввв ааввоаввва вввоооиввв вввпввоввв ввиоввппвв ввсввввовв восоосасов всюоопооси □□ввввввса □□ввввввоо
80% впвввввввв □□□□ввсввв □□□□□впав □□□□вапава ввпавовопа воопвовпао ввавпаппвв впспвсввпв □□□вввпввв ваввавввва □□ВВВВВВВВ □□□□вввввв ввпаппвввв ввапваопвв ввоовввпаа ВВ2ОВВВОПС ввопвпппвв ввопасвввв □□□□вввввв □□ВВВВВВВВ
ВВВВОГ1ВОВВ ввввопвввв
вввасавввв ввввоовввв
90% вввооооавв □ввпасдивв ввопввооов вввппопввв ввасввспвв ввааввссівв
ввоввввпвв всоввооссо вооооопоов ВОВВВВВВОО ВВІІВВВВІ 1ВВ восоаоопов восаооооов □пввввввоа
□ [ЗВВВВВООО □□ввввввпо
вввасавввв ввввсовавв
ВВВВС.1ПВВВВ ВІШПГІВВІ ваввппвввв ВВВООС.1ОВВВ
100% ВВВІЗВВІ ІВВВ ввоаввізовв вваввввпвв впаоооосав ВОООООС1СЮВ □□авввавап ВВВІЗВВІЗВВВ ВВПОВВІЗОВВ вваввввсвв воаопоаапв ваасосаапв □□ввввввоо
□□авввват □□ввввввпо
138
Розділ 3. НеПропні мережі
3.9. Нейронна мережа Хопфілда та її застосування
139
Образ, що тестується Відсоток зашумлення образу Вигляд перекрученого образа Результат розпізнавання
□□□а □□аааааааа
□□□а □□□а □□ааааааас □□ааааааас □□ааааоаса
50% □□□□а □□аасааваа
□□□□□а □□□□□□а □□□□а □□ааааааас □□ааааааса □□□□□ааасс □□□□ааааас □□□ааааааа
□□□□а □□аааааасзс
□□ааааааас
□□ааааааас
60% □□□□□□а □□□□а □□аааааааа □□□□□□□□□□ □□□□□□□□□□ □□аааааааа
□□аааааааа
□□□а □□ваааааа
□□□□□□□а □□аааааааа
□□ □□ааааааш
□□аааааааа
□□ааааааса
70% □□ □□ааааааса □□□□□□□□□□ □□□□□□□□□□ □□аааааааа
□□ааааааас
□□аааааааа
□□□□□□□а □□аааааааа
□□ □□аааааваа
□□аааааапа
□□□а □□ааааааап
60% □□□□□а □□□□□□□а □□□□□□□□□ □а □□аааааааа □□□□□□□□□□ □□□□□□□□□□ □□аааааааа
□□ааааааас
□□□ □□ааааааас
□□□□□а □□ааааааас
□□а □□аааааааа
□□а □□ааааааас
□□ааааааас
90% □□□□а □□□□□□□□□□ □□□□□□□□а □□□□а □□ааааааса □□□□□□□□□□ □□□□□□□□□□ □□аааааааа
□□□□а □□аааааасс
□□ааааааас □□ааааааас
□□ааааааас □□ааааааас
□□аааааааа □□аааааааа
□□ааааааас □□ааааааас
□□ааааааас □□ааааааас
100% □□аааааат □□□□□□□□□□ □□□□□□□□□□ □□аааааааа □□ааавааяа □□□□□□□□□□ □□□□□□□□□□ □□аааааааа
□□ваааааас □□ааааавсс
□□ааааааас □□ааааааас
□□ааааааа □□аааааааа
140
Розділ 3. Нейронні мережі
3.9.6. Ефект «перехресних асоціацій»
Ускладнимо задачу і навчимо нашу НМ Хопфілда ще
(а)
(Ь)
одному зразку: а саме букві «П».
Буква «П» дуже схожа на вже існуючі
в пам’яті НМ букви «И» і «Н» (а). Тепер
НМ Хопфілда не може розпізнати ні одну
з цих букв навіть у неспотвореному стані.
Замість правильно розпізнаної букви вона
видає наступне зображення (при зашум-
ленні образа від 0 до 50%) (Ь):
Воно схоже потроху на кожну з букв
«И», «Н», «П» і не є правильною інтер-
претацією жодної з них.
При зашумленні від 50 до 60% на ви-
ході НМ з’являється спочатку представле-
не зображення (6) у злегка перекрученому
вигляді.
Починаючи з 65% зашумленості, на ви-
ході НМ стабільно з’являється негатив зо-
браження (с).
Описане функціонування нейронної ме-
режі відомо як ефект «перехресних асоці-
ацій».
□□□□□а
□□□□
□□□а
□□□□
□□□□
□□□□
□□□а
(с)
При цьому символи «А» і «Б» розпізнаються безпомил-
ково при перекручуванні до 40%. При 45 — 65% на виході
НМ з’являються злегка зашумлені інтерпретації зображен-
ня, схожі на негатив букви «Б» (але дуже перекручений), або
ж негатив образа, що тестується. При перекручуванні 70% і
більш НМ стабільно розпізнає в образі, що тестується, його
негатив.
3.10. Нейронна мережа Хеммінга
141
3.10. Нейронна мережа Хеммінга
Коли немає потреби, щоб мережа в явному вигляді дава-
ла зразок, тобто достатньо, скажімо, отримати номер зраз-
ка, асоціативну пам’ять успішно реалізує мережа Хеммінга
[20]. Дана мережа характеризується, порівняно з мережею
Хопфілда, меншими витратами на пам’ять та об’ємом обчи-
слень, що стає очевидним з її структури (рис. 3.14).
Мережа складається з двох шарів. Перший і другий шари
мають по т нейронів, де т — число зразків. Нейрони першо-
го шару мають по п синапсів, з’єднаних входами мережі (що
утворюють фіктивний нульовий шар). Нейрони другого шару
зв’язані між собою інгібіторними (від’ємно зворотними) сина-
птичними зв’язками. Єдиний синапс з позитивним зворотним
зв’язком для кожного нейрона з’єднаний з його ж аксоном.
Ідея роботи мережі полягає в пошуку відстані Хеммінга
від зразка, що тестується, до всіх зразків.
Зворотний зв’язок
Вхід 1-й шар 2-й шар Вихід
Рис. З 14. Структурна схема мережі Хеммінга
142
Розділ 3. Нсйроппі мережі
Відстанню Хеммінга називається число відмінних бітів в
двох бінарних векторах. Мережа повинна вибрати зразок з
мінімальною відстанню Хеммінга до невідомого вхідного си-
гналу, в результаті чого буде активізовано тільки один вихід
мережі, що відповідає цьому зразку.
На стадії ініціалізації вагових коефіцієнтів першого шару
та порогу активаційної функції їм будуть присвоєні наступні
значення:
х$
и}ік=—, г’ = 0...п — 1, к = 0...т — 1,
= к = 0...т-1,
де х£ — і-ий елемент к-ого зразка.
Вагові коефіцієнти гальмуючих синапсів в другому шарі
приймають рівними величині 0 < Н < ^/т. Синапс нейрона,
зв’язаний з його ж аксоном, має вагу +1.
3.10.1. Алгоритм функціонування мережі Хеммінга
Алгоритм функціонування мережі Хеммінга такий:
1. На входи мережі подається невідомий вектор, виходячи
з якого розраховуються стани нейронів першого шару (верх-
ній індекс шару в дужках вказує номер шару)
(п— 1 X
^2 и’чхг + Т3 І , = 0... т - 1.
і=0 /
Після цього отриманими значеннями ініціалізуються зна-
чення аксонів другого шару
2. Обчислити нові значення входів нейронів другого шару
т— 1
42) (?+1)=Уз (р) - ю ’
к І, у = 0... тп — 1
3.10. Нейронна мережа Хеммінга
143
та значення їх аксонів
(р + 1) = / 8{2} (р + 1) , і = 0... т - 1.
Активаційна функція / має вигляд порога, при цьому ве-
личина порога повинна бути достатньо великою, щоб будь-які
можливі значення аргумента не приводили до насичення.
3. Перевірити, чи змінились виходи нейронів другого ша-
ру за останню ітерацію. Якщо так — перейти до кроку 2.
Інакше — кінець.
З опису алгоритму видно, що роль першого шару досить
умовна: використавши один раз на кроці і значення його ва-
гових коефіцієнтів, мережа більше не звертається до нього,
тому перший шар може бути взагалі виключений з мережі
(замінений на матрицю вагових коефіцієнтів).
Переваги:
— невеликі витрати на пам’ять;
— мережа працює гранично швидко;
— надзвичайно простий алгоритм роботи;
ємність мережі не залежить від розмірності вхідного
сигналу (як в НМ Хопфілда) і в точності дорівнює кількості
нейронів.
3.10.2. Аналіз результатів експериментів
Наведемо результати експериментів з НМ Хеммінга в за-
дачі розпізнавання букв російського алфавіту.
НМ Хеммінга прекрасно справляється з задачею розпізна-
вання образів для експериментів з рівнем шумів від 0 до 45%.
В цьому діапазоні усі еталони розпізнаються без помилок.
При 50% зашумлення образи розпізнаються нестабільно,
часто виникає «переплутування» і на виході НМ з’являється
зовсім другий еталон
При 80 — 90% зашумлення образ починає інвертувати-
ся і при зашумленні 100% ми бачимо повністю інвертоване
144
Розділ 3. Нейронні мережі
зображення початкового. Хоча людина може розпізнати з
легкістю інвертований символ, програма не вміє цього роби-
ти, бо вважає, що сам символ зображується тільки чорними
точками. З цікавості можна було б навчити мережу розпізна-
вати інвертовані зображення символів одночасно з неінверто-
ваними. Для цього необхідно процес розпізнавання розбити
на два етапи: спочатку НМ працює в нормальному порядку
і обчислює виходи другого шару для оригінального (можли-
во зашумленого) зображення. Потім оригінальне зображення
інвертується і процес розпізнавання ініціюється знову. Потім
максимальні значення виходів, які вибрані з двох випробу-
вань, порівнюються та вибирається більше.
При зашумленні 80 — 100% НМ Хеммінга переплутує
символи, що подаються, з найбільш схожими еталонними.
Наприклад, при 100% зашумленні літера «П» схожа на тов-
сту смугу і програма розпізнає символ як «1».
Теоретично, другий шар повинен працювати, поки його
виходи не стабілізуються, але на практиці кількість ітера-
цій штучно обмежують, так було зроблено і в представлених
експериментах.
Мережі зі зворотними зв’язками є перспективним об’є-
ктом подальших досліджень їх динамічна поведінка відкри-
ває нові цікаві можливості.
Зрештою, можна зробити таке узагальнення. Мережі Хоп-
філда та Хеммінга дозволяють просто та ефективно вирішу-
вати задачу відтворення образів з неповної та перекрученої
інформації. Невелика ємність мереж (число образів, що запа-
м’ятовуються) пояснюється тим, що мережі не просто запа-
м’ятовують образи, а дозволяють проводити їх узагальнення,
наприклад, за допомогою мережі Хеммінга можлива класи-
фікація по критерію максимальної правдоподібності. Разом з
тим, легкість побудови програмних та апаратних моделей роб-
лять ці мережі привабливими дія багатьох застосувань [20,30].
3.11- Нечіткі нейронні мережі. Властивості. Застосування
145
3.11- Нечіткі нейронні мережі. Властивості.
Алгоритми функціонування. Застосування
3.11.1. Принципи побудови і структура систем
нечіткого керування. Загальна характеристика
Багато комплексних процесів являють собою багатопара-
метричні системи і є істотно нелінійними, а в ряді випадків
нелінійними в часі. Для застосування більш складних мето-
дів керування часто не вистачає інформації про процес і на-
дійні математичні моделі, що описують процес. Знання про
хід процесу, на які спирається оператор, реалізуються ним у
вигляді правил «якщо — то», що мають нечіткий інформацій-
ний зміст. Цей же принцип використаний при автоматизації
керування процесами на базі нечіткого контролера.
Останнім часом нечіткий контроль на основі застосуван-
ня теорії нечітких множин став однією із самих досліджу-
ваних тем. Основна ідея теорії нечітких множин полягає в
тому, що приналежність елемента множині описується не за
допомогою точних понять (належить (не належить)), аза до-
помогою будь-якого значення функції приналежності (ФП) в
інтервалі [0,1].
Кожний логічний зв’язок асоціюється з відображенням
[0,1]2 —> [0,1], що дозволяє визначити значення істинності
логічного виразу.
Розглянемо деяку імплікацію —»і/)].
Для оцінки її істинності можна використовувати різні
функції, деякі з яких наведені в табл. 3.13.
Ідея нечіткого контролера вперше була представлена
Мамдані (Матсіапі), після чого вона одержала широкий роз-
виток, в основному в Японії.
У випадку нечіткої інформації, недостатніх вихідних да-
них задача керування процесом не розв’язується традиційним
7і
146
Розділ 3. Нейронні мережі
способом, і необхідно перейти до формулювання задачі нечі-
ткого керування. Нечіткий контролер дозволяє вирішити цю
проблему шляхом завдання експертом нечітких правил виду
«якщо — то».
Наприклад: «якщо X є велике позитивне число і У є мале
позитивне, то С є позитивне середнє» (для випадку контроле-
ра з двома вхідними сигналами X і У і однією вихідною змін-
ною С). Терми «позитивне велике», «позитивне середнє» і
«позитивне мале» являють собою так звані лінгвістичні змін-
ні і є невизначеними описами значень вхідних змінних X і У
і вихідної змінної С.
Кожне лінгвістичне правило інтерпретується початко-
вим відношенням, що у свою чергу визначає в загальному
випадку відношення між нечіткими вхідними значеннями і
нечіткими вихідними значеннями.
Таблиця 3.13.
Варіанти функції належності імплікації
Ім’я автора [фі -> [-ф]
Гедель ґ 1, якщо [ір] < ['ф] [ [*ф], інакше
Лукашевич шіп{1 - [ір] + [ф]; 1}
Гоген ґ 1, якщо [<р] = 0 шах |1; інакше
Кліні-Дінс тах{1 - [ф];[Ф]}
Заде тах{1 - [ір]; тіп([ф]; [ф])}
Рейхенбах 1 - [ф] + [ф]#]
3.11- Нечіткі нейронні мережі. Властивості. Застосування
147
3.11- 2. Загальна характеристика систем
з нечіткою логікою
Апарат нечітких множин і нечіткої логіки вже давно з
успіхом застосовується для вирішення задач, у яких вихідні
дані є ненадійними і слабко формалізованими. Сильні сторо-
ни такого підходу:
— опис умов і методу рішення задачі мовою, близькою до
природної;
— універсальність: відповідно до теореми ГАТ (Еиггу
Арргохітаїіоп ТЬеогеш), доведеної Б. Коско (В. Ковко) у
1993 р., будь-яка математична система може бути апрокси-
мована системою, заснованою на нечіткій логіці;
— ефективність (зв’язана з універсальністю), що підтвер-
джується рядом теорем, аналогічних теоремам про повноту
для штучних нейронних мереж.
Разом з тим, для нечітких систем характерними є і певні
недоліки:
— вихідний набір нечітких правил формулюється екс-
пертом-людиною і може виявитися неповним чи суперечли-
вим;
— вигляд і параметри функцій належності, що описують
вхідні і вихідні змінні системи, вибираються суб’єктивно і
можуть виявитися такими, що не цілком відбивають реальну
дійсність.
Для усунення, принаймні частково, зазначених недоліків
було запропоновано створювати нечіткі системи адаптивни-
ми, коректуючи, в процесі їхньої роботи, правила і параме-
три функцій належності. Одними з самих вдалих прикладів
таких систем є нечіткі нейронні мережі. Нечітка нейронна
мережа формально за структурою ідентична багатошаровій
нейронній мережі з навчанням, наприклад, за алгоритмом
7*
148
Розділ 3. Нейронні мережі
зворотного поширення помилки, але сховані шари в ній від-
повідають етапам функціонування нечіткої системи [34]:
— перший шар нейронів виконує функцію введення нечі-
ткості ЦиггіЯсаІіоп) на основі заданих функцій належності
входів;
— другий шар відображає сукупність нечітких правил;
— третій шар виконує функцію приведення до чіткості
(веГиггійсаІіоп).
Кожен з цих шарів характеризується набором параметрів
(функціями належності, нечіткими вирішальними правила-
ми, активаційними функціями, вагами зв’язків), настроюва-
ння яких виробляється, по суті, так само, як і для звичайних
нейронних мереж. Нижче розглядаються теоретичні аспекти
створення подібних мереж, а саме, апарат нечіткої логіки і
власне нечіткі нейронні мережі стосовно до задач прийняття
рішень в умовах невизначеності.
Увівши поняття лінгвістичної змінної і допустивши, що в
якості її значень (термів) виступають нечіткі множини, Заде
запропонував апарат для опису процесів інтелектуальної ді-
яльності, включаючи нечіткість і невизначеність виразів. Це
дозволило створити фундамент теорії нечітких множин і не-
чіткої логіки, а також передумови для впровадження методів
нечіткого керування в інженерну практику.
Нечітке керування виявляється особливо корисним, коли
досліджувані процеси є занадто складними для аналізу за до-
помогою загальноприйнятих методів, чи коли доступні дже-
рела інформації інтерпретуються якісно чи неточно. Нечітка
логіка, що надає ефективні засоби відображення невизначе-
ностей і неточностей реального світу (і на якій засноване не-
чітке керування) ближче до людського мислення і природних
мов, ніж традиційні логічні системи.
3.11- Нечіткі нейронні мережі. Властивості. Застосування
149
3.11-3. Математичний аппарат нечіткої логіки
Використовуваний у різних експертних і керуючих си-
стемах механізм нечітких висновків у своїй основі має базу
знань, формовану фахівцями предметної галузі у вигляді су-
купності нечітких предикатних правил вигляду:
Пі: якщо х Е Аі, то у Е В} ,
Пг : якщо х Е А2 то Є Дгі
.........»
П„ : якщо х Є Ап то у Е Вп,
де х — вхідна змінна (ім’я для відомих значень даних); у —
змінна висновку (ім’я ддя значення даних, що буде обчислене);
А та У — функції належності, визначені відповідно на х та у.
Наведемо більш детальне пояснення. Знання експерта
А —» В відбиває нечітке причинне відношення передумови
і висновку, тому його можна назвати нечітким відношенням
і позначити через В :
В = А -+ В,
де «—» » називають нечіткою імплікацією.
Відношення В можна розглядати як нечітку підмножи-
ну прямого добутку X х У повної множини передумов X та
висновків У. Таким чином, процес одержання (нечіткого) ре-
зультату висновку В' з використанням даного спостереження
А' і знання А —> В можна представити у вигляді компози-
ційного правила нечіткий «гпосіие ропепє»
В' = А' • В = А! • (А В),
де • — операція згортки.
Як операцію композиції, так і операцію імплікації в алге-
брі нечітких множин можна реалізовувати по-різному (при
цьому буде відрізнятися й одержуваний результат), але в
будь-якому випадку загальний логічний висновок здійсню-
ється за наступні чотири етапи [33, 34].
150
Розділ 3. Нейронні мережі
1. Введення нечіткості (фазифікація, Гиггійсаііоп).
Функції належності, визначені на вхідних змінних, засто-
совуються до їхніх фактичних значень для визначення сту-
пеня істинності кожної передумови кожного правила.
2. Логічний висновок.
Обчислене значення істинності для передумов кожного
правила застосовується до висновків кожного правила. Це
призводить до однієї нечіткої підмножини, що буде призначе-
но кожній змінній висновку для кожного правила. Як прави-
ло, до логічного висновку звичайно використовуються тільки
операції тіп (МІНІМУМ) чи ргосі (МНОЖЕННЯ). У логі-
чному висновку МІНІМУМУ функція належності висновку
«відтинається» по висоті, що відповідає обчисленому ступе-
ню істинності передумови правила (нечітка логіка «І»). У ло-
гічному висновку МНОЖЕННЯ функція належності виснов-
ку масштабується за допомогою обчисленого ступеня істин-
ності передумови правила.
3. Композиція.
Усі нечіткі підмножини, призначені до кожної змінної ви-
сновку (у всіх правилах), поєднуються разом, щоб сформу-
вати одну нечітку підмножину для всіх змінних висновку.
При подібному об’єднанні звичайно використовуються опе-
рації тах (МАКСИМУМ) чи вшп (СУМА). При композиції
МАКСИМУМУ комбінований висновок нечіткої підмножини
конструюється як поточечний максимум по всіх нечітких під-
множинах (нечітка логіка «АБО»). При композиції СУМИ
комбінований висновок нечіткої підмножини формується як
поточечна сума по всіх нечітких підмножинах, які призначе-
ні правилами логічного висновку
4. Приведення до чіткості (дефазифікація, сІсГиггіГісаІіоп).
Використовується, якщо потрібно перетворити нечіткий
набір висновків у чітке число. Існує значна кількість методів
приведення до чіткості, деякі з яких розглянуті нижче.
3-11- Нечіткі нейронні мережі. Властивості. Застосування
151
Приклад. Нехай деяка система описується наступними
нечіткими правилами:
Пі : якщо х Е А, то ш Є О;
ІІ2 : якщо у Е В, то го Е Е;
Пз : якщо г Е С, то и Е Г,
де х, у та г — імена вхідних змінних; їх — ім’я змінної виснов-
ку, а А, В, С, В,Е,Г — задані функції належності (трикутної
форми).
Процедура одержання логічного висновку ілюструється
рис. 3.15. Передбачається, що задано конкретні (чіткі) зна-
Рис. 3.15. Ілюстрація процедури логічного висновку
152
Розділ 3. Нейронні мережі
На першому етапі на підставі даних значень і, виходя-
чи з функцій належності А, В, С, знаходяться ступені істин-
ності а (аго), а (уо) та а (до) для передумов кожного з трьох
приведених правил.
На другому етапі відбувається «відсічення» функцій
належності висновків правил (£), Е, Е) на рівнях а (а?о),
а (уо) та а (го).
На третьому етапі розглядаються функції належності,
усічені на попередньому етапі, і здійснюється їхнє об’єднан-
ня з використанням операції тах, у результаті чого утворю-
ється комбінована нечітка підмножина, що описується фун-
кцією належності (ш) і відповідає логічному висновку для
ВИХІДНОЇ ЗМІННОЇ IV.
Нарешті, на четвертому етапі знаходиться, при необхі-
дності, чітке значення вихідної змінної, наприклад, із засто-
суванням центроїдного методу: чітке значення вихідної змін-
ної визначається як центр ваги для кривої /іц (ш) :
/ IV (гг) (іи>
_ п____________
гГ° / № (їу) йго
р
Розглянемо наступні найбільш вживані модифікації алго-
ритму нечіткого висновку, вважаючи, для простоти, що базу
знань організують два нечіткі правила виду
ІІ! : якщо іЄ Аі і у Є Ві, то г Є Сі,
Па : якщо х Є Лг і у Є В2, то г Є С2,
де хтау — імена вхідних змінних, г — ім’я змінної висновку,
Аі, Ві, Сі, А2, В2, С2 — деякі задані функції належності.
При цьому чітке значення го необхідно визначити на основі
приведеної інформації і чітких значень х0 і уо-
3.11- Нечіткі нейронні мережі. Властивості. Застосування
153
Алгоритм Матсіапі
Даний алгоритм відповідає розглянутому прикладу на
рис. 3.15. У розглянутій ситуації він математично може бути
описаний у такий спосіб [34]:
1. Введення нечіткості.
Знаходяться ступені істинності для передумов кожного
правила: Аі (т0) , А2 (М, В\ (уо), В2 (?/о) •
2. Логічний висновок.
Знаходяться рівні «відсікання» для передумов кожного з
правил (з використанням операції МІНІМУМ)
«і = Аі (гго) А Ві (г/0);
а2 = А2 (т0) А В2 (уо),
де через «А» позначена операція логічного мінімуму (тіп).
Потім знаходяться «усічені» функції належності
Сі = (а! А (г));
Сі = (а2 А С2 (г)).
3. Композиція.
Проводиться об’єднання знайдених усічених функцій з ви-
користанням операції МАКСИМУМ (позначене далі як «V»),
що призводить до одержання підсумкової нечіткої підмножи-
ни для змінної виходу з функцією належності
МЕ(^) = С(г) = С((г)7СІ(г) =
= (оц А С] (г)) V (а2 А С2 (г)).
4. Приведення до чіткості.
Проводиться для одержання г», наприклад, центроїдним
методом.
7’
154
Розділ 3. Нейронні мережі
Алгоритм Тзикатоіо
Вихідні посилки — як у попереднього алгоритму, але тут
передбачається, що функції Сі(г), 6*2(2) монотонні (рис.3.16).
1. Введення нечіткості (як в алгоритмі Матсіаш).
2. Нечіткий висновок. Спочатку знаходяться рівні «відсі-
кання» О] і а2 (як в алгоритмі Матсіапі), а потім рішеннями
рівнянь та а2 = С2 (г2)
визначаються чіткі значення (21 та г2) для кожного вихідно-
го правила.
3. Визначається чітке значення змінної висновку (як зва-
жене середнє 2і та 22) : +
~0 = -----7----•
«і + а2
Рис. 3.16. Ілюстрація до алгоритму Ткикатоіо
3.11- Нечіткі нейронні мережі. Властивості. Застосування
155
Алгоритм 8и§епо
8и§епо і Така§і використовували набір правил у наступній
формі [34] (як і раніше, наведемо приклад двох правил):
Пі : якщо х Є А] і у Є Ві, то г1=а1х + Ьіу,
П2 : якщо х Е. Аг і у Є В2, то г2 = а2х + Ь2у.
Опис алгоритму 8и§епо (рис. 3.17).
1. Введення нечіткості (як в алгоритмі МатНапі).
2. Нечіткий висновок. Знаходяться «і = А] (гго) А Ві (уо),
а2 = А2(хо) А В2(уо) і індивідуальні виходи правил:
іі — ОіТо + Ьіуо;
і2 = а2хо + Ь2уо.
Значення змінної висновку визначається центроїдним ме-
тодом і дорівнює
Отії + о2і2
г0 =---------------.
Осі + ос2
Рис. 3.17. Ілюстрація до алгоритму Зичено
156
Розділ 3. Нейронні мережі
Алгоритм Ьагзеп’а
В алгоритмі Ьагзеп’а нечітка імплікація моделюється з
використанням оператора множення.
Опис алгоритму (рис. 3.18).
1. Введення нечіткості (як в алгоритмі Матсіапі).
2. Нечіткий висновок. Спочатку, як в алгоритмі Мапкіапі,
знаходяться значення:
«і = Аі(х0) А Ві(у0\,
а2 = А2(х0) А В2(у0);
а потім визначаються часткові нечіткі підмножини:
аіСі(г) а2С2(г).
3. Знаходиться підсумкова нечітка підмножина:
№(г) = С(г) = (аіС^г)) V (а2С2(х)\,
(у загальному випадку п правил: Цг(г) = С(г) = V (аіСДг))) .
4. При необхідності проводиться приведення до чіткості
(як у раніше розглянутих алгоритмах).
Рис. 3.18. Ілюстрація до алгоритму Ьагзеп’а
3.11- Нечіткі нейронні мережі. Властивості. Застосування
157
3.11-4. Методи приведення до чіткості
1. Вище вже був розглянутий один з даних методів — цен-
троїдний. Приведемо відповідні формули ще раз. У загаль-
ному випадку:
/ г • С(г)йг
_ я__________
го /С№ •
я
для дискретного варіанта:
п
І=1
го — — —
І=1
2. Перший максимум (Гігбі-оЕ-Махіша). Чітка величина
висновку знаходиться як найменше значення, при якому дося-
гається максимум підсумкової нечіткої множини (рис. 3.19, а):
го = гпіп |г |с(г) = п х С(1/)}.
3. Середній максимум (Міск11е-оГ-Махіпіа). Чітке значення
знаходиться за формулою:
/ гсіг
20 =
с
де С— підмножина елементів, максимізуючих С(рис. 3.19, б).
и
а б
Рис. 3.19. Ілюстрація до методів приведення до чіткості:
а — перший максимум; б — середній максимум
158
Розділ 3. Нейронні мережі
Для дискретного варіанта (С дискретне):
=
4. Критерій максимуму (Мах-Сгііегіоп). Чітке значення
вибирається довільно серед множини елементів, для яких С
досягає максимуму:
го - тіп {г |с(г) = тах
5. Висотна дефаззифікація (Нещіїї веіиггійсаііоп). Еле-
менти області визначення О, для якої значення функції нале-
жності менше, ніж деякий рівень а, у розрахунок не прийма-
ються, і чітке значення розраховується відповідно до виразу:
/ г С(г)сД
26 =
со
де Со — нечітка множина а -рівня (див. вище).
3.11.5. Ефективність нечітких систем прийняття рішень
Можливість використання апарата нечіткої логіки базує-
ться на наступних результатах [33, 34].
1. У 1992 р. \Уап£ показав, що нечітка система є універ-
сальним апроксиматором, тобто може апроксимувати будь-
яку неперервну функцію на компакті Ц з довільною точні-
стю, якщо використовує набір п (п —♦ оо) правил:
Пі : якщо х Є Аг та у € Ві, то г Є Сі, і = 1... п,
при наступних умовах:
— гаусових функціях належності:
А, (х) = ехр
(\ 2
х — од \
)
3.11. Нечіткі нейронні мережі. Властивості. Застосування
159
Ві(у) = ехр
)2
СДг) = ехр
1 / г - о,з \ 2
2\ (За /
— композиції у вигляді добутку:
[А, (ж) апб Ві (у)] = Аі (ж) Ві (у);
— імплікації у формі (Ьагвеп):
[Л£ (х) алеї Ві (у)] -> Сі (х) = А, (х) Ві (у) Сі (г);
— центроїдному методі приведення до чіткості:
52 ааАіВх
»=і
20 = —п------->
ЕАВі
І=1
де «ІЗ — центр Сі.
Інакше кажучи, \¥ап§ довів теорему: для кожної дійсної
неперервної функції д, заданої на компакті V і для довільного
є > 0 існує нечітка система, що формує вихідну функцію
/ (х) таку, що
нирЦу(ж) - /(х)|| є,
де || || — символ прийнятої відстані між функціями.
2. У 1995 р. Сазіго показав, що логічний контролер Мат-
сіапі також є універсальним апроксиматором при:
— симетричних трикутних функціях належності:
1 - Іщ — ®|/а , якщо |«і — ж| а»;
0, якщо |а, — х| > а,;
1 — |6, — УІ/д, якщо |6і — у| /Зі',
0, якщо |Ьі — у| > (Зі',
Аг (х) =
Вг(У)=
160
Розділ 3. Нейронні мережі
Iі Iе* гІД,., якщо |сі - г| $ 7»;
0, якщо |сі — г| > 7<;
— композиції з використанням операції тіп:
[Лі (х) апй Ві (у)] = тіп (Лі (х) , Ві (у));
— імплікації у формі МатНапі і центроїдного методу при-
ведення до чіткості:
Е с\ тіп {Лі (х), Ві (у)}
20 = -------------------->
Е тіп {Лі (х), В, (у)}
»=і
де Сі — центр Сі-
Взагалі кажучи, системи з нечіткою логікою доцільно за-
стосовувати в наступних випадках:
• для складних процесів, коли немає простої математичної
моделі;
• якщо експертні знання про об’єкт чи процес можна
сформулювати тільки в лінгвістичній формі.
Системи, що базуються на нечіткій логіці, застосовувати
недоцільно:
• якщо необхідний результат може бути отриманий яким-
небудь іншим (стандартним) шляхом;
• коли для об’єкта або процесу вже знайдена адекватна і
легко досліджувана математична модель.
Відзначимо, що основними недоліками систем з нечіткою
логікою є те, що:
• вихідний набір нечітких правил формулюється експер-
том-людиною і може виявитися неповним або суперечливим;
• вигляд і параметри функцій належності, що описують
вхідні і вихідні змінні системи, вибираються суб’єктивно і мо-
жуть виявитися такими, що неповністю відбивають реальну
дійсність.
3.11. Нечіткі нейронні мережі. Властивості. Застосування
161
3.11-6. Контролер Мамдані
Першим контролером, в якому була використана нечітка
база правил та нечіткий логічний висновок, був контролер
Мамдані [38].
Розглядається система з п входами а?і, ж2,..., з домена-
ми Х1, Х2, ..., Х„ й однією керуючою змінною у з доменом У.
Щоб створити придатні правила для бази даних (БД) нечі-
ткого контролера, множини Хі, Х2, Хп і V повинні бути
нечітко розділені, тобто розділені на нечіткі множини на Хі.
Звичайно множини Хі визначаються інтервалом дійсних
чисел, а самі нечіткі множини визначаються трикутними
функціями
д : Хі —» [0,1], х = 1 - тіп {є - |ж — ж0| 51} ,
де є > 0.
На границях інтервалу [а, Ь] :
: [а, 6] —> [0,1], х =
1, якщо х < Хо
1 — тіп {є • (х — а?о); 1} , інакше.
Такий вигляд функції обраний тому, що обчислення з НК
значно спрощуються при використанні кусочно-лінійної фун-
кції. На рис. 3.20 показаний розподіл 7 множин, що асоці-
йовані з лінгвістичними термами: велике негативне (IVІ, —
= Не§аІІУе Ьаг§е); середнє негативне (Ж/ = Ие^аііуе Меап);
негативне мале (N8 = Ие^аііуе Зіпаїї); приблизно нуль (2 —
= 2его); позитивне мале (Р8 = Розйіує Зіпаїї); позитивне се-
реднє (РМ — Ровіііує Меап); велике позитивне (РЬ = Розіііує
Ьаг£е).
База правил складається з правил, що мають наступну
форму:
Яг : якщо (ай Є д£*) і (х2 Є і ... і (хп Є Д,"^ ,
то тоді у Є Біг,
162
Розділ 3 Нейронні мережі
Рис. 3.20. Розподіл 7 множин для лінгвістичних термів
де в,, — лінгвістичні терми, обумовлені нечі-
ткими множинами Ціг , що відповідають нечіткій
розбивці МНОЖИН Хі,Хі,...,Хп і У відповідно.
В нечіткому контролері реалізовано алгоритм логічного
висновку Мамдані, який розглянуто вище.
Приклад. Задача балансування переверненого маятни-
ка. Ми використовуємо кожну з множин Хі,Х2,...,Хп і У-
Множини є доменами кута в, кутової швидкості О і сили Р,
що змушує маятник прагнути до вертикального стану.
В якості бази правил використовуються 19 правил, пред-
ставлених у табл. 3.14, де, наприклад, третій рядок читається
так: якщо в є приблизно нуль (2) і £1 є мале негативне (N3),
то Р є позитивне мале (Р5). Так задається процес фазифікації.
Спочатку процес логічного вирішення обчислює кожне
правило незалежно. На цьому етапі ми обчислюємо значе-
ння Д^Г(ЯЦ,), де V = 1,П, тобто З ЯКИМ ступенем змінна Хц
відповідає лінгвістичному терму, асоційованому з нечіткою
множиною Тобто Жі,..,а;п повинні відповідати термам
..., а значення р^г (у = 1,п) повинні сполучатися.
Це досягається визначенням
3.11. Нечіткі нейронні мережі. Властивості. Застосування
163
Таблиця 3.14.
База правил нечіткого контролера
/ф N1 ІЇМ N8 2 Р8 РМ РЬ
ІЇЬ Р8 РЬ
ІЇМ РМ
N8 км N8 Р8
г т N114 N8 2 Р8 РМ РЬ
Р8 N8 Р8 РМ
РМ NМ
РЬ т N8
Величина аг показує, з яким ступенем виконуються умови
правила Ег- Вихідне значення правила Ег — це нечітка мно-
жина керуючих змінних, отримана шляхом відсічення вихі-
дної нечіткої множини ціг з ФП аг правила Ег-
Математично це можна записати в такий спосіб:
у -> тіп (жі), - - -,(хп) , д}”’ (у)} .
Після того, як усі правила будуть обчислені, усі НМ треба
об’єднати в одну НМ, використовуючи процедуру узяття ма-
ксимуму (тобто операцію об’єднання). У результаті процесу
логічного вирішення одержуємо наступну нечітку множину:
у = тах [тій (жЦ ,..., (жп), (у)}] .
На останньому етапі ця НМ повинна бути перетворена в
чіткі значення за допомогою процесу «дефазифікацїї». Це мо-
жна зробити одним з вищерозглянутих методів:
164
Розділ 3. Нейронні мережі
1. Метод максимуму критерію (тах сгіїегіоп теііюсі).
2. Метод середнього значення максимуму (тісМІе о£ тахі-
та теїИос! = МОМ).
3. Метод центра ваги області — центроїдний метод (іЬе
сепіег о£ агеа шеіЬос! = СОА).
На рис. 3.21 представлені кроки мінімаксного контролера
Мамдані.
Метод СОА гарантує плавний контроль (керування) у по-
рівнянні з двома іншими методами. Його недоліком є ком-
плекс більш складних обчислень.
Приклад. Розглянемо нечіткий контролер, що керує ав-
томобілем.
Керування полягає в тому, щоб уникнути зіткнень з пе-
решкодами. Якщо перешкода виникла попереду, то нечітка
множина, зображена на рис. 3.22, визначається процедурою
логічного вирішення, керуюча дія якої може бути інтерпрето-
вана як повернути «вліво чи вправо». Оскільки методи СОА і
МОМ допускають значення нуль як керуючу дію, то машина
рухається вперед, поки не відбудеться зіткнення з перешко-
дою (це істотний недолік!).
Описане відхилення відбудеться, якщо нечітка множина
буде опуклою, і воно може бути інтерпретоване як пред-
ставлення єдиного значення в інтервалі. У наведеному вище
випадку метод дефазифікації повинен вибирати між різними
керуючими діями (у даному випадку між двома трикутними
зображеннями на рис. 3.22), а потім трансформувати кожну
множину в чітке значення.
Принципова структура нечіткого керування наведена на
рис.Ж23, де показані функціональні компоненти фази-конт-
ролера, що викону ють процедури фазифікації на базі лінгві-
стичних правил, композиції бази правил і логічного висновку,
а також дефазифікації. Розглянемо детальніше ці компонен-
ти (рис. 3.23).
3.11. Нечіткі нейронні мережі. Властивості. Застосування
165
МОМ
Рис. 3.22. Приклад невдалої
дефазифікації
Рис. 3.23. Структурна схема нечіткого керування
166
Розділ 3. Нейронні мережі
3.11.7. Нечіткий контролер на базі нейронних мереж
Для проектування нечіткого контролера повинні бути за-
дані лінгвістичні правила і ФП (функція приналежності) для
представлення лінгвістичних величин. Специфікація гарних
лінгвістичних правил залежить від знання експертом систе-
ми керування. Але переклад цих знань у нечіткі множини
задача аж ніяк не формалізована, і потрібно зробити вибір
на підставі, наприклад, форми ФП. Якість нечіткого контро-
лера (НК) досягається шляхом зміни форми ФП.
Штучні нейронні мережі (НМ) являють собою високопа-
раллельну архітектуру і складаються з аналогічних обробних
елементів, що взаємодіють через зв’язки, що задаються вага-
ми. Використовуючи НМ ми можемо не тільки апроксимува-
ти функції, але і вивчати (досліджувати) об’єкти керування,
застосовуючи навчання і самонавчання. Проблема полягає в
тому, що на навчання витрачається досить багато часу і при
цьому не завжди гарантується результат. Але можливо впро-
вадити раніше набуті знання у вигляді правил уже навченої
НМ для спрощення процедури навчання.
Сполучення НК і НМ дозволяє об’єднати всі їхні перева-
ги й уникнути їхніх недоліків. Цей підхід використовує НМ
для оптимізації скінченних параметрів звичайного НК або
для добування правил з даних. Вибір ФП, що представляє
лінгвістичний терм, більш-менш довільний. Для прикладу
розглянемо лінгвістичний терм «приблизно нуль». Очевидно,
що відповідна нечіткій множині ФП повинна бути унімодаль-
ною, досягати свого максимуму в значенні нуль. Правильний
вибір функції приналежності став основною і найважливі-
шою задачею НК.
НМ пропонує можливість вирішення цієї проблеми. Метод
прямого поширення (сигналів) у НМ припускає вибір форми
ФП, яка залежить від декількох параметрів і може бути ско-
регована в процесі навчання. У якості ФП можна взяти симе-
З.П- Нечіткі нейронні мережі. Властивості. Застосування
167
Рис. 3.24. Дефазифікація з використанням монотонної
функції приналежності Тзикапюїо
тричну трикутну форму, що залежить від двох параметрів,
один із яких визначається значенням, у якому ФП досягає
максимального значення, а другий — довжиною інтервалу.
Дані навчання повинні бути розділені на т непересічних
кластерів /?і,..., Кг. Кожен кластер Ні відповідає вирішаль-
ному правилу Ні. Елементи кластера представляються у ви-
гляді значень у формі (X, у), де X — [ж і,..., хп] ~ вектор
вхідних змінних, а у — вихідна змінна.
Ми розглядаємо динамічну систему 8, що керується однією
змінною С, і її стан може бути описано п змінними Хі,..., хп.
Лінгвістичні значення змінних моделюються функціями
приналежності, а керуючий вплив (керування), що приво-
дить систему до бажаного стану, описується нечітким керу-
ванням «якщо — то». Щоб одержати вихідне значення (тоб-
то керування), необхідно вирішити проблему дефазифікації,
для чого ми використовуємо монотонну функцію принале-
жності Тзукамото (Тзпкатоіо), див. на рис. 3.24, де дефази-
фікація зводиться до застосування зворотної функції.
168
Розділ 3. Нейронні мережі
Така функція приналежності д характеризується двома
точками а і Ь із ФП д(п) = 0, д (6) = 1, і вона визначається
як
якщо х Є [а, Ь] V (х Є [Ь,«] А а > Ь);
„ 0, інакше.
Дефазифікація здійснюється таким шляхом
х — д 1 (у) — — у (а — Ь) + а — а + у(Ь — а); у Є [0; 1]. (3.56)
Для наших цілей ми повинні обмежити монотонну ФП,
щоб представити лінгвістичне значення вихідної змінної. Для
вхідної величини звичайно використовують трикутну чи тра-
пецеїдальну ФП.
На рис. 3.25 представлена структура нечіткого нейронного
контролера.
Модулі Хі і Х2 тут представляють вхідні змінні, і вони по-
силають свої значення у свої д-модулі, що містять відпо-
відні ФП. д-модулі зв’язані з Д-модулями, що являють со-
бою нечіткі правила «якщо —то». Кожний р-модуль передає
всім зв’язаним з ним Д-модулям значення ФП щ (а\) її вхі-
дної величини Хі. Д-модуль використовує операцію перетина-
ння і знаходить тіп{/іу (ж»)} , і передає це значення далі —
І
у ^/-модуль, якій містить ФП, що описує вихідне значення,
^/-модуль, використовуючи монотонні функції приналежно-
сті, обчислює величини Гі Й і/-1 (Ті) і передає їх у С-модуль,
що обчислює вихідну змінну — керуючий вплив С згідно фор-
мулі (3.57), тобто використовує алгоритм центру мас (СОА):
£ Гі^1 (Гі)
С='^—п--------, (3.57)
І=1
3.11- Нечіткі нейронні мережі. Властивості. Застосування
169
Рис. 3.25. Структура нечіткого нейронного контролера
де п — число правил виводу; Гі — ступінь, з яким правило
Ні виконується. Як неважко побачити, система на рис. 3.25 .
нагадує послідовну багатошарову НМ, де х-, К- і С-модулі
виконують роль нейронів, а ц- і ^/-модулі відіграють роль
адаптуємих ваг зв’язків мережі.
3.11.8. Поширення помилки в нечіткому
нейронному контролері
Одна з проблем конструювання нечіткого контролера —
це вибір відповідної функції приналежності. Дану проблему
можна вирішити за допомогою інтеграції методики навчання
НМ і архітектури нечіткого контролера.
Стандартний метод складається в додаванні ще одно-
го модуля в архітектуру, з огляду на необхідність корекції
помилок. Ми розглядаємо обчислення керуючої змінної за да-
ними виміру вхідних змінних як послідовну процедуру в ба-
гатошарових НМ, де вхідні сигнали поширюються в прямому
8і
170
Розділ 3. Нейронні мережі
напрямку(Іеесі Сотані), але якщо дійсні значення виходів від-
різняються від бажаних, то помилка поширюється в зворо-
тному напрямку з урахуванням величин, розрахованих під
час прямого ходу.
Нехай вхідні виміри задані в підінтервалі дійсних значень
Будемо визначати ці виміри шляхом лінійного
відображення Іп в інтервал [0,1] — область визначення фун-
кції приналежності, тобто будемо інтерпретувати це відобра-
ження як представлення лінгвістичних значень:
М : -* [0,1]
(так зване М8Г-відображення).
Відповідно до цього будемо відображати інтервали трапе-
цеїдальною чи трикутною функцією приналежності (ФП). У
такій постановці розглянемо для простоти один шар основ-
них правил.
Звичайно правила пишуться в такій формі:
Рі (жі),.. .,Рі (ж„) С).
З кожним значенням Хі ми зв’яжемо значення ФП ц, (ж,).
3.11- Нечіткі нейронні мережі. Властивості. Застосування
171
Розглянемо тепер повну архітектуру нечіткого контроле-
ра. Вона приведена на рис. 3.26.
Вона складається з наступних компонентів:
1. М8Р — модулі, що реалізують процедуру фазифікації,
2. Т — модулі для агрегації вхідних даних,
3. 8 — модуль для агрегації вихідних даних,
4. РЕРІ/2 — модуль, що виконує процес дефазифікації.
Т-модулі здійснюють операцією мінімізації (перетинан-
ня), 8-модуль операцію максимізацїї (об’єднання) відповідно.
На рис. 3.26 контролер має 2 входи а~і і а?2 для п’яти пра-
вил, де М8Р задані як /ф,... /4, * = 1,2.
Значення, отримані Л/5Р-модулями, передаються спочат-
ку Т-модулям, а потім через 5-модулі до процесу дефазифі-
кацїї. Вихідний сигнал а порівнюється з бажаним вихідним
сигналом сґ( і визначається помилка <5. Проблема полягає в
настроюванні вхідних і вихідних Л/57?-модулів.
Процедура навчання
Помилка <5о!) є комбінацією бічного зсуву доменів 5^ і
залежить від форми функцій Ці помилки поширюються
в зворотному напрямку в 8 і Т-модулях відповідно.
Будемо розглядати наступні два методи дефазифікації:
метод центра ваги (СОА) і метод середнього значення ма-
ксимуму (МОМ). Після того, як отримали чітке вихідне зна-
чення а = О ЕРІ/ 2 (8), ми повинні визначити сигнал помил-
ки як різницю сг — Сті між вихідним значенням і бажаним
вихідним значенням
Розглянемо МОМ-процедуру дефазифікації.
Існує 4 можливості для вихідної величини приймати не-
вірне значення:
1. Якщо бажане значення розташоване під вершиною 8,
але зсунуте трохи вліво чи вправо (рис. 3.27, а);
8*
172
Розділ 3. Нейронні мережі
Рис. 3.27. Групування а таким чином, щоб змінити
форму нечітких множин Т
Рис. 3.28. Можливі випадки розташування о, відносно 5
2. Якщо бажане значення належить області визначення
нечіткої множини Тг, що генерує вершину 8і, але не розта-
шовується під вершиною 8 (рис. 3.27, б);
3. Якщо бажане значення не належить області визначення
нечіткої множині Ті, що генерує вершину 8, але воно як і рані-
ше знаходиться усередині області належності 8 (рис. 3.28, а);
4. Якщо бажане значення сг{ не належить області визна-
чення 8 (рис. 3.28, б).
3-Н- Нечіткі нейронні мережі Властивості. Застосування
173
У двох перших випадках вершина 3 згенерована правиль-
ною вихідною нечіткою множиною Т, але вона зміщена. Ми
припускаємо, що тільки Ті впливає на невірне значення ви-
ходу сг. Цю помилку можна виправити, змінюючи форму Т»
таким чином, щоб положення вершини Ті співпадало з сг( (пе-
реривчасті лінії на рис. 3.27).
У третьому випадку вершина 8 згенерована невірною ви-
хідною нечіткою множиною Тг. Ця помилка відбувається че-
рез вхідні нечіткі множини, отже ми спочатку повинні змі-
нити функції належності р-модулів так, щоб перевірити, що
вершина З згенерована правильним модулем 7}.
Припустимо, що вершина З, згенерована модулем 7, і сгь,
належить області приналежності 7,. Отже, ми повинні збіль-
{0 ) 1 ’ •
у на виході і зменшити величину
іпіп на виході Ті. Потім застосовуємо процедуру агре-
гації в 5-модулі таким чином, як і в двох перших випадках.
У четвертому випадку, коли не належить області визна-
чення 5, робимо висновок, що в нашій базі правил присутня
помилка.
Це може бути або у випадку, коли не існує правила, що
покриває область визначення сг{, або правило не відповідає
дійсності. У цьому випадку ми повинні запропонувати прави-
ло, що відповідає даній ситуації. Ця процедура реалізується
не автоматично, а виконується користувачем.
3.11.9. Алгоритм нечіткого поширення помилки
Опишемо алгоритм нечіткого поширення помилки в нечі-
ткій нейронній мережі.
1. Після того як пристрій ЕЕЕІ/2 згенерував сг, він пе-
редає на зворотному ході правильне значення і фактичне
значення виходу сг в 5-модуль.
82
174
Розділ 3. Нейронні мережі
2. Перевіряється умова приналежності <7( області визна-
чення 5. Якщо вона не виконується (тобто сг( області ви-
значення 5), то експерт повинен додати нове правило в базу
правил, і поточне вихідне значення повинно бути скориго-
ване перед початком процедури навчання. У протилежному
випадку переходимо на наступний крок.
3. Якщо 8-модуль передає в зворотному напрямку ст і стІУ
то висота 8 (/ітах) і максимальна висота Н (Ті) кожної нечіт-
кої множини, що не відповідає вершині /ітах, належать Т-мо-
дулям Ті.
4. Кожен 5-модуль перевіряє:
а) Якщо висота Ті дорівнює висоті 8 : Ні = Нтах і ст( не
належить області визначення 7}, то посилаємо Нтах, , Н (Ті) і
понижуючий сигнал всім підключеним до Ті р, -модулям.
б) Якщо Н (Ті) — Н (8) — Нтах і сі належить області ви-
значення Ті, але сг( сг, то змінюємо форму 7} таким чином,
щоб сг4 визначало положення максимуму замість ст.
с) Якщо Н (Ті) ± Н (8) = Нтах і сг4 належить області ви-
значення Ті, то посилаємо значення висоти Н (8), Н (Ті) і під-
вищувальний сигнал, усім р -модулям, підключеним до Т,
приймаємо Н (8) як іпіп | ц? > = іпіп {цк (Ті)} і змінюємо
к=ї,К V 1 к
форму Ті таким чином, щоб тах Н (8) досягався саме в точці
сті, замість точки а.
д) Якщо Н (Ті) Н (8) і Оі не належить області визначе-
ння Ті, то перериваємо поширення помилки в цьому модулі.
5. Кожний д-модуль перевіряє:
а) Якщо надходить понижуючий сигнал і (х3) —
— Н (Ті), то змінюємо форму так, щоб (гг7) Нтвх.
б) Якщо надходить підвищувальний сигнал і (зу) <
< Н (Т3), то змінюємо форму д^ гак, щоб дР (х^) = Н (8).
На рис. 3.29 приведена ілюстрація описаного алгоритму.
3.11- Нечіткі нейронні мережі. Властивості. Застосування
175
Отже, ми представили
алгоритм Васк ргора§аііоп
в нечіткому контролері,
шляхом застосування те-
хнології навчання НМ.
Алгоритм навчання визна-
чає модуль, що відповідає
за помилку в сигналі
на виході і поширює ін-
формацію в зворотному
напрямку через нейрон-
ну мережу, що дозволяє
модулю змінювати його
нечіткі множини (тобто
їхні ФП). Тут немає не-
обхідності вводити ваги
Рис. 3.29. Регулювання а шляхом
збільшення (зменшення) форми
до правил. Кожне правило однаково важливе. При зміні
нечітких множин семантика кожного правила, запропонова-
ного експертом, не змінюється, але помилки, що виникли в
результаті моделювання, постійно усуваються, і скоректовані
правила легко піддаються інтерпретації.
3.11.10. Застосування нечітких нейронних мереж
для апроксимації функцій
Нечіткі системи є універсальними апроксиматорами фун-
кцій. їх можна розглядати як тришарову нейронну НМ пря-
мої дії. Перший шар тут представляє вхідні змінні, середній
(схований) шар — нечіткі правила і третій — вихідні змін-
ні. (Іноді використовується 5-шарова архітектура, де нечіткі
множини представлені в нейронах 2 — 4 рівнів). Нечіткі ней-
ронні системи апроксимують п-вимірні невідомі функції, що
частково визначені навчальними даними.
Апроксимація функцій, заснована на локальних навчаль-
них стратегіях, є однією з областей застосування НМ і зокрема
8**
176
Розділ 3. Нейронні мережі
нечітких НМ. Однак нечіткі НМ мають переваги перед зви-
чайними НМ, тому що можуть використовувати попередні
знання у формі нечітких правил, у той час як останні навча-
ються з нуля.
Нечітка нейронна мережа архітектури АМГІ8
Розглянемо як приклад гібридну систему з механізмом
логічного висновку, запропонованого Сугено на базі правил
«якщо — то» [35, 36] (див. розділ 3.11.3), яка отримала на-
зву мережі АГ4ГІ8 {АЛарітие їїеіиюгк — Вазесі Ригху Іп/егепсе
Зузіет). Дана система може бути успішно використана для
настройки функції належності та настройки бази правил в
нечіткій експертній системі. Нижче представлено модель не-
чіткого висновку Сугено та структурну схему мережі АЬІГІЗ.
АГ4ГІ8 мережа використовує наступну базу правил:
якщо х — Аі та у — Ві, то Д = а\х + Ьіу + п;
якщо х = Д2 та у — В2, то /2 = а2т + Ь2у + т2,
де Аі та Ві є лінгвістичними змінними.
Шари даної нечіткої нейронної мережі виконують такі
функції (рис. 3.30).
Шар 1. Кожен нейрон даного шару є нейроном, що пе-
ретворює вхідний сигнал а; чи у за допомогою функції нале-
жності (фазифікатор). Найчастіше використовують дзвіно-
подібну функцію
МДі (ж) ‘
1
(3.58)
чи функцію Гауса
цАі (х) = ехр
(3.59)
3.11- Нечіткі нейронні мережі. Властивості. Застосування
177
---- б
Рис. 3.30. а — схема логічного висновку Сугено;
б — еквівалентна структура нейронної мережі АГ1ГІ8
Шар 2. Кожен нейрон в цьому шарі позначений як П
здійснює множення вхідних сигналів, моделюючи логічну
операцію АN^ і посилає на вихід сигнал
Юі = Мл (^) х Мв, (у), і = 2- (3.60)
По суті, кожен нейрон представляє активуючу силу правила.
Фактично будь-який оператор Т-норми, що узагальнює опе-
рацію АИВ, може бути використаний в даних нейронах.
Ш а р 3. Кожен нейрон в даному шарі обчислює нормова-
ну силу правила: 7,,.
йї=--------—, і =1,2.
и>і + ггг
83
178
Розділ 3. Нейронні мережі
Ш а р 4. На даному шарі в нейронах формуються значен-
ня вихідних змінних:
Оі = йЦ/і — йй (а,іХ + Ьіу + г,). (3.62)
Ш ар 5. В останньому шарі отримується вихідний сигнал
нейронної мережі та виконується дефазифікація результатів:
— оуегаїї оиіриї = . (3.63)
Нейронна мережа архітектури АИРІ8 навчається за допо-
могою методу градієнтного спуску, який в контексті нечітких
нейронних мереж буде детальніше розглянутий у наступному
розділі.
Алгоритм навчання нечіткої нейронної мережі
Відтворення бази правил та настройка параметрів
функції належності. В подальшому розглядається підхід
до навчання нейронних нечітких мереж, запропонований в
[35].
В існуючих системах з нечіткими нейронними мережами
одним з найважливіших питань є розробка оптимального ме-
тоду настройки нечіткої бази правил, виходячи з навчальної
вибірки, для отримання конструктивних та оптимальних мо-
делей нечітких систем з подальшим використанням в пра-
ктичних системах. Переважно нечіткі правила описуються
експертами чи операторами згідно їхніх знань та досвіду про
відповідні процеси. Проте, в разі розробки нечітких систем,
деколи досить важко чи навіть неможливо отримати чіткі
правила чи функції належності (тетЬегєіїір (ипсііопз) вна-
слідок неясності, неповноти чи складності систем.
В таких випадках найбільш доцільним вважається генеру-
вання та уточнення нечітких правил, використовуючи спеці-
альні навчальні методики. Наданий момент широко застосо-
3.11- Нечіткі нейронні мережі. Властивості. Застосування
179
Рис. 3.31. Схема моделі нечіткої нейронної мережі
вується алгоритм зворотного розповсюдження помилки для
нечітких мереж, що дозволяє генерувати оптимальні моделі
нечітких систем та бази правил. Даний алгоритм був запро-
понований незалежно Ічіаші (ІсЬіИааИі), Номура (ЬІотига) та
Вангом і Менделом (\Уап§ апсі Мепсіеі) [35].
Основними характерними рисами даного підходу є те, що
настройка параметрів нечітких правил здійснюється без мо-
дифікації таблиці правил та, крім того, алгоритм працює у
випадку поганої активації нейронів, що відрізняє його від по-
передніх методів.
Без втрати узагальнення розглянемо даний алгоритм на
моделі, що містить дві вхідні лінгвістичні (а?і,а;2) та одну ви-
хідну змінну у. Алгоритм реалізується для нечіткої нейронної
мережі архітектури АКРІ8, що базується на моделі нечіткого
висновку Цукамото (див. розділ 3.11.3). Схема мережі наве-
дена на рис. 3.31.
8***
180
Розділ 3- Нейронні мережі
Нехай ми маємо базу правил, що містить всі можливі ком-
бінації А1г та Д2і і' = 1,т, д — 1, к такі, що:
Правило 1: Дц> Аі — >Уі,
2: Дц> Д22 = >У2>
к: Дц> Аа-= >Уь
к+1: Аі2і Д21 = >Ум,
2к: Аг» Азк = ► Узкч
(г-1)Л+>: А» Д27 = ► У(і-і)к+і,
гхк: Дім Аа= Уг.к,
де Дн та Ац — нечіткі множини відповідно на Х\ та Хг, та
— дійсне ЧИСЛО З У
Даний набір правил можна навести у вигляді таблиці:
Д21 Д22 д2> ... А?к
Дп Уі Уз Уз ... Ук
Л12 Ум Ук+2 Ум ... Узк
... ... ... ... ...
А. ... ... У(,-ІМ ... ...
... ... ... ... ... ...
д1г У(г-і)м ... ... ... Угк
Виходячи з вищесказаного, якщо нам дано набір величин
(хі, х2), то згідно нечіткої баз правил величина у може бути
отримана на основі методів нечіткої логіки.
Позначимо величину ступінь виконання умов
= Аі (яч) А2і (х2) - (3.64)
Згідно з центроїдним методом вихід системи у визначається
так , .
т к г к
И 52 ^(і-і)к+іУ(і-і)к+з 52 52 Ац (ті) Д2_, (т2) у^іук+}
і=1 3=1 і=1 3 = 1
52 52 іці-і)к+з 52 52 Ац (ад) а2] (х2)
і=1 3=1 1=17=1
(3.65)
3.11- Нечіткі нейронні мережі. Властивості. Застосування
181
У разі навчання системи за допомогою навчальної вибірки
(хі, %2, у*), помилка системи може бути описана як
г (у* - у)2
Виходячи з опису нечітких величин для Ац маємо аи —
центр функції належності та Ьь — ширину для даної фун-
кції, аналогічно для Л2> маємо агу та Ь2д. Згідно з методом
градієнтного спуску для мінімізації помилки виходу Е мо-
жна записати формули для розрахунку коефіцієнтів ац, я2^,
Ьгі та у(і_і)*;+у (г = ЇЕ> З = наступним чином:
дЕ
\ / дАц \ _
дАц ) \даи(і))
= аи (І) - а
— Я1І (0 +
к
а(у* - у) Е (у(і-і)*+7 - у) а2і
л=і
т к
(3.66)
Ьи(1 + 1)-Ьи(і)
/З (у* - У)
Е (У(і-1)к+7 ~ у) А2і
— Ьи («) +
г к
Е Е \і-і)к+і
І=Ц=1
(3.67)
182
Розділ 3. Нейронні мережі
= а2з (і) - а
‘‘!'(1+1) = ‘,2>(і)-°^Ло =
(дЕ\ Ґ ду \ /дН^ї)к+і\ / дА,
^ду) \дН^1}к+з) \ дА2з ) \да2з
О (У* “ У) Е (У(і-і)к+> - у) ЛН
= а2з (і) +
(3.68)
= Ь2з (0 - ІЗ
<>2, (< + ') = (0 - /ЗдДї =
оЬ2з (І)
( ду А (дІг(і-і)к+з>
дА2з )
(З (у* - у) 52 (У(і-і)к+з - у) А
= І>2_, (І) +
І=1_______________
т к
52 52 \г-1)к+]
і=13=1
г к
Е 52 і\і-і}к+і
(і-1)к+і
(3.69)
дЕ
У(і—1)к+з (і + 1) — у^і)к+і (2) 7 —
оУ(і-і)к+ї (Ч
9£\ ( ду \
ду) \ду(і-і)к+з(і))
и\,^(У* -У)^(і-і)к+з
- У(і-і)к+з (і) +-------------------
= У(і-1)к+і (І) ~ 7
(3.70)
Е 52 ^(і-і)і+л
і=1 і=1
де а, 0, 7 — величини швидкості'навчання, а і — означає
ітерацію в процесі навчання.
3.11. Нечіткі нейронні мережі. Властивості. Застосування
183
Застосування методу ШІ-Масахару
з використанням функції належності
у формі функції Гауса
Розглянемо застосування методу в разі функції належно-
сті у вигляді функції Гауса. Для нашого випадку застосуван-
ня функція належності Гауса для двох змінних хі та х2 може
бути записана як:
Дії (гг]) = ехр
(3-71)
(3.72)
(а?і Ці»)
2аіі
Ац (х2) = ехр І ~^2
\
Тоді величина узгодження нейронів (ступінь виконання
умов правил) може бути записана як:
(з?1 Яіі)
(х2 — а2і)2
Крім того, враховуючи (3.71) (3.72) маємо:
дАи _ (а?] -аіі)Дц (хД
даи (і)
дАи _ (а?і -аи)2Дн (зд)
їі(і—1)к+3 — ЄХр
2(7^
— ехр
. (3.73)
.2
(3-74)
даи (і)
дА2і _ (а?2 ~ аг>) А2] (т2)
5а27 (0 <^1з
дА2і _ (т2 -а2,)2Д2Да:2)
(3.75)
(3.76)
(3.77)
(І) 4,
Підставляючи (3.73) — (3.77) в (3.66) — (3.70), отрима-
ємо такі формули корекції величин (і = 1,г, ] = 1,/с) для
184
Розділ 3. Нейронні мережі
алгоритму навчання нечіткої нейронної мережі з функцією
Гауса:
Он (і + 1) = Лц (і) +
к
а (у ~~ У) (я-і — ан) 52 ^(і-і)к+з (у(і-і)к+ї ~ у) (д 78)
а1і 52 52 \і-1)к+з
»=17=1
<7]і (і Ч- 1) = СГіі (ї) +
Р (У у) (я-і а1») 52 ^(і—1)к+з (у(і—1)к+з у)
________________________Ї=1___________________________
г к
стіі 52 52 \і-і)к+з
І=1 7=1
Й27 (і + 1) — Я27 (0 +
г
° (у — у) (^2 °27') 52 ^(і-1)к+і (У(і-1)/с+7 ~ у)
і=1
а2з 52 52 ^(і-1)*:+7
і=17=1
<Т27 (* + !) = (<) +
(у у) (^-27 а27') 52 ^(і—1)к+і (у(ї—1)/с+7 ~ У)
_________________________г=1___________________________
г к
а2з 52 52 \і-і)к+з
і=17=1
У(і-1)к+7 (і + 1) = У(і-1)к+7 (1) +
7 (у* - у) Ь(і-і)к+з
т к
52 52 ^(і~і)к+з
і=1 7=1
(3.81)
(3.82)
3-11- Нечіткі нейронні мережі. Властивості. Застосування
185
Результати практичного застосування АМГІ8
Нейронну мережу АИЕІ8 було використано для прогнозу-
вання макроекономічних показників.
Вхідні дані:
Х1=ІСЦ(0) — індекс споживчих цін;
Х2—ЮЦ(0) — індекс оптових цін;
ХЗ=КУУЕ(-7) — кредити, що вкладені в економіку;
Х4=М0(-7) — грошовий агрегат Мо;
Х5=М2(-7) — грошовий агрегат Мі-
Вихідна змінна: у — ІСЦ(+1).
Навчання проводилось градієнтним методом з довжиною
кроку а — 0,1; (З = 0,1 та 7 = 0,1. Кількість ітерацій 1900.
В процесі експериментів варіювалась кількість правил —
12, 20, 40. Навчання, як і раніше, проводилось на ковзному
вікні, розмір вікна — 12 точок, а тринадцята точка — про-
гнозована. Кількість таких вікон — 10.
Результати експериментів наведені нижче.
В табл. 3.14 наведено результати прогнозування для 12
правил після навчання на першому вікні, в табл. 3.15 та на
рис. 3.32 — результати прогнозування на останньому, деся-
тому вікні. В табл. 3.16 результати прогнозування після на-
вчання для 20 правил, а на рис. 3.33 — відповідні графіки
реальних (ІРС РО) та прогнозованих значень (ІРС РО) ве-
личини ІРС.
Підсумкові дані по результатам прогнозування на всіх 10
вікнах для 12, 20 та 40 правил наведені в табл. 3.17, а та-
кож на рис. 3.34. 3.35 та 3.36. Графік середньоквадратичного
відхилення прогнозного значення (М8Е) індексу споживчих
цін для різної кількості використаних правил наведено на
рис. 3.37.
186
Розділ 3. Нейронні мережі
Таблиця 3.14.
Результати прогнозування для 12 правил після навчання на першому вікні
Роіпі ІРС НО ІРС РО ОЕЬТА ОЕЬТА*2
4,6 4.600000000 4.567278543 0.032721457 0.001070694
14,2 14.200000000 14.357384453 0 157384453 0.024769866
9,1 9-100000000 8.705500321 0.394499679 0.155629997
6,2 6.200000000 6.257630514 0.057630514 0.003321276
4,6 4600000000 4.673767284 0.073767284 0-005441612
9,4 9400000000 9575363191 0.175363191 0.030752249
7,4 7 400000000 7.707435637 0.307435637 0.094516671
3 3.000000000 2.834451722 0.165548278 0.027406232
2,4 2.400000000 2 270216084 0-129783916 0.016843865
0,7 0.700000000 0 971526590 0.271526590 0 073726689
0,1 0 100000000 0.838782353 0-738782353 0.545799366
0,1 0.100000000 0.876361720 0-776361720 0.602737520
2 5 700000000 5.363240690 0.336759310 0.113406833
ТОТАЬ 3.617564382 1.695422870
М8Е 0.375879288
Таблиця 3.15.
Результати прогнозування для 12 правил після навчання на десятому вікні
Роші ІРС ВО ІРС РО ОЕЬТА ОЕЬТА"2
0,7 0.700000000 0.934338721 0.234338721 0.054914636
0,1 0.100000000 0.788645481 0.688645481 0.474232598
0.1 0.100000000 0.794611158 0.694611158 0.482484661
5,7 5.700000000 5221854658 0-478145342 0.228622968
2 2.000000000 1.675199421 0 324800579 0 105495416
1,5 1.500000000 1 334093282 0.165906718 0.027525039
1,2 1.200000000 1.241237782 0.041237782 0.001700555
0,9 0 900000000 0.990382146 0.090382146 0.008168932
2,2 2.200000000 2.316603454 0.116603454 0.013596365
1,2 1.200000000 1.073362814 0.126637186 0.016036977
0,1 0.100000000 0.795806328 0 695806328 0.484146446
0,8 0800000000 0.966980696 0.166980696 0.027882553
0,1 0 800000000 0.911253250 0.111253250 0.012377286
ТОТАЬ 3.935348841 1.937184432
М8Е 0.401786058
3.11- Нечіткі нейронні мережі. Властивості. Застосування
187
Таблиця 3.16.
Результати прогнозування для 20 правил після навчання на першому вікні
Роіпі ІРСКО ІРС РО ОЕЬТА ОЕЬТА"2
4,6 4 600000000 4.318448238 0.281551762 0079271395
14,2 14.200000000 12.006129321 2.193870679 4.813068558
9,1 9 100000000 9.844594158 0.744594158 0.554420461
6,2 6.200000000 6.299323821 0.099323821 0.009865221
4,6 4 600000000 4.395669343 0.204330657 0.041751018
9,4 9.400000000 9.566300726 0.166300726 0.027655932
7,4 7.400000000 7.527174879 0 127174879 0.016173450
3 3.000000000 2.924084211 0.075915789 0.005763207
2,4 2 400000000 2597729668 0.197729668 0 039097021
0,7 0 700000000 2.261446624 1.561446624 2.438115560
0,1 0.100000000 2.221404773 2.121404773 4.500358211
0,1 0 100000000 2.424357880 2.324357880 5.402639554
2 5.700000000 4 397473051 1.302526949 1.696576452
ТОТАЬ 11.400528365 19.624756039
М8Е 1.278826156
Рис. 3.32. Результати прогнозування для 12 правил на десятому вікні
Рис. 3.33. Результати прогнозування для 20 правил на першому вікні
188
Розділ 3- Нейронні мережі
Таблиця 3.17.
Підсумкові дані по результатам прогнозування на всіх 10 вікнах
для 12, 20, та 40 правил
12 правил ІРС НО ІРС РО ОЕЬТА
5.7 5.363240690 0.336759310
2.0 1.606193073 0-393806927
1.5 1.394963575 0.105036425
1.2 0.962540606 0.237459394
0.9 0.805087709 0.094912291
2.2 1.989793547 0.210206453
1.2 2.088157944 0.888157944
0.1 0.802739862 0.702739862
0.8 1.229643436 0.429643436
0.8 0.911253250 0.111253250
МБЕЬТА 0.350997529
М8Е 0.54175
20 правил 5.7 4.397473051 1.302526949
2.0 2.518034556 0518034556
1.5 1.307538474 0.192461526
1.2 2.414532756 1.214532756
09 2.338645782 1.438645782
2.2 3.005689095 0.805689095
1.2 1.511555783 0.311555783
0.1 2.454072972 2.354072972
0.8 2.258117947 1.458117947
0.8 1.865751522 1.065751522
МОЕЬТА 1.066139
М8Е 1.425167
40 правил 5.7 5.369751156 0.330248844
20 2.673130677 0.673130677
1.5 2.454889444 0.954889444
1.2 2.383138172 1.183138172
0.9 2.262107445 1.362107445
2.2 2.549820865 0.349820865
1.2 2.436449713 1.236449713
0.1 2.439473989 2.339473989
0.8 2.221949834 1.421949834
0.8 2.159535975 1.359535975
МБЕІ.ТА 1.121074
М8Е 1.484835
3.11- Нечіткі нейронні мережі. Властивості. Застосування
189
Рис. 3.34. Результати прогнозування на 10 вікнах
для 12 правил
Рис. 3.35. Результати прогнозування на 10 вікнах
для 20 правил
Рис. 3.36. Результати прогнозування на 10 вікнах
для 40 правил
190
Розділ 3. Нейронні мережі
Рис. 3.37. Графік середньоквадратичного відхилення прогнозного
значення (М8Е) індексу споживчих цін для різної кількості правил
Це свідчить, що застосування чіткої нейронної мережі для
задач прогнозування економічних показників в порівнянні з
нечіткою є більш доцільним. Проте перевагою нечіткої ней-
ронної мережі АЬІГІЗ є те, що процес навчання для неї від-
бувається значно скоріше, ніж навчання класичним градієн-
тним методом.
Результати експериментів свідчать, що найменше значе-
ння СКВ (середньоквадратичного відхилення) досягається
при кількості правил 12 (М8Е — 0,54175). Зростання ве-
личини СКВ прогнозу з ростом кількості правил може бу-
ти пояснено недостатньою кількістю ітерацій навчання пра-
вил (1900). Для порівняння наведено відповідне значення для
нейромережі ВР (Васк Ргора^аііоп) класичним градієнтним
методом в цій задачі: М8Е = 0,2129.
Основним недоліком нейронної мережі АМГІ8 є те, що в
процесі навчання налаштовуються лише параметри функцій
належності нечітких правил. Проте параметри функцій ви-
сновку /к (ж) правил йі, Ьі та в ході навчання не змінюю-
ться. Це обмежує гнучкість алгоритму навчання, та потен-
ційну можливість нейронної мережі АКЕІ8. Даний недолік
буде усунено в алгоритмі навчання більш перспективної ней-
ромережі Т8К.
3.12. Нечітка нейронна мережа Т8К
191
3.12. Нечітка нейронна мережа Т8К
Узагальненням нейронної мережі АЬІГІЗ є ННМ (нечітка
нейронна мережа) Т8К (Така§і, 8и§епо і Кап§’а).
Узагальнену схему висновку в моделі Т8К при викори-
станні М правил і N змінних х^ можна представити в насту-
пному вигляді:
Ні : якщо а?і Є А^\ х2 Є Є А^, то
N
Уі =ріо +
і=і
* Нм : якщо Хі Є А^ ; а?2 Є А^\..., хп Є А^л/), то
N
УМ = РМО + У^^РМіХ],
з=і
де А^ — значення лінгвістичної змінної Хі для правила Нь з
ФП (функцією приналежності)
. (^) /х \ _____1_______
МД \Хі) — .(*:) >
((к) \ 4
(3.83)
і = Т^-,к = Ї^М.
У нечіткій мережі Т8К перетинання умов правила Нь ви-
значається ФП у формі добутку, тобто
При М правилах висновку композиція вихідних результа-
тів мережі визначається за наступною формулою (аналогічно
192
Розділ 3. Нейронні мережі
висновку Сугено):
У(^) =
м
52 у’кУк (ж)
к=1________
М
У ™к
к=1
(3.85)
N
де ук (а?) = Рко + 52 Ркз^з- Присутні в цьому виразі ваги іик
7=1
інтерпретуються як ступінь виконання умов правила: и>к —
— / (т), що задаються формулами (3.84).
Нечітка мережа Т8К, яка реалізує висновок згідно (3 85)
задається багатошаровою структурою мережі, представле-
ною на рис. 3.38. У такій мережі виділяють 5 шарів. ,
Рис. 3.38. Нечітка нейронна мережа Т8К
3.12. Нечітка нейронна мережа Т8К
193
1. Перший шар виконує роздільну фаззифікацію кожної
змінної х„ і = 1,2,..., IV, визначаючи для кожного к-го прави-
ла висновку значення функції приналежності Цд > (х.) відпо-
відно до функції фаззифікації, що застовується, наприклад
(3.83). Це параметричний шар з параметрами с^к\ Ь^к\
які підлягають адаптації в процесі навчання.
2. Другий шар виконує агрегування окремих змінних
Хі, визначаючи результуючу ступінь приналежності пік =
= Цд (х) для вектора х умовам к правила. Це непараметри-
чний шар.
3. Третій шар являє собою генератор функцій Т8К, у яко-
N
му розраховуються значення ук (х) = Рко + 22 Рк^. В цьо-
5=1
му шарі відбувається також множення функцій ук (х) на іХк,
сформовані на попередньому шарі. Це параметричний шар,
у якому адаптації підлягають лінійні параметри (ваги) рко-
Ркі для і = 1, IV, к = 1, М, які визначають функції наслідків
правил.
4. Четвертий шар складають 2 нейрона-суматори, один
із яких розраховує зважену суму сигналів ук (х), а другий
м
визначає суму ваг 22 и'к-
к=1
5. Останній, п’ятий шар, складається з єдиного вихідного
нейрона. У ньому ваги піддаються нормалізації й обчислює-
ться вихідний сигнал у (х) відповідно до виразу
м <к\
, £ (X)
------• (3.86)
22 ™к
к=1
Це також непараметричний шар.
9‘
194
Розділ 3. Нейронні мережі
З приведеного опису випливає, що нечітка мережа Т8К
містить тільки два параметричних шари (перший і тре-
тій), параметри яких уточнюються в процесі навчання.
Параметри першого шару 6^) будемо називати не-
лінійними, а параметри третього шару {ріу} — лінійними ва-
гами.
Загальний вираз для функціональної залежності (3.86)
для мережі Т8К задається так:
1
М N
Е П дї’ М
/с=13=1
(3.87)
У (ж) =
Якщо прийняти, що в конкретний момент часу парамет-
ри умов фіксовані, то функція у (гг) є лінійною відносно змін-
ної Хд.
При наявності N вхідних змінних кожне правило Нь фор-
мулює (/V + 1) змінну лінійної залежності уь (я). При М
правилах висновку маємо М (№ + 1) лінійних параметрів ме-
режі.
У свою чергу кожна ФП використовує 3 параметри
(с, сг, Ь), які підлягають адаптації. При М правилах виснов-
ку одержуємо ЗМN нелінійних параметрів. У сумі це дає
М (^^ + 1) лінійних і нелінійних параметрів, значення яких
повинні визначатися в процесі навчання. Це дуже велика ве-
личина.
З метою скорочення числа параметрів, що підлягають
адаптації, оперують з меншим числом незалежних ФП.
Зокрема, можна прийняти, що частина параметрів ФП однієї
змінної Цд (тд ) фіксується, наприклад, сг^ і Ь^.
3.12. Нечітка нейронна мережа Т8К
195
Структура мережі Ванга-Менделя
Якщо як вихідні функції ук (х) в правилах висновку ви-
брати Ук, ТО ми одержимо структуру НИМ, що називається
нейронною мережею Ванга-Менделя (див. рис. 3.39). Це чо-
тиришарова структура, у якій перший шар виконує фазифі-
кацію вхідних змінних, другий — агрегування (перетин) умов
правила, третій (лінійний) — композицію М правил висновку
(перший нейрон) і генерацію нормалізуючого сигналу (дру-
гий нейрон), тоді як один нейрон останнього шару формує
вихідний у (х) сигнал
м
М Я <іл
ПЛ (^)
і \ Л=1
У (*) =
Е П № (*,-)
к=іі=і
(3.88)
Рис. 3.39. Нейронна мережа Ванга-Менделя
9*
196
Розділ 3. Нейронні мережі
Відзначимо велику подібність структури обох мереж.
Частини, що визначають умови правил — перший і другий
шари — у них ідентичні (тобто вони відповідають компонен-
там правил «якщо...»), розходження виявляється в представ-
ленні наслідків правил («то...»). У мережі Т8К вихідна фун-
кція представляється поліномом першого порядку, а в мере-
жі Ванга-Менделя константою = Ск, де величину Ск можна
інтерпретувати як центр ФП наслідку.
Таким чином, нейронна мережа Ванга-Менделя є частко-
вим випадком нейронної мережі Т8К.
Завдання обох мереж полягає в знаходженні такого ві-
дображення пар даних (т, </), при якому очікуване значення
ф що відповідає вхідному вектору х, формувалося б вихід-
ною функцією мережі у (х) .
Навчання нечітких нейромереж, так само як і класичних
чітких мереж, може проводитися як відповідно до алгоритму
навчання з учителем, при якому використовується цільова
функція Е — | £2 (У ~* тіп, так * за алгори-
і=і ' '
тмом самоорганізації без учителя.
Гібридний алгоритм навчання
нечітких мереж
Розглянемо гібридний алгоритм навчання ННМ, який за-
стосовується як для мереж Т8К, так і для мереж Ванга-
Менделя (у яких усі рк3 = 0, а рко = ^)
У гібридному алгоритмі параметри, які підлягають ада-
птації, розділяються на 2 групи. Перша з них складається
з лінійних параметрів рк3 третього шару, а друга група — з
параметрів нелінійної ФП першого шару. Уточнення параме-
трів проводиться в два етапи.
197
3.12. Нечітка нейронна мережа Т8К
На першому етапі при фіксації окремих значень параме-
трів функції приналежності (в першому циклі — це значен-
ня, які отримані шляхом ініціалізації), розв’язуючи систему
лінійних рівнянь, розраховуються лінійні параметри по-
лінома Т8К. При відомих значеннях ФП залежність для ви-
ходу можна представити у вигляді лінійної форми відносно
параметрів
м / N \
Ук (ж) = 52 Шк ( Р™ + 12 РкЗХ3 •) , (3-89)
к=1 \ Л=1 /
де
П № (^)
<= Л —к = ^М-
£ п Лг) (^)
г=17=1
(3.90)
При розмірності навчальної вибірки £ (аАа(')), (/ = і,
2,..., £) та заміні вихідного сигналу мережі очікуваним
значенням отримуємо систему із Ь лінійних рівнянь
вигляду:
’ ... юпх^ ... •••
Ш21 «'л37'1’ и’21Х^} ••• ^гл/^ї2’ ••• ™2МХІЇ
(3.91)
92
Рю
Рп
Рік
Рмь
Рмі
Рмн
</(І)
198
Розділ 3. Нейронні мережі
де іг'1у означає рівень активації (вагу) умови г-го правила при
пред’явленні 1-го вхідного вектора х1. Цей вираз можна запи-
сати у матричному вигляді:
Ар = <1.
Розмірність матриці А дорівнює Ь + 1) М. При цьому
кількість рядків Ь звичайно буває значно більшою за кіль-
кість стовпців (/V + 1) М. Рішення цієї системи рівнянь мо-
жна отримати як звичайними методами, так і за один крок,
використовуючи псевдоінверсію матриці А :
р = А+<1,
де А+ — псевдоінверсна матриця.
На другому етапі після фіксації значень лінійних пара-
метрів рі~у розраховуються фактичні вихідні сигнали у^\
І — 1,2,..., Ь, для чого використовується лінійна залежність
у(ь) = Ар. (3.92)
Після цього розраховується вектор помилки є — (у — (1)
та критерій ь
в=і£(Н^)-<«(0)2-
л 1=1
Сигнали помилок спрямовуються через мережу в зворо-
тному напрямку відповідно до методу Васк ргора^аііоп, аж
до першого шару, де можуть бути розраховані компонен-
ти вектора градієнта цільової функції відносно параметрів
,Ь^. Після обчислення вектора градієнта робиться
крок спуску за градієнтним методом. Відповідні формули на-
вчання (для самого простого методу щонайскорішого спуску)
приймають вигляд:
сУ° (п -!-1) = (п) - , (3.93)
3.12. Нечітка пейронна мережа Т8К
199
а<‘>(п + 1)=а<‘>(п)-ч<,^, (3.94)
Ь<‘>(" + 1) = ^’(п)-%^, (3.95)
де п — номер ітерації.
Після уточнення нелінійних параметрів знову запускає-
ться процес адаптації лінійних параметрів функції Т8К (пер-
ший етап) та нелінійних параметрів (другий етап). Цей цикл
повторюється доти, доки стабілізуються всі параметри про-
цесу.
Формули (3.93) — (3.95) потребують розрахунку градієн-
ту цільової функції відносно параметрів ФП. Остаточний ви-
гляд цих формул залежить від вигляду ФП. Наприклад, при
використанні узагальненої функції Гауса
р* =;—(3-06)
І + Стг)
відповідні формули градієнта цільової функції для однієї па-
ри даних (х, с?) приймають вигляд [27]
дЕ
= (у (я) - <9 $2 ( РгО + ^Рг^з ) •
г=1 \ з=1 / де}
дЕ
А \ Щ
= ІУ (*) - а) > , Рго + > Ртз^з —щ
г=і \ л=і / д&і
(3.97)
дЕ
дЬ^ ~ м / N
= (у (*) - <і) 521 Рго+52 Ртзхз
г=1 \ з=\
ди'г
дЬ^'
9**
200
Розділ 3. Нейронні мережі
Т-Г • 0и>' диі'г
Похідні
отримані на основі залежностей
(3.84), приймають наступний вигляд:
дій1, _ бгк’т (хз) ~ (хз)
дс(^ [т (яу-)]2
диз’т _ 5ткт (х^) — І (х?)
до^ [т (^)]2
ди’’г _ бгктп (х^) — І (х])
д^ = [™ (^)І2
(3.98)
для г = 1,2, де 5Гк — дельта Кронекера, І (х^) —
N М N
= П мд} (хзУ т и>) = Е П м? (ь)-
>=1 ь=1г=1
3.13. Нечіткі нейронні мережі з самоорганізацією
201
При практичній реалізації гібридного методу навчання
нечітких мереж домінуючим фактором їх адаптації вва-
жається перший етап, на якому ваги підбираються з
використанням псевдоінверсії за 1 крок. Для урівноважен-
ня його впливу другий етап багаторазово повторюється у ко-
жному циклі.
Представлений гібридний алгоритм — один з найбільш
ефективних способів навчання нечітких мереж. Його харак-
терна риса полягає в розділенні процесу навчання на 2 відок-
ремлених у часі етапи. Якщо врахувати, що розрахункова
складність кожного алгоритму оптимізації нелінійно зале-
жить від кількості параметрів, які піддягають оптимізації,
то зменшення розмірності задач оптимізації значно скорочує
об’єм розрахункових операцій та підвищує швидкість збіжно-
сті алгоритму. Завдяки цьому гібридний алгоритм виявляє-
ться значно ефективнішим в порівнянні із звичайним граді-
єнтним методом.
3.13. Нечіткі нейронні мережі з самоорганізацією
Розглянемо нейронну мережу з самоорганізацією, де на-
вчання відбувається без учителя.
Алгоритм самоорганізації відносить вектор х до відповід-
ного кластеру даних, які пред’являються центром сг, вико-
ристовуючи змагальне навчання, як і в мережах з самоорга-
нізацією Кохонена.
Базова форма алгоритму самоорганізації дозволяє точно
знайти положення центрів Сі відповідних груп даних (класте-
рів), на які розбивається вихідний багатовимірний простір.
Ці центри надалі можуть використовуватися у гібридному
алгоритмі навчання ННС в якості початкових значень, що
значно прискорює процес навчання та гарантує збіжність до
глобального мінімуму.
93
202
Розділ 3. Нейронні мережі
1. Алгоритм нечіткої самоорганізації ^-середніх.
Припустимо, що в мережі існує к нечітких нейронів з цен-
трами в точках Сі (г = 1,2,..., к). Початкові значення цен-
трів можуть бути вибрані випадково з області допустимих
значень відповідних компонент векторів х.), і = 1,7У, із на-
вчальної вибірки. Нехай функція фаззифікації задана у фор-
мі узагальненої функції Гауса, що виражається формулою:
У-а, (х)= С2ьГ‘ (3.99)
1+(М
Вектор хд що подається на вхід, належатиме к різним
кластерам, що представляються своїми центрами Сі зі сте-
пенем Цц, де 0 1 і Иу — цаі (хд) . Сумарна степінь
приналежності до всіх груп повинна дорівнювати 1, тому
к
= М]. (3.100)
і=і
Функцію помилки, яка відповідає такому представленню,
можна визначити як суму відхилень від центрів Сі з ураху-
ванням функцій приналежності зі степенем т. Отже,
к р
е=13Е^ііс*-х^і2’ (3101)
і=1 7=1
де т — це ваговий коефіцієнт, який приймає значення на
інтервалі (1,оо) (звичайно цілі). Мета навчання з самоорга-
нізацією полягає в такому підборі центрів с$, щоб для заданої
множини векторів хл, що навчають, забезпечити досягнення
мінімуму тіпЕ1 при виконанні умови (3.100).
Рішення цієї задачі можна отримати методом множників
Лагранжа:
3.13. Нечіткі нейронні мережі з самоорганізацією
203
Використовуючи метод множників Лагранжа, отримуємо
наступні умови оптимальності:
^ІЕ = 2 £ «5 Цс. - х,|| = 0 Сі 52 = Е
7=1 7=1 7=1
ЗВІДКИ
Сі = Ц—- (3.103)
7=1
к ____
Із умови 52 Цд= 1, ^’ = 1, IV знаходимо
де гіу — ||сі х7Ц.
Оскільки точні значення центрів Сі на початку процесу
невідомі, то алгоритм навчання повинен бути ітераційним.
Опис алгоритму ^-середніх
1. Виконати випадкову ініціалізацію коефіцієнтів иу, ви-
бираючи їх значення з інтервалу [0,1] так, щоб виконувалась
умова (3.100).
2. Отримати к центрів сг у відповідності до (3.103).
3. Розрахувати значення функції похибки у відповідно-
сті до (3.101). Якщо її значення виявиться меншим за вста-
новлений поріг є (Е є), то потрібно закінчити обчислення.
Знайдені значення сі є шуканими. Інакше — перейти на крок 4.
4. Розрахувати нові значення иг] за формулами (3.104) та
перейти на крок 2.
Таку процедуру нечіткої самоорганізації назвемо нечі-
тким алгоритмом ^-середніх (С-теапз).
9***
204
Розділ 3. Нейронні мережі
Багаторазове використання ітераційної процедури приво-
дить до досягнення мінімуму функції Е (але не обов’язково
глобального). Найкращим може вважатися таке розміщення
центрів, при якому вони будуть розміщуватися в областях,
які включають найбільшу кількість пред’явлених векторів х5-
(тобто в центрах мас). При такому підборі центрів вони мо-
жуть представляти вектори даних х7 з найменшою сумарною
помилкою. Тому початку ітераційного алгоритму ^-середніх
оптимального розміщення центрів повинна передувати про-
цедура їх ініціалізації. До найбільш відомих алгоритмів іні-
ціалізації відносяться алгоритми пікового групування та рі-
зницевого групування даних.
2. Алгоритм пікового групування.
Алгоритм пікового групування був запропонований Єге-
ром і Філевим [27].
При використанні N вхідних векторів будується сітка, яка
рівномірно покриває простір цих векторів. Вузли цієї сітки
розглядаються як потенційні центри &, для кожного з яких
розраховується пікова функція:
р
т (0) = 22ехр 1
л=1
ІІ^-х,І|2Ь
2<т2
(3.105)
де <т — це деяка константа, яка підбирається окремо для ко-
жної конкретної задачі.
Величина т (і?) розглядається як оцінка висоти пікової
функції. Вона пропорційна кількості векторів Хд, які потра-
пляють в окол потенційного центра д. Мале значення т («9)
свідчить про те, що центр & розміщений в області, в якій
зосереджена найбільша кількість векторів {хД .
Коефіцієнт <т має незначний вплив на кінцеві пропорції
між т (19) для різних значень •&.
3.13. Нечіткі нейронні мережі з самоорганізацією
205
Після розрахунку значень т («?) для всіх потенційних цен-
трів відбирається перший центр Сі, який має найбільше зна-
чення т (&). Для вибору наступних центрів необхідно ви-
ключити Сі та вузли, які розміщені в безпосередній близько-
сті ВІД Сі.
Це можна зробити шляхом перевизначення пікової функ-
ції за рахунок відділення від неї функції Гаусса з центром в т. Сі.
Позначивши цю нову функцію через тпєи) (#), отримаємо:
піпеи, (#) = тп (ї9) - т (сі) • ехр { - 247^" | 106)
ВІДМІТИМО, ЩО ця функція має нуль В ТОЧЦІ Сі-
Потім ця ж процедура повторюється із наступним цен-
тром С2 І Т.д.
Процес знаходження наступних центрів Сг, Сз,... реалі-
зується послідовно на модифікованих значеннях тпеиі ($),
які отримуються при виключенні найближчих сусідів центра,
який було знайдено на попередньому етапі. Він завершується
в момент локалізації всіх центрів, які використовуються в мо-
делі нечіткої мережі.
Метод пікового групування ефективний, якщо розмір-
ність вектора х не дуже велика. Інакше число потенційних
центрів зростає лавиноподібно.
3. Алгоритм різницевого групування.
Алгоритм різницевого групування — це модифікація по-
переднього алгоритму, в якому вектори х? розглядаються як
потенційні центри &. Пікова функція £> (хі) в цьому випадку
задається у вигляді:
Р(Хі) = Еехр(-І|Хі7^2ІІ-У (З-107)
І (^) . )
206
Розділ 3. Нейронні мережі
де значення коефіцієнта га визначає сферу сусідства. На зна-
чення О (хі) значним чином впливають тільки х7, які знахо-
дяться в межах цієї сфери.
При великій щільності точок навколо х, значення фун-
кції Р (хі) велике. Після розрахунку значень пікової функції
для кожної точки х,, відбирається вектор х, для якого міра
щільності Р (х) виявиться найбільшою. Саме ця точка стає
першим центром Сі-
Вибір наступного центру Сг можливий після виключення
попереднього центру та всіх точок, що лежать в його околі.
Так само, як і в попередньому випадку, пікова функція
перевизначається так
В™™ (х,) = Р (хі) - Р (сі) - ехр <
ІІХі-сЛ26]
(?)2 /
(3.108)
При новому визначенні функції Р коефіцієнти гь позна-
чають нові значення константи, яка задає сферу сусідства
чергового центра. Звичайно дотримуються умови, що гь га.
Після модифікації значення пікової функції шукається но-
ва точка х, для якої Рпеи) (х) —> шах. Вона стає новим цен-
тром.
Процес пошуку чергового центру відновлюється після ви-
ключення всіх компонент, які відповідають вже відібраним
точкам. Ініціалізація завершується в момент фіксації всіх
центрів, які передбачені початковими умовами.
У відповідності до описаного алгоритму відбувається са-
моорганізація множини векторів х, яка полягає у знаходжен-
ні оптимальних значень центрів, які представляють множину
даних з мінімальною похибкою.
Якщо ми маємо справу з множиною навчальних даних у
вигляді пар векторів (х,, сі;), так як це має місце при навчан-
ні з учителем, то для знаходження центрів, що відповідають
3.13. Нечіткі нейронні мережі з самоорганізацією
207
множині векторів сЦ, достатньо сформувати розширений ве-
ктор: [х,, <1і] —> X,.
Процес групування, який проводиться з використанням
розширених векторів хг, дозволяє визначити також і розши-
рені версії центрів Сі-
З урахуванням того, що розмірність кожного нового цен-
тра дорівнює сумі розмірностей векторів X і <1, то в описі цьо-
го центру можна виділити частину р, яка відповідає вектору
х (перші N компонент) та залишок д, що відповідає вектору
СІ. Таким чином можна отримати центри як вхідних змінних,
так і очікуваних вихідних значень с£ = [р*, <&], і = 1,2,..., К.
У випадку застосування правил з одним виходом вектори
сі і ц зводяться до скалярних величин д. і ? відповідно.
Таким чином, при використанні правил виводу Ванга-
Менделя процес самоорганізації дозволяє відновити функцію
/ (х), яка апроксимує множину даних (а;,, <4), і = 1,2,..., р.
Використовуючи введені вище позначення, формулу для
вихідної величини можна записати у вигляді
К п
Ел* П 1*Ак (Хі)
= --------------- (3109>
£ П ^Ак (х,)
Іс=1 і=1
Ця формула приймає такий вигляд:
/(х) =
К
Е 9. ехр
і=і
(3.110)
Згідно з нею всі центри підбираються оптимальним чи-
ном. При цьому інші параметри (б^сті), менш критичні для
збіжності алгоритму, можуть підбиратися ефективно гібри-
дним методом при невеликій кількості ітерацій.
208
Розділ 3- Нейронні мережі
4. Алгоритм нечіткої самоорганізації Густафсона-
Кесселя.
В класичному алгоритмі ^-середніх (с-теапз) нейрон-
переможець вибирається на основі звичайної евклідової від-
стані між вектором х та центром с кластера, тобто:
(1 (х, с) = ||х — с|| = д/(х — с)т (х — с). (3.111)
Визначена таким чином відстань враховується у форму-
лі (3.101) при обчисленні критерій Е. При такому заданні
метрики відсталі між двома векторами множина точок, рів-
новіддалених від центрального нейрона-переможця приймає
форму сфери з однаковим масштабом по всім осям. Якщо вхі-
дні дані утворюють групи, форма яких відрізняється від сфе-
ричної або якщо шкали значень окремих координат вектора
значно відрізняються, то в цьому випадку метрика вигляду
(3.111) стає вже неадекватною. В такому випадку якість кла-
стеризації можна значно підвищити за рахунок використання
удосконаленої версії алгоритму самоорганізації, що називає-
ться алгоритмом Густафсона-Кесселя [27].
Основні зміни відносно до базового алгоритму ^-середніх
полягають у введені в формулу розрахунку метрики д. (х, с)
масштабуючої матриці А. При такому масштабуванні відс-
тань між векторами х і центром с визначається за формулою
(1 (х, с) = ||х — с|[ = ^/(х — с)т А (х - с). (3.112)
Введена матриця масштабує одиничний вектор є? —
= [0,..., 0,1,0,..., 0] наступним чином
||єі|| = у/е[Аеі = Таїї, (3.113)
де аи — діагональний елемент матриці А.
В якості масштабуючої звичайно приймається симетри-
чно додатньо визначена матриця, тобто матриця, у якої всі
З 13. Нечіткі нейронні меі>ежі з самоорганізацією
209
власні числа — дійсні та додатні. В новому масштабованому
просторі довжини власних векторів матриці А (ж^і,..., і/*.)
перетворюються наступним чином
у/ц^П2 = = у/Хі, (3.114)
де Хі — власне значення.
Аналогічно до базового алгоритму ^-середніх мета навча-
ння мережі з використанням алгоритму Густафсона-Кесселя
полягає в такому розміщенні центрів, при якому мінімізує-
ться наступний критерій
е=52 22’ <3-115)
і З
де відстань між та центром с, визначається з урахуванням
масштабування так
й(х7,Сі) = у/(Хз~Сі)т А(хі-сі). (3.116)
Рішення задачі оптимального розміщення центрів за алго-
ритмом Густафсона-Кесселя відбувається аналогічно до ал-
горитму ^-середніх, але враховуючи матрицю масштабування.
Опис алгоритму Густафсона-Кесселя
1. Провести початкове розміщення центрів у просторі да-
них. Створити елементарну форму масштабуючої матриці А.
2. Сформувати матрицю коефіцієнтів приналежності всіх
векторів Ху до центрів Сі, і = 1, К шляхом розрахунку зна-
чень игі за формулою
(3-117)
V /<Р(х4,с.) у-1
А,
де сР (х^,Сі) визначається згідно з (3.116).
Якщо для деякого ] = 1, (ііу = 0, то приймаємо иц = 1, та
Пу = 0 для всіх ] 7^ І.
210
Розділ 3- Нейронні мережі
3. Розрахувати нове розміщення центрів у відповідності
до формули к
Е Ч"х5
с, = Ц------. (3.118)
Е^
5=і
4. Згенерувати для кожного центра матрицю коваріацій
5, : дг
= 52 и% “ Сі) ~ С£)Т- (3.119)
5=1
5. Розрахувати нову масштабуючу матрицю для кожного
і-го центра (і = 1, К) за формулою
А, = >/<1еІ (8і) • 8"1, (3 120)
де п означає розмірність вхідного вектора х.
6. Якщо останні зміни положень центрів та матриці ко-
варіації 8і достатньо малі по відношенню до попередніх
значень та не перевищують заданої на початку порого-
вої величини є, то завершити ітераційний процес, інакше —
перейти на крок 2.
Описаний вище алгоритм навчання паралельно генерує
усі центри нечітких нейронів, які підлягають самоорганіза-
ції, та зв’язані з ними масштабуючі матриці. Після закінче-
ння процесу навчання як положення центрів, так і значення
елементів масштабуючих матриць фіксуються та можуть ви-
користовуватися при експлуатації мережі.
5. Адаптивний алгоритм самоорганізації нечіткої
мережі.
Алгоритм самоорганізації ННМ (нечіткої нейронної ме-
режі), який був розглянутий в попередньому розділі, потре-
бує апріорного знання центрів, які будуть представляти дані.
Тому більш універсальним являється адаптивний алгоритм,
який автоматично вибирає число центрів К в режимі оп-ііпе.
3.13. Нечіткі нейронні мережі з самоорганізацією
211
Адаптивний алгоритм був розроблений тільки для гау-
сівської функції (6 = 1) з використанням узагальненої ННМ
Ванга-Менделя. В результаті його реалізації визначається
число центрів та їх розміщення в частині, що відповідає умо-
вам (множина векторів та висновкам.
Даний алгоритм можна описати наступним чином [27]:
1. При старті з першої пари даних (хі,ф) створюється
перший кластер з центром в точці хі = Сі- Приймаємо
та потужність множини £і — 1. Нехай г означає гра-
ничну евклідову відстань між вектором х та центром, при
якому дані будуть трактуватися як ті, які належать до ство-
реного кластеру. Для збереження загальності розв’язку при-
ймаємо, що на момент початку навчання існує М кластерів
з центрами Сі, Сг,.. •, См та відповідні до них значення ю, та
Ц, і =
2. Після зчитування к-бі пари (х^ф,), що навчає, роз-
раховуються відстані між вектором х*, та всіма існуючими
центрами Цхд; — с,|| для і = 1,2,..., М. Припустимо, що най-
ближчий до точки Хк центр — це Сік- В такому випадку, в
залежності від значення Цх*, — с,^ ||, може виникнути один з
двох випадків:
а) ЯКЩО Цх*, — Сік II > г, то створюється новий кластер
См+і = хь при чому чпм+і (^) — Ьм+і (к) — 1. Параметри
створених до цього кластерів не змінюються, тобто и’і (к) —
= и<і (к — 1), для І = 1,2,..., М. Кількість кластерів збіль-
шується на 1: М —+ М + 1;
б) якщо |]хд — бк II г, то дані включаються в г-ий кла-
стер, параметри якого необхідно уточнити у відповідності до
формул;
иіік (А) = Шік (к - 1) + 4;
Цк(к) = Цк(к-1) + 1-
212
Розділ 3. Нейронні мережі
сгк (А:) =
Сік (*-!)• Цк (А; - 1) + Хк
Цк (А:)
тоді як інші кластери не змінюються, тобто при і гк .
Ьі (А:) = Ьі (к — 1); іі)і (к) = и>і (к — 1); с, (к) = с, (А: — 1).
В іншій версії алгоритму фіксується положення центрів
сгк після ініціалізації, та їх координати вже не змінюються.
3. Після уточнення параметрів нечіткої системи функція,
що апроксимує вхідні дані системи, визначається як:
л £вд(*)ехр{-Ь^а£}
/ Р) = V---------;-------тг
££,(А,)ехр{-1ї^И-}
і=1 1
При повторі вищеописаних етапів алгоритму до к — р з
уточненням кожного разу значення М простір розділяється
на М кластерів.
Цей алгоритм кластеризації нагадує за своєю ідеєю іє-
рархічний агломеративний алгоритм кластер-аналізу (роз-
глядався у главі 2). Він називається алгоритмом самоорга-
нізації тому, що розділення простору даних на кластери про-
ходить самостійно, без участі людини При малому значенні
г кількість кластерів зростає, в результаті чого апроксима-
ція даних стає більш точною, однак це досягається за раху-
нок більш складної функції та збільшення об’єму необхідних
обчислень при одночасному погіршенні узагальнюючих вла-
стивостей мережі.
Якщо значення г дуже, велике, то навпаки, обчислю-
вальна складність зменшується, однак збільшується похиб-
ка апроксимації. При підборі оптимальної величини порога
г потрібно дотримуватися компромісі' між точністю відобра-
ження за обчислювальними затратами. Звичайно оптималь-
не значення г підбирається методом спроб та помилок — з
використанням обчислювальних експериментів.
3.14. Застосування нечітких нейронних мереж
213
3.14. Застосування нечітких нейронних мереж
для апроксимації функцій
Нечіткі системи є універсальними апроксиматорами фун-
кцій. Нечіткі нейронні системи можна розглядати як три-
шарову нейронну мережу (НМ) прямої дії. Перший шар тут
представляє вхідні змінні, середній (прихований) шар — не-
чіткі правила і третій — вихідні змінні. (Іноді використовує-
ться 5-шарова архітектура, де нечіткі множини представлені
в нейронах 2 — 4 рівнів).
Нечіткі нейронні системи апроксимують п-вимірні невідо-
мі функції, що частково визначені навчальними даними.
Апроксимація функцій, заснована на локальних навчаль-
них стратегіях, є однією з областей застосування НМ і, зокре-
ма, нечітких НМ. Однак нечіткі НМ мають переваги перед
звичайними НМ, тому що можуть використовувати попере-
дні знання у формі нечітких правил, у той час як останні
навчаються з нуля.
Нижче буде розглянута модель, яка називається
ХЕЕРЕОХ (Иеиго-Еиггу Іипсііоп арргохітаіог), заснова-
на на нечіткому перцептроні.
Нечіткий перцептрон можна розглядати як тришарову
нейронну мережу зі спеціальними функціями активації і по-
ширення та нечіткими множинами ваг. З іншого боку, перце-
птрон можна розглядати як нечітку систему, представлену у
вигляді архітектури НМ.
Система ИЕГРЕОХ — це спеціальний тришаровий нечі-
ткий перцептрон з наступною специфікацією:
1. Вхідні нейрони, позначені як хі,..., хп, нейрони схова-
ного шару як 7?ь..., Нк- нейрони вихідного шару — уі,...,
- • •іУт•
2. Кожне з’єднання між нейронами х, та її, позначається
лінгвістичним термом Ад .
214
Розділ 3. Нейронні мережі
3. Кожне лінгвістичне з’єднання між нейронами В? та у3
позначається лінгвістичним термом В3кг.
4. З’єднання, що виходять з одного нейрона мають одна-
кову позначку і одну і ту ж саму вагу протягом усього часу.
Такій же умові задовольняють з’єднання, що входять у вихі-
дний нейрон у3.
5. Нехай Ьх ц — маркіроване з’єднання між вхідним ней-
роном х і нейроном В (нейроном правил — гиіе пеигоп). Тоді
виконується наступний наслідок:
для всіх нейронів В, В',
таких, що (\/х Ьх К = Ьх<п') => В — В'.
Це визначення дає можливість інтерпретувати КЕРРНОХ
як просту нечітку систему.
Кожен прихований нейрон реалізує нечітке правило
вигляду: «якщо — то». Якби цей наслідок не виконувався, то
існувала б можливість
для нечітких правил,
що представляють одна-
кові лінгвістичні терми,
розвиватися по-різному
в процесі навчання.
Якби цей наслідок
був відсутнім, то ко-
жне правило могло б
мати індивідуальну ФП
(функцію приналежно-
сті), що призводить до
невірної інтерпретації
бази правил і є вкрай
небажаним.
Рис. 3.40. Структура системи КЕГРНОХ
На рис. 3.40 представлена архітектура ИЕЕРНОХ.
3.14. Застосування нечітких нейронних мереж
215
Алгоритм навчання системи NЕЕРКОX
Для задачі апроксимації функцій ми можемо використо-
вувати алгоритм навчання з учителем, тому що правиль-
ні значення на виході відомі для навчальної вибірки даних.
Якщо ми використовуємо систему, що складається з нечітких
правил для апроксимації функцій, то зможемо використову-
вати попередні знання, а це означає, що ми вже знаємо зручні
правила для визначених областей і, отже, можемо включити
їх у нейронну мережу. Інші правила повинні бути знайдені за
допомогою процедури навчання.
Якщо ж у нас немає апріорних знань, то починаємо із
системи МЕРРНОХ без прихованого шару і навчаємо усі без
винятку правила.
Для навчання будемо використовувати ФП, яка описує-
ться трьома параметрами: а, Ь, с.
ц : П -> [0,1],
М М = '
якщо
якщо
Є [а, 6];
Є [6,'с];
(3.121)
0, інакше.
Для навчання можна використовувати також і будь-яку
іншу форму ФП. Щоб почати процедуру навчання, ми по-
винні точно визначити початковий нечіткий розподіл кожної
вхідної змінної. Це не потрібно для вихідних величин, для
яких нечіткі множини будуть створені в процесі навчання.
Якщо нечіткі множини не задані, то тоді потрібно чітко ви-
значити початковий діапазон для функцій приналежності
(тобто |с —а|).
Розглянемо структуру алгоритму.
Маємо систему ПЕЕРНОХ з п вхідними нейронами
Ті,..., хп, к нейронами прихованого шару /?і,..., /4 та т
216
Розділ 3. Нейронні мережі
нейронами вихідного шару уі,..., ут. Задана також мста на-
вчання Ь = {(зі, іі), («2,, (зг, іг)} , що складається з г
зразків, кожний з яких складається з вхідного зразка 8 Є Е^
та зразка і Є Е^ (ціль навчання), та множини обмежень Ф.
Алгоритм навчання, ціль якого створити к нейронів правил
ХЕРРНОХ, складається з наступних кроків:
1. Вибираємо наступний зразок {«,0 із Ь.
2. Для кожного вхідного нейрона Хі Є Еі знаходимо ФП
Мд таку, що дФ = тах^ {м>1 («і)} •
3. Якщо не існує вузла правила /? з ш(яі,Я) - /$,
гп(хп,К) = то треба створити такий вузол і з’єднати
його з усіма вузлами виходу.
4. Для кожного з’єднання з нового вузла правил треба
знайти зручну нечітку вагу відповідно до наступної проце-
дури. для функції приналежності, зв’язаної з нейроном ви-
ходу Уз знаходимо ФП таку, що — шах < (Іг) >
та } (іі) 0,5. Якщо не існує такої нечіткої множини, то-
ді створюємо Упеи> таке, що (іі) = 1 і додаємо його до
нечітких множин, зв’язаних зі змінною виходу та множиною
Ш (Я, у) = Риєш.
5. Якщо залишилися ще необроблені зразки, тоді йдемо
на крок 1 наступної, (і + 1)-ої ітерації, інакше закінчуємо
створення правил.
6. Ми обчислили базу правил. Визначаємо значення ви-
ходу для кожної змінної виходу кожного правила, заданого
таким чином, щоб його правило мало ступінь виконання біль-
ше, ніж 0.
Алгоритм навчання з учителем для нечітких множин си-
стеми МЕРРВОХ відбувається циклічно шляхом навчання
множини Ь, продовжуючи наступні кроки, поки не виконає-
ться критерій зупинки алгоритму навчання.
3.14. Застос}'вання нечітких нейронних мереж
217
1. Вибираємо наступний зразок (я,/) із £, пропускаємо
його через систему ИЕГРНОХ і визначаємо вектор виходу.
2. Для кожного нейрона виходу у, визначаємо різницю
між бажаним і дійсним значенням виходу: 6Уі =іі~ оУі .
3. Для кожного нейрона правил В з виходом Од > 0 ви-
конуємо наступні процедури:
а) Для усіх у Є І7з, визначаємо зміну для параметрів а,
Ь і с нечіткої множини ге (Я, уі) , використовуючи швидкість
навчання <т > 0. Якщо гс (Д, уі) (£,) > 0, то
АЬі = а • 6Уі • (с - а) он- (1 -ге (Я, у,) (*«)); (3.122)
Да, = о (сі — аі) • Оц + ДЬ,; (3.123)
Дсі = — о • (є» — аі) од + Д6{. (3.124)
Якщо хи (В, уі) (іі) = 0, то
АЬі = о - ЬУі (с-а)- он • (1 - гс (/?, уі) (іі)); (3.125)
Да» = згдп (іі — Ьі) сг (с — а) Оц + АЬі; (3.126)
Дсі = —зідп (іі — Ьі) а (с — а) • Он + АЬі- (3.127)
Застосуємо вказані зміни до функції ге (В, уі), якщо це не
порушує задану множину обмежень Ф (якщо вага IV (В, уі)
застосовується і до інших зв’язків, то виходить, вона повинна
бути змінена більше одного разу).
б) Визначаємо помилку правила
Еп = он (1 - од) - £ (2 • (В, уі) (іі) - 1) 1-5,1; (3.128)
уЄЦз
в) Для кожної ваги ге (х, В) з ги (х, В) (ох) > 0 визначаємо
зміни для його параметрів а, Ь і с, використовуючи швидкість
навчання а > 0
Д6 = о • Ед (с — а) • (1 — ш (х, В) (ох)) єі&п (ох — Ь); (3 129)
До = — сг Ец • (с — а) (1 — ги (х, В) (ох)) + Д6, (3.130)
Де — а • Ец • (с — а) • (1 — хи (х, В) (ох)) -І- Д6. (3.131)
10і
218
Розділ 3. Нейронні мережі
Застосовуємо зміни до ваг, якщо це не порушує задану
множину обмежень Ф (якщо вага иі (ж, /?) застосовується і
до інших зв’язків, то виходить, вона повинна бути змінена
більше 1 разу).
1. Процедура закінчується, якщо буде виконаний критерій
зупинки, інакше йдемо на крок 1 наступної, (г + 1)-ої ітерації.
Алгоритм навчання правил вибирає нечіткі правила, за-
сновані на визначеній раніше розбивці вхідного простору.
Ця розбивка задається початковими нечіткими множинами.
Якщо алгоритм створює дуже багато правил, можна обро-
бляти їх, визначаючи індивідуальні помилки, щоб надалі за-
стосовувати тільки кращі правила.
Кожне правило описує визначена кількість зразків неві-
домої функції.
Якщо правило видаляється, то це означає, що ми його
більше не беремо до уваги.
Для поліпшення трактування, кількість правил у проце-
сі навчання повинна скорочуватися. Результат досягається
шляхом зрушення ФП, що може призвести чи до збільшен-
ня, чи до зменшення області її визначення. Для того, щоб
цього не сталося, потрібно перед початком процедури навча-
ння задати кінцеву множину обмежень. Як критерій зупинки
можна взяти критерій, який застосовується в алгоритмі на-
вчання звичайних НМ: навчання триває доти, доки помилка
не припиняє зменшуватися протягом визначеного числа іте-
рацій.
Обмеження, що накладаються на нечіткі множини:
1. Нечітка множина не повинна перетинатися зі своїм сусі-
дом. як праворуч, так і ліворуч під час навчання. Перевірити
це можна порівнянням: чи залишилися всі параметри три-
кутної ФП менше (більше) свого правого (лівого) сусіда.
Якщо ми цього не передбачимо, то нечіткі множини можуть
3.14. Застосування нечітких нейронних мереж
219
перетинатися, що призведе до плутанини в інтерпретації, хо-
ча при відсутності цього обмеження можна домогтися деяких
поліпшень.
2. Асиметричне навчання. У випадку, в якому навчання
проходить асиметрично, під час навчання змінюється тільки
та частина функцій приналежності (ліва чи права), у якій
розташовані значення вхідних перемінних.
3. ФП перетинаються в точці 0,5. Якщо ми приймемо це
допущення, то дві сусідні ФП будуть перетинатися в точці 0,5
і сума функцій приналежності для виходу буде дорівнювати 1.
Якщо ми цього не приймаємо, то сума не буде дорівнювати 1.
4. Фіксовані ваги наслідків. Застосування цього правила
означає, що ваги наслідків фіксуються і рівні 1.0. Відсутність
обмеження означає, що ми повинні навчити ваги наслідків.
5. Ваги наслідків в інтервалі [0,1]. Це означає, що ваги
під час навчання завжди знаходяться в цьому інтервалі В
іншому випадку, ваги можуть приймати будь-яке значення.
Приклад: прогноз тимчасових рядів
Як приклад, що показує можливості системи ПЕРРВ.ОХ,
ми розглянемо хаотичні тимчасові ряди, задані диференці-
альним рівнянням Маккі-Гласса (Маскеу-СІазз)
дх 0.2 • х (і — т)
ді 1 + ж10 (і — т)
— 0.1 • х (і).
Ми будемо використовувати значення х (/ — 18), х (і—
— 12), х (і — 6) і х (і), щоб спрогнозувати значення х (і + 6).
Навчання даних проводилось з використанням процедури
Рунге-Кутта з кроком 0.1. Як початковий стан тимчасово-
го ряду було взято х (0) = 1.2 і т = 17. Було створено 1000
значень між і — 118 і 1117, де перші 500 використовували-
ся вже в навченому вигляді, а інші 500 будуть настроєні в
процесі навчання
10*
220
Розділ 3. Нейронні мережі
Рис. 3.41. Лпржсимація тимчасових рядів Маккі-Гласса із системиНЕРі’ПОХ
Система КЕЕРНОХ, яка повинна була апроксимувати ча-
совий ряд, мала 4 вхідних і 1 вихідну змінну. Кожна змінна
була початково розділена на 7 однакових трикутних нечітких
множин, де сусідні функції приналежності перетиналися на
рівні 0.5. Ми використовували процес дефаззифікації МОМ
(теап-о£-тахітит), тому що система КЕЕРКОХ представ-
ляє звичайну систему Мамдані.
Ця система мала 105 регульованих параметрів. Також вво-
дилась швидкість навчання а, початкове значення якої 0.01,
що потім збільшувалося на 1.1, якщо помилка зменшувалася
протягом 4 послідовних кроків. Якщо помилка або не зміню-
валася, або зростала, то швидкість навчання сг домножува-
лась на 0.9. Навчання припинялося, якщо помилка правила
не зменшувалася протягом 100 ітерацій. Система ХЕЕРКОХ
з найменшою помилкою зберігалася під час процесу навчан-
ня і відновлювалася після навчання.
Рис. 3.41 представляє апроксимацію даної системи після
216 ітерацій. Значення 1 — 500 являють собою відтреновані
дані до процесу навчання (дані, отримані раніше), а значен-
ня 500 — 1000 являють собою множини, отримані в результаті
3.15. Нечіткий перцептрон як загальна модель
221
навчання. Процедура процесу навчання створила 129 правил
(у даній конфігурації максимально можлива кількість пра-
вил 74). Значення помилки в раніше отриманих даних 0.0315
і відповідно 0.0332 у даних, отриманих під час навчання. Час
навчання при використанні пакета 84 N 4Нга8рагс склав 75
секунд.
3.15. Нечіткий перцептрон як загальна модель
для нечітких нейронних методів
Розглянемо загальну модель багатошарової нечіткої ней-
ронної мережі (нечіткий перцептрон). Мета даної моделі по-
лягає в наступному: ми не зацікавлені в тому, щоб роби-
ти процес фаззифікацїї багатошарового перцептрона цілком,
а хочемо дати можливість мережі використовувати рані-
ше отримані знання й інтерпретувати результат навчання у
формі лінгвістичних правил. Шляхом введення додатково-
го обмеження у визначення нечіткого перцептрона, він мо-
же сприйматися як звичайний нечіткий контролер. Таким
чином, можна створити нейронний нечіткий контролер типу
ИЕГСОН (ПЕшаІ Еиггу СОМгої) [38].
Навчальний алгоритм для нечіткого перцептрона не є по-
слідовним, як це було при навчанні нейронних мереж, тому
що тут як функції активації найчастіше використовуються
не диференційовані функції і-норми і 1-конорми.
Тому метод градієнтного спуску тут не застосовано.
Розглянемо 3-шаровий нечіткий перцептрон з п вхідними і
т вихідними нейронами. Нехай Ь - мета нашого навчання, що
складається із зразків р = , де Є Нп, № Є Нт
Нехай и Є 43 і № описують бажане вхідне значення нейрона
и, заданого вхідним вектором №, і нехай о£р) описує дійсне
вихідне значення нейрона ц. Нехай змінна гапдеи визначає
102
222
Розділ 3. Нейронні мережі
різницю між максимальним і мінімальним значенням на ви-
ході нейрона и. Нечітка помилка для нейрона и і даного
р визначається так
/ (/р) _ о(р) \ 2
Е^ = 1-ехр -р----------М -/З
І І гапдеи і
де 0 Є П — масштабний коефіцієнт.
Масштаб 0 використовується для регулювання чутливості
нечіткої помилки, він робить помилку більш-менш відмінною
від бажаного і дійсного вихідного значення.
Розглядаючи 3-шаровий нечіткий перцептрон і мету нав-
чання Ь, алгоритм зворотного поширення помилки визнача-
ється в такий спосіб:
1. Вибираємо будь-яке р Є Ь та вводимо вхідний вектор
г(р);
2. Обчислюємо
№ =
8§п - о[р)) для и Є Е3]
* для и Е Е?.
3. Визначаємо
ДрИ/ (и,у) = / 4Р), пе#>) ,
и є Еі, V Е Е;, і, у Є М, д — і + 1.
(3.132)
Повторюємо ці кроки для всіх р Є Ь, поки загальна по-
милка Е = 52 52 не буде досить малою.
рЄЬиЄІ/з
Зміни у нечіткій вазі IV (и, г>) визначаються за формулою
(3.132) і залежать від сигналу 6 нейрона V, а також можуть
залежати від активації аи і від вхідної величини мережі пеі.
Звичайно нечіткі множини представляються параметричною
функцією приналежності таким чином, що зміни специфіку-
ються в термах цих параметрів.
3.15. Нечіткий перцептрон як загальна модель
223
Мінімаксний нечіткий перцептрон
Розглянемо 3-шаровий нечіткий перцептрон, використо-
вуючи оператори тіп і тах в якості <-норми і і-конорми.
Дефаззифікацію будемо проводити методом центра простору
(СОА). Ваги предикатів визначимо як Ду — И7 (і^, иД, щ Є
Є І/1, гід Є [/2) а ваги наслідків визначимо як = IV (гід, ик),
гід Є (/2, Чк Є ^з- Кожна нечітка вага визначається трику-
тною функцією Ду, яка задається трьома елементами /у, Су,
г^, такими, що інтервал [Цд,Гу] являється областю визначе-
ння нечіткої МНОЖИНИ І Під (від) = 1, Ніз Ціз) = (гу) = 0>
і для всіх функцій приналежності виконується нерівність
Ц3 -С Сід -С Гід
{х Цд) / (Су /у) , ДЛЯ Є [/у , Су] ,
Ми (ж) = (Гу - ж) / (Гу - Сід), для Є [су, Гу];
0, інакше.
Аналогічне визначення має місце і для функції принале-
жності іУдк. Ми будемо використовувати навчальну мету Ь із
зразками р = (г^р\ , такими, що Є [0,1]п, Є [0,1]™.
Якщо значення на виході вихідного нейрона повинно бути
збільшене для досягнення бажаного значення, то область ви-
значення нечіткої множини, що відноситься до наслідку пра-
вила, повинна бути розширена. Цього можна досягти збіль-
шуючи г чи зменшуючи І, додатковий параметр с повинен
бути змінений так, щоб він наближався до відповідного вхід-
ного значення. На рис. 3.42 зображено приклад, що ілюструє
вплив цієї стратегії для наслідку правила.
Якщо вихідне значення повинне бути збільшене, і ми по-
чинаємо із ситуації, зображеної пунктирними лініями, то ми
досягаємо нових нечітких множин. Обчислення, що викори-
стовуються для поширення зразка в цьому прикладі, такі ж,
як і для нечіткого контролера Мамдані.
10**
224
Розділ 3. Нейронні мережі
Рис. 3.42. Настроювання функції приналежності
Представимо процедури обчислення нечіткої помилки по-
ширення, використовуючи метод дефаззифікації СОА.
Покладемо Е = 0 і для кожного р Є Ь повторюємо насту-
пні кроки:
1. Вибираємо будь-яке р Є Ь, яке ще до цього не було
обране під час процесу навчання і поширюємо вхідний вектор
2. Обчислюємо 6и для всіх ІД СІ [/2 і обчислюємо загальну
помилку Е.
3. Визначаємо зміни параметрів для нечітких ваг. Для усіх
зі швидкостями навчання сгг,сгс,сгг Є Я отримаємо
^р^зк ’ ^ик ' (рук ^ук) т
^р<ук °с ' ^ик ' (Рук Іук) і
^р^зк — ' &ик ’ (Рзк Сук) ,
для усіх ФП Ріі зі швидкостями навчання г^, рс. тр Є Я обчи-
слюємо
^р^гЗ Рі ‘ $из * (рзк ^зк) і
&рСіЗ Рс ' ^из ' (<р)к р)к) >
^р^гЗ Рт ‘ &из ' (Рзк ^зк) •
Критерій зупинки алгоритму такий: закінчуємо навчання,
якщо помилка Е досить мала. Такий вигляд архітектури ви-
користовується для апроксимації функції за заданими зраз-
ками даних. У результаті отримуємо множину правил виду
«якщо — то».
3.15. Нечіткий перцептрон як загальна модель
225
Спеціальний нечіткий перцептрон
для задач керування
Модель НЕГСОИ (НЕигаІ Гиггу СОМігої) походить від
загальної моделі нечіткого перцептрона і також використо-
вується для задач керування. Навчальний алгоритм є мо-
дифікацією алгоритму нечіткої помилки, що поширюється в
зворотному напрямку, і навчання може відбуватися в інтер-
активному режимі.
Система ИЕЕСОН — спеціальний 3-шаровий нечіткий
перцептрон з наступними особливостями:
1. Вхідні нейрони позначені як Єі,...,єп, нейрони прихо-
ваного шару — нейрон вихідного шару — 7].
2. Кожне з’єднання між нейронами єг і Яг відмічається
лінгвістичним термом
3. Кожне з’єднання між нейронами та вихідним нейро-
ном т] відмічається лінгвістичним термом Віг,дг Є {1,.
4. З’єднання, що ви-
ходять з одного нейрона
Єі, мають однакову позна-
чку і ту ж саму вагу про-
тягом усього часу. Такій
же умові задовольняють
з’єднання, що входять у
вихідний нейрон г/.
5. Нехай ЬЕц — маркі-
роване з’єднання між вхі-
дним нейроном х і нейро-
ном В (який називається
також нейроном правила
— гпіе пеигоп). Тоді вико-
Рис. 3.43. Система КЕРССЖ
із двома вхідними змінними
нується наступний наслідок: для всіх нейронів її, В' таких,
що (УхЬЕІІ = => /? = В'.
10’
226
Розділ 3. Нейронні мережі
Це визначення дає можливість інтерпретувати ИЕЕСОН
як просту нечітку систему. Кожен схований нейрон представ-
ляє нечітке правило виду «якщо — то». Якби цей наслідок
не виконувався, то існувала б можливість нечітким прави-
лам, що представляють однакові лінгвістичні терми, «розви-
ватися» по-різному в процесі навчання. Якби цей наслідок
був відсутнім, то кожне правило могло б мати індивідуальну
функцію приналежності, що призвело б до невірної інтерпре-
тації бази правил, а це вкрай небажано. На рис. 3.43 пред-
ставлено архітектуру системи ПЕРСОМ. Розглянемо процес
навчання системи МЕГСОГЕ
Навчання нечітких множин
Нехай нечітка помилка Е = е - 8§п (^орі), де е описує ве-
личину помилки поточного стану і визначається з множини
лінгвістичних помилок правил, е Є [0,1]. Е містить у собі
інформацію про напрямок необхідних змін. Ця інформація
міститься в знаку невідомого оптимального вихідного стану.
Саме значення т]^ не відомо, але наявна інформація про те,
більше воно чи менше нуля. Тепер розглянемо зміну вели-
чини Е. Нехай Е — нечітка помилка в момент часу і, а Е'
нечітка помилка в момент часу 4 4-1. Тенденцію помилки т
визначаємо як:
' 1, якщо (|Е'| |Е|) А (Е' • Е 0);
т = < 0, якщо (|Е'| < |£7|) А (Е'
— 1, якщо (£' • Е < 0).
Приведемо алгоритм зміни функції приналежності преди-
ката і наслідку.
Нехай 8 — динамічна система з п змінними стану
Є] Є X? і однією вихідною (регульованою) змінною г] Є ¥
{¥ = {Утіп, Утах}) • Для КОЖНОЇ ВХІДНОЇ ЗМІННОЇ Єу ВИЗНаЧЄНІ
3.15. Нечіткий перцептрон як загальна модель
227
трикутні нечіткі МНОЖИНИ V-}, І Є {1, . Для кожної не-
чіткої множини задане обмеження Ф, яке визначає, можна
робити зміни чи ні. Центр функції приналежності позначи-
мо як с. Для налаштування функцій приналежності систе-
ми НЕЕСОИ з к нейронами правил застосовуються наступні
кроки (поки не спрацює умова зупинки):
1. Визначаємо Е і 8§п (^оре) для поточного стану;
2. Визначаємо так звані абсолютний внесок асг та відно-
сний внесок ге,- кожного вузла правил г у вихідне значення
ог (рг — значення на виході вузла правил Д.)
асг = і/іг (ог),
ог — асг
ГСг = ----------,
Утах Утіп
де и'^г (ог) визначається шляхом застосування процедури де-
фаззифікації СОА
Е У П1ІП (ог, Цг (у))
, . уЄУ, ^г(ог>0)
' г' : 7 7 і
Е тт (°г> (у))
уЄУ, і^г(ог>0)
3. Визначаємо значення на виході ог та застосовуємо його
до динамічної системи З для досягнення нового стану;
4. Визначаємо нечітку помилку Е' і тенденцію т помилки
відповідно до нового стану системи 5;
5. Визначаємо зсув для наслідку нечіткої множини и^т
= т • 8£П (т^) • |Е'| • ог • |ог - аСгІ • СТ,
де ст > 0 — швидкість навчання. Змінюємо Ф (і/,,.), якщо це
не суперечить множині всіх обмежень.
6. Визначаємо зсув предиката функції приналежності
(хі поточне вхідне значення Єї)
= т • 8£П (т^) - |£/| • ГСг ІЛі - с}? • сг;
10***
228
Розділ 3. Нейронні мережі
7. Змінюємо //у, якщо це не суперечить усій множині
обмежень Ф •
Ми описали навчальний алгоритм, що оптимізує нечіткі
множини шляхом їхнього зсуву.
Даний алгоритм намагається модифікувати якнайменше
параметрів, щоб підтримувати процедуру навчання в стійко-
му стані. Заміна модифікації довжини основи нечіткої мно-
жини на її зсув є позитивним моментом, тому що можуть
бути виявлені зайві НМ, що просто співпадуть потім з яки-
мись іншими НМ
Класифікація об’єктів за допомогою
моделі ХЕГСЬА88
Метою моделі ПЕЕСЕЛ88 (НЕиго Еиг/у СЬА88ійег) є
одержання нечітких правил з множини даних, які можна роз-
ділити на різні класи [37]. Нечіткі правила описують дані у
формі:
/ї : якщо є3 Є має функцію приналежності /4і,л2 —
//2, , хп — дп, то зразок належить класу сіг де — нечіткі
множини.
Задача ЕЕЕСЕЛ88 полягає в тому, щоб визначити при-
належність до класу вхідного зразка. Тут приймається,
що перетин двох різних множин є порожньою множиною.
Розглянемо більш детально архітектуру моделі ПЕРСЬ А88.
Система ПЕГСЬА88 має 3-шарову послідовну архітекту-
ру. Перший шар включає вхідні нейрони, у яких представля-
ються вхідні зразки. Активація нейрона звичайно не змінює
вхідне значення. Прихований шар включає нечіткі правила,
і третій шар складається з вихідних нейронів кожного кла-
су. Активація для нейронів правил і для нейронів вихідного
3.15. Нечіткий перцептрон як загальна модель
229
шару із зразком р обчислюється так
= тіп {XV (х, П) (а<р)) } ,
4Р)= ЕИ/(с,/ї)(а^)
ЛеП2
чи альтернативно
— шах
с Лє(/2
де И7 (ж, /?) — нечітка
вага з’єднання вхідного
нейрона х з нейроном
правила К, а XV {П, с) —
нечітка вага з’єднання
нейрона правила Н з
нейроном вихідного
шару с. Замість за-
стосування операцій
максимуму і мінімуму
можна використовува-
ти інші функції і-норми
і £-конорми відповідно.
База правил являє со-
бою апроксимацію неві-
рне. 3.44. Система КЕРСЬАЗЗ у вигляді
3-шарової нейронної мережі з двома
вхідними нейронами
домої функції і описує класифікаційну задачу, де <р(х) —
— (сі,Сг,...,с,п) така, що с, = 1, с7 = 0, V? і і х належить
класу с,.
Нечіткі множини і лінгвістичні правила представляють
апроксимацію і визначають результат системи МЕЕСБА88.
Вони отримуються з множини вибірок шляхом навчання.
Обов’язково повинно виконуватися правило, що для кожного
лінгвістичного значення може існувати тільки одне пред-
ставлення нечіткої множини.
230
Розділ 3. Нейронні мережі
Навчання в системі КЕЕСЬАЗЗ
Система ПЕРСЕА88 може бути побудована за частковими
знаннями про зразки. Користувач повинен визначити кіль-
кість початкових нечітких множин і задати значення к —
максимальне число вузлів правил, що можуть бути створе-
ні в прихованому шарі. Для навчання ми будемо використо-
вувати визначену раніше трикутну функцію приналежності.
Розглянемо безпосередньо алгоритм навчання.
Розглянемо систему НЕРСЬА88 з п вхідними нейронами
к ктах нейронами правил і т вихідними ней-
ронами сі,...,ст. Також задана навчальна множина зраз-
ків Ь — {(рі, й) > - • •, (РвДз)} , кожний з яких складається
з вхідного зразка р Є РІп і бажаного зразка і Є (0,1)т.
Навчальний алгоритм, мета якого створити к нейронів пра-
вил системи НЕГСЬА88, складається з наступних етапів:
1. Вибираємо наступний зразок (р, і) з £;
2. Для кожного вхідного нейрона Хі Є знаходимо таку
функцію приналежності р^, що
(*) Г (»)/ Л
Мд = тах Н
7Є1.--Л1 І )
3. Якщо, як і раніше, вузлів правил залишилося менше
ніж /стах і не існує вузла правила Н з Ж(хі,К) =
..., Ж (жп, /?) = р^, то створюємо такий вузол і з’єднуємо
ЙОГО З ВИХІДНИМ вузлом Сі, ЯКЩО Іі — 1;
4. Якщо ще залишились неопрацьовані зразки в Ь і к
ктах, то ідемо на крок (1), а інакше стоп;
5. Визначаємо базу правил за однією із трьох наступних
процедур:
а) «Просте» навчання правил: залишаємо тільки перші
к правил (зупиняємо створення правил, якщо було створено
к ~ &шах правил);
3.15. Нечіткий перцептрон як загальна модель
231
б) «Найкраще» навчання правил; обробляємо зразки в Ь
і накопичуємо активації кожного нейрона правил для кожно-
го класу зразків, що були поширені. Якщо нейрон правила К
показує більше нагромадження активації для класу С^, чим
для класу Сд, який був специфікований для наслідку пра-
вила, тоді змінюємо наслідок Я на Су, тобто з’єднуємо Н. з
нейроном виходу сл. Продовжуємо обробку зразків у Ь далі
й обчислюємо для кожного нейрона правил:
= 22 ан ' єр>
рєд
1, якщо р класифіковано вірчо;
ер 1
— 1, інакше.
Залишаємо к нейронів правил з найвищими значеннями
Уд і видаляємо інші нейрони правил із системи ПЕЕСЬА88.
в) «Найкращий для кожного класу» алгоритм навчання:
діємо так само, як і в попередньому випадку, але залишаємо
для кожного класу Су ті найкращі [^] правил, наслідки яких
представляють клас Су (де [т] — ціла частина від х) .
Алгоритм навчання нечітких множин
Алгоритм навчання з учителем системи ПЕЕСБА88 по-
винен адаптувати нечіткі множини, пробігаючи циклічно че-
рез усю навчальну множину Ь і продовжуючи нижче описані
кроки, поки не виконається один із критеріїв зупинки.
Кроки:
1. Вибираємо наступний зразок (р, і) з Ь і поширюємо його
через систему ПЕГСЕА88 та визначаємо вихідний вектор с;
2. Для кожного вихідного нейрона Сі обчислюємо значен-
ня <5С1
— Е Ос, •
232
Розділ 3. Нейронні мережі
3. Для кожного нейрона правил К із ар > 0
а) обчислюємо значення 6р
6р = ап • (1 ~ йй) • У? (К, с) <5С;
сЄІУз
б) знаходимо таке х', що
IV (ж', Я) (ах’) = тіл {IV (ж, /?) (аг)} ;
гЄРі
в) для нечітких множин XV (ж', /?) визначаємо 8а, 6Ь, <5С, ви-
користовуючи швидкість навчання о > 0
< 5Ь = а • • (с - а) - (ах- - Ь);
< 5а — — сг - <5д • (с — а) + <56;
< 5С = а • - (с — а) + 6Ь,
і застосовуємо зміни до XV (х', Е);
г) обчислюємо помилку правила:
Е = аг - (1 - ар) У2 (2- XV (Я, с) - 1)<5С.
сЄРз
Як критерії зупинки можна взяти, наприклад, такі:
1. Помилка протягом п ітерацій не зменшується;
2. Припинити навчання по досягненню помилкою визна-
ченого (бажано близького до нуля) значення.
Розділ 4
МЕТОД ГРУПОВОГО УРАХУВАННЯ
АРГУМЕНТІВ У ЗАДАЧАХ
ПРОГНОЗУВАННЯ Й ІДЕНТИФІКАЦІЇ
4.1. Основні принципи і загальна схема методу
Метод групового урахування аргументів (МГУА) був за-
пропонований наприкінці 60-х — початку 70-х р.р. академіком
О.Г. Івахненко (Інститут кібернетики НАН України) [15 — 18].
Цей метод використовує ідеї самоорганізації і механізми жи-
вої природи — схрещування (гібрвдизацію) і селекцію (добір).
Нехай є вибірка з N спостережень вхідних векторів Х(г)
та вихідних V (г) :
{Х(1) ¥(1)}
{Х(2) ¥(2)}
{Х(А) ¥(АГ)}.
За результатами спостережень
треба визначити Г(.т), причому
структура моделі Г(ж) невідома.
*(*) Цх)-? у(0
Хї(<) .
^(0 .
Рис. 4.1. Задача ідентифікації
моделі
Найбільш повна залежність між входами Х(г) і виходами
¥(і) може бути представлена за допомогою узагальненого
полінома Колмогорова-Габора.
Нехай є вибірка X = {«і,... , тоді такий поліном має
вигляд-
N N N
У = а0 4- аіХі + У2 У? У^ У^ а^кХіХ^Тк + ...
і=1 7=1 «СІ *=1 7^’ ^^3
де ВСІ коефіцієнти Оі не відомі.
234
Розділ 4. Метод групового урахування аргументів ...
При побудові моделі (при визначенні значень коефіцієн-
тів) в якості критерій використовується критерій регулярно-
сті (точності): к
* І=1
Нам треба знайти таку модель, для якої є2 —> тіп.
Розглянемо основні принципи та ідеї МГУА.
Принцип множинності моделей: існує множина моде-
лей на даній вибірці, що забезпечують нульову помилку (до-
статньо підвищувати ступінь полінома моделі). Тобто, якщо
є N вузлів інтерполяції, то можна побудувати ціле сімейство
моделей, кожна з яких при проходженні через експеримен-
тальні точки буде давати нульову помилку
є2 = 0.
Як правило ступінь нелінійності беруть не вище п — 1,
якщо п — кількість точок вибірки.
Позначимо 8 — складність моделі (визначається числом
членів полінома Колмогорова-Габора).
Значення помилки є2 залежить від складності моделі.
Причому в міру росту складності спочатку вона буде падати,
а потім зростати. Нам же потрібно вибрати таку оптимальну
складність, при якій помилка є
буде мінімальна. Крім того,
якщо враховувати дію пере-
шкод, то можна виділити на-
ступні моменти:
1. При різному рівні
перешкод залежність є2
від складності 8 буде зміню-
ватися, зберігаючи при цьому
загальну спрямованість (ма-
Рис. 4.2. Залежність є2
4.1. Основні принципи і загальна схема методу
235
ється на увазі, що з ростом складності вона спочатку буде
зменшуватись, а потім — зростати).
2. При збільшенні рівня перешкод величина ішпє2 буде
зростати.
3. З ростом рівня перешкод величина 50 = аг§ тіп є2 буде
зменшуватись (оптимальне значення складності буде зміща-
тися вліво). Причому Є2(5'о) > 0, якщо рівень перешкод не
нульовий (див. рис. 4.2).
Теорема неповноти Геделя: У будь-якій формальній
логічній системі існує ряд тверджень і теорем, які не можна
ні спростувати, ні довести, залишаючись у рамках цієї систе-
ми аксіом.
У даному випадку ця теорема означає, що вибірка завжди
неповна. Один зі способів подолання цієї неповноти — прин-
цип зовнішнього доповнення. В якості зовнішнього доповнен-
ня використовується додаткова вибірка (перевірочна), точки
якої не використовувалися при навчанні системи (тобто при
пошуку оцінок значень коефіцієнтів полінома Колмогорова-
Габора).
Пошук найкращої моделі здійснюється в такий спосіб:
1. Уся вибірка поділяється на навчальну і перевірочну:
^виб ^навч ^переві
2. На навчальній вибірці визначаються значення
3. На перевірочній вибірці 7Уперев відбираються кращі мо-
делі.
Вхідний вектор має розмірність /V (X = {.ті,..., т/у}).
Принцип свободи вибору (неостаточності промі-
жного рішення):
1. Для кожної пари хг та х^ будуються часткові описи
(усього С^) виду:
— або = </? (ті, х}) — ао + агх, + а3х]у з = 1... (лінійні);
236
Розділ 4. Метод групового урахування аргументів ...
— або у^ = у) (хі, х3) = од + Хі + а3х3 4- агіх2 + аі3хгх3 4- а33х2,
5 = 1... (квадратичні).
2. Визначаємо коефіцієнти цих моделей по МНК,
використовуючи навчальну вибірку. Тобто знаходимо
) * * • ) У ) * “ " ч № 1^11)'**) О'і] • • • • ) № № *
3. Далі на перевірочній вибірці для кожної з цих моделей
шукаємо оцінку
1 Мирее Г /<л“] 2
^=— £ У^-Ук ,
1Упере.в к=ї
(де ¥(к) — дійсне вихідне значення в Л-тій точці перевірочної
„(«)
вибірки; ¥к — вихідне значення в &-тій точці перевірочної
вибірки відповідно до 5-тієї моделі) і визначаємо Р кращих
моделей.
Обрані Уі подаються на другий ряд (рис. 4.3).
Шукаємо
гі = <р{2} ІУі,Уз) =
- а(2) 4- А 4- Л 4- А2 4- «(2)7/ 4- л(2)7>2
— а0 та^ у,+ а2 у3 г а3 у, т- угу3 г а5 у3.
Оцінка тут така ж, як на першому ряді. Добір кращих
здійснюється знову так само, але Р% < Р\.
Процес конструювання рядів повторюється доти, поки се-
редній квадрат помилки буде падати. Коли на шарі ш одер-
жимо збільшення помилки є2, то припиняємо.
Якщо часткові описи квадратичні і число рядів полінома
5, то одержуємо, що максимальний ступінь полінома к = 25.
На відміну від звичайних методів статистичного аналізу, при
такому підході можна одержати досить складну залежність,
навіть маючи коротку вибірку.
Існує проблема: на першому ряді можуть відсіятися деякі
перемінні Хі і х3, котрі впливають на вихідні дані.
4.1. Основні принципи і загальна схема методу
237
Рис. 4.3. Структура багаторядного алгоритма МГУА
У зв’язку з цим запропонована така модифікація: на дру-
гому шарі подавати уг і X], тобто:
- о(2) 4- А -І- п(2)т 4- А2 4- х 4- а(2)т2
•2/ — Од г уі і £^2 &3 ^3 Уі ^4 Уг*^з .5 *”з *
Це важливо при високому рівні перешкод, щоб забезпечи-
ти незміщеність моделей.
Виникає два критерії добору кращих кандидатів частко-
вих описів, які передаються на певному шарі на наступний
ряд (шар) [15—16].
1. Критерій регулярності (точності)
а) = м- £ (у* - у*(і))2;
І=1
^пр п
Е (Уг - У‘(<) (®))
XV _ »=І
238
Розділ 4. Метод групового урахування аргументів ...
2. Критерій незміщеності. Беремо усю вибірку, поділяємо
на дві частини Кі, Я2, де Я = Я] + :
Перший експеримент-.
Ні — навчальна вибірка, Т?2 — перевірочна;
визначаємо виходи моделі у*, і = 1, /?;
Другий експеримент.
В.2 — навчальна вибірка, Я\ — перевірочна;
визначаємо виходи моделі у**, і = 1, Я,
і порівнюємо.
Критерій незміщеності.
1 "
Пзм ~ 7? 52 ~Уі
і=1
Чим менше пзм, тим більше незміщеною є модель.
Такий критерій визначається для кожного часткового
опису першого рівня і потім знаходиться пзм для рівня в ці-
лому для Р кращих моделей
п = 1.\"п(1)
зм р / - Пзм,і'
*=1
У ряді варіантів Р = 1. Аналогічно на другому шарі об-
іг)
числюємо п3м.
І процес селекції здійснюється доти, поки цей критерій не
перестане зменшуватися, тобто до досягнення умови
п£2 —» тіп.
Переваги метода МГУА
1. Можна відновити невідому довільно складну зале-
жність по обмеженій вибірці. Число невідомих параметрів
моделі може бути більше, ніж число точок навчальної послі-
довності.
4.1. Основні принципи і загальна схема методу
239
2. Можливість адаптації параметрів моделі при одер-
жанні нових даних експериментів (зокрема використовуючи
РМНК).
Алгоритм самоорганізації МГУА і його застосування в за-
дачах прогнозування і РО
Багаторядний МГУА. Існує два підходи при виборі час-
ткових описів і побудови МГУА.
• Точнісний;
• Робастний.
При першому підході в алгоритмі МГУА при виборі описів
використовується критерій регулярності послідовності або
точнісний критерій, що визначається в такий спосіб
Навчання відбувається на вибірці А, перевірка на В, де
В
ув — фактичний вихід на вибірці В, уі — прогнозування по
моделі.
Цей критерій досить гарний і застосовується на практи-
ці. Перший підхід використовується для одержання найбільш
точної моделі по вибірці даних.
В основі робастного підходу лежить застосування дифе-
ренціального критерію несуперечності
Де Уі > У і ~ Це виходи моделі, які побудовані по вибіркам А
і В, відповідно.
Цей критерій — критерій узгодженості моделей, ефектив-
ний при зашумлених даних.
240
Розділ 4. Метод групового урахування аргументів ...
Щоб одержати найбільш гострий глибокий мінімум за цим
критерієм вибірки А і В вибираються так, щоб виконувалась
умова |Д| « |В| і їхні дисперсії були приблизно однакові, а
взаємна дисперсія була якнайбільша.
Наступне питання про вибір предикатів (перемінних), що
вводяться в модель.
Насамперед, для кожногоХі = {х},х^,... ,х^} — вектора-
стовпця (деяке спостереження) виконується процедура нор-
малізації:
Змінах Яцпш
2. Хг = --------------
З'і.тах Я'і.тіп
(є 10; 1]);
3. х'і =----Х- ~~-----
*^г,тах Я'ідпіп
(Є [-1-.1]).
Ми визначаємо попередні коефіцієнти кореляції вхідних
спостережень з виходом
N
Е {уз ~ у) (Хіз ~
з=і
РуХі — І--------------;--------------
/ N „ Л „
л/Е (Уз ~У) Е Сщ -*і)
у 7=1 7=1
Далі перевіряємо гіпотезу про те, що коефіцієнт кореляції
відмінний від нуля.
У модель вибираємо ті перемінні, для яких руХг > 0, де 0
— деякий поріг. Якщо є необхідність досліджувати нестаціо-
нарні процеси, можна використовувати підхід з виділенням
трендів.
4.2. Багаторядні поліноміальні алгоритми МГУА
241
4.2. Багаторядні поліноміальні алгоритми МГУА
Багаторядні алгоритми МГУА застосовуються для рішен-
ня некоректних чи недовизначених задач моделювання, тоб-
то у випадку, коли число точок у таблиці дослідних даних
менше числа аргументів, що входять у синтезовану модель.
Методи регресійного аналізу в цьому випадку незастосов-
ні, тому що не дають можливості побудови єдиної моделі,
адекватної процесу за межами інтервалу інтерполяції. За-
стосування багаторядних алгоритмів МГУА не обмежується
зазначеною областю некоректних (недовизначених) задач.
Вони успішно застосовуються й у випадках, коли вихідних
даних досить для застосування однорядних МГУА, однак
при цьому багаторядні часто виявляються кращими.
Вважаємо, що початковий склад аргументів, з якого по-
чинається процедура багаторядної селекції моделі процесу,
будується на так званому нульовому ряді алгоритму, що ор-
ганізується по-різному в поліноміальних і гармонійних алго-
ритмах. Наприклад, у класі алгебраїчних функцій найбільш
загальною моделлю є поліном Колмогорова-Габора від к пе-
ремінних:
к к к
<7 = а0 + 52 + 52 ]Е2 + - • •
і=1 і=1 7=1
який являє собою суму лінійних, квадратичних, кубічних і
інших членів. Після перетворення всіх наявних у ньому до-
данків одержимо лінійний поліном:
(] — 0,0 + ... + о,пхп.
Члени цього полінома і складають початковий набір
аргументів, побудований на нульовому ряді багаторядного
алгоритму.
11‘
0
242
Розділ 4. Метод групового урахування аргументів ...
У випадку різницевих моделей до аналогічного виду зво-
диться модель, отримана за допомогою перетворення усіх
вхідних змінних, їхніх запізнювань і заданих нелінійних фун-
кцій від них.
Багаторядні алгоритми, як правило, працюють за насту-
пною схемою (див. рис. 4.3):
1-ий ряд — на основі даних таблиці спостережень буду-
ються часткові описи від усіх попарних комбінацій початко-
вих даних (перепозначених) аргументів, що наближають по
МНК вихідну змінну у :
Уі= / (жі, т2), у2 = /г (жі,х3), • • •, Ук = А (яп-і, хп).
З цих моделей вибирається деяке число кращих за зовні-
шнім критерієм селекції.
2-ий ряд — отримані змінні приймаються як аргументи
— входи другого ряду, і знову будуються всі часткові описи
від двох аргументів:
гі = (уі,уг), 22 = 9?2 (уі,Уз), • - -, 2,1 = ірі (уг'-ьуг).
З них за зовнішнім критерієм відбирається Р2 кращих мо-
делей у якості змінних наступного ряду і т.д. Ряди нарощую-
ться доти, поки знижується значення зовнішнього критерію.
Кожний частковий опис може бути лінійною
/ = Яр + Я\Хі + О-2Хк
чи нелінійною
/ = а0 + Яі.Ті + а2хк + а3ХіХк 4- а4х,2 + а$хк
функцією від двох змінних, коефіцієнти яких можна визначи-
ти по МНК, маючи відповідну кількість точок спостережен-
ня в навчальній послідовності. Виключивши проміжні змінні
після останову алгоритму, одержимо модель, число коефіці-
єнтів у якій значно перевищує число точок.
4.2. Багаторядні поліноміальні алгоритми МГУА
243
Опис алгоритму
Перша гтперацгя. Крок 1. З множини виходів X — {ті,
х%, - ,хп} вибираються пари аргументівхіг х3 і складаються
часткові описи виду
= (р(хі,хі),
і /У, = 1,ДГ,
при цьому використовують часткові описи квадратичного ти-
ПУ: (і)
ук — ао 4- агХі + а^х^+
4- а^ХіХ-, 4- ацх2 4- а^х2.
Число часткових описів 1-го ряду дорівнює М = п(п — 1)/2.
Крок 2. Використовуючи метод найменших квадратів
(МНК) для кожного опису знаходяться по навчальній вибірці
оцінки невідомих коефіцієнтів ао, а.і, а-;, а^, ай, а]3.
Крок 3. За критерієм мінімуму є2 на перевірочній по-
слідовності відбирається Рі кращих моделей, тобто реалізу-
ють процедуру селекції. Величина Р3 називається свободою
вибору, при цьому Рі < М. Виходи цих моделей служать
аргументами-входами для конструювання моделей другого
ряду-
Крок 4. Знаходиться є2(0) = пйпє|(0).
т-а ітерація. Крок 1. Конструюються часткові описи
виду:
Ук — ао 4- а1 уі + Уі +
і (т ^1) , (т) 2/ , (тп) 9/
+аг3і Уі Уз 4- аУ ’Уі (т - 1) 4- а^’у2 (т - 1),
Крок 2. Для кожного опису, використовуючи МНК, зна-
„(гп) Ат) (т) (»") _(гп)
ходяться відповідні оцінки а0 , а, , , ай , а^ .
11*
244
Розділ 4. Метод групового урахування аргументів ...
Крок 3. На перевірочній послідовності знаходиться для
кожного часткового опису величина критерію
, N пер гу
^пер І=1 ' 7
де Мпер — обсяг перевірочної вибірки.
Крок 4. Знаходиться є2 (т) = тіп є2 (т). Перевіряється
к
умова є2 (т) > є2 (т — 1), де є2 (т), є2 (т — 1) — величи-
ни критерію точності для найкращих моделей (т — 1)-го і
т-го ряду селекції відповідно. Якщо так, то кінець. Шукана
модель вибирається з часткових описів (т — 1)-го рівня, на
якому досягається мінімальна помилка є2 (т — 1). Інакше пе-
рехід до конструювання наступного ряду часткових описів.
При цьому провадиться добір (селекція) Е кращих описів.
Заключний етап. Рухаючись від кінця до початку і ро-
блячи послідовну заміну перемінних, обчислюються вирази
для шуканої моделі у початковому просторі описів.
4.3. Комбінаторний алгоритм МГУА
МГУА має особливості, що дозволяють поліпшити про-
гнозування моделей складних об’єктів і надати їм об’єктив-
ний характер:
1. Самоорганізація фізичної моделі для пізнання об’єкта
досліджень і декількох нефізичних — для довгострокового
прогнозу.
2. Вибір класу рівнянь і виду опорної функції виконує-
ться за допомогою ЕОМ, що перебирає багато варіантів за
критеріями вибору моделі.
3. Вибір множини вихідних і вхідних перемінних, а також
«провідної» перемінної доручається ЕОМ.
4.3. Комбінаторний алгоритм МГУА
245
4. Перемінні, що погано прогнозуються, прогнозуються в
другу чергу.
5. Можливість прогнозування при неповному інформацій-
ному базисі.
6. Самоорганізація фізичної і прогнозуючих моделей мо-
жлива при сильно зашумлених вхідних даних.
У комбінаторних алгоритмах виконується перебір усіх мо-
делей із заданого базису з вибором кращої з цих моделей за
заданим критерієм селекції.
При переборі складність часткових моделей, тобто число
аргументів, поступово нарощується від 1 до максимального
числа п (числа аргументів базисного набору функцій).
Таким чином, загальна схема комбінаторного алгоритму
включає наступні операції:
— по МНК визначаються коефіцієнти всіх часткових мо-
делей при складності з = 1... п;
— для кожної з них обчислюється значення зовнішнього
індивідуального або комбінованого критерію селекції;
— єдина модель оптимальної складності вибирається за
мінімальним значенням критерію.
Опорним набором аргументів є п членів деякого полінома
заданого максимального ступеня від заданого числа перемін-
них. Наприклад, повний поліном ступеня 2 від п = 6 змінних
<7 = оо + а^Хі + 02X2 + О3Х3 + 0.4X4 + 05X5 + ОоХв+
+а7Хі + авХхХг + 09X1X3 + 010X1X4 + 011X1X5 + аі2хіх6+
+013X2 + 014X2X3 + 015X2X4 + 010X2X5 + 017X2X5+
+0ЮХ3 + 019X3X4 + 020X3X5 + 021X3X0+
+022X4 + 023X4X5 + 024X4X0 + 025X4 + 020X5X0 + О27х|.
II2
246
Розділ 4. Метод групового урахування аргументів ...
Іноді до складу аргументів потрібно ввести зворотні ве-
личини 1/хг, їхні ступені або інші нелінійні функції. У будь-
якому випадку повний поліном є лінійним за коефіцієнтами,
для визначення яких застосовується МНК. При цьому ступе-
ні і коваріації початкових перемінних розглядаються як «пе-
репозначені» лінійні аргументи.
Спочатку визначаються всі моделі при 5 = 1, тобто з одно-
го аргументу (усього С^):
2
91 = а0, 92 = 01^1 > - • • ; 928 = 027^6-
Далі розглядаються всі моделі при 5 = 2 (усього С^У
929 = ЙО + СЦХ1, 9зо = До + 0,2X2, - - - ,
9г = а0 + а27^6ї • • > 9? = О,\Х\ + 0,2X2, - . . ,
Як = 0.1X1 + 027^1,. . . , 9п = 026^5^6 + 027^6-
Таким чином, загальне число Рп всіляких часткових мо-
делей, побудованих з п аргументів повного полінома методом
повного комбінаторного алгоритму, обчислюються:
п
Рп = £с^ = 2”-1.
5=1
При великому п приходиться застосовувати доцільне усі-
кання перебору. Максимальна складність т задається чи-
слом точок початкових даних, довжиною навчальної послі-
довності: якщо ІЯА < п, то т = І\'д.
Структура комбінаторного алгоритму
У структурі кожного з алгоритмів МГУА можна виділити
три основних блоки [15,17]-
1. Перетворення початкових даних відповідно до обраної
системи опорних функцій, у якій шукається модель.
4.3. Комбінаторний алгоритм МГУА
247
2. Генерування повної або неповної множини часткових
моделей, що ускладнюються, в обраному базисі.
3. Обчислення значень деякого критерію селекції, що має
властивості зовнішнього доповнення і послідовного добору
часткових моделей, кращих за цим критерієм.
Блок формування базису.
Якщо задані виміри деяких вхідних перемінних хі,...,
об’єкта, що моделюється, і максимальний ступінь полінома,
то число доданків п у повному поліномі ступеня <7тах ВІД V
перемінних визначається однозначно:
(сГщах + «) ! - (Отах) !
і)!
Сам повний поліном записується в наступному загально-
му вигляді: п V п
у=52 аі П 4° = 52
і=і і=і і=і
де кожен узагальнений «лінійний» аргумент х, є нелінійною
функцією початкових перемінних г3 :
V
ж’ = ПгГ-
7=1
Отже, {жі}— базисний набір опорних функцій.
Описана процедура дозволяє сформувати матрицю вимі-
рів узагальнених аргументів Х^хп\ де N — число точок ви-
мірів.
Ці точки розділені на три послідовності: навчальну (Л)
довжиною перевірочну (В) довжиною й екзамена-
ційну (С) довжиною N0- Причому
N а + N в + — N.
II**
248
Розділ 4. Метод групового урахування аргументів .
Блок перебору часткових моделей.
Основні операції:
— формування структури чергової часткової моделі;
— формування відповідної нормальної системи рівнянь;
— вирішення отриманої системи (оцінка коефіцієнтів мо-
делі).
Формування структур часткової моделі формалізується
за допомогою структурного вектора сі = {ф,ф,... ,с?п} :
якщо елемент ф цього вектора приймає значення 1, то від-
повідний г-й аргумент включається в часткову модель, якщо
0 — не включається.
Використовується схема зміни двоїстого вектора за прин-
ципом роботи двоїстого лічильника, в останній розряд якого
додається одиниця.
Формування нормальної системи рівнянь, що відповідає
черговому структурному вектору, можна виконати формаль-
но: зі стовпців повної матриці X, зазначених одиничними еле-
ментами сі, складається часткова матриця Хе, а потім обчи-
слюються елементи Х^Хе, Х^у.
В комбінаторному алгоритмі досить один раз обчислити
матрицю повної нормальної системи, що містить елементи
всіх часткових нормальних систем:
/ лАг Х1 Хі х?х2 - Хі’Хп ( хТу
хтх = Х2Х1 х2х2 - х2Хп , Хту = Х2У
\ хпх1 хпх2 • ХпХп к ХпУ /
Для одержання будь-якої часткової нормальної системи
досить взяти елементи матриці ХТХ, що знаходяться на пе-
ретині рядків і стовпців, зазначених одиницями вектора сі, а
також відповідні елементи вектора Хту.
4.3 Комбінаторний алгоритм МГУА
249
Для вирішення кожної нормальної системи Х^Хеае =
= Х^у, тобто для обчислення оцінок коефіцієнтів часткової
моделі, можна застосовувати будь-які процедури розв’язання
систем алгебраїчних рівнянь.
Блок добору за критеріями.
Розглянемо питання про обчислення значень критеріїв се-
лекції для довільної часткової моделі з вектором коефіцієнтів
а, оцінки якого вже отримані на вибірках А і В окремо.
Критерій незміщеності:
п2зм = (у А - У в) (у А - У в) =
/ - \т -'Т-' /- - \
= ( аА — аві X X І а.д — ав ) ,
де уЛ, ув — оцінки вихідної величини, отримані за коефіці-
єнтами ал, ав; ХТХ — сума матриць ХЛХЛ і ХсХв-
Критерій регулярності:
/ а\т / А\
д2(5) = (ув-Уві (ув-Ув) =
„Т- „ _Т„т„
= УвУв — 2авХву в + авХвХвавУв>
де у в — початковий вектор вимірів вихідної величини на по-
_А
слідовності В; ув — оцінки виходу на В по моделі ал.
На послідовності С
т т
А2 (С) = УсУс ~ 2а,уХсУс + аИ'ХсХсУ|у,
де ац/ — оцінки коефіцієнтів часткових моделей, відібраних
по п2зм і А2 (В) після перерахування на об’єднаній послідов-
ності А О В = IV.
1Р
250
Розділ 4. Метод групового урахування аргументів ...
Селекція моделей, як правило, виконується в процесі пе-
ребору. Для цього запам’ятовуються значення критерію для
заданої свободи вибору Г перших моделей, а потім величина
кожної наступної моделі порівнюється з кращим з Г значень.
В алгоритмах самоорганізації застосовується добір по
двох і більше критеріях.
Як правило, кілька критеріїв застосовуються послідовно:
за критерієм п2зм відбирається Р\ найменш зміщених моделей,
потім за критерієм Д2 (В) — Г моделей самих точних на пере-
вірочній послідовності, де Е < Е\. Використовується також
інформація послідовності С за критерієм регулярності.
Так само в алгоритмах МГУА звичайно виконується ще
один етап обчислень — оцінка якості відібраних кращих мо-
делей.
Помилку МНК, обумовлену після перерахування коефіці-
єнтів на IV, також можна виразити через нормальні матриці
В2 (IV) = (у^ - (у^ - у^ =
т „Т -т „
= УіуУуу ~
де виконується рівність
Т „ Т „т „ /„Т „ \ -1 „т
а^уХц/Хи/аи/ = ац/Х^Хи/ І Х^/Х^у І Хц/у^л =
_ ~т ~Т -
= а^Хц/Уіу.
Селекція продовжується доти, поки не досягається міні-
мум критерію незміщеності. Потім відбирається найбільш ре-
гулярна модель.
4.4. Алгоритм МГУА з послідовним виділенням трендів
251
4.4. Алгоритм МГУА
з послідовним виділенням трендів
Нехай є залежність, яку потрібно відновити у =
= / (ті,..., хп). Ранжирують перемінні за коефіцієнтом ко-
реляції вхід-вихід р : хі >- х2 хп <-> руХі >
> Рух, > • • • > Рух„ Далі шукаємо першу залежність
так: у = Ч>\(хі) — тренд 1-го порядку. Потім шукаємо рі-
зницю Д^у = у — (ті) - <р2 (я-Д — тренд другого по-
рядку. Тобто помилка першого порядку визначається як де-
яка функція, що залежить від х2. Потім знаходимо помилку
М^у — ір2 (я-'г) — Д(2)У = <Рз (я-'з) • Зазначений процес продов-
жується доти, поки відповідна помилка не буде мінімальною
за заданим критерієм:
|Д(т)у| < боа-
Такий же підхід можна застосувати, якщо у є функція
часу і залежить від ряду перемінних Хі,..., хп.
У (і) =
= / (^1 (*), - ,хп(і) ,хі(і - Ті),..., хп (і - тп)).
Використовуючи метод ковзного середнього, можна виді-
лити тренд к
К *—4
і=0
Далі знаходимо залежність Ду (і) = (х'і (і)) і викори-
стовуємо відповідний МГУА для визначення невідомої зале-
жності і так далі. У результаті одержимо представлення
У (і) =
— У (0 + V3! (ті (£)) + У’г (ж2 (і)) + - • - + <Рк (я* (£)) -
11***
252
Розділ 4. Метод групового урахування аргументів ...
4.5. Нечіткий метод групового обліку аргументів
і його застосування в задачах прогнозування
макроекономічних показників
Принципи самоорганізації методу
групового обліку аргументів
Побудова систем самоорганізації по методу групового
обліку аргументів (МГУА) базується на наступних принци-
пах [15]:
1. Принцип самоорганізації моделі. При послідовно-
му збільшенні складності структури моделі значення зовні-
шніх критеріїв спочатку зменшуються, досягають мінімуму,
а потім залишаються незмінними чи починають збільшувати-
ся. Перше найменше значення комбінації критеріїв визначає
єдину модель оптимальної складності.
2. Принцип зовнішнього доповнення. Задачі інтер-
поляції відносяться до некоректно поставлених задач, що
мають багатозначне рішення. Для однозначного їхнього рі-
шення необхідне завдання адекватного зовнішнього допов-
нення — зовнішнього критерію оптимальності. Під зовні-
шнім критерієм будемо розуміти критерій, що обчислюється
з використанням інформації, не використаної при оцінці па-
раметрів. Внутрішні доповнення, тобто критерії, що не вико-
ристовують ніякої додаткової інформації, при дії перешкод
не можуть вирішити задачу вибору моделі оптимальної скла-
дності.
3. Гьоделівський підхід при самоорганізації моде-
лей. Теорема стверджує, що для будь-якої системи вихідних
аксіом (зовнішніх доповнень першого рівня) завжди можна
задати таку теорему, для доказу якої недостатньо даної си-
стеми аксіом і необхідні нові аксіоми — зовнішні доповне-
ння. Стосовно до моделей самоорганізації ідеї Гьоделя мо-
4-5. Нечіткий метод групового обліку аргументів
253
жна інтерпретувати в такий спосіб: по мінімуму заданого
зовнішнього критерію можна вирішити всі питання про ви-
бір опорних функцій, структури і параметрів моделі, крім
питань, зв’язаних з алгоритмом обчислення і способами ви-
користання самих критеріїв.
4. Зовнішні критерії селекції моделей. Рівняння ре-
гресії вибирається за критерієм мінімуму незміщеності — не-
суперечності, відповідно до якого потрібно, щоб моделі, по-
будовані по частині таблиці А, якнайменше відхилялися від
моделей, побудованих по частині В. Критерій мінімуму не-
зміщеності є базовим, тому що несуперечність моделей є обо-
в’язковою властивістю оптимальної моделі.
5. Розбивка таблиці даних на частини. Основний
критерій мінімуму незміщеності вимагає розбивки таблиці
даних на дві рівні частини А та В. Звичайно таблиця ви-
хідних даних поділяється на три частини: навчальна А, пе-
ревірочна В и екзаменаційна вибірка С. Навчальна вибірка
використовується для одержання оцінок параметрів моделі
(наприклад, коефіцієнтів регресії), а перевірочна— для вибо-
ру структури моделі.
6. Гіпотеза селекції. При використанні принципу селе-
кції в кібернетиці необхідно дотримуватися наступних пра-
вил:
— Для кожного покоління (чи ряду селекції моделі) існує
деяка мінімальна кількість комбінацій, які відбираються.
Вони називаються свободою вибору і забезпечують збіжність
багаторядних селекцій моделі оптимальної складності
— Занадто велика кількість поколінь приводить до інду-
циту (інформаційна матриця стає погано обумовленою).
— Чим складніше задача селекції, тим більше потрібно
поколінь для одержання моделі оптимальної складності.
254
Розділ 4. Метод групового урахування аргументів ...
7. Принцип збереження свободи вибору. Свобода ви-
бору забезпечується тим, що на кожний наступний ряд селе-
кції передається не одне рішення, а декілька кращих, відібра-
них на останньому ряді. Д. Габор сформулював цей принцип
таким чином: приймати рішення в даний момент часу необхі-
дно таким чином, щоб у наступний момент часу, коли вини-
кне необхідність у черговому рішенні, зберігалася б свобода
вибору рішень.
8. Застосування евристичних методів. Евристичний
характер самоорганізації моделей особливо виявляється при
виборі опорної функції окремих моделей, критеріїв селекції
моделей, способу регуляризації, способу нормування перемін-
них, конкретній реалізації послідовного збільшення складно-
сті моделей-претендентів.
9. Одночасне моделювання на різних рівнях спіль-
ності мови математичного опису об’єктів. Основним мо-
ментом у цьому принципі є використання багаторівневого мо-
делювання для рішення задачі прогнозування.
Самоорганізація відноситься до емпіричних методів моде-
лювання. Ці методи у своїй області застосування мають деякі
переваги в порівнянні з теоретичними і напівемпіричними
методами побудови моделей. У тих випадках, коли ми спо-
стерігаємо параметри досліджуваного об’єкта, але не знаємо
структури і механізму взаємодії між елементами складної
системи, поводження якого визначає значення параметрів,
підхід самоорганізації виявляється єдиним надійним засобом
побудови моделей прогнозу. За допомогою самоорганізації
рішення можна визначити, навіть якщо іншими способами
одержати результати неможливо. Моделі, отримані за допо-
могою самоорганізації, мають специфічну область застосу-
вання й особливо ефективні для короткострокового прогно-
зу. Фізичні моделі, отримані на основі математичної теорії
4 5. Нечіткий метод групового обліку аргументів
255
об’єктів, які спостерігаються, можуть мати тільки цілком
визначені пізнавальні цілі (ідентифікація і довгостроковий
прогноз). Тому побудова моделей відповідно до нових об’є-
ктивних методів самоорганізації уможливлює замість допу-
щень і грубих помилок запропонувати моделі, що ґрунтую-
ться на надійній інформації й отримані за допомогою само-
організації.
Постановка задачі
Задано множину вихідних даних = {У, Хі,..., Хп} ,
Хп Є Пм, де п — кількість змінних, а М — кількість то-
чок спостереження. Необхідно за допомогою нечіткого МГУА
(НМГУА) синтезувати рівняння регресії у — / (х1}... ,хп),
адекватне вихідній множині даних, причому отримана мо-
дель повинна бути найменшої складності.
У якості експериментальних даних для обчислення інфля-
ційних процесів були узяті наступні макроекономічні пока-
зники на період із січня 1995 року по лютий 1997 року:
• індекс споживчих цін (ІСЦ);
• індекс оптових цін на промислову продукцію;
• випуск промислової продукції;
• роздрібний товарообіг;
• кредитні внески в економіку;
• середньозважений курс долара;
• грошовий доход на душу населення;
• грошовий агрегат МО;
• грошовий агрегат М2;
• середньомісячна заробітна плата;
• ставка НБУ;
• кредиторська заборгованість між підприємствами;
• зміни обсягів валового сукупного продукту.
256
Розділ 4. Метод групового урахування аргументів ...
У результаті виконання роботи необхідно побудувати аде-
кватну модель, що визначає залежність показника ІСЦ від
інших макроекономічних показників, що має найменшу скла-
дність і використовується для прогнозування інфляційних
процесів.
Нечіткий метод групового урахування аргументів
Побудова часткової моделі НМГУА. Для побудови
часткової моделі НМГУА використовувалася лінійна інтер-
вальна регресійна модель [9], що задається таким чином:
У = В1&1 + В2^2 + . . . + Вп2п,
де 2$ — деякі відомі перемінні, В і — інтервали, які можна за-
дати трикутними нечіткими числами і записати таким чином
у вигляді центра а, і ширини с, :
Ві = (Од, Сі) .
Виходячи з цього, У можна розрахувати так:
Відношення вкладеності двох інтервалів Ві і В3 (Вг С В3)
можна задати наступними нерівностями:^ — с, а, — с,, с^ +
+Су (Хі + Сі.
У нашому випадку змінні 2, зв’язані зі змінними і х3
для відповідної часткової моделі НМГУА так:
21 = 1, 22 = Хі, гз = Ху, 24=Х1,...,
*п-1 = Хі Хп=ХГг
Розглянемо метод оцінювання лінійної інтервальної регре-
сійної моделі. Нехай є М спостережень п +1 перемінної, при-
чому п з них — незалежні величини, а (п + 1)-а залежить
від інших, і цю залежність (а?і,..., хп, у) ми намагаємося ви-
значити. При цьому Хі = (х,і,...,а;ім) і У = —
4 5. Нечіткий метод групового обліку аргументів
257
вхідні і вихідні вектори точок спостереження. Тоді оціночна
лінійна інтервальна модель для часткової моделі НМГУА має
вигляд:
= -^оо Т Аожі "Г Аихз Т А20хі Т • • • -Ь Агг_|ТіЛ:^ + Аггх^.
Побудова робиться з урахуванням наступних вимог:
1. Задані значення у3, що спостерігаються, включаються
в оціночний інтервал У*.
2. Ширина оціночного інтервалу повинна бути мінімаль-
ною.
Ці вимоги можна звести до задачі лінійного програмуван-
ня в наступному вигляді (для /г-тої точки спостереження):
тіп(со + сі • + ...
• • - + СС2+1-1 ‘ ‘ *| + сс?+1 ‘ > И-1)
«О + • ^кі + • + аС%+1
— ^со + Сі • |Хц| + ... + Ук\ (4-2)
Од + - Хкі + . . . + <>С2+1 +
+ (со + сі - |Лн| -І-... + Сс2+1 ‘ і) (4-3)
Ср > 0, р=1,с^+1.
Виходячи з цього, при відомих значеннях перемінних Хі
і величини у, отриманих у результаті М вимірів, ми прихо-
димо до задачі пошуку коефіцієнтів моделі (для всіх точок
спостереження) у такому вигляді:
/ м
тіп І со • М + Сі • Е|Хь|+...
\ к=1
М \
• •+• Е Iх" • 11+ Е Іхь І • <4-4)
к=1 /
258
Розділ 4. Метод групового урахування аргументів ...
при обмеженнях
«0 + «1 • ^кі + ... + ОсС2 • Хт —
(со 4- Сі - |ХИ| 4-... 4- сС2+і |х[.
(4.5)
«о + О] • Х^г 4- ... 4- 0:^2 Х1' 4-
▼+1
+ + С1 ‘ 4-... 4- Ук\ (4.6)
/с = 1,М; Ср^О, р=1,С^+1,
де к — номер виміру, дані з яких використовуються.
Завдання полягає в тому, щоб мінімізувати область зміни
вихідних значень ¥ за рахунок відшукання таких значень
ширини інтервалів — шуканих коефіцієнтів с, і таких зна-
чень центрів інтервалів а<, і = 1,СЗ+1, які забезпечували б
мінімальне розсіювання величини ¥ одночасно з виконанням
умови, що всі вимірювані значення шуканої величини зна-
ходяться в цьому інтервалі. Ця задача є задачею лінійного
програмування. Для її рішення перейдемо до двоїстої задачі.
Вона запишеться в такий спосіб:
шах
м м
У^ &к — &к+М — 0
*=1 к=1
м м
-^кі ’ $к Х^г ' <5к+Л/
к=1 *:=!
(4-7)
(4-8)
м м
к=1 к=1
4.5. Нечіткий метод групового обліку аргументів
259
л; м
&к + У $к+м А/
к=1 к=1
М М М
У + У |Хь| 5к+м У |А/й|
Ь=1 к=1 к=1
(4-9)
м м м
<5й^0; к = 1,2М.
Це задача лінійного програмування. Вирішивши двоїсту
задачу симплекс-методом і одержавши оптимальні значення
двоїстих змінних, ми зможемо знайти й оптимальні значення
шуканих змінних с, і а», г = 1, С>+і, а разом з цим і визначити
шукану модель математичної залежності.
Опис ряду селекції
Щоб одержати моделі другого ряду необхідно задати
опорну функцію, аргументами якої є функції-моделі, отри-
мані у попередньому ряді.
У нашому випадку опорна функція задавалася також по-
ліномом другого (г-того) ступеня від двох змінних, тобто
У^'+1 = / (К*> , де А: — номер ряду.
У кожнім ряді після генерації всіх можливих моделей за
комплексним критерієм у площині критеріїв відбиралися Г
кращих моделей, що беруть участь у подальшій генерації.
Критерієм зупинки процесу генерації є близькість середнього
260
Розділ 4. Метод групового урахування аргументів ...
критерію моделей ряду на двох сусідніх рядах роботи методу,
тобто:
-є < -N^л<є.
При генерації моделей може виникнути явище индуцита,
що зв’язане з тим, що після ряду ітерацій Р моделей к-го
ряду стануть майже нерозрізняні між собою (стануть колі-
ніарними). Для боротьби з цим явищем вид опорної функції
не змінюють, а замість одного з аргументів беруть модель
попереднього ряду, тобто = / (X*1, Кі*) •
Загальний опис алгоритму
1. Вибір загального виду моделі, яким буде описуватися
шукана залежність.
2. Вибір зовнішніх критеріїв оптимальності і свободи ви-
бору.
3. Вибір загального виду опорної функції (для багато-
рядних алгоритмів МГУА).
4. Покласти нульові значення лічильнику числа моделей
к і лічильнику числа рядів г.
5. Генеруємо нову часткову модель. Визначаємо значення
основних критеріїв на ній. Присвоїти к = к + 1.
6. Якщо к Ср, то к = 0, г = г + 1. Складаємо середній
критерій моделей ряду т А^. Якщо г = 1, то переходимо на
крок 5, інакше — на крок 7.
7. Якщо £> то йдемо на крок 8, інакше ви-
бираємо Р кращих моделей відповідно до зовнішніх критеріїв
і переходимо на крок 5.
8. З Р кращих моделей за критерієм регулярізацїї виби-
раємо кращу модель. Відновлюємо аналітичний вид кращої
моделі, використовуючи гьоделівську нумерацію.
4.6. Аналіз різноманітних видів функцій приналежності
261
4.6. Аналіз різноманітних видів
функцій приналежності
У перших роботах, присвячених нечіткому МГУА [8, 9],
розглядалися функції приналежності нечітких коефіцієнтів
трикутного вигляду. Оскільки нечіткі числа можуть мати й
інший вигляд ФП, важливим є аналіз інших класів ФП в за-
дачах моделювання на основі МГУА. В роботі [14] розглянуті
нечіткі моделі з гаусівськими та дзвоноподібними ФП.
Нечіткі числа з гаусівською ФП
Назвемо нечітким числом В з гаусівською ФП нечітку
множину з ФП вигляду
у в (ж) = е-2’( . (4-Ю)
Таке НЧ задається парою чисел /? = (а, с), де а — центр, а
с — величина, що характеризує ширину інтервалу (рис. 4.4).
Нехай оціночна лінійна ін- . .
НУ)
тервальна модель для частко-
вого опису НМГУА має ви- 1 _ ~
гляд (4.10). Тоді задача ста- / \
виться так: знайти такі нечі- / \
ткі числа А,, тобто параметри а--------7——V-----------
(сНігСі), ЩОб / \
1. спостереження Ук належа- ---------
ло даній оціночній множині І * *
Уі уг
Ук зі ступенем, не меншим за
Рис. 4.4. Підмножина рівня а
а, 0 < а < 1;
2. ширина оціночного інтервалу рівня а була б мінімальною.
Ширина оціночного інтервалу рівня а дорівнює (див.
рис. 4.4):
<іа = У2 - Уі = 2 (у2 - а),
262
Розділ 4. Метод групового урахування аргументів ...
де (т/2 — о) визначається з умови
(4-11)
Звідси с?о = 2с • V— 21па.
Отже цільову функцію можна записати у вигляді:
м ІИ
тіп У2 = тіп 22 2Ску/—21па =
к=1 к=1
М ті
= 2у/-2\патіп 2222 С, 1^1- (4-12)
к=1 і=1
Так як 2 у/—21п а — додатна константа, що не впливає на
набір Сі, який мінімізує цільову функцію (4.12), то можна
розділити цільову функцію на цю константу та отримати ці-
льову функцію у початковому вигляді.
Тепер розглянемо першу вимогу: р (гд) а.
Вона еквівалентна ехр | а. Ця нерівність
зводиться до системи нерівностей вигляду:
ак + ск\/-21па ук; ак - сьУ-21п а ук. (4.13)
Враховуючи, що
п п
Як = 2 Яі^кі, Ск = 2 Сі Ц&І,
і=1 і=1
задача знаходження нечіткої моделі зводиться остаточно до
задачі ЛП наступного вигляду:
(м л/
с0 м+Сі 22 м +
к=1 к=1
м м м \
+ Сз 22 кь + С4 22 |4і| + С3 22 |4,| І > (4-14)
к=1 к=1 к=1 /
-1.6- Аналіз різноманітних видів функцій приналежності
263
за умов:
2
ао + о,\Хкі + ... + а5іс^+
+ (Со + С\ |ж*і| + ... + С5 |ж^|) • 21па ук
а,о + а^Хкі + ... + а^х“кз
— (Со 4- Сі |хн| + ... + С5 |х^|) • а/—21па ук
к = 1,М.
Для розв’язання цієї задачі, як і у випадку ФП трикутного
вигляду, можна перейти до двоїстої задачі вигляду:
См м
Е ~ Е ' $к+м
к=1 к=1
(4-16)
за умов-рівностей (4.8) та умов-нерівностей:
м м
Е ^к+е ^к+м
1=1 к=\
м
у/—21п а
м л/
У2 $к+м
к=1 к-1
м
ЕІ^НІ
А^-1__
21па
л/ м Е
Е 1^11 • ^+Е 141 ’
(4-17)
<5*^0, 1,2М.
Цю задачу можна розв’язати стандартними методами.
264
Розділ 4. Метод групового урахування аргументів ...
Нечіткі моделі з дзвоноподібною
функцією приналежності
Розповсюджений клас нечітких чисел становлять НЧ з
дзвоноподібною ФП вигляду
"«м =
Таке НЧ В задається парою
чисел В = (а, с), де а — центр, а с
— величина, що характеризує ши-
рину функції (рис. 4.5).
Для нечіткої моделі:
V = Ао + Дія:, + Аях^
+А3ХіХі + Д4ГГ? + А5а;2
відповідна задача ЛП для знаходження невідомих параме-
трів (а», Сі) має вигляд:
(м м
Со • М + Сі і^ьіі + Сг 5 Іа:іу|"Ь
Ь=1 к=1
м м м \
+ Сз £ |хн а^-І + С4 £ |^| + С5 52 1 , (4.18)
к=і *=і /
р(х)
а ~х
Рис. 4.5. Дзвоноподібна ФП
за умов:
ао + а^Хкі + ... + а,5х‘^+
/1 — о?
+ (Со + Сі |я:н| + ... + С5 |х^|) у ~ Ук,
2
Оо + СІїХкі + ... + <і^,х^—
І ~| _
- (Со + Сі |гги| + • • • + С5 |х^-|) у — Ук',
к = ї^, Сі > 0, і = Д5.
(4-19)
Перейшовши від неї до двоїстої, можна знайти шуканий
розв’язок за допомогою стандартних методів ЛП.
4.6. Аналіз різноманітних видів функцій приналежності
265
Адаптація нечітких моделей
При прогнозуванні з використанням методів самооргані-
зації (зокрема НМГУА) виникає проблема корекції отрима-
ної моделі в процесі її використання для прогнозування при
одержанні нових експериментальних даних.
Оскільки повний перерахунок моделі напряму потребує
великих обчислювальних затрат, більш раціональним є ада-
птація коефіцієнтів знайденої на попередньому етапі опти-
мальної моделі методом МГУА. У роботі [8] розглянуто та
досліджено алгоритм адаптації на основі методу стохасти-
чної апроксимації.
Метод стохастичної апроксимації дозволяє просто врахо-
вувати нові дані, що надходять, і належить до рекурсивних
методів структурної ідентифікації. Оцінка Рп+і вектора па-
раметрів на кроці (п+ 1) за умови, що відома оцінка вектора
Р на кроці п, визначається так:
Рп+і = Рп~ Рп^п, (4.20)
де Фп — функція, яка залежить від Іп (рп) — скалярного
критерію якості ідентифікації (наприклад, інтегральний се-
редньоквадратичний критерій); рп — величина кроку.
Умови збіжності методу:
ОО оо
1. рп —> 0 при ті —> оо; 2. рп = оо; 3. У^ р„ < оо.
п—0 п=0
Якщо за критерій оптимізації взяти критерій І(Р) =
= (у — Ф (X, Р))2 , де Р = (рі,р2,... ,р*;) — вектор шуканих
параметрів нечітких коефіцієнтів, то
Ф =
дГ
ді
дрк
(4-21)
дрк
12і
266
Розділ 4. Метод групового урахування аргументів ...
У випадку лінійної моделі відносно параметрів Р = [р*]
рекурентне співвідношення (4.21) для пошуку невідомого на
(п 4- 1)-му кроці параметра р*. запишеться так:
рк [п + 1] = рк [п] + рп (уп+і - Ф (X [п + 1], Р [п]) • хк [п + 1])
п = 0,1,2...
4.7. Експериментальні дослідження нечіткого
МГУА та застосування в задачах
макроекономічного прогнозування
У роботах [7, 14] проводилися дослідження алгоритмів не-
чіткого МГУА з трикутною ФП в задачах прогнозування ма-
кроекономічних показників України. В якості вихідної вели-
чини, яка прогнозується, було обрано ІСЦ — індекс спожив-
чих цін. В якості істотних вхідних змінних за результатами
регресійного аналізу були обрані наступні змінні ІСЦ пото-
чного періоду; ЮЦ поточного періоду; грошовий агрегат М2
(лаг — 7); об’єм кредитів, вкладених в економіку (лаг — 7);
офіційний обмінний курс долара на поточний період.
Наведемо деякі з отриманих результатів виконаних екс-
периментів.
1. Результати структурної ідентифікації на вікні прогно-
зування розміром у 15 точок, з яких 10 було виділено на
навчальну й 5 — на перевірочну вибірку. При ідентифікації
на наступний етап синтезу передавалося 10 кращих моделей
поточного етапу.
Використовуваний частковий опис:
А)0 + Аи х\ + ТІ02 х2 + ^412 Зц • х2-
Величина СКП: 0,7119462.
2. Результати структурної ідентифікації на вікні прогно-
зування розміром у 12 точок, з яких 7 було виділено на на-
вчальну й 5 — на перевірочну вибірку. Останні 3 точки, пред-
4.7. Експериментальні дослідження нечіткого МГУА...
267
ставлені на графіку, прогнозовані у покроковому режимі без
адаптації коефіцієнтів моделі. При ідентифікації на насту-
пний етап синтезу передавалося 10 кращих моделей поточно-
го етапу.
Використовуваний частковий опис:
Лоо + Лої Хі + А)2 2-2 + -А12 • Ті • Х2 + Лц • + А22 ' х\.
Величина СКП (на вибірці, що складається з навчальних
і прогнозованих точок): 0,249623.
3. Результати структурної ідентифікації па вікні прогно-
зування розміром у 12 точок, з яких 7 було виділено на на-
вчальну й 5 — на перевірочну вибірку. При ідентифікації на
наступний етап синтезу передавалося 10 кращих моделей по-
точного етапу.
Використовуваний частковий опис:
Лоо + Лої • Хі + Ло2 Х-2 + -<412 ' Хі Х2 + Ац Х{ + -422 ’ %2-
Величина СКП: 0,116168.
4. Результати структурної ідентифікації на вікні прогно-
зування розміром у 12 точок, з яких 7 було виділено на на-
вчальну й 5 — на перевірочну вибірку. При ідентифікації на
наступний етап синтезу передавалося 10 кращих моделей по-
точного етапу.
Використовуваний частковий опис:
Лоо + Лої Х1 + Ло2 • Х2-
Величина СКП: 0,7151176.
5. Прогноз 10 точок за допомогою моделі, синтезованої
єдиний раз, без покрокової адаптації коефіцієнтів.
Використовуваний частковий опис:
Лоо + Лої Хі + Лог • Х2 + Л12 • Хі %2 + Лц • + Л22 • х%-
Величина СКП на прогнозованих точках: 0,990959
12*
268
Розділ 4. Метод групового урахування аргументів ...
6. Прогноз тих же 10 точок, що і в пункті 5, за допомо-
гою покрокової адаптації коефіцієнтів прогнозуючої моделі
(адаптація використовувалася у випадку виходу реального
значення змінної, яка прогнозується, за прогнозовану смугу).
Використовуваний частковий опис:
Лоо + А)1 • Х1 + А)2 • х2 + Л12 • Х1 х2 + Лп Х1 + -^22 ’ х2'
Величина СКП на прогнозованих точках: 0,813633824.
7. Прогноз 11 точок за допомогою покрокової адаптації
коефіцієнтів прогнозуючої моделі (адаптація використовува-
лася у випадку виходу реального значення змінної, яка про-
гнозується, за прогнозовану смугу).
Використовуваний частковий опис:
Лоо + Лої • Х1 + Ло2 • х2 + Л12 • Х\ • Х2 + Лц • Тд + Л22 • х2-
Величина СКП на прогнозованих точках: 0,88312.
8. Прогноз тих же 11 точок, що і в пункті 8, за допомогою
моделі, синтезованої єдиний раз, без покрокової адаптації ко-
ефіцієнтів.
Використовуваний частковий опис:
Лоо + Лої + Л02 • х2 + Л12 Х1 • Х2 + Лп • Тд + Л22 ’ Х%-
Величина СКП на прогнозованих точках: 1,16648.
Аналіз результатів
Як видно з наведених нижче графіків (рис. 4.6 — 4.9)
ідентифікація структури моделей з використанням нечітко-
го МГУА дає досить високі результати при прогнозуванні
навіть для моделей з лінійними частковими описами. Для лі-
нійних моделей СКП не перевищує значення 0.72, для описів
вигляду
Лоо + Лої Х1 + Ло2 • х2 + Л12 • Х1 • а?2 + Лді • Тд + Л22 Х%.
' СКП не перевищує значення 0,3.
4.7. Експериментальні дослідження нечіткого МГУА...
269
Найкращі результати структурної ідентифікації та про-
гнозування отримані на вікні розміром у 12 точок ( тобто
при розмірах вікна, отриманих за допомогою регресійного
аналізу) при використанні квадратичних часткових описів і
максимальній можливій свободі вибору (на кожному етапі
синтезу обиралися 10 кращих моделей).
Довгострокові прогнози величини ІСЦ в результаті вище-
описаних експериментів мають високу якість (як для моде-
лей з покроковою адаптацією коефіцієнтів, так і без неї), що
свідчить про можливість успішного застосування нечіткого
МГУА в задачах довгострокового прогнозування макро-
скономічних показників для економіки перехідного періоду.
Особливо цікавим було порівняння результатів прогнозування
з використанням моделей, які адаптуються, та без адаптації.
В усіх експериментах точність прогнозу з адаптацією кое-
фіцієнтів моделі виявилася дещо вищою. Так при прогнозі 10
точок (з 09.1998 по 06.1999) СКП для моделей з адаптацією
й без адаптації склала відповідно 0,813634 та 0,99096.
При прогнозі 11 точок (з 02.1998 по 12.1998) СКП скла-
ла 0,88312 та 1,16648 відповідно. Ці результати свідчать про
доцільність застосування адаптації для коригування коефі-
цієнтів моделі за даними, що знову надходять та дозволяють
уникнути великого об’єму обчислень, пов’язаного з повтор-
ним синтезом моделі. Однак слід відзначити, що в умовах
економіки перехідного періоду залежність між вхідними й
вихідним процесами може істотно змінюватися на коротко-
му відрізку часу й адаптація коефіцієнтів моделі може не
дати бажаного ефекту, тому що поточна модель стає неаде-
кватною, і тоді потрібен синтез нової моделі. Отже, для під-
вищення точності прогнозу необхідно визначити деякий ба-
ланс між адаптацією існуючої моделі й синтезом нової моделі.
Зокрема, значна помилка прогнозу є сигналом для синтезу
нової моделі.
122
270
Розділ 4. Метод групового урахування аргументів ...
Приклад 1.
Прогнозоване значення Точне значення Відхилення Квадрат відхилення
-0,53722196 -0,09862794 0,33996608 0 0,09862794 0,00972747
0,829243012 1,267837031 1,70643105 1,2 0,06783703 0,00460186
0.751614352 1,19020837 1,62880239 0,9 0,29020837 0.0842209
0,605627406 1,044221425 1,48281544 0,9 0,14422143 0.02079982
0,540008112 0,97860213 1,41719615 1,4 0,42139787 0,17757616
0,177188037 0,738594019 1,3 1,3 0,56140598 0,31517668
-0,00701998 0,431574042 0,87016806 0,2 0,23157404 0,05362654
-0 55478555 -0,11619153 0,32240249 0,2 0,31619153 0,09997709
0 847198903 1,285792922 1 72438694 1,3 0,01420708 0,00020184
-0,23758945 0,201004569 0,63959859 0 0,20100457 0,04040284
-0,15179696 0,286797055 0,72539107 0 0,28679706 0,08225255
-1,35272226 -0,91412824 -0,4755342 -0,9 0,01412824 0,00019961
-0,03090259 0,407691428 0,84628545 0,2 0,20769143 0,04313573
3,396947499 3,835541518 4,27413554 3,8 0,03554152 0,0012632
5,722489177 6,161083196 6,59967721 6,2 0,0389168 0,00151452
СКВ 0,24962329
Розмір ковзного вікна: 12 точок; розмір навчальної вибірки: 7 точок;
розмір перевірочної вибірки: 5 точок; останні 3 точки прогнозовані.
Частковий опис, використовуваний при синтезі моделей:
Ао + Аі ’ ті + Аг ’ х2 + Аг' хі ’ х2 + Аі ’ хі + Аг ‘ х2-
Рис. 4.6. Графіки прогнозованих і точних значень (приклад 1)
4.7. Експериментальні дослідження нечіткого МГУА...
271
Приклад 2.
Прогнозоване значення Точне значення Відхилення Квадрат відхилення
0,741907027 0,820953513 0,9 0,9 0,07904649 0,00624835
1,4 1,530499329 1,66099866 1,4 0,13049933 0,01703008
0,852220261 1,07611013 1,3 1,3 0,22388987 0,05012667
0,2 0,276785899 0,3535718 0,2 0,0767859 0,00589607
0,2 0,284920755 0,36984151 0,2 0,08492076 0 00721154
1,104810941 1,202405471 1.3 1,3 0,09759453 0,00952469
0 0,135304494 0,27060899 0 0,13530449 0,01830731
-0,87951073 -0,1034006 0,67270953 0 0,1034006 0,01069168
-1,76330477 -0,98719464 -0,2110845 -0.9 0,08719464 0,00760291
-0,40601665 0,370093479 1,14620361 0,2 0.17009348 0,02893179
3,007468704 3,783578834 4,55968897 3,8 0,01642117 0 00026966
5,433833205 6,209943335 6,98605347 6,2 0,00994334 9.89Е-05
скв 0,11616784
Розмір ковзного вікна: 12 точок; розмір навчальної вибірки: 7 точок;
розмір перевірочної вибірки: 5 точок.
Частковий опис, використовуваний при синтезі моделей:
А10 "Ь Ал ' 3-І "Р А)2 ’ "Р А]2 ’ Т] * Х2 + А1 Хі 4“ ^22 ’
12**
272
Розділ 4 Метод групового урахування аргументів ...
Приклад 3.
Прогназоване значення Точне значення Відхилення Квадрат відхилення
3.96 4,4 4,84 6,2 1,8 3,24
2,36 2,8 3,24 3 0,2 0,04
2,51 2,95 3.39 3,3 0,35 0,1225
1,61 2,05 2,49 1,5 0,55 0,3025
1,36 1,8 2,24 1 0,8 0,64
1,36 1,8 2,24 1 0,8 0,64
2,01 2,45 2,89 2,3 0,15 0,0225
2,06 2,5 2,94 2,4 0,1 0,01
0,91 1,35 1,79 0,1 1,25 1,5625
-1,24 -0,8 -0,36 -1 0,2 0 04
СКВ 0,81363382
Прогноз 10 точок було отримано шляхом прогнозування наступної
точки за допомогою моделі з коефіцієнтами, які адаптуються на кож-
ному кроці.
Розмір ковзного вікна: 12 точок; розмір навчальної вибірки: 7 точок;
розмір перевірочної вибірки: 5 точок.
Частковий опис, використовуваний при синтезі моделей:
До ~Р -Дії Т] "Р А? ’ "Р Аг Ті • Х% + А1 • Ті “Р Л22 • т2.
Кількість описів, які передаються на наступний етап синтезу: 10.
Рис. 4.8. Графіки прогнозованих і точних значень (приклад 3)
4.7. Експериментальні дослідження нечіткого МГУА...
273
Приклад 4.
Прогнозоване значення Точне значення Відхилення Квадрат відхилення
0,447247747 1,376050257 2 30485277 0,2 1,17605026 1,38309421
0,35431648 1,297410503 2,24050453 1,3 0,0025895 6,71Е-06
-0,82637542 0,102427091 1 0312296 0 0,10242709 0,01049131
-0,7749941 0,150991763 1,07697763 0 0,15099176 0,02279851
-1,02358967 -0,09478716 0,83401535 -0,9 0,80521284 0,64836772
-0,66598734 0,260363951 1,18671524 0,2 0,06036395 0,00364381
1,197507568 2,12504098 3,05257439 3,8 1,67495902 2,80548772
3,6 4,4 5,2 6,2 1,8 3,24
2 2,8 3,6 3 0,2 0.04
2,15 2,95 3 75 3,3 0,35 0,1225
1.25 2,05 2,85 1,5 0,55 0,3025
СКВ 0,88311896
Прогноз 11 точок було отримано шляхом прогнозування наступної
точки за допомогою моделі з коефіцієнтами, які адаптуються на кож-
ному кроці.
Розмір ковзного вікна: 12 точок; розмір навчальної вибірки: 7 точок;
розмір перевірочної вибірки: 5 точок.
Частковий опис, використовуваний при синтезі моделей:
Аш + Аі' Ті + Др ' Тг + Аг • • Тг + Аі ’ хі "Ь Аг ’ х2-
Кількість описів, які передаються на наступний етап синтезу: 10.
12і
274
Розділ 4- Метод групового урахування аргументів ...
Результати експериментів
з різними ФП
З метою дослідження впливу на якість прогнозування ви-
ду функцій належності нечітких моделей було проведено екс-
перимент з моделювання невідомої функції з використанням
програмної реалізації описаного вище алгоритму НМГУА з
використанням різних ФП.
У якості вхідних даних було взято наступні макроеконо-
мічні показники (дані з квітня 1996 р. по червень 1999 р.):
номінальний ВВП (НВВП);
відсоток зміни індексу споживчих цін (%ІСЦ);
відсоток зміни індексу оптових цін (%ІОЦ);
індекс реальної промислової продукції (ІРПП);
ставка рефінансування НБУ за минулий місяць (СР).
Вихідною прогнозованою змінною було значення номі-
нального ВВП у наступному місяці.
Параметри моделювання: Масив вхідних даних розміром
28 точок було розбито на 11 вікон (проміжків) даних, за яки-
ми будувалася модель. Розмір кожного вікна склав 12 точок,
кожне наступне вікно було отримано зсувом на один місяць
відносно попереднього.
Після цього здійснювався прогноз НВВП(+1) на 5 кроків
вперед.
На кожному етапі синтезу НМГУА обиралося 7 кра-
щих повних квадратичних моделей часткових описів Спів-
відношення критеріїв регулярності та незміщеності у визна-
ченні похибки часткових описів 0,7/0,3. Для гаусівської та
дзвоноподібної функцій приналежності задавався рівень зна-
чимості 0,7.
Результати експериментів наведені в табл. 4.1, 4.2.
4.8. Порівняльний аналіз результатів прогнозування
275
Таблиця 4.1.
Точність прогнозування в залежності від типу ФП
Номер вікна М8Е
Трикутна ФП Гаусівська ФП Дзвоноподібна ФП
1 1669,862 1655,426 1652,184
2 458.4141 449,6609 447,6822
3 830,1062 826,8912 826,1713
4 1362,054 1353,997 1352,193
5 1858,873 1845,201 1842,133
Середнє: 1235,862 1226,235 1224,073
Таблиця 4.2.
Порівняльний аналіз гаусівської та дзвоноподібної ФП
__________з різними рівнями значимості.________________
Рівень значимості М8Е з гаусівською ФП М8Е з дзвоноподібною ФП
0,3 1368,135 1365,201
0,5 1366,106 1363,162
0,7 1361,489 1361,162
0,8 1361,796 1358,851
0.9 1359,482 1359,201
4.8. Порівняльний аналіз результатів
прогнозування за чітким і нечітким МГУА
Було проведено порівняльні експериментальні дослідже-
ння чіткого й нечіткого алгоритмів МГУА в задачах прогно-
зування макроекономічних показників. У якості змінної, яка
прогнозувалася, було взято ВВП України. В процесі експе-
риментів змінювалися об’єм вибірок, співвідношення між об-
сягом навчальної та перевірочної вибірки, кількість кращих
моделей, які передавалися на наступний рівень.
Деякі з отриманих результатів наведені нижче.
] 2***
276
Розділ 4. Метод групового урахування аргументів ...
Приклад 5.
У цьому прикладі використовувалася вибірка з 49 точок,
з яких ЗО було виділено на навчальну, 19 на перевірочну. При
ідентифікації на наступний етап синтезу передавалося 7 кра-
щих моделей. Використовувався повний квадратичний опис:
у — Л0Ч-Лої + Лог Ч-Лц -х%+А22 Лі2’Хі -Х2.+Лої 'хі
Результати прогнозування наведені на рис. 4.10.
Величина СКП на прогнозній вибірці:
558174 — у нечіткому алгоритмі МГУА;
1071791 — у чіткому алгоритмі МГУА.
Приклад 6.
У цьому прикладі використовувалася вибірка з 49 точок,
з яких 35 було виділено на навчальну, 14 на перевірочну. При
ідентифікації на наступний етап синтезу передавалося 7 кра-
щих моделей. Використовувався повний квадратичний опис:
у — Ло + Лої-Хі + Ло2 ’Х2 + Лц-Х? + Л22 Л12-Ті-Т2. + Лої 'Х1
Результати прогнозування наведені на рис. 4.11.
Величина СКП на прогнозній вибірці:
249863 — у нечіткому алгоритмі МГУА;
521658 — у чіткому алгоритмі МГУА.
Приклад 7.
У цьому прикладі використовувалася вибірка з 49 то-
чок, з яких 25 було виділено на навчальну, 24 на перевіро-
чну. Останні 5 точок представлені на графіку, прогнозовані у
покроковому режимі без адаптації коефіцієнтів моделі. При
ідентифікації на наступний етап синтезу передавалося 7 кра-
щих моделей. Використовувався повний квадратичний опис:
у = ЛоЧ-Лої’-Ті Ч-Лог'^гЧ" Лц-а?} Ч-Лгг'Т^Ч-Л12-Ті-Х2.Ч-Лої-Хі
Результати прогнозування наведені на рис. 4.12.
Величина СКП на прогнозній вибірці:
1061710 — у нечіткому алгоритмі МГУА;
1652718 — у чіткому алгоритмі МГУА.
4.8. Порівняльний аналіз результатів прогнозування
277
278
Розділ 4. Метод групового урахування аргументів ...
З наведених результатів бачимо, що нечіткий алгоритм
МГУА виявляється точнішим за чіткий алгоритм МГУА. Це
пояснюється наступними перевагами нечіткого МГУА:
— відсутня проблема поганої обумовленості матриць,
оскільки нема необхідності застосовувати МНК, а задача ЛП
завжди має розв’язок;
— отримуємо інтервальну, а не точкову оцінку прогнозної
величини, що дозволяє оцінити точність одержуваних про-
гнозів.
У залежності від параметрів, що варіюються в експери-
ментах, можна зробити наступні висновки:
— велика кількість вхідних параметрів безсумнівно підви-
щує якість прогнозів як в чіткому, так і в нечіткому алгори-
тмах МГУА;
— при однаковій кількості вхідних параметрів зміна спів-
відношення між навчальною та перевірочною вибірками
(збільшення навчальної та зменшення перевірочної) веде до
погіршення результатів прогнозу. Зокрема, нечіткий метод
дає ширший інтервал значень, чіткий — більш згладжену
криву;
— застосування нечіткого МГУА в задачах прогнозування
економічних процесів зі складною динамікою та невідомим
функціональним взаємозв’язком між процесами є цілком ар-
гументованим і дозволяє отримати відносно високу точність
прогнозу;
— використання адаптації коефіцієнтів знайденої нечіткої
моделі за поточними даними дозволяє підвищити точність
прогнозування на 15—20%.
— результати прогнозування за нечітким МГУА практи-
чно мало залежать від типу функцій приналежності Є деяка
перевага гаусівської та дзвоноподібної ФП перед трикутною.
4.9. Метод прогнозування багатовимірних випадкових процесів 279
4.9. Метод прогнозування
багатовимірних випадкових процесів
на основі комплексування аналогів
Нехай є деякий багатовимірний випадковий процес х (і) =
= [ат, (і)]л=ї-^ , і = 0,1,..., Т, заданий у вигляді матриці спо-
стережень X = ||Ху||, де х3 — ознаки процесу, і = 1,7 —
рядки, що відповідають моментам спостережень. Необхідно
по даній вибірці спостережень X спрогнозувати стан процесу
в момент часу (7 + 1), тобто знайти х3 (Т + 1), і = 1, т.
Один з методів прогнозування — це метод комплексува-
ння аналогів. Він базується на наступній гіпотезі. Якщо ми
на передісторії знайдемо деяку ситуацію А3, що збігається
або близька до спостерігаємо! в поточний момент х3 (ї), то
є всі підстави за прогнозований стан х (і + 1) вибрати насту-
пний за аналогом стан процесу, що позначимо через хі,
І = 1,771.
Такий підхід виправданий у випадку, коли в базі даних
накопичена досить велика статистика, і для кожної можливої
ситуації можна знайти близький аналог (чи аналоги).
Він широко використовується в метеорології, чи прогно-
зуванні погоди і кліматичних змін. Точність прогнозу може
бути підвищена, якщо використовувати не один, а декілька
аналогів.
Розглянемо формальну постановку методу. Нехай є ви-
бірка даних X — {.Ту}, де г = 1,ТУ — рядки спостережень,
] = 1, т — ознаки. Припустимо, що {Лі. А%,..., Л/у} — ряд-
ки, що спостерігаються, а В — останній (поточний) рядок,
що описується набором .т^, і — 1, т ознак. Потрібно знайти
значення процесу в наступний момент часу (ТУ + 1).
280
Розділ 4. Метод групового урахування аргументів ...
Ідея методу полягає в наступному. Серед рядків
розшукуємо Г (Р > 1) найближчих аналогів до
рядка В. Як міра близькості А, й В може бути використана,
зокрема, евклідова метрика:
= ||х.4і - хв||.
1. Розглянемо випадок, коли число аналогів 2 (р = 2).
Нехай найкращими аналогами для В виявилися Аі і А2,
для яких с?(Ді,В) сі(А2,В') < тіп с!(Аг, В).
Нехай х3 — значення рої змінної, прогнозоване по А і
(тоото наступний стан за рядком АД х- — значення 7-ої
змінної, прогнозоване по А2. Тоді прогнозоване по
в
значення X, визначається з виразу:
стану В
Аі Аі
х} 1% + Хі І?
І^І2
(4.22)
Тут /я = гі(А1,В), = Й(А2,В).
Вираз (4.22) можна розглядати як сплайн-апроксимацію
п -А1
по двум аналогам. Причому, якщо 1[‘ —> 0, то х3 —» ху .
2. Розглянемо тепер випадок довільного числа аналогів Р
(1 <р<72-1).
У цьому випадку прогнозоване значення змінної х3 визна-
чається так:
(4.23)
де розглядаються аналоги А,, і = 1,Р, р = (ЦАк,В).
Зазначемо, що якщо 1^ —> 0, то —> х3 , що цілком ви-
правдано.
4.9- Метод прогнозування багатовимірних випадкових процесів 281
У методі комплексування аналогів виділяється два етапи
[17|:
— етап навчання (чи настроювання системи прогнозуван-
ня);
— етап прогнозування.
Перший етап. Навчання.
На цьому етапі розглядається ковзний рядок В, що займає
положення і, і = 1, N (див. рис. 4.13).
Нехай число аналогів Р = 2.Для ковзного рядка В, що
знаходиться в положенні і, визначаємо два найближчих ана-
логи. Нехай ними виявилися і Аг-
Знаходимо сплайн-апроксимацію згідно (4.23). Позначимо
її через їу (Аі, Д2) •
Далі порівнюємо її з дійсним значенням х^, оцінюваним
по рядку В (тобто в рядку, що слідує за В).
Обчислюється помилка прогнозу
Дху = - хі} (Аі, Л2)і
Величини Ату = — Ху(А], А2)| записуються в допо-
міжну матрицю розміром N х т, по якій обчислюються час-
ткові ковзні критерії:
N
= (4.24)
І=І
Як критерій вибору оптимального рішення використовується
критерій несуперечності ковзного середнього СУ, що забез-
печує
1=1
На етапі навчання вирішуються задачі вибору оптималь-
ного числа аналогів Р — Рорі і числа ознак т = торі так, щоб
забезпечити тіп СУ (т, Р).
Ї71,К
282
Розділ 4. Метод групового урахування аргументів ...
Рис. 4.14. Етап прогнозування
4 9. Метод прогнозування багатовимірних випадкових процесів 283
Зазначена задача є комбінаторною задачею дискретної
оптимізації без обмежень, але з огляду на те, що число змін-
них у ній всього 2, пошук оптимальних значень можна здій-
снити шляхом перебору. Задача спрощується в зв’язку з тим,
що число аналогів Р обмежене (К С 3 4- 4), тому що експери-
менти показали, що при великих значеннях Р точність про-
гнозу знижується.
Після того, як на етапі навчання були визначені т° і Р°,
переходять до етапу прогнозу.
Другий етап. Прогнозування.
Ковзний рядок В займає крайнє нижнє положення г = ТУ,
визначаються для нього найближчі аналоги, наприклад Аі
в
І Ак, І ЗДІЙСНЮЄТЬСЯ ПРОГНОЗ = Хі(Аг,Ак) відповідно до
формули (4.23) (див. рис. 4.14).
Робота алгоритму комплексування аналогів приведена на
рис. 4.13 і 4.14.
Постановка задачі прогнозування
повторюваних випадкових подій
Функція мети У при прогнозуванні процесів не задається.
Вибірка містить тільки компоненти характеристичних векто-
рів матриці X. Чим більше кореляція між сусідніми рядками,
тим більше гранично досяжний час упередження прогнозу
процесу і тим ширші патерни.
Для рішення задачі прогнозування повторюваних випад-
кових подій необхідно крім матриці X задати також матрицю
векторів вихідних величин У. Для цієї задачі важливо, щоб
були корельовані стовпці вибірки X и вибірки У Кореляція
між рядками вибірки звичайно відсутня.
Для правильного прогнозу подій необхідні повнота і ре-
презентативність вибірок X и У.
284
Розділ 4. Метод групового урахування аргументів ...
1. Алгоритм не може прогнозувати подію, занадто далеку
від інших подій, зафіксованих у вибірці даних У, тобто ви-
бірка даних повинна містити повний набір подій усіх видів.
Вибірка даних є повного, якщо вона містить весь набір типо-
вих видів (кластерів) функціонування об’єкта спостереження.
2. Вибірка повинна бути репрезентативною. Це означає,
що кластери матриць X и У повинні збігатися за часом.
Для встановлення повноти і репрезентативності матри-
ці X и У піддаються автоматичному поділу на кластери за
одним з відомих критеріїв, наприклад, з використанням іє-
рархічного алгоритму кластер-аналізу.
Постановка задачі прогнозу повторюваних випадкових по-
дій може мати як загальний інформаційний вид, так і більш
спеціалізований причинно-наслідковий характер. При інфор-
маційній постановці повинна бути задана вибірка характери-
стичних векторів а, що містить результати вимірів всіх змін-
них, котрі можуть бути виміряні за N + 1 інтервалів часу.
Крім того, необхідно задати матрицю У, що містить N ряд-
ків. Потрібно прогнозувати вектор події У на N + 1 крок.
Наприклад, вибірка містить результати тестування 30-ти опе-
раторів, а відомі результати діяльності тільки 29-ти опера-
торів Потрібно дати прогноз результатів роботи останнього
оператора за даними 30-го характеристичного вектора.
Причинно-наслідкова постановка застосовна тільки для
деяких практичних задач. Тут вибірка X містить спостере-
ження причин подій числом N + 1. Наслідки наведені у ви-
бірці У тільки для перших N спостережень. Потрібно дати
прогноз наслідку для останнього (А + 1)-го вектора причин,
що повинний бути відомий Наприклад, вибірка X містить
спостереження способу обробки і метеоумов за N + 1 рік
Дані про врожай представлені у вибірці У тільки за N років.
Потрібно прогнозувати врожай на (А” + 1)-й рік.
4.9. Метод прогнозування багатовимірних випадкових процесів 285
Алгоритм прогнозування
повторюваних випадкових подій
Для прогнозування подій потрібно вирішити наступні за-
дачі:
— вибір оптимального числа комплексуючих аналогів Р =
= Р'орі'у
— вибір оптимальної множини ознак т = торі,
— вибір оптимального вектора функції мети ¥ = ¥орі.
Ширина патерна Ь. = 1 не підлягає зміні і дорівнює одно-
му рядку вихідної вибірки. Тому доцільно виконувати пе-
ребір компонентів вектора мети ¥. Спосіб зменшення числа
множин ознак, що підлягають перебору при прогнозуванні
подій, показаний на рис. 4.15
Тут бере участь не одна, а дві матриці даних — X и У, а
замість різниці прогнозів розраховуються різниці характери-
стичних векторів:
— |.Ту (^) (^1> -^2)|
Далі обчислюємо і заповнюєм матрицю ДХ = ЦДтуЦ.
Обчислюємо часткові критерії несуперечності ковзного се-
реднього N
сц = ^£|Дгц|,
І=1
а потім і повний критерій несуперечності ковзного середнього
7П
7=1
Показники СУ використовуємо для визначення опти-
мального числа ознак торі і числа аналогів Рор( Знаходимо
торі і Рор(, для яких СУ (торі, Рорі') = тіп СУ (т, Г).
286
Розділ 4 Метод групового урахування аргументів ...
4.9. Метод прогнозування багатовимірних випадкових процесів 287
Ці процедури ілюструються на рис. 4.15. На цьому етап
навчання закінчується, і ми переходимо до етапу прогнозу-
вання.
Другий етап. Тут задано характеристичний вектор
X (/V + 1). Потрібно спрогнозувати значення ¥ (її + 1)
(рис. 4.16).
Нехай Гор1 = 2. Для рядка В в матриці X знаходимо
два найближчих аналоги Ат і А}., далі в матриці У визна-
чаємо відповідні рядки у (Аг) і у (Ак). Здійснюємо сплайн-
апроксимацію і знаходимо У/у+і - ¥ (Аг, АД відповідно до
формули (4.23).
Розділ 5
ЕВОЛЮЦІЙНЕ МОДЕЛЮВАННЯ ЯК
МЕТОДОЛОГІЯ ВИРІШЕННЯ ЗАДАЧ
ШТУЧНОГО ІНТЕЛЕКТУ
5.1. Основні ідеї і механізми
еволюційного моделювання (ЕМ)
Еволюційне моделювання (ЕМ) сформувалося в роботах
Л. Фогеля, Оуена, М. Уолша. 5
Основна теза підходу, названого ЕМ — це замінити процес »
моделювання складного об’єкта, моделюванням його еволю-
ції. Він направлений на застосування механізмів природної
еволюції при синтезі складних систем обробки інформації. З
появою навчання Дарвіна в 1859 р. термін еволюція здобу-
ває сучасне тлумачення: «біологічна еволюція — історичний
розвиток організмів».
У своїй теорії походження видів Ч. Дарвін відкрив і об-
ґрунтував основний закон розвитку органічного світу, охара-
ктеризувавши його взаємодією трьох наступних факторів
• спадкоємної мінливості;
• боротьби за існування;
• природного відбору.
Дарвінівська теорія дістала підтвердження і розвиток у
генетиці та інших науках. Одним з найбільших еволюціоні-
стів, нашим співвітчизником 1.1. Шмальгаузеном були вису-
нуті наступні необхідні і достатні умови, що визначають не-
минучість еволюції [2]:
1. спадкоємна мінливість, тобто мутації як передумова
еволюції, її матеріал;
іі
5.2. Моделювання механізмів еволюції в складних системах
289
Рис. 5.1. Взаємодія факторів еволюції
2. боротьба за існування як контролюючий і направляю-
чий фактор;
3. природний добір як перетворюючий фактор.
Сучасний погляд на фактори еволюції і їх взаємодія пред-
ставлені на рис. 5.1.
5.2. Моделювання механізмів еволюції
в складних системах
Найбільш вживаною, глибоко дослідженою на різних по-
пуляціях і в різних конкретних задачах є наступна спроще-
на схема еволюції: породження нащадків, їхня оцінка і добір
кращих (селекція)
Розглянемо наступні приклади.
13і
290
Розділ 5. Еволюційне моделювання ...
Приклад 1. Еволюційна стратегія пошуку.
Мета: мінімізація /(х), х Є X.
Спадкоємна мінливість:
Популяція — послідовність{хі,х2,. • •, х3,..., хп}
Розмноження — х}і = х3 + г = 1... кг, і = 1... п;
Змагання — за значеннями / (х^).
Селекція (відбір) — N особин з імовірністю за значеннями
/(х). Тут — реалізація випадкового механізму (мутацій);
|£,і| характеризує інтенсивність мутацій. Величина рівно-
мірно розподілена в інтервалі [—1; +1].
Дану просту схему можна легко удосконалити, уводячи за
аналогією із природними закономірностями залежність чи-
сла породжених «нащадків» від значень оцінюючих функцій
батьків чи залежність інтенсивності мутацій від значень оці-
нюючих функцій особин.
Зокрема можна запропонувати такий метод, що одержав
назву «генетичного» Тут, як і раніше, популяція складається
з точок, кожна точка характеризується не тільки своїм поло-
женням, але і дисперсією ймовірнісного розподілу, за яким
породжуються нащадки. Розмноження здійснюється по на-
веденим у прикладі 2 формулам. Відмінність від приклада 1
незначна, однак введенням інтенсивності мутації (параметр
х*) у генотип, з однієї сторони істотно різноманітять спад-
коємну мінливість, а з іншого боку — посередньо залучають
інтенсивність мутацій у відбір. Тим самим параметр х* ви-
значає головний фактор еволюції — зміни, що не задаються
ззовні насильницьким методом, а регулюються за значення-
ми мінімізованої функції.
Приклад 2. «Генетичний метод пошуку».
Мета: мінімізація /(х).
Спадкоємна мінливість-
ПОПУЛЯЦІЯ — СуКуПНІСТь{Хі, Хр ..., хп, х*}
5.2. Моделювання механізмів еволюції в складних системах
291
Розмноження — Х]г = X] + Х*^і, X* = (х* * Т]]г)° , де £]г —
рівномірно розподілена в [—1; 1]; — рівномірно розподілена
В [0; 1];
а —
1, з імовірністю 1/2;
<
—1, з імовірністю 1/2.
Змагання — за значеннями за значеннями / (х^).
Селекція (добір) — N особин, найкращих за значеннями
/(*)
Приклад 3. «Автоматна модель еволюції» (рис. 5.2).
Мета: мінімізація (А|х°) — функції вартостей прогнозу-
вання послідовності {х°}.
Спадкоємна мінливість:
Популяція — кілька скінчених
автоматів.
Розмноження — список випадко-
вих змін:
1. убрати стан;
2. додати стан;
3. убрати зв’язок;
4. додати зв’язок.
Змагання — за значеннями функції (А|х°).
Селекція — за значеннями функції (А|х°) -
Приклад 4. Еволюційний синтез структури.
Мета: багатокрітеріальна багатопараметрична оптимізація
(х, у) —> тіп , х Є X, у Є У.
х,у
Спадкоємна мінливість:
Популяція — кілька гіперграфів
Розмноження — за списком випадкових змін:
1. додати (1 ребер;
2. видалити (1 ребер.
13*
292
Розділ 5. Еволюційне моделювання ...
Змагання — за значеннями функції <^(х,у).
Відбір — за значеннями функції <^(х, у).
Зауважемо, що приклади 3,4 реалізують еволюційні алго-
ритми структурного випадкового пошуку.
Формалізація класу структурованих моделей
Формалізація, що викладається нижче, базується на ос-
новних моделях системного підходу й аналізу, використову-
ючи категорії «об’єкт», «властивість», «відношення» [2].
Структурована модель Р (СМ Р) — це сукупність об’єк-
тів (елементів) /і, і Є І із властивостями дг і відношенням
між ними 5, що утворюють цілісний складений об’єкт, тобто
такий, який здобуває властивість ії, що є наслідком власти-
востей елементів і відношень, але не властива цим елементам,
узятим окремо.
Структурована модель Р здійснює відображення Р вхі-
дних функцій х (і) Є X дискретного аргументу і (і Є Тоо ;
і — —1,0,1, 2,...) у вихідні функції у (і) Є У того ж аргумен-
ту за допомогою набору операторів, із сукупності /, І відпо-
відно до відношення 5, що визначає порядок проходження чи
застосування /і, і Є І.
Якщо при відображенні СМ Р вхідної функції х (і) Є X у
вихідну у (і) Є У використовується набір операторів /і,---,
є {/, 1} то у (і) = [/і,..., /№ 5, х (і)] є суперпозицією
функцій /1, ..., /дг ПО відношенню 5.
Відношення, що фіксує набори функцій суперпозиції із
сукупності /, І (і порядок їх проходження при формуванні
вихідних функцій у (і) Є У), назвемо структурою СМ Р.
Таким чином, поведінка структурованої моделі Р визначає-
ться двома основними компонентами: сукупністю операторів
суперпозиції /, І і структурою 5. У залежності від конкре-
тного завдання типів цих компонентів розглядаються різні
класи СМ Р.
5.2. Моделювання механізмів еволюції в складних системах
293
Множина К = {({/, Дп},5т) | С {/,/}; $т Є 8}
із СМ Р називається класом (/, І,8) — структурованих
моделей із заданою сукупністю операторів суперпозиції.
Структуровані класи різні, коли різні типи операторів су-
перпозиції і (або) типи структур. Окремі класи СМ широко
відомі і добре досліджені, до них відносяться:
• класи функцій алгебри логіки, побудовані на різних си-
стемах елементарних булевих функцій (КНФ і ДНФ). Вирази
для 8т відповідної моделі Р визначаються при цьому видом
КНФ чи ДНФ;
• класи ортонормованих функцій;
• клас неорієнтованих і орієнтованих графів, мережі
Петрі, скінченні автомати (детерміновані і ймовірнісні) і так
далі.
Рис. 5.3. Класифікаційне дерево структур С-моделей
ІЗ2
294
Розділ 5. Еволюційне моделювання ...
На рис. 5.3 наведене класифікаційне дерево структур
С-моделей.
Сукупність операторів /, І називається функціонально
поєною, якщо будь-яке відображення Р можна представити
суперпозицією /, І на деякій структурі вр.
Клас Кр називається функціонально повним, якщо його
сукупність /, І є функціонально повного системою чи містить
функціонально повну підсистему [2].
Сукупність 8 називається структурно повною, якщо до-
вільне відображення Р можна представити суперпозицією де-
якого набору операторів /, І зі структурою в Є 8.
Клас К3 : ({/,І3},8) називається структурно повним,
якщо его сукупність 8 є структурно повною при деякому на-
борі операторів з {/, І3}
Твердження 1: Довільний клас К3 : ({/, І3} , 8) включає
клас Кі : ({/, Д} , 8і) тоді і тільки тоді, коли 8і С 8 і {/, р} С
Таким чином, будь-який клас А, що включає структурно
повний клас, сам є структурно повним. Аналогічне твердже-
ння вірне і для функціональної повноти класу.
Твердження 2: Довільний клас К : ({/, 1} , 8) включає
клас Кр : ({/. Ір} , 8р) тоді і тільки тоді, коли {/, 1} З {/, Ір}
і 8 З 8р.
Клас К називається повним, якщо він структурно і фун-
кціонально повний.
З тверджень 1 і 2 випливає наслідок: Довільний клас К є
повним, якщо він містить хоча б один К§ і Кр. Отже, пов-
ний клас К містить хоча б одну СМ Р, на якій реалізується
відображення у (і) = р (.т (і)).
Структурована модель Р%, що реалізує відображення
у (і) = Р (х (і)), і є Тоо з точністю до називається ^-на-
ближенням структурованої моделі Рр
5.3. Етапи процесу еволюційного синтезу
295
5.3. Етапи процесу еволюційного синтезу
Аналіз задачі синтезу функціонального відображення Р у
вигляді СМ із бажаними властивостями на основі формалі-
зації еволюційного моделювання дозволяє виділити наступні
етапи:
— вибір (завдання) класу С-моделей перетворювача Р;
— вибір (завдання) критеріїв синтезу ^-наближень і послі-
довності ^-наближень перетворювача Е;
— синтез ^-наближення перетворювача Р на часовому ін-
тервалі по звуженню вхідних і вихідних функцій, заданих
на інтервалі Тс, при і Є Тс С С Т;
— синтез послідовності £ -наближень перетворювача Р
(СМ-Г) на часовому інтервалі Т на основі збору нової ін-
формації і додаткового коректування процесів синтезу ^-на-
ближень.
При цьому формування довільної С-моделі здійснюється
за допомогою змін деякої С-моделі класу К на основі його
списку РЗ (режимів змінювання).
Кожна структурована модель складається з функціональ-
них та структурних елементів. Виходячи з загальноприйня-
тих понять структурні і функціональні елементи С-моделі
поділяються на прості та складені. Складені елементи деком-
позуються на прості елементи. Таким чином, будь-яка модель
складається з набору простих та складених, структурних та
функціональних елементів; причому для С-моделей одного
класу цей набір однотипний. Зміни елементів С-моделі базу-
ються на наступних типах дій:
— усунути один елемент із С-моделі та суперпозиції Е;
— додати один елемент в С-модель та суперпозицію Р.
Зміна на елементному матеріалі С-моделі називається
складеною, якщо вона являється композицією простих змін.
13**
296
Розділ 5. Еволюційне моделювання ...
Прості зміни першого типу на структурному елементі на-
зиваються структурними.
Прості зміни першого типу на функціональному елементі
називаються функціональними.
Проста зміна другого типу на структурному елементі на-
зивається функціонально-структурною.
Проста зміна другого типу на функціональному елементі
називається структурно-функціональною.
Зазначимо, що поняття «проста зміна» несе відносний ха-
рактер і на більш детальному рівні декомпозиції прості еле-
менти стають складеними у класі СМ Р = [{р, /} , V], в яко-
му будь-яка функція {/, 1} СМ-Р є суперпозицією функції
д Є {з> /} за структурою ь Є V, яка є елементом 5.
Нехай поведінка довільної СМ-Д Є К за деякою сукупніс-
тю її вихідних функцій описується деяким критерієм <2, екс-
тремальне значення якого відповідає бажаній поведінці У*.
Тоді критерій <2 задає відношення переваги у класі С-моде-
лей: СМ-Д >- СМ-Д2, якщо <?(Уі) < <2 (У2), де Уі — вихід
моделі СМ-Д, У2 — вихід моделі СМ-Д.
С-модель Рі Є К називається локально ефективною,
якщо вона отримана в результаті змін С-моделі Рг-і Є Д на
основі списку РЗ та справедливо відношення (Уі) < (^ (Д) •
С-модель Рі Є К називається ефективною, якщо вона є
^-наближенням.
Для еволюційного підходу принциповим є випадковий ха-
рактер РЗ, що виявляється таким чином у ймовірнісному ви-
борі конкретної зміни зі списку РЗ.
Розглянемо більш детально ймовірнісну реалізацію РЗ.
Складена зміна зводиться до багаторазової послідовної реалі-
зації простих змін на одній ітерації, тому досить розглянути
використання базових змін Д моделі. Ймовірнісна реалізація
5.3. Еіапи процесу еволюційного синтезу
297
РЗ конкретного структурного (і відповідно функціонально-
го) елемента С-моделі з ¥с = Р (тс), що приймають участь у
суперпозиції виконується так: здійснюється ймовірнісний ви-
бір у С-моделі структурного елемента і суперпозиція сусідніх
структурних елементів для структурного елемента, що дода-
ється, а потім детерміноване чи ймовірнісне функціональне
(параметричне) довизначення С-моделі по елементу що до-
дається, так, щоб СМ-Р) як і раніше належала класу К.
Виконання структурно-функціональної зміни починає-
ться з ймовірнісного вибору ФЕ із сукупності {/,7} Є К,
а потім здійснюється детермінований чи ймовірнісний вибір
сусідніх структурних елементів, тобто структурне довизна-
чення ФЕ, що додається, з тим, щоб зг Є 8.
Ймовірнісну реалізацію функціонально-структурних і
структурно-функціональних змін наведено на рис. 5.4.
Рис. 5.4. Ймовірнісна реалізація функціонально-структурних
і структурно-функціональних змін
ІЗ3
298
Розділ 5. Еволюційне моделювання ...
Аналіз процедур випадкового пошуку
Як вже зазначалося вище, процес синтезу ^-наближення
перетворювача Г у заданому класі СМ носить рекурен-
тний характер. Етап синтезу сукупності я (2^) локально-
ефективних ^-наближень, використовуваної для прийняття
фактичного рішення, складається з окремих кроків форму-
вання С-моделей. кожний з яких включає операції, приведені
на рис. 5.5.
Кінцевим результатом № кроку процесу синтезу є форму-
вання моделі С/у, а результатом послідовності N кроків син-
тезу — послідовність Сі, Сг,...,С^.
Кожна модель (N = 1,2,...) синтезованої послідовно-
сті є ^-наближенням перетворювача Г за заданим критерієм
з якимсь Єдг 0.
Рис. 5.5. Етапи алгоритму синтезу С-моделей
5 3. Етапи процесу еволюційного синтезу
299
Єіу =Р , де <21/7 — <21 (уси) — вихідна функція
моделі, <21 — <21 (у*) — вихідна функція бажаного перетворе-
ння, р — деяка метрика (відстань). Очевидно, мета синтезу
буде досягнута, якщо єдг —> є при N N (є).
Однак у загальному випадку ідеальний перетворювач Г*
і його бажане функціонування невідоме, а, отже, невідомі
значення <2; і посчідовність є. Апріорі відомо, що є екс-
тремумом (тіп чи тах) по С. Тому при синтезі на А-му кро-
ці локально-ефективного наближення справедливе співвідно-
шення є/у < Єлі-і- Використовуючи властивості опуклості й
адитивності функції р (ФпФілг) легко одержати аналогічні
співвідношення, що не містять :
{<2ш > <21,N-1 при <2і = шах <21 (С);
СеК (5.1)
<21/7 < <21,N-1 при <2; = ШІП <21 (С)
С Єл
Таким чином, мета синтезу буде досягнута, якщо послідов-
ність (А =1,2,...) є послідовністю послідовного полі-
пшення чи містить підпослідовність, що задовольняє одному
зі співвідношень (5.1) при N > N (є).
Подібна ймовірнісна процедура наближення до оптималь-
ного рішення визначається алгоритмом А — випадковим по-
шуком, що зв’язує наступні рішення:
• С)у = А(С/у..і) у найпростішому випадку;
• С)у = А(СЛг_і,С'дг_2, ... при урахуванні ре-
зультатів попередніх кроків.
У загальному випадку алгоритм А включає роботу двох
великих операторів на кожному кроці пошуку.
1. одержання інформації про поведінку критерію якості <2
у просторі пошуку;
2. ухвалення рішення про те, яке С рекомендувати в яко-
сті вихідного на наступному кроці пошуку.
13***
300
Розділ 5. Еволюційне моделювання ...
Збір інформації здійснюється за допомогою к пробних
кроків , і = 1...к в околі ВИХІДНОЇ ТОЧКИ С/У-і, вибір
якої здійснюється випадково. Нехай на А'-м кроці довільно-
го к-го етапу синтезу С-моделі до моделі Ск, обраної із суку-
пності локально-оптимальних моделей тг (/^), застосовується
режим змін Гі, обраний зі списку РЗ.
Позначимо цей процес записом (Гі)лг С3кде і = 1... г,
І = 1... к, N = 1... N (є). Результат виконання дії оціню-
ється за критерієм Сі після функціонального довизначення
зміненої С-моделі. Таким чином ми одержуємо нову СМ:
= (Гі);у (5-2)
При цьому використовується список РЗ. Як відзначалося, він
складається з базових (простих) змін і складених, частина з
яких є багаторазовим повторенням базових змін. Кратність
(глибина) РЗ — число д > 1 — є характеристикою реалізації
такої складеної зміни.
В описуваних далі еволюційних алгоритмах використову-
ються наступні чотири типи списків [2|:
• Класичний — складені зміни відсутні, список РЗ скла-
дається з базових змін, ймовірнісна реалізація яких не вико-
ристовує топологічних характеристик.
• Напівкласичний — список РЗ є класичним, але складе-
ні зміни реалізуються додатково випадковим вибором числа
9-
• Модифікований напівкласичний — при реалізації РЗ
напівкласичного списку використовуються топологічні хара-
ктеристики.
• Ієрархічний — список РЗ містить у собі складені змі-
нило у тому числі є багаторазовим виконанням базових, а
також такі РЗ, реалізація яких здійснюється як з урахуван-
ням топологічних характеристик, так і без них.
5-4. Основні алгоритми структурного випадкового пошуку
ЗОЇ
5.4. Основні алгоритми
структурного випадкового пошуку
на основі еволюційного моделювання
На відміну від відомих алгоритмів випадкового пошу-
ку, які працюють у параметричному просторі, у процеду-
рах еволюційного синтезу пошук локально-ефективних мо-
делей здійснюється в просторі СМ заданого класу К. Звідси
випливає істотна особливість у розроблюваних еволюційних
процедурах — це структурний випадковий пошук, що вима-
гає розробки спеціалізованих пошукових алгоритмів у класі
структурних моделей.
У заданому класі К перехід від моделі С^-\ до моделі
С/у здійснюється на основі реалізації випадкової зміни Г* зі
списку режимів змін, що відповідають заданому класу К.
При цьому елемент випадковості виявляється як у ймовірні-
сному виборі ВІДПОВІДНО ДО розподілу Р] (С) моделі С/У-1 із
сукупності 7Г (Р^), так і в ймовірнісному виборі відповідно ДО
ймовірнісного розподілу Рг (Г) конкретного режиму зі списку
РЗ.
Опишемо роль даних джерел стохастичності в еволюцій-
ному синтезі при їхньому поступовому підключенні.
Усі такі списки РЗ розрізняються простими змінами про-
стого, або складеного елемента:
• додати структурний або функціональний елемент;
• усунути той же елемент.
Ці РЗ характеризуються протилежним напрямком пошу-
ку в просторі С-моделей.
Відповідно до двох основних тактик випадкового пошу-
ку (ВП) множина можливих алгоритмів поділяється на дві
групи з лінійною і нелінійною тактикою.
Розглянемо ці алгоритми.
302
Розділ 5. Еволюційне моделювання ...
5.4.1. Випадковий пошук з лінійною тактикою
Лінійна тактика пошуку характеризується тим, що дія
(результат зміни С-моделей у даному випадку), що привела
до синтезу локально-ефективної моделі, зберігається. У про-
тивному випадку здійснюються кроки в просторі можливих
дій або визначальних їх керуючих параметрів а і ф
Для довільного класу С-моделей це приводить до насту-
пного виразу:
Скм = (ГОуу Ск^-і) =
' Ск^-1) + (Г»)л^
якщо <2 ((Гі^С^дг-і)) (5.3)
)(Гі)]ЧСкІГІ_і^
якщо ((Гі)лгС^_п) <
де записом “'(ІДдг відзначена дія забування синтезованої
моделі, що не виявилася локально-ефективною; і =
= і=Й-іЄ(ад'
У результаті здійснюється повернення до попередньої мо-
делі і повторне формування нової моделі з викори-
станням нового РЗ Гф
Різні модифікації алгоритму відрізняються умовами ви-
значення нового РЗ Г- у випадку невдалого кроку пошуку:
1. Г' = Гг (тобто напрямок пошуку не змінюється);
2. Г' / Г» — РЗ міняється, тобто міняється напрямок по-
шуку;
3. умова на Г< відсутня; відповідно до ймовірнісного роз-
поділу Да стохастично реалізуються випадки 1 або 2;
4. Г' — Г», якщо Єї е„; Г' Г,, якщо Єї > еп, де Єї —
кратність використання Гі.
Одночасно різні модифікації алгоритму відрізняються
критеріями збереження напрямку пошуку (відповідного РЗ)
у випадку вдалого кроку.
5.4. Основні алгоритми структурного випадкового пошуку
303
При цьому важливі умови відносної величини зсуву (тоб-
то ймовірнісної реалізації Гі) :
• параметри ймовірнісної реалізації зберігаються;
• параметри реалізації змінюються на основі інформації,
отриманої в результаті пробних кроків
Процедури випадкового пошуку з лінійною тактикою реко-
мендуються в умовах «гладкості» функції (£, коли значення С}
при переході від однієї С-моделі до іншої міняються незначно [2].
Необхідною умовою ефективності пошуку є:
— імовірність синтезу локально-ефективної С-моделі велика;
— імовірність випадкового вибору вдалого РЗ теж не мала.
5.4.2. Випадковий структурний пошук
з нелінійною тактикою
Нелінійна тактика пошуку характеризує тим, що дія (кон-
кретне застосування С-моделі), що привела до невдалого кро-
ку, забувається, а та, що привела до локально-ефективної мо-
делі — заохочується випадковістю. У реакції на вдалий крок
пошуку і складається основна відмінність між випадковими
процедурами з лінійною і нелінійною тактикою.
Для довільного класу С-моделей це приведе до виразу
Скк = (Гі)?/ Ск(ту-і) =
_ (Гг)лг С^дг-!), ЯКЩО С ((Гі)лгСк(лг-і)) (5.4)
ЯКЩО С((Гг^С^_1))<^_1,
де позначення збігаються з виразом (5.3).
Різні модифікації (5.4) відрізняються способами визначен-
ня конкретного РЗ Г' у випадку вдалого кроку пошуку. Тут
застосовуються умови вибору Г'. описані у випадковому по-
шуку з лінійною тактикою, а також деякі способи, що приво-
дять до окремих випадків типу випадкового пошуку «з пар-
304
Розділ 5. Еволюційне моделювання ...
ними пробами». В останньому випадку при невдалому кроці
пошуку випробується режим зміни (РЗ) «протилежного на-
прямку», тобто інший РЗ пари, що відрізняється простим за-
стосуванням того ж структурного або функціонального еле-
мента. При цьому у випадку невдачі допускається спроба Г,,
невдача по якій приводить до забування режиму Г,.
У даному випадку процедура (5.4) записується у вигляді:
Скьі = (Гі)лгС'*.(лг-і) =
(Г«^ Сц/у-і) + (Г«) дг
якщо (<2 ((Г^С^/у-і)) (Зм-і') А
а (<2 ((г.) „ С^дг-і)) < ;
< -,(Гі)ЛгС'*:(ЛГ-1) + -І (Г^ууСїцдГ-І), (5.5)
якщо (<2 ((Гі^С^-і)) > л
А (<? ( (Гі) н і
(П)лг С*(лг-і),
, якщо (<2 ((Г.^С^лг-і)) < <2^-1)
Практично, у процедурах (5.5) використовують два про-
бних кроки у напрямку пошуку. Очевидне узагальнення да-
ної процедури — проведення декількох пробних кроків, з яких
робочим вибирається крок, що дає найменше значення С^.
Процедури випадкового пошуку з нелінійною тактикою
рекомендується використовувати в тому випадку, коли функ-
ція С} не виявляє гладкого лінійного характеру, і, більш того,
значно змінюється. У подібних умовах синтез локально-ефе-
ктивної С-моделі доцільно вести шляхом випадкових блукань
або «заохоченням випадковістю».
Для ес])ективної роботи алгоритмів даної групи єдиною
важливою умовою є те, щоб імовірність випадкового вибору
вдалого РЗ була не мала.
5.5. Навчання й адаптація процедур пошуку
305
5.5. Навчання й адаптація
процедур пошуку
Ефективність розглянутих процедур структурного випад-
кового пошуку як з лінійною, так і з нелінійною тактикою
знижується при зміні характеру функції у процесі пошуку
в заданому класі К, тобто з появою ситуацій «пружності»,
«горбкування» і т.ін.
Крім того, у процесі еволюційного синтезу за певних умов
відбувається перехід на інший критерій у результаті чого
характер нової оціночної функції якості може не відповідати
умовам оптимальності використовуваної процедури пошуку.
У таких умовах ефективність описаних процедур СП підви-
щується за рахунок самонавчання й адаптації.
У табл.5.1 наведені відомі алгоритми покрокового нав-
чання параметрів вектора пам’яті XV пошукових процедур у
класі С-моделей, що використовуються в розроблених еволю-
ційних процедурах синтезу ефективних ^-наближень.
Специфіка структурного пошуку виявляється в тім, що
г-та координата Р^ вектора імовірностей вибору напрямку
пошуку — це імовірність вибору режиму ЗМІН 1 і : /< =
= Р-2 (Гг) на У-ому кроці пошуку, що задана дискретно. В ал-
горитмах навчання передбачена безпосередня зміна Ро (Гг),
і — 1... А;, а також їхня зміна через вектор параметрів
XV, що називають вектором пам’яті — Р% .
Розподіл Р2 може мати довільний вид у залежності
від XV: експоненціальний, лінійний, релейний, східчастий,
синусоїдальний, гаусовий і т.ін. У табл.5.1 наведені алгорит-
ми навчання імовірностей вибору Гг зі списку РЗ при довіль-
ній залежності Рг від И7 [2].
306
Розділ 5. Еволюційне моделювання ...
Таблиця 5.1.
Покрокове навчання параметрів структурного випадкового пошуку
Назва алгоритму навчання Рекурентний вираз Особливості алгоритму Еволюційний алгоритм
Покоординатне експопепційпе навчання = А,/’(Л’~,,+ + (і-А)\ Експопепційний ха- рактер зміни імовір- ності параметра ЕПА, ЕРА, МАКІ
Покоординатне навчання довільним законом Р1(Л') = Р2(Ж1(^,)); - де 6 > 0 Не здатний постійно шукати найкращий напрямок зміни (^. Не враховує отрима- ний результат вели- чини С]. Запам’ятовує і збері- гає весь попередній досвід. ЕПА, ЕРА,
Пропорційний алгоритм навчання іут = и<('ї’1)- — 6 Дфдг-і, де і> > 0 Запам’ятовує і збері- гає весь попередній досвід в усередненій формі, чутливий до визначення найкра- щого напрямку. ЕРА
Самонавчання з забуванням — 6Д де 0 к 1 При = 0 пошук повинний бути рівно- ймовірпим. МАК2
«Скептичне» самонавчання іг/"’ = - -6(Д Забезпечує в серед- ньому перевагу най- кращому напрямку. МАКІ
Позначення: 6— параметр швидкості адаптації;
6х — коефіцієнт пропорційності;
к — параметр забування;
<1 — параметр скептицизму.
5.5. Навчання й адаптація процедур пошуку
307
По тим же алгоритмам покрокового навчання можна ко-
ректувати також величину робочого зсуву д і число спробних
кроків /, тобто кратність використання РЗ в описаних раніше
алгоритмах випадкового пошуку.
Відзначимо, що в цілому параметри імовірнісної реаліза-
ції різних РЗ, параметри забування к, пропорційності 6' і ске-
птицизму <7 взаємозалежні.
Оскільки аналітичну залежність цього взаємозв’язку
одержати неможливо, а експериментальна визначається кон-
кретними умовами, доцільно коректувати ці параметри в
залежності від конкретної ситуації в процесі синтезу ^-на-
ближень.
Глобальність структурного пошуку
Вищерозглянуті алгоритми структурного пошуку ефе-
ктивні у випадку одноекстремальних функцій.
Задача відшукання глобального скстремума на основі ре-
алізованих ними тактик не вирішується, тому що діють меха-
нізми закріплення знайдених «успішних» напрямків пошуку.
Тому у випадку багатоскстрсмальності функції необхідно
вводити механізми зміни або «розгойдування» початкових
умов синтезу. Це досягається використанням третього дже-
рела випадковості — тобто ймовірнісним вибором С-моделі із
сукупності тг (7^) на кожному кроці формування нової моделі
12].
На відміну від попереднього, далі вважаємо, що
Лк(іч-і') (^) = {£*(лг-і)> • - • > Сь(л-і)} ,
де к — номер етапу синтезу, N — номер кроку синтезу, І —
обсяг сукупності 7Тд.(дг_]) (7^) .
/
308
Розділ 5. Еволюційне моделювання ...
Випадковий вибір моделі Сцм-і) в реалізованих вище ал-
горитмах приводить за N кроків синтезу до випадкового і
незалежного «обстрілу» заданого класу К. У зв’язку з тим.
що при цьому сукупність тгкк (7^) формується за наступним
правилом:
Сну = <
якщо <2
(Г.)
якщо
^*N-й
(5-6)
де / . \
^-1 = (^(ЛГ-І) ) ’
то алгоритм забезпечує попадання в окіл глобального екс-
тремума при N —» оо і досить розумному розподілі Рг (С),
тобто розподіл Рі (С) повинен відповідати структурі класу
К і заданій на ньому функції С^).
Тут необхідний адаптований розподіл Р\ (С) до конкре-
тної ситуації, що здійснюється по алгоритмах покрокового
навчання (корекції), які описані вище.
Імовірнісний вибір С-моделі із сукупності 7Г (Г^) звичай-
но супроводжується умовами, виконання яких приводить до
таких модифікацій:
і ГЧ' = П3..
— модель на кроці N формується з тієї ж моделі, тобто до-
пускається крок локального пошуку;
2. С^_, С^_]
— модель на кроці N формується з іншої С-моделі, здійсню-
ється крок глобального пошуку;
5.5. Навчання й адаптація процедур пошуку
309
3. — с3!Ч_1,
якщо і і-
^N-1 РлГ-1>
якщо і > і, де і = 1,2,... — кратність використання моделі
в якості вихідної, у результаті реалізується іц кроків
локального пошуку на базі моделі С'^_І;
4. умови на С'^_1 відсутні; відповідно до ймовірнісного
розподілу Рі (С) стохастично реалізуються випадки 1 і 2.
Накладення третього джерела стохастичності приводить
до комбінування в алгоритмі випадкового пошуку (5.4) —
(5.5) різних модифікацій ймовірнісного вибору С-моделі із
сукупності 7Г (Р() , породжуючи при цьому цілу сім’ю проце-
дур структурного ВП.
Приведемо одну з можливих процедур, що допускають ба-
гаторазове використання С-моделі у випадку алгоритму з не-
лінійною тактикою:
= (Г1)лгС^7У_1^ =
(Гі)^! + (Г,)/у-і Р*(?у-і)>
якщо ((? ((Гі)^! С3к{М_^ Р^-і) Л
А (і < і„);
“ (Гг)уу-1 р£(ЛГ-1) + (П)уу-1 Р*(ЛГ-1)>
якщо (Р ^(Г»)ЛГ_1 С3^^ £ л
А (і > і„);
ЯКЩО Р ((Гі)^] < Р^-1-
310
Розділ 5. Еволюційне моделювання ...
Модифікації при вдалому кроці Параметри ймовірнісної реалізації РЗ зберігаються 1 о •* я * Д -с О > 45 о- Н Іі • г;=г„ г>г,; Г' = Г, з імовірністю рі; г,= (Гй якщо 1 < 1п-, | Г', якщо 1 > 1п Параметри ймовірнісної реалізації РЗ зберігаються Параметри ймовірнісної реалізації РЗ змінюються !(д)с7 оілоініїшоипе ? оїпяв "-^1 _ [_д, !“? 1 оїпяв = '-уо
Модифікації при невдалому кроці 7 А н_ Г • = Г, з імовірністю РІ; г, _ (Гй якщо 1 < 1п-, [ Г', якщо / > 1п (^\-1 С*(Л'-1)+1(Г,)Л,_1 Сцц.1}, ЯКЩ0(Фу_| 1(Гі)лг_і Сцл-1), якщо(<2у-і ^N Флм); (Г')С^_,), ЯКЩО т спробних кроків по парі РЗ протилежної дії Є1,., = (?£., * С^.і с1'. = Ск якщ0 1 1т Л‘_1 [СЦь якщо і > і„, С^.і= СІ/-] з імовірністю Рі(С); оПіяв ’,"Л,7^(;л) ’"л/б) оШхв V? '-"аоіляв
Рекурентний вираз і % х—х % а якщо (2ц-! (Я,.,; ЯКЩО 7 6*$ * о II 7 . Лі ттттіт — ї-А'Лі (Гі)лг-іС*(лг-і> якщо Су-» (Р|)^Ц«-1р якщо С}ц-\<С)ц-1 якщо 0^ <2;_і; (Г^л-^Сцлі-і). ЯКЩО С^.і}є{С{,С2...,Ск} = ^ V СУ СУ а о & 3 м М к к 4 і Ез 7 7 с-7 Х-Г
Назва структурного випадкового пошуку Локальний пошук з лінійною тактикою: дія, що привела до локально-ефективної моделі, зберігається Локальний пошук з нелінійною тактикою: дія, що привела до локально-ефективної моделі, зберігається Глобальний пошук з лінійною тактикою: Гл обальний пошук з нелінійною тактикою:
5.6. Моделі систем класифікації і розпізнавання
311
5.6. Скінченні автоматні моделі для прогнозування
та деревоподібні вирішальні моделі
систем класифікації і розпізнавання
5.6.1. Клас автоматних моделей
(скінченні автомати Мілі)
Розглянемо клас детермінованих скінченно-автоматних
моделей у класі детермінованих скінченних автоматів
Мілі. Як відомо, детермінований скінченний автомат Мілі
Дг{ЛЛ} заданий вхідним алфавітом Хд = {ті,... ,хр},
вихідним алфавітом Уд = {уі,---,у9}, множиною станів
5д = , $„.} , функцією ВИХОДІВ Уі+1 = /у , фун-
кцією переходів 5І+1 = /з , де Хі, ¥і І Зі — відповідно
вхідний символ, вихідний символ і стан автомата в момент
часу і, і — 1,Т. Таким чином, скінченний автомат реалізує
автоматне відображення символів (слів), складених із симво-
лів вхідного алфавіту, у сигнали, складені із символів вихі-
дного алфавіту, характер відображення залежить від поча-
ткового стану $о, У якому подається перший символ сигналу
Ед : Хк —> Ук ($о), де к — довжина слова.
Задача ідентифікації у вигляді автоматного відображення
Ед припускає наявність навчальної вибірки вхідних і вихід-
них сигналів, що знаходяться у відображенні Е, яке невідомо,
і наближає відображення Ед Є Ф, де Ф —клас автоматних
відображень. Орієнтуючись на застосування еволюційного син-
тезу, будемо розглядати в якості Ф-класу СМ — зв’язаних
скінченних автоматів з числом станів, не більше X, — авто-
мат А, який визначається функціональним базисом і структу-
рою 8д. Остання задається графом С = (V,!)), де V— сукуп-
ність п вершин, О— сукупність дуг, які з’єднують вершини.
Функції / сукупності реалізують часткові відображення
вхідного символу х Є Хд, у вихідний у Є Уд і розташовані
у вершинах графа, — число різних функцій /. При та-
312
Розділ 5. Еволюційне моделювання ...
бличному представленні структура задається 5-підтаблицею,
а кожній функції / відповідає рядок у підтаблиці.
Використовуючи визначення еволюційного синтезу, сфор-
муємо список базових змін скінченного детермінованого ав-
томату.
Для цього необхідно визначити прості елементи. Фун-
кціональні елементи — це функції набору {/^а}, що пе-
ретворюють символ алфавіту Ха в символ алфавіту Ід, у
даному випадку це перемикальні функції. При заданих р і
д — розмірностях, відповідно вхідного і вихідного алфавітів,
множина перемикальних функцій має потужність рд.
Функція зміни полягає в додаванні чи усуненні простих
елементів сукупності {/, /д} , що не змінюють структури ав-
томата і не виводять його за межі даного класу. Фіксуючи
рівень деталізації розглянутого класу моделей, припускає-
мо далі, що функції / Є {/,7} є простими елементами.
Проста функціональна зміна автомата зводиться по визна-
ченню до усунення деякого елемента / (ц) із суперпозиції
/ (щ), / (^2)(ц») • Ясно, що така зміна може відбува-
тися без зміни структури лише у випадку заміни / (уї) на
/*(№)//*)•
По визначенню проста структурно-функціональна змі-
на — це додавання функції /* в зазначену вище суперпози-
цію. Вона реалізується без зміни структурних елементів лише
в тому випадку, коли здійснюється заміна / {уі) на /*.
Структурні прості елементи автоматних моделей — цс
елементи множин V = {г>і, и2, і В — {Ф, ф,..., ф}
графа С = (V, 7?).
Тому прості структурні зміни — це усунення вершини
з множини V, а так само усунення дуги з множини В.
Відповідним чином формуються функціонально-структурні
зміни, що зводяться до додавання вершини або дуги у відпо-
відні множини.
5.6. Моделі систем класифікації і розпізнавання
313
Як відомо, у зв’язному автоматі для будь-якого вхідно-
го символу існує перехід у наступний стан. З урахуванням
цього структурні і функціонально-структурні зміни на дугах
не можуть бути реалізовані окремо. Однак, реалізованими є
зміни, що полягають у зміні структурного елемента «верши-
на + перехід». У результаті одержуємо список базових змін,
приведених у табл. 5.2, який будемо називати «класичним».
Результатом виконання А1 є заміна Д, = (і^) в супер-
позиції і символів вихідних функцій, формованих у вершині
ц Є 8а- При виконанні А2 міняється частина суперпозиції і
тієї сукупності вихідних функцій, у формуванні яких брала
участь усунута вершина и?, починаючи з першої появи в
суперпозиції.
Незмінною залишається частина суперпозиції і вихідних
функцій до першого попадання в Уу у випадках ЯЗ і А4.
При необхідності список РЗ збільшується шляхом реалізації
складених змін, одержуваних багаторазовим використанням
базових РЗ. З цією метою ймовірним вибором здійснюється
завдання д > 1 кратності виконання базових РЗ. В цілому
це приводить до збільшення потужності зміни вихідних фун-
кцій скінченного автомата за одну реалізацію РЗ. Список РЗ
є класичним, але при реалізації обраного РЗ допускається
його «/-кратне виконання, що приводить до складеної зміни.
Такий список РЗ і називається «напівкласичним».
Якщо при реалізації напівкласичного списку РЗ врахову-
ються топологічні характеристики автомата, то такий список
РЗ відрізняється обов’язковістю фрагментарної зміни авто-
мата. Як топологічна характеристика, що відображає стру-
ктурні особливості автомата використовується «зв’язність»,
яка конкретно виражається в ступенях вершин графа — стру-
ктури ((5+ — число вхідних і — число вихідних дуг вер-
шини V).
Відповідний список РЗ приведений у табл. 5.3.
14і
Класичний список базових змін
Таблиця 5.2.
РЗ Тип зміни Реалізація Формалізований вираз Результат
А1 Функціональне: усунення функціонального елемента В суперпозиції обираєть- ся елемент= який змі- нюється на 4 -> /• такий, що/**/., Змпіепа перемикаль- на функція стану автомата та супер- позиції
А2 Структурно- функціональне: додавання функціонального елемента В суперпозиції /, («) обираєть- ся елемент 4 такий,що А = А, при й змінюєть- де к - кількість станів автомата Д-»/* такий, що/*хД, /*є{/,7} Змінена перемикаль- на функція стану автомата та супер- позиції з додаванням
АЗ Структурне: усунення структурного елемента В маршруті суперпози- ції обирається ц; переходи (ум) та (^,1^1 змінюються на(ц4,цл1) ,ук#Ум (ум) + (и,,^) Усунення V, із авто- мата та суперпозиції
А4 Функціонально- структурне: додавання структурного елемента В маршруті (ці,ц*) суперпози- ції' обирається «у; на перехід (^,^0 додається вершина?; з переходами (у,-,у) та^,^) (УіУ»і)-*(уіУ) + (^я-0 Додана вершина у
314 Розділ 5. Еволюційне моделювання ...
"* , Таблиця 5.3.
Напівкласичний список РЗ
РЗ Тип зміни Реалізація Формалізований вираз Результат
А5 Складене функціонально- структурне: додавання зв’яз- ного фрагмента з д вершин В сукупність вершин Vдодає- ться елемент д вершин з пере- ходами, які зв’язані між собою тазвершипами Уз урахуван- ням топологічних характерне тик зв’язності V', такі, що 8+(?;0>1, > = п + 1,...,п + р; в 1 •1 ? ^п+9 ) — 15 (^п+ь^п+й* ч'Уп+д) — 1 Доданий підграф з вершин У„+1,...,Уп+я умови на топологічні характеристики заг безпечують зв’язність автомата
А6 Складене структурне: усунення зв’язно- го фрагмента, якій складаєтся з д вершин В сукупність вершин V, які приймають участь в суперпо- зиції, обирається д зв’язних вершин, які усуваються з ура- хуванням їх топологічних хат рактеристик У - V', У' = У\ {^,... такі, що 8"(г')>1, І = 1,...,п-д Усунений підграф з вершин у^...ууІ9 з виконанням зв’яз- ності по топологічним характеристикам
А7 Складене з структурного та функціонально- структурного У сукупністі Р переходів усу- нені кінцеві вершини та дода- ні інші П —> Р', такі, що <і, = І = -д-, = (Цун,ук) = (у'„,у'к), Уи = «4> * «ь 3 = Ь-д,...,Ь-, Г($)>1, Ь-(у'к)>1 Зміїїені кінцеві вер- шини у переходів 3 виконанням зв’язності по топологічним ха- рактеристикам
316
Розділ 5. Еволюційне моделювання ...
5.6.2. Деревоподібні вирішальні структури
систем класифікації і розпізнавання
Останнім часом з розвитком програмних технологій де-
ревоподібні вирішальні моделі одержують широке поширен-
ня в задачах генерації формальних описів класів, організації
структур даних і т.ін.
Сукупність структур даного класу С-моделей складають
множини скінченних зв’язаних орграфів Д = (У, Г>), де V =
= • .і’п}— множина вершин, £> = {ф,ф, -., Ф} —
множина дуг (орієнтованих ребер); як звичайно, орграф вва-
жаємо ордеревом, що росте з кореня г?і, якщо він зв’язаний,
не має контурів і єдиний маршрут з до будь-якої V, , і = 1, п,
є шляхом (щ, Уі) = {щ = угі — уІ2 — ... — = гг} .
Число вершин, що складають маршрут (щ, уг), дорівнює
а і збігається з номером рівня аг = а вершини Уі.
Будь-яке дерево характеризується наступними параме-
трами: числом п елементів множини V; максимальним рів-
нем у Є V; розподілом вершин по рівнях; кількістю 6~ дуг,
що виходять з кожної вершини, тобто ступенем виходу для
кожної вершини. Максимальний рівень дерева називають йо-
го висотою атах = /і-
Дерево називають рівномірним, якщо кількість дуг уа, що
виходять з вершин а-го рівня, однакова і є функцією а :
("“) = / (а) = і/ (а).
Дерево абсолютно рівномірне, якщо (г,) — сопзі (не за-
лежить від а). Рівномірне дерево з точністю до ізоморфізму
визначається скінченною послідовністю натуральних чисел
{щ, і/2,..., і//і}, де /г — висота дерева.
Вершини вирішального дерева у3, і = 1,п, відрізняються
реалізованими перетворювачами Д, що входять у функціо-
нальний базис /, 7.
5.6. Моделі систем класифікації і розпізнавання
317
Як перетворювачі в різних вирішальних деревоподібних
структурах використовуються ^-місцеві предикати, описи
об’єктів, булеві змінні, лінгвістичні змінні. У результаті де-
ревоподібні С-моделі являють собою ті чи інші вирішальні
функції. При цьому задача побудови булевих вирішальних
дерев зводиться: до мінімізації систем булевих функцій; до
мінімізації в класі ортогональних ДНФ; до пошуку булевих
функцій, які мінімізують середній ризик помилки.
Ефективною вважається модель з мінімальною імовірні-
стю помилки навчальної вибірки. Такий підхід розглядається
далі в еволюційному алгоритмі, що розпізнає.
Нехай на множині X припустимих символів задане скін-
ченне число підмножин Уі,..., У« (класів) таких, що
к=1
Кожен сигнал х визначається значеннями характеристик
(а?!,..., хп) таким чином, що їхня сукупність дає опис У(х)
сигналу х (характеристики х3, і = 1, IV, х3, Е С П назива-
ються ознаками).
Неважко помітити, що в деревоподібній вирішальній стру-
ктурі будь-який маршрут І задає сукупність характеристик
сигналу, що складають деякий опис У/ : Зі (х) <-» (уі, ні).
Визначимо структуру О у такий спосіб: зіставимо кожній
дузі, що виходить з кінцевої вершини Є V мітку з номером
к — 1, К класу, до якого відноситься опис Д (а?) сигналу по
х3 Е Xе і Ус = к, де (Xе, Ус) — навчальна вибірка, відома
апріорно.
У результаті сукупність маршрутів дерева, що закінчу-
ється мітками к, визначає опис У (Ук) класу сигналів У*, а
сукупність маршрутів дерева в цілому визначає сукупність
{У (Ук), к = 1,К] описів усіх К класів, і таким чином дере-
во визначає розбивку \¥а припустимих сигналів X на мно-
жини Уі,Уг,... ,Ук- Оскільки описи -І(Ук) формуються за
142
318
Розділ 5. Еволюційне моделювання ...
апріорною інформацією (Xе, ¥е), що звичайно не є вичерп-
ною, то можливі х Є ¥к, для яких (х) 7^ 7/ (х) Є 7 (¥к). Тоді
розбивка \¥а характеризується імовірністю помилки класифі-
кації сигналу X, що має ймовірнісний розподіл Р (X) :
Р(Щ) = £ Р(х), (5-7)
Де к
Хпом = □ {х : 7 (х) ± 7 (я) Є 7 (П)}. (5.8)
к=1
Звідси випливає задача синтезу такого дерева Д*, для яко-
го сукупність {7 (¥к), к = 1,К} забезпечує імовірність по-
милкової класифікації, не більшу £ із заданою імовірністю
або мінімізує імовірність помилкової класифікації
Р {Р (ЖЛ) £} > 1 -1] або тіп Р (Ж*.).
Неважко помітити, що сукупність {7(У^), к = 1, К] кін-
цевих маршрутів є підмножиною суперпозицій функціональ-
них перетворювачів з прийнятого базису /, 7. Кожна супер-
позиція визначається конкретним набором /і, і = 1,...,кі,
застосованим до вершин маршруту (тл,^,... , г^), їхньою
черговістю і довжиною кі маршруту. Усі ці фактори визна-
чаються зазначеними вище параметрами Д-структури, тому
синтез необхідного дерева Д* і відповідно розбивку IV* до-
цільно проводити шляхом структурних змін деякого дерева
Д* на основі списку РЗ.
Переходячи до формування списку РЗ деревоподібної
структури, відзначимо її специфіку, зокрема ієрархічність.
Вона приводить до того, що функціональні перетворювачі
(ФП), приписувані вершинам з меншим номером рівня бе-
руть участь у більшій частині маршрутів дерева і тому більш
істотні для класифікації реалізованої деревом.
Таким чином, рівень дерева, на якому реалізується РЗ, є
параметром, що характеризує ступінь зміни дерева, і тому
враховується при складанні списку РЗ.
5.6. Моделі систем класифікації і розпізнавання
319
Відповідно до визначення еволюційного синтезу сформуємо
список базових змін Д-структури. Функціональні елементи
деревоподібної С-моделі — це функції набору /, 7, що є ха-
рактеристиками сигналів х Є X (тобто ознаками). Ці ознаки
можуть бути як логічними, так і дійсними функціями різної
складності, що є принциповою відмінністю деревоподібних
моделей від скінченно-автоматних, породжуючи множину
класів, що відрізняються функціональним базисом. Прості
функції цих базисів визначаються, як функції Є {/, 7} не
декомпозовані далі без порушення класу моделей. Тоді про-
ста функціональна зміна деревоподібної моделі зводиться
по визначенню до усунення деякого елемента /„, / = 1,1, із
суперпозиції /іі, /і2, . • •, /п, реалізованої маршрутом (г?і, ьі).
Проста структурно-функціональна зміна деревоподі-
бної моделі зводиться до додавання /^ в суперпозицію
/іі, /і2, • • • і /іі- Положення елементів /іу у суперпозиції в обох
випадках визначається випадково.
Структура рівномірного дерева, на відміну від структу-
ри кінцевого автомата, складається з одного типу просто-
го елемента: вершини V з вихідними ребрами. У резуль-
таті маємо наступну структурну зміну — усунути вершину,
і функцінально-структурну зміну — додати вершину в де-
рево. Оскільки кожна вершина деревоподібної вирішальної
структури є одночасно і функціональним елементом / Є
Є {/, 7}, то, очевидно, будь-яка структурна зміна дерева є
його функціональною зміною. З іншого боку, функціональні
і структурно-функціональні зміни (Д1, Д2) дерева, включаю-
чи усунення елемента /^ із суперпозиції (маршруту), можуть
приводити до зміни маршрутів і залученню інших функ-
ціональних елементів, тобто на іншому елементарному ма-
теріалі.
Список базових РЗ складається зі змін, приведених у
табл. 5.4. Він привабливий тим, що його реалізація найбільш
проста, однак, як показує аналіз РЗ типу Д5, однократна ре-
алізація Д1 — практично ніколи не приведе до такої фун-
кціональної зміни дерева як використання РЗ типу Д5.
14**
320
Розділ 5. Еволюційне моделювання ...
Результат Заміна функціонального еле- мента вершини у, на інший елемент суперпозиції. Перерозподіл маршрутів. Додавання в суперпозицію елемента із збереженням по- переднього на іншому місці. Перерозподіл маршрутів. Скорочення маршрутів, які проходять через вершину V, . Скорочення дерева па кількість маршрутів, які проходять че- рез (т>-1) гілку рівня (І +1). Продовжешія маршрутів, які проходят через вершину «]+1. Продовжешія дерева на («-!) маршрутів, які закінчуються у доданих гілках (вершинах^) Тчхзттп тттолм гтгуЇхг ттг» отгггат-ч- позиції (маршруту) елементів. Перерозподіл маршрутів.
Формалізований вираз Л -> /* так,що л(ЛЩ)),; = і7 /„->/• так, що (/‘*/ц)Л Л (4=Л, «»Є(«ьЦ)) ; 4» Г є {/,/}, > = Ї7 б" п в” в1 так. що /іж/,4.30 V £ Т* + + т ►і?
Реалізація В суперпозиції (/ц) маршруту обирається елемент 4 = / (ч) > якій змінюється на ГєЦ), В суперпозиції (/,) маршруту (Уі,^Л обирається елемент /і =Ж), такий, що існує/#=Д, при змінюється на Гє{/,7}, У маршруті (і^) обирається змінюється на/,(?^+і) У маршруті обирається V ; на ребро (^,^1) Є додається вершина V Ау-1 ребром (и,г4) так, що = 1.^-1 Р с\ггтрг\гтттлт г її ( і. X С'іїагіАР'гм'я ^Ч, 1 який змінюється наД+І, а /0+1 змінюється на
Тип зміни Функціональне: усунення функці- онального елемен- та з суперпозиції маршруту Структурно- функціональне: додавання функці- онального елемен- та в суперпозицію маршруту (г?і,«,) Структурне: усунення струк- турного елемента з маршруту («!,«() та дерева Функціонально- структурне: додавання струк- турного елемента в маршрут функціональне: усунення двох функ- ціональних елементів
1 РЗ 1 сч СО
5.6. Моделі систем класифікації і розпізнавання
321
5.6.3. Методика синтезу скінченно-автоматних
прогнозуючих моделей
Відповідно до результатів досліджень в умовах макси-
мальної апріорної невизначеності доцільно починати синтез у
класі графових С-моделей з найпростішим функціональним
базисом, що складається з перемикальних функцій, тобто в
класі скінченно-автоматних моделей.
Опишемо методику еволюційного синтезу ефективних
^-наближень у даному класі С-моделей при розв’язку задач
прогнозної оцінки параметра [2].
Еволюційний синтез починається з завдання конкретного
класу скінченних автоматів і здійснюється при конкретизації
параметрів і часткових алгоритмів формування автоматів у
процесі СП, і передбачень щодо очікуваного значення пара-
метра.
При відсутності інформації щодо максимального числа
станів п і вимірності р вихідного алфавіту визначення цих
параметрів, типу списку РЗ, а також параметрів, що регла-
ментують процеси синтезу скінченних автоматів і фактичні
передбачення, базуються на попередніх обчислювальних екс-
периментах з пакетом програм прогнозної оцінки (ПППО) у
діалоговому режимі [2].
Основна стратегія діалогу припускає поступове ускладнен-
ня алгоритму еволюційного синтезу і його програмних ре-
алізацій. Тому при відпрацьовуванні параметрів р, </, і п
доцільно максимально спрощувати алгоритм синтезу. Це до-
сягається при наступних вихідних параметрах і процедурах.
• Значення вимірностей вхідного і вихідного алфавіту ви-
значаються за дискретними значеннями наявних реалізацій
вхідної і вихідної функцій (тобто передісторії) і апріорно-
го припущення максимальних і мінімальних їхніх значень у
143
322
Розділ 5. Еволюційне моделювання ...
майбутньому. З урахуванням бажаної точності апроксимації
значень прогнозованого цілого параметра визначається ба-
жана і гранично можлива значність р і д, що апробуються
обчислювальним експериментом.
• Початковий клас детермінованих автоматів при обробці
параметрів р і д задається числом станів, що не перевищує
20. Далі у випадку незадовільних показників синтезу (недо-
статня точність, незадовільний час синтезу і т.ін.) можливий
перехід у більш широкий клас з великим числом станів авто-
мата. Максимальне значення п визначається встановленими
значеннями р і д на основі співвідношень, що враховують об-
сяги пам’яті ЕОМ.
• Як вихідний автомат вико-
ристовується довільний автомат із
класу для апробованих значень р, д,
і п,... у режимі діалогу. У випадку
р = д = 2, це автомат, зображений
на рис 5.6.
• У найпростішому випадку Рис. 5.6. Вихідний автомат
обсяг сукупності 7Г (/^) фіксований і дорівнює 3. При
цьому передбачається, що вихідний імовірнісний розпо-
діл Рі (с) = {Рц, Різ, Різ} моделей С 3 7г(/^) рівномірний
Ріг = 1/3, і = 1,2,3.
• Тип списку РЗ, обраний з чотирьох можливих, визначає-
ться серією експериментів, що задається в діалоговому режи-
мі (максимум чотири серії). У будь-якому випадку вихідний
розподіл Рі (Г) — рівномірний, при якому конкретний РЗ
обирається рівноймовірно.
• В якості функціонала С}, що оцінює ефективність ав-
томата по вхідній функції хс (і), береться середня вартість
помилки прогнозу автоматом (Ь 4- 1)-го значення вихідної
5.6. Моделі систем класифікації і розпізнавання
323
функції уг, тобто
р(с,ь)= $2
«єУ(О
де С (£і, £)) — вартість помилки прогнозування символа & €
Є Ус (і), коли реальним є символ Є У* (і); — число
помилок типу (£, £}); Ь — число зроблених прогнозів; матри-
ця вартостей помилкових прогнозувань ||С,у|| = {С (&,£,)}
задається в діалозі. Можливі варіанти Сприведені в табл. 5.6:
Таблиця 5.6.
Варіанти матриці С
Ціль передбачення Елементи матриці С
Мінімізація модуля помилки передбачення <7 = 1 4-м
Мінімізація СКО с.=^-С
Мінімізація СКО при рівноцінному передбаченні сі3 = ' р р' «/ТУ /ТУ Н II /ту /ту
Мінімізація СКО при нерівноцінному передбаченні мТ1 II Н о МГ
• Адаптація основних параметрів процесу синтезу авто-
матів як випадкового пошуку здійснюється в такий спосіб:
— Розподіл Рі (С) на наступних кроках синтезу визнача-
ється за формулою
де Су — показник ефективності автомата Сі Є тг (/^) за фун-
кціоналом Сг,
14***
324
Розділ 5. Еволюційне моделювання ...
— Розподіл Р2 (Г) у найпростішому варіанті рівномірний,
але можна вибрати режим, при якому імовірність г-го режи-
му Г, збільшується на величину 1 /п при кожному успішному
кроці синтезу (формування локально-ефективного наближе-
ння), вибір того чи іншого варіанта навчання Р2 (Г) задається
в діалозі;
— Параметри кратності використання С-моделі і РЗ при
первинних налагоджувальних експериментах вибирають рів-
ними 1. Надалі можливий вибір інших кратностей: 2, 3 і т.д.
• Адаптивність алгоритму СП на у-му кроці синтезу оці-
нюється частотою синтезу локально-ефективного автомата
Ру = ЦЗ, де і — число локально-ефективних автоматів, 7 —
загальне число синтезованих автоматів.
• Процес синтезу закінчується при синтезі ТИ-автоматі в
або при синтезі т локально-ефективних автоматів. У най-
простішому випадку р = 0.33, що відповідає т = 5 і М = 15
й-
• Процес конкретного прогнозування значення параметра
здійснюється при пред’явленні значення чергового вхідного
сигналу хь+і (і) автоматові з найменшою величиною . У
діалоговому режимі можна задати інші правила одержання
прогнозної оцінки:
— автомат вибирається із сукупності л (Р?), обраної від-
повідно до розподілу імовірностей Рі (С?);
— за правилом більшості.
Як функціонал фг, що оцінює якість фактичного перед-
бачення параметра, узятий відсоток правильних передбачень
при фактичному прогнозуванні, тобто
= ~ 100%,
Ф
де фп — число правильних передбачень; ф — загальне число
всіх передбачень, зроблених до моменту і.
5.6. Моделі систем класифікації і розпізнавання
325
• Найбільш обережна стратегія припускає перехід на но-
вий етап синтезу сукупності 7г (7^) при першому ж помилко-
вому передбаченні. Це пов’язано з істотними витратами на
синтез.
У протилежному випадку число припустимих помилкових
передбачень за час Т оцінюється по залежності С,)?, у якій
визначається число передбачень (1т за час Т, а також бажане
число правильних передбачень <1*тп.
5.6.4. Методика синтезу деревоподібних моделей
для розпізнавання та класифікації
Як було зазначено вище, деревоподібні С-моделі широко
використовуються в якості ієрархічних систем прийняття рі-
шень. Суттєва відміна деревоподібних моделей від автома-
тних полягає в функціональному базисі, який характеризує-
ться значно більшим різноманіттям та складністю реалізова-
них функцій.
Опишемо загальну методику еволюційного синтезу ефе-
ктивних є -наближень в цьому класі С-моделей при вирішен-
ні задач розпізнавання (сигналів).
1. Клас деревоподібних правил рішення при фіксованій
структурі моделей характеризується сукупністю вирішаль-
них функцій, що складають функціональний базис та при-
писані до вершин дерева. В найпростішому випадку фун-
кціональний базис складає сім’я гіперплощин х3 — а® = 0,
І = 1, /V, які перпендикулярні до координатних осей в про-
сторі ознак (де N — вимірність простору ознак). Таким чи-
ном, N гіперплощин розбивають простір ознак на 2ДГ гіпер-
паралелепіпедів, кожний з яких входить в область, що від-
повідає одному з класів сигналів. Вибір найпростішого типу
вирішальних функцій обумовлений інженерними вимогами
простоти реалізації та економічності.
326
Розділ 5. Еволюційне моделювання ...
2. Сукупність деревоподібних структур як друга компо-
нента класу визначається мінімальним та максимальним роз-
мірами дерева. Фіксація числа вершин дерева приводить до
фіксації рівня і (висоти) дерева, що в свою чергу визначає
розміри ієрархічних систем ознак, що реалізуються різними
маршрутами дерева. Для заданого числа ознак класифіка-
ції N висота Г бінарного дерева оцінюється співвідношен-
ням і* — [/од2•№] + 1, де знаком [гг] позначена ціла частина х.
Оцінка довжини навчальної вибірки то може бути визначена
із виразу
и , 1 ,
т° ? п (5-9)
де д — число листків дерева, які відповідають міткам класів
об’єктів; є — точність; /3 — надійність розпізнавання [2].
3. Формування початкового дерева (або декількох дерев,
які складають початкову послідовність 7гє) здійснюється рі-
зними способами в залежності від наявної інформації про
динаміку вирішальних функцій. При незначній динаміці гра-
ниць, що розділяють класи об’єктів, та репрезентативній на-
вчальній вибірці Xе доцільно синтезувати дерево по вибірці
Xе одним з відомих методів. В іншому випадку, при значній
динаміці границь класів недоцільно задавати відразу поча-
ткову структуру, яка б давала найкращу класифікацію на
вибірці Xе. В цьому випадку за початкові структури вибира-
ються дерева, що генеруються випадковим чином із заданого
набору ознак, рівень і* дерев визначається співвідношенням
(5.9) із п.2.
4. Об’єм сукупності я фіксований і дорівнює К. При-
пускається, що початковий ймовірнісний розподіл рі (с) =
= [рп,Рі2> - - - ,Рік] дерев в сукупності 7ГЄ — рівномірний:
(ріі = І,і = 1,К")
5.6. Моделі систем класифікації і розпізнавання
327
5. Використовується описаний в розділі 5.6.2 список РЗ,
що містить чотири режими змін Гі, і — 1,4, початкові ймо-
вірності яких Р2г — Р2 (Гі) — однакові.
6. Ймовірнісна реалізація кожного РЗ включає також
ймовірнісний вибір рівня, на якому буде здійснюватися РЗ,
у відповідності з розподілом д — [д\,д2,... ,ді], де і — число
рівней (висота дерева), а також рівноймовірний вибір верши-
ни дерева на вибраному рівні для реалізації режима зміни
(РЗ). Вихідний розподіл доцільно задавати нерівномірним,
з більшими ймовірностями вибору рівня дерева, який роз-
ташований ближче до кореня. Як показали експерименти, у
випадку структур із і = 4, високою вартістю ознак та обме-
жених часових витратах доцільне покрокове корегування в
процесі синтезу [2].
7. Для оцінки ефективності роботи вирішальногоо дерева
по критерію навчальна вибірка Xе поділяється на визна-
чальну 2опр та оцінювальну 20Ц послідовності Xе — 2опр, 2ОЦ.
Рішення дерева, які отримані на послідовності 2опр, викори-
стовуються для ототожнювання листків дерева з тими кла-
сами, сигналів яких в даному листку більше. Опис сигналів
інших класів, які приводять до того ж самого листка, вважа-
ються помилково класифікованими. Сума вартостей (штра-
фів) помилок по всім листкам дерева визначає штраф дере-
ва Р^. Аналогічна сума вартостей помилок по послідовності
2ОЦ дає штраф Р^. В цілому класифікація деревом навчаль-
ної послідовності оцінюється виразом фі = + Р^ + А®,
де Р^ — штраф за складність дерева, який визначається як
сума вартостей всіх ознак, що приймають участь в класифі-
кації Xе. Матриця вартостей (штрафів) задається апріорі на
основі наявної інформації про цілі класифікації.
8. Оптимальне функціонування дерева визначається та-
кою сукупністю порогів ознак, при якій Р — тіп. При цьому
328
Розділ 5. Еволюційне моделювання ...
використовується довільний алгоритм випадкового пошуку,
оскільки процедура вимагає вирішення задачі багатопараме-
тричної оптимізації і пов’язана із значними часовими витра-
тами. Підбір здійснюється зверху униз від кореня дерева.
9. Адаптація основних параметрів процесу синтезу дере-
воподібних вирішальних структур здійснюється так:
а) у випадку синтезу локально-ефективного дерева із дере-
ва С™ , яке вибрано із сукупності 7Г у ВІДПОВІДНОСТІ 3 Рі (С) =
= (Рц, Ріг, • • -, Рік), на наступному кроці синтезу (г + 1)
маємо Р1/с (г + 1) = Р1к (г) + Ні, Р1з (т + 1) = Рі7 (г) -
З ¥= к, з = 1,к,0 < Ні < 1;
б) у випадку синтезу локально-ефективного дерева за до-
помогою РЗ Гі, (г = 1,4) із списку РЗ при виборі режиму
Гі із ймовірністю р?і на наступному (т + 1)-му кроці коре-
гуємо ймовірності Ргі (г + 1) так: Р2; (т + 1) = Р2І (г) + /і2,
Р2І (т + 1) = Р2> (т) - / і, 3 = М, 0 < к2 < 1-
10. Оцінка адаптивності алгоритму синтезу як випадково-
го пошуку і закінчення процесу синтезу деревоподібної стру-
ктури здійснюється згідно п.10,11, що наведені в розділі 5.6.2.
11. В процесі фактичної класифікації в алгоритмі ЕРА
(еволюційний розпізнавальний алгоритм) здійснюється по-
стійний контроль за відсотком правильних рішень (класи-
фікацій) Р по надходженню нових вхідних сигналів. При по-
казі сигналів контрольної послідовності Якоитр Є Xе вста-
новлюється порогове значення Рпор, в околі якого визнача-
ється смуга допуску є. Якщо при фактичній класифікації
Р Рпор + є, то здійснюється перехід на новий етап синтезу
моделі. Дана методика структурного синтезу деревоподібних
рішаючих моделей класифікації і розпізнавання реалізована
в алгоритмі ЕРА, який розглядається нижче.
5.7. Еволюційний розпізнавальний алгоритм — ЕРА
329
5.7. Еволюційний розпізнавальний алгоритм — ЕРА
ЕРА представлена блок-схемою на рис. 5.7. Робота ал-
горитму починається з блоку 1, у якому задаються вихідні
значення параметрів: Ь — число розпізнавальних класів; рг,
і = 1,А — штраф за складність і-ї ознаки, у = 1,£ —
елементи матриці штрафів С; рх,к (к = 1... 4) — імовірність
вибору дерева; ргл (А: = 1... 4) — імовірність вибору РЗ; дк
(к = 1... 5) — імовірність вибору А?го рівня дерева; і Н? —
величини підкріплення імовірностей вибору дерева і режиму
випадкових змін (РЗ) відповідно; Рпор — граничне значення
відсотка правильної класифікації. Тут же вводяться визнача-
льна й оцінююча послідовності {^т} і {^оц} > та 1Х довжини.
У блоці 2 створюється вихідна пам’ять із трьох дерев,
складених випадковим чином з ознак вихідної системи ознак.
Градації цих дерев також підібрані випадково. У блоці 3 від-
бувається вибір дерева Ак з пам’яті відповідно до розподілу
імовірностей Рі = (рп,Рі2,Різ) Вибір режиму випадкових
ЗМІН (РЗ) ПО розподілу Імовірностей Р2 — (Р21,Р22>Р23,Р24)
провадиться блоком 4. Здійсненням обраного режиму випад-
кової зміни (блок 5) завершується синтез дерева, що відразу
ОЩНЮЄТЬСЯ при пред’явленні І {Яоц} -
Блоками 6 — 11 і 13 здійснюється підбір оптимального
функціонування синтезованого дерева. З цією метою в блоці
6 вибирається вершина дерева, у якій знаходиться ознака з
градацією а, що підлягає зміні. При цьому використовується
розподіл імовірностей дк (к — 1... 5). На основі інтервалу мо-
жливих значень ознаки в блоці 7 вибирається нове значення
а (використовується рівномірний розподіл усіх значень гра-
дацій). У блоках 8 і 9 дереву пред’являються визначальна й
оцінююча послідовності.
За допомогою штрафів за складність і помилки розпізна-
вання в блоці 10 обчислюються рО), Р = рО) _|_
/г(2) _|_ /?(з) у блоці 11 отримане значення Р порівнюється зі
330
Розділ 5. Еволюційне моделювання ...
значенням Р*, що є максимальним для дерев, що зберігаю-
ться в 7г. Якщо Р < Р*, то отримано дерево, що ефективно
розпізнає навчальну послідовність, тому в блоці 12 воно запи-
сується в я замість дерева зі значенням штрафу Р*. У про-
тилежному випадку після перевірки на закінчення підбора
оптимального функціонування блоком 13 керування переда-
ється знову на блок 6. Підбор закінчується після здійснення
80 змін градацій (порогів) ознак дерева. Інформація, нако-
пичена під час підбора і зміни структури, використовується
ДЛЯ ЗМІНИ Ймовірнісних розподілів Р1 І Рі в блоці 14.
У блоці 15 відбувається перевірка на закінчення етапу
структурного синтезу: чи синтезовано 20 дерев? Якщо ні, то
знову здійснюється структурна зміна дерева, обраного з тг, і
підбирається оптимальне функціонування.
Блоками 16 і 17 реалізується етап використання кращого
дерева з я для класифікації сигналів контрольної послідовно-
сті {Яконт} • Так, у блоці 16 пред’являється об’єкт контроль-
ної послідовності, у блоці 17 відбувається відновлення {7ОП}
і {^оч} • Обчислюється відсоток правильної класифікації Р.
Якщо Р Рпор + є, то етап використання закінчується і по-
чинається знову етап адаптації. Якщо ж Р > Р„ор + є, то етап
використання продовжується.
Обчислювальні експерименти по дослідженню впливу
найбільш істотних факторів на ефективність еволюційного
синтезу проведені при рішенні задач розпізнавання об’єктів по
кривим, фактична і формальна постановки яких описані далі.
Вони підтверджують основні методичні положення ево-
люційного синтезу відносно ймовірнісної реалізації режимів
змін деревоподібних структур (доцільність первісного вибо-
ру рівня, на якому проводиться зміна), а також необхідність
і ефективність покрокової корекції (навчання) параметрів
ймовірнісної реалізації процесу синтезу. Визначена також
стратегія щодо оптимальної довжини навчальної вибірки; во-
на встановлюється спробним експериментом.
5.7 Еволюційний розпізнавальний алгоритм — ЕРА
331
Рис. 5.7. Блок-схема ЕРА
332
Розділ 5. Еволюційне моделювання ...
5.8. Розпізнавання об’єктів за кривими
При вивченні радіофізичних полів радіолокаційними ме-
тодами як характеристику відбитого поля широко використо-
вується перетин зворотного поля розсіювання. Ця узагальне-
на характеристика несе інформацію про конфігурацію об’є-
кта, що відбиває форму, розмір, параметр руху і т.ін. При
цьому експериментальна інформація звичайно фіксується у
вигляді характерної часової, частотної чи фазової залежності
ефективної площі розсіювання / (і, гі, <р), де (1 і </> — деякі
параметри, що відбивають розміри об’єкта, його форму чи
параметри руху об’єкта; і — час.
Як приклад ефективної обробки радіолокаційної інфор-
мації алгоритмічними і програмними засобами еволюційного
моделювання розглянемо задачу розпізнавання об’єктів, що
відрізняються параметрами гі і </?, за кривими / (І, гі, </>) [2].
Задача 1. Класифікувати об’єкти п’яти класів по їхніх
характерних кривих (і, гі, </?), і = 1... 5. Кожна група об’є-
ктів одного класу представляється шістьма кривими / (і, (Г),
що відрізняються параметром гі при фіксованому значенні
9? = Повний набір таких кривих при шести значеннях па-
раметра гі для об’єктів 1-го класу представлений на рис. 5.8, а
Значення гі зазначені в умовних одиницях. На рис. 5.8, б при-
ведені криві, що відповідають деякому представленню ко-
жного з розглянутих класів при фіксованому гі. В цілому 5
класів об’єктів представлені ЗО кривими, що випадковим ви-
бором (із імовірністю 1/2) розділені на навчальну і контроль-
ну послідовності. Відзначимо, що кожна крива при машинній
обробці задається 41 дискретним відліком: і = 1... 41.
Задача 2. Умови формування кривих, описаних у задачі
1, наближені до реальних: на кожну криву / (і, гі, <^і) діє нор-
мальна перешкода, тобто /і (<тп) = +&, де — г-тий відлік
5.8. Розпізнавання об’єктів за кривими
333
вихідної кривої (рис. 5.8), & Є N (0,<т„). При цьому на кожну
з ЗО вихідних кривих накладено 40 нормальних перешкод, і
розпізнаванню підлягають 1230 кривих п’яти класів — по 241
кривій від кожного класу.
Навчальна послідовність при вирішенні даної задачі ви-
користовується та ж, що у задачі 1. З усієї сукупності 1230
кривих відібрані ЗО в оцінюючу послідовність, а інші ввійшли
Рис. 5.8. Характерні залежності ефективної площі розсіювання /(і, ф<р)
а — об’єктів 1-го класу в динаміці параметра <1 (в умовних одиницях виміру)
б — об’єктів 7-го класу при фіксованому значенні (1 (номер класу зазначений
поруч із кривою)
-10-------1------1-------Ю-----------------1------1------:
7 8 9 10 І.У-ОД- 7 8 9 10 І.У-ОД.
а б
Рис. 5.9. Характерні залежності ефективної площі розсіювання /(1, фір)
для об’єктів 2-го класу при семи значеннях параметра ір
а — параметр <2 = 17; б — параметр <1 = ЗО.
334
Розділ 5 Еволюційне моделювання ...
Задача 3. Класифікувати об’єкти чотирьох класів по ха-
рактерній залежності ЕПР (і, <1, <р), і — 1... 4, причому ко-
жен клас представлено 8 значеннями параметра (і і 13 значен-
нями параметра у?, разом 416 кривих. Характерні залежності
У (і, </, ір) в динаміці параметра <р для двох значень <7 зобра-
жені на рис. 5.9(а, 6), а також на рис. 5.10 (а, б).
У навчальну послідовність були відібрані по 6 кривих
(при різних значеннях параметра Л і при ір — </>і) з (£, ф ір),
З = 1... 4. Інші криві (у кількості 392) були розбиті на кон-
трольну й оцінюючу послідовності.
Вихідна система ознак по описаних кривих у кожній із
задач формувалася таким чином. З кожної кривої / (<) буду-
валося 12 наступних моделей:
і./(0; 2./'(«); з./"(*);
4- <*У/ (о = д; 5- <*У/ (<) = х;
4 ’ 2
Рис. 5.10. Характерні залежності ефективної площі розсіювання /(і, гі,ір)
а — об’єктів 3-го класу при зазначених значеннях параметра ір (</ = ЗО);
б — об’єктів 4-го класу при зазначених значеннях параметра ір (4 = ЗО)
5.8. Розпізнавання об’єктів за кривими
335
Остання модель будувалася для 4 значень т. Для кож-
ної моделі розглядалися наступні ознаки: число змін знака;
число локальних екстремумів; максимальне і мінімальне зна-
чення; середнє значення М и середньоквадратичне значення
о для дискретних значень кривих; число Л/2/п2; < лінійний
спектр» (сім значень). Останній утворюється в результаті
розбивки інтервалу між мінімальним і максимальним зна-
ченнями на 7 підінтервалів і підрахунку частоти влучення
значень кривих у кожен підінтервал. Перераховані ознаки,
обчислені по 12 моделям, дають вихідну систему з 168 ознак.
Результати розпізнавання об’єктів
У результаті застосування описаного алгоритми ЕРА при
експериментально встановлених розподілах РЗ й імовірно-
стях вибору рівня дерева отримані наступні результати [2].
Задача 1. Побудовано вирішальну функцію, що безпо-
милково розпізнає об’єкти навчальної послідовності, і більш
90% об’єктів контрольної послідовності. Дерево, що реалізує
цю вирішальну функцію, зображене на рис. 5.11.
Рис. 5.11. Деревоподібна вирішальна функція, синтезована в задачі 1.
1,5 — вирішальні вершини; і відповідає номеру класу
336
Розділ 5. Еволюційне моделювання ...
Рис. 5.12. Деревоподібна вирішальна функція, синтезована в задачі 2.
У„і= 1,5 —вирішальні вершини; і відповідає номеру класу
Задача 2. Дерево, син-
тезоване ЕРА, приведене на
рис. 5.12. Результати розпізна-
вання — на рис. 5.13, де зо-
бражена гістограма відсотка
правильного розпізнавання Р
від Де п-2 — дисперсія
нормальної перешкоди, 8 —
величина постійної складової.
Такі ознаки, як положення
екстремумів чи наявність
осциляції, при дії перешкод
виявляються малоінформа-
Рис. 5.13. Гістограма відсотка
правильного розпізнавання Р
тивними. Ефективність розпізнавання об’єктів в умовах
указаних перешкод з ст 0.85 можна вважати задовільною.
5.8. Розпізнавання об’єктів за кривими
337
Рис. 5.14. Деревоподібна вирішальна функція, синтезована в задачі 3.
]іг і = 174 — вирішальні вершини; і відповідає номеру класу
Задача 3. Дерево рі-
шень, побудоване ЕРА,
приведене на рис. 5.14.
Результати розпізна-
вання представлені на
рис. 5.15—5.17 у вигляді
гістограм відсотка пра-
вильного розпізнавання
Р від ф. Як випливає з
гістограм, при ір < ф]
масмо Р — 100%. Варто Рис. 5.15. Гістограма відсотка правиль-
звернути увагу на зна- ного розпізнавання об’єктів 2-го класу
чення Р < 25% при 9?і ~ у>б (для об’єктів 2 і 3-го класів) і
при </? и </?із (для об’єктів 3 і 4-го класів). Перша обставина
є наслідком того, що відповідні криві майже не містять
осциляцій і це утрудняє розпізнавання об’єктів 2-го і 3-го
15'
338
Розділ 5. Евочюційпе моделювання ...
Рис. 5.16. Гістограма відсотка правильного розпізнавання
об’єктів 3-го класу в залежності від параметра ір
Рис. 5.17. Гістограма відсотка правильного розпізнавання
об’єктів 4-го класу в залежності від параметра ір
класів. Причина другого падіння — різке збільшення значен-
ня середньої складової в кривих, що відповідають об’єктам
3-го класу при ір = <^із, причому за характером динаміки ці
криві мало відрізняються від кривих, що відповідають об’є-
ктам 2-го і 4-го класів при <р — <р7 і <р = Інші помилки
розпізнавання при <рц <р ф7 й <р — <р\% в основному є
наслідком схожості кривих, що відповідають об’єктам 2-го і
4-го класів (в першому випадку), а також об’єктам 3-го і 4-го
класів (в другому випадку).
5.8. Розпізнавання об’єктів за кривими
339
Висновки: Проведені експерименти свідчать що викори-
стання ЕРА дозволяє успішно вирішувати задачу розпізна-
вання радіолокаційних об’єктів при наявності нормальних
перешкод з невідомою дисперсією, а також при невідомій
складній багатопараметричній динаміці відповідних кривих.
Перевагою даного підходу, на відміну від відомих, є швид-
ке переналаштування класифікуючих функцій відповідно до
мінливих умов радіолокації |2].
15*
ГЛОСАРІЙ
ГІІПС88 Іпсісх — 100
Адаптація процедур структурного пошуку — 305
Алгоритм глобального випадкового пошуку — 307
Алгоритм випадкового пошуку з лінійною тактикою — 302
Алгоритм випадкового пошуку з нелінійною тактикою — 303
Алгоритм навчання в методі потенційних функцій — 40, 41
Алгоритм навчання по Байєсу — 51
Алгоритм навчання Хебба — 105
Алгоритм нечіткого виводу Мапкіапі — 153
Алгоритм нечіткого виводу Ьагвеп — 156
Алгоритм нечіткого виводу 8н§епо — 155
Алгоритм нечіткого виводу Тзикашоіо — 154
Алгоритм нечіткого поширення помилки — 173
Алгоритм нечіткої самоорганізації’ Густафсона-Кесселя — 208
Алгоритм пікового групування — 204
Алгоритм різницевого групування — 205
Алгоритм обчислення оцінок — 28
Алгоритм самонавчання Кохонена — 109
Алгоритм самонавчання на основі методу потенційних фун-
кцій — 82
Алгоритм спряжених градієнтів для навчання нейронної ме-
режі — 96
ГЛОСАРІЙ
341
Асинхронна корекція — 132
Асоціативна модель навчання — 49
Аттрактор — 130
Вирішальне правило — 35
Генетичний алгоритм навчання — 100
Гібридний алгоритм навчання нечітких мереж — 196
Градієнтний алгоритм навчання нейронних мереж «Васк
ргора&аііоп» (НМ ВР) — 90, 92, 102
Дисперсійний алгоритм самовільної класифікації — 69
Еволюційний розпізнавальний алгоритм ЕРА — 329
Ємність запам’ятовування — 143
Ієрархічний алгоритм кластер-аналізу — 77
Імовірнісний ітеративний алгоритм навчання — 59
Карти ознак, що самоорганізуються — 115
Класи структурованих моделей — 292
Комбінаторний алгоритм МГУА — 244
Критерії відбору часткових описів в МГУА — 237
Критерій незміщеності МГУА — 238
Критерій точності (регулярності) — 237
Лабіринтна модель навчання — 49
Лінійна інтервальна модель — 256
Метод комплексування аналогів — 279
Метод максимального значення критерій — 157
Метод потенційних функцій — 39
Метод розділяючих поверхонь — 26
Метод середнього значення максимуму — 157
Метод центра ваги — 157
152
342
ГЛОСАРІЙ
Методика синтезу деревоподібних структур для розпізнаван-
ня — 325
Методика структурної ідентифікації (синтезу) прогнозуючих
моделей — 321
Метрики кластеризації — 66
Мінімаксний нечіткий перцептрон — 221
Мінімальне дистанційне розбиття — 77
Модифікований алгоритм самонавчання Кохонена — 114
Мутації — 101
Навчання нечітких правил — 216
Нейронна мережа "Васк ргора§аііоп"(НМ ВР) — 89, 92
Нейронна мережа Хопфілда — 130
Нечітка нейронна мережа АИРІ8 — 176
Нечітка мережа Ванга-Мснделя — 195
Нечітка нейронна мережа Т8К — 191
Нечітка нейронна мережа НЕЕСЬА88 — 228
Нечітка нейронна мережа з самоорганізацією — 201
Нечіткі правила виводу — 153, 155, 156
Нечіткий алгоритм МГУА — 256
Нечіткий апроксиматор (НЕЕРЕОХ) — 215
Нечіткий контролер Мамдані — 161
Нечіткий контролер на базі нейромереж — 166
Нечіткий нейронний контролер ПЕРСОН — 221, 225
Нечіткий перцептрон — 213, 221
Основні механізми еволюції — 288
Основні етапи структурного синтезу моделей — 295
Поліноміальний алгоритм МГУА — 241
Потенційна функція — 39
Правильна кластеризація — 78
Принцип зовнішнього доповнення — 252
Прості зміни — 296
ГЛОСАРІЙ
343
Процедура дефаззифікації — 157
Процедура корекції ваг — 103, 104, 91
Процедура фаззифікації — 153, 154
Режими змін — 313
Рекурентний вираз для обчислення похідних помилок ней-
ронної мережі — 92
Рекурентний алгоритм самонавчання на основі методу сто-
хастичної апроксимації — 85
Свобода вибору — 254
Схрещення батьківських пар — 101
Спряжені напрями — 97
Спрямляючий простір — 43
Статистичні моделі розпізнавання образів — 34
Статистичний алгоритм навчання — 62
Структурована модель — 292
Структурно—повний клас моделей — 294
Тест — 29
Тупиковий тест — 29
Умови збіжності імовірнісного алгоритму навчання — 61, 62
Умови зупинки методу МГУА — 244, 260
Умови зупинки синтезу структури — 324
Функціонали якості кластеризацїї — 66, 67
Функціонально—повний клас СМ—моделей — 294
Функція активації — 89
Частковий опис — 242
ЛІТЕРАТУРА
1. Айзерман М.А., Браверман 9.М., Розонозр Л.И. Теоре-
тические основи метода потенциальних функций в задачах
об обучении автоматов разделению ситуаций на классьі. —
Автоматика и телемеханика, 1964, т. 25. №6.
2. Букатова И.А., Михасев Ю.И., Шаров А.М. Звоин-
форматика. Теория и практика зволюцинного моделирова-
ния. — М.: Наука, 1991. — 206 с.
3. Васильєв В.И., Распознающие системи. Справочник. —
Киев: «Наукова Думка», 1983. — 298 с.
4. Вороновский Г.К., Махотило К.В., Петрашев С.Н., Серге-
ев С.А. Генетические алгоритми, искусственнне нейрон-
ньіе сети и проблеми виртуальной реальности. — Харьков:
«Основа», 1997. — 112 с.
5. Гаврилова Т.А., Хорошевский В.Ф. Бази знаний интелле-
ктуальньїх систем. — СПб: Питер, 2000. — 384 с.
6. Журавлев Ю.И. и др. Распознавание образов и распозна-
вание изображений // Распознавание, кластеризация, про-
гнозирование. Математические методи и их применение. —
М.: Наука, 1989.
7. Заенцев И.В. Нейроннме сети. Основнне модели. — Воро-
неж, 1999.
8. Зайченко Ю.П., Заєць І. О. Синтез і адаптація нечітких
прогнозуючих моделей на основі методу самоорганізації. //
Наукові вісті НТУУ "КШ". - 2001. - №3. - с. 34 - 41.
ЛІТЕРАТУРА
345
9. Зайченко Ю.П., Заєць І. О. Застосування рекурсивних ме-
тодів ідентифікації в задачах синтезу нечітких прогнозуючих
моделей. Праці Міжнародної конференції з індуктивного мо-
делювання. — Львів. Травень 2002. — с. 59 — 64.
10. Зайченко Ю.П., Кебкал О.Г., Крачковський В.Ф. Нечіт-
кий метод групового урахування аргументів та його застосу-
вання в задачах прогнозування макроекономічних показни-
ків. // Наукові вісті НТУУ «КПІ». - 2000. - №2. - с. 18-26.
11. Зайченко Ю.П., Моамед Мухамед, Шаповаленко Н.В. Не-
чіткі нейронні мережі і генетичні алгоритми в задачах макро-
економічного прогнозування. // Наукові вісті НТУУ «КПІ».
- 2002. - №4. - с. 20 - ЗО.
12. Зайченко Ю.П., Приходько А. В., Чичирин А.Е. Модели-
рование и прогнозирование макрозкономических показате-
лей Украиньї на основе метода самоорганизации. — Вестник
Харьк. Гос. Политехнич. Ун-та. Випуск 72. Системний ана-
лиз, управление и информационньїе технологии. — Харьков,
1999. - с. ЗО - 32.
13. Зайченко Ю.П., Бережной И.Е. Применение генетичес-
кого алгоритме для обучения нейронньїх сетей в задачах зко-
номического прогнозирования. — Вестник Харьк. Гос. Поли-
технич. Ун-та. Вьіпуск 70. Системний анализ, управление и
информационньїе технологии. — Харьков, 1999. — с. 152 —
157.
14. Зайченко Ю.П. Нечіткий метод індуктивного моделюван-
ня в задачах прогнозування макроекономічних показників. —
Системні дослідження і інформаційні технології. — 2003. —
№3. - С. 25 - 45.
15. Ивахненко А.Г. Непрерьівность и дискретность. — К.:
Наукова Думка, 1990
16. Ивахненко А.Г., Юрачковский Ю.П. Моделирование си-
стем по зкспериментальньїм данньїм. — М.: Радио и связь,
1986.
346
ЛІТЕРАТУРА
17. Ивахненко А.Г., Мюллер И.А. Самоорганизация прогно-
зирующих моделей. — К.: Техника, 1985.
18. Ивахненко А.Г., Зайченко Ю.П., Димитров В.Д. При-
нятие решений на основе самоорганизации. — М.: Советское
радно, 1976.
19. Искусственннй интеллект. Справочник. Книга: 2.1 Под.
ред. Д.А. Поспелова. — М.: Радио и связь, 1990.
20. Короткий С. Нейронньїе сети Хопфилда и Хзмминга.
21. Короткий С. Нейронньїе сети: алгоритм обратного рас-
пространения.
22. Короткий С. Нейронньїе сети: обучение без учителя.
23. Кохонен Т. Ассоциативная память. — М.: Мир, 1980.
24. Куссули 9.М. Ассоциативньїе нейроподобньїе структури.
— Киев: Наукова думка, 1990.
25. Минский М., Пайперт С. Перцептроньї. Пер. с англ. —
М.: Мир, 1971.
26. Нильсен И. Принципи искусственного интеллекта. Пер.
с англ. — М.: Наука, 1985. — 373 с.
27. Осовский С. Нейронньїе сети для обработки информа-
ции / Пер. с польского И.Д. Рудинского. — М.: Финансн и
статистика, 2002. — 344с.
28. Прикладньїе нечеткие системи. Пер. с англ. / Под ред.
Терано. — М.: Мир, 1992.
29. Сотник С.Л. Лекции. «Основи проектирования систем
искусственного интеллекта».
30. Ф. Уосермен. Нейрокомпьютерная техника. Теория и пра-
ктика. — М.: Мир, 1976.
31. Ципкин Л.З. Обучение и адаптация в автоматических
системах. — М.: Наука, 1976.
32. Шлезингер М.М. Лекции по математическим методам в
распознавании образов. — Киев, 1999. — 169 с.
33. Якушкина Н.Г. Нечеткие нейронньїе сети. // Новости
искусственного интеллекта. — М.: 2001.
ЛІТЕРАТУРА
347
34. Н. Риііег. Іпігогіисііоп іо Иеиго-Еиггу бузіетз. Асігапсез
іп ЗоЙ Сотриііп^ Зегіез. Зргіп^ег — Уег1а§, Вегііп, 1999.
35. Іап 8кг, МазаКага Мггитпоіо. А Келу арргоасЬ оЕ пеиго-
Еиггу 1еатіп§ а1§огііЬт Еог Ішіт§ [иггу гиіез // Гиггу 8еіз
апс! Зузіетз. VI12. 2000.
36. .ІуК-8Кіпд, Еодег }апд. АКЕІ8: Асіарііуе — Кеїлуогк
— Вазесі Гиггу ІпЕегепсе Зузіет. ВерагітепЕ о£ ЕіесЕгіса!
Еп£Іпеегіп£ апсі СотриЕег Зсіепсе. ІІпіуегзііу о£ СаІіЕогпіа,
Вегкеіеу, 1995.
37. Ка.иск Б., Кіашопп Р. Кеиго-Гиггу СІаззійсаЕіоп іпіііаіігасі
Ьу Еиггу сіизіегіпц. Верагітепі о£ Сотриіег Зсіепсе, ТесЬпісаІ
ІІпіуегсіїу о! Вгаипзс1і\уеі§. Сегтапу, таіі: утлу.си/іи—
Ьз.сіе/ папск
38. Ааиск Б., Кіашопп Р., Ктиге К. Гиггу Сопігоііегз апсі
Кеигаї Кеїхуогкз. ВерагЕтепі о£ Сотриіег Зсіепсе, ТесЬпісаІ
ипіуегзііу оЕ ВгаипзсЬлуеі§. Сегтапу, таіі: «гїт.си/іи—
Ьз.сіе/ папск
39. КоЬегі НесМ—КіеІзеп. Кеигосотриііп§. .ІоЬп \¥і!еу апсі
8опз. Іпс. Кєуу Уогк, 1993.
40. ¥.Р. 2аусІгепко, І. О. 7аеіз. ТЬе Гиггу Сгоир МеіЬосІ
о£ Паіа НапШіпц апсі ІЕз Арріісаііоп Ео ЕЬе Тазкз оЕ іііе
Масгоесопотіс Іпсіехез Еогесаз1іп§. — 8АМ8, 2001, Уоі.
рр. 1 - 11.
ЗМІСТ
ПЕРЕДМОВА .......................................... З
ВСТУП .............................................. 5
Розділ 1. Основи математичної теорії розпізнавання
образів ........................................... 21
1.1. Основні етапи розвитку й аналіз сучасного
стану розпізнавання образів ................. 21
1.2. Короткий екскурс в історію розпізнавання образів 22
1.3. Математична постановка задачі розпізнавання
образів ..................................... 24
1.4. Синтез евристичного алгоритму розпізнавання
образів ..................................... 26
1.5. Алгоритм розпізнавання на основі обчислення
оцінок ...................................... 28
1.6. Метод розпізнавання образів на основі статис-
тичної теорії прийняття рішень .............. 34
1.7. Метод потенційних функцій.................. 36
1.8. Синтез екстремальної моделі (алгоритму) РО ... 47
Розділ 2. Моделі та алгоритми навчання та
самонавчання в задачах розпізнавання образів ... 49
2.1. Класифікація моделей навчання. Формальна
модель навчання ................................... 49
2.2. Алгоритм навчання за Байєсом .............. 51
2.3. Імовірнісні ітеративні алгоритми навчання . 59
ЗМІСТ
349
2.4. Самонавчання в інтелектуальних системах.
Постановка задачі кластер-аналізу.
Критерії і метрики кластер-аналізу ..:....... 66
2.5. Дисперсійний алгоритм самонавчання (мимовіль-
ної класифікації) з незаданим числом класів .... 69
2.6. Агломеративний ієрархічний алгоритм
кластер-аналізу ................................ 77
2.7. Алгоритм самонавчання на основі методу
потенційних функцій............................. 82
2.8. Рекурентні алгоритми самонавчання на основі
методу стохастичної апроксимації ............... 85
Розділ 3. Нейронні мережі.......................... 88
3.1. Структура та математична модель мережі .... 88
3.2. Градієнтний алгоритм навчання нейронної мережі 90
3.3. Побудова рекурентного виразу для обчислення
похідних помилок ............................... 92
3.4. Прискорення збіжності алгоритмів навчання
нейронних мереж. Алгоритм спряжених
градієнтів ..................................... 96
3.5. Генетичний алгоритм навчання
нейронної мережі ............................... 100
3.6. Удосконалення градієнтного алгоритму
навчання ...................................... 102
3.7. НМ, які самоорганізуються.
Алгоритм навчання Кохонена .................... 105
3 8. Застосування НМ у задачах прогнозування
в макроекономіці............................... 120
3.9. Нейронна мережа Хопфілда та її застосування . 129
3.10. Нейронна мережа Хеммінга................. 1^1
3.11. Нечіткі нейронні мережі. Властивості.
Алгоритми функціонування. Застосування .... 145
3.12. Нечітка нейронна мережа Т8К .............. ^1
3.13. Нечіткі нейронні мережі з самоорганізацією . - - 201
350
ЗМІСТ
3.14. Застосування нечітких нейронних мереж
для апроксимації функцій ..................... 213
3.15. Нечіткий перцептрон як загальна модель
для нечітких нейронних методів ............... 221
Розділ 4- Метод групового урахування аргументів
у задачах прогнозування й ідентифікації........... 233
4.1. Основні принципи і загальна схема методу . 233
4.2. Багаторядні поліноміальні алгоритми МГУА ... 241
4.3. Комбінаторний алгоритм МГУА .............. 244
4.4. Алгоритм МГУА
з послідовним виділенням трендів ........... 251
4.5. Нечіткий метод групового обліку аргументів
і його застосування в задачах прогнозування
макроекономічних показників ................ 252
4.6. Аналіз різноманітних видів функцій
приналежності ................................ 261
4.7. Експериментальні дослідження нечіткого МГУА
та застосування в задачах макроекономічного
прогнозування ................................ 266
4.8. Порівняльний аналіз результатів
прогнозування за чітким і нечітким МГУА........ 275
4.9. Метод прогнозування багатовимірних
випадкових процесів на основі комплексування
аналогів ..................................... 279
Розділ 5. Еволюційне моделювання як методологія
вирішення задач штучного інтелекту ............... 288
5.1. Основні ідеї і механізми еволюційного
моделювання (ЕМ) ............................. 288
5.2. Моделювання механізмів еволюції в складних
системах ..................................... 289
5.3. Етапи процесу еволюційного синтезу ....... 295
5.4. Основні алгоритми структурного випадкового
пошуку на основі еволюційного моделювання .. ЗОЇ
ЗМІСТ 351
5.5. Навчання й адаптація процедур пошуку. 305
5.6. Скінченні автоматні моделі для прогнозування
та деревоподібні вирішальні моделі систем
класифікації і розпізнавання............ 311
5.7. Еволюційний розпізнавальний алгоритм — ЕРА 329
5.8. Розпізнавання об’єктів за кривими . 332
ГЛОСАРІЙ .................................. 340
ЛІТЕРАТУРА ................................ 344
ЗМІСТ ..................................... 348